\"\n ]\n },\n \"metadata\": {},\n \"output_type\": \"display_data\"\n }\n ],\n \"source\": [\n \"# This may take about 2 minutes to run\\n\",\n \"\\n\",\n \"plt.figure(figsize=(16, 32))\\n\",\n \"hidden_layer_sizes = [1, 2, 3, 4, 5, 20, 50]\\n\",\n \"for i, n_h in enumerate(hidden_layer_sizes):\\n\",\n \" plt.subplot(5, 2, i+1)\\n\",\n \" plt.title('Hidden Layer of size %d' % n_h)\\n\",\n \" parameters = nn_model(X, Y, n_h, num_iterations = 5000)\\n\",\n \" plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)\\n\",\n \" predictions = predict(parameters, X)\\n\",\n \" accuracy = float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100)\\n\",\n \" print (\\\"Accuracy for {} hidden units: {} %\\\".format(n_h, accuracy))\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"**Interpretation**:\\n\",\n \"- The larger models (with more hidden units) are able to fit the training set better, until eventually the largest models overfit the data. \\n\",\n \"- The best hidden layer size seems to be around n_h = 5. Indeed, a value around here seems to fits the data well without also incurring noticable overfitting.\\n\",\n \"- You will also learn later about regularization, which lets you use very large models (such as n_h = 50) without much overfitting. \"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"**Optional questions**:\\n\",\n \"\\n\",\n \"**Note**: Remember to submit the assignment but clicking the blue \\\"Submit Assignment\\\" button at the upper-right. \\n\",\n \"\\n\",\n \"Some optional/ungraded questions that you can explore if you wish: \\n\",\n \"- What happens when you change the tanh activation for a sigmoid activation or a ReLU activation?\\n\",\n \"- Play with the learning_rate. What happens?\\n\",\n \"- What if we change the dataset? (See part 5 below!)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"\\n\",\n \"**You've learnt to:**\\n\",\n \"- Build a complete neural network with a hidden layer\\n\",\n \"- Make a good use of a non-linear unit\\n\",\n \"- Implemented forward propagation and backpropagation, and trained a neural network\\n\",\n \"- See the impact of varying the hidden layer size, including overfitting.\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"Nice work! \"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"## 5) Performance on other datasets\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {\n \"collapsed\": true\n },\n \"source\": [\n \"If you want, you can rerun the whole notebook (minus the dataset part) for each of the following datasets.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 26,\n \"metadata\": {\n \"scrolled\": false\n },\n \"outputs\": [\n {\n \"data\": {\n \"image/png\": \"iVBORw0KGgoAAAANSUhEUgAAAYAAAAD8CAYAAAB+UHOxAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXd4VGXah+9zzvT0QhqBhBZK6NJBihSliIK6dt3PgmUt\\na9u1rK4odtG1u+jqWlZQEVQUpUuRGnqHkB5CSO9TTvn+GIiEmUkCpEHOfV16wZzyPmcS3ve8T/k9\\ngqZp6Ojo6Oi0PsTmNkBHR0dHp3nQFwAdHR2dVoq+AOjo6Oi0UvQFQEdHR6eVoi8AOjo6Oq0UfQHQ\\n0dHRaaXoC4COjo5OK0VfAHR0dHRaKfoCoKOjo9NKMTS3AbURHh6uxcfHN7cZOjo6OucNW7duzdc0\\nrU19zm3RC0B8fDxJSUnNbYaOjo7OeYMgCOn1PVd3Aeno6Oi0UvQFQEdHR6eVoi8AOjo6Oq0UfQHQ\\n0dHRaaXoC4COjo5OK6VFZwHp6Oi4qapysXbFEfbuzCE0zMYllyXQLj6kuc3SOc/RFwAdnRZOcVEV\\nzz66mIpyB06HgijCulVHuPnOQYwc17m5zdM5j9FdQM1IYUElBXkV6G05dWrjm8+3UVpchdOhAKCq\\n4HQofD5nM5UVzma2Tud8Rt8BNAOZaUV8+OY6co+WgiAQEmrlzgeGk9AjorlN02mBbN2YiaJ4viRI\\nksDenTkMHBbXDFbpXAjoO4AmprzUwQtPLiErvRiXS8XlVDh+rJzXZ67g+LGy5jZPpxGpKHeSk12C\\n06k0tyk6OoC+A2hy1q5IRpZVj89lWWHpov3cdOegZrBKpzGxV7n4z3sb2LYpE0lyv3NNmZ7I5df0\\nQhCEOq+/aEg7Nq5J9dgFKIpGYp/oRrFZp3Wg7wCamIy0Ilxe3gAVRSM9tagZLNJpbN57bQ3bN2Ui\\nu1QcdhmHXWbRd3tZ9tOBel1/7a39CQy2YjJLAIgimMwSt941CJufqTFN17nA0XcATUxsfAjGDRke\\ni4AoCbSLC24mqy5sVFWjIK8cs8VIYJClScfOyy1j/+5cXK6auz6nQ+bHb3czfkq3OncBQcFWXnp3\\nKutWHmHPDj0NVKfhaJAFQBCET4ApwHFN03p6OT4a+AFIPfHRAk3TnmuIsc83Ro7txKJvd3ssAAaD\\nyKVTuzeTVRcu2zZl8t8PN1FV6URVNDp2CePuhy8mrI1fk4x/7GgZBqOIy+W56ysvc6DIKgajVOd9\\nrFYj4yd3Y/zkbo1hpk4rpaFcQP8FLqvjnLWapvU98V+rnPwBAgItPDFrAjHtgjCaJEwmibA2fjzy\\n9FgiowOb27wLisMHjvPB7LWUFLlTKGVZJflgPrOe+NVrHKYxiIoJQHZ5H8s/wIxk0L2wOs1Hg+wA\\nNE1bIwhCfEPcqzUQ1zGUl96ZSkFeBYqi0ibSv17BQJ0z44dvdntk3KiqRmWFkx1bshgwtH2j29Am\\nMoDuvSLZv/tYDTeQySwx9ZpeuFwqSxftZ83yZBRFZeDwOKZM74l/gLnRbdPRacoYwDBBEHYB2cCj\\nmqbtbcKxWyRN5YZobHZuzebnBXspyCunU0I4U//Um9j2zR/POJpZ4vVzp0MmJ8v7scbgvr+N5ON3\\na2YBXX5VT8ZOTODFp5aSnvpHYsCyRQfYvC6dWf+aogd4dRqdploAtgHtNU0rFwRhEvA90MXbiYIg\\nzABmALRv3/hvaDrnxpIf9zH/fzuqq1QL8ivZviWLvz83ns5d69WVrtGIjg2kIK/C43OT2UBU26Zz\\nt5ktRv7y6Egqyp2UldoJDffDZJLYtjmTzPTiGvEgWVYpLbGzaskhJk/3CKfp6DQoTeKA1DStVNO0\\n8hN/XgwYBUEI93HuHE3TBmiaNqBNm+adQHRqp6rKxfwv/5j8ATRVw+lQ+GLOlma0zM0V1/SuTp08\\niSAKWKxG+g2MbXJ7/PxNRMUEYjK5bdq1NRuHXfY4z+VU2LYps6nN02mFNMkCIAhClHDCyS0IwqAT\\n4xY0xdg6jUfKoXyfQcz0lIImC7T6IqFHBHc+MIyAQDNmiwGjUaRD5zD+8dJl9cq8aWz8/M2IkvfY\\nj5+/HgPQaXwaKg10LjAaCBcEIQv4J2AE0DTtQ+Bq4B5BEGSgCrhO0xXQznssVgOa6v3HKEkiotj8\\nge1Bw+MZMKQ9ucfKsFiNhITamtukakZc0pEli/ajKjUD1WazgUsmJjSTVTqtiYbKArq+juPvAu82\\nxFg6LYcOncOx+pmwn+bGMBhEBg6LaxELAIAoiUS3DWpuMzyIbhvEDbcN4Kv/JCEI7gwlQRQYPaEz\\nfS5q29zm6bQC9EpgnbNGFAUeemoMLz+9DEVRcTpkzGYDoW38uHnGwHO6d1mpnb07czAYJHr2jcZi\\nNTaQ1S2LSy5LoN+gWLZuzESWFfpeFNukAWqd1o3Qkj0xAwYM0JKSkprbDJ06cNhdbNmQQWF+JXEd\\nQunVLxpROvvw0uLv97LgfzuRDAIgoKoqdz00ggFDzs+sMEVR2b45i707jxIQZOXiSzrSJjKguc3S\\nuUARBGGrpmkD6nWuvgDotCT27z7GG7NW1sgsAjCZJF5+74rzrnbCXuXihSeXkJtThsMuIxncsZHb\\n7xvK0JEdmts8nQuQM1kA9Dp0nRbF0p8OeEz+4PaPr115pBksOjd+/HY3OVkl1emeiuzuAfGfdzdQ\\nUe5oZut0Wjv6AqDToigurPT6uSyrFBV4P9aSWbcqxUMJFNzxkx1J2U1qS2pyAauWHGLXtmxUpXlT\\ndHVaBnoQWKdFkdg3hoy0Ig8BNYvFQI/eUc1k1dmj+KqF0DRkLwqhjYHD7mL2cytJPeIuvRFFEavV\\nwOOzJhAVowecWzP6DkCnRTFhclcsFiOnauMZDCIh4TYuGtyu+Qw7S/oPjvVa7KWqGr36N02q59xP\\nt5JyOB+nQ8HpULBXuSguquKNWStpyTFAncZHXwB0WhSBwVZmzp7EoBHxWCwG/PxMjJ7Qmadfntgi\\nqnfPlOk39MU/wIzxFNtNZonJV/UkNKzxi9JUVfPqhtI0KC6sIkPvQteq0V1AOi2O8Ah/7n3k4uY2\\no0EICbXx0ttTWbb4ALu2ZhMYbGH85G707BvTJOOriurT1SSKAuVlvgPRDruL3TtyUGSVxN7R+Afq\\n8hQXGvoCoKPTyPgHmpl2XR+mXdenycc2GCWi2gaSk1XqcUx2KcR3CvV63bZNmXzwxlpEUQQ0FFnl\\nqhv7MvHKxEa2WKcp0V1AOjoXODffOahagfQkJrPExCt7eBWdK8ir4IPZa6vjBfYqGZdLZcHcnRzY\\nm9tUZus0AfoCoKNzgZPYJ5rHnh1HQo8IrDYj0bGB3HrXYKbf0Nfr+WtXHkH1IvLndCgsXbS/sc3V\\naUJ0F5BOiyUro5jVSw9TXFRFr/4xDBkRj8ms/8qeDQk9InjqxUvrdW5RQaVPKe/zsRZDxzf6vyad\\nFsma5cl8Pmcziqyiqho7t2bz0/w9PPPqRL1fbiPTvVckG9akejSrMRhFEvtEN5NVOo2B7gLSaXGU\\nlzn4fM5mXE6l2hXhsMsU5FWwcN7OZrbuwmfAkPaEhtlqNPsRBLBYjEyY0q0ZLdNpaPQdgE6LY9e2\\nbK+9BGRZZePaNG6+c1Ct1+/ffYzvv97F0awSoqIDuPK6Pvqb6xlgMEo8/cpE5n+5nY1rU1EUjT4X\\nteXaW/sTGGxtbvN0GhB9AdBpcWi1yNT46kB2ks2/p/HR2+urBeVKi+3868VV/PnuIQwf07Ehzbyg\\n8fM3cevdg7n17sHNbYpOI9IgLiBBED4RBOG4IAh7fBwXBEF4WxCEZEEQdgmC0L8hxtW5MOnSo43X\\nIKQkCQwcFufzOlXV+GLOFg81UadD4X//2YKiC6Dp6NSgoWIA/wUuq+X4RKDLif9mAB800Lg6Fxg/\\nLdjDU/cvqqEFBO689cBgK9Nv8F1MVZBXgd3u8npMllVyc8oa0lQdnfOehuoJvEYQhPhaTrkC+PxE\\nI/iNgiAEC4IQrWlaTkOMr3NhkLQhgx++3oXTWfMNXpIEpl3bmzGXJWC1mXxeb7UaURXvLiJVUbHZ\\nzs+2kqqqsWV9OquWHMLhUBg8PI7RE7pcsG0ydZqOpooBtAUyT/l71onP9AVAp5pF83d7bQZjNElE\\nxATWOvmDW3IhoXsEB/bm1ihkEkWBuE5hBIc2nPiaw+5i3aoUtm3KxD/AzJjLEuiWGNlg9z+Jpmn8\\n+811bN+chcPhTsvMSivit6WH+efrk7Dqi4DOOdDi0kAFQZghCEKSIAhJeXl5zW2OThNSmO+7GUxh\\nXkW97nHXQ8MJj/DDYjVgMIhYrAZCw2wNKi5XUe7k6Yd+Zt5/t7JnRw4b16Ux+7kVjZKieuRgPts2\\nZ1ZP/gBOp0J+XgUrfznY4OPptC6aageQDZwq5h574jMPNE2bA8wBd0/gxjdNp6UQ1zGU3duPenwu\\nSSLt4kPqdY/gUBuvvHcFe3bmuNNAYwLp3S/mnJrUn87ihXsoyK/4o2mN5g40//zdXkaM6USbSP8G\\nG2t7UpbXXZHLqbBxbRqTp/dssLGamuQDeWxYk4qqaQwaFke3npEIpwd/dBqVploAfgTuEwRhHjAY\\nKNH9/zqnM+36Phzcm1sjBmAwiETFBNKtZ/3dK6Ik0rt/W3o3UsOVDWvSPDqWnWTHlizGN2CxlNEo\\nIUqC19iG8TzsjwBut9YXczazduURXE4FDfh9VQr9BsZy10MjvNaA6DQODZUGOhfYAHQVBCFLEITb\\nBUG4WxCEu0+cshhIAZKBj4B7G2JcnQuLTgnhPPz0JcS0C0IUBQwGkcEj4nj8+fEt6s3Q5wQlgNDA\\nk9fgEXFIXnYvZrPE6Eu7NOhYTcXBfcdZtzIFp0NB0wDNXem9fUsWO5Kymtu8VkVDZQFdX8dxDfhL\\nQ4ylc2HTvVcUL70zFadDxmAQG9R1UxtOp8LOpCwqyp0k9IggJjbI57nDx3Tk5+/24jq90YoG/QfF\\nNqhd0W2DuPK63nw/b1e1LpLZYqBbYiTDR5+fhW3rf0vB4ZQ9PnfYZdauOEL/Qedf68/zFb0SWKdF\\n0pSqn4cPHGf2c+7+uKqqoWnQf3A77v7rcK8L0MQrerB1YwbHj5XjsMvVu5WrbuxLaLhfg9s3ZXpP\\n+g2MZcNvqTicMv0HtTuv/eWyrIKP6J6v7mU6jYO+AOigqlqr9bs6HTKzn1tJVWXNArLtmzNZ9vMB\\nLp3aw+Mai9XIs69NYvP6dHZsycY/wMSo8V2I6+i9u1ZD0LZdMFff3K/R7t+UDBoWR9KGDA+1UbPZ\\nwJCRHZrJqtaJvgC0YnYmZTP30yRyskux2oyMndiVadf3wWBocdnBjcbOrdm4PZQ1cToUlv180OsC\\nAG7BtGGjOjJs1PnphmlOel/Ulm6JkRzYm1u9CJjMEu07hjB4RHzzGtfK0BeAVsqubdm8++rq6oyb\\nqkoXSxbt5/ixMv7y2Mhmtq7pKC9z+KweLsoqZM+/5pP44FXnjbvF6VRwORVsfsYWa7MoCvz1ydFs\\nWpfO2pXJqKrGsNEdGTayQ6t6+WgJ6AtAK+Xrz7Z5SC64nArbt2SRl1tGm8iAZrKsaUnoEeHdHa2q\\nBOXnsP3pBchllfR9+pamNu2MqCh38OkHm9i+KRNNg9BwG7fcNajRUmHPFVESGTqqA0NH6S6f5kRf\\nblspRzNLvH4uSQLpKUVNbE3z0bZdMP0GxtZsmq6qSKpCx/3bkCvs7H71a2S7s/mMrANN03jpH8vY\\nvikTWVZRFJW83HLeeXk1h/Yfb27zdFow+gLQSvHVVlHTICSsdTX9uOfhEUyaEI+lqhyD00FYbib9\\n1/6MX/mJRVIQqMjIRdM0jq3dxe7Xvib586W4yqua1M60IwW899oannpwEf9+cx1Z6e6F+sCeXI4f\\nK/OQ0HY6FRbO1Tuo6fhGdwG1Ui6d2p0fvtlVQ2ZAEAVCwmx07BLejJY1PaIkMunq3pTe/xyqw1NO\\nWnXJGAJsLB71Vwq3J6M4XEgWExsfeIcJv7xMxNDERrdxx5Ys3nt9jbtyVnPv4JI2ZvDQU2PIyij2\\n2esgM6317OZ0zhx9B9BKmXRlD4aN6ojBKGK1GTGbDUS3DeSxf45tscHDxsQc7E/ctBFIlpqKo5LF\\nRNy0Eex7cz75SYeQK+xosoJcXoWrtJJlU55CdXkWNTUkqqLyn3c3/FE5izt11+lQ+M+7Gwlr4+cz\\neBoe0XC6RBcqGWlFLP5+Lyt+OUhpcdPu6pobfQfQShElkf+7dwjTrutNekoRwaFW2ncIaZWT/0mG\\nf/QIcnkVR5dvQzIbURwuosf2Y/hHj/BN3PWoXuIAmqJwdMU2Yi+rvU/xuXDsaFkNNdBTKSmuon2H\\nUCxWIw67zKkZrSazxNRrejWaXec7qqrx8Tvr2fJ7OoqqIYkCcz/dyu33DWVoK6lH0BeAVk5wqK1B\\ndfLPZ4x+Vsb9+ALl6bmUHs4isEss/nFuETq5wu79Ig1cpd5lrBvMLpNUo79BjeFVDYvFwJMvXMpb\\nL60iL7ccSRRRVY2rbuxD/8G6rIIvNqxOJWl9RnU23Eln6H/e3UC3npEUF1bx04I9HMsqJa5TKFOm\\n9ySmnW+JkPMRfQHQafFomsbKXw+xeOE+SourCDO46Hr0APERFno8MJ3IEQ37lusfF1k98Z8k8uJe\\n5Czf5nGu4nQReXHjvWW7KqrI+3op1spyXJKFU3tlCgLEdwolINBCQKCFF9+eytGsEiornLSLD8Hc\\nhHIa5yPLfznofWelaXz7xXa2rE//I+aSVcKW9ek8+sxYujZC45/mQo8B6LR45n6ylXn/3Ur+8XKc\\nToWcSpE1/glsX32YJZf9nX3vLGx0Gwa9fjcGfyuC+Mc/GYOfhR73T8MWHVave1QdLyJl3krSf/gd\\nucpR5/muskoWDbyXpCc/puuaXzG4nIiyO0htthjwDzRz10MjalwTExtE565t9Mm/HlRVeE/tlWWV\\nzevSvMZcPnl/YxNa2PjovyWthJTD+Xzz+XZSk/PxDzBz6eXdGTe5W4vXACotrmLlrwdxnaa/rxoM\\nJPcYSMjqH0n6+xw63TQOc0jjFa+F9u7E5ZvfZ+esLzi2ZjfWyBB6PnINHa4dU6/rd8z6kl0v/g/R\\nKLlf3TWN0V8/U2vsYP97P1CedgzF7sQPB0OWfcvxth2oCgll2H2TGXvTYH2iPwf6Doolb9EBj/RZ\\ng1HC17+K/NxySkvsBAZZGt/AJkD/7WkFHDmUx8tPL6tO+bRXyXz75XYy04u4/b5hPq/b/Hs6C+bu\\nIC+3nLA2fky7rjdDRzat9k1qciEGo+SxAABUBIagAaLRQM6KbcRfPapRbQnu1p5RXz51xtdl/bqZ\\n3a/MRbE7UU4JJay6eiZXH/kCa6R3EbmUuStQTgk8GxSZmIzDkCUSlZGA2Tz8jG3R+YNJV/Tg91Up\\nVJQ5q9NoTWaJDp3CSEnO93qNBhiNF47j5MJ5Eh2fzPvvNo+2gk6HwobVqeQfL/d6zaolh/jo7d/J\\nySpFdqnkHi3jk/c2snTR/qYwuZqAILPPAKikyO43NQFE0x/N0VVZYc8b3/Jtxxv5KvxKVkx/huL9\\n6U1jsBf2vjnfaxBZU1WOfLXC53WnPlMNVJWMhesoz8htKBNbJYHBVp5/cwqXTEwgrI0fMe2CuObm\\n/jw2cxyhYZ6y3qIo0KVbG6w2k5e7nZ/oC0ArIOWw97cZySBy5JDnMUVR+faL7V4XjQVf7WxSzfYO\\nncMICrZwenaqqMhEp7mbomuKSsy4/tXHVt8wi23PfEp52jEchWVk/LCeRYP/0iyLgOqSKTmY6fWY\\nYndSlVPo89out03EYPNesV20L40fB9yNPa+4QexsSooKK0k7UoDD7ll0Vx+OHS3l1x/2sXTRfgry\\nKs7JluAQKzfdMZA3PprOS+9MZcKUbhiNEvf9fRQ2PxMms1sixGwxEBhk4c4HfO+Yz0caxAUkCMJl\\nwFuABHysadrLpx0fDfwApJ74aIGmac81xNg6dWOzmSgt8Z7G6E0SojC/wuckr6Fx/Fj5WafDyS6F\\nlUsOs2b5YRRZY8jF8Uy4vJvPtypBEHjkmbG88swyKsuduCrsaEBQ/jE6pexCspoZ+eWTGGxun2zR\\nnlQyf96EcmqQVdOQK+1se/oTLpk/86zsPhtKjxxl8ci/Ys/3Pkkb/K0eGUyqolCelosp0EbXOyaR\\nvnAtuWt3e1YoqxpyuZ39731Pv2f/3EhPUJO0IwWkJhcQEmqjZ7+YM1buLC918P7sNRzadxzJIKGq\\nKhOv7MG06/rUu/7k68+3seynA2iqhiDAN59v56ob+zDxyoatxm4fH8IbH09n45pUjh0to318CAOH\\ntW/SRkVNwTk/jSAIEvAeMB7IArYIgvCjpmn7Tjt1raZpU851PJ0z55KJCSxesNdD/dNkNtDdS7N1\\nm58ZxYdEsiyr+Aec3RZYVVRefXY5qckF1buLRfP3sH51KjNnT8Ji9e7yiIoJZPa/p7F/Ty4FuaUY\\nk1NQthXgd+m1dPm/iTVSNnPX7vYxuMax1bvOyu6zZcW0Z6jKLQQvLizRbCSgUwyxkwdXf3bkq+Vs\\n+ut7KFVOVFkhYlgiIz9/nN/veJ3sJUke91DsTrKXbm30BcDpkHnzhVUkH8wDDURJwGQy8Pis8bRt\\nF1zv+7wxayVpKYUoslod0/nl+/0EBloYN7lbndfv3ZnDip8P4jrt93jBVztJ7BNN+w4N25DHajUy\\n5tKEBr1nS6MhXECDgGRN01I0TXMC84ArGuC+Og3E5Vf3ome/GIwmCbPZgMVqJCDQzGPPjvPa8tDP\\n30Sv/p5veJIk0i0xksBg32JxLpfCxrWpLJy3k41rU2v0zd25NZu0I4U1XEsul0JhQQVrlifX+gyi\\nJJLYJ5qRE7oy9N6JjPj4UXo+di0I1JBiMIcFIvp4MzUFN50sQsnBTMpSjnqd/AESbpvI5DX/QpTc\\nLobsZUn8PuMNHPmlyBV2VIeL3LW7+fWSRwgf1A3R5OVdTRCwtT0z3aYjh/J54/mVPHT7d7z0j6Xs\\n3ZlT5zXffrmdw/uP43QoOJ0K9iqZ0lI7r89c4TM+czqZaUVkphehnC5Y55BZ9N2eet1j1ZJDXvP2\\nXS6FNSuO1OseOjVpiP1MW+BUJ2cWMNjLecMEQdgFZAOPapq2twHG1qkHBoPIg0+MJjuzmCMH8wkM\\nttCzb+1b+DsfGMbrM1eQlVGMKApoKkS1DeSehy/2eU1ebhnPP/4rjioZu13GYjHw1SdJPP3yZbSJ\\nDGD7liyPNoDgji1s2ZDBhMu7+7y3q6KK0sPZWCNDMIUEsPH+t0n53woEUUAwSPR+6iZ6Pfon2k0Z\\ngkfAAJBsZno8MK2Ob8pNWWoOuev2oKkqWYs3kbV4E4IoEn/1SAa8MgNLeN3uL2dxOaJBwpsjTTQZ\\n6D/rNowBf1Rg75j5OUplzdoATVaoPFZIYOdYBEkCan53ktVE4oPT6/VMALu3H+Xtl39z7wQ1KCyo\\nJOVwPjffMZCR47v4vG7N8mTPLCwNKsudpBzKp3O3NnWOffxYGZIkgpdvpKSofvo7FeXe8/Y1zd0P\\nQefMaSqH1jagvaZp5YIgTAK+B7z+xgmCMAOYAdC+ffsmMq910LZdcL237H7+Zv752iRSkwvIyS4h\\nKiaQDp3DavXVvj97HaUlDrQTb4V2u4zDqfDB7HU88+pErDYjogiqF+FKq827+0fTNHbO+oJdr8xD\\nNEioThljgA1XWWWNFMmdMz/DYDHR4/5pjP/pRZZNeRJN09BkFdBof8Uwut1b+8ZUU1V+v3M2KXNX\\nIkgicqW9RvPyI18uJ2fVdqbt+aQ65uCLkN4d0bw9KOAX2wZTsD+aqqIpKqLRQMmhLK/nqk4ZZ0kF\\nI794grW3vowgiWgaaC6Z/rNuq3cVtKZpfPbhJq+B/a8+2cqw0R0xGCWv19m9LNrgVo8tL6vfxNu2\\nXbBHvv1J6itYd9HgdiQfyPNwZZotBvoN1CUvzoaGWACygVO//dgTn1WjaVrpKX9eLAjC+4IghGua\\n5pGComnaHGAOwIABA+q3v9RpNDp0DqND57orXYsLK8lILaye/E+iqRrpqYUUF1UxYkwnli8+iHra\\nxCiKAiPHdvJ634P/XsTuV75GqXRUvzsqXkTZ5EoHO57/nO73XUnkiF5clzOfrJ834igsI/LiXgR3\\nj6vzGQ58uIjUr3/zen9wu5rseSWkzFtFwm0Ta72XwWrmohfuYOsTHyGf8mYvWc0MfP1uNvzlLZI/\\nW4JidxHUrT2WNkE48j2b9KgOF6XJ2fS470raXjqAo0u3ojhdxIzrjyWsfoH4kkOZ7H77eyJ/3o4p\\nNJJj7TqjGP+I42hAZnqx15+zIAjEdQglPcUzW8nlUujYpX5V0FFtA+maGMHBPbk1dhMms8T0G/rU\\n6x4Xj+3E0p8OUJBfgXziHkaTRHTbQF3z6CxpiBjAFqCLIAgdBEEwAdcBP556giAIUcKJV0dBEAad\\nGLegAcbWaSE4HIrPqmJRFHDYZWLjgn1WrnpLRwXY+eL/3G/i9cBZXFF9rsFqJv7qUXSdMaVekz+c\\nyNevYyy5ws7R5Vvrdb8e909j1Ff/IHxgVywRwUSP68+ly15j71vfkfzfJShVTtA0SvanU5p81Kvr\\nCuDAnEXkrNqO0c9K3LQRdLx2TL0n/7Tv1vBDv7tInrOI8KPpdNi/jUErF2Ku+iN9UlVVnzswgBtv\\nH1CdDnkSs9nAuElda40Hnc4Dfx/F4BHxGI0SRpOEf4CZG24bwLBR9SsuNFuMPPv6JCZemUhElD9R\\nMYFceW0vnnzxUr2X8FlyzjsATdNkQRDuA5bgTgP9RNO0vYIg3H3i+IfA1cA9giDIQBVwnaZp+tv9\\nBUSbSH+sVqOHiwHAajPRJtKflMP5Xt0Aqqqxaslhrr31Io9jlUfr/55g9LfW6ZqpDUdhWZ3nCEYD\\nfu0i6n3P9lOH0X7qH7nj+VsPUbDloMcuQ6ulp4Bmd7Hr1XlEj+lX73EB5CoHa//v1RopsQZFRlJk\\nOu3ZzL6BYxAEaBMZQFRMoM/7dE2M5PHnJzD/y+2kHSkgKNjKpGmJXOxj1+YLs8XInQ8O55a7B1NZ\\n4SQoyOLN7qTSAAAgAElEQVQ1CaE2bH4mrr6xL1ff2PeMrtPxToPEADRNWwwsPu2zD0/587vAuw0x\\nlk7LRBQF/nzvED6YvbY6yIgAJpPEn+8ZjCgKlBbbfe4SqqpcaJrmEWMIiI+iLKXuTBXJZqbn3671\\nuF6utHPo019Jn78aY4CNhDsn027KUK+xjIjhiWT9vAlqeTcRDRIJd0zyebz4QAb73/2e0sNZRAzv\\nSbe7L8caEVJ9vGDbYTSfSjO+KU89dsbXHFu9E8HL9y0A4bmZmM0GDCaRvzzmO7B/kk4J4fz9ufFn\\nbIM3zGaDrmHUQtB/CjoNRv9B7Xj8+Qksmr+b7Ixi2rYP5vKre9EpwZ2q2KFzWI200FNpFxfsdVLu\\n99z/8fuM2TUyZASTAVOQH67SSiSzEdWl0OP+afT+23U1rnWVV7Fo8L2Up+dWX5+zagedbhrHsA8e\\n8hjrolm3cWzVDg/ZBkESMfhZ0GSF4f95jKAusV6fIWPRen67bhaqS0aTFXLX7mbfv75jyoZ3Cerq\\n9lH7tWuDKIles4Nqo82guvPkNU3DWVSGZDVjsJprXcgAZFkBNGY9voQbb7uIEWM7n6FVOuc7+gKg\\n06B0Sgjnr096V8gMDrUxalxn1q48UsNVZDJJXP9/A7zf74axyBVVbH3yP8iVDjRVJf7qkQz74CGU\\nKgeVOQXY2oZTmZVPRVYe/u3/KArb/85CylOP1XC3yBV2kr9YRte7Liesb80JL7R3JyatfYukv8/h\\n+Pq9GANtdLltIiGJ8UhmEzHjL8Lo793nrbpk1t76Sg13i2J3ojhc/H73G0xa9SaA+x6BNndD+VMm\\naMliQlNVVKenK0g0G+n9xA1exz1J5uJNbLzvbSqPumMpMeMuwuBv9dqsRgMKI2JRFA1FUcCh8Nmc\\nzQSH2ejZN6bWcXQuLPQFQKdJuenOQUTFBPLLD/soL3XQLj6EP93Sn25eKpJP0vXOKXS5bSJVxwox\\nBftj9HNPwkZ/K6nf/EbSEx8jCAKqSya0byfGfPtP/Nq24chpaponUR0uMhdt8FgAAML6dubSJa+e\\n8XPlbT7gPe1T0zi+bg+Kw4lkNiFKEpetnM3yKU9ReTQfwSChOlwkPnQ1osnA7lfmoTic1emn5rBA\\nxi16odZAdu663ay6ZmaNxSdr8Sav5wpmIy4kDvesKUPtdCj88M1ufQFoZegLgE6TIooCEy7vXmvR\\nl9frJAm/tjULjtIXriPp73NqpFnmbznIL6Mf5qqDnyEaffx6i4LvY2eJIAo1agZqHqRGhk9Ql1im\\nH/gvhTuScRSUEta/C+ZQdxC2w7VjSPt2NYrTReykIUQO7VHn2Nv++d+a2ke+zJBEzAN7sT64Ow7R\\nM+vn2NFSL1fpXMjoC4BOg6FpGpt/T2fxwr0UF1XRpXsE067rfUZ6MWfCjuc+rzH5g1sZtOp4ETmr\\ndpBw20S2/H2OR4WtaJCIu6ruwOeZED6wm7vZy+mIAlGj+yKdJu0sCAJh/TxrIYO7tafv0zef0djF\\ne1LrPgn3d2MLsiHYrOCluKuxfk46LRd9AdBpMOZ/uYNlP+3HccK/n7Q+nV1bs3nyhQnEd6pfwZAv\\nNE0j/bs17P/gR5xFZbSfOoyyVO/ZQZqiUpqcTcKdk0mbv4b8rYeQy6sQJBHRZKTPUzf6DOSeLaJB\\nYtRX/2DF9GfQZAXVKSPZzBhsZoZ/6Blwbkj84iKx53kWkZ2OYJSISYwlqMSK83g56imCfyazxJXX\\n9fZ6XVFhJYsX7mX3tqP4B5qZMKU7A4e1r7eCp07LRWjJ6fgDBgzQkpI8VRB1Wh6lxVU8fOcCr527\\nuiZG8OQLl57T/dff8yZHvlxenaEjWoygaDWE4E5i8LcwYfHLRI7ohaooZC3eRMaP6zEG2Oh8ywSv\\nvv+GoiztGAfn/ETp4Wwihvagy20TMTeyCF3Gj+v57fpZdbqBJKuZK3bMQQsP46O3fufAnlxEUcDm\\nZ+LmGQMZMNQzzlCQV8EzD/9EVZVcLeRmNhsYOa4zN905sFGeR+fcEARhq6Zp3rMqTkPfAeg0CIcO\\n5CEZvLduTD6Qd073Lt6XRvLny2pMcKrdhWCQwCDCKcVlotFAYKe2OArL+GnY/VRkHCdsQAL9/nmL\\nV5dLffFWo3ASV3kVKV+toGD7YYK6tqPXo3+q9un7ojwjl8xFGxAkifZTh2KLqZ+qZ9XxItK/W4ur\\nvIqY8RcR1rcz7acOI2HGZPa/tcDndaLFyPA5D1fvfB57dhwV5Q7sVTIhYTaf9RnffLGNinJnjYxS\\nh0Pmt2WHuXRqN9pENl4fZp3GR18AdM6Y3JxS9u48hsVqoN/AWKw2EzabEV9R0HNtopH1y2Y0xXNh\\n0WQFc3gQokHCWVyOpmq0vWwg4QMSWH3DC9WyDpWLCshZvpXxi18maqR3N4cv8rcdYtOD73F8w14k\\ns5GO149l0Oy7MQW53+rLUo7y09D7kSvtyBV2JJuZ7c9+xmUrZhN+kXct+R3Pf8Gul77iZD/LzQ+/\\nz0Uv3UHig1fVakvqN6tY++dXQRTQXArbZ35G+yuGMeqLJ+l+z1QOzfnZ6y5AMEhckzoXW2RIjc/9\\n/M34+XvvOAbuXd2mtWleywkEAfbsyGHMpfoCcD6jLwA69eakouS6VSkIuDN6Pn1/I395bCS9+sVg\\nNErYq2q6ZEQRBgw7N1VXyWpG8CEZYAkLZNreT6g6VuiWVxYE5kZe5aUjmION97/NlTs/rve4xQcy\\n+GXUQ9VuJ6XKyZEvl5OfdJArtv0bQRRZ+3+vYi8oqdb9Pylat2zSE0SO6o052J8ut00kYog7myd3\\n3W52nWgQfypbn/wP0aP7EtrHu7xCVW6hW9bh1OtcMpk/biD5s6V0+b/LCEyIpXh3ao10VNFsJG76\\nxR6Tf32Y++lWn7VkAue+sOs0P7qCkk692bAmlfW/peJynmgMYpdxOhTee20NVRUuHvrHJZgtNScF\\nVYPN69LPyQ0UN/1ir1WtktVMwp2TEUQRW0w4xgAb+UkHfaZ4Fu9LR/ah9Algzy9h4wPvMC/6aua1\\n/RMrr3rWY6JWnS7KUnLIXpqEs6ScvI37vTZ9secVkz5/DYc++YVfxz3K9pmfAbD/gx/dInCnoThc\\nHPz4Z5+2pX6z2uvncoWdfe99D8DYhc9hiw3HEGB1VwP7WQjt3ZFh7z/o8761sWVDhs9jiqLRb2DD\\nBtJ1mh59CdepN0sXHfDakQkNNv2extiJXYmI8iczrbjGMYdd5oM31vL6v6edVeaILSqUIe89wMb7\\n3kZT3NWyBn8L4QO60f2+K3GWlJPz205Eg4Q5NBBN9S60IBgkRIOXVE3AVVbJjwPvoSqnoLoatyrH\\nuxCdXGEnP+kQ4QO7Uqesj6qhVDrY/eo8Ot4wFkdBqXeJBlX1KgddbV9pJYq37x5wlbiVPQPio7j6\\nyJfkLN9GWdoxQnt3pM2QHmedrXO6tPepXHZFd2x+Z9caVKfloC8AOvWmwkfzD5dLoaLcSWmJnZws\\n78VEpSV2jh0tJbrt2TWTT/i/iUSP6UfK/5bjKC6n7YQBxIztz8GPfmbzQ+9Xt0xUZQWjvxW5vKae\\nj2gyEH/VSJ8LwKFPfsGeV+xViuF0DDYztpgwLGFBBHZuS/G+9Dqv0WSVjIXraH/5UI6v2+1Rv2Dw\\ns9Bu8hCf18eM68+ul7/y0CkSjYYaaqOiJNH2Us/snLLUHA5+9DPlqTlEXtybzrdM8ClrcZJe/WLY\\nkZTlsV4ZTRJTrq5fIxqdlo3uAtKpNz37xSBJnm+TJrOBbomRtYqPCdSpTVYnAfFR9HnqJga9djdt\\nxw8gb/MBtjzyAYrdiau00v2WXOnAfrwY0WTE4G9FMEgY/K0EdW3HkHcf8HnvrMWbPArGfD6LJNLh\\nmlEADP/4UQx+FndGUi1oaGiaRuc/X4o1OqxGj1/JYsK/QxTxJ+7pjfBB3Yge2x/J9kfQVjQaMAX7\\nu3sj10LmTxtY2Ot29s7+ltSvfyPp73NY0O1WKrJrd8vdcPsAbP4mjEb3NCGcUHe96Y6BWK2++wfo\\nnD/oOwCdenP51T3ZuDYNe5Wzuq2j0STRKSGcLt3bIAgCkTEBZGd4ujJs/mai29aeGnmm7Ht7AbIX\\nfzqAKsuEJMbR4bpLCO3biZix/RFE3+87lja1V8GKJgOS2YRkNTHuh1nV/XwjhvTgiu1z2DP7W/K3\\nHkKTZYr3p6Oe5q4RDRJxV47A6Gfl8s3vs+ulr0j9ehWCKNLp5vH0+tt1SGbfLhVBELhk/rMcnLOI\\nAx8swlVeRfvLh9L7iRuwRYX6vE5xOFl904s1Fje5wo5id7Lpr+8xeu7TFO9NQ7KaCOwSW8NdFBEV\\nwMvvTGX54oPs332MsDb+jJ/SrVrdVef8Ry8E0zkj8nLLWTh3J7u2ZWM2Gxg1oQuTruxR3U82NbmA\\nl59eiuxSkWUVySBikEQe+scYuveKalBbfh7xAMfX7/V5XLKYuHLXxwR2blvnvXLX7+WXMQ+h+ZCr\\ntkSGMOabZ4gYlogo+X7bd1VU8fOw+ylLyXG7awQBg9VM9/unMeClO+p+qDPAUVTGvre+I+27tRj8\\nLHS763I63TK+hn3Zy5JYdc1Mr6qggkHE4G9DUxQ0RcWvXQSXfPtPQnp2aFA7dZoWvRBMp9FoE+nP\\njL8O93m8Q+cwXnpnKit+OUhqciGxccGMn9y1UQqGoi/pR/7WQ6gOl9fjoslA4a4UylJzqMjMI6x/\\nF59VwJHDEomdNITMH373etwWFUrUxXXXEBj9rEzZ9D6pc1eStmAtpmA/ut4xmahRf/S9Lc/IdQu+\\n2V3EThp0VgVqjqIyfug3g6rcourn37g3jcyfNjBm/rPVb/Le6idOoskqruLy6r+XHsxk8aiH+FP6\\n3DrjAzoXBg2yAxAE4TLgLdwtIT/WNO3l044LJ45PAiqBP2uatq2u++o7gObH6VTYtDaNpI0Z+PkZ\\nGTW+C10TfUs3NyVVx4tY2OM2HIXeA8+SxYQx0OYOuGoaaBrhg7szftELXltHVh0v4tv4GzxSPw02\\nC4PevJeud04+Z5v3v/8DWx79EE3V0BQF0WykwzWjGfHJYwiC4E4t3XQAY6CNNoO6+XRbbZ/5Gbte\\nmYtqr7n4GfwsXLr0VSKGJgLujmhzI6/yCB77wuBnYfCb95Jwx7k/q07zcCY7gHMOAguCIAHvAROB\\nHsD1giCcrmE7Eehy4r8ZwAfnOq5O4+Owu5j52GK+mLOJHVuy+H11Kq8/t4Lv/re9uU0DwBoRwuWb\\n3yO4Z7znQVFAcTixHy9GLq9CrrAjVzrI27CPzY9+6Hn+iftd/NnjHqqeikvGVVpBycHMc7K3NDmb\\nLY99iGJ3ojpdaIqKUukgbf5q0r5dza5X5zEv+hpW/ek5llz6N76Ju56C7YcBqDyaT96m/dWLXdp3\\nazwmf3BP+Fm/bK7+u8FmYdiHDyHZ/iimkywmn4V1coWd0uTsc3pOnfOHhnABDQKSNU1LARAEYR5w\\nBbDvlHOuAD4/0Qh+oyAIwYIgRGuaVnezV51mY8miA+TmlOFynvCLa+7GIb/8sJ/hYzrV2kj8dIoP\\npJP2zWoki4m2EwcR2qtjg9gY0DGGK3d+TNLjH7H/nYWIZmP1BOtNmUKxO0n+bAlD333A69u1OSzQ\\nndFzSixAc8lseezfbH36U8L6dGLsD8/X6PNbfZ6qVlcknwwSn8qR/y1HlT1jDHKFnc2PfICzqMzd\\nRezEDkQuq+KXsY8QMTSRY6t2VD9blz9fViMb6FREgwGDX83dTacbxxHSswP73llIWWoO0aP7Urjr\\nCBkLf/doYmPwt+oxgFZEQywAbYFTX42ygMH1OKctoC8ALZj1v6X8MfmfgqpqbNucyaQrE+u8h72g\\nhF/HPUbRziPVn239xyd0umkcI/7zWINICguCwMBXZtDnyRso2pvOoTk/kfy/5eDD/604XKgu2WvW\\nzd7Z33it1AVQ7U7ytx1ixRVPM2XDuzWOpXy9is1/fQ9nSQWaqhE7aRAjPn60hiicq6zSZ5C5Mjvf\\n6+dyWRVHl21Fk5XqhSH5i6VEje6Lwc/itX9xh2s9W3KG9unEiI8frf570Z5Usn7ZXLPXsiRiDLAR\\nd7XvdFSdC4sWVwcgCMIMQRCSBEFIyss7NxVJnXPEx9xc3ylb0zR+Gf1wjckf3CJuKXNXkjpvFUdX\\nbmfRkHv5wn8y8zvfxMGPf+Zs41KmIH8ihyVScjjL5+QP7o5cp0/+mqZhzyumLO1Y7c/kUijcnULx\\ngT9kErKXbGHd7a9RlVtUvfvIWryJJeP/VuNZYicNweDvGXuodTxFRTtt16BUOshdvZOYCQPdb/uC\\n4E5TtZgYNPseAuLrzrYK6dmB8T+9iH+HKASDhCCJtBnSgykb3sFg0St8WwsNsQPIBtqd8vfYE5+d\\n6TkAaJo2B5gD7iBwA9inc5YMH92RhXN3oiieP4aLBtct8Ja3aT+lh7O8HlMdLnbM+oLytNxq4bay\\nlBw2//V9ylJyGPDi2adMBveII3/zAZ8ZMJbIYAp3HqkWXstYtJ6N971N1fFid38BAd/tHXFLShz/\\nfQ+mQBu2mHC2Pf2pRxGZ6pQpOZTJ8Q37iBzm3ilFj+mLX3wUJXvSzvrZqu8vKwyf8xClh7PJ+mUz\\nRj8L8X8aXa/J/yTHN+6jIjvfXZQmCBRsPUTOqh10ufXcejfonD80xAKwBegiCEIH3JP6dcANp53z\\nI3DfifjAYKBE9/+3fDp3bYPiRQ9GQ8OvHjowJQcza51Iy5KPejR0kSvt7PvXd/R67FrMIWeXOpr4\\n16tJ/nwpePe2kLtuDz8Nv59x3z+PaDS4m6nUswoYQC6tZNOD77HxvrcJ7de5xm7gVDRVZcO9/6L0\\ncDaS2Uinm8djP1Z0No/kgcFmwRTsT8SQHtVKo2fCsTW72DXrf2hOGeUU+YsN975FxNAeBCW0q+Vq\\nnQuFc3YBaZomA/cBS4D9wDeapu0VBOFuQRDuPnHaYiAFSAY+Au4913F1Gp/liw96ncAlUWT96pQ6\\nrw9KiPWZbYKA125e4JYwLtiefCameox7eg/eGpwQaPv9rjfdDdW9Tf6SWKuvS660ozhc5G85iOLw\\nHjNQqpwU7UpBqXLgLC7nwL8XucXg6osgYAj0DCYDJNw5qdaCtLrY/+5CZC+9A1RZ5tAnv571fXXO\\nLxqkEEzTtMW4J/lTP/vwlD9rwF8aYiydpuP4sTKvnzudis9jp9JmSA8CE2Ip2p3isZAYA6woTtlr\\nKqPmkrFGnH2D8sLdKQg+OlydSlVOAc5TCqFORTQaGPDKDMyh/mx78j9UZheA4FlYpSkqotGEIIo1\\nC9IEwUP8SKuH0FzNCzTksiqvh0r2+ZZqrg9Vx4u9ijNpLgV7bqHP6xwOmS2/p5OdUUx0uyAGD4/D\\nbNF1gc5XWlwQWKd+bFqXxmP3fM+fp3/Jg7fNZ/nPB846eOqLTgnhiF7E3ywWAx06160HIwgCly17\\njRAvTU5Up0LsxEFIpwUcBVHEPz6K4MT4s7bbYLPUWgF7Ek1V8Y+L8HpMAI58vpT079Yx+J37ubHs\\nJ6w+mqposkLbCQMw+FsxBtiQLCYks+9J0eeuyONEwedCdnRlnXWUteLtuwd3GmjbCd57/ebmlPHI\\njAV8Pmczi7/fx5cfbeHhGQs5ln0GuxqdFoW+AJyHrF2RzMfvrOd4ThmaqlFcWMXXn29jwVc7GnSc\\niVcmYjytKEoUBax+JgYO92wg7g1TaIDXFEfF7iRz0UZC+nZCspkx+FswBFjxi4tk3E8vIggCitNF\\n1i+bSPl6FZU+tPm9EdS1Hba2tS9QgiTSZmgi/Z79MwYvOfWKw0nB1kNkfL+ONTe+yIa73ySou/dn\\nNlhNJNwxieuPL2DSmn8x/eBntBnq3S8vWoz4x0W6nznA6l4MfKTCnl6QVsO+KmetzW3qoutdl2MO\\nDaihYiqajfi3jyDuqou9XvPhG2spL3XgsLt3Mg67TEWZg/deX3PWdug0L7oW0HmGqmp88/l2nI6a\\nEc6TBVqTpvdsMKneyOgAnpg1gc//vYm0I4UIAvTq35Y/3zMYk6l+/uei3ak+8+o1WaE8NYfJa9+i\\ncFcK/u0jiBrVB0EUyV23m+VT/+EuVNI0FKdM4oNXcdFLd9RZOyAIApd8N5PFox5Cdbr+yJU/kd1j\\n8LdiCrQx8rO/498+kgGvzCDpiY8RRAGlyuku1jplNyVX2En5aoW7uEsU4ZTiKUESMYcFETtpMKIk\\nVWcW9Xz4GvI3H/CUYFA1Eu6YREifTriKK/CLi6B4fwZ73/iW0sPuxDjRbMRoszD0wwdZddVMr88o\\nmiSOr9tNzLiLav0ufGEO9ufypA/Z/ux/SV+wFkGS6HTTOPo+fbPX+ElJcRUZaUUeXiNNg5ysUgrz\\nKwgN9zsrW3SaD30BOM8oL7VTWel9QjUYRHKySujYpeHkejt0DuOfr03C6ZARRaFa9bO+iEZDrY0A\\n5AoH9rySGqmHztIKlk1+Atdp/u/dr31NytyVdL//Srr/5UoMVt8NzUN6duBP6XNJ/eY3So9kE9y1\\nPYpLpjz1GCGJ8cRNH4FkNiFXOZAsphMLj0DJ4WxKvWT1aIpaI15wMnUyYmgPRn7xhEdAtt3kIfR8\\n7Fp2vzwXwSihOmR3dTKw47kv0DSNdlOG0PPha0i4bSJdb5+EpmmUHMhAdckEJ8a7K5Ul0WtNg2gy\\n1nAlOQpLOb5hH8YAGxHD/1AszV6aRNKTH1OyLx1rdCi9H7+ehDsmIwgCtqhQhn/4MMM/fNjn91j9\\nM3EoiD4WXkF0x4V0zj/0BeA8w2IzIfhIT5FdKkHBjaPieLYNwIN7xGEOC/QtRqbh4d5J/26t93aE\\nmkZF5nG2//MzUr/+jcm/v11rto/R30rCbRO9HnMUl7N95ufsfeNb9xu/qkE9AscnMfhZmLbvU2yR\\nvrX4+z1zC93uvpzDn/7K9mfdPYFP7TiW/t1ashZvwj8ukkuXvoZfbBuCT3MztZs8hMyfNnj0HRZE\\nkYjhPQHY8fwX7HrpK0STAVVWECWJ/i/eji06lDU3v1xdZ1GeeozND39AeVouF71we72fFSA8wg//\\nADOFBZ6y0labiYiohld71Wl89BjAeYbJJDFkZLyHb16SBDomhBPWpmVtwwVBYPS8p32qWmqqSpuB\\nXWt8drKi1hdKlYOSgxmkzT8737OztIIfL7qbPa997Z6QT06uqua1wbs3VJeMs7DuTChrRAgVmXke\\n1bwnUaqclB7OZsWVT1d/Vp55nINzfuLwp7/Sb+atWNsEI51QLxVNBiSbmVFfPolkMpK+cB27X51X\\n3RVNqXTgKqtk0/3vsOra56sn/5PIFXb2vjkfh4/sJ18IgsBt9w3FZJaqQxaCACazxG33DkE8g8VT\\np+Wg7wCaAEVR2ZmUTU52KVExAfQZEIvBcPZr780zBlFcVMWBPbkYJBFV1YiODeS+v41sQKsbjogh\\nPbjkh+dZOe2ZGhOhZDUTM74/wT3ia5zfZkh3JIupVgljudxO+oI1dLph7Bnbc+CDH6nKKfCdKSQK\\nCJKE5qNOAdxa+t4E32qco2lUZudTmZ1fuy6/olJ8IIOSg5mkzF3B7lfmgSQiCAKaojJw9t1oikru\\nml0EdIqh64wpBHSIBmDXq/N8f08+xhTNRop2HqnRo6A+9OoXwz9euoyfF+whK72YmPbBTJmeSHyn\\nsDO6j07LQV8AGpnC/ApmPbGEinIHTqeCySRh8zPxj5cuO+u3dbPZwKPPjCUnu4TsjBLaRPoT19G3\\nK6Il0H7yEC5b8TqbH/mAwu3JGAP96HbP5fR95haPc6NG9SGkd0cKtyf73gkIAsYg9/enndD6r63l\\n46mkfbem1h0GqoamyV5z+cHtfgnuGY9fbBuftzi2eidrb3+NqqMFbheTKNS6uxCNBjIXb2LP7G9R\\nTmtws+XRf3PFjjn0uG+ax3VVR72LyNWGYndgDju79pxxHUO599GW+aKhc+boC0Aj8+Gb6ygqqEQ9\\n8Y/fXiXjdCi89/oannnFu3+6vkS3DSK6bVBDmOkT2aXw/de7WLXkMJWVTmxWI6oGQcEWLp3anVHj\\nu9R7+x91cW+mbq67FcTJ+oHtz37GwX//hKvM0+9ssJqJu3IEq659jozvf0dVFCIv7sXQdx8kpI4a\\nAoOtHnESrfp/NW0zSljCgxjz9TM+Ly0+kMGyyU+4G9HUE9XhImfFNq9v86qskPzfX7noBU99pDZD\\nE6nIXl1v1xWA6lJYMe0ZJq35F7Zo/e29NaPHABqR0hI7Rw7mV0/+J1FVjfSUQooLPSe2lsY7r6zm\\n1x/3U17mQFU0ysudVFY4ycku5atPkvjkvQ2NMq7BZmHgq3dxU8kiev3tWiSr2a1aaZCQrCa6/eUK\\nNj7wLukL17klJVSN3DW7+XnY/ZRn5NZ67+gxZ+b6OJ3Lkz6sdsGAW/K6eH96dV7+nte/8XiLB/fi\\nYQiwekhMGPws9Hhgms+qZM0lY88r8Xqs3zM315oN5RVVozw9lzU3v+S+v6ah1qNwTufCQ98BNCL2\\nKpe7ktaLK1mSROxVZygN0IgUFlSSkVJISJiN9h1CEASBzLQi9u065rUnALhTAzeuSePyq3sRGd14\\nWSADXp5B51svJeN7d7/e9tNGkL/lIAc++LFmcFXTUOxO9v7rOwa/4VtuKmJoIoJR8qnNXxsGm4WS\\n/Rn4RYfhLClnza2vkL1kizvdFejz1I0UbDvs1eevuRQ63zme2ElD2PrER5QczMQaGUKvx6+n291T\\n2f3yXAq2H/aom3BX53rv8BfcI56Jq95gxfR/UplVf/l0TVbIXbebj19azsZtuciySnznMG6+cxCd\\nEhoujbih0DSNNcuT+eX7fZSVOuiUEM5VN/Zt8a7Plo6+ADQi4RH+WKxGj6ItAKNRIiLKvxmsqomi\\nqHzy3kY2rU3FYJRQFY3wSD8efWYsRw7n1yn+L4pwcG9uoy4AAMHd42qkSO57ewFyuadOjuqSyV27\\nuydvx9kAACAASURBVNZ7RQxPRDRIKGexAKguGVuUWxJi+RVPk7dxP6rTVa0DtHPWl4T07IAgiR6L\\ngMFmIbhHHO0mDabdpNN7JkHXuy9n/3vfUyUXVy9OksVEYKcY2l8x3KdN4QO60v+5P/P7Pf9C87Lz\\n8IWswrY1ybjM7lhK6uECXn56Kf98bRKx7c9ei6kx+PLjJNYsP1z9b2nntmz27znGE7MmNGjdS2tD\\ndwE1IqIocMuMQR5VsyazxC13DUKsryZMI/Ljt7vZvC4Nl0ulqtKFwyGTk1XKazNXEBhkqdO/L4gC\\nNv+GbSCiqWqdukb+HaK8atkgCAR08K2Jr2kae9/8Dk0+c5eHIIkEJbQjuEc8xfvTyU86WF3cdRK5\\nwk5Zag6iFy0gwSjR6cZxPu9vDglg6rZ/0/XOyVgiQ7DFhpP48DVMWvtW9Q7DF+EDu/n8WZ0q91DD\\nVoORClPNTCaXU+GHr3fVOlZTU1RYyeqlh2q+SJ1oTzrv063NZ9gFQPPPQBc4A4fF8diz40jsE01I\\nmI0evaN45OmxDB4R39ymAbDspwMeVZyqqlFwvIKgYItHvcHpCIJA7/5tG8SWY6t38kO/GfzXOIEv\\nA6ew8cF3vUoWA3S5ZYJXUTXJaiLx4Wt8jpHy1Qp2vzzXpxS1N0SzEYO/lcCEWMYtmgVA6eFsRIP3\\nSdmeV8Lob56pqTEkCChVDtJ/+L3WsawRIQx990Guz5nPtRlfc9Gs2zD61x20DkmMJ3p0X49FUbKa\\n3TGU0/WOTEaSew320CHSNDhy6MwzixqTw/vzkHykTbc0W883dBdQE5DQI4K/zfT95tdQOBwy639L\\nYde2bAKDrFxyWUKtPlJN06go954OKUoCpcV2/v7ceJ5//NdqAbDTueJPveqtC1QbxzfsZenkJ6q1\\n+eUKOwc/+pmiPalMXDHb43xrZCjjFr3AqmtmnpjMBTRFYfBb99XaIGXnC/9DrvRdX3AqotHA2EUv\\nIJdW4NcugvBB3ap1iIK6tvO5iPjFhqM55Zo5RJqG6pTZcPe/iBrZ54w6d9WXSxbMZNvTn7ozp8qr\\nCOndgcFv3Ev0mH5Ej+nHjuc+p/RwNkHd22OYOp4NG4rAy881NKz2+oYzRXYpbNucRU52CVExgVw0\\nuN0ZSYr4+Zvw5Ys0W/Up7FzQv70LhPIyBzMfW0xJkR2HQ0YQBdb/lsKfbu3P+MndvF4jCAJRbQO9\\nyvnKLpX2HUIJa+NHVNsA0o9472TlTRrg/9u7z8CoqrSB4/9z77QUSCghJCGhV+m9SZUizYptbeta\\nV3FfV3fVRddVd9Vde0FXLGvvDSxIU6nSQQRCJ5QAIZXUqfe8HyZEwswkk0ySScj5fSGZuXPvyTBz\\nz73nPOd5qmPjA2/6llW0O8lcm0rWxt20HNDF5zUJY/pyxbHPOLF6Ox6Hk/gRPTFFVlxzt7gKcfOG\\ny03Sef39ri+I6ZpMq+E9yFi5rVwdAFOkjb4PXUvqnK/8Fpox3B72vreYfg9cE3Q7gqVbLQz6zy0M\\n+s8tSCnLJc1LHN+fxPH9y353ONx8se5zn31YrCamXnxOjbUpM6OQf93/PSXFLux2NzabiQ/e3MAD\\nj08mLj64ObBuPeOxWHTsJeWH28wWnTETO9dYWxsjNQR0lvjq463kZBXjcHiv6KQhcTo9fPzWJvLz\\n/BcVAbjy+gG+cxQWncEjUsoWqkVF+Q8z1HWNyCBKQwYje9OewM9t3B3wOc2k03pUb5ImDKz05A9U\\nqc5AREJzb6EXjwdnfpHPvMT4Lx4h5YLh3iGiKBvmmCj6PXo9nX9/Po5s/2kipNvD3rcWeheHASUZ\\nOeSlHsSZXxR0u4JRWcZUq9XEvY+cR2zzCGwRJiIizZgtOhde3ot+g2uuHOR/n1lBXp4de+mdht3u\\n5mSenVeeXhH0PnRd456HxhMVbcEWYcJs0bFYdbr2aMVFV4QW0tvYhXQHIIRoDnwMtAPSgMuklD6X\\nikKINKAAb5VWt5TSf0xbDSnMd5CXW0xcfHSjqVa0dmUabj8Tm5ou2LIxnVHjO/l9Xd9BbfjjPefy\\n0dubOJ6eT2SUhQlTu3LB5b3Lthk/pSv7dmWVdS6n73v46A410v6I1s1xnfQ9CWq6Xmlu/1Oyt+xl\\n/T3/JWPVNsxREXS5cQp9/3EdptPGxQf88wYWT5vtkyPHH0d2AcuueZyDX67AcLqxxcUy8N830enq\\nCQCYm0Qy9qO/4zxZiCM7n8g2cWXJ6ZKnDyV3R5rfKmDF6Vls+sdbpH2yjIJ96WXrzZr17sDYTx8i\\npnOboP7eULXr2IJnX7+E/buzKClx0bFLyxrr0MGbQjptf45PYj9pSA4eyCEvt4TYZsElL2zboTnP\\n/+9SftmQzsncEjp0aUn7TmoRW6hCHQK6D1gqpXxCCHFf6e/3Bth2rJSyVmdsHHYXr734M5vXHcZk\\n0jE8BhOnd+OS3/VrvMmqKlkg6nZ5iIuP5t5HJhDbLMLv+zRgSDIjx3Vg+dJ9SEMiNIE0JGMndaZJ\\n0youQvJjx9Zj7Dh3MscTTxBz4ijJ+7Zjsxd7a+JG2Uia5L9C1enydqTx3bl/KltJ63C42PHCF2Su\\nTWXyD0+XXREnjO3H2I8fZOklD1W6DsBwudj/0Q9lOXVKjmWz+tZnvbnzrxxXtp0lJhpLTPnhjB53\\nXsyO57/A5acDMBwufn38A5//m9yt+/lm6B3M3P+ez/5qyvZfjrFwfiq5OcWc0yeBSTO606lb4JQW\\nobCXuNE14W8ZDJomcNhdQPDZa81mnYHDUmqsfUroHcAFwJjSn98GfiJwB1DrXn56Jdu3HMXtMnC7\\nvF/aRd/sxBZhZvqlvcLVrDoxZGQ7fvh+N54z7gIMQ9J3gP8onaULdvPpO5uQSDylC4Fu/8somjUv\\nPwlYXOSi6znxtGrdhMyMQn5efgCXy8OKpfv4ceEeLpjZi+kzq/f+Lpy/g8/e3+IN8WvSjKLIpmS0\\n7cyg9YtpEaUx4bsn0AKEMZ5u0z/e9okY8tidZG3YReaaHbQa9tu4dsL4/kGVjETik1DNU+xg099e\\nL9cBlD3ncLL/ox858PGPmCKttJkyhAMf/+i/Ew7QMbsKitn77mK/eX9C9c0X25j38daycMqjh0+y\\nbPFeHn56Sq2kc46L966DcfhZB2OLMBMXr1JIh1uoHUC8lPJY6c/HgfgA20lgiRDCA7wqpZwb4nF9\\nZGcWsX3LMVyu8l9Yp8PDd19uZ+rFPc/qu4ALL+/NlvVHOJlXgtPhQWgCs0lj5jX9aOqnRsCmtYf5\\n6K0N5WKr9+3K4vHZi3hizgVl79XyxXt457X16LoASdlYrpf3tfM/+5WENjFVvjorKnTw6Xtbyq00\\nlrqOB528q6/ilqemVzqWfcqJVdv85sMxXG4y16SW6wA0swnNbCpfxL0KCg9mYHg8CE0ja91O0hdv\\nRLea2ffBEgr2Hi27C9EjrN6Vcmd2NgGSzIF3jiBr/a5qtasiBfl2vvpwK67T7nrcbgOPx8nHb29i\\n1r2ja/yYmia49tYhvPrsynKfM4tV57pbh5zV38eGotIOQAixBPAXszb79F+klFIIEWjAYaSUMl0I\\n0QpYLITYKaX0m8xdCHEzcDNASkrwJ5TMjEJMZq3cB/wUh92Nw+GusVKJ9VF0Eyv/en4aq37azy8b\\n0olpFsHYSV0CjpN++dEvPiuUDUNyMreEnduO06N3AofScnn3tfW4nB4qOlU6HR6++XxblTuAndsy\\n0HUNF+XbIYE9BwvKTv5SStxuA5NJC9gh2Fo1o+RYjs/jmtWM7Yxi7ppJp8PlY9n/0Y8+C7mCYWnu\\nvXL9cebDpC9cj7vE6Y1SPPNuocSB0DU0m6Us+6hmNqFZTN67FT8dltA1n6IwNWHH1uPoJoHrjD9X\\nSti6Kb3Gj3fKwKEpxD4ygfmf/Er64TySkmOZMbNXrQ07KVVTaQcgpQwYwC6EyBBCJEgpjwkhEoAT\\nAfaRXvrvCSHEl8BgwG8HUHp3MBdg4MCBQac4jE9sgjvAmK4twoy1mhWtGhKrzcy4yV0ZN7lrpdtm\\nnfCfeMyQkoxjBfToncAPC3b5nVj2pzrhoGaLHjDThG7SkFKy6OtU5n+6jaJCJ9FNLMy4rDcTpnb1\\n6Qh63T2T1bc955NNU2gabS/0TaMw5IU7yN2RxsmdhzFcbjSThsfhRgiB0DUik1qimXTy9x8tN1dg\\nirTS888z2fPm96R/v77SNQXSkLQe0wf7iTyc+cWkTB9Gp+sn8u2wO/2+VrdZ6Pz7SX72FBrve+3/\\n3TYFGGKTUlKQ78BqM4X0/enUNY4/P+g7ZKaEX6hnxfnAdcATpf/OO3MDIUQUoEkpC0p/ngg8EuJx\\nfTRrHkmfQW34ZUN6uSEFi9XEjJm91O3mGVonNmX/nmyfx4UQJLbxppjOzSnxyWTql4AO1YjI6N6r\\ntd/1PSaTxtBz2zHv4618++X2sjuVgnwHn767CYfd5TOn0+F355G9ZS+pc+aVReJoFhMTvnnMb3io\\npWkU09e+zIlV28jevJeolFYkTxmC82QRhtNFREILHFknWXrR38nevBfNYsJjd9Lp95Ppfd+VzB90\\nW3ALyoSgeZ+ODHz8pnIPn//TMyy54IHf7loE2OJiGf/Vo0RUUGayunr2ScDwM+xkMmkMH93O5/FN\\n6w7z3tz1nCwNIe4zMIkbbh9GdJPQJ/2V+kNUlnOlwhcL0QL4BEgBDuINA80RQiQCr0sppwghOgBf\\nlr7EBHwgpfxXMPsfOHCg3LBhQ9DtcTo9vPPqWtYsP4CmaQgB0y7pybRLewY9ltxY/Lr5KC888VO5\\nYSBd10hs05RHn5uGEILF3+7kk3c2+U1mdzqLVeeBxydXKzPjti1Hef7xn5AGuFwebDYTzVpEcu8j\\nE7j3j/N8Qk8BbDYTL717md80FcVHs8hYuQ1LbDQJY/tWmkMnGPl70yk+mk3sOW2xtfB2jp93vZb8\\nPZUPnegRVqaufJ4W/XwXLEkpyd+TTl5qGk06JHqTyNXi5/SXDem89J9lSClxuQxsNhMt4qJ44InJ\\n5cI/d27L4OlHl5b/bJg0EpN++2wo9ZcQYmOwofYhdQC1raodwCn2EhcF+Q6aNY+o0pLzxubn5Qf4\\n4I0N2EtcGIbknL4J3HznCKJLQztLSlz8bdZ8TuaW4PF4Pye6LjCZNDweA49HktyuGdfcPJgu3VtV\\nux0n80pY/dN+crKL6dK9Ff0GJ3PiWAEP//U7vymzrTYTjz47rUoZSKWUpH26jNSXvsSRW0jy9GH0\\nvOtSbHHVy3q5/q+vsuOFL8oVefen590zGfTkrdU6Rm3IzSlm9U/7yc0poWsP73t9ZnnSf/1tIbt3\\n+I7mWm0m/vzAOLr1DBTrodQHjb4DUIJnGJLc7GIiIs1+FwGdzCvh03c3s+HnQwAMHJbCZdf0o0mM\\nDcOQ6LWU0bSo0MGdv/+sLJz3dCazxktvzyQiMvhFS6tve5Z97y0pmyPQrGassdHM2DyXyNZVv3Ox\\nZ+bxVd+bsGeeDFjwHeA656Kgwljrg4XzU/ns/c0B7/jMFo0rrh/IeVMqn2NSwqcqHcDZPzOqVEjT\\nRIW1iWNiI7hx1nBunDXc5zldr72hgKhoK/0GJbN5/eFyncCpxUBVOfnnpR5k7zuLyhVaMRwu7Dn5\\nbH3sfYa+MKvK7bPFxXLhltfYMPt19ryxwG9cv7VlTFAnfyklWet2krl+F5EJzUmeNhTdWrMptiuz\\n8OsdfPBmxamVdV0jrlX4a1goNUd1AEq9deOsYcx50kXqtgxMJg232+Cc3q35/R/LF1NJ/fU48z7e\\nytEjJ0loE8MFl/WiR+/fSjamL9rgk44AvBW6Dn65slodAHg7gZFz76Fgz1FO/LyjXEipKdJGn/uv\\nqnQf7mI7i6beT/aG3RgeA82so1vMTF7yFM37dKxWu6rKMCSfvbelwm2EJoiMstCrX4Lf56WU7Npx\\ngqwThSS3bVZrlbpysoo4kVFIfEITnwWLStWpDkCpt2wRZu7++3gyMwrIOFZAfEJTnwySa1em8fqL\\nq8uGLU7m2dm/O4sb7hjGsFHtAW8BeU3XMfysZjCdmSe/GsZ/9QjLrn6MY0s3o1lMGC4PPe66hB7/\\nd0mlr904+02y1u4sWydg2MFNCYum3s/lhz7ym4m0phUVOgKW/QTvurWUdrHMuneM3yJGOVlFPPHg\\nYk7mliDxdgbtO7bgzw+Ow1ZDa28cdhevPLOSbZuPYjLruF0e+g5K5ub/G1Ej6cgbK5UNVKn34uKb\\n0LNvos/J3/AYvDt3nc+YtdPp4f3X15cVOm970Uik9J1L0COsdLlpaoXHNtyeSquTWWKimfD1Y8w8\\n8D5Tlj3HlRmfM+DRG4KKltnz5oKyk//pXAXFZKzaVunra0JEhLnC0p8DhqbwyDPTAqZvfv7xn8jM\\nKMRud+Owu3E6POzbk8W7c9fVWBtff+lntm0+Wla5zuUy2LLhCO+8urbGjtEYqQ5AabAyTxT5DRMF\\n7+rkExnexW62uFhGvHY3us1SVqrRFG0jbmh3etx5sd/XH1mwls+7X8/b1km813Qaa+96GY/Df/Gc\\nUyLim9O8T8egKnid4iryn6pbCIEz1/9ivZpmMusMHOp/FbcQcPFVgVMuHz+az9HDJ33Wi7hdhjdD\\nbTXqLp+psMDBprWHfdK8uJwe1iw/4FMnQAmeGgJSGqyICFPAhWoewyAi8rfhh45XnUfrUX3Y/+FS\\nHLmFJJ43gISxff1epR9dspEfLn24LGW0u8jOrrlfk783nQlfB7WEJWhxg7qRuTbV53HD6SZuaPca\\nPVZFbrlrJBnHF3Bo/2/Z3IWA3904iKTkwKGyBfl2b7lGP0NIhvQWngk1FDsvt8Q7B+QnIkzTNAry\\n7TU21NTYqA5AaTAK8u0sX7qPI2m5pLRrxrnjO9Gxc0v27Mws1xFomqBDpxbEnJEEL6pNHL3+ckWl\\nx9lw32s+9QI8JU6O/bCZvNSDNZqrZ/Czf+T78+7xRiiVDjWZIm10u/0CIlo1q+TVNcds1nn0mWkc\\nSstlzfIDNI21MWp8p0rrA7Rp2yxgupCYWFuN1BeIaxUVsKMXAmLVZHC1qQ5AaRAO7s/h8QcW4XEb\\nOJ0e1v98iHmf/srt95zLi/9eXm4oSEpZ7fTUALnb0/w+Lkwa2Zv3VqkD2LH1GN/PTyU3q5huPeM5\\n/8IeNG/5W9htq6E9mLL8OTY/9BaZa3cS0boZvf5yBR2vDq2GtNPpIW1vNharTtsOzXG5DL79Yhs/\\nLdqD0+GhZ78EZl7dzycNdEq7ZqS0C77jiYgwM+3ic8ql7ABvVbmrbhhYI6uGrTYzE6Z1Y/E3O32y\\nik69+By/K8KV4KiFYEqDcN8d8zh2xLd2cUysjeJiJy5n+avQJk2tPPfmpT6rXIPxccoVFB/J9Hnc\\nFB3BhG8eo/Wo3n5e5WvBvB188cGWcicts0XnwX9Pom370KpZ5eUUs2zJXjKOFtCxa0uGj+lQlu12\\n+ZK9vP/6eoQQGFISFW2hSVMrR4/kl0X7CE0QEWHin89Nr3AdSDCklKz8YR9ff7aN3JxiEpJimHlN\\nP3r1Swxpv6czDMnXn21jwVfejsYWYWLapT05/4IeKjXFGdRKYOWsknWikPvumF9hqOKZzBaNW/98\\nbsDJzYrsePFLNtz/Wrmi7kLTiGobz6V73gkqNLOo0MGfbvjcb5tNJo0n5syodkGUXdszePrRHzA8\\nBi6XgcWqY7WZeOg/55OTVcxTjyytNH8TeEt6jp7QietvHVqtdoSDYUjsJS5sEWaV4DGAqnQAKgpI\\nqfcMQ1YUpeiXy2nwytMr2LblaJWP1/2OC+l601R0mwVzTBSmKBtNu7Rh8tKngo7LP1XrwB+32+DV\\nZ1dVuV3gfS/mPLUch91dFhXjdHgoLHDy5pw1PkMxFe7LI9m+5VjlG9YjWumCNHXyrxlqDkCp9+Li\\no2kSYyM707dovNmiB7wzcLsMXnh8Gc++cTFR0cEv+BJCMOTZ2+nzt9+RvWkPtvhmNO/TsUpDDWaL\\n7nf18SkH9mZTmO8oS7wXrIP7c/wmyJOGZNf2DOKqWNqxSVPfVNlK46HuABoYp9NDdmaR38pnZysh\\nBDf/aQRWqwmtNP+QrgusNhNX3zQIizXwJKBEsm7VwWod1xYXS9KkQbTo26nK48yBah2UtUtKHJVk\\nEvXHMAwCNUVKaN+xedBXx1ariUkz6i7UVKl/1B1AA+HxGHz67maWLvDWixUIJkzryiVX9fW7PP9s\\n061nPI8+N5WF81M5fDCPtu2bMXF6d1q1bkLb9s351/3f+ywUAnC7PBQWOPzssXaZzTp3/HUUTz/y\\ng9/nPYbkhcd/4v5/TqxSDHvbDi3QAgxDtevUghmX9WbT2iPloqI0XRAdbcVud6FpAmlIDANGT+jE\\n4BE1X35SaTjUJHAD8d7r61m2eI9PGNx5U7tx+bX9w9iy+uHNOT+zYuk+n3hxq83E3Q+Oo+s5weew\\nz8wo4IM3NrJ1czqaEAwYmsJVNwygaWzwK3xPWfXjPl57YbXfGvAms8bYSV24+sZBVdrnxjWH+O+z\\nK3G7DAxDYjJpmMwasx+bREr75uzbncnb/13L4bQ8hBD0GZDE9X8cgs1mYsuGdBx2Nz16t6alyux5\\nVlJRQGcZe4mLO6771O9Yt8WqM+edy7A0gprHFcnMKOTBu77BXuIqO9maLTodu7TkvkcnBD2Ek3/S\\nzv13zKOoyFU2hq/rgtjmkTzx0owqvc9FhQ5efGIZu1JPYHj8f880XTB4eFtGT+hULoNpZQ6n5bLo\\nm50cP5pPxy4tmTitW7n1BeBdhatrQhVFamTqrB6AEGIm8A+gOzBYSun3bC2EmAw8D+h4S0U+Ecpx\\nG5vsrCJ0XfjJZekdH8/NKalSdayzUVx8NA8/PYVP39vC9i1HsVhNjJnYmWmXVK0c6NIFu3DY3eUm\\ncD0eSWGBgzUr0xg1vlPQ+5rz5HLvKuUAJ3/wRuKsWZHGpnWHGXd+V668fkBQ+05u14w/3DEs4PPb\\nfznG4m93UpDvoM+AJMaf36VKE+FK3SsscLBi6V4O7MshKTmG0RM6E9us6nedVRHqZeM24GLg1UAb\\nCCF0YA4wATgCrBdCzJdS7gjx2I1Gs+aReAIstzcMSWwzFckBEJ/QlDv+MiqkfezYetzvXILD7mbn\\nrxlBdwDZmUXs3pEZME3CmZwODz98t4tR4ztWmHsnGF98+EvZginwRg4tXbCLR5+ZWq1hLKX2HT18\\nkkfv+x63y4PT6cFs1vjui+385eHz6NQ1rtaOG9LsoZQyVUq5q5LNBgN7pZT7pZRO4CPgglCO29hE\\nRlkYNrq9T95zi0Vn1PiOWG0qEVZxkZNvPv+Vf9zzHU88uIj1qw9WmsbZn5ZxUX6jbEwmjeZxweec\\nyckuwmSu2tfL7THYtOZwlV5zpuzMIr77ovxaAJfTQ8FJO199vDWkfSu1Z+4LqyguduIsHeZ1uQzs\\ndjevPLWiWp/jYNVF+EgScPqn+kjpY0oVXHvLEIaMbIfZrBMRYcZs1hg+pgNX/aFqE4hno6JCBw/e\\n9Q1fffwrB/Zmk/prBq+9sJo3Xvq5yvuaMK2b39wymiYYfV7noPYhpcTp8OAMkKo6EIE3RUMotm5K\\nR/j5Vns8kvWrD4W0b6V2FBY4OHQg129Z0YJ8h98UKDWl0iEgIcQSoLWfp2ZLKefVdIOEEDcDNwOk\\npFR9Gf/ZymzWufHO4Vx5wwCyM4toERdNVHTd1o2tr76fn0pebkm5dMEOu5u1K9KYMLVblcoTdujc\\nkt/dOIj3X1+PZtJAek/ot/55ZMCCKKfLOFbA048sJS+3xJuq8oxvtcWq07t/Els3ppdd7Z2i6RoD\\nhiYH3VZ/dJMWcM5Dr0ZeJKX2SVnBSnfhXftRWyrtAKSUoaUlhHTg9E91m9LHAh1vLjAXvFFAIR77\\nrBMVbT0rJ/MK8u0s/W4X27Yco1mLSCZM7UaXHq0q3P7IwTyat4xk3aqDfnPFu90Gi7/ZycVX9fGJ\\nkKnImImdGXJuO1J/PY6uaXTvFR9U9I9hSP7998XkZBX5Dfts2tTKJVf3Y/jo9jw2exFHD5/E4XAj\\nhDdiafKM7iQkxQTdTn/6D0rmnVd9K3GZzTojx3YIad9K7WjS1EbrpKYcOZjn85wtwkxiiHNCFamL\\n2MH1QGchRHu8J/4rgMqrZSuNRnZmEQ/d/S32Em+pPwRs2XCES3/Xl0kzepTb1vAYvPvaepYv3YvZ\\nrON2B14ZaxiSn1ccYM2KA/QdlMwtd40IOnVwRISZ/oOrdjW+a3sGRQUOvyd/AJfboH2nFlisJh54\\nYjIb1xxiw+qDRERZGDW+E526BT/Z53S42bH1OG63Qfde8WUXBdFNrVx3y2DefnUdhsfA45FYbSbi\\nE5ow7ZKeVfp7lLpz46zhZenO3W4DTReYTBo3/2l4reY9CmkdgBDiIuBFIA7IA7ZIKScJIRLxhntO\\nKd1uCvAc3jDQN6WUQZVVUusAGodXnl7BulVp+LvT7T8kmSt/P6Asb/28T7byzefbyk1ynuoAKvoo\\nmy06547ryHW3DqnJppez6sf9vPPqWuz2wGP/8QlN+PfLF4SUwnjL+iO8/PQK73yBlHg8ksuu6cfE\\n6b+ldTh+NJ+VP+wj/6SdXv0S6Tc4uVqpsZW6k51ZxOJvd3JgbzZJyTFMnN6d1olNq7wftRBMaVBu\\nueLDgCdNISAi0sK/np9GsxaR/PHqTygu8q3NK4R3mOPMcfXTmS06r7x/ea0VEEk/nMdDd39XYdpq\\ni1Xn0WenVeuLDZCTVcS9t8/zyfhpser85aHzKhw2UxoHlQ5aaVAqymUkpXdC99svt2MY0u/JH7wp\\nH2Zc1oshI9sGvtKVkpIAr68JScmx9OjdGnMF4Z9CiJAKpa9Yus/vwjKn08PC+b61hRWlIqoDUGpV\\nUaGTvNySCmOZh57brsIIFY/HYPsvx9B1jRYBJnM9bsmIMR24/rahAUMprTYT0U1qdwJ91r2jtrQp\\nSAAAEDZJREFUGX9+14DzElaricQ21Z/ozcku9r+4THrXHihKVTTuBDJKrcnJKmLu86vZnXoCIbyr\\nmX//x6Gc08c3382lV/dl+9ZjZJ0oCrjiuWmMd7Xzpdf05X8vr/GpP9t/SHJZpM+4yV34ceFun8R5\\nF11Z+5lTzWadK28YyIBhKTz50BLcbm/CNk0TmMwaf5g1LKQ2dDsnnp+XH8BxxpCZyazRw89729AU\\n5jv48K0NrFt1EMMjOadPAr+7cSDxCdUbMlMqpuYAlBrndnm459avOJlbUi47p8Wq88Djk/3G5btc\\nHpYv2cN7r23wzehp1bnlrpEMKC3vuOrHfXzyzmby8+2YTBrjJndh5jX9y4Z+DEPy7RfbWPDVDoqL\\nnMTERnDxVX0YPSG4hVzVYRiSBfN2sGh+KoUFDpJSYpk4vRt7UjM5uN+b22XyBT1IrkLBdX9cLg+z\\n7/ya7MyisjsBoQkiI8089uKMWs8dU5tcLg9/mzWf7MxiPJ7Sv610DujxF6cT2zz4ldiNmZoEVsJq\\n7co03nzpZ5+JXSFgwLAUZv11dMDX/rIhnTlPLUcIgZQSw2MwcXp3Zl7Tr1zkjJQSh92Nw+5i9U8H\\nOHL4JG07NGfk2A5ERlnKtvG4jVrPhlmQb+epR5ZycH8O8rQbGItF509/G0PPvjVXHB28K0c/eWcT\\na1em4fFIevdP5Irrf4uUaqh+XnaA/72yxvfuxqQxaUZ3LlNpz4NSZ9lAFcWf9MMn/Ub1SAmHD+RW\\n+No+A5N48a1L2brpqDdvfZ8EmrfwvfITQnD8aD5PPLgYt9vA5fSwblUaX330Cw/+ezIJSTEIUfup\\nkI+n5/PQPd9hL/HN1ep0evjwfxv51/M12wFEN7Fyw+3DuOH2wNlAG6Kd2zN8Tv7gXdCX+uvxMLTo\\n7KcmgZUa16p1NFab/2uLYMIfrTYzg4a3ZeS4jn5P/uC9up/z5ApKil1lYZdOh4fiIievPle9guvV\\n8ebLa/ye/E85ciivVpN5nU1axEX5T6AnqNJKbiV4qgNQatyg4W0xW3SfmrgWq860S2tmNWrGsQLy\\ncot9Hj91l1GQb6+R41TE6fSwJ/VEhdtERlpCWvTVUBiG5JeN6bz93zV8/PYmjhzyTWtQmZHjOvpd\\n9Wqx6Kp2cS1RQ0BKjbNaTcx+bBIv/WcZmccL0XSBrmtce8tgunSvmYVKHo8R+MQqvNkvw81k1hh/\\nfpda2XdBvh0pf4uOCie3y8NTjyxl/55sHHY3miZY8u1OLrqqD1MuPCfo/TRvEcmse0cz58kVZdcO\\nbo/B5df2r7HPjVKe6gCUWpHYJobHXphBxrECHHYXSSmx6DUYgpmQFIPNZvI7ZhzXKrpOomEsFp3O\\n3Vuxe0eG3zQUfQcmceEVfWr0mEcO5jL3+dWkl15ht05qyk13DqddxxY1epyq+GnRHvbtzioLuzUM\\nidPp4Yv3f2Hg0JQqTU737p/ES+/MJPXX47hdBt16xpdN6is1Tw0BKbUqPqEJKe2b1+jJH7z5+W/6\\n0wgsVr1s2EDXBVariRtnDa/RY1XkhtuHEhll8Q554a3xq5sEf5g1jFn3jqnR/Dv5J+388/6FHNyf\\ng7s0adiRg3k8/sAicnN8h8PqyrLFe31SUwAYsno1CMxmb8rs/kOS1cm/lqk7AKXB6tUvkYefmsr3\\n83eQfiiPdp1aMGl69zoNh2yd2JT/vHwhPy3ew56dmSQkNmHc+V1rpQ3LFu/xuwrY7TZY+t0uLr26\\nX40fMxhuj//Fe9IwcLurn/ZCqX2qA1AatMTkmLCHQ0Y3tdZJquUDe7P9JppzuwwO7M2u9eMHMnRk\\nO77+bBuuM3IcmUw6fQe2CVOrlGCoISBFaSDapMT6DZPUTRptUmqvaEhlJk7vRvOWkeVqVlutJoaN\\nal+lamxK3VN3AIrSQIyZ1IXv56f6VD/TdY3zpnYNU6u8qRoeeWYqyxbvYd3qQ0REmBk7qTP9h4RW\\n3lKpfSoVhNIgORxuVv6wj/WrDxIRaWHspM706pd41sfc79l5gleeXklBvh2BIDLKzC13jaR7L39l\\nu5XGSOUCUs5qJSUuHv7Ld2RnFpVFn1itJs4d35Frbh4c5tbVPiklx9LzkVKS2CbmrO/0lKqps4Iw\\nQoiZQojtQghDCBHwgEKINCHEr0KILUIIdUZXQrLo61SyMorKhR46HG6WL9nLkYMV5xo6GwghSGwT\\nQ1JyrDr5KyEJdRJ4G3AxsDyIbcdKKfsG2zMpSiBrlqf5RJyANxxx87ojYWiRojRMIU0CSylTAXUV\\notQpTff/eRNC1HrBF0U5m9RVFJAElgghPMCrUsq5dXTcBk1KydqVaSz6eieFBQ569Utg6sU9G31m\\nxHPHdeTz97f4FIDXhGDgsJQwtSp4xUVOMjMKadEyiuimtVuiUlEqUmkHIIRYAvgLMZgtpZwX5HFG\\nSinThRCtgMVCiJ1SSr/DRkKIm4GbAVJS6v+XuTa9+9p6Vizdh9PhzXeTdaKQn5en8fDTU4mLjw5z\\n68Jn/JSubPj5EIfScnHY3QjhTR8w47LexCfU36IoHo/Be6X/p7pJw+P2MGBoCn+4YxgWq4rIVupe\\njUQBCSF+Au6RUlY6wSuE+AdQKKV8qrJtG3MUUMaxAmb/6WuflZ+aBsNGdeDm/xsRppbVDx6PwZb1\\nR9i07jARkRbOHdex3i86+vDNDfzw/e5ydy5mi86AIcncdve5Qe8nM6OABV/tYO+uTFq1bsr5F/ag\\nY5eWtdFkpQGqVxXBhBBRgCalLCj9eSLwSG0ft6HbsfUY/qZWDAN+2Zhe9w2qZ3RdY8DQlLI6wfWd\\n0+nhh4W7fYatXE4PG9ccoiDfTpOmlad2TtuXzWOzF+F2efB4JIcO5PLLxiNcf9tQRozpUFvNV85S\\nIXUAQoiLgBeBOOBbIcQWKeUkIUQi8LqUcgoQD3xZOlFsAj6QUn4fYrvPelabCS3A5LrVWrtlDpWa\\nV1jg8M6E+WEy6eRkFQfVAbz137XlUmBL6a2E9s6r6xg8oi2GIVn5wz7WrkzDajMxZoJ3Ra4K1FD8\\nCTUK6EvgSz+PHwWmlP68H6jZpOiNQL9Bbfjfy2t8HjdbdEZP7ByGFimhaNrU6rfaFXizebZsVfmc\\njtPp4eC+HL/PCWDX9gw+eGMDmScKy9ZI7Np+gsHD23LjnXWXIltpOFTMXD0VEWnh9ntGYbHoWCw6\\nQnjvCjp2acmUi4KvsqTUDyazzuQLe2A54+7NYtUZOa4DUdGV573XBD5lNk+RUrJ5/RFOZBSWXyBn\\nd7N2VRr792SF0nzlLKVCD+qxvoPa8PRrF7N2ZRpFhU669mhFt57x6na+gbrgst4AfP/VDozS4Isx\\nEztz+XUDgnq9yazTq18iv246imGUH0+yRpjZveOE33TRLqeHTWsP06GzmihWylMdQD3XNMbGhKnd\\nwt0MpQZomuCiK/ow/ZKenMyz0yTGVi6FcjCuv20oj/x1AcVFThx2N2aLjq4J7rx3NO+/sd7va4QQ\\nNVqZTDl7qA5AUeqYyazTIq56i/mat4jkP69cyLpVaezfk02r+GhGju1IdFMro87rxJFDeT7lGXWT\\nxuAR7Wqg5crZRnUAitLAWCw6I8d2ZOTYjuUeP3d8J9avPsjeXVnlFshNu6QnickxYWqtUp+pDkBR\\nzhImk8Y9D53Hti1H2bjmMFabiRFjOtT7BXJK+KgOQFHOIpom6N0/id79k8LdFKUBUDNDiqIojZTq\\nABRFURop1QEoiqI0UqoDUBRFaaRUB6AoitJIqQ5AURSlkVIdgKIoSiOlOgBFUZRGSnUAiqIojZTq\\nABRFURqpkDoAIcSTQoidQoitQogvhRCxAbabLITYJYTYK4S4L5RjKoqiKDUj1DuAxUBPKWVvYDdw\\n/5kbCCF0YA5wPtADuFII0SPE4yqKoighCqkDkFIuklKeqlC9BmjjZ7PBwF4p5X4ppRP4CLgglOMq\\niqIooavJOYAbgAV+Hk8CDp/2+5HSxxRFUZQwqjQdtBBiCdDaz1OzpZTzSreZDbiB90NtkBDiZuBm\\ngJSUlFB3pyiKogRQaQcgpTyvoueFENcD04DxUkrpZ5N0IPm039uUPhboeHOBuQADBw70tz9FURSl\\nBoRUEEYIMRn4KzBaSlkcYLP1QGchRHu8J/4rgKtCOa6ihIvT6WHjmkOcOFZAYnIM/Qa1wWSuWmF3\\nRakvQq0I9hJgBRYLIQDWSClvFUIkAq9LKadIKd1CiDuAhYAOvCml3B7icRWlzmUcK+Cf93+P0+7G\\nbndjizAREWnhwScmV7vIu6KEk/A/alM/DBw4UG7YsCHczVAUAP7+5285dCCH078ymibo3C2Ovz02\\nKXwNU5TTCCE2SikHBrOtWgmsKEHIzizi6JGTnHm9ZBiSfbuzKMx3hKdhihIC1QEoShAcdjeaJvw+\\nJzSBw+H2+5yi1GeqA1CUILRObII5wGRvkyZWmreMrOMWKUroVAegKEHQdI1rbxmMxXpaJyDAYtG5\\n/rahlAZBKEqDEmoUkKI0GkNGtqNZi0i+/vRXjqXn06ZtLDNm9qJD55bhbpqiVIvqABSlCrp0b8Xd\\nfx8f7mYoSo1QQ0CKoiiNlOoAFEVRGinVASiKojRSqgNQFEVppFQHoCiK0kipDkBRFKWRqtfJ4IQQ\\nmcDBcLfDj5ZAVrgbEWaN/T1o7H8/qPcA6ud70FZKGRfMhvW6A6ivhBAbgs22d7Zq7O9BY//7Qb0H\\n0PDfAzUEpCiK0kipDkBRFKWRUh1A9cwNdwPqgcb+HjT2vx/UewAN/D1QcwCKoiiNlLoDUBRFaaRU\\nB1BNQognhRA7hRBbhRBfCiFiw92muiSEmCmE2C6EMIQQDTYKojqEEJOFELuEEHuFEPeFuz11TQjx\\nphDihBBiW7jbEg5CiGQhxI9CiB2l34E/hbtN1aU6gOpbDPSUUvYGdgP3h7k9dW0bcDGwPNwNqUtC\\nCB2YA5wP9ACuFEL0CG+r6txbwORwNyKM3MDdUsoewFDg9ob6GVAdQDVJKRdJKU8Vgl0DtAlne+qa\\nlDJVSrkr3O0Ig8HAXinlfimlE/gIuCDMbapTUsrlQE642xEuUspjUspNpT8XAKlAUnhbVT2qA6gZ\\nNwALwt0IpU4kAYdP+/0IDfTLr4ROCNEO6AesDW9LqkdVBKuAEGIJ0NrPU7OllPNKt5mN95bw/bps\\nW10I5u9XlMZKCBENfA78n5QyP9ztqQ7VAVRASnleRc8LIa4HpgHj5VkYT1vZ399IpQPJp/3epvQx\\npRERQpjxnvzfl1J+Ee72VJcaAqomIcRk4K/ADCllcbjbo9SZ9UBnIUR7IYQFuAKYH+Y2KXVICCGA\\nN4BUKeUz4W5PKFQHUH0vAU2AxUKILUKI/4a7QXVJCHGREOIIMAz4VgixMNxtqgulE/93AAvxTv59\\nIqXcHt5W1S0hxIfAz0BXIcQRIcQfwt2mOjYCuAYYV/rd3yKEmBLuRlWHWgmsKIrSSKk7AEVRlEZK\\ndQCKoiiNlOoAFEVRGinVASiKojRSqgNQFEVppFQHoCiK0kipDkBRFKWRUh2AoihKI/X/4ZB+p5aK\\nKJAAAAAASUVORK5CYII=\\n\",\n \"text/plain\": [\n \"\"\n ]\n },\n \"metadata\": {},\n \"output_type\": \"display_data\"\n }\n ],\n \"source\": [\n \"# Datasets\\n\",\n \"noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure = load_extra_datasets()\\n\",\n \"\\n\",\n \"datasets = {\\\"noisy_circles\\\": noisy_circles,\\n\",\n \" \\\"noisy_moons\\\": noisy_moons,\\n\",\n \" \\\"blobs\\\": blobs,\\n\",\n \" \\\"gaussian_quantiles\\\": gaussian_quantiles}\\n\",\n \"\\n\",\n \"### START CODE HERE ### (choose your dataset)\\n\",\n \"dataset = \\\"gaussian_quantiles\\\"\\n\",\n \"### END CODE HERE ###\\n\",\n \"\\n\",\n \"X, Y = datasets[dataset]\\n\",\n \"X, Y = X.T, Y.reshape(1, Y.shape[0])\\n\",\n \"\\n\",\n \"# make blobs binary\\n\",\n \"if dataset == \\\"blobs\\\":\\n\",\n \" Y = Y%2\\n\",\n \"\\n\",\n \"# Visualize the data\\n\",\n \"plt.scatter(X[0, :], X[1, :], c=Y, s=40, cmap=plt.cm.Spectral);\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"Congrats on finishing this Programming Assignment!\\n\",\n \"\\n\",\n \"Reference:\\n\",\n \"- http://scs.ryerson.ca/~aharley/neural-networks/\\n\",\n \"- http://cs231n.github.io/neural-networks-case-study/\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {\n \"collapsed\": true\n },\n \"outputs\": [],\n \"source\": []\n }\n ],\n \"metadata\": {\n \"coursera\": {\n \"course_slug\": \"neural-networks-deep-learning\",\n \"graded_item_id\": \"wRuwL\",\n \"launcher_item_id\": \"NI888\"\n },\n \"kernelspec\": {\n \"display_name\": \"Python 3\",\n \"language\": \"python\",\n \"name\": \"python3\"\n },\n \"language_info\": {\n \"codemirror_mode\": {\n \"name\": \"ipython\",\n \"version\": 3\n },\n \"file_extension\": \".py\",\n \"mimetype\": \"text/x-python\",\n \"name\": \"python\",\n \"nbconvert_exporter\": \"python\",\n \"pygments_lexer\": \"ipython3\",\n \"version\": \"3.5.4\"\n }\n },\n \"nbformat\": 4,\n \"nbformat_minor\": 2\n}\n"},"license":{"kind":"string","value":"mit"}}},{"rowIdx":1392,"cells":{"repo_name":{"kind":"string","value":"dtamayo/rebound"},"path":{"kind":"string","value":"ipython_examples/HyperbolicOrbits.ipynb"},"copies":{"kind":"string","value":"2"},"size":{"kind":"string","value":"68225"},"content":{"kind":"string","value":"{\n \"cells\": [\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"# Loading Hyperbolic Orbits into REBOUND\\n\",\n \"\\n\",\n \"Imagine we have a table of orbital elements for comets (kindly provided by Toni Engelhardt).\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 9,\n \"metadata\": {\n \"collapsed\": false\n },\n \"outputs\": [],\n \"source\": [\n \"from io import StringIO\\n\",\n \"import numpy as np\\n\",\n \"import rebound\\n\",\n \"epoch_of_elements = 53371.0 # [MJD, days]\\n\",\n \"c = StringIO(u\\\"\\\"\\\"\\n\",\n \"# id e q[AU] i[deg] Omega[deg] argperi[deg] t_peri[MJD, days] epoch_of_observation[MJD, days]\\n\",\n \"168026 12.181214 15.346358 136.782470 37.581438 268.412314 54776.806093 55516.41727\\n\",\n \"21170 2.662235 2.013923 140.646538 23.029490 46.292039 54336.126288 53673.44043 \\n\",\n \"189298 15.503013 11.550314 20.042232 203.240743 150.855761 55761.641176 55718.447145 \\n\",\n \"72278 34.638392 24.742323 157.984412 126.431540 178.612758 54382.158401 54347.240445\\n\",\n \"109766 8.832472 9.900228 144.857801 243.102255 271.345342 55627.501618 54748.37722\\n\",\n \"\\\"\\\"\\\")\\n\",\n \"comets = np.loadtxt(c) # load the table into a numpy array\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"We want to add these comits to a REBOUND simulation(s). The first thing to do is set the units, which have to be consistent throughout. Here we have a table in AU and days, so we'll use the gaussian gravitational constant (AU, days, solar masses). \"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 10,\n \"metadata\": {\n \"collapsed\": false\n },\n \"outputs\": [],\n \"source\": [\n \"sim = rebound.Simulation()\\n\",\n \"k = 0.01720209895 # Gaussian constant\\n\",\n \"sim.G = k**2\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"We also set the simulation time to the epoch at which the elements are valid:\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 11,\n \"metadata\": {\n \"collapsed\": true\n },\n \"outputs\": [],\n \"source\": [\n \"sim.t = epoch_of_elements\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"We then add the giant planets in our Solar System to the simulation. You could for example query JPL HORIZONS for the states of the planets at each comet's corresponding epoch of observation (see [Horizons.ipynb](Horizons.ipynb)). Here we set up toy masses and orbits for Jupiter & Saturn:\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 12,\n \"metadata\": {\n \"collapsed\": false\n },\n \"outputs\": [],\n \"source\": [\n \"sim.add(m=1.) # Sun\\n\",\n \"sim.add(m=1.e-3, a=5.) # Jupiter\\n\",\n \"sim.add(m=3.e-4, a=10.) # Saturn\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {\n \"collapsed\": true\n },\n \"source\": [\n \"Let's write a function that takes a comet from the table and adds it to our simulation:\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 13,\n \"metadata\": {\n \"collapsed\": false\n },\n \"outputs\": [],\n \"source\": [\n \"def addOrbit(sim, comet_elem):\\n\",\n \" tracklet_id, e, q, inc, Omega, argperi, t_peri, epoch_of_observation = comet_elem\\n\",\n \" sim.add(primary=sim.particles[0], \\n\",\n \" a = q/(1.-e),\\n\",\n \" e = e,\\n\",\n \" inc = inc*np.pi/180., # have to convert to radians\\n\",\n \" Omega = Omega*np.pi/180.,\\n\",\n \" omega = argperi*np.pi/180.,\\n\",\n \" T = t_peri # time of pericenter passage\\n\",\n \" )\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"By default, REBOUND adds and outputs particles in Jacobi orbital elements. Typically orbital elements for comets are heliocentric. Mixing the two will give you relative errors in elements, positions etc. of order the mass ratio of Jupiter to the Sun ($\\\\sim 0.001$) which is why we pass the additional `primary=sim.particles[0]` argument to the `add()` function. If this level of accuracy doesn't matters to you, you can ignore the `primary` argument.\\n\",\n \"\\n\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"We can now set up the first comet and quickly plot to see what the system looks like:\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 14,\n \"metadata\": {\n \"collapsed\": false\n },\n \"outputs\": [\n {\n \"data\": {\n \"image/png\": \"iVBORw0KGgoAAAANSUhEUgAAAU0AAAFCCAYAAAB1po8RAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XlwXNWdL/DvUbdaLaul1r7vliyveLdsDFiGYGPMQFYq\\nA2QjE4ZJwstMXjKEMATXo8IkpDI1ZKYmkwqQhCUBQjwODhibJcLGE8sLXvAia98X093aet/O+8OS\\nIoxs60rd9/by/VSpqnVb0vldkL86595zzxFSShAR0cwkaF0AEVE0YWgSESnA0CQiUoChSUSkAEOT\\niEgBhiYRkQJ6rQuYCyEE50sRUVhIKcV0x6O+pyml1Pzj0Ucf1bwGnhPPSe0Pl8uFs2fPoqWlBT6f\\nLybOaeLjSqK6p0lE2ujt7YXFYkFhYSFycnK0LkdVDE0imjG/34/m5mZ0dHRg8+bNMBqNWpekOoZm\\nCNTV1WldQsjxnKKDmudkt9vR3t6O9PR0bN26FQkJ4bm6F+n/n8TVxu+RTAgho7l+omgQDAYxMDAA\\ni8WCsrIymM1mrUsKOyEE5GVuBLGnSUSX5fF48N577yEzMxNLly5FYmKi1iVpjj1NIpqWzWZDd3c3\\nsrKyUFxcrHU5qmJPk4hmLBAIoLu7Gw6HA9XV1Zg3b57WJUWUqJ+nSUShY7VasX//fgghsGjRIgbm\\nNDg8JyIAwMDAAPr6+pCZmYny8nKty9HUlYbnDE2iOOfz+dDe3g4pJSoqKmAwGLQuSXO8pklE0+ru\\n7obVakVeXh7y8/MhxLQ5QVPwmiZRHAoGg+jq6kJjYyOKi4tRUFDAwJwhDs+J4ozL5UJ7ezuMRiPK\\nysqg0+m0LinicHhORAAu3uwZHBxEcXExsrKytC4nKjE0ieKA3+/H6dOnYbFYcN1118XlQhuhwuE5\\nUYwbGxtDR0cHMjIyUFhYGLaFNmIJh+dEcUhKib6+PlitVpSXlyMtLU3rkmICQ5MoBnk8HtTX16Ok\\npASLFi3iQhshxOE5UYyZWGgjLS0NFRUVWpcTlTg8J4oDE3MvudBGeLGnSRQDLBYLWltbkZeXh9LS\\nUt7smSP2NIli2ODgIFpbW1FQUBD3C22ogT1Noijl8/nQ0dGBQCCAiooKJCUlaV1SzGBPkyjGWCwW\\n9PX1ITs7m8+Nq4wXPoiiiJQSXV1dOHjwIMrKylBYWMjAVBmH50RRwuPxoK2tDYmJiSgvL4dez4Fi\\nuHB4ThTlJuZeFhQUIDc3V+ty4pqmoSmEKAbwLIA8AEEAv5RS/kwIkQHgJQBlADoA3CmlHNGsUCKN\\nBAIBHDt2DD6fD6tWrUJycrLWJcU9TYfnQoh8APlSyhNCCBOAYwDuAPAVAFYp5RNCiAcBZEgpvzfN\\n93N4TjHL6XSira0NSUlJqKio4HBcRVGzR5AQYheA/xz/2CSlHBwP1nop5cJpvp6hSTFpcHAQAwMD\\nKC0tRUZGhtblxJ2oCE0hRDmAegBLAXRLKTOmvGeTUmZO8z0MTYopbrcbJ0+ehNls5txLDUX8jaDx\\nofkrAL4lpbQLIS5NQiYjxbzR0VG0trbCYDCgpqaGU4kilOahKYTQ42JgPiel/OP44UEhRN6U4fmF\\ny33/jh07Jl/X1dWhrq4ujNUShd7UdS+rqqqQmpqqdUlxp76+HvX19TP6Ws2H50KIZwFYpJTfnnLs\\nxwBsUsof80YQxTK73Y7u7m7OvYwwEXtNUwixEcB+AB/g4hBcAvg+gMMAXgZQAqATF6ccDU/z/QxN\\nilpDQ0P4y1/+goULF6KyslLrcmiKiA3NuWJoUjQKBoPo7u7G2NgYKisrue5lBGJoEkUIl8uFtrY2\\nzJs3D6WlpdxzPEJF/N1zonjQ3t6OxsZGrFu3jnuORzH2NInCLBAIoLOzE06nEyUlJTCbzVqXRFfB\\n4TmRRhwOB9ra2pCeno6ioiJuQxElODwn0sCZM2fg8/lQXl6O9PR0rcuhEOGfPaIQ8/l8aG5uhtVq\\nxYIFCxiYMYbDc6IQGh0dRUdHB7ehiHIcnhOFWTAYRE9PD4aHh1FRUcFHIWMYQ5NojrxeL44ePQop\\nJdatW4fExEStS6Iw4vCcaA6Gh4fR2dmJ3NxcFBQUaF0OhQiH50QhJqWcHI5XVVUhJSVF65JIJbx7\\nTqSQw+HAO++8A4/Hg8WLFzMw4wyH50QKTOwKOW/ePFRXV2tdDoUJh+dEczR1ZaLq6mquTBTH2NMk\\nuorh4WF0d3fDZDJxZaI4caWeJq9pEl2B1WrF4cOHkZqaioqKCgYmsadJNJ1gMIiuri44HA5UVlYi\\nOTlZ65JIRVzliEiBiYWCU1JSUFpaypWJ4hBvBBHNUGdnJ86cOYPa2louFEzTYk+TCBeH4xMLBRcX\\nF3Oh4DjH4TnRFUwMx00mE0pKSjgcJw7PiS6npaUFdrsdpaWlyMzM1LocigL8k0pxKRgMor29HV1d\\nXZg/fz4Dk2aMw3OKOxyO09VweE407sMPP0RfXx+Ki4t5d5xmhaFJcSEYDOL48eMYGxvD+vXrYTQa\\ntS6JohSH5xTz3G43WltbkZycjNLSUuj17CvQlXF4TnHLarWip6eHw3EKGYYmxSS/348PPvgABoMB\\nCxYs4LPjFDIMTYo5Ho8Hzc3NcLvdWLZsGYfjFFK8pkkxZWhoCF1dXSgsLEROTo7W5VCU4jVNinnB\\nYBC9vb0YGRnhyuoUVgxNinperxcHDhxAVlYWli1bxoWCKaw4PKeoNjo6io6ODmRlZaGoqEjrcihG\\ncHhOMUdKif7+flgsFlRWVsJkMmldEsUJ9jQp6rjdbpw+fRppaWmoqKhAYmKi1iVRjGFPk2KGw+FA\\nY2MjdDodqqurIcS0v9dEYcPQpKhx4cIF9Pf3o6qqiiurk2Y4PKeIFwgE0NnZCY/Hg8rKSiQlJWld\\nEsU47ntOUcvtdmPPnj3w+/2oqalhYJLm2NOkiDXxdE9ubi4KCgq0LofiCG8EUVSRUqKnp4dP91BE\\nYk+TIorT6URzczNSUlJQUVHBp3tIE7ymSVFhbGwM77//PnQ6HaqqqhiYFJE072kKIZ4GcBuAQSnl\\nNePHMgC8BKAMQAeAO6WUI9N8L3uaMWJwcBCDg4MoLy9HWlqa1uVQnIv0nuavAGy95Nj3ALwlpawB\\n8A6Ah1SvilQRDAbR1tYGm82GhQsXMjAp4mkemlLK9wAMXXL4DgC/GX/9GwCfVLUoUoXD4cDevXsh\\nhEBNTQ0MBoPWJRFdVaTePc+VUg4CgJRyQAiRq3VBFFrDw8Po7OzEokWLUF5eHrZ2pJTwer0AAL1e\\nP/nYJfc6p9mK1NC81GUvXO7YsWPydV1dHerq6lQoh2ZLSom+vj7YbDZUVVUhJSVlTj/P5/PB5XJh\\neHgYAwMDMJvN8Hq9aGpqQn5+PhITEzE8PIyEhARkZWXB6/Wip6cHVVVV0Ov1sFqtyM/Pn7wsYDQa\\nYTab+Ux7nKmvr0d9ff2MvlbzG0EAIIQoA7B7yo2gcwDqpJSDQoh8AH+WUi6a5vt4IyiKuN1udHZ2\\nQgiBysrKWe3dMzIyAqfTCbvdjra2NrjdblRUVCApKQlerxeFhYVISkpCQkICDAYDdDrdtAHo9/vh\\n9/sxNjYG4OKjmh9++CHcbjeSk5ORmJgIr9eLiooKzJs3jz3TOHOlG0GREprluBiay8Y//zEAm5Ty\\nx0KIBwFkSCm/N833MTSjhMvlwsGDB5GXl4elS5cq6slduHABLpcLVqsVra2tqKysREFBAUwmE0wm\\nU8gDLRAIwG63w2KxICEhAW63GyMjI6iqqkJ6ejo3aosDER2aQojfAqgDkAVgEMCjAHYB+D2AEgCd\\nuDjlaHia72VoRgGbzYbu7m6UlJQgMzNzRt/j8Xjw4Ycfor+/H01NTVizZg3y8vI0GTr7/X5cuHAB\\nwWAQdrsdXq8XRUVFyMzM5DA+RkV0aM4FQzOySSnR29uL4eFhzJ8/f0Z7jzscDrS3t+PQoUPYsGED\\nCgsLkZ6eHjHhFAgE0N/fD6/XCykljEYjsrKyYDQatS6NQoihSapzu904fvw4srOzUVFRcdUhrcVi\\nwZEjR5CamoqioiLk5+fPKGS15Ha70d7ejmAwiLy8PA7dYwhDk1TldDrR1NQEAFi+fPkVe4ljY2Po\\n7OyE1WpFSkoKVq5cGXWPT/p8vskVmQoKClBQUMAbR1GOoUmqsVqt6OnpQWlpKTIyMi77dYFAAOfP\\nn8f+/fuxZcsWlJaWRn0vze12w2azwev1Ij09Henp6VqXRLPE0KSwm7qc29WuX7a3t6OnpwdpaWkh\\nmasZaVwuFxobG5GZmYmioqKo/2MQjxiaFFZ+vx/79+9HRkYGrrnmmssOr/1+PxobG3Ho0CFs3749\\nphcWllJiZGQEIyMjmDdvHnJycrQuiRRgaFLYuFwutLS0wGQyoays7LLX8np6etDS0oKMjAwsWbIk\\nbnpfHo8H58+fR15eHnJycnitM0owNCksJm5+XO36ZW9vL9566y2sXbsWixcvVrHCyCClhM1mg8vl\\nQkZGRsxdjohFDE0KqWAwiPb2djidTsyfP/+y21EEg0GcOnUKQ0NDWLNmDVJTU1WuNLLYbDb09/dj\\n/vz5nNcZ4RiaFDKBQADnzp3D4OAgNm3adNlhdiAQwIEDB9DT04M777yTy76N83g8sFgsSE1N5dqh\\nEYyhSSHhdrvR2tqK1NRUlJSUXHb+pc/nw7Fjx6DX66Ny3mW4+f1+NDU1IS8vD1lZWVqXQ9OI9JXb\\nKQqMjIxM3tAoLS29bGD6/X4899xz8Pv9WL16NQNzGnq9HgsWLIDf78fo6KjW5ZBC7GnSVZ0+fRoe\\njwc1NTUwmUyX/Tq/349Dhw4hKSkJa9euVbHC6DTxHLtOp4vp6VfRiD1NmpWJGz5jY2NXDUyfz4fd\\nu3fDaDRizZo1KlYZvXQ6HXJzcxEMBuFwOLQuh2aIoUnT8vl8aGpqgpQStbW1VwxMADh58iT8fj9W\\nrlwZMSsSRQODwYC8vDzY7XbY7Xaty6EZYGjSxzgcDjQ2NsJsNqOysvKqE7Kbm5sxOjqKT33qU7yG\\nOQt6vR5msxn9/f3w+/1al0NXwdCkj+jt7cWf//xnlJSUzOg6W0tLC15//XWsX78+bp7yCQej0YiS\\nkhIMDw8jGAxqXQ5dAUOTJvX29sJms+G6666b0Qo9brcb58+fx6c//enLTnCnmTMajUhMTER/f7/W\\npdAVsGtACAQC6OjogN/vx6JFi2bUYwwGg9i/fz/Ky8tRUlKiQpXxIS0tDU6nEy6XK+IXYY5X7GnG\\nObvdjsbGxsm5gzMdYp86dQqtra1YtOhjm4TSHAghkJOTA4fDweubEYqhGcfsdjsOHDiA5ORklJWV\\nzfiut9PpRGdnJ+6++26u2hMGer0eRqMRAwMDWpdC0+DwPE5NrLC+ceNGxc9Av/HGG6ipqeGz02Fk\\nMpng8Xjgdru5uEeEYWjGmak7RNbU1Cj+B9nV1YWBgQHcfvvtYapw7lwuFxwOB7xeL+x2OwwGA8bG\\nxmAymSClhF6vR0pKCnQ6HdLS0iK2t2w2mzE2NgaDwRCxNcYjhmYc8Xq9OHXqFNLS0rBw4ULFU4SC\\nwSDOnDmDT37ykxE1vcjv92NoaAi9vb0IBoOw2WwoKiqCTqeDwWDAvHnzkJiYiKSkJPj9fng8Hjid\\nTthsNuh0Ouj1ephMJmRlZUXUzRe9Xj+5Fmd2drbW5dC4yPnNp7Dyer1obGyElBLV1dWzemqnoaEB\\nAFBYWBjq8mbF5XLh7Nmz8Pl8EEKgoKAAWVlZM17kt6SkBIFAAG63G1arFX19fXC73SgoKEBaWlpE\\n/GEwm80YHR1FIBDggwMRQvvfCgo7u92OtrY25OfnIzc3d1Y/IxAI4MyZM7jppptCXJ1ydrsdra2t\\nsNlsKCgoQFlZ2ax7iDqdDikpKZNB63A4cOHCBYyMjCA5ORl5eXmaPhaq0+lgNBrhdru54nuE4CpH\\nMW7ihk95eTnMZvOsf05rayu6urqwefPmEFanjN/vR2dnJ86dO4clS5agqKgobIsbu91uWCwWeDwe\\n5ObmarrqvJQSfX19yMvLi4jebzzgIsRx6sSJE3A6nVi5cuWcrtUFg0H8+te/xvbt25GXlxfCCmfO\\narWiubkZgUAAa9asQVJSkirtjo6OYnR0FEIIFBYWatbrdDqdSEhI4J10lXBpuDgTDAbR1tYGIQRW\\nrVo155sb7e3t8Pl8mgVmX18fjhw5gry8PGzcuFG1wAQuPqGTn58Pg8GAjo4O+Hw+1dqeymg0wuv1\\ngp0E7bGvH2N8Ph9aWlqQnJyMa665JiQ9o+7ubnziE58IQXXKdXR04OTJk9i8ebNm80L1ej1ycnJg\\nMBgwODiI7Oxs1Xt8CQkJCAaDcDqdvLapMfY0Y8jEI5EZGRkoLy8PSWBaLBZ0dnairKwsBBUq09LS\\nglOnTmHr1q0RMZHebDbDbDZjaGgIbrdb9fa5KEpkYGjGCJvNhr1796KwsBD5+fkh+7lnz55FUlKS\\n6jcgGhsb0dzcjC1btkTUdbzU1FSYTCaMjIyoPlQ3GAyQUnLpOI0xNGPA4OAgenp6cPPNN4d8d0O7\\n3Y66urqQ/syr6e7uRk9PDzZs2BBRgTkhNTUVycnJsNlsql9jFELA6XSq2iZ9FEMzikkp0dnZCavV\\nioULF4Z8CDs0NISRkZFZz+2cDbvdjubmZixYsGBGa3pqJS0tDUajEVarVdV2uX+89hiaUcrr9eL0\\n6dPw+XyoqakJyz+m999/Hy6XS9Xnnk+cOIHk5GSUlpaq1uZspaamIiEhQdVN0RITE5GQkMC76Bpi\\naEYhj8eDY8eOwev1Yv78+WF7vE4Ioepk9ubmZgwPD6O2tla1NuciISEBKSkpcLvdql5nFELA6/Wq\\n1h59FEMzytjtdpw/fx5VVVVYvXp12CZbB4NBDA4OhvSm0pX4/X50dHRg5cqVUbWiz8RNMjV7mwkJ\\nCQgEAqq1Rx8VPb+dBJvNhtbWVpSXlyMnJyesbTU3N6Orq0u1VX+6u7vh8/lQVFSkSnuhlJqaCp/P\\np9pK61wqTluc3B4lTp06NbmHjxpBFgwGsXr16rC3M9HW4cOHVb9LHyoJCQlISkqCz+dTZWrW+CN+\\nkFJyj3kN8M9VhJNSor29HQ6HAwsXLlSt5zexJqUaBgYGkJWVpdljmqGQlJSk6oR3KSX3ENIIQzOC\\n+f1+NDU1IRgMora2VtUnQk6cOKFae83NzcjIyFClrXDR6/WTvU01GAwG9jI1wtCMUB6PB42NjUhJ\\nScH8+fNVv4blcrmQmZkZ9nb8fj96e3uxePHisLcVbjqdTrUbNAxM7TA0I5DNZsO+ffuQn5+P4uJi\\n1dt3u92qrSFps9kibpuJ2dLr9aoOmbVacSneMTQjjM1mQ3d3N9atW6fZvjBWq1W1nm1zc3PMbOOg\\n0+mg0+lUmbOZkJDABYk1wv/qEaS/vx8WiwULFizQtOc1MDCA4eFhVdry+XyYP3++Km2pQQiBYDAY\\n9j86QggO0TUS0T1NIcQtQohGIUSTEOJBresJl2AwiNbWVgwPD6t6h/xyUlNTsXTpUlXaslgsMbU+\\n5MQOkmrgo5TaiNjQFEIkAPhPAFsBLAHwt0KIhdpWFXqBQAANDQ24cOECampqkJiYqHVJ8Hq9qi0M\\nMTIyosqd87GxMaxduxZ2uz1sbQQCAbz22mt4/PHH8ac//SmsN4Um2nrsscfC3hZ9VCQPz9cBaJZS\\ndgKAEOJFAHcAaNS0qhDyeDxoaWlBUVERiouLI+YpD4/Ho0po+nw+pKenq/KH4vXXX8fRo0fx+uuv\\n48477wz5zw8EAti6dSsaGhrgcDiQkpKC2tpa7N27N+TXbNVsiz7uqv9KhRAPCCG0mERXBKB7yuc9\\n48digsPhwPnz55GTk4PS0tKICUwAWLZs2eQe5+EUCATQ19cX1ja+9rWvIS0tDV/4whcAAPfccw/S\\n0tJw3333hbSdPXv2oKGhAXa7HVJK2O12NDQ0YM+ePSFtR+226ONm0tPMA3BECPE+gGcA7I2kLSB3\\n7Ngx+bquri4qHsXr7u6G1WpFeXl5RK4ZaTAYVLkzq9frQ75o8qW+//3vo6GhAS0tLZOPOZaXl+Oh\\nhx4KaTvHjx//2KIdDocDJ06cwG233Ra1bcWL+vp61NfXz+yLJ55hvdIHAIGL1xZfBNAC4HEA82fy\\nvbP9ALAewBtTPv8egAcv+RoZbQYHB+Ubb7whrVar1qVcVnd3t3ziiSfC3o7b7Zb/9m//FvZ2du7c\\nKfV6vTSZTFKv18udO3eGvI3du3dLk8kkAUx+mEwmuXv37qhuK16NZ8u02TSjMeH4DxkY//ADyADw\\nihDiiZlF86wcAVAlhCgTQhgAfB7Aq2FsL6yklOju7obFYsHmzZtVedpmtgYHBzE6Ohr2dnQ6HZKT\\nk8M+r/GVV15BamoqfvjDH8JkMuEPf/hDyNvYtm0bamtrJ7fnMJlMqK2txbZt28LWlk6ngxAirG3R\\nxwl5lZG2EOJbAL4IwALgKQC7pJS+8bvbzVLKsE2yE0LcAuBJXLz2+rSU8keXvC+vVn8kCAaDaG9v\\nRyAQCOuiwaFy+vRpWK1WbNq0KextvfTSS7jtttvCOu3ogw8+QEFBAbKzs2GxWDAwMBCWKVWBQAD/\\n9E//hKamJnzzm9/Etm3bwvb/OhAIYOnSpbjppptwyy23hLWteDS+ktS0E2FncuEqE8Cn5fhd7AlS\\nyqAQIqwXUKSUbwCoCWcb4eZyudDQ0ICysjJUVlZGxYRknU6n2uR2u92OwcFBVFZWhq2NZcuWTb7O\\nzs4O25NWOp0OS5cuxZYtW8J+bTEhIQFZWVl4/PHHI2J743hy1eG5lPLRSwNzynvnQl9S7HC73Whu\\nbkZOTg4qKiqiIjCBv97ZV0NNTY0qlwLU0t7erspkfYfDAZ1Ox8DUQCTP04xqY2NjaGtrQ3Fxcdjv\\nEIdaVVUVzp1T5++h0WjEwMCAKm2Fm9PphMPhwPr168PeVktLC5KSksLeDn1c5EwOjCE2mw1tbW2o\\nrKyMusAELt7EsNvtqiw8UVVVhba2NlU3JguXpqYmZGZmqvIYbH9/f9SvQRqtGJohdu7cORw7dgwL\\nFixQZWm1cNDr9WhtbcXg4GDY20pPT0dubi76+/vD3la47d27V7XV7oeGhrBu3TpV2qKPYmiGiJQS\\nnZ2dCAaD2Lhxo+aLbszVmjVrwvqc9lQmkwmnTp1Spa1w8Xq9sFgsuPXWW1Vp7/Tp01G5CV0sYGiG\\nQCAQmHziZNGiRapuSxEuZWVlsFqtqrR1/fXXo7OzEy6XS5X2wuHw4cMwGo2qBdn777/P9TQ1wtCc\\nI6fTicbGRiQlJWmyLUW4GI1GvP/++6q0lZKSgqKiIjQ2RudaLFJKvPrqq7j55ptVac/tdsPn8/GR\\nSY3Exr9wjbhcLuzfvx8GgwGlpaVRM6VoJgoLCzE0NKTamo3Lly/Hu+++G5VbOOzfvx9paWm49tpr\\nVWmvsbERZWVlk08fkboYmrM0NjaGpqYmrF27FtXV1VqXE3J5eXkoLi6GxWJRpb3S0lIsXLgQb7/9\\ntirthYrX68Xbb7+N1atXqzZcfv755/n0j4YYmrNgtVqjekrRTGVnZ6t6g2b16tUYGBiIqjvpzz//\\nPJKSknDLLbeo1qbT6cRdd92lWnv0UQxNhc6dO4fe3l7U1NRE7ZSimVL7rvbE2qJvvvmmqrs6ztbx\\n48fR3NyMe++9V7VLM2NjY2hpacGGDRtUaY8+jqE5Q1JKdHR0oL+/HwsWLIiL60kbN26EwWCA0+lU\\nrc3NmzfDaDRi165dqrU5GzabDbt378bGjRtRUFCgWrvPPvsscnJy4uL3L1IxNGdgYkqR3+9HXV1d\\n3PzC6vV6lJSU4PTp06q1KYTArbfeCo/HE7HXN91uN55++mlkZGSofge7ubkZW7ZsUbVN+iiG5lX4\\nfD40NTXBYDDE1JSimZo3bx727dunapsmkwmbN29GZ2cnDh06pGrbVxMIBPDkk09Cr9fjG9/4hqpt\\nDw8Po6mpCZ/73OdUbZc+Kr4SQKHh4WHU19cjIyMDZWVlMTWlaKbq6uqQmZmJoaEhVdstLCzEzTff\\njCNHjuDw4cOqtn05Xq8Xjz/+OMxmM/7hH/5B9T+gv/jFL7BgwYKYeHgimjE0L2NsbAzt7e2orq5G\\nfn6+1uVoRq/XY+nSpTh+/LjqbZeUlODuu+/GgQMH8Pbbb2t6c+jChQt47LHHUFZWhnvvvVf1SzTB\\nYBCHDx/GjTfeqGq79HEMzWlMrFJUVVWF8vJyrcvRXFVVFV588UV4vV7V287MzMQ3v/lNtLS04MUX\\nXwz77pXTqa+vx5NPPolVq1bhnnvuUW1P+KmOHj2KjIwM/M3f/I3qbdNHXXW7i0gWju0u+vv7YbFY\\nUFVVFfWLboTSzp07UVpaijVr1mjSfjAYxIEDB3DkyBGsWrUK119/fdj3S7fZbHjqqacgpcSNN96I\\ntWvXhrW9K7nnnnvwuc99DnfccYdmNcSTuW53EReklDh16hRsNtvkVBv6q2uvvRY7d+7E8uXLwx5W\\n00lISMCmTZuwfPlyvPDCC2hpaUFNTQ2uu+66kD8dMzg4iAMHDqChoQHXXXcdbr75Zk2vI545cwYX\\nLlzATTfdpFkN9FfsaeKvG5/5/X5UVFQwMC/j0UcfxerVq3H77bdrXQpOnz6N48ePo6urCxs2bEB1\\ndTVKSkpm/fP8fj/Onj2Lv/zlL+jo6MA111yDTZs2obCwMIRVz853v/td3HDDDRyaq+hKPc24D02/\\n34+WlhYYjca4vUM+U93d3di1axfuu+++iNlqoaWlBefOncPZs2dhMBhQXV0Ns9mMxYsXIyMj47J3\\nuN1uNzo7O9HT04Oenh6cPXsWJSUlyMnJwe233x4xl2ZeffVV/OpXv8LLL7+sSQ8/XjE0L2N0dBQd\\nHR3Izs6OiB5FNPjTn/4Eo9GIT3ziE1qX8hFSSpw9exYWiwUnTpxAIBCA3W6HEAI5OTkYGhqC2WyG\\n0+nE6OgokpKS4Ha7sWTJEmRkZGDVqlXIycnR+jQ+IhAI4Mtf/jI2btyI+++/X+ty4gqvaU7D4XDg\\n0KFDqK4BvJVUAAAODElEQVSuZmAqsH79evzzP/8zli9fHlEhI4TAkiVLAGByv3afz4eBgQFIKWGz\\n2SZ3bkxLS0N6enrEL+L72muvITc3F3//93+vdSk0Rdz0NAOBAPbs2YPjx4+juroaCxYswPz582E2\\nm8NcZew5ePAgOjo6cNddd/FyRph0dnbiq1/9Kn75y1+ioqJC63LiTtz3NAOBALZu3YqGhgY4HA4k\\nJydj3bp1eOutt7QuLSpt2LABjY2NePfdd1FXV6d1OTFHSon//u//xsaNGxmYESguJrfv2bMHDQ0N\\nsNvtkFLC6XTi6NGj2LNnj9alRaWEhARs2LABL7/8suqPV8aDvXv3Ynh4GI888ojWpdA04iI0jx49\\n+rGdFR0OB06cOKFRRdFv8eLF+NKXvoSdO3dGxdqX0eL8+fP44Q9/iG9/+9sRf801XsV8aI6MjGDX\\nrl0fmwCdkpKCFStWaFRVbFi3bh30ej2efvpprUuJCS6XC//+7/+O+++/Pya3UIkVMR2avb292LRp\\nE6699lps2rQJJpMJQgiYTCbU1tZi27ZtWpcY1YQQ2L59O7q6unDy5Emty4lqwWAQjz32GKqrq7mV\\nRYSL2f7/gQMHcMstt+CRRx7Bgw8+iGAwiD179uDEiRNYsWIFtm3bxs2pQiA7Oxv/+I//iGeffRZp\\naWm8cTFLv/jFL3D8+HHs3LmTMxIiXExOOTpw4ADuvvtu3HffffiXf/kXDSqLP6dPn8ZPfvIT/OhH\\nP1J1+4dYsGfPHrzyyiv46U9/ivT0dK3LIcTZE0G///3v8Z3vfAe/+c1vOB1GZQ0NDXjvvffwla98\\nBZmZmVqXExWee+45/O53v8NTTz3FhywiyJVCM2auaQaDQTzxxBN4+OGH8dprrzEwNVBbW4tNmzbh\\niSeeQFdXl9blRLz33nsPe/bswYMPPsjAjCIx0dOceEZ34omfuax2Q3P33HPPobu7G3/3d3+H3Nxc\\nrcuJSM888wzeeecdPPbYY7wOHIFiuqfp8Xjwta99DSMjI/jggw8YmBHgC1/4Am699VY888wznAt7\\nCSkl/ud//gc7d+7EAw88wMCMQlF/9/wzn/kM8vPz8corr3AdzAiyYsUKjIyM4Oc//zm+8Y1v4Jpr\\nrtG6JM15vV787Gc/Q1dXF379618jOztb65JoFqI+NFetWoUdO3bE3da60WDTpk2oqanBCy+8gPb2\\ndmzfvj1un3IZGhrCI488AovFgmeeeYY7SkaxmLimSZHN4XDgBz/4weQyZ/E2rea9997DM888gy1b\\ntuCzn/1s3P7hiCZxNeWIIlMgEMCBAwdw8OBB3HDDDbj++uu1LinsPB4PnnvuOfz2t7/Fv/7rv6K2\\ntlbrkmiGGJoUMTo7O/GDH/wAN9xwAz7zmc/EbK/zzTffxK5duzB//nx85StfQUZGhtYlkQIMTYoo\\nPp8P7777Lg4ePIjS0lLcfffdMXMTz2q14oUXXsC+fftw3333RcQmdKQcQ5MiUkdHB37+858jPT0d\\nW7duxcqVK6P2uWun04mf/OQnOH/+PG677TZ8+tOfhtFo1LosmiWGJkW01tZW7Ny5E2fOnMEDDzyA\\nFStWRM1iKhaLBW+++SbefvttFBYW4vOf/zwWL16sdVk0RwxNinjBYBCHDh3CiRMnYLPZkJ2djbvu\\numtyM7RI09XVhX379mHnzp1Yt24d7r//fuTn52tdFoVIRIamEOKzAHYAWARgrZTy/SnvPQTgXgB+\\nAN+SUu67zM9gaMagpqYmPPvsswgEAqipqUFZWRk2btyo+XXP0dFRHD58GE899RSSk5Oxfft2bN68\\nGVlZWZrWRaEXqaFZAyAI4BcAvjMRmkKIRQB+C2AtgGIAbwGoni4dGZqxzeVy4dixY3jqqaeQl5eH\\nJUuWoKCgAKtXr1ZlFSUpJfr6+nDy5Ek8//zzSE5OxsqVK1FdXY0bbrgBycnJYa+BtBGRoTlZgBB/\\nBvB/p4Tm9wBIKeWPxz/fA2CHlLJhmu9laMaJkZERnDlzBi+99BL8fj+Ki4uRnp4+GaL5+flITEyc\\nUxvDw8Po6OjAwMAATp06hf/93/9FeXk5li1bhtTUVGzbtg2pqakhOiOKZNEWmv8B4C9Syt+Of/4U\\ngNellDun+V6GZhwKBALo7e1FfX09+vr6Jj8fGhrC+vXrkZGRgcHBQdTU1CAjIwN2ux1CCGRkZMDl\\ncqG1tRX5+fmw2+1oaGhASkoKRkdH0d/fD7PZjOuvvx5lZWVIS0vDihUrovaOPs2eZvueCyHeBJA3\\n9RAACeBhKeXuULSxY8eOydd1dXVcRzMO6HQ6lJaW4otf/OLkMbfbjfb2dkgpMTQ0hP7+foyOjmJ0\\ndBStra0IBAIoKSmBz+dDa2srzGYzzGYzVq9ejcWLF6OiogJms5kBGafq6+tRX18/o6+NxJ7mpcPz\\nNwA8yuE5EaklGtbTnFrcqwA+L4QwCCEqAFQBOKxNWUREH6VZaAohPimE6AawHsCfxm/4QEp5FsDL\\nAM4CeB3A19mdJKJIofnwfC44PCeicIiG4TkRUVRgaBIRKcDQJCJSgKFJRKQAQ5OISAGGJhGRAgxN\\nIiIFGJpERAowNImIFGBoEhEpwNAkIlKAoUlEpABDk4hIAYYmEZECDE0iIgUYmkRECjA0iYgUYGgS\\nESnA0CQiUoChSUSkAEOTiEgBhiYRkQIMTSIiBRiaREQKMDSJiBRgaBIRKcDQJCJSgKFJRKQAQ5OI\\nSAGGJhGRAgxNIiIFGJpERAowNImIFGBoEhEpwNAkIlKAoUlEpABDk4hIAYYmEZECDE0iIgUYmkRE\\nCjA0iYgUYGgSESnA0CQiUkCz0BRCPCGEOCeEOCGE+IMQIm3Kew8JIZrH39+iVY1ERJfSsqe5D8AS\\nKeUKAM0AHgIAIcRiAHcCWARgG4D/EkIIzaokIppCs9CUUr4lpQyOf3oIQPH469sBvCil9EspO3Ax\\nUNdpUCIR0cdEyjXNewG8Pv66CED3lPd6x48REWlOH84fLoR4E0De1EMAJICHpZS7x7/mYQA+KeXv\\nwlkLEVEohDU0pZQ3X+l9IcSXAdwK4MYph3sBlEz5vHj82LR27Ngx+bqurg51dXXKCyWiuFZfX4/6\\n+voZfa2QUoa3mss1LMQtAH4K4AYppXXK8cUAXgBQi4vD8jcBVMtpChVCTHeYiGhOhBCQUk57Azqs\\nPc2r+A8ABgBvjt8cPySl/LqU8qwQ4mUAZwH4AHydyUhEkUKznmYosKdJROFwpZ5mpNw9JyKKCgxN\\nIiIFGJpERAowNImIFGBoEhEpwNAkIlKAoUlEpABDk4hIAYYmEZECDE0iIgUYmkRECjA0iYgUYGgS\\nESnA0CQiUoChSUSkAEOTiEgBhiYRkQIMTSIiBRiaREQKMDSJiBRgaBIRKcDQJCJSgKFJRKQAQ5OI\\nSAGGJhGRAgxNIiIFGJohUF9fr3UJIcdzig48J/UxNEMg0v8nzwbPKTrwnNTH0CQiUoChSUSkgJBS\\nal3DrAkhord4IopoUkox3fGoDk0iIrVxeE5EpABDk4hIAYbmHAghnhBCnBNCnBBC/EEIkTblvYeE\\nEM3j72/Rss6ZEkJ8VghxWggREEKsuuS9qDufCUKIW4QQjUKIJiHEg1rXMxtCiKeFEINCiFNTjmUI\\nIfYJIc4LIfYKIcxa1qiUEKJYCPGOEOKMEOIDIcT/GT8e0efF0JybfQCWSClXAGgG8BAACCEWA7gT\\nwCIA2wD8lxBi2ovKEeYDAJ8C8O7Ug0KIRYjO84EQIgHAfwLYCmAJgL8VQizUtqpZ+RUunsNU3wPw\\nlpSyBsA7GP/9iyJ+AN+WUi4BsAHAN8b/30T0eTE050BK+ZaUMjj+6SEAxeOvbwfwopTSL6XswMVA\\nXadBiYpIKc9LKZsBXBqIdyAKz2fcOgDNUspOKaUPwIu4eD5RRUr5HoChSw7fAeA3469/A+CTqhY1\\nR1LKASnlifHXdgDncPHfUESfF0MzdO4F8Pr46yIA3VPe6x0/Fq2i+Xwurb0H0VP71eRKKQeBiwEE\\nIFfjemZNCFEOYAUudj7yIvm89FoXEOmEEG8CyJt6CIAE8LCUcvf41zwMwCel/J0GJSoyk/OhqBWV\\n8weFECYArwD4lpTSPs3864g6L4bmVUgpb77S+0KILwO4FcCNUw73AiiZ8nnx+DHNXe18LiNiz2cG\\negGUTvk8mmq/mkEhRJ6UclAIkQ/ggtYFKSWE0ONiYD4npfzj+OGIPi8Oz+dACHELgO8CuF1K6Zny\\n1qsAPi+EMAghKgBUATisRY1zMPW6ZjSfzxEAVUKIMiGEAcDncfF8opHAx/+/fHn89ZcA/PHSb4gC\\nzwA4K6V8csqxiD4vPhE0B0KIZgAGANbxQ4eklF8ff+8hAF8F4MPFYcc+baqcOSHEJwH8B4BsAMMA\\nTkgpt42/F3XnM2H8j9uTuNhJeFpK+SONS1JMCPFbAHUAsgAMAngUwC4Av8fFUUAngDullMNa1aiU\\nEGIjgP24OGtDjn98Hxf/IL+MCD0vhiYRkQIcnhMRKcDQJCJSgKFJRKQAQ5OISAGGJhGRAgxNIiIF\\nGJpERAowNImIFGBoUkwTQqwRQpwcfwQ0ZXyR5cVa10XRi08EUcwTQvw/AMnjH91Syh9rXBJFMYYm\\nxTwhRCIuLtzhAnCt5C89zQGH5xQPsgGYAKQCMGpcC0U59jQp5gkh/gjgdwAqABRKKR/QuCSKYlyE\\nmGKaEOILALxSyhfHN1k7KISok1LWa1waRSn2NImIFOA1TSIiBRiaREQKMDSJiBRgaBIRKcDQJCJS\\ngKFJRKQAQ5OISAGGJhGRAv8fIZ3Pkw1x1G4AAAAASUVORK5CYII=\\n\",\n \"text/plain\": [\n \"\"\n ]\n },\n \"metadata\": {},\n \"output_type\": \"display_data\"\n }\n ],\n \"source\": [\n \"addOrbit(sim, comets[0])\\n\",\n \"%matplotlib inline\\n\",\n \"fig = rebound.OrbitPlot(sim, trails=True)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"Now we just integrate until whatever final time we’re interested in. Here it's the epoch at which we observe the comet, which is the last column in our table:\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 15,\n \"metadata\": {\n \"collapsed\": false\n },\n \"outputs\": [\n {\n \"data\": {\n \"image/png\": \"iVBORw0KGgoAAAANSUhEUgAAAU0AAAFCCAYAAAB1po8RAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl81NW9//HXSYYsJEDIQhL2JSwCKiCCLaKxIBChRcGl\\nautGobeiUotaFG9BbUsRr8rVKxd64boUEREU8crmEgGFgALRIEHWhASyEkK2yWzn90dCfgECZCDJ\\n+c7k83w88jCZzEzeDpN3zvku56u01gghhKifANMBhBDCl0hpCiGEF6Q0hRDCC1KaQgjhBSlNIYTw\\ngpSmEEJ4wWY6wOVQSsnxUkKIRqG1VnXd7vMjTa11k3/MmjXLyM/1pUxWy2PFTBfLU1BQQGpqKllZ\\nWXg8HktksuLr1BgfF+LzpSmEv9Fak5mZyebNm+natSsdOnRAqToHPcIAn56eC+FvHA4Hhw8fJiAg\\ngLFjx9KiRQvTkcRZpDQvQWJioukI57BaJqvlAetlOjvPyZMnycjIIC4ujtjYWEtksgKrZVIXm79b\\nmVJK+3J+IQA8Hg+7du2ivLycQYMGERYWZjpSs6eUQp9nR5CUphAG2e12Dh06REBAAN27dycoKMh0\\nJMGFS1Om50IYUlhYSFZWFh06dCA6Otp0HFFPUppCNDGn08nu3btp2bIlvXr1IjQ01HQk4QUpTSGa\\nUHl5OQcPHgSgT58+BAYGGk4kvCWlKUQTycvL4/jx43Tq1InIyEjTccQlkh1BQjSyyspKMjIycLvd\\ndO/eneDgYNORxEVcaEeQnBEkRCMqLS1ly5Yt2O12+vTpI4XpB2SkKUQjycnJITc3l65du9KmTRvT\\ncYQX5DhNIZqQ0+nkyJEjeDweunXrJsde+iCZngvRRIqKili7dm3N4URSmP5HRppCNACtNcePH6eg\\noIC4uDjatWtnOpK4DDI9F6IROZ1ODh8+DEC3bt1kZSI/IKdRCtFIjh49WnPsZVxcnKx72QzINk0h\\nLoHWmuzsbDIzM+nSpQvx8fFSmM2ETM+F8JLD4eDQoUPYbDa6du2KzSYTNn8j03MhLpHb7Wbt2rXs\\n2rWLgQMHMnjwYHJzc40uFCzMktIU4jzcbjejR48mJSWFsrIyQkNDSUhIYNOmTXKwejMm2zSFOI+1\\na9eSkpJCaWkpWuuaFYo2b95sOpowSEpTiPPYtWsXZWVlZ9xWXl7O7t27DSUSVmC8NJVSi5VSuUqp\\n72vdNksplaWU2ln9McZkRtH8VFZWsnTp0nOugR0WFsaAAQMMpRJWYLw0gf8FRtdx+8ta60HVH+ua\\nOpRovg4ePMjw4cPp1KkTP//5zwkPD0cpRXh4OEOHDiUpKcl0RGGQ8R1BWustSqkudXxLDnoTTW7l\\nypVMnTqVZ599lqlTp+LxeFi7di27d+9mwIABJCUlyWrrzZwljtOsLs01Wuurqr+eBdwPnAK+BaZr\\nrYvreJwcpykaRHFxMb/97W/Zu3cvy5YtY/DgwaYjCYN88TjNN4DntdZaKfVX4GVgUl13nD17ds3n\\niYmJlruwvLC+Q4cOcccdd1BcXMz27dvlUhTNUHJyMsnJyfW6ryVHml58T0aa4rKsWrWKxx57jGee\\neYY//OEPciqkAHxjpKmotQ1TKRWntc6p/nICkGYklfBbJSUlPPvss6xbt46PPvpIpuOi3oyXplLq\\nXSARiFJKZQKzgJuUUgMAD3AE+L2xgMLvHD58mJ///Of06NGDlJQUIiIiTEcSPsQS0/NLJdNz4a2P\\nP/6YRx99lEceeYTp06cTEGCFo+6E1fjC9FyIRuVwOHj22Wf55JNPWLlypUzHxSWTP7PC73377bf0\\n7duXI0eO8PXXX0thissipSn82rp167jzzjsZMmQI7733Hm3btjUdSfg4mZ4Lv+R0OvnrX//KihUr\\nWLZsGUOHDjUdSfgJKU3hd1JTU3nqqacIDw9n8+bNREVFmY4k/IhMz4VfSU5OJjExkYSEBFasWCGF\\nKRqcjDSFX3C73bz00ku8/fbbrF69mhtuuMF0JOGnpDSFzysoKGDKlCm4XC6++OILuXaPaFQyPRc+\\n7YMPPqBv374MGjSIVatWSWGKRidnBAmfpLVmwYIFvPbaa/z+97/nj3/8o+lIwo/IGUHCrxQXF/PY\\nY4+Rm5vLxo0b6dixo+lIohmR6bnwKatXr2bkyJF07NiRNWvWSGGKJielKXyC1pqlS5cyadIk7rnn\\nHv72t7/RokUL07FEMyTTc2F5FRUVzJgxgx9++IFt27aRkJBgOpJoxmSkKSzt0KFDjBs3Dq01n3zy\\niRSmME5KU1jWggULGDJkCA8++CDz58+nZcuWpiMJIdNzYT0ul4s5c+awbt06lixZwq9+9SvTkYSo\\nIaUpLCUnJ4epU6fSunVr/u///k8uRSEsR6bnwjLefPNNxo0bx0033cTixYulMIUlyUhTGKe1ZtGi\\nRbzwwgu8+OKL3HPPPaYjCXFeUprCqJKSEp544gkKCgrYsWMH8fHxpiMJcUEyPRfGpKenM378eOLj\\n43nvvfekMIVPkJGmMGL+/PnMmTOHhQsXMn78eNNxhKg3KU3RpBwOB3//+9/ZsmULS5cuZcSIEaYj\\nCeEVKU3RZI4fP860adOIiYnhww8/pFWrVqYjCeE12aYpmsRbb73FxIkTufnmm3n99delMIXPkpGm\\naFRaa5YsWcILL7zAvHnzuOOOO0xHEuKyGC9NpdRiYByQq7W+qvq2tsByoAtwBLhTa11sLKS4JKWl\\npcycOZPc3FxSUlLkUhTCL1hhev6/wOizbpsBfKa17g18ATzd5KnEZTl48CB33XUXUVFRvP3221KY\\nwm8YL02t9Rag6KybxwNvVX/+FnBrk4YSl2XRokXcdNNNTJ48mb/85S8EBQWZjiREgzE+PT+Pdlrr\\nXACtdY5Sqp3pQOLi3G438+fPZ/369SxcuJCkpCTTkYRocFYtzbPJJSctrqioiCeffBKbzcby5cub\\nfLENt9uNy+UiICAArTUejwen00lAQACBgYE196usrCQ0NBSoueIgADabjYAA4xMv4QOsWpq5SqlY\\nrXWuUioOyDvfHWfPnl3zeWJiIomJiY2fTpzh008/Zf78+YwdO5ZHHnmkUcvH7XbjdDopKSkhJCQE\\nt9uNx+PB5XLh8XgICwtDKVVTnqcpVXU11tq3n36c1rrmeZRSuN1ugoKCCAwMrHmu048X/ik5OZnk\\n5OR63dcS1z1XSnUF1mitr6z+ei5wQms9Vyn1Z6Ct1npGHY+T654b9tFHH/H4448ze/Zs7r///gZ/\\n/tMF6XQ6a0rMZrPhdrtp2bJlzQixoYpaa43L5ar52uPx1BRqSEiIlGgzYenrniul3gUSgSilVCYw\\nC/gHsEIp9RCQAdxpLqGoi8PhYN68eezcuZMvv/ySrl27Nsjzut1uioqKsNlsZ0yvw8LCCA0NPWOq\\n3RiUUnVe5dLj8aC1RmuN0+nE7XZjs9mw2WxSoM2MJUaal0pGmmbk5eXx1FNPER0dzXPPPUdYWNhl\\nPZ/b7cZut2O323E6nbhcLqKiomqmyFZUu0ShqmxPj0Kh6v9p7dq17Nq1i4EDB5KUlGTZ/xdxrguN\\nNKU0hVfWrFnDk08+yVNPPcUDDzxwWdNiu93OiRMnKCkpITY2lpCQEIKDg31y5OZ2u9Fao5TC4/GQ\\nlJRESkoKZWVlhIWFMXToUNavXy/F6SOkNMVl01qzcuVKFi1axN13382DDz54Sc/jcDiw2+2Ul5cT\\nGBhIaGgoLVu29Ks91x9//DH33nsvpaWlNbeFh4ezbNkyxo0bZzCZqC9Lb9MU1udwOJg7dy579+5l\\nyZIldOzY0evncLlclJaWcuzYMSIjI4mMjPTbg95TU1MpKys747aysjK+++47KU0/4D9/3kWj+PHH\\nH5k8eTJ2u53Fixd7XZh2u52ioiJycnIA6NWrF3FxcX5bmAADBw48ZzuvzWbj/fff5z//8z/P2Dsv\\nfI+UpjivXbt2ceutt9K7d2/++te/1hwUXh8ej4eioiL27t2L2+0mPj6eiIgIbDb/n9wkJSUxdOhQ\\nwsPDUUoRHh7ODTfcwH/8x3+wb98+7rrrLj777DNk05Jvkm2a4hynt1+++eab/Pu//ztDhw716vGl\\npaWcPHmSkJCQZlOUZzu993z37t0MGDDgjL3n27dv57XXXqO0tJQpU6bI6aYWJDuCRL05HA5efPFF\\n9u/fz5w5c2jfvn29H1tZWUl6ejrR0dFER0cTHBzciEl9m8fj4ZVXXmHjxo2MGDGCP/zhD4SHh5uO\\nJapdqDRlei5qpKenM2bMGBwOBwsXLqx3YWqtOXHiBLm5uXTu3JkOHTpIYV5EQEAA06dP5/3338fl\\ncnH33Xfz6aef4vF4TEcTFyEjTQHA999/z8yZM+nZsycvvfRSvQ8BKi4u5tSpUwQHBxMZGdksp+IN\\nYffu3fzxj3+kX79+zJ07V0adhsn0XJyX1pqPP/6YJUuW8Mwzz3i1/bKoqIgjR47QpUsXIiMjGzFl\\n81BSUsLChQvZunUrs2fP5sorrzQdqdmS0hR1qqio4LXXXmPPnj38/e9/p0OHDvV6nMvlIi8vD4/H\\nQ1xcnIwuG9jmzZuZO3cugwcPZubMmXWeCy8al5SmOEdhYSHjx4+nW7duLFy4kJYtW9brcUVFReTm\\n5hITE0NkZKRPnvLoC44fP86kSZO44ooreP755y/7/H7hHdkRJM6Qnp7Oww8/zH333cebb75Z78Is\\nKSnh+PHjREVFERUVJYXZiOLj41m9ejVxcXH827/9G9nZ2aYjiWoy0mxmNmzYwIIFC5g+fTrXX399\\nvR9XWFjIqVOnaN++vewZb0Jaa1atWsWSJUu47777uOuuu0xHahbk3HOBw+HgmWeeIScnh1deeaXe\\n6196PB72799PaGgonTp1ku2XTUwpxcSJEwF44403iI+P54YbbjCcqnmT34BmoKSkhL/85S+kpqay\\ncuVK2rZtW6/Haa3Jzs7G4XCQkJAgy5oZNHHiRPr378+MGTMoLy9nzJgxpiM1W7JN089lZGTw6KOP\\n0qdPHzZu3FjvwvR4PGRnZxMQEED//v2lMC2gd+/evPrqqyxevJiFCxeajtNsyTZNP7Z161Zefvll\\npkyZws0331zvx7lcLjIzMwkJCSE+Pl52+FhMRkYG9913H7///e+55557TMfxS7JNs5nRWvP000+z\\nbds2/vu//5s+ffp49dgDBw7gcDjo1q2bFKYFdenSheXLl/PYY48RGRkpU/UmJtNzP1NZWcncuXMp\\nLCzkn//8p1eFCXDs2DFatmzJlVdeKYVpYXFxccybN49Fixbx1VdfmY7TrMj03I/k5+fzwgsv0Llz\\nZx577DGvF/rNzc2loqKCzp07+9XlJ/zZ/v37mTRpEn/+858ZO3as6Th+Qw5ubwa2bt3K448/zg03\\n3MD06dO9LsyDBw+SlZVFx44dpTB9SM+ePZk5cyaLFy/m2LFjpuM0C/Lb4QfWr1/Pgw8+yKRJk7j9\\n9tu9nlaXlpZit9vp06ePHIfpg0aPHs19993Hs88+e861iUTDk9L0YW63m8WLF7Nq1SrWr1/PTTfd\\n5PVzOJ1OsrKy6NKli5zf7MNuvfVWrr76ambMmIHD4TAdx6/JNk0fVVZWxrx583C73Tz11FO0atXK\\n6+dwuVwcOnSIyMhIoqOjGyGlaEpOp5PbbruNpKQkpk6dajqOT5Ntmn5m586d3HvvvbRv357Zs2df\\nUmFC1U6EkpISKUw/0aJFC958802++uor0tLSTMfxW1KaPiY1NZW5c+fys5/9jClTplzymTolJSUo\\npRgwYEADJxQmRUdH8/jjjzNnzhxKSkpMx/FLMj33EVpr1q5dywcffMD06dPp16/fJT+Xy+Vi//79\\ndOrUSS6r4KdeeeUVfvjhB/7nf/5Hjoa4BD47PVdKHVFKpSqldimltpvOY4rL5WLhwoWsX7+eOXPm\\nXFZhAuzbt4+IiAgpTD82ZcoUCgsL2bRpk+kofsfSpQl4gESt9UCt9RDTYUwoKSlh3LhxpKenM2fO\\nHGJjYy/r+QoLC8nPz6ddu3YNlFBYUVhYGH/7299YtGgRpaWlpuP4FauXpsL6GRtNdnY2zzzzDL/6\\n1a946aWX6r3C+vm43W5ycnIYPHiwrFrUDPTv35+hQ4eyZMkS01H8itULSQPrlVI7lFKTTYdpSrt3\\n72bWrFlMnDiRhx9+uEEOOs/NzaVVq1YyLW9GJk2axMaNG/n4449NR/EbVj/9Y5jW+rhSKgbYqJTa\\nq7XeYjpUY/J4PLzzzjt8/fXXPPnkk/Tu3btBnre4uJjjx49z9dVXN8jzWY3D4SAzM5PKykpSUlKI\\niori8OHDpzfoU1RURPv27Tl69Cg9e/aktLSU6OhoYmNjCQwM5Morr6R169Z+t9MkPDyc2267jU8+\\n+YRx48b53f+fCZYuTa318er/5iulPgSGAGeU5uzZs2s+T0xMJDExsQkTNiyXy8Ubb7zBihUrWLFi\\nBXFxcQ323IcOHSI8PNyvTpMsKipi27ZtZGZmUlJSQnl5OYMHDyYiIoIePXrQr18/WrVqRcuWLQkI\\nCCAgIIDy8nIA8vLycDgcFBQUkJmZyaFDhzhw4ADDhg2rWeWpvgs2W90DDzzA7t272bx5MzfeeKPp\\nOJaUnJxMcnJyve5r2UOOlFItgQCtdalSKgzYADyntd5Q6z5+c8hRaWkpr776KsHBwTz66KOEhIQ0\\n6HMfOXKEvn37+vxI4+TJkxw4cIANGzYQGBhIQkIC8fHxDBw4kNDQ0Mt67qKiIvLz89m0aRNaa4KC\\ngujduzfXXnutz28DTk1N5dVXX2XRokVyHfV68MnrniulugEfUrVd0wYs1Vr/46z7+EVpHjt2jHnz\\n5nHttdfy61//usGL7aeffvL5UyWzs7PZs2cPX3zxBQMGDGDAgAEkJCQ02sjZ5XKxc+dOsrKyyMnJ\\noXPnzowcObJB/5g1tT/96U/Ex8fz5JNPmo5ieT5ZmvXhD6X50Ucf8fbbb/PYY481yqaF/Px8cnNz\\n6devn08uKnx6Cv7ll18ycuRIrrvuOlq3bt2kGbKzs0lLSyMjI4PY2FhuueUWnxytbdmyhXnz5rFi\\nxQqvlw5sbqQ0Lerzzz/n7bff5q677uKWW25plJ+xZcsWOnbsWO9L9lqFx+Nh27ZtrFq1iptvvpnr\\nr7/e+CpMeXl5bN++ncLCQrp3787111/vc3+IZs2axXXXXUdSUpLpKJYmpWkxbrebd999lz179vCn\\nP/2p0Q40Ly0t5fDhw/Tv39+nfrlzcnL4r//6LxISEhg9enSD7hBrCPv37+ebb74hNjaWa665hpiY\\nGNOR6i0tLY1XXnmFRYsW+fx22sYkpWkhpaWlLFiwAK01jzzyyGUfsH4hhw4dIiws7LLPImoqHo+H\\n1atXs3//fq655hpuuukmy+64crvdfP755+zfv59bb72VDh06mI5UL1prpk2bxvDhw7njjjtMx7Es\\nnz333N/k5eXxq1/9iqCgIKZPn96ohWm32zl16hRRUVGN9jMaksPhYM2aNaSlpXHXXXcxYsQIyxYm\\nQGBgIKNGjWLixImsXr2azz77DF/4A66UYvDgwXz00Uemo/gs674r/cz+/fuZM2cO06ZNY9q0aY0+\\nNdqzZw9aa584LtNut/Piiy9y7NgxnnrqKbp06WI6Ur3FxcVx9913U1ZWxvr163E6naYjXdQ999xD\\nYGAgGRkZpqP4JCnNJrB161Zef/11HnroIcaPH9/oP09rTUBAAD179mz0n3W58vPzWbBgAf3792fy\\n5MkEBwebjuS1tm3bkpSUxLFjx/jiiy9wu92mI12QzWZj5MiRbNiw4eJ3FueQ0mxEHo+HhQsX8uGH\\nH/LUU09x5ZVXNsnPLS4uJigoyPLnmFdUVPDOO+8QFhbG+PHjfWJUfD5BQUHcf//9KKV45513LF+c\\no0aNIjk5GbvdbjqKz5HSbCROp5NXX32VTz/9lJkzZzbpjoKCggLLH8hut9v5xz/+QY8ePZg8ebJP\\n7d0/n8DAQH7xi1/Qtm1bUlJS8Hg8piOdV1xcHHa7nXfffdd0FJ8jpdkITp06xUsvvUSbNm344IMP\\naNOmTZP9bLvdzr59+yy9A8jtdrN69Wrat2/PuHHj/KIwT7PZbNxyyy2kp6fz5Zdfmo5zQQ888ACF\\nhYWmY/gcKc0GlpWVxd///neuuuoqHnrooSY/c6S4uJjo6GhLT3WXLVvGTz/9xEMPPeSXxwq2aNGC\\niRMnUlJSwoEDB0zHOa/hw4ezc+dOueSvl6Q0G9Dq1auZMWMGEydOZOzYsUZGUCUlJZbe+3zw4EEy\\nMzOZNGmST56KWF9t2rRh0KBBfPLJJ5SVlZmOU6eIiAi6devG7t27TUfxKVKaDSQ5OZkNGzbwu9/9\\njmuvvdZIBq01J0+etOySZg6HgwULFnDjjTfSvn1703EaXefOnRkxYgSbN2+27PbNK664QrZreklK\\n8zJ5PB7ef/99Nm/ezPPPP290Pc8TJ04QEBBg2cN21q1bx8CBAxk2bJjpKE2mb9++ZGZmkp6ebjpK\\nnQYPHszRo0d94sB8q5DSvAzl5eUsWLCA3NxcnnjiCeM7XzIyMnC5XEYznE9GRgaff/4548aNMx2l\\nSQUGBnL77bezd+9eS17grE+fPkRGRnLs2DHTUXyGlOYlOnHiBHfffTcej4eHH374shfAbQhBQUH0\\n6tXLdIw6ffbZZ0yYMKFJjySwisjISJRSfPfdd6ajnEMpRf/+/UlLSzMdxWdIaV6CzMxMXnnlFaZM\\nmcLUqVMtsQfY4/FQWlpqyQPad+3axZ49e5rVtPxsSUlJnDhxglOnTpmOco7+/fvLziAvSGl6KTU1\\nlQULFnDnnXcyduxYyywqUVZWRmhoqCUPNdq1axcTJ060ZLamcvrf5ttvvzUd5RwdOnRg3bp1pmP4\\nDGv8xvsAj8fDu+++y8qVK3n44Yeb7JTI+jpy5Igl99Du3buX77//niFDhpiOYtxNN91EaWmp5U5d\\n7N27Nx07duTkyZOmo/gEKc16cLvdLF26lJUrVzJt2jQ6depkOtI5XC4XERERpmOc46effuIXv/iF\\nXx+TWV/h4eFUVFRYbiqslKJbt24cOXLEdBSfIKV5EXa7nX/+859UVlby7rvvGt9DfiFWO9+8vLyc\\nL7/8kuuuu850FMsYPny45UaagJSmF6Q0L+DEiRPMnz+fdu3a8dBDD1n2+EetNRUVFZbYg1/b4cOH\\n6dixY6NdzsMXxcXFkZ6eTm5urukoZ2jbti1btmwxHcMnSGmex/bt23nyySf5+c9/zoQJEyyzw6cu\\nFRUV2Gw2y+1o2bhxI1dccYXpGJYSEBDAgAEDKCkpMR3lDHFxceTn55uO4ROs2wQGpaWlsWrVKm67\\n7TaGDx9uOs5F5ebmkpOTYzrGGbTW5OTkSGnWIS4uznLbNa+44gpLHDrnC6w1NDFMa82mTZvYsmUL\\njz76qM9cLCskJITevXubjnGGw4cPY7PZ6Natm+kolhMbG4vL5cLj8VhmBtO6dWsqKyux2+2EhISY\\njmNp1vgXswCXy8WqVavYuXMnU6dO9ZnCBKisrLTc9tYff/yR8PBwv1ors6GEhobSunVrS80OlFJE\\nR0fLFL0epDSpKp3p06eTlpbGww8/bMlDdy7E4XBYrjQrKioYOnSo6RiWZbPZKCgoMB3jDIWFhaSk\\npJiOYXnNvjSLi4tZuHAhw4YNY+bMmZYrn/rIy8szHeEc27dvl5VzLqBHjx6WOxmhf//+lj6kziqa\\ndWkeO3aMBQsWMGjQIO644w7L7X2ur5KSEstsGzstLCzMcmdNWYnT6bTccnFRUVGyins9WLollFJj\\ngFepKvfFWuu5DfXcmzZtYtOmTdx6663079+/oZ7WiOjoaMLCwkzHqOFwOMjPzycyMtJ0FMuKj4+3\\n3AyhZcuWVFRUmI5hedYantSilAoAXgdGA/2Au5VSfRriubdt28aCBQu47bbbfL4woeo0TyuNNE8f\\naG+lQ1hKSkq49tprLbOmpc1ms+T1g6xW5FZknd+0cw0B9mutM7TWTuA9YPzlPKHH42Ht2rXs2LGD\\nN954g379+jVIUNOsdOgKwMmTJy13rvmnn37Kt99+y6effmo6CgDBwcGW2+FYWFjIoUOHTMewvIv+\\npimlHlVKmbjoTAfgaK2vs6pvuyROp5Ply5eTk5PD7373O8teR+dSHDhwwFI7Xex2u2V2ckyePJnW\\nrVvz29/+FoDf/OY3tG7dmilTphjNZbPZsNvtuN1uozlqS0hIkJMR6qE+2zRjgR1KqZ3AEmC9ttBv\\n6OzZs2s+T0xMrPMaPXl5efzjH/9g2LBh3HnnnZaaNjaEdu3aWWqkGRYWZpltrM888wwpKSkcOHAA\\np9OJzWaja9euPP3006ajWe7SJFrrZntcbXJyMsnJyfW670VLU2v9rFLq34FRwIPA60qp96naMXPw\\ncoJeRDbQudbXHatvO0Pt0qxLfn4+S5cupW/fvkyYMMEv3xTh4eGWGmkWFRVRWFhoOgZQtXrPc889\\nx5133kl4eDh2u53nnnvO+JlKHo+HqKgoS/0Bb86lefaA67nnnjvvfes1PKkeWeZUf7iAtsAHSqkX\\nLyfoRewAEpRSXZRSQcCvgY+9eYIjR47w9ttvM2LECH73u9/57RsiICDAUqXZuXNnS6249MEHH9Cq\\nVSv+9re/ER4ezsqVK01Hwul0Wu5iZllZWWRlZZmOYXkXHWkqpaYB9wEFwP8AT2qtndV7t/cDTzVG\\nMK21Wyn1CLCB/3/I0d76Pj41NZWNGzcyceJE46OKxuZ2uy011QsMDOT777/n+eefZ9CgQSQlJRkd\\nUc2YMYP58+cTHR3NPffcY4nTF10ul+W2HwYEBNC6dWvTMSyvPts0I4EJWuuM2jdqrT1KqUa9HqvW\\neh3g9UoU7777Lps2beKFF14gJiamEZJZS2ZmJgkJCbRq1cp0FNxuN7feeiubNm1i3bp1hIWFMXTo\\nUNavX2+sOGsfZB8dHW2JxZoLCgosdxplSEgInTt3vvgdm7mLTs+11rPOLsxa36v3yK8puN1u1qxZ\\nQ0VFRbPQudRpAAAWK0lEQVQpTKha1ssqh/isXbuWlJQUnE4nWmtKS0tJSUlh7dq1pqNZTseOHU1H\\nOENZWZllduBZmXV2uV4mu93O8uXLsdvt3Hfffc2mMKHqeudWOf1t165dlJWVnXFbWVmZ5daPNC03\\nN9dS230BSktLpTTrwS9K8+jRoyxevJjo6Ghuv/12y4y6mkpwcLBlSnPgwIHn/OKFhYUxYMAAQ4ms\\nyYrXqN+6datckbIefL40c3NzmT9/PjExMYwaNcpv95BfSGVlpWWuOZOUlMTQoUNr1tIMDw9n6NCh\\nJCUlmY5mGW63m8rKStq3b286yhni4uK46qqrTMewPEsv2FEfK1asYMqUKfTq1ct0FGOCgoIss3hs\\nYGAg69evZ+3atezcudMSe8+tprCwkLKyMkvNiOx2O3a7XRZZqQefL80JEyZY7i92U7PaRbECAwMZ\\nN24co0aNIiAgQArzLKdOnbLc5oqCggJiYmIsdWaZVfn8K9TcCxOqthlWVFRY6gB3qDq/ujluLrmY\\nXbt2WW6x63379lkuk1X5fGmKqpFdixYtLLcWolKKyspK0zEspbS0lA4dOljuGlQHDhyQP3D1JKXp\\nJ/Ly8jh69OjF79iElFIEBgZaaiUf03bv3k1QUJDlpsFOp5NRo0aZjuETrPUvJy5Znz59LDc9h6op\\nuow2q7jdbjweDz179jQd5RwZGRl+f7pxQ5HS9BOxsbGUlJSYjnGO0zuBrLK+pkl79+4lMDCQNm3a\\nmI5yhrKyMoqLi4mLizMdxSdIafqJNm3aUFxcbMnRZlBQEHa73XQMozweDydPnqRHjx6mo5xj06ZN\\nOJ1Oy20ysCp5lfxEcHAwdrudEydOmI5yDpvNhsfjadbbNvfs2YPNZrPkaK64uJjrr7/edAyfIaXp\\nR5RSlluj8bTQ0FDKy8tNxzDC6XRy4sQJS44yoWrP+bBhw0zH8BlSmn5k4MCBlt3pcnrbplXOkW9K\\nO3bsICYmxpKLyJSXl5OdnW3ZQrciKU0/Eh0dTWFhoWWnwWFhYZSXl1tqweTGVlRUhNPppHv37qaj\\n1Gnr1q20b9/eUqd0Wp2Uph8JCgqidevWltyuCVUrg5/eKWTFHVYNraKigi1btnDVVVcREhJiOk6d\\nvvnmG1mt3UtSmn5Ga01KSorpGOfVsmVLoOr8a3/m8Xg4dOgQPXr0sOzlol0uFwUFBdx7772mo/gU\\nKU0/c8UVVxAYGGjpkVxoaChaa7/evrlr1y6Kioosdx2g2tLT02nXrp0lLv/hS6Q0/Uzbtm1p1aqV\\n5a4/U1tgYCCtW7emqKjIL4/fzMjIICAggEGDBln6fO4dO3YwePBg0zF8jpSmH+rQoQPZ2edcIt5S\\nAgICaNu2LZWVlX5VnMePHyc1NZU+ffrUbIqwIrvdzvvvv0+/fv1MR/E5Upp+KD4+ntTUVMuXUVBQ\\nECEhIZw4cQKn02k6zmVLT08nKyuLUaNGWe76P2fbvXs3N9xwg+Uu7uYLpDT9UEhICG3atCEzM9N0\\nlIsKDg6mXbt2FBUVWfLc+frQWpOZmUlhYSG9evWy7J7y2r766itGjx5tOoZPktL0U8OGDbP8FP00\\nm81GREQEDoeDU6dO+dTiHm63m507d5KRkcGQIUMstxhHXbKzsykoKJDrAV0in7/chahbTEwMWmsK\\nCgp8Yu9oUFAQbdu2JTc3l8rKSiIjIy1/mYzCwkLS09Pp1KkT7du3x2bzjV+nJUuW0K9fP5/JazUy\\n0vRj3bt354cffjAdo94CAgKIj48nPDycrKwsy07XXS4XBw8e5OjRo3To0IHOnTv7TAGVlJRw+PBh\\nEhMTTUfxWVKafiwuLo7U1FSfu5Z1aGgocXFxuN1usrKyLHUZj4KCAtLS0sjPz6dfv3507drVdCSv\\nfP7554wYMcLncluJJUtTKTVLKZWllNpZ/THGdCZfFBISwtixY9m/f7/pKF4LDg4mIiKC8PBwSkpK\\nOHbsmNHyLCoqIi0tjbS0NBISErjuuut87nztsrIy2QHUAKw8p3hZa/2y6RC+rlu3bmzcuJHi4mKf\\n2ElxtoiIiJpts8XFxRQWFtK6dWtatWrV6AeOOxwOioqKyMnJoaSkhP79+9O3b1+fXaz3X//6F717\\n9/aJbdxWZuXStO6pFD7EZrPRs2dPfvjhB59daFYpVbNj6+TJk1RUVFBYWFiz8yg4OLjBdhq53W7y\\n8vKoqKigoKCA4OBgevToQVhYmKXP7rmY0tJSvv76a5544gnTUXyelUtzqlLqt8C3wHStdbHpQL6q\\nS5cufPTRR/To0YP4+HjTcS6ZUqpm8QuHw0FpaSlFRUWcOHGC2NhYKisradu2LTabjRYtWly0SD0e\\nD3a7neLiYgICAjhy5Ajh4eFA1emo11xzjeX34NfXJ598wrhx4+QwowagTC3soJTaCMTWvgnQwExg\\nG1CgtdZKqb8C8VrrSXU8h7bywhRWcvjwYQ4fPsxNN93k0yOmurjdbiorKykoKCAkJIS8vDxatGiB\\n1hq3211znntUVBSFhYWEhIRQXl6O0+kkMjKS0tLSmjNj2rRp4zN7wuvr+PHjvPzyy8yaNavmj4K4\\nMKUUWus6f1GMvTu01jfX867/BNac75uzZ8+u+TwxMVEOpTiPbt26kZGRQUZGht/tOQ0MDKRly5Z0\\n7twZgHbt2gFVl5lwOp0opQgLCyM0NJRWrVoRFBREYGAgNpvN7/6A1GXhwoWMHj1aCvMCkpOTSU5O\\nrtd9jY00L0QpFae1zqn+/HHgWq31PXXcT0aaXjh58iSbNm1i5MiRll5MQjScHTt28Nprr7Fw4ULL\\nnw9vJRcaaVp1N+CLSqnvlVK7gRuBx00H8gcRERG4XC4+++wz01FEEygrK+PDDz9k1qxZUpgNyJIj\\nzfqSkab3Kisr+eyzz7jmmmsseTlZ0XDeeecdQkJCuOOOO0xH8Tm+ONIUjSQ4OJhrr72Wb7/91q9X\\nTm/u1q9fT2pqKr/85S9NR/E7UprNULt27ejQoQNbtmwxHUU0glOnTrFmzRpGjhzpE8vU+RopzWaq\\nX79+7N69m3379pmOIhqQ1pp33nmHMWPGMGaMnH3cGKQ0m6mgoCAmTZrE3r17fW5BD3F+GzZswOVy\\nkZSUZDqK35LSbMbatGnDwIED+frrr2X7ph/48ssvWbZsGffff7/fnMlkRVKazVyXLl2IiYlhxYoV\\nPrViujhTXl4eGzdu5MEHHyQiIsJ0HL8mpSkYMGAAWmu+++4701HEJSgrK2PRokX88pe/5MYbbzQd\\nx+9JaQqCgoK48847yc/PJz093XQc4QW73c4bb7zBVVddxc9+9jPTcZoFKU0BVBXnjTfeSHp6OgcO\\nHDAdR9SD2+3m9ddf59ixY3I8ZhOS0hQ1wsLCGD58OEuXLuXIkSOm44gL0FqzbNkyWrVqxdy5c5vF\\nwiNWIadRinPk5eWxefNmhg4dWrNkmrAOj8fDihUrKCgoYPLkyQQFBZmO5HcudBqllKaoU2FhIcnJ\\nyVKcFuPxeJgzZw4lJSXMnj1bzvhpJHLuufBaVFQUiYmJLF++nJ07d5qOI6i6dPDSpUsJCwvjz3/+\\nsxSmITLSFBd0+PBhduzYUXNRMWGG3W7nrbfeIjg4mN/85jd+t7q81chIU1yybt26ccstt3Dw4EF2\\n7NiB/JFqegUFBUybNo1WrVpx3333SWEaJiNNUS8Oh4N169Zx7NgxHnroIdn50ESOHDnCv/71L7p0\\n6cK9997rs5cP9jWyI0g0CIfDweeff47dbicxMbHmypCicWzbto3169dz11130adPH9NxmhUpTdGg\\nDh06xPbt2xk8eDAJCQmm4/idyspK5s2bR2lpKdOnTycmJsZ0pGZHSlM0uJMnT7J06VIiIyOZMGEC\\nwcHBpiP5hczMTJYvX050dDQTJkygTZs2piM1S1KaolGUl5ezY8cOcnJyGDZsmBzPeRmcTicbNmxg\\n165djB8/niuvvNJ0pGZNSlM0qmPHjvH111/TunVrhg0bJtfX9lJWVhYLFy7E4XDwzDPPyOjSAqQ0\\nRaNzOBwsW7aMsrIyRo4cSc+ePeV86IuoqKhgw4YN/Pjjj4wZM4arr75a9o5bhJSmaDL5+fls3boV\\nrTXXXXcdsbGxpiNZjtvt5tNPP2Xjxo2MGDGCUaNGyXXJLUZKUzQprTUHDhxg+fLlJCQkMHr0aDk8\\niarXJS0tjc8//5ygoCAGDx7MkCFDTMcSdZDSFEaUlZWRnp7O3r17iY+P55prrmmWl2LQWpOcnMw3\\n33xD27ZtGTVqFD169JDNFxYmpSmMcjqd7Nmzh40bNxIVFUVSUhJxcXF+XxpOp5PU1FS++eYbysvL\\nGTBgAKNHj/b7/29/IKUpLKGsrIwff/yRgwcPYrPZ6Nu3L927d/e71XpOnDjB8uXLycvLo0ePHlx/\\n/fV06dJFytKHSGkKS9Fak52dzdatW0lJSWHs2LH07NmT9u3b++ze44qKCtLT09m9ezf5+flER0dz\\n44030qNHD9PRxCWwZGkqpW4HZgNXANdqrXfW+t7TwEOAC5imtd5wnueQ0vRxxcXFHD58mAMHDlBW\\nVkZISAiDBg2ie/fulr92d1lZGfv37yctLY21a9cyduxYBg4cSM+ePWUlIh9n1dLsDXiAhcATp0tT\\nKXUF8C5wLdAR+AzoWVc7Smn6l6KiItauXYvWmrKyMjp27EhcXBzt2rWjQ4cOxqe3LpeL7Oxstm3b\\nRlZWFi6Xi+7du9OrVy86duxIVFSU0Xyi4ViyNGsCKPUlML1Wac4AtNZ6bvXXa4HZWuuUOh4rpemn\\nKioqOHr0KDt37uTHH3+kU6dOxMbGEhsbS0hICJ07dyYiIqLRitTlclFYWMjx48f5+uuvCQsLIzc3\\nl5iYGMLCwujUqRNDhgyREaWfulBpWvFfvAOwtdbX2dW3iWYkNDSUXr160atXLwBKS0vJyckhNzeX\\nNWvW0KpVK2w2GxEREbRs2ZLi4mKuvvpqQkNDadmyJQEBAQQHBxMaGkpAQAABAQForfF4PLhcLpxO\\nJ6WlpRQWFhIUFERJSQklJSX88MMPuFwuAgICiIiIIDo6GpvNxg033EDHjh1lHVHRuKWplNoI1D4l\\nRAEamKm1XtOYP1v4l/DwcBISEkhISGDYsGFA1RJqJ0+e5Pjx46Snp1NUVER2djYVFRXs27cPrTUx\\nMTG43W48Hg+7du2ib9++hIeHY7PZqKysJD8/n8GDBxMeHk5UVBTDhw8nJiaGzp07yyhS1KlR3xVa\\n65sv4WHZQKdaX3esvq1Os2fPrvk8MTGRxMTES/iRwhcFBwfXTNkHDBhgOo7wYcnJySQnJ9frvlbZ\\npvmE1vq76q/7AkuBoVRNyzciO4KEEE3IkhdWU0rdqpQ6ClwHfFK9wwet9Y/A+8CPwKfAw9KMQgir\\nMD7SvBwy0hRCNAZLjjSFEMIXSWkKIYQXpDSFEMILUppCCOEFKU0hhPCClKYQQnhBSlMIIbwgpSmE\\nEF6Q0hRCCC9IaQohhBekNIUQwgtSmkII4QUpTSGE8IKUphBCeEFKUwghvCClKYQQXpDSFEIIL0hp\\nCiGEF6Q0hRDCC1KaQgjhBSlNIYTwgpSmEEJ4QUpTCCG8IKUphBBekNIUQggvSGkKIYQXpDSFEMIL\\nUppCCOEFY6WplLpdKZWmlHIrpQbVur2LUqpcKbWz+uMNUxmFEOJsNoM/+wfgNmBhHd87oLUeVMft\\nQghhlLHS1FrvA1BKqTq+XddtQghhnFW3aXZVSn2nlPpSKXW96TBCCHFao440lVIbgdjaNwEamKm1\\nXnOehx0DOmuti6q3dX6klOqrtS6t686zZ8+u+TwxMZHExMSGiC6EaEaSk5NJTk6u132V1rpx01ws\\ngFJfAtO11ju9/b5SSpvOL4TwP0optNZ1bia0yvS8JpxSKlopFVD9eXcgAThkKpgQQtRm8pCjW5VS\\nR4HrgE+UUmurv3UD8L1SaifwPvB7rfVJUzmFEKI249PzyyHTcyFEY/CF6bkQQvgEKU0hhPCClKYQ\\nQnhBSlMIIbwgpSmEEF6Q0hRCCC9IaQohhBekNIUQwgtSmkII4QUpTSGE8IKUphBCeEFKUwghvCCl\\nKYQQXpDSFEIIL0hpCiGEF6Q0hRDCC1KaQgjhBSlNIYTwgpSmEEJ4QUpTCCG8IKUphBBekNK8BMnJ\\nyaYjnMNqmayWB6yXyWp5QDLVh5TmJbDaPyJYL5PV8oD1MlktD0im+pDSFEIIL0hpCiGEF5TW2nSG\\nS6aU8t3wQghL01qrum736dIUQoimJtNzIYTwgpSmEEJ4QUrTC0qp25VSaUopt1JqUK3buyilypVS\\nO6s/3jCZp/p7Tyul9iul9iqlRjVFnjryzVJKZdV6XcYYyjFGKZWulPpJKfVnExnOppQ6opRKVUrt\\nUkptN5RhsVIqVyn1fa3b2iqlNiil9iml1iul2hjOY4n3UG1Smt75AbgN+KqO7x3QWg+q/njYZB6l\\n1BXAncAVQBLwhlKqzo3aTeDlWq/Luqb+4UqpAOB1YDTQD7hbKdWnqXPUwQMkaq0Haq2HGMrwv1S9\\nLrXNAD7TWvcGvgCeNpwHDL+Hzial6QWt9T6t9X6grgJq8lK6QJ7xwHtaa5fW+giwHzD1i2mqrE8b\\nAuzXWmdorZ3Ae1S9PqYpDP/+aa23AEVn3TweeKv687eAWw3nAfPvoTNIaTacrkqp75RSXyqlrjec\\npQNwtNbX2dW3mTBVKbVbKfU/TTnVq+Xs1yILc69FbRpYr5TaoZSabDpMLe201rkAWuscoJ3hPGD+\\nPXQGm+kAVqOU2gjE1r6Jqjf4TK31mvM87BjQWWtdVL1t8SOlVF+tdamhPE3mQvmAN4DntdZaKfVX\\n4GVgUtOntKRhWuvjSqkYYKNSam/1SMtqTB+TaLn3kJTmWbTWN1/CY5xUTyu01juVUgeBXsBOE3mo\\nGll2qvV1x+rbGpwX+f4JmCj5bKBzra8b7bXwhtb6ePV/85VSH1K1GcEKpZmrlIrVWucqpeKAPJNh\\ntNb5tb409R46g0zPL13NdhalVHT1DgeUUt2BBOCQqTzAx8CvlVJBSqlu1XmafA9t9S/daROAtKbO\\nAOwAEqqPcAgCfk3V62OMUqqlUiq8+vMwYBRmXhuoet+c/d55oPrz+4HVJvNY5D10Jq21fNTzg6qN\\n4keBCuA4sLb69tP/mDuBb4FbTOap/t7TwAFgLzDK0Ov1NvA9sBv4CIg1lGMMsI+qHWIzLPA+6lb9\\nmuyi6ggII5mAd6natFQJZAIPAm2Bz6pfrw1AhOE8lngP1f6Q0yiFEMILMj0XQggvSGkKIYQXpDSF\\nEMILUppCCOEFKU0hhPCClKYQQnhBSlMIIbwgpSmEEF6Q0hR+TSk1uHqx3yClVFj1os19TecSvkvO\\nCBJ+Tyn1PBBa/XFUaz3XcCThw6Q0hd9TSrWgauGOCuDnWt704jLI9Fw0B9FAONAKCDGcRfg4GWkK\\nv6eUWg0so2p1ofZa60cNRxI+TBYhFn5NKfVbwKG1fq96zdOvlVKJWutkw9GEj5KRphBCeEG2aQoh\\nhBekNIUQwgtSmkII4QUpTSGE8IKUphBCeEFKUwghvCClKYQQXpDSFEIIL/w/sYlalxXOMt8AAAAA\\nSUVORK5CYII=\\n\",\n \"text/plain\": [\n \"\"\n ]\n },\n \"metadata\": {},\n \"output_type\": \"display_data\"\n }\n ],\n \"source\": [\n \"tfinal = comets[0][-1]\\n\",\n \"sim.integrate(tfinal)\\n\",\n \"fig = rebound.OrbitPlot(sim, trails=True)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"REBOUND automatically find out if you want to integrate forward or backward in time.\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"For fun, let's add all the coments to a simulation:\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 16,\n \"metadata\": {\n \"collapsed\": false\n },\n \"outputs\": [\n {\n \"data\": {\n \"image/png\": \"iVBORw0KGgoAAAANSUhEUgAAAU0AAAFCCAYAAAB1po8RAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XlwXFeZN/7v0Wa11Nr3XZYsWYvlXXZwcBDBiTEJGDKE\\nJAwTYCCZFMP8mGIIBF5qSAHzDlAMTOadClsKQoaEACY4iRPHWRzHZLESW4s3SZa19KJWd0ut3td7\\n+57fH7Y0lrV1t7r73m49nypVSa2+957W8vS55znnOYxzDkIIIaFJkbsBhBCSSChoEkJIGChoEkJI\\nGChoEkJIGChoEkJIGChoEkJIGNLkbsBqMMZovhQhJCY452yxxxO+p8k5j+nHd77znZhfQ+6PtfAa\\nE+l1er1eDA8PK/41Tk1N4Uc/+hEEQUi63+VyEj5oEpJs/H4//H6/3M1Y0c9//nOUlJQgLS2hb1jD\\nRkGTEIUJBAIQBEHuZizL7/fD4XDglltukbspcUdBcwVdXV1yNyHm1sJrBBLndaanp6O4uDiiY+P1\\nGnt6erBp0yZUVVXF5XrXk/N3yVa6f1cyxhhP5PYTshiLxYJAIICKigq5m7Iozjl+8pOf4ODBg9iw\\nYYPczYkJxhh4siaCCEk2kiQhNTVV7mYs6fjx4+jp6UFjY6PcTZEFBU1CFEYURaSkKPdfc2RkBHff\\nfTcYW7QjlvSU+5shZI2anJyE2+2WuxmLstlsuHz58ppMAM1aW3MFCEkAxcXFyM/Pl7sZi3rzzTex\\nc+dOZGZmyt0U2VBPkxCFUeqYZiAQwA9/+EPs3LlT7qbIioImIQoTDAYVOabZ29uLD33oQ2hoaJC7\\nKbJS3m+GkDUuGAwqcpXNa6+9ho997GNyN0N2FDQJUZjJyUm5m7CARqPBzMwMtm7dKndTZEdBkxAF\\n4ZxDpVIhPT1d7qbM893vfhfl5eWKHDaIN/oJEKIgwWAQubm5cjdjHpfLhWAwiHvvvVfupigCBU1C\\nFESJmfMTJ06gs7MTpaWlcjdFEShoEqIgSlsNJEkSjh07hv3798vdFMVQzm+HEAK/36+osnCHDh3C\\nuXPn1uw688VQ0CREQZRWgHhgYABf+9rX1uw688UoImgyxlIYYz2Mseeufl3AGHuZMTbEGDvGGMuT\\nu42ExENGRgZKSkrkbgaAK1OfhoeHceutt8rdFEVRRNAE8BUAF6/5+iEAr3LONwI4DuCbsrSKkDhT\\nUiLo+eefx759+5CRkSF3UxRF9qDJGKsG8BEAj13z8EEAv736+W8BfDze7SJEDqIoKiJoer1e/OAH\\nP8DevXvlboriyB40AfwUwIMAri3BXsY5NwEA59wIgOY6kDVBkiRFZM9PnDiBu+66ixJAi5B1gStj\\n7DYAJs55H2Osa5mnLrmnxcMPPzz3eVdXV8LsA0PIYiYmJlBRUYHCwkLZ2sA5x+HDh3H//ffH/FpO\\npxNqtVr2RNOJEydw4sSJkJ4r6x5BjLH/C+AzAEQAKgA5AP4CYCeALs65iTFWDuB1znnrIsfTHkEk\\nqYyNjaG4uBg5OTmytaGnpwePPPIIHn/88ZgFM1EUMTU1BQAoLS1VxJDEtRS7RxDn/Fuc81rOeQOA\\nuwEc55z/HYDnAXzu6tM+C+BZmZpISFwpIRH07W9/G7W1tTELmBaLBYODg1CpVCgvL5f99YZLefWn\\nrvgBgD8yxv4egAbAp2RuDyFxIUmSrGXhLBYLgsEg/uVf/iXq5w4Gg7BarXC5XKipqUFeXmLOJFRM\\n0OScvwHgjaufzwDYJ2+LCIk/uQsQP/fcc9i3b1/Ut9vw+XwYGBhAWVkZamtrFZHsilTitpyQJGQ0\\nGmW7XfX5fPjzn/+MO+64I2rnlCQJU1NTMJlMaGxsRGVlZUIHTEBBPU1C1jpRFJGVlSVbJvk3v/kN\\ndDpd1KYZiaIIg8EAh8OBlpYWRVajj0RyvApCkoAkSbLuQnn69Gn88Ic/jMq5zGYznE4nioqKUFNT\\nI/uUomiioEmIQgSDQdluzYeHh6HT6bBv3+pSCZIkwWKxwGq1orKyUtapU7GS2IMLhCQROacbPf74\\n47jzzjtXdQvtcrlw7tw5AEBTU1NSBkyAepqEKIbP54MoinG/rtVqxaOPPore3t6IjpckCXa7HQ6H\\nA9XV1SgqKopyC5WFgiYhCuHxeOD1euN+3eeeew6f//znUV9fH/axoiji8uXLSElJQUNDQ9Ike5aT\\n/K+QkAQhxy6UkiThySefjCgBZLFY4HK5UFZWhoKCghi0TploTJMQhZAjEXT06FGoVKqw9jOXJAlG\\noxE6nQ6lpaVrKmACFDQJUQw5EkHf+c530NzcHPKUILvdjpGREaSlpWHz5s1QqVQxbqHyUNAkRCHi\\nXYBYq9VCEIR55RWXwjmHzWbD1NQUCgoKUFxcnPAreyJFY5qEKITBYMC6devidr0nnngCd955J7Kz\\ns5d9niAIGBwcREFBAerr69dEsmc5a/vVE6Ig+fn5yMrKisu1rFYrnnrqKbz00kvLPs/hcMBqtaK8\\nvFwxG77JjYImIQqRkpISt+z5I488AlEUUVtbu+j3JUmCXq+HzWbDxo0b49oDVjoKmoQoRLyy55xz\\nnDhxAj/72c8W/b7NZoPD4UBWVhYqKyvX/O349dbmSC4hChSv7Pm7774Lt9uND37wg/Me55zDarVC\\no9EgNzcXxcXFFDAXQT8RQhRAEATY7fa4VAP6z//8T3zxi1+cl/32er3Q6XTIzc1Fe3s7BctlUE+T\\nEAWIV8V2rVaLP//5z7jtttvmHnM6nZicnERWVhbKy8spYK6AfjqEKADnHMXFxTG/zu9+9zvcf//9\\nqK6uhiRJuHz5MlJTU1FdXU3JnhBR0CREAeIxnikIAh577DE899xz8Hg8sFgsyMnJQUlJCfUuw0C3\\n54QogCiKMb89//Wvf42GhgaUl5fj4sWLKCwsREVFBQXMMFHQJEQBBEGIeRLou9/9LpqamiCKIjZv\\n3rziSiCyOHqLIUQBbDYb/H5/1M8bDAZx9OhRPPvss/B4PPj617+O8vLyqF9nLWGcc7nbEDHGGE/k\\n9hMyy2QyISUlJapLFYPBIG655RZ0d3fD4/EgIyMDe/fuxbFjx2TbViNRMMbAOV+060+354QoQCxW\\nAz377LNzARMAAoEAuru7cfTo0aheZ62hoEmIAkQzaHLOMTExgddff33B9hlutxt9fX1Ruc5aRUGT\\nEAWI1pSjQCAAo9EISZLwwQ9+cEGyJzs7O6wq7WQhCpqEKMDk5CSCweCqzuF0OtHf349169ahpqYG\\nBw8exI4dO5CVlQXGGNRqNXbv3o0DBw5EqdVrEyWCCAnD7N9btKcHnTt3Dhs2bIho+whRFDE1NYVg\\nMIiioqJ55+jv78eFCxcwOjqKrVu34sCBA5QECsFyiSCackRIGILBIDjnUa97mZ6eHtE5fT4ftFot\\n0tLSUF9fP2+CvMfjwdjYGO666y4KlFFEQZOQMPj9/qivoOGchz2myTmHXq9HMBhEVVXVohPVLRYL\\nOjs7KWBGGY1pEhIGURSjfms+W+Eo1POKogij0Qiv14uKiopFA6YkSZiZmaEtKmKAepqEhMHpdCIz\\nMzOq5xQEAT6fL6TnzszMwGAwoLq6GuXl5UsGWoPBgOzsbGRkZESzqQTU0yQkLH6/P+rjmYIgrLiE\\nMhgMYnp6Gk6nEzU1NcjPz1+2ZzowMBC3TdrWGuppEhIiURQBIOrViFJSUpZdD+73+zEwMICSkhLU\\n1NSseH2n04nKykpUVlZGtZ3kCgqahITI4/HA6XRG/bzLVW23WCxwuVxYv3498vLyQjqf2WxGaWlp\\nNJtIrkG354SEKBAIQK1WR/28wWBwQUZeFEVotVoYDAZUVVWFHDA9Hg9sNhuKioqi3k5yBfU0CQmR\\nz+eLSc3L63uaFosFTqcTeXl5qKmpCeuaY2NjkCQpLvsNrVX0kyUkRGazOSZB02Qywel0QpIkWCwW\\nmEwmFBYWoqCgIKzrSZIEURTR0dER9TaS/0U9TUJCxDmPye15fn4+AGBwcBDFxcVoaWmJqKdotVqR\\nlZUV9SlRZD7qaRISounp6ahPNwIAh8MBq9WKwsJClJaWRnxrrdfrKQEUBxQ0CQnB7AqbnJycqJ0z\\nGAxiaGgIU1NTc5PVI2Wz2aDVakNOGJHI0e05ISHwer3IycmJ2rpzt9uNmZkZFBQUICUlJaLqRtey\\nWq3YtWtXVNpGlkc9TUJCYLPZ4Ha7V30ezjnMZvPc+GVpaSksFsuqEkyCIMBut6O4uHjV7SMro54m\\nISGIxtxHj8cDi8WC9PR0dHR0zK0L55yvqhKRwWBAYWEhVTOKE+ppEhICn8+3qsy5y+XCyMgI0tPT\\nUV5ePhcwJUlCXl5exLf9nHOcPXs2qmOtZHnU0yQkBMPDw6ipqQn7OFEUodfrkZaWhubmZqxbt27e\\n91e7oZrVasXGjRtRUFAQ8TlIeChoEhICxhiqqqrCOsbv98NkMkEQBNTU1CwaHBdbQhmOqakplJWV\\nRXw8CZ+sQZMxVg3gCQBlACQAv+Kc/xdjrADAHwDUARgH8CnOuV22hpI1z2q1LlrsdykTExNwuVyo\\nrq5e9jhBEBDpPlcOhwN+v5+mGcWZ3GOaIoCvcs7bAbwPwD8yxloAPATgVc75RgDHAXxTxjaSNU4Q\\nBGg0mpBugYPB4Lze5UqB1uVywWq1RtSuoaEhMMZisrSTLE3WoMk5N3LO+65+7gIwAKAawEEAv736\\ntN8C+Lg8LSTkSi+zurp6xdtol8uFvr4+pKWloa6uLqQiwJmZmRHVvRRFEenp6WhtbQ37WLI6ihnT\\nZIzVA9gK4BSAMs65CbgSWBljtDaMyGZqagqCICz5/dnVQh6PB01NTcjNzQ353JEmgqanp5Gfnx/1\\nTd7IyhTxE2eMqQEcAvAVzrmLMXb9IA9tbk5ko9frlwyEgiBgZGQEaWlpWL9+fdgBMJJEkCRJmJyc\\nxMaNG8M6jkSH7EGTMZaGKwHzfzjnz1592MQYK+Ocmxhj5QDMSx3/8MMPz33e1dWFrq6uGLaWrEWB\\nQAAVFRULHp+ZmYHT6URZWVnEU36CwWDYRUAmJydhNpuxbdu2iK5JFjpx4gROnDgR0nNZpJm7aGGM\\nPQFgmnP+1Wse+yGAGc75Dxlj3wBQwDl/aJFjudztJ8nvP/7jP9DS0oLbbrsNwJWe3vT0NCYmJtDS\\n0rKqdeNnz55FaWlpWMU6Ll26hJKSEpqbGUOMMXDOF82wyT3l6EYAfwvgHGOsF1duw78F4IcA/sgY\\n+3sAGgCfkq+VZK1zu91oaGgAcCXZMzU1BbVajS1btqy6Qnp6enpYQdfr9cLn883V4CTxJ2vQ5Jy/\\nBWCpQaB98WwLIUvxer0oKiqCw+HAxMQECgsLUVJSEpVzZ2RkhLU3+eTkJEpKSmiakYzknqdJiKK5\\n3W6MjY1hZmYGDocDjY2NUV2BI4piyIkgQRDQ29uLwsLCqF2fhE/2RBAhSqbRaFBRUQGVSoXKysqo\\nb1gmSVLIGXeLxYLt27cvWL9O4ot6moQsYWJiAmfPnkVmZibq6uqiHjCDwSC8Xm9I5+WcY2pqiraz\\nUADqaRJyHVEUMT09DUmSYLfbY1Z2LRAIwOFwhPRcq9WK9PT0sNa/k9igniYh13C73ejv70daWhqq\\nq6vBOceGDRtidr1Qy8319vbSLpMKQUGTEGBuz3GLxYLm5mYUFxeDMYbh4eGYLVUMdTzT6/WiuLgY\\ntbW1MWkHCQ/dnpM1TxRFjI6OAgAaGhrmBUm73Y6mpqaYXTeUoGk2m1e1tS+JLgqaZE1zOp2wWq0o\\nLi5Gfn7+vMAkSRI8Hk/YxYdDFcq6c0EQYLVa0d7eHpM2kPDRWxdZkzjnmJ6extDQEIqKilBYWLig\\nJ2c2m2Gz2WI2L9JiscDpdC77nEuXLsHv94e9Pp3EDvU0yZrj8/kwNTWF9PR0bNu2bclbZK1WG9G+\\nQKHKzMxctqfJOYckSWhra4tZG0j4qKdJ1hSv14uxsTEwxlBeXr7smKLBYIjpRHLG2LLrzu12OzIy\\nMminSYWhoEnWBEmSoNfrMTU1hfXr16O6unrZ5weDQfzxj39EX18fjhw5gmAwGPU2rVSAeDYBRJSF\\nbs9J0hNFESaTCS6XC42NjSuODwaDQezfvx8nT56EKIro7e3F7t27cezYsVVtt7vYdZY638zMDAYH\\nB2OWuSeRo54mSWpWqxXj4+PIzs7Gxo0bQ0qoHD16FN3d3XM7RbpcLnR3d+Po0aNRbZvT6VxyGpHD\\n4cC2bduompECUdAkSYlzDpvNhqmpKRQVFSE/Pz/kANTb2wu32z3vMbfbjb6+vqi20WazLRo0RVGE\\nzWZbtFo8kR/dnpOkM7tvT25u7oLJ6qHYtm0bsrOz4XK55h7Lzs7G1q1bo9ZGzjlKSkoWraU5NTWF\\ngoIC2jRNoainSZKKz+eD0WhEdnY2ysvLIwo8Bw4cwM6dO6FSqcAYg1qtxu7du3HgwIGotXOp1UCS\\nJOG9995DUVFR1K5FooveykjSmJiYgNPpRG1tbUh7ji8lNTUVhw4dwqFDhzA1NYWtW7fiwIEDUU8C\\nLRbQbTYb6uvroVaro3YtEl0UNEnCm93oTBCEVQfMWaIo4uabb45Z9nqpzLnZbKbCHApHt+ckofl8\\nPpw7dw4AohYwgSsbqMVyYrvVaoXVap33mNvthiiKyMvLi9l1yepR0CQJy+VywWQyoaqqKiZVgGJZ\\n8DcjI2PBuGV/fz+ys7NpmpHC0e05STicc2g0Gni9XjQ0NMSkR2i1WmOejLm2qHAgEABjLGYVlUj0\\nUNAkCUUURUxNTSEjIwPV1dUxm5YzmzWPlWAwOC/YT01Nobq6OqztfIk86PacJAyPx4P+/n6sW7cO\\nlZWVMQuYoigCQEznSV475Wg2kUXrzBMD9TRJQrDb7bDZbGhubl6y6k8wGITNZoPf78fMzAzWrVsH\\nk8mEwsJCWCwWFBQUwOfzQa1WIyUlBZmZmcjKyoJKpYJKpZobE3W5XOCcx/T1OJ3OuYTP6Ojogp4n\\nUS4KmkTRJEnC2NgYAoEANmzYsGDteCAQwMTEBDwez1xgzM7ORlFREbKzs1FZWTkvGEmSBEEQEAwG\\n4Xa7547PyclBMBhEZWUlAoFAzAoPz7Lb7XO1Om02G00zSiAUNIliCYIAs9mM7Oxs1NXVzbtddjqd\\nGBwcnOsdNjQ0YOPGjSHdUs+OG+bm5gLAXKB0OByYnp7G6Ogo1Gp1TMcYCwoKoFKp4HA4kJWVRbfm\\nCYSCJlEkt9uNixcvoqmpCfn5+XOP22w2jIyMwOv1oq6uDmVlZVEJbBkZGSguLkZxcTF8Ph8CgQAm\\nJyeRmpqKioqKqK4Gmq3InpaWBpPJhLKysqidm8QeBU2iODabDQ6HA62trXMZbJ/PB51Oh5GREWzb\\ntg0lJSUx3Z1xdqL89PQ09Ho9cnJyonbLPpsEstlsMBqNaGxsjMp5SXxQ9pwohiRJGB0dhcFgQGVl\\n5VzAtFgseOeddxAIBLBv3z6UlZXFNGBOTU0hMzMT6enpqKioQFlZGQKBALRaLQRBWPX5RVGc62UW\\nFxfT1rwJhnqaRBFmxy+zsrJQW1uLtLQ0SJIEnU6Hc+fOYe/evXFZXji7jPHa5FFmZibKy8thsVgw\\nNTWF3NzcVc3hdDqdMJvNUKlU2LRpUzSaTeKIgiaRndfrxYULF7B+/fq5VTiSJOH06dMQBAG33HJL\\n3KbjeDwe+Hy+Rb9XVFQEl8sFp9MJSZLmEknhSk1NBWOMamYqlE6nW/b7dF9AZGW322E2m9Ha2jov\\nYL7xxhtQqVTYvXt3XOcv+v3+Zccu1Wo1CgsLYbfb4fF4IrqGIAgwmUyUMVcgvV6PJ598ctnnUNAk\\nsuCcQ6fTQavVorKycq44hiiKOH36NAoKCtDW1hb3nlggEFhxH6HZFUnT09MRBU6j0YjU1NRlt+8l\\n8ffuu+/i1Vdfxd/93d8t+zwKmiTuRFGE0WhEeno6Wltb5wWpkZERuN1udHR0RHWaT6hsNltIU5hS\\nU1NRWVkJh8MRduCcmZnBli1bIm0iibJgMIjDhw/jT3/6E+64444Vi6ZQ0CRxFQgEcPbsWaSkpKCs\\nrGxeT3JkZASXL1/G3r17ZQmYAJCenr7kMs3rpaWlIT8/H16vN+Ss+myQvXbuKZGP0+nEM888g5SU\\nFHz/+98PaZyagiaJG7fbjcnJSWzYsAFlZWXz6kZaLBaMjY3hpptukjU5MtsDDtXs1CSn0xnS88fG\\nxpCSkhLzte1kZWazGQ8++CByc3Px0Y9+NOSxc0rdkbgwm82YmJhAa2vrvDqSwJXbo8uXL6OysjLk\\nXl4szCaBwl1hlJubC5vNBqfTuWz73W43tFotGhsbY1rgmKxseHgYR48exX333YcdO3aEdSwFTRJT\\nkiTBYrFAEAS0tbUt+m5+6dIlzMzMYNeuXVG9rtPphMPhmCvQAVxJ4mRlZSE7O3tBIsbr9UKSpIiu\\np1ar57arWKqnbDabsWPHDtjtdtmGH9Y6zjmeeOIJDA0N4Z/+6Z8i2luegiaJmWAwiKGhIWRnZ6Om\\npmbRlS8+nw96vR579uyJyjYPNpsNOp0OVqsV69atg1qtniv/JkkSOOeYmZmBwWBARkYGCgoKUFRU\\nhLS0NLjd7ojnXqalpSE1NRVer3fR3mYgEIDdbsfGjRvhdrtX+zJJBARBwHPPPQeHw4Evf/nLEQVM\\ngIImiRG/3w+z2YzS0lIUFxcv+TytVov09PRVr/bxeDy4ePEiHA4HqqursWPHjhVvgZ1OJ6xWK4aH\\nh1FcXAxBEFY1JzQ7OxsOh2PR3qbBYEBxcTE45zShXQYGgwGPPPIIdu3ahQceeCCscevrUSKIRJ3T\\n6cS5c+eQn5+/bMAUBAH9/f3Yvn37qq6n1+vx1ltvQaVSYe/evWhubg5pzDAnJwe1tbWor6+H1+vF\\n0NDQqv6ZGGNIT09fkEkXRRFnzpyZmxTvcrkivgYJn1arxeOPP47m5mZ84hOfWNXvGKCeJokyu90O\\nu92OlpaWFddnm81mVFVVRXxLDFwZDx0bG8P27dtRUlIS0TlUKhVqa2uh1+ths9mQk5MTcY8zMzMT\\nNpsN69atmxuOmJ6exrZt25CVlQW73U5JoDh65plncPHiRXzyk59ES0tLVM5JPU0SFZxzjI+PL6hQ\\ntJyenp5V7fg4PDyMsbEx7NmzJ+KAOWt2nLG0tBRms3lun6BwpaSkQKVSzR0vSRLMZvPc+BljbFVv\\nEiQ0kiThyJEjeOGFF3DnnXdGLWAC1NMkUTAbGMLZIdLtdiMtLS3iWpJmsxmDg4O48cYbozJNSRRF\\nVFdXzwU0i8UScc3O1NRUCIKAjIwMzMzMzCWigCtDErR8MrasViueeuoppKam4r/+67+i3rOnniZZ\\nldlxScYYKioqQk5yzK6/jiQpIkkSenp60NraGrXCwGazGYFAAMCVeZez2fRIpKengzGGYDCId955\\nZ97qH0EQVj2mRpZmNpvxrW99C1arFffdd19MhkKop0ki5vP5YDabUVNTs2zCZzEGgwH19fURXXdg\\nYADp6enYsGFDRMcvJi0tbd62E3l5ebBarcjOzg67t8kYQ0pKCqxWK+rr6+f9bPx+PwXNGDl79iye\\nfvppfPrTn8bevXtjdh3qaZKIWK1WDA4Ozu2rEy63242CgoKwj5MkCcPDw2htbQ372OXOqdPp5gWz\\ntLQ0qFSqJWtrriQ1NRUGg2Fux0ngf8d9aWJ7dHHO8eyzz+JrX/saPve5z8U0YALU0yQRmF0y2NTU\\nhKysrLCPDwQCMJlMESWB9Hr9XIWhaHG5XKirq1vQA8zKygp5Tfli5+Scz7s1F0URDQ0NtL1FFImi\\niKeeegpjY2P49a9/jerq6phfU9G/PcbYhxljg4yxS4yxb8jdnrWOc47Lly9jenp6Xg3McPl8PlRU\\nVEQUPPR6fVQDJnBlHGyxKkUpKSlIS0ubW4IZjp6engUT9mk8M7rsdjvuuusuTExM4Otf/3pcAiag\\n4KDJGEsB8N8A9gNoB3APYyx68wZIWCRJgtFohEqlQn19/apWtUxOTkY8wdtisUS05a3T6URnZ+ei\\n12WMzbuNnhUMBvHyyy/j+9//Po4cORJy8HS5XFCpVOjt7cX3vve9uWMpaEaPRqPBd7/7XRw4cADf\\n+MY34jojQcm357sADHPONQDAGHsawEEAg7K2ag0KBAIYGBhAZWUliouLV71GXK1WR5wEcrlcEY2h\\nvvjiizh9+jRefPFFfOpTn5p73G63Y2pqasHUp2AwiP3796O7uxtutxvZ2dnYvXs3jh07tuKYpF6v\\nx0MPPYTe3t55xz755JNR2aN9rXvyySfx7LPP4qtf/SpuuOGGuF9/xZ4mY+yfGGPhj9ivXhWAa3c4\\n0l99jMSRz+eD0WhERUUFSkpKolJUAwAuXLgQ9jHBYBB5eXkLSsst57777kNubu7cFgaf+cxnkJub\\ni/vvvx/AlYTUxo0bFxx39OhRdHd3z41NulwudHd34+jRo8tez+Px4NVXX0Vvb++CYw8fPhxxFSVy\\nZXjo0KFDeO211/DlL39ZloAJhNbTLAPwHmOsB8CvARzjCqqg+vDDD8993tXVha6uLtnakmwsFgsM\\nBgMaGhqiOt+tsLAwoi1wZ8vMheNb3/oWuru7cfnyZQiCgLS0NNTX1+Ob3/wm3G43xsbG8L73vW/B\\ncbO9xGu53W709fXh9ttvX/J6586dg0ajWfTY8+fP44477gir/eQKq9WK73znO8jPz8dPf/rTqG/n\\nfOLECZw4cSK0J3POV/wAwHBlbPFpAJcB/F8AjaEcG+kHgBsAvHTN1w8B+MZ1z+EkNmw2Gx8bG+N2\\nuz3q59ZoNPzXv/512McFg0H+yCOPcFEUwzrumWee4WlpaVytVvO0tDT+zDPPcM451+l03GQyLXrM\\n888/z9VqNQcw96FWq/nzzz+/5HXcbjc/fvw4P3z48KLH/uIXv+A+ny+sthPOjUYj/8d//Ef+xS9+\\nkfv9/rhc82psWTQ2hZQIunoS49UPEUABgEOMsR+FFpoj8h6ADYyxOsZYBoC7ATwXw+sRXHkTHR0d\\nxfT09LwPJyp8AAAgAElEQVRlhdEkCAJqa2vDPi4lJQUFBQWw2WxhHXfo0CHk5OTg3/7t36BWq/Hn\\nP/8ZJpNpbqnkYg4cODC3fTBjDGq1Grt378aBAweWvM7k5CTa2tpw++23Y9euXXMrg2aPfd/73keJ\\noDC9/PLLeOihh7B//3788pe/VMaY8FLRlP9vb+4rAM4AOAbgTgDpVx9PATCy0vGr+QDwYQBDAIYB\\nPLTI92PxJrNmBYNBbjQa+fj4OBcEIWbX0Wg0/Lnnnovo2GeeeYafO3curGPOnj3Lp6amOOecT01N\\n8Z6eHn7p0iVus9mWPU4URf4P//AP/N577+XPP//8sj1cj8fD+/v7eTAY5JxzPjExwe+44w7+ve99\\njz///PPc6/XywcHBsNq91r3wwgv8hhtu4C+99FLcr41lepqhjGkWAriDX81iXxNsJcbY0oM7UcA5\\nfwnAwlF6EnWBQACXLl1CSUkJamtro5bwWczsEsVIlJeXY2JiAps2bQr5mI6OjrnPCwoKMDY2hvz8\\n/BXHxURRRE1NDT7/+c+vODd0aGgI5eXlc3NP7XY7tmzZgm9/+9sAriSIFNFLSgA+nw8///nPMTAw\\ngEOHDq24pW68rRg0OeffWeZ7A9FtDpHD7AqdgoKCiOZAhkutVmPdunUIBAJhB5Lm5mY8//zzER07\\nO9e0pKQkpFJyf/3rX6FSqVYMmG63GwaDYV4gP3/+/Lxk1/T0dNjDCmuR3W7HF77wBTDG8Jvf/Cai\\nhGGsKXZyO4kPu92O4eFh5Ofnx+0dPTU1FZIkYWxsLOxji4qKkJeXh97e3rCPvXTpEux2O+rq6lZ8\\nriRJ6O/vR3t7+4rPNRqN2Llz57wJ/36/f976+IyMDJSXl4fd5rVkZGQEX/7yl7Fv3z78/ve/V2TA\\nBChormlutxsWi0WWrXNbW1vh8XgiOnb79u04f/58WKuKdDodVCoVmpqaQhp6OHnyJERRxM0337zs\\n89xuNzwez4IJ9/39/fPehARBiGid/lpx+PBhHDx4EPfeey8eeOABRe+jREFzjdLr9TAajaiuro6o\\n2tBqZWVl4ezZsxEdW1dXh/Lycrz22muzCcFl6fV6mEwmVFdXh5S9npqaQnd3Nz70oQ+t+Pzx8fF5\\nY5mz11OpVGhra5t7LBAIUOZ8EZxzPP7443jiiSfws5/9DLfccovcTVoRBc01hnOO6elp+P1+VFVV\\nyZacaGxsRFZWVtiT1WfdfPPNsNlsOHny5JLP4Zzj4sWLEEUR27ZtC6kkm8/nw5NPPomamhrs3Llz\\n2efOzMxgZGRkQbWm7u5u5OTkzOstzVZyJ//L4/HgwIEDOH78OH75y1/GvKRbtFDQXEOCwSCGh4cR\\nCASwfv36sJYjRltqairUanVE45rAlc3Qbr/9dly6dAl//etfF3xfFEXo9XqkpaWhuro6pIDpdDrx\\n2GOPQaVS4a677lrx+WazGe9///vn9TI55zh//vy8VUOBQABer1fRt5zxNjk5ifvvvx/r16/Hf//3\\nf0dUT0AuFDTXiGAwCJPJhPT09AW3k3Lp7OxEX19fxJuYFRUV4eDBgxgeHsZf/vKXuYLBs28OszU/\\nQwlWly9fxmOPPQa1Wo0vfOELKwZZm80GSZIWbLcxOjoKURTR1NQ095jH45nbSoMAv//973HXXXfh\\ntttuw6OPPppwG83RW98a4PF4oNVqUVZWFvValKtRXFyM0tJSjI+PR7x1RWlpKe6++268+OKL+O1v\\nf4vW1ta5LXlDKTBitVrx0ksvQavVYuvWrbjllltWfEOZrfS+2Kqmp59+Gjt27FgQqJU211Auf/rT\\nn/DTn/4U999/P+655x65mxMRCppJzufzwWQyIT8/X5aEz0o2btyI1157bVUVzbOysvDJT34Sp0+f\\nxsmTJxEIBNDe3o4NGzYsOgwxMzODwcFBDA8Pw2w2o7y8HJ/73OdCnqOq1WphMpnmTZoHgMHBQQSD\\nQezbt2/e436/P+J91JOF1+vFgw8+CL1ejz/+8Y8RlwZUAhZK9lGpGGM8kdsfC8FgEEePHkVvby8a\\nGhqwY8cO1NbWKna6iyRJePnll1FYWIhdu3ZFfB6v14uLFy+iqqoKXq8X58+fh9FohMvlQmpqKhhj\\nkCQJoiiCc47c3FzU1dWhs7MzrB0tJUnChQsXUF9fP2+aFuccP/7xj1FZWYm//du/nXeMVqtFXl5e\\n1CvzJIqZmRncf//9mJiYwMsvvxz36W2RYIyBc77obQr1NJPI9YVzVSoVOjs78dprr8ndtCWlpKSg\\ntbUVJ06cQHt7e0Ql6CwWC4aHh9HR0TF3/Pr16wFcSQhZLBa43W4wxpCbm4uCgoKIe7VmsxnZ2dkL\\n/vFffPFFCIKAu+++e8ExgUBgzfY033rrLfzrv/4rbrvtNnzlK19Jik3l5M8GkKi5vnCux+PBmTNn\\nViycK7e6ujrU1dXhL3/5S0jzLq+l1WphtVrR1ta2aMCd3Zq3oaEB69evR1FRUcQBUxRFmEymBeOT\\nJpMJPT09+PCHP7wgKEiSBI1GsybnaL7wwgu455578NnPfhZf/epXkyJgAhQ0k8rp06cXrJKZLZyr\\ndHv27EFubi7efvvtkJ4vSRImJydhs9lQWVkZlwxsb28vGGPzeo3BYBD/8z//g8rKSmzfvn3BMYIg\\noLi4OGkCRihEUcSPf/xj/Pu//zuef/553HvvvXI3Karo9jxJWCwWnDt3DhkZGfOmt2RnZ2Pr1q0y\\ntiw0GRkZ6OzsxAsvvIC6urpldxaUJAmjo6NwuVzo6OiIS0Dy+XxIS0tbsDXGr371K6hUKnzuc59b\\n9Di/36/IBFysOJ1OfOQjH4EkSTh8+HBIhVESDfU0k8DMzAx+8pOfoKOjA+9///uhVqtDLpyrJBUV\\nFdi3bx/+8Ic/LLlSSBAE9PT0IDMzE5s3b45bD2526+Bre5mHDx+Gy+XC3XffvWQ7IqnGlEiCwSCO\\nHDmC733ve3jsscdw2223YceOHTh27FhSBkyAsucJr6enB0888QT279+PD3/4w5AkCUePHkVfXx+2\\nbt2KAwcOJNyt4cjICF566SV8/OMfnzd+6HQ6odfrkZeXF9f5pg6HA1qtFu3t7XPzPk+ePIlXX30V\\n991336Lb/86amJhAVlZWUvY2r088AkBLSwvOnj2b8KuflsueU9BMYENDQ3j00Uexe/dufPrTn5a7\\nOVHV09OD8+fPo7OzE62trbDZbDAYDMjLy4vrRHHOOY4ePYqdO3eitLQUkiThpZdewptvvokHH3xw\\nxWA4ODiImpqaqG5MpxRHjhzBPffcM28cXa1W4/e///2ym88lAppylIQOHTqEd955B1/60pcW3YI2\\n0W3fvh0pKSl455135qoGbd26Ne41Fqenp1FTU4PS0lIEAgH88pe/hNfrxTe+8Y2Q5l3q9Xo0NDTE\\noaXxd+bMmYh27Ex0FDQT0PHjx/Hmm2/is5/9bFIGzFlbt26FKIo4cuQIduzYEfZ0pNUSRREGgwHN\\nzc3QarV47LHH0NHRgY985CMh9RwFQUBNTU1SjmkKgoCKigpkZmbC6/XOPZ4oicfVoNvzBCKKIn7x\\ni1/AbrfjgQceCGslS6IJBoMYGhqCSqVCWVkZjh49CqvVio6ODnR2dsal4IhWq4XP50N3dzc0Gg26\\nurpw4403hrx/ktPpxMzMTEiV4hOJ2WyGwWBAaWkp7r333rkxzezsbOzevRvHjh1LuHH069GYZhIQ\\nBAG/+93vMDQ0hIceegj5+flyNylmfD4fDAYDBEFAU1PTXICcmJjAM888g+LiYrS2tmLLli0x2wDO\\nYDDgiSeegN1ux86dO3HTTTeFnQ2enp6e65ElC4vFgosXL6KxsRGVlZVzy3YTOfG4GAqaCc5iseBX\\nv/oVKisrcc899yT16hKv14vh4WHk5OTMLYW8Fuccp0+fxvnz5+H1etHZ2bnkaqBIjI+P4+zZs3jp\\npZfQ1NSEj370oxFXYEqmzLkkSRgfH0cgEEB9fb2stVjjgYJmArPZbPj5z3+OjIwM/PM//7Mi6mDG\\nitPpRF9fHzZt2rRioOGco6enByaTCadPn8amTZuQm5uLjo4OlJSUhPxzCgQCOH/+PGZmZvDee+8h\\nIyMDWVlZ2Lx5M/bs2bOqnuypU6fQ1taWcPUiryeKIi5evAin04kbbrghKXqSK6GgmaDOnz+Pw4cP\\n4wMf+EDCbAUQKZ1Oh5mZGTQ2NoadIfd6vRgcHMTly5dhMBggiiIyMjJQU1MDt9uNuro6WCwWFBQU\\nwGq1QhRFuFwumEwmcM7BOceOHTuQn5+Pbdu24eLFi2hoaFhVpp5zjjNnzmDLli0JfWfgcrmg1WpR\\nUFCA8vLymA2HKA0FzQQ0Pj6Oxx57DDfccENST9+YXRLJOUdlZWVUbrN9Ph+Gh4fBGMPg4CBKSkqg\\n1WpRWloKl8uF4uJiZGZmory8HGVlZfNuNXt6epCSkrLqDHAgEMD4+Diam5tX+3JkMz09jVOnTmHP\\nnj1JnXRcDAXNBPPKK6+gp6cHd955Z9LO8QOuBBaDwQCn04mWlhbZe2Q+nw8XLlxAW1sbVCrVqs7l\\ncDhgs9kWre6udJxzGI3GufYn48T8lSwXNJN3gCxBnTp1Cq+//joOHjyY9AHz0qVLCAQC2LRpk+wB\\nE7gyxaimpmbVARNI3GrtoijirbfewvT0NJqamtZkwFwJTW5XiGAwiEOHDsFqtYa82iRReTwe9PT0\\noKWlRTG7EM7MzEAUxagVmXA6nQmXNfd6vRgfH0d1dTVqa2uTOum4GvRTUQBRFPHss89iaGgIn/nM\\nZ5I6YBqNRgwNDWHz5s2KCZiiKOLkyZOorKyMWqLDYDAkVNJEr9fjzJkzKC8vR319PQXMZdCYpswc\\nDgcOHTqEgoICfPSjH0346jDLGRsbgyAIKC8vV9Q0HJ1OB5/PN2/b3dWQJAlDQ0NoaWlJiMBpNBph\\nNBpRU1ODoqIiuZujCFSwQ6FcLheeeuopMMZw8ODBpH13n13D7XA40NLSoqixPo/Hg5mZGbS3t0ft\\nnH6/HxkZGYoPmLNzVHNzc7Fp06akfsOOJvopyWR0dBSvvPIKduzYgZ07dyr+HyxSgiBgdHQUgiCg\\no6NDcW8MGo0GVVVVUQ0YiZAE8vl8GBkZQWpqKhobG5P27y8WKGjKYHJyEocOHcKOHTvQ2dkpd3Ni\\nxu/348yZM6ivr49r0eBQjY6OwmAwoLW1Narn9fl8il5maDAYYLFYUFVVtebmX0YDBc04O3PmDPr6\\n+nDXXXclXfWba01PT2N8fBxtbW2KLC4iCMLcssBo0+v1i66bVwKj0YiBgQFs37494bL7SkFBM44u\\nXryIl19+GZ/61KeSOmBqNBr4fD40NDQoMmACVwJbUVFRTOYhpqamKm5+YyAQgFarBQDcdNNNipgX\\nm6goaMaBJEl4/fXXMT09jS996UtJO6VIkiRMTEzA4XCgsbERWVlZcjdpURaLBS6XK6rJn1mCIECl\\nUinq9tzn8+Hdd99FUVER2traaPxylZQ1Kp+EJEnCyZMn0d/fj9tvvz1pA6YgCBgfH4fFYkFbW5ti\\nA6YkSXjvvfdQUFAQk6SU3+9XVMC02Wy4fPky2tvb520MRyJH8zRjyOfz4ZVXXkFmZia6urqS9pYo\\nEAigv78fJSUlqKurU/Q/psFggNfrRWNjY0zOPz09DVEUUV5eHpPzh4pzjpGREYyPj2PPnj2KfRNT\\nKpqnKQOfz4cjR47A5/PhtttuU9xUm2hxOBy4ePEimpubFZ+J9fl8mJqaQltbW8yuYbPZZE+wiKII\\nrVYLxhj27t2r+OlPiYaCZgyYzWa89dZbaGpqwubNmxXd81qNiYkJ2Gw2bNy4UfZAEYoLFy6gpqYm\\npj3+6elpWVfVuFwuvPPOO2htbUVVVVXS/u3JKTm7PzKy2Ww4cuQISkpKYrqHjdy0Wi0cDgfq6uoS\\nImBOTk7CZrPFdL27JEnIy8uTbcaA1WrF+Pg42tvbUV1dnbR/e3KjnmYUDQ8PY2BgALfeeiuqq6vl\\nbk5MiKKIiYkJzMzMoKOjIyGW3omiCLPZjD179sR0mESu5ZOcc/T394Mxhubm5qiUtiNLo55mlOh0\\nOhw/fhybN29O2oApCAIGBgbg8/mwdevWhAiYwJXfTVFRUcyDic/ni/v4oSiKGB0dRUpKCjZu3EgB\\nMw4S469e4fr7+2EymXDPPfcoqnpPNHm9XvT09KC5uTlqNSfjYWJiAmazOS7LVeO9fHJqagparRZV\\nVVVoaGig2/E4oZ7mKnDOce7cOfT09ODGG29M2oBpMpkwODiI9vb2hAqYkiRBr9ejuro6LrMXxsfH\\nEa8pcBaLBWNjYygrK1tTG54pAc3TjJAoijh9+jQAYPv27cjIyJClHbE2NjaGQCCAsrIyxS6JXIpe\\nr4cgCHFbB37u3Dls3Lgxpn8Ls7fjkiStif3H5UJ7BEWZKIp4++23YTKZ0NnZmZQBMxgMQqPRwOl0\\noq6uLuECpsfjgcViQU1NTVyuFwgEkJGREdO/hUAggIsXL2JmZgbNzc0UMGVCY5phcjqdOHv2LEpL\\nS7F3796kvC0KBAJzRTc2bdqUcBPzOed48803sXnz5rglq3w+X0yTMBaLBUajEeXl5SgtLY3ZdcjK\\nZPtvYIz9iDE2wBjrY4z9mTGWe833vskYG776/VvlauP1vF4v/vrXvyIjIyNhtjIIl9/vR29vL1Qq\\nlSKLBofCbDajpKQkrksZY5kEMhqN6O7uRnV1NQVMBZBtTJMxtg/Acc65xBj7AQDOOf8mY6wNwJMA\\nOgFUA3gVQNNig5fxHNM0mUwYHR1FfX09Kioq4nLNeLNarRgcHERra2vC3Y7P8vv9GBwcjPu2Ghcu\\nXEB5eXlUVwMJggC9Xg9RFFFXV5eUw0BKpcgxTc75q5xz6eqXp3AlQALAxwA8zTkXOefjAIYB7JKh\\niXOsVitOnTqFqqqqpA2YGo0Gk5OTaG9vT9iACVzJYJeVlcV9vqTL5YpqT9Pr9eKNN96AIAjYsGED\\nBUwFUcqY5t8D+P3Vz6sAvHPN9yauPiYLnU4Hk8mEm2++GTk5OXI1I2YkScL4+DgEQUB9fX1CV8PR\\narUYGxvD/v3743pdURSRl5cXtcLDVqsVExMT2LJlS0JN8VorYho0GWOvACi79iEAHMD/4Zw/f/U5\\n/weAwDn//SKnkJXBYEB/fz+6urqgVqvlbk7UBQIB6HQ6uN1utLW1JcwKn8WIogir1Yobb7wx7mPN\\n0dpIjXOOCxcuwGazYfv27Qn9BpbMYvpfwjm/ZbnvM8Y+B+AjAG6+5uEJANfOE6m++tiiHn744bnP\\nu7q60NXVFX5DryNJEkZHRxEIBHDrrbcm5a2Rz+fD0NAQsrOz0dHRkfBJrdmlknLcDXi93lXfmguC\\nAI1Gg3Xr1mHXrl1J+TenZCdOnMCJEydCeq6ciaAPA/gPADdxzi3XPD6bCNqNK7flryCOiSBJknD5\\n8mWYTCa8733vS+je11Lcbjd6e3vR1tam+BqYoTCbzZicnJQt26/T6aBWqyOu9jQ9PY2zZ8+ivb0d\\nZWVlKx9AYk6RiSAA/w+AGsArjLEextijAMA5vwjgjwAuAngRwJfilSIPBAK4fPky1q1bhxtvvDEp\\nA+bk5CQGBgawZcuWpAiYkiTh7NmzKC4ulm161OjoaMQ9dZPJBKPRiNbWVgqYCYKWUV4liiIGBgaQ\\nmpqK1tbWhL9dvR7nHMPDwwCAysrKpBmj1el0CAaDqK+vl+X6kiRhaGgo7Hm7giCgp6cHBQUFqK+v\\np9txhaHtLlbgcrkwOTmJqqqqpOh9XW92+1ZJktDQ0JA0/6ButxtWqzWm21esJJIaml6vF+Pj48jK\\nysKGDRsScgHBWrbmg6bP58Pw8DAqKyuTMmB6PB5MTEwgGAxi48aNSdODliQJp0+fxqZNm2QdRgl3\\nJdDo6CicTidqa2sTouI9WWhNB02bzTa3x00yTu/weDy4cOECKisrUVUl21TXmJicnERmZqas+/EA\\noQfN2T3hjUYj2traEnoBwVq3Zu8LXC4XNBoNSkpKkjJgWq1W9PT0zG2wlUx8Ph+mp6exbds2uZsC\\nnU63Yk93dsfOYDCI3bt3U8BMcGuypzkzMwO/34/29vakzJDP9qCTdYK0RqNBRUWF7GOznHOkpKQs\\n+zN2OBw4d+4cSktLZUtWkehKvoixAqvVCovFgoaGBqSmpsrdnJjIyspCTk5OUr6+wcFBTE9PY+PG\\njXI3BYFAAHl5eYtuCSxJ0txqqy1btiTNbAWyhoKmJEmwWq1ISUlBY2NjUmcs5e6BxUogEIDX68Xm\\nzZvlbgqApcczBUHA4OAg7HY7brjhhqS8m1nL1sRvczZgCoKAsrKypMkgrzVarRbl5eWK2YvJ6/Uu\\nKDxss9kwMTGBkpISbNq0if7WklDydreuEkURTqcTKpWKNqBKYEajEYFAIK6FhVditVrn3ZpPTk7i\\nrbfeQk1NDf2tJbGkDpqSJMFutyM1NTUpEyJrhSiKePfddxV3lzA1NYX09PS5zc5cLhf27dunmJ4w\\niY2kDZqCIMDr9SI3N5cG4ROcTqfD9u3bZZ+Tea3ZoR4AeO211wAAGzZsiHvxYxJ/SRk0JUmC1+tF\\nenr6oplNkjjsdjvcbjcqKyvlbso8Xq8XPp8Po6Oj2LlzJxoaGhTVCyaxk3RBMxgMQhRFqNXqpM0i\\nrxWBQAD9/f2ora1V1GyHYDCI7u5uGI1GNDU1KaoHTGIv6bLnkiQhPT2d3vWTgFarRVZWlqLGCL1e\\nLzQaDbKysuK+eRtRBuW8fUcJBczk4HK54PF4FLFUcpZOp8OpU6dQWloalWrtJDElXU+TJD5JkqDR\\naFBbW6uIVU2SJEGv18PlcmHbtm1Qq9WoqKiI2kZqJLEkXU+TJL6+vj4EAgFFFLZwOp148803AQAt\\nLS3Iz8+Hz+ejgLmGUU+TKIrH44EkSbIWFp41u5VuTU0Namtr5x4Pt4YmSS4UNIlicM6h0Wiwfv16\\nWRcjBINBnD17FhkZGWhsbFywVHJ2/i9Zm+j2nCiGXq9HWlqarFN4/H4/Ll++DMYYmpqaFgRMAJiY\\nmKD5v2sY9TSJIni9Xrz33ns4cOCAbG3QaDSYmZlBTU0NiouLF31OMBgEALo9X8Oop0kUQavV4v3v\\nf/+iPbtY45xDr9fDYDCgrq5uyYAJXOmJlpaWKmqyPYkv6mkS2U1NTYFzjpKSkrhf2+FwYHx8HLm5\\nudi1a9eKU5wWKwdH1hZ6uySycrlcGBwcRH19fdwXJdhsNgwMDEClUqG+vj6kOaGUOSfU0ySyGh8f\\nR0FBQVwDkSRJGBkZgSiK6OjoCCtTb7VaaevdNY56mkQ2MzMzSElJQXt7e9yu6ff7ceHCBUxNTaG5\\nuTmsgClJEkwmE/U01zjqaRJZiKIInU6HpqamuN2WG41GTE9Po7y8HB0dHWEf7/P5UF9fT0mgNY5+\\n+0QWp06dQmZmZlwmsXPOodPp0N/fj7q6uogTTj6fj5JAhHqaJP5sNhuysrLQ2NgY82s5nU5MTk4i\\nPT0d+/btW1UBEEoCEYB6miTOgsEgtFotmpubY761rc1mw9tvv43MzEysX79+1RWTqBwcAainSeJs\\nZGQE+fn5Md23SRRFGAwGuN1u7N27NypDAJIkYXh4GPX19atvIElo1NMkcWO1WjE4OBjT/X78fj/e\\nffddWCyWsLPjK5031LmcJLlRT5PEhSRJmJiYwAc+8IGY3ZZbLBZMTk6iqakp6quLfD4f7WpKAFDQ\\nJHEyMTEBtVqNvLy8qJ9bkiRcunQJBoMBN9xwQ0wy8pQEIrPo9pzEnNlshkajQXV1ddTP7fV6MTw8\\nDJVKFbXxy6WuQ9ONCEBBk8SYJEnQ6XSoqamJ+m252WzG8ePHUVRUhLq6upjVuJwdWqCeJgHo9pzE\\nmNFoRH5+Purq6qJ2ztmNzjweD2666Sbk5ORE7dyL8fv9yMrKoiQQAUA9TRJDbrcbU1NT8/bXWS2v\\n14vXXnsNgiCgubk55gETAAKBAEpLS2N+HZIYKGiSmOCc4+TJkygsLIzabbPFYsHIyAg6OjrQ2NgY\\ntzXgNJ5JrkW35yQmTCYT6uvrUVNTs+pzBYNB9PT0zFVEivfYos/nW7aaO1lbKGiSqPP5fDCZTGht\\nbV31uTweDzQaDQoLC1FXVxfzpZeLsVqtMcn8k8REQZNEFeccFy5cQE1NDTIyMlZ1rrGxMeh0OnR0\\ndMhW+Nfj8cDpdMoSrIky0ZgmiaqJiQnYbLZVJU6CwSDGx8fh9XqxZcsWWSulC4JA683JPBQ0SdQE\\nAgFYLBbceOONEZ/DarXizTffRFpaGlpaWmKygigcVEOTXI+CJokajUaDsrKyiBM1ZrMZExMTaGxs\\nRHV1tSIqpNPySXI9GqghUXHp0iVYLBZs2LAh7GMFQcDp06dRWFiIpqYmrFu3LgYtjAzV0CTXk/+t\\nnCQ8QRBgt9vR0tIS9n4/LpcLw8PDyM/PV1zA9Hg8mJiYiNnyTJKYqKdJVk2r1aKqqirshM2FCxcQ\\nCATQ2NiI3NzcGLUucqIooqGhQe5mEIWhniZZFbPZDJ/Ph4qKipCPEQQBo6Oj8Pv9aG5uVmTABK6M\\nZ2ZnZ8vdDKIwsgdNxti/MMYkxljhNY99kzE2zBgbYIzdKmf7yNJEUcTbb7+NysrKkG/LJycn0dfX\\nh6ysLGzbtk3RQYmSQGQxst6eM8aqAdwCQHPNY60APgWgFUA1gFcZY02ccy5PK8lSdDodduzYEdJt\\nOeccJpMJer0eNTU1KC8vj0MLV8fr9YbVgyZrg9w9zZ8CePC6xw4CeJpzLnLOxwEMA9gV74aR5dnt\\ndrjdblRVVa34XJfLhd7eXng8HmzdujUhAqbH48H09DQlgcgCsgVNxtjHAOg45+eu+1YVAN01X09c\\nfYwoRCAQQF9fH+rq6lacS+lwOHD58mVkZmaioaEhYYJQIBBAfn6+3M0gChTT23PG2CsAyq59CAAH\\n8ETZR+8AAAj8SURBVG0A38KVW/NVefjhh+c+7+rqQldX12pPSVag0WigVquXrWUpSRIGBwcBABs2\\nbEi4TckEQaDKRmvIiRMncOLEiZCey+QYKmSMbQLwKgAPrgTSalzpUe4C8PcAwDn/wdXnvgTgO5zz\\n7kXOQ0OdceZwOKDRaNDW1rZkJXO/34+xsTHYbDbs2LEjYXqX19JqtcjLy5N9GSeRB2MMnPNFs5uy\\nJII45+cBzA1sMcbGAGznnFsZY88BeJIx9hNcuS3fAOBdOdpJ5pMkCRqNBrW1tUsGTJ1OB6vVioqK\\nCrS0tMS5hdHj8/kSYuyVxJ9SJrdzXOlxgnN+kTH2RwAXAQgAvkTdSWU4c+YM0tPTF+19zW4+NjY2\\nJmspt2jw+/1wuVyrLm1HkpMigibnvOG6r/8dwL/L1ByyCJfLhbS0tEULC9tsNuj1euTk5ODGG29M\\n+A3I3G43JEmSuxlEoeSeckQSwOxteX19/YK14RaLBefOnYNarUZdXV3CB0zgyuulSu1kKYroaRJl\\nGxkZgUqlmnfLHQgEMDY2BgDo7OxMqpUzXq9XsUs7ifyop0mW5Xa7MTg4OG9ljMfjwblz5+B2u9HU\\n1JRUAROg5ZNkedTTJEvinEOj0WDPnj1z1cu1Wi0cDgcaGxuTcvK3KIoQBIGSQGRJ1NMkSzIajcjI\\nyEBRURFEUcTw8DBGRkbQ1NSUlAETuLLdxszMTNh1QcnaQUGTLGpmZgbnz59HbW0tLBYLLl26hOzs\\nbHR1dSmqUHC0McaohiZZFgVNsgDnHAaDAY2NjbBarTh9+jTKysrCKgGXqHw+H7KysuRuBlEwGtMk\\nC5jNZgSDQQSDQbhcLtx8880JuRQyEj6fj9ack2VRT5PM4/F4MDIygsnJSQBIqMpEqxUMBiEIQlIP\\nP5DVo54mmSNJEl544QWoVCp0dXUlXGWi1QgGg/jDH/6AkydP4vbbb8eBAweSYqI+iT5ZqhxFC1U5\\nip5AIIA33ngD09PT+Ju/+Zs1NeUmGAxi//79OHXqFDweD7Kzs7F7924cO3aMAucatVyVI7o9J5ie\\nnsaFCxeQlpaGT3ziE2sqYALA0aNH0d3dDbfbDc45XC4Xuru7cfToUbmbRhSIguYaJkkSRkZGcObM\\nGdhsNjQ3N6/JlTC9vb1wu93zHnO73ejr65OpRUTJKGiuUW63G8PDw0hNTcWWLVuQkpKyZjcR27Zt\\n24JpRtnZ2di6datMLSJKRkFzDbJYLHj99ddRUFCAqqoqmEwmdHZ2rrjfT7I6cOAAmpqakJqaCsYY\\n1Go1du/ejQMHDsjdNKJAlAhaQwRBgMFggNfrRU1NDbKzs+cqGFVWVsrdPFn95Cc/wYsvvoiuri5s\\n3bqVsudrHCWCViHUzZaUzuPx4OTJk/B6vWhubkZ2djY0Gg1GR0cxNDQkd/PiYrnfpd1uxwMPPIBv\\nf/vbuP322xM2YCbL3+tK5HydFDRXkAx/hGazGaOjo9i2bRtaWlqQkpICURRhs9nQ2dmJN954Q+4m\\nxsVyv8uBgYFFq9InmmT4ew2FnK+TJrcnMVEU0dfXh0AggB07dsxb6aLT6VBUVJS01YrC4fP5oNPp\\n0NTUJHdTSAKgoJmknE4ndDodysvLUVlZOS/JMzk5CYfDgY6ODhlbqBxnz55FdXX1mpufSiKT8Ikg\\nudtACElOSyWCEjpoEkJIvFEiiBBCwkBBkxBCwkBBcxmMsX9hjEmMscJrHvsmY2yYMTbAGLtVzvat\\nFmPsR1dfRx9j7M+MsdxrvpdMr/PDjLFBxtglxtg35G5PtDDGqhljxxljFxhj5xhj/9/VxwsYYy8z\\nxoYYY8cYY3lyt3W1GGMpjLEexthzV7+W7TVS0FwCY6wawC0ANNc81grgUwBaARwA8ChL7P0fXgbQ\\nzjnfCmAYwDcBgDHWhiR5nYyxFAD/DWA/gHYA9zDGWuRtVdSIAL7KOW8H8D4A/3j1tT0E4FXO+UYA\\nx3H195rgvgLg4jVfy/YaKWgu7acAHrzusYMAnuaci5zzcVwJNLvi3bBo4Zy/yjmXrn55CkD11c8/\\nhuR5nbsADHPONZxzAcDTuPJ7THiccyPnvO/q5y4AA7jyOzwI4LdXn/ZbAB+Xp4XRcbUD8/+3d/+u\\nVWRhGMe/z+KGFbWTjfg7YmmhsFhoE6xEIaUKIoqlKPbRykpLsV1tLBSxSQI2gtgIouAPFP0DVDDW\\ngrgij8UZYQgxcIzrZCbPp7r33Lnwvkx47px7z5wcAP5tDXfWY0JzHpImgDe2X8x5aQPwpvX8XTM2\\nBCeBO83jIfU5t5e39LeXH5K0FdhJ+fAbtT0LJViBv7ur7Jf4fgHTXurTWY/LdnG7pLvAaHuIclLO\\nA5OUqXnvLdDnOdszzTHngC+2b3RQYiySpNXAbeCs7Y/zrF/u7bpCSQeBWdvPJI0vcOhv63HZhqbt\\neUNR0g5gK/C8+R5vI/BE0m7KFdfm1uEbm7El60d9fifpBGXqs681/A7Y1Hq+5PtcQO/OWQ1JKyiB\\ned32VDM8K2nU9qykdcCH7ipctL3AhKQDwEpgjaTrwPuuesz0fA7bL22vs73N9hhlOrfL9gdgGjgs\\naUTSGLAdeNRlvYshaT9l2jNh+3PrpWngyED6fAxsl7RF0ghwhNLfUFwDXtm+3BqbBk40j48DU3Pf\\n1Be2J21vtr2Ncu7u2T4GzNBRj8v2SrOCKVNabL+SdIvyK94X4FTPN/S8AowAd5sfxx/aPjWkPm1/\\nlXSaslLgD+Cq7dcdl/VLSNoLHAVeSHpK+VudBC4BtySdpKz+ONRdlf+bi3TUY26jjIiokOl5RESF\\nhGZERIWEZkREhYRmRESFhGZERIWEZkREhYRmRESFhGZERIWEZgyapH8kPW9uCV0l6WWzX2jET8kd\\nQTF4ki5QNntYSdny71LHJUWPJTRj8CT9Sdm44xOwp6/30cfSkOl5LAdrgdXAGuCvjmuJnsuVZgye\\npCngBjAGrLd9puOSoseyNVwMmqRjwH+2bzb/ZO2BpHHb9zsuLXoqV5oRERXynWZERIWEZkREhYRm\\nRESFhGZERIWEZkREhYRmRESFhGZERIWEZkREhW/IjtgecSmH+AAAAABJRU5ErkJggg==\\n\",\n \"text/plain\": [\n \"\"\n ]\n },\n \"metadata\": {},\n \"output_type\": \"display_data\"\n }\n ],\n \"source\": [\n \"sim = rebound.Simulation()\\n\",\n \"sim.G = k**2\\n\",\n \"sim.t = epoch_of_elements \\n\",\n \"sim.add(m=1.) # Sun\\n\",\n \"sim.add(m=1.e-3, a=5.) # Jupiter\\n\",\n \"sim.add(m=3.e-4, a=10.) # Saturn\\n\",\n \"for comet in comets:\\n\",\n \" addOrbit(sim, comet)\\n\",\n \"fig = rebound.OrbitPlot(sim, trails=True)\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {\n \"collapsed\": true\n },\n \"outputs\": [],\n \"source\": []\n }\n ],\n \"metadata\": {\n \"kernelspec\": {\n \"display_name\": \"Python 2\",\n \"language\": \"python\",\n \"name\": \"python2\"\n },\n \"language_info\": {\n \"codemirror_mode\": {\n \"name\": \"ipython\",\n \"version\": 2\n },\n \"file_extension\": \".py\",\n \"mimetype\": \"text/x-python\",\n \"name\": \"python\",\n \"nbconvert_exporter\": \"python\",\n \"pygments_lexer\": \"ipython2\",\n \"version\": \"2.7.10\"\n }\n },\n \"nbformat\": 4,\n \"nbformat_minor\": 0\n}\n"},"license":{"kind":"string","value":"gpl-3.0"}}},{"rowIdx":1393,"cells":{"repo_name":{"kind":"string","value":"wathen/PhD"},"path":{"kind":"string","value":"MHD/FEniCS/ShiftCurlCurl/CppGradient/Efficient/.ipynb_checkpoints/Untitled4-checkpoint.ipynb"},"copies":{"kind":"string","value":"1"},"size":{"kind":"string","value":"10513"},"content":{"kind":"string","value":"{\n \"metadata\": {\n \"name\": \"\"\n },\n \"nbformat\": 3,\n \"nbformat_minor\": 0,\n \"worksheets\": [\n {\n \"cells\": [\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"from dolfin import *\\n\",\n \"import numpy\\n\",\n \"nn = 1\\n\",\n \"mesh = UnitCubeMesh(int(nn),int(nn),int(nn))\\n\",\n \"order = 1\\n\",\n \"parameters['reorder_dofs_serial'] = False\\n\",\n \"Magnetic = FunctionSpace(mesh, \\\"N1curl\\\", order)\\n\",\n \"Lagrange = FunctionSpace(mesh, \\\"CG\\\", order)\\n\",\n \"print Magnetic.dim()\\n\",\n \"def boundary(x, on_boundary):\\n\",\n \" return on_boundary\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stderr\",\n \"text\": [\n \"DEBUG:UFL:No integrals left after transformation, returning empty form.\\n\"\n ]\n },\n {\n \"output_type\": \"stream\",\n \"stream\": \"stderr\",\n \"text\": [\n \"DEBUG:FFC:Reusing form from cache.\\n\"\n ]\n },\n {\n \"output_type\": \"stream\",\n \"stream\": \"stderr\",\n \"text\": [\n \"DEBUG:UFL:No integrals left after transformation, returning empty form.\\n\"\n ]\n },\n {\n \"output_type\": \"stream\",\n \"stream\": \"stderr\",\n \"text\": [\n \"DEBUG:FFC:Reusing form from cache.\\n\"\n ]\n },\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"19\\n\"\n ]\n }\n ],\n \"prompt_number\": 11\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"B = BoundaryMesh(Magnetic.mesh(),\\\"exterior\\\",False)\\n\",\n \"numpy.sort(B.entity_map(1).array().astype(\\\"float_\\\",\\\"C\\\"))\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"metadata\": {},\n \"output_type\": \"pyout\",\n \"prompt_number\": 6,\n \"text\": [\n \"array([ 2., 4., 5., 7., 11., 12., 13., 15.])\"\n ]\n }\n ],\n \"prompt_number\": 6\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"E = EdgeFunctionBool(mesh)\\n\",\n \"print E.array()\\n\",\n \"VertexBoundary = numpy.zeros(mesh.num_edges())\\n\",\n \"VertexBoundary[E.array()] = 1\\n\",\n \"print VertexBoundary\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"[False False False False False False False False True True True True\\n\",\n \" False False False False]\\n\",\n \"[ 0. 0. 0. 0. 0. 0. 0. 0. 1. 1. 1. 1. 0. 0. 0. 0.]\\n\"\n ]\n }\n ],\n \"prompt_number\": 13\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"B = BoundaryMesh(Magnetic.mesh(),\\\"exterior\\\",False)\\n\",\n \"print numpy.sort(B.entity_map(0).array().astype(\\\"float_\\\",\\\"C\\\"))\\n\",\n \"bb = numpy.sort(B.entity_map(0).array().astype(\\\"float_\\\",\\\"C\\\"))\\n\",\n \"print numpy.sort(B.entity_map(1).array().astype(\\\"float_\\\",\\\"C\\\"))\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"[ 0. 1. 2. 3. 4. 5. 9. 10. 14. 15. 19. 20. 21. 22. 23.\\n\",\n \" 24.]\\n\",\n \"[ 2. 4. 7. 11. 13. 15. 20. 27. 33. 40. 45. 46. 49. 52. 53.\\n\",\n \" 55.]\\n\"\n ]\n }\n ],\n \"prompt_number\": 14\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"B = BoundaryMesh(Magnetic.mesh(),\\\"exterior\\\")\\n\",\n \"B.entity_map(0).array()\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"metadata\": {},\n \"output_type\": \"pyout\",\n \"prompt_number\": 16,\n \"text\": [\n \"array([ 0, 1, 5, 2, 3, 4, 9, 10, 14, 15, 19, 20, 21, 22, 23, 24], dtype=uint64)\"\n ]\n }\n ],\n \"prompt_number\": 16\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"\\n\",\n \"vert 0\\n\",\n \"\\n\",\n \"edge 1\\n\",\n \"\\n\",\n \"edge 2\\n\",\n \"\\n\",\n \"edge 4\\n\",\n \"\\n\",\n \"vert 1\\n\",\n \"\\n\",\n \"edge 0\\n\",\n \"\\n\",\n \"edge 2\\n\",\n \"\\n\",\n \"edge 6\\n\",\n \"\\n\",\n \"edge 7\\n\",\n \"\\n\",\n \"vert 2\\n\",\n \"\\n\",\n \"edge 5\\n\",\n \"\\n\",\n \"edge 7\\n\",\n \"\\n\",\n \"edge 10\\n\",\n \"\\n\",\n \"edge 11\\n\",\n \"\\n\",\n \"vert 3\\n\",\n \"\\n\",\n \"edge 9\\n\",\n \"\\n\",\n \"edge 11\\n\",\n \"\\n\",\n \"edge 14\\n\",\n \"\\n\",\n \"edge 15\\n\",\n \"\\n\",\n \"vert 4\\n\",\n \"\\n\",\n \"edge 13\\n\",\n \"\\n\",\n \"edge 15\\n\",\n \"\\n\",\n \"vert 5\\n\",\n \"\\n\",\n \"edge 3\\n\",\n \"\\n\",\n \"edge 4\\n\",\n \"\\n\",\n \"edge 18\\n\",\n \"\\n\",\n \"edge 20\\n\",\n \"\\n\",\n \"vert 9\\n\",\n \"\\n\",\n \"edge 13\\n\",\n \"\\n\",\n \"edge 14\\n\",\n \"\\n\",\n \"edge 16\\n\",\n \"\\n\",\n \"edge 27\\n\",\n \"\\n\",\n \"vert 10\\n\",\n \"\\n\",\n \"edge 19\\n\",\n \"\\n\",\n \"edge 20\\n\",\n \"\\n\",\n \"edge 31\\n\",\n \"\\n\",\n \"edge 33\\n\",\n \"\\n\",\n \"vert 14\\n\",\n \"\\n\",\n \"edge 27\\n\",\n \"\\n\",\n \"edge 28\\n\",\n \"\\n\",\n \"edge 29\\n\",\n \"\\n\",\n \"edge 40\\n\",\n \"\\n\",\n \"vert 15\\n\",\n \"\\n\",\n \"edge 32\\n\",\n \"\\n\",\n \"edge 33\\n\",\n \"\\n\",\n \"edge 44\\n\",\n \"\\n\",\n \"edge 46\\n\",\n \"\\n\",\n \"vert 19\\n\",\n \"\\n\",\n \"edge 40\\n\",\n \"\\n\",\n \"edge 41\\n\",\n \"\\n\",\n \"edge 42\\n\",\n \"\\n\",\n \"edge 53\\n\",\n \"\\n\",\n \"vert 20\\n\",\n \"\\n\",\n \"edge 45\\n\",\n \"\\n\",\n \"edge 46\\n\",\n \"\\n\",\n \"vert 21\\n\",\n \"\\n\",\n \"edge 43\\n\",\n \"\\n\",\n \"edge 44\\n\",\n \"\\n\",\n \"edge 45\\n\",\n \"\\n\",\n \"edge 49\\n\",\n \"\\n\",\n \"vert 22\\n\",\n \"\\n\",\n \"edge 47\\n\",\n \"\\n\",\n \"edge 48\\n\",\n \"\\n\",\n \"edge 49\\n\",\n \"\\n\",\n \"edge 52\\n\",\n \"\\n\",\n \"vert 23\\n\",\n \"\\n\",\n \"edge 50\\n\",\n \"\\n\",\n \"edge 51\\n\",\n \"\\n\",\n \"edge 52\\n\",\n \"\\n\",\n \"edge 55\\n\",\n \"\\n\",\n \"vert 24\\n\",\n \"\\n\",\n \"edge 53\\n\",\n \"\\n\",\n \"edge 54\\n\",\n \"\\n\",\n \"edge 55\\n\"\n ]\n },\n {\n \"metadata\": {},\n \"output_type\": \"pyout\",\n \"prompt_number\": 13,\n \"text\": [\n \"array([ 4., 7., 11., 15., 15., 20., 27., 33., 40., 46., 53.,\\n\",\n \" 46., 49., 52., 55., 55.])\"\n ]\n }\n ],\n \"prompt_number\": 13\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"b = SparsityPatternBuilder()\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [],\n \"prompt_number\": 33\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"B = EdgeFunctionBool(mesh)\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [],\n \"prompt_number\": 2\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"B = BoundaryMesh(mesh,\\\"exterior\\\")\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [],\n \"prompt_number\": 12\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"bb = B.entity_map(2).array()\\n\",\n \"print bb\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"[ 0 3 4 6 7 9 10 12 13 15 16 17]\\n\"\n ]\n }\n ],\n \"prompt_number\": 15\n },\n {\n \"cell_type\": \"code\",\n \"collapsed\": false,\n \"input\": [\n \"k = 0\\n\",\n \"VertexBoundary = numpy.zeros(3*bb.size)\\n\",\n \"for face in faces(mesh):\\n\",\n \" if face.index() == bb[k]:\\n\",\n \" k = k+1\\n\",\n \" print \\\"\\\\nface\\\", face.index()\\n\",\n \" for edge in edges(face):\\n\",\n \" print \\\" edge\\\", edge.index()\\n\",\n \" VertexBoundary[kk] = edge.index()\\n\",\n \" kk = kk+1\\n\",\n \"VertexBoundary\"\n ],\n \"language\": \"python\",\n \"metadata\": {},\n \"outputs\": [\n {\n \"output_type\": \"stream\",\n \"stream\": \"stdout\",\n \"text\": [\n \"\\n\",\n \"face 0\\n\",\n \" edge 1\\n\",\n \" edge 2\\n\",\n \" edge 0\\n\",\n \"\\n\",\n \"face 3\\n\",\n \" edge 4\\n\",\n \" edge 5\\n\",\n \" edge 2\\n\",\n \"\\n\",\n \"face 4\\n\",\n \" edge 1\\n\",\n \" edge 7\\n\",\n \" edge 6\\n\",\n \"\\n\",\n \"face 6\\n\",\n \" edge 5\\n\",\n \" edge 8\\n\",\n \" edge 7\\n\",\n \"\\n\",\n \"face 7\\n\",\n \" edge 9\\n\",\n \" edge 10\\n\",\n \" edge 6\\n\",\n \"\\n\",\n \"face 9\\n\",\n \" edge 8\\n\",\n \" edge 11\\n\",\n \" edge 10\\n\",\n \"\\n\",\n \"face 10\\n\",\n \" edge 12\\n\",\n \" edge 13\\n\",\n \" edge 0\\n\",\n \"\\n\",\n \"face 12\\n\",\n \" edge 4\\n\",\n \" edge 14\\n\",\n \" edge 13\\n\",\n \"\\n\",\n \"face 13\\n\",\n \" edge 9\\n\",\n \" edge 16\\n\",\n \" edge 15\\n\",\n \"\\n\",\n \"face 15\\n\",\n \" edge 11\\n\",\n \" edge 17\\n\",\n \" edge 16\\n\",\n \"\\n\",\n \"face 16\\n\",\n \" edge 12\\n\",\n \" edge 18\\n\",\n \" edge 15\\n\",\n \"\\n\",\n \"face 17\\n\",\n \" edge 14\\n\",\n \" edge 17\\n\",\n \" edge 18\\n\"\n ]\n },\n {\n \"metadata\": {},\n \"output_type\": \"pyout\",\n \"prompt_number\": 24,\n \"text\": [\n \"array([ 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])\"\n ]\n }\n ],\n \"prompt_number\": 24\n }\n ],\n \"metadata\": {}\n }\n ]\n}"},"license":{"kind":"string","value":"mit"}}},{"rowIdx":1394,"cells":{"repo_name":{"kind":"string","value":"getsmarter/bda"},"path":{"kind":"string","value":"module_4/M4_NB3_NetworkClustering.ipynb"},"copies":{"kind":"string","value":"1"},"size":{"kind":"string","value":"24094"},"content":{"kind":"string","value":"{\n \"cells\": [\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"
\\n\",\n \"
\\n\",\n \"\\n\",\n \"
\\n\",\n \"
\\n\",\n \"Combine clusters such that, given a cluster with centrality measures $[x1, x2, x3, x4]$, and another cluster with centrality measures $[z1, z2, z3, z4]$, the following holds true:
\\n\",\n \"$x1 = z1$
$x2 = z2$
$x3 = z3$
$x4 = z4$
\\n\",\n \"> 8. Print the size of each cluster, in descending order, after performing the cluster merging in the preceding step.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"# Your code here.\\n\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"
\\n\",\n \"\\n\",\n \"
\\n\",\n \"
\\n\",\n \"\\n\",\n \"\"\n ]\n },\n \"metadata\": {},\n \"output_type\": \"display_data\"\n }\n ],\n \"source\": [\n \"def show_examples(size, width):\\n\",\n \" # Calc the depth needed\\n\",\n \" depth = int(size/width)\\n\",\n \" # Load the images and labels\\n\",\n \" images, labels = mnist.test.next_batch(depth*width)\\n\",\n \" # Config Subplot\\n\",\n \" f, axarr = plt.subplots(depth, width)\\n\",\n \" for d in range(depth):\\n\",\n \" for i in range(width):\\n\",\n \" axarr[d,i].imshow(images[d * width + i].reshape(28,28))\\n\",\n \" # Fine the index where value is 1\\n\",\n \" axarr[d,i].set_title(np.where(labels[d*width+i]==1)[0])\\n\",\n \" axarr[d,i].set_axis_off\\n\",\n \" f.set_size_inches(width*2, depth*3)\\n\",\n \" return\\n\",\n \"show_examples(20,4)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {\n \"deletable\": true,\n \"editable\": true\n },\n \"source\": [\n \"### 1.2 Prep for test set embeddings\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 11,\n \"metadata\": {\n \"collapsed\": false,\n \"deletable\": true,\n \"editable\": true\n },\n \"outputs\": [],\n \"source\": [\n \"LOG_DIR = 'tmp/tb/1'\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {\n \"deletable\": true,\n \"editable\": true\n },\n \"source\": [\n \"# 2. Modelling \"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 12,\n \"metadata\": {\n \"collapsed\": true,\n \"deletable\": true,\n \"editable\": true\n },\n \"outputs\": [],\n \"source\": [\n \"n_features = 28*28\\n\",\n \"# Four Layer the autoencoder\\n\",\n \"#dimensions = [512, 256, 128, 64, 2]\\n\",\n \"dimensions = [512, 256, 128, 64]\\n\",\n \"learning_rate = 1e-4\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {\n \"deletable\": true,\n \"editable\": true\n },\n \"source\": [\n \"### 2.1 Define the graph\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 13,\n \"metadata\": {\n \"collapsed\": false,\n \"deletable\": true,\n \"editable\": true\n },\n \"outputs\": [],\n \"source\": [\n \"tf.reset_default_graph()\\n\",\n \"\\n\",\n \"\\n\",\n \"##\\n\",\n \"x = tf.placeholder(tf.float32, [None, n_features], name='input')\\n\",\n \"\\n\",\n \"current_input = x\\n\",\n \"n_input = n_features\\n\",\n \"\\n\",\n \"ws = [] # list of all the weights \\n\",\n \"\\n\",\n \"# Building the Encoder\\n\",\n \"for layer_i, n_output in enumerate(dimensions):\\n\",\n \" #print('Creating weights with {} by {}' .format(n_input, n_output))\\n\",\n \" layer_name = 'encode_layer' + str(layer_i)\\n\",\n \" with tf.name_scope(layer_name):\\n\",\n \" w = tf.Variable(tf.truncated_normal([n_input, n_output], stddev=0.1), tf.float32, name='w')\\n\",\n \" h = tf.nn.relu(tf.matmul(current_input, w))\\n\",\n \" # Tensorboard Recording\\n\",\n \" tf.summary.histogram('weights', w)\\n\",\n \" tf.summary.histogram('activation', h)\\n\",\n \" ws.append(w)\\n\",\n \" current_input = h\\n\",\n \" n_input = n_output\\n\",\n \" \\n\",\n \" \\n\",\n \"\\n\",\n \"z = tf.identity(current_input, 'inner')\\n\",\n \"## Test \\n\",\n \"#embedding = tf.Variable(mnist.test.images, name = 'test_embedding')\\n\",\n \"\\n\",\n \"\\n\",\n \"## Building the Decoder \\n\",\n \"wd = ws[::-1] # Reverse the weights \\n\",\n \"dimensions_d = dimensions[::-1][1:] + [n_features]\\n\",\n \"\\n\",\n \"for layer_i, n_output in enumerate(dimensions_d):\\n\",\n \" layer_name = 'decode_layer' + str(layer_i)\\n\",\n \" with tf.name_scope(layer_name):\\n\",\n \" w = tf.transpose(wd[layer_i], name='w')\\n\",\n \" h = tf.nn.relu(tf.matmul(current_input, w))\\n\",\n \" # TB summary\\n\",\n \" tf.summary.histogram('weights', w)\\n\",\n \" tf.summary.histogram('activation', h)\\n\",\n \" current_input = h\\n\",\n \" n_input = n_output\\n\",\n \" \\n\",\n \" \\n\",\n \"y = current_input\\n\",\n \"y = tf.identity(y, 'output')\\n\",\n \"\\n\",\n \"\\n\",\n \"## Measure output performance and optimiser\\n\",\n \"with tf.name_scope('Cost'):\\n\",\n \" cost = tf.reduce_mean(tf.squared_difference(x, y), 1)\\n\",\n \" cost = tf.reduce_mean(cost)\\n\",\n \" tf.summary.scalar('Cost', cost)\\n\",\n \" \\n\",\n \"with tf.name_scope('Training'):\\n\",\n \" optimizer = tf.train.AdamOptimizer(learning_rate).minimize(cost)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {\n \"deletable\": true,\n \"editable\": true\n },\n \"source\": [\n \"### 2.2 Training\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 14,\n \"metadata\": {\n \"collapsed\": false,\n \"deletable\": true,\n \"editable\": true,\n \"scrolled\": true\n },\n \"outputs\": [\n {\n \"name\": \"stdout\",\n \"output_type\": \"stream\",\n \"text\": [\n \"Epoch: 0 Cost: 0.18830522894859314\\n\",\n \"Epoch: 1 Cost: 0.0434880293905735\\n\",\n \"Epoch: 2 Cost: 0.02912084572017193\\n\",\n \"Epoch: 3 Cost: 0.02431577816605568\\n\",\n \"Epoch: 4 Cost: 0.020580973476171494\\n\",\n \"Epoch: 5 Cost: 0.01844988390803337\\n\"\n ]\n }\n ],\n \"source\": [\n \"batch_size = 128\\n\",\n \"n_epoch = 5\\n\",\n \"epoch_cycle = 500\\n\",\n \"n_iter = n_epoch * epoch_cycle\\n\",\n \"\\n\",\n \"sess = tf.InteractiveSession()\\n\",\n \"tf.global_variables_initializer().run()\\n\",\n \"\\n\",\n \"\\n\",\n \"#tf.summary.image('input_images', mnist.train.images, 10)\\n\",\n \"# Image must be a 4d tensor? what? \\n\",\n \"#saver = tf.train.Saver([z])\\n\",\n \"merged_summary = tf.summary.merge_all()\\n\",\n \"writer = tf.summary.FileWriter(LOG_DIR)\\n\",\n \"writer.add_graph(sess.graph)\\n\",\n \"\\n\",\n \"for it in range(n_iter+1):\\n\",\n \" batch_x,_ = mnist.test.next_batch(batch_size)\\n\",\n \" optimizer.run(feed_dict={x:batch_x})\\n\",\n \" \\n\",\n \" if it % epoch_cycle == 0:\\n\",\n \" epoch_value = int(it/epoch_cycle)\\n\",\n \" cost_value = cost.eval(feed_dict={x:batch_x})\\n\",\n \" print('Epoch: {} Cost: {}' .format(epoch_value, cost_value))\\n\",\n \" \\n\",\n \" # Record variables and write to disk\\n\",\n \" if it % 10 ==0:\\n\",\n \" s = sess.run(merged_summary, feed_dict={x:batch_x})\\n\",\n \" writer.add_summary(s, it)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {\n \"deletable\": true,\n \"editable\": true\n },\n \"source\": [\n \"# 3. Reporting\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {\n \"deletable\": true,\n \"editable\": true\n },\n \"source\": [\n \"### 3.1 Cost of test set\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 15,\n \"metadata\": {\n \"collapsed\": false,\n \"deletable\": true,\n \"editable\": true\n },\n \"outputs\": [\n {\n \"name\": \"stdout\",\n \"output_type\": \"stream\",\n \"text\": [\n \"Cost of test set: 0.018090857192873955\\n\",\n \"Test to Train ratio: 0.9805404543876648\\n\"\n ]\n }\n ],\n \"source\": [\n \"test_x = mnist.test.images\\n\",\n \"test_cost = cost.eval(feed_dict={x:test_x})\\n\",\n \"print('Cost of test set: {}'.format(test_cost))\\n\",\n \"print('Test to Train ratio: {}'.format(test_cost/cost_value))\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {\n \"deletable\": true,\n \"editable\": true\n },\n \"source\": [\n \"### 3.2 Visual Inspection\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 16,\n \"metadata\": {\n \"collapsed\": false,\n \"deletable\": true,\n \"editable\": true\n },\n \"outputs\": [],\n \"source\": [\n \"test_out = y.eval(feed_dict={x:test_x})\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 17,\n \"metadata\": {\n \"collapsed\": false,\n \"deletable\": true,\n \"editable\": true\n },\n \"outputs\": [\n {\n \"data\": {\n \"text/plain\": [\n \"\"\n ]\n },\n \"execution_count\": 17,\n \"metadata\": {},\n \"output_type\": \"execute_result\"\n },\n {\n \"data\": {\n \"image/png\": \"iVBORw0KGgoAAAANSUhEUgAAAXQAAAC7CAYAAAB1qmWGAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAFQdJREFUeJzt3XmQleWVBvDn9AKN7M0O3WwKKHEBacCIJhiIUUcHmaTc\\nZqaIZUKYjI5WnKpQTCVqYlJq4lIZt6AyYI0jY0ZUoiaKyCBGaWyQrdltISzN1iCr9HbP/NGXqZZz\\nGm73Xfp+L8+viuru0+fe773Ny+mP+26iqiAioujLae0GEBFRarCgExEFggWdiCgQLOhERIFgQSci\\nCgQLOhFRIFjQiYgCwYJORBSIpAq6iFwjIhtFZIuITE9Vo4haG/s2RZG0dKWoiOQC2ATg2wB2APgE\\nwK2qui51zSPKPPZtiqq8JB47BsAWVa0AABGZC2ASgCY7fRtpqwVon8QliZp2AsdQo9WSgqdi36as\\nkmjfTqag9wOwvdHXOwCMPd0DCtAeY2VCEpckalqpLkzVU7FvU1ZJtG8nU9ATIiJTAUwFgAKck+7L\\nEWUM+zZlm2QGRXcCKG70dVE89hWqOlNVS1S1JB9tk7gcUcawb1MkJVPQPwEwREQGiUgbALcAmJ+a\\nZhG1KvZtiqQWv+WiqnUicieAdwDkApilquUpaxlRK2HfpqhK6j10VX0bwNspagtR1mDfpijiSlEi\\nokCwoBMRBYIFnYgoECzoRESBYEEnIgoECzoRUSBY0ImIAsGCTkQUCBZ0IqJAsKATEQWCBZ2IKBAs\\n6EREgWBBJyIKBAs6EVEg0n4EHaVebo8eJrb+wYFurrSrT/h5z3vG5uat3+rm1n9xKOHnJUpG7cRR\\nbnzfSHtKVEGVurm51TZeuGyvm6tt25hYbO2G0zUxa/AOnYgoECzoRESBYEEnIgoECzoRUSCSGhQV\\nka0AjgCoB1CnqiWpaBQ1qL/qUjfe/oHtJrbh3KeTvl7OBPv7/cpVN7u5nX450MTk41VJtyFbsG+n\\nTm73biZWN6TIzd12/TkmVtO3xs2dONz2t2k9F7m5K0/0N7EHP7rezR0wT0ysTcdL3Nxs6/OpmOVy\\nlaruT8HzEGUb9m2KFL7lQkQUiGQLugJ4V0SWi8jUVDSIKEuwb1PkJPuWyxWqulNEegJYICIbVPWD\\nxgnxfwxTAaAA9v0xoizFvk2Rk9QduqrujH/cC+A1AGOcnJmqWqKqJfmwK7uIshH7NkVRi+/QRaQ9\\ngBxVPRL//GoAv0hZy0KQk+uG84r7mljFlGITe/8Hj7iPL8zNXPFYfMnLbnzX3GoTm/D6v7q5Q+5e\\nmtI2pRv79pnVj/dnYB0aZPvmweE2r+3gw+7j646fMLFbL1zu5u6p7mRio5xl+wDQJWeLiX126TI3\\nd+6Jr5vYsOdq3dy6K0eaWM6ST93cTEjmLZdeAF4TkZPP81+q+ueUtIqodbFvUyS1uKCragUAf3Im\\nUYSxb1NUcdoiEVEgWNCJiALB/dBTJG+AHdTceKe/vLn8tt8l9Jw5aOfGH9x/sYltPtrTzR3Swe75\\nPKP7yoSufzp98+zg1+wbnnVzH3rquyZWv+mzpNtAmXHgdjtI+MUwP3f0lXbf8BjsUvpNVXZPfwDI\\n6xgzsf/50zj/YvZpMajwAjf1vm++YWI/7vaRm/veQPviNkzr6uYOe/64ifk7smcG79CJiALBgk5E\\nFAgWdCKiQLCgExEFggWdiCgQnOXSTHl9ervxIfMqTWxe73lJXau8ps6Nl35/hInpp+Vu7hddupvY\\n5Tf/i5u79OdPNqN11ti2/vLoo/9uZy60+05Sl6I0OHrTZW688B/sgSpDCo4l/Lz9Cr4wsYPt/c3M\\nquba2WJF7+1yc+u7dTQxqbN9DQAeaHODiW0Z6S/9v2WA3WpgZ+8ubu7aaf71Wgvv0ImIAsGCTkQU\\nCBZ0IqJAsKATEQVCVDO3ULWTFOpYmZCx6yXLW/K89MGn3NxYGhb8XrN+shvPm/jXlF8LAIqWdjCx\\nZ4sXp+Va1/cblfLnLNWFOKwHnAXh6Ze1fbuJPflrv2UH1ns/UOHmts+rMbFjdf6+48ed+Oq1A02s\\nQ4XfrqI/2TO569dtcnObQ8fZ17v5dn9OyMPf+IOJvTB0UMLXymnf3o3HjiU+kHyqRPs279CJiALB\\ngk5EFAgWdCKiQLCgExEF4owFXURmicheEVnbKFYoIgtEZHP8o79ZMFEWY9+m0CSy9H82gCcBvNgo\\nNh3AQlV9SESmx7/+aeqblxmxb9qTuwHglft/Y3ObOHQihsSXAH9t7l0m1neJszz+dX9pcrpseOxC\\nE4s9viijbciw2Qi8bx++ZbQbP1pk7+Umd/FnuZyTU21iv6+40s099hd7cMU59TavV9mX7uNjm/w2\\nJEv+Yg91yfmev9VBv7yDJnbZKv+wmuUH+5tY7Xi7DUimnPEOXVU/AHDglPAkAHPin88BcGOK20WU\\nduzbFJqWvofeS1VP/hraDaBXitpD1NrYtymykh4U1YaVSU2uqhGRqSJSJiJltbD/dSPKVuzbFDUt\\nLeh7RKQPAMQ/2pOI41R1pqqWqGpJPuzBwkRZhn2bIqul+6HPBzAFwEPxj/ZI7SxVdYddzj/rZ4+7\\nud7J9s0xfvUtbnzIz1abWOy4PT0807qU7jSx1472dHMnd2iyzkVdZPv2se+ONbGqi/zV4rH+dlBy\\nxRE7wAcA5VX2DIDjS+zgJwB0qbCD+20O21HRnMWfuo9P10YkeYMH2tgx/2fzi8GXNuOZW28A1JPI\\ntMWXAXwMYJiI7BCRO9DQ2b8tIpsBTIx/TRQp7NsUmjPeoavqrU18Kwt3IiJKHPs2hYYrRYmIAsGC\\nTkQUCBZ0IqJAtHSWS9ar+qGdzQIAb//8tybWOcffrL85vOX83mwWIDtmtHjqttnT3d+susTNndxh\\nQbqbQ81UdZE9NKLvqF1u7qhu9pCUd/96vpv7ZUUnEytaVevmttt11MRkp50R5ewGkFYnBnUzMRlq\\n2woA15fbpf/HY36NKD040MSOfWNf8xqXQrxDJyIKBAs6EVEgWNCJiALBgk5EFIggBkXz+tilyVN/\\n4q/Ybs4A6KNVdn/wV5/6lps79L/XmVh9lg5+UrRVX+vvcZ578SET27HPP5/j3E777fNu6OzmDnzX\\nbjyWu2iFm5v4qQDpEbvSP9tg3yV2G48R/T53c9vm2AHfE+qXyg177WacxeCgKBERJYkFnYgoECzo\\nRESBYEEnIgpEEIOi6x/ua2Kvd3qriWz7O6yy3j+w9vXH7ABo99kfu7mZXvmWDhWP2NW1bw54sons\\nxO8FymvqWtgi8hy4IN+N9+/qrHDs4E8CeH+tXRU65I/+IL58tKoZrWtducvs5AQAOD7JDpZuqvL3\\ndB/VeZuJPV8+zs2NbWvfjNalH+/QiYgCwYJORBQIFnQiokCwoBMRBSKRM0VnicheEVnbKHa/iOwU\\nkZXxP9elt5lEqce+TaFJZJbLbABPAnjxlPjjqmo3F28FFw6wez7HmrEIefr2G9x41yZmtERdzojh\\nbnzd39sZLc35OZZW+7Mv7p/2IxPLR1nCz5tGs5HlfdvT47odbrz+KvvvYPvjl7m5A96187JylpW7\\nudqMtrW2L6/29++vL7QzrXq0P+bmfv6lnf1SU1Xg5vZanV0/nTPeoavqBwAOZKAtRBnFvk2hSeY9\\n9DtFZHX8v63+DkBE0cS+TZHU0oL+DIBzAYwAUAng0aYSRWSqiJSJSFkt7K5tRFmGfZsiq0UFXVX3\\nqGq9qsYAPAdgzGlyZ6pqiaqW5MNuYUmUTdi3KcpatPRfRPqoamX8y8kA1p4uP91ePc8u829qKK9e\\n7SDGxhf9w3G7I0KDojn2gGAAOHSb3Tv7pV81Nd7XLuHLeT/H2+dPc3PPe3dpws/b2rKtb3vyJtoD\\nngGg18f2MOetC8XNLdhnt7vQusxt0ZDbybYVAOQc2wfrdu9xc2NXjDCx7RP9e9TRQz8zsTY5/oYd\\nSysHmFj+Yf/fV+f/zK4accaCLiIvAxgPoLuI7ABwH4DxIjICDQPgWwHYaQxEWY59m0JzxoKuqrc6\\n4RfS0BaijGLfptBwpSgRUSBY0ImIAsGCTkQUiCAOuGiO0aW3m1jR77NrpPpM8gYUm9jGO4vc3PLb\\nfudEk59i5/0cz7snOrNZomz0Sn92RsUxOxOj7UF/louWZW7yTt7A/jZYXePmHrrczjCpKxjk5u7/\\nmxMmdnG/z93cjnl2nUDpLnstAKhdb2fgFC3y25tteIdORBQIFnQiokCwoBMRBYIFnYgoEGfdoGj1\\n1o6t3YSEbf+3y9341X+3zMTm9Z6XljZMWHOzGx8www4y+UN1lIwtT9j9zDsf3ezmllXYQb7OdoV/\\nWuV26WxiNcXdTKzycn+bibr2dkuJwVduc3OHFhw1sXa5tW7u1iO2DXVrbFsBoP+C4yaW8+FKNzfb\\n8A6diCgQLOhERIFgQSciCgQLOhFRIFjQiYgCEcQslxx4y5v931WTxtsZIkumfN3N7faHVSYWO25H\\nwJsiJRe68SODO5jY0J/YE9ff6f+0+/ha9eaTJP+7edi8H5vYkLtK3VzOaMkMbzuFH2yxfQUADl3x\\nNRPb+qDft2WUzdXl/vN6h6dUf+dSN3XvpfkmVtPVHjdT38E/TGPauEUmdm3HNW7uO0fta5i90c4K\\nAoDYKjujpXiRPwUoKjNaPLxDJyIKBAs6EVEgWNCJiAJxxoIuIsUiskhE1olIuYjcHY8XisgCEdkc\\n/9g1/c0lSh32bQqNqHN6+1cSRPoA6KOqK0SkI4DlAG4E8H0AB1T1IRGZDqCrqv70dM/VSQp1rExI\\nTcsbeXPnchOLwQ7ENNeM3WNNbF+NHdAEgJja341PFL/l5nbMaZPQ9XOa+H3bnNdWWm0Hqe795T+5\\nuYX/Ea194U9VqgtxWA/4G4A7otC3Nz09xsQuuGCHm9vdWQr/yQ5/z++8ZXYLjHb7/FpwvLf9kcrY\\nL9zcu87/XxO7o5Nt79Y6f3LB5lq7RP/Xn13n5m6v6GFiXVfZAVwA6PHs2dG3z3iHrqqVqroi/vkR\\nAOsB9AMwCcCceNocNPxDIIoM9m0KTbPeQxeRgQBGAigF0EtVK+Pf2g2gV0pbRpRB7NsUgoQLuoh0\\nAPAqgHtU9XDj72nD+zbu/9dEZKqIlIlIWS3sDn1ErY19m0KRUEEXkXw0dPiXVPXkPq174u9Bnnwv\\ncq/3WFWdqaolqlqSn4KzLIlSiX2bQpLILBcB8AKA9ar6WKNvzQcwJf75FABvpL55ROnDvk2hSWSW\\nyxUAlgBYA/z/9IoZaHiv8RUA/QFsA3CTqh443XOlaybAw5/b5ekXtEnPFPtUzDxJ9lrlNXbZ9Pfm\\n3e3mDn2kwsTq97g3nJHXglkuWd+3PUf/PNiNX97Tnni/+mA/N3dblZ2J2a/wkJubn2M3ephWvNjN\\nrVE7yyTXecdq8eFh7uPf2mC3y+j1pv+/n66Lt5pYXeVuNzfqEu3bZ9zLRVU/BNzNUgAgMz2YKA3Y\\ntyk0XClKRBQIFnQiokCwoBMRBSKI/dBnjLZLg3c839PNfX/U8yaW6FL8dHrvS7sU+9db/CXPXX5Y\\nY2Lnbrf7ZgPctzzqcjt1MrEO19iBbgD44ysXmdiFfSqdTD9+vM7/d9CpzQkTq3e2ugCAdw7YNqzY\\nU2RiRzf62+Oc/5TdJqBu23Y3199R/ezGO3QiokCwoBMRBYIFnYgoECzoRESBYEEnIgrEGZf+p1Im\\nl0c3xTvtfOvf2hPBAaBmoB3dT4UeC+1S5u5LdplY3efb0nL9UDV36X8qZUPfxhg7w2TLbe3d1DYH\\n7L1cj3H+jJiDx9uZ2NHd/kEvfRfZ5y3YX2tiee/bQ2moaSk74IKIiKKBBZ2IKBAs6EREgWBBJyIK\\nRBBL/5tDl5eb2IAsGJ/hMmZK2rI1JnT+zr5u6rFL7D7psqy7m1u064iJxVYva2bjKBN4h05EFAgW\\ndCKiQLCgExEFIpFDootFZJGIrBORchG5Ox6/X0R2isjK+B9/r1eiLMW+TaFJZFC0DsC9qrpCRDoC\\nWC4iC+Lfe1xVf5u+5hGlFfs2BSWRQ6IrAVTGPz8iIusB+EeJE0XI2dC363baLSUAoG0TcU8sVY2h\\ntGvWe+giMhDASACl8dCdIrJaRGaJiH8ECVEEsG9TCBIu6CLSAcCrAO5R1cMAngFwLoARaLjLebSJ\\nx00VkTIRKatFdQqaTJRa7NsUioQKuojko6HDv6Sq8wBAVfeoar2qxgA8B2CM91hVnamqJapakg+7\\nyyBRa2LfppAkMstFALwAYL2qPtYo3qdR2mQAa1PfPKL0Yd+m0CQyy2UcgH8EsEZEVsZjMwDcKiIj\\nACiArQB+lJYWEqUP+zYFJZFZLh8C8DZWfzv1zSHKHPZtCg1XihIRBYIFnYgoECzoRESBYEEnIgoE\\nCzoRUSBY0ImIAsGCTkQUCBZ0IqJAsKATEQVCVDVzFxPZB2Bb/MvuAPZn7OKZw9fVegaoao/WuHCj\\nvh2Fn1NLhfraovC6EurbGS3oX7mwSJmqlrTKxdOIr+vsFvLPKdTXFtLr4lsuRESBYEEnIgpEaxb0\\nma147XTi6zq7hfxzCvW1BfO6Wu09dCIiSi2+5UJEFIiMF3QRuUZENorIFhGZnunrp1L8RPi9IrK2\\nUaxQRBaIyOb4x8idGC8ixSKySETWiUi5iNwdj0f+taVTKH2b/Tp6r+2kjBZ0EckF8BSAawEMR8NR\\nX8Mz2YYUmw3gmlNi0wEsVNUhABbGv46aOgD3qupwAJcB+Of431MIry0tAuvbs8F+HUmZvkMfA2CL\\nqlaoag2AuQAmZbgNKaOqHwA4cEp4EoA58c/nALgxo41KAVWtVNUV8c+PAFgPoB8CeG1pFEzfZr+O\\n3ms7KdMFvR+A7Y2+3hGPhaSXqlbGP98NoFdrNiZZIjIQwEgApQjstaVY6H07qL/7UPs1B0XTSBum\\nEEV2GpGIdADwKoB7VPVw4+9F/bVRy0X97z7kfp3pgr4TQHGjr4visZDsEZE+ABD/uLeV29MiIpKP\\nhk7/kqrOi4eDeG1pEnrfDuLvPvR+nemC/gmAISIySETaALgFwPwMtyHd5gOYEv98CoA3WrEtLSIi\\nAuAFAOtV9bFG34r8a0uj0Pt25P/uz4Z+nfGFRSJyHYAnAOQCmKWqv8poA1JIRF4GMB4Nu7XtAXAf\\ngNcBvAKgPxp237tJVU8dYMpqInIFgCUA1gCIxcMz0PB+Y6RfWzqF0rfZr6P32k7iSlEiokBwUJSI\\nKBAs6EREgWBBJyIKBAs6EVEgWNCJiALBgk5EFAgWdCKiQLCgExEF4v8AJ2R4mt+8ujwAAAAASUVO\\nRK5CYII=\\n\",\n \"text/plain\": [\n \"\"\n ]\n },\n \"metadata\": {},\n \"output_type\": \"display_data\"\n }\n ],\n \"source\": [\n \"index = 60\\n\",\n \"plt.subplot(1,2,1)\\n\",\n \"plt.imshow(test_x[index].reshape(28,28))\\n\",\n \"plt.subplot(1,2,2)\\n\",\n \"plt.imshow(test_out[index].reshape(28,28))\\n\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"### 3.3 64D Compress output for tensorboard\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 20,\n \"metadata\": {\n \"collapsed\": false\n },\n \"outputs\": [],\n \"source\": [\n \"compressed = z.eval(feed_dict={x:mnist.test.images})\\n\",\n \" \\n\",\n \"metadata = 'compressed_metadata.tsv'\\n\",\n \"test_labels = mnist.test.labels\\n\",\n \"\\n\",\n \"with open(metadata, 'w') as metadata_file:\\n\",\n \" for i, v in enumerate(test_labels):\\n\",\n \" c = np.where(v==1)\\n\",\n \" metadata_file.write('{}\\\\n'.format(int(c[0])))\\n\",\n \" \\n\",\n \"\\n\",\n \"np.save('compressed_output', compressed)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {\n \"deletable\": true,\n \"editable\": true\n },\n \"source\": [\n \"#### 3.4 2D Compressed Visualisation\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {\n \"collapsed\": false,\n \"deletable\": true,\n \"editable\": true\n },\n \"outputs\": [],\n \"source\": [\n \"sample = 1024\\n\",\n \"compressed = z.eval(feed_dict={x:mnist.test.images})\\n\",\n \"labels = mnist.test.labels\\n\",\n \"metadata = np.empty(len(labels))\\n\",\n \"for i, v in enumerate(labels):\\n\",\n \" metadata[i] = np.where(v==1)[0]\\n\",\n \"\\n\",\n \" \\n\",\n \"for i in range(10):\\n\",\n \" index = np.where(metadata==i)\\n\",\n \" plt.scatter(compressed[index,0], compressed[index,1], label=str(i))\\n\",\n \" \\n\",\n \"plt.legend() \\n\",\n \"fig = plt.gcf()\\n\",\n \"fig.set_size_inches(18.5, 10.5)\\n\",\n \"\\n\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {\n \"collapsed\": true,\n \"deletable\": true,\n \"editable\": true\n },\n \"outputs\": [],\n \"source\": []\n }\n ],\n \"metadata\": {\n \"kernelspec\": {\n \"display_name\": \"Python 3\",\n \"language\": \"python\",\n \"name\": \"python3\"\n },\n \"language_info\": {\n \"codemirror_mode\": {\n \"name\": \"ipython\",\n \"version\": 3\n },\n \"file_extension\": \".py\",\n \"mimetype\": \"text/x-python\",\n \"name\": \"python\",\n \"nbconvert_exporter\": \"python\",\n \"pygments_lexer\": \"ipython3\",\n \"version\": \"3.5.2\"\n }\n },\n \"nbformat\": 4,\n \"nbformat_minor\": 2\n}\n"},"license":{"kind":"string","value":"gpl-3.0"}}},{"rowIdx":1397,"cells":{"repo_name":{"kind":"string","value":"OceanPARCELS/parcels"},"path":{"kind":"string","value":"parcels/examples/tutorial_sampling.ipynb"},"copies":{"kind":"string","value":"1"},"size":{"kind":"string","value":"252044"},"content":{"kind":"string","value":"{\n \"cells\": [\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"# Field sampling tutorial\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"The particle trajectories allow us to study fields like temperature, plastic concentration or chlorophyll from a Lagrangian perspective. \\n\",\n \"\\n\",\n \"In this tutorial we will go through how particles can sample `Fields`, using temperature as an example. Along the way we will get to know the parcels class `Variable` (see [here](https://oceanparcels.org/gh-pages/html/#parcels.particle.Variable) for the documentation) and some of its methods. This tutorial covers several applications of a sampling setup:\\n\",\n \"* [**Basic along trajectory sampling**](#Basic-sampling)\\n\",\n \"* [**Sampling initial conditions**](#Sampling-initial-values)\\n\",\n \"* [**Sampling initial and along-trajectory values with repeated release**](#Sampling-with-repeatdt)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"### Basic sampling\\n\",\n \"We import the `Variable` class as well as the standard modules needed to set up a simulation.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 1,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"# Modules needed for the Parcels simulation\\n\",\n \"from parcels import Variable, FieldSet, ParticleSet, JITParticle, AdvectionRK4\\n\",\n \"import numpy as np\\n\",\n \"from datetime import timedelta as delta\\n\",\n \"\\n\",\n \"# To open and look at the temperature data\\n\",\n \"import xarray as xr \\n\",\n \"import matplotlib as mpl\\n\",\n \"import matplotlib.pyplot as plt\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"Suppose we want to study the environmental temperature for plankton drifting around a peninsula. We have a dataset with surface ocean velocities and the corresponding sea surface temperature stored in netcdf files in the folder `\\\"Peninsula_data\\\"`. Besides the velocity fields, we load the temperature field using `extra_fields={'T': 'T'}`. The particles are released on the left hand side of the domain.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 2,\n \"metadata\": {},\n \"outputs\": [\n {\n \"data\": {\n \"image/png\": \"iVBORw0KGgoAAAANSUhEUgAAAYsAAAD8CAYAAACGsIhGAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAfO0lEQVR4nO3df5BV5Z3n8fcH/En7W9TBbkBnQ7lj3I0/KKLr7pSRmCDbFdwtextqE8msU0xEqpKdsBMcquiFXXbNLkmmrE5r2OiKjlHAxEixGKU0rMmUUdH4i8aOHQ3Q0CshJkK6/THY3/3jPg23L7f73gvd93YfP6+qU/fc73mec58TIl+e5znnOYoIzMzMhjKu1g0wM7PRz8nCzMxKcrIwM7OSnCzMzKwkJwszMyvJycLMzEpysjAzqyJJkyX9VNJ2SdskfTXFz5K0WdIb6fPMQerPktQhqVPSkqq1289ZmJlVj6RJwKSIeFHSqcALwA3Al4F3IuL2lATOjIhvFNQdD/wKuA7oAp4H5kVE+0i32z0LM7MqiojuiHgx7R8AtgP1wBxgTSq2hlwCKTQD6IyINyPiQ+ChVG/EHVeNHxkJ0vgYp+Nr3QwmcGqtmwDAhONGR96vG/9RrZvAySd8WOsmAHDCye/XugkAjK/rq3UTAOg79aya/fYvX/7tvog451jO8dlrp8Q775T3Z/rLl3+7DcgvvDoiVheWk3QBcBnwLHBeRHRDLqFIOrfIqeuBXXnfu4BPl9WoYzRmk8U4Hc/JJ0yudTO4bNxnat0EAKafcXKtmwDA5WcfqHUT+NT5u0oXqoKp/6yj1k0AoO6qP9a6CQD0/vmNNfvt0869c8exnuOdd97n/24u7xpOO/fO9yNi+lBlJJ0C/BD4WkTsl1TOqYsVqspcwuj456iZ2ceIpOPJJYoHIuJHKfx2ms/on9fYW6RqF5D/r+QGYM9ItrWfk4WZWRUp14W4G9geEd/OO7QBmJ/25wOPFqn+PDBN0oWSTgDmpnojzsnCzKy6rga+BFwr6aW0zQZuB66T9Aa5u51uB5B0vqRNABFxEFgEPE5uYnxdRGyrRqPH7JyFmdlYFBE/p/jcA8DMIuX3ALPzvm8CNo1M6wbnnoWZmZXkZGFmZiU5WZiZWUlOFmZmVpKThZmZleRkYWZmJTlZmJlZSU4WZmZWkpOFmZmVlJlk0dTcSHvHFvb3dtDesYWm5sZaN8nMLDMysdxHU3MjrW0rqaubAMCUqfW0tq0EYP3ajbVsmplZJmSiZ7F8xeJDiaJfXd0Elq9YXKMWmZllSyaSRcPkSRXFzcysMplIFl27uiuKm5lZZTKRLFqWraKnp3dArKenl5Zlq2rUIjOzbMlEsli/diOLFi5l547d9PX1sXPHbhYtXOrJbTOzYZKJu6EglzCcHMzMRkYmehZmZjayMtOzMDMbKyTdAzQCeyPikhRbC1yUipwB/CEiLi1S9zfAAeAj4GBETK9Ck50szMxq4F6gFbivPxARzf37kr4FvDtE/c9ExL4Ra10RThZmZlUWEU9LuqDYMUkC/h1wbVUbVYLnLMzMRpd/BbwdEW8McjyAJyS9IGlBtRrlnoWZWRnGHXiHCU8/VG7xiZK25n1fHRGry6w7D3hwiONXR8QeSecCmyW9HhFPl9uwo+VkYWY2/PYdzcSzpOOAfwtcMViZiNiTPvdKegSYAYx4svAwlJnZ6PFZ4PWI6Cp2UFKdpFP794HPAa9Vo2FOFmZmVSbpQeAZ4CJJXZJuTofmUjAEJel8SZvS1/OAn0t6GXgO+D8R8ZNqtNnDUGZmVRYR8waJf7lIbA8wO+2/CXxqRBs3CPcszMysJCcLMzMrycnCzMxKcrIwM7OSMpMsmpobae/Ywv7eDto7ttDU3FjrJpmZZUbZyULSeEm/lLQxfT9L0mZJb6TPM/PK3iapU1KHpM/nxa+Q9Go6dkdaAwVJJ0pam+LPDrZmymCamhtpbVvJlKn1jBs3jilT62ltW+mEYWY2TCrpWXwV2J73fQnwZERMA55M35F0Mbl7hT8JzALaJI1Pde4EFgDT0jYrxW8Gfh8RnwC+A3yzkotYvmIxdXUTBsTq6iawfMXiSk5jZmaDKCtZSGoA/jXw/bzwHGBN2l8D3JAXfygiPoiIt4BOYIakScBpEfFMRAS5pXlvKHKuh4GZ/b2OcjRMnlRR3MzMKlNuz+LvgL8B+vJi50VEN0D6PDfF64FdeeW6Uqw+7RfGB9SJiIPk1nE/u7ARkhZI2ippa8RHh0+0q7tooweLm5lZZUomC0n9b3N6ocxzFusRxBDxoeoMDESsjojpETH98MgWtCxbRU9P74CyPT29tCxbVWaTzcxsKOX0LK4GvpBe5fcQcK2kvwfeTkNLpM+9qXwXMDmvfgOwJ8UbisQH1EmrLp4OvFPuRaxfu5FFC5eyc8du+vr62LljN4sWLmX92o3lnsLMzIZQMllExG0R0RARF5CbuH4qIr4IbADmp2LzgUfT/gZgbrrD6UJyE9nPpaGqA5KuTPMRNxXU6T/Xjek3juhZDGX92o1cfNE1nDbhIi6+6BonCjOzYXQsCwneDqxLqyXuBJoAImKbpHVAO3AQuDUOTzDcQu7dsycDj6UN4G7gfkmd5HoUc4+hXWZmNswqShYRsQXYkvZ/B8wcpNxKYGWR+FbgkiLx90nJxszMRp/MPMFtZmYjx8nCzMxKcrIwM7OSnCzMzKwkJwszMyvJycLMrMok3SNpr6TX8mL/WdJuSS+lbfYgdWelFb07JS2pVpudLMzMqu9eDq+6ne87EXFp2jYVHkwreH8XuB64GJiXVvoecU4WZmZVFhFPU8GSRnlmAJ0R8WZEfEhuCaY5w9q4QRzLE9xmZh8bH/WMo+eZU8os/fuJkrbmBVZHxOoyKi6SdBOwFfh6RPy+4HixVb0/XWajjol7FmZmw29f/wrZaSsnUdwJ/BPgUqAb+FaRMmWt0D0SnCzMzEaBiHg7Ij6KiD7gf5Ebcio02KreIy4zyaKpuZH2ji3s7+2gvWOL379tZmNK/ysfkn8DvFak2PPANEkXSjqB3KKrG6rRvkzMWTQ1N9LatvLQe7inTK2ntS23jqGXKjez0UbSg8A1wERJXUALcI2kS8kNK/0G+KtU9nzg+xExOyIOSloEPA6MB+6JiG3VaHMmksXyFYsPJYp+dXUTWL5isZOFmY06ETGvSPjuQcruAWbnfd8EHHFb7UjLxDBUw+RJFcXNzKwymUgWXbu6K4qbmVllMpEsWpatoqend0Csp6eXlmWratQiM7NsyUSyWL92I4sWLmXnjt309fWxc8duFi1c6vkKM7NhkokJbsglDCcHM7ORkYmehZmZjSwnCzMzK8nJwszMSnKyMDOzkpwszMysJCcLMzMrycnCzMxKcrIwM7OSnCzMzKwkJwszMyvJycLMzEpysjAzs5KcLMzMrKTMJIum5kbaO7awv7eD9o4tNDU31rpJZmZFSbpH0l5Jr+XF/qek1yW9IukRSWcMUvc3kl6V9JKkrdVqcyaSRVNzI61tK5kytZ5x48YxZWo9rW0rnTDMbLS6F5hVENsMXBIR/xz4FXDbEPU/ExGXRsT0EWrfETKRLJavWExd3YQBsbq6CSxfsbhGLTIzG1xEPA28UxB7IiIOpq+/ABqq3rAhZOLlRw2TJ1UUNzOr1IfvncSOVy8qs/SuiQVDRKsjYnUFP/cfgLWDHAvgCUkBfK/C8x61kj0LSSdJek7Sy5K2SVqe4mdJ2izpjfR5Zl6d2yR1SuqQ9Pm8+BVprK1T0h2SlOInSlqb4s9KuqCSi+ja1V1R3MxshO2LiOl5W9l/oUtaChwEHhikyNURcTlwPXCrpD8fhvaWVM4w1AfAtRHxKeBSYJakK4ElwJMRMQ14Mn1H0sXAXOCT5Mbk2iSNT+e6E1gATEtb/5jdzcDvI+ITwHeAb1ZyES3LVtHT0zsg1tPTS8uyVZWcxsyspiTNBxqBfx8RUaxMROxJn3uBR4AZ1WhbyWQROX9MX49PWwBzgDUpvga4Ie3PAR6KiA8i4i2gE5ghaRJwWkQ8k/5HuK+gTv+5HgZm9vc6yrF+7UYWLVzKzh276evrY+eO3SxauNTv5DazMUPSLOAbwBcioneQMnWSTu3fBz4HvFas7HAra84i9QxeAD4BfDcinpV0XkR0A0REt6RzU/F6cpMz/bpS7B/TfmG8v86udK6Dkt4Fzgb2FbRjAbmeCSpo+vq1G50czGxMkPQgcA0wUVIX0ELu7qcTgc3p38q/iIivSDof+H5EzAbOAx5Jx48DfhARP6lGm8tKFhHxEXBpuu/3EUmXDFG8WI8ghogPVaewHauB1QDjx51UtItmZjbaRcS8IuG7Bym7B5id9t8EPjWCTRtURbfORsQfgC3k5hreTkNLpM+9qVgXMDmvWgOwJ8UbisQH1JF0HHA6BbeVmZlZ7ZRzN9Q5/U8SSjoZ+CzwOrABmJ+KzQceTfsbgLnpDqcLyU1kP5eGrA5IujLNR9xUUKf/XDcCTw02uWNmZtVXzjDUJGBNmrcYB6yLiI2SngHWSboZ2Ak0AUTENknrgHZyt3/dmoaxAG4h9+TiycBjaYNc9+t+SZ3kehRzh+PizMxseJRMFhHxCnBZkfjvgJmD1FkJrCwS3wocMd8REe+Tko2ZmY0+mVjuw8zMRpaThZmZleRkYWZmJTlZmJlZSZlYddbMzI4k6awyivWlZ+iG5GRhZpZde9I21Fp744EppU7kZGFmll3bI+KIRx/ySfplOSfynIWZWXZdNUxlspMsmpobae/Ywv7eDto7tvj922Zm8J8kfX2oAumh6JIyMQzV1NxIa9vKQ+/hnjK1nta23APkXrbczD7GvkTupXUDSPpL4JyI+O/lnigTPYvlKxYfShT96uomsHzF4hq1yMxsVHhvkBcp3Q98sZITZSJZNEyeVFHczOxj4r3+V0nki4gPyC30WrZMJIuuXd0Vxc3MPia+BTwqaWp+ML3ZtK+SE2UiWbQsW0VPz8CeVk9PLy3LVtWoRWZmtRcR64HvAi9I2ijpv0r6b8A/ABX9BZmJZLF+7UYWLVzKzh276evrY+eO3SxauNST22Y2Kkm6R9JeSa/lxc6StFnSG+nzzEHqzpLUIalT0pJSvxURa4ALgXXA8cD7wLyIeKCSNmfibijIJQwnBzMbI+4FWoH78mJLgCcj4vaUBJYA38ivlF5C913gOnKvo35e0oaIaB/qxyLiQMFvVSwTPQszs7EkIp4m91bQfHOANWl/DXBDkaozgM6IeDMiPgQeSvWKknRV/2uxj5WThZnZ8JsoaWvetqCMOudFRDdA+jy3SJl6YFfe964UO4Kk/wKcA3yvsqYXl5lhKDOzkfTehyfw8p7J5RbfFxHTR6AZxRYEjEHK/gPw58CvhuOHnSzMzEaHtyVNioju9GzE3iJluoD8jNVAblXZI0TET4CfDFfjPAxlZjY6bADmp/35wKNFyjwPTJN0oaQTgLmp3ohzsjAzqzJJDwLPABdJ6pJ0M3A7cJ2kN8jd7XR7Knu+pE0AEXEQWAQ8DmwH1kXEtiF+58Uy2lKyDHgYysys6iJi3iCHZhYpuweYnfd9E7CpzJ/6M0mvDHFcwOnlnMjJwswsu/5pGWU+KudEThZmZhkVETuG61yeszAzs5KcLMzMMkrSsI0eOVmYmWXXc8N1IicLM7PsKvbE91HJzAR3U3Mjy1cspmHyJLp2ddOybJVXoTWzj7tzJP31YAcj4tvlnigTyaKpuZHWtpWH3sM9ZWo9rW0rAZwwzOzjbDxwCsPQw8hEsli+YvGhRNGvrm4Cy1csdrIws4+z7ohYMRwnysScRcPkI95HPmTczOxjYtjmLDKRLLp2dVcUNzP7mDhi+ZCjlYlk0bJsFT09vQNiPT29tCyr6H3kZmaZEhGFb+M7aplIFuvXbmTRwqXs3LGbvr4+du7YzaKFSz1fYWY2TDIxwQ25hOHkYGY2Mkr2LCRNlvRTSdslbZP01RQ/S9JmSW+kzzPz6twmqVNSh6TP58WvkPRqOnaHJKX4iZLWpvizki4YgWs1M7OjVM4w1EHg6xHxZ8CVwK2SLgaWAE9GxDTgyfSddGwu8ElgFtAmaXw6153AAmBa2mal+M3A7yPiE8B3gG8Ow7WZmdkwKZksIqI7Il5M+wfIvZ2pHpgDrEnF1gA3pP05wEMR8UFEvAV0AjPSO2VPi4hnIiKA+wrq9J/rYWBmf6/DzMxqr6IJ7jQ8dBnwLHBeRHRDLqEA56Zi9cCuvGpdKVaf9gvjA+qk1wa+C5xd5PcXSNoqaWtEWe/rMDOzYVB2spB0CvBD4GsRsX+ookViMUR8qDoDAxGrI2J6REw/PLJlZjZ2SLpI0kt5235JXysoc42kd/PKLKtRcw8p624oSceTSxQPRMSPUvhtSZMiojsNMe1N8S5gcl71BmBPijcUiefX6Urrr58ODNv9wWZmo0VEdACXAqT53N3AI0WK/iwiGqvYtCGVczeUgLuB7QUrFG4A5qf9+cCjefG56Q6nC8lNZD+XhqoOSLoynfOmgjr957oReCrNa5iZZdlM4NfD+frTkVJOz+Jq4EvAq5JeSrG/BW4H1km6GdgJNAFExDZJ64B2cndS3RqHJxhuAe4FTgYeSxvkktH9kjrJ9SjmHttlmZnV1ERJW/O+r46I1UXKzQUeHOQcV0l6mdwIzOKI2DbcjaxEyWQRET9n8MWoiq47EhErgZVF4luBS4rE3yclGzOz0ajno/G8+LtTyy2+LyKmD1VA0gnAF4Dbihx+EZgaEX+UNBv4MblRmprJxHIfZmZj0PXAixHxduGBiNgfEX9M+5uA4yVNrHYD8zlZmJnVxjwGGYKS9Cd5K1zMIPd39e+q2LYjZGZtKDOzsULSBOA64K/yYl8BiIi7yN3oc4ukg8B7wNxa3/TjZGFmVmUR0UvBg8cpSfTvtwKt1W7XUDIzDNXU3Eh7xxb293bQ3rGFpuZRc3uymdmYl4meRVNzI61tKw+9h3vK1Hpa23I3Y3nZcjOzY5eJnsXyFYsPJYp+dXUTWL5icY1aZGaWLZlIFg2TJ1UUNzOzymQiWXTt6q4obmZmlclEsmhZtoqent4BsZ6eXlqWrapRi8zMsiUTyWL92o0sWriUnTt209fXx84du1m0cKknt83Mhkkm7oaCXMJwcjAzGxmZ6FmYmdnIcrIwM7OSnCzMzKwkJwszMyvJycLMzEpysjAzs5KcLMzMrCQnCzMzK8nJwszMSnKyMDOzkpwszMyqTNJvJL0q6SVJW4scl6Q7JHVKekXS5bVoZ77MrA1lZjbGfCYi9g1y7HpgWto+DdyZPmvGPQszs9FnDnBf5PwCOENSTd/mlplk0dTcSHvHFvb3dtDesYWm5sZaN8nMPr4mStqaty0oOB7AE5JeKHIMoB7Ylfe9K8VqJhPDUE3NjbS2rTz0Hu4pU+tpbVsJ4GXLzWxY9B7sY+sf3iu3+L6ImD7E8asjYo+kc4HNkl6PiKfzjqtInSj3x0dCJnoWy1csPpQo+tXVTWD5isU1apGZ2eAiYk/63As8AswoKNIFTM773gDsqU7ristEsmiYXHwob7C4mVmtSKqTdGr/PvA54LWCYhuAm9JdUVcC70ZEd5WbOkAmhqG6dnUzZeqRw3ldu2r6v62ZWTHnAY9IgtzfwT+IiJ9I+gpARNwFbAJmA51AL/AXNWrrIZlIFi3LVg2YswDo6emlZdmqGrbKzOxIEfEm8Kki8bvy9gO4tZrtKiUTw1Dr125k0cKl7Nyxm76+Pnbu2M2ihUs9uW1mNkwy0bOAXMJwcjAzGxmZ6FmYmdnIcrIwM7OSnCzMzKykkslC0j2S9kp6LS92lqTNkt5In2fmHbstrZTYIenzefEr0iqLnWk1RaX4iZLWpvizki4Y5ms0M7NjVE7P4l5gVkFsCfBkREwDnkzfkXQxMBf4ZKrTJml8qnMnsIDDKyn2n/Nm4PcR8QngO8A3j/ZizMxsZJRMFmm9kncKwnOANWl/DXBDXvyhiPggIt4i90DJjLRa4mkR8Uy6f/i+gjr953oYmNnf6zAzs9HhaOcszut/9Dx9npvig62UWJ/2C+MD6kTEQeBd4OxiPyppQf8qjhEfHWXTzcysUsM9wT3YSolDraBY9uqKEbE6IqZHxPTDo1tmZjbSjjZZvN3/Io70uTfFB1spsSvtF8YH1JF0HHA6Rw57mZlZDR1tstgAzE/784FH8+Jz0x1OF5KbyH4uDVUdkHRlmo+4qaBO/7luBJ5K8xpmZjZKlFzuQ9KDwDXk3vzUBbQAtwPrJN0M7ASaACJim6R1QDtwELg1Dk8u3ELuzqqTgcfSBnA3cL+kTnI9irnDcmVmZjZsSiaLiJg3yKGZg5RfCawsEt8KXFIk/j4p2ZiZ2ejkJ7jNzKwkJwszMyspM8miqbmR9o4t7O/toL1jC03NjbVukplZZmTifRZNzY0D3pQ3ZWo9rW25aRO/48LM7NhlomexfMXiAa9UBairm8DyFYtr1CIzs+IkTZb0U0nbJW2T9NUiZa6R9K6kl9K2rBZtzZeJnkXD5EkVxc3Maugg8PWIeFHSqcALkjZHRHtBuZ9FxKgZT89Ez6JrV3dFcTOzWomI7oh4Me0fALZzeK28USsTyaJl2Sp6enoHxHp6emlZtqpGLTIzKy29v+cy4Nkih6+S9LKkxyR9srotO1ImhqH6J7GXr1hMw+RJdO3qpmXZKk9um9mw6eUAL/b9tNziEyVtzfu+OiJW5xeQdArwQ+BrEbG/oP6LwNSI+KOk2cCPyS2fVDOZSBaQSxhODmY2SuyLiOmDHZR0PLlE8UBE/KjweH7yiIhNktokTYyIfSPT3NIyMQxlZjZWpMVU7wa2R8S3BynzJ3mvnp5B7u/q31WvlUfKTM/CzGyMuBr4EvCqpJdS7G+BKQARcRe5FbhvkXQQeA+YW+vVuJ0szMyqKCJ+TvGXvuWXaQVaq9Oi8ngYyszMSnKyMDOzkpwszMysJCcLMzMrycnCzMxKcrIwM7OSnCzMzKwkJwszMyvJycLMzEpysjAzs5Iykyyamhtp79jC/t4O2ju20NQ8al4wZWY25mVibaim5kZa21Yeeg/3lKn1tLatBPCy5WZmwyATPYvlKxYfShT96uomsHzF4hq1yMwsWzKRLBomT6oobmZmlclEsuja1V1R3MzMKpOJZNGybBU9Pb0DYj09vbQsW1WjFpmZZUsmksX6tRtZtHApO3fspq+vj507drNo4VJPbpuZDZNM3A0FuYTh5GBmNjIy0bMwM7OR5WRhZlZlkmZJ6pDUKWlJkeOSdEc6/oqky2vRznxOFmZmVSRpPPBd4HrgYmCepIsLil0PTEvbAuDOqjayCCcLM7PqmgF0RsSbEfEh8BAwp6DMHOC+yPkFcIakmj44NmYnuPvig309H3TuqHU7fkbncJ1qIrDvqNvx3nA14xgVf7TlmK6tYq9V7ZeGvq4nqtaOkTACf2Y1/cfx1GM9QV988HjPB50Tyyx+kqSted9XR8TqtF8P7Mo71gV8uqB+sTL1DPZfWBWM2WQREefUug3DSdLWiJhe63aMhKxeW1avC7J9bUcrImYN06lU7PRHUaaqPAxlZlZdXcDkvO8NwJ6jKFNVThZmZtX1PDBN0oWSTgDmAhsKymwAbkp3RV0JvBsRNV2/aMwOQ2XQ6tJFxqysXltWrwuyfW01FREHJS0CHgfGA/dExDZJX0nH7wI2AbOBTqAX+ItatbefImo6DGZmZmOAh6HMzKwkJwszMyvJyWIYSZos6aeStkvaJumrKX6WpM2S3kifZ+bVuS090t8h6fN58SskvZqO3SFJKX6ipLUp/qykC6p4feMl/VLSxoxd1xmSHpb0evqzuypD1/Yf0/8XX5P0oKSTsnJtVmUR4W2YNmAScHnaPxX4FbnH+f8HsCTFlwDfTPsXAy8DJwIXAr8GxqdjzwFXkbvf+jHg+hRfCNyV9ucCa6t4fX8N/ADYmL5n5brWAH+Z9k8AzsjCtZF7iOst4OT0fR3w5Sxcm7fqbzVvQJY34FHgOqADmJRik4COtH8bcFte+cfTf5CTgNfz4vOA7+WXSfvHkXvKVlW4lgbgSeDavGSRhes6Lf2FqoJ4Fq6t/yngs9LvbgQ+l4Vr81b9zcNQIyR1xy8DngXOi3SPdPo8NxUb7JH++rRfGB9QJyIOAu8CZ4/IRQz0d8DfAH15sSxc158CvwX+dxpi+76kOjJwbRGxG1gF7CS3TMS7EfEEGbg2qz4nixEg6RTgh8DXImL/UEWLxGKI+FB1RoykRmBvRLxQbpUisVF3XclxwOXAnRFxGdBDbmhmMGPm2tJcxBxyQ0rnA3WSvjhUlSKxUXltVn1OFsNM0vHkEsUDEfGjFH67f8XI9Lk3xQd7pL8r7RfGB9SRdBxwOvDO8F/JAFcDX5D0G3IrZF4r6e8Z+9fV/7tdEfFs+v4wueSRhWv7LPBWRPw2Iv4R+BHwL8jGtVmVOVkMo3SHyN3A9oj4dt6hDcD8tD+f3FxGf3xuuqPkQnJr1z+XhgYOSLoynfOmgjr957oReCoiRvRfchFxW0Q0RMQF5CYxn4qIL47160rX9v+AXZIuSqGZQDsZuDZyw09XSpqQ2jQT2E42rs2qrdaTJlnagH9Jrgv+CvBS2maTG8N9EngjfZ6VV2cpubtOOkh3mKT4dHKLbf8aaOXw0/YnAevJLQPwHPCnVb7Gazg8wZ2J6wIuBbamP7cfA2dm6NqWA6+ndt1P7k6nTFybt+puXu7DzMxK8jCUmZmV5GRhZmYlOVmYmVlJThZmZlaSk4WZmZXkZGFmZiU5WZiZWUn/HxBwloDiCsncAAAAAElFTkSuQmCC\\n\",\n \"text/plain\": [\n \"
Python 3.6 Jupyter Notebook
\\n\",\n \"\\n\",\n \"# Finding connected components using clustering\\n\",\n \"\\n\",\n \"\\n\",\n \"Note that this notebook contains advanced exercises applicable only to students who wish to deepen their understanding and qualify for bonus marks on the course. You will be able to achieve 100% for this notebook by only completing Exercise 1. Optional, additional exercises can be completed to qualify for bonus marks.\\n\",\n \"
\\n\",\n \"\\n\",\n \"\\n\",\n \"### Your completion of the notebook exercises will be graded based on your ability to do the following:\\n\",\n \"\\n\",\n \"> **Understand**: Do your pseudo-code and comments show evidence that you recall and understand technical concepts?\\n\",\n \"\\n\",\n \"> **Apply**: Are you able to execute code (using the supplied examples) that performs the required functionality on supplied or generated data sets? \\n\",\n \"\\n\",\n \"> **Analyze**: Are you able to pick the relevant method or library to resolve specific stated questions?\\n\",\n \"\\n\",\n \"> **Evaluate**: Are you able to interpret the results and justify your interpretation based on the observed data?\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"#### Notebook objectives\\n\",\n \"By the end of this notebook, you will be expected to:\\n\",\n \"> \\n\",\n \" - Find connected components in networks (using the techniques of hierarchical clustering, modularity maximization, and spectral graph partitioning); and\\n\",\n \" - Interpret clustering results.\\n\",\n \" \\n\",\n \"#### List of exercises\\n\",\n \"> - **Exercise 1**: Understanding hierarchical clustering.\\n\",\n \"- **Exercise 2 [Advanced]**: Interpreting the results of hierarchical clustering.\\n\",\n \"- **Exercise 3 [Advanced]**: Summarizing clustering results based on modularity maximization and spectral graph partitioning.\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"# Notebook introduction\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"Community detection is an important task in social network analysis. The idea behind it is to identify groups of people that share a common interest, based on the assumption that these people tend to link to each other more than to the rest of the network. Specifically, real-world networks exhibit clustering behavior that can be observed in the graph representation of these networks by the formation of clusters or partitions. These groups of nodes on a graph (clusters) correspond to communities that share common properties, or have a common role in the system under study.\\n\",\n \"\\n\",\n \"Intuitively, it is expected that such clusters are associated with a high concentration of nodes. In the following examples, you will explore the identification of these clusters using the following approaches, as discussed in the video content:\\n\",\n \"\\n\",\n \"- Hierarchical clustering (using a distance matrix)\\n\",\n \"- The Louvain Algorithm (using modularity maximization)\\n\",\n \"- Spectral graph partitioning\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"#### Import required modules\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"import networkx as nx\\n\",\n \"import pandas as pd\\n\",\n \"import numpy as np\\n\",\n \"\\n\",\n \"%matplotlib inline\\n\",\n \"import matplotlib.pylab as plt\\n\",\n \"from networkx.drawing.nx_agraph import graphviz_layout\\n\",\n \"\\n\",\n \"from collections import defaultdict, Counter\\n\",\n \"import operator\\n\",\n \"\\n\",\n \"## For hierarchical clustering.\\n\",\n \"from scipy.cluster import hierarchy\\n\",\n \"from scipy.spatial import distance\\n\",\n \"\\n\",\n \"## For spectral graph partitioning.\\n\",\n \"from sklearn.cluster import spectral_clustering as spc\\n\",\n \"\\n\",\n \"## For Community Detection (Louvain Method).\\n\",\n \"import community\\n\",\n \"\\n\",\n \"\\n\",\n \"import sys\\n\",\n \"sys.path.append('..')\\n\",\n \"from utils import draw_partitioned_graph\\n\",\n \"from utils import fancy_dendrogram\\n\",\n \"\\n\",\n \"plt.rcParams['figure.figsize'] = (15, 9)\\n\",\n \"plt.rcParams['axes.titlesize'] = 'large'\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"## 1. Data preparation\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"You are going to read the graph from an adjacency list saved in earlier exercises.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"call_adjmatrix = pd.read_csv('./call.adjmatrix', index_col=0)\\n\",\n \"call_graph = nx.from_numpy_matrix(call_adjmatrix.as_matrix())\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"# Display call graph object.\\n\",\n \"plt.figure(figsize=(10,10))\\n\",\n \"plt.axis('off')\\n\",\n \"\\n\",\n \"pos = graphviz_layout(call_graph, prog='dot')\\n\",\n \"nx.draw_networkx(call_graph, pos=pos, node_color='#11DD11', with_labels=False)\\n\",\n \"_ = plt.axis('off')\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"## 2. Hierarchical clustering\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"This notebook makes use of a hierarchical clustering algorithm, as implemented in [Scipy](http://docs.scipy.org/doc/scipy/reference/). The following example uses the average distance measure. Since the graph is weighted, you can also use the single linkage inter-cluster distance measure (see exercises).\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"def create_hc(G, linkage='average'):\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" Creates hierarchical cluster of graph G from distance matrix\\n\",\n \" \\\"\\\"\\\" \\n\",\n \" \\n\",\n \" path_length=nx.all_pairs_shortest_path_length(G)\\n\",\n \" distances=np.zeros((G.order(),G.order())) \\n\",\n \" \\n\",\n \" for u,p in dict(path_length).items():\\n\",\n \" for v,d in p.items():\\n\",\n \" distances[list(G.nodes)[u]][list(G.nodes)[v]] = d\\n\",\n \" distances[list(G.nodes)[v]][list(G.nodes)[u]] = d\\n\",\n \" if u==v: \\n\",\n \" distances[list(G.nodes)[u]][list(G.nodes)[u]]=0\\n\",\n \" # Create hierarchical cluster (HC).\\n\",\n \" Y=distance.squareform(distances)\\n\",\n \" if linkage == 'max':\\n\",\n \" # Creates HC using farthest point linkage.\\n\",\n \" Z=hierarchy.complete(Y) \\n\",\n \" if linkage == 'single':\\n\",\n \" # Creates HC using closest point linkage.\\n\",\n \" Z=hierarchy.single(Y) \\n\",\n \" if linkage == 'average':\\n\",\n \" # Creates HC using average point linkage.\\n\",\n \" Z=hierarchy.average(Y)\\n\",\n \" \\n\",\n \" return Z\\n\",\n \"\\n\",\n \"def get_cluster_membership(Z, maxclust):\\n\",\n \" '''\\n\",\n \" Assigns cluster membership by specifying cluster size.\\n\",\n \" '''\\n\",\n \" hc_out=list(hierarchy.fcluster(Z,maxclust, criterion='maxclust'))\\n\",\n \" \\n\",\n \" # Map cluster values to a dictionary variable.\\n\",\n \" cluster_membership = {}\\n\",\n \" i = 0\\n\",\n \" for i in range(len(hc_out)):\\n\",\n \" cluster_membership[i]=hc_out[i]\\n\",\n \" \\n\",\n \" return cluster_membership\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"Below is a demonstration of hierarchical clustering when applied to the call graph.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"# Perform hierarchical clustering using 'average' linkage. \\n\",\n \"Z = create_hc(call_graph, linkage='average') \"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"The dendrogram corresponding to the partitioned graph is obtained as follows:\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"hierarchy.dendrogram(Z)\\n\",\n \"plt.show()\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"You will notice that the full dendrogram is unwieldy, and difficult to use or read. Fortunately, the `dendrogram` method has a feature that allows one to only show the `lastp` merged clusters, where $p$ is the desired number of last `p` merged clusters.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"plt.title('Hierarchical Clustering Dendrogram (pruned)')\\n\",\n \"plt.xlabel('sample index (or leaf size)')\\n\",\n \"plt.ylabel('distance')\\n\",\n \"hierarchy.dendrogram(\\n\",\n \" Z,\\n\",\n \" truncate_mode='lastp', # show only the last p merged clusters\\n\",\n \" p=10, # show only the last p merged clusters\\n\",\n \" show_leaf_counts=True, # numbers in brackets are counts for each leaf\\n\",\n \" leaf_rotation=90,\\n\",\n \" leaf_font_size=12)\\n\",\n \"plt.show()\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"This dendrogram can help explain what happens as a result of the agglomerative method of hierarchical clustering. Starting at the bottom-most level, each node is assigned its own cluster. The closest pair of nodes (according to a distance function) are then merged into a new cluster. The distance matrix is recomputed, treating the merged cluster as an individual node. This process is repeated until the entire network has been merged into a single, large cluster, which the top level in the dendrogram above represents. You can now understand why this method is agglomerative.\\n\",\n \"\\n\",\n \"The linkage function is used to determine the distance between a cluster and a node, or between two clusters, using the following possibilities:\\n\",\n \"\\n\",\n \"- **Single:** Merge two clusters with the smallest minimum pairwise distance.\\n\",\n \"- **Average:** Merge two clusters with the smallest average pairwise distance.\\n\",\n \"- **Maximum or complete:** Merge the two clusters with the smallest maximum pairwise distance.\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"Now, you can finally retrieve the clusters, based on the analysis of the dendrogram. In this post-processing, there are different ways of determining $k$, the number of clusters to partition the data into. Scipy's hierarchical flat clustering function - \\\"``hierarchy.fcluster()``\\\" - is used to assign cluster membership by specifying a distance threshold, or the number of clusters required. In the function definition (above), you have been provided with a utility function, \\\"``get_cluster_membership()``\\\", which does the latter.\\n\",\n \"\\n\",\n \"Selecting the number of clusters $k$ is, in general, an ill-posed problem. Different interpretations are possible, depending on the nature of the problem, the scale of the distribution of points in a data set, and the required clustering resolution. In agglomerative clustering, as used in the example above, you can get zero error for the objective function by considering each data point as its own cluster. Hence, the selection of $k$ invariably involves a trade-off maximum compression of the data (using a single cluster), and maximum accuracy by assigning each data point to its own cluster. The selection of an optimal $k$ can be done using automated techniques or manually.\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"Here, identification of an appropriate cluster is ideally done manually as this has the advantages of gaining some insights into your data as well as providing an opportunity to [perform sanity checks](https://joernhees.de/blog/2015/08/26/scipy-hierarchical-clustering-and-dendrogram-tutorial). To select the cluster size, look for a large shift in the distance metric. In our example with dendrograms plots shown above, say a case has been made for an ideal cutoff of 3.5. The number of clusters is then simply the number of intersections of a horizontal line (with height of 3.5) with the vertical lines of the dendrogram. Therefore, 3 clusters would be obtained in this case as shown below.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"fancy_dendrogram( Z, truncate_mode='lastp', p=12, leaf_rotation=90.,\\n\",\n \" leaf_font_size=12.0,\\n\",\n \" show_contracted=False,\\n\",\n \" annotate_above=10,\\n\",\n \" max_d=3.5)\\n\",\n \"plt.show()\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"opt_clust = 3\\n\",\n \"opt_clust\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"You can now assign the data to these \\\"``opt_clust``\\\" clusters.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"cluster_assignments = get_cluster_membership(Z, maxclust=opt_clust)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"The partitioned graph, corresponding to the dendrogram above, can now be visualized.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"clust = list(set(cluster_assignments.values()))\\n\",\n \"clust\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"cluster_centers = sorted(set(cluster_assignments.values()))\\n\",\n \"freq = [list(cluster_assignments.values()).count(x) for x in cluster_centers]\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"# Creata a DataFrame object containing list of cluster centers and number of objects in each cluster\\n\",\n \"df = pd.DataFrame({'cluster_centres':cluster_centers, 'number_of_objects':freq})\\n\",\n \"df.head(10)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"\\n\",\n \"
\\n\",\n \"Exercise 1 Start.\\n\",\n \"
\\n\",\n \"\\n\",\n \"### Instructions\\n\",\n \"\\n\",\n \"> 1. How many clusters are obtained after the final step of a generic agglomerative clustering algorithm (before post-processing)?\\n\",\n \">> **Note:** Post-processing involves determining the optimal clusters for the problem at hand.\\n\",\n \"> 2. Based on your answer above, would you consider agglomerative clustering a top-down approach, or a bottom-up approach?\\n\",\n \"> 3. Which of the three linkage functions (i.e. single, average, or maximum or complete) do you think is likely to be most sensitive to outliers? \\n\",\n \">>**Hint**: Look at this [single-link and complete-link clustering](http://nlp.stanford.edu/IR-book/html/htmledition/single-link-and-complete-link-clustering-1.html) resource.\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"Your markdown answer here.\\n\",\n \"\\n\",\n \"1. \\n\",\n \"2. \\n\",\n \"3. \\n\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"\\n\",\n \"\\n\",\n \"
\\n\",\n \"Exercise 1 End.\\n\",\n \"
\\n\",\n \"\\n\",\n \"> **Exercise complete**:\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"\\n\",\n \"
\\n\",\n \"Exercise 2 [Advanced] Start.\\n\",\n \"
\\n\",\n \"\\n\",\n \"### Instructions\\n\",\n \"\\n\",\n \"> In this exercise, you will investigate the structural properties of the clusters generated from above.\\n\",\n \"\\n\",\n \"> 1. Assign the values from your \\\"cluster_assignments\\\" to a Pandas DataFrame named \\\"df1\\\", with the column name \\\"cluster_label\\\".\\n\",\n \">> **Hint**: The variable \\\"``cluster_assignments``\\\" is of type ``dict``. You will need to get the values component of this dict, **not** the keys.\\n\",\n \"> 2. Add a field called \\\"participantID\\\" to \\\"df1\\\", and assign to this the index values from the previously-loaded \\\"``call_adjmatrix``\\\" DataFrame.\\n\",\n \"> 3. Load the DataFrame containing the centrality measures that you saved in Notebook 1 of this module, into \\\"df2\\\".\\n\",\n \"> 4. Perform an inner join by merging \\\"df1\\\" and \\\"df2\\\" on the field \\\"participantID\\\". Assign the result of this join to variable \\\"df3\\\".\\n\",\n \"> 5. Perform a groupby on \\\"df3\\\" (using \\\"cluster_label\\\" field), and then evaluate the mean of the four centrality measures (using the \\\"`agg()`\\\" method). Assign the aggregation result to \\\"df4\\\".\\n\",\n \"> 6. Review \\\"df4\\\", and plot its barplot. \\n\",\n \"> 7. Merge clusters which share the same mean values for a centrality measure into a single cluster. Assign the smallest value of the labels in the set to the merged cluster.\\n\",\n \">> **Note**:\\n\",\n \"Combine clusters such that, given a cluster with centrality measures $[x1, x2, x3, x4]$, and another cluster with centrality measures $[z1, z2, z3, z4]$, the following holds true:
\\n\",\n \"$x1 = z1$
$x2 = z2$
$x3 = z3$
$x4 = z4$
\\n\",\n \"> 8. Print the size of each cluster, in descending order, after performing the cluster merging in the preceding step.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"# Your code here.\\n\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"
\\n\",\n \"\\n\",\n \"
\\n\",\n \"Exercise 2 [Advanced] End.\\n\",\n \"
\\n\",\n \"\\n\",\n \"> **Exercise complete**: \\n\",\n \"> This is a good time to \\\"Save and Checkpoint\\\".\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"## 3. Community detection\\n\",\n \"Community detection is an important component in the analysis of large and complex networks. Identifying these subgraph structures helps in understanding organizational and functional characteristics of the underlying physical networks. In this section, you will study a few approaches that are widely used in community detection using graph representations.\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"### 3.1 The Louvain modularity-maximization approach\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"The Louvain method is one of the most widely-used methods for detecting communities in large networks. It was developed by a team of researchers at the Université catholique de Louvain. The method can unveil hierarchies of communities, and allows you to zoom within communities in order to discover sub-communities, sub-sub-communities, and so forth. The modularity QQ quantifies how good a \\\"community\\\" or partition is, and is defined as follows:\\n\",\n \"\\n\",\n \"$$Q_c =\\\\frac{1}{2m}\\\\sum _{(ij)} \\\\left [ A_{ij}-\\\\frac{k_ik_j}{2m} \\\\right] \\\\delta(c_i, c_j)$$\\n\",\n \"\\n\",\n \"The higher the $Q_c$ of a community is, the better the partition is.\\n\",\n \"\\n\",\n \"The Louvain method is a greedy optimization method that attempts to optimize the \\\"modularity\\\" of a partition of the network via two steps:\\n\",\n \"\\n\",\n \"1. Locally optimize the modularity to identify \\\"small\\\" communities.\\n\",\n \"2. Aggregate nodes belonging to the same community, and create a new network with aggregated nodes as individual nodes.\\n\",\n \"\\n\",\n \"Steps 1 and 2 are then repeated until a maximum of modularity produces a hierarchy of communities.\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"### 3.2 Spectral graph partitioning\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"Spectral graph partitioning and clustering is based on the spectrum — the eigenvalues and associated eigenvectors — of the Laplacian matrix that corresponds to a given graph. The approach is mathematically complex, but involves performing a $k$-means clustering, on a spectral projection of the graph, with $k$=2 (using an adjacency matrix as the affinity). A schematic illustration of the process is depicted in the figure below.\\n\",\n \"\\n\",\n \"**Optional**: You can read more about [spectral graph processing](https://devblogs.nvidia.com/parallelforall/fast-spectral-graph-partitioning-gpus/).\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"Now, apply spectral graph partitioning to your call graph, and visualize the resulting community structure. You can read more about [Scikit-Learn](http://scikit-learn.org/stable/index.html), and the [Spectral Clustering](http://scikit-learn.org/stable/modules/generated/sklearn.cluster.SpectralClustering.html) function utilized in this section. Spectral graph partitioning needs input in the form of the number of clusters sought (default setting is 8). There are various approaches one can take to optimize the final number of clusters, depending on problem domain knowledge. Below you will use a value of $k=9$.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"# Create the spectral partition using the spectral clustering function from Scikit-Learn.\\n\",\n \"spectral_partition = spc(call_adjmatrix.as_matrix(), 9, assign_labels='discretize')\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"pos = graphviz_layout(call_graph, prog='dot')\\n\",\n \"nx.draw_networkx_nodes(call_graph, pos, cmap=plt.cm.RdYlBu, node_color=spectral_partition)\\n\",\n \"nx.draw_networkx_edges(call_graph, pos, alpha=0.5)\\n\",\n \"plt.axis('off')\\n\",\n \"plt.show()\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"print(spectral_partition)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"\\n\",\n \"
\\n\",\n \"Exercise 3 [Advanced] Start.\\n\",\n \"
\\n\",\n \"\\n\",\n \"### Instructions\\n\",\n \"Compute the size of each the clusters obtained using the spectral graph partitioning method.\\n\",\n \" \"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"# Your code here.\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"\\n\",\n \"\\n\",\n \"
\\n\",\n \"Exercise 3 [Advanced] End.\\n\",\n \"
\\n\",\n \"\\n\",\n \"> **Exercise complete**: \\n\",\n \"> This is a good time to \\\"Save and Checkpoint\\\".\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"## 4. Submit your notebook\\n\",\n \"\\n\",\n \"Please make sure that you:\\n\",\n \"- Perform a final \\\"Save and Checkpoint\\\";\\n\",\n \"- Download a copy of the notebook in \\\".ipynb\\\" format to your local machine using \\\"File\\\", \\\"Download as\\\", and \\\"IPython Notebook (.ipynb)\\\"; and\\n\",\n \"- Submit a copy of this file to the Online Campus.\"\n ]\n }\n ],\n \"metadata\": {\n \"anaconda-cloud\": {},\n \"kernelspec\": {\n \"display_name\": \"Python 3\",\n \"language\": \"python\",\n \"name\": \"python3\"\n },\n \"language_info\": {\n \"codemirror_mode\": {\n \"name\": \"ipython\",\n \"version\": 3\n },\n \"file_extension\": \".py\",\n \"mimetype\": \"text/x-python\",\n \"name\": \"python\",\n \"nbconvert_exporter\": \"python\",\n \"pygments_lexer\": \"ipython3\",\n \"version\": \"3.6.6\"\n }\n },\n \"nbformat\": 4,\n \"nbformat_minor\": 2\n}\n"},"license":{"kind":"string","value":"mit"}}},{"rowIdx":1395,"cells":{"repo_name":{"kind":"string","value":"mjbommar/cscs-530-w2016"},"path":{"kind":"string","value":"samples/cscs530-w2015-midterm-sample1.ipynb"},"copies":{"kind":"string","value":"1"},"size":{"kind":"string","value":"19277"},"content":{"kind":"string","value":"{\n \"cells\": [\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"# Midterm \\n\",\n \"\\n\",\n \"### Goal\\n\",\n \"\\n\",\n \"I will explore whether a network-theory driven approach shown to improve the efficiency of an agricultural extension program is sensitive to the models and parameters originally used.\\n\",\n \"\\n\",\n \"### Justification\\n\",\n \"\\n\",\n \"Social networks have been shown to be important vehicles for the transmission of new agricultural methods or 'technologies' (Bandiera and Rasul 2006, Conley and Udry 2010). These types of dynamics and time-varying agent behavior are best captured with through network modeling.\\n\",\n \"\\n\",\n \"My project is based off a recent paper which used network modeling in conjunction with a large-scale field experiment (Beaman et al 2014). I wish to test the robustness of the findings of their model and so will employ a similar network modeling method.\\n\",\n \"\\n\",\n \"### Background on base paper\\n\",\n \"\\n\",\n \"Beaman and co-authors aimed to improve the rollout of an agricultural extension program using predictions from network theory to optimally select 'seed farmers'. 'Seed farmers' are the select farmers in a village that the agricultural extension program trains. Because it is costly to train farmers in this way, it is most efficient to pick seed farmers such that their adoption of the agricultural technology will lead to the greatest spread of the technology throughout the village. \\n\",\n \"\\n\",\n \"Beaman and coauthors first elicit the social networks of various rural villages. Then under the condition that the extension program only trains two farmers in each village, they take every possible combination of two nodes in a village network and simulate an information diffusion process for 4 periods. They take a measure of information diffusion at the end of each simulation and the pair of nodes which gives the greatest diffusion is their optimal seeding pair. \\n\",\n \"\\n\",\n \"Their findings are then used in a field experiment where a random half of total villages are seeded according to their simulated optimal seeds while the other half is seeded according to the extension program's default procedure, usually based off of a field officer's own knowledge of the village and its influential farmers. They find evidence that network-theory informed seeding leads to increased technological adoption over baseline seeding procedures. \\n\",\n \"\\n\",\n \"### My extensions and measures of interest\\n\",\n \"\\n\",\n \"I wish to recreate and expand upon their simulations in the following ways:\\n\",\n \"- I will compare optimal seeds found with their method against optimal seeds found with an extended process of information diffusion. The extended process will include the possibility that households can reject a new technology even after being exposed to it by multiple connections. The original process assumes that a household will automatically adopt a technology after the number of connections who have adopted the technology passes a certain threshold\\n\",\n \"- I will also sweep across the number of periods simulated and the alpha which the adoption threshold is normally distributed around to see if this produces alternate optimal seeds.\\n\",\n \"\\n\",\n \"### Outline\\n\",\n \"\\n\",\n \"The original paper looks at rural village in Malawi. I do not have access to their network data but I have a dataset of social graphs from 74 villages in South India. Though there may be differences in network structure between villages in these two locations, I will assume they are reasonably comparable.\\n\",\n \"\\n\",\n \"First, I will recreate results from Beaman et al by selecting all combinations of node pairs in a subset of 25 villages. For each pair, I will run them through a information diffusion simulation for {3,4,5,6} steps. I will also sweep through values {1,2,3} for a alpha parameter. Each household has an adoption threshold, T, which determines whether they adopt the new technology or not. If X number of connections have adopted the technology and X=>T, then the household will adopt the new technology in the next period. Each household independently drawns a threshold from a normal distribution N(alpha, 0.5) bounded positive, so sweeping through alpha parameters will push up and down the distribution of household thresholds T. \\n\",\n \"\\n\",\n \"To mitigate stochasticity, I will repeat 2000 times, and take an average measure of information diffusion (given by percent of households adopted at last step). The pair of nodes which give the greatest information difussion are my theory-driven seed farmers equivalent to those found in Beaman et al. I will examine whether the determination of these optimal seed farmers depends on the number of steps run and the alpha parameter used. Then, I will run the same simulations except using the extended information diffusion process described above. I want to see whether seed farmers selected through this method are different than those selected by Beaman's process. For the midterm, I will concentrate on coding the re-creation of method from Beaman et al.\\n\",\n \"\\n\",\n \"\\n\",\n \"### I. Space\\n\",\n \"I will model space with an undirected social network. Each node represents a rural household and each edge represents a social connection. \\n\",\n \"\\n\",\n \"### II. Actors\\n\",\n \"Each node in my network is a household. They are modeled simply and have only a few properties:\\n\",\n \"- id: household id\\n\",\n \"- adopted: whether they have adopted the new technology or not\\n\",\n \"- threshold: the threshold above which they will adopt the new technology in the next period. This threshold will be drawn from a normal distribution with mean alpha and standard deviation 0.5 which is bounded to be positive.\\n\",\n \"\\n\",\n \"In each step, each unadopted household will count the number of connections who have adopted the new technology. If this count exceeds a household's adoption threshold, it will also adopt the technology in the next period.\\n\",\n \"\\n\",\n \"### III. Model Wrapper\\n\",\n \"I will wrap my model in a function which loops through each village, and in each village, loops through every possible pair of nodes. Then, I will sweep through my parameters, number of steps and alpha. I will repeat this under the alternate information diffusion process. I will also determine and collect optimal seeds here.\\n\",\n \"\\n\",\n \"### IV. Initial Conditions\\n\",\n \"Each model will start with a list of adopted households. In the first step, only seed households will be in this list which will be read in through the wrapper.\\n\",\n \"\\n\",\n \"### V. Model Parameters\\n\",\n \"My model will have the following parameters:\\n\",\n \"- network: adjacency matrix that is read in from wrapper\\n\",\n \"- alpha: parameter determining distribution of adoption threshold\\n\",\n \"- HH_adopted: list of adopted households, in first step these are seed households given by wrapper\\n\",\n \"- HH_not_adopted: list of all not adopted households\\n\",\n \"\\n\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 1,\n \"metadata\": {\n \"collapsed\": false\n },\n \"outputs\": [\n {\n \"name\": \"stderr\",\n \"output_type\": \"stream\",\n \"text\": [\n \":0: FutureWarning: IPython widgets are experimental and may change in the future.\\n\"\n ]\n }\n ],\n \"source\": [\n \"#Imports\\n\",\n \"\\n\",\n \"%matplotlib inline\\n\",\n \"\\n\",\n \"# Standard imports\\n\",\n \"import copy\\n\",\n \"import itertools\\n\",\n \"\\n\",\n \"# Scientific computing imports\\n\",\n \"import numpy\\n\",\n \"import matplotlib.pyplot as plt\\n\",\n \"import networkx\\n\",\n \"import pandas\\n\",\n \"import seaborn; seaborn.set()\\n\",\n \"import scipy.stats as stats\\n\",\n \"\\n\",\n \"\\n\",\n \"# Import widget methods\\n\",\n \"from IPython.html.widgets import *\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"## Household class\\n\",\n \"Below is a rough draft of the household class. It only has one component:\\n\",\n \"\\n\",\n \"- constructor: class constructor, which \\\"initializes\\\" or \\\"creates\\\" the household when we call Household(). This is in the __init__ method.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {\n \"collapsed\": true\n },\n \"outputs\": [],\n \"source\": [\n \"class Household(object):\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" Household class, which encapsulates the entire behavior of a household.\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" \\n\",\n \" def __init__(self, model, household_id, adopted=False, threshold=1):\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" Constructor for HH class. By default,\\n\",\n \" * not adopted\\n\",\n \" * threshold = 1\\n\",\n \" \\n\",\n \" Must \\\"link\\\" the Household to their \\\"parent\\\" Model object.\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" # Set model link and ID\\n\",\n \" self.model = model\\n\",\n \" self.household_id = household_id\\n\",\n \" \\n\",\n \" # Set HH parameters.\\n\",\n \" self.adopted = adopted\\n\",\n \" self.threshold = threshold\\n\",\n \"\\n\",\n \" def __repr__(self):\\n\",\n \" '''\\n\",\n \" Return string representation.\\n\",\n \" '''\\n\",\n \" skip_none = True\\n\",\n \" repr_string = type(self).__name__ + \\\" [\\\"\\n\",\n \" except_list = \\\"model\\\"\\n\",\n \"\\n\",\n \" elements = [e for e in dir(self) if str(e) not in except_list]\\n\",\n \" for e in elements:\\n\",\n \" # Make sure we only display \\\"public\\\" fields; skip anything private (_*), that is a method/function, or that is a module.\\n\",\n \" if not e.startswith(\\\"_\\\") and eval('type(self.{0}).__name__'.format(e)) not in ['DataFrame', 'function', 'method', 'builtin_function_or_method', 'module', 'instancemethod']:\\n\",\n \" value = eval(\\\"self.\\\" + e)\\n\",\n \" if value != None and skip_none == True:\\n\",\n \" repr_string += \\\"{0}={1}, \\\".format(e, value)\\n\",\n \"\\n\",\n \" # Clean up trailing space and comma.\\n\",\n \" return repr_string.strip(\\\" \\\").strip(\\\",\\\") + \\\"]\\\"\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"## Model class\\n\",\n \"\\n\",\n \"Below, we will define our model class. This can be broken up as follows:\\n\",\n \"- constructor: class constructor, which \\\"initializes\\\" or \\\"creates\\\" the model when we call Model(). This is in the __init__ method.\\n\",\n \"- setup_network: sets up graph\\n\",\n \"- setup_households: sets up households\\n\",\n \"- get_neighborhood: defines a function to get a list of connected nodes\\n\",\n \"- step_adopt_decision: method to step through household decision\\n\",\n \"- step: main step method\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {\n \"collapsed\": true\n },\n \"outputs\": [],\n \"source\": [\n \"class Model(object):\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" Model class, which encapsulates the entire behavior of a single \\\"run\\\" in network model.\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" \\n\",\n \" def __init__(self, network, alpha, HH_adopted, HH_not_adopted):\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" Class constructor.\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" # Set our model parameters\\n\",\n \" self.network = network\\n\",\n \" self.alpha = alpha\\n\",\n \" self.HH_adopted = HH_adopted\\n\",\n \" self.HH_not_adopted = HH_not_adopted\\n\",\n \" \\n\",\n \" # Set our state variables\\n\",\n \" self.t = 0\\n\",\n \" self.households = []\\n\",\n \" \\n\",\n \" # Setup our history variables.\\n\",\n \" self.history_adopted = []\\n\",\n \" self.history_not_adopted = []\\n\",\n \" self.percent_adopted = 0\\n\",\n \" \\n\",\n \" # Call our setup methods\\n\",\n \" self.setup_network()\\n\",\n \" self.setup_household()\\n\",\n \" \\n\",\n \" def setup_network(self):\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" Method to setup network.\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" ## need to flesh this out. will network be an input given from wrapper? \\n\",\n \" ## what do I need to do to set up network?\\n\",\n \" g = network\\n\",\n \" \\n\",\n \" def setup_households(self):\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" Method to setup households.\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" num_households = nx.nodes(g)\\n\",\n \" # Create all households.\\n\",\n \" for i in xrange(self.num_households):\\n\",\n \" self.households.append(Household(model=self,\\n\",\n \" household_id=i,\\n\",\n \" adopted=False,\\n\",\n \" threshold=stats.truncnorm.rvs((0 - alpha) / 0.5, (alpha) / 0.5, loc=alpha, scale=0.5,size=1) \\n\",\n \"\\n\",\n \" \\n\",\n \" \\n\",\n \" \\n\",\n \" def get_neighborhood(self, x):\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" Get a list of connected nodes.\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" neighbors = []\\n\",\n \" for i in g.neighbors(x):\\n\",\n \" neighbors.append(i)\\n\",\n \" return neighbors\\n\",\n \" \\n\",\n \" def step_adopt_decision(self):\\n\",\n \" \\n\",\n \" \\\"\\\"\\\"\\n\",\n \" Model a household evaluating their connections and making an adopt/not adopt decision\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" will_adopt = []\\n\",\n \" for i in HH_not_adopted:\\n\",\n \" adopt_count = 0\\n\",\n \" for j in get_neighborhood(i):\\n\",\n \" if j.adopted:\\n\",\n \" adopt_count+=1\\n\",\n \" if adopt_count >= i.threshold:\\n\",\n \" will_adopt.append(i) \\n\",\n \" \\n\",\n \" \\n\",\n \" \\n\",\n \" def step(self):\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" Model step function.\\n\",\n \" \\\"\\\"\\\"\\n\",\n \" \\n\",\n \" # Adoption decision\\n\",\n \" self.step_adopt_decision()\\n\",\n \" \\n\",\n \" # Increment steps and track history.\\n\",\n \" self.t += 1\\n\",\n \" self.HH_adopted.append(will_adopt)\\n\",\n \" self.HH_not_adopted.remove(will_adopt)\\n\",\n \" self.history_adopted.append(self.HH_adopted)\\n\",\n \" self.history_not_adopted.append(self.HH_not_adopted)\\n\",\n \" self.percent_adopted = len(HH_adopted)/len(households)\\n\",\n \"\\n\",\n \"\\n\",\n \" def __repr__(self):\\n\",\n \" '''\\n\",\n \" Return string representation.\\n\",\n \" '''\\n\",\n \" skip_none = True\\n\",\n \" repr_string = type(self).__name__ + \\\" [\\\"\\n\",\n \"\\n\",\n \" elements = dir(self)\\n\",\n \" for e in elements:\\n\",\n \" # Make sure we only display \\\"public\\\" fields; skip anything private (_*), that is a method/function, or that is a module.\\n\",\n \" e_type = eval('type(self.{0}).__name__'.format(e))\\n\",\n \" if not e.startswith(\\\"_\\\") and e_type not in ['DataFrame', 'function', 'method', 'builtin_function_or_method', 'module', 'instancemethod']:\\n\",\n \" value = eval(\\\"self.\\\" + e)\\n\",\n \" if value != None and skip_none == True:\\n\",\n \" if e_type in ['list', 'set', 'tuple']:\\n\",\n \" repr_string += \\\"\\\\n\\\\n\\\\t{0}={1},\\\\n\\\\n\\\".format(e, value)\\n\",\n \" elif e_type in ['ndarray']:\\n\",\n \" repr_string += \\\"\\\\n\\\\n\\\\t{0}=\\\\t\\\\n{1},\\\\n\\\\n\\\".format(e, value)\\n\",\n \" else:\\n\",\n \" repr_string += \\\"{0}={1}, \\\".format(e, value)\\n\",\n \"\\n\",\n \" # Clean up trailing space and comma.\\n\",\n \" return repr_string.strip(\\\" \\\").strip(\\\",\\\") + \\\"]\\\"\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"## Wrapper with parameter sweep\\n\",\n \"\\n\",\n \"Below is the code which wrappers around the model. It does the following:\\n\",\n \"- Loops through all villages we wish to examine\\n\",\n \" - Pulls network data from a csv and puts in the appropriate format\\n\",\n \"- Loops through all possible pairs of nodes within each village\\n\",\n \"- Sweeps through alpha and number of steps parameters\\n\",\n \"- Runs 2000 samples\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {\n \"collapsed\": true\n },\n \"outputs\": [],\n \"source\": [\n \"\\n\",\n \"## cycle through villages:\\n\",\n \"## (need to create village list where each item points to a different csv file)\\n\",\n \"num_samples = 2000\\n\",\n \"\\n\",\n \"for fn in village_list:\\n\",\n \" village = np.genfromtxt(fn, delimiter=\\\",\\\")\\n\",\n \" network = from_numpy_matrix(village)\\n\",\n \" for HH_adopted in itertools.combinations(nx.nodes(network),2):\\n\",\n \" HH_not_adopted = [node for node in nx.nodes(network) if node not in HH_adopted]\\n\",\n \" for alpha in [1,2,3]:\\n\",\n \" for num_steps in [3,4,5,6]:\\n\",\n \" for n in xrange(num_samples):\\n\",\n \" m = Model(network, alpha, HH_adopted, HH_not_adopted)\\n\",\n \" for t in xrange(num_steps):\\n\",\n \" m.step() \\n\",\n \"## I need to collect adoption rate at each final step and average over all samples\\n\",\n \"## I am not sure where to fit this in\\n\",\n \"\\n\",\n \"\\n\",\n \"## I also need to write a function which determines optimal seed pairing\\n\",\n \"\\n\",\n \"#######\\n\",\n \"#######\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"## Results\\n\",\n \"I hope to present charts which list optimal seed pairings at each parameter level and information diffusion process. This means optimal pairing will be given for alpha = {1,2,3} for each of num_steps = {3,4,5,6} and this will be done for both the original information diffusion process and the extended process.\\n\",\n \"\\n\",\n \"## Hypothetical results\\n\",\n \"\\n\",\n \"I expect that the optimal seeding is dependent upon the alpha parameter though I suspect it may not be as dependent upon the number of steps parameter.\\n\",\n \"\\n\",\n \"I am more interested in whether optimal seeds given by the extended information diffusion process are different than those given by the original process. I am actually not sure but I suspect that they will be different. If so, they could provide improved predictions to test in the field which hopefully may lead to even more efficient seed farmer targeting.\"\n ]\n }\n ],\n \"metadata\": {\n \"kernelspec\": {\n \"display_name\": \"Python 2\",\n \"language\": \"python\",\n \"name\": \"python2\"\n },\n \"language_info\": {\n \"codemirror_mode\": {\n \"name\": \"ipython\",\n \"version\": 2\n },\n \"file_extension\": \".py\",\n \"mimetype\": \"text/x-python\",\n \"name\": \"python\",\n \"nbconvert_exporter\": \"python\",\n \"pygments_lexer\": \"ipython2\",\n \"version\": \"2.7.11\"\n }\n },\n \"nbformat\": 4,\n \"nbformat_minor\": 0\n}\n"},"license":{"kind":"string","value":"bsd-2-clause"}}},{"rowIdx":1396,"cells":{"repo_name":{"kind":"string","value":"ppyht2/tf-exercise"},"path":{"kind":"string","value":"012. Unsupervised MNIST/Unsupervised MNIST.ipynb"},"copies":{"kind":"string","value":"1"},"size":{"kind":"string","value":"59721"},"content":{"kind":"string","value":"{\n \"cells\": [\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {\n \"deletable\": true,\n \"editable\": true\n },\n \"source\": [\n \"# Unsupervised Learning on the MNIST dataset \"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 8,\n \"metadata\": {\n \"collapsed\": true,\n \"deletable\": true,\n \"editable\": true\n },\n \"outputs\": [],\n \"source\": [\n \"import tensorflow as tf \\n\",\n \"import matplotlib.pyplot as plt\\n\",\n \"import numpy as np\\n\",\n \"import os\\n\",\n \"from tensorflow.examples.tutorials.mnist import input_data\\n\",\n \"% matplotlib inline\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {\n \"deletable\": true,\n \"editable\": true\n },\n \"source\": [\n \"# 1. Loading the data set \"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 9,\n \"metadata\": {\n \"collapsed\": false,\n \"deletable\": true,\n \"editable\": true\n },\n \"outputs\": [\n {\n \"name\": \"stdout\",\n \"output_type\": \"stream\",\n \"text\": [\n \"Extracting MNIST_data/train-images-idx3-ubyte.gz\\n\",\n \"Extracting MNIST_data/train-labels-idx1-ubyte.gz\\n\",\n \"Extracting MNIST_data/t10k-images-idx3-ubyte.gz\\n\",\n \"Extracting MNIST_data/t10k-labels-idx1-ubyte.gz\\n\"\n ]\n }\n ],\n \"source\": [\n \"mnist = input_data.read_data_sets(\\\"MNIST_data\\\", one_hot=True)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {\n \"deletable\": true,\n \"editable\": true\n },\n \"source\": [\n \"### 1.1 Plot a few examples\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 10,\n \"metadata\": {\n \"collapsed\": false,\n \"deletable\": true,\n \"editable\": true\n },\n \"outputs\": [\n {\n \"data\": {\n \"image/png\": \"iVBORw0KGgoAAAANSUhEUgAAAeMAAAMzCAYAAACV1no+AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XmcFNW5//HvM8MAAoKAiMgiKItr1LjvGjTiEreYRJMb\\nETGYqIlGk2hiboxJrjGbue7KFYPmejX+1AhR4kbcF1xRWWRxQUEEwQVEtpk5vz+mqerToWd6ppdT\\nXfN5v168fE6fmq7HeabmTNXpOmXOOQEAgHBqQicAAEB7x2AMAEBgDMYAAATGYAwAQGAMxgAABMZg\\nDABAYAzGAAAExmCcw8ycma0ys/8qcPtLM9s7M+tQ7vzQOtQzfdpQ07Fm9lnm64aWOz+0DsdoE2PR\\nD5+ZOUnDnHPzN9J3qqRbJH3HOXdT1uuDJb0tqc45V1+hVFGAjdUz89rnkjb88N/hnDsjq3+wqGdi\\n5dbUzIZL+oOk/STVSnpB0g+cc3Oa+zokA8dok9T8VVFuZtZT0s8kzQydC0piF34pp8ZmkiZLGiNp\\npaRfSJokabuQSaFo7eoY5TJ14X4r6SpJy0InAiDmnHveOTfBOfeRc269pD9LGmFmvUPnBhSKwbgA\\nZraXpD0k3RA6F5TME2b2gZndk7nkhfQ4SNIHzrnloRNBUdrVMcpg3AIzq5V0naRznHONofNBSRws\\nabCaLmO+L+m+NH0QpD0zswGSrpV0fuhcUJR2d4wyGLfsLEmvOeeeC50ISsM594Rzbp1z7hNJ50oa\\nImn7wGmhSGbWR9JDkq5zzt0eOh+0XXs8RlP9l0aJjJR0sJkdlWn3krSbme3qnDsnYF4oHSfJQieB\\ntst8wPIhSZOdcwXdIoOqkvpjlMG4ZadJ6pzVvkfSXZImBMkGRTGzHSXVSXpd0iaSfiNpkaTZIfNC\\n25lZd0kPSnraOXdR6HxQnPZ6jHKZugXOuU+ccx9s+CdpnaQVzrlPQ+eGNukr6W+SVkh6S03zUsdk\\nPoWL6nSCpD0ljcks7rHh36DQiaFN2uUxyqIfOcxsjaS1kq5yzv1nAdtfoqYPi3SS1NU511DmFNEK\\n1DN92lDTMWq63amzpB2cc2+VOUW0AsdoEwZjAAAC4zI1AACBFTUYm9koM5tjZvPNjA9OpAA1TRfq\\nmT7UNJ3afJk6sxjGXEmHS1qopsXZT3HOzSpdeqgkapou1DN9qGl6FXNr016S5m/4MISZ3SHpOEl5\\nfyg6WifXWV2L2CWKtUartM6tzXe/XqtqSj3DK2U9JWqaBByj6dJCPSPFDMb9Jb2X1V4oae/mvqCz\\numpvG1nELlGsaW5qc92tqin1DK+U9ZSoaRJwjKZLC/WMlH3RDzMbJ2mcJHVWl3LvDmVGPdOHmqYL\\n9axOxXyAa5GkgVntAZnXPM658c65PZxze9SpUxG7QwW0WFPqWVU4RtOHYzSlihmMX5A0zMyGmFlH\\nSSer6QHfqF7UNF2oZ/pQ05Rq82Vq51y9mZ2jpjVhayXd7JybWbLMUHHUNF2oZ/pQ0/Qqas7YOTdF\\n0pQS5YIEoKbpQj3Th5qmEytwAQAQGIMxAACBMRgDABAYgzEAAIExGAMAEBiDMQAAgTEYAwAQGIMx\\nAACBMRgDABBY2Z/aBLTVR6fv67Wf+fU1ebets9ooXu8avL6/r+oVxYM6fOT17Z61jn72e+S+z4i7\\nz/L6hv1gWt5c0Da1I4Z67dk/6pl32wN3mhPFt279hNeXW/98Ftav9tpfeuiHUTzsL+u8Pnvm1YLe\\nE+XVof9WXnv94C2i+JOhm3h9y3d1Udxl8Aqvb8vuK6P4ge0m5d3fY2vqvPYZj4+J4u1//JbX17Dc\\n/93SWpwZAwAQGIMxAACBMRgDABBYu50zrtl00yiu39Wfq6p58pWi33/9Ybt77Ydv+Z8o/tY7h3l9\\nH+9f3FxDWvUf7c/JNKox77brXf7tjuu6LO/XZW+Z/R6573PdURO9vj/+/VtRXPvoy3nfH82rHTok\\nio+/9xmv7+/dFxT0Huudf07R3M9JtgEd/DnGN466Lor/eYg/X33JNadG8ZZX+nmi9Wp79/LaKw8a\\nFsULj/APxK0Gx8fv9dv9n9fXp6Y+ijev9euZrUbmtRvlsuL8Dum83mvPPeLGKH7ooK5e3x/P/o8o\\n7vjgi828a74cAQBAUAzGAAAE1m4vU7/xu+2j+H9H3eD1/WqbLxb9/m+f5N8mk31ZZFTvGV7f7fI/\\nro8mMxf1818YuvHtKuHQTT7z2hecszaKBzxa6WzS461vxzUe0/09r6+wi83lcWSXj7321V9ZGDeu\\nrHAyKVHzhe2iuNt1H3p9k4Zcl7v5xt9DHb32c2vj9uOre3t9P330a61N8d9suuVKr33Vzn+L4s1q\\nPvf6lo6Lb5Ub8GDr98WZMQAAgTEYAwAQGIMxAACBtZs543d+7S+tOP3YK6J4/vra3M2L9rsv/a3l\\njdCsPpM6+y8cnH/bqz+Ob404u+ccr+/R1d2ieMtaf1m87TsW9vfoKW8e5bXt+R4FfR2at81Vb8SN\\nM8Ll0ZIp298dxcdqz4CZVI9l4/zfuQO/Fd+qePuQh72+19fFtyh96+XTvb4OT8THWrfF/icJuk+e\\nHsWNa9Z4fcP1fCszbtlv9YUorunSxevrv2txwylnxgAABMZgDABAYKm+TF3bvXsUn3HCQ15fF8v+\\niHxhT3lpSfZH93fv9FROb/7VYVC8Rw4eHMVTu+3o9bk18W1I1iHnR75DPEWx/MD+XlfvJxdFceMS\\n/1aM/mtYhakUsp908+VZJ3p9fx1xWxS/Vd/N6zv9nu9G8VZP+Zcuu7y3KordSzO9vvovxSvjDbps\\nrtc3fuBjBeW84Ff+5detf/FsQV/XHnxwb3zL6Mt7Xpt3u1rzzwN/vuD4KB7w1Zm5m+cV8va3xs/9\\nW5uKfbIXZ8YAAATGYAwAQGAtDsZmdrOZLTWzGVmv9TKzh81sXua/+Z8CjsShpulCPdOHmrY/hcwZ\\nT5R0jaRbs167SNJU59zlZnZRpn1h6dMrzucHjoji83rmX7Pwz4u/nPPKJ23a36oh8Rz1oA6JniOe\\nqCqoae06/+kta1x8+4M/5y/NuXh4FA89/7m879mhv7/0qPssnl/s9U9/DrFxXfzEltzbJhJmoqqg\\nni3peLj/lKZvj/phFHd5fZHXt+2i/DV2eXukDv96KYofe92/Ralx4L8KyFIaPMm/Pa65/RVhoqqw\\npuOGx5+VaWzmO7PHf53ltfvdVvg8cVq1eGbsnHtCUu4z/o6TdEsmvkXS8ULVoKbpQj3Th5q2P239\\nNHVf59ziTPyBpL75NjSzcZLGSVJndcm3GcIrqKbUs2pwjKYPx2iKFX1rk3POmVne6xHOufGSxktS\\nd+tVpis6G/fuEYV9Pu2Z+dt47WEq78PiL332K157uF7Ks2UYzdW0kvXs8vdpXnu3kedF8ewTrvH6\\nttklvoxZs+mmXl/9rvHjnr5yo3+L2+eNneKvM/9GiZmfxbc6vXqdfztL73viJ281rvSf7JI0ST5G\\nm9PxgReiuL6Z7VrDdo9ve7vpSzcX/HU3fRr/jsi9XSqEpByja4/0L/Xv2vnGvNtu/1i8xNqwW1/3\\n+hoSfgxVQls/Tb3EzPpJUua/S0uXEgKhpulCPdOHmqZYWwfjyZJGZ+LRkiaVJh0ERE3ThXqmDzVN\\nsUJubbpd0rOSRpjZQjMbK+lySYeb2TxJh2XaqBLUNF2oZ/pQ0/anxTlj59wpebpGljiXkvvqAYU9\\ntWPzf3VqeaMC1G9S2IUGW1FXkv21VbXWdPsrlkTx7KP9+d3bh98RxXteea7X98YR1xf0/jU5f5s2\\nbjYvblz2mNe386h4/mvbsfO8vtxl8sqtWusZwvv/Gf/cHNR5ndfX3NKKN10bf85jC5V/KdRqqWnH\\nFeu99jYdsn/2/ds7Zx9yUxR/4/5RXt+i/9kpijf7a/tcXpQVuAAACIzBGACAwFL91Kadu7xX0Ha5\\nKz01J/uB0rmXIz84al3u5hvV/7HE3D1SVerfeieKP2n0L4HtWBNfLiv0snQxXj8ovuT2hYt/4PUN\\nvrh9XmZLiuxj9M0Jw7y+mXvGtzPVyHK/MoouW7az19PvjjeiuDTPeEsHe3q6197/HxdE8UVf+ofX\\nN7b7wij+f9s+6L/R5VntnJnwOz7rE8XX/uJrXl+Pf7wWxZWeHio1zowBAAiMwRgAgMAYjAEACCzV\\nc8b3Lt0tik/Z9IG820353RVee8yZJ0TxjOf9pTJdv/jpPcP/uNbr+8Ve9+Xdx3oXzzR1Wbw673Yo\\nzBn3jvPas0++NlAm0gP/8Qev/d2LDwiUSfuUPUcsSXPHx09rm3XQeK/Pv30p51a2rN6JL+zn9Q1f\\n/mJRObYXw86Ol7C947Ajvb4/HRw/ae0XX7/T6/t6t/yLiWX3nXzFdV7frgPPieIBN/pLbCZ9mdpc\\nnBkDABAYgzEAAIGl+jL1x5cNjuI//H4Hr+/HvWdFcbcafwWu/zd0StwY6nV5t0M0Hlr4LUpXfxw/\\nLUbPvZZ/QxRk2wv8h8uP3e/QKJ4w6NG8X7eswZ8iOHVevNBRw2+38PrqHomfprVsnP/Upu+ff3cU\\nf2vTxV7f/Cv2ieKh5/t5ovTePXdXrz3r0Cvb9D6vrI3PTUZc6/+ccDNi62UfP5I0+JE4vu2/d/H6\\nbjww/kW78Hj/5rHnRl4Vxb1r/FsaX/7h1VG896pzvL4+11fXLYacGQMAEBiDMQAAgTEYAwAQWKrn\\njDs+8EIUP/bpPl7fhK/Hc4xjR/pzjBf2np33PWst6+8X19xzXnw1Vvi2aL0Fl20XxTOvetjrm752\\nYBRfd/lXvb6eE+N5pRrlXz518/H+/NP1q+P3Oe6yP3l9T530xyg+ZeoPvb5O978gFO/N2+LbFmcf\\ncrXXV+iR9m69Py980ffjWnV6hTqVU8Pyj7z2JvfGT9gbdq+/7TcP/X4Uj7nBf4Rz9m1PY86Z4vU9\\n8GD8M5K9lG5ScWYMAEBgDMYAAASW6svU2ezZV7320Kyrjk/U9fD6Ht/9tCj+YN9uXt/ne8ZPBjl8\\n2Bte35VbPZ13/zc+cHgUbytudym1zv+IL3P9ZLm/Olfdgg+juOei0tzukP0A9N1Hft/rm3N4vOrT\\nooP9Q2yb+0uy+3ahuacvzc56alZzT1/KlX1petyYc72+Tv/i0nQS1T76chRfNvEbXt/J51wTxTt3\\n9qeZ7nurZ3kTKzHOjAEACIzBGACAwBiMAQAIrN3MGTfHrV/nv5C1XOWWzUzv/uvOnf0XsuaM365f\\n43UN/8vHUewv9oa2cPv6y+nNGxf/KG/xr45e32bPvF/WXLZ4uM5/If54gC4//jav6+YbvhTF1XC7\\nRUhzLo+Pr9kHXeP1Ffr0pVyHPRDfvjScOeKqs+mB/tOdGrMWKn19zcDczasKZ8YAAATGYAwAQGBc\\npm6lDlv2jeK79xqf0xtfHr1x2YFeT8PMOeVMq91ZcHTOA+W/HF/GnHqg33fVy8dHcTnq0OO2nLmM\\n38fhMV2Xe11X7LFlFHfjMrVnzTF7ee07vnJNni3b7saRE6P4vhf9pz01uvznJm+fFD/Rq35B/pXa\\nUDzr4A9Law6PV9J6epcbvb7sCYnxc/f3+rbSLFUTzowBAAisxcHYzAaa2aNmNsvMZprZuZnXe5nZ\\nw2Y2L/Pf6rrDup1qVKOoZ7pwjKYLx2j7VMiZcb2kC5xzO0jaR9LZZraDpIskTXXODZM0NdNGdaCe\\n6cIxmj7Us51pcc7YObdY0uJMvNLMZkvqL+k4SYdkNrtF0mOSLixLlgny4ahtonh4Xce8202Z5D8l\\napCeKVtOrVGjGjnnXpaqu56Df+4va7nk1HiZw5Gb+NuOfOj/ovjqj/1lFW+7+ogo3vKh/LdAvf2t\\n/l579YD6KH78qCu8vjqLl1Bd71R2aTlGb77W/z4O6NCp5Ps4eJN4OdtDN/Hn+pu7JeqETieXPJd8\\n0nKMtkb2Z3Fm/WqQ1zf36BuyWrlLn8a2/FP+38fVoFVzxmY2WNJukqZJ6pv5JSBJH0jqm+fLkFDU\\nM32oabpQz/aj4MHYzLpJulvSec65Fdl9zjknaaPnAGY2zsxeNLMX12ttUcmidKhn+lDTdKGe7UtB\\ntzaZWZ2afihuc87dk3l5iZn1c84tNrN+kpZu7Gudc+MljZek7tarAhftymt9t/yXSZY0xJdKt7nF\\nv/2hPnfjgNJYzwOnnB/Fb3zl2rzbnd3Tv7Xp7F/E7ZpfFL6Sk8+/nLrexWusFf4exanWmi741b5R\\nPLjDy15f48bHmn/Tmqc2Nfd1P3z/gCj+55wdvL6hc18p6D1LpVrq+emUoV675pbNC/q6Vf38Go35\\nzpQonrzZP3O2zv8794R5x8T7fmp6QftOqkI+TW2SJkia7ZzLntSZLGl0Jh4taVLp00OpuaZfcNQz\\nRThG04VjtH0q5Mx4f0nflvS6mW340+Nnki6XdKeZjZW0QNLXy5MiSqmhaWVs6pkuHKMpwjHaPhXy\\naeqnlP86wcjSpoNy66AOcs5RzxThGE0XjtH2ieUwW8m+vDxv388WHRXFLJlXWSP+Z1UU79zjDK/v\\n9YNuqnQ6kdtX+rdEbfb0u1GcpM8RBJM15uTOERc+3174XP+jq+Pbzm5YdIjXt/zKwVE89J5pBe67\\nfftSv7le+9Ir/lbQ1+XO12fXvrmq/275jv7XfWeTPFtWH5bDBAAgMAZjAAAC4zJ1K1230/+1vBEq\\nzr00M4q3Hbep13fQCT+I4hsv/W+vb/uOpf97dFnWLW7XXf5Vr6/nomdzN2/XesyPL0/+ZYX/cPjR\\n3Re06T1/+H78xLQXrtvN6+szLZ5mapjlX2LtoiVt2l97dsere3rtnx/2YhTXWW2b3vOVdf6F6jHj\\nz43iAb/NXcnwrTbtI4k4MwYAIDAGYwAAAmMwBgAgMOaMW+kLHRuyWv6cyPlbPhzFPzrke15f7WP+\\nUn8on8aVK732ZrfG87QXTz3B61t+aPyEmKVfXuf1zR55Y0H72/6RM/32z+NVCnu+xxxxczb7a/z9\\neeosf2nF5uaMd3xsXBT3eqiz19f7nhlx30r/+98glNKw017y2l+89LwovuPUP3t9O3aMh5upq/0l\\nZM98fHQUj7hutdc34KVkPPGu3DgzBgAgMAZjAAACs6YncVVGd+vl9rbqXs1t4c/2i+LpZ1/t9W33\\naLzy0/Az/dsmGletUhJMc1O1wn2U/zEorZCGela7UtZToqZJwDGaLoXWkzNjAAACYzAGACAwBmMA\\nAALj1qZWGnBZ/DH7Yy7b3esbqleiuNDnzQAAwJkxAACBMRgDABAYgzEAAIExGAMAEBiDMQAAgTEY\\nAwAQWEWXwzSzDyUtkLS5pGUV23F+SclDqlwuWzvn+pTijRJYTyk5uVRdPaWopquUjO+hlJx6SlVY\\nU47RZiWqnhUdjKOdmr3onNuj4jtOaB5SsnJprSTlnpRckpJHWyQpd3IpjSTlnpRckpLHBlymBgAg\\nMAZjAAACCzUYjw+031xJyUNKVi6tlaTck5JLUvJoiyTlTi6lkaTck5JLUvKQFGjOGAAAxLhMDQBA\\nYBUdjM1slJnNMbP5ZnZRhfd9s5ktNbMZWa/1MrOHzWxe5r89K5DHQDN71MxmmdlMMzs3VC6lEKqm\\nSalnZr+pqSnHKPUs4b4TUc/MfhNf04oNxmZWK+laSUdK2kHSKWa2Q6X2L2mipFE5r10kaapzbpik\\nqZl2udVLusA5t4OkfSSdnfk+hMilKIFrOlHJqKeUkppyjEaoZ2lMVDLqKVVDTZ1zFfknaV9JD2a1\\nfyrpp5Xaf2afgyXNyGrPkdQvE/eTNKeS+WT2O0nS4UnIpdpqmsR6VnNNQ9czqTWlnumqZ1JrWsnL\\n1P0lvZfVXph5LaS+zrnFmfgDSX0ruXMzGyxpN0nTQufSRkmrafDvYZXXNGn1lDhGi0E9NyKpNeUD\\nXBmu6U+jin203My6Sbpb0nnOuRUhc0mjEN9DalpeHKPpwjHqq+RgvEjSwKz2gMxrIS0xs36SlPnv\\n0krs1Mzq1PQDcZtz7p6QuRQpaTUN9j1MSU2TVk+JY7QY1DNL0mtaycH4BUnDzGyImXWUdLKkyRXc\\n/8ZMljQ6E49W0zxCWZmZSZogabZz7oqQuZRA0moa5HuYopomrZ4Sx2gxqGdGVdS0wpPmR0maK+lN\\nSRdXeN+3S1osab2a5k7GSuqtpk/QzZP0iKReFcjjADVdCnlN0vTMv6NC5FLNNU1KPdNWU45R6pm2\\nelZLTVmBCwCAwPgAFwAAgTEYAwAQGIMxAACBMRgDABAYgzEAAIExGAMAEBiDMQAAgTEYAwAQGIMx\\nAACBMRgDABAYgzEAAIExGAMAEBiDMQAAgTEYAwAQGIMxAACBMRgDABAYgzEAAIExGAMAEBiDMQAA\\ngTEYAwAQGIMxAACBMRgDABAYgzEAAIExGAMAEBiDMQAAgTEYAwAQGIMxAACBMRgDABAYgzEAAIEx\\nGAMAEBiDMQAAgTEYAwAQGIMxAACBMRgDABAYgzEAAIExGAMAEBiDMQAAgTEYAwAQGIMxAACBMRgD\\nABAYgzEAAIExGOcwM2dmq8zsvwrcfqyZfZb5uqHlzg+tQz3Tpw01vTSzvTOzDuXOD63DMdqEwXjj\\ndnHOXSxJZjbczCaZ2Ydm9pGZPWhmIzZs6Jyb4JzrFi5VFCCqpySZ2Xgzm2NmjWZ2WvaG1LNqeDXd\\nwMxOzfySPmPDa865SyTtWNHs0FrZv3MPzAy22f+cmX1VSu8xymDcss0kTZY0QlJfSc9LmhQ0IxTr\\nVUlnSXo5dCIoHTPrKelnkmaGzgVt55x70jnXbcM/ScdI+kzSA4FTKysG4xY4557P/CX2kXNuvaQ/\\nSxphZr1D54a2cc5d65ybKmlN6FxQUr+VdJWkZaETQUmNlnSXc25V6ETKicG49Q6S9IFzbnnoRAA0\\nMbO9JO0h6YbQuaB0zKyrpJMk3RI6l3JjMG4FMxsg6VpJ54fOBUATM6uVdJ2kc5xzjaHzQUmdqKYr\\nHY+HTqTcGIwLZGZ9JD0k6Trn3O2h8wEQOUvSa86550IngpIbLelW55wLnUi58TH/AmQ+GPKQpMnO\\nuYI+fg+gYkZKOtjMjsq0e0nazcx2dc6dEzAvFMHMBko6RNKZgVOpCAbjFphZd0kPSnraOXdR6HxQ\\nPDPrqKarQiapzsw6S1rHJc6qdZqkzlnteyTdJWlCkGxQKt+W9Ixz7s3QiVQCl6lbdoKkPSWNybnv\\nbVDoxNBmD0laLWk/SeMz8UFBM0KbOec+cc59sOGfpHWSVjjnPg2dG4pyqtrBB7c2YDD+d2slvWRm\\nv5Yk59wtzjlzznXNvvfNOfeuJJnZGDP7JPN1nFklj1dPSXLOHZKpafa/xyTqWSX+rabZMvW9aUPb\\nzC5R073layWlfu6xCm20ns657Zxz/3Z1I63HqLWDeXEAABKNM2MAAAIrajA2s1GZNX7nmxkfbkoB\\napou1DN9qGk6tfkydeZG+7mSDpe0UNILkk5xzs0qXXqoJGqaLtQzfahpehVza9NekuY7596SJDO7\\nQ9JxkvL+UHS0Tq6zuhaxSxRrjVZpnVtrebpbVVPqGV4p6ylR0yTgGE2XFuoZKWYw7i/pvaz2Qkl7\\n525kZuMkjZOkzuqivW1kEbtEsaa5qc11t1hT6pksxdZToqZJwzGaLi3UM1L2D3A558Y75/Zwzu1R\\np07l3h3KjHqmDzVNF+pZnYoZjBdJGpjVHpB5DdWLmqYL9UwfappSxQzGL0gaZmZDMssLnixpcmnS\\nQiDUNF2oZ/pQ05Rq85yxc67ezM5R07rNtZJuds7NLFlmqDhqmi7UM32oaXoV9aAI59wUSVNKlAsS\\ngJqmC/VMH2qaTqzABQBAYAzGAAAExmAMAEBgDMYAAATGYAwAQGAMxgAABFbUrU2Js9fOXvPdozaN\\n4sbtP8v7ZT0nd/HaPeatihvPv16a3JB48/+6m9e+df8JUfzLMWO9vprHX6lITgDaB86MAQAIjMEY\\nAIDAqu4ytXXyn0Iyd/yOUfzwIVd5fYM6bJL3fWoUP16y8QDn9b1bvzqKr152iNc35cE9o3jolW96\\nfQ1LlubdH5Kpw9bxmvtvfOkmr69RjVG8ya8We31rDy5vXqi8Pac3RPGUGw7w+vrc8Gyl00E7w5kx\\nAACBMRgDABAYgzEAAIFV3Zzx27eO8NrP73d1FO/58HleX5/H6wp6z1XHrvDahw+eE8V/2HKa1/eH\\n0XF75in1Xt9Jd58bxdv+6LmC9o2w5n9nQOgUEEju5082rf0oio/73uNe3/MPDI3i+nfeLW9iaJc4\\nMwYAIDAGYwAAAqu6y9SzDpjotff47Y+jePg1z7TpPXve4rfndO4cxccO/5bX1+fG96P4L4Me8/pe\\nOzm+tWrUzt/w+roc/V4Uu3r/8jaA1llxyj5R3P32tk0JNe6+nde+sPctebaUhn83vpdtyEVcpt5g\\n7ZF7eu2Hb7oh77Y7Tzgnijeb699O2uN/mdbjzBgAgMAYjAEACIzBGACAwKpuzjhX3+fi25JcM9u1\\nRuOaNXHjtTe8viX7xvHQ8Wd6fXOPjudLpu50l9c34oqzonjYD/zbpRBO912Xh04BBajZyZ/fvfG3\\n/x3F/7HV+V5fvz8V9tmR7a6aVXxi8GQvIZvr9bHXRPHihtVe36XnjIri6Tf7T9/zWE67mV/6fR+L\\nlyde36+711f72br4Lef6nwFoXLky/5uWEWfGAAAExmAMAEBgVXeZetc/n+O1By6YF8UNuRuX2fBx\\nL3jtEVfHl6LnnXi91/ePY+PLamc/+AOvr9P9/vugcv60w51RXGe1Xt/6rEtgs58b4vVtow/Kmhd8\\nb1zQ1Wt/oWN8++Hpp0/x+h68fqsobvz8c69v1Vf3juI/9bsuZy9x/e9Y2dPrGTphSRRX+vdMknV5\\n3n9y3c5Pjo3i1w+ckPfr+tb6q59dN/DRuHHJo8qnJuf8sbnL4n85b3AUD+64zOtb0Rj//ExftbXX\\n9+JZu0WxPftq3vcvNc6MAQAIrMXB2MxuNrOlZjYj67VeZvawmc3L/Ldnc++BZKGm6UI904eatj+F\\nnBlPlDTMyjlHAAAgAElEQVQq57WLJE11zg2TNDXTRvWYKGqaJhNFPdNmoqhpu9LinLFz7gkzG5zz\\n8nGSDsnEt0h6TNKFJcwrr63+6N+2kKT5m+E/fCmKh24yzuube+SNUbz7r17y+mbcX968ciWtppXU\\nYcu+XruzrY/i9c7/23TyqvjEY/iNi72+JC1omtZ61m4/LIpfP/zanN54zm+HTou8ngdrB0Zx7pOZ\\nOpwZz/3mfkYg2y//drLX3nresy3mW0rVUtOG5R957aE/7xHFbz2y3u+r82tRbmN6vJO3r0bxZwmO\\n6+rPJ4/qvlcUdyx5Vvm1dc64r3Nuw2+nDyT1bW5jVAVqmi7UM32oaYoV/QEu55xTM7dem9k4M3vR\\nzF5cr7XF7g4V0FxNqWf14RhNH47R9GnrrU1LzKyfc26xmfWTtDTfhs658ZLGS1J361WqRbISKftp\\nTH2eqvM7j4zDy7f0b2U6RruXM61CFVTTaq/noq9v67V3aeY61IzVA6K4/q13ypRR2VT/MXrdqijs\\nVtM572a/mv8Vr9115VtRXNunj9f32E735n2fzxrjlfeG3POp15f/BpqKSvwx2jD/7Sg+87zzvL4P\\nd80/3Fxyyu1RfEK3vD+qZfHrD7/otbvMiy9bV3I6qq1nxpMljc7EoyVNKk06CIiapgv1TB9qmmKF\\n3Np0u6RnJY0ws4VmNlbS5ZION7N5kg7LtFElqGm6UM/0oabtTyGfpj4lT9fIEueCCqGm6UI904ea\\ntj9VtxxmpdV06eK13Y7b5tlS+nj7blG82Tz/qSRz18dPCRle509U1vbdIoobllR2vgRIig79t/La\\nJ275ct5tG1w8i/v5vf6HirsqnjP+fK/BBe//gvcPjeLG6TzRqVib3Pu81x6Uf7pef/llvCTlrX33\\n9Ppm/zprucqcpzYN3SZelnbKds3sIEf2bW0vf22Y19fw1lu5m1cEy2ECABAYgzEAAIFxmXojPvta\\n/GSX3X4y3ev781YTo7gm55pJY3NPum5mLZeB/4gfZv3e0f6tGA0fftjMe6K1Dvj2Sy1vlPG/M+OV\\neLbR9Ga2RCnM/b7/9JyxPabk2VLa55V4haw+N/irY2VP+4y4ZIYKNe9nO0RxnQr/OUFp5U7VDR+X\\nf+rusBnx787mnuCUe/tS9qXpxrffbW2KZcGZMQAAgTEYAwAQGIMxAACBtds547VHxx+fv/7aK72+\\n4XX5b6nI/mz999/fz+s5pMfsKP5q148LzuXGAfGcV8N0f97jG299OYqXXTbE6+v0T39ZTWxc9u1p\\nQ7u87/dl/T2a+xSfrs/6t7WhvDp9Yi1vlPHIrrdE8YQZO3p9R3aLn+y2fUdqmCZLz/J/547u8Yes\\nlv+5nJs+3SaKp9xwgNfXp8JP4SoEZ8YAAATGYAwAQGDt5jJ1TdeuXjv70nTuQ6/nro+f3nLUIz/w\\n+gZNiv9+6fwPf4WZBf32jeJLT9vG65t+ztV5c9vp6W9H8V92n+j13TA4ay348f7X7TklfirK8DO5\\nZJ3Pp1/5QhR/b7PHvb7sSYHZ6/zHzfV79KONbofyGHTTHK9962mbR/Gp3f0HwPeo2SSKz++Vu2IS\\nl6aTIPsWM0nSZt3zbuvei6eP3Hr/WUnv/mSPKP7mN/7l9fWoiS9N/3ixfwl7/jcHRXGfucm7LJ2L\\nM2MAAAJjMAYAIDAGYwAAAms3c8Zzf7Oz1x5e92QU//GjEV7fE8fGy+INf/vFgvdRvzh+gojrsE3e\\n7f6+qpfXHvS116P4Eu3u9a3/cjxf8lm/Oq/PXzgTxVrS0M1rN854I1Am7VPDsuVe+45jD47iS87v\\n7fUNHbY4in85ZJLXt3/nws4xtrnrTK+9/Yx3orheaIvseeJdH/jA67t0i39Gce7Slfu8GH9u5rNV\\nnb2+GQfHn++pyTl/zH6X+57zl7wcNndaYUknBGfGAAAExmAMAEBgqb5MvfTs+KPuL570R6/v7lX9\\noviJ4/wVfOrffqdN+3vzD/GtTc+d/Iec3vjSy4WPfd3rGa78tyXVPRRfJu/ZpqxQqDEPnuG1h+v5\\nPFuiEhrmvhnFw7/7Zt7tzjn7HK/9ysXX5d326o/jJ0ONuHiW11e/cmXu5mitrNuXsi9LS/4Kd+tz\\nHnD3/B63NfOm+VfJy36fy798h9f36598K4q3+v0zSjrOjAEACIzBGACAwBiMAQAILNVzxpseG9/+\\n0K3GX/Jy6ifx7Uv1b73Tpvdffsa+Xvuxb8TzxNnL9Un+7Uzb/8xfvq+hTXtHoTqcvqSg7Tp+VNvy\\nRkic2rWu5Y0yrnjyiCgevpLPBJSaffZ5FI//dLDXN67HO1H85Vknen2/3faeKN6tU/7FZ/d8+RSv\\n/cmM+Ja3YRP843xQ/aIoroZb1TgzBgAgMAZjAAACS/Vl6j8P/1sU1+T8rz5z525RvJUK/9h74wG7\\nRvH3Lvi719evNn5azPR1/oWRG846KYrrlr1U8P7QetbJn5IY3D1e2Sl3BR+k29KGVV57+yvinwWm\\nh0qvflH89KX7T/Kn8e4aNCqKnflf9/jvt4vi3Tr5t5xtN+WsKB7+Hf820Oy1DKu9nvxmAgAgsBYH\\nYzMbaGaPmtksM5tpZudmXu9lZg+b2bzMf1mTogo0qlHUM104RtOFY7R9KuTMuF7SBc65HSTtI+ls\\nM9tB0kWSpjrnhkmammmjOlDPdOEYTR/q2c60OGfsnFssaXEmXmlmsyX1l3ScpEMym90i6TFJF5Yl\\nyzb60/vxbQy3DH7E6/tsu3UFvcfKk/fx2uf96vYo/mrXj72+Me8eEsXv/sp/ElSnR/IveVlJNaqR\\nc+5lqfrqWaiGvXbw2v8zaHwU579ponpV8zFabisb/duespfYTKq0HKMNs+Z67Y5ZU8Fnz/P7jujy\\naRSvcf7nbbrN8Z9Wl1atmjM2s8GSdpM0TVLfzC8BSfpAUt+SZoayo57pQ03ThXq2HwUPxmbWTdLd\\nks5zzq3I7nPOOUkbvfPezMaZ2Ytm9uJ6rS0qWZQO9Uwfapou1LN9KejWJjOrU9MPxW3OuQ1LpSwx\\ns37OucVm1k/S0o19rXNuvKTxktTdehW+VE4JPPvasLiRc5n6/H0fjuK/nnaU1/fZwPhz90+M85++\\n1KMmfvrS0IfGeX3bnx+vrNXp42Rclt6Yaq1nuW26IHQGbdfuamrxMfr5qPxPW5rw0X55+5Ks3dUz\\ny64P+0/hGv7H5D9xqRQK+TS1SZogabZz7oqsrsmSRmfi0ZImlT49lJpr+mOaeqYIx2i6cIy2T4Wc\\nGe8v6duSXjez6ZnXfibpckl3mtlYSQskfT3P1yNBGppujaee6cIxmiIco+1TIZ+mfkqS5ekeWdp0\\nUG4d1EHO5a5/E6GeVYhjNF04RtunVC+Huf2fPoziy/bb2ev7+eYzovi7/3VN3vd4dm1Xrz06a554\\nuwtmen0Nq/yl91Bdev/Ps6FTQIE69N8qimft9795t7vrgf299hBR4ySoNf8mwx++f2AUDx/TPpcL\\nZjlMAAACYzAGACCwVF+mbpj/dhQ/f9xQr2/7y/eI4vq1/rdh0+nx7Uv97/vA6xs+L34geRpXc2pv\\n9vrDuVG8ZSue3oXk+rRxdRQPmcTUUVK8/5P4NrMDOvvTBZPzTpG3H5wZAwAQGIMxAACBMRgDABBY\\nqueMs9W/867XHnLyu3m29DWUIxmUVc2Tr3jtY/vvmXdb5omr0+c7xbc23buqm9d35fe/E8Udn0vu\\nsrTtzfqsu0Q7mz/0PPf+4CjeUrMrlFGycGYMAEBgDMYAAATWbi5TA0iPjg/El5+vH+bftthRXJpO\\norqsu8zWuHqvr9f1XdXecWYMAEBgDMYAAATGYAwAQGDMGQMAym6r38e3EZ50hP8o5i7zlkWxP5vc\\nfnBmDABAYAzGAAAExmVqAEBF1Yx8z2u310vT2TgzBgAgMAZjAAACYzAGACAwc85VbmdmH0paIGlz\\nScta2LwSkpKHVLlctnbO9SnFGyWwnlJycqm6ekpRTVcpGd9DKTn1lKqwphyjzUpUPSs6GEc7NXvR\\nObdHxXec0DykZOXSWknKPSm5JCWPtkhS7uRSGknKPSm5JCWPDbhMDQBAYAzGAAAEFmowHh9ov7mS\\nkoeUrFxaK0m5JyWXpOTRFknKnVxKI0m5JyWXpOQhKdCcMQAAiHGZGgCAwCo6GJvZKDObY2bzzeyi\\nCu/7ZjNbamYzsl7rZWYPm9m8zH97ViCPgWb2qJnNMrOZZnZuqFxKIVRNk1LPzH5TU1OOUepZwn0n\\nop6Z/Sa+phUbjM2sVtK1ko6UtIOkU8xsh0rtX9JESaNyXrtI0lTn3DBJUzPtcquXdIFzbgdJ+0g6\\nO/N9CJFLUQLXdKKSUU8pJTXlGI1Qz9KYqGTUU6qGmjrnKvJP0r6SHsxq/1TSTyu1/8w+B0uakdWe\\nI6lfJu4naU4l88nsd5Kkw5OQS7XVNIn1rOaahq5nUmtKPdNVz6TWtJKXqftLyn5Ux8LMayH1dc4t\\nzsQfSOpbyZ2b2WBJu0maFjqXNkpaTYN/D6u8pkmrp8QxWgzquRFJrSkf4MpwTX8aVeyj5WbWTdLd\\nks5zzq0ImUsahfgeUtPy4hhNF45RXyUH40WSBma1B2ReC2mJmfWTpMx/l1Zip2ZWp6YfiNucc/eE\\nzKVISatpsO9hSmqatHpKHKPFoJ5Zkl7TSg7GL0gaZmZDzKyjpJMlTa7g/jdmsqTRmXi0muYRysrM\\nTNIESbOdc1eEzKUEklbTIN/DFNU0afWUOEaLQT0zqqKmFZ40P0rSXElvSrq4wvu+XdJiSevVNHcy\\nVlJvNX2Cbp6kRyT1qkAeB6jpUshrkqZn/h0VIpdqrmlS6pm2mnKMUs+01bNaasoKXAAABMYHuAAA\\nCIzBGACAwBiMAQAIjMEYAIDAGIwBAAiMwRgAgMAYjAEACIzBGACAwBiMAQAIjMEYAIDAGIwBAAiM\\nwRgAgMAYjAEACIzBGACAwBiMAQAIjMEYAIDAGIwBAAiMwRgAgMAYjAEACIzBGACAwBiMAQAIjMEY\\nAIDAGIwBAAiMwRgAgMAYjAEACIzBGACAwBiMAQAIjMEYAIDAGIwBAAiMwRgAgMAYjAEACIzBGACA\\nwBiMAQAIjMEYAIDAGIwBAAiMwRgAgMAYjAEACIzBGACAwBiMAQAIjMEYAIDAGIwBAAiMwTiHmTkz\\nW2Vm/1Xg9mPN7LPM1w0td35oHeqZPtQ0XdpQz8My9Ww0s8PKnV+lMBhv3C7OuYs3NMxsvJnNyRT/\\ntOwNnXMTnHPdKp4hWiOqp5ltbmZPm9lyM/vEzJ41s/03bEg9q0Z2TQ/M/HLO/ufM7KsSNa0Sub9z\\nv2RmL5vZCjN7y8zGbehzzj2Sqee7QTItEwbjwrwq6SxJL4dOBEX7TNLpkvpI6inpd5L+YWYdgmaF\\nNnPOPemc67bhn6Rj1FTnBwKnhjYwszpJf5d0o6Qekr4h6Qoz2yVoYmXGL6ACOOeulSQzWxM6FxTH\\nObdG0hxJMrMaSQ1qGpR7SVoaMDWUzmhJdznnVoVOBG3SS1J3SX91zjlJL5jZbEk7qOnEKJU4M0a7\\nZGavSVojabKkm5xzDMQpYGZdJZ0k6ZbQuaBtnHNLJN0uaYyZ1ZrZvpK2lvRU2MzKizNjtEvOuS+Y\\nWWdJJ0jqGDoflMyJkpZJejx0IijK7ZJuknRlpv0959x7AfMpO86M0W4559Y4526XdFHa56PakdGS\\nbs1c3kQVMrPtJN0h6VQ1/aG8o6SfmNnRQRMrMwZjQKqTtE3oJFAcMxso6RBJtwZOBcXZSdJc59yD\\nzrlG59wcSfdLOjJwXmXFYFwAM+uYuaRpkurMrHPmwz+oMma2j5kdkKnpJmZ2oaS+kqaFzg1F+7ak\\nZ5xzb4ZOBEV5RdKwzO1NZmbbqukT8q8FzqusGFAK85Ck1ZL2kzQ+Ex8UNCO0VSdJ10paLmmRpKMk\\nHe2cez9oViiFU8UHt6pe5o+p0yVdJWmFmub/71bTHHJqMRj/u7WSXjKzX294wTl3iHPOcv49Jklm\\nNsbMPsl8XWOYlNEMr57Oucedc7s45zZ1zvVyzh3snHtiw8bUsyr82zEqSc657ZxzE3I3pqaJt7Hf\\nuXc653bKHKcDnHMXOucaJcnMRmbq2VdNtyamgvE5BwAAwirqzNjMRmWWiZxvZheVKimEQ03ThXqm\\nDzVNpzafGZtZraS5kg6XtFDSC5JOcc7NKl16qCRqmi7UM32oaXoVs+jHXpLmO+fekiQzu0PScZLy\\n/lB0tE6us7oWsUsUa41WaZ1ba3m6W1VT6hleKespUdMk4BhNlxbqGSlmMO4vKXtFlIWS9m7uCzqr\\nq/a2kUXsEsWa5qY2192qmlLP8EpZT4maJgHHaLq0UM9I2ZfDzDz6apwkdVaXcu8OZUY904eapgv1\\nrE7FfIBrkaSBWe0Bmdc8zrnxzrk9nHN71KlTEbtDBbRYU+pZVThG04djNKWKGYxfUNMqKUPMrKOk\\nk9X0BBxUL2qaLtQzfahpSrX5MrVzrt7MzpH0oKRaSTc752aWLDNUHDVNF+qZPtQ0vYqaM3bOTZE0\\npUS5IAGoabpQz/ShpunEcpgAAATGYAwAQGAMxgAABMZgDABAYAzGAAAExmAMAEBgZV8OEyiHml13\\n8NrXTBofxYM75F8CsNb8vz8vXLJrFN81czevb8tJHaO42/+b1qY8AYSx6qR4ye57/3yF13fQDT+O\\n4oGXPet/YRufZFgszowBAAiMwRgAgMC4TL0R2ZdAB41/2+ub8cddorjbnc9VLCf4Gjap89pXfnho\\nFG9Su97r+80WL8UN15i3z9tO0vpDGqJ49u/9/X/n9+dG8RY3+V/n1q9rJnMAldD1rnhq6Xid7/U9\\n/ec/RvHXnzjb66t58pXyJpYHZ8YAAATGYAwAQGAMxgAABMac8UYs+mX80fZ/DvA/9v6Fbw6O4u6T\\nO3t9jWvWlDUvxOzZV732nD2y+jr4P9bH7vTtKH7/kM28vhW7rI3in+7zT69vx04Lo3ivTv7tDi/8\\n/Noo3nnzc7y+gb9+prnUAVRY9vyxJJ145ilRvGyfTby+rZ6sSEr/hjNjAAACYzAGACAwLlNvxOnD\\n4kvTDTm3wly4/UNRPHHvY72+msfDfCQePldf77enz4riLaf7226ZFd+tLby+SUP2jOKet33q9d2y\\n9b+i+Csn+pelX/1tfFjl5gKgeTWbbuq3u8Yr6uUeTw3LlrdpH4s/7h7F6/s3NrNl5XBmDABAYAzG\\nAAAExmAMAEBgzBm34PV1/tKKv7j/a1G83fx3vT5mB9Ol/u0FUfzc0/v6nVlzxif08JfDnDHghPg9\\n3vF/RgD8uw4DB0TxHvf5SxBf2ie+12hh/Wde34FT42VpB91d6/V1feKNuLFFb6/vkX2uj+Jj/viT\\n1idcBpwZAwAQGIMxAACBcZm6Bf9atb3XrlsZ//1Sv+j9SqeDClp00X5RPOeb13h9tRb/HIy+7Xte\\n3+B3ch5WnkL1I3f32lNuvSGKO8i/XPhcvMiZzpt1stf33W2fiOKxPT7w+rJvK3yzfrXX963Xx7Qu\\n4VaqudO/rLnZremvaSVlX5aWpN3+EU8JXdpnZt6ve7+hk9d+cuSVUTzgiG5e348/2C2Kn126udc3\\nY11c360mzvD6GhQGZ8YAAATGYAwAQGAtDsZmdrOZLTWzGVmv9TKzh81sXua/PcubJkqJmqYL9Uwf\\natr+FDJnPFHSNZJuzXrtIklTnXOXm9lFmfaFpU8vjBvvPCqKZ4zz5wqv7puKG5gmqp3VNJ/aHUdE\\n8fqrPvf6nh7xpyhuVEevb88XvxHFgy95vkzZFWyiKlzPlQP870fuPHG2fbKm+Z7b7Y682zW4vF3a\\ntoP/ZJ3m3qcUbthma689+dbeebYsm4lK8TE65/I+Xvv+Le6L4qmr/Z+ln//nd6K4532zvD4NiBe0\\nnf0D/4lsbx87Pm5s6S9VvN1N8ec8tl6RjM8DtHhm7Jx7QtJHOS8fJ+mWTHyLpONLnBfKiJqmC/VM\\nH2ra/rR1zrivc25xJv5AUt8S5YNwqGm6UM/0oaYpVvStTc45Z2Z5LzCZ2ThJ4ySps7rk2yxR1m6e\\n/8PtnRen/26w5mpajfXMtvr4vbz2b66IL2Xt28mv+1pnUfy1+Ud5fVuO+TCKGxpD3QxRmHIco71u\\ne8Fr7979nHh/+a9Y/5tuo+LbmRbP9y9durr41qYRw/zbCOfM7R/F3bdc6fX1676i8ASy/GrIvVF8\\nYrfZXt9kHdCm9yyXajxG1x4dPwXtXwf+2euburpHFP/u1G97fd2ffi6Kc4+0mrr45+A3h97t9b22\\nbk0U/8fV53t9g6+JV81rZnakotp6ZrzEzPpJUua/S/Nt6Jwb75zbwzm3R5065dsM4RVUU+pZNThG\\n04djNMXaOhhPljQ6E4+WNKk06SAgapou1DN9qGmKFXJr0+2SnpU0wswWmtlYSZdLOtzM5kk6LNNG\\nlaCm6UI904eatj8tToA6507J0zWyxLkkRs1ay9tXuzZvV9VIfU1r/EnLd34VzxPPGnOt19fYzIzR\\nF+4+L4qHnftc3u1CC1FPV+/f4tf36mfa9kb/HYfD9Fb+/eW0h2tRwdsWasxP4ycAPfK937fxXUoj\\njcfokt3ronhQB3/pynPePjyK6xZ86PU1donnvedduovXd8tX4+O5s/k/k9/7SXz89rvT//lMyjxx\\nNlbgAgAgMAZjAAACS/99Om1Qsz7/ZepBN82J4mTf0NJ+ZV+WlqQZY7JXUctf21yXH3l7FP9+xje9\\nvt7/k4xVe1A6Aw9f0PJGaLPBkz+J4qXfWeX1TR72QBTfMdVf5fOGBQdH8fydrvf6DplxYhR3+aH/\\nyfFuM5M7tbQxnBkDABAYgzEAAIExGAMAEBhzxpK0185e87Sj/5V300+/NCyKu925vGwpoe2OOXKa\\n167Jmif+3fLtvb6nlm8bxV/d8mWv77Tu8RKMjT/ynxJ0w/snRXGn+/2lIVGdlqzcNHQKqdY4PX7i\\n0vE/usDr2//C+Jj9Q84Tlk7eKV6m9KDXT/D6uh63OIob1qxRNePMGACAwBiMAQAIjMvUkvT8617z\\n6SPjS5erp73q9X20ffz3i7+GDJLijeO38tpHDhgTxbWvzvP6Gj+PL0Xfs/WeXt/ce9+L4t9s8ZLX\\nd8O5WasE3d/mVJEgn34Sr/R0zKune32ba26l00m1ulWNXvvoHq/m2dI3css5Xvu52p55tqw+nBkD\\nABAYgzEAAIExGAMAEBhzxhtRvyieRzxhztcCZoK2qH9vode2rHZj7sbZX7fgPa/9j3v2i+LffNef\\nMx606UdRvLSDfxjlPtEIyVTbdwuv/dyXro7iQ6adWel0Uu+zr+0dxdf/4Uqv76OGeL5+x2vO8vqu\\nP+O6KL6kzyyvb9Twb8WNV2aWIs1gODMGACAwBmMAAALjMnUrHXHs81E8+9KAiSCovwx6LIqP7XOU\\n11e/+IMKZ4O2+GzfwV67d80mYRJJqbVH+7cKnvnru6P4w4auXt9Pfz0uigdMfMbrm/bN+FbTgzq/\\nWcoUE4UzYwAAAmMwBgAgMAZjAAACY864Besbar324T1mRPG8ASO9vvqFiyqSEypj9aD1efumru4U\\nxW7N2kqkgxJbvn3+X38Ns3mCU1t02GZwFI+4dLrXd1y3+NbBw/7zfK+v18Rn4/fYeqDXd3jXu6J4\\nYb1/TNasip/U1ND6dBOFM2MAAAJjMAYAIDAuU7fkyj5e89AbV0Txj87Y2usb9EsuU1ezhkO/6LX/\\ndli88k+N/OmKqxYeFn/dx4uF6rN6hD+9UJ91obPvi9V+0TOMd0+Kn5h2/1b3en3b3HVeFA/7y7PK\\nZ9ZP+3ntXTvFU0Lb3P0Dr2/Y3GltyjOJODMGACAwBmMAAAJrcTA2s4Fm9qiZzTKzmWZ2bub1Xmb2\\nsJnNy/w3PU95TrFGNYp6pgvHaLpwjLZPhcwZ10u6wDn3spltKuklM3tY0mmSpjrnLjeziyRdJOnC\\n8qUaRqf7X/Daj67pHsUHHfWK1/fOLyuRUUm023rmqt1xRBRv+qt3vb7dOsZ/q76w1nl96y7uG8Wm\\n4HPG7foYbY0O/baM4qmH+k8OempNjyjeZNLzCqwq69l/1IIoPnH+4V7f8Avi35f+0SStOGWfKP77\\nEVfm9MZzxls8Z0XnmFQtnhk75xY7517OxCslzZbUX9Jxkm7JbHaLpOPLlSRKp0Y1op7pwjGaLhyj\\n7VOrPk1tZoMl7SZpmqS+zrkNpwQfSOqb52vGSRonSZ3VZWObIBDqmT7UNF2oZ/tR8GBsZt0k3S3p\\nPOfcCrP4coFzzplZ7pWHDX3jJY2XpO7Wa6PbVJNznviPKJ52uH85ZfROY6O4ccYbFcupLZJSz89P\\n2Ntrd1jdGMWdlnzepvf8eKfuXnvZF/On+ZfjbojifTv5t7PMXh+v9nP6BH/FoIFP+0+WSYKk1DTJ\\nXK/4UvSgDv5AdcQz8bE9RK9WLKd8qqGeVtfRa+/b++0ofuFj/9bPj0/ePYo/2tl/nxe/eUUU98h5\\netaQyfETnYbf7k8bpklBn6Y2szo1/VDc5py7J/PyEjPrl+nvJ2lpeVJEqVHP9KGm6UI9259CPk1t\\nkiZImu2cuyKra7Kk0Zl4tKRJpU8PpeaaPjpBPVOEYzRdOEbbp0IuU+8v6duSXjezDSt//0zS5ZLu\\nNLOxkhZI+np5UkQpNTStMkQ904VjNEU4RtunFgdj59xTkvJ9nnxkntdTq9+D8bds1Uh/OuaNH3aL\\n4uFjlUgd1EHOucTUs25lvdeeMCGehx/QwZ87qsn6MWz8t5sjClOT86Oc/T7PrvWXvDz/snOieOBN\\nyZsj3oBjtHDvnNg7dAotStox2qwaP80utfESo/cN/6e/7e+ae6P4WB/yj+94PcPPeiluNKZ3mVJW\\n4AIAIDAGYwAAAuOpTa206d+ei+Ivf/HHXt/Pj/17FN+1y6FeX+Ors8ubWJWqe+Qlr/29E8+M4kU/\\n95h5jEsAACAASURBVC9F77xFvNLVLYMfadP+zlq0v9d+4v7donjwpE+8vt7T8z9ZBtWpoVP+6Y2u\\nT3atYCbp4Nb6T766fmq86taPv/am1/fQ53VR/N/v+atzrbs0Xhlt+OMv5uwk1XfbRTgzBgAgMAZj\\nAAACYzAGACAw5oyLMPSvH3vtB/ffMYpX/X6N17fJERVJqeq5l2ZG8VYn+H3Ls+JjtLvaZrXXGqT4\\nlqXG3E2ROgcd/loUf9zo/yxs8eLKSqeTOsPOjT9Tc8S5uzaz5fteqzan3R5xZgwAQGAMxgAABMZl\\n6iLkPpnp0wPieBPvoiqAEDoM8Z8cdF7fO6L4imX7+hs//3olUgI2ijNjAAACYzAGACAwBmMAAAJj\\nzhhAar15Wn+vvV1dpyj+20z/9riheqUiOQEbw5kxAACBMRgDABAYl6kBtEuu0UKnAEQ4MwYAIDAG\\nYwAAAmMwBgAgMHPOVW5nZh9KWiBpc0nLKrbj/JKSh1S5XLZ2zvUpxRslsJ5ScnKpunpKUU1XKRnf\\nQyk59ZSqsKYco81KVD0rOhhHOzV70Tm3R8V3nNA8pGTl0lpJyj0puSQlj7ZIUu7kUhpJyj0puSQl\\njw24TA0AQGAMxgAABBZqMB4faL+5kpKHlKxcWitJuScll6Tk0RZJyp1cSiNJuScll6TkISnQnDEA\\nAIhxmRoAgMAYjAEACKyig7GZjTKzOWY238wuqvC+bzazpWY2I+u1Xmb2sJnNy/y3ZwXyGGhmj5rZ\\nLDObaWbnhsqlFELVNCn1zOw3NTXlGKWeJdx3IuqZ2W/ia1qxwdjMaiVdK+lISTtIOsXMdqjU/iVN\\nlDQq57WLJE11zg2TNDXTLrd6SRc453aQtI+kszPfhxC5FCVwTScqGfWUUlJTjtEI9SyNiUpGPaVq\\nqKlzriL/JO0r6cGs9k8l/bRS+8/sc7CkGVntOZL6ZeJ+kuZUMp/MfidJOjwJuVRbTZNYz2quaeh6\\nJrWm1DNd9UxqTSt5mbq/pPey2gszr4XU1zm3OBN/IKlvJXduZoMl7SZpWuhc2ihpNQ3+Pazymiat\\nnhLHaDGo50YktaZ8gCvDNf1pVLH7vMysm6S7JZ3nnFsRMpc0CvE9pKblxTGaLhyjvkoOxoskDcxq\\nD8i8FtISM+snSZn/Lq3ETs2sTk0/ELc55+4JmUuRklbTYN/DlNQ0afWUOEaLQT2zJL2mlRyMX5A0\\nzMyGmFlHSSdLmlzB/W/MZEmjM/FoNc0jlJWZmaQJkmY7564ImUsJJK2mQb6HKapp0uopcYwWg3pm\\nVEVNKzxpfpSkuZLelHRxhfd9u6TFktarae5krKTeavoE3TxJj0jqVYE8DlDTpZDXJE3P/DsqRC7V\\nXNOk1DNtNeUYpZ5pq2e11JTlMAEACIwPcAEAEBiDMQAAgTEYAwAQGIMxAACBMRgDABAYgzEAAIEx\\nGAMAEBiDMQAAgTEYAwAQGIMxAACBMRgDABAYgzEAAIExGAMAEBiDMQAAgTEYAwAQGIMxAACBMRgD\\nABAYgzEAAIExGAMAEBiDMQAAgTEYAwAQGIMxAACBMRgDABAYgzEAAIExGAMAEBiDMQAAgTEYAwAQ\\nGIMxAACBMRgDABAYgzEAAIExGAMAEBiDMQAAgTEYAwAQGIMxAACBMRgDABAYgzEAAIExGAMAEBiD\\nMQAAgTEYAwAQGIMxAACBMRjnMDNnZqvM7L8K3P7SzPbOzDqUOz+0ThvqOdbMPst83dBy54fW4xhN\\nF47RJuacC51DopiZkzTMOTc/57XPJW34Zt3hnDsjq3+wpLcl1Tnn6iuXLVqSW08z21zSJEnbSaqV\\nNFvSj5xzTzf3dUiOPMforpImSNpeTTUd65ybntU/WByjiZSnnuMlHSxpmKTTnXMTC/m6asaZceF2\\ncc51y/w7o+XNkVCfSTpdUh9JPSX9TtI/OGOqXmbWUU1/YP2vmmp6i6RJmddRnV6VdJakl0MnUikM\\nxmhXnHNrnHNznHONkkxSg5p+gfcKmxmKcIikDpL+2zm31jl3lZpq+6WgWaHNnHPXOuemSloTOpdK\\nYTAu3BNm9oGZ3ZO55IUqZmavqelAnyzpJufc0sApoe12lPSa8+fcXsu8DlQFBuPCHCxpsJrmGd+X\\ndB+XNaubc+4LkrpL+qakpwKng+J0k/RpzmufSto0QC5AmzCgFMA590QmXGdm50paoaYPirweLisU\\nyzm3RtLtZjbbzKY7514NnRPa5DM1/WGVrbuklQFyAdqEM+O2cWqak0I61EnaJnQSaLOZkr5gZtnH\\n5BcyrwNVgcG4BWa2o5ntama1ZtZN0p8kLVLT7ROoMma2j5kdYGYdzWwTM7tQUl9J00LnhjZ7TE0f\\nxPuBmXUys3Myr/8rXEooRub47Kymk546M+tsZqker1L9P1cifSX9TU2Xpt9S09zxMc659SGTQpt1\\nknStpOVq+qPqKElHO+feD5oV2sw5t07S8ZJOlfSJmm5dOz7zOqrTQ5JWS9pP0vhMfFDQjMqMRT9y\\nmNkaSWslXeWc+88Ctr9E0vlq+iXf1TnXUOYU0QptqOcYSX+W1FnSDs65t8qcIlqJYzRdOEabMBgD\\nABAYl6kBAAisqMHYzEaZ2Rwzm29mF5UqKYRDTdOFeqYPNU2nNl+mNrNaSXMlHS5poaQXJJ3inJtV\\nuvRQSdQ0Xahn+lDT9Cpm0Y+9JM3fMHluZndIOk5S3h+KjtbJdVbXInaJYq3RKq1za/PdI92qmlLP\\n8EpZT4maJgHHaLq0UM9IMYNxf0nvZbUXStq7uS/orK7a20YWsUsUa5qb2lx3q2pKPcMrZT0lapoE\\nHKPp0kI9I2VfDtPMxkkaJ0md1aXcu0OZUc/0oabpQj2rUzEf4FokaWBWe0DmNY9zbrxzbg/n3B51\\n6lTE7lABLdaUelYVjtH04RhNqWIG4xckDTOzIZmHeJ+spsfRoXpR03ShnulDTVOqzZepnXP1mTVg\\nH5RUK+lm5xwLs1cxapou1DN9qGl6FTVn7JybImlKiXJBAlDTdKGe6UNN04kVuAAACIzBGACAwBiM\\nAQAIjMEYAIDAGIwBAAiMwRgAgMDKvhwmAITy4PvT2/R1py44yGsv2XdFKdJBG9TuOCKK53ynp9fX\\nZ/iyKO5x1PyK5VQOnBkDABAYgzEAAIGl+jL1796eFsW7dvIXTB9y33eiuPfz/reh903PljcxtEnN\\nrjtE8ZzzOxf8dQP6fhzFR281w+u78ZUDo7jffR29vk3//nIUu/XrCt4fKuvzE/wnCD557Y1Fv+et\\nWz/hv/B+HB549pleV5e/TxNKJ/uytCTtd/urUfz33q/n/brb3+jvte884eAobpg9r0TZlQ9nxgAA\\nBMZgDABAYAzGAAAElqo54/f+cz+vvWPHl6J4vWvw+uYefUPcd5Tft/aS+ij+4kM/8PrqltRFcdf3\\nzevb4ppnWpkxctV07RrFb07Y1ut7cN/ronhAh028vkY1tml/5498I36Pkf577LH1uVG81R+obZLM\\n//M+UfzmN25oZsvSy52TPlDxHDLzx8XLvX2puXnibN/adLHX/lvH6hreODMGACAwBmMAAAKrrvP4\\nFmz+er3XXtawOu6r3SR380id1eZtzx2V/zaJtW69117y4/o8W0ovrBkYxZfeforXN/DBVVFsz76q\\n9uydC3aJ4tcPvDKnt5Py+ahhbRTPq+/m9W1WsyaKR9T5tW7O/2/vzsOjKtI1gL9fSEgAQQlgCFsC\\nJEGiI4s4AzKiXmAQhgs6oyJuOKKgogJ6VXDGBUcZR1FmVBwuigL34jLXDVxGVNQBkVVFZJFNdgib\\nyL5kqftHmnNOtZ5Op7c6ffr9PY8PVamTPp/5OFS6qqvqaOPIhr4p9oKXLyV6aDqU7d3s6aqCtwwG\\n4hPfXT5Bq6fKU8h3xkRERIaxMyYiIjKMnTEREZFhvpozrvX2Iq2+fby9vWHDEFOFnRZfo9Wbnrrf\\nKs8oesf1+zIlQ6u3SM9wuRJocYp9usjvb3pGa9v6B3tuu8ec27W2gmu/dn1NP8ofZ5+yc0FnfW79\\n3+1escpdHrpNa6u7xZ6vr/nBYq0tvXkzqzz0k0+0tt61D0YeLMWVc544FltcVkfwqU0/2R7TwTl/\\n3Wtk+7jFRP7Gd8ZERESGsTMmIiIyzFfD1MFufdDeQemNR57Q2nIcS53SPtR3fFFTN1vl7j1u0dpK\\nBtrLZK5uu0Rrm76qk2ss2fWOWOW57V7T2mo4NvIa+Av9NT/vbe80lPkvffjVjyqO2D+n7Kt2a23F\\nD9lD+AXPh3+ylsqypyuypDTEleQlLe9ZFdfXb/3azVq9YOQCq7xufLF+cYhhaqJY4DtjIiIiw9gZ\\nExERGVZlZywiL4rILhFZ7vhatoh8JCJrA3/WD/Ua5C3Mqb8wn/7DnKaecOaMpwB4FsA0x9dGAZit\\nlHpMREYF6vfGPrzonDbNnldc+YD+9zanlj33m95nj9ZW8Zy9PWWtGfpyqZYz7PKixs31tpJlrrFI\\npr2VY/+Cq/TGMvvUKNmvL7XJLInLPPEUJEFOy3/cr9ULRixwuRKocWYbq7ypXwOtbeltzwRfbkmD\\nPWE/8PveWlvhQyussse35JuCJMhnVXLm19PqoZYTOQUvQ5q3wJ7vdc4DA/pyqYK33P8+NZmj9C8M\\nCCuUWJoCH+Q0kVaV6p8HkRPu2xN7UZXvjJVScwD8EPTl/gCmBspTAVwS47gojphTf2E+/Yc5TT2R\\nfpo6Ryl18vDIEgA5bheKyBAAQwAgC7UjvB0lQFg5ZT6TBp9R/+Ez6mNRL21SSikRUSHaJwGYBAD1\\nJNv1OpOm/+Ilrf7JyiLXa9/ddbZV/vGZFlpbnTd2un6fOm6fKlS+YnV1Q0yoUDn1Sj7XTjlHq799\\noX3SS/DJTKGGmMfs7miVD97dRG886D7tkEy8/Iw6h42n5UW2y9aGx9tq9VDDz7XfWhjWazpPYqqK\\nPkx+IOzvi0YyPKOJ1v8TfVe+olVLXK70pkg/Tb1TRHIBIPDnrtiFRIYwp/7CfPoPc+pjkXbGMwEM\\nCpQHAZgR4lpKDsypvzCf/sOc+lg4S5teATAfQBsR2SoigwE8BqCniKwF0CNQpyTBnPoL8+k/zGnq\\nqXLOWCk10KWpe4xjiathr9+o1Vde+6xVbpmepbUNPnUz3DjbJj7cSmv7YIk9n1y2aUtEcSaCH3K6\\nuuckrV6BEMdyhbDkB3vef90V+odd2uwvtMpq0zb9fo5tO01LpnyuG99ZqztPPKqO84cNtcrhzgPH\\ni7aUCu7z1dWRTDmNtQzRn+XSMGe9G8x3PzUvGXAHLiIiIsPYGRMRERnm61ObnBot1cc6dl511Co7\\nT3ACgPnH7WGSxzb10doea/mmVb75tO+1tqeH2dcWTdCaPD1snYxmH9WHlC+qdSii13mnzUyrXNEm\\naBGUY9elkdvP15pW/ck+oavmrORaQpFozuVLkQ5L/+SEpRDLl2Ih0jgpMuvH2dMXpepLra0ixOLE\\np/edYZUbVOMkNy/iO2MiIiLD2BkTEREZxs6YiIjIsJSZM677qj7H1KfpPVY5a48+n5y90p5/VIu/\\n1dpuvH6kVX7hofFa28qr7eVSZx++XWtrMYZzxrE0/hr9GJ1bb7H/Kl961lKtbWzj6Je+jG8yV6sv\\nn2ifKDT6miFam8zT75/q5k6IbJtL5zxx8OlL8eCc2waYw3hKy9KXk2a2POhyZWgvvdrLKjfHF1HF\\nZBrfGRMRERnGzpiIiMiwlBmmDpb7pPuQRqgNX+pPsT8+f2VffVevb7pMtcrv3/C41jbomzutcq23\\nF4UZJblaoJ+oVOgYxVwedGk/nOv6Mkf7/9IqN7xrg9Y2rdU7VjlT9N19zq5pl8dN15fBDB9qnx6T\\nisue9OFeINIh30QMTTtFOpye6Dj9QLVtrdW/6jzFUUvN94ip+X9NRETkIeyMiYiIDGNnTEREZFjK\\nzhnHwukv6dtoootdbJaut2XevsOuvB3HoKhaas2w5+8PB50Oe+6D9jz/X66ZprX1rr3PKrfN0OeT\\nD91+wCpnz4pFlMllezeJ6Pt6NWkf40hCi3Ru23liFADUhtlTo/wgzfG+MNJTm5Id3xkTEREZxs6Y\\niIjIMA5TR6HOV/quWv+5up9Vdp4GBACX5NpDYDPRIL6BUUy0GGMvf/vrmmu0tt7jnnH9vvfavWSV\\n/9D0cq2tbNv2GEXnXV4+8WjdePt0oEjjrP0Wh6WjtfV+ve48mSl4WNrZtvC4PiXU9LMjMY/NFL4z\\nJiIiMoydMRERkWHsjImIiAzjnHEUynaUaHV1v700Y/PLR7W2nnW+s8r//M+RWlvWO9we0+vSj4W/\\nvuK70jpWWZWVxSMcz3HOxVZn+0vtZCbEflvJ4OVLkc4TO5czcSlT9FrU31f1RT/jYIV+2lPGD/ac\\ncXlUEZnHd8ZERESGsTMmIiIyjMPUMeQ8VP7GNVdrbR8Wv2mV1W279W98B5Qgu249T6sPGva+VX5x\\nch+tLfcpe2nT3jP1XYFCuWvlFVY5e+ea6oaYlJrMcQzjDwj/+7p2XmmVd0Z47+Ch6Jb3rLLK0/LC\\nP4npuk3drPKGx9tqbVzO5A1bTujLQstX+uf54jtjIiIiw6rsjEWkuYh8KiIrRWSFiAwPfD1bRD4S\\nkbWBP+vHP1yKVgUqwHz6C59Rf+EzmprCeWdcBuAupVQxgM4AholIMYBRAGYrpQoBzA7UKTkwn/7C\\nZ9R/mM8UU+WcsVJqB4AdgfJBEVkFoCmA/gAuDFw2FcBnAO6NS5Q+c2v+Z1r9JeQl7N5pSINS6ivA\\nv/mUjJpaffWz7azymr76Npbzjtnb6x3K1xdHbH7Anl9eNjR4+0v3U2ZqvXBateKNlheeUeec6nX3\\ndNPapuXNcf0+rS1op1DnHG7I76vGUqpQr7+zi33alsnlS6nwjKaJvlQw3FObMiTZFzC5q9acsYjk\\nA+gAYCGAnMA/AgBQAiAnppFR3DGf/sOc+gvzmTrC7oxF5BQAbwAYoZQ64GxTSikAP7srgogMEZEl\\nIrKkFMejCpZih/n0H+bUX5jP1BLW0iYRyUDlX4rpSqmTa3R2ikiuUmqHiOQC2PVz36uUmgRgEgDU\\nk+y4HhN9+Pf6EocDefZwR7Op32lt5Xt/iPp+kpmp1Tf+saNVfjjvZa3tuCq1yqM/0U/yKUJid+BK\\nlnxGatvITlr9u75/t8oVQdfe8j/2DlB12+u7As2+9AXH9+lD306Xre+l1U+Zv9EqJ2pQzUs5DV4W\\nhAnuw9ShhBrejpRzaNo5LO01XspnPFQo0ethntrUOONHra1GsZ3PZF/mFM6nqQXAZACrlFJPOZpm\\nAhgUKA8CMCP24VGsqcpfpplPH+Ez6i98RlNTOO+MuwK4FsC3InLykxL3AXgMwD9FZDCATQCucPl+\\n8pDyyvdqzKe/8Bn1ET6jqSmcT1N/DkBcmrvHNhyKt3SkQynFfPoIn1F/4TOamny1Hea+NvpH4r8a\\nZs8VTrihjdb28eXn2JXd4c8frx9eZJVP7bhHa/u2/bNWuVTps4WP7P6lVS66hac0xZrqYi9fmnzL\\n30NcqVt2k71kqeInM8ru88TLT9gTW4f76B+SqTh4MOz7+1Hw1pGtu9nz8pGemhQp56lQAFAwMvYn\\nQ1Hi9KilP1t3/66hVW7u9zljIiIiii92xkRERIb5api62dgvtPrng+2DqG+vv1Zru/1jvR6+D11b\\nDlXYw5Ud3xmhtRXdyqHpeErfe8gq15XSoNYMROKtQ6db5UdX9tbamt9knzFUcXBvRK+fKpxDw62h\\nDxvHYtg61FB0ATgs7UVb383Xv3BneN/XdvZQrd76syOxCcgD+M6YiIjIMHbGREREhrEzJiIiMkwq\\ntzhNjHqSrX4lZpbJbX7wPK3+2h/sjW3aZkQ2pzjzsH6c6AuX/9YqV3yzKqLXjLeFajYOqB/c1jBW\\ni8l8hlJ/XrZWn5o/y/Xath8PdW07Y6y9XWL56nXRBxYHscwn4N2cppJUeEZTSbj55DtjIiIiw9gZ\\nExERGearpU2htBijL3u6e0znONzFm0PTqWZfV31HtX441/XaQnzl2ubfY8yJyGv4zpiIiMgwdsZE\\nRESGsTMmIiIyjJ0xERGRYeyMiYiIDGNnTEREZBg7YyIiIsPYGRMRERnGzpiIiMgwdsZERESGJfTU\\nJhHZDWATgIYA9iTsxu68EgeQuFjylFKNYvFCHswn4J1Yki6fgJXTw/DGzxDwTj6BJMwpn9GQPJXP\\nhHbG1k1FliilOiX8xh6NA/BWLNXlpdi9EotX4oiEl2JnLLHhpdi9EotX4jiJw9RERESGsTMmIiIy\\nzFRnPMnQfYN5JQ7AW7FUl5di90osXokjEl6KnbHEhpdi90osXokDgKE5YyIiIrJxmJqIiMiwhHbG\\nInKxiKwWkXUiMirB935RRHaJyHLH17JF5CMRWRv4s34C4mguIp+KyEoRWSEiw03FEgumcuqVfAbu\\n65uc8hllPmN4b0/kM3Bfz+c0YZ2xiNQAMAFAbwDFAAaKSHGi7g9gCoCLg742CsBspVQhgNmBeryV\\nAbhLKVUMoDOAYYGfg4lYomI4p1PgjXwCPskpn1EL8xkbU+CNfALJkFOlVEL+A9AFwCxHfTSA0Ym6\\nf+Ce+QCWO+qrAeQGyrkAVicynsB9ZwDo6YVYki2nXsxnMufUdD69mlPm01/59GpOEzlM3RTAFkd9\\na+BrJuUopXYEyiUAchJ5cxHJB9ABwELTsUTIazk1/jNM8px6LZ8An9FoMJ8/w6s55Qe4AlTlr0YJ\\n+2i5iJwC4A0AI5RSB0zG4kcmfobMaXzxGfUXPqO6RHbG2wA0d9SbBb5m0k4RyQWAwJ+7EnFTEclA\\n5V+I6UqpN03GEiWv5dTYz9AnOfVaPgE+o9FgPh28ntNEdsaLARSKSEsRqQngSgAzE3j/nzMTwKBA\\neRAq5xHiSkQEwGQAq5RST5mMJQa8llMjP0Mf5dRr+QT4jEaD+QxIipwmeNK8D4A1ANYD+GOC7/0K\\ngB0ASlE5dzIYQANUfoJuLYCPAWQnII5fo3IoZBmApYH/+piIJZlz6pV8+i2nfEaZT7/lM1lyyh24\\niIiIDOMHuIiIiAxjZ0xERGQYO2MiIiLD2BkTEREZxs6YiIjIMHbGREREhrEzJiIiMoydMRERkWHs\\njImIiAxjZ0xERGQYO2MiIiLD2BkTEREZxs6YiIjIMHbGREREhrEzJiIiMoydMRERkWHsjImIiAxj\\nZ0xERGQYO2MiIiLD2BkTEREZxs6YiIjIMHbGREREhrEzJiIiMoydMRERkWHsjImIiAxjZ0xERGQY\\nO2MiIiLD2BkTEREZxs6YiIjIMHbGREREhrEzJiIiMoydMRERkWHsjImIiAxjZ0xERGQYO2MiIiLD\\n2BkTEREZxs6YiIjIMHbGREREhrEzJiIiMoydMRERkWHsjImIiAxjZxxERJSIHBaRR8O8fkzgeiUi\\n6fGOj6qH+fSfCHI6WEQOBb6vIN7xUfXwGa0kSinTMXiKiCgAhUqpdUFfOwLg5A/rVaXUjY72fAAb\\nAGQopcoSFy1Vhfn0H5ec1gAwBsANAOoCWAfgIqXUj6G+j8wLlRcRuQ7AVAA3KaVecHw9Hz57Rn3z\\nW0UCtOND7CvMp7+MAXAegC4ANgM4E8AxoxFRVESkPoD7AKwwHUsisDMmoqQW+Ed7BCp/wdoU+PJy\\ngyFRbPwFwNMArjAdSCJwzjh8c0SkRETeDAyRUHJjPv3jFwDKAFwWyOkaERlmOiiKnIj8EkAnABNN\\nx5Io7IzDcwGAfABnANgO4F0/fXAgBTGf/tIMwKkAigC0BHAZgIdEpKfRqCgigfn/5wDcppSqMB1P\\norAzDoNSao5S6kTgwyDDUfnAtzUcFkWI+fSdo4E/H1ZKHVVKLQPwKoA+BmOiyN0KYJlSaoHpQBKJ\\n7wYiowCI6SAoZpjP5LYs8KdzaQiXiSSv7gAuEJGTv0xlA+ggIu2VUrcZjCuu2BlXQUTOBJAB4FsA\\ntQA8AmAbgFUm46LIMJ/+o5RaLyJzAfxRRO4A0ArAlQAGmo2MInQ9gCxH/U0ArwOYbCSaBOEwddVy\\nALwG4ACA71E519hXKVVqMiiKGPPpTwMB5AHYC+A9APcrpWabDYkioZT6USlVcvI/ACcAHFBK7Tcd\\nWzxx048gInIMwHEATyul7g/j+gcB3AkgE0AdpVR5nEOkamA+/SeCnP4BwHhUvtsqVkp9H+cQqRr4\\njFZiZ0xERGQYh6mJiIgMi6ozFpGLRWS1iKwTkVGxCorMYU79hfn0H+bUnyIepg4szF4DoCeArQAW\\nAxiolFoZu/AokZhTf2E+/Yc59a9oljb9EsC6kx+GEJFXAfQH4PqXoqZkqizUieKWFK1jOIwT6rjb\\nmtpq5ZT5NC+W+QSYUy/gM+ovVeTTEk1n3BTAFkd9K4BfBV8kIkMADAGALNTGr6R7FLekaC0Mvdqj\\nypwyn94SbT4B5tRr+Iz6SxX5tMT9A1xKqUlKqU5KqU4ZyIz37SjOmE//YU79hflMTtF0xtsANHfU\\nmwW+RsmLOfUX5tN/mFOfiqYzXgygUERaikhNVG4/NzM2YZEhzKm/MJ/+w5z6VMRzxkqpMhG5DcAs\\nADUAvKiUWhGzyCjhmFN/YT79hzn1r6gOilBKvQ/g/RjFQh7AnPpLKubzyKX255nmTvhvra31azdb\\n5YKRyXlCXyrmNBVwBy4iIiLD2BkTEREZxvOMiSipOYelgZ8OTRMlA74zJiIiMoydMRERkWHsjImI\\niAzjnHEUNjzWRavPuPJJq1yUkaW1/WbVJVY5vcfm+AZGlEK2d6tyD35LkzmRnVJHFG98Z0xERGQY\\nO2MiIiLDOExdhbSzz9DqjSfZe7K/33yC1nZc2T/OfRVHtbZLcr+xyu+ifixDJEo568Z3tsrrB0x0\\nve66Td20eu23FsYtJr+Sc87U6je88q5VvrTOD1pb9+WXWeVavTbENzCf4TtjIiIiw9gZExER3aKF\\nhAAAEYdJREFUGcbOmIiIyDDOGQPYf3VnrZ41qMQqv952stZ2apq9ZOnhPWdrbe8+Z89PHW2kL7e4\\nZeB7UcdJlKqCt7wMNU/stLPLgXiEk1LWDDpFq/evs8cqVwRd+9FZ/7TKfS8YorWl/fvrmMeW3rSJ\\nVS75bZ7rdQ0nzY/5vWON74yJiIgMY2dMRERkWMoMU5f2OEerl9x83Cov6vw3rS1TMqzy/ON1tLZB\\nH9pDL2fctUJra3jYHgo5fJk+rPbUgp5WuQhLwg2b4sy5bKO8dk3X64401tv2DzwU3uuLvuPTod32\\n36e2o9fr12bYf+9OFDbR2tLmxn6Iz+ucQ9PVOYnp/GFDrXJtcClTtP7W+38i+r5RL07T6k9d2Nsq\\nl23ZGtFrOoelAeDEtBpW+Ysznnb9vjPaD9Prdy6zyhXHjkUUS6zxnTEREZFh7IyJiIgMY2dMRERk\\nmK/njGvknG6V88eu1No+ajrPKu8qL9PaOn5hzwu3HntCaytatsgqB3+s36nO6/pcVdHrVYZLUXDO\\nLwZveai6trfKG/SpI7zX1d7SNC9dnxdOc/yuWhEy2+7Sgn7fdb7OA+eeq7Vlpx+2yiOy39Xa+jXV\\nr00F4Z7GxC0vvalblv5v55NZ7p/JCFfw8qVQ88ROa/r/Q6sXH7zNKre61xvLnvjOmIiIyDB2xkRE\\nRIb5epi6okWOVX6u6Qda28ayI1a538R7tLaWf/nCfo04xUbVt/3u86zygGs/0dqG1R9vlf8xpoPW\\n1qeuvSymbc3g3z+jHzqL1MOnL3ZtazfvBq2eh2/jHY7ndO28suqLAMxbUKzVC7AgHuGQj9Qr3ms6\\nhJ/gO2MiIiLDquyMReRFEdklIssdX8sWkY9EZG3gTx7Qm0SYU39hPv2HOU094bwzngLg4qCvjQIw\\nWylVCGB2oE7JYwqYUz+ZAubTb6aAOU0pVc4ZK6XmiEh+0Jf7A7gwUJ4K4DMA98YwrpioUbLPKn9w\\ntLbWdrjC/qUy7/92aG3l8Q3LuGTJqerSTqvPvuMJq3xqWvBcr72V5N0N9LnGCo/OxtxXom+Z2jhz\\nv1VuffePWpu++E6XLPmsrml5c8K6rmCk/+aIvZTTMeMGafXeDzwb1vdlSA2tvnu83d1k940+LuCn\\nSwfDjaVfC2vAAYtaFWltZd9vjDquSET6r1SOUupkD1YCICfUxZQUmFN/YT79hzn1sajfMiilFADl\\n1i4iQ0RkiYgsKcVxt8vIQ0LllPlMPnxG/YfPqP9EurRpp4jkKqV2iEgugF1uFyqlJgGYBAD1JNv1\\nH4R4cJ4M8qcVl2htSzq9bJU3vLVca/vgvy6wyjVnpcwJS2Hl1GQ+07Sy+++RwUNSpWFGuei4vuPT\\nDS8Pc7lSV/DfW7R6+CfS6AvnlqOuo6a/ZgSS4hl1Wje+c9BXlrpem6InM5l5RoNeIdzd6IKfu4oY\\n/M2qu0WfsPnS8btGh0z3uIJjGdXwG6t8ceF5WlvNJBumngng5ETCIAAzYhMOGcSc+gvz6T/MqY+F\\ns7TpFQDzAbQRka0iMhjAYwB6ishaAD0CdUoSzKm/MJ/+w5ymnnA+TT3Qpal7jGOhBGFO/YX59B/m\\nNPX4ejtMp8ZX6XNwAz74jVV+pdUsrW3wC/Zc1W++1rclPP3P9pIatTj1tihMJJn/jVa/8fvfWeXX\\nCt4Nvtzyk7mqMOe4xl70O62evym801xCLTui8K0fMDHsa+NxMlPO/Hqubc4tN/24lCpZZP5L30L2\\nf/fa870dmnwe0Wvub5mh1RtF9CrR8+YCTCIiohTCzpiIiMiwlBmmrjh8WKsfuTTLKrd56iatbXX3\\n563ywnNe1trwtl0smnGL1tTyTXvvroyPv4w0VHJx6KGmVnnQI720tqn5s4Ivr7b6rxzU6j/c1MYq\\nl69YHfXrk3lHLrV3PdveTV/KNisvxDC5YzewXiPbxzyuVHBarWNWOT2vudZWtinqpXwRO/2KzVpd\\nhT9bElN8Z0xERGQYO2MiIiLD2BkTEREZljJzxsHK9+y1yoXX7dXa+hfbS/zqPb9Ha3u42TtWecMl\\nk7S2sb+25xgnf3yR1tbmH/bOdeVrv48gYqrx6VdWuWTsuVpbxxuut8pLO0+L6PUn532k1ds9aC9r\\ny7siopekKuhbYLpvf9n6tZu1egEiW17U8p5VVnlumKdCUWy83/YNq/zp7FO0tls+uc79G51T+0HL\\nFkfWj+xZdzr+11ytXhPbon7NSPCdMRERkWHsjImIiAxL2WHqUMpXrrHK+7rqbSPaXm+V117fUGv7\\n8MonrPLdA/QD7qf1tpflTHz8Uq0t+6XwdnoiW+Z7+k48zd6zy/3Oulpr2/igvcPO0vNeDPseX503\\n2Sqf+dxtWlvRrYvCfh2KXqS7XgXvqjWNQ9PVp68AC3limlOo09O61zqita35rft6IufrlKpy1+tC\\nvbcMeZKbBP0PGsJ3xkRERIaxMyYiIjKMnTEREZFhnDOupvJVa61yq3vXam23vjLEKu99tFRrm9f+\\nVat83SPPam0dG9xulZuM+yImcaayiuXfafUWl9vlsx+5Q2t7+5onrXJBRqbWlplmzzMN/rU+1zgX\\nWaDEcW5jCYR/ahPniKNXd7N+LtmXx+1yh0z3E9EiPT0t1OvE4jWCX6fdo19rbWu+b22Vy9esj+h+\\nkeA7YyIiIsPYGRMRERnGYeoYqlhqL2dq8Ht9GLPNX4dZ5dWXTdDanrjZXkLzzGs9tbayLVtjGaLn\\n1WhkH+393QOttLbC26M/UD7/T/oysts+sacIXnjp71pbs/RaVrlv3W+0tmljR1jllvdxaVqkmsxx\\njB8OcL/OuXMWAOx8y/3acHf1qo7rNnVz1A7E5DWTRea/9GWED1xt70y3cbg+/vvt+ZORbP7aWH9+\\nz77W3t0v/34OUxMREaUMdsZERESGsTMmIiIyjHPGcVJx7JhWb/u3HVZ5Xt8Mra1nraNW+W85p+kv\\nlGJzxhuHFlrlD/o9obVdtfS/rHKDyZHN06Y3baLV6/95g1Vukp4ZfLmlbU3999ayOsrlSqoObYnS\\nBPfrfrJEabtdDD7Raf0A960VI7Xh8bZWuTai/+xCMpP59ucnClbo2412HXBH8OU/62ALvT52wHTX\\nazPEXlo1/POBWtvCHk9b5VPTaoZ176qU1TXzbPOdMRERkWHsjImIiAzz9TB1jXr2EIpq1Uxrcy5D\\nSoSDZ+dY5fOz9B1tagh/JzrpxRuescp56fqw0++Gf2KV572Xr7WVley0yjvvOE9rS+ux1yrf1eZj\\nre2yU0oiivOs9hut8nH3y6gaejVpr9WdJy6F2kkrHsPS5w8bqtXD3fEr1ZQf0Jd5NXg+vOmjBkH1\\nSfe3+tnrghXhS63+8OL/sMpPNvk8rNcI9vqhxlq9cOpBq5zIAWv2AkRERIZV2RmLSHMR+VREVorI\\nChEZHvh6toh8JCJrA3/Wj3+4FK0KVID59Bc+o/7CZzQ1hfPOuAzAXUqpYgCdAQwTkWIAowDMVkoV\\nApgdqFNyYD79hc+o/zCfKabKOWOl1A4AOwLlgyKyCkBTAP0BXBi4bCqAzwDcG5coI7TzyjOt8sH/\\nOKy1tbwyvvdW57XT6n968iWrXBE0EzH9QEOrXGPnj1qbPrscvTSkQSn1FeDNfJ7jWF0UfD7LXQ2W\\nW+Ue85drbUcq7G/smqXPK0V60ovTwuP6crSjD+Ra5TRENu8cK8n8jIbiXE503T16WzxOY3LOWZtc\\nvuT1Z9RL0sR+ttNCvLfMkBpa3XmKk3PpVOCFjKjWbUUkH0AHAAsB5AT+EQCAEgA5Lt9GHsV8+g9z\\n6i/MZ+oIuzMWkVMAvAFghFJK+widUkrB5YNnIjJERJaIyJJSfu7UM5hP/2FO/YX5TC1hLW0SkQxU\\n/qWYrpR6M/DlnSKSq5TaISK5AHb93PcqpSYBmAQA9SQ7oVubZP1o3+6+jm9rbfc9erVVbj1OP4y+\\nfN++sF4/eDenkr55VvnxeyZpbd2yTri+zrjnr7DKuVu+COve0fByPs94zT7d6vPLxmltDWvYpyh1\\n+MlmO6VWKdSQVHXMP26/zqOt9GU3afg6+HKjvJzTSDmXEwWf0tQLdj70U5p0wcuenKcv7ezi3dOX\\n/JjPeHjvu7Os8hO57v92Bv8b4Jy66l9nj9b2eEd7SV0DfcYrrsL5NLUAmAxglVLqKUfTTACDAuVB\\nAGbEPjyKNVX5yzTz6SN8Rv2Fz2hqCuedcVcA1wL4VkROHg56H4DHAPxTRAYD2ATgCpfvJw8pRznA\\nfPoNn1Ef4TOamsL5NPXnAMSluXtsw6F4S0c6lFLMp4/wGfUXPqOpydfbYZ42d6NVXn5U3w5z5fX2\\nETGfXakvW/n0YLFV7nfqV66vX1dKtXpBhvupP875x2ETb9Xamk20T0GJfhFOciu4c4FV7pmvb0n4\\n5a+mhPUaoeaHgr2w396Gr3VNfQrulg8HWeUiLArr3pR4BSMXuLb1Gtk+6CvenSem6ms+3dGFXWQu\\njljgdphERESGsTMmIiIyzNfD1GU77J2RFvUv0NraDr3AKr818Cmt7cFGSx01999X0pCl1f+y1x7e\\nfvMf+phJ44/tU4WarNU/gp/qQ9NumozT/3p26jrcKrfs+73W1qfRt1b5g91naW3Llra0ymkN9XWX\\nRXdssiuN9dOeilZwaJrIy+os22aVR24/X2sb32RuWK/hnKoCgNP/bU9XlUcRW3XxnTEREZFh7IyJ\\niIgMY2dMRERkmK/njJ3KNm7W6i1H2/U7R3eJ+f0aYb5WT+Tcg1/IF99o9SaOqfbjT+jXvtO8g1Uu\\n27JVayvETrjR8rL3h+qGSEQGlW3bbpXnT9U/84HR7nPGf97d0Sq/P/HXWlujNfODL08IvjMmIiIy\\njJ0xERGRYSkzTE3+Fjw0TUSp5fRn9SWj/Z49N6zvC55SNIXvjImIiAxjZ0xERGQYO2MiIiLD2BkT\\nEREZxs6YiIjIMHbGREREhrEzJiIiMoydMRERkWHsjImIiAxjZ0xERGSYKKUSdzOR3QA2AWgIYE/C\\nbuzOK3EAiYslTynVKBYv5MF8At6JJenyCVg5PQxv/AwB7+QTSMKc8hkNyVP5TGhnbN1UZIlSqlPC\\nb+zROABvxVJdXordK7F4JY5IeCl2xhIbXordK7F4JY6TOExNRERkGDtjIiIiw0x1xpMM3TeYV+IA\\nvBVLdXkpdq/E4pU4IuGl2BlLbHgpdq/E4pU4ABiaMyYiIiIbh6mJiIgMS2hnLCIXi8hqEVknIqMS\\nfO8XRWSXiCx3fC1bRD4SkbWBP+snII7mIvKpiKwUkRUiMtxULLFgKqdeyWfgvr7JKZ9R5jOG9/ZE\\nPgP39XxOE9YZi0gNABMA9AZQDGCgiBQn6v4ApgC4OOhrowDMVkoVApgdqMdbGYC7lFLFADoDGBb4\\nOZiIJSqGczoF3sgn4JOc8hm1MJ+xMQXeyCeQDDlVSiXkPwBdAMxy1EcDGJ2o+wfumQ9guaO+GkBu\\noJwLYHUi4wncdwaAnl6IJdly6sV8JnNOTefTqzllPv2VT6/mNJHD1E0BbHHUtwa+ZlKOUmpHoFwC\\nICeRNxeRfAAdACw0HUuEvJZT4z/DJM+p1/IJ8BmNBvP5M7yaU36AK0BV/mqUsI+Wi8gpAN4AMEIp\\ndcBkLH5k4mfInMYXn1F/4TOqS2RnvA1Ac0e9WeBrJu0UkVwACPy5KxE3FZEMVP6FmK6UetNkLFHy\\nWk6N/Qx9klOv5RPgMxoN5tPB6zlNZGe8GEChiLQUkZoArgQwM4H3/zkzAQwKlAehch4hrkREAEwG\\nsEop9ZTJWGLAazk18jP0UU69lk+Az2g0mM+ApMhpgifN+wBYA2A9gD8m+N6vANgBoBSVcyeDATRA\\n5Sfo1gL4GEB2AuL4NSqHQpYBWBr4r4+JWJI5p17Jp99yymeU+fRbPpMlp9yBi4iIyDB+gIuIiMgw\\ndsZERESGsTMmIiIyjJ0xERGRYeyMiYiIDGNnTEREZBg7YyIiIsPYGRMRERn2/15Eq87eY5CpAAAA\\nAElFTkSuQmCC\\n\",\n \"text/plain\": [\n \"\"\n ]\n },\n \"metadata\": {\n \"needs_background\": \"light\"\n },\n \"output_type\": \"display_data\"\n }\n ],\n \"source\": [\n \"# Velocity and temperature fields\\n\",\n \"fieldset = FieldSet.from_parcels(\\\"Peninsula_data/peninsula\\\", extra_fields={'T': 'T'}, allow_time_extrapolation=True)\\n\",\n \"\\n\",\n \"# Particle locations and initial time\\n\",\n \"npart = 10 # number of particles to be released\\n\",\n \"lon = 3e3 * np.ones(npart)\\n\",\n \"lat = np.linspace(3e3 , 45e3, npart, dtype=np.float32)\\n\",\n \"time = np.arange(0, npart) * delta(hours=2).total_seconds() # release each particle two hours later\\n\",\n \"\\n\",\n \"# Plot temperature field and initial particle locations\\n\",\n \"T_data = xr.open_dataset(\\\"Peninsula_data/peninsulaT.nc\\\")\\n\",\n \"plt.figure()\\n\",\n \"ax = plt.axes()\\n\",\n \"T_contour = ax.contourf(T_data.x.values, T_data.y.values, T_data.T.values[0,0], cmap=plt.cm.inferno)\\n\",\n \"ax.scatter(lon, lat, c='w')\\n\",\n \"plt.colorbar(T_contour, label='T [$^{\\\\circ} C$]')\\n\",\n \"plt.show()\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"To sample the temperature field, we need to create a new class of particles where temperature is a `Variable`. As an argument for the `Variable` class, we need to provide the initial values for the particles. The easiest option is to access `fieldset.T`, but this option has some drawbacks.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 3,\n \"metadata\": {},\n \"outputs\": [\n {\n \"name\": \"stderr\",\n \"output_type\": \"stream\",\n \"text\": [\n \"WARNING: Particle initialisation from field can be very slow as it is computed in scipy mode.\\n\"\n ]\n }\n ],\n \"source\": [\n \"class SampleParticle(JITParticle): # Define a new particle class\\n\",\n \" temperature = Variable('temperature', initial=fieldset.T) # Variable 'temperature' initialised by sampling the temperature\\n\",\n \"\\n\",\n \"pset = ParticleSet(fieldset=fieldset, pclass=SampleParticle, lon=lon, lat=lat, time=time)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"Using `fieldset.T` leads to the `WARNING` displayed above because `Variable` accesses the fieldset in the slower SciPy mode. Another problem can occur when using the repeatdt argument instead of time:\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 4,\n \"metadata\": {\n \"tags\": [\n \"raises-exception\"\n ]\n },\n \"outputs\": [\n {\n \"ename\": \"RuntimeError\",\n \"evalue\": \"Cannot initialise a Variable with a Field if no time provided. Add a \\\"time=\\\" to ParticleSet construction\",\n \"output_type\": \"error\",\n \"traceback\": [\n \"\\u001b[1;31m---------------------------------------------------------------------------\\u001b[0m\",\n \"\\u001b[1;31mRuntimeError\\u001b[0m Traceback (most recent call last)\",\n \"\\u001b[1;32m\\u001b[0m in \\u001b[0;36m\\u001b[1;34m()\\u001b[0m\\n\\u001b[0;32m 1\\u001b[0m \\u001b[0mrepeatdt\\u001b[0m \\u001b[1;33m=\\u001b[0m \\u001b[0mdelta\\u001b[0m\\u001b[1;33m(\\u001b[0m\\u001b[0mhours\\u001b[0m\\u001b[1;33m=\\u001b[0m\\u001b[1;36m3\\u001b[0m\\u001b[1;33m)\\u001b[0m\\u001b[1;33m\\u001b[0m\\u001b[1;33m\\u001b[0m\\u001b[0m\\n\\u001b[0;32m 2\\u001b[0m \\u001b[1;33m\\u001b[0m\\u001b[0m\\n\\u001b[1;32m----> 3\\u001b[1;33m \\u001b[0mpset\\u001b[0m \\u001b[1;33m=\\u001b[0m \\u001b[0mParticleSet\\u001b[0m\\u001b[1;33m(\\u001b[0m\\u001b[0mfieldset\\u001b[0m\\u001b[1;33m=\\u001b[0m\\u001b[0mfieldset\\u001b[0m\\u001b[1;33m,\\u001b[0m \\u001b[0mpclass\\u001b[0m\\u001b[1;33m=\\u001b[0m\\u001b[0mSampleParticle\\u001b[0m\\u001b[1;33m,\\u001b[0m \\u001b[0mlon\\u001b[0m\\u001b[1;33m=\\u001b[0m\\u001b[0mlon\\u001b[0m\\u001b[1;33m,\\u001b[0m \\u001b[0mlat\\u001b[0m\\u001b[1;33m=\\u001b[0m\\u001b[0mlat\\u001b[0m\\u001b[1;33m,\\u001b[0m \\u001b[0mrepeatdt\\u001b[0m\\u001b[1;33m=\\u001b[0m\\u001b[0mrepeatdt\\u001b[0m\\u001b[1;33m)\\u001b[0m\\u001b[1;33m\\u001b[0m\\u001b[1;33m\\u001b[0m\\u001b[0m\\n\\u001b[0m\",\n \"\\u001b[1;32mc:\\\\users\\\\gebruiker\\\\documents\\\\github\\\\parcels\\\\parcels\\\\particleset.py\\u001b[0m in \\u001b[0;36m__init__\\u001b[1;34m(self, fieldset, pclass, lon, lat, depth, time, repeatdt, lonlatdepth_dtype, pid_orig, **kwargs)\\u001b[0m\\n\\u001b[0;32m 284\\u001b[0m \\u001b[1;32mfor\\u001b[0m \\u001b[0mi\\u001b[0m \\u001b[1;32min\\u001b[0m \\u001b[0mrange\\u001b[0m\\u001b[1;33m(\\u001b[0m\\u001b[0mself\\u001b[0m\\u001b[1;33m.\\u001b[0m\\u001b[0msize\\u001b[0m\\u001b[1;33m)\\u001b[0m\\u001b[1;33m:\\u001b[0m\\u001b[1;33m\\u001b[0m\\u001b[1;33m\\u001b[0m\\u001b[0m\\n\\u001b[0;32m 285\\u001b[0m \\u001b[1;32mif\\u001b[0m \\u001b[1;33m(\\u001b[0m\\u001b[0mtime\\u001b[0m\\u001b[1;33m[\\u001b[0m\\u001b[0mi\\u001b[0m\\u001b[1;33m]\\u001b[0m \\u001b[1;32mis\\u001b[0m \\u001b[1;32mNone\\u001b[0m\\u001b[1;33m)\\u001b[0m \\u001b[1;32mor\\u001b[0m \\u001b[1;33m(\\u001b[0m\\u001b[0mnp\\u001b[0m\\u001b[1;33m.\\u001b[0m\\u001b[0misnan\\u001b[0m\\u001b[1;33m(\\u001b[0m\\u001b[0mtime\\u001b[0m\\u001b[1;33m[\\u001b[0m\\u001b[0mi\\u001b[0m\\u001b[1;33m]\\u001b[0m\\u001b[1;33m)\\u001b[0m\\u001b[1;33m)\\u001b[0m\\u001b[1;33m:\\u001b[0m\\u001b[1;33m\\u001b[0m\\u001b[1;33m\\u001b[0m\\u001b[0m\\n\\u001b[1;32m--> 286\\u001b[1;33m raise RuntimeError('Cannot initialise a Variable with a Field if no time provided. '\\n\\u001b[0m\\u001b[0;32m 287\\u001b[0m 'Add a \\\"time=\\\" to ParticleSet construction')\\n\\u001b[0;32m 288\\u001b[0m \\u001b[0mv\\u001b[0m\\u001b[1;33m.\\u001b[0m\\u001b[0minitial\\u001b[0m\\u001b[1;33m.\\u001b[0m\\u001b[0mfieldset\\u001b[0m\\u001b[1;33m.\\u001b[0m\\u001b[0mcomputeTimeChunk\\u001b[0m\\u001b[1;33m(\\u001b[0m\\u001b[0mtime\\u001b[0m\\u001b[1;33m[\\u001b[0m\\u001b[0mi\\u001b[0m\\u001b[1;33m]\\u001b[0m\\u001b[1;33m,\\u001b[0m \\u001b[1;36m0\\u001b[0m\\u001b[1;33m)\\u001b[0m\\u001b[1;33m\\u001b[0m\\u001b[1;33m\\u001b[0m\\u001b[0m\\n\",\n \"\\u001b[1;31mRuntimeError\\u001b[0m: Cannot initialise a Variable with a Field if no time provided. Add a \\\"time=\\\" to ParticleSet construction\"\n ]\n }\n ],\n \"source\": [\n \"repeatdt = delta(hours=3)\\n\",\n \"\\n\",\n \"pset = ParticleSet(fieldset=fieldset, pclass=SampleParticle, lon=lon, lat=lat, repeatdt=repeatdt)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"Since the initial time is not defined, the `Variable` class does not know at what time to access the temperature field.\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"The solution to this initialisation problem is to leave the initial value zero and sample the initial condition in JIT mode with the sampling Kernel:\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 5,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"class SampleParticleInitZero(JITParticle): # Define a new particle class\\n\",\n \" temperature = Variable('temperature', initial=0) # Variable 'temperature' initially zero\\n\",\n \"\\n\",\n \"pset = ParticleSet(fieldset=fieldset, pclass=SampleParticleInitZero, lon=lon, lat=lat, time=time)\\n\",\n \"\\n\",\n \"def SampleT(particle, fieldset, time):\\n\",\n \" particle.temperature = fieldset.T[time, particle.depth, particle.lat, particle.lon]\\n\",\n \"sample_kernel = pset.Kernel(SampleT) # Casting the SampleT function to a kernel.\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"To sample the initial values we can execute the Sample kernel over the entire particleset with dt = 0 so that time does not increase\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 6,\n \"metadata\": {},\n \"outputs\": [\n {\n \"name\": \"stderr\",\n \"output_type\": \"stream\",\n \"text\": [\n \"INFO: Compiled SampleParticleInitZeroSampleT ==> C:\\\\Users\\\\GEBRUI~1\\\\AppData\\\\Local\\\\Temp\\\\parcels-tmp\\\\95267e2b33bce749036c721bfb587691_0.dll\\n\",\n \"WARNING: dt or runtime are zero, or endtime is equal to Particle.time. The kernels will be executed once, without incrementing time\\n\",\n \"INFO: Compiled SampleParticleInitZeroAdvectionRK4SampleT ==> C:\\\\Users\\\\GEBRUI~1\\\\AppData\\\\Local\\\\Temp\\\\parcels-tmp\\\\7e5de9a8e76698139bc7c407a0d61d6f_0.dll\\n\"\n ]\n }\n ],\n \"source\": [\n \"pset.execute(sample_kernel, dt=0) # by only executing the sample kernel we record the initial temperature of the particles\\n\",\n \"\\n\",\n \"output_file = pset.ParticleFile(name=\\\"InitZero.nc\\\", outputdt=delta(hours=1))\\n\",\n \"pset.execute(AdvectionRK4 + sample_kernel, runtime=delta(hours=30), dt=delta(minutes=5),\\n\",\n \" output_file=output_file)\\n\",\n \"output_file.export() # export the trajectory data to a netcdf file\\n\",\n \"output_file.close()\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"The particle dataset now contains the particle trajectories and the corresponding environmental temperature\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 7,\n \"metadata\": {},\n \"outputs\": [\n {\n \"data\": {\n \"image/png\": \"iVBORw0KGgoAAAANSUhEUgAAAZkAAAEKCAYAAADAVygjAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAADa90lEQVR4nOydd1hURxeH39lGk46gItjF3nvvvRt7iRpLYkzUGFuM0Zhoihpji93Yu8Ya7L13xa4ICCIgTTpsme+PRXQDKvmCirrv8+wjzp65d+6F3d+dOWfOEVJKzJgxY8aMmdeB4m0PwIwZM2bMvL+YRcaMGTNmzLw2zCJjxowZM2ZeG2aRMWPGjBkzrw2zyJgxY8aMmdeGWWTMmDFjxsxrwywyZsyYMfMOIITwEEIcEkLcFEJcF0IMTW13EkLsE0LcTf3X8QX9mwkhbgsh7gkhxryxcZv3yZgxY8ZM9kcIkRvILaW8KISwBS4A7YA+QKSU8udU8XCUUo7+R18lcAdoDAQB54BuUsobr3vc5pmMGTNmzLwDSCkfSSkvpv4cC9wE3IG2wPJUs+UYheefVAHuSSnvSylTgHWp/V47qjdxkuyEi4uLzJ8//9sehhkzZt4BLly4EC6lzPlfjtG0WRkZER6XyfP5XQeSnmtaKKVc+E87IUR+oDxwBnCTUj4CoxAJIVwzOLQ7EPjc/4OAqpka1H/kgxOZ/Pnzc/78+bc9DDNmzLwDCCEC/usxIsLjOHP+h0zZqkTPJCllpVeMKQewGRgmpYwRQmTm0BkZvRFfyQcnMmbMPPVDZvLDacbMf0IiMRj0WXIsIYQao8CsllJuSW0OFULkTp3F5AbCMugaBHg89/+8QHCWDOoVmH0yZrIt/v7+3LhxA4PB8EIbvV7PsmXLaFa/Ec3qN2L58uXo9Rl/oP39/WnXsjUWGg221jb06/0xUVFRr2v4ZswYkRKDITlTr5chjE9FS4CbUsrfnntrO/Bx6s8fA9sy6H4OKCKEKCCE0ABdU/u9dswiY+aNodfr2bdvH8uWLePmzZsvtPPz86NaxSqUL1WWRjXqkT9vPvbt25fOTkpJ148688vX4ynsq6Owr46fv/qW7p278s+oydjYWGpXq4Hd1SBWlmzHvCLNCN1/lmYNGqWzNWMmK5FIDFKXqdcrqAn0AhoIIS6nvloAPwONhRB3MUaP/QwghMgjhPgbQEqpA4YAezAGDGyQUl5/PVdsinm5zMx/5ubNm5w+fZo8efLQqFEjlEplOpsHDx7QqF5DdE+ScVE68lVCAM1btWDF6pUm9nq9nqYNGlMq0ZVuebqgQHA74SGdO3zExauXKVCgQJrtiRMnOH34GJPyNEetMB6jgq0n4/d74+3tTdmyZUlJSSElJYVVq1aRT1rR2bUEADZK+DRXeYY/OMThw4epX7/+a75LZj5cJPLVAvLqo0h5nIx9KwANM7APBlo89/+/gb//80D+JWaRMZMhUkquXLlCXFwclSpVwtLSMp2NXq+nT68+7Ny+k3yWnkQbnqCwVXDg8AETMQDo2aUHBWNdqW1XHgCtVXXW7N3DvHnzGDJkCElJSURERLBr1y5SohJo4FYmrW8xm7yUTcxHh3btKVy0CLGxscTGxuLr60tFlVuawABoFCpKq11p2bKlyflVKPjYvaxJmxCCYpZO3Lx50ywyZl4jWSMy7ypmkfkASUlJQaVSoVBkvFp669Yt2rZqR1RYFJYqS2J1McxfNJ8uXbqY2C1evJjjfx+jl2031Ao1ABdiLtGtUzeOnz5OWFgYISEh3Lhxg/MXzjM6T5+0vmqFipqaMowdMZrRo0eTkJCQ9l5JG890Y3JT2XPZ9wrJ2hRsbW2xtbUlV65chD+ISWcbJZPo2rUrDRo0QKPRoNFoOHLkCFe37DHZQCCl5GZiBCNLlsz8zTNj5t8iJdJgFhkzHwBHjx5l6OfD8LlxFStLawYMGMDPv/6ERqNJs9Hr9TRt1BSPmMLU1DRBCEG4DGNgv4GULl2aYsWKERYWRlBQEL/98hvllWXTBAagnFUZ5l1ciFqtNjm3pdCg/IcL0EKosbS0pHf/Pjg7O+Ps7ExKSgrfjhpLkiEFS4VxXFJKbhiCmTF7Jn379k3rHxkZSeH8BbkcG0g5W2PgzOXYQO7pItkzbx4ODg5ptq1bt6bk9p2sCb1GS+fCpBj0rAu/iVsBT+rUqZNl99iMmQwxz2TMvMtcvnyZX36ays3rNylfsTyjx46kWLFiJjbXrl2jVYvWlDDUoG2OT0mUcWxZupPHjx+zcvUKwPhlvmXLFrQxerwsSqX1dVG5kj+lKDWq1SA+MR6dzviB0QgN5ZxKm5xHgQKN2oKBAwdRsmRJcuXKhZubGz06d+dWoh/FrQumnetCym36fzaQn37+yXSsl32Y/5c3DaxKYqXQcDrpLgpXa7p162Zi5+TkxLZdO+jeqQubY68hAYNGwfa/d5oIDECOHDk4dvokI4cOZ6D336hVarp27cIv06eZQ5nNvGYMSH3i2x7EW+ODy11WqVIl+a5sxoyMjGTdunUEBwdTq1YtmjRpkm6J6/Dhw7Ru2ZY8+pLY4kqMCCFEeYvDRw9SoUKFNLs+vfpwcctdvNQV09q0MgXv+GVUrlaJ0NBQAgMDSU5OJo/ag2b27U3OczvpGiEuAXTu1pm8efPi7u7Orp27OLnxBE2sG6Z9Ud9P8uOKzTV8A3xNvryPHz9OmxatKa7Jj5O05b54hHDRcPz0iXSCYDAYWLFiBUvmLSQ+Lp52nTsybPgw7OzsMrxPer2eCxcuIISgQoUKGQYemDHz/yCEuPCqzZGvonz53PLIkb6vNgTs7X/6z+fLbphF5i0gpeTcuXOEh4dTtWpVnJ2d09mcOXOGJo2bYYMbJFmSYhlGibJF2btvt4kTvkzJcnDPDTdVwbS2IO0NZP7HtG3fGn9/fwICArh60YfKmia4qjxMzrM3bjWexfNQsmRJPD09sbOzY8oPU2iXowdWCuu08R7S7eL7WRPo3bt3Wt+YmBhqV69NwqN4PPR5iVHGck/ry7ad26hbt266a3r48CFLFi/hgV8AterVpmvXrhkGFJgxk13IGpHJJY8c6v1qQ8Decep7JzLm5bIs5smTJ0RFReHh4ZHhE7W/vz9NmzQnNCQcC5U1sYnhfDv+W775ZmyajZSSrp2745xcFkdVPlCD1Bm4dek448aNo27duvj7+3P//n2u3bhKA6sBJudwUxXk6N3j/P67L56enuTLl4/8BfPxOOChicgkGxLRq5M5dOgQLi4uae2J8YksnruEorIUGmGJv+IOOQu5pHP829nZcfbiWTZs2MDRQ0fxyOdBv0/6kTdv3gzvjbu7O99N+O7/uq9mzLyzSAkfsOPfPJPJJFJKkpOTsbCwyHANPzY2lk/69Wf7ju2oVBqsra2YM2cWnTt3NjlG6VJlCfMzYKvIjxACnSGRKMUl1m9cTcWKFQkICODkyZOMGfktxZTtTM4Vo3/I/eSjGNACYGlpiTZFR1VNZ6wVz5aSnujDeOhwhsDgB2nLa/fu3aNS+coU1Jcjr6owCTKWW+IM7Xq2Ys4fs9Nd686dO1n4xyLiYuNo37kdAwYMwMrK6l/fNzNm3mWyZCZTzk0eOdDl1YaAvcvs924mY97xDy9NW2IwGJg06QccHR2xsclBgQIF2bJlSzq7bt26s8f7GDbKYlhRlJRYR/r168/JkycB0Gq17N27F3+/gDSBAVAprLDQutO6VVtcXV2pXLkyQ4cOJSUlfYoJiaRAgfycPXuWsLAwEhISGD58OP6qM2il0T5FJvJAfZ5hI4aZ+G8KFy7MkeOHcammYb92DbdynOCLbz5j5uzf051HCEHr1q3Z4b2dQ8cP8uWXX5oFxoyZ/xMhDQhdUqZe7yMf9HLZmjVrGDt2LA8ePCBXrlxMmDCBQYMGmcwexo8fz6yZf6BNsUGjtOfRwwR69eqNnZ0djRo1AiAwMJADBw5io/DCWBsI1Moc6LSOtG7VBitrS4KDg5FSohY2CBvTmZBSWOLq6sboMV+TL18+PD096dSxC1EP7+OkKgSAQeqJUd/ju69GUrly5bS+U36aTER4BOvXr8fOwomYpEgG9B3AiBFfpbvesmXLsvfgniy/j2bMmHkZ5uWytz2GN8rT5bLNmzfTu/fHJCbqASVgwNpaya+//sLgwYMBSE5OxsnJGb3WAYV4psc6fRz2jgqKFy9GYGAggYGBSIMKJ2vTcN4UfQxSFcpHnTrg6elJrly5+Gr4CJxFJSyUxuUtKSVPxDVGf/c5I0eOTOt79epVGtRrhMZgh0ixIkEZQs3a1flr2+Z0e1AAHj9+TEBAAIUKFcLRMcPqq2bMmPmXZMVyWYWyzvKod8tXGwK27ivfu+WyD3YmM27cOBIT9Yg08VCSkKBnxIiv2bNnD8HBwTx48ICEhASsNC4mfRUKC6KiwhBCULNmTXLmzMkfc+ehNySjVFg8Z5jAx316MXv2M5+HpaUlXwwZiqUuLwppgV4Tgat7Dj799FOTc5QpU4YHQf5s2bKFR48eUatWLapVq/bCPR05c+YkZ87/VFvJjBkzrwMJZFGq/3eRD1Zk/P0DMM5gnkdBUlI8vr6+5M2bl1KlSrFmzVoMUotCPJs9SJlMvXr12L//WWZgR0cnpk2dgU7rhFJhgV7GoLJKZNSoUSZn6NOnDyVLlmTunHmEhITQslVf+vXrh42NTboxWltb07Nnz6y8bDNmzLxxJOIDXi77YEWmUKGC3Lx5H9NbYCBXrlz4+PikzRhKlizJxIk/oE22QiHU6A2JqC2S+OGHSSbHGz/+W4oWLcLUX6cTGhZKwwYNmfj9BDw8TPelAFSuXJllyyunazdjxsz7iDTPZD5Efv75Z7p27Upiog7jjEaPlZWSyZMnmyxJjRgxAkdHR378cQohIY8oV64M06dPpXr16ibHE0LQtWtXunbt+mYvxIwZM9kbKRG6lxcke5/5YEOYW7duzdq1aylaND9KZTL58uVmwYL59OvXz8ROCMEnn3yCn58viYkJnD17mtq1a7+lUZv5r0gpuXz5Mrt27SIkJOSV9mFhYZw8eZKwsIwq2poxkwlk6kwmM6/3kA9WZADatGnDrVs30Wq1+PndN/s/shFPxeDkyZMkJ7/4KTAlJYXx34wjd043bKysadO8Jbdu3crQNiwsjJqVq9CqXiMmDfwSr4KFGPnViAwrY2q1WgZ98glF8hfgs46djf/2H5CWHPSfBAYG8tXQodSuXIleXbpw7ty5/+/CzbyXCIM+U6/3kQ9aZMy8eXx9fblw4QIpKSkvtLl58yYlihajRb0m9G7TBfdcedi8eXOGth9374n3onUMc6jJtPztsL3ymDo1ahEcHJzetlsP3EOSmFeoMd/lrsr8os3YvnwNK1euTGf746RJXNm1l3Vl6jG3UCXWlanHxZ27+XHSpHS2vr6+VClXjshdO+ktJbmvXqFlw4Zs3/5GSqibyfZ82DOZD3afjJk3S1BQEJ3af8Ttm7fJobEmUSYze96cdD4snU5HoXwFqGkoSHXbYgghCEgKY3HEAU5fOIuXl1ea7b1796hctgLT87dDo3jmXlwRdgb7WsVp37EDSUlJJCUl8fjxY36d/BMrS7XB4jnbM9FBrEy4T+dePVAoFAghUCgUzP5tBnOLVSO/tW2arV9CDMPunWfRsmXY2NhgY2ODtbU1kydOJNfNG3xa8Fk10LORkfwU+pg7/v4vLA5nJvuTFftkKpa0lSfWZ+4QVqUPv/R8QoilQCsgTEpZKrVtPfD0g+EAREspy2XQ1x+IBfSA7k3tx/lgHf9msoa1a9cy+fvJBAQGUKZkaX78ZXK6UsZSSlo1bYlLqA1funRHKRQEJ4cxuP+neHl5Ub58eaSUREVFsWnTJlQJkhquxdP657N0paJFAZo3bY6LqwtRUVFpr0KWLiYCA+Bl4crirdvZtMV09mOr1KARpmHrDmorHj9+zKxZszAYDBgMBqSUGPR6cltYm9jmtrAmKjaWjh07mrRbK5WsrVbFpK2yoyPRt+7w6NEj3N3d/91NNfN+ISVC9+KZ+79kGTAHWPHs8DItMZoQYjrw5CX960spw7NqMJnB/IhlJh1SSs6cOcMPP/zAzJkzX+ggX7hgIcMGDcXrcWF62XbD4Z497Vu35/DhwyZ2J06c4FFgMHVyVEApjH9yeSxcKa8pRoumzfH09MTCwgJnZ2cGDRqERUr6P0tnlS1JCQm4uLhQuXJlunTpwoABAwjVx6H7xzKDb0ok3Xv35Pbt2wQEBBAaGkpkZCQOOZ3xiTN14B968oBPh3xOYmIiycnJaLVadDoddapV50D4QxPbA+EPqVq+ApcvX+bEiRPs27ePrVu34pE3Lw8TTYtSxeh0pOj12NvbZ+qem3nPyaLlMinlUSAyo/eEMSy2M7A2awf/3zDPZD5ApJQvzBwgpaTvx/3Y+ddO3GV+dKoUxn8znrUb1tKy5bPUGAaDgQnjJ9DYoiFuGlcAilkVxSAN9O7em4pVK/LgwQMCAgKIiIjAXeOa7pzOKgeEFDRo0IBcuXKRO3duVCoVY0aMIl6fhI3SWGvGICU++iCmzpxOjx49TI4RHBDIogun6eJUDlulJSeifTmT+IBL3+/A09PTxHbe4kX07tqd5g4FyKvOwbmkMPxVySwZOybdffjl9xm0aNyEMF0ypW0c8ImP5q+IILxX76Ns2bImtpGRkUwdPYqiOWxxtbQgUa/n1/t+fNShAzly5Mjkb8XM+4tEvCQJbxZSGwiVUt594UBgrxBCAguklAvfxKDMIvOBIKVkzpy5/DLlF4JDgylepDi//vaLiXAAbN++nb3b9tLCohPq1CwHBfGie5furF63mqCgIO7fv8/NmzcJjwjHLZerSX9Pi7zsDznI3bt38fT0pEqVKjg5OTFj2m/E6uKxVT3LbHDH8IBR345m2LBhJsd44OfP3CUrqWNRHCulhnPJvjgUdKNTp07prmvd5o2MHjGSccuXkZicRM0q1dk390A6gQFo2bIlR0+fZN7sOdz0D6BZgzYMGDgwXWVOgKpVq3Li7Blm/DqVjVevUqpqdU6M/DpdWWswZnHw9/Wl44wZ5LO3JzAmhoYNGzJr/vwX/j7MfED8u7QyLkKI553GC/+FGHTj5bOYmlLKYCGEK7BPCHErdWb0WjE7/t8DwsPD2bRpE3FxcTRr1oxSpUqls/n1l6lMn/w7JQy1cFC4EKp7wA1xnE3bNtKoUaPUMG4/BvQbiO6ygmJWpsk+t0atIVJvXMrVaDTkz5+fgPsBdHPshJPaKc3uXqIvDz1COH/F9B5P/G4Ci2YuoLqmDDmU1lzT3iPOUcu5S+extbU1sZVSsn37dhbPW0h8bBztunR8ZT0bKSUGg+Gtll6Ojo7m5s2beHh4vLBwm5l3iyxx/Be3lqf+LJopW4vqV155PiFEfmDnU8d/apsKeAhUlFIGveo8QoiJQJyUclqmBvYfMIvMO86uXbvo2rkbzkoPFHo1EQTQr39ffvt9etrylE6nw9XFjYq65tgpnwlCoPY29y0u4eBsh7+/P3q9HiUqqtjUorhVGZPz7E7awrDvvqRr1664u7ujUCiY8uMU5k+bRwNNXZxUTgSnPGJ/8iGWrl5KmzZtTPpLKdm2bRvzZv1BVFQUrdq24sthQzOcRZgxk13IKpE5vbRwpmw1NXz+X5FpBoyVUqave2583wZQSCljU3/eB0ySUu7O5GX835iXy7Ip4eHhfDVsBJu3bEZKSZs2bfl95m/kypUrzSY+Pp5uXXtQXN8Ie9wA8JQVWL5kJfkKeGJra8udO3fw8fEhNiYWO1snk3M4K/NwJfYIDZvUp2vXrhQpUoTHjx8zddI0ChuKoVZoAAjRPiRREc+XX36JhcWzLNNjx41FqVQybeo0YqJiyO2Wi99//z2dwIAxc0K7du1o167da7hbZsxkY6QEnTZLDiWEWAvUw7isFgRMkFIuAbryj6UyIUQeYLGUsgXgBvyV+uCpAta8CYF5ejIzb5grV66wdu069Ho9nTp9RJUqpuGver2e2rXq8uQBFJTNEUJwbPs1qp+uya07N7CwsODJkycsXrwYa+mAvdItra9aWOCSXIQRw7/GgB6NRkOhQoVQqpTE6CNNZjIR+mAqV6rM+vXr09qklNy7fY8NazeQV1EAnSqFIF0Am7ZsNBEYMArH6LGjGTl6JElJSVhZWb0woMCMmQ8WKSGLHP9Sym4vaO+TQVsw0CL15/tA2X/avAnMIpOFSCm5ceMG8fHxlC9fPsPiYpMnT+HnKb9gYcgFEhbMW8Snnw3k16m/pNl4e3sT8SiGvNRHKIxf2rlEeXxD9lK2bFmioqLScmnZCVf4h6tCKIwRWwsXL8DT0xOlUsnUX6cx7YffKKGrhb0yJ6G6AG6Ls2yZvMm0rxDMXzSfTz//lL1792JnZ0enTp1wdnZ+4XUrFAqsra1f+L4ZMx8672vKmMxgFpl/wctCf+/cuUObNu14+DAYlVKNEAb+XLaUtm3bptn4+voyZfJP5BTVUKmM4bl6mZ+5c+fhlssVnU7HvXv3OHDgACLBFqExPZe1dCMhIYrWrVtTtGhRPDw86N9vADGGcOwUxsJqOplChMaXWaOWU6DAsx3oX48cgY2NNT9P+YXgkIcU9yrB2mmradiwYYbXU65cOcqVK/dfbpcZM2YAY1qZNxLCnC0xi8wr0Ov1/PjjZGbOnEl0dBRlypRl9uxZJpmY9Xo9Deo3JCZShYWiMEIKtPo4unfvycWL53F0dOT+/fvMnTsXjXRBlbr/A0ApNKh1Lnz99dcAuLq64uTkRLgiPJ2oSatYfvppisleEY1Gw8e9+pBTFEDo1ESq/OnUuSNNmjQxuQ4hBIM/H8zgzwe/rltlxoyZjJB80CLzQe/4P3XqFA0bNsTV1Y2aNWuyf//+dDZDhw5j2tQZJMRaYKHy4Ma1IJo1a86lS5fSbP7++29iYxOxULqkiYJamQOptaF06TK4ublRvXp1Vq1ahVabPqOwQikYMmQI0dHRhIaG4uPjQ25PJ0K5hFYmoZPJhBquoLbVp0tp0rFjR27fvcUXk/rw8dg27Du0m0VLFpp9I2bMZBtSZzKZeb2HfLAhzEeOHKFFixYkJup5VrRMxapVK2nfvj1g3PeQO3ce0Dsjnst5pdPH4JrLhjx5cuPv78/jx49RK+2wtzSNhU/UhuGe35rBgz+lUKFC2Nra0rx5S5ypiIXSDgCtIZ5weQ6fa1coWLBgWt/Hjx/zxZChbN26BYOUtGrZmtlzZprzYJkx8wbJihDmSkXU8szvLpmyVbUK+c/ny2689uUyYfx2Pg88lFK2EkI4AeuB/IA/0FlKGZVqOxb4BGOW0C+llHtS2ytiTAxnBfwNDJVSSiGEBcZEcRWBCKCLlNI/M+P6+uuvSUzUI8RT57yCxEQd/fp9wp49e3jw4AF37twhOVmLpdp0g59CWBAW9piSJUtQvnx57O3tmfn7LAxSh0IYb6mUEpVFEt9++yO9evVK67t48UL69x+IbWpEWKwuhBm/zzARGICcOXOybv2atFon5pmJGTPvMO/pLCUzvAmfzFDgJmCX+v8xwAEp5c9CiDGp/x8thCiBMda7JJAH2C+EKCql1APzgIHAaYwi0wzwxihIUVLKwkKIrsAvQBcygY/PNdJfvpLoaGMm4Hz58uHl5YW/fwBS6k1mMggtbdu2YePGDWlNyckpLFu6EoPWHgVKhDqWgoXz0rlzZ5MzdO/enSZNmrBjxw70ej2tWrUy2fvyT8zikvUkJSVx//59cufOjaOj4yvtU1JSMBgMWFpavtLWjJl0mH0yrw8hRF6gJbD4uea2wPLUn5cD7Z5rXyelTJZS+gH3gCpCiNyAnZTylDQ+1q/4R5+nx9oENBSZ/FY2frH/8xcvsbe35/Hjx1y4cIFdu3YxePBgVJo4DIYUpDSg08ehVCfx7bfjTHr+/vsMlvy5gCo1CuJVxpnxE0dy/PixdHtLAFxcXOjbty/9+/d/qcCYyRwHDhygS/uPaFynHtOmTiM2NvaFtr9Nm467ay5a1K5PPve89Ov1MUlJSRnahoaG0qldO+xtbbG3taNxnbrcvn37hceWUnLkyBGWLFnCuXPnMqy4aeZD5MP2ybxux//vwChMv83dpJSPAFL/fZph0R0IfM4uKLXNPfXnf7ab9JFS6jDWUUi3oUMIMVAIcV4Icf7x48cAjBv3DdbWSqQ0Dk1KA9bWCr7++muT2cOMGb8xZuzX2Dro0BqCKVOuIHv37kmXiVcIwUcffcSBg/s5e/Y0I0aMMO8d+T9JTExk+rTp1KhYlQa16rJy5UoML/gA/jZtOj07dMHqbDClApRsnraQmlWqERcXl852w4YNzJr8Mz951mZugYYsKtqcu/uOM2zIF+ls9Xo9jevWxeLyLbZWaIh3lSaUCI6ifq3aPHmSvlxHREQEVcuXZ2Cnj9j102Q+atqU5g0bkpCQ8MLrjIqK4siRI9y9+6KkuWbeCyRgkJl7vYe8tuUyIcTT6m0XhBD1MtMlgzb5kvaX9TFtMGYxXQhGxz9A//79iY6O5ocffkSn06FQCIYNG8o333xj0lepVDJu3DjGjRv3z8Oa+Zf4+vpy8OBBHBwcaNWqVYYJL7VaLQ3r1CfJP5JqFoVJMej4fuhYjh48wqI/F5vYRkdHM3HCBCblbYGLxphSv4KtJ3PCjjFt6lS6de9OQkJC2uv7b76lt3Nx3C2NCTlzqDR86laWAStXUrp8OaytrVEqlSgUCq5du0ZyWASflqie9tDROXcBrifGMnv2bL744gtsbW3Tql4OHTyYIrFPGFO+DEIIdAYDY27d5fsJE/hl6lSTcUsp+fH7iUyfNo2iTnYEPImjTLnyrNvy10s3vZp5V5Gg073tQbw1XqdPpibQRgjRArAE7IQQq4BQIURuKeWj1KWwp1WkggCP5/rnBYJT2/Nm0P58n6DULKT2vKCgzz8RQjBy5EiGDRtGWFgYLi4uGS5tmfnvSCkZ9fUoFs5fgJdNAeJkIoMHfcau3X+nS6nz119/EekXwmCnpihSv9yL23jww/r1FC9dArVazePHjwkLC8PHxwdXhU2awIDx91rF0oNff/yJ7ydNMjm2pUKFe3HTCEAHtSVCp2fIkCHpxt3M1SOdT8xLY83E775j/PjxCCGwtbXFzs6OkOBgDtetlWavUij4zNOdAYsW0aJVK/LkyUOePHmwsbFh48aNrPpjNnvqeuFmpUFrMDDlph+f9OrJ1r+9040jNDSUmb9N5+Thg+TOm5fBw0aY7NMyk815OpP5QHltIiOlHAuMBUidyXwtpewphJgKfAz8nPrvttQu24E1QojfMDr+iwBnpZR6IUSsEKIacAboDcx+rs/HwCngI+Cg/JcL4Wq12hwW/H+SnJzMwoUL2bh6AxaWlvQd2JeuXbumq2nv7e3N6iUrGezcBevUjag34+/TvnU7jpw4SmBgIAEBAfj7+7Nx3XpKKPKkCQyAhUJNAaUrI0aMAIxC4uLiQo4cOYjRJqTbtBqhjadi5UoMHvoF1tbWWFlZYW1tzZTvJ3H61kM+srRLs70VF46DkxPXz51BCIFer8dgMHDmzBm+HfIleilRPnfsCwnR9O7Th1KlSvHkyROePHlCZGQka1evwlJpet02ShUxsbHUq1cvrc3Ozg6NQc+kUnlwszImIFUrFIzyykX1fYd5+PChyd/jo0ePqFaxPA1dYIi7Bb4hwXRt25Ipv83i4z59/s/fnJk3jnw//S2Z4W3s+P8Z2CCE+AR4AHQCkFJeF0JsAG4AOuDz1MgygM94FsLsnfoCWAKsFELcwziD6fqmLuJDR6fT0aRBEx7dCKaEohhaqWP04NEc2n+IRUsXpdklJSUx67eZVFIVTxMYgOI2BdkTdJwiRYqktQkhsM1hi6MyvaswXq1lzpw5dO7cGScnJ5RKJVJKypYohXfUDZo5lkAhBI+Sn7A//h7bZuyievXqJseYPmsmtavXQIekYg43/BOfsC7qNr/9MYf8+fOb2BYqVIjFf8zjRz8feucqgIVCweawB0RZWzB37tx0S32P/P3ZHPyI7h7PJt3rHj6iRYsWfD5sGMHBwWmvDSuWkTtVYJ5ipVKi0uvw9PQkX758FCpUiEKFCnH75nUaOxv4qUpOAOq6Q2VXK3qMGE637t3RaEyPYyY78v76WzLDGxEZKeVh4HDqzxFAhgmzpJSTgckZtJ8H0lXiklImkSpSZrIGg8HAnNlzmPnbLB5HPKZWjZr8PO1nypQxrS+zY8cOAm74096qDQphFIWChvz8uXolSdokHj9+zO3btwkICECNilbO6ctc2FjmoO+gATRv3pz8+fOTN29eQkNDKVOiNLcTgvCyzotBSk7F3iLRQs/AgQNNko4KIdjuvYv2rdpwOGgHDhobghOj+HXatHQCA1C8eHFOnTvLzz9OZsnJU+QrWoA1YzbToEGDdLZCCHbu3cPE8d8xdvVqUrRa2rZty9Gff8rQlzRz/nwa1qnDjcQkSlhYcCExibt6A8fmz083U1ZKyfa9f1HO6dky36XIOBSW1oz+6nP8/Py4f/8+mzZtIiUmiq+bmlb5LO1sia1acPv2bUqXNi0uZyYb8oEvl32wO/4/VOLj41GpVC/0P40cMZJ1izdQTlTFVmmPf8o9borLnDl/hiJFihASEsL169eZNHES+BionKOiSf+dkd74GwIoVaoUXl5eeHl5ERYWhvfqHfR2aIUydb9RcHIY6+L2EBz6KN2X9r59++jb82NEioFkvZZc7rnZ8NemDEsfg9Hnc+3aNSIjI6lUqRI2NjYZ2r1uIiIiWPbnn9y9eZOylSrRs2fPdFU/wbgEVr1SBWrkUNLIxYb78Sks8otg9qLF6fZVNa1Xm/bCj46F7NPaEnUGym0O4PodX3Lnzv3ar+tDJkt2/BdQyDMTMjfjVPVNNu/4N/NucuXKFQb1/5SLly+iEIK2bdoxb+EfODk9qy8THR3NvHnzaWPVFSuFMfy6uGUZEhMSqF+nPknaJCIjn8VVlLYume48eis9axevpUOHDmltOp0O/3t+/Hl2O14iHwmKZHwS77Bk+dIMZwWNGzcmIDgQHx8fLC0t8fLyeummVCFEtniid3Z2ZkRqotOXkTt3bs5dvsqcWTNZd/gweUp6snPRcCpXrpzOdsiIUQzr14tKrlbks9WQrDcw6WIktWvVMgvMO4KUIHUf1sP885hF5j0gLi6OW7dukStXrgxry4eEhFC/TgMKaMvR0qo/OrRc3n2epo2acfLMCe7evcvVq1fZs2cPGoNFmsA8JY/aA7+4O3Tp0ZlSpUpRqlQpHBwcqFe7HoHJQXhY5EVKyc3EW8SrE2jZsqVJf5VKxQ7vnXh7e7N7lzdOLs6s6LMhXSqd51Eqle91qYGcOXPy/Q8/vtKudevW3B09jibff08+ByuCniRQpWpVVq5e9wZGaSZLkKTf9/0BYRaZd5xff5nKpEk/kENtT1zyE+rWrcPaDWuws3sWQbVo0WJySk/yq40zDw1KSipqsufqcmxsbNBqjaVhlUolQipIMSSjUTxbTovQP6ZFy+YsWLDA5NwbNm/g4x4fo0xQojNosXd2YO+2vRkuxSkUClq2bJlOgMy8mq++HsmAQZ9y/fp1cuXKlS5Iwcw7gFlkzGQ3pJQcO3aMc+fOkS9fPlq3bp3uy3vLli388sM0yhhaY6W1Qy90XDt2mt49+zDpx4lcvXqVq1evsmblWly1ReC5ZWEhBE4qN8o28qJr166UKVOGYsWKMaDfAE7sOERFZU1sFDl4kHKfm/IKf4yekW6MTZs2JSgkiMuXL2NhYUGpUqXMudZeE7a2tlSrVu1tD8PM/8uHu1pmdvxnR5KSkmjetCVXLl3DSu+KXh2H0krHsRNHTJaYalarQ8wlS1xVhdLadDKF44nLMWCM/tZoNOTMmRMRbkUVi+Zpdgap55BhLcdOHTHxZ6SkpDDq69EsWbKY5JRkihQsyu9zZtC4ceM3cOVmzGQvssLxX9FTIU+PzpzjXzPk5Y5/IcRS4Gk2lVKpbROBAcDjVLNvpJR/Z9C3GTATY22TxVLKn//Ndfy/fNBFy94GQUFBfPbpYIoULkatmnXYunVrOptffvmVGxf8ya9rQi4q4K6tgzIqF21bt2fBggUMGTKEunXrcu7cWSwVdiZ9VUKDlcaG6dOnc+3aNeLi4rh+/ToGx0Ru6s6QYIghWv+Yi+ynVu1a6RzmGo2G32fNIDommqjoKK7fvmYWGDNm/iuGTL5ezTKMWej/yQwpZbnUV0YCowTmAs2BEkC31Mz3rx2zyGQh8fHxeHt7c+DAgTQ/x/M8evSICuUrsmHFPhKCnblzIZaPe33C1F+f5baKi4tj0YIlOOq8EOLZr8dZ4cX1G9f59NNPWbFiBTqdjsJFChEu75ucI8bwGCsbC7744gtKliyJWq3G3t6eM+dOU7FtUc4odnArxzF6f9mFzVs3vvBalErlWwsFNmPmvUKC1Cky9XrloaQ8SiZTZ/2DKsA9KeV9KWUKsA5jFvvXjtknk0WsX7+eTz7pj4U6B1IaEEo927dvo2bNmmk206ZOx5Boh73SmD/LQumAhcGBcd+OZ9/+fdy5c4eAgAAUqChiYbr3VCBQq9WcOHmaihUrIoTgwYMHVCxfGb+kMzjo85IgnxCi9mH2zJkmmxYB8ubNy8o1K1//jTBjxsw/EGDItK/SRQjx/Hr+wtQEv69iiBCiN8YCkSOeFoJ8joyy3FfN7KD+C+aZzCvQarVMmDAB15yuWFlZ06xZc27evGli4+vrS7++n6DWe6LQ5kWp80QX70Tz5i25fv063t7e/P7776xYsQq13jTLrlphjdQp8ff3p2bNmvz444+0bd+GKMUdk3okkXpfShQvQaVKldKc656enly+epE2/esiiwbj1cSJHd7bTCpxmjFjJhsgReZeEC6lrPTcKzMCMw8oBJQDHgHTM7DJVMb618EHPZPx9/dn2rRpnDt3jlKlSjFy5Mh0u8p79/6YHTt2o0u2RAhnDh04S/Vq1bl+4zru7u5IKZk79w8U0g6V8tn+Eo3Knuj4R5Qq9WxGolFbYquIw+q5kjcGqUdjqeDAgQN4eBiTUMfGxlK7Zl2CAg6jSnQGywSSNRHsWHUo3TW4u7vz+8z0kV8fElJKQkND0Wg0JptLMyIsLIzZM2dx8shR8np6MGT4sAw3QT4lNjaWtWvXcvPadUqXK0uXLl3My4hm/h0SZOZnMv/+8FKGPv1ZCLEI2JmB2Yuy3L92PtjosmvXrlGjRg2Sk/VotQaUSoGFhYI9e/akLXE9ePAAL69ioHcx8Y/oZTSe+VyxsrLE19eXhIQErNR5sNHkMTlXoj6A9h81ZeDAgRQrVoybN2/SskUb7AylsFDaY5A64rhHxRpF2bPXNMW7Tqdjx44dnD59hgIF8tOtWzfs7e0xY8q5c+fo/3Ff/P390UsDNatVZ8nK5RluSg0ODqZqhUqUVtpTxdqVoOQ4tkbdY/6fS/joo4/S2fv5+VG3Rg0KKy0prrbGJyWehwoDx86cJk+ePOnswZhZYdmSJTyJjKRZmzZ06NABleqDfpZ7p8mS6LK8SnlySI5XGwKWY2NeeT4hRH5g53PRZbmfFoIUQgwHqkopu/6jjwq4gzFv5EPgHNBdSnn9X17Ov+aDFZlGjRpx8OBxhHjmu5BSi7t7Tj755BP8/f25ePEiN67fRaNyMzmG3pCASpNAw4YNKFy4MCkpKfy5dBVWolCaGBmkjkR5Fx+fKxQq9CzEeMWKFQwbOhyDXpCsTaRhg4asXrPSLCDP4e3tzYxfpxMc9JBadWsz5ttvMtyAGBISQkmv4nS1K0tV+wLopJ5dUde5aRPHtds305UcGDpkCIF/HeKT3M+qmt6MC+f3qKsEBD9EqVSa2Ldt3oJctwPo7V44rW1h4G30Vcuxan36HfdLFi9m7Fdf0Sm3G45KJbuionErUYIdu/ek85E9RUpJTEwMNjY2ZjHKhmSJyLir5InB6XPYZYTVt9GvCmFeC9QDXIBQYELq/8thXP7yBwal1uvKgzFUuUVq3xYYqxUrgaWpCYlfOx+syFhbW5OUpDDZPCilRMp4wOgod3Nz4/LlK6gVeUw3GSri6D+gB7NmzQSMmYvbtW3P0SMn0SfbABKhiWHQoP5MnWZaFRGMfp579+7h7OyMq6truvc/ZObPm8/EMd/SxKosrhoHriUFcFEXwLlL58mXL5+J7ZQfJ3Ngzhr65nzmv5RS8m3ATso3rImjoyOxsbHExsYSExPDzctXmZi/FkVsTP1iPa5swWClwcLCApVKhVKpRKlUEhQYyO5qzbFWPvvyj0hJosulQ4wZNw4XFxdcXFzImTMnFhYWtGjShNUVypLfxrhsqjMY6O9zg2FTp9GzZ89017p582a+GfEVD0NCsLCw4LPPPmPij5PNYpONyDKR+TRzD5FW30WaE2S+L9jZ2ZGUFINR1J8isbCwJDo6CktLY+2TVi1bcfjwSfRaa0CJ3hCPhSaFYcOGpvVSKBT8tXULmzdvZs2atVhZWtHvk74v3F+iVqspXrz467u4bEZERAQjvxrJ5s2bMBgMtG/Xnmm/T08nsMnJyYwb8w2DHBqT28LoW8ln6YohUtKza3eq1KhGYGBg2ivsUQhd3Uw/j0II3BQ27N27F2dn57TKlba2ttjY2PA4JcFEZJIMOlKEpEeXLqjVavR6PTqdDq1Wy7rVa0gx6E1EJsVgQOoNTJw4Md11lrSzTRMYMFbHbOvixMypv2JnZ0ehQoUoWLAgVlZWHDx4kCGf9OW3cu5Ur1yWoIQUxqxextjkZKbO+P2F9zIxMRG1Wm0WoncI+Zp9MtmdD/Yv9YsvvmDKlJ9JTDRWVZRSYmmp4JNP+qUJDMDGTRsZPvwrli9fTkpKMuXKVWD+/D/SJXdUKpV07tw5Xar2Dx2dTke9WnWxCVXziUNHBHBmz1VqV6+Fz81rKJXGyLqbN29y6NAhRIohTWCeUsY6H3PP7uTClUt4eHiQN29eGjVqREREBJdPXKWxLJ4209Qa9ATIGE6fPp2uBs66desYN3goXjbOOGus0Rr0rAi9RtPGjVm0aBH/RGh1LD95ni89iiGEwCAly0Pu03/AAH6fM5uIiAjCw8MJDw/n8OHDrJ01K90xnqRo8bl3m7Ztn21JyJMnDzIpkZFFc1LD1biZ1sPGghnl8tB40SIm/jg5XXDBmTNn+OrzTzl/xQeNWkWP7t2Y9vtscuTI3Fq/mbfJvwphfu/4YJfL9HpjEazVq9dgZWVFUlIiLVu2ZNWqVSYi8xSDwYBer3/h2vqHhk6nY9GiRaxYYtwY2qVHFz4f8nm61P07duxgWJ8h9MrR2mTJcenjLYicakJDQ0lKSkprVytUTC7QG0vFszQcZ2Pu8LCIngNHD5kcIzExkYplypM7Rkl928IkG7TsiL1J4Rrl2LTtr3RjllIyacJEpk+bRgF7F4LjoilboTwb/tqSYVRaREQEjevWIyksnOJWdvjER+Ocz4M9hw6aJCB9ej8KeXrypaszTXMZfXhhScl8fOUac5cvx83NDV9fX+7fv4+vry/bN65nXc1CFLU3zXhdccdlajVtTo0aNShbtixlypQhISGB6hXLM6m8Le0K2hGZpGfixWiS85djm/fezPy6zPyfZMVyWYU8anm8v2OmbG1+ePzeLZd9sCLzlJCQEG7fvk2hQoUyjEgykzEd23Xk0uFLlFGUQimUXDfcIGcxVw4fP4wQgrt373LhwgXmzZuH/mocTR1rmfQ/FH2Ghy5RtG3XluLFi1OiRAmKFy/OwH4DCDp2g/b21bBUaHiUHMnS6AMsW7+KZs3SZ9OIjIxk8qQf2LZlK5aWFnzcvx/Dhg9/6cNAVFQUV69eJU+ePCblnzPCYDBw4MABbt++TcmSJalXr94Lk4BevHiRts2b46pS4qRWc+5xON98+y2jxo5NZ9ulXVuKB1yhb5FnQSX3YxNpffAWDjldefjwYVq7rY0VvQpa833VZ8uLKXpJxb+COHz6PF5eXibH9vPzY9ovUzh/+gSe+Qsy9Osx1Kplev/NZI4sEZncann8E+dXGwI2k0PNIvOu8y4kyHybpKSksG3bNu7fv0+FChVo2LBhuiit8+fP07x+M7rl6IJKGFdcDdLA2icbyFkwJw8ePCA2NhYw1pJxVTkx0M10GXF93G6+nfU93bt3N2mPi4vjk4/78re3N/YWOUiSWib/PIVBnw56jVeddWi1Wvbv309MTAz16tXDzc0tQ7tLly7RuG4dvi7qQsPcDtyJSeSHm2EM+HoMI0aNIjIyEh8fH65cucLc335lTGFoXcB09tR6VyBuVRrStWtXKleuTMGCBbl37x61q1WmVzEFTfKpuB6u45fzKcycv9S8lPt/kDUio5FH+7hkytb250dmkXnXMYvMiwkICKBOzTooEzTYah14rHyER+G8HDi8P23t//Hjx4wbN46z687QIEc9k/5nYs/hbxtA+w7tqVixIhUrVqRw4cKUL10Ot2h7qluXQwjBmfir+FuHcPPurQyXJgHCw8MJCwujUKFCLywV/a5z7tw5Jn4zhrPnzpM3T26GjR5L7969082UJoz/lqDti/mlyrMlvXitgVJr76EVKpKTkwFwcnLCzlpDj/yJjK72LGT29MNkBh4R+AY+SvfAEBkZydatW4mPj6d58+YULlwYM8/IEpHJpZFHP85cFKntrw/NIvOu8yGLzKNHj9BqtXh4eGS45NO4fmOizydS2qIiYPRhnEjZj2cVd3LlduP06dP4+voCkFudi64upk/GB5MO8/H4PgwfPtykPSQkhGFDhvLX9q0gJa1btub3OTPNy5OZJCQkhPKlS/JJQTVdC9kSmqjjh8uxFKrdjPlL/uTatWucO3eOs2fPsnntCvZ3caKo8/P7vyQF5j9mxfotNGnSJG0p0dvbm55dO1G/sBp7jZ7tN3QM/nIY3/8w5W1darYjq0TmSK+MZ7T/xG5akFlk3nU+RJG5f/8+Pbr0xOeaD0qFkjx58rB89TKqVKmSZhMXF4ezkwtdbPuhem6DaqQunF1PNpIztwvVq1enWrVqlC9fnh5de1BWX5qSlsZs4b7J9zmmO8Ed3zvkzJkzw3E8/VszFzb799y9e5fvxoxi/4ED2NvZ0m/gZ4waMyZdKHOtyuX40iOI5oWeBWBEJOrxmv+IFD1YWVlRqVIlKlasyJ+L57Oth5JqnsZjPI43UGuRgVVbdpt9OKlkhciUz6WRR3rmypSt/fTA905kPtgQ5g8FrVZLvdr1cYzypJG6FwIFDx/eo0mjpmz+axM3b97k1KlTnDhxAp1Wyz/z6AkEzs5OPHz40EQcDh45SJeOXTgfdBGlQomdox271u56ocCAWVz+C0WKFGHt5vQRc//k869GM3HEp5RwUZPPXkVsioGRR5P4qEMH2n7UhVOnTnHq1Clmz55NxTxQzfPZUmROGwUDKuhYt3qFWWSyEinA8OHmIjaLzDtMZGQk34wdx6aNm1EoFHTt1oUfJ/9gEl7r7e2NTFBSSF0urS2vugjBCfdp1KgRYNy3UaNGDdRCw+3HPpS0LA8YZx63DVfp2r1rOoEoWbIkPjd98PX1RafT4eXlZRaRbEDXrl154H+fOj9Nwd3egofRSbRs2ZIFS5djbW2d5vxfvXo1K38anK6/RinR6dLXQjLz3/iQN2Oal8veUbRaLWVLlychUEFuQ0kkEKzwwaWwJafOnuDatWucOnWKFStWEHolloqWjUz630m+SN66dixctCDNR3P37l3q1KyLrdYem2R7Ii1Csc9jx9ETR3BwcHgr12nm/yMuLo67d++SJ0+eDCPcoqOjKejpzoG+Ckq4GbNexCVLai6WzPpzE02aNHnTQ86WZMlymaulPNQlc/5Hxzm+5uUyM6+f5ORkpk6dxp9LlpGSkkLHjzowYeJ3ODo+29C1fft2oh/FU0w2RSiMT0mFZS3O3diAra1tWmVOZ2dnEg3J6KUepTB+mUgpeWLxiPH9vsTT0zPtmEWKFOGe3102bNiQFsLcunVrcwqTd5AcOXJQvnz5F77v4ODA7HkLaDx4IJ1Lg71Gx4YbKhq3/shcbvs1YJ7JfEBkh5mMMRGnTBdO+pRmTVtw8cTN1BLMKp4o7mHnLrhy9RIJCQmcO3eOn376iYATcRTUmNZCuas9Sb6qdgwZMoTq1avj4eFBu9btuXjUh/z6MihQEqS4iW1+DWcvnEGj0WQ4hveZuLg44uLicHNz++CX+Pz8/Fi7di3xcbG0bNWa6tWrf/D35HmyYiZTztVSHvzI89WGgPO8u+/dTObD9Ua9BfR6PRMnfo+TowsqlYpSJcty4MABE5tz585x+sQZ3A01sFHmxFrhSC5ZidCAaPLly4ezszPNmjXjyJEjxBCS/hzWcQwbNowuXbrg6emJEIJNf21k+MQhRHve51Gua3T7sj3HTh59LwRGSsn169fx8fHBYDC81DYmJoaeXbqSK6crxQsVwatAIfbs2fPSPocPH6ZxnbrkdXWlYa3a6X5f7zoFChTgm2++YfKUn6hRo4ZZYF4HqQkyM/N6HzHPZLIQX19fzp07R548eahVq1a6mcqXXwxl1bKNWBuKoBY2JOhDiVfc5dDhA+TLl49Lly4xb948Tnhfx0NVzaRvmPYGFnmfMGBgfypXrkzx4sWpVKEyOZ7kI48ogQQeyqtoXR5z1/f2eyEgr+LixYt0+6gzMZHRKBBY2tmwav1aqlevnqF9y8ZN0F8PoK9raWyUai7GPGJW6CUOnThO6dKl09nv2bOHnp0682nuQpS1c8YnJpL5j+6xdO0aWrZsmeE5EhMTWbduHWdPniRfwYL07dfvhbv+zWR/smQmk9NK7u+QP1O2ORfeeu9mMmaRyQIMBgP9PxnAuvXrsdI4oJdJuLo5c/DggbQNhzExMeRyy01ORXWUimdhozEp/sQr/ElKSkhrs1I6UMyilck5QhTn+fr7AXz11VdpbX5+fgzoN4ijx48A0LBBIxYtWfBOb3JMTk7mwIEDJCYm0qBBAxM/1PPExcVR0DM/nWxKU9WuAAAXYx+w8skF7vr5miS8TElJ4fz587Rq3JSlXi1QK56Vd1gfeoOwojn5csRwVCpVWhp9tVrNgN4f011lTx3n3Gn2JyNDWSNjuXQjfUHByMhI6lSrhlNiAjVzWHMvRcvhiCj+3rfvpSWezWRfskpk9rUt+GpDwHXJjfdOZMwe3VeQnJzMzz//zJIlS0lJSeGjjzry/fff4+z8LOHd4sWL2bx5O1aiKAqdEiElIUFhtGvXgR9++J5r165x/PhxdFpQWpmmSLFQOqJVBjN5+g+UL1+e0qVLU6VyNcJCruMivBAoiNL7k2gZSu/evU36FihQgP2H9qZlMX5RipZ3hRMnTtCudVtcVHZYCDV9Y4OZNmM6AwcNTGe7adMm8qudqGb/7MNb0S4fJ2PvU7NmTaytrYmIiCAiIoK4uDgAClg5mAgMQAELezYfPsKeg/vTnUMBVK1hOmOp4piTUSfO0LhxYzw8PHB3dydv3ry4u7uzad06immTmViyaNqy067gED7t25cL165leM06nQ5vb28CAgKoVKkSVatWNS9ZvW+Y68l8uMTGxrJixQrOnz9PqVKl6Nu3b7qU761bteHkqXPoki0AwdIla/D23s21az5YWVmh0+mYMWMmpDigUBm/wIQQaMjJhQsXaNGiBQC5cuXCIFPQGZJQKZ6JQbKMolHjhiYzlCNHD9G7Vx9OndqGEIKiRYvy14oDuLhknGTvXRcXMC4ztW3Zmo421SlhY3SSPrZ6wpgRo8jjngeDwcCtW7fSXpcvX6amZf50x8mlsiM4JpyCBQtSsmRJnJ2dcXZ2Rq1W88OEiTzRJWOveib0FxPD6Na7JwM/+xStVptWsEyr1TKg98fcjXtCKbtnfxP34mOwt7LmyZMn3Lhxg5CQkDRfkLVSyYqqFUxEolluNyYfOcmJEyeoVq2aSYnngIAAmtSri70uEa8cGqY/jqNEhUps2bHzvc3X9iEiEUj54bq/P1iRCQwMpHLlKsTFJZCQkISVlQWTJ0/m5MmTFCtWDDA64U+eOoU+xRFFapiw1Kt5GBRKrVq1SEpK4t69e6Sk6LC3LPqPMwgsLCz588/FNG3aFCcnJ0aNGsOi+cuw1hVCrchBvC6UJGUg479bbdLTw8ODQ4cPEBUVhU6ne+ku+uzOvXv3mPLDFM6cPI1nfk9Gjh1FgwYN0tnt3r2bXGqnNIEByKmxp4KmAG1bt8GAcVk3V65ceHl50aRJE07uO4zWoE+bneikAR99KMuWr0zbaPo8j0NC+XHlOno4FcNZY82R6AecT4ng0k9TyJUrfdqPcRMnMv27iUzIX4r81rY8SIxjWtAtJk2ZzJfDhhnPqdMREhLCw4cP6d6xAwl6vckxtAYDSSlaatWqhbW1NaVLl6Zs2bKULVuWlUsW0cZO8kWxfGm2n573YdrUXxn37fj/74abyZZk1UxGCLEUaAWESSlLpbZNBVoDKYAv0FdKGZ1BX38gFtADuje1LPfB+mQ6derM1q07MRieXz7RUbJkEYYMGYKvry/79u3j2tW7qJSmtSB0+hhsbCV169bFy8uLq1d9OH7kIhYib9pTbIruCXY5k3nwwD+tzWAwMGPGDKZPm0F4xGMqVqjE9N+mUqNGjTd1+W+UO3fuUL1yNcqoilJY7UmYNoLjKZeYOW8W3bt35+bNm5w+fZpTp07h7e2NfbSSQe6my1OHoq4QU8KSn379CS8vr7RNoVJKOrZtz52Tl2hkXQSFEBxMuEeuMoXx3r83wyUnKSULFy5kwaw5REZG0qBxI76b9D358+fPcPxSSmZMm8bPU35Cr9WiUKkYMWoko8eOzfD4v/7yCztmz2RWSS80qUEf8/wCuGLnRL/PPuPy5ctcuXKFK1euEB0djUYh8GlfAUvls6fcC+FxfBuQxPV799MdPzw8nHlz53LqyAHyeORj8NDhVKhQIbO/DjP/B1nhkynrbC13t/znQ2jG5Fl55aXnE0LUAeKAFc+JTBPgoJRSJ4T4BUBKOTqDvv5AJSll+L+/iv+fD1ZkcuTIQUKCRIhnH3Dj/pV4ANRqNa6uroSFRqBSmEYHKdXxTPx+DCNGjACMRbAqV65KxONYdEkWKFR69CKabdu20rBhwzd3cdmMHl26E7rPn1q2FdPagpJDWBv1NypLFTExMQA4OjpSrlw5Th8/yei8nXBQGcsK6Ax65kTuYs7KhRlGc+l0OpYsWcLqP1dg0Bvo+nEPBg4cmOWRdTqdjoiICJycnF5aDE2r1dL9o484ceQI1V2cuBufgD6HLXsOHTIJxpBScvnyZepUr8aV1mVQKZ4J1vWoBDofvkXNBo2oXbs2derUoXLlykRHR1O9UgVqOupplkfN3Sc65t+K548ly+jYsWOWXq+ZZ2SVyHi38Hq1IeC+6vIrzyeEyA/sfCoy/3ivPfCRlLJHBu/5YxaZ189TkXF0dOLJk+R0IqNUJnPnzp20nfBFi3gR/DAKpA0gMMh4rGx03Lt3z8RHEh8fz6pVqzh44BD5C+Rn0KCBFCyYuYiSd42zZ88ybvQ4zl84j3sed0Z9M4pevXqZPN0nJCRQyLMgHTQNyak29XP9+nAx7bt0oEmTJlSrVo2iRY2O8l9++plpU36lmpUXlqi4oPOjXK1KbNq65YUbV7Mjly9f5vz58+TLl48GDRqY+GGep3qFcnRUxdC5gPHvSErJ1xcC8bPLRZJWx/Xrxgg2CwsLcuV0poFDEr/WeFaX5GxIAp+eTcQv6NELz2Hmv5EVIlPG2Ub+3bR4pmw91l4IAJ4XgYVSyoX/GFN+XiwyO4D1UspVGbznB0QBEljwz+O+Ll6bT0YIYQkcBSxSz7NJSjlBCOEErAfyA/5AZyllVGqfscAnGNcMv5RS7kltrwgsA6yAv4GhUkophLAAVgAVgQigi5TSPzPj+/jj3ixYsJjkZIkQAiklGg20bduRAgUKpNkdPXaE3r0+5viJY4CgWPFiLF++LJ0T3sbGhkGDBjFo0LtRwfH/5eLFizRu0JjKqkp8ZNWR8McRjB4ymrCQMGrWrsmBAwfYv38/p06dAq0kwjnaRGQS9IkoNErmz5+Pra2tybFHjx1DnXp1Wb50GQnxCUzv9BVt2rR5pwQGoFy5cpQrV+6VdvP/XE7TBvU5GZ1MMSsFR6K0JNg6cujQYRwcHIiIiOD48eMcO3aM5Qv+oGsl08JXVXJZQ3IkN2/epFQp0++ba9eu8fu0X7h1/SolSpdj+MgxFC+euS86M1nMv4suC/9/RU0IMQ7QAatfYFJTShkshHAF9gkhbkkpj/4/5/pX43pdMxlhfKy1kVLGCSHUwHFgKNABiJRS/iyEGAM4SilHCyFKAGuBKkAeYD9QVEqpF0KcTe17GqPIzJJSegshBgNlpJSfCiG6Au2llF1eNq6nM5n4+HiaNWvGpUuXEUIJGChYsACHDh1KF2EGxn0uWq3WJHT5Q6Rdq3Y8Of6EstZl0toidZGsDV+HTuoQQlCuXDkaNmyIRqNh6ezFfJSjCc5qB5IMyXjHH6Ni6+osXb70LV5F9iEyMpKVK1cScN+XytWq07FjxwyX+xrUqMrHOR7SssAzYU7QGSi2/C5KKxsaNmxIkyZNaNKkCSEhIbRv1YzPy6mpllvFiYc65l/VsWvvAZMaQmZeTZbMZJxs5M7GJTNlm2/Duf9ruUwI8THwKdBQSpnwor7P2U8E4qSU0zI1sP/Aa5vJSKN6xaX+V536kkBboF5q+3LgMDA6tX2dlDIZ8BNC3AOqpK4j2kkpTwEIIVYA7QDv1D4TU4+1CZgjhBAyE8ppY2PD0aNHOXfuHD4+PhQtWpRatWq9cI/C8+nz30fi4+P59ptvWbliFSkpybRs2ZKpv0018SVER0dz6tQpmqpNM/Q6qZywVFvyy4xf6Ny5s8ksz9nJmUkTJ2GjsuJJUiwd2rdn7vy5b+y6sjtOTk4MHTr0lXYDvxzOD8M/o5KbFW7WKnQGyZSL0ZQtW4YylaqyZ88etm3bZjxmDgum1rOmcwlrAGp5WpDbJp5xI4ez78iJ13o9ZjJGyte3T0YI0Qzjd2jdFwmMEMIGUEgpY1N/bgJMem2Deo7XGsIsjFOEC0BhYK6U8owQwk1K+QhASvkodeoG4I5xpvKUoNQ2berP/2x/2icw9Vg6IcQTwBnTNU2EEAOBgYBJ1mEhBFWqVPngn+6klLRo2pJHVx9TW9kctYWam97XqH68OqvXrebo0aPs3r2b06dPozAoCLMLw+m5JbA4fRwooU+fPlhbW5sc+6sRX/HZ4M/w8/PDzc3tg58J/r906dKFW9d9qDVjBiXdbPGLSqR4qdLs/Gs7zs7OSCm5d+8ee/bs4csvv6Cdl+l97lDMiuFzz2AwGEyWH6Ojo5n6y0/8vW0TNjY29PxkMAMHDnznliizNTLr8pIJIdZifEh3EUIEAROAsRjdEvtSH5JPp67u5AEWSylbAG7AX6nvq4A1UsrdWTKoV/BaRUZKqQfKCSEcMF5gOkfVc2T0W5AvaX9Zn3+OYyGwEIzLZS8b8/tKeHg4KpUqw7owZ86c4ebVmzRTd0aRGghRzqIa+yK2UrduXQAqVqzImDFjcHFxYdK3k8iRnAN3jTsx+hiOphxjwMAB6QTmKVZWVpQoUeK1XduHgBCCiT9M5othX3H58mXc3d3T9nM9fb9IkSIUKVKEHyaMwz9aR1HnZ5Fw/tF6VNJArly5aNq0Kc2aNaNWrVq0bdGY0jbB/F5XEpMEP00fxYUzJ1n054q3cZnvJRL+sVXiPxxLym4ZNC95gW0w0CL15/tA2SwZxL/kjWzGlFJGCyEOA82AUCFE7tRZTG4gLNUsCPB4rlteIDi1PW8G7c/3CRJCqAB7IPK1Xcg7yOXLl+nb+xNu376FxEDNGrVYtvLPtGUwrVbLli1bcDC4pAnMU/KqCuBVvTDrNqzF1fWZ09nd3Z1Rw0eyK+xvLCwsGPz5YCb9+EZm3h88zs7OrwyLH/TZ54zcMI/lzZU4WCqISNQz6mgyrdp1QG1hye7du1m1yhh8VKeQmkU9LdOWiWsWkBSfsYlR34ynSJEi6Y6dkJCAUqk0ZyT4lxhe43JZdue1zYmFEDlTZzAIIayARsAtYDvwcarZx8C21J+3A12FEBZCiAJAEeBs6tJarBCiWmowQe9/9Hl6rI8wbkj6IGcqGREeHk6Deg0Rdx1ppOlDI00fHp2No3aNOixYsICOHTvi4uLC1KlTCU4M5J+3LkYTQZt2rU0EBqBTp07cD/QjNDyU8Khwpvw85Z0obBYUFMTSpUtZv359Wj6zV5GYmMjp06e5c+fOax5d1jF+wvd41etA6aVR1FmfSNml0ZRv1pU169azatUqQkNDOXv2LFUrlKZTaaWJH9JGI6iZT8GuXbtMjnnr1i2aNqiJs5M9jva2dOnQitDQ0Dd9ae8mMnNp/t/X/GavM7qsDEbHvhKjmG2QUk4SQjgDGwBP4AHQSUoZmdpnHNAPYxjeMCmld2p7JZ6FMHsDX6SGMFsCK4HyGGcwXVOnhS8kOxQtyyoCAgLYsmULer2etm3bpnvy/O233/hj4jJKUdek/UDcauJkFB4eHjRt2pSmTZvyw8Qf0T9QUEpVCZVQcTflOn6am9y+d/uFmZDfJX6ePIWfpkyhkkNe4qWOu/HhbNr6F/Xr139hnz+XLuXr4cPJZWVDeEICRYp5sf6vLbi7u7+wT3bi8ePH+Pn5UahQoQx9Yd+NH0fUkVlMa2G6V6zEtDj8IiVeXl40bdqUGjVqMPzLTxlVP44BNQXJOpiyR8H+IE8uXr31XvtvsiK6rJSDrdxS58VVSp/Ha8ex9y4L8we7GfNdZ+GChXw1fAQuigIgBeHSj2/Hj2PM2NHodDrOnz/P0C+HEX9VRWGN6R/4Vd1hen7dnu+//z7tKTYyMpIvBn/B5i2b0Rv01KlVlz8WzMXLK3M7ld8kiYmJTPxuAiuWLScxKYnmzZrx87RfyZcvX4b2Z86coW3jZvyUrx7OGqPf6GpsKL+HXSDwUTBWVlbp+pw8eZL2zVswrVB5CtrYoZMGVjz05ZqDJWcuXXzh2FJSUtixYwe+vr6UKVOGJk2aZNsv4YCAACqVK8nCNgaaF1Oh1cNvx/WsuePEwM+HsW/fPo4cOUJSUhKtygj++uyZj0dKSfXfrJgydyNNmjyLNtTr9Xh7e3P0yCFc3XLTq1evd7qeTlaJzObamUv/U2znUbPIvOu8KyLz5MkTHj9+jKenZ7p9E0FBQXgVKU4pWmGtsAcg2RDPJf0WatSuxvnz59NStjir81DTov2z/GlSzwk2sueQN5Uqpf9b1uv1GAyGl6ZPedu0bNKM8Mv3aWNXGmuFhiMxd7jAI3xu3TAJbIiJiSEwMJBvRo3B9nIgnXOZ7lUY43uAPJVKUbBgQZRKJSqVKu3f/X97UydJ0MW9UJq9Xkq6+hzD++hhypZN70N9+PAh9WvVwlGbQgkrC87FxpMjjzt7Dx/OtiHwhw8f5tNPehH3JIrEFD3ly5Xjz9Ub8PAwukeTkpLo0a0T1ZTeDG9k6rzuv9JAgnt7vvvuO0qWLElKSgptWjQiPPAq7Sok4RduwY6Lko1bdlCvXr23cHX/nawSmU21Kr7aECi+68h7JzLZfyH9AyMpKYlBAz9j48YNaFRWCIWBKT9P5rPPPkuz2bp1Ky7KfFhL+7Q2C4UNzroCXLp4ia5du9KoUSOqV69Oo/qNuf7oGB6GEujR4a+4QuXqlTMUGAClUvlWUpQYDAbu3LmDlZXVC2ckkJqy5fRZJudthyo1UKGdc3kehcTQonlzHBwdefDgAYGBgWlCqxYKPnYvl+5Yaim4dOkS169fR6/Xo9fr0el06PV6FCkpdCls2kcpBNY6A5UqVaJw4cIULlyYQoUKpf37+6+/0FCjZEhq1JeUku9u3+O7ceP4ffbsrLlRWUy9evW4ee8B9+/fx9ramty5c5u8b2lpSeu2HVk/8wjDGyWntesNkv03DTw8uZGNGzfi6upKXnd3HPS3OPW9Mq0w3+7Levp93JV7fsHZdkb3upFSoNd/uGl/zCLzhpFSEh4ejrW1NTY2Nune/3TQYHZvOUZB0QKVwYJEXRRjRn5LcnIyCoWCo0ePsmfPHqyS3IyR8c+hUqkZOmwoEyZMSGs7eeYEEyd8z1+b/kJjoWHAJ30YNWrk677Mf8XBgwfp16sviXHxJOu0FCvmxZqN60xyv+n1eq5fv87MmTPxVDmmCcxTSli4sfnyZYqU8KJIkSI0aNAADw8PPDw8CAoK4o8pU2liKIyFwvgnH5wUg582Bn+/wAwzPPz6yy8cmL3ApCpmSFICIfpkPv/8cwIDA7l37x6HDh0iPt6YVFUpBD80rJ1mL4SgX948DFy79oUio9Pp2LVrV9qG4LZt277xyC0hBIUKFXrh+126dOGXyRP4alMoQ+oaSNRKJu/RUKJsZY4uWcnhw4c5dOgQ3ts38N0gJcrnEn42LatEvTqBq1evZirVzvvK69yMmd0xL5e9QQ4fPsyA/oMIDAoEKWnVqhWLlyxKW+J5WqK5oGiBSjz7oonS+ROUcgYDOvLnz0+FChXYtcObcsp2WCmMyzDJMp5rYgenz518p/akPHjwgLIly/BRjpoUs/bEgOR4rA8+Fg+Zu3AeZ86c4eTJk5w+fZrY2FgAHNTWTC/cFcVzUVErIs7Q+ItujB33TbpzGAwGenfrwYl9B6ltnYdEqeNgzAN+nj6NAQMHZDiuJ0+eUL1iJfIlG2hs78rj5ERWhwcydOwYRjwn0lJKQkNDuXHjBs2aNOFkg1pYPTcTfJCQQIcTZ6laqzZ169albt26VKtWDWtrayIjI2lUpxaK6Aiq2au5Eq8nRKo5dOJktiuhHRoayoRvx7B921Y0GhXdevRh/ITvTfZGNW1YgwHlLtG+iqnvpshXsHPfaUqWzFxqlexEViyXlbS3k+uqVc2UbZm9+9+75TKzyGQRUkouXbpEUFAQFStWTBeBdOfOHSpWqISVvjBWSlckOuK5T4nyHsyf/wdnzpxh3759bN6wlRKWpqnbEw1RRFqf58Klc2kZC+bNm8/IEaNwFgUQUhCBH2PHjeabDL5kszMTxn/H0fk7aW1fzaT9lwdrCdNGo1AoKF26NDVq1KBGjRpUr16d3t16YhkQS1uHslgp1Bx7cpfdibe5dvtGunDrp0gp2b9/Pzu3bcMmhy09e/d6pRhHR0czZ9Ys9u78G5ecLgz68guaNm36QvtWjRtTJCiA/vk90s75w+173LN3RKjUXLp0Kc3fVaVKFVIS4ikcG8JP5Z/VIfrtZghB+cqwacfOf3MbswV//vknC6YOZf9YiZXGeD2rjmqZdjA3V2/4vpNlpbNEZOzs5Jpq1V5tCJTbty9biExqIuNXYcioOFq6Y5lF5r8TFhZG0ybN8PX1Q6O2Jj4xin59+zFn7uy0D9aQz79g7bK92CqeLQFJaSAo4RAGqQWM+dGSEpLJr2qIleJZ2PBj/Q3qtC3G2vVrTM7r5+fH5s2b0ev1tGvXLltFggUEBLBo4SIe+AVQs24tevXqlS4jQEBAAN07d8Ptvopa9qbJIFZFHKDRgLaMHz8+Xbbm6Ohohg35kg0bN6DV66lVtTqzF/yRLhPxm8bPz4/6NWtSQKWkhIWa8wlJJNracejECZydnXny5AknTpzgyJEjHDlyhMvnz7K/aWk8czybtcZq9VTceZW4hMR3Yu/R8+j1ej7p050De3fRqrzgfriKa0EK/t5zMMNAiXeBrBCZEnb2ck3VzIlM+f17s4vIJGHc9P6yJwOllNLzJe8bj2UWmZeTlJTE3LlzWb16LRqNmkGDBvLxxx+bODEbNmzM2VM3UOOGEAKD1KFXBjHi6y8pUKAAly9fZvmylSgS82KjMi3zG6G7yIDPjMW2ihYtypIlS/l6+GgctMWxVNgTJ4OJ1/hz5tzpbCUiL+Pw4cO0a92OEprCOEo7/MVDDE6CE2dO4ufnx/bt29m2bRtXrlwBIL9VLobkbpcmyMkGLb+GbuD0xbMvveanzvqsLlL2X0hISGDjxo3cvXuXsmXL0q5duxdG6rk6OrClRr50IlNu6yW+Hj2ajz76iAoVKqTdl7i4OKZPncpfG9agVqnp8nFfvvxyaLa6foBLly5x7Ngx3NzcaNOmTYYh4u8KWSUyq6tUz5RthQN7sovIXJJSvnRzT2Zs4AMXGYPBwP79+7l27RpFihShefPmJk+POp2OWrVqc/3abVKSjUmkNZZaWrVqxtq1awHjLMbDwxMbZXGTAmgp+ifEJfsBBqysrHByciY2HBzVz562DVJHuP4kd+7eNlmD//vvv/lp8i8EBQZRvWZ1Jkwc/84IjJSSwvkLUTmhJEWsCqS17Yg+gL94SExsDAqFgpo1a9K2bVuaNm1Kz649UD1KoaqlF0mGFI4mX6NO60Ysec/LAQwe0J/Yo978WDZPmpBMvx7MlsfJPIqIQq/X4+npSYcOHWjTpg3fjPwKt7ggBnpZozVIZt5IwL54Zbbs+PudXIp6F8gqkVlRqWambCsf8s4uImMppUz6rzbwAYvMkydPqFOnDn5+/iQn67GwUJEzpwsnThwnVy7jbGPr1q307t0PbZJt2odYSgMGwmjazFi34/r16yQmJONgVcbkg67Tx2NhG82Ro4coWrQokZGRlCxRCl28HVYiN3qZTLLyAR06tWLJ0kVv5V68Du7fv0/lMpX4zLGHyf0ISg5hW/w+fpszg5YtW5IzZ86092JiYpgx/Tf+2rgFa2tr+g76hE8++eS9D3mNjIykYe2aqGMiqWKn4mq8gUdSzcHjJ7CysmLHjh1s2bKFvXv3kpKSQgknSw53zJd2X1P0kprbHrFu516qVs2cY9nMvyMrRKa4rb1cUalWpmyrHP47u4jMeCBBSjn9vx7r/f4Uv4RRo0Zx+7YvcXF6dDpBfLyewMBH9OrViz179jB37lwmTvyexARp8mUphAK9TsXRo0dxcHDgk08+wc7eDp0h1uT4BmUM3bp3pXjx4iiVSnLmzMn5C+do9VFNtNZ3yJE7iok/jmHR4gVv+tL/by5dukTXj7pSpngZenbrybVr19Lek1Jy+vRpJk+eTGxCLHoMJn2TDckULFiQPn36mAgMGH1RE76fyOUbVzl5/jQDBgx47wUGjLVkzl3x4ZvZC3Dr+imDf57BtTt38fDwwMXFhb59+7Jjxw7Cw8Np06ol7QvZmvwtapSCerk1nD59+oXn+NAeIrMnAoPM3Csb0QuY989GIUT/1ArGmeaDncnY29sTG6szWeKSUiJlfNr/1Wo10mCBWmma90ltGcfSpcYEkwB79uyhY8ePUBjsMejVKDVJ2NmruXDx/Aujnd41jhw5QtuWbSmtLIubyo1HumCu668xf/F8rl+/zpo1a7h//z4WFhY42jrgpStArRyVEEKQYtCyKd6bkT+N4dNPP33bl/JOMnPmTE4snMIftUyDfhpt8eORwp4BAwbQo0ePtBLLhw4d4puvh3Lm0jXy5HTk8y+HMWrMN29lo+27TNbMZBzknxVqv9oQqH50Z3aZyVyRUqaL1kgteX9RSpnpePQPVmRsbW2JjzekExkhEtm/fz/FihVDSknRol5ok61RCEsADDIeOwcFQUGBJpvmbt26xZzZc/C970fDhvXp379/hrVb3lUqlKmI6wNXilgVTWu7mXCDo7FH0As9DRs2pHv37rRv357Y2Fga129MfEQsLipH7sc/oH3HDixZtuSDmKG8DiIiIihRpBDfl7OmQ2E79BL+vPmE2beSKFW+EgcPHsRgMFChQgXq1q3LyiULmFHfkpaFLbkbqWP44WRqdejLL9NmvO1LeafIKpFZWr5OpmxrHNuRXUTmNMZy9o8yeC9DAXrhsT5UkenZsxcbNmxBr3/2pSeEjvr1a7Nv3960tsOHD9O1azcSEhIxGAzkzp2LrVv/eic3lr2M5ORkkpOTM8yxZTAYUKlUfOb6uUnNmRRDCksjFhMYFJjmx3q+z7FjxwgKCqJKlSoZ1iZ53RgMBnbv3s3+vftwdnGmV+/eJpVRX8TFixf59cfJXL92jRKlSjJq3DgqVsxc7qnXyYULF+jfuwcPg4LQGQyULFGCpavWUqRIEUJCQli3bh2rV6/mxuULTKhjy+BKz0K/Q+L0VF7xhAfBoelCws28mKwQmWI5HOTicvUyZVv7xLbsIjKdgJEYs+QHPNfuCuzJTFRZWp8PVWTCwsKoWrUq4eFRxMcnYmNjhbW1JadPn6JAgQImfQwGA9euXUOj0eDl5fVeRfLExcUx5LMhbNi4AYPBQNHCXvyxcC61atVCq9WyZ88eVq5cyZaNW+ji3A1H1bP9O2HaME6ojhEUEvSSM7wdtFot7Vu14fb5K1S1cCMKLSdjHrBy3RpatWr1wn5Hjx6lQ6vWdHPJT2lbJ67FRbHmsR+bd2xPqxL6NpFSEhgYiEqlIk+ePBnalCjkycJaSZTLZRraXPbPJ2zZdzzdnpXIyEiOHDlCjhw5qFevXrZOjvqmyRqRcZQLy9bLlG3dk1uzhcgACCE+BqYDp4HLGH34nYCJUsrVmT3Ou7XbKwtxdXXl1q1bbN68mcuXL1O8eHE6d+6cYT4xhUJBmTJl3sIoXz8d23bE/1wwLa16oBGWBD64R/MmzWn/UXt2797N48ePcXZ2pnyF8hy/c4xGisZYKaxI0CdwRneKL7/+8m1fQoasWrWKBxevM9mjQVqes9o5POjb62OCQoIzzA8mpWTM8K8YnNuLhi7GkHKvHI44qDSM/WoEJy+8eH+VlJK9e/fy18aNaDQauvXqRfXqmdsb8W8QQrxyNla2fAVOPjxiIjKPYvU8jIyjUaNGdOvWjZ49e1K5cmX+mDuHcWNHUa2AFVEJkpBENX/t2E2FCplLTW/m1UhAvnRPY+YRQiwFWgFhUspSqW1OwHogP+APdJZSRmXQtxkwE2ONr8VSyp9fOm4plwshtgDtgZJAPNBNSvmvdrO/cCYjhPgbGCyl9P83B8zuvCup/t8Et2/fpkqFarS06IFSPHMIX0w4zh2tD+07tKNnz540a9YMhULB0CFDWb58OY5WjkQnRTNg4ACm/TbtjfhZtm7dyo/jv+euny8lihZjwpRJNGvWLEPblJQUmtStT/lHCmo7ms5Kh97eTpKNGqVSiVarTXvpdDp0Oh0C2F2tDRaKZ/cjxaCn2ZkdzPj9d0qUKEGJEiXInTv3c2HtkgF9+3Jk507aOjuRIiVbHj/m02HD+HbCxNd1S17IxYsXadagDj/X1tCqiCV3InSMOJJCgUoN0AslO3bsIDk5GU9PTxKjQjj6qYYCTsbf4RYfLaMP2eAbEGye0ZA1MxmvHI5yQZkGmbKtf2rLS88nhKgDxAErnhOZX4FIKeXPQogxgKOUcvQ/+imBO0BjjGXrz2EUjBv/zzX9G142k1kG7BVCLAd+lTI194mZd4Y7d+4wZ/Zc7t/zo3a9mgwcONCkyuW5c+ewUziYCAyAiyo3bpUd2bBhg0n73Plz+fGnHwkICKBAgQLY29vzJli/bh1fDvycTnaV6J67NHdCH9GzUzeWr1tFo0aN8PHx4cKFC1y8eJELFy7g4+ODQmeglHvldMcyCEG1atVwd3dHrVajUqlQq9Vpr1nTfyMoMY5CNs+uLTAxDguFkqFDh6a12dvbU6JECYoXL46lpSV7tv7FpooVsE7dzNshT246TJ1Gj94fp1t+fd1UqFCBzTu8GTdyGJ/tuUqenE58PmwsX40YiUKhIDo6ms2bN/PjxPF8VpU0gQHoUFrNzLM6Dh06ZFKM7Cl6vR6FQvFeLRm/CbIqPFlKeVQIkf8fzW2Beqk/LwcOA6P/YVMFuPe0crAQYl1qvwxFRghRHbiZmdxkr+KFIiOl3CCE2AV8B5wXQqyEZ5sfpJS//deTm3l97N+/nw5tO5IHL6z1Diw4sZI5s+aye683x48fZ926dRw+fBglKrSOKajFs6WVcEUw7Wu1yPC4jo6Ob7wc8/gx4+jpUJ1iNkYfREW7AiiFoGfnbsSlJKLT6QBwcHCgYsWKDB06FL1ez5YlK6nq4ImN0nhtp6MfoHbIwdatW18YymulsWDW73P4Ll9ZnDWWRKQkMSv4FuMnTqTfgP7cuHHD5LVz507Cw8IYWLBAmsAAOFtYUDdnTnbv3m1SC+hNUbt2bY6evpDhe0/3dx07uBvXxPSJOC1JYMuWLVSoUAEXFxcAdu7cyfgxw7hyw5c8ro4M/WoUI74eZY4WzBTi36T6dxFCPL/UslBKufAVfdyeRoFJKR+lOuf/iTsQ+Nz/g4AMd/AKIX7AONMZBnTJ7MBfxKt8MlqM63AWgC38Y4edmWyJlJIB/QZS3FAHV1U+UIC7LMq18KOULV0OvdTh5eXFxIkT8bnsw8kDeyghKmEtcuCnu0WYRRBDvhzyti8DMDrw7wX44eVlutxQzMaduEcJjBw9igoVKlCxYkXy589vsoSVkpDEsJWrqGSfl0hDEgHJT9i1x/ule0VGjhlNVGQkfefNw8XKhvDEeD799FNGfzMWhUKBm5sb9evXN+kzetQogjdtTHes0NgYpk+fTlxcHO3bt6dw4cIm78fExLBixQquXbqAV6nS9OnT940KeLPWHZk5fi99KkpUSuN9C4gycDZAy5EFC1i8eDGNGjWiTJkyrFwyh0XdtDQZrOb6o1gGLfqRxIR4vpv4wxsb77uKlKA3ZFqMw1+T4z8jlXtR1NcJoA7G5bX/fuKX+GSaAb8B24FJUsqErDjh2+Z98MkkJSWxbNkytv21AycnJz77fBC1aj1LWxEYGEgJr1LUVfQ0WdZ4on/MNdV+Dh07SJkyxjQ4er2e36b/xh+z5/Ek9gmNGzVmyi+TX1rEKis4fPgwy5b8SWJCIh917USHDh3SvvyllPj4+LBu3TrWrVvHQ/9AvvZsRX6rZ5kCbsUH4625y417t196nlu3bnHo0CGcnJxo3bp1ukzQLyI2NpYHDx7g6en5ypDfu3fvUq1CBf4sW5oCqYEjl6Ki+fyqD4WKFUtLBFqmTBk6dOhA+/btsbe3p26NapS2UlDFTs2lOB1nopM5dPwERYsWfdnpsgydTkfbFo2J8rtIz9IpRCYK5p9TMOrbH6hdtx7r169nw4YNPA72Y3Y3JT2rPhNnv3BJ9ekaHoZEpAuiiIiIICkpiTx58rzzy2pZ4ZMpauMkZ5VMv/SYEc3PrX/l+VKXy3Y+55O5DdRLncXkBg5LKb3+0ac6xqiwpqn/Hwsgpfzp317Pv+VlInMM+FRKef11D+JN8q6LTFJSErVr1OHhvQjskvKhE0mEq28z8YfxtG7Tmq1bt7Jx40bOnTlPE5tPUIlnztvHugckFgzkyvVLb/EKjDVkFsycRyVNMTSouKy/R9laFfl52i9s2LCBdevWcePGDZRKJY0aNcLVJSdHdu7jY8eaeFg645cYxvKok/w8Zzq9evV6q9fylGV//snQIUOo6OKCVkpuPIlmzYaNNG3aFH9/f7Zu3cqWLVs4fvw4Ukqc7WzpnteOESWf1R1afDeUiy6F2LXvwBsbt1arZfPmzfy9dSM57B3o3XcA1Z6rfSKlxDOPM/s+i6Owq6lg5BkNf/19kJo1jckfg4ODGfRJT44eP4lGpSBvXnfmLlhOjRo13tj1ZDVZITJFbJzkrBIvrkP0PC3Or/t/RGYqEPGc499JSjnqH31UGGcmDYGHGJfDur+J7/cPdp9MdiYhIYGwsDBy586d7ilx4cKFTBzxC4V0DdKeEpMMsVxM2YReGn0TZcuWJTEuCUOwDV6Kaggh0MpkLos9TJz6zVtN7RIQEEDp4qX4MmcnciiNswqd1DMzeB3hKdEA1KlTh65du9KxY0dcXV2RUjJ75ix+mjyFqOgocjrn5LtJE19Y1fJtERkZyb59+1Cr1TRt2jTDcPjQ0FC2bdvG0M8Hc6x5GXJaPnsISNTpKb39MknJydkq/Uub5g1o5XKUfjWfjel2iKTSFC1JWihVqhStWrVi66bVdCgTwdh2CixUsPWcjs+Xq7h45Wa2q/SZWbJGZJzl78UzJzKtLqx9VXTZWoxOfhcgFJgAbAU2AJ7AA4wbKCOFEHkwhiq3SO3bAvgdYwjzUinl5Jec56KU8qVx7JmxAbPIZCv0ej2jR41h/vz5KBVqEJJvvhnDqNGj0gSlScNmPDiWgqvKdH3fR7eDTn1aM3bsWAoUKMDjx49p2awVvnfuY6d24XFiEL1692LuvDlv1Vm7ZMkSFoz9nQ45TDc2Ho2+SGwxJWs3rH3hF5KUkoSEBKytrd/5ZRg3J0c2VPMkfw7LtLbwJC01/r7KwSNHqFGjRra5xhMnTtChdRNmdEimeSkFVx9KvthkQcvOn+GW253t27dz5MgRPJ0ld2fZmIx76HJJzirDmTBxUlpbcHAwCxfM4+4tH0qWrcSAAYPSJU3NLmSVyMwolnG4/T9pfXFNttiMKYRIBO6+zASwz0zRsg92M2Z25PuJk1i+cB2ehsZosCbZEMPPP/5GeEQEarWKvXv3cunCZTxVpilOpJSorAR9+vRJC5fNmTMnZ86f5vLlywQGBlK+fHk8PDzexmWlER8fz+nTp3kcFwk5TN9LVKRQp26Tlz7xCiEynB28i/To2ZMZf2/it/IeKIVASsnU68FYqFXUqlWLihUr8sUXX9ClSxcsLS2RUuLt7c3a5UvR6XS079Kdjh07vpEZT82aNVm3eScTvxlB/9XXyOeei2GjxzFw0CCEEAwbNoz58+ezf+XX6YSxpLuWP7dvoW69BlSvXp1bt27RpFEdOtZU09gLjp44Tvk5v3Pk2JnX7gd8W0jeyYipYpmw0WfmQOaZzBsiJSWFCd9NZOGiRSQkxFOvbn1+n/lbWjEyg8GAo4MzebS1sVA8yx8Wpw/FL/kwChVUr16dYsWKsXblBorJZlgp7JBSEmq4hTZXML5+d9/aLCUxMZHly5fjvcObnK45GTR4EJUrG/epPHz4kDlz5rBgwQKioqKwUGno6tyYYtb5AQhNieDPqL8584pKmO8T8fHxtGvRjHvXr1HZxZYrUfG4eOZn3Zat7Nq1i9mzZ3Pjxg1cXFwYOHAg4aGPOLzjL/oXtkSjFCy/n4xXtbqs2bg5W8x4bt68Sf1aFbn3uxIrzbPxNJ2cxMFrOqSUxuJ99haM66JgQMtnwRQ/r43lelwt1m7Yltam0+nYsWMHx44eJlfuPPTq1ZvcuXO/0WuCrJnJFLZ2llO9Mt4S8E86XF6VLWYyWYlZZLKQhw8folAoMvwwdOzwEYf2ncbSUACl0JCgC8ZgFcb582cJDAzk4MGD/PjjZEpbdjUtfiaT8DX8TWhYSFryyjlz5jBm1FjsLVxJ1idg52SD955db+0LOj4+ntrVa5MQFEchChAv47mqvc7nw4bge9+XjRs3YjAYaNeuHcOHD0cIQYc27bFX2KARagLjQ5g7fy4937AT32AwsH79etavXAVAt49706lTpzcm1FJKzp49y7Vr1/Dy8qJmzZomIdiHDh1i1qxZbN++nRwqwaWuhbG3MM5cknQGGnqHMn/tlnQh1W+Lj3t2JsBnN+Pb6nCwESw8KDgekJP9h05y/vx59uzZw7x5c4nZ7onFc0IUGqWneL/HhIRFYm1tTWJiIi2bNyAu8h7t6mjwDYbtR2LZuHk79erVe6PXlFUi86tXy0zZdry80iwy7zqvQ2SuXLlC9249uO/nB1JSvEQJ1q1bkxaK6uvrS5nS5XFRVEM8t7s+MuU68bpgDAbjrNNCbYW7ojq2ymciFam7T75Kao6dOGJyzidPnnDq1Cns7e2pWrXqW/WzzJw5kwXfz6OlVZO0L8kIbSTLw9ZilcOKAQMG8MUXX5jsfNdqtRw+fJikpCTq1av3xjMDSynp2bUblw4epaWtcRlxZ0wglRvXZ8XaTOf+eyNMnDiRu+tnM7OWm0n71IvhiEZ9+PmXX9/SyEzR6XTMmTObVX/OJz4hgZZtOjBm7Pi0DZ0GgwF7O2tuLslJLqdnn4Pr/inU+CKEFL2S8uXLY2VlgaXuJtume6JQGP+edp98wvCZidz1DXyjf+tZITKFrF3kL0UzJzKdrqzIFiIjhFBJmRpJ9B8x+2RegVarZcuWLXh778bNzY3+/T8xSVsfHR1NvXr10SbYYaX0AgF3bzymdu06nDhxPK2glzBYIv6xfm4hnMiZz4LZc2ZSvXp1Dh8+TO+efdHqSmCtcCbeEEq06jbrpnqnG5e9vf0Lc3e9aXb+tZMiopDJDMxZ7USuHG4sWLeQli3Tf8DUajWNGzfOkvOfOnWK36dOJ8DPn2q1ajJi1Nev9D+dPn2ao3v380ehulgojB+D2o55+cx7N2fPnqVKlSov7f/gwQN++3Uq506eJF/BAgwdOfK1lUAuVKgQ5wzp84g9jNeSeM+XlJQUNBpNBj3fLCqVimHDhjNs2PAM31coFPTo3o2xS7ezaHgOVEpBcork22WJtGnXkQIFi3Dq1CkuXzjOih/ypQkMQNPqdih+j+T69euULl36TV1SlmF4957lzwJZkiX1g88J4evry7Zt27h582a695KSkqhdqzYDBnzG6pVbmTVzIeXKleevv/5Ks1m3bh1Sb4mFyhkhBEIINEoXIiPiKFKkCO3atWPjxo0kaZ8gpan7T6ri6fhRB1q0aIGjoyPt27dn+86/KFjVijjHq5Rp6MahIwey9T6D2NhYHoc/JkFvuldXSolWoXthOvqsYtOmTbRu0hzLMw9pGJ2Te5uOULlcBfz8/EzsDAYDgYGBHDlyhD///JOxY8dSzcolTWAALJUqqlq5MGbMGP7880+OHj1KUFAQBoPp783X15cq5csT5b2b3ihx97lJ6yZN2LJly2u5xrZt23IuLJFDQXFpbZcfJ/LX/Vi2bNlCwYIFmTFjBvHxxqqujx8/5odJE2nfojHDvxzCnTtZsnE7S5g6fRbhshRF+0bSaXIihftEYJWrFsuWr2LKlCkcOnSIChUrkpRi+q0sJSQl67OFmP4/SESmXtmILBvMB7tclpKSQrdu3fj7b28sLCzRapOpVq0a27dvT4tgmjt3LmNGj0eb/Cws02BIRqWJ46sRX3H79m0OHjxEQowaK7WpHyZRF0SzljUZOXIkZcuWpX27jpw7eQNrWRCl0BCne4hO85Br16++9aivl3HlyhV+m/obvnd9qVarOsO/Goa7uzvh4eHMmjWL2bNnEx0dja06Bz2cO2GrtEVKyeVEHx66hHL99vXX5pjW6/Xkd/egj3V5vGyeLSVtfnyJR3nVVKxamfv373P//n38/f1JSUlJsxFCUMPBne8Kmwr4xHsnOB0dzPOfC41GQ4ECBShYsCAFCxbk/OnTlI2KYWD+Z9FQF6MimRIahG/g61nOOXr0KN0+6kBuS4FGpeBuZCIL/1yOjY0NP/30E4cPH8bZ2ZnevXuzYc0KGuaRNMoLVyMky66nsGnbrmxRD+cpV69e5c6dO5QqVYpixUwDmZYuXcrCmaPYPdsDa0vjvfxzewQLdlpx4dKNNxrokBXLZQWtXOSPhVtnyrbHtWXZZbksCGPGlwz5N7krP1iRGTduHDNmzCIpSSJSQ0gtLKBr106MHz+ee/fu8dlnnxMYEIVSYZqKJEkbDOgpVKgQTk5O+Fy9jZWikInTVq/yZ+eubdSubaztnZCQwFfDR7BixQqSU5KoUqU6f/wxm/LlM11g7o2ze/duunzUlRKKUjgqnHnEQwKFP23at2H9+vUkJCTQvn17xo4dy8H9B/nxhx/Ja5OHGF0sNo45+Hvv3+nydWUlAQEBVCxVlt/zdzBpD0qK4vv7u7CwtaZQoUJp4vD8y9rampJexRidpzzl7YwCdeFJCFMfXebm3TvExcWlCdTzL19fX7RxcSyvVJ0CNs/isKWUND93gks3X9/GQ61Wy7Fjx9DpdNSuXRsrK6u0906dOsVPP/3E3r93MLiiLd/XeZZFeufdRH6548Sl67ezRSTaq9Dr9fT/pBf7du+kaQ07/IJ13AuSeO85+MYr0maVyEwq3CZTtr2u/ZldROYRMI8XzGiklN9n+lgfqsi4uOQkMjLexBEvpQHTFG0CtdIRpcLmORuJUhPN/v17qV69OjqdjqpVqnH3ThDojB9soY6mQqVSHDy4P92HWkqJwWDIVju6M0JKSeH8hSn2pDQeFvnS2s/FneJq4iW69ezG6NGjTT70ERERnDp1CmdnZ6pVq/bavtCelnZesGABm9ZtYHaxLtgon2VGuBjzgOMOkZy9cvGlxzl48CA9OnfBQaFBAjFSy5qNG14ZwVS5TBl6CjW1XJ4lu32iTaH5icN07t6dAQMGULt27bfyhe7u6sTONhoKOz7z4RikJN+8cO4FBKU54d8Frl69yvHjx3Fzc6NVq1YZFpp73WSFyBSwcpGTCrXNlG3v60uzi8hkajd/ZvhgfTIJCQmkF2mjT2XhwoUcPXqUJUsWY2GpN/GlGGQCrq450/I7qVQqjhw9zLCvBpLT3UAuDxg9dii7d/+d4ZeMECLbCwxAWFgYYWFh5NWYbugtalkcJydnVqxYke6p0tnZmVatWlG9evX/6wtWq9WyfPly2rVsQ48u3dm/f7/J+/7+/kyaNInChQtTr149du7cScGCBVkdfp5kgzEQJiIlji0x1xg2+utXnq9BgwY8eBTMws3rWLxlPQHBDzMVIvvlyJH8EfyA0KQkAJL0eqbdv0ehAgXZunUrdevWpXDhwvzwww88ePDApO++ffvo1aULH7VuxYoVK9Bqs7ZMk7OTI2Hxpj6kJ8mSZK2WGzfSlw5JSkoiODg4rVxCdqJMmTIMHjyYjh07vhWByToEBpm5VzbC7JP5f3k6k2nZsiW7dx/k+QA7KbVUrFiGc+fOpv5fMnz4cBYsWIhGkwOBAQtLFQcPHnjj0/bXQWRkJJcuXSJPnjwUL148rV1KybZt2+jUsRM9nPphqXiW+iQo5QEBbvfwueWTpWPR6XQ0b9yMoKu+VFQXJMmQwsnk2/Qd3J9iJYqzbNkyDh48CBjFoW/fvrRv3x4pJb279eDgwYO42TgQEh/NyFEjGffd+Nc2k5BS8sPE7/lt+jQ8bO0Iio2hcaNGLF21CiEEW7Zs4c8//+TQoUMIIdLGe8PnKmsWLaSPhxM2KgUbQmLIWbw023fvybIHj5kzf2f9zIlsbGWDnYUCnUEydH8M2+4mE5OYQv369RkzZgwNGjRgwrdjmTfvDzQKUKg1fDthEoM//yJLxvG+kDUzmZxyQsHMzWT63liSXWYyTlLKyCw51ocqMnfv3qVKlaokJWlJTtai0ahQqxUcOXI4XX1zf39/jh49iouLC40bN37ny9JKKZkwfgK//TYDF6tcPEmOpHjJYmz6ayMHDhxg6tSp+Pj4YGttSx6Rl1rW9VEJFYmGBA6k7ObbX8ZleZLNTZs2MXbQV3zm1BylME6wY3WJTPJfjVbqKFiwIH369KF3797ky5cvXf+HDx/y8OFDihUrlrZp9XUTExPDzVQfjLu7e7r3/f39Wb58OcuXL8fPzw8rpYIjTSvibGH8+9EZJJ3P3GPivIW0a9cuS8ak1+v54rOBrFu7hop5bbkRlkipsuVZsmIN69ev57fffiM4OJi8ud3IaxnLsg4q8jkquBaip/tmyffTF9KtW7csGcv7QFaITH6rnPK7Au0yZfvJzcXZQmSykg9WZABCQkL4448/OHPmLGXLlmHIkCF4er4y39s7z4YNG/ii/zCqiRZYKWwwSANXU04QJO8SnxRHyZIlGTlyJK1bt6Z3j94cO3oMZysXwhJC+ezTz/h1+q9ZPkv45OO+RHvfpY6D6R6IJWF7aTOkG5MmTXpnqzAaDAbGjRvHxVVLmFe5iMl7f94LJrxKA+YtXpKl5wwMDMTHx4d8+fKZzLqTk5NZsWIFw4Z8yrnPbSjo/GwGtfeOlh8ue3DuSvpw/g+VrBKZcfnbZ8p24K1F753IfNCbMXPlysWkSZNebfieMWvGHArry2GlMQY0KISCUprq3I+9zsqVK+nRo0eaiOz03om/vz8PHjygZMmSODs7v5Yx6Q0Gnujj07VrNZJq1aq9swIDxk2I1apV48jq5eneC0nSIl/DTj0PD48MQ+MtLCzo1KkTXw0dQgEn03taKpcS/wdB6fro9Xr8/PxwcHB4pwIHsgtSkt38LW+U1/bJFUJ4CCEOCSFuCiGuCyGGprY7CSH2CSHupv7r+FyfsUKIe0KI20KIps+1VxRC+KS+N0ukfgMKISyEEOtT28+kFvP54NFqtWzdupUZM2Zw9OhRkz0fBoOBoAeBWClM0yCrhAp7GwcqVqyYbpaSP39+6tSp81oEJjg4mH79+rF81QqOR1/nUfKzZeBLsfeIlgk0aZK5qoL/lSdPnrBgwQK+GTuWrVu3ZqkzvFmzZvgnpuD9MDyt7faTeNb6hbB02TL69+9PcHBwlp3vZdjb25MrpzMnA0yT6O67qyUpIY6WLVvi7e2NwWDgr7/+onD+3DSsWY7CBfLSsU0zIiOzZKn+g0Jm8vU+8tqWy1LLgOaWUl4UQtgCF4B2QB8g8rkqbo5SytFCiBLAWqAKkAfYDxSVUuqFEGeBocBp4G9glpTSWwgxGCgjpfxUCNEVaC+l7PKycWXnejJZQUBAAHVr1UMXK7DSOxItgileuiir161i3bp1zJ8/H7/7/hTQFKeydcO0fuG6R/hYHOFhyENUqqyd4EZHR6PX601EKi4ujqlTpzJt2jR0Oh1ffvklhQoWZPTI0bhb5yRRn4zeArbt2vFG9hL5+PjQuF59Slo54CEsuJgSjVUeN/YfPZJledUuXLhAx9atyCH12KpV3I6O5edp07l9+zazZ89GrVYzatQovv76a5OSBhERESiVShwcHLJkHABr1qxmzNBBTGkoqZBHyUFfPd8fgbYfdWPXrl2EhITg4eFBfFQIm/pDrcIK4pMl3+5ScldWYM/B41k2luxMViyX5bPMKUfn65gp28/vLHjvlsvemE9GCLENmJP6SleP+p81p4UQe4CJgD9wSEpZLLW9W2r/QU9tpJSnUsuLhgA55Usu6n0Xmfp1GhJyPpGCSmPwgpQGLml3E64PRKfXUadOHbp3786P30/GOu5/7Z1leFRHF4Df2d24QYAIhKBBg7u7aynuDoUipaWF9itQXIuUAsUpUIq7u0MgeHBIiBBIICFuuzvfjw0Ji5QACZLcl+c+u5k7M3dm2b3nnjNnzsmMgz4nkTKM++Iai5ctpE2bNqk2lgcPHtCzSw9Onz2NECrcixRl4bJFnDt3jl9//ZVHjx7Rrl07Jk6cSN68eQGD8Dl58iSWlpZUrlz5nbyuPD09mTdnLoH+AdSoV5t+/fun+MZcsVRpqoSraOKQGzA4R0z2vUSF7u0YP3Hiu079jeh0Ok6dOkVMTAxVqlRJEib37t1j5MiRrF+/HmdnZ8aPH0+pUqX4tk8vrl2/jl5C1coV+WvZ36m2brh7925mTBzDfW8fipcowc+jx1O+fHni4+PZuHEjP/0whD5lQhjRIPmhQ6uT5B+r4dDJCxkiLUNqCBlX82zyxxQKmUGKkHnPixjMWMcAd8BXSpnphXOhUsrMQoi5wBkp5arE8iXAbgxCZrKUsm5ieTXgJyllUyHENaChlNI/8dw9oIKUMtkmYSjvC/QFcHV1LfPgwYO0nG6ac+fOHfz9/SlevLiRdhAWFoaTgxM1TLqhFsk3hjBdENfUBzh55njSIvDTp0+Z9+c8Du0/Qq7cORk0dBBlypR55VrvS0JCAgXzFSBvVHbKW5VAILgcdYMDYSeJ08VTuXJlZsyYYZRP/kP4d80avu37DfVtC+CoscIzLpBA8wTOeHq81swXHx9PQEAAfn5+XLt2jR+/G8bmUo2TPNsAbkaGMCfSh5ve91NljCnh1KlTfP/995w5cwZLUw1jyzrSPn9mEvSSBTdC2BJqyrVbd1Nd23wdjetVpU++szQtZizoq85UMXTckiQvtCdPnjBl0nj27NyClZUlXXoOpH///l/EfrC3kTpCxkEOd02ZkBl8Z0G6EzJp/k0VQlgDG4GhUsrw//BKet0J+R/l/9XGuEDKhcBCMGgybxvz50poaChftfiaC54XsTHLTGhMEEMGD2bi5AmEh4ezcuVKEhK0CBPjj0Wgxtra2sjLKEuWLPw66ld+HfVrmox1586dqKNVVLZOFlylrd25G/uAah1rs3DhwlTzUIuPj2fIwEF851SNvBaGheny5Gbho9P069OXSlUq4+fnZ3Q8fvzYOD6ZUKGXoH5hSDopCfAPoGXLltSrV4/69euTP3/+N447Li6O06dPo1arqVSp0nsJgsqVK3Pq1Cl69ezJ48Ob6VzAHgCNSvBdsawcPvSIPXv20LRp03fu+10pX7kW2w9dpGmx5LWbx+GSyw9i6NixI4sWLaJNmzbM/n0SNXI/ZUkXPSGRknHzRnD54lkWLv47zcf4JSABXSos/AshCgJrXyjKC4ySUs56oU5NYCvwPELsJinlJ/VuSlMhI4QwwSBgVkspn4eofSyEcH7BXBaUWO4PvOgO4wI8TCx3eU35i238E81ldkC6XZXs2rk79z2f4K5vhSpWRQ6imT9nMQcO7efq1avExcVhaWaNn/YGuUzcAYPZx191jdZtU/YklVo8ePCArGR6pTy7iSO2Nrap6gJ948YNLIRJkoB5TlXr3MzYup2NmzdhZWWV5HFVrFixpPfPjz7durM16D6tnQyx1nRSz5qguxQpWZwrV66wdasha2Pu3LmTBE7t2rWxtzcIgV27dtGjc2eym5ujlXqe6SX/btpElSpV3nk+Qggy2dmQI6vFK+eK2GpeiTCdVgz8djDlly5i+OZndCijx/+Z5Le95vTp252sDtlZuXIlAwYMoG4xFfN6mPPcj6iSmw63Hzbw08jRRimVpZQEBARgZWVF5syZ33DV9ElqOBBKKW8BJQGEIR5WALD5NVWPSynT/ikkhaSZkEn0AFsC3HgpYuc2oBswOfF16wvl/wghfsew8O8GeCQu/EcIISoCZ4GuwB8v9XUaaA0c+q/1mM+dBw8eMG/efG7fvEPlqhXp3bt30o8xJCSEAwcPUFK0QZVo0jEVljjrSnL10gn6D+xPx44dsbKyoma1WkTpgjGNtSHKIgg7ZyvG/Db6o87FxMSE6+F3qGNZKWm8Ukr81Y/pXzF18674+PjwJDwUrbMOjSrZRBOqjaF0mdJs37ubTJky/adgW/7PaurWqMn5B6Hk0ljiGfWUfMWKsn3PbszNzbl37x779u1j3759rF27lkWLFqFSqShbtiwVK1Zk+aJFzC1WlJKJa0DHg5/QskkT7vv5vZfjQLkKlZi39V8GSpk0bq1essf7KZU+UoiVbNmycfLsBaZOHk+frbvIkiULP00YRseOHRFCMGrUKJo1qk1L11NG7azNBZULCI4ePZokZA4cOMCgAb0IefqE2Hgd9erWZsGivzOMS3Qa3JTqAPeklJ+97T8tvcuqAseBq8DzYEo/YxAU6wBXwBdo8zx8gRDiF6AnoMVgXtudWF4WWA5YYFinGSSllEIIc2AlUAqDBtNeSvmfBvTPdeH/zJkz1K/XEGvpgjrBBq3pU7CK4rynBzExMaxcuZIpE6ZR1rSTUbtI/RPCHK7g7XsvqSw8PJx//vnHkPekfHlatmz50aIUhIWFMXLkSObPn4+1uTUupk5UtiiFWqi5EOdFnKPE87JnquQFOXbsGOPHj2f//v1YmZhT174AbbKVRCVUhCZEM+XREWYtXcBXX6VsI1xcXBzbtm3D19eXcuXKvTHIpVarxcPDg3379rF//35Onz5NUydHJhRzN6r33a3bdB07jq5du77z3OLj46lQqgSFZQh93GyJ1UlmeoVyPjiG0KgYBg4cyMSJEz9adIM38cvPPxF9ZS7TOyaXSSnJOySWh89U1KpVi/Lly/PXvJksH2pOwzKmRMVKRq2O4/KTAhw57vHpBp8CUmNNxsXMQQ5xSZlDzY/35z0AXlxTXpho7n95XEuBC1LKuS+V18RgPfLHYPH5QUrp9X4jTx0y9I7/j0lsbCwbN27kxo0bFC1alFatWhkF/XMvUoLw+9Zk0iSHTHmUcIl480eEhYcCYKI2o6C6LnYvpGf2k+do1LUyC/6a99HmIqXkxIkTnDhxAicnJ1q3bo2NjQ1bt25l4MCBBAYGMnToUH7++Wf+mD2HVStWodVqad2uDf8b9b8PcsWVUnLgwAHGjRvH8ePHcXBw4IcffqBly5Z0adeRB/fu42iZifthj/hh+HBG/TYm1eb9JoYNHUrsju18ky+vUfn4O3epPGQoQ4YMea9+Q0NDmTD2N7Zu3ICJiYYOXXvwzcCBjB8/njlz5pA9e3bmz59Ps2bNCA8PZ8OGDTx+/Jhq1apRpUqVjxIF2sfHh3Kl3VnUM4GmpdTEJsCkbbDFy4EmLdqyfft27t+9yZAWVkzqkazR6XSSAv2j2Lr7BCVKlAAMZs+xo0dy9NgxHLJlod+A7+jf/5tPmp4gtYTMoBQKmRH35731ekIIUwwCpKiU8vFL52wBvZQyUgjRGJgtpXR7XT8fC0XIfAQCAgKoVLEy0RF6tDGmaCzisLYz4czZ0zg5OfHw4UNy58pLQdOWiBe8m+L0ETzQHmDajKk0btyYa9eu0aVjN7JqC2GOHZEmD4m3fILnxfOvjZ2VFiQkJNCqRSvOnTxHTpGTaHUUgdpHlC5XmoMHD1K8eHEWL15MuXLl3qv/+Ph4lixZwobVazExNaVr7+60b98eIQQ7duxg/PjxeHh4kCNHDn766Sd69+5tlFflypUrPHr0iDJlyqRZdIKXOXjwIP3bt+PfkiUwTYxMEKXVUv/YCXoMGMC0adNSPaPj2bNn6d27N9euXaNu3bpcOu9B5eym5LLUsctXR8mK1fh345aP4oV29OhRBvTtytMnwcTG66lSuSKLl6/B2dnwMNSofjW6lrpK2+rGa0y1RoSRs/hX9OvXDwcHB2pUq8h37axoU8cGn8B4fpoXRv1mPZk4aZpRO71ez5MnT7C1tcXc3Jy0JDWETA4zBzkwR9sU1f3F+8+UCJkWwEAp5Vt3KQshfICyL3vcfkwUIZMK3L59m4kTJnHe05PChQsxcuQIoyCbLVu24ti+q9io8ySVhWvv4pzHkqxZ7Tl79iwJ8VoKW36FWiTfjKJ0T9A73MP7QbIp7OLFi8z6fTb37/lQo3Y1Bg8ehINDcl6TtGbevHnM+HkGjS0aoU7MxXMr5jYHww4yZvwYhg8f/t6mOZ1OR4M69Xl01ZuKZgXQSi3H426St0RBgkOfcvnyZfLkycPIkSPp2rXrZxP+XUpJ25YtuXP2LG2zZSVBr+efx0EIOztu3b9P4cKFWbBgAdWrV0/V68bHxzN16lQmjx3Nn/Wy0NLNsOcmTitptSucLj9Nol+/fql6zTchpcTPzw8LCwuyZctmdG7KlElcOzCV5UOTBcKzSD25uj8hKtZgSbcw1zDg68xMGuiUVOdxSALFOvly39s/aW3y33/X8MvIHwgLC0Onh+7duzNl6u9plpY5tYTMgOwpEzL/80mRkPkX2CulXPaac07A48TlhPLABiDXp1yr/nIDQn1Ebty4wb///su5c+d4+f/q8uXLlClTjo3rDuB7N47d289QrVqNpFwo0dHR7Ny5HSuVcbZEK1VObty4TlxcHIMGDaJixYo8xSupf73UEq65Rf8BxjeJUqVKsWLlco6fOsL48eM+qoABWLVsFUVVRZMEDEABczdsLW0+eO1n9+7deF+9TW/7epSwzkMZGze+sW/IyWMnCAsL4++//+b27dv06dMnTQWMlJKjR48yf/58jhw58sr/+csIIfh30yaGz5iBp2surrsVYPKiRdy4e5cdO3YQExNDjRo16NmzJ0+epN4DpampKS1atCCrrSUt8idnbzXTCAYUNWH9qlfuQWmGEAJXV9dXBAxAnz79OHXHgu+XxHD5fgL7L8bReGwsvXr3ISQkhK1bt5LDOQsNKhqHOnK0NyFHVhUTJ07Ew8OD3bt388N3/Vk0zhnf4xU4v6UUNy9tZth33xq1i4qK4q+//qJ3726MHfsbAQEBaTr3lKBHpOh4G0IIS6AesOmFsv5CiOdh0VsD14QQl4E5GNapP6kmkeE1mcjISB48eICLiwt2dnZGdePj42nTpi0H9h/A1NQSrS6OggULsG/f3iTX1Xp163P6+E3MNMk/rnjtM9TmIbjmyomXlxd6vSSHVXUjLUWrjyVEf56YGEMmzpCQEBo1aMKtm3ew1NgTHveIZs2asnL13x/F5JFSKpapiKO3A3nMk7UyKSVrov7l8OnDH5RnZ9jQ77iz6hT17Y1TLfwbcpwOY/rz7bffvqFl6hEWFkajOnUJ8vHF3SoTXlHPyOLqwp5DB997LSk6OpqxY8cyY8YM7OzsmD59Ot26dUv2GtNqiY+Px9LS8i09vcrVq1dpWbcqnu0zG61d7LofzaKnuTh08vNYWA8MDGTSxN/Yv2cndna2dO89iL59+yYFPu3RtT2F7Y7zXccXQg9F63BpepPoRG3HxkrDjJ8L0Lll8ppkcEg8xZt44usXiK2tLU+fPqV6tYq4ukga1HHA62YkW7b7sm37bipVqvTO404NTSa7mYPs5/yf0a6SGPNgbrrbjJlhNRkpJT///DMODo5UqlQFJydnBgwYYBQUceLEiRw8cBRdQmZio81JiLXlutc9unXrzrFjx/jrr784cvQIJupMRn2bqO0ICw8je/bs/Pzzz1SpXIVovW/SE7GUkhj8ad26dVIbe3t7znic4uCRvfyxeBKXrlxgzdp/PisBc/z4cXwCfPCIPIdOJm/Quxt7F5vMNhQpUuSD+ndwdOQZ0a+UR6riUqSxSSk5e/Ysf/75J9u3b3+vAJc/ff89WR49Y3GBynznUpRFBSrjGBzO8O+GvXNfz7G0tGTy5MlcuGAIxdKjRw9q1arFhQsX+LZfX7LY2WKfyY7yJYpz4sS7xQQrWrQoaktbdtxL/twSdJIZHs+46e3HyZMn33vcqYmzszNz/ljAjTt+nDnvRf/+/Y0iaw8a+iMz1oSz+1Q4UkoePU2g96QntGrVCl9fXzZt2oStrQ3FCxlrO9nsTTEz0dGoUSOGDh1Kx47tKF/GhHUrqtOrayF+n1iW6RNKMWBAr7dqpGmJlCk70iMZVpOZPXs2v/zyP6Kj9QihQkqJhYVg8OBvmThxIsHBwRQt4k54mArVCxqIlDritMnRcoVQY22aDxN18pdfp48jQeVDeHgYarWaoKAgqlSpRkhwOCRYIjXRODhn5uTJ4x9tcTql+Pv7s/Cvhdy5eYdK1SrRvXt3dDodP/74I4sXL8bV1RUHewcCvANw0bsQrYnmoe4he/bvoXz58u99Xa1Wy5AhQ1g0/y/6ZW9MAcscSCm5EHmX3fFX8PF/YLTA/zJxcXF83bwlF8+ex93SkQBtBLEWag4eO/zaJGcvkpCQwMOHD/Hz86NhvXosK1oTB7Pkaz2Jj6G711Eiol8VgO+KXq9n6dKl/Pjjj8RFhlPdOTNjS+Qgq5kJuwNCGe0VxAmPc+8UF+zMmTO0aNyAqtlNyW2pZae/xD5HXvwfP8HPz4++ffsyefJkVCoVy5cv58LZE+RxK0TvPv1wcXF5+wU+Env37mX4sIH4+PojhIouXTozbfrspP/3bl3a4ZbtIt/3To7ddscnmqrtLuBWoCg3b95EJeLZs7kxxd2Tf1d6vSRf8Q1cuXqL7Nmzv9OYUkeTcZS9nVKmyYzz/SPdaTIZVsi4uLjw8GEI4oW1BSn1CBGLubk50dHRgMBU44TqhThgUkoS9IFs2LCeMmXKsHHjRkaPmoBalx2VMEEvtejVj+jeswOzZ89KaqfVatm1axc3b96kSJEiNGrU6LOL7XT27Fka1mtITpEXW11mgk0CCVUFoxd6nj17xrBhwxg9ejSWlpYcPnyYEydO4OjoSLt27T7ILTkoKIj27dtz+PBhGjduzIWz5zGXGuL1WizsrFm/ecNbIzFPmjCRTbMXM9SpKppED72tT67xKI8ly1avxN/fHz8/v9e+Pnr0KOkpVy0Em8s2xtYk+cEiQhtPK889hEdGppo307lz56hbrQrnmhbHXJ38RP/7jUfoqjTij/l/vVN/z549Y+3atUkuzDVr1iQqKorRo0cza9Ys7O3tMRE6KmeX1HXVcvmJmo039ezce/C9PQHTAiklz549w9LS8pV1t+vXr1OzRiWG93Kiae2s3LgXxc8z/Oj/7c8MHfo9er2ekiUKMeW3/FStlOxAEB2tpUDpDXh7+yeZuVNKaggZZ1NH2TOFQmainyJkvnieCxkLCwvi4tRGdmwpJVJGMWjQIPLnz8/GjZs4c/oyKl7w79dHUcTdlUuXLgKGJ9MffhjO/PnzsTC3JiY2kjZt2rB48aI083hJK4oXKYG9nzN5zZKfos9EHSXE5hF79u2hZMmSqX7NM2fO0Lp1a54+fcr8+fPp3r07Wq2WCxcuYGpqSokSJVK0T6JI/gK0Jz8FrZLNavF6Hb281pAgjfOmWFtbJ4WTcXFxMXqdOXUa2e8F0i1H8mew3O8mawJuY+/owJAhQ+jXr98Hh90/ePAgo3p3YU15Y03i4MNnrFU7sefIsQ/q/0UuXLhAs0b1+SpPFNMaJGvca67Essg3D6c9r6TatdKaK1euMG7s/zh75gw5XLIzeMhPRumif/99Bts2/8G6FdWxsNAgpWT8tCtcv2PPjh373/l6qSVkujumTMhM9leEzBfPcyFTpUpVTp8+jyG8mgEpteTP78rt27cAg+mobJmyREVpiY3VY2oqUGu0HD586JWIxc+ePePu3bvkypXrtR42nztPnz4lZw5X2lr1TAoDA/BMF8IZk4M8DErdhFpSSubPn8/QoUNxcXFh06ZNHyTE3HLlpZdpUfJYvmAmkXp631zHuMkTKVKkSJIwednB40V8fX2pVrESeVRmuJtYcz0hiru6GMZPmczff//NwYMHsbGxoW/fvkljfx8CAwMp4paf4/UKYmuarCmPvuRH1ibtmfb7zPfq903kcs7G9q91uL2Qblmrl2SfEYHfw8epmqvmU6LVaunRozMHDuyheuXseN18holJJnbuOvDOpjJIPSHTLYVCZko6FDKfz6ryR2bmzN+pVas2sbFapBQIIbGwUDF37h9JdVxcXLh56yZLlizh9OkzFClSmH79+r1242OmTJkoW/bL/W6o1Wp0Oi06tKhI1sDi9HFGCbTeh+vXr7P4r0U8fvSY+o0b0Lx5cwYPHsyqVato0qQJK1eu/KCAiQEBAUgVbAu+xmDX6kmaz4ln3hQuVIhhw1K+aO/q6sq1WzdZvXo1Xleu0KZYMTp37oyNjQ1du3blwoULTJ8+nVmzZjF79mw6duzIDz/8QLFixd5pzM7OznTo0IG+e7YxomBWnC1N2fQghH/vPaa85wXCw8NTNWSMlZUFoTHhQLKQiYqX6HT6z85s+yFoNBpWrvyX69evc/78eb4Z5Er16tU/afpuScZOv5xoIso4R5kyZeRzrly5Ilu3bi3z5MkrGzduIs+cOSPTM97e3rJP776ySIGiskGdhnL//v1Sr9fLHTt2yCJFikgNGlnEooTsbj9I9sgyWHaxHyBz2+aTkydNfu9rrl27VtpZ2cqa9hVkM/ta0i1THmlraSMBOXbsWKnT6d67b71eL1etWiUzZcokzc3NpatzDlk8Wy7ZyamMrOlUWGbNZC8vXLjw3v3/F97e3nLw4MHS0tJSArJhw4by0KFDUq/Xy5iYGDlh3DhZvICbdM+fX47+9VcZGRn5Sh9arVZOnTJFurm6SHtbG9mmeTM5btw4qVarZbFixaSvr2+qjXfihPGybkFbGfJzFhk9KquM+jWL7FvOQlqaIN3d3eWuXbukXq+Xe/fulc0b1pZli7nJgf37SB8fn1Qbw5cIcF5+4D3H0cRB/pB9cIqO1Lje53ZkWHNZRsPb25uypcvhlJAPR3IRoQ/lNufJkcuZGzdv4ObmZog1NvMP/H0eYq/JysNYPxo2asCqNavea5NlbGwsORyz09qyHtnNDGslUkr+DtpKg+5NmT9//nvPJygoiG+++YZNmzZRuXJlli9fTq5cudi4cSNnT50md768dOnSJc2990JCQpg/fz5z5swhKCiI0qVLo4+NxT78GT1cHFELwd8BQUQ4OnM0MdfM29i/fz+tW7fGysqKHTt2GEWPeF8SEhLo3qkdB/fvpUpuc64+1pI1R176DBjMhAkTuHfvHkWLFCbssQ+j6+oo6CDYfl2w6oo5pzwukjt37g8ew5dIapjLHE0dZaes7VNUd2bgnHRnLlOETAahZ/deeKz3orBJspvxM10wR6I2Mn3mNAYMGICJiQlSGvaa+Pj4ULJkSQoVKvTe1zx58iRdmnekm01zo/Kb0fd5XCCKQyeOvFe/mzdvpl+/foSFhTF+/HiGDRv2yU0+sbGx/P3334wbNw7dk2D21qqEOtFsp5eSjhevM3HRkhQnG7t27RpNmjThyZMn/PvvvzRr1ixVxnnjxg0uX75M7ty5qVChAkII4uPjmTt3Lv8b+QPHvzWjWPZk09Kve/RE5O3IvL+WpMr1vzRSS8h0SKGQmZ0OhUyG3YyZ0Th+9DhOqjxGZZnU2bCxsqVx48ZJmooQgooVK9K+ffsPEjBg8OKK1sbw8oNMjD4Wm/dYbwgNDaVLly60atWKnDlzcuHCBYYPH/7JBQyAubk5ffv2ZeDAgdTP4ZQkYABUQlDVxhIPj5Tvvnd3d+fs2bMUKVKEli1bMmnSJIYNGUSBXC6UKJSfaVOnkpCQ8M7jLFy4MO3bt6dixYpJa1empqY0btyY7FmsjAQMQMuiklPHDr/zdRReQBqSlqXkSI8oQiadEB8fz6hfR+PkkB0rS2uaNW7O7du3kdIQhyssLIxIXahRmwQZR5w2Ns0SRxUuXJgEtJyLuJpUFqWL4ZzWi97f9Hlju7CwME6fPo2fn19S2Z49e3B3d+fff/9lzJgxnDlz5oNC2KQVrq6ueCfoXim/G6/F1dX1NS3ejJOTE0eOHKFRo0aMG/ULwfv+YVEZUya4adm1YCpd2qcsfHxKyJYtG08jtETEGt/p7gRLnoWFcfz4caSU3Lp1izYtG5PJ1pLcLtkY+9vo9xJ2GQn5Dkd6JMN6l6U3unTqxsk958mnq46psODOoduULV2OPPlyc+XKFWxtbbmuO0smXTZs1JlJkPFck6do1rRZmqTCjYmJoV27doSEh3LW7hrXI7yxU9twP9KXQYMHvdZsJKVkzK+jmfn7TByt7AmKDqVatWpkc3Zg+fLlFClShG3btr3iPv458dVXXzFi2DBWPwigbU5nBLDZP5CTDx+zsG7dd+7PysqKZs2aEXn1BDOrOiaVr8pmTrnNB7l69eo7e7a9jixZstCkcSOGbt/H7OZ6rM0EN4P0/LIHwrVaqlevTsmSJfHzvs2P9eOZPUbwKPwZIzdPp+/dmyxbufbtF8nApFctJSUomkw64P79++zauZPC+trYqLJgJizJrSmJTVx2/P0CWLBgAY8ePWL81N84w3aOyfXsj19FqbqFWbxsUaqPJywsjAYNGrBjxw7mzZvH46dBLF63jJ/njubGnZtMmDzxtRssV61axYo/F/OD01d8m7kx/3NuR+Cp26xesYoff/wRT0/Pz1rAAFhYWLD/6FGOWthS89g5ah4/x7oYHVohaNmyJU+fPn3nPi+cPU0jF+NIA2ZqFdVyWJOa64sLlvyN3rUe+SZJis/SUHeRCSPHTicwMJD58+cT4OdDy+KxDKuvwsFWUNxFxbo+CWzfvg0fH59UG0d6RGbg2GWKkPlCuH37Nl+1aEUmW3ty5czDtKnT0OkMZpnLly9jp3FALYwV02xqV8qVKU+/fv2wsLBg8JDBPAp+xMGT+/Hx9Wb9pnVYW1u/7nLvzePHj6lZsyanT5/mn3/+4ZtvvkGtVlOnTh3atm37n8nV/pgxiwaWJbHTGPblmKo0tM5WDY2Jhl9++SXNE1SlFgULFuTEuXPcuHcPrzt38bp7l+3bt3Pz5k3q1atHaGjo2zt5gVz58nMjwrhMSolXSNxb47K9C9bW1qxet5lb9x6wYfdJfB8GMWDgICwtLenfvz+Vy5eiflHjW4aVmaB4Tg1XrxpMolqtlqlTJ1MovwuOWe3o1O4r7t69m2pj/BKRgFam7EiPKOayL4CAgAAqlq+MbUxe8qkaEB8cxbRxczl54hSuuXOyatUqIiKiKGKpQ/VCLLYozVOKlahl1Je5uTnu7u4vX+K9uH//Pr+M+IWDBw+S2S4T7bt0YPXq1QQGBrJ9+3YaNmz4Tv0FBQdjr8lvVGahMsXcxIywsLBPns/+XXFySo6fVb9+fTZv3kzLli2pX78++/fvT/Eu+x49e1Fi+jQqZw2jRR5b4vSSGRee4BcalSYZUR0cHF4b9dqtcHHO3TxNqzL6pLK4BInn3Ui6d+9O586deeh3n+B7R1nWS0/2zCpWHd9H9SpH8bzklZQpMyOSTuVHilBcmD8Tnjx5wqpVq/Dz86dKlco0b948Kcz/8OE/snbeXlxkciBDrYzHM/YfNKZqWrRowb3b3jy5G0UefXlMhTmB2tv4mV7k8rVLqfq0+5zAwEBKuJeggC4/Bc0KEKmL5Ej4MSJVURw4fOC9cnf06NKNwN1eNLJPnufd6Ids01/A2//BJ921nVrs2LGDVq1aUapUKfbt2/efIW5exMPDgwG9unPf2wetXk/pkiW4cvMOJiYm7N27N03iyr2Mt7c3FcoWZ1LzGDpUUBEcAT9uMiFAFsQ5Zz62bduGmngCFtpia5lsDh28TEfmUgMZP2EyYNB2tm7dytkzp8jh4krnzp0/u2jkz0kNF+asJo6yRaaUuTAvfaK4MCukAefOnSN/Pjcmj5rPqj/20bfHYCpWqExUVBTR0dHs3bUPS62jURuNMMXeypn169ezbt06jp08QsMO1fGQ6zkUuxir4jEcOLw/TQQMwB+z/8BV5qSCVTkyaexwMctB6yxfAbz3xr1mX7XgUMhlNgaf4Ha0P0fDrvJP2DFm/TknXQgYgKZNm7J+/XouXLhAo0aNiIiIeHsjoHz58py/ep0b97x5EBDIkVNnOXXqFGZmZtSoUeOd89C8D3ny5GHnnkOsulMSu291FPtNjUOpTuw7dIL169fzzz//ULaAtZGAAahTVM+RA7uIjo4mMjKSGlXLMf23Ptg9XYrHznEUKZQvVdeWPjtSuB6TXp/3FU3mI/B8o97WLdvJmjULAwZ+Q4UKFQCDbb1A/kLEBmTBTuOaVBaoO4N9DhP8A/yJj0sgu6YYribJDzh6qcNLbOLytYvkzZs3uVyvR6fTfVAa5JRQp1ptbK5bkc88r1H59vjdzFszj7rv6Enl7+9P2bJlMTMzo0nDxlzyvEiuPLn5bviwD8pT87myadMm2rZtS6VKldi9e/d7r435+vpSv359fH19Wb58Od7373HqyAGccuSk/7dD3poi4X2Jj49Ho9EYCf+7d+9StUIJvOdqMNUkC5qRq2OYvTMeoTbDNWcO3J2DWfu/5Eyeaw5FMXOXPZ6XbiaVnTlzhqVLFhAW+oR6DVvSuXPnT7ImlyqajMZRNk2hJrPiqaLJKLyBBw8e4OXllbQY/5yYmBgqV67KiB9+4+whb7avP03d2vWZP38BAHfu3OHhw4fYqnMmtRFCYCfyE+AfyMCBA1m8ZBFhpt481XkjpZ54GY2f6gzVa1Q3EjAAKpUqzQUMgFshN4K0wUZlOqkjKDronTWZ6OhoWrRoQXR0NLt27WLeX/M5df4Ma9b/my4FDECrVq1Ys2YNp0+fpkmTJoSGhrJ161YWLVrErVu3UtyPq6srx48fx83NjR6d2+Px9xRam1zB+fZ2GtWuxrp169Jk/Kampq9ol/nz56dS5ar0WSh5/EyPTi9ZfyqeZcdMWLBwKQMGDCDkSQBDW1kaeRe2q2mJv78f9+/fB2D+vD9p/VV98pgfpKH7NdYs+YX6dasRGxtrdD2dToeXlxe+vr5pMsfUwhAgM3U2YwohfIQQV4UQl4QQrzwtCwNzhBB3hRBXhBAfHpPoA1EW/lOIlPK1brd+fn583ao117y80GhMMDc3Y9myJTRp0gSA5cuX43P3Edb6IggTQ/sEfVaGDB7CihXLuXTpEglxOrCUwAu5bdCRP39+ZsyYAYCbmxvf9BuI553jqNUmdGzbgTlzZ6f9xF+DlBKViZpz4Z5kU2cln3leYvWxnIw7TeUqlcifP//bO3mhr549e3Lx4kW2bdv2WW6wTCvatGmDVqulU6dO5MrujLtDJnJaavjl+2e0bteePxcuSlEunWzZslG/Tm3cdd7Mr58pqbxGTlO6DPqGVq1afbQ03ivXbOSHYd9S6Lt/0ep0FC9agC3bF1KlShUAThzZTXyCsXedTg/R0bEULVqUUqVKcfWKJ+dWFiCfiyFpWYeGkqbf+bJq1Sp69+4NGNa2Bg7ojYlaS3hEHO7u7vy9av1rUy+86bf7MdGlrsGolpTyyRvONQLcEo8KwPzE109GhtdkpJTExcW9Evrk+bk//vgDJydn1Go1hQoVZufOnUbn69Spy/VrAZiRH40uNzHhNrRr256LFy9y7tw5/vxzAap4e6MvuYnKCvRmhIeHM2DAAFxzufJMfz/pvF7qiNTcp0ev7kll1apV49r1K4SEhhAe8YwlyxZ/cAj+9yEhIYHevXszf/586jasy+0s91jwdDErnq2mRONSrN34bk/OEydOZO3atUyaNCnFcb3SE+3btyeXsyP/K+bIuiouzCjlxLEGbpzcuYU1a9akuJ9jh/bRpYilUVkZJzMsVXpu3LiR2sN+I9bW1ixYuJynoREEBYdy5rxXkoABaNepJ1PXxxOfkPx7W7A9ijx58jBgwACePXtGQVeTJAEDoFIJujSyZOmiPzh//jyenp707NGRxZNzc2Vvee4crULVkqG0aNbA6He8Y8cOypRxR6PRkD9fTubN+/ONv/M33QNSi4+4JtMC+DsxiPQZIJMQ4pO69WVoIbNixQpy5HDB0tISBwcH/vjjD6Mv2pQpUxg58n+EPtFjqs7B/btPaNu2HQcPHgQMASAfBQZjIrImCRETtTW6eEtKly5D+fLlue51DZ2MM7qulBJLKzOWLVvG77//zt59u9HbBRKsOcNTcYWHqkNUqFaCQYO+fWXM1tbWH8UcBoZYYVOmTKFJg6Z8O3AQnp6etGjRgqVLl/Lrr7+ya9curt++jn+gP0+fPeXv1X9jY2Pz9o4T2bJlC//73//o1KkTP/74YxrO5PPl+vXr6GNj6JAvObSPtYmafnlsWbl4YYr7yZw5M4FRxqbaOK0kJCrukyQkMzExee0606BBQ7B2roB731AG/RlJ3RGR/LHTlE1b9/D777+zZMkSYrXmr9zwHz9N4OLlq5QrV47KlcrRtVU2qpS1T7yWip++yUNkxGNOnz4NGCJZ9+nThRHfuRD8oAeL5pZh/rwJzJr1e1KfhofIOeTKlR1raysKFcrHqlWrUv2zkIA+hQeQVQhx/oWj72u62yeE8HzNOYAcgN8Lf/snln0yMqy5bO3atQwYMJCYGD1gwdOnUYwc+TMAgwYNQqvVMmnSJBLiLFGpDDd1tbAgIU5PmzbtcHHJzu3bt9ElmGBjbqyKq1RmFC5chAkTxhETE0O/vgPQ6h3QqCyQUhKte0jmbLZJ6w0FChTA58F9duzYQUBAAJUqVfrkedcfP35MudLlsI62w1nnwpnT51i0YCEJMoG//vqLvn2Tv9/vmjcdDGl0O3fuTLly5Vi0KGVmofRIbGwsFiaaV+ZvqVERGxOT4n56DxzKr4N7U9VFh6OVGp1eMu5U6GcRPPRFTE1N2bhlFx4eHpw9e5Z6Li40bdo0KVV5xYoV0atsWLYthB7NDRYAn4dxzF0fwZKlqzA3N2fC+F8plM/41iWEwMFeT+3atSlQoADPQh8xaUxpGtYzONOULe3A0nlVaN52EoMGDUGj0fDHH3NYuGgGa9a2o3iJ7Jw65UO/3t9jbm5O69atU3Xe+pSrKU/esvBfRUr5UAjhAOwXQtyUUr6Yq/t1P6RP6t2VYYXMr7/+SkyMDpG0S15NdLSO4cN/ZNu2bTx48IDw8AjMTYz3MaiEGeHhweTOXZny5cvz94qV6KUWVWI/Uko0ZvF8++0AvvrK4NIbGBjIr7+OwtokC1pdHLZZLNmzZ4/RjcXMzIyvv/76o8w9JYwbO57MEdmoYF4VEhWnbConLpmcpU+fNwe3fBOhoaFs27aNuLg4ypcvT8uWLbGzs2PLli1YWFik8ui/HEqUKEEUKk49jqCyo0EL1EvJ3z7htBw2KMX9fP3111y7fInys36nhLM13qGx2GZxICrhEeXLl2fLli1UqFCBiIgIfH19yZkz5yfb3CqEoEKFCkkeli+iUqnYvHUPLZs34M8NvjhlMeX89TB+GzuBjh07AobNyVu3T6dDi+xJv6GQZ/FcvhFN586defz4Md73b1GxvLHbf6GCmQkPD6No0aLkypWLc+dOs2tPb4oVN6RlrlIlD7/PasqkCeNTXcik1l1eSvkw8TVICLEZKA+8KGT8gZwv/O0CpG7u9Hckw7owm5tbEB+vNrrRGzK5RVGuXDlcXFzYuXMX6DOjEsnmKZ0+ijLlCnL69CkABg0azIrlq9HH2yKEBqGOwDG7LZcuXTRaMwkJCeHUqVNkzpyZSpUqffb7PvK55qNERHmymiTv/JZSsiFmJZe83m2D5/bt2+nUvhN5LXNigpqrobeQAk6cOvHJNbbPgX379tGh9dc0z2mHi6lgg89TgnVq7vsHvLMgePLkCZ6enjg7O1O8eHG8vLxo1qwZAQEBNGlYj8OHDuFoa8rj8Hh69e7FlOmzPjttBwyu+KdOneLZs2dUqVLFKIhrZGQklSuVpphbAl1bOfA0NIEpC/xp0LgzU6cZzGF16lSlc1szWrfMl9Tuxs0QGrTYTc1a9fH39+fSpQuEhE0yugeEhERTvOh0nj0z7F9KDRfmzGoHWcu6XYrqbg6f+8brCSGsAJWUMiLx/X5grJRyzwt1mgDfAo0xLPjPkVJ+UhfNz/tOl4a4ueUHXg7JrsfZOTtnz55l06ZNjB37G6ZmMej1hkVBnT4GE7M4JkwYn9RizpzZzF8wh2KlnMmZ14whw/py7pzHK4vy9vb2NG3alCpVqnz2AgbAxtaWGBltVKZFS7wu4Z32dISFhdGpfSfa2zbkK6vaNLWqwQCnjphpTD/a2tLnTv369bl4zYu87fryrGITmvcdxNOISKZNm/bOfWXNmpUGDRpQvHhxAIoWLYqHhwc5XXJw58wezvcx52JvEy72tcBjx99MmjAutaeTKqhUKqpWrUrTpk1fiRJubW3N0WNnyV+sM6PmRLNsqyU//jyTKVNnJNUZOXIMP4/2ZPe+B8TH6/DwfEyPb04yesw4Nm/ejIeHB7lyuXDunLH78/Fj93B3L5Kqc0lFF2ZH4IQQ4jLgAeyUUu4RQvQXQvRPrLMLuA/cBRYBA1J1Mu9BhtVkdu3aRZs2bRLXZNSADgsLNfPm/Um3bt0Aw5P7vHnzmDBhIo8fP6JgwULMmDGdRo0afdI5pDZhYWEkJCQk5ZXx9vamTu06hPqF0TxTG8xUZuilHs/4M2Sv6MDOvTvf0mMyq1evZurQCbSyqmNUfjjcg3I9qzNt+rvfSDMC3bt3Z9WqVZw6dSpV9grlcXFkVaN4SmdPtpDfCNbSdL3gYXDIB/f/ObJz507GjBnJpUvXyZ07B99/P4J+/fonaS7Lly9j7NiRzJrTjNJlcnLs6D2+H7aDZUtXJ8XdSw1NJpPaQVa3Spkmsz3izZrMl0qGXZNp3Lgx69ev56efRnDnzh1cXXMybtw42rVL/jIIIRg4cCADBw78hCNNOwICAujepQcnTp5ACEFBt4J07NqBCRMmoNfrqVqnKhuPrSaHlQtP456Qv2A+lq9a/k7XSEhIQP0ahVmNioR4JdnVm5g9ezaHDh2ia9euXLx48YPXrR4Fh1Igq7HpzS2LmkdPQ9Dr9V+Edv2uNGnSJGm/2uvo3r0H5uYWjBk9gbt31uDuXthIwKQmGe1h/kUyrCaT0dHpdBQuUATLIHsKakqhQo1P/E3ORR+meKnibNy4kTx58hAQEMCFCxfImTPnewVhfPToEW5589Mr89dkNjHc5GL18SwL28y67RuoXr16Ks8s/XDw4EHq1q3LkCFDmDVr1gf1VbtKeTo73KBD8eTQLFtuxPHTMQ1Xb3ljZ2eHXq/n6tWrCCEoVqxYhvX4e5HU0GTs1A6yqmXbFNXdFfmnoskopA8OHjxIdEgs5UySTTF5zYoQLB/Stm1b8uTJA0COHDk+KJy8k5MTrVp/zfxVayhrVwxTYcJ17T1atf+aatWqffA80jN16tTh22+/Zfbs2bRo0YJatWq9vdEbGDd1Jl81bcCTmFgq51Tj4a9j7LE4wmO0uLu789133zF/zgxIiEDqQWOZiZX/blQcM1KJjPYw/yLpT0dWSBE+Pj7YyFfTLtuRBZ/7Pql2naCgIHbs3EGREkWpNaARZXtUZdPuLcz7a77ypJwCpkyZYohL1qMHPj4+HD9+HD8/v7c3fIkqVaqw7/AJrtjVZ/CprJyzqsOBo6c4ffo0lpaW/PLT90yu9ZRrQ3V4DdMxunIQzRrVS3GUaIU3Y0haJlN0pEcUTSadc+7cOUb8MJLzF87j5ODE8JE/0KlTJ7y8vPAOv01Ju6pJic6klISaPqJSlV6pdv2hQ4cSGRnJ6tWrKVIkdb12MgKWlpYsX76c2tWr4l7QDffs9tx5Ekm9evVYuuofLC0t395JIiVLlmTV2o2vlA8cOJAjS3+iWdFkV+avS2j41ws2bNhAjx49UmUuGRmZgdOWpZkmI4RYKoQIEkJce6HMXgixXwhxJ/E18wvnRiZGDr0lhGjwQnmZxKijdxOji4rEcjMhxNrE8rNCiNxpNZcvlUuXLlGnVl2entVTSX5N1sDC/DjoZ1xyuDBnzhwyZ83EKe0enmgDeaZ7wkXtcTRZBG3bpsx+/DZ27tzJmjVr+OWXXxQB8wFcvHiBAlks8Wybhx11s3CpdU7ir59i2ODUcUh5+vQpBbPqXynPZRPL48ePAYiKimLp0qWMHDmCtWvXEh8fnyrXzii8Q1iZdEdamsuWAy+7aYwADkop3YCDiX8jhCgCtAeKJraZJ0RSHuH5QF+SI4s+77MXECqlzA/MBKak2Uy+UMaNGU9uXQlymxbFXGVJNo0LZdQNCQ+LYOfOnTzw96HvTz24Z3+RK5bHqde9Oqc9TqXKDvyIiAi++eYbihYtyogRI1JhNhmXv+bMYny5rGQxNxgeLDQqxpfJxD9r/iUuLu4trd9OjRo12HrLjIQXQgXHaSXrLsaxaNEi5s6dS9GCedn851AsvKYzf1wfypUqypMnbwoErPAiEok+hUd6JM2ETGI8nZcd8FsAKxLfrwBavlD+r5QyTkrpjWEjUfnE6KG2UsrT0rBy9vdLbZ73tQGoIzKgkV+n07FgwQJKlyhLIbci/O+X/xEWFgbABc8LZFUZL9pbqeywtcpEgQIFMDU15Zf//cJdnzv4Bfoy54/ZH5QGV0qJj48PwcHB/Pzzz/j7+7No0aKkuFQK78eTkFBcrI0t21kt1CAl0dHRb2iVcmrVqoVbsQo0Xa5i2zUtW69qabRURf4ipdFoNIz4fhB9yj5lc584fm6sZv/AWCo7+jH6f8rDQ4qQhlBBKTnSIx974d9RShkIkPj6PGbJmyKH5kh8/3K5URsppRYIA157hxRC9H0e1TQ4OPh1Vb5YenTryZjhk5C3HLHxK8jKWZspW6ocw4YN49Hjx4Tqg4zqx+qjiNPG4OTklKrjOHToEPlz56OUeylyueTirz8X0LNnTypVqpSq18mI1KxZg83ekUZlB/wiyeXikioRloUQbNi6i3ZDpvGXd0kWPShF9x9ncuTEWS5cuECCXsWg2iqj+t/V0rNp4wbA8KCzdOlS6tWsQM0qpZk58/dXEoxldGQK/6VHPpeF/zdFDv2viKIpjjYqpVwILATDPpn3GeCnJDIykg0bNvDgwQPKlStHgwYNUKvV3Lp1i82btlCONqjVhhAtdtKR8w+2MGvWLKpVq8YFj/NYaG3IpnYhWoZzQ3WCXj16vXe639dx//59WjVvRT3z6uTNlAsdOk6En+XsyTOfRcKoL50xEyZTo3IFQuNDqOlkysUnscy+HMKajZtT7bM1MTGhf//+9O/f36hcp9OhUqvQvbRgkKCD6OgoVqxYwb7dW7l/ZT/DG8ZjqhH8uXo0u7ZtZM+BY59lXLSPjQS06XbF5e18bE3m8fMEOomvzx+z3xQ51D/x/cvlRm2EIZSyHa+a5754bt68Sd7c+fhlyEQWTdhMt/Z9qVi+MlFRURw5coRMwhn1CwE8hRA4qd1o3aoNR48eZeWaFTzKdo09sYvwENvo3L8dM2ZOT9Ux/jV/AUVMC5DPIjdCCDRCQw3byjwNfMqZM2dS9VoZkQIFCnD2wmXMa7ZjfrgzV7KUJCpBx6lTp9L82mZmZjRtWI9p+5OFmV4vmbAbTMws6N69O3t2bmH/jzpalNXQqKSarUN1PHt4LSnBX3x8PAsXLqRFk9q0b92MHTt2ZLB9IynVY9LnZ/KxNZltQDdgcuLr1hfK/xFC/A5kx7DA7yGl1AkhIoQQFYGzQFfgj5f6Og20Bg7JL/Sbe/HiRaZP+53bt+5QqXIFfhj+Pa6uhjwYnTt2xSoiHw7qQqABmSDx8TpGMfdi+Pr5Yqq3hpfW6RNMIylUuCAALVu2pEWLFkRFRWFhYZEmT5Y+9x+QGeOUCEIIspra4+/v/4ZWCu+Cq6sr02cmp9vu2bMn06dPp0OHDknBMNOK2fMWU7dmZY7NCaWsSzxH7ppglTUf97yPMGbMGMIuz8PCNFkIqVWCliVj2Lp5A40aNaJZ4zokhFylT11JRIxk+LdHOXm8L5OmJD/sSCnx8/NDrVZ/0ObfzxFD0rIv8taUKqSlC/MaDAKgoBDCXwjRC4NwqSeEuAPUS/wbKaUXsA64DuwBBkopn4dI/gZYjMEZ4B6wO7F8CZBFCHEXGEaip9rnSGxsLBs3bmTRokXcu3fP6NyePXuoVrUGhzZfJei6GeuWHqBE8VLcuXOHoKAgrnldI6uqQFJ9IQTZKMLDgEcMHToUe0cbfPWX0UsdUkqe6B4QjDe9+/Q2amNtbZ1mpouqNavyQBgLkzh9PD6RfpQtm64iZHw2TJs2jcyZM9O3b190upejiacu2bNn57LXHYZP+huX+uOY9tdGjp/xxM7OjsqVK+P37FVvRC9/PUuXr8TR0ZHH3ufZM8qUttXM6VXfgmMTzVi0cB4+Pj4AXLhwgbKlilCudBFKFHOjWuUy3L59O03n9FERoBf6FB3pESV2WSoQGBjIkSNHsLW1pV69ekbeVJ6entSr1wCVtEDoNUQnPKF3n17MmjUTgHx53NA+csZak5yG+0nCDTT2ocTERhH2LIIy5p1RieTngUh9MNGON/B+cJcHDx7Qvk1Hrl69gkZtQqbMdixfuYyaNWum6hz/i4iICPLmyotTXDZKWxcjRh/LOe0l6n5Vj0VLF3+0cWQ0Vq9eTefOnWnfvj0WasiRKw+9+vQld+7cH20MsbGxuOV1YUyzCLpWUyME7L6sp8ciNSN++Y0li+bRt3owg5sbbxptOyWaXOX70LdvX2pWr8TkfhZ0qGuLXg9/bQ1j1ibJrTsPMDMzQ6vVMn36VBYv/JOQ0HBq1KjKhIkzXrv3KrXXAFMjdpmVOqssZP7mQJ0vciH673QXu0wJK/MWAgMDmTZtGt9//z27du1Crzd+2hg/fjx58+Zj4Dc/0KVzL7I758DT0xMwLJo2bdocEeOMhbYg5vp8ZFKVZvnSlcyYMYM//vgDP38/rNTGnl626pwEBwfz9ddfkztXboL1N5POSaknRHOTzl0NWQJz5crFaY+T3Lp7k/OXPPD2vf9RBQyAv78/YZFhxOfQcdryAned/Php0kj+eocc9QrvTqNGjchiY4n/8a0UDzhIyN5FlCtZjMOHD3+0MZibm7N73xH+OOlK/h9UFB6h4bt19mzaupsffviBVl+3JSD01dvM/YexzJw5k8KFC1OxkI5O9e1QqQQajWDg15nI66Rn27ZtAAwe1J/dm+fw90QHLm0qSiW3O9SuVQVf3+RcMMePH6dqlbJoNBqyO2dl3LjfXqvh3blzhyNHjhAaGpp2H8pLSCS6FP5Lj2RoTeb48eOMHPkz169fJ1++vIwbN84ozPehQ4do3rw56M2Ii9NiYaWidOmS7Nu3F1NTU44dO0aTxs1Q63MmZc+M1z7DKlMMFy9eYNeuXXw35EcyqUobjSEqIYBncbeR6BGoyG/ZFI0wSz6vC8LM5TG379zg9u3bVK9aA1WcFapYK2LNgnErnIeDh/e/U0iRtEKn01G1alXu3LmDl5cXjo6Ob2+kkCr8MvInvLcv5s+amZKe3vf6RDHKy4Sb9x58VK8+KSU3b94kISEBd3f3pNQBd+7coXKFkuz81Ywy+U2QUvLvsThG/mPCilXrmDRpAtVyX2Fk16xG/Q2YFsjaI3qKFi3KtSue3N1XFjub5CXkkTN9Udu3ZPqMWVy6dIn69WowdXQRWjTMwT2fSL4f5UXp8i2YOWsuYMhM26FDay5fvkjevFm4ceMx3333Pb/+Otroczp69CirVq0gJjaaZk2/on379h+sWViqs8j8Fg3eXhG4GrUm3Wkyn4sL80fn8OHDNG3alJgYHaDG0/MqX3/9NStWrKB169bodDratWtPfKwlapU5GjXEx0g8z19i2rRp1K1bl1G/jkafYIOJJtm7y1STiSfBgUmLlxphCcZJMhGoKV6iBBs2rGPc2Ans3nQce1kcldCglbFEaG4xYtgowOBZ5P3gPps2bUpyYa5Tp84nzf9x48YNlixaQtDjIHToOHPmDKtXr1YEzEdm19ZNTCliYXSTrJ/LkmEng7h//z758uX7j9apixCCwoULv1Lu5ubG/IUraNq/J3mcBJHROrQqW3bs3kGJEiUIDw9n0qje/NRZolIZ5pGglew7H0+1arXw9fUlb04zIwEDUKOsNf3HLObS5Ws8DPBmaN88tGlucJYpXMCOFX+WplSt5YweM55MmTLRq1dX8uSO5J9VPTExURMYGMlXXy+iYMHCSTmkJkwYx6LFfzJgYDWsbcyYPuN/qfLZGHb8p8/1lpSQYTWZMmXKcPGiF+IF918ptWTObMXIkSO4du0aa/5Zi4psRu11+mgSdCEYfEZUWJrmwExjvAc0Tu9D565tqV+/Pt269cBKXwhTtW3iNfREqW4wc84kunfvTlRUFJ06dmH//v1YmWUiMjaUAQO+Ydr0qZ/l/pK1a9fSt1c/CmkKYikt8Yr2Aht4EPAgVcLRKKScKmVLMDR7EPVyJT/FxOkkRVYGcu32PZydnf+j9cclNjaWs2fPYmFhQdmyZZMekrRaLbWqV8TB4gGDv7YkQSuZtiYai6xl2LxtD35+fpQuWYTbu0tgaZHsuDJ2ni+bj6jJlNmB27cus2FpZcqXNv4dFq68g9AwFdmyZePxY3/u3RmIpWXy733b9tvMnHWX2bMXEBcXR+vWX3Hhys84ORk8JePjtWSyHvzBmoWF2l7msaiboro3otYrmkx6wcvrOq9OX01IyFOGDx+OWq1GrwdT9asLiW5ubsyc+TsXL15k6pRZSJ19Uh2dPhZUCUybNg1bW1uEEHTp0g0zmQ19ghphHk7pssXp1KkTAFZWVmzZugk/Pz/8/PwoVKgQ9vb2H+ETeHdiY2Pp36c/jc0bkc3EEKzB3aIYu2N3sWzZMgYM+OTpxDMUXfsMYPrEkVRytsDaVIWUkpmeoZQoUeKzEjBgWLupUaPGK+UajYY9+48yY8Y0vvvrHzQaDW07DGLw4CEIIXB1daV+/fr0GnWWaT+44JTFlE37g1m8IYTjJ89RsGBBunfryCmPG0ZCJuhJLKHPdHTs1Bl/f3+io4ONBAxAjuw23LlzJymvUaPG7kkCBsDUNLVujwZd5kMRQuTEEFrLCUM8zYVSytkv1amJYWuId2LRJinl2A+++AeQYYWMs7MzDx4EYvwR6LG1tcXX1xcbGxty587Do4dRqIVh7UNKPWYWOkaN+pUmTZpQv359Dh06jOf5yyTEmqNSS6QqnDlzZmNra9BcWrVqRcmSJVm+fDnBQU9o3KQRjRs3fsWdOGfOnOTMmZPPGQ8PD+xM7JIEDBjMJAVEATav26wImY9Mnz59uOBxmlL/rqdaTmtuPInB92kkLdvm/dRDeyesrKwYNWoMo0aNee35JctWM3LED5T5ejkxsXGULe3O5q27KVjQsBfs+x9GUqd2VRyymdKikQv3vCP4Ycx1+vXvz/Tps9DpdOTJ44KHRwDlyyfvwVm3/hbNm31Ft+692LNnD2c9dqbJ/CSklnuyFvheSnlBCGEDeAoh9kspr79U77iUsmlqXDA1yLBC5tdf/8fgwUOIjtYhhBop9VhaqhkxYgR2doanma1bt1CnTh30umi0WpDE0bx5Czp2NHh2mZiYsG/fXrZu3cqWLVvJnDkzvXv3emVzXN68eRk79pM+TKQKVlZWxGpjkSbG2l2cPg5bG9v/aKmQFqhUKv5aspzhI/+Hh4cHOXLkYPfu3UyZMgVbW1uePHyAmbkFnbr3pmHDhp+l+TUlWFhYMGv2n/w+8w8SEhIwMzMzOl+sWDG2bN3NL798z7cjtuHkmIUBA4cwfPhPAKjVambMmEOnLn0Z9G1JChawZ9duH44cfcypU1txdnamWrVq5M79Nzt3XKFJU8Pv9+aNwFSagURHwof3Yoj3+Dz2Y4QQ4gaGGI4vC5nPigy7JiOlZM6cOYwZM4bY2FhMTEz4/vvvGTVqlNGPMTo6mm3bthEcHEyNGjXSfHf154yUklw5cuEWVYCilkUBiNHHsD12G0v+WUKTJinbC6CQdsTHx5PHxYksRDKwrDUxCZL51/R81bk3k6fN+NTD+6ScO3eO+fPnEBDgR6VK1Rk4cBDZsiWvuZ45c4bWrVvi4pIJaxszLnj6EBoa/sFrJGZqO5nDsmqK6npH7krR9RLzZx0D3KWU4S+U1wQ2Ygi79RD4IXGz+ycjwwqZ52i1WkJCQsicOTMmJib/0TJj4uHhweqVq0nQaqlWvSrffvstkWGRONk4Y6O24UG0D4MGD2LCpAlf7JNyemLnzp2M7NeRI21tMFEb/j9CYvSUXfmMsxevkjfvl2VK+9gkJCRw9OhRYmJiqFGjBnZ2dqkiZJwtK6eo7oPIPQ+AFxP1LEwM8JuEEMIaOApMkFJueumcLaCXUkYKIRoDsxPzd30yMqy57DkajQYHB4e3V8yAjP1tHLOmzSKfKIAKNSsXrUSn1nLuwjkCAwN5+vQp1atXx8XF5e2dKXwU9u3eRZt8IknAANhbqKiX14KDBw8qQuYtmJiYULduyjzBUo5hO2YKefJfQk0Y3GE3AqtfFjAAL2o1UspdQoh5QoisUspPlmEuwwsZhddz//59pk2ZRgvLtliqDC6yhc3c2Rq9jujoaBo0SNnmMoWPSyZ7ex7HvrqH6lG0JHPmzK9poZDWGAJkpop3mcAQs/GGlPL3N9RxAh5LKaUQojyGqC5PP/jiH4ASVkbhtezevZvcZnmTBAyAqcqMvCo3tm7Z+h8tFT4lXbt159+bcVx6HJ9UtvNuDGd9wrh65TKliuQnv6szA/v3ITAwtRa2Fd5GShMwv4UqQBegthDiUuLRWAjRXwjxPBFQa+CaEOIyMAdo/6mj0yuajEISnp6enDx5EmdnZ9RqNQnyVY8YnUr3WYSzUXg9+fLlY/7i5XzVpycFs+qIStDzOEoCkl1LpzCljiVZLFWsuLKWqhV24nnleqpk11R4MzL1vMtO8PpkjS/WmQvM/eCLpSKKkFFAq9XSvnV7Dh88grPKlWh1JKHaYCIiIyhk546DiSGA5zNtKPd1d+jQscMnHrHCf9GmTRuaNm3KiRMnMDc3x9HRkUplirOrsw1WiXlfJtfR8Gh7DEuXLmHYsO8/8YjTOxK9TJ/BL1OCImQUWLhwIR6HPWlo0g61MHwlbumucEVzlgNxu8iuyoEaDX4xPsz5cw758+f/xCNWeBsWFhbUq1cPgPXr11M1r3WSgHlOPVcdh04dZWfBQhw6sA/7rNno2rXbZ78p+EskNXb8f6koQiaDIaXk2LFjbN28FUsrSzp17sSyRctx0xdHrUn+OriZuXOLSxw5eZhbt26h1Wpp2LAhWbJk+Y/eFT5HcufOjVdQPHpphuoFN/NzAQmceXSGm55H+bpgHH6RJpSaNom//1lP48aNP+GI0xvv5F2W7lCETAZCSkmPbj3ZuWUXTgl50au1zJn1B9ZWNmQSxm7IAoFapcbc3DwpSq3Cl0nZsmVxypmfEQfv8Ws1E6xMBdtuxrPiUhzFnOI52tsKjdqwi76du56O3TrxIOAxer0eDw8PLC0tKVOmjLIP6j2RgF4qmoxCOiMmJoa1a9dy/pwnBQsVoEuXLpw7d45dW/ZQTbRCY2bYeJpLV5g9wavBxBMnjUvSjcQv4T529nZJ8aEUvlyEEGzZtY9venfHbe4BNCpB7lw5KV8mD/3z3Ubzwp6ayrk1ONvAtKlTmTNzGq72gogYPSqLzKzdtINixYp9wpl8oUiJ/jVONBkFRch84eh0Onx8fMicOXNS9OagoCAqlquE7pkaq9hs7DI/xNjR46hTtzbOCfmSBAyAtToT2S1yY+Gk5nDIVrLF5yDWNIpHwpeda3YqT6/phKxZs7J+yw7Cw8OJiYnBwcGB1i0aEau9ZVRPSkng03CmTvqNvf1VlHE1RHdedS6Qpg3rcNcngGfPnrF48UKuXz5PwaKl6N2nL05OTm+4skJGzyej7JP5AoiNjcXPz4/4+Hij8vXr15PdyYUyJcrjkj0nX7X4mrCwMEb+9DPqJ3YU19cnn2kpiupr4RhdiK1btqKV8a/0b2quYfykcfy5Yg61+1eiz6hu3L53m8qVUxYKQ+HLwdbWFkdHR4QQdOjam9lnTQiPTd5Gsemalog46F5OUsbVcHsQQtClvBoXm3iWL19OyWIFub1vErWsduB7ZAqlihfi+nVDjEa9Xs/+/fuZOHEi//zzDzExMZ9knp8bUupTdKRHMnzsss+BR48ecfjwYWxtbalXrx6mpqaA4Qc7etQYZs2ahUCNEJKfRv7EyJEj8PDwoF7thuTX1cBO7YRWxuMrzlGwYnY8znlQWtcUK1Vybgyd1LInaiGWplbUMmuDhcoagCfah3iKAwQE+mNtbf1J5q/waZBSMnhgP9avWUWjQib4R6jwChJUrlKZqqq9DKxubOj4anECFx9bM7B6FD82Tk5VMfegngNPKrN2006aNapDyMMb1CuawNWHptx8ZMb+QydwczOEzzp37hwr/15CVGQETZp9TYsWLV5Je/H8nvQ5aNFCiA+OXaZWmUtLs1wpqhsZezvdJS1TNJkUIKVEp3uzd8itW7dYvXo1J06c4GWhHRYWxqhRo3EvWpyKFSqzcuVKozoTJkwkb558DBvwKz06f0OO7Dnx9PQEYOrUaSyYvZQ8uvoUlC1w1dZmxqQ5LFiwgN+nz8RRWwQ7tcFMoRGm5JYVOXToMJERkeil1mgcenSYmJjy0y8/cjhhPZc5iqc4wHn2s27DWkXAZECEEPwxbyFHTl+gfNfJ9Bn1F/ceBNCmfRfWXrVAp0/+nj6Nkhy7C8EhYfSubnzb6FlVsOfAMb7p14fM2mucG6dnckcNO3/QM7h2OP17dwZg9qzfadmkFtnC/6WExU4m/NKTdq2bJ/22Hj58SOcOX2NlaY6NtQU9unUgKCjI6Fq+vr5Mnz6d3377Lel38jLR0dHcu3fvs9KiFE0mA/GiJnP37l2mTp3KuXPncXd356effsTd3T2pblRUFN99N4yVK1cSHx9H+XIVWPDXfEqUKAEYNjF26tSZHdt3YG6WCa0uBhcXZw4dPoijoyPR0dGUKlWG4IAo1LpsSBLQmjyiQ6c2zJ//J8eOHaNZ45Zk01fCRGVIXRyu9Udr+wBfPx+yO+XAKbYKlqrkmFORuiC89UeQOkkhkzrYq429wi7pN+NepiC+F4MoJmojhMGmfkd6UKi2C1u3b8bPz489e/ZgYWFB8+bNkxKsKSiAIRJxo7rVEU+v0atcHBGxkpknzGnRoS/Lli3myLBY8jsmaxn+IZKCI+IxM4F9v1pSLl+yZhKvlWTrE8uUabP4ZcT3XJhrh6uDQUOKT5BU/TGG0VOW06BBA0oWL0TzSnEM65AZvR6mrAzlyDUbPC9eR6PR8M8/qxn0bT++qp8NWyvBhj0hfN2mM7/P/AMhhEHzH/0Lf86di62tGRER8Qz9bhj/+9/o99aKUkeTMZPmpikLIhsddz/daTIZVshcvnyZqlWrEhurQ6eTqFRgbq5m165dVK9eHYA6depy5vQFdAnmgBq9jMbcUsv16164uLgwY8YMfhszGbUue9LNXEswFasUZf/+fSxcuJCRw8dioSuY9CXXywSeJngwe84sViz7m3sXI7A3KWA0Ru/YfcTrI5FSUsaiq9EPRCcTuBy7llKlShHkFUs+dZWkc3H6KC6LLdy9d5t2rdtz/eot7HEmQvUUOwdrjh4/jKOjY9p/yApfPHFxcSxbtoydm9dgYWlFl57f0LRpU378YSjeJxezsqcWE41Aq5P0WqHBwu0rDh/cx5pvoiiTN1nIJGglmXtEEpsAtUuasndiVqPrzN0WyeIj2ciTvzBhASc4+GfyRlApJdW/CeS7n/+kXr165MvryoG/3SmS36B1h0VoqdLuCkuWb6JmzZpMnTqJjevmsmJeOVyyW/HAL5Iu/c/Rredwhgz57r0+h9QQMiqVqTTTpMwxIjbBTxEyXzrPhUzt2rU5cuQUhsjZBqRMwM0tN7t27cTLy4t27dojtVmMbvJShFOjZgXq1q3L5MlTiY/KhIna+oU+9ITFXqNgwQL4+vpjpsuJlUl2ozEER18gTh+KQI2jaUkymeQ2Oh+gPUHD5tU5duQkNuGFyfSCthKi9ca+aCzbdm6hRLFSWEXlIAt5iNVH8Mj0Ct8O68+Y30YjpeTUqVNcuXKFvHnzUq9ePVQqxTqq8GHExMTQsW0Lzp05SYX8Jpy7n0CxkuVYu3EHkyaO497xP1k5QKBSGX4z8/Zp+feaG1+368bGZb9xdKqxWXbMygjm7dITHhnLyG5ZGNXb+CHo+1kP+WPdU4QQVC+fid1LSxudn77Ih3X7NdSoWZd//lnOrrXVcS+crPl7XnpKryFe3L3n917zTS0hY6pJWTqRuIQARch86TwXMhYWFsTFqY0FiJRIGZX0txCmmGmMv/Q6fRQJulAMW6xU2Ji7oUk0dT3vIzzOiwYN6uH7wBe/e5HYmuQ3Ps8lZs6eSmRkJGN/nUo2XQWEMAiAOH0EjzlJ4KOHHD9+nA5tO5FF6461KhsR+sc81XixfedWatasiZ+fH+N+G8+B/QfJmjUrw4YPpV27dp/FgqlC+ubatWtcv36dggULJpmPIyMjaVi3OnHP7lO/aCxXA8y56Kth/6ET5MmTh9yuzvw1QNC4vDkA3o+01Pgpih17jnHz5k0Wzx7K3lnJT/xSSir19qNY+ZaEh4fz7NEJdi42zkw7eYE3c1cFgzAhJCSEUO/2aDTJD1PRMVpci20mNvZVr8qUkCpCRphKE03Wt1cE4rWB6U7IJN5YM85RpkwZKaWUjo5OUggLqVJZJx1CWEoTE1O5bNkyOXPmTGlqai7NNC7S3CRn0mFpnlkOG/a9jIiIkP37fyOtLZxkZsuSSYeVaW7p5lZQ6vV6efv2bWllaS2zmpeWLtZ1ZA6rWjKzhZvMmze/1Ol0Mj4+XtauVVfa2zhLR9OS0sG8qLS2tJWLFy+Wzzl8+LCsUa22dHbMIevWri9PnjwpFRQ+V7Rardy+fbscPXq0XLZsmYyMjEw6d/r0aensmFlWLWEvm1bJKjPZWsi5c+dIKaWMjY2VhQrklt93dpIBOwtL3+2F5LdtHWWJYgVkQkKCDAsLk5kzWcuT68vJaK86MtqrjvQ9UU3mcskkT5w4IaWUsmzZYvKfRdVkhF/HpGPZ3MqyatVy7z0f4Lz8wHuOQCNNNI4pOlLjep/b8ckH8LGP50Jm4sSJ0tLSWgphlShgrKSlpbUcMmSIfE6zZs2llWUmaapxkmaa7NJEk1lmypRZBgYGSimlDAoKkq6uuaSdjaO0NM0pbayyS2trWyNBsGvXLumQzVHa2dhLSwtrWaZMOenj45N0PiEhQW7YsEF27tRFDh40RF6+fFkqKKRXYmNj5c6dO+W6devkkydPjM4FBgbKrp3bSitLM2ljbS579ugkg4ODk85v2rRJZs5kJTs0zyX7dsgtHbJay19+/inp/N69e6VDNls5Z0oF6XGgsZw5oZzMltVWHj58+L3Hmxo3fdBIjTprio70KGQyrLlMp9MxcOBAVqxYgZmZBXFxMbRs+RXLly/DzMwQxykuLo5Ro0azaNEioqOjqV27NrNmzaRAgeSF+sjISFasWMHRo8cpUCA//fr1eyWKrU6n4+bNm1hZWZE7d+6POV0FhXRFUFAQGzduJDo6miZNmlCoUCGj86dOnWLqlHHcunWDIkXd+emnUZQvX/69r5ca5jIhNFKjtnt7RUCrC0l35rIMK2SeExwczJ07d8iTJw/Ozs6fcGQKCgqfG6kjZNRSpUrZPjS9PjzdCZkMH7ssW7ZsZMuW7VMPQ0FBIV2TPjdapoQML2QUFBQU0px0ups/JSgbJxQUFBTSFIlEn6LjbQghGgohbgkh7gohRrzmvBBCzEk8f0UIUfp1/XxMFCGjoKCgkOboU3i8GSGEGvgTaAQUAToIIYq8VK0R4JZ49AXmp9oU3hNFyCgoKCikKZJUCpBZHrgrpbwvpYwH/gVavFSnBfB3ogf2GSCTEOKTejRluDUZT0/PJ0KIB596HKlIVuDJpx5EGpFe55Ze5wXpb24pi9H/3+wFbcq2/IO5EOLFXCQLpZQLE9/nAF6Mj+MPVHip/evq5AAC32G8qUqGEzJSynTlSiaEOJ/eXB6fk17nll7nBel7bu+LlLJhKnX1unhRL+9BSUmdj4piLlNQUFD4MvAHXtzp7QI8fI86HxVFyCgoKCh8GZwD3IQQeYQQpkB7YNtLdbYBXRO9zCoCYVLKT2YqgwxoLkuHLHx7lS+W9Dq39DovSN9z+6RIKbVCiG+BvYAaWCql9BJC9E88vwDYBTQG7gLRQI9PNd7nZLiwMgoKCgoKHw/FXKagoKCgkGYoQkZBQUFBIc1QhMxngBAipxDisBDihhDCSwgxJLHcXgixXwhxJ/E18wttRiaGjrglhGjwQnkZIcTVxHNzRGKaTCGEmRBibWL5WSFE7o84P7UQ4qIQYkc6m1cmIcQGIcTNxP+7Sulobt8lfhevCSHWCCHM08vcFD4ynzqhjXJIAGegdOJ7G+A2hrARU4ERieUjgCmJ74sAlwEzIA9wD1AnnvMAKmHwl98NNEosHwAsSHzfHlj7Eec3DPgH2JH4d3qZ1wqgd+J7UyBTepgbhs173oBF4t/rgO7pYW7K8fGPTz4A5XjNfwpsBeoBtwDnxDJn4Fbi+5HAyBfq7038ITsDN18o7wD89WKdxPcaDLuyxUeYiwtwEKj9gpBJD/OyTbwRi5fK08Pcnu8at0+87g6gfnqYm3J8/EMxl31mJJoNSgFnAUeZ6OOe+OqQWO1NoSNyJL5/udyojZRSC4QBWdJkEsbMAn7EOPpfephXXiAYWJZoClwshLAiHcxNShkATAd8MYQjCZNS7iMdzE3h46MImc8IIYQ1sBEYKqUM/6+qrymT/1H+X23SDCFEUyBISumZ0iavKfvs5pWIBigNzJdSlgKiMJiQ3sQXM7fEtZYWGExf2QErIUTn/2rymrLPcm4KHx9FyHwmCCFMMAiY1VLKTYnFj59HUE18DUosf1PoCP/E9y+XG7URQmgAOyAk9WdiRBWguRDCB0PE2NpCiFV8+fN6fl1/KeXZxL83YBA66WFudQFvKWWwlDIB2ARUJn3MTeEjowiZz4BEj5slwA0p5e8vnNoGdEt83w3DWs3z8vaJHjp5MOSO8Eg0YUQIISom9tn1pTbP+2oNHJJSpumTo5RypJTSRUqZG8Pi7iEpZecvfV6Jc3sE+AkhCiYW1QGukw7mhsFMVlEIYZk4pjrADdLH3BQ+Np96UUg5JEBVDKaCK8ClxKMxBhv1QeBO4qv9C21+weDFc4tEj53E8rLAtcRzc0mO6mAOrMcQbsIDyPuR51iT5IX/dDEvoCRwPvH/bQuQOR3N7TfgZuK4VmLwHEsXc1OOj3soYWUUFBQUFNIMxVymoKCgoJBmKEJGQUFBQSHNUISMgoKCgkKaoQgZBQUFBYU0QxEyCgoKCgpphiJkFDIswhD92lsIYZ/4d+bEv3N96rEpKKQXFCGjkGGRUvoB84HJiUWTgYVSygefblQKCukLZZ+MQoYmMZyPJ7AU6AOUklLGf9pRKSikHzSfegAKCp8SKWWCEGI4sAeorwgYBYXURTGXKShAIwwh7d0/9UAUFNIbipBRyNAIIUpiSBBXEfjueZRhBQWF1EERMgoZlsTIwPMx5O/xBaZhSNaloKCQSihCRiEj0wfwlVLuT/x7HlBICFHjE45JQSFdoXiXKSgoKCikGYomo6CgoKCQZihCRkFBQUEhzVCEjIKCgoJCmqEIGQUFBQWFNEMRMgoKCgoKaYYiZBQUFBQU0gxFyCgoKCgopBn/B/3Ei2Tht4fTAAAAAElFTkSuQmCC\\n\",\n \"text/plain\": [\n \"
\"\n ]\n },\n \"metadata\": {\n \"needs_background\": \"light\"\n },\n \"output_type\": \"display_data\"\n }\n ],\n \"source\": [\n \"Particle_data = xr.open_dataset(\\\"InitZero.nc\\\")\\n\",\n \"\\n\",\n \"plt.figure()\\n\",\n \"ax = plt.axes()\\n\",\n \"ax.set_ylabel('Y')\\n\",\n \"ax.set_xlabel('X')\\n\",\n \"ax.set_ylim(1000, 49000)\\n\",\n \"ax.set_xlim(1000, 99000)\\n\",\n \"ax.plot(Particle_data.lon.transpose(), Particle_data.lat.transpose(), c='k', zorder=1)\\n\",\n \"T_scatter = ax.scatter(Particle_data.lon, Particle_data.lat, c=Particle_data.temperature, \\n\",\n \" cmap=plt.cm.inferno, norm=mpl.colors.Normalize(vmin=0., vmax=20.), \\n\",\n \" edgecolor='k', zorder=2)\\n\",\n \"plt.colorbar(T_scatter, label='T [$^{\\\\circ} C$]')\\n\",\n \"plt.show()\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"### Sampling initial values\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"In some simulations only the particles initial value within the field is of interest: the variable does not need to be known along the entire trajectory. To reduce computing we can specify the `to_write` argument to the temperature `Variable`. This argument can have three values: `True`, `False` or `'once'`. It determines whether to write the `Variable` to the output file. If we want to know only the initial value, we can enter `'once'` and only the first value will be written to the output file.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 8,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"class SampleParticleOnce(JITParticle): # Define a new particle class\\n\",\n \" temperature = Variable('temperature', initial=0, to_write='once') # Variable 'temperature'\\n\",\n \" \\n\",\n \"pset = ParticleSet(fieldset=fieldset, pclass=SampleParticleOnce, lon=lon, lat=lat, time=time)\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 9,\n \"metadata\": {},\n \"outputs\": [\n {\n \"name\": \"stderr\",\n \"output_type\": \"stream\",\n \"text\": [\n \"INFO: Compiled SampleParticleInitZeroSampleT ==> C:\\\\Users\\\\GEBRUI~1\\\\AppData\\\\Local\\\\Temp\\\\parcels-tmp\\\\a7be8026cea52a1209527ece608da439_0.dll\\n\",\n \"INFO: Compiled SampleParticleOnceAdvectionRK4 ==> C:\\\\Users\\\\GEBRUI~1\\\\AppData\\\\Local\\\\Temp\\\\parcels-tmp\\\\a89daffb525400878a75fcf5f9700e46_0.dll\\n\"\n ]\n }\n ],\n \"source\": [\n \"pset.execute(sample_kernel, dt=0) # by only executing the sample kernel we record the initial temperature of the particles\\n\",\n \"\\n\",\n \"output_file = pset.ParticleFile(name=\\\"WriteOnce.nc\\\", outputdt=delta(hours=1))\\n\",\n \"pset.execute(AdvectionRK4, runtime=delta(hours=24), dt=delta(minutes=5),\\n\",\n \" output_file=output_file)\\n\",\n \"output_file.close()\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"Since all the particles are released at the same x-position and the temperature field is invariant in the y-direction, all particles have an initial temperature of 0.4$^\\\\circ$C\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 10,\n \"metadata\": {},\n \"outputs\": [\n {\n \"data\": {\n \"image/png\": \"iVBORw0KGgoAAAANSUhEUgAAAZMAAAEKCAYAAADXdbjqAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAACpDUlEQVR4nOyddXgVRxeH37lxNyKQEBII7u7u7u5QvIUWh34tFChQCoVCKVLaYsUdirsGl+AQiAOBuCf33vn+SHrhEqChJEDIvs+zT2B2ZnZ2CfvbmXPmHCGlREFBQUFB4V1QfegBKCgoKChkfxQxUVBQUFB4ZxQxUVBQUFB4ZxQxUVBQUFB4ZxQxUVBQUFB4ZxQxUVBQUFB4ZxQxUVBQUMgmCCH+EEKECiGuv+a8EELMF0LcF0JcE0KUe19jU8REQUFBIfuwHGjyhvNNgYJpx0Bg0XsYE6CIiYKCgkK2QUp5HAh/Q5XWwEqZijdgK4TI/T7GZvg+LvIxkStXLunh4fGhh6GgoJANuHjx4jMppeO79NG4SSkZ9iw2g9d7eANIfKFoqZRy6VtczhUIfOHvQWllj96ij/9EjhMTDw8PLly48KGHoaCgkA0QQvi/ax9hz2I5e2Fqhuoaih6JUsoK73A58Yqy9xIzK8eJiYKCgsL7RCLRajXv63JBQN4X/u4GhLyPCytioqCgoJCVSIlWm/S+rrYD+FwIsQ6oDERJKbN8iQsUMVFQUFDIUiQSrVRnSl9CiLVAHSCXECIImAQYAUgpFwO7gWbAfSAe6JspF84AipgoKCgoZCkSmUliIqXs+i/nJTAsUy72lihioqCgoJClZJ6YfMwoYpIDSU5OxtDQEJVK2WakoJDlSInUfvpiorxNchDHjx+nQulymJuZY2dty+ivRpGcnPyhh6Wg8Okj1Rk7sjGKmHwCXLlyhZ5dulOxVDk+69uf27dvp6tz/fp1WjdvSemnDswt0I/RTi05tGoHA/t+9gFGrKCQk9AiNQkZOrIziph8xISHh/Prr7/yv//9j71796LVatPVOXr0KHVr1Cb+yENqRuQl9O/rVK1YhUuXLunV+2nWbGqbF6W8VQEMhAoHIyt62tVky9atPH78+H3dkoJCjkPKVJtJRo7sjGIz+QBIKTl//jzPnj2jcuXKODg4pKtz9uxZmjVqQmHTPNhpzFjz6594lijE3/v3YGpqqqs38osv6WBdmbJW+QHwMs+NhTChd9ceNGvTEn9/f/z8/Lh52Ye+TvX0rmGqMia3pQMPHz7ExcUla29aQSHHIiEH2EwUMclkoqKiiIiIIG/evBgYGKQ77+fnR4vGzYgMDcPB2JoHMY/43/++ZtzECbo6Ukp6dO5GW4uKlEsTiaZSy283DvG/r7+mVu3a+Pn58eDBA65cv0a/gvpLVeWs8rPx7inuzvPF3d2dfPny4e7pwd2wEAqbu+rqxWoSeRT7jIIFC2bR01BQUEAqYqLwAlJKkpKSMDExQYj04W9iYmIY1H8gO3buwMzIBBMzU35aMI9OnTrp9dG2RWsKRdlS37EmQggiLGL5+Ye5lC5XlvLly+Pv78/p06cJe/KUsnkb6NqqhIqaZkVYOG8Bc376CQBTU1OMVAaEp8SSy9haV/dZSjR5XHLjFxyg89i6f/8+lcpVxCbSnHJWBQhPiWF77EX69O1Lrly5suqxKSgoQLY3rmcExWYCr7RFvHju+6nTcLLPhZWlFUXyF2LLli3p6vXq1oOAIz5Mdu3Ed7k70cWkEkP7D+L06dMApKSksH//foL8AqhnXVInSHZGltQ1LUq7lm1wcnKiYsWKjBgxgqTk5HTR2bRS4unhyblz5wgNDSU+Pp4vv/qKzTFnidekhmuIUSewLeYCw0d+qef66+XlxZETR4kqYc6U4I2sTTlH3zFDmTt/3js9OwUFhTcjpBahTszQkZ3J0TOTtWvWMGnit9zz98U9txsTv/0fAwcN1Jt5TP5mEusXrWCITQOcHW25HR/MwN79sba2pkGD1JlDYGAghw8d5jvXThirjADIb+ZCvaTitGvZBkMzY0JCQpBS4mRkg+qlmY21oRkuTs58OW5U6pKUuzvdOnbhXMw9qlgXAkAtNRxLvMXQCaOoWLGiru20Gd8THhbGlPXrcbKwJzQunAEDBjBy1Mh091u6dGn2HNqX6c9RQUHhTSjLXJ80mzdv5svBX9DVpjoFC9bHLzGUaeMnodVqGTJ0CABJSUnM//lnRjm1xMHICoCiFm600JSjb/deeBb2IjAwkMDAQOxUFjoh+Yc8xvZoEzU0atQId3d3XFxcGDtyNCFJ4eQxsQdSl74uJPsxdOznDB8+XNd2/ZaNNKzXgOuRwdhLc24mBVOpRhUGDRqkdw0jIyN++/N3ps+aib+/PwUKFMDOzi4rH52CgsJbIRE5YJkrx4rJ1G8m08G6MoXM8wDgaeZMN1Gd8WPGsnffXkJCQggICCA5IUknJP/gYepEWNAp8gtB9erVcXR0ZOmviwlPicH+hbo3k4Lo1qsH8xb8rCszNTVl9BdfUdO8CHYqC66qA1A7mjBo8GC9a5QqVYqHAX5s2bKFR48eMbVGDapUqfJKew2Ao6Mjjo7vlMNHQUEhK5DA+wtB/8HIsWJy/+EDerjq56BxN8lFTHwcvr6+uLm5UaJECTau3cDj5AhcjJ9/7d9LCKFunTr8fWCvriyXfS6WzFlAU4sy5DKy4kq8H1c1Qfw+drTeNfr06UPx4sVZ8utiQh89pk/zL+jXrx8WFhbpxmhubk6PHj0y+c4VFBTeLxKhLHN9uhTyKsj98EeUsvTQlT1MfELe3K74+PjoZgAli5dg3rQfaWdVCVcTe27EBbA79gq7p+zV62/i/yZSoGAB5s+ex5Mnd6jTrC7ekzaQN29eXqZixYpU/LNiunIFBYVPEanMTD5lvps+lX7deqNCUMg8D36JoWyI9mba3B/0lpK+GjUSWztbfpz+A0EhwZQtVYYdP+6iatWqev0JIejSpQtdunR537eioKDwMSMlQv3ekmN9MHKsmLRs2ZLf/1rOt+P/xx/3D+OZNx+zFs5Nt6wkhKBf//7069//A41UQUEhWyOVmcknT6tWrWjVqtWHHoaCgsInjlDEREFBQUHh3VBmJgoKCgoK74iQMkfMTJRwKgrvxNq1aylVpATWFlbUqFSNI0eOfOghKSh8XEiJUCdn6MjOKGKikA4pJWfPnmXq1Kn8/PPPr813snTJUkYNHkGt2Hz8L3c7CgWa075lW44ePfp+B6yg8LGj1WTsyMYoYpIDkfLlEJL65/r37kvrRs05+fNWNk1fRhGvQvz999969bRaLd99M4letjUpZpEXSwMzKlh70cqqHN99/W1W34KCQjZCIrTaDB3ZGcVmkkOQUrLwl4X8OOMHgh6HULxwUWbM/oHmzZvr1duxYwdHdu1nnFNrTNJijVUx8aJ7l26sXvsXQUFB+Pr6cvv2bZ6FPcPdSz+ESyFzV3bd2P3e7ktB4aNHCaeikF149uwZmzZtIjY2liZNmlCiRIl0dWb/OJtfZ8yli3UV3LwcuBUdRO8uPVi3dSMNGjQgJSWFhw8f8vPsn6hi5KUTEkiNW2b5xIiWLVsCYGxsjIeHBwYGBulCzfgnPiW/h2fW37SCQrYhZ3hzKctc2Zy///4bL4/8rJy0gN2zVlOnak1GfTlSbylLrVbzw/SZ9LSpST5TJwyEASUs89HSshw9OnXFy8sLMzMzChcuzMlTp5HpMqmAqZkps2bNIiAggISEBO7cucM3337LmqhTPEqKQErJ/YRHbIs5z/+mKMtcCgovIqQ2Q0d2RpmZfKQ8e/aMMV+NYvOWzWi1kjatWjP755/0crXHxcXRo0t3BtjXx9PMGYBm1mX56c9V5PVwx8rKirt37+Lj40NsTAwuzvqh6QuYuRD97BS1G9ajS5cuFCxYkKdPn/LztNlU0hbEVGUMwP34R0QSz/DhwzExMdG1H//1BAwMDZg9azZRMdHkcXbhp19/VjaCKii8iJSgTvnQo8hyFDH5AFy9epX169ahUWto37EDlSpV0juv0WioV7MODs8MGO/SFgNUHD7iQ80q1bl+5yYmJiZERUWxbNkyXIxsdUICYG5gQhVjL8aMHI1aajA2NqZAgQKoDAx4nBSBi8lzQfFNeEzFihVZv369rkxKie/d+8xct4FSJvmIVyVzMy6QDVs26QkJpIaaGTt+HKPHjiExMREzM7PXhshXUMixSAnZ3LieEZRlrkxESsmNGzc4d+4cKSmv/hKZ+f106teow6Vl+7m+/DAtGjRlwtjxenX27NlD4tNoOthVwdbQAitDM1rbVYKwJEqXLo2zszO2traMHj2axISEdNdQCRX169XjwYMHxMfHc/PmTaZ8P5WVkcd5mPCEFK2Ga7F+7Ii9yLdTJ+u1FUKwaOli9h8/TKMxXen13Rf4+j+kUaNGr71vlUqFubm5IiQKCq9BaDUZOrIzyszkLZBSvvaFeffuXTq0bkdoyGPMDE2Jk0n89ucyWrduravj6+vLzOkzGefSGhvD1PwltTUlmLlwMbmcHVGr1dy/f59Dhw6RT2OT7lqFTXLjEx9Ky5YtKVSoEHnz5mVg/wEEJj4jr2kuABK1yZxN9mXZmBV4ej43hI8aPQpzc3N+nPEDgQ+CKVGkGKt+W0P9+vVfeT9lypShTJky7/K4FBQUgFQD/Kc/M1HE5F/QaDTM+H46C36ez7OIcCqUKcfsn3+iZs2aenUa12tIFU0+BjpXRyUEDxIe06d7L7wvnsPOzo4HDx6wcOFCSpjm1QkJgKWBKWWN3Rk9OjWJlpOTE/b29jxICU0nXoGqCKbPmE737t11ZcbGxvTr1YfSFh6YSSOuJPnTtlP7dDMJIQRDhw1l6LChWfWoFBQUXoUkR4hJjl7mOnPmDM0aNCGviyv1atbh4MGD6eqM+nIka37+nQFWdZnr1Y/ij2xo1bQFly9f1tXZvXs3qngNNa2LoUp7+ec3c6GcsQdlSqUuS1WtWpXVq1cTn5yY7hoaA/j888+JjIzkyZMn+Pj4YJnHnq2R54hRJxCnSWRXxEViTNW0b99er2379u25efc2bcb3pdrnrdl1aC+Lly1VlpwUFD4a0mYmGTmyMTl2ZnLs2DHaNG9FM8sy9Derhd/9ULq07chvK/+gbdu2AERGRvLH77/zde72WBmaAVDB2otITTztW7UlV24n/Pz8ePr0KUXN3dJdw8nIBi/PAnw2ZCAFChTAysqKls1aEJIUTh4TewBCk6O4kuDHH19tw8bGBgBDQ0OOnjrOV5+PYPK2DUippVWLVpxYsA1TU9N013F1dWXkyJFZ9agUFBTeASElQvHmeneEEAbABSBYStlCCGEPrAc8AD+gk5QyIq3uBKA/oAGGSyn3pZWXB5YDZsBuYISUUgohTICVQHkgDOgspfTLyLi+HjOB1lYVqGRdEAAnYxusDMwY8tkg9u3bR0BAAHfv3sVILXRC8g8FTJ05FHqNgsUKU7ZsWWxsbPj151+I1yRhbpDq8SSl5JomkPFfT6Fnz566tkt+W8KgAYMoZuWOkHAjxp/Zc38if/78etdwdHRk9fo1rErbL6LMNBQUsjHZfNaREd7HzGQEcAuwTvv7eOCQlHKmEGJ82t/HCSGKAV2A4kAe4KAQopCUUgMsAgYC3qSKSRNgD6nCEyGl9BJCdAF+ADpnZFBXfK7SxrWTXlkRc1dCg1N3k+fLl4/ChQtz2D+IaHU81obmunoPkp7QvFVL1mxYqyvTJKtZsGItdU2LYa4yxjvZF8t8jnTqpH+Nrt260bBRI3bu3IlGo6FFixZ6e0deRhERBYVsTg6xmWSpmAgh3IDmwPfAP+swrYE6aX9eARwFxqWVr5NSJgEPhRD3gUpCCD/AWkp5Jq3PlUAbUsWkNTA5ra9NwC9CCCHfFMkwDbfceQhOCqOgeR5d2ePkSBxs7Qh9+lT3Eh814iuWr95CO6tKOBlZcyX2IYfjb3D060V6/c2eO4eqNarx++LfiIuJpkenwQweMjjd3gyAXLly0bdv338booKCwidBzvDmymoD/DxgLPDik3SWUj4CSPvplFbuCgS+UC8orcw17c8vl+u1kVKqgSjA4eVBCCEGCiEuCCEuPH36FIDRE8ayOeYcj5MjAAhLiWF99BlGjh6lNxuY9dNseo8axIr4k4x5uJJ7eRPYtXc3pUuXfvkadOjQgT0H93H87ClGjhqJubk5Cm9PQkICc2bPoVr5ytSrUZtVq1ahzQH/GRU+USSglRk7/gUhRBMhxB0hxP20lZ2Xz9sIIXYKIa4KIW4IId7bV2uWzUyEEC2AUCnlRSFEnYw0eUWZfEP5m9roF0i5FFgKUKFCBQnQ/7PPiIqKZsa075EaLVokw0eMYNwE/X8fAwMDJkycyISJEzNwCwpvwtfXl8OHD2Nra0uLFi0wMzNLVyclJYX6teqS6BdOVRMvkrVqvhsxgeOHj/Hbn8s+wKgVFN4VCWr1O/eSZn9eCDQk9aP6vBBih5Ty5gvVhgE3pZQthRCOwB0hxF9SyizPvJWVy1zVgVZCiGaAKWAthFgNPBFC5JZSPhJC5AZC0+oHAXlfaO8GhKSVu72i/MU2QUIIQ8AGCM/I4IQQjBo9iuEjhhMaGkquXLleuSSl8O5IKRk3eixLFy+hhFU+YrQJDBs0hF17d6cLJbN161bCHz7mc/vGOjfrohZ5mbZxE6PGjaZIkSIf4hYUFP47/8xM3p1KwH0p5QMAIcQ6Upf6XxQTCViJ1OUVS1Lfh++uZBkgy8RESjkBmACQNjMZLaXsIYT4EegNzEz7uT2tyQ5gjRDiJ1IN8AWBc1JKjRAiRghRBTgL9AIWvNCmN3AG6AAczoi95EWMjIxwdXX994oK6UhKSmLp0qVsXrMBE1NTeg/oS5cuXVCp9FdP9+zZw5rfV/J17nZYGKS6Nl+NfUi7lm04euo4gYGB+Pv74+fnx8Z16ymhyqMTEgBTlRHFLPNy8uRJRUwUsicZjwicSwhx4YW/L01bWYFXmwIqv9T+F1LfiyGAFakeru9ljfhD7DOZCWwQQvQHAoCOAFLKG0KIDaSqrBoYlubJBTCE567Be9IOgN+BVWnG+nBSvcEU3gNqtZrG9RsRfjuIaiYFSdaq+ebzsRw9eISlf/ymq5eYmMiCn36mpklhnZAAlLb0ZMtDbwoWLKgrE0JgZWmFvUF6U164Ng5nZ+d05QoKHz8Zs4ek8UxKWeE15zKyrN8YuALUAwoAB4QQJ6SU0RkdwH/lvYiJlPIoqV5bSCnDgFcGhJJSfk+q59fL5ReAdBmfpJSJpImRQuag1WpZuOAXFsz9mdCwZ9SoVp3pP86kVKlSevV27txJyK2HDHdogkqkvvxLaPMxec1aElISefr0KXfu3MHf3x9jDOjsXDPdtaxMLeg9fABNmzbFw8MDNzc3njx5QqliJSkbH0QRcze0UnIm5jYxBkk0adLkvTwDBYVMJfOWuV5nCniRvsDMtBWa+0KIh0AR4FxmDOBN5Ngd8DmVuLg4DA0NX2sfGj92HNv+WE8ry3LkcrLm0pWH1KlRG+8LZylYsCCPHz/mxo0bzJszl+KqPDohgdTlqIJGLmzYsIESJUpQtWpV+vTpQ2hoKAfW7KCCVQEMhAEAAYlPiSSeqVOn6hni3d3d2bh1E3179EbEXiBJk4KLa24ObD2EkZFRuvEqKGQLMkdMzgMFhRCeQDCpKzHdXqoTQOrH+gkhhDNQGHiQGRf/NxQxySFcvXqVoQMGc+HyJVQqQdtWbfhlya/Y29vr6kRGRrL410VMzN1Ot0mzjm1xYjUJ1K9dl/jkRMLDU/0bBFDVJr39ItFEw9oVa2nXrp2uTK1W0+b+Q+ae301pg7zEiCQuxPuybPkfr/ToatiwIf4hgfj4+GBqakrhwoWVzZsK2RYpQarfXUyklGohxOfAPsAA+CPNPDA47fxiYCqwXAjhQ+p/03FSymfvfPEMoIjJJ0BsbCy3b9/GxcUFN7f0McIeP35M/dr1aGxaki6evUjSqtl97BLNGjbhhPcp7t27x7Vr19i3bx8WmOjt9gcoYubK2UhfOnTrRIkSJShRogS2trbUrVmHu/EhFDLPg5SSszH3iFAl0rx5c732hoaG7Niziz179rB39x7sHRxY2qd3uhAyL2JgYKCEwFf4NJDo77R7l66k3E1qFJAXyxa/8OcQ4PXJh7IQRUyyOT/O+pFpU6aSy9SGsIQoatWuxep1a7C2ttbVWfbbMkqYuFE9bSZhbmBAO9sqfHt9DRYWFrpEXgYGBhhIQYImCTOD58tgAcnPaNKsKUuWLNG79vrNG+jToxcmcQYka9VY2duwb/v+Vy6hqVQqmjdvnk5oFBRyBDlgz60iJh8pUkpOnDjB+fPnyZcvHy1btkz3kt6yZQs/T5/NKKcW5DKyJlmrZvOFs/Tr2Ydvp07m2rVrXLt2jfWr11ID/VmASgjymTrhWrMoXbp0oVSpUhQpUoRB/Qewes9J2ltXwtbQEp84fw7FXefQuAW8TOPGjQl8FMyVK1cwMTGhRIkSynKUgsKryBSTyceNeMttGdmeChUqyAsXLvx7xQ9IYmIiLZs05/bVGxQ2ys0Took2SubIiWN6S0N1qtXEy8+UclYFnrfVJjPedyUpaV7VxsbGODo64hhrwgDnhrp6aqlh6qPNHD59jJIlS+rKk5OTGT9mHMuWLSMpOYnCBQoyZ8E8GjZ83lZBIacghLj4BlfdDFHeXSW9xxlnqK7x50nvfL0PRY5OjvUhCAoK4vMhQylRsCj1atZh27Zt6erM+mEWYdcDGOvYinZ2lRli15AK6rx0aNWWJUuW8Pnnn1O7dm3Onz9PLiNrvbamKmOsTCyYM2cO169fJzY2lhs3bhBmnsTOiAuEpcQQlBTGn+FHqVazup6QQKr4/PTzXCKiIwmPjODa7RuKkCgovCvaDB7ZGEVMMpG4uDj27NnDoUOHdHaIF3n06BGVylXg7mZvmiUVxeO+IcN6D2T2j7N1dWJjY1n+2+/UNy+BwQtut7Wsi+Nz8waDBw9m5cqVqNVq8nsV4FKcvtdfQOJTjCxM+OKLLyhevDhGRkbY2Nhw+pw3Tg2L8nP4XlYnnaHVkK5s2LrptfdiYGCAhYXFa88rKChkEAlSrcrQkZ1RbCaZxPr16xn02UDczHORolUTJRPYvH0r1atX19X5afYcipGbNnap8ag8zJzwMHPi26+/Yf+B/dy9exd/f39MVEao3PR/sVRCYGxkxJlT3pQvXx4hBAEBAVQqVxEZcY7iJm48SYnkYPx15i78Od2eDDc3N1b8tSrrH4SCgsJLCNB++rbE7C2F74GUlBS+mzQZN+c8WJlb0qppC27duqVXx9fXl0H9BjDEviFDbRsywr4p7U0r0KpZC27cuMGePXuYN28ea1f9RQkTfdfdXEbWWGKMn58f1atXZ9q0abRo3ZKjsTd40Z7lHX2X4kWLU6FCBZ2R293dnYtXL1Gya21OO4SQXMmBLX9vp8cLmR0VFBQ+AqTI2JGNydEzEz8/P+bO/okrFy9TtHhRvhw9Ml0gwc969+PyvtP0tqqOjZU55y7do2a1Gly9fg1XV1eklCz69VfKmXuS1zSXrl1xC3fswi9TosTzKDAWxmY8to2kkPnzwJIpWjXJRpJDhw6RN29qpISYmBjq1qzN/KC9FMKZUINYHqY85dCqw+nuwdXVlZ9+npvZjyZbIaXkyZMnGBsb623CfBWhoaEs+Hk+p46ewM09L1+MHEHFihXf00gVciQSpDIz+XS5fv065UuX487G05QItCJ45xWqVazCqVOndHUCAgLYvn07fe3r4GrigKWBGfVsS1FClYf6detRqlQpLC0tmfvTXCxk+r0VDqY29OjRg+PHjxMaGsruA3s5lHCDwMTUDalJ2hS2Rp2jRo0aOiEBsLKywvvCOWb+No/i/evR97vh3Ht4P52xXAHOnz9PmWKlKJy/IO558tKobgOCgoJeWTckJIRypcpw/LcdFPEzJ+7wA5rUa8imTa+3HSkoZApaVcaObEyOdQ1u3qgp5ldjqGv7fOZwIfo+J4wf0L1vL/z8/Lh06RKx90MZnbeNXh9XYx+yKfoc1evWxMvLi+TkZLat3MAY59YYqVJjT8VqEpn+aAsXr12mQIHnrrsrV65k9JcjMZIGxCTGUb9+fZb/tRIbG5v3cv/ZgT179jB31hxCgoKpUbsm4/83EQ8Pj3T1Hj9+TPHCRWltXp5yVgVQSw2Hoq/hax3N9Ts304XCHz7sC25uPEk7u+dRux8kPGZt4lkCHgVhYGCQ1bemkM3IFNdgV0N5aqhVhuqa/S8y27oG59hlrhOnTvC/3O31yspa5Wf5vcN89913uLm54ezsTKg6ihStRicSAAHqMHr366NbXtJqtTwKCOaXU3upZJSfFKnhVNI9Bg8drCckAL169aJr167cv38fBwcHnJycUHjO4kWLmTz+fzQxL0VZ46Jc23GJSlsqcv7yBfLly6dX949lv1PcxI0K1l4AGAtDmtiUZWbIVtq3b4+trS0xMTG648alawx2bqzXR34zFzRRanx9fSlUqNB7u0+FHEY2n3VkhBwrJrbWtoSnxGJp8DzQYJQ6DnNTM55FhGFqmpp7o23L1vx15gStrStgZWjGhej7nE3wZeGIDbp2KpWKDVs3sXnzZjat3YCpqSnL+0167f4MIyMjihYtmrU3+BERFhbG2FFj2LRpE1JqadumLT/OnZNOSJOSkvh6wkSG2DUgj0mq7SOfqRPaMC09unSjUrUqBAYG6o7QkMe0yVVFrw8hBI7Cin379uHg4IC1tTVWVlZYWVlhYWFBREos+UwddfWTtSnEJydgZ2eX9Q9CIUcic4jNJMeKyZAvhrJqzm/0N6qDmYEJydoUtkafZ8Bnn+mEBGDNhnWMGTmamStWkJCUSOVyFdj36/50QQoNDAzo1KkTnTp1et+38lGjVqupW6M2Ds8MGOvUCiEEhw9cp1bVGly7dR0DAwP8/Py4desWR44cQSRpdULyD6XNPVhwbhcXr14mb968uLm50aBBA8LCwrhx0ofasrjOwy1FqyFIRODt7Z0uB8u6desYN/grPMycsDW0QC017Ii6SN26dXF0dERBIWvIGa7BOVZMxo4bh/8DP75bswY3KyeCY57SvHlzZvz4g149MzMzflm0kPkLF6DRaJScGmmo1Wp+++03Vv++ArVaTcfuXRj2+bB0IeX37NlD4tMYOtg30b3w29lVZk7IDgoVKsSTJ09ITEzU1TdWGZKoTcZU9Tz8xJOUSKpWq8ah40f0Yn8lJCRQvlRZ1kecprp5YZK0KRyI96Fm3TrphASgc+fO3L55ixmz55DX0okn8eGUKVeWP1evyOSno6Cgj8zmbr8ZIcca4P/h8ePH3LlzhwIFCrwyfLvCq+nYtj3Xj1+krmlRDIQBJxPvYFXIhSMnjiKE4N69e1y8eJFFixZhfCOa9o5V9dr//ewCd+2iaN2mNUWLFqVYsWIULVqUgf0GEHziJu1tK2OqMiYkKZxlEYdZvn71KzMthoeHM+27qezYug0TE1P6DOjLl1999UbRj4iI4Nq1a+TJk0cvbbCCwstkhgG+XG4jebK/Q4bqWnz/JNsa4HO8mCjok5yczPbt23nw4AHlypWjfv366byiLly4QIt6TZjg3AYjVerkViu1/BCyDRsPJwICAoiJiQFSc5nkMbJjXN52en0sjjjI+HlT6NZNP1FcbGws/Xv3Zc+ePdiYWpKgTeH7mdMZNHhQFt61gsKryRwxMZbH++T694qA1cxH2VZMcuwyl0J6/P39qVO9FpbJhuSWNizRzMe5QF4OHDmIpaUlAE+fPmXp0qUUMnLRCQmASqgoa+rBxfBgevXqRfny5SlfvjxeXl6UK1mG7RHnaWBdEoHgSPR1Yk3VetkY/8HS0pL1mzfy7NkzQkNDKVCgwGtTDCsoZAskijeXwqfFo0ePSElJIW/evK/MOzKw72eUSslNY7syAGilZOWDY7Rr3Ran3M54e3vj6+sLgKdpepfmcFU8o8eM5quvvtIrP3rqOF99PoJvdqxFSknL5i05/stWPUeHl8mVKxe5cmXsa05B4WMnJ3hzffpyqcCDBw+oUbkaRQoUokyxUpQsXJxz587p1YmNjeX4yRPUtS6uK1MJQUOrkhw7cpTDhw9TunRpZs2axYEDB0iwhNPRt9FKiZSSq7EPuZUUTI8ePdJd38XFhbWb1pOQlEhichKbtm1W7FMKOQZJqgE+I0d2RpmZfOKkpKRQv1Zdyqtd6ezWBYGKy7G+NGnYmI1bNnHr1i3OnDnDqVOnSElJQaD/Cy0QODg4EBwcrDebOXj0MF07dGZv0FUMVQZY2lqzc8/fb3SxVbIwKuRIpFCWuRQ+bsLDw/nfhK/ZsmkzKpWKTl06M+X7qXr53/fs2YNpkop69s9dZctbeXE11o8GDRoAkCdPHqpVq4aJyogT0TepZ5taV0rJ0bibdO7aJZ0QFC9enKs3ffD19UWtVlO4cGFFLBQUXkNOWOZSxCSbkpKSQu3qtbB/pmKwdX0kkoPrDlL/5ElOep/m+vXrnDlzhpUrV2KTnD5laF6TXDhVK8jipUt0NpR79+5Rp0YtHkaE4aK1wpdnmLrYMGnK5FeOQQiBl5dX1t6ogkJ2Rwqk5tOP+6aIyUdIUlISs3+czao/VpCcnESb9u34ZvK3eiE/duzYgfppHJ3sG+lmBN3sajDt9kasrKx0mR4dHBxQJybqxReTUnJHPmFS369wd3fX9VmwYEHuPrjPhg0bePDgAZ+VK0fLli0xNFR+TRQU3gVlZqKQJcg0o/XL+zf+oUPrdgSev0MLixIYGxpxYs1Bauzdx8Wrl4iPj+f8+fP8smAB+aWD3tKSEIJiZm4kF7fh888/p2rVquTNm5f2rdqy7PQh6pkXx0gYcCrhLqZ5bGjbtm26a1tYWNC3b98su/ePgdjYWGJjY3F2dlaW5hSynH8M8J86n75V6CNCo9EwZfIUnOwdMTQ0pFzJMhw6dEivzvnz5zl/5iz9HeqS38wFNxMHuthVIzkkinz58uHg4ECTJk04euwY95Mep7vGE8NYvvzySzp37oy7uztCCNZv2Ui/r7/guLU/u41v02BgO46dOoGxcfrlr+yGlJIbN27g4+ODVqt9Y93o6Gi6deqKi6MThfMXpJCnF/v27Xtjm6NHj1KvZh1yO7pQt3qtdP9eCgr/Slqgx4wc2RllB3wm4uvry/nz58mTJw81atRIN/P4aviX7PtrGx2sK+NkZMO1WH82Rnuz/8hB8uXLx+XLl1m0aBFPjt2hp1NtvbaHIq5xzSqU/gM+o2LFihQtWpTK5StSQetObetiaIHDUT7cMn3Krft3Pgmh+DcuXbpEl/adiA6PQiUEZtbmrF6/lqpVq76yftMGjYm9Gkxrm4qYqYy5GR/I2qjTHDt94pWJx/bt20e39p1pYVUOL7PcPEh4zM7YS6xYt5rmzZu/8hoJCQmsW7eOs6fO4FHAk779+uHs7Jyp963w/siMHfBlHM3kwXYeGarruPR2tt0Br4hJJqDVahn82UA2rN9AYSs3niRHYuFow75DB3T7KaKjo3F1ycPXudthbWiua3s0wod9sdeITojVleUxsefrfB31rrEm8hTtxvVl5MiRurKHDx8ypP8gjp48BkDDeg1YtGxJtt7DkZSUxKFDh0hISKBevXqvDQ0fGxtLfncPWpiUobxVas6Ya3F+bIo9x72Hvnrpe5OTk7lw4QLNGzThO7fOGIrnxtC9EZdJKmnNiFFfYWhoiJGRke5n/559qBGfj9KWnrr612P9OWkdyLVb19ONKTw8nBqVq2EUqaaQcCZUxHA9MZC9B/crqYGzKZklJgda5//3ioDT7zezrZgoNpN/ISkpiVk//MCqP1aQlJxMm3Zt+fa7STg4PA/ctmzZMo5u28+3eTpgqjJGSsm+yCt0atuBb6ZM4vr165w8eRIjjUpPSCA1OZNx0m3mTJtD2bJlKVmyJNUrVWVv5GXqWZfEQKg4F3OP20kh9OrVS6+tp6cnew/v10XdfdOO8uzAqVOnaNuyNbkMrTEVRvSNDWH2T3MYOGhgurqbNm0ir6GDLjEWQGlLT87H+VK9enXMzc0JCwsjLCyM2NhUoXY1ttcTEgBXI3uWHznE/sMH011DIBjoVUOvrKhFXhbd3kujRo1wc3PDzc0NV1dXXF1d2bBuPQ4RhnSxr62zxeSPvseA3v24ctPnnZ+PQjZFyWfy6RMTE8PKlSu5evEyRYoXo0/fPnpftADtWrUh5OJ92piXxtjYkBPrj1Jj7z4u+VzBzMwMtVrNr/N+oYFZCV3YdCEEDWxKMebicpo1awak7gKP1yQSmRKHrZGFrv/7iY+p16Ce3ozj4LHD9O/Vl6/PrEElBIULFubAioOvDS+S3UUEUpeHWjdvSWfLKhS3SPUwCzWPYvyoseRxzYNWq+X27du648qVK1QyTv+152RgzfXoUPLnz0/x4sVxcHDAwcEBIyMjpnw7mVhNgl5CtNspIXTr3YNBQwaTkpKCWq0mJSWFlJQU+vXsQ1BSGJ5mz5epgpPCsDK1IDIykhs3bvD48WOdrcZEGPFV3lZ6Rv3yVgXY4neOx48f4+LiklWPT+EjRiKQ8tM3T+dYMQkMDKR65aq4qK3wwIHNf3vzw/SZHDt1nCJFigCpxvBL3heY6NwGg7Qv2k7GVVnwZA81atQgMTGR+/fvo1JLGrrqp+c1QIWFqTnLf19M48aNsbe3Z+K48Sz/bQ1trSribGzD1Vg/DsVd58g3C/Xa5s2bl/1HDhIREYFarc7WiZvu37/PjGnTOXvqDPk88jFqwljq1auXrt7evXvJbWyvExIAJ2MbKhh70LplK7SkLse6uLhQuHBhGjVqxKn9x/RcnjVSwy3tI5avWKXbkPkiTx89YenKjTQzL42tkQUXYh9wSz5m7Yzpr3zRf/PdJGZ9PZVeqlq4mNjxJDmSDdHeTJ3xPSO+HAGk5nV5/PgxwcHBdG7bkSSZoteHWmrRaLU5woal8HqUmcknzPhRYymhdqGF3fPlySORPvTs3J0Bwwbh6+vLgQMHcBf2OiGB1FlHCRM3jj64Q43aNWnRogU3fK5z+uwdPEyddF+lN+MDsctlT5cuz3ePT5sxnVxOTvw8Zy6hj59SsVwF/p6zhzJlyrxyjNk9lezdu3epWrEKVU28aG5WlBCfcDq37sC8RfPp2q0bt27dwtvbmzNnzrBnzx7s4gzgpVu2MjSnTq3aTJ81k8KFC2NrawukenG1b9WWxacPUMu0CCoEJ5PuULRcSerXr//K8fw4dw4FixZm0c8LCY8Ip36T+nhP3fjaGcOQoUOIj49n5vcz0KSoURkZMGbMaIaPGK6rY2hoqFvuGjpiGKt/XEo+EyedwB2O9qFa1arpZrwKOQiZM1yDc6wB3tbKhrFOrbA1fL7klKxVM/L+H0gkRkZGqTnKwxOZmLeDXh9rIk/RbmxfRo5KXZqKiIigeqWqmEZqKWqQm6faGM4n+LJp25bXvthyAj06dyPmiC+N7crqyh4mPGHRk30YmBoRHR0NpIpmmTJl8D55mv+5ddQtA6ZoNcwL280vq5a+0ntKrVbz+++/89efK9FqtHTp3Z2BAwdm+ixArVYTFhaGvb39G5NupaSk0KV9J44fOUYRCzceqSMwsjXnwNFD2dopIieTGQb40g7mck+zwhmq67r6ynszwAshMvKFo5VSRmakvxw7MzExNiZJq78kkSxTMDI05PbdO7qd4SUKF2N35CUaWJfEQBhwNuYed5JD6NX7uTHczs6O81cusnr1ak4cPkYFz3wsHjggXZ74T4Vz587xzbiJXLh0EdfcroyeOJaePXvq2Qri4+M5fOgwn1nquzh7mjmDVtKiRQsaNWpElSpVKFSoEEIIfpgxkzkzZlHNtBCmwojzKQ8pW6MiTZs2feU4DA0NGTRoEIMGZW3iLENDwwy59xoZGbF5x1auXLnChQsXyJcvH/Xq1cPA4NMPpaHweiQC7ccZTiUk7XjTtMkAcH/DeR1ZNjMRQpgCxwETUkVrk5RyUpoargc8AD+gk5QyIq3NBKA/oAGGSyn3pZWXB5YDZsBuYISUUgohTICVQHkgDOgspfR707j+mZmM+nIkJ1fvoad9TVRChZSSTZHeuNUvwaq1f+nqBwcH81nvfhw/eRwQFC9SjKXLl712aepT59KlS9SvXZdm5mUoYelOSFIE22Iv8OXXo6lWozqHDh3i4MGDnDlzBpEi6Z27rp5rbawmgakhmwl58ggrK6t0/Z85c4YVfywnIS6eNh3b0apVK+VlrPDByIyZSSl7C/l3o2IZquu+/sL7nJlcllKWfdc6urpZKCYCsJBSxgohjICTwAigHRAupZwphBgP2EkpxwkhigFrgUpAHuAgUEhKqRFCnEtr602qmMyXUu4RQgwFSkkpBwshugBtpZSd3zSuf8QkLi6OVk1bcPPqdbzMcxOQ9BQn9zzsO3zglevb0dHRpKSk6LkE50TatmiN8YVwats8z3vyODmCmf5bSJFqhBCUKVOG+vXrY2xszPJffmOAfX2cjG1I0CSxLvIMpZpX5fcVf37Au1BQyBiZJSa7Ghb/94pAvg3n33g9IUQT4GdSZwzLpJQzX1GnDjAPMAKeSSlrv1wnrZ6plDLxTePJSJ1/yLJlLpmqUv/sxDNKOyTQGqiTVr4COAqMSytfJ6VMAh4KIe4DlYQQfoC1lPIMgBBiJdAG2JPWZnJaX5uAX4QQQmZAIS0sLDh47DDnz5/Hx8eHQoUKUaNGjdfGanoxrPunSFxcHN9M/B+rV60iKTmZFs2a88NPP+qt9UdGRuJ9xpsBVnX02roY22FubMr0n36gU6dOei7MuewdmDL5OyyNzIhMiKFd23b8svjX93VbCgofBZlhgBdCGAALgYZAEHBeCLFDSnnzhTq2wK9AEyllgBAifUrU54wRQsRLKee8ftwZExLIYptJ2s1fBLyAhVLKs0IIZynlIwAp5aMXbtaV1JnHPwSllaWk/fnl8n/aBKb1pRZCRAEOwLOXxjEQGAjoRckVQlCpUiUqVaqUCXebfZFS0qJxM+JvhzLEpkFqXpOjt6heuSqr1v7F8ePH2bt3L97e3hhqVQQYP8XF5LnbVaQ6Dq0B9OnTB3Nz/U2ZX40ayeChQ3j48CHOzs45fmankAORmRZ3qxJwX0r5AEAIsY7UD+qbL9TpBmyRUgYASClD39BfT6DMy4VCiM8ARynljLcZXJaKiZRSA5RJU8utQogSb6j+qqct31D+pjYvj2MpsBRSl7neNOZPlWfPnmFoaKhzrX2Rs2fPcvf6LSY4tUElUjdXtbSrgH/wbmrXTp0hly9fnvHjx5MrVy6+/2YKdoaWeJnlJiwlhvXRZxg4YEA6IfkHMzMzihXL2JqxgsKnhgS02gzb/XIJIV6M97Q07f0FL3w8pxEEVH6pfSHASAhxFLACfpZSrnzNtRKklPGvKF8FXAI+HjH5ByllZNrNNQGeCCFyp81KcgP/KGcQkPeFZm6kehoEpf355fIX2wQJIQwBGyA8y24kG3LlyhUG9O7HrTu3kUhqVKvB7yv/1C1fpaSksGXLFtwNHHRC8g8lzN3JU8GLNRvWpbpJp+Hq6sq4kWN47L8fE2MThg4bxnfTprzX+1JQyE5oM77M9ewNNpOMfDwbkuqQVJ9Uh6UzQghvKeXdV7RN+OddrNehlElCCHVGB/zihbMEIYQjkJImJGZAA+AHYAfQG5iZ9nN7WpMdwBohxE+kGuALAufSDPAxQogqwFmgF7DghTa9gTNAB+BwRuwlOYVnz57RoG59mpqWopd7DzRSy6Eb16hTvRZjJo5j//79HDx4kOjoaOwNLZEOUs9mFCQi6NRmgJ6QAHTs2JEOHToQExODubl5tkmeFRQUxP79+7GwsKB58+ZYWlr+a5uEhASuXr2Kvb09hQoVeg+jVPjkyLxlrtd9cL9c55mUMg6IE0IcB0oDrxKTOcB2IURHKaX/P4Vppoc353N4BVkZMCY3cEQIcQ04DxyQUu4iVUQaCiHukWpImgkgpbwBbCB1/W8vMCxtmQxgCLAMuA/4kmp8B/gdcEgz1o8Exmfh/Xx0+Pv7M3fuXGbPns29e/fSnV+5ciVFjPNQ1bowBkKFscqQprbliH0UweDBgzl//jydOnVi48aN5CtSgM2R3sRqEkjWpnA40gdfzVN69+79ymsLIbC2ts42QjLz++kUK1SUZRN/4ofh3+Cex40jR468sc0ff/yBq3NuerToSLXylalWsQrBwcHvacQKnwr/JMfKyPEvnAcKCiE8hRDGQBdSP6hfZDtQUwhhKIQwJ3UZ7NYrxyXlRlIN+heFELuEENOEENOBU8Dst73PHLsDPruzdMlSxowcRVkLTwSCy3EPmfjN14wdPw61Ws2FCxcYOeJLcj9UUd+ulF7bv8JOUH9oe7777jvdTCQ8PJwRw75g05bNqDUa6taszYLFCylcOGM7d98nCQkJTP52Eiv/XEFCUiJNmzRh5uxZ5MuX75X1z549S8uGTfnSsbku4sHd+GBWRZ8k6HEIZmZm6dqcPn2aVo2bM9ihIXlM7NFILfuirvAkt4bzVy6+dmzJycns3LkTX19fSpUqRaNGjV6bUVPh4yczXINL2FrJzTXLZahukV3H/801uBmpbr8GwB9Syu+FEIMBpJSL0+qMAfqSOrtYJqWc96ZrCiGsgLZAcSAO2C2lfOuXpCImHylRUVE8ffoUd3f3dOFBgoKCKFaoKCOdW+BkbANAZEocM0O2ULF6FS5cuKALVVLAPDdfubbUiYZGapj+ZBs7D+2hQoX0v7MajQatVvvGsCEfmmaNmhJ66QFNLctgZmDMqZjbXFUFc/32TT0Hg+joaAIDA5kwdjyce0ITe/3/0D+F7MSjclHy58+PgYEBhoaGup/7d++l0DNr6r0gxFqpZcqjzRw4eZjSpUunG1dwcDC1q9XEOB7chC2+mlDs3Z05dOzIJ+9a/qmSWWKyqUb5DNUt+vex97lpsSpwK6PhUv6N7LFGkYNITExk2KAhbNi4EUtjM1LQMm3G9wweMlhXZ9u2bZSyzKcTEgBbIwvKm3ly+fJlunTpQoMGDahatSqN6zVkfcRpaloUIVmr5kC8D+WqVHilkAAYGBh8kB3nWq2Wu3fvYmZm9toZBqQ6FFzwPsc3Lu10ATib25XnydMomjVthq2dLQEBAQQGBuoE1VAY0CbXy04vYCgFly9f5saNG2g0GjQaDWq1Go1Gg0xUU9VZf6+XSqgwSoYKFSrg5eWFl5cXBQoU0P2cM/NHCifmonmaaEkpWRN0im8m/o+ff5mfWY9KIZshpUDzkYVTEUJMJXXZ7EvgjRu9M4oiJu8ZKSXPnj3D3NwcCwuLdOc/HzyUq7tP822eDlgYmBKcFMbk8f8jMSkRlUrF8ePH2bdvH4VF+lhRhoZGjPh8BJMmTdKVnfA+xZRJ3/HXlq2YGBvTc0Qfxowdk6X3+LYcPnyYfr36kBgTT5I6hcJFCrNm4zq92GYajYYbN27w888/42ZgpxfJGaCwUW52XrlIwWKFKViwIPXq1SNv3rzkzZuXoKAgFkybQ3VtUYxVqb/yoclRBGsj8b8X8MqIB7N++IEts5dTmuehYMJSYoggnmHDhhEYGMj9+/c5cuQIcXFxAKgQ/OjVR1dfCEEDyxIsXrvutWKiVqv5+++/dRtnW7dujYmJyX9+lgofJx9h1OBTQC1ebZj/TyjLXO+Ro0ePMmzgEAICA9BKSasWLVm0bIluaeaf1L7f5OmApcHzhFcXY+7z1+PjJMkUPDw8KFeuHPt27WFsnjbkMk5dPolSx/Hjk52cPHc6W+3pCAgIoHTxUnSzqUYx87xokRyLvs4loxAWLl3E2bNnOX36NN7e3sTExABgY2jBNM/uqF7wPFsXeZomw7sw8euJ6a6h1Wrp2bU7J/YfoZyhB4kihXPxvvzw048MGDjgleOKioqicrmK2McYUc7Yg0h1HIcSbjDq67GMfkGMpZQ8efKEmzdv0rhRY3707IWx6vkS4dPkKKb7b6JqrerUrl2b2rVrU6VKFczNzQkPD6dujdokhkbjKXIRIqKINVVz/PRJJcrwR0JmLHMVt7GW66qknxm/ilL7D2bbtL2KmGQSUkouX75MUFAQ5cuXx9XVVe/83bt3qVy+Ip2sq1DSwoNEbTI7oy9iWMSe+YsWcvbsWQ4cOMDfm7YzM79+et7gpDCWx57gzKVzuh38ixctZvzosZS18EQlBZfiHzJu4jjGv+Jl+jEz6dtvObVkJ+1s9f+zTXm4jicpUahUKkqWLEm1atWoVq0aVatWpVfXHhg+jKOZdVlMVUacib7LoeSb3LhzM50b8z9IKTl48CA7t+/A0tKSHr16/qvoRkZGsmD+Avbt3E0ux1wMGfE5jRs3fm39pg0aY+oTTUPb0rprrg8/TWweQ1TGBly+fFlnj6pUqRIJsfFYBCbT2aG6zqa1O+IihhVzs+3vl510FD4EmSIm1tZyTZUqGapb5sABRUyyC1khJqGhobRo3IygB/7kNnPgXnQQffr25edf5uteEiM+H869jWdoYfvcEKeRWsY/WEm8JglIjf+lTkhmRJ4WuJk8DzuyL/IK1vUK6EUzBnj48CGbN29Go9HQpk2bj8rzyt/fn2VLfyPAz59qtWrQs2fPdDvk/f396dapK25+Kmrb6gdH+PPpYep+1oZvvvkmXXThyMhIvvx8OOs3bkCt0VCjclUWLPmVEiXeFGAh63n48CG1qtXAUWNBbq01D0UYwt6M46dP4ODgQFRUFKdOneLYsWMcO3aMS+cu8D+PTuQyem6cT9AkM9F/NXEJ8dnG7fpTJjPEpJi1jVxTOWNiUvbg/vdpgL8kpXyjm1lG6ujqKmLyZhITE/l14a9sXrsBIyMjeg/sR+/evfXcPZs2aIz22jNa2lZAJQTxmiQWhx2g55cD8PT05MqVK6xd8RfNTUpTzko/x8nPj/+mef+ODBw4kEKFCvHH73/wv9HjaWZehtwmdvgkBHAq8R6nz535qMTiTRw9epS2LdtQ3swTJ2HFLe1jkmxVnDx7mocPH7Jjxw62b9/O1atXAchv7sJI1+e505O0KUx9tIkzF8+98Z7/MZp/TClx4+Pj2bhxI/fu3aN06dK0adPmtZ5xDjZ2jHBomk5Mxj5YwdhxY+nQoQPlypXTPZfY2Fhm//gjG9dswMjIkB59ezN8xPCP6v4/NTJLTP6qVDVDdcsd2vc+xSQBSL9B7YUqgI2U8sPmM/lYeVFMtFotBw8e5Pr16xQsWJCmTZvqfQ2q1Wrq1qxN7L1QqpkWJEWr4WjiLao0qcXKNauB1FlJfncPpuXtpjPuAlyPDeDPRwdJlCmYmZmRy94B1zhLejo99xBK0CTzXcgGbt69rbdGvnv3bmbPmEVQYBBVqlXh60nfZBshkVJS0KMADdWFKWmZT1e26ukxbmseERUTjUqlonr16rRu3ZrGjRvTo0t3TB4nU82sIInaZA4l3KRmy/qffJj6wZ8N5PZ2bzraVdUJxq7wC1whkNCIMDQaDe7u7rRrl5rXZdzIMRAYSy3zIqillsMJN8hXsSg7du98bbRrhXcjs8RkZYXqGapb8cie9ykmr3ebfI5GShn079VysDdXVFQUDerUIyzgCfkNHAnSRjDOzpTDJ47qcoLv2rWLJ3cDGe7QVGfsLWbhxuStG2jVqhWPHz/mxo0byBQNRi95F1kZmpHL0ZH9Rw9SqFAhwsPDKV28FDsjLlDJwotodTx74q/StWu3dMbWZs2a0axZs/fyHDKbhw8fEhkeQYnc+tGZa1oV5V7EE/7880+aN2+Oo6Oj7vzx0yeY+9NPbNuwBXMLc8YM/Ib+/ft/iOG/V6bPmkntU7VY8HQfHjgQoko1wJ89fQEzMzN27tzJ1q1bWbRoEfPmzcPVxIEJ7u11wpHfzJkZp7dx7tw5KlfOmIFX4f0jP9Ic8C+GUMkMcqyYTBw3AdOgJEY5NNf959wecZ5+vfoyYtSX3L9/nz+W/U4xVR49ryFjlRGFjFw4fvw4lSpVon///qxbtYbb8cEUtXguCufi79OxWyeKFi0KgKOjI94XzjL5f9+ybO8+bKxtGDp6FJ9/8fn7vfF34PLly/w4/Qdu3bhJydKlGPv1eJ2dQkrJ2bNn+e2334iJj0UttXoCG69NIn9+T/r06ZOuX2trayZNnsykyZPf0518HNjb23PZ5wq7du3Cx8eHggUL0rZtW51rcN++fenbty8xMTF079Yd4f1EbwZiKAwoaurK2bNnFTH5qBFvE+gx25JjxWT9uvUMt2us95+zoXUpxh1YwZ4DewEwNjLG2NwzXdsEEy2/L/6d9u3bA9C8eXO6duhM1ZSCOKtsuKkJIdQ0nvVfT9Br5+7uzh8rl2fdTWUhx44do22L1tQzL059k/z4Hval5q7qLPptCTdu3GDNmjU8ePAAExMTHOwdOBh1lSa2ZRFCkKRN4WD8Db7634R/v1AOw9DQkDZt2tCmTZvX1rGysqJ+g/qsP/dbunOhMiad56DCx8fHODPJbHJs0CCtVqM344DUHc4qlYrDhw8TEhLCQ7+H3NY85kZcAFJKtFJyOvoOYSKeFi1a6No1btyY0+e98epYlfCy5nQc259LPlde66aaHRk1/CvaWlWknm1J8pu50NC2NC0sytGnWy+mT59OgQIF+PPPP3ny5AnnLl/ggW0Ms8N2sSr6BFNCNlG9RV0GDhz4oW8j29KjRw/uJoVwLvoeWinRSA1Ho64TbZhEy5YtP/TwFP6FTAr0mKmkpe3INHLszKR169Yc3XeNdnbPlweORd+gcYNG1K1bV1e2dec2enXtwfanF0nWqHF0ceLA1oPpdikXKVIkW4fMSEpKIikp6ZUxpLRaLZd8rtDb6zO98rJWnqx/dpLgoGCdnQnAxsYGn9s3OHHiBEFBQVSqVImCBQtm+T28jFarZe/evRzcdwAHRwd69uqll2nzdVy6dImZU6dzw+c6xUoUZ/w3EylfPmOxlbIKBwcH9h06QJ/uvdgRdAGNVkuxosU4tO6I4s31kSMlaLQf5Xf7OSBjESgzQI715goNDaVmleoYx2jxlA4Eq6IINYjl+OmTeHrqL21ptVquX7+OsbExhQsX/qQ8Z2JjYxk+9HPWb9iAVqulSMFCLFjyKzVq1CAlJYV9+/axatUqtm7czIR8HXA2ttW1DUh8yl9J3gQ+/vjCsqekpNCmeStuXrhGKQM3YkQSl+IfsnrdX3qzypc5fvw4bZq3pL55CQqYuvAg8QkH433YumuHLuvkh0RKSWBgIIaGhuTJk+dDD+eTJzO8uYpY2smlpetkqG7t09vepzfXZSll2czqL8fOTJycnLh26zqbN2/m6pWrtC1ahE6dOr0yXpZKpaJUqVKv6CX707FNe6KvBvGta0csDEy4HPGQ5o2b0rp9W/bu3cvTp09xcHCgbPlybLh/hr4OdbE0MCVaHc+2mAt8MXbEh76FV7J69WoeXLzFyFzNdHG8ypt60rdnb4Ieh7wy/pWUkrFfjqKNZUUqWHsB4G7qiKXKlHFfjcb70vnXXk9Kyf79+9m8fhPGJkZ079WTqlUztrfgbRBCZGh2pfDxIAH5yiSJHxxHIcTI152UUv70Np29du4lhNgthPB4m86yGyYmJnTr1o0fZv1A3759XykknzJ37tzhnPdZOttVw8rQDJVQUd6qAJVM8rN+zTrq1KnD9u3bCQkJ4dSZ09Tv3IKpIZuYHbaL6Y+20KJXe0aPHf1exrpt2zbKlyyLjaU1VcpVYu/eva+tm5yczJ9LfqeqsZdeQEhPM2cMEyRubm64uLjg4OCAtbU1ZmZmGBkZoVKpOHf5AqUtPfT6K23pybkrF5k/fz4HDx4kJCSEF2f0Ukr69+nHgC69ebbzOoGbL9KmcQumTP4u05+DQvbkY7SZkJoTxZLUXPGvOt6KN81MlgP7hRArgFlSypS3HqrCB+Xu3bv8umAhfr4PqVa7OgMGDsTOzk53/vz58zgZ2WD40h4ZT1MXRMlcbNiwQa/8l8ULmTpjGv7+/nh6emJjY8P7YP26dQwfOIx2VhXp7FKKe48f0aNjV1asW02DBg3w8fHh4sWLXLp0iYsXL+Lj44NI0ZLPKf1GMamCKlWq4OrqipGREYaGhhgZGemOebPnEpoShesL4WxCUyIxFoaMGPF8FmZjY0OxYsUoWrQopqam/L15B+Nyt8E0LchjVXVhZv44h569e6VbNlXIeXykrsGPpJRTMquz14qJlHKDEOJv4FvgghBiFS/kBX7bKZDC++XgwYN0bNuequYFcVHZsvXCCn5dsJC/9+3h5MmTrFu3jqNHj2IsDEnMlYyp6rkR957mCTVqvNquYGdnpydI74Nvxv+PrjbVKGSe6gJb1io/KqGie8euxKUkoFarAbC1taV8+fKMGDECjUbDxmV/UcbSEzOD1CWtKzEPMLG1YNu2ba/N2WJqbMLy2YvpbVcLG0MLotTxbI4+x7ffTab/gP7cvHlT79i1axdPQ0NpYl9OJyQA1obmlLBwZ+/evQwZMiSLn5DCx80HmXVkhEwd1L/ZTFJITeNoQuq0562TzCu8f6SUDO4/kG421Slukbq+XgEv1oeepGyp0qRoNRQuXJjJkydz46oPy44dprlFWWwMzTkXe5+bmhDWfiSbKVNSUrjv/4CCBevrlRc2dyXucTxjxo2lXLlylC9fHg8PD51zhJSSpPhEvl+1mhIW+YiWCYSoI/h73543Jv8aO34c4eHhzFi0GFsTSyKTYhk0eDDjJ45HpVLh7Oys5+0HMG7sWC7+sT9dX2FxUcyZM4fY2Fjatm2Ll5eX3vno6GhWrlzJ1YuXKVayBH369nnvQq2Q9XzE3lz1/71KxnmtN5cQognwE6kJ66dIKeMz88IfiuyStvdNJCYmsnz5cnZv24mdvT0Dhg6iRo0auvOBgYGULlKCqa5d9DzPAhOfsSzqCAePHaZUqVIIIdBoNPw05yeW/LKIyOgoGjVsyNSZ31OgQIEsvYejR4+y4vc/SYhPoH2XjrRr1073kpdS4uPjw7p161i3bh3BfoF8mbcV+Uyfh2C5Gx/MfpO73Lx/543XuX37NkeOHMHe3p6WLVumi1z8OmJiYggICMDd3T1d1OKXuXfvHpXKVuALxya4GKeKgW/CYxY/2UfBooV1AS1LlSpFu3btaNu2LTY2NtSoUo08Gms8hAOBRPJA85Tjp09QqFChDI1RIevJDG+uQhb2cn7xRhmq2/T8+k8vBL0Q4gQwWEp54/0OKWvJ7mKSmJhInRq1SPALp7yRBzHaBI4l3Obr776hRauWbNu2jY0bN3Lx3AVmFeiNyQtLL7fiAjltF8xFnysf7gaASd98y9L5i6huUggTYcjZlAeUqlGeGT/+wIYNG1i3bh03b97EwMCABg0a4JTLkaO7DtDDtiZuJg74JYTyV9RJZv4yh549e37Qe/mHP//8k+HDvqCQtRsaqcE//inrNq2ncePG+Pn5sW3bNrZs2cLJkyeRUmJraUNVkwK0cKio6+NwpA+xxS3Yezj9LEfhw5AZYlLQwl7OL/b6PDgv0uzCuk9PTD5VsoOYxMfHExoaSu7cudO5sC5dupRfJv7AIPsGullHWEoM0/w3kKxNtR2ULl2a5LhE8kSa0cauEiohSNAksTj8IKOmf83gwYPTXfN94e/vT6miJZiYux1WhmYApGg1TA/cRGhSJAC1atWiS5cutG/fHicnJ6SULPh5PjOmTSc8KhInh1x8O2Xya7MkfijCw8M5cOAARkZGNG7c+JXegU+ePGH79u18MfRzvsvXBWvD5zOlZG0Kox+sICk56Y1LcQrvj8wREwc5r2jGxKTFxbXZVkxy7D6TjxGNRsPEceNZvHgJpgZGqNEyfuIERo8d8zwY5cYtlDPy0Fu+cjCyws3MkfrdWjBhwgQ8PT15+vQprZq24Pt7W8hj5sD96GB69Oz5wUOaHDx4kOJW+XRCAmCkMqCaVWHCyhmyZsO6dFGUhRAM/3IEX4wYTnx8PObm5h/lxlF7e3s6d+78xjrOzs4MHDiQiWMnkKhN4cV4A0laNQKBt7c31apV+yjvUeG/8TEa4IUQMaRug0l3CpBSyvThMN6AIiYfEVO/m8KOPzcy1qkVdkaWPEmO5JcZc3n67BmGRobs37+fa5eu0MxB/8NFSonGBPr06aNzQ3V0dOT0eW+uXLlCYGAgZcuWJW/evB/itnTExcXh7e1NaGw42Oqfi1elULNOvTfmPhdCfDJ7gXr07MHetfvpYV8TlVAhpWRnxHmMDQ2pUaMG5cuX54svvqBz586YmpoipWTPnj2s+mMFarWajt060759e2UGkw2QfJyeS1LKt95L8iaUZa73RHJyMt9Nmszvvy0jNi6OenXq8uO8ObqkV1qtFkc7Bz63b6wXsuRufAiLg/eiMZBUrVqVIkWKsPmvDQx3aoqjsQ1SSk5F3+a8aRB3HtzTywD5PklISGDFihXs27mHXE6ODBw6iIoVU+0BwcHB/PLLLyxZsoSIiAhMDI3p51SfEpapnmYhSeEsfLYX74vns00SsHclLi6OFo2bcef6LQqYueCf+JTc+d3YtG0Lf//9NwsWLODmzZvkypWLgQMHEvroCXu37KK6SUEMhQHeyb6Uq1OZ9Zs3KjOYLCQzlrm8zB3kj4Uzlp+o3ZXVH2SZSwhhBxQETP8pk1Ief5s+lJlJJhIcHIxKpSJ37tzpzvXs2p07xy4zwLIuVrameF+8S42q1fE+f5bAwEAOHz5MVEw0Ts76GwHzmNhhaGJE6JNHuiCMpUuVZuK48bhbOhOdEoeJjQW79u7+YEISFxdH7Wo1UYfEUMYwL8+0oTTd1IghX36Or68vGzduRKvV0qZNG7766iuEELRv3ZbDyTcxVhnhH/eEhYsWvnch0Wq1rF+/nrUr/wKge5+edOzY8b08RwsLCw6fOMq5c+e4fv06hQsXpnr16gghGDx4MIMGDeLIkSPMnz+fGTNmYCIMmerZHfO0PTMVtV7MPrKLo0ePpnNVVvj4+EjDqQAghPgMGAG4AVeAKsAZoN7b9KOISSZw9epV+nTrxYOHD5BIihctzoq1q3Qunr6+vhzYt59JuTtilJbat4FdaZ6ERlGkUGHUWg0Alibm6ZJsXY8NoGL5CnrRfId9PowePXtw5swZbGxsqFy58gcTEoBly5ahDYllgF093VdySXN3Znw/A1MLM7744gu++OILvZ3ggY+COXr0aKp3Wp06/+p+m9lIKenRpRvnDp6iuklqROOJQ0axa9sOVq39672MQQhB5cqVX5nYSghBvXr1qFevHpMnT+bA/A06IQEwUhlS2jAve/fsVcTkI0d+/MmxRgAVAW8pZV0hRBHgrWMBKWLyL6SkpLBlyxYO7t2Po7MTffv30wunHhkZScO69WlsUpL+bpWRSE4E36ZerTocPXlclzjKSWWtE5J/KGLmSriDhjnz51K1alWOHj3KgF79aK4pSz4TR+4mhLA/3odds3anG5eNjQ1NmjTJ8vvPCLu37aT8S04BLsZ25LVyYsGa32jevHm6NkZGRjRs2DBTrn/mzBnmzppDgJ8/VWpUY9TY0f9qH/L29ubIvkOMc2qNcdq/S1mtJzN3b+fcuXNUqlTpje0DAgKYM2s2Z0+dIV9+D0aOHZ1l2Q4LFCjALqP0q+4RKbHc971PcnKyEob+I0f7cVsTEqWUiUIIhBAmUsrbQoi3Xib4KLdlvk98fX3Zvn07t27dSncuMTGRerXqMGnYOKL+vsPFP/dTqWwFtm7dqquzbt06PA2dqGpdGJVQYSAMqGNTHONoLQULFqRNmzZs3LiRwIRnqKVGr/8ATRit27WlWbNm2NnZ0bZtWzbu2EJIYcFqtTeJFezYf+Qg1apVy/Ln8F+JiYnh6bNnxKgT9MqllCQKdZaHSd+0aRMtGjWD04+p8iw3N9efoEKZ8jx8+FCvnlarJTAwkGPHjvHnn38yYcIEShi66oQEUlMyFzdwZfz48fz5558cP36coKAgtFr9F7mvry8VypTn9sZTVHmWG3nyEc0aNGHLli1Zco+tW7fmYeITbsUF6sr8E59yMdaXLVu2kD9/fubOnUtcXBwAT58+Zcp339GiUVNGfD6cu3fvZsm4FDKORGTo+EAECSFsgW3AASHEdiDkbTvJsQb45ORkenfryd49e8lvnRv/2CdUrFKJTdu26DyGFi5cyJJJcxloX1+XldEvIZSl4Qf54qsR3LlzhyOHj1AZD5o56CdP2vjsFHa1CzJmzBhKly5Np3YdeHrhIa2sy2NpYMa56LvsTfThyvWrH9zL6k1cvXqVebN/4sE9XypVr8KXI7/C1dWVZ8+eMX/+fBYsWEBkZCS2xpaMdm2NnZElUkqORd/khvUzrt+5mWUGYo1Gg4erOx2NK+Bl9txOtSv8AuH5VJSvXJEHDx7w4MED/Pz8SE5O1tURQlDa0pMBufVnR0tC9uET568XFdjY2BhPT0/y589P/vz5OXfmLI4B0Nz++b/5vfgQNmsu4xfknyVLjsePH6djuw7YCDOMhAGPEsP5fcWfWFhYMGPGDI4ePYqDgwO9evVi7aq/KCicKWToQogmnDPx99j2keRjyW5khgE+v1kuOc0rY9kwu19f/kH3mQghagM2wF4pZfK/1X+RHLvMNW3KVG4ducikPB0xVhmisdKw5sopvvpiBOP/N5H79+/z67xfqG6cXy+9r4eZE8bJgmnTplGgQAE883vic8ufJrKcrp5Garmvfcqar37V5bTYsGUTY0aOZubKlSQkJVCjcjUOLjz0UQvJ3r176dqhM3UsilHCyI7Lqw5R5o/ltGzbivXr1xMfH0/btm2ZMGECRw4dZtqUqeS3zkNEcgxmdlbs2r07Sz2NgoKCiI+Nw8tV3+GhnEV+Zl/axu37dylQoAClSpWiTZs2OjHInz8/5ubmFCtUhNvxQRQxT7VR3YoLIoBwHj16RGxsrE6IXjxOnz5NYnQ8Y93b6l3Tyyw3sSHHCAkJeaN783+lVq1aBD0K5sSJE6jVamrWrImZWepenUaNGnHmzBlmzJjBgnnzqWtbkjaOqUtu5chPXkMHhg0Ygs+dG4rn1wdC+xEb4F9ESnnsv7bNsTMTV6fc9DGvoRdqPEodxzcP1qBJ8wo3EYZ0cqpBFZvny4dSSqY93sKWfTuoWrUqarWaGlWqofWLppZ5EbRScjjhJs6lPNh7aH+6/7xSSrRa7Ue/P0BKSSFPLxqri1DM4rng7Xx2nsOR1+jcvSvjxo2jePHiunNhYWGcOXMGBwcHqlSpkmUvLq1Wy4kTJ1iyZAkb121gRv6eesZpn1g/LuQK5fzVS2/s5/Dhw3Tt2AUrYYIE4khm3ab11KlT543typUoQ5WI3JSwzKcri9MkMvHBarp078qAAQOoWbPmB3lxO9s7MsSmAU7Gz70CtVIyIXA1DwP9yZUr13sfU3YmM2Ymnma55JQCrTNUt9eNP95npsWTUsoar9i8+J82LeZYm0lMXCxWBmZ6ZRYGpkiRGrLk+PHj/LpsCceSbhOvSdLV8Y65i3UuW6pUqQKAoaEhB48eptnQzuw2vs0B83t0HtmPHXt2vfJlIoT46IUEIDQ0lNDQUIqa639lV7YuhIOdPStXrtQTEkjNU96iRQuqVq36n16kKSkprFixgjbNW9G9czcOHjyod97Pz48pU6bg5eVFnTp12LVrFwU887M5wptkbWq6nYiUWP6Ou8pX4/49aVe9evUIehzMn1vXsGLbWgIfBf2rkAB8NW4Uu+OvEpESC6SGQdkccZb8+fOzbds2ateujZeXF1OnTiUgIECv7YEDB+jWqSttm7di5cqVpKRkbpoge3t7otX6MVkTtckkpSRz8+bNdPUTExMJCQnRhfFXyApSvbkycrxPpJT/RIddJKW0fuGwAha/bX85dmbStkVrOBdKQ7vSunOno27jny+ZE2dPA6lf52NGjmbZ0t8oZuVOhCaOGINk9h3an+5Fmh0JDw/n8uXL5MmTh6JFi+rKpZRs376dTu078r1ndywMdPuYuB0XxDErf67e8snUsajVapo1bELQtftUNM5PgjaFk4l36Dv0M4oUK8ry5cs5fPgwkCoCffv2pW3btkgp6dm1O0cOH8HR3JYn8RGMGTuW/337vyybGUgpmTL5O+bMnoOzuR2hcRE0aNiAFX+tQgjBli1b+PPPPzly5IjOxbdv375cv+bDisV/UNO0MKYqI84lPyBfmUL8vf/NYfHfhp/n/cyiqT8xwK4+ZgbGaKSW9c9OcjnOj/jkBOrVq8e4ceOoV68e30z8ml9/XYQBKgyNDZn03WSGfSSpBz4WMmdm4ign5c/YzKTvzd/fu81ECHFJSlnupbJrUsq3ylWeY8Xk3r17VK9cjWKGeShg6EiAJpyLiQ85eOQQ5crpPVf8/Pw4fvw4uXLlomHDhhgZGb2m9+yBlJLJ305i7pyfcLdyJjQhgsLFirJ+y0YOHTrEjz/+iI+PD9bmVhQxyUM3hxoYqQyJUSfwW8Qhxkz/H4MyOVjkpk2bmDhoJF84NMFApE6YY9QJfPtwDclSTf78+enTpw+9evUiX7586doHBwcTHBxMkSJF9PbkZCXR0dHcunULNzc3XF1d05338/NjxYoVrFixgocPH2IsDJni2U0Xl0wjtfwctofZvy+gTZs2mTImjUbD0IGDWbt2Lfmt8xAc94xSZUuzYs0q1q9fz08//URISAh5nHNjkaCip0NtHIysCE4KY0XEcX5cPI+uXbtmylg+BTJDTDzMHOW3nm0yVLf/rWXvc5lrCDAUKADcf+GUFXBaStn9rfrLqWIC8PjxYxYvWsTlc5coWrI4Qz8firu7+wceYdazYcMGxgwcwWCHBtgYWqCRWraFn+V8nC8xiXEUL16cMWPG0LJlS/r06MWJYyfIbeFAUGwog4YMYdbsWZn+1d+/d19i9tyjjl0JvfKlT/bT4vNuTJky5YNuzHwXtFotX3/9NXsXbWSAcwO9c4cjrmHfojhL//gtU68ZGBiIj48P+fLl05tFJyUlsXLlSj4fMoyJedvj+IJt5UZcAKesg7hy81qmjiU7k1li8rVH23+vCAy8/dv7FBMbwA6YAYx/4VSMlDL8bfvLsd5cAC4uLkz+7q03emZ7fp33Cw3NS2JjmOoCbSBUtLSryKnIW6xatYru3bvrxGLH7l34+fkREBBA8eLFcXBweFPX/xmNVkuUJi5debJxas727CokACqViipVqrDz9w3pzkVq4rF5af9RZpA3b95XegqamJjQsWNHRnw+nFxG+jM4VxMHAoO9M30sOR0pMy8HfFrSwp8BA2CZlHLma+pVBLyBzlLKTa8el4wCooBMmYpm2f9QIUReIcQRIcQtIcQNIcSItHJ7IcQBIcS9tJ92L7SZIIS4L4S4I4Ro/EJ5eSGET9q5+SLtTSeEMBFCrE8rPyuE8Miq+8lOpKSksG3bNubOncvx48f19kxotVqCAgOxNdTPOGisMsTBMjWH+suzDg8PD2rVqpUlQhISEkK/fv1YsXolxyJvEJL0/IPoYowvETKeRo0ylqXuXYmKimLJkiVMnDCBbdu2ZapRukmTJjzTxnAp5oGuLDgpjJORN/lzxXI+++wzQkLeep/Yf8LGxganXI74Jj7WK78ZF0j5smXfyxhyGjKDx5sQQhgAC4GmQDGgqxCi2Gvq/QDs+5f+Tqb9jBFCRL9wxAghot/m/iBrZyZqYJSU8pIQwgq4KIQ4APQBDkkpZwohxpM6vRqX9lC6AMWBPMBBIUQhKaUGWAQMJFVpdwNNgD1AfyBCSuklhOhC6gN8c0KJTxx/f3/q1ayDSQLkUdkyN3kWBYoXYuXa1axbt47FixfjHxSAt40Z+c1cdO0eJjxBayT0QsVkFpGRkWg0Gj0xio2N5ccff2T27Nmo1WpGjx5Ngfz5GTdmHG7mjiRoklCbwO79e95LqBAfHx/q16mHp0EuHLWWbP5tDd/nncrh40czJW6YiYkJf+/bQ5sWrTjy7CamBiYEJzxj/qJfuHPnDgsWLGDt2rWMHTuW0aNH64XaDwsLw8DAAFtb23ceB6R6FE6fNYMvhwynpboc7ia5uJ0Qwr64q+yeuTdTrqGgTybNTCoB96WUDwCEEOuA1sDLbnpfAJtJjbf1Wv7x5sqsUPRZJiZSykfAo7Q/xwghbgGupN58nbRqK4CjwLi08nVSyiTgoRDiPlBJCOEHWEspzwAIIVYCbUgVk9bA5LS+NgG/CCGEzGmGoBf4rHc/SiQ509i+DABaqeW3awco4JmfFI2aWrVqMXbsWKZP+Z41EScpbuTGU3UUx+JvsfiP3zA0zLxfCX9/f/r36ssZ7zMIIShRrDhL/lzG+fPn+eabb3j8+DGdO3dm+vTp5M+fH4AePXty6tQpzM3NqVat2lt5OV28eJFf5/9CSGAwdRrVY9DgwRl+Affv2ZeGRsWpblMESHVSWBV4nB9mzGTa9O/f+t5fRfny5fELCuD06dMkJCRQvXp1nWgMHTqUCRMmMHnyZJYsWcK0adMoW7Ysg/sN4Matm0gk1apU4/eVf2aKXa9b9+7Y2dsz47vv2e93nNKlS7N36v5/jUmm8Pa8ZT6TXEKIF3NkLJVSLk37sysQ+MK5IEAvIJwQwhVoS2rE3zeKSWbzXgzwactPx4ESQICU0vaFcxFSSjshxC+kRq1cnVb+O6mC4QfMlFI2SCuvCYyTUrYQQlwHmkgpg9LO+QKVpZTPXrr+QFJnNri7u5f39/fPytvNcu7du0dQUBClSpXS+9qPiooij7ML3+ftrhdzKiDxKcsiDnPszEmdMTYsLIxfF/7K8YNHyOvhzrARX1C+fPl01/qvpKSkUKRAIUomuVDXujgqIfCOvsuWMG8S1clUq1aNOXPm6PbrvCvr1q5l2MCh1DYvgoOBFdfVQTwzT8L74rlXLs8lJycTHBxMYGAg169fZ8yXo5jp0VPnSQbgnxjKVnGVu36+mTLGjHD69GlGjRqFt7c3pobGtHOoQhXrwmiklsPR17ll9pRb9+9kqugrvJ7MMMC7mzrJMe7tM1R3+L3Fr72eEKIj0FhK+Vna33sClaSUX7xQZyMwR0rpLYRYDux6nc3khTYmQHvAgxcmGFLKKRkadBpZ/hsphLAkdcr1pZQy+g1eQK86Id9Q/qY2+gWpyr4UUr25/m3MHysRERF0bNOeK5cu42xuT0DME4YPH860Gd8THR3NqlWrSElRY/DSMzYQKiwtrfS8ehwcHPjm22/g22+yZKx///03JgnQyP75Pp7qNkW5HhdApS4NWLp0aaZ5hCUnJzN82HAG2NfD3dQRgLLk56+wEwwaMJCq1asRGBiodzx58kTPlmQkDJAv/epopJag4GDatGlDw4YNadSoEV5eXq8dd1JSEmfOnMHAwICqVav+pxd+tWrVOH36NP369ePK5uNUt0nd/2MgVDSxLcPd8L3s3buXFi1avHXfCh8GCWgyZ5krCHjRq8KN9AEZKwDr0n5HcwHNhBBqKeW2N/S7nVRD/EUg6Q313kiWiokQwohUIflLSvlPSNUnQojcUspHQojcQGha+eseVFDan18uf7FNkBDCkNQAZW/t0pZd6NezD5pbYUzK3QEDYUC0ZTwLFy5j/6ED+Pj4kJSUhLWpBaeiblPLNlU4pJQci7tFu24Z+zLKLPz9/XFR2aQr9zB1wsbKOlNdi2/duoUphjoh+YeKZgVYsn0Xm7emBu/8x8OpZMmSuj//c/Tv1ZfjgTepZ1MSSBWSAzE+lChbimvXrrF9+/bU8Xt46ISlXr162NvbA7B79256d++JvaEVGqkhXpXCxq2bqV69+lvfjxACWysbPEwc053LrbJNFxFZ4eMnk0LQnwcKCiE8gWBSbczdXqwgpdQlDXphZrLtX/p1k1K+cz6LLBOTNI+r34FbUsqfXji1A+gNzEz7uf2F8jVCiJ9INcAXBM5JKTVp3gVVgLNAL2DBS32dAToAh7OzvcTf35/Fvy7G985dKlWvQv/PPsPOLtXZLTw8nAOHDjLFrQsGItWOYG1oTnPrcvx17QSDhwymW7duWFhYUK9WXR5GPMNZa8V98RQjR0u+/W7Se70XIyMjrkT40tamkm7pSErJfZ7SvUrm5v3w8/MjLCYCdS4NhuK5jSVKHUe5cuXYtX83tra2bxSwlWtXU69WHe5GPMEJK+6kPKJwqWLs2rcbU1NTfH192b9/P/v372f9+vX89ttvqFQqKlSoQJUqVfhj6e8Mcmygc2q4HhtAq2Yt8AsK+E8G/EpVK3Ng7Q4aSKkbt0ZquRJxn64mJv/SWuFjIzNeSlJKtRDic1K9tAyAP6SUN4QQg9POv3UIlDROCyFKSinfKaxFltlMhBA1gBOAD8/tTxNJFYQNgDsQAHT8Z4OMEOJroB+pnmBfSin3pJVXAJYDZqTaUb6QUkohhCmwCihL6oykyz+eDq/jQ+WA/ze8vb1p1qgp5c08yaOy5Z7mCYEGkXhfOEdCQgKrVq1i7ozZzPTsqdcuMPEZm8VlvXX96Oho1qxZwwNfXypWqkSbNm3e2679qKgoJkyYwKJFi7AysyC/iTONrEpjqDLgeNwtYhwF569czBQPrePHjzNt2jQOHDiAuZEpNa2L0cK+PCqhIlIdx6KwA8z/cxFt22Zsw1hSUhI7duwgICCAihUrvjZYo1qt5ty5c+zfv58DBw5w5swZKlp50dtFP8vpH5FHGf7jRHr16vXW95acnEz50uWwfQa1LIqSotWwL+YqD5OeEJMQx7Bhw5g+ffp72+2fU8kMm4mbiZMc4dYxQ3XHPvj1Q4RTuUnqx/sDUpe5/gn0qIRTeRMfSkwSExPZvHkzt27donjx4rRr1w6TF74wy5UoTZkwRypYe+nKtj47y2WNP2FREQCYGZkwyLkRBc2fJ5zaFnGOgu2qsHDxr+/tXqSUnDx5kpMnT+Li4kKHDh2wsrJi+/btDBs2jEePHvHll18yceJEFsyfz5oVq0lJUdO+cwf+9+037+TiKqXk4MGDTJ06lRMnTuDk5MTo0aNp06YNPTp3w9/3IY6mtvjFPGb0mDFMeg8zsq++/Iq7q0/Q3EH/HbAh4jRtv+7PiBEj/lO/ERERTJ08ha2btmBkZEiPvr0YOmwY06ZNY/78+eTJk4dFixbRsmVLoqOj2bRpE0+ePKFmzZq6fPIK70ZmickXGRST8R9GTNxJE5AXy6WUAa9u8Zp+FDHJeoKDg6lVtQaWiQa4aW0JFJEkWEhOeJ/CxcWFkJAQvDzyM8ujF6oXvIlCk6OYHbKdGbN/oFmzZly/fp2+3XtTx6Iozoa23EoJ5p54yrlLF14ZGyorSElJoUPrdlw8fY5iRq5EqOJ5kBhK2YrlOHToEKVKlWLZsmVUrPjfvBKTk5P5/fff2fTXeoyMjen1WR+6dOmCEIJdu3Yxbdo0zp07h6urK+PGjeOzzz7T5fUAuHbtGo8fP6Z8+fJZtlv/ZQ4dOkTfDt0ZlaslRqrUZbZEbTL/e7CGAZ8P4scff8z0vTJnz57ls88+4/r16zRo0ICL5y7gZeqCrdaMGylBVKpRlY3bNiteX+9IZoiJq4mTHObaKUN1v3648H2GU3k59LzuFP8hBL0iJpnA3bt3mTXjB65cvEyhIoUZPX6MXrDIjm07EHfKnxZ2z11vt4Wd44lzCjYOdpw9exZNspofCvTC7IW8HA8SHrPT4Dp3Hj6PwXb58mUWzP0Zvwd+1KhTk8+Hf4GTk1Om3s+b+PXXX1n4zY8Mcmigs09ciL7PmtDjfDt1MmPGjPnPS2oajYbG9Rvy+Lof1YwLopYajiXdJn/pwjyNCOPq1at4enoyYcIEevXqpTez+5BIKenQuh0+Jy9S1cQLjdRyIvEOxvYW3H/oS9GiRVm8eDG1atXK1OsmJycza9Yspk2aQg/n2pSzKgBAilbD4vADfDl9AoMGDcrUa+Y0MktMhubJmJj8z+/9iUlmk30DHr1Hbt26xbp16zh//jwvi+/Vq1epUqEyT3b7UCsiL8nHAqhfq64uF0d8fDw7du2gnrV+AMN6NiW4cfMmSUlJfPHFF1SrWpVdUZfQpvWfrE1hb9w1+g8eqNeubNmy/LFyOYdPHmXKtKnvVUgA1i5fTS3TInqG7vJWBbAxt3pn28yePXt46HOXQfYNKGPlSQVrL4Y5NObU8ZNERUWxcuVK7t69y4ABA7JUSKSUHDt2jEWLFnH06NF0/+YvI4Rgw9ZNTFowg8iyFiRWtmfen79y1/ceu3btIiEhgdq1a9OvXz+ePXv2xr7eBmNjY1q3bo2thTVlLfPryo1UBtQyLcKa5asy7VoK74YWkaEjO5Pj58CxsbH4+/vj5uaGjY2+K2tycjLdOnXlyMFDFLRyJSDhKR4F87Nr326dS+jEMeNpaFaC2mmuuF7muXEwtKJbxy645M3DjRs3QCvRSP09sFokpmamnD17Fkj11mrZpDnT72zB1SwX92NCaNGyBSNHjXwPTyHjaLSv/pVXGaj+9aX7bxw+eIgSKle9jYOmKiPK2RWky6jB9OzZ8w2tM4eoqCga12/IowdBeBo74pf8FKd8edh/5OAbbT0GBgZ0796d7t31o3Y3b96cunXrMmXKFObMmcOOHTuYPXs2vXv31tk01Go1ycnJmJubv6rrf+VVQTAFoNW8xb5rhSxDkmmuwR81OXZmIqXkm4n/w9U5N01rNiBvbleGD/tCL7jfzBkzuHfyKt/m7kgv65pMdGqLiX8CA/r25/jx4yxZsoTDR49Q7oWvQoCSFvkIi4wgT548TJw4kZrVa3Ag+qruZSul5GC0Dx3bd9C1sbe35+TZ0+w8vJfxC6dx/upFVq3766Na8z5x4gQPgvzYG34ZzQuRbi/HPsTCxopixdLFnHsrnJydiZDx6cpjDJIyNAOTUnL27FkWLlzIzp07/1OgxrEjR2Pkn8DYXC3pZFOVMblaYhaUzOivRr11X/9gbm7OzJkzuXTpEoULF6Zv377UrVuXS5cuMWTgYOysbbCzsaV8yTKcPHnyrfouXrw4ZtbmXI3105VppIa9YZfwDfTj1KlT/3ncCpmHlBk7sjM51may4Of5/Dx5Fn3t6mBnZEmMOoFVkcdpM6gbU7+fxtOnTylXojQ9zKrpbYaL0yQywXeVLk+8qcqYYa5N9YImhqXEMDt0J+FRERgYGBAaGkrdGrVRh8eTT+WAn/YZJo7WHD157L0ZiTNKUFAQvy1Zyv0796hcoyp9+vRBo9EwduxYli1bhru7O84Ojjx+GEwxg9xEGCTim/SY3fv3vlNcJ7VazYgRI/ht0RKGujalkLkrUkouxvjyd8o1/AL99QztL5OUlES7Vm245H2BIqauPNZGkWIuOHT8yCuTab1ISkoKISEhBAYG0rhBIybmaYedkaXufKQ6jukhW4hNSB8i/23RarX88ccfjB07lvjoWIpZutPRoSpWBmZcjn3I1pjznLlwlsKFC2e4T29vb1o0aYaXiQu2GlNuah6R29ONR8+eEBgYyMCBA5k5cyYqlYrly5dz7pQ3XkUKMmDgQNzc3P79AjmYzLCZ5DFxlp+5ZCz+7NSABdnWZpJjxaSAuydtKa0nAqHJUcwI3IyhiRHx8fEYCQP+59FJL++DRmoY9WA56zduoHz58mzZvIWFU+fQ364u1obmxGuSWB15kvo9WjJn3vO9mmq1mt27d3P79m2KFStG06ZNP7pc8GfPnqVpwyaUNfMgt7DhnvYJ/pow1EJLZGQkI0eOZNKkSZibm3PkyBFOnjyJs7MznTt3fid339DQULp06cKRI0do1qwZl85ewFQakqJVY2pjycatmyj7L6HRp38/nQ0//UF/h7q6TZ37I68QVdCE5X+tJCgoiMDAwFf+fPz4sW7WqEIws0AvvVTF8ZokJvitJiY2BlNT01de/205f/48darXYnq+7hi9EEdtd+Ql3NuU59cli96qv8jISNavX69zDa5Tpw5xcXFMmjSJefPmYW9vj0oDHoaOFFQ58UhGcTnRj30H9/9nz7ucQGaISW5jZ9kvg2IyPVARk2zDP2JiZW7Bt3k66r00tFIy4v5vDPv8c7y8vNixZRuGN6JoZf/8P5t31B3u5onF+9L51DZaLePGjGPxokU4W9gTGhdOx44dWfTbkvcSOj0zKVu8NGXD9fe6bAg9yR2jZ+zZv5cyZcpk+jW9vb3p0KEDYWFhLFq0iD59+qBWq7l06RLGxsaULl06Q/slihYoTPOUonofBylaNaN9l6N+KfmUpaWlLoyKm5ub3s85P/yI8fVomtk998bbHXaBA+FXcXBxZMSIEQwaNOidw8EfOnSIL7sPYoiNfuZFn1h/7uZP5NCJI+/U/4tcunSJZo2aUkzjRAen5+FdzkXf5bpTJBeuXsq0a31qZJaY9HHOmJjMDMq+YvLxLMi/ZyqVr8jVe35USws5DnAjzp/ihYoyf/58ANq1a0fVipWJijiBl8qRYBnJ1cQA9v92QNdGpVLx45wf+fqbr7l//z758uXD0TF9TKWPnbCwMO753qO/u36ok1q2xbkffyLThURKyaJFi/jyyy9xc3PjzJkzumsYGhq+9ZJZijpFz8MMUoMjGhka8sPMWRQrVkwnGi87WrxI0aJFqV65Kk8iosmHPQFEEGIYxW/Lf2flypWMHz+e77//noEDB+rG/l8oVqwY/tFPSLBM0nMHv50YTPkKDf9Tn6+jXLlyqISgpm1xvfLyVl5suL2KyMjITMuVovBqcsIne441wM+YM4u/4y5zMPIaAYlPOR51g/VR3syeP1dXx83NDZ9bN+g4rj/ami7UGtSaazd9Xhmq3dbWlgoVKmRLIYFUbyS1RkOy1Ddax2uSsHwhUdN/4ebNm4wc8RU9OndjxYoVRERE0KtXL4YNG0ajRo24ePHiO4lVcHAwqAQHI67qeZSdj7lP0cJFGDlyJE2aNKF48eJvFBIAd3d3bt69Tf8pX+LSvix9vxvOrXt36NWrFwcPHuTixYu0aNGCefPm4enpSe/evfHxefuQRrlz56Zr1y78HnEEv4RQItVxHIi4wqmIm5y/dIHo6LdOdPdGLMxTl2BfJFmbglar/eiWWz81Ur25RIaO7EyOFZNKlSpx/PRJTGvnY6fxDZIrOrDn0L50KWJtbW0ZOWokf21cx+Qp3723neZZgZ+fH4MHDKJ0kRI0b9iEgwcPIqXk77//pnr16kiNlh1hz/fSJGvV7Iu7Rt+Bn/3na27YsIHqlapyZ+1J5NFgZo2cjIdbPlavXs2UKVPYsWOHLpjl2yKl5K+//qJEiRIEPw4h1CKRXyMOcCD8Cn9FnuTvxKssW/nnW/drZWXF4MGD+WXRQoYMGaIXqLFcuXKsWbOG+/fvM3ToUDZt2kSpUqVo2rQpR44cQUpJYmIi30/7nuIFi1K0QGEmffstcXHpjfe/Ll1Mn7FD2SQv8WPoDkRlF76dMplTp05Ro0YNAgMD07X5r/Qd+Bn74q6Rok39WJBSsiP8PFKjpVq1auzZswcpJfv376dpg8aULlKCIQMHk91z/3wsKN5cnyAfa6DHrObhw4dUKl+RCoYelDDNy+PkSPbEXsEpb25u3b5FwYIFmThxIgvnLeCxfzCuJg7cjQ2mcdPGrFyz+j9tRkxMTMTNJQ+f2dTVecRJKVkQ/Dd1e7Vk0aK3MzK/SGhoKEOGDGHLli1Uq1aN5cuXky9fPjZv3szZ02fwKJCfnj17Zrm3XHh4OIsWLWL+/PmEhoZSrlw5UuKTMHyaRF3z4qgQHIu/hYGnLSe9T2VoFnDgwAE6dOiAhYUFu3bt0oum8F9JSUmhR+duHNh/gEKWrgQlPSOPR16GDB/G999/j6+vL8WKFiU04BFNLMvgYmzL9cQALqoDOHfpPB4eHu88huxIZthMnI2dZfdcXTJUd+6j+dnWZqKISQ7hs779efT3NZq/ENIlMPEZPwXtYNZPPzJ06FCMjIx0ezX8/PwoU6YMRYoUeUOvb+bUqVP0ad2Vrxya6ZVfjfXjvmcih04e/U/9bt26lUGDBhEVFcW0adMYOXLkB1+qSUxMZOXKlUydOpW4x5FM8eyqi7OmlZJ5YbuZt2JRhpNaXb9+nebNm/Ps2TPWrVtHy5YtM2Wct27d4urVq3h4eFC5cmWEECQnJ/PLL78wYcw4Rudtg6vJcwHeGXGBfK3KsXjZ0jf0+umSWWLSNYNi8nM2FpMcu8yV0zh57ASlzPT3W+Q1zYWdpTXNmjXTzTyEEFSpUoUuXbq8k5BAqtdUXEpCup3x8ZpErKzfPsdHREQEPXv2pF27duTNm5dLly4xZsyYDy4kAKampgwcOJBhw4ZRzqaAXsBOlRAUEs6cO3cuw/2VKFGCs2fPUqxYMdq0acOMGTP48osR5HfLRzGvIvw4axYpKSlvPc6iRYvSpUsXqlSpovOSMzY2plmzZjhY2ekJCUAps3wcP3rsra+j8AIydQd8Ro7sjCImnwjJyclM/nYSbs55sLawpE3zVty9e1cXZyoqKorQlEi9NgmaJOKSE8iVK1eWjKlo0aIko+FE5A1dWYw6gaOJt+k/ZOBr20VFRXHmzBk9m8HevXspUaIE69atY/LkyXh7e+ulIf5YcHd355kqvX0kVBWLu7v7W/Xl4uLC0aNHadq0KZO//pYLfx2kq2ElmiQXZuUPi+naMWNfuxnB0dGR2OR4ErXJ+uNOjiQyMooTJ04gpeTOnTu0ad4KawtL3Jzz8N2kyf9J1HIS8i2O7EyOdQ3+1OjTozc3Dp+nt2V1rC3NOXvhLpXLV8Q9vwfXrl3D2tqa7QkXcDPJhbOxLYnaZDZHnaNly1b/2QD+JhISEujcuTNh0REctLnFhTB/7A0tuR0dxBfDv3jlco+UksnfTGLu3Lm4mNsTGh9OjZq1cMztxPLlyylWrBg7dux4pTfdx0Lbtm0Z89UojkXdoIZ1EUBwJuoONyIe0qBBg39t/zIWFha0bNmShyd86OZYU1eez8SJqYc24ePjQ8mSJd953A4ODjRt2pTNx8/S3rYKpiojHidHsDPyAslGklq1alGmTBke3ntAPfNifO3SnmhNPJt/WcX9O/dYte6vdx7Dp0x2n3VkBEVMPgEePHjA7r//ZnKeThin7aZuYFuaR4kR3AsKZvHixfTq1YtlS39j0jffYmloRmRiDE2bNmXpH79l+niioqJo2bIlJ0+e5Ndff2XgwIEcPXqUsLAwqlev/lqPuNWrV7Ni4TLGu7TB1tCCZFs1q08fY3/sfsaOHct3332XaTvQswozMzMOHz9Kn269+PrWWgSC3Llzo42ENm3acOjQobd2Cjh/5iwlTPPqlRmpDChi4caFCxcyRUwAfl/xJ/169WXy3vXYmloRp0lkyqzv6du/HytWrOCbr/9HCYM8NLArDYCVoRl9jerw3c4N+Pn55VgjfUbICaZpRUyyCXfv3mXi2AkcOXIEOxtbBn0+hJGjUg3PV69exd3MUSck/1DcIi8OJfLrclp8MWI4AwYN5P79+zg7O2fJnpgnT57QpEkTrl+/zpo1a+jSJXUppn79+v/adsGceTQzL4OtYeq+FmOVIV2canArKYivv/76oxeSfyhcuDBnLp7VhWnJnTs3+/fvp1WrVjRs2JBDhw691WzQ06sAB7ioVyalJCgp7F/jjr0NlpaWbNiykdDQUEJDQ/Hy8tI98yFDhrBz83Zcb+pHIjZRGeFplYebN28qYvIaJKDOAWKi2EyyAcHBwVSvUg316WBGOjSjLaX544eFdGrXgeHDh9O/f3/uRQSlCxsSqAmnWCl9u4KpqSklSpTIFCF58OAB3Tt1xcXBiSIFCjF50iSqV6/O3bt32blzp05IMsrTp09xMNI3zJupjDExMiEqKuqdx/u+cXFxIXfu3AA0atSIrVu3cuPGDRo1akRkZGSG++nXvx8+iQFciL6PVmpJ1qawPewcT+MismTfk5OTEyVKlEgn3kVLFCNQE65XlqLV4B/7hIIFC2b6OD4lcoLNRBGTj4Rnz54xb948xowazZYtW/TCp8+f9zOljfLSyK4MdkaWeJo585ldXXbu3MmSJUto0KABJUuVZE34SSLVcailhjNRtzmf8IBhX3yeJeN99OgRVStWIfqoL0OtG9AsuSi/z/qVx0GPOHjwIE2aNHnrPuvUq8vFOF+9svsJj7CytsrWm0X/oWnTpmzevJmrV6/SuHHjDAtk7ty52XNgH5fsnjAxaA1fB64l3ssME0szatWqxZUrV7J24Gl8PuILziX4cibqDmqpITIljrWRJ6lRq4YiJm/gn3wmijeXQpZz/vx5ingVYuP0ZdxZcZwJA7+iRpVqxMXFER8fz8G9Byho6KzXxszABE+bPGzcuJENGzZw5OQxyrarzfSQLYz0/ZMH7knsP3wgU5dBXmTBzwsobpCHpnblyGVsjZd5bka4phrV/+tyR8u2rTkYdpUNT09xOz6II1E+rIw8wbyF81+ZACo70qJFCzZu3MilS5do2rQpMTExGWpXqVIlrtz04d5DX4IeBXPy7GlOnz6NiYkJtWvXfus8KP8FT09P9h3azwP3REb6/sn0R1so164O6zZtyPJrZ2syuPs9u9tVlE2L74F/NrTt3fE3drkcGDhkEJUrpwZUlFJSvFBRqsa5Ud4qNVqvVkr+CD1ETC4IDApCnZRCA7vStHJ8HvwwRavhu0cbuHDtMvnzP0/OpdVq0Wg075Q+NyM0rFUPL19jSlp66JUvijzI3L8Wv7XnUlBQEBUqVMDExITmTZpx5eJlPDw9+HLMyHfKk/KxsmXLFjp16kTVqlXZs2cPlpaW/97oFQQEBNCoUSMCAgJYvnw5D3wfcPzQEfLkdWPY8M//NXT/fyU5ORlDQ8NPRuRfR2ZsWsxl6Cxb2GZsyXdFWPbdtKgY4DMJf39/YmNjKVKkiN4muoSEBOrUqE28fxjljPIRoQ2l+eYmTJs1g8FDBnPv3j0eBYdQ1q22ro1KCOpYFef34EMMGzaM4sWLM2rEV7jFOFDG0pMYTSI7oi9Qs1YtPSGB1CjG7+M/eIHCBQm4dYmSeOjK1FJDcNyzt56ZxMfH07p1a+Lj4zl06NBHuX8ks2nXrh1r166la9euNG/enG3btnH8+HFCQ0OpVatWhpNjubu7c+LECRo0aEDPrt0pbZOf0qb5eOZzgwab6rLo96V06tQp08ef3dIrfEhyStpeRUwyiJTylXk1AgMD6dqhMzeu38DcyBRhYsCSP36jefPmACxfvpxE/3AG2zfQtS9l7sHIEV+yfMXy1PXuZA0SCS9kV1dLDV4FvJgzZw4ABQsWZPjgYay6exwjQ0O6de3K3AU/Z/l9vwopJSojAw6GXcHN2J6SFh7EaxPZHnWBqtWq4uXl9e+dvNBXv379uHz5Mjt27MgRQvIPHTt2RK1W0717d9xcXPH4f3vnHVdl9T/w9+EyLusiOJiCgODeK/femZqVmivnz8yW9XVku8yBOStnjsrMXEiuNLU0TVHce6LgAEFE9rj3/P64VwRHYmw4b1/P697nPOec53wAn89zzvkMnQtOGjvGxb/Py717M3/xgmzlcilbtizt2rTF5moKA8q2yij3s3LjrVGjefHFFwtV+ueSiL4EKJPiPUfNBlJKUlJSHgn5cf/aN3O/wdPVA41GQ+2qNdi0aVOW653adaB0qIHP3V9honNPXrasz4A+/Thy5AgHDx5k8XcLqGdRIctDoZylA6XN7Lh37x6jRo3C08uLvffOZFxPl3p2Jp2m/5BBGWXNmzfnyKnjRMdEE3PvLguXLMY2h6Hh/wtpaWkMGzaMefPm0aZjO/62vca4az/y+fXV+HWsxy9rn239/KuvvmLVqlVMnjw523GrihN9+vTBw9mNHqUa8IZTB/o6NOFD1178sX4zK1euzHY/u7btoLF91tlMBetymOvNOHPmzBNaKfKLkrBnUqKVyfLly/EpXwFbG1s8nN34Zu43WZTK9GkBfP3xV/S1bMjsikNpHOvBwN792LFjB2AMZBgXGUMHh1oZqWL9bNyoZ1GBBnXr07BhQ06cOsm99MQs95VSIqwtWLp0KTNmzGDj75vZKy7zXcx21tzdz+SIQCo+V53Rj7HEsrOzy/P9kPvExMQwbepUXujUlbfeeJOQkBC6d+/OkiVL+Oijj9i8eTMnz50m7EY4UTF3WPbTD1nCtT+NwMBAPvzwQ/r168fYsWPzUJLCy+nTp0lNTMmSpE1rZkkrbWWWLvg+2/04OjkSq88axiXNoCc+NVElvipgJGDI5lGUKbFz31WrVjHuzffoV6oZPr6dCEuJIuCjSQCMfnM06enpTJ08hVGO7XGxNDqY1bDzItmQyoDer1LGzZnz58/jZVb6kaUIF8tSVK9ajU++/IykpCTeHfkmtdO8cbKwR0rJ3ntnsXa0zdhY9vf352LoZTZu3Mj169eZ2rhxgefljoiIoFG9Bril2lPF3JVLh/fTbMFCUgxpLFiwgBEjHsTWcnJyeub+jx8/Tv/+/WnQoAGLFi3K1nJOcSQ5ORkrjcUj8lsKC5KTsu9b8/rboxkzbDQVrd1wMLfBIA38Fh1c7DfIiwqGoj7tyAYlVplM+uRzXtI1wteUM9xTW5a+NOGDcePZELTBuKEeF4+Lc1ZPZR9rF+5G7aV+k0Y0bNiQlT+uIFGfgo0p9aqUkpP6G4x44x169uwJQMTNW3zy0cd427tyLz0Rc3stG7dszvIAsbKyolevXvkk/dOZ9PmX+KY40cvpuYwyb8tyrE89zPDhw5+5v5iYGIKCgkhJSaFhw4b06NEDBwcHAgMDsba2zs2hFylq1apFmrmB84nX8bcx+tIYpGRv0nmG9nsr2/306tWL40ePMXnGTCrYuxCZfBfHsqVJvZVOw4YNCQwMpFGjRsTFxXHt2jXKly+PTqfLK7EUD1H8VUkJNg22s7blU/dXMpQAGBXBmxcWUb9BfTw8PNi2eStjXLrhYvVAoQTfu8BVnzR27d0NwLtvvs2Gn9bQzroathotB5IvEetoIPjIoSx7Gnfu3GHfvn04OjrSuHHjQv/G6Ofly0vUobz2QURhKSWf3PyVkJNHn8l/5bfffqN/335UsnXHEnMORZ9HCsnf+/YW+AysMLBt2zZeefFl6tn64GDQciDuPInm6Vy9EfbMD/yoqChCQkJwdXWlZs2anDp1im7dunH9+nU6t+/Izl27KGVlx93keIYOG8r0mV8XihD+hZXcMA121JSTre16Z6vu+nvfKNPgokZl/0pciLpBLTvvjLLLyRF4uZfnwIEDCCEImBbAt5Nn8rJ9IzysynAmMYzf4kNY/cW6jDYz5syi/nMNWfTtAu7FRtBtcC/eHTPmkc1xJyenIrXBrNPpuBeTda8nVaaTkp76TD4RsbGx9O/bj5Gl2+GlLQdAZ9taBNzckG97P4WdDh06cPz0CZYtXcatGzfpX6oF06ZNIyAggC+++OKZ+ipTpgwdO3bMOK9WrRrBwcE0atiQg9v3Mt7DGETzXnoiP6wIxKm0Ex998nFui6TIhDINLuZ8PvlLBvbuB4CftRtXkyNZfe8AU+d+nbH89P7/3sfW1pZpX00h/PINalapxk+LV9KmTZuMfoQQ9OvXj379+hWIHLlBbGwsaWlpGXlNrly5Qkx8LOtuX8Vb64yNxgqDNLAl9gitWrZ6pqi3GzduxM/WLUORADha2NHYrhI//7SC2rVr57Y4RRJPT08+zvRQj4iIYPLkyXTr1i3HTptlypQhNTGFAS6tMoJo6sxt6GXfiLmz5yplkg8U9c317FC411rykC5duvDDqhUcLhPFp9d/5S+7UGYv+pZBgx6Y4wohGPXGKEKvXyNdn87hk8fo3LlzAY46d7l+/Tqd2nbAzdmFCh6e1K9Zl4CAAOrUqUNUdBR1Wz/H5zfWsDh2F19GrCPey5IlPy57pnukpaVhzqPLKBaYkZaa+pgWCoDZs2fj5ubGwIEDSUpKynF/t+9EUc6yVJaycpYORN2NxmAoCY+6gkVKma2jKFNiZyZgVChdunR5esViiF6vp13LNvjGOTCp/KtohIbgyAtMHDeB6rVrsnbtWry9vbl+/TqHDx+mfPny/2kW0alTJ94aNZoo21qUsTCu/yfpUzmUGsr7L03PZamKDw4ODixdupR27doxYcIEZs2alaP+GtSpx/FrV2io888oOx4firNjWeLi4nBwcMBgMHDixAmEENSoUaPEWtjlNvdNg4s7JVqZlGR27NhB+t0kupRunVHW2KESF1Jv0uOVV/D2Nu4lubu75yhir4uLCz1f6sVXP/1Mc6dqWAkLQlJD6dG7F82bN396ByWYtm3bMnr0aGbPnk337t1p3br10xs9gSkzAujWqSvxhhR8tS5cSY5g893DJKYlU716dd59913mzphNWkIyBimxcbBj5ZpVykAil8itWYcQohMwG9AAi6WUUx663g8YZzqNB16XUh7LlZs/hRK7zFXSCQ0NxUVT6pFyD3Mnrl4OzbX7REZGsnHTRqrUqk6j/3ueKoNasmZzIN8tmKfefLPB1KlT8fPzY/DgwYSGhrJnzx7CwsKeuZ+mTZuyc8+fmDd3Z5PlaWRjZ/7cu5t//vkHGxsbxr8/lo6yChPK9mBiuZ60SvOlS4dO2Y5qrHgyxuRYMlvHvyGE0ADfAp2BqkBfIUTVh6pdAVpKKWsCXwALc1+ix6NmJsWcgwcPMvF/4zl0OARXZxfGjHufV/v149SpUxyNvsArDo0yvPellFzgNt2aNs61+7/zzjvEx8ezYsUKqlZ9+O9e8TRsbGxYtmwZrZq1oIpfJSo4unEzIZp27dvxw88/YWNjk+2+ateu/dhw8W+88QbLP5lLzUwRoOva+3JMH8aaNWsYPHhwbohSopG542nSELgopbwMIIT4BegOnM64j5T7MtXfD3jkxo2zQ57NTIQQS4QQkUKIk5nKnIQQ24UQF0yfjpmuTRBCXBRCnBNCdMxUXk8IccJ0bY4wvc4KIayEEKtM5QeEEBXySpaiytGjR+nQph1lz6QztuwLtE/245N3P8DT3YM5c+agK12KRVE7uZIUwfWUaH6N+YdUnVmuRZndtGkTK1euZOLEiUqR5IAjh4/galOaz7z68KZjRz51e4XwvWd4+43sOzX+G9HR0ZTTPOrP4qDXEhERAUBCQgJLlixhwvjxrFq1ilRlPPFMPEM4lTJCiEOZjhGZunEHMk9Lw01lT2IosCWXRHgqebnMtQx4ON3eeGCHlNIP2GE6xzRV6wNUM7X5zjSlA5gHjAD8TMf9PocCMVLKisBMYGqeSVJEmfTZl7SzqU7TUlXQmdvgb+PO8DJtibsXx6ZNm7gSdpXeY4YQpDnJirQD1OnTmr8P7MsVj/S4uDhef/11qlWrxvjx43NBmpLLN7Pm8KJjI+w0xt+LpZk5PXQNWPnLSlJSUnLcf8uWLTmlv4E+U9rnNIOeg3fPs2jRIr755hsq+frx7fipnFy8ky9GT6BO9VpERUXl+N4lAYnEkM0DiJJS1s90ZF6mety68GOnPEKI1hifkeMedz0vyDNlIqXcDdx5qLg7sNz0fTnQI1P5L1LKFCnlFeAi0FAI4QropJT/SOMO1g8Ptbnf1xqg7f1ZS0lCr9czf/58GtWpT41KVflo4ocZ6WCPhBzG39otS/2ylg442jng7++PpaUlEz+cyLkrFwi9fo1Zc2c/kw/Jw0gpCQ0N5fbt23zwwQeEh4ezaNEilfsih9y5cwcni6wBNO001kgpSUxMfEKr7NO6dWtqNKjN/Og/OBYfytG4K8y7s40qtatjbm7Oe2+9Sz19eYY6tqZz6bq87tiecjGWfDhhYo7vXSKQxhA52TmeQjhQPtO5B3Dj4UpCiJrAYqC7lDI61+R4Cvm9Ae8spbwJYPq878n2pOmbu+n7w+VZ2kgp04FY4LFPQiHEiPvTxtu3b+eSKIWDYa8NYeYHk6l/uxwdk/zZsXA9jeo1YMyYMURE3OJaclZ5Y9MTSUhLxsXFJVfHsXPnTvwq+FKvem0qeHiy6Nv5DBkyhMaNc2//paTSslUrQuIvZSk7lXANT/fyuRIRWAhB4KYg3pw0jnOeCVzwTuL9qR/x9/59HD58GIMZtC5VPUv91nbVWLtmLWB8oVmyZAktGzejSb1GzJwxk+Tk5ByPqzghs/nvKRwE/IQQ3kIIS4yrOUGZKwghPIF1wAAp5fk8EeYJFJYN+CdN3/5tWpftKZ9pqrgQjLG5/ssAC5L4+HjWrFnD1atXadCgAR07dkSj0XDu3Dk2rA/kI9eXsDIzhibx1jozI2wDs2bNonnz5mw8eBhHczsq2bgTnRbHr/f+YejQof85TezjuHz5Mr2696SvrinV3MqTLvVsig4heO/+JyYVU2SfL6dMommjJiTFpOFv6crV5Ei23z3Kr+vX5trP1sLCgpEjRzJy5Mgs5Xq9Ho2Z2f0lmAflGEhMTOCHH35gU9BGju7cTyvrKpgLDcu++pYN6wLZ8ddOFfcLkzVXLniaSCnThRCjgd8xmgYvkVKeEkKMNF2fD3yM8aX6O9PfRnp+xfrK75lJhGnpCtNnpKn8SdO3cLJaI2Se1mW0EUKYAw48uqxW5Dl79ix+3hWZO3Yy++cG8eaAETR7rikJCQn8+eefVNS6ZigSML41NtD50bvXy/z1118s/fkHtlqc5b3QZcyM2swLw/oQMCN3nQUXzJtPQ5uKVLfzRAiBhZk53cs0JOZWFPv378/Ve5VE/P39CTl2mGp9W3DUPYb0uk4k69PYt2/f0xvnECsrKzq178gfsScyygxSsvXuEay0WgYNGsSmwCBeL92BWnbeVLP1ZLhTG8LPXM6SSK5kk915ydPfc6WUm6WU/lJKXynlJFPZfJMiQUo5TErpKKWsbTryLWhkfs9MgoBBwBTT54ZM5T8LIWYAbhg32oOllHohRJwQ4jngADAQmPtQX/8ALwE7ZRGNR3DkyBFmTZ/BpfMXadC4Ee++PwZPT08ABvcbREuNHy0cjOlsDVKy9OIOataoydVrV3Eys31kce828TSrYsy616NHD7p3705CQgLW1tZ58qZ47fJVyoms1kBCCFytHAkPD39CK8Wz4OnpyYzZMzPOhwwZwvTp0+nbty81a9bM03t/t2g+rZq2YO6d3/EQjlxKj6CMtxtXdgXz6aefcnD5NizNHjxKzIQZ1czc+GvXn7zwwgt5OraigNEDvkg+mp6JvDQNXonxQV9JCBEuhBiKUYm0F0JcANqbzpFSngJ+xWgvvRV4Q8oM05LXMW4mXQQu8cDU7XugtBDiIjAGk2VYYSQ5OZm1a9eyaNEiLl3Kuva9detW2jRvRdwfF6l7szSnf9lDvVp1uXDhApGRkZw4dYKmugdZ+MyEoJ2uJpHXb/HOO+9gXUbH9rvHSJd6Yy6V+KscTrzC0GHDMtoIIbCzs8uzJYcmrZpxxpB1HzDZkMr5uHDq1y+S0bQLPQEBATg6OjJixAj0ev3TG+QANzc3Tp0/w5TFs+g49lUWrFrG/kMHcHBwoEmTJsSZP2pRFmOWhKu722N6K4EIMAhDto6iTInNZ5Kb3Lx5kz///BOdTkf79u2zWC+FhITQpUMnnDUOOJhZczLuGkOGG/NIAFT29addqh/VbD0z2my9c5ijFjeIS0ogITaOrysOznAsBAhNimSD5jjnrlzk6tWr9O/9KieOH8fS3AL7Ug58/8NSWrVqlasy/htxcXFU9PLBR+9Ei1LVSdAnsz3xBC17dGDhksX5No6SxooVK+jfvz99+vTBQmjwrODFsBHDqVChQr6NITk5Ge/yFWhnXoVG9v4I4FRCGL/E7ePMhXM4Ozvn21jygtzIZ2KrKSMra7tmq+7hxB9UPpPiys2bN/npp5+IjIigdZs2dOrUKUtiq8lffsXkr76iss6TeEMydwwJbPp9M/Xq1UOv19OzW3e6WdWhrr0PAIl29Zm97GdcPdywtLTkWtg1qnq3yXLP+nYV+SP8OK8O6s+eHX+xO/ZMhjWNQRrYlXiKPq+/CoCXlxd79u/l+vXrJCUl4evrm+8b3uHh4cTExxJTwYnAtOPYO9jz7ocfZEntq8h9OnfujIOtPSFBu6lv58sBTvPt3G9ZF7Q+R3G8ngWtVsv2XX/Q+8WX2XbrBOZmGixsrQjcGFTkFUluIZHoydvZY2GgRCuTPXv28NnEjzl1+jS+Pr58+PnHdOr0wM9y586d9OrekxrWXjgYtKxd8gsVa1Vm4++bsbS0ZPfu3cyaNoMJrj1xMOWJOBJ3me5duxF8+BCbN2/GEJ9KXVefjD5tNFa00FZi4tgJpMp0zIUZ8fpk7M0fOAreSY/Dx9uHxYsXc/78eVo3b8nFmEjKGew4b4jAo1IFxk3IuqqXk2CMOUGv1zNkyBB0Oh1/7dmtHiD5SMDUAKppPXjVqXnGC4SfuTPDBg3h4tXL+fZSUb16dU6eO83Zs2dJS0ujevXqhT6TaH5T1JewskOJVSa7du2iV7eePG9Xh5a6doSGRzLg5VeZt3QhL730Enq9ngF9+jHAoTmVbY0GZR1kbRYc/4OAgADatWvHF598RnOtf4YiAahj70NQaHDGw93loRwSAFbCgtq1arFi9S9M/mIS6zcfoE+pxliaWRCXnsTG+CO8/4HRIczf35+LoZdZt24dV69e5f0GDWjbtm2B/mc9c+YM3y9aTFTEbdLQs3//flasWKEUST7z27pAOtlUyqI0qtl6svrWAS5fvoyvr2++jUUIQZUqVfLtfkUJowe8UibFloljJ9BTV5969hUBKG1hj51Gy1uvjyY0NJSTJ0+SHp9C5fIPLJM1woymWj++/OgzPvzwQ6yEOS+Xa/pI3w5ae3q81psOHTow9LUhXE2OzMg0qJd6/km9yLi3P6VixYrM+e4bBvUbwKfbV+Ns68TN+ChGjnqd/8tk729tbV1oMjmuWrWKkUNH8JyNHw7Cmn2xZynnWIaePXsW9NBKHDa2NiQlZY2RlS4NpKanPVMASEXeo5RJMeb4yRO86J41oKG/tRu3wiP53//+h0ajwU5YPeJ0ly71+Pn7MfnraRw5coQfZyykofRHI4wzhYjUu0SkxxIQEIBOp0MIwZCBr1Hfxhed1HLMEIZfnWoZysHW1pY1gesICwsjLCyMypUr4+TklH8/iGcgOTmZUSNGMrJ0e8prjSl+mzlUZUH0dpYuXcqoUaMKeIQli6Gvj2DGhEn4WruiNbNASsm2mCPUqlULV1fXgh6eIgPj3KS4U2KVSXk3d8JTovC3ebDXcDM1BicHRy5dvYy9vT3+Pn6ExF2ivs44e0kxpLE7+RyfTJtM165d6dChA3/v2s2co1uoo/EigRT+STzPjDkz0emMfhcvvvgitWvXZvmy5UTfjmJwlw/o0qXLI2a65cuXp3z58hRmgoODKW2py1AkYDRVbmRVkQ2r1yllks8MHz6cg/8c4IvVa6hk78H1pCgi4+7wkk/uRH1W5A4StWdSrBk7cTwfj/mAQRpr3KyciEyN5Zd7+xg7fiwODg4ArF6/hk7tOnA45iqOwpaTidfo2v15Xn3VaEllYWHBxt83s2HDBjZt+A0Px1JMHvr9I05kPj4+fPb5Z/kuY25ja2tLYnrKI7O1JEMKdvaFczZVnDEzM2PxsiWM//ADgoON+3Rbtmxh6tSp6HQ6bl67jlarZdCwwXTq1EmFtSkwJHrSCnoQeU6J9TORUvLNnLl88dkXpKYkozE359333mPiRxOz/KdLTEwkKCiI27dv07Jlyzz3Ni7MSCnx9vCiabo3TUsZN1vj9UnMidrKghVL6No1e7b0irwjNTWV8q7uWCRI2jrWJNWQzp6Uc7w6dCDTvg4o6OEVOXLDz8RK4yDdbZplq+6V+M3Kz6SoIYTgzbff4vU3RnHnzh0cHR2xsLB4pJ6NjQ19+vQpgBEWDoKDg/n5xxWkp6fTtEUz4pITWHdvPwf1V3A0t+fMvWu8+dabdOnSpaCHqgC2b9+OjcGCMZ5dMxxd6+p9mDR/ASPfeB0fH5+n9KDIC9QGfAnA3NyccuXKPb1iCeSLz75g7tczaaStiDlmvPH9D6QIPQdCDnLz5k2io6Np0aIFHh75lhlU8RS2bt5CbXPPLBETbDVaqtt7sWPHDqVMCgSj22Jxp8QrE8XjuXz5Ml9PC2CcSw8czI1mps10VZlyaz2JiYl07NjxKT0oCgJHJyfOikdjZd3TJ+Ho6PiYFoq8xhjosfjPTJSbquKxbNmyhZp2FTIUCYC1xpIGWl82BG74l5aKgmTQa4M4mHApS1K0Y/GhnI+5xvFjx6nmVwUv1/KMHP5/3Lx5swBHWrLIbuLeooyamSgyCAkJYe/evbi6uqLRaEiWqY/USRV65RBXiPH19WXRsu8ZMWQ4rtZOpBjSiNMnAfDj1wvoUboRdlbW7N8QzHObG3Ls1IlcydaoeDKyhFhzKWWiID09nVdf6cPuP/6kirUH0TKe6ynRxMXFEaqtSgVr455SROpdQpIuMf/VvgU8YsW/8fLLL/P888/z999/o9VqcXZ2pn6turzl/nxGIrWeVo34IWY3S75fwpj3xhTwiIs7EoNUeyaKEsDChQs58dchJjj3wMKU5GjP3VMEJR9ifvR2Ktq5YS40nLl3jdnfzKFixYoFPGLF07C2tqZ9+/YArF69msqlPLNk5ASopHHhn91/s6lyJXZs+4PSZUszcNCgQu88WxQp6ktY2UEpkxKGlJLdu3cTFLgBaxsb+vXvx4+Ll9FaWzVDkQA0dajCtoQT7Pj7T86dO0d6ejqdOnWidOnS/9K7ojBSoUIFridFYbCXmGXyoQpNiuTS/rMc3hNMDY07R0UKAVMC+PnXlcrUO1dR1lyKYoaUkqGvDeH3DZupZ+FFitDz7ey52Nva0cAyq3m0QGBuZo5Wq6V3794FNGJFblC/fn08fLwIDA+mi0MdLIUFx+KvsO/eWdwsnXjHs0dGbLk62gq81n8g4bduYDAYCA4OxsbGhnr16ikP+v+IxJiHqLijlEkxJSkpiVWrVnH4UAh+lfwZMGAABw8eZHvQFt4v+2DtvLGtP1+G/sp2m2P4W7tnvLkeiw/F3lFHpUqVClIMRS4ghGDTti0Mf20oH/3xCxozM7zKe1LXuQ7VI0plKBIAX2sXdInWTJs2jVnTZ+BkYU9SegraUrasCwqkRo0aBShJEUVKDFJtwCsKOXq9ntDQUBwdHTOiDUdGRtK0YWNsE83wkWUINtvBl59+Qdt2bahvUSHL2nk5SweqOHiSWtqC2dFbqCJciNEkcTo5nN+2bFJvo8WEMmXKsH7jBu7du0dSUhLlypWje5dupN9KzFJPSknUvRgmfz6J0a5d8NKWRUpJcNwFOrXrQGj4tcdGilA8mZKSz0T5mRQBkpOTCQsLIzU1q6nu6tWr8XT1oHGdhni5l+elHr2IjY1l4rgP8ErUMcKxLe2cajGwVAtamPsTFLiBFP2jb0jmVhZ8/tUXTF8yF/9Bzek5bjBnL56nSZMm+SWiIp/Q6XQ4OzsjhGDg0NfYnXyWJP2Dv6sj8ZdJNqTRyNYPL21ZwDizaaTzR2fQsn379oIaepFGSkO2jqKMmpkUAm7dusWuXbvQ6XS0b98eS0tLAAwGA599/CmzZ83GXGgwCAPjxo9j7ITxBAcHM3LICAY7tsTH0YVkQyob9h2kT69XCD4YzNtOnbPco5muMusi97Ev4TzNSlWllCk75KWkW4QmRtK1a1fs7Ozo3r17vsuvKBh69erFzu07mLRiJdVtPYmVSdzS36Vz585YHIh6pH4pjQ1RUY+WK56G2oBXmJBSYjAYHslBcp9z585x6NAhvLy8aNq0aZalodjYWGbOmMFvazdgZ2/HsFH/R//+/TPqTJn0FV9N+orKOk/iDcnEyEQ2bt1EvXr1mD4tgJXfLeO9cs9T2sKeyNRY5gfMRedYij27/qKNTVV8rF0A0JpZ8qLDc4zbtRwpJamO6VnGmC71WFhY8v4HY5kyZRo1dF6kyHQuJt5k1ZpfsbOzy6OfnqKwIoTguwXzeOvdt9m1axelS5emW7duBAUF8fG+sbSQVTEz7afE65M5fe8aLVu2LOBRF02K+qwjO5TYEPQAFy9e5Otp0zl2+CiVq1ZmzNj3qV69ekbdhIQE/jfmfX788UeSUpJo1qgps+fNpVatWoDR2e+1fgPZvGkzlew9uJESjaNbWX7fsR1nZ2cSExNpVLcBdtGSRtqKJOqT2ZF8mi59ejD3u2/YvXs3rzz/Im+V7ZwxUzgcd5kt+hNcvhaKp6sHw3StcLd6YI57OekWCyK3I/UGBju3pYpt1iCLU26sx7tWJRLPRDCodEvMhBlSSoLuHsLuufKsDQokLCyMrVu3Ym1tzQsvvJCRyEuhAEhLS6NdqzbcOXeDRpa+JBtS2Z1ylr5DBzB1eskKY58bIeg1ZlZSa5m9YKiJKZdVCPqixrFjx2jdvBWNtRWpb+XMtbCztFjfjMBNQbRo0QKAl3q8yN2jYUxw6YmtRsuBy+dp06I1x04dx8PDgzmz53D4j3/42PUlLM3MkVKy8XYIQwa8xqZtW/jpp58wj06lv2ObjJmIv407ny1ZSvVaNVix/EeaaP0zFAlAXXsfNl49iLW1NVJKXMtkTTrlZuVEcloKdWrX4Xjo1SzK5G5aAncNifyyehWvvtyHKSc34Kd1JSw9GqvS9uxctAAwZnUcPnx4Xv+IFUUUCwsLtu38g6VLl7J+1RpsbB349v8W8fzzzxf00IokEonBUPytuUrszKRz247oTibSslS1jGshcZc45HCLdRsDOXXqFK/1HcBn7q9kCef9a/Q+bOq707ptG2ZO/Zre1g3xs3HLuJ5qSGPs5R/w9a/IrbAbdLWrQxOHylnGMDd8I2cTr2MpzHm5XNNHrs+8uZE6nZrwz+69dNPUorqdZ6YxXuS0Wxzrfgukbs061BTu1LX25k56HFsTjjP0nZF8/OknSCnZt28fx48fx8fHh/bt22NmpuwtFIpnITdmJmZmltLSPHtpLlLSrquZSVHj73/28pFbryxlte28WXp2R0a4kIrWrlkUCYCPRTl+3raDLb9vxUpYYONpleW6uTBHI8zw9vbGQmNOxK3YLNellCSYp7N48WLi4+OZ9/kMGkn/DFv/iNS7ROhjWbx4MXv27GFgn37E65PwtnbmYuJNNiccZf3PG3B1dSX48EEmff4la7fvoKxbGaa+NzPDwVAIQdOmTWnatGmu/twUCsUzIkvGnkmJfVV1KuXInbT4LGV30xPQWlqxdOlSZs6cSaSMI82Q1Qrjkj6SN8e8TVxcHMNGjmBfwvks14/GX6Gib0U2bdrE2vXrOJR8mfOJNwDQSwN/xB7HtqwDgwcPZtSoUVSoXYk50Vv56+5JNseE8M3trcycMwudTkfXrl1Z+1sgNyubsSx5LzE1rNm0bQutWrUCjMtV8xct4HzoRfYe3E+fPn2UX4hCUeiQJSIEfYld5po6eSrLps9jiGMrbDVakg2p/BSzhzYDXmD6zK8B6NX9Ra7sPcHzdnWxM9eyP+48f6dd5PjpE7i4uHD79m2aNHgOh0RzKgkXbnGPI0mhbNy6KcNHY8sWo+exTNWTlJZM5SpVWLlmFV5eXoBxE3/Dhg1sDAyilKMjg4cNKdF55hWKwkRuLHMJYSHNNaWyVTddH1Vkl7lKrDLR6/W8M/ptli9fhqtdGW7GR9OzRw8WLl2MlZVx6SolJYXPPvmUJYu/Jz4hgXZt2jJt5nT8/f0z+ouPj2f58uX8s3svPn6+DP+/EY9EXdXr9Zw9exZbW1sqVKiQn+IqFIockDvKxFyaaxyyVTddf0cpk6JCZtNggNu3b3PhwgW8vb1xdXUtwJEpFIrCRu4oE400M8ueH5fBcK/IKpMSuwF/n7Jly1K2bNmCHoZCoSjWFO39kOxQ4pWJQqFQ5DnKmkuhUCgUOSP3rLmEEJ2EEOeEEBeFEOMfc10IIeaYrh8XQtTNE5Eeg1ImCoVCkecYsnk8GSGEBvgW6AxUBfoKIao+VK0z4Gc6RgDzck2Ep6CUiUKhUOQpMrdC0DcELkopL0spU4FfgIfDfHcHfpBG9gOlhBD5YllU4vZMQkJCooQQVwt6HLlIGaC4xgUvrrIVV7mg+MnmlQt9/A7pZbJZVyuEOJTpfKGUcqHpuzsQlulaONDoofaPq+MO3HyG8f4nSpwykVIWK9MtIcShompK+DSKq2zFVS4o3rL9V6SUnXKpq8eFt3jYtyM7dfIEtcylUCgURYNwILNHtAdw4z/UyROUMlEoFIqiwUHATwjhLYSwBPoAQQ/VCQIGmqy6ngNipZR5vsQFJXCZqxiy8OlViizFVbbiKhcUb9kKFClluhBiNPA7oAGWSClPCSFGmq7PBzYDXYCLQCIwOL/GV+LCqSgUCoUi91HLXAqFQqHIMUqZKBQKhSLHKGVSCBBClBdC7BJCnBFCnBJCvG0qdxJCbBdCXDB9OmZqM8EUMuGcEKJjpvJ6QogTpmtzhClblhDCSgixylR+QAhRIR/l0wghjgghNhYzuUoJIdYIIc6afneNi5Fs75r+Fk8KIVYKIbTFRTZFHiGlVEcBH4ArUNf03R44jzFcwjRgvKl8PDDV9L0qcAywAryBS4DGdC0YaIzR3nwL0NlUPgqYb/reB1iVj/KNAX4GNprOi4tcy4Fhpu+WQKniIBtGJ7crgLXp/FfgteIgmzry8O+moAegjsf8UmAD0B44B7iaylyBc6bvE4AJmer/bvoP6wqczVTeF1iQuY7puzlGL2WRD7J4ADuANpmUSXGQS2d64IqHyouDbPe9qJ1M990IdCgOsqkj7w61zFXIME336wAHAGdpshE3fZYzVXtSyAR30/eHy7O0kVKmA7FA6TwRIiuzgLFkjWJXHOTyAW4DS01LeIuFELYUA9mklNeB6cA1jGE4YqWU2ygGsinyDqVMChFCCDtgLfCOlPLev1V9TJn8l/J/a5NnCCGeByKllCHZbfKYskInlwlzoC4wT0pZB0jAuPTzJIqMbKa9kO4Yl6zcAFshRP9/a/KYskIpmyLvUMqkkCCEsMCoSFZIKdeZiiPuR/w0fUaayp8UMiHc9P3h8ixthBDmgANwJ/clyUJT4AUhRCjGCKdthBA/UfTlun/fcCnlAdP5GozKpTjI1g64IqW8LaVMA9YBTSgesinyCKVMCgEmC5fvgTNSyhmZLgUBg0zfB2HcS7lf3sdkEeONMXdBsGnpIU4I8Zypz4EPtbnf10vATillnr4JSiknSCk9pJQVMG6y7pRS9i/qcplkuwWECSEqmYraAqcpBrJhXN56TghhYxpTW+AMxUM2RV5R0Js26pAAzTBO8Y8DR01HF4xryDuAC6ZPp0xtJmK0mjmHyULGVF4fOGm69g0PohxogdUYwywEAz75LGMrHmzAFwu5gNrAIdPvLRBwLEayfQacNY3rR4yWWsVCNnXkzaHCqSgUCoUix6hlLoVCoVDkGKVMFAqFQpFjlDJRKBQKRY5RykShUCgUOUYpE4VCoVDkGKVMFCUWYYzWfEUI4WQ6dzSdexX02BSKooZSJooSi5QyDJgHTDEVTQEWSimvFtyoFIqiifIzUZRoTGFsQoAlwHCgjpQytWBHpVAUPcwLegAKRUEipUwTQvwP2Ap0UIpEofhvqGUuhQI6Ywy1Xr2gB6JQFFWUMlGUaIQQtTEmInsOePd+VFyFQvFsKGWiKLGYItnOw5g/5hoQgDEplEKheEaUMlGUZIYD16SU203n3wGVhRAtC3BMCkWRRFlzKRQKhSLHqJmJQqFQKHKMUiYKhUKhyDFKmSgUCoUixyhlolAoFIoco5SJQqFQKHKMUiYKhUKhyDFKmSgUCoUix/w/jWZNpxJXbzMAAAAASUVORK5CYII=\\n\",\n \"text/plain\": [\n \"
\"\n ]\n },\n \"metadata\": {\n \"needs_background\": \"light\"\n },\n \"output_type\": \"display_data\"\n }\n ],\n \"source\": [\n \"Particle_data = xr.open_dataset(\\\"WriteOnce.nc\\\")\\n\",\n \"\\n\",\n \"plt.figure()\\n\",\n \"ax = plt.axes()\\n\",\n \"ax.set_ylabel('Y')\\n\",\n \"ax.set_xlabel('X')\\n\",\n \"ax.set_ylim(1000, 49000)\\n\",\n \"ax.set_xlim(1000, 99000)\\n\",\n \"ax.plot(Particle_data.lon.transpose(), Particle_data.lat.transpose(), c='k', zorder=1)\\n\",\n \"T_scatter = ax.scatter(Particle_data.lon, Particle_data.lat, \\n\",\n \" c=np.tile(Particle_data.temperature, (Particle_data.lon.shape[1], 1)).T,\\n\",\n \" cmap=plt.cm.inferno, norm=mpl.colors.Normalize(vmin=0., vmax=1.), \\n\",\n \" edgecolor='k', zorder=2)\\n\",\n \"plt.colorbar(T_scatter, label='Initial T [$^{\\\\circ} C$]')\\n\",\n \"plt.show()\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"### Sampling with repeatdt\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"Some experiments require large sets of particles to be released repeatedly on the same locations. The [`particleset`](https://oceanparcels.org/gh-pages/html/#module-parcels.particleset) object has the option `repeatdt` for this, but when you want to sample the initial values this introduces some problems as we have seen [here](#repeatdt_error). For more advanced control over the repeated release of particles, you can manually write a for-loop using the function `particleset.add()`. Note that this for-loop is very similar to the one that `repeatdt` would execute under the hood in `particleset.execute()`.\\n\",\n \"\\n\",\n \"Adding particles to the `particleset` during the simulation reduces the memory used compared to specifying the delayed particle release times upfront, which improves the computational speed. In the loop, we want to initialise new particles and sample their initial temperature. If we want to write both the initialised particles with the sampled temperature and the older particles that have already been advected, we have to make sure both sets of particles find themselves at the same moment in time. The initial conditions must be written to the output file before advecting them, because during advection the `particle.time` will increase.\\n\",\n \"\\n\",\n \"We do not specify the `outputdt` argument for the `output_file` and instead write the data with `output_file.write(pset, time)` on each iteration. A new particleset is initialised whenever time is a multiple of `repeatdt`. Because the particles are advected after being written, the last displacement must be written once more after the loop.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 11,\n \"metadata\": {},\n \"outputs\": [\n {\n \"name\": \"stderr\",\n \"output_type\": \"stream\",\n \"text\": [\n \"INFO: Compiled SampleParticleInitZeroSampleT ==> C:\\\\Users\\\\GEBRUI~1\\\\AppData\\\\Local\\\\Temp\\\\parcels-tmp\\\\d441e19c77676cd806da7f8e4c974550_0.dll\\n\",\n \"INFO: Compiled SampleParticleInitZeroAdvectionRK4SampleT ==> C:\\\\Users\\\\GEBRUI~1\\\\AppData\\\\Local\\\\Temp\\\\parcels-tmp\\\\d1281aa8d15fe9594b477ca71b782dce_0.dll\\n\"\n ]\n },\n {\n \"name\": \"stdout\",\n \"output_type\": \"stream\",\n \"text\": [\n \"Length of pset: 10\\n\",\n \"Length of pset: 10\\n\",\n \"Length of pset: 10\\n\",\n \"Length of pset: 10\\n\",\n \"Length of pset: 10\\n\",\n \"Length of pset: 10\\n\"\n ]\n },\n {\n \"name\": \"stderr\",\n \"output_type\": \"stream\",\n \"text\": [\n \"INFO: Compiled SampleParticleInitZeroSampleT ==> C:\\\\Users\\\\GEBRUI~1\\\\AppData\\\\Local\\\\Temp\\\\parcels-tmp\\\\01fc394199c11f84c25331b4797a64a0_0.dll\\n\"\n ]\n },\n {\n \"name\": \"stdout\",\n \"output_type\": \"stream\",\n \"text\": [\n \"Length of pset: 20\\n\",\n \"Length of pset: 20\\n\",\n \"Length of pset: 20\\n\",\n \"Length of pset: 20\\n\",\n \"Length of pset: 20\\n\",\n \"Length of pset: 20\\n\"\n ]\n },\n {\n \"name\": \"stderr\",\n \"output_type\": \"stream\",\n \"text\": [\n \"INFO: Compiled SampleParticleInitZeroSampleT ==> C:\\\\Users\\\\GEBRUI~1\\\\AppData\\\\Local\\\\Temp\\\\parcels-tmp\\\\1dcf704643338d59fe9815a88cd8967c_0.dll\\n\"\n ]\n },\n {\n \"name\": \"stdout\",\n \"output_type\": \"stream\",\n \"text\": [\n \"Length of pset: 30\\n\",\n \"Length of pset: 30\\n\",\n \"Length of pset: 30\\n\",\n \"Length of pset: 30\\n\",\n \"Length of pset: 30\\n\",\n \"Length of pset: 30\\n\"\n ]\n },\n {\n \"name\": \"stderr\",\n \"output_type\": \"stream\",\n \"text\": [\n \"INFO: Compiled SampleParticleInitZeroSampleT ==> C:\\\\Users\\\\GEBRUI~1\\\\AppData\\\\Local\\\\Temp\\\\parcels-tmp\\\\0364537a5edb2a00eaf61893bcae1143_0.dll\\n\"\n ]\n },\n {\n \"name\": \"stdout\",\n \"output_type\": \"stream\",\n \"text\": [\n \"Length of pset: 40\\n\",\n \"Length of pset: 40\\n\",\n \"Length of pset: 40\\n\",\n \"Length of pset: 40\\n\",\n \"Length of pset: 40\\n\",\n \"Length of pset: 40\\n\"\n ]\n }\n ],\n \"source\": [\n \"outputdt = delta(hours=1).total_seconds() # write the particle data every hour\\n\",\n \"repeatdt = delta(hours=6).total_seconds() # release each set of particles six hours later\\n\",\n \"runtime = delta(hours=24).total_seconds() \\n\",\n \"\\n\",\n \"pset = ParticleSet(fieldset=fieldset, pclass=SampleParticleInitZero, lon=[], lat=[], time=[]) # Using SampleParticleInitZero\\n\",\n \"kernels = AdvectionRK4 + sample_kernel\\n\",\n \"\\n\",\n \"output_file = pset.ParticleFile(name=\\\"RepeatLoop.nc\\\") # Do not specify the outputdt yet, so we can manually write the output\\n\",\n \"\\n\",\n \"for time in np.arange(0, runtime, outputdt):\\n\",\n \" if np.isclose(np.fmod(time, repeatdt), 0): # time is a multiple of repeatdt\\n\",\n \" pset_init = ParticleSet(fieldset=fieldset, pclass=SampleParticleInitZero, lon=lon, lat=lat, time=time)\\n\",\n \" pset_init.execute(sample_kernel, dt=0) # record the initial temperature of the particles\\n\",\n \" pset.add(pset_init) # add the newly released particles to the total particleset\\n\",\n \" \\n\",\n \" output_file.write(pset,time) # write the initialised particles and the advected particles\\n\",\n \"\\n\",\n \" pset.execute(kernels, runtime=outputdt, dt=delta(minutes=5))\\n\",\n \" print('Length of pset at time %d: %d' % (time, len(pset)))\\n\",\n \" \\n\",\n \"output_file.write(pset, time+outputdt) \\n\",\n \"\\n\",\n \"output_file.close()\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"In each iteration of the loop, spanning six hours, we have added ten particles.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 12,\n \"metadata\": {},\n \"outputs\": [\n {\n \"name\": \"stdout\",\n \"output_type\": \"stream\",\n \"text\": [\n \"[ 0 0 0 0 0 0 0 0 0 0 6 6 6 6 6 6 6 6 6 6 12 12 12 12\\n\",\n \" 12 12 12 12 12 12 18 18 18 18 18 18 18 18 18 18]\\n\"\n ]\n }\n ],\n \"source\": [\n \"Particle_data = xr.open_dataset(\\\"RepeatLoop.nc\\\")\\n\",\n \"print(Particle_data.time[:,0].values / np.timedelta64(1, 'h')) # The initial hour at which each particle is released\\n\",\n \"assert np.allclose(Particle_data.time[:,0].values / np.timedelta64(1, 'h'), [int(k/10)*6 for k in range(40)])\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"Let's check if the initial temperatures were sampled correctly for all particles\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 13,\n \"metadata\": {},\n \"outputs\": [\n {\n \"name\": \"stdout\",\n \"output_type\": \"stream\",\n \"text\": [\n \"[0.4040816 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816\\n\",\n \" 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816\\n\",\n \" 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816\\n\",\n \" 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816\\n\",\n \" 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816\\n\",\n \" 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816]\\n\"\n ]\n }\n ],\n \"source\": [\n \"print(Particle_data.temperature[:,0].values)\\n\",\n \"assert np.allclose(Particle_data.temperature[:,0].values, Particle_data.temperature[:,0].values[0])\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"And see if the sampling of the temperature field is done correctly along the trajectories\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 14,\n \"metadata\": {},\n \"outputs\": [\n {\n \"data\": {\n \"image/png\": \"iVBORw0KGgoAAAANSUhEUgAAAZkAAAEKCAYAAADAVygjAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAADzh0lEQVR4nOyddXRU1xaHvzszcZIQIQlxCCG4BXd3p0WLFC2UFrdCi7sXKBQrUtzd3d09SoR4IJ6MnPfHpBOmCfLeCy0y31qzkpzZ51pm7u+effbZWxJCYMCAAQMGDHwIZP/2ARgwYMCAgc8Xg8gYMGDAgIEPhkFkDBgwYMDAB8MgMgYMGDBg4INhEBkDBgwYMPDBMIiMAQMGDBj4YBhExoABAwY+ASRJcpMk6ZQkSY8kSXogSdKgzHZbSZKOSZL0LPOnzRv6N5Yk6YkkSX6SJI3+x47bsE7GgAEDBj5+JEnKD+QXQtyUJMkSuAG0BnoAcUKIGZniYSOEGPW3vnLgKdAACAWuAZ2EEA8/9HEbRjIGDBgw8AkghHghhLiZ+Xsi8AhwAVoBazPN1qIVnr9TEfATQgQIITKAzZn9PjiKf2InHxP29vbC09Pz3z4MAwYMfALcuHEjRgiR7//ZRqPGpURsTNJ77i/wAZD2WtNyIcTyv9tJkuQJlAWuAI5CiBegFSJJkhxy2LQLEPLa36FApfc6qP+TL05kPD09uX79+r99GAYMGPgEkCQp+P/dRmxMEleuT34vW4X0TZoQovw7jikPsAMYLIRIkCTpfTadk9E/MlfyxYmMAQN/zUO+55fTgIH/C4FAo1HnyrYkSTJCKzAbhBA7M5sjJUnKnzmKyQ9E5dA1FHB77W9XIDxXDuodGOZkDHy0BAUF8fDhQzQazRtt1Go1a9asoXGd+jSuU5+1a9eiVuf8hQ4KCqJ1sxaYGBtjaW5Bz27diY+Pz9E2MDCQ9m3aYGVugaOtHcOHDCUlJSVHW6VSyebNm+nVtSvDhw7lwYMH7zw3Q8DNF4QQaDTp7/V6G5L2qWgV8EgIMe+1t/YC3TN/7w7syaH7NcBbkqQCkiQZAx0z+31wDCJj4B9DrVZz7Ngx1qxZw6NHj95oFxgYSGXfipQtUZr6VWvj6erBsWPHstkJIej4VXtmDv+ZQv4qCvmrmDF0HJ3bd8x2E09MTKRG5apY3Q1lffHWLPVuTOTxqzSuWz+bbXx8PDUqV8H69lM2lKjJ/AJlub11F1+1yj5Pmp6eTuO6dZk9dCiO16+TsG8ftatUYcOff+Z4bseOHaNi6VLI5XLcnRyZM2vmW0U0MTERPz8/0tPffgMy8PEiEGiE6r1e76Aa0BWoK0nS7cxXU2AG0ECSpGdoo8dmAEiS5CxJ0kEAIYQKGAgcQRswsFUI8e6noVzA4C4z8H/z6NEjLl++jLOzM/Xr10cul2ezef78OfVr10P1Kh17uQ1DU4Jp0rwp6zas17NXq9U0qtuAEqkOdHLugAyJJylhtG/7FTfv3qZAgQI62wsXLnD59DkmOTfBSKbdRjlLd34+fohDhw5RunRp0tPTycjIYMOGDXgIM9o7FAPAQg7fOZXlx4DjLFiwgHLlyiFJEpIksWXzZoorzOju4g2ADSaM8yxJpytnOXLkCL6+vpiammJqasr69etJCQhgRfHiyDPdbw3t7ek3YABt2rbF3Nxc73i7tGvLxGIu/NmyMs8SUxg3fw5JCYlMmDJF73plZGQwbNAPrF+/nrxmJiSrNPw8fgI/Dh7yxv9DXFwcQgjs7Oz+23+hgQ+KQLxbQN69FSHOk/PcCkC9HOzDgaav/X0QOPh/H8h/iUFkDOSIEII7d+6QlJRE+fLlMTU1zWajVqvp0bUH+/fux8PUnZeaV8gsZZw4fUJPDAC+6dCFgokO1LAqC4DSrAobjx5h6dKlDBw4kLS0NGJjYzlw4AAZ8SnUdSyl61vEwpXSqR60bd2GQoW9SUxMJDExEX9/f3wVjjqBATCWKShp5ECzZs309q9ARneX0nptkiRRQG7B0KFD9dpNZXJ+KFBCv78ko6DClMaNG+u1WygUjCtSRCcwAN6WljjIZDRu3Bhvb2+srKywtrZm95bNDPZypJGzVgSKWlvwa2l3Wi1cyKixYzEzM9NtY/TwYTw6sosLLTyxN1Xw7GUaPadNwjG/Mx06dNA7hoCAAPr2+Iar128iSVCqRHF+/2M9xYoVy/Y/M/BvkDsi86liEJkvkIyMDBQKBTJZzt7Sx48f06p5a+Kj4jFVmJKoSmDZimXZbm4rV67k/MFzdLXshJHMCIAbCbfo9HUnzl8+T1RUFBERETx8+JDrN64zyrmHrq+RTEE141KMGTaKUaNG6c13FLdwz3ZMjgprbvvfIV2ZgaWlJZaWljg5ORHzPCGbbbxIo2PHjtStWxcTExOMjY05ffo0d3ce0VtAIIQgQJ3E/PnzKVWqFEIIhBBs3riRB0dP0/I1W40QBKpS+emnn3ByciItLY20tDR2bNpEokr/BiKEIFGlIi0khICAAF69ekVSUhIWChm+tUrp2bqYmyIy0rC1tcXBwYF8+fJhY2PDhTOnudSmEPam2q+od15TfillzZypk2jXrh0KhbY9PT2d+rWq07NABht7OiGTYP3D5zSsU5NHfoFYWlrq7e/gwYNM+WU0Dx4/o7CXJ6N/mUK7du2yXUMDuYgQCI1BZAx8AZw9e5ZB3w/m3sO7mJma06dPH2bMmo6xsbHORq1W06h+I9wSClHNuCGSJBEjoujbsy8lS5akSJEiREVFERoayryZ8ygrL60TGIAyZqVYenM5RkZGevs2lYyR/20K0EQywtTUlG69e2BnZ4ednR0ZGRmMGzmGNE0GpjLtcQkheKgJZ/6ihXz77be6/nFxcRTyLMjtxBDKWGoDZ24nhuCniuPI0qXkzZtXZ9u8eXOK793Pxsj7NLMrRIZGzeaYRzgXKsCgQYP0Is1Kly5NyT1F2f4ikBYO7iSplax84UfhEiWYMmWKnm3FihXp17kz9R0dsc28jgcjIjC1s+Opv79OyNVqNa2aNOJ6TBDeVlkutNDkNFQyOf369SM+Pp6YmBjCw8ORIXAy17+GhfOa8vDMI4yNjbG3tyd//vxIkoQDCfxQLmspR8+SeTj5IpGNGzfSr18/XfuBAwfo260D8xrIqFHfjKuhYQzq35309DQ6d+6it6+MjAzWr1/Pvh0bMTM3p0uPfjRr1swQkfe/YhjJGPiUuX37NjOnz+bRg0eU9S3LqDEjKFKkiJ7N/fv3ad60BcU0VWmV5ztSRRI7V+8nOjqa9RvWAdqb+c6dO1EmqPExyXIX2Ssc8MwoTNXKVUlOTUaV+eRuLBlTxrak3n5kyDA2MqFv334UL14cJycnHB0d6dK+M49TAylqXlC3rxsZT+jdvy/TZ0zXP9bb91i26xB1zYpjJjPmctozZA7mdOrUSc/O1taWPQf20fnrDuxIvI8ANMYy9h7crycwAHny5OHc5YuMGDSEvocOYqQwomPHDsycOyfbjTNfvnycPHeWIQMGsuT8IYwVRnTp1Ik/F8zPZtuoUSN6DBhA23nzqOjgQExGBlFqNQeOHtUbKcrlcsZOnEyrxo2wNpJT18mGpwmpTHgczshRo/h5wkSdrUajwcvNhWtRyVRwsNC1HwlJpHjxEjRt3ZYXL17w4sULbt26RRO77CPSElZqBgzoz7Rp03B1dcXNzY3LZ0+woKGM5kW0YtjI25gVRkoG/TxGT2RUKhWtmjYgLfwmvSqkk5wuGPHdac536sOM2fOy7Ss+Pp5du3aRlJREo0aN8PHxyWbzZaNBqFP/7YP41/jicpeVL19efCqLMePi4ti8eTPh4eFUr16dhg0bZnNxnT59mhbNWuGsLo4lDiRIEUTIH3P67EnKlSuns+vRtQc3dz7Dx8hX16YUGRxKXkOFyuWJjIwkJCSE9PR0nI3caGzdRm8/T9LuE2EfTPtO7XF1dcXFxYUD+w9wcdsFGprX0918A9ICuWNxH/9gf70b8vnz52nZtAVFjT2xFZYESC+Q7I05f/lCNkHQaDSsW7eOVUuXk5yUTOv27Rg8ZDBWVlY5Xie1Ws2NGzeQJIly5crlGHjwv6JWq5HJZO98gg8LC+PMmTPY2tpSr169bCO5vzh58iTjRgzn+t27uDo4MGj4CH4cPDjb9jdu2MDIH/ozuoQ1JWzNOBmezG9PEjhx9jylS5fW297Ab9px/itr5DLtNoQQ1Nkeh1eVhpibmxMaGkpISAhBAX6EjbLF0iRrX0II8kyMo1bt2nh6euLh4UFMTAwXD/zBhR/UKORa27hkQfGZEtduP9Sbbzty5AidO7SjbnE5tuZqdt/Q0KvvAKbNmJPj+YeEhBAdHU2xYsVynOf72JAk6ca7Fke+i7Jl84szZ759tyFgbT39/97fx4ZBZP4FhBBcu3aNmJgYKlWqlGM00JUrV2jYoDEWOEKaKRmmURQrXZijxw7rfTlLFS8Dfo44Kgrq2kKVDxGe0bRq04KgoCCCg4O5e/MeFYwb4qBw09vP0aQNuBd1pnjx4ri7u2NlZcW0ydNonacLZjJz3fGeUh1g4q/j6datm65vQkICNarUIOVFMm5qVxLkifgp/dmzfw+1atXKdk5hYWGsWrmK54HBVK9dg44dO34SN5p/i+PHjzN/+lQCAwPwrVCR0b9MoHjx4no2Qgjq16qORfQjhpQ2RS6D3+6lE2jkyoWrN3RzNwClixZiesVo6hTMEsCb4SpabEynSMmyBAcH8+LFC4zlginNFQyqre/o6LhGQ2r+erRo0QIPDw8cHR1p3KA2OwZmUK2wVthjEwVVpyhYuWEftWvX1vWNi4ujR9evuXTpEvntTImIVzF12mz69O3Hx0zuiIyTOHOq27sNAWub2QaR+dT50CLz6tUr4uPjcXNzy/GJOigoiEYNmxAZEYOJwpzE1BjG/TyOn34ao7MRQlDQsxBShBs2Co/MNg2hsvN07deWWrVqERQUREBAAL8u/JW6Zn2QpKwRjlKkcTZ1HUbGCtzd3fHw8CA8NByC81DcpLLOLl2TyknlJoJCgrC3t9e1jx0zlpVLVlFYlMBYMiVI9hQ7LxvOXTyLiYmJ3vmkp6ezdetWzp46i5uHGz179cTV1TXXrqeBd5OSksKsGdPZumEdao2Gtu07Mmbsz9lGfhs3buTnof1Y1VxGRVcFdyLU9N6v4fsx0xjw/UAgM3R66GDkj1Yzu6X+6KrKPCW3w9Bb7OpbQOLKJP0HhbkHVZyJq8G0mfPw9PTE2tqa5o3r4Gl6mxnfmmFqLPHwuZIWE1JZ/edu6tXLir5Vq9XMmjWd3xYv5EVkHFUrlWHqjAXUqFEjty/be5ErIlPGUZw52eXdhoC13XyDyHzq/K8iI4QgPT0dExOTHF0niYmJ9OrZm7379qJQGGNubsbixb/Svn17vW2ULFGaqEANljJPJElCpUklXnaLLds24OvrS3BwMBcvXmT0iHEUkbfW21eCOoyA9LNoUAJgamqKMkNFJeP2mMuybiiv1FGE5b1CSPhznXvNz8+P8mUrUFBdBldFIVJEIo+lK7T+pjmLf1uU7Vz379/P8t9WkJSYRJv2renTp49eiK2BT5M/Vq9myoSxhEZE42Rvw8iffmHA9wP1Pmd+fn5UqVCa/b1UlHOTIYRg6y0No49Y8iwwlPj4eIKCgti+fTs3jy3jxCj9fSw6omLMFiVp2o8plpaWSOpkwjc5YmKUtZ+Vh5M55Fee3fuP6fY/YvggLp/awK9D7SjkZsKeM68YujCOI8fOUrZsWV1fIQSbNm1i2dL5xETHULN2XX76aTzu7tkjE/8fck1kTnR4tyFgbb/IIDKfOjmJjEajeWM4r0ajYcqUqcybN5fExCTc3NyYN28ubdu21bNr3rwF507fQCEckUkKlOokVPIwjh49TNWqVVEqlZw8eZJ2bdrjKKuhLx7KYOJVT1CpM3RtcowpZdZBz+6VOhScQ9i0ZQOenp7Y29szcsQoNv6+E291TYwkEzJEKk/kpxj2yw+MGDFc7xjv3LnDiCEjOX/pPLZ5bflh0A8MHzEsV+cwDHz8CCFIS0vD1NT0jXNN27dvZ0C/nhS0l5OUpiFdlodtuw5QpkwZnU1CQgKebvk5MUpNKXft9yc5TVBlipzegybj6upKUFAQV69e5c7lfTxcru8WPn0nnXaT41Bhhru7O87Ozly+dJYn2wvjYJvl0luwKYZ70ZVZv3G7rm3KlIls+nMxE4Z44uZszo6DEWzaG8/Va7dxdnbWO9ft27ezZs3vJCcn0aRJa77/fiB58uR5r2uVGyJTrnQ+ceZom3cbAlZOKwwi86nzushs3LiRMWPG8Pz5c5ycnBg/fjz9+vXT++KNHTuWXxf+hjLDHAkFGpGGwjiZPXt2U79+fUA7mVm4cBEsZD5oawNpSVVGYWKRjJm5KeHh4QghMJIscLeoo3dMyapIZDYRjBo9HA8PD9zd3fm6XQfUYQ7YKrwA0Ag1YfJz/DJ9BAMHDtT1VSqV9OvzHVu2bMHK1JaEtDj69OnDvAVz3yicBgy8D2lpaVy+fBkzMzMqVKiQ4+dpy5bNfP9dT9pXlLAxU7L5mjF1G7dl+cq1uu9RSkoK7q6OnJ1pTmHXrHme75ckEZRenuIlSxMcHMzjx49JjPXDb3dRvX1ce5BCy2HB+BTzxc3NDUdHR/5YvZxbh6vj7JQ1uh4+5QmWji2ZOTMr6GDkyGEcPLCJoYNKkdfGhHXrnxIeYcrZs5feaz4wd0TGXpw53PLdhoCV8x8GkfnU+UtkduzYQbdu3UlNVQNyQIO5uZxZs2YyYMAAQDvfYGtrh1qZF5mU9eVQqZOwtpFRtGgRQkJCCAkJQWgU2Jrrh/NmqBMQiki++rot7u7uODk5MXTIMOyk8pjIte4tIQSvpPuM+uV7RowYoet79+5d6tauj7HGCinDjBR5BNVqVGHXnh05Ri5FR0cTHByMl5cXNjY5Vl81YOCDEBwczKZNm0hMTKBZs+ZUqVIl2whpyZJfmTNtLGPbK/DKL2fbBTWHbplw+dodHB0dAe18pqeHM3c3euL42khm/sZo1hwxxsXNi+fPnxMcHIyHixG3j+o/rJ28EE2/MU+oXacprq6umJubM3/+LG5f74KtjVZQhBC0bX+Yb7r+pLfm6k3kjsjYibOHmr3bELB0Wf/ZicwXu05m7NixpKaqkXTiISclRc2wYcM5cuQI4eHhPH/+nJSUFMyM7fX6ymQmxMdHIUkS1apVI1++fPy2ZClqTTpy2WsT47IUuvfoyqJFWXMepqam/DBwEKYqV2TCBLVxLA4uefjuu+/09lGqVCmehwaxc+dOXrx4QfXq1alcufIb3Rv58uUjX77/q7aSAQP/Ex4eHowe/faS8d9//yOFCvmwbPFcIi+EU6N2Iy79PkInMADW1tb06dOHTuP+ZOFQO7zdTNh9+hVzNiRw7MQ5nasuKCiI8r4lSEtXY2qS5Tl4+DQRhdyEy5cvExoaSkZGBnVqu+kEBrSphFq1cOPMmWPvJTK5ggByKdX/p8gXKzJBQcFoRzCvIyMtLRl/f39cXV0pUaIEGzduQiOUyKSsJysh0qlduzbHj2dlBraxsWXO7PmolLbIZSaoRQIKs1RGjhypt4cePXpQvHhxlixeSkREBM2af0vPnj2xsLDg75ibm/PNN9/k5mkbMPCv0ahRIxo1avRWm+kz5jJ7tgNtxywgPCKOapXLsmvPBr25IE9PT6pXr8HQSU+YMdobK0sjLt2IY/7KUHbvPUqlSpUQQrB7925++WVgtn0EBSfj4OCcrf3DIZC+4LQyX6y7rHjx4jx6FPDaSAaEUOPoaE14eLhuxDBnzhwmTJiMMt0MmWSEWpOKkUkax48fo0qVKq/1FWzZsoXZs+YSGRVJvbp1mTBxfLZEkQYMGPj/SUhIoP93Pdm//yCWeYwxMjZj9pxFfPXVVzobtVpN8WLe9OjmRr8+JZHLZVy99oLOXY9x7vyV98pMkCvuslI24tzebEmScyRPgR2fnbvsixWZffv20bFjR1JTNWhHNGrMzOQsWvQrPXv21NkLIVi9ejVTpkwjIuIFJUuWYu7c2f9a3L4BAwayiI+P5+XLl7i7u+cYJenv70+nTu0IDw/BysqUhAQVv/22gpYt328iPldEpmRecX7X+90vLLz3G0TmU+f16LK9e/cycuQo/P39cHV1Y/LkSQb31GfOXyUMwsLC8PX1xcnJ6a32UVFR+Pn5UahQIRwcHP6hozSQ2zx58oSkpCRKlSr1xpQ/OZErIlPCWpzfWe29bC18Dn12IvNFx7i2bNmSx48foVQqCQwMMAjMR4QQgtu3b3Px4sW3VoXMyMjg55/Gkj+fIxZm5rRs0ozHjx/naBsVFUW1ChVpXrs+k/r+iE9BL0YMHZZjKWSlUkm/Xr3w9ixA/3bttT9799ElB/07ISEhDB00iBoVytO1QweuXbv2v524gQ+Cj48Pvr6+/5XA5CaSRv1er8+RL1pkDPzz+Pv7c+PGDTIyMt5o8+jRI4oVLkLT2g3p1rIDLk7O7NixI0fb7p2/4dCKzQzOW405nq2xvBNNzarVCQ8Pz27bqQsuEWks9WrAL/krsaxwY/au3cj69euz2U6ZNIk7B46yuVRtlniVZ3Op2tzcf5gpkybleE4Vy5Qh7sB+uglB/rt3aFavHnv35lxC/erVqzStVxd7a2vKFC3CmjVrchQ6A58LQhtd9j6vz5Av2l1m4J8jNDSUr9t8xZNHT8hjbE6qSGfR0sV07NhRz06lUuHlUYBqmoJUsSyCJEkEp0WxMvYEl29c1Zus9fPzo0Lpcsz1bI2xLCuAY13UFayrF6VNu7a64mLR0dHMmjqd9SVaYvKa7ZWXoaxPCaB91y66bMsymYxF8+azpEhlPM2zin4FpiQw2O86K9aswcLCAgsLC8zNzZk6YQJOjx7yXcGsII+rcXFMj4zmaVCQ3iLGmzdv0rB2LYYXcqBu/rw8TUhl8pMI+o0Yw9DX1kn9xb1795g7fRr3797Cp2hxho0Zq5dd28CHJTfcZb7FLcWFLe+3CbOSp9+6P0mSVgPNgSghRInMti3AX1+MvMBLIUSZHPoGAYmAGlD9U265LzaE2UDusGnTJqZOnEpwSDClipdkysyp1Kmjv0hOCEHzRs2wj7TgR/vOyCUZ4elRDOj9HT4+PpQtWxYhBPHx8Wzfvh1FiqCqQ9aqbw9TB3xNCtCkURPsHeyJj4/XvbxM7fUEBsDHxIGVu/eyfaf+6MdSboyxpD85nNfIjOjoaH799Vc0Gg0ajQYhBBq1mvwm5nq2+U3MiU9MzFZJ0lwuZ1PlinptFWxsiLxzjzp16uDi4oKdnR329vbs37mDAQXs6VBAO7+Tz9SY38yM6Th1Ct//+KNeAtIrV67QrGF9BvhY0qGAKddDLtGoTi227t6b7RqDNn/ezp07iY2NpU6dOnq5vgz8iwiBpHrzyP2/ZA2wGFiXtXmhS4wmSdJc4NVb+tcRQsTk1sG8DwaRMZANIQRXr17l6NGjWFlZ0aFDhxwnyJf/vpyfR4yjulFValpWJdgvhDYt2rB7/269NO8XLlzgRUg4bW2zcrE5mzhQ1rgITRs1wcjUmIiICJRKbUbFouZu2fZlp7DkYUoE9vb2FCpUCBsbG9RqNZvWrEelUaOQZYmHf0Ycnbt9w6gxozE1NcXU1BQjIyNKFyvOvaQoSllmLQA89eo53w38njnz9Ytx1a5SlRMxYTR1zEq4eCImjEply7Hsj9UkJyeTnJxMSkoKowYNIiw1lQKvrXVKUKlQCUFKSgrXrl0jNjaW+Ph4LBQyptYuobevgpZmqNNSqVixIgULFsTZ2RkXFxe2rF/DL6Ws6OitzeDgm88cZ3M5Pw0bzKWbd/S2cfnyZVo1bUzF/Ea4mGmYP208DZu1YsUf6wzphT4GcskVJoQ4K0mSZ07vSdovV3ugbq7sLJcwiMwXiBDijZkDhBB8270n+3ftx0V4olJk8PNPP7Np6yaaNctKjaHRaBj/83gamNTD0Vj7VF7ErDAaoaFb5274VvLVpQCJjY3Fxdgh2z7tFHmRhETdunVxcnIif/78KBQKRg8bSbI6DQu5dqW2RgjuqUOZvXAuXbrop0wPDw5hxY3LdLAtg6XclAsv/bmS+pxbE/dly8i7dOUKunXsTJO8BXA1ysO1tCiCFOmsGpN9tfrMBfNp2qAhUap0Slrk5V7yS3bFhnJowzG9omGgrZUye9RICuexxMHUhFS1mlkBgXTq0IHVf/6ps1OpVDSuU5t78RF6JZijUjNI14C9vT1+fn6cOXOG+Ph4FBI089WvcNrE3Yo+p+7yww8/ULBgQTw9PXFzc6Nju9YsqGFMMy/tdsdX0dBszwG2bt2azSV58+ZNRg/7gdPnr2BrnYfeffvxy4TJemW4DeQmAkmj+Sd2VAOIFEI8e+OBwFFJkgTwuxBi+T9xUAaR+UIQQrB48RJmTptJeGQ4Rb2LMmveTD3hAG1Y99E9R2lq8jVGmVkOCuJD5w6d2bB5A6GhoQQEBPDo0SNiYmNwdNIP63U3ceV4xEmePXuGu7s7FStWxNbWlvlz5pGoSsZSkfW0/1TznJHjRjF48GC9bTwPDGLJqvXUNCmKmdyYa+n+5C3oyNdff53tvDbv2MaoYSMYu3YNqelpVKtYhWNLTuSY8r1Zs2acvXyRpYsW8ygomMZ1W9Knb99slTkBKlWqxIWrV5g/azbb7t6lRKUqXBgxPFtZa9BmcQjy96fd/Pl4WFsTkpBAvXr1+HXZMj07hULBmAkT+aZdG/KbG1PZ3oqQlHR+ehDOgIHfM3vefJ1tamoqRQp6EJCQQWn7rCSQQYkZmBnJ+eOPP0hOTta1u1rKaeaVVcfHwkhG/+Jyfps/m4oVK+Lu7o5CoSAgIIDG9WszoYaazaOtCE3QMGrPMvqFPOeP9ZuynVt0dDQ7duwgOTmZJk2aUKxYsWw2Bt7Bf5dWxl6SpNcnjZf/F2LQCcj+T8yimhAiXJIkB+CYJEmPhRBn3/fA/lcME/+fATExMWzfvp2kpCQaN25MiRIlstnMmjmbuVMXUExTnbwyeyJVz3konWf7nm3Ur18/M4w7kD49+6K6LaOImX6yz93xG4lTa125xsbGeHp6EhwQTCebr7E1stXZ+aX6E+YWwfU7+td4wi/jWbHwd6oYlyKP3Jz7Sj+SbJRcu3UdS0tLPVshBHv37mXl0uUkJybRukO7d9azEUKg0Wj+1bIFL1++5NGjR7i5ub21cNuOHTsYO3woIeERmJqaMGDA94yfPFmviiXA3Nmz2fLrDFZXs8fB3IjYNBX9LsZQt+t3jJ80WVfX5ciRI6xdMJWrXfRz7O14ksyPx2JJUgoUCgWenp6gzqClazRTG2Rdy6R0gc+vadx5+FTvuPft20f3bzrQuJicvCZqdt2T6NazLzNmzXtnOerPhVyZ+C9qLi79Ufi9bE2q3Hnn/jLdZfv/mvjPbFMAYYCvECL0XfuRJGkCkCSEyLlOdi5iEJlPnAMHDtCxfSfs5G7I1EbEEkzP3t8yb8Fc3Y1ApVLhYO+Ir6oJVvIsQQhRPiHA5BZ57awICgpCrVYjR0FFi+oUNSult5/DaTsZ/MuPdOzYERcXF2QyGdOmTGPZnKXUNa6FrcKW8IwXHE8/xeoNq7OtqBZCsGfPHpb++hvx8fE0b9WcHwcPynEU8SUghCAxMRELC4s3CqNGo+GnkSP4fdkynK3MCE9IoXuPHsxZ8KueIKlUKjxdnFhaQ04td614ZKgFzfe8onbH7yhcuDB+fn74+/tz/sRBFjeGJj76rrEqyxIxdi1L5cqVKVy4MG5ubvTo2pH9fVRU8NDO6cQlC6ouNGLVpv16c25CCJYtXcqiBTMIDY+iUvkyTJo+Xy/t0qdKbonM5dWF3svWuOq9/1VkGgNjhBDZ655r37cAZEKIxMzfjwGThBCH3/M0/mcMIvOREhMTw9DBw9ixcwdCCFq2bMWChfP0JuCTk5PJ7+RCEWVdrOXayWylSOeubB+/TBmLpaUlT58+5d69exw7fJyWlvqZnlM0iZxM3UTrdq3w9vbG29ub6OhoZk+aQyOjNhjJtDeiCGUYl8RJXkS90It+EkIwa8Ys5syeQ0JiAvkdnZgyY6phUWsuk5CQQGBgIB4eHm8U5RMnTtChbWuaFDDB2VTF3udQrHw1tuzcoydIg3/4HuP765lUN2tRYlK6oODcBNy9ihAUFKRzw1XylDg3VF+M5pxQc000ZOny1Tg4aOfZpkyewM61c1nQRUkxVxn7b6oZsUXBkePnsoVbp6WlsXv3bgICAihTpgyNGjX6qIvm5YrIFDETl1d4vpetcc3H7wph3gTUBuyBSGC8EGKVJElrgMtCiGWv2ToDK4UQTSVJKgjsynxLAWwUQkz9H07nv8YgMv8Cd+7cYdOmzajVar7++isqVtQPf1Wr1ZQoXopXz8FOFEOSJGLFY4wdknn89CEmJia8evWKlStXMnv8IkqKJnr9gzPu4K+6igY1xsbGeHl5EeAXSA3jdtlGMsalUjh/+ZyuTQhB/7792bppG66yAqgUGYRmBLN95zYaNmyY4/loNBrS0tIwMzP7YtwoHyORkZFs2rSJmOho6tarR506dbL9P/z9/alSoSwTaqjpWMpEOydzXOBUtgl//LkZIQQRERGsWLGCM1tmcvg7/bmE+SdU/HJATboKrKysKFSoEE8e3eXOdAWe+bKi2BYdUXE5uSGbt+/TtQUGBlK/TjUKOmRQtoCak3clTKw9OHT0DFZWVvyd9PR0Xr16hb29/b8WIZcrIuNjKi4v93gvW+PaTz+7tDIGkclFhBA8fPiQ5ORkypYtm2MKi6lTpzFj2kxMNE4gIEMRxXf9+zJr9kydzf79++nZpT+uSv2bhL/qKE4FrImPjycqKgoAK8mBimb6paCfq+7iXt2C5St/1yUOnD1rDnMmz6OYpjrW8nxEqoJ5KF1g597t1KuXPUPs7du3dSHMX3/9NXZ2dtlsDHya/BVddurcZezyWtKrT1/GT5yiF132V2nlo/2VlHbR3uATUgVVFiro8f1Y8uTJw9OnT7l16xb+Dy4T9pt+lcm7zzU0nClo0aYzhQsXxtvbm1/nz6ChTwCj2muDP4QQfDsvGefSPZg1OyuEXKVSMW7sKJYv/x0JDZaWlkyaMotu3br/A1dHn9wSmSvL3jxH9zpGdf0/O5ExRJf9F7wt9Pfp06e0bNmasLBwFHIjJEnDH2tW06pVK52Nv78/06ZOJ59UGYVC+6VUC0+WLFmKo5MDKpUKPz8/Tpw4gZRiiWSsvy9z4UhKSjwtWrTQ+c179+xDgiYGK5l20lclMog19ufXkWv1ygwMHzEMCwtzZkybSXhEGEV9irFpzoYcBQagTJkyejU8DHw+lCtXjqOnLrzVxsrKimUr/qBRnx60KQ15TVRsu2tMi7adGDNmjO57kJSUhJuLA+HxGpxtskYbV/w0mJqYc+jQIf744w8AjBSwf6SLzkaSJIa3M6bZ+D/4pmsPvLy8sLCw4KcxI7h+bgPX1hXAzdGYaw+S6fLTj9jZ2ecYDbls6QJiYqKoXacRw4aN1CuE9nEg4J8JYf4oMYxk3oFarWbKlKksXLiQly/jKVWqNIsW/aqX6l+tVuPh7klCnAJjmR2SJKFUJ6GUhXLz5nVsbGwICAhgyZIl7N9+HjuFfvRXTPoDXikDAXBwcMDW1pawgFgKyRvriVq44jxzfpukt1Zkx44ddO/ag3yyAkgqI+IUQXzdoR3LV/5ucF0Z+L8JDQ1ly5YtJCUl0axZM8qXz/6QPWrEEC4dXsmy7iq8nSQO3dHQd7WcHXuPUq1aNRITE7lz5w4N69chcqsjZiZZYvQgSEm1wZEkp2nvQ46OjiS+iuH+tqK4OGSNrHaciGfFEQdOnr6sa5szZya//zaLMd+74+5izrYDkRw7n8qVq7ezVYm9evUqmzb9iUqlok2br3J0JeZEroxkCpuIK0vyv5etUcPgz24k80WLzKVLlxg3bhz37t3H27sQEydOpH79+nr2Awf+wNo1f6JMN0OSjFBrUjAySeX8+XO6tB379u3jmy7fYqzRL1CWnBGCiniUyqyUEhby/DiZ+erZxake0qV3U6ZMmYK1tTUqlYriRUuQFGaEHcWQ0M7JyOxe8tTvMaam+q6JsLAwtmzZQmJiIk2bNqVChQq5dr0MGHgXarWaqVMmsmTRQuJeJVGySEGmzFxI06ZN9eyaNKxJbY/7DPsqD6D1DPRekAT5mtCsRWv8/f25c+cORw/tJOKYfgj9s+dpVOn+hAKFilOgQAFcXFxYv24VV/dXw90la2HrwHGPcPPpxMSJk3VtU6dOZunSBfToVgQjIxl/bnhGw0atWLx42TuFJndExlhcWfT2khJ/YdQ4xCAynzp/icyZM2do2rQpqalqsoqWKfjzz/W0adMG0K57yJ/fGdR2SK/lvFKpE3BwssDZOT9BQUFER0djJLfC2lQ/Fj5VGYWLpzkDBnyHl5cXlpaWNGnSDDt8MZFrJzqVmmRixDXu3b9DwYIFdX2jo6P5YeAgdu/eiUYImjdrwaLFC3FxccGAgY8RIQRKpfKNmQP8/f2pX6c6RVyUlPVUcvyuHMnMhaMnzmNtbQ1o52M83BzZO8eBkt5Z4rFkazQrDygoWKg4gYGBPHv2DE9XI24d0c/hdvRsFEMmBvJV++54eHhgYmLCqFFDuHKhC46O2rmgxMQMqtfeysaNe94ZZp0bIlPe20hcWWD/bkNA0TzisxOZDz4nI2nvzteBMCFEc0mSbIEtgCcQBLQXQsRn2o4BeqHNEvqjEOJIZrsv2sRwZsBBYJAQQkiSZII2UZwvEAt0EEIEvc9xDR8+nNRUNZL01+S8jNRUFT179uLIkSM8f/6cp0+fkp6uxNRIP8RSJpkQFRVN8eLFKFu2LNbW1ixc8CsaoUKWWc5ZCIHCJI1x46bQtWtXXd+VK5fTu3dfLDNDjhNVEcxfMF9PYADy5cvH5i0bdSngDa4vAx87kiS9NTWNl5cXD58EsH37dgIDAxnXqQxNmzbVC7FWKBT8Mn4KHX4aw8wf7ChZyIzDFxOY9kc8R46d0YVEP3v2jOpVy6FUajAyynK/PQtMIiU1g0WLFunqEH3VzkcnMACWlsa0/8qLffv2/nNreb7gOZl/YuJ/EPAI+CtGcTRwQggxQ5Kk0Zl/j5IkqRjQESgOOAPHJUkqLIRQA0uBvsBltCLTGDiEVpDihRCFJEnqCMwEOvAe3Lt3n+ynL+flS20mYA8PD3x8fAgKCkYItd5IBklJq1Yt2bZtq64pPT2DNavXo1FaI0OOZJRIwUKutG/fXm8PnTt3pmHDhuzbtw+1Wk3z5s3fWp3RIC65T1paGgEBAeTPnx8bG5t32mdkZKDRaLK5KQ3895iZmek9dOVEv+/6Y2efj/lzpxL8PITyvuU5fHSq3pobb29vypT1ZeysZ0waXghTEzl3Hr5iwcowdu46QJUqVYiKimLx4sXcvZO9FlFSkgonZ/Ns7R8EwRctMgghPtgLcAVOoM0Kuj+z7QmQP/P3/MCTzN/HoF2x+lffI0CVTJvHr7V3QpvcTWeT+bsCiCHTBfiml6+vrxBCCA8PTyFJZkImy6N7SZK5sLa2FhqNRvzFDz/8KPJY5BUmivzC1MhNGMnthLm5hbh9+7Z4HY1GI7Zt2ybq1qknKlSoJObMmSOSk5OFgQ/P8ePHRfvW7UT9GrXE7FmzRUJCwhtt586eI2wtrYWHrYOwNDMX337TTaSmpuZoGxERIb5q1UqYGhsLY4WRqF+jpnj8+PEbt63RaMTp06fFypUrxdWrV/U+RwZyn5iYGNGsaX1ha2MhfArlE06OtmLt2jV6NrGxscLW1kqcPNpJvIodIl7FDhE3rvQQ9vZW4tmzZ+/cB3Bd/J/3QV8vuVDttH2vV27s72N7fWiR2Y7WlVX7NZF5+Teb+Myfi4FvXmtfBXwFlAeOv9Ze47Vt3QdcX3vPH7DP4Tj6onXZXXd3dxdCCLF8+XJhYaEVlr8ExsIij5g8ebLeh0ylUokpU6YIe/t8Qi6XC1/fCuL8+fPCwIcjJSVFzJk9R1QpV1HUqVZTrFu3TqjV6hxt586eI5ys7ER35ypisHtdUdnBW5QsUkwkJiZms92yZYvwyGsvfi/eXOz37SQ2l24nqjsWFP169c5mq1KpREkfH9HFw0ccrtxEnKjaTPzoVVLkt88nXr58mc0+JiZGVChdWhTOZy/aeBUQ7jY2olGdOm990IiLixOnT58WT58+/S+ujoG/ExoaKu7evSvS09NzfH/fvn3C1tZKNGxYRLRoXlxYW1uIVatWvte2c0VkCsqFarvNe70+R5H5YO4ySZL+qt52Q5Kk2u/TJYc28Zb2t/XRb9BmMV0O2ol/gN69e/Py5UsmT56CSqVCJpMYPHgQP/30k15fuVzO2LFjGTt27HucgoG34e/vz8mTJ8mbNy/NmzfPMeGlUqmkXs06pAXFUdmkEBkaFRMHjeHsyTOs+GOlnu3Lly+ZMH48k1ybYm+sjVgqZ+nO4qhzzJk9m06dO5OSkqJ7TfxpHN3siuJiqk3ImUdhzHeOpemzfj0ly5bB3NwcuVyOTCbj/v37pEfF8l2xKjqXZfv8BXiQmsiiRYv44YcfsLS01K1EHzRgAN6JrxhdthSSJKHSaBj9+BkTx49n5uzZescthGDKxAnMnTOHwrZWBL9KolSZsmzeucuw6PV/wMXF5a0BMc2bNycoKJRDhw6hVCr5Y03jf/g6C1Cp/sH9fVx8yDmZakBLSZKaAqaAlSRJfwKRkiTlF0K8kCQpPxCVaR8KvF6tyhUIz2x3zaH99T6hmVlIrYG49zk4SZIYMWIEgwcPJioqCnt7e728XAZyDyEEI4ePZPmy3/GxKECSSGVAv/4cOHwwW0qdXbt2ERcYwQDbRsgyb+5FLdyYvGULRUsWw8jIiOjoaKKiorh37x4OMgudwID2/1rR1I1ZU6YzcdIkvW2byhS4FNWPAMxrZIqkUjNw4MBsx93YwS3bnJiPsTkTfvmFn3/+GUmSsLS0xMrKiojwcE7Xqq6zV8hk9Hd3oc+KFTRt3hxnZ2ecnZ2xsLBg27Zt/PnbIo7U8sHRzBilRsO0R4H06voNuw8eynYckZGRLJw3l4unT5Lf1ZUBg4fprdMy8G4sLS2zzY/+YwhA82VF8b7OBxMZIcQYtPMsZI5khgshvpEkaTbQHZiR+XNPZpe9wEZJkuahnfj3Bq4KIdSSJCVKklQZuAJ0Axa91qc7cAmta+1k5hD3vTEyMjKEBf+PpKens3z5crZt2IqJqSnf9v2Wjh07ZsszdejQITasWs8Auw6YZxYie5QcQJsWrTlz4SwhISEEBwcTFBTEts1bKCZz1gkMgInMiAJyB4YNGwZohcTe3p48efKQoExBCP1MDLHKZHwrlGfAoB8wNzfHzMwMc3Nzpk2cxOXHYXxlmpUn63FSDHltbXlw7QqSJKFWq9FoNFy5coVxA39ELQTy17Z9I+Ul3Xr0oESJErx69YpXr14RFxfHpg1/YirXP28LuYKExES9jMVWVlYYa9RMKuGMo5k2EstIJmOkjxNVjp0mLCxM7/P44sULKvuWpZ49DHQxwT8inI6tmjFt3q9079Hjjf8btVr9USee/OIQX+7E/7+RVmYGsFWSpF7Ac+BrACHEA0mStgIPARXwvdBGlgH0JyuE+VDmC7TzNuslSfJDO4LRLwFo4IOhUqloWLchLx6GU0xWBKVQMWrAKE4dP8WK1St0dmlpafw6byHlFUV1AgNQ1KIgR0LP4+3trWuTJAnLPJbYyLMnQ0w2UrJ48WLat2+Pra0tcrkcIQSli5XgUPxDGtsUQyZJvEh/xfFkP/bMP5AtPHXurwupUaUqKgS+eRwJSn3F5vgnzPttsbbWymt4eXmx8relTAm8RzenApjIZOyIek68uQlLlizJ5up7ERTEjvAXdHbLGnRvDntB06ZN+X7wYMLDw3WvrevWkN9MP9TXTCFHoVbh7u6Oh4cHXl5eeHl58eTRAxrYaZheUbuCvZYLVHAwo8uwIXTq3DlbyPCK5b8zY/IEAsMi8fZ04eeJ0/jmHdFcBj40wjCS+dAIIU4DpzN/jwVyTJgltKmns6WfFkJcB7JV4hJCpJEpUgZyB41Gw+JFi1k471eiY6OpXrUaM+bMoFQp/foy+/btI/hhEG3MWiKTtKJQUOPJHxvWk6ZMIzo6midPnhAcHIwRCprbZS9zYWGah2/79aFJkyZ4enri6upKZGQkpYqV5ElKKD7mrmiE4FLiY1JN1PTt21cv6agkSew9dIA2zVtyOnQfeY0tCE+NZ9acOTmufyhatCiXrl1lxpSprLp4CY/CBdg4egd162YviS5JEvuPHmHCz78wZsMGMpRKWrVqxdkZ03OcS1q4bBn1atbkYWoaxUxMuJGaxjO1hnPLlmUbKcuFYO/RXZSxzXLz3YpLQmZqzqih3xMYGIi/vz/bt28nIyGe4Y30q3yWtDPFSJ3OpEmTqF+/PkWLFsXBwYEVy39n7oRRrKhriq+TC5fCMug/dABGxsZ06JBzZH9QUBBCCDw9PQ3h8h+KL9xd9sWu+P9SSU5ORqFQvHH+acSwEWxeuZUyUiUs5dYEZfjxSLrNletX8Pb2JiIiggcPHjBpwiS4p6FCHv0UOfvjDhGkCaZEiRL4+Pjg4+NDVFQUhzbso1ve5sgz1xuFp0exOekI4ZEvst20jx07xrffdEfK0JCuVuLkkp+tu7bnWPoYtHM+9+/fJy4ujvLly2NhYZGj3YcmNjaWNX/8wbNHjyhdvjzffPNNtqqfoHWBVSlfjqp55NS3tyAgOYMVgbEsWrEy27xBo9o1aCMF0s7LWteWqtJQdMNTUlRZLhgbGxtEejI7WuelfP6s/+3JoDQmPsrLrQdP9bZ7//59en7TnufBwUgSOLu4smr9FkNS1L+RKyv+C8jElfFvXqT6Oopv0z+7Ff8GkflCuHPnDv16f8fN2zeRSRKtWrZm6fLfsLXNqi/z8uVLXJ3daGnWETNZ1kK1mymXibIMJU2ZRlxcVlxFSfPiNMirPyjdk7qfWStn07ZtVvkBlUpFq2YtuX/1Lj6SBymydO6lPmXV2tV89dVXOR6vWq3m3r17mJqa4uPj89k9ZUdHR7P414VcOn0aZ3d3vh88JMecc/v27WNwz65sqZsPD0tj0tUaJtyII9qlNIuXr+LRo0c8evSIBw8esHLlCuKHuOpdq6QMDZ6/hdOnX39KlixJyZIlKVCgABXKluSXaml0LasdGW6+o2TsGWOe+AfnWNvl7t27hIeHU7Zs2Y8wy/GHI1dyl3nKxJVx2ct+5IRRnwyDyHzqfI4ik5SUxOPHj3FycsqxtnxERATFfIpTQFkGd0URVCh5qrmOVWEFF69c4NmzZ9y9e5cjR46wZ9M+2lh20e+vDOOC6gQdurSnRIkSlChRgrx581K7Rm0amdbHzcQVIQSPUh9z2+geQSFB2UZKGo2GQ4cOcfjAIWzt7ejeo3u2VDoGcmbenNlMmTgRj7xmhL5KoWKlSqzfsl3vAQHAp6Abv1bMoIpr1rU/EpDK9ydTSBcKEhISdO21ChpxuKf+iK/TdkHTAbPp06ePri06OpqvWjUhyP8x3k5G3AhMo1+//kyfNfezE/6cyBWR8ZCJK2PfU2T6fX4iY6gn84kza+ZsJk2aTB4ja5LSX1GrVk02bd2o9zS6YsVK8gl3PI2KA2CMnOKyahy5uxYLCwuUSiWgXRMkCRkZmnSMZVk3qlh1NE2bNeH333/X2/fWHVvp3qU78hQ5Ko0Sa7u8HN1zNEdXnEwmo1mzZtnqgRh4N0OHj6BPv+948OABTk5O2YIU/mLchKl8N+x75tcSVHQ25kJoOkPOpLFy3SZatGjB8+fPuXfvHosXL6Zw0pls/b2t0vjll1+4cOECpUuXplSpUsyZMRHfPPc5+osGuUxJTJKg8dIVFC9VNlt6GKVSyb59+3jy5AklSpSgadOmhgi3v/hyg8sMI5mPFSEE586d49q1a3h4eNCiRYtsN++dO3fSp1t/fNT1MZNZoRYqAqXLlK3nzaQpE7h79y53795l4/pNOLz0poCxfuzE1fRDlK7vQ8eOHSlVqhRFihShT88+XNh3GV95NSxkeXieEcA1zXlOnT2ZrV47aF1ht2/fxsTEhBIlSnwRT7cfM5s2bWLm5F94GhBMscJe/Dx5hl7hPIDTp0/T/5uWXO0rw0iu/X+pNQLfJelYuBQjPDyciIgIAMyMIHK2EWavFdDbd1fDgtslOHPplq7txYsX1K9TFVujeCoXSOfsMxPUJvk5evJCthHXp0SujWRGv+dIZsDnN5IxiMxHSFpaGk0aNePOrfuYqR1QGyUhN1Nx7sIZPRdTtco1SbhlioPCS9emEhmcT12LBm30t7GxMfny5UOKMaOiSROdnUaoOaXZxLlLZyhZMqt2R0ZGBiOHj2LVqpWkZ6TjXbAwCxbPp0GDBv/AmRv4JxBC0LxxPVSh1xlSSYNMgoVXZWTYl+LIibPIZDKioqI4ePAgPw3tR/AU/XVI14I0NP5VhWfhUpQsWZJSpUpx5OAuyue9w7QOct0+Bq4BqUB7lv6+Wm//d+7cYcG8Gfg/e0TJMhUYMnQUhQoV+icvwXuTKyLjLhOXR73fxL/xwLdP/EuStBr4K5tKicy2CUAfIDrT7CchxMEc+jYGFqKtbbJSCDHjvzmP/xWDyPzDhIaGMnXKNI4fP4mjowPDRwyldevWejYTJ07it9lrcdFURcoMD45WP8TaK4OBPw7g3r173Lt3j0vnr1DauDlWMv0qgFdUG5k0fTyNGjWicOHCpKSkUKxIcawTXPCQFSVDpOMnu0nJaj7sP7Q3x+NUq9WkpaX9a5FaBj4s6enpLFr0K9s2/IEQgnaduvPjj4P0Iv3UajXeBVxY0S6WWoWz1i4N3CK4m1YKGztH7t69S2hoKHIZRP5uQV6LLDEKjtZQ/mdB4PMXunoxJ0+epOPXLRna1oQKPkacvqvk94NKjp88ny1MHrTZDqKjo/H29v5XMnLkmsiMeE+R+fGdIlMTSALW/U1kkoQQc97STw48BRqgzZRyDegkhHj4vufxv2IQmVwkOTmZs2fPYmxsTM2aNfXWdIDWpVC6VBnUyVaY4oBSk0K60XPG/TyaESNHANpJ/CKFi5MnrjgW8izx0Ag1d1I3I1BjaWlJyZIliY99SWqQCQXllXR2CZpogszOEh4Zprf/0NBQxowcw4EDBzEzM6Nn756M+3msIZWOgbeyf/9+enbtwPc1VBRx1LD3gQlXwq24cOWWLsosJiYG5/yORC4zw8o8S2RCYzX4DEkhXQVubm6UKFGCB3evMreXjNbVs6IXF+9O5PRzX3bvO6prS0hIoG/vrhw9ehxHezPiXqmYMm0mffr0++dOnlwSGTeZuDT0/cpEmAxNfef+JEnyRJsk+L8RmSrABCFEo8y/xwAIIaa/14H9Hxgm/nOJLVu20KtXb0yM8iCEBkmuZu/ePVSrVk1nM2f2XDSpVljLtfmzTOR5MdHkZey4nzl2/BhPnz4lODgYGQq8TfTnTyQkjIyMuHDxMr6+vkiSxPPnz/EtW4HAtCvkVbuSIl4RYXSPRQsXZhM4V1dX1m9c/+EvhIHPiubNm3Pi7GWWLVnI7ZBAKrWox6J+3+nNs9jb29O6RWPmHTrFhHZZ7rLZBwR169ahZp2GPHjwgLt37xL2IpYWVfQXl7avZc7P355m9erVFC1alKJFi9K3d1csVDfx31cECzM5D/1TaT1sFB4eBWjYsKGurxCCrVu3snHDapTKDFq26kDPnj3fWjztn0cCzXvPVdpLkvT6U/DyzAS/72KgJEnd0GabHyYyC0G+hgsQ8trfoUAl/gEMI5l3oFQqmTJlCkt/W0piUhK1atVi/vx5FC1aVGfj7+9PqZKlMRYeKOTaJ7QM1SuEcRSXLl3g+fPnPHnyhKlTZqBI9sRMoZ8BNiT5NAUKuVChQgWKFSvGjRs3uXD4Li5kZQCOVT3Dpkg6t+7c0OsbFhbG7FlzOHPqHO4ebgwfOdSQPNHAP05oaCh1alamgE0SlTxTOfPMjHiVHSfPXCZfPu2IXK1WY29rxY3fbHB3yHq+vfwonSajo0hKzQrBMjeVEXq0DBZmWdFpa/dGs/9WIfbsO6ZrGzCgDxfP7ePHni6YmMhZsSEcMysf9u8/mi2y7cGDB5w6dQo7OztatWqFufm7i5blzkhGLi4Nyp4lIidMRiT/LyMZR7S1tAQwGW29rp5/6/M10EgI0Tvz765ARSHED//l6fzXfNEjmaCgIObMmcO1a9coUaIEI0aMyLaqvFu37uzbdxhVuimSZMepE1epUrkKDx4+wMXFBSEES5b8hkxY6QQGwFhhzcvkF5QokTUiMTYyxVKWhBlZIqMRaoxNZZw4cQI3N20S6sTERGpUq0Vo8GkUqXZgmkK6cSz7/jyV7RxcXFxYsHB+bl+aTwohBJGRkRgbG78zkikqKopFC3/l4pmzuLq7MXDI4BwXQf5FYmIimzZt4tH9B5QsU5oOHToY5qlywNXVlXsP/di5cydPnjzhh44laNWqld6IQi6X06t3Lwb99ifrRubB0lxG9Es1I1akMWHyTFq1as2jR484efIke7at0BMYgMIeppxdcJoSJUpQuHBhbG1t2bN7E/dO1sYyj3bk3ry+E7XaXeXw4cO6cHkhBAMG9GX37u00bVyQ0LBkhg79gX37DlO+/D8QyCVAvP9I5r/fvBCRf/0uSdIKYH8OZm/Kcv/B+WJHMvfv36dq1aqkp6tRKjXI5RImJjKOHDmic3E9f/4cH58ioLbXTcADqMVL3D0cMDMzxd/fn5SUFMyMnLEwdtbbV6o6mDZfNaJv374UKVKER48e0axpS6w0JTCRW6MRKpLww7dqYY4c1U/xrlKp2LdvH5cvX6FAAU86deqkmzw1kMW1a9fo3f1bgoKCUAsN1SpXYdX6tTkuSg0PD6dSufKUlFtT0dyB0PQkdsf7seyPVTlmHggMDKRW1aoUkptS1MicexnJhMk0nLtyGWdn52z2oI2cWrNqFa/i4mjcsiVt27bVq2H/pZOens6A73qya9cuvFzM8QtNoXfvPsycPV+XvTstLQ03VweOL/WgaIGsEcCI+aFcfuaEU343nj59ytOnT/mqeX5Wz9cXirnLnnLgjDk9evTCy8uLx48fs3rVbA7ua0WePFrR2733KZOn3OPJ08BsWcNfJ1dGMq5ycXFgnncbAqZjEv6XkUx+IcSLzN+HAJWEEB3/1keBduK/HhCGduK/sxDiwX95Ov81X6zI1K9fn5MnzyNJWXMXQihxcclHr169CAoK4ubNmzx88AxjhX4aDbUmBYVxCvXq1aVQoUJkZGTwx+o/MZO8dGKkESpSxTPu3buDl1dWiPG6desYPGgIGrVEujKVenXrsWHjeoOAvMahQ4eYP2su4aFhVK9Vg9HjfspxAWJERATFfYrS0ao0lawLoBJqDsQ/4JFFEvefPMp28xg0cCAhu07RK39pXdujpBgWxN8lODwsm3ulVZOmOD0JpptLVnjt8pAnqCuV4c8tm7Mdz6qVKxkzdChf53fERi7nQPxLHIsVY9/hI9nmyP5CCEFCQgIWFhZflBhFRkYSFBSEt7d3jqPPpb8tYfaMsfzc25ZCbqbsPp3IlmNpXL56S/cAsWnTJlYuHcXeNfrrt/qPus2m3aGoVNow/jx5jJg3ux4d2me5uIUQVK62hXXr97x1JJsrIuOiEBcGZM9hlxNm416+K7psE9pKw/ZAJDA+8+8yaN1lQUC/zHpdzmhDlZtm9m0KLEAbwrw6MyHxB+fL+VT/jYsXL5L99BWEhoYyceJEXF1dtdEzkipbvRK5QkOvXr349deFgDZlyvPgEM6euYg63QIQSMYJfN+vv57AAHTr1o1OnTrh5+eHnZ0dDg4OH/ZEPzGWLV3GhNHjaGhWmlLGxbi/9yYVd1bg2q3reHh46NmuXrmKMmbOVMmrXTtkLClobVuK68H7adu2LTY2NiQmJpKYmEhCQgKPbt9lgmd1vW0UzWNPkv9LbGxsMDExQaFQIJfLkcvlhIaEcLhyEz37do4edNi1E++JE7G3t8fe3p58+fJhYmLC0EGD2FCuNJ4WWrfpV67O9L73kC1btvDNN99kO9cdO3bw07ChhEVEYGJiQv/+/ZkwZeoXITaOjo5vzYHWf8D3eBYoyJJFs4nYFU61Gi25dGW03gi1devWDB/2I9v2hfJVcxckSeLclRgOnozD3z8AmUxGQEAAw4Z+j5Gx/gOHJEkYmyh02S4+OJo3j5b+G4QQnXJoXvUG23Cg6Wt/HwSyrZ/50Hz+n+Y3YGVlRVpaAlpR/wuBiYkpL1/GY2qqDTls3qw5p09fRK00B+SoNcmYGGcwePAgXS+ZTMau3TvZsWMHGzduwszUjJ69vn3jAkYjIyO9wIHPndjYWEYMHcGOHdvRaDS0ad2GOQvmZhPY9PR0xo7+iX55G5DfRPt062HqgCZO8E3HzlSsWpmQkBDdK+pFBB0d9R/6JEnCUWbB0aNHsbOz01WutLS0xMLCguiMFLwtsubE0jQqMiRBlw4dMDIyQq1Wo1KpUCqVbN6wkQyNGnN51tckQ6NBqDVMmDAh23kWt7LUCQxoq2O2srdl4exZWFlZ4eXlRcGCBTEzM+PkyZMM7PUt88q4UKVCaUJTMhi9YQ1j0tOZPX/BG69lamoqRkZGX4QQNWnShCZNmrzxfTMzM/YfOErHDm2YtigYM1MFMXEqNmzchru7NoLN1dWV7/oPZtXqabRoVggjI+33/fyFUGJi0t46isktxAeek/nY+WLdZVOnTmXatBmkpmpHKUIITE0levXqwaJFi3T2qampDBkylLVr15KRkU6ZMuVYtuy3f+TD+TmgUqkoW7IMFpFGVDUvgwRcSb1LdN5E7j26j1wuJygoiEePHnHq1CnW/raK8W76D2vBaZEsCduPZKLAzc0NV1dX3NzciI2NJfjCXUY419WNNJUaNaND9nHs/Olsi/s2b97M2AGDGO9aBTtjc5QaNX9E3kNWpiC7DmSfK+3eqTOpF6/zo1sRJElCIwSzgh/g0awhCxYvIjY2lpiYGGJiYjh9+jSbfv2V7RXK6m1jTWAwi/0CSNdkRU45Ozsj0lIZ7mVDO097XXtUagYNTj0lLDIqW3DBlStXGPr9d1y/cw9jIwVdOndizoJF5Mnzfr7+zxmNRsOtW7dQKpX4+vpmc00qlUratm1BUNB9WrfwICw8lb37/dmwYSuNGjV667Zzw11WztlIXOiT971szSfFGNLKfOr8JTJqtbYI1oYNGzEzMyMtLZVmzZrx559/6kYxr6PRaFCr1W/0rX9pqFQqVqxYwbpV61CpVHTo0oHvB36frTbMvn37GNxjIF3ztNBzOa6O3omUz4jIyEjS0tJ07UYyBVMLdMNUlhWVdDXhKWHeak6cPaW3jdTUVHxLlSV/gpw6loVI1yjZl/iIQlXLsH3PrmzHLIRg0vgJzJ0zhwLW9oQnvaR0ubJs3bUzx3mB2NhYGtSqTVpUDEXNrLiX/BI7DzeOnDqZLR2+SqXCy92dHx3saOSkdQNFpaXT/c59lqxdi6OjI/7+/gQEBODv78/ebVvYXM2Lwtb6YbS++25TvVETqlatqktSmZKSQhXfskwqa0nrglbEpamZcPMl6Z5l2HPoKAbejUaj4ejRo5w8eRw7u3x07dr1jcEbr5NbInO+t8172VpMjjaIzKfO39fJRERE8OTJE7y8vHKMSDKQM+1at+PW6VuUkpVALsl5oHlIviIOnD5/GkmSePbsGTdu3GDp0qWo7ybRyEZ/LuTUyyuE2cfTqnUrihYtSrFixbSL8Hr2IfTcQ9pYV8ZUZsyL9DhWvzzBmi1/0rhx42zHERcXx9RJk9mzczempiZ0792TwUOGvPVhID4+nrt37+Ls7KxX/jknNBoNJ06c4MmTJxQvXpzatWu/MQnozZs3adWkCQ4KObZGRlyLjuGnceMYOWZMNtsOrVtRNPgO33pnzUsEJKbS4uRj8uZzICwsTNduaWFG14LmTKyU5V7MUAt8d4Vy+vJ1fHx89LYdGBjInJnTuH75Au6eBRk0fDTVq+tffwPvR66ITH4jcb6X3bsNAYupkQaR+dT5t3OXfexkZGSwZ88eAgICKFeuHPXq1csWpXX9+nWa1GlMpzwdUEjauQGN0LDp1VbyFczH8+fPSUxMBEChUOCgsKWvo37Fxy1Jhxn360Q6d+6s156UlESv7t9y8NAhrE3ykCaUTJ0xjX7f/bPpRP5XlEolx48fJyEhgdq1a79xcvvWrVs0qFWT4YXtqZc/L08TUpn8KIo+w0czbORI4uLiuHfvHnfu3GHJvFmMLgQtCuiPnlocCMGxYj06duxIhQoVKFiwIH5+ftSoXIGuRWQ09FDwIEbFzOsZLFy2OlvVTQPvJndExlic7WH/bkPAcsYLg8h86hhE5s0EBwdTs1pN5CnGWCrzEi1/gVshV06cPq7z/UdHRzN27Fiubr5C3Ty19fpfSbxGkGUwbdq2wdfXF19fXwoVKkTZkmVwfGlNFfMySJLEleS7BJlH8OjZ4xxdk6DNhxUVFYWXl9dnm1/t2rVrTPhpNFevXcfVOT+DR42hW7du2UZK438eR+jelcysmOXSS1ZqKLHJD6WkID09HQBbW1uszI3p4pnKqMpZIbOXw9Lpe0bCP+RFtgeGuLg4du/eTXJyMk2aNPlosyH/W+SKyDgZi7Pd3y+K1HJWmEFkPnW+ZJF58eIFSqUSNze3HF0+Deo04OX1VEqa+ALaOYwLGcdxr+iCU35HLl++jL+/PwD5jZzoaK//ZHwy7TTdf+7BkCFD9NojIiIYPHAQu/buBiFo0awFCxYvNLgn35OIiAjKlixOr4JGdPSyJDJVxeTbiXjVaMyyVX9w//59rl27xtWrV9mxaR3HO9hS2O719V+CAsuiWbdlJw0bNtS5Eg8dOsQ3Hb+mTiEjrI3V7H2oYsCPg5k4edq/daofHbklMme6vl/Jaqs5oQaR+dT5EkUmICCALh2+4d79e8hlcpydnVm7YQ0VK1bU2SQlJWFna08Hy54oXlugGqeK4cCrbeTLb0+VKlWoXLkyZcuWpUvHLpRWl6S4aTEA/NMDOKe6wFP/p7pcVX/nr8+aobDZf8+zZ8/4ZfRIjp84gbWVJT379mfk6NHZQpmrVyjDj26hNPHKCsCITVXjs+wFGWpt2G/58uXx9fXlj5XL2NNFTmV37TaikzVUX6Hhz52Hc5zDiY+PJyoqCk9Pz892dPl3ckNkyjoZizPfOL2XrfXckM9OZD7/YPsvHKVSSe0adbCJd6e+UVckZISF+dGwfiN27NrOo0ePuHTpEhcuXEClVAL6AiAhYWdnS1hYmJ44nDxzkg7tOnA99CZymRwrGysObDrwRoEBg7j8P3h7e7NpR/aIub/z/dBRTBj2HcXsjfCwVpCYoWHE2TS+atuWVl914NKlS1y6dIlFixbh6wyV3bPEIp+FjN7lVGz6c42eyKSmpjKwfy927NiJvZUxiekwfuI0Bnw/8IOc62eHkHJtMeaniEFkPmHi4uL4acxYtm/bgUwmo2OnDkyZOlkvvPbQoUOIFDleRmV0ba5G3oSnBFC/fn1Au26jatWqGEnGPIm+R3FT7VoPIQRPNHfp2LljNoEoXrw49x7dw9/fH5VKhY+Pj0FEPgI6duzI86AAak6fhou1CWEv02jWrBm/r16Lubm5bvJ/w4YNrJ8+IFt/Y5mGtWvW8uCxH1WrVqVKlSps27yelGcHeDZBg41FOg9fCNpOHY2Lq1u20s5/odFo3poT7EvDsBjzC+JzcZcplUpKlyxLSoiM/JriCCBcdg/7QqZcunqB+/fvc+nSJdatW0fknUR8Tevr9X+afhPXWlYsX/G7bo7m2bNn1KxWC0ulNRbp1sSZRGLtbMXZC2fImzfvv3KeBv43kpKSePbsGc7OzjlGuL18+ZKC7i6c+FZGMUftKvikdEGlZUpKVGlIWFgYt2/fRqVSYaKA4OlG2OXJulFuv6Fh1dNyHDtzRdem0WiYO2cWvy6YTVhEPOVL+zBl5kK9+i+fGrniLnMwFac6vN/8o81if4O7zMCHJz09ndmz5/DHqjVkZGTQ7qu2jJ/wCzY2WQu69u7dy8sXyRQRjZBk2i9/IVGdaw+3YmlpqcvJZGdnR6omHbVQI5eyCkq9MnnBzz1/1KXfAK1Lxi/wGVu3btWFMLdo0eKLSGHyuZEnTx7Kli37xvfz5s3LoqW/02BAX9qXBGtjFVsfKmjQsgNLl69GkiRSUlK0i2m/64bd3xILFHGCW1tvM3z4cCpVqkSlSpVYtWIpR7YvYe9gNcVcLTh4K4hunduwffeRHOd41Go1arX6Iysw9mEwjGS+ID6GkYwQAiHEG90JjRs15eaFR9iofJAkBa9kfli5SNy5e4uUlBSuXbvG9OnTCb6QREFj/fQ2z5QX8ahkxcCBA6lSpQpubm60btGGm2fv4akuhQw5obJHWHoac/XGlS/iC/53kpKSSEpKwtHR8Yt38QUGBrJp0yaSkxJp1rwFVapU0bsmKpUKDxcHdvdOpKxb1ud16kENK69ZEx2fpAuhNjWWeDjPHHf7LLtVJzM4GFad3fuP69qSk5MZOXwQ6//cQGpaBlUrlmXuwmX/TG2X/5LcGMmUcTAVJ79yf7chYLf02Wc3kjE4Tf9B1Go1EyZMxNbGHoVCQYnipTlx4oSezbVr17h84QoumqpYyPNhLrPBSZQnMvglHh4e2NnZ0bhxY86cOUMCEdn3YZ7E4MGD6dChA+7u7kiSxPZd2xgyYSAv3QN44XSfTj+24dzFs5+FwAghePDgAffu3UPzWn6wnEhISOCbDh1xyudAUS9vfAp4ceTIkbf2OX36NA1q1sLVwYF61Wtk+3996hQoUICffvqJqdOmU7Vq1Wyiq1AomDJ9Dl+tNObPK2puhWiYchB+u2jGiTMXSUhI4OrVq4wfPx5rc4WewABUKSzn0sWLzJkzh1OnTvHq1Su6dGxDvN8uHqywI2GvK92rBtG0cV2CgoKyHV9aWhpnz57l2rVr7/z/frRkJsh8n9fniGEkk4v4+/tz7do1nJ2dqV69eraRyo8/DOLPNdsw13hjJFmQoo4kWfaMU6dP4OHhwa1bt1i6dCkXDj3ATVFZr2+U8iEmrq/o07c3FSpUoGjRopQvV4E8rzxwloohgDBxF6V9NM/8n3wWAvIubt68Saev2pMQ9xIZEqZWFvy5ZRNVqlTJ0b5Zg4aoHwTzrUNJLORG3Ex4wa+Rtzh14TwlS5bMZn/kyBG++bo93+X3orSVHfcS4lj2wo/Vmzbqqi7+ndTUVDZv3szVixfxKFiQb3v2fGtK+0+FI0eOsGjuNEJCnlOhcjVG/TReLyVPWloaLvntuTIJCjhkfe6XHc1g/A6J2FdZ+elsLOWEbXHBSJF1Ux21Mgkjzx7MmDlH17Zz5076f9cTj/ymJCQrQWbJlm17KF06qx7QhyZXRjL5zMTxtp7vZZtv+ePPbiRjEJlcQKPR0LtXHzZv2YKZcV7UIg0HRztOnjyhW3CYkJCAk2N+8smqIJdlhY0mZASRLAsiLS1F12Ymz0sRk+Z6+4iQXWf4xD4MHTpU1xYYGEifnv04e/4MAPXq1mfFqt8/6UWO6enpnDhxgtTUVOrWras3D/U6SUlJFHT35GuLklSyKgDAzcTnrH91g2eB/noJLzMyMrh+/TrNGzRitU9TjGRZ5R22RD4kqnA+fhw2BIVCoUujb2RkRJ9u3emssKamXX6d/cW4SDaKRG49zF5QMC4ujpqVK2ObmkK1POb4ZSg5HRvPwWPHvois3VMmj2f3+nks6q6hhJuM/TdUDFovY+/BE3h5eXHjxg02bNhA8L1dnJytn2Zl+9lkflor0fGb3pQuXZq8efPyTeev2LPQA99ieRBCsPlQHD8vfYV/YKjeQ1RoaCi//baIhw9u41OkJAMG/JCt9tD/Sm6JzLFWBd/L1mHVw89OZAwzuu8gPT2dGTNmsGrVajIyMvjqq3ZMnDgRO7ushHcrV65kx469mEmFkankSEIQERpF69ZtmTx5Ivfv3+f8+fOolCA301/EZiK3QSkPZ+rcyZQtW5aSJUtSsUJloiIeYC/5ICEjXh1Eqmkk3bp10+tboEABjp86qsti/KYULZ8KFy5coHWLVtgrrDCRjPg2MZw58+fSt1/fbLbbt2/H08iWytZZX15fKw8uJgZQrVo1zM3NiY2NJTY2lqSkJAAKmOXVExiAAibW7Dh9hiMnj/N3ZEClqvojloo2+Rh54QoNGjTAzc0NFxcXXF1dcXFxYfvmzRRRpjOheGGd2+lAeATfffstN+7fz/GcVSoVhw4dIjg4mPLly1OpUqVPdp5o7LgJWFnb0G3+LELCo6lYrgRbd86ncmXtqLxx48b4+PhQ0XcnKWkazE2zRjzHbmSQpjRl9uzZqFQq5DL4rr0jvsW0EQeSJNGpqR0rdydw+PBhWrZsCcCDBw+oV7cG7Zo58nXjvFy9dZAK5Vdy5OipbIEPKpWKCxcukJ6eTvXq1TE318+A/cEw1JP5ckcyiYmJrFu3juvXr1OiRAm+/fbbbCnfGzZoxMVL11ClmwASMkUa+Z1tuX//HmZmZqhUKkqWLE14YAbGiry6fkJoiE25DWj9yE5OTkRHxeBsWhOFLEsMElRB1GpSlB07t+vaQkJC6Na1B5cuXUKSJAp7F2bNutVvjRb61ElNTcUtvwvtLKpQzEI7SRqd8YrfYg6ybvOfaDQaHj9+rHvdvn2baqaedHPWd41ti7zBTeMYSpcpjZ2dne5lZGTE5PETWF6kKdaKLKFf9uIWjg2r0Lf/dyiVSl3BMqVSSZ9u3fnZ2YcSVlmficdJLxn25DqFSxQnLCyMiIgI3VyBuVzOukrlKGKVlTdMLQQ1zlzk4PETVK5cWa/Ec3BwMA1r18JalYpPHmPORydRrFx5du7b/1mvqO/+TXsi/Y4ztYcpjjZy1h9LYdF+wc3bD7GxseHRo0eMHDGYhqUD+aFzfr2+7YY84cTVNEqXLk2xYsW4eeMSXVqbMODbrJxrqzcGsu+UBUePndW1Xb58mfbt22Bvb4KZmYInT2JYunQFX3/99VuPNTdGMqXtzcXRFu+XE85pzT3DSOZzISQkhAoVKpKUlEJKShpmZiZMnTqVixcvUqRIEUA7CX/x0iXUGTbIMsOEhdqIsNBIqlevTlpaGn5+fmRkqLA2Lfy3PUiYmJjyxx8radSoEba2towcOZoVy9ZgrvLCSJaHZFUkafIQfv5lg15PNzc3Tp0+QXx8PCqV6q2r6D92/Pz8mDZ5GlcuXsbd050RY0ZSt27dbHaHDx/GychWJzAA+YytKWdcgFYtWqJB+zDk5OSEj48PDRs25OKx0yg1at3oRCU03FNHsmbtet1C09eJjohkyvrNdLEtgp2xOWdePud6Riy3pk/DySl72o+xEyYw95cJjPcsgae5Jc9Tk5gT+phJ06by4+DB2n2qVERERBAWFkbndm1JUav1tqHUaEjLUOqenEuWLEnp0qUpXbo061etoKWV4IciHjrb767fY87sWYwd9/P/dsE/AVb+sYHp06bw1bRlvEpIoEH9Opw+O1f3PyhTpgx9+w1k9uQBDOggkMu13724VyrO306lffsOhIaGcujQIWKiI+myvoXe9ju3c2fwz3tYtWoVPj4+uLi40Lp1cxbOr0mTJtqb/Z27kbRp2xtfX18KFnw/V9b/Q26NZCRJWg00B6KEECUy22YDLYAMwB/4VgjxMoe+QUAioAZU/5SYfbEjma+/bs/u3fvRaF53n6goXtybgQMH4u/vz7Fjx7h/9xkKuX4tCJU6AQtLQa1atfDx8eHu3XucP3MTE8lV5+rIUL3CKl86z58H6do0Gg3z589n7pz5xMRG41uuPHPnzaZq1ar/1On/ozx9+pQqFSpTSlGYQkbuRCljOZ9xi4VLf6Vz5848evSIy5cvc+nSJQ4dOoT1Szn9XPTdU6fi75BQzJTps6bj4+OjWxQqhKBdqzY8vXiL+ubeyCSJkyl+OJUqxKHjR3N0OQkhWL58Ob//upi4uDjqNqjPL5Mm4unpmePxCyGYP2cOM6ZNR61UIlMoGDZyBKPGjMlx+7NmzmTfooX8WtwH48ygj6WBwdyxsqVn//7cvn2bO3fucOfOHV6+fImxTOJem3KYyrPcRjdikhgXnMYDv4Bs24+JiWHpkiVcOnMCZzcPBgwaQrly5d733/FJoVKpaNK4Lurkp/RubUliipoFG17Ssu23zJw1V2eX38mOAxt88fHKynIRHJpMuXpHSc/IikarVNGFo0f0y0qM+ekM+RwaM2HCxDceR66MZOzMxeFmf38IzRnn9Xfeuj9JkmoCScC610SmIXBSCKGSJGkmgBBiVA59g4DyQoiY//4s/ne+WJHJkycPKSkCScr6gmvXryQDYGRkhIODA1GRsShk+tFBcqNkJkwczbBhwwBt4sAKFSoRG52IKs0EmUKNWnrJnj27qVev3j93ch8ZXTp0JvJYENUtfXVtoekRbIo/iMJUQUJCAgA2NjaUKVOGy+cvMsr1a/IqtH54lUbN4rgDLF6/PMdoLpVKxapVq9jwxzo0ag0du3ehb9++uR5Zp1KpiI2NxdbW9q3F0JRKJZ2/+ooLZ85Qxd6WZ8kpqPNYcuTUKb1gDCEEt2/fpmaVytxpUQqFLEuwHsSn0P70Y6rVrU+NGjWoWbMmFSpU4OXLl1QpX45qNmoaOxvx7JWKZY+T+W3VGtq1a5er5/uxkJ6ezpo1a9i/dyvmZuZ06daHFi30K6yOGzeGm5c3sW5xWcxM5aSlq+k15DYFfZoz4PtBPHv2jLVr16JW3WfVyqZ625+/4ArxL0uzYMGvbzyG3BKZQ0193m0IuPx5+537kyTJE9j/l8j87b02wFdCiC45vBeEQWQ+PH+JjI2NLa9epWcTGbk8nadPn+pWwhf29iE8LB6EBSChEcmYWajw8/PD3j4rQiY5OZk///yTkydO4VnAk379+v4jw/B/g6tXrzJ21Fiu37iOi7MLI38aSdeuXfW+/CkpKXi5F6StcT3yGenPc80KW0mbDm1p2LAhlStXpnBh7UT5zOkzmDNtFpXNfDBFwQ1VIGWql2f77p2fVB6s27dvc/36dTw8PKhbt67ePMzrVClXhnaKBNoX0H6OhBAMvxFCoJUTaUoVDx5oI9hMTExwymdH3bxpzKqaVZfkakQK311NJTD0xRv38bmTkZHBtz26cPToYcqUzMed+zHUrlOXtWs36UqB+/v7U7lyOa5d7YatjVlmPzV16m1l1qzlNGnS5I3bzw2RKWVnIQ42Kvpetm6bbgQDr4vAciHE8r8dkydvFpl9wBYhxJ85vBcIxAMC+P3v2/1QfDCRkSTJFDgLmKCd+9kuhBgvSZItsAXwBIKA9kKI+Mw+Y4BeaH2GPwohjmS2+wJrADPgIDBICCEkSTIB1gG+QCzQQQgR9Lbj+ktkBg8ezO+/ryQ9XRu5IoTA2BhatWrOli2bdfZhYWF069qd8xfOARJFihRh7do1lClTJjcu0yfHzZs3qVOzDhUU5SlgUoAYVSyXlZcZNm4Y1WpU48SJExw/fpxLly6BUtDGrgFFzLPENkWdym9xm3kR+QJLS8ts27906RJrV68hJTmFNl+3pWXLlp/tDfTOnTs0qluHqnZmFDGTcSZeSYqlDacuXCJv3rzExsZy/vx5zp07x9rff2NDfQfKOZjpbaPctlAOnr1EiRL695v79++zYM5MHj+4S7GSZRgyYjRFi77fje5TJCAggMePH1O4cOEcC6+NHj2CnTvW069fSczNjfhjzSNcXEqwY8eetz7A5IrI2FqIAw2LvZet+5br//NIRpKksUB5oK3I4cYuSZKzECJckiQH4BjwgxDi7N/tcpsPKTISYCGESJIkyQg4DwwC2gJxQogZkiSNBmyEEKMkSSoGbAIqAs7AcaCwEEItSdLVzL6X0YrMr0KIQ5IkDQBKCSG+kySpI9BGCNHhbcf1l8gkJyfTuHFjbt26jSTJAQ0FCxbg1KlT2SLMQLvORalU6oUuf4m0bt6aV+dfUdq8lK4tThXHppjNqIQKSZIoU6YM9erVw9jYmNWLVvJVnobYGeUlTZPOoeRz+Laowuq1q//Fs/h4iIuLY/369QQH+FOhchXatWuXo7uvbtVKdM8TRrMCWcKcotJQZO0z5GYW1KtXj4YNG9KwYUMiIiJo07wx35cxonJ+BRfCVCy7q+LA0RN6NYS+JIQQHDlyhI0b15KenkarVl/Tvn37d+blyy2R2d+g+HvZemy99j+JjCRJ3YHvgHpCiJQ39X3NfgKQJISY8y7b/5cPFl2WqaRJmX8aZb4E0Aqondm+FjgNjMps3yyESAcCJUnyAypm+hGthBCXACRJWge0Bg5l9pmQua3twGJJkqScVPzvWFhY6NJV3Lt3j8KFC1O9evU3rlF4PX3+50hycjLjfhrH+nV/kpGRTrNmzZg9b7beXMLLly+5dOkSjYz0s+raKmwxNTJl5vyZtG/fXs+NaGdrx6QJk7BQmPEqLZG2bdqwZNmSf+y8PnZsbW0ZNGjQO+36/jiEyUP6U97RDEdzBSqNYNrNl5QuXYpS5Stx5MgR9uzZo91mHhNm1zanfTHtOpDq7ibkt0hm7IghHDtz4YOez8eKJEk0btyYxo0b/yv7F+LDrZORJKkx2ntorTcJjCRJFoBMCJGY+XtDYNIHO6jX+KAhzJJ2iHADKAQsEUJckSTJUQjxAkAI8SJz6Abggnak8hehmW3KzN//3v5Xn5DMbakkSXoF2KHv00SSpL5AX0Av67AkSVSsWPGLfbr7CyEETRs148XdaGrIm2BkYsSjQ/epcr4KGzZv4OzZsxw+fJjLly8j08iIsorC9rV5liR1EsihR48e2Ra4DR02lP4D+hMYGIijo+MXPxL8X+nQoQOPH9yj+vz5FHe0JDA+laIlSrJ/117s7OwQQuDn58eRI0f48ccfaO2jf53bFjFjyJIr2eq8vHz5ktkzp3Nwz3YsLCz4ptcA+vbt+0nNgX30iNzLSyZJ0ia0D+n2kiSFAuOBMWinJY5lPiRfzvTuOAMrhRBNAUdgV+b7CmCjEOJwrhzUO/igIiOEUANlJEnKi/YEs01UvUZO/wXxlva39fn7cSwHloPWXfa2Y/5ciYmJQaFQ5FgX5sqVKzy6+4jGRu2RZQZClDGpzLHY3dSqVQsAX19fRo8ejb29PZPGTSJPeh5cjF1IUCdwNuMcffr2eeMKajMzM4oVez+ftIGckSSJCZOn8sPgody+fRsXFxfdeq6/3vf29sbb25vJ48cS9FJFYbusSLigl2oUQoOTkxONGjWicePGVK9enVZNG1DSIpwFtQQJaTB97khuXLnIij/W/Run+Vki4G9LJf6PbQnRKYfmVW+wDQeaZv4eAPxzSd9e4x9ZjCmEeClJ0mmgMRApSVL+zFFMfiAq0ywUcHutmysQntnumkP7631CJUlSANZA3Ac7kU+Q27dv8223Xjx58hiBhmpVq7Nm/R86N5hSqWTnzp3k1djrBOYvXBUF8KlSiM1bN+HgkBXV5OLiwsghIzgQdRATExMGfD+ASVP+kZH3F4+dnd07w+L79f+eEVuXsraJnLymMmJT1Yw8m07z1m0xMjHl8OHD/PmnNvioppcRK74x1bmJqxUQFJ2/nZE//ayXAPMvUlJSkMvln3VGgg+B5gO6yz52PtiYWJKkfJkjGCRJMgPqA4+BvUD3TLPuwJ7M3/cCHSVJMpEkqQDgDVzNdK0lSpJUOTOYoNvf+vy1ra/QLkj6IkcqORETE0Pd2vWQntlQ37gH9Y178OJqEjWq1uT333+nXbt22NvbM3v2bMJTQ/j7pUswjqVl6xZ6AgPw9ddfExASSGRMJDHxMUybMe2TKGwWGhrK6tWr2bJliy6f2btITU3l8uXLPH369AMfXe7x8/iJ+NRuS8nV8dTckkrp1S8p27gjGzdv4c8//yQyMpKrV69SqVxJvi4p15uHtDCWqOYh48CBA3rbfPz4MY3qVsPO1hoba0s6tG1OZGTkP31qnybi/dL8f675zT5kdFkptBP7crRitlUIMUmSJDtgK+AOPAe+FkLEZfYZC/QEVMBgIcShzPbyZIUwH0Ibeicyw6TXA2XRjmA6Zg4L38jHULQstwgODmbnzp2o1WpatWqV7clz3rx5/DZhDSWopdd+ImkDSSIeNzc3GjVqRKNGjZg8YQrq5zJKKMqjkBQ8y3hAoPEjnvg9eWMm5E+JGVOnMX3aNMrndSVZqHiWHMP23buoU6fOG/v8sXo1w4cMwcnMgpiUFLyL+LBl105cXFze2OdjIjo6msDAQLy8vHKcC/vl57HEn/mVOU3114oVm5NEYJzAx8eHRo0aUbVqVYb8+B0j6yTRp5pEugqmHZFxPNSdm3cff9bzN7kRXVYir6XYWfP98g767Dv32eUu+2IXY37qLP99OUOHDMNeVgCERIwIZNzPYxk9ZhQqlYrr168z6MfBJN9VUMhY/wN+V3Wab4a3YeLEibqn2Li4OH4Y8AM7du5ArVFTs3otfvt9CT4+77dS+Z8kNTWVCb+MZ92ataSmpdGkcWNmzJn1xvTuV65coVWDxkz3qI2dsXbe6G5iJAuibhDyIly3aO91Ll68SJsmTZnjVZaCFlaohIZ1Yf7cz2vKlVs333hsGRkZ7Nu3D39/f0qVKkXDhg0/2ptwcHAw5csUZ3lLDU2KKFCqYd55NRuf2tL3+8EcO3aMM2fOkJaWRvNSErv6Z83xCCGoMs+MaUu20bBhVrShWq3m0KFDnD1zCgfH/HTt2vWTrqeTWyKzo8b7pf8psv+sQWQ+dT4VkXn16hXR0dG4u7tnWzcRGhqKj3dRStAcc5k1AOmaZG6pd1K1RmWuX7+uS9liZ+RMNZM2WfnThJoLbOPIqUM5lrtVq9VoNJq3pk/5t2nWsDExtwNoaVUSc5kxZxKecoMX3Hv8UC+wISEhgZCQEH4aORrL2yG0d9JfqzDa/wTO5UtQsGBB5HI5CoVC9/P4wUPUTJPo4OKls1cLQcd75zh09nSOhbPCwsKoU706NsoMipmZcC0xmTzOLhw9ffqjDYE/ffo03/XqStKreFIz1JQtU4Y/NmzFzU07PZqWlkaXTl9TWX6IIfX1J697r9eQ4tKGX375heLFi5ORkUHLpvWJCblL63JpBMaYsO+mYNvOfdSuXftfOLv/n9wSme3Vfd9tCBQ9cOazE5mP35H+hZGWlka/vv3Ztm0rxgozJJmGaTOm0r9/f53N7t27sZd7YC6sdW0mMgvsVAW4dfMWHTt2pH79+lSpUoX6dRrw4MU53DTFUKMiSHaHClUqvLGeulwu/1dW2Gs0Gp4+fYqZmdlbC07dvn2b65evMtW1NYrMQIXWdmV5EZFA0yZNyGtjw/PnzwkJCdEJrZEko7tLmWzbMhISt27d4sGDB6jVatRqNSqVCrVajSwjgw6F9PvIJQlzlYby5ctTqFAhChUqhJeXl+7nglkzqWcsZ2Bm1JcQgl+e+PHL2LEsWLQody5ULlO7dm0e+T0nICAAc3Nz8ufXT61vampKi1bt2LLwDEPqp+va1RrB8Ucawi5uY9u2bTg4OODq4kJe9WMuTZTrCvMdvq2mZ/eO+AWG643ohBDcuHGDsLAwypUrpxO1zxEhJNTqzzNrxftgEJl/GCEEMTExmJubY2Fhke397/oN4PDOcxSUmqLQmJCqimf0iHGkp6cjk8k4e/YsR44cwSzNURsZ/xoKhRGDBg9i/PjxuraLVy4wYfxEdm3fhbGJMX169WDkyBEf+jT/K06ePEnPrt+SmpRMukpJkSI+bNy2WS/3m1qt5sGDByxcuBB3hY1OYP6imIkjO27fxruYD97e3tStWxc3Nzfc3Ny0lROnzaahphAmMu1HPjwtgUBlAkGBITlmeJg1cyYnFv2uVxUzIi2FCHU633//PSEhIfj5+XHq1CmSk7VJVeWSxOR6NXT2kiTR09WZvps2vVFkVCoVBw4c0C0IbtWq1T8euSVJEl5eXm98v0OHDsycOp6h2yMZWEtDqlIw9YgxxUpX4Oyq9Zw+fZpTp05xaO9WfuknR/5aws9GpeXI1idx69YtfH21T/NRUVG0btGQqBeBFPEw5eK9RLp26878BUs+Wtfi/8uHXIz5sWNwl/2DnD59mj69+xESGgJC0Lx5c1auWqFz8fxVormg1BSFlHWjiVcFEZpxBQ0qPD09KVeuHAf2HaKMvDVmMq0bJl0kc1/ax+VrFz+pNSnPnz+ndPFSfJWnGkXM3dEgOJ94j3smYSxZvpQrV65w8eJFLl++TGJiIgB5jcyZW6gjsteiotbFXqHBD50YM/anbPvQaDR069SFC8dOUsPcmVSh4mTCc2bMnUOfvn1yPK5Xr15Rxbc8HukaGlg7EJ2eyoaYEAaNGc2w10RaCEFkZCQPHz6kccOGXKxbHbPXRoLPU1Joe+EqlarXoFatWtSqVYvKlStjbm5OXFwc9WtWR/YylsrWRtxJVhMhjDh14eJHV0I7MjKS8eNGs3fPboyNFXTq0oOfx0/UWxvVqF5V+pS5RZuK+nM3zv2SSVGbU716dapVq8bRQ7up5BHMtJ6WyGQSL5PUNB2bQJ9Bs+jTR///ERERwYkTJ8iTJw+NGjX6x6u/5oa7rLi1ldhcudJ72ZY6evyzc5cZRCaXEEJw69YtQkND8fX1zRaB9PTpU3zLlcdMXQgzuQMCFckEUKysG8uW/caVK1c4duwYO7buppipfur2VE08cebXuXHrmi5jwdKlyxgxbCR2UgEkIRFLIGPGjuKnHG6yHzPjf/6Fs8v208K6sl77zOebiFK+RCaTUbJkSapWrUrVqlWpUqUK3Tp9g2lwIq3ylsZMZsS5V884nPqE+08eZgu3/gshBMePH2f/nj1Y5LHkm25d3ynGL1++ZPGvv3J0/0Hs89nT78cfaNSo0RvtmzdogHdoML093XT7nPzEDz9rGySFEbdu3dLNd1WsWJGMlGQKJUYwvWxWHaJ5jyII9SjF9n37/5vL+FHwxx9/8PvsQRwfIzAz1p7P+rNKJu61pFGztly8eJF79+5hZiwRucsdM5OsUcvhqylM3+PIhct3dG1z585iyuQJ1KloS3yCmseB6ezYtf8frb+UKyJjZSU2Vq78bkOgzLFjH4XIZCYyfheanIqjZduWQWT+f6KiomjUsDH+/oEYG5mTnBpPz297snjJIt3NY+D3P7BpzVEsZVkuICE0hKacQiOUgDY/WlpKOp6KepjJssKGo9UPqdmqCJu2bNTbb2BgIDt27ECtVtO6deuPKhIsODiYFctX8DwwmGq1qtO1a9dsGQGCg4Pp3L4TjgEKqlvrJ4P4M/YE9fu04ueff86Wrfnly5cMHvgjW7dtRalWU71SFRb9/lu2TMT/NIGBgdSpVo0CCjnFTIy4npJGqqUVpy5cwM7OjlevXnHhwgXOnDnDmTNnuH39KscblcQ9T9aoNVGpxnf/XZJSUj+JtUevo1ar6dWjMyeOHqB5WYmAGAX3Q2UcPHJSFyhx584dGtWrQshmR731OTeeptNoRCTlKtakfPnyWFlZsXTxTM6t8sLVURv4cujCS/pPjyXo+Qu9YJhbt26xfPkSIl6EUq16Pfr06Yu1tTW5QW6ITDEra7Gx0vuJTNnjRz8WkUlDu+j9bX4+uRDC/S3va7dlEJm3k5aWxpIlS9iwYRPGxkb069eX7t276/mO69VrwNVLDzFC+8XRCBVqeSjDhv9IgQIFuH37NmvXrEeW6oqFQr/Mb6zqJn36a4ttFS5cmFWrVjN8yCjyKotiKrMmSYSTbBzElWuXPyoReRunT5+mdYvWFDMuhI2wIkgKQ2MrceHKRQIDA9m7dy979uzhzh3tU6unmRMD87fW3XTSNUpmRW7l8s2rbz3nvybrc7tI2f9DSkoK27Zt49mzZ5QuXZrWrVu/MVLPwSYvO6t6ZBOZMrtvMXzUKL766ivKlSunuy5JSUnMnT2bXVs3YqQwokP3b/nxx0Ef1fmD9qZ/7tw5HB0dadmypV6IuEajoWhhDxb0UdKgfNZDx/cL47kR6o5MYcKdO3eQhJIxvZwZ08tZb9u1+gTx06RVtGihLbm8detWfhzYh/7d3SjoYcbeI7E88JM4f+Fatrm2xMRE7t69i5OT01vnoF4nt0RmQ8Uq72Vb7sSRj0Vkbgkh3rq4531s4AsXGY1Gw/Hjx7l//z7e3t40adJE7+lRpVJRvXoNHtx/Qka6Nom0samS5s0bs2nTJkA7inFzc8dCXlSvAFqG+hVJ6YGABjMzM2xt7UiMARujrKdtjVARo77I02dP9HzwBw8eZPrUmYSGhFKlWhXGT/j5kxEYIQSFPL2okFIcb7MCurZ9L08QJIWRkJiATCajWrVqtGrVikaNGvFNxy4oXmRQydSHNE0GZ9PvU7NFfVZ95uUABvTpTeLZQ0wp7awTkrkPwtkZnc6L2HjUajXu7u60bautq/PTiKE4JoXS18ccpUaw8GEK1kUrsHPfwTdmD/8YOXbsGF06tqV3ExOKuMs4cEXDrSAzzl+6gYODAxkZGXT4uhV1ijziu6/13Z/1+j7i0t1UihcvTokSJTh8aC+7VpfDt1TWyP+7UfcoWKwzEydO1rXNmTOLadOmUMjLnuDncZQpU5aNG7e/M2FrbonMuvLV3su2wqlDH4vImAoh0v5fG/iCRebVq1fUrFmTwMAg0tPVmJgoyJfPngsXzuPkpB1t7N69m27deqJMs9R9iYXQoCGKRo21dTsePHhAako6ec1K6X3RVepkTCxfcubsKQoXLkxcXBzFi5VAlWyFmZQftUgnXf6ctl83Z9XqFf/KtfgQBAQEUKFUefrbdNG7HqHpEexJPsa8xfNp1qwZ+fLl072XkJDA/Lnz2LVtJ+bm5nzbrxe9evX6bCON/iIuLo56NaphlBBHRSsFd5M1vBBGnDx/ATMzM/bt28fOnTs5evQoGRkZFLM15XQ7D911zVALqu15web9R6lU6f0mlj8Wnjx5wvLflxD2PIAKVWrTu3cfPRfXzp07mfpLP86s8MDYSPs58A9No1LXp3zbsx9+fn5cv34dhZTA04v682RnL8cw6JcgZs1ZTJEiRXj48CGjRvZn144WuLtZoVSq+Xn8RULCbNm378hbjzM3RKaopbVYV776e9lWPH3wYxGZn4EUIcTc/3tbX6rI9OvXj7VrN5CRge5LK5drqFWrKsOHD8fPz48VK1by4H4QRnJ9/26GMoY8VgoqVqxIkSJFWLfuTzRpdhjJsxbcZfCCnr3bs3DhAl3b8+fPGTfuFw4fOoyVlRU//Pg9P/zwwydzM7116xYzp87k4YOHlCpTitFjR+vmQYQQXLlyhRUrVrD+j3UMc+mLQsqKsvJPDeZp/lCu373xbx3+R4lKpWL//v3cu3cPb29v2rRpky2EOTExkW86d6Jk5FUGl9V/8h5xKYYyvca9sSaNEOKTGuX8hVqtpsPXrfB7fJmuTcyJSxCs2v2SCZNn8t13A4DMjAW+JXh2oQ5GRlnfoa17Q/lx3B2SklUAWFoaM39OPb7+KitrdVqaimIl13D33mOcnfVdcq+TOyKTV6zxfT+RqXzmwMciMk+BMn+vTyNJUm8gnxBi+vtu69OaWcxFNm/eTEaG0HNxqVQSx48f5/jx4wCZvvTsaxYsLE1ZtUqbYBKgWbNmtGv3FUpNKhq1EXLjNPJaGzH2b5Fe7u7urFu35oOd04fkzJkztGrWipLy0hRWFCHwYBDV91Vn2cplPHjwgI0bNxIQEICJiQl2dnZcSrpJ9TzlkSSJDI2SK6o7jBgw+t8+jY8OhUJB69atad269RttLC0tqVu/AReWX8v23q0XiRycNo3o6Gi6dOmiK7F86tQpfho+iCu37uOcz4bvfxzMyNE/fTKlrOVyOVu27eHAgQMcPLCbPFZWHDn+rV6mBQ8PD0qXKs2MJX6M/dEbmUwiMjqNWb8Fs+S3VRQpUoQnT54w/pdRuLrqB4+Ymiqwt89DbGzsW0Umt/gE18mkvqEA2nrgJvDeIvPFjmQsLS1JTtboiYz2qS+V48ePU6RIEYQQFC7sgzLdHJmkjc/XiGSs8soIDQ3Re+J8/Pgxixctxj8gkHr16tC7d+8ca7d8qpQr5YvDcwe8zQrr2h6lPORs4hnUkpp69erRuXNn2rRpQ2JiIg3qNCA5NhF7hQ0Byc9p064tq9as+mRGbR8bsbGxFPP2YmIZc9oWskIt4I9Hr1j0OI0SZctz8uRJNBoN5cqVo1atWqxf9Tvz65jSrJApz+JUDDmdTvW23zJzzvx/+1RylfDwcNq2bUZUxHMKuFty8240gwYPZfz4SboR3MiRw3n18jSzZ9TU9bt7L4qvOx4mODj8rYETuTWSWV225rsNgarn9n0sI5nLaMvZv8jhvTtCiPeuTfPFisw333Rl69adqNVZNz1JUlGnTg2OHTuqazt9+jQdO3YiJSUVjUZD/vxO7N69i+LF369m96dCeno66enpOebY0mg0KBQK+jt8r1dzJkOTwerYlYSEhujmsV7vc+7cOUJDQ6lYsWKOtUk+NBqNhsOHD3P86DHs7O3o2q2bXmXUN3Hz5k1mTZnKg/v3KVaiOCPHjtWtVv83uXHjBr27dSEsNBSVRkPxYsVY/ecmvL29iYiIYPPmzWzYsIGHt28wvqYlA8pnPb1HJKmpsO4Vz8Mjs4WEf+oIIbh9+zYRERGUL19eb74PtAtJq1QuT62a9rRoXoCAgJfM//UO06fPo1u37m/YqpbcEJkiefKKlWVqv5dtjQt7PhaR+RoYgTZLfvBr7Q7AkfeJKtP1+VJFJioqikqVKhETE09ycioWFmaYm5ty+fIlChQooNdHo9Fw//59jI2N8fHx+SR93G8iKSmJgf0HsnXbVjQaDYUL+fDb8iVUr14dpVLJkSNHWL9+PTu37aSDXSdsFFlRPFHKKC4ozhEaEfqWPfw7KJVK2jRvyZPrd6hk4kg8Si4mPGf95o00b978jf3Onj1L2+Yt6GTvSUlLW+4nxbMxOpAd+/bqqoT+mwghCAkJQaFQvNHNU8zLneXV0yjjpP+EXvqPV+w8dj5bcs//tHfW4VEdXRx+ZzfuBiEQLLhLcHd39wLFCkVKP6xKgaLFKe5S3N3d3R2iBKLEZWW+PzYkWaQEGoFkX5777O7ce+fOhN37u3PmzDnBwcGcPHkSKysratWq9UUHR/1cAgICmDt3NmfPHsfFxZXvvhtC1aof9/hKGZGxl4tL1UrWsTXP7fgiRAZACPENMB24ANxAl7KlPTBWSrku2fVkVpEB3dP71q1buXHjBkWKFKFDhw7vjSeWkWlYtyEel19QUlkJE2GGd9wTrmvP0Lpdaw4cOEBAQACOjo645XHD/1EA9czrY64wJ0oTxdG4wwwcPZCRo0emdzfeYcWKFcwc+Tu/5KiREOfsUWQA0wMu4fPyxXvjg0kpqVquPPUiFNR1SnQpPxrowxErLeeufnh9lZSSQ4cOsX3zZkxMTOjcvTuVKydvbURK07ldK8q8PslA98Tvsl+4hhKLX2Jt70Tnzp3p1q0b5cuXZ/7f8/h5zEgq5TUnJEryMtqY7bsPULZs8kLTZ3RSQmQKWdnLxaU+nLcoKbXObf/X6wkhlgPNAH8pZfH4MgdgI5AH8AA6SClD3nNuI2A2uhxfS6WUkz/WHiGENdAaKAZEAvuklJ+0mv2DIiOE2AcMlFJ6fEqFXzpfS6j/tODhw4dUKFuJpqZdUSbxBLsWdYZHqtu0btOKbt260ahRIxQKBUO/H8qqVauwN7fndcxr+vbry18z/kqTeZYdO3Yw4dc/ePz8KUULFub3ieNo1KjRe4+Ni4ujQc3alPFTUN1ef1Q69OEuYiyNUSqVqFSqhE2tVqNWqxHAgUotMFUk/j3itBoaXdzNzFmzKFq0KEWLFsXFxSWJW7ukb69enNyzh5aODsRJybaAAAYMG8Yvv49NrT/JB7l27RqN6tRgcnUTmhUw41GQmh9PxpG3XB00Qsnu3buJjY0lV65cRIe85NQAE/I66P4Pt91WMeq4JU89X2TIEc2nklIis6hknWQdW/v8to+JTA0gAlidRGSmAsFSyslCiNGAvZRy1FvnKYFHQH10aesvA52llPc+p0+fwr95l60EDgkhVgFTpYyPfWLgq+HRo0fMm/s3z548p3qtqvTr108vy+Xly5exUdjpCQyAk5ELzuXt2bRpk1753wv/ZsKkCXh6epI3b94UC93xMTZu2MCQfoNob1OOLi4lePTKj27tO7Nqw1rq1avH7du3uXr1KteuXePq1avcvn0bhVpL8Rzl36lLKwSVKlUiR44cGBsbY2RkhLGxccI2Z/oMfKIjyGeZ2Dfv6AhMFUo9N2FbW1uKFi1KkSJFMDMz4+CO7WxxL4tF/GLeNtldaDPtL7r2+OYd82tqU7ZsWbbu3s/PI4bx3cFbZM/iwKBhYxj+4wgUCgWvX79m69atTBj7K99VJEFgANqUMGb2JTXHjx/XS0b2Bo1Gg0KhyFAm47RAm0LeZVLKU0KIPG8VtwRqxb9fBZwARr11TAXgyZvMwUKIDfHnvVdkhBCVgfvJiU32MT4oMlLKTUKIvcBvwBUhxBpAm2T/jP96cQOpx5EjR2jTsi3ZKYSFxo5FZ9cwb87fHDi0nzNnzrBhwwZOnDiBEiNU9nEYi0T7faDiBa2rNXlvvfb29mmejvnX0T/Tza4yhS11cxDuNnlRCkG3Dp2JiItGrdath7Czs8Pd3Z2hQ4ei0WjYtmwNFe1yYanU9e3Cay+M7azYsWPHB115zU1MmTNrHr/lLoWjiRlBcTHMefGAX8eOpXffPty7d09v27NnD4H+/vRzy5sgMACOpqbUzJKFAwcO6OUCSiuqV6/OqQvvX5NkZ2fHt99+y+ljB8ga/W4gTjOi2LZtG2XLlsXJyQmAPXv28OvoYdy895TsWe0ZOnwkP/5vpMFbMFmIT3FhdhJCJDW1LJZSLv7IOc5vvMCklH7xk/NvkwPwTvLZB3jvCl4hxHh0I51hQMfkNvxDfGydjAqdHc4UsCaJyBj4cpFS0rd3P4poa5DVKDcoIIcsyJ3AU5QqURqNVFOoUCHGjh3L7Ru3OXf0IEVFOSyEFc/VD/A39eH7Id+ndzcA3QT+E8/nFCqkb24obJmDCL8oRowaSdmyZXF3dydPnjx6Jqy4qBiGrVlLOVtXgrUxeMaGsvfg/n9dKzJi9ChCgoPptWABTuaWBEZHMmDAAEb9NAaFQoGzszO1a+vb10eNHMmLLZvfqetVeBjTp08nIiKC1q1bkz9/fr39YWFhrF69mjvXr1KoeAl69uyVpgLeqHlbZv96iJ7uEiOl7u/mGaLlkqeKk4sWsXTpUurVq0fJkiVZs2weSzqraDDQmLt+4fRfMoHoqEh+Gzv+I1cxICVotMkW48BUmvh/n8p9aEL+LFADnXntv1/4X+ZkGgEzgF3AuA8szPnqyAhzMjExMaxcuZKd23fj4ODAd4P6U61a4opib29vihYqTk1FNz2zRqgmgDtGRzh++hglS+rC4Gg0GmZMn8H8uQsIDQ+lfr36TJzyZ7IDCH4uJ06cYOWyFURHRdOuU3vatGmTcPOXUnL79m02bNjAhg0b8PXw5n+5mpHHPNE19UHkC/abPObek4f/ep0HDx5w/PhxHBwcaN68+TuRoD9EeHg4Xl5e5MqV66Muv48fP6ZS2bKsKFWCvPGOI9dDXjPo1m3yFS6cEAi0ZMmStGnThtatW2Nra0vNKpUoYa6ggo0x1yPUXHwdy/EzZylYsOC/XS7FUKvVtGxSn5Dn1+hWIo7gaMHCywpG/jKe6jVrsXHjRjZt2kTAi+fM7aykW8VEcX4eKKk83QTfl0HvOFEEBQURExND9uzZv3qzWkrMyRS0dJBzir1renwfjS9v/Oj14s1le5LMyTwEasWPYlyAE1LKQm+dUxmdV1jD+M9jAD5l5f7n8m8icxoYIKW8m9qNSEu+dpGJiYmhepUa+D4JwiYmN2oRQ6DxQ8aO/5XmLZqzY8cONm/ezOWLV2hg+S1GInHyNkDtRbSbNzfvXk/HHuhyyCyavYByJoUxwYgbmieUqubO5L+msGnTJjZs2MC9e/dQKpXUq1ePrE5ZOLnnMN/YVyWnmSPPo/1ZFXKOyfOm071793TtyxtWrljB0O+/x93JCZWU3At9zT+bNtOwYUM8PDzYsWMH27Zt48yZM0gpcbSxpourDT8WS8w7tPTxK6455WPv4aNp1m6VSsXWrVvZt2MzVrZ29OjVl0pJcp9IKcmV3ZHD30WQP6u+YGQfBdv3HUtwBX7x4gX9v+3GqTPnMDFS4Oqag78XrUrT/C8pTUqITAFLBzmn6IfzECWlyZUNnyMy04CgJBP/DlLKkW+dY4RuZFIX8EVnDuuSFvf3TO3C/KUSFRWFv78/Li4u7zwlLl68mLE/TiGfuk7CU2KMNpxrcVvQSN3cRKlSpYiOiEH7wpJCikoIIVDJWG6Ig4yd9hMDBgxI8z69wdPTkxJFijMkS3uslLpRhVpqmP1iA4FxrwGoUaMGnTp1om3btmTNmhUpJXNnz2HSnxMJeR1CFscs/DZu7AezWqYXwcHBHD58GGNjYxo2bPhed/hXr16xc+dOhg4ayOnGJclilvgQEK3WUGLXDWJiY7+o8C8tGtehmdMpeldNbNPDl5JyE1XEqKB48eI0a9aMHVvW0aZkEGNaKTA1gh2X1QxaZcS1m/e/uEyfySVlRMZRziqSPJFpdnX9x7zL1qOb5HcCXgG/AzuATUAuwAvdAspgIUR2dK7KTeLPbQLMQufCvFxK+ee/XOealPJf/diTcwwYROaLQqPRMGrkaBYuXIhSYQxC8tNPoxk5amSCoDSo2wiv03FkNdK3799W76Z9z+aMGTOGvHnzEhAQQNNGzXj66Bk2xk4ERPvQvUd3/l4wL10na5ctW8aiMbNoY6W/sPHU62uEF1ayftP6D96QpJRERUVhYWHx1ZthnB3s2VQpF3msEtMJB8aoqLLvFsdOnqRKlSpfTB/Pnj1Lm+YNmNkmlsbFFdzylQzeYkrTDt/h7JKDXbt2cfLkSXI5Sh7PsdRr99BVkiwVfuD3seMSyl68eMHiRQt4/OA2xUqVo2/f/u+s0v9SSCmRmVn4/e72b9P82j9fxGJMIUQ08PjfDgFsk5O0LNMGyPwS+WPsOFYt3kAubX1MsCBWG8bkCTMIDArC2NiIQ4cOcf3qDXIZ6Yc4kVJiZC7o2bNngrtslixZuHjlAjdu3MDb25syZcqQM2fO9OhWApGRkVy4cIGAiGCw0t8XrYijRs0G//rEK4TIMItlu3brxsx9W5hRJidKIZBSMu3uC0yNjahWrRru7u4MHjyYjh07YmZmhpSS/fv3s37VctRqNa07dqFt27ZpMuKpWrUqG7buYexPP9Jn3R1y58jGsFE/069/f4QQDBs2jIULF3Jkzf/eEcZiOVSs2LWNmrXqULlyZR48eECDejVoW9WY+oXg1NkzlJk3i5OnL6b6PGB6IfkqPaYKf/wQNMmpyDCSSSPi4uL4/bexLF6yhKioSGrVrM2s2TMSkpFptVrs7RzJrqqOqSIxfliE5hXPY0+gMILKlStTuHBh1q/ZRGHZCHOFDVJKXmkfoMr2gqfPH6fbKCU6OppVq1axf/d+smTNQv+B/SlfXrdOxdfXl3nz5rFo0SJCQkIwNTKhk2N9ClvkAeBVXBArQvZx8SOZMDMSkZGRtGrSiCd371DeyZqbIZE45crDhm072Lt3L3PnzuXevXs4OTnRr18/Al/5cWL3dvrkN8NEKVj1LJZClWryz+atX8SI5/79+9Su5s6TWUrMTRLb0/DPGI7dUSOl1CXvszXl544K+jZNdKaYvD6cuxHVWL9pZ0KZWq1m9+7dnD51gmwu2enevQcuLi5p2idImZFMfgtHOa3Q+5cEvE2bG2u/iJFMSmIQmRTE19cXhULx3h9D2zbtOH74AmbavCiFCVHqF2jN/bly5RLe3t4cO3aMCRP+pIRZJ/3kZzKGp9p9vPJ/mRC8ct68eYweOQZb06zEaqKwcbBk/8G96XaDjoyMpHrl6kT5RJCPvETKSG6p7jJo2Pc8ffaUzZs3o9VqadWqFT/88ANCCNq0aI2twhITYYx35Ev+Xvg33dJ4El+r1bJx40Y2rlkLQOdvetC+ffs0E2opJZcuXeLOnTsUKlSIqlWr6rlgHz9+nDlz5rBr1y6sjATXO+XH1lQ3colRa6m7/xUL1297x6U6vfimWwc8bx/g15Zq7CwFi48Jznhm4cjxc1y5coWDBw+yYMHfhO3KhWkSIXoVoqFI7wBe+gdjYWFBdHQ0TRvXISL4Ca1qmPD0Bew6Gc7mrbuoVatWmvYppURmaqGmyTq27Y01BpH52kkNkbl58yZdOnfl2fPnICVFihZlw4Z/ElxRnz59SskSZXBSVEIkWV0fHHeXSPULtFrdqNPU2JwcispYKxNFKlj9jNzljDl99qTeNUNDQzl//jy2trZUrFgxXedZZs+ezaI/FtDUvEHCTTJIFcwq//WYW5nTt29fBg8erLfyXaVSceLECWJiYqhVq1aaRwaWUtKtU2euHztFU2udGXFPmDfl69dm9fpkx/5LE8aOHcvjjXOZXc1Zr3zatUBEvZ5MnjI1nVqmj1qtZt68uaxdsZDIqCiatmjD6DG/Jizo1Gq12NpYcH9ZFrI5JP4O7nrEUWXwS+I0SsqUKYO5uSlm6vvsnJ4LhUL3fTpwLpQfZkfz+Kl3wnc9KiqK2bNnsWvnRkxMTOncpTd9+/ZNURNiSohMPgsnOaVg8kSm/c3VX4TICCGMpIz3JPqPGOZkPoJKpWLbtm3s338AZ2dn+vT5Vi9s/evXr6lVqzaqKBvMlYVAwON7AVSvXoOzZ88kJPQSWjPEW19+U+FAltymzJ03m8qVK3PixAl6dOuFSl0UC4UjkdpXvDZ6yIZp+99pl62t7Qdjd6U1e7bvoYDIpzcCczR2IJuVM4s2LKZp03d/YMbGxtSvXz9Frn/+/HlmTZuO53MPKlWryo8j//fR+acLFy5w6tAR5uerialC9zOobu/Kd/sPcOnSJSpUqPCv53t5eTFj6jQunztHbre8DB0xItVSIOfLl4/L2nfjiPlGqoh+8pS4uLh/zYmSVhgZGTFs2A8MG/bDe/crFAq6dunMmOW7WPKDFUZKQWyc5JeV0bRo1Za8bgU4d+4cN6+dZfX43AkCA9Cwsg3av/w5evQo9erVQ61W07B+TRys/fllYHZiYjRMXzKO82dPsGrNBr3rqtVqTp8+rRtxV6+eZuGQkqL9+p7lLwEpEiU104vM06dPuXPnDgULFkzIKviGmJgYatWsxb37j4iOlBgZC+bNm8fatWto3bo1oMuwKTVmmBolpsU1UToRHPQwQYyEECiEMdLorSRpRpG0bdeGJk109trWrVuza48df/w+gSdPblGqdEn+GDefcuXS/cHmg4SHhxMQGEAWjf5KdSklKoU61bMObtmyhQG9+tDUpgh1TbJwc8tJyv/zD+evXNIbOWm1Wnx9fXn27BnPnj1j1apVVDJ3ShAYADOlERXNnRg9ejTdu3cnX758uLm5kT17dr2R4tOnT6laoQIN7RzoYWvPk9v3ad6gAQtXrKBNmzYp3seWLVvy45DvOe4TQW1XncfEjYBotj8LJ+rhNtzc3Pjxxx/p168flpaWBAQEsHDB31y7cJY8+Qvx3fdD0myB58eYNn0OHdo+o2Cva7gXsuDC3Uiq16jNylVrE9z169auRExcgN55UkJoeBQNGjTAyckJFxcXjHjB/hWVEsSoVhUnSjU4wK1btyhZsiSgCxbapk1zHB2MsLU1pXt3P6ZNm0GfPmnr/i7fu+D+iybFGpxpzWVxcXF07tyZffv2Y2pqhkoVS6VKldi1a1eCB9Pff//N6FG/oopNdMvUamMxMolg+I/DefjwIceOHScqzBhzY/15mGi1D42aVmXEiBGUKlWK1q3acvncPSykG0phQoTaF7WJL3fu3kp3r69/4+bNm8yYNoOnj59SqVplfhg+jBw5chAYGMicOXOYO3cur1+/xtrYiq6O7bFWWuuSSEXfxtfpFXcf3k21iWmNRkOeHDnpaVGGQpaJpqStAdfxczXGvWL5BFHx8PAgLi4u4RghBFXscvBbfv2FgmOfnOXC6xck/V2YmJiQN29e3NzccHNz48qFC5QKCaNfnkRvqGshwUx85cNTb+9UMV2eOnWKzu3a4GImMDFS8Dg4msUrVmFpacmkSZM4ceIEjo6O9OjRg03/rKZudkk9V7gVJFl5N44tO/d+Eflw3nDr1i0ePXpE8eLFKVxY35Fp+fLlLJ49kgNzc2JhpvtbLt8VxOzNMPD7H7lx4wb79+/h+x6ODOuj75HWd+QtQuNK0KNHD/Lnz0+LFo2ZON6dVi10Lv9PnoTQuMVuDh06+U5enfeREuYyN3MnOSF/82Qd2/XOyi/FXOaDLuLLe/mU2JWZVmR+/vlnZs6cQ0yMRMS7kJqaQqdO7fn111958uQJ3303CG/PEJQK/VAkMaoXgIZ8+fLh4ODA7VsPMVfk05u01Rh5sGfvTqpXrw7o7MfDf/iR1atXExsXQ4UKlZk/fy5lyiQ7wVyac+DAATq260RRRXHsFY744Yu38KBF6xZs3LiRqKgoWrduzZgxYzh25BgTxk/A1TI7YepwLO2t2Hdo3zvxulIST09P3IuXYlYe/dGDT0wIfzzbi6m1RcJo5O3NwsKCYoUKMyp7GcrY6ATqauhLpvnd4P7jR0RERCQIVNLt6dOnqCIiWFWuMnktE/2wpZQ0vnyW6/dTb+GhSqXi9OnTqNVqqlevjrm5ecK+8+fPM2nSJA7t281Ad2v+qJFoEtrzOJopjxy4fvfhF+GJ9jE0Gg19vu3O4QN7aFjFhucv1Dzxkew/eCwhI+2UKZN5eH0p8yboWx+qtT7D9TuvEz4XLerI+VNd9I6ZNOUSseqKzJgx+6NtSSmRGZe/RbKO7X5nxZciMn7AAj4wopFS/pHsujKryDg5ZSE4OFJvIl5KLfoh2gTGSnuUCsskx0iUJq85cuQQlStXRq1WU7FCJR4/8gG17octjF9Ttlxxjh078s6PWkqJVqv9olZ0vw8pJfnz5KdwaAlymuZOKL8ccZ5b0dfp3K0zo0aN0ktDHRQUxPnz53F0dKRSpUqpdkN7k9p50aJFbNmwibmFO2KpTIyMcC3MizN2wVy6ee1f6zl27BhdO3TETmGCBMKkin82b/qoB1P5kiXpJoyp5pQY7DZUFUfjsyfo0KULffv2pXr16ulyQ8+R1YE9LUzIb584h6OVktwLAnni6ZMwCf81cOvWLc6cOYOzszPNmjXTi37x8uVLShQvxII/C9G4Tla0Wli2wYvZKwK5fuMeHh4eLF++nAf397Flg7778JLlt7j3IBfLlq3+aBtSQmTymjvJcflaJuvYHneXfykik6zV/Mkh08bpjoqK4l2RFgghWLx4MadOnWLZsqWYmmmQMnEplVZGkTVrloT4TkZGRpw8dYJhw/uRJYeWbDlh1JihHDiw7703GSHEFy8wAP7+/vj7++Nqor+gt6BZERwcHFm9erWewAA4OjrSrFkzKleu/Fk3WJVKxapVq2jVtAVdO3bhyJEjevs9PDwYN24c+fPnp1atWuzZswc3NzfWBV4hVqtzhAmKi2Bb2B2GjfrfR69Xp04dvPxesHjrBpZu24jnC99kucgOGTGC+S+8eBUTA0CMRsNfz56QL68bO3bsoGbNmuTPn5/x48fj5eWld+7hw4fp3rEj7Zo3Y/Xq1ahUKZumydHBHv9I/aV/obGSWJWKe/feTR0SExPDixcvEtIlfEmULFmSgQMH0rZt23fCK2XLlo1t2/fw8/RXFK1zjoI1TvPPHsGBg8exs7OjdOnS/PTTT1y+8pIXfhEJ56nVWjZuek6jRskzX6UMAq1M3vYFYZiT+VzejGSaNm3KgQPHSOr7IKUKd/eSXL58Kf6z5IcffmDRosWYmFgh0GJqZsSxY0ffucF+jQQHB3P9+nWyZ8+u5/QgpWTnzp20b9uerg69MVMkhj7xifPC0/kJtx/cTtG2qNVqGtdvhM+tp7gbuxGjjeNc7EN6DexD4aJFWLlyJceOHQN04tCrVy9at26NlJIenbty7NgxnC3teBn5mhEjR/Dzb7+m2khCSsn4sX8wY/pf5LS2wSc8jPr16rF87VqEEGzbto0VK1Zw/PhxhBAJ7b13+xb/LFlMz5wOWBop2PQyjCxFSrDrwMEUe/CYPXsWG2ePZXMzS2xMFai1kqFHwtj5OJaw6Dhq167N6NGjqVOnDr//MoYFC+ZjogCFsQm//D6OgYMGp0g70gqtVsujR48wMTHBzc3tnf3Tpk1h7txp9O9TBDs7U9ase4KDYwF27dqPkdHH/Z5SZiSTRf7ulryRTK97y76UkYyDlDI4RerKrCLz+PFjKlSoSEyMithYFSYmRhgbKzh58sQ7+c09PDw4deoUTk5O1K9f/6tPSyul5Pdff2fGjJk4mWcjNDaYIsUKs2X7Zo4ePcq0adO4ffs21hbWZBeuVLOojZEwIlobxdG4A/wy5ecUD7K5ZcsWxvQfzncOjVHGe+CFq6MZ57EOlVTj5uZGz5496dGjB7lz537nfF9fX3x9fSlcuHDCotXUJiwsjPvxczA5cuR4Z7+HhwerVq1i1apVPH/+HHOlgpMN3XE01X1/1FpJh4tPGLtgMa1atUqRNmk0GgZ/148N6//B3dWae/7RFC9VhmWr/2Hjxo3MmDGDFy9e4OrijKtZOCvbGJHbXsGdlxq6bJX8MX0xnTt3TpG2fCmcOXOG1auXExERRtOmrenQoUOyf8MpITJ5zLPI3/K2Stax395f+kWITEqSaUUGdHbd+fPnc/HiJUqVKsn3339Prlwfjff21bNp0yYG9xlGJdEEc4UlWqnlVtxZfORjImMiKFasGCNGjKB58+b06NqD06dO42juhH/UK74b8B1Tp09N8VHCt9/04vX+x9SwK6FXvsz/EC2+78y4ceO+2iyMWq2Wn3/+mWtrl7GgfAG9fSuevCCwQh0WLF2Wotf09vbm9u3b5M6dW2/UHRsby+rVqxn2/QAuD7LEzTFxBHXokYrxN3Jy+eb9FG3L10xKiczPeVon69h+D5ZkOJHJ1OtksmXLxrhx4z5+YAZjzsx55NeUxtxE59CgEAqKm1TmWfhd1qxZQ9euXRNEZM/+PXh4eODl5UWxYsVwdHT8t6o/G41WS6gm8p1ylYmkUqVKX63AgG4RYqVKlTi5btU7+17GqJCpsFIvZ86c73WNNzU1pX379gwf+j15HfT/psWzKfHw8nnnHI1Gw/Pnz7Gzs/uqHAe+FKTkS5tvSVNS7ZcrhMgphDguhLgvhLgrhBgaX+4ghDgshHgc/2qf5JwxQognQoiHQoiGScrdhRC34/fNEfF3QCGEqRBiY3z5xfhkPpkelUrFjh07mDlzJqdOndJb86HVavHx8sZcoR8G2UgYYWtph7u7+zujlDx58lCjRo1UEZgXL17Qu3dvVq1dzZnXd/GLTTQDXw9/wmupW4CXFoSGhrJo0SJ+GjOGHTt2pOhkeKNGjfCIjmO/b2BC2cPQSNY/f8nylSvp06cPL168SLHr/Ru2trZky+LIOU/9ILqHH6uIiYqgadOm7N+/H61Wy/bt28mfx4W6VUuTP68rbVs0Ijg4RUz1mQqZzC0jkmrmsvg0oC5SymtCCGvgKtAK6AkEJ8niZi+lHCWEKAqsByoA2YEjQEEppUYIcQkYClwA9gFzpJT7hRADgZJSygFCiE5Aayllx39r15ecTyYl8PT0pGa1WqjDBeYae16LFxQpUZB1G9ayYcMGFi5cyPNnHuQ1KUJ5i7oJ5wWq/bhtehLfl77JmhD9FF6/fo1Go9ETqYiICKZNm8Zff/2FWq1myJAh5HNzY9SIUeSwyEK0JhaNKezcuztN1hLdvn2b+rVqU8zcjpzClGtxrzHP7syRUydTLK7a1atXadu8GVZSg7WxEQ9fhzP5r+k8fPiQuXPnYmxszMiRI/nf//6nl9IgKCgIpVKJnZ1dirQD4J9/1jF6aH8m1pWUza7k2FMNf5yElu06s3fvXl6+fEnOnDmJDHnJlj5QLb+CyFjJL3uVPJZlOXjsTIq15UsmJcxluc2yyFG52ybr2EGPFmU4c1mazckIIXYC8+K3d/JRv51zWghxEBgLeADHpZSF48s7x5/f/80xUsrz8elFXwJZ5L90KqOLTO0adXl5JRo3pc55QUot11UHCNR4o9aoqVGjBl26dGHCH39iEWFPVm1OImQoz8Qdlq5YTPv27VOsLZ6envTu3ovzF88jhILiRYuxeMUSLl++zK+//srLly/p2LEjEydOTPAMioiI4OzZs1hYWFClSpVP8rq6evUq8+fMw8/Hl5r169B/wIBk35grlSlL1TAFTbPmAXTOEZO9blCxZ0cmTJz4qV3/IBqNhnPnzhEdHU3VqlUTxOTp06eMGTOGzZs34+LiwoQJEyhTpgzf9/2WO/fuoZVQrUolFq1YnWLzhvv372f6xLE8e+5ByVKl+On3CVSoUIG4uDi2bt3KqP8Npa97MKMbJj50qDWS/OOMOHb2WqZIy5ASIpPLLIscmUyRGWwQmc+8iM6MdQooDnhJKe2S7AuRUtoLIeYBF6SUa+PLlwH70YnMZCllvfjy6sAoKWUzIcQdoJGU0id+31OgopQy0SahK+8H9APIlSuXu6enZ2p2N9V5/PgxPj4+lCxZUm90EBoaSras2ahp/A1KkXhjCNX4c0d5hLMXTidMAgcFBTH/7/kcO3yC3HlyMnjYYNzd3d+51ueiUqkolK8gbpHZqWBZCoHgZuR9joSeJVYTR5UqVZg+fbpePvn/wob16/m+33c0sCmIs5ElV2P98DNTceHqpfea+eLi4vD19cXb25s7d+4w8ofhbC/TJMGzDeBBRDBzIjx48PxZirQxOZw7d44ff/yRCxcuYGFixLhyznTKb49KK1l4P5gdISbcefgkxUeb76NJ/Wr0zXeRZiX0hb7aTAXDxi9L8EILDAxkyqQJHNi7A0tLC7r3HsSAAQO+ivVgHyNlRCarHJEreSIz5PHCDCcyqf5NFUJYAVuBYVLKsH/xSnrfDvkv5f92jn6BlIuBxaAbyXyszV8qISEhtG7ZlmtXr2Ntak9ItD9Dhwxh4uQ/CQsLY82aNahUaoSx/p9FoMTKykrPy8jR0ZFff/uVX3/7NVXaunfvXpRRCqpYJQpXWaviPInxpHqXOixevDjFPNTi4uIYOmgwP2Srjpu5bmK6AnlY/PI8/fv2o3LVKnh7e+ttr1690o9PJhRoJSiTNEkjJb4+vrRq1Yr69evToEED8ufP/8F2x8bGcv78eZRKJZUrV/4sIahSpQrnzp3j2969eXV8O90KOgBgpBD8UMKJ48decuDAAZo1a/bJdX8qFarUZvex6zQrkTh38ypMctMzmi5durBkyRLat2/P7BmTqJkniGXdtQRHSMbPH83N6xdZvPTjK+ozAxLQpMDEvxCiELAxSZEb8JuUclaSY2oBO4Hn8UXbpJTp6t2UqiIjhDBGJzDrpJTb4otfCSFckpjL/OPLfYCk7jCuwIv4ctf3lCc9xyfeXGYLZNhZyR7devLsaiDFtW1QxCjIQRQL5izlyLHD3L59m9jYWCxMrfBW3ye3cXFAZ/bxUdyhXYfkPUmlFJ6enjhh9055dmNnbKxtUtQF+v79+5gL4wSBeUM1qzxM37mbrdu3YWlpmeBxVaJEiYT3b7a+3/Rkp/8z2mXTxVrTSC3r/Z9QtHRJbt26xc6duqyNefLkSRCcOnXq4OCgE4F9+/bRq1s3spuZoZZaXmslG7Zto2rVqp/cHyEEdrbW5HAyf2dfURsjnj9//p6zUp5B3w+hwvIljNj+ms7uWnxeS/44aEbffj1xypqdNWvWMHDgQOqVUDC/lxlv/IgqF9BQ4H9bGDXmd72UylJKfH19sbS0xN7e/gNXzZikhAOhlPIhUBpA6OJh+QLb33PoaSll6j+FJJNUE5l4D7BlwP23InbuAr4BJse/7kxS/o8QYga6if8CwKX4if9wIUQl4CLQA5j7Vl3ngXbAsX+bj/nS8fT0ZP78BTx68Jgq1SrRp0+fhB9jcHAwR44eobRojyLepGMiLHDRlOb2jTMMGDSALl26YGlpSa3qtYnUBGASY02kuT+2LpaM/eP3NO2LsbEx98IeU9eickJ7pZT4KF8xoFLK5l3x8PAgMCwEtYsGI0WiiSZEHU1Z97LsPrgfOzu7fxW2lf+so17NWlzxDCG3kQVXI4PIV6IYuw/sx8zMjKdPn3Lo0CEOHTrExo0bWbJkCQqFgnLlylGpUiVWLlnCvBLFKB0/B3Q6IJBWTZvyzNv7sxwHyleszPydGxgkZUK71VrJgedBVH4rxEpqkSVLFs5evMbUyRPou3Mfjo6OjPpzOF26dEEIwW+//UbzxnVoleuc3nlWZoIqBQUnT55MEJkjR44weOC3BAcFEhOnoX69OixcsjrTuESnwk2pLvBUSvnF2/5T07usGnAauA28Cab0Ezqh2ATkAryA9m/CFwghfgZ6A2p05rX98eXlgJWAObp5msFSSimEMAPWAGXQjWA6SSn/1YD+pU78X7hwgQb1G2ElXVGqrFGbBIFlJFeuXiI6Opo1a9Yw5c9plDPpqndehDaQ0Ky3eO71NKEsLCyMf/75h6dPn1KhQgVatWqVZlEKQkNDGTNmDAsWLMDKzApXk2xUMS+DUii5FnuXWGfJ1ZtXUyTJ1qlTp5gwYQKHDx/G0tiMeg4FaZ+lNAqhIEQVxZSXJ5i1fGFC7p+PERsby65du/Dy8qJ8+fIfDHKpVqu5dOkShw4d4vDhw5w/f55m2Zz5s0RxveN+ePiIHuPG06NHj0/uW1xcHBXLlKKIDKZvARtiNJKZd0O4EhBNSGQ0gwYNYuLEiWkW3eBD/PzTKKJuzeOvJIGOpZS4DY3hxWsFtWvXpkKFCiyaP5OVw8xo5G5CZIzkt3Wx3AwsyInTl9Kv8ckgJeZkXE2zyqGuyXOoGflsvieQdE55cby5/+12LQeuSSnnvVVeC531yAedxed/Usq7n9fylCFTr/hPS2JiYti6dSv379+nWLFitGnTRi/oX/GipQh7ZoWdUWLIlJeqG8SZvSQ0LAQAY6UphZT1sE2SntlbXqZxjyosXDQ/zfoipeTMmTOcOXOGbNmy0a5dO6ytrdm5cyeDBg3Cz8+PYcOG8dNPPzF39hzWrlqLWq2mXcf2/PLbL//JFVdKyZEjRxg/fjynT58ma9as/O9//6NVq1Z079gFz6fPcLaw41noS/43YgS//TE2xfr9IYYPG0bMnt18l08/dtaEx0+oMnQYQ4cO/ax6Q0JC+HPcH+zcugVjYyM69+jFd4MGMWHCBObMmUP27NlZsGABzZs3JywsjC1btvDq1SuqV69O1apV0yQKtIeHB+XLFmdJbxXNyiiJUcGkXbDjblaatuzA7t27efbkAUNbWjKpV+KITqORFBwQyc79ZxLyuty/f59xv4/h5KlTZM3iSP+BPzBgwHfpmp4gpURmcDJFZvSz+R+9nhDCBJ2AFJNSvnprnw2glVJGCCGaALOllAXeV09aYRCZNMDX15fKlaoQFa5FHW2CkXksVrbGXLh4nmzZsvHixQvy5HajkEkrvcyZsdpwPNVHmDZ9Kk2aNOHOnTt07/INTurCmGFLhPEL4iwCuXr9yntjZ6UGKpWKNi3bcPnsZXKKnEQpI/FTv6Rs+bIcPXqUkiVLsnTpUsqXL/9Z9cfFxbFs2TK2rNuIsYkJPfr0pFOnTggh2LNnDxMmTODSpUvkyJGDUaNG0adPH728Krdu3eLly5e4u7unWnSCtzl69CgDOnVkQ+lSmMRHJohUq2lw6gy9Bg5k2rRpKZ4e+eLFi/Tp04c7d+5Qr149bly5RJXsJuS20LDPS0PpStXZsHVHmnihnTx5koH9ehAUGEBMnJaqVSqxdOV6XFx0D0ONG1SnR5nbdKihP8dUe3QoOUu2pn///mTNmpWa1SvxQ0dL2te1xsMvjlHzQ2nQvDcTJ03TO0+r1RIYGIiNjQ1mZmakJikhMjlMs8pBOTok69ifn/+dHJFpCQySUn50lbIQwgMo97bHbVpiEJkU4NGjR0z8cxJXrl6lSJHCjBkzWi/IZqtWbTh16DbWysR0wGHqJ7jktcDJyYGLFy+iilNTxKI1SpF4M4rUBKLN+pTnnommsOvXrzNrxmyePfWgZp3qDBkymKxZE/OapDbz589n+k/TaWLeGGV8Lp6H0Y84GnqUsRPGMmLEiM82zWk0GhrWbcDL28+pZFoQtVRzOvYBbqUKERASxM2bN8mbNy9jxoyhR48e74R/Ty+klHRo1YrHFy/SIYsTKq2Wf175I2xtefjsGUWKFGHhwoXUqFEjRa8bFxfH1KlTmTzud/6u70irAro1N7FqSZt9YXQfNYn+/fun6DU/hJQSb29vzM3NyZIli96+KVMmcefIVFYOSxSE1xFacvcMJDJGZ0k3NzNiYFt7Jg3KlnDMq2AVJbp68ey5T8Lc5IYN6/l5zP8IDQ1Fo4WePXsyZeqMFBfxN6SUyAzMnjyR+cUjWSKzATgopVzxnn3ZgFfx0wkVgC1A7vScq/56A0KlIffv32fDhg1cvnyZt/+vbt68ibt7ebZuOoLXk1j2775A9eo1E3KhREVFsXfvbiwV+tkSLRU5uX//HrGxsQwePJhKlSoRxN2E+rVSTZjRQwYM1L9JlClThlVrVnL63AkmTBifpgIDsHbFWoopiiUIDEBBswLYWFj/57mf/fv38/z2I/o41KeUVV7crQvwnUMjzp46Q2hoKKtXr+bRo0f07ds3VQVGSsnJkydZsGABJ06ceOf//G2EEGzYto0R06dzNVdu7hUoyOQlS7j/5Al79uwhOjqamjVr0rt3bwIDU+6B0sTEhJYtW+JkY0HL/InZW02NBAOLGbN57Tv3oFRDCEGuXLneERiAvn37c+6xOT8ui+bmMxWHr8fSZFwM3/bpS3BwMDt37iSHiyMNK+mHOnJ2MCaHk4KJEydy6dIl9u/fz/9+GMCS8S54na7IlR1leHBjO8N/+F7vvMjISBYtWkSfPt8wbtwf+Pr6pmrfk4MWkaztYwghLID6wLYkZQOEEG/CorcD7gghbgJz0M1Tp+tIItOPZCIiIvD09MTV1RVbW1u9Y+Pi4mjfvgNHDh/BxMQCtSaWQoUKcujQwQTX1fr1GnD+9ANMjRJ/XHHq1yjNgsmVOyd3795Fq5XksKyhN0pRa2MI1l4hOlqXiTM4OJjGDZvy8MFjLIwcCIt9SfPmzVizbnWamDySSyX3Sjg/z0pes8RRmZSS9ZEbOH7++H/KszN82A88XnuOBg76qRY2BJ+m89gBfP/99x84M+UIDQ2lcd16+Ht4UdzSjruRr3HM5cqBY0c/ey4pKiqKcePGMX36dGxtbfnrr7/45ptvEr3G1Gri4uKwsLD4SE3vcvv2bVrVq8bVTvZ6cxf7nkWxJCg3x85+GRPrfn5+TJr4B4cP7MXW1oaefQbTr1+/hMCnvXp0oojtaX7okiT0UJQG12YPiIof7VhbGjH9p4J0a5U4JxkQHEfJplfx8vbDxsaGoKAgalSvRC5XScO6Wbn7IIIdu73YtXs/lStX/uR2p8RIJrtpVtnf5V+jXSUw1nNehluMmWlHMlJKfvrpJ7JmdaZy5apky+bCwIED9YIiTpw4kaNHTqJR2RMTZYYqxoZ7d5/yzTc9OXXqFIsWLeLEyRMYK+306jZW2hIaFkr27Nn56aefqFqlKlFar4QnYikl0fjQrl27hHMcHBy4cOkcR08cZO7SSdy4dY31G//5ogTm9OnTePh6cCniMhqZuEDvScwTrO2tKVq06H+qP6uzM6+Jeqc8QhGbrBGblJKLFy/y999/s3v37s8KcDnqxx9xfPmapQWr8INrMZYUrIJzQBgjfhj+yXW9wcLCgsmTJ3Ptmi4US69evahduzbXrl3j+/79cLS1wcHOlgqlSnLmzKfFBCtWrBhKCxv2PE38u6k0kumXXvPguTdnz5797HanJC4uLsyZu5D7j725cOUuAwYM0IusPXjYSKavD2P/uTCklLwMUtFnUiBt2rTBy8uLbdu2YWNjTcnC+qOdLA4mmBpraNy4McOGDaNLl45UcDdm06oafNujMDMmluOvP8swcOC3Hx2RpiZSJm/LiGTakczs2bP5+edfiIrSIoQCKSXm5oIhQ75n4sSJBAQEUKxoccJCFSiSjECk1BCrToyWK4QSK5N8GCsTv/wabSwqhQdhYaEolUr8/f2pWrU6wQFhoLJAGkWR1cWes2dPp9nkdHLx8fFh8aLFPH7wmMrVK9OzZ080Gg0jR45k6dKl5MqVi6wOWfF97our1pUooyheaF5w4PABKlSo8NnXVavVDB06lCULFtE/exMKWuRASsm1iCfsj7uFh4+n3gT/28TGxtK2RSuuX7xCcQtnfNXhxJgrOXrq+HuTnCVFpVLx4sULvL29aVS/PiuK1SKraeK1AuOi6Xn3JOFR7wrgp6LValm+fDkjR44kNiKMGi72jCuVAydTY/b7hvD7XX/OXLr8SXHBLly4QMsmDamW3YQ8Fmr2+kgccrjh8yoQb29v+vXrx+TJk1EoFKxcuZJrF8+Qt0Bh+vTtj6ur68cvkEYcPHiQEcMH4eHlgxAKunfvxrS/Zif8v3/TvSMFslznxz6Jsdsee0RRreM1ChQsxoMHD1CIOA5sb0LJ4om/K61Wkq/kFm7dfkj27Nk/qU0pM5Jxln2yJW8kM95rboYbyWRakXF1deXFi2BEkrkFKbUIEYOZmRlRUVGAwMQoG4okccCklKi0fmzZshl3d3e2bt3K77/9iVKTHYUwRivVaJUv6dm7M7Nnz0o4T61Ws2/fPh48eEDRokVp3LjxFxfb6eLFizSq34icwg0bjT0Bxn6EKALQCi2vX79m+PDh/P7771hYWHD8+HHOnDmDs7MzHTt2/E9uyf7+/nTq1Injx4/TpEkTrl28gpk0Ik6rxtzWis3bt3w0EvOkPyeybfZShmWrhlG8h97OwDu8zGvBinVr8PHxwdvb+72vL1++THjKVQrB9nJNsDFOfLAIV8fR5uoBwiIiUsyb6fLly9SrXpXLzUpipkx8op9x/yWaqo2Zu2DRJ9X3+vVrNm7cmODCXKtWLSIjI/n999+ZNWsWDg4OGAsNVbJL6uVSczNQydYHWvYePPrZnoCpgZSS169fY2Fh8c68271796hVszIjvs1GszpO3H8ayU/TvRnw/U8MG/YjWq2W0qUKM+WP/FSrnOhAEBWlpmDZLTx/7pNg5k4uKSEyLibOsncyRWait0FkvnreiIy5uTmxsUo9O7aUEikjGTx4MPnz52fr1m1cOH8TBUn8+7WRFC2eixs3rgO6J9P//W8ECxYswNzMiuiYCNq3b8/SpUtSzeMltShZtBQO3i64mSY+RV+IPEmw9UsOHDpA6dKlU/yaFy5coF27dgQFBbFgwQJ69uyJWq3m2rVrmJiYUKpUqWStkyiavyCdyE8hy0SzWpxWw7d316OS+nlTrKysEsLJuLq66r3OnDqN7E/9+CZH4t9gpfcD1vs+wsE5K0OHDqV///7/Oez+0aNH+a1Pd9ZX0B9JHH3xmo3KbBw4ceo/1Z+Ua9eu0bxxA1rnjWRaw8QR9/pbMSzxysv5q7dS7Fqpza1btxg/7hcuXrhADtfsDBk6Si9d9IwZ09m1fS6bVtXA3NwIKSUTpt3i3mMH9uw5/MnXSymR6emcPJGZ7GMQma+eNyJTtWo1zp+/gi68mg4p1eTPn4tHjx4COtNROfdyREaqiYnRYmIiUBqpOX782DsRi1+/fs2TJ0/InTv3ez1svnSCgoLImSMXHSx7J4SBAXitCeaC8VFe+KdsQi0pJQsWLGDYsGG4urqybdu2/yRiBXK78a1JMfJaJDGTSC19Hmxi/OSJFC1aNEFM3nbwSIqXlxfVK1Umr8KU4sZW3FNF8kQTzYQpk1m9ejVHjx7F2tqafv36JbT9c/Dz86Nogfycrl8IG5PEkfLvN7xxatqJaTNmfla9HyK3SxZ2t9VQIEm6ZbVWkn16ON4vXqVorpr0RK1W06tXN44cOUCNKtm5++A1xsZ27N135JNNZZByIvNNMkVmSgYUmS9nVjmNmTlzBrVr1yEmRo2UAiEk5uYK5s2bm3CMq6srDx4+YNmyZZw/f4GiRYvQv3//9y58tLOzo1y5r/e7oVQq0WjUaFCjIHEEFquN1Uug9Tncu3ePpYuW8OrlKxo0aUiLFi0YMmQIa9eupWnTpqxZs+Y/BUz09fVFKmBXwB2G5KqRMPI58/o5RQoXZvjw5E/a58qVizsPH7Bu3Tru3rpF+xIl6NatG9bW1vTo0YNr167x119/MWvWLGbPnk2XLl343//+R4kSJT6pzS4uLnTu3Jl+B3YxupATLhYmbPMMZsPTV1S4eo2wsLAUDRljaWlOSHQYkCgykXESjUb7xZlt/wtGRkasWbOBe/fuceXKFb4bnIsaNWqka/puSeZOvxxvIso8m7u7u3zDrVu3ZLt27WTevG6ySZOm8sKFCzIj8/z5c9m3Tz9ZtGAx2bBuI3n48GGp1Wrlnj17ZNGiRaURRrKoeSnZ02Gw7OU4RHZ3GCjz2OSTkydN/uxrbty4Udpa2shaDhVlc4fasoBdXmljYS0BOW7cOKnRaD67bq1WK9euXSvt7OykmZmZzOWSQ5bMklt2zeYua2UrIp3sHOS1a9c+u/5/4/nz53LIkCHSwsJCArJRo0by2LFjUqvVyujoaPnn+PGyZMECsnj+/PL3X3+VERER79ShVqvl1ClTZIFcrtLBxlq2b9Fcjh8/XiqVSlmiRAnp5eWVYu2d+OcEWa+QjQz+yVFG/eYkI391lP3Km0sLY2Tx4sXlvn37pFarlQcPHpQtGtWR5UoUkIMG9JUeHh4p1oavEeCK/I/3HGfjrPJ/2Ycka0uJ631pW6Y1l2U2nj9/Trmy5cmmyoczuQnXhvCIK+TI7cL9B/cpUKCALtbYzLn4eLzAwciJFzHeNGrckLXr137WIsuYmBhyOGennUV9spvq5kqklKz230nDns1YsGDBZ/fH39+f7777jm3btlGlShVWrlxJ7ty52bp1KxfPnSdPPje6d++e6t57wcHBLFiwgDlz5uDv70/ZsmXRxsTgEPaaXq7OKIVgta8/4c4unIzPNfMxDh8+TLt27bC0tGTPnj160SM+F5VKRc+uHTl6+CBV85hx+5Uapxxu9B04hD///JOnT59SrGgRQl958Hs9DYWyCnbfE6y9Zca5S9fJkyfPf27D10hKmMucTZxlV6dOyTp2pt+cDGcuM4hMJqF3z2+5tPkuRYwT3YxfawI4EbmVv2ZOY+DAgRgbGyOlbq2Jh4cHpUuXpnDhwp99zbNnz9K9RRe+sW6hV/4g6hmvCkZy7MyJz6p3+/bt9O/fn9DQUCZMmMDw4cPT3eQTExPD6tWrGT9+PJrAAA7Wrowy3mynlZIu1+8xccmyZCcbu3PnDk2bNiUwMJANGzbQvHnzFGnn/fv3uXnzJnny5KFixYoIIYiLi2PevHn8MuZ/nP7elBLZE01Lvx7QEu7WhfmLlqXI9b82UkpkOidTZGZnQJHJtIsxMxunT54mmyKvXpmdMgvWljY0adIkYaQihKBSpUp06tTpPwkM6Ly4otTRvP0gE62Nwfoz5htCQkLo3r07bdq0IWfOnFy7do0RI0aku8AAmJmZ0a9fPwYNGkSDHNkSBAZAIQTVrC24dCn5q++LFy/OxYsXKVq0KK1atWLSpEkMHzqYgrldKVU4P9OmTkWlUn1yO4sUKUKnTp2oVKlSwtyViYkJTZo0IbujpZ7AALQqJjl36vgnX8dAEqQuaVlytoyIQWQyCHFxcfz26+9ky5odSwsrmjdpwaNHj5BSF4crNDSUCE2I3jkqGUusOibVEkcVKVIEFWouh99OKIvURHNZfZc+3/X94HmhoaGcP38eb2/vhLIDBw5QvHhxNmzYwNixY7lw4cJ/CmGTWuTKlYvnKs075U/i1OTKles9Z3yYbNmyceLECRo3bsz4334m4NA/LHE34c8CavYtnEr3TskLH58csmTJQlC4mvAY/Tvd4wDJ69BQTp8+jZSShw8f0r5VE+xsLMjjmoVxf/z+WWKXmZCfsGVEMq13WUaje9dvOHvgCvk0NTAR5jw+9ohyZcuTN18ebt26hY2NDfc0F7HTZMFaaY9KxnFHnqN5s+apkgo3Ojqajh07EhwWwkXbO9wLf46t0ppnEV4MHjL4vWYjKSVjf/2dmTNm4mzpgH9UCNWrVyeLS1ZWrlxJ0aJF2bVr1zvu418SrVu3ZvTw4azz9KVDThcEsN3Hj7MvXrG4Xr1Prs/S0pLmzZsTcfsMM6s5J5SvzWJG+e1HuX379id7tr0PR0dHmjZpzLDdh5jdQouVqeCBv5afD0CYWk2NGjUoXbo03s8fMbJBHLPHCl6GvWbM9r/o9+QBK9Zs/PhFMjEZdZSSHAwjmQzAs2fP2Ld3L0W0dbBWOGIqLMhjVBrr2Oz4ePuycOFCXr58yYSpf3CB3ZySmzkct5Yy9YqwdMWSFG9PaGgoDRs2ZM+ePcyfP59XQf4s3bSCn+b9zv3HD/hz8sT3LrBcu3Ytq/5eyv+yteZ7+yb84tIRv3OPWLdqLSNHjuTq1atftMAAmJubc/jkSU6a21Dr1GVqnb7MpmgNaiFo1aoVQUFBn1zntYvnaeyqH2nAVKmgeg4rUnJ+ceGy1Whz1SffJEnJWUbUW2LMmHF/4efnx4IFC/D19qBVyRiGN1CQ1UZQ0lXBpr4qdu/ehYeHR4q1IyMiM3HsMoPIfCU8evSI1i3bYGfjQO6ceZk2dRoajc4sc/PmTWyNsqIU+gPTLMpclHevQP/+/TE3N2fI0CG8DHjJ0bOH8fB6zuZtm7Cysnrf5T6bV69eUatWLc6fP88///zDd999h1KppG7dunTo0OFfk6vNnT6LhhalsTXSrcsxURjRLkt1jIyN+Pnnn1M9QVVKUahQIc5cvsz9p0+5+/gJd588Yffu3Tx48ID69esTEhLy8UqSkDtffu6H65dJKbkbHPvRuGyfgpWVFes2befhU0+27D+L1wt/Bg4ajIWFBQMGDKBKhTI0KKZ/y7A0FZTMacTt2zqTqFqtZurUyRTO74qzky1dO7bmyZMnKdbGrxEJqGXytoyIwVz2FeDr60ulClWwiXYjn6IhcQGRTBs/j7NnzpErT07Wrl1LeHgkRS00KJLEYos0CqJEqdp6dZmZmVG8ePG3L/FZPHv2jJ9H/8zRo0ext7WjU/fOrFu3Dj8/P3bv3k2jRo0+qT7/gAAcjPLrlZkrTDAzNiU0NDTd89l/KtmyJcbPatCgAdu3b6dVq1Y0aNCAw4cPJ3uVfa/e31Lqr2lUcQqlZV4bYrWS6dcC8Q6JTJWMqFmzZn1v1OsCRUpy+cF52rhrE8piVZKrTyLo2bMn3bp144X3MwKenmTFt1qy2ytYe/oQNaqe5OqNuwmZMjMjGVQ/koXBhfkLITAwkLVr1+Lt7UPVqlVo0aJFQpj/ESNGsnH+QVxlYiBDtYzjasw/GJkoadmyJU8fPSfwSSR5tRUwEWb4qR/hbXKdm3dupOjT7hv8/PwoVbwUBTX5KWRakAhNBCfCThGhiOTI8SOflbujV/dv8Nt/l8YOif18EvWCXdprPPfxTNdV2ynFnj17aNOmDWXKlOHQoUP/GuImKZcuXWLgtz159twDtVZL2dKluPXgMcbGxhw8eDBV4sq9zfPnz6lYriSTWkTTuaKCgHAYuc0YX1kIl5z52LVrF0ri8F1sg41Fojl0yAoN9mUGMeHPyYButLNz504uXjhHDtdcdOvW7YuLRv6GlHBhdjJ2li3tkufCvDzQ4MJsIBW4fPky+fMVYPJvC1g79xD9eg2hUsUqREZGEhUVxcF9h7BQO+udYyRMcLB0YfPmzWzatIlTZ0/QqHMNLsnNHItZimXJaI4cP5wqAgMwd/ZccsmcVLQsj52RLa6mOWjn2BrgsxfuNW/dkmPBN9kacIZHUT6cDL3NP6GnmPX3nAwhMADNmjVj8+bNXLt2jcaNGxMeHv7xk4AKFSpw5fY97j99jqevHyfOXeTcuXOYmppSs2bNT85D8znkzZuXvQeOsfZxaWy/11DiDyVZy3Tl0LEzbN68mX/++YdyBa30BAagbjEtJ47sIyoqioiICGpWK89ff/TFNmg5l/aOp2jhfCk6t/TFkcz5mIz6vG8YyaQBbxbq7dyxGycnRwYO+o6KFSsCOtt6wfyFifF1xNYoV0KZn+YCDjmM8fH1IS5WRXajEuQyTnzA0UoNd8U2bt65jpubW2K5VotGo/lPaZCTQ93qdbC+Z0k+Mze98t1x+5m/fj71PtGTysfHh3LlymFqakrTRk24cfU6ufPm4YcRw/9TnpovlW3bttGhQwcqV67M/v37P3tuzMvLiwYNGuDl5cXKlSt5/uwp504cIVuOnAz4fuhHUyR8LnFxcRgZGemJ/5MnT6hWsRTP5xlhYpQoNGPWRTN7bxxCaUqunDko7hLAxl8SM3muPxbJzH0OXL3xIKHswoULLF+2kNCQQOo3akW3bt3SZU4uRUYyRs6yWTJHMquCDCMZAx/A09OTu3fvJkzGvyE6OpoqVaox+n9/cPHYc3ZvPk+9Og1YsGAhAI8fP+bFixfYKHMmnCOEwFbkx9fHj0GDBrF02RJCTZ4TpHmOlFriZBTeigvUqFlDT2AAFApFqgsMQIHCBfBXB+iVaaQG/yj/Tx7JREVF0bJlS6Kioti3bx/zFy3g3JULrN+8IUMKDECbNm1Yv34958+fp2nTpoSEhLBz506WLFnCw4cPk11Prly5OH36NAUKFKBXt05cWj2Fdsa3cHm0m8Z1qrNp06ZUab+Jick7o8v8+fNTuUo1+i6WvHqtRaOVbD4Xx4pTxixcvJyBAwcSHOjLsDYWet6FHWtZ4OPjzbNnzwBYMP9v2rVuQF6zozQqfof1y36mQb3qxMTE6F1Po9Fw9+5dvLy8UqWPKYUuQGbKLMYUQngIIW4LIW4IId55WhY65gghngghbgkh/ntMov+IYeI/mUgp3+t26+3tTds27bhz9y5GRsaYmZmyYsUymjZtCsDKlSvxePISK21RhLHufJXWiaFDhrJq1Upu3LiBKlYDFhJIktsGDfnz52f69OkAFChQgO/6D+Lq49MolcZ06dCZOfNmp37H34OUEoWxksthV8midCKfmRsx2hjOxp6nStXK5M+f/+OVJKmrd+/eXL9+nV27dn2RCyxTi/bt26NWq+natSu5s7tQPKsdOS2M+PnH17Tr2Im/Fy9JVi6dLFmy0KBuHYprnrOggV1Cec2cJnQf/B1t2rRJszTea9Zv5X/Dv6fwDxtQazSULFaQHbsXU7VqVQDOnNhPnErfu06jhaioGIoVK0aZMmW4fesql9cUJJ+rLmlZ50aSZj94sXbtWvr06QPo5rYGDeyDsVJNWHgsxYsXZ/XazV9Ups+kaFLWYFRbShn4gX2NgQLxW0VgQfxrupHpRzJSSmJjY98JffJm39y5c8mWzQWlUknhwkXYu3ev3v66detx744vpuTHSJOH6DBrOnboxPXr17l8+TJ//70QRZyD3s3CWGEJWlPCwsIYOHAguXLn4rX2WcJ+rdQQYfSMXt/2TCirXr06d+7dIjgkmLDw1yxbsfQ/h+D/HFQqFX369GHBggXUa1SPR45PWRi0lFWv11GqSRk2bv20J+eJEyeyceNGJk2alOy4XhmJTp06kdvFmV9KOLOpqivTy2TjVMMCnN27g/Xr1ye7nlPHDtG9qIVemXs2UywUWu7fv5/Szf4gVlZWLFy8kqCQcPwDQrhw5W6CwAB07NqbqZvjiFMl/t4W7o4kb968DBw4kNevX1Mol3GCwAAoFILujS1YvmQuV65c4erVq/Tu1YWlk/Nw62AFHp+sSrXSIbRs3vC9v+MvgTSck2kJrI4PIn0BsBNCpKtbX6YWmVWrVpEjhysWFhZkzZqVuXPn6n1Jp0yZwpgxvxASqMVEmYNnTwLp0KEjR48eBXQBIF/6BWAsnBJExFhphSbOgrJl3alQoQL37t5BI2P1riulxMLSlBUrVjBjxgwOHtqP1taPAKMLBIlbvFAco2L1Ugwe/P07bbayskoTcxjoYoVNmTKFpg2b8f2gwVy9epWWLVuyfPlyfv31V/bt28e9R/fw8fMh6HUQq9etxtra+uMVx7Njxw5++eUXunbtysiRI1OxJ18u9+7dQxsTTed8iaF9rIyV9M9rw5qli5Ndj729PX6R+qbaWLUkODI2XRKSGRsbv3eeafDgoVi5VKR4vxAG/x1BvdERzN1rwradB5gxYwbLli0jRm32jli8ClJx/eZtypcvT5XK5enRJgtVyznEX0vBqO/yEhnhz4ULF9Kkf5+CBLTJ3AAnIcSVJFu/91R3SAhx9T37AHIA3kk++8SXpRuZ1ly2ceNGBg4cRHS0FjAnKCiSMWN+AmDw4MGo1WomTZqEKtYChUJ3U1cKc1SxWtq374ira3YePXqERmWMtZm+SUOhMKVIkaL8+ed4oqOj6d9vIGptVowU5kgpidK8wD6LTcJ8Q8GCBfHwfMaePXvw9fWlcuXK6Z53/dWrV5QvWx6rKFtcNK5cOH+ZJQsXo5IqFi1aRL9+id/vT82bDro0ut26daN8+fIsWZI8s1BGJCYmBnNjo3f6b2GkICY6Otn19Bk0jF+H9KGaqwZnSyUarWT8uZAvInhoUkxMTNi6Yx+XLl3i4sWL1Hd1pVmzZgmpyitVqoRWYc2KXcH0aqGzAHi8iGXe5nCWLV+LmZkZf074lcL59G9dQgjy5bHCz88vPbr1UbTJH6YEfmTiv6qU8oUQIitwWAjxQEqZNFf3+35I6Tq8y7Qi8+uvvxIdrUEkrJJXEhWlYcSIkezatQtPT0/CwsIxM9Zfx6AQpoSFBZAnTxUqVKjA6lVr0Eo1ivh6pJQYmcbx/fcDad1a59Lr5+fHr7/+hpWxI2pNLDaOFhw4cEDvxmJqakrbtm3TpO/JYfy4CdiHZ6GiWTWIHzhlUWTjhvFF+vb9cHDLDxESEsKuXbuIjY2lQoUKtGrVCltbW3bs2IG5uXkKt/7roVSpUkSi4NyrcKo460aBWilZ7RFGq+GDk11P27ZtuXPzBhVmzaCUixXPQ2KwccxKpOolFSpUYMeOHVSsWJHw8HC8vLzImTNnui1uFUJQsWLFBA/LpCgUCrbvPECrFg35e4sX2RxNuHIvlD/G/UmXLl0A3eLknbv/onPL7Am/oeDXcZy/4s/i99T5JZBSd3kp5Yv4V38hxHagApBUZHyAnEk+uwIpmzv9E8m0LsxmZubExSn1bvS6TG6RlC9fHldXV/bu3QdaexQi0Tyl0UbiXr4Q58+fA2Dw4CGsWrkObZwNQhghlOE4Z7fhxo3renMmwcHBnDt3Dnt7eypXrvzFr/vIlysfpcIr4GScuPJbSsmW6DXcuPtpCzx3795N105dcbPIiTFKboc8RAo4c+5Muo/YvgQOHTpE53ZtaZHTFlcTwRaPIAI0Sp75+H6yEAQGBnL16lVcXFwoWbIkd+/epXnz5vj6+tK0UX2OHzuGs40Jr8Li+LbPt0z5a9YXN9oBnSv+uXPneP36NVWrVtUL4hoREUGVymUpUUBFjzZZCQpRMWWhDw2bdGPqtBkp2o6UcGG2V2aVta06JuvY7WHzPng9IYQloJBShse/PwyMk1IeSHJMU+B7oAm6Cf85Usp0ddHMtCJTokQJ7t59kmQkA1JqyJbNHl9fH4QQTJkyhQnjJxEXY4oQJmhlDMam0ezevYs6derEnyP5559/mDf3b0LDwmjbtg0//jg8XezgKUnp4mVw8clFTpM8CWUqqWJTxGq8fDyTvUI7NDSUnNlz0smmETlMdQtKQ9URLA3awqnzp9NkpfrXgJeXF6tWrsTf7wUWNrZMnTqVX375hfHjx//nugMDA6lUsQLmEV7s6GpDdmslryK09NilpkH3H/jlt7H/vQNpTEhICLNmzeDA/h3Y2NjSs9d3dOnSJcXNrikhMnbKrLKWZfJEZmf4v4qMG7A9/qMR8I+U8k8hxAAAKeVCofsDzAMaAVFALylluq50zbQis2/fPtq3bx8/J6MENJibK5k//2+++eYbQCcg8+fP588/J/Lq1UsKFSrM9Ol/0bhx43TtQ0oTGhqKSqVKyCvz/Plz6tapS4h3KC3s2mOqMEUrtVyNu0D2SlnZe3DvR2pMZN26dUwd9idtLOvqlR8Pu0T53jWY9te0FO1LRqFnz56sXbuWc+fOpchaobyuzqxtHEfZ7IkPVfcD1DTbLHgREPyf68+opJTI1EimyOz+F5H5WvmybTapSJMmTdi8eTPFihXAxERD/vw5Wb58WYLAgM52PGjQIF688EWj0XDv3t0MJTC+vr7Ur9OAbFldyOWamzIlyjJt2jTKlClDYFAgletWZGvkOk5qD7EjZgOmBZSsXLvyk66hUqlQvudrpkSBKs6Q7OpDzJ49m+zZs9OjRw+iP8EB4EO8DAihoJO+WayAo5KXQa/RarUfOMtASqEzxX98y4hkWpEBndDcvn2LmJhoHj16RMeOyXvayAhoNBpq16hDwOVwWlj0pKV5b8yeOTJm5Bjc3Ny4efMm+w7u4+GTB/y1YipHTh/mwpULZMmS5ZOu06hRIx5HehCiCksoi9HGcVfzlDbt2qR0tzIMtra2rFixgocPHzJmzJj/XF/lcqXZ/UDflX7Pwzhcs9olxE/TarXcvHmTW7duZdgbXnrwiS7MGY5M612W2Tl69ChRwTGUN040xbiZFiVAvqBDhw7kzZsXgBw5cvyncPLZsmWjTbu2LFi7nnK2JTARxtxTP6VNp7ZUr179P/cjI1O3bl2+//57Zs+eTcuWLaldu/bHT/oA46fOpHWzhgRGx1Alp5JLPhrGnYolLFpN8eLF+eGHH1gwZzqowpFaMLKwY82GrQbHjBQiM4t2ph7JZGY8PDywlu+mXbbFEY9nHil2HX9/f/bs3UPRUsWoPbAx5XpVY9v+HcxftCDTro35FKZMmaKLS9arFx4eHpw+fRpvb++Pn/gWVatW5dDxM9yybcCQc05ctqzLkZPnOH/+PBYWFvw86kcm1w7izjANd4dr+L2KP80b1092lGgDH0aXtEwma8uIGEYyGZzLly8z+n9juHLtCtmyZmPEmP/RtWtX7t69y/OwR5S2rZaQ6ExKSYjJSypX/TbFrj9s2DAiIiJYt24dRYsWTbF6MwsWFhasXLmSOjWqUbxQAYpnd+BxYAT169dn+dp/sLCw+Hgl8ZQuXZq1G7e+Uz5o0CBOLB9F82KJczZtSxmx4S5s2bKFXr16pUhfMjMyE6ctS7WRjBBiuRDCXwhxJ0mZgxDisBDicfyrfZJ9Y+Ijhz4UQjRMUu4eH3X0SXx0URFfbiqE2BhfflEIkSe1+vK1cuPGDerWrkfQRS2VZVuc/IowcvBPuOZwZc6cOdg72XFOfYBAtR+vNYFcV5/GyFHQoUOHFLn+3r17Wb9+PT///LNBYP4D169fo6CjBVc75GVPPUdutMtJ3L1zDB8yKEXqDwoKopDTuzMCua1jePXqFQCRkZEsX76cMWNGs3HjRuLi4lLk2pmFzDwnk5rmspXofLWTMho4KqUsAByN/4wQoijQCSgWf858IRLyCC8A+pEYWfRNnd8CIVLK/MBMYEqq9eQrZfzYCeTRlCKPSTHMFBZkMXLFXdmIsNBw9u7di6ePB/1G9eKpw3VuWZymfs8anL90LkVW4IeHh/Pdd99RrFgxRo8enQK9ybwsmjOLCeWdcDTTGR7MjRRMcLfjn/UbiI2N/cjZH6dmzZrsfGiKKkmo4Fi1ZNP1WJYsWcK8efMoVsiN7X8Pw/zuXywY35fyZYoRGPihQMAGkiKRaJO5ZURSTWTi4+m87YDfElgV/34V0CpJ+QYpZayU8jnwBKgQHz3URkp5Xupmzla/dc6burYAdUUmNPJrNBoWLlxI2VLlKFygKL/8/AuhoaEAXLt6DSeF/qS9pcIWG0s7ChYsiImJCT//8jNPPB7j7efFnLmz/1MaXCklHh4eBAQE8NNPP+Hj48OSJUsS4lIZ+DwCg0NwtdK3bDuZK0FKoqKi/nP9tWvXpkCJijRbqWDXHTU7b6tpvFxB/qJlMTIyYvSPg+lbLojtfWP5qYmSw4NiqOLsze+/GB4ekoXUhQpKzpYRSeuJf2cppR9A/OubmCUfihyaI/792+V650gp1UAo8N47pBCi35uopgEBAe875Kul1ze9GTtiEvKhM9behVgzazvlypRn+PDhvHz1ihCtv97xMdpIYtXRZMuWLUXbcezYMfLnyUeZ4mXI7ZqbRX8vpHfv3lSuXDlFr5MZqVWrJtufR+iVHfGOILera4pElhBCsGXnPjoOncai56VZ4lmGniNncuLMRa5du4ZKq2BwHYXe8T/U1rJt6xZA96CzfPly6teqSK2qZZk5c8Y7CcYyOzKZ/zIiX8rE/4cih/5bRNFkRxuVUi4GFoNuxf/nNDA9iYiIYMuWLXh6elK+fHkaNmyIUqnk4cOHbN+2g/K0R6nUxVezlc5c8dzBrFmzqF69OtcuXcFcbU0WpStRMoz7ijN82+vbz073+z6ePXtGmxZtqG9WAze73GjQcCbsIhfPXvhgsjcDyWfsn5OpWaUiIXHB1MpmwvXAGGbfDGb91u0p9rc1NjZmwIABDBgwQK9co9GgUCrQvDVhoNJAVFQkq1at4tD+nTy7dZgRjeIwMRL8ve539u3ayoEjp77IuGhpjQTUGXbG5eOk9Ujm1ZsEOvGvbx6zPxQ51Cf+/dvleucIXQAyW941z331PHjwALc8+fh56ESW/Lmdbzr1o1KFKkRGRnLixAnshAvKJAE8hRBkUxagXZv2nDx5kjXrV/Eyyx0OxCzhkthFtwEdmT7zrxRt46IFCylqUpB85nkQQmAkjKhpU4Ugv6AvMr/H10bBggW5eO0mZrU6siDMhVuOpYlUaTh37lyqX9vU1JRmjeoz7XCimGm1kj/3g7GpOT179uTA3h0cHqmhZTkjGpdWsnOYhtcv7iQk+IuLi2Px4sW0bFqHTu2as2fPnky2biS545iM+TdJ65HMLuAbYHL8684k5f8IIWYA2dFN8F+SUmqEEOFCiErARaAHMPetus4D7YBj8iv95l6/fp2/ps3g0cPHVK5Skf+N+JFcuXIB0K1LDyzD85FVWRiMQKokHndPUaJ4Cby8vTDRWsFb8/QqkwgKFykEQKtWrWjZsiWRkZGYm5unypOlxzNP7NFPiSCEwMnEAR8fnw+cZeBTyJUrF3/NTEy33bt3b/766y86d+5MyZIlU/Xas+cvpV6tKpyaE0I51zhOPDHG0ikfT5+fYOzYsYTenI+5SaIIKRWCVqWj2bl9C40bN6Z5k7qogm/Tt54kPFoy4vuTnD3dj0lTEh92pJR4e3ujVCr/0+LfLxHdiv+v8taUIqSmC/N6dAJQSAjhI4T4Fp241BdCPAbqx39GSnkX2ATcAw4Ag6SUb9L8fQcsRecM8BTYH1++DHAUQjwBhhPvqfYlEhMTw9atW1myZAlPnz7V23fgwAGqV6vJse238b9nyqblRyhVsgyPHz/G39+fO3fv4KQomHC8EIIsFOWF70uGDRuGg7M1XtqbaKUGKSWBGk8CeE6fvn30zrGysko100W1WtXwFPpiEquNwyPCm3LlMlSsvy+GadOmYW9vT79+/dBoNB8/4T+QPXt2bt59zIhJq3FtMJ5pi7Zy+sJVbG1tqVKlCt6v3/VGvOujZfnKNTg7O/Pq+RUO/GZCh+pmfNvAnFMTTVmyeD4eHh4AXLt2jXJlilK+bFFKlShA9SruPHr0KFX7lKYI0AptsraMSKaNwpyS+Pn5ceLECWxsbKhfv76eN9XVq1epX78hCmmO0BoRpQqkT99vmTVrJgD58hZA/dIFK6PENNyBqvsYOYQQHRNJ6Otw3M26oRCJzwMR2gCinO/z3PMJnp6edGrfhdu3b2GkNMbO3paVa1ZQq1atFO3jvxEeHo5bbjeyxWahrFUJorUxXFbfoF7r+ixZvjTN2pHZWLduHd26daNTp06YKyFH7rx827cfefLkSbM2xMTEUMDNlbHNw+lRXYkQsP+mll5LlIz++Q+WLZlPvxoBDGmhv2i0w5QoclfoS79+/ahVozKT+5vTuZ4NWi0s2hnKrG2Sh489MTU1TbO+vI+UiMJsqXSShc2aJuvYa1GrM1wU5i9l4v+Lxc/Pj7Vr1/Ly5Uvq1q1Lo0aN9BKOTZgwgT//nIi5qT0IDQqFhoOHDuDu7o5Go6FZsxaIaBfMjXS5VEwUuVi5fA05c7piYmKCt483+U3L6F3TRpkTz4BHfNOzO8eOnCDA7wHOSt1iRim1BBs9oE8PXZbA3Llzc/7SWXx9fYmOjiZfvnxpPtHu4+NDaEQoDnkcOK+6hpWVNaMGjdFL0Wwg5WncuDGO1hb4nN5J2wJWPH4gKf/3XDZt3/Wf4px9CmZmZuw/dIJunVozbqcfJsYKpNKKbTs3UKNGDUKCA/F9tOCd8569iGHbzJnMnDmTltWt6dpAZ25VKGBQWzt2nw9i165dtG/fPk36kZpIJBpSd7T5JZOpReb06dOMGfMT9+7dI18+N8aPH0+jRonrR48dO0aLFi1Aa0psrJolS5ZTtmxpDh06iImJCadOnWLK5GmYCjdQ6SbfY9SvadKkKdevX2Pfvn1EhEVjFy8wAAphjFKVlZEjRiHRIlCgIQ4jEp/YVDKKvHndWLp0KY8ePaJGtZp4xwaiiLEkxjSAAkXyMmaMvnUwvezYGo2G3r17Y2Njw6nTp3B2dv74SQZShOnTptAglxl/17JLeLCo4WLEgG+/4cFTzzR72ChevDjXbz/iwYMHqFQqihcvnvAg1rPXt1SpOJcOVVW45zdGSsmGU7EExthy9OgmJk36k7J5br1TZ5FcIkPN52VUU1hyyLQic/z4cZo1a0Z0tAZQcvXqbdq2bcuqVato164dGo2Gjh07ERdjgVJhhpES4qIlV6/cYNq0adSrV4/ffv0drcoaY6NE7y4TIzsCA/wSbvpGwgIs9a8tUFKyVCm2bNnE+HF/sn/baRxkSRTCCLWMIdzoIaOH/wboPIueez5j27ZtCS7MdevWTdf0zffv32fZkmX4v/JHg4YLFy6wbt06g8CkMft2bmNKUXM9MWmQ24LhZ/159uwZ+fLlS7O2CCEoUqTIO+UFChRgweJVNBvQm7zZBBFRGtQKG/bs30OpUqUICwtj0m99GNVNolDo+qFSSw5eimXVDxXTrP2piW7Ff+YVmUw7J+Pu7s7163cRSdx/pVRjb2/JmDGjuXPnDuv/2YgC/fwpGm0UKk0wOp8RBRYmOTA10l8DGqv1oFuPDjRo0IBvvumFpbYwJkqb+GtoiVTcZ+acSfTs2ZPIyEi6dunO4cOHsTS1IyImhIEDv2PaX1O/yPUlGzdupN+3/SlsVAgLacHdqLtgDZ6+nikSjsZA8qlarhTDsvtTP3fiU0ysRlJ0jR93Hj3FxcXlX85OW2JiYrh48SLm5uaUK1cu4SFJrVZTu0Ylspp7MqStBSq1ZNr6KMyd3Nm+60C6/wZSYk7GXOkg85rXS9ax9yM3Z7g5mUwrMmZm5sTFKfW+xLrsdJEAKJVKtFowUbroHaPRRpHHzZGZM2dw/fp1pk6ZhVLjmnCMRhuDWuGNn98LbGxs2LZtG927f4OpyIJWpUSYhVG2XEkOHNiHsXGiwHl7e+Pt7U3hwoVxcHBIo7/GpxETE4NLVhcamTQii7EuWIOUkv0x+xg+cTgDBw5M5xZmLhYtWsTyiWPY2sgOKxMFUkqmXA7hknEhjp05n97NSzaRkZFMnz6NHVv/wcjIiA6dezFkyNAvIhxRyoiMvcxjXvfjBwIPIrd+8HpCiJzoQmtlQxdPc7GUcvZbx9RCtzTkeXzRNinluM9recqQaUUmb143PD390K3j1CGlBmtrY7y8vLC2tiZPnry8fBGJUmERv1+LsVkkCxbMpVu3bqhUKho2bMTVKzdRxZihUEqkIow5c2bx7beJ4fKfPXvGypUrCfAPpEnTxjRp0uSrXAl96tQperTuQQuTlnrlT2Ieoyql4vCJw+nUssyJVqvlu7692bZlM9VzWnE/MBqvoAhadejMunXr0rt5GYKUEBkzpb3MbZE8R4xHEdv/TWRcABcp5TUhhDVwFWglpbyX5JhawP+klM3+S5tTkkw7J/Prr78wZMhQoqI0CKFESi0WFkpGjx6Nra3O02Xnzh3UrVsXrSYKtRoksbRo0ZIuXXSeXcbGxhw6dJCdO3eyY8dO7O3t6dPn23cWx7m5uTFuXLo+TKQIlpaWxKhjkMb6oWJitbHYWNukY8syJwqFgkXLVjJizC9cunSJHDlysH//fqZMmYKNjQ2BLzwxNTOna88+NGrUKN1NT5kXiQbVf69FF+/xTezHcCHEfXQxHO/964npTKYdyUgpmTNnDmPHjiUmJgZjY2N+/PFHfvvtN70fY1RUFLt27SIgIICaNWum+urqLxkpJblz5KZAZEGKWRQDIFobze6YXSz7ZxlNmyZvLYCB1CMuLo68rtlwJIJB5ayIVkkW3NHSulsfJk+bnt7N++pIiZGMqdJW5rColqxjn0fsS9b14vNnnQKKSynDkpTXAraiC7v1At2o5u6ntzrlyLQjGSEEQ4cOZdCgQQQHB2Nvb683R/IGCwsLOnXqlA4t/DK4dOkS69asQ6VWU71GNSJjIzkTeZoniidYK63xjPJg8JDBNGnSJL2bagA4fPgwjiYaTnTIirFS97DUupCWcosX0u+7Qbi5uaVzCzMnn+Bd5iSESLpafHF8gN8EhBBW6IRkWFKBiecakFtKGSGEaALsQBemK93ItCLzBiMjI7JmzfrxAzMh4/4Yz6xps8gnCqJAyZola9Ao1Vy+dhk/Pz+CgoKoUaMGrq6uH6/MQJpwaP8+2ucTCQID4GCuoL6bOUePHjWITLqgW46ZTAL/bSQjdO6wW4F1Uspt71wpiehIKfcJIeYLIZyklOmWYS7Ti4yB9/Ps2TOmTZlGS4sOWCh0LrJFTIuzM2oTUVFRNGzY8CM1GEgP7BwceBXz7hqql1ESe3v795xhILXRBcj87+tk4pMyLgPuSylnfOCYbMArKaUUQlRAF58y6D9f/D+Qfiv6DHzR7N+/nzymbgkCA2CiMMVNUYCdO3b+y5kG0pMe3/Rkw4NYbryKSyjb+ySaix6h3L51kzJF85M/lwuDBvTFz88vHVuauUhuAuaPUBXoDtQRQtyI35oIIQYIId4kAmoH3BFC3ATmAJ3SOzq9YSRjIIGrV69y9uxZXFxcUCqVqOS7HjEahQYLC4v3nG3gSyBfvnwsWLqS1n17U8hJQ6RKy6tICUj2LZ/ClLoWOFooWHVrI9Uq7uXqrXspkl3TwIeRKedddob3J2tMesw8YN5/vlgKYhAZA6jVajq168TxoydwUeQiShlBiDqA8IhwCtsWJ6uxLlXza3UIzzSP6dylczq32MC/0b59e5o1a8aZM2cwMzPD2dmZyu4l2dfNGsv4vC+T6xrxcnc0y5cvY/jwH9O5xRkdiVYaAmQayMQsXryYS8ev0si4I8r4xakPNbe4ZXSRI7H7yK7IgRIjvKM9mPP3HPLnz5/OLTbwMczNzalfvz4AmzdvppqbVYLAvKF+Lg3Hzp1kb6HCHDtyCAenLPTo8Q05c+Z8X5UG/gPJMIVlWAwik8mQUnLq1Cl2bt+JhaUFXbt1ZcWSlRTQlkRplPh1KGBanIfc4MTZ4zx8+BC1Wk2jRo1wdHT8l9oNfInkyZOHu/5xaKUpiiRrwC77qrjw8gIPrp6kbaFYvCOMKTNtEqv/2WxwSU9RPsm7LMNhEJlMhJSSXt/0Zu+OfWRTuaFVqpkzay5WltbYCX03ZIFAqVBiZmZGx44d06nFBlKCcuXKkS1nfkYffcqv1Y2xNBHsehDHqhuxlMgWx8k+lhgpdakmOhbX0uWbrnj6vkKr1XLp0iUsLCxwd3c3RAz4TCSglYaRjIEMRnR0NBs3buTK5asUKlyQ7t27c/nyZfbtOEB10QYjU93C09yaIhwIWAfGV8lmlBjo01v1DFsHWwoVKpSe3TCQAggh2LHvEN/16UmBeUcwUgjy5M5JBfe8DMj3CKMka2qq5DHCxRqmTZ3KnJnTyOUgCI/WojC3Z+O2PZQoUSIde/KVIiXa9zjRZBYMIvOVo9Fo8PDwwN7ePiF6s7+/P5XKV0bzWollTBb2mR1j3O/jqVuvDi6qfAkCA2CltCO7eR7Msyk5HryTLHE5iDGJ5KXwYu/6vYan1wyCk5MTm3fsISwsjOjoaLJmzUq7lo2JUT/UO05KiV9QGFMn/cHBAQrcc+miO6+97EezRnV54uH73sgYBj5MZs8nY1gn8xUQExODt7c3cXFxeuWbN28mezZX3EtVwDV7Tlq3bEtoaChjRv2EMtCWktoG5DMpQzFtbZyjCrNzx07UMu6d+k3MjJgwaTx/r5pDnQGV6fvbNzx6+ogqVaqkVRcNpBE2NjY4OzsjhKBzjz7MvmhMWEziMoptd9SEx0LP8hL3XLrbgxCC7hWUuFrHcfiwIdL25yClNllbRsQwkvkCePnyJcePH8fGxob69esn5NHQarX8/ttYZs2ahUCJEJJRY0YxZsxoLl26xLc9+5FfUxNbZTbUijiuHblM+zYduHT5EmXRj/Sdy6go9yLP4GlyHzdtccwVVgAEql8QJF7RtGlTrKysaNmy5TvtM5Axadu2LSePHaLE7LU0LmyMT7iCu/5mNGpch7yKg+8c72onCQxMt+gkXzGGiX8DH0FKiVar/WAOmIcPH3LlyhVy585N1apV9UxMoaGhTJ8+g21bt2NlZcWg77+jW7duCcf8+edE/pzwJ7ZmLmiIQypjOXBwH+7u7kydOo2Fs5eTV9MAU4UVMZowpk+ag729HSeOncRZXRRbI90aFiNhQh5ZiWPHVgESrblar41aNBgbmzDq55FMmTSVHKZuqIWKAHzZvGUTVlZWqfPHM/DFIoRg7vzFDBoynOPHj9PY0ZHmzZuza9cuZv16igHV4lDGp0QOipQcuR/H1Jo107nVXycZdZSSHDJtqH+AJ0+eMHXqVC5fvkLx4sUZNWokxYsXTzg2MjKSH34Yzpo1a4iLi6VC+YosXLSAUqVKAbpFjF27dmPP7j2Ymdqh1kTj6urCseNHcXZ2JioqijJl3AnwjUSpyYJEhdr4JZ27tmfBgr85deoUzZu0Iou2MsYKXeriMLUPahtPvLw9yJ4tB9liqmKhSIw5FaHx57n2BFIjKWxcFwelvlfYDe12irsXwuu6PyVEHYTQ2dQfy0sUruPKzt3b8fb25sCBA5ibm9OiRQtsbAy5YAwkolKpaFyvBiLoDt+WjyU8RjLzjBktO/dj0tTMlS4gJUL9KxWm0swkeUFko2KfGdIvf+28EZmbN29SrVo1YmI0aDQShQLMzJTs27ePGjVqAFC3bj0unL+GRmUGKNHKKMws1Ny7dxdXV1emT5/OH2Mno9RkT7iZqwmgUtViHD58iMWLFzNmxDjMNYUSRi5aqSJIdYnZc2axasVqnl4Px8G4oF4bn8ccIk4bgZQSd/Me+umfpYqbMRspU6YM/ndjyKesmrAvVhvJTbGDJ08f0bFdJ+7dfogDLoQrgrDNasXJ08dxdnZO/T+yga+e2NhYVqxYwd7t6zG3sKR77+9o1qxZpnMESQmRUShMpGm8xeFjxKi8DSLztfNGZOrUqcOJE+fQRc7WIaWKAgXysG/fXu7evUvHjp2Qake9H5YUYdSsVZF69eoxefJU4iLtMFZaJalDS2jMHQoVKoiXlw+mmpxYGmfXa0NA1DVitSEIlDiblMbOOI/efl/1GRq1qMGpE2exDiuCXZLRSrD6OQ7FYti1dwelSpTBMjIHjuQlRhvOS5NbfD98AGP/+B0pJefOnePWrVu4ublRv359FAqDn4cBA59CSomMiVHy0onEqnwNIvO180ZkzM3NiY1V6guIlEgZmfBZCBNMjfSf/DXaSFSaEHRLrBRYmxXAKN7U9aaOsNi7NGxYHy9PL7yfRmBjnF9/PzeYOXsqERERjPt1Klk0FRFCJwCx2nBecRa/ly84ffo0nTt0xVFdHCtFFsK1rwgyusvuvTupVasW3t7ejP9jAkcOH8XJyYnhI4bRsWPHTPe0acBAapEiIiNMpLGRU7KOjVP7ZTiRybSPtra2dvCO77rE2NiEFStWMHPmTIyNdSawpBgbS4YPH054eDgDBvRHilC9/SpNKPny5WPv3r1s37EdjTKIGHWIrnapJUrrTRZnB3r16sXAgQMpXa4oAcoLhKieEqx5QIC4wJy5s7GxsaFp06bs2ruD3BVNCbK9TIFq1hw8vJ9atWoBkDNnThYvXcQzzydcunqBTp06GQTGgIEvDplSof6/TnRP75lnc3d3l1JKOXHiRGlhYSWFsJQKhe7VwsJKDh06VL6hefMW0tLCTpoYZZOmRtmlsZG9tLOzl35+flJKKf39/WWuXLmlrbWztDDJKa0ts0srKxt59uzZhDr27dsns2ZxlrbWDtLC3Eq6u5eXHh4eCftVKpXcsmWL7Na1uxwyeKi8efOmNGDAwJcBcEX+x3sOGEkjpVOytpS43pe2ZVpzmUajYdCgQaxatQpTU3NiY6Np1ao1K1euwNRUF8cpNjaW3377nSVLlhAVFUWdOnWYNWsmBQsmTtRHRESwatUqTp48TcGC+enfv/87UWw1Gg0PHjzA0tKSPHnypGV3DRgw8B9ICXOZEEbSSGmbrGPVmuAMZy7LtCLzhoCAAB4/fkzevHlxcXFJx5YZMGDgSyNlREYpFYrkrUPTasMynMhk+sWYWbJkIUuWLOndDAMGDGRoMuh8SzLI9CJjwIABA6lOJl7xn2m9ywwYMGAgbUg57zIhRCMhxEMhxBMhxOj37BdCiDnx+28JIcqmSpc+AYPIGDBgwECqo03m9mGEEErgb6AxUBToLIQo+tZhjYEC8Vs/YEGKdeEzMYiMAQMGDKQqkhQK9V8BeCKlfCaljAM2AG+HTW8JrI73wL4A2Akh0tWjKdPNyVy9ejVQCOGZ3u1IQZyAjBp/PaP2LaP2CzJe33KnQB0HQZ28Jf9gJoS4kuTzYinl4vj3OQDvJPt8gIpvnf++Y3IAfp/Q3hQl04mMlDJDuZIJIa5kNJfHN2TUvmXUfkHG7tvnIqVslEJVvS+cx9trUJJzTJpiMJcZMGDAwNeBD5B0pbcr8OIzjklTDCJjwIABA18Hl4ECQoi8QggToBOw661jdgE94r3MKgGhUsp0M5VBJjSXZUAWf/yQr5aM2reM2i/I2H1LV6SUaiHE98BBQAksl1LeFUIMiN+/ENgHNAGeAFFAr/Rq7xsyXVgZAwYMGDCQdhjMZQYMGDBgINUwiIwBAwYMGEg1DCLzBSCEyCmEOC6EuC+EuCuEGBpf7iCEOCyEeBz/ap/knDHxoSMeCiEaJil3F0Lcjt83R8RnMRNCmAohNsaXXxRC5EnD/imFENeFEHsyWL/shBBbhBAP4v/vKmegvv0Q/128I4RYL4Qwyyh9M5DGpHdCG8MmAVyAsvHvrYFH6MJGTAVGx5ePBqbEvy8K3ARMgbzAU0AZv+8SUBmdv/x+oHF8+UBgYfz7TsDGNOzfcOAfYE/854zSr1VAn/j3JoBdRugbusV7zwHz+M+bgJ4ZoW+GLe23dG+AYXvPfwrsBOoDDwGX+DIX4GH8+zHAmCTHH4z/IbsAD5KUdwYWJT0m/r0RulXZIg364gocBeokEZmM0C+b+BuxeKs8I/Ttzapxh/jr7gEaZIS+Gba03wzmsi+MeLNBGeAi4CzjfdzjX7PGH/ah0BE54t+/Xa53jpRSDYQCjqnSCX1mASPRj/6XEfrlBgQAK+JNgUuFEJZkgL5JKX2BvwAvdOFIQqWUh8gAfTOQ9hhE5gtCCGEFbAWGSSnD/u3Q95TJfyn/t3NSDSFEM8BfSnk1uae8p+yL61c8RkBZYIGUsgwQic6E9CG+mr7Fz7W0RGf6yg5YCiG6/dsp7yn7IvtmIO0xiMwXghDCGJ3ArJNSbosvfvUmgmr8q398+YdCR/jEv3+7XO8cIYQRYAsEp3xP9KgKtBBCeKCLGFtHCLGWr79fb67rI6W8GP95CzrRyQh9qwc8l1IGSClVwDagChmjbwbSGIPIfAHEe9wsA+5LKWck2bUL+Cb+/Tfo5mrelHeK99DJiy53xKV4E0a4EKJSfJ093jrnTV3tgGNSylR9cpRSjpFSukop86Cb3D0mpez2tfcrvm8vAW8hRKH4orrAPTJA39CZySoJISzi21QXuE/G6JuBtCa9J4UMmwSohs5UcAu4Eb81QWejPgo8jn91SHLOz+i8eB4S77ETX14OuBO/bx6JUR3MgM3owk1cAtzSuI+1SJz4zxD9AkoDV+L/33YA9hmob38AD+LbtQad51iG6JthS9vNEFbGgAEDBgykGgZzmQEDBgwYSDUMImPAgAEDBlINg8gYMGDAgIFUwyAyBgwYMGAg1TCIjAEDBgwYSDUMImMg0yJ00a+fCyEc4j/bx3/Ond5tM2Ago2AQGQOZFimlN7AAmBxfNBlYLKX0TL9WGTCQsTCskzGQqYkP53MVWA70BcpIKePSt1UGDGQcjNK7AQYMpCdSSpUQYgRwAGhgEBgDBlIWg7nMgAFojC6kffH0bogBAxkNg8gYyNQIIUqjSxBXCfjhTZRhAwYMpAwGkTGQaYmPDLwAXf4eL2AaumRdBgwYSCEMImMgM9MX8JJSHo7/PB8oLISomY5tMmAgQ2HwLjNgwIABA6mGYSRjwIABAwZSDYPIGDBgwICBVMMgMgYMGDBgINUwiIwBAwYMGEg1DCJjwIABAwZSDYPIGDBgwICBVMMgMgYMGDBgINX4P6BPNwQPuSuBAAAAAElFTkSuQmCC\\n\",\n \"text/plain\": [\n \"
\"\n ]\n },\n \"metadata\": {\n \"needs_background\": \"light\"\n },\n \"output_type\": \"display_data\"\n }\n ],\n \"source\": [\n \"Release0 = Particle_data.where(Particle_data.time[:,0]==np.timedelta64(0, 's')) # the particles released at t = 0\\n\",\n \"\\n\",\n \"plt.figure()\\n\",\n \"ax = plt.axes()\\n\",\n \"ax.set_ylabel('Y')\\n\",\n \"ax.set_xlabel('X')\\n\",\n \"ax.set_ylim(1000, 49000)\\n\",\n \"ax.set_xlim(1000, 99000)\\n\",\n \"ax.plot(Release0.lon.transpose(), Release0.lat.transpose(), c='k', zorder=1)\\n\",\n \"T_scatter = ax.scatter(Release0.lon, Release0.lat, c=Release0.temperature, \\n\",\n \" cmap=plt.cm.inferno, norm=mpl.colors.Normalize(vmin=0., vmax=20.), \\n\",\n \" edgecolor='k', zorder=2)\\n\",\n \"plt.colorbar(T_scatter, label='T [$^{\\\\circ} C$]')\\n\",\n \"plt.show()\"\n ]\n }\n ],\n \"metadata\": {\n \"celltoolbar\": \"Raw-celnotatie\",\n \"kernelspec\": {\n \"display_name\": \"Python 3\",\n \"language\": \"python\",\n \"name\": \"python3\"\n },\n \"language_info\": {\n \"codemirror_mode\": {\n \"name\": \"ipython\",\n \"version\": 3\n },\n \"file_extension\": \".py\",\n \"mimetype\": \"text/x-python\",\n \"name\": \"python\",\n \"nbconvert_exporter\": \"python\",\n \"pygments_lexer\": \"ipython3\",\n \"version\": \"3.6.11\"\n },\n \"pycharm\": {\n \"stem_cell\": {\n \"cell_type\": \"raw\",\n \"source\": [],\n \"metadata\": {\n \"collapsed\": false\n }\n }\n }\n },\n \"nbformat\": 4,\n \"nbformat_minor\": 4\n}"},"license":{"kind":"string","value":"mit"}}},{"rowIdx":1398,"cells":{"repo_name":{"kind":"string","value":"rishuatgithub/MLPy"},"path":{"kind":"string","value":"torch/10. JPEG - CNN + AlexNet.ipynb"},"copies":{"kind":"string","value":"1"},"size":{"kind":"string","value":"1910035"},"content":{"kind":"null"},"license":{"kind":"string","value":"apache-2.0"}}},{"rowIdx":1399,"cells":{"repo_name":{"kind":"string","value":"Luke035/dlnd-lessons"},"path":{"kind":"string","value":"gan_mnist/Intro_to_GANs_Solution.ipynb"},"copies":{"kind":"string","value":"1"},"size":{"kind":"string","value":"209536"},"content":{"kind":"string","value":"{\n \"cells\": [\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"# Generative Adversarial Network\\n\",\n \"\\n\",\n \"In this notebook, we'll be building a generative adversarial network (GAN) trained on the MNIST dataset. From this, we'll be able to generate new handwritten digits!\\n\",\n \"\\n\",\n \"GANs were [first reported on](https://arxiv.org/abs/1406.2661) in 2014 from Ian Goodfellow and others in Yoshua Bengio's lab. Since then, GANs have exploded in popularity. Here are a few examples to check out:\\n\",\n \"\\n\",\n \"* [Pix2Pix](https://affinelayer.com/pixsrv/) \\n\",\n \"* [CycleGAN](https://github.com/junyanz/CycleGAN)\\n\",\n \"* [A whole list](https://github.com/wiseodd/generative-models)\\n\",\n \"\\n\",\n \"The idea behind GANs is that you have two networks, a generator $G$ and a discriminator $D$, competing against each other. The generator makes fake data to pass to the discriminator. The discriminator also sees real data and predicts if the data it's received is real or fake. The generator is trained to fool the discriminator, it wants to output data that looks _as close as possible_ to real data. And the discriminator is trained to figure out which data is real and which is fake. What ends up happening is that the generator learns to make data that is indistiguishable from real data to the discriminator.\\n\",\n \"\\n\",\n \"\\n\",\n \"\\n\",\n \"The general structure of a GAN is shown in the diagram above, using MNIST images as data. The latent sample is a random vector the generator uses to contruct it's fake images. As the generator learns through training, it figures out how to map these random vectors to recognizable images that can foold the discriminator.\\n\",\n \"\\n\",\n \"The output of the discriminator is a sigmoid function, where 0 indicates a fake image and 1 indicates an real image. If you're interested only in generating new images, you can throw out the discriminator after training. Now, let's see how we build this thing in TensorFlow.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 1,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"%matplotlib inline\\n\",\n \"\\n\",\n \"import pickle as pkl\\n\",\n \"import numpy as np\\n\",\n \"import tensorflow as tf\\n\",\n \"import matplotlib.pyplot as plt\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 2,\n \"metadata\": {},\n \"outputs\": [\n {\n \"data\": {\n \"text/plain\": [\n \"'1.1.0'\"\n ]\n },\n \"execution_count\": 2,\n \"metadata\": {},\n \"output_type\": \"execute_result\"\n }\n ],\n \"source\": [\n \"tf.__version__\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 3,\n \"metadata\": {},\n \"outputs\": [\n {\n \"name\": \"stdout\",\n \"output_type\": \"stream\",\n \"text\": [\n \"Extracting MNIST_data/train-images-idx3-ubyte.gz\\n\",\n \"Extracting MNIST_data/train-labels-idx1-ubyte.gz\\n\",\n \"Extracting MNIST_data/t10k-images-idx3-ubyte.gz\\n\",\n \"Extracting MNIST_data/t10k-labels-idx1-ubyte.gz\\n\"\n ]\n }\n ],\n \"source\": [\n \"from tensorflow.examples.tutorials.mnist import input_data\\n\",\n \"mnist = input_data.read_data_sets('MNIST_data')\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"## Model Inputs\\n\",\n \"\\n\",\n \"First we need to create the inputs for our graph. We need two inputs, one for the discriminator and one for the generator. Here we'll call the discriminator input `inputs_real` and the generator input `inputs_z`. We'll assign them the appropriate sizes for each of the networks.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 4,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"def model_inputs(real_dim, z_dim):\\n\",\n \" inputs_real = tf.placeholder(tf.float32, (None, real_dim), name='input_real') \\n\",\n \" inputs_z = tf.placeholder(tf.float32, (None, z_dim), name='input_z')\\n\",\n \" \\n\",\n \" return inputs_real, inputs_z\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"## Generator network\\n\",\n \"\\n\",\n \"\\n\",\n \"\\n\",\n \"Here we'll build the generator network. To make this network a universal function approximator, we'll need at least one hidden layer. We should use a leaky ReLU to allow gradients to flow backwards through the layer unimpeded. A leaky ReLU is like a normal ReLU, except that there is a small non-zero output for negative input values.\\n\",\n \"\\n\",\n \"#### Variable Scope\\n\",\n \"Here we need to use `tf.variable_scope` for two reasons. Firstly, we're going to make sure all the variable names start with `generator`. Similarly, we'll prepend `discriminator` to the discriminator variables. This will help out later when we're training the separate networks.\\n\",\n \"\\n\",\n \"We could just use `tf.name_scope` to set the names, but we also want to reuse these networks with different inputs. For the generator, we're going to train it, but also _sample from it_ as we're training and after training. The discriminator will need to share variables between the fake and real input images. So, we can use the `reuse` keyword for `tf.variable_scope` to tell TensorFlow to reuse the variables instead of creating new ones if we build the graph again.\\n\",\n \"\\n\",\n \"To use `tf.variable_scope`, you use a `with` statement:\\n\",\n \"```python\\n\",\n \"with tf.variable_scope('scope_name', reuse=False):\\n\",\n \" # code here\\n\",\n \"```\\n\",\n \"\\n\",\n \"Here's more from [the TensorFlow documentation](https://www.tensorflow.org/programmers_guide/variable_scope#the_problem) to get another look at using `tf.variable_scope`.\\n\",\n \"\\n\",\n \"#### Leaky ReLU\\n\",\n \"TensorFlow doesn't provide an operation for leaky ReLUs, so we'll need to make one . For this you can use take the outputs from a linear fully connected layer and pass them to `tf.maximum`. Typically, a parameter `alpha` sets the magnitude of the output for negative values. So, the output for negative input (`x`) values is `alpha*x`, and the output for positive `x` is `x`:\\n\",\n \"$$\\n\",\n \"f(x) = max(\\\\alpha * x, x)\\n\",\n \"$$\\n\",\n \"\\n\",\n \"#### Tanh Output\\n\",\n \"The generator has been found to perform the best with $tanh$ for the generator output. This means that we'll have to rescale the MNIST images to be between -1 and 1, instead of 0 and 1.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 5,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"def generator(z, out_dim, n_units=128, reuse=False, alpha=0.01):\\n\",\n \" with tf.variable_scope('generator', reuse=reuse):\\n\",\n \" # Hidden layer\\n\",\n \" h1 = tf.layers.dense(z, n_units, activation=None)\\n\",\n \" # Leaky ReLU\\n\",\n \" h1 = tf.maximum(alpha * h1, h1)\\n\",\n \" \\n\",\n \" # Logits and tanh output\\n\",\n \" logits = tf.layers.dense(h1, out_dim, activation=None)\\n\",\n \" out = tf.tanh(logits)\\n\",\n \" \\n\",\n \" return out\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"## Discriminator\\n\",\n \"\\n\",\n \"The discriminator network is almost exactly the same as the generator network, except that we're using a sigmoid output layer.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 6,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"def discriminator(x, n_units=128, reuse=False, alpha=0.01):\\n\",\n \" with tf.variable_scope('discriminator', reuse=reuse):\\n\",\n \" # Hidden layer\\n\",\n \" h1 = tf.layers.dense(x, n_units, activation=None)\\n\",\n \" # Leaky ReLU\\n\",\n \" h1 = tf.maximum(alpha * h1, h1)\\n\",\n \" \\n\",\n \" logits = tf.layers.dense(h1, 1, activation=None)\\n\",\n \" out = tf.sigmoid(logits)\\n\",\n \" \\n\",\n \" return out, logits\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"## Hyperparameters\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 7,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"# Size of input image to discriminator\\n\",\n \"input_size = 784\\n\",\n \"# Size of latent vector to generator\\n\",\n \"z_size = 100\\n\",\n \"# Sizes of hidden layers in generator and discriminator\\n\",\n \"g_hidden_size = 128\\n\",\n \"d_hidden_size = 128\\n\",\n \"# Leak factor for leaky ReLU\\n\",\n \"alpha = 0.01\\n\",\n \"# Smoothing \\n\",\n \"smooth = 0.1\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"## Build network\\n\",\n \"\\n\",\n \"Now we're building the network from the functions defined above.\\n\",\n \"\\n\",\n \"First is to get our inputs, `input_real, input_z` from `model_inputs` using the sizes of the input and z.\\n\",\n \"\\n\",\n \"Then, we'll create the generator, `generator(input_z, input_size)`. This builds the generator with the appropriate input and output sizes.\\n\",\n \"\\n\",\n \"Then the discriminators. We'll build two of them, one for real data and one for fake data. Since we want the weights to be the same for both real and fake data, we need to reuse the variables. For the fake data, we're getting it from the generator as `g_model`. So the real data discriminator is `discriminator(input_real)` while the fake discriminator is `discriminator(g_model, reuse=True)`.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 8,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"tf.reset_default_graph()\\n\",\n \"# Create our input placeholders\\n\",\n \"input_real, input_z = model_inputs(input_size, z_size)\\n\",\n \"\\n\",\n \"# Build the model\\n\",\n \"g_model = generator(input_z, input_size, n_units=g_hidden_size, alpha=alpha)\\n\",\n \"# g_model is the generator output\\n\",\n \"\\n\",\n \"d_model_real, d_logits_real = discriminator(input_real, n_units=d_hidden_size, alpha=alpha)\\n\",\n \"d_model_fake, d_logits_fake = discriminator(g_model, reuse=True, n_units=d_hidden_size, alpha=alpha)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"## Discriminator and Generator Losses\\n\",\n \"\\n\",\n \"Now we need to calculate the losses, which is a little tricky. For the discriminator, the total loss is the sum of the losses for real and fake images, `d_loss = d_loss_real + d_loss_fake`. The losses will by sigmoid cross-entropys, which we can get with `tf.nn.sigmoid_cross_entropy_with_logits`. We'll also wrap that in `tf.reduce_mean` to get the mean for all the images in the batch. So the losses will look something like \\n\",\n \"\\n\",\n \"```python\\n\",\n \"tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=labels))\\n\",\n \"```\\n\",\n \"\\n\",\n \"For the real image logits, we'll use `d_logits_real` which we got from the discriminator in the cell above. For the labels, we want them to be all ones, since these are all real images. To help the discriminator generalize better, the labels are reduced a bit from 1.0 to 0.9, for example, using the parameter `smooth`. This is known as label smoothing, typically used with classifiers to improve performance. In TensorFlow, it looks something like `labels = tf.ones_like(tensor) * (1 - smooth)`\\n\",\n \"\\n\",\n \"The discriminator loss for the fake data is similar. The logits are `d_logits_fake`, which we got from passing the generator output to the discriminator. These fake logits are used with labels of all zeros. Remember that we want the discriminator to output 1 for real images and 0 for fake images, so we need to set up the losses to reflect that.\\n\",\n \"\\n\",\n \"Finally, the generator losses are using `d_logits_fake`, the fake image logits. But, now the labels are all ones. The generator is trying to fool the discriminator, so it wants to discriminator to output ones for fake images.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 9,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"# Calculate losses\\n\",\n \"d_loss_real = tf.reduce_mean(\\n\",\n \" tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_real, \\n\",\n \" labels=tf.ones_like(d_logits_real) * (1 - smooth)))\\n\",\n \"d_loss_fake = tf.reduce_mean(\\n\",\n \" tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_fake, \\n\",\n \" labels=tf.zeros_like(d_logits_real)))\\n\",\n \"d_loss = d_loss_real + d_loss_fake\\n\",\n \"\\n\",\n \"g_loss = tf.reduce_mean(\\n\",\n \" tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_fake,\\n\",\n \" labels=tf.ones_like(d_logits_fake)))\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"## Optimizers\\n\",\n \"\\n\",\n \"We want to update the generator and discriminator variables separately. So we need to get the variables for each part build optimizers for the two parts. To get all the trainable variables, we use `tf.trainable_variables()`. This creates a list of all the variables we've defined in our graph.\\n\",\n \"\\n\",\n \"For the generator optimizer, we only want to generator variables. Our past selves were nice and used a variable scope to start all of our generator variable names with `generator`. So, we just need to iterate through the list from `tf.trainable_variables()` and keep variables to start with `generator`. Each variable object has an attribute `name` which holds the name of the variable as a string (`var.name == 'weights_0'` for instance). \\n\",\n \"\\n\",\n \"We can do something similar with the discriminator. All the variables in the discriminator start with `discriminator`.\\n\",\n \"\\n\",\n \"Then, in the optimizer we pass the variable lists to `var_list` in the `minimize` method. This tells the optimizer to only update the listed variables. Something like `tf.train.AdamOptimizer().minimize(loss, var_list=var_list)` will only train the variables in `var_list`.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 10,\n \"metadata\": {\n \"scrolled\": true\n },\n \"outputs\": [],\n \"source\": [\n \"# Optimizers\\n\",\n \"learning_rate = 0.002\\n\",\n \"\\n\",\n \"# Get the trainable_variables, split into G and D parts\\n\",\n \"t_vars = tf.trainable_variables()\\n\",\n \"g_vars = [var for var in t_vars if var.name.startswith('generator')]\\n\",\n \"d_vars = [var for var in t_vars if var.name.startswith('discriminator')]\\n\",\n \"\\n\",\n \"d_train_opt = tf.train.AdamOptimizer(learning_rate).minimize(d_loss, var_list=d_vars)\\n\",\n \"g_train_opt = tf.train.AdamOptimizer(learning_rate).minimize(g_loss, var_list=g_vars)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"## Training\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 11,\n \"metadata\": {\n \"scrolled\": true\n },\n \"outputs\": [\n {\n \"name\": \"stdout\",\n \"output_type\": \"stream\",\n \"text\": [\n \"Epoch 1/100... Discriminator Loss: 0.3476... Generator Loss: 4.4379\\n\",\n \"Epoch 2/100... Discriminator Loss: 0.3773... Generator Loss: 3.6476\\n\",\n \"Epoch 3/100... Discriminator Loss: 0.4128... Generator Loss: 2.9022\\n\",\n \"Epoch 4/100... Discriminator Loss: 1.3566... Generator Loss: 1.9196\\n\",\n \"Epoch 5/100... Discriminator Loss: 0.5184... Generator Loss: 6.9337\\n\",\n \"Epoch 6/100... Discriminator Loss: 1.8136... Generator Loss: 1.5963\\n\",\n \"Epoch 7/100... Discriminator Loss: 1.3852... Generator Loss: 2.7554\\n\",\n \"Epoch 8/100... Discriminator Loss: 1.4262... Generator Loss: 5.0319\\n\",\n \"Epoch 9/100... Discriminator Loss: 1.6795... Generator Loss: 4.5466\\n\",\n \"Epoch 10/100... Discriminator Loss: 2.1964... Generator Loss: 0.6939\\n\",\n \"Epoch 11/100... Discriminator Loss: 1.3391... Generator Loss: 1.0769\\n\",\n \"Epoch 12/100... Discriminator Loss: 2.0142... Generator Loss: 1.4427\\n\",\n \"Epoch 13/100... Discriminator Loss: 0.6645... Generator Loss: 3.5429\\n\",\n \"Epoch 14/100... Discriminator Loss: 1.9441... Generator Loss: 2.2589\\n\",\n \"Epoch 15/100... Discriminator Loss: 3.1723... Generator Loss: 0.7948\\n\",\n \"Epoch 16/100... Discriminator Loss: 1.6960... Generator Loss: 1.7192\\n\",\n \"Epoch 17/100... Discriminator Loss: 2.5293... Generator Loss: 1.7526\\n\",\n \"Epoch 18/100... Discriminator Loss: 0.8310... Generator Loss: 2.8067\\n\",\n \"Epoch 19/100... Discriminator Loss: 1.1654... Generator Loss: 1.2197\\n\",\n \"Epoch 20/100... Discriminator Loss: 1.8485... Generator Loss: 1.1577\\n\",\n \"Epoch 21/100... Discriminator Loss: 1.1272... Generator Loss: 1.4185\\n\",\n \"Epoch 22/100... Discriminator Loss: 0.7266... Generator Loss: 2.6219\\n\",\n \"Epoch 23/100... Discriminator Loss: 0.9997... Generator Loss: 1.5696\\n\",\n \"Epoch 24/100... Discriminator Loss: 0.7488... Generator Loss: 3.1071\\n\",\n \"Epoch 25/100... Discriminator Loss: 0.9664... Generator Loss: 1.3132\\n\",\n \"Epoch 26/100... Discriminator Loss: 0.9947... Generator Loss: 2.1388\\n\",\n \"Epoch 27/100... Discriminator Loss: 1.2071... Generator Loss: 1.8175\\n\",\n \"Epoch 28/100... Discriminator Loss: 0.7611... Generator Loss: 2.3673\\n\",\n \"Epoch 29/100... Discriminator Loss: 0.8222... Generator Loss: 2.3087\\n\",\n \"Epoch 30/100... Discriminator Loss: 0.9604... Generator Loss: 2.3985\\n\",\n \"Epoch 31/100... Discriminator Loss: 1.1468... Generator Loss: 2.0511\\n\",\n \"Epoch 32/100... Discriminator Loss: 1.2076... Generator Loss: 1.5616\\n\",\n \"Epoch 33/100... Discriminator Loss: 1.1870... Generator Loss: 2.2151\\n\",\n \"Epoch 34/100... Discriminator Loss: 1.0174... Generator Loss: 1.8403\\n\",\n \"Epoch 35/100... Discriminator Loss: 1.1196... Generator Loss: 1.4938\\n\",\n \"Epoch 36/100... Discriminator Loss: 0.8838... Generator Loss: 2.5240\\n\",\n \"Epoch 37/100... Discriminator Loss: 1.1113... Generator Loss: 1.9427\\n\",\n \"Epoch 38/100... Discriminator Loss: 0.7654... Generator Loss: 3.5077\\n\",\n \"Epoch 39/100... Discriminator Loss: 0.6580... Generator Loss: 2.7958\\n\",\n \"Epoch 40/100... Discriminator Loss: 1.2465... Generator Loss: 1.9984\\n\",\n \"Epoch 41/100... Discriminator Loss: 0.9223... Generator Loss: 1.9843\\n\",\n \"Epoch 42/100... Discriminator Loss: 1.0616... Generator Loss: 2.2574\\n\",\n \"Epoch 43/100... Discriminator Loss: 1.3891... Generator Loss: 1.5796\\n\",\n \"Epoch 44/100... Discriminator Loss: 0.9016... Generator Loss: 1.9284\\n\",\n \"Epoch 45/100... Discriminator Loss: 0.8242... Generator Loss: 2.7717\\n\",\n \"Epoch 46/100... Discriminator Loss: 0.7974... Generator Loss: 2.0371\\n\",\n \"Epoch 47/100... Discriminator Loss: 0.9277... Generator Loss: 1.6320\\n\",\n \"Epoch 48/100... Discriminator Loss: 1.1799... Generator Loss: 1.9311\\n\",\n \"Epoch 49/100... Discriminator Loss: 1.0351... Generator Loss: 1.4160\\n\",\n \"Epoch 50/100... Discriminator Loss: 0.8978... Generator Loss: 2.0509\\n\",\n \"Epoch 51/100... Discriminator Loss: 0.8651... Generator Loss: 2.2080\\n\",\n \"Epoch 52/100... Discriminator Loss: 0.7782... Generator Loss: 2.2180\\n\",\n \"Epoch 53/100... Discriminator Loss: 0.9958... Generator Loss: 1.9843\\n\",\n \"Epoch 54/100... Discriminator Loss: 1.0633... Generator Loss: 1.4747\\n\",\n \"Epoch 55/100... Discriminator Loss: 1.0347... Generator Loss: 2.0532\\n\",\n \"Epoch 56/100... Discriminator Loss: 1.0908... Generator Loss: 1.8969\\n\",\n \"Epoch 57/100... Discriminator Loss: 1.0056... Generator Loss: 2.0256\\n\",\n \"Epoch 58/100... Discriminator Loss: 1.0669... Generator Loss: 1.7931\\n\",\n \"Epoch 59/100... Discriminator Loss: 0.8461... Generator Loss: 1.8467\\n\",\n \"Epoch 60/100... Discriminator Loss: 0.9207... Generator Loss: 1.9543\\n\",\n \"Epoch 61/100... Discriminator Loss: 0.9859... Generator Loss: 1.7968\\n\",\n \"Epoch 62/100... Discriminator Loss: 1.1813... Generator Loss: 1.6643\\n\",\n \"Epoch 63/100... Discriminator Loss: 0.9457... Generator Loss: 2.2089\\n\",\n \"Epoch 64/100... Discriminator Loss: 1.0183... Generator Loss: 1.8519\\n\",\n \"Epoch 65/100... Discriminator Loss: 1.0323... Generator Loss: 2.1944\\n\",\n \"Epoch 66/100... Discriminator Loss: 0.7799... Generator Loss: 2.6862\\n\",\n \"Epoch 67/100... Discriminator Loss: 0.9300... Generator Loss: 2.2780\\n\",\n \"Epoch 68/100... Discriminator Loss: 1.0825... Generator Loss: 1.6308\\n\",\n \"Epoch 69/100... Discriminator Loss: 1.0393... Generator Loss: 1.7590\\n\",\n \"Epoch 70/100... Discriminator Loss: 1.2438... Generator Loss: 1.7331\\n\",\n \"Epoch 71/100... Discriminator Loss: 1.0732... Generator Loss: 1.9556\\n\",\n \"Epoch 72/100... Discriminator Loss: 1.0529... Generator Loss: 1.7048\\n\",\n \"Epoch 73/100... Discriminator Loss: 1.0301... Generator Loss: 1.6153\\n\",\n \"Epoch 74/100... Discriminator Loss: 1.0944... Generator Loss: 1.8231\\n\",\n \"Epoch 75/100... Discriminator Loss: 0.9399... Generator Loss: 2.0286\\n\",\n \"Epoch 76/100... Discriminator Loss: 1.1016... Generator Loss: 1.5947\\n\",\n \"Epoch 77/100... Discriminator Loss: 0.9712... Generator Loss: 2.0750\\n\",\n \"Epoch 78/100... Discriminator Loss: 1.1852... Generator Loss: 1.4842\\n\",\n \"Epoch 79/100... Discriminator Loss: 1.0053... Generator Loss: 1.3980\\n\",\n \"Epoch 80/100... Discriminator Loss: 0.9162... Generator Loss: 2.0734\\n\",\n \"Epoch 81/100... Discriminator Loss: 1.3742... Generator Loss: 0.9680\\n\",\n \"Epoch 82/100... Discriminator Loss: 1.0276... Generator Loss: 1.8480\\n\",\n \"Epoch 83/100... Discriminator Loss: 1.0645... Generator Loss: 1.5863\\n\",\n \"Epoch 84/100... Discriminator Loss: 1.2115... Generator Loss: 1.4543\\n\",\n \"Epoch 85/100... Discriminator Loss: 1.0001... Generator Loss: 1.9772\\n\",\n \"Epoch 86/100... Discriminator Loss: 0.8218... Generator Loss: 2.1147\\n\",\n \"Epoch 87/100... Discriminator Loss: 1.1014... Generator Loss: 1.5176\\n\",\n \"Epoch 88/100... Discriminator Loss: 0.8500... Generator Loss: 1.8422\\n\",\n \"Epoch 89/100... Discriminator Loss: 0.9565... Generator Loss: 1.6739\\n\",\n \"Epoch 90/100... Discriminator Loss: 1.2104... Generator Loss: 1.4702\\n\",\n \"Epoch 91/100... Discriminator Loss: 0.8567... Generator Loss: 2.1475\\n\",\n \"Epoch 92/100... Discriminator Loss: 1.0398... Generator Loss: 1.5363\\n\",\n \"Epoch 93/100... Discriminator Loss: 1.2562... Generator Loss: 1.2255\\n\",\n \"Epoch 94/100... Discriminator Loss: 1.2859... Generator Loss: 1.3106\\n\",\n \"Epoch 95/100... Discriminator Loss: 1.0269... Generator Loss: 1.8969\\n\",\n \"Epoch 96/100... Discriminator Loss: 0.9509... Generator Loss: 2.1518\\n\",\n \"Epoch 97/100... Discriminator Loss: 1.0212... Generator Loss: 1.9379\\n\",\n \"Epoch 98/100... Discriminator Loss: 1.0222... Generator Loss: 1.9024\\n\",\n \"Epoch 99/100... Discriminator Loss: 1.0340... Generator Loss: 1.5095\\n\",\n \"Epoch 100/100... Discriminator Loss: 1.0565... Generator Loss: 1.4482\\n\"\n ]\n }\n ],\n \"source\": [\n \"batch_size = 100\\n\",\n \"epochs = 100\\n\",\n \"samples = []\\n\",\n \"losses = []\\n\",\n \"# Only save generator variables\\n\",\n \"saver = tf.train.Saver(var_list=g_vars)\\n\",\n \"with tf.Session() as sess:\\n\",\n \" sess.run(tf.global_variables_initializer())\\n\",\n \" for e in range(epochs):\\n\",\n \" for ii in range(mnist.train.num_examples//batch_size):\\n\",\n \" batch = mnist.train.next_batch(batch_size)\\n\",\n \" \\n\",\n \" # Get images, reshape and rescale to pass to D\\n\",\n \" batch_images = batch[0].reshape((batch_size, 784))\\n\",\n \" batch_images = batch_images*2 - 1\\n\",\n \" \\n\",\n \" # Sample random noise for G\\n\",\n \" batch_z = np.random.uniform(-1, 1, size=(batch_size, z_size))\\n\",\n \" \\n\",\n \" # Run optimizers\\n\",\n \" _ = sess.run(d_train_opt, feed_dict={input_real: batch_images, input_z: batch_z})\\n\",\n \" _ = sess.run(g_train_opt, feed_dict={input_z: batch_z})\\n\",\n \" \\n\",\n \" # At the end of each epoch, get the losses and print them out\\n\",\n \" train_loss_d = sess.run(d_loss, {input_z: batch_z, input_real: batch_images})\\n\",\n \" train_loss_g = g_loss.eval({input_z: batch_z})\\n\",\n \" \\n\",\n \" print(\\\"Epoch {}/{}...\\\".format(e+1, epochs),\\n\",\n \" \\\"Discriminator Loss: {:.4f}...\\\".format(train_loss_d),\\n\",\n \" \\\"Generator Loss: {:.4f}\\\".format(train_loss_g)) \\n\",\n \" # Save losses to view after training\\n\",\n \" losses.append((train_loss_d, train_loss_g))\\n\",\n \" \\n\",\n \" # Sample from generator as we're training for viewing afterwards\\n\",\n \" sample_z = np.random.uniform(-1, 1, size=(16, z_size))\\n\",\n \" gen_samples = sess.run(\\n\",\n \" generator(input_z, input_size, n_units=g_hidden_size, reuse=True, alpha=alpha),\\n\",\n \" feed_dict={input_z: sample_z})\\n\",\n \" samples.append(gen_samples)\\n\",\n \" saver.save(sess, './checkpoints/generator.ckpt')\\n\",\n \"\\n\",\n \"# Save training generator samples\\n\",\n \"with open('train_samples.pkl', 'wb') as f:\\n\",\n \" pkl.dump(samples, f)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"## Training loss\\n\",\n \"\\n\",\n \"Here we'll check out the training losses for the generator and discriminator.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 12,\n \"metadata\": {},\n \"outputs\": [\n {\n \"data\": {\n \"text/plain\": [\n \"\"\n ]\n },\n \"execution_count\": 12,\n \"metadata\": {},\n \"output_type\": \"execute_result\"\n },\n {\n \"data\": {\n \"image/png\": \"iVBORw0KGgoAAAANSUhEUgAAAW4AAAEICAYAAAB/Dx7IAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXd4XNWZ/z9nRhr1YjU32ZZccTeugOnNQGjJwpIECKQB\\nGyAJJYH9pUE2m00hhRbKJkDC0kJvIQSMDbhg3Hvvsq3eR2Xa+f1x7p2500fVGut8nkfPSDP33jma\\n8r3v/b7veY+QUqLRaDSa5MF2vAeg0Wg0mq6hhVuj0WiSDC3cGo1Gk2Ro4dZoNJokQwu3RqPRJBla\\nuDUajSbJ0MKtOe4IIexCiFYhxOje3FajOVERuo5b01WEEK2WPzOBTsBr/H2zlPK5/h9VzxFC/AIo\\nlVLeeLzHotHEIuV4D0CTfEgps83fhRAHgG9JKT+Mtr0QIkVK6emPsWk0gwFtlWh6HSHEL4QQLwkh\\nXhBCtADXCSFOFUJ8JoRoFEIcE0I8JIRINbZPEUJIIUSZ8ff/GY+/J4RoEUKsFEKUd3Vb4/GLhRC7\\nhBBNQoiHhRDLhRA3duN/miqE+NgY/2YhxBcsj10qhNhuPH+FEOIO4/4SIcQ/jH3qhRCfWPYpFUK8\\nLoSoEULsF0LcannsFCHEOiFEsxCiSgjx266OV3Nio4Vb01d8EXgeyANeAjzA94AiYCFwEXBzjP2/\\nCvwEKAAOAf/V1W2FECXA34EfGM+7H5jf1X9ECOEA3gHeBYqBO4CXhBDjjU2eBr4ppcwBZgAfG/f/\\nANhn7DMM+LFxPJtxvNXASOAC4AdCiPOM/R4GfiulzAXGA690dcyaExst3Jq+YpmU8m0ppU9K2S6l\\nXC2lXCWl9Egp9wFPAmfF2P8VKeUaKaUbeA6Y1Y1tLwU2SCnfNB77A1Dbjf9lIeBAianbsIXeA75s\\nPO4GpgghcqSU9VLKdZb7RwCjpZQuKaUZcZ8K5Eopf2ncvwf4S8jxJgghCqWULVLKVd0Ys+YERgu3\\npq84bP1DCHGSEOJdIUSlEKIZ+DkqCo5GpeX3NiA72oYxth1hHYdUmfiKBMYeygjgkAzO5B9ERcug\\nri4uBw4JIZYKIRYY9//K2G6xEGKvEOIHxv1jgNGGhdIohGgEfoiKygG+DkwBdgohPhdCXNKNMWtO\\nYLRwa/qK0HKlJ4AtwHjDAvgpIPp4DMeAUvMPIYQgILZd4SgwytjfZDRwBMC4krgcKEFZIC8a9zdL\\nKe+QUpYBVwL3CCHOQp1Mdksp8y0/OVLKy4z9dkopv2wc73fAq0KI9G6MW3OCooVb01/kAE2AUwgx\\nmdj+dm/xDjBbCHGZECIF5bEXx9nHLoRIt/ykAStQHv1dQohUIcS5wCUonztDCPFVIUSuYce0AD4A\\n43nHGYLfhCqZ9AErAZcQ4i7jOexCiOlCiDnGftcLIYqklD5jP2keU6MBLdya/uMu4AaUsD2BSlj2\\nKVLKKuAa4PdAHTAOWI+qO4/GdUC75WenlLITuAy4AuWRPwR8VUq529jnBuCgYQF90zgGwCTgI6AV\\nWA48KKX81CiNvASVKD1gHPMJINfY7xJgu1GR8wBwjZTS1f1XQnOioSfgaAYNQgg7yva4Skr56fEe\\nj0bTXXTErTmhEUJcJITINyyPn6AqNj4/zsPSaHqEFm7Nic7pqFrqGmAR8EXD+tBokhZtlWg0Gk2S\\noSNujUajSTL6pMlUUVGRLCsr64tDazQazQnJ2rVra6WU8cpVgT4S7rKyMtasWdMXh9ZoNJoTEiHE\\nwUS31VaJRqPRJBlauDUajSbJ0MKt0Wg0SUZcj1sIMYng6cljgZ9KKf/YZ6PSaDQ9xu12U1FRQUdH\\nx/EeisZCeno6paWlpKamdvsYcYVbSrkTo7+xMWX4CPB6t59Ro9H0CxUVFeTk5FBWVkZwY0PN8UJK\\nSV1dHRUVFZSXl8ffIQpdtUrOA/ZKKRPOfmo0muNDR0cHhYWFWrQHEEIICgsLe3wV1FXh/jLwQpQB\\n3SSEWCOEWFNTU9OjQWk0mt5Bi/bAozfek4SF21h373Lg5UiPSymflFLOlVLOLS5OqIa851Rvh4Mr\\n+ue5NBqNZoDQlYj7YmCd0eN4YPDxb+CdO473KDQaTRTsdjuzZs1i6tSpzJw5k9/97nf4fGpNiDVr\\n1vDd7363x8/x+OOP87e//a1L+5x22mndfr5nnnmGo0ePdnv/3qArMye/QhSb5Ljh6VA/Go1mQJKR\\nkcGGDRsAqK6u5qtf/SrNzc3cf//9zJ07l7lz5/bo+B6Ph1tuuaXL+61Y0f0r9WeeeYZp06YxYsSI\\nhPfxer3Y7fZuP2coCUXcQogs4ALgtV575t7A6wav53iPQqPRJEBJSQlPPvkkjzzyCFJKli5dyqWX\\nXgrAxx9/zKxZs5g1axYnn3wyLS0tAPz6179m+vTpzJw5k3vvvReAs88+m+9///vMnTuXBx98kPvu\\nu48HHnjA/9gdd9zB3LlzmTx5MqtXr+ZLX/oSEyZM4Mc//rF/LNnZaj3ppUuXcvbZZ3PVVVdx0kkn\\nce2112J2TP35z3/OvHnzmDZtGjfddBNSSl555RXWrFnDtddey6xZs2hvb2fx4sWcfPLJTJ8+nW98\\n4xt0dqquwWVlZdxzzz3Mnj2bl1+O6DB3m4QibimlEyjs1WfuDXxu9aPRaGJy/9tb2Xa0uVePOWVE\\nLj+7bGqX9hk7dixer5fq6uqg+x944AEeffRRFi5cSGtrK+np6bz33nu8+eabrFq1iszMTOrr6/3b\\nu1wufz+k++67L+hYDoeDNWvW8OCDD3LFFVewdu1aCgoKGDduHHfccQeFhcFStn79erZu3cqIESNY\\nuHAhy5cv5/TTT+e2227jpz/9KQDXX38977zzDldddRWPPPIIDzzwAHPnzqWjo4Mbb7yRxYsXM3Hi\\nRL72ta/x2GOP8f3vfx+AwsJC1q1b16XXKBGSe+ak16Oibo1Gk9QsXLiQO++8k4ceeojGxkZSUlL4\\n8MMP+frXv05mZiYABQUF/u2vueaaqMe6/PLLAZg+fTpTp05l+PDhpKWlMXbsWA4fPhy2/fz58ykt\\nLcVmszFr1iwOHDgAwJIlS1iwYAHTp0/no48+YuvWrWH77ty5k/LyciZOnAjADTfcwCeffJLQOHtC\\nn3QH7Dd8bvBpq0SjiUdXI+O+Yt++fdjtdkpKSti+fbv//nvvvZcvfOEL/OMf/2DhwoW8//77MY+T\\nlZUV9bG0tDQAbDab/3fzb48nXC+s29jtdjweDx0dHXznO99hzZo1jBo1ivvuu69btdexxtkTkjzi\\ndumIW6NJEmpqarjlllu47bbbwmqZ9+7dy/Tp07nnnnuYN28eO3bs4IILLuDpp5+mra0NIMgq6WtM\\nkS4qKqK1tZVXXnnF/1hOTo7fg580aRIHDhxgz549ADz77LOcddZZfT6+5I64vR7tcWs0A5j29nZm\\nzZqF2+0mJSWF66+/njvvvDNsuz/+8Y8sWbIEm83G1KlTufjii0lLS2PDhg3MnTsXh8PBJZdcwi9/\\n+ct+GXd+fj7f/va3mTZtGsOGDWPevHn+x2688UZuueUWMjIyWLlyJU8//TRXX301Ho+HefPmdavK\\npav0yZqTc+fOlf2ykMKjC6BmB/ysEfQMMY0miO3btzN58uTjPQxNBCK9N0KItVLKhOojk9wqMaJt\\n7XNrNJpBhBZujUajSTKSW7hNf1snKDUazSAiuYVbR9wajWYQktzCrSNujUYzCElu4fZH3Fq4NRrN\\n4OHEEG4dcWs0A5aqqiq++tWvMnbsWObMmcOpp57K668fn9UPly5d2qPOgAOF5BVuKQORtva4NZoB\\niZSSK6+8kjPPPJN9+/axdu1aXnzxRSoqKvrsOSNNazfpjnDHOt7xInmF2+cN/K4jbo1mQPLRRx/h\\ncDiCZhOOGTOG22+/Ha/Xyw9+8APmzZvHjBkzeOKJJ4DYrVbXrl3LWWedxZw5c1i0aBHHjh0Dwlu9\\nvv322yxYsICTTz6Z888/n6qqKg4cOMDjjz/OH/7wB2bNmsWnn37KgQMHOPfcc5kxYwbnnXcehw4d\\nAgKzIxcsWMAPf/jDfn7V4pO8U96tvrb2uDWa2Lx3L1Ru7t1jDpsOF/8q5iZbt25l9uzZER/7y1/+\\nQl5eHqtXr6azs5OFCxdy4YUXApFbrS5YsIDbb7+dN998k+LiYl566SV+9KMf8dRTTwHBrV4bGhr4\\n7LPPEELw5z//md/85jf87ne/45ZbbiE7O5u7774bgMsuu4wbbriBG264gaeeeorvfve7vPHGGwBU\\nVFSwYsWKXl0AobdIXuH2uiy/D7xLGY1GE86tt97KsmXLcDgcjBkzhk2bNvkbODU1NbF7924cDoe/\\n1Srgb7Wan5/Pli1buOCCCwC1qszw4cP9x7a2UK2oqOCaa67h2LFjuFwuysvLI45n5cqVvPaaWh/m\\n+uuvD4qur7766gEp2pDUwm0Rax1xazSxiRMZ9xVTp07l1Vdf9f/96KOPUltby9y5cxk9ejQPP/ww\\nixYtCtpn6dKlEVutSimZOnUqK1eujPhc1haqt99+O3feeSeXX345S5cuDVtsIRH6qiVrb5DEHrdF\\nrLXHrdEMSM4991w6Ojp47LHH/PeZbVoXLVrEY489htutvr+7du3C6XRGPdakSZOoqanxC7fb7Y64\\nuAGo6H3kyJEA/PWvf/Xfb23JCmrR4BdffBGA5557jjPOOKM7/2a/k7zCbRVrXVWi0QxIhBC88cYb\\nfPzxx5SXlzN//nxuuOEGfv3rX/Otb32LKVOmMHv2bKZNm8bNN98cs4LD4XDwyiuvcM899zBz5kxm\\nzZoVtULkvvvu4+qrr2bOnDkUFRX577/ssst4/fXX/cnJhx9+mKeffpoZM2bw7LPP8uCDD/b6a9AX\\nJG9b17q98LCR9Lj2FZhwQd8+n0aTZOi2rgOXwdvW1Rpla6tEo9EMIhISbiFEvhDiFSHEDiHEdiHE\\nqX09sLh4dTmgRqMZnCRaVfIg8E8p5VVCCAeQ2YdjSgydnNRo4iKlDFvfUXN86Q17Om7ELYTIA84E\\n/mI8qUtK2djjZ+4pOjmp0cQkPT2durq6XhEKTe8gpaSuro709PQeHSeRiLscqAGeFkLMBNYC35NS\\nBtXtCCFuAm4CGD16dI8GlRBeHXFrNLEoLS2loqKCmpqa4z0UjYX09HT/5KLukohwpwCzgdullKuE\\nEA8C9wI/sW4kpXwSeBJUVUmPRpUIesq7RhOT1NTUqDMGNclNIsnJCqBCSrnK+PsVlJAfX6wzJ/WU\\nd41GM4iIK9xSykrgsBBiknHXecC2Ph1VIuiIW6PRDFISrSq5HXjOqCjZB3y974aUIEFNprRwazSa\\nwUNCwi2l3AAkNKOn39B13BqNZpByYsyctC6qoNFoNCc4ySvcuhxQo9EMUpJYuC0et7ZKNBrNICJ5\\nhdunywE1Gs3gJHmF27RHhF1H3BqNZlCRvMJtinVqpva4NRrNoCJ5hdsU69QMHXFrNJpBxQkg3Ona\\n49ZoNIOK5BVunxtsqepHR9wajWYQkbzC7XWDPVX9aI9bo9EMIpJXuH0eJdq2FL2QgkajGVQkr3B7\\nXYZVkqIjbo1GM6hIYuG2WCU64tZoNIOI5BVun8eSnNTCrdFoBg/JK9xeN9hT1I+2SjQazSAiiYXb\\nBXaHLgfUaDSDjuQVbtMq0eWAGo1mkJG8wm1aJbocUKPRDDKSV7jNmZM64tZoNIOM5BVur0d73BqN\\nZlCSxMLtMqpKUnWTKY1GM6hIaJV3IcQBoAXwAh4p5fFf8d3fZEovpKDRaAYXCQm3wTlSyto+G0lX\\n8Zq9SuJ43B1NcGQdjDun/8am0Wg0fUjyWiW+BKe8b3wRnr0Smir6b2wajUbThyQq3BL4UAixVghx\\nU6QNhBA3CSHWCCHW1NTU9N4Io2FtMhVLuNsb1e2RtX0/Jo1Go+kHEhXu06WUs4CLgVuFEGeGbiCl\\nfFJKOVdKObe4uLhXBxkR0yqJVw7odqrbijV9PyaNRqPpBxISbinlEeO2GngdmN+Xg0oIn1tF22Y5\\noJSRt3MZwn1kXf+NTaPRaPqQuMIthMgSQuSYvwMXAlv6emBxsbZ1BfB5I2/nalO3R9dH30aj0WiS\\niEQi7qHAMiHERuBz4F0p5T/7dlgJ4HUbE3CMwphoJYGuVnXrdkLNzv4Zm0aj0fQhccsBpZT7gJn9\\nMJauYVolZsTtdUNqRvh27jZIz4eORpWgHDqlf8ep0Wg0vUzylgOaVonNtEqiVJa4nDBsOqTl6coS\\njUZzQpCcwi2lpcmUcdEQrbLE5QRHNow8WQu3RqM5IUhO4TaTjGaTKYjhcTvBkQUj50DVVnC3988Y\\nNRqNpo9ITuH2utSt2Y8bokfc7jZwZCrhll44tql/xqjRaDR9RHIKtxld26zlgDE8bke2Em7QdolG\\no0l6klO4zTau9tTYEbeUSrhTMyFnGOSWauHWaDRJT3IKtz/iTokdcXs6lT3iyFJ/j5ythVuj0SQ9\\nySncfo87TnLSbcya9Av3HGjYD231fT9GjUaj6SOSVLgNkbZbywEjRNzmrElTuPNK1W1bXd+OT6PR\\naPqQ5BRu0xYxm0xB5Ijb7FOSmqluTVvF09m349NoNJo+ZOAIt88L//ghbHsz/rZBEXdq8H1WzM6A\\njmxj+zRjWy3cGo0meRk4wm2zw+aXYe+S+NtG9LhjWSVGxJ3iULceV8/GqtFoNMeRgSPcAEPGQOPB\\n+Nv5rZI4U95Dk5P+iFsLt0ajSV4GmHCXQcOB+Nv5rZJ4HrdhlaQawp2ihVuj0SQ/A0u488dA4+H4\\nCx5YZ07GmoDj97jNiFsnJzUaTfIzsIR7yBglyi3HYm/nnznpiD0Bxy/cZlWJTk5qNJrkZ2AJd/4Y\\nddsQx+dOtMmUO9Qq0clJjUaT/Aws4R5Spm7jJSgjNpmKYpXYUgOCrZOTGo3mBGBgCXdeKSASiLgt\\nddy2GIsFu9oC/jbo5KRGozkhGFjCnZIGuSPjV5ZYZ07GKgc0F1Ew0clJjUZzAjCwhBsSq+VOuMlU\\nqHDr5KRGo0l+EhZuIYRdCLFeCPFOXw6I/DFds0riTXk3+5SAEnrQyUmNRpPUdCXi/h6wva8G4mfI\\nGFUOGMvOsM6cjDnlvS3QpwTAZlPb64hbo9EkMQkJtxCiFPgC8Oe+HQ5GSaBUE3GiETRz0gbCFiXi\\nbg3UcJukpEVfn1Kj0WiSgEQj7j8CPwR80TYQQtwkhFgjhFhTU1PT/RH5SwIPRN/G6nGDiqKjLaRg\\n9bhBWSs6OanRaJKYuMIthLgUqJZSxlzzS0r5pJRyrpRybnFxcfdHNCSBSThWqwSUGEdcSMEZmHxj\\nYk/TVolGo0lqEom4FwKXCyEOAC8C5woh/q/PRpQ9TIlrrJJA0+qw2QO30SbghEbcKQ6dnNRoNElN\\nXOGWUv6nlLJUSlkGfBn4SEp5Xd+NyAb5o2KXBPrcKtoWwtgnNbE6btARt0ajSXoGXh03xC8J9LoD\\n/jYoqyQ04va41H06OanRaE4wuiTcUsqlUspL+2owfuJNwvG6AzMmwYi4Qzxud8iyZSY6OanRaJKc\\ngRlxDymD9gboaI78uGmVmNhTwuu4QxcK9m+rrRKNRpPcDEzhNtu7Rou6ve7AjEmIXA4YuoiCiU5O\\najSaJGdgCre/JPBA5Md9npCIO5ZVopOTGo3mxGJgCne8BRW8rpCIO6ULEbdOTmo0muRmYAp3xhBI\\ny0vcKrFHKAcMXSjYuq1OTmo0miRmYAq3EMouSdQqsaVGSE5qq0Sj0ZyYDEzhBigoh/p9kR8LLQe0\\np0SPuMPquHVyUqPRJDcDV7iHlCuPO9KSZF5X8AScSB632ygHDKvj7kLE7fPBe/dC9Y7Ex63RaDR9\\nzMAV7oJyJcbNR8Ifi2SVhEXcreo2tI67K8nJtlpY9Rjs6Nu1I04o3B3wz/+EtvrjPRKN5oRl4Ar3\\nkHJ1W78//LEwqySSx90Gwh5YINi6baLJyc4WdatFKHGOroPP/gS73j/eI9FoTlgGrnAXmMIdwecO\\nnTlpi+JxO7ICjahM7Glqf1/U1uLBxwAVeWsSo71R3dbvPb7j0GhOYAaucOeOVD52Q6SI2xO/yVTo\\nQsEmKcZ+3gQSlKbd0laX2Jg10NGkbqMlljUaTY8ZuMJts6uJOBGtEld4k6nQJGboQsEmXVnp3R9x\\na+FOmA4j4q7TEbdG01cMXOEGZZdEirgjNZkKs0oiLFsGAc87kQSl6XE7tXAnjN8q2QdSHt+xaDQn\\nKANbuIeUQ/2BcAHwehJoMtUaWbhNiyWRBKWOuLuOGXF3NoNT5wY0mr5gYAt3QTm4WsIFwOdWCUmT\\niE2mokTcpnAnZJUYHrfbCe72xMc9mDE9btAJSo2mjxjYwm2WBIbaJYlMwInmcZvJyURmT5rCDTrq\\nTpT2RnDkqN91glKj6RMGtnAXRKnlDrVKIjaZagufNQldS052WoRbX/YnRkcjDJumauh1glKj6RMG\\ntnDnjwFEeMQdapWYEbfVC3e1hvcpgUByMqGI2xn4PSTifnVtBVuONKEJob0RMgshf7S2SjSaPmJg\\nC3dquqrnDou4I6yAA8ElgXE97q5aJcGzJ3/65haeXRljXczBSkcTZORD4TgdcWs0fcTAFm4I7xIo\\npYqugybgGNG36XP7vODpCO/FDV1PTmYPU79bZk+2u7w4XV4a2/upy6CrDT74aWAdzYFMRyOk50PB\\nWF0SqNH0EXGFWwiRLoT4XAixUQixVQhxf38MzM+QsmCrxOxJEtpkCgI+d7Re3NC15GRnK+SNBGEL\\nskrqnEr0G9v6aSWdQytg+YPqdiDjcakrnYx8KBinTnyt1cd7VBrNCUciEXcncK6UciYwC7hICHFK\\n3w7LQkE5OGsCk2FMcQ5tMgUBUY/Wixu6PnMyLQcyCoKSk/VOJfpN7f0k3Oaklmir3g8UzBrudMMq\\nAV1ZotH0AXGFWypMszfV+Om/619/SeABdWvaIaFNpiAg6tF6cUMXk5Ot6hhZRSERd38Ld4O67Rzg\\nwt1uEe6Csep3naDUaHqdhDxuIYRdCLEBqAY+kFKuirDNTUKINUKINTU1Nb03Qr8AGJGbOdEmtBwQ\\nLBF3lF7c0PXkpCNbVUlYhbtV7dtvVol/NmJL/zxfdzEn32Tkq4ogW4pOUGo0fUBCwi2l9EopZwGl\\nwHwhxLQI2zwppZwrpZxbXFzceyMMreU2BTdiVYnpcZsRdw+Tk52tkBYu3PWGx93u9tLpibBCT2+T\\njFaJPcVoEqaFW6PpbbpUVSKlbASWABf1zXAikJ6nPGYzQRnJKjFF3BvqccdoMpVoHbcjKzzidgb2\\n7Re7JFkibr9VkqduC8ZCnfa4NZreJpGqkmIhRL7xewZwAdC/izAOGQONh9Tv/uRkBI/bFHV3DOFO\\nNOL2utU2jhxDuOv9iy+YVglAU3/YJe2Wxk0DGfMEk5GvbgvH6ZJAjaYPSCTiHg4sEUJsAlajPO7+\\nXYQxZwQ0H1O/+8sBI1SVhJYDRuxVkmDEbfrkjiyVnJRevzDVWyLuxn6JuJuCbwcqVqsEVEmg2wmt\\nVcdvTBrNCUhKvA2klJuAk/thLNHJHQ4Hl6vf/R63tclUqMdtRtwRqkpsKYCIn5w0j5GWDSnp6ve2\\nOsgsoM7pYkhmKg1t7tgJyr1LlNhOvTL2c8WjPYmsktTMQK18oZFYrtsLOcOO37g0mhOMgT9zEiBn\\nuIrm3O2xrZIwjztCxC2EEv14VkmnJeLOLFS/Gz53XWsnY4vVSaGxLcYJYNkfYOn/xH6eROhIIqvE\\n9LdBRdzQO7XcB1fCzvd6fhyN5gQgeYQboPlo5JmToVPeXa2AgJSMyMdLSUvAKjHFPydMuOudLsYW\\nKf88ZnKytSoQLfeEZKkqaW8M2CQAeaVq1mljL/R0Wfo/8N4Pe34cjeYEIK5VMiDINYS7pTJwX+ia\\nkxCIxg1LA1uU81IiEbfLsCWsEbezlnaXlzaXl7KiLGwijnC3VCa20k4svJ7AWAa6VWI2mDKxp0Ju\\nKTT0gnA3HoKmCnXCTXHE316jOYFJkoh7hLptORaIqkNXeYdANN5aDVkl0Y/XlYjbrOMGaKvz9ykp\\nynaQl5Ea3eN2dyjrwNPeM/E2E5Ip6UlileQH35c/uucRt88HzUdA+gLVRYONtnr43Ukqb6IZ9CSH\\ncOdarBJvAlPenbWQHWMSkN0RPznp97izlVeemgltdf6KkoKsNCXc0SJuayVFotUgUvpLDgP7GjZJ\\n3ijV8TCR+vPjRXtTsMcNqpSzpxF3a1Xg/RqsvU8Or1KBy7Y3j/dINAOA5BDutFwlnC2VcZpMmcJd\\nDVnxhDueVWIRboBM1a/ErOEuyHKQl+mIbpVYhTtRn3vPh/DrMcFCb+6bP1rdDmS7pKMx2CoBNXuy\\ntbJna3Y2HQ78HrqoxmDhyFp1e2DZ8R2HZkCQHMIthEpQthyN0mQq1CqpiWOVOLpWxw3KM3fW+mdN\\nFmU7yM9IpSlaVYnVj0804q7crOwQs6EWQIfRYCp/lLrtHKC13D6vGnuoVTJkjLptquj+sa32yGCN\\nuI+sU7d1uwNzGjSDluQQboBcYxJOpHJA65R3d7tK5mUVRT+WPS2BiNsJiMAkHmPau9mnpCDLQX5m\\nuFVS1dxBdUtHiFWSYMRtto5tiRCtD7SIW8rgKhdrgykr+YZw98QuMSPuIeWDU7ilhKPrYNgM9bc5\\np0EzaEke4c4Zpjy+eFPenUZnwuweJic7W1W0bVamZAWsEofdRnZaSsTk5HdfWM//e21z9yJuc+yt\\nln3Nlq6mAA6UksC9i+G34wORdEdInxITM+JuPND952o8rCL5YdMHp3A37Fefgzk3KNvwwKfHe0Sa\\n40wSCfdww+M2BDdikym3skkgtlWSSHLSbOlqYkTcdU4XhdkOhBDkZ6TS3OHG5wv04thb46SquVNF\\n3Gbliym+8TCFuyVCtJ5nWiUDJOKu2qauWsxL+PaQ6e4m2cPUFU5PI+78UappVcPB4LVFBwPma1w6\\nD8acpn1uTRIJd+4IJRROYymsiG1dPQHx643kpLVJVWYhuFppbmmlIEsJcl6mAymhpUN56x1uL7Wt\\nnbR0uJWpLKbjAAAgAElEQVRwmzMHE464DaskNLGZkhGwfgZKSaA5xupt6jaaVWKzKdHtSUlg42HI\\nG62E2+fumV+ejBxdr8pBS6ZA2elQt0f73IOc5BFus9eFmagKSk7a1a3XHRD2WOWACSUnnaqG28So\\n5fa01PiFOz9DjcFcNPhIo6qcaO7wqKuD/NFKdBP1uM0Fia1WiVmpkZZr/N1D4a7e3ju10C2GcFRt\\nVbehDaas5PegJFDK4IgbBp9dcmSt8rftqUq4QUfdg5wkEm5jEo4pOhFXwHEnGHEnkJzsDLFKjIjX\\n11ZHUbbqMJhnCrfhc1c0KOFu6XAjW6sgZ6jyfBOJuKWMbJWY08jTDeFONOLe/2lAVE3WPwePnw6v\\nfjuxY8SiJSTiDu3FbaUnk3DaG9TVT/7owKIag6kk0OuBYxth5Gz197AZkJanfe5BTnJMeYfAJJxI\\nwm2d8u6sVf1FUqP0KYEEZ062QvbQwN9GxG1vrwtE3JlmxK2E+4gh3F6vV4lw9jAVLSdSx93RaCln\\nDElsZuSrMdsdiQm3pxP+70vqeLO/Buf8GNY8BUt/qb70h1eBsw6yCuMfKxpmxF2/T1XyhPbitjJk\\njBLgjubACShRzIqSvFHq5G1PG1wRd80OtYbqyDnqb5td+9yaJIq4sw2rxPQ3IyUnfR5llcSySaD7\\nHjeQ5WkKE25zEs6RRrVkWiFNCOmzRNwJCLfpb+cMV9GsufiAtXFTWm5iVknNDpV8HX0qrP8/+MMU\\nJdozvwLXvgxINdmnJ7RWQe5INQ29Zoc6wdhSI/dANytiumPRmPvkj1J+eUF5YBm7wcBRIzE5Ynbg\\nvrLT1ZJwzUePz5g0x53kEe4Uh5q96K8qsQces9lRPbYNqySWTQIJVpWEetzKKhkiWijKNpKTGerW\\nnIRjWiUlwhDq7KFKdBOxSkybZOg0dVIxxd46GzEtJ7Gqksot6vayB+E/VsJJX4BzfwJXPqYqE7JK\\nYNc/4x8nGp0t6sQ27hz1d9U2dYLJyFeTpULxlwRGsUs6WwMteUNpNCNuo459sNVyH1mnrpJMfx+0\\nz61JIuGGgF1id4QLhD1VedytCQh3IsnJUI87Ix+JoEA0U5AV2eM+0tCOEFbhHqYi7kSsEjPiHmas\\nw2x6yNaIOz03MaukcrOKfAvGQvFEuPoZOPNu9ZrZbDDxQlWH7Y3R2TAW5thGn6aSr9XbwntxW8kv\\nU7eREpReNzx2Kiz5ReR9mw6r/yWzQP1dMFZF3INlObQja2HkycGdLodNV5ZR5abjNy7NcSW5hNtM\\nUFptEhNbqoraEoq405DeTjYejiKoUobXcdvseBy55BMoB3Sk2Mh02P0ed0VDO+WFWRSbwp0zVEWh\\nXY24QfncZkvXDItVklDEvRmGTg2+KrEyYZEa0+FVkR/f9Hd49VvRj2968LkjoHiSSoKG9uK2klmg\\nXstIEfeeD5UdYvbiCKXxkPK3zRN1QbnquGid4NQVnLXw+i3w5/PhD9PhV6OPf+TafBTevTu8n4u7\\nQ50UrTYJqPe1cDzU7u6/MWoGFEkm3IbPbY+QU7WnqO55bXWxZ00CpKQhpI8vPfoJmysiiKq7DZBh\\niw13puSSJ5x+qwRUSWBTuxuXx0dVSweTh+dSgtUqMapKQrv+hWJG3CVT1G1LVUDwu+JxSwlVmwMn\\ngEiMO0ed6KLZJVvfgM0vB/dMsWKKZs4wdYKo3hbei9uKENFLAjc8p25r90Te1ywFNOlpSeC7d8Hm\\nV1QUP+ZU9Tp8+vvuHau32PIarP5f2LM4+P4ja1XexkxMWimaADU7+2d8mgFHcgl3bpyIu7UKkIl5\\n3IADN/vrnOGPW3txW2iz55KP0x9xg5qE09jm5lhTO1LC5OE5lIhGOlPzVCVIer4akytOpOysUdvm\\nlaq/WyvDKzVCrRIpYflDwZMxmg4rER02PfpzpeVA2ULY9a/Ij9fuUrfRej9bhbtkinrdG/ZHj7hB\\n+dyhEbezDnb+E1KzVAMxs5WulcbDgVmj0LOSwO1vw7Y34Ox74Ia34EtPwim3KNuoekfXj9dbVG5W\\nt3s+CL5/1z9VO4fyM8P3KZ6kXk93R9+PL1lpPgrPXBpcXpsoUqp9l/TC0oN9QHIJt7mEmT2CcNtT\\nA1n2BIU7FY+/hC8I044IWWy41ZbDEFsr2WmBiF9F3C7/cSYPz6VENOJ0GDMdTd83ns9tWjxpOUYL\\n26rwaeRpOcHCXb8PPvgJrHwkcJ8pAmZDomhMvAhqd4ZXaHjdAVHc+1HkfVuOKY81PR+GGlcI7Q3R\\nPW4IRNxWb3rLKyovceqtxv+zN3gflxPa64Mj7rzRSsy6GnG3N6hoe9h0WPj9wP1zvq5mJa56rGvH\\n603M92z3B8Gvz673YczCyCWURRNVRU/oa3ai8env4e3vdW/ffR+revfu1LwfXK72W/5goI3GACKu\\ncAshRgkhlgghtgkhtgohuvkq9gKxhNuWGqgtjmOVSEO40/D4S/iCiLJKfCPZFNjaEJbEqNloyqwo\\nmVCiIu7mFKNG2oyW4/ncbXVKuIVQFktrZaCla6jHbX65zQh2+9uB+yq3ACIgqNGYcKG63R0Sddfv\\nV5fn6Xmw/+PIfUFaq1S0LQSUTA3cH80qARVxu51qJReTDc/B8Jkw5Qr1d6hna1aUmOWEoCyx/NFd\\nF+73f6TsqCseDf78ZBXBjH+HjS8Gj81KXyZC3R3qBJo7Uq3yU71d3V+/T90/6eLI+xVNVLfm1VF/\\n4ayF9+6N3V9dSvj0dz1vTbDrfVh8P2x4IXrVUSzqDPvNfE27wpqn1fff03F8T+pRSCTi9gB3SSmn\\nAKcAtwoh4qhCH2FWlUSySuwpgf4ZsRpMAY1uJbwO3BxtjHCpGdqL26DBl0UewZfz+ZnK465obMcm\\nYHh+OsNsjTTahqgNzCg0Xi23sybQjyRnmFp+LTTiTs9VUZZ5YjFrnBsPBqK2yk1QOC5s7GEUjoPC\\nCerLYcUUgtlfUyebo+vD922pDOQbsksCS7vFskrMtrRml8DKLWpG4Kxr1VgQUBcSPVon31jpaklg\\nxVp1klj4PXWiCOWU76gv6Nqnwx+TEp44Az68P/wxV1vPFogAVQPv88Cpt6m/zROp+b5MXBR5v8Lx\\ngICaPhJujyuyfbT1dSVksVrL1u2BxT+HLa92//mbjqgksjnLuTvWWJ0RCNR00QZz1sH2t+Dk62DK\\n5fD5//bOot+9SFzhllIek1KuM35vAbYDI/t6YBExq0oiRtwpStQgdi9u4HCTiiKHZdvCrJI2l4ff\\nvWNMekjLCXqs1pNBtmwNSjTmGT25KxraGJqbTqpNUEQDdcIU7gQjbms1TPZQJY6hHrc5HtMuaTwE\\nwq5WUt/xjrqvcnNsf9tK2elQsSY4cVprJLzmfQsQke0Sq3ALEUioxoq4zah594dKoNc/q07A065S\\ns1zzRgW+aCbWyTdWik9SiblE1/I0q2dO+U7kx0smw9hz1Bc0tESytVq9psv+AIcsVTjOWnh0Abzw\\nlcTGEA2zpG/iIhg6PTAxaud7UDQpuH7biiNTvS59FXF/+DPVHsFMmpuY1T9V26Lva145tVZ377m9\\nHnj1m2quxZV/UvdVx3i+qOPoZsS94Tn13HNuhDPuUt+31f/b9efvQ7rkcQshyoCTgbA6MiHETUKI\\nNUKINTU1feQJZRYofzpachLU47G8VuBgo7rsOr0sh6ONwcK9uaKJfUeMyD0kaq30ZGJDBq1Ck5/h\\nwOXxsbe6ldIhGdDegAMP1dKMkhPwuL0edZkeFHFH8rhDGk01HlLJzNGnKruko0lF37EqSqyMnK3+\\nF2v0WrtbnSCHlMGIWdGF25zJCqqyxPq/RqKgXF16Lv0lPDwbVj0Oky4KTLsvHBdulTQdVu+r9blA\\nJVY9Heqkkwi1OyGjIPaM2lO+o6y2He8G319t9HuxO+Ct25S14fXAyzdC0yHYtwSOboj9/LEqiio3\\nq9dlSDlMOB8OrVTR5sHl0aNtk6JJgRNtPLyexO2GlkrVIsHnhkOfBT9mvuaxxLCuh8K97A/qdbj0\\njzDpEkB0XXx9hv8v7CpaTzSJKyWsfQZGnaJO6MNnKltx5Z8CV7oDgISFWwiRDbwKfF9KGVaTJqV8\\nUko5V0o5t7g4TnKwuwihRC1ictJIGJo+cQz2NajJN2PyU2jp9AStG7mv1kmmMN7kEOE+1pmufrH0\\n1zYn4eyobGFkfobfrqn0GSKWiMfdXk9QNUz2UHWWbzmmEmepxvOawmgmTxsPKwti8mUqItn2lro/\\nXmLSxCwzs9ZQ1+5SpWYA486Fw58HlyC6nKpCJscipmbEHcsqcWTB9zfD19+DK/4EZ/8/OO++wONF\\nE1QkbvWTGw9D3sjgySegenUgwpNOLiccXh3+3DU7VRVGLMafp6pbDq0Mvt9s1HXFo+q1+fjX8MFP\\n1XNf/Bslup9F8UB9XtXQ65G50d//SqN002aD8Rco2+SDn6rbaP62SdFEFVXGKzUFeP5qeOHL8bcD\\nlZDzutXJyvp6tDcGRLl6a+R9IeAtt3ajmgNg62uqkmbG1erKoqC86xF3c4U6uZedrq7EE70y2f+J\\nEvy5Xw/cd8Zd6jv64f0DJlGZkHALIVJRov2clPK1vh1SHPJGRW4gZUbc8SpKgD31SqiHZal/3xp1\\n7691ko3xtyU52e7yUu0x+nBYhNvsV9Lp8VE6JNP/YT3qNUTWkaOsjFget3k5ao24QQmOVQz9Vokh\\nAo2HlHCfdKn6+5PfqttErZKiSaqCxeyHIaWKes3E17hzQXqDBdJaCmgycRFMvjyyf2wls0CJ7snX\\nqpK8ovGBxwonqBOC9ctes1NF/qFkDFH/Y+jEmaW/gqcWKY/SSiLCbbOrY4ZGz1Xb1Il0xtUw6zpY\\n/kf47FGYfzMsuFn5oFteDZ8Q5PPBW7fD5r8b1T8/DX9On095/eb7NWq+mt6+5RX1vpfOjz3m4olq\\nMpJ1MeVIHF6trpz2fBC/9tuMtmd+BUbODRZu83MydJo6TrQFLUyLwtkNkXO1KU961ILAfSVTuh5x\\nm1dvky9Tt4n63GufUa+9mTAHGH0KTP0ifP4E/G4i/O3K8CuRfiaRqhIB/AXYLqU8zjMVgIt+BYv+\\nO/x+MwqPU1FS1dxBjaHLJZkqMrf63PtqWsnE8E4twl3f5qJRGn9bhTsjEP2PHJLhrxk91GnYGjab\\nMXEmRsQd2orW7EpYsyPYN7ZaJZ5OFZHnj1Ze5/BZyibJLAwW1VjYU9R+ZsTdWqUifVPkSuerKNRq\\nl0QS7pxhcM2zsT3ueBQai06YX7jmY2oiUaQaZlD3H/48cAns86mJLNILxyzi66xV0VJRHOEGGHGy\\n8pytglS9NXBFsegXykYac3rgM7jgZhUdf27xQKWE936ovNKz/xNOu00Jwv5Pgp+v8YA6WZnCbU+F\\ncWer3ydcGHmimRV/ZUmcGZQrHlRXa7ZUJcqxWP6QirbPvEsJ1rGNAYvA/JzMulZFs9EmaPmtkm5E\\n3NXbVIRsDQJKJqursa7UrJtR/8SLVP4rEeH3upVVNv3q8ODw6mdU35/T71BXYW/emvhY+oBEIu6F\\nwPXAuUKIDcbPJX08rugMn6G+YKHYLFZJDDZXNOGSatsi47050mgVbifZoh03qaqniUGD00UThnVi\\n8avzMgPCXTokwz8d/IDLktgMae363uZj3P6CpVojVLhNUTQn5Zj4I+4Wo9RKBqo1zMhi2PS4VlEQ\\nI2fDsU3qQ2teTppWSYoDys8IntFnTncP9Z17ivmc5hfOrK6YeFHk7cvOUNUGFZ+rvys+V5fHECzc\\nZqRVPDH+GEbMUrNmzdfB61GVFaaHnzEEbl2lJu+YgULBWNXEa81TqsKk8TC8dpNKZp16G5x1j7KF\\nCsbCW99VEaWJv+becoVklmnG87chcDKK5XPX7oHt78D8m1SFxIYXgsdgpaUK1vwFZn5ZjXf0qeqk\\nZPraFWvVldHoU9Tfof3eQX3OnTXqSrOtLjzZ+/p/qJYK0TDfu1Dhlt7g5PXR9fCvH8eI+nerQCev\\nVK1ElUjEXbdHfaZK50V+fOgUOO+nqjqpbo/KRRwnEqkqWSalFFLKGVLKWcbPP/pjcF2htt2sKIkj\\n3EeacAn1pctN9eFIsfmtErfXx6H6NjLpoF2kB+1X53TRFCHizrNG3Pkq4nbb0qnqTMFrrkUZspjC\\ne1sqeXvjUbXEGQSsEqMDYVAfcGsUa11MIbRUzhTuRBOT/kHPVh/Wqq0W4baI3LjzVHLHLNWLFHH3\\nBrmlqmGVVbhzSwPRbihjTlUW1H7DxtnyqsoH5IwItjtMa6D4pPhjMAMCswSyfp96bYZaatXTssN7\\nwJzyHRXVP3e1SrxuewPOuBsu/IU6iToy4fKH1eu4xHK1WLlZJc+s/+O0q+ALvw++VI9GVqFKusby\\nb1c+rLzq+TfD3G8qmy1amd4KI9o+4y7196j5gFC2gJQq4i6da7yWURKG5vtnirvVLvG4YOMLsOSX\\n0X35YxvVCdJaAmq+PtbnW/ZHWPFw5BJOcxyF44yqp5MSi7jNE1G8ORBjz1K3+z+Of8w+IrlmTsag\\nyqk+CG2pBTG323q0iWFDlADafG5G5KVTYQj3ofo2PD5Jjq0DJ8HCHS3izs8MROUj8lXE3ZZWDAha\\nO40sfnp+kMe9r1bVgh+sMyIfZ40SoQyjhDCjIHAFYY24HZaI218qZ0TcxZNUAm3BLTH//zDMBkZH\\n16maYEd2YKITqE6CEKgrbqlUQmCOtbew2QKVJZ5ONd1+4oXRrx7S81RUdmCZirq2vqGi1dELgiPu\\nWuN/yk2ggrVwvLKGTOE3E3DRTh4mY05Ton9whYpWb18H5/0keOxlp8Pcb8DKRwNXMMc2qfct1fJZ\\nS02Hed+MnICPRPGk4FpuZ20gsGipUhH2ydeqipoxpynRjWSXtNbA6r+oyUimbZWRr05ah1aoQMFZ\\nrRLasRKGpnCXLTSOa6ksaTkGSHUCOxilsdexjep9tb52BeMMu8N4PneHUTYp4MOfR65eqdujrg4A\\niicrWyfalYZJ9TZ1Ii2Kc3VWMlVZkqHWVz9ywgh3h1f9K3vaYqx8g4q4y4cZ4u5xMXJIhj/i3lej\\nvLzhGV5afeERt5sUZGpWUMSd5bDjsEkuyNpL+oc/gj0f4spQPnuzWa1iae0qpWS/8TwHzD4pbbUq\\n2jarJ2y2QNRtjbhtNiXeHc2BGm6rIJ18XXjNczyGlKkTxZG1gYoS65dmSJn6spsNqcxSwK7YMYlS\\nOE594Q4uV7MsJ8SxC8rOgIrV6kvsrIZpXzK8/kOBWZA1O8L/p2jY7Eo0zIi7aqs6ocaL1oWAa1+B\\n721UkXW09+DC/1YngVe/pSyVrtTcR6NoQiDirtsLD8+BX5fD42eokkWvKzC5Rwh18ji6Lnxi1YqH\\n1NXFGXcH3z/6VJXcNGvYzUqkkimRhbt2t/pcmolVq6haZ1Ku+1v4vh6XSgYPnxV8f4pDibA5IWjf\\nUjVJ7qL/UdZWaOLX1aZONKb9VnISIMPnCYRSvV3tk5IWezubTX329n183NoLnzDC3e5VX8xNjY6o\\n21S3dFDV3Mm44YZwezsZmZ/hT07uq1GRcEmahxaZhtsbuJxrcLqw2wRkDgkSbiEET6c9wP96f6Ii\\nmTGns3fGnUBg9Xdra9ealk6cLuXLBSLu2nCLxxTu0BI7s9FU4yEl2vESWPEQQtklR9YHV5RYmbhI\\nRZMdzcrj7m2bxKRwgoqMtr+jbI9oiUmT8jNVrfG/fqwi5QmLlE8NKnIDFY0mkpg0GTFLCarXo0Sk\\ncHxwRByNrKL4J01Hpkri+jzw/DWqsVaPhXuSOvE3HoKXrlPv55k/UMHCkbUq0WZG0AAzrlGVRJ89\\nHhAdZy2s/rOyaayVPqAsD7dTJVftaQErrmRK5IRh3W51svc3S7MkKE3hHneuKl0NbTFQvU29n5Gq\\nk0omB04UO95R/vXcb8LC7yr75YBlJqc5L8H8v80Tb7xGYlVb1fMkwtiz1PtnXmH0MyeMcLcZEffn\\n1VF6UIO/hesEU7g9nYzIz6C6pZNOj5d9NU4Ksxzk2DpxynQa2gKLLdQ5XQzJTEVkBAs3wAx2syXv\\nLPjhXvjK83hLlb/n97Aty5ftrQkU8e+vNX63Tnc3McUxtFLDbDTVeKjr0XU0Rs6Bmu0quWdGKVYm\\nLFJfqH1LjFmTQ8O36Q2KJqgk1MYXlSg7IiyDZmX0KSq6q92lap4dmYEv/bEN6mTZcjR+KaCVESer\\nErvaXcEVJb1F4Tg1G9C0YXos3MaJ9vlr1NXFVU/BuT+CG9+B/3cEvvhE8PYZ+Srq3vQivHePsplW\\nPqoSq2feHX780aeq24PL1GtrJuzNhGGov167R72PZnWX0xpxG3mZs/9TRfehSUrzZBtRuKeoqqmO\\nJjWrdMKFaixn3K0aj717V2CCkRlZm1aJabXUxPC5O1vU8a29d2JRfnx97hNHuI337LNqO07TWw7h\\nzQ1HyU1PYepo40PldamEIlDZ1MG+2lbGFmeR7mvDSYZ/ZRtQEfeQTMPbtQq3y0mObGXS7LP8VR+5\\n6cqfbO6weNyeDnB3+MV6ZH4GB+tiCLffKgnxks2e3Obkm95g5JxAu4BIEfeoBerks+t95ZtaPfDe\\npNCI9tzOQHVFLNJyAgnFaf+mbjOGqOn1RzcEyuS6ItzmZfqBZSr672qyNxEmX6Y6FKZkxK99j4dZ\\nLVO9Dc6/T0WzJvbU8MlLABf8l7JPPn8CXvwqfP6kqlOO9DrljQx8zqx9wSMlDM3ZioXjVTldWm64\\nVZJZqJKeI06GdX8NthqObVT7DCkPH4cZCa/9q7rCmGzMXXBkwkW/VKK86SV1n1lHbkbcKQ41plgR\\nt/lYvMSkScFYlTzfp4W723S4vXR4bfgQ1PmyWXeoIWybutZO/rmlkn+bU0p6mnHpaxHuIw3t7K91\\nMrYoG4e3HSdpNDgDEXe906X6cIcKt9FKNjW/1H9XTrqyL4IiboCOJvbVtJKWYuO0cYUciGWVmBF3\\nJKukrV5Fkr0l3NYVViIJtz1Fzerb+Q9VlZDdRxF3oeUyPZFyOICTLlGVJOPPC9w3YpaKuM2Kkq5Y\\nJYXjVTJz4/Pq70S/yF3l/Pvg7p09T/LmjVafnWlXwWnfTWwfm03VoV/8G3UydrUqeyUaZtRdOjdw\\nX+E4laS2+tzmbEXzfcwuCbZKmo8ELJTZN6h9j6wLPH5so5r1G+lkYwr3ioeVZTP+/MBjJ12qToCf\\n/EZVxdTtVjaideZz8UmxI27z/0j0CksIZZcc+DSxmau9zAkh3A1tLqoooDlzDFLYWb0/vD3nK2sr\\ncHl9XLtgdCD5YCQnAbZXtlDb6mJscRYp3jacMiPIKqlviybcRi1nXiBJmGuUCPqTk+aXs6OJ/bVO\\nyouyKC/Ooqalk1anU1kfUSPuCFZJ7S4VIfeWcGcXKwEQ9uhNjSYuCvzffRVxZ+QrESqenPj/tvAO\\n+N6G4ITS8FkqWj68SolLpNmX0bDZghOUQxO8dO4qQsTtqZMQNpuqYvnS/3Y9YbzgZrjuVZVQjXWC\\nGneushqssxntqeokbxVu8wrHtNuyh4ZH3GaZ37R/U177st+rqNvrgaot0a9AhpSpKxRnNYw9O7gB\\nnBDKfmk4oKLuuj3BQQAo4W84GL2ypHqbypNYWwjHo/ws9Z04Dmt/nhDCXe908YjnSlZf8CrTRuax\\nKkS4fT7J858fYn55AeNLclT1gLCDt5NheekIAct2q3rTscXZ2N1O2kinIcQqCRJu8xLPLMI3V+fB\\nGnGbVkmgtasp3GWFKho4csTw/UIj7tJ56pIx9AOYlqv8QQhvd9oTyk5XX95oGfXx56sKC+g7jxvg\\n3B/D+T9LfHubLXzMZoJy2xvq9etqAte0XxzZgdXlBzLpuZGj1EQYf55q4RuL6f8O310fnlMJnYpu\\nJupMbzm7JIJwlwbGfNY9KtG46gkVjHg6Au9dKDZ7wMoxbRIrEy9SJ+yPfxPw2a0UG5Ul0SYrVW1V\\n1SddeR3N5PlxKAs8YYTbTQp5+QXMKytgw+FGOj2BGVUr9tZxsK5NRdsmKWng6SQtxU5xdhqf7VNi\\nP7bAgfB20irTqTesEp9P0mCNuH3uwDRgc9WdnIBwp9ptZKTaafZbJSpq9rQ1cKi+jbHFAeGuqTQy\\n7aHCPWyaiiRDI3Hraii9FXEDXPJb+Npb0R/PLAhEXL09a9LKnBvjN1eKh+lTdzTFr8mNtX/J5O4L\\n4omEzRb5s1Yy2Vgqz2hCZs5WNBOTWRbh7mhSV5bW8tWF34NJX4B//Uj57BDb8y+ZooKHSREmbptR\\nd+NBZeeFBjzmcQ+uiHzs6u1dT0TnDlefr62vhxUs9DUnxKfSFNiCrFTmlRXQ6fGx5UhgpuJzqw5S\\nkOXgomkWwbE7VI0rqsdIu9tLik0wOltF0i57Bo2GVdLU7sYnCQg3BN6o5gpVgx1SMpaTnhIWcdfV\\nVuPxScqLshlTqComGmoM4c8MEehomP1KhC2xSSWJkpatxDkWJ12qXre8XnzeviCzIHhiUlcxo76+\\nsklOFEyh2/yyuq3brQTTtGyyS5SIutsDpYB5gVwQQsAXH1Pv1dqnlXUSKrhWTr9DWULR+u1PXBTI\\n1xSGRNwF5SrRvC1CcNJarRKe3Xm/T/kPlU95eA6se7bf/O4TQrgb/MKdxrwyJayf71fCWt3cwb+2\\nVXHVnFLSUiylgnaHvxG/maAcXZBJqiewbFm9U0XMdf7jOwLJQr9wHw2ySUxy0lMCEbfhUzfUKTum\\nvCiLrLQUinPScNYby63FWfzBjyncOSOCeqn0C6f8B3zns96fNdkXmFFzd4S7YJzyYKd+qXfHdKIx\\n9mw1EeXdO2HxfymLwiq8Zp6mtdoi3CF2S3oe/Puzyr8eNiO8nYCV4okw/arojwsBF/xcWYyRLJcp\\nV8LhzwJXySbmVPdEa7itzP0G3PyJOlG8dRv85YL4MzR7gR7O3hgY1Le5EUL1DbHbBONLslm8vYqG\\nNqkN/iYAACAASURBVBevrK1ASslX5odc6qWk+RvgmMJdXpTlfxNb0kf6I24zSVmQ5YCU0Ig7cnVH\\nbkZqWMTd0lgLTGJcsbJJyguzkIkucGxiJmV6q4a7K9jswZM5+gCvT2ITBK3r2S1GzFLLT3WlosTE\\nZlP10JrYpKbDda/BP+6CTx9Q91m9ZX8td03kiNtk2DS44e34dfuJUH6GshgjMeUKWPILtejIgpsD\\n9/srSrp5hTVsOnzjn2r+wZG1vfN/xCHpIm6vTwaaNxnUOzvJN0QbYF5ZAWsONvDUsv3MLyvghW+f\\nokTZit3hT/KZlSVji7PU9OnUTI7lzaTeEOy6VnXrr+OGQO+RpoooEXdqoI47JQ1SMmhvrmdIZqq/\\nv8mYggzmtixRkUaklbwjYW7Xm/72AOKaJ1bykze39PxAJ18P59/f+xNoNMGkOOCyh9R0fmEPrjwx\\nhPsfn22g7ug+YzWjKIntUfP63poqnqgqlra9GXx/9TYVOMVaISkeQsCsr8AXHujZGBMk6SLuu/6+\\ngU6Pj8euC0wGaHC6GZIVsA2+c/Y4Jg/P4aKpwyjJjTJd2UhOAozIM4U7Gz5bDGVnkC2yOHhUJV3M\\niLsw2wFYIm6XUwl4BK85Nz2FinrLJVN6Hh5nvXoOg/lpB5nAQVwzf0vCpkfaiSvcB+ucrDnYQE1r\\ngmtJxiK7BE7/fs+Po4mPEKrn+PxvB1f4GCK9bP02SgoPUpg7/Pgne6deqRbcaKkKVEdVbUu6E3zS\\nRdxbjjazqSJ4UYJ6p4tCi3CPKsjka6eWRRdtCEpOzhyVz8zSPM4qbFF9DsafT0GWwy/YZvIzKOJu\\nb1DN/iGicAdF3AAZ+ciOpqDIf37DO7RLB/uHd6G9ud8qOfGE+4NtarLGwbq2oMlPmiQhtCzTsP+K\\naUQ0H0HmRrBJ+pspVwBS2WiguiLW7NDC3ddUNnVQ2dyBx9IAqt6cjt4VLMnJ4pw03rztdEbUGaVC\\n488jP9NBU7sbr09S73SR5bCTnmpXU3ntaYZwG75dBKskN8OSnAS8jlzSPS0B4e5spfTIu7zrO4V9\\nLTESMqEMnQan3Bq5JCrJ+dfWKtJS1EdyY0WMpd40yYE9lTZ7HkWiiaGyhvqU2KtT9Qslk6FoEq7N\\nr/Pehx9Q+8eFdLjdfOxYeLxH1iWSSrhbOty0dnrw+iSVzYGuZP5ZjV3Bkpz0s2exmqFVOI4hmalI\\nqUoB652ugBUjRGASjplYjFAel5ueisvjo8Ot6smdtmzyhNOfmGTra9jdTl7wnBOY+p7QuB2qN0Oi\\nVSgDBI/Xx23Pr2Ptwcj1rrWtnaw5WM/1p4xBCNh4OMZSb5qE+Muy/byz6Wj8DfuQGvIZn9HCUBrY\\n2dGDpe16kcbyi7EfWsEZn16H9Li5yf4LfrUlH3mcWrR2h6QS7iqLWFcYrVillKoBVFeF25KcBFT0\\nvf8Tfw8E80RQ73SFWTEB4TZmTeZEiLhDZk82kkOZqGR6yzI163Ld36BoEgczpweaTfUAKSWPLtnD\\nnuqWLu/r8fp4btVBfvbmFv6++jDbjjYHtbTtDfbVOnln0zGeWr4/4uMfba/GJ+FLs0sZV5zNJh1x\\n94hdVS384t1t3PX3jRyu7/vytEh0uL1UuHOYIg6SKrysro9ebfHEx3t5afWhHj/n4fo2fvDyRtpc\\nkRvNATzTdDICsJVMoujO5Vx4wcVsPxZuwQ5kkkq4jzUFhNvsod3S6cHjk8HCmggpaapxu8mhz1RX\\nOkO4zcqPxjZXcMQNhnA3qunumYUR+zXnGB0CzUZTS4q+SoUsZuT734JnLlULAMz+GmVFWYH2rj1g\\nyc5qfvv+Tv664mCX9lt9oJ7LHlnOj17fwourD/PDVzdxyUOfcsmDn8b88HeVnZXqhLJ0R7X/KsTK\\n+1srKR2SweThOcwszWdjRWOXI6A1B+q5/YX1UbtDDiRW7Knl2j9/1mdjfWjxbjJT7dhtgp+/E2HB\\ng15gZ2ULC3/1UcSmbqAWLamWeeS51HJ365uzqGgIP4m8v7WS/3lvBz97ays1LT1LTD/28V5eXlvB\\nkh2RV5ivbOrgT1vTePSkZ8i86V+I3BFcMWsEGal2XuyFE0d/kbzCbaxaU28t1esKoRH3ng9VuVLZ\\nGQAUZAZH3AURI+6jUWcvhvYr+aShkFuz/6DKpo5tUD75zC9TVpQVWFChm0gpefgj1SdiTRQrIhK/\\n/9dOrn58JU1tLv507Wy2//wiPrrrLP7riqnsrm7l0SW91yTeFG6ny8uKvbVBjzk7PXy6p5YLpwxD\\nCMGsUXnUtrqCFnFOhN+8v5O3Nx7l52/3jVD1Fl6f5L63t7J8Tx2vrauIv0MX2VXVwrubj3HjwjK+\\ne94EPthWxUc7urHiehwe+mg3Rxrbue+trfh84SfZtQcbqJWBRlpHZRFLdgQvM1bT0sl/vraZscVZ\\nuDw+/rIs8hVZIrR2enhzvboKXrIzwnJmwJ8/3YdXSq5cdKE/4MpJT+XSGcN5a8PRwHKDA5ykEu5K\\nQ7jzMlL9EXe9dXJMV7AkJwHY+5FqzJ+myvXyjdXbG9uUx12QGcUqiSLc/g6BHW7aXV6W7anljJNG\\nqLKp29fCtz+CrCLKi7KobO6gqd0d8TiJsHJvHesPNTKmMJOdlc2BdrIx2F3VwiNL9nD5zBF8eNdZ\\nXDJ9ODabYGxxNtefWsaXZo/kyU/2sddYFQjgkY92c+4DS8MqPo42tnPb8+tiVoLsrGphTGEm2Wkp\\n/GtrsIh8sqsGl8fHhVNVedbMUcoL7YrPvbuqhc/311NWmMlLaw7zzy2VCe/bFVo7PT22kd7aeIRd\\nVa3kpKfw9IoDEUWvJzxoRNvfOn0s31hYzrjiLO57a1vEKx0rbS5PxJNlc4ebdzcdCxrn3ppW/rH5\\nGFOG57Kpook3NoSveL7uYAOejEBtdMqQUSy2CLeUknte3URrp4cnrpvDpTNG8OzKA/6Jb6FUNLTx\\nya7IkTTAWxuO4nR5GVecxdKdNWGva4PTxfOfH+KyGcMZVRBs23x5/micLi9vbzy+OYFEiSvcQoin\\nhBDVQohemBXRM441dVCY5aC8KIuKRhWlmmLRZY87xRFITjYfUy0lLT1+zeMdbWqn3e2lINsq3PkB\\n4Y7St8MacX+6u4ZOj48Lphh1oznD1GwxYM4Yc4p+eCvaRHlkyR5KctL4yRem4JOw/lB8f/hX7+0g\\ny5HCfZdPJdMRXs7/nxdPJj3Vzn1vbUVKyR8+2MUD/9rFvlonL4RcUv5p6R7e2XSMf2w5FvX5dla2\\nMG1kHuecVMIH26qCJlH9a1sVQzJTmWu8FicNy8Vht3XJ535u1SFS7YKXbj6V6SPzuPe1TUE5ka6y\\n5UgThyxXQm0uDw8t3s2C//6Qyx9ZHiZwGw83ss2o+4+Fy+Pj9x/sYuqIXO6/fCr7apx8sju6GMWj\\n3eXluj+v4vYX1rPmQD07K1v4hxFtD8ly4Eixcf/l0zhU38Zdf9/IO5uOcrDOGWZDfbCtivN+9zHn\\nPrCUPdWtQY/9v9c2c+vz63joo8CajY8t3Utaio2/fmM+M0vz+PU/dwRZa1JK1h1qJLfY+H6k5XHK\\n5HJW7K2jzaUKDP6ybD8f7ajm3otOYsLQHG49ZzxOl5enlx+I+L/e//Y2vv7M6ojvq5SS51Yd5KRh\\n6ji1rZ1sDXk//rryAG0uL/9xdng/lNmj85k4NJsXP+++XeLy+HolX5UIiUTczwAX9fE4EqKquYNh\\neemMHBJYJ9Ksse6yx21PC1gl+5aoW8vqIVkOOw67zb+AcHDEna8WKW1viFgKCJZVcNrdfLi9ipz0\\nFOaXhzdxOnl0PmkpNlbureva+A3WHmxgxd46bjpzLAvGFmATRK3cMFm5t47FO6r5zjnjo16pFOek\\ncfeFk/h0dy3feGY1Dy7ezdVzSjltXCHPrjzojzobnKqtAKgEYyScnR4O1bcxaWgOi6YOpc7p8o9x\\nb00r/9xSyfmTh5JiVx9HR4qNySNy2XA4MeFud3l5dV0FF08bztDcdP745Vl0un3c/fLGLkezda2d\\n3P7Cei59eBln/nYJZ/92Cfe8somzfruU33+wiwVjC6mob+OKR5az9mAD1S0d3PnSBq54dDlfe2pV\\n3Kj2pTWHOVzfzt2LJnHpjBEU56SFCZXPJzna2M7KvXW8u+lYzAj/t+/vZNmeWpbuqOaqx1fypT8t\\nJ8uRwrdOD/RVP31CEV9fWMa/tlVy2/PrOeu3S5n18w/4+tOf8/Di3dzy7Fq+/bc15Kankp5q5wev\\nbPSfWD/aUcU7m44xMj+DBxfvZsmOaioa2nhj/RG+PG80xTlp/OTSKVQ1d/L4x/v8z1nR0E5taydD\\nRxjzDfJKOfekElweH3e8tIGFv/qIX7y7nTMmFHHjaWUATBqmPh9PL98fdtVY73SxZEc1Xp/kpdWH\\nw16HTRVNbD3azLULRnPWxGKECLZLnJ0enllxgPMnlzBpWE7Y/kIIvjxvNBsrmiKegL0+SVO7m8Y2\\nF3WtneyraWX5nlpeXnOY/353G1c9toLp973Pvz+xsl+qU+LOnJRSfiKEKOvzkSTAsaYORuanU5qf\\nwQdbq/AZNdbQnYjbkpzct1R157MsUyWEID8z1W8VhHncJnE87sZ2N4u3V3POpBJS7eHnybQUO3PL\\nhoT5vi6Pj0921XDe5JKofTtcHh8PLd7NkMxUvrpgNJmOFCYNy40p3D6f5H/e287wvHS+vrAs6nYA\\n1y4YzUurD7NkZw1Xzynl1/82g492VPOtv63h/a2VXDpjBP/32UE63D4Wji9k2Z5a2l1eMhzBdem7\\njQhu0rAcThtXiMNu4/2tlcwozeP259eTnmrjrguDe4rMKs3j5bUVeH3S38ogGm9vOkpLh8fftndc\\ncTY/vnQyP3p9C09+uo9bzkqsv8p7m4/x4ze20Nzh5nvnTWBIZiof76rh7U1HmTI8l8evm82cMQXs\\nqW7hm39dw1ee/Iy0FBudHh9XzhrBGxuO8sraCq47JXIz/naXl4cX72Ze2RDOnliMEILrTxnD7z/Y\\nxZ7qVsYWZfHU8v384YNd/gWlAX5+xVS+dmpZ2PFW7avj6RX7ueHUMdxz8Um8sf4of19zmMtnjgj7\\nPvzssqnce/FJ7KpsZfORJjYebmTdoQaW7KwhLcXGDy+axLfPGMu7m47x/Zc28PTy/Xxl/mh+8sZW\\nJpRk8+p3TuPLT3zG915cz6njChECbjpTnRzmlhVw6YzhPPHxXr548kjKi7L8n8GyMeWwBsgbyfzy\\nAvIzU1m8vZqzJxXz40snc8GUodgs7+9t50zg/a1V/G3lQW49JxAZv73xKB6fZGxRFi98fojvnD3O\\nf6IHeH7V/2/vzMOiuu4+/jmzsAz7joBsAiKKRBZxQeMWozHVmmiqklRT39rGNtqkTZq8yfs8Xd40\\na/smbVNba2x9qk3aqrWJ1WjVbBo1NSYuURHUiiB7FGWRRc77x50BhmFANmGG83keHmbu3LlzfjP3\\nfs/v/s7v/E4+7kY988aE4+1mJCXCl/dySlk1Xaud8rsPz3O1psHqmG25LzWcl3ad4dE3j/J6diqJ\\nod7N3/MTm4+Tbyc7x8WgIznch4fGRZEa5YeUXV/Toqv02pR3IcQKYAVAZGTfzOorrqwlNdKXCD93\\n6m82UV5Vx5c19bjodXi4dGESC7QMTkqpCXfsnTbTcf09XFo87i4Kt4eLAZ3Q4rcV1fXMSLK/+MCE\\nYYG8vCvHahB046GL/GT7KX7/9fSWEAvaLeHmTwvY9UUJB8+VU11/kyfuHt4c7kiP8mPr0QIabzZZ\\nndgW3jl+meMFlbyyMEWbUNQBBr2O17NT2Z9bRnZmFDqdYFpiMFEBJtbvv8CMESFsOHiROxOC+EZW\\nDAfyPuHg+XKmJVrbmlOseTDDQ7zwcjMyMS6AXV8U03iziVNF11i/LJ1QH+vMnJShvmw4eJG80qp2\\nPaTWbDqcT1ywp9UdzZKxkXycV8HLu3LIiPYjLarjkrUnCyt5ZNNRksN92LQws/miXTYxBimlVecZ\\nF+zFtpUT+cHfjiEEPDMniegAExfKq/n9R+dZPDbSprMpu17Hs9tOUHq9jl8vSW0+3pLMSH79Xh6v\\n7jnL1ZoG9ueVM3V4EDOSQojy9+D5naf58+F8c357yzFr6ht5YvNxhvqZ+OHsREwuBpZkRrIk0/61\\n52rQkxzhQ3KET/N+lebFQnzMYzrz7ghj+/HLvLwrh6P5Vyi8WsuWR8bj7Wbkdw+lce+v9rPrixK+\\nlj6UMHNxNoCnZifyUW45C3/7MW8szeBo/hVMLnpNuAF8InAx6NixahJuRr3dO73kCB+mDg9i7Yfn\\nWTI2srkD2nq0gBFDvFk9PZ5vb/yU93LKmq+LazcaePvYZeamhDXf6U4dHsyre8/yZXU99Y1NrP3w\\nHHNGD2FMpP3Klr4mF9Yvy2D1W58z79cH+J97k7hYUc26/ReI9Dfx3/ckYtTr0AmBp6uBMF93wn3d\\nCfVxw8Vwe4cLe+3TpJRrpZTpUsr0oKAeFGuxw42Gm1ypaWCIOVQCcOlKrTmH29j1anKWKe+lp7R1\\n8WKn2uziazJSa771tS/c7YdKdDrtxz14vgKDTjBluP3vZFxsAACHzreESyzhh02HrdP7dp4s5onN\\nx8kpucZXx4Sz9qE0HmnlUaZH+1Fdf5Mzxbb53BVVdfxsx2lGDPFm/phbq6kdE+jBQ+Ojm70inU6w\\ndHw0R/Ov8tPtpyivquObk2LJjPHH5KJn3xnbcElOcRXuRj2R5gGhu0eGUnCllg0HL7I8K8ZG6KH1\\nAGXH4ZKTZu8xOzPS6hwQQvD8/cmE+7rz6J8/63QK/ZoPzuHlamDTN1tEu/Wx2uLn4cIbyzJYtzSD\\nmEAPhBB8+85hXKyosRoYlVLy139fYsYvPuC9M2X8cFaiVQcT6OnKvJQwth8v4tOLV3j+vmTWL8sg\\nOzOKrPhAHhoXxZni6zYpdy/uPEP+lzW8vGB0u2MUt4qPydgs2hZbn5ufjKtBx44TxTw4LrK50xvq\\nb+JXi8cwMsyblVOt72Ii/ExseWQ8bkY9i9YeYufJYlIifDF4BmklT83Fp8J83TtNJHj6nhFU1TXy\\nf3u0FeTzSqs4VlDJ/anhzBgRTIi3KxsPadeFlJKX3j1DbcNNq05ramIQUmqO0yu7c2hqgqdmJXb6\\nfUwYFsiOVZMYG+PPs9tO8vuPLrBkbCQ7Vk1ixeRhPDwxhqUTork/LYLxwwKIDDDddtEGB8oqsQxI\\nhPq4E+6rCUDh1Vq+rG7oeiogtNSyzt2t/Y+dYrNL6xOsqx43aJklUmrCbPEE2mN0hA8eLvrmOPcX\\nlys5VXSNqAATH5wta55AIaVkzfvniAn04P0fTOW5+cnMHBlqdatpGexsGy5papJ8/2/HuFLTwCsL\\nR3cafuiIhekReLoa2HQ4n8RQLybGBeBm1JMVF8i+06U2Mb6ckmskhHg2t3NGUgg6AcnhPvzQzsUU\\nE+CBl5vBbo4waHHH53eext2o574xtnUwvN2MvL4klfKqeh7/6+d2sxUulFez80QR2eOiOvydOmPm\\nyFBiAj347QfnkFJSdr2OZX/4N09uOU5CiCc7VmfxyBTbsM2q6fF8LX0o/1yVxeKx1h3QV1LCtA7l\\nUMug2cd55Ww4eJGHJ0aTae70e5MQbzdeWpDCpPhAnmzz+0xOCOKfqyYRFeBh8764YC/+vnIi8SGe\\nlF2v085FnQ4ePQIpi2758xNCvMjOjGTT4XzOllzn758VoBMw944wDHodizIi+TC3jPyKGl549wwb\\nD+XzX1kxzZ09wKgwHwI9XVi3/zxbjhbw8MRom0wSewR5ubLh4bH8bH4yG5dn8tz8ZDxcB1Y9PocR\\nbksOd2uPu/BKLV9W15mr9nURvbkgztndWvH3dupbWybh6HXC+oK2CLedyTcWLJNw7uogTALaUmcZ\\nMf7Nce4tnxZi1AvWZKehE4JNh7WLdn9eOScKK/nW5Fi7whvu606ot5uNcK/bf573c8p4ds4IRob1\\nbJFaLzcjC9I0oVwxObZZaKYlBnO58oaNt59TXEVCSEu4I9DTlY3LM1m/LMOut6LTCSYnBPGXI5f4\\n+e4cm1K+AK/szuFAXgU/njvSymtsTXKED8/eO4L3cspI+989PLjuMJsOX6S+sWXAb+2H5zDodXwj\\nK7pL30Nb9DrBNyfFcqKwktf25jL7tY84eF5r319WjNfWO22Hof4mXlww2qpypAUPVwPzU8PZfqKI\\nK9X1XLvRwBObjxMb6MGTd3fuQXaXWaNC+dPyzC53ZEFerry1YhxPzhrO18d3YeHdNjw2IwFPVwM/\\neecU2z67zKT4IIK9tGtt0dih6ITg4T9+wu8+OM+D4yJ5Zo71Igg6neDOhGBOFl7D193Iyg5i2+2h\\n0wmWZEaSFT8wS0vcSjrgm8BBYLgQokAIsbzvm2WLJYc7xNsNT1cDviYjhVdruFLTXY/bLNyXDrfr\\nbQP4mcXAz2S08mqbhdtOmMSCZdr79BGdF9eZMCyAc2XVFF6t5R+fFzJjRAhJYd5MTwzmb0cuUdd4\\nkzXvnyPE25X5qfa9fCEEaVF+VsL9Wf4VXno3h1kjQ3nIzsBZV3l0WhxPzU7kKykt38HURM3O1uGS\\niqo6yqvqbOLUE+ICCfKyszCxmVcWpLAwLYJf7csje92h5nMA4N2Txax5/xyLx0byQEbHi0p8fXw0\\n73w3ixWTYym8Wsszfz/J0vWfUFnTQMm1G2z5tJAH0iOahaEn3JcaTqCnK6/uycXfw8jb353I0gnR\\n1udPF1mSGUl9YxNbjhbw03dOUVRZy88fSLEZBB4omFwMrJwS13F1zk7w83DhezPi2Z9XTuHVWu5r\\ndc4P8XFnemIw58qqWZAWwU/mjmo3nDXNfD5+b0YCPu7dv5MaiNxKVsni29GQzrB43JZBrHBfdwqu\\n1NrOarxV9Ob3yJvtxrehZTamzfFdvbWi8Z2UqYwKMNHYJInw6/wWbXys1rM/v+M0FdX1zR5t9rgo\\ndp8q4cWdOXx8roJn7hlhvQRbO6RF+fHPE0UUXq1lf24ZL+w8Q6iPGy8uGN3zlWXMBHi62mRrhHi7\\nkRzuw97TJc2j95YZk50NMLaHu4uelxakMDYmgGe3nWDCC3sZFe5DZow/b35yiZShvvxo7q2V47QM\\nyj1593C2Hi3k6a0nmP+bA4wK96GxqYkVk3pnZR83o56fzR/FicJKVk6J6xVxTQz1Ji3Kj1/uzeXa\\njUa+M3VYh4NszsKD46LYeOgiJdfqmJlkvUD1s3OSGBcb0GGnOHtUKH98OIPJ8b0/5tbfDKzATQcU\\nV9bi5WbA0xxrivBzJ7ekisrabnrcFuEWOojOancXy3Ftji+EFloJ6ngF8efmJ9N489ZyOpPCvPF2\\nM7D9eBGBnq5MTtBOtklxgUT6m1h/4AI+7kYWd5A1YCHdvO7m/NcPUHq9jvQoP164f/Rt8TqmJQbz\\ny325VFTVEeDpSk5J94XbwoK0CFIjffnH55f5+Fw5fzjwH3xNRtZkp3baibVFCMH9aREM9TfxrT8d\\n4e1jl5l3RxiRAb233NTMkaHMHBna+Y5dIDszksf/esycWdGNlesdEKNexxtLM6iorrPpACMDTHwj\\nK6bD9+t0ginDB0Ap2T7AcYT72g2GtEoZC/c1sdtceL9bMW5LqCQ8rXkx37ZYPO12j7/8X+BiG5Ns\\njVGvo5OMu2b0OkFmbAD/OlXC/DFhzTnflljbCzvPsHR8VHPH1REjhnjjZzLSJOEXD6Qwf0x4r3na\\nnXH3yFBe25vLU1tP8JvsVHKKr+NnMhLk2XFYpDNigzx57K4EHrsrgWpzYbGedERjY/zZ9p2J/HJv\\nHqunx3f+hn5mzugh5JZWsTAtol+yGPqL6EAPotsuO6hwIOGuvEGoT0veaLifO5bkhR553LFT7O7i\\n2xzjbuf4nr3fk09OCGLP6RIWpFnHbLMzI7lW28DySbF23mmNUa9j5+rJeLa6Q7ldJIV586OvJPGj\\nd7SSohcrqhke6tWrHUdvjfBHBXjw8wdSeuVYfY2rQW83A0cx+HAY4S6qvGF1ux3h1yLi3YpxWxYi\\niJ9pdxfLcbt1/G6wOGMoY6P9bcIKXm5Gm7Sszmg7oeV2smxiDDUNN3np3RztuXlKs0Kh6B0cQrgb\\nbjZRVlVn7XG3mrXVLY87cjx89wgE2r9NDvJyxcvNQFxwxyGR3sKg1/UoFjyQWDklTpvivS+PpCG3\\nuIK9QqG4JRxCuEuv1yElVjHu1h53t2LcQnQo2qClNR16ejqmAZp2NdB5/K4EsuICrSZGKBSKnuMQ\\noxzFbVIBQavJbYnf+tqZfNEbeLgabtvAnrMhhDbg2llNFIVC0TUcS7hbJfQLIQj3dcfT1dDllDCF\\nQqFwZBwiVFJUqdXeHtJmwC3Cz725CJRCoVAMFhxCuIsrb+Bm1Nnk7T4+M4Er1d1f8kuhUCgcEYcQ\\n7qJrNxji424Ta+5psSSFQqFwRAa0cNfUN7LndCmfXbzSq1OSFQqFwpEZcMJdUVXHB2fL2HemlH1n\\nSqmpv0mwlyuLMvpmVR2FQqFwNAaMcN9ouMmitYc4VnAVKc0rg9wRztyUMMbG+Peo8L9CoVA4EwNG\\nuN2MeqIDTEwdHsy0xGBGhnn3qIaxQqFQOCsDRrgBXl00pr+boFAoFAMeh5iAo1AoFIoWlHArFAqF\\ng6GEW6FQKBwMJdwKhULhYCjhVigUCgdDCbdCoVA4GEq4FQqFwsFQwq1QKBQOhpCWpdJ786BClAEX\\nu/n2QKC8F5vjCAxGm2Fw2j0YbYbBaXdXbY6SUgbdyo59Itw9QQhxREqZ3t/tuJ0MRpthcNo9GG2G\\nwWl3X9qsQiUKhULhYCjhVigUCgdjIAr32v5uQD8wGG2GwWn3YLQZBqfdfWbzgItxKxQKhaJjBqLH\\nrVAoFIoOUMKtUCgUDsaAEW4hxCwhRI4QIk8I8VR/t6evEEIMFUK8J4Q4JYT4Qgix2rzdXwjxSQk1\\nDQAAAzxJREFULyFErvm/X3+3tbcRQuiFEJ8JIbabnw8Gm32FEJuFEGeEEKeFEOOd3W4hxGPmc/uk\\nEOJNIYSbM9oshFgvhCgVQpxstc2unUKIp836liOEuLsnnz0ghFsIoQdeB2YDScBiIURS/7aqz2gE\\nvi+lTALGAd8x2/oUsFdKGQ/sNT93NlYDp1s9Hww2vwa8K6VMBFLQ7Hdau4UQ4cAqIF1KOQrQA4tw\\nTpv/CMxqs61dO83X+CJgpPk9vzHrXrcYEMINjAXypJTnpZT1wFvAvH5uU58gpSySUh41P76OdiGH\\no9m7wbzbBuCr/dPCvkEIEQHMAda12uzsNvsAk4E3AKSU9VLKqzi53WhLIroLIQyACbiME9ospfwQ\\n+LLNZnt2zgPeklLWSSkvAHloutctBopwhwOXWj0vMG9zaoQQ0cAY4DAQIqUsMr9UDIT0U7P6ileB\\nJ4GmVtuc3eYYoAz4gzlEtE4I4YET2y2lLAReAfKBIqBSSrkbJ7a5Dfbs7FWNGyjCPegQQngCW4Dv\\nSSmvtX5NajmaTpOnKYS4FyiVUn5qbx9ns9mMAUgF1kgpxwDVtAkROJvd5pjuPLROKwzwEEI82Hof\\nZ7PZHn1p50AR7kJgaKvnEeZtTokQwogm2puklFvNm0uEEEPMrw8BSvurfX3ARGCuEOI/aGGwaUKI\\njTi3zaB5VQVSysPm55vRhNyZ7Z4BXJBSlkkpG4CtwASc2+bW2LOzVzVuoAj3v4F4IUSMEMIFLYj/\\ndj+3qU8QQgi0mOdpKeUvWr30NrDU/Hgp8I/b3ba+Qkr5tJQyQkoZjfbb7pNSPogT2wwgpSwGLgkh\\nhps3TQdO4dx25wPjhBAm87k+HW0cx5ltbo09O98GFgkhXIUQMUA88Em3P0VKOSD+gHuAs8A54Jn+\\nbk8f2pmFdvt0HPjc/HcPEIA2Cp0L7AH8+7utfWT/FGC7+bHT2wzcARwx/97bAD9ntxv4MXAGOAn8\\nCXB1RpuBN9Hi+A1od1fLO7ITeMasbznA7J58tpryrlAoFA7GQAmVKBQKheIWUcKtUCgUDoYSboVC\\noXAwlHArFAqFg6GEW6FQKBwMJdwKhULhYCjhVigUCgfj/wHR4MZc4lp7GgAAAABJRU5ErkJggg==\\n\",\n \"text/plain\": [\n \"\"\n ]\n },\n \"metadata\": {},\n \"output_type\": \"display_data\"\n }\n ],\n \"source\": [\n \"fig, ax = plt.subplots()\\n\",\n \"losses = np.array(losses)\\n\",\n \"plt.plot(losses.T[0], label='Discriminator')\\n\",\n \"plt.plot(losses.T[1], label='Generator')\\n\",\n \"plt.title(\\\"Training Losses\\\")\\n\",\n \"plt.legend()\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"## Generator samples from training\\n\",\n \"\\n\",\n \"Here we can view samples of images from the generator. First we'll look at images taken while training.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 13,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"def view_samples(epoch, samples):\\n\",\n \" fig, axes = plt.subplots(figsize=(7,7), nrows=4, ncols=4, sharey=True, sharex=True)\\n\",\n \" for ax, img in zip(axes.flatten(), samples[epoch]):\\n\",\n \" ax.xaxis.set_visible(False)\\n\",\n \" ax.yaxis.set_visible(False)\\n\",\n \" im = ax.imshow(img.reshape((28,28)), cmap='Greys_r')\\n\",\n \" \\n\",\n \" return fig, axes\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 14,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": [\n \"# Load samples from generator taken while training\\n\",\n \"with open('train_samples.pkl', 'rb') as f:\\n\",\n \" samples = pkl.load(f)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"These are samples from the final training epoch. You can see the generator is able to reproduce numbers like 1, 7, 3, 2. Since this is just a sample, it isn't representative of the full range of images this generator can make.\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 15,\n \"metadata\": {},\n \"outputs\": [\n {\n \"data\": {\n \"image/png\": \"iVBORw0KGgoAAAANSUhEUgAAAZwAAAGRCAYAAABR3wXnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJztvXm8VWP//38dUyhSpyQNjkqIQiEhRbjJlBAyz9OdebzN\\nxc2NDLd56jZ8jPUl85QxkQZDQklEE5JUQqbz++P3WG/PrX111jp7r2uvfXo9H4/z8Hose6+99rrW\\nWlfv136/31dFdXW1E0IIIdJmuVIfgBBCiGUDTThCCCGCoAlHCCFEEDThCCGECIImHCGEEEHQhCOE\\nECIImnCEEEIEQROOEEKIIGjCEUIIEYbq6urYf5WVldXOOf0V6a9Lly7Vzrk5ScZA41Ie41JZWRnt\\nR3/F+0v1XqmoqLC/DHzXsvhLeq8kinCqqqq8/6+iosL+RDzGjRvnnHNfFrqfpY2LSE4xxqWqqira\\njygeqd4rK6ywgv0tqyR9jie9V2SpCSGECELiqXy55f6ao/7880/TnBGTNgQt5L21/Rzi+0zfdxXp\\n0bBhQ9Pz588v4ZHUffLdD8tyM9/ffvst1f0nec75XsvtvFd++OGHIMdVKIpwhBBCBEETjhBCiCAk\\nttR81pIvFIsTrhU7jIvzg1ecz5SNFh7ZaOFYlu2zfKRtoSc533GelYXYaIVQSGKYIhwhhBBB0IQj\\nhBAiCEVLOA9llzmXG/oyZ/7XX391zvkznXgsccLnpFltK6200hLHIkREnGvOl5FUakaNGmV6m222\\nMX3AAQeYfvjhh4MeUzFo0qSJ6e+++y7va/iM+f33302HzO5KE981l8YzXRGOEEKIIGjCEUIIEYTE\\nllrQIiGPBbHGGmuYnjdvnunll1/eOefcTz/9VOO+4xR78jVxwk7ZaH+xyiqrmG7atKlzzrlvv/3W\\ntv3yyy9537fjjjua/vHHH03ffffdpr/55hvTO+ywg+ksWhyvv/666R49etT4+kJstPXWW8/0lClT\\nanx9dL88+uijtq1v376m//jjD9P77rtv3n2Uo43Gc+yz0UhSG40WHM8hX7/iiiuaTrvgtBgU695S\\nhCOEECIImnCEEEIEIbGlFtKqYBhHzTC1WbNmptdaay3nnHMbbbSRbRsxYoRphq60zurXr2+aVs/C\\nhQtN//zzz6YjK+Lvx5I026Muw/M1a9Ys55w/M4vnk9lQZ511lulevXqZph1Bsnie49hoxYI2Wpzr\\nLyocbNCgQd7/z3th+PDhxTjETJBGr0e+Zp111jHdokUL06NHjzbN7Dg+Q+bMmeOcy70naOnFOXba\\n2Xy28eeHDTfc0PTEiRPz7t+XncdjS4oiHCGEEEHQhCOEECIIRSv89NlfhfQk4nsbNWpkmhbA5ptv\\nbjoK9RYvXpz3/0+YMMH01ltvbfqtt97Ke+zMOqMFx5CVtlu5ZZ6Eol69es455/r372/bXnjhBdNR\\nFptzzj300EOmhw0bZvof//iH6XvvvTeV4ywVvuumEFs2zutPO+0055xzd9xxR97PPOeccxJ9ZrmQ\\n9LzSWhowYIDp6667znSrVq1M77HHHqb5zJkxY4Zp2p+dO3c2/cQTTzjnnPv+++9t26WXXmqaWXV8\\nDjEz9+KLLzY9ZMgQ0127djXN+88HbTRCCzApinCEEEIEQROOEEKIICS21BjGMRPJVyTpg2Etsx74\\nXvZEY7Hnsccea3r99dc3HYWpX3751xLbH3/8sentttvO9AcffGB6tdVWM83iRFp61CxIpNVGO2TV\\nVVc1HacQta7BMf3000+dc7l2ALMLef7ff/9900cffbRpXnfPPfecaV8mYVaIY9/47Ne0s+54HiMW\\nLFhgmvdfXYIWLr+vrxiZ9zKzy2iR8ZnAwuQrr7zSNK1T7ofXyP777++cy7Wt+EzitcKfAqLsNuf+\\nsrCdc+7AAw80PXToUJcPX9ZtGijCEUIIEQRNOEIIIYKQ2FLzhZ2FwGwIhp20XXbeeWfTzLZo3Lix\\n6SjEXbRokW1r27Zt3v1xtbzI8nEu15aJ09eKltrqq69u2nee+PpyxZeR+NFHH5nm948KcjnOH374\\noenbb7/d9Jprrpl332T69OmmW7dubdpnqTHDkcVvIeB4p21XJGXq1KnOudzzzELBd999N/gxhWDu\\n3LmmaZX77E8+T6IsMudy7Xra/B07djRNy47WHD+LFli0nZ9Py4sZunz2rbzyyqa32mor0yNHjjTN\\ne5LP2TSe6T7K/+knhBCiLNCEI4QQIgipFH7Gya7xvYa2A20vZjJFvbmcy11l8+2333bO5RZNderU\\nyTRtHFoHDGmZBRJnxTvf8fr6DfF4Q5BGTzeeu969e5tmDylmlUUhe/fu3fPuj+cqjo3J13BFV14j\\nzF4LbaORrNloZNKkSc455zbZZBPbxrGoq8tt0EbjPcEi8XHjxpmmRTZ27FjTp556qmle7w888IBp\\nX5H63nvvbToqwCXRs8y53GeGb2kO/nTAY4zG2Lnc51MhGZ3qpSaEECLzaMIRQggRhIKWJ0jDrmG4\\nywwkhoNdunQx/fTTT5uOrJP33nvPtrGvGi0falptvrbgxPe94/SQC5kR4lzxxoUZfoMHDza95557\\nmqY1yR5SUdYMw3jaBMy2icPll19umueTn9+8eXPTs2fPNs3sHI5Rlq2vtKBVlI+6WrDsu2dpozG7\\nkNmXvGbYa47XHl9Dy5fXGAtFuQxHVGzLImley3xusb8g980C92uuucY0M+YKoZD+mIpwhBBCBEET\\njhBCiCAUlKWWRq8nhrL77ruv6Z122sk0Q0wWX6299trOuXgFa+utt55pWj0+a4UWEF9DXVlZaZrF\\nZeXKoEGDTDPb5qCDDjJNS4vf+d///rfpfBkx7I3HXlFRkahzuXYoNdu10yI788wzTd92222maZtk\\nfdmIc8891zT7cJUCWs1p4+vRmDY+e5ya1z4zHnlNMnOW+DJa+ZyjdRmtxMksS/ZJo53NzDTuj9Yg\\nj7dYtnEhz31FOEIIIYKgCUcIIUQQilb4WSxoXdGuYXEas8e40t7o0aOdc85VVVXZNlo022yzjWn2\\n42IGnM9yiVMEx8ySOAWMWYch+GGHHWaa/aT2228/08zUqckW6dOnj2kuJ0G91157mWaxKWH/OloJ\\n3A8tkdBZgiTOkhUhbbSarlH2EEsb2lMhiZN1y+cDX0MrmKuC8vnks5/4nKO9HC2bwkww9knbdddd\\n8+6D5++GG24wzWy4tJe7iIMiHCGEEEHQhCOEECIImbPUmK1CS4XQ9mIGRxTW9u3b17axuO2pp54y\\n/fLLL5tmRogv7CxWr7isw8w0ZgDSLrv++utN0z6gBVdTcRhtClqdXGWSPfFYkMvMtGnTpplu166d\\naVqgtCRKaalloZDSt7RERKn6pxVSTFgIPkuN+I6tWNmPLHyO7jNa/j179sz7mbz3XnvtNdMsNk2j\\nOL+QnwsU4QghhAhC5iIc/kuBC6PxXwH8Fy7rab766ivnnHM9evSwbfzRjJqRUZx/wZRrxJKUk08+\\n2TS7L7MzLhd18tUu1AQjTMLIh3AsGLEccMABpr/++mvTbK2T9dqbkLCTcBSRJu3WXe7Eqb3xwXqX\\nQqIyRpJ8zkUw6o9qc5xz7qGHHjK9zz77mGbNFDtKsyUVWzwlpVjPQkU4QgghgqAJRwghRBAyZ6kx\\nn/zCCy803bJlS9NNmjQxTdsnarnCH54/++wz05MnTzYdp31GnB8U64LVNmzYMNP8PrQM7rjjDtPF\\naJHB9kRMDrj55ptNH3fccaY5/rQjaI0OGTLENK8j1vCErC3JIuwknO9ccGxptdWlbtpx7ll2ZY6s\\n+rjvjYNvEbjonPNZRXbbbTfTXKRt/Pjxpnv16mX6kUceMU07kM+zOGNbrO+tCEcIIUQQNOEIIYQI\\nQuYsNYaaDGWZgURLZf/99zcdtbG59dZbbRstN9aVxKk3SGqjxWldkhXYfZuwVQxrVo4//njTrMNJ\\nAi0aru/OVkRHHnmkadoKzLxhxuLEiRNN81pgls/QoUNNM4Mxi6RtY7Vv336p/58ZgHXVUosDWyOR\\nNLL4aHVFVjOfH7SER40aZZo1i+zgHrX4ci63Pod1aqXKzFWEI4QQIgiacIQQQgQhc5Ya8XWOZmdW\\nhoavv/76Eu+7//77TbM9C7OYfOElt8cJNX02WhYLSFm8+eKLL+Z9DY+VbYGmTp1qmotAEdoEUTEp\\n14ZnMeb//d//5X0fbTGOBbtys/CX2Yts+5F1G42kbV0xOzAfvC84tp988klqx5R1aJXzuvV1hY5z\\nv7du3dp0o0aNTEdtaQ499FDbxjY3XOSRBfD8yYHZvddcc41pZrJ16dIl73Gl/XxShCOEECIImnCE\\nEEIEIROWmq+DLRcmYshIa+yNN94wHXV9btGihW1jHyLuY8GCBabZv8u3YFEhWR1ZsdEILUrfd+B2\\nFocOHDjQNG2vNm3amL7vvvuW+MxocSnnnLvnnntMczz5+cyY49rsZMqUKXm3i/w0bdp0qf+fmWl1\\n1UaLc8/yPNAqT2qP8/W0i7fcckvTXCQysohZoPvggw+aZsH6F198YZqLwXXv3t30rFmzTNNGK9Uz\\nSRGOEEKIIGjCEUIIEYRMWGqE9grD0fPPP9/0559/brpz586mI5ts5syZtu2QQw4xzb5bTz75pOkx\\nY8aY9i0i5mtLnkW7rBC233570wzln3jiCdN33XWXaWYM1kSnTp1MX3vttaZ9fZ2YnSOKAxckzMfz\\nzz9vOovZlcXAZxtT01KLc7/7zhX3Q4v4lVdeMb3tttsuoVnofNhhh5mmtc2lCpixxkJR3qutWrUy\\nzaL6OAsUstiavQ+ToghHCCFEEDThCCGECEImLDWGoCw8owXGlQoZDu69996m33//fedc7qqVhP2R\\nWOzIYq6k65rXNZgFw75mhx9+uOkkNhrx2Q7s/XTggQeaXlbOeUiYYRj1x2vQoIFtY3EgrZY4y3mU\\nC3FW/GRRJ3uW8fnE19Nypy3M17CQdueddzbNDLOowPqKK66wbZMmTTJNq43LsNB+Puqoo0wzM/eZ\\nZ54xTQvOZ6MRX5ZoUhThCCGECIImHCGEEEFI7I2knblCG4Wavb823XRT048//rjpKGON2SAMgdlX\\n7Z133jFNS60uZePUhvfee880l3Zgi//awoxCfg5Jo/17KaGNwh50IWGmFK9vWmYRF110kWmu8krb\\npVj3SKmy4JJmmtFO5Hb2paN1xecTswLHjRtnmkWbLJ6OrLY111wz7zGydyCzazmW//vf/0xzeQJm\\nrzHTjPYan4VEK34KIYQoKzThCCGECEJiSy3t0Jc2GnsYcYVO9jtjf64o24bZaMy6efPNN/PuQ/wF\\nzzOLY4cMGWL6n//8p2lm55BoqQjnnOvZs2fsz69rlmZSGy0Nm4mWmm9Fz3yfecQRR5i+/PLLi3Is\\nvs8qFb6iRy5x4sti3XHHHU0PHz7c9FlnnWXaZyMz05PnIcokY7EnC9mZXcsVjDmW7GPIbDs+T0uV\\ngagIRwghRBA04QghhAhCKoWfxbIFGCZSs1CK/YGilfkmTJhg21gkGme5AR91ta/U0mARJs8zC2t5\\nLpjVtmjRopSPrm6SxrVFm5SrpUafxXuB9lEaNlrW8C3T4euf1r59e9OPPfaYaRZGcwmIdu3amWZm\\n2GabbWaamWS77babc865uXPn2jZmvbHYk2PFYlMeY1VVleldd93VNG1xwow1X1/JQlCEI4QQIgia\\ncIQQQgQhFUutEFvAZ12xbX63bt1Mz5gxw3QUyjJ7Y+LEiab79etn+qqrrkp0XMuKjUZoR1LXteLM\\nZZXIpu7atattY8/CZQ1fLzVe77NnzzbNrC/aa1E/NOec22KLLUy/9dZbpnfaaSfTfJ5FllmjRo1s\\n2y233GKazzB+Dq1BHjuXQWAvNd/zzFf4WSwU4QghhAiCJhwhhBBBSGyp+Va+9JE0u4uvYZbEiBEj\\nTL/xxhumW7dubTpq4z158mTbxgKrl19+ucbjWhaz0UR6sPfVlClTanw9szF5/acJ+wqKJeESKCyG\\n5vOBVhuh5c9Vi7n8QJRd69xffdA++ugj28YlCdhjjTYan8VczoBZbbQASchrThGOEEKIIGjCEUII\\nEYTEllrSAqBi2VLMvGAmBe2zaFU6FobG+fykNppst79IarEua8Sx0UgoGy0kbIvPayTLq4jyHmcG\\nWhyOOeYY03feeafpQYMG5X39bbfdZrpLly7OudzC6SZNmpj2rc7ps8Xmz5+f9/WNGzc2zYJUwn5y\\nLB4uBEU4QgghgqAJRwghRBBK1kstqRXD/fjey1X3kpDURhN/IRutdjB7knaxDxZnJs0qK7UFTOus\\nXK6XpOeJzyTaaEnhcioRtNF81llSK9ZnoxGfjVbIs1ARjhBCiCBowhFCCBGEiiShY0VFxRzn3Jc1\\nvlAkYZ3q6uqmNb/Mj8YlFQoaF41JKuheySaxxyXRhCOEEELUFllqQgghgqAJRwghRBA04QghhAiC\\nJhwhhBBB0IQjhBAiCJpwhBBCBEETjhBCiCBowhFCCBEETThCCCGCoAlHCCFEEDThCCGECIImHCGE\\nEEHQhCOEECIImnCEEEKEobq6OvZfZWVltXNOf0X669KlS7Vzbk6SMUh7XCoqKuyv1OennMelsrIy\\n2o/+iveXqXtFf8nvlUQRTlVVVZKXixoYN26cc0VYDGpp41JRUWF/cVh55ZXtr9gst9xy9pdlijEu\\nVVVV0X5E8Uj1XhHJSXqvZPvOF0IIUWdYodQHIIoDI5JffvnFNFd0ZZTjW+n1559/rvH13M5o5Y8/\\n/ljqMf755595t6+44oqmf/vtt7yv4efUr1/f9MKFC5f6mXGJGwGmQcOGDU3Pnz+/ZMfhXLxrxAfH\\nyDfWYtlGEY4QQoggaMIRQggRBFlqdQTaaMRntcWxP3yWCrfXZKP5oHXjs9EIj5G2X9LPivOdQlNq\\nG40Uch5kqdUOXp+rr766c865k046ybb17t3b9AMPPGD61ltvDXB0xUURjhBCiCBowhFCCBGE1C01\\nn6UjiovPNlq8eHHe15fC8ohjba200kqmf/3117yv+f333xPts5DMq9C0bdvW9NSpU2u9n+WXX960\\nz/Zs0KCBc865RYsW2Tbf+dlll11Mv/DCC3lfz3Eh5XT+Q+HLilxhhf//kXzjjTfatqFDh5qeMmVK\\nugeWMopwhBBCBEETjhBCiCCkbqmlYaO1adPG9DfffGM6ynZi1pMvhF9llVVM+6wA2hJZtwMLyb5K\\nann4CjXj2GERzGiKbIS/a9p+a6yxhukffvjBNO0ivpdjGsc+5HtLSSE2GuF5ueCCC0wzs2nVVVd1\\nzuVaaqRJkyamL7nkEtNnn3226W7duplm9mBlZaVpn723rNlrvvts4403Nh2dwzfffNO27bzzzqZ5\\n7/G69tmmvnuiVCjCEUIIEQRNOEIIIYKQDR8BtGjRwvTMmTPzbm/UqJHpBQsWmI56UjVr1sy2ffbZ\\nZ6avvPJK01tvvbXpDTbYwDRD3Xfffdf0/vvvb/rbb781TUupnLJxCjlWWiQ+GjdubHqTTTZxzuVa\\nOx9//LHpV1991fSXX/7VeHattdYyzWshsoKcc27OnDmm49h7vu+dBbuhmPB78rrn9/z++++dc7nj\\nyT51F154oWnaPjy3vs7fs2fPNs37i9b0euutZ/rDDz/0fZWy5h//+Ifpl156yTSzdydPnmz6+eef\\nd8459/7779u2pk2bmu7atavpe++917TPNs7ada0IRwghRBA04QghhAhC5iw1WifkmGOOMU1L67jj\\njjO9zTbbOOecu+OOO2wbrbDWrVub7tSpk2mfLUDbjZkiLVu2NH3ZZZeZzrqNViwYvnfo0ME0F7fa\\nfPPNTR999NHOuVwbYauttjIdWW7O5VoAtF84dkcddZRp9iGjdfPee+/lPa5p06bl+UZ1G5+tEmWY\\n0Xbma6+44grTJ5xwgmlmPtG6o37ttddMP/3006ZpMWXZRouzZEYcRo8ebZrW8bx580yvs846pj/6\\n6CPnnHPnnHOObWP23+uvv246TmZaMfoeFhNFOEIIIYKgCUcIIUQQMmep+bjmmmtMM4ODBZxRKHnu\\nuefaNq6mWK9evbz7ZqjJjB1aBHfeeWfez+zfv7/phx9+OO8+QxOnj1bSglBmhq277rqmeX4POeQQ\\n07SxomyouXPn2jbaKSx2ZHZT8+bNTfN7MMONdsfEiRNN06Zg5tuygm98eW1E2VH77LOPbTvvvPNM\\nMzOUVhstaN/90rdvX9MnnniiaVrmLOCmffrTTz/lPfaQxLHRmK235557mmY22gcffGB6tdVWMx0t\\nQ+Ccc+PGjTMd/XTgKzT32f+E9wqzRWk/8/Oj+zMEinCEEEIEQROOEEKIIGTaUlt77bVNX3755aa/\\n++470wwZo4JPhq4s+qNm2B5lhjiXayO0atXK9CeffGI6yoZzzrnhw4ebLqWNRjujWMdBW8ZXWEZ7\\ncdasWaZpe02YMME5l2tBsH8XrU6O3eeff573WPiZtB54Dn788UfTzFR89NFH836nUvZSK1ZGVBwO\\nPPBA05FNzUJpns+FCxea5jHSgqFlxPuV+6Fl98Ybb5jeYostTHPJA5K1VUR5PHyeMBNvjz32MM2e\\ncryGaUUyYy2yLn2v9cFrn4Xxt912m2neBxzbOPskBa0KW+t3CiGEEAnQhCOEECIImbDUGLrRLunc\\nubNpZhoxlGWx33PPPeecyy0SpRXAjDJ+JsN/Wjq0iNizi8fiW1HThy9MLRR+T56fJEsG/B0eK9/L\\n/nU9evQwTVuK2WuRBfrVV1/ZNl9/KGb7MKvmrbfeMs3zT3uHmVS0DJg96KOUdmjaNtpee+1l+qab\\nbjIdjSktEl5HtB+5JATvF76G48Vrh0W+zB702WgkCzYa4fHwXLGomQWz3E5rjMuq9OnTx3S+a4Gf\\nybHy9QXkPh555JEaX+8jjUJ2RThCCCGCoAlHCCFEEDJhqTHTjNljtEtYeEiLYOzYsaa3224755xz\\np556qm0bOXKk6U8//dQ0w0WGvWyZzrbhtGsYSiclrX5rtLx8mTTFglkwLPA84ogjTLOfXXQ8HFuu\\nFNm7d2/TG220kWlamrRxXn75ZdM+K8z3vWkr8Dxloc9UMeH9MmzYMNO8/iL7mP3leO8888wzpn0r\\nq7J4k9mjtMZ5v7DIt5yW88gHrStauCyepaXFc8h+kL7lM/LBceX9xPddf/31pmlF83rv16+f6Qce\\neGCpn1lMFOEIIYQIgiYcIYQQQSiZpebLEmPYyQwrFgGyCJShbNTLi1YMQ3ifbeIrAqUV0LNnT9Ns\\nM86snwEDBpgu5Up7xcrs8dkcO+20k2kWEvJ8tWvXznRUQEubhUW1tOiouVIlbR/2W+N15PvetIB4\\nDdQ1G43nn1bn9OnTTTdp0mSJ17MHHQsY46wiyfuS9hp7D+64446mTzvtNNPlaKP54LXEYlhCy5HL\\nnZBoGY4ZM2bYNo6rz0bzZX1y1VxmlDLTlFmcvoy4YqEIRwghRBA04QghhAhCUEvNl5VCy6NBgwam\\nGYIyNGRxJvtAjRo1yjmXm2n27rvvmqbV5oMhJYs633zzzbzHwpUQy4k4SxgQZrjwPHIsuE/abpEF\\n9uSTT9o2jjMt1WgMncsdOy5nwD5pcexDWkBpFd6GxFcozevy6quvNs1sT1ovN998s3POuXfeece2\\nxeldxs/nSqz169c3zYzQSy+91PS//vWvvPssF+LcN9zue56wx1qUXeucc0OHDnXO+ceB25lde/DB\\nB5tmJhtXWGXhNYtxQ1rLinCEEEIEQROOEEKIIJQsS43hN0PGTTfd1PSxxx5rmj2YmEnD1T+j8HHM\\nmDG1Pi72AGMIzCUJaPuEbC1fG3w2ZtIwmq+nXcKsGa4iSKIiT47hzz//bPq9994zzXNLG43ZiIVY\\nAOWUGcWxo33C7//QQw+Z5jXKvmbMDNtyyy1Nf/3118653PvFl13JY2Fx7ogRI0zz3PJaYFZp1pYb\\nSIpvdWA+B8aPH2+aRZ20PNkPkPdTtM+2bdvaNvax4/iwZ1vHjh1N8z7juHHplc0228z0K6+8Yppj\\nkobVpghHCCFEEIJGOIwe+C82zrZnnHGG6VtvvdX03LlzTTPPnAt9RT+4+dq8UPv+5c/OrUcddZTp\\no48+2jTrg7Kw/vrSKNa/6PkvH0YkN954o+nTTz/dNKO9KFmA/2LimDPxgGPkq89aVuC/oHlNR13R\\nnXNuhx12MM3FttjOhv/6HjhwYN595oPvY30UF1RbY401TPO+YD2b71/Q5Q6/C7vWc3FBPrcYsfO5\\nke8eZTdpRpSMVpmYwyQc3kOEyVkXX3yx6RdffNE0x1wRjhBCiLJFE44QQoggBLXUmCjAeoDox0vn\\n/O1h2EKD66IzHM0XmjLspY1Gu4I2Q9++fU1fd911ptdcc03Tn3322RKfsyzBUNvXmZYhfmTHsMUJ\\n7RcubseQvl69eqZpry2LMJmCbYM4FuwAfMMNN5jm9ZrEYuVruTDe+eefb5rjxfqsM8880zQ7uicl\\nax2l+dxgDRTbMPGc8D7YYostTLds2dI0bdGorvDwww+3bbQz+RyiJcrnHI+R0MZjchZ/6mCCQhoo\\nwhFCCBEETThCCCGCkLqlxsXVaIuw+2+HDh1Mc9Ez1mrE6QpcE746lJNOOsn0zJkzTQ8aNCivHjdu\\nnOlSdoUuFRwLhvXsOszWGc2bN3fO5daG8P9zkTzaP4UsdOc73izYMkuDXZ7ZroTX3+OPP26aNRz7\\n7ruvabazSfKdea6ouW+OC+9FLipWjPvVueyNF58bvPc/+eQT08zAZW0UszGZseZbrC7fZ7KtE7tS\\n83N8sOXNYYcdZpo2WnSvOpebYVeshRwV4QghhAiCJhwhhBBBSN1SY7j2wgsvmGamy7///W/TXJio\\nWGF5BLM3mJnBrtTMAGLIfNVVV5n+73//W/CxlDPsdMsCzz322MM0F3uKigA33nhj28YCX9omHHO2\\n6Jg3b57ppAVpPlsmacfsENCWOuuss0z7CpifffZZ0+uuu67pSZMm1erzef5p19Fq8Y0Xs6DYQuf5\\n55+v1bExiJf3AAAgAElEQVRkEZ57Xu/MwGQRKIstCZ8/JDq3PK+0mVloy+Jp/vzAbGDCfdIu43Y+\\nr4tloxFFOEIIIYKgCUcIIUQQUrfU2KGUxWDnnHOOaYaGzGpjP6HawnCRhYSHHHKI6bXXXts0LSKG\\nqbvuuqtpZnsw864u9YlyLtc+YJjOQjVaQLRgmCUVdcalzUKrgeeZfahoc3Hs4vSv4/59mYRZsdFo\\nUXJBs+HDh5tmUSevUWY7scdabeF9we7GPJ+01GjN0A7nONYleI9PmTLFNC33e+65x7TvGvP1O4te\\nz//PZyI18Vl3hFZf9+7d8+6T45kGinCEEEIEQROOEEKIIKRuqU2fPt00F05jy23aXrvttptpWgqk\\nprCP4Sj7ELHAk+25+fkMgdlviNYZLR2+t5SkUdzILC4W59Im7dmzp+mbbrrJNK22yA7jUgbt27c3\\nTfutS5cupmkRJV0GopwKcnk9MxuvV69eptl7zlecydfQdqvpejjwwANN33nnnaZp0/iur1NOOcV0\\nsWy0LC9qyHuCiz9yITyeBxaBJilkpnXHceC+WUjK5xY1i635DBsyZIjpkMW1inCEEEIEQROOEEKI\\nIKRuqe2+++6mGfIzjGPYTFvmpZdeMr355pubZi8pFrtF66jffPPNto3WTZMmTfIeI4+FyyDwMx9+\\n+OEa31tKinUctE6YPcVwnCt+0rKkjUXbLSpC5PlkZiBbtXPpiQULFpimTZpGNmBWrNHx48eb5vn3\\nFUFzGYIHH3zQdNTm3rnc5T9YwBkVjdI6jsOMGTNMc2XRYtm6WbPRCO0q2msbbrihad4fnTp1Mu0r\\nmM3X45FjxucW7bVoJV3nnDv77LNN82eMrC3roQhHCCFEEDThCCGECELqlhoz09i+nivksaiNGTsM\\nTVlsyCUMaLudcMIJzrl49ghDzbfffts0i7aYecJQtq4VePpg9hiXE+jTp49pZo8dccQRprmKZ5Qd\\nuP7669s2Zuywrx5XjYxTVFtOSw/EgUXQPOfsR8Y+XMyCog3Tu3dv08ymYt9AZorWBK0hFpsuy/iK\\nOjt37mx6k002Mc3rvE2bNqZZhBnZibQVWYDL/ma8P+OQhXtFEY4QQoggaMIRQggRhNQtNfLVV1+Z\\nfuWVV0zTomFfH2Y9jR492jSz3dq2bWs6n5XG0JHhaLdu3UyzBxj7evky6eoyvu/M7ClaY8w8o+3J\\n/USZURy3sWPHmmY2mq9QzmdfFMsayIodx2t4l112MU170Wepsd/cqFGj8u7fl6kZES0l4VyuHZRG\\n37m0Mw9LBa8l2pn77bdfrfZHq7QQsnCNK8IRQggRBE04QgghghDUUiPs5cMMnBEjRphmyM3XHHfc\\ncabzWV3s2bXKKquYZnFUnIKoLGR1FBOeC1qHcZg9e7bpMWPGmPadF7ZCjwrkWFT7zjvvmGamGy2d\\nOL2nCrFlsji+PA5mY/Kav+WWW0wzg4nXdP/+/U1zhdrzzjvP9BNPPOGcK91SAr7xqqtWWynI2jWu\\nCEcIIUQQNOEIIYQIQlBLjeExNVtos8CMmTHstxWtIOmcc4MHD867z2KQhRC0mPhstDhhd6tWrUwz\\nw4xZOMxYY+Fn9F6uGsqi3sWLF5vmmHM8fcdVyBixmDeLWYgsPGbfrhdffNE0LbJbb73VNDP/2G+w\\nHCyqcjjGcoH3B6+hUq12qwhHCCFEEDThCCGECELJstQILTUfX3zxhemrr746zcMpS5jZwzCa2xlG\\n005iwaAvY4nn3/e5hx56qGmuVhlZdixG5DH+8MMPNR5vGoSw0ZJmCfkytHguaI1edNFFhR6iWEYo\\nlY1GFOEIIYQIgiYcIYQQQciEpSYKx5fZ4wuj2aeOmiTNAGPh4TPPPGM6yo6JE9LzexRStJb0vczg\\nKSZcEZXWoW+8lKEl6jKKcIQQQgRBE44QQoggyFKLSdZ6EtWGON/Bt7JpHAvI16stiU2UtDiNx0t8\\nNqGPtKysOKsy1oVr6+/Uxe8kCkcRjhBCiCBowhFCCBGEiiThbkVFxRzn3Jc1vlAkYZ3q6uqmhexA\\n45IKBY2LxiQVdK9kk9jjkmjCEUIIIWqLLDUhhBBB0IQjhBAiCJpwhBBCBEETjhBCiCBowhFCCBEE\\nTThCCCGCoAlHCCFEEDThCCGECIImHCGEEEHQhCOEECIImnCEEEIEQROOEEKIIGjCEUIIEQRNOEII\\nIcJQXV0d+6+ysrLaOae/Iv116dKl2jk3J8kYaFzi/dWvX9/+SjEulZWV0X70V7w/3SsZ+0t6rySK\\ncKqqqpK8vGAqKirsry4ybtw454qwGNTSxmX55Ze3v2WJTTfd1P6SUoxxqaqqivaTl+WWW87+ypnA\\n92iq90pS6soYFkLSe2XZPVNCCCGCskKxdsR/4SRdRdT3Xuok+/e9tpBjzDq+7/bHH38E+6wsMWrU\\nqESvX2WVVVI6kvz8+eefQT8vH9G/zH3HwnFee+21Tc+cOdN0Vse/UHg9/Pzzz3lfk4UxLDcU4Qgh\\nhAiCJhwhhBBBKJqlVoh1VazX1PTaLIT/af24Gue78bPXWGMN0/PmzSv6Z5UbPtski6ywwl+37e+/\\n/17r/dRkCXGcaaMVclwNGzY0PX/+/Br3WSqSXg/lYDNnAUU4QgghgqAJRwghRBASW2o+S8iXXbYs\\nESeszsq5+eGHH2p8jWyC8MSxpZLaaCuuuKLp3377rXYHFoM4x5VlG81Hs2bNTH/zzTd5X1Os++Pu\\nu+92zjl3zDHH2DbW0KU5fiFQhCOEECIImnCEEEIEIbGlFtJaKbcCziwdSz6SHl/Wv09dJKldxrYq\\n++67r+nHHnvM9Kqrrmp6q622Mr399ts755x75plnbNunn35qevHixaZ32WUX0/Xr1zd96aWX5n3N\\ntGnTTP/4448xvkl28dlohfDLL7+Y5hhG9lnfvn1t2/HHH2/6wgsvNE2rtHnz5qY//PBD0xxvvr5U\\nRauKcIQQQgRBE44QQoggFK3wMw18lg5DUIaGxbCAuO+OHTua/uijj0wXUmwnSgszftLoMxca9vwa\\nNmyYad4LvEd4fY8cOdI559yCBQtsG/Xee+9t+uCDDzbNDtzjx483vcMOO5j+73//m+BbZNcmLybM\\nQOzUqZPpfv36mY4sShbIRplrzjm38sorm+Y5o6aN9uuvv5q+6aabTJ900kl538vrI43nnCIcIYQQ\\nQdCEI4QQIggFWWpxwmBfuBbHzlhppZVMV1ZWmp49e/ZS38fPYYYOs264b26nRTFhwgTTdSHM53dm\\nqJ3GPjnue+yxh3POuZtvvtm2MbxnlhR7WH3xxRemi5VVk0UbzXcfNWjQwLQv02vRokV5t/Me4Gue\\nf/75JT7Xd22/9957pq+//nrTvKc6d+5s+pBDDsm7nzjUhfurJjbZZBPTH3zwgekHHnjAdNOmTZ1z\\nzr300ku2bfr06ab5fHr99ddNMwON19Po0aNN00bzFeqnnb2mCEcIIUQQNOEIIYQIQkGWWtJlBRiu\\nMexj9gZXFrziiitMn3vuuaYZus+YMcP01KlTnXPOtWnTxraxSI0FVOzpxNfT6nn00UdNZz0zjRl1\\nH3/8sWme86Q2Gu0ywv2wt9Nmm21metasWabbtWvnnMvNvDnvvPNMH3XUUaaPOOKIJd7nnHNjxowx\\nnXQ5hVJyzTXXmD7zzDPzvsZ3H/lsNJ8Fx/uI2zmOtCxrun9pAd14442mWeDJ+yVOfz5fhumywLvv\\nvmv6tNNOM81zG233PSufffZZ099++61p9nvjdbD++uubXmuttUzzZ4mQY6IIRwghRBA04QghhAhC\\nYkutkMI5hvAMARkaMrz87LPPTNPe2njjjU0zA2fhwoXOudzVLKNtzuXadb7suUaNGuU93mLBwq1i\\nwv5JxcJnwTEjpmXLlqZ33nln07RuIivtu+++s20spOX5P/3000337NnTdI8ePUyzODGLWWfkrLPO\\nKvo+eb54jfJcrLPOOqZ/+ukn0/msYW7j/X3OOeeY3nDDDfMey7hx4+IetnNu2bPRyBZbbGG6qqrK\\nNC3P6N7iTwFff/216auvvto0sz5pOV911VWmaa9xPyTpmPD+T4oiHCGEEEHQhCOEECIIiS01n4XB\\nENBXjEbY8pth/IABA0zvvvvuptnXiRlmUaGUc39lrM2cOdO2rbvuuqZpEdWrV8807TVafWmE/2wj\\nXq5ccMEFpmnpsCiNRZuDBg1yzjl35ZVX2jaec4boHP8+ffqYPvvss00fd9xxpmndFUJaVmfSYuc4\\nGUO+/fA80hqeO3euaWYVRmPAsTj//PNNb7DBBnn3TYuuLlGsfm4cw4EDB5pmZhrPIZ+dUbHtnnvu\\nadvYd22fffYxPWLECNMsFKW9lsbPArLUhBBCZB5NOEIIIYJQtOUJ4thoPmgRsJCT7dbZ74whJguh\\nIpvslVdesW0dOnQwzZ5FtNqY9cTiqDSg1VRO0HJi4R+tG/Z2Gjx4sOnIGuIqh4QFo0ceeaRpWhO7\\n7rqraVp3hVhqtFB8x1YoSbPoCrFxaZcxa7GmouXGjRubPvbYY01zzPk9TjjhBNMs8C0WpVqqoJDP\\nYtYZ+8udccYZpmnjsx9d//79TR966KHOudwiWo7rpEmT8u6bmW7ct++5zHNM4pyDQixVRThCCCGC\\noAlHCCFEEDK34ictBWagMcSkdcNMjchqof0W9VdzLrcIinD72LFjTRcSYtOOSMuu8VEsS4LnhQV+\\n7M/E88tzN2fOHNPMQozo2rWraVp0tCYILQNaoIVQl1vix+n9F1kvbJXP4mjCa5iWdSFWuo8sjEvS\\ne4jXJItk8137zvnHJ3o9l2N57LHHTH///fd5j4u2W779/V0zYzdphnEhKMIRQggRBE04QgghgpA5\\nS42hLDOgttxyS9OvvvqqaVpw7JsWQXuNYSTfx2y4u+66qzaHvQShbTRSLEuCY+HrzUXbk6F/vl51\\nHE8W2J5yyil538fvceedd5rO+lIRWYbWZL9+/ZxzuWNBeP4vvvhi0zWtuFsbSpWZ5iPpMXDJjCjT\\nzLnc70X7mRYce0NGWZfMxOzdu7dp3m/sQUkLjtlw/Bzet7TX0rbRiCIcIYQQQdCEI4QQIgiZs9QY\\nyjIbitsnTJiQd3sEw1hmQNFO4GqKbPmdhXC+mPA7J13xk8V+7J9Ezew1Fs3yczfaaCPnXK4td8AB\\nB5hmoZrv8y+//PJExy7yw3E5+OCDnXO5BbaE5/+ee+4xncY9Ui73Ha/h6dOn531NixYtTPN73Xrr\\nraavvfZa07SaoyUh9tprL9vG4mb+bMBlWNgDr3v37qZZaL799tub5mq6cVZqLRaKcIQQQgQh0xEO\\nf4Tmj2jsfpsP/gv8mGOOMc1/4TNvnQu91TWSRjWELWf4IyMjyI4dO5rmInn83CiC7NWrl21jrQKT\\nAPivbY5zsWpvlhV4Hhl5vvzyy6ajf637frAfMmSIaY5nnI7WdZUvv/wy73Z2gWfCEO8P33uZcHDu\\nuefm/Ne53OcZx4c1U+wizWNhmx0+544//njT7OKeNopwhBBCBEETjhBCiCBkzlIj/DGLlgrD+Hw/\\nNrZq1co0W6Wsueaapk899VTThdhOSfF1aQ2BL4HAZ6nwR1Hm6q+22mqmORZNmjQxzVqEaCEv7o/t\\nVLp165Z3fyeffLLppF2Xk1LKcUkbntPPP//cNBdYi+CPzBdeeKFp1nawFcrXX39tmrZrTffo3ykX\\nm44/1PMHfLaBYof67777znRtv5evbQ2fj6yl4jjQrp48ebLpfDWLIVCEI4QQIgiacIQQQgQh05aa\\nLyz3hehRKBnVfTjnXNu2bU2zbc39999ftOOMiGMLlLLeII6NRpg9w4XudthhB9MjR440Ha3H7lxu\\nRs62227rnMttT8MWHX379s17LGw5lDblUgcSF1o8zFpijUhkU77zzju2beDAgaZpB/Ha5rXDz4lz\\njxLaQN98802Nry8VtKhoY/E80GZkp/Q0ryv+zOB79vDYafWxDigkinCEEEIEQROOEEKIIBRkqaXd\\n4TVp5kpkEbCQiUVYzMxI43hLmV2T9FzF+f7Mjjn88MPzfhazYBo0aJB3P9ddd51zLtcC4Gtpe7JQ\\nN8vZSnEpJHMrKbTLaP2wpUqnTp2WeF/UNdo5fydoHjs1ixJ5LfB7+zIMs2yjER4/LURmfbKb9okn\\nnmiaz0i2qKkt3B9bQjGLtGHDhqY5VszYZcf9kCjCEUIIEQRNOEIIIYJQkKWWdmZP0v03btzYOedc\\ny5YtbRsL1saOHWuaoXHIws+0SNt+inOOauo6y3PORde4kFQ0hs7lZkmVKyELVrmQFzsD00bjPXXL\\nLbc455z7/vvvbVvS68hXlMjvzWNkxhztOx5X1hZjW3nllU3ToueiZzzftK5Y4Fzb4lbeN3wf98de\\nk7Q2uegae1PGsTzTQBGOEEKIIGjCEUIIEYRMF34m5eyzz3bO5WZvMOT3ZW+IMPCc77nnnqaZvcPF\\n9T799NNUjydr1k1cfEtF0D4+44wz8r6e3/Oiiy5yzhWWPUW7h9aMrwiU9hS30x5i9hctrFLBY9hy\\nyy1Nv/7666Z57rmswz//+U/T7Ds3derUpX4ms/9YyN6+fXvT9913n2mOMeESI+yTx3Mfx17z2YpJ\\nUYQjhBAiCJpwhBBCBKEgS43hNDMj0sBnf3DlyKglPkPEmTNnmh4/frzpkJkZoWndurXpr776qoRH\\nkgt7Ob3wwgum2Saf45W25VVONhqhNUkrh5lKPpipWdu17Gn3sIDX12eMTJs2Le9r+J2yYKMRHif7\\nCPI8LF682DSzAjfddFPTn3zyiWmeBz6vGjVq5JzL7VHIvoNcHoHwWuaxzJgxI+9rSJxnYbHGRBGO\\nEEKIIGjCEUIIEYSCLLW0bTRfBgxthPPPP980Q88IhsMff/yxaWbF1DV7LUs2GuFqk2+99ZZpZt5w\\nVdY0KNfMNOLL7ho0aFDe7fzO7FVXE7R61l9/fdPMdpo/f37e4/Kd565du5rmsghZhsf/n//8xzTP\\nz2WXXWaaRdI33nijaT5naCGyCJp975IcFws8BwwYkPdYsoAiHCGEEEHQhCOEECIImV6egEWb/Kx1\\n113XNAuSotcwXGVRW7t27UxPnDixuAfrStefaGlkyUJiVg/73bG/1sknn2z6iSeeMF1IK/uQ2ZTF\\nJM7YNWnSxDRb1Pvey2LBLl26OOdyz0+UJeVcbo81ZlgVch3RRmNWHe/TUl+ncbn99ttNc6VUnk/i\\nWx01iY3G63e//fYzzfPqW2IiCyjCEUIIEQRNOEIIIYKQ6eUJfJ/FbJxu3bqZjiwthufPPvusaWZv\\n0f4qls2SFRuttm3Q04Z9nfr372+axYPsN1Ws85kVGy2pvRnnNbym2UOQq6vyfmAb/dVXX32J/XFJ\\nCF8/tDj4Xu/LrCoXOIY8VzyXTz75ZF791FNPmR41apRpFmo2a9bMOefc9ddfb9vmzp1revDgwabL\\nxXokinCEEEIEQROOEEKIIGRieQJaQIR2EJcW6N69u2kWoUUr8L322mu2jaEpM3pYsFYsspKllgUb\\njdbDgQce6Jxz7pxzzrFtzFLj8TIzim3q6wJxLJBCMupYnJlkn6WyYLNq/S4N33EyQ7BXr1417oeZ\\nmcsSinCEEEIEQROOEEKIICS21JKG/I0bNzZNu4T4wlTaMqeddpppFoSyFXjU0ptFUNtss43pYcOG\\nmU6jGLCUNhrtiTjZRTy3kRXpXG7mTSFw//PmzXPO5S49wCUJaEXOmTPH9KxZs4pyLOVEGplHNV3f\\npbKzsmCjxckc7Nmzp2mu8lmOWWKlRhGOEEKIIGjCEUIIEYTElhrD8zjhqM9Gi4Ov2JN9i7bbbjvT\\nV1xxhXPOuUsvvTTR5yQtyPOtZljKEJu2FC3HOBTLRiO0S6ZPn+6cc2633XazbVxiok+fPqYfeeQR\\n04WMC/t0lVOBYamLh4vVey9LPfyWRpxjY9arKAxFOEIIIYKgCUcIIUQQUumlVogV4ns9rYbWrVub\\nZrjLvmpJSPo9aAf98ssviT6LLfqLSRwbjYWvadhovvOVbykInreHH3447z4KOc9JbTSfTZp1im1d\\nFbKPcizk9FEulmC5oQhHCCFEEDThCCGECEJFknCxoqJijnPuy/QOZ5lknerq6qaF7EDjkgoFjYvG\\nJBV0r2ST2OOSaMIRQgghaossNSGEEEHQhCOEECIImnCEEEIEQROOEEKIIGjCEUIIEQRNOEIIIYKg\\nCUcIIUQQNOEIIYQIgiYcIYQQQdCEI4QQIgiacIQQQgRBE44QQoggaMIRQggRBE04QgghgqAJRwgh\\nRBiqq6tj/1VWVlY75/SHvw4dOthf0vd26dKl2jk3J8kYaFzS/yvGuFRWVkb7qfVfRUWF/aX5fZdb\\nbjn7K/W5r+Ev1Xsl7fOdZP9ZOpal/SW9V1ZwCaiqqnJz585N8pY6Q0VFhWkuWvfwww+b7tSpU6J9\\njhs3zlVUVBS8+uCyPC5pUIxxqaqqivZT632ssMJft+dvv/1WyOEslfr165teuHBhovf67gsfyy33\\nl6ny559/JvosV4SVOv9+r/D4fefbN4bLL7+86d9//9207zuuuOKKpn/99delHiePhfuOc47jjAn3\\n/8cff+Q93jgkvVcSTTjlQsOGDU3Pnz8/72s4KLxAePKJb+CSTjIimxQyMSwNPpR4bfHzfA+uNCcZ\\nEmeSSTqx+Ej6QItzLydllVVWMf3zzz+b5rHFuR44Vpy0Fy1alGg/JHq9b+x5rRAee5xJvZBri/tP\\n/N5av1MIIYRIgCYcIYQQQUjdUlt55ZVN//LLL2l/nHMuXuhNW8Bno4llh0JsoqURx6KNY82UgpVW\\nWsm07zeHtM5bRLFsNEIbjZYXf2Phs4oWku/7/vTTT3m3c/8+GyufXclz7/s9yfe7EWnQoIHpH3/8\\nscbPj2PHFTLminCEEEIEQROOEEKIIBRkqflS90goG02ILOLLUqItQRuDdk+poY32//7f/zO9zz77\\nlOJwUoffl9lgtJZ8dpJvuy/zraZML9poPvufFiCfv/xMn9WXFB5DIRmdinCEEEIEQROOEEKIIBRk\\nqflsNCHyZdmcdtpptu366683XYuK87LBZz9wu+/7r7rqqqaLZY2QKCOO9g3HjcdYl2y0OJaQL7sw\\nTgGsr3sBWXPNNU0zEy+yyZhR5rNffTYXX0NrkNt9GXNpZ+wqwhFCCBEETThCCCGCUCd7qWWBYvWe\\nyiK+/mCrrbaa6e+++840bZqIwYMHm2Z2EPtc1QWrLel3oO0Rx0bjWJxxxhmmJ0yYYLp9+/amBwwY\\nYLpJkybOudxzPnPmTNPrrLOOaV7DHM9yvLbjWGFx3uu7x7n92GOPNX3fffeZpqXWs2dP01Gxb9Om\\nTW3bt99+a7qysjLv9nnz5i2xD+ecmzRpkmlmDNOu9WVG+u5zFX4KIYTIPJpwhBBCBCEVSy2N/mks\\ncmKGBcO+gw46yDnn3IsvvmjbPvnkE9P16tUzTauD/YaKRRathjiFunHgd+N59LVIj17vsx14XNOm\\nTTO9ySabmP7hhx/yfn454etT5RuX7bff3vSbb75perPNNjP91FNPmZ46darpgQMHmub54mfly6Bq\\n06ZN3mMcOXKkaY5do0aNTH///fdL7C+LcBx834VZYosXLzbNc+m7DvlMGjZsmOl+/fqZpl3KJU4+\\n/PBD55xz33zzjW2jzUm93XbbmabN+fXXX5v+4osvTNMW8/Vho46zxk9SFOEIIYQIgiYcIYQQQUhs\\nqcUJrWijMXMp6fK1hHYYQ0baYZHtFicLha9ZsGCB6R49epiOwtu/fw7tnUMPPdQ0s1CySFIbbeut\\ntzb99ttvm2ahGu0GWqkM36Pzxcwbnv+uXbuaHj9+vOljjjnGNDNy2Ncr6zRv3tw0r1viG5dXX33V\\ndOvWrU1fc801pnl/de7c2TTHi9bkjBkzTK+99tpL7IPj9vTTT5v+8su/VhFmNlyrVq1MX3zxxaaZ\\nNZU1fAW1XHraZ//6niFcVoLPxa222so0n520LpklFl0LtM44Js2aNTPNnw46dOiQ9zvxnmQ2KI+d\\nz1a+d4sttjA9ZswYVwwU4QghhAiCJhwhhBBBSGypJc1QKMRGIwcccIBpZpMwHI2yQ3ytxX2hMS0F\\n2gKPP/646UceecQ0C+n4mrrGW2+9ZZq2D7MEGY4TjkGEz+qk1dSuXTvT1157rWlmVPGaaty4cd59\\nZgVagYVk19Hq+N///md68803N33XXXeZHj58uGlmXDFrKbLgrr76att25ZVX5v18Wp20V5g9yky6\\noUOHmk76vWlP0bItVu9GWv6+55lvJVBfhiy/I6/JDTfc0HTLli3z7jMqwCWR3emcc59//rlpZgLS\\nLuN54nHRPuT5Y3Eoj50WKTNGuU8WrSZFEY4QQoggaMIRQggRhMz1UmMoy6wRZslMnjzZ9AYbbGA6\\nyuaYNWuWbWNmVE2r7Dnn3Lbbbmv6hBNOWGLfzjn36aefml5jjTVq3Ge5km+JAedyQ3kfHANakBEM\\n9Tnm77zzjmmfXcdi3qzja/ceZ+kBXq+0Zh599FHTzIxs2LChadokzKrkuY4y2Zjd5ltpklma7L3G\\n/V1yySWmmeGZdLxo96QBzxMtKmaAsfDS10fMZ13xvmEGLLPE2OuOllpktXHs2T+Nz54uXbrk3Tft\\nNRYJv/baay4ftFxpN3JseQ4KWZVWEY4QQoggaMIRQggRhExYaszYYDYS7ao+ffqYfuyxx0wzG+bI\\nI490zuWGvSygYijtg9YBW+z7VsijXVHXYHEa29rfeeedpn1ZPrQj99tvP+eccw888IBtu+GGG0wf\\nffTReffnaxd/++2313jsWYH2CrOE4iw9wHuBvcyIzx6i3cP98PxGx8Dj8mWUMWvKV/x9xx13mG7R\\nooVp9nij9VMqfJlezJZMulIrrSg+zzgOLKRlnzxaVJEFNnr06Lz7Y1Yij4WWHi3SiRMnmua59/U9\\npD4JNtQAAAz/SURBVHXm6zlXyDNPEY4QQoggaMIRQggRhJJZahtvvLHpm2++2TQLL08++WTTxx9/\\nvOmrrrrKNC217t275/zXudyMF4a3viUJGGr6bLRlhdmzZ5v2nQtmEt54442maanssMMOzjnn+vfv\\nb9u4yiH3TfvAx/3331/ja7ICbQyuoMmsS59942sPz8JIFhkyO4ma1zr74K211lrOudwsJf5/wr52\\nvgLqnXbayTS/KzO+mLHG7+TLjksD7p/jw+PxFY/z+vStgsrzzSUEfD0Iq6qqTEc98/hzAovOaQcy\\nAzdO5iyz3Vjs/vHHH5v2FbMWa0wU4QghhAiCJhwhhBBBKMhS87XqjsNHH31k+pZbbjHN7AwWD/I1\\nLAjk9k033dQ5lxuuMuyMY9ccccQRNb4mDsVaXbOU0K556KGHTNPSPPjgg02zyO2NN95YYj/sx8Vs\\nGF8Wle/6uueee0wfdthhMb5J6eB3+Oqrr/K+xnfvsK/cZ599ZprXNy1jXme0RpgFxWymyELy2Wgs\\nSOR9weOlFUZrhn3w+D24T99yDSHxnXufzesrAmUxLJeDmD59uuktt9zSNAsymQ0anZNx48bZNva/\\n43gzA5c2Go+dmnYcr0WfdeZbubkQe00RjhBCiCBowhFCCBGEgiy1QkIrtlj/17/+ZTrKnHEu1wqg\\njcawluFrp06dnHO52SYMR9ddd928x8LvwaLSQki6jEMpYYYNz123bt1Mc7wGDx5smlYbX0+bLLLX\\n2Pqcq3ZefvnlplnUyZVAeYwHHXSQ6VNOOcV0Fotw49wjvkLKKVOmmPa1yKeNRvvOl1WYryce30dr\\nhssWcDy5bAVXmnzwwQdNn3322aZPP/1003GKrwmtQV9fukLw3af8XN+55DVJy4kr5dJqY59Gngdm\\nHUYZfb5iWdqW3EfHjh1N85pjhiA/h89WngO+t1g2GlGEI4QQIgglq8PhD8977bWX6dtuu800f7Ti\\nv5569eplmvnkEZyNueiRD76+WD/w+/7VmkX4Lyj+S/ruu+82zX/hMqrgGPFfvvz+G220kXMuN8GA\\nEQ7P/3nnnWeaC3oR/uuTESwTRMopUSPO9cHX8F+q/Nd3nP3wXEcLe/F8sls3WzudddZZplkHxXPO\\ndj3z5s0z7avtiJN0lEZUE6dTt+94eMy8xtj6h9+dY8Vz62shE0UwrFfiQmh8H+89nmMmIXA/vk7Q\\nceptfLVXSVGEI4QQIgiacIQQQgQhFUuNP6b5usOyJQoXlGJIR7uMC1AxTM3Hq6++apo/XjK3nRRS\\nT+SjnCyde++91zTbCXGMfGua+xaKotUTtXHxJWSwFQhrFeLAug62X6E1m0XiXHP8UZg1Try2mDSz\\n/vrrm2Znbtow/NzIvonaqfz9/1944YWmn3nmGdMcW9aZkCuvvNI0ExFYC+LrUpw2cTp1+6C17Gtz\\nw7ZFL730kmmOG2up+LyMEl98bXb4E0FUd+hcbtsofs4TTzxhmueYz1BeWySNFkOKcIQQQgRBE44Q\\nQoggpGKpxVlkifnhPubMmWOa9kJNWRIvvviiaS4K5SPrWWRp42sPw7qZnXfe2fTzzz+f9/XM7Wf7\\nmUsvvdQ5lzturE9g6E5bLk5Iz067WbfRSJxsILacoX3Deie2nPnggw9MN2vWzDTtE1rTUTYT77Pr\\nrrvO9FNPPWWaGU5x7hfaOm3btjVNS2311Vc3zcyuNCzupPAYfF2taXXRfiasDaN1xfdusMEGptdb\\nbz3nXG52GW00trZp3ry5aXbIZwYwrxUuxhanxsZ3DgqxPxXhCCGECIImHCGEEEEoWeFnHBjqMduM\\nWVUMDaOCUHZiZRaPj379+hV0nHUVFvU9+eSTeV/DMWIGz5lnnmk6GiNfJ9ozzjjD9DbbbJP3c2jT\\nMmOKHcWzCK2IOAV2tBq7dOlieuHChaaZyRctbuecc5MnTzZ97LHHmj7ppJNMP/fcc6aHDBninMs9\\nh8OHDzfty6TiPeeDrajGjh1rmuNOG41kwUbz2UZ8Da/3zp07m6bNS+vshRdeMM1nFG3OKMONmaC0\\n65iNts8+++Q9rt133900C6yJL4vWV5hLeE0nRRGOEEKIIGjCEUIIEYRMW2pkxIgRptmTixZBtNAX\\nC68Y0pI0OkTXNb799lvTPXr0MM1CXYb+7FFVUyYTrU4WbDJLjSE9x5EFjsyMyyJJMyCZBcVecizO\\nZCdhFs2y39n5559vmt3Yhw4dajo6vz/++KNtYzYci2ppo3DhNI6Lr+s0radnn33WtM/uTjtrNE6f\\nQ1/hJV9Pa5FWKK3oqIO9c85NmDDBNO3Kt99+23S0MCUz0DgO3HejRo1M0/Ik77//vmmOM68bZtLx\\nueizgwsZH0U4QgghgqAJRwghRBDKxlJjcRoX/WKoF2XyXHHFFTXujxk9xYJ2kK8QrFwZM2aM6UMP\\nPdQ0i2xJTbYFe235bDRmCkV26d+3Z504fQUJLTWeZy4J8O6775pmNhjvBS6exgXuaKtE55FjReuU\\nxYcsAr7gggtMR4vrOZfbfn/SpEmmaTex/xevCxZ2MwuPvciKhc8S8mXHcUx8bfrZU45F7bxvWABL\\nuzqy0Zz7y2qj5casN2q+htmF//nPf/J+Di1v2mg+y5D3Ga9j34J0cVCEI4QQIgiacIQQQgShIEuN\\nq9ylXYAXp91/9BquCOqjd+/eBR/T36lrNhphqP3aa6+ZZhEuVwg999xzTUd2aIcOHWwbM5TiFJgx\\nG45ZWlknjo1GaD+xZx37adHqat++vWmfNclVVNlvLrJMDjnkENvGVT6ZAcjstcMPP9z0kUceaZrX\\nPy1Qn03q6xuXho3mg+c7Tn8xbqcVxT5lzB7jUggtWrQwzeclz0mk+T7fyp4vv/yyafaMZL86FtfS\\ngvOtXOqD17EKP4UQQmQeTThCCCGCUJCllrU+VlGYyJDWB62IL774IrVjquvQSmB24KBBg0zfdNNN\\nzrnc7BlfoRq56KKLTJeTjUaSttqnjdW1a1fTXHqgZ8+eptnanlbU008/bXqttdYyfdxxx5mO7t+Z\\nM2faNhZm8thPPPFE0xw7Wjy00Wjr+IpTeT34zhP3n0Z2Is+3LwPN118snxXmXG7vOI4Ps9d4rtgn\\nL7L4eI5Z9EtrmxZ2tHqrc7kWGY+Ly0HQwkx6jgvpdacIRwghRBA04QghhAhC2RR++mA4GIWJvqwn\\nhoJsFS5qz+23326aKw3SAovO+7777lvj/mbMmGH6sssuK8YhlpSk9gOv59GjR5umTbzxxhubHjVq\\nlGlmsrH/1q677mp65MiRpqOiQFp3zNoaMGBA3n3wGGfPnm36hhtuMH3LLbeYpr3KHm8+C46kXeSb\\n1PL02Wu0ulhgOW3aNNNceoM2GolsTtqmzOhkfz1fHzvum9YcVxyNsxQDKdYqrIpwhBBCBEETjhBC\\niCCUpaXG1t0DBw40Xb9+/aW+j0WKIYnTDr1cYbEc+6pxtcrIpmFmDIsUaRl8/vnnqRxnueDLfGJB\\n5iWXXGKaFguvM2ZEcbVWFv899dRTzrncTEO+lsWefA0tFWZ7Dh482DSLwll4Snw2WqnwWfE+fNYS\\nzxszBGm1de/e3TQzzLbddlvnnHMdO3a0bVtvvbVpZpqxvx6XLeD3YDEuP3/RokWm4zyfZKkJIYQo\\nKzThCCGECEJZWmrs68NeThEM+dhKO99rQ1DXbDQfe+yxR6kPoezxrbjJbDBaVLzWfT2x2E+Lfbke\\nfPDBJfbHpQciy825XIuU29nzi8fCdv1ZxtcXjPesz2rz9SOjFcrzwwJYWma0mtu0aeOcc2699daz\\nbVxKhfYbi1ZpofIzeVy+64Pf1WevFetnAUU4QgghgqAJRwghRBCCWmqrrbaaaV/hUxyYeUGLIAoZ\\nGdrTRisku0KIQoljS9ACpjVCfNldtOO4H173tGHuuece55xzd911l23jMhBcZXfKlCl5P7MciWOR\\nxclAo7XP99LeYp86FjUzw4yrnUZwjLmsB+21FVb46/HNlVyTZtv5CliTLmEQB0U4QgghgqAJRwgh\\nRBCCWmoM+4oFrYOotxCzRIYMGVL0zxSiNsTJ7vGtgumDNh3vhTjks0mi/mrFpFhFg8UiaR8xHrPP\\nRiO+fbL3GX8W4M8L9erVW2IfXO7AZ5vSXuO48tjjvIbficdbrHFThCOEECIImnCEEEIEIRVLLU62\\nTBoUo5V51sJ/UTfhcgMszEx6zSUtwivF9e37HN8Km1kolI6zAmkcK4q9BmlXchkIZg5GVpfPLqOl\\nR3x2Kj+HffR8q3zyO9GujWMlxkERjhBCiCBowhFCCBGEiiRhdUVFxRzn3JfpHc4yyTrV1dVNa36Z\\nH41LKhQ0LhqTVNC9kk1ij0uiCUcIIYSoLbLUhBBCBEETjhBCiCBowhFCCBEETThCCCGCoAlHCCFE\\nEDThCCGECIImHCGEEEHQhCOEECIImnCEEEIE4f8DUFXK4jYBfhMAAAAASUVORK5CYII=\\n\",\n \"text/plain\": [\n \"\"\n ]\n },\n \"metadata\": {},\n \"output_type\": \"display_data\"\n }\n ],\n \"source\": [\n \"_ = view_samples(-1, samples)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"Below I'm showing the generated images as the network was training, every 10 epochs. With bonus optical illusion!\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 16,\n \"metadata\": {},\n \"outputs\": [\n {\n \"data\": {\n \"image/png\": \"iVBORw0KGgoAAAANSUhEUgAAAZwAAAKhCAYAAABkTRjXAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXeYJFX1ht8N5CXnoOQsGQUJIiwZJEsQkCA5iiig/iSD\\nkSBZMQFKlChJQFAykkFyEgmSRHKG+f2B79zps1PbXT09vSOe73l4mp7trq766txb3wn33GE9PT0k\\nEolEIjHYGD6uTyCRSCQS/xvIB04ikUgkuoJ84CQSiUSiK8gHTiKRSCS6gnzgJBKJRKIryAdOIpFI\\nJLqCfOAkEolEoivIB04ikUgkuoJ84CQSiUSiKxhZ58OTTDJJz1RTTcWwYcMAGH/88QF48cUXAZh2\\n2mkBeOGFFwCYddZZAXjnnXcAeOmllzwOAG+99RYAE0wwQcPvfPTRRw3/PmLEiIZ/n3rqqRs+9+GH\\nHwLw6quvAjDDDDMA8PrrrwPw/vvvA/Dvf/8bgCmnnBKADz74AIDhwz9+7r788ssv9fT0TNsKF6NG\\njeqZcsope7kYb7zxGriYbrrpAHj++ecBmG222VriQk49brtcvPLKKwDMOOOMDVy89957Df/eHxdv\\nvvkm77zzzrBWeBgbF16jdvG/zMX/ol04XwjHufODXNSdLwabi1bmi3btQsS5s9N28eabbwIwcmTj\\nFD+u7aLWA2f66afn0EMP7b3In//85wAsscQSAMw888xAIUcSfe/JPvDAAwC8/fbbADzxxBMALLjg\\nggBsscUWANx9990AXH311UAh4fjjjwfg8ccfB+Cee+4BioFMOOGEDZ//4he/CJSb5E179tlnAZh0\\n0kkB2HfffZ9slYvpppuOQw45pJeLk08+GYAll1wSgFlmmQUY06B8LxcPPvhgw7n9/e9/HysXV111\\nFQBvvPEGACeeeCIAjz32WAMXL7/8MgATTTRRS1w888wzAEw22WQcc8wxrdLQwIUTinZRl4v7778f\\nKIMscvGVr3wFgHvvvbdfLk444QRgTLuoy0Vfu2iXi2Z2ER/Gg20Xcvavf/0LgIknnhiA1157baxc\\naBeTTjopxx57bC0ums0XVXbRbL6QiwUWWKBfLqrmi0cffRSAv/3tb8DA5ou6djHttNNy8MEH9/5W\\ns/lCu5CLKaaYAoCHHnoIKPdZLhZaaKF+udAuvM8nnXQSUMZItIs4RlZYYQWgcO+/y8Vkk01Wyy4y\\npJZIJBKJrqCWh/P2229zzz33cN111wHlKTjXXHMBRTWpqlZffXUAbr31VqC4b5/+9KcBuPLKKwHY\\nd999ATj77LMBuOuuuwD405/+BBQlsvDCCwPlKevnttpqKwAOOuggoDz1l19+eYDe81Ud/vWvfwXg\\nySc/dmi23377OjQAH6ufe+65h+uvvx4oLqxceI6RC39bl1YurrjiCgD22WcfAM455xwA7rzzTqCo\\nNtX6IossAhR1pqL56le/2sCF3//CF77QwIXq8JZbbgHgqaee6uUiuuHd4sIwQhUXXuOf//xnoLld\\nbL311gAceOCBbXGx3XbbDRoXqu3VVlutXy4ML/3xj3/slwuvpYqLKrs45JBDanHxj3/8A2jPLuJ8\\n0cwu1lhjjQYuquYLuWg2X3zmM59p+B093mgXrc4XctGOXbz99tvce++9vcfWY5hzzjn75SLahU2W\\n43zh3Kld3HHHHQD85S9/Acp8oQfU6nwhFzfccAMA8803HwA333wzAE8//TRQ3y7Sw0kkEolEV1Dv\\nMc3HSah55pkHgM9//vPAx3E8KJ7Cd77zHaAkwD71qU8BcOGFFwIlEWU8UTUljPlusMEGACy66KIA\\nPPzwwwCcccYZQCkOOP/884ESD5177rmBkiDz6W9cfJlllgFKctC4aR0MGzaMkSNHMu+88wLwuc99\\nDiix1sjFc889BxQuLr74YqAonZ/97GdA4UJFo3rYcMMNgaJgH3nkkX65OO+884ASJ1dBTTPNNA1c\\nGBdfdtllG7h44YUXehOCg8VFtItWuTABv/766wPFy4t2YeLz3HPPbYsLr//FF1/sGBfmI7bbbru2\\nuFBZRruQi1btYrHFFgNg9tlnb4mLvmOkLheeZ6vzxT//+c8GLuJ8YQ7opptuauCi1fki2oXzhR7X\\nYHIxbNgwRowYwfzzzw/AZz/7WWBMu/j2t78NjGkXl1xyCVDySnGM6BnHMaJno0d95plnAsUu5GLx\\nxRcHxhwjP/3pT4GS99Lz8fqfe+65Xl5aQXo4iUQikegKank4r776KhdffHHv0/jaa68FSnXRpptu\\nCpSnn7FRY7MqBuPExrl92q611loNv6caUAVYPmlVmTmjd999Fyi5ohgLNh5urHf06NFAUQWqyjp4\\n9dVXueSSS3q5MDbrNW622WZA4UL15rnpbcmF31eFrb322g2/14wLY8BWeMmFnKqEIhcrr7wyUNTi\\nRRdd1FsCOVhcWJW45pprDogLPagqu2iXi7520Q4Xf/jDH9hhhx1a4sIxYl6r03YxUC60i3a5aGW+\\nMFcjF9pFnC/8vvNFMy70EpqNkWbzhVx4z9rl4rLLLqscI1ZgRi7ifGFeSS60iy996UtAKY+uO3d6\\n7R5HjzpyseqqqwLFLi699NLe5SitID2cRCKRSHQFw+psMT3XXHP1HHHEEb1PP5/KVr6YpzA+bK22\\ntfzTTz89UGKi22yzDQCXX345UCoofKp7PJ/2LiLziTrTTDMBJd7t0101YLWKsVz/XYVkbPmAAw4A\\n4Iknnri9p6dnyTpcGE+Wi0MPPbTh2ueYYw6geDjtcqFas34+cuEaKLlwMasKSi6s43dxnOdh3uuA\\nAw7g2Wef5d133215Udtcc83Vc+SRR3LjjTe2xYVrDowPb7vttgBcdtllY+VCT0kVF7lQyUa7sHJH\\nLuRKLsy/HHDAATzzzDMD4kKP5rDDDhsrF/7d2HnkQrtwrdNAuWjVLhwj+++/f1t20c35InLhGNEb\\niWMk2oWf833VGDnwwAPbtgurvqrGiDkUOdA+HCPLLbccMKZdNJsvtAvX4zh36uFU2YVcmDN0rVTf\\nubOOXaSHk0gkEomuoJaHM/nkk/d8/vOf71VhKgWrQ4w/ujbAKjFX6qrqfLWW3PfrrrsuUJ7CKg6/\\nbzzRVbFWl6mgfCqvuOKKQFmla/zRahdVotVtv/3tbwGYZ555WvZwJptssp6ll16694nvGoONNtqo\\ngYtrrrmmXy5UMl676y38exUXo0aNAko9vlwYo5ULP7/SSis1cGWdvvFoubBa5fTTT2eDDTbg3nvv\\nbVm9dZqLgdpF5EK1r11UcaFK/P3vf/8/w4Vj5Pbbbx90LgY6XzQbI16b349jpNl84eciF/3NF+1w\\nsdRSS/V6S3YKsPrUvKF24RzbbO7UO7QqzbWRXlucL7zf2oU5vKr5Qi48PysCtYszzzyT9ddfv2Uu\\n0sNJJBKJRFdQq0pt5MiRTDPNNL2qTc/BqhLjkL5X2ViV4tPZGKtPb5+qruT1c9acG4/0qWxtujFg\\nFYqfV7n6765QdlW1uQFr3o2v18F4443HdNNNNwYXVv8Ye/W9yua+++4DikozxqoSkQtXu6tgVIce\\nVy7sweTf/b6fV6HIhauxzRFELg499NDeYw2UC6uItItmXJiri3ZRxYXXpBprlQv/XS60i0svvRSA\\n7373uwPmQgXriu527aJVLjyuCtZ8RV0utItOcuFvOi7bnS/iGInzRdUYqTtfRLvQs+o7X7TDxfTT\\nT99rF1VjxPdyoV24VijOF6ussgpQ7MJuHV6bx213vrDDSZwvXDt1yCGH1OIiPZxEIpFIdAW1PJzp\\nppuO3XbbjY033hiA0047DSgxWOOOPm2tcFhqqaWAUjVilZDrYYQxU5WLNeaqNTubGvu1msjj+j1j\\nula1qBqtKNt8882BolyMHdfBdNNNx+67786Xv/xloHBhDyO58Jys/nC1tVUjk08+OVDNhVxaWWd1\\nSeTCunu58HvGZu0fpVKKVVR6gdNOO23tPlED5cJzNoZufyfzi5EL7UIu7JHl5yIX/q5cWOFj1ZFc\\nRLvoBBennnoqUNZNtGsXrXKhXVRxEe3CMRK50C4GykU788XSSy8NlHHpfBHXBlXNF1VctDtfRC6m\\nmWaajtuF1+o56eXZFaVVu7DHWat24e96D8z9OF/IRafmi/RwEolEItEV1KpSm2qqqXpGjx7dGxP1\\nqWtc0vUM1oYbK/VpaXWISsWnsdVjVtio5n/5y182vFf5GNN1pbl9fqyk8Jp8ahtjtNrE3xM+oY85\\n5piWq9TkwpioqqkZF3a2dmWvSkUu7EtkVUkVF3qN5j2quNADMpbraxUXI0aM4KyzzuL5559vuQJn\\nyimn7Bk9enTvOcuFFTMD5UJ7U7XJhe/tV1bFhRzISVzjMDa7OPPMM9viwnNWQcqF6x1Uy3KhV+fq\\n97pcVNmFithcQDMurE5zfYZoxy7ifBHtwnFnvsh9aPQ0rKCKXIyr+cJ7N2LEiHFmF86dnqvn5tiL\\ndmGOsIqLaBe+xrVy2kXsmzZ8+PBadpEeTiKRSCS6glqByGHDhjH++OP3KtL11lsPKFVkrgj277/7\\n3e+AomztaOvT2XyCcUWfukcffTRQ4pd2l7XSwk6rqnVjs+YA4upqV8W6M92PfvQjAI466qiPSagZ\\nj+3LhcrDNQFVXLjWRwVTlwuPJxdWZrXKhSucjdW7Y2F/XNTp/gofq5wJJpig1y5a5cK1BHa0bcaF\\nnWvNd6jeq7hwD49YuaUq9N/luFNcTDjhhJV2oU27bkIujInLhbF871erY6QZF7GiT09mMLiomi+s\\ngNIu1llnHWDg84XHs19Yq/OFXFTNFz/84Q8bfmcgYyTahVx4H+PcqV24t497eDWzizhfyIXRAD2X\\naBeOEXM2chXt4sgjj2yLi/RwEolEItEV1MrhzDDDDD1bbLFFr0q315BrCozVqzyNN/oUd02Bq1Xt\\nAnv44YcDpROp37diQhVmzPW2224DSv2+FRfuEeE1Gcd2BbLVMipef3fvvfcGYJdddmk5hzPDDDP0\\nbL755r0q3Rhs7Nqq8miVix/84AcNn49cqM5VNtbNV3EhjN1anSQXqry+XPzgBz/gySefbDk+XcWF\\nytX3VXZh51pj5lVcqNa8hrp2MRS4EOY/zU/UtQu50C5Ume3ahWPEKqrB4OK/Zb7QLjbZZBOg//mi\\nLhfTTz99z+abb947d3rtejoi2oW5FNfdVNmFn49caBe+xrVQzezC41SNkW9+85u1uEgPJ5FIJBJd\\nQa3kxYQTTsi8887bu6ugcUSrQuxoaqxUlaVCsDLD2m5r0ffaay+gKBuf/tblG1N1Va1xRave3OfC\\nfcDtDu1T3xXwqgsVjR1b/X5dLuaff/7ePci9piouVBbGSuXCVdKnnHIKAHvuuWcDF7GjrVzYFdYY\\nrGsGqrhwRXHkQvTlQv7rcDHffPONwYWrpX1txkW0i8iF52VnY+2vyi70nFTC2m2rXEw88cQd48Jq\\noVbtohkX2oX3Vy6iXTTjIq66Hwwu3G3SHEzdMRK5+PrXvw6UvETVGKk7X+hhWWk6tvmiLhcTTTQR\\nCyywQG+ngDhG5ML722y++M1vfgPAHnvs0fC9OEbk3MiLHk3VfOH3tAs7EJhXE+3aRXo4iUQikegK\\nauVwZp555p6dd965VzFYz65S9Olr/x3XBFgDrhIxTulT3fp6j2dc0+PqKXkc45HGE41r2gPJPeyt\\ncbeflRUeVmi4gtkqtauuuqrlHM7MM8/cs9NOO/UqSVfyqhTlwu6vVodELszxqHQ8N7kw9h+5sFLL\\neLXXUsVF7OEkF1YA9eXi1ltv5bXXXms5Pl3FheesmotcaB8qpIFyYX6rmV0048IY/vDhwzvGRat2\\nIRwjA+XC6IL5Mceme9gPNhednC/kIs4XVVzE+UIbH2+88YDW7SLOF+1yseOOO/Z6GM3sQi60jzhG\\nondYxYX5K6vgnC/iGPF3q+zC/Jbc+/2RI0dy2223tcxFejiJRCKR6Apq5XA+/PBDXnvttV7PwRin\\nT01VlWsM7JV0ySWXAB/vGghlLwWVj72MXIVrvNAqERWLT2NjsXZzVan4fc/LmndXyRqPtNbcVbUq\\nmLpcvP76673n7m/Kga8qDhVJ5MJ9aIw7ezzPsYoLVZr18nKhWnRtgd+XC2O2KiB/R0/36aef7uWl\\nU1yoMCMXrjAfKBfahXFpO9vas6tVLvycXDzzzDMD5sIKrThGIhcXX3wxUHafrRojrdpF5EK7iN+X\\nC3M8Kls/17cjQTtcdGK+qLKLeF8jF3p1decL7ULvo7/5ol27sBrQrstWFcqFuRa9OcdItAu50AO1\\nZ1rkQi/RMVI1X8TvR7vwHsp5u3aRHk4ikUgkuoJaHs7w4cOZeOKJe+OP7snhU8+noauq7evj0zhW\\nF/nUtGrFWnNVnR1TrbxRqajajLFarWKuwO/7Oev/fZqrLt1b3XUBxjvrcGHs1H0oVE2uIfDcVEle\\nuxU1VpHIhZzJpbmAyIV9plZYYYUGLozZGxOWCxWNsWBjtubLDj74YOBjhWVceKBc2N+pigvtolUu\\nvBb7P0UuvMZoF5ELOZML7SJysdZaa9X2fiMX9vtqxoXnJhdxjAyUiyq7kAuhV+iK94MOOgj4eJ+W\\ndu3C+SKOkVbni2gXrc4XzezC41bNF44R5wvtYu21127LLiaZZJLe++XcqV14LXEPH+3Aa3OOkwvt\\nJ84X0S7s9lA1X3g+zeYL7eLAAw/s5aKOXaSHk0gkEomuoJaH8/rrr3PNNdew4IILAuVpbMzbp6kx\\nWP99hx12AIpyiB2VrTV37cKiiy4KlAoM+0ottthiQKkW8Xf1sKxKueiii4BSuWE81HjmzjvvDMC+\\n++4LlJhwO1y44lelIOTCGKzXGLkwfyAXcuY5yYWKKnJhtYhcqBKtcpELFY9xcrnYfvvtgbKb4euv\\nv94b+67LhXYhF/7G6quv3lEutAsrqSIXwrh05EK7aMbFG2+80RYXV199dW/vq8hFHCOtcuHnzAF0\\nigu9D3NJnud2223XwMVA7MIx4jWIuvOF7+vOF3GMOF9U2YXzhfB8BsrF1VdfXTlGXAdjDsV/r7KL\\nyIUdAawys5pMLvx7tAvnC6sbL7zwQqBwEe3CvaTc8bPuGEkPJ5FIJBJdQS0PZ7zxxmPGGWfsraiw\\nplwVptI455xzgLK/xfe//30AvvWtbwFwxhlnACUmapdW48U+bY1jWnljTNc+UvYZUr25Wt94plVp\\nv/71rwFYcsmPl9joLcR95NvhwgosY6cqD9XV2Wef3cCFPYj0rk4//fSxcqHXZqy3GRfGdF2VbYWe\\nykg1ZwddVyj3jRGrZupyEbswN+NCu9hnn31qcaFdWHnTjAvtIlalWRnmOoxOcTHTTDONMUbkwjFy\\n1llndZWLOEZiJZYr16u4mGOOOdq2C8dIq/NFHCNnnnlmw7Vb5WYeYaDzhVw4X7iXjGtgzDF1YozE\\n+cI1gPLejAu7SJt/jnbhehtzh63OF3Kht+IY0ft0DOuFmmucffbZa3GRHk4ikUgkuoK29sNREVhD\\n7lM0xqON2W+xxRZAibnG1dMqTWOqPn1VWSohn7rGx62oMc6ognJVrE9j+1Dp0ey3335AiQ2rvNvh\\nQg/CWnSVplzsuOOOQFEKW265JVB6WTXjQg7kRKVRxYXHU0FFLuxbZ4xWLqx6Oeuss3pzZIPNhXbR\\njAsVrFxEu1Clu5eM+8R7PHMI9rGKdiEXqkjtohNcuF4hjpFmXNh7rZldNOMijpF2uTjnnHPa5qLu\\nfOEYsQeb596p+UK7iPOFnoxjxPlCr3OgdjHBBBP0ehDaRczRRbtwx0/twgo9ufBzzbhoNkacL+wS\\n3apdnH322bW4SA8nkUgkEl1BrV5q448/fs+0007L1ltvDYy5Ytc4pOrO6iRXCrsHgxUYKh9jgCog\\n44zuUmk1ixU6KiR39nNlsbFZVYMKyaezMVhX87pK19jt/vvv33IvNblQgbiWQy7MF0Uuzj//fKBU\\npVg1Yt5JLswBuL/F9ddf38CFlVtyIWeuJariwqqkBx54APi4jr7v8d566y1OOukknnnmmZYDs+3a\\nRatcGPeOduFxhjIXV111VQMX2kXs3uwY8f62aheDxYVr0/R8x4Vd+L7T84WdmK3QkgsjMHLhfKFd\\neLy33367bS6q5gu5iN2bzzvvvAYu9CaiXZjXinYRudDDkgs7CpjLiXZxzz33ACVnM1C7SA8nkUgk\\nEl1BrRzOiBEjmHzyyXvr3TfaaCOgdBR1hfDPf/5zoCgXa8B9qlshpXL1ae3KXysv3H3QWKx/d/Xt\\nnXfeCZQYrXFHn8o+te02a1zc87QyyKd1XS4mm2yy3rivO+J5TsZETzrpJKAoi0UWWQQoK3dVvCoU\\nV6Iba9f7kgtjsZEL74ExWs/LTtkq26mmmgoosVtXFsvFa6+91quG6nJh/Fi7aJWLaBeq+GgXcuHx\\nW+VCu4jKthtceN/kwrzBiSeeCBT1bW4uctHMLppx4f2vaxfes05w4XwRuYh24XzRzC7kwmuMY6Rq\\nvtAu4jpCuXB9TpwvtAt312yHi+HDhzNq1KjK+UK7OOGEE4Axx4j5Jz0hr00unAO1g6r5wrlPLhZe\\neGFgTLtwjLgPj3m0OEZeffXVWlykh5NIJBKJrqCWhzPJJJP0VgxB6UhrnND44U477QSUSgpVnErD\\nuKWro10H41NctWUtuXFKj+dx/L7Kx/i1sVif6ldeeSVQFIy71e29995Aqaoy7tkqF8sss0zv6mW7\\nsMqFvZHsauDKXyu3VO1y4b9HLlRbcmGMtYoLFbFcWI3k380pqGw322wz4OO9yeXC1cmtYtSoUSy7\\n7LK9XGgX5uyaceE1uNaomV34OblQQTfjwri0djEuuFCRyoX3cbC48Pz1AlT/jpHBtAvHiIhjxDxC\\nM7sYrPnCHG7VGDFC0h8X9iJrFaNGjWK55ZbrrU6rmi923XXXBi70+rxm73fVfBHtwvVf2oUejlw4\\nFozy1J0vPvroo95zaQXp4SQSiUSiK6jl4Uw44YTMNddcvXt8WON9wQUXAKWyYtlllwVK9UjcP9t4\\no09f44c+nVVrdrY98sgjAVhuueWAolxUi7/97W8B2HTTTYFSkRO7TPt96+49jkqmDiaYYALmmGOO\\nXgVgrNWqEn9bhaeCifuqG1uXC+PKcqFa0yOSCzn2Gsx3nHbaaUBRIpEL74VcxF0N2+Fi/PHHZ/bZ\\nZ++1C3N2sQpNLlS20S6quNDLi1wcccQRDdfiNagK5UKP1mpGvY3B5EK7cIxUcRHtwvtY1y6quPB4\\njpFucuF8YX8w7aJqvoh24X1sdb5Q7TcbI3bhqBojgzVfzD777L2VenG+sArNc3Zui3ZhzsUOBa7f\\nMdci9Oq0i8iF3Ea7sKu0++/oifn9aBdGjVpFejiJRCKR6ApqeThvvfUWd999d2882NiqCkTVZKxX\\nJWInU6s+rMxyfYxVKCoWn752APD39Jiuu+46oMTkrdSxT5hPez9n7btxSc9LpVIndyPefvtt7r33\\n3t4qEGOmKtPIhSt/jRvX5cIeS8bgq7iwOkUurC5xHc9WW23VwIXnZYz2+uuv711FXJcL48HahVyo\\nIFvlwhXevvd+Ri7kXi68Rldly4UdcD1O5MLz7iQX0S4cI1bKNePCaqTIRZVd1OWiyi46yYXzhbbW\\nbL6o4sIx0eoYiVw0GyPRLuJ8Ebm44YYb2rYLv2e+qWq+iHOnHQbifOF7owBGCyIX5tflItqFXqec\\nV80X5oJcm3TttdfW4iI9nEQikUh0BbU8nEknnZQvfOELvfG+3XbbreHfYx28ysPd5Nx/xLigdfj2\\nA/LfXVk8evRoAP7yl780HNd9vY2x/uIXvwBKHyHVg8e3Ss6ad/sOGQdXXdSBXBgHtrrEOPOGG27Y\\ncM4qD5VIMy5UXa44lwvX70QujLHa6dbKEbm3OsUKILmw6rAvF6qiTnGhBxq5UKF6rcbuW7ULufB8\\nVXXjmosVVlihY3bh+oy6XNi5wGuSC6uTzI92wy7ifOEx43zRaS48rnkSr8n5wjxE3O0yzhd+z1xR\\nO1yMGjWqgYtddtkFKLmYDTbYoOGczdlMMcUUQPFIjcbIhf3nHENysfLKK/fLhfOFOcQquzA36Hog\\nufB7cnHHHXfU4iI9nEQikUh0BbU8nHfffZfHH3+8VwkY6/TpqeKw1txVqyuuuCJQKhzsH2X9vRUb\\ncW9s3/u0P/744wHYZpttgFKNYpzRKhUrLVSVft+4pKpChbPSSisB8Ktf/ao2FypEz0kuVCRy4cpe\\nfyty4dqlyIXrOaq4sE/VUUcd1S8X7uuuglVFGstVzeltjB49ujfO3ykuol3Ihavr2+XCaznuuOMG\\nxEW0i4Fy8dhjj/VWCblDonHuunbhGLE6qRkXxx57LFA6Lh999NEN3KhgW7ULvY2B2IXzhfdDLlTl\\nvqqi684XzcaI81SVXbQ6X3ieK620Um0u3nvvPZ544oneMaJdVM0XcqHXZqXceuut18CFdmF0xzWF\\nVWPEa492oZenXRidimNEuzBqMHr06N5cWCtIDyeRSCQSXUEtD2f88cdnttlm682pWLkgrMnWc/Bp\\nbqWNq1mNM/q0NU/hinCrmnzqW7GharTPj3vQ2zvN31EN2O1Vhe33Tz75ZKA8te2AWgeut3BfCat7\\n4r7pKgFVntUlKhu5UGn4Xq7kwh5XVszIrZV2rXIhp5ELle3aa6/dq7JahWuS6nIR7cI1BXJRZRdy\\noV3Ihb9Tlwvj1YPBhRWW7XLRbIzU5UL764ZdOEacL7QLUTVfeI56Qq3OF1VjxOqygY6RvvNFu1xU\\n2YXj2FyKecxW5wu5sPuzVW2RCysFv/a1rzUcX06skpMLOXWMmP9q1y7Sw0kkEolEV1C7W/Rkk03W\\nq8Ksczfup8djhY57jlv/blzZqjBrw12VbZxx3XXXBcoeDA8//DBQlIfxU+PLqjvjmZ6He6GrcDbZ\\nZBMAvv71rwNlZbO18H6+VS4mnXTS3jUDHityYVWKK3etf49cyKVcGH9eZ511+uVC5WH9fOTCa/I8\\nzjjjDKDFNDz4AAAgAElEQVQoKSuE5MLfX2ihhXpVUqsYPnw4k0wyyRh7bciFynbzzTcHYP/99wfG\\ntAvXqGgX9sCr4iLuguhq/iouPI+zzjoLKHYhF+702NcuBpuLKrsYKBfN7KIZF52wC8eI6rvb84Vj\\npNX5Io6Rsc0X7XAxatSojo0RuYx2IRfua/TQQw8BJSpkxZ55SrlwbZR95pwL5cJK08jFwgsvXIuL\\n9HASiUQi0RXU2vFz2LBhLwL12qT+d2HWnp6eaVv54Ceci5Z5gOSiL5KLguSiILn4GLUeOIlEIpFI\\ntIsMqSUSiUSiK8gHTiKRSCS6gnzgJBKJRKIryAdOIpFIJLqCfOAkEolEoivIB04ikUgkuoJ84CQS\\niUSiK8gHTiKRSCS6gnzgJBKJRKIrqNW8c9iwYT3hPVBabMf38XMifr6f3wHKZkTNfqfq+FXHrTq/\\nnp6el2q0tvlEt2jo6enp/+b0g25xUXX/BhvJRUFyUTAUuXDr57rbJwwUrXJR64EDjZO7u795cV6s\\nu8752fj6/vvvf/zjIxt/3n93F0I7qEaDir/jTn3igw8+6Pd7fs738Xjvv/9+272Oqh6ezT4fH6oR\\nnrPXWoV2H779fX+gA7cZF/H4cZBUfV97036aHb/qOGMRHGP8vR0u+n4v2lyzybFVu3CM2N232XHk\\nWFRNSH6uvzHSzAaboa5dtCAQgTKPOO6bfb4TAnWwx0g8t3hfquBOne630+y4rd6TTs0XdT0cxhtv\\nvF7Diwbo+2jcVRNM1YlqOPF9fLBEeNw4yOOD0X+PD6a6GD58eOU1tDrpNfvtyHHV95q9b4Z2OWjl\\n+/Gc40Budk3+e3zQtDqJx883u4aBTiZ97SIeKz5Iqrhodo7NuIifrzpOq+/bxUDsotkx/HucL1r5\\n7TrolF0MGzas8pyaCYyq345z6UAfNIPtJWYOJ5FIJBJdQS0Pp6enh/fff7/36Rg9jmbKpOrzPqUN\\nE8TjG1pz8yI3TPJ9VIe62KpAww7R9W6mKpqhb1iirkJspuaqwn/+ZryWZuHC6CnVzas1Q9/raPUY\\nVZ5w5MQwQVT1cjHxxBMD8NZbbwHVYchWPduBKuMPP/yw9xjxGqt+I6r8GPKK4eZoD15THCPaSTxe\\ntIsYemvV42qGduyiVU/Ya62yC+1GLrz/kYtoF1XXMFC76OnpaTl/HcdvtIvIiWMgpiH8vBumuXlm\\n1Vjw783C1m1Hhdr6ViKRSCQSNVG7aGDEiBFjqJ6q9zGp79NWlSZ8mvq5N998EygKxa1lfaoap/Tz\\nUa3F84kqLz7N263oqJMwq1I2VZ6J8JrMQ/ka49e+j95d33Ntdi0Dwdi4aBa3jvcxHsdrkQvtQY+m\\n6r6OGjUKgFdffbXfzw0WxpbDEVWqPd5HEW1Ur90xol3IoUrX4/h3v9dqXrWTdlF1rRHxc3GMiBip\\nmGSSSYDqQgqvcaKJJgLKPNMtu2hljFTl/OSgai7zfvt3t5B2e2/HUMxzTzHFFAD861//AqqLkzqW\\n3xzQtxOJRCKRaBF1t5juGTly5Bgln7EMOv67UFn4tFWB+lSeccYZgfLUfeWVVwCYd955AXjppZcA\\neOKJJwCYc845AbjrrruAEtP1qa7qUwmLqBZ9/9FHH93e09OzZHMmPuaijiKqKuX0vepMbuRC6NUt\\nvPDCADz44IMAvPHGGwDMMMMMAPz9738HCvf+u1wYz65CHzVae41BVfy5WWll5GKmmWYC4MUXXwTg\\n85//PACPPfYYUOLQW2+9NQCnnnoqANNMMw1Q7qd2IHe+j7H9FryQWlz09XDqepZ6/46pySabDCh2\\n8elPfxoo3HpNn/3sZwH429/+BhSv7lOf+hQADz30EFDswn+PSxBEf1GL//w3YLtoNX8R1fy0007b\\ncO6LLbYYAM888wxQPJYNNtgAgIsuuggo845j4OWXXwYKp3IY819V6MYYiTmYWGk7xxxzAPDUU08B\\nMHr0aKDcf69p1113BeDEE08Eij3Ilffdz8utnLViF/95bYmL9HASiUQi0RW05eH0eQ8UNRbjxSoG\\n/66KV2XNN998ADz33HMALL/88kB5yi6xxBJAqcBQ7enR6PHoCV1xxRVAqcgwLunTWmUccz59FowN\\n2MOJykXIga8xF6MXJxezzz47UFS73pyf1wO67777APjHP/4BFHV2xx13AGNW6jVTtO2qt77x6WYq\\nTrvwvsbKOxXqBRdc0PC5jTbaCCgeysMPPwwUu1G5qmxnnXVWAO69915gTO/Pe6AX2Od6Gs6rHQ8n\\noqrqyPsRX/33xRdfHCje3QILLAAUG59nnnkaPj/LLLP0e83a+HXXXddwbbECVOVblUscTLvwfjhe\\nhXaxxhprAHDllVcCZT5Yc801gcLJk08+CcDSSy8NwD//+U8ArrrqKgCmn356oIyR559/vuH3vAdy\\nETEYYyTmqbwf0cP13LbYYgsAfvOb3wBlbt1qq60afveee+4BigekrZ911lkAzD333EAZS/fffz9Q\\nOI9Ro3j+dcdIejiJRCKR6ApqV6n19PSMoUhjlZHwvTF0VbyehpUUCy64IACf+cxngPK0nm222QC4\\n/vrrAVhllVWA4rmoVHyvInnggQcafj+uw+lUXX1/x2pWkaXSNB6twvRajNEbn5YDlYaq7Etf+hJQ\\nlKexWa9dD0l19+9//xsoXHSq6qQVxN/wHFS03u9YNaRdqGD1iB9//PGG13XXXReA3/72twDsueee\\nAJx++ulAue/mhvwdPaJOrz3pew3Ro4m8+zk9Uz1X845TTjklAMsttxxQ7ML7rfd34403ArDSSis1\\nXKNennYhh+Y9VM6O0ao822CgyotyjKju5cJzW3TRRYGi2r0mPRWvTbs488wzAdhuu+0AOP/884FS\\n7eg9kDPV/GDYRRXibzhGfHX866F4v5wz11prLaDMsTFn53xx2mmnAfCd73wHgF/96lcNv6NdaY/O\\nH5GLdit708NJJBKJRFcwoOadcTV11XoKVZtVR8alzU/4tI7qzTj0HnvsAZTcjmpPhaqyjXFt451+\\nLq7b8DxV2lX1+3VQtcLcc1GR6uWp0jx3FafXqCpXzX/7298GSnWKXL7wwgtAicFatfSnP/2p4Xzk\\n0N+JimXYsGFtqZf+1J9cyK8K1oo6VZSqbeeddwbK/Vep6tlqJ17DEUccARQP2Modla5c6+moArU7\\nOVDZxvzWiBEjOtawMtqFr+aj9PLMR+qpeK7ayzLLLAPAdNNNB5Tczn777QcUzsx/Oub0jJdc8uMU\\nZezK4BiJub2+a+Ta4WJsdhGr0Kaeemqg2Il2YV5C719vbrXVVmv4vK8/+clPgHLN5inMj8r50Ucf\\n3XB8Iy4eJ67367uWpdNjRA/GOUhb1tbl4utf/zpQcrrmXlZddVWgRDKs9D3yyCMBuPrqq4Hi8Zrn\\n8nfNe66wwgpAicDIgfZnfs3zGTlyZGWHhv6QHk4ikUgkuoJaVWrDhw/vGTly5BirX0VsH68682mp\\n56HHM//88wNFgXjcz33uc0BRqj71fXobs3300Ucbfu+WW24Bisr3qe55ejyv2e8NZB1Osw4CsZeR\\n6srKKtciyZHK1uqir3zlKwBce+21QFFhd999N1Di1H/+85+B4hEZm1UhqQpVIyqWfqrTfB1wBU4V\\nF8bO/fw3vvENAJ5++mmgeBp6eXow3//+9wE46KCDgKLir7nmGqCo/N/97ncAbLvttgCsv/76QLE/\\nq5XkQPuKSq2T63Cit6ftmaPRw1Fh+l5Vr8f67LPPArDeeusBcNtttwHFjhwT2tHNN98MFK/SNUt6\\nUtqN1+7f+4yJXi7aWYdTxy7M2fi5HXbYASjjXrvQ49WmDzjgAAB+8IMfALDUUksBpZrtW9/6FlDs\\nYpNNNgFgyy23BMp8pB3p/entVXVs7wQXVV1P9FD87e9973tA8Wj1kJ0r//KXvwDF6zcSokdrdaK5\\nG+3AdTpWABpl+uMf/wiUfJb2ETtV5DqcRCKRSAxJtOXhxKe0T+HY18mnolUlxiVVuK4gV8Wp6lQY\\nxmBXX311YMzqImP0Po1VyFZWGLN1VX6zzaree++9jq3DUbHE+npj73p1Koq55poLKMrF6jRzNXpn\\nX/ziF4HC8a233gqU9Rnms7wnXrvfl5uqzar8WzvqrQpxXZbwGsxjuf5GVRXXiDzyyCNAWWsS1ypZ\\nfWSeQy60L9cqGfc2vxFVXF+0w8XY1uGYt1Ctq2i9Jivz9OKtOtJD1n7M1Xg/9Yy0N9dfyNHZZ58N\\nFE71oD2OMf3YfaHvWP/www8HZBdx3ohd4v138wRe09prr93w7+YP9AK0C71FuTNqcO655wKw4oor\\nAvDLX/4SKJ6NXqHeg3bh7/SXuxqsMRLXIHk/9UC+/OUvA+W+ez/9vlw4n3iNerhy4Rg544wzgJIT\\n8rhWucmFax776yJdh4v0cBKJRCLRFbRVpRY7lerZCCsbfLoad95www2BojSNqdv/x6epT2vjyRde\\neCEAK6+8MjDmqmy9BZ++t99+O1A8Iv/eaq+kgSDmtVRHqnDVtDkclYSei9dsnsE8l96aFVdf+9rX\\ngKKMVX8zzzwzUJS0MXrfV/W9E3U6YFehqpeeHoTemN6X9/Woo44CYLfddgOKJ2x8+pvf/CYA3/3u\\nd4Gi2n/9618DRc3rIetBqQo322wzoFT06AH1x0G8ljroj8PY/Vlv25ybeYpll10WKBWa5iv0UK06\\n1PPRA3Z9hXahvQntwnuiXRgl8HwcewPdDXdsiB6gv6XK1vvS8zUfudNOOwHFkzFHu/vuuwNw6KGH\\nAnDppZcCcPzxxwNlftBjcb6yalHOzIdcfPHFQOftoi+q+gg6Ps29GMGQiwMPPBAo16zna47GsbHX\\nXnsBxWszf2XkJHYO2HzzzYGS7zTPdeyxxwLV+yn1PedWkB5OIpFIJLqCAXWLjp1thU9dX10rouej\\nslC1mdvx3+0GrWIV9kYSxuJdg2JHVH83rratWmPQiRxOlRKUo7jaXZXmKvrYQ00OrDKzOs0Yvlzo\\ntV122WVA8d4uv/zyhmuWa9Vk3Duorx10Kj4d/xb7yXmfvDa9PNW+Mfff//73DedoRZZrCszxeRwr\\nb1S2XruetjlAX+MuimIgVWp93je8ClW29091H9W35+61uB5LjuxQoT0Zm9fuVOteo9EC778ekmOh\\nan2W/98Nu9CzdV2OFXdes7lfbTzmkJ1PtAur3/bZZx+grPPSk3LsmadQ/XfaLsbGRaxidM4yr22+\\n6gtf+AIw5jo+Ix8eR8/V/KWdBrQTvTq7zzvPmAd3bGh/kYvspZZIJBKJIY1aOZxhw4YxbNiw3vhd\\n3Cs8xiF9yuqJGKtXvbu2IK4Jsbok7nehglGZqPZVfeYzrNTw943d+lSOO0hW7TtfB1W7BqraVFle\\nq/FiVZuxVa9Rta6Cdb1N7HhrhZ7dY08++WSgKBvXJI3L3mnCSplYDWYVo+snYq89Falx7XXWWQeA\\nH//4xw2/5wpz497GsfWE/vrXvwKlIktU9Q8bSD4rKsCqzsh6eeYvHSOqbHN42pEK1RyN1UvG8LUz\\n15S4jsuuwnrQ5oiq7KK/KrWBoopLrymOQ+3Cyr24s6fjXY7sJu5aFDkzD2H+y3Vf2tdNN90EFG9P\\nDIZdVMHjaesxGuNcqX04b+gFauN6uNqFa9fMZ59wwglA6TIvF4sssghQ1jKa+xHem5jLqctFejiJ\\nRCKR6ApqeTh2io77a0fV5t+NjfrUVbWpUP2ecUOVr9Vt5jtU6x5XdWf1kkpHVaBisuJLD6eq6qQT\\naiWqId97TZ6b1UJ6ZeZiVCy+eq12wtY7MIar0rAPlPX13gO9yLjuI9bRd6MTrlxY428llhzohVm1\\n6LoIY/GqL3M5rrLXDjyO6s1cnty5Gj/uCRQ78Eb11glOqjqoex+0i9gHzjGjDev1eT8dS3q6cuq/\\nW3VkDsf1HUYHvHZfYz4zYjDsw98yX2D1otdm9WrsEm40wEo9q9L05pwvvNaf/vSnQFl/I6eqeSM1\\n2kXM+VblctpB9Hzj3z1nIxqeox6JHqr5ab07PSArL/Vw9HiN+hgBOe6444CS/zZS4nnF3o/meAbK\\nQXo4iUQikegKaudw+nZKjZ6NSsGnok/JuBra+KCqTqVqTFVFYzzTp6u/qwowbqm61wtQGXk+xslV\\nNqq52K22E6hSMJEbFYhq3pzOnXfeCZSqJD0ir02larxZBWQloLF7lavKuIqLqh0IB4KqvV98r0fj\\nWgJj9a4lcR3OKaecApRrtupID9bOuao61+XYg02PyOpHc3Zx75mYQxyMfEXsyiHifidW6qlI9YDt\\nHOAKcr1685jmNcx3+vmFFloIKL34vP/aj1yohK3UivnNwYgCRL49J/OR3kcr67bffnug3G89HCuw\\nvDb3vTnvvPOAMj9Y3aadeO16Mr43hyyXnRwjVb3U4to180quq/G+68XvvffeQFmj5H0yx2NVmz3V\\nfvaznwGlms3qNrtzOEbiTrB6k0ZeBjpG0sNJJBKJRFfQ1jqcKtUT96pXfakYjDOq1vU0jFfbgUBP\\nyHp8V47rAekxnXPOOUDxElyfobJRpanmzafEvUD8XDvdovu8b+BEjlSOVp/56gpy1bte3KabbgoU\\nL00lojcXPRx/56STTgKKKpNz9y6v6hIdY/edWGNQ5dkYf/Y3VfdWF6nSvZ92BrDqzO7QsTef3aPt\\n/qsqlCvj3KpDf1+7ELEvVd01BnIxfPjwSjWvzWnLXrNjxi4IqnXzGa7LMTpgLk8vzWiCHoowZq9d\\nGE1wF0ztIkYR+uNioOuzquxCby2uDbO3nhwZ2TA/pV3oBWoX5n693+6bY1dp74FRBHN+sWO2iF0Y\\n2rWLVrgwj2VVmZ7HxhtvDBS7sEuHHN11111Aqegz4mFe1DVIduB2jOgJ6Qmb23GMmF/z/Jw72+Ui\\nPZxEIpFIdAVtrcNptdrLld2uoladWTuuqlLRGpP1qaqyiPFOn+YqGlWAaxFUtO6jopdh1VKsrutk\\nzD5WJcX4sNdovzerzOxtJRdW2ujluYZEJaxCdm2Bq7GN/RqblWur1uKOfdFb7eQag7jHh16ZalzP\\nxnN2PxPvmyrLXJ6VWK63kRvX57jeQiWrl2gc21yjKk070H5i/q1dLvrb9yTaRdxzxb3pzb3Y00qv\\nX+70BvSU/bycahdWcBrTN9en968XYPVT9LQ7mbsRcYz43mpW748VWjfccANQPNhYVRb3CtKjcbxb\\n3aiXt++++wJl7B1yyCFAuXbnB7n0HnXKLvpD7HHo+DdapDfn3j8//OEPgZKrdYx5P50H7Ctn1Ecv\\n8JhjjgHg8MMPB8oaSdfjeDw59vyqPJtch5NIJBKJIYm21uGIqtXUcf8TKxyMHxuLVdXFLtFWRpjr\\n8akfd/y02klV5+898MADwJj19NETq+oOUAdVvYW8lrgOxhi7n3NHRmOu1te7HsPvWWGjIlXxqGhc\\ni+C1Gvc2ByAGq1N23y7iInam9v6YdzCvoCest2YPtQsuuAAo+SsrrYxH68Go9tzN0JXmXqsethVg\\nqsS490unOiP/J9cxxt+g2GTseO56COG1GdO3ak3vX/vSu9NutCc5dNdLr1XFa57C48SV7fG8B6Lq\\nq8ZItAu9ce1BToxcmLe66KKLgFLBadfoXXbZBSjj36jBnnvuCZTu0Xr3eov2E7PreLN9s9pFfxW+\\ncYzouToHOkZcq6j37/21Ai+Okf/7v/8DynxxxRVXAMVb/NGPfgSUvJVzqlEHq+C0i7F1zq6D9HAS\\niUQi0RXU3g8HxozjxX1PfK9HY1WZytZYqU9vKytU//7dp7816D5tVXPGfFUyVnComHx6e57G6v2e\\nGEg8tqo6La7gj2t+jBubp7j77ruBomg9jorVa7HSywotlYvHt3LH45s3855ETjqp6uP/xxyOv61H\\na1dn33tfXPXsTo/ai5VVKmAVsRV/qjLtRY/J83G/HdWjnnMnV5KLqvUV8bfizp/mH1ThevGqcD0V\\n12vJqdek0tUutAPtyLGh96CdOdbi+ptO7odTNUa8Br1xczJGNPy8nqyVfOabXKfje+cd81ff+973\\ngJLzMTck3PXSqlrnq2Z7R9WFlX59jxn59/7a7898pB6OY0Qvz64bnrNrlMz5aU+OJcec88wll1zS\\ncG1GCcyPmzuO81m7XKSHk0gkEomuoHaV2ogRI8ZQQz51fZqqNMzBqET9vPkFPRYrJVTv1s2734Ur\\ny61Ndy2J8WirmFR1Kqa4e2FUmQNVb2OLa6tcjQe7LsZrVoX57+YZVPPGl61SMRavZ6NHJCceXw7t\\nH2ZVm78bVVsnUbW2QPuI6y6MmceOFO5q6OpolaprCIzZmwNUoaoO/bsqUftzz6DIhajKu9RF33xW\\nPIYeh+dgdZF2ECso5UqFq/fmuhxj9v6eXlu0Cz0gK7RiH7k4ZgajA4XwmHEXVPvCeZ+0XfOZO++8\\nMwB/+MMfgJLX1C70gBwj5jfk2jUpRlRiX7rYkaKqa0gnIyIxj+Uc5TVYuenf9e7NU5qP1IPZcccd\\ngTJGzA27Hs9qMz0YPSHtyu4cfq7ZtdflIj2cRCKRSHQFbXUaULGqilQKKhIVpepKz8dVrXo4xhHd\\nB8W4sipddafH5FPfPR78XdVf3N1QbyFWhMQ8hvjwww9rdxqoUiyem9esRxN34lPZ6KXpFbqq3n83\\nz+HaAr0+lY7cec2qPZWziiVy0d++J+2sKB8+fHil2tFePGfVduxAIDfG7uVuv/32A0plletwXFNg\\n7s61BSpV1Zv5C5Vs3NUyVqv1RTtcjBgxorJq0ftpZaV5Ta/d++97x0DM3Tmm9GTk1DyEduHY0X6M\\nGjTrPNHfDo+d2vFTOEbivkd6vL6XC++TdmEvPb00OwboFfi9ww47DChcOV+Yy5GD2EndsdMpuxjb\\nGNEuHCN6HML5Qg/ZaICf33///YEy/q1Gs0O29uL6HM/DdV6OEcde3LPKMTVQLtLDSSQSiURX0FaV\\nWpWHYKzUdTaxQsc8hZUV1sv79FTt+Tnh8VQmPoVVPMaxrWE35iuimo87lA4EVcfwN628i+sdjN2v\\nueaaQMk32CXBSjy5skOBawlUvqp4j2udflwxHM9LDEaVWkTkwvukAnWNietrrFK0v5P7mcTOt+Yx\\n7CJtfymP72p7PaCoYCM3VetE6qK/dTjCc1Chep9Uqno4rrbXDqw+07b1dPUe7aWnMpZDVbqVnHIT\\n1/1Ebqp2eOwktAu9Lz0bVbywe7j5C/MSv/jFL4BSnahXZw8+111ZqSlX2oX253zm/a5an9Xpys6+\\nkH/vixxou1Yrur7G++v6GdfV+O+nnnoqUCo43YPMMeJxzfUYlfJexN5poj/PPTsNJBKJRGLIoVYO\\nZ/jw4T2xsqQvVGs+nY0bmrOxOkQPxteYl1AJG4/2vapQlefqej0lP6fH5LmqWHwqVymVdnI4Y/l3\\nYMyd83xvJZWxdz0W49aqOL25WK2kUlGRWIUiB8arY5eFZpVZ7eZw6nARO2cvtthiQPHuYg8r981R\\n4RrP9hpVf37PHlnCz5nDqbKDTuWzRowYUbkyO1YlqTTlInbCdgzEseIY0C5Uxu6KqV24/4ncyUFU\\nrtEu+tuRstM5nJjvdIzIjWNAu/Ac/bz73siFY8eczr333guUPJZegNfm52Ieq1llVifHSLQLvTDn\\nUF/lwjnU++u52QvNiIc5Pz1cOw7ozekJxV5pdrLo00G/4fwGOkbSw0kkEolEV1C7l1pPT88YT2Wf\\nhno4sftu3NvDp7OfV2n49DZnozIxXqla92kdczp9zxNKXDT2ePM4cc1DXfTlogqeQ+xQbDVJhB2Q\\nXUfjugo5VoH4qnK1466/U6VYm+262C764yK+jxVQ3n/PXXXmSnJ3RbWnmmtIXH+lWpMLqyJjNVr0\\ncKvWEnSKi48++qhyR0ffqzy1fb2/aBd+3kquO+64Ayi5nciBY0a7cCz5O1XViRFV3c/ropUx4jnF\\nfaq0CyMbyy+/PFD2iLIq1a4LRlK833Ki5yQ3cu9rq3mqTo6RKvvwfuqVRy70YM1fmgO2C7idAbQX\\nufXajQ5oD44R58Q63n87SA8nkUgkEl1BWzmcqqoNn8aqIt/HqjBVvDFXVwDrCekhGcu1h5YKxt/T\\n8zH3UxWLjedZpfY/+OCDjuVw+nwOGHNVtRwZo/UaXK9jrN46ebmxz5jHU6HImUq5qit0lbrvey3t\\nxqdbVT/eV9WX72P1mte20047AWVtkXZg3ziPE1Wa5xE7ITdT9f2outrrLapW6Edl6/0S2oVenPZg\\nLke70IORM1ffezy509vzc9pJvOZW7GKgOZxm9mH+IvaZi3bh97/61a8CZT2N84rdpeM6q9gnLkZi\\nqlR8p+yizhjxmvV4tHn/Hsf5XnvtBZT5wc8bFfDa9Zzi71ft/dMKMoeTSCQSiSGHtjoNNKvRj0/P\\n2J3Zf1e1+RRXcaj6VfF+3kqcqOLia1U/KOHv9XPtHfNwqn47duH1c9bBe26xSiSiao+fGKNvhrGo\\n/Y4p2WYqP94v1xyZz4jqLNpfvJ/azdhWirdynn0+V9vDqUL8zchBtBfX5XgtsUtC5C4q1ZjPjCq/\\n6t7EHGCf8x9ndmFFp5EM73vVWKjiaizjv6Xz7PO5jlXsVdmFiH0g7URiHtv7pUcbPx+5cE6OkZAq\\nT7fZnJ8eTiKRSCSGFNrycGJeIqomn4Lx734+7g0T8xsqEOOVPrVj7N/jxpXBVZ0Eqq7Vp/3bb7/d\\ndi+1iGa8RhVXtbdQlSLpb2/xvu+rfq8ZJwNZYxCVfYyJx9+Kn497g0Q78d/1cGNupqqyJiL+ztgU\\ndztc9M3hVFUFxvfx8167YyHmN7xWx0Ss8IpcNOsw0Yq9fvjhhwOyi2bVgfHc4hiJ1bCRuyq7aNVj\\nqcrxdnKMxPEdKyebeTqRC+0icqNdxB5orc6Jcf+sZt5ZejiJRCKRGFKoXaU23njjVa7ErVK4VWqq\\nWU3N+gkAACAASURBVI1//H7c16ZZxUf0GqrUf59qto5XqbWKZhUxEVUx/IFiIBU4dVF1jVXeW7Nr\\nbPd7VQrbf6vLRX+dBlr4Xr/nUvf+Rm+wrrofm721q+o7hbpjJH6vipsqVNnFQKoXq45ddc5Vn3dO\\na8VL7/v3VsdIVeVef+eXHk4ikUgkhhzq5nBeBJ4cvNMZ55i1p6dn2lY++AnnomUeILnoi+SiILko\\nSC4+Rq0HTiKRSCQS7SJDaolEIpHoCvKBk0gkEomuIB84iUQikegK8oGTSCQSia4gHziJRCKR6Ary\\ngZNIJBKJriAfOIlEIpHoCvKBk0gkEomuIB84iUQikegKRjb/SMGwYcM+6W0JXqrR2uYTzUXdxoSD\\neS7jGslFwWByEZtqDvUuKGkXBa1yUeuB8z+AT2qvo0RinGDEiBGVHY1jx+PYwbiqs7Fott9R7A5f\\n9f1W90/6b3kQDmVkSC2RSCQSXUF6OInEJwCt7g3TbXz00UeVe7LE3Stb9STi9+PxJ554YgDefPPN\\nfo+jZ/X+++83/L3Z7r1Djdv/RqSHk0gkEomuYEh5OFFhVO3wF2O68e+JxCcVre5WWZUH6bZKH9vv\\n6WFUeRb+XY8kIu7kO9tsswHwz3/+E4BRo0YBxdPps7Nvv8f1XPW4Ep1HejiJRCKR6Aq66uGoWCaa\\naCKgKByVxXjjjffxSY38+LT67gEO8N577wEw6aSTAkWJvP766w2f8/tvv/12w/H/m9DMe2tW8fPf\\niKo8RLPYfqtcDNU8R39wjHjt2vJkk00GlGtQvfu5mL+YfPLJAfj3v//d8Dk5evfddxuONxiIttzq\\n/XMcTzDBBA3vJ5xwQqBcy2qrrQbAY489BsBCCy0EwCuvvALA/fffD8AMM8wAwAcffADAM888A8A7\\n77zT8Pcqb/C/wX5a5XhcXUt6OIlEIpHoCgbVw4keSqwqMcYq5p57bqB4OrPMMgsA00wzDVAUzlNP\\nPQXA448/DsC//vUvAJ5//vmG41Upq6GsUGJcevzxxwfg85//PAB33XUXUK5Bb89r9+//TfmsqvUW\\n0VPx/ac+9SkAXn755X6P99prr/V73KF4371/0YN59dVXgeLpOBa8timmmAKAzTffHIB//OMfQOFI\\nr//uu+8GYOqppwbgpZdeAsYcG7FibDDgfYjzQrNcTYx8rLTSSgAstdRSANx4440AnHnmmUCZD/z8\\nn//8ZwDmmmsuAI4//nigcC4399xzD1DugV6i0BMaSqhac/SFL3wBKNwIvcN4bd1CejiJRCKR6AoG\\nxcOJ6kmFoiozFzP99NMDJc68zDLLAOUpPNVUUwEw3XTTAfDpT38agIsuuqjh91SJ/p7qMFalqAbG\\npVKpqsSLeSk5+OxnPwsUpWt8ep555gHgd7/7XcPx5Cp6PFVKaFyiKq487bQfdxdSpatUt956awBu\\nvvlmoOQfJplkEgD+/ve/A0Upa296QjFHYMx+XMSz/c233noLKJ6s98e8xejRowF46KGHgDJWDjjg\\nAKAoWO3HVyu1fL/44osDcM011zT8vnDMGHV44403BnyN/k5V3iDmavQs9Dy+9KUvAeV+r7vuukC5\\n73osW221FVDupx6w1zLrrLMCcN555wGw2WabASX3c8sttwDw8MMPN5yfdqUdeo+cv7qJyJ124H1y\\nvpBD5zjHkhz89a9/bTjuTDPNBBR7GewcT3o4iUQikegKhtV5grXagE6PRrXm01iVvdxyywFFQfh0\\nNk+x5JJLAuXpuvDCCwNwww03NPzOJZdc0vD+97//PVCUk8rWp32sRukHt/f09CzZyjW224xPNSdU\\nbRdeeCFQPBSVrde+wgorALDIIosAcOyxxwKl8uYPf/gDUNSgcWw9Jq/Z12b3fTAaE0bVJBfawVpr\\nrQWUWLxqzb/r3a288soALLjgggCcdtppADz55Met8IxPn3POOcCY9197VNWJKk4Ggws9VtWyalyv\\nfs011wSKB+u16uUZHTC3M//88wNw+umnNxzHnM+ll14KFM/XCi2Pe8UVVwDFPqpUfCe4iDmcWJU6\\nxxxzAPDcc88BsMQSSwDl/u+1115A8YSswPOaPXfnHzm69957vQYAjjrqKABuuukmoHgwjp04VvrO\\nGz09PV1p3hlzunpzp5xyClDGzmc+8xmg5Lt/+MMfAiUvvsEGGwCw6qqrAvDII48A8LOf/Qwoc3aM\\n/rSa02uVi/RwEolEItEVdNTDibkb49DG0lUyKgk9nZlnnhkoMVtjpsYfH3zwQaBUk6h8b731VqBU\\n3liRYzza+LjKRuXjU7ufax80D0f15mpoYcXdDjvs0PD3+eabDyiKVtV15ZVXArDlllsCpWptww03\\nBIoKvO+++4Ci/uK6jWYYTPWmattoo40AePHFF4Hinanqf/7znwOw0047AcW7U8X95Cc/AeD//u//\\nAHjiiScA+NznPtfwO1G9aV9jsYMGdJKLmDvRu9ej0XO5+OKLgaJA9d6//OUvA8WzNa/5gx/8AIDv\\nfve7QPFg9t57b6B4A/6eY/C6664DytgwP1LFTV0u+uZwYpWq72NuxHnC8a+Kd+x4v/XK9NL+9re/\\nAWXc+6r3t8466wAlmiAnRkqcV1zPoz15PrE322COETnSG3cOtRrReWH55ZcHCodGTJxXnCM33XRT\\noMyFfk97c86Maxpjv7kqpIeTSCQSiSGFjlap6dGoKGMPI2Ec0Uorlac5F+PZqnnr7VUkUcmq6uad\\nd16gVGIYvzZe7u90sxpJZeKqZxWKCkZlaz7hm9/8JgDHHXccUDhV2V5//fVAuXbXDujRqOL0HjyO\\ninW99dYD4IILLujYNbYK14zowZx//vkN/77YYosB8Mtf/rLhVQ/nO9/5DlAqblSkjz76KAC33347\\nUKqNDj74YKBcu/kNlbVVkddee20nLq8lqJZVnJ6TeQTPdZVVVmn498MPPxyAb33rWwDsvPPOQLEP\\n8xfmOc03nHDCCQD86le/ajgPczpWselN3HHHHUBnx0jslqGX5Tj3XB3fSy+9NFAiF1aVmdPxWmaf\\nfXagjHfnCz0hufF3zXM6hhZYYAGgeAOOUeeNfry72tdeF1bYeU6ei56H+W1t3rnvxz/+MVCuYfvt\\ntwfgG9/4RsP3nGNfeOEFoHhKcnnEEUcA5VrNgzr/DBTp4SQSiUSiK+hoDkf1pqJQgara9EBUICoM\\nY7TGj32qWyOusjFWG5WI8WqrlFyPEb2JcVGlFtciGac2H6GyMN9gbN76epWLlTk77rgjUJSsytj8\\n1lVXXQWUnI+/r3pU3Y+FA2Bwq9RU497HjTfeGCjVSc8++yxQPGS5U62r7r/2ta8BxX6M7Vuxc/bZ\\nZwPFTrxm49Jy0SxO3Uku/E29bteSaLO77babxwGKF+AYULVHBWs14/rrrw/Aj370IwDmnHNOoKzj\\nMT9hbi+OCZX0YFSpxfyV80XM7Tp/eE3mYrbddlugjBU5MXdrvsNr9PMPPPAAUO6z9iA3f/zjHxu+\\nF9dCOb/07Vgx2FVqscuGUR7zl3ZZcU50vF9++eVAqWYzD3rkkUcCJe9lrufAAw8ExhwD2kOr6/cy\\nh5NIJBKJIYWO5nDiPhN6LMaJp5xyyo9/9D+KRuWiijNeaCxfD8eYvWsIXKNiVZPxSKvZ/F2huh8X\\nq+zjLoSeg6pLRWpOxTUDVimp4sxHGGNVgZoPMy6uclW1qWBj14VxgdjLTpVv1ZBrB1yHo3o/9NBD\\nAfjqV78KwMknnwzANtts03AcqxxVg/6OKi+uzxgXnbU9JxWl98tcn/mt733ve0DpqrH66qsDhavD\\nDjsMKNwcdNBBQIntm8szJ6BSNeenIq6qSuvUSvOqvW76/qbwHPVY9XD0iM1zOpbM3ay44opAyQla\\neWVln/ZgzthqNq/dXJEejV6enpCeVze7z3vtVpXddtttwJgVnHpp2oljxrGgJ2zUQK/PDibmCPWA\\n49zZ6fkiPZxEIpFIdAUd9XBip2LVjZ1LVVeLLrooUJSDcUg9l1jF4loDPSef5v5dhaKCVak021Gw\\nmzAnE3tVqVhdK2BeQy/QlcJnnXUWAMcccwwAv/3tb4ESv1522WWBMSts5HIo7A3k/dOzNeZu5Yy9\\nrrQXFavK1y4McmaHAbmJa4/iGiSVs9yPCy78TW3U9Q/asp6HObq1114bKHu6GC3Qq/vLX/4CwE9/\\n+lOg5PCM8evh6hX4PvbQUtl2uk9YX47jOJSD6GWZ2/W73i8jJOaCtW3tQW/OnKCekXanPWhvVqtp\\nF7GjgGNGe+1mzz3nSs/duUwPxqpCPRPnC+3C/LkdCfR0rOR0nnE+8r7H/ZQ6jfRwEolEItEVDEq3\\naJWHno6VVOZihE9h8xU+zVW0Kho7EpiXMO/h9/RwhDHYodQhWVXkuVmppyLZc889gRKrN94sRyoc\\nV5TbB8r1GnoLKhi/5yr+obAXjApWVeW5mbMzR6cqM46tmnM9hjkcvYOvf/3rQFm/Yfxaj2nGGWcE\\nSiWYGJddomPHY/OQX/ziF4FSGWUuxnyEY2uTTTYBSkxfNf+Vr3wFgF122QUonSd+85vfAKVr9J/+\\n9KeG81Hlx114B4oRI0aMkduNff1U1bE7s3kLe+lp49r8GWecARQ7MZ+h9+bv6i3oGelBee1GCWI3\\n+zhvjIt5xHPx2owKnXvuuUBZj+eYip6NuT67isuha5LMFVo1e+eddw7WpQDp4SQSiUSiSxiUHI7q\\nzaexnopxaqGKtxLDeLVPc1fHqmT1Cty/wp3/VGsx9qqiHgo7P8ZzUY2rYFRhxk5VXyqQmNux0kaF\\nY4We127ceyjuw26eyXPzvlqhd8ghhwAl36DytRrJ72kf9gNT9duhQG5djyWGAhfaoivKzWc4Jrxm\\nq5H8nF3DzXP5d8eOeSy9PNdlmBvSy4s5JNFpe/noo4+a7rTruNXb1x707lxf57zyi1/8Aij5TVW9\\neUzXban6zVPZjd7cnzkdx5Zr2Twfx1rMPXXDfmIFn70Tzdl5DZ67c6ydKOK6Gr1Gqxldy+Z8Mdie\\njUgPJ5FIJBJdwaDkcFTxxgtVtKorY/KuHLdqTSXi6ns9H6tPrNAx3mgew+ol17YY5xbjch1O3PvD\\n9+ajVGX77LMPUCr2VLKqLGOxvqrCXJ1/2WWXNXzfuPRQUPPCa49719v7TAXr+irzG8bwvX+u17LL\\nuOrdfIU5G5Wv6zWGQrWi90NbdozojcVOx3KhnajqVbB6utrB008/DRQ7EGussQYAxx9/PFC8gHhe\\nnR4jPT09lV5T7KYg9PKtzNMLM9cjZ37fHK5c6aloHx7fCk87q1vRJ3dGSrwXcUfYvtW33RpXjn97\\n6RkZcT2eNu6YcO5z/vCa7DDgWJFjx4xz7WAjPZxEIpFIdAWDuh+OMVmfulaHqDzMM6jGrGIzHml+\\nwqey8UpzQ65FcTW+T2nVX6zQ8nUsK8wHfcfPuEeLqt6Yut6aFTW+2mnAa7XnmiuIt9tuO6DsfxHr\\n90Wr97sbe33E93HtkEpWO5Aj77tegB6sSnj33XcH4Oqrr244flwf1qqaHwwuvD+OEW3aV/NX5qnk\\nxH2SvK/f//73gZKPULk6tqxGcodY7c7v+yqXjo0qbtrZD6cKcmCFnRV6qno7mzv+nR9cY2TFnVx5\\nPD0j8xZes/OM+QpfHWNWvfl7wnmn7zzSrR0/495B3p/oHbqOz7nTNWyuOfLv3m979jmW4hism8vL\\nXmqJRCKRGFLoaA7Hp6IKxVioCkOPQzWmsnB/bVVc7D/mjnwqXZ/esReSSte/x1xBp1dRtwMVipzE\\nVc7mLaxacx8K1whYiWX1kvmN2GcqVqkNhbVIIqomOfAcVWF6wuZ47EShfbmb5a677grAyiuvDBQ7\\niN5C/P1xUcGnUvXVc9Nm7XFlbN7qQyu2PFcVq9/X09Fe7JwtjC4YBYgrybWbuONjJxF51rvzPtit\\nWc/FcW8O11yvXr0cyJU5HPNYdg2XU7kyb2Gu2M7akVPnFe1yXKzri5w5b3gOvrc60fse1/eZu7NS\\nOO6uGrvHD9aYSA8nkUgkEl3BoKzD8dVqEdW2K8mNxarKzVu4rsYOAnoyKhXXFBivFLHTgE9vlVOn\\nV0+3g6imVbSem4rlrrvuAsqOjPZAUsHYR85qlS222AIonZajhzOUPBsRuYjemDBWby7mgAMOAErv\\nNPf4cKW5XFnBIxdy7e+Nyw4UUS2rRPV8rS7U6xPmJfbff3+gdPm1OmmPPfYAyh5B3/72t4Hi/Zm/\\nkAvPI67u7/QY6a+XWoxgRA8mrr+y4koVbqWe6/XsPKHaN7/p2HK+iWpee1L1m++I+yX1lz/p9lzi\\nb8f8s+dqPzk7qlsFaV5Kjl3jtu+++zZ8zqjTYCM9nEQikUh0BYOyDsfYeYwHG2t15bfKQ4VrhZVK\\nR8/FdTw+hf27VUlWm5gDMj4du9COS0RFpNry3Mw3yYW9s9zvxhXCJ510ElC8R9ciGY92PxQxlPrJ\\niar1GDHfpP1YSaNnu+mmmwJl3xxj9K6zcD8UY/1xLdS45CLmOYVK1Yot/10bN49lTseuDK5A117M\\nY1nVaMeBX/3qV0DJUziWrE4bTETP1fvh/XU8+2q+0gosx4j95rR9e63FfJd95GIORo7NZzhmzBXZ\\ntSHuehq90qGwtk1OnS/MW9lncocddgDKtelN6vn6vluejUgPJ5FIJBJdwaB4OHoWehxxL3kViv2g\\nnnjiCaD0kbI3lupeBbPRRhsBZYWwcW1Vmwol7l4Yu9SOC0RPI57LEkssAcAdd9wBlPUX5r1OPfVU\\noHTeNv5sp2RzPENp/5tWEXN/2oGdKVS8xuz1eKwuMo9lZZ/2ZH5ELoYC4lowPRlfHTt66eZkvO/a\\nshV8dsR2Jbndol1LYgcKKzyvvfZaYMyuD3HMdBJV3r1QpZvT9X6594sehxERcztW3tl9Y/nllwdK\\nFVr0cOyk7nFOPPHEhvOrqtgaCvNHhHkq1+WZfzIfZYcBezFqJ1Z66tl0u1IzPZxEIpFIdAWD0mlA\\npWCcUDVlfNrYqetwjM2r7tx32zUDKhPX8RirtW7fWKsKySoXPaoaOZxB7zQQ8wlR7cmRFTfu/Kiq\\nN65tzF4vQO9ODydWI9VFN1ZRRy7iuinh/ibu6WGFlvamd3fBBRcAZWX4UOSiKodjpaac2A9O2/Wa\\n7JhtjsZqxlj5qUdsXtTKLvfZURnHCqxmqMPF8OHDe8Ybb7wxqkT9TecH80yObzsOeK16Fno0vtf2\\n5dKKLPsSer+dJ8wFW+UoN3qTek6uCxRxdX+frvNd6zQQ144J5wnz5kZ9zFN5rl5rvObo4baL7DSQ\\nSCQSiSGFQVmHE3f086lsHygrY4wzG7M1Lq1K8+ms4nF1vVD1+Rr7hw2F6rQq2BdMzlRX5iP0WFT3\\ndgV2v4sf//jHQInF6hnJhWsXrrnmmkG8ioEhxs7jfup6de49P8000wCl0/aBBx4IlP1v9GTiLqmu\\nvlfZjkvEMaIXplfuuVuFZk7v7LPPBorH6+dct6X6v/LKK4EytuKOolaA+rnBzEv09PQ0dPeIat1x\\n77mYc7ObvJ/zPvp3r+2hhx4CynxhDz29P+3B/XX8HceS85BeghxFr89/H5fzSazkdKzYlUHuXG9j\\nPvMnP/kJUMaIXDrfONZcu2b3jsFCejiJRCKR6Ao6msPp8zmgKAMVgxUU7j/hHh+xp5KqPXY6Vd1Z\\nhaQqVKn4tI4KpcY1DnoOx2vUI/FajTubz3JHP/NZekSuMbAa6eijjwaKJ2RV20CVazfi03qk0TO1\\nw4Q7PRqP1kOxylG1ftxxxwGw1VZbASVHaL4i9g2ri8HgQjvwvlqJp+1q06py15zYbcMOAuZ67Kxs\\nF+BDDz0UKJV92oWecz/5iJaubyDdomOlZuycruo20qFa33jjjYEx8056OHGnX8eWeU6PZ+cKvUrn\\nh7jraVVX+b45qP/sZNq1HI5RAMfIueeeCxTbdj2ea9G8RqNDdihxnZZ7inVq36zM4SQSiURiSGFQ\\nPBwR9wSPuwwaW9WTWW211YCyQ6MKyBitisOneuxKLQYQax10DyfCa4jcWIll/sFYrfFnoRLudEeB\\nbqi3CHM03l89X9eO6NG4Hssea95vY/v/TVxYXRQ7TpjDiXmGX//610CxC9drWbmputdOYuWf3kDc\\nG2gwPRy9uNi1O+71YgWm4zmuNbESz3OXMz/vuhuPGzueRC7iNcdOJVWfGzZsWNc8nIi4fkq7cPdk\\nIyJ2oDAqIGfNukS3i/RwEolEIjGkMKgejohP5Rgj9e9xXYb/rtKNCikq2A4o2q55OM32eY+vQo7i\\nTp6dRjfVW+xRFavXfI3315i/lXliEDoeDzoXquuY31CR+u9xLKlQ3R3VXI3qvqpzersYzHyW1xa9\\nPj0kPY9oHzEHGD1cudFOPF7kJuazqvaSGjFiBB9++GFXx0gzT9Rrjp/z74PdJSE9nEQikUgMKXTF\\nw+nz/X7fx55nKgqVjvX0VbH5DirarudwWoUqLVbUDBbGRXy6hd8Byp4fp5xySjd+dpxyEb3+uEeL\\nFVzm/Ko85nGZz4rjvuoc4/iO126OJ3a4roqYRES1H9838yLivw/FMSKsXjT/PdhIDyeRSCQSQwpd\\n9XD+CzBkPZxuYyirt24juSio20tt5MiRvR5EVSSjz7HHeryY14x9wKr6wjXrBt3MA4s5xhEjRvDB\\nBx+kXfRBejiJRCKRGFKo20vtJeDJwTiRIYJZa3z2k8xFHR4gueiL5OI/6Onpeen9998fg4t218nF\\nKsa6VapVlVrNPKt43P8cJ+2ioGUuaoXUEolEIpFoFxlSSyQSiURXkA+cRCKRSHQF+cBJJBKJRFeQ\\nD5xEIpFIdAX5wEkkEolEV5APnEQikUh0BfnASSQSiURXkA+cRCKRSHQF+cBJJBKJRFdQq7XNJ70B\\nHfBST0/PtK188JPORTYmLEguCpKLgk5w4RbRndpQMW7x0OpW0q1uNV71uVa5qNtLbVBRd3/1QcAn\\ntddRIjFOMGzYsDG6PNftpVbVzTnue1N13FYnXRG7WXdqT6Fhw4aNsU+N5zTzzDMD8PbbbwPw8ssv\\n93uMuEeQe4ZNPPHEAPz73/9u+PcqTjzOFFNM0fC9OAc328OsLjKklkgkEomuYJzshxOfmvHvrSqJ\\n6D52wEPK/XD+gwydFCQXBeOCiziuVfN6B6r4Zp7TlFNOCcArr7wCFE/G48T9dZphILufRu8s7joa\\n58Jm5xa9sgkmmACA9957DxjTk4mfn2222QD4xz/+0fA7hvw8TpW3mfvhJBKJRGJIYZzkcJrtGV4F\\n9zR/8803gTE9nE/yVgvxWv+XEBXuRBNNBJR49xDI/XUNg+DVdx11zzl+7q233gJg0kknBeD111/v\\n93vmS1577TWg5Ds8XtVOoXU9nTqIv121C6oeSrTx2WefHYAnn3yy4fOHHXYYAPvttx8A77zzTsPv\\nmhPyWvWo5PD555/v97z0bMRkk00GwKuvvlrrukV6OIlEIpHoCsZJDic+zWN8UU9mvfXWA+DMM88E\\nYNppP65YnmaaaYDylI0VH5NMMgkAb7zxRt1TyxzOfzAuYvVx7/iqnJ6fixU7ft6qJNWhnzP2X9cu\\nBpOLgZajRkQPqNOe8UDyFvG+xmupKhGOOZuVVloJgMsvvxyAhRZaCIDddtsNgL322guAb3zjGwCc\\ncsopAEw33XQA3HPPPQ3Hi/NPn/NveI0ctsOFXpa/XVUNFj0RcyxPPfUUAJNPPjkA8803HwA33XQT\\nAHPNNRcAG2ywAQDHHXccAL///e8BWHPNNYHC6bvvvtvwO44duXJujefZt/Kvp6cncziJRCKRGFpo\\nK4fTbtxYBaMHooei57LYYosBsOqqqwJw6623ArD66qsD8K1vfQuAm2++GYBzzjkHgIUXXhiARx99\\nFIBtt90WgH322QdoHuv9b0JVlcgnAVXrHvSI47Xr6WpXcS2BKs73ejaDGaOvi2b5zKp/dwypdOeZ\\nZx4AvvzlLwNwxBFHACWW36eaCCgx+09/+tNAUc6DkSOM11J1TXo2fn733XcH4JFHHgHKuHd8P/PM\\nMwD86U9/AuCWW24ByrhfZpllAFh//fUB2GijjQBYeeWVgZKPOPDAAwGYf/75gZIneeKJJxrOp+/1\\ntDvuYk5k7rnnBuCll14Cig17H370ox8BMOecczZcg977Zz7zGaB4bX/+85+BMlc+9NBDAOy9995A\\nsYuHH3644Xe22WYboHCmp+S/P/fcc0DxvBxzPT09La9vgvRwEolEItEldCWHo0LQk3nhhReAEs9U\\naUw11VRAeYr6PT2cddZZB4DzzjsPKE97n+Z+X2Xr54zRetyqVbwMwRyO5zzLLLMARbGeddZZQOGk\\n095bN3M4UUHqgfSnpqAo0aeffhqAddddF4Abb7wRKJ6uuUCrmuSuroofl+twjJV77QcddBBQvDNj\\n+17blltuCZSYvYr31FNPBQonrkWpm+PpJBdVORLfzzDDDEDJI8wxxxwALLfcckCJkEw44YRAmUf0\\nTLbYYgsAjjrqKADOPvtsAE444QQArrzySgDWXnttoHgTrvpfYIEFGj7nvKI91eWivyrcOP9WRTDM\\nqSyxxBJA8VBuu+02oIwR8916cTvuuCNQ5gs9I/Ng2o2VfF6bn3OsPfjggw3n57159tlnPc/M4SQS\\niURi6KArHk5V5YzwHFTxBx98MABHH300ADvttBMA11xzDVCersZ2rci47rrrAHjssccAePHFFwHY\\ndNNNG447lvj4oHs4Vb+tSjMeamxd700ls8MOOwClMkeVb5XKiSeeCJR4drux5m6o+lht5rm6IlyV\\npWe89NJLAyVevcoqqwAlH+G6iwceeKDh79qJaxv0cOMq6iqMy9X1vpqzsXJTj+UPf/gDAKNHjwaK\\nUtWrlyvHzsknnwyUMaSdaG9xfUe7TRr/c+5tceFYENpHXO1uhOTb3/42UPITX/3qV4GS4zUfS4Jg\\nNwAAIABJREFUYRRAL9Cc8VZbbQXA4osvDhSvYI011gCqc36d5MK1ZY5/vTV/23/XDpZaaikA7rjj\\nDqB4rl6Lnq3e2+GHHw7A+eefD5Rrdyw415577rlAGYOOIXNBcV3QhBNOyDvvvMOHH36YHk4ikUgk\\nhg660mkgxmZ7f/w/8WkViNVmxh9nnXVWAG644QagKFTVnVUsKhs/r0dz//33AyVmG1XjuKjw8jfj\\nmgM5uO+++4ASm1eV7brrrg1/F//617+AwpEKtVX1Pi4Q74MKVhU377zzAiUXo5rbc889gcKRSlaV\\nrnf3uc99DijqzVj8BRdcABRP2sqscYloi1FNX3vttUCp2Nxwww2BUnG31lprASX2rnevElUR6yFb\\nDaVy1Ut4/PHHO3xl1ajKG8mFa0N8r7fmuVrF6v3dbLPNAPj73/8OlHlAz/jOO+8ECneuytczOu20\\n04DiFbh+J3ZUdqy1W6XWN7LjfTY346vnam720ksvBYrH4dzneNcuYgcC81DOpUZK9thjD6BEfxZd\\ndNGG73teesbm22MUQrzzzju1cqLp4SQSiUSiK+hqLzUVrE9JlcOKK64IFJVvBYa5G3MvVpsYj3SV\\nrR1OjWOqCsxrqAar1gF0s0+Z8WlVnF6eHKja5MrYqkrXyjtXT5u/slpEBVunNr7bqFKHU089NfD/\\n7J11vC1V+Yefey8pgnQKF6S7u0s6pQQkpCQlpFNAUEo6Lt3SId2ohEiXdEhKh4Xy4/7+wOeus9c5\\nc3fNnr0vvs8/+3P22Xv2zJo1M+/3rQWTTTYZkKwuz4tW+q233gqkLKRLLrkESBk8Khm34/m3ZkVL\\n1XOR952qknwsVDaef9W751sr/4QTTgDg4osvBpJ3wLiDFqxKRwvZY/b/eg3qLQTWTu1JTtF1lm9/\\n9tlnH/HbkK6N3Bo/6aSTgHTdL7PMMkCK3W2zzTZAqlGyZslMvbPOOgtIWY55TZLzRb71rW+NGNdm\\nGDx48Ijr0m1bS2Qmnhhz8/p2H73nXX/99QBsvPHGQKrHMcabx69VPN539t9/fyDFAI3tOQ8OP/zw\\nmv1xXsZ6OEEQBMEoQUez1Ir802Zg+FTWipt66qmB5Gs1394MGqtw9dnrv9RHb4aO1r6ZOE899VTN\\n/oxkOdfK6nC0JHxVZVlz5DHaGfu8884D0tjpe9VHv+iiiwIpe+3cc89tZ/cqzVJT5emb1/fuq751\\nYy9mq/mqwjG7SD+1qvG4446r+b5+6ZHUY9XQjSw16x+sq9Cy1Wo/+uijgRR7UcE4plqwxr1Uyosv\\nvjiQLFbjHdau1KOMXmpF5CpLj4XHbh2M14IqQ+Xi3FcdqmROP/10IKkIY4SOsWrDei7jpe5HroBV\\ne82OxZAhQ/plunmPMqaWj1XeyVoVZ3bqJptsAqR7pfPDz5vF5v3BTF7vH6o3vQv2p/P3vSaLGDx4\\nMF999VXU4QRBEAS9RUcVTlFsRN+6FohV0Vos+lL11eqT14998MEHA3DRRRcByRKZcsopgaR89I82\\n4p8GGD58eGUKR7Xnq/tuDCbPYtHKMnNLNac1l1cUtxvDqcKqtzOEx6afWWWjAvH/WnEqWBWL51fF\\nrNXmfNIi1mJutm9YN7ouqFjMyFPJ2tPKvmJmVGmJGsfyGnMMfvnLXwL9lUyVXReKrkPnuvEl98nz\\n7rFZ7a6VbgxYq95aEdWcWapm8pl5teCCCwLp/uL8MMNrpZVWAuC2226r2U/vlRNNNBGffPIJX375\\nZdvzwvOtGvfYvH5V9x6DPdVU6capb7jhBiDV11hrpHdIJew8Ms7lNef/jY9b0+a1aBzUbMgB1iIL\\nhRMEQRD0DpVkqZlZIz6lzULz6akFk/veffpaRavicTtmWmjZ5r75kcRsgO7U42jZaMnYF2ruuecG\\nkjWmj9fMLD9nB2w74/Zdn6LXcT6o0sxONGtIH3teJ2MHAWN5+vZVso6B88l5olWWd+LtBXKfvcdg\\nHOGJJ54A0ly3DuPGG28EUvzSMTVGYz2O65/oFfD3utEpu+g69HyYQWWc0qxCsX5GJaOat3u08Q2V\\nrMrIDE/VX16rpNI2xqOyKVoHJ89aa4a8nsXXxx9/HEhjZO2gdTTGZD027wcqGu+ZxoI8Nut1XBfH\\n+4e/6+fsVOF8coy9Fh1L+8rpWTHG3PDxN/XpIAiCIGiRUhROUYfTvB+TT2ezi3wa65O3it6nq7nk\\n5tm7op8WibnqW221FZCy3fIMsNzq7+YaMrmFqcWjdafv3mMyHz5fnVC/tyoh9zf3Irmq00+sinN+\\naK1bW+Ixar37f3upOWb2zlIN2HHA2iW/Z/eFXlI6eY2aKj2vu9A379gY59hwww2BNC/03ecWby+s\\nAWS2Wb4iq+fD8+T9YIMNNgBSnNNMKuMNxnydJ6p+7wfGQY1/qYzsYOHYe19xO52ozyrquqL6dt9V\\nZcaVnA/GXLyHmsXo5+xM4hpAv/rVr4Ckyoz9OYbOG+eVXiZ/x/lkPY/3mb7dIJq5n4bCCYIgCCqh\\nFIWT54qLud35etj6Ba2K1ceuP1CrzGwTffwqGut0/L077rgDSNagvn7pZu+0nLwmyX3Tun/kkUeA\\nFMtxLFwLJM8SMavFrJVRAS1YLUiP3RU8/fvee+8FUn2WlvGBBx4IpBifdRjGbpwnKmWr6XN/c5Xz\\nol7PNMfCTC0tVS1SM6ccG63xpZdeGkh95IyLmrllDMf5ow+/KnU3kAWsItVKdl923XVXIMUn/J6r\\nYi655JJAUrqOkda9NWx2SN5iiy2AFONT4aiM7MFmfMRry3oe46hlrRDbdyycD3phnNuuyWOfQOPW\\nKiCPyXugx2y9lXEse6cZB/PaOPvss4F0f1E1LrXUUkDqK+f+mdFntxf337Fo9toJhRMEQRBUQikK\\nJ++zI/odzbyx2tVMBy2dNdZYA0gWqyt52iPNp7x+af+vH9Ou0caC8gr2PDumFxRPPmb6WO0XpiWj\\npTps2DAgqQOtOq32gVYT7DUc77yCW1WnktESPeaYY4C05ryWr2OjJWrWkX5naxfcflHfqyrPf1HP\\ntPz/Wv1mFxlnsGbEfoJeA553lY3xKa89LV/rcKqOWw00xioOPSDOYfvCicdkvZ1Zi8budtttNyAp\\nIM+3SsisNjO+dthhByDVrJkZ5phbm+J8zHs+tpOd1nd7kM6D58uaxBNPPBFI94HrrrsOSDE7Vy21\\nu4b3Uq8dOw/Ye02vgceqojFW5N92Wdhjjz2AlLHnNZXPm+ilFgRBEPQ0Hek0kK9zop9SS1X/of18\\ntFDtbWT9hNkl+jV/9rOfAamq9s477wRSlpMZFtZz+FTOfbDdXPGzCH3z+lzNsNGHmnck0Kdv5bB1\\nGWVZ7Z2srndeeExaUWYLafWp5uz26+etflYZm4njdvVDm22k/7uoW3g9quw0oOq3HsKYi8dkDy3H\\nSJWnAjrnnHOA1IVBZew1U7SSZ6O0MhZ5dmB+/Rm/cO5rrV966aU176uMje1Zi6aiNaZjRp+Znioj\\n7zt2YTDjyu051na0cDt5h/c+86jteaEXxuvY+Lb3TJWIKk8V6Dyx04DXgO/bT9AxV72peBdY4Ovb\\n3AEHHACkTD9jgvZyVPmo+orWkIpOA0EQBEFPUWqW2oiN/vepbS64mTb6E4888kggZWL4FNZCMeNK\\ni2PrrbcG0lPXjAk/5/o5fl60Gpqthu0G+Zo9Bx10EJCsMK1ErTH9166H0QsZeI1iJbmvKhAVjP3k\\n9PE7L8xq9FiNY/n+PvvsA6Rsozwjq2jVwl6I6Xl+HQs7DWilW29hxp3xCtW9qs96ip///OdAipc0\\ne4xljkm+6qwxEc+r9VjGI6yTUfk4FsZqVDZW2esh0bORZ6vaK00r/aGHHgLSfcN6LRW23RzyFUjL\\nnB+e77yezjlthwFX/jSG473PzgB2g7bbwhlnnAGkrDOPTa+Rmb977703kBSzSsZjVOnYxcV7d1HN\\nZaOEwgmCIAgqodQYjr5RlYe+T/3MosWjhatF6/eM5Wjt6Us199x4h1lrWn1aRlq4LVgkXYvhiOrQ\\neJVjYqaNqyAajzKjq+yq6DLjFrlVlK8B5KvzQgtWrHK204TK1Q4UWmlarL7q8/e1yrhFszhGebzA\\nGjS7PG+55ZZAuibsHv6HP/wB6N9t2HVztKTr9RWsRzNjMXjw4OFjjjlmP4XgHDdGYz2McSgVxtNP\\nPw0kleZ59Zitk5lvvvlq/m92o14Cx9Zryrot6360/vtWz/fd36J508688Hzk14LKx1oyYy16hfK4\\nuNmHegM873ZpseuGysYOA2a7eQ5UVq4wWpTNmMfDXeMnYjhBEARBT1Gqwsmf0j4F9f/ps9UfqWLx\\naauFoi/Vp3e+up1WnBaKT3vz5P3dFiqDu65wHEOtNlWex6I/2h5IdiIom05a9XmVdV61rPK1NsFY\\noPPFzCutv3wdlDyWl8dwcuutXryiG+vhODZeS6oAsxFVLlaWq/bsrK4SMr6h6m+XMsbCY7R7sx4K\\nr3OtctW7PfI8r9brmXmn4jUzyxjNNddcA6SaEjO+rHUx+9GuDa63lcfJiuZHs2pv9NFHL8zUU9V7\\nLP7fDhFm4hmvtAbR+WF2ovuu18h5s8oqqwApDuY92RpHYz+ujqwnxS7U22+/PZDUYb62USicIAiC\\noKfoSB2OCsUMGnsbGWMxS0WLxQwNfbeux26fIH25WrrmlPt/4xz6F7WQW+gv1nWF4zGYoaPletdd\\ndwGp1siVIPNeXGXRCas+j+V4rHkHXWN0joGV5XbOdkVX54sq0POtpWyHAa2xVrONuqFwVGNmn2nJ\\nmtnpSp+S1xxZWa5lWlamVbNjoY+/L8ZwjPlqxdv/ywwrr3ePzfNpvMGeaMY7rBHRk7LffvsBSQ2o\\nhO07Z5zDOIbZbY3Wa7UyL4rWrfJ9r3PVumrOfXRdI5Xs0KFDgdQ9wdpGlY4dB1QyvqqM9aRY36eq\\ntDbOOLldX/ocj2PgayicIAiCoHcoVeH41FPh5FaV61poSVx55ZVAqoo208ZsFatf9XtqKdmTzae4\\na5dbkZz78JugawpHa9+xssOA1pr+bscsH5OyqaLTgGjdqWisAXC1S2sOrKNQ4ZpxY5zC7eRjY+ZX\\nqyqwSoXjMbjP1l3YJ9CVF/3ba0qL2XoMlbDegT77B7Rei1SGwhGPVUXr39437OKsQt13331r/q/S\\n8T7w2GOPAUk5GQ855ZRTgGTFm/WoerD6vlmajeGMNtpoI8bX86Vy9Risx1OpqFjNvLMz/hxzzAGk\\n7FXHyNojx9L7h10WvKb0GugNcL9ee+01oP96Xe5vHge1A3YonCAIgqCnKKXTgORPb5+Sud/SDqj2\\nAzPTyjx5eynZP8jv689WwfhUN5vJLLf871EBx87+YFoe+lpdtdKaAbNDeqFKvlm0jrTinSd2hLAz\\nhVaf1c52Dz7zzDOBlJXoGNhHygwdf0eLuChLrRfQKyDGK7xmVP1mZtk12mPRctV7YFbTANlEQOO1\\nJu3yf//3f4XryXhseiaMExiDVZGamamaM5NK5atyMd7pNeRYnHzyyUCKf9ldXmVjZ22z1UTFXUaG\\n3/Dhw2tqoFR1bnuxxRYDUicRlannXS+OPfXsqWbPvZtvvhlIPRhV/Waj2X3c+Lj3EePpziMVjnE1\\nYzjGjPJO/HkXiXqEwgmCIAgqoSNZaq5X4tNYS9W6CS0Ys0a0dPRTaqlaWe5T3rVhVC5aCfo9pYnu\\n0Dmlx3Bcz8Q+cKKFII6R2SFarH7O2gFrkVSBuYVaVkynE3GL3GLMV4C1olxL0Hmiz11l7Oe03t2O\\nqqBoHaRW6cRYWBtiHzEtRzM6neP62rUwvaY8Nqvt3Z59B3MF3GztURFljoUKV6VhPEJPhta7VfTG\\n8LxWzD6zp5oZXMY7vRasXdJqt2uD5B6YohWM+xxXU3GL/35nuN+FdC3kfR5Vup4/98nzZ+cJ/6/C\\nsDean3PeOI/MctNj4tg7hiog18Oxzsv6ILPXjBGqOv3NiOEEQRAEPUVHFI5oOfgbuT/Zp7ydB/Td\\nTzvttECy8otW4usAHctSK7Io9aGq5rTerCjWYtHa14I1W00LqMiSbZUqOg0Uve+8ySu+zWYUlU5e\\n01B2jKaTY6Ea91hVf1qWxq3sruC1sPbaawPJmre7cB6/KoqftEon67O8P2i1e3/w73wFTjO4XDfL\\n2iPHyEy9IorGpqheLJ9nzY6Fyqjvb9RToMannOu5AsqzyVSHiy++OJDGRIVinMpjURl7zfmaZ3T6\\nu/nquZGlFgRBEPQkHVU4Us/Kyusy3Kf8exVkYnWtDscxMFZjFok+WP3Y+uwdi3p9wlqlytqTAbYH\\nJAtXqyq3PItWryw7c6+bY5H31nOte+OXxgCKvAjdnheDBw9u+rfz2Gx+DHl2Yx6rzedFo/Oh2XnT\\nTgzH3yg6P7miKFol9cADDwRSjVLeGcB7aJ99BlL9j0omv9fmca0i1XfYYYdx8skn8+abb4bCCYIg\\nCHqHShROtyjqWzQSut5Lrc/2ge7V13TTqu81enks2l2BsVnKHItm40u5Gmj0+vZ3/H5R9qJZbGYE\\n5vQd61ay1AYPHjxQx+mRfq8og67RrEMzAE844QQgKZui+pm8l1+uHov2O2I4QRAEQU/xjVY4LdAz\\nCqfb9LJVXzUxFol2xqLeyq/tdjzP41f57xbd64q+l9fK9Y1ntFqHk1PUFaXePhcpkRwzfu2knX/O\\nY89VYlFmXr5fY4wxBv/5z3/46quvQuEEQRAEvUOzCud94PXO7U7XGTp8+PBJGvngN3wsGh4HiLHo\\nS4xFIsYiEWPxNU09cIIgCIKgVcKlFgRBEFRCPHCCIAiCSogHThAEQVAJ8cAJgiAIKiEeOEEQBEEl\\nxAMnCIIgqIR44ARBEASVEA+cIAiCoBLigRMEQRBUwmj1P5L4pjcmBD5oorXNN2os8qZ8zTQmnGii\\niYYPHTqUxx57rNR9qPf/iSeeGEjLKneKaN6ZiLFIxFgkvlHLEwwaNKhfp9kOba/tXkdue/DgwQwe\\nPLjuvjf6f7fX6PfE7+Xfzxl99NFHdI5tlqFDh3LvvfcW/n/IkCH9Vh4ciLHGGmvEao4DMeaYYzLm\\nmGOO+Hvddddl3XXXbW5ng65Rbw42S34NlL39UYn8Gmv2/lAVPbk8QauLj+VL07ZAx5YnqGpBNX8n\\nX2533HHHBVIL9nqt4MtoQ9/qsTa6MNc444wDpGWWi5h//vkBeOSRRxr6/XbUXliyibLGwrn7+eef\\nl7G5lpcryBkV50WjS443u7DfN0rhBEEQBKM+bSmcFpZw7nWaVjhaQ1oE+dKtzVr7U089NZAWTCqL\\nySefHIB33323oc83a725KBXAt771LQD+8Y9/+H+32fgOt/G9Rsn3s4hR0ZLtFKPCWOQKeYIJJgDg\\n448/Bhjhtm13wbdeGItG457isX/xxRc17/dR8y3tRyicIAiCoKdoKkstpyxlM9FEEwHw4Ycf1rw/\\n9thjA8nvWOSrb9QSHmOMMYD+KqQdtJ7ee++9Af/vPuW+0zzW4v/ff/99oL96bNSvXESubBZffHEA\\n7rvvvpr3+yqVZuj7Ha0olYP/W3PNNQG4/vrrm95mJ6inbIL2aXU+1dsmFM8PY7n//Oc/gXTNqHz8\\nvwrIazKPGfo7KuF6scJGaDSGUkR+7G7PY/P9RRddFIAXX3wRSPcV733+vt/zXlt0jI3GVesRCicI\\ngiCohKZjOO1YLPUsk1lmmQVIT2VTYFdddVUA7r//fiDFOaaaaioAbr75ZiA9pT/66KOW9o8mYjhj\\njjnm8KmmmopXX321oQ2rrlQs77zzDgAzzDBDzedeeuklgH4pyk899RQAU0wxBQBbb701AL///e+B\\npIjM3Prkk09qvp/HK4rib57fXvBPd4uHH34YgAUW+Hoq/C+PRU4rY9GoddyopyL/nNf9+OOPDyQr\\nfpJJvi6p22WXXQDYY489gP5eCb+nWvD9evvTTpyzHvn17xh6bJNNNlnNvruv4403HpDupd5nnn/+\\neSAdm8dqHCv3vPi3+1vvHEYMJwiCIOgpKq3D8am64IILAvDHP/4R6P/01Eo/5ZRTAHjllVcAWGWV\\nVQCYe+65Adhrr72AFBv47LPPANh0002B9LTX2tc6GIkftekstSmnnBJIlkS98fTz+pfdB6vmVXdm\\nqani9EO7/dVXXx2AddZZB4B99tkH6O+DreczLsrYacWS3WGHHQA49dRTgfbjTjPOOCOQxqQIj9Hf\\n8Xy7H4cccgjQ31efF7ydccYZAGy33XbA1yrwyy+/7AmFo1X+6aef1rzvteJ8Urlq3b/55pvuF9B4\\n7KDIui9jLBpVMnn9lOfLOa9n46ijjgJguummA+Ctt94C4Lvf/S4Ac8wxBwBLL710zfa85hwz56tj\\nWk/pdHJe5LFdr4W//OUvAMw888xAUjKvv/51zbr3yCWWWAKAk046CWBEYbb3wFzZSD0VWnQ/CYUT\\nBEEQ9BQdUTh57rcWhBaolsR3vvMdIFUSq1wWWmghICkVn6r596w89ql98cUXAyn2c9hhhwFN9doq\\nvdOA6s1XFYsWyTPPPAPA0UcfDSRVd8sttwBp36+88koAzjvvPAAuuugiAB566CEA7rjjDgC23HJL\\nAM455xwgqb7cIqmnfMq03hrNzFElas2r1iaccMKaz3m+nWeXX345AJtssknN5/L41IEHHgjAFVdc\\nAcDLL78MwLBhwwDYdtttB9yvKhVO7ou3a4bHpvJVtZ1//vkA7LzzzgCsuOKKACyzzDJAmkeOZbsZ\\nY50YC2MwqrQBtgOkeMXyyy8PMKJ33zHHHAPAFltsAcCTTz4JwJlnngkkpTTXXHMBcO211wJJwah8\\njBU7D7yGirJxOzEW3ifyLDKVx7LLLgukOPWuu+4KwMEHHwzAeuutB8ADDzwAJAV09913AymG67zS\\nw2GNUgMdBYreD4UTBEEQ9A4djeEUNY/zqbrNNtsA/ZXMb3/7WyD50m3QqBo44ogjgGTReAxud7HF\\nFqvZnpldWlK/+c1vavavzxh0rJfa9NNPD6QaAP3M8847L5CssD//+c9AslzNyLvkkkuAZN3ttNNO\\nABx77LEAbL755kCy6nbccUcgWTK33347UFxrUKV/WvRLX3bZZUDK5Jt99tkH/PzTTz8NJBX4y1/+\\nEoBnn30WSL56FbPH5DF67M63q666CuivmHKqGAt/2/mhJTrnnHMCsOeeewJJ7anOjNHou//Tn/4E\\nwNVXX13zf+dbnn3ULFXELfJ9y7uC5+dJz4ixF2OJl156KZCuKeNfd955JwAzzTRTzXaXWmopIKnI\\nvFNBnv1a5lh4TN6j7AQw6aST1vztNbPyyisDqXbReaOi3XDDDYEUy/Ga8f6hInLMvAYcizzGXFbG\\nXiicIAiCoBI6onByv2OuNLbaaisADjroIACuu+46IPmZtSj2228/IFm2Po1VMhdeeCGQaln0a2vx\\n6OM1/tFAtlTTCqcoPqFFYNxJC0ILdckllwRSZpR1Mmaf/PWvfwVSPMpMvHPPPRdIlpDqQAW1wgor\\nACl2I/l5LrvGAPr3rNLa0hrLyWsLitqkG5tTmdiZwlifinjvvfcG4Be/+AWQxt555fa1BuuNweDB\\ng/nqq68qUTie15/97GdAOu8qWf8+8cQTgWSNm200dOhQIJ1/vQN+z/quVivcpcyxMCaT14zVw/O4\\nxhprAGnuq3Q9v2ajqfKMzTgvVf/WW/m+NS525yjqM1bmWOTLd3iezDb0mLwPqFi9zr3X+rlpppkG\\ngB/84AdAuq94zzRrzZozlZLHOJJ6m6L3Q+EEQRAEvUMldThaksYXzJ9XsWjl61988MEHgWLLQr/m\\naqutBsAJJ5wApKw1t6Mf3Nz1BmhK4VinAf27sLrPZuj5qjIxU8ZMOrOK9K3m6lArULWnWjNLRYvH\\nGidjNnl8wu3Vy7dvx3rTWrMOwow8rXPjVWbcFHWudWyN7RTh/+2+oDK25kkFbf1Gs1SZpebc9vXt\\nt98GUoaV14ZjYzabamHWWWcFksr3WnvuueeA4kywRulGTVJez+X8UtkatzL2l2d4ei3YMd3PPf74\\n40B/he2Y16OdTgO5us6vT983FqMiUbkYp1TtO188Zu+N3/ve94DUqcTzb0zY+0B+X8nvX/n7OaFw\\ngiAIgp6iEoWTP7XNCdcStZOAcQx9p/l6Klo2G220EQCHHnookOpyjAlpyfg7d911V6O72rDCGTJk\\nyPCxxx57RHxAS0Ofuu+77/pOv//97wOpHkdlpD/ZMVL9mVdvfY2W63LLLQf0t8byTJq8b5TWohZy\\nfv6riFuodI3l5VlH+XwpQivPmiS7L6h0VT6nnXYakOIjzWZoVWHVa0n22Q6QLMuiMXIMfve73wGp\\nHkvLVRXw6KOPAu3X45Q5Fo2up+V9wX12jnt+tdpVsqp8Mz2PO+44II2VnzeTz9hgXq9XlNHXyWvE\\nY8pjOr5vrZD3NO+FxknNvPvDH/4ApHuomXpmNxobsnO7Ki/30IjzKRROEARBMErQ1no4ReRWtBaK\\nGTNaoPr4ffrutttuQKoIz1EV+LTVavd9LRZVhnEPM8Pa6CLdj6+++qpmPZV8LZ98vRszqLSmzNjL\\ns0NES0PL1DiV1fjGpfIMLH25jo3Kyf//8Ic/BOCCCy4oPK52yTP3ckvWWIuWpnGtZmtEPLbtt98e\\nSPEM42NaiVq4Oda46N/uBmYVeSySd6hwzueV6GarWVui5eu1ZcynnoXaDZpdT8tYb77KrvcTa9p+\\n9atfASku4ef0Jjhm3h+8jhtd66WMayTHa8R9yNfg8br2/KnixPlz2223AWmeGLvze46VXe6Nd9t1\\n3mPLM3rLmjehcIIgCIJK6GgMJ7fO5plnHiD5C421aIloafh/8+z1M/oUtzvsvvvuC8A999wDpGrr\\nvDI4t1xGcsyldxoo6iunTzZfFVPMTrG+YoMNNgBS9bSvWntmqXmsZjVpvas68lqXvFas+A3zAAAg\\nAElEQVRFyshSK7IY/U196u77bLPNBtBvjSE/p9VltpsdJay+tm9Uo2sU5RTVhXSzW3S+kqP1FNZX\\n2CVcS9ZYokrWXntlWeXd6CtnppVruuTxDa12MXar8rWmzY4Fqgfrb+w4kY9RWWvA/PdYGhoLr41c\\n6bivxqut41Pp5F0U9CapoFUwdiDZfffdgVTH4/1Iz4h/6y3y76IYT8RwgiAIgp6iLYVTr8urFoJP\\nZZ+mWtnWYZhHrwVrfzDz57VgrrnmGiA9pX36Wmtw1llnAbD++usD/S2WBtZnKV3h5Fkn7nO9cffz\\nKhXz8PPeSnk+v6+LL744kNYccix8tUpfC7jPcbW94qe1IMbmisj91vmYuB0t1R//+MdAyuATK8y1\\n9owF2nGgVXpp9VN76hl/0EI1a9ExNMPTvnLOt1bXJMqpciy8b2i1zzfffG4XSMf8/vvvA3DyyScD\\nKQtSpWqHgfvuuw9I1frHH388kMYmrzWpF2PqxFh4TahQjEv6vuffa8JO6d6LVfvOAzuj6z3Qe+S1\\nZVabnhC7enif0fvkPdvv54TCCYIgCHqKtrLUipSNfsc8W8wsE2sDtFxeeOEFICka/dNmq5lPry/W\\n+pvc72jNiiv/6cvPV7VsdMXBdqhnEdRD681qaOMLKhQtE+MfWndaMqo8/daLLLIIkPzbqspOUKRs\\n8hU8tSCLujTfeOONQLLuVX32avN8en7NUmpV2Rj/KMoc7AYes5at59V4VZ7ZZ0amaj7PfhuVyFfu\\nza9b45/Ocetw8ro9/2+Nku/bkcBaNl+7cd7zFVk9Nu8jrnd06623AuleqZLxvJt9qjLxmltrrbWA\\npIidP6pDx8K+dGbHem3lMd5WCYUTBEEQVEKpWWp5jYBWuU9ZV+Izi8z6CGM5rlJ3//33A6kTgZaw\\nMaDTTz8dSFkrZr+Z1WZ8oujYRqJwmo7hFNVRlE2eMePYOjaOqRaP/mrVoeqyKGNvgFhQx9aub1Rh\\nHn744UCy3vRbi6rN+aC6M6vNLDazGJtlwgkn5NNPP+XLL7/segzHmMypp54KpGNzXjj/rJZfdNFF\\ngaT+R4UsNa15PRfG5Mwic857H7ALtFa93Ra8zxj3sJefcRFf/dyRRx4JpDq+RudnJ8bC33YfrddT\\nsZp5qxdp2mmnBfpnI3oN+Dm7jtvdQ2644QYgdS5x3RxjQ86nvBNKTsRwgiAIgp6i6RhO346nOfk6\\n3D6t9Sfav8esEfv9uJKnmRNW5WvR6KvXd2+WiWt8uCaMnZfdv6K+YWX6aIuUTZ4R12jfqCLybtRa\\nefpc7UDg2BvHuOmmm4B0bkayeiHwdWxIi7BZPG9Weo/EGhrpdrR03UdrTcw++/Wvf12zHdcvscra\\nmgTrN5rFc1VmZ4pWMfvI+IJWvz5+LVnPv9eI157H0mossUryWo+VVloJSMeoOnftILsqqFS05v3c\\nxhtvXPO3cQjHwm4MZr9uttlmQOp7WCV5ZxIz8qy7MsbivU/Vp1dIPN9mclq/Y/zb+KRxMd93bKzn\\n8j6l0irKdhzZ82AgQuEEQRAElVBKDKdo1Uu79Lr2vFaalsf+++8PJEtUyzRfv8Yq2RVXXBFIfmyt\\ndS1b+0bVqxAeCaXV4eR+YK00LYdG1yXJ18nw2FRQZvRp4erX1ldrPMueSWKevVluOa34p4vW+GhV\\nUeZrAllvYw+0fL5Zc6AVaEeCPffcc6S/U68+q5t1OI6hx66XwPe9Vo4++mggZR9qwWqxlpVl1Mna\\nE+eqnguvEbPM7Padx3ZVLM4Hx0blqxow1nvOOecAqQfjuuuuC/TvPl2PTo7FwgsvDCTV5uqleVai\\nStf7gorEMfP/xkPtNu1cz1fT1evkvVkF5OejDicIgiAYJWirDie3YI256IPdYYcdgLQGjNa0/kgz\\nIvTRW1tiZwGr5PVbm7FhPMMalSeeeAJoS9m0jatLqjQcEzsja6Go4lQiWjDWKmlty29+8xsAttlm\\nGyBZMHZXMM5gb7UZZpgBgE022QRIFemOifn3ZviVWZPkNqwQ91ibZfPNNweSNeW+ulJormzMFNRS\\ndV65zlK9eVFWFX4n0OJ1TIYNGwakuMNJJ50EpHmzxBJLAGnMtNarqD1rFRWsmVbeB9x3Yytmr3p/\\nMa7g9413+Wofwtdeew1IWWjel+xH5tj1QpzLa8c5aRaa6ksvkXFxYzWqPa8Ra8q8L5mF5tipZPzb\\ne+nZZ59d83v1lE2zhMIJgiAIKqEthZNbS/qN9StraVgd6zrae+yxB5Cq3u0oYG8jLZJddtkFSIrH\\nzKxDDjkESKvc5T7XPCOsCusuX3nTTtjrrLMOkFYjVbG4j2Z2aVHYO80YjGOlpbLddtsBqZ+cGTVa\\nha4Mmvv4/Zzf76QKNFMq70zdKFrxKhMt0qJ9NlPQ6mjHxjFudT9efvnlERXa3UIrXEvXLtDON2Mz\\nqj69B157ncjMLAuVhTFdr+dpppkGSN0VtOa1wrW28+vaayRfvXLttdcGUj3WMsssA6TOJGY95p2a\\npaz7x8gyuvR0eC/T46FStWuK90LvtWapqmhUSCpix9KuHd4fjAkaWzZWYx1fvkZVWYTCCYIgCCqh\\npSw1rfHcr6cloKXgetv6m32q6j9U4Vhf4Xo2WiBaKFr9Wqw+xf2emRjGN/JOyvVqEfr4+JvOUtN6\\n9re0GOz/ZRzB/1sXY2admXezzz47kCwKYzT2mfvRj34EpFiNx6TqsxJdpWNNk10cjJ/5ef3fAxxX\\naR2Sm609coy03rT2GvUfq4ycd8arcvUp+r/rZXD1wno4vuaZVLk1ntes+LmyFE4ZY2HMzevWeeJ9\\nw/NlDDDPblVBOxb+nSta4xYPP/wwkOKbxoKclypos18bpcxuHLmKcizy+Ld1NJ5f183So+Lcd0wc\\na2vr7DxhrNm4mYrKWHO+NlnRNdjs/SIUThAEQVAJpdbh+OrT15iMdRBa+2azacXvtddeQIrN2PfL\\np68qwKeyPl2VjtafT/98vQwtnwaykdquw/HYcmtdC0SfrCpMa0tlogKxh5HvOxbm1+u79ff0vdq3\\nzriGlolj0Kkag9FGG63lLgriMVmPoZqrh+dZ1WgswA4WVm23mmnTDYWTd9DO1Xoen/S8q9qsvndM\\nnXftKp0yxyI/JnvjqUjsB+e145x2rqv+vQ+Yoef5NkZjpqZ1WWYzOkatZvJ1Yl7kHhNjO3pvrMPy\\nVUW7wgorAGnuW5PmteS9147adtxXNapwzABWXTbaIzIUThAEQdBTlKJwfBpbva6V7lPV7BLjE2be\\n2AvJ+pqf/OQnQIp/+H8tIGM+Wj5FcYg2Oji3rXByqy1f1XLfffcFkiVqB2R9trkS0Wo3C8WsKeMO\\nxnYuuuiimt9v1Zrv5CqX1h7ZOSJXaVY3m1HnmDhWRee7aA7b6eK8884D+q9uWoRjrDVYpcLJa4ac\\nD67xpMp3juc99jxma06uvPJKIPnk26WTHZJVKo77EUccAaQYsHNaT4adju0o4DHrBTBu4Wq54ljU\\ny8DKu3wM0Gm9Y/PC3/b8+rdrPqlA7JDutaW6y9dD8ppTKXlvdt44ts3WMkYMJwiCIOhJSl0PR3wq\\nm8tttoidT824MP/dp7f9oLQ89LVaj6OlYdxD/2WuZPLV8wY4jpq/+4xBUwpnoLhFkR9Yi1QLxTGx\\nUtwsM7PKjjnmGAAOPvhgIHXCNg+/CMcor78o6ndXtL9lWG9aqPa+EmsCHAPnSxF51wb7g9mBIl+b\\nXuvO79mr74033gCar7OoUuHYH1AFm6/k6avzyM+tttpqQFJCZjfldDOGU896zs+D581aNvuBudaT\\nY+E8s1blqaeeApLSOfPMM4E0Rjmtdiipcl6Ykafi9Tr2uvYacv6ogPSU+P38Xun9K1fKRffOovtI\\nKJwgCIKgpyhV4eQWigpFi1QLxHx3OxhbP/HYY48Bab3uPA5RZIloyZjZVW+/RkLLMZxGfyPvZGsv\\nNI/JrLQXX3yx5v2y6igarY1px3rLx8Lf0kevxWnVfKOoYKyKdj2TfGzsiOsKkFp7zpN6Pd7szmCV\\ndi9kqdlpILdstUjvvPNOINWsdao/XC90zvbasaZE691rxdd2q+TNECuKf/XCWBjf9BrIj9m4Z94R\\nPf+7KuUbCicIgiCohKYVzuDBg/ut7JkrjrwuRwtXn6tVsHl8we3l1lnR7zS6/koVCkffuSpOGu2c\\n3GvdfNux3lyXyLoKsTbA3P9cwWqtOb+KstIk9ydvsMEGQFopcv311wdSLZRW3dJLLw2krMd6vvtu\\nWrIj+R2g+vlSZnV9r8z1VinTC9AsRRl0eR1P0dzOr5129ycUThAEQdBTdDSG06uMZD9LW/GzbAui\\nU+RqpJN1OGVRlCnjOjjXX389kGqY8nPgyo/Wh9Wjl8eiar7JY9HNTgO9en/IaTerNRROEARBUAkd\\nqcPpNNbf1KtJaYHSFE5OUXZYkbXeKEUWR7M1DzllWG95JozkmTJFnSHyLKFWqqChuFK8HnvuuScX\\nXHAB77777jfWqm+WbnZd6BStXoO9pPYaVUjt3m+KCIUTBEEQ9BTNKpz3gdc7tztdZ+jw4cMnaeSD\\n3/CxaHgcIMaiLzEWiRiLRIzF1zT1wAmCIAiCVgmXWhAEQVAJ8cAJgiAIKiEeOEEQBEElxAMnCIIg\\nqIR44ARBEASVEA+cIAiCoBLigRMEQRBUQjxwgiAIgkqIB04QBEFQCaM18+FvemNC4IMmWtt8o8ei\\nlxoTdpsYi0SMRSLGItHTzTsHDRrUb832btJnf76pvY4qYfDgwSO60XaCRufNkCFDRnQa7gatzO1G\\n93mfffZhn332aWW3ukIV13nZ95Oi7Tm/e+neNaoRLrUgCIKgEjqyHk69NReqXt2u6PcGeL/09XDK\\nWn8i31f/9lXr2P+7hkijY5xvvxV3QdXn1bHNx2SyySYD4J///GfN5z766KOWfmdUdJ2UdS7KmBcb\\nbrghAJdddtmAn5t44okB+OyzzwD497//3eruVsqoOC86RU+71IIgCIL/PUbJFT/bZSTWX8dW/GyW\\nfLXMscceG0jWn6th/v3vfweSwpliiikAePfdd2s+3yydsN48BpVHEUOHDgXg7bffBuAnP/kJACef\\nfDIA0047LQAzzDADkMbi97//PQArrbQSAIsssggABx98MACffPJJI7vZj25asmeccQYA22233YD/\\nL1pJtlP8L1n1+TWYeyv+l8aiHqFwgiAIgp6iqbToXqdRv3UnYgzN+sxzyzTPfPH/k046KQCLLbYY\\nAHPPPTcA448/PgA333wzkKz5Qw89FKBfxlNunVUdb4H+ysZ9mnrqqQF44403gKRYvv3tbwMw1lhj\\nAbDpppsCcNRRRwFwzTXXALDKKqsAcMopp9T8/f3vfx+ABRdcEIAHH3yw1OMpk6JYX65sHJt//OMf\\nNZ+fZ555AHj88cc7up/NMnjw4H7HlMfeenURSJWNtBuHDULhBEEQBBXRUYVTL7Mqt+r1mX7xxRc1\\n/x9zzDGBpAZ8/c53vgPAp59+CiTLyQytov3oBPW2nR+r1pJKxFetccfiu9/9LgCzzTYbAEsvvTQA\\nn3/+OQDvv/8+AKeeeiqQxsQx/Ne//lWzf+5H0VhVQa7u1llnHQD+9Kc/Aclav//++wG46667AFh5\\n5ZUBuPvuuwHYeOONgRS7UfXddNNNQBrTZ555plOHUojjvP766wNw+eWXj/TzRRmUzn1jcqutthqQ\\n4lT77bcfkJRwr/HVV1+NOA/O+bKUgmM03njjATDXXHMBMP/88wMpK85rZZxxxgFS3PP5558HYJpp\\npgG6cy2UhdeUY6tXYJJJvq5jf/313igxDIUTBEEQVEJHs9RyZaFVrSVq1tL3vvc9IGUlLb744gBM\\nP/30QLJgzTLSEvnLX/4CJH+2Vn0bFlTpWWq5snEstEhUMv7t2JiJZWxGy9Y4hFb8lFNOCcCNN94I\\nJKteq84xV000er47kYGz6667AnD22WcPuI8TTDABkCzWZZddtuZzY4wxBsCISnuz2R555BEgZehp\\n4eqD97VVhdvJbKRc4bqvhxxyCJAy7C666CIAVlhhBSApWbMQxx13XADmnXdeAJ544olmdqNh2hkL\\nj7FZJWFM7o9//CMA9913H5DuG15Dxgi9rzjnn376aSDNF2OFM844I5CuKRXRsGHDgPpxz25kqXme\\nvSZUtksuuSQAf/vb34A0j8477zwAttlmGyDdS71n1qOJuHhkqQVBEAS9Q0diOPlTUctGv6KW6kwz\\nzQTAXnvtBSQf7AcffFDzqrV/7733AsnHb12GyiavTelm9ktuHfm3Y+EY+L4ZWdNNNx0Am2++OZDi\\nFldffTWQxujOO+8EkrVoptc777wDJN9/rvYck6rqNvpy/PHHA/3HQgvVMbEjgFb9nnvuCSRFe9JJ\\nJwGpPkfL1zFzLP/617926lCapshSVLWr6vyc8SyVr9mHsv/++wPw8ssvA7DTTjsBnVM2ZaDy0Aov\\nwpidc3SZZZYBUhzLOe18Ea//fIy9XxjP9D7k2O68884AvPbaawBMNNFEAHz44YcATD755DW/P1Dm\\nXafIO4l4b5twwgkB+PjjjwE4/PDDAbj22muBpPKnmmoqINWszT777ABccMEFQPIiGBd1+6rFsu+h\\noXCCIAiCSuhoDEdLUz+jFsLMM88MwAEHHACkp68W0EMPPQTAe++9BySf7UILLQQkP+Ydd9wBwG23\\n3QYkv7aZWy1U2ZcWw8ljN1oo7rsWkkrEY996660BmGOOOYBUd2PNyVNPPQUkS0Sr7s9//jOQMm/8\\nPa26vK9Yn2rpAfe/k/5p98GYi/vi+TLrUEszj/U4ZmeddRaQeqe9+OKLAOyyyy5A6s3VrpXWylg0\\n2wEgV315DYgWq+ffOKdK1zFceOGFgRTXKpsy50V+jRxxxBEA7LvvvkCKS/qqR0NV7xjnMSGVrfeB\\n6667DoBVV10VgGeffRaANddcE0hj533K+eV8LOpLWGUMJ1fI9p/zuheVcq7+ci9QjopJJb3DDjsM\\n+LtFRAwnCIIg6ClKjeHoG9Wq9tX8dzMpfCr/4Q9/AFJmlnEIfae33norkHLIjeVo9asC9D/6PZ/u\\n7WYntYOWgdaTVpJKQ7/0m2++CSRfq9bZBhtsACRLVavsscceA5Ilo0rQQjZzR9+unzP+kXcg6Ebt\\ngfvqseZj5asWap7dpAV64oknAknpPPDAAzWf72YML1c2RZZifmxeK7nCefTRR2v+vuWWW2q26/f3\\n2GMPINUo5dTrXl5Wd/NGyGO8Bx10UM0+bLTRRgCsvfbaQFKsnn89IXZX2HHHHYE0JmZFbrvttkC6\\nv3gt6XExIzDv9VfPC1AlxxxzDJDU31prrQWkOKYeD71K1n2577/4xS9qtuexOs/MEDWmaFxVJX3P\\nPfeUchyhcIIgCIJKKEXh5BaqSkcrT5+8T1ufmr4/yyyzAHD++ecDcNxxxwHJ0tBaM5/e6lkzslQH\\nL7zwApCe9lVQZLnmufv5q1lIfk7ra4EFFqh539oA1ZudCIxrqHC0/l555RUgja1j4fY6qfrqWcf6\\nyI3N1dtOUQ2TMRvn15lnngmkOi4Vs7UGKu1uUjRPcoXpec3rLYxnOYZaoKKq1xdfRD3l0gllUxTP\\n8n3Ja8WcB875o48+Gki1ScsvvzzQ//way73qqquAFBsS1+fxWtPj4n3JWpVe6Lkoe++9N5DmuN4B\\n1b2ZmsapvM71/qhw/F2vDRWR8SqzHx37hx9+uKn9rEconCAIgqASSo3h+FRVgfgU1XLR2jaWY72F\\nykb/oZaPVp1qwG7B9hczBuTvaOXl2Wmd7KXWROU+kCxXj91j8VULRh+r2O/JGI6qTmtfH7/WXq5s\\npJNjUc86rqdsxH0rqvDWitN3bwW5lu0NN9wAdKfWqIhmlYPKJu9EoMrP1Z/K1up5aTRb7oc//CEA\\nl156aVP72QhFc60ozuUx2BFAZWMNmjEZrxXjll4zbse6GjFT68orrwRSDZMemd/97nc1n889NWXM\\np2avO4/Fe5s9FfXuXHjhhUDycJjFaBd5M3l32223mu95LOeeey6QYofifK1XM9UsoXCCIAiCSihF\\n4eSdiFUq+gH9255IrmK44oorAskvrYWiZaEFs9xyywHw5JNPAsna14Ixw8KskyLff5VrwBT1kbN7\\ngseqL9YxULlcf/31QKqS1sLVmnN7VkFrAWnp+H9VZx5nqzIbqVXcR9Fat0raWgEtU7MXretSGY8K\\nx1qEMR4rxLVM8xiOKs8MLlE559Z+TieUjXgMjWbIvfTSS0DKsPzpT38KpD5yduNwPqicnfu5qsv/\\ndrt2svjBD34w4P5UEfurd0/yfftKWkfjPVDVpudEBew6Sr/97W8B2GyzzYCU+bn77rsDaX4M0Ceu\\nzSMbmFA4QRAEQSWUGsPxqWgMxYwZn57mcuuDn3XWWYEUl1ChqHDWXXddIFlzZqXob9Sqc/tup97+\\nVcEAVclAslC0+ow7qOZ837iUY2LfOddXUdGoHkXF4/f1g0u+2mIvka/VoyWshZorV+eXPn4zbIwh\\nunaQGTz5iqOjEqo4x8Lzp4J1Pjh//Ftl040VXnPqKcxcCZlpeeSRRwJJwZills8HPR15Rqi/u/32\\n2wOpXssYTjdp9HwYm3HOq+btL+k8cI7bxcW1oFTIziMzgY2L27HC+1ARefZks4TCCYIgCCqh1Dqc\\nPF6hRaJC8X0VjPnuWvmu/Ghcw95YWrD6G/VD2lvJ7BUpWj2xCuuuyE/t+/pc875gWq7GavIVOR0j\\nYzjmz1un8/Of/xyA9dZbD0jWoRQprrIYNGhQw9ssmi9a5XaQMEPGGiWtNTtna7X5fftLabU5Fvri\\ni+ZBL1j/jWIHiiuuuAJI15Yqzu7idumQ/Nh6Oa6V75P3EeMOufLNv5fHbnzfeh6zGGVUOv9mt5qh\\ne8kllwAppqPXx/uEmb52Xci7J5jl1iitKhsJhRMEQRBUQqlZauJTVKtci0NL0+wh8+2NU7z66qtA\\nUjb6C83YMtNizjnnBJIayPuJPffccwPuXxVWXb0MnFzJ2B9O36k9z1zJ0+7PZtYYs7HOxvetw9Hi\\n1dLx+3n2Sdlj0Yx1WNRPTOvcTgEqHNcr0W/t57V89V+bbeR6Ko61nSouvvjitve9W3gN6WtXKauQ\\nzWa0o7qfy3uyVa1smlG+ReT1fXYU8f7geTZ+YWxm0UUXBdLY6Q3w2jJGfM4557S1f93AMTHjV0Wb\\nqz69A7fffjuQVhDOqUrlhcIJgiAIKqHULLX8Kak1nlvV5orbH0yr3L/zHHOtMfPz9fEby8mr7ev1\\nN6sC9yGvl9Da8v/GWuyIrdWmMjE+lfdAMiPP+h3f13pze3l36LyKv0rytea1xlTCVkObzXjggQcC\\naR7k3chVeXZONobjdsxmtA9VXo/h2PRSV+B62AU8P68e27Bhw4D+a8Z4zEXnvVMWbpnb06o3W1Wv\\ngPcD45gqXzOxVMgqGev/rMMZlXHu2zHALgyiAnY9pSKqmvuhcIIgCIJK6EgdTj2FodVlxoN1O1qw\\n9oXy83Y8tVOBqkGLxew2fbdVdosuIlcSuXXvGKlMtET82/iF6+Hoj9b69xiXWGIJIPlyrbJXXaoC\\ni7ovVIk+ds+fNUOu6WH8wewzLVrHxrH02F3/RAvXGJ9xMCvUjWfYV0o6XVXdCY466iigv8LRe2B8\\nVC9BruZcQyhfO6aba0Y1+9vGevPO2Ntssw2QVnz1WjKTy67iZnB5baiwRwUcM2uO7Exi5ma973U7\\nIy8UThAEQVAJpSocqff0VNFo6fp5FU9eLe2qmNbhmIXmuhaufqd/uyoaycAx40rr3qwRa43yjKt8\\nlVS7w3rsVgqrBvfZZx8gqT99+HaFzVfRzOlGPYZWt2NgVpljY/2MY5OPlf2hHDOzGO25t+yyywJp\\nDKxZMBYko1JtipapXZ1zxerfZicWrbujspH8c6oG6z06SbNWthmdxuqsSbrvvvsAuPbaa4G0Do7x\\nDbt7LLXUUjWfN+aTr7qak68g28354T449+0rd9JJJwEpk2/mmWcG0rxYY401ar7fLULhBEEQBJXQ\\nEYVTRG5J5GuH5/5FlZA+VhWPvv/TTjsNSP2iqq45GJm1YJzK7tDWHOW1A3a69dhULsYxjE94DFou\\nqkOz0U4//XQA3nrrLSD5r6XIiuuGxeNvao25dr1xp5tuuglI3YHFeeC8UQXaWcAxdqxUg3nX6SJl\\nU2W9VrOolPfaay8gxSXEa6XZfc7nRRXKplFUJqp+FWrel9C4patfHn744UC6pqym1yNifNT55LGb\\n4Zn3EytSPt1EL4GZu3lXFu+lfs77RKMUxXryTNFmCYUTBEEQVEJLCqfVTIei/mK5halF4d/GMbS+\\ntOa05vXN3nbbbTXb6wVfq1kkxqFc10IFowLSP52v8GfPNNWAsRwzrlQFvuarnUqRiuxmdpLZZPbI\\ncmx+9rOfASlDz7iE2WbWT2jVqfquu+46APbbbz8gVVerDowRzjvvvEBarz2vx+mmRetczmN1Wqp5\\njzQtTTP0clTSqkGvId83DrLYYosBKcOrynmhMjWGpzpfYIEFgBTTsweax+IY2QV6pZVWAtJYeR/w\\n+wsvvDCQ1tVyLPxdY371KKN7Qlnk+2HH9FNPPRVIqrBoPSTnvp4X1V/R6qbtrhEUCicIgiCohEHN\\nPKkHDRpU8+FmlUTReie5jz3//CmnnAIka19LeKeddgLg2WefrdleG0/hR4YPH75AIx/MxyIn71Rr\\nNwRrSjxm62i0QLbeemsgdRDQT20tktadfmmtQbs0GN/IuzQ0yuDBg/nqq68YPnz4oPqf/pp6Y9HA\\n9wH48Y9/DCSFseWWWwJJ/VlFrdIRVYDKSOVkN3K35xg3q+6qHIsinAd2/73//vuBdJ4dI+szVHM3\\n3ngjkDI5rXmy03qzNDsWfdXAkksuCaSswXz8vb69VsxGtRuHc95jcD64rpbr5HzQL3kAACAASURB\\nVKiY7NZhTZKKyXnheknWsOQx4D7HMeD+9sK8ELPVvIbMXlXBeN8p8iJtvvnmAJx//vkt/X6jYxEK\\nJwiCIKiEthROyz+a1RDkPnStNP2KV155JZBiNg899BCQfPT2ZtO6b8O/WprCyVWctQN5ZoxWnRaI\\nGXh2RnYdC1f8s5LcqmljQFbf1+sL1stWfa6AHTNrDlR9rmJqnMvvOY/yTha5f9rPa9HaBaJoRdB2\\nxsLOAGaXtYr7akaW2Un5teQ8Uc3ZhUNl5Fhab2ONU6Nx2U7OC2N1doN2HuTdEjy/ZqMZy7P+Riv/\\nvPPOA5JXwFiNatEYUKt0wwuQnx+7hOvlyWvNxJok41157LddQuEEQRAEPUVXFI4xGK2wfK0Y13ix\\ny6tWvL2S9OX++c9/BlKXaDPBmlU4fdRIaQqnz+dq9sm/zZzaaqutgFRXYfaaVpjWtzEa/dIqJDNr\\n8nqKoqy0RvZ3+PDhXfVPF1XRF8WjrEnK1Z1jmCsbx6ooE0dGG200vvzyy5bGIu/SXBb2GXT1U+MS\\nHqPxCuNaRf0NW800LXNe5F4A17lynRrrqzwm57ZWvNfGE0884b4Bqe+g9xEzRV13y99T7TUa58zP\\naTeukTyjV8+I9wWzWPMVg/Ps17I7pIfCCYIgCHqKriicPtsDUhzDehstmPnmmw9IXX/1yVqZfvzx\\nxwOpF5f+6DYoXeEUoZWtxaElolVuzyy7Q5t556udbrVw8vhVu5ZLK9ZbL9Q/9aWszridsGSL9q3e\\nGObqz2vHeZNfA0XbM07abP/BMsaiSG15TahMXPfm0ksvrfm/c10VZ4zXLDXra3xVkeg9MLvNmqNW\\n6QUvgMd08803A+l+YN2eY+X86BShcIIgCIKeoiWFk6+t0KpFW1R/41Pa2gHjHfla9cZwmrVgR9Id\\ntmWFU8+arvd/lY5olfm+efauBaLSMX5RVEPQKr1UY1A2RWsDdaPewjiF3RPcB2tLzD7qFZoZi8GD\\nBw8fffTRR8zNornv9ez9wM9fc801QIpTWpdlTMb7hEpGxVOUeVW2Aq/yGinad9/PPSZ6icqOIRYR\\nCicIgiDoKboawxnJ7wD91+awlkC/cwfWoq8shtMsZa/UV29732SF0yzfxLHoZpZao0pjiimmAJLC\\n0Xov6hc4kv0Ayu8PNyrMi7JW+q13zkLhBEEQBD1FpQqn17KYBqA0hdP1tcPbHOtWrLduH3O7jAo9\\ns7pNmQrH2I2Kxb/zPl9lk8dw9ZxY69YoZc6LTtVtVUUonCAIgqCnaHY9nA+A5paO60MPKxsZ2sRn\\nRzoW3bby2xzrZsYB/jsW3T7mdinY/5bGov296UlKGQvnZh6Lqcq6z7NTm1U2/6XUeTGqKpv/0vBY\\nNOVSC4IgCIJWCZdaEARBUAnxwAmCIAgqIR44QRAEQSXEAycIgiCohHjgBEEQBJUQD5wgCIKgEuKB\\nEwRBEFRCPHCCIAiCSogHThAEQVAJTbW2abQx4ZRTTgnA22+/3cIulc9kk00GNLQE9QfDhw+fpJFt\\nRpPGRIxFoltj0amF+HJGhbGoik6Mxdhjjw2kpaFHFRodi6a7RQ8ZMmSglTLbotVOqR3oTtxwt+ix\\nxx57+HTTTTdi1dGcccYZB4C///3vZe1bpTRzMQ0ZMmT4WGONxT/+8Y9O7lLDjMorOxax0EILAfDQ\\nQw+1tZ1udBHvNeqNQaP3lWbHYvDgwW3/Zqdo9/ejW3QQBEHQU7S0Hk5ZazdMPfXUALzxxhsAfO97\\n3wPgzTffBOBb3/oWfX/vgw8+aGi7bexfz674mVtl//rXv4C0jnvZdNOS7bV1k5pVe2OPPfYoq2zr\\n0c150ajXoGy14Hx0e31eR3m1lzPuuOMC8Pnnnzf1vVA4QRAEQU/R1oqf+pP1LxeRWyZzzDEHAM89\\n9xyQ1ipX0ahwtCwMiGrxasFcd911QAqUbrDBBgP+fpGFMgAtK5x99tkHgF/+8peNfH3EWDg2vUY7\\n1lu3/dHNUk8RfxMt2VZpZyzylTbbxXmWX98TTDABwIiYYn5evY/42um4xX/3NeYFoXCCIAiCimhL\\n4TSKFsh3vvMdAD755BMgpQCaPu3/m+Wxxx4DYJFFFgH6ryRYxACWbc/GcKqmG9bbFFNMAcBnn30G\\npPP4/vvvA3DVVVcBsPfeewOw7bbbArDmmmsCMP/88wNJMedzu15sqCgltcqxePzxxwF47bXXANh9\\n990B+O53vwvA7373OwBWXnllAG655RYAVlllFQBuvvnmmu1NPvnkALz77rs17zeqNmaccUYAXnzx\\nRaC3rHrPp3HMbbbZBoAtttgCSMf4pz/9CYAdd9yx5vvGQVull8aiXSJLLQiCIPhG0ZLCaTSL6KOP\\nPgJgwgknrHlfhTPLLLMASeH4lG0UrbOJJ564ZrttPK2bVjiNjoXHaFFsr9NJ661ISZgZc+655wKw\\n0047AbDddtsBsMMOOwDw6aefAikOttFGG9X87fkvK1bQzlgYXzQOKbnCcJ8//PBDAMYbbzwADjvs\\nMCBZ7yqc+eabD4DZZ58dgEkm+bpeefnllwfgoosuyo+h5vMPPPAAAOOPP36jh+Z2mh6LTmUdul2v\\n//vvvx9I2a8qZNXdwQcfDMCzzz4LwKuvvgokRd3s/aKdsfD8+5qrrSeffBKAueaaq6l9qoe/7zXo\\n3157+b1z1llnBSisN5RQOEEQBEFPUUkMR9Zaay0AbrjhBiBZqq1mamkh33HHHUDy5bdB12M4WhxH\\nHXUUkMZIy/fUU0+tt19A+xliVfqnVbpLLbUUkI5R699Y21tvvQXAVlttBcCDDz4IwEQTTQSkOi3H\\nbtdddwUaj+kV0YmMPWMr77zzDpAyqszU/Mtf/gLA4YcfDsAXX3wBwH333Qek2jVVg2Ol9T7zzDOP\\n9PeXXHLJmu01Si/ELVQF3//+94GU7Xr99dcDMNtss/n7QLLel1lmGQBeeOEFoP0uIL0wFs1irePq\\nq68OJIVrjHDhhRcGYIEFvr4NOnb16v1C4QRBEAQ9RVPNO4sosqLy962bkWHDhgGwyy67AMlyyfH7\\nxoTOOussIFm41157bXsH0EU85rXXXhuA4447DoBpppmm5nP6dE8//XSgvz/cDJwTTzyx5v95F4de\\nQNW28cYbA0nxGu9QkRj30L+tj/7222+v2d7f/vY3AL797W8D8N577wFw6aWXAvDDH/6wZrtVUnRN\\nGFfw/3vuuScAJ598MpB853l/Or+fKyS//8QTTwAw00wz1XxeBeQ106yy6SWshnfsjMF4HzBO6jGb\\nhbrooosC8PTTTwO919FiZDTaPcVMTz0ir7zySs37jpn3Hf92DIw1ez8xVqjybrdfYiicIAiCoBJa\\nUjgbbrghAJdddhlQHC8oel/LwpoDfar64n1V0VxzzTU1fxsL0rrTv9huXn0VaJ2vtNJKQIpD5VlM\\nOWaraLWpFlddddUBv+8Y64uVJpZq6BgqkRtvvBGA448/HkhWux0j7r77biDFbIzhFJF3Unb71qzo\\n4+8m+TXh36eddhqQVH9uyeY9rlRIZhtdccUVQOri4fkXLeTNN9+8hKNojrKUxNChQ4GkhP/whz/U\\n/N+ss2OPPbbm/8YlrrzySqC/Vd+LPPPMM0DKKqynbLz+rd9yzD3v9fDzXmPegx3TI444AoDddtut\\noe0V/k5b3w6CIAiCBiklS83K7mZ95H7vkEMOAVLdxT333APA2WefDaTsI5/ic845Z83nzXIqoXdX\\nx7LU9KVbJW/cyhqCegrnpZdeApJv3+0tvvjiQFIDjoFxDS1g+0v5fj06kYHjPhvDMavQfdfidB/t\\nHFGvBkBFtP766wOw3nrrAcmyNQPn6quvbmQ3+1HGWHjef/WrX7W0D+LYTT/99EBS/TPMMAOQMj4f\\nfvhhoH+fMeeb32uWbmRmaaVPOumkQLofeP8wg2/rrbd2H4GUqef9xE4ml19+OZDuVw30WByQMsbC\\nOOYll1zS1G+LsRhjfz/5yU+AFLt9+eWXgZSV6DE2qnxE74HXVE5kqQVBEAQ9RUc7DTRKngFhpbkV\\n5j7FzbyxN9K+++4LwG9+8xugvo+/CK2+Dz74oHSFo1X1gx/8AEjWlTEcq6J/9KMfASkrRN/pSSed\\nBMCvf/3rAbdvjystXDHuoWViZk49VlxxRR588EE+++yzjluydoYYc8wxgWSx+rraaqsBKfbiPHDe\\nqQrtN3bkkUcCKSZoHc4ee+wBwAorrNDU/g0aNIjhw4f3RL3FdNNNB8Drr78OwPbbbw/AKaecAsCm\\nm24KJK+AYygqI2MCrV4r3VQ43qusHfGYzD7zvNux/fzzzwdSzFClrLIxBuz9rFEPTS/NC5Wqno88\\ntif+vddeewEpC817r16F/Br0/mJt00ji9aFwgiAIgt6hrRhO2eue+LS1lkR/5LrrrgskJaOFa675\\nVFNNBaQMrmb3R7Vx6623drzTgFaXdRMew2233QakbDQztor6gWmVOVZaLB67mXtFVls314BRmXjs\\nZmCZfaQisd7KTL48VqjV/9vf/hZIKi+vv/jjH/8IpMr0nGmnnRZIGT453bRkrY63fsaq+uWWWw5I\\nFm1R1bzzwWM0c884aKMMHTqUd955hy+++KJrY5H3WvTYnAd6C2SzzTYDUl85u4nfe++9QKrXsqtD\\ns1Q5Lzx2X417Oue9NlR/RTFh7xt2YDe263aXXXZZIHmRGu3GEAonCIIg6Cna6jRQlrLRN6+FayaP\\nnXFdk0PyHPN6Oer1Yk633nprK7vdFGYp5Zk0WuOuZ9KoH9kxsoOyWM/hdszQ0VKWemPWCTwPZlKp\\nbEQry64I/q31ZgW5VtmZZ54JJP+yOKbzzjsvkHz7c889N5Cq8aVI2fQCxuDyim+zFvNrMO9Obd2O\\nVnyRsqm3Po6xo14gP2Yzp+zWsfTSS9f8304TZm45dtYBtppl2wlU9XYH91ifeuopIGWzLbbYYkC6\\np/30pz+t+X4Rd911F5Biy8ZuHDPnm6pQFej9q11C4QRBEASVUEovNS3Ojz/+uKnvFa1bYvW8T+98\\nzQ6/Zy2LMZ6iOoteqCi+8847gaQsiirO6+Gxq+78O1+nXQs3z8zKK9arxH1zDLSuPBbjTsbk8r5N\\nef8xffRad2apud1DDz0UgJ133hlI1dNWTe+3334lHVkxxhfMOmwU41IqC8fOY899+pL77htd76be\\n2kFmZnWT/PdVZSqVc845B0hdF+w+7hio8uy2kc9H6WaPNT0g4uqlqri8js7uKvZYrLemmN0avLbM\\nEPXerdKxb2HZhMIJgiAIKqHpLLUhQ4aUtpKi/mgrys28+PGPfwyk6lmfwmYr+T3/XmeddYCU6eUx\\nmbWi77YBur4ezkh+D0g90LR87ZXmMWudtao6pZMZOFppWuNFfZ/sQPHzn/8cSPUU+tzdTu57V8XZ\\nt84xMr5hXEslXe8aKHMsrLe68MILR7od41VvvvlmzT7m3X5ztNaff/55INXnqALapdmxKFMZ5V0T\\nXBV1wQUXBFLdlvEula/eBc+7XaVVkdaDNUsVWWqef+e63RNEFWYtoWPjMeVqzT6UZi3aqcQuHcZP\\nvbfqVaiXkRxZakEQBEFP0XQMpyx1A+mpq0UiWn9mXPlUzVdFFC1Zn+buoz2XeoF2/cJ2HNCqs6ZA\\nup1h04jyVXHqQ7fq3bVZtKrMjLnggguA/tXQ/l1kbZmdZudk6y7sHmx36m7EJJzb1ju4T3k2kuf5\\n97//PZDiEfWwTsc4htX4+fxTIakGW7XyR8aQIUMYd9xxW952blX7t/uuircGzfl09NFH13z+0Ucf\\nBVIvtosvvhjojdhujvt80EEHATDPPPMA6ZrI99nPu8qtWatm9pqRaR2X80i1r+K2L6W1cXZ1yeOm\\n7RIKJwiCIKiEUrpFj+TzQHHevDGbm266CUj58WZquJKf3X7NyLCOwz4/K664IpCe/mY5mVPeREeE\\njsVw6tU5FKFlqgq0al5fvXEQ4xq+32iNUhGd9E8fdthhQIrRWPWsctGq0p/sec0z7IrWQTIzzPnh\\n2Ocrifq3faba9U9D82Ph+XEf7LKQ97pyn41j5XPaeaXF6lpVft4uCyomLWbp021jpPvbybHIj8k5\\nnMfu7J1m3MEY7s033wyk9bPsquDYGMszlpMrp6K/i+jkWHjvm3DCCQF47LHHgBSrsY7GzEu9A14j\\njpXXVt59w7i4tWn2mcuzXVWnebZjfj+LGE4QBEHQU5SqcPp0Xa55X7+hlsUA2wXS0/eRRx4B0lPc\\np7RrOohPYS1elY9Pd/3h+vKtsvb9AeIqlWWpaZnoMy16XyvfrCOtPi0LLY16+ffNUkUGjrE3/c9m\\nDaloPT+5NV5kgRrXMi6iAhKzmexgYa8+Y0WSV563MhYqEn3lRbiWS1F3Z68Bj9VrxBiP1fV2W9D3\\nn2PcQjWQd2jP46JFVNk/TKva2Iz9BVVvjp3q0KxWu0V7P9CDYp/CPN7ZqNch9xq0MhZFnoei950X\\nV111FZBigMbojNnYNVycP14DnmfH1N8x3mXX6WOOOaah43HMVVahcIIgCIKeopROA6Kyyaug7d+T\\n14r025n/PuX1wWvFFdUc5Bkbft61YMxWEpXNCSecAKQqXq3IKrE+JremtTQcO7OO8hoVx6TZrr+d\\npF5PKo/J87/yyisDyeqyuln/ssq2aDu5wtHizZWNnzOmp7Wnrz+njIy/espGjD+piDyGfE56DMY/\\n/Z51FHZTyFEVuA7K6quvDsC2224LJGVjBfrbb79ds/+txh7bIR+LW265BUid1j0/7rtjsdBCCwEp\\nG9IsNmM93h+cV94/6sVsirwRrVAUU83fN5PTPn96j/R4uK+5srHXmmPj+TMO5vfsAn3ssccC/ed8\\nUWduUdk0SyicIAiCoBJKjeHoT7bu4bjjjgNgk002AYrXaJCiLJEiZeT7WirGBFQDWtB5Hyqf9lq6\\n3Yjh5OQZV1o4ZmzlaKFoCZdtgXbSV28PtPPOOw9InSDMlHEtDnuhaW17Xl0DxN5YWltmNw4bNqzm\\n9/J4l/Mgz/Arsto6MRZ53NLqd6+hfK6bpWQcyn2eYoopAHjllVcG/B0/Z9ZTvl3nmdu3Ar2IKmI4\\n7rMrthrTy5WKn/N8XnnllUCKa/g9rxUVk906nBf1FE7uselzP2l7LKyXsdee88H7gXN54403BlLN\\nmt1YHBP/9tpwX72fqOqmn376mmPwd3KvgDGgRrNcI4YTBEEQ9BSlxnBce961XbRki2I2OUWZVvW+\\n75r2VhIfeOCBAEwyySRA/9jSHXfcAaQeblVSZE1piWhpFCkb6ZSy6QSeP18POOAAoH+38JdffhlI\\nq1kaa1PJaN153qwZWX755YHiTCutNF/tNODv7rPPPgAcfPDBLR9js+RZZ3Y8z8+nlqiZWWbU6buv\\n103DWrc8o8v6CuMS3ei6UBQfUsmqgI03+XkVi+c7XytGzG60A/LTTz8N9L+2Gqi3aehzrWCtmErH\\n7u7WJDovjL256rEdBMzEK9pnYz/5yp1+z/f1IuTxsbLXzQqFEwRBEFRCqQpHa0yL06wjLYr11luv\\nqe3VqwDefPPNgfTUNzvF/+f1G2JX2SrIVVuuunJfar1MmLyyvFG6kW0keTah9RCuIuiKjOeeey6Q\\nFIzKxliL3Ra0zvTRG3+w3ssxssZA/7eWs4rGTEGzmbpBXmO2wQYbACnjymvJtX7MUsqzF3fbbTcg\\nrQllN3FVpQonzwDzGlJdVkk+F71WjK0aq9EK93rOa4gcG8kzsewjlnfebpROXjvWCKq+PA+u9eWx\\nutaPY1KkPIzVGZvLu3BIrnjya9T5UTahcIIgCIJKKCVLLbcAfCpb9bz//vsDqT+UvvnrrrsOSGt1\\naN394he/AJLfWuvPDBozeorWeimq2s33cwDLpWNZavlKnFoqZmY5ZnmvrBz3udOdbtvJwCmqsleZ\\n6Cf2GFz7xZqSG264AYBnn30WSErG82Qml5ZrPg/srWfFub594x9mKfXZf6A7vdTE+KPzwAw9a9jM\\nQlpiiSVqvmdfOlX7NttsAyTfvWvTP/nkk0D/FWCtefKcGBs0Symnyk4DqrM111wTSH2/PP9mpdpJ\\nwLiG59FjyLPLWqXV6vr/7kNDY+G9yxib8Wjj1F4LOd7r8sy9qogstSAIgqCnaErhDBkyZPhYY43V\\nb635bxClKxytIn2ixhns52XsxrVecmtMy9PaAuMcnaYKS7ZIWajyVES5IinCTtrGgFTGjnUTXcNr\\n6GQdTqP7Yhdg54kxHnvsWV9hPMvuDVbp2ynZeZV3rmiUbigc99XOydZb2fdLRa3yKIq1lG31VzEW\\nxq3shJ135TD+6bo57dLpayQUThAEQVAJHV0PZ1ShT9foyjoN5P5gq+tdD8X1S8zoci3yqnyzZVpv\\njXZO7lXKHAv7BFpZXjVmctrdoR55TKdKhdPrdHIsvGasMbLrgurNWsKy7gcbbbQRkDJ+myUUThAE\\nQdBTtOTIzatUc7pZ89EMZWWvtIL58fZCskeWmEef15aMivSKsmnVP10m3VI2orIZYC2oASnKVusk\\no8r9o5N4zZit9swzzwDwwgsvAMlD0uh5rIfKptPXSCicIAiCoBLaiuH0gsU4EG3sV+XdorVQtCSt\\nw9B3blZS1YSvPhFjkYixSMRYJCKGEwRBEPQUTcVwRhttNCaccMIRueGNKggVhzUn9VaLq7faXD16\\nTXGNDH2v1ln0qmpshk754PMeWqMivXp+I27SW9TrIzmqEgonCIIgqIRmYzjvA693bne6ztDhw4dP\\n0sgHv+Fj0fA4QIxFX2IsEjEWiRiLr2nqgRMEQRAErRIutSAIgqAS4oETBEEQVEI8cIIgCIJKiAdO\\nEARBUAnxwAmCIAgqIR44QRAEQSXEAycIgiCohHjgBEEQBJUQD5wgCIKgEppq3tlui20bVH7++eft\\nbKaTfNBEa5tvdIuGdlqvf1MaDUq0oU/EWCRiLBI9uTzBAgsswAILNLTcTLf4pvY6qsuQIUNGdAxu\\nlUGDBjFo0CBGG200Rhutvy1T9H697XXq80E1DB48eMS6T52k0+e/2fk7EP/rc7StBdjmnntuAJ54\\n4gn/D/SeZesk+fLLL+t9tPIF2MqmrHNQpfU2xhhjAPDvf/97pJ974IEHAFh00UXb+bmmCUs20Ytj\\nkc/5evOp6Bqpd+3k/+/FsegWPalwgiAIgv9dmtKHM8wwA8cddxxrrrkmkJSNtLtYkLLbRcnKogFl\\n842h19RlX1w22xie57meshl99NEBOPHEEwfcnstzt0ruSoxFyKqlUcVRdH/Iv5fPJ+fPf/7znwE/\\nX7SdZv8f1CcUThAEQVAJbcVwuk0HFNEoH8Mpi3b802UtBf3WW28BcM011wCw0047tbW9IhZaaCEA\\nHnrooQH/301fvWM55phjAvDxxx+XufmmaXYsRhtttEIPQ6/GfIvuKxHDKT5nEcMJgiAIeopKFc5U\\nU00FwNtvvw3AzTffDMB6660HpDqdL774AoDnnnsOgPnnnx+AI488EoDNNtsMgMknn7xme0V8+9vf\\nBuBvf/tbvV0cZRSOVthPf/pTAH79618Do1aWmufb83LYYYcBcNBBBwHlx/JapZuWrGNwzjnnALDn\\nnnsC8MknnwAw33zzAXD55ZcDSQU+//zzALzyyitl7k5LY+Gc9Drs1Tq8Zq+dXlY4RZl6ZcU9c0Lh\\nBEEQBD1FU1lqQ4YMYfzxx+fDDz+seb9e3vsee+wBwCKLLALAtttuC8AEE0wAwCOPPALAlFNOCcA4\\n44xTs73XX/+6HlPLY+mllwZg7bXXrvmcVv97771X8/sNKJuO0W6cadZZZwXgmWeeAZIVJldffTUA\\nRx11FJBUpMc8xxxzAPDwww+3tR/tMOmkkwJp399//33g66xHgM8++wyAAw88EOg9n34VmBlnzZi1\\nRqr8F198EYCPPvoISCrh9ttvB2DaaacF4JZbbgHSGDZRg9YRBg0aNGJfcmVTdgxH6937ymuvvVbz\\nOwsvvDCQ7jc77rgjACeffDKQ7jvOR7Pb6mVRdgO9Qk8//TQAM800EwDXXnstAPfffz+Q7rmO8T//\\n+U8geRe8Bn/0ox8BsM466wBprP71r3+Vut+hcIIgCIJKaErh/N///V8/dQNJcWht5Rx77LFAUh7G\\naLTiZpllFgAee+yxmu+ZmZMz0UQTATDJJF+3PdP61xLRqtNqLLKgrL/oRN3F2GOPDSSLQooyuFSJ\\nU089NQB33XUXANNMM81If0eL5O677wZg/PHHB1JcS9XYTdXgeXz33XeBNO4zzjgjAMsvvzwAe+21\\nFwB///vfgfpWeSfPX1WogF944QUA3nzzTQAuuOACAGabbTYAttxySyAd6w477ADApZdeWrOd/Dx3\\nuwZtZPOu0TnptSHGrU477TQALrnkEgAefPBBAOacc04gKWtV/yabbAIwor2WMUMz/xxzlc5cc80F\\npA4X3biGvB84L9wH73lPPfUUQL+WO4svvviA21PZuJ2XXnqp5m9rLMtWNhIKJwiCIKiE9jrR/ReV\\njVljWrJaFvrstThyfvjDHwL1OxX4vurh1FNPBZLC0gpo1KrrpGWsslHVeexFtSmqs2WWWQZIyqQe\\njpGWi1ac7xsX2XnnnZva/zLRGtt6660BuOyyywC48847geRn9v+rrbYaAMsttxyQ6mPMxPv9738P\\npPN80003ASne5f9VidIrWW992X777YF0nq666iqgf6zu3HPPrXnN8drTMjWLbVRWf2anemwzzzwz\\nAPvttx+QMq3WX399IMVk/LxxTOebcYlVVlkFSGP0xhtvAEkl6oVwPqlwqmCsscYC0nl03+See+4B\\n4NVXXwX6K5tGyeeXf//2t78FkldChfXyyy+39Ds5oXCCIAiCSihF4YjKRqwUL8JYjJk3WqAqIrPb\\nrMvQtzrZZJMBSUEZxzj99NOBxrNKOtW7rS9Fqk7MhFGd7bbbbkCx5eK+ouhygQAAIABJREFUrr76\\n6kAa83feeQdISueAAw4Ako+3SnKFqoJxX8y4UsHk1paK5dFHHwWSCnBMNthgg5rvqYgmnHDCmu3Y\\nO0sL+LrrrmvzyMrHuEGewVUULyias84Dv2f8QWvdrKWq6Zul1ve9vq8ei7Fc41l6CYYOHQokZaOy\\n/etf/wrAeOONB6RMqzPOOANI1rrXmPV7ZrM5Nqp/e0MaQ+xGdmt+Xr2eVXt6c3ztFMbZy15KIRRO\\nEARBUAmlKpxm0Qerv1JLSAXj31oqa6yxBpB8+X7/iiuuAJJF2yjd8OlrhavqPMYpppgCSNadaJ0V\\nZdxp8Tpm1h74ea24KnGftUxzlWd2WhFasFtssQWQagVWWmklADbddFMgxbmK/Mvux9FHHw30psJp\\nturezDznbq4Szj//fCBZ/Vr73aLvfK1XE2R3BI/JGiTVmnPa82q848ILLwSSEl5rrbUAWGyxxYBU\\nq6YStuu4XRi89rwP7bvvvkCKETfabbodHn/8cQDmmWeemvedHwsuuGDNbxcpj0bj4PXolLoLhRME\\nQRBUQle7RWvtazmYGfHBBx/4e0CyjKxJOPTQQ4HU5ddq+lw15DRQn9O1XmoTTzwxkOJX1tUY5ygi\\nt77yHmvDhg0DksVrrEeKalnK6BNl9fuZZ54JpHqbIivLOIQWZ7MUnXfHJq/naGK7PdszSyvf7DYz\\nsYyPtnvsOVWMhXPYbFSzGV1hWOv7kEMOAVI38byDhUpKdeD1b78556d96FRA6667LpDqArfZZhsg\\nzWMpYyzqxZG9L6j+vI6LYrzGvfT6nHfeeUBSc0sttRSQOpOY0VeE/zdeZtac2WsSvdSCIAiCnqKr\\nMRyzRbQcrJq2ctj+QObN67vXL22MQCu9nlrT4imqyq6C3LeqhZorjxVWWKGh7eXKRkvJnkr2hSqy\\niHJlM2TIkNJqN4wnGbMx9rb77rsDaQzMCmpV2UiRf3vVVVdta7u9jOe/6BjtyF5FRmaz5NdCHuNR\\nvavO9IA4j6zvUtmYxbr//vsDaW77uSWWWAL4//bOPN63udzj73OcdAhlSskQKrMMSZFMkaSIuIYy\\nZHZD3FDqkswKTZJS5jGEzEXGRCVk7KqkNFHIkFucc//ovs93/56z11lr/aa96Xn/s1977/Vbw3d9\\n1289n+8zwSKLLAKU6tXm43g8832MWovKpp94P1ZffXWg5JC5emOEp2oudr0VFYgrGo5R7J+kv+vq\\nq68Gpo8sjhhZqh82KpsZ9TsajVQ4SZIkyVDoSeFES7JOMWhlabEYmWEklVn25t+YZ2MvENdu119/\\nfQCuv/56oPh8mjJMKy9alrE/u2urWneuW1edo2pOtOLi9ion16FVEfrNqmol9UPdeG3iWrnnqFXu\\ntah0u8V5aP6VlrDWoj6ApoxHNSDx3MyXqOLMM88EulfzvVZ0Hi0PR6rqvnlM6wJqZfs9cdlllwFl\\nLFTQVn3Wh+Ocd7XAaEX9oieddFLHfrTex2Llw7kqVrS2Ppz/jyreSF0j+VzRqKuFpiJyHsVnVl9Q\\nVR6hx29bqy8VTpIkSTIUWiuckWv8bS0BLVkjL8yijVaUNYy0hLfYYgugrLUusMACAJxxxhn/uoj/\\nVwdt+1YMw5KN+1Zh2J8mRonUWQyOfV08vWu3VtRWFQ6qCuxIqnrBH3nkkQB84hOfAIovrtfxN3In\\nVhd3zb7tPB2PysZVAVV/XSdPrXej18aqWvjUqVNbqyR9KUbaWVXeXDN9u/o9VXGuDqiMPK6RVQcf\\nfDBQnnv9F4cffjhQvldi/bJ+9+1pgvfbYxtdFlHRxB5gdbi6EJWN1+g8q6LbsUiFkyRJkgyF1gqn\\nlzV+FYqRM5FoWdrTRav/Yx/7GACXXnopUCrsGpHVlmFasloUqjEjslxnbtqZ0TXVOovmvvvuA4q1\\np78rZqoPEvOm7r33XqBkcJvx368K1uYcRPT5mV9h1V/ztV4MGEmlNW4kVhWxSnivPrl+WPVN9+Hc\\n1LrfdNNNgeKPNI/L/8ccMxWOaL1bkcLajocddhhQVlgkKpux7JYaq8pH380OO+wAlA6vbfHZjLj/\\n2MerX6TCSZIkSYZCa4Uzo6iTOvyca+vWKrJGmhapUWq/+c1vgOKbMWJDS8iokm4rmg7SgnENVKtK\\nv9XDDz8MlEoAWqJ2KaxjtI6ro+Fxjed3DXhQyma0eaGycU3e++Q1xHFv61Mz32Ldddcd9f/Wodp4\\n442B4guwkvYgqers2hTnphFWRi2Zr1E1531m6vIrhhWJN2HChGkqO+aERGKtNPtsWSvP6DJ9t1ba\\n1jfjmHlN3n/vgRUFXGlxZUSF5Hb6jqM6HDnm/fbnLLbYYkC5Vr/jPBd/2q3U/BxXgZqiWtRfFdF/\\nrm+oXxUqJBVOkiRJMhTGpJaa1p/9s+2PouXrWqoWhpnpxxxzTMd+7H+jJWTPD2PMu7BC+lZLrSqy\\nRevLn/YeN2qtas09RpPUWabxuP7umO2+++51n29dJ6pKMZonYWRVrHTsuRllZmSVytftnTf7778/\\nUPokRcxNcI3+pptuAopPoG3e1ljUUlMRq1S1OI3cigpHa15rvYqq2nlNFU8/xyIe02taccUVgeLn\\n1B/pasCuu+4KwFFHHQXAzjvvDBRr3PlkV8z11lsPKMomVriIuWxWMLFHVRyr2WefnWeeeYYXXnih\\nb2OhgrFrqf6p+Bz7Heh20W8ViV2Yvf/mb8W8Pp/dOJZ1ZC21JEmSZFwxJrXUzAW55JJLAHjwwQeB\\nUifIjGDXcq0jFPEtvOWWWwJFMe24445AeVtXWXWDJFoGWv9aqvqp7r777o7tq8616Vp7lT/KelKD\\nzCWoOrYK1jwsFYjnEqsAe/+NlFGxmi+x7bbbAtNnSbs/P2dEl/tvq2zGEiPpjKg66KCDgKICHJND\\nDjkEKH6NOlzD1y+qZe1Y+ky1zWnrhjinvX/OVTu++kxsv/32QLmvWulRIYn+rujPcjvVgWPivNEP\\nFlcV/FzbHkZN8LtOZasvJWLlaqstOCZGasY+NvHaHauobMT5NKjviVQ4SZIkyVDoyofjG97aZ0bQ\\ntNgPAGuttRZQLBpzTKz+6s/zzz8fKJ38xOOa12HNNS1o12hj18wZqIXWPhyznmOnzoiRUlaidZ3Y\\nSKu6CJ6meG/M31B1uM5tf4y6+97NWr3qrc6PUEdUeZdffjlQ8nbsFWRUkXkWWr7m+1gR15p9TRml\\n/l3ffTixj9GIzwNlztubRfbbb7+OzztG+jPqqFIw8ZqtqKwfRNqOxcSJE6dFk6oc6vjgBz8IFF+e\\nfgjvt+fqCol+UM/d741FF10UqM4pcdVB32FV7ksVg/TtGa3mNUT0h/odp4qP52xlk2222QaAY489\\n1vPp2M7POdZtKxekDydJkiQZV/QlSq3bWkMLLbQQANdddx1QLBUtGH8aZWTsuG91LV0tXyN6Yr2x\\nFufV946f1nsy4sZupa6VqkBiFem2+RHm8dx1110df9eSNR/HHh91jMcul3FN3bV317vtdmn/kqpe\\nQZG6qufDGIs555wTmL6qd+yTdOuttwLlWrVI9flExSSqxlVXXRUoPkSVtzimVTX3BjkW5q55Ld4X\\nz10Vp7L58pe/DJQcFtGvYZ5OvJ/xfvt722duEGPhd1dVjy+/L1Rn+vJiTUb9U/akqqr67P5uvvlm\\noKxatSUVTpIkSTKu6CpKzfVj+5wYhTRtpyEfQwvCn0Yrueavv8GfVjj+4he/CJT8i2jxGIFhFWIV\\njlFObdchB4HKJtZS06+wzDLLdGzf1MrS8tVyida/aP1r6QySQWevR6vPNXd7/ujT0+9x4YUXzvB8\\nYv8c96t1OKh6UqPhGrx131xzj6hsxDkvXrsqwGfDKKall16643dxLPqdWd4E/QrnnHMOUHw3Rt65\\ngmHUmhUDYi0082a8NudjVcUA/x8Vjj4n1cMwIvakLq/G7w99OH4Hx+9IfblVFSniisoDDzzQw1k3\\nJxVOkiRJMhR68uFES8G1VN++Khzf2sbNn3DCCR373W677QA44IADgJJXs8IKK3Rs5+e1SK2U6jq0\\nForr4dZq23zzzTv2M4M6V3334YiqLq5PR+tqww03BMqY6b9SzVVZLK65r7zyyv+6kP+39mOPmKb0\\nY31aq8nIvF5xftlPx4xzr9H7GvNt9BXGasDOfbP3q+rUDWKtPvoXrfxw/PHHA9Nb5VHdxXlg9OHR\\nRx8NlOoOPiPRStfXE+vcjWVklh07vZ/3338/ALvtthtQVj78v9a+12IF5bPPPttzrTqvjt9jHk5T\\nBjkW3i/vT4Nz8TiNtvc7O45ht6QPJ0mSJBlX9LWWWqzbE3MN9NG4rrzVVlsBxZq3ntjyyy8PlLev\\nSuSGG24Aytv5uOOOA0qUW8T1aK3FBpUGBqZwxOquWmteo7S1VOoyh81NMfqpKb1Yb71WSo54v6Mf\\nrM4ijWv09gQy/8uIHCN0PN84b8ciYk8f3d577w0Uq937rVpbYoklgO47ubatLDDInKStt94aKNes\\nD1fV5v33e8Tn+bbbbgNKNem2HYm79T0OY17ol6rrwNkUxyZ+70Sq8sSqSIWTJEmSjCv64sNxH0aR\\nrLTSSh1/N2JGhWIugb4Xt7NvhtnN66+/PlDW7H3rxn4ZkR6ipQaucIweca1+zz33BKqjg6KfTEvW\\n7auUTa+MpzycGDXW1N9gV0M/F7PmmzKexmKs6cdY1OU9GX1mRN6JJ54IlOoc8XtFBWS0bKwKHY8T\\no11jBfem9DIWTb+jrJriOavu2vYAq1sJ6ZVUOEmSJMm4Yij9cGI136rM3/j3qs+95z3vAeCaa64B\\nuo+TH8XKGLjC6RY7P2qlW2tpULwUrHrnlfle5jzV1fSKiuqlMBb9opexaFq13W6W+mZ22WUXoDwD\\n1hezeri1FGPVjl6rd9QxlvNCH4xz1ZUTK1QcccQRQBm7pnRbNSYVTpIkSTKu6KvC6fbt2JZoKVVF\\nRZmF2yLLftwqHLHbZdPqwBEj+upqJr2YrHrng/PPCC9zUVzTl1iJoI4X01i0JVYFsaumtf4i3YxF\\nXZdRf8bKJLF/klUzjII1p62q02yL8wSqV1iqlNFLeV60JRVOkiRJMq4Yig8ndtjrV35GvzDy4+mn\\nnx73CmdYDNN623fffQH4/ve/D8AWW2wBFJ+L1ResN+bavjko5mPFfkn9op9jMaxVgEHRzVjEnA7H\\nwKhUe0HFvCkxItNKI/Zbisq139Tdq1Q4hVQ4SZIkybhiTH049u+u6zXftJ9JjLOvq6U0yv9fMgqn\\naURQFWNpvXm/rZllLbaqzp0xr8K1/L322gsoGevd0s+xGHRF7UEzjLpyvc7dOqruQdsKGalwCqlw\\nkiRJknFFW4XzKNCsMfmLk4WnTp06b5MNX+Jj0XgcIMdiJDkWhRyLQo7Fv2j1wkmSJEmSbskltSRJ\\nkmQo5AsnSZIkGQr5wkmSJEmGQr5wkiRJkqGQL5wkSZJkKOQLJ0mSJBkK+cJJkiRJhkK+cJIkSZKh\\nkC+cJEmSZChMarNxVQG6F3tBwhE81qK0zUu6REM3hQlfrKX355xzTqCUu4/nn0UaC/9OY1HX2O3f\\naSzqaDoWrV44VbzYXjTrr78+AFdeeWX810u11tHAmTBhQmW1bvus/+1vfwOad2asqxrscfwZ52HV\\n5+P52Y8lMv/88/Poo482OtemaJx57H6/nCdPngyUsfjHP/7R6HzcftCVmmHwhkm3+49jUTVPR871\\nQfNiNeKqyCW1JEmSZCgMpePnoK26PjL0fjjj1YIZxpKa88JOnj/72c+A0hnWDo9NFXTd0m5cIqk6\\nXztMqg4G0fHzla98JVDdtbKt0ohdNZtSd8/syjliuXFoy0j9Ult11xjvd9XnXvGKVwDwzDPP+PeB\\n9waq6hUUFWnTVQOfrZVXXhmAhx9+GIBHHnkEgC233BKA0047DaieV/HeZD+cJEmSZFwxEIVT52wb\\nx7xkOn42JVpt0tZ6m9G6tn6FZZZZBoCf/OQnQL0i0Yry856jn9t8880BOOecczwPzx2Aj3zkIwD8\\nz//8DwA333zzqMdbdNFFAfjVr34Vr4upU6e2GouZZppp6iyzzDLdeNZRNRbRkpxtttkAuOqqqwBY\\nffXVR/1cxGfSMdJijWPmWD/33HOj7mcQ3U/7vfLRtANw3d+rfIMyCIVT9TyOsj+gjKEq7TWveQ1Q\\n/KWvf/3rAdhggw0A2GWXXQC44oorANhqq60AuOaaawDYZJNNgHLNTebV888/nwonSZIkGV8MxYfT\\nbwbo9/i3UzhV9EPhtL1P0bL0c1rnWvurrroqADfccAMA3/3udwFYeOGFATjzzDM79qO/5M477wTK\\nuvUPf/hDAOaee24A/vSnP416Xr1YslEx1Fnf73//+wG4/vrrATjkkEMAuPfeewE49thjO4533nnn\\nASUSUL/Xfvvt1/G70XZarCqm+eefH4A//OEP8ZpHvb5+zAvv54j1/6a77ApVQJxfnsess84KwNNP\\nPw0UX47z5sknn+zYXzfKt+33Rbf+UD/nNb3hDW8A4AMf+AAAp556KgCLLLIIUFICbrvtNgC23npr\\nAH73u98BxZdT509LhZMkSZKMK15UCse37EUXXQTAe9/73o7/u2754x//GIB111230X5HWBMDVzh/\\n//vfgRIt8qUvfQmAffbZB4B3vvOdAPzxj38EimUbz1Wi5bHiiisCcPvttwPdW4+9WG9t1+bjerTb\\nO0YxL8LImaOPPhqA1772tQBstNFGHZ/XStPHc9BBB3Xsxwgs83D6ZdWP9vc3velNAPziF79otB+V\\nkWPjuarqXJv3/16rSuorX/kKAGeffTZQrtExdgy0cH12nEcLLrggAL/97W87zqsf0YuDjsz0Gp0/\\n8803HwCnn346AN/73vcAuO+++4Diz1Ipq3ifeuopoNqfMp4SP/XhqGi85pe//OVA+R6JCsX7v9Za\\nawElN/E3v+lMSfQZjD5ASYWTJEmSjCv6Ummgile/+tUA/PnPf+5pP3vuuScA//Ef/wGUNXzfulpK\\n5nFcdtllwPSRP77Ff/CDH3Tsfxg5MK4X33XXXUBRMHfccQdQIq4+9KEPASVaRCtNy/XDH/4wAGed\\ndRYASy65JFAsGqNPtETOP/98ALbYYov+X9QIRqs0IHXj6/+9TzEPx7Ez0uZHP/oRAF/84heBomhF\\n6+uWW24BiuVqhJf704r3OH5OK7Af2faOhcqmqXWvH0HfjEpYRSvux+gk/VP/+Z//CZRotpi34Xwy\\nv+b3v/89UMZExaQv4O9//3vXz4mKdEReU1f7qUIr3Z9zzDEHAJ/73OeAcm033ngjUCKzVI0PPfQQ\\nAH/961+B4hfbeOONAfj1r38NTO/nasvI56LfY+Bc9Vz9Gee0+N34hS98ASjfiYsvvjhQVoeWWGIJ\\nAPbaay+g3MtuSYWTJEmSDIW++HC0wrQQIq6JalW1zVEwWsQ8CS2ZaEmL16SlY/RJA/ruw9EiePbZ\\nZzt+am17DVpj+nDe/va3A9PH5S+77LIA7LvvvgCsvfbaQLFwXZvXmlxppZWAkovSlDbr0y972cum\\nzjXXXNOUbLcZ4jF6SRwjlY9jqPX1vve9Dyh5N87DTTfdFCh+M/0UztfHHnts1POIlmibsZg4ceLU\\nSZMmVWb8ty10e9111wHl/t50000A3HrrrUAZE31EO+64I1DuwU9/+lOgRB+prH0W9RXpA9DXY/Sa\\n6kCG4bdo6+NRlTkPjNBzPvksOOaXXHIJUMbEMV1zzTUBWG211QD45S9/2XEeMaquzVjMPPPMU+eZ\\nZ57pVFKvhY+j/9P7Hr93qiJIP/WpTwFFETs/9t57b6A8Q6pCx/Zb3/pWx37Th5MkSZKMK/riw6lS\\nNiqTv/zlL432o7W2wgorAMW6822sBV2lbMS3umvzY4k+FS1QVVrM5P3mN78JwIUXXghMb6kstdRS\\nAGy//fZAWXtXAcWMY39qxXdba6sJL7zwAo8//vi0+9JW2cTIqSrc/wILLADAZpttBsAOO+wAFOV7\\n6aWXAmWMVDgS52NUViOj5dqutU+dOrVjjKO13tSSVekaUfWud70LKHkRWuWxzpcKx2tQzemv0ML2\\n2dQfql/sPe95DwDrrLMOUCzabi1wM9Hb4DXVWf/zzDMPAN/4xjeA6SOyzJ+xTti73/1uoESn+czF\\nGmqOperP+TPyvNqOxz//+c9RfUBt96NPbaGFFpp2LiP389a3vhWAe+65Byg+4vhMOue9/46lqwA+\\nW/q9dt99d6C6hUdTUuEkSZIkQ2EgUWrRujKePeZlaP3Zn8a1VSNk3vGOdwAlCsnPaXFogcS3rVbA\\nIKz5OqLFoaWoD8W8Bq10M8ddL1aJqPa02lxzP+qoowD46Ec/2vH/aCl5HkadaMEOgmjVR+p8OnVW\\nXlRO5t8Ytaaac54dc8wxwAzrgY2637hW3w0TJ05k8uTJ01nFbbFGmvlZqnvzcCKqCK9ZFed9X2yx\\nxYBi7Ts/tLpVwlrE5mP0Gk3VTT1F72fVnPK+GUVm7om+HK1yf1577bVA8Tu48uGzpno0skuFVOUD\\nHov+X16zysN8uze+8Y1AUTyeqxXY9WtZK01ls8YaawAlctf7ZE7bz3/+c6DMP5W29Qi7JRVOkiRJ\\nMhRaKZxZZ52VJZdcclrkSxVaAFoMEuv8mAG+4YYbdvzft7D1fUSr3zV7a2aJb3cVUmQYvWe89jPO\\nOAMo68Na+Vph999/P1CiRGLuh3k1V199NVCi2MwcV9m4Tu32Hs//P/jgg0B11FE/qVpz7zWfxbpP\\nRg9ZYUILVave42jBNs3/6SdTpkyZ5kPsBmupqWDN2zICrw7zddZbbz0ALr74YqBU6FYFeo5xPvSa\\na9ILsXZZVeVkVfuBBx4IlAg+n3utcH15oq/ZzxuRZ/7eySefDBR/l7X1hpGnV/fdZJTYpz/9aaAo\\nGhWvdQHN0/MZNELYsXXVyXw/lbhqcttttwXK95PKSB+0UWwjz7vN+KTCSZIkSYZCK4Xz7LPP1qqb\\nGeGb0CgR1wvj2/3EE08c9fNW0B3Rca/jp+vT5p5UHX8YmJmrJeFPoz1cQ61ap9YC1aqP68hGi+y/\\n//5AqQLr+rdWv9biMPxZVQqnW2WpKnTd2jV777+qzuOaS2CkTbcMMiO8ClW/qt376N+1xqtYeuml\\nO7Y3umz22WcHyv13laAqF868iwsuuKCLq+gN1VddhRJXOGJdLxWPqt5rjJFVqn+Vjj5iq3G48hK7\\na/aaMzMjquaZ989qCEaT+f0Qo19V+T4zKpK4yqB6M5rthBNOAIqvxu1VRo5p0/OuIhVOkiRJMhQG\\nWkstYsdHI7S0GESLxcitWPX1lFNOAUqHRlWC1r9Z965LDsNnU4Vr5q6JX3755UBZQ62L3tHaq8Ix\\n0kqLdeXuvvtuoLse992M14QJE6ZdUxz3bsdf605cr951112B4q8yIsvILhWOY97WIu11vnQzhqp9\\n0Q+lcjn00EOBUpPNqEZVvVa/98Dt9Fv4d8eiKi/LPDCfuZjDNAg8F8/N3j3ef/+ugvX++/2g+rP+\\nl/XkVPla6foztN5VNl/72teAsvpQlZ0/MtetXzl+sY+N5xZzDe1n44qF88XoQn03jqWV0Y844gig\\nqEWrKVgN2nqDRgjHnkEeL6q9bnOSUuEkSZIkQ2GgCsf1xc985jNAqfZcVSlAq94IDCMlrAqsFRfR\\nEmratXAYGFklnqMqTItBy1NLx7yJVVZZBai+Bq03I3litnRVpF4dPfTP6XkfopWm/0r/lH4x/Vb6\\nKfRb2CNGq+8tb/lXWbyYx9XmPLrJI+lG4Vhdwxwj57r318g8e9JHFam/wnwvLeBYFVqqlG/MdZNu\\nx6IJWsjzzjsvUBSOxzOK1cg9o1jjs2N9OXPdHDt9Qq6EqBodGxVO7IsUx9jjvfDCC337bqlSB34/\\nOCYPPPAAUNSa52b0qc+MY+P9XW655YDSDVc/uD6e73//+0AZq6qVlahs6s6/ilQ4SZIkyVBopXAm\\nTZrEq171qukqH1fh29NaR3F9UHxrmt1slqtv+braaf5fVaClMx5wbVUrvao6gnWdVHfmElRFs3nN\\nxueL0U1We30xYS00o9H0U3gt5ghojbm+rFVm5M0hhxwClK6XUU02pdvIvilTpky7DzEPqyonyXwb\\nLdU777wTKDkh+j+15mN3VCOv9BFahcF5ZF3CbhlklKNjouKI9QD13Wjtu73zwO0OO+wwoHzvqPJU\\nd/r2rNTuWDk2satlVYXlbtXNSOXrXK+KPnSu6oMzJzHOdfvYWC3B+/Sd73wHKCsmRh+qiBwjV14c\\nG1VgvEbHukXl/VFJhZMkSZIMhVYK5/nnn+exxx6rVRxy3HHHAcWHU/W5WCcoouXj+qQ/fQurtFyr\\nH2S8fFv0M6hEosWrZWL0iOvNWnMHH3wwUOLp7QyqFb/TTjsBJQ7fbqdW/TW+/sWA68wrr7wyUCJt\\nzLeJa/eHH344UGrxWS/M9W6tNn0Adv6sUhn9nDfRp1ZXbcHIKi1Xo8S8Vv9uxYnY40Vl5LyyX1LT\\n2lfd9jBqQ1QIsbJIjIjSX+HvPgPOkxjZFStOqGSsN6Y6MMfIytoqnEFXppg6deq0c44+NRWPf3cu\\nqiyc2yoY67xZZcE8P78DVX0q5Ntvvx0oUWt2+rSavdtXobKJ97Ctby8VTpIkSTIU+tLxswpzRVxP\\nNmqtqUKqw1hyFZTWwUUXXdTtLvve8bMOI7Fcg7d2WuzDvskmmwDFwtHq0yekyjMj2L4Y3a69D6Oz\\no3gNrjs7JkYrmT9hJJZjZJa0f9fP8brXvQ4oY/Lxj38cKOvhTWutST/GIqqzGXw+HhuYPl/DMdMC\\nNkPcLqhub37FNttsA1TnmDRlEPPCsfGc/V1/phF722233ajbqw6d+wcccABQngHzs6666iqg5HM5\\nb4zI8xlsWgtvkM+Iz7c/reKtapPPfvazQMlRjHk8XpM10bxmx8qigej2AAAgAElEQVRK2j5TKpkq\\npVs1j7PjZ5IkSTKuGEgejm9J8yN825o/YU+XKmLtooj5NlYc0AoYi/43dXiO+lh22203oESl2ckz\\n1gUzgsb6TuI6tZZOtIjN84kWrGNkhz+V0yCostLj+q8RMvbkMEdAJeLYeO5aqq7lb7TRRkCx3l3z\\nd2yM/Io1uaqse6OaBlExucpibFqVIT4TWqr6cvT5xLV477fPhp+P56Nicn55b8xtMnK0n3hfPWet\\ncf2XnrNVM4zc00/h5+1zo9JREZmd//a3vx0o9chUznZNdWx7qfLdlviMqBz0xenLNZ/O+xYrWVsl\\nWuI8cl54v/1eiZUKHOs6H15VNZGmpMJJkiRJhsJAFI6WhBFSRkR8/vOfB0qdsT322AMoMeFaU+ae\\naGUZZeJbXl+Qlsl4iEaLaH0ZB28UmrWLtExde9XCOPfcczv+b5UFP6cV5tgZvaLPJ1aV1VJyjFQ2\\ng8xZ0uqJkU9R6diNUB+LikSr3PphZs97DdEK0+dj/yX/b/6Ox6vKx9G61MIeBFWKs2nuR9yPlrDq\\nIFZQj/tbfvnlgaIOxGcq5sAY0aWymXnmmfu2guC5aa0bneZc9rk3R0VrXF+LFSR8NlQ2PjMqJP1b\\n5qpYJy5GXKkChqlw4jPi2Pp36wMahWr9yVh3zrkc57TXpur3+8Br9xkzErRtzbxufYCpcJIkSZKh\\nMBCFY7SQlqcZ477NjYzQx+PvWhj24zYyQ9xPr9muw8DIKhVGFdFqNL7eunMqGf0WjuExxxwDFEvD\\nvu5G6mmxWjXYmkoyCGUTreqqysSeq7kD1rJS0WhxfvKTnwRKdJFKyPwJFYw5J0ataZU7BrEWljiW\\n/l912M8q41HluW/rgnnMGEWkdW5OknNfa95rMQ/D+RYtXv0fqse6qgtVqwUxr6gXHFeVjQrTa9bf\\n6Tm6nfky5us5t93fiiuuCJRcNTt52lVXf4jXoprzeydWbxhELcbY1dR5seSSSwJlzuqjMXJTf6b+\\nym9/+9vA9F2VxWfOKg3OE//uvHA+Vvn2qhip0LPjZ5IkSTLuGGi1aLOczQ0wQsIopNhzXOzYGd+c\\nRnKNJ6qs4RgZ1dRq1iqr6qwa13o9jmOjBWV1Yf1jWoveCytx94vRKiT7u+es2tN/dN555wGlCrRr\\n7+bJGDnlfDDDXOWrlee8MuLG9ei6sdaqG0R0Y7SWI1aYsAKF16xfQhVnfTDVm1a5fg4jsL785S8D\\nxZr3vts7JuauxP44MUpNmuYPzYiqKgZR2ahoVb5eo1a6vhgrTKhU/LzKR1+c88ZnJKq0WKsx+tMi\\n/ahEUVWN2efRigPm3TkGO++8M1C+H1REPs/33nsvUOaHeTaumDgmPhtHHnlkx3HbXlO3FSlS4SRJ\\nkiRDYSgdP7UMVDZ1uIYbLQ0jN8YTdRVljcSJtZOqiLlH0fJYdtllgWIdqho8rtnYrvU7ZqqDfisb\\nmZGacN1YS1Mlo/WuMnFd2+39ad6E69pGL2nptq0cIFUWbT/W7uO+/ek1bbnllkCJwFJlWf/NnBO3\\n875p/ZuFbx6G+V7mMmnBxugj54s9YyQqm352/Iz+K8fXY3r/jGbVmveZMS9KP4RzO0YfGs2q2jMC\\nVL9YpOraqlYjRt7TbudIlZJwf35H+ryus846AJx44okdv9vd1Hlifp9qT/+4ylUf3kc+8pGO3+uu\\no2osuq29lwonSZIkGQp9UTjHH388UNZaI23XB12rjZx//vnA4PwQg0ArraqHvKhs9G8YRaIVZoTW\\nPvvsA5T1aNdmtRKtlOzY6NNxDV5l1G9GqoSYC+KxtcIvvvhioFQEMFLLnkFaTUYP2QXTeaRS6lWJ\\n1GX/d3uMkX3e4+e9bx5bxaqisA5cVLLWJYzRRv5uFWCj32KEnnkYkVirzfPuh7KpOlYVVtVwTqtk\\nvFZ7wqhwVb5a2/aeUtHUfe/UKZlur6MJdXlXqneVqr44vxeMWvV3n3/9YCpllZHRbiqgpj2iqq41\\n83CSJEmScc1Aq0W3xdwQq7xGFl98caDE3w+AvleLrusBEi1M/RlGnb3tbW8DylqtXS/NWdEadM1W\\nC7rX6KJ+VMKNvhGre5tToIIxw9z1ZuvBuQZvZM+gKkrURRD2Yyz0nXjN3i/vt9dufpVKVx+PCsio\\nJa14fTp2y7Uu3SOPPAIUxWsE11lnnQV0Pz/6WSFZ5bLIIot0nLO/77777gBsvfXWQPl+MDrR3CXV\\nm5Gdqsc6P0NVZF5ThllRXSWrn9P54+9+f9gt17E0otPvCVdYqqLlqujXM5IKJ0mSJBkK40LhGDtu\\nzLhrs6Jlq8UyQIbWD0eLwUxyI3G07vVnVOFYWK9Oa1CL1egmc6FcD29KW+ttwoQJ0yLkTj755FG3\\n0z+h9TVeiJZw9Ld1MxZGkanq6o454vMd/19wwQUBOOmkk4CSu6Yfy9p7UanYw97999AjqoNuxqLu\\nO8Zr1Uo3f8aoRH3D+iOtS2guk6re742mqq3Or9pv5TtyLOp8OPHvfkfGXKK4vWPptTkWcZ7F84h/\\nb0sqnCRJkmRcMS4UTsTIDN/mBx54YE/7ixUOZsDQFI6WiNdqPTAtU/uu131+UD3oh7k+3c/aZU2o\\n81/E/w9zLCR2dI1jpA+nykeoMlJNavFGf0W08ofhz2qKimfppZcGSjZ97A3kM1B1X6tyimLFbmmS\\nmzJ16tSBjkXbZyJubzRa0w6vjp3zLVYfryMVTpIkSTKuaK1wJk2a1FNdpSaYHW8F3EExivJppXB6\\nyTjuFbOq7RXTb9pYb3PMMcfUVVZZZVr9rsiwFUzb40YrP+ak9GLJVp2Dx9AStQK6fopYmcLtzcew\\nwnZd5F6dn6KKqrX9NmMxyyyzTF100UWnKZOmxxyrZ6otg/BnVSnW+Lu1Eo1OtEeQeTkqmzg/2q6M\\nVPmOIqlwkiRJknHFuPLhdGuNNUXFNIOabEPz4Yx3+mHVj9hX0/109ble0eozVyF2fuzHWr15E912\\nlez28/1WDWPhzxqxP8+hn7vtmm7Gom2txbpoxhHn0vRUuqLueKlwkiRJknFFW4XzKDB6YsFLg4Wn\\nTp06b5MNX+Jj0XgcIMdiJDkWhRyLQo7Fv2j1wkmSJEmSbskltSRJkmQo5AsnSZIkGQr5wkmSJEmG\\nQr5wkiRJkqGQL5wkSZJkKOQLJ0mSJBkK+cJJkiRJhkK+cJIkSZKhkC+cJEmSZChMarNxXTG+8VZc\\nrwsea1Ha5kV7kU0YyyKN440ci0KORSHHojCQ4p0ve9nLeO1rXzvt9wkTJnRUEf3/Lnhtdvmvk5g4\\ncVq/j27w8/F8qphpppmmVWENdF3rqOmx/x1wLKruy/LLL8/yyy9f+flJkyZN60AI/6qoa1Xd0Xjl\\nK185rY9ME2adddZp1ZdHHm+++eZjvvnma7yfXohjNKzjVf0+DGabbTZmm222oR7z34UZfKc1Yljz\\nIZfUkiRJkqHQUz+c2WefHYCnnnqqY7uqHuKxk2Jdb3nfuHPMMQcATz755Az3V/X5Fl32xqwfzqB7\\nAbVlEMsFjzzyCACve93rRv2/XQUXXHBBAP70pz8B0/cEec1rXgPAH//4x6an2MGNN94IwDvf+U5g\\n+vkRjzeIjp/2jn/uuedmuL9eO7uOdT+cXrrixnM/44wzAPjQhz7UsZ33y++Jxx9/vKvjteWl0Buo\\nX/vJfjhJkiTJuGIgHT/jWzMqkW7fqn5OC/h3v/tdx37b7meU4/dd4dRd+0c/+lEALrjgAgBuueUW\\nAM4991wA9thjDwDuuusuAD75yU8CcPjhhwNw8MEHA/C9730PqO5VXqcGI22st5lmmmmqqhZKV8qm\\nytJz9hz33XdfAD73uc91bH/DDTcARZl0S5Uylz333BOAL33pS8BLyzlcNw/qet73YyzmnHNOoLkS\\n0d/28MMPA7DBBhsAcN111wHlnLfaaiuAaX6iU089FYCZZ54ZKAq6X4zlvKi7T8MmFU6SJEkyrhiI\\nwhkUWjr/+7//CxQLWmstWm/+vv322wPwrW99q+Nzo9BK4XSzPu3avef4hz/8ASjXpH9ixHE6fq+6\\n1qOOOgooVrn+rjhGTa28bqw3ra6dd94ZgBNOOAFgWgRZ9MGN+DwAK664IgA//elPGbm/aMW97W1v\\nA+ADH/gAADvttBMAc801FzD92ET/mJFojz76aMd2VbyUFE4ddasPwxwLfXTzztuZqRCj+vQB6xNe\\ndNFFgaKImqqAV7ziFQA888wzjbZ/Mc6Lqvvrd6vq02ej398XqXCSJEmSodCVwhlWgqeWqcdbfPHF\\nATj00EOB4s8wmsnt9H+st956wPQ+AhnFsh14lJq+DqOT/uu//guA1VZbDYBFFlkEgIUWWggo69H6\\ncJZddlmgjI38+te/BopF4vr1VVddBcCdd94JDMaH41i09RM12O+ofz/55JMB+MxnPgPAQw89BMCB\\nBx4IwH333QfAhRdeCJR5c8UVVwDwhje8ASiKZ8cddwTgpJNOGvV4/bBkB/XMOD+cT1r5zo8YBee1\\n/+IXv+g4H/2iv/nNjFPRBmnVv/WtbwXg+uuvB4raf+KJJxp93lUC/aLe/7/+9a+jbh+jZFdddVUA\\nfvjDH466/Sg5h63HYqyS410tWHLJJQH4/e9/DxR/6xJLLAHAHXfcQTfnmQonSZIkGVe0Km0jvvVi\\nLoHRIAsvvDDQPndAi8Moot133x2ATTfdFICll14aKBb0uuuu2/H7gw8+CMCZZ57Zsd/NNtsMgG9/\\n+9tAUQ+u9RrtMgii1W9u0jzzzAOUsTJHRWtdC/XVr351xznr89H6czuvRWstZh0Pw6KqUjb6TJwv\\nVVb0Jz7xCQCOPPJIoCiQs846C4BtttkGKMrG/fz5z38Gylh9+MMf7tiv98CxjqhsFltsMQB+9atf\\nAf0ds15zUfxpxQWfBXNPbr755o7jqKRf//rXA2V+3H333R37d+3e+RdVpfvrJZ+mjs9+9rNAUajm\\nad1///0z/Jxz3RUMvz9USFXKJn7eMahSNtKP64/7qPIvumrTFu/f/PPPD8A+++wDlGfPyMBLLrkE\\nKHPdZ6kuN7JXUuEkSZIkQ6GnKLVe1yP9fLRMVl555Y6/azlrxemnWHPNNYGyDnnttdcCZY1f5XLb\\nbbcBxfL191EYuA/nK1/5ClByTFRzCyywAFDW2L2Wxx57DIC//e1vHfvZa6+9gJKHM7L22MjP6Z9w\\nf45VHWMRgaNSfvnLXw6U++78ete73gWUa1f5asmq6rQajVI67bTTgOL7q2K0KMcpU6YMdSyiMt14\\n442BonwPO+wwoFiqRnB97GMfA4pyVrGogFZffXUAbrrpJqBE+hmNdOWVVwJlno1llJrfA0Ytap3H\\nqMWf/exnQPF/xohMrz36gLzPrhI4r3784x8DRVnVfa+Nhyg1r8UIu7nnnhso12KE6C9/+UugKGTV\\n5Nlnnw2UMdMPVhXZV/Wdnz6cJEmSZFwxJnk4viVdO3Wd8aCDDgKKJaOSMX/G/xvJdcwxxwAlcsto\\nJK0039qqhrXXXhuATTbZBCgKacS65cAUTrSeXafWmncN1e3qaqq5nfk3Wi4bbbQRUCwUI388rpZv\\nHW2st4kTJ06dPHnydBFRTeeW69ZWjvD+R/9FxPyqZZZZBijzyOMed9xxAOy3337A9FZblb9Cbrzx\\nRnbccUfuv//+vtdSq2OFFVYAioXqHN9yyy0BplXbvvTSS4FyjU8//TQAyy23HDC9f/WrX/0qUBS2\\nfs+f/OQnQPGDeS8cs9lmm41nn32WF154YeCRWV6b+Vj6E7xGq2oYjVi136rjOqY+Y6p+1eTFF188\\nw/1uuOGG3HjjjTzxxBMDUzhNx8xnZaWVVgLKfPA5P/roo4HyXav/01w5lZCrBHURplW5calwkiRJ\\nknFFXxRO1ds4/t11RmshmSez3XbbAeWtqRV2+umnAyUHJb5VtYyNyDGT3d/NRDfjXWbwFh+YwnEs\\nHAPX2lU23frBohq49dZbgRKV5LW6jm0kVhXzzDMPTzzxBP/85z+Htj7turFWuKhUq3rdRDWoInY/\\n/l0fQB1VVc6HsVYfFfCb3/xmoKj5448/Hig+m3vuuQeAyy67DCiRXj4jPhuq+XXWWQcoysnVAvO0\\nfHa89tGqNTz//PNMmTJl4GOhMjVXRJ+c99dqGt3WRtP3YzTrscceCxR/59e//vVG+xkP1aKNRrNP\\nmXk2jpn317/r23VsrScY53zdcdOHkyRJkoxrusrDidRZ51pLrpW69up6YqyNZnSZlkhEn4tva/0g\\nvqVd89WCsT5QXVz+IDEfQrW1/vrr97Q/LQ3X3LXmja9XyejfcI3XfB4juETl5Zh2cz7dqjQVrvk2\\nWl9VfXNE61uVF5Wr+2mK82csssE9pupMf4URm9aJ0ydzzjnnAPC1r30NKPffc/YZ8H7qv1QVWH9O\\nReTYVzHMPk3//d//DZT7am2zqHTqqPIBuoLyne98p+PvTZXNeMDnXsWrb8/IPpWvz5Dfgd5n/d1d\\nRKMB3VcVSYWTJEmSDIW+KJwqXHt3fdH4dmPCL7/8cqBUFPj5z38OwHe/+91R9xffur61o1WukvLt\\nrTUwTD74wQ8Cpc+N57711lv3tF+tPsdAP4cW8Kc//WmgWMJGcsXclEjTCrmjMXHiRCZPntw4x2fk\\n5wC++c1vAiWixo6cTZWGY+D21gl7y1saueOmEY8366yz1nbk7JZ4LOeF0WUqEvO03M5qCz470dp3\\nv37O/eqfcnVA9a/Pr6oqeT9pahXvvffeQLHGXQFp6mcQx8woVStSqALOP/98YPpnath1zrrBaFR7\\nR5lLtMUWWwBwyimnAKV3lPk2PhtGtVZVcK8bg27nRyqcJEmSZCgMVOEYGeVbVCtKa+u3v/0tUN6W\\nKpH4dtUq8/Pvfve7gRKBEYnVoc2mjlFIg7RktJ7EmkXmGPzlL39ptb9oHcbKAtaJs36dVai1lOP5\\n9JMpU6a0VjdQOnh6XzxnfXxanrGuk/PAMdEvpY/OGnuxo2eVYtLyVYk7f7q5pqaMrFEGpUaeFdBj\\nV0zv6+233w5Mb2G6H8dC1fiOd7yjYzvngX4zt/OaXfNvmq/VhqZW8YknnggU5RqrvNfh9lZANhfN\\nah76OZ0f+oys4tDvzqC9EOesFa033HBDoPQM8tytnuB273vf+4CiEo1e1Wc7CCU7I1LhJEmSJEOh\\nK4VjDw6zmquIWam+pbXOVRoxT0JLUwvE9WatO+Pw6yJn4ts7WqyrrLIKUNaxB4Fj4E/9VG3RajMi\\nzzVYfzfqxLH1mszKtlJyXb+TXohWex2qL+dR9C9YEVlr3+hFa2Rp/WuRmple5aeqirCJPr5+9Itv\\n6n/S0tQa9746Fj4Dsf6f16BvTiWjOtCa91r0RTnWrhLEaxyEsmmKYxarP3stfk+YgxSffz9vRKg9\\noKxIoppbY401gJLDYgVt51X0Cfezz1MXfWY6PqeCedOb3gQURevfzVmMUbDOE/3jsWr4sEiFkyRJ\\nkgyFVgpn4sSJzDLLLNMpG62oQw45BIADDjgAKNZ3VBb6L3xruw5pNrSRVlo4ViTw7W30mxZuU6J1\\nYR2hQaK15k+jyTz3aMFEf1Xs+aG1tdVWWwGlh4yq086fWsZ+ztpYgyRWCqhTPGY/WxHCauBGMS61\\n1FId25uXpTI2B+VHP/oRUKz7Oiuyyv/h9r0om8mTJ7Poooty7733Ntpe5aGfUz+U99PoQcfISE/X\\n4n0W9X/pD/OnmHPis+XnvGdtI8AGgeOv79f7pN9T5WHuScyzilFm9reJvaOcZ66k2BlUBRUVTT/9\\nHL1W1reStisWqnuj1awH52qQkZqueFgleqxIhZMkSZIMhVYKZ8qUKaPma2gRaj2peKqifHzLu6Z6\\nxhlnAPDGN74RgLXWWgsodaTcn7Hn9nYxys3ja8momCLRDzLIKCSrKBg9oipTsXguXpu11RxD1Zcq\\nwAoF5tW4nZaP98V+Ox7HsdaS1aKeUYXdtlbYUkstxVlnnTXNEh25rxmh/8KsaKOJzJtwDLTStN6M\\n0PnCF74AwA477AAUC7ZO4agOzfOIlSh66Xr43HPPNVY3UCpBeM2OiXkTVojQmneM9Plcc801QMm7\\ncV557SrbPfbYA6j2e3rcqnwsewP1k7r75N/14diZ1bHxGfCajcSy548KxjGUj3/840BZDbCHjArK\\n6+y1+2Y/8ZxcGdHvaDSaVeONyHVOx9xHvzPHilQ4SZIkyVDoS7Vo37ZHHHEEUCzOEZ8Dpre2tUwW\\nXHBBoLzFjZPX4tRKM+JKa8+oEv/uOnhbS2zE+XVdLXq06rpQrGU7LLq2qi/HOHktUP+utaYvRstU\\nv0ZUD6oBOz+6fu12jpX7c42/yqJtWwm3Gwv4vPPOA2DzzTcf9f+uqavK7OnhOra5K+9973uBcg/c\\nrle/hGqvl6rAMeKtqoK6z46Rk1Z/Nhop9naKuSWxorb9bex74zMS1UBVrlMVg6iQ7LPiOUS1tcsu\\nuwDTV333mfAaYr6O/9e699ly7ruqoBpwvvn9UhcFO4xq0XU9mxwrv0PtHWaEp2NrtXF9Pf0mq0Un\\nSZIk44q+dvzUQtCaiz3m9ZmYde9at3kTZstrYZiToNLRYt1///2Boh604szGFi0efzaw4nruh6P1\\n5LUZHaTlaldKr2nbbbcFSoRe7NSota6lo/9JvKaLLroIKFWiXbfWAjIqSWvOLO4qf1Yv1pv+BdeP\\n29I0VyFGJakCrB927rnnjvq5qjybeNxXvepVPPXUUzz//PMDs2RjVry/myfhs6OPxvmistl0002B\\nErllnpV5NlrpVlOoqhdWNeZRuQ/CqleduULhc+0zc9pppwElMi/iuUWFY2TWAw88AJQox8MPPxwo\\nY+azYg0/fUNG3VYxzD5J4rXGahuuYLiyYV6e2zmWMZ+rV9r2SUqFkyRJkgyFrioNVGXeGnFjDoHW\\nlfkzvoWtFGC0iT+NMnONPq57f+pTnwKKBatS0qpzO1WBMepVa7Faj/3o9RH7mbg+rG9G7DluRJ7r\\nyq7Buh8VjtafVnlES3jNNdcEynr1nnvu2bGddee0HlU4/cy/0I+kf6EKrz0qUqlTNt7XmOfjfIx1\\n46I1uNlmmwGlp0zVcc0H6YWmOUFGQsW6g87NmENihKfbeS1GWnlfjWqKlrHPiMq2ac5SP/F7IlYs\\nVrVrjTs2UeFUnZt/32233YCiWFSHjo0/9as6Bvq7xhLvk8+988Dnd4TiBIpPTpWmYnYsfSb7rXDa\\nfnemwkmSJEmGQiuFM99887HNNttM85lEv4Jx7a4jain4f9dSY+0i824kWqxaQuakXH311R37sU+7\\n+RrmJkQLWvVRp3yaMtNMM01XJ86IPRWEtdOMUtMvtfPOOwOl/peROF6zdZ6qLE8VkBaQdaNc23ds\\nN9hgA6DUkzJKTWXVj4rZEyZMYPLkydO6U5rXILEydrwvKg59eJ5b7NDqud9yyy1AsfZ+8IMfANNX\\nPq7y4UVls+yyywIlx0k/WzdMmDCBSZMmTdeBc7TtRqKvzb977d5Hr8nctGjtW2Hb6gtGeEUV6O+D\\nzEGTWWaZhcUXX5w77rhj1P/HqszeJ++r/7e3VMwhcUxUf+K1mq/ls2IkoNU5PJ7+zejvsIJFP5g0\\naRJzzz1345we75PVu33OXcGIqzOeu1Gv4ucefPDBrs67H3UFR5IKJ0mSJBkKXUWpRWvJt61vQyuS\\nfv7znwdKtr0VbX0rx7emCiRah/5dS9bIHNcttVC07vXpxHXrqpyDET6pnqPUPJZdBU899VSgRI14\\nDm6nEjIKSaJl6nqzOUmue7t//Q3eC7uoei9OP/10AC6++GKgRPpdeeWVo15fLxE4TTP1vTbXl6uq\\ndmuNGwUZ5533X79E0+q+Md/D8/ZerLXWWlx77bU8/vjjfY9GigrHa/GcY6TnfvvtB5T7ZjSk+Tb2\\ntDfis9+9nvqRk1SHOWauhMQxkK9+9asA7LTTTtPObTRiPUHnj/f9zW9+M1BWUFSJ+r3i99MwIvaq\\ncHXH77bY08u5q//y/e9/f8e5qvaqnvdumWuuuXjyyScbR3KmwkmSJEmGQl/ycLRA7Fao1X7QQQcB\\nxdfi2r3+itj/QuI5mTtiXoWdIo2n9y2u1adlHdc3G1xrzwrHSDv7iqy22mpAqe/kOcV8Gs9t1113\\n7fi7/ir9IH7ONf6ohIxO01pU6fg5fUqej50f49j0w3rzGLHrZESFo5VmpJWKR7+X52hOyQUXXADA\\nwQcfDJQxUi24du/v1lBTFTa4rr5Z9VVr4bGmnnNXq3uTTTYByly3vpf30fqCVT2A+k0/xsK5qt/R\\n1YCodKv8BipZ50msjD3iXIGidPycYxyrQ3sPjCytqks4Yv+txmK0OoVN1bjbxU6wUe1bb85VINW7\\n1aUHVRU8Kw0kSZIk44q+VhqIfSb0sWiJWE3YKCCjkrR4Yi00/+7bW8vUePqq3uMxx0BiRrOMsD57\\nVjiite7aq+pOhWOF7BjVpmUiVZnh3dIii7+x9bbccstNveyyy6bF/sdxb1t92ftkRE+VGtTa04K1\\n++FDDz3Usb0+QGu3WXVaqqzM+eefn0cffZR//OMfPdeVi/2OovXu9lrdjpXq0Kx3K0n47Fgbq+pZ\\n6DeD9Fs4Nv70+6Nqrlr12bpzjrFRtPbRsgOoUbT6blQyp5xySsdx4vfPDKpZD82HU4Vz17w/qyn4\\n++WXXw6UMTHCs98+vlQ4SZIkybiitcKZkfWmErFGkUrCyCotUdcVzTU5+uijgRInH6NTtFDXXntt\\noLylY55GW0ZZV++bwpHYn8QxGpZFGmkaV9+L9eY1es1NlU20bMX5o3KO801cyzdiz+3r5om9i/w5\\nMmLshRde6KslGyPjovLxnK32q5Kxz4lVOcw5stpGW4s1Wu+DUL5tI/Y8dtUKRdv9xL/7veR8iPOy\\nha/X7YaucKoq75uvY97doYceCkzfTbcfVVVGIxVOkiRJMvPxf9wAAAKoSURBVK5oXUttypQp096y\\nsSKAlqERWvbycD1RC/See+4BSk01o5mi1W0+hJFf9nRwHTvSNiu21+zZJt0xoxocK2Uj/coYnhFN\\nrSjvl5UJjD5T+Vo13DpzRm5VWb5G4DhvjOQyB6oKlU3b829CnJMqGyPvYu00FZAKx/mj8tEfoV+0\\n27X4USKuutpPHU2ekfj/bqsg1HUONV+rSnEPagxGo62Ki7lGVuMw3+aKK64AisIxWs35Yn3KplFx\\ngyIVTpIkSTIU+hqlJjEq6Rvf+AZQckxirasqn5A/rY1mTouW7BprrAFQWatJRaWqaGDd992HM96J\\ncf0yjPVp64Hph4iomK07Z8fHKuvMeWfNLSMEY9VnfYHXXnvtDM9Pf2UvY1HlK5Ho2zOvRgvWSCtX\\nCZzD/r0qryfuPz7nKia7pjZlPERmDZsq3854GIuqmmpxnnWraPrt20uFkyRJkgyFgSicBvsBmq+Z\\nGjev76dqDbbtfkfZ/t9O4VTRD+tNP4UKI1aBrvK5aX2bm2RlimOPPbbpKc2QqMDr1rWHack6J60A\\nYe272MOl1/334PsZc6t+vDCWYxGjX0ecUz8P05hUOEmSJMm4onWU2ozycHy71kWLuZ3RRObnVHXg\\ntObSaOcC03e/S8YW70v0nayzzjpAyS0R54+Z31//+teBUkfOn22J80uqsvwjTSKs+o3Hi/Xe+hVV\\n1Gu+TjIcqr5Dq3yAVYqnKa4iVX3XVtH2GUmFkyRJkgyFtj6cR4HfDO50xpyFp06dOm+TDV/iY9F4\\nHCDHYiQ5FoUci0KOxb9o9cJJkiRJkm7JJbUkSZJkKOQLJ0mSJBkK+cJJkiRJhkK+cJIkSZKhkC+c\\nJEmSZCjkCydJkiQZCvnCSZIkSYZCvnCSJEmSoZAvnCRJkmQo/B+upgo4r1EqBAAAAABJRU5ErkJg\\ngg==\\n\",\n \"text/plain\": [\n \"\"\n ]\n },\n \"metadata\": {},\n \"output_type\": \"display_data\"\n }\n ],\n \"source\": [\n \"rows, cols = 10, 6\\n\",\n \"fig, axes = plt.subplots(figsize=(7,12), nrows=rows, ncols=cols, sharex=True, sharey=True)\\n\",\n \"\\n\",\n \"for sample, ax_row in zip(samples[::int(len(samples)/rows)], axes):\\n\",\n \" for img, ax in zip(sample[::int(len(sample)/cols)], ax_row):\\n\",\n \" ax.imshow(img.reshape((28,28)), cmap='Greys_r')\\n\",\n \" ax.xaxis.set_visible(False)\\n\",\n \" ax.yaxis.set_visible(False)\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"It starts out as all noise. Then it learns to make only the center white and the rest black. You can start to see some number like structures appear out of the noise like 1s and 9s.\"\n ]\n },\n {\n \"cell_type\": \"markdown\",\n \"metadata\": {},\n \"source\": [\n \"## Sampling from the generator\\n\",\n \"\\n\",\n \"We can also get completely new images from the generator by using the checkpoint we saved after training. We just need to pass in a new latent vector $z$ and we'll get new samples!\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": 17,\n \"metadata\": {},\n \"outputs\": [\n {\n \"name\": \"stdout\",\n \"output_type\": \"stream\",\n \"text\": [\n \"INFO:tensorflow:Restoring parameters from checkpoints/generator.ckpt\\n\"\n ]\n },\n {\n \"data\": {\n \"image/png\": \"iVBORw0KGgoAAAANSUhEUgAAAZwAAAGRCAYAAABR3wXnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\\nAAALEgAACxIB0t1+/AAAIABJREFUeJztvXncVeP+/39lKkNUd0WGuqkopShThkPGhCRDiHAKIc4R\\nMs8+jqGjrylk5nA6KJKZIkNIQkKEBkPzqJCp3z+/9fa8tS73Wvfe+9pr3/fr+XjsR6/Hau21rr2u\\ntfZ1X6/9fr+vWitXrnRCCCFEoVmt2A0QQghRM9CAI4QQIggacIQQQgRBA44QQoggaMARQggRBA04\\nQgghgqABRwghRBA04AghhAiCBhwhhBBhWLlyZeJXWVnZSuecXnl6dezYcaVzbl6aPlC/lEa/lJWV\\nRceJfa211lr2Kvbnbd26tb0Kfa5atWrZqwrvL+izssYaa9ir2H0S8tW2bVt7pX1v2mdlDZeC8vJy\\nt2DBgjRvEX/BhAkTXK1atWbkehz1S37JR7+Ul5dHx4n9/0022cT0tGnTYvdZbbU/DIjff/89l+b8\\nJQ8//LDpDh06pHovP1+SMll16tQx/eOPP6Y6l3OuoM9Kw4YNTc+ePTvXUwUlbT+QkSNHmm7evHmq\\n96Z9VmSpCSGECEKqGY4QhWb11Vc3/dtvvxWxJfmhvLzc9PTp001zVrPWWmuZ/vnnn03nMqvZfPPN\\nY88VR9pZDUn713TaWU3v3r1NP/jgg6nemxbOanKZMYRinXXWMf3DDz9U+TgtWrTIR3MSoRmOEEKI\\nIGjAEUIIEQRZaiJT5MtGy5fdkCu00QgtG9pou+yyi+lx48ZV+byV2Wikfv36po855hjTt99+u+lC\\nBi38FYW20ZJw2GGHmR4+fHgRW1KRfN3XaS1DBrOkRTMcIYQQQdCAI4QQIgiy1ETeyFJkTzFtNOK7\\nJmuuuaZpWmrjx48P0zCw0UYbmR47dqxptpfal1tUneDnTWKj+XKm1ljjj6/YX3/9NU+tKy652Kua\\n4QghhAiCBhwhhBBBkKUmUnP99debHjhwoOmq2mi0aGrXrm36p59+Ml2vXj3Ty5cvN/3LL79U6Zyh\\nYATYwoULTdNGI7RdCm1RHnDAAc455+rWrWvbLrnkEtNMCGVbkvRXlllvvfVML1u2LC/H9NlMxYru\\nyyqa4QghhAiCBhwhhBBBqJaWmq82VVpY18sXsVPsaKxQ0EahjZaP45111lmmI5vHOec22GAD05dd\\ndpnpvffe2/Q555xT5fOG6DvaaGkpdPteeOGFVbY9+uijpln37JVXXjHdtWtX06Vio5F82Wg+eI/x\\nO0T2mmY4QgghAqEBRwghRBCqlaUWTWU5jW3fvr3pTz/91DSnt0kSsmhv7LHHHqZfffXVKrU1S/zt\\nb38z/dprr8Xuk297p0GDBqavuOIK0+uuu67pFStWmD755JNNH3rooVU+bxYtUCYH8r7ccsstTU+Z\\nMiXv540i/Hy1sXit9tprL9O0rLlP1iMG08AF8ubNm2eaSbLff/+96UWLFpn2XZMhQ4aYPu2002LP\\nG/VFdbXfNMMRQggRBA04QgghglCSlhotAJah/7//+z/nnHP9+/e3bb5y9x07djQ9efJk07Tjunfv\\nHquPPfbYqjS7oCxdutT0+uuvn+q9PhutkNAyWHvttU3T9mQUVT4i44pBkhVMfZZuIWw0MmbMGOec\\nc/vss0/s/7/11lum2V+0ke+44w7Tw4YNM51LdGixaN68uekvv/zSND8L7URy6623mmbkJG3h8847\\nz/Suu+5qmsnBgwYNcs798V3mnHMTJkwwzeUr7rnnHt9HySya4QghhAiCBhwhhBBBKBlLjTYa7ZWL\\nLrrINGskRTAJi9YFI0YYdUbbY7/99jNNC26nnXYy/fXXX5ueNWuW6dDRUGlttJBEpfgZgcZEQtpO\\nrVq1Mt2oUSPTAwYMKGQTC0a+VjDNF3we+vXr55yraClPmjTJ9GOPPWZ6wYIFpm+88UbTd911l+kX\\nX3zR9OzZs/Pe3kI/U7TRiM9G4xITtMB4DRlpyBVUubIqo+CiZGeudMp7iM9Kly5dTB9xxBGxbcwa\\nmuEIIYQIggYcIYQQQcibpeZb8S4XOGXltPKCCy4wTRstmnL7Sqk//vjjphkxwn34OR544AHT06dP\\nN80otTPOOCPBJ/mDhg0bptq/OhAlvzGSrl27drH78vqXYp2urENbKrKQ4p4h5/zP8WGHHWb64IMP\\nrnT/XMhaom7Pnj1Ns21csoNW1/PPP2+aS2zMmTPHNJNJ46CNRnr06GGaPxfUqVMndnu+8LUnCZrh\\nCCGECIIGHCGEEEHIm6VWiOk0p26bbrqpaUZk0WqLrDFG3Xz00Ueme/fuHfs+MnbsWNMsic8EtyVL\\nliT7ADHMnz+/yu8tdXzRPj4YDViq0CJs1qyZ6WnTphWjObGkjaT7/PPPTdOyWbx4cd7aVAxorTdt\\n2tQ0Ez8ZuXrqqaeaHj16tGlG9NFG22233Uxz6QceP6qrx0jc6667zjS/E3018C6++GLTl19+eew+\\nuZBL5KVmOEIIIYKgAUcIIUQQCp74maSWlI+tttrK9BtvvBF7HE5927Rp45yrmHjFaBAfnErvuOOO\\npkeMGGGapcjLy8srPaZYFdpIvOY+WIeqVKHV/O233xaxJbnBmoVnn3226XzVT9t9991Nv/7661U+\\nTi4wKpb2IKMr+/bta5rfQ0xMZl21Tp06meZ3y8SJE02zrlr0XHBZAz43w4cPr/RzdOvWzXQhLLVc\\n0AxHCCFEEDTgCCGECELBLbW00Wu0WhjJwWiYL774wvR2221n+tlnn3XOVUzISlKLidFrbO8tt9xi\\nmqtSZi0ZLYvwukeJhWVlZZW+j/WsFi5cmP+GFZFCJOEVEq5ESnuT1hnttVwolo1G+Ll89iCTKpkw\\nu/3225vmdwi/K9555x3TaSIwaen54Dl33nnnxMf+M4WuXacZjhBCiCBowBFCCBGEgltqaadlTGbi\\nezm9f+6550wzei2KHmMU2Ycffmia5fEZMTJ06FDTF154oen/9//+n+lCJLZWZ2rXrm06sl0YBeTD\\nV2OtOlAK9xCjSplgzecvKqHvXGFW9gy5JEFaaIu+/PLLpg855BDTjEx78803cz4nl/Lw/VzAdjFJ\\n/quvvoo9pu8aU+cSYexDMxwhhBBByNwCbBxJp06danrDDTc0zRh1lkuJ4tW5KBqrQp9//vmmOZJf\\nffXVpgcPHmyaVVy/++67FJ9CsO84s4yDgQI1sUI0Z368t4sB820YtMN+KfSsIwuzGl/1e34/cZE0\\nLqJGV2WHHXYw7ZtV8Dss6n8G2HD2Qs37hvqbb76J/1CAQQtvv/127D6cvXK2o2rRQgghMo8GHCGE\\nEEHInKXm44cffojdHmdBcNrJRYr4QzbXAI/yd5yrONWVjVZ1tt12W9NxFbJ5nbmgXSn8sJ5v8vWD\\nbNof2yPb6L333rNtLN3C7TUNBknwO2bRokWmZ82aZZrfT3vssYdp9smee+5p+v777489ZmRjcRG3\\nVq1amU4SeOOrIk0mTJgQuz8/t+9cuTyjmuEIIYQIggYcIYQQQSgZSy0Nffr0Md2hQwfTXDjtqaee\\nMp2FqJjqximnnLLKNl/U0/jx44O0qRgw2ogLc5F82YiMMKPF47u/ly9f7pxz7rbbbrNtNdlGI778\\novr165tu2bKlaX638N6mpcYFHRs2bGiaNlYUYcuyWj179qy0vcxNTBLpyZ8dGEWa5L7J5ftSMxwh\\nhBBB0IAjhBAiCNXKUosSkq6//nrbxqkxS1HIRss/jLw5/vjjV/l/RsM0a9Ysdnt1i1Kj1ZIkiozb\\nBw0aZPrcc8+t9FxMjuaiXaxqHC1S6Nwfz0tcFKGIZ/r06abHjh1rmhXnfbB/aH8ykfKMM85wzlVc\\n8JHJo7TxeK/069ev0vPTuqOlFlmrf7VPvtAMRwghRBA04AghhAhCtbLUosqsrHLLaSGj10R+YOVg\\nJnDGwUW8GElTaguTpYGfjZaaD1+1dEYS0QIh++yzj2lWQCdMVhw+fLhzrmKUWk3GZ3n6rOC0HHro\\noaYZPcsFJT/++GPnXMVosRYtWsQejwuzsX6kD99z5qs6XQg0wxFCCBEEDThCCCGCUPKWWpMmTUzH\\nrRMeTVGdS1ZjSFQOryOTGX1ly6PIM9aYKnYZ/lDkspgYbZLNNtvM9Nprr2365ptvNs1INpa8pz1T\\nt25d0xdffLFzrmJEVBZgVN2yZcuCndfXP/mKnJwyZUqsZn8yOTqCzxgTRvnTQZIlLvhdSWs1ZMSu\\nvoGFEEIEQQOOEEKIIJSkpcbkpMqWEBgxYoTpmriaZCGgxcDExgYNGsTuH9VKmzx5cmEblkGS2BW+\\nEvb9+/c3/emnn5pu166daa46yUg2LnnAyCO+d/To0ZW2LQ5aQIw8zJf1FNJGy8Jqq3E2GrnoootM\\n33nnnaZ537DG29y5c2OPQxutWGiGI4QQIggacIQQQgQh05Yao54YkbFw4cK/fB9tDNb3qmzqKpKx\\nzTbbmGY5+3333dc07YlRo0Y55/K3smV1Y+ONNzb94osvmqZFxXu6Tp06ppk0SKvZF3n2wgsv5NZY\\n57emk9TES1s3j/XH5syZk7SJiSmFpONrr7220n18S19kDc1whBBCBEEDjhBCiCAUzVJLkhBH6+DZ\\nZ5+t9JjRcXr06GHbZs6cWdUmCg+8prvvvnvsPrR3HnnkEedcxYgg34qKhYDRc5XZscXg22+/NU0r\\nrF69eqZpB++1116mudJjIaOs2J+svcaVXZNE5KWNZCuEjUayukwJIw4ZgeajVJb10AxHCCFEEDTg\\nCCGECELRLDVOZVlWncloRx55pGmW8yaDBw82feGFFzrnlOBZaFgTjZGE7NMPP/zQdJTMyCTFkGTR\\nRiM77rijadp/tFLmzZtnmpbWpptuWrB20UZjhGGS1SXzRS616EoZLvvhg4nUpXJtNMMRQggRBA04\\nQgghgpCTpcYS6LlEHdFSYDTatGnTYs/F+k0DBgyo8nlF1XjqqadMs19OOukk03fdddcq+zDyJmsl\\n8YtJVGvOuYoW5aJFi0zT3spXAnNk33HlSCZCcpkA1swLad+UilWUb1gj0rdMBaM+8wXvPybdVlaz\\nMima4QghhAiCBhwhhBBByMlSS2KjnXHGGaZvueWW2H2uueYa09ddd51pWgdMAGvatGmqdoow0EYj\\n0X0SMtmzVGE0GC3I5cuXm+byAIQJuc2aNTPts6Uqi95jOfv999/f9GuvvfaX76tucJXN+fPnBz8/\\n66SxpmQhkj15/xUi6VYzHCGEEEHQgCOEECIIBU/89NloPsrKykxzKskS7ozY8dkOItukLVNfquSS\\nuJjkfu7cubPp5s2bV+lcjEajjd2oUSPTuazCyXZNnz7dNO2bLCd4hrTRWrVq5ZyrmOhO67N9+/am\\nWWuvEBRiORHNcIQQQgRBA44QQoggZG7Fz7lz55pu0qRJ7D4sw17IkuyicFRnG4347KG6deua9iXB\\nJrGZ3njjDdNpn4Xo+D67zLc9rR365Zdfxm4v9GqeubB48WLThbCufP0/ZcqUCv8698fyHklJct/w\\nM/GzJoH9nxbNcIQQQgRBA44QQogg1EoTEVKrVq15zrkZhWtOjaTZypUrG1W+mx/1S0HIqV/UJwVB\\nz0o2SdwvqQYcIYQQoqrIUhNCCBEEDThCCCGCoAFHCCFEEDTgCCGECIIGHCGEEEHQgCOEECIIGnCE\\nEEIEQQOOEEKIIGjAEUIIEQQNOEIIIYKgAUcIIUQQNOAIIYQIggYcIYQQQdCAI4QQIgwrV65M/Cor\\nK1vpnNMrT6+OHTuudM7NS9MH6pfS6JeysrLoOHrl76VnJWOvtM9KqhlOeXl5mt2DUKtWLXuVGhMm\\nTHAuD4tBFbNfVlttNXtllbRtzEe/lJeXR8cR+SPYsxLye2X11Ve3V0Quz1UubS/0s5LdbwkhhBDV\\nijXSvoGjZr5WC11jjT+a8euvv6Z6b8olslMdI5d21RR+//332O1rrbWW6Z9//jmv50x7D/raKPIL\\n/yrO8jVP0s5CfM/5+O2331bZ5mvXBhtsYHrJkiWx+7C966yzjukff/wxdh/fedN+XyZBMxwhhBBB\\n0IAjhBAiCKktNd90at111zW9fPnyVMcMZVelnQpWNxstF5sgrb1IGy2yMPr372/bbr755iq3q9AW\\nRwhCWjahyLKNRpK0k/tsuOGGpufMmVOQNiXFZ6P5+OGHHyrdx3cv+u5LBjekRTMcIYQQQdCAI4QQ\\nIgipLTUfPhutEJFenNLFRXiQkJEzvsisrNgnuZybfef7PNy+5pprmo6uxX333Zf3dpUqhY6MTBOJ\\nxX0re56qM7xnee3nzZtXjOZUSllZmekFCxZU+ThJrDPeF7ncI5rhCCGECIIGHCGEEEFIbanVqVPH\\n9E8//VTp/oWI9KrqlI7Wwfrrr2/6+++/N92wYUPTS5cuNc2kKR++BMdSsox8dlndunVN83oR7t+t\\nWzfTXbp0cc45d9JJJ+W9XdWNfD0vtNG22WYb05MnTzYdXdN8Wc1JrNYs990vv/wSuz1Lbea1XLRo\\nUez2I4880vTJJ59seu+99zad5GcJ3/ZcylhphiOEECIIGnCEEEIEIbWllsRGKzac8vXo0cP0lVde\\naXrTTTc1fc8995i+9957Tffq1cv0jTfeaDqJRVAqNsKf8bXVZ6Nxav7KK6+Y3nLLLU3Pnz/fOefc\\nueeea9vuvvtu04wO8iXWsV1pohRrKox2Y5RV/fr1V9mHNvLMmTNN++w9X40tHpv9mMSyy/LzkqRt\\nvujCtdde2zS/O3nPM2k+SjJ99NFHbRv7h7XUpkyZYvqiiy4yPX36dNNPPvmk6R133NH0119/bTp6\\nPp3z24okFwtWMxwhhBBB0IAjhBAiCDklfma1HDmnoFdccYXprbbayjSnxnvssYfp66+/3vTgwYNj\\nj59kip01W8C5wtgWPE7nzp1Nf/7556aXLVvmnKs4dV+8eLHptJYLE2yTRA/WRBiFSZukRYsWpvv0\\n6eOcq9hXY8eONf3pp5+a7t69u2n2OS3NcePGmWZ/1atXzzQjq0jWnpe09dNoo9Euo4223nrrmd5h\\nhx1MX3LJJaanTp3qnKtoT7ItfFbatm1r+o477jDNfhgwYIBpLlVw3XXXme7du3f8hwL5+q7XDEcI\\nIUQQNOAIIYQIQmpLbeONNzb93Xff5bUxuRJN+2idcTrK6f+zzz5r+v777zc9d+5c00lWxcsivulv\\nIWwLHn/XXXc1zSTPyOL8/9c/d875E2/ZR7RlmjRpYpr2RSlZaiEjsXhNjzrqKNPbbrut6SghdOut\\nt7Zt7du3N73RRhuZvvbaa02z7Xy+mBRO25P2qe8aZM2eT2Kjsc2MHluxYoXpVq1amaalzOU5+Czs\\nvPPOzjnnateuHXtORmjy/LTxaFvyPmC0YhIbjeSrTzTDEUIIEQQNOEIIIYKQ2lKbNWtWIdpRZTjF\\n3GmnnZxzFWsJMfGKds27775revz48bH7pCWJZULboVCEtCQ4re/UqZPp559/3vTs2bOdc87tvvvu\\ntu2hhx4y7WsvbYKoHptzzv3rX/8yHVkQzjk3bdq0VG0PTaGThBkFtddee5mmDc56Wo0bN3bOVbSD\\n+Lx8+OGHpn19x+coiV3GPiW+hHK2J6R9mqRPeN/SuqKdyEi/6Hr/eR8uLRDVY9xkk01i/59Joow+\\n5PEuvvhi01zxM5d7i9fDl/ibBM1whBBCBEEDjhBCiCCkttQYPcFpcMgIHNYtokUVJbCxThCn8Jxe\\nMhqnEEmQPqpD7S8mpTECifcGbc3bbrvNOVfRZvNNy7l9l112MX3DDTeYZlRP165dTQ8ZMsR01hIJ\\n/0whVvbkEhJchoC2I62Xhx9+2DlXsd5geXm5aSYT8tmh5ncA7+0kNlTW+ijJdxivN/fh5+L14f7c\\nzrqOtMBef/1155xzLVu2tG28PxhlSEuN9SCjROu/+hxpyddxNMMRQggRBA04QgghgpC35QlCTo9p\\nR3AqGyUYfvnll7aNUWy0HPbcc0/TSUpy5wKn6oU+VwgYLcTP9thjj5lm0mDUB0ymY1+wP2lBnHDC\\nCaYZSUXYv6RBgwamFy5cGLtPaHit8mWj+WwdJsoeffTRpl999VXTUeLn7bffbttat25tmhFWLIW/\\nZMkS07RRaRmRXFYCLURkmu+8Sb7DfBGVSSxEXrcXX3zRNJcNeOqpp5xzzn3yySe2jUumTJo0yTQj\\n4/79739X2pZ8kcvxNcMRQggRBA04QgghgpDT8gQhYXRNt27dTD/xxBOmIxuHERs++4GWDst254ss\\nr2BYFfh5zjnnHNOsw0Ubi+XsI/vy5Zdftm2MtmEyG+s9MWGR/UgY7TN06FDTWbHRSL7uA9o0tCN3\\n220307Q0v/jiC9NcAfLggw92zlW0rV566SXTH3zwgWnuw8/hs1f5TC1fvtw0o0Z5nFwsxrQk6YdC\\nJJzy+eCSDTNmzDB9+eWXO+ecGz16tG376KOPTPM6se4jreVcEjPJ5ptvbjpfSdWa4QghhAiCBhwh\\nhBBBKBlLjdEwrOvUqFEj09EUM6pH5FxF+4ERYm+99ZbpQiyzUB1sNNo1tC4fffRR0wMHDjTNFVJp\\nSURW2iGHHGLbaIWxVlS7du1M+2w0WgaXXXaZaV8EZXWGic/8/IcddphplsVnYmcUCbX99tvbNtYV\\n5DNHWynJ8he+iLVSidL0WYVpn2teK9amY907Xudhw4Y55yr+hEBLsm/fvqbZr0zGjmy5XClEbULN\\ncIQQQgRBA44QQogglKSlxig0TiUje62srMy2ccrPlfCYVFgd6pvlC1/5+M0228w0rz+v3XbbbWe6\\nc+fOps8//3znXMX6dbQJmjZtapoWka8kOi1TLlVw0003xba9OsPrRcuSibKsYceIp2bNmjnnKlon\\ntJfZtzwPI6VqwrOTiz1+5plnmmYyLq02XsMjjjhilWMwGo2Rbvyei0u0di4bq6cSzXCEEEIEoWRm\\nOJydMFCgY8eOpr/66ivnnD9PoH///qa//fZb09XhB/58wfwk5mzwx3z+OM2/oLhPVCHauT9mJJw9\\nMaiAeSLRX91/bosvT4M/xNYUONvjX7ODBg0y3bx5c9P8q5glat544w3nXEWXgEEFXASMMx/+8M+/\\n1KlD5tVkmV69epn25cfwusXlBG666aamfQ7EAQccYJqzHVbOzwKa4QghhAiCBhwhhBBBKBlLjT+s\\n0RaYPn266che4XSeFVpfeeWV2OPVdM477zzTBx54oGmWnPFV+aUd9sILL5geMWKE6ciOYbVolq1p\\n1aqV6VtvvdU0cxFoO/hs0poC+4K5GEuXLjXNQADuH7dIGvuFwRwMFOD1533BAA5f7k0uFKtEFK3K\\nXL4rzj33XNPPPPOMaV5bHj+6zmmrajMg4YEHHjC9//77m85XDlQupXM0wxFCCBEEDThCCCGCUDKW\\nGuG0klPTKJ/joYcesm2sZsxIt5rOihUrTDMajNP7Sy+91DQj05jDNHLkSNO0Mhm9Fk3B2W+c3jNn\\nhBFVtHFo3TH3JopMrKmwv6pajoXXmRWCec1pMdEOZRRUIeyvYkWQxt2/zqVvz+uvv276lFNOMb3l\\nllua5vWMrv/w4cNtGyPXjjnmGNNt2rQxzTJUUXkc55xr0aKFaS6olwtagE0IIUTm0YAjhBAiCCVp\\nqXF6z4WKomnlkUceadv23nvv2PfFResUitCRNpyCM3KI9iP3oXVGq4sL3dEO6NOnj2lGo/H4jF6K\\nrrWv5Mbpp59u2hdR1alTJ9O07hhVJf4gzX3G+5MWGatIczuTdhmxRts1ywsQ+qpdk0K0+emnnza9\\nww47mH777bdNR1Y3S3kxWvPjjz82zZ8Ovv/+e9Ndu3Y1fd999+Xa7LyiGY4QQoggaMARQggRhJK0\\n1FhPiMmcrVu3ds5VnI4ySo11t0JO80OcizaBLwFvv/32M83p/dVXX236jjvuMM0K0aw9RwuO+KoI\\nR/YdbbGpU6eafvzxx03zWtHSofXBCLt8ka914POJz5bKt13VsGFD06z4Xa9ePdOs58W++Oyzz/La\\nlhCErKDM54CJuVEdO+cq2thRBWhu4/NMa5ORaYx04/ffqaeeavrmm29O/wHyjGY4QgghgqABRwgh\\nRBBKxlJjBBTXA2eEUzTFZLTMggULTGfRNskXSWwCJqFxOk598sknV3ocRrgx8oyWCiOZIgts5513\\ntm1bbbWV6cgKdc65tm3bmj7nnHNMF7r0fRbtIJ+NlsRSS7MP+4W1v/ic0aY58cQTTTMasabBa8xn\\nyHd/MjKN0WZcbqVDhw7OuYpLg/C779hjjzXNZ48/MzCRm3XyuNwEtyd5nmiv57LkgWY4QgghgqAB\\nRwghRBBKxlJjZBKnprRaoikuE6VefPFF0/kqz12qsJYcI5C4hAOtMF+0G5PMfHCaHvXL3//+d9vG\\n+mm0PZ977jnTXLXysMMOM33vvfdWev4skkt0GfdPErFGi4f3PW2y6PqynD3fR5uGNjUjDLNoRYaC\\n3z29e/c2fdBBB5m+4IILTDPq0nedI6uNdpnPzoxbHfTP21kPj1FybHsS8rVyqGY4QgghgqABRwgh\\nRBBSW2ohayT5znX33XfHbo+SrGbMmGHbQiZ5lRKLFy+O3U4bLV8WUHQu1t2ijde9e3fTrP10ww03\\nmGZUT6mSr+fFZ4f4agUyaolJnlHyIW02QhuNK0fSmi1FSy3Jfc1rwnp9PjuTq+ZyiQ0mpjMJ86ij\\njjJNCyxaYoLLbtAWSxKtyGUqaF2/+eabptu1a+fiYAJptFJvPtEMRwghRBA04AghhAhCakutWDXI\\nGNXBqA3us2zZMuecc0OHDrVttBbEHySxFdL2Na0eRphFUYM8Hmtz0bo588wzY/eZNGlSpefPckn8\\nfEKbmEmBtNRIs2bNTK+//vqrHIfXauHChaYHDBhg+r333jNd6tc2SftpLfv279mzp2nWKRw8eLDp\\nKVOmmD7//PNNM7GTq3JeddVVzjnnevToYdsuuugi077INN4TJ510kmmuzksbzWfN0UYrxPOkGY4Q\\nQoggaMA7uEq3AAAgAElEQVQRQggRhEwnftKi6dKli2lGUpAoCoqJbCKeQtgi7C9aDFESaP369W0b\\nbTTyzjvvmGZCnI/qYKOl/Qzcn9eR14sWC22yyHZ27o9lJmgfzZ0713QuSdNJVtXMAkx0ZnQXrzEj\\n1piA/sQTT5hmTTmuiMs6gbQlr7vuOtPDhw83PW7cOOdcRfuNkWZc1uCee+4xTWuVddKOP/5400nq\\nvRW63qRmOEIIIYKgAUcIIUQQMm2pcSr+zTffmGbkGfeJpvETJkywbdtss41p1gDL8jQ/NLQMaLn4\\n8E27OU3nFL9jx47OOb+N5iOJjVNKNprPZkproxFeZ14vJnvyeaHd8t///tc5V7HGFm2XtO3i/ll+\\nvthm2miE18yX+Om7P2lhMtmScJVbMnDgwFW2jRw5stJzNm3a1DTrnjHS01cPLeQzpBmOEEKIIGjA\\nEUIIEYTUlhprMc2fPz/Ve3OJKPrggw9MM3mNkU+MsBF/De2dJDYa8fUdj/nYY4+ZnjlzZsrWVR98\\nUVA+GGlG+8R3zWlT8vny1crjPlFkFe0vap4/bbuyTC51AWk5+q5bvmEEnO871PeM5WtZgXyhGY4Q\\nQoggaMARQggRhNSWWlobjeQy/WadKE7pGzdubDrOUit0YmCpJLj9mUK0lcesyTYaKURkXi5wiYiW\\nLVs65yra1bRvQrYrJEm+E3z7+BImQ5GvuofFSpjWDEcIIUQQNOAIIYQIQtESP9NO6ZiIFZW7d865\\nyZMn/+X70k6Zk8D3prWmCl2rqCaTxbpquSRPFuJcjEh8//33q3yuyqDVzHZloV/yZT+l3Z4limXB\\naYYjhBAiCBpwhBBCBKFWmulRrVq15jnnZhSuOTWSZitXrmyUywHULwUhp35RnxQEPSvZJHG/pBpw\\nhBBCiKoiS00IIUQQNOAIIYQIggYcIYQQQdCAI4QQIggacIQQQgRBA44QQoggaMARQggRBA04Qggh\\ngqABRwghRBA04AghhAiCBhwhhBBB0IAjhBAiCBpwhBBCBEEDjhBCiDCsXLky8ausrGylc06vPL06\\nduy40jk3L00fqF/Sv2rVqmWvUP1SVlYWHSf2tdpqq9mr2NenhF56VjL2SvuspJrhlJeXp9ldVMKE\\nCROcy8NiULn2y2qrrWavJNSqVavSVz5gu9Iem+9dc8017ZWEfPRLeXl5dJxY1llnHXslId/Xtlik\\nvdf+RNGfFVGRtM+KLDUhhBBBWKPYDRD5h389ckVX3+quv//+e6XHXH311U3/9ttvptdee23TP/74\\n418eg3+dsy1s7wYbbGB60aJFlbbLBz/Tzz//XOn+VfyLu1J43dim5cuXm15jjT8ew19//TX2OLxe\\nSWY59erVM83rGNePvn7hjJBtZ//zvdS+eyoLKwz7Pm/Wjlkd0QxHCCFEEDTgCCGECIIstWqIz87w\\nWTFJLADaKMRno9GiirTPLmJ709poPqsvLYWy1JK0if3CdiSxOn3WpO868nptttlmzjnnhg0bZtuO\\nPPJI0926dTN92223mabVxj713V9JrNQk1m++8B3fd+2T2GVZtdGyZvVphiOEECIIGnCEEEIEQZZa\\nNaFu3bqmf/jhB9O52Ew+klhztCSSWENVJV+fz2f35YovimuttdYyvWLFCtNJbI8k0Ya0h55//nnT\\n5513nuklS5Y455zr3bu3bZs5c6Zp2mj169c3vXDhwtjz52LZ5vLefJHlyLqqkrW2a4YjhBAiCBpw\\nhBBCBEGWWjXh+++/N80oIlpOaZMHfay77rqmly1bZjpJAmOW8EVJFeoc7IuffvrJdJLoLl8kW4MG\\nDUzPmzcvdv+XX37ZdL9+/UxHSbunnHJK7LFJZL8551ydOnVMM+qtssTfP5MkmjJt1F51Icnz6btn\\n+d7atWubZgJ0sa6lZjhCCCGCoAFHCCFEEKqlpVZq1k6++eWXX0z7Er9803FGIzF5kMe5//77Tfft\\n29d08+bNTU+ZMsU064ZVFfbpvffea/rEE080nTZiLYStkDbx09dH3If39Ny5c00zUpGf7dtvvzXd\\npk0b00OGDFll2wcffBB7DNa4a9q0qenp06ebTmup+ShWZFWxkiRpgUe6c+fOtm3GjD+KMdPO/Oqr\\nr0zz2jdq1Mg0q5FPnTrV9OGHH256+PDhse0qxDXQDEcIIUQQNOAIIYQIQslbaoySueSSS5xzFa0F\\nJthFFoJzFZMjOWWtbvhsGeomTZqYpv3CfY477jjTnLJzmt6hQwfTvL6VnT+JjcTkxH/+85+mC5HY\\nWih8kUf77befaSZpJin3T3jNd911V9OtWrUy3aVLF9NR9Nqrr75q23zXk+efNGmS6fXXXz9VG5NQ\\nLGvLd+/lqw20zvi9tNFGG62yz8SJE22b77pyaRB+522//fam+TzzPO+//75pRgKut956phmZmC80\\nwxFCCBEEDThCCCGCUJKW2sUXX2z6qquuWuX/fVPg/v37m/bVr+rUqZNpRuyUKr7kRl8UE60E2i83\\n3HCDaVpqrKvFvqDttXTp0lWOzWibXr16mX7rrbdMH3zwwaYZebfPPvuYfuyxx0xnrW6UcxWTZJl4\\nx89DGy1JiXzfPj6L5fjjjzfdsGFD02effbZzzrnnnnsu9jybbLKJaUapfffdd6YXL14c+95c+iIL\\n/Zi2Db7PzmvYrl0702eeeabpzTff3PTTTz/tnKv43cOEXkaRjh07NnY77brWrVubpqW3YMEC082a\\nNTM9bdo004WI9tUMRwghRBA04AghhAhCSVpqcTYa4fSW1gWniJx2cv9Zs2blo4nB8U3pk0QO8b20\\nZT7//HPTtGJYt402UY8ePUyPGjXK9AsvvOCcq2ijlZeXm77mmmtMR/abcxXtiBEjRph+8sknTefL\\nfqH1lU9YMy1J7askJfIZScb+2nHHHU2zxlq9evVijxlFKtE6feKJJ0wz0o0WDPuREWt81vJFqdRS\\nY7QsnxUmSbdt29Y0I8ZIZG9NnjzZtg0dOtQ0E219x2P/MEmXSaC0onk/cX9f9G4udRg1wxFCCBEE\\nDThCCCGCUJKWmo/IdmDkDC0HTsmZJMcpaCFsgRAkWXqA035GnfC9rMnEJDBeU+7P6Jj33nvPNCPf\\non1ol82fP9807RomEvI8O++8s+lvvvnG5Zt81HuLg5FBtNcYRUaLMgnsR0aP8Vy0WK6++mrT7du3\\nNx0lfE6YMMG28VmYPXt2bNt577AtpfrsRPC7gs+Bz67m9eYyAC1btjRNW5L78Bry+NG9PW7cuNj/\\n588CLVq0iN3OxE/uc8stt5hmX7Fmom81VyJLTQghRObRgCOEECIIJWOpnXPOOZXuE01TmUj4r3/9\\ny/TWW29tmglOO+ywg2laBKWEb9rPKJ8kyVt870cffWT6nXfeMc1IGVpdnLKPHz/edDTd5zSeK4XS\\natt0001jz8MIm3yVwWekIqPt8gmtKEbd0XJMC61hJgU2btzY9GeffWaa9/dNN91kOvrMX3/9tW2j\\npTZz5kzTPju20M9LoZNA+Xz47ivfKqiM7uL9w+vJemS+unNMqv7kk0+cc86NGTMm9n20UPms0MY7\\n8MADTX/44Yem33jjDdM+C5nXm33Lz5pLtKBmOEIIIYKgAUcIIUQQMm2pcUrHaSfhFDCayh566KG2\\njXWKGA201VZbmWbSX77smtD4rAdOf7ki55dffpnqmLTLaFMyqoUrB/K8cZYaYZQMYY0nX1RPLpYL\\nbZAQVirtL+L7PL5oIN6vtDq22WYb07RDmTRLK+9vf/ubc865jz/+uNLz+EresyYhr2cSizJJPxba\\nUvPZQ74ahL73+pLKeQ3Z/1y19tZbbzUd9Se/h/i9xehOWmpM2PTdN/xMjMjz9VUu0Wg+NMMRQggR\\nBA04QgghgpBpSy3JlI779OzZ0zlXMRqtb9++pjk1pkXDcvtfffVV1RpbAiSx0Qiv1xdffGGaES7c\\nx1fOPG71T0JLZ/fddzfNZNN+/fqZ9lkxjLBidJgPHifEyqE+SzHJqqzchwmEtG+4+irr2tHWueuu\\nu0w//vjjq5yHx6ONxtp3tGZYe9AXzZULxVr9k3aZL1qL8N7bf//9TdNGY/8zeZnLFkSRZDw/ryuv\\nB59D2mtz5swxfe2115pmXyX56SBfSxIQzXCEEEIEQQOOEEKIIGTaUmPUjQ8mJEZ1g+68807b5rMo\\naP+wlld1wGcBpC31zuu15ZZbmmaE36effmo6iY0VwSiZbt26mWZ9Ktqbr732Wmy7eJwk5w+R7JkE\\nn1Xk0+w7JhNyFdsLL7zQNKOZhgwZEnucuG2s8bbHHnuYZjLhpZdearpDhw6mfYmivAf53PEeLFaU\\nWhJ8NprPkmX9Mq6m2qZNm9h9eK0i25vRn7xmvkgzRuPynExCpRVbrGhczXCEEEIEIdMzHC7u5MvD\\nYL7B//73P+ecc4MGDbJtLCdC+NcVy6xUB3x/kaUtScFyMvyL+bLLLjMd/fCcBPbbaaedZpp9xL/g\\nNtxwQ9OcYfGHUP5Ayx/HfX3KWQ1nO4WqdJzkB2cfvqCZTp06md5zzz1Ns7+4CNj1119vesqUKaYH\\nDx7snKs4k+EPyzw2r8/cuXNNM1CBf3EzUMRXFockyUXKwmyH8F7deOONTfP6sCzNI488YprBBE2a\\nNDEdVfPmLJb3Nfft3r27aT7bdGwYkMByR8Va2E4zHCGEEEHQgCOEECIImbbUONVjlVtaBJyaHnHE\\nEc65ink1Pk444QTTIXIwQpIve4K2SFTF1rmK1g1/NH7ppZdMx1mgf//7323bNddcY5qWC/ucQQDP\\nP/+86YkTJ5pmAAPbSHyfO0RpmyT3ls/e8OXH8AffnXbayTStF+aF+Ij6gIEatC65AB/zd7g9euac\\nc+6JJ54wzXIsvvI3/Hzch9esWDZakurr3M6csVdeecX0jBkzTLMPaT/S/o3y0Hhf016jhcySULTu\\n+Oy9++67ptnPxfrO0wxHCCFEEDTgCCGECEKmLTVOWc8880zTzBUYMGCA6WHDhjnn/NE9tCsefvjh\\nvLUza+SS0+Czd5gLwIXRrrrqKtOcytNWOPbYY51zzt1xxx22jRYW28W13FmVmH3KyJuOHTuaZhSO\\nzzLgAla0fUJG6vyZJLYnry3tJ9pr3E6b5oMPPjDNZyeyQ1kKpV69eqZpf7GMCquxv/3226a32247\\n06NHj45tI6Pd2Be0b7MQmebrE1/JG9pejJz1PUN877bbbmu6a9euzjnnysrKbBuvE21mX0Tn2LFj\\nTdP+5nuLdV01wxFCCBEEDThCCCGCkGlLjQwdOtQ0K+Eed9xxpiurLl3dStj4yCWpi5E0tKVYxfmB\\nBx6I3WfkyJGx2x999FHnnHO33XZb7P/TcmFSKe2XUaNGmT7rrLNMs4r0/fffb9pny9D6KCZpbSNG\\nndH2onXGCsSXXHKJaZaiWbp0qenIgmRf0ArdbbfdTDM5lNFwjFI855xzTJ9yyimmGWHKPt1oo41M\\ns1+ylvjpOy9tMUbusc28VrNnzzbNZGdGj0WRfrSNGzdubDpKDHWu4vVjFCevMRN5+WynKUOVTzTD\\nEUIIEQQNOEIIIYJQMpbaGWecYZrWSVQ/zTnntthii1Xex+geVlStzuQSceWbao8ZM8Y0+4LJfoxk\\nIlG003777WfbuKb7f//7X9O0A1mJmgmJtCB4L5Cs1N1KUhU6yf68trTRWFWYC9kxEZHXlwmHzZs3\\nd84599Zbb9m2N9980/Trr79umtYl7SBaYQcddJDp8847z/TBBx9s+vPPPzfN6DnfImPFjB6sDFpX\\njLJjZBgjzJioydqE06ZNMx1dWyYx832skcdjM6KTFlxVq7kXCs1whBBCBEEDjhBCiCCUjKXGZLNm\\nzZqZjrPRfO/zWT41hVwifmjjcEkCJhv6iKKgWBqfFg0jsHbZZRfTrCfF5ETWbEv7mbIQ9fRXJEna\\n5UJn559/vmnax7169TLNaCb2Y2SHPv3007aNCYd8zhgZx2hPWjlc+JDnHDFihGmW1/dZZ2xDliNL\\nfXX5+Flol9WvX980IzNZDzKyvWiD8plg8ii57777TDNaMYmNFnKpAs1whBBCBEEDjhBCiCCUjKXG\\naTkjaSqDdkFNgVFEtKJ8qy2mJclxaJdECXJHHXWUbeO664cffrhplnOntcJIKlqjviggH6FtNF9p\\n+1ysC9pM1LzmjF7j9dp0001NR+vdM2mRllufPn1Msy8aNGgQezxGqXE5A35W3o8+2PZirUyZBEZL\\nMgmUmnYxIy15HWi1RXXQaNFNmDDBNJchYF/xmeR18q2UzPtSK34KIYSodmjAEUIIEYSSsdQIozbi\\n4CqINZHvvvvOdCEspCRTcE7fo2gnRs8wiooROwcccIDpU0891TSjnmhHMJKKlpqvrl4xI9MKbV3w\\nszE6yme1RTYZrz8tLF7///znP6ZZe4010xixxqg2ntO34qfvc2QtkpBt9lnLXAKiS5cupvm9xdp0\\nV1xxhenoWvlWe2XiJ/uN157t4vWj1acVP4UQQlRrNOAIIYQIQslYaix9TjhlfOONN5xzzo0fPz5I\\nm7JKSBuC52IpdtpH0T5McGMSKJckuOiii0wzqZf1uLhCYvfu3U2zThjthtatW5tmbSnCtlcH2C9M\\nFuT2yJr0WS1MGmTtu8MOO8w0a6Oxzxlt6Is043afjZY1S823dAIpLy83zeuw//77m6b927dvX9MD\\nBw50zlVMkG3VqpXprbfe2jQjdxmJyBpvbGOxbDSiGY4QQoggaMARQggRhExbaizzzRUMOa098MAD\\nTTOZUBQOX7QVI5CYHHjttdc65yomA3KFQkbecDXR22+/3TTfO2jQINO0i2ijEZ+NRkLU2fNZMLSW\\nCmF7xCXhOvfHc8Rz+iwsrgR64oknmn7kkUdM0yalZXT22WfHtoXnzXqNuwhfHzIJlM8BoyiZqMmV\\nO1kbcM8993TOOTd69GjbxmU9+Kww6TdJDb4soBmOEEKIIGjAEUIIEYScLLUk0+AktZB801RuZw2h\\nuXPnmh43blyyxlZz0iZ1scaTr4Q5E84Y+eLra+7D5MzevXs75youZcBjcDtXrWRCHNvI+4KWmu9+\\nZA2rqVOnxu7juwfzie+68bnIl7XE+4H4+qAypk+fbnrfffc1zeURhgwZYpoRiUmiznx9kTVLyLek\\nAu3cqEadcxXvN35X3X333aa3224709H33M4772zbRo0aZZp1JGnR0dLjc5g1NMMRQggRBA04Qggh\\ngpCTpZZkulu7dm3TvigiJuyxDtGkSZNMs2bTxRdfbHrp0qXJGlvN4fTeZ6/RDmAkjY8kNloSKlt1\\n8MEHHzQ9ZsyY2Pf5bJYk9gGTE33JoSGsG5/t4VvCgPisHB/sd989UBk//PBD7Pt470ycONH0/Pnz\\nTeeSvJllGy1J23h9aGEyIZT1zp555hnTkU3GqEk+z76VRfO19Eih0QxHCCFEEDTgCCGECELBEz99\\nNhrh1J2akS7vvvuu6aZNm5r21WMqJIzeSmJNhYBJspzGE14fX6Kab39O6+PqpP2ZuGRDTvsZXda4\\ncePYtiSJpGMZfL6XqyjOmjXLdJL7sVAksT18dlmS65ykFH1VnxHf+0aOHFnpe5kEzKUKSMuWLU0z\\nsisLJLlmPpuX156r1qbBZxtnbemBJGiGI4QQIggacIQQQgQh07XU2rZtW+k+hV5FMY6s2GgkSS2w\\ntFFqSepekSuvvNL0pZdeajrOSqIdwBVKk8ClBBYvXhy7D63ZJBQz8TOtRZskmZr9lWQZgMpIUube\\n1y7aaD7rJ2s2mg9eB1/koM/+9UUjxi3ZkDYZ2NcnWUui1QxHCCFEEDTgCCGECEKtlNPqec65GZXu\\nKNLQbOXKlY1yOYD6pSDk1C/qk4KgZyWbJO6XVAOOEEIIUVVkqQkhhAiCBhwhhBBB0IAjhBAiCBpw\\nhBBCBEEDjhBCiCBowBFCCBEEDThCCCGCoAFHCCFEEDTgCCGECIIGHCGEEEHQgCOEECIIGnCEEEIE\\nQQOOEEKIIGjAEUIIEQQNOEIIIcKwcuXKxK+ysrKVzjm98vTq2LHjSufcvDR9UOh+qVWrlr3y/XlX\\nX311exX72he6X8rKyqLj6JW/V6aeFb3SPyupZjjl5eVpdheVMGHCBOfysPpgPvtlzTXXtFcSatWq\\nZa/K9qlbt6698kWS86clH/1SXl4eHUfkj0w9K9WF1VZbzV5pSfusrJH6DCKTrLPOOqZ/+OGHSrf7\\n+Pnnn1Odlzfpb7/9FrtPtKrs4sWLUx07CVqxNgxrrbWW6bT3SKnAP1pq0n31+++/BzuXfsMRQggR\\nBA04QgghgpDaUsvytDNqz8KFC21bgwYNVvl/51yV/Mos47PLGjVqZHrGjD+s1o4dO5p+7733qnxe\\nn41W2X1Cq++nn34yHXJ6T+rUqVOU85YK1dVGI77vsyx/55Ua1etbVwghRGbRgCOEECIIqS21Qkwp\\nN998c9PTpk0z7Qt1bdu2remJEyeu8v+00RgZVb9+/ZzaWYrQRiNJbLQNN9zQ9Jw5c0yzX9Zdd93Y\\n7d9///1fHpsWIEOw27dvb/r999+vtI35grZeoaCN67MOr776atMXX3xxwdv0Z2QfrYquQ/7QDEcI\\nIUQQNOAIIYQIQiYSP2mjJWGnnXYyvcYaf/0R/vGPf1SpTTWJ1Vdf3TSjzmijkbXXXtv0smXLTPfv\\n39/0rbfeajqKSKONtvHGG5tu3ry56alTp5pu3bq16enTp5tmxBTbm4sdFCJqMUkEXiFsNNqeH330\\nkel9993XOefcFVdcYduOOeYY07yebHuLFi1M0zqdP39+nlosqiua4QghhAiCBhwhhBBByISl5rNC\\nXn/9ddODBg0yfeWVV5qOS/LkMYYNG5bfxmYU3zX0RfpxH1/ypg9fkiltNLJixQrnnHPbb7+9bTvo\\noINMH3XUUaafe+4505Hl45xzd911l+lPPvnE9Msvv2w6iY3Gc/HeKFbCaa4k6XdakI0bNzb9xRdf\\nJD4PLcc+ffqYLkYkXRZRdF8yNMMRQggRBA04QgghglAQS+3yyy+P1Sxx/ssvv/zRCESa/frrr6Z3\\n2203077EPB4z4sILL4w9T3UmyTSe15n785rnC1owZWVlzjnnBg4caNs6d+5smpFuvqjCG2+80TSj\\n1xiBtXz5ctO+61FKFqvvsxHf5zzrrLNMn3POOaYPP/xw09ddd51zrmKCb7169UzXrl079tg8Hu3t\\nmlBvzUeS56+qtlva92XZ3tMMRwghRBA04AghhAhCwS01wil3jx49TDMCac899zQdRTc551y/fv1M\\n33333bHHv+eee5xzzl177bWp2lud4ZS6EPYik0BZE2/o0KGmo6UQFixYYNtouTFh8KWXXjJ93HHH\\nmWYk3aGHHmp6yJAhprNmHzjn3HrrrWea1mESfDZaEmhBfvbZZ6bHjh1rOooa9NnbfP7Ylrlz55ou\\nhB1b6rDPR44cafrOO+803aZNG9M33XST6bgahA0bNjTNe/++++4z3a5dO9NMjH/iiSdM8/5btGhR\\nJZ+iMGiGI4QQIggacIQQQgShaImfI0aMMP3CCy+Yvu2220yfcMIJpllLi1NJ2gGnnHLKX54zSXn4\\n6kYhIlYYJbb//vub/ve//22aFtg333zjnHNuq622sm1ckoC2HOu6sW/nzZtnmrX3tt56a9Pjx483\\n7VvdlduZBFmoOmBpbbRC8Mwzz8Ruj6tDyH6jvcN9uU9NeY4qg8/ZmDFjTNPy5T18/vnnm+b9P2DA\\nAOec/7uK22nFcTuT4Xv27GmaP1cU67tQMxwhhBBB0IAjhBAiCDlZarnYNXwvI2B8iX9du3Y1TauF\\nK1f26tXLOefcgw8+GHsMJrL9+OOPqdqbdaIlAJyrWOssFxvN178sZ8+kQUahMfk2LqqQfeirzfbP\\nf/7TNK02RsP5Vg7l8WkZ8DNx+QUmWdYU4iLMHn30UdO8hrw+IZZyyBK+eoS8JpMnTzbdqFEj0/fe\\ne69p3ofU55577l+en9ebbWH/MQF+gw02ME3LuW7duqZp9YZM2K1Zd44QQoiioQFHCCFEEHKy1HKx\\na3zvXbJkiWmWs6dNRuuEU8MttthileNxCsppL1ctzGLCYFpoLeWSbEh8kV60N6MINOecmzlzpun/\\n/Oc/VT5vhC9RlfcIE9hOO+0000wm9tVYo/XAY9YUIpty1KhRtu2AAw6o9H2+ZSiqK7xnGK3H+o7R\\n0ijOOVenTh3T/P7hM0SLmMeJvtu++uor27bJJpuY5nPOZ4/JodyfNjeTQ7nyK/cpNJrhCCGECIIG\\nHCGEEEHIxIqfPt544w3TvlLp2223neldd93VOVcxiorRW6effrrpYpXw9kW85BPaaLl8TloAviUk\\naG8effTRpn3LSVQG20vNZENGl+23336mmUxMW9EXtUcbjZ+jpvDOO+845/6odZcURg8y+bDUoc3F\\ne5/WLu/9Jk2amOb3DPGtwnrzzTeb5qqp0VIeTHT3sdlmm5lmvTyep3nz5qZHjx5tmhac79kuBJrh\\nCCGECIIGHCGEEEFIbamFtKKSJJgxOiRuf9Zju+aaa0xz6tihQwfTjLTiVJPTatYS+/TTTyttIwkd\\nEec7ny+ZzFcna/311zfdqlUr023btjWd7wQyX7vIc889V+lxfPdRoZduyCK0W9PU0OK+aS24UoH3\\nmO9+22ijjUyz/h4TyVkbzXcPX3DBBaZp+cYtT0B4LzOi0PeTA+/xSZMmmWYkG6N3C41mOEIIIYKg\\nAUcIIUQQUltqhbaEWBMorny6c8599913pjk1jGDEyBdffGGatYQ41W3fvr1prpDHSCdGdWyzzTam\\nDz/8cNOPP/547PGzmFiatiQ57QNG57z55pux2yv7/Px/JsqxTtonn3ySqo0+VEL/DxjJx6jCyrjq\\nqqtMZ2HJhWJB6+r11183zahM1ljjfc7IM1/9wMrgasZnn322aZ9tzKU8aAd+/vnnsfvXr1/f9OLF\\ni6YBafsAAAiPSURBVE3n6ztMMxwhhBBByFweDmc4H3/8sWn+ON20adO/PAZLONxzzz2mfTkww4cP\\nN+2bVXGEZ6AA/2rgzIelI0LAfKT333+/0v35w2baytmzZ882zWvKchzMa4muHWej0UJTzlWcJR57\\n7LGm8zXD8ZH1WWi+YH5Jt27dTMc9D7wO/FF67Nixpvnjd025hhEsA9OyZUvT9erVi92fwSj77rtv\\nlc55++23m+Yik0ly+ujSdO7c2fTAgQNNX3311aZZKqoQaIYjhBAiCBpwhBBCBCFzlhrtHea7EP6A\\nz9yPCRMmOOcqlnxIUrKElkMSGHzQpUsX0/xBNjRJbDSSywJ0tE58Ngptl+iHVlYlpv1IaLW98sor\\nVW4j8dk+NcECcq5i0ESnTp1MR5Yln6G99trL9Ntvv23al5fCH8j5w7lv/1KHP/bPmjXLNO1/Wvq0\\n1BicxB/zaeNvu+22zjnnHnvsMdtWXl5e5fbyu6px48amBw8eXOVj5oJmOEIIIYKgAUcIIUQQMmep\\nMSfDF1vOKClfNdbKoP11yCGHmPbZazz2oEGDTD/55JOmGbfOdc1DlE1hiZ+FCxfG7sPpdWUlNJyr\\n+JlpTdIu4fXiPjvuuKPpaPrORe98jBkzJvbYuVg0NcU6I3x2mJdGK2fFihWr/H+SckKEfc6F7qor\\ntCe5QCQXHIxsMecqfrc8/PDDpnlvs8wWLcp8tJFRZ8y98eUB+fLjcrHgiWY4QgghgqABRwghRBAy\\nZ6kNGzbMdBKLrLJ9ItvAuYpRNA8++KBpWl49e/as9JyXXnqpaU5fmbQYuvqwz0YjtNF8kVuc6jOZ\\ndJ999jHdu3dv0yzXwSicDTbYwHRkGTDZlDYCrxUT1Til9y2i5luwjZZSoReVyjqvvfaaado9EWlt\\nNFLTytzwWh144IGmjz/+eNO0GVmGi5Yj7W2WjXr33Xedc87tscceto3PLau2++5rPitsI+09JpMS\\nPlv5stGIZjhCCCGCoAFHCCFEEDJnqTG6iXZVksXYImjR0EZjNM4jjzximvXbOKVkQhzfywXImPCV\\nNoG0mCSpgXXccceZ7tevn2n2C5NwaYdNnTp1leOxEjTXYKftyag/JsT52uiLqqGt4Pus1bkOGO/F\\nDz/80DRtz8g+o02TtpZWTbMreZ+wBqMPJnCymjzvVX5HRdWazzzzTNt26qmnml66dKnpBx54wDTr\\nS55++ummWePNZ6Px+4/fnYV4JjTDEUIIEQQNOEIIIYKQOUttww03NE1bhBFOaaBd4EtkJIzS6dq1\\na+w+U6ZMiT0mKSsrM82S5lkhyaJkRxxxhGn2BZMHr7zyStPffPON6YkTJ5qOaqkxco3RgOeee67p\\nZs2amaZdSXuNNg4/B6NqGDXEBL0zzjjDdHWz0Qgjkniv05qO7l32S6HL09dkkkSALVmyxDlXcSHI\\nf/zjH6bfeust06+++qppRiLyOyxJgjd/Oig0muEIIYQIggYcIYQQQcicpUZYV+iKK64wfckll/zl\\n+5IsSUA41Y2WOHDOuXHjxpn2WVC0KLhPMW002pJz5swxnaQ22cYbb2z6hhtuMM3127/88kvTSSyY\\nyD7gOf/3v/+ZPvroo02z3lOS9vpqyD300EOma1pyonMVo/0YKUUiS22LLbawbUzkFeGJ7M0333zT\\ntvHnBC6H0r1790qPl7VITM1whBBCBEEDjhBCiCBk2lLjFJD1y4YMGWL6lltuMX344YdX6dhNmjQx\\nfdRRR5lmQpaPJNFeoaGNRnz2H7cz0uzWW281PXPmTNNt2rSpUrsYXcYVP5lsxig1ntNXm85n6fHz\\nJUnQqw7QDmWEX2UwMdTH3LlzTdOCq4l2ZSHZYYcdnHMVbTTaYlwGwfc8kyzYaEQzHCGEEEHQgCOE\\nECIImbbUfHDFTyYnRlFNTLrklL9v376mb7755lXe9+ft1Q3aUvzMvkgWJlu2bNkydjvrMBEeJzov\\na6ntuuuupmmj9ejRw/TLL7/s+yix5/HBGm+8HxjNmEVrNC1M9mQNrcqYN2+eaSaB8lo1btw4x9YJ\\nH7TGou8zbmPk4AcffGC6WPdsmpWV/4xmOEIIIYKgAUcIIUQQStJS8xElBzKihtAuS7LKISNFWEK/\\nVO0XljNnrTGWSue14GemdeUr8U9ozSxevNg559y3335r27j0weTJk03TDk1ilyVJbPNFUoVelbXQ\\n0IJM0kcRffr0MZ2k9pbIL9GSBM45d8IJJzjnKvYfa6aNGjUqVLO85BL5phmOEEKIIGjAEUIIEYRq\\nZalVRtq6QiwhzhU/aTX57Lhi4vuctNEYXcYEV26ndcjj8DP7rJvIRiM8D5NHx44da/rII480zdUp\\nfcmJWUtsKyZcZTXNCrmiuDDxPOq3yFpzzrkHH3ww7+csVo013ZVCCCGCoAFHCCFEEIpmqRVjSpfL\\nebjiZRbh9WSioy/qiKv8MamPEX5cHoLHZ9QXE0K/+OKL2P3jrjvPv9NOO5necsstTSep8UWyVord\\nuYoWZZKVFbP4GUQ6ktQ4I5988onpKDmdy2sUgmLdW5rhCCGECIIGHCGEEEEomqUmuyC/0IpJm7zn\\nS5Rdvnx57HZacIyMSoPPauCKn2lhbbQk9lUI0rajuj8XTKZmFGh1gve2L+qT9QgZvbn33ns75yqu\\n2MolOPJ1f5x55pmmQ9aP1AxHCCFEEDTgCCGECEKNSvysziSZajPqzGeX+eByBrTgih1VxfNnxUYT\\nfqqrjebDd09y9Vvew7169Sp4m5wr3jIsmuEIIYQIggYcIYQQQaiVxgapVavWPOfcjMI1p0bSbOXK\\nlY1yOYD6pSDk1C/qk4KgZyWbJO6XVAOOEEIIUVVkqQkhhAiCBhwhhBBB0IAjhBAiCBpwhBBCBEED\\njhBCiCBowBFCCBEEDThCCCGCoAFHCCFEEDTgCCGECML/B2p+AB2SZaWtAAAAAElFTkSuQmCC\\n\",\n \"text/plain\": [\n \"\"\n ]\n },\n \"metadata\": {},\n \"output_type\": \"display_data\"\n }\n ],\n \"source\": [\n \"saver = tf.train.Saver(var_list=g_vars)\\n\",\n \"with tf.Session() as sess:\\n\",\n \" saver.restore(sess, tf.train.latest_checkpoint('checkpoints'))\\n\",\n \" sample_z = np.random.uniform(-1, 1, size=(16, z_size))\\n\",\n \" gen_samples = sess.run(\\n\",\n \" generator(input_z, input_size, n_units=g_hidden_size, reuse=True, alpha=alpha),\\n\",\n \" feed_dict={input_z: sample_z})\\n\",\n \"_ = view_samples(0, [gen_samples])\"\n ]\n },\n {\n \"cell_type\": \"code\",\n \"execution_count\": null,\n \"metadata\": {},\n \"outputs\": [],\n \"source\": []\n }\n ],\n \"metadata\": {\n \"kernelspec\": {\n \"display_name\": \"Python 3\",\n \"language\": \"python\",\n \"name\": \"python3\"\n },\n \"language_info\": {\n \"codemirror_mode\": {\n \"name\": \"ipython\",\n \"version\": 3\n },\n \"file_extension\": \".py\",\n \"mimetype\": \"text/x-python\",\n \"name\": \"python\",\n \"nbconvert_exporter\": \"python\",\n \"pygments_lexer\": \"ipython3\",\n \"version\": \"3.5.3\"\n }\n },\n \"nbformat\": 4,\n \"nbformat_minor\": 2\n}\n"},"license":{"kind":"string","value":"mit"}}}],"truncated":false,"partial":true},"paginationData":{"pageIndex":13,"numItemsPerPage":100,"numTotalItems":47214,"offset":1300,"length":100}},"jwt":"eyJhbGciOiJFZERTQSJ9.eyJyZWFkIjp0cnVlLCJwZXJtaXNzaW9ucyI6eyJyZXBvLmNvbnRlbnQucmVhZCI6dHJ1ZX0sImlhdCI6MTc1MTY2OTA5OSwic3ViIjoiL2RhdGFzZXRzL2NvZGVwYXJyb3QvZ2l0aHViLWp1cHl0ZXIiLCJleHAiOjE3NTE2NzI2OTksImlzcyI6Imh0dHBzOi8vaHVnZ2luZ2ZhY2UuY28ifQ.ixviquVIpqRjlRfR5vEVUhv9P-92uJCokV_FW4U6wjjHF-yvk55hI9JWcKNKsiQ27Q_QYJLeTVUR87YeagnXBA","displayUrls":true},"discussionsStats":{"closed":2,"open":0,"total":2},"fullWidth":true,"hasGatedAccess":true,"hasFullAccess":true,"isEmbedded":false,"savedQueries":{"community":[],"user":[]}}">
repo_name
stringlengths 6
92
| path
stringlengths 7
220
| copies
stringclasses 78
values | size
stringlengths 2
9
| content
stringlengths 15
1.05M
⌀ | license
stringclasses 15
values |
|---|---|---|---|---|---|
fionapigott/Data-Science-45min-Intros | neural-networks-101/Neural Networks - Part 1.ipynb | 6 | 20311 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Neural Networks - Part 1\n",
"\n",
"2016-06-17, Josh Montague\n",
"\n",
"Motivation, a little history, a naive implementation, and a discussion of neural networks.\n",
"\n",
"\n",
"## Logistic regression\n",
"\n",
"Recap of the structural pillars of logistic regression for classification ([previous RST](https://github.com/DrSkippy/Data-Science-45min-Intros/blob/master/logistic-regression-101/Logistic%20Regression.ipynb)).\n",
"\n",
"<img src=\"img/NN-1.jpeg\"> "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's see an example where logistic regression works. Consider some two-dimensional data that we'd like to classify. "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"%matplotlib inline\n",
"\n",
"from mlxtend.evaluate import plot_decision_regions\n",
"from sklearn.datasets import make_blobs\n",
"from sklearn.linear_model import LogisticRegression"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"samples = 20\n",
"\n",
"X, y = make_blobs(n_samples=samples, n_features=2, cluster_std=0.25,\n",
" centers=[(0, 0.5), (1.5, 0.5)], shuffle=False, random_state=1)\n",
"\n",
"# fit the LR model\n",
"clf = LogisticRegression().fit(X,y)\n",
"\n",
"# plotting decision regions\n",
"plot_decision_regions(X, y, clf=clf, res=0.02)\n",
"plt.xlabel('x1'); plt.ylabel('x2'); plt.title('LR (linearly separable)')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"print('The model features are weighted according to: {}'.format(clf.coef_))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## A different view of logistic regression \n",
"\n",
"Consider a schematic reframing of the LR model above. This time we'll treat the inputs as nodes, and they connect to other nodes via vertices that represent the weight coefficients.\n",
"\n",
"<img src=\"img/NN-2.jpeg\"> \n",
"\n",
"The diagram above is a (simplified form of a) single-neuron model in biology. \n",
"\n",
"<img src=\"img/neuron.gif\"> \n",
"\n",
"As a result, this is the same model that is used to demonstrate a computational neural network. \n",
"\n",
"So that's great. Logistic regression works, why do we need something like a neural network? To start, consider an example where the LR model breaks down:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"rng = np.random.RandomState(1)\n",
"X = rng.randn(samples, 2)\n",
"y = np.array(np.logical_xor(X[:, 0] > 0, X[:, 1] > 0), dtype=int)\n",
"\n",
"clf = LogisticRegression().fit(X,y)\n",
"\n",
"plot_decision_regions(X=X, y=y, clf=clf, res=0.02, legend=2)\n",
"plt.xlabel('x1'); plt.ylabel('x2'); plt.title('LR (XOR)')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Why does this matter? Well...\n",
"\n",
"\n",
"## Neural Networks\n",
"\n",
"### Some history\n",
"\n",
"In the 1960s, when the concept of neural networks were first gaining steam, this type of data was a show-stopper. In particular, the reason our model fails to be effective with this data is that it's not linearly separable; it has interaction terms.\n",
"\n",
"This is a specific type of data that is representative of an XOR logic gate. It's not magic, just well-known, and a fundamental type of logic in computing. We can say it in words, as approximately: \"label is 1, if either x1 or x2 is 1, but not if both are 1.\"\n",
"\n",
"At the time, this led to an interesting split in computational work in the field: on the one hand, some people set off on efforts to **design very custom data and feature engineering tactics so that existing models would still work.** On the other hand, people set out to solve the challenge of **designing new algorithms**; for example, this is approximately the era when the support vector machine was developed. Since progress on neural network models slowed significantly in this era (rememeber that computers were entire rooms!), this is often referred to as the first \"AI winter.\" Even though the multi-layer network was designed a few years later, and solved the XOR problem, the attention on the field of AI and neural networks had faded. \n",
"\n",
"Today, you might (sensibly) suggest something like an 'rbf-kernel SVM' to solve this problem, and that would totally work! But that's not where we're going today. \n",
"\n",
"With the acceleration of computational power in the last decade, there has been a resurgence in the interest (and capability) of neural network computation.\n",
"\n",
"### So what does a neural network look like?\n",
"\n",
"What is a multi-layer model, and how does it help solve this problem? **Non-linearity and feature mixing leads to *new* features that we don't have to encode by hand.** In particular, we no longer depend just on combinations of input features. We combine input features, apply non-linearities, then combine all of those as *new* features, apply *additional* non-linearities, and so on until basically forever. \n",
"\n",
"It sounds like a mess, and it pretty much can be. But first, we'll start simply. Imagine that we put just a single layer of \"neurons\" between our input data and output. How would that change the evaluation approach we looked at earlier?\n",
"\n",
"<img src=\"img/NN-3.jpeg\"> \n",
"\n",
"\n",
"### DIY neural network!\n",
"\n",
"**Reminder:** manually writing out algorithms is a terrible idea for using them, but a great idea for learning how they work.\n",
"\n",
"To get a sense for how the diagram above works, let's first write out the \"single-layer\" version (which we saw above is equivalent to logistic regression and doesn't work!). We just want to see how it looks in the form of forward- and backward-propagation.\n",
"\n",
"Remember, we have a (``samples x 2``) input matrix, so we need a ``(2x1)`` matrix of weights. And to save space, we won't use the fully-accurate and correct implementation of backprop and SGD; instead, we'll use a simplified version that's easier to read but has very similar results."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# make the same data as above (just a little closer so it's easier to find)\n",
"rng = np.random.RandomState(1)\n",
"X = rng.randn(samples, 2)\n",
"\n",
"y = np.array(np.logical_xor(X[:, 0] > 0, X[:, 1] > 0), dtype=int)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def activate(x, deriv=False):\n",
" \"\"\"sigmoid activation function and its derivative wrt the argument\"\"\"\n",
" if deriv is True:\n",
" return x*(1-x)\n",
" return 1/(1+np.exp(-x))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# initialize synapse0 weights randomly with mean 0\n",
"syn0 = 2*np.random.random((2,1)) - 1\n",
"\n",
"# nothing to see here... just some numpy vector hijinks for the next code\n",
"y = y[None].T"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This is the iterative phase. We propagate the input data forward through the synapse (weights), calculate the errors, and then back-propogate those errors through the synapses (weights) according to the proper gradients. Note that the number of iterations is arbitary at this point. We'll come back to that. "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"for i in range(10000):\n",
" # first \"layer\" is the input data\n",
" l0 = X\n",
" \n",
" # forward propagation\n",
" l1 = activate(np.dot(l0, syn0))\n",
"\n",
" ### \n",
" # this is an oversimplified version of backprop + gradient descent\n",
" #\n",
" # how much did we miss?\n",
" l1_error = y - l1\n",
" #\n",
" # how much should we scale the adjustments?\n",
" # (how much we missed by) * (gradient at l1 value)\n",
" # ~an \"error-weighted derivative\"\n",
" l1_delta = l1_error * activate(l1,True)\n",
" ###\n",
" \n",
" # how much should we update the weight matrix (synapse)? \n",
" syn0 += np.dot(l0.T,l1_delta)\n",
" \n",
" # some insight into the update progress\n",
" if (i% 2000) == 0:\n",
" print(\"Mean error @ iteration {}: {}\".format(i, np.mean(np.abs(l1_error))))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"As expected, this basically didn't work at all! \n",
"\n",
"Even though we aren't looking at the actual output data, we can use it to look at the accuracy; it never got much better than random guessing. Even after thousands of iterations! But remember, we knew that would be the case, because this single-layer network is functionally the same as vanilla logistic regression, which we saw fail on the xor data above! \n",
"\n",
"But, now that we have the framework and understanding for how to optimize backprogation, we can **add an additional layer to the network (a so-called \"hidden\" layer of neurons),** which will introduce the kind of mixing we need to represent this data.\n",
"\n",
"As we saw above in the diagram (and talked about), introduction of a new layer means that we get an extra step in both the forward- and backward-propagation steps. This new step means we need an additional weight (synapse) matrix, and an additional derivative calculation. Other than that, the code looks pretty much the same."
]
},
{
"cell_type": "raw",
"metadata": {
"collapsed": true
},
"source": [
"#### fall-back data ####\n",
"# convert to/from raw nbconvert\n",
"X = np.array([[0,0],\n",
" [0,1],\n",
" [1,0],\n",
" [1,1]])\n",
"\n",
" \n",
"y = np.array([[0, 1, 1, 0]]).T"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# hold tight, we'll come back to choosing this number\n",
"hidden_layer_width = 3\n",
"\n",
"# initialize synapse (weight) matrices randomly with mean 0\n",
"syn0 = 2*np.random.random((2,hidden_layer_width)) - 1\n",
"syn1 = 2*np.random.random((hidden_layer_width,1)) - 1"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"for i in range(60000):\n",
"\n",
" # forward propagation through layers 0, 1, and 2\n",
" l0 = X\n",
" l1 = activate(np.dot(l0,syn0))\n",
" l2 = activate(np.dot(l1,syn1))\n",
"\n",
" # how much did we miss the final target value?\n",
" l2_error = y - l2\n",
" \n",
" # how much should we scale the adjustments?\n",
" l2_delta = l2_error*activate(l2,deriv=True)\n",
"\n",
" # project l2 error back onto l1 values according to weights\n",
" l1_error = l2_delta.dot(syn1.T)\n",
" \n",
" # how much should we scale the adjustments?\n",
" l1_delta = l1_error * activate(l1,deriv=True)\n",
"\n",
" # how much should we update the weight matrices (synapses)? \n",
" syn1 += l1.T.dot(l2_delta)\n",
" syn0 += l0.T.dot(l1_delta)\n",
" \n",
" if (i % 10000) == 0:\n",
" print(\"Error @ iteration {}: {}\".format(i, np.mean(np.abs(l2_error))))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Ok, this time we started at random guessing (sensible), but notice that we quickly reduced our overall error! That's excellent!\n",
"\n",
"**Note:** I didn't have time to debug the case where the full XOR data only trained to label one quadrant correctly. To get a sense for how it can look with a smaller set, change the \"fall-back data\" cell to code, and run the cells starting there!\n",
"\n",
"Knowing that the error is lower is great, but we can also inspect the results of the fit network by looking at the forward propagation results from the trained synapses (weights)."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def forward_prop(X):\n",
" \"\"\"forward-propagate data X through the pre-fit network\"\"\"\n",
" l1 = activate(np.dot(X,syn0))\n",
" l2 = activate(np.dot(l1,syn1))\n",
" return l2"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# numpy and plotting shenanigans come from:\n",
"# http://scikit-learn.org/stable/auto_examples/svm/plot_iris.html\n",
"\n",
"# mesh step size\n",
"h = .02 \n",
"\n",
"# create a mesh to plot in\n",
"x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1\n",
"y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1\n",
"xx, yy = np.meshgrid(np.arange(x_min, x_max, h),\n",
" np.arange(y_min, y_max, h))\n",
"\n",
"# calculate the surface (by forward-propagating)\n",
"Z = forward_prop(np.c_[xx.ravel(), yy.ravel()])\n",
"\n",
"# reshape the result into a grid\n",
"Z = Z.reshape(xx.shape)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8)\n",
"\n",
"# we can use this to inspect the smaller dataset\n",
"#plt.plot(X[:, 0], X[:, 1], 'o')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Success! (Possibly... depending on whether Josh debugged the larger network problem :) ). If only one quadrant was trained correctly, go use the smaller dataset!\n",
"\n",
"\n",
"# Wrap-up\n",
"\n",
"The stuff in this session is just a very basic start! The limits to the increasing complexity are now at the hardware level! Networks can be amazingly complicated, too. Below is an example from a talk I saw - note how interestingly the layers are *building* on each other to represent increasingly complicated structure in the context of facial recognition. \n",
"\n",
"<img src=\"img/3l-face.png\"> \n",
"\n",
"It's not clear how you'd encode \"this is a face,\" but once you see how the first layer's \"atomic\" components are assembled into abstract *parts* of a face, and how those *parts* are combined into representations of kinds of faces, it seems more believable!\n",
"\n",
"## Don't actually do it like this\n",
"\n",
"And, as you probably guessed, what we've done above isn't how you use these in practice. There are many Python libraries for building and using various neural network models. And, as you might expect, many are built with an object-oriented expressiveness:\n",
"\n",
"```python\n",
"# pseudo-code (that is actually very nearly valid)\n",
"nn = Network(optimizer='sgd')\n",
"nn.add_layer('fully_connected', name='l0', nodes=4)\n",
"nn.add_layer('fully_connected', name='l1', nodes=5)\n",
"nn.add_layer('fully_connected', name='l2', nodes=2)\n",
"nn.compile()\n",
"nn.fit(X,y)\n",
"```\n",
"\n",
"In Neural Networks - Part 2, we'll look at some of these libraries and use them for some learning tasks! (*hold me to it!*)\n",
"\n",
"In addition to using optimized libraries, there are many other issues and topics that go into developing and using neural networks for practical purposes. Below is a bag-of-words approach to some terms and phrases that you'll invariably see when reading about neural networks.\n",
"\n",
"\n",
"## Neural Network Word Salad\n",
"\n",
"- GPU (graphical processing unit)\n",
" - The matrix manipulations needed for large network training are typically bottlenecked by the compute throughput of a CPU. Starting in ~2013, people figured out the computer graphics chips were much faster at computing these steps and are now the go-to hardware for training networks. CPUs still work! They just tend to be an order of magnitude slower.\n",
"\n",
"- architecture\n",
" - We only looked at so-called \"fully-connected\" networks - that is, every node was connected to every other node downstream. This is not the only way to design the layout! \n",
" - Among many others, so-called \"convolution networks\" are very common in image recognition tasks; each layer combines a *region* of the previous layer's outputs into a single node in the subsequent layer.\n",
" - There are still other choices to be made in designing a network: the number of nodes in a hidden layer, the activation function, and more. \n",
"\n",
"- batching\n",
" - If you're training a network on the entirety of the internet's search queries, you can't exactly feed it all forward and backward through the network at once. The concept of batching is deciding how much of the input data to feed forward (and backward) before updating your weight matrices.\n",
"\n",
"- training epochs\n",
" - the magic numbers in our ``for`` loops above were chosen arbitrarily. A lot of work has also gone into deciding how to optimize the convergence of network training. \n",
"\n",
"- regularization\n",
" - Neural networks, too, can suffer from overfitting. There are tactics to \n",
" - \"dropout\"\n",
" - \"pooling\"\n",
" \n",
"- \"deep learning\"\n",
" - lots of layers\n",
" \n",
" \n",
"## Links\n",
"\n",
"To save you some time if you want to learn more, here are some of the references that I found the most helpful while researching for this RST:\n",
"\n",
"- [Hacker's guide to Neural Networks](http://karpathy.github.io/neuralnets/)\n",
"- [Deep Learning Basics: Neural Networks, Backpropagation and Stochastic Gradient Descent](http://alexminnaar.com/deep-learning-basics-neural-networks-backpropagation-and-stochastic-gradient-descent.html)\n",
"- [A Neural Network in 11 lines of Python](http://iamtrask.github.io/2015/07/12/basic-python-network/)\n",
"- [A Neural Network in 13 lines of Python](http://iamtrask.github.io/2015/07/27/python-network-part2/)\n",
"- [Intro to Neural Networks](http://www.slideshare.net/DeanWyatte/intro-to-neural-networks)\n",
"- [Single-Layer Neural Networks and Gradient Descent](http://sebastianraschka.com/Articles/2015_singlelayer_neurons.html)\n",
"- [Tensorflow Playground](http://playground.tensorflow.org)\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.1"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| unlicense |
PepSalehi/tuthpc | Untitled5.ipynb | 1 | 16328 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# MPI and cluster computing"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"What is large-scale and cluster computing?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"* MPI: the message passing interface (`mpi4py` and ...)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"* GPU: graphics processing-based parallelism (`pyopencl` and `pycuda`)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"* Cloud computing (`cloud`, `mrjob`, and Apache's `mesos`/`spark`/`hadoop`/`zookeeper`/...)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We'll focus on `mpi4py`, as it's probably the most stable and active of the python MPI modules, and generally provides the most in terms of classic scalability to instutional class resources."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Getting started with `mpi4py`"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"* Typically not an `easy_install` -- thanks MPI"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"* Getting started: say `\"hello\"`"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Writing hellompi.py\n"
]
}
],
"source": [
"%%file hellompi.py\n",
"\"\"\"\n",
"Parallel Hello World\n",
"\"\"\"\n",
"\n",
"from mpi4py import MPI\n",
"import sys\n",
"\n",
"size = MPI.COMM_WORLD.Get_size()\n",
"rank = MPI.COMM_WORLD.Get_rank()\n",
"name = MPI.Get_processor_name()\n",
"\n",
"sys.stdout.write(\n",
" \"Hello, World! I am process %d of %d on %s.\\n\" \n",
" % (rank, size, name))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"* Executes with `mpiexec`"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Hello, World! I am process 2 of 4 on hilbert.local.\r\n",
"Hello, World! I am process 1 of 4 on hilbert.local.\r\n",
"Hello, World! I am process 0 of 4 on hilbert.local.\r\n",
"Hello, World! I am process 3 of 4 on hilbert.local.\r\n"
]
}
],
"source": [
"!mpiexec -n 4 python2.7 hellompi.py"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"* Coding for multiple \"personalities\" (nodes, actually)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Point to point communication"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Overwriting mpipt2pt.py\n"
]
}
],
"source": [
"%%file mpipt2pt.py\n",
"from mpi4py import MPI\n",
"\n",
"comm = MPI.COMM_WORLD\n",
"rank, size = comm.Get_rank(), comm.Get_size()\n",
"\n",
"if rank == 0:\n",
" data = range(10)\n",
" more = range(0,20,2)\n",
" print 'rank %i sends data:' % rank, data\n",
" comm.send(data, dest=1, tag=1337)\n",
" print 'rank %i sends data:' % rank, more\n",
" comm.send(more, dest=2 ,tag=1456)\n",
"elif rank == 1:\n",
" data = comm.recv(source=0, tag=1337)\n",
" print 'rank %i got data:' % rank, data\n",
"elif rank == 2:\n",
" more = comm.recv(source=0, tag=1456)\n",
" print 'rank %i got data:' % rank, more"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"rank 0 sends data: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]\r\n",
"rank 0 sends data: [0, 2, 4, 6, 8, 10, 12, 14, 16, 18]\r\n",
"rank 2 got data: [0, 2, 4, 6, 8, 10, 12, 14, 16, 18]\r\n",
"rank 1 got data: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]\r\n"
]
}
],
"source": [
"!mpiexec -n 4 python2.7 mpipt2pt.py"
]
},
{
"cell_type": "code",
"execution_count": 45,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Overwriting mpipt2pt2.py\n"
]
}
],
"source": [
"%%file mpipt2pt2.py\n",
"'''nonblocking communication\n",
"'''\n",
"from mpi4py import MPI\n",
"import numpy as np\n",
"import time\n",
"\n",
"comm = MPI.COMM_WORLD\n",
"rank, size = comm.Get_rank(), comm.Get_size()\n",
"\n",
"pair = {0:1, 1:0} # rank 0 sends to 1 and vice versa\n",
"sendbuf = np.zeros(5) + rank\n",
"recvbuf = np.empty_like(sendbuf)\n",
"\n",
"print 'rank %i sends data:' % rank, sendbuf\n",
"sreq = comm.Isend(sendbuf, dest=pair[rank], tag=1337)\n",
"rreq = comm.Irecv(recvbuf, source=pair[rank], tag=1337)\n",
"\n",
"# rreq.Wait(); sreq.Wait()\n",
"MPI.Request.Waitall([rreq, sreq])\n",
"if rank == 1: \n",
" time.sleep(0.001) # delay slightly for better printing\n",
"print 'rank %i got data:' % rank, recvbuf"
]
},
{
"cell_type": "code",
"execution_count": 46,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"rank 1 sends data: [ 1. 1. 1. 1. 1.]\r\n",
"rank 0 sends data: [ 0. 0. 0. 0. 0.]\r\n",
"rank 0 got data: [ 1. 1. 1. 1. 1.]\r\n",
"rank 1 got data: [ 0. 0. 0. 0. 0.]\r\n"
]
}
],
"source": [
"!mpiexec -n 2 python2.7 mpipt2pt2.py"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Collective communication"
]
},
{
"cell_type": "code",
"execution_count": 52,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Overwriting mpiscattered.py\n"
]
}
],
"source": [
"%%file mpiscattered.py\n",
"'''mpi scatter\n",
"'''\n",
"from mpi4py import MPI\n",
"import numpy as np\n",
"import time\n",
"\n",
"comm = MPI.COMM_WORLD\n",
"rank, size = comm.Get_rank(), comm.Get_size()\n",
"\n",
"if rank == 0:\n",
" data = np.arange(10)\n",
" print 'rank %i has data' % rank, data\n",
" data_split_list = np.array_split(data, size)\n",
"else:\n",
" data_split_list = None\n",
"data_split = comm.scatter(data_split_list, root=0)\n",
"\n",
"# some delays for printing purposes\n",
"if rank == 1:\n",
" time.sleep(0.001)\n",
"elif rank == 2:\n",
" time.sleep(0.002)\n",
"print 'rank %i got data' % rank, data_split"
]
},
{
"cell_type": "code",
"execution_count": 53,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"rank 0 has data [0 1 2 3 4 5 6 7 8 9]\r\n",
"rank 0 got data [0 1 2 3]\r\n",
"rank 1 got data [4 5 6]\r\n",
"rank 2 got data [7 8 9]\r\n"
]
}
],
"source": [
"!mpiexec -n 3 python2.7 mpiscattered.py"
]
},
{
"cell_type": "code",
"execution_count": 70,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Overwriting mpibroadcasted.py\n"
]
}
],
"source": [
"%%file mpibroadcasted.py\n",
"'''mpi broadcast\n",
"'''\n",
"from mpi4py import MPI\n",
"import numpy as np\n",
"import time\n",
"\n",
"comm = MPI.COMM_WORLD\n",
"rank, size = comm.Get_rank(), comm.Get_size()\n",
"\n",
"N = 10.\n",
"data = np.arange(N) if rank == 0 else np.zeros(N)\n",
"if rank == 1:\n",
" time.sleep(0.001)\n",
"elif rank == 2:\n",
" time.sleep(0.002)\n",
"print 'rank %i has data' % rank, data\n",
"\n",
"comm.Bcast(data, root=0)\n",
"if rank == 1:\n",
" time.sleep(0.001)\n",
"elif rank == 2:\n",
" time.sleep(0.002)\n",
"print 'rank %i got data' % rank, data"
]
},
{
"cell_type": "code",
"execution_count": 71,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"rank 1 has data [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\r\n",
"rank 2 has data [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\r\n",
"rank 0 has data [ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9.]\r\n",
"rank 0 got data [ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9.]\r\n",
"rank 1 got data [ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9.]\r\n",
"rank 2 got data [ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9.]\r\n"
]
}
],
"source": [
"!mpiexec -n 3 python2.7 mpibroadcasted.py"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Not covered: shared memory and shared objects"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Better serialization"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from mpi4py import MPI\n",
"\n",
"try:\n",
" import dill\n",
" MPI._p_pickle.dumps = dill.dumps\n",
" MPI._p_pickle.loads = dill.loads\n",
"except ImportError, AttributeError:\n",
" pass"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Working with cluster schedulers, the `JOB ` file"
]
},
{
"cell_type": "code",
"execution_count": 47,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Writing jobscript.sh\n"
]
}
],
"source": [
"%%file jobscript.sh\n",
"#!/bin/sh\n",
"#PBS -l nodes=1:ppn=4\n",
"#PBS -l walltime=00:03:00\n",
"cd ${PBS_O_WORKDIR} || exit 2\n",
"mpiexec -np 4 python hellompi.py"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Beyond `mpi4py`"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"* The task `Pool`: `pyina` and `emcee.utils`"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Writing pyinapool.py\n"
]
}
],
"source": [
"%%file pyinapool.py\n",
"\n",
"def test_pool(obj):\n",
" from pyina.launchers import Mpi\n",
" x = range(6)\n",
" p = Mpi(8)\n",
" \n",
" # worker pool strategy + dill\n",
" p.scatter = False\n",
" print p.map(obj, x)\n",
" \n",
" # worker pool strategy + dill.source \n",
" p.source = True\n",
" print p.map(obj, x)\n",
" \n",
" # scatter-gather strategy + dill.source\n",
" p.scatter = True\n",
" print p.map(obj, x)\n",
" \n",
" # scatter-gather strategy + dill\n",
" p.source = False\n",
" print p.map(obj, x)\n",
"\n",
"\n",
"if __name__ == '__main__':\n",
"\n",
" from math import sin\n",
" f = lambda x:x+1\n",
" def g(x):\n",
" return x+2\n",
"\n",
" for func in [g, f, abs, sin]:\n",
" test_pool(func)"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[2, 3, 4, 5, 6, 7]\n",
"[2, 3, 4, 5, 6, 7]\n",
"[2, 3, 4, 5, 6, 7]\n",
"[2, 3, 4, 5, 6, 7]\n",
"[1, 2, 3, 4, 5, 6]\n",
"[1, 2, 3, 4, 5, 6]\n",
"[1, 2, 3, 4, 5, 6]\n",
"[1, 2, 3, 4, 5, 6]\n",
"[0, 1, 2, 3, 4, 5]\n",
"[0, 1, 2, 3, 4, 5]\n",
"[0, 1, 2, 3, 4, 5]\n",
"[0, 1, 2, 3, 4, 5]\n",
"[0.0, 0.8414709848078965, 0.9092974268256817, 0.1411200080598672, -0.7568024953079282, -0.9589242746631385]\n",
"[0.0, 0.8414709848078965, 0.9092974268256817, 0.1411200080598672, -0.7568024953079282, -0.9589242746631385]\n",
"[0.0, 0.8414709848078965, 0.9092974268256817, 0.1411200080598672, -0.7568024953079282, -0.9589242746631385]\n",
"[0.0, 0.8414709848078965, 0.9092974268256817, 0.1411200080598672, -0.7568024953079282, -0.9589242746631385]\n"
]
}
],
"source": [
"!python2.7 pyinapool.py"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For emcee, see: http://dan.iel.fm/emcee/current/user/advanced/"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"* Loooooong import times: `MPI_import`"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"* Interactive MPI: `pyina` and `IPython.parallel`"
]
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"$ ipcluster mpiexec -n 16 --mpi=mpi4py"
]
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"from IPython.kernel import client\n",
"mec = client.MultiEngineClient()\n",
"mec.activate()\n",
"\n",
"%px from mpi4py import MPI\n",
"%px print(MPI.Get_processor_name())"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"* Working with schedulers directly: `pyina` and `ipython-cluster-helper`"
]
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"from pyina.launchers import SerialMapper\n",
"from pyina.schedulers import Torque\n",
"from pyina.mpi import _save, _debug\n",
"\n",
"def host(id):\n",
" import socket\n",
" return \"Rank: %d -- %s\" % (id, socket.gethostname())\n",
"\n",
"print \"Submit a non-parallel job to torque in the 'productionQ' queue...\"\n",
"print \"Using 5 items over 1 nodes and the default mapping strategy\"\n",
"\n",
"torque = Torque(queue='productionQ', timelimit='20:00:00', workdir='.')\n",
"pool = SerialMapper(scheduler=torque) \n",
"res = pool.map(host, range(5))\n",
"\n",
"print pool\n",
"print '\\n'.join(res)"
]
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"from pyina.launchers import Mpi\n",
"from pyina.schedulers import Torque\n",
"from pyina.mpi import _save, _debug\n",
"\n",
"def host(id):\n",
" import socket\n",
" return \"Rank: %d -- %s\" % (id, socket.gethostname())\n",
"\n",
"print \"Submit an mpi job to torque in the 'productionQ' queue...\"\n",
"print \"Using 15 items over 5 nodes and the scatter-gather strategy\"\n",
"\n",
"torque = Torque('5:ppn=2', queue='productionQ', timelimit='20:00:00', workdir='.')\n",
"pool = Mpi(scheduler=torque, scatter=True)\n",
"res = pool.map(host, range(15))\n",
"\n",
"print pool\n",
"print '\\n'.join(res)\n",
"\n",
"print \"hello from master\""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"* Issue: conforming to the `multiprocessing` interface: ..."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We are in the tall weeds here... "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The other end of the spectrum is [high-performance parallel](Untitled6.ipynb) instead of large-scale parallel."
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.9"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| bsd-3-clause |
MadDataScience/DAT4 | DS_Lec13-ANN.ipynb | 1 | 500355 | {
"metadata": {
"celltoolbar": "Slideshow",
"name": "",
"signature": "sha256:bb30774b7c8076d6bcb249ec4b0009fd22aaaa8b806b858a513774e7fd9e518d"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"`caret` and Neural Networks\n",
"========================================================\n",
"Instructor: Alessandro Gagliardi \n",
"TA: Kevin Perko"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"`install.packages(\"caret\", dependencies = c(\"Depends\", \"Suggests\"))`"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Last Time:\n",
"--------------------------------------------------------\n",
"\n",
"- Principal Components Analysis\n",
"- Eigenvalue Decomposition\n",
"- Multicollinearity\n",
"- Dimensionality Reduction\n",
"\n",
"### Questions?"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"1. `caret`\n",
"2. Neural Networks"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"An introduction to `caret`\n",
"========================================================\n",
"(slides lovingly adapted from Max Kuhn's presentations)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"The `caret` Package\n",
"--------------------------------------------------------\n",
"The `caret` package, short for Classification And REgression Training, contains numerous tools for developing predictive models using the rich set of models available in R. The package focuses on\n",
"\n",
"* simplifying model training and tuning across a wide variety of modeling techniques\n",
"* pre\u2013processing training data \n",
"* calculating variable importance \n",
"* model visualizations\n",
"\n",
"The package is available at the [Comprehensive R Archive Network (CRAN)](http://cran.r-project.org/). `caret` depends on over 25 other packages, although many of these are listed as \"suggested\" packages are are not automatically loaded when `caret` is started. Packages are loaded individually when a model is trained or predicted."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%load_ext rmagic"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"prompt_number": 1
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Test/Training Set Split\n",
"--------------------------------------------------------\n",
"We decide to train on 75% of the data:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"require(\"caret\")\n",
"require(\"mlbench\")\n",
"data(Sonar)\n",
"set.seed(107)\n",
"inTrain <- createDataPartition(y = Sonar$Class, p = 3/4, list = FALSE)\n",
"## The output is a set of integers for the rows of Sonar that belong in the training set.\n",
"\n",
"trainDescr <- Sonar[inTrain,1:60]\n",
"testDescr <- Sonar[-inTrain,1:60]\n",
"\n",
"trainClass <- Sonar$Class[inTrain]\n",
"print(length(trainClass))\n",
"testClass <- Sonar$Class[-inTrain]\n",
"print(length(testClass))"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"Loading required package: caret\n",
"Loading required package: lattice\n",
"Loading required package: ggplot2\n",
"Find out what's changed in ggplot2 with\n",
"news(Version == \"0.9.3.1\", package = \"ggplot2\")\n",
"Loading required package: mlbench\n",
"[1] 157\n",
"[1] 51\n"
]
}
],
"prompt_number": 2
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"source": [
"By default, `createDataPartition` does stratified random splits."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Filtering Predictors\n",
"--------------------------------------------------------\n",
"In order to avoid multicollinearity, we remove predictors to make sure that there are no between-predictor (absolute) correlations greater than 90%:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"print(ncol(trainDescr))\n",
"trainingCorr <- cor(trainDescr)\n",
"highCorr <- findCorrelation(trainingCorr, 0.90)\n",
"# returns an index of column numbers for removal\n",
"\n",
"trainDescr <- trainDescr[, -highCorr]\n",
"testDescr <- testDescr[, -highCorr]\n",
"print(ncol(trainDescr))"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"[1] 60\n",
"[1] 57\n"
]
}
],
"prompt_number": 3
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Transforming Predictors\n",
"--------------------------------------------------------\n",
"The class preProcess can be used to center/scale the predictors, as well as apply other transformations. By default, centering and scaling is done:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"xTrans <- preProcess(trainDescr, method = c(\"center\", \"scale\"))\n",
"trainDescr <- predict(xTrans, trainDescr)\n",
"testDescr <- predict(xTrans, testDescr)"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [],
"prompt_number": 4
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"To apply PCA to predictors in the training, test or other data, you can use:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R \n",
"xTrans <- preProcess(trainDescr, method = \"pca\")"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"prompt_number": 5
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Cross-Validation\n",
"--------------------------------------------------------\n",
"`caret` gives us an easy way to do cross-validation during the training of our model."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"trControl <- trainControl(method=\"cv\", number=25)\n",
"logFit <- train(x = trainDescr, y = trainClass, \n",
" method='glm', family=binomial(link=\"logit\"), \n",
" trControl = trControl)\n",
"logFit"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"Loading required package: class\n",
"Generalized Linear Model \n",
"\n",
"157 samples\n",
" 57 predictors\n",
" 2 classes: 'M', 'R' \n",
"\n",
"No pre-processing\n",
"Resampling: Cross-Validated (25 fold) \n",
"\n",
"Summary of sample sizes: 151, 151, 151, 150, 151, 150, ... \n",
"\n",
"Resampling results\n",
"\n",
" Accuracy Kappa Accuracy SD Kappa SD\n",
" 0.742 0.491 0.189 0.371 \n",
"\n",
" \n"
]
}
],
"prompt_number": 6
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R -w 960 -h 480 -u px\n",
"resampleHist(logFit)"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAA8AAAAHgCAYAAABq5QSEAAAEJGlDQ1BJQ0MgUHJvZmlsZQAAOBGF\nVd9v21QUPolvUqQWPyBYR4eKxa9VU1u5GxqtxgZJk6XtShal6dgqJOQ6N4mpGwfb6baqT3uBNwb8\nAUDZAw9IPCENBmJ72fbAtElThyqqSUh76MQPISbtBVXhu3ZiJ1PEXPX6yznfOec7517bRD1fabWa\nGVWIlquunc8klZOnFpSeTYrSs9RLA9Sr6U4tkcvNEi7BFffO6+EdigjL7ZHu/k72I796i9zRiSJP\nwG4VHX0Z+AxRzNRrtksUvwf7+Gm3BtzzHPDTNgQCqwKXfZwSeNHHJz1OIT8JjtAq6xWtCLwGPLzY\nZi+3YV8DGMiT4VVuG7oiZpGzrZJhcs/hL49xtzH/Dy6bdfTsXYNY+5yluWO4D4neK/ZUvok/17X0\nHPBLsF+vuUlhfwX4j/rSfAJ4H1H0qZJ9dN7nR19frRTeBt4Fe9FwpwtN+2p1MXscGLHR9SXrmMgj\nONd1ZxKzpBeA71b4tNhj6JGoyFNp4GHgwUp9qplfmnFW5oTdy7NamcwCI49kv6fN5IAHgD+0rbyo\nBc3SOjczohbyS1drbq6pQdqumllRC/0ymTtej8gpbbuVwpQfyw66dqEZyxZKxtHpJn+tZnpnEdrY\nBbueF9qQn93S7HQGGHnYP7w6L+YGHNtd1FJitqPAR+hERCNOFi1i1alKO6RQnjKUxL1GNjwlMsiE\nhcPLYTEiT9ISbN15OY/jx4SMshe9LaJRpTvHr3C/ybFYP1PZAfwfYrPsMBtnE6SwN9ib7AhLwTrB\nDgUKcm06FSrTfSj187xPdVQWOk5Q8vxAfSiIUc7Z7xr6zY/+hpqwSyv0I0/QMTRb7RMgBxNodTfS\nPqdraz/sDjzKBrv4zu2+a2t0/HHzjd2Lbcc2sG7GtsL42K+xLfxtUgI7YHqKlqHK8HbCCXgjHT1c\nAdMlDetv4FnQ2lLasaOl6vmB0CMmwT/IPszSueHQqv6i/qluqF+oF9TfO2qEGTumJH0qfSv9KH0n\nfS/9TIp0Wboi/SRdlb6RLgU5u++9nyXYe69fYRPdil1o1WufNSdTTsp75BfllPy8/LI8G7AUuV8e\nk6fkvfDsCfbNDP0dvRh0CrNqTbV7LfEEGDQPJQadBtfGVMWEq3QWWdufk6ZSNsjG2PQjp3ZcnOWW\ning6noonSInvi0/Ex+IzAreevPhe+CawpgP1/pMTMDo64G0sTCXIM+KdOnFWRfQKdJvQzV1+Bt8O\nokmrdtY2yhVX2a+qrykJfMq4Ml3VR4cVzTQVz+UoNne4vcKLoyS+gyKO6EHe+75Fdt0Mbe5bRIf/\nwjvrVmhbqBN97RD1vxrahvBOfOYzoosH9bq94uejSOQGkVM6sN/7HelL4t10t9F4gPdVzydEOx83\nGv+uNxo7XyL/FtFl8z9ZAHF4bBsrEwAAQABJREFUeAHs3QecXVW59/F/eie9t0nvIT0QIAQIHaIG\nMKIgKHopKnJBAYH7KojC9Yr3UhRFugoiIlINNSGUkJBCeiEJk94bSUhP3vXs8YTJZGZyzpmz99nl\ntz6fYc6cs/cq3zVkz7P3KpUOuiQSAggggAACCCCAAAIIIIAAAjEXqBzz9tE8BBBAAAEEEEAAAQQQ\nQAABBDwBAmB+ERBAAAEEEEAAAQQQQAABBBIhQACciG6mkQgggAACCCCAAAIIIIAAAgTA/A4ggAAC\nCCCAAAIIIIAAAggkQoAAOBHdTCMRQAABBBBAAAEEEEAAAQQIgPkdQAABBBBAAAEEEEAAAQQQSIQA\nAXAiuplGIoAAAggggAACCCCAAAIIEADzO4AAAggggAACCCCAAAIIIJAIAQLgRHQzjUQAAQQQQAAB\nBBBAAAEEECAA5ncAAQQQQAABBBBAAAEEEEAgEQIEwInoZhqJAAIIIIAAAggggAACCCBAAMzvAAII\nIIAAAggggAACCCCAQCIECIAT0c00EgEEEEAAAQQQQAABBBBAgACY3wEEEEAAAQQQQAABBBBAAIFE\nCBAAJ6KbaSQCCCCAAAIIIIAAAggggAABML8DCCCAAAIIIIAAAggggAACiRCoGrVWTp06VbNmzYpa\ntakvAggggAAC5Qqcfvrpat26dbnHVOTDF154QZs3b65IFpyLAAIIIIBA6AQuv/zyjOpU6aBLGZ2R\n54ObNG6oX//k6jzXguIRQAABBBDIncCCJcs089N1euVfr+cu02I5TZgwQdde/R1d960Li73LSwQQ\nQAABBKIt8MRzY3XZldcqkyA4ck+A+/ftpcsuPCvaPUXtEUAAAQQQKCawYPEy/eapN4u9k/uXo844\nmetn7lnJEQEEEEAgYgLMAY5Yh1FdBBBAAAEEEEAAAQQQQACB7AQIgLNz4ywEQiXw3kczVaXjCD3p\nhoGQEEAAAQQQQCB7gV8/9FeNvvK2wzK44c7fqvtpl2jF6nWHvc8PCCAQPQEC4Oj1GTVG4AiBJ//x\nmq69/AI9/MwrR3zGGwgggAACCCCQvcD1P39Ab38wTe/+7QG1adks+4w4EwEEQiFAAByKbqASCGQv\nsGv3br305ge64/ortHrdRi1csvywzO5+8C/qNPxrOvbsb+mRYgFyae//8rd/0oN//ueh8++8/0n9\n4S8vej+f8rUfys5pPuhLGvvOJM39pFD2Xv0+Z6v9CRfpfx/526HzJkyaoRMuuEathnxF19z2G1kd\n7Q+Ih//68qFjxn84Xd+8/heHfuYFAggggAACYROwa9fkGfM0/q/3qmnjBl71Pt+5S1fd+mu1Hjpa\njY49Vxdd8/+0bfvn3menff06/ebhZ9Ru2IUaeN53vOulfTBr/mJd/IPbdfmPfqlmA0fpS9+9Res2\nFK3KXl5+Xqb8BwEEcipAAJxTTjJDIHgBC36PH9BL9erW1pjzTnVPgb8IMp964Q09/vd/6en7fqpn\nHviZbvmfh1S4YrXKen/dxi3asGnroUas3bBJG7cU/bxo6UrvDvgj/32T+vfsokuuu1PnnHKcVk36\nh/73v76vH//yQW3a8pnWrN+oC67+L33na+dp1muPa7kbLvZ7F0QP7dfTq0sq86deeFMDe3dN/ch3\nBBBAAAEEQiNgm6T85x336/4n/uFdP+sfU/dQ3e597O9avHSVpr/yiCb+40HNdMHtMy+/7X2+eNkq\n/f3Vd7ynxbf94JvetdKui7t27/GOad6kkea/9We1aNpI3/3J/3jnlJffoUJ5gQACORMgAM4ZJRkh\nkB8BG/781fNO8Qof477bcvB79+7zfn7+tXf19VEjNaRfD3Xv1F4vP3K3atWoobLeP1oLrvv2hTrv\ntGFq7i7cD931I13/na+qRvVqKmjTUrVq1tB6F0Db01+7sH/ronPUuGF9PXjn9RpxXD+dP3KY90eC\nPaXev3+/XnjjPV10blG9j1YunyOAAAIIIBCkwNh3Juv9qbN14qA+7ubxHw8r2q6rT/7mVjVr0lA1\na1RXl4I27ubvpkPHXPn1UWrfpoW+cuZwtXVDpsd/+LH3WZUqVXTb97+pRg2O0Y//42t65e2J2u0C\n46PldyhjXiCAQE4EIrcNUk5aTSYIxETAhk/ZRXrWgiX6r3se8VplQehLb72v0WedrAVuOPQVY849\n1NrBx/bwXpf1/qEDy3hhF/JUWr9pi0666Aeav3ip+rknwhbUHjh4wCtzyL/LsWNtvlRqztS5pxyv\nf77+rvfHQvdO7dSqeZNUdnxHAAEEEEAgNAKtmjfWvx7/lbZ8tl19z/qWLjz7ZHcj9wSvflWqVNYP\nb79P70z6WE0bNdDeffs0uG/3Q3UfNrDXodcD3EinxW4EVad2rdSra4E3Wss+7OyC5tq1amjpyrXe\n9/LyO5QZLxBAICcCPAHOCSOZIJAfgadffFMjTxioVx79b/3zoV94X/95xVfdXNuixbAa1q8r2180\nlcZNnObNQyrr/cqVKmn3nr2pw2VBbvFkd68t2VDnC676L93w3TFaNfkfeuup/5UbLeZ92Z3tBUu+\nKHP5qnXuifME77yvnX+aFwBbEGzDtUkIIIAAAgiEUeDYHp29UUyd2rfWz677lq685dfavHWbV9Wr\nbr3HPcWtp1ljH9fs15+Q3fR1l8BD6ZPCFYdez164xBslZW98uny1d7PYXi9zge/nO3erbatmbj5x\n+fnZ8SQEEMidQOXcZUVOCCAQtIANf77kK2e4u8odDn1dc+mX9fq7H8kCz5EnDHIB53ve4hw7d+3W\nd276lSq5ILes95u74VyTPp7rAtmD3oJaqWFbJdu1fcdO7y0Lvmu6IdUWiO/es8cben3K8f01bfZC\nzVtU6B3zPw89rRnzFnuvzzp5iPfanlpfePYI7z3+gwACCCCAQJgFbLpPy2aN9YOf/p9XzY2bP3ND\no/t6Q6BtW6Q33ptyaOqRHfD0i295P8901755i5Z6w6jtfVsoy67Jdo219TlOGNTbmz50tPzsXBIC\nCOROgCHQubMkJwQCFbBVmOd+slSj/j0kK1W43a0e1LebHnv2VW+O7pRZC9ThpDGqX6+OLnbzlnp3\n6+juRrdQae83rF/PXZTHeitb1q9XV2efPDSV7WHf27VurssuOEvHnvNtNXZPfHt2KfAWuVr46XJv\nXu8vb/wPDR51pfcHQ2dXnz//323e+TXcXCnLc8Wa9d4fDodlyg8IIIAAAgiEUMBGPz3yq5u869pF\n55yiH1/5NV3v9gV+4Ml/eMHsV844ScWf+tpaF3bdtaHRv//FDd584HUbN3vXvdvvfVzXucW1GrhF\ntV597Fdea4+WXwhJqBICkRao5O5CFR+1EfrGnH7KiXr9sV+Gvp5UEIEwCXy2bYe3UEd1t2BV8VTW\n+zaPOLXdQ/HjS77e8flO74ly7Vo1S36kfe7Cv+PzXSq+cqYdZFsfnXHSYO/J9REn8QYCCRWwqQq/\neepNPfTI474ITJgwQW8+/yfd/sNLfcmfTBFImoD9+bxx81Y1cXOAi6eCE7+qlx6+yxvaXK9ObaWm\nDn3ktlK61F3/bAVom0Zk04WKp7LyK34MrxFA4EiBJ9yDGzXpqssvv/zID8t4J3JPgA8cOOD9g1NG\ne3gbAQTKELA70dpx5IelvV+5cqWM/j+z4dVlJfsDwZIt1PXn51/XB1Nn6e4br8wo/7Ly5n0E4iJg\n/x/u3fvF/Hs/2rXPLVSX+v/Rj/zJE4GkCdiUopL/T+3ff8BbOMsWebQFtFJpq3tti0Wmjk99T31u\n30vLr/jnvEYAgSMFbLvOxhmuqRq5J8AF7dq4YSP1jmw97yCAQKgF7ObVHjdPuHr16qpcmeUHQt1Z\nVC5wAft/o037Dnr9jTd9KXvixIm68CtfUtMmjX3Jn0wRQKBIYM/ePapWtZoXzBY3sSe8dqOrerXD\nR2IVP4bXCCCQucDqNWt1328f1JgxY9I+OXJPgLt276nXX3897QZyIAIIIIAAAmEXWLBggX7zm9/4\nVk17uvydK6/W7bff7lsZZIwAAggggEDQAk888YR27ixanDXdsnkMk64UxyGAAAIIIIAAAggggAAC\nCERagAA40t1H5RFAAAEEEEAAAQQQQAABBNIVIABOV4rjEEAAAQQQQAABBBBAAAEEIi1AABzp7qPy\nCCCAAAIIIIAAAggggAAC6QoQAKcrxXEIIIAAAggggAACCCCAAAKRFiAAjnT3UXkEEEAAAQQQQAAB\nBBBAAIF0BQiA05XiOAQQQAABBBBAAAEEEEAAgUgLEABHuvuoPAIIIIAAAggggAACCCCAQLoCBMDp\nSnEcAggggAACCCCAAAIIIIBApAUIgCPdfVQeAQQQQAABBBBAAAEEEEAgXQEC4HSlOA4BBBBAAAEE\nEEAAAQQQQCDSAgTAke4+Ko8AAggggAACCCCAAAIIIJCuAAFwulIchwACCCCAAAIIIIAAAgggEGkB\nAuBIdx+VRwABBBBAAAEEEEAAAQQQSFeAADhdKY5DAAEEEEAAAQQQQAABBBCItAABcKS7j8ojgAAC\nCCCAAAIIIIAAAgikK0AAnK4UxyGAAAIIIIAAAggggAACCERagAA40t1H5RFAAAEEEEAAAQQQQAAB\nBNIVIABOV4rjEEAAAQQQQAABBBBAAAEEIi1AABzp7qPyCCCAAAIIIIAAAggggAAC6QoQAKcrxXEI\nIIAAAggggAACCCCAAAKRFiAAjnT3UXkEEEAAAQQQQAABBBBAAIF0BQiA05XiOAQQiLTAhu2Rrj6V\nRwABBBBAIC8Ca7dK67dJO/fkpXgKRSDnAlVzniMZIoAAAiETWL1F+u5jUqM60jnHSqf3khrXDVkl\nqQ4CCCCAAAIhE5jyqXTNk1LXFtL23dLefVKdGlLdmkXf31so/eQ86atDQlZxqoNAOQIEwOXg8BEC\nCERfYNde6dbnpJvPlZodI42dJV35uNSztXRmb+m4TlIVxsJEv6NpAQIIIIBATgW27ZJ+PVZ69ntS\n+yZFWe8/UBQI73CfWUB86TDpv1+VTuvJjeWc4pOZrwIEwL7ykjkCCORb4MG3pb5tpBO7FtXE7mJf\ndYr0rrtr/cI06b43pCEdi+5et22U79pSPgIIIIAAAuEQ+NMH0knu2pkKfq1WdsO4fq2ir1Qtz+0r\nPfWh9IORqXf4jkC4BXjuEe7+oXYIIFABAQtyZ69wAe+ph2dS3d36s7vVvxoj3fsNqUFt6bI/Spt2\nHH4cPyGAAAIIIJBEgWUbpXfmS9884eitv8gNf353gWRzhUkIREGAADgKvUQdEUAgYwFbsOOBN93Q\nZzc3qWa1sk9vUV+6Yrg0xl3An5tS9nF8ggACCCCAQFIEfj9O+sbxUj031/doyY758gDJnhiTEIiC\nAAFwFHqJOiKAQEYCBw+6p7tuTtKFg6UuzdM71Y61+cE254mEAAIIIIBAUgU+XCxtdDsnnOsWjUw3\nfWWgNLVQsifHJATCLkAAHPYeon4IIJCxwF8nuXlKlaSLXFCbbrJVoYd3k/45Nd0zOA4BBBBAAIF4\nCezbLz00vmitjEwWiKxVveim85Pvx8uD1sRTgAA4nv1KqxBIrMCCNdKL06UfnZM5gQ2Dfulj9jrM\nXI4zEEAAAQTiIPC8WxyyfWOpf/vMW3N+P2n+aumTtZmfyxkIBClAABykNmUhgICvAjv3uO0YXnEr\nUZ4uNXFPdDNNNh94UAcXQLsgmIQAAggggECSBDbvcFseTZb+Y0R2rbYFJi8+Tnr8vezO5ywEghIg\nAA5KmnIQQMB3gd+5LY+ObScN65x9UV8bWjQMes++7PPgTAQQQAABBKIm8IQLXM/sI7VskH3Nz3Ln\nr9rsdmBYmX0enImA3wIEwH4Lkz8CCAQiMMFtwTBvlZu3NKJixbVzQ796tpb+NbNi+XA2AggggAAC\nURGwYcuTP5W+7p7gViTZvOFLhrmnwO9WJBfORcBfAQJgf33JHQEEAhCwp7W2aMf/+5JUo5wtj9Kt\nij0FfvYjaf+BdM/gOAQQQAABBKIr8Hs3guryEyVbzKqi6dQe0mduR4UpLqAmIRBGgcAC4G3btunW\nW2/VsGHD1K1bN5144om6+uqrtWaNW7GGhAACCFRAwJ78Nqwj2dPbXCTbOql9E+nNObnIjTwQQAAB\nBBAIr8D4+dIet/rzGb1zU8dKbheGy05gLnBuNMnFD4HAAuCrrrpKLVu21Msvv6x58+Zp7NixGj16\ntEaNGuVHu8gTAQQSJDBunjSie24bbE+Bn3GLgdiewiQEEEAAAQTiKGAjqB6ZIH1/ZG5bd0IXyQLh\n9xbmNl9yQyAXAoEFwKtXr5YFwY0aNVLlypVVt25dnX766WrRooV27tyZi7aQBwIIJFDA9ix8f5F0\nco4D4D5t3FPl2tI7bm4xCQEEEEAAgTgKTCmU2jSUurXIfetsSPUT73MjOfey5FhRgaoVzSDd8+1J\n78UXX6wvf/nLXhC8Y8cOTZo0SW3atFGtWrXSzYbjEEAAgcMEbNGOjk2z2/bosIxK+cG2c3jY3RnP\n9dPlUoriLQQQQAABBAIXsCe0J3b1p9iBBUXX5rfdKK3TevpTBrkikI1AYE+Ar7vuOl1//fVatWqV\nN/x55syZ3nzg+++/P5t6cw4CCCDgCYx3F9ZT3IIbfiTbE9hWtJy02I/cyRMBBBBAAIH8Cex1I6gm\nLZFsuLJf6bx+kgXAJATCJBDYE2Br9PHHH+99pQOwe/du7dmz54hD9+93/7eSEEAAASew0/0TYcO3\nrj3dP46Lh0pPT5KGdvKvDHJGAAEEEEAgaIFphVInN4KqgZvu41ca0F769b+Krte5WGHar3qSb7IE\nAg2AS6MdNGiQpkyZcsRHTzzxhLdgVskPFi5kNn1JE35GIKkC738iHdtWqlvTPwEbGvb4e9LHy6R+\n7fwrh5wRKEtg0aJFuuuuuzRjxgxt377dmzo0YsQI3XjjjapePQd7lpRVMO8jgECsBd5z11C/hj+n\n4Czo7dlamlrof1mpMvmOwNEE8h4AP/fcc6XW8T/+4z9kXyXTGWecUfItfkYAgYQKjHNbN5yZo20b\nyiO8zC3k8dcPCYDLM+IzfwQOHDjg7Zbwu9/9Tvfee69q166tzZs3y24S27SiBx54wJ+CyRUBBGIt\nYPvcT3QLSH7rJP+bObSjNNkNtfY72Pa/JZQQFwE3uy2YtHTpUn33u9/VOeeco8mTJx8q9IYbbjj0\nmhcIIIBAugJbPpfmr5aOC2BospWxcK20bVe6teM4BHIjsGXLFnXr1k32xNd2T7BdFBo3bqxrrrlG\ndl0lIYAAAtkITHf/fLRvLDWqk83ZmZ1jU4hswUq2FczMjaP9EwjsCfAvfvELXXTRRd6Kz1deeaV3\nJ3v48OFavHixf60jZwQQiK3ABLc90fHuolo9gH/FqlUpevprd7BZyTK2v1KhbJhtHVilShXddNNN\nGjx4sBcEb9q0Sc8884wuueSSUNaZSiGAQPgF/Fz9uWTrmx9TNM/Yblr3aFXyU35GIHiBAP50LGqU\nrf6cGr788ssv67zzztPjjz8efIspEQEEYiEwzq0q+Y3jg2tKaggXAXBw5pRUJPDss8/q+eef15w5\nc7R+/Xo1a9ZMt9xyi4YOdSu0kRBAAIEMBWz48wdu+PM3hmV4YgUOt5FUdhOZALgCiJyaM4HAAmBb\n7Orqq6/Wf//3f6t169b6xz/+oQsvvNDbFilnrSEjBBBIhMCardJq92WrSwaVBrs5TH98R7I/HGxr\nJBICQQlUqlRJo0eP9r7SKdMWx7JAuXhas2aN6tQJYKxj8UJ5jQACoRSYuVxq1VBqWi+46g1x19AH\n3pRsTQ0SAvkWCCwA/tnPfubt/3vw3xMAOnTooJdeekl33nlnvg0oHwEEIiZgT3+Hd5ObDxlcxW2e\nVMsG0tyVUh+38jQJgXwKzJ49W/fcc48ee+yxI6rxwx/+UHv37j3s/UmTJmnq1KmHvccPCCCQTIF3\n3YYqJ/q4929pqj1aShu3S+s+k5q5IdEkBPIpEFgAbI0866yzDmtrq1atZCtbkhBAAIFMBN52AfD1\nZ2ZyRm6OtWHQk9wQLgLg3HiSS/YCXbt29bZGKi0HG2VVMi1btsxbg6Pk+/yMAALJEnALy8u2ELwv\n4CUE3EAW2VNgu4ae3y9Z5rQ2fAIBPj8JX+OpEQIIRE9g8Tpp7778zCNKXbyjp0aN4yZg+/+2aNEi\nbs2iPQgg4LPArBWSLUplX0En7xrK2rdBs1NeKQKBPgEupXzeQgABBDISGO/2/j2lR0an5Ozgri7e\n2O62QrI5yC3q5yxbMkKgTAGby3vHHXeU+nmXLl107bXXlvoZbyKAAAKlCXjDn7uW9on/7w0qkO4Z\nK+12MzRqVPO/PEpAoCwBAuCyZHgfAQRCKWDzf++6KH9Vs2HQH7o72F8ekL86UHJyBJo0aaIGDRpo\n4sSJuvnmmw9reMOGbhUbEgIIIJCmgC3DY8Off3Nxmifk+LBa1aWebhukqW4P4mGdc5w52SGQgQAB\ncAZYHIoAAvkVmOVWrjymltS2Uf7qMcRt5fDyxwTA+euBZJVsK0D//Oc/15e+9CW1bdtW3bq51d9I\nCCCAQBYCs90ijo3qFi3omMXpOTnF21LQ3UQmAM4JJ5lkKcAc4CzhOA0BBIIXGDc/f8OfU621rZfm\nrpJ27km9w3cE/Bd44YUXCH79Z6YEBGIt8F4eVn8uCWr7AdtCWCQE8ilAAJxPfcpGAIG0BWz/XZu7\nNKJ72qf4cmBNN2+pl1tkd2qhL9mTKQIIIIAAAr4I2PDnk/I0/zfVoOZu/QwbybVgTeodviMQvAAB\ncPDmlIgAAlkITPlUKmgiNa2Xxck5PsWGcH3k6kNCAAEEEEAgCgI2cqluTalNHqcQpZxSw6BTP/Md\ngaAFCICDFqc8BBDISuCdBdJpPbM6NecneRdvhnDl3JUMEUAAAQT8EbDhz/l++ptqma2l8SHX0BQH\n3/MgQACcB3SKRACBzAXsCfDAgszP8+MMhnD5oUqeCCCAAAJ+CdgUorAEwL1aSes+kzZs96u15ItA\n+QIEwOX78CkCCIRAYNFaqX7tcAx/TnEwhCslwXcEEEAAgTAL2HxbW7+iXeNw1NItbq8hHdxiWG41\naBIC+RAgAM6HOmUigEBGAtPcnoG2+nKYkg3hYiXLMPUIdUEAAQQQKE0gTMOfU/UbyjU0RcH3PAgQ\nAOcBnSIRQCAzgekhDIB7tpTWuiFcGxnClVlncjQCCCCAQKACtvrz8JBtIW5TmmYtl/bsC5SCwhDw\nBAiA+UVAAIFQC9jFcd5qqW/bcFWzsvvXc7AbwjWZhTzC1THUBgEEEEDgkMCyjdIBt42g7aIQplSn\nhtTd3Ui2EV4kBIIWIAAOWpzyEEAgI4GZ7g5x1+ZSreoZnRbIwUM6Mgw6EGgKQQABBBDISsD2rB9Q\nkNWpvp/ENdR3YgooQ4AAuAwY3kYAgXAITF8m9Q/Z/N+UzKACaYar3979qXf4jgACCCCAQHgELAAO\nyw4KJVWOs3nALIRVkoWfAxAgAA4AmSIQQCB7gWmF4Q2A69aUOrun0xYEkxBAAAEEEAiTgN2cnbNS\n6tcuTLX6oi4tG0g2FHqhW6WahECQAgTAQWpTFgIIZCSwaYe0fpvUrUVGpwV6MEO4AuWmMAQQQACB\nNAVmr5A6Ni0KMtM8JfDD7CmwPaUmIRCkAAFwkNqUhQACGQnY6s9259r2DAxr8vYDZiGssHYP9UIA\nAQQSKxDm4c+pTund2q0G7QJ1EgJBChAAB6lNWQggkJFAGLc/KtmAdo1dgO7eLNxQ8hN+RgABBBBA\nIH8CYV4AK6XSywXA81ZJ+91K1SQEghIgAA5KmnIQQCBjgSjcvbZGDbWFPHgKnHH/cgICCCCAgD8C\nNoVog9unPsxTiKzltpaGzQX+ZK0/DuSKQGkCBMClqfAeAgjkXcCeqNrWR83r570qR62AN4fp06Me\nxgEIIIAAAggEIjDVXZMGuB0UwjyFKAXRty3DoFMWfA9GgAA4GGdKQQCBDAW8oVsh3f6oZFN6tnKr\nWLq713v2lfyEnxFAAAEEEAheYJpbQ8MC4Cgk5gFHoZfiVUcC4Hj1J61BIDYC3sW7IBrNqVFN6tBE\nmr86GvWllggggAAC8RaIwvzfVA/0cU+AbbumgwdT7/AdAX8FCID99SV3BBDIQsD2LpzrLobHuoti\nVFKfNgzhikpfUU8EEEAgzgK2r27DOlLTetFoZf1aUuO60pL10agvtYy+AAFw9PuQFiAQOwG7E9wh\n5HsXlkT35jAtL/kuPyOAAAIIIBCsQFQWkCyuwjDo4hq89luAANhvYfJHAIGMBaYVRmfuUqpxtpXD\nfHfXfZ97ek1CAAEEEEAgXwJR2EKwpI2NoprNfsAlWfjZJwECYJ9gyRYBBLIXmL5M6heRxTtSrbQV\nq9s1KgqCU+/xHQEEEEAAgSAFdu4p2lLIRiVFKdk84JmMoopSl0W6rgTAke4+Ko9A/AS27pRWbZF6\ntIxe2+wCPosLePQ6jhojgAACMRH42N1A7uF2JqheNVoNauLmANuewMs2Rqve1DaaAgTA0ew3ao1A\nbAVs6FZfNxSqSgT/dbJ6z2IIV2x/N2kYAgggEHaBKM7/TZkyDzglwXe/BSL4J6bfJOSPAAL5FPDm\nLhXkswbZl23zgOetkvYfyD4PzkQAAQQQQCBbAdtCcGBBtmfn9zzmAefXP0mlEwAnqbdpKwIREPDu\nXkds/m+K1YZvtWoo2RYUJAQQQAABBIIUWLNV2rVXKnD70kcxedOIGEUVxa6LXJ0JgCPXZVQYgfgK\nLN9UNPTZgsioJvYDjmrPUW8EEEAg2gJTPpUGFUS3DS3qF9V9tVsHhISAnwIEwH7qkjcCCGQkEMXt\nj0o20NsPmDvYJVn4GQEEEEDAZwEbQTWgwOdCfM6eYdA+A5O9J0AAzC8CAgiERsDmLvWP6PDnFKIt\n4jHXzQM+wDzgFAnfEUAAAQR8FrC1J2a4XQgGRPwaagHwTG4i+/zbQvYEwPwOIIBAKATs4m0rKEc9\nAD6mltS0nrRoXShYqQQCCCCAQAIE7MZrGzd9yK5BUU42D3g2AXCUuzASdScAjkQ3UUkE4i+QunjX\ncwtJRT0xDzjqPUj9EUAAgWgJ2BSiqK7+XFy6bSNpx25pw/bi7/IagdwKEADn1pPcEEAgS4GP3fDn\nQR2yPDlkpzEPOGQdQnUQQACBmAtMKXQBcIyuoTPdcG4SAn4JEAD7JUu+CCCQkcD0ZdKxbuhTHFJq\nEY+DB+PQGtqAAAIIIBBmgc92Sis3Sz1ahrmW6dctdQ1N/wyORCAzAQLgzLw4GgEEfBDYuUdast5d\nvFv5kHkesmxQW2pYp6hNeSieIhFAAAEEEiRgC0jaDeQqMfmrvrdbCMvWBCEh4JdATP5X8YuHfBFA\nIAiB2Sul7i2k6lWDKC2YMpgHHIwzpSCAAAJJF7Dtj+Iyhcj6smNTadMOaat7sk1CwA8BAmA/VMkT\nAQQyEvh4mbt73S6jU0J/MPOAQ99FVBABBBCIhYAtgDWoIBZN8RpRqZJkWwoyDzg+fRq2lhAAh61H\nqA8CCRSYEdcAmEU8EvjbTJMRQACB4AQWuy33alWXmtcPrswgSmIecBDKyS2DADi5fU/LEQiFwLZd\n0qotUjc3BDpOqZGbA2xbOhVuiFOraAsCCCCAQJgEbPXnOA1/TtkyDzglwXc/BAiA/VAlTwQQSFvA\nhjj1ckOd4rJ4R/GGMw+4uAavEUAAAQRyLfDREmlwTLY/Km7Tpbm02t0c3+5ukpMQyLUAAXCuRckP\nAQQyEvDm/8Zk+6OSDe/j2jWLYdAlWfgZAQQQQCAHAhYc2hBoW3MibsluitvOEHPcIpkkBHItQACc\na1HyQwCBjARmuACxX8wWwEoB2B8lM9nKIcXBdwQQQACBHArY9kd2o7ValRxmGqKsGEUVos6IWVUI\ngGPWoTQHgSgJ2DYHm7ZLnd1QpzimpvWkmm5rp+Wb4tg62oQAAgggkE+BKZ/Gc/hzytQbRcVN5BQH\n33MoQACcQ0yyQgCBzATiuPpzSQGGQZcU4WcEEEAAgVwIfOQC4CExnP+bsrHFMZdulHbuSb3DdwRy\nI0AAnBtHckEAgSwEvAA4hnOXilP0bePmAXMHuzgJrxFAAAEEKiiwaK1Up0b8tj8qzmJDu7u7IHje\nquLv8hqBigsQAFfckBwQQCBLAVsAq3/7LE+OyGkM4YpIR1FNBBBAIEIC3tPfjhGqcJZV7el2ieAm\ncpZ4nFamAAFwmTR8gAACfgqs3Srt2S+1beRnKfnPu0V9qVIlt9fx5vzXhRoggAACCMRDIO7zf1O9\n1NsFwKwEndLge64ECIBzJUk+CCCQkYA9/Y3r6s8lIVjJsqQIPyOAAAIIZCtg2x8tWe9WgHZTbOKe\nbCukhW649/4DcW8p7QtSgAA4SG3KQgCBQwK2/dGxMZ//m2qsBfqz2cswxcF3BBBAAIEKCEwpdNdP\nd12pGtPtj4rT1KoutWnoguA1xd/lNQIVEyAArpgfZyOAQJYCSXoC3MsN4ZrpAn4SAggggAACFRVI\nyvDnlFNv96Sbm8gpDb7nQoAAOBeK5IEAAhkJ2L641d2d6+ZufmwSUmt393rXXmn9tiS0ljYigAAC\nCPgpYAtgDY7x9kcl7ewmMvOAS6rwc0UECIArose5CCCQlUCSnv6mgGyu1my2Q0px8B0BBBBAIAsB\nGwrcoLbU7JgsTo7oKQTAEe24EFebADjEnUPVEIirgO3/29fNX0pS4gKepN6mrQgggIA/Ajb8eVCC\nnv6aYqM6Ur2a0tIN/piSa/IECICT1+e0GIG8CyTxCbAFwMxhyvuvHhVAAAEEIi0w2QXAQxIWAFuH\ncRM50r+2oas8AXDouoQKIRBvgcXrpIbubq7d0U1S6txMWuP2PrbtK0gIZCKwaNEi/eQnP9Ebb7yh\nf/7znxowYICuuOIKrVjBmPpMHDkWgagLfLZTWrZRskWhkpZsP2BuIiet1/1rLwGwf7bkjAACpQgk\n8emvMVR2/9r2dPsZspBHKb8UvFWuwNVXX61+/frp3nvv1UMPPaSxY8dqzJgx+s1vflPueXyIAALx\nErDtj2xbvSoJ/OudJ8Dx+l3Od2sS+L9QvskpH4FkCyRp/9+SPW13sAmAS6rwc3kCW7duVfPmzb2A\n9/zzz9dxxx2nZs2a6YwzztDy5eytVZ4dnyEQN4GkbX9UvP/aNJJ27pE2bC/+Lq8RyE6ganancRYC\nCCCQucD+A0UrIf/47MzPjcMZNmzt8ffi0BLaEJRA/fr1tXv3bn3zm9/0At6aNWvqscce07x58zRs\n2LCgqkE5CCCQZ4GDByULgL91Up4rksfi+7Qt+htiRPc8VoKiYyFAAByLbqQRCERDwLZvaNmgaDXH\naNQ4t7Xs1kJasl7as8/tg8y/vrnFjXFuf/vb3/TBBx+oe/fu2rJli5544gmdeOKJOu+882LcapqG\nAALFBRa462ejulLTesXfTdbr1DBoAuBk9bsfreVPMD9UyRMBBEoVSOr83xRGjWpSQRNpwWrJ7mST\nEEhHoFKlSjrhhBO8Qxs3bqw77rij3NO2bdum/fv3H3aMvbdvn7vzQkIAgUgK2NPfJK7+XLyzbBrR\nG7OLv8NrBLITIADOzo2zEEAgC4GZbsriVwZmcWKMTklth0QAHKNOzUNTZs+erXvuuccbDl2y+B//\n+Mdau3btYW9v2LBBjRq5SXQkBBCIpMBHLgC+Yngkq56zSndyuymsdrsp7Ngt1amRs2zJKIECBMAJ\n7HSajEA+BGzY7zz35PP/uXmwSU52B/vlGUkWoO25EOjatavuuuuuUrP6/e9/f8T7EyZM0FtvvXXE\n+7yBAALhF9jqtj9asbloL9zw19a/Gtrq1z1aSnNXSYMTuBeyf7LJy5lVoJPX57QYgbwIzHMXrI5N\npVrV81J8aAq1hbDmrpRsQRMSAukI2D7Atu/voEGDvHnAI0eO1K9+9Sue6KaDxzEIxEDAhj/3T+j2\nRyW7zxtFtaLku/yMQGYCBMCZeXE0AghkKTB9mTSgfZYnx+i0ejXdIibHFC2GFaNm0RSfBA4cOKBR\no0bp0ksv1fjx4zV37lw988wzql27tq6//nqfSiVbBBAIk8C0Qjf/t2OYapS/uqQWwspfDSg5DgIE\nwHHoRdqAQAQEJi+RBhZEoKIBVNGGQc/mDnYA0tEvwlZ97tatm0aMGKG6deuqcuXKsoWwrrnmGi1d\nujT6DaQFCCBQroBNH/rQXT+Hdir3sMR82KOV9Ilb4mDf4ev8Jab9NDQ3AswBzo0juSCAQDkCG93G\n9eu3Sd3d3B1S0TyuDxdLXxqABgLlC9jCVVWqVNFNN92kwYMHe0Hwpk2bvKfAl1xySfkn8ykCCERe\nwK4Vdu2sXyvyTclJA2q63RTaN5bmu22h7GYyCYFsBAiAs1HjHAQQyEjA5i/Z01+3mwvJCdhF+5EJ\nUCCQnsCzzz6r559/XnPmzNH69evVrFkz3XLLLRo6dGh6GXAUAghEVmD8fGlEt8hW35eKp4ZBEwD7\nwpuITAMLgH/+85/rJz/5iXcn2/YwtDlMPXv29C7iAwbwGCQRv200MrECtn3D8Z0T2/wjGt68vlTZ\n3QxYvUVq2eCIj3kDgcMEbB/g0aNHe1+HfcAPCCAQawHb7ufjZdKPzo51MzNunC0m+Rr7AWfsxglf\nCAQ2B/jVV1/V/v379cYbb2jJkiWaOHGiFxBffvnlX9SGVwggEDuB/QckWwCL+b+Hd61dwJkHfLgJ\nPyGAAAIIfCHwwSdu9We3eGTthO+e8IVI0avUE+CS7/MzAukKBBYApypkK1jaapb169fXwIEDvS0d\ntm93EwRJCCAQSwHbr6+Ve8rZoHYsm5d1o2zo1hy3HRIJAQQQQACB0gTG2fDn7qV9kuz37O+Jhu6r\ncEOyHWh99gKBBcBt2rTR8OHDNW7cOD366KNejR944AHt3r3bW9Qj+yZwJgIIhFnA5v+yYf2RPeQ9\nASYAPhKGdxBAAAEEtOVzaYFb6GloRzBKE7CbyIyiKk2G99IRCGwOsC3isXPnTs2cOdNbxMMq17Rp\nUz311FPp1JNjEEAgogI2//cHIyNaeR+rXdBE2uz+wLE/cng67iM0WSOAAAIRFJiwwK2d4bY+qh7Y\nX+rRQrJh0NPcTnDn9YtWvaltOAQC/d+qVq1ah61aOWbMmDIVxo4dq8mTJx/x+fLly494jzcQQCCc\nArb90Qa3/VG3FuGsX75rZRdwu4N9Ytd814TyEUAAAQTCJGCrP3/9uDDVKFx1sevnnz4IV52oTXQE\nAg2AS2MZNGiQpkyZcsRHnTp1Uo0aNY54/5VXXjniPd5AAIFwCtjw5wEFbsXjwCZbhNOhrFp5Q7jc\nMGgC4LKEeB8BBBBInsDaz6QVm4oWwEpe69NrcauG0t790jpn1eyY9M7hKARSAnkPgJ977rlUXQ77\n3qVLF9lXyWSLZ5EQQCAaAmx/VH4/2R3s348r/xg+RQABBBBIloA9/T3J7f1bhZvH5Xa8N4rK3UQ+\nlQC4XCc+PFIg7/9rtW/f/sha8Q4CCERegO2Pjt6FNjR8ubvLv3PP0Y/lCAQQQACBZAi84wJgVn8+\nel+zneDRjTiidIHAngDfdttt2rp1a6m1uP/++0t9nzcRQCC6Amx/dPS+q1pF6tJcmr+aoW5H1+II\nBBBAIP4CdlP0s51SH7dXPKl8AXsC/K+Z5R/DpwiUJhBYADx06FBde+21evDBB1W1amDFltZm3kMA\ngQAE2P4oPeTUVg79GQyTHhhHIYAAAjEWGDdPOpm9f9Pq4c7N3EKbbrHNHbulOkcuG5RWHhyUTIHA\nItHzzz9f8+bN08qVK3XFFVckU5tWI5AgAZv/+/2RCWpwlk21O9jPfpTlyZyGAAIIIBArAZv/e8t5\nsWqSb42pVEnq2Uqa4TaIGdbZt2LIOIYCgQXAZnfjjTfGkJAmIYBASYHU9kfd3RxXUvkCPV0AvOAl\nyeZMs+BJ+VZ8igACCMRZYMEat2uCC+o6u6kxpPQE+raVZhIAp4fFUYcE8r4I1qGa8AIBBGIjwPZH\n6Xdl7epSa7edw0L3hw8JAQQQQCC5AuPd8GcWv8qs/1MBcGZncXTSBQiAk/4bQPsR8EHAhj8P7uBD\nxjHNsq9b7GSO28qBhAACCCCQTIGDB6V3Fkin9Ehm+7NtdRc3D3iNW2N3265sc+C8JAoQACex12kz\nAj4KsP1R5ri2lcPMFZmfxxkIIIAAAvEQmOWuAY3qFI0IikeLgmlFZRfJ2Dxg8yMhkK4AAXC6UhyH\nAAJpCbD9UVpMhx1k213MdhdvewJAQgABBBBInsA49v7NutMZBp01XWJPJABObNfTcAT8EWD7o8xd\nj6klNa0nLV6X+bmcgQACCCAQbQEbOfX+QrY/yrYXCYCzlUvueQTAye17Wo6ALwI2/3cQ838ztrWn\nwAzhypiNExBAAIHIC9iN43aNi26ERr4xeWhAF7dq9trPmAecB/rIFkkAHNmuo+IIhE+A7Y+y75M+\n/97KIfscOBMBBBBAIIoCb7P6c4W6zbYQ7N6yaCpRhTLi5MQIEAAnpqtpKAL+C7D9UfbG3jxgVoLO\nHpAzEUAAgQgKLNtYtI/tGb0jWPkQVZlh0CHqjAhUhQA4Ap1EFRGIigDbH2XfU7b6Z303F/jT9dnn\nwZkIIIAAAtES+Osk6csDpepVo1XvsNXWthNkN4Ww9Up460MAHN6+oWYIREqA7Y8q3l3MA664ITkg\ngAACURGw/Wtt5NSoflGpcXjr2bWFtHqLtJ39gMPbSSGqGQFwiDqDqiAQZYH5q93+hQ2kBrWj3Ir8\n1t32A2YhrPz2AaUjgAACQQn8bbJ0ngt+a1UPqsT4lmPzgHu4/YBnM5Uovp2cw5YRAOcQk6wQSLLA\nW3OlE7omWaDibWcOU8UNyQEBBBCIgoAtGjlhgRv+PCAKtY1GHbmGRqOfwlBLAuAw9AJ1QCDiAvv2\nS++6PQxP7RHxhuS5+rYXcG33JGD5pjxXhOIRQAABBHwV+PtH0pl9JNsHnpQbAW8e8PLc5EUu8RYg\nAI53/9I6BAIRmOzmMHVsyh6GucC2ecAzuYDngpI8EEAAgVAKbN0pvTFHumBQKKsX2UrZPOCVm5kH\nHNkODLDiBMABYlMUAnEVsOHPp/WMa+uCbZe3HdKKYMukNAQQQACB4AT+OVU6ubtkq/+TcieQmgc8\nh3nAuUONaU4EwDHtWJqFQFACtuLix8ukE5n/mxPyPm1ZCCsnkGSCAAIIhFBgx27plRnSVweHsHIx\nqJI3D5ibyDHoSX+bQADsry+5IxB7AVvEY1BB0dzV2Dc2gAa2qC9VqiStcsO4SAgggAAC8RJ4cbo0\ntJPU3P1bT8q9AAth5d40jjkSAMexV2kTAgEK2PBnFr/KLTj7AefWk9wQQACBMAjs3iv9c5o0ZkgY\nahPPOnRz84BXuIUk7Uk7CYGyBAiAy5LhfQQQOKrA2q3uQuOeVA7qcNRDOSADAbuDzX7AGYBxKAII\nIBABgVdnSnaDs02jCFQ2olVMzQOezTDoiPZgMNUmAA7GmVIQiKXA2/OKFvKwCw4pdwI8Ac6dJTkh\ngAACYRCw7QKfmyJdfFwYahPvOtg1dCYBcLw7uYKt48/WCgJyOgJJFnjTbeMwktWfc/4r0LqhtGef\ntPaznGdNhggggAACeRCwbY86NJU6NctD4QkrknnACevwLJpLAJwFGqcggIA0f3XRYk227x4p9wJ2\nAWcIV+5dyREBBBAIWuDAAemZSTz9Dcq9e0vmAQdlHdVyCICj2nPUG4E8C9jwZ/b+9a8TvGHQy/3L\nn5wRQAABBIIRmLBQalJP6tkqmPKSXopNy7IgmP2Ak/6bUHb7CYDLtuETBBAoQ2C/u5s93gXArP5c\nBlAO3mYOUw4QyQIBBBDIs4Btaffg29LVp+a5IgkrnmHQCevwDJtLAJwhGIcjgIA05VOpXWP2MfTz\nd6F9E2n7Lmnjdj9LIW8EEEAAAb8E9rqFr+58SfrmCcz99cu4rHz7uGlEMxlFVRZP4t8nAE78rwAA\nCGQuYMOfefqbuVumZ9gFnO2QMlXjeAQQQCAcAvbkt63b8ujcY8NRnyTVortbn2S52w/48z1JajVt\nTVeAADhdKY5DAAFPwC4mH7knwMO7AeK3gDcMmjvYfjOTPwIIIJBzgfHzpRnLpOvOyHnWZJiGQNUq\nzANOgymxhxAAJ7braTgC2Qm8u0Aa0F6qWzO78zkrfQFvISz2MkwfjCMRQACBEAisdPN+f/eWdNso\nqVb1EFQooVVgHnBCOz6NZhMAp4HEIQgg8IWAN/yZvX+/APHxVUe3Z+TmHdKWz30shKwRQAABBHIm\nYHu43/mi9O3hRfv+5ixjMspYgHnAGZMl5gQC4MR0NQ1FoOIC67dJn66XhnSoeF7kcHSBSpWk3m2Y\nB3x0KY5AAAEEwiFgT347uJuXZ/UJR32SXIsebiskmwe8k3nASf41KLXtBMClsvAmAgiUJmBPf09y\nc39tbg0pGIHerQmAg5GmFAQQQKBiAm/NlWavlK49vWL5cHZuBGw/4B5u7+Xpy3KTH7nER4AAOD59\nSUsQ8F3ALu6nMfzZd+fiBdgcplkshFWchNcIIIBA6ATsSeND44vm/dasFrrqJbZCtmbJtMLENp+G\nlyFAAFwGDG8jgMDhAgvXSHv2ulUV3dYCpOAEOjeT1rmh55/tDK5MSkIAAQQQSF9gl7s23v5P6Ttu\n3m+B28OdFB6B/i4A/pgnwOHpkJDUhAA4JB1BNRAIu8AfxkmXniBV5l+NQLvKvHu5YdBz3LA6EgII\nIIBAuATsyW+zH0in9pBO7x2uulEbyRaT3L7b3Uj+DA0EvhDgT9kvLHiFAAJlCHy4WNrhFpGwCzwp\neIG+biGsaUuDL5cSEUAAAQTKFhg7S7rhaelv35O+fnzZx/FJfgW8YdBcQ/PbCSErnQA4ZB1CdRAI\nm8CBA9IjE4qGdtmqxKTgBfq1k2YwDzh4eEpEAAEEShHY4Z4o/vIl6cXp0j0Xs+JzKUShequ/u4ZO\nJwAOVZ/kuzIEwPnuAcpHIOQCb8yRGtaWBnUIeUVjXL3OzaVN292X2xOYhAACCCCQP4G5q6Srn3DX\nxTrSvd+Q2jbKX10oOT2B/gUEwOlJJecoAuDk9DUtRSBjgT37pD994J7+npzxqZyQYwF7CsxCHjlG\nJTsEEEAgA4GnP5R+/oL0/ZEuCD5VqsaWgBno5e/QJnWl+u5G/qK1+asDJYdLoGq4qkNtEEAgTALP\nTyvaQ68rKz/nvVuOdQHwzGXMw857R1ABBBBIlMDBg25v3xXS36dIu91qz7/9ptTIPf0lRUsgNQ/Y\nRlSRECAA5ncAAQRKFdi2S3ruI+n/vl7qx7wZsIA9Abb+ICGAAAII+CtgQe8sF/S+u1B6z301dk8Q\nh3eTLhossRaGv/Z+5W7bIdmc7a8O8asE8o2SAAFwlHqLuiIQoMBfJ0knuQt+q4YBFkpRZQrYPLM9\n+6W1W6Xm9cs8jA8QQAABBLIUmOkWG5ywwAW9n0hN60kndpX+190EbsG/uVmKhue0Y9tKd7/irqNu\nald1op/wdEyeasKvQJ7gKRaBMAvYfnmvz5YeujzMtUxe3ewp8HQ3DPqsPslre5Jb/P7772vhwoW6\n6KKLdNddd+nll19W7969dd9996lx48ZJpqHtCGQlsM/dTFzm9u/9dL20dIP7bl/utS1sdZILeu91\nQS83GrOiDe1JtapLnZpKc1ZK9jSYlGwBAuBk9z+tR6BUAVv4alS/oj8GSj2AN/Mi4AXAbisHAuC8\n8Oel0P379+vmm2/Wn/70Jz3yyCOqUaOG3nvvPb322mv6/ve/r6efdpuQkhBAoFyBxeukKYVFQa4F\nuqu3SC0bSAVNir7OPVbq4IKj5seUmw0fRlzAAl/bDokAOOIdmYPqEwDnAJEsEIiTQKG7Ez7lU+nR\nK+LUqni0xQLgR9+NR1toRXoCu3btUq9evVRQUKBZs2bphhtuUL169XThhRfqueeeSy8TjkIgYQI2\nzNUCnUlLpMnuq4b7a3dYF2lwh6I5oO3clJKqrOCcsN+KosD3wbelbyeu5TS4pAABcEkRfkYg4QIW\nYH1tqGTDhUjhEmjmnk7Udv1iQ/bauycXpPgL1KlTRw0bNtQPf/hDdevWTVdeeaW+/vWv680339Rl\nl10WfwBaiECaAvZUd9q/g95ZyyXbvWBoJ+mCQVJr1rJIUzHeh3Vv6Z7+u3U0tu502yLVindbaV35\nAgTA5fvwKQKJErA/Gpa54OqnX0pUsyPVWFvIY4brJwLgSHVbhSr7y1/+0pv3+8EHH6hr164qLCzU\nNddco1NPdRuRkhBAQC+4Lfts4Ubb6ua0ntJN50h1agCDwOECVSpLfdpIH7u1NE52i3ySkitAAJzc\nvqfleRCwu46rNhfNNapZLQ8VKKfIAwfcapevS5efJNlFghROAdsP+J35bo52/3DWj1rlXqCS23fl\n/PPP977Syf3ee+/V5s3uH5piaenSpdq7121iSkIgRgIbt0v3jJV27pEedAMiGtSOUeNoii8CdpNk\neiEBsC+4EcqUADhCnUVVoyuw1604aXeo/za5aCjWYrcIRwM3/KatW8DV5iK1c99Tr4/Jw7Acq993\nH3XDa90d8xHdo+uchJrbPOD735Rsn0r2o0xCj5fextmzZ+uee+7RY489dsQBxx9/vHbudHfbiqUZ\nM2Zo0aJFxd7hJQLRFrA9en/7lvQldzNwjNvbtTI3bqPdoQHV3hbAem5KQIVRTGgFCIBD2zVULC4C\ntqfgoxOKnvr+n9taIbWvru3nunSjG3LsvhasLtp2aIV7aNOmoXTJMGlgQTACduf8jhekLm6+1C3n\nBVMmpWQvYE84mtSVPllbNMct+5w4M8oCNhTatkQqLQ0Z4qKBEsmeIm/c6P6xISEQcYHP3TXrdy7w\nne+um3d8hX8HI96dgVe/rXvosN+NeLPReKm/xwKvBAXmXeCoAfA3vvENnXHGGbrgggtUt677q4uE\nAAJpCcxb5fbRHS/Z09UbznLzTtoefprtMWhfQzoe/v47LmC282yxo0tdIDyg4PDPc/nTZ+4h0W1u\nIdlOzaVrR/JEMZe2fuZld7BtDpMt8kKKv4A9ubVg157ibt++XW3atNGIESN04403xr/xtBCBYgKz\n3R6u//Nq0WrOv73Ure4csqlExarKyxAL2DBoWzCNADjEneRz1SofLf9LLrnEW3zDtmC4/PLLNX78\neDf07uDRTuNzBBIrYE9273pZ+sVL0nluL90H3EW6ZPBbHo4tzPD7y6QvD3Tfx0v/+ZT7h7qwvDOy\n+2yDmzt1w1+LAuwfnk7wm51ifs5KLYSVn9IpNUiBA25y/qhRo3TppZd619+5c+fqmWeeUe3atXX9\n9dcHWRXKQiCvAs9PdU98/yl9392stS+C37x2R6QLt5vIFgCTkitw1AD47LPP1rPPPuvNHRo2bJh3\nF7pz5866/fbbtWqVe8RFQgCBQwK27+Blf3Qr9Lo5vbaPrq1GmU2yuZ0WCP+hWCB8/dPSTLf6by6S\nDf25weV3Vh+36NWJuciRPIIU6OtGE8xxT0JsGBcp3gJbtmzxtj+yJ742Cquym+jYuHFjbxVoW9iK\nhEASBD5w09cvfcjdFL686OlvEtpMG/0TsADYdlOwxT9JyRQ46hDoFIttu/DJJ594gXCrVq20bds2\n2UIbd999ty6++OLUYXxHILEC23ZJ1zxZ9PTWVurNRUoFwsO7upV/3dDoB95yT2pdxha4nuqC62z2\nsVu8rmjY87dPkk7vnYtakkfQAra9h91kmevuQdqWDqT4CjRq1EhVqlTRTTfdpMGDB3tB8KZNm7yn\nwDZCi4RA3AXWuFFV977untjdLjWqE/fW0r4gBGwtjebHuPVX1kg9WgVRImWETeCoAbBtp/DHP4V7\n38AAAEAASURBVP5Rdhf6sssu09ixY9WlSxevHbYtw49+9CMC4LD1KvXJi8ADb0rfHi7lKvgt3ggL\nhG11ZvuataJowaw/PyL1d4H2GS6IHVSQ3gqYq7e4ha7+Lv3wDGlY5+Il8DpqAt4w6GUEwFHrt2zq\na6Ownn/+ec2ZM0fr169Xs2bNdMstt2jo0KHZZMc5CERGwNbQuPNF6RvHs+ZBZDotIhVNraVBAByR\nDstxNY8aANsF17ZaOP30072hV1b+unXrvDvSvXr10n333ZfjKpEdAtETsO0Y7MmqLXbld7InfvZ1\nzZ6ip8JPfyjd94Y0slfR3rC73Pt2x3y1fbmAN/V9lXtdw/0fbys9+xGk+91u8j9cwLZDenqSWzH8\n8Lf5KYYCtoLz6NGjva8YNo8mIVCmwB/GSS0bsO95mUB8kLWALYT1V3cNvfi4rLPgxAgLlBkA79rl\nxnO6NHHiRC/I3bPH/VXtki3Ice211+qss87yFsVq0qSJ9z7/QSCpAlvdSsq2JcPPviJVL/P/qNzr\n1KpeNBTahkPbVkqvzZaufFyq64bHtnCrS9sfDfa9W0v32n231Q737HP7D7uhP6ToC/RqXbQV0u69\nLAYT/d6kBQggUFLApv3YQkW2kCQJgVwL2IOEn7vRBbvcNbQmq4nnmjf0+ZX55/q5556rt99+22tA\nrVq1DjXE7kS3bt1ad9xxx6H3eIFAkgXs6euZLgjtlsctadq5+aDfPVn6jhuCbcOly0q2tRIpHgK2\nAmpXt32VbQsysCAebaIVCCCAgAmsdAs1/vZN6e6vFm0JiAoCuRawBxbd3d9ttrhoye0oc10W+YVP\noHJZVXrzzTe1d+9eb36vfU997du3T8uXL1fXrl3LOpX3EUiMwNvzii7Ul7j5SWFI5QW/Yagfdcit\ngA1ln+HmAZMQQACBuAjYSCV7MmdranRsGpdW0Y4wCvQvYDukMPZLEHUqMwC2J71Vq1bVU0895X23\n1/ZlWzCQEEBA2rRDemi89OOzpapVEEEgeAELgD8mAA4enhIRQMA3AZtSZIGvTe8hIeCngC0kmqvt\nJf2sJ3nnXqDUaHbSpEnq16+fV9rJJ5/sPe21J77Fv2w1aBICSRb4v9el846VOjVLsgJtz6dADze/\ne/kmaXvRkg35rAplI4AAAhUWeHOO2+N8lXTt6RXOigwQOKpAFzeNaON2af22ox7KATETKHUOcM+e\nPfXYY495Tb3//vu94c8l292xY8eSb/EzAokReMMtOLXJ/aN58ZcS02QaGkKBKu4WZk+3GNbMFWxr\nFcLuoUoIIJCBgC3maKOqfv01FiXKgI1DKyBg08ZsDY2phYw4qABjJE8t9QlwvXr11L9/f69Bffv2\nVePGjTVw4EDZYlhvvfWWatSooYYN3ZKyJAQSKGB3Ch+eIP3IDX22AISEQD4FbDsk5gHnswcoGwEE\nKirgNhjR/74mXX2qZIs6khAISiAVAAdVHuWEQ+Cof77/6Ec/8rY72r17t0499VS9//77shWibSEs\nEgJJFLCL9FcGSgVNkth62hw2AQuAmQcctl6hPgggkImArWa/zU3lOLlbJmdxLAIVF7D9gKe77bbs\nJgwpOQJHDYCfeeYZvfTSS96TX3vq+8ILL+gb3/iGbJVoEgJJE3j/E+lztyX214YmreW0N6wCNodp\ns1uQbcvnYa0h9UIAAQTKF/jTB25K0XFyC62WfxyfIpBrgYZ1pBb1pXmrc50z+YVZoNx/ag4ePCjb\n9qhu3bp68cUXdcEFF3ht2bNnj2yYNAmBpAm8OlM6v2h9uKQ1nfaGWMBWg7Y5TCQEEEAgagK2Cq+t\nqXFK96jVnPrGRcCGQU8rjEtraEc6AuUGwLYV0nHHHafzzz9ff/3rX709gR955BE9+eSTOu2009LJ\nn2MQiI3ACrfa7pJ1DNGKTYfGqCE2hIuLd4w6lKYgkCCBP7unv18/nqe/Cery0DV1UIE0pTB01aJC\nPgqUGwBbuX/5y1904YUXekOee/XqpVatWmnatGksguVjp5B1OAVemC6d05c9f8PZO8mulRcAuzlM\nJAQQQCBKArPc098NPP2NUpfFsq62m8KKzdLWnbFsHo0qRaDUbZCKH2fB7hNPPKE1a9a4CeJfzBC/\n9957ddZZZxU/lNcIxFbA5v2+PU/647di20QaFmGB5m7+Uq3qUuEGFmeLcDdSdQQSJ/Dnie7pL3N/\nE9fvYWuw7ejRt03RYlgjGIoftu7xpT5HDYAvv/xyXXHFFRoxYoSqVv3i8M6dO/tSITJFIIwCr82S\nhnSQGrnFEkgIhFGgvw2Ddk+BWZ08jL1DnRBAoKTArBWSbSt4ao+Sn/AzAsELDHJ/49laGgTAwdvn\no8QvItpSSrdFsD777DPdfPPNsvnAJASSKOD+N9BLH0s/dvv+khAIq4ANg/6XW6RttNuii4QAAgiE\nXeAvtvKz21GBlZ/D3lPJqJ/NA7b56KRkCJQ7B9iC3jPPPFOPPvqobOVnEgJJFJi8RKpXU+rRKomt\np81RETi2rTTH7aW5b39Uakw9EUAgqQK27+86e/rbM6kCtDtsAjaVqE4NabFb7JQUf4FyA2Br/rZt\n2/Sd73xHjRs3Vvfu3Q99jR07Nv46tBABJ/Cie/o7qj8UCIRboK67SdO+iTR3VbjrSe0QQACB1NNf\nm3tJQiAsAjYMmtWgw9Ib/taj3CHQVvTtt9+uW2+99YhaZDoH2ALpu+++W+PGjdPGjRvVtGlT9enT\nRz/96U/VokWLI/LnDQTCILD831sf3f7lMNSGOiBQvkB/tx/wdDcPuK97GkxCAAEEwihgT3/XbOXp\nbxj7Jul1smHQf5ssjRmSdIn4t/+oAfCxxx7rKezbt09btmxRgwYNDlsMK12iq666Sscff7xefvll\nL4/PP/9cEydO1KhRozR5svttIyEQQoEXp0vnuv8FqlYJYeWoEgIlBGwe8MMTpMtOLPEBPyKAAAIh\nEfCe/rqVn3n6G5IOoRqHBOzm8Z0vSTvdrE/bWYEUX4GjDj4pLCz0hkDb/r8PPvigrrvuOu9JbqYk\nq1evlgXBjRo1cgseVFbdunV1+umne09/d+5k461MPTnef4Edu6Vxbuujc4ruAflfICUgUEEB28tw\n2UZp+64KZsTpCCCAgA8Ctk7B6i3Sacz99UGXLCsqUN09Fuzp1nv5eFlFc+L8sAsc9Qnwt7/9bY0c\nOVJ33HGH1q9frxtvvFHnnXeeRo8era5du6bdPnvSe/HFF+vLX/6yFwTv2LFDkyZNUps2bVSrVq20\n8+FABIISeH222/qoI1sfBeVNORUXsCcqfdwd7Onu4n1S+v88V7xgckAAAQTSEPiL2/f3Yp7+piHF\nIfkSSM0DPr5zvmpAuUEIuD+Xyk62DdKcOXP04x//WDVruhVWXGrXrp3GjBmjt99+u+wTS/nEnhxf\nf/31WrVqlWwBrZkzZ2rYsGG6//77SzmatxDIr0Bq6yMWv8pvP1B65gKpecCZn8kZCCCAgH8CtkDf\nys3SyF7+lUHOCFRUwOYBT/20orlwftgFyn0CbNsg2VDlWbNmHWrHgQMHvHm8tjdwpsnmANtX8TRo\n0CBNmTKl+Fve6/vuu0//+Mc/jnh/4cKFR7zHGwjkWiC19VH3lrnOmfwQ8FfA5gHb3HUSAgggECaB\nF6ZJX3WLCzH3N0y9Ql1KCrRrLO0/WHSzpnXDkp/yc1wEyg2ArZG/+tWvNHz4cHXo0EHVqlXTH/7w\nB/Xs2dMbBp0LhOeee67UbK699lrZV8l0xhlnlHyLnxHIucALLoDg6W/OWckwAAHbCmn3vqJVVlvU\nD6BAikAAAQSOIrDNrUtg28tce/pRDuRjBEIgYE+Bp7inwATAIegMn6pw1AD4ggsuUO/evfXKK69o\n79693tzfLl265Kw67du7xxUkBEIkYFsfFW6QTu4WokpRFQQyEBhY4IZwFRatYJ7BaRyKAAII+CLw\n1lzpOLemRp0avmRPpgjkVMCuoa+5dWC+NCCn2ZJZiASOGgBbXbt16+Z9hajeVAUB3wRsmNY5fdn6\nyDdgMvZdoJ/bD3jiIgJg36EpAAEE0hJ4zc2ku/rUtA7lIATyLtDfPZu7Z6y0d79UjW0w894fflSg\n3AD48ccf94Y8z507V7YPsD35/da3vqXvfe97Ge8FfNttt2nrVrfzeSmJhbBKQeGtvAh87vZ+e2eB\n20v123kpnkIRyImAzQP+nVun0BZzc0s5kBBAAIG8CSxcUzQtw/ZYJSEQBQEbqdCxqTR7hWTBMCl+\nAmUGwDfccIP+/ve/6/vf/76376+tAm2B8N13362pU6fqySefzEhj6NCh3pxe20u4atUyi80oTw5G\nINcC9tSsl9tLtT47c+WalvwCFGhYR2pWT1rg/vBkIbcA4SkKAQSOEBjrnv6e0fuIt3kDgVALpLZD\nIgAOdTdlXblSI9ENGzbo4Ycf1uTJkw8b+mxBrO3j26lTJxUWFqqgoCDtgs8//3zNmzdPK1eu1BVX\nXJH2eRyIQJAC9vT3lO5BlkhZCPgjMKDA7Qe8lADYH11yRQCBdAR275XedZt3/P6ydI7mGATCI2Dz\ngG0Y9HdPDk+dqEnuBCqXltWnn36qNm3aHBb8po5r2LCh+vbtq/nz56feSvv7jTfeSPCbthYHBi2w\n3a1SacNd2Pw8aHnK80OA/YD9UCVPBBDIRMCC356tpMZ1MzmLYxHIv0CX5tKWz6X12/JfF2qQe4FS\nA+Dt27ercePGZZbWqFEjbdvGb0SZQHwQSYH3PpFs6fua1SJZfSqNwGECNt9u4Vppl3sCQ0IAAQTy\nIWAr6Z7ZJx8lUyYCFROw9TNSOypULCfODqNAqUOgraL79+/Xli1bSq2zbYdEQiBuAu+4QQ3n949b\nq2hPUgWqu3/du7eQZi6XhnRMqgLtRgCBfAms2iytcNsKDuXfn3x1AeVWUMDmAX/o1oY5i5s4FZQM\n3+llBsAffPCBbLhzWemb3/xmWR/xPgKRE9i8o+hp2WD3jx0JgbgI9C+Qprl5wATAcelR2oFAdARs\n8auRvaQqpY41jE47qGlyBewJ8G/fcg8FD/B7HLffglID4JNOOkkbN24st6116zKho1wgPoyUgM1T\nGtaZ/d4i1WlU9qgCNg/YFvEgIYAAAkEKWMDw5lzpV18NslTKQiC3ArYjSOsG0tyVUh+28cotbp5z\nKzUAtm2KbJ4vCYGkCNjw54uPS0praWdSBGwRj01udIN9NXJbI5EQQACBIAQmL5FaucChDX9KBsFN\nGT4KpLZDIgD2ETkPWTMwJQ/oFBkugXWfScvdPCX2egtXv1CbigvYIh793FNg2w6JhAACCAQl4C1+\nxd6/QXFTjo8CNgx6SqGPBZB1XgQIgPPCTqFhEpjg9v49sSvzO8LUJ9QldwID2rt5wIW5y4+cEEAA\ngfIEbMSJbSl4UrfyjuIzBKIh0KOltHZr0UiqaNSYWqYjQACcjhLHxFpgvBv+PKJ7rJtI4xIs4AXA\nPAFO8G8ATUcgWIE35hQFv2wpGKw7pfkjUNlFSnYdnfqpP/mTa34ECIDz406pIRFY6bZpsBWg+7QJ\nSYWoBgI5FmheX6rnFvJYsj7HGZMdAgggUIrAa271Z7aNKQWGtyIrkJoHHNkGUPEjBAiAjyDhjSQJ\n2OJXNkzL5kqSEIirgK0GPYW713HtXtqFQGgEZrmhz9WqSN1ahKZKVASBCgvYPGDbUvDgwQpnRQYh\nESAADklHUI38CIx3839PZp5SfvApNTABG77FQliBcVMQAokV4OlvYrs+1g1v7HZ+beK+5q+OdTMT\n1TgC4ER1N40tLvCpGxK6e6/Uo1Xxd3mNQPwEjnVPgOe5C7f9vpMQQAABPwQ+3yNNXCyd2tOP3MkT\ngfwKDO7g5gEX5rcOlJ47AQLg3FmSU8QEWPwqYh1GdbMWsMVourshiTOWZ50FJyKAAALlCtiOChYk\n1HdrDpAQiJsA84Dj1aMEwPHqT1qTgYDN/z2Z1Z8zEOPQKAsMKODudZT7j7ojEHaB8fOk4UwpCns3\nUb8sBXq1lpZukLbtyjIDTguVAAFwqLqDygQlYPM4qlWVOjYNqkTKQSC/AraIB8O38tsHlI5AXAVs\n799F64qeAMe1jbQr2QJVXMTUz00n4joaj98DAuB49COtyFDAnv6y92+GaBweaYFOzaTtu6V1n0W6\nGVQeAQRCKGDX1GGdi1aADmH1qBICORHwhkGzo0JOLPOdCQFwvnuA8gMXsGXs313I6s+Bw1Ng3gUG\nutWguXud926gAgjETuAdN/+Xm8qx61YaVEKAecAlQCL8IwFwhDuPqmcnYPsUNqgttWmU3fmchUBU\nBZgHHNWeo94IhFdgzVbJvmx4KAmBOAs0P0aqW8MN918b51Ymo20EwMnoZ1pZTMBWf2bxq2IgvEyM\ngM0Dnr5MOnAgMU2moQgg4LPAOLf41Uldpcr8RemzNNmHQYCnwGHohYrXgX+uKm5IDhESsOHPHyxi\nqFaEuoyq5lDARj60qC/NX5PDTMkKAQQSLTDO3VQ+tUeiCWh8ggRsq68pzAOOfI8TAEe+C2lAJgK2\nD6oNYWlaL5OzOBaB+AjYPOBphfFpDy1BAIH8CXy6Xtq9V+rRKn91oGQEghTo06ZoxfPP9wRZKmXl\nWoAAONei5Bdqgffc4lcndAl1FakcAr4KMHzLV14yRyBRAt6UIvb+TVSfJ72x1d0Wmr3dnsDcSI72\nbwIBcLT7j9pnIGDDn9//pGiuUgancSgCsRLo6Z7ULNvotkTaFatm0RgEEMiDgAXApzD8OQ/yFJlP\nAbuRzI4K+eyBipdNAFxxQ3KIiMCcVVLDOlLLBhGpMNVEwAeBqlXc3Ws3hMsWwyJFU+B73/ue1q5d\nG83KU+vYCMxz19Qa1aQOTWPTJBqCQFoCNg/4I+YBp2UV1oPcg3wSAskQsOHPtlIlCYGkCwwqcHev\n3cWb/x/C/5uwbt069ejRQ/Xq1VPNmjW9Cq9atUqvvfaahg0bpieffDL8jaCGsRTwnv52j2XTaBQC\n5Qq0bihVdY8Ql26Q2jcp91A+DKkAT4BD2jFUK/cCFgCfSACce1hyjJyAbYc0dWnkqp3ICjdr1kyv\nv/66evbsqYcffljz58/XmWeeqQkTJhD8JvI3IhyNtilF7yxgR4Vw9Aa1yIeADYPmKXA+5HNTJgFw\nbhzJJeQCC9y2L7WqS20bhbyiVA+BAATs7nXlStLyTQEURhEVFhg4cKD+/ve/65lnntEtt9yiPXv2\nVDhPMkCgIgIfL5Oaud0UmFJUEUXOjbIA84Cj3Hvub6BoV5/aI5CewPv29JfVn9PD4qhECNhTYPYy\njE5X165dW/fff79OOOEEffLJJ6pSxU3mJiGQJ4F33OJXI1j8Kk/6FBsGgX7tpHmrpV1uGzBS9ASY\nAxy9PqPGWQi851Z/vvX8LE7kFARiKmAB8L9mSl8ZGNMGxrRZ5557ruxr9uzZuvnmm/XYY48d0dKL\nL75Yq1e7v8yKpS1btqh1a7d3BwmBCgrs2y/ZNfUPJ1QwI05HIMICNd0CcD1aSjPcaIihnSLckIRW\nnQA4oR2fpGYvWS/ZfKVOzZLUatqKQPkC/dtL//Mvaa/7Y7YaDxPLxwrhp127dtVdd91Vas2efvrp\nI963OcNvvfXWEe/zBgKZCti8x45u5efGdTM9k+MRiJfA4I5F62kQAEevXxkCHb0+o8YZCtjw5xMY\n/pyhGofHXaC2mxPfyf0RO3tF3Fsaz/ZVr15dLVq0iGfjaFWoBWz15xGs/hzqPqJywQgMdDeSJy8O\npixKya0AAXBuPckthAI2VIsAOIQdQ5XyLmDDoKcW5r0aVOAoAosWLdIVV1yhQYMGqXv37ho5cqTu\nvPNOFsM6ihsf517A5jvaE+CTuuU+b3JEIGoCtgXS/oPSChaUjFrXsQhW5HqMCmckYP8o7djt5mm0\nyug0DkYgEQIDCgiAw97RBw4c0KhRo3TppZdq/Pjxmjt3rrcatC2Kdf3114e9+tQvZgITF0m920j1\nirakjlnraA4CmQsMZjukzNFCcAZPgEPQCVTBP4F3Gf7sHy45R16gmxtBu2G7tGlH5JsS2wbY4lXd\nunXTiBEjVLduXVWuXFmNGzfWNddco6VL2cw5th0f0obZ8OeTefob0t6hWvkQYD/gfKhXvEwWwaq4\nITmEWOB9N/z5yhEhriBVQyCPApXcXsD93VYO0wqlkb3yWBGKLlOgUaNG3pZHN910kwYPHuwFwZs2\nbfKeAl9yySVlnscHCORaYNsut2bASunmc3OdM/khEF0Bu4b+z6vSbjc9oIZbGZoUDQEC4Gj0E7XM\nQmDtVmn9tqLhWlmczikIJEIgNQ+YADi83f3ss8/q+eef15w5c7R+/Xo1a9ZMt9xyi4YOHRreSlOz\n2Al84G4oDyqQarkF9EgIIFAkYP8/dHWjqWYsl4Z0RCUqAgTAUekp6pmxQGr4sz3lIiGAQOkCNnzr\n0XdL/4x3wyFQyf0jNnr0aO8rHDWiFkkUeGsu+4Ynsd9p89EFUsOgCYCPbhWWI5gDHJaeoB45F7Dh\nzyey/VHOXckwXgK2l6d9zVsVr3bRGgQQyJ2ArRXw6QbJFvwhIYDA4QL2/wU7KhxuEvafCIDD3kPU\nLysBu1iv2Cwd6+ZmkBBAoHwBG9Y4xW1tQkIAAQRKExg/r+iGctUqpX3KewgkW6DAbYe0Z5+0yv3d\nSYqGAAFwNPqJWmYo8L5b/fn4TlIVfsMzlOPwJAoM7ihNJgBOYtfTZgTSErDVn0/pkdahHIRAIgXs\nKTDX0eh0PeFBdPqKmmYgYMOfT2D4cwZiHJpkgZ5un+xVW6QtnydZgbYjgEBpAss3Ff3b0Mft/0tC\nAIHSBVLzgEv/lHfDJkAAHLYeoT4VFrA/4hevl2x1WxICCBxdwEZKDGjPMOijS3EEAskTsOHPJ3eX\nWFAyeX1Pi9MXsGvoHLdNmA2FJoVfgAA4/H1EDTMUsK0ahrihKMxVyhCOwxMtYMO3PmIYdKJ/B2g8\nAqUJjLPhzy4AJiGAQNkC3nZIzYu2Qyr7KD4JiwABcFh6gnrkTOD9RW6xjq45y46MEEiEgA3fmrZU\nOnAgEc2lkQggkIbA/NVS5UpSZ/eHPQkBBMoXYBh0+T5h+pQAOEy9QV0qLLB1p2QXbLZqqDAlGSRM\noFEdqdkxbjsk9/8PCQEEEDABW/zqVBa/4pcBgbQE7G9PdlRIiyrvBxEA570LqEAuBd5zqz8P7ShV\nr5rLXMkLgWQI2NQBLt7J6GtaicDRBGw0yDus/nw0Jj5H4JBAh6bS7r1sh3QIJMQvCIBD3DlULXMB\nu1if3C3z8zgDAQTcwnEuAGYeML8JCCBgAjOWF40KadkADwQQSFeA9TTSlcrvcQTA+fWn9BwKbNgu\nFW5g9ecckpJVwgR6tpTWbJU27UhYw2kuAggcIfC2W/2ZvX+PYOENBMoVYB5wuTyh+ZAAODRdQUUq\nKvDuAmlYZ1Z/rqgj5ydXoLK7Itj2YVNZDTq5vwS0HAEnYFu5THQLSg5nRBW/DwhkJDCgQJrNdkgZ\nmeXjYALgfKhTpi8C77gA2PYqJCGAQPYCNnxrMgFw9oCciUAMBCYtkbq2kGxxPBICCKQvULu6+3/H\nrZo+000hIIVXgAA4vH1DzTIQWOuGbdrQzWPbZnAShyKAwBECqe2Q9rMd0hE2vIFAUgRs9Wf2/k1K\nb9POXAvYehpTCnOdK/nlUoAAOJea5JU3gfHu6e9Jbu9fG8JJQgCB7AUa1JZauUVv5q7KPg/ORACB\n6Ars2C1NXyqd4K6pJAQQyFxgUAE7KmSuFuwZhAvBelOaTwLe6s8Mf/ZJl2yTJsBehknrcdqLwBcC\ntp3ggPaSDeUkIYBA5gKdmkmf75FWb8n8XM4IRoAAOBhnSvFRYPkm6bOdUu/WPhZC1ggkSIBtHBLU\n2TQVgRIC3vDnHiXe5EcEEMhIgOtoRlyBH0wAHDg5BeZagKe/uRYlv6QLdG8prd8mbXRbi5EQQCA5\nArYF2idrpSEdk9NmWoqAHwK2ngbzgP2QzU2eBMC5cSSXPArY3eqT2aohjz1A0XETqFRJsjlMH7Ea\ndNy6lvYgUK6A3VA+oYtUrUq5h/EhAggcRcCmEdhK0Hv3H+VAPs6LAAFwXtgpNFcCi9dJBw4WbdeQ\nqzzJBwEEXABsd68JgPlVQCBRAuPmSSNYTyNRfU5j/RGoU0Pq7OYCsx2SP74VzZUAuKKCnJ9XAW/4\nM09/89oHFB5PAQuApy+T2A4pnv1LqxAoKbByc9G0h37tSn7CzwggkI2ATSXgRnI2cv6fQwDsvzEl\n+CjgDX/mbrWPwmSdVIH6taQ2DaU5K5MqQLsRSJbAqzOl03tLNgWChAACFRcY6gLgDxZVPB9yyL0A\nAXDuTckxIIF5bp/SWm6bhoImARVIMQgkTIBVLBPW4TQ3sQL73DzFN+dIZ/VJLAENRyDnAu3d36d2\nP6lwQ86zJsMKChAAVxCQ0/Mn8M4C5irlT5+SkyBgw6BZCCsJPU0bky7wvntK1bGp1KJ+0iVoPwK5\nFRjaSZq0JLd5klvFBQiAK25IDnkQOOgWvmL+bx7gKTJRAt1aSJvcVki2JRIJAQTiKzDWDX8+u298\n20fLEMiXwHEWAC/OV+mUW5YAAXBZMrwfagFbVa9JPamVm6NIQgABfwS87ZDcU2AW8fDHl1wRCIPA\nmq3SkvXSsM5hqA11QCBeAn3bSks3Slt3xqtdUW8NAXDUezCh9R/vhj+z929CO59mBypgw7emFAZa\nJIUhgECAAv9yT39H9pKqVgmwUIpCICECVVyk1d+trP4Rw6BD1eMEwKHqDiqTjoBty/L+QhcAs/pz\nOlwcg0CFBAa2l6YVSnv2VSgbTkYAgRAK2PX0DRa/CmHPUKU4Cdgw6A8ZBh2qLiUADlV3UJl0BKYt\nldo2kpq6IdAkBBDwV6BuTal7S2lqob/lkDsCCAQvYIvztHZTieyaSkIAAX8EBneUpi+TbLV1UjgE\nCIDD0Q/UIgOBCTb8mae/GYhxKAIVEzjezQ2cyF6GFUPkbARCKGDDn9n6KIQdQ5ViJVC/ltuys7Fk\n69eQwiFAAByOfqAWaQps31W0qfgpPdI8gcMQQKDCAhYA2/CtA264JAkBBOIhYKu7z18tndQ1Hu2h\nFQiEWWCIGwbNdkjh6SEC4PD0BTVJQ+CtudLQjlI9NyyThAACwQjYdINmx0hzVgVTHqUggID/Aq/N\nkuxmcvWq/pdFCQgkXcD+dmU7pPD8FhAAh6cvqEkaAq+64Vpn90njQA5BAIGcCtgWKQyDzikpmSGQ\nN4GDB6WxLgA+h71/89YHFJwsgYImkvvfTks3JKvdYW0tAXBYe4Z6HSEwzz19shUr+7g91UgIIBCs\nAPOAg/WmNAT8FLCtzZq4kR32RzkJAQSCEfBWg3YLz5HyLxBYAPzzn/9c+/bt00F32/H2229Xz549\ndeGFF2ratGn5V6AGkRBgsY5IdBOVjKlAh6bu7rW7fV3I3euY9jDNSpIA19Mk9TZtDYuADYOezHZI\noeiOwALgV199Vfv379cbb7yhJUuWaOLEifrJT36iyy+/PBQQVCLcAp/vcXv/ulVoT+8d7npSOwTi\nLMBT4Dj3Lm1LisCmHdIMtxrtCHZTSEqX086QCPR1IxgLN0pbd4akQgmuRmABcMp47ty5uvTSS1W/\nfn0NHDhQ3bt31/bt21Mf8x2BUgXedotfDSqQbCl5EgII5EfA5gF/wHZI+cGnVARyJPDGHGl4N6lm\ntRxlSDYIIJCWQNUqUv920kcMg07Ly8+DAguA27Rpo+HDh2vcuHF69NFHvTY98MAD2r17t+rWretn\nG8k7BgLe4lcs1hGDnqQJURbo1Vpau1Wy7VNICCAQTYGxLCYZzY6j1rEQ8OYBMww6730Z2OL3zz77\nrHbu3KmZM2dq/fr1XsObNm2qp556Ku8IVCDcAgvWSLv2Sv3cXTMSAgjkT6Cyu2U61O1laKtBj+qf\nv3pQMgIIZCfw8TKpVnWpa4vszucsBBComMDgjtKD44oWda0S2GPIitU5jmcHFgAbXq1atTR06NBD\njmPGjDn0uuSLDz/8UDZcumRau3Ztybf4OeYCdrf6TLY+inkv07yoCNg84JemEwBHpb+oJwLFBWzx\nq7MZTVWchNcIBCpgU/naN5Zmunn4/dsHWjSFFRPI+72HQYMGFavOFy+rVKmiatWqHfFVqVKlLw7i\nVewFdrrFr95dKJ3RK/ZNpYEIREJgoLtg26iM7bsiUV0qiQAC/xbY7Ba/mrZUOrUHJAggkE8BG0n1\nIcOg89kFCvQJcGktfe6550p7W4MHD/a+Sn74pz/9qeRb/BxjgXHzioY+N6wT40bSNAQiJFDDLZxz\nrFvJcvKn/CEdoW6jqgjo2Y/czWS3k0KdGmAggEA+BWw7pJ89L119aj5rkeyyA3sCvG3bNt16660a\nNmyYunXrphNPPFFXX321atTgX+Jk/wqW3/p/zWK4VvlCfIpA8AK2GrTNAyYhgEA0BD5z2668Plu6\noPRBd9FoBLVEICYCBU2kg64tSzfEpEERbEZgAfBVV12lli1b6uWXX9a8efM0duxYjR49WqNGjYog\nG1UOQmCRm+5tF+2BBUGURhkIIJCuwBA3fMuGUu7dn+4ZHIcAAvkUeGFa0dZHjRhNlc9uoOz/3955\ngElVZG34Q4IkAUkiQUGUIMFAdg2AoBgIgopgWDCBrmnZNYE5oa5rQtHVX1cXE4IsK4gBECQKkiSD\nqIAIKFkyCPOfr68NPTM90z0zHW746nnuTPcNdeu8dftWnapT54jAIQIhM2iFQzrEI9UfUqYAr1u3\nDlSCy5cvjyPMlShDH7Vv3x5VqlQJeYdOteC6n/sJMPRRBzm/cn9FqYSBI0AnHidUAuhRVkkERMDd\nBOhLY9Q84PLm7i6nSicCQSLQ8gRbSqR1wGmr8pStAeZMb48ePdClS5eQErxz507MmDEDjA9M79BK\nIhBJgGGPJi0DXusduVefRUAE3EKA3qCnmRl0s1puKZHKIQIiEI3A6G+BpvY7rVI22lHtEwERSAeB\nxuZL4/HRwDazdOSgslJqCaRsBviOO+5Av379sHbt2pD5M+MBcz3woEGDUiux7uYJAl8tBRpVB2Su\n5YnqUiEDSIDrgL/WOuAA1rxE9hKBfb8D/52t2V8v1ZnKGgwCRQoDp1tUhVnmUFIp9QRSNgNM0Vq1\nahXaUi+m7ug1AnR+dWUrr5Va5RWB4BDgbFLZksCStUD9qsGRW5KKgJcI0PFV3SoAne4oiYAIuIvA\nmXWAsfYbPfdkd5UrCKVJ2QxwEGBKxsQQ+HEDsGmHmWzVTEx+ykUERCA5BOQNOjlclasIJILAgYMI\nhT7q3iIRuSkPERCBRBNgOKQl64DtexKds/KLRUAKcCxCOp5yAmHnV4UKpfzWuqEIiEAeCITXAefh\nEp0qAiKQIgITbSlR1XJAvWNTdEPdRgREIE8Eihe1SCdmBj31uzxdppMTQEAKcAIgKovEEdhoM79s\ntDuemrg8lZMIiEByCJx0DECHdT9tTk7+ylUERCD/BD6YAWj2N//8dKUIpILA2XUdp6+puJfucZiA\nFODDLPTJBQSGfwOc3xAoI494LqgNFUEEYhPQLHBsRjpDBFJNgDNKpY4ETj0u1XfW/URABPJCoLmZ\nQS9b73iDzst1OrdgBKQAF4yfrk4gga27gHGLgG5NE5ipshIBEUgqgbPNicfU5Um9ReAznzJlChhK\nsFevXli3zhaMWdqxYwd691acuMA/HDkACM3+Ku5vDnS0WwTcQ6CYuSPmWuApakdTWilSgFOKWzfL\njcCIWUBb84R3dKncztIxERABNxFoZLEMN+8EVm9yU6n8VZZHHnkETzzxBNq3b48OHTpg/fr1OHDg\nAFauXOkvQSVNQgjMXQUw/BGtM5REQATcT4Bm0Az/qZQ6AlKAU8dad8qFAD3gfWahjy5rlstJOiQC\nIuBKAm3rA+MXu7Joni/U1q1bUblyZTRs2BBXXnklnnvuOXTp0gXbtm3zvGwSIDkEOPt7uWZ/kwNX\nuYpAEgg0qQn8uNEZTE5C9soyCgEpwFGgaFfqCfxvDvCnk4BKR6X+3rqjCIhAwQgwhqEU4IIxzOnq\ncuXKgUrws88+Gzqlbdu2uP/++9G1a9ecLtH+ABNgXO5fbGykTb0AQ5DoIuAxAkULAy1ryww6ldUm\nBTiVtHWvqAR27QM+nitvlVHhaKcIeIDA8RUdx3Xzf/JAYT1YxOHDh6NWrVqHSn7RRRdh8ODBIZPo\nQzv1QQSMwIczzZLKZn+PUO9Oz4MIeIqAzKBTW1229FpJBNJLYNQ8oJn17aqUTW85dHcREIH8E6AZ\n9JdmBt3Y1gQrJZZA8eLFcckll2TKtHnz5uAWLVFh3r59e6ZDy5Ytw8aNZmOn5FsCs1cCq2wt/oCO\nvhVRgomAbwmcbvGA/zEG2GCvbllDJr+aNUaYfMa6Qy4E9loM0ZGzgSta5nKSDomACLieQBtTgKdY\n6JX9B1xfVF8UcOHChTl6gS5cuDCybkfYlGChQoV8IbuEyE7gd/vdDR4P3NwWKGLmlEoiIALeIlDY\nNLIzzHHdZHmDTknFaQY4JZh1k5wIjJkPNKwO1Cif0xnaLwIi4AUCFUoDdaoAX38PnGWhkZSSS6BO\nnToYOHBg1JtknS3mSZMmTcL48aYhKfmSwHCLonBcBaDpYUt5X8opoUTAzwRoBv2faUDXJn6W0h2y\naQbYHfUQyFJwpmj4N0APzf4Gsv4ltP8IhM2g/SdZeiVasWIFrrvuOjRt2hT16tVDu3bt8PTTT6N8\neY0cprdm3HF3mkwyjGDfNu4oj0ohAiKQPwKnHges3WKO7H7L3/W6Kn4CUoDjZ6UzE0zgi4XAiccA\nJ1RKcMbKTgREIC0E6Ml9/hqAYc2UEkPg4MGD6NSpE66++mpMnDgRixcvxtChQ1GyZEn069cvMTdR\nLp4m8NpEoPPpwDHyo+HpelThRYDO6840C6pJy8Qi2QSkACebsPKPSuDAQcdbpWZ/o+LRThHwJIES\nxRyHdmq8E1d9DIFUt25dtG7dGqVLlzbvvkegQoUKuPnmm7Fq1arE3Ug5eZLAvNXAd+vN83MzTxZf\nhRYBEchCoLWFMFMbmgVKEr5qDXASoCrL2AToLbba0UC9Y2OfqzNEQAS8Q4Axgd//GrjoFO+U2c0l\npZkzHVrdfffdaNasWUgJ3rx5c2gW+KqrrnJz0VW2JBPgQPJL44Cb2gLF1JtLMm1lLwKpIdDI/OJs\ntGUN67YCx5ZLzT2DeBfNAAex1tMsc0YG8MEMW/vbIs0F0e1FQAQSToChHH7mGqZtCc86sBkOGzYM\nLVq0wJIlSzBmzBj88MMP6N+/P7p37x5YJhLc1v1aBIWqNpDcorZoiIAI+IUAnfXTDPormUEntUo1\nZphUvMo8GoFJ5uK9XEmgUY1oR7VPBETAywQYyoEmXOPNyqNnKy9L4p6yM3xR165dQ5t7SqWSpJPA\nxh3AsJnAizICSGc16N4ikBQC51gbyrBmV2iiKCl8malmgJOGVhlHI7B7H/DaBOD6c6Id1T4REAE/\nEGhrZtBfLvGDJJJBBNxJ4PWJQMdTgSpyfOXOClKpRKAABBpWA7btAtZsLkAmujRXAlKAc8Wjg4km\n8M50J05h/aqJzln5iYAIuIVAXYsHzLRsvfNff0VABBJHYP5PwNJ1QHfNDiUOqnISAZcRYExgmUEn\nr1KkACePrXLOQmD1JmCshT669uwsB/RVBETAdwToDItm0EoiIAKJI0DHV4PM8RVj/srxVeK4KicR\ncBsBKcDJrREpwMnlq9wjCNBb5Z/PBMqWiNipjyIgAr4k0La+jV4vBdhhVxIBEUgMgZFzLN5vGaDV\niYnJT7mIgAi4kwAtJffuB1ZtdGf5vF4qKcBer0GPlH+CrQfcZet/L2zskQKrmCIgAgUicIytTaxu\nHmpnryxQNrpYBETgDwI/2XrAD83x1V/OFRIREIEgEDivITBqXhAkTb2MUoBTzzxwd6Tjq9e/Am5t\nD9C9u5IIiEAwCNAZlsygg1HXkjK5BPbYTNDDI4E+Zvqs2KDJZa3cRcAtBC6wSaMJZknFfrRSYglI\nAU4sT+UWhcCQaUDzWkDYMU6UU7RLBETAhwS4hmnWSjXePqxaiZRiAi9bSJQG5hmWSwuUREAEgkGg\nfCmgyfHAOPnTSHiFSwFOOFJlGElgpa1d4AyQHF9FUtFnEQgGgaOKA42rA1OWB0NeSSkCySDANnTJ\nWuDmtsnIXXmKgAi4mQDDnckMOvE1JAU48UyVYwSBkOOrPwFl5Pgqgoo+ikBwCNCEa8z84MgrSUUg\nkQR+3gL8awJwXyfgyKKJzFl5iYAIeIFAoxq2fNAKyvBnSokjIAU4cSyVUxYCHLXe+zvADrCSCIhA\nMAk0PwHYvgdYsCaY8ktqEcgvgf0HgMdHAb3PAmpWzG8uuk4ERMDrBDqdBnw81+tSuKv8UoDdVR++\nKQ09Pr8xyRxftZPjK99UqgQRgXwS6NoEGDErnxfrMhEIKIHXJjqe1DWIHNAHQGKLwB8EuPZ/3mpg\n0w4hSRQBKcCJIql8MhH4z1SgRW2gTpVMu/VFBEQggATaNbA1jOsAmnMqiYAIxCYwbQXwzQ/AHefH\nPldniIAI+JtAiWJAG1OCP9VyooRVtBTghKFURmECDNo90dy29z4zvEf/RUAEgkygWBHg4lOAjzQL\nHOTHQLLHSeCX34AXxwL9OwIlreOrJAIiIAI0g6Y/jQMHxSIRBKQAJ4Ki8jhEgLHKHv0Y6GuxCuX4\n6hAWfRCBwBPoaI33pGXAtt2BRyEAIpAjAXZuB44GujeXBVWOkHRABAJIoEZ5gNvU7wIofBJElgKc\nBKhBznLQOIAe61rXCzIFyS4CIpCVQFnzBH+WxQX+ZF7WI/ouAiIQJvD2FIDhwy6xdfNKIiACIhBJ\n4GILiTRabWgkknx/lgKcb3S6MCuBsQuB738FbrLZXyUREAERyEqgm3XqGc9w3+9Zj+i7CIgAfxtc\n+3v3hWIhAiIgAtkJnHEisHYrsNKWGioVjIAU4ILx09V/EPhpM/D6V8AAW7PE9X5KIiACIpCVQHUz\n36JjvC+XZD2i7yIQbAJffw8MnWFhj7oBpW0GWEkEREAEshIobFobvcJrFjgrmbx/lwKcd2a6IgsB\nzuYwVuF1ZwPHVchyUF9FQAREIIJAt6ZyhhWBQx9FAMvXA899DjzYBTimrICIgAiIQM4EqABPMEez\n9LmjlH8CUoDzz05X/kHg1QlArYrA+Y2ERAREQARyJ9DYfAQULwrMtBAvSiIQdAK/bAMeHgn0s3BH\nJx0TdBqSXwREIBaB8qWApjWBsYtinanjuRGQApwbHR2LSWDycic4923tY56qE0RABEQgRECzwHoQ\nRADYsceWDX0E9GwFtKgtIiIgAiIQHwGGFRz9bXzn6qzoBKQAR+eivXEQ4Mj1S+b1uf/FAIN0K4mA\nCIhAPATOqgOsM0ceK36J52ydIwL+I7D/gM38/g9oZU5tLrLOrJIIiIAIxEuA0VYK2cnzf4r3Cp2X\nlYAU4KxE9D0uAoxVyHW/PVsCJ8psKy5mOkkERMAhQEcenU8HRswWEREIJoFnPgVoykjfGUoiIAIi\nkFcCnU4DPp6b16t0fpiAFOAwCf3PE4E3JwMVSjud2DxdqJNFQAREwAjQkcesH4EN24VDBIJF4M1J\nwEZ77v9+QbDklrQiIAKJI9C6HrBgjb1LdiQuzyDlJAU4SLWdIFkZp3CKrf29/bwEZahsREAEAkeg\npC2baN8QGDkncKJL4AATGGPr9tiG0uNz0cIBBiHRRUAECkSg1JFAF7Oken1igbIJ7MVSgANb9fkT\nnOsNXhxra5cuAcqVzF8eukoEREAESICN99iFwC6Fc9ADEQACn5jyO3SmLR+6FChTIgACS0QREIGk\nEqBDyUU/A0vWJvU2vsxcCrAvqzU5Qv24wVn3O6AjULNicu6hXEVABIJDoNJRwGnHA5wVUxIBPxP4\ndL4pvzOApy+3WL9l/CypZBMBEUgVgWJFgN5nAa9NTNUd/XMfKcD+qcukSsJ1evdZuIZb2gGNqif1\nVspcBEQgQAToBOhDmxWjV3klEfAjgc8XAO9OB/7R3ZTfsn6UUDKJgAiki8C5JwP0Kj9pWbpK4M37\nSgH2Zr2ltNSMVXjvMODy5gDDlyiJgAiIQKIIVLbZsEubAS9/magclY8IuIfAF2bi/46UX/dUiEoi\nAj4k0KcN8MYkRxH2oXhJEUkKcFKw+ifTfb+bs47/OrEKGbZESQREQAQSTYDrmNbbDDCdAymJgF8I\njFsE/Gcq8NRlwLHl/CKV5BABEXAbAVpm1q4sp5J5qRcpwHmhFbBzMzKAgaMdky3FKgxY5UtcEUgh\nAcYFvq09MHg8sGd/Cm+sW4lAkgiMXwy8NcWUX1vzW/XoJN1E2YqACIjAHwSut+VEw2w50bbdQhIP\nASnA8VAK6Dkv/9EZ/VuHgAKQ2CIgAikj0LCa4xBryLSU3VI3EoGkEKDyy1i/T9rMbzUpv0lhrExF\nQAQyE+BAG9cDDzGrE6XYBKQAx2YUyDPetpHrxeZW/YHOAGdnlERABEQg2QSuPweg2ejKjcm+k/IX\ngeQQoEM3Dh4/aTO/1csn5x7KVQREQASiEbiyFTB5OfDT5mhHtS+SgFSbSBr6HCJw11An1u9AG70u\nUUxQREAERCA1BMpabNQ//wkYZLHGlUTAawQ46zvYnLm90weoIeXXa9Wn8oqA5wmULg5c0QJ4/SvP\ni5J0AaQAJx2xt27ABpzrB6beB7AzqiQCIiACqSRw4SnA7weBseY9V0kEvECA/jI46ztrJTDiVqCk\nBo69UG0qowj4kkCn04A1NgM8d5UvxUuYUFKAE4bS2xmxAX/RZl3mrwGeuQIoXtTb8qj0IiAC3iVA\nh1hvTAa2Wwg2JRFwMwFGSnh8lNPh/Ke1neVLubm0KpsIiIDfCXDZIpcTvTYRYN9eKToBKcDRuQRq\n7wGbbXnyE2DdVvP6fClwlJlQKImACIhAuggwnEPreqYEy4wrXVWg+8ZBYIcN0Az4CChSGHi0q5YM\nxYFMp4iACKSAwBknOn35z2VJlSNtKcA5ognGgXCcX/5/RA14MCpdUoqABwhwLTBNSumMT0kE3EZg\nw3ag3wdAnSrAPRc5SrDbyqjyiIAIBJdAr7PMH8E0YNe+4DLITXIpwLnR8fmxnXuBe4cBR5vJ1v2d\ngKI2iq0kAiIgAm4gQAd8N7R2HGIdNCsVJRFwC4Gft5jy+z5wQSN7Rs3UUEkEREAE3Ebg5Kr2jmoM\n3GdWKvsPuK106S+PFOD010FaSkDl907z9nySjV4zzu8RehLSUg+6qQiIQM4EzjwJKFfSRrGn53yO\njohAKgnMXum0ndedDVzSJJV31r1EQAREIG8EGBapQmnHx0/ervT/2VJ7/F/H2ST8cQNw+7sAO5d9\n22Q7rB0iIAIi4AoCdOZxn1mnTF8BDLX4qkoikC4CdCYzZCrw3OdmOXWxs0Y9XWXRfUVABEQgXgJ3\nXgCw3z/8m3ivCMZ5UoCDUc+HpPxsga1XGubECetpI0NKIiACIuBmAqWONC+75pxvzLcKjeTmevJz\n2bbuAvoPBxb9DLx0NdCoup+llWwiIAJ+IlCsCPBgF2DkHGDmD36SrGCySAEuGD/PXL1nP/CPMc4P\ngKEa2jXwTNFVUBEQgYATYGgZeqh/00IjqQEP+MOQYvEXmtJ7yxCgvq2nG3iZY5Kf4iLodiIgAiJQ\nIAKVjnKsqf75GbB6U4Gy8s3FUoB9U5U5C7Jqo9OA08nVi1cC1cvnfK6OiIAIiIAbCVQ9Gnj4EoAN\n+BJ5hnZjFfmuTDQZfPxj4K/nA9eYV/JChXwnogQSAREICIF6xzrLHh8YAfy2OyBC5yKmFOBc4Pjh\n0FiLAUZnVz1aAndYI05TCCUREAER8CIBhpy5+0JThP8H/LTZixKozF4gsNcsph4aCUz5zgaNrwKa\n1PRCqVVGERABEcidQJv65r/AtsdsYO9AwKMrSAHO/Vnx7FGGDXnWZkqGzbIZkx7AuSd7VhQVXARE\nQAQOETi9JnBja2CArclkLFYlEUgkgbmrgJv/A1Qpa23nFQBNB5VEQAREwC8Eep0JMMzgoLF+kSh/\ncmg+MH/cXH3VnJXAqxOBujZbMuhK4Miiri6uCicCIiACeSLQ1kaw6ZhogMU3fNaUlNLF83S5ThaB\nbAQ27wT+NQFYvh7oY9ERWtbOdop2iIAIiIAvCNxzEXD1a0BFG+C76gxfiJRnIaQA5xmZey9Yu8Ua\n8ImOaeD15wBnnOjesqpkIiACIlAQAl0tBuvmHUDNvwMrn5ESXBCWQb6W1lL/mwu8/zVw8anA3zpo\nqVCQnwfJLgJBIMAZ4Hf6mG8DU4K32XrgPq2BIuYnKEhJJtA+qO3d+8w76iRb4/ueE57htV5Sfn1Q\nrRJBBEQgBgEO9D1pnnlvMpPVb1fHOFmHRSALATpTu+Ud4JsfLb5vT8fRlfxkZIGkryIgAr4kUNys\nQ9+8DthkA8n93gd+2eZLMXMUSjPAOaLxxoHxi4E3TPltWtNmf3sBR1u4ECUREAERCAoBKsF0UvSP\nT4E/nQRcd7Zm8IJS9/mVk4PGNHeetRK4oTVwTt385qTrREAERMC7BLh86IHOZgVjMYJvexe4/bzg\nTKBJAfboc8uR639NdAr/kAW4pndUJREQAREIIoHTjje/B38GBn9ps8Fvm+d78xTNkA9KIhBJgOt8\nPzZz588XmCfUesDrvR1nMJHn6LMIiIAIBI1A59OBk6s5Yd9oTXXDOf43iZYC7KGnfN/vwJdLgFHz\ngD02gt2zlbw7e6j6VFQREIEkEuBI9l2m+E610DUPWwibDo0c5x6Fj0jiTZW1Jwj8uAEYMRuYvsJp\nM58xx2nVLK60kgiIgAiIgEPgpGOAl6+x5SCfW+xzM4ke0NHxhu9XPlKAPVCzdG71yXyAMX0b2AjN\ndWcBDAWiJAIiIAIikJkAzaBPrgq8MBa49R3gQbOQOaZM5nP0LRgEZq8EPrJQgKs3AR1PA966Xs7S\n3FTzHJDggNWJ1vHuYjNQSiIgAuklUOpI4L5OjqXM7WYSfVt7oJV5xD/ChwPJUoDT+6zlevcZ3zuz\nvSt+Bc5rYCGNrlZHLldgOigCMQiMMvPH4dYhLm0v+acuz94ZXrDGcQTBkdDjK8bIzCWHuZ6Rs1v8\nz3jftSq5pGBpLAZ9IXBpCAcNbx0CNK7hzAhzrXChQmksmG6ddAIMj/XND87vnLP/3Zo65s5etQTg\n7/oLe46Z2lj4rzIlnM9e//vPzyzO8qfAKcc5FhsXnQp8cFPypWLs8BdtcIz/+T6gqadS4ghssWUG\nXIqyzX6HLU8E6K3fK4mTTUxVZR2CTjZgyIFk1uUrtl10CnBBY6BcSYeRH/6mTAHevn07nnzySUyY\nMAGbNm1CpUqV0KhRIzz44IOoUkULWPkwseHmiDW3uatM2S1ro9bWKHAGo2jA3JOTh1L6CNAr6uOj\nnPsvXQdM7g9UOiq+8uyyDtuTnwBzVgI79wL/vt5C1bhAmXzWOlwDRwPNTwAmLgXengqseMpMfMo5\ncr06wVkb2MJGO7u8aE4hbnf/EoPfD5gDn4HAb7udtYz0BP9JPzn1CT+p7RtafVt9TrNZpiHTnFnh\n823f+Y3if57DeaXz/4oVKzBw4EB8++232LFjB6pXr47WrVvjrrvuQrFixdJZNFfce9VG4OsfbLMZ\nxdWbzULqeKBvG4Brw72cqPz++XVnbR49tl75L2DxE8BxFbwsldM2PPhfq6/7gYbVge32/jp5gOPQ\nk07sEp2m2XMxaZnjHI/3HXQV0L2F3e8rp0249+JE39G/+c3/CVhifYIq1j/N6jxu736g/r1mOmsz\niO1sMPa1ifZ7tN/mHee7n8fTY4CZ9g7hUsO9trH9528uyInrmLLaAAAgG0lEQVSWGc90B1aZBc3H\n84Dr3wRaWP+J1jR+8LGRMgW4b9++aNWqFUaPHo1y5cph165dmD59Ojp16oSZM2cG8hlj/MFFa53G\ngN4o120FTj3OPDrXAnqf5a0OWiAr8A+h6TCAcSQzMoBrzwZqlPc2DXYm2zwJzHvEMU17xxSHG/8N\nvNc3tsMYMmhtCtl5DW0G5hYnNA2dEr1xbfpHVdnxqW8jmpzZXWu/NVhZuc7lfZt1oLUFj//0rNNJ\n6n2m/QbfcF7ybl4rSK+NHBz79lHgSGus+77lbEusDpQcAmVLOCPXHL3mWtBPFwA3/8dxHHiBKcI0\nmXbzrPBBayjYTg4ePBgvvPACSpYsiS1btuDtt99Gv3798NJLLwWuqvme+dY64l/b75a/3YP2vWVt\nJ4wRZ/u9OtubtSLv+8iJTXzNn5wjp5hsj9nA5Gu9sp7pre8zf3Q60sfa4CMH/LlE4SL7fc5blXg5\n3psOPP+FzTJf4sz8lrD3JK0CjjKfAQx91X2w816Q5Uxs9oPGOgPjha3N+c0mbC5t5gxwh698Y7Ip\nSeeY1U07Z08z68te+rLxtvPc3C96wZ6PjdudPgtLfts7ZiFmg/icfAp6oukzfxu3t3eWX36xCOBg\nAa3oOEtMqxSvvm9TpgCvW7cOVIKLFHFuWbp0abRv3x6DBg3C7t27UaKE9VJ8nDiSy1GUlaZccKOS\nQdPmY8s6Zjh92ljn/FjvPkjxVB09cD76P4AzipztpuLhhpnBeMqe0zmzrCF/wBQnOt85YAMavV53\nTGs5iOHVREdrL17pKL+U4aozbJDGOiaLbbCGJmO5JZ7DkcHHujlncTaVI+3jFjud09yuTfqxQs6g\nEmPeMfB7UXsVLVzj3PV7+y0+ffnh8Dm0vmCHmr9VNyvA81c7sb87veCMXB9pMnHWXSk6ATbkN7e1\nTpoNVE35zlnn9PJ4oHZlRyGmN31u5c2E2i1p69atqFu3bmjGN1ymChUq4Oabb8Zll10W3uXb/2w7\nv7eBix/sNxra7POaLc4sKH+j7KR6vR3JqfJoTXN23cNH6dht0LjD3736qXF14JGRNqP9qjPo/9YU\ngLJSSU1k4rv+nmH2nn/cMR1nn4vK9puTnHAvvNcR1i7sP5DIuzp50cSaAzWV7X5+SIw8cu9wC7VZ\n0vntLbX64vp6LrthH4GJM8CRfQQqTyWLOXXrnOHOv7S45LrXcHq2hw2aPhv+pv9hAnQ0SZN2brQS\npEd9tp98/7LfV6+qo8d45Zm37lJqEkewe/TogS5duqB8+fLYuXMnZsyYETLl8oPyS+WHCh7XP/D/\nZnvx8gX4gzXWVHa3WoebI2C17EHhDBRHxrjO0C/reWI9RTQraTTAiTfGl8tnC2z06Hlg/N3enum+\n60Nn5JqKPRtRNgRcM8Hg4l5NxeytQIUwMtFZCWdF40mciYxM7IS4QqGwzggV2nPq2azKKVZHk52R\nTZa1uv02uc7laqs/Ntrb9zgdzfDMS6Q8bvpM1vQKv/RJZ0aj3dPO+8dNZXRjWfiMt7WRa258Pr/7\nxbb1wGhjudz+8zjfz1SGL7RnhbPI6UpsLwvblMvdd9+NZs2agYPHmzdvxtChQ3HVVVelq1gJvS/b\nTdYDt4228Tt/q2w/uY8DFyfYdpLVB83X2eEqYR1rvyeaIP7fV4cHFF+ZYBEgTMnweqJcv9k7loNQ\nlUxBpOMdez2HZpMSKRuVar7vw/2s9g1soPMT+z2XdO7CJTH0+3CiDYAlMj0xypTD2QCXqHCW++Pb\nDw+u5nQf9h+4TIeDxbyOIbrIyS2J7SUT18ee19D5bbKcNCMPK8B8n9JMnwNTlPulcc7yk9r223Vz\nos8IDt6HeS+zNoDvHaWcCVCH4cYByhXWftIs/qulFo7Q+lG0qKJCTIu7y5rlnEe6j1gzn5p0xx13\noEWLFpgyZUrI5Lls2bI444wzQqZdqSlB3u+yZrMzS8sK5ouU/3db48PPu/Y6DRGVXDbW7DBzcTh/\nSOzsly9tI39H/dFYV3BeBm42s8s7nbxdMXulY3bEmW4mmiNyNJZrMd38A3FKm/Nf1judeXDNCxuw\n+0e429QnZ0kOH+HoHhsxKvJ8wbFRpml+oxqHz8npE72Ul7KOaddBFkPOFEl2ZrmuZr3NUKY7Uamh\nFcYHX9tsqdUVUyX7nTJxluXzhdbRvtMZwWbnm+vE3D6zRN4zjO+p9ztLJ2gWWsdFnSaHrrv/VrBn\ngBs7beH0yzZThP9Qivk5nQowyzRs2DD897//xaJFi7BhwwZUrlwZ/fv3D7Wp4TK77T/XCrJ9pEVC\nuM0M/f+jPd1h704eZ0eTMwvheqhodUF/A2fWsfWvNuhW3TrcQW07/3KuDdI8BfR4xemc09ybS0u8\nnjjIdMd5zlptKsH9zrd2w54BPjNsaxKVaGFHq5h/T3aWlXECYssuW7I0x7FEa2jvz+n27uSgZ6IS\n+wNvTQFuaecMStIT/d8/MKuqGGNV3azN5MAz16/TCuvSl4CRpji7pQ2iyTPT4GucNpImsdX7OdZ8\nzhHHodnAS+2/MeVM+wk2sDDnEffHk+Wz2GCA9eWucCy++r5tjiVvDUul/7kR4EAk+4aR/cNffnN+\nX/yduznZqyF1iWuAuUWmpk2bYtasWZG7Qp9ffPFFjBhh2kSWtHz58ix7kveVo0DsvJe00UmacXDt\nCJVbNsisdNrAU+ENbab8BrWRjqcGyOb3g5nP/MmUETpS8HL63jrJnNEvbPIVKmxKSE1bx7Q6cRKx\nQ/D5AqcBobdKdhSTnfhsD/uLs25q+DfOGrSeLeO/K5VHmijSdJiKA50mhBXO+HNJ/Jl0bMFUzWZ7\n1291BrDoPIqJpmp0oENFmDN/NIkKmUe3cI679S8H2l6yjtVce+aoaPzftU5ny63l9Uq5aALP7aw6\n7ihxIXuBdu3aNbSFS7Rw4UL07t0b//73v8O7Dv2ntRWXHUUmmlJXq2Y9/hQlWo1wgJDvE87wUcGh\naVz4O2flKlj7WdGUXa+uIUs2SjrhmdLfQgUZS76j6KyJfRGvJ876sp3k4AcHJcctcnwYPHJJYiUr\nYm3y090d67Oxdg8OurxiCtzVf0rsfSJzo3k1Faqbz3X2ciaM64xzU4DZZnIy4NU/Az2ti8x3ebOH\nnTXLtJhzQ2pSywaPZ9iM+kBnMCHsmbxJzcOl4yRAvw9s6/CHs6TnHTPpZDg2O3zXgn9iH+6Bzs6g\nP2XgwEgiB2IKXkJv5cDBD25ZnaS5TYqUKsDRhP/oo4+i7cZtt90W2rIePO88e7OkKHFtAzelghNo\nbi/P/0x1Amx3Pt0c0cy3NcBfHzbtKvgd0pMDOyh0qHTfCMcRC029y1hHLxGJDeK1bzgzkTQxqXK7\nmWk+5VgTJCL/3PKgtQM7XHQuQ/P+eAd3aEbEBmTWQ4dz55q1kbNNlrMP70vHp0J2UxMnZMnBdV/8\nvMfqi2nkHMdqY8iNznc2huy0UBF2sydZDoqwnFzDymfxrqFO8HpHCv31M4E6deqEPENHk/H999/P\ntnvSpEkYP358tv3J2hG29klW/kHJl7OTbhmISRRzzsQy/i/bl3/1MgeL053JhmS8azlpseqfjndw\nWidxYCuZiUp3pPdg3p+WD7klWhtyMoDKLxMHjC5s7JiWOnvS/7ddA5vssQFXOovijDqTPZro3jL0\nMfTnDVP+GbnknoucfZtfNgs/22gy7WYnWK9/ZZYVM52lixwop1dyRrJgP0DJvwT4/KY1HX/88Wm9\nv26eGgJsxGlSyvXRXB/z6282w/ZE7HUxqSld/u/CmU06fljzrONBmB55E2VORTOcCXc78dduP89Z\nE8T4hclOXNdz+oNO56R7c2ekno6+4klUmmn2FJloOeGGGR4q8VXL2Xol62SE1/barlDiTBUb6cjE\nNYfc7+bEzhU7XPQ5wLiLP2/xV5w+N7NPd9kY/kghBNNdC7p/fgjMXmnLbOw9/MlfnXfsja0dZ2YT\nluQnt9jX8B3J93mylV+WhJ6R6Z3/7SmO9VarxxxfArmVkmvbWcbHPnaWDZEDw/LRQ71bUpUyjvLL\n8nB2lF60bWwcXLIQThw4j3TaxmVHdJoVawAgfH26/tP/xybrm04eACx70rFSoVKs5G8C9nimJikO\ncGo4u/kuVIIe7ermEua9bMXtF3RMBRvd7OeYcNHcl6bziUg1LV+a5oQT4yVOXh7+lrz/H9pIKNdo\n07M1Ez1a93zVcRbSyMqQW6K5F2eAh0wFrmjphChhbNofn8ntqtQcY2PM2fpP5juzwCGF2My0mVqd\n6HgkPc9GucmcMSM5c+32+JDPfGYhqs45PHNA7+pcL9jldEcu/fUHAcUB9kc9SgqHAJU9OvPiOm9u\nTGwnItfhO3u99/dem/2keTdnEKkctqkHvNMndzloLjrgYqDP28AYa59odUUnUn89P/frUnn0qTHO\nhMW4O50+DgcTWGcDhluZ/+aUhAo7Q8zR9JVLAxlCkfK81juVJc37vdbawDHX24fXW39wk4VzNEVY\nyd8EUqYAKw6wvx+koErHNW10RDT7YYdAv/cd74iJ4HGKjbIOsBUCj3dzzJFfm5iaDgI7JnTEEZnY\nmMXjfZSDHM/3BC4fbEqwNX5sxGc95A5P31zbS4+fDao6jlA4a0rFl4nHnrnC+D7qKP+c1Q+HznDO\ncOdfmmrVrHS4bHTEx1l4Jf8QUBxg/9SlJHEI0Lniu9OdGU/G5OV60o/nAP/o7n1CVO4/usXxKkxp\n6laJzwLqyjNsIN0GvaetcHxn0AEc83JNsnaF689Pr+lsLNeefZmXRzW3CYD+HYHG9znet+mAbNET\n7rf0ox8CKvi0XuNgBJ2AusFqzTV179OCpEwBpkOOIMcB9unzE3ixnrjUYoq+aaO8NlrIxoGerd/r\nmxgsjG95rq357WxKG2crW9uoath0NzF3iJ5L6/p2zxdMGTTlkI03HV9wjdazpiDGk7j+iWEf3Jbo\n+GT6d07IIyqK4xebqVr7w6Wk6dZy481ZVHqhjVzHdfgsd31iiA96GJ14j9PJoKk6vZwq+YdA0OMA\n+6cmJUkkged6WJvyuRNHlAOl82zwkUuI/JJOtoHWvCa2QZEmxHm9Ppnn97vAcRLV8hFnsPiZTx2L\nqpG3Zb4ro0gwHBIdjnFds6uU+MxFPfStv82+/83a0RGzHPNnRnmRD4NDeHz7IWUKsN/jAPv2CZFg\nuRLo0Ngcev3NMZcNm3hzhDQRiQo1QzT8tNnpGKTKYzbXSr1xrc2EPmNrfWwmmOFJuC4ma3zfRMiY\nyjxubus4KKNzMa5fmmcNOdfQRibu5+aVdNEpjsXByf0dU3WGXvvybq+UXuWMh0AQ4gDHw0Hn+IsA\nB3X/1sFfMvlZGkZ0mPmgOYW0rcuLzoDre32Ak6tll5oDzNy8kuh8jFZudCLJfg5nsd2+/MkrbN1c\nzpQpwF6MA+zmilPZ3EOA8c+SucYlHd4Tacr0gynAfktXmZkZNz+lW9vZut+WjjM2Ovlix1LJXwS8\nGAfYXzUgaURABGrZ4PjWwf7kQL8n3JSCQyBlCjCRRosDHBzUklQEREAEkkMg0hNncu6gXNNJIFoc\n4HSWR/cWAREQAREQAS8TOMLLhVfZRUAEREAEREAEREAEREAEREAERCBeAlKA4yWl80RABERABERA\nBERABERABERABDxNQAqwp6tPhRcBERABERABERABERABERABEYiXgBTgeEnpPBEQAREQAREQAREQ\nAREQAREQAU8TkALs6epT4UVABERABERABERABERABERABOIlIAU4XlI6TwREQAREQAREQAREQARE\nQAREwNMEpAB7uvpUeBEQAREQAREQAREQAREQAREQgXgJSAGOl5TOEwEREAEREAEREAEREAEREAER\n8DQBKcCerj4VXgREQAREQAREQAREQAREQAREIF4CUoDjJaXzREAEREAEREAEREAEREAEREAEPE1A\nCrCnq0+FFwEREAEREAEREAEREAEREAERiJeAFOB4Sek8ERABERABERABERABERABERABTxOQAuzp\n6lPhRUAEREAEREAEREAEREAEREAE4iUgBTheUjpPBERABERABERABERABERABETA0wSkAHu6+lR4\nERABERABERABERABERABERCBeAkUifdEt5y3a9cufPrpp9mKs2bNGlSuXBnFihXLdiwIO9atW4ey\nZcuiZMmSQRA3m4wbN25E0aJFQwyyHQzAjq1bt+LgwYMoX758AKTNLuL27dvBd8MxxxyT/WAA9uzZ\nswebN29G1apVAyBtdhH3798PvgOPO+647Ac9sofP74YNG5Ja2m3btuHDDz/E7t27Q+1lUm/m88yD\n3uYmqnq///571K5dO1HZBTIftv2rVq1CrVq1Ail/ooRmP0LvxoLTTMe7kXphhw4d8lT4QhmW8nRF\nmk/+6KOPwBdm1jR8+HC0adMGFSpUyHooEN8/++wz1K9fH8cff3wg5M0q5OTJk0PKX4MGDbIeCsT3\nuXPnYt++fWjRokUg5M0q5HfffYfVq1fj3HPPzXooEN/Z4HzzzTfo1KlTIOTNKiQ7LqNGjULPnj2z\nHvLMdzbF7dq1Q5MmTZJSZr4fBg8ejPnz52P9+vVo3bp1Uu4TlEzHjBmDhg0benrQxQ119eqrr6Jv\n375uKIpny8ABwCFDhuDaa6/1rAxuKPjSpUv1bkxARaTj3cgB5DvvvBOlSpWKWwLPzQB369YtqnDL\nly/HjTfeGNiRRM4AduzYEa1atYrKx+87OfPP0c/OnTv7XdSo8r333nvYuXMnbrjhhqjH/b5z3Lhx\nmDFjBu666y6/ixpVPio1nAUIqvxU6FasWBFY+aM+FFl28h15xx13hCyoFixYIFZZ+OT166ZNm8D+\nSPPmzfN6qc6PIMDOclDfWxEYCvSRs5ZTp04VxwJRhN6NBeQXvtwr70atAQ7XmP6LgAiIgAiIgAiI\ngAiIgAiIgAj4moAUYF9Xr4QTAREQAREQAREQAREQAREQAREIE5ACHCah/yIgAiIgAiIgAiIgAiIg\nAiIgAr4mIAXY19Ur4URABERABERABERABERABERABMIEPOcFOlzwrP/pBbVixYqhUDhZjwXh+6+/\n/oqjjjoKJUqUCIK42WRkCBiGQSKDIKbffvst5ASpXLlyQRQ/5ACMjkD4Dghi2rt3L+gIL6hhoA4c\nOBDy3lmtWrUgVn+eZN6xYwf4vAQ1YkKeYOVyMtvcMmXKoHjx4rmcpUOxCDB8T1CjV8RiE+9xepBn\nKNAaNWrEe4nOi0JA78YoUPKxyyvvRt8owPmoI10iAiIgAiIgAiIgAiIgAiIgAiIQIAIygQ5QZUtU\nERABERABERABERABERABEQgyASnAQa59yS4CIiACIiACIiACIiACIiACASIgBThAlS1RRUAEREAE\nREAEREAEREAERCDIBKQAB7n2JbsIiIAIiIAIiIAIiIAIiIAIBIiAFGAPVvbzzz+Ptm3bomfPnti+\nfXs2CR566CFcfPHFuPHGG0EPi35LX3zxBS688EK0a9cOS5cujSrewYMH0aVLFyxatCjqcS/vjCX/\nwoULceutt6JTp0748ssvvSxq1LLHkn/06NHo2rUrrrzySixYsCBqHl7fuW/fPpx//vnYsmVLNlF+\n+OEHdOvWDa1bt8aIESOyHffDjtzknzVrVujd2LlzZ7z55pt+EFcyuIAAn7k+ffrg7LPPBtvYrGnD\nhg1o1arVoe2TTz7Jekqgv8fiF+t4oOFFCB/r/f75558fegb5PK5duzbian2MJLBy5UqwnYiWYvUz\nol0T1H2jRo3CfffdF1X8yy677NDz+Oijj0Y9J207zX26kocITJs2LePSSy/N2L9/f8agQYMy+vfv\nn6n0n376aUbfvn1D++xFmHH99ddnOu71LxbuJ6Np06YZ1vHPmDdvXsZZZ50VVaSnn346w0LCZMye\nPTvqca/ujCW/hQLKaNKkScbGjRszLDRU6FnxqqzRyh1Lfv4uTjnllAxyWLx4ccYFF1wQLRtP71u+\nfHmGdcIzjj766FA9ZxWmQ4cOGXPmzAkdO+2000K/laznePl7LPnPPPPMjNWrV2f8/vvvGW3atMmw\nQUAvi6uyu4TAwIEDM5577rkMU9QyrrjiigzrIGcqGdvbfv36ZezZsye0WWiuTMeD/iUWv1jHg84v\nLH+s9/u9996bMXLkyEPPYfg6/c9MgH1l9pUaNmyY+YB9i9XPyHZBgHc89dRTGbVq1cq45ZZbslHY\nuXNnRvPmzQ89i+yfuSlpBjhtQw/5u/GUKVNwySWXoEiRIqFZjgkTJmTKiCN+9kCG9jEm8M8//5zp\nuNe/cMbXOvVgvFtTdLBt2zZw5DgymWIMU35w7rnnRu72xedY8n/99dewAQLwP7cPP/zQF3KHhYgl\nP38X9oLFt99+C84E+jEu9Pr16/Hqq6/i5JNPDmPJ9J8x0fkbYZxXUwYxc+bMTMe9/iWW/O+9914o\nHmbhwoVRqFChUHxgr8us8qefwOTJk3H55ZeH4s1zViNr2zt37lwceeSReOGFF/Ddd9/hiCPUvYqs\ntVj8Yh2PzCvIn2O93/kc0jJo8ODBodjwQWaVm+yM+ZuTlUasfkZu+QbtGPsZfNaiJVrgValSBa+8\n8gq++uorsE12U9Ib2k21EUdZGOy8fPnyoTOpBG7atCnTVWXLlkWZMmVCiu9tt92Ghx9+ONNxr3+J\nlJ+ykIHNdh4Sy0bfcc8998BG6g/t89OHWPLT3MlGNkMKIF84NJP3U4olP5VfmjT95S9/CT37NlPj\nJ/FDspjVA+rXrx9VLnZ8ihcvfuiYzRJn+n0cOuDhD7nJT7Fq1KgRku6ZZ54B5bcRaA9Lq6K7hUDk\nuyfa72rXrl2hAZdGjRrhhhtuCHX43FJ2N5QjFr9Yx90gQ7rLEM/7nUoG20GzgAsNgFLRU8pOwCwp\nQ4PE2Y8Akc8ij2ftZ0a7Jqj7rrvuutCEXDT5uSykVKlSsFl2vPvuu3jkkUeinZa2fUXSdmfdOF8E\nqOCGX2hscCtVqpQtnx9//DG0BpIj0c2aNct23Ms7IuWnHGbqiooVKx4S6Yknngh1evljM1PJ0Azo\nSSed5JuZwFjy82XDmXEzjQ8xOf3002HmPKFBkUOQPPwhlvxm8h6a+eXsr5nAom7duqG1siVLlvSw\n1PEXnTPefC+Ek5kgoXLlyuGvgfnPgT+u/+dssJII5IcArYhobcXEtWvhdw8HmKL9riIHm838OfTs\nnXPOOfm5tS+vicUv1nFfQsmjUPG83+kDI5xsKQy4PrNHjx7hXfofB4Hwsxg+NWs/M7xf/3MnQF9E\n3Jioi9BC9cEHH8z9ohQe1QxwCmEn4lY0bZwxY0Yoq+nTp6Nx48aZsuUMIEe23nrrrZCzjkwHffCl\nQYMGoIkzRzhp/kxnV8WKFTskma35RMeOHUNKMPezwfCTKVos+an80iqAfNgJ42eawvslxZKfAwAc\nrWXiSDg/0ww2KIkm4Kzv8DPAAYGcZov9yoSKyK+//ooPPvgg07vBr/JKruQQ4BKDZcuWhTaaPsdq\ne239L7755ptQYXgdZ4KVDhOIxS/W8cM5BfdTrPc7+0N0EBoeBNVzmL9nJVY/I3+5Bu+qoUOH4qWX\nXgoJvmLFihyXbaWLjGaA00U+n/elZ9+xY8eGPPxyLdzHH38cyoken6n88RjNN3r16hXaX7t2bQwf\nPjyfd3PfZTTroXdfjiqxkxte7xyWnyP2HGVi4voOMqFS5JcUj/y9e/cGN86AP/DAA6E1a36Xf8iQ\nIeBoN03fjzvuOFxzzTWh9U833XSTrwYAcqrHSPnNAVzoN8LlAOwMVatWLafLfLM/LP+dd96Jxx57\nLNTQmoOTkHzk0b59e9/IKkHSQ4DP1u23346XX34ZtCjhc8YoC/S4TouTq6++GuaAKLQOmFY3fvXA\nnl/60fgxr3r16oG+TXI6nt/7+fW6aO/3yOeQy374TPL9Twsomp8qxUcg3I6wHxGtnxlfLjor3B9n\nP53L8Lgcj4MxnJhzUypkM0UZbiqQyhIfAZpk+GlmLz6pD59Fx1ccDfXT7O5h6WJ/iiU/Z3+5Rc6O\nx87VO2fEkn/v3r0hxT+ozwdrkh2gyPXA3qldlVQE3EsgVtvL0IR+dL6XqBqJxS/W8USVw+v55PZ+\n50wwOfpp8D8d9RWrn5GOMnnxnly2Wbp0adcVXQqw66pEBRIBERABERABERABERABERABEUgGAa0B\nTgZV5SkCIiACIiACIiACIiACIiACIuA6AlKAXVclKpAIiIAIiIAIiIAIiIAIiIAIiEAyCEgBTgZV\n5SkCIiACIiACIiACIiACIiACIuA6AlKAXVclKpAIiIAIiIAIiIAIiIAIiIAIiEAyCEgBTgZV5SkC\nIiACIiACIiACIiACIiACIuA6AlKAXVclKpAIiIAIiIAIiIAIiIAIiIAIiEAyCEgBTgZV5SkCIiAC\nIiACIiACIiACIiACIuA6AlKAXVclKpAIiIAIiIAIiIAIiIAIiIAIiEAyCEgBTgZV5SkCIiACIiAC\nIiACIiACIiACIuA6AlKAXVclKpAIiIAIiIAIiIAIiIAIiIAIiEAyCEgBTgZV5SkCIiACIiACIiAC\nIiACIiACIuA6AlKAXVclKpAIiIAIiIAIiIAIiIAIiIAIiEAyCEgBTgZV5SkCIiACIiACIiACIiAC\nIiACIuA6AlKAXVclKpAIiIAIiIAIiIAIiIAIiIAIiEAyCEgBTgZV5SkCIiACIiACIiACIiACIiAC\nIuA6AlKAXVclKpAIiIAIiIAIiIAIiIAIiIAIiEAyCEgBTgZV5SkCIiACIiACIiACIiACIiACIuA6\nAlKAXVclKpAIiIAIiIAIiIAIiIAIiIAIiEAyCEgBTgZV5SkCIiACIiACIiACIiACIiACIuA6AlKA\nXVclKpAIiIAIiIAIiIAIiIAIiIAIiEAyCEgBTgZV5SkCIiACIiACIiACIiACIiACIuA6Av8PwycY\nwmHPHH0AAAAASUVORK5CYII=\n"
}
],
"prompt_number": 7
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Tuning Models using Resampling\n",
"--------------------------------------------------------\n",
"Resampling (i.e. the bootstrap, cross\u2013validation) can also be used to figure out the values of model tuning parameters (if any).\n",
"We come up with a set of candidate values for these parameters and fit a series of models for each tuning parameter combination.\n",
"For each combination, fit $B$ models to the $B$ resamples of the training data.\n",
"There are also $B$ sets of samples that are not in the resamples. These are predicted for each model.\n",
"$B$ sets of performance values is computed for each candidate variable(s). Performance is estimated by averaging the $B$ performance values."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Tuning Models using Resampling\n",
"--------------------------------------------------------\n",
"As an example, k-Nearest Neighbors has the tuning parameter $k$\n",
"\n",
"We can train over 5 values of $k$: 5, 7, 9, 11, and 13.\n",
"\n",
"$B = 25$ iterations of the bootstrap will be used as the resampling method. \n",
"We use:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"knnFit <- train(x = trainDescr, y = trainClass, trControl = trControl,\n",
" method = \"knn\", tuneLength = 5)"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"prompt_number": 8
},
{
"cell_type": "heading",
"level": 2,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"The `train` Function"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%R print(knnFit)"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"k-Nearest Neighbors \n",
"\n",
"157 samples\n",
" 57 predictors\n",
" 2 classes: 'M', 'R' \n",
"\n",
"No pre-processing\n",
"Resampling: Cross-Validated (25 fold) \n",
"\n",
"Summary of sample sizes: 151, 151, 150, 151, 150, 151, ... \n",
"\n",
"Resampling results across tuning parameters:\n",
"\n",
" k Accuracy Kappa Accuracy SD Kappa SD\n",
" 5 0.8 0.584 0.168 0.349 \n",
" 7 0.782 0.547 0.169 0.352 \n",
" 9 0.776 0.533 0.177 0.366 \n",
" 11 0.775 0.531 0.171 0.356 \n",
" 13 0.774 0.532 0.194 0.395 \n",
"\n",
"Accuracy was used to select the optimal model using the largest value.\n",
"The final value used for the model was k = 5. \n"
]
}
],
"prompt_number": 9
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"The Final Model\n",
"--------------------------------------------------------\n",
"Resampling indicated that $k = 5$ is the best value. It fits a final model with this value and saves it in the object:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R \n",
"knnFit$finalModel"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"5-nearest neighbor classification model\n",
"\n",
"Call:\n",
"knn3.matrix(x = as.matrix(x), y = y, k = param$k)\n",
"\n",
"Training set class distribution:\n",
"\n",
" M R \n",
"84 73 \n",
"\n"
]
}
],
"prompt_number": 10
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Other Tuning Values\n",
"--------------------------------------------------------\n",
"If you don\u2019t like the default candidate values, you can create your own."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"knnFit <- train(x = trainDescr, y = trainClass, method = \"knn\", trControl = trControl, \n",
" tuneGrid = expand.grid(k=seq(1,21,2)))\n",
"knnFit"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"k-Nearest Neighbors \n",
"\n",
"157 samples\n",
" 57 predictors\n",
" 2 classes: 'M', 'R' \n",
"\n",
"No pre-processing\n",
"Resampling: Cross-Validated (25 fold) \n",
"\n",
"Summary of sample sizes: 151, 150, 150, 151, 151, 151, ... \n",
"\n",
"Resampling results across tuning parameters:\n",
"\n",
" k Accuracy Kappa Accuracy SD Kappa SD\n",
" 1 0.84 0.678 0.163 0.327 \n",
" 3 0.803 0.592 0.147 0.298 \n",
" 5 0.81 0.612 0.128 0.256 \n",
" 7 0.771 0.532 0.154 0.308 \n",
" 9 0.778 0.541 0.146 0.29 \n",
" 11 0.779 0.548 0.142 0.282 \n",
" 13 0.781 0.552 0.168 0.334 \n",
" 15 0.736 0.458 0.166 0.334 \n",
" 17 0.724 0.43 0.175 0.357 \n",
" 19 0.723 0.426 0.152 0.315 \n",
" 21 0.716 0.413 0.15 0.312 \n",
"\n",
"Accuracy was used to select the optimal model using the largest value.\n",
"The final value used for the model was k = 1. \n"
]
}
],
"prompt_number": 11
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"plot(knnFit)"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAeAAAAHgCAYAAAB91L6VAAAEJGlDQ1BJQ0MgUHJvZmlsZQAAOBGF\nVd9v21QUPolvUqQWPyBYR4eKxa9VU1u5GxqtxgZJk6XtShal6dgqJOQ6N4mpGwfb6baqT3uBNwb8\nAUDZAw9IPCENBmJ72fbAtElThyqqSUh76MQPISbtBVXhu3ZiJ1PEXPX6yznfOec7517bRD1fabWa\nGVWIlquunc8klZOnFpSeTYrSs9RLA9Sr6U4tkcvNEi7BFffO6+EdigjL7ZHu/k72I796i9zRiSJP\nwG4VHX0Z+AxRzNRrtksUvwf7+Gm3BtzzHPDTNgQCqwKXfZwSeNHHJz1OIT8JjtAq6xWtCLwGPLzY\nZi+3YV8DGMiT4VVuG7oiZpGzrZJhcs/hL49xtzH/Dy6bdfTsXYNY+5yluWO4D4neK/ZUvok/17X0\nHPBLsF+vuUlhfwX4j/rSfAJ4H1H0qZJ9dN7nR19frRTeBt4Fe9FwpwtN+2p1MXscGLHR9SXrmMgj\nONd1ZxKzpBeA71b4tNhj6JGoyFNp4GHgwUp9qplfmnFW5oTdy7NamcwCI49kv6fN5IAHgD+0rbyo\nBc3SOjczohbyS1drbq6pQdqumllRC/0ymTtej8gpbbuVwpQfyw66dqEZyxZKxtHpJn+tZnpnEdrY\nBbueF9qQn93S7HQGGHnYP7w6L+YGHNtd1FJitqPAR+hERCNOFi1i1alKO6RQnjKUxL1GNjwlMsiE\nhcPLYTEiT9ISbN15OY/jx4SMshe9LaJRpTvHr3C/ybFYP1PZAfwfYrPsMBtnE6SwN9ib7AhLwTrB\nDgUKcm06FSrTfSj187xPdVQWOk5Q8vxAfSiIUc7Z7xr6zY/+hpqwSyv0I0/QMTRb7RMgBxNodTfS\nPqdraz/sDjzKBrv4zu2+a2t0/HHzjd2Lbcc2sG7GtsL42K+xLfxtUgI7YHqKlqHK8HbCCXgjHT1c\nAdMlDetv4FnQ2lLasaOl6vmB0CMmwT/IPszSueHQqv6i/qluqF+oF9TfO2qEGTumJH0qfSv9KH0n\nfS/9TIp0Wboi/SRdlb6RLgU5u++9nyXYe69fYRPdil1o1WufNSdTTsp75BfllPy8/LI8G7AUuV8e\nk6fkvfDsCfbNDP0dvRh0CrNqTbV7LfEEGDQPJQadBtfGVMWEq3QWWdufk6ZSNsjG2PQjp3ZcnOWW\ning6noonSInvi0/Ex+IzAreevPhe+CawpgP1/pMTMDo64G0sTCXIM+KdOnFWRfQKdJvQzV1+Bt8O\nokmrdtY2yhVX2a+qrykJfMq4Ml3VR4cVzTQVz+UoNne4vcKLoyS+gyKO6EHe+75Fdt0Mbe5bRIf/\nwjvrVmhbqBN97RD1vxrahvBOfOYzoosH9bq94uejSOQGkVM6sN/7HelL4t10t9F4gPdVzydEOx83\nGv+uNxo7XyL/FtFl8z9ZAHF4bBsrEwAAQABJREFUeAHt3QecVNXd//EvLL03AekK0pEiCoIIImLv\nGmPjQcVCLM+TZlRIotHY9S9RozFR0VhTjBGIYgXEKFIVBQSlSBGlSC9L2f/53XGWhZ3d2TIzt8zn\nvl7Lzt6595T3Gfa399xzz6mQ5zaxIYAAAggggEBGBSpmNDcyQwABBBBAAAFPgADMBwEBBBBAAAEf\nBAjAPqCTJQIIIIAAAgRgPgMIIIAAAgj4IEAA9gGdLBFAAAEEECAA8xlAAAEEEEDABwECsA/oZIkA\nAggggAABmM8AAggggAACPggQgH1AJ0sEEEAAAQQIwHwGEEAAAQQQ8EGAAOwDOlkigAACCCBAAOYz\ngAACCCCAgA8CBGAf0MkSAQQQQAABAjCfAQQQQAABBHwQIAD7gE6WCCCAAAIIEID5DCCAAAIIIOCD\nAAHYB3SyRAABBBBAgADMZwABBBBAAAEfBAjAPqCTJQIIIIAAAgRgPgMIIIAAAgj4IEAA9gGdLBFA\nAAEEECAA8xlAAAEEEEDABwECsA/oZIkAAggggAABmM8AAggggAACPggQgH1AJ0sEEEAAAQQIwHwG\nEEAAAQQQ8EGAAOwDOlkigAACCCCQtQE4Ly9Pu3bt4hOQBgFzNV+21Avk5uamPlFS1O7du7V3714k\n0iDAZ7Zo1KwNwPPmzdNPf/rTomV4p8wCP/nJT/TVV1+V+XxOTCywZcsWnXvuuYnfZG+5BO666y5N\nmjSpXGlwcmKBoUOHJn6DvcraAEzbI4AAAggg4KcAAdhPffJGAAEEEMhaAQJw1jY9FUcAAQQQ8FOA\nAOynPnkjgAACCGStQKWo1/ydd97RihUrClVz5cqVWrBggZ555plC77GjfAILFy7UK6+8oiZNmpQv\nIc7eT2DHjh1avnw5n9n9VFLzw+zZs2WD3MyXLbUCq1evDvxntkKFCho2bFhqK16C1HJudVsJjgvl\nIRZgL7nkEg0YMKBQ+Q384IMPVu3atQu9x47yCTRu3Fh169ZV5cqVy5cQZxcSaN26NZ/ZQirl31Gn\nTh3Vq1dP1apVK39ipLCfwCGHHBL4z6xdiFlM6N69+35lT/cPkb4CtmdRhwwZouHDhxdytGfT7C/e\nBg0aFHqPHeUTWLdunewXGgG4fI4Hnm3Pqa5du1b2Bw5bagU2bNigqlWrqnr16qlNmNRkV8BNmzYN\nvIQfcxdwDzjwHwsKiAACCCAQRQECcBRblTohgAACCARegAAc+CaigAgggAACURQgAEexVakTAggg\ngEDgBQjAgW8iCogAAgggEEUBAnAUW5U6IYAAAggEXoAAHPgmooAIIIAAAlEUIABHsVWpEwIIIIBA\n4AUIwIFvIgqIAAIIIBBFAQJwFFuVOiGAAAIIBF6AABz4JqKACCCAAAJRFCAAR7FVqRMCCCCAQOAF\nCMCBbyIKiAACCCAQRQECcBRblTohgAACCARegAAc+CaigAgggAACURQgAEexVakTAggggEDgBQjA\ngW8iCogAAgggEEUBAnAUW5U6IYAAAggEXoAAHPgmooAIIIAAAlEUqBTFSmWiTnv2Si9Pk5aslVo2\nkIb1z0Su5IEAAgggEBUBroDL2JLDnpAmfyEN7CC95ALx+Y9KeXllTIzTEEAAAQSyToAAXIYmt8C7\neqP0p+HSMe2l//xMOqi29PbnZUiMUxBAAAEEslKAAFyGZt+2UxrSJXbi7a9J322SDj1I2uL2syGA\nAAIIIFASAQJwSZQOOKb3Ie6q91Np2ldSY3fl+/T70q2vSke3O+BAfkQAAQQQQKAIAQZhFQFT3G7r\nbn5iuLsKvlfq21b6fJX04a+lpnWLO4v3EEAAAQQQ2CdAAN5nUapXnZpJX90nbdgm/fQFqV6NUp3O\nwQgggAACWS5AF3Q5PgDVKseuegd2lKYuLEdCnIoAAgggkHUCBOAUNPmx7lEkGxnNhgACCCCAQEkF\nCMAllSrmuM6uO3rLDmn5+mIO4i0EEEAAAQQKCBCAC2CU56U9D0w3dHkEORcBBBDILgECcIram27o\nFEGSDAIIIJAlAgTgFDU03dApgiQZBBBAIEsECMApbGi6oVOISVIIIIBAxAUIwClsYLqhU4hJUggg\ngEDEBQjAKWxguqFTiElSCCCAQMQFCMApbmC6oVMMSnIIIIBARAUIwCluWLqhUwxKcggggEBEBQjA\nKW5YuqFTDEpyCCCAQEQFCMBpaFi6odOASpIIIIBAxAQIwGloULqh04BKkggggEDEBAjAaWhQuqHT\ngEqSCCCAQMQECMBpalC6odMES7IIIIBARAQIwGlqyAFucYYpLFGYJl2SRQABBMIvQABOUxt2aS5t\nZonCNOmSLAIIIBB+AQJwGtuQbug04pI0AgggEHIBAnAaG5Bu6DTikjQCCCAQcgECcBobkG7oNOKS\nNAIIIBByAQJwmhuQbug0A5M8AgggEFIBAnCaG45u6DQDkzwCCCAQUgECcJobjm7oNAOTPAIIIBBS\nAQJwBhqObugMIJMFAgggEDIBAnAGGoxu6AwgkwUCCCAQMgECcAYaLN4NvWJ9BjIjCwQQQACBUAgQ\ngDPUTNYN/f7CDGVGNggggAACgRcgAGeoieiGzhA02SCAAAIhESAAZ6ih6IbOEDTZIIAAAiERIABn\nsKHohs4gNlkhgAACARcgAGewgeiGziA2WSGAAAIBFyAAZ7CB6IbOIDZZIYAAAgEXIABnuIHohs4w\nONkhgAACARUgAGe4YeiGzjA42SGAAAIBFSAAZ7hh6IbOMDjZIYAAAgEVIAD70DB0Q/uATpYIIIBA\nwAQIwD40CN3QPqCTJQIIIBAwAQKwDw1CN7QP6GSJAAIIBEyAAOxTg9AN7RM82SKAAAIBESAA+9QQ\ndEP7BE+2CCCAQEAECMA+NQTd0D7Bky0CCCAQEAECsI8NQTe0j/hkjQACCPgsQAD2sQHohvYRn6wR\nQAABnwUIwD42AN3QPuKTNQIIIOCzAAHY5wagG9rnBiB7BBBAwCcBArBP8PFs6YaOS/AdAQQQyC4B\nArDP7U03tM8NQPYIIICATwIEYJ/gC2ZLN3RBDV4jgAAC2SFAAA5AO9MNHYBGoAgIIIBAhgUIwBkG\nT5Qd3dCJVNiHAAIIRFuAAByQ9qUbOiANQTEQQACBDAkQgDMEnSwbuqGTCfE+AgggEC0BAnBA2pNu\n6IA0BMVAAAEEMiRAAM4QdEmyoRu6JEocgwACCERDgAAcoHakGzpAjUFREEAAgTQLEIDTDFya5OmG\nLo0WxyKAAALhFiAAB6z96IYOWINQHAQQQCBNAgTgNMGWNVm6ocsqx3kIIIBAuAQIwAFrL7qhA9Yg\nFAcBBBBIkwABOE2w5UmWbujy6HEuAgggEA4BAnAA24lu6AA2CkVCAAEEUixAAE4xaCqSoxs6FYqk\ngQACCARbgAAc0PahGzqgDUOxEEAAgRQJEIBTBJnqZAjAqRYlPQQQQCBYAgTgYLVHfmm6Npc2bZdW\nrM/fxQsEEEAAgQgJEIAD3JhcBQe4cSgaAgggUE4BAnA5AdN5OgE4nbqkjQACCPgrQAD217/Y3OmG\nLpaHNxFAAIFQCxCAA958XAUHvIEoHgIIIFBGAQJwGeEydRoBOFPS5IMAAghkVoAAnFnvUudGN3Sp\nyTgBAQQQCIUAATgEzcRVcAgaiSIigAACpRQgAJcSzI/DCcB+qJMnAgggkF4BAnB6fVOSunVDb9wm\nrfw+JcmRCAIIIIBAAAQIwAFohJIUYUAHacoXJTnS32P27JW+2VhR67f4Ww5yRwABBIIuQAAOegv9\nUL4wdEPb1JnXPyf9ZlxNHf37SnpqSkhwKSYCCCDggwAB2Af0smQZ9G7ove7K9+jbpUMaSX++ZLNm\n37Zbf5okvTOvLLXlHAQQQCD6AgTgELVxkLuhv90ktW0iXTFQuu/N6srLk+4+X5ocgm7zEH0EKCoC\nCERIgAAcosYMcjd01UrS6g3SiKekBjXz9MJHFfXfL6WaVUIETFERQACBDAq4X5tsYREo2A3dvH5w\nSr1wtfSHtyQr05ufSSd13KuxH1bQF27/yoeCU05KggACCARJgAAcpNYoQVni3dAX9i3BwWk+ZMsO\naexUeVe6I1zX8+BO0tSF0riZOdrruqDf+qVUrXKaC0HyCCCAQEgF6IIOWcMFpRv63fnSVWNjeE8M\njwVf+8nKd+PQ7bpiQJ4+Wxl7n38RQAABBAoLcAVc2CTQe/zuhl6xXnrkbWnLTunWs6T2TRNz9W27\nV4+8m6Nh/RO/z14EEEAg2wW4Ag7hJyDeDZ3Joufulp79QPrZi+5xo3bunu/FRQdfK1fHg12Qdl3U\nq5i9K5PNRF4IIBAiAQJwiBorXtRMd0PPXCpdPTY2Febjw6Uze0kVS/DJsUD9gRsJzYYAAgggUFiA\nLujCJoHfk6lu6HVuOsnH35O+/NbNcDVE6tWmdDT9D4tdNZ9/ZOnO42gEEEAgGwRKcB2TDQzhq2M6\nu6FtVqtXZ0kjn5FaN5SeuKz0wddED28prXBd0BbI2RBAAAEE9hcgAO/vEZqf0tUNbc/uXv+8NO0r\n6aGLpEv6SZVzysaS4z5dRx0ifeTSYkMAAQQQ2F+ALuj9PULzU6q7oW3A1NNTpQ/dPdsr3TO9x7ln\nelOx9XePJY2fI53aPRWpkQYCCCAQHQGugEPclqnqhrYFE6582g2squAWUnDdzakKvkbbu400f1Vs\nRHSIqSk6AgggkHIBAnDKSTOXYHm7oe2Z3l/9TfrXTOm2s6Vrj3dzN1dNbfmruD6Wnq1dl/bi1KZL\naggggEDYBeiCDnELlrUb2p7pffEjacInsXu8p/eQKrir33RtNhraFmY4vnO6ciBdBBBAIHwCXAGH\nr832K3Fpu6FnLHFTSLru5lUb3CNGw6UzeqY3+Fph+xwqzV4mWeBnQwABBBCICRCAQ/5JKGk39Fr3\nKNAdr0l/fFf636HSzafZsoGZqXytalIHN2XljKWZyY9cEEAAgTAIJO2CXrt2rWbPnq3PP/9cGzdu\nVI8ePXTEEUeoRYsWYahf5MuYrBvanun99+xYl7Nd7f7q1LI/VlQezH6uG9pGWPdrV55UOBcBBBCI\njkCRV8AWbG+66SZ1795dDzzwgBeA161bp8cee0wDBgxQz5499e677nKKzXcBuwqe8kXhYtjo4+ue\nkz52A6DK+0xv4dRLt8cCrz0PvMf9QcCGAAIIICAlvAJ+//33dc8992jkyJG6/fbbVbly5UJWc+fO\n1b333qsXX3xRf/7znwu9z47MCTR0Xcl3jJNec1e6Jx8unXOE9NT7sck0rhwkDeqYubIUlVPDWlLz\n+tKny2Ojoos6jv0IIIBAtggkDMDdunXT+PHjizWwY/7617/KuqjZ/BOweZr/PCUW3Oze7t0T3OAq\n1zFxSX+3/3KpRhX/ynZgznYVbKOh7bEkNgQQQCDbBRJ2QderV6/ELo0aNSrxsRyYeoFH35F+fUZs\nNPNPnnWB2DVdFddh8ZPBwQq+VvNj7HGkRak3IEUEEEAgjAIJA3DBikydOlXHHXecOnXqpA4dOuR/\nvfHGGwUP47VPAtXdFa59XT3IdUOfI425OLj3WZu5LmgbEb3gG5+wyBYBBBAIkEDCLuiC5Rs+fLiu\nuOIKDRo0SJUq7Tu8XTvXn8jmu4DNsWyPFz16qWTPBJ9wn9Q/wE3jdUO7q+COB/tORwEQQAABXwX2\nRdQExcjLy9OmTZu80dAV0jlVUoK82VUyAZtlytbq/dEfpUa1pfPc2rsjjyvZuX4cZY8j3ePuU19+\nrB+5kycCCCAQHIFiA7AF3RNPPFFPPfWULr30UlWpEqARPcEx9L0kQ7pI9hWG7bAmsRmxvl4ntXJr\nDbMhgAAC2SqQ9B7w5s2bNWLECDVs2FAdO3bM/+IecLZ+ZMpfb7sK/oDBWOWHJAUEEAi1QNIAfNtt\nt+njjz/2Jt2wx47iX3369Cl1xd98802dcsopGjJkiBYsWFDofHv06ZxzztHFF18se87YtsWLF+vc\nc8/17kG/8sorhc5hR/gE7B61PY7EhgACCGSzQLFd0AZjM2HtdfMZLlu2TLm5uTrssMNUsWLSuF3I\n1K6kR40apbfeestL66qrrtKUKVPyj9u9e7dGjx6tjz76SEuWLNHPf/5z/ec//9G1116rO++8U61a\ntdIJJ5ygwYMHqzSPSeVnwIvACHR1s5h+u1H6bpPUuE5gikVBEEAAgYwKJA3AixYt0nnnnedNRVmz\nZk1ZoHzwwQd19dVXl6qgdsVr01da8LQvm+rSAnr8vrKNsLZBX5988okWLlyo2rXdiCK3ffPNN955\n9vqYY47xrsaHDh1qP+63vffee4UmBVmxYoXWrFmjrVu37nes/WD12LVrV8L3Ch3MjlIJmOv27du9\n9i3qxN6tKuu9z/bqtO57ijqE/QcI2P8P+9wm+jwfcCg/llLAPrPmaxcbbKkV2LNnT+A/szahlF34\n1ahRo1DlrVc2Jyen0P5U7EgagO1K9fTTT/e6oC1w2hXq+eef780H3blzyRd4tWDYoEGD/DJbWlbp\nZs2aefvsw3/mmWd6V7wbNmzQfffdp++//17VqrkHR3/Y6tevXyjIxt+zcyzYFtzsfGv8RP+pbB//\n4Qpqpfa1+RY3cv7INrv07zmVdUq3XanNOMKp2efVtkSf5whXOyNVM1t+H6SPOuifWfvD1nppD4wh\n6ROJpZw0AM+bN08TJ07Mv1Lt37+/LrvsMtl80aUJwHXr1tWWLW5NvB82u0IqOIvWzJkzNWPGDO/L\nMGzSD1uFadu2bfFTvL+iGjdunP9zwRdnn312wR+91/Pnz9fDDz+cfzVd8AC7+rb/cPEr7YLv8bp8\nAmZrvSWJ5hCPp3yM+9vtkckumFSqorrV43v5XpyA/RLbsWMHn9nikMr4nv2hXrVqVVWvzoexjIRF\nnmY9NkH/Pdu0aVMdfPDB+p//+Z8i65GON5LezO3atavmzJmzX95277Zg8NzvzSJ+6NKli5eOBT3r\nfrZfJvHuZzvFfmHbVbFtdrlvr+0XuP2HsFWY7DwL0jYjF1v4BSq7Hp0j3JzQ09wKSWwIIIBANgok\nvQK2FZFs8JPNhGUDoexq2ILjGWe4CYhLsTVp0sQb3Xzaaafpu+++81ZbstOti/vkk0+WXcFa+sOG\nDZN1J1u+FnxtxSUbFW1/+dsI6ubNm5ciVw4NsoA9jvTefGlo1yCXkrIhgAAC6RFIGoBtAFabNm1k\nz/3aPVVbI/iSSy4ptnuxqKJaULVpLW3AVXwk9RNPPJF/+N13362dO3d6acffHzhwoOzLAnDB+8H5\nJ/EitAJHHSr94S1pe25sPuvQVoSCI4AAAmUQSNgFPW3aNPXo0cNLzoLfRRddpGeffVbjxo2TBUnr\nli7rRBzW7RwPronKa/dhEr1P8E2kFe59tlRiF9ehMX1JuOtB6RFAAIGyCCS8ArbBVU8//bSXng1i\nsiH6B26HHuouX9gQKKeAzWVtk3Ic6xaSYEMAAQSySSBhALYRa/bMrm12z9WmoSy42T3coA8rL1he\nXgdXoG9b6c9uNPRu9zhwpfQ8ahfcylMyBBDIaoGEXdAmYvdc7csGX8Vf23d7LOiGG27wuqOzWo7K\np0Sgnnvu/ZBG0pyvU5IciSCAAAKhESgyAJ966qneKOTPPvvM+24jku2rVq1a+uCDD9SvX7/QVJKC\nBlvAW5yBuaGD3UiUDgEEUi5QZAB+++23vXu/F154offd7gPbl02SsXz5cu+RoZSXhgSzUsAWZ/jQ\nBWD3qDcbAgggkDUCRQZgm0bQHheyx4ZsAQS7J2wjo21CDXumd8IEt6o6GwIpEGhSV2pQU/p8VQoS\nIwkEEEAgJAIJB2EVLLs9u2uTY9iUlPb4kXVBP//8897EGQWP4zUC5RGw0dB2FdyVeVbKw8i5CCAQ\nIoEir4CtDvFpI20ZwRNPPNFb3cYGYB1//PFlfg44RDYUNYMCFoA/WJjBDMkKAQQQ8Fmg2ABs3dA2\nR7PN3WzrAk+dOtUrrq1q9PXXX/tcdLKPkkAbNxK6ovs0Lt5/QasoVZG6IIAAAvsJJO2Cvuaaa3T4\n4Ydr8eLFWrp0qS644AJvaUJblpANgVQK9HODsf67SDr0oFSmSloIIIBAMAWKvQK2It94440aP368\nNyDrnXfeUbdu3bxngNu2dTMosCGQQgHvcSQXgNkQQACBbBBIegVsCHYFbFvr1q01evRo7zX/IJBq\ngc7NpA1u+edvNkgHx1amTHUWpIcAAggERiBhAJ4xY4a3TGBxpbRlAocMGVLcIbyHQKkFjnbd0B+4\nq+Dzjiz1qZyAAAIIhEogYQA+7LDDNGbMGK8iTz31lFauXOktQWjdzu+9956ee+45dezYMVQVpbDh\nELDR0C98SAAOR2tRSgQQKI9AwgBct25dDRgwwEv30ksv1axZs2Qjn23r37+/1q1bJ5spa/jw4d4+\n/kEgVQI9Wkl3jZfWb41NzpGqdEkHAQQQCJpA0kFYOTk5Wr169X7lnjt3rho1cs+NsCGQYoEc94k8\n6tDYpBwpTprkEEAAgUAJJA3AN998swYOHOjNfHXttdeqffv2XgW4/xuodoxUYbzHkVicIVJtSmUQ\nQKCwQNIAPGLECE2cONHrerau6TvvvNObBatatWqFU2MPAikQOPIQad5KaevOFCRGEggggEBABRLe\nAz6wrL169ZJ9sSGQCYGqlSW7FzxtsTS4UyZyJA8EEEAg8wIJr4CnTZvmrXxkxbHuZ+t2PvDrjTfe\nyHxpyTFrBOKzYmVNhakoAghknUDCK+DOnTvr6aef9jAefvhhbx3gA2UOPdSNlGFDIE0CfdtJj70n\n5e6WqiT8lKYpY5JFAAEEMiSQ8FfbggULvHWAiyvD/fffr6FDhxZ3CO8hUGaB2m6IQfsm0qxlUl9m\nPS2zIycigEBwBRIGYOtufuyxx4otNRNxFMvDmykQsLmhbXEGAnAKMEkCAQQCJ5AwANtoZ5two7ht\nx44dxb3NewiUW8CmpXzuv9LevbGlCsudIAkggAACARJIOAirYPlsBaRjjz3WWwWpa9eu6tSpk5o0\naaIJEyYUPIzXCKRc4KDasUUZ5q5IedIkiAACCPgukPAKuGCpRo4cqWHDhmnevHmyAFyrVi09//zz\n3sQcBY/jNQLpEPCWKHSTcnR3jyWxIYAAAlESKPYKOC8vTxs3btSoUaN04oknKjc3VzfccIOOP/54\nbzKOKEFQl2AK9Hfd0HYfmA0BBBCImkCxAbhChQqqWbOmF4S7d++uqVOnevW3hRm+/vrrqFlQnwAK\ntHBrgFSvIi3cfzryAJaUIiGAAAKlE0jaBX3NNdfo8MMP1+LFi7V06VJdcMEFevfdd/XRRx+VLieO\nRqCMArZE4X9dN3T7pmVMgNMQQACBAAoUewVs5b3xxhs1fvx4VapUSTYgq1u3bho3bpxsbWA2BDIh\nYLNifUA3dCaoyQMBBDIokDAA29XtFVdcoQ8/dCuju82ugG1r3bq1Ro8erb59+3o/8w8CmRCwK9/t\nudLy9ZnIjTwQQACBzAgkDMCHHXaYGjdurPPPP98b+fzQQw9p3bp1mSkRuSCQQMC6obkKTgDDLgQQ\nCK1AwgDcsGFD3XXXXd5AqwcffFDTp09Xu3btdOGFF3rd0DY6mg2BTAp494Hphs4kOXkhgECaBRIG\n4HieFStW9OZ7tud+ly1b5j1+ZOsBd+jQQTNmzIgfxncE0i7Qtbm0eqO0ZnPasyIDBBBAICMCxQbg\ngiWoXLmyateuLZumcufOnd4zwQXf5zUC6RRwfwt6c0J/6EZDsyGAAAJRECg2AO91k/C+/fbbGj58\nuJo1a6axY8fqoosu0qJFi9SvX78o1J86hEggvjhDiIpMURFAAIEiBRI+B7xmzRrdfffdevHFF1W1\nalVdfvnl+vTTT9WyZcsiE+INBNIt0Ku1dN/r0qbtUp3q6c6N9BFAAIH0CiQMwHaFu2rVKj377LPe\nfV+bEYsNAb8FqrhPa083J/S0r6QTuvpdGvJHAAEEyieQsAvaupft6nfIkCGKB985c+Z4V8Xly46z\nESifgNcNzX3g8iFyNgIIBEIgYQBOVDKb+/n1113/HxsCPgr0OVT6ZLm0Y5ePhSBrBBBAIAUCJQ7A\nKciLJBAot0DNqlKnZtL0JeVOigQQQAABXwVKHIBbtWqlU045xdfCkjkCJmBLFPI4Ep8FBBAIu0CJ\nArCtgtSjRw+dfvrpuvfee/XZZ5+Fvd6UP8QCR7sAPG2xtGdviCtB0RFAIOsFkgbgX/ziF95zwDb5\nxuDBg/XBBx/o1FNP1fLl7kYcGwI+CNSvKbVpKM352ofMyRIBBBBIkUDSAPzyyy97yw/aUoT169fX\nv//9b1188cXeBB0pKgPJIFBqAbsKZnGGUrMF5oQtO6RH35HuniB95B4rY0MgGwWKDcC26MLu3btV\nq1Ytvfbaazr33HM9o9zcXG9aymwEo87BEDimPfeBg9ESpS/Frj1uidNfSxaED28hDblX+sf00qfD\nGQiEXaDYAGzPANvav3bv96WXXvJWQ3ryySfzJ+gIe+Upf3gFmtaV6tWQ5q0Kbx2yteR/fFc6t7d0\n+bHSsR3cIhtjpGemSmu3ZKsI9c5WgUrJKm4rIf3tb3/Trbfeqi5dunhLFM6aNcvrjk52Lu8jkE6B\n+BrBnd1jSWzBFMjdLS1fL634XlrpvtvrcXMkm1vvkj9JbRtLfxwm1awmbXVXxI1qBbMelAqBdAgk\nDcA1atTQoEGD1KZNG82bN09z58715oRu0cL1HbEh4KOAzYp1x2vSlQN9LARZewK2TORKF2S9YPtD\nwF3hvn+/VWpWX2rhvlo2kHofIlnvxROTpFdvkK55RnpwojR1odTcHcOGQDYJJA3ANgra1v6dOHGi\nNwq6T58+evTRRzV16lQWZ8imT0oA63roQZJbsEtL17pR0Y0CWMAAFmm9C4hffOOuNGtLhzUpXQET\nXc3ala0F3RpVYkG2hQuy8UBr35vUcVe7drl7wLbTXRl3uUU6uJ60aoOb3ex2qVLOAQfxIwIRF0ga\ngG0UtF35FhwFfcstt3ijoC+77LKI81C9oAv0d4OxbDQ0ATh5S33qnhy8+e9S91bSCx9KN54q/WRw\n4fMOvJq1AGtXt4muZs86IhZwLQCXZrtqkHRmT2nyF7GpRRvS9VwaPo6NiECxAZhR0BFp5QhXwx5H\n+qN7nOXioyNcyRRUzYJnvzvcIz+/kbo2d4HYBd/T/p/kHnTwBrNZd3FRV7NHum5ju7It6mq2rMVr\n4rqiT+0uvfiRZCOjK3MFXFZKzgupQLEBuOAoaOtytkk44qOgR40aFdIqU+woCXRxA7AsuHy70QUI\n9ws9iJt1kb86M9YV++M+6SmndQ9vdOsk21rJ9lXw9SY3uGmBGy3evaX0+Luxx3+sK7q6u2p9+3Pp\nrF6xe7NlvZotj7nN7W23Ej5b4ZaadOs9syGQTQLFBmCDYBR0Nn0cwldXu7/Yt53rhv5SOsd1hwZt\nW7zGDTQa6waKDXL3q93VZtsb3fPL7hnYbi2KLmlRwXTDNvfIztrq2uv+18aD7OYfgq1LWnWrS3Xc\nl32v7UYVx1/bAKjG7p7vpy7IXTXQ/QHg7rvaz/b87dX9pbN9djuijTRzKQG46E8E70RVIGkAtlHQ\nw4YN07Jly/TFF1/oxBNPVMWKxT4+HFUr6hVQAVuc4aVpwQzA//ucG6l9rtTxYMmC8X0XSD99QRp+\nTOwqdbO7Oi1pMLWgenDdPWrZdF+wtX0WcKtWLlnj9Pu99NgwN+rY3Te30cl+B18rtV35Pvx2ycrP\nUQhESSBpAF60aJHOO+88ff7556pZs6Y3M9aDDz6oq6++OkoO1CXEAj3coKK7Jkh2hWiTcwRpq+L+\nh81eJt3/uht17AJnjrti/25TrIQ2Sjh+lWrfkwVTG/G9dm2uGrtnZ8uynXekdIjr7rXBWHbv9fQe\nZUkl9efYHydmYt3iDWqmPn1SRCCoAkkD8FVXXeXNhPXuu++qXr16+uijj3T++edrwIAB6ty5c1Dr\nRbmySMAeXznKDRSyJQpPPjwYFbeVmibOjQ1s+vMkafzPYs+/3vsfaVBHNwlFP3/KeUQbyb6CtNlt\nhF7uKnjWUtct3iVIJaMsCKRXIGlfsj2C9Jvf/EYNGzZUTk6O+vfvL3v86P33309vyUgdgVII2KQc\nQVmcwSaVuHpsrJv32Svd867ufu+Fj8VmfrIu5/93USkqliWH2h8Fdh+YDYFsEkh6Bdy1a1fNmTNH\nRx11VL7LlClT9H//93/5P/MCAb8F7FGZB9+QtuXGJoXwozzWtfvklNg6xdcev29Q0TMuCK/6Xm7s\nROwq2I+yBT3PXm1idkEvJ+VDIJUCSQPwyJEjdcIJJ3jTUbZq1cqbEcu6os8444xUloO0ECiXQLXK\nbmUd95jNx4tjXbzlSqyUJy9xg6uech1CNlnFMDeq2LqYD9xswBNb0QIHuVHZ9dz930Xfln6GrqJT\n5R0Egi2QtAv61FNP9WbBOvLII1WlShXddNNN3jSUlSu733hsCARIwBZn+K8b3ZupzZ49vs/d073l\nH5Jdgf/5ssTBN1PlCXs+R7j7wHRDh70VKX9pBJJeAXfs2FFvvfWWRo8eXZp0ORaBjAv0aSv9aVL6\nZ1Wyx4Zs9qZ35rnpFHtJ1w2JTWqR8QpHLEO7D/y3jyWbrIQNgWwQSHoFbKse2QpIbAgEXcCeh23r\nHrOx0bTp2HbuigXeEU+5+7x5bkUfd8VrU2DajFJs5RewWwjWBb3d3cdnQyAbBJIG4CZNmnjPATd2\nDx/aesDxL1sdiQ2BoAl43dDucaRUbvZI0YRPpMuelL5eJ/3hktgiBkF75jiVdfYjLXtmulOz2OIM\nfuRPnghkWiBpF7R1Pd94441euXbu3KmqVd3krW5r3769951/EAiSgD2O9PyH0v+eEBt1XN6yvb9Q\nGusGWNk807efE1tAvrxpcn7RAvY8sN0H7utuJ7AhEHWBIq+A161bp4svvlg7duxQ3759va9XX31V\nY8aMkY2GbtCgQdRtqF8IBWw0rQXLz1aWr/D2SNENz8XuSV7vgvmd5xF8yydasrN7u8FsDMQqmRVH\nhV+gyAB83HHHeaOeO3XqlF9LGwFdt25dHXPMMfn7eIFA0AT6tXOjocvYDW3zNY/6p/TQm9K5burG\nh113s011yZYZAVvXeYe7177ajTBnQyDqAgkDsM3/vNdNPPv000+rfv19DzDa/eDHH39ctWvX1syZ\nM6NuQ/1CKlCWx5HskSKbJnKUe6ToaNf9aY8UDewQUoCQF9tGQ3MVHPJGpPglEkgYgD/55BN17969\nyAQGDRqk6dOnF/k+byDgp0CrhpIN6LERtck2Wzf38ffco0Suu9mW7Xt6hFuo3i1SkJPwf0ay1Hg/\nFQIWgGcsSUVKpIFAsAUS/prp06ePJk+eXGTJp02btt/UlEUeyBsI+CTgdUMXMymHdXPas7xXukeK\nbPvL5dJF7pEim1GLzV8BG4j1ibsHb6PP2RCIskDCANyyZUt16NBBl156qTZv3pxf/23btsmmplyz\nZo169AjIWmb5peMFAvsEbDR0ovvA9kt9/Bz3SNFfpOXrY/d4rzkutqbuvrN55aeALc3Y3PVGzP/G\nz1KQNwLpF3AddYm3cePGec//2mjntm3bas+ePVq8eLEGDhwouwKuaDPLsyEQUAFb4m7SfOnYu6TK\n7qP6rxukOV+7R4qmukXt60m/d6OaD3WTdrAFU6B3G3cf2HVDd20ezPJRKgRSIVBkAK5Ro4b+85//\nuAXA13prAFtmvXr1UrNm7kl5NgQCLLBui1vz9rfSyMGS/SK3K+E+v5OO7xx7Prg7o5oD3Hqxotnq\nSLaO8v8cE/iiUkAEyiyQMAB/+umn3nO+Ng1lo0aNdNpppyXMwCbmeOONN3TmmWcmfJ+dCPgh8Iab\nOfXeC9zVrxvFfNFjLggfInV30xxecaz7TvD1o0lKnWdn93f+iu8lm3fbuqTZEIiigOucK7zZs76/\n/OUvdd1113krH+3evTv/oNzcXM2fP1/33nuvbLDW99+7/yVsCARMYKtb+N66L5+/OvZI0Sb3s3VL\ns4VDwEah2x9Ns5aFo7yUEoGyCCS8Am7durVefPFFTZkyRaNGjdKMGTO854GrVaumFStWeNNQ2jKF\n9n6dOnXKki/nIJA2gTN6ukUS/iS1+jjWBX3dX2OPJTGhRtrI05KwPY40aylLPKYFl0QDIZAwAMdL\nduyxx3qPI9kArK+++kobN25U165dVb06fUJxI74HT6B2NfeI0TWxdXrf/jx2JWULKLCFS8BuHbzg\nHhVjQyCqAsUG4Hilc3JyWHwhjsH3UAjUrCqNuTgURaWQRQg0rRt7LnvpWsmmqGRDIGoCCe8BR62S\n1AcBBMIpEF8dKZylp9QIFC9AAC7eh3cRQMBHAeaF9hGfrNMuQABOOzEZIIBAWQVs4Nz8VVLuvgcx\nypoU5yEQOIGkAdjWBH7mmWe0ZYub3YANAQQQyKBA9SrSYU0kW5+ZDYGoCSQNwJdcconGjx+vNm3a\naPjw4Zo0aZLy8vKi5kB9EEAgoAI93eIMPA8c0MahWOUSSBqATz75ZP3973/Xl19+qX79+umuu+5S\nu3btdNttt2nVKtc3xIYAAgikUYD7wGnEJWlfBZIG4Hjpli5dqkWLFnmB2OaDtlWSjj76aG/Cjvgx\nfEcAAQRSLdC+qfT9VmnNvoXZUp0F6SHgi0DSADxmzBhv8g2bD7pKlSre3M/vv/++7r//fj377LN6\n8MEHfSk4mSKAQPYIxGfFyp4aU9NsEEg6EYctQfjAAw/ohBNOKLQEYZcuXfSHP/whG5yoIwII+Chg\nzwPPWCqd2M3HQpA1AikWSHoFfPvtt3vTUcYHXl199dX6+GM3ya7bbKUk64ZmQwABBNIpcISbltIG\nYjH+M53KpJ1pgaQB+KqrrvLmgN67d69XtsGDB+uCCy7Q+vXrM11W8kMAgSwVaFDT/cFfS/pidZYC\nUO1ICiTtgp42bZqsG7rCD2u5WfCdN2+eXnvtNe+xpEiqUCkEEAicQPw+cMeDA1c0CoRAmQSSXgHX\nqlVL06dP3y/xyZMnswzhfiL8gAAC6RbgcaR0C5N+pgWSXgHfcccdGjJkiHr16qWWLVt6E3F06tRJ\nZ5xxRqbLSn4IIJDFAl1bSF+tkbblSjXcDFlsCIRdIGkAPvPMMzVjxgzZo0dbt26VDcqyWbF27Nih\nSpWSnh52H8qPAAIBEaicI3VtLs12g7H6HxaQQlEMBMohkLQL+p133tGIESP00EMP6YknnpDNjNWk\nSRNNmDChHNlyKgIIIFB6AbqhS2/GGcEVSHoJO3LkSA0bNswbeNW1a1fZPeHnn39eZ599dnBrRckQ\nQCCSAhaA/z0rklWjUlkoUOwVsD37u3HjRo0aNUonnniicnNzdcMNN+j444/3ZsTKQi+qjAACPgq0\naijtcWvBrPzex0KQNQIpEig2ANujRzVr1vSCcPfu3TV16lQv2wYNGujrr79OURFIBgEEECi5wBFu\nVqyZS0t+PEciEFSBpF3Q11xzjQ4//HDvWWBbkMGeA3733Xf10UcfBbVOlAsBBCIsYLNivfW5dEbP\nCFeSqmWFQLFXwCZw/fXXe+sB24hnG5DVrVs3jRs3Tm3bts0KICqJAALBEujZSvpshbR7T7DKRWkQ\nKK1A0gDcsWNHVatWzUu3devWGj16tPr27VvafDgeAQQQSIlALffryO4Fz2M58pR4koh/AkkDcIsW\nLTR37lz/SkjOCCCAwAECvdu41ZGWHLCTHxEImUDSAGzP/J533nlq3LixbPnB+NfEiRNDVlWKiwAC\nURHo1cYNxHITcrAhEGaBpIOwrMv5xhtvLFTH9u3bF9rHDgQQQCATAh2bSqs3Shu2SfVqZCJH8kAg\n9QJJA7DNAc2GAAIIBEmgouu7s8FY9jjS8Z2DVDLKgkDJBZIG4JNOOkmrVxdehPO+++7TCSecUPKc\nOBIBBBBIoYDNijVrKQE4haQklWGBpAH4tttu82bAsnLZTFifffaZ/va3v6l3794ZLirZIYAAAvsE\nLAA/88G+n3mFQNgEkgbgPn367Fcnm4ZyxYoV3jPBNjiLDQEEEPBDoHEdqVZVt0Thd1Lbxn6UgDwR\nKJ9A0lHQByZv80MvW7bMm57ywPf4GQEEEMikgF0F231gNgTCKJD0Ctju83777bde3Sz4rlu3TpUr\nV9ajjz4axvpSZgQQiJCABeBXZkg/OipClaIqWSOQNADfdddd2rlzZz5I9erVZcsSVqlSJX8fLxBA\nAAE/BLq3lO4cL+3YJVWr7EcJyBOBsgsk7YK2530nTJjgTT/Zv39//elPf9KcOXPKniNnIoAAAikS\nqOqCrj0T/OnyFCVIMghkUCBpAL7qqqu8+7179+71ijV48GBvRaT169dnsJhkhQACCCQW8GbFWpr4\nPfYiEGSBpAF42rRpeuSRR7z7vlYRW45w2LBheu2114JcL8qGAAJZIsBArCxp6AhWM2kArlWrlqZP\nn75f1SdPnqw6ddwzAGwIIICAzwL2CNJWN0zl200+F4TsESilQNIAfMcdd2jIkCEaNGiQLr30UrVs\n2dIbgHXGGWeUMisORwABBNIj0Kt1bFas9KROqgikRyDpKOgzzzxTM2bM0Pvvv6+tW7fq9ttvV5s2\nbdJTGlJFAAEEyiBg94E//FI6+fAynMwpCPgkkPQKeNOmTRo7dqyGDx+uG264QfZY0scff+xTcckW\nAQQQKCxg94Fnfy39MFa08AHsQSCAAkkDMKOgA9hqFAkBBPYTsCUJD64rzf9mv938gECgBZJ2Qdso\n6MWLF6tChQpeRWwU9Lx587xR0HZVzIYAAggEQcDuA89eJnVpHoTSUAYEkgskvQJmFHRyRI5AAAH/\nBXofIs1Y6n85KAECJRVIegUcHwXdq1cvbwT0pEmT1KlTJzEKuqTEHIcAApkQsCvfZWulLTvcKknV\nMpEjeSBQPoGkAZhR0OUD5mwEEMiMQI7rzzvczQ09y3VDH9shM3mSCwLlEUjaBW2J23zQV1xxha6/\n/notWrRI55xzjv71r3+VJ1/ORQABBFIuYKOhZy1NebIkiEBaBEoUgG0JwgceeMALxOeff74aN26s\nI488Mi0FIlEEEECgrALetJTuCpgNgTAIFNsF/eGHH+qxxx7TP/7xD7Vr107169fXp59+KluSkA0B\nBBAImkDz+lLFCtJyt1ZMywZBKx3lQWB/gYRXwF9++aV69Oihyy+/3Au89tjRM888o7p16xJ89/fj\nJwQQCJiAXQXPWBKwQlEcBBIIJAzANvvVqlWr1KdPH3Xt2lXNmjVLcCq7EEAAgeAJeN3QS4NXLkqE\nwIECCQOwPXL01Vdf6ZhjjtH999/vBeDf/e53ys3NPfB8fkYAAQQCJdDTTcjx2Upp155AFYvCIFBI\nIGEAtqNq166tESNG6L///a+3EIPdA/7iiy+8gVi2IMOaNWsKJcYOBBBAwG+BGlWktge5ILzC75KQ\nPwLFCxQZgAueZhNv3HfffVqxYoXuvfdeb33gqVOnFjyE1wgggEBgBJgVKzBNQUGKESh2FPSB51Wq\nVElnnXWW93Xge/yMAAIIBEXAuqHHvOlKMzAoJaIcCBQWKNEVcOHTyrbnzTff1CmnnKIhQ4ZowYIF\n+yXywQcfqG/fvvt9LV++XBMnTtTRRx+d/2WDw9gQQACB4gQ6NJXWbpHWby3uKN5DwF+BUl0Bl6eo\nmzdv1qhRo/TWW29p2bJlsmUOp0yZkp+kBdnJkyd7P7/33nt6+OGHvbmn7Tnkm266SSeddJL3XtWq\nVfPP4QUCCCCQSMAWb7PVkWYukU7omugI9iHgv0DGArBd8fbs2VP16tXzvjZu3OiNqq5SxY2YcFvF\nihVlwXXr1q1eoJ4wYYK3f/bs2d7Arz/+8Y+66KKL1KRJE2//gf+MGTPGG7ldcP/69etl+dj3A7c9\ne/Zo165dCd878Fh+Lp3Azp07PXdrU7bUCeTl5Xn/ZxJ9nlOXS3RSat+wsqbOz9ERzdzqDEk2+8za\nUx7bt29PciRvl1Zg9+7dgf89u3LlStlCQzNnzixUPZsFsnLlyoX2p2JHxgKwDeBq0GDf1DQWiNeu\nXVvoGeO//vWvGjp0qJo2dX1IbsvJyZH94rHAa49FWUC2JRIP3E4//XQveBfcb+sY2yxeiY634Ltt\n27aE7xVMg9elF7D/cDVq1JCNGWBLncDevXu9PxoTfZ5Tl0t0Ujq6vfTSzEqqWbOSW8+8+HrZ7xi7\nGKCHrXinsrxrf9wE/TNbp04dDRw4ULb40IFbOn+PZew3pM2itWWLuynzw2Z/aTZq1Cj+Y/73p556\nSn//+9/zfx4/fnz+61mzZmncuHG68MIL8/fFXxx66KHxl/nfDc4ep4pfZee/8cMLC+5FvXfgsfxc\ncgFztb8Y0/VXY8lLEq0jLQBbrwKf2ZK1a7OGUgP3t/qy76uofezv+SJPtM+s/b7AtkiiMr9Rwf31\nE3RXixMWhLt161bmepblxIz1EXbp0kVz5szxrmatW9h+mRzYKN9++61Xh9at3c0bt9kxNmjLrlRt\ns+eQMw3kZcw/CCAQSgFmxQpls2VNoTMWgK0L+eKLL9Zpp53mjYK+5557PGQbjBVf2nD+/Pne1Jdx\nfftr/8c//rHOPfdcHXfccWrevPl+78eP4zsCCCCQSMACsK0PzIZAEAUy1gVtlR85cqS3rrB19cQH\n6DzxxBP5LoMGDZJ9FdyGDRumSy65xBscUbNmzYJv8RoBBBAoVqBbC+mO16Ttbhbd6rHxnsUez5sI\nZFIgY1fA8UpZt3M8+Mb3JftuxxN8kynxPgIIHChQxV1idGomzfn6wHf4GQH/BTIegP2vMiVAAIFs\nEuA+cDa1drjqSgAOV3tRWgQQKKUA94FLCcbhGRMgAGeMmowQQMAPgTbuacedu6RvNviRO3kiULQA\nAbhoG95BAIGICNANHZGGjFg1CMARa1CqgwAChQV6tXHzQi8tvJ89CPgpQAD2U5+8EUAgIwK2MMOn\nK6Q9ezOSHZkgUCIBAnCJmDgIAQTCLFCnutS8njRvVZhrQdmjJkAAjlqLUh8EEEgo4I2GXprwLXYi\n4IsAAdgXdjJFAIFMCxxxiDRjaaZzJT8EihYgABdtwzsIIBAhgU4HS6vco0gbWfI3Qq0a7qoQgMPd\nfpQeAQRKKJDjftsd7uaGns3iDCUU47B0CxCA0y1M+gggEBiB3q4bmseRAtMcWV8QAnDWfwQAQCB7\nBHq3cfeBl2RPfalpsAUIwMFuH0qHAAIpFGhSV6rhliVcsiaFiZIUAmUUIACXEY7TEEAgnALMihXO\ndotiqQnAUWxV6oQAAkUKsDpSkTS8kWEBAnCGwckOAQT8FejeMjYjVu5uf8tB7ggQgPkMIIBAVglU\nd/eA2zdxc0Mvz6pqU9kAChCAA9goFAkBBNIrwH3g9PqSeskECMAlc+IoBBCIkIC3PjATckSoRcNZ\nFQJwONuNUiOAQDkEDnNd0Bu2Sms2lyMRTkWgnAIE4HICcjoCCIRTgFmxwtluUSo1AThKrUldEECg\nxAK9Wkuzlpb4cA5EIOUCBOCUk5IgAgiEQcAGYs1y94Hz8sJQWsoYRQECcBRblTohgEBSgQY1pcZ1\npAXfJD2UAxBIiwABOC2sJIoAAmEQYFasMLRSdMtIAI5u21IzBBBIIsB94CRAvJ1WAQJwWnlJHAEE\ngizQtYW02K2MtC03yKWkbFEVIABHtWWpFwIIJBWonCNZEP50hXvBhkCGBQjAGQYnOwQQCJbAoY2k\nZz+sor9NzxELNASrbaJeGgJw1FuY+iGAQJECX6yW7prguqHX5uiT5RV16C+ljduLPJw3EEipAAE4\npZwkhgACYRK44FHpqSukzTsqaORxu3XzadKYN8NUA8oaZgECcJhbj7IjgEC5BJrUlY5pL53Ta5ee\nmpqj4zpJqzaUK0lORqDEAgTgElNxIAIIRE2gQ1Ppz5Olnx6/QxVc5X76gtTG3RNmQyATApUykQl5\nIIAAAkEUuPVsNwp6lDRtUXXl7qmgrTul3XukPXulHC5PgthkkSoTH7FINSeVQQCB0gjYdJTLHpAu\nOipXIwft1qSb5AKxG5g1PhaES5MWxyJQWgECcGnFOB4BBCIlYM8C92q1Rz1a5amSe/2bMwjCkWrg\nAFeGABzgxqFoCCCQeQGCcObNszVHAnC2tjz1RgCBIgUIwkXS8EYKBQjAKcQkKQQQiI4AQTg6bRnU\nmhCAg9oylAsBBHwXsCD82zO5J+x7Q0S0AATgiDYs1UIAgdQI2ONIBOHUWJLK/gIE4P09+AkBBBAo\nJEAQLkTCjhQIEIBTgEgSCCAQfYGCQfhOnhOOfoNnoIYE4AwgkwUCCERDIB6EbbYsJuuIRpv6WQsC\nsJ/65I0AAqETsCD8GzcwaxdBOHRtF7QCE4CD1iKUBwEEAi9AEA58E4WigATgUDQThUQAgaAJEISD\n1iLhKw8BOHxtRokRQCAgAgThgDRESItBAA5pw1FsBBAIhkDBIMzo6GC0SVhKQQAOS0tRTgQQCKxA\nPAjbOsIE4cA2U+AKRgAOXJNQIAQQCKOABeFfu6UMCcJhbD1/ykwA9sedXBFAIIICBOEINmoaq0QA\nTiMuSSOAQPYJEISzr83LWmMCcFnlOA8BBBAoQqBgEP79uFi3dBGHsjuLBQjAWdz4VB0BBNInEA/C\neXkSQTh9zmFOmQAc5taj7AggEGgBC8Kj3cAsgnCgm8m3whGAfaMnYwQQyAYBgnA2tHLZ6kgALpsb\nZyGAAAIlFiAIl5gqqw4kAGdVc1NZBBDwS6BgEL7jNQZm+dUOQcqXAByk1qAsCCAQaYF4ELZKEoQj\n3dQlqhwBuERMHIQAAgikRoAgnBrHKKRCAI5CK1IHBBAIlQBBOFTNlbbCEoDTRkvCCCCAQNECBOGi\nbbLlnUrZUlHqiQACCARNIB6E7X7w6H+60lWQVq6PDdB67H+kOtWDVmLKk0oBroBTqUlaCCCAQCkF\nLAjfeIr0l8nSZyuk/3eRdE5v6YqnpO25pUyMw0MlQAAOVXNRWAQQiKLAB4ukH/eVereRXpomVXV9\nk3b1O/Z9afEaac1mKXd3Zmu+6Ftp/ioel0qnOl3Q6dQlbQQQQKAEAhVc13PDWrFpK//4rrR0rbTk\nO2nbTmnuSmnT9thXRXfJVNcFZgvOtavte20/J9pnx1Ypw2/5212X+DyXb6UcaeZS6aNf0x1egmYs\n9SFlaJpS58EJCCCAAALFCPRrJz0xSfr3bOnSftLfp7sA6K4+X/+5uxquvO/EHbukjT8E483ue/7r\nHdLX6/YFatu/2e2z7xVdcK/jgnU8SOd/L7CvYFB/eZo7b5v04shYvve/Lt36qvTghfvKwavUCBCA\nU+NIKggggECZBapXcfeAL5eufFr6hwu+rRpIn9+5f/C1xKu5YGxfTeqUPCsL2vEr6HhQjv+83A34\nstfx/RbUP/zK5d/Q/SHwhHTIQe5e9ADpqrElz48jSy5AAC65FUcigAACaROwLuWXfrjqTGUm8aDd\nuIRB+zf/kprXiw0Em7FE+smzscFhdh/6oNqpLBlpEYD5DCCAAAII5AvccILU9pfSdy7gtm/qBmJ9\n466AB8UC8dCubrBYn9j95/wTeFFmAUZBl5mOExFAAIHoCTRyg8FWj4l1c691QfiNn0u/Pcvdox4u\n7XTd2Vc8Kb38ceZHZUdP2g1yi2KlqBMCCCCAQNkF7J60XfUW3OrXlK4b4rqmj5Ce+UC63AXiS9yA\nsaFd3EAvLuUKUpX4NWwlpuJABBBAAIFm9aWbT5N+c6Y0eUFsgJY9x8xWegECcOnNOAMBBBDIegG7\nP3zX+dLIwdILH0n/94J7ZnlF1rOUCoAu6FJxcTACCCCAQEGBI9pI9vXefOmB190jTI1c97R7dHg7\noIcAAA7kSURBVKmN+85WvAABuHgf3kUAAQQQKIHAcZ2kYztIEz5xXdR/d9NqHhKbVKQEp2btIXRB\nZ23TU3EEEEAgtQK2sMQZPaWnroiNor72r9JzH1f3JvtIbU7RSI0AHI12pBYIIIBAYARsFLWNkP7z\nZdLuPRU0wq3s9KK7T2yPMbHtEyAA77PgFQIIIIBACgXq1ZCGH71Nf7hEWubmqrZHl/7juqj37E1h\nJiFOigAc4saj6AgggEAYBJrWlW46VbrtbGmqe2Tp6rHS+wvDUPL0lpEAnF5fUkcAAQQQ+EGgXRPp\nzvOka4+X/uZm0/rf56VPl2cvD6Ogs7ftqTkCCCDgi0DP1tLD7muSm8jjoTelZm7xh8uPlQ51qy9l\n00YAzqbWpq4IIIBAgAQGdZQGtHf3hT+VRv9T6tlKGtbfjaB2XdbZsNEFnQ2tTB0RQACBgArYo0un\n95CevNxdCdeXrn9Oevw9aeP2WIGnuyURH3gjtm/XnoBWoozFIgCXEY7TEEAAAQRSJ2CPLl18tHt0\nyQXivDzpSvfo0s9edHNNPy21aywtXC11ulnasiN1efqdEgHY7xYgfwQQQACBfIG61WPzS//eDdZ6\n1q26ZMG3cR3pwQtjKzQ9OSX/0NC/IACHvgmpAAIIIBA9geqVpRO7Snf/SPp8Zax+R7rpLddvjU5d\nCcDRaUtqggACCERGwJ4dtm7p/7rnhkcMlOz+7+kPSf3aRaaKYhR0dNqSmiCAAAKREaiUE7v67ezu\n+749T9qwzT2ydJG7Ku4WmSoSgKPTlNQEAQQQiJZAo1rSSnfVu3iNVKuq1NyNko7SxhVwlFqTuiCA\nAAIRE6jsroQ7NI1YpX6oDveAo9mu1AoBBBBAIOACBOCANxDFQwABBBCIpgABOJrtSq0QQAABBAIu\nQAAOeANRPAQQQACBaAoQgKPZrtQKAQQQQCDgAgTggDcQxUMAAQQQiKYAATia7UqtEEAAAQQCLkAA\nDngDUTwEEEAAgWgKEICj2a7UCgEEEEAg4AIE4IA3EMVDAAEEEIimAAE4mu1KrRBAAAEEAi5AAA54\nA1E8BBBAAIFoChCAo9mu1AoBBBBAIOACBOCANxDFQwABBBCIpgABOJrtSq0QQAABBAIuQAAOeANR\nPAQQQACBaAoQgKPZrtQKAQQQQCDgAgTggDcQxUMAAQQQiKYAATia7UqtEEAAAQQCLlAp4OUrV/Ea\nNWqkqVOnaujQoYXS2bZtm9avX68WLVoUeo8d5RNYsWKFGjZsqOrVq5cvIc7eT2DPnj0y29atW++3\nnx/KL7B69Wrv81q3bt3yJ0YK+wksXbpUbdq02W9f0H6YNWuW3nrrrYwXq0Ke2zKeawAy/Pzzz/XY\nY4/pkUceCUBpolWEK6+8Ur/61a/Url27aFXM59ps2bJFF154ocaNG+dzSaKX/e23367+/ftr8ODB\n0auczzUaNGiQJk2a5HMpgpk9XdDBbBdKhQACCCAQcQECcMQbmOohgAACCARTgAAczHahVAgggAAC\nERcgAEe8gakeAggggEAwBbI2ANso3YEDBwazVUJeKhvIUq9evZDXInjFr1Klik477bTgFSwCJTry\nyCN5IiJN7XjOOeekKeXwJ5u1o6DD33TUAAEEEEAgzAJZewUc5kaj7AgggAAC4RcgAIe/DakBAggg\ngEAIBQjAIWw0iowAAgggEH4BAnD425AaIIAAAgiEUIAAHMJGC3KRzz//fB199NHel03vx1Z+gVtu\nuUUTJkzIT+jNN9/UKaecoiFDhmjBggX5+3lROoHc3FydeOKJ+v77770T16xZk//Ztc9wQfPSpZzd\nR996663eaP2rrrpKy5Yt8zD4zBbxmbC5oNkQSIXA1q1b84466qi8HTt2eF+7du1KRbJZm8bmzZvz\nLr300ryDDz447x//+IfnsGnTprzevXvnuaCRN2fOnLwBAwZkrU95Kr5w4cK8Y489Nq9+/fp5a9eu\n9ZKaOHFi3s9+9rP8z69b/KI8WWTlua+//nreNddck+85YsSIPD6zRX8UuAIu4g8TdpdeYO7cuWra\ntKm3yMXkyZOVk5NT+kQ4I1/AVuu66KKLdPnll+fvsyvenj17es9Zd+/eXRs3bpRdybGVTsBWP3r8\n8cfVuXPn/BNnz56tqlWrasyYMVq0aJEqVuTXYz5OCV9Yz8E999zjHW2roa1cudLrpeEzmxiQT1hi\nF/aWQcC68GrWrKmuXbvq+eef1+9+97sypMIpcYFWrVrppJNOiv/ofbflCBs0aJC/zyY8cVdw+T/z\nomQCrudAnTp12u9gW6K0QoUK6tatm2xFL/sjkq10AracY506dbzAe8MNN+i2227zltDkM5vYMdLr\nASeuMnvTJWCzNMVnarKZheyv4d/+9rfpyi4r07VfcLYsYXzbvn27bN1rtvILWLCIb7b28gsvvMBs\neXGQUnxfsmSJbPYr60mw3wPuVgqf2SL8uAIuAobdpRd4+eWX89dX/vLLL/fr3it9apyRSKBLly5y\n937l7ip53c979+6VTVHJVn4Bd/9X06dP9xL64osvvCvh8qeaXSmsWrVK5513nsaOHSt3j92rPJ/Z\noj8DXAEXbcM7pRSwq1+7Z2ldd/YLzP4TsqVWoEmTJrr44ou9nobvvvsu/35banPJztTcgDfdfPPN\n3n1gN3BIr7zySnZClKPWd9xxh9flPHz4cC+Vtm3byg0g5DNbhClzQRcBw+6yC1gXaa1atcqeAGcm\nFbCBV5UqVWKgUFKp0h9gXaa1a9cu/YmcUawAn9nCPATgwibsQQABBBBAIO0C3ANOOzEZIIAAAggg\nUFiAAFzYhD0IIIAAAgikXYAAnHZiMkAAAQQQQKCwAAG4sAl7EEAAAQQQSLsAATjtxGSAAAIIIIBA\nYQECcGET9iCAAAIIIJB2AQJw2onJAAEEEEAAgcICBODCJuxBAAEEEEAg7QIE4LQTkwECxQssX77c\nO2Dnzp2y6SXZEEAgOwQIwNnRztQyoAK25u8ZZ5zhle7VV1/Vfffd570eNGiQTjjhhP1KvW7dOm+5\nPFupp7jtV7/6lUaPHl3cId6iAx07dkx4zC9+8QtWsUoow04EUivAYgyp9SQ1BEolMG3aNPXt29c7\n58MPP8xfQcZ2TJ06VU8//bQuu+yyUqVpCwrYurZsCCAQbAGugIPdPpQuogJz586VXYFacP3nP//p\nvX7yySf185//XAsWLPBqfeONN3qr83z77bcJFWzVqe7du6tevXre+qtr1671jrN0LHDb9vXXX+vU\nU09Vw4YNvbzOPfdcffbZZ957u3bt0vXXXy9bLL13797eClbeG+6fhQsX6ogjjtBBBx2kX/7yl4pf\nda9cuVJ2hdysWTMdfvjhevfdd71TPvnkE9kKOKeccopXl40bN+ryyy/3yta6dWtWbYrD8h2BAgIE\n4AIYvEQgUwIdOnTQxIkTvSD2zDPP6PXXX1fdunU1adIk2RJuttk6qhbULEgeuK1Zs0ann366Fxzn\nz5/vnXvXXXd5h9l95HgwtqUL27VrJwv4derU8ZbY27Fjh3fc4sWL1bRpU82bN89bu/mmm27Kz2b8\n+PFeN/Q777yjcePGycpomy03aV3htm7uddddpzPPPFO2Buz27dv13HPP6aijjtL999+vN954Q7Ym\n9FdffeW9/v3vf+/9nJ8BLxBAQLawNxsCCPgk0L59+zwXvPIWLVqUd9xxx+WXYuDAgXkvv/xy3tat\nW/PcFWSeuz+c54Jqnvudlbd79+68xx9/PM91Xee5K03vy853V9Te+e7KOW/UqFF5q1evzqtYsWKe\nu8/s7f/+++/zcnJy8lzwzPv444/z3JKR+fm5K9m8rl27ej+7q/A8d186/73bbrst7+STT85zg8W8\n/FesWJH/Xo8ePfIeeeSRPNd9nlezZs38/e6qPq9NmzZ5r732Wp4L+N5X/pu8QAABT4ArYP4KQ8AH\nAevKveWWW7xRz7aI+a9//Wu5AOkNnnKBM79ENWrU0MMPP6yf/OQnsm7d+OaCoHdVa1fS9jVgwABt\n2LBBlm58sytcFwRVv359b5d1VdvVcHyzbuT4Zu/Fr4xtX/y+tL22rmi7yl22bJlatmyp5s2b225v\ns+PsPdtatGjhfbd/zjrrLO9q+YorrlCTJk28K3Ub5c2GAAL7BAjA+yx4hUDGBNyVqNeVa8HT7sF+\n8803Xne0vbb3Cm7W1XzkkUfK7gnHN+vq7devn3eenWtfM2fO9O7Nxo+x+8O23wKzbVu2bPG6hOPv\nFzdQq2Agty5q66q2+8EWbOPpWTp2P/mQQw7xkixYbgu2dj/bjn/hhRe8buyxY8d6x/EPAgjEBAjA\nfBIQ8EHAApoNYrJBUT/72c+8+7P23b4s0B24/eEPf/Dupcb3DxkyRDaCevbs2d4uu/960kknae/e\nvfFDZFfPxxxzjHdPdtOmTXrggQfkuq/z3y/uxVtvveUFbAu2NkjMBlfZvWkLtn/5y1/s1pXmzJnj\nBf2CV8vxNF966SX96Ec/8kZju+5r7yo9/h7fEUAgJkAA5pOAgE8CFsDcPVQvdxtI1blz5yJL0qpV\nq/2eza1evbruvPNOr+vZrqJt4JO7L1zo6tkC99tvv+0FTuuStuBepUqVIvOJv2EjtK1s1mVto5iv\nvvpqL+1nn31Wjz76qLdv6NCh3mt37zh+Wv73Sy+9VO6esBe0rezuXrTXJZ1/AC8QQEAV7E4wDggg\nkHkB655t1KiRFxCXLl3q3a8tbSns8SC7SrXHjA7c7L+2BUwbCV2pUiW5AV1q3LixlixZ4n0/8PgD\nf7bHlOwcuz984GYjrS2YF9eNbefYfeXc3FzvCv/ANPgZgWwXIABn+yeA+kdawK5ErdvZBmm98sor\n3pWrPSfMhgAC/gsQgP1vA0qAQNoE7Ap0ypQp3v1aG5Rl01tadzAbAgj4L0AA9r8NKAECCCCAQBYK\n8KdwFjY6VUYAAQQQ8F+AAOx/G1ACBBBAAIEsFCAAZ2GjU2UEEEAAAf8FCMD+twElQAABBBDIQgEC\ncBY2OlVGAAEEEPBfgADsfxtQAgQQQACBLBQgAGdho1NlBBBAAAH/BQjA/rcBJUAAAQQQyEKB/w9/\n7wCD8T3G4gAAAABJRU5ErkJggg==\n"
}
],
"prompt_number": 12
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Predictions\n",
"--------------------------------------------------------\n",
"Since the output of `train` contains the final model object, you can use its `predict` methods as usual:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"head(predict(knnFit$finalModel, newdata = testDescr))"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
" M R\n",
"[1,] 1 0\n",
"[2,] 0 1\n",
"[3,] 0 1\n",
"[4,] 1 0\n",
"[5,] 0 1\n",
"[6,] 0 1\n"
]
}
],
"prompt_number": 13
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"source": [
"However, `predict`, can have nuanced syntax depending upon the model in question. Instead, we can use `caret` functions `extractPrediction` and `extractProb` to handle all of the inconsistent syntax. \n",
"\n",
"It can also handle multiple models at once."
]
},
{
"cell_type": "heading",
"level": 2,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Using `extractPrediction` to Get Class Predictions"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"predValues <- extractPrediction(list(\n",
" knnFit,\n",
" logFit),\n",
" testX = testDescr,\n",
" testY = testClass)\n",
"testValues <- subset(predValues, dataType == \"Test\")\n",
"str(testValues)"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"'data.frame':\t102 obs. of 5 variables:\n",
" $ obs : Factor w/ 2 levels \"M\",\"R\": 2 2 2 2 2 2 2 2 2 2 ...\n",
" $ pred : Factor w/ 2 levels \"M\",\"R\": 1 2 2 1 2 2 2 2 2 2 ...\n",
" $ model : Factor w/ 2 levels \"glm\",\"knn\": 2 2 2 2 2 2 2 2 2 2 ...\n",
" $ dataType: Factor w/ 2 levels \"Test\",\"Training\": 1 1 1 1 1 1 1 1 1 1 ...\n",
" $ object : Factor w/ 2 levels \"Object1\",\"Object2\": 1 1 1 1 1 1 1 1 1 1 ...\n"
]
}
],
"prompt_number": 14
},
{
"cell_type": "heading",
"level": 1,
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"Using `extractProb` to Get Class Probabilities"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"probValues <- extractProb(list(knnFit, logFit),\n",
" testX = testDescr,\n",
" testY = testClass)\n",
"testProbs <- subset(probValues,\n",
" dataType == \"Test\")\n",
"str(testProbs)"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"'data.frame':\t102 obs. of 7 variables:\n",
" $ M : num 1 0 0 1 0 0 0 0 0 0 ...\n",
" $ R : num 0 1 1 0 1 1 1 1 1 1 ...\n",
" $ obs : Factor w/ 2 levels \"M\",\"R\": 2 2 2 2 2 2 2 2 2 2 ...\n",
" $ pred : Factor w/ 2 levels \"M\",\"R\": 1 2 2 1 2 2 2 2 2 2 ...\n",
" $ model : chr \"knn\" \"knn\" \"knn\" \"knn\" ...\n",
" $ dataType: chr \"Test\" \"Test\" \"Test\" \"Test\" ...\n",
" $ object : chr \"Object1\" \"Object1\" \"Object1\" \"Object1\" ...\n"
]
}
],
"prompt_number": 15
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Evaluating Performance\n",
"--------------------------------------------------------\n",
"For classification models, there are functions to compute the confusion matrix and associated statistics. There are also functions for two\u2013class problems: `sensitivity`, `specificity` and so on.\n",
"\n",
"The function `confusionMatrix` calculates statistics for a data set. The no\u2013information rate (NIR) is estimated as the largest class proportion in the data set. A one\u2013sided statistical test is done to see if the observed accuracy is greater than the NIR."
]
},
{
"cell_type": "heading",
"level": 2,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Confusion Matrices and Statistics"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"knnPred <- subset(testValues, model == \"knn\")\n",
"confusionMatrix(knnPred$pred, knnPred$obs)"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"Confusion Matrix and Statistics\n",
"\n",
" Reference\n",
"Prediction M R\n",
" M 22 4\n",
" R 5 20\n",
" \n",
" Accuracy : 0.8235 \n",
" 95% CI : (0.6913, 0.916)\n",
" No Information Rate : 0.5294 \n",
" P-Value [Acc > NIR] : 1.117e-05 \n",
" \n",
" Kappa : 0.6467 \n",
" Mcnemar's Test P-Value : 1 \n",
" \n",
" Sensitivity : 0.8148 \n",
" Specificity : 0.8333 \n",
" Pos Pred Value : 0.8462 \n",
" Neg Pred Value : 0.8000 \n",
" Prevalence : 0.5294 \n",
" Detection Rate : 0.4314 \n",
" Detection Prevalence : 0.5098 \n",
" Balanced Accuracy : 0.8241 \n",
" \n",
" 'Positive' Class : M \n",
" \n"
]
}
],
"prompt_number": 16
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"logPred <- subset(testValues, model == \"glm\")\n",
"confusionMatrix(logPred$pred, logPred$obs)"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"Confusion Matrix and Statistics\n",
"\n",
" Reference\n",
"Prediction M R\n",
" M 14 5\n",
" R 13 19\n",
" \n",
" Accuracy : 0.6471 \n",
" 95% CI : (0.5007, 0.7757)\n",
" No Information Rate : 0.5294 \n",
" P-Value [Acc > NIR] : 0.06052 \n",
" \n",
" Kappa : 0.3045 \n",
" Mcnemar's Test P-Value : 0.09896 \n",
" \n",
" Sensitivity : 0.5185 \n",
" Specificity : 0.7917 \n",
" Pos Pred Value : 0.7368 \n",
" Neg Pred Value : 0.5937 \n",
" Prevalence : 0.5294 \n",
" Detection Rate : 0.2745 \n",
" Detection Prevalence : 0.3725 \n",
" Balanced Accuracy : 0.6551 \n",
" \n",
" 'Positive' Class : M \n",
" \n"
]
}
],
"prompt_number": 17
},
{
"cell_type": "heading",
"level": 1,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Neural Networks"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"History of Neural Networks\n",
"========================================================\n",
"* The Neuron Doctrine (1899)\n",
"* The Perceptron (1943)\n",
"* Parallel Distributed Processing (1986)\n",
"* Deep Learning"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"THE NEURON DOCTRINE ~1899\n",
"--------------------------------------------------------\n",
"<img src=\"assets/Ramon_y_Cajal.png\" width=350/> \n",
"Santiago Ramon y Cajal (1852-1934)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"<img src=\"assets/golgi.png\" /><UL>\n",
"<LI>Neurons are the fundamental processing unit of the brain</LI>\n",
"<LI>Receive input from many sources</LI>\n",
"<LI>Direct output to many other neurons</LI>\n",
"</UL>"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"<H2>The Model of Neuron (1943)</H2>\n",
"<TABLE>\n",
"<TR><TD><IMG SRC=\"assets/pitts.png\" width=200 />Walter Pitts (1923 - 1969)</TD>\n",
" <TD><IMG SRC=\"assets/pitts-mcculloch.jpg\" width=400 /></TD>\n",
" <TD><IMG SRC=\"assets/McCulloch.png\" width=200 />Warren McCulloch (1898 - 1969)</TD>\n",
"</TR>\n",
"</TABLE>"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"<H2>Parallel Distributed Processing (PDP) (1986)</H2>\n",
"<TABLE>\n",
"<TR><TD><IMG SRC=\"assets/Rumelhart.png\" width=200 />David Rumelhart (1942 - 2011)</TD>\n",
" <TD><IMG SRC=\"assets/pdp.png\" width=400 /></TD>\n",
" <TD><IMG SRC=\"assets/McClelland.png\" width=200 />James McClelland (1948 - )</TD></TR>\n",
"</TABLE>"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"<H2>Deep Learning</H2>\n",
"<img src=\"assets/AI_01-test-3.jpg\" width=600 />\n",
"Geoffrey Hinton (1947 - )"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"What Are Artificial Neural Networks?\n",
"--------------------------------------------------------\n",
"(this section lovingly adapted from Vincent Cheung and Kevin Cannons)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"* An extremely simplified model of the brain\n",
"* Essentially a function approximator\n",
" - Transforms inputs into outputs to the best of its ability"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"- Composed of many \"neurons\" that co-operate to perform the desired function"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"\"Neurons,\" in this case, can be thought of as logistic regressors."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"What Are They Used For?\n",
"--------------------------------------------------------\n",
"* Classification\n",
" - Pattern recognition, feature extraction, image matching\n",
"* Noise Reduction\n",
" - Recognize patterns in the inputs and produce noiseless outputs\n",
"* Prediction\n",
" - Extrapolation based on historical data"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Why Use Neural Networks?\n",
"--------------------------------------------------------\n",
"* Ability to learn\n",
" - NN\u2019s figure out how to perform their function on their own \n",
" - Determine their function based only upon sample inputs\n",
"* Ability to generalize\n",
" - i.e. produce reasonable outputs for inputs it has not been taught how to deal with"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"How Do Neural Networks Work?\n",
"--------------------------------------------------------\n",
"\n",
"* The output of a neuron is a function of the weighted sum of the inputs plus a bias\n",
"\n",
" $$ Output = f(i_1w_1 + i_2w_2 + \\ldots + i_nw_n + bias) $$ \n",
" \n",
" \n",
"* The function of the entire neural network is simply the computation of the outputs of all the neurons\n",
" - An entirely deterministic calculation"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Activation Functions\n",
"--------------------------------------------------------\n",
"* Applied to the weighted sum of the inputs of a neuron to produce the output\n",
"* Majority of NN\u2019s use sigmoid functions\n",
" - Smooth, continuous, and monotonically increasing (derivative is always positive)\n",
" - Bounded range - but never reaches max or min\n",
"* Consider \u201cON\u201d to be slightly less than the max and \u201cOFF\u201d to be slightly greater than the min\n",
"\n",
"<img src=\"assets/logistic_regression1.png\" />"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Activation Functions\n",
"--------------------------------------------------------\n",
"* The most common sigmoid function used is the logistic function\n",
" - $f(x) = \\frac{1}{(1 + e^{-x})}$\n",
" - The calculation of derivatives are important for neural networks and the logistic function has a very nice derivative\n",
" * $f\u2019(x) = f(x)(1 - f(x))$\n",
"* Other sigmoid functions also used \n",
" - hyperbolic tangent\n",
" - arctangent\n",
"* The exact nature of the function has little effect on the abilities of the neural network"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Where Do The Weights Come From?\n",
"--------------------------------------------------------\n",
"* The weights in a neural network are the most important factor in determining its function\n",
"* Training is the act of presenting the network with some sample data and modifying the weights to better approximate the desired function\n",
"* There are two main types of training\n",
" - Supervised Training\n",
" - Unsupervised Training"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Supervised Training\n",
"* Supplies the neural network with inputs and the desired outputs\n",
"* Response of the network to the inputs is measured\n",
" - The weights are modified to reduce the difference between the actual and desired outputs"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"# Unsupervised Training\n",
"* Only supplies inputs\n",
"* The neural network adjusts its own weights so that similar inputs cause similar outputs\n",
" - The network identifies the patterns and differences in the inputs without any external assistance"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Where Do The Weights Come From?\n",
"--------------------------------------------------------\n",
"* Epoch\n",
" - One iteration through the process of providing the network with an input and updating the network's weights\n",
" - Typically many epochs are required to train the neural network"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Perceptrons\n",
"--------------------------------------------------------\n",
"* First neural network with the ability to learn\n",
"* Made up of only input neurons and output neurons\n",
"* Input neurons typically have two states: ON and OFF\n",
"* Output neurons use a simple threshold activation function\n",
"* In basic form, can only solve linear problems \n",
" - Limited applications\n",
"<IMG SRC=\"assets/pitts-mcculloch.jpg\" />"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"How Do Perceptrons Learn?\n",
"--------------------------------------------------------\n",
"* Uses supervised training\n",
"* If the output is not correct, the weights are adjusted according to the formula:\n",
" - $w_{new} = w_{old} + \\alpha(desired - output) \\times input$ \n",
" _<small>$\\alpha$ is the learning rate</small>_"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"Example: \n",
"Given input: $[1, 0, 1]$ \n",
"and initial weights: $[0.5, 0.2, 0.8]$"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"Assuming Output Threshold = 1.2 \n",
"$1 \\times 0.5 + 0 \\times 0.2 + 1 \\times 0.8 = 1.3 > 1.2$"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"Assume Output was supposed to be 0 \n",
"-> update the weights\n",
"\n",
"Assume $\\alpha = 1; \n",
"\\\\ W_{1_{new}} = 0.5 + 1\\times(0-1)\\times1 = -0.5 \n",
"\\\\ W_{2_{new}} = 0.2 + 1\\times(0-1)\\times0 = 0.2 \n",
"\\\\ W_{3_{new}} = 0.8 + 1\\times(0-1)\\times1 = -0.2 $"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Multilayer Feedforward Networks\n",
"--------------------------------------------------------\n",
"* Most common neural network \n",
"* An extension of the perceptron\n",
" - Multiple layers\n",
" * The addition of one or more \u201chidden\u201d layers in between the input and output layers\n",
" - Activation function is not simply a threshold\n",
" * Usually a sigmoid function\n",
" - A general function approximator\n",
" * Not limited to linear problems\n",
"* Information flows in one direction\n",
" - The outputs of one layer act as inputs to the next layer"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"XOR Example\n",
"--------------------------------------------------------\n",
"<img src=\"assets/perceptron-xor-task.png\" />\n",
"\n",
"*N.B. This is impossible for logistic regression and exemplifies the difference between a linear and non-linear model*"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Backpropagation\n",
"--------------------------------------------------------\n",
"* Most common method of obtaining the many weights in the network\n",
"* A form of supervised training\n",
"* The basic backpropagation algorithm is based on minimizing the error of the network using the derivatives of the error function\n",
" - Simple\n",
" - Slow\n",
" - Prone to local minima issues"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Backpropagation\n",
"--------------------------------------------------------\n",
"* Most common measure of error is the mean square error: \n",
" $E = (target \u2013 output)^2$\n",
"* Partial derivatives of the error wrt the weights:\n",
" - Output Neurons: \n",
" let: $\\delta = f'(net_j)(target_j-output_j)$ \n",
" $\\frac{\\delta\\ E}{\\delta\\ w_{ij}} = -output_i\\delta_j$ \n",
" <small>j = output neuron; i = neuron in last hidden </small>\n",
" - Hidden Neurons: \n",
" let: $\\delta_j = f'(net_j)\\sum{\\delta_kw_{kj}}$ \n",
" $\\frac{\\delta\\ E}{\\delta\\ w_{ij}} = -output_i\\delta_j$ \n",
" <small>j = hidden neuron; i = neuron in previous layer; k=neuron in next layer</small>\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Backpropagation\n",
"--------------------------------------------------------\n",
"* Calculation of the derivatives flows backwards through the network, hence the name, backpropagation\n",
"* These derivatives point in the direction of the maximum increase of the error function\n",
"* A small step (learning rate) in the opposite direction will result in the maximum decrease of the (local) error function: \n",
" $w_{new} = w_{old} - \\alpha\\frac{\\delta E}{\\delta w_{old}}$ \n",
" where $\\alpha$ is the learning rate"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Backpropagation\n",
"--------------------------------------------------------\n",
"* The learning rate is important\n",
" - Too small\n",
" * Convergence extremely slow\n",
" - Too large\n",
" * May not converge\n",
"* Momentum\n",
" - Tends to aid convergence\n",
" - Applies smoothed averaging to the change in weights: \n",
" $\\Delta_{new} = \\beta \\Delta_{old} - \\alpha \\frac{\\delta E}{\\delta w_{old}}$ \n",
" $\\beta$ is the momentum coefficient\n",
" $w_{new} = w_{old} + \\Delta_{new}$\n",
" - Acts as a low-pass filter by reducing rapid fluctuations"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Local Minima\n",
"--------------------------------------------------------\n",
"* Training is essentially minimizing the mean square error function\n",
" - Key problem is avoiding local minima\n",
" - Traditional techniques for avoiding local minima:\n",
" * Simulated annealing\n",
" - Perturb the weights in progressively smaller amounts\n",
" * Genetic algorithms\n",
" - Use the weights as chromosomes\n",
" - Apply natural selection, mating, and mutations to these chromosomes"
]
},
{
"cell_type": "heading",
"level": 1,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Neural Networks in Practice"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"library(nnet)\n",
"library(devtools)\n",
"source_url('https://gist.github.com/fawda123/7471137/raw/c720af2cea5f312717f020a09946800d55b8f45b/nnet_plot_update.r')"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"SHA-1 hash of file is 3e535ef9cbcad648f0fffb89a8879e12c09be1e7\n"
]
}
],
"prompt_number": 18
},
{
"cell_type": "heading",
"level": 2,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Unsupervised"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"eight <- data.frame(X1=c(1, rep(0, 7)), X2=c(0,1,rep(0,6)), X3=c(0,0,1,rep(0,5)), X4=c(0,0,0,1,rep(0,4)), \n",
" X5=c(rep(0,4),1,0,0,0), X6=c(rep(0,5),1,0,0), X7=c(rep(0,6),1,0), X8=c(rep(0,7),1))\n",
"eight"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
" X1 X2 X3 X4 X5 X6 X7 X8\n",
"1 1 0 0 0 0 0 0 0\n",
"2 0 1 0 0 0 0 0 0\n",
"3 0 0 1 0 0 0 0 0\n",
"4 0 0 0 1 0 0 0 0\n",
"5 0 0 0 0 1 0 0 0\n",
"6 0 0 0 0 0 1 0 0\n",
"7 0 0 0 0 0 0 1 0\n",
"8 0 0 0 0 0 0 0 1\n"
]
}
],
"prompt_number": 24
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"library(nnet)\n",
"eight.net <- nnet(x = eight, y = eight, size = 3)"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"# weights: 59\n",
"initial value 19.013140 \n",
"iter 10 value 6.037264\n",
"iter 20 value 2.095977\n",
"iter 30 value 0.048524\n",
"iter 40 value 0.000155\n",
"final value 0.000067 \n",
"converged\n"
]
}
],
"prompt_number": 37
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"plot(eight.net)"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"Loading required package: scales\n",
"Loading required package: reshape\n",
"Loading required package: plyr\n",
"\n",
"Attaching package: \u2018reshape\u2019\n",
"\n",
"The following objects are masked from \u2018package:plyr\u2019:\n",
"\n",
" rename, round_any\n",
"\n",
"The following object is masked from \u2018package:class\u2019:\n",
"\n",
" condense\n",
"\n"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAeAAAAHgCAYAAAB91L6VAAAEJGlDQ1BJQ0MgUHJvZmlsZQAAOBGF\nVd9v21QUPolvUqQWPyBYR4eKxa9VU1u5GxqtxgZJk6XtShal6dgqJOQ6N4mpGwfb6baqT3uBNwb8\nAUDZAw9IPCENBmJ72fbAtElThyqqSUh76MQPISbtBVXhu3ZiJ1PEXPX6yznfOec7517bRD1fabWa\nGVWIlquunc8klZOnFpSeTYrSs9RLA9Sr6U4tkcvNEi7BFffO6+EdigjL7ZHu/k72I796i9zRiSJP\nwG4VHX0Z+AxRzNRrtksUvwf7+Gm3BtzzHPDTNgQCqwKXfZwSeNHHJz1OIT8JjtAq6xWtCLwGPLzY\nZi+3YV8DGMiT4VVuG7oiZpGzrZJhcs/hL49xtzH/Dy6bdfTsXYNY+5yluWO4D4neK/ZUvok/17X0\nHPBLsF+vuUlhfwX4j/rSfAJ4H1H0qZJ9dN7nR19frRTeBt4Fe9FwpwtN+2p1MXscGLHR9SXrmMgj\nONd1ZxKzpBeA71b4tNhj6JGoyFNp4GHgwUp9qplfmnFW5oTdy7NamcwCI49kv6fN5IAHgD+0rbyo\nBc3SOjczohbyS1drbq6pQdqumllRC/0ymTtej8gpbbuVwpQfyw66dqEZyxZKxtHpJn+tZnpnEdrY\nBbueF9qQn93S7HQGGHnYP7w6L+YGHNtd1FJitqPAR+hERCNOFi1i1alKO6RQnjKUxL1GNjwlMsiE\nhcPLYTEiT9ISbN15OY/jx4SMshe9LaJRpTvHr3C/ybFYP1PZAfwfYrPsMBtnE6SwN9ib7AhLwTrB\nDgUKcm06FSrTfSj187xPdVQWOk5Q8vxAfSiIUc7Z7xr6zY/+hpqwSyv0I0/QMTRb7RMgBxNodTfS\nPqdraz/sDjzKBrv4zu2+a2t0/HHzjd2Lbcc2sG7GtsL42K+xLfxtUgI7YHqKlqHK8HbCCXgjHT1c\nAdMlDetv4FnQ2lLasaOl6vmB0CMmwT/IPszSueHQqv6i/qluqF+oF9TfO2qEGTumJH0qfSv9KH0n\nfS/9TIp0Wboi/SRdlb6RLgU5u++9nyXYe69fYRPdil1o1WufNSdTTsp75BfllPy8/LI8G7AUuV8e\nk6fkvfDsCfbNDP0dvRh0CrNqTbV7LfEEGDQPJQadBtfGVMWEq3QWWdufk6ZSNsjG2PQjp3ZcnOWW\ning6noonSInvi0/Ex+IzAreevPhe+CawpgP1/pMTMDo64G0sTCXIM+KdOnFWRfQKdJvQzV1+Bt8O\nokmrdtY2yhVX2a+qrykJfMq4Ml3VR4cVzTQVz+UoNne4vcKLoyS+gyKO6EHe+75Fdt0Mbe5bRIf/\nwjvrVmhbqBN97RD1vxrahvBOfOYzoosH9bq94uejSOQGkVM6sN/7HelL4t10t9F4gPdVzydEOx83\nGv+uNxo7XyL/FtFl8z9ZAHF4bBsrEwAAQABJREFUeAHs3QegHVWdP/AD6b0ACZ2AgCJFULBgQ6UI\nrGXXFde1oVj+1hUVuy5iAQV777i6YO+gIq4oWEFUpElogZBCQnpv/M9nwnmZN5l7372v5LXzg5fb\nZs7M/ObM7/vrZ6f7I4VMmQOZA5kDmQOZA5kDO5QDO+/Qo+WDZQ5kDmQOZA5kDmQOFBzIAJwnQuZA\n5kDmQOZA5kA/cCADcD8wPR8ycyBzIHMgcyBzIANwngOZA5kDmQOZA5kD/cCBDMD9wPR8yMyBzIHM\ngcyBzIEMwHkOZA5kDmQOZA5kDvQDBzIA9wPT8yEzBzIHMgcyBzIHMgDnOZA5kDmQOZA5kDnQDxzI\nANwPTM+HzBzIHMgcyBzIHMgAnOdA5kDmQOZA5kDmQD9wIANwPzA9HzJzIHMgcyBzIHMgA3CeA5kD\nmQOZA5kDmQP9wIEMwP3A9HzIzIHMgcyBzIHMgQzAeQ5kDmQOZA5kDmQO9AMHMgD3A9PzITMHMgcy\nBzIHMgcyAOc5kDmQOZA5kDmQOdAPHMgA3A9Mz4fMHMgcyBzIHMgcyACc50DmQOZA5kDmQOZAP3Ag\nA3A/MD0fMnMgcyBzIHMgcyADcJ4DmQOZA5kDmQOZA/3AgQzA/cD0fMjMgcyBzIHMgcyBDMB5DmQO\nZA5kDmQOZA70AwcyAPcD0/MhMwcyBzIHMgcyBzIA5zmQOZA5kDmQOZA50A8cyADcD0zPh8wcyBzI\nHMgcyBzIAJznQOZA5kDmQOZA5kA/cCADcD8wPR8ycyBzIHMgcyBzIANwngOZA5kDmQOZA5kD/cCB\nDMD9wPR8yMyBzIHMgcyBzIEMwHkOZA5kDmQOZA5kDvQDBzIA9wPT8yEzBzIHMgcyBzIHMgDnOZA5\nkDmQOZA5kDnQDxzIANwPTM+HzBzIHMgcyBzIHMgAnOdA5kDmQOZA5kDmQD9wIANwPzA9HzJzIHMg\ncyBzIHMgA3CeA5kDmQOZA5kDmQP9wIEMwP3A9HzIzIHMgcyBzIHMgQzAeQ5kDmQOZA5kDmQO9AMH\nMgD3A9PzITMHMgcyBzIHMgcyAOc5kDmQOZA5kDmQOdAPHMgA3A9Mz4fMHMgcyBzIHMgcyACc50Dm\nQOZA5kDmQOZAP3AgA3A/MD0fMnMgcyBzIHMgcyADcJ4DmQOZA5kDmQOZA/3AgQzA/cD0fMjMgcyB\nzIHMgcyBDMB5DmQOZA5kDmQOZA70AwcyAPcD0/MhMwcyBzIHMgcyBzIA5zmQOZA5kDmQOZA50A8c\nyADcD0zPh8wcyBzIHMgcyBzIAJznQOZA5kDmQOZA5kA/cCADcD8wPR8ycyBzIHMgcyBzIANwngOZ\nA5kDmQOZA5kD/cCBDMD9wPR8yMyBzIHMgcyBzIEMwHkOZA5kDmQOZA5kDvQDBzIA9wPT8yEzBzIH\nMgcyBzIHMgDnOZA5kDmQOZA5kDnQDxzIANwPTM+HzBzIHMgcyBzIHMgAnOdA5kDmQOZA5kDmQD9w\nIANwPzA9HzJzIHMgcyBzIHMgA3CeA5kDmQOZA5kDmQP9wIEMwP3A9HzIzIHMgcyBzIHMgQzAeQ5k\nDmQOZA5kDmQO9AMHMgD3A9PzITMHMgcyBzIHMgcyAOc5kDmQOZA5kDmQOdAPHMgA3A9Mz4fMHMgc\nyBzIHMgcyACc50DmQOZA5kDmQOZAP3AgA3A/MD0fMnMgcyBzIHMgcyADcJ4DmQOZA5kDmQOZA/3A\ngQzA/cD0fMjMgcyBzIHMgcyBDMB5DmQOZA5kDmQOZA70AwcyAPcD0/MhMwcyBzIHMgcyBzIA5zmQ\nOZA5kDmQOZA50A8cyADcD0zPh8wcyBzIHMgcyBwYmVmQOZA5sI0DS9duCAtWrQvz49/K9ZvCxi33\nFz+O3HmnMHH0yLDHxLFh9/g3fdyosNNOO23bMb8bkhxYtm5jMRfmr1wbVm6I82HztvkwIc6H3SeM\nCXtMGht2GTc6z4chOQP69qJ2uj9S3x4ij545MLA54BGYu2JtuH7RirAigu7ajZtDs4di/MgRYeKY\nEeHQ3SaHfaeMDztnIB7YN7jNszMfKGDXLVwRlq/f2PV8GLVzGD9qZDEfZk3N86FNdg/rzTMAD+vb\nny9+VbRq/nzPkrBw1fqwbvOWthgyZsTOYbfxo8Oj9p4eJo8Z1da+eeOByYE1GzeFq+9ZWgDw2k3t\nzYfRI3aKlvCY8Og4H6aOzfNhYN7hgXVWGYAH1v3IZ7MDOXDfmg3hyrsWh6XRzdgTmhRdkSc+aEYG\n4Z4wcQDsy938mzmLwtK1G5t6QLo6VaGKp8zaNUwfP6arTfPvw5wDGYCH+QQYrpfP0vnxPxeEtZs2\n9woLxo7cOTx51m5hZowPZxp8HFgX58HF18/ttRPnHXnifruGvSaP67Ux80BDjwM5C3ro3dN8RV1w\nYHV0O1922729Br4Oty66K6+6+74iZtjF4fPPA4wDYv7mQ2/S+hjO+MPcJdGa3tCbw+axhhgHMgAP\nsRuaL6c5ByTY/DnG+Hrqdq47igSuP0WhuyXnNdaxZ8B+d838pWFJHwClrOk/xvmw6YFM+gHLgHxi\n/caBDMD9xvp84P7gwLyY3bpg9bo+O/TiNevDncvW9Nn4eeDe5cDCOB/uWbGuRzHfZmd0XwT225eu\nbrZJ/m0YcyAD8DC++cPx0q+PpSXcxX1F62Od6A2xnClbwX3F4d4d9/p7V/RqKKJ6durIb8zzocqW\n/PkBDmQAzlNh2HBgecxyVdfZU9q8aVNoVj4vxszyyTSwOaAEbUfcJ4l+965eP7CZkc+uXziQO2H1\nC9vzQfuDAzpcrYkJN3X08699IXz3kx8Mo8eMDVu2bAmTpk0PRzz+yeE/3vCOMCp+l2jJgnnhfS98\nZnjrl78TZuyzX/q606v60XmxscduuQylE18G2od743xo5A3paj5s2rgxfO9THwo3X/2H4rIOffTj\nwzNfeWYYOWr0dpfpGBq96KCWKXOgzIFsAZe5kd8PaQ4siM02mnW4OvIJx4fP/O6G8Lk/3BTe862f\nhbmzbw6/+ub/dPDktz/4Vvjgy/4jrFy6pOO7Rm8cK9PA5sCCaJVubpIw12w+/P4n3wuL7r4rvONr\nPyj+5t0+O/z+J99veMELswXckDfD+YcMwMP57g+za1+5oXX38/hJk8Pu++0fNm3c6kr2evVlPw1n\nfurC4LeuaHWsM840sDmwoo1wRHU+7HPwIeG0M98eLd5Rxd+eBxwUZv/tmoYXrNQpU+ZAlQPZBV3l\nSP48ZDmw4YFG+o0ucMGc28OlX/1s2LJ5c1g07+5w543Xh2e99s3F5lyLb/zs1xvtut33m3PpyXY8\nGWhf9GQ+7H/YwzouZ/3aNeGPP/tR+I83vqvju+qbLff3XeJf9Vj58+DhQAbgwXOv8pn2MQfWrFwR\n5tx8Q4gZVmHZooXB53vvmhMmT9+1j4+chx+IHGhlPvCMfO4trwn7H3pEOPr4kxtextq1a8Nf/vKX\nsN9++4Vdd83zqSGjhtkPGYCH2Q0fzperWX4zOuCwI8MrP/ipjk1+9c2vhW988N3h7Isv6fiu1Tcj\n4vKFmQY2B3o6H4Dvp97wiiIj/hXnfqL5xcbkg7n3zA1z584NEyZMKIB4n332CWPH5sSs5owb2r/m\nGPDQvr/56kocmDS6vRVqAPL8O25tWnJUGr7TW2vFZhrYHGh3BavyfFCK9rm3vLbImH/Nhz9Xm/1c\nvvqR92+LAa9evTrceOON4bLLLgt//vOfw8KFC7s1x8rj5/eDkwNZSgzO+5bPuhsc2H3imHDHstUN\nM6FZNKuWLytGXrNiebj0ws+Gg446plsLrVuoPdPA5oB7dOuS1Q0zoZvNh19962vh3rlzwhs+/T9h\n/bp1xZ+ErLHjJ9Re9M5rV4ZDDz00rF+/Ptx1111hw4YNBejOnz8/+GMJc0/vu+++Yfz48bVj5C+H\nHgcyAA+9e9qtK7I6kDVx1crqabwh1sKi0TvvHJfZG1nUMM6IAmswW3bqMMePGhFWN8hIve6qX4fX\nHXdkcd0TJk8JBxx+VHjRO88tPrfzz+jofd4zr4LTDsv6ZdsZcT5Yxao78+GX//uVcN/8e8IbTnxk\nx7kf/rgnhTM/+dWOz+nNTps2hlFrV4SbbloYjj322HDIIYeEBQsWhDlz5oR77926CMS6COL//Oc/\ni78ZM2YUYLz77ruHnePzNxDIalFKqbTutGzjhrjYhJK+UTHUwrM0Myq3M6N8mJTXxW7rduXlCNti\n19DbeFF8qLTjWxR7GGsY0KgucsROO4Vxo3YuFhw/bMbkAIwHI/3i1oVBP+i+pDGb14fnHHVgGDFA\nhGdfXutgH/tXt98b7opNMvqSdlq7KsxYdlfYGK3e0aNHhyc84QlFHNgx16xZU1jErGKJWmWyLYuY\nZTxx4sTyTzvsvUUqtNKc/0DTkkYLS0h5GDdyRJg6dlQgH/aIys1OUWZkas6BDMDN+TNkf6XR/mX+\nsjB3+dqwJr5vh1iRe00aGx6xx7QIyiPa2bXft71n5drw2zmLG3ZA6ukJ7rxlc5i+elE49qEHhl12\n2aWnw+X9+5gDLLpf37m4z/pB77R5U9h4541hxsgtYdq0aWHp0qUFmALhUdFlnUhrU9Ywq5h1XG11\nai4B4j333DOMGNH3zxwL9+8LlsWQzZqGHoJ07tVXXoXdJ4wNx+w1LUzMuRBV9nT6POLsSJ2+yR+G\nPAf0RP71HYuK9niaxbdL9lm6dmOhFe87ZXwYFRcfHyw0KQqExWs2hGVtNGFo59om77wljFs2v9hl\n5syZ7eyat+0HDgCIpes2FPO5Lw4/csOasHHOzWFizHzeY489itivJKxly5aFvfbaq8NKZC2ycn0H\naMeMGVNYxxtjy0vEOhYrvv322wN3tZhxX2VQC0f9+s5FYU5Uzq1r3C6xkj1f8+IqU3tNHhvGRMs4\nUz0HMgDX82XIfrs+WruXzF4QFyXoeacmTeavj+6pA6ZOiLG0wfGQEXTc5/NWNu4D3N2bT5g/Ytex\nYcWS+8Lm2MxDvWfZyunuuHm/vuXAjNizm4vVfO5N2mnThjBx8Zyw8+aNhet55cqV4dGPfnSYN29e\n8F5CljhvlUaOHFl4Tw444IBiDrGGV61aVVjF+pQD7zvvvLPInravsqbesoo3RsD99g33BGsZt6+a\nd76SdXGsmxavDHvHfIgJo3K6UWfubP2UAbiOK0P0O+3wfnHbwrAiPly9SQvj+rr7Thk3aCzh0dFi\nt1DC3TH21x0PQB3vuN2e+qCZYZeJ4wo3okxWIDx9+vS6zfN3A4gDPDgzY8zy7uXRWu2GR6juUsYa\nc9X8sGX1igJ8bUP5Y7UeeOCBRT0wIAW2zeaIecTtDIzty/oF3Mh7JUysYlY1q3ncuHHFb935B/he\nfse9Bfh2Z/9G+3Dz7xVBOFvC23MoA/D2PBmy3/xx7pI+SUCSvGWVof2iO3qwJF6IYx8wbXzhhu+O\nm608SaaMGRmeuN+uYZcI6iyRxYsXF0KSgBxImazlc87vO3OAB+dB0yeEe6JStj7O556QqoHH7bNL\nGLtlQ7jvvvuKocwFz8by5cuLciRWq1jvokWLwpQpU8KkSZOaHtK8EkPef//9QwptAF0WMQvZuBK5\nWNe+485u1yq+dsHSMGfZ2h5bvtUL8XxZBvSAaRMGjXyoXkNffc4A3Fec3cHjegg9eI3KFpQX/ePe\n5b2m4Vcvj/tul/GjB1UZAstHDNu6sITupsjDdmhM3H+PWH7xhAfAN+1L2BKIkydPLoRjV8I17Zdf\n+5cDI2PWOk8OZVKSYqOM30ZnqbPWjJh8ZD7sFsMcan0BIhK/nTp1agG2LFhWMA/JkiVLCiBWetRq\nTJeVS7FjFQNy45lzyDElc7GKubmFQFjRXSnGS2O2s6TMniqjxUnU/CP0JUQzfdz2yzXWbF77VVcy\nrnanAf5lBuABfIN0yXnwgx8cnvKUp4S99967OFMP12GHHVYkaqgnRID3Oc95TrjjjjvC4x73uOK7\n6j+/v/u+sCQmX/UVEVYE14HT+6dcorvXxR09a+r4onxCNjgPZFeCd3y0lqaNGxWzwKeGo+JfNf5N\nUBCsrBBZr1yImQYHByhlPDmUSfN5S7yXXc6HWJ43JZbfPDxWBTxiz6kdlQFAzzOJeEW4mgEiq3fW\nrFkFiK5YsSL440qWgNVOzgBlG6in7GifxYqTVQyA77777uIP2ANrLu86+sv8pcHyjH1F1kFZtWFz\nOGiXiZ2Ugd6UcX117n05bgbgvuRuD8f2QBLmZ511Vnj+859fPDynnHJKeNKTYsH/mWcWo2vw/h//\n8R/hT3/6U3jsYx9bC8DcPzfEWt/uxrcsPr5zC6UPhNXeMeuxCkg9ZEOf705QEqAHReVBeZVaRr2c\n1T6zili6E6LLWrLOg3eZFI6YOaX4mxa1+TrLQv0md6B7xw3IsulJbK7PGZAP0IkD7qmGEpRJCUTm\nxsj4XZwKnebDrnE+HBy3MR+OjH+su/J8AHa33HJLMTZg5GoGipRpn1m93MmUau5kIO23Rl6sTidZ\n+SD+ayxWMY+L7Gk1xsh7Y7OKU9wZGKdzTSWJXa0OZR3s0XEup/0qp1B8bCYrPA8SIMulSb0l4+rO\nZTB8l+uAB/hdos0CXA+Xovzf/va34aqrrupI7Hjd614XHv/4x4crrrgiaO7+1re+dbsr+mfMRPxD\njP925WB908nHhjPOuSAccsyxHWNYZu0XX/9i+O+LftrxXaM3yu4fGWv/Hrpb1+vlNhpjqHx/7bXX\nFkKVdULYPvShDx0ql5avow0O/OpXvyruP+BjrSLdsFh+xx9/fJE4pcTIc51yBh75yEc2BblWDw/U\n1RVTBlPiVtqXUkie+Fuyaafwm1gbX6egb9ywPvz0S58KFiYZN3FSoVQ+KHaI+883/3eYsuuMNFzx\n2oqsODw26Th6z2md9usNGddpwEH0od4fMYguYKifKm34G9/4RnjYwx5WaMZXX311B/i69k98Yusq\nLAC4ESmx6Ap8q/uujr2Qf/DpC8LVv7wkTJu5R/Xn2s+O4VgZgEMhbLn9aP2sHsK11RhfLXPzl4OS\nA0CXAuYVCLJUr7/++kKhnj17dhFO4h1RnnTllVcW8eAbbrih+L6nF8zKpfg95CEPKVzcwJirG5mP\nrHN/9+/5oLBxVH0S2MXnnxMWz5sbzvr8RWG/Qw4LLNzLvvGlcO5Lnh3e8qVvh2kzZoZ2ZIV2t1Xq\nDRlXHXOwfB48HRQGC0f74Dx1wZEByZ0psaddWtmNmt8b//S76G4aFy3iD7d1uO4cq60DDJKNk7Uj\nC5b3QhJOpuHHgXIC3j333FMwQFxYbgdATMlT3NNHH3108fttt90W7ox1vr1FAE4TECB/4oknFoBc\nDoms3Fif9b143t3hqh99J5zxnvML8HU+Fpw45cWvDDP2mRWuufzS4hTbkRWNaq17KuN6i1c7epwM\nwDua49043pvf/OaigTsr+L/+67/aHiEtrNDOjseccEo47cy3FzGfdvarc2O1s/9Q2ZZAZfFwL0q+\nEedjEWcaXhwoK8wsYcQylWwFFFnBiWQ2S7BE1113XZGslX7rrVfAC/xPOOGE8JjHPGZrguDO9Y7Q\nebfNLizcqqvZucw65PBw543XFafVjqxo5InrqYzrLf7s6HHqOb+jzyIfryEH/u///i98/etfD//4\nxz/CprgG6eGHHx4uueSScOqppzbcp39/aPSI9e9Z7eij81YQtKwPLmiCWPZrXeejHX1u+Xg7jgNl\nCzgdVSjil7/8ZZHbIXSkJClZpA960IMKlzULWJxYz+i6MdJY3X2VSCUJzN/8m+eF+2oqJCRdTZpW\n38986m4zwm3/uLYbh99ePgw+GdeNy26wS7aAGzBmIHxNcL/kJS8JH/zgB4tkCRmO733ve8P/+3//\nryhdaPUcZXDuKJI1nGkrB7ihZcLKQGXtpJrQzJ/hw4FyDW55RaObb479oR/o/ZwypRNXKNm77bZb\noXD/8Y9/3C6BKm3XW6+bYqJVHe190EPCkoXz6n6K388P+xzc88TC3pJxtSc5CL7M0nIA36Q3vOEN\nRVnBK17xio6z5IImzJUmtUrltP9W9+nudr+9/LKO2sfujjFU9gPASkC4HlnDSIOOTMOHAyxN4Qgk\nzpkWV2DVqhE/+OCDizrd8lKEvCbHHHNMYfkqJWIJ91X4QhnjL3/6o9obsteBDw5rohFwy7V/7vT7\n5uiJk5y5/6FHdPq+lQ9jKuWMvSXjWjn2QNwmA/BAvCsPnNMXv/jFwD1Trrvj2vRAfv7zn+905p/+\n9KdrS5BsZCH6HUHKCW792zWF0nDRRRftiEMO6GNwOysFAcSSsShOORlrQN+yPjm55EIGxCm5Siji\nhz/8YaGYqf395z//2enYYsSPetSjiooHTV3+9re/dfq9Nz44vjjwQ/aOC0LEZTSrJOHq9HefF778\n7jeGOTddX/y8dtXK8JWzzwoz9t4vHH38KdVduvy8a2xwUqbeknHlMQfT+wzAg+ludfNcZ8Z2ibo3\n9TVtWb823HzNHwqF4XnPe1542cte1teHHNDjU5a4GcX3uKHF29SDVmsyB/RF5JPrMQfKiVjAFFGq\n5XUgVvDcuXMLZa344oF/eE2AMIvY79zWvUFK484999zwr//6r+Hf//3fwz7TJ8cVm+oXaHn0yc8I\nJzzvjPCld70hvO5JR4W3PO0JYVNsd/mq8z8TRjToqtXoHHWd2yc2Nsm0jQO5Ecc2XgzZdx44SxAu\niuvg9iWNu39juOorHw+f/tSnOg6jDlFd43AlFg/3ocb7ykCUnhCos2IrwkzDgwNqb8VykVpfjXOQ\n50IXO7kdsp4lWT784Q8vfiv/A3y5itEjHvGIjra05W1afS8c8qIXvSh8//vfLxZ2OP/884s8hZW7\n7R82jt/qKm801qrly8L4SRGsu5nnYdGSpx28x6BZNa0RH3rz+2wB9yY3B+hYtO1DY3cqzeL7imi3\nj9h3Zjjl5JPDc5/73OIwHtSbbrqpiGUBoOFI3M8STbgfkxuaQOauzzQ8OFC2gMu9npUDffe73y2Y\ncNBBBxVJeqlUqcwZLmrbor/+9a9Fn/Hy762+14qSy5nrWXKgdrapN/QRu08L4+KSms1o4pSp3QZf\niaD6QOu1nWkbBzI3tvFiSL/bLy44oHdtX9H0uDjBAdMmFi4zC0M8+clPLkBGyQUFQM/XH//4x311\n+AE7booDa6QCgLmjuaWVJGUaHhzwDCSrUSJWSqgCfnq4I/NiVvSKVGPBiUO6WQFiipt9Up/n9HtX\nr8qeJHZpS4lOP/30orLCe+Mevv/efZorop+2PuqZOnMgA3BnfgzZTztHEHz0XtPDpLgkWG/TxLhQ\ngbEtYEDAWLP01a9+ddFUQHYn4aKJyDOe8Yzw+te/vrcPP6DHI3gl4bB8xP8IUKsj5WSsAX3bevXk\nKKApE1oink5XiaxolkBYPTBPEY9JHR155JFFUxdLDnJpp4zqum3L3330ox8NJ0fP1K677lrsA8wt\n6oIoB8qenOMxsUfztAiUvU1jo2X9qNgjnpcsU2cOZI505seQ/kQLPXbv6WFsLz4IVgo6btZucXm+\nbdmNRxxxRLEG6Tve8Y4i8UgXKHFoC0d8/OMf72i5N6SZXbo4wpdrkeUrCYs1LN5nGbpMw4MDKRPa\nHCgrXxTT5IYGhrOiFdwo2UpSn4Ua1BYDaX3hm4UyKL9WUVPqA4DNPc+hUsZkkQN1q3ehCVE5f9y+\nu4TxUaHuLRL2OnbvXcLMHVSJ0VvnvaPGyQC8ozg9QI6zZ8xCPPFBM2K8p+cPmfrix8cH1uLjVbI0\nIstXExEPuDIK7i/JH+JYQChlhFb3HWqfxYHV/7JAkus5lyQNtbvc/HrKceCyhevZ+PWvf92RGc8K\nprA2Us4s5iCZj/vaXEqZ1NWjWwfY2uAXX3xxeOc731ksumBcPQX0JkeSv9L7tL8w1akH7d4rIGwJ\nz0fuOT0If2Wq50AG4Hq+DOlvd4kPGRCeGYFzVHQbt0v2sa7nk6Plu09cvLyOaPwSSwDtBRdcUGwi\n+eMPf/hDAcTcaMpyxKaGOhG+YnYpEYsVQvBpxIAPmYY+B5IFXHel+jJfdtllxU8AFjA2soJtZCzx\nXG5jWfa33nprp2EtbShbWtIVhdeSiLpt2cfSpkiJE/d3HVGsTz5wZtg7ro09phuJmxKurI38xP12\nLRKv6o6Rv9vKgQzAw3QmeEBOfNDMjriPOE1XxHUtRmQ9z5MigO9SKaqv7q8EicvNmqPvete7ip+V\nPVx66aVFzSOAtjrL2972tuquQ+ozQQmE1f9yM7KGWTDaDQ7X7PAhdYNbuJiyBex92XXMrfy9732v\nYxT9oFm3zbqmUV6FepBypjSPPve5zxXrDJtbYssXXnhhofQC7de+9rUdx1DulDKgO74svZk8ZlR4\nygEzwqOj+3jXKCu6ypC2q3CUUqMj95gSTokAnt3OJYY2eJvrgBswZjh9vXnL/eHe1evD3BVrw8LV\n68K6TVvi+sGapu8U/4uJGhGcWbx7R/f1zAlji2SrVvkjDsXKZfXRxv/nf/6n2JVWLlP6jDPOCF/5\nyleK2kia+1AlLkHWrmQsr1yNrGJrwyZrZqhee76urRz46U9/WmRAs0wRSxdxQysJ4h3iMUIsYDFb\n7uZmZP5I6gLoP/jBD4qFWyQ7WsDlrW99a/jMZz5T7P72t7+9iB/7oKRJIlartCU+u4vWrA/3RPmw\nIK7nu2ZjXOf6AfkQ4uvYGM4C0rxhhVctAnGm1jiQAbg1PuWtesABAoKgQO9///uL5BFWoaXYaPvf\n+MY3wgtf+MIig9paqazmoUZieq6X20/cTocjlBZnZ7FkGtoc0IRD3gOl9KqrriqWBExXLKEKIFt8\nBclwpriq202gnLYtv1JseZTe+MY3FiVMvEmesQ984ANF7Ne2vEyvetWrit1Y30984hM7krDKY+X3\nO54DWVXZ8TwfdkcEskmIvOc97ylqggkOYCQ7WKYmcPLedr/73e+GHI+4AC2+zgKWgZoScXIy1pC7\n1Q0vKLmhJSdqTVom3bHKbmjzhJdEI5tmpC+8lq8SHFm8J510UmH9ppCPxD+rpyFKr9hwyoBuNm7+\nbcdwIAPwjuHzsD8KV5oHn/uVoFFKQctXE4uANMtgv/32K7I39aodSkT4ScJK2dBJAE+fPr2IDdd1\nQBpK15+vZWvyVOJDNfkOKFuuslwjrJ6eG7pRtcBXv/rVwpqVUMWiPu6448JvfvObwoqm4CI1wAlw\nDz300CIXIZ1Dfu1/DmQA7v97MCzOQJxLzSGSMPL3v/+9SAJhCe6zzz4dPJDRedpppwUxq6c+9akd\n3w+FN8qRCFRWSQJgwJyt4KFwd7u+hmQB21IyXgJJn2XEWxihagVLVKxawWrINbThrpbVzH0tqQoQ\nn3feeR2dtqwdnrKvKXop5ux4mQYGBzIAD4z7MCzOAtDK3kRa7mkwD4A0mz/22GM7ePCtb30ryOb8\nxS9+UYBT1Vro2HCQvWEBA2BCUTvC1E5QSZI2la12Nhpkl51P9wEOAMhEPD8S88p0/PHHdzTlSN+z\nguUPJIVNdrTtNLR505veFC655JJiuUtjWdiBFwk95SlP6ciS1sADQHvWMg0sDmQAHlj3Y8ifjeQj\nAoEWz/qVGYpkgFrCMJGGAZKVuN8kZfXFeqjpWDvq1XVQJvyVrWDxPi08LdKQaehygJtZnS9Smld2\nN/vOPKCkpZWTfKdUiBUsK1oDm6OPPrqweDXYUNLHvUyp0+nqnnvusUvgatYKNlnYypXK4F9slP8Z\nEBzIADwgbsPwOQkCQ90jotVzS4tToYsuuihI0kp02GGHFVYiC/Goo44KH/vYx9JPg/I1xYGrbmgX\nk9zQSWgOygvMJ90lB5JLePfdd98OgFm3z3rWs2qtYIoqL5E5JEmRtYvUlj/zmc/sWPJTDoXYcIr7\n2j4lQHZ5cnmDHc6BDMA7nOX5gNzQVmBB3NCvec1rCo3d57PPPrsAYu8Ra5l77V/+5V+KWkmLiA9m\nSm0pWTqyov0h1jHrqFHCzWC+5nzu2ziQANi9ribemQuymJUVAVakvldPdS1dVQ1cc801HbkUlDVr\n+0q8QoBWLXDqNQ18baMhx1AJ4xQXOoT+yQA8hG5mTy5Fsf2StRvCbUtXh2vnLw2/v/u+4u8v85aG\n25asKn6zTW8Ri5bLjYCRwfmpT32qED7G54ouu+F895Of/KRoaamd5axZszoSTfw2mCglYhGO3M5i\nv4lYwTJhMw1dDpQTsZKVWr5aeQAWaNCaUmKWVYuA7ytf+crwvve9r9O8P+uss4J8CQTQPRsUuORF\n4V2i2K1evTooVyp33yofs5X3xly2bmO4I8qHv85fVsiG30UZcU2UD7dG+bA4NuroTfnQyjkNhW1y\nI46hcBd7cA1rY1eb2fEBuj0+WOs3b4ldsDbHB6nzgNpFj42W6JjYEeuAaePDgdMn9UqzdgImdb8i\ndAArt7PWeoST2kbrCJeJINFk3u9iYo362Zb3GWjvxbslxbCAJKC5dkTIyWjFA2VamYYeByhcFE70\nzW9+s+gAV57jspUtmqBj3I033lh4fyQknh7X770z9n2eM2dOUXr0kY98pGi+YRzPAiAWK7YNkvBo\njgFfzxgLOH1XbNDiP+tjV7zbl66KMmJ1IRvIh80V+RDFQ9Etz3KDs6ZOCAfvMjHoJ52paw5kC7hr\nHg3JLWirNy1eES69dUH464JlYWnUbrWYq4Kvi/fdmvjg2eavC5aHn81eEG5ctKLHGi+XGdBF1113\nXeGO1RmKZUhbVxtcdZ2JH6ulZUlKNvnyl79c7D+Y/klWsOsHwin7mVUsNpit4MF0N9s7VxZpIolY\nqS1l+o5Syv3M42NuAE/gi2zvty996UuB9Zvowx/+cAHKCXzTGr9+l3zlmQHSQjmqD1ohyuBtEXgv\nnT0/WrnLwn3RO7Y6yocq+BoLHq+NQL18/aZw3cIoH25dGP4eZcqm+Axnas6BDMDN+TMkf10fwfSK\nOxeFa+ODtSI+NHWg2+jCbbtiw6YCtH99x6IeP2SsP9mhHvhkGQAgQoSwAUhVsr1aYr2kX/rSl3bK\nnq5uOxA/p4YchCKLp+yGdr2S02SJZxp6HOAqNrdRNRPaMyC7WQhG4uGb3/zmjoRF25svSpK0lUzu\nZEAs45k3KFEK76TPFNpUgy+bOmVLp9+rr4CTe/lPc5eGZVE+bIrn1SrZclWUD9fduyJcfvuiQNZk\nasyBDMCNeTMkf2H5/vL2e8Ndy9eGDe0gb4UbG6IqfHdszv7dG+eFDdF13RNKNcDcZTR0TTv0hJaA\nxSLQkq+OLr/88nDOOecUSVsHH3xw3SYD8rtkATs5wjHVePrs2lnGuSQJN4YmpUQsIGueI/W7+jdz\nS0s01B+9ulQn8NR2MnlMNKwRH9bUJtX/8hqlWvsy97ifLcKArr322obJfpSAn0cL9vala4qQVHmM\ndt5virJl/qp14Zs3zA3CXJnqOZABuJ4vQ/Jbmi3wXbxmQ+E26ulF0nbFhH4dremNPQBhbrkEoIQM\n1xtLUPYmUi+psUAd6XlrQXOCjLstCbS6bQfKd+K7GnHIegXAXOplizeVJA2U883n0bscSIlYkhDN\nAx4flixgfPnLX170bubdkc2caoW91xlOCRs6/PDDw9e+9rVim2TRmv/NVjkCwOLNrGe5FKkRTLo6\nyvlv5ywu5MPmNqzetH/da8Th8Ks77i3kRN3vw/27DMDDaAb8Y+GKYtlBwNlbZKyFcYmyv8fYT09I\nMlWyDNJiDBrHf/vb3y6G/b//+79CONUd47jjjiusSK49FkDKDK3bdqB8x8olTFn5XNLl8iMCWgOG\n8ncD5bzzefScA2mep5GsZKQpDW+OrGfWrM//9m//VtQEe3/qqacWCVj28axoM5lauqZxJF01W+NX\njgH3tLknvKPSIFnTxvjn4pVh7sq1vaKcp3PyKn58dcyWzrQ9BzIAb8+TIfmNEgLZzlxDvU20ZVnU\nyph6QqnRAMswdb569rOfXQgb437xi18MEk7qCIiJpVr0QZOCtAJM3bYD4Tvnm6wZXbHKcWDnp1Vh\nquccCOebz6H3OJAsYOtjSzr0+YILLiiSCtNRhCDMfQqoHtEpxmteaNFKObVvSlJk3con6IoofLrR\nyaMA7OqKuZ1Xx7jtDYtWxnBS78sHIsdawvNXbq157+och9PvGYCHyd3+R7RQZTH2FRnbMXpCLFgl\nOEi5hfgveuc731k0HPBe/9sf//jH3tbS73//+8Kd9/nPf75w09VuNAC+FAfmekbc0KzdlFjjO6DM\nFZ9ie77LNDQ4wBLVRlKpkUx+imd1PWilSNzJlDA1wQhQ/+xnPyvKiViu3NeIMpdCOMUXXfwjEYyi\nylp2HC1fb47Wr+SpviJZ0j31kvXVufXnuBmA+5P7XRxbnEZ8NMVCbe6B0aBdxxska1K8SDaxdXWr\nK6fYRhLEgtV9r30uXL2+0KQds7tkxZakyauXTXThhRcWNZM+P+MZzyjKltJv1dcPfehDRZN6dZSE\nFlfdQCMWCAKwYoHuc1I4fC/jVRw8W8G4MXRIqZCQibmti5UucGrBq0Qhs75vuv/mCItZX2exW3M7\nEdez+dIOeS6OOeaYorXl7fGcZi9e3qXreeXSbU0+2jlW2nb5+o3becl6S8alYwy21/bu2mC7ukF+\nvur33va2txX9YQGvuI0Myac//enFK2A588wzCxCWCSlRyTJlVZq/am1Yt7HrTOU3nXxsuOnq3xe7\n33Pb7PC5t742vPu0p4YPvfy54c+/+El12O0+r40JWTIfe0qPecxjCoFCy/eAJlITKcaLCB29cxuR\nWFoCXoknzazmRmP09fflbOjy4gzpuADYfU+WTvo+vw5ODshjsJiCelz9zz3LMpbrAJilK8M5EY+O\n55u7WLJWStrjNSorbmn7Vl4dWzLXpjETonyo945t3LA+/OAzHw6vecIR4ZznPS2cdcpjw2ff/Oqw\nfPG9HYdoVVboM3D38jUd+3nTWzKu06CD6EMG4AF+swAw0KEp6wkLlLivEJelGJFyBsQK5oKt0rwY\ne2mnls/+F1/wnnD4Y48L53z75+Fl7/tY+N8Pnh2W39cY8OxTxHpiEkdPiWsMwCIWABBKZL1gLjeg\npPF8M3Di1lM3Sciwmt/whjekYQbEq+tIbugUByZgE3EVAuny9aff8uvg4sAnP/nJotWqGK5uZymr\nX0xWVnw5B8DvADeR59r8QOZ/2lbowty+5ZZbOoUv0n6tvPKmTdx973D/iPrOVReff06444brwlmf\nvyicf+nvwnk//k3Y75DDwrkveXZYeu/C4hDtyIo6Bb03ZFwr1zoQt8kAPBDvSumcuJbUBKp55YaV\n4atWFHmYn/CEJ3Rs/YUvfKHIluz44oE3OtS0Q4D9yae9IDzqqU8vdps2Y2YYG0sc5tx0fZfDrFjX\n3rEaDchqTYoFK7gcHwXKeMB9iwddkYQuCgyrg9ttoBBwTdZLatCQADmdYy5JSpwYnK8SCk+Pnaxe\n97rXFasWcT0Ls3ABJ1Kjm8qNgCkFO813PaDf/e53F9nQlElleigpqeY/97S2rd2lUZOn1e66eN7d\n4aoffSec8Z7zC9C10ch4rFNe/MowY59Z4ZrLLy3Osx1ZsWrD9pZ2b8i42gsYBF9mAB4EN4mmq3SA\ntlx+cMunrj1dWrCg/L337Xaj8UA8/EknFQ+b/W/80+/CmhXLw4EP22qV+q4R6SfdW8Q95ZpZuWXL\nXvyUIHKerEOJLF0RC+S73/1u4b4TYx4IJT7ch64v1WPWuaFZyZJ2UsZ0V9eZfx84HFCfS0H++te/\nXpQYfec73+lYl7dcisSTI+mQYmnBhZTZbP5rziGcwiouK6JiwalfuLKknljB62KCVB3Ni2EoyveU\nXWds9/OsQw4Pd954XfEMtiMr7m8Qae6pjNvuBAfJFxmAB8GN0pLOQ8YV9V//9V/bnTF3lUxhVnJa\n5q+8UU8qjxbMuT188Z2vD8976zlh/KQp5WFr35frCms3aONLAKtkAnG7pYYDPnOdacCBJKQ87WlP\nK943+8daqywFsXTxr2qnoWb79tVvXcWBHTdbwX3F/b4bVy27UiGd3X70ox8FDWPKpGlGIhYw17K1\nsFm5SFaz+mDznqL2ile8olhYwW9yA+yTiKfINhK82iWK7U0PWNXVfSVdTZq2S/Xr4vPU3WaEZYu2\nuqDTBq3Iip2CpRu2p57KuO1HHBzfZAAe4PdJ4gYN+jOf+UywKors50suuaTjrHXDOfvsswvwBdJ1\nNNJyRt2g+XfcGj740ueEp7/8v8KjT35GSyPcHrtWiVlbXKE3SBw3CRvJJ8k6MDbrwuLjyILldQlo\nxY+lf7i2tby0csyJJ564nWAsbbpD3pYBmEXDIlafWaYUy+bOzDTwOcAbpTLBvWW1Wsu6StzGCYQp\nWNbFTkmDPlOohSXUA/PWzHpg0RKhl9TXuTymkqXZs2c3zYkob0+uOMfHPvaxYcni+tyOvQ96SFiy\ncF55t473SxbOD/sc/NCOz63Kim0ZDh27ht6QcdtGG1zvMgAP4PtFEL/kJS8psiE1bhc70gFHkwma\nsraLGrHrHysW5EGtc62OHzWi7au8d+5d4fxXPC/8y0tfG5707Oe3vP+YOKOs8MJaB5zVdX1bHqi0\noYQsgkdcrOyKtsnpMb6mXAN9/OMfD5/97GeL9139o1xLGQiX3xOf+MSuNu+z37mYy+7lOjc0UGax\nJwHdZyeTB+4RB3h/xGz1a6bcAd/Uf7luYG5o4RVKZMpqNh90xEqhJn3CKZ6JWL+AuUrmBwWuKytY\ndrW6Y0lgPEg8SQ/Zf7/qcMXnvQ58cFgTZdAt126rRPDD5rhQyNW/vCTsf+gRxXbtyIpRFWOgt2Rc\ncSKD8J8MwAP4psnaBbrcT4m4oGnIeseyillzxx13XNHMQRzFX4oppn12G7/9A5t+a/TK7fyYU55Z\nJGKtWr4s+Nu0setOV3tMmRA+9rGPFS4x5RVKirjIeuru1TgASVKqLuF27rnnFt2C/G6lmFaPJamN\nd+HKK68sGiFofLGjiTBlDbmPqA6Afe+es4ZSco7vMg0cDrg3LEpeKlm93M4JRBudpd8lTupGhcwD\nrupyGKnoUvXA3KBcp6YcdWM2soKNwXPGJS6enOrreZAkfI3ZtF5JxXZDSrg6/d3nhS+/+40dCZhr\nV60MXzn7rDBj7/3C0cefUuzTjqyYNnZrAmk6WG/JuDTeYHvdKd6cOq/AYLuOfL5NOKAF3BVzFsWG\n6Ns/ZOXd1AGfcc4FYey4CeG9L9je5XzGey4Ij336v5d36fR+ZEywGLfw9jBq3coCKD71qU8V7qW0\nkeQnAkcstjukYw/wlZTEwhD3KpMaS648v0vSarU7kAxUHbhYIcA4gX157L58z3XIeuEeRxqvKC9J\nSTbp2GLdFKyUHZ6+z6/9ywEAqqZXRruQUKvzW1e3cmtViy3wbsl9qCpaEg/NDx4fCVmNSOzZ/LCC\nGOtameL73//+cMMNN3TsYnxLHqbz3DRqbFg144CwZWRncEw7XH7xheE337uoowzxkGOOLYB53MRJ\n4Y7r/96yrBgRn8vH7jM9PGj6tjWR0zGG62sG4GFw5/V//skt84N+0H1JU8aMDPutuzfMjYlOSYiI\ng7HaNQpJRPPnLiZM2iXWLQsfOJ1wwgnb7c5Vr9GBMg3uOy69Vom3gVv/vPPOC295y1ta3a3H22ko\nUs7mlpDD5e5aykTAczFqqJ9pYHCAB8UKRkJAP/zhDwvFqZUz04ZSCCSRWKw5LaRUR6ldpTkvDNVI\nSZS0JUzDItfIw1wqk7iz/c31RCywLQccGZZvXyGUNileecHGT5pcPNudfmjxw6TRI8OpB+0exnUj\nJNbiIQbdZtkFPehuWfsnLAnrwbtMDDTQvqIRceiD4jEeEcFB0hANXntF8U1avtckNMSvX/ziFxdJ\nKNzV7RBBhIBwXdtNWc6Oy5otu/JaOQbrWuN7MeWTTz65lV16ZRtKAtd6ckY1ckMrRcPXlCnbKwfP\ng3SLA6xLWcovfOELw+Me97jCKuW1aIUokS996Us7NrV4CI+OjOlE4v5lSglb5qdypjqSpMfiFYP2\nVwVfHfT+93//txP4GuehMXnzyL13DaMr8dnqMSZOmdpt8CV59p0yLoNvhakZgCsMGaofD4punylj\n67vd9MY1Tx4zKoL8pGIoIAkExVRZBl65dn/1q18VwClWhoCoVprca7TyVoggStneah/r4rZizyxg\nvyW3bitj24ZwE1v/+c9/XuxbzrpudYx2t2Pt+kvXApAJ07qsZ7Fg68dm6j8OsDJPOumk8JGPfKSY\nv+ZK6l/e1VlpCsP1m8r1jAOAWaSUx7T4BoAvU0rAs0ThpZdeWpTSpd/lD2gyYww5EKzfMh1//PFF\nXgRQRrxTidQgC9XMmjo+TB9f74JO2/bkdVL0jh2627bmIz0Zayjtu+1ODKWryteyHQdGjdg5PHqv\n6WH8yM6a9XYbduOLcSN3DsfsOS2MjsdI9KQnPakAFWCRGmXQ/CWSAGIWqvIM8VpAo9uPhCT1gF0R\ngZESXNLaweV9AJgyKGM7voYG7ZBMVi5zLmyZqmlpxHbGaHdbrvrUBct5s4IJ+iqJ7/Em7AjFoHrs\n/DkU80o3NfOO+xkIV63VRnzSbEMSVCozE/P97//+72Jz88z8T0BbHSO1I+VdEoKwJKH5IgFxVixR\nksyUFm5I+0rOVIWgCQ2QBuoSvVJ82VxSrYB2jnPuUVE+TBzd+/JhTJQLR86cEiZEF3SmzhzYJjE7\nf58/DUEOzJw4Nhwxc3LwQPQWKSt4aNRs95o8rtOQtGyWLuEkAURDDdarhBXg5nuduwiD5zznOYVW\nDlRkZRISNPlmJLs6gXdaK7W8PStZyQWStOIY7VBadSYJPAllfUnlemDHaeSGxjfnVBW2fXlueeyt\nHOAd4d2hPF511VXF6mOt8kb8Xlgj3TeldcYTVkjEgk2Kpe/KliplMAEnq1m2NOv17W9/e6EopjHs\nw01t4RIucvtwbZs3vFLJ8jbfJC16hhJNHzc6HB0V6d6UD8JfD9l1Yk68SkyuvPaeJK4MnD8OTA4c\nEsHy4XtMDWOj1dpTYvkC9COidltHNHo1th5ypQ9AWG3wnTGR6IorrujYRR0z7VxcjKAg4NTzev+C\nF7ygY7vyGxnQQBJx3aWeyuVtCCraPxIbs5hFO+T43Nmslte+9rUdWaPtjNHqttU4MAHJJZ0EZnkc\nbv1cklTmSN++B2IaY5x22mnFIiGUSCU9rZLOaxYDSTkLLFbNdABiuSUlgJblnsicSOT5kAXPQyRR\ni4cneUxsY65ajpSyC9hToh7LWXIXoE8hDp/lYwjTVGn/qRPC4/bdJXS3eU95PPJB7snD99imZJR/\nz++jkpWZMPw48JBdJ4XH7D09yFrepv+2x4fJcV8uqyNmTm26IwHjYZdg9Jvf/KZwR9P+CQ/dq1LM\nyyBf/OIXC/CluSdXmYUoaPXPfOYzC5AuH4wgSwILwCcLobyNRRg0wkf66so+bZcIywsuuKBYj1Xj\ngmp8rt3x6rZ3vWLhyT3pmsUVWT5Vsh0hWvdbddv8uWccME+1OVXKo0RI+ETTi1bJnASMciCQeypm\nrKEGKlu8KcGw+CH+A1SRLHnPBtDnIUo1436TO0BxlQ/BJa4WmHLmWTNPKb/leWR73iPKcSPad8r4\ncPz+M8LUsaOia7rRVs2/nxRd2UfuPiU8MsqITI05kMuQGvNmyP+yesOmcN3C5WHuirVhdVyrs6uC\ncM/ihPhg7TlxXHhYfLgmthHTEf8SS/Xgy/iUgKUTDwHFMk4Cqcx0iVkEHwsikYQSa/sCIcRa5mo2\njjFS7+i0fXo99dRTi+QVn7kPlX20Szob2Y9gZIG0Wmfc6nHUIwPiVH5E8BKmapSrJJau3CrF8Kq/\n588954BacpYrj82nP/3pTpnLrY6uPaqSO8RrA8DLQGveCsXUkWx3oOo5Mc/LBEjNd7Hocra/mnKW\nMtISlgWclDrz1rFbTRhbF9f3vv7e5eGOZWvDmo2biuVGy+dQ935CLDGaMWFMOCp62abExMxMzTmQ\nAbg5f4bFr6siEM9ZtibctXxNWBUfNK1ZtjzQn0VyRvw/TBg1MpYRjA/7xVKCSd18sLjgaOqsYvFh\nGjqBxArWOCAla1WZrlRJrKtsLQNClik3nUSr1JyAdt/IQgFkXHSsS/W+Ceiqx2v22TnMipY3cPzK\nV74STj/99Gabt/WbpCvXkspZ8EcSDaWi6i7kUeAKZfGU3ZhtHTBv3JADQJHlytPw/e9/v7AaG27c\n4AdeEx3rkDlnNS4NO6rEIk5KJsXOvQW64rgAukzyKCQJ8hIJjXA3A1oALRfC/AG0qV+0xjSJJCPK\nom+X1kTlnGwgI1ZGWUE2xNYCke4vkrdY2dzN+8Q8kP1iNvXUSrerdo83nLbPADyc7nYL17oxLifI\nGt70wIM/MgoOWq0s6t4gAkFcVZJRskKBJ8EhTlVe37h6vAtj60ju5KTR+507GxCzUliLhA/BRODV\nEavBdiwI2cTJkq7bttl3eulqIq8OVPej3iBCVBcsSkQ6/+uvv75QKOqUCqtDcUf2tiXeG9cyWMcA\nfkIVkpxkO2vhKObeLsk5UF5kPCQXQTikSqxcYIvUoYs18w5VCfCa1xTRBK76mFPM5CfwzhjLfKaw\nSWgUlknHLz9v1bHb+UwukA/khCsbGcFXdnO5AqKd8Yb7tvVSarhzZRhfP6AV+9k19o/2531vgS+2\nimOJ24pfpvIegk5ClUQqNY6NSmxYm4QMSyJlj2pUT6s/44wzijFZjdUFG8q3E2gRUo7RHcGaxmK5\nK50SU2aF9gYRpiyusoLRKBva8ZSRcEXXJWr1xvkMtzEkKckgBoK6VLFAuzNHxF8pZgn8NHapA1/W\nLYWUV0ioRSlRFXwl42kbKQbstfxsPPvZzy68II7nufBcpaRHgJyOz2Pj2aqrK2/3HlPIuZbJBj3m\np8XM6Qy+7XJx2/bZAt7Gi/xuB3IgtZRULpQsOAkvhAnBwToGPs1ILaQsae7gRCxczfC5+tIyhum3\n9Gp7oA2sCSfu6O7SFTGbW1xabJuLvTtu7fKxWUGseCUmCLgSpmWruLy9bkeO3ehay9vm9405IP4u\n0U/cl+u4bt3txntv+0WIQ2cs3hX03Oc+t+g+VS73SVvz6AivlNu0pt8omM7H/uZAUrIoabKleUjM\nFft6LzlQiIUrm+KQwFZ8mNJLUbVvqhxIx8mv/cuBbAH3L/+H7dE16pBwBLRYpUg8V7KUZBXJJeXW\nfHWMUmYkyURSVbJUNDIgPLmm65p0GEcdrfgp4rruyXKExx13XNEwAwgSgmJyPSEWT7m8BI+Uq9SV\nWTkORcI1J2unJ8cervtSBnlh8NH77oKvMApwTOBrjgPZKvhSHFUGaMdaBV9Z0QD1W9/6VpEABlDN\n10TCFLxHANXiJMb2nABWCiW3cwLfVMNuX8siljttpfHya/9yIANw//J/2B6dNk5AETbAMHV9Yv0B\nVjFP1ghw7YpYy0CcMGPRIkKKJQKgxGqrJI4muQaxGKy73F2iOHAFa2ygVlS5SnfJWFzQ5eSbZm5o\nsUEKS+Jfd487XPfTyQpo8jiYhxSq7hAXsHFkpiPWqPixXANEQbJEIaDXAUusv0zmKTe1BRTc+3Q/\ngWo1yQ74Ok6qhQfyXNfGTOELQO5Yni9knmjLyt2daeBwIAPwwLkXw+5MxGIlXdHixW3L9Y1crrKi\nCSJlRgRRV8QK4E4moMoWsYQpIKZ8qUzc1AQesii6tn49IQJQ1uvnP//5brv6KCCEJYGeyLnjQyMr\nl/BOHZbSPvm1OQdks4upyiYWS+UtSW7/5ntu/yv3sB7NMpgRt685S5kCpqxZ5WJcysnzkkbR/QUK\nxqYAAEAASURBVMoCCcqNhDKStatsrxGxirmoeW7sT5lkuSfQ9lx5fnhPysQKBtzVOHN5m/x+x3Ig\nA/CO5Xc+WoUDhJTyCIJKPLWcZKI0CUATcDKdG7lhK0MWXYCUdnz5y1/uEKqEk5pOLl7NPRLpLJRW\nppFh+r3vfS/91K3XD33oQ0Vdp1ggK6RRb99mgzvH5Ma0Hfc2oVp2TZf3l3zD7VhWYMq/5/edOcAV\nyzuiA5ulJy+++OIi+a3zVq19ohTxnkjKQ+Yz8JWLIDtejoNsaO7iMikdkmktBPOf//mfHUmFPEPA\ntRx+oYy5/2XibWEBIwpEIqALfNNv6XuvEvzkCpTHLv+e3+94DmQA3vE8z0escICwUvsqvpWac6RN\nCCNxYYKFq7i6xFrarvpqPMJGEwRxWe44BMQkbomrpv7OMkyT61EWbLl2sjpuK58tMpGAl9tPx692\niBAvA7B9U+Z43Tg8CHiYreA67nT+zhwCXhKYKHU9XfdZhnNS6LibWbus6YMOOiicHrP2qy5fgCzL\n2hKdSuqSi7rsZpbIp0LAPEDyHMo18L5LiYeuI7mZzQMlSOWxbFsmCY+pfK38fX7fPxzIANw/fB+Q\nR1Xjt3jN+jAnFt3ftnR18ee971JdcF+dOFeaP5YcIVkmblnxNSDEspRo0gqlOmPgfWGMk4mPpYQr\n1qL6SZYF1zPgJzQRIZYAtJXj1G3DlchyEQvUyrCVVZ7SOASv8yu73ZvFge0HgMW9KTGZ6jlgmcnk\n5lV7LhbbEzIej0ciC36whuUASO4rk3wH3bTMNQoA7457mqjcklIfZ5YxJRGZByzjMgFlSV/JsmaJ\nUy49I83IfAfw3bGCN8fuG/et2VA05Sjkw5JVRXOORavXhw2xLjhT+xzIZUjt82xI7aGrzfxV68Ls\n+1aFRRFoIwaHjfGfTVtb3RRN2dUB6wmr7u/AuK7wnpPGFh1w+oIR4qjAT42rTNEqERySs7jYCFPg\n3IxYIIQZ0n2LdcDNLf7LVZjiqiwRdZjit1zdxifQkoXS7Bhd/WZlJ4tLcLVXk28a7SuhjKDkAUgk\nfsiCKQvr9JtX15qSbcrfD/f37rd7ICQhDqt2u5mV2Aq/JFSJ+6ZkOXyvCwFonsHiFReWm4AcmyJY\nnrvisuK4iJfnc5/7XFEOVXwR/3noQx9a3N+kYNnX3E3H516WUGZOd0WU3Msvv7zw+iSQb7SPYyyM\nAHtrBNsFq9aHzfGzJhzkQ2rEMWrETmFEFBDTYgesA6dPCHtPHt8rizk0Oqeh9H0G4KF0N9u8loUR\neP8yf1lYvn5jWLepNQ12bARjCzE8Ii5btntc3rAvSC0wFyyLOLVlLB+HpcfNx+VGkCVXXXmb8nvW\nLWtULLVs9bAsxOdkQydBxtLw3h8LJbn6yuN1573Ysgxp8V1uw67OWRKOc1DalIhVRSCWv0u/eWXh\nU05YWHiTKRRueUBJ8dE4xfq7PeWN9qAs2lTuU+Wz8Sl4gJc1y31sDspl8Ju8BvOgTO6rUIV7LsnK\ndmXljzIGfFm9VRJPlrCo3je1pqxuU/2sw5rzN1caEWv3L/OXhiVrN4S1LcoHTTkmxc5YR8Ve8XvH\n1pQ95XWjcxsq32cX9FC5k21cB6v3rxF4r5izuNBuWwVfh1gXtd9744P5mzsXh5sXr+ywINs4fJeb\nPv7xjy8sUEClQUKVACOXNCvgipi41VUjDa5ogoBgS1aIMe1PYAFiNZk+E3KEIAL0Yna9Qc961rOK\n8ySMuQnrSqPKx6kmYvmtWRzY7ywrQrvVZDX7DGUClABG2EJJ0Nlnn91jQDAmT0od+Jo/EqqAG4Ur\nLQmoR3NqpKFrWhV83QPzM3k2KIrGokyl5CtlbnXtSGX7A1/7UzRarUMXbtGStZxtX54LNy5aEX51\nx73hnpXrWgZf+3NF3xcB+6q77wv/iAu9cFtnasyBDMCNeTNkf/ndXfeFG+IDpsl6d2lNXCnlz/cs\niQ/poo6FG7o7VnU/SSUsDNYoYVaXXARoJGcRZso/0mIM1bF8tm1aNUgZRirXKG9rYQXgqwlDOd5G\nCHKHl+Ox5f3aec+K4WoU/1MaxRprRMDUtsnlaDvfUQ6alZEoSaqzkhodZ6h+735KrOMaBpoy4HtC\nEpde/vKXF6sJVROi5BiI/ZorSoq4ixNRIpMXRTgh5Rmk39MrN3l5XB2yeGZSTFebTPe/TEBaw5lk\nZcqG1qa1FQLys2bNqo0FXzNvafjrguVFz+dWxqrbhlL/1wjAP509P4NwHYMe+C4DcBPmDLWfuLl+\nHzXTO+KqJht7QTPdHJXbe1auDX9bsKzXLWGgmRp1ANdGVh0XNEADOuJajUiNZxJm3JHJyq1uT/Cx\nVrgrExBLePGe+7pcJlXdt9XPBLVew+ecc05xjXX7UUII3KqF0pVb3O8AuizM68Yfqt9RWGQX6w1u\n/mjjWQbEdq+bd0VSFbe/bHnPUCIgJrYsZiu+bB6WCWimpQGrYFneTq7BFdGTw0OTSEyX5V62llOd\ncdqGUlhW0NT5AvlWkxQpA+a24yfyLF9/74peSaoiYpau3Rh+Gz1t2RJOHO78mgG4Mz+G9CeZi3dG\n8JVI0VvkIbt58aowOyZp9DYRQuo1CT0dsRqBCheczGVJMJaRI/jqSFIXYAOwBHMzes973lNsJ9Er\nkRaChK4YXqNjpG27epWVrfmHeDcLu+7a6tzQALbOgk/Hc33GG45WMEvT/bLykKxzZUZlAEs8auVV\nst/psYxI0pvEvORCti+LE8DfGWPyMpt5Nqpkzgp3JM+JbPi6hCeW9ZVXXlnc//I6vVzn5jM3caIy\nUKbvAGiZlNG1agVTcuVZUAjRPSvWFM9y70kHCxZuVdL/EdcVzrQ9BzIAb8+TIfkNd/Pfo0tofYzR\n9DYZ87qFK8LqDb1fAkOjJ4xYrBJZyhp/+TqU4Zx44omFcNQUIbUELG/Dik1JJwRbK6VGMlM1xC8T\ngck6VVuc3Ivl31t9T8ATfgSr+B9XaZnqANh24o91Mci0Lze080rCP30/lF/FWd1b3hINNnQ4o4y0\nS6xMiXmsZo00qvONu9mc+NKXvlSUfjUaX0Z68tooSat22QLQsvNltrtPYsNpbhpTYhUyTnIx+8yS\nLlMVgMWBZUI3mx/l/Vntch0WLVkarp63LMZ7ux+WKo9bfs/bdkusslgaY8OZOnOg/Rnaef/8aZBw\n4KYY8125vvcBMl2+hbolbvQFaWZBILJCgHAjkrCiCQZwZH0QylUCTv4Q4VcVsNXtfb7ooos6lUSl\nWJz9JcbI1NZdqTvEwiIslanoYFSuK3UclnH5HAljVjCh2YhYNsC7bD012nYofK+TVUq0kx2vHrdd\nAtxKlLR11EyjLkQB/LQzFb9vRhSqVGdL6ZOMVQZR85iyBVz9znvDfWz+JoBN1rB7WHZ7A+m0jXMA\nwOXf0wIMvDWtEIUC2F99291hRR/KB2sIU9IzdeZABuDO/BhQn7hJua3KtaMeOPEoWZ2Its9NC6BY\nanVuKpmJd8aGGr3pWqpj1Jzla8P6PtCgHUu8ihUhvslt24xkqUowAYp12caEGMHH8mg1Xma75GoE\nivgOCJFEMecGTFPNcbPzq/tNrFGmtM5MMrwRoc3irXbF6gqA7Ss7ti55zW9Dhdw//JJ5LLxAIUqL\n1bd6jUIbYvtqtNX2lsEsZSWnscSAy2Vs6fvyq3PSSS2NI/kvZTLbTqmY+es59mwLZ/DeJErlaax3\nZUXmVJkoV6lftO/lJFTnBzd0Oy1V949u6PvuH9NlaGrl0iUd11U+p1bfL1y9LhoBGztt3lsyrtOg\ng+hDBuABfLMIBWvbEsweWEka6guf/vSnF68yLM8888wCjCV7eKAl9lRpQaz3baXU6E0nHxtuuvr3\nxe4L5twePnnmy8O7/v3EcM7znx7uuP7v1WG3+7wugq9i/b4iwpXFSeAQts2I4AO0BJ76ynKMlXBL\nTT6Ud7RqvarNZZWySMUAubAJ0yRAZ8+eXShCwL877SzF7sQv9bFmEROuLNmqUuU78cFmCWHAw3VW\nhXMzng2m37h3NbngMdDR7LLLLutQiFq5Dm5kCXxK3qrWohamr3zlKzs11njve99blKp1NTYFzJxD\nPDfuYyIKkS5v7p04PfBN3pS0TfrMAqdcVN3o4v/2LVPV00GBA2zmdiu0bOOWsNPoMbWbbtywPvzg\nMx8Or3nCEeGc5z0tnHXKY8Nn3/zqsHzxtthzq7JCGGzuirWdjtNbMq7ToIPoQwbgAX6zADAXkaXK\n3vGOdxRu2PPPP784a5Yw6ytpxICBBl4lna7abRX31bPfHI454ZTw3u9eFv7t1W8Knz7rldVht/ss\n1iMrui+Jm5aQkrySMkwbHY8APOGEEwqtnYAuW4QyolNcTt/dZmBWHl9yE7cdIUq4EqLGpRAkCxlQ\nA39WaLWtZnmsuvfusy5YYriuUyy7CqKEMhdls2QsYzv+UEzGkh0s/k75kcj2iU98oiNjvY6n5e8k\n6XH5yheo3hvPGStXLa3VidKzZLEOTTW6Ivcj1a1L1rM6F2INc0kDRc8ob45zMI+qVLa6Wbuo/B1Q\nTc972pdyXiZd3FjqyUtW/q3uvVaSsUVI3U/h4vPPCXfccF046/MXhfMv/V0478e/Cfsdclg49yXP\nDkvv3Zog1qqs2JqQtW674/SGjNtu0EHyRQbgAX6jCFvN3pXYXBgzZ8Wn0oPJRQlIJPKoAeSqtrxa\nlXSyaZde+9EvhkedvLV2cksUGls2txY/Xrqus4up3eO2sv1xxx1XZCOzOGWiNiOZ1HoxqwclAFPv\nXPuwqAlKArKVdYftw8vAysF7FjA3IfIKeCkFqRwFMLOyCMx2FmQguFlRXM1im2pLy1m4jteKG9px\njdNqQo5xBzoBFd4L1wRAJbJ1RaxJoOp+8x6ZB2XSbAXgAknxXTXDKcudla0tZFcEWMtNXsR9Pae+\nF1/2jIrdUsyEi8ox4fLY1VWMnKt5xOuBWP7msnmYyHfV+cFr1mo29OLYWKeOFs+7O1z1o++EM95z\nfgG6thkZlYZTXvzKMGOfWeGayy8tdmtHVui6V6XekHHVMQfL5wzAg+BOAVnZwB7gsjacTp17NSXz\nVN1ptmnF/ZzGSq8Tp04rhMRF578nXPjet4XnvfWc9FPTV27oviYPrDgvfrAWqxZA3fGVp7BYue3L\nMeRjjz222BxQAfRWiKWUao4JXcIuEWFuHGCsPApJmKIEuIcUqFaI8Gbls2Q++tGPdjqG/VnAaoQJ\n+EaET9yVBPhgJ0qSxiV4TUHhceC+bEZ4A1jdB21AzZUyAWTAzKJ+/vOfX3gauG+TSxdYfvvb3+6U\n9FTev/yeYpcapAhB4DsvCSUB/ymCvCW8Mo2IxS0xK5FrvuCCCwpgT0lZwlCUg6obuvoMyAvxXVer\nh5Edy9fUe63m3TY7TJsxM0zZdUY6pY7XWYccHu68cev6x+3ICl346qinMq5uzMHwXQbgQXCX1DQS\n7OKaOjVVibb9/ve/v3Cfced4cMvU3SJ48Z/J03YJ02fuEf7885+ETRvrNeXysVatWh0uvfTSIltZ\nFnIrpT7l/Vt9D6BYlywJGaXVhhV147BSCV0uXTWi3M4UmtSdiPWahGjd/uXvKADJMtKxqLqsHXe0\n8AAhmKxkx1XiwrWstrQVUlJiyTuuUzWbiSgfEna6ivOJTzuH5E5N+w+mV8qRDGX5DdzBMuFT3L3u\nOtxXrmSZxS984Qs76lzTtixo/DQ/JSyZQyxq1nHKXsZrc4S12RWZ4ymPANACfDyn6Dl3nghztU55\nTmN7ZikV5Xg/a9i1UPISANueq7valjIpDWk81yRfhBVsbKDtPCmHxnNurk9oZvnK1Wm3Tq+SribF\n57+Opu4WczEWbXVB+711WVHv6u6pjKs7x8HwXQbgAX6XZPHS4i19RuBzwXlwkESfsiDn2mJtVWOG\nVirpDo2KiRn/8tLXhLd99bvh5mv+EGb/tXni09ZjxNVSYpkFQCSUuMVll/rjhmU5csmJbfYUFACZ\nmDABw9JoxdUq7gs8uSWBG0GJb0nQtuqKdq2veMUrOlz+koF0Q6oS4UuwEsSsEkQY6q5EWFsXtisS\n+9daEc8I5WQlteKGtj3B35N65a7Ory9/d63ipe6VZ+ALX/hCRwimelzWnCQ2HgptI3k7ygQEJV/J\naFeulshckEn9+99vTUDEV4lwVZBL25dfAaQcgkRaQwqLOIbnAJCboylslLarvqo/Tspqck+z4ClZ\nfisDMKWLxcjDkcj9dR2eO54TLm/eHft57tTGexYpmSmvIHlPtmza3i1s3L0PekhYsnBeOkSn1yUL\n54d9Dn5ox3ety4rOxoEBekPGdZzIIHuz7Q4OshMfDqdLaOsxq6kAi8rDLBuT8PagSbJhec2dO7d4\n+Cwwzz3H1VmmsSPbu80b168L3/7oBwqt1jgjYsnOzH33DwvvuqM8bP37aCUDRMJBnEqMNQkUgMst\nJzGIFk4wJGCmiRNaklgItVYJwPEAGJtlRAh1RYBbbA84OSahRFg5T0Kc5doqcRGynBDr7Iorrije\nV//BCw08uBBPOumkjmO96U1vKs7jXe96V3WXjs/2Zc1RroCppg2W1COExf+6umZ1z4PRDQ10uZlZ\nfABEZnIdUWgkJkpK1IbS81AmbnyKlXtT7myWtuFVSglLSoZYx8krkrZp9MqtnVpIAn7lZFza5j8w\nViOe5n+jMVjdQBvxbKQ6dXNaEqHrT25s2/js+S/HgSmfztszQOEzJvnBVV03P9I54dXfrv6TYbej\nvQ58cFgTx7jl2s4x883i2r+8JOx/6BGhXVmxc3zGytRbMq485mB6355kHkxXNgTO1fq0QJellYiw\n8ICeddZZxSu3HIuOUOZe0jSiStPHja5+1fTzqDFjw503/aNIwLChLMg7bvh7OOio5jE3217x80vC\nD3/4wyI2STASIgBSYovMU650oAn8kgZvG8DHGgV+BC9gJlDEtAlPAsV4dUQ5AVCAu1mjjvK+BB0g\nxEt8401gCSNKQNkVWN6v7r1zTRmvkniarc7EEmJdsY50LcIDAvx973tfYSW9/vWvrztEYQnZDo/E\nEvWSftnLXla4s4FwM5LAQwi3c03NxtsRv5133nmFlSqhDaAoF6oSTw+FlFeDC7PshgUw3Nb2NZ8k\ns9UR5ZbiiswJTT1SiVrd9uXveHhSljkPCiuU9WluO1/lTF0Ra5S1mkjcmQWeyDhAmJXtOUEptgyE\nuyL74NOsGJemoCQ3OCWZJ4ocuekvf64FaQlXp7/7vPDld78xzLlpq1K6dtXK8JWzzwoz9t4vHH38\nKaFdWTFlTOfM796ScV3xYaD+ntcDHqh3po3z8jDRJNPDVd31rtiE48q4AlJXpUjqgM8454JwyDHH\nhtuv/1v45gXvDeJA46LFeNLzXxoe9dStll51/PR5VHR1L772yvCGl7ygsHwtQp+sccJNbIwQqBLg\nJLiAC6ECaJKwqW7rM+GqhIMLlxUoscVxWNUEmu+Su7du/+p3XJWSaICjP0DvNTXEqG7f6DMw50Z0\nbtyEZQul0T6+B6YyndM145Xvyi5t/BGfTpaZhCTKF6tLSIIC0oxYUACYotYOrYodztRvprkzMt7j\nCaNGhIlxzddkRbUzXlfbukZLQ0p+khgllgvQygToJKbpw1wFIQqNhCtue/2XmxGwfd7znteRM8HF\n3cjKro5DYeQ6TW5c95xSxeXLauf56YrMd/kLnl/Eo2XemTvV6+pqLL87B8ooD4+559U9546nuCcF\nzPE06lBdgZ7xny8Mp73lnLC+gfPo8osvDL/53kVh+X2Liu3JB8A8buLW1ZlalRVs30ftNS0cstvk\nYpx2/ulKxrUz1kDaNgPwQLobfXQuhOdPbpnfrVZza1auCOMntfbAWIj7aQfvHv5w1ZVF9i4gpeGy\nfpOVRkACgQQkzS4ZIAG0BB7cbEng1e0HEJIwY5EQwM2SdcpjEE4pOzqNIWs6JVCVt2303vlSgoCI\n1yTwGm1f/V4NsJh+uka8kiTEq+HaucrVvyYCALwKBC8rKtU1p9/Lr86NxcMb0RU4KFu7Iy7ccXds\nmqC2e3O0ni3gASfkEwDhEZHXe04aFw6YNiHsNn50r4AxNyyrlRdETN3cKRNrk8sfj6rJcjqbAWxJ\niNXuUeUx0nueEq7pFO54+9vfXiQypt+bvZofQhfVuDr+84S4b1Wyj3OmKPsDsinmW9220efy/KZw\nUmbNiZT74HdKo/ngeJ4bnqMymNsW/5KnSIjrU1GR+cWdS0JXJYSrli8rZEHd9TnnrmQFxe3kA2eG\nSRUruNH1DofvMwAPh7scr/EvcY3Pf8RlxrZPgeg9Bhy2W1ygYK/pxYC0ezEwlhs3muQX7sDUw9hD\nzHpLbt92z4LwI5ABO8EGtBJw1o1FQAMeSS1AmbXB0iwTkHKeFIdELGkWdatEsIq7OR/WiHKkdgmI\nfOQjH+kAhyRYuVm5R8sACuS5OlntSmrKJVHV47L0XXMjoFaj+df5y8K9sTGD3r2t0LiYXyDE8Yg9\npoVdIhB3lygTLFf3UKlWOVaLh1zFEtHK98ax8ILFLBdiVnSztkK8HeZkUpAAt5g6PrdCQhTlPAH7\nAV7H5+p3LxLQpvde62KxdcfzbOCDPxax+DY3MgVK+MLcAsBCERK0yiEPLmzHkbzmmIl8597LqFfH\n7nmQAChmjvSKtxhDb66Ulo6dXg+YOiE8cdY293r6fji/ZgAeJnefG/Fnty7olhXcCotYv7TbCfG1\nTOLTtG0ZpQQId7HXFK8jvGjyklV6gwhVbujUkcj4zYCZUCLEuewAJ6uXopCsG4KKVdFI6687Z8KZ\nQHZcscd2MqvL4wGds88+u8PC8ZtkMXHxsntbLFJWL2B59atf3RHTLI/lPbcpgc2Krl7P7LhajdWy\nLKrRHWLdPHyPqeFB0SLG83bo4x//eJCMJj9APD2FKcTmzz333MJVyr1bJuEHrlUxTMpUqyTpSFZy\nStQC9MrmWI2tEFCjLKQ5Zf4IPQBFv4nPpt9aGc/8sj93cfpzbcnCdp8oY1fEBDL32XlTbn1/6qmn\nFvO0vIqW8ZxLItvhDyWDxQ3I5WBQ1mSFJ+Ilu3T2gi6t4LR9u6/mxwkHzAjT2sxHafc4g237DMCD\n7Y714HxvjWv2/vmepb2+JOHoETuHY/acGg7eZWtMqHqKFreXLEPIEbAptgroWMiJWHKs5t4grjbW\nLM2fFUuoAWYWOOuE67FVi0RmLOArg15X5yjDW/MNRPgpJesuiaUDGsI9kTij5CIxR8AqG1fNJ6tG\nvXi5NCbt41WGLgFcLrH509wl4fZlq7vVsKU8Nrf0/lPjGs777tISCLtHEgxZn1ztF8ZOb0IHFJgP\nfOADtasSce2/6lWvKtzTrqMdopyZC8l6xSfla41yJ4xtniRr1itrnKekHWLFprgsxS65z3ljnA/Q\nrBJlKpVRUVjV+UtupKSkBT/sa05SyKqgnzwdkti4nLnzbSMEYRzemSpZD/jKu5b0+pKEQhaHz5gc\njtx9azev6nGH8+cMwMPo7nsA/zh3aZgdgbi3XE0jorGzf3QtdSV0gYVYMEtGyY0EokTAgnafhAiN\nHRATIj0hAjfFdVnidQDa3QQwQAH8WMypTWD1XFkuqTWo621WalTdt+4zFyyXYRmIWdosOPE+sU+A\ngs+uVRekKkhxkeO1hiTo+hiWuDqGJ3qLCNuDp08Mj4zJNs0sYYqXRhGyz/FG0pT3CWjSXEjnhdeu\nXTJRI36nbete3Wcx3xT7BECszGQ9U2JYsGWwTYpa3Xh131HUkhWL/+k9AHY9FM6UNW1bLuRqglka\nF9AnJcq5WemMImvhCUsuIh4bFm3VLe/ahHYomDLlJfghljbPkGM3or8tWFbMCbH/3qA4HcKMCWPC\niQfMLPIHemPMoTRGBuChdDdbuBat4H4zZ3G4e/naHoPw6Ii+e8dEnCfOas0S4T6T1MSFJnkIKJdd\noawzAiIJX1YaS68nQMztpgEBK0M5B2HYCrFy7MsSqQq4uv2BjWMQbgCCq935q9lmgSBLGHZnrdry\n8bgb8dG46kETcdtqUsGl6rwlubG0lHKpeS4TIJA1vSqMLObC2k0N0l/LO7Xxfkz0iADgAyMQ1xEA\nEatmAQMH/AK85kOV8JASw+qtU6Cq29d9Np9kO+O/8SQBOh6vSALcstu2bozqd8ZhwSaQdW51lmza\nj9WdwiI8QWLQ9m1EFCV140i8l7tYmEF2uJr5ZqTaQFhFQpvKAM+PMjduZ/H11Ku80Rh/vmdJ+GcM\nSWzqIQjziOwxaUw4fv8ZTZWxRucxHL7PADwc7nLlGgmkvy5YXljCYsPdofEjR0QBOyEcFeN+1eL6\nZuMRdIQPIAFSBARhViaZm5JIkotYEhQgbhU8y2N5f2fMruWiZW0A4TLoV7etfnYOqW7Xb6yIWTHZ\nhsXZagIYAKd0cClq2uH6u6tUyHYGWBLJxCJ1cErxdOfn3FJdsrg6wc99Las4Eetz+cpVYfZOk8KS\ntZ1jq2mbnr5OlhNw0MwwflRn9yolQba3+nYJQdzPySotH5NnwXmz4JpZbOV90nv3LFmzXnkFeA3M\nt1bnkDkCVIE0TworNJFEJ2O1SjwRlEtkXOGMrhL7WOxJIWHpmjfqxoU1ysoCoMWrBO6OQUHjVTDn\ngDfFg8JL6XB8SX5d0Q3RM3JDTMxqNRmvOp7mP/tNGV8oYiPjMTPVcyADcD1fhsW3C+MyhX+JWa+y\nX1tdsGFstG4mjxkZHrHntLD7xM71me0wjVXDRUuAALjjjjtuu90JFfGuFHMDPK209dtuoPgFAUgQ\nivc96UlPqtuk4XeAlhBPBBA03KiCKEFN+LFMCXzu9mTNp33Lr/Z3/SwhSghB2hVApESacj2vFXPE\nUMW4EwEI1o7YMwtc9jSXKyLAL/vrjWHx6CnRC5L26N3X6HkMD41Z8Y98ICseL7hPnYskMHxhiVeJ\nJQ+YTz/99C554ToS0LJk03u8b8b38jFZrfhfdhn7nIAXb8vg6x61U5pG2Slfp2tPbu/yedS9Z+k6\nNovZNdXNDZax5yJt61lSO+2ZYQlTxlQbIEotVzZXfyt0X1wl6S/zl0YlbUOMC7fmJZEPIiHzyN2n\nhH0mj8uWbxeMzgDcBYOG+s9c0tYLlgW7aM36aHXGxurxn+R+Uvc5OmqwlNjdxo8p3Ip7TopdrHYi\nYntGmgFYnICwkHRD8NaReBhLLmn+QBSgtGsZpaXdgB0gb4eq5R4sieOi0tDMjZjGJ0TFXSVJsVyd\nf50wTdsb2+9AQVckyWkAARmLNV/XrYnFxDXtWIlcqxaZsolZQ6zwibGu+7v/mBPW3N+zewjk7o9z\nZeeoSNQRQfwvsS58+X2LC5cz1zNrrmyxp/0oFCwzFn3VlZsSoRLAJrdxGRjTOI1exUopO5KYyoDb\naA5RpCzWkLwwxuVBobw1u3fl41PE9JdOY/BIsPxbIeED2fN116iMzDOBxPJ9lqglji7xEEl05K42\nh8rEEj47Ztazwlsh93hhLEuTwLlgVWyQEz9vjBnT5APdbWSUA6NiKIqcmDZ2dOEV23vy+KJWvJXx\nh/s2GYCH+wwoXf+mKEyXxfV8uZ0SAKfOR1PHjooPVUThXiZWLveymJeYVerJW3cY1gTwSSUpEqE0\n6m8FBNN4LFkWLUtLAlM7JNtU3BIYAgUKQRKArYxjH+DLJS2piBvbNQEkoOL7ZO3XjSfOzBoi0Fm4\ns2bNKqyftC0LnJVvbCUqKVvW7+KVhLp9f/rrK8PSqXuFdTXm78de++Jw6GOeEE74zxenYYuF1994\n0qPC5/94c9F60A/G+dxbXh3XiT08nPqSV3VsW35j7sxcvzQ896lPLnheZ5W6B4CDBZ+ANgFssmpb\nicGn4wJUoGPfT3ziE0WNLDClhPC4dEXOUXMLfESUgaT4Udqq4ZJG4zm+GG6aq+KuLNKuiJKh/Io3\no8wv80LLTMmESrbMRUQ5Exbhmk6WrTwDymxKtCsfUwhAGKMVXpT3896qalvlw6aiQUs8wUImjB89\nIkyNzTVGRes3U3sc6BygaW/fvPUQ4wCA3TVauTuyVJ57DBABUuURgJEgASJVAjr+xLZswy0nDkro\nAnGuuK5I6YYVmTQvAODJPdfVfn5nNTgeIGNJyWiVqaq0qRW3JMuJwiFLlcKhUxe3oGsuE2GLJ9zN\nQBXoAwECGUghFlCyglICGMUAWLEygYj9JWCx5IyDbPvJr349POu1b+62e/DOG/8RLo7rRN9z2y0F\nABcD1/xDifvmJZcV15p+dnwgBkgARWoiwnpPQJe2bfbq3lG80l9yIQNMOQQACY/Rs5/97KKDVrPx\n/Ia33MVKhYxjPqXGMe5Rq+DrfnH3J/A1Z7tqOKNbFeClLNSRY4uVOyeWuOs3/3kV9M02Fz0HZ555\nZvEspDr26lgyz7mteZwaZWBX90mfWbmarewSWktkTPvl18YcyADcmDf5lx3EAcAEJPThteQioQzo\ngHIdEUZcbFx8BCY3nXIjAkWCTLMEF+5dwl/MjFub0Go1JkfYK/UBmqxLGcdcuv5Y1eXuTXXn7TvC\nmHB2bQSupLDkNkz7iA2LNfqrEuUDiHOpAuQEzIR9AlnKSbKG1F/jLxelntFcogccdmS3wdf5/O4n\n3w3HRwv55mv+WD297T4/5KhHFADonroer6z4ROW4dfouvbpXgDWBaxls/VZHlA7lRgl8JbyJgzfa\nPo0BAGXLU64cB+AKOyBg1xWApnHcB/c3uY7NRSV1FI86ch/NJwpXmQCtuZKSt3gw8E3SIqKg/vjH\nPw5qxM0B81KZEl4h18GaTp+LL+M/ytLUArOglatl6l8OZBd0//I/H73CAQ3iJeBwceqQJHGnKwI8\n4ruEDgI4hEyzPtC2tcSd46jHFB9tlexHuAFvMTXC0/EJeclZKV7bbDwJUuLfSDMKikerxMoliMtx\nbII8ubNTElLZhZnG9t2K3Q8Om8fWLzTPBb0+KjT7PWSbu3TdmtXhtz/4ZicXtPG+fu67wvSZezR0\nQdtm543rw9R5N3nbkFibdSAL+BoBV91g7gnrLoEULwULsat7y3q0D8+DOcMzIVSRvA1AvM4jUz0H\nc0l2f7I+Abl9ywpH2oeCAHir8XDHUSJGyQTmarwRr4ZngcLJKpch/tWvfrX4jUL5/e9/v/AM8Xwk\nch11Hh5hHn8y0DP1Lwfq1cj+Pad89GHMAV2jxHkJL40X1G92RawDliTwI7QJTtYM4QWU6ghIckcj\nyS4JvOu2rX7HFQ0YWDmsJDE4QOw71myjY5bH4X5VKoJkBrcTk5NMBLQAbSIWkxjjcccdV4AFK5CF\nQzizpOzj/ApAa2A9prFCTK/Zcv+Wjr/74/vu0tZUnc57AySxcBaxxCT3wR9LUf0yEATIxbl23rXh\nJ1agOHICX/dERnAz8KWMiIfyDgBfwCeUwTOSwJdl2Qr4OjFenAS+vDEUpCr4Ak9KgfhwGXxZpngA\nsJOr275JmWOhpy5x7mkCXy5lK0N5BoB0mXhL6oj3yDWX68jrtsvf9T0Hsgu673mcj9AmBwAJq5I7\n2UpA3Kk0/6o7rTqs37mBASNLhNCynzgta6C6CAHhrCyEMLoi9toFooCtK2L5OkeCWizZuASgRgms\n42SlaHXYjHTGYgWx+pVlEfbGaIUcj+VP4UAARPyQUPc9FyOLrEpaZO715JExdntY9aeOzw9/8lO3\nS8K68off7vi9nTeLF98X/hAVIfeFZwKx7Py5P+WYJ7BJbmavySqugljd8fWFTolJ9qV81bVbTPs6\nvnmFX+45cAPa4urc2IiS0NUyj2k8lme6FuMBX/MkkeOITQtVlAloOkYjRcE5UA7N6bROMKXP2BRU\nx+H9QLalaKWkNWBvXlTL5SgHFDRWsOS0TP3Hga6lTf+dWz7yMOYAYUyovfCFLyxieIQjq6Eus7PK\nJsJJuQgrRjyOgALCulopdyl3AhL/BaZibeLOgKKreKHjce0RuMYWV039rVnhLKE7Y/MPbsauao7F\nJ4E4q0izBefZLDubIGZhc5tyuQKROqCt8kQJlLIUPHn9wx5b/bnPPq+P7muZt7owsdYoOY2SfwCN\nv7Jl6MRsXwbkBNLABlFkkkUIrJW3NZsn+MZD4pUCw+pNQEepQuaAxLpW5oL7J56PWO1pPBY2RZKS\nleLzxUbxH/OOwkWRakaulUJg7n/yk58sNvVsmNeJV8ZOQAvQUxmaeQGEq5axQXQi0x0rA3Az7vf9\nbxmA+57H+Qg94IA4lRWFtCIkEAnzM844o6URWVxigoQTgcXlBmglUHF1pmYWAJkwI0jF/o6LbtxW\niPXB6gJqrF4WOxJ/Zq1wh7I4gXLZGqqOzQUu6Qdou0YABEgAPAHK1cxi6wpoCX/Wl2Oxgljg3JNi\n6cml6thj79+2Wk71XHr7857TpxaWL8tPL2uxSlnJQgbJIu7qmLKK/SX3btoej/CGoiPrGb9kATdL\nhsNb94rLmqvXPTMOsKQ4+R6JHwPlrgjApmQt27Kk3XvnAniVIyVyf4QDAC9gbYV4ATwD+JYIoFLS\nUgzZvMBfx3VNCYBtzw1dB8CeKfxUblVWSNMx8uuO4UBOwtoxfB40R1Fkv7UOeKv7UmmSpcT6u8YP\nmEmWInCt/0qYt0uAWLJUio0RiBojcE8jbmsCmrXNimmFZPGmuKPYcHnxAxaW0hECUtZzXVIYpYBF\nS4ASnKwbLkPn1oj8lkDDubqGqiUlxswSdM1lAsrv+OCHw+pdZ4X7R2yvf7daB2zMLpOw4nWPXzI3\n3H71VUWtL8WAooOcL6XqRS96UXEteAWs/CUXarFhN/7BvzqLGZ/FfBHQkdmc+AyIUsaxmK94bPqt\n0SkAft6PxGPjUSpYw+X4vHG4wyl9KWTQaMzy9+aEuDbPDNKkhBfHeXLfU0rSUpcUBsBO0UotLO3j\neI0UknZaUxoL6RVAPpATqRGHJUh1wMrUPgcyALfPsyG3x6oNm8KcZWvCnOVr4sOl3jQ2WvBPJB2v\nYMGE2NN339jbdb8pccWXWHTfH0TosBAJSy5GVm0jd2ZX5yfuy42LCEjlMSxXgOk4BDTXdCtECLMm\nWJ9c0VW3pcQswJOsHm7kZGnVjc8aQ4CEQGcFsW6cI4BORND7zKpK9IIXvKCImydr2RiEM9cqBUDZ\nSmxdFZbvcXDYMqr7rUTT8Zq97rxpQ5i0YHYYsXljUfb1mc98pnDdA46UqObalJ9ZLi8pKKz9BMbp\nFUAn8G52zFZ+E29lKSaQxm8uXjxzD3lAugJK52Of5FlQbuT83NtE5sGsWbOKudTMA5K2L78CWY1p\nzHXKFmXltNNOC1/60pcKd/sVMWeBkqC0zPmzclN3NOdFOUjE21CeN+l7FnQrrSn1i78rygYywnrR\njre1h8v9D8iHncK4kTsXrSf3i8tRTo0dsTK1xoEMwK3xaUhutTo+TNfFRdjnrlwXvN8q9htfKpts\nQux6s+fEceFhsdfrxKj59geJJWraIfOX1dpqokzduXI7ll12YnOEF5BgLRKgXRHBLemHJZQSh5KF\nkqyjZmMASfFMgEBoy3JlQXEzyghvRECfNc+VzlLS9zeBNyCR0MWFzUoigK08lKy6aYceHW5f1fU9\nb3TsVr7fbeSWsPm2rbW0tpdQJw4t+/n0WGpmkQAAgyhSFl5QXkPRqCO8BMjqrpVtsVSNRQGpKj11\n+7fyHWA2XgJn4FclFrpQRVIIHDspPLbF+wS8KU5dHaPZZ3ObIgXkXZ+uVl7xiNKlHEnWPHd76uzm\nPNOqV5K9kqXvOOaREEcdicmffXZ9a8p1mzbHpQmXhzuXrS0U8y1dCYh4AN4yyw9apGVKPynqddc5\nUL/LADxQ70wfn9edcQH2a+NCDCvWd08IW5Dh4XGB7f2n1deT9vHpFwJISz7CD7BwufaEWIgEewKw\nNFad6zglQgHA5DItC+C0b/U1CWogSCgCGuBbJdZNSt6SmAVY6wjIs25Y8+m8WcysSe0duT25MVlf\n6o7TOQKZhx39yPCz2QvCiqh49QURxMfvv1u48drO5S5i+JQVYKL8yvXrU53cv4AEOL/lLW+prWGl\nUHD1p6Qn90dnM9efrGWvyaWdrrm71+g8gXECZIqMc3WMKjl34QB/rca3y2O4Bo1TAKL34rTCCDKz\nxZoRTwjLV7meBD7zVmMWZM6IW0sMTOtg+75sHftcpkatKedHpfyPcVnCFXGhllaAtzym95Oion50\nXLBlVlwrPFNjDmQAbsybIfuLRdhptq2ucNKIEaNia7qjoiV86IzmmZyN9u/p9zKHARBAZBXo/dtT\nYjkQ7mXBTahxNforf9/sWAQ2VydrCuAlApoANglYArWOvvzlL3dkqCpRuuCCCzo2k/XKuk3xPz8A\nCoIbcPEKqCfl5gbChCyLHrHO9IlGt9y3MlwzLy7oHuN5vUl6QB+62+Tw8GgFsRK59csud/F7XZwQ\ni1dbREqG1xRPB8xinhZo4EJH7jPvgOtDwgTc/+W4e/FD/AcopYxmAMRFnEAZeJbPJ+3T3VfnynPi\nfFpJ3Ko7jnNi9SZlizfg05/+dOF+NidZtUiSl7I3PKEIAGZ5DSh5bMwtNdDJPe78WMd1XgJKZGpe\nYg6h25euDlfPWxq6u1RpMUj8xzw4OK4J/ai9p6ev8muFAxmAKwwZ6h+tavLHuUu2NlPvhYsdHVdC\nedjMqeGwGV1njPbC4bYbgkUkLsyNLAYm/gVk2iGJUOLBXM8AQwySEGtGrFgWj1hhcoVyibPu7O89\nwVZHXKmsNqDIfdzIhQ5M0zq+XK4aawBepUeJWLesXX/ogx/8YMeqUpqYiPGVwea4GN9MCVvi/L+/\n+75wWxS43bFy0jmUX4UpZk4cE044YGbHijjlRDXbAgRAI56JJAmx0PFRTBMQA1YENJTM4IXGJQm4\nga4cgGqnJ7xVyiUL2b5Aqa4emIufApMUEwoTwOqtBLBkMXv1Z54k939xYaV/KHzurex8c0q5ke5o\nicTLZW4j1wNM7ZOs8FT/zKOSmnWYI3iQqJogmL73ypoWwhBznrtibfjl7fUNPMr7tPoeCB+y68Ro\nDWcQruNZBuA6rgzR76z/e8Wdi8OaGNvpTZKA8YR9dw17Tt7WeKA3x29lrJNOOqlI9GHpcMnWxbzU\nUwJaFiSgLQNTK8ewjRgvYdYoqYbLV1wONYu9+R2AiOE6Z27FOgI+5RKUtA1Li4WkoYLrksktAYzl\ng9TFyspNrkvflQW0zwgIE7gL4tzoKQhHWVssWfnUA2cWyTlbj7D1X3W3qcGFb1hb4u8UB14Fblux\nT52xkMxfdaqs5ypxA/u+mqnOQmYNcsEa3++NGlwoHVJ2hsp8AcLJUnYv3R/j9pQoA0A4AXJ6pQRQ\nlJwzS53Lmeu5TLwmiQ/4RMkSduEBMhcpcxQKfOERQsC3rKhRVFK2f3ls7/HdcT/+hS+HX91xb1i1\noXflgzXEj91nlyBBK1NnDoyIbquzO3+VPw1FDigb+PWcRX0S87PqjUW7D4jxYCum9Adx37F8WQMS\nl1ighJBmHiwLLjyWBGHGyqm6klllQJXAJuRY1bKgWaiEJ0sbEdDcm8biWq7G+oxhGwKV8OYubGSR\nE/x+E+MDBo7rWIm4UNXwAoJErFeJTBdeeGEB8CwmLkouZ4Am6cc1yyjmFTC+a3WeyriqxCpz3zZs\n2hIF76aOZSir23X1eUwUsvtGBeyJs3arXbaSxep8WKiOSflxvSwvXgPgrN5VKQ3FgQKlRIlixatR\nbpvovgCacmczv7OaAZF7CMSAXB1xuyrnQYCa58T9R17xy/11vrwZVeJupoihut+r2/vMo2JesFqT\nx0Xdt/3Vk/OWsPIlWzm++5bOyT2WsYzS+VlMRNY+JYNC6c9Y+GZf8yAluNkPv+uUUr/NmjUr/HeE\ngYec9K9h2YbeDUcUx47Xfl+UD/vFKopcroQj2yhbwNt4MaTf3bgotmWM8T4LavcFRU90kfl4+A6K\nBxNmBGS7iVBJOAEyIEWYJkHXjC9ik1ypBK9j+0OsDkIwuXX/P3t3An9XVd0LfEPmkJFAwiAQZpGi\nVetQrZiKbR1rRapWnxr1taKgWEV5RR+g1ScKbaniVCmDgiIqiFrnIaJ1qto6owwyhiEh80AG4O3v\nCeufnZNzp/+Q5J/clc8/995zz9lnn733Xb+1fmvtvaMMCpLn5HwLcbQTAAtkCCBFLwKmcqcgoEWJ\nU8ao8gAAnhxjgYIF6ICc4YGG5VkHcAEsdW0nty5fk3565/IMxBvS+k3zTNqdXn2HYpySE24envsd\nkLeiWZ2MfcBOEAaBNlRHf8cff/xA5q5dfc4888zKGLFMJ+OqSYCsVbBQ+NpB+wBlzENpyJTXAine\ndVDPwC9i9MAR0JXUbXmt96a/lcAPLHnM4TUrw5/PvhuKMA7CU2YQMBy1GyNPwlXMh2fA6W9iaVVj\nmkSGdPUh/yfjuRVzc9Z5H0gH/smfpd3GjswUImb5w/aemh67f5+Kjv7w2gfgsjV2sPfoNEkn1heW\n7Ul4Vd6bhmA6TgiFb3edcv5ffMdD/fzv7qg2045jI/E6PWdG/+WR+zZ6QIO9H0VGIfJAeTeUdjeK\nzbkW1fD6yrxylgUrhiooP/UAdJSwuFwocsqy3ApRvfUbARCx6larOvAMxXv98Z5DeEToQSAL5D0P\npcyTt0F77BaFirYAg/qpJwYgygHWFHM3CUIWWrhl+dqcoJUXxsgZsBvy2KknafFiJOCZG37YnntU\nmfDdejbltC9gwEgBGDxfsUgrhxGxbsskWjUrvExgK9vdAhJYAG1G0KuO62dedTspY6PORXnzHgEv\nA6EU7SZUEeOtXby+vM57xoBrA4wDmN0ryqtf0+1nRiSWR/lAmAEZ09VKqrlM3lJ2JGnV76Oul//0\nunTvmAn1r7b4vHJpNvxmzGxrZG1xQe3D1Dxt8ZmH75MmjdvENvh6uHRc7Vaj5mMfgHfwrqJsLJ7A\nA6OAATJFj5oM4UGhsHhMJV0Z35tSsCDTz/dmmrGdnPr0J6RXvv3cdNRjnjBw2tpVK9P//eu/SC8/\n8z3p6Mc3xynjZDTkkw/aK+0/iFiwegPawSRC8ex4UTKOI+ZHyfESeAE8XYo3PIOo72BeYyvCAFUg\nR4lEnJCHAix5VaUC5AWH11q/r8SiV7ziFQPequ/VFZ1exu20jTghbxfgB/jbkF38F6CoXywiAay1\njRWYtEcncKrXa21egGHpvZk2zdT0ujx2cCfieVY+mjFx3KDmgQNT8UztxUv1HIAEcKCWxYQ9D1Dw\nfYAVOvriTLuHyACWQc3wDCAGpq4H2k0ecOmB6wuAhKZlqJUiGYyBhcqPpCyJXCjfoYjntpiG+saz\nMgwDpONeQ7kHMDZ2gn73DCGtVngTPpIH0JT1vGH9uvSFC85P37j8kjRpytSqXw495pHpRW8+M03f\na3N2v3t00hVjMovzxAP2TIfmzOhShkPHleWNpvd9AN7BeyuAhOKlBACKxA2KPoTnQMGbrtLkAf93\nnu/7P3nBjU7SBMAXnvmm9JNvfiW95pwPdARg5R+Ts6HN/2slYn0SgwAXJRzeTavzHadMPS9gEUsE\ntK3ArF6OaSwUuut5V5GkUj+v28/6I9Z/ppAjw5YSlWgE9AiqmIIXe/YdoBHPLAW9evLJJ1ceWBzn\nZfFsedCukSFcUuTiwpGohO5FPYqZin9qU94R4yCm4ABmrIE4OC94RxBhg8hyBhSARx2Bkqk8Mr6t\n/ASEiXZm5Hg2wljzmQHij9FhTmwYJLzp008/vUpuimt8BwDdh5QMQXUg/2dKmLbDFAgJ6APCmMI6\nNYF6dUIX/8lsNj+b8YQilwU+N8deS1G3AGOv8RfGXXnuYN4bL4wxz6fd/Z6MLdPRvnfrksaFeD76\nzrekxQtvS887+U3VDlobswH11UsvqPaHPu2CK9LM2XMGqtKNrjgkzwt+8twtp94Nh44bqMQoe7Np\nRI+ySu9K1fWjp6gpc+/F0ErwtcsMRd0uzrhozbpBNdlPv/WVNC4nc+xz0MFdX78434uFz9sAtig3\nyi+8lHYFUQaejXKg9FC95bO2u7bVdxZ5EOcTUwWAZ+VkEzHGwYo+4FnLPEWnolEZBeoMLClL2c2U\nJ4o6wFMboAn1I0bjzW9+84CCVxexRRRyLMcYVLJpOdgN7AeaNDZ8cA2AYlxYYSroZnXjFRJArf38\nUXKMg/COqxO203/ai8crmU07MWKMF16tZwJWAb6qyMg455xzqjnB4v7a0fOg57Ub+vltb3tbdY45\nz9pp/vz5VV9bRcp7ZQT4KjPay3vGLdDm+RqnjIMAX0DNcBks+DIuTCm65JJL3KrygGWoN8Xj9VPE\nxKuTH/wPaAs9RfzctYwQxkWMr/L8Vu+1qbYpxXhYMXP/vC741vkBixfemr579afSOV/87oC3OzYb\nls94+avTtT/+Qfrx1784sG1lt7oCo1KX4dBx9TJHy+fNKZejpca7YD39KFGrfmxlHA/AmRtZLtLQ\n1DxN1FLTeeWxFUsWp8/923vTCa87rTzc8f1dS5ZXnibKnFKl9Ovg6zn88FFl5i2K98UcV4kiAJOC\nHir4RmWtJiWxSTtK7okl++L7Xl8ZPDKKeRTANpS1cgCyMAHPk/Iun/2f/umfqu95d3GNZwUGwDzA\nVzm8MWVQsgsWLKj6mHdGoTMkYtGRT3ziE9UcWsrV4gyxApJxUlLOygPqO4qoa7AYQic+a89IplJP\nAKudPRuP1tjQ3sCXt4zqDwBCr8qLkFmM9fD83p944omVIWfOcZ3idc28efOqLGjg6z5CFcEiAToZ\n0uFF99p2EqfUH/gCGdOqzHduAt92Zbu/saF9iDFGH6CzeeqMsjIxLM5rV2Z85/e5en3ztKOFN1xX\nebh1qtm1c486Jt30659XxfSiK+QUNMlQdVxTmaPhWB+AR0Ev8ZYoKN7TKaecMlDjk046qZo/ipLm\nkbHw0ax1RSMJq1e55B9PT3/16jdUcZ9ert2QrXUJQgQNSxHycFB4QDaAlrfIs+DlhhLt5T69nktB\nob7dk6epTkMBJM9FOVPaALL0rtSN8cBzBaJYCh54SZNiLMQ+eVv1DOp4NmUwFnjM4p2Ex2uur+Qr\n9LX4mSknPCQx9Oj7+pSjHQ2A9TnjC1hoQ8uAWuEK2ABbtLpNLGQs23ie+GyqDuBEVTeJ57SQB/C1\nVKl+QnlbWczqUhLagBcjqZ69jraPedPannE0mLWc1Uu/AkZUuf79/Oc/P7BYSlO9Ox0D4J6FYA3o\nAsYdg0tIBtsRwKsN/L785nj2TSI7HpNAX9yd3zeJpKupM2c1fZVm7D07LVu0KXbei67YZEJsXeRQ\nddzWJY6OI30KegfvJwqI4jZvERXlh4aWtJwgJeFH5I/iRXNSPibnl4qj16m5P/zy59Ldt91ctcz/\nXPONtGblinTjL/47zTnwoLTXfge0bbFly5amN+eEGUpVHXiB5h9SRjzRocZg2968w5eUO4VIoaM5\ngT+l3moRjA7FVTQ5Raj99RMPraQqgaR4pn4jFKR2QIuqC9DhybUThpdkLoClb8VDKV6fZcCiZHnW\nkm2ATNyjbtRQ3owEY4QHvyMIIBTzFp/miaFVzQV+6UtfWhkac+fOrZgCY93zWHjElBtGDU8SyNSF\nd8wQwXjoV14yg8ViE8IhfktAhyFrHKgDcb7+IPoQeIWHXh3s4T/eNuNYe+s/924FhD0UW4U5PINy\n9ScjEm0f48Gz8N4xKrxsnrJ2NTbkImAa/DEyMDB+m1a/2it7/03pmQ85/KFpyV0LG6u45K470gFH\nPCz1qiseaIg0D4eOa6zkKDjYT8LagTuJpQtwKWxUGkGz2WTdDy8sYscpYvGwoM8cC/mPvOj+3as7\nx4EjCevuW2+uYj9x/W3XXZtm7btfes6Jb0iP+bNnxOHG1zGTq86fAABAAElEQVTrVqfpeQs63p2Y\nlcQkio1ypTgAc3jGKEZeEEqVh1gHjcYbDNNBCtwKRBQ2Cl+CzGCFgqPAxYF5VvNzzFHcPuhnCl2c\nUhwzlhSMewFM3jkgL0V/Ut7aET0KeChN7ak815jzS7FrO14jwACu9WSvKFcdKWXtvqOI9v/0pz9d\nGWvGxlk5Rh9zgNWVYekc4Qrfe1YgYqzot9e//vXVo2hrx8U4m5KWlMWQcY3ziP4SDjB9T/uG8Ix5\n2b2KhEKgzugiDE6AX/5Oey2zPN+zMVYII/vv/u7vKnD3O/N8Yv/eez4gLMObwVUKw48RaN41FsFY\nWpn3ht6wx4zytOq9hKuTj314esP7L0lHPOqxA9/flw3K05/7lHT8Saeme9fkJT1znDikk64wFemE\nh23ePnO4dFzcf7S99gF4B+4xlJlEFVmeQS9RNKgxnpDdZELaAfB3b1mcrluyKTs3zm96DQAupyE5\n7x//13PS8TkLstM0JOfOGfdA2u2W31RgW33OCS4Mg/C6KBDb0JmrSkGgBylMypVSBSKUH88QTWtB\n/lYUrfKHIrwCNDJlZclHQDBYAYy2h0OjehZC2fFSJQaFxPKTntVz8tZCUImUI5rUVBrl8OJikQ7n\naatIsuLxoJpjkRAGjox4z0Mh14VxFuOk/t32+oyeZ/zw4jEm2AI5AZ6Z90bEvmMeNapd28Ryn8aH\nqUdApwQb7RsGkH6QnMYr1EZispZz9NsimCTshXn1zmu1YlR1cov/TGViHAgH+a2qk/yM+N22uKyn\nwwzZq666aiDUsCCHPvyegCgjpRQ5Fn5DjDiesrbAKEiAq9dp3cz90uppW04pirJ+8KWr01XvPzfP\ngvhglQVtqtGlZ5+RVtyzOL3+fRelMbltS+mkK/bN64Q/7bB9Bi4ZLh03UOAoe9MH4FHWYYOp7o1L\nV6X/vGVJ2vggMLQqY6gAjOp+Yl7z9bA8z49C5BmGUhSXYjS0SkCRUCabV0zLdbGIBsVCwQAUmdEU\nCtCRgDIYRVl/dvXj8aD4JX4Bs148FgpdXNvUpBJ4gXFspFDe0/OIQQMabWI1J4lHYpauZ1T5nvBq\nxXhLwSQAn1C6MnhjHivPER0eVGR5nffKF5sUBwc63Yp9YS1lSsbqi2IhhW7LaDoPyApJ8HLRyrEB\nASCOWLbrhApikwGfeZoo3o985CM+Vv2GJQIuwNa4MJ54V8S4A0KlACSUve3/wgjCzJiPLc7cy9jC\nagBv5TAg0ejlIjnlfbt5z1ACrP78FuJ96aWX5WAHnv3sZ1dTjLAkkR2Ofidoa7+rGJ9xrXY25ifu\nvW/6zq1Lt1pwJc77+icuTt/+zMfT8nsWVYcY6PPPOLsxP6QTAD8q7572iLyNaV82tUAfgHeBkWBB\nhS9cl+M+LbIdh6sJ7AFrpRsLNYSINwG3oAXRqTxi9F834jp0Ma8PUMmsplgBGEueZy2DkiIRtwPM\noXi6KT/OseoShcxz4FnwRNsJRSc2GZ6Ycyk0VDN6TxKROZdNUs6DVdeghF1D2Xou02owAJ6JN0fC\n+2WM8NiA7U0ZuIksWUDlD8hrj3It4Oqk/B8aFqPQjmJdn8F24cq16ebla9M9eVqZHD6bNmT7KuXK\n5Y0WUpqZF+Kwtq9FVyaO3VS/uEc3r56T8cGgIGhgYRbeO9GWDAXZ4Txhbal9GDw8QX9yIbALxoJn\nEiPW/6h2f0S7aMO6aEt9h+LHSpiXG1N0gLjwhGxq3nc7QTGjghly2lw5neL6UZ6xHOBaAm0YVHGe\nV/2KBTDejReG6LycwW1OMToao0RioRhjhGGpHdynLjLktaexZfWzq397R7U3eP288vOq5Tm2PHVa\nZfyVx7t9Pznrhz87ZHbac1L3xl+3ZY/W8/oAPFp7rsd6f+fmxen6vO3cSMohebcTi/E3CdABGEEr\nUpg8k6HQy1aQkl0ayxtGgor78/B4gmKlFDkPoVVsNOprfiYgJh/4wAcGPLL43qvnALwxJ9MxXr3s\nZElXwICxwEsD4mjlJoklEXmyvDsKlWGhPSSG8eCCVvQcnkGmu/Pdn8TSmN5TpABbwg9allDQsYtO\ndSD/p/7KlltQF8B77eKVOVyxKjHaWk0ZieusbESpzs39bjvKboGYUYb6R4cT9eQ1Gh9BG/NGxdO1\nJ08Z8GJAeIeOhQBic709l2v0AyAkxoAygHkp+kaZ4SFjIoR1ADrGQTiBaGt0NyYC0JWinjxl1Dlh\nEAmt6KtS9CEjCdCWIOuz8VqKPgSMxoI/ABnvIyGMJ8tI8awy5Hm/jEFlMdzit1CW2/Re7oCyQ36S\n9//9Rd4nvPf5ElFC59d9p0zM9POczifuQmf0AXgX6exl9+YVbG7IayNnxToSwvt9ahfWLY+Hkgjl\nxxOWgMSLHS7h2QBnilScj9KmwFFwvBsUc9B0kQAWlCwvW9xV/WTjxgIKwEJsMnbRUVd1Nx93/vz5\nW1SdV8UToXzR5XWlHCejmsWM0aDqhhnQNiGSrCLLNY4BKyAtFspzI8BDdnfE+dDMkosIgyKoWp+d\n4568Qm0Rsign6X0/7xO9PI+TTqGKuCZeecTTJoxLj9lvRnrItK0XdIjzvGpXbRKbB/AWJawFvcpj\nZSAQ9LqxYXpQ3Yvj4UkiYmDxGLEOAZxobV4pD7vu6esT7RZT0IwF/Q3QQhhAgBjYEcAmoUpclyFk\nCg+mQx8TK9CZ48sYqAOtPINgf6qT838MggDAEmgdqxsLcU28lgAL9BkIDAfgjoI3fuO3FdcA77lz\n5w6sjua4DGjT5EJWr9+YvnT9XdWyo3FsOF9tWfrkg/ZO+07dMTLwh/PZhlJWH4CH0nqj7FpLUv4y\n74o0mHnB7R6VJ2Snk3ZLUNavZ7FTJuEFoH55GbyckRIUo4UrJMqg5nhNqENKmfcRi4OgOylzIMeb\nooBLOhegAjWJW62EocHLci3PtCn2LYM31vQG4jzwJjGNpoyJUqiYBKA9NyvWyKCOfWF9D5B5bkTC\nkXmWIUCd1wfgyC3L16Qf3r5kyCGK8WN2S4/NG68fPmvLtX7jvjxP3juAI7w9tL8xoP0xATw6decl\nE+1Xj13qH3QsDzVE+wBFFDAxlsTlAXqIcjAPFsgg6FzGADBvEuMEsConhOFiLABhBgyjiQfqWOmZ\nO5+Bpp4lyHrvuT3vYMR99B/BIqDdTat661vfulWZjErtoE21o+k+JTjbwKME/N9k3fDTO5d1vRNW\nt/VnoNkp60l5z/C+bNkCfQDesj126k9iPd/6/aJ0e96cYbiopvzbSnP2mFB5v+PGbFaI3TYk5QWI\neamEMkSP1j2XbssbzHmA2AbnPB7KrUzgKcvjJckytitPN0k6QASYUNS8svCylSluxxOjGCUQUabO\nqYMBb1b9eLkMBUligCxE1m6ZNCYhCMA4Jj4ZoH7llVcOJAbxGAEIivOu1femL153VxQ35Fcg/Oh9\n8/zevbaO8dtQAdVMeK+MD8/COAFs6gwgxKnrHi8wY/hgIrQj4GQwhQQjICThmbUV4JE1LBZK9G0Y\nUvrE1o9l20VZXhlQ4c2i8Rk37tEkjBnAWgdacdvhFn2HwSDK1x7GUClhtGBKMCYh5fM7xuAp6yjO\nL1R1UzbIBrF2T9xmq9dpEzbtgtRtiGKrAnbiA30A3ok7t+nRZLNede3CaueToYKwn/2snFDxjJx4\nNYaZOwRB2wLioAZ5JwCiVBBDKL7rS9HXEoLCAysvpPB5WjwdSo73UCaAmYYSyj6uQ4GjUD0PgAUw\nPCAGh/JQlBQjmtLncnGJSLLixQTgyy4HwqUo232D6o7YMJA577zzKvBwvvblsQE9hsFD//DR6Vs3\n3zPstOPknJRlwf19cswvBH1rIRGCxvWZoE3FyjER2qIOvM7h0TM0eLzA2XnaCoDqA+EFIKmMENS7\nseR783IBdoQPlMOgAZz6OYDWa7xvSoSKsstXeQwS5oQn6kBYnjdc7/1OgkGolynBUdLYTTnm7LnU\nR5zYOCAMOQZdiDBMPWERO/al6+9MdkgaDhCeMWFcetYR+6TBGOdRz535tQ/AO3Pvtng2P7Jr8vaE\ntilcP8hfGU9nnz0mpj85cFaaMIgs2BZVq5So+GAoQN4Oz2Lu3LmtLhmW41/84hcTDy0MAIW6J0oT\nOErmofzEFk0VQvv543HGwgeAgKizGJupL8DGloKSsShG8UJxWNQkZU/QyTwsErHBoBp5ipFV6zr3\nJBQtClkyWMQYgQ2F6jNmAfjzBC1liUZFe1LMQO9nP/t5umX8zLR43ZbzR6vCh+G/PSeNS0/P8z3t\nEwwAX/3qV1elmp4jtg4c0Pu8VOGAiPvGrRkTGIfwOo0BbUNi3rNzMAnGS9DKytTeYsruxegg+g/L\n4DxAzXMUN40QSHVS/k8bMXbCmxVjxo5ElrHYuilQppg5HrSzMACjQliipMaj3KG+6kfTnIRRIpEx\nymTg8fzDM46x43vto7+JMoxz44gYp2jouuHAE/7erfdU+0LX94KuLuziv7HZIN978oRMO8/aYlZE\nF5fuUqf0AXiX6u7ND+tH9tu8DdmvF63Msb+NXVu7HN0p48amo3LMF824e1akIyHAjGKlmMXuKGMK\nGCANp5jiVE5/UTZwk9gS2bSOyTxF2UmM8oo+psDqQlEDbcpQUg6ql9dcxjGBM49JAphpM8opVzlC\nwfPW0PClR83zYQSgbHnTIdbe5tGGYubxoB95eRKFALKktAsvvLCiuHnhP7t5YfrlivvSfZsmF0VR\nw/YqL+CR+05PN/3wmgoIAZu1q3miAEo/onl5ZaXwSvUz0OCp82zV3zWShlDGgET7utZzBohiAhg6\nPGTGjTZkeMT35X0YK2LJAbRe/el73xHetjne+sYxmfHmCYfclA0qWdcXX3zxQIyeYSX2/jd/8zcD\nnmecP5hXYMlYYKSEoRXlAE4sAMZG5r1ztCt2Rf4B8TzqFCK3oTR29EcwJ3GOV+P1xmWr08/uXF5t\n1tBtYh5tYBriEXvmhUByZrx5431p3QJ9AG7dNrvEN6abmHZyY56ixNq16ELdKQa6E7MCnZAzGQ+Z\nOTkvtDG1mn6yLRqIhyGzk/VPKVDklEypVAZTD0lUvNEyKQXVy0NoNXXIfUxn4oVSWrzPEqRb1UMS\nlgQYwiv2TECBQgUmngmlClzUwepAaNeSjqZceWzEohVN4A+cGQa8XwKIlcfrDarV3FbgdsF3/ifd\ns3ZzLLm6YJj/G3//xnTSUx9b0Y9ACfXOkGJA1EFR8h2wQKOWgpEI71P7AGEeLIAFgJ6Rl2v9ZcAS\n3l2UAZTdL3IMPLu+ZwBp91bCoxTvZ9wwhMTQedBNgjbnEStXHxDPKraPVWnqq6ZyymPGCC+eN1tS\n687xPHEfY0SiGEOAMcmgM6YYkF49Ly84hAHp9xTid6TdW8m6jfdn3bCqWkmPbrg3f74v/w5LAboT\ns27AdszN+/0ekZPwphRrAZTn9t9v2QJ9AN6yPXbZTzxiU5WW5tjP8nUbqh+axpiQf1Qz8qILM3Os\n1+tIebydGp4yoTjQvd7ziCg5XksvlJ95m5KoSm+Cl2lKUF35t6oTZUu5UuCyqsV+m8Q90JnodEAg\n1gtIKVRervrz4swfBdCUo7oBp1e+8pXVc0nKAtoRP2UcoLXbifsuWLB5hyb1RFcDCmW/7T3/nF73\nrxekabOa52y3K7uX71bnhRu+/OF/Ts9/2nGVp6oedYAEbjxerEBdIhEKEAEdwqM///zzK2OMESTD\nG3gDSIxDzJ1lGAFPhgxRhpXCMBnKkn3Nc6wLI09b6wfvga6yu0kK1JfGF085DDtxVhnoYtL1BLv6\nvX3m9RsHwgcR0nCct6vvtRVaHu1MJK/xdgGvecmAmMjgjkxtceCgmQF3GUPWhrzgTqItlq/bWOkH\nemJtBmMwHPqBbrDAxvbSD53qv6N+3wfgHbVn+vVqbAHgC8h4PwHE4nTifu2AmPKlrMvpPLwp3mwo\n6cYbtjgI4MTPlBdrGZenmu5CefNkgDDgBUCUKgXoOOVZTpNRF89E2TmPAuX9oaplAfOGbLFHmaJE\nGQyAxn3Mgy09NIYKZQv8ARnRPspfPXlmWps3Yd/9weScst7nvfbl6eg/PnZgo3XfLb37rvTGv3hc\n+vAPrk3jJkxM1ge+5srL06rlS9NDDjsyPet/n5z2O+TwspiB9+OX35WmLLtj4HO8CTDh1fJcy0Uq\n4n1Qpbxcm5AwRNQfIGpLgOb5UckklpzUtgAovGztxAsEbHb/MX4II8p83xg3mIP5eTqYtbgJIwiY\n9urBam/zw2V5R9szgDAuYuFN401/MyAAr/qH6GvP7RmxJATQRzIVA1RbYIWEJWKdcG1ozJF5ORMa\nVR/CiAmWxLFWjEqc338duRboA/DItW2/5BFuATQkhcWroqh4GyhXCjvEXFtKlGdBnMcjoMR7VaxR\nZrzyRMSDJfZY9AEoB1hQtsTcVB5uKWK1sYgDI4ByNNeXEgbq4nQoU3StLHCKWb3NoaVs0eTAWgIY\nz45X51rimXiTkpsAv5glBatMipusnHVg2jBlS6q3+iL/1wmAbU155guekd52xZfS9OxBf+fqK9KP\nvvz59MYPfiyK2OJ1zL2r0vS7rq+MCvfn/fMOPVMArfqXAhDVPbxZIAOAGCSME8DL8AkDTGa3fAHf\nMWqUHclbwE6cNPoa8EgCMz2JaG8shvYW7+VZ6kM7jolZD0U8p7HHeIj6MAaMSaum6SftYQwzDkp2\nQBvMnTu3Ata65+yamJtszBuDxhCWJe7DeNHnJNiWeBaxcW0U0m7Ftjin/zoyLdAH4JFp136p27AF\nWPoSZXgOgApdSPGZBxtKjUJDFYuTDbeIwwFUVCgDIDKarVMsntskwISXpl48G8p63oOeiudAiQOY\nEDR5JxpUIpYdnSheSh3gMTwAE1ABRgDg7879tzT74OZktk4AvCpT2HffelM68tGb1le++Te/TGe/\n8vnpg9/bFJ+O+sbrisV3pfe+6m8q+htwlAIUAWsJtN6jWYFJXfQz0C4lwIURxCDR/56XYAnQq0Ff\nx3W+N3XIbkXeM1YYRTxmMVM7NDGMhkuEBIwF21FGtjZGA22sz70P0U8BvOrfSsR4jRMMgila/hiA\nN2VmCCPEIItNPbAN5drmQFquQAgjD4j3Zdu3wGZXYdvfu3/HfgsMSwtQ4v6Aju3/AFsoYR6jRBgx\nv5ESgCtmKBnGe0pUYhBavJWYP2zKEKoa+HofNKHrKUyASijZTuDrPCBdZk2jWhkFvD4rJlknWjLb\nugfZANc0yU+/+ZV0z8LbBr6y52vIzNlzkr+QBXmXnIc/6SnxcavXdfeuq+L2PDWerPrxWL1HH+uf\nbgXNynMLINcuPGUCZGQLhweoXFngdfB1LpA+66yzKsoaQxFzj8XkZV2jfIdTeLCnnHJKRT+bkiUU\n4p7GJCNRiMGSkmL76hDeers6GCuMOIaDsQ5AAbApWgBYGYDd2IoEtCjP2GP4hYEXbRbf91+3XQv0\nAXjbtXX/TiPUAqx9MVDUbAm8qFfJL7wa8dAmZTwcVUKFl1sP8kx42u0A2H0jRum9MoBUSHhKPlOy\nygTMnQRoo7x5ODxG93BtCC9432J5xji+5esDORN+s/f9QPG+PE8c+GfXfD299WObln8sv4v3s+fM\nHsgcR7PyygAEAPZXer9N02GiHK+SqgJ8fUZD8/CBDSq+BBLH6tSta0J4pTzdMicAuJtSxJgC0sMp\ngFB/8G7f9773VauuYSsAsYxrlLKYs0Qq7dNJgCsAxvAYH7GgBgCOrRCxHe7rWf1FezBOTPeK9tIG\nxkkYgJ3u3f9++FqgT0EPX1v2S9rGLcCzMy1oQbb8Q9B2lBiKkXIT06N8CIUkUacpCSau7/XV1BOL\ncxBTWyx6QRlSbqhpipW3URdgJKubQmY0AJDISJW4E9scBqXKa7FpQAhjQxzTVCieH3AKuj3OKV8p\nXMDCu1s557C0cdJm2rM8rxMFLQmLLPj0ZemzH/yX9OaPfKJlApbzNq5ekWYv3uS1agvGQfSH70uR\nkNYEzLx/3pqlQj1nKTxfFCraPYwvsVVxZf0t+aruZUtQk4wFrHx3xhlnVPOKg7IVC+aZltRwec9e\n3gM24ZHwsuNaFDvvHW3OI46pQeL+pj+ZLobVaSUxfnzPc9Yu2k5+A3qaGBexEIkxWRp4jI1YGcy5\nrkX992XbtkAfgLdte/fvNgwtgFKTkBQr/yiSdW9XoUh+Km8DDC3rGHMnKWg06FAtftv+SeAhpp/I\nhiY8TjFEmaoAgpIts53Vh4daztF0rpgtJUlZAxyZsxToxz/+8SpJhzL3DEEdVjer/cdLBhy8KIrZ\nKlq8zHh2py+4fmF6+HHPqF256WM3APyfn/t0+tR7351O/dClVRZ0Y0EPHvzV965Jh+2+eoBCVz9G\nEg8fRc7z9wdQWj2X/vI8jAhgK87uLzJ5w0hxS0CC2ta+PETxXXR+eLQMG7kA2prBwyCwq5B7A71g\nMrQZyr4dCLZ7bkYU4I1M7jjXOFUmQygMA4aDhVJkZMc2l4w29Lj5001MSjk/2lxe9DxKXlsFe8Iz\njnwEYK/NQrRdJAI6Vjfw4rz+68i2QGdOa2Tv3y+93wJdtwDFAniBaQhvVpZpq2Qn54mDmqJBIbuW\nd8RrprAAcSfqM+5VvlKipgUBFIZAUIDOccz0oTe96U3p3HPPrbxcWc7zcsINxQcc1DsWSGBQiAUD\nWp4Zheo871sJT0m9gY1yrLxU1sEzoqN5myX48tjvWHtfOvzxeRegPZp3LWp1T8cX3X5r+ti7/m96\n/fsuSjP2npOnIm3KYJ4yfet5vPdnevQX378mXfb1L1TApr0ZJ/4ofLF59ecNopZjBSuAHBnSaFvP\n4q8U3i0qVwKb5zO1KxK4gGnMjw0WRLIWdkIsFm0N1ACs+xOAxxMVS5U57v7i1QwsmdLdijHmOQB8\nKeppzDAg6owI44DX7Q9LAIjN7XVvBoJxYJnLsn9L75z3C8yxO8adRVewBu7J2EEx1+PAxp+QTIwN\n32sX46ov264F+h7wtmvrHfZO993/QLo77wd724o8bzS/Wu3mgWqa/W5JJMwqN7PzjkcPmTYp73w0\nccgbL/TaEJKr0LuWBgxh6Uto4SX0KrwT01aCzqSMeAc80k7CU6PoAYbzUccRW2u61pxSCz6gh83h\nlRjkWuDMiyljkBQoOpSYL8p7okB5fv7cVzvwvFuJMoF5GSsNDxE1CYCnzpyV3vfV76f7x47fqphO\nHvCVH/in9JWPfmSr6z74vd+kCdm7K2Xj2tXpbS89Pt1+/W8r8JGk5nlKAUZoeB5cUzt6DoYJIJZA\nxqC4KWf6AmmebbAOnhkDQoCI8gCWfXzFg3mWgI3IF7DPs35vEkYa0HMf9bO4hf5qJ1gNwFsHOkCJ\n2sWEhBferpz4jqeuvcpFM+Q0AGJT3khsU+ke1rp+3eteVxklpqgxVAkjDCATxxiHIWhv4zkEY4Ix\nqItFehatWZduX7E23blq3YMbucg0px0eyPohx5TzIhwHTJ9c7YzW33ih3oKtP/cBuHXb7PTf2JTh\nhrwM5W8W50SNjZuWmWv30BPH7J4mjRtTrQF9WF7rdaTXeaUgeAUUYQggojzFuoYqElRQvLFYAo+A\np1TSxeU9AIH4HMqQwispvPI8YMB7QSszHihlXp/reSp1o4FiBj626vM9peg5Zcfy3gn6mddO0MoA\nphRg7VliPrDvUOy8Gl6OeKdpN8Qc1z86/n9VywtWB0bov32nTEyfPffMavMKt6DgYwUxwFZSztqg\nvuCEaxhKjByChsZYMGZkuqN4AQpvmKBbtXEJgq5517veVbUvNgLtzQhizPiLmDODrhSerMxkWdFE\nn1lLu0zkMw60u3rUPXTlAV5jqRfgLevgPQAFxBK1Qkw5sv8vY4bBpS0ZZn4XZgHIfwhDrtyYwXPH\neFKWusdcYZ+jfb0ngPemZWvSr+5ekVZv2Jh1xObEvE1nbPm/VbEY6/aDfuisqf0dkLZsnsZPfQBu\nbJad/6Dtxn5w25Jq27ENGYh7kXG771YtTfn4/fdMsyZv7UX1UlbTuWg0Ci9iWc5BqaHjulk2r6nM\ndscCoChdghIFcmXSCorbesMEkEloQhfycClJCS8AHdA2iXmgaFf0ptic5DGeWGzGQNHzyClVHk4o\nfso26EYJZQCdQpfgBQx4hQwVQBuCmrY7DxoTWEk64h0BDDv5WMpx2b3r01dvuDsr1k0748S1w/U6\nKSviYw/KWxJm5kRWrhgnYVTEzkjAU1tHLNf3nk27o2v1S8T5Peu8TOG7RnsDD+K4Nmd4MF60l/ZF\nIUtUMx8czQyQPL8V0epziZUDKEtA9l4dxIRR3QT4o60ZCqhtwBssSnVC/o8xAHjF74dTeOU8eOMt\nDBesDQ8fE+C5Gar6ndGqnqRM6KtvzKDdyvnmjEDxcLIiL0f7w6wfeL7r7utNP4zNfTgtL035+P1n\npjnZCOtL6xboA3Drttlpv0ElfT//uFbmXZCGIpMy9XTcwXunvbOSHQ4BaFYpQueFsMopE8pvpAXd\nyYuM+6MuKW+bKQA6QkmhjUMJNtUJEIh3UtS8PmBL+TMeJNWgzpUDZMUqeXg8PUIB+k4MkQetLPHr\noG5RkoAJzaoOZeYzSlx5wEniFwFuYq3OA35oy5CfLFyafpV3w6ovrh/fD/YVMXnIzD0qAFYG2lgb\nin0T8eqSBZibKWjGSxhA1Un5v9JLlgHOgClpU/1jlSuAG0DN+HDs4jydCNDrK4AoqxkVC+CBEk84\n4syAq1V/8mSxEbKGnYO2Zszo19KzdQ6A8zqSIgxjrWoMSxh7EqwwC/Pnz6+MNeDPICTq3GpjBt9H\n8p/3BJBvGDsxffvmxdWa8JuODu5/3vATDpiVDsrUdF+aW6APwM3tstMeXZIt2i9nz2ew+3zWGwbt\n9KSDZqUDpg3+R8aq52EGFewevA+xLMpzWwiKl5IGcJQ8ECvjqE11iEQoiyeg91784hdvkSjjGkDI\nk+eliAOSSy+9tFKWlKP1ggE1qe9ME9NIAA3wBEhAQzy0FN6b8oF1CVDKR5kDbJR1/boNeferb/5+\nUVq4assVqsqyB/N++oSx1V7AwhUhwFWyGK+RSIai7EN4vdpBHZsSmMRzHRf7JZ4VUxAJdDxEQEqw\nBJENL1SBlkbHK1v78boZQwwdop/FbwOQIwkMfVtS+tXJD/7n/oxD41Td/PGatXMZZy2vGc73DIKz\nzjprCyB2f8/iO+0d1Dy63mf10h6l4VBS1Op36FFHp/9aM3yJWPYNf2xmyg7fsznePpxtMhrL6gPw\naOy1QdZ5ed7F5Gs33j1kz7d++6l56zGesB2TehFeCm+C9xMiO5XFHqAUx4frVXzVRuq8T0q3ngjV\n6j6UGQA1vUjiD6+jk1DkAKcOrK7jgQEkyxPyWGSsopXrEmUAe14sUC0FiPG2yYIFCwYW93A+uttm\nDOqOjuUd18UWc1f+ZuGwGWTGwrOP2LfaurJ+L8DgmdUJgKHxS2aDtynzmOFRJtzVy/HZs5Sxet6g\nGDCPFx0v4Y2njbZluIQEUGszXrV2aiXKkgyFyld3f2LpjrcS5QHhOp3NOw7Ab3Vtr8cZB4xG88Hj\n2aOMv//7v6+yutUnxpDvjN8y3u23F1tl3j9mXFqz3+Fp/e69/Y7jnq1e98iG2JNzOKJPR2/dQn0A\n3rpNdsojEiqA78KVw+vtRGPtM2VC+vND5nSVIX3eeedV2Zw8sxAeHJDoJhM5rmn3itLl+bD+eUS8\n6zJOWr+WV0BBRpJKeFOyX1F+Fi0QS0UlAw9eL2AtlXtZpnMp63br7AJhXpkyZbeKbdYzc+sL56sn\nz0uiUcSMJYTx3IOSBLgUsGQw3h7vXl3EB5tAYGMGdZ6wDHiJeYOR7OikWdkAE/edOqE1qGEExHLR\nxuK3ALI0Znj7DI2g1vVHhASiXowV8c/oK8eFDni9NjkI6lostN4/2jpiyOhizEX9HONE/zd5wIwl\n05kkzBH9C8gZDTzoksWpTnjwP/fQb3VgNoZKQCyv6ea9sA2vV509l12YwkBgxNoKUYJWhDhi7eyy\nbDsorclhglU26dhjpkB8+fWwvDc2nnbYnGrP4GEpcCcppA/AO0lHdnqM3y9dnb532z1pfY8JFZ3K\nje9txv24nHRxWBuqyTQRCjcUhGvF6wBvHXii3E6vgMeSguWKUAFETddShBS46RYASXw2EqGczwNT\nlvNknpbZ1rxPoEk5e++cuXPnVglb3oeg+wA/IPR8TSIuGlvHxRQZbcDb4hUClIjjlddTqqYr8X7E\ncwFKKTwtGbJofYaC2DVPkUdJ0ZdeY3kdEJbtel3Oil+5vrfELB7O3BmT0yPmzGj0fMv7eK+/gaN+\nYnCZ5iO+WxcZygAvksnq33sez4vNsIyjNpVkJmZOxO+bFrEA7hL9gCXq29xfho02DU+3NNZ8B2iF\nQ4wdIo6PvXGeNtXe4d0Hhe013sdUoOri2n8SDD1rHZw9eycRV2egqCOgxYKIt/N84xmUYwqT+cwM\nR/HrUoDz9Xfek1btdWB6oGFqWnnuYN9LzPrDfaenY2Zv3hZxsGXtTNf1AXgH7k0WbUx3CfrQj817\ni0/ILjXloNxogPKOjNN4NEr6P667M2c0btqyLo4P9ysr91lH7LPVptzoQJZ5KATKQkzz6quvruZo\ndqoHxYhmcz5gkoEquahOx5blAB80I8UJVLVVCablud7zKCkn3qKsY15zO2+ct0NZU+ahoHkXnhGw\n8u4CCOr38ln2qecCImhBWdKShmxVB7SVSQA7kKH8IwGLsvY5lG91Yv4PABgXsSk7b1NskohpmyrD\n42onK9dtSNfmaWm35ES99TlGbE54k0zILu/43Mb7TZ2Yjtpras/hB2PWOt3EszDM6nQwyr8MEQAq\nyWgMk7LvGURXXHFF5d1LTsIaRFgjkrfqz6Dt0cs8cR64+KjwRGm8afuI8zYxB4wsq2qh1Hnusstb\nLQhjXAUYl8AsAa98lrKe4ttNwMwIi/ERmfGum5eZBe1j/Br36mLKWcTUHZd5L++gXAWOcfCNzIBs\nmDyy4Cg3QHiinCc8XDqubLfR9L4PwDt4b1FMKC8Uoh8NQEbX+hER1q6YZCS0UBpox1IW58Srb9y4\nKK3J8b6RFFnRT8mxYIt2EGskX3TRRQNKTd0AoY0KAGRdKCm0Mc+OYgEavJq6l1deR2kDMUpUUo5F\nLwBuLyIGBiwpQiAqkalbEeNFI5eKmzKPhRCayglamRI1jQSIU0RBtXpex3hmJT3rHsAdyPPEgEeI\nsoAVT5AAJPNYQ7Sj+OfjH//4ONT2lUe8OBtsxs7StRuqGDFfe3zuw5mTxqW98vSzvSZPGBKliBGJ\n+arqhUKug3BUkjHkHGPIswQTUZ6vTRgrwSRoR4aQ30ZTYhSmQhZwHQCNzbmZ2RDLrf+Woj7ximEw\npiPr/DWveU0SYinrFec2vXoWuQh1cDamwmCtX+eZGFI8ZkaJ+vLkGZjGC4ZEXzO4PPeHP/zhai50\nADHDlPfO2MM8LF29Nn3uN7c1LsxS3nvl0iVpyoyZA+BfftfNeyzZsQfmhM1aVvRw6Lhu7r8jntMH\n4B2xV4o6UQ4UCBqJ5ctqZ3mzuIk4lh8wReDHFwk5RREVtfijPOWkk5z69CekV7793HTUY56Qfv+r\nn6fz3/iqLS5560evylvR7bPFsfqHR+0zPb37Da+pQDYUGwUhG/finHRFeDBiaOgydacYSlq6Oqn2\nH8uespB1qj2UF8sI1k7t6aNEIAsdEB6oeaODEd4wYA1BS2IjYvpQHC+TXhhSvC5AEKKttA1aXZzT\nQgklCIj7xhxh1zA+lMloEEcmgA0NXRcgj5KlwHcUYTBY4ILw4MXcw7uLOvosVhuMBPC1UhWDhUeH\nzi6v8XyM1aB9g7aP8uQeALi6Jw3cga5xFb+vuKbdqxgsY1NCFMFg2OmojFG3u77pO8aWGHQdmIUS\nytyJ8lpgi01gmPGsjQceOqNEJr6FSK688soBj5jBcuKJJ6YXnfT69PNled/o3TaHUaLcDevXpS9c\ncH76xuWXpElTplbG8KHHPDK96M1npul7bVokphddcWRepMPUpFKGQ8eV5Y2m930AHgW9JaFHvJKC\nEC8Mr8hxysKPjrVLEaNqecmlfCMnX6EUO0kJwN/61KUVCL/4tLcNXDY+e9alohv4onjzs+98M/3r\n615RHVHfSPxB6aJ5W1n1LlA2sGFsWAhDVrB5wWKpIyGmoogvui/Ae97znjfo28hCpfh4JZ41DAqg\nwSMJCtPUKt4tZVl6zTwm5/FoiLpQlgCWl4aKjNhyWUltBJB4hzw+Xi/vt0kYO2jIpuUGm87fFse0\nAYOKUUnE44FCfYGLGEsSy4wJIQhen/FujGlzRlA5vvRrsCfaB+BgLBircdw9oy/cA4sy2PGG/pf0\npH9RwOoWIQD3GQ5Rb+AawKzvhSLogpIRKe/luRghDNhYElM7agfysre8Mz35hBeXlwy8/+g735IW\n572hn3fym9JBR/1B2ijEcukF6ZqrLk+nXXBFtTd0L7pCmOovj9w0xgdukt8MVceVZY2m92NHU2V3\n1br64YgHUTqlh4u+ssiCqSwUKyrHsnt1AF41iAU3bvntr9Mhx/xhWrl0cW723dJe+z2kq+afte+m\nua5OZtmK2daFQqAMgQ0vEV0LOAKk6ucP92ftyIhB2bonr4KCGqwAD8qP8sZI8NJ5HGh03j3aWB8S\nypkE+PK0KOm6tySpB5UpvIAWR82X3jSjC5iIJVsbmmIG0sBJ2UClLsCcEbQjAbB2O/nkkytvFYhG\nLBetW0qMJYlxPECxXV5mJCqhZHmvGIUwgEqQLbcrjHK1p2vmZrpZf0lGch4PdjBJgfqKMWCREYCi\njtbextYMlzAq1NefxCoSuQE8ceNIkhtvV9v4rWECbspxcn+AtxTjZNb+zWN/8cJb03ev/lQ654vf\nHfB2x2ZD8Rkvf3W69sc/SD/++hfTn73o5akXXbHuwfFf1sH7oeq4enmj5XPfAx4FPUVB+fFIHPED\ns5BDkwAUFi7LNug6533mN7fnpeU6r3pVesDveMlfpVUrllW3ufuWm9LTX/aq9Nev/4em225xbNFt\nt6TTnn1sdQydyjAAbuhWSlWm5vYUKyZRsEAKUAKxoUhkKzMkJOzURRybYg+POL7n6YtVx0IScbz+\nKlvXmtPoaMpXm4r7Mxx4fMAZIEkgs2QiD7BV9rU6yCVA5+4Iwhixxy/mBoNjlTAJdgQVLUapf+QG\nlIIJAHKMuCZRrt+La/1m6qLt9b3+0p4hDDEsAQobO1IaPHFON6+MABR55BKIbdtpqbxXN+V0e44x\nLRGM+H0BYoY6I42nrG29AmZhEvpBG2ojcvrFn0mHPeLR1fvyv59nNuuyd5+Z3v2F75SHq/dXnn9u\nuufO29PfvuNfUi+6Ysr4MemvH7a1MT9UHbdVBUfJga1J/1FS8V2lmhKExJbEJk19QGvFhtsUe8RV\ntQcFy6MCekOVgx52THrFme9JZ1+9IJ35iS+kr19+cVqxZHOsslX5m3ZR2vwtpeMPMIi5ib1tL6EE\ngQ/w5SkOFXwjjsiLagJfwEHh1cHX83cTYwQkwIlXRVCP4ruR4IO6Bb4AwzrVkSnPy3VuXQAKj6cV\nVVk/f6Q/AwXPRzASYpYxdiUZioFiSeosCm+JYVIH5qgvwBEfbgJf5xiLQCpYiLiOF81Y1KZArf59\nnNfp1bMIG0QSnL2iTQHSLyMhJSuGumeYYEOMT8/iT58z4IxFf1igAcnsSZNIurJzVpPM2Ht2WrZo\nE+j3pit226q47aXjtqrIdjjQ94C3Q6N3e0vKiYdjnVdxMSLOZGqB2I/v/dBQnTxfiTeseCBdyud/\ne0danDdf6CSlB1w/99wTX5z+6KnPSPNaxIri/HszZX31u99S/fh5f378daEIKA11Vn+eYGR3188d\nrs8UoEULiMzs+fPnV+8H+x/KUuYrOrc+r5J34TtKvhTgJ9GI4RQxTlQngK2vIQxEJNwFjQrgbRgv\nQxwAUfLuAchR3M5HOQJZho429sx1oGd0UNDafnsKtgaIEgYFYwPNDJTPOuusCiTUE4VqnL/kJS/Z\nKkbPsBM3j2dB9/NgtX8pDBR9ofxSXD83U7nyKCL84Rw0NADHNokda8vBirCQTG/lYimsa+43PZyC\n7jYW1Fl/a1uZz6h4bVg3uDyPNsPa+P0d9cwX5K2ztl7D+ubf/DL96ymvSP/81R9tVd1Pv/fdVTz4\nhW9861bftdMVVko74WGbx95w6bitKjFKDvQBeAfuKPP4/IhQkKEEKCpeHMXjRwaQecasWnSmuBiP\nrJQFNy1Kv1+2NRCW53gfAHzYwx+VvnjRh3Ks58Q0bsKmKU3vnH98etpL/jY9+rhNcaf6tfH5wOmT\n8rKUm7Ij4xiFJkmJkmAgoBn98AJc4jyvFAavB30mNjpv3ryKDmyKaZbXtXrPCwJW7gmc0ILKHooA\nO9SpmKo5vCEUoBhb6XlR7GL1BHUcsUUAzLNTFgESFLPsaX3OqApB3wfIUOiR4WxMONfzLcgZ5TxC\nSp5xYDzwJuv5AOoIqCS5bS/hgapvGGeA0LgmwJDnJgktxgcDBesDqI0h15fCCFJWtGV8JxNaXxtP\n+t+1pLyfz5GkhJbWDzxfcX3tySP2WxuKqLt1wpVnfGOtZCcPRowtzEC5brWx4ndVbxflG09i0YBW\nNjQv3DFtJmeB/Oj2JdWmHNWH4j8JVycf+/D0hvdfko541GMHvrkvt8/pz31KOv6kU9Oj/vTPe9IV\ns/PUtWfmtQJChkvHRXmj7bUPwKOtxxrqS1H5YUWiT/2U3+aFFex+1Ew0bT47ANg0pLNf+fz0mD9/\nVjruBS9NN/ziv9N7/vaF6V+/+dM0cXJz3E0p/ITH5tWwHrb3prWJN5fc/I63w3sD0BQKS54SrXsq\nrha345EwLljuYnQloDXdAdgCL4qJIhUzpXyHIsBU0gswt5gIAXjmXZYKkDHEM3au/gEsTasy8U4A\ncXhtwCCe33vPCBRCTJkydSpE1i1q3TWMHPXTRpQ0oXhLg4MCB0Q88e0lETd3/xIMgYIscmtYl5nc\nDBOAiDXRXsYLA66VaHtgEwlacV6Z+Ws8MIJK0GbQyF4GxAw+GfKAXVmdFjCJe7R6xTyYLgUoCSPK\nIjr6uEk8J2++BFrvGVx1atz4YGTICldPzAeKGWsgSRPgh2AdeMjaXfKjZ751+Zpk96OmbUl/8KWr\n01XvPze95pwPVlnQa1etTJeefUZacc/i9Pr3XZTG5HbqRVccM3ta+qP9ZkZ1un7tpOO6LmgHO7EP\nwDtYh4xEdZbn1Y2+cv1dHfd+LQH4+v/5Sfrkee/MWdB528IM7i85/R/T45/+nLbVm5yXJPyLQ2en\nGRPHtz2v05eSRAAXZSGGKp4JoOqKRzm8IvTt3Ewl8pRY9bb0o8CtC0zMFZVVPFThpUlkobQku6gX\n76Osl7qgLSk4zAVFyHgIsG5VB+eZ3xvg6zyeF6AIMVXKNB0irijTVYYrL1wczbVodvXh5QgBEIuM\nlCAOgCnq8Mark2r/2S/4jrxu+B15pyTbVm54cAnTsXkv6CmZRpyT1/7eN+/1alqJ9uhW1AmAEteF\nl8t4BCI8X8YMAPRc2pCYbqXtHY92D6+5OiH/B8wkqzXF453D+NDG6Gj9My+zKwAW0NXjsxgHgCZp\njWHVKsku7t3NK8CXES2TmwDA97///ZUBVwdaYYRomyhbcl1FGaON818sXWmMaCegHWONt80QYfRF\nMphyGL2R+8CIdY4NOT7/uzvSqvWbWIi4X7x+/RMXp29/5uNp+T2LqkMM9PlnnF3NC3agW10xcczu\n6U/zQj379PcIjqZNfQAeaIqd+81Xb7gr3T6IjRhWLV+WJk+d1tJSL1uNQrbg+kgJb4WXJzZKSfNo\nOy3iQYmiYYEiYOaJDlZM+aGMgRclVgIAb4vHS7ETmbCh+EwXqcdiyzrw5lCyAb6UaMSPGRjuZ91i\n3jyRLYyKdj4P2bXuDyzQ4pSx76Ic4Fsui8k79p22KYXCt1nHL/Ka0Iy2tRvua8uaTB47Ju2Rs1qP\nzozHQXkt6N07ADFaHAB6LQVVzmgwnYqhBYwZULHgiilYRBa9xVKCui7LiPcA2gpiwLxJUPCxLzHw\niWU/3RcQG0+lAD3jTttIcqt71eW57d4zlICsv0suuWSr6UDltZiAANoAWZ/b3dsiK7HwCGDXDpiP\nm3Kms/GFsSHl8wPn+D1895bFeR3wzSurlfWJ9510QafvWy1VG+Xviq99AN5Fev3O7MmIBa/duGUi\nynA9vs23bTm239RJw1Vk1+WEZwN4TMUJ8GoqgJcUCWCAjVIFYpR2O+FhNtGelGU9CUt9gDWhQFGa\nrYQ3JykrJDwtZQBwsUvgYN1koCp2yBMuBSCb/w3kLfQBqBkpnjVAvaTAgYxpKyUlvjp7uf+VV0vj\n8bZa/7m8Z/neutCWpXxc3vd1+sRx5VdbvC9BIr5gCHhOzwCEsRgSleZmRoOg1PVPgCYQRqsSIAus\n0bolC+E7fQuAmrxz92MgkTq9zNBhXAV7UJ304H/aE2AzcppEW+vPujfL6+SRlhL1Auz6TZKl7RMB\nbblOc3lNu/elZ6uODAflXX755RXjEMuzMiAxCaQcu0tzkqbd0lZno2skZHxmTh7/kD3ToW02axmJ\n++7oZW49W39Hr3G/foNqAbTP/hkcb8i7InWKBfd6AwTkfrl8HvD2EApMIlJsxYZ+pQh5AehO4GkF\nMR4OQKMMeTUyyUtqGiXrWoobqM7LFKUEFl5b6XVRnmKFrZJznE+U1w58UcHix4Ryd7+YhuOZAKn7\n8tQod7Fd4EPZAg7XENsl8vCBM6r7rJxFDLBjVyfXih2qM+UOQCQ6Uf6ehfK9JscAl+b9ogczNtbd\n90DFrlDgrfaFFt8PD62qdP5PvXiDNlAg6HUZ6jx2gMp7462bI6rf9KkMf/0DsGP6jdwA4F5OrQHK\n+plhZRyUwijiCaJsga0+D1DV1owy1/rOfUPUl2GD5tYv+iH+gK7xFQl3cQ0GwxhAoZe0sf7TJ+YL\ne2U4eo6YShbXd/sabeF8hiIA9uwAGDMSAKw+zkWHl7S7vbwPnjk5/WbRqnRfHhfDLXvl9eEPntk6\nf2S47zdayut7wKOlp4ahnihFSvKeLqYk9XK7GdnrEfudPG5LRddLGUM519rJ4RUBIFN1OgnwRWeb\n70l5ijsDZUo25FWvelVF3YYCRzlTyGJuFGoZV41rKOFItBEnDko6vo9X9wYAhBeovKZzxZR5wOhi\n2bRASB2BLy9RNnMAse+AtiQbiTgMEs8GZMPTitWTJCQBsjETJ6dP/uq2qNaQXzEh8zITsm/BhAAl\nRlDppVL+6sf7V3/JZaZZ8dCEFoCS9yHONx0PcGony3TayCLEuZ4pFqSI4wwaoCb7uBTlSbIizhFv\nrrc/kJWDwHgwBsJrdQ3DgOHgnsRY4HWXIOs9oynGT3Vi7T8et0VF5DwQMXBGSb2+tcu2+ghQw/CT\nCS9xDSNkXMk0tttWiPAN44b4Pu61Ie9+9fXf353uXLVliKA6cQj/yQ15eg5NTWuzT/QQih/Vl/YB\neFR3X++VX5Fje5/5zWarvvcStrzCXrDWdp2Y44HbQwAvACa24TvttNOGVA1ALPmLBwoYABfgpWxL\nb9lNIgGM980r4i1HYhPvg8dZF0o9YrS+43218noAJE9VmUF/A18AD6TUCygwCNDJFD2QUw+ev/tb\nxIVhEeKYugG4B8aOS7+6d2xaknc7Gk6ZNn5sOu4QyXjjqvazKAWjIITXaPocKpznKcYrTu+Z/JVA\nrQ88Hy/Sd56Nd2p6F1Dn+YfoK2Vrs1L0E8OEh1mKc3m5RHmA1rGgkBk0yiSuBY5i6eoUEu2v/8vj\n8X03r/rRuJVYR4AnGh6QdivKEH4gVsGT5c5wY8CZzhdTsHxvjIfhUB+nazZsTJ/+9cJh84LtkPbM\nw+ekqX3w1fRbSR+At2qSnf+ArMev3bDJEx4s2YR23jPTVsdmb4ei3R7C4+BxAh7eTKmMe60PBYay\nrXtQwE8MEoiZMmU6DK8NGACVMqGI54LiBZAylAMYKUMJYEC9VIRlEky9vjx59/Ns7tMUFwQewAZg\nAQKZu2KorjnllFMqD5N3beGWMikp5n/+521L09I0flC0c72+9c/CEX+WQfim39+4xZxmWdpW7eKx\n8hDNW2dU8Mj0QQhvdG728HmQniFkQU440zZi5MAFuNdpfrS+qU5lea5nfOjHAFljBwXsuDqYGgR8\nifaqe7M+85aNgXqegXHCYMJUlJ5yVViX/1122WWVt4oxQCGjj8vkuU7FRJ6ChCsMCGEcov7R88YF\nYQSGx62NjZlSwhNetHr9kIB4RgbdPzloVto75wf0pbkF+gDc3C47/VEg/JM7lqXblq/teZ9glNL+\neSN28/m2h+drigZlSJFIwqG8w/PsteMoad5imf1KgfJ8KFueWTuhiFF/6iRLVXmWuVS3UtDZlKKy\nASaanMKmYCVelWJPWXtAOxdV7lnbCW8WmARlCzyUKV5q2os62S4v6GeK+OFPODZ9K2/Cft/uI8Nc\nSLp5xF6T040//l7Vlp7ZxgSxGpkEIZsXAAfgF6JuQEPSWGTuxnfxCphiAwpeogSt8G71m/EASAEZ\n77cUMdzzzz+/AnAeK/bh1FNPrehn7aQP0foREy6vjffaWTlALcZKfIeK1q9AfTAesXitRDPjiRHy\nnve8p2qnKL/dKwMyYtb2BvbsvHZ0vXLLnAX9YOy2GuPrMx39szuXVQv49JqYNSmHIebsMTE9Jq8J\nYMpaX1q3QB+AW7fNLvHNotXr0i/ztJNFeeN12a+tEjDGZDCYNG73PO9zQjp69tTqB7Y9GggNbI1d\nila2J0U4GOFBif+KwYVQWJSvGJn3AVjxfavXMv5mlTJgAFQAA3CWbcqjoazdDxi7fykMCMAJgHho\nRMyXIu1WAI9ro2z1kHCDtuX58cQt3EHWPeShafWYzZ5lt/fo5bzxG+9Ne9yek6HyvS0Wom4od/Fe\nNGnQu8rU3kAXoHrfSTAMNmwgPH9ePTYA+xCJUNrUOXUPD9ACSAwE6lk8l6FDHEfLdhL3MPaAGE8c\nLR4GkGt57Tzz+oYPncr1PWNQQl2MbatoMV7UtZ14doYY0eeM01g5Detg7+WQJrCO78rXJTlf5NeL\nVgxkx2+8v5kzy/ZWQjdjw47Oi21IyjTe+9K+BfoA3L59dplvxX7uyskXpivZOWn9g17J+OwlTJsw\ntpo8PztnMu6xHS3a8Ax1CrrQxgS9CsXJ46UwQ1DDsSVgxNGAbz0pJ86vv8YevwCv3GnIvcR7KXwS\nsTmLd0jCUg+KX0xOfUpPMO5B6SoXFcuDkSzEK29KAItrlKfcoEll9lo9i0IHgOe+7/1p49xj0v1j\nx8clI/K628YNafl/fyf94z+8qarvC1/4wsoIKBUzLxfw8nqDIi0rg0kAKkEbe/UHNEvAc422EpYo\n585iDxgkjJNS9LlMd+DJEEArR1Ywr1g7dRKGl9AH7x7jIByBjQgDyPWeT9/NzVRv0/O1uodnsxuU\nTViI8YnRYCC0Et4vYCVi0trUdDhGnN+ORT9ChFAkmBGhm3ZzjJ2DMbs7G+v0w7KcLc9DBsXjMvJO\nHT+uWphlTtYP/Viv1upe+gDcfVv1z9yOLUDB8UzReuJXnajhelXRhQCvnKrCS5Gcw1MgaDlKFC3c\nyduI8mNuK7Aut1osV3xyLmAw9aSVAGVKExgADd6bJCCgQMHXBYCoN4/RdTxAsVGAEqIOlGzQ4coC\nxIc+5onpZW99V9ot17ku57325enoPz622uc1vlt6913pjX/xuPThH1xbrQ3+wy9/Ln3j8kvS6hXL\n0wFH5D2I84buFmtpku9+vh09UQAAQABJREFU+mNp742rKiVfAm/dQ4zYbB1oAWfpKbsHelgb+QM4\nASSmXvEUm0SCldh9aeSoj4QnQCUjHVvBWAKaFgFpRYGX5YvPi0MTxhdjR78xEMIA8l2vHr5ryL//\n+79X4AnUGWJi5pifJpGoJw5MPJNxYQxgVoBszKX2vfa2njlBmWvLvmz7FugD8LZv8/4de2gBdBwP\niXKRiMRyR+d2KzxLIBkg5DrgysspE5soI0pp3rx5Wxxvdx/KN3b04ZlG3BCY8oRCgg6Mz/VXwMgD\nAbRWMQovPM7zPaODl1auAFZ6WnEuL0s9UJ8oVqDAe/JsQAaY3Tl+Zpqw39y4ZIvXTgC8dNHd6f/N\nf156+xVfTtP2nJUuevtpadIeU1PTrjgKHrt2ZZp29+a2AEpAUNuFZwt063OEXcsLrXuzPpfeqfJM\npYl+OPPMM9NZZ53l8q0E/W8slMDoJMlywApzEIuiAK2YO7tVQbUDkVWs7YEj2h+Qi+OixYMSd5lz\nGE3+ugF41wBOsVxtBMht1WhFsLpoV2NHHzPOjDsiMcyz+w1FXNo5QhzqWZ5bL7P/eWRboA/AI9u+\n/dKH0AI8UvQZxSIuF1MnuimySdma78gTqCdshRfLG45dh7q5hzV91a2MGwaQu56yBA681VZCAVLY\nDATxZ+DdrQASHo97yvql7GVxlwo/yqJ4JdwwXv72PR9M+xz20Phqi9dOADx2/IS0evmyNGXGpgX1\n//2MU9OkXO6L3nTmFuXEhzVL70mf/X+nVclBspNL6t85vFDGQgm08T4Mmiir1SsDBQMgBkouvPDC\n9PKXv7zxdAyH/nZNKTxXlDQDJzLhsS6t1pUur/U+4sg8e2ssB4NifABoGesx79v5rbK8fdck6GVr\nmmNxCG8fpVwfW7x41Dhwj0xo86WNVWPLGAvhuTNw1cXvLMA5vu+/jnwL9FPURr6N+3cYRAtIFjrn\nnHOqK02pOe+887oqxUINgLr0DgEc4A2lWBYkVsqzoPR7AV/xVMoVyDIO3I+XGnQxhU4RdxIJWsCX\nB9wL+CqXsqc4/ZWiXrwm8WfTnmJFJ4oZAIrftZOffvMr6Z6Ftw2ccu+aTQuGOAAwge8dv78+XfWB\nf0q333BdeuMHPjpwbv3N6vxs4t2UvFioKV1BH2tztHy7eHa9vKbPjAqxTt4+ylXGt3ZFydcFMAFr\ny1GiikMYbAwZoOu9/tQfaN+mcRPXxatn04+WuNT2PGFjA6jxsBlpDBB9wRNleGFJnA/kXd+uHTyP\n+onlMjAkVRm7MpxLRoCRpZ8ZGv48r/EJgGVClwCs3QCwuhgXxmxftm0L7L5tb9e/W78FOrcARQp8\nKa+rr766K/AFota4pfwCfHlQkqnE85qUaMTqYqGHzjXbdAZFSkmTeZmypsQAQIAvZdoN+FL2DAZ1\nU+ZwiXajlMWDtQHPnyIOD2fcuE529wPp/gfuH/h7IL+vy/p196Y5Bx2SNuTXX37vmvrXA59nzpxR\nxVkpeV4iUPMHPLyaLlTG5Qcu7PGNJCf9j93QD7KIAU6TaAdtLzu6jEuHdwzsiHKUUY9BN5XpmHgy\n6hrA8rIZQiHugwo2FlHb4d07BwgzUrAY7dpCH4oJW0EMlW2sCy+EV+xejM0QQEwiq7veHmUox6Id\nfdn2LdCnoLd9m/fv2KIFWOFiY+hBoEFhl9Z902WSa3gzAX7OEdMC4ryuVhLx217jX4BE7IxSBrTu\nEVM/3Mt9eU2dxAIQjAvXMx5kSA9GKFXKm8JHwaI7Kd46aPDGeD+8w3T4o9LEvZqzfDtR0OMmbDl1\n6dc//M/0of9zcrVXdAlm8Sz3LluS9lu+KRZqNbE6CDjPdTxEnnHQz+El659eRNhCMpzxYOwAKeDc\nSow1bQd8SwHkAYbaTV93I8YHale5GBUA2dQuykJ184jrdLjrJEaVYFq/N2/YdDzGH2A2bxztbix5\nHsIg8HsyJrRvfdqeTOvYmKGXmHe9Lv3Pg2+BTqbw4EvuX9lvgR5aAKUrs5kCo3xjRaJWRfAaeFHO\nDwF8vIt2wOtcilXSDpCPRJUoo9PrggULKnBD/1KcoTx5JLKn6zG5pvIs/AB8CYq4E/gCEwlY4r3o\ndUqboi1jinEfypinRfHy8Hji2oQxA5g/+clPpol3rUpP+qvnxyU9vd7061+km3798zTvhBdX1+13\nyOFp1bKlac3KFWmPadO3Kuv3v7s2XfXpiyrgP+OMMyovHE0MiCPjGYhIWPIHQEvRpwHGJTi3Cheg\nnWVCAyP3EQcFiKW3V5bvuAQ6oCVRLcQY4SnzUNVTiAC920mMPQl+pidhNYwTyXBNokx/kZDmlbjO\nH1AExOEtl2Wos7HDkOM5v+IVr6hey6l54QEbD9gQ8W2GWRgEjDKJiAzfGMflPfrvR74F+gA88m3c\nv0OHFqA0KGfSbiqJ74EPj7Ok91CG9S0BndskABuQUT4SpHoRoB9eEe8hlBZPBbXYjQCHWPNX/A4V\nGqJscVvGiGxcoImirmftOp/xAGQt9sDLmpepcEq5NAAAG3YgvE5rZVt85E+eszE96S9PSBlh4tZd\nv87Ye0761L+enR7+pKck77/xyUvSQw5/aCP4KvS2a39ZxcaBq/WOAR5Q5b0BF0CqHQOMvcZ7npvn\n98fjK0WbNwGz6Tfz58+vkr7e8pa3VGNFEhKWABg2iRAAQwxAYVRCYox51YY8yKDx45ymV32ACdGP\n4rxiu/qqlQBHf9rB+I4kMEaWP+0lVl43IoROGJIW2MAu2FFJf9t8gQePCg8xRhg3EvW0e4gyATAG\ngEFnXPVl27VAn4Ledm29Q99pey3EISkHILLKL7300mqJwaaG4u1SZiW1WmYfN13TdAx9TKFKXOrk\nKZfXiyvHHr/lcQrfFJZuxHN6XmIHHEkvFCZg5/3UF5bQJrwuBoZ5xDxZLAEPq53w/Mr5vwAB9QzQ\nKPNrfvCj9LM1Yxr3fu2Ggv7axy+qgFcdDjzyYek5r3p92v/QzUo96mZJwqMn3Z9e9tfPrbwznr7k\nunLtZgrfZ31ZBzcGCVo9ADnA2TgomY+4n1cgC6yAM7CJzHmeolXU6vcor/Ve2cZaOc7iHMCl3G6F\nR425UFcGYsSWO10PEAFxLCsZ5wNpdWhiTORM2C3K2OZVM3a0QyToMUZsWwmoLYgSwtOO9ckt9ALU\nm8RCHHflhTju6i/E0dQ8gz7WB+BBN93OceFglqL8g7zUnFWxhiKmyojN8W4oTZQzMKsLgLqpWIwB\nKDlPfKtXkaUsU9XGCE1JWe3K4z3UPdFO05Yocxsq8DotGAFAmoQhgAoEQmhW3hPvvBdlr1wACzyi\nnmKgvBpzix0D3AABXW4zjttWrm2qTlfHANS9q1elSVNa07Kz8mYdzzpin7Qu3zu8NMaAVcwo+xJE\n9QcgBgCdDCPGEICqA7Nj8exND4HKxRRo16CzGTZ1rw9zAJQima8sC6XfS7aw8a3/jVvZ13Uvtiy7\n/p4H65n0aynuD1wBbSnGqDW2JQhq59e+9rXVanHalvEhMc3SnNaXDvE7NEaJbOySkXFsMEtR0g82\n4/DMfWnfAn0Abt8+O+23w7EZw6P3nZnXh26d6NSq8XglpgWJbVpkA9VaF+eUiofnIhGmV1CKctGB\nFFOnRTHi/PKVccCbCgEQPNkAcfQk6lgcESjwKsTfgsKM67yivoEPr9nazGKW3XpGZTnlewaK+wIM\nSg+tK/5rwQYKF1ja+CCob9fesfLe9O2bF6W1Gzdn6pZlDvW9zRge/5A906F7ThkoCgXOE9MuJ598\ncuWVo6bLBDoxbP08NxtnDIVeRLkWaimBWaa1GGlTXyhbewF946oEZkaeUEfEUaMe9b6P4+1ePaM6\n6Hs0djex5LI8RhQgRo+XnjmjjUcsVhxg57ck8z9+UyeddFKVNS3jHw1u3KLjSwHAgFi9YoW5oWzG\nYE/offqbMZRN3PJ9H4BbNs3O+8XyvJbrNTcvTvfkhdabl1bv/OxsW9sR2nKuFxC2D+wb3/jG6gZo\nWDvbhPCIAK+4VwjgpRi7zUKN68pXAEl5mY7By+xFIi4b11BUqHLKGdUbMeH43isQQRNSeDwKcV/X\nUZZlxnR5zWDe87CVh7qmgD0bZgBwibFattB7bWwlpbp8+6ZF1W43gx0D9fLKz7Ed4ZgMxKVQ9ihQ\nxhBv1F7AQA5wlh4nDy7WiAZcQxFeKPo+5v0CIW0GqHm7rUR7MhR4m6VoU0DaLku5PN97/YROZ7Tx\nolvFo+vXlZ+NIYag5ygNCsBpbDG8jANtabeomJ7EyDMGGBUMiEj2irJ5+4xGArw37rZ7Ns4Wp+HY\njvC4Q/bOa8kPrf+injvjax+Ad8ZebfNM63Is53O/zfuDbticPdzm9K6+Ov6h+6XpXewJ/OxnP3tg\nmcV/+7d/q5JF3ADwUhalMqQoTP+gNIYiofgoqG68ZxQ1D0EWq9is7fwoNZ4HCjsWx1cnyTVoQGUD\nd0lQkrGARwglzpNHG0bSVnw32FfeEEXMc2SgzM3eorbyHpipC3BGd/LKAVmTiPt/7ca7M824oenr\nQR/bI7Mif37onJb7RKvbc57znIouR3vaZIDhwJPnuZVTgoAdQ8YzlO3aa+W0F8YB+CgHXcsA8BkQ\nl16z92UyFuPFjkTaNwSA82rR2kFn64fynDg3XiXWAU+eKybGsw1G0OzaSXuVNH7E003dMoavuOKK\nKubrHgxYx/3OjGt1DfFZqIc8+jGPTd9avCG12vUorunlVRiivydwc4v1Abi5XXbKo2sz6H71hrvS\nkuwBD6fsOWlc5QlPHtesUHg2FCggovwoImDoOIVQAhOlxGtsNc2kl3q7H49aWeK1pVC8lLAsUtmv\nlJDFCMILM6XIqkMBvqbvUHzKiUSodsrWvSh881B5xDy+oKzLenT7nsfDg+LdULoMFMAkhhn14MkA\nFZSlNtS2nUBraWZBvppBeM0wGWTox6dl8J2Z2ZF2gjmwbzLw1S4WmBC/9GxACsDw+EI8L2PMOBqM\n96gc7aHvGFlAUDy81RQh9Qtg9ioxioFV3ptRVoKc54gEsJLOFtvmxTtfHWQ5S4YTk4++i+fs5dVY\nZcwYEyWNrx7GqvvJCUD9iyerA8MBM1IyIp5twYI8vS57vhsPOjqtfKD3sFK7ek/Pu6k9NTNlfU94\n61bqA/DWbbLTHvlOppVuWJoX5B/mJ9wtl3fwjMnp2IP2qgCrLF4MzhQIysJ8RAojPF4//BBAITba\naeGNOL/TK8AT9+WlUlCAUGaweJzs1FJhKYsi5M2oo4QhcUHgS9plh1YnNPzHY0KvKhe4t8oubbh0\ni0OAlxLl7XjPQKHQed2lWIgBXeqcE088sVqYofy+3XuG2ZezYSY0MZSxYdvKJ+S4775TJ7W73cB3\nAOKss86qEoW8l8Vr/1pt5jl4oTxXBkWI73jN2mAwBs3nPve5ak1lY1BfGxdeuxGgjBkJIy2uYRgB\nuXIecXznVZ8xHHjKmArjiUExXItfAFVj3F+9btqLofbc5z53II+B9+23EeNb21uQY8WUvdO6aXtX\nQFzWfzje7zd1YmWk7/7gb2o4ytwZyugD8M7Qi108g308F+SY30gl3fB8npwBeL9C+Yp9Visv5fpZ\nnYgXKSO0nJ/IO+RVmmIxFOFVS4RSPsVtuguPNu4fZVOGqFkUHNpTxrEYGSVMKZsqxEMK4ak4pxd5\n29veVgGLayh4CWe9CgOBweBZKEjeC2+XMq3L/Pnz0yWXXFIp9YsvvriizevndPq8ev3G9F8Llw5s\nvN7p/PL7CWN2S3tNnpAel8F3+iDifUAR1W9c6AtTZSLT2LNjMgBxOW6AB6MGENezmMu6Nb3/0Ic+\nNLCbkDEAVHnE3QiAM87qQKcOjEcgWNLZwLmst3u4F8AGwFgYxhWPufSa4/m7qVOcY8woq07jGztY\nILkX6k6EAD72sY8NJIR96/s/SreMmzlie0Q3JeVFvXfl1z4A78C9L36HMvOjibmfEkq8l8zEqkVp\nyXRE16HozAf0Q64L6vn2nPk6kiLx5mmHbZoaIdEG4BLZt7J+S0+G9yIxpmmVn1Z1pGCsamTHF9N6\nxEIlbCmXog5xX+cCYZ6HjGBWv+lHre7Hu1EuzyuEl1Lu8RvH273yenm/hIIDLL0IxQ54JcV4JswA\nr6nJg2YomF8qS1tCkLZx7mDF/RbmMfKLu/OmDes2JJ7x5lbdutTJY8ekPcbnWP3e09JBmQEZincD\ntIACoBWv/OxnP7vFs6ibvtbnJXOiVownjEAv2cX2RX7HO95RPZS4/Ze//OWOdH20gPHGUCvHiu8Y\nd4zJ+vQgBoQ+Ckrbe8Yhj1+/2dVIfkEpyojYcgnOQLuTMCTryYyuUT/JWNrWeFe+94yY//jFDenu\njZl6HkEPNaalleNkOHVcp3bZEb/vA/CO2CtFnVBy6EWZvCxngOxHboqJZBU/ossuu6zysvy4xHf8\nlUKZfuX6uxoXXijPG+r7yTn55qlz90qPe8QfVFSzpA/JVoAshKfAgGinLAELBWf1I4kuLHqGRxkT\njPIiEYoSkXzE2+QdWYKwU/wzyuBlat+6zMvx1G49I9fyvsNbtrIXT7hb0Ze8eJnVRKxRfLJVLBy1\nb16ppCueMYWrLYZLlt27vpqqdMeqdWnl+g1pw32boHhszmqeMn5s2mfKhPw3MVGqQWUO9d4oXNm7\nFjyxkhMDxgIadRFDlVwnzFCK6VyAuNs+E4N2DyL+7HfU7bPE1KLy/vEeYNZDBPFd+RrJT4wLSVBi\n0kAaYLcSz1Z6yvEeLY9uDvF7wb6QiP3Gd35HAN/cYM972eVXpBX7HZnWPtjHcV79deXSJdVOWN22\nUf36iWN2T3968N7VuCm/Gw4dV5Y3mt73AXgH7y1WNgudRcwLErvxQwUuEljQaWgsXkErxfPbxSvT\n929b0tab0QynPv0J6ZVvPzcd9ZgnpNUrlqePvvMt6bbrrk0TsmJ/6t+8PD3hmc/t0FoPpE+e+4/p\nB1/4TEXxAdr4sQJc4FiChEQoigAFWK4IVaf3lEEhAyNJLgwQU0mUXyodmZ+8E985vxuJKUrOjbpS\niNparK5b4bG6Rn9R5jzhboQyBLwUJtE+aNF2sfCPfvSj1dq/PJ2XvOQlyeedRbTfP/zDP1SLReiP\ns3KMmLcafVM+p6x5HrFxVEpkpnda9ELs1EpRMS8WRXvuueeWRbV9j30Kg6l+ImPA+OF1thNePS+Q\nkcqgQj2jrMNbjldeM8DW500SCWDhNWN+eNk8ZuBsPGmrkg73OzMt7Ld33pNedsa70+7jtk6c27B+\nXfrCBeenb1x+SbXoit/Gocc8Mr3ozWem6Xtt2nSkF11xTF6k44/2m7nFIwyHjtuiwFH0oQ/Ao6Cz\neGhoVGCDekU1E3vkUgKUP+/LlBfxtDoNKfb7+2Wb45qtHrkEYOC7x/QZ6XknvymtWLI4nf2K56f/\nc+Gn0rQ92+9Oc8+N16ZD0uoBrxflSwksyFmWKFKeG++B94ImLsXzMSI8B0UCYGUj15+nvCbeK5tC\n5oGK23YjqH1UHOFxikczZBg35kN2K0CU4uTFMjLC82h3PUOBd09JEgaDPu4UC3/Vq15VsQraypQo\nn3dGkV1sQwVsSD1eWX9eWfQ84jBi4ntzsXmi7doUIJnTKxOeWE9ZMls3or8xNYCMgQCcSkEvC7N0\nilGHJ2zcmSPc6nz3A6J1Ohtt77smMU5iFgBvGctgnBunXsnKaXPShpnN1DY9sHjhbZUeOOioP0gb\ns9Hy1UsvSNdcdXk67YIr0szZcypDvVtdMTvnCjwzT0uqy1B1XL280fK5D8CjoKcoIV4RsPDjiy3a\nrCokmQONZo6tmBKFUveIPp/n/S7O0006SQDwkY96XDrxj4/KW8z9JI0ZmzcVz9TR2AbruKm8MevX\npN1/95Mqniq+5AfPwi0lEqFY5mhWlj+gbYpzlte1ek953pSTT8SZwzhpda7jABP4hjcBsIE+Gpf0\nulQlT4tB4XnUo52gjHm8QZ9S0qYMdUq6oeRNa1JHCppBgwnYmUW/oqC1KfCwg5RQQysx1gAUr7IU\n/YM5aWWYWXOZ4cYwBFhCOPIrupHwYJ3LiKsvhYn+FadvWr+5LJ+nq+76lkEQ4Fie0+q9cSz5qw7M\nsueN9VbCK+apn3Da29M+R/zBVqctXnhrOv2vjkvnfPG7A95unPTPJ70sHfPEeem4F7y0J10xNYcv\nTnjY/lHMwOtQddxAQaPsTXt+ZJQ9zM5aXclEFBAlfMopp1QrMXlW3iXvUNyMWIAdCDmvjH+urwFg\ndXKb/5bfsyhNzIrgSxd/OH31sn+vABTlNO95m+7T5tK0dMWq9Pc5tsYbUAfer8xd3h3F0i4Rql25\nrb6LBQkk7nQDvtiCWHxemTxt9fvCF75Q3YKC72V6i/sCUxR7O/B1DuAFwETfoSgBcCfh4WADlOF+\nQLib6zqVu6N/b8zoq+c///mVp8mbRO23Yie0qXO0MTDT14SHjJXwPY8Y8JSUNhASd5aop439nhho\nDJ5OYnwzHIE38OVtoqXDuENzY2cYmmjhVuL3DYTEf7FajNIyd6LVdY47z7j1hy0IYcBgzJRpTAdI\nC2ER9fT3tDXNyZkLb7iu8nCDao5yvc49Ki+ckrel7FVXbMkRbC5xqDpuc0mj610fgHfw/kJx8XBl\nxqJsecJ29LHAvuzPMpmJtc3irXucvT7iyqX3pNXLl6Uldy1M//zVH6Tf/feP00fe8vfpic9+Xho3\nfkLb4ngB6idu7f1ICuXByqcEu6GpI86sThQwg4DnGTFASgogdytizeY1a/f6zjVRhvgkRRhUN/aC\nx9ttjJo3Jqas7ylXrMKuJNpLjoO1rNHDstKxPta4biWME+yA5DTGS0zl4iGLt/rN8IgBbwCxfte2\nDERAagtDi7Q4r5MAV+EPvz0esXnvQi2l9+mz++v7VsDKIEMlK4vhwZiI+nWqQ9P3npPn7U9ZficE\n/QzkMQrG7cbcDk0i6WrqzOaQ04y9Z6cbfvHT1Luu2BqCt4eOa3re7XFsc9rc9rh7/55tWwCdbKPt\nd7/73ZWVzVOzd66FFlj5lJHYF6VCLrzwwurHVQe+sRlsepHJU6dVHuwzX3lSmjx1evrDY49L+849\nJP3q+9/pWMzsvWZVHkq9Dh0v7PEEsVpKRMyYcukkKFuxNsIzZ8AAXx60eCyZl7OeuxV7rlIcFCT6\nsA6ojAMJZpQ48KUEKXdeVv3cVvcEOtZ05k2ZyrWrgW+0i5DFe9/73mqus77jLZnmxmNsJ9oZqNlZ\nam6e941eJn5XAI6Xy3MNg1X8lbGrT8XmedqxN2+7+zDA3Icoi/fNuItQUVzLE+V9lsAc33lVP3Q1\nA8L4ieUhy3N6eV+yJMG8uN5sAaIt6ZLDs15pEvs8M8KbZMldd6QDjnhY1g+D1xXKHS4d11TH0XCs\nD8A7cC9RwEC3TLRBQbNkeQAsXKDLM0JNUh4X54UY6mLaSC+CctotK4OJk6cMXDYmK5n197aOJ8WJ\nU/JUpJEWFLspSuJk8zqApnN55DF3lFKkWHkhvuNBE9Q9hdSN2M7tggsuqE7lPZfUItqTx8Y4ABAy\nck2JQmd2S23zdinwf/mXf6mukfluLOzqYtqQtkDzmuutTdvR/tFeMsvR2fIM9FV4oJEIpw+Vw9Bh\n8MSuUQw2WdLBXkR5Ta8MrBgHxppr1a8eFuEFG7uRfFcvC5jzUI0VdQLmg5XS0AN0ITx0ElPvrGDW\nJPsfdmRak6/73U83Gfhxzn15fP7X1/4jHXz0w6vYcC+6YkIxJVF5w6Xjom6j7bWfhDXaeqyhvuKt\nqE5KoEl+lRdW+FFe5aiTRBKWaUgfePNr0pwDD66yH2/PsaC3v/hZ6V2f/Vbac59muirKftQ+09Mj\n9pkRH0fkNeK1nRbJKOdCqgg6ES0ZYvEFlB9PAWXejZj6dfzxx1enmgIWxhFPShKM8nhQ6M1eQD3u\nrRz0KRpSYhgl2S6LN67blV55pdYyxi5oGxnT3fafdtJHQgdAsszEx9owZCXTSWgMIGZAff7zn+84\npQiAL8hMSwA2I0oCmLWtebPhaauDMWJ8zM2eeZPwWHnLYsg8VmNhMCK2zdBkrFtDgMi+V6Y2FOK4\nccmq9N1bl6T7alnczv3Bl65OV73/3PSacz6YZEGvXbUyXXr2GWnFPYvT6993UU7SHNuTrjhy1pT0\nhAOaaW33ayWddFyr63b0430A3tF7aBjqt3jNuvSNGxelNRub5xDGLUoAXnLnwvT+U1+dVq9cXsWD\nX/iGt6Yn/uUJcWrj66S8MtJT8kT72Xu0jxM3XtzlQaBJoXRaaINni14O4Y2UBkp8TxGio8MrivOb\nXilRnhSJOaMSWyw3SFEqS1yeYu00/7OpfOvxyvpVFrqaJ92X5hYwBqwAh4nQ1tiCbqcPRYnaWf8B\nY+9DMCG82dNPP71arMJxU6KwTZ2Eh8tLBxgymjE06icRTEJUPUsa2BsvQY+X5TOqJY8pi1fcKou7\nvKb+npGiHOUzWI1Rbcc7NlY9/6q8DOkXr7uz5UI9X//Exenbn/l4lXClfAb6/DPOruYF+9ytrhg/\nZvd07IGz0gHTJ7usL7kF+gC8CwwDP+D/yD+wRWvW9/y0q5YtreI8u9eoo6aCmpaaazpvsMd4F+g9\nSq3VoiPKpgBlsxLKD/VY0suo4Vj6j7eJ0uwkPFLUPy9Hgo4lPyX48KAot5hS1aRIO5Xt+1gakYJ8\n+9vfnt761rd2c9kuf86HP/zh9NrXvrYC0Je97GXJ516m8GhAfcgbBsS841LekZerjKx5fSIHo5PE\nFpjOm5s93DDagK98jRibUQ4vWey3KW8isvaNY/kD7cZ9lFe+lomHPGCeMEFDY1fURXb41264O922\nsn2IaVVOzBTzbTXGO+kKuyI9+4h907gMxH3Z1AJjzsrSb4yduwUo9XEZJBauWptppt6edfzESVU8\nuNNVrNtHZvp5Vp5oPxIipipuZjpOK0qWZc9rjKQqigX41r1bq/+gAyk+GaydBOjyPpRvGouVmtDb\n2hVlybuuT23pVGZ8rx42IBC7ZySgDHlbfemuBRhQ6GfsAW9P/4vblglInUoCKHIDxGuBN/o3qGlU\nLc/VMYYdrzGSmFqVa1wZHwCXR+wzbxiIopIdj5wEZUjKArTqUM8T8ByuQ7tLzBLaECfuVpQdiWTK\nj3ZhVABgTIvntozs7RmA2+0DPD5T9MZ8K2mnKySCHp1Xwep2p6xW99jZjvdNkZ2tR1s8j8Xy7Vgz\nUmJP4INn7DEixZvCQfmYagTomgQ4A6+gElGI9m+tC6UTXqsYXTdC6VFksqYlYFFCYskoPdNXWnkE\nncr2TBQyb9xz8cIYDH3prQV4hgAFGANLr+be9ioMNUmP+oDXKnkLVWtd71goRdawPIB2YjwA6RgX\nYq4xLh2TMW06YQlmQFnMVw5AXRh5xrNzrHgXZdXPa/ocHq/vykSsMCJi8ZlY27upjOE4Nn3iuHTk\nrE3e93CUt7OU0feAd5ae7PAcfux7ZwC+bcXatP6+LVem6nBpx69lPtsLeHKP2dYdC84nACUx1rmZ\nyms1RxflB1hDeMkUaV14IzG1g9darktdP9dnQG1xA9NHeKe2yWMEtPPCm8ppOmYKE9pRnRgC5nmH\nd9J0fv9Y+xbQdrKkzfnlCV966aVVyCCApv3VW37rt4I9MYZ4rlgKC2XIXgZ+poPxGoFiGdooS+FJ\n81R5wsaRsAdDLgSgY3IYYRgWIlTks3vIVygB2mcAytAUTxY2CYCPMpteec+RC6FOEW7xTOLnvOIT\nTjihuhf9YDesezcOr36wVemTcuwXCPdlyxboA/CW7bFTf5qYk6RmTBiXbs8gvDH/2IdDJmTq+biD\nZ48I9Ux5sdApH2DVJDyd8Bp4MLyX8Fbq55tuQsmJ5QLWVkJh8losRyhZi6ITu+NRoxOHKhaSEK90\nH9m2vezCM9R778zXAxt9BoyFGSw0gX5F8dfDEN20AwAUcwW2VrsyDhlOANIc4gg78JKb4s5AHGAC\nX+DJGy2NLAYgSluSVBl7FpcFssqPequLz8rzJ9MaoJcg3fRMrpeFbawZ+2GYAl7j0H3F0Ikw0l6T\nx1dG+ob7h0c/jB+zW3riAXul/adNaqreLn+sn4S1Cw6Be3JW9NdyVvTaDlnRnZrG/OLH7z9zRLIa\nKRhKjnKz4lRdeA2o21Bc5TSL+rk+A2qJVJS0rOcmEeO1XKTVjHgHpjtRcLzmbmLFTWXWj8lyBgy8\nI1NAJHT1ZfhbwNh5wQteUIEVilpbm5M9VLEa1+te97qqGIacRXKAKjCUH1BPkhK6ANoAUJ9LhKon\nWxnLxh2mpRTxYGxLWaYxiqoG6DzwbsZljH1jWdgkPGfZ1wxM8Wi/s5BOWdFxXqfXPTIz9sg8JfHw\nPPWoL80t0PeAm9tlpz46edzYtN/UiWnZvRsqOrpXY3dc3hNWPPlJB+6V9snlDLdQMsAVvSdJpC5o\nW94spUZkIMc+vPVzfeZJo6kJL7burYitiR3GkpGUNwqTmP9JgQ9VeDRoTMlkvA9xbcq1LyPTAjw9\ni2p861vfqvrWXtlWuipp4MHcWZ8BUGOEkQjAlAtob8oLZwAztHUkUwFd7xl1aF/X8HpLAYjqxThk\nJIYY3yh15YXnzKNlSFhC0rnK78TKqFNkXqOgY/wbi4DfwjR+QyE84QOmT0or121I67Jx0GvipoSr\nGXmf6D/J830PzLknfWndAn0Abt02O/U3k7J1evDMrCgyLc3iJe0yIH1vQ+2pE8amh8/Jyz9mz7fX\nFbaU0Y2Y60vM9Q1rPa4zVQRYhki44Xm0E8qSzM1x5FLRoAZRy+KvMqcpOsdOPfXU6nwLMaCKhyrm\ncloDGNWovmLanZTmUO/Zvz5VoQhxYdPFJC9ZKU7/x7SgwbYRgwy1LfELHey9ebo8TACL8mVwoZj9\n8WBlUfvOOAPg6Om6GBP+lAesCdoY2PosZuweQBcdzmMWM65T2/VyGQfOI2UmtNCN35r2UP9SJmS9\nQD9MGT8urc764YH8r5N+EI6aMn5Mle38xw/ZM03rx3zLJm183wfgxmbZNQ7unn/MPNnD95xSJWiJ\nEfuhjcnHxW7GZ2vbj8r8vYOzJQt4H7XvzGqhDdeOhIjd8YDFcusJLix2CwcQwGyNXwqlnZg7zMNV\nVniy6Dtl8V4ALgVGAVFskTlthat3vvOd7Yru6juUJU9M3FCsTQZt3ajoqqD+SYNqAf2u/fUt1uTK\nK6+sgFBYYyj9wGvkPWJWABnjzdgBssS4cpzRBXABP28W3ewYT7Q+vl2nHN4w79bvIASg82IjLhwg\nbvoScAXOrZIKgXfkSRjrwJsYkxdddFE1xa5p+0VgPzN7sijk2VMmVFOVXOe3H/rB67ScV3JgjvFu\n0g95/++pk9KYzJL1pXML9GPAnduof8Y2aoFYQAOlVyZSUVq8WJY8oaSAbyeh8CI7GpUNiNHMMQeT\nZ2JKiFfHKDG0n7JjoY5O92j3vV2MUJ9oQ4lWYpJ92X4tYK6wrQb1NQC2nnQnA65dbYGsmC5jjjDY\nrMYFlOu7Y/F4zSWPtZ15ugxCINckxqGxi7ouxdhHgwNSEmOcgSGbPo6X1wBaz04AeIQ+GAuobZn9\nWKC+bPsW6APwtm/z/h0bWgCdx5pH0cZUCaeh7kz/CErOd87pJEA71oyWwcp74PkSyg/wloknFBeF\nZH6v3Y2GIsqx0hBlS/GiP/9/e+cCZldR5fuCvDqd7nQ65E0gHQghAUMggygCDg6PGcKHXOAOMIAK\nl4c8rwIJCMhTeRlGkU9BlKCCMgzI5YKAfggKAl4+wEGiBCVgAoEknXcnnXcCt37Vqc7u3fs86pzq\nTJ/T//Ulfc7Zu3btfX5n71pVq9ZaVcyyduWcU8cWR4DfhMVLmAbAu5mQIpyRShVGs4S0YeZGmd53\n333mtNNOc/cS58JMjBnZC4oShYgQVpfPG5/jqINrTQpzxYRX4QSGUIZ7lrlmOq+MjtOCZYkObLrz\nyv1OmBLPhp+3Th+rz11HQIk4uo6tai6SAI0HypfGIKl8mUvDicYrX+ZRi1G+nBbPU4RGEfMbDQwj\nXEzbjBSSyhenGJQmirlc5YtZkoaRRhEPVUYwUr7up+gWf/AXYMR6zDHHuBhzlOfDDz9c8rVxT5EA\nhtEtCpPlQ7HWcH+hJLGmYH725m6vfDkh9xoOhbmEe5d7hxErStcLo2N8F1DMnJPv1GT9G1Cw+Bsk\nz+GP8SNj5qDpnHrhGvmMZUiy/QlIAW9/5jpjggAmNJQVGaGSiooRMcoMofHC1Jd0oEpU0ektscOY\nBxEaKLxGiQU96KCDOs2TEV+M8sczNG3u61RxgQ0zZ850I1+UOekkMetljUYKVKPdXUwAsyuhYFdd\ndZW7T0488USXi9t39EJPTzgQ1hZGlyg/VsvyCV+Yl6XjiCLGM9vH9XIO7k2mXfBryHduzMaMbJOd\nRo7H1I1DIgqZUTzlsBixLV2f96LmOG8J4r1PVOKnatgm2X4EpIC3H2udKUUAD1IefEaeviGgCM4y\nKEUEsxi5fX0P3m3M8Qdlztq/Pp6SuV2cZXCwylKEzMmi6FHweFdnOcXkOFWnzSjcs846y20nhriY\nlXM6VaIN240Ao0sWWiA+GMXGe2KyvX9A6IXQkWNOGQWLEuS+4370wn1M+kksMJidOT+CEqajhs8B\nijg5OvXH8sr9jxJOxzLTaUSJM7Jl2gPfCRy4fOfV15F8fpIKOL02sC+v1+1DQHPA24ezzpIigLmM\neSlGCDRKCKNWzHe+9550GEkd3uEj8ZeY85JeozQ4jJpzCaOfm266ye3GJHnAAQfkKpp3O45dKHhM\neDTkpEEsZ04x78m0s0sIEJNNghQ6YZhzGR0zHVKK/OhHPzLnnHOOOxTnJpJmZIUccf/joZ+8ZzkI\nSwwjauank2Znfy0obO515pyTwtwy0zN0Ol944QWnkFH0Pn0rpm58KRByS3NtCL4R3idCo2CHZLv+\nkQLerrh1MgjQy8crk5Gnz0rFiJfRqBfmT2mI8gmNEP8x+1EXJkB694wu8q3xi6OMj+/FS7lU72Qa\nQhKAMGrCfM71p82E+a5f+7oPARTRySef7DqFmGtJxMI8cSly7bXXuiUlOZbQJFZo8skvkvVx36AU\nUappQaFy/2O25n1aeF5Il5oeMaNwCWNiVIxyJ8a3yc4PY6bGOoQwik7G/XIerEY8O+VYgdLXqM+F\nCSgOuDAjlYhMgOB/Gh3MdChOzGUoMwTlSaOVL2MRzid4FpPhCqGRoqHx2a4YzSbnvFyhrX8Yofr0\nj6y7e/755yd3F/2ehRkYuTOSIc6UhlSNV9H4ul1BTMSEKDF/z8iUjhkjUBz2vLm42ItmeUQcCLmv\neaWTeMIJJ3Sqh2kR6saTGvGhdyhLrEBsZzESPnM/J0fEfMZCxDOQdLrC/Ex6Vka4hEJhomYETnmU\nLGWpO9m5ZZSOGZxYYO9ZXex3VbnyCEgBl8evao7+yCrEFTY15YLW9WbeyjVm7sq1Zr5dtGHxmg1m\n3aY2r8l+dlWT0MYoDYj5Xcy2mIdpgPBW9oqUUQLZr7ISCtBokDgDczENE4obcyGOVXigUi9l8Er1\nZrf0ufGGxiEG5U+oyO23354uUtRnEmpcfvnlriyJNmbMmFHUcSrUvQlwT+Gsx32FhYYpEhQT1pTQ\nzhU5l/FUxqzNfcvokrrTgvmX+59ngv/MyXIPU94rS5JwoIgZ0TK14kfEPC84LzKS9k6H1M+xzENj\nlSFJh0/UQeeC/yh0zNB8X4RrZOqHeeykL4bbufUPz0zLhs1moV0taZ5tG+baNuL9re3DWts+0H6Q\nyKfc9iF5zp7wXibonvAr5/mOKNc5y1vN31essXlfP7JLkfEwdTyApDY1ZMWyCni3xlozbnB9e1ac\njiXzf6KnjeMVShNzMQ+9N6GRnYeQkLSgVGkEUZ68p/FhbisZP4npF5McDUousyEjVUYCNGKcn2sJ\nFY7FEYZOAJ0EOg8+qUFoXSrfvQkwH8qIkPuO6RDihZOjxmKuHmXH/YKpGPn2t79tLr744k6H+lE3\nzwKdUkbQjHYZsTJ6Zr8X7nHi2rn/fUcV5YiSR5EmhU4DCprtvMeqNM/6SyCM7FH+CCZyOr6sdXzX\nXXe5bf7Phs0f2bah1bYRa1zbQPuQzg2NOxlLDpJDusmuCT7eZs7qqjS1/rqq5VUKuFp+ycDvQY/1\nb8tWm9lLVrtc0Gmlm6s6lHGdXcxh4tB6M2FIvUtLl6tscjuNkB+B0nNHiXnB4SUZgsR2eumEctAI\n0cDQgLCYAfNZSWHujvkuhMxCuTIbYd7DEYXjGU2ECscwQqADgYMMDXSWc01ovSrffQlgzvXTCygr\nzNLeYbDYq2b0iZ8Aig/liac06++mhfvLhy4lk81w72NKJlSPUa0XRpooVxSx9zvA6xqzNx1VL5Rj\nRM134bnzq4dhCfJhfezDisTUjX8uOe/f7Sh3VnOLad2wpejlS1HGA/r2NuMHD3A5oXtvHWX769Fr\nRwJSwB159IhP9Gpfmr/UmZM2Fqt5U2TIATtiQI35x6YhptBDRi9+9uzZzuzFg+176jQOjEaTSpNR\nJh7FzF1RlkaD+SwamyxhtSIaHHr3KMgsYY6YBo55sFLCTPCKpdGkU4A50mfYyjqXtlUXAX5zlh9k\nZEiI0be+9S1zySWXBH1JfBa4zzElcz8TcsQINC1+2UC2Y4pOrprEs4AyRxGnk3egsDGbc3+zDyWK\nOTspWJwIVfLCaD65lCHPF51LzNcf2+fy5Q+Wm/db1jmrmD8m5LW37akPtXnmP2fbBxZ2kGQTkALO\n5lK1Wxn5PjVnkVm6dqNddqE8obfLvM/xE0c581NWbd67GQXJPJVvPDAlk5zAz63RYNB7ZyUYxMdN\n5nMK8SZtzHXemzp9DTh0MULmfDSAfrSQLpfrM3O9NLp0FljA/LLLLstVVNurmABJVnDYo4N46qmn\nGsKNuEeLFZz/uN+5z7HG8BmLTlKYJiHzG3O/3K+YorPOwZwxDofcz0nhWUERcwzzz+n9PCd0KBBG\nxXQKvPh1qt94Y5Z5v2aIWb5ukzU1l9tCGGshM+bEvUYbVl+TdCYgBdyZSdVu2WxHis/OXeJGvuU/\nWm2YUMIj62vMPzUNNX3sHFBSULZ4B9MzR/n6h58GiLkxhO2Yp70nKD114mgxieUTRgPeXIZDVzLR\ngD+OtICs9oLpj3y3mI6LFUbV1Mv1M2rBc/vQQw8t9nCVq0ICeN6T5QrrDM5KzAvnssxkfX1WYsKk\nzb2F+Ze0kekOJlMuZHJDeAbyrXPNM8OIGBNyUjgO0zSd33lb53yT+3nPaB5HMS9EBFx3/fVm5m/+\nYHYYPKLszrmvl9ehtX3N4bsNc5315Ha9t7/DdVYEomcQeGNRi/NuLtHqnBOS94IcZZch8+J78/Tk\nee/npfC+xFSMYwkKNLkkIHNQmMVQwvkEZ5XnbKgIgnk5qxG8+eabDev5IjhLsfhCscKcGyMJrg3z\nHiZEn7ig2DpUrvoIYBImVInRK+keiRXGCc/PpRb6xox4mUsmdzRTITghMpqmg+eFzirPBqZgTMbs\n8+FJvox/xQmLe5+4XkbW3sTMK/PBjHgJVfJWJ38cr5i0+e+XJuR8CzbuYPb+xyPNjr07xx0njw19\nj+PWOvt/TENt6KFVX14KuOp/4rYvuNKGGL26YEXJczr5MDGaZtFuRsKYmlCQeFYi3suZ9/TmaYAY\nSRD3i2Imcw/baZy8Vydl8wmjUpxJaJySZjR/zCOPPGJYzxchLSSjlmKF+TkaVRxeGAEzOg81Wxd7\nLpWrPAJYWr7whS84xygUMctMYs7N5X+Q/obcW1h9mO/FioMHPwlAkjmiqQ8FyrPDKJfpGz9Vk66P\nz5ic6RwwmsZEjjJFOA9OilwzHWDfCXY77R/mfDkWZ8Le/QeY9UObzMAhbWsF+zIxXmkfiLbYqX8/\nU99v26ISMequ9DqkgCv9Fyzy+l/9cIVptjG9XSWb7LB6kw1jIgwB5evNzZyPnjijW0aUmMxQnvTq\nCTvC+zkrT3Ou6ySxAf8R1nRlhJ0UzHfMtSHM14bM2WKGI58zDd/VV19tfvKTnyiuMQlX7x0B7meW\nNMR5kHsdR0BMx4TyJBVpLlzcn8zhkgKT/M/cz4Q8eaEOlKaPAGAES+gRfgj5hOcIiw3/mUf2ihil\njPKlXka9SaETwLmW7lhrWnboY6drumaudrNtH9ZYJTxucF3y9D3+veaAu/EtgCMFozBMVT7eFAcM\n3hNTSO+WtHdpYYTJQ+iF3ucTcxbacKO2hBp+e+zXAXb0O7D5HbNhdUt71YxqaTi8eYzePebgYke7\n7RXZNyhG74HMiBkzcVJoTBgJUI5RLyPhYoWsXMzzotDxeuazRAQKEcAaw7wu87BYcrjn0vO6WXWg\nFEnM4adSrrzySnPjjTd2KEo0wLytc7hZ93uHwhkfeOaIQCD8L614k8Xxet7QNNms3Ra9lNzd/n71\nCuvEOKixYEeg/YDUm1rbPhxh54IH9+/bvidWG9deYYW9kQLu5j8YDyUhEMSdYq5FIZN0/bvf/a4b\nZfIge7niiitcrzmteAikf+n95QVj+aYd9Rlz5g23mZ13H2+u/7dtDhq+/mPOvsgc+j9P9R87ve7w\n8Uem/7L5pmbNCrePHjfKEMExBMUbMtp1Byb+YB7GrMYcsR/l+t1wgA9zYTjIeEcWvz/XKyY+ymPy\n4xqZ22O0IRGBYgmg4PAiZroCczHOVr7DnK8O5oGJXWckjPzgBz9onzrhM1YkvKK55+nE4tHPPR4q\nTPXghIgyT5uhqWtTTZ1pHdJkPu7V2Ty8aeMG88Q93zPPPvhT07+u3iny3SftZ0657FrTMGSYWbV8\naVBbMWVEg5k8YlCHrxCjjetQYQV9kALu5j8WDwzhCDhaoBgIqSH8Jj0nxJwSDiIoap/hxn+1F99f\n6jLZ+M+5Xr0CnrD/gWajVWRe/v7n183dV/xvc/1/PuUeOr8967Vvq+0lL3u/fRejAYL+09fbXqDI\nN5jscIZC8N5Mm/pwJkGZMvLHdFeMwJHECihtRi+wxbwoEYFQAig5pi8eeOAB55tAp5klKgsJ9yoL\nI+CxzD396KOPdsjmxjytz9qGqRglnL73C53D7+c+JwYfZZyUtQ3WiWvQyOSm9vf33XiVWbrgA3PC\nhdPNmImfMJutafvpn91jfv/og+byex4yg4YOC2orRtbZdLPjRrTXz5sYbVyHCivoQ8e4kQq68J5y\nqYTQ4G1JrmPmJMmkk6XMLrjgArcCS1r5wokcriFCb7ufdc7gP+/vv/lqc8Z13yqofDnHlj5tHp2Y\ngonNZe4363pDrofGzStflHm6AcI8h/JlZOznhwvVj4c0oVA0SiRWoAMj5VuImvbnIoAzEw5Zt956\nqxu5EgJHAo+kL0TWsTwneEUzssVahEMWZlkvzDP7tKvM6fpFS/z+kFesT3jzp03kW/psi15I1rd0\nwXzz4mMPmzOvn+GUL/t62ymaqWecZ4bt0mRee+Yp1z6EtBVZ02Ax2rjkdVfSeyngCvi1eAhxWkLx\nEKaQFnIl07PNSnFH2Q02BKBU+c3PZ5rhu4wxkw/5p6Kq6NWvxvXgyeQTS6H5eTIaqXTIB44vKGfO\nhSkwrZyzLpqVaaZNm+bKsiC7D1fKKqttIhBCAKc/FnLgeWWhDqZK0nG66fomTZrkzNZ0VDE3Y+FJ\njlJJ1eqfe55zRsXlSNKMTRjTxznCjha8O8c0Dhue2fFumjjJzJs9q8NlFNNW2OCnDsf4D+W2cb6e\nSnuVAq6AX4yHmlEeS+595Stf6XTF9LxPPPHEnI5N5cT9vvTLR8zBx/5rp3Pm2kAjQo82lpAfl/ld\nRuLpRBgXXnih80JlH+WyRv/J68CblDhk5ugoi+JGGUtEICaBI4880vkSMNrESQufDeaH8wm+HSSN\n4V5GYdOx9Iqb5wk/BfYhTDMVGlnnO5dX5pQhBKnB/s8SnK7qG3fK2uVMzyuXNHfYV0xbsYPJ9uQu\nt43rcCEV9CFeS1lBX7qSLpUkEvfff7+58847nZMGc0R+YW3/PcjIg+kql5CXtRSZN/vPprVlhZn8\n2cOKPrzX1kai6APyFMTk5hdOwJSdFEYX3//+990mPKPpoOQT4i0x9zGCoDEjm1Ho6jb56tc+EUgS\n4N4iGsGvqES8OmtI5xN8ODBhI9ynjIQZESOMWv09zjasXqUKc8leeMbSGez8vtF7TDDLmxf4jx1e\nlzcvNLuM36t9W7FtRdb4N0Yb134hFfZGCrgb/2A8HMwl8VDigEXWp2984xtu2TC/MgrxfpirMGPl\nEtz/S5HXn3vaTPncP9t5n21hA4XqKfVcWfX6VY5wsCKjjxdMfMyvIXfccYeZOnWq35X5ikMMXqmE\nZbDkGh7S5c5LZ55IG0UgQYAELkQkXHfddc7XAAVLbvEsT2R/2PTp0w2WHYS54JNOOqk9kgDrjbfy\nMN1C2F0pgq+Et1LRjtT3zXY83HncnmatbYPe/q9tc9Kcb4v1zn71N0+asXvv0376YtuKPqnBQKw2\nrv1CKuyNFHA3/sFwDkLp+qxOXComaJwoeFARAvkxKeElnUtYlaQUWfD3ObaXm39kma53SInnStdD\nOBBmNuZ0k+sE44Tic9jSUF100UXpQzt8/uIXv+iS6GO+w5KAMpaIwPYiwH1HrD5WKp5TFvagw0gM\nfy4hxNAn5sC6wyIQCHVhvfF+DixekgxDzFVfejv1+FEwCnDYgH6ZhmEcrk6/5hYz85pLzXtvtYVK\nrWtdbe69broZNnqM2f/wbR3fYtuKxpqOnflYbVz6O1bK5+yuT6VcfZVfJyuupIWHL+klSSap9Kon\n6WNG1NWYGrv273q7DGGILHpvro37Pa3oQ/rZxRhG2nOVKziZkI8ZSaaa5HuyUANJBZgjwwydSzDT\nMfeGwqbhw8tZ+Zxz0dL2ribw+c9/3pmkiRcmexZTKijlrHuS0Sl+HThwcd/+8Ic/dDmfv/71rztP\nf/Klk6SDjHK8FpsGM/kdUcDEIWNBq7cGMixXZKpKy6ePOta0rlxh7rn6EtOyrG3Rh4mf/Iw5f8ad\nplciZK+YtoLpqdEDO7YPsdq49HVXymfFAVfKL1XGdZIG7pdvLzTkg+5KabB5Xj+/58iC6wMXuga/\nxi8xvShRhBAN5sEwI++1114urWWuekhsgOLGvEZZRtOlZN7KVb+2i0CpBFB6mKKZRsFEfd9997WP\ndtN10hHlPiYGHiEM8Utf+pJ7z0pKZMVDGBVnLUjidub449foZjdxyK+2fGSW2CVK80lry0pTWz+w\n3Xydr2zWPkzdR+8xQksTJuDIBJ2AUa1vccLac6c6E9NBKs2ql/Xz2sOeo7ftvZcjL7zwgpsjIyWk\nV77UhwMVypdUluSUziU0aMQKo3xJmk9ZKd9ctLR9exOgE0kH82tf+5pb9QgvfOaIs1JFEppDjLCf\nXjr77LPN008/7S6ZrHI+DzoRAMTKh4g3QXMMqy/tNXSg6Zuan03XV9cwqGTlixvorg39pXxTUMtr\nLVOV6WP3JbCHTYLeUNN1Mw4D+/WxSn6bd2UpJPBM9uZ0v14w9dDDx+GERAJkDMol55xzjhsh0JiR\n1g9lLBGB7kYAEzPLZZJUhwQe19t1eDFNMx+bFtawJuqB0TLmYmL9mfvlWSAsEcFXgjCnLCWers9/\nToYi0VltGlRrBtt1e7tKWAVpb6vkJR0JSAF35FG1nwg1+PTOg01t79I8ovOB6d97R/PJUY2mrz1H\nqYKJGVMxgrenXwKQEQKNC3PfhCRleS/jiELiD+aT8PBkneGk41qp16TjRKArCRC7jym5qanJPP74\n485TH9NwWri3H374YZdsBiWNExcZ35iiwTKEEDPsQ/bSx2d9RvF7Zy7q3NHOz37Ktg91fWNt/TkA\nABo6SURBVOO3D/iG7Du8wQzI4W2ddX09ZVvpLWZPIVRF33O4dZDaZ/hAwwMRSwgrwHy188D+ZVVJ\nwgJ68D5dHpURskHSDASlmgxFchvtHxostpOcAMWN81bSdO3L6VUEuiMBnAqJUScRBw6DOGdhdk4L\nTod3332324yliNW68KQm/JBnBpk9e7YzJ7sPBf6kPaEpzipF+9uOdMz2gemvCUPqzO5ahjDzF4nX\nEmdWr43djcBEqyynjBxkauyotVxh5ItC38f2bssReu7e/MbCE8jMmTNdyAbvSRfJKCAtbMfJioaI\nsA2UcdK0li6vzyLQHQkw18vcLiGGZGsjzM4n5EheLzkBMFcjKGs8q4kpZj4YwYpER7RYU7R/VjBh\n+4QfY+163gfvupP15WDWtjyhfcD3ZMrIxvIqquKjy2+FqxhOtX61CUPqzYGjBxu8lkt9zAbaYzFZ\n7TM8O41dsewwH+NEgqBMMTE/99xzbmUZtt10002Z6SKJH2QdVhodcjn7kTLHSESg0ghgDr799tvN\nT3/6U/cM4KRFEg6vGP33ueaaa8yZZ57pPrJKEo6GOCYyV4zQGX377bfd+0J/ko5YvgPMMbs21JrD\nxw4zg2r6WNN0oVqy99dbU/a+dunBA2wbIclNQGFIudlU/Z41GzebWc0t5oNV61wMYFaauCQEnsUB\n9sEaVdffrunZYOeLynfqouePB6df45fRMKZkevYs53bvvfcmL8E5nLAkG/GRzGOxRnAyVrhDYX0Q\ngQokgC/E8ccf75bVxNGKeGHmib0wYj322GNdKBPbGDnfdtttruNKpADmZZwYyfOcTwhjYg4aofPr\nV13yx6y3i7j8ZXGLmbtynVm7abOx0YwFZYCNJyaxx37WytZgHTMl+QlIAefn0yP2tlpF/N7Kteb9\nlrWm1T5odirWPmxtTxvOGfafGdCnt+sZj7GhBPWRHiwWQ/AxjpjdUMSk2sPbkwaEeeGkkH6P+V0c\nTkjNSUpJev8SEag2As3Nzc7y89JLLxlM1A899JCbJ/bfE0V76KGHuvljtqGA6bASxocwui20djDP\nmw9rIo6YaIMsWWsTdNA20Eastm0FbUObMv7YOW+h8DE372L9QMZYb+pBqWxXWXVqWxsBKWDdCR0I\nbNrykRsNb7YjUIS4Xnq1uRK2dzg44EPy4feJBIiRJCSCRPbJ5diolsQFhGqgnHFIyXJUCTi9iopA\ntyfAvU66VTJhsdwmUy0+BzoXj5ImTSvpaFGCLPaAU5c3QfMckTUrnxDixIia0TIKu5DQLpAxi3aC\nLnpve168m8uJgCh0zmrerzngav51S/huKFrmfsjpzH/ex1a+XBbzvAgPPr3vJmtiQ/nyOa18r776\nanP00Ue7hoLFKKR8HTr9qXICJNrA85mYdhQspubTTz/dLezAVydBB88CI2Qcr8iSRbw8HVmEFZWW\nLl3q3uf64x2xmAMuxnmLDjmmZdoGcsw3Ws9pKd9cdAtvlwIuzEglIhPwSeRpVOh1M4dLXCMOWD4H\nNKdkHph8uN/85jfdPuZ7yYcrEYGeRICY9t/97ndO4eKkxfSMT0gzfvx4l1kLfwhyQzN3zHu/2hFe\n0Yykc4l3xMKZMe3wlesYbY9HQAo4HkvVVAQBcuGibBFy0OLFiUMVDQZhRDQeCD15RsbPPvusi/PF\nOeuwww5z+/RHBHoaATqpxAuz8AJOWoTlMT+MHHjggc78zDNEGBPRAY2NbaE/TPXkWzvYj4CpBwuU\nZPsSkALevrx7/Nm8k8iwYcOcee1nP/uZY8LavzhWISzQjUma0TAjZHr7o0aNcvv0RwR6KgGyXvGc\nsMQm878k72B+GMEr2q8ONn/+fLeEoU/QwWeSd2SJHwGzLxmKlFVW2+ITkAKOz1Q15iBANitMXcQ8\n4tFMTCOCWc2HEpEjF7Mz5jRiIZkr9ua0HNVqswj0GAIoVZ6X73znO+5Zwjx93nnnOTMz6wbzzCCM\nem+55ZZ2Lkz78EylRSPgNJHt+1kKePvy7rFnwxkEszJCnueTTz7ZvWdOlx49cswxx5grr7zSeXw+\n9thjLmG926E/IiACHQh89atfdSFEOGDhpMVomFExiWtOPfVUV5bO649//GPnXEXCG9YOTku/fv2c\nfwXbNQJO0+n6z1LAXc9YZ7AEfMA/CTf8XC7J6PFqZgUkTM5PPPGEi+tlLpg0exIREIHcBFC6zAsT\nekRWLGLkiY1H6fpnjI7sI4884irBDI3lKS3eDM2yhMV4QqeP1+fSCUgBl86u6o4kxm/p2g3mPRt0\n/+6KNe4/79nm44JL+dLMW+HRjCmZhBu8x5mE5dhQzMxt4ZhFInoaiTFjxpRyGh0jAj2OAB1XniE6\nsx988IE55JBDzIMPPuhSs6KYEfwsfMINTNNpb2dvhua5RAnnki02+8aytRtdUg7XPixvdck5lqzZ\nYDbauGBJOIHycwmGn1NHdCMCZLVZ2LrezFnWapZYRWufQbPJ/tm8Ne8cSdmJAyYnLHF/4+yqJqPq\na1wGnGK+Bg5U5KdFSCbPPBQK95VXXnFOI8Q20uu+6KKLzB133FFMlSojAiKQIFBbW+s6s/vuu68L\n02NK5+KLL3bhSQcffLDBCeuuu+5yC5UQecDyniTwIAwQ8SNg3mOGTn7m2Wy2CvYdq2wXtW4wW+xn\nknDQPvhEHH167WB62Qai0WbAGjd4gBk9sDbKYg5cT7WLMmFV+y+c5/s1W8X7x4UrTcuGTWb95uJ6\nsDVWGbMQwz/YZctG2OUN8wkOV5iVkRtuuMGt1ML8Lw85PXbWOMUh6+c//7lLPJ+vLu0TAREoTICM\ncaeccooh3A8zNKsnYXUiPIn5Xj5PmDDBZcgiUxaybNkyZ8Lm/Z577un2u+12tPvHhSvM8nUbzboi\n2weSctTbzFj72Vzxo21qSq/kqU/SmYBM0J2ZVP0WRr2vW8X73HtLXe+2WOULmPW297vYPpjPz1tq\n/ro0f/YcnEAQTM0kBCCdHvmfechRvmS9evPNN6V8HSX9EYHyCUydOtVZlyZOnOhi6ImzJ4Ulyhfr\n04033ujC+lg72DtdJUe8ftvsJavMs3MXmw9Xry9a+XL1mKKXWYX94vxl5s92oRfM1pLcBKSAc7Op\n2j0vvb/MvGkfMJKslypr7Uopr3y43D6kS9oXbkjWRX5a5pNIGkCOWnrCKF163+SqZX6K+V6UsUQE\nRCAeAbJjvfzyy86RkQQ25I8mVIlnEAWLNQrHRzrFzPuSgQ4FjbD/tQUrzOuLWlzO51Kvik7961YB\nPzlnoZRwHohSwHngVNsu5nP+YHumc+2qJpsi9Ey32M7th6vXmT8tWtnBe5KQB5w95s2b58Ii4Mhc\n7wknnOCUMuuZEhLhEwVUG2d9HxH47yaAYxXLGJJHHacr1hrGaxohXInoA8IC/cIN3hFr8Y61dgnC\nVVGcqmhilq/bZH5vLW0aCWffEVLA2Vyqciuei/Os8sWRIpbwkP11aauZY500vJC3liUDSQqA0sfx\ngwYAYX3fe+65xxfVqwiIQBcRYMTLaJcwJHwvSOvaZL2mERZqmDFjhnnrrbeckyRm6I01dWZ93RDn\nXOUKRfhDS0Mn/c92XWFJZwJywurMpCq3YG7+1TuLzKoNm7vk++F4cdS44WbenL8Zsu5ceumlrqdN\nogCcPHjAiVX0oRFdchGqVAREIJMAvhakq0Txoox9uBFZ5+go7zp2N/P/lqw3W/rVZh5f7kaWND1i\nt2Fu9aRy66qm4zUCrqZfM893ecvO+a7uIuXLaVmo+42Fyw3OHWTjwcyF0xXKl3lf8jpL+eb5gbRL\nBLqQwN577+38MY488kinfIk+QJ555hlnkXrXWrC29GmbB+6Ky2AN4VnNWuwhzVYKOE2kG30mVpbe\nKjmUvSxevNiMHTvWPProo24T64HSi91vv/3MWWed5Uy/vqx/xTNxnk2oEc/w7Gvu+PrOkpXmB/fM\ndEqYPSz0TcpJzFx8D4kIiMB/HwFWSCJMadq0aS6PtL+Sh3/xC/Nuy3pjdmxTyn57+nX1iuUdfD3S\n+wt9bl6z3g4COi6NGKuNK3Tu7rpfCri7/jL2usgMdcUVVzjnJRQvYQTHHXec827klaXGzj77bPO9\n733PBddj7k0mYPdfbZGN9y0m1GjaUZ8xb736B3fY8uaF5kdXfdVce9JR5tsXfMn89bWXfXU5XznH\nyq3PF/NPrM6CB7REBESgexBg5MvcL7H33vO5ae99zAY8KjNk08YN5tE7/91c+Nl9zA2nHmOmTz3I\n3HXZBaZl6eL20sW2FUyDfbBqXftxvInVxnWotII+SAF38x8LBUzA/IUXXmiuuuoqt+oJDxBCCAGL\nHPg1dJlnTS5o778ama5CU8U9dvftZtRue5jr//NX5rjzLzU/vm662WJHtPmkT01/M+mgQ513M+nx\nuGaJCIhA9yNAsg6e0REjRpjdJ00xDUOGZl7kf8y4wcx9c5aZfvcDZsZTL5lbHn/ejJn4CXPz//pX\ns2Jxszum2LaizSHLjrRTEqONS1VZMR+VirKb/1TkTyaX6+TJk10uZeJqidtDWNiAUSZr5rJAN/Ov\n3jSd/FpksgkVzE0jm9oy5dTY87Qss/G+H9mlBE3+W2bsxL1dfC9JNiQiIALdlwDTVrNmzTK3/eJX\nmUt+Ll0w37z42MNW8b5oFfQw90V69+ljpp5xnrOIvfbMU+aIU84wIW0FWffSEqONS9dZKZ81Aq6A\nXwrTMvM3mI98vB6XvX79epdknTlhElps2rTJmaLTX6kY83P6mOMvmGZ+/38eNN+fdq657dzTzBeu\n+Kbp07ewk8Yn9pviMlyl69NnERCB7kdg6NCh5rOHHZF5YQvenWMahw1vV77JQk0TJ5l5s2e5TSFt\nBVn4sqTcNi6rzkrYJgVcAb/SZZddZkgtxyiYhBZeiOsj5Ie4WzyPWYbML27gy/BaShD8O396zTlc\njBw7zj6EI1yPt5AJmnPlesDYJxEBEeh+BHLl5GFkW9+4U+YFDxo6zKxc0maCDmsr2haASFdabhuX\nrq9SPue3J1bKt6ji6/ztb39r7r//fpdZCq/iSZMmmSeffNIcffTRbpUTklx4mTJlilm1apX739DQ\n4De7lUraPxTxBkX70O03m8vvedCMmfAJ8z/Ou8RM+5dPmzl/etVM2P/AvDXsaJ2vJCIgApVDgJWM\nsmT0HhPM8uYFWbvs9oVml/F7Ob+QsLai8wg4RhuXeZEVsFEj4G78I5GXlSX8br31VrPrrrua3Xbb\nzaWQO/fcc52SJbXj888/7+Zc+RqMgI844giTVL5sr+kd9jOvWdViPrIrGfGAIczRjLEmpyUfznef\n8/2p6Z0/lCHfsdonAiKw/QnU2iQZWbLzuD3NWtsGvf1fr3TYTQf91d88acZa7+nQtiLdQY/VxnW4\nwAr6ENYyV9AXq4ZLveSSS5zS/fKXv9z+dTAxjxw50kyfPt0wf3PllVe6sCRM1L/+9a9d6rn2wlvf\nDO7f5rSV3p7r88DBO5lxk6eY1+xDhqB457z+qpnyuX/OdUj79saaPu3v9UYERKD7ExhSm90+4HB1\n+jW3mJnXXGree+sv7ousa11t7rUREcNGjzH7Hz7VhLYVDf06tg+x2rjuTzn7CpWKMptLxW3F9Jx0\n0Ep+gfdtEo4X7ApIhUKRiAM+84bbzMRPfsbM/csb5v/aUKQV1tSEHP5vZ5jPHndSstpO7/tYU9Yh\nuw4xYwZ1TTq7TifUBhEQgbIJkCDjd3OX2mUHs1dHe+Y/fmKef+QBFwnByWgfUMz96+rduYttKzB0\nf2rnRjNx6EB3XOiffG1caF3dpbwUcHf5JbrwOlC8v3x7YUl5oOnx+get0CWSD/qY8SNMP5mhC6HS\nfhHoNgRwnHz8bwvNivWdQ4SSF9nastLU1g/MDFmiXKG2gnzQ5IuvT42Ck+foae9lgu4Bv3jfXjua\npoZak+1qkR9AscqXWsY09JfyzY9Te0Wg2xFgXnbPnepMrwIOlHUNg3IqX75UobZi+IAaKd/Ury8F\nnAJSrR8x+9T36zqnd0a/e5VoWqpW5vpeIlApBHYfXGcGdmH7wOh38ojSTM+VwrCU65QCLoVaBR6D\np+Pk4Q2mnx0NxxZG2PsMH2gGWCUsEQERqDwCPMOfHDXI9O+C6aPe1jdkvB1hD6rJdvaqPFrxrjh+\naxzv2lRTZAK7Nw4wYwcNKGhqCjltL2vX3nVgf7OH7UFLREAEKpfAzgNrzYQhdQZnylhCVXhZTxq2\nLS9BrLqroR4p4Gr4FYv8DqxQ9KnRjWYXO1dbaL6nmCr7Wu07xs4tHzJmiKFuiQiIQGUT2HfEIDda\nZdRartDGjKqvMf+y+/DgZEDlnrtSjpcXdKX8UhGv82Pr9fj6ohYzxy7CzRJhpUitNVWNGzzA7DfS\nOmZI+ZaCUMeIQLcl8ObiVebNJavMmhLbB5L/0Dk/wIYd9baJfCTZBKSAs7n0iK3NdpnCPy5caVih\npNgFG2rsXBHOGv8wqtGMqKvpEZz0JUWgJxJYtnajbR9WGFZTW2fX+i5GmEvGIXPfEQ1mFzs1JctY\nfmpSwPn5VP1eYgBZL3jOslazZO0Gu+SgMZvsn81bM7STJ7av7cHSiR1a28+OeuucWUmj3qq/NfQF\nRcAtyNK8ZoN5x1rLFrVuMFtse7HJ5hWgfSCrc29r/epjp6JoJxqtkxVWsdF2LjmGCbsn4JcC7gm/\ncpHfcbNVvCttMD5mJ6+AeZAIIRhkU0zKlFQkSBUTgSokwKpqbe3DZttJt+rXKmPahNq+tn2wyTX6\n2NGvJIyAFHAYL5UWAREQAREQgSgE1GWJglGViIAIiIAIiEAYASngMF4qLQIiIAIiIAJRCEgBR8Go\nSkRABERABEQgjIAUcBgvlRYBERABERCBKASkgKNgVCUiIAIiIAIiEEZACjiMl0qLgAiIgAiIQBQC\nUsBRMKoSERABERABEQgjIAUcxkulRUAEREAERCAKASngKBhViQiIgAiIgAiEEZACDuOl0iIgAiIg\nAiIQhYAUcBSMqkQEREAEREAEwghIAYfxUmkREAEREAERiEJACjgKRlUiAiIgAiIgAmEEpIDDeKm0\nCIiACIiACEQhIAUcBaMqEQEREAEREIEwAlLAYbxUWgREQAREQASiEJACjoJRlYiACIiACIhAGAEp\n4DBeKi0CIiACIiACUQhIAUfBqEpEQAREQAREIIyAFHAYL5UWAREQAREQgSgEpICjYFQlIiACIiAC\nIhBGQAo4jJdKi4AIiIAIiEAUAlLAUTCqEhEQAREQAREIIyAFHMZLpUVABERABEQgCgEp4CgYVYkI\niIAIiIAIhBGQAg7jpdIiIAIiIAIiEIWAFHAUjKpEBERABERABMIISAGH8VJpERABERABEYhCQAo4\nCkZVIgIiIAIiIAJhBKSAw3iptAiIgAiIgAhEISAFHAWjKhEBERABERCBMAJSwGG8VFoEREAEREAE\nohCQAo6CUZWIgAiIgAiIQBgBKeAwXiotAiIgAiIgAlEISAFHwahKREAEREAERCCMgBRwGC+VFgER\nEAEREIEoBKSAo2BUJSIgAiIgAiIQRkAKOIyXSouACIiACIhAFAJSwFEwqhIREAEREAERCCMgBRzG\nS6VFQAREQAREIAoBKeAoGFWJCIiACIiACIQRkAIO46XSIiACIiACIhCFgBRwFIyqRAREQAREQATC\nCEgBh/FSaREQAREQARGIQkAKOApGVSICIiACIiACYQSkgMN4qbQIiIAIiIAIRCEgBRwFoyoRAREQ\nAREQgTACUsBhvFRaBERABERABKIQkAKOglGViIAIiIAIiEAYASngMF4qLQIiIAIiIAJRCEgBR8Go\nSkRABERABEQgjIAUcBgvlRYBERABERCBKASkgKNgVCUiIAIiIAIiEEZACjiMl0qLgAiIgAiIQBQC\nUsBRMKoSERABERABEQgjIAUcxkulRUAEREAERCAKASngKBhViQiIgAiIgAiEEZACDuOl0iIgAiIg\nAiIQhYAUcBSMqkQEREAEREAEwghIAYfxUmkREAEREAERiEJACjgKRlUiAiIgAiIgAmEEpIDDeKm0\nCIiACIiACEQhIAUcBaMqEQEREAEREIEwAlLAYbxUWgREQAREQASiEJACjoJRlYiACIiACIhAGAEp\n4DBeKi0CIiACIiACUQhIAUfBqEpEQAREQAREIIyAFHAYL5UWAREQAREQgSgEpICjYFQlIiACIiAC\nIhBGQAo4jJdKi4AIiIAIiEAUAlLAUTCqEhEQAREQAREIIyAFHMZLpUVABERABEQgCgEp4CgYVYkI\niIAIiIAIhBGQAg7jpdIiIAIiIAIiEIWAFHAUjKpEBERABERABMIISAGH8VJpERABERABEYhCQAo4\nCkZVIgIiIAIiIAJhBKSAw3iptAiIgAiIgAhEISAFHAWjKhEBERABERCBMAJSwGG8VFoEREAEREAE\nohCQAo6CUZWIgAiIgAiIQBgBKeAwXiotAiIgAiIgAlEISAFHwahKREAEREAERCCMgBRwGC+VFgER\nEAEREIEoBKSAo2BUJSIgAiIgAiIQRkAKOIyXSouACIiACIhAFAJSwFEwqhIREAEREAERCCMgBRzG\nS6VFQAREQAREIAoBKeAoGFWJCIiACIiACIQRkAIO46XSIiACIiACIhCFgBRwFIyqRAREQAREQATC\nCEgBh/FSaREQAREQARGIQkAKOApGVSICIiACIiACYQSkgMN4qbQIiIAIiIAIRCEgBRwFoyoRAREQ\nAREQgTACUsBhvFRaBERABERABKIQkAKOglGViIAIiIAIiEAYASngMF4qLQIiIAIiIAJRCEgBR8Go\nSkRABERABEQgjIAUcBgvlRYBERABERCBKASkgKNgVCUiIAIiIAIiEEZACjiMl0qLgAiIgAiIQBQC\nUsBRMKoSERABERABEQgjIAUcxkulRUAEREAERCAKASngKBhViQiIgAiIgAiEEfj/lnKWNW0TZ8UA\nAAAASUVORK5CYII=\n"
}
],
"prompt_number": 20
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"plot(eight.net)"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAeAAAAHgCAYAAAB91L6VAAAEJGlDQ1BJQ0MgUHJvZmlsZQAAOBGF\nVd9v21QUPolvUqQWPyBYR4eKxa9VU1u5GxqtxgZJk6XtShal6dgqJOQ6N4mpGwfb6baqT3uBNwb8\nAUDZAw9IPCENBmJ72fbAtElThyqqSUh76MQPISbtBVXhu3ZiJ1PEXPX6yznfOec7517bRD1fabWa\nGVWIlquunc8klZOnFpSeTYrSs9RLA9Sr6U4tkcvNEi7BFffO6+EdigjL7ZHu/k72I796i9zRiSJP\nwG4VHX0Z+AxRzNRrtksUvwf7+Gm3BtzzHPDTNgQCqwKXfZwSeNHHJz1OIT8JjtAq6xWtCLwGPLzY\nZi+3YV8DGMiT4VVuG7oiZpGzrZJhcs/hL49xtzH/Dy6bdfTsXYNY+5yluWO4D4neK/ZUvok/17X0\nHPBLsF+vuUlhfwX4j/rSfAJ4H1H0qZJ9dN7nR19frRTeBt4Fe9FwpwtN+2p1MXscGLHR9SXrmMgj\nONd1ZxKzpBeA71b4tNhj6JGoyFNp4GHgwUp9qplfmnFW5oTdy7NamcwCI49kv6fN5IAHgD+0rbyo\nBc3SOjczohbyS1drbq6pQdqumllRC/0ymTtej8gpbbuVwpQfyw66dqEZyxZKxtHpJn+tZnpnEdrY\nBbueF9qQn93S7HQGGHnYP7w6L+YGHNtd1FJitqPAR+hERCNOFi1i1alKO6RQnjKUxL1GNjwlMsiE\nhcPLYTEiT9ISbN15OY/jx4SMshe9LaJRpTvHr3C/ybFYP1PZAfwfYrPsMBtnE6SwN9ib7AhLwTrB\nDgUKcm06FSrTfSj187xPdVQWOk5Q8vxAfSiIUc7Z7xr6zY/+hpqwSyv0I0/QMTRb7RMgBxNodTfS\nPqdraz/sDjzKBrv4zu2+a2t0/HHzjd2Lbcc2sG7GtsL42K+xLfxtUgI7YHqKlqHK8HbCCXgjHT1c\nAdMlDetv4FnQ2lLasaOl6vmB0CMmwT/IPszSueHQqv6i/qluqF+oF9TfO2qEGTumJH0qfSv9KH0n\nfS/9TIp0Wboi/SRdlb6RLgU5u++9nyXYe69fYRPdil1o1WufNSdTTsp75BfllPy8/LI8G7AUuV8e\nk6fkvfDsCfbNDP0dvRh0CrNqTbV7LfEEGDQPJQadBtfGVMWEq3QWWdufk6ZSNsjG2PQjp3ZcnOWW\ning6noonSInvi0/Ex+IzAreevPhe+CawpgP1/pMTMDo64G0sTCXIM+KdOnFWRfQKdJvQzV1+Bt8O\nokmrdtY2yhVX2a+qrykJfMq4Ml3VR4cVzTQVz+UoNne4vcKLoyS+gyKO6EHe+75Fdt0Mbe5bRIf/\nwjvrVmhbqBN97RD1vxrahvBOfOYzoosH9bq94uejSOQGkVM6sN/7HelL4t10t9F4gPdVzydEOx83\nGv+uNxo7XyL/FtFl8z9ZAHF4bBsrEwAAQABJREFUeAHsnQmAHEX1/1+SzbXJ5s4mgYRsgIQbuUFQ\nCch9qyiI+OOSG0FAwBMD+FcRPFBAUEBuEFDkEBBEQEAUkPsO5ICQO9lsjk32CPzrU8vb1PZ2z/Ts\nzmZmZ96DTc/0dFdXv65+33fVqx4fOxIj44BxwDhgHDAOGAfWKgd6rtWr2cWMA8YB44BxwDhgHPAc\nMAC2gWAcMA4YB4wDxoECcMAAuABMt0saB4wDxgHjgHHAANjGgHHAOGAcMA4YBwrAAQPgAjDdLmkc\nMA4YB4wDxgEDYBsDxgHjgHHAOGAcKAAHDIALwHS7pHHAOGAcMA4YBwyAbQwYB4wDxgHjgHGgABww\nAC4A0+2SxgHjgHHAOGAcMAC2MWAcMA4YB4wDxoECcMAAuABMt0saB4wDxgHjgHHAANjGgHHAOGAc\nMA4YBwrAAQPgAjDdLmkcMA4YB4wDxgEDYBsDxgHjgHHAOGAcKAAHDIALwHS7pHHAOGAcMA4YBwyA\nbQwYB4wDxgHjgHGgABwwAC4A0+2SxgHjgHHAOGAcMAC2MWAcMA4YB4wDxoECcMAAuABMt0saB4wD\nxgHjgHHAANjGgHHAOGAcMA4YBwrAAQPgAjDdLmkcMA4YB4wDxgEDYBsDxgHjgHHAOGAcKAAHDIAL\nwHS7pHHAOGAcMA4YBwyAbQwYB4wDxgHjgHGgABwwAC4A0+2SxgHjgHHAOGAcMAC2MWAcMA4YB4wD\nxoECcMAAuABMt0saB4wDxgHjgHHAANjGgHHAOGAcMA4YBwrAAQPgAjDdLmkcMA4YB4wDxgEDYBsD\nxgHjgHHAOGAcKAAHDIALwHS7pHHAOGAcMA4YBwyAbQwYB4wDxgHjgHGgABwwAC4A0+2SxgHjgHHA\nOGAcMAC2MWAcMA4YB4wDxoECcMAAuABMt0saB4wDxgHjgHHAANjGgHHAOGAcMA4YBwrAAQPgAjDd\nLmkcMA4YB4wDxgEDYBsDxgHjgHHAOGAcKAAHDIALwHS7pHHAOGAcMA4YBwyAbQwYB4wDxgHjgHGg\nABwwAC4A0+2SxgHjgHHAOGAcMAC2MWAcMA4YB4wDxoECcMAAuABMt0saB4wDxgHjgHHAANjGgHHA\nOGAcMA4YBwrAAQPgAjDdLmkcMA4YB4wDxgEDYBsDxgHjgHHAOGAcKAAHDIALwHS7pHHAOGAcMA4Y\nBwyAbQwYB4wDxgHjgHGgABwwAC4A0+2SxgHjgHHAOGAcMAC2MWAcMA4YB4wDxoECcMAAuABMt0sa\nB4wDxgHjgHHAANjGgHHAOGAcMA4YBwrAAQPgAjDdLmkcMA4YB4wDxgEDYBsDxgHjgHHAOGAcKAAH\nDIALwHS7pHHAOGAcMA4YBwyAbQwYB4wDxgHjgHGgABwwAC4A0+2SxgHjgHHAOGAcMAC2MWAcMA4Y\nB4wDxoECcMAAuABMt0saB4wDxgHjgHHAANjGgHHAOGAcMA4YBwrAAQPgAjDdLmkcMA4YB4wDxgED\nYBsDxgHjgHHAOGAcKAAHDIALwHS7pHHAOGAcMA4YBwyAbQwYB4wDxgHjgHGgABwwAC4A0+2SxgHj\ngHHAOGAcMAC2MWAcMA4YB4wDxoECcMAAuABMt0saB4wDxgHjgHHAANjGgHHAOGAcMA4YBwrAAQPg\nAjDdLmkcMA4YB4wDxgEDYBsDxgHjgHHAOGAcKAAHDIALwHS7pHHAOGAcMA4YBwyAbQwYB4wDxgHj\ngHGgABwwAC4A0+2SxgHjgHHAOGAcqDAWGAeMA2s4ULuyUeYuXyVz3N+yhmZp+uhj/2NFzx4ysE+F\njBnYT0a7v2H9e0uPHj3WnGifSpIDS1Y1+bEwZ9lKWdboxsPqNeNhgBsPowf0lTFV/WR4/z42Hkpy\nBHTtTfX42FHXXsJaNw4UNwd4BWYtXSmvLVgqSx3ormxaLZleisqKXjKwby/ZbOQgWW9wpfQ0IC7u\nB5xj7xgPKGCvzFsqdQ1N2cdD755S2bvCj4eaITYecmR3WR9uAFzWj99ufrmzap79cLHMW94gq1Z/\nlBND+vbqKSMr+8iOY4fJoL69czrXDi5ODtQ3NctzH9Z6AF7ZnNt46NOrh7OE+8pObjwM6WfjoTif\ncHH1ygC4uJ6H9WYtcmBRfaM8+f5CqXVuxs5QlXNF7rVBtYFwZ5hYBOfibn5i5gKpXdmU0QOSrauE\nKj5fM0KGVfbNdqj9XuYcMAAu8wFQrrePpXPv23NlZfPqvLCgX0VP2b1mpIxy8WGj7seBVW4c3Pba\nrLx1HO/IruNHyLqD+uetTWuo9DhgWdCl90ztjrJwYIVzOz/83vy8gS+XW+XclU99sMjHDLNc3n4u\nMg4Q82c85JMaXDjjmVmLnTXdmM9mra0S44ABcIk9ULudzBwgweZZF+PrrNs57iokcP3XCd2PLK8x\njj1Fu+/5ObWyuAuAkqzp/7jx0PxJJn3RMsA6VjAOGAAXjPV24UJwYLbLbp27YlWXXXphfYPMWFLf\nZe1bw/nlwDw3Hj5cuqpTMd9MPVrkgH1a7YpMh9hvZcwBA+AyfvjleOuvuakluIu7ihrcPNHX3XQm\ns4K7isP5bfe1+UvzGoqI9o555G/YeIiyxb5/wgEDYBsKZcOBOpflyrzOztLq5mbJNH2eGDOWj1Fx\nc4ApaGvjOZHoN39FQ3Ezw3pXEA5YJayCsN0uWggOUOGq3iXcxNFDN/xe7vrtxdKnbz/56KOPpGro\nMNnys7vL4Wd9X3q7fUqL586WH//fIfKda++U6nHjdXebLfNHZ7vCHiNtGkobvhTbl/luPCR5Q7KN\nh+amJvnz5T+Xt557xt/WZjt9Vg45+Uyp6N2n3W1yDQq9UEHNyDgQcsAs4JAb9rmkOTDXFdvIVOFq\nq8/tIVc+/bpc9cybcsGfHpRZU9+SR2+/sZUn/7r7T3Lx8YfLstrFrfuSPnAto+LmwFxnla7OkDCX\naTz8+74/y4IP3pfv33C3/5s9bar8+76/JN7wPLOAE3lTzj8YAJfz0y+ze1/WmN79XFk1SEaPnyDN\nTS2uZLbPPXy/nHn59cJv2WiFm2dsVNwcWJpDOCI6HsZN2kS+cub3nMXb2/+ts/5EmfrS84k3zFQn\nI+NAlAPmgo5yxL6XLAcaPymkn3SDc2dOkwf++Dv5aPVqWTD7A5nxxmvypW+e6w/HtXj2725KOrXd\n/tU29aQdT4ptR2fGw4TNP9V6Ow0r6+U/D94jh5/9w9Z90Q8fZ/S9RI+27+XCAQPgcnnSdp9ZOVC/\nbKnMfOt1cRlWsmTBPOH7/PdnyqBhI7KeaweUHgfSjAc8I1edd5pM2GxL2W6PfROZsHzZcqmvr5fK\nysrEY+yH8uOAAXD5PfOyvWOK5Wei9TffSk6++PLWQx69/Qa5+eLzZcptf2vdl/ZDL7d8oVFxc6Cz\n4wHwvfysE31G/Ik//U3Gm50/f56MGbOjHHHEEfKNb3xDtt1224zH24/lwQGLAZfHc7a7dByo6pPb\nCjUA8pzp72accpTEWNaKNSpuDuS6glU4HpiKdtV53/QZ86f94qrY7Ofw7tcfN1bOPvtsefDBB2W7\n7baTrbfeWq688kqpq6sLD7PPZcYBA+Aye+DlfLujB/aVTHYpFs3yuiX+b/4HM+WB638nE7fevkML\nrbNQu1Fxc4Bn1CvDWs6ZxsOjf7pB5s+aKcdOuUQaVq3yY2ZVfXLFq9VLF3sAnjZtmjz00EOy4YYb\nyre+9S1nFY+Ro446Sp566qniZpb1rks4YGp6l7C1+zXK6kCsictcWWoaN7q5sFCfnj3dMnsVfg5j\ntRNY3dmyYx5mZe9esiIhI/WVpx6T0ydv5e97wKDBsv4WW8tRP/ip/57LP73lI1nHVsHJhWUFObba\njQdWserIeHjklutk0ZwP5ay9dmjt+xaf2U3O/O0fW7/rhx7NTVJRXyf//ve/Zdddd5W9997b/y1Y\nsEBuuOEGueaaa+TGG2+UjTbayLunAeSRI0fq6UWxZbUoplJRupNlGxvdYhNM6evtQi14lkY55XaU\nkw9Vti52Ts/LliPMiV2ld/AC91JRjm+Bq2FMwYCkeZFYCv179/QLjm9ePUgA4+5If393nlAPuiup\noXaBHL/rNtLLKS9Gxc2BR6fNl/ddkYyupF6N9TJozjve+zJixAj59Kc/LT0jY+PJJ5/0QHznnXdK\ns3NvH3zwwXL88cfLHnvs0e7YruxrtG0WqaCU5pxPipYkLSxBykP/il4ypF9vQT6MccpNjwzeheh1\nyvW7AXCZPnk02v/NWSKz6lZKvfucC2FFrlvVT7YdM9SBcq9cTi34sR8uWyn/mrkwsQJSZzv4cXOj\nvPDX2+SCM0+V4cOHd7Y5O7+LOYBF99iMhV1WD7rH6mbpXztb+q1Y7AGJEqbrrbeejwHH3Rox4Vtu\nucWD8Ysvvijjx4+X4447To455hgZO3Zs3Cldsg8L9+W5S2S6W1gkyUOQdGG8CqMH9JPt1x0qAy0X\nIolNfr+p6BnZU5o/UhP5Ebf+6dRFbmpEjuALRyjn+O7iFfKIsx66W4GBdZxmjnDoKqqU1fLWf5+U\nGTNmdNUlrN08cmCUGw/rDnLWWh7bDJvq1bRK+q6o9bsAX6Yhvf/++zJ16tTwsNbPgwcPllNOOUVe\neOEFef7552WfffaRSy+91APx/vvvL3/961+9hdx6Qhd8IBz16PT58ubC5TmDL93Bkzajrt7LmFyK\nnXTBrRR9kwbARf+I8tvBBge4f39vnix0rqVMZRmzXZVzKWR/++uzBEDvLoRbbAenmQ91rrJ8E9r+\nTusOk40mTZJHH33Uz/vM9zWsvfxzYDvnyRnWv30N585eqYfzhlQunuXAfc2btnLlSgFk33jjDZk9\ne3bGSzBV6aqrrpI5c+bItddeK0uWLJEvfOELMm7cOPnud78r7777bsbzO/Jjk7N873pjtssFyVym\nM03bS1ylsT+/OduHt9IcX47HGACX0VPHWn3IxUBzdSllY9HjMxc4q7j7lF4kkeyz643wCVnZ7i3t\n77jd9lq/WtYdMdRPM3n22WezCti0bdtxXcsBwiifGz9CBuQxnNKvV08ZuWyOVDgLOCSs4IEDB3pL\nGCsXUM1GWM1HH320PP300x64v/rVr3oX9SSn6O2+++5y6623yiqXid1ZAnz/4SzfpDyQjrb/pAv5\nmCUczz0D4Hi+lOTe52fXSm0XWKu1K5vkuQ9rOzRftlCMHl7ZRw6cNFoGuwzvzhJt7F4zUgY7q7q3\nqw3M1JK3335b5s6d2+Xuws723c5v4QDJQwdtNMZ7RjrrjmbWwK4O0EcPGhDLXizfT33qUz4m/J//\n/EewitPSJptsIr/85S/lww8/lNtuu0169eolRx55pKyzzjpyxhlnyKuvvpq2qXbHvTRviSxYkf9l\nNOvcrIpnZi22NbLbcVzEADiGKd1xF5r1alfDOImYXkQC0hpnWNKRue+nTTKLyZTsTlTZu0L23mCU\njB/cX7BYcqW+7pyxLhltD2f5EktUmjhxoo/ZEeebN2+e7rZtkXOgn8vi3WuDapkwpNJl9OY+Hqis\nRfbv5ydU+2loSVOJeFdnzZol22+/vTQ2NgogTOZzLtSnTx857LDD5JFHHpH33nvPx43vuusu2XLL\nLWWnnXbyFvLy5ctTN1nrwknTa+vzbv1qBxa62RbTa5PnSetxmbbZZFymc4v1t9xHWbHeSQn2Czcm\n7qr//ve/rXc3f/58mTBhgtx9992t+1i/9itf+YpccsklrfuiH16ZV+cyPVvm9kZ/y8d3Ei9embc0\nH02t1TZwR+/mrNfPrDfczXXu693S2SygSieoqwf0kZ3HDZPPO/CNVlQaMmSIfP7zn/fzPonfGXUf\nDqCU4Y7mDzAl4z/reHDT80Y4j8qnxw73AI41DRHrTaIPPvjAu6EBzKVLl/qEKwCmI4Q8+PGPf+yT\nu+69914ZNWqUnHTSSd4Tw1Qm5Eg2et1NNcp3aCq8ZqNbnOT1BcvaWcH5lHHh9brLZwPgIn5SO+yw\ng0+2+NKXviQAb0NDg0/COOigg/yWrv/vf//zk/tJ+kmiOpcMweT5jhKLj6ehluvk34WV5tqdOYbE\nrHGDK2XfDUf7OO6OLkkLq3iYE6RVDqD5I2lrPVdcY4d1hnqLdz93bM2QAdIzZq4jgpdKRw8//LB3\nEdbWtmTBdqaPdu7a4wDjYZ2q/rLPhqO8h2THscOkxo2PYf3bjoexbjxsN8YpW87iPWDiaFl/aNvx\nMGBAexd0RcWakMdbb70lNTU1ssEGG3hPyWuvvdapm8QdfeCBB8o999zjwZhErX/+85+y4447esv4\nN7/5jcSNRaYkpvFesQ52NiUhk6xY0dgs8yPrIudLxnWKcQU82eYBF5D5aS6Ndbvbbrt5rZb5g//6\n17982TpcUNDpp58un/3sZ+Xxxx/32ZHf+c532jX79sJlPgaTTb/+9r47y3EXXiqbbL9zaxsss/b3\nm/4gP7r1/tZ9SR+wFMgw3nRk9vVyk9oolf0k2BCb0ykkm222Wancmt1HDhyg7CSKcxKRRIWXC0uQ\nnAEsYizafBGACQhTbQuvGcrFF7/4RV/kg6pcfP/ATRl6wiVKNcUsodnU2CD3X3O5sDBJ/4FVHoA3\ncBXijjj3RzJ4RHWbbqaRFVu4Ih3bOSU2pHzIuLC97vR5jTrWnXpdRn2lYs7NN9/skzb4/Nxzz4mC\nL2xAq4UA4CRCu80GvtFzVyytk7uvuFSee+RvMnTUmOjPsd+5BtcyABYZOnSo91LwXBB4JNr0798/\nlm+2s3Q5gDcE71VIZDWzNCGEFUwsmClH1IMmiQrLubq6LbiF5+fyGYAlHMLfokWL5KabbvJgjFKP\nl4aVmXb4wtdiwZfr3HbJhbJw9iw55+pbZfwmmwsW7sM3XyM/PfbLct41d8jQ6lGSi6yg3G2U8iHj\nom12l+/mgu4GT4qKSgh0XEyDBuVuXS5zWYi50hv/fVr69OvvLOJf5HRqR66V0wW6ycEIXla90Zic\nxYK7yYPLczd5b0MCEMmUVyIjmupXuKZxFfft29cr2cSF803IERaAwNVNXWo8ZxdddJHc+/dHYi+1\ncPYH8tQ9d8pxF1ziwZeDKlzf9zvmZKkeVyPP/+MBf14usmJlQuGfzsq42BvoBjsNgLvBQzr33HOF\n6QdMXWCqQa6kCyvkct72e+4nXznzew6E12T3pjk/zo2V5rxSOwYApu4v2a7E3ciGzpSlXmr3b/fT\nwoGqqqo2rMAlDOCSqKeEFQzhIQGEOYbEy0yuaz23o1vqUV933XW+yMfmW20d28zs96Z6Czfqaubg\nmk22kBlvvOLPy0VWJHniOivjYm+gG+w0AC7yh0T8BrcRa4dSFYc4zt/+lvsC8WvvNpNesbXXg2K4\nknormCpy//33+4zYqCuyGPppfehaDkQBmKsxNlDQlIj9akEOgBl3NC5qQLirlTb6R9Z0HJF0VTU0\nvp75kJHVsmRBR6bYtZcP3U/GxXGrY/sMgDvGt7Vy1rJly+TYY4+Viy++2BdwX3/99b3LiCkGubio\nKpzba21Rs5vXaNTCAYTsnnvu6ZUmCiVkKz1ofCs9DsRlQgPAeEXwkCi9+eab+tFPHyJpj2NYkKGr\nqTkhSWzsxI1l8bzZsZdfPG+OjJu0aexvuezMl4zL5ZrFdKwBcDE9jUhfzjrrLAF0TzzxxNZfcEFT\naemcc85p3Zftw9pckaS5frmwtJpRyzxQnh8xN1WYcD8alQ8HANuoFdzkEpkYD+HqRnhHwilCJEix\nEhIVr0JwzjfnqCddX7swttl1N9xI6p0R8M4LbecRr3ZFQ0jOnLDZlrHnZdrZ1/EjpHzJuLDN7vTZ\nsqCL+Gn94Q9/aNc7Xui4ifVXXHFFu2N1BwvRd/Wap/5aLnbVu2GFLF66WB588EHZa6+9vLtN+1Fu\nWxLmcCGSgUqVImr4YgWH7sdy40k53i8AjKWnRIyXTGj2ke2soQmAdued10wBZErSihUr5J133vFT\nlViEIV9EH1AMp02bJhWVQ6Tho2GuLmJbcCTh6ujzfybXnn+2nHLJ73wi1srly+Tmn50v1WPHy3Z7\n7JdzdyhYElK+ZFzYZnf6bBZwd3paHezrKCo8uepNXU09VjdJ71Ut5e8osUesupwtPpQlXJCHHnqo\n/OUvf/HCllhfVybXdPUztvZz50DczIV+LrmRBD0WVFBasGCBnyqk35meQ6EK5gm/9NJLbX7TYzqy\nxQKn/CXgC1U4pbmnW7c4jnba92DZ82vHyTU/PEtO321rOe/AzwlhplMuuVJ6BUVF4s6N7uvjSreO\nc8VLjNZwwApxrOFFyX5C2/3b1LluWbCujc/2ci/yoLlT25Xu22KLLbwrvWQZnOHGZs6c6V2LzPXE\n+sXqQbDWuApIRuXBAZ478/dDAoBZwYhsZIBQa4YTF95ll13CQ70VTAEe6HOf+5xX6tockMMX6kOT\n3BWtE71s5ARpqlyTGBbX5PK6JVJZNciP37jfs+1j0ZIDJ42R3g6IjVo4YJwog5HA3MPNXHUqisV3\nFaHdbjJiYDvw5XoUF4hzm3dVX4qpXbJa4T8AjBVM/J6sV6r/GJUHB+IsYMB32LBhQk3ojTfeuJUR\nCxcuFCzhkPCiYAmzYAOWKxZsRwiQpzBMFHxpq7pHQ9YFKAYOHtJh8CURdOLwgQa+kQdnABxhSKl+\nHe9WeBlR2bfLbo86udtMGJc4pYFCFKzc0tXTKrrsBjvYMPE/ppRQz5spZMz1xKUYFbIdbN5O6wYc\nIN6LEhYlxgHvBVsUMyWdF6zf2VKoYquttvLgiTWdqwJHshXgHff+ESrZZctN3WIkuc35D/uX7TNL\ndW40vO2c6GznlMPvBsDl8JTdPbJowE7rDvMLC+T7lge6FWNou1fPHl5T54WOI4DogQceaJOQEndc\nKe3D3QwI77HHHvLYY4/57FebklRKTzj7vTAG4qxg8iQgXNQbbbRRa0OLFy9uTcxq3ek+kITFcShv\nr7zSUgQj/D3uM1bz888/L6+//nqi9UqBH6zs7V2NZhYdyTf1c0s7ssAJXjKjthwwjrTlR0l/Qwvd\n2a3s0pG1b5MYw5q4k91yfkP7t2Q3Imyo5pNEaO5MvCc2Wi5E1jMCGFfjfffd512PCEadmlQufCjn\n+4xORYIXuJuxfHFDM0ZQzJTirGB+A4DXXXdd//5g1WYiFF6mBDKVCc9LnNU8evRoD+y0w9KcLMvJ\nEoz5IsJeO7tlGsP1svPVdim0YwBcCk8xh3tYx2Uhsuh4/zxkRTO/+LPuhR05oK1rm4XIk6ZM6EIS\nZHWylGI5EMKVbPAvfOELPg7MPZsVXA5Pfs09xlnAKGGMDYCYxTpCK5g5weQKRAlX9tZbb+1rw2PV\nJtUYp80nnnjCK3m4r4k5R4l3Ebd2SISp9ndLK+YDhAc4IN9hnWFC+MsongMGwPF8Kem9w91LBgiP\ncsDZ27mNcyXOqXbn7u4sX9bRjaNtttmmzapNegwJJAA0xDSMTOsY6zndfYv1g4A95JBD/BrBCEPK\n/yFk1Q3Z3e/R+p+ZA3EWMGfw/HVKEiAdFud4++23YxslxIOXCasWJVbLWOrBZFWz2AJts7Qhyh8z\nIaKE65nFH6KEYr2vWwt5bFU/6duBxE0SroY5j9iu40f4xKto+/Z9DQcMgNfwoqw+8YLstcGo1rgP\ncZpshOuaGBHree7tAHx4ZFJ99PywqID+hiAgxrXpppv6XWRkUisZd1mpElYLApj1nJlmwhqxrH6D\nIpJkwZQqL8r1vpIAmCIcgC5uaCi0ggHWpPEBcO60004+uYtpRSh4JFixDjWzDgBpLGXOx9KOEmMx\ndHlHfx/Ut7d8fv1q2cm5j0c4WdE/hXwgHMVUo63GDJb9HICb2znK1fbfe01x1H637SkHDpCYhctp\n4rCBMtJt+zm39Mfuv15uP7GbPu4l1pdqgnMjbTlqsGwzZqi3fjk3G6HZY/GGJfY4BxBGK//MZz4j\n77//vo9NobUjpOJcddmu0x1+xxqhqhGKBlYL7mj4w30T04vLku0O92V9TMcBliCkolWUKMrCSmfE\nc4nHMv4ZI5ofwLzxmpqa2PEBCDPNjXwKgBwQZ0tWNRYyLuo4xZZxx+9JyZLaR8YkuR1MH6qmmM8n\nsWHefZUPbAHr9Vxoq0U+DJExVf19Qqa2Y9tkDlghjmTe2C954gDTj+IEAcKGwgIPP/xwqysWYYNr\nrNQIQYqQxVI56KCDfOEFBCDWCu7ofC3AXmp8K6X7ISYbdRdzf1iq7733nveIbL755l5RIzSjbmPW\nlUZJSyJKSnI+xFiiPTKfiQPHEZ4pDQPF/W771h4Hsvsd115f7EolyoE4VzS3ipaPoNh3331bBcKM\nGTN8sYBSYwVWCbFflpoDeJmSBOEGTHIzlhoPyv1+krw7FMggaZGcCECXKUG4iJWIBSsY6z7dYv3i\nRVFizjFKXRL4brDBBq3vmp5j28JxwAC4cLwvmysjUHCzxRGZnrjKAGmtCIR7mrgw1mKpEO48Ml6x\nhL/4xS+2ZkNTDQk3ZFx1olK5d7uPFg4kxYEBSyxcxoEuzECNaA1LMGaYShQSU4pefvllXyOaqX9Y\nyVi/06dPb3esnocSmPQe6jG2XbscMABeu/wu26shUEILgCQkJVyzCA4SUIgLQySU4JqOm4qh53W3\nrU5HAoDvvfdeb9UgZJkLSjEGo9LmQDj+wzslPwBlE7ewJmNhybIcoVJoBQPUTz/9tOAt4jjCOAB4\nuL4w5ymA62dmJmSL++r1bLt2OGAAvHb4bFdxHMDKVaFAZmY4BYLKPlT4Yc4iLmmSViAyPLGQS4EU\ngHfddVdv8VIaECL5ZtGiRR2u8VsKvCmHe0iygLl3LF/c0CicmrWM0op1C+EhAZyJIVPPmZkEADZj\nCWAnjBF9T0K3Nd6loUOH+rbsn+LhgAFw8TyLku8JgMsap0po/gq07GPuIoKGAgH77bdfq8DAQtbV\nYPTc7rjFFc89QyRiURsaggcoHqVk7fsbs3/acIDs4yQLlDiw1oNWbwjzfElKVHrjjTd8ZStyCYjl\nspIS7wpgTC6Fkiq5+p1M6Q033FC/2raIOGAAXEQPoxy6gkABbCA0dEBZtXz2UaZSQQrXmgoOpjJR\nR1p/49juRghGtYKZhnTPPfe03oImY4VWS+uP9qEkOMDzT3JDY9kS12UcqBuam544cWKr1wjXM+MD\nVzLZ0rSHwoonJSwzqdXmlGlUuwrfMd1v28JzwAC48M+g7HpAAQEVCAgQBVkYgYBh2pLSZptt5jV9\nvjOn+MEHH0zM8NRzinmrALzXXnv5OdBkrEIkyKCM4Io2Kl0OJAEwd6xuaJKyNAGR9wTLWQlw1SlJ\nWMLPPPNMm9CFJvXp8WzxIBkVJwesEEdxPpe13quPHPDVrmqS2ctXyYwlK2T6knr5YOlKmb+iQVY2\nrfb96euq4UTdWx3pKEKFeJi62nChsd6pZnqizTO9QoEZ1+36668vM1zSCb9hIdCPaNJJR/qyts/h\n3rlPEmyoWoRlP3nyZN8N3JPE8shmNSpNDlCMRTOdo3fI88e1zNjnM6EJkq0UjDme5EQAmfdHQzba\nDsActs37gbeJ6U1QZ94XFOO6hmaZswz5UO/kwwp5/xP5UO/kA/KDQj75kA96P+WwtUIc5fCUM9wj\n4Dp18XKZVrtCGlZ/JKuaeZnankC56H5OIADA6w+tlA2HVbVWxWl7ZG7fSLDSuCfxLqzdMJZF0ghu\n6JB0ST/2IVw0azo8ptg/c9+4Be+880659NJL/VQS+oyQe/bZZ2WLLbbw2a3Ffh/Wv9w5QKIhwBlH\neED23ntvIdYLaOLxAXBrXNiGWQNqyXIclnS4pjTgi+WMmxri+N12282DNVYyvzEHPaw1HdeH6L6G\n5o+cbFjuZMQKLxuQD6sj8sGJBwe+Pf1ygzVDBsgkVzmLetJG2TlgAJydRyV5BBrr24uWyRsLlsny\nxuZ2oJt004DxwN4VssnIKtl4RJVfZzjp2Gz7sWZxKWvWJ/EuNP9wKTYEC3McQyJjmmlLEC453Lmc\n112I+8NViJDE2p06daoXsvSf0pzEudX67y73ZP1MxwHcxn//+98TD/7sZz/rxwBWMNYkVeHwljAm\nCM3ouxI2QBU1xn9Y0CUEW84liRFLepdddvFjLzw/7jPK4DRn5b4yt87Jh9XS7L6nIcCYZQ0nDRsg\nm1UPkgrn8TFK5oC5oJN5U7K/NDgt9sn3F8rURcul3mm46V6tFnZwLJbygvoGWbiiUdYb3L/DIIyA\nAYg06QRXNNYfWn9YC5crh+4zQEtd2BwLgCGEsKK7A2HZUFwBawQXIwJSq4VxD1g6ZMRqnLw73JP1\nMR0HULooGxkmTXEmzxrQIwcAy5Z3gzGgi5YAsIz1aI4AOQWMIy1FSVucFxbc4FzeD94zwh8oteHs\nA84Jqdkpxs/MWuyV8xW4l8MfU3xu9PKhUeYtb5Bxrka0gXAy00w9SeZNSf6C5fvItPnyft1KaYz6\nmnO440bnhyJGfNcbs4UXrqMEsIZl93DPkeUJMCtRhEBBWvchRNTyRXCh4auLTo8p1q0mYtG/cI1g\nvmPR43pnWopRaXKA5x8lBWRixDx/vEGALWNbCddzSIAooQxc1kqMn7ha6iT5kWeB8kfWNNs44noP\nvTvPuZ3rvaIdd0yafc1Otsxx+SS3vz6rNYckzXnldowBcBk9cTRbwHdhfWNOVm8SixANxIQem7FA\nmjoBwhSPR3BAxLBYLQhXHFV+lDRhSb+zxVo84IADfO1cvlOIgHhXsRP3hcDFHcl8YGLCYfIMU1E0\nQa3Y78X6lzsHMhXkoDWAknV8eRd0XKCQsehCSIAlYz50SwPIUaDWc1B2+R3vy3PPPdfOCkc5/9fM\nhV4+rA6AX8/vyBYd/9Hp872c6Mj5pX6OAXCpP+Hg/l6dt9RnNa/RqYMfO/iRtnA1vTyvroMttJym\nLli+kYCC9r/nnnv6OKk2rHEs/a7bPfbYw1cR4jsCixgb7rpiJrWCAVuWhvvLX/7S2l0SbHBV4pI3\nKj0OJE1F0gxixj6Zzuo2Zo4wgBlaw3AF4CW5SolYsRbz0H3RLd4mKmzh5tYpcHrM2wuXyaxlK/Oi\nnGubbBetbJTnZteGu+zzJxwwAC6TobDETTEi2xnXUL4JbZks6sXuResoAUhMwVDS4gL77LNPm6kN\n//jHP2LBFbc1fxCW5d/+9je/5rC2V2xbBWD6RW1orYql/TQrWDlRetskCxilC1Krl9KUJFbh1QkV\nSsIvUdJZBNH9cd8pS8n4muGm9WnYZoVLxHzdJWQSWso3IXI+dOEqpjAZteWAAXBbfpTst1edhUpC\nRVcRbXONzhDVfZjzC6Hd45olgQQLVwnXbVIWKQLr85//fGtCy+OuZq5mS+v5xbINAfjggw8W+soq\nUErU+aVISTgHVH+zbffmQFJyncZlFYDJg2C8k6SnRJIiMV61lnU/ymemxCo9ji3ncjyxZlzYTAV8\ny1m/zIboKlrpkj076yXrqr4Vsl0D4EJyP8u1mRNK8gRApMTLSXxILabbbrtNdt99d/9SHnnkkfLm\nm2/qoa1b5vrOXdH12uc8V7QDTbozFLqiuVcsAGKmTJ9QQlCF1bJ0P1v4RR1pzYhmyhLuu2Ij7R8A\ny5Qjslbvu+++1m4ipFmkwWLBrSwpiQ+MaV2EI+mG8OBE6ztzLIlZFKQh4zl0RzNWUOhyIRRbYs2M\nw+ee/59Mc96xbLbvstrFba6by/U4tq6hqZ2XLF8yLte+FMvxNg2pWJ5ETD9wNfGinXPOOQK44qIC\nXJhgf+aZZ3rNlSxa3LLf/va3vQVFYYevf/3rbVr7YKmrXOOyGrPlKn97351l3EabyMh1x8mH702V\nW38+Re79/W/kuUf+Jr379JV1N9yoTbvRL7iih/bvI8PcX0cJLR6BorEtABjXNMCKsNDCHYAwsbIw\ng1qvyfmcQ7KJ/hFXJkbGb8VCZLxC3BtJNljBhx12WGv3uF9chLgLi6nfrR20DzlxAOAkmRCrFqVS\nLd6wEZ453h8qpIUeEZQxEqjYRxshISMYH+FUvfD3pM/IEzwt781bJMv6DHSmcft3o6mxQe69+jK5\n4uyT5N/3/1kevuVaee+VF2TS1ttLv8oWb1VaWdHkfNEDeveS0QPXlNbMl4xLusdi39+e48Xe4zLr\n33e/+10PJqeddpp8//vf9y/tJZdc4rnAi3zHHXe0li7ENRVXZWe2i72knUiv7L3t0gtki10my4V3\nPCTH//jXcsvFU6Ru0QL9OXbrYz0uiaOzRJKIavTco94TABoWqACkX3zxxcTLbb/99q2rLwF2LOaA\nW7dYKHRDEwdm/WOsHyWyWVnJxqYkKUe655b4LZn9ZDGjYLKKEYAaR+paRnFUAlwZB7wLgG9o/eox\ngHvoqtb92bYkhI2o2VA+7hlfueq2Sy6U6a+/Iudcfatc8sDT8rN7n5Dxm2wuPz32y1I7v2WqXC6y\ngqlJUcqHjIu22V2+GwAX+ZPi5bv55pu9lXv99dfLn/70p9YpO1hGYanG3//+97L//vu3uyNquOZC\nvOi7f+XrsuM+B/nThlaPkn4uNjvzzbbTIOLaXLoqt2vFtcG+cO1grAEqA0GUqwwzPakcRSGOJMJd\nP3nyZB/34r4effTRdnOKk87t6v0hABPbI+uVymAh8YzDCkfhb/a5+DlAiOHJJ5/0mf0kX/G+8pyT\nErGiMX+OQ/GkgAbzfUNgJplKF2rAataEqly50tQr3mO1cPYH8tQ9d8pxF1ziQZd2K5wCsd8xJ0v1\nuBp5/h8PeKUgF1lBVa0o5UPGRdvsLt8NgLvBk6LmMQkTxG2SpjBcc801PoaICzpKVL7KhXghttlt\nb/+ycd4b/31a6pfWyYafaskyztQWVbLyQdGCAi+//HKrhk/sSi1kroVgygRSHItiosIKKyKT5ZyP\n/qdpg/7A6/r6en/4oYce2hrb1/PpO1YRU1GMuhcHCJFoch1KI+BLuAFKeo9D61at5ZqaGg+806ZN\na2UA8gBPEX9K/K61oHVfmi0JUnE024WhUL4Hj6hu93PNJlvIjDde8eM3F1nxcUKkubMyrl0Hu8kO\nA+Bu8KDOPfdcn6SDi/mMM85o1+Orr75afvCDH3grOa7YemdmHs2dOU3+8INvyde+c6FUVmVP9AgF\nSLuO5rgDzV/jWrT71FNPtbaAVauAyk6SOcKYWeuBn3xAeaHQPdYHhOWMNVxoCq1g4vlMn8KaCQnh\nbclYIUeK/zNTfLTM6EYbbSSEQ3SaEb3XbP9Md8LYJybMn7qmOZ6xTBYz+3hH+B3C1d0RK5gCHHFE\n0lXV0Ja1u6O/DxlZLUsWtK3WlkZW9BCqRbenzsq49i12jz0GwEX+nFig/qabbpIrr7xSrrrqKm8h\nIaSVbrjhBpkyZYoH37D+q/7OtoIVFDpAc6a/Kxd/4zA56IQzZKd9D07VwjuubOS+++7baq2mOinD\nQRSpQOBAuN/eeeed1qMBVP2NnVgbURde68GffCD+pvV1iQfff//9Wc+JtpHP7yEAc69Y/qz4FBJK\nA8pFGB8Of7fPxcMBwhx4V/DYMDbx1uAqDgGU3hLfDxXIuDtQhZJM/lCxZbqeWtJ4UAB4Jabd5TJO\nmNL3SkIexdiJG8viebO16TbbxfPmyLhJm7buSysr4qA+HzKutSPd7IMBcBE/MADn2GOPlYsvvthn\n+zIF4aKLLpKTTjrJL1bAy3bqqafK7bff7jNlmboQVz2p0mUe5krzZ70vl5z4NTngG9+U3b58ZOrT\nq/r18VOEEDC77rprp5OesBrC1ZCYZqUuWzpFPehQuCUV6ghvgOkcuAM5D6uB5KdMLuzw3Hx/JrlG\nBS3CNFobmushyFmAolB9zPc9l2p7AB9eGrwrWLiMsTBfIXrfSW5onc/LOMetrOv5cj4KG1ZvSMx/\n17KtjOdMORGcB5jfc889/r2i0E2vj+LrQjProR6l94Vnw8vJauehYWbEhM229PtzkRW9I8ZAvmRc\nmw52oy8GwEX8sM466yw/7+/EE09s7SUuaF5qpiZhFZPdizuWGIr+hQDFiSMr+7aen/YDbudP73eI\nT8RaXrdE+GtuWlMQIKmdwb17CPFo+kLpSJJIsALCtUuTzk3aT8ZoKMhw7SlhMTItSwkLBEDNRsTQ\niAtrDWpc2NHSfNnayMfvXB8lQ6ckkQ197733trF4uA73TzY092dUfBwgUfCJJ57w04fwWKB8JiVa\nae8VNPW7bpmepOAcLrSAwhh1R3NO1ArG/R3nCWLskMS55ZZbyiGHHOIVWZT3lQvmune7PQiTcHX0\n+T+Ta88/uzUBc+XyZXLdlHOkeux42W6P/XyXc5EVQ52CHlK+ZFzYZnf6bOsBd6en1cG+UgLu8ZkL\nXEH0zMKbecDHXXip9Os/QC76enuX83EXXCq7HHRoYi8qXILFjRedJ0ccsI9PGqNYBm5zBQ1cZ7jP\n4+buJjb6yQ+0Ea4dTHYzgkSJ+cFhwRJcdFTFSkNYLSTMQFgYKDRrk4jbIViZE4nwRYDDp7AoCf2h\nahGKTdIUlrXZZ7vWGg5g8eJyZowyTY4QR+iVWXPkmk9Yqo+7kEnStDgUrqjHg2QsroXVqlaytohV\nS06DKnLh+0FOwS233CI/+clPfAgHlzhTGrkG78wNd/xFfvDHO6S5R7yn7B+3XS9P/PnW1mmIm2y/\nswfm/gOrZPprL6eWFb2cArHLuGGywbCWRDTtezlvDYDL4OlT//m+d+YI9aC7kgb3dQvML/lAvnjI\nwf5lJ4kEwPjDH/7gBQBCB8IFjAssKWad1EdAMpqIBWAq4a4LrViAjJhvGnrrrbeEZQ8hLFIWglDr\nOM35nTkG7wBzmpUfRx11lAdhne+tbWNlEXbQmte637aF4QCAi1LEuCNMwKpecXWao70DLJ9//vmM\niXVhbgDn0y7tP/TQQ4IiG3VDcwxLdmqRDqxiVhTD4v3Zz34mWMUkcX7ve9/z+zmOMUd9gVtdNb0e\nk7Z1a3xn9nDhBausGuQtbq6XK1X1qZD9J46W/h0IieV6re5yvLmgu8uT6kQ/ScLaaPhAQQPtKurl\nmp7orrHLp3fyVi+T69HGAc3DDz/cT484/fTTPbgRo8JKQKOnQEFaAsxDwaMFOvR8YuT8KVH2LwRk\n3R+3xSpQixOLAWub89cGaRxYE22IA//1r39td2nc5gj9pUuXtvvNdqxdDjDdh/EH+OK9AOzSgC+9\nBLSzZbVrXgDHY+3i7QHkmRceXRubYyBmQOD5oW8ouExRIl+E/AG+v/TSSx7EKc1KAhhhrF/84hdy\noFvSc9ORg6RPJD7b0uqafwcOHtJh8EXyrDfYZXQb+K5hqPtkANyGHaX7ZaJz+wzuF1/tJh93Pahv\nbwfyVb4pAAQXF+UxEQhU6MGlOsVla+NiZcoU1iXFNUiwQqjgjktD4XqntIslEZIWtNB9CMi0CzJQ\nlo8Mbp0uwio0CMuuJgQs/FD3IYllFF4g+zVK8Cqb8I6eY9/zywHAkXgvyiVeHkIWoScm09UIN1C1\nSimbq5rjWJRBvTGALNeNi/GS0EQS4vHHHy/XXnutLzMJ8FJ7mhK2AC/XxwNFXskpp5wiJ5xwgu9K\nzZBKGVbZNj6rfczHtsp5xzZzIG/UlgMGwG35UbLfevfqKTutO0wqK+LjPJ258f4VPWX7dYZKH3cN\nJZLFvva1r8lxxx3X6lolKQvrl0xutHSyu9HEiXWRSAUAMi0oG6mlynEAldaN1vNwO+s0DfYBZGmt\nWQQdyVlYpRACi353NYUuR5JzUATCNYL1+lgzuKI7UnZQ27BtxzlARjKVrQBAvC2MNQXHbK2iOIUK\nHTMF8OpkozBODODzzoRWMDMfUG7xDuFuBmCJ9/JHhjRJmfSZdpiPTIjjM5/5jD9Hr93Tecd2dPJh\nYJ/8y4e+Ti5sNWqwDHAuaKO2HFgjMdvut28lyIFRrgj6lqMGCS9EvohpBbiv1h3UUgwgbJcYJhnQ\nZPYCsAgqsjqxLCEm3yPISNRi2gZAeuCBB/oELmJXSUSGKEJGiUQSXLMhkYAVCkauiYWQlshi1brT\nAB4u6a4EPQA/rHYVt0YwfccNiaISTdBJe192XMc4QHiAsUvIhM/EY/G2EGtNQ1itYbiF57jTTjv5\nsZ50vnpi8IwoCGMxA6oAMErld77zHQ+8F154oZ/2RDY/WfQ6152kLeaVk5GN4nr00Uf7a5KXESUW\nUdnOKdL5lA+EvzYeMdASr6LM/uR7utGTcLLt7n4c2MSB5TZjhkg/Z7V2lrB8AfQtnXabRCwWgZaP\nCwyrDvBAcFAAQJOycIchYMjUxBIEiIgbA7RU+YojBIxWEyJmG7fEG67cUEAiiHIBUepOUxwD4jwS\nYBCkXUHcK7FdjQPDL+Y8x7nPiTUCwFGloyv6ZW2KD5swvvDeYH1iPeaSyY/iFyqJgCiKKUpXpqlK\neELUExN6cDj/17/+tQdelFzGClnYuJuxcMluDl3itEOo55vf/KYPX9x1113tsqj1OU8YMkA+s97w\nDhfv0XbYIh/IPdlmzNBwt30OONB5KRw0Zh+7Bwc2HlElnx47TMha7mha1iB3Li6rLUe1uGoz3Tlg\nC6h+6Utf8lo4CU8ULSAuHCabHHHEEf441sUFtBFcJJEgQH7+85+3uwQavcbQyCSOxkaxMvbYY4/W\n8wC3NHOEW09wH5jyA5DTFueThR1W4wqP7cxn4sAId7XSSbhinec///nP7Zol6QcXe9T13u5A29Fp\nDqAUEe8FAInF4hnh2aQlxjnel3DpQbKRydCHdL5vXHtYvnocc8BRxngfyINgZS8y9bHK8RZhjSuh\nmIXTlLgHkiIZ+7xzmUCfNtYbXCl7TKiWIf3c0qAdFBBVzpW91ejBsoOTEUbJHLBpSMm8KflfVjQ2\nyyvz6mTW0pWyoml1Qpn0NWzgXRzgXqx1BvaXT7mXa2AOMR0EGC43XMyXXXaZtyR1ShEZnsxbjBKJ\nWVjCuhwfMTMyN4khK5HQwjJvENZumESlxwD+CFElgI4ylrkSJfMUILHkw1h0rm3FHU/CGG5zreeN\n9U+p0Wi2N+diieOGRBgbdQ0H8DIwXQcPC/FVxmnoUcl2VUCXojGhkonyGZaOpG1AMYl4vuRFkA/A\nGEYRPNq5kb/61a/68A3jOOwTIR3c0OpdYrwyP5hxhBXO9dPSKreIy2vz62T6kpVS39QsbjZjVmK9\n3+oBfWVr52Ub7BIzjTJzwAA4M3/K4tflDohnLqmX9+vqZbl70Zyh5162lreN5Az3v1tIu8JrxuPd\nVIKqDr5YuFSJzZ599tn+D7cuWZsIKrJ7cZ/FEbEzMqs18QTtngxO3HAQgknjp7jssFKiRLJWmDGd\ndFz0vOh3XH3MqYRQCLBCEIr5IJJpsOKZ5wkBAMT7SPyJFt/AGud+EKjZLJp89K2c2oC3zAnnDw8L\nwFtTU5MTC7BCcVuHFeAA8ajCBFACwFwzSowzrFbyDxjz//d//+cTpwhBkMSIZwlXto4NlDIynbHQ\nmStO7sIVV1zhvUfnn3++L1ubyeKOXl+/1zvlHNmAjFjmZAWyoQWMP3YWMvLBVehy7uZxLg9kvMum\nHhKpdqXt2LY9BwyA2/OkrPc0ueUEsYabP0lqqnBWJVotWdT5IKzaww47TH7729/KV77yFd8kWcYI\nC1zNuF2TAA0Ax4LWaRwcR0bn7373Ox+fVSGGiy9OYBLDC0v7ZQL9TPcagjnCB8APY26Zzs30G9YQ\nApS4s1o1xBvJJj/55JPbnQow46YMLap2B9mOnDiAMojVS2U1FCyUwjSZytGL0IYqjPxG9jrPVUMm\nejwZ+tE4P99vc8UxsGR5JwjdoLgCqqGrGdc2iVr0kSl9tEXiIEoZ12FRCOYnUy8ebw2xYQC7M4Rc\nQD4gJ1AZKtx1yG4OZ0B0pv1yO9cAuNyeeBHcL8lW1IAlvgnAQEzPYMoPwEPGdDiNKNplMjtxNSuY\ncg6JKMccc4wHb4QPcVtczVFCKHG+EtnUmjGq+9JsmdqBa08ToRCMYRGQNG3EHUOxBNpRS+WXv/yl\nVy7iYteABVYwCTZhzC+uXduXnQMkAgJ6uG3xkABWxNtzJcYlyp4Sbe2yyy6t88t1P9ZxGF7gHbjz\nzjt9wQwSDJkO9+Uvf9n3g3HLOxGWV0URxDtEyAJvCQANyEJYz0yRotKVelTYP3ly+jnLHG/UtRww\nAO5a/lrrCRxgviJWMHFVteCIE+sUJYQJ7tdMhACjLi7WBgTwbrvttn56EwkzobAK2wlrP7Mft2BY\nYSs8NttnXOhaQCMfFgaCE4VCs2yx9ilRCW8Q5FFC0GOp6fHR3+17Og6QZ4AygxcCQGNMJHliMrXI\n8yNMoYQFy6pIPKOQUJ7Iyidmi9LFbAGAG0/KQQcd5BVKBX+UVM2XIORBmxBKIPXWyRsA4FVpI5TB\nd9phrn043nFXa2Z/2B/7XBgOGAAXhu92VccBXGNM7SE5hAIDEHFhhAqCEAAGiLMRSS5YC+EqSWj9\nJJ4knR8CJ+0j5DriauRcBDfWCITQBPg7Irw5H1c8ruXQ1cicUzwGX//61zmkDQH+JKFhrUXdm20O\ntC+JHAhDE0w90/nfiSck/BBdEARgxAUc580h1EC5USxero/CyApFJFVFwZrnjyJGNrMmLDJOsNYh\nxhwgD5F1TeY/SgRubMYE2fLhu8GxuWRy+4btny7hQH4Ce13SNWu01DlAgggCD61e5+citABTtHli\naLh5sxFWA1o+FoEKIkAJaxhgilsjGSEVum31/GzXivsdF7Am12DRMEVEs6Xjjs+0j/vGFaqubY6N\nWyNY28BViQC2KUnKkfRbjbljeTIWiJN2FHwBRBQxJbwYWJpR8OW5kt2Oa5lKVSiPlGxlHxarWrfh\n2GT8EkOG8IQQQmG8koyFgsm1Gfu0feSRR3pXN8qnKmQot2TtK7HwiFFxcMAAuDieQ9n2AiuAWC0x\n3ZCIAzM1CTBiGgbAlo0AIjKiyT5VixBLA8uWxCy1UrWd6BQOrGKdvqHHpN3iwiaBDMGLIMS1TmJM\nroTljBAOAZyqWMSAk3iA65sYoFF6DgBYlGck6xylh0S6EKTStyQ+BMGYC8cOShlWrRJgf9NNN/lw\nAnN5cUFTGIO1s6lipceq4oUiqgQAh/OBSbYCePHyAK6Me7wmZ555pgCuvFNRKzqcfgSIxymlej3b\nrj0OGACvPV7blWI4AGDhcgZAyPYNCXcbggzBBgBFATQ8NvxMVuiPfvQjufvuu71FzDUQWrjlEERa\nSAOwixbqwCXeUWI6EMlgmvxFbC8sP5i2XWK9Oq2KcxC0gCzTUeIIIQw4ayw67hjbt4YD5A6gqOHS\nJRMeN7FWVVtzVLpPTAcib0E9OJzFuNVkKPZT9pGViZhGxFhmGt7ll1/emtkMgOpUMs3k1y3toYwB\nqFi07Gc86MpL7GNcUxGLpEbGSFyuAACvIE6bZgXDhcKTAXDhn0HZ9wA3HQCLRULFnpAQNFqJChcf\nQJqNAFxdB5jYKUUMyJBmygZzO0n6wroGIBF+molNu1gqKAQdJUAdy1oFMJYJlnUuhEs9LN7AuUxF\nQaGII4Qw14tWAos7ttz3UexEAZPkNpQ1rbmcK28YK+QvhIoPQMvYQiEiyXCDDTbwKw7hhcHNfOml\nl3rAZ4wCnAqkCsDahxDQ2UcMV93S4fX4jT4Q77399tszJi6GVjBKSFeVVaVPRuk4YACcjk9lcRRz\n/BbWN8hMN+n+vdoV/o/P7NN5wV3FCIQRruY//vGPcuWVV7a5DCB5gFuzFCuFOZKPu7nE2YgkEwSh\nEjE33H4sAIF7j2xVklu4LtZAmKyl7kk9tyNbXOBYKhACk/KatJuGcIlyTujSJA5MwQaEfhwBwMSB\nuUej9hyAl2TLsz40ShJV2QDLjhKWKAoh8VclxhKJg1ijNa5wB+tfs8UqxeIGbFGWILwkYaIdz49k\nWaYAAEAASURBVDwknjMgrcTxCqBaGY7feBe4DtXhom3oubrlndCiHexjXn0utNpV31hU3+iLcnj5\nsHi5L86xYEWDNLp5wUa5c8CyoHPnWUmdQVWbOctXydRFy2WBA1qHwdLk/mluKXXji7JThIOasCMr\n+8qGbl3hdar6+Qo4XcEIqvuQ7Yvb7uCDD253CS1wgNVC8lYYK2t3sNtBe2SGQoAUwAj99Kc/9bE3\n/Q333I9//OM2brq0Wdi+wYR/cCVTaERdirjU1epJOMXvBigQ6Jqtyvmcd/3113uPQNy5WPcoKZxn\ntIYDWKNkDPMs8LbEJUetOTrdJ7wnYYwfgMSyxuolvkomPOteT5482T97LNjQ4sRDE7qEcTOTNwAx\ntgFgxrZawljQKInqncHLwrx5kg65JgoFoZVoXkP0bvCsANpKJJ5lin0z7uY5gH3Xge3c5Q2y2n2n\nCAfyQQtx9O7VQ3o5ATHUVcDacJgbf4Mq87KYg/axlLe9pjgq5Ru0e0vmwDwHvE++v0jeceC70Gm2\njavdy+VerE+w15/IZ/bx25JVTTLb1Y3+wFnFg/r2zqkWdHIv2v5CFirxKhJKSIyJghUgCsgQD0YA\ncWym+B3Zo1ppiIQuBBnHE/dDQBI/1VKWWKlkMCOQmFdLjBArhHM6Sghm7gmLGysMNzFxw9ASiWub\nY1AONJ6H5YT7lIxdvAFxRJyQ6xDXVEsr7rhy2gcYUuwCjwJjAeDDo9IZQtHRamwAGsv/obwRRgF4\nb7zxRvne977nrV+uwzgNi7/gmYkWbcG9rMU7GHMkY2lCFm0AxLjMyZXgM/eDgkptdJK6GNMAMOMl\nmnnN+UqMR8Y17wJEO0lz4LF2n/pgkby5cJkDYeTDR+3lg2sDMEY+LG1oltnLVnkLudJVz2PBFhuH\nns2J/xgAJ7KmdH/A6n1pbp38b+4SD6pq7aa542Z3LqXoZi9d5bXc4W4N0Xy/ZGj6CAjWOiX2qSCk\n/SNGipWHBcJUJYAttCb0OLaAElq8Wh8AIICofcYi/v73v+8FIhYIwgmBzdJuXAe3HvG5bO698JrR\nzwhUKm4BBrihscQQpKGLPHoO33E1hkCN8KSACXFt7X94HvdKbI9tZ0EmbLe7fkYZIQseaxJ3c0eL\na4T3D5AyxY1neeutt/p65BTeoESqVngLPRCMJxLx1AMCUBJ3Dt3LtM/zVOVMgZdxpxYw56NA8Bt5\nBWRQM13v//2//+e7h9WMOxxLOqq0hv3nM+3CGwjvQJwS+8aCpfLfDxfLopVNrd4wf0KWf7CQV7pF\nHGY75Z4+j3BeM+pFG8VzwFzQ8Xwp6b1Pzlzo47xYtp0h53ly7uj+svuEkV3ykh177LE++YQkkygI\n02+Al3nCCBFctToHOO6eOE61fqxeKgXFEYlO3/jGN1qnaQBmZGf/4he/iO1DXBuZ9mE9aQYqsUgs\npjiwRNBy3ygIHAcR30UIY6kn9Z8pJvxp/DlTX0r1N3iHCx+QgXcodHgFOkvwFcWMpD4S67jOoYce\nKjgRsU6jxO+EH8KEOjwvAF4ckYQIsCthFYcxfebMM1aYsgeQMxdYxwbn4BUiREN1OE3Y0rai27B4\nDO9WuIDJ87Nr5W3nFetsXJewFUsaHjBxjHdRR/tg390KbsaE8uEAGum/nUtp+pJ670rq7J07r5N8\nuMyV0nOWtGr4nW0zPP+6667zbjxivXHJRwgfMqQRrmj/JLuoxRC2w2diXWo1kqyUNKWJZCesZQAb\nCxhXMP3AwsZl3VkiA5usa/qCAoHbkgpKUcJCwlIJhTdClWINSdnQtIFygaKBUlKOxPMi3gr4ahnI\nfIAvViyKGO5ewJd56ihIrMUbB77wHkUrfH5Y4XHgy7uDYhYmdHE+4MsYUGJcUrSD/YRowqlqHIO3\nhHGTJhtey79yHu3oGORdfm3+0k6DL+2i39c6C/pfTuEngcuoPQcMgNvzpGT3kLk4w4EvbqJ8Ee/V\nWwuXy1SXpNEVhLWHJQHwJBEuPeZeAr6AsLqbw+OxHEKrEEshDtT1HIpqYPH8/Oc/9zFghB7uPhJj\nEIKdIWLKoZWCIKcQf5TipiOhIFBoIYkQwOU6JQkgIcEIK5I4PlZdZ0IH8Bh3M6t2McbIFeC5sfoW\n2fok1CURfdCYLsfQjxD09DzGIG5y4vua5cxvmlwYekcYi4xbluHEMxNmQ3MOCinKRrgKE/vjCGAP\nXeUoCx8urffvcv6kg/hELZT0V926wkbtOWAA3J4nJbmHNT1fnlcnDS6RIt9Em6/MWyorGuOnyHTm\neggirFGEGa7hJCKeOtllnGJZ4prDoogSiS+aVQyoc1wm4tosA3jttdfKZZdd5t2/ADHuaKzRE044\nIdPpGX+jbYp2aH9I1EHAhxQHwFj8xI/Dgv/hOXwGgFEesLDLhQAdXLgkrjH3lmQrBbGO8ACLlwpk\nTBVCCSThicx8njnjLFOcFVAFKJVQiiiLyjYkEqBwUZMXEG1TXct6DsmBvAcU29DpUzzjKJG5jwKa\nZsobCoF6hZYsXSbPzFzg47fRNjv7nVAXiZ61Kxs721TJnd92RJTc7dkNKQfedEkVy1yWYlcRC3WT\nuNEVRIwKtx9Vqi644ILESwBYJKZgHaDRh0u96UlM11ChhnsQyyMTkVGKMCdTlEIK/CHkELIIZATl\nEUcckamJjL8Rt9b6w1hwCFp1o2Ol4EoOLXWNARKHTCKAB2CPWkhJx3fn/bhvsVIV8AA6PB0KLLne\nG+5rFCOsW5LyqF71+9//Xo4++mifAwC46/NKahtvBuCqhIs6aokDnihcjFniwjxXXObabxRECIWP\nMpeUsfzhD3/o29GEQ8YvLveQ8K7QVhormLHNWIYaBgyV5U35V861byRuoqQbteWAAXBbfhTVN+Yu\n8pLgolTixcXa0zgg1W+IKbKm7Ve/+tU2MSc9h2SKGW7qUD5dS9p2uJ1Zt1IaXAZkVxAAyD1TpAP3\nXxIBiLgJEVJkBAPaoSUIOFGAQwnhrXOBdV90S1u4uCGSoJh3iVVEVi2CkipEgDpWUnitaDtJ30mu\nAeQhBC5udOLUCGMEdxhH5BgsM33+fI+jcnBDo6gw95YpQYAOQBa6VeP4krQP65K4Lu8SLmEKW8Bj\neK3giXuXZ5WJeD+JPysR8wW0Q8LbAahiyaIwqLWrz5tjVQlDBuB9IewB8GPdkoDFHxRVsmgDUCVT\nOg15a9qd01A1Qj6OWOjR85fVLu5Urse8FaucEdC2UEy+ZFy0r93luwFwET8pMmApzchUHF5stF1i\ngMRD2WK9kYyBoGB+KGBNYfcozXVTAlY1Z9duv73vzvLmc//2p8+dOU1+e+YJ8sND95ILjzxIpr+2\nZo3TaPv6fZUDXybrdxURh8MaYXoSBTYyEYCGUgLPqCAVJqwgpNWKwILK5ormOig9oSAFaFlxhna5\nFu0wH5TpINSXzjUJiv6Q3cr5EJYYbvQ4NzQWGha+zkX1J0T+4TyUgmhiT+SwbvuV6T1YkChZWH3E\ne+My5bPdIGOD58czg9+EFwBQlCmuoQSQkk2tFqruD7coTy+++GLrLoA1PIcxQ/Yx83XxxMRZ0gr2\njCcSBcmw5h0HqCHNkkYRhJALUWJ8k4iX5tkD5MPXmyAf9WwZd9G2mhob5O4rfyGnfW5LufBrB8o5\n++0ivzv3VKlbuOa6aWUFYbBZro5ASPmScWGb3emzAXCRPy0AGMF/2mmn+fmqvOSUuoMABSw4rWSD\nqzLOAqPSVa5TCv445VzZfs/95KK7HpYvnvptueKck7NyilgPCRddSQhGFlo46qijstaFZu6tTk1C\nWIeARTUktTxwF6Ypy4drUwUf90iBDyxVXN3E3EjcgrCmcCcyVShqvfoDEv7BOseFDnhCCrLRNgAa\npi9lckNzPhZbmoxYju1OBDBp7LSmpsZnuBN2SEuAG7FUPCEUNSGmztKYPE/mWPM9DE2g2IbjJek6\nxOVDbwrxY7VUGR/EqAF1lAVVAKNtadYzih3KNP0jCUwJYEUG6PkoINxPSLTBGEnjhua8ASPHyMe9\n4gH4tksulOmvvyLnXH2rXPLA0/Kze5+Q8ZtsLj899stSO3+ev2xaWUEvP3SFOqKUDxkXbbO7fDcA\nLvInhRVz8803+xjo9a4MIdMeNLkEbRztH0FNrWNc1ay0EqXFHUh++Oav/iA77ttSCvIjB+wfrU4X\nP6511bK6mk455RQPwBQ/yAYwxEIBNXiGsqLufPiK9q2EVaLzhHVf3BbLRa0UfqdNpnDgAgV4UYIQ\nmjwbgBlBiBWk0zzi2ozumzx5cmuRDgQxgjQU7ByPByQbACOkEfjRc6PX6y7fARoUJaxIXP+EAFhm\nkmeZhlBOKZaBG5n5uyheJNiR4MeYAsQB9zAjnX1YyPrOJV0Hl284tQ1FTStMoaShAALGKIQKynFt\nMbbwnuACR0E47LDD2h2GG5rpZtw3ruo4Sxc3NP3RWHK7RoIddU0OGt14jdLC2R/IU/fcKcddcIkH\nXX6vcMmH+x1zslSPq5Hn//GAPyUXWVEXcUHTQD5knO9IN/wn3cjthjdWSl0GZAESLLZQ+Os98sIS\ny0HQxrlm07iftS3dDhwy1IPIrZdcINdf9F352ncu1J8ybnFDrw26+OKLvYXJHOFswAnfcO/CR4CQ\nubcIYwAqjBni9k1DxApDiwtQV3cl19KpUwhPhAtuSWKyJONoWcxs1yHmrAoCwEOfQ0FLGIJYJdZa\nEnFt5oZmU1KSzi+m/Vh98BlFCd4Tq1WAy9ZPzgVoyfplwXr4AhAD5hR70aIVAKUmc9Em4QDAF29G\nJuK9C1fpoj2UA4jnTZyaDHxCKBpiSGoPRQ4PF14QrHGI9zs8DwBmnAHCUJwbmixt7jvuN39S8A+u\n4Tia/d5UGVo9SgaPqG73c80mW8iMN17x+3ORFVThi6POyri4NrvDPgPgbvCUWMEH4Y22f8YZZ7Tr\nMZoyc1TJysWdE3VJdXQSPPGfQUOHy7BRY+TZh+6T5qbs0wimz5jpgfG8887zy/2162wed1AKEBCl\nAH0aTR+hjRBGoJFtTNk+YmsqgBGkYQwvU1cBfoSg0uNu/qkmzug+EuQAeqZPIUDxVCCICSlgOWcj\nQJtpRwAGzxS3Kwk8EMAKOKRJxiJRJy40ke36xfI7z4l75z5QRHHhxhW0iPaX54lrGX7zDAA1XM9U\nySJzPXx+KFAAvI4jPBgApoYDom2H3xkzgJ0S4IvFzH5yM2gnbg6wHh9uv/Wtb/mwBTWetS+EIML7\n1TiwuqGjiVi0h5LC71E3NB4axiHeE2QGCskrCWORpKsq9/7H0ZCR1bJkQYsLmt/Ty4r2ljbnd1bG\n0UZ3JAPgIn9qTIVgCgLZv1dddZUXuCSOQMxVZFqMEklHaPFhwhG/sVJJR6h3n75ywDdOk+/+8S55\n6/lnZOqLz2dtpqlhlXe9UjQAxQBBBsCh4eKKxdWnq75kbSzFAVj8CGhcimmIYgdUxUK40Q/qSQNk\nStT6DS1N3R/dIrwBR+4PUis1DuhQjBDQhAfgBfFF4oO4CcmGzURYRFjcagHhHsWigtJkQ1M/GhBJ\nYwll6kehfsNjAfji5WCBDOLq8CQT4VommYocCXIn4DPvjM7t1WembaCQ8RzC6V6MXQU4PS5ui4Ub\n8pZrAZYk9gGUuJzDet5xbeg+phmhyLFmMPeoU4xQJEJFgPeb8av5CHyPKn/cE0oFISsWhuD9wPWO\nNY8yT2Inld3wBNQ6izqOxk7cWBbPmx33k9s/R8ZN2rT1t/Syor0FnA8Z19qRbvbBALiIHxjAgosM\ndyvCB+uJ2BDl8Hi5SLLB0iT+xAt5+eWX++kyWAkh9avI7TEDonf86ideq6WdXs56G+UyJee9Pz1s\nNvYzWrMS/UBg4g5DILCEG1WESCBCCAJiCBYUB8r83XnnnTlbalgavMC0TYH6NETSmmYccx7JWQhr\nJQBOrQ/dF7fl2lhjSoCvLhen+8ItghVBSXINFgrPDfBHQGc6jyQgFBgt/oDAR/EgBk5sMZvCgCWd\nyVUd9rFYPqPQkJWMVQpfUVgAxdBqjfYVS5FViXBNM20HoCEur3N7o8fzHcUI8GV8KnEeQJqNAPow\nXoyyQ0gDEGVsAL6aVJWtLVzkvBtMm1PXOjygHUi9NHxmbAK6jAs+w6ff/OY3fmUk8g+w+PkNzxCK\nCEtvYvmjXOJFY7lPlEEyv+FnaMnSvtK6G24k9U4GvfPCs7rLb1c7K/q5R/4mEzbbUnKVFdGFGfIl\n49p0sBt9yU0yd6MbK4WuEgMCdE888cTW28EFjUDFRcUWYU72LZYdySS4ZaM0zK1YlAv17ttPZrz5\nqk/A4DyyIKe//rJM3HpN0lJSe7Pefbv1J4AB4YeQQ7AgLMgGZR4vGjnTMFSA0G+yPbH0cLkiQPj9\nkEMO8VZ+NBO49SLuA7Ew5s7iVsPyTkMINpKzSJIiWQVQU8uK/hJfTUMoEGTIKmG1PO4EcCbC0sGq\n+dWvfuUtElyIWNOAbJJLmesgmPEiQJyPe3Py5Mk+5pzpeihC8DkTDzOdv7Z/wxKF/7hKeU54LHgP\nkgivD9Yc/IG3xM5JgEMx08z0uHPhCfNQNX7PMTU1Na2VpuLO0X2AI/Hi0OOBgoTCgLLMmAhBU8+L\n2zJ2mWrENDZyOcI8Dx2TeAIIWxA6YSoeQIsCjhcEJRx5gIKHpc9zhmfHH3+8B1piynh6uM/rXSIn\n9005S8Yp79mMN171+6J9I+Hq6PN/Jteef7bMfLMlZLJy+TK5bso5Uj12vGy3x36Sq6wY7JYxDSlf\nMi5sszt9ttWQutPTSugrwgBNMnxxw0Pfr3NTINy6v9mmIjEP+LgLL5VNtt9Zpr32ktx+6UWCRdvf\nTWvY+8hvyI77HBQ22+7zR81NcuV5p8kL/4yfo4vliQBgHmscIYCoc0yWK7Er7ikUcJyDlUE7xNTQ\n4IlhqWWIq5JscIQLRUnSEoINKxjgRzgpYZ2mcUNyPLHZ0BpCOdIkKm0vaYv1gwDmfiGeI8U+qMKk\nRCIVygtKCe7Yxx57zPeVZ4+So1PT9PjolvMRzFh3udDyxmYhSUfHToULZwzo3cuvBR115ebSbtKx\nWJWAGLxA6YCHSUlQgBKgQ2gG3pAZztKSqqQkXYP9CqB4IZTwRHC9NPdFMlg4dY1nRt+5NsCYlnCL\noyQwp5wpdlipeGBIuqNveC5wc9N2lBj3KCZcGw8ObmW8SeGYRTlhfKCkovChpOJ94d3hfQGUz/zB\nFNnhsGNdGco1Yz+81j9uu16e+POtUrdogd+NfACY+w9sWSgirawgWLPjukNlk5GDwuZTfc4m41I1\nUoQHGQAX4UPJd5cQnve9M8cvmJ1r2/XLlkplVboXpqpPhayz7EPZc/fdvEBMuhYWGe62uCkWcefg\nIqTaFIIJYYT7LYzXcQ6WEu0itBFcABju+7SEMEfwh4R7DmUBYE5DzAOdMWNG66GAZbbKSa0Huw+4\nCbFa1KXMdBXW/yWOiQBG4OsCACgmWHgAD8IJ8GCKVBJxPNYeAIEAzkRMW5vuFu74wBVNYG73aqeU\nsICH+9/nEwDCvVwIgaUo1x86QEZW5mdNaLwQKF94IACXJJczIIWnA8WFYxlHxDlz4TXKkia0wQvG\nDlajxtoz8QfQwnqE7xDjA8UQqzdJCQ7bY+yi8KFE4SoHNHk+WPw8z5BQBnRKE8dhseIeB3gBXNrC\nKqYvccVI8ASg3PHsGU9409iSgMX45j053tW3vvftOZJtCuHyuiVeFiS9D9lkBYrbvhuOkqqIFRze\nb7l9NgAukyf+P7fG56tumbEWkdE1N735yCrZft1hHiAR9IClEgCBgA0tTOJjxKgAnY4QVggJamjy\nuN+ZnhFNRkGgqvsWAYmbe/LkybGXIw5IzDC0unELkz2dlhB4FEdQIiNWY3q6L9uW+C5xOm0H4X7+\n+ed7S4n2QgDFVavzTxGsWFNJcVKEPr/hZo0j5mi+OGeJzF/RINTuTUP9XX4BIY5txwyV4Q6IO0qh\nBwGgoYhKlDgGheTGG2/0P8Ejsv5RdHIhxmU4bQi+UcYy5GtSe4xf4u6h25owBt4SjdfquYwnxiih\nApQn/vjMWEVxCIlzuWc8FNw/52JJc286HnmnwmlSPGveISxcLF3CUJptjYJAPJzxDGiTLwDvyDYm\nMQtQR+HTdaWpFf/c7CV5XSktvD8+rz9kgOxa0zJ1KvpbuX43AC6TJ48b8cF353bICk7DIqxftNsB\nbqtEjBXtXAmrBtcXmZehBUuci+SyuCIiem4uW4ALdyTCCgAFmImZqsVCW2jxCC/6hGBjXi3xNACK\nhR9Clx+/p0nK0T4i9MK5yQg5nbOpx6TZIlhRGHQeL8oEFgzJdiGhxJB4g7XEfZE1jdCNEkIdKx03\na9SKmepWq2G1LBbV6Ahh3WwzZohs4CziNC5cvQbgQiIcXgtiplj4oQuV4wCtn/zkJ8K0Lo7Bs0Hc\nk1hrroRLF2tQCeDLVhxDj2UbZzkzZxvrVUFWgRZvSKhwcj5gT5yXEAtjj6puAC7PL7S+qZql0424\nZwCbKXO4rJVUuVPlhexrxh3vEt4ixj45I8ccc4x/D0nUov9Mi8IVHc6Bx0v2wNS5Wa1gvXauW8bH\nnutXy9Ac81FyvU53O94AuLs9sU709123Zu+zH9bmfUnCPr16yvbrDJFJw1tiQmEXcRVSu1nBDyuD\nhCysvF/+8pdtLFZ+Q7BmWvEobDvbZ0AYawcXNlYkAIT2f//993sLCGGMyy8UkoAHMUesGgQUblBc\ne4Bz1MLJdH0Uj9DKIfM7DhQztaG/Ya0RH0SgQwhqvAZMTYNwnSNksXCUz0lKA/FuAC4Euf/OWizT\nlqxIVS/cXzDhH9zSE4ZUymfWG54KhHke9J3YNMoQHgoASol5tLhKAQueCcoHLlvi6x0hAA2lRp83\nyhbKEe7nNES2MZn6KAv84XkggS4uwxwwVGuWrX4GdElAxIIm+SppTIXhDPpHWAKgJplKlUMUEMYn\n/OPZ33HHHX6KG94mkpuY8gc/cXXzLnAceQVMXeR9iBLrAT/5/uK8L0lIyGKL6kGy1egh0UuW/XcD\n4DIaAgjn/8yqlakOiInp5YN6ucyKCc61lEno4g5jhSKd1wjIqTuMKRJkcmOhKqHxE/cEoDtDCFpc\niwg5hFAmIgEMQY+FgXDNlACGMMX9FyaARdvGsgOEVdhzz/AgSeBGz4/7DniS/YoQhrBiKSiBSxZl\nQZdHVF5itQPEIQFCnI/ghl5zYYnnXHgiX4SwnTRsoOzgkm245yTCK4ElSsgAQKWfagFivQG8ZPQS\nPjj11FN9HLMjXgS9PpYhVmUYogDwAauQeEewTqNuY75rbD48HjexgmsItKGCEx7PvdAP/ri3JGKu\nOAVDINzFAD3XQmnQ4hqAKM8TXmHZwp/TTz/dZ0QrwOItIQbMOERJI4M66v0I+/DS3CV+TBD7zwe5\n4SDVA/rKXuuP6nA9gnz0o1jbMAAu1ifTRf2iFNwTMxfKB3UrOw3CfRz6jnWJOLvWjMzaW+K/CFmN\nV3ICU4x02g2CAus3TEJB2CA0AJaOEoIXQYubkESuXAg3OdnFFFUglodrG+sjdJ/THqCKlUIMj3gx\nc5pZuAELj2xWJQAGt3xnCNDCtYhFrnFMgK6mpsYrBddcc413P8JvCKsb6zsk4sbEClf06O3HQlL2\na3hOLp/7Oo8IALyhA+I4wisBuAB29IM/7gElibglyWXqPgVQMgFVXPvRfSh+5AmEY4uELZQkdRsr\n4OJKVgtT2wGwAGoAEEUHxQa3NdXQcukbbnSSD/HIYAlnIs1e5hiuTZIg1iwxYZRE4tBY4+zHfY0i\nxhxfkrNQrrhnPAZkV8NL6smjfOB+zuZBePbDxfK2C0k0dxKE8YiMqXIZ1xOqMypjmfhQ6r8ZAJf6\nE465PwTfi3PrvCWcVAc25rQ2uyorejkBO0C2dnG/6OT6NgdGvmA5htYowIGrEZcvhKDASgiTXBCA\nTC8iBtgRIoZKkgzZsmnnCet1UBjIzFVC4E52SVwIbuYuIwhJqsESCa0rjgdwca3ijiTuR5Yt8Vfm\n/HaUcIPCK6wirklBkTCmCSjcc889XtHBKoJQZABhnVPKPdUtWy5Te1TJ4pVtk4E62q/oeYPICZg4\nSip7r8kJwArDtUoWM7xBIQMMcMUCvCSwqfv05JNP7rDLPuwLChhhB54XliN/KFL0Ifq8UKQAOFy9\noTXL+4LXQAlAw3WdycLXY3VL3gOFYlAEUM6yEV4MwjQQ19MEQ/qN9wiARhkgqQpXMxYyihWWL+2j\noDEuUDyZ2sc0Jdz99JkxmI1ed56R111iVtpkvGh7FP8ZP7jSK2IV7v01iueAAXA8X8pi7zy3TOH/\nXNYr2a9pF2zo56ybQX0rZNt1hsroge3jSGkYR0YviSJKxPewerBUlXAJY/0CMkoIDyxIsjdzdeXi\nvgWcmK6StmKWXheLBQGnBHjQVlwfsEgQtlS2Qugj7JMSwBCgJNaQAIY3AKDMRrRPLE+zXTkekIEv\nCHclLHEyxLGSARAIwQvgYcH//YXXZVHfIc4Lomfkd+s8j7Kpy4rfwWXFQ/AAQMCNiyVHX0hWw32K\nRYdVCZhQs1ndp/7ElP+gsKk1yxaLlj+sbb1/bYrrw78o0EYToTiPNsLpSjx7ktyS5ibrNcItY5sY\nPot0oLylJRQTVRLIW2Dcwz/AFIUUpRKvC9Y8+QYcT3+Z74sHhAQ+it5oX1G8SEwkFEKYJxstqm90\n8qHWKWmNiXOEo22QD0JC5lajB8u4Qf1zUlKibZXDdwPgcnjKGe4RlzTrBZMFu6C+wcWKXHk+94+6\nn3q5IE4fp8GixI6s7OvdiutU9cvJ6o27PMICoaSJSoArWZrEfkNCeFFUQ12q+huWNJZeLolNgCLu\nYVzaXDstYbnR36jrGYtW12LO1haZvriHEYAkUzGXGTehxog5H0sfKxUrEHcigpJ7D+8RtzbKBK7E\nKJFgQ2wRa01BB4AncUmtX4T3ZptvIXe9OlPqPwYmO05c42PHm54JigOC+IBJo6V+aZ23zgBhrDlA\nkfKqWOiAHkl69D1OoYn2jnGgQAvY6OcwtKHnaJY74I6yg2VIMlKN87pks14Zlzwrrhc+I9y7uWRf\nowCRxIfr+fDDD9eupdoSvkCJYpyTk4AXhWdJWU5VCAl94A6H4CMZ8bjWUXApShIS+0mABLDhQRri\nGc9z09JI4Jy7vMGHrZpcxjTyAd2tooer9e5CUciJof2cB8F5xcYOqhRyAYyyc8AAODuPyuaIZidM\nl6xq8m4nBWBeJKYQDOnX271U+XUlkewEQITgSiwLCzJKWE8UHuCckCg+QbIObt40REyMWDOxZyyI\ntIQli4tUCQGOcMKSYv5lGtIELz2W83B5Yu0jZHF1c39YtAhLJa5Fhjhgj9WG1UOWK2AaEu2wmg4u\ncYQ9SWUKHghcBDJt9B1WLbVD1pVVMebvr795jGz2aRffPOKY1qZZeP3svXeUq//zli89yA+0e9V5\np7p1YreQ/Y89pfXY8ANjZ6N+ToC//Yq35ABL+I9FiYsXbwQKRtTyh6+4ihVcQ6DFFRslrPqoNYul\nGh5L6ACvAPuzEfzHXcs9hnFjFKPQS5OtHe6BMcaz4i8t0W+UUSxZgBfAxCWPEsEfigW8gVDaCGnw\n3KkIhrU7ZcoUn4gVdz0UQdokOTFXYlW1FvnQ7Au0uBfAy4TKPk4+9O3tgDi/8iHX/nXH47OPxu54\nV9bnDnEAgB3hrNy1NVUeYYLlggZP5itEXBWgAoxCyw+XJQIN6w/rlSxRCPcwVhUWI0CcLbnlqKOO\n8hYiLjysxSiI+UZj/gG4sKToAwRoIMyJyQLOaQQaygYJPppNS8IP7lCsMv6ihEuZRBt4g9XMdBeu\nT2xQ5wJjNaJ8AOQIe44hwYnzIObMkiXN+UxdAkR+9Ls/St+BbiqPA/aOELWDb3PrRH/43jsegJPa\nQIl7e84CecZ5D1AOeNbMXaVvxCgBWoqDACYhyMIXQDAkgAYlAoUrjM/yOZoIhQcAoFHC+ue8NOCL\nZcnYI4s5VAzhM31PS3g4iM+jNKYFX66NBYu1zP3zXtAG90gxF+6L8AN8UCJEg4WNwoCFzLxf3iu8\nNXH3yxgmqZBxyNjLhbByKbYyXPrkcpodm4EDZgFnYI79tPY4oMXk9YqAL3M2SSKJI9yYlIlEWIeE\nVUm8DNdmJiLWCMAB4GmtZ9oL43IIM1yVxGUR0FgiUWsurg+4wkPLCkGbdi4q7SFAcU0CXJkSwAAm\nhDXATB+xsunvab+4WrbZfe+4rkkaC/iWi38kk7bZwS1R6Xjn1opOsoC5wAdvvy4/Onx/7zbFpQ4Y\nqmVLZrnGOLUzxCa1IhTAo5YtngZ1o+uxcVtADDAC3CHaQznCasxG8JK+YXHSDoqVksbP9XumLaEF\nViJiWhBzc1EeMhFKFdn2hEY4l5wAFpXg2fGsIVX+8IbAR1zJ9JdpfFjMnIOihbJGG0n9hS8UmqG9\ntJ6bTH233zrHAQPgzvHPzs4jB0gywXWqsVYEF/MWjzvuuMSrACxYCaHFw8FYtmR/JgE4x3CeupbT\nxB85BwvkcTevWQm3JtYOljnCEWGfBkyx1vU+aQvwTgMwHIuA5X6j7lB4gbWFtYlSwb1xrIIR59LH\n79/4V1l/80/xtR0BwA0uzjx+481af1tVv0L+dfftbVzQ/HjTT3+YFYBX1tXKXRec5S133OvEgSFc\npQBA1JrFko+z3PxJWf7hOQBY6r5n/BCnx0OSiXgOZOKTWUxsnYQunYPLeVrwIlMb+hu8xq3OvQJ0\nmRLKsP6JheOWpw94ZVjVSbOkeXYALQSY4znh3hhjWMqANgoVXh2SrXi2xK0BdCzmJIsdJQNvBFXp\njArLAQPgwvLfrh7hAEIJ7T3MfiYb+rrrrosc2fYrwAigqitbf8UlzTQUrXmr+9ki9LAOASud8hH+\nnvQZ4awucCwsLBKENhY1AljjtEnnsx/LD+Gq4AhYYNGnsaA5Hzcp19EMV/ZB8AH3KQlOgBnWEe5n\n+ktMk/4uG7upfNQnflH7FgCul3EbbdrSoPu3wQHwk3+9o0MA3LOpQYbMbolXaoN4N3Dps3ABlinf\n09Rh1vPjtngU4D+gpQSYMnc3E3EeFjOEQgOPULAUxFGKyHqGb2kIBQgvCd6bJM8KAIjlSrgF0CQx\nkHg4LuQoMS5RWuAPfMItTvsk9AHuuJxxQTP2IYCVsUG/k6a74d4mAx0gT+pjtB/2vWs4YADcNXy1\nVjvBAcCJmB1WiRLaPOCayaLgWLKEqRZF9nRIgBIuOlyDIQGcCGosJayItBS6kZmTS38R2mSu0n+u\nB7hnIhWEegxCPmmpRj1Gt7gfieEpwBD75Q8rEEsOix7hHkfzh42Xiqr48otpXNDaZhoLuHF5nYxe\nNF1PSdzSXwVjtvqXxisAv4nnh3FjrMhsYQg8BMyd5VkxvlB+aEdj9HQ2l0z3yy67zM/RZZzWBHFa\nvWm8FhTjwNPDsz766KN95nLcsXpOuLgHYMksATKrsXCpna4Z2cwKgGfwAoCGdJ+2FW5RVghRkDth\nVDgOZA5OFK5fduUy5gDCGFfaSSed1MoFhBfZriQ9ZSIENto91i1ArCCE5YClijsSAaiEFQZo4i5k\nfnJaQjArES/E/YsAxxLBuuN6WC9qSemx4RaLJrTMcSfSjySiLRJxyAjHU4ClQ1yXP/bheiTDFWtJ\n71vb4jtWNgA9e+YM3d3l24WON2S1q6WfdEGAA2ud+8OdD4jxXHDVU+yE8YDSAZ8BWm0PnhDHD8EX\nyz8b+MI/rkG8mQUgcHsTkw7BlzZ4lmmIMcXCCpQfjQIqFjYxWqYwcT9U98IjQdZy9NjotXR5Q7wY\nuLYBX/pL3xV8OUc9Rrw7GgJhXCaRJkBi8RsVjgOWBV043tuVs3CAbFAACksBQQt4kCCDQM+2ljBg\nSOEDiLgymbcIGwQVxfARbFgstI01wbQkABuhRoJWNsL6JH6JOxECDAF4BDngjKJAghgCFxdhNFNX\n2ye2h/WlMWyyU7HCUDaw0ABU3KppBSVAy70DYlyXPgJaAA5/CP+b//mMNGoHunhL0RZ4D4BgsXFf\ngASu3xBIk7qBIsVz5y8klAkUGIBb48r8jkcA13wSMY6oxoW3AK8F1i+E6z5U7mgb3qUh4s6ESbhP\nrbHNeViZVPjCW8J4Y54uLuq0oE4bWLVYwYxVxgFAzrXwujAGtWwmygvjGOI3FAmUQJSROAKAGSOA\nNM/EqDAcMAu4MHwv2qsyyZ65fgtdUQ7++My+QhELHiAw1RJAgAKoAElaooQl5zENRxN8cD0jyBBi\nv/71r71VQcIXsTh14WVrn5hd2C+sEiWydknQwlJ73MUUydqOEuAKgFNeENBUQkkghosAxaUeB74A\nEH9YOyQzUZmL6VkIaKpiAfxYjIADW6xEeHbFFVdIn8Z66bG6Y8sOah9TbZ3CU92vwrvVcfUCQNwv\nigWKB+Ux+SPmD9gBCigqIS+SrgNPeIYh+HIsZUfxgGB1MrUJ3gJGADm8hB+AOcqJgi9jg6lvalWj\nxDBlLE0/ULLgO/N2NbyB5U58lWvQ7pQpU7xlT9w3F/DlHn/729/68qn0Dfc1yiH9Q2EIk8vUAoYH\nel+AMvcWRyhBADVek1yIWgFUzkM2ULin1lXJYilDo45xwGLAHeNbSZ21vLFZZi6pl5l19a4IR7MT\nRK7QAv84os6z+98V46iQ9Vxt1/GD+0uVm3S/tgmLCdebWpxcHwsGa1FBNW2fqCaEwMTlq4TblkIV\nAAPLIZIglZRFquewxSrB1azCO1opCQuN3xGm9BPQ5Lp6fNhW3GdAgL5hCSEwSSpDeEIUtMDlHp37\njMKCi5ProAhQ/5qEH9zjJ5xwgnuovaRuzCT5qHfHSonG9TNuX8/mRqma6xafX7HMJwthbaGw0B+m\nwQCKbHEDY3EqwRvAEgWFPyxl/Rw+Mz0+ly28w0oG6DXOjOsZ74ASCg18y0ZY0cT5UexQ3Mg+x+LF\nGwIIYu1Sp5nr5EoALMlZKFKMSdonV4FxhEJB7BYgVs8J7eOBYazAP8YvY4/EMuZ+xxHKCgoCioOO\nqbjjqBf/vpMNyAjWi6b9lhouH38iH3pI/4qevvTkeLcc5RBXEcsoHQcMgNPxqSSPWuFeplfcIuyz\nlq0SPrdAbvKtktIzwFW9WWdgf/mUq/U60JUaXNvElAuSqZSwAhAi6n7T/Wm2lOujFnGYOUtyDCCK\ncMX1h1WWjXCvAnpKgAmWGQCTlgBnEsyi52USoCRbYSXjcsXSoQ8IVQQzCzZMnjxZalwykAI1rnsU\nAKh+8GhpGDI66zNP2/+444ZKg/SY2eKiR3ECRBDe9IElKKlVDPDBf/gMEKtHIa499nEsygWg2RWE\nQgO40Y9MCWAoBFi4WMpM52EckR3PfaDgoehkOj9T37GqqQ2OS5xrAOIAK38oD3hTGO/EqMNkwzDr\nm3eCqVBMx0uaiseYAaiTSlOual7tliaskxlLVnrF3NVVyUpUzWP5QRZpGVwART1rB4vsAAPgInsg\na6s7M5askBfcQgxLG7IDb1yfiO1t4xbYnjA0t2o6cW3lug9XMaX5sAYgQPOuu+7y7tdc2+J4XNBY\nv1jZSoAYVhIuutA6Q2gh2LDm1AWa5ObTtuK2CFKEqLoLw2N06onuA0jjYshYgyRfcf/0BxBnOTqs\nN1yvgC+ABzGNS6ecsG/8hpNkWs/BstQpXl1BCOLdxg+XF//9pLdmuQYKAHFSJWLx1157rc/axk2O\n8kE8Ete+ro6lx+oW9zWufr0v7hl3L2CnVnJoMYfPVNtIu6Vtnr1ayrqF37j56Qvt03eAjhKnhDUy\nWZPZrk0RGSxfxhZjHE8NFjXPFwIsCU/AHwq4EC5RrwCArHOIGbckrhFiyTTfFwsavsHDkOY4pfw/\nblnCpc7dnAZ4w3P5XOUU9e3cgi01bq1wo2QOGAAn86Zkf2ERdjTbzq4D27tnD9naWcKbVQ9e67xC\nuCCANAmFDhBjJM7WUbr++ut9nBSBhODF+sAaxiWJRaSAn6Z9XMecg4WOi1gBBYtVY8Usx4cLNkoA\nOoJVgR1lAPdiKNhxL8IDBDOAAGhpwg0gR5KaghTZs1ibtAMBVswRfWfRMnl+tlsUIs8xPGpAbzZy\nkGzjrCDikMRdIYAC65BMZyUWFiCLG2UEpQEwA9Rwt3NPqjRwPKBEyEE9C9wPLuC4uCpgTtyZLaDF\ns+O5KjinSQDTPka3XJ/5tvQXVzmJgrj3UZLUwxA9J9t3nhVjl0IcPOcrr7zSlxHlPABXV2TCOsfT\nwfhCCUABI8kOIh+AdwLCU4B1CxFnD5VIv/OTf/T5ANKANTStdoU8N7tWOrpU6SdN+wUZJrk1oXcc\nm65Ou55XTlsD4HJ62u5eWdXkP7MWtxRTz8O993EroXxq1BDZvHpQHlrLrQkEMi5AFU6cTdEEpvKk\nFYQIYqwF3LkIfoAtBL5MPeIaCEsEFyCAizB0RZMYFS2UQXtcg8xYjYECxFHiGASogigCFyHPfuZH\nIzi5NgBPjE9d5Uzduvrqq1ubA8CwMhV8+YF2OJc4/78/WCTvOYHbESun9SLBByB+1MC+suf6o1pX\nxMH9rC5j3PWAMP1Ry40+UiwFEOB+8TAAxAAm8U8senhMVjGAqsSz1/vWfWyJkQJMKEDkDaCgRIkQ\nA8co8ewIATAe9Pnrb7ls6adaymzVgsaaTiKuebTLxmcqEx4AFtEgv0EJoNc58SgTJJfBJzwjKHR8\nh+ApoMxYgZi+RcIZSg6ekSRiLGppyllLV8oj0+YnHZrzfpSxTUYMdNawgXAc8wyA47hSovtY//fx\nGQ5oXGwnn0QCxufWGyHrDOqfz2ZTt0Vhf6YRKQFIxMBw8yoBWMRHyRYFaBH+Cm56TNwWywnQQ5Bh\nuSEIAV5c3nExPrKN1V0I+ALCSfS4y44m2QYhjZUSJRSMxx57rM1uhCxAQdwX8OG+sIAQzCSNhQoA\nJ958881trB+OU0uZ3wFhBO5cNzY6C8JO1volK/fZcFSb5SrhIfcKoEJYvBQ9wSug04sADcorUtkJ\n4tnwvABieATPQw8E90/MOEqAFTwAcDgmVDz0WKxD+MoWAhwpWsHz5LphAhjjhTg1+9VC1HZy2dI2\nzxmlQEEZgEbZIIuaKUGALuAbnRYEjwBTCE8B/GAf3hnawiughDWO0gKp4kOYI1NRGGLO9GObXT4n\nj06fL8sb8ysfWEN853HDhQQto7YcMABuy4+S/cZUogfenesW116T+ZvPmx3qlivcb+JoYUHuQhBx\nXLJOsSZJXMJ9WVNTk1NXEMRYQrgSAXEAHGBgGhNxuRAAaBhhR5ZqGJ/lGNzH6iYF7AC9JKKwAkk1\nXAcQjoI6CUdhXWLAV6e70CbXwVLGzYwlBdEWVhzJO2E5QgQ+QBMlQPi5D2tlussL6GhYoq977uu6\ndaI/7QRt3BgANAARgAwekZCF4Ic/oQeDaWcsSsB9QhzLeSgjSgAKYBWCK+3iqsXCBpiimeF6Llss\nXyxgpbhQAFY08Vfm3/IZMAeMsdSxFlEm1KUdWuXaZtot94XSALhTBQ2lhOcUjgOeMeMMws0MiKMM\nEndmbPEb9w8xnYuxD9FfwJnxgNeDbRwxbv7hpm71mrStLGzIL/jq9cgZ2WcDN3e5AImb2odi3BoA\nF+NT6YI+vbFgqY/3rf7kRc33JZwn2mc+brEW4sGACxo77jcEOwIwrdsQoQ3QIuAQdlgbSdM0Qh4R\nxzzwwAP9ubirQ0LgUwFJ29G4mh6DqzAEad2vW63fy3dcpoAHQh9LDgGNu1itNY4hPqouSpJ2mPuL\nAEYwA1gIVAqKAB4hSFFoJEkI/3/27gTerqq6A/+GzCEhISEJYUoYZBBRa+tQbTV1qFrt4NBqHbFa\nR+y/ImqdAHH4o1CrFWut/GtQC9ZKnXG2KNShdagziihjmEJC5hn++3se62Xn5Nzx3YS85K58Xu69\n556zzzn77Lt+a/3W2mtr9/o81eT7N6/KHtCWPLezi5TXfAyKcUZOuLlvfu5H54S88nzaLAXQAkkC\nAK1h674YFLJ5g5JGLWM0ePiYDP0Tgk62H5ACNPrKZ/Fe+QCMr3Z9XdK52vT8zUMOMaasw2u+NIDF\nYFhS0Gpd2AR9XRfnD0AOUPaKaelXjFH3GN5yZIvbDnSNjYj5AllgS0pv15gwLgE4D7gp4S+u73Pf\n/G66ffrctC3tGgM6q4d073kz04MOG1LR0edehwBc9sYe9p6lzmNRWIBiIRSE9+985zt3WEPW5H8F\nKuKHWN6KdVk/88tcJzgX1diVMitbuX9y/MJqke5BnAf1S2H2WhGK4qF0KGSKXjsvf/nLK4U1luuy\ntJxavBS0KUxl5STt8j54IzwTVLVrJ7xqSVTtBO3pOTMkgIzrp4DRyhRteMrRhozXpUuXVrStbaaa\nAP4Aq4svvnjUi9If2hQf7CQKLVy3akNO0Mpzb3MG7JY8dupJWjxcCXjmhh8754AqE77J662fy3UA\nC8YFcb8KTRAAZ3pZ0PfAwnzhSF6zj37AOqBf9b1xwZDSV4wP03D0dSvRx4De/sS+cga86jerC8mw\nZ9AxViREibEDL9OmytKorc5RbvcsGUMlODOofO42R6FsL94LbQB3bfDe9VkU1PCcebthCDFMUPll\nhnS0E6+ey3/+5Nq0ehuYbC1rVq5IM2YfNNp26z2bv5mZvd8nZJZs2qTtnvigdFzzGff8rUMA3sOf\nkfmFSjLKeGXZA2ReEu8mhEKTsetHGMotvvNqSsFl196WNm5tX7Hm9Mc/ND3/7PPSiQ/cXud4w9o1\n6Y1//tj0vDPfkU56yO+Vze70Hg35iEUHp8N6jAVTUjxaniXQBJg8uW6EEioToXhEvAaAZzpPCNpQ\nH0Z8LLb3+srwOe+886okKuCANgSOpVB2lkL0PNwLcf6mZKs4ThxXHDCyut1DPS4se5oBRl796leP\nJjaZrsJDD6r6rFx5qSwiYkyY0wxcepENuQDDyo2bq+ILm/LY4ROL56ERZ+eQQz/zwN2f+GswFoDN\nc+GZW+GH52naDbHNfFoeMopWhq9nHSKxKwqzAGIxYZ5/k5cPZPQf0A5hyAJlSwKKSQNm3i7gZdDY\nV1lRhi2Da6xiPJjfa+qPZ2scodoDoP0Ool/Gci59YJwz4BjkxkXTeIpzrMjVrL589S05N2Tn39yW\nzZvSZy84P331oxemaTNmVkzLMSf/VnrGq89Msw6eH01Ur510xYTMPj3siDnpmJwZXcogdFzZ3nh6\nPwTgPfxpASJWOtrRD0smKGVbKiJxMz9otXabPOAf5Pm+/5cLbnSSJgD+1zNflb73tS+ml577Tx0B\nWPsn52xo8/+aBBAAWtfYSyKUtihVngpFwjsCaGUfNJ1PVSILLFC+hJLGFCgRORZ5xSteUVGkrHfX\n4n54HT6XwhhQ/jGqKjkvj6oUnhdaltfFw0NnAxbKGt2IAi3vUwKTeDQg4+XwGtHQYpPEPFBgER6Q\nV4pYjJgnNBbPq7zusbwXv4wKTu7jRS96UeUp8uzEsxmX5YIZjCmVvPQP8TwBL1rWtByGEI/Y/Rkj\n4sqLc/xf/4XYl4ETog1GkrnJRP+IS5tyRoxPxi6auyz8Un3Zx39+t9b7ZUA94xnPqIwN47EU11Qm\ngJXAHPR8uX+v7+kPGed+Q8ZEjCvT0b55/YrGoiwfeuvr0/JlN6SnnPqqtOjE+6StmW7/0kcuqNaH\nfs0FH0sHzV8wehnd6Iqj87zgRyweSRKLAweh46Kt8fa6fYSOtyvfR66XwhR7omi8RynFD0cXmPPJ\niq57S2X3qNnaj3z/v76YJmWFdsiio7o+XI1Y3hzqF1VIofSiPACt++Htl4lQXV9AsSNPBn3IS+WJ\nuhZeFM9Dwla/goIGkPrc86DU1B7mwaAuI2MVuCrOACCcDyAAas8RCElCcl1AOYpJuCaesmlNPEMJ\nXRG/k0nMQ+Ml6SNzRUvwdawVeQJ8fRYrdn28O2vU1gsu2Gd3i0xeYAmMeLbmb3tWQO9JT3pSVfMY\nQAA+yhko61egrK94yKhcBk2AMvpZ/zNeTMuRPY2JEA5g3MRUnWtykpb4MkBE1yqc8drXvrbaL/pB\n//J6XYMpXGMVqx4xxNwLbxt70SSeGyPEH4O7FOyQ50cAqN9UmRdQ7tvqvZBIhEXsEwbt7TPmZ/Dd\nmbpfvuz6dMWn/iOde+kVo97uxNxnf/S8l6Qrv/vt9N2vXJoe84znVafrVldgVOoyCB1Xb3O8fB4C\n8Dh4UpQORUPBiHWFADoUnrgahdRK+plQv3rF8vTpf/nH9JoPfDSd9+JntWp6p+23rFiVvvPTK3fa\nXt9A+fEAgFO3iVD1Nrr5DCRlGaPtGQW8DEwBOrKsytRNW+U+piEBM/RoAC7FCCSBKiABns7HEOGJ\nU+jijDwRgIgmlHBUGlRxDh6+Z46uda1AiCInYs0Uue/C87XdNB79GsI790ckDwGePQGAXQ+K3PUD\nEl47wwLAimMzItyfqUSMnaDQGSa8VPSwkAsjpBT9bx9eLADmFXtl1HnVV1gKx8kJEHdumkf8spe9\nrAIqv6uyP8tzdfPeONAWat2zlE1fZqV300bsE4aGzww5hgVq2Xb9h0UJ9guQG3edBIAD9rULJ6cp\nc3cEfMcuu/qqysOtU82+W3ziyeman42EXnrRFXIKmmSsOq6pzfGwbdekvI2HOx9H18hipnR5wTFP\n0uX7cfMCUNKKT/jB84jqlrEkrF7lwje/Lv3ZS06r4j69HHvb7csrBco7k7Tk2mQqU6a8T3Me/fFK\nUeso18ge7uU8vexrOhHqO6oEORaAihm2M1w6nUOMmdJTZaoUgCoZi8ej3CIL31zl888/v1KYvC99\nwrNtAt9oC6DoJ+Ad4KvwP28OmAOnEOOgLLZASWs/hEFQzpWO7ffUK+PLeA55znOeMwqGDEvhA5St\nLOioZcyAwiTIpq6Db7TjlQepbYU9eNUMV2MAUImXYx/Q3E3g67wMJ9nD+rhfca1LcvY78HVeTEm/\n4OsaGBHGA3E/DNd4j+HAKoQAX6ELRkoUKzFOZU4bl8YSxkFddf2+avXI/Ow4Pl4lXc08aMeQSXw3\ne978dMdtI+Uxe9EVrdK8xqrj4rrG2+vQA97Dn5iszQ9/+MOVtctrUtXGj0hGK+XtR+UP6KLaLFkm\ncQS9FKJAQi/ynS98Ot16w7XVIf/3ja+m9WtWp1//+AdpwZGL0sGHHtG2qa1btlbX07QTJUKpUXwU\nA1AqK/c0HTOobUCQp8qDinKVFDnFzGvlIfcqFD0Q1t+8ah5oXc4666yK5gQEPCrKj6FEZNWec845\nVWZ1/TifUeZimahaXg3wEZfk0ZchB/0qLl1SzwC5FAqZtyM7m9GzJ4gYObBlHAENzwUlbJzzWCll\nhSmW5mxvHisKlsf8/Oc/v/o9YBPKOG95TwxSfe8YBp7jTSPTV7KGjcN6DBblzajxnIyLfkU4wthG\ns3u98MILR8Gz3zYdh/0Cvvon7lt/iKMDYQafsaI/I/tZrJx3LJ5cit8Dg7RaG3vhIWlr+eXd7w+/\n1wlpxS3LGr7Jc4xvuSkdcdy9U6+64q6GSPMgdFzjRY6DjcMkrD34IfnRAFwxspgCIQuXkvCjKulo\nsR20XtBQ5W197qqb063rOseBIwnr1uuvrWI/0cYNV12Z5i48NP3pi09LD3zMH8Xmxtc1t9yYLv2H\ns6sVa8TbKIhOQhkAM1Q0zwUoq2VcV5Cd2un2e8vGUTxxbc7PY5cM1I9I7uHdAAxzW4nMaHFiwIJO\n5gXxfD0/HlaZ7cqb4+WKRYagSk25oWz1g+dNbJd0Z3uILHl9F4LibgJZnrqEsEFk9Ma5xvrKaFQK\nEXgQhUfK+DzPnddvrq77RE/HvhgULEuZ2f6Zz3ym8p71kzxlhfFsAABAAElEQVQCoItFEGtmKDFC\nnEP/6ScsiO9cA7Dk+Y6FppdNzctmZLlWz7U0jMbSX3IG0Oqu3T0DLoYK485vDTMSY7rVeQC3fjP+\nI8685uDFacsBIx51eZyEq1Mfft902nsvTMc94EGjX23L53/dkx6Znvyy09PG9et60hWmIj313oeN\ntjUoHTfa4Dh7MwTgPfiBUTyyN82XjB8xxY1apGDLmr/tAPiK65anq1as63inAcDlNCQHvflZf5qe\nnLMgO01Dsu/U9Xek6bdd420lqFYABXzci8+dlEQc656BkzgmCp4X9+xnP7ux+H4c0+0rGpLXSyGH\noON4K/2IZ+Ta0MyYCdeOFgS8IZSyWC5QNk8XJRzesH0cB3woV/WSCVpZv4WI+Ykph4jt/tVf/VV8\nrF55b5KS6iIGiWIts4Hr++zuz+V86Tg3MAlDxrY3vvGNVa6D9wBSFrFxRPQxL1kfmc6CDXL/9inn\nBRs/USEKgGERMCD6HwDzkOVToL37EW1iQVTPYhhLnAT+YxGeLcAFrDxZSXkMO6xBGCHdtm/cGCt+\nQ0Flx7HrZy1IG2dvN+Biu9dvf/5T6RPvPS/PgnhflQVtqtFHzjkjrc6hpr99zwfThAzopXTSFQtz\nnfDHHXvI6CGD0nGjDY6zN0MAHmcPrJ/L/fXKtem/r1uRtmbF307GCsCo7oflUoTTN66uKELeTSmA\nlJfOo5OtagoI+pcVz3Ovx67LY+vvUexoNx7MkhxrMzUnFGx931afKU1eEbouRMlBn3nk3QqjiHJE\n/fFG3CdF1yQMJaBDgDTF+qY3vamim+v7mxpj+k2IrF7eWwjgoOjDOIvtXvUF0ClFvFt2teSdXvrK\nurBKmZKJmS0oCymU7ff63r0bB3UBEBgJwBrCMGIgEcfII+AREvfPqAHGss4BTcwl9j3w4dXW+8lz\n8ywYJGKqKHH90q6SlvbqwogD3May400Vi+lM9X2bPksy0xcBtPHeWHFfvQjwF+Lh3UsQNJ4lOKGm\nS2Mv2vQbmrPomPTDVdt2KrgS+3zl4qXp65dclFbdPjKHmoF+yhnnNOaHdALgB+TV0+6XlzEdykgP\nDAF4HxgJCip89qqbBl5kvd511oBV6SbqvfrR80iAUikUAg8egNRF8QMxb5QgRaQNQN6tIpK1SoHK\nEsUUALEo21g/V3yW2MZzCaHEFK5oV8PZvhQaBe4aUXvmn6JEUaXizQCzSSSmyfYlYpHiugpQqLJV\ninglwwL4oA0p+FJkcZdZutiC0uiREYz+LgW9L/YHqFrJ5gy2y9ZsSNfmili352llcvjUi872FbTL\nCy1kUMuFOBbNml4VXZk6cXtlo1Zt1reXc4F9xygDkDFWsADqe0uWI+5T7gPDRr+LpaPsY3/7uCfG\njL4XPyf6kIFW9/p8B/jQ/PpEQmPQuahZQAqcOonnjyZ3P6huBlMrAJeYVQdZYzyqf3U6V/k9Q8r4\nNH4WL15cGQDCEBGqsK9nz1tuYpz0r3CEV9XPPvWLm6q1wctz1N+vXZXZrZkH9j2XfHrWD485en6a\nM21yvel99vMQgPeRR3/5tcvTr/Kyc7tSjs6rnTxi8bydTgFsFF6QQFIKz4RHXMayy+/L9xSqaSSU\nMFCnzCjfbqk4ipiyopRQz+J95paGaBvYRWzW/haxD68r9vPqWtwPzwdtTFkD/BDVm0yxkYzTpMR5\n3qjoOBfwdj2AxXtgVE+aibbjVVWrmGIU22S9SjrSfohkLAZPiKxcix24troA3iuXr8nhirWJ0dZq\nykgcp7IRpbo4P3fLUXYLxADHqlEhwBUQ8kQjJACMGVCmJ0mKIkDUAhNADtsAgBg9PM4QxwDTAFwZ\n1OWzif2wLcAcaKHmnc9Y0i4gNlaBnGcLpJpEGEFCmPEA/CVAEmDcBLRBmze11bTNGBSC4MViM/yh\npf1u3J/rN46I91ghv49Oxqr70d+lfC+v//vjvE54b/522ULn9wtnTM30887TnTofuffuMQTgvffZ\n7nBn6kB/KZebW5cV664Q3u+jO1i3PA7AVZ/6A4ABMcXSj0iqUtUIdUyBAq8At07tScDiiVPEFLVY\ndXhPjgWmEWsH+KhmdDlvk0Kse5hxPl4V78McXiBdF98BQQlZ0T4KlPKmeMU6TRMJQCqPf8ELXrCD\n8VB+pw3GSWmYSBAD6gTDIEYqzmrfkNtykt638jrRq/I46RSqiGPilUd84JRJ6YGHzk6HH9ieujcG\nGAnxfPS/jHi0MuBgLIjPEgaTpDxgIRYaIjFRvBYNDThR1foqDDzPUrY7BkCIoS76RpIf5kJltHLG\ngH1dhwxm12SsMqJ4i2HwOB7gKujiWOUlPTOg6zrL8VM/d9NnbQD6Emi9t60+dlDrUe9bJjxDBij7\n/Rj3Zb5AeS59wqAQQ2bk8db1Xci6zVvT5391S1V2NLYN8tWSpY9YNC8tzCtmDWV7DwwBeHtf7PXv\nlKT8SV4VqZ95we06hydkpZNWJSjrx1IUqDvKuBQKl8fSyuMo9+3mPUWPEkYnAxzJS6V32E0b9hFn\nRm0CakAmsYpCayfOAzgYF+j0JqFAZbISNDmwLkWSFs+4LmLnJX0PkMQ/gQkvmnHAwwtPCMhRuECC\n8JTFLIPyvm7V+vSdG1eMOUQxecJ+6UF54fV7zZ1Rv+TqM6Bg4LjGELFScW3PXFjCtaKQw0hjMEhI\nK71Hho9nWxpsDKMwerTtOS3N05fqc7R9Z8qWvhIKKNvwXSn6j0GEJnbNrt8xpit536sY3+HJxiug\nZfjFs+nUJoCP2LfMcOOaIQFM43mXbTCyGA/OzeiJDPw6M+KYn2fd8P2b7+h6JazyPO3eM9CslPX7\nec3woezYA0MA3rE/9upPYj3/9Zvb0o15cYZBUU1s6AUHTKm830kT9u+p/8KjjHhoHCwBCqjsqgId\nPBtxZmDgPY+2BIW4jsWLF1cgBdx4rKhbHgSPhacGmIEZmrop3ssjk4nrr6wnTBFSiuGtyGKWOIRu\ndN/EecpCFbbxXExxKecA83bRtLwbEvFl11gmtaF5gTBRhAJrIHP7lnUb06VXjRRUqL4c439A+LcX\nHpROOHjmDi25FlRyCVw8cf2qL3h7IUCFgQaMeZsMEXFrGeJBzUuqYti4T4JNkNVsbrAQBQFKDCdF\nJ8LbM1fbVDDGjkSlEMYgoI2/oJABMGDjYTJa0N6uT/ydYdcEeoyJujcLcJsKf8T5u331vE2xImLN\npWHS1MaSHP8uY9I8ZiEA/e2aShHnF6q6Jhtk4v6DEmsByw3pNkQxqPOOh3aGADwentIAr1E26yeu\nXJaUpxzrbwz4zs0JFX+Uf1wTmLl9isShSGYqm+DJ8TZLqrT8ftDveVuAUpawlXKAGkpbghTl3kmA\nnGxaHo1YpHrCQIa3gSI1/xboUuIACaCK4QV1qn0KkzHAww6a1nZKFDXLaAjhZZvPSbSJtgYqPEje\nft0r4jWrDgVUxE5/ef2N6Xsr8lq2mX4cpEzPSVkK7h+SY37EffBYS8aDR4aqRT+HoQVcAChKnpEh\nvkoYZPpFEhovN5KKAKLYvWzhWNzBuSRuic+GoIg9V94f+h4I6+MAWaDLEOhGACuvGiADMnFr3itP\nPkB3UAxO0/VE6KLpOwYLkNcfIfUYuDHEuDOe9GldsGOf/9XNyQpJgwDh2Tk08cTjDkm9Guf169pb\nPw8BeG99sm3uy4/sG3l5QssUbu7zV8bTOeSAqen3jpybpvSRBdt0eZQiIK4rQ14O5VZ6LE3Hj3Ub\nKo9y4pmjjlGiwAqY2hYCaCn6Ms4a3zW9Uow8JUov5vCKJ/KkUKXAw3kIZU7Bl3FEcUAsgcSu8pyS\nkVDspQBWAAYEIpZafs9zZxA8KBsYLznvn3OgtXOmb3l8t+/nTMvr0ub5ntYN5rGVz9T9+EOhAmL3\nrvazpDdjAO0uhstbjsIyYu1iuoCUMRMi4coCFxFaMFZkjMtEF6fVHqkzAnF8p1fPjlHlOjwbbIW5\nqwwrhVaAsGfIo3SN9tkVYtxgaxgprQSgGmPCGsEURNW5OEafqhJGrDIVDEJ875Un/M3rb6/Wha6v\nBV3u1+79xPzc502fkmnnuaOzItrtv69+NwTgffTJ+5H9Ii9D9rPb1uTY39aurV2O7oxJE9OJOeaL\nZtw/03yDFsoUjSjZpKT4AB9PA1U7SHEe3hDQo2wBL2AICSo5Ym+2AzGKjNcpC1fNYgrZvqXnGm00\nvVLuvFLKHCA779Ict4z4p2Psw/t2jSVVH0DKa0ctl/NeHcerlJzE6wyP0XbCkPna93+SZpyYF4KY\nvvNUsJG9xva/vIDfWjgr3XnTNZWhEa3xyjELMtEZIMpPmsvMsMAYAF7GFgEWjI7oT6yE+1K+s6wa\nBniwJPofUGIZSgMmzt3uFRAFLYuaDYNPcQ/11QEZKrxeshQFDBglbWFsGEBCFtiNQYj7EfdlHDaJ\nMIj7xiJF/5QGHeOgXoPauNW3xlsro9bv7td3rEs/vHlVWrd5W9eJebSBaYjHzTkgnZQz480bH0rr\nHhgCcOu+2Se+Md3EtJNf5ylKrF1FF+pOMdCdmi37KTmT8eiDpqdj58yspp/s6g4CxOhgCqYEYsqN\n4injhv1ci3YBLy9JpisPi8JqJQAC5RkCNGVeNykxVLE4oZibBKHSc43ju3mVnMXjK5O+gHK9yhLg\nB8QxZSfaBlg8QbR4iNDDhsNPTBsnTIlNu+R12n53pqnX/jhlJTPavli5Zwl4ee/uRQwdoDbF0cvC\nJY4DLsYELy/YhNHGu3wDTM29DqD1yqgrvVdTkWRZo6cl01mpKUo3Np2GxwmIGUoMRUC8ePHiHeZp\nNx3XahvDSntNWfD6LMaT+3CNPGPGqXh62WfaV5CDcRCi/yS+MVrqBkXsE6+btt6ZdcPaqpIe3bAx\nf95WPE/7Ad2pWTdMzjkgi/N6v8flJLwZGYSH0rkHhgDcuY/2iT14xKYqrcyxn1WbtlQ/NDc+Jf+o\nZueiCwflWK/XXeHxdupgykaBAR5TKB7HUJiUdj2ZpFN7lA/lxjNE1YrntQPesj2lJq3tGgYBZWsK\nVCQ4lftSxowE9LVrFZuV/IU6ds0UJQ8naNLy2PK9mGZ4VM5r+ovzLsmen7rQJXBpS0KXLN+4Rm3x\n7M2hRftunZTnGc8/Kt01cefpUeV5x/p+v21b0gHLr0uTN44sBAA41ErWXzxOMV7GQUzlAqj1JCif\nzc8OoJD49I53vKPjpXmujDTeI1DCGPBkQxhT1vptqngmVqyUpesxDc0z19/dCM8SeHu2nhlg91ef\nTtSqLZS2ay7j5bGvPgPsGIFgY/QL48tnxhYvuKSZHWufMo/CORiGrgkNHQlqcZ6mV2Np1aatlX6g\nJzZkMGZWhX6gGxTYuCf0Q9P1jpdtQwAeL09qeJ0V+FI0ADRoSd1CsfM2JCJ530qALnqSZ82bAbzd\nKsayTRm3PI8yLlzWK7YvulJ2MsVlqot4rPgc4fHxnLUj1qzusczkUiKBysIbpffaCoAABJAFxmLW\nsrOVc0Q3lkYLyvvv/v78dNiDHpFdl5376l0vf1466XcfPrrQumtaeest6ZWPfXB6/7evTJOmTK3q\nA3/jPz+a1q5amQ4/9vj0xBecmg49+l7l5Y++n7L61nTdN79aGQToZOd3/5KsxIUDcMOLGz2weOO+\nosayzd7H9C0gF/FfRpQKWWLCjvHqfKh4BhDAZYSEweP5MwZQxiHAnTdu//e85z19L9CBAhc6YDQa\nk56hZ9MUczVGeLDGZ1NWs/sKatt1lYlYjAvjC6DaL+hmRkTcJwMgsuvdp9+O0IlxIZu8qVhM9Mfw\nddf2wBCAd23/DlvfRT1AWfE0Qvk6DdBCB8ucDo/RdjQzRUjh8BLEviiysQjvCGVdJjrJMLY8odKW\nvCaiEIQM4LrYl+fCg7UQQCkAlGdYF0pdAhDgL0G1vl/52X36C2Xsuxe+7d3pIY//03K30fedANjS\nlGc+7Y/Smz72+TRr7rx0+ac+lv7nC59Jr3zfh0fbKN9c97MfpbOe+SeVB8noQdU2gUx5TP2960cH\nA24CQCRuoeXdF+OHx0k8f0aKFcQAIKAu2Q1AJckL4BGeslABZkCClRCD60Q516tFVQf0+J9s9wBi\nz4yhCExdE+DFkhjLkTRVNs944MVjCErD0vOPueX6ALhiPAijg1Ep8S3usSnjWR+huQE46noo90wP\nDIn6e6bfh2cdYw+gdv3xhnnF6GQKjWKmjFFuQNg0Itt9NiVjrMAbl83Dcm6x2KA2eZs8nDAKLE8o\nu7dJeCASfergC9TR1E0rFqG5Q1EDoagAJgHMfTYlgNnPXylH3uv48mNP7+/MCQIvecd7K/B14JF5\nTdiL3n5WyzZmHTy/AjmxTNfYTgCHZ1rGZr0HEvpVLF3c3jPk1RFgqd+BJUDx7COJDsNQgq/9xdQl\nrAFh37suxhDDDBias429KClbx/UrrhszA0iNF3+MNl4nIG1KFpMAaH+x6iZ62D0BZIBuPPgsxisR\ni2EoN0H7AcCS+ozJ0ijVb/pLctcQgPt9umM/bgjAY+/DYQv3YA9EjA3wRkIVwA1lL8aHju2Hau7m\ntqw/i7YMjzXAF/AC4FbCI6eMS6FwgSkR83YfITwndHUIELIIgL+6SACT4ARc0Ks8KAqZkqa4b5q9\nc73uso3vf+2L6fZl28HSmq8hB81fkPyFXJZXybnv7z8yPu70ih5VfxrQeCb+xCABCyOGxwpk/aFo\n2xlIDBbHl/3CYOHhMYJMPwJqgAWABeVfvyhZ5+Lx6GhTnxgowNf5eZatjqu308tn4881AUEx3jKj\nPdpxXgYIr7YJeGM/3xkLwFa8FxA7tgRgMe8Q/SWmHMVabAfSxHYswq76fVQnGf7XsgeGANyya4Zf\njKceAF4UL6u/pGcpZPGwmOZTZoMO6v54XJRiCQwoUNfhtS4oWF5Rub8YLlAmKMnyO9tagQLlCTyA\nGm8I5QlQFOevCzoWGL76Xz+ejpy9XUHX98vVkHMm/J2jm+8q3o9uzG/EgX/4ja+kN3z4U+XmHd67\n1+tz1i2aFAD5K4VBgGq1n5AC78+fbXUwrveLPg9qFoWsxKRpQwTFilI2b7gJzHimKo2FJ+kY+QFi\nqDxgID0oYZR5tqhoz6dJACaGpjSymvaLbQHAxonnzpgxBoLeN17KewP4JQDrY54zw4gX7PczlN3f\nA0MA3v19PjzjAHsAAJmaQvnwLtCVvAiJKqZbAGBCyYjPivkBzKbs134uS8KOeamEh0YBAkSK0XeA\nAFVcCmUXnrLtgIZCVeNZdScJSXWJZR15PRSu+y4Njfr+5Wcr5AAiyl//LDr80LZV0B7wyMftlIR1\n+Sd3LPhx2cf/LX3yff+QXv2Bi9OcBa3rYs84YHr6x6VLKw9LgRF9X4p7cD/+6gKEAUWsbFTG2+2r\nj9HSEonEPCVnqW8d8XfziwFpPQygH170ohdVyzwCvte//vXVtCgGnHZU55K4JRY/FhEWcc2Atz4X\nW7vGoniwMcr4kKSGCjd+29Wodqx+CdF3YaAZHwT4aiM8bdn2dUFDMwyGAFzvmd33eQjAu6+vh2ca\nYA+w3AEvmpX3yKOMuKDTUGT+fA+8xEeJz2hGyilihdUXffwn7ghgCcUva5aIKaqzTFDUMmBRy2hg\ngBDX4nveGUMB5ayqUyhS39WFku5FJBJJKgLWRNzz2c9+dvrk5z+XHvHUZ/bS1A77/venP54++c/v\nSqe//99aZj/HAXduXF+Bm3Ke6jKjmk3x4e3Vvfw4Jl7Rq/6aJLw7gINyf97znleVmJSkpp+tlkSE\nBxZn+l4NbcI4QtvLQucBy4L2vYx1JSujEtuSJUuqEqRKV/Yq+ps3LcRQGlrRDjaGIeQ6Q4QKxLc9\nY/fDW7VPSSXHvl5LT1mM1xgjwBzY+004NgAY1ay/SzbAdQQA17+rGhv+t8t7YMJZWXb5WYYnGPbA\ngHoA8EqeEe+l3FCbPJZWHgNPFzCz9imhoADFy3gnPGWgV0/WaXe5ABSQokQpNPN0X/nKV44eEtm6\n4owESABnHhmFVwrvTPxNO9YnLhVkuV+n97xo90Cp895UlAImkYB15plnVgUZzGvduHlLOvn3lqRJ\n+bx1+fbnP5XmH7EoHXPydk91YwbBL33kgvTHebrRiltuSu/6m79Kp77z/Xm/xWnzplzONP9NLgo9\nRJuoazT1kXNH6g6jfdHg/iSZid/yXj071w5UPdNuPPsSvD1T81m1gwkBrLy6mCur3rZtwIhx5Lnx\nxhlHQcsaA54b0HRt+s33DDZ0fp0Oj3ssX40p52RsOa5+H2K7xioavj7ePHc0MiDl8bsPnrN2hE2w\nAaXoKyBPjJ/F2Yhw7c4JWI177yMXwnvnL0MwrsE59DljtfyuPNfw/a7rgaEHvOv6dty0vC1ntt6a\n14O9YfX6vDrOpqoIx10VSblf2i/fhSo38/OKR4cfOC2vfDR1TAsv9NspQA/dCMwoDsq7l0xVylmS\nDm8BMAVVhzLmcaD0KOlWHkdctylFkrooaEqOMm+6DnatAggA1utleSEBHnspvCteTtCT3YKv87of\nCpXiDHCQUW0ebOl1Uc7qIrsvlDiadeMP/jelrVvKS+n6/dc+9qG0eeOG9I6/fvoOx7zvmz9PU/Jz\nKeWAyZPSbx1zZDUf2VxnnmdMsQJyp5xySkW3MhYU24gsXUaW541aBUTAtBvheQJZf9pjYOlzzwrg\nOj/WwspK4sN1EPRZkRTjwDUBLZ67+uCMLMDWJK6X5yoR0DF1MT7QyqXXWt8nPhsDQhSOYRwaX1Zu\n8ry14XkT16q/POsoXQrAPV9jG73tmFL0S8mwON64APL62PFNokjPbes3pRtXb0g3r91090IuEgRp\nh7uqVY4OzkU4jpg1vVoZbbjwQlMvNm8bzgNu7pd9YqtFGa7OZSh/vnxNVdlGmbl2MnXC/mnapLzy\nS64BfWyu9bo76rwCSIBJyQAe1GUrRdju2uvfUfCUM6VUCk+j1Tne8pa3VHNO7U8ZymYlFH9TIlT1\nZf6P50uBl2JKEW+0SXh3vDreGQUJaCl39YYJT0V5wRBA5hzh7cZ2XpGqWRRtWbwCCJ1z0Ser8oKx\n7654XZhXQ3rcsQsq4BcGYHAwFtCj4vEMgzA+XKuENffCUyY8SnHRoNDdB8PL5zCcMBFhgNTvATAC\n0ogdM7IYRI4hvEjepj/fxZ/PwhR/+Zd/OVqRSia55CwebAh6HEDWS6X6HpA6hrervbEII8R5xHGB\nuLHnHiw9GbFd7InxyBAA4HGd2IaIrwN1xmApPGDhD8wJNqIUwHvNHevTT29dndZt2Zp1RHv9oCoW\nY9160CfMnTlcAanszBbvhwDcomP29s2WG/v2DSuqZce2ZCDuRaxwozTlQw6bk+ZO35nG7KWtVvsC\nRp4H5UGBAUVW/aBFzAwQ8xxK4WEo6BHKGg1pvilR7ECxDUDQ5PGU7VCAwK8UIKJ4BAAARtoovVZe\nyhlnnFHF7KK2s31QqQFYpu/I+AUKTddgmUJeICAA/gCamGpD6d6xcXP60tW3ZsW64xzh8jrH8n5a\nVsQPX3RwOnTmtOr6XvziF1f9FdOmgCaAsnKTqUARGtDfpm+J5Xr+wCekLKnoe4yIBDPx3OgDIMMQ\nYWD5A1CmiMXzFYoAwq28vTgXQwzIOzaoXoaBLHKlPgFd0LtxjFfP1LMBvAzGQQpPFch69ZtwPWFA\nYmUYBOY4+y7WjGb4XHN32KNuuLk2hi0jxzgxro3HansuR/udrB94vpu29aYfJua2DsylKR9y2EFp\nwd1LUlaNDv/bqQeGALxTl+z9G1BJ38o/rrGuAztt4oT0qKPmpXmZnh6UoMIkJVEmrH3lAjspy0Gc\nGwDwtEuFr11emAQe8WOiDvQjcxnKbkScmgdWCi+LJ6c9ipKnVZ6TIow1bxWFQFGH9+wYRoCFDFxr\nk2AHlFwMb1iSWNRO1p9AJeR7y1amn+bVsOrF9eP7fl8Rk0cfdEAFwNGG/mUQKPpgylDEcHlzDA6e\n+r/8y7+MJl3xyPQDpoAxVHp1krmW5sxq1CxKVuzTmCH2FWoAPBKrAPOSnFBlxarwBGUeYzO6iXny\not/1rndVeQdxL5K1JLOVnrf3i7MXr+1u2o22+nllVPCIy3GDNseYhJHII3ZNvHOGSohpVvqoFGyE\ncR4Gzu3rN6evX7u8qglf7tfre97wQ4+YmxZlanoozT0wTMJq7pe9duuKbNF+9Te3pfVbx+75oLCv\nXbU+zc5rv87KC2+PRczfVSaQtc77ULEI+OxKZcYr4g1KnKHQQkHHfVDsPDdeMs9APJAn3kooPMoN\neHilpANoHAMcP/CBD1RxRsDAg6YQAXIIcAKUtvFiZfOiUNGDPC9AJTZYF54fRQq0grJ1b5KviPYY\nN2XBBeu13pZj/mM1xOrXMmvKxPSIRfN2oCCdH4sQta3FJxkJPDivEqAYOvYDngwFHjCvXx/qCwaL\nxRyAJ2YB4BEGGq8QWGISGD4qlAEqTAUGQtz34osvrr63nefnfI71rHiujg1Pumo4/+e5W3qSYRTV\nyYwXfwAr6HLX7TqNIcajtoLhiLYG9ep6GSR+GwHC7t92/ek6jDUeuOsyjkPcr/FVimvW3/adMWde\n+sQvllUro5X79POefrhxzYYqbDU3M2ZD2bkHhh7wzn2y125ZlVcx+fKvbx24wp05eWLlCaOlexUW\nunmvLHDAhZ4dJHVHuQMsAE/JOE9J97a6XnN3UaOEZyG5KTweitU18tx4YGK08Z39AQFFF0BoG2Xp\n/AAQpQloTzvttIrm9j1xHrWjS0FB87hbXTPKFvCaxiLRKwAEyIi5+ux6ZUarp1wXS8z9588Ho3C1\nbSz88XELq6Ur6+fyWalIsdU3vOENFWDoEwJc9YlXoKscp+pWYRRhDlCkKGf3K45dCiMJlRr9BOiB\nb1De9jUtSzJW9JH+YRCV4tk5J/qagQbQgvY3R/id73xnNYYcg86W2BaGQNlOvAdqrt19RYzZq/ED\n1MciWAV9RRgCPmsTAJuTHkVP7OM7Isu6bkTKLUDjT5o+I20+4sS0MuuJQcoBOW/kETkcMaSjd+7V\noQe8c5/slVskVHzjuuXp9hz7HbRszusI35FjRkfntUC7XY6MV0ehSV7iDVGo4pMRg+r1GoEd5c6T\nLVfY8ZmCoVTtE8q3Xftve9vbRus785xMIQrF7jgKDrADX1OcAFwpvA9eUAhwdp/heTA0gJA2QglT\nkOKN5rNS2u6F5yVe2XTNPF7e8NOe9rSq/9CMroto11J/ARy8ReeU0KXtUiTSnThvZkI7WmIuOy19\nyYSMJfNyPoCQxPQMwq2E0WLJPFWrFB0BTPFsGGOAD9Uu/g5wxYmNFQaFZCH9hSEx/Sz607l4tChs\nY4gYT6YmlfcLlBhGAVpBzS7JFHWI8ecaMDEAuOx7fa5dHrrzecZA33bX2SSOZ/TZX3vGAY9UDNm4\nBPC+C4B0/hgTTe2V29ybtpyDYec+nMM41y7R39oPQ8a+QLgUxuFVmS1ZdeAhad3+gwsnxTnkmKzY\nsCUdlcMSE3L+yFC298DQA97eF3v1u9+sXJe+ecPtaXOPCRXddorFuB+cky6OndM+45PiQY0CNB5E\nr0sC8lAoapRbKO5SSXZ7vbEfZUfpUeqUMwo3kmss5xcFHJwDsAMDABcCfCk0yj3eU96liNe6zxDH\n8+QCML2+6lWvqvqFdwQsZT03iRgjrxhIMS7q4j6Au/4hkoaAseSd8Njrx/i8Nd+fbNerclb8ms3b\n769p3/o2Hs7i2dPT/RbMbun51o/hrYuPf/SjH60Aqqn6l3sBKhgD8XCGTEwfAziMFUaLcSAu69kE\nxe18DCRgXxdJXueee+7oZkzHKTn7GlOin8IrH90hvwFSPEpMg/MpJqLEaYjcAIlhQNn3PPJ4vrFP\nt6/uu/SWvWeolMZEtCUTOsDW2HUP5iEb08aZMcnABcwh9qu39cVv5tWTJh+0y9aIlph1/4Wz0snz\nZ8VlDF9zDwwBeA8eBjxE9KOqSqFIxPG8R4Wh1ySkSLoJoejrpQ8pgs9ddXPOaBy89xvn9SrO88Tj\nDmn0gsXMWOuUAspWFaqSti3b8Z4SBISUC6XGm+tXoWmPIqK0KTLZ1DyWkuoGAPqO90B5ySatU3Xa\nIZR0GBEjW0baP+uss3ZIePGdBCrJQKV4nrysEPfGG2wn5s+KoQJUHq34uOdc9ol7Ar4BzOVqTGKF\nwMtx7WRNZjKuzNPSrsuJepiNVlPTpmSXd3IGxENnTk0n5mlp/YQfLBjBa7UcIA9QgZVS0PHGiFfx\nb7HfCy+8sCr9GXFNz9Ufg+7000+vfg8KoHiOxDMFmqXoM/2kShhxDhnlTasCGSOAV2az84QwyBgQ\nGIoQiU/KifLMfe8ZA2N/8d5rvwajGK/xq32vgBlT4o/IEzB2jQ+GpaIj+olhUp7TWMLSlPLJH/06\nrbxzQrlp4O/lBghPlPOEB6XjBn6xu6nBIQDvpo7u9zQUg/mS6DIeDECW/BELuJtuIJYo85NQEqz1\nUpZLvPr1YBKvynbr72VFPzJTkIp2hEhc4c1Reqg6oFYCL8scFcej4zVQpCWoRDvdvmpbPIxyomQk\nqwDedsKAEQ8kjAMebKdj7MszA8YAtJxn6zuiRjQPrRTKUHJRKbxsMeom8bzFQilfYgUfyWoMr1Kp\n+o5RpqgIAfqRPe0zGtR5xVm7ER7x8mywGTsrM324KYMxdnpyHl8H5aS7gzPdfHBO4sJ8jEVkGCtu\nAswCSKI9IPP3f//3FTMB2IKaZcSZVqX6WHh/vhPf1Y5YOsVOeHp+G6WxZTsmxfYAfb8Zv7WgsJ1b\nhrbxE+d1XF0YETxxY5cwcGRctzJ0jG37BjCX4FyGOern6eZzzBmXhGZsCJ/wfj176wXH7wrTg1GI\nPlm7eWv6bE682tCBHVuzckWaMfugtv3R7jqNlYcfObcq2FHuNwgdV7Y3nt4PAXgPf1p+SBQFupYV\nTsGinQIgeHNAgLeICi3jYnFrqMX/yVNOOsnpj39oev7Z56UTH/jQ9Juf/iid/8oX7XDIGz70ibwU\n3Uglnh2+KD484JBZ6T45pgh4UcWUl0QhYIge44V1mwhVNLvTW4qV0nS/QLOeCLXTAS02mBqj+hEx\n5QU13KvUKU3H8z7Ekk0PiWfFKytpSwoR+OqXVgIwAVRQhmKIEmYCFLxqx3zaaFsiWyxrWLbrOLHV\nAPPyu3vyvQpeQhMWSGBAutcAI2OFZxfzsV0ndsRz86yMf5R9eP36g7esrnaAImASu/Ud8Ab0zsf4\nk0RlnBLAJOwAuJwv+rj6ss1/YsIocIYbMSYZDDziXiQSwEpQ9j68+V7asq++ZLQzRoUkoj98594w\nJrz7WzNZcMX1Kxqno23ZvCl99oLz01c/emGaNmNmNdaUKX3Gq89M1nomveiK43ORDlOTShmEjivb\nG0/vhwA8Dp4WBUGR+0FRooCW2M5iZ6kDNj9WhRl4TaV8NWc+oxQ7SQnA//UfH6l+WM98zZtGD1Pv\nt5NSmrZlfZq2bCQ2ad+wukcb6eGN4yljgEE58qDr1FkPze20q36jiAkqEZD2KuhTnlcpQA5dGhKx\nbsYTJUv0i1rDkWltm+eLiubBW70oBIB47oAnYsOO97zFIiU0xUIQvD9hiiZxrzw7xsqeIoAWJW+u\nMjB91rOeVQGgfjHOY7zpU2NdKEM2N8BVfEL/u2d9yZMKj9aYQW8DH4JeNpaEDoB6CBDGUkjyIjxX\nc6eBei/CEzcO0L/Es3zzm99ceeS9tNO0LwD2rMs/VHaMpaZjOm0zxjA3wG/rwmPS6snbV1cqj/3Q\nW1+fli+7IT3l1FelRSfeJ1cw3VLVBf/GJz6aXnPBx6q1oXvRFcJUf3L8zuNvrDquvObx9H5s/NF4\nutNxfK0UMCoJvVp6uH6Az33ucyuPmGJGySnSUBcUU69y3S9+lo4++f5pzcqc7LTy9qrObyjDdm1t\numu/0a+7BV/t8hLdIyVLsVKyPBleKQZAzHhQ4IsGRr8BJEqZ0u4HfHmZdfCVJKW4Rullir8CyNID\nofADfD1XFDjvTFKSOCePlhInlDtaM8DXNqDOw+ZpB/hSqqZLRXzUfqXwhpoSjMp9dvd7mc0Akffr\nuUhYc+/odH3p+RCMij6QGQ58ebiKTgBfYt4vah7VyoP122BUxRhEy2qjBF/HAWZUffyusEnGXX0/\n+7YTv1HToyRjEcBmmUMGVZkR366NVt/5bWh/8eLFVfa3mLj545Kp3Gv0kfEigasbEXMX9tH/1986\nkrBXP275suvTFZ/6j/T8N51bga/vJ+YY8x897yXVQhzf/cql1SG96IpNeYw3yVh1XFOb42Hb0AMe\nB0/JUnfXZHqLJQyEoqxg/dLRTLxEdHQoJvtc8vMb0+pNnUG49IDf8uw/S2tXj6wteut116THP/dF\n6c//9rX1U+70ef8tm9LsZT/fYTtlxNqWIAL4KAnX51p5ZLtTJN5IwKGYeVyUfj/XgDYWHwSaIbx0\nSi2Ed2W+K1aCNxYGjP5QeIISpLBNJ2oScX80JjAKQHfd2BDeoSkwwXYAccDtXpyHgq7nAjifspuR\n0Nd0zt25jaeumlWIe5ANzhuy3VQjXh8DKUCMccFQOyVnLbcTfaPcJxCPucB+F2Lt4p/GH2+X4ie8\ncMZe0L2WbuRdhxHU7lz17zwHBVwCxN2HZQ/L5TLrx4zlM4/dWCPuQV9JRDMO3L8+Y4BEqEo/6GN9\nS1639JJ07P1+u3pf/vejy7+W/u3tZ6a3f/bycnP1/j/PPy/dfvON6a/f8g+pF10xY/KE9Of3Pnyn\n9saq43ZqcJxsGDEvx8nF7ouXidJSlECpPXSdH7PYF+uXMvUXyoiCZS0H7TaW/lp075PTgx/7x+m4\nBzwoXXvlT9LbTnlKeuxzXpgOnLNj/KZ+ji35GlGt8SP3Q6f0AqgoWZ6YeLapOypeAYtWSSv19sfy\n2eIHUXiB5xDLBfbaJiUNAOOeHK/fJZOFUP6mungmFHKALwAVc+axuZ76AvVxvFdxSAl4IYwYdDOW\ngNem30IkH7kmitg55AnwjkvhIet/CrpbT6k8fpDv9WFZTpMXB+zEZ2Utm7tK9JvMb+ECCwwAMX2N\nFQjwLK9Lf6OZ3SMwlyjHMGVsMZgAOzA866yzqrEXx0pmxEhE9TKFS6zgVK/jHfu3e8VKGduAX8ze\nbxfoM/7qz6RdO91+5/fOIMS0YFD85rAD+tL2MF5atpfHS5NIupp5UPPvffa8+enqH3+/Oqw3XbGd\nIYtz3lM6Ls5/T74OAfie7P0O52ahWjYNlQawiLgS6xp1xIqP2sS8yfPPP7/6gdc9H5mrvcqzX/vm\n0UMWnXCfdK/7/076/te+kJZ0WMj9xuwt89haCdBCv/pjPEQCFEVLkbgPtCCFRVl5HYTIvo56wRY6\nkEXcr7jG8G60ATjQ2bxUSlsiD7Ak5oYGvekzGlqck6CDL7vssuq+ebUloKBLgUeI44CD/qszHMBE\nmUwABWDtQ+maWnXiiSdGE9UrL91572kAlpFd9iEAfvrTn14ZSJ6/5DRjXVhFXzDUYp4r8JaY5pku\nzrQsQTkDXkwRhiGEsUIYJcYYz1aGNGrYeRguGBHnl9jFiIpwBGrfs65nskfb7V6NWyEK2eiu1XhX\nGIRRxojqVxgYPFnPNv78jni5kbjWa9vrVm+vD14ee/i9TsjrP283KsvvrAt9xHH3rjb1oivq8Dso\nHVde23h6P6Sg9+CnRXlTwuix8KAoV/P4eE4RKxP388NEzfGM0E6lXHbNbek3d6wvNzW+Dwr62Ps+\nIF36wX/OsZ4Xp0lTRqY0vfWUJ6fHPfuv028/6vGNx8bGA7auT7/8wiWVkhOro9AkjFCA/QqwUFRB\nxqYMX7SrzFieUCfhATjONQAnnsGSJUs6Hdbye0qbAiyFt8l74ul6PiE8WMAYz852lDKw4P1RyqW4\nT0BMsZZUtrCDZ27KjilnZV+aluQcvER0t+Qt7Yfoq5IR4SHzCOvAHPvvjldeoXnWIfpHTJcxyWsl\nchkYSkBFIRFGjeftWH0X/ayPgSevr+wXbWiX18t7dpwELkLpizlHTJ5XbSlEnqtzuBbnI9qQ0Qyk\n+xHGAno1mBdtMMB8rhvKZfuuMQA2XtHIQiZx7+X+vb5nvNMhktvu/Zg/SfsfsninJiRcnfrw+6bT\n3nthxYTFDtvyM3ndkx6Znvyy09MD/uAPe9IV8/PUtSfkWgEhg9Jx0d54ex0C8Hh7Yg3XS/FQ5qUH\nVe72i1xYwepHnSAwANg0pHOe/xfpgX/4xPSopz0nU00/qBZgf/fXvp+mTm+d5MG6fVCuhnXveQeW\np6/e82KAn0QZioQXxxMrvZWdDuqwAaUKnHg5Ci5I0FGsIjxO82clczkH2puX0Gt2a3kJPBiJNqWY\nJgRMmu4DHVgq2XpRCAAATABiK0FlMiBCysxt2wDEWdkDBlb+li5dWgFyXI/zl2sHAwSxZR7lPSG8\nXpRjMAReLRjBUIhkMnN/eZ3GtdCEMRPP1DUbN7aVHnR5LxgJU2z0Vcx11R8qiEUlLb8VuRT6i/FK\ngDXvF+sEJFHVBCgrXykZsF9hLJtuFfeNrZAbgDXxeyhB1nu/j7GKfuDBqxvA4GJo6Dv36bfjGry/\nftX6ZPWjpmVJv/35T6VPvPe89NJz31clYm1YuyZ95Jwz0urbl6e/fc8H04Rs/PSiK06ef2D6nUMP\n6vnWOum4nhvcQw4YAvAe8iB25WWsytWNvvirWzqu/VoC8K/+73vp39/11pwBnZctzOD+7Ne9OT3k\n8TsX8y+ve3ouSfjYY+an2VM7e6ZxnDiVzFWJJChinxkT/dJp2pXsxSsKT3Bxpilj6bo4b6+vvBie\nZjfCu1DcI0DQMahf2d1NAkgkGgU4xD7uQ8wfmBB0ptgkoUADOHxmHJgHrCiEvpQhrQ+ImCrwDwHA\nwKld8pn1gm9aszHdtHZjtXjHlruLNEzMtXxnTJ6YC+tPSQvzWq+mlTACuhXPIaZJASOlI2V0Y27c\nD4+Ix6kPbXMv6GpACQgBSDAr9XMCHM8aAxRJa+U+vMrLMuUfzwWr4BrQwjzS8IhdD29c1nUU9GDA\nYTp4jP0IQFW0g7GBjSH6re6199O2ezW1DNh61oxOwMrrN05Q9/GMGJBhuOgrjIsFOT7zy5vS2s3b\n2ZvyOr5y8dL09UsuSqtuH0n0YqCfcsY51bxg+3WrK6bmQhx/kAv1HDJcI3i0e4cAPNoVe/ebL119\nS14abPv8x27vdu2qO9L0mQd2lQ1KIT/u2AXdNt12PyBsOg+lJ8aFekOf8uD6FRQ0ICwTwHjMnRLA\nUL/dxO3QoZQsmtp1h1B+pra0Eh4PUGklgEfZSaEGwpvhNcl4jeIbtgNq4CqWyasW3wwQlnQmREGE\nNXjGFHYpwGBZHiM/zoVbGG0btmxry5pMnzghHZCzWk/KjMeiXAu600Ic1+T4rKIVxLncD1AUYgHK\nkpZcvzAD7zDyHqxqBDR4pkIKrUQ/A5R66clyf+MoKpHpA543Q8fY4nmjnl0TMVaMmai2BdQYEF6b\nBDWMZal7s6jvaLPpuG63MQI8+/jDjngPSBlwYdhYxMJ1R71xnnswCOaTR7KgbeHVX5EXarlqxbq2\nl9JJF3T6vl2p2rYn3ou/HALwXvxwy1u7OXsyYsEbtm5PUCm/H+t7i29bcuzQmSMlE8faXqvjKWIU\npgxmylrijezP8HZbHdduO8VNGQFQCk0CjaxYr5deemnlQbQ7ngLkLUXtaEUhwstynGk/YthNghYt\nY8Eocp4ZkOA1ASqGSHjfqNOSslZ8QsZ1eFJAheIVSxVTlsREgAwvmZfoeMqaAg9Zl+eK/2+ulsbj\nbVX/Ofatv6oLrSzlgw+bk2ZNnVT/uvosKczUoIhfon/dIw9XQqH1foGgwiLi2eHBAj/fu0eAbL8Q\n9xRZ0faJPrftpJNOajQa9ZNzRh8GRRttir0r8yr7OeLwxkf0L0ZCKMWYqwMtI6pkJaLNXl+FVQJc\njcd4b3y2kjJpzzxhDAJvH2PAoAkWhYEQyYjaYsTpx5V5lTRLla7LRteukMmZOXnI4XPSMR0Wa9kV\n596T2xwC8J78dAZ8bZfnOM/VeVWkTrHgXk+7Xz7gqOwBPTwDMGV1TwjlLmuaEmb9UziU91gTwNrd\nCxoXQEemrX1NwQrF7TNFSCHWBRCh3kuPnifOew5xL5K70LKEokTPimuiWcNzr89h9QzOPvvsKinM\nfrLmCZpSzBrtKkOXYWBfyvcbeWxYB3YsY6PVutDACyMQhobYPIOF18aDlznuXtXOtqACYSBIdotj\nGFioYiUleXjua3E2fPQJ0efo4qBXGSoMKBRsXbTFiIswh/3q4MZjlc0PjMvnWW+r38/6nYddto3e\nxqAA3V5F6CamdTESGCE+2+69bUSYo5x+x9gD+OR/l61IP79tbWNJymqHMfxn0Y7HHD2/I0syhlOM\ny0OHADwuH1t/F41SZOUOek3g2dnrEfudPmkk5tjf1fV/lLgawCE8H95AKTwtXgsFzVMSG+MZhMdU\n7tvte4qfVwt8ZZPKykZ/lt4FQ6CpHjCly/MNr8o5w2spz48uBTSuk+cKjCntEO1TrkAbNSvZplzU\nQfKV6xF7tm4wCW+cctb2hKnT07//dOwJP3FNmJAl2RBbWDAhPEPeIkHhmi7HaBB3FStHjUtYEw5w\nH/avx8MdK0aLJjaFTFyzLsAXxRqgzYt2v6jbumAXol42ml48HOCXCVEyq8cq2jZGgGrpzXpmGAr9\n4NkEzc0QQL93u2hGXJ8xxfgjDBNjMeh2xogERWLMYUiCiWBEBuBv2XZn+spvbk03rx1JSqsOGMB/\nckMen0NTB05pZkcGcIpx28QQgMfto+vvwlfn2N4lP1/W38ENR1kLVm3XqTkeeE/IkjylKCx6nqKK\nU92K0o6SUoAC0DaXFzD3K5KGIuYaXh9aWsGMoKCdg5IPsT/gEectheeOjo6sWYApkQqQieGGAnUM\ncBb3RFVqC/UYgmIFXOYQi3cCbVQ0z+iuiZPSTzZMqBZLj/0H8XpgTtJ6VPZ2GGb60/PRH66doSQj\nWIER/c7ri2xgwBsFOMrr4PHLBEdBCzmoIiZjmudaF8aKOLP7I+5Xv4nbAt2SNmaARIY54Ebn9yuo\nf4xEHWi1X3+29XMASos5RGya1y4+fsopp9R3bfmZNw9YiXHDIGSIMPSMMVRzsFMoeHQ/UaAEqxCy\nfsvW9PGfLRuYF2yFtCfca0GaOQTf6OIdXocAvEN37BsfZD1++eoRT7hfyhHRPCdnwKKdKdrdLQCK\n90eRUCwXX3zxqJfX67UolMAL4Rn3KwAh4mzaQInHkpE+AwLThACy6wVIPLRyipD9QnhtAUaAvb6m\nMCD3FwDtOO0CGpnSJZhQ6JSwuDAw4hEBiv++YWVacdekMdHOcb31Vwl5j1p8cLri8m9U96FvzbVl\nJPF2JQK5J/N9gWVkBpft8EoBmHtiZISYgoS2FkcGoqUwTAAaIwcYB+jEwhf6PcT8aM8tWAVGQX2a\nWewbr8C0DBvY7hzGj9rP/WZJi5HLYFf+MkQmNo8/jLrY3upVrgBjCzsDcEtQltMQWe+SwmIuu3Fp\n37J/wxO+bd3mMQHx7Ay6v7dobpqX8wOG0twDQwBu7pe9fisQ/t5Nd6QbVm1I6/P7XgSldFiO6ZjP\nd094vqhkVjsFA8TQykflMoy9CmXLm4rs0VbHi9XyLFGcqGxUH48UADpWhrE4ayh78UMeZwglx+vj\nbRAgYI5plKiUAMZTRUuiTCnduKamNYWjXa/X5MxiXl0JCq7DOVxDZN/axkvTHm950Un3Tz9avS1t\n23/XMBeSbg5PG9Idv7myinOa1wucGDuA0fQj9GdM/SnvSX/4Dh0bfVp+7z0jw1Qr/Q7cw7MFLJEI\nxchw3gBYz0zd7bI0Iy8acBKxYRnX+l5ctO7N+uw5KQwiHFAX18qT1Z45tv2Ie5Jwpo+ILGVx4Rg7\n7dpkmEgOI1gXvw2xbmNAeMK1E/eHfQgpM+Rj2+ZMR//w5juqAj69JmZNy2GIBQdMTQ/MNQFMWRtK\n6x4YAnDrvtknvrlt3ab0kzzt5La88Lrs122Fh1B2wISsXKZN2j/P+5ySTpo/s/qBld/vrveWrYvS\ngGJrKMlehZehElKZANOqDdNSlEVsJYCvnAoE+ChRgEDRU3rAJpKFKFYlFoFBJwHcDAteIAW6JNPt\nlGWTRyReyRAJ8Im2nQegh4fJG+bpTTrhd9KWaTsXTInjBvE6YVP2xn7zw/T6PB3KfYtPq4FdGifl\neQAl4EXXB/C6bh6b/izjs3UavmynfM/bt+ZveMquATuAjnYOrAUQj4xwfatIieNaCcPPtLJ47p6t\nsRiVthwnUQwQl/Ruq/bq2yX2yQaPcAiDicFWzuWuH+Oz/mEUkkiuMlPA2HD/8iMI1sQ5QhhGrr9J\nVuQEvZ/dtno0O37rndsZhHL/bG8ldDM27KRcbOPQzIDEMyz3G77fsQeGALxjf+yzn8R+bsnJF6Yr\nWTlp890WuDrSB06ZWE2en3/AlDzv856zaCXehOKgoGQE9yISfsznDa+w07H2bVfX2vFlYQOfKbKg\nISMJxnbCg0YD89jCwxn5prf/ebJlBTBJVkExAhiJV+W0LEaBudToVnHBQxYdld72sayAJ+/aKWP7\nbd2cLnrr69IPrrisikminIMGLe9YzFK2uKlBJch6H1Oxyv17fa+/9Ht4pfoDwJqeIxEKIAkZRJ/x\ndBkC7YRhwCCKRC73oGa7UqDiriE8WCVCxd97EfFwBTUC1MXBjV/1slsJoAW4BNgCXYaK/IZ6rFee\nQAA8pqEpnl6eB2N2azbW6Yc7crY8DxkUT8rIO3PypKowy4KsH4ax3rLXOr8fAnDnPhrucQ/3AC9T\nvDditOaJogG7FYU0eCNNdCePB4DJRi1F9rK4YTvhlVGUIRR9xHTR5GVGMuABkiESwJQ3jAQwYBMA\nEPv0+soTo2gX5yxYXrNpR8AkKFjA4zyX/+Sq9KT/5+9G63yX53nXy5+XTvrdh6fHPON5o5tX3npL\neuVjH5ze/+0rq2O+84VPp69+9MKkiP8Rx52YnvP6t1bFWkYPKN5cfcVX0gmzs2LO8VYi2xeoAouY\nj8xri6Sg4tCe3+p/wOmeY+5sgKnYLbYESxAiacofT821oMeJeKgxgQpvJ+heniZDi+h3zxMN/pa3\nvKUKV8TxvGrUsnhrtyIHQEnMchxifzAsZcw22gOogJVIWJOdr79NAYu4cPVl/k/CV1x3OW7j++Hr\n7umBIQDvnn4enqXPHqAo0K+8FEqUJ0epdiOoXnRjnZZ1rLYkBfFQohpQtGnOZGSkxrb6K7AUGy4l\nKhCJu5Vgj0JsRx9api48G0pfBiwvKpQkcChjvOU5u3lPWfP0eJkU8+Ne9Io0/4T7NR7aCYBX3nZr\nsjTl2R/7QrU05QfPfk2adsDM9PRXvqGxvZXX/Tp97t1vqQAX8I7VyHASfSReHiDL02OU8TJjHnHj\nxeSNgF7GcySvobt5wgAKOEdIwzmAcBPQlW0zwEwhi2lE2pL1zeBihBmD5j2HAEUesapf3VC0jCbJ\ne8ax90QWu6TDMKyibQlocS5Tu4QrSrpZHkPUxmbMlgtimENvjAxl9/bAPccn7t77HJ5tHPaAWKXV\nfohYHYtdXLSTUMIqGYWSLfeXmBLL3GkvYoOxjzrAncDXvijLUoABkLS9pJfL5Jdy/3hPSQf4MgrM\ng3WN9dV3AHpUABPXBRSSaboBNNeDdvenEtJDnv3SNFJ6Ia6i+9d5hx2R3vLxL6UZs0fKWt6Zqck7\n72ydxLfprv2q6+7+DNv3ZDDUvVn9HMlE2/dMFfhaYtB39b4r99MmYNXvPEz9zdgx7xao82r1k+8w\nHBE3Ldso3/O4lQkFYJ4F5dw3PgAAQABJREFUCth18Fq16dW0KB6xxDHPDhXvPpQK9ezbjWkgbbwC\nbqs1ob4xJyhjxUy0E6IdwG+fCLMwLACrfARzqwOAUealCE0MAbjskd3zfugB755+Hp6lxx6gxEy/\nIWJhsTJNu2YscP/BD35wtMJRuS/FJJ4bVaUoKUqoBGnAR3G1U4japERjnqnP2qaII/5mG88J5RwK\nz7a68EJ4pADS/gwCn3sRCUHmdQJ+nh2PDPVN4fKYTGfifQMyFKnY8f73fnC6c0qzt8MD3pSBZNEJ\nIwk7rmXj+nXpG5/46CgFbdtNv/lV+sQ//X268eqr0iv/6UNpziGH2ryzbNqQbvzyx0dp56CfIwEO\nwJhmBEhcY/z53C4RaucTpeocf/EXf1GBXaeYq37zHKMuslAEY0mSmiz38DbNp62DVdO5zWVWJjOM\nL1OK6pnS4rnoY96r8xM5A5LEZOMDy3YilivLWlyXoPXFnG0LKUMf4fHydI21oOdjXwxOGHCdWJo4\nZvg62B4YAvBg+3PY2hh7AI0mfhnxKRnE5ny2EwlZaNxQfuW+aDqUblSCiu/Keba2AV3AxUNqJ2Wc\nLfaTxBKK3DagS/m1E94ymjPocXG6fjJm4xwMCh4xYGNE8JgZF4CkTnWuWnhc2jZ5ehy6w+sIAK9P\nRxy/3bPalAH48k9+bAcAvvbKn6TvfuXz6Tt5ubonPv/U9PAnNycH3ZUBeO7Nv9jhHD64Lh6/mDWA\nY8QAFH1Xv96dDm6zAY1s0QYFWVSD6iTitZHoZF/A79p4v4RXuCQnWzVlnlc7FP+p123VrBBUM++1\nLlgI08FMQ4vQAsPLUohyG8RkW4nny2uO8Ie+UgkOTe19mZcg7ozREWMX+2d8iVmHBDD7rO87GS1x\n3PB1cD0wBODB9eWwpTH2AMse5QeUKDweXavYKaB+8pOfXFF84a2Up6fYKbimpBfWfunBUlxiy7GY\nQtlO/b0Ym3OHAJFQorahQHlSnYR3FyUTXScPqBuhgMUx0YlAlwcT3lQ3x9vn51unpQXHHN+4e6cY\n8KQpO4LDz77z3+mf/+7UZK3oJuC89fpr07YfX9GRyo2LwQQEGAMFfz776xSPjTZ4sJKVGGXdMApo\nZ2AU/Sh5Tb9GOcxevEPeLHANUW7zBS94QXzc4RUbYFqd+HV4omLSQiimRrWihI0/92d6WQiW6MMf\n/nBFnUdslzHBmDVesCS8e/HjEEZuGW7xW+nkhcexw9fB9MD+g2lm2MqwB8bWA6oaURbAl9UuBtcE\nvhSVeBuAFnurgy8FJgmG0mkCX15mCb6uGr3dDfgqdFCCr2NL8HW93YCvuHOALy+pDr48edfPm5FV\nq/hHLGAAXGznrfN0AzRcS5MALUYC5WsaFA/tlz8eWRKwaf9O26752Y/TZR/fPv3r0KPvldbesTKt\nX7O68dDbb7qx8s5M13INkoMASxNYa8C9e/YoU54pIwy97v5lqqNYeXOyqAFk0/1LPjrttNMqTzj6\nufHi7t5ovIkLA3mib7EHAfgy1rEL3QiKGSMTAkhj6lxsi1fUu1wFQGialPOLSQNgoC/xKqYKxTFe\nsTUKipiGJ2xCxIN5vOV1Rhw4amH7bQXQO6ZOrXfTV44byuB6YJiENbi+HLbUZw+gDMVuCXBVUq8u\nFBFAZck3CU9HkkvM9WzaRwGI+vEUWbu1eqMdgBhVhmJbvFLUSzJNyVvrJO4vYnji3JLMzNsFOuK2\nlGQTld6pXUoZwAE3tHtQuzyciLvympzjyu9+Kz30CU9KEzrEHJvOOXvegvQf7z4n3ff3H5m8/+q/\nX5gOv1deWODAnRc8cPwvv/8/ldEioc59i8FT/LKF9Rcv3h+w8Od90/0ztGLf+nUBofCW45VHCMx4\nnxdddFFbWld7wA9wm9frOeunMhdAvFi2PGOmnTAsjGXnljTHYBOXvixPD2plnDEAeMKy8k2ZM19b\nVjXjzApQL3/5y6swTD0mDugljsmoZlQyTFyjkI2kLWOKuGbUvrCE31GAthAIQzaMGOd0LUPZfT0w\npKB3X1/v0We6pwpxSLqJGJx4GaVTCkUGeCnAJuFN8oS10060LU5WSi+LNzR529oSrwOqpbIuz+E9\nzxOAK+xxySWXVF+7buDfq1CYzgkweJNi1l5LoVBR6uLS9hcXRY0CAwDxj+//QJr/0Mc2rv3aDQX9\n5Ys+WAGvcx6ZY8V/+qK/TYcdc1x5CdX7qRP2S5d/6J/S+857++h34rLWKKb8GQsSg8paz4AWUJSA\nHO8DKEYb6/CGQcJL1J4iGTxBAN0uxur8xmM5vztO0214wf6ATgJXrI4l/orNMJ+9kwBOK0bJfzAF\njegrFdn0HZanFGNLAhh2hHjGjE0GnuI1PkdylnnPQDuEQep4AuBj1aT4Pl4V4rglF+K4ZViII7pk\nIK9DAB5IN47fRvopRXmfXGpOVayxSGRlUo7AC21cJiGh5QBvgHP9XGLFqL1uYnzlPNtoR4Yyarcb\ncW0RDyz3pwjVbg7hoVFm4rSUKLovEqHQ3EuXLq125Z2K+7UTsbjw7AAsBQ482gk6XCY2Dw74iAGa\n/iIOSbSHxpWIYzGOG9ZsaNdc2+8A1cZ1a9O0Ga2vaW5erOOJxx2Szs3enUIoQd9LWhO/dD9A1XUB\nYlPN2hky+rP0lgOYyzBA/aKdUzlRfaioBWGUhKccrwyaMgGM8aIv45qjXQwLg6EbMcbRwhgIIsQC\n8Dz/bsRvQwIhQw0tThgPvHoJW+XiH/pRHWv3GgJMsUKMNAaF0EV9zJZJaJgcgB3Uu3b6KUVJP1iM\nA/APpX0PDAG4ff/std8OYjGG3154UK4P3Xlebr0TTdkwF5ISR0fKCo04lakW6EPbmoQCVIO3U7Zy\nHMvyL0HSdl5AK2CP4+KV8oxyg7HNK6qOogIIgKGdd2bheav+EArUakCEggK0FD+PUF8A2qAIq526\n+M/5MQTAX/tKYeofQBtTo8QUvY+4301rNqavX3tb2pDrf+8KsRjDQw6fk46ZMxJXlbUre5dxQhgI\nvDwg4VkzVFw7ZsC1AsluBQAHGJcArV8IWh/gi9E35QXEeTxPgAyMvTIGXFu0Yz/XxXhzrd2I8ewe\nI5YLkFHTvTxj168MJZpaPJoYN3IHMBtlHWf78ZT1J2GoWqbQ9cph8BrV2nxvzJRhmZh2NZbFGKwJ\nfchwMQbd21GGANyxi/a+HVblWq7fuHZ5uj0XWh+prdP7PbJtLUf4mLzuay8gLJ5F8RIVhKL8H+WA\nMgtvodqh+I9i4PFSjt0KD4SHXMYUAVBULWrXjmMktADPsQhPHvVMwtNfnOfjAshO8cRO5xWnBLzu\nB4ir4MXDMe2E0RFgJ/M1Fg4o2/z6NbdVq930OwbKturveUDGxgRV+u8WMWBzVoFSiHilxCVJVb4H\npvoFEOunsWTlMooCkLVv7FkMQvyZ8dev6GuFMIzFbgwF8V+gF546A1Moop2333RtQFWyImMuFl3Q\nBsNGUQ+MB1H8Q9GOeP48bscJhRDjgQFE9JHfVfQHwD500eJsnC1Pg1iO8FFHz8u15NvPb64uZB/9\nbwjA+9iD35RjOZ/+xU1p7ZbtU2nG2gVPPuHQNKuLNYElhohNEgknFAlvQDJJU4ITD9GyauKvvYIV\nZVfOs3VOSgc1XLZFAfECgBgvZZCJUDwq3mjEXnndqNaxinsAvGhxICCuGrSm4iUqQbkv/SeTlpfU\nJOL+X/71rZlmHPGWmvbpZ9sBmRX5w2MWNK4TDRCBA2o0ROKQJffQxNdcc01V5QtYAF8xU3/lM4vj\nen3VNrDiSfKG616zayuNtW7a58kGjV2+1g0HrIdxHkDHSy3p4m7OFfsYT/rLs43a1p61aXmoflS3\nFb9Mh4pYNkNBzgNDADOCaQlhIISHPn/hoelXUxekVqsexTG9vApDDNcEbu6xIQA398teuXVDBt0v\nXX1LWpE94EHKnGmTKm9n+qRm2hDA8WgAB1BicYtviWU1TX2wD0+JkunVS4j7KufZ2qZNXjZFTtk4\nP5AOhRjHdfNKmaHygB/QcC6vzhFCSVLIQV+iYDsV54hjW73yaBgw+pFxAUScN4SnLYuWMDb0c6fi\nCiszC/KlDMLrB2SQoR8fl8H3oMyOtBJ9fvbZZ6c3velNo/2Pdo4l94AgqlW5Tc9Jf1uWEdUanlur\ntjtt13+WopSpHB5jHOO6nC+A2Wt40AyaXsR1BiAbJ96jh0tjCIDyXPsV16vPtFOGSdDsS3JWvj5T\njatkP4yHd7/73aMrdjm3RDFU+1377Z/WLTgmbW5RJa3f65w1ZWJ6dGZDhp7wzj04BOCd+2Sv3XJ5\nppWuXplLFA74DpGMR82enh6+6ODK6yqbN/+TQqBUgYakIJnOQKQuwPaZz3xmVUCj/l23n3mwvE7e\nTimyYMV++xWeqyxY99CNiBHHnMxOawp3ak8mrHrCwMAUo5jCE8cBBwo36HxJThRyPVs29q+/Msy+\nkA0zoYmxjA3LVj40x30XzhyZm1o/T/0zqlRiVIwF1C7AiKplxoyQBLrVvTNwFmdamjHXSwy1fl7J\nd6pH8RL1VTfCkALIPM643m6Oq+8DhN13iHCMspXuhxfbrwBZv60ynmtuu74E/uZFhxHB8GAQGs9E\nqEbxjvWzF6aNM3OC2P6953V0uu5DZ46EJPYfwz12Osd4/H4IwOPxqfVxzdbxvCzH/HZV0g3P5xEZ\ngA8tlC9rP6oC+bGjTAFkXXg4vJKIDde/b/rMiwVwvELKGWUpRmaqUVndx7E8Q4UWmoTSQxdS/rzj\nAM1yXwpfbKxbQQnHNchMDa+02+NjP1OweCe8Ml42Ct90lFLM/zS/FMtAALFM59IbL/dv9X7d5q3p\nf5etHF14vdV+Tdun5OlGB0+fkh6cwXdWj/E+tLyYaFCl2jdugEncA08PSNgHCHpmPGbPpd4fTdfX\ntM30JHWUsSyRANi0X30bEBM2CWbD98aN68F6hNdcfl+2wagwt9eUJMLoNGYZVeEpxyvgdH/RD2U7\nrd4rWqLvXGOIfAD0NOo98h8YZ+LQ8jBc66X/9Y20dv7R6c6JrZmLaK+f13pSXj9t7I3HDAF4D36q\nMnhRRhRqZPICCO8tLGACviShl73sZdWPCOXkx900Jxb1fGPOfN2VIvHmcceOTOQ3pSiscUqGcqoL\nxcUyjwzh+veUFYqaBwi8A2ib2nKsYg887lLE/PxRYs5HofFiAVqZCFVOxyiP55mIQ3crwETMmnSz\npnBTu8BGohKjwjUC3iaPT3UoijUyXjELTbWHm87RtA3QLctj5Me3rk6rNm1JPON2HvH0iRPSAZMn\npJPmHZgWZQakX++GMSU+ijIPaVpyz/UxSgCx8QCITQkS8wRWvYrfCqYAEBsb3QoQU7u7FONLSCCm\nBgHqAGOv8ccAFfoAupGJ79n6DSzO3n1d3KMx6/7iLwC6XXjG1Lu4v2iTEclQCyPTPTN6xYb//Vs/\nTOun5mIq+Xy7SmJaWjlOBqnjdtV178p2hwC8K3t3AG2L7wAWU0hY6gCZxyOOY3oCOok1b3qDRA9J\nOLGKUJyeMv3ir3J1nwHF+aLd+uv0nHzz0PnT0/1PuFdjbDf2Fz8966yzqnq2tlFWQNYfZdxPIlQ5\nzzbOI+NVUX4JSrzsVsJQCA+yvo81frtVzowJxRNIN2sK18/Fm0VxUtA8FMDb6tySbWQPEx68+283\nxaZ+rk6f79i4OZmqdNPaTWnN5i1py7YRKJ6Ys5pnTJ6YDpkxJf9NTZQqkBirMLbEQ4UKQni49SX3\n4jtJe4A4cggwLIC4F29WW54ZA0ZJyF7uQ9WpyESOa/IqTg3oWrXlPhmSnrUKbLLkiex8987g6law\nNgHGAc5ejQeGCuNcbBc9jXZnwBDHYVVCXv6K09KDnvXStGX/1r8R+65ZuaJahrLVvUV7rV6nTtg/\n/cFR86pxU+4zCB1Xtjee3g8BeA9/Wn6wskTFFE2pUe2G9U0xm09roj6vD3C1Uj6/WL4mfeuGFW29\nGd1w+uMfmp5/9nnpxAc+NK1bvSp96K2vTzdcdWWakn+wj/7L51XlC9t2V/6Bf+TtZ6Sv/fuHG3fj\neUq+WZJpUnE0SoAREYqh8aAWGyMRinfAOMEClFJOcSq3l+950speuoYmEUsu51g27RPb3v/+91cF\n9H0GnlE4Ib5v92r6DQ+cISImyZNqZTAYDzJZo4gIhS1+101BknbXsKd8Jy4rJhqhCoBikQHMQpMw\n2gBxGFD6Xry+TE5rOi62AV+lUOUH1KuwxT5Nr56DAi0RDy5ZHs+EkdzKeIr25CnISAaWRIUqhhRv\nOjxmYG1c9CISwIBsTEPC9vjtAXhGumsv5X65rOiLz3lP/p3vGN6wz5bNm9JnLzg/ffWjF1ZFV/xW\njzn5t9IzXn1mmnXwSCZ1L7ri5Fyk43cO3Z446ByD0HHaGY8yBOBx8NTMYRRX9MNUnB7VTMQWWbko\nSxm+6C/0Zz1eKfb7mzu2W7ytbrkEYOB7wKzZ6SmnviqtXrE8nfNXf5H+7l//Ix04Z26rw6vt3/vq\nF9J7T3/x6D6sZQuTKxoQSR+jX3bxhjWPoqOIKVXKrUyEEmsFWCWIL85UXngWrU6BwmTMlMeV+/Is\nFFzoRoB40NSulfJsRw9Gm4CDF8UQ8OziGcf39VeKWqwwwF0ogjHWCqzrx4+Xz56pLPh4hsaQjGkA\n2cr74gnrz5jOZpwAVeDTSYCcZCV0vuUAuxVGLxCOMWSMevYEAHo+5Vhtatd0MjWoXQPxXoJUme0d\nCWDatl+AM6akF/FbAuZYFtQvL1yS25JnvCA97rkvbGyKHli+7IZKDyw68T5pazZYvvSRC6r1oV9z\nQZ46Nn9BZah3qyvm51yBJ+RpSXUZq46rtzdePg8BeBw8KZ4iStOPD/UVSgUNKcmJh4BuNbfWj1NM\nq5TP5Hm/y/N0k04SAHz8Ax6cXvy7J+Yl5r6XJkyclJMi908TJ3UXI7vuFz9NZz39CRUNZtqNODVl\n2E4oVcqB0qLEoiKUz+2E12PpuDImTOFRjO3E9JaYP2k/5w8lGseJ33YLojwXx9sfOHa6X8+wmvaR\nj5G8w9NmXLUTSTUo5vDWJZbJA9hbRZwVKMp/CAHKxrYx0ko8e0Ac6zP7rfCIy3mvTccCboVgLFih\nHGO3woDyPInxauxGMRnjQRihk+GJwTLewtO1eANPtZWxEdcGgAOMy9couBH7dXq9Y+6idOeMHb1S\nxyxfdn163Z89Kp176RWj3m609c6XPTed/LAl6VFPe05PumJmDl889d4j2dfRltex6riyrfH0vj3p\nP57uZC++VnVfJVb5wcmqVdWGmJLC25XAQigPUw/sV9Jfm2uUU7Vzm/9W3Z5LGmZq9/NL35++9G//\nX0URoZyWPGXkPG0OrWgqihJlWKcBgYzroqjQ5ZQjsCqvtV3b5XdANzJPYzsQxwa0E0xBeEn2A9jo\nzhLE0YfdgC9lDzyBL2WJCm8Fvmg2oI92tK/iEvV5qK2uW4IOY8t5eLsXX3xxVXy/1f57w3ZjAzCJ\n0YrPEvSsXAdxYfHhJjGuVKkCSIAYGMo49lvhEaOom0SIxxQo0+A8Q6xNN+I6MBM8cCAi34CxLInO\nmBIeQFMz0loBqpCCet2odyIzG2h3MrD8bvSTv1IAuft3DREjx8y0yszer0Xm87Krr6o83KCay3Ms\nPvHkdM3PfpR61RWtkvrGquPKaxtP74cAvIc/LZ4PD9d0FD8sP261XVnpMkBLbwAA+ZHVYzy93uKa\nlbendavuSCtuWZbe+aVvp1/+4LvpA69/RXrYHz8lTZo8pW1z8w6eV8XUJFqJzwbQdkqEattow5di\npaVCAe6KzaOOm4Qy5E2Vx6DysQoRx3McD6aTxxLto40jAxk4NK0p7FmYw4tiA+pAoJdqWBJ1Yt4o\ng0bIQbLRviD6S7Ihg+iFL3xhlRXO2wSwjJBycfl6f/hdqBsO+ACx/td3DC79b/zUARGYWgrwb/7m\nbyojtxXIl+fShrCA6T/GGFqXkSAHQbiIMez8jDXX4zfaJKecckplLLzxjW+svpbMJ66vVGevwkgz\nVrBDAcCMPZ8Zm2hz49JvEqOyukUOnaSrmQftCO5xLbPnzU9X//j7OTGrV12xMwTfEzou7uOefm3P\ne93TV7ePn58VK0FE8oQfI6/JNBOLfAMNtJXkHfEcwoL34wd+pUzMSqIXmT7zwMrbesLzX5amz5yV\n7v/wR6WFi49OP/3W5R2bmX3gzIoORz9TQjx0Xscg45RipTGVIi4IuLZKmNJXjJYSfCl11xXJO9qh\nTNWc7kYYP54PaVpTmLFkioupQmhp/cBo6hZ8Kc7FOZYd4OueeVr7CviWz8DSepdffvnoKkTi9/qy\nm+UcGYFoYOMxDC5eKaUPlOvGKs8XCPrdlUxJeT31987BMA4R1wX05p5HYqS25BzEmIl9y1cxblOC\nQiw9WJ/REN9181oa587LoHFdjExi/JtVMX/uyOd6m9Z5ZoQ3yYpbbkpHHHfvrB/61xXaHZSOa7rG\n8bBtCMB78FNCvwFdRSpCUNAs2Ve96lWV9wt00b2sdZ7y0qVLY9fRV9NGehGU037Zo5w6fbs3afH2\nzRs7L1/X67l6uS77utcochHHmmq0ZMmS+LjDq5KGvJOI8VJCEqZ4uejoUmSkdiOSa4LqpjApyhAe\nD08L4DMSeMVit62MgziufEWZAvhY+Yb3p4RiP1R92e54fs9gApyxXi3g9BtQ9xr120lQsJ4FIPYs\nGGNCBgw3/VwCMXBXrxoIR3JUp/aFQyLOzKvEegi1MOiCUdEWEI6s56Y2TTl0fuKaVApjfPQjwDak\nZHnQ8SRyJVqViDzs2OPT+gzcv/z+iIEfbW3LxuX/fvlz6aiT7lvFhnvRFVPy76+UQem4ss3x9H6Y\nhDWenlaLawUupmO0ij/+NBdW+J9c5aiTRBKWaUj/9OqXpgVHHlVlP96YY0FnP/OJ6f/95H+lOYcc\n2raZBxwyK93vkJEfeNsd+/jSjzXm2cbhlLAKP01CYQdQ+p6n8uhHP7ra9bLLthegt0EMEHvQSRT1\nUOSARJEU7yW+8HyALgZCbDgUr++7FZSrBCvPlLHAwJJBPpSRHkD5m3IWaxzbKgteCAAIdisMJdO/\nJMNhKzwz7II29DvBNkmyUj6yFXVcns8Y4FlHWAI1HYU5ymQtx6DGsSF1Gtx3aGJTD1HYBJ2szGhT\ngZ1qhzb/MQTdXzn2xcWxMzxkY/jXK9amK65fkbblMVeXb3/+U+kT7z0vvfTc9yVZ0BvWrkkfOeeM\ntPr25elv3/PBnKQ5sSddcfzcGemhRzTT2vVzl5876bhy3/H0fgjA4+lp9Xmty9dvSl/99W1pfV4J\nqZ2UALzi5mV5OtFL0ro1uTBGjgc//bQ3pIf9yVPbHZ6mTZyQHpkn2s8/oH2cuG0jLb4s59nGLpK9\nzIVuEvNkYy6p7ylCCpGgHnk/IRQuOr+ToCaV+SNiuSoZ8b60JWuXx4OKbJXo06l93pzsV8J7oXQB\n+VB27gGsh+UFASkRzzSHuBUTsnMLI1uApelOsRSi6T88ZHS1cXHqqadW0+C6obu1yOBj+BFhFwDH\n+yaMM98FQGOyjMmm8Ix9hXBcF2EYYEYc04vwuGM+cGT288R5/sCft70hF1m59KqbWxbq+crFS9PX\nL7moSrhybgb6KWecUyVc+tytrpicZ1M8/Mi56YhZ7Wc3aHNfkSEA7wNPmvX4ufwDu239iLLq5ZbX\n3rGyivPsf7dX0O7YplJz7fbv9rtynm0cI65Xgmhsp1xQziWlWHoiEmXEZUuhtCNWV24v38s8F4sk\nYmiymXm8lBvvQoy2FQNRttP0Hj2IYuUlEd4RDwWgD6V1DzBQnvKUp4zGagGZufH1oiytW9j+DS/R\nMzVFDYXM4wXEQgGoaIlfp59++vYD2rzz7GIqkjEhtBGeLqNQiCJiwbxQIQ1jqC7GAxDGbhGePkAt\nY7v1Y+qfhS4ilCEmjX6u9EH2jP0WUOTG85evvjXdsKZ9iGltNsTFfFtNmeukK6yK9MfHLUyTMhAP\nZaQHJpyVZdgZe3cP+PFP2n//tGzthkwz9Xavk6fmVVrysZ2EdftbmX6emyfaD1JkkNapYV6A7XWh\n9ChlCoZQFDyQEhhZ/uGB2Edym2SndqJN86yJOKzEGMqRknZtEqyaFGi7NuM7CpKXG3FB02DQmN1Q\nntHGvvrq2WENxEjN+2V0qScNcJQQbfIsW/WVsQKIeL7oaIlenomsZgVZeNw84qZM93qbvHFjEahj\nSIyZmJLnPTaGoeiPB4+RYQDWx5DpRUDzoosuqsas6+FBC4METV4/d/0zwOdNE+05D30gKUwcHCC7\nNmVkb8wA3G4d4Mm5X8KQqJ/H53a6QiLoSbkKVrcrZTW1vzdu66xZ98a73gfvSbF8K9bsKrEm8FGz\nd7bix3K+cp5ttMMrpLDqAsh4HiFoP8lP5bQkoFkm7FCGPOl2QgGrTkQoH0kyaMol2WsG7qFY27XR\n6rsLLrigmppCEQMAyxbGHO9Wxwy379gD4uy8QklTIRIRPbMoxhHbu3kFbEBYrgCP07MGfNgPNHS5\nYESr9urjytQpzziEYcCjFsYgDEL0Mu+7LrxjU64CcLFB1tHuVkpvuSkRi6FBorZ3t+32ut+sqZPS\n8XNbF1Dptb29Zf+hB7y3PMkO9wE85mUAvmH1hrR52461YDsc2vHrGdl6thbw9B6zrTs1LKu0nDpE\ncVGqdU+BxxhWvjbN8aSAgVoIT4OSK4Vn087TdG4KnidDgC+PS/JMfapX2W4370855ZQqyYe37n54\n2a3qHXfT3r68j3EhH4B3h+HgCYvF8hxRuJEI1Usf+b3wDoExI84Y0I6SmMal2Qntxo5naswBOM/Y\nK489PEivPGXXzBt1zabE8VglBJZjF1A7p4QqIsMaaHdTKhVwRxzZ9aLUiWuLkqaLMwMU+sFqWBu3\nDlY/WKr093PsFwgPZcceGALwjv2xV3+ampOkZk/J1aIyCG+9m6Yd6w1PydTzo46aP3DqmbKL2Jdr\npCAonjLTFUCqllSW3kMRooTrwnMQ8woBou0SWgA9hRlty0Y25Yh3MxbRnoIM6v0ScUbJXBT6UMbW\nA2KtpinFnG9eJ0ZBUpw+70eMOwlxQMqY5FGal+8VSHptNSZQvsYRsIxxBHRLcbxxyIC0Hy8VIAPh\nEuDlCPg+piR5dZzt7YRxItMbwPsz3oj7EvMGxLK/fRZGOnj65MpI33Jnj7GqFhcxOa8V/bAjDk6H\nHTiSiNZit3128xCA97FHPzMD8KEzp6brVrWP93TTLeb8PuyIOQOP66DdVLUqhVK1xnAIWhD1GPFe\nCmRJpoWbMpCV5CsLbqCn63HlaBe9zVMWQ4zs0bNymkQ/FYmizXh1T6aSoLUJj9dSiGP1pqP94Wuq\nPFa1lC/L08wAGaNLMRPGnDnAQeX22lfGF7CMhKn3vve91dx7njag5yWXCyhoH0DzouN5K64CWOvP\n23HAXciFBywJzDisYrNFIh6PF5jGPHjLDAqhBJXd6p4i3suLVy/AdTEahGT8fgB5XNP0SRPT4hyu\nujYv3jJWED4gM2O/s/CgdPScwYamWt3neNw+BODx+NTGeM1+ZED4jo1bKjq6V2N3Ul4TVjz59488\nOB2S2xmkSDAJ7zDaNfc3MpBtA6hKc4ZQHsoSxnSP2O6Vcixjw7Y1KWKKDfBSqGeeeeZoPE6d7ahF\n7Nh+xZrNCoDw2ilz8cRBtNvv9ezNxwE9c6fLRTfMqQXKpt3UQxi99gXQA+yXXHJJNV8XuPMmea/a\nDjDTrjEJ5ExTI0AYs1JSzLYzDNDDvFT7aF8iF6As8wxMJTJOjVftqostXh3UsrbqwpCMWC+wdU3G\nIGDmmWtfn4XwhI+YlVf12rQlbcrX0WvipoSr2Xmd6N/L832PzGA+lNY9MATg1n2zV38zLVunRx10\nQDV3d+3mkRhnuwxInWFB7ZlTJqb7LpiVHnTYQdXC7IPsJPNsxVlLMaXEGsIh6thG7Mo2sTGeb12h\nxf6oZ0otBEVd0oCyqWOBBrFj1cR4FgSl2U3STbTd6tU9vPa1r60UJuVsmhRDYyi7rgfQt1Y3AmCX\nZeAFVjxRRVTkB3jWYxElKzEaxo5FFHitAE0GdkxNC4MQFY2xsQ/KF7gat3UBijL2edraMm7De+U5\n+x5QW2HMuPQdWhoI2xYlJuvtMvrsS0qwBcr+jMk6czQlh6vohxmTJ6V1WT/clf910g/CUTMmT6iy\nnX/38DnpwGHMt/4odvo8nAe8U5fsexu2ZRf41nWbqtjPLetGkjD84HKkKP/LwJuTKBTXOPzAaWnB\nAVPThOwBD1rKebbRtlVivvCFL1QfKS5gGglRNiow3642cr0SllieCkOE8pScQjGLK5sKdO6551ZL\nOvp+cY75xXq0Pvcjrtk8y6jVjWY0d7k0APppd3hMbz3AoMJkhBcIcFTSUuZxLAIglQkFjm9961ur\n9hl0YSB6znINgCrvOBZBcE7hlHbjAB1tvjDwJIAT6Id3LbbMQAx6W2yXZ1xOuasOzP/x0CX5EftF\ncRfGgtkD2o5M/2qn2n935t/IbbmYj9yRm9duSuu3bKsAmX5I+Z3ckoOzx6vAxoKsJ4bzfGsd2Obj\nEIDbdM7wq93TA5RD1PiNM4qVxjqr4rdipSE8AcBGcbQSXogYcYhjxHUlPKELyVFHHTWqjNCJT33q\nU6vtPJByyka1scf/gLepJkE9or3r1HqPTQ53H0MPiHeKuZe5BQprWE+737iwywGQ5m4z7FTmIsYO\nIBbOIMapOK3iG7EONe/YMWWiVbVz8R8DDnUeyYjA15gKT9fvw+8mchUANHalXsCF5x2GLICWGU4Y\nJIwC7BFq229kKLu3B4YAvHv7e3i2Wg+w4AFhSRPzDCJpisIsi26gFMVSOylNiTf1NoEhZSMRRbWp\nEF5AzAemEMXgyvnDsV+3r8pjSgTirVNqkrjOOOOMbg8f7reLegAA8no//elPj55B/BQtHaA2+kUP\nb4wXdPdLXvKSUSPO4fIPAL+EKkwLBsaYtJ1gRKI8arWh4T/7A20xX2L8CqPEbADZ0Iw7IEsAqbrY\n9d8HALYPEMcsEW2rCufaGAOubyi7tweGMeDd29/DsxU9wHso59n6ioIAvhQI5RIl/XwnliYTtFW8\n1z7kiiuu2KHghm1iZUBX9nNJ/TkX74QSApaWd6zHwxzfrVhY3IpVlBtjAf2plOFQ7vkekG0s9i4G\nG9N5AJvKZoqqoJL7Ed7skpyHwKOOBR204/lLegK0xoOxFkDpe56y5Kd2xp4x6bp4taYqaUc8mXfM\nm12cQyXGbyxbyFj1fVRucx4iBqwIDaMQDe33pW10uWvipZuTPJTd2wNDAN69/T08W9EDElFMuwih\nFHjEFBq6NjwF31MynbwF+1E+vI5S1Gkuqbv4jhKj3IAzQd91c444vnylGHkRij8Q7fLeVVMayp7T\nA0AH2PIiTW0zBlC4H/rQh6p4rbyCfgSQmpOLhhbfLWOxWBVGXXitEYt2HsAIoNtR0fYDjn4v9gei\n2sDoGGfuhfdqTjyR9W/+bxnXFVMOqtq1RIKYdnwH4LU1lN3bA0MA3r39PTzb3T2ABo5klegU8S6K\nS2UrXkqImFUor9jW9GpKhZhWKWJkrTJeeScR61XrV2H/foSXzkCI+J5zmio1pPT66c3dc4wcAzFh\nhh4KmRFmNSWGlPrLgLpXAWy8S3PG0bz15w8Ugeji7LUa+87pfPIFeMv2b8fuAE3TjQAp9sifODNm\niPGHYpeIRRiTQjthANq3KRM6trvfbn5jvfbJcP/2PbB/+6+H3w57YPA9gK6L8njR+sc+9rFKAZXF\nNSgsiVOlNxH7l6+oNYlc4QHEdwCWcmoSnk7Ema0prMpVP+KclG4oNxQ0evP/b+9c4OSq6jx/IN1J\np9PPvJ90h7zBgGQQo6tMHEEEV0ZkV8Som2xwQUA+yyNERBxEJ2AYXBSM4sYJIDDM8BlY0GEdHo6M\n4bN8hiAvQSEEAsE8yLOTzqPzgD3f05zi1u2q6jrVp2NX9e//Sbqqbt176t5v1T3/c/7n/yjUkZby\nOTomPgEypuGh7tdE+QRqAKOY/cAs9FOZXTMLJjQpOdNNtoMpnEGan/WihEmugZc/sctJT//kcTxn\niYYZtleWKFC/VENsOWvRXvhNe8e/5GDAV2JiPx//y/WyDCM5tASkgA8t737/aQsWLOgyS128eLEb\n2XuvZyDRMZA0gZlBPsFEjcKm48KMlhSUN16huYR2vTcsOYSXLFmSa7dut5EXmAQgmDHpTHF+IU2h\npHwIsPZJTO2ll16aOWkck/jt4A9QipAvnN8FIUrJNd9kWyhSPztlOwM2FCBWFH7PfLZfGkke5/fl\nWJZWmLmiwDE7c/9gSvemZ47Hs5+ymcl15uTgAsVMGyj95JJP+jP1uncISAH3Dle1moMAyomcykmh\nig3rrsliCswoMQPmE5Ttb2xyBRLv03EQD5nurAhTyiU4SPnkGnRieCyXIszMr363kiezbDpMZk6S\n8iOA8mP2yPq9Xxvl+0QJp2tHF3t1KHQyXl188cV5Z5YsjbD+i6BECX8jRpfzIVyO2SsDRQZ4uQRT\nNrNhnwKT2TNx5pjS/Vo2s10GnJi8UfpIcgaM34VXzulBbK7P1La4BBSGFJdn2bZGsD2pKbfZ/217\n92UqopDdpslmtGm2gfY8Hm5Hy6VIMs7WH084EVmikqYvcu3m80LG6YSCDHQgOKUQOsQjM4ZkmUE6\nJmYHabn55pszsZqYp0lmECoMFEjs772zeU42JGbckvInwGwRq4hPcIEy/O53v+symYVeHYNDPODx\nd8gXhsbAEZ8HX6wBBczaLaFLeDTzu0ZJ8pumHa9Ek+eCGRpTujd5kw4TxY453P/GiQAgpaufkTOA\n9NYllDafx8DXJ+lIts9z7tG2jgNm2x5b4cn2EXsOkIzDGN8/0DcMtX1Eqf1D+vP6y2sp4P7yTee5\nzj02q82qre3m1W02CbwtU7jX3ljp3NAkvqqxncAgmxHryOZaM3lovSvgnafJLpuTcbb+TZxGmI16\noZMhxMjPQPx2HlF6rJHhMU28JorXj9qZqTBb8EKnQueSFtZqMQsieHxihuMzQwRzN+uFvrO88MIL\nzU033RTShPYtAwL4BrCWmnTow0HvtttuC84jjVkXk/Tpp5+e18+Az/OJZlD4c6yPBLNhlB4DPRQx\n7fAea7+EOqXvE5wWGZyiSBF+29wr3Ave5Mx9Q0pU7pFkJi78MXAaJDyP7UnpsKUJX91m45m37nJ9\nA/3DwdRSMUNysuWRQ7rV1gSfOqwuepra5DlV0nMp4Er6NgOuhRnvS1t2mhc37TTkgk4r3XxNoYzr\nqqvMjBH1ZvpwW5KtmxkxnQuzzaRXMzGKrAV7obNhtJ4WzGYUXWCET+dAB5LM8sN272Tij2VWne6c\nMOPhcEOHxkwVh6nQxAukqVy0aJFrg86NnNF0rJLKJMDsFW9mqh55mTlzplvnDy0dyQAShU6ccDo+\n17fN79wn28D/gSUUFC7C75aZLIoYZcqaLTNc0lymC0t4ZerbxTeBGb1fomG5BqdDll+YaSNYloid\nZ9/TTjvNbeMzX92+yzy3sc20dxwsunwpyniIrZI21VZAOnpkg6l69xpco/rThYAUcBcklb+BUe3j\nazeb9bb49r5iNW8KC3U+R9u80H/ZOjzvTcbaFSZiP2OkCTwzucnpRBBG9ElnFLYxiscZBXMZsYm8\nn8v0RpKL5PoYZjbCgZLCuhbKmw6Vz2Qmnc/Mljwu+fyzn/1sZq2Y6yHUgzAWSeUTWL58uctw5U23\nDNzInEUGrRBhfZYsXDfeeGPOUpgMUPFr8I5Q/I6T2dr8ZxHnjiL2Mb2EJTEjTno5M+glpM8rXR6p\nJubvQ7JlYVb3yzTcG8REI1zXIBvu9MSbW13JUqxipUiVHamPsBXTPmb7h0FVYZamUj6vXI9RHHC5\nfnMlnjcz339dvdGst0nV06akkCY5doddE3p5yy5ncspVoCEZZ4sC/eY3v+k8NL3yJXEBo3gv5GhG\nuWF2I16SWQAKOtf6KoqUkbsXZsZpr2c6NUKYfOdJekrCP4oV1tSYOfvYShQ3nR/XJekfBLC6kOoR\nxz18D7C64KyF1YbZZLGC4kbhseyCl3I6PI7ZLh7Zfu2Z2GTugbQ1h6UX7gna41yw5nDfcG68x33G\nrBgHL3JI89vHYsPMm1A9FDy/Ybb52S6fTTwxg1nOYcXG3Wbdzo4e1QNmXI9l7YVNO8y0YfUq0JDn\nhyIFnAdMJW4+YD0tH3ltk6t8lFrGKflyqaS02TpmtNhKKEkljOKi2gqCUxXVYryy5YZnpO07ITJX\nUfkFkzMdB4oXExudRC6hs8FZJim0l96f2QEdGYIDCjViixVmEGQY8t7Z8+bNc3HGuQYDxbap/cqT\nAL8jqimxTsvgEPMsPgWYe1Fixf4mSLtKW5iiOc77MXgqKFva9gNLHlG23hTt9+MRJYuXNQNMZrbM\njFHEDBoZjGKp4R7Cb4L7hXPEf4Fz5j7j940Vx1uDuE922P02DBpqttjEcKXNe5Nn2PmcfoYKa0fY\n/kHm6K58pIC7MqnYLc9uaDOvbd9d9HpvsSAoT8bMemz9YHcIYQ/eqQTzMfGyXtnSceAYwnoTzlN4\nEGMyo2NC8aKAc3U4yXN55JFHXNiG34aiTOZ3Zjuza0b6SLqmsNtY4M/SpUtdVixmBJwLpeu4Bkn/\nJcCMFzMuyssP/rDCUOSA3zMKrxjBkxkL0LXXXuvC1rwnsj+WmS2zWmau/P4wDxdKEYmyRdEyyOUY\njmUWjfJGwWOe5jfMbJgBKrNvTNL4RVCUgtetra3O23rtHlsooqbBvHNY59qzP6eePuK4hdc0g3RJ\nNgGtAWfzqNhXhA48ZE3Pu6yy7A0ZUj3AnHTkSPPtry80P/zhD91H4PzBrNMrVGYAKEY8Ln2tXW5+\nZst+n+7OjZG7D61gXzq+OXPmZB1G8gHCnhCcstIZsrJ2Tr1gne7OO+90W+nAyDKUXqNOHaKX/YwA\n4WyXXHJJZo0VUzHFEBhAFitYhFCCrDEzGE0KM1bWg4kNRkjF2l02OH88TloMPH0pRBS6tzxRHxuF\njvC7xoMfBY4DVv2w4ebf1m43b1d3xgr79mI9DrZe0n/ZMsKMqe+d9mOd56FuRwr4UBP/M33eb1/f\nbF6xoUa9KQfeetP8j1M+4sIcCNHxGXn4TNa/cIjCLI2yJeYw1JGJUT2dhRdmEsy2k6Znwiyo8YrQ\nfjK7lj8u1yNrYxRs8CFNdFpkF0qbCXMdq239jwAhaQz0sN4gKFEGnuedd17RMEhZiWmY5ZG0JL2Z\nMU0TtpdW1Oljkq/9Wq83mTNQxWRN2J53XGQQzEycRB7L//XfzRt7rcE48uw3eU5j6mrMJyer4EOS\nSVxbQ7JlPe8xAYLrUQCsj3phTZLwATI4kVUK81P6vx/9+mOI9d1g12F6W7btf8dMmn6UU4Be+aIk\nMaFhrqMzQCnihRmqfDl3b9b214HTVVL53nrrrRnli8m7WOXLjBzTt1e+dKx0VFK+nrQe0wT4fTOj\n9NWzMOtSDxgvf6/g0sekX99www1u7TZX+lJCnfyyCs5W3D8hwm+Xc8M3AisTs2pCnZLr1fQjZAAb\nNnyEeXbNn7pVvju3bXVr1CHnkdy3rWO/2Wr9RZISq49LtllOzzUD7uPfFqaqH//4xy7FHKNY4mUx\n4/7gBz9w5qTkzc7sDyXnza/+0gikf/yNrd3G8l126ofNgmv+zoybNNV8++z/7A/PPH76K18zc/7L\n3Mzr9JP9+zrMwA2vmuZ3OtyNinLEjMY6FyEV3PClCiYz71BFG5jkMM15YUbi01fiCcpsO72+5vdN\nPpJcgWxFnCeDBbgyM5GIQDEEUI4oXb9swTF4R9977715M7ol28Vk/LnPfc7MnTvXrTEn3yMLFlWN\nvNkYCw0DxVKE8yQUCkctb9rG4YvffMfAWrO1YYwZNKS+S9Pc079cdrN59O7bzOC6zuQgk2YeZ75w\n+d+YxuEjzY6tm4P6ilmjG82xo5uyPidGH5fVYBm9kALu418WNwvmJ2aRmJBQNJhh08qF2SGemqSV\nY90nKSve2Owy2SS35XruFfD04z9k9lnPSi+vPv+0ueWKi8y3//FBd9P57bkeB7ZvNQPXv+LOD9MW\n67vM0HsiOL4wUvaCCTuZ0ABTGs4tsELpMwjJl87St8EjyfJxsEIw85FbOiS0xB2oPyJgCZCohQGw\nTziDosRKlQ6NywWL3zeJOkhXic9CUnCo8k5f3PMMwH3u5+R+xT7HUYvfuY8R5rjdjaPM3qbcoXW3\n/+2VZvO6N82ZFy40LTPeZw7Ymf5Ddywz/37f3WbRsn8yTSNGBvUVY+oGWTP06KzTjdHHZTVYRi+U\nwLaPf1komzvuuMOtofIcJ6S08uUSvKdvWvnyHjlcQ4RRMcH4CIr459deZeZfvaRb5cv+HYfZ5O62\no+jJaJ12vNChcc1JSc58Gdkzu/ajesz13SlfwjZIucdgBWm1JjrWe3OxS36unotAPgI+u9TnP/95\nZ6nBURAz9U9+8hMzz4awFRLiypctW2YoTILZ2Zu1OYZBNwqaMCOsXaR1JV96qYLyZnmG9hBM0ger\nO+/1dJub1601K+6/x1z/4IrMvV9l17pPm/9V88eVT5iVjzxoTv7C/KC+on1fVyfQGH1c+tzL5bXW\ngMvgm+KGIUCe2V0y440/ddZ2cNpg7TKXdNgQgFLl4Tt/ZkZNaDHHfvSvimqienCtC68o1VSW/hDy\n8WIq80K7PqSJbXRe3gxPTWGKIxQSYo5pwytf4jGZQUv5FqKm94ohQMIOLDU+tpbZJnWBSWnpzcj5\n2mEQ+f3vf98NpH1KSr8vXvh+0I3i9PH1/v3Qx2QfQqKRGmtaziXrVq8yzSNHZZRvcp/WGTPNmhez\n16WL6SvecSUcki11Pu9pH9e1xfLYIgVcBt8TRd5xWvKZdNKnzPoT60iEFOQSmyujZHn8F/9sPvLX\n7xX57q6hXCkjuzsm3/soRpxHvDBaZ2bthTVlX0KNQurJYuR+n+QjCpoybaTxY5aPB6hPwZfcT89F\noFQCePeTOY30pV7wK0A5E4tbSLDKfP3rX3c+Ccl9mbUmQ+FwGkxW/yrUZq73iGn2Qjve2uW3+Uec\nruqbh/mXWY+Ynrdv2pi1rZi+4jBzWNYx/kVP+zjfTrk9SgH38W+MUmUk/ic5BOYs1pXSSoNC8Ji+\n8gl5WUuRNS8+b9rbtpljT/x40YcPsIothjCrTXt+eicr2ifmco11KEEw3ZHmspBQl/Wss85yMxE6\nNJJ50NlJRCA2ATyQiQu+5ppr3ECP9n9j43pxnsSEXEioKc3v9JxzzslSslh6MEcjzKax4CQtQ4Xa\nTL+XnAHjBJavfxg/ZbrZunFd+nD3euvG9WbC1KMy7xXbV+SaC8To4zInUmZPpID78BfG7A8PXcIU\nuPkITWCmR6whNw6CMwXejVRqySe1NklGKfL0bx4ysz52iqmqHlj04aV+VvoD6LCSwrX7sCAUro8H\nJrcz4Uf5hM6KNWOS4COYn1Hcuaov5WtD20UglAAWlquuusrcf//9mWUjTMfMcu++++6CzRHOxP1M\nLL136uIATNs+NzQx8Sw7lSLcR5wfQh9TPzC3K9C4ydPMbvv+y797zwGSYw7ae+rJh//FTDz6GF46\nKbavqE5NBmL1cf48yu1RCrgPf2Nk20HxnHvuuZmzJJk7o2GcPhDWixjRFkpXR1WSUmTdq6vsKHdG\n0KHDS/ys5IcQj4tzlRdmrH6AQRWX22+/3b0FG8KT8gkdHqx8MQWULpWWunPSyteetotAKAG89XEM\n9NmoMPlSxhLri3cczNUmqU9JvHHllVdm3uZ10kGLTFp+IJ7ZqYgnOD35MoYoQPqHXHYrHK7mfes6\n87NvXWpe/8PvXct72neav796oRk5vsUcf9JpmU8rtq9orskezMfq4zInUmZPpID78BdGiAzmGT9a\n5VRxxMLR45ZbbnFnTtmyZHxsrssZbTPQUDA7VDa8/poZ3Tqp6MMGDTjckO2mJ4LiJQlGUrzp+Z57\n7nGzCt4jJrrQDOCXv/yly4Pr19IwURN+QecjEYFDSQAHK+5ZsrZ5warFa4on5BJ+p6wdY93i0Qte\n0qwzIyhwTNGFFLk/Lv3ozdDMsOsOf9vks1zNPvWvzclzF5hlV11iLvrYcWbRp080B+zy0PnXLzUD\nrE+Gl2L6Cpanxjdk9w+x+jh/HuX2qDjgcvvGSjjfA9YL6xcvrzfkg+5NaRxUZU6fNqZHVU/SNX5x\nPvNpIVlDQ/AIpePy5rj0NTFrWLx4sdvMrIE1cl96Lb2vXovAoSKAomQgiPOfF+LXMVPjHJhLGFzj\nYEnMOo8ISpPoAGavCPdHaGY5rEx+oEus8lO2qU27s7NUucYTf9rbbKWl+oaSB7GYuj81ZbQZXOKS\nWOJUKuappgMV81XmvxCcLKYNqzOxHKRyfdIAa8OaYj+jJyXHnn322UxIEZ+BmYzOhdALn9CAmQGd\nRy7lSwf38Y9/PKN8SZLPDELKN9c3pm2HmgC/XQaGeON7EzC/z9mzZ7tBYq7zITyOlLPki0bpIljB\nMEV7yxjFF7qzgqXb9jNgtqPIjxrRYAam1mfTx9Q1NpWsfDFxH9E4WMo3BVUKOAWkUl9OGVpnGmve\nMxnFvs6GQdWu8Hap7bKWhXNUUsgAhjc04UbezEZqvlwpLVHSlDTEZI+Q0Yqc2N5zNNmunovAn5MA\n4XJkrvO/YxQgYUus++bybOY3/NOf/tT5fRCChDQ1NRmWn7xgiu4u1tjvy2MyFInPb22qNUNrs9dn\nk/v39Hm9tY4dbZW8JJuAFHA2j4p9VW3XZ2ePG2pqq0rziC4EhlJjHxjbbAbazyhVSLGZFOIeGenj\ntUzmKoTSbb7IQ3JflG5ra6vLGMR2Qo7o4JKJ55P767kI/LkJUMOaDG9YbBAU79VXX23OOOOMjGk5\neY44IbJujEMm6SkRav2iiJFdu3YVXXyE/ZmB+xk0g9/D7frsB23/UDcwfv+Ab8j7RzWaIXm8rTmf\n/iql95j9lVgZX/co6yB1zKgGww0RSwgrwHw1riF3OrtiPgcHlWS4BQ5WLS0tLsUk4RYIXqPz5s1z\nz5N/SOROxReyDqFwcdQio5BEBPo6AbI/UauaTFleWA/GJE3GtrRgESIKgtBEkslg0sYUzSNC4hqq\npRUjHONnwZQuZAAwdPBAc7wdSMfsH1j+mj68zkyyFjhJVwLxeuKubWtLHyQwwyrLWWOaSvKKTl8O\nM18U+jF2dFuq4KVMrlsvjMrnzJljTjnllIyTCCk2k44rfl/KGuLUQudBqk7KD+ZLx+mP0aMI9CUC\nWHlY3yW0zmeR43eMz8OvfvWrLqeKIxbe0zhlMehEiVLwxAuFG5KFFvz2XI9eAbO8wwwamdg0xHzk\niGF5k3PkaiffNvoHfE9mjWnOt0u/3y4F3A9/AtOH15sPjR9q8FrGOaIUabDHYrI6ZlSnCayUNjjG\nx+j64+l4zj//fPPQQw+5TeR2ZlabFBxOMDn7jGDks2UNGJOcRATKkcCXvvQlF9OOHwOClz+KdsmS\nJV0uhyUWfv/MnFGerCVTnhNhuQZnxmIk6YiVjCc+orHWnDRxpGmqqbam6WJa6rpPvTVlv9+WHjzB\n9hGS/ASkgPOzqeh3Wu1I95RJo9wItc6GBRRzn7EPa0RTrTmJYyc2D+kRI9Z9vXMVDdGJkCWI+sfI\nuHHjXNFz9+LdPyhsOimfkJ6ZAA4oPll9cl89F4FyIkCY3cqVKw3Z3RDujUWLFrk0s+ncz1iEULY+\n3SWDUO/zgPMh/7sTPwNmPx/S5I8ZU19jTp08yjpO1dt7vqpoRTzE9iUTrUPXybZ/mD5cTgfCS7IA\nABfESURBVFeeZ75HxQHnI9OPtrfvO2Be377bvNG227TvP2BNuvbm548VnDPsPzOkusqGEdSaFhtK\nUG89nnsqdBB0Nl4wxSG+zi/p8tKdAgkJGP1jcmZ/wjO+/OUv+yb0KAIVQQAT8te+9rVMsh0uCqdE\n4tnxjfCC2Zga4ITZ4ZxFljcGowjx72R+82Ztf0zykePJiY7g7JgsdJLcb/f+g65voI/YafsK+obO\nAi/vvNs/HGYwN0+wfiAtVvk2pbJdJdvS82wCUsDZPPr9q/0H7XqQveEO2NE3Qlwvo1q8qGMJDleY\nj1GkXkilSc5mtjGSZ20YZywvrH15UzSms8cffzxT9s3vo0cRqCQChB6hiH25TbJgEUOMM5YX7pMz\nzzzTkNKRQg44NHqfCu4pHLryCfcaGeOYaTMbLiY/Ov0C/QP9BHdvlR2d493ckwiIfOfXH7bH61X7\nA61+cI0oWtZ+yOnMf57HVL4gpNBCUvkSSkF1I7bhhEUVJK98WZsiGYdXvmT8oYPxNVf7wVeiS+yn\nBFheIe7d5y5H2X7iE58wN910U4YISpnwPEzShN5RspTc6cjGjRu7xNZnDrRPuNe8GRpP6ORyUHK/\n5HMG5I3WAkbfQA7pZus5LeWbJBT2XAo4jJf27iEBikdws3vBlIwJzScRIBWlT6uHOQ3TmA/JmDt3\nrvN0zlf32LepRxGoFAJYhViq8eZh7pOLLrrIzJ8/33lBc50UJfnRj37kZsGEIqVrB3sP51xMvCMW\ng9/kfZlrX22LT0AKOD5TtZiHAKa0559/Putd1q68gwkje8KPkGXLlrlOh86DmEVqId9xxx1Zx+qF\nCPQHAjgjUvWLMpxebrUlOElK452tiBYgk9ZXvvIVZ0nya8Us9zCQTVqcfBs8+hkwz9M+F2yT9C4B\nKeDe5avWEwQwpyXl+uuvN+vWrXObGNVT/xSZZxNu0JFgEiNjD+XckiUZ3U76IwL9iABmZZQuda29\ntzPrvXhOY3pGGLxy3zA7RgF7SxFhe+ScziV+Bsx7UsC5CPXuNing3uWr1t8lQHIBn1KSTWT8wZEK\nwQSNhzMzYVLu3XbbbW47ZddQ0L4KktuoPyLQjwmQCYsYedZ+EeLfccqirB9CVADlOxnMJv0kKGCS\njPV1O9s/yRlwrvf9fnrsHQJSwL3DVa0mCFDj16/jsplEATiOIGTxwSOa4uKs9/pk8+TEZdSeHKG7\nA/RHBPo5ARQueaRxuEJY2sFhiwQ2hDBdccUVTkFfd911hnKHCNakp556qoujFVXF/IxaM2CH6pD+\nkQI+pLj754clTc9vvvmmW6uCBOUCUbh33nmnm/m2tbU5z8wbbrjB3Hvvvf0Tlq5aBIog0Nra6kzP\nZ511VmZvEthQ3IF80Czv4DVN7LCf5TLDZSaclLQndDIne3I/Pe8dAlLAvcO1LFslxm/z7g7zuk3I\nsXrbLvef52zzccGhF5bMTUsC+csvv9yNwhl5Y16+4IILzBe/+EVXjIGkAWTHIqZRIgIiUJgAa7xk\njiMEyRdkwFmLJRucHXFcXLFihcupjqJFsESlawd7Bc37hTyhD9rsG1t273NJOVz/sLXdJfDZtKvD\n7LNxwZJwAkrEEc6soo4gq8369r1m1ZZ2s8kqWquDzX7750BnqhuXlJ04YHLCEvc32aahHGvT1JEh\nqzthRkvML4IZ+rLLLnNem4QekUryM5/5TCYb1oQJE5y3pl/bcgfpjwiIQFEECN8jKxY5pBEGs6wL\nUymM+sN4UPt80Tg2zpkzJ2N6ZqnnhRdecMfhTe3zUbMB7+mNVsG+YpXthvYOc9C+JgkH/YNPxFE9\n4DAzwHYQzTYD1uShQ8z4htooxRzcCVX4HyngCv+CC13eRqt4n1q/3bR17Dd7DxQ3gq2xyphCDH9h\ny5aNtuUNCwlZdjBp8Z+ctT5JPNtxFvEjcbw3c1V+KdS23hMBEcgmwOyWbFj4U3jBmrRgwQLnGc0j\n2bEQTNh+DRmTtS+KQkGTo446yu3DbPep9dvM1j37zJ4i+weSctTbzFjH2UIM421qSj/zdg3qTxcC\nMkF3QVL5G5j1Pm0V729e3+xGt8UqX8jstaPft+yN+diazeaPm3fmjS/khvbrSSQJ8MqX5PLMfFG+\n3JzELkr5Vv5vTlfY+wRQnoTsoYS9UBsbz2kGwMyIfb3gNWvWuExZ7Jc0QXtHrBc37TCPvvaW+dPO\nvUUrX9rCFL3FKuwVa7eY5ze2GczWkvwEBlxtJf/beqcSCax4Y4tZZU1KHT1Yt9lvb6z1O/fY9eF9\nptUmYE+OdLnJX3rpJYfurrvucvlmeUF4BA5XeGRSvQizGcXFJSIgAnEIEC+MYxamY/wpELLPESuM\npzSxxMx8MVHjpHXEEUe456tXr3b3JffmtsFDze837SzaKpbrzDFRY7peu2O3W7YqZskqVzuVvk0m\n6Er/hhPXx035/960Qflbd7m1nMRbJT9lbXjmyAZrcmrKKOEHHnjAdQDEKy5dutS1jemL3LQIuW0J\niSDsSCICItA7BPCAps6wd6xi7Zd1YmLyKfKAEvZVkHDewiq1u2GU6Wge49Z3Y5wVniIttoraiS3D\n3TpxjDYrqQ2ZoCvp2+zmWvBcXGNLiuFIEUuwMP1xc7ubUdPmY4895pQv+WvxwkQojeaVr0+fJ+Xr\n0OiPCPQaAZZ6nnjiiUwsMGldMUMzEOeRJSIiEQgNxAy9r6bOdNQPj6Z8uTB6mj9ZS9nzb7X12nWW\nc8NSwOX87QWcOzU9n7VrMj0xO+f7ONp8buMO88rra50XJl6VxCFizkJIDoAQgoSC9iETbqP+iIAI\n9BoBEt2QstLnWOeDMEfjqEU9bYTqY9U1g82eprHmnapqty3mH5arXrZRFtvs2rAkm4AUcDaPin31\nB+tUsbPjQK9dH4W6/2PNepca7zvf+Y6r1OIz7DADxhz2ve99r9c+Xw2LgAjkJtDc3GwefPBBs3Dh\nwswOzHxJkPPzn//cDZBXsyxV3VnGMLNTxCfUEGaQLskmIAWczaNPvWLkWldX5zwb/Ynh4DRx4kRz\n3333uU04MhHrd9xxx5lzzjnHbNq0ye+aecQzcY1NqBHP8JxpOutJR02DWXLD/zLE/5JCktJpw4YN\ncw5ZSc/MrIP0QgREoNcJYHVasmSJwSmSJDgIudfpR267/XazvarWmMMHFDyPndu2OvN1wZ0KvLlx\n1147Cei0hvndYvVxvr1ye5QC7sPf2AknnODyup555pkufKCjo8OQI/n00093jyS3oPrJzTffbMg4\nhbIj/2taNth432JCjS479cPmD092VlbZunG9+d9X/k/zN2edar5/wX8zf1z5RLrZLq8JUWoa3+pS\nTJL2jhqmJItnwCARARH48xM4++yzXREUX66QZaLnVq8xO/fszXly+/d1mPuW3mAuPPEYc83cT5uF\np/0n8+PLLzBtm9/K7F9sX8Ey2Js79mSO40msPi6r0TJ6IQXcx78sEqtTFYjqJldeeaUzF7G+inDz\nEErgR7Q4UmBaSguZrkJTxd1/y41m7JFTzLf/8f+aM86/1Cy/eqE5aGe0haSmdog5/q8+YUg5yfky\nuvVm6ELH6T0REIFDRwBrGU6SZMNCJs2cZWrqG93z9J9/uP4a89oLz5mFt9xlrn/wcXPdA4+Zlhnv\nM9f+9/9qtr3VGdVQbF/R6ZDVVdHH6OPS510ur6vK5UT763liOqIQPbF7PKcKCjG0CGEFFLEnvpYU\ncoQXeNN0kheZbEIFc9OY1knusBr7OW1bNlmFf9AMMIV/MuMmT3XlBBlpS0RABPomAVK+Pvzww+bi\niy82+8ZOyekYuXndWrPi/nus4l1hGoePdBdSZf05Tpv/VWcRW/nIg+bkL8w3IX0FWffSEqOPS7dZ\nLq8L96blchUVfp6YlnGkIJ4vWZ6P+rrE2mLinTZtmss2hSl6+vTpWUSKMT9nHWBffPaCy8zSy75q\nVj/3O/Pq7581X7riu6Z6YPdOGlNmHG3OPlYm5zRPvRaBvkYA6xQD+OW/fSbnqa1bvco0jxyVUb7J\nnVpnzDRrXnzObQrpK8jCl0t62sflarMctskEXQbfEuE7M2bMcLNg0sp5efTRR80zzzzjvBkXL17s\nauzyPnF+SSklHdwrz6x07YyZONnehKPdiLc7EzSfyQhZIgIiUD4Ehlslm0uY2dY3D8v1lmkaMdJs\n39Rpgg7rK0jN0VV62sd1bbE8tmgG3Me/p1//+tcuVIDyYngVz5w50xWw/9SnPmXWrl1rZs+enbmC\nWbNmGZyf+N/Y+N6aDpVKQgRF+083XmsWLbvbtEx/n/nMVy8xl31ytln1zJNm+vEfKtiUUs4VxKM3\nRaDPEcjXP4yfMt1s3djVp4QLwPFqwtSjnF9IWF+RPTmgrRh9HO2Uo2gG3Ie/NRKjkyuZ+Flyth55\n5JGGGNvzzjvPKVm8o0lssX79encVy5cvNyeffHKW8uWNmqqwr3nXjjbzts2Sww2GsEbTYk1Om/60\n1r0u9KemqnAoQ6Fj9Z4IiMChJ1BbnfueHTd5mtlt+6CXf/cfWSfFAP3Jh//FTDz6GBPaV6QH6LH6\nuKwTLKMXYT1zGV1YJZwqpcRQuueee27mcjAxjxkzxgXVU9/zG9/4hgtLwkRNVSGqnqRl6OBOp630\n9nyvG4YOM5OPnWVW2psMQfGuevpJM+tjp+Q7JLO9uUYm6AwMPRGBMiAwvDZ3/8By0rxvXWd+9q1L\nzet/+L27kj3tO83f24iIkeNbzPEnnWZC+4rGQdn9Q6w+rgww5zxFFWPIiaX8NmJ2TjpoJa/gDZuE\n47e2AlJ3oUjEAS+45u/MjA982LxmHa/+jw1F2mZNTchJZ883J55xVrLZLs+rran7o0cMNy22OpJE\nBESgPAiQIOPfXttsyw4ezHnCj/zDreaxf77LRUKwA/0DinlwXb3bv9i+goWwD45rNjNGNLjjQv8U\n6uNC2+or+0sB95VvohfPA8X7i5fXmx0lpKJkxOtvtO5OkULcn5462gySGbo7VHpfBPoMATyTH3hp\nvdm2t2uIUPIk29u2m9r6hpwhS+zXXV8xxJq6T508ytSnZsHJz+hvz2WC7gff+MABh5tWWxIszBWr\nE0yxype9WxoHS/n2g9+TLrGyCLAuO21YnRlgHwtJXWNTXuXLcd31FaOG1Ej5pgBLAaeAVOpLzD71\ng3rP6Z3Z71ElmpYqlbmuSwTKhcCkoXWmoRf7B2a/x44uzfRcLgxLOU8p4FKoleExeDoeO6rRDLKz\n4djCDPuYUQ1miFXCEhEQgfIjwD38gbFNZnAvLB9VWd+QqXaG3VST29mr/GjFO+P4vXG8c1NLkQlM\nah5iJjYN6dbUFPKxA6zV6oiGwWaKHUFLREAEypfAuIZaM314ncGZMpbQFF7WM0e+l5cgVtuV0I4U\ncCV8i0Vew2F2jeeD45vNBLtW2916TzFNDrTat8WuLX+0ZbihbYkIiEB5E3j/6CY3W2XW2lOhjxlb\nX2M+OWmUyZfso6efUe7Hywu63L/BEs6fVJVPb2gzq7a2G0qElSK11lQ1eegQc9wY65gh5VsKQh0j\nAn2WwAtv7TAvbNphdpXYP5D8h8H5CTbsqMom8pHkJiAFnJtLv9i60ZYpfGr9dkOFkmILNtTYtSKc\nNf5ibLMZXVfTLzjpIkWgPxLYsnuf7R+2Gaqp7TnwdlEIWEvGIfP9oxvNBLs0JctYYWxSwIX5VPy7\nxABSL3jVlnazaXeHLTlozH7758DbnTlbMR0NtCNYBrEjagfZWW+dMytp1lvxPw1doAi4giwbd3WY\nV6y1bEN7hzlo+4v9Nq8A/QM9RJW1flXbpSj6iWbrZIVVbLxdS45hwu4P+KWA+8O3XOQ1HrCKd7sN\nxsfs5BUwNxIhBE02xaRMSUWC1G4iUIEEqKrW2T8csIN0q36tMqZPqB1o+webXKPazn4lYQSkgMN4\naW8REAEREAERiEJAQ5YoGNWICIiACIiACIQRkAIO46W9RUAEREAERCAKASngKBjViAiIgAiIgAiE\nEZACDuOlvUVABERABEQgCgEp4CgY1YgIiIAIiIAIhBGQAg7jpb1FQAREQAREIAoBKeAoGNWICIiA\nCIiACIQRkAIO46W9RUAEREAERCAKASngKBjViAiIgAiIgAiEEZACDuOlvUVABERABEQgCgEp4CgY\n1YgIiIAIiIAIhBGQAg7jpb1FQAREQAREIAoBKeAoGNWICIiACIiACIQRkAIO46W9RUAEREAERCAK\nASngKBjViAiIgAiIgAiEEZACDuOlvUVABERABEQgCgEp4CgY1YgIiIAIiIAIhBGQAg7jpb1FQARE\nQAREIAoBKeAoGNWICIiACIiACIQRkAIO46W9RUAEREAERCAKASngKBjViAiIgAiIgAiEEZACDuOl\nvUVABERABEQgCgEp4CgY1YgIiIAIiIAIhBGQAg7jpb1FQAREQAREIAoBKeAoGNWICIiACIiACIQR\nkAIO46W9RUAEREAERCAKASngKBjViAiIgAiIgAiEEZACDuOlvUVABERABEQgCgEp4CgY1YgIiIAI\niIAIhBGQAg7jpb1FQAREQAREIAoBKeAoGNWICIiACIiACIQRkAIO46W9RUAEREAERCAKASngKBjV\niAiIgAiIgAiEEZACDuOlvUVABERABEQgCgEp4CgY1YgIiIAIiIAIhBGQAg7jpb1FQAREQAREIAoB\nKeAoGNWICIiACIiACIQRkAIO46W9RUAEREAERCAKASngKBjViAiIgAiIgAiEEZACDuOlvUVABERA\nBEQgCgEp4CgY1YgIiIAIiIAIhBGQAg7jpb1FQAREQAREIAoBKeAoGNWICIiACIiACIQRkAIO46W9\nRUAEREAERCAKASngKBjViAiIgAiIgAiEEZACDuOlvUVABERABEQgCgEp4CgY1YgIiIAIiIAIhBGQ\nAg7jpb1FQAREQAREIAoBKeAoGNWICIiACIiACIQRkAIO46W9RUAEREAERCAKASngKBjViAiIgAiI\ngAiEEZACDuOlvUVABERABEQgCgEp4CgY1YgIiIAIiIAIhBGQAg7jpb1FQAREQAREIAoBKeAoGNWI\nCIiACIiACIQRkAIO46W9RUAEREAERCAKASngKBjViAiIgAiIgAiEEZACDuOlvUVABERABEQgCgEp\n4CgY1YgIiIAIiIAIhBGQAg7jpb1FQAREQAREIAoBKeAoGNWICIiACIiACIQRkAIO46W9RUAEREAE\nRCAKASngKBjViAiIgAiIgAiEEZACDuOlvUVABERABEQgCgEp4CgY1YgIiIAIiIAIhBGQAg7jpb1F\nQAREQAREIAoBKeAoGNWICIiACIiACIQRkAIO46W9RUAEREAERCAKASngKBjViAiIgAiIgAiEEZAC\nDuOlvUVABERABEQgCgEp4CgY1YgIiIAIiIAIhBGQAg7jpb1FQAREQAREIAoBKeAoGNWICIiACIiA\nCIQRkAIO46W9RUAEREAERCAKASngKBjViAiIgAiIgAiEEZACDuOlvUVABERABEQgCgEp4CgY1YgI\niIAIiIAIhBGQAg7jpb1FQAREQAREIAoBKeAoGNWICIiACIiACIQRkAIO46W9RUAEREAERCAKASng\nKBjViAiIgAiIgAiEEZACDuOlvUVABERABEQgCgEp4CgY1YgIiIAIiIAIhBGQAg7jpb1FQAREQARE\nIAoBKeAoGNWICIiACIiACIQRkAIO46W9RUAEREAERCAKASngKBjViAiIgAiIgAiEEZACDuOlvUVA\nBERABEQgCgEp4CgY1YgIiIAIiIAIhBGQAg7jpb1FQAREQAREIAoBKeAoGNWICIiACIiACIQRkAIO\n46W9RUAEREAERCAKASngKBjViAiIgAiIgAiEEZACDuOlvUVABERABEQgCgEp4CgY1YgIiIAIiIAI\nhBGQAg7jpb1FQAREQAREIAoBKeAoGNWICIiACIiACIQRkAIO46W9RUAEREAERCAKASngKBjViAiI\ngAiIgAiEEZACDuOlvUVABERABEQgCgEp4CgY1YgIiIAIiIAIhBGQAg7jpb1FQAREQAREIAoBKeAo\nGNWICIiACIiACIQRkAIO46W9RUAEREAERCAKASngKBjViAiIgAiIgAiEEfj/96OeWCldcqQAAAAA\nSUVORK5CYII=\n"
}
],
"prompt_number": 54
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"hidden_sums <- function(i) {\n",
" return(c(sum(plot.nnet(eight.net,wts.only=T)[['hidden 1 1']][c(1,i+1)]), \n",
" sum(plot.nnet(eight.net,wts.only=T)[['hidden 1 2']][c(1,i+1)]), \n",
" sum(plot.nnet(eight.net,wts.only=T)[['hidden 1 3']][c(1,i+1)])))\n",
"}\n",
"t(sapply(c(1:8), hidden_sums))"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
" [,1] [,2] [,3]\n",
"[1,] -53.493462 -78.163640 -97.705215\n",
"[2,] 41.023794 -1.851191 1.150396\n",
"[3,] 25.064062 94.200762 101.144791\n",
"[4,] -75.822102 104.801736 -84.204842\n",
"[5,] -1.921834 -98.268453 136.608166\n",
"[6,] 44.748766 140.694407 -113.532087\n",
"[7,] 137.462885 -64.387803 -13.907567\n",
"[8,] -127.439960 87.422128 70.566624\n"
]
}
],
"prompt_number": 41
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"t(sapply(c(1:8), hidden_sums) > 1) * 1"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
" [,1] [,2] [,3]\n",
"[1,] 0 0 0\n",
"[2,] 1 0 1\n",
"[3,] 1 1 1\n",
"[4,] 0 1 0\n",
"[5,] 0 0 1\n",
"[6,] 1 1 0\n",
"[7,] 1 0 0\n",
"[8,] 0 1 1\n"
]
}
],
"prompt_number": 42
},
{
"cell_type": "heading",
"level": 2,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Supervised"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"nnet(trainClass ~ ., data=trainDescr, size = 3, decay = 5e-4)"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"# weights: 187\n",
"initial value 97.094228 \n",
"iter 10 value 48.353877\n",
"iter 20 value 10.988537\n",
"iter 30 value 5.351126\n",
"iter 40 value 2.336103\n",
"iter 50 value 1.836484\n",
"iter 60 value 1.572561\n",
"iter 70 value 1.422582\n",
"iter 80 value 1.325231\n",
"iter 90 value 1.268751\n",
"iter 100 value 1.228825\n",
"final value 1.228825 \n",
"stopped after 100 iterations\n",
"a 60-3-1 network with 187 weights\n",
"inputs: V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14 V15 V16 V17 V18 V19 V20 V21 V22 V23 V24 V25 V26 V27 V28 V29 V30 V31 V32 V33 V34 V35 V36 V37 V38 V39 V40 V41 V42 V43 V44 V45 V46 V47 V48 V49 V50 V51 V52 V53 V54 V55 V56 V57 V58 V59 V60 \n",
"output(s): trainClass \n",
"options were - entropy fitting decay=5e-04\n"
]
}
],
"prompt_number": 138
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"library(nnet)\n",
"nnet(trainClass ~ ., data=trainDescr, size = 3, decay = 5e-4, trace=FALSE)"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"a 57-3-1 network with 178 weights\n",
"inputs: V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14 V16 V17 V19 V21 V22 V23 V24 V25 V26 V27 V28 V29 V30 V31 V32 V33 V34 V35 V36 V37 V38 V39 V40 V41 V42 V43 V44 V45 V46 V47 V48 V49 V50 V51 V52 V53 V54 V55 V56 V57 V58 V59 V60 \n",
"output(s): trainClass \n",
"options were - entropy fitting decay=5e-04\n"
]
}
],
"prompt_number": 43
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Tuning Models using Resampling\n",
"--------------------------------------------------------"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"The number of hidden nodes and the decay can both greatly affect the success of a neural net.\n",
"`caret` to the rescue:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"eights <- rbind(eight, eight, eight, eight, eight, eight, eight, eight)\n",
"eightTrain <- createDataPartition(y = seq(1:nrow(eights)), p = 7/8, list = FALSE)\n",
"trainEight <- eights[eightTrain,]\n",
"testEight <- eights[-eightTrain,]\n",
"is(apply(testEight, 2, factor)[,2]"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"[1] \"character\" \"vector\" \"data.frameRowLabels\"\n",
"[4] \"SuperClassMethod\" \"EnumerationValue\" \n"
]
}
],
"prompt_number": 82
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"nnetFit <- train(x = trainEight, y = apply(testEight, 2, factor),\n",
" method = \"nnet\", #trace=FALSE,\n",
" tuneLength = 3)\n",
"plot(nnetFit)"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"# weights: 11\n",
"initial value 8.673728 \n",
"iter 10 value 4.999045\n",
"iter 20 value 4.999025\n",
"iter 30 value 4.999004\n",
"iter 40 value 4.998983\n",
"iter 50 value 4.998960\n",
"iter 60 value 4.998937\n",
"iter 70 value 4.998913\n",
"iter 80 value 4.998887\n",
"iter 90 value 4.998860\n",
"iter 100 value 4.998833\n",
"final value 4.998833 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 10.609366 \n",
"final value 5.000000 \n",
"converged\n",
"# weights: 51\n",
"initial value 16.708649 \n",
"final value 5.000000 \n",
"converged\n",
"# weights: 11\n",
"initial value 18.270834 \n",
"iter 10 value 4.881627\n",
"final value 4.875318 \n",
"converged\n",
"# weights: 31\n",
"initial value 9.803649 \n",
"iter 10 value 4.779104\n",
"iter 20 value 4.775880\n",
"final value 4.775879 \n",
"converged\n",
"# weights: 51\n",
"initial value 8.163138 \n",
"iter 10 value 4.727742\n",
"iter 20 value 4.727095\n",
"iter 20 value 4.727095\n",
"iter 20 value 4.727095\n",
"final value 4.727095 \n",
"converged\n",
"# weights: 11\n",
"initial value 25.260746 \n",
"iter 10 value 5.002238\n",
"iter 20 value 5.001798\n",
"iter 30 value 5.001298\n",
"iter 40 value 5.000723\n",
"iter 50 value 5.000053\n",
"iter 60 value 4.999265\n",
"iter 70 value 4.998320\n",
"iter 80 value 4.997166\n",
"iter 90 value 4.995726\n",
"iter 100 value 4.993876\n",
"final value 4.993876 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 11.097899 \n",
"iter 10 value 5.005318\n",
"iter 20 value 5.005263\n",
"iter 30 value 5.005208\n",
"iter 40 value 5.005151\n",
"iter 50 value 5.005092\n",
"iter 60 value 5.005032\n",
"iter 70 value 5.004971\n",
"iter 80 value 5.004907\n",
"iter 90 value 5.004842\n",
"iter 100 value 5.004774\n",
"final value 5.004774 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 4.646928 \n",
"iter 10 value 4.267219\n",
"iter 20 value 3.518633\n",
"iter 30 value 3.511242\n",
"iter 40 value 3.507777\n",
"iter 50 value 3.506980\n",
"iter 60 value 3.506815\n",
"iter 70 value 3.506137\n",
"iter 80 value 3.505601\n",
"iter 90 value 3.505180\n",
"iter 100 value 3.505060\n",
"final value 3.505060 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 17.716435 \n",
"final value 7.000000 \n",
"converged\n",
"# weights: 31\n",
"initial value 14.860389 \n",
"final value 7.000000 \n",
"converged\n",
"# weights: 51\n",
"initial value 18.894532 \n",
"final value 7.000000 \n",
"converged\n",
"# weights: 11\n",
"initial value 10.486567 \n",
"iter 10 value 6.166966\n",
"final value 6.107471 \n",
"converged\n",
"# weights: 31\n",
"initial value 10.622843 \n",
"iter 10 value 6.080145\n",
"iter 20 value 6.047568\n",
"iter 30 value 6.045179\n",
"final value 6.045150 \n",
"converged\n",
"# weights: 51\n",
"initial value 20.397641 \n",
"iter 10 value 6.065362\n",
"iter 20 value 6.046806\n",
"iter 30 value 6.038947\n",
"iter 40 value 6.038931\n",
"final value 6.038931 \n",
"converged\n",
"# weights: 11\n",
"initial value 18.367755 \n",
"iter 10 value 7.003787\n",
"iter 20 value 7.003490\n",
"iter 30 value 7.003159\n",
"iter 40 value 7.002789\n",
"iter 50 value 7.002371\n",
"iter 60 value 7.001894\n",
"iter 70 value 7.001345\n",
"iter 80 value 7.000705\n",
"iter 90 value 6.999949\n",
"iter 100 value 6.999040\n",
"final value 6.999040 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 10.628473 \n",
"iter 10 value 7.005315\n",
"iter 20 value 7.005244\n",
"iter 30 value 7.005170\n",
"iter 40 value 7.005094\n",
"iter 50 value 7.005014\n",
"iter 60 value 7.004931\n",
"iter 70 value 7.004843\n",
"iter 80 value 7.004752\n",
"iter 90 value 7.004656\n",
"iter 100 value 7.004554\n",
"final value 7.004554 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 23.789082 \n",
"iter 10 value 7.000137\n",
"iter 20 value 6.999516\n",
"iter 30 value 6.998706\n",
"iter 40 value 6.997600\n",
"iter 50 value 6.995996\n",
"iter 60 value 6.993468\n",
"iter 70 value 6.988926\n",
"iter 80 value 6.978673\n",
"iter 90 value 6.939879\n",
"iter 100 value 5.680219\n",
"final value 5.680219 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 25.633738 \n",
"final value 1.999999 \n",
"converged\n",
"# weights: 31\n",
"initial value 10.080237 \n",
"final value 1.999993 \n",
"converged\n",
"# weights: 51\n",
"initial value 17.377625 \n",
"final value 2.000000 \n",
"converged\n",
"# weights: 11\n",
"initial value 6.951183 \n",
"iter 10 value 2.467581\n",
"final value 2.467580 \n",
"converged\n",
"# weights: 31\n",
"initial value 14.092601 \n",
"iter 10 value 2.334016\n",
"iter 20 value 2.332511\n",
"iter 20 value 2.332511\n",
"iter 20 value 2.332511\n",
"final value 2.332511 \n",
"converged\n",
"# weights: 51\n",
"initial value 6.625965 \n",
"iter 10 value 2.257854\n",
"final value 2.257832 \n",
"converged\n",
"# weights: 11\n",
"initial value 10.746226 \n",
"iter 10 value 2.000334\n",
"iter 20 value 1.999931\n",
"iter 30 value 1.999457\n",
"iter 40 value 1.998888\n",
"iter 50 value 1.998191\n",
"iter 60 value 1.997314\n",
"iter 70 value 1.996175\n",
"iter 80 value 1.994635\n",
"iter 90 value 1.992436\n",
"iter 100 value 1.989065\n",
"final value 1.989065 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 12.589536 \n",
"iter 10 value 2.003197\n",
"iter 20 value 2.003129\n",
"iter 30 value 2.003059\n",
"iter 40 value 2.002985\n",
"iter 50 value 2.002907\n",
"iter 60 value 2.002825\n",
"iter 70 value 2.002739\n",
"iter 80 value 2.002647\n",
"iter 90 value 2.002550\n",
"iter 100 value 2.002447\n",
"final value 2.002447 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 18.386290 \n",
"iter 10 value 1.989134\n",
"iter 20 value 1.982939\n",
"iter 30 value 1.969454\n",
"iter 40 value 1.934161\n",
"iter 50 value 1.657039\n",
"iter 60 value 1.592682\n",
"iter 70 value 1.589571\n",
"iter 80 value 1.588750\n",
"iter 90 value 1.588673\n",
"iter 100 value 1.588590\n",
"final value 1.588590 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 15.481109 \n",
"final value 5.999955 \n",
"converged\n",
"# weights: 31\n",
"initial value 9.886870 \n",
"final value 5.999996 \n",
"converged\n",
"# weights: 51\n",
"initial value 15.410244 \n",
"final value 6.000000 \n",
"converged\n",
"# weights: 11\n",
"initial value 11.167058 \n",
"iter 10 value 5.611302\n",
"final value 5.610677 \n",
"converged\n",
"# weights: 31\n",
"initial value 9.435758 \n",
"iter 10 value 5.523095\n",
"iter 20 value 5.522773\n",
"final value 5.522773 \n",
"converged\n",
"# weights: 51\n",
"initial value 24.495347 \n",
"iter 10 value 5.502849\n",
"iter 20 value 5.480956\n",
"final value 5.480955 \n",
"converged\n",
"# weights: 11\n",
"initial value 11.593586 \n",
"iter 10 value 6.010395\n",
"iter 20 value 6.010344\n",
"iter 30 value 6.010293\n",
"iter 40 value 6.010241\n",
"iter 50 value 6.010190\n",
"iter 60 value 6.010139\n",
"iter 70 value 6.010087\n",
"iter 80 value 6.010036\n",
"iter 90 value 6.009984\n",
"iter 100 value 6.009932\n",
"final value 6.009932 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 9.066718 \n",
"iter 10 value 5.294354\n",
"iter 20 value 4.528664\n",
"iter 30 value 4.497458\n",
"iter 40 value 4.495742\n",
"iter 50 value 4.494949\n",
"iter 60 value 4.494880\n",
"iter 70 value 4.494804\n",
"iter 80 value 4.494757\n",
"iter 90 value 4.494713\n",
"final value 4.494702 \n",
"converged\n",
"# weights: 51\n",
"initial value 17.588226 \n",
"iter 10 value 6.002329\n",
"iter 20 value 6.002177\n",
"iter 30 value 6.002007\n",
"iter 40 value 6.001817\n",
"iter 50 value 6.001601\n",
"iter 60 value 6.001354\n",
"iter 70 value 6.001068\n",
"iter 80 value 6.000730\n",
"iter 90 value 6.000324\n",
"iter 100 value 5.999827\n",
"final value 5.999827 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 17.727503 \n",
"final value 7.000000 \n",
"converged\n",
"# weights: 31\n",
"initial value 14.519545 \n",
"final value 7.000000 \n",
"converged\n",
"# weights: 51\n",
"initial value 15.424997 \n",
"final value 7.000000 \n",
"converged\n",
"# weights: 11\n",
"initial value 25.985396 \n",
"iter 10 value 6.278687\n",
"final value 6.269723 \n",
"converged\n",
"# weights: 31\n",
"initial value 21.975306 \n",
"iter 10 value 6.323554\n",
"iter 20 value 6.198427\n",
"final value 6.198169 \n",
"converged\n",
"# weights: 51\n",
"initial value 17.058147 \n",
"iter 10 value 6.196971\n",
"iter 20 value 6.182819\n",
"iter 30 value 6.182382\n",
"final value 6.182379 \n",
"converged\n",
"# weights: 11\n",
"initial value 13.526453 \n",
"iter 10 value 6.998069\n",
"iter 20 value 6.996839\n",
"iter 30 value 6.995166\n",
"iter 40 value 6.992752\n",
"iter 50 value 6.988968\n",
"iter 60 value 6.982249\n",
"iter 70 value 6.967576\n",
"iter 80 value 6.918539\n",
"iter 90 value 6.213270\n",
"iter 100 value 4.618646\n",
"final value 4.618646 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 8.729255 \n",
"iter 10 value 7.005703\n",
"iter 20 value 7.005660\n",
"iter 30 value 7.005617\n",
"iter 40 value 7.005573\n",
"iter 50 value 7.005529\n",
"iter 60 value 7.005484\n",
"iter 70 value 7.005438\n",
"iter 80 value 7.005391\n",
"iter 90 value 7.005344\n",
"iter 100 value 7.005295\n",
"final value 7.005295 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 31.683383 \n",
"iter 10 value 7.004576\n",
"iter 20 value 7.004468\n",
"iter 30 value 7.004352\n",
"iter 40 value 7.004227\n",
"iter 50 value 7.004091\n",
"iter 60 value 7.003944\n",
"iter 70 value 7.003782\n",
"iter 80 value 7.003604\n",
"iter 90 value 7.003406\n",
"iter 100 value 7.003183\n",
"final value 7.003183 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 14.618582 \n",
"final value 7.999983 \n",
"converged\n",
"# weights: 31\n",
"initial value 14.177186 \n",
"final value 8.000000 \n",
"converged\n",
"# weights: 51\n",
"initial value 11.583555 \n",
"final value 8.000000 \n",
"converged\n",
"# weights: 11\n",
"initial value 8.990453 \n",
"iter 10 value 6.605450\n",
"final value 6.574753 \n",
"converged\n",
"# weights: 31\n",
"initial value 14.336989 \n",
"iter 10 value 6.531526\n",
"iter 20 value 6.510687\n",
"iter 30 value 6.510639\n",
"final value 6.510638 \n",
"converged\n",
"# weights: 51\n",
"initial value 22.857913 \n",
"iter 10 value 6.616519\n",
"iter 20 value 6.529219\n",
"iter 30 value 6.443550\n",
"iter 40 value 6.443114\n",
"final value 6.443114 \n",
"converged\n",
"# weights: 11\n",
"initial value 10.313407 \n",
"iter 10 value 8.006229\n",
"iter 20 value 8.006132\n",
"iter 30 value 8.006031\n",
"iter 40 value 8.005924\n",
"iter 50 value 8.005811\n",
"iter 60 value 8.005690\n",
"iter 70 value 8.005562\n",
"iter 80 value 8.005425\n",
"iter 90 value 8.005277\n",
"iter 100 value 8.005117\n",
"final value 8.005117 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 27.776048 \n",
"iter 10 value 8.001621\n",
"iter 20 value 8.001059\n",
"iter 30 value 8.000358\n",
"iter 40 value 7.999456\n",
"iter 50 value 7.998251\n",
"iter 60 value 7.996562\n",
"iter 70 value 7.994027\n",
"iter 80 value 7.989842\n",
"iter 90 value 7.981806\n",
"iter 100 value 7.961527\n",
"final value 7.961527 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 29.203238 \n",
"iter 10 value 7.999132\n",
"iter 20 value 7.998097\n",
"iter 30 value 7.996618\n",
"iter 40 value 7.994329\n",
"iter 50 value 7.990340\n",
"iter 60 value 7.981827\n",
"iter 70 value 7.953952\n",
"iter 80 value 7.436207\n",
"iter 90 value 4.600000\n",
"iter 100 value 4.522029\n",
"final value 4.522029 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 10.871622 \n",
"iter 10 value 6.996968\n",
"iter 20 value 6.996864\n",
"iter 30 value 6.996752\n",
"iter 40 value 6.996633\n",
"iter 50 value 6.996505\n",
"iter 60 value 6.996366\n",
"iter 70 value 6.996217\n",
"iter 80 value 6.996055\n",
"iter 90 value 6.995879\n",
"iter 100 value 6.995688\n",
"final value 6.995688 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 12.854428 \n",
"final value 7.000000 \n",
"converged\n",
"# weights: 51\n",
"initial value 11.720122 \n",
"final value 7.000000 \n",
"converged\n",
"# weights: 11\n",
"initial value 8.855860 \n",
"iter 10 value 6.263145\n",
"final value 6.262857 \n",
"converged\n",
"# weights: 31\n",
"initial value 12.187882 \n",
"iter 10 value 6.192021\n",
"iter 20 value 6.189036\n",
"final value 6.189036 \n",
"converged\n",
"# weights: 51\n",
"initial value 7.239005 \n",
"iter 10 value 6.156232\n",
"iter 20 value 6.155381\n",
"iter 20 value 6.155381\n",
"iter 20 value 6.155381\n",
"final value 6.155381 \n",
"converged\n",
"# weights: 11\n",
"initial value 9.751729 \n",
"iter 10 value 6.999946\n",
"iter 20 value 6.999245\n",
"iter 30 value 6.998423\n",
"iter 40 value 6.997445\n",
"iter 50 value 6.996257\n",
"iter 60 value 6.994782\n",
"iter 70 value 6.992898\n",
"iter 80 value 6.990399\n",
"iter 90 value 6.986920\n",
"iter 100 value 6.981732\n",
"final value 6.981732 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 19.312728 \n",
"iter 10 value 7.004163\n",
"iter 20 value 7.004030\n",
"iter 30 value 7.003888\n",
"iter 40 value 7.003733\n",
"iter 50 value 7.003566\n",
"iter 60 value 7.003382\n",
"iter 70 value 7.003180\n",
"iter 80 value 7.002955\n",
"iter 90 value 7.002704\n",
"iter 100 value 7.002420\n",
"final value 7.002420 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 20.386776 \n",
"iter 10 value 7.004795\n",
"iter 20 value 7.004744\n",
"iter 30 value 7.004691\n",
"iter 40 value 7.004636\n",
"iter 50 value 7.004580\n",
"iter 60 value 7.004521\n",
"iter 70 value 7.004461\n",
"iter 80 value 7.004399\n",
"iter 90 value 7.004334\n",
"iter 100 value 7.004266\n",
"final value 7.004266 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 22.265627 \n",
"iter 10 value 15.998731\n",
"iter 20 value 15.998712\n",
"iter 30 value 15.998693\n",
"iter 40 value 15.998673\n",
"iter 50 value 15.998653\n",
"iter 60 value 15.998632\n",
"iter 70 value 15.998610\n",
"iter 80 value 15.998588\n",
"iter 90 value 15.998565\n",
"iter 100 value 15.998541\n",
"final value 15.998541 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 21.407812 \n",
"final value 16.000000 \n",
"converged\n",
"# weights: 51\n",
"initial value 15.705263 \n",
"iter 10 value 6.315596\n",
"iter 20 value 6.145859\n",
"iter 30 value 6.144857\n",
"iter 40 value 6.144843\n",
"final value 6.144843 \n",
"converged\n",
"# weights: 11\n",
"initial value 16.293926 \n",
"iter 10 value 9.534451\n",
"final value 9.499919 \n",
"converged\n",
"# weights: 31\n",
"initial value 16.330965 \n",
"iter 10 value 9.688788\n",
"iter 20 value 9.175265\n",
"iter 30 value 9.165602\n",
"final value 9.165120 \n",
"converged\n",
"# weights: 51\n",
"initial value 14.528910 \n",
"iter 10 value 9.169283\n",
"iter 20 value 9.108662\n",
"iter 30 value 9.107292\n",
"final value 9.107290 \n",
"converged\n",
"# weights: 11\n",
"initial value 17.456383 \n",
"iter 10 value 16.009586\n",
"iter 20 value 16.009536\n",
"iter 30 value 16.009486\n",
"iter 40 value 16.009435\n",
"iter 50 value 16.009384\n",
"iter 60 value 16.009333\n",
"iter 70 value 16.009282\n",
"iter 80 value 16.009230\n",
"iter 90 value 16.009178\n",
"iter 100 value 16.009126\n",
"final value 16.009126 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 13.370069 \n",
"iter 10 value 6.435933\n",
"iter 20 value 6.160126\n",
"iter 30 value 6.157456\n",
"iter 40 value 6.154745\n",
"iter 50 value 6.154614\n",
"iter 60 value 6.154309\n",
"final value 6.154295 \n",
"converged\n",
"# weights: 51\n",
"initial value 24.108535 \n",
"iter 10 value 6.995909\n",
"iter 20 value 6.346121\n",
"iter 30 value 6.167736\n",
"iter 40 value 6.164743\n",
"iter 50 value 6.156578\n",
"iter 60 value 6.154791\n",
"iter 70 value 6.154623\n",
"iter 80 value 6.154152\n",
"iter 90 value 6.154130\n",
"final value 6.154089 \n",
"converged\n",
"# weights: 11\n",
"initial value 16.449487 \n",
"final value 9.000000 \n",
"converged\n",
"# weights: 31\n",
"initial value 18.163770 \n",
"final value 9.000000 \n",
"converged\n",
"# weights: 51\n",
"initial value 9.078179 \n",
"iter 10 value 8.999803\n",
"iter 20 value 8.999802\n",
"iter 30 value 8.999800\n",
"iter 40 value 8.999798\n",
"iter 50 value 8.999796\n",
"iter 60 value 8.999794\n",
"iter 70 value 8.999792\n",
"iter 80 value 8.999790\n",
"iter 90 value 8.999788\n",
"iter 100 value 8.999786\n",
"final value 8.999786 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 21.130651 \n",
"iter 10 value 7.502028\n",
"iter 20 value 7.339857\n",
"iter 20 value 7.339857\n",
"iter 20 value 7.339857\n",
"final value 7.339857 \n",
"converged\n",
"# weights: 31\n",
"initial value 15.218695 \n",
"iter 10 value 7.333072\n",
"iter 20 value 7.295429\n",
"iter 30 value 7.294624\n",
"final value 7.294598 \n",
"converged\n",
"# weights: 51\n",
"initial value 18.877172 \n",
"iter 10 value 7.528185\n",
"iter 20 value 7.297149\n",
"iter 30 value 7.220824\n",
"iter 40 value 7.220043\n",
"final value 7.220037 \n",
"converged\n",
"# weights: 11\n",
"initial value 9.406574 \n",
"iter 10 value 8.970409\n",
"iter 20 value 8.926541\n",
"iter 30 value 8.136637\n",
"iter 40 value 5.076649\n",
"iter 50 value 5.057555\n",
"iter 60 value 5.016040\n",
"iter 70 value 5.013796\n",
"iter 80 value 5.012965\n",
"iter 90 value 5.012937\n",
"final value 5.012916 \n",
"converged\n",
"# weights: 31\n",
"initial value 16.774179 \n",
"iter 10 value 9.001849\n",
"iter 20 value 9.001424\n",
"iter 30 value 9.000915\n",
"iter 40 value 9.000295\n",
"iter 50 value 8.999519\n",
"iter 60 value 8.998517\n",
"iter 70 value 8.997169\n",
"iter 80 value 8.995259\n",
"iter 90 value 8.992344\n",
"iter 100 value 8.987375\n",
"final value 8.987375 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 17.525798 \n",
"iter 10 value 7.873848\n",
"iter 20 value 5.066852\n",
"iter 30 value 5.013790\n",
"iter 40 value 5.013069\n",
"iter 50 value 5.011775\n",
"iter 60 value 5.011715\n",
"final value 5.011703 \n",
"converged\n",
"# weights: 11\n",
"initial value 8.168237 \n",
"iter 10 value 3.999176\n",
"iter 20 value 3.999164\n",
"iter 30 value 3.999152\n",
"iter 40 value 3.999139\n",
"iter 50 value 3.999125\n",
"iter 60 value 3.999112\n",
"iter 70 value 3.999098\n",
"iter 80 value 3.999083\n",
"iter 90 value 3.999068\n",
"iter 100 value 3.999053\n",
"final value 3.999053 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 31.068493 \n",
"final value 4.000000 \n",
"converged\n",
"# weights: 51\n",
"initial value 22.757584 \n",
"final value 4.000000 \n",
"converged\n",
"# weights: 11\n",
"initial value 24.444726 \n",
"iter 10 value 4.175260\n",
"final value 4.171580 \n",
"converged\n",
"# weights: 31\n",
"initial value 17.248785 \n",
"iter 10 value 4.056994\n",
"final value 4.053473 \n",
"converged\n",
"# weights: 51\n",
"initial value 22.146053 \n",
"iter 10 value 3.998396\n",
"iter 20 value 3.990404\n",
"final value 3.990404 \n",
"converged\n",
"# weights: 11\n",
"initial value 19.151843 \n",
"iter 10 value 4.004540\n",
"iter 20 value 4.004377\n",
"iter 30 value 4.004203\n",
"iter 40 value 4.004018\n",
"iter 50 value 4.003819\n",
"iter 60 value 4.003604\n",
"iter 70 value 4.003372\n",
"iter 80 value 4.003120\n",
"iter 90 value 4.002844\n",
"iter 100 value 4.002541\n",
"final value 4.002541 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 9.263435 \n",
"iter 10 value 4.004570\n",
"iter 20 value 4.004515\n",
"iter 30 value 4.004458\n",
"iter 40 value 4.004400\n",
"iter 50 value 4.004340\n",
"iter 60 value 4.004278\n",
"iter 70 value 4.004213\n",
"iter 80 value 4.004146\n",
"iter 90 value 4.004077\n",
"iter 100 value 4.004004\n",
"final value 4.004004 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 7.736685 \n",
"iter 10 value 3.998352\n",
"iter 20 value 3.997465\n",
"iter 30 value 3.996231\n",
"iter 40 value 3.994396\n",
"iter 50 value 3.991384\n",
"iter 60 value 3.985596\n",
"iter 70 value 3.970647\n",
"iter 80 value 3.889083\n",
"iter 90 value 3.397467\n",
"iter 100 value 3.319148\n",
"final value 3.319148 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 19.030289 \n",
"final value 10.000000 \n",
"converged\n",
"# weights: 31\n",
"initial value 13.516618 \n",
"final value 10.000000 \n",
"converged\n",
"# weights: 51\n",
"initial value 11.345462 \n",
"final value 10.000000 \n",
"converged\n",
"# weights: 11\n",
"initial value 12.555017 \n",
"iter 10 value 7.382475\n",
"iter 20 value 7.106459\n",
"final value 7.106459 \n",
"converged\n",
"# weights: 31\n",
"initial value 11.793963 \n",
"iter 10 value 7.055665\n",
"iter 20 value 6.816820\n",
"iter 30 value 6.815147\n",
"final value 6.815146 \n",
"converged\n",
"# weights: 51\n",
"initial value 14.381127 \n",
"iter 10 value 7.841802\n",
"iter 20 value 7.053894\n",
"iter 30 value 6.781306\n",
"iter 40 value 6.778841\n",
"final value 6.778777 \n",
"converged\n",
"# weights: 11\n",
"initial value 16.963772 \n",
"iter 10 value 9.987234\n",
"iter 20 value 9.981880\n",
"iter 30 value 9.973003\n",
"iter 40 value 9.955381\n",
"iter 50 value 9.904226\n",
"iter 60 value 9.246035\n",
"iter 70 value 4.086422\n",
"iter 80 value 4.025535\n",
"final value 4.025414 \n",
"converged\n",
"# weights: 31\n",
"initial value 10.140596 \n",
"iter 10 value 10.000948\n",
"iter 20 value 10.000123\n",
"iter 30 value 9.999022\n",
"iter 40 value 9.997475\n",
"iter 50 value 9.995139\n",
"iter 60 value 9.991227\n",
"iter 70 value 9.983479\n",
"iter 80 value 9.962396\n",
"iter 90 value 9.821719\n",
"iter 100 value 5.098902\n",
"final value 5.098902 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 15.082355 \n",
"iter 10 value 8.014953\n",
"iter 20 value 4.051294\n",
"iter 30 value 4.023400\n",
"iter 40 value 4.022750\n",
"iter 50 value 4.022660\n",
"iter 60 value 4.022348\n",
"iter 70 value 4.022083\n",
"iter 80 value 4.021937\n",
"iter 90 value 4.021889\n",
"iter 100 value 4.021622\n",
"final value 4.021622 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 10.452651 \n",
"iter 10 value 5.998285\n",
"iter 20 value 5.998248\n",
"iter 30 value 5.998210\n",
"iter 40 value 5.998170\n",
"iter 50 value 5.998128\n",
"iter 60 value 5.998084\n",
"iter 70 value 5.998039\n",
"iter 80 value 5.997991\n",
"iter 90 value 5.997942\n",
"iter 100 value 5.997890\n",
"final value 5.997890 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 10.581240 \n",
"final value 5.999939 \n",
"converged\n",
"# weights: 51\n",
"initial value 16.032967 \n",
"final value 6.000000 \n",
"converged\n",
"# weights: 11\n",
"initial value 11.410167 \n",
"iter 10 value 5.528984\n",
"final value 5.528843 \n",
"converged\n",
"# weights: 31\n",
"initial value 16.322416 \n",
"iter 10 value 5.452224\n",
"final value 5.448848 \n",
"converged\n",
"# weights: 51\n",
"initial value 8.792933 \n",
"iter 10 value 5.410156\n",
"iter 20 value 5.409336\n",
"final value 5.409335 \n",
"converged\n",
"# weights: 11\n",
"initial value 8.209523 \n",
"iter 10 value 6.002492\n",
"iter 20 value 6.002241\n",
"iter 30 value 6.001961\n",
"iter 40 value 6.001646\n",
"iter 50 value 6.001290\n",
"iter 60 value 6.000880\n",
"iter 70 value 6.000404\n",
"iter 80 value 5.999840\n",
"iter 90 value 5.999161\n",
"iter 100 value 5.998323\n",
"final value 5.998323 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 16.662172 \n",
"iter 10 value 6.002486\n",
"iter 20 value 6.002232\n",
"iter 30 value 6.001945\n",
"iter 40 value 6.001616\n",
"iter 50 value 6.001236\n",
"iter 60 value 6.000788\n",
"iter 70 value 6.000252\n",
"iter 80 value 5.999599\n",
"iter 90 value 5.998781\n",
"iter 100 value 5.997725\n",
"final value 5.997725 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 19.960198 \n",
"iter 10 value 5.995669\n",
"iter 20 value 5.993329\n",
"iter 30 value 5.989221\n",
"iter 40 value 5.980296\n",
"iter 50 value 5.949377\n",
"iter 60 value 5.324430\n",
"iter 70 value 4.669766\n",
"iter 80 value 4.661141\n",
"iter 90 value 4.659221\n",
"iter 100 value 4.657522\n",
"final value 4.657522 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 15.975060 \n",
"final value 4.999995 \n",
"converged\n",
"# weights: 31\n",
"initial value 16.780503 \n",
"final value 5.000000 \n",
"converged\n",
"# weights: 51\n",
"initial value 20.878886 \n",
"final value 5.000000 \n",
"converged\n",
"# weights: 11\n",
"initial value 22.547605 \n",
"iter 10 value 4.913364\n",
"iter 20 value 4.909096\n",
"iter 20 value 4.909096\n",
"iter 20 value 4.909096\n",
"final value 4.909096 \n",
"converged\n",
"# weights: 31\n",
"initial value 20.696130 \n",
"iter 10 value 4.809347\n",
"iter 20 value 4.807352\n",
"final value 4.807351 \n",
"converged\n",
"# weights: 51\n",
"initial value 18.020127 \n",
"iter 10 value 4.758789\n",
"iter 20 value 4.756006\n",
"final value 4.756005 \n",
"converged\n",
"# weights: 11\n",
"initial value 7.959249 \n",
"iter 10 value 5.001124\n",
"iter 20 value 5.000678\n",
"iter 30 value 5.000171\n",
"iter 40 value 4.999590\n",
"iter 50 value 4.998915\n",
"iter 60 value 4.998120\n",
"iter 70 value 4.997170\n",
"iter 80 value 4.996012\n",
"iter 90 value 4.994567\n",
"iter 100 value 4.992712\n",
"final value 4.992712 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 6.948163 \n",
"iter 10 value 5.005423\n",
"iter 20 value 5.005374\n",
"iter 30 value 5.005325\n",
"iter 40 value 5.005275\n",
"iter 50 value 5.005224\n",
"iter 60 value 5.005172\n",
"iter 70 value 5.005118\n",
"iter 80 value 5.005063\n",
"iter 90 value 5.005006\n",
"iter 100 value 5.004948\n",
"final value 5.004948 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 17.236488 \n",
"iter 10 value 5.003747\n",
"iter 20 value 5.003685\n",
"iter 30 value 5.003622\n",
"iter 40 value 5.003555\n",
"iter 50 value 5.003485\n",
"iter 60 value 5.003411\n",
"iter 70 value 5.003333\n",
"iter 80 value 5.003251\n",
"iter 90 value 5.003164\n",
"iter 100 value 5.003072\n",
"final value 5.003072 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 25.767144 \n",
"final value 6.999993 \n",
"converged\n",
"# weights: 31\n",
"initial value 9.134123 \n",
"iter 10 value 6.999763\n",
"iter 20 value 6.999761\n",
"iter 30 value 6.999759\n",
"iter 40 value 6.999756\n",
"iter 50 value 6.999754\n",
"iter 60 value 6.999752\n",
"iter 70 value 6.999750\n",
"iter 80 value 6.999747\n",
"iter 90 value 6.999745\n",
"iter 100 value 6.999742\n",
"final value 6.999742 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 23.678110 \n",
"final value 7.000000 \n",
"converged\n",
"# weights: 11\n",
"initial value 11.577876 \n",
"iter 10 value 6.283029\n",
"final value 6.272815 \n",
"converged\n",
"# weights: 31\n",
"initial value 13.302911 \n",
"iter 10 value 6.215106\n",
"iter 20 value 6.200026\n",
"final value 6.200003 \n",
"converged\n",
"# weights: 51\n",
"initial value 12.642082 \n",
"iter 10 value 6.193970\n",
"iter 20 value 6.184632\n",
"iter 30 value 6.184379\n",
"final value 6.184378 \n",
"converged\n",
"# weights: 11\n",
"initial value 10.955348 \n",
"iter 10 value 7.008606\n",
"iter 20 value 7.008539\n",
"iter 30 value 7.008471\n",
"iter 40 value 7.008401\n",
"iter 50 value 7.008330\n",
"iter 60 value 7.008259\n",
"iter 70 value 7.008186\n",
"iter 80 value 7.008111\n",
"iter 90 value 7.008035\n",
"iter 100 value 7.007958\n",
"final value 7.007958 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 13.086127 \n",
"iter 10 value 6.998996\n",
"iter 20 value 6.998086\n",
"iter 30 value 6.996860\n",
"iter 40 value 6.995117\n",
"iter 50 value 6.992437\n",
"iter 60 value 6.987806\n",
"iter 70 value 6.978052\n",
"iter 80 value 6.947004\n",
"iter 90 value 6.519557\n",
"iter 100 value 4.506551\n",
"final value 4.506551 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 7.342172 \n",
"iter 10 value 7.001387\n",
"iter 20 value 7.001017\n",
"iter 30 value 7.000570\n",
"iter 40 value 7.000018\n",
"iter 50 value 6.999314\n",
"iter 60 value 6.998385\n",
"iter 70 value 6.997095\n",
"iter 80 value 6.995179\n",
"iter 90 value 6.992036\n",
"iter 100 value 6.985979\n",
"final value 6.985979 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 8.893524 \n",
"iter 10 value 4.997188\n",
"iter 20 value 4.997097\n",
"iter 30 value 4.997001\n",
"iter 40 value 4.996898\n",
"iter 50 value 4.996788\n",
"iter 60 value 4.996670\n",
"iter 70 value 4.996543\n",
"iter 80 value 4.996407\n",
"iter 90 value 4.996259\n",
"iter 100 value 4.996100\n",
"final value 4.996100 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 17.936721 \n",
"final value 5.000000 \n",
"converged\n",
"# weights: 51\n",
"initial value 6.133998 \n",
"iter 10 value 4.999525\n",
"iter 20 value 4.999516\n",
"iter 30 value 4.999506\n",
"iter 40 value 4.999496\n",
"iter 50 value 4.999485\n",
"iter 60 value 4.999474\n",
"iter 70 value 4.999463\n",
"iter 80 value 4.999451\n",
"iter 90 value 4.999439\n",
"iter 100 value 4.999426\n",
"final value 4.999426 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 14.350507 \n",
"iter 10 value 4.870926\n",
"final value 4.869503 \n",
"converged\n",
"# weights: 31\n",
"initial value 12.452700 \n",
"iter 10 value 4.773509\n",
"iter 20 value 4.771592\n",
"final value 4.771592 \n",
"converged\n",
"# weights: 51\n",
"initial value 7.744401 \n",
"iter 10 value 4.722915\n",
"final value 4.722235 \n",
"converged\n",
"# weights: 11\n",
"initial value 17.077757 \n",
"iter 10 value 4.991619\n",
"iter 20 value 4.988949\n",
"iter 30 value 4.985211\n",
"iter 40 value 4.979598\n",
"iter 50 value 4.970240\n",
"iter 60 value 4.951684\n",
"iter 70 value 4.900179\n",
"iter 80 value 4.626554\n",
"iter 90 value 4.086041\n",
"iter 100 value 3.906687\n",
"final value 3.906687 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 22.137904 \n",
"iter 10 value 4.908607\n",
"iter 20 value 4.411717\n",
"iter 30 value 3.930598\n",
"iter 40 value 3.919484\n",
"iter 50 value 3.912386\n",
"iter 60 value 3.908797\n",
"iter 70 value 3.908248\n",
"iter 80 value 3.907990\n",
"iter 90 value 3.907230\n",
"iter 100 value 3.906797\n",
"final value 3.906797 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 8.982054 \n",
"iter 10 value 4.998880\n",
"iter 20 value 4.998160\n",
"iter 30 value 4.997203\n",
"iter 40 value 4.995867\n",
"iter 50 value 4.993867\n",
"iter 60 value 4.990548\n",
"iter 70 value 4.984029\n",
"iter 80 value 4.966237\n",
"iter 90 value 4.842527\n",
"iter 100 value 4.058323\n",
"final value 4.058323 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 8.994385 \n",
"iter 10 value 6.997719\n",
"iter 20 value 6.997601\n",
"iter 30 value 6.997471\n",
"iter 40 value 6.997325\n",
"iter 50 value 6.997163\n",
"iter 60 value 6.996980\n",
"iter 70 value 6.996772\n",
"iter 80 value 6.996535\n",
"iter 90 value 6.996261\n",
"iter 100 value 6.995942\n",
"final value 6.995942 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 20.877544 \n",
"final value 7.000000 \n",
"converged\n",
"# weights: 51\n",
"initial value 18.251895 \n",
"final value 7.000000 \n",
"converged\n",
"# weights: 11\n",
"initial value 25.760391 \n",
"iter 10 value 6.363395\n",
"final value 6.353131 \n",
"converged\n",
"# weights: 31\n",
"initial value 13.660612 \n",
"iter 10 value 6.283886\n",
"iter 20 value 6.271493\n",
"final value 6.271477 \n",
"converged\n",
"# weights: 51\n",
"initial value 16.050385 \n",
"iter 10 value 6.249999\n",
"iter 20 value 6.239089\n",
"final value 6.239018 \n",
"converged\n",
"# weights: 11\n",
"initial value 11.294569 \n",
"iter 10 value 7.008551\n",
"iter 20 value 7.008489\n",
"iter 30 value 7.008427\n",
"iter 40 value 7.008364\n",
"iter 50 value 7.008300\n",
"iter 60 value 7.008235\n",
"iter 70 value 7.008170\n",
"iter 80 value 7.008104\n",
"iter 90 value 7.008037\n",
"iter 100 value 7.007968\n",
"final value 7.007968 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 10.564469 \n",
"iter 10 value 6.086679\n",
"iter 20 value 5.125211\n",
"iter 30 value 5.116156\n",
"iter 40 value 5.106074\n",
"iter 50 value 5.104425\n",
"iter 60 value 5.103682\n",
"iter 70 value 5.103319\n",
"iter 80 value 5.103164\n",
"iter 90 value 5.103124\n",
"iter 100 value 5.103052\n",
"final value 5.103052 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 11.567648 \n",
"iter 10 value 7.004807\n",
"iter 20 value 7.004763\n",
"iter 30 value 7.004719\n",
"iter 40 value 7.004674\n",
"iter 50 value 7.004627\n",
"iter 60 value 7.004580\n",
"iter 70 value 7.004531\n",
"iter 80 value 7.004481\n",
"iter 90 value 7.004430\n",
"iter 100 value 7.004377\n",
"final value 7.004377 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 17.745229 \n",
"final value 7.000000 \n",
"converged\n",
"# weights: 31\n",
"initial value 27.255976 \n",
"final value 7.000000 \n",
"converged\n",
"# weights: 51\n",
"initial value 7.829178 \n",
"iter 10 value 6.999873\n",
"iter 20 value 6.999872\n",
"iter 30 value 6.999871\n",
"iter 40 value 6.999871\n",
"iter 50 value 6.999870\n",
"iter 60 value 6.999869\n",
"iter 70 value 6.999868\n",
"iter 80 value 6.999867\n",
"iter 90 value 6.999867\n",
"iter 100 value 6.999866\n",
"final value 6.999866 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 16.305536 \n",
"iter 10 value 6.246216\n",
"final value 6.214667 \n",
"converged\n",
"# weights: 31\n",
"initial value 21.012069 \n",
"iter 10 value 6.207481\n",
"iter 20 value 6.148654\n",
"final value 6.148532 \n",
"converged\n",
"# weights: 51\n",
"initial value 14.524318 \n",
"iter 10 value 6.187450\n",
"iter 20 value 6.145487\n",
"iter 30 value 6.145297\n",
"final value 6.145291 \n",
"converged\n",
"# weights: 11\n",
"initial value 14.821245 \n",
"iter 10 value 6.986710\n",
"iter 20 value 6.979144\n",
"iter 30 value 6.964012\n",
"iter 40 value 6.921950\n",
"iter 50 value 6.604091\n",
"iter 60 value 5.077008\n",
"iter 70 value 4.085006\n",
"iter 80 value 4.057073\n",
"iter 90 value 4.057032\n",
"iter 100 value 4.056914\n",
"final value 4.056914 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 16.496305 \n",
"iter 10 value 6.988034\n",
"iter 20 value 6.978545\n",
"iter 30 value 6.946733\n",
"iter 40 value 6.298307\n",
"iter 50 value 4.105334\n",
"iter 60 value 4.062246\n",
"iter 70 value 4.060198\n",
"iter 80 value 4.056404\n",
"iter 90 value 4.056215\n",
"iter 100 value 4.056021\n",
"final value 4.056021 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 16.292015 \n",
"iter 10 value 7.004158\n",
"iter 20 value 7.004092\n",
"iter 30 value 7.004023\n",
"iter 40 value 7.003952\n",
"iter 50 value 7.003877\n",
"iter 60 value 7.003798\n",
"iter 70 value 7.003714\n",
"iter 80 value 7.003626\n",
"iter 90 value 7.003533\n",
"iter 100 value 7.003433\n",
"final value 7.003433 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 13.198909 \n",
"final value 6.999966 \n",
"converged\n",
"# weights: 31\n",
"initial value 15.066457 \n",
"final value 7.000000 \n",
"converged\n",
"# weights: 51\n",
"initial value 8.135236 \n",
"iter 10 value 6.999689\n",
"iter 20 value 6.999685\n",
"iter 30 value 6.999681\n",
"iter 40 value 6.999677\n",
"iter 50 value 6.999673\n",
"iter 60 value 6.999669\n",
"iter 70 value 6.999664\n",
"iter 80 value 6.999660\n",
"iter 90 value 6.999655\n",
"iter 100 value 6.999650\n",
"final value 6.999650 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 11.236554 \n",
"iter 10 value 6.285577\n",
"final value 6.283343 \n",
"converged\n",
"# weights: 31\n",
"initial value 10.281890 \n",
"iter 10 value 6.208128\n",
"iter 20 value 6.206116\n",
"final value 6.206112 \n",
"converged\n",
"# weights: 51\n",
"initial value 12.583298 \n",
"iter 10 value 6.186108\n",
"iter 20 value 6.180127\n",
"iter 30 value 6.180018\n",
"final value 6.180018 \n",
"converged\n",
"# weights: 11\n",
"initial value 16.486685 \n",
"iter 10 value 5.787473\n",
"iter 20 value 4.961948\n",
"iter 30 value 4.939719\n",
"iter 40 value 4.925720\n",
"iter 50 value 4.921076\n",
"iter 60 value 4.919906\n",
"iter 70 value 4.919646\n",
"iter 80 value 4.918189\n",
"iter 90 value 4.917911\n",
"iter 100 value 4.917819\n",
"final value 4.917819 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 23.143967 \n",
"iter 10 value 7.003616\n",
"iter 20 value 7.003361\n",
"iter 30 value 7.003076\n",
"iter 40 value 7.002755\n",
"iter 50 value 7.002391\n",
"iter 60 value 7.001972\n",
"iter 70 value 7.001485\n",
"iter 80 value 7.000910\n",
"iter 90 value 7.000220\n",
"iter 100 value 6.999374\n",
"final value 6.999374 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 14.131431 \n",
"iter 10 value 7.002261\n",
"iter 20 value 7.002105\n",
"iter 30 value 7.001932\n",
"iter 40 value 7.001737\n",
"iter 50 value 7.001516\n",
"iter 60 value 7.001262\n",
"iter 70 value 7.000967\n",
"iter 80 value 7.000617\n",
"iter 90 value 7.000196\n",
"iter 100 value 6.999676\n",
"final value 6.999676 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 16.802538 \n",
"final value 7.999999 \n",
"converged\n",
"# weights: 31\n",
"initial value 9.725303 \n",
"iter 10 value 7.999852\n",
"iter 20 value 7.999851\n",
"iter 30 value 7.999850\n",
"iter 40 value 7.999849\n",
"iter 50 value 7.999848\n",
"iter 60 value 7.999847\n",
"iter 70 value 7.999846\n",
"iter 80 value 7.999845\n",
"iter 90 value 7.999844\n",
"iter 100 value 7.999843\n",
"final value 7.999843 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 9.409114 \n",
"final value 7.999958 \n",
"converged\n",
"# weights: 11\n",
"initial value 15.578559 \n",
"iter 10 value 6.068243\n",
"final value 6.000450 \n",
"converged\n",
"# weights: 31\n",
"initial value 13.121039 \n",
"iter 10 value 6.212629\n",
"iter 20 value 5.912302\n",
"final value 5.912201 \n",
"converged\n",
"# weights: 51\n",
"initial value 10.497421 \n",
"iter 10 value 6.045483\n",
"iter 20 value 5.920286\n",
"iter 30 value 5.738367\n",
"iter 40 value 5.731880\n",
"final value 5.731572 \n",
"converged\n",
"# weights: 11\n",
"initial value 11.393880 \n",
"iter 10 value 8.007523\n",
"iter 20 value 8.007453\n",
"iter 30 value 8.007382\n",
"iter 40 value 8.007310\n",
"iter 50 value 8.007235\n",
"iter 60 value 8.007158\n",
"iter 70 value 8.007080\n",
"iter 80 value 8.006999\n",
"iter 90 value 8.006915\n",
"iter 100 value 8.006829\n",
"final value 8.006829 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 22.192156 \n",
"iter 10 value 7.107534\n",
"iter 20 value 3.287414\n",
"iter 30 value 3.208704\n",
"iter 40 value 3.193053\n",
"iter 50 value 3.187582\n",
"iter 60 value 3.181107\n",
"iter 70 value 3.180873\n",
"iter 80 value 3.180827\n",
"iter 90 value 3.180764\n",
"iter 100 value 3.180724\n",
"final value 3.180724 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 30.470275 \n",
"iter 10 value 8.004948\n",
"iter 20 value 8.004879\n",
"iter 30 value 8.004806\n",
"iter 40 value 8.004730\n",
"iter 50 value 8.004651\n",
"iter 60 value 8.004567\n",
"iter 70 value 8.004478\n",
"iter 80 value 8.004384\n",
"iter 90 value 8.004284\n",
"iter 100 value 8.004176\n",
"final value 8.004176 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 11.813650 \n",
"final value 4.999939 \n",
"converged\n",
"# weights: 31\n",
"initial value 28.453694 \n",
"final value 5.000000 \n",
"converged\n",
"# weights: 51\n",
"initial value 6.263991 \n",
"iter 10 value 4.999879\n",
"iter 20 value 4.999878\n",
"iter 30 value 4.999878\n",
"iter 40 value 4.999877\n",
"iter 50 value 4.999876\n",
"iter 60 value 4.999876\n",
"iter 70 value 4.999875\n",
"iter 80 value 4.999874\n",
"iter 90 value 4.999874\n",
"iter 100 value 4.999873\n",
"final value 4.999873 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 19.377885 \n",
"iter 10 value 4.796844\n",
"final value 4.796586 \n",
"converged\n",
"# weights: 31\n",
"initial value 12.740293 \n",
"iter 10 value 4.706322\n",
"iter 20 value 4.703720\n",
"final value 4.703719 \n",
"converged\n",
"# weights: 51\n",
"initial value 8.773290 \n",
"iter 10 value 4.660740\n",
"iter 20 value 4.659767\n",
"final value 4.659767 \n",
"converged\n",
"# weights: 11\n",
"initial value 9.362009 \n",
"iter 10 value 5.007494\n",
"iter 20 value 5.007452\n",
"iter 30 value 5.007410\n",
"iter 40 value 5.007368\n",
"iter 50 value 5.007326\n",
"iter 60 value 5.007284\n",
"iter 70 value 5.007241\n",
"iter 80 value 5.007199\n",
"iter 90 value 5.007156\n",
"iter 100 value 5.007112\n",
"final value 5.007112 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 16.918922 \n",
"iter 10 value 4.998888\n",
"iter 20 value 4.997985\n",
"iter 30 value 4.996783\n",
"iter 40 value 4.995102\n",
"iter 50 value 4.992587\n",
"iter 60 value 4.988428\n",
"iter 70 value 4.980372\n",
"iter 80 value 4.959467\n",
"iter 90 value 4.847961\n",
"iter 100 value 4.022003\n",
"final value 4.022003 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 16.631602 \n",
"iter 10 value 5.005070\n",
"iter 20 value 5.005029\n",
"iter 30 value 5.004987\n",
"iter 40 value 5.004944\n",
"iter 50 value 5.004900\n",
"iter 60 value 5.004856\n",
"iter 70 value 5.004811\n",
"iter 80 value 5.004764\n",
"iter 90 value 5.004717\n",
"iter 100 value 5.004668\n",
"final value 5.004668 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 18.591129 \n",
"final value 8.999965 \n",
"converged\n",
"# weights: 31\n",
"initial value 13.791790 \n",
"final value 9.000000 \n",
"converged\n",
"# weights: 51\n",
"initial value 9.611425 \n",
"final value 8.999977 \n",
"converged\n",
"# weights: 11\n",
"initial value 11.703770 \n",
"iter 10 value 7.696615\n",
"final value 7.696414 \n",
"converged\n",
"# weights: 31\n",
"initial value 8.952654 \n",
"iter 10 value 7.633668\n",
"iter 20 value 7.631491\n",
"final value 7.631490 \n",
"converged\n",
"# weights: 51\n",
"initial value 10.680464 \n",
"iter 10 value 7.611229\n",
"iter 20 value 7.609113\n",
"final value 7.609112 \n",
"converged\n",
"# weights: 11\n",
"initial value 10.808767 \n",
"iter 10 value 8.993926\n",
"iter 20 value 8.991775\n",
"iter 30 value 8.988884\n",
"iter 40 value 8.984777\n",
"iter 50 value 8.978455\n",
"iter 60 value 8.967429\n",
"iter 70 value 8.943356\n",
"iter 80 value 8.853570\n",
"iter 90 value 7.575159\n",
"iter 100 value 6.715215\n",
"final value 6.715215 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 14.936637 \n",
"iter 10 value 9.004841\n",
"iter 20 value 9.004789\n",
"iter 30 value 9.004734\n",
"iter 40 value 9.004678\n",
"iter 50 value 9.004621\n",
"iter 60 value 9.004561\n",
"iter 70 value 9.004500\n",
"iter 80 value 9.004436\n",
"iter 90 value 9.004369\n",
"iter 100 value 9.004300\n",
"final value 9.004300 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 16.523150 \n",
"iter 10 value 9.004249\n",
"iter 20 value 9.004193\n",
"iter 30 value 9.004134\n",
"iter 40 value 9.004074\n",
"iter 50 value 9.004010\n",
"iter 60 value 9.003945\n",
"iter 70 value 9.003876\n",
"iter 80 value 9.003803\n",
"iter 90 value 9.003727\n",
"iter 100 value 9.003647\n",
"final value 9.003647 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 15.891145 \n",
"final value 10.999951 \n",
"converged\n",
"# weights: 31\n",
"initial value 13.080646 \n",
"final value 10.999995 \n",
"converged\n",
"# weights: 51\n",
"initial value 9.219027 \n",
"iter 10 value 6.308620\n",
"iter 20 value 6.232465\n",
"iter 30 value 6.232144\n",
"final value 6.232143 \n",
"converged\n",
"# weights: 11\n",
"initial value 20.839197 \n",
"iter 10 value 8.320368\n",
"final value 8.310985 \n",
"converged\n",
"# weights: 31\n",
"initial value 10.583249 \n",
"iter 10 value 8.287341\n",
"iter 20 value 8.283798\n",
"iter 30 value 8.283767\n",
"iter 40 value 8.282681\n",
"iter 50 value 8.281399\n",
"final value 8.281348 \n",
"converged\n",
"# weights: 51\n",
"initial value 15.078775 \n",
"iter 10 value 8.497957\n",
"iter 20 value 8.237499\n",
"iter 30 value 8.227747\n",
"iter 40 value 8.204202\n",
"iter 50 value 8.201482\n",
"iter 60 value 8.199272\n",
"final value 8.199189 \n",
"converged\n",
"# weights: 11\n",
"initial value 15.341920 \n",
"iter 10 value 11.001600\n",
"iter 20 value 11.001102\n",
"iter 30 value 11.000506\n",
"iter 40 value 10.999777\n",
"iter 50 value 10.998862\n",
"iter 60 value 10.997669\n",
"iter 70 value 10.996043\n",
"iter 80 value 10.993677\n",
"iter 90 value 10.989907\n",
"iter 100 value 10.982972\n",
"final value 10.982972 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 9.955797 \n",
"iter 10 value 6.375691\n",
"iter 20 value 6.241141\n",
"iter 30 value 6.240277\n",
"iter 40 value 6.239797\n",
"iter 50 value 6.239760\n",
"iter 60 value 6.239543\n",
"iter 70 value 6.239436\n",
"iter 80 value 6.239349\n",
"iter 90 value 6.239320\n",
"iter 100 value 6.239300\n",
"final value 6.239300 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 19.896657 \n",
"iter 10 value 11.002862\n",
"iter 20 value 11.002701\n",
"iter 30 value 11.002523\n",
"iter 40 value 11.002323\n",
"iter 50 value 11.002096\n",
"iter 60 value 11.001835\n",
"iter 70 value 11.001532\n",
"iter 80 value 11.001174\n",
"iter 90 value 11.000741\n",
"iter 100 value 11.000207\n",
"final value 11.000207 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 20.785450 \n",
"final value 5.000000 \n",
"converged\n",
"# weights: 31\n",
"initial value 10.350695 \n",
"final value 5.000000 \n",
"converged\n",
"# weights: 51\n",
"initial value 9.797825 \n",
"final value 5.000000 \n",
"converged\n",
"# weights: 11\n",
"initial value 17.048600 \n",
"iter 10 value 4.895483\n",
"final value 4.891138 \n",
"converged\n",
"# weights: 31\n",
"initial value 19.052525 \n",
"iter 10 value 4.789923\n",
"iter 20 value 4.787095\n",
"final value 4.787092 \n",
"converged\n",
"# weights: 51\n",
"initial value 10.079322 \n",
"iter 10 value 4.740833\n",
"iter 20 value 4.739379\n",
"final value 4.739378 \n",
"converged\n",
"# weights: 11\n",
"initial value 19.108232 \n",
"iter 10 value 5.005972\n",
"iter 20 value 5.005901\n",
"iter 30 value 5.005828\n",
"iter 40 value 5.005753\n",
"iter 50 value 5.005675\n",
"iter 60 value 5.005595\n",
"iter 70 value 5.005512\n",
"iter 80 value 5.005425\n",
"iter 90 value 5.005334\n",
"iter 100 value 5.005240\n",
"final value 5.005240 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 13.562621 \n",
"iter 10 value 5.005376\n",
"iter 20 value 5.005327\n",
"iter 30 value 5.005276\n",
"iter 40 value 5.005224\n",
"iter 50 value 5.005170\n",
"iter 60 value 5.005116\n",
"iter 70 value 5.005060\n",
"iter 80 value 5.005002\n",
"iter 90 value 5.004943\n",
"iter 100 value 5.004882\n",
"final value 5.004882 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 13.339248 \n",
"iter 10 value 5.001483\n",
"iter 20 value 5.001282\n",
"iter 30 value 5.001053\n",
"iter 40 value 5.000787\n",
"iter 50 value 5.000475\n",
"iter 60 value 5.000102\n",
"iter 70 value 4.999646\n",
"iter 80 value 4.999075\n",
"iter 90 value 4.998336\n",
"iter 100 value 4.997340\n",
"final value 4.997340 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 11.134067 \n",
"iter 10 value 9.243710\n",
"iter 20 value 7.285528\n",
"iter 30 value 7.245812\n",
"iter 40 value 7.231656\n",
"iter 50 value 7.231393\n",
"final value 7.231393 \n",
"converged\n",
"# weights: 31\n",
"initial value 14.130867 \n",
"final value 12.000000 \n",
"converged\n",
"# weights: 51\n",
"initial value 14.415938 \n",
"final value 12.000000 \n",
"converged\n",
"# weights: 11\n",
"initial value 15.019432 \n",
"iter 10 value 9.069689\n",
"final value 9.063171 \n",
"converged\n",
"# weights: 31\n",
"initial value 17.508841 \n",
"iter 10 value 9.261632\n",
"iter 20 value 9.055988\n",
"iter 30 value 9.055626\n",
"final value 9.055625 \n",
"converged\n",
"# weights: 51\n",
"initial value 11.303518 \n",
"iter 10 value 9.017983\n",
"iter 20 value 9.011319\n",
"iter 30 value 9.010274\n",
"iter 40 value 9.009455\n",
"final value 9.009346 \n",
"converged\n",
"# weights: 11\n",
"initial value 18.239316 \n",
"iter 10 value 12.007304\n",
"iter 20 value 12.007242\n",
"iter 30 value 12.007180\n",
"iter 40 value 12.007116\n",
"iter 50 value 12.007051\n",
"iter 60 value 12.006985\n",
"iter 70 value 12.006917\n",
"iter 80 value 12.006848\n",
"iter 90 value 12.006777\n",
"iter 100 value 12.006705\n",
"final value 12.006705 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 16.014808 \n",
"iter 10 value 12.005794\n",
"iter 20 value 12.005717\n",
"iter 30 value 12.005637\n",
"iter 40 value 12.005553\n",
"iter 50 value 12.005466\n",
"iter 60 value 12.005374\n",
"iter 70 value 12.005278\n",
"iter 80 value 12.005176\n",
"iter 90 value 12.005068\n",
"iter 100 value 12.004953\n",
"final value 12.004953 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 13.391025 \n",
"iter 10 value 9.413596\n",
"iter 20 value 7.286503\n",
"iter 30 value 7.242636\n",
"iter 40 value 7.239833\n",
"iter 50 value 7.238170\n",
"iter 60 value 7.237712\n",
"iter 70 value 7.237671\n",
"iter 80 value 7.237563\n",
"iter 90 value 7.237521\n",
"iter 100 value 7.237438\n",
"final value 7.237438 \n",
"stopped after 100 iterations\n",
"# weights: 11\n",
"initial value 15.087301 \n",
"final value 7.999988 \n",
"converged\n",
"# weights: 31\n",
"initial value 14.180092 \n",
"final value 8.000000 \n",
"converged\n",
"# weights: 51\n",
"initial value 7.621209 \n",
"iter 10 value 5.807104\n",
"iter 20 value 5.756148\n",
"iter 30 value 5.755560\n",
"final value 5.755556 \n",
"converged\n",
"# weights: 11\n",
"initial value 9.112559 \n",
"iter 10 value 6.884039\n",
"final value 6.883875 \n",
"converged\n",
"# weights: 31\n",
"initial value 10.731645 \n",
"iter 10 value 6.824275\n",
"iter 20 value 6.820743\n",
"final value 6.820727 \n",
"converged\n",
"# weights: 51\n",
"initial value 18.479336 \n",
"iter 10 value 6.806358\n",
"iter 20 value 6.796743\n",
"iter 30 value 6.796679\n",
"final value 6.796679 \n",
"converged\n",
"# weights: 11\n",
"initial value 11.006901 \n",
"iter 10 value 8.003946\n",
"iter 20 value 8.003643\n",
"iter 30 value 8.003313\n",
"iter 40 value 8.002951\n",
"iter 50 value 8.002551\n",
"iter 60 value 8.002107\n",
"iter 70 value 8.001610\n",
"iter 80 value 8.001047\n",
"iter 90 value 8.000405\n",
"iter 100 value 7.999663\n",
"final value 7.999663 \n",
"stopped after 100 iterations\n",
"# weights: 31\n",
"initial value 8.823275 \n",
"iter 10 value 8.001656\n",
"iter 20 value 8.001172\n",
"iter 30 value 8.000591\n",
"iter 40 value 7.999875\n",
"iter 50 value 7.998973\n",
"iter 60 value 7.997794\n",
"iter 70 value 7.996188\n",
"iter 80 value 7.993872\n",
"iter 90 value 7.990248\n",
"iter 100 value 7.983840\n",
"final value 7.983840 \n",
"stopped after 100 iterations\n",
"# weights: 51\n",
"initial value 11.581945 \n",
"iter 10 value 8.001224\n",
"iter 20 value 8.000881\n",
"iter 30 value 8.000470\n",
"iter 40 value 7.999967\n",
"iter 50 value 7.999334\n",
"iter 60 value 7.998511\n",
"iter 70 value 7.997393\n",
"iter 80 value 7.995779\n",
"iter 90 value 7.993242\n",
"iter 100 value 7.988684\n",
"final value 7.988684 \n",
"stopped after 100 iterations\n",
"Error in train.default(x = trainEight, y = apply(testEight, 2, factor), : \n",
" final tuning parameters could not be determined\n",
"In addition: There were 50 or more warnings (use warnings() to see the first 50)\n",
"Error in train.default(x = trainEight, y = apply(testEight, 2, factor), : \n",
" final tuning parameters could not be determined\n"
]
}
],
"prompt_number": 86
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"nnetFit <- train(x = trainDescr, y = trainClass,\n",
" method = \"nnet\", trace=FALSE,\n",
" tuneLength = 5)\n",
"plot(nnetFit)"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAeAAAAHgCAYAAAB91L6VAAAEJGlDQ1BJQ0MgUHJvZmlsZQAAOBGF\nVd9v21QUPolvUqQWPyBYR4eKxa9VU1u5GxqtxgZJk6XtShal6dgqJOQ6N4mpGwfb6baqT3uBNwb8\nAUDZAw9IPCENBmJ72fbAtElThyqqSUh76MQPISbtBVXhu3ZiJ1PEXPX6yznfOec7517bRD1fabWa\nGVWIlquunc8klZOnFpSeTYrSs9RLA9Sr6U4tkcvNEi7BFffO6+EdigjL7ZHu/k72I796i9zRiSJP\nwG4VHX0Z+AxRzNRrtksUvwf7+Gm3BtzzHPDTNgQCqwKXfZwSeNHHJz1OIT8JjtAq6xWtCLwGPLzY\nZi+3YV8DGMiT4VVuG7oiZpGzrZJhcs/hL49xtzH/Dy6bdfTsXYNY+5yluWO4D4neK/ZUvok/17X0\nHPBLsF+vuUlhfwX4j/rSfAJ4H1H0qZJ9dN7nR19frRTeBt4Fe9FwpwtN+2p1MXscGLHR9SXrmMgj\nONd1ZxKzpBeA71b4tNhj6JGoyFNp4GHgwUp9qplfmnFW5oTdy7NamcwCI49kv6fN5IAHgD+0rbyo\nBc3SOjczohbyS1drbq6pQdqumllRC/0ymTtej8gpbbuVwpQfyw66dqEZyxZKxtHpJn+tZnpnEdrY\nBbueF9qQn93S7HQGGHnYP7w6L+YGHNtd1FJitqPAR+hERCNOFi1i1alKO6RQnjKUxL1GNjwlMsiE\nhcPLYTEiT9ISbN15OY/jx4SMshe9LaJRpTvHr3C/ybFYP1PZAfwfYrPsMBtnE6SwN9ib7AhLwTrB\nDgUKcm06FSrTfSj187xPdVQWOk5Q8vxAfSiIUc7Z7xr6zY/+hpqwSyv0I0/QMTRb7RMgBxNodTfS\nPqdraz/sDjzKBrv4zu2+a2t0/HHzjd2Lbcc2sG7GtsL42K+xLfxtUgI7YHqKlqHK8HbCCXgjHT1c\nAdMlDetv4FnQ2lLasaOl6vmB0CMmwT/IPszSueHQqv6i/qluqF+oF9TfO2qEGTumJH0qfSv9KH0n\nfS/9TIp0Wboi/SRdlb6RLgU5u++9nyXYe69fYRPdil1o1WufNSdTTsp75BfllPy8/LI8G7AUuV8e\nk6fkvfDsCfbNDP0dvRh0CrNqTbV7LfEEGDQPJQadBtfGVMWEq3QWWdufk6ZSNsjG2PQjp3ZcnOWW\ning6noonSInvi0/Ex+IzAreevPhe+CawpgP1/pMTMDo64G0sTCXIM+KdOnFWRfQKdJvQzV1+Bt8O\nokmrdtY2yhVX2a+qrykJfMq4Ml3VR4cVzTQVz+UoNne4vcKLoyS+gyKO6EHe+75Fdt0Mbe5bRIf/\nwjvrVmhbqBN97RD1vxrahvBOfOYzoosH9bq94uejSOQGkVM6sN/7HelL4t10t9F4gPdVzydEOx83\nGv+uNxo7XyL/FtFl8z9ZAHF4bBsrEwAAQABJREFUeAHsnQeYU0X3xt/Jwi69Su+9Se8gbQEFUT5R\nPruCilhBRf1/tk+xYtdPVFQEURAFsaCiCEgXLCBVioIsvSOwwFJ2c//vmZCwPVuSLcmZ55lNcnPv\n3Lm/m82bMzPnHOOwQIsSUAJKQAkoASWQowRcOXo2PZkSUAJKQAkoASVgCagA6wdBCSgBJaAElEAu\nEFABzgXoekoloASUgBJQAirA+hlQAkpACSgBJZALBFSAcwG6nlIJKAEloASUgAqwfgaUgBJQAkpA\nCeQCARXgXICup1QCSkAJKAEloAKsnwEloASUgBJQArlAQAU4F6DrKZWAElACSkAJqADrZ0AJKAEl\noASUQC4QUAHOBeh6SiWgBJSAElACKsD6GVACSkAJKAElkAsEVIBzAbqeUgkoASWgBJSACrB+BpSA\nElACSkAJ5AIBFeBcgK6nDD8C27dvtxd96tQp7Nu3L/wA6BUrASWQgoAKcAokukEJBJbAoUOH0L9/\nf9voV199hZdeesk+v+SSS/DGG28kOdmuXbtgjMHJkyexfPlyNGjQIMn73hfDhg3DqFGjvC+TPFas\nWBGbN29Osi2rL8aNG4cePXqkOLxz586YOHFiiu2JNyTu/44dOzB69OjEb+tzJRD2BFSAw/4joACC\nTeCXX35Bhw4d7GmWLl2Kjh07ZuiUTZs2xfz58zO0b17cKXH/Fy1ahFmzZuXFbmqflECuEVABzjX0\neuJQJ7BmzRo0bNgQN910Ez7//HP7XCzK+++/Hxs2bPB7+X/99Zc9VnZ0HAcjRoxApUqV0KVLF4hF\n6S3btm1D3759cd555+Gee+6B2+32voUFCxagefPmKFWqFC6//HIcOHDAvidW+CuvvIJu3brZ9665\n5hrExcX5jsvMk549e2LChAmoW7eu7d/bb79tD/f2X6x6uWb5MXH99dcjPj4eN998sz1vjRo18MIL\nL2TmdLqvEggZAirAIXMr9ULyGgEZPv7hhx/QrFkzfPjhh/j+++9RsmRJK0R16tSx3f3yyy+tsIq4\nSh05cqTvMmQYesuWLfa1iNrChQsxb9483HXXXfjuu+98+91www2oV68eVq1aZYeu9+/fb9+Tx0sv\nvRQPPvgg1q9fb8/tHbaW955//nk8/PDD9jgZLp46daqvzcw8keHuyZMn49tvv8XYsWNx33334ciR\nI7Yv0n8ZEn/qqacgw9bvvPOO/TGyadMmO0w+c+ZMPPvss5DXWpRAuBFQAQ63O67Xm2MEIiMjIRbe\n1q1b7TxqQkIC6tevb7cVLFjQ9kMsW7FYE9fUOvjFF19g8ODB1oq++uqr0bp1a7ubzC+LMD/66KOo\nUqUKHn/8cd/hckyTJk3s/HPRokXtPomFe8CAAejTp4/tT+/evRETE+M7NrNPROTF2pd5bfmRIVav\nt7hcLsj55ZqLFStmH2VR2pIlS1C7dm3IjwGxnrUogXAjUCDcLlivVwnkFIGdO3firbfesquen3nm\nGWvx/fPPP3jsscdw9913227IsPDw4cN9XRLhkmHq5EWsTK/oynveOWWxHKtWrYoKFSrYQ0SEpUqR\nYWoZBk++kEv6JaV8+fL2Uf6IQMrQcPIiQ9exsbHJN+P48eNWaL1veM8vr6WtM2fOeN9K8XjZZZfZ\nBWa33HILTp8+jRtvvNEuTIuKikqxr25QAqFMQC3gUL67em25SiAiIgIHDx60AlimTBns3r3bDkfL\nc3kvM6V69epYt26d75C///7bPpftItqHDx+2r0UYvW5O7dq1Q6dOnex55dxSZai5cuXKdl9Zbe2v\nyFC5WPCJi1jyYsHWqlXLtzkjbXl3FlcsmROWfsvQ9TfffGPnkL3v66MSCBcCKsDhcqf1OnOcgMx9\nyvzvFVdcYed3S5Qo4ZvvLVeuXKb6IwudZI5WBFYEUYadpcg5ZOhX5pilfPrppz7rs1evXpAV2CtW\nrLDvTZo0yQ45J16kZd9I548MmYtl+sQTT9hzy5yuDDeXLl3azjunc2iSt8QqlnlhKdLHK6+80rpb\nyeKx5BZ6kgP1hRIIYQIqwCF8c/XScp/AypUr0aJFC9sRWQjVuHHjLHXqkUceQeHCha3oiRtT+/bt\nfe2IMIuPrVjDE7gaWR6lyP7PPfecXTUtIvfyyy/bRVCZsb6LFCmCr7/+GjKfXLZsWSuWixcvtgup\nChUq5OuDvyfyQ0QseGEhi8ZEkMW6lr7KHPG1117rrwl9XwmEHAHDRSBOyF2VXpASyCMEZJhV3INk\nQZYscqpZs2a2eiZWpCxkSk1EZbhbRDJ5kSFjGaJO7b3k+6b3+tixY9ZqFfHMShHLW4af5YeBFFnl\nLXPAMjKgRQmEIwEV4HC863rNSkAJKAElkOsEdAg612+BdkAJKAEloATCkYAKcDjedb1mJaAElIAS\nyHUCKsC5fgu0A0pACSgBJRCOBEJegCW4gK4zC8ePtl6zElACSiBvEwhpAZZgARIK0Bu0IG/fivDr\n3ZNPPmndUMQVRao3ZV/4kci7V7xx40YbArNRo0aIjo7G77//nnc7qz1TAvmMQMiGopRwfhJ43huY\nPjv3ZSsTyDz9NUP7HQJOJwCfM4pg6ax5YmSnGyF3rASTGDNmjC/frPiDZrWIi8vb372BH36fgb2H\n9+A/A/+LKzpdmdXm9LizBCToRvfu3fHBBx9YP14JCLJ69eokYSwzA8s5sBrOb8xjfHw3UKAQzCVf\nwhTwuCVlph3dVwmEAoGsf+Pl4asX30IJTiCB5yWWbXbKEWZoa/IoMLAt8P39wADGwL9mDBB3Ojut\n6rFCQLL3SExjSVsnUwWZCeyQnOBjk/6Dz376BFP+Mx0znpiL+8beidkrZibfTV9ngoAkepgzZw6G\nDh1q/X8lsYP4Mf/444+ZaOXcrg5F15nSAabV/TCXs43SjeDMHw7HzV+1WpRAGBIISQtYgh5IGrhA\nlHnrgcf/BfRp6mltWC9gLyPqLYsButTP3Bnemw+cOJW5Y4Kx9zXMDV+hZDBaznibMj1w9OhRm49W\ngkRIwH9JzSfDnFkpC9bOxdxnlyCqYBSKRBWhCP+IcbPfRe+WfTLV3LK/fsXidQsydUwwdm5QtRH6\ntr4kGE1nuE358SpV8g1LBC8J6PHnn39iz549GW4jyY5/fwPT4y2YCm3sZtPtNbjn3gEcYSrC0g2S\n7JreC7umY8Xr6e2Sc+815Y+TgjoclnPAQ+tMISnAgb5Fya3dTfuAvibzZ6lXgUPYKRPOZL6hbB5R\nKDKbDQTgcEn+PmjQIJsFp3jx4jYnrEwZZFWASxctjZOnT1oBlu7FnY7jj50Tme5p2RLnoVG1Jpk+\nLtAHVCrtSZgQ6HYz055MCUjKQslaJLmKJSSlpBQsUCAbXxtnkt2TfzawS1n4ZyrTKDOXErx9Xdlg\nEbxeacv5hEDIR8KSlGtLly61cWezck9EfG94D7isFdC5HjCWxtGiP4GFD/NrIwvfG1npQzgcc+DA\nAZtGT1LoZTZRgfD5ZOEkO//7nyv+i3+OHcLIyY/gzdvHon6VjFtW4cA5s9cooS8feughSBzrgQMH\n2v+lq666KksL5pyTB+F8fy1M8zuBsk3h/PwE6KIAV59Jme2W7q8EQoKACnAGbqOI8CPTOHzMx/oV\ngbt6AoU8+dQzcLTukhoBSVIgdTCTzEuRHLWS1UcWzWV1LvibX7/CF0umojCHoIdceDta1fEMddoT\n6J8sEZBVz82bN/fFnm7atCkkq5Jsy0pxTh2Gs+gBwB0PU7E9cD6HcF2ZS82YlfPqMUogLxJQAc6L\ndyUM+iSCK64ta9eutZavJKnfsGGDnQcOg8vPN5d40UUX2SFoSR8oixrFdWzJkiU+Qc43F6IdVQJ5\nkIAKcB68KeHSpVdffdWmx5MMOZJfdtq0aahbt264XH6+uE4RW+8qaBmZkHSHshpaixJQAtknEPIC\nnH1E2kIwCciKVnF3yW6qvGD2UduGTWeYXZc+5agElEBSAirASXnoKyWgBJSAElACOUIgJANxiL/i\nfffdh5YtW1r/xddeey1HYOpJMk5g/PjxqFatWooqc8NalIASUALhQCAkLeA33ngDCxYswGeffQbx\nN61fvz4+//xzG3UpqzfVLUGVttP1iF4tpmtWW9HjvAQk8pVELPOWhx9+GOKCJPcpq8Xh8c4PswH6\nr5prr4aJispqU3qcElACSiDoBELSAr7tttvsYhEJJCBVvujFKs5qSbiL7ooTeHQhIKE/PShezWpL\nepyXgARzKFKkiK3ijjR9+nSMHTvW+3amH531G5DQuQdw5gycdeuRUK4KHM4ta1ECSkAJ5FUCIWkB\ne2F/+umnePnll3H++edDhjyzEuzfPYeCey/jxq/1tOqc4evLaGSNoiXczHsmfcwOAZkqkCmDG2+8\nMcvNxDdqhoh3GeawaxfbhvutMXB27ETEqGey3KYeqASUgBIIJoGQjqNmGKpKYtguW7bMRvLJkvvE\nfort7edugZEAHIzv4OylAJ/bnKFnCQN43D8Z2jWoO0W86xlKD+pJMtj4mjVrsHnzZhtlKYOHpL5b\nhQo+8ZUdTO9ecJ59PvV909nq/mQK3O++n84eOfOWq2cPuP77SM6cTM+iBJRArhAIaQvYS1SGpMX6\nldR3mS3OGg47U4AjvuOXOhMYONv4ugZf7+DrKpltTfdPTkDCHEoYyvffz57oJdx1D0y9unDdO8ye\nIuG/I+0csOsxxgzVogSUgBLIgwRC0gKW4Waxdtu3Z6g7FnkugeSzUgyzILmGU3QrU3CZBxi/U3wX\nqfhmhWVqx3z11Vd48803U3srU9tcz4xEQgPGF165CsxtyFjDZWBefyVTbejOSkAJKIGcJBCSAiyL\nrh5//HHMmDEDx44dw0cffYTLLuPEbRaL6yoKbmceTKsXI/i8QhYb0sOSEDjDBVObNm2CxBfObjGM\npBWxK4ZJhld7VkG3bJHdJvV4JaAElEBQCYTkEPSJEydw66234tdff7XwLr/8chvDNqtB/oN6B8K4\n8Y0bN6Jjx442ElYYY9BLVwJKIEwJhKQAe+/l8ePHEUVf0GzlL/U2po9KQAkoASWgBAJIIKQFOICc\ntCkloASUgBJQAgElEJKBOAJKSBtTAkpACSgBJRAEAirAQYCqTSoBJaAElIAS8EdABdgfIX1fCSgB\nJaAElEAQCKgABwGqNqkElIASUAJKwB8BFWB/hPR9JaAElIASUAJBIKACHASo2qQSUAJKQAkoAX8E\nVID9EdL3lYASUAJKQAkEgYAKcBCgapNKQAkoASWgBPwRUAH2R0jfVwJKQAkoASUQBAIqwEGAqk0q\nASWgBJSAEvBHQAXYHyF9XwkoASWgBJRAEAioAAcBqjapBJSAElACSsAfARVgf4T0fSWgBJSAElAC\nQSCgAhwEqNqkElACSkAJKAF/BFSA/RHS95WAElACSkAJBIGACnAQoGqTSkAJKAEloAT8EVAB9kfI\nz/uXXXaZnz3C7+0RI0Zgy5Yt4Xfh6VzxtGnTMHny5HT2CL+3du3ahbvvvjv8LtzPFet3SkpA9957\nL7Zt25byjXy+pUA+73+ud//w4cO53oe81oHY2FgkJCTktW7lan9OnjyJU6dO5Wof8trJ5TNy9OjR\nvNatXO+PfqekvAXyOQnF7xS1gFPea92iBJSAElACSiDoBFSAg45YT6AElIASUAJKICUBFeCUTHSL\nElACSkAJKIGgEwj5OeDly5dj//79QQN56NAhzJw5M2jt58eGt2/fjoULF2LTpk35sftB6fOqVatw\n5swZ/awkoiv/lzt37lQmiZjIU/1OSQaEL3fs2IEFCxZg48aNKd8MwBZjDC666KIAtJS5JozDkrlD\n8ubeX3/9Nfbs2ZOkc/IP/u6772LIkCFJtgfyxcGDB1G2bNlANpnv2xImxYoVQ1RUVL6/lkBdwJEj\nR2xTJUuWDFST+b6d06dPQxbs6f9P0lup3ylJecirYH+niJdCp06d0KpVqxQnv+WWWxAREZFieyA2\nhIwFXKRIERQvXjwJE1k5165dO9x///1JtgfyhaxYLFWqVCCbzPdtyZeq3I9gfWjzIyBZBS2lUKFC\n+bH7QemzrGo9ceJEiv/boJwsHzWq3ykpb1awv1MKFy6Mv//+O8c/iyEjwL169Upx19avX2+hFi1a\nNMV7gdogH4xgth+ofuZkOyI28oEuWLBgTp42T59LBpqk6mfl3G2Kj4+HWMHK5BwTeabfKUl5yKu4\nuLigfqeUK1cO5cuXxzXXXJPy5EHcoouwgghXm1YCSkAJKAElkBYBFeC0yOh2JaAElIASUAJBJKAC\nHES42rQSUAJKQAkogbQIqACnRUa3KwEloASUgBIIIgEV4CDC1aaVgBJQAkpACaRFQAU4LTK6XQko\nASWgBJRAEAmoAAcRrjatBJSAElACSiAtAirAaZHR7UpACSgBJaAEgkhABTiIcLVpJaAElIASUAJp\nEVABTouMblcCSkAJKAElEEQCKsBBhKtNKwEloASUgBJIi4AKcFpkdLsSUAJKQAkogSASUAEOIlxt\nWgkoASWgBJRAWgRUgNMio9uVgBJQAkpACQSRgApwEOFq00pACSgBJaAE0iKgApwWGd2uBJSAElAC\nSiCIBAoEse2watpZ8y6cmO+A43tgGl4H02J4WF2/XqwSUAJKQAlkjoAKcOZ4pbq3s+J/cI5ugek7\nBXDccD5tAxQuB9PgmlT3141KQAkoASWgBHQIOgCfAWfrTJh2jwKnjwAJJ2EGzIKzZUYAWtYmlIAS\nUAJKIFQJqAAH4s5GlaL4xsJZ8w6ceXfb51aMA9G2tqEElIASUAIhSUCHoANwW03jm+AsuBcoVBqI\n2wdn7u0wnV8IQMvahBJQAkpACYQqARXgANxZU+NCIKoknFmDgVJ1geINYSp1CEDL2oQSUAJKQAmE\nKgEdgg7UnS3XEihZB6bPJ1wJvRvOqcOBalnbUQJKQAkogRAkoAIcqJtK0UXRijCRxWCqdAVivg9U\ny9qOElACSkAJhCABFeBA3dTjuyjAlT2t1e7PVdDfwqFLkhYloASUgBJQAqkRUAFOjUpWth3bBVPM\nI8CmZC2gSAVg989ZaUmPUQJKQAkogTAgoAIcqJt8QizgSr7WjFjBf0/3vdYnSkAJKAEloAQSE1AB\nTkwjG88dWsC+IWhpp3IXIHYbnNjt2WhVD1UCSkAJKIFQJaACHKg7m3gOmG0aVwRMzYsBtYIDRVjb\nUQJKQAmEFAEV4ADcTsedwAAcBznvWzFpa7UuhrNjPpz4uKTb9ZUSUAJKQAmEPQEV4EB8BE7sYfKF\n86zVm7g5U6gsUK4FsG1O4s36XAkoASWgBJQAVIAD8SGQ4eezK6CTN+dZjPV18s36WgkoASWgBMKc\ngApwID4AFGDj9QFO1p45rxknhA2c/auSvaMvlYASUAJKIJwJqAAH4u4nXwGdrE21gpMB0ZdKQAko\nASWgQ9CB+Aw4yVZAp2izWk/gwCo4cQdSvKUblIASUAJKIDwJqAUciPvuR4BNgcIw1aKBLTMCcTZt\nQwkoASWgBEKAgApwdm+i4zD70V6biCHdpmoxMhYTNDju+HR30zeVgBJQAkogPAioAGfzPrtOcVi5\nUCmYiMh0WzLFqzJdYU1g56J099M3lYASUAJKIDwIqABn4z47Oxei6OpRwJEYOCcP+W3JiBW85Ru/\n++kOSkAJKAElEPoEVICzeI+dTV/AmXUTEkrUA8o0gvPNZXAOb06/tUodGDFrn//90m9F31UCSkAJ\nKIEQIKACnMWb6Cx5BObqX+COLAFTvTdM6/vhrBmTbmvGuGBqXcr40BqYI11Q+qYSUAJKIAwIqABn\n9SYX45wuQ026TjIGtKQhLF4TOHPCf2s1+sDZtQjO6WP+99U9lIASUAJKIGQJqABn9dZWvoBD0IPs\n0U78STirRsPUvMhvayaqJEyljsDWH/zuqzsoASWgBJRA6BJQAc7ivTVtH6HFewyFYz4Flj5GUe0E\nU/tfGWuNw9C6GCtjqHQvJaAElECoElABzuKdFbcj1yVfIK7mVTBdXoJpcnOGWzJlGgIFi8HZ+1uG\nj9EdlYASUAJKILQIqADn0v3U+NC5BF5PqwSUgBLIIwRUgLN5I5jniC2YzLdStTvwz0Y4x3dn/lg9\nQgkoASWgBPI9ARXgXLqFMoRtanDR1t8amCOXboGeVgkoASWQqwRUgLONXyzgLJaa/eBsmw0n4XQW\nG9DDlIASUAJKIL8SUAHOxTtnila0UbSwY14u9kJPrQSUgBJQArlBQAU4N6gnOqcuxkoEQ58qASWg\nBMKIgApwQG52FhZhnT2vqdAGiD8B59D6gPREG1ECSkAJKIH8QSBHBXjWrFm4+OKL0atXL2zYsCEJ\noZ9++gkdOnRIUrdv3479+/dj5MiRuOSSS/D2228nOSZUXmh86FC5k3odSkAJKIGME8gxAY6NjcWj\njz6KyZMn45VXXsHQoUOT9LJjx45YsGCBrSK4ZcuWRbVq1XD77bfjwgsvxPTp0yEifeAA8++GWuFq\naGfPL3BOHQ61K9PrUQJKQAkogTQIFEhje8A3i8XbsmVLlCpVytYjR47g9OnTiIz0JLJ3uVyIiorC\n8ePHrVDPmDEDCQkJ2LhxIwoVKoQpU6Zg7NixKFKkSMD7lq0GHa6CNlkfgpZzm4JFgSrdgJjvgQbX\nZKs7erASUAJKQAnkDwI5JsA7duxAmTJlfFREiMWarVy5sm+bPJk4caK1eCtWrIhdu3Zh7969GDNm\nDJo2bQqxkpcvX44CBVJ2e/jw4Vi9enWStkTMy5cvjz179iTZHsgXhfgj4dChgzjjyt45XMU7otja\nF3C0BIWYaQszVU4BkbOiALfBmS6n4JThj4JcLGfOnLE/rkw2f5jk4iUE/NTyY1KKfCa1eAg4/PEa\nHx8f1P/P/MhaDJNgfmflRybynSI1WN8pO3futNrzwQcfpMAjU6deQzHFm9nckFLJstlgWoeXLFkS\nx46dS8EXFxeH8847L8Xu48ePx2effWa3Fy1aFG632wqwiK5Yw3PmzEGfPn1SHPfGG2+k2LZ+/XqM\nHj0aIubBKrF/uFCyzHkw2T5HRbh31URhZwsTO3TOcHedM9TdK7l7Peo2cbqbABGcXjcNMtxEwHc8\nePAgSpQogYIFCwa87fzaoHz2RXCKFy+eXy8h4P0W8T18+HCq3wMBP1k+alDEN5jfWfkIha+rYqyJ\nhgTrO6VKlSp4+OGHMWjQIN85c+JJJk2trHepSZMmWLlypf0SkuFnEdbkvyrE2pVSo0YN+yjAK1Wq\nhKNHj9rXYhHLF3uoFlObWZL+/jpTl+d+hmIbTdF9EXD9Hx8XUYT/m6kmdGcloASUgBLIBQI5JsAV\nKlTAddddZ1czyyroF154wV6uLMb68ssv7XOxWM8///wkGGT4ecSIEejXrx/KlStnh6GT7BBKLyp3\nAWK3wYndnvGrOkgB7g44P9GbqRYfaRGD27QoASWgBJRA3iaQY0PQguGOO+7ALbfcYudwZdGVlPfe\ne88+yp/u3bvb6tvAJ126dLH1xIkTeW8BVuKOBuC5cUUANS9mfOjpQPO7M9SiYWbDhAcowpVo/fJ3\nTMI9PGwNhfhvbqudoSZ0JyWgBJSAEsgFAjlmAXuvTYadveLr3ZaRxzy3+jkjnc7KPrUuhrNjPpz4\nuIwd3YK7rfAIrvtTPudaH9frHIamKLv/x+2xGWtG91ICSkAJKIGcJZDjApyzl5f/zmYKlYUp1xJg\nkgZ/xdlEgX3JM+8bwblgV18+n8nHG1k/4tH0jnLzuZvTyuItpUUJKAEloATyDgEV4EDci0C729jF\nWOmnKXQYj8T9MIVWhp+54tl0Ze3GWsxzQfLoGs76KsV3Hve9lY8cmtaiBJSAElACeYOACnDeuA9J\nemHOa0YlNXD2r0qy3fvC4ei0+yHuMpCV67bSK4YLsyJeoxDfwGNoJbufphDvT+8IfU8JKAEloARy\ngoAKcHYp27Hd7EXCSq0LaWVJctwU0ScpvI0pqleldmTq28Q6dk3ke9V4/BDWSRRiWTGtRQkoASWg\nBHKFgApwrmDPwEmr9QIOrIITl9RcdUbzWIqwkdXOZ8uh2EN4a8b/8MY3r2Lzbk4Mp1EMo366BrO+\nS/H9i80M4iPdl7QoASWgBJRAzhNQAc555hk6oylQCKZaT2DLDN/+7mkUTI5Ku0ZSgOmxJOVY3DFc\n+/LlNsBJpdKV0Xx4ffy0fpHnzTT+GgYGi6AVLfPH7ve5cJoBPJxtaeysm5WAElACSiAoBFSAs43V\noRoGfgjadksWY8XMhOOOh7OEIjmFovk8T5coH8XTU/6LwT1vxd2X3IteLS7Cmjc34YVpT2foqkwr\ntkcBNu0pxFyw5R7Dc5zI0KG6kxJQAkpACWSTgApwNgEG83BTrCpQshacXxbCLaEmn6VYlk96xrjT\ncWhS/Xz8uGoW2t3fFM9OHYm/dv2FJesX4/hJ/4H/xZJ2XcH6Idvl7m5ZrEVXJi1KQAkoASUQXAIF\ngtu8tp5tAmX6w5k4Fa4Ho2Hqp2ytff2O+M+HI1CsUDH88vJqPDH5EWuQz1j2NV764jnUKF8TLWu3\ntrUxhbpAROq33JSkuHNI2vmTAvwGh6WnU5Q5zyyRtrQoASWgBJRA4Amk/m0c+POEcIscgg5SEXcj\n56UOMJ3eApps5lnqpDjTtd1uxLZXnkO3ZTvxz1tNMLhsMTy/cAWKFi+F+IR4rNu2Fiv+Xo7xc97D\n1n0xEBH2CnKdSnVTtCciH/EmRZhxQNyPUYDbsg5lLZ1iV92gBJSAElAC2SCgApwNeME81EmgAD5B\n4WtuGGTjUsaHZjirVvelOOXejyfggu2nUXbhIriLFEHzYf+Feel/wFNPWGu3Wa0WkDqo5y12SHrV\nlhVWkEdNewqxJ46iRe1WHkGu0wYVSlXwte/qTfG/gHUi+zGY/biOlUPV3sVfvh31iRJQAkpACWSJ\ngApwlrAF/yCHGgrOz5phfDzTB87sm4Dzb4WJPBvq6mwXYsa/Bfe9d6H+UQfOVzOAp0fCGZZSqGX3\nooWKolOjC2yV1/uP7MdKWsdiIX84dxwKRxamIHuGq0WYixcubq1fpx9FmFax8y2HpdkfsYq1KAEl\noASUQPYIqABnj19QjnZPpdj9QbGj6BlZJhfFCdpKHYGtPwD1aIaeLWLNHk44iV474uGePgrm2qvh\nPPs8F239CvfYcTA9e8DUru3dPcVjuZLl0LtlH1vlzZi9W6wYz145E69NfxFVylb1DVc3eaopCi6P\ntAkeUJN9u4t9q5SiSd2gBJSAElACGSSgApxBUDm1m7OY4vsZBe5tClzhRGetzcVYvz0Hk0iA35/1\nDu7uQfP0NZrLzz8DU7UK3IuXwDwz0h7ofuRxoBD9iUWIo7vDVKlit6f1p2aFWpA6oONAJCQkYP2O\nddZCnjR/Ajbv2YRGVRujxa2t0Xxja9S9vT5c/Tk8LkPThdJqUbcrASWgBJRAWgRUgNMik9HtAQxF\n6WzkUO/LFF9WUy5pB0zpBnAiS8DZ8ytMxXaYv2YuWi2LQd3YcjDzfoDzwUdw/7GOfr1j4LqQE7hS\nbr0Fzrr1cObOo5/vCOC88zxCHE0xLpfsBPaAc38iIiJwfo2mtl7fYzDiTsVhdcxKayG/duZ5HGpz\nEM1WtkSLmRyyvqE1qvZPX9zPtazPlIASUAJKQAioAOeRz4Gzl+L7KMX3PxTfuql3yhsfOqFcK/z9\n9CPo71RlWMk3YMqUoRVM1U6lmMaNGDe6EZy77gBWMrTl3PmMBX07UKOGxzLu3hWmJIe4/ZTCUYXR\nvkFHW2VXCX8pc8crli7Hp59ORMRnEWjZg2LctjVqlK6FEiVK+GlR31YCSkAJhDcBFeA8cP8l+pRb\nhFeGcznVm2ap0h1Y8x42PnADmhxyo+yXH8AUL57m7onfMBKtq2ULGFbnXq6k+m0ZnB9pGXOuGCLS\n0bSKu1wAU7Ro4sPSfF6meBn0bN7bVuc2pi+eug0rpizH/NVz8Xvx31C5YhW0rtvWziE3rdkcUQWj\n0mxL31ACSkAJhCMBFeBs3/XshaK07kb/pfC2ofU7wE9nHIP4VacRf3gJKn0wL8Pim7xVw+FldGgP\nw+qcPg0s/RluirHz5hiPSEdTjDt34orryOSHpvpatL3GVdVRvV919J8wAHHfn8Tfl/+JNVGrMHXx\nZDwz9QnUr9zAirGssm5QpSFcLg3ClipM3agElEDYEFABzuVb7bzKDnARk7kr/Y44J0/C/fiT2HDg\nNIp2LodqlWumf0AG37Ui260rIlidEyfgLFoMZ+YsOK+8TmucQUCiuwNt28AU8P9RMfSQMncDpzrH\noeGHTdB4STNcM/wGnL7+FNbErLJD1qO/fRV7D+9Bs5otfCusq5WrnsHe6m5KQAkogdAh4P9bNXSu\nNUhXkvVIWO5PuOKZoR9dTDEoVmRaxTl2DO6HHsOJ8mXwTKkC+KDehcD2uUDNPmkdkqXthoE8zEVs\nm9U5cgTOAgb3mPIZV1i/BHNBZztnbIex0+ssz+xUZ77El9xwLY2AexRQsHEUWt/RDm0uamf7deT4\nESvG4oP8+ZIpSHAn+KxjidIlw9talIASUAKhTkAFOJfusLOAQvUlxZejvum58TiHDsF9/39g2rXB\n+5WOoF/xy1CkYXOubub8b4AFODEKWZhl+l8CsDoHDsCZtwDu9zhfvG8fTI9uFGPGpubccXrFdOX1\ndeB18oeGewivcyDrVcwvUbQkujeNtlWO33VwpxXkpRsW453vR1OAy/qsY7GUZQGYFiWgBJRAqBFQ\nAc6FO+qsoyC9TnHiwmVTNu0OOLt3wz3i/2Au7YdtPdvj14/ux7jhk2CiisBZ/RacQ+u5Ajp9EUy7\n9Yy/Y8R96d8MAMLq7NrlWbz1EsfO4+LOuTXVrZtqg4bTyGYQRbgvr5m+zQ6f2yAeDHPpLZXLVoHU\nfm3p60y3rr92/WkF+aufp0FCZtapWNdnIYsvsrhIaVECSkAJ5HcCKsABuYPpjB8na9/ZQyHioivX\nwxSmOsneTPTS2bIF7gcfhrlpEFz9+mL8xw/j6q7XowjFV4qpdaknPnQOCHCibsFUrgxzA5drs0of\n7Urqx5/iOHNBjxj37AEUTmmxShrFiJEU4JW8fgmz+RUZDOd1JJv+ldXa9as0sPWqLtfi9JnT+GPb\nGivI7858EzsP7qBvcjOfhSyBQ7QoASWgBPIjARXgHLxrzjGKj7gb3cjqmQ5N9ewSPMP96ONw0V3I\ncHHU6i0rsX3/Vjxx9TPn9q9xEZwNk7ji6TAt4lLntufgM1OrFswQCuCQm+Gs3+AJ+HHvAyjMuWQ7\nj9ybw9TlqbyJimlB4eVItjOdLESAGTPEDGZNw/spsmAkWtahfzGrlNi4WEbn+t0K8je/fgnJh+zN\n7iQrrCW8phYloASUQH4goAKcQ3fJuhs9TqFpTwH6V9ondeif62Y8Z9djtH7beERn7KwxuKn30CRD\nr6YgFatqd2DLd0DDa9NuMIfeMY0aQqpz5+04tWAhCv62HO6hdwLVqtnFW0YCfpTy/FCQ+NaGLldO\nNCvF2H0DXw8hl4v9d1YSRHRp0s1W2Xvv4b1YsXkZlm36FRKas3iREj5Bbl6rpU1A4b9V3UMJKAEl\nkPMEVICzy1xCUfpZFSyncF7iH2qmuSPtEzoULvfro+F67mnfAicJOemiYnVt0j3lgRIfegnDZzW4\nml2gquWBIkPI7qbnA/Qjdo24B1i23DNM/f54QEQ6mnGpu3BFdbFijMBFHoyQ6fT3DEsn0Cp28RDT\nOOMXIikU+7TuZ6sctXn3Jmsdz1j2NV764jnUKF/TJ8iSC7lAhH7kM05X91QCSiCYBPTbKJh0z7bt\nnkSR2UJxeSNtrXZ/+x2cCR/B9eqLMBzalRKfEI8Pf3wfIy7juHUqxZSoCadoJS4jXgJUSbSqKZV9\nc2OTDfjRvh2t/nbnAn4wFKbz1higRXPPnLEE/KgbhYjRFOE5rE+QEQ1/M5Q1C95IdSrVhdSBna+y\n/NZtW2sFefyc97B1XwxEhL1D1rKfFiWgBJRAbhFQAc4meWOP9/xNrSn3PIrvNxRfao6JSm0Pis7k\nT5lr9zv6A7/GFH8U1LPl29+mo1q5GpBQjmkVWYzlbPmGmY7yngAn7nOSgB9cPe0s/gnOrDlwXv2f\nFWibsal7W/obF4AzkUxuIi+OrFvXpSwuehZrt1mtFrYO6nkLjp88DknhKDGsZXV17ImjzH/cyiPI\nddpArGktSkAJKIGcIqACHETSktPX4Ypf12tpW3Pud8fC+flX5v5l5ClJqnC2nDh1Ap8unIQXBvPg\n9EplCu+ad+DEbmdoymrp7Zln3jNcJW169wJYnaNHPQE/pk7zBPyQeNTR3YE+jFk9xuX58SKLtdJZ\ntJbRCytaqCg6NbrAVjlm/5H9Nt2iCPKHc8ehcGRhCjIXfLGKMMt8sxYloASUQLAIqAAHiayzm1bc\nfym+j1E8PCPKSc7kuN023KOzJcZj+XJONHGZumgyOjToZOcwE29P/ty4IuCUawln9k1wStWna9O/\nYLhCOr8Uw6xJ4ucMVufgQU/Aj3ETgD17YLp3A5p2h/uNJkB1sryLLKsE7spkxXTvln1slVZj9m6x\n1vHslTPx2vQXUaVsVd9wdZPqTSErsrUoASWgBAJFQAU42yQdXwvOdj6VlzRk3f9HsbiZlUkWkhcn\nPh7up58Djh+ndcwwj1FJx6YPHD2A75Z/g7fv4BJhP8U5tsPjDyyLsBoNYoCONxkg4yBMHlgZ7afr\nKd42ZctyyPlygFWCkIiPsTObQwinjtNc7Y6EG3vAdXVd+iGTK+NnB7qIT7HUAR0HIiEhAet3rLMW\n8qT5E7B5zyZIEBCvhVyvMn/sZGDxXaD7qO0pASUQOgRUgANwL62L0QNsiFpoRXgfBeI+WmyXpGzc\nJlV47AmuiC4K1/PPpprkYNK8D3Bx60txXonzUjaQbIuznALeYSScv6bCHP4TTocn6Y97R74U4MSX\nJnPh5npOArM6MTFWjPHP03CP4YTwe93Jtwcirg3ekLtE2zq/RlNbr+8xGHGn4rA6ZqW1kF/56nnm\nQz4IcXPyLuiSSF5alIASUAKZIaACnBlaaezr0Jg1VSm4L9PyfZZ1Ml+fSLmzExtLy/gRmNoMYPHA\nfalaULJS9+eNSzD+no9TNpDaFsNbWKgMTKsHGB+arj4x3wMHVsG9iCEsS9Vh4OWztXh1yHB1fiym\nZk2YW7gqi9XZ+Cfck+bCeexBxD9bGuZWWsXXUpCTBfwI9HVKPOr2DTraKm0fij1kxVgSSnyycCIi\nyNYzd+yZQ5Z411qUgBJQAukRUAFOj05G39tpYJ6m8E6kBUzhdc3io/j7ilV8tsj8pk2q0KkDXEOH\neDeneBw3+90kISdT7JBsgyRkcGb8G+aaZTCdnuNqag7hVu8NQ99gHNnMSBXLmHFpCnBiD5ziNeh7\nS0EuVZvCXJe1Ni3wwslazNsvTYP6iHi6PvD07Uh4czWcd+ch4X1a/J34A6MvhVgCfpQuHfSLkIxN\nPZv3tlVOtn3/NivIC9bOhaRcrFCqos86Tm8Ve9A7qidQAkogzxJQAQ7ErZHFy6tZY2n5MtSiiaEA\nnzzXsCQwsOJ7WX+4rvr3uTeSPZOcuRJy8vGrqeYZLIZii07PwPmsMyBWbpXuQOsHaO3y1pZvZVsx\n/OsknKYg/826yT46ks7wCGM5F2aiBa+VfNZiNrSo80OJuLsZnJuawT3+bjjTfufc93y4x03gj496\njL7FMJhduaI62eK2YF2X5DSW2r/9ALi5wG7jzg12/njq4sl4ZuoTqFmuNprVaIGOjTujQZWGcLk4\nZ69FCSiBsCagApzd289IWOYWg4ROFF5OWYKhiN3LmXiA1rAU5++/PUkVbh5skyp4tqb+V0JODuo5\nJNPRmkyDayg616Te6NmtJiKSi8Maeiq3WVGWKF50X7KWMq1lZ9PnwGE+mghrJRtrJdfxDGMXq5Lq\nkHm6J82BNyWGdMQwrgT/V1uulm7LCzsN0+RXOL9yAdfb7wDNm3lCYXbqyIVbQVi5lco1irg2qtbY\n1mu63YBTZ07hl/VLrQ+yWMd7D++BpFn0zh+LcGtRAkog/AioAAfgnpu6FAFxO7qVjYkgcPpWsvw4\nf6zzJFVgSEbTtUu6Z1r4x3ybik/y5OZUsat4S7CjUqsxROTZEztx+62VbMV450KAuYdx6h84JThk\nnXheuURNWGHPqQ6ncx7hHcE5eGdxJNxvXcDwnLR+34oD/mTAj9k/egJ+tGOgj+jugETnYvamnCpR\nBaPQqnYbtKzVGsWLF8eR40d888efL5mCBHdCkvljGd7WogSUQOgTUAEO0D02FdlQ4wNAOzfFtzwt\nsN88SRUef5ShFT1DwWmdSlxeJswZi3v7P5jWLjm63RSmGS+1YvtzonyGk9sypyxD2IfW0bL/GqAL\nlFOU6QmTDWHnaGeTncxQe13tKMSc9naGM+DH5b3gerIXf0DEegJ+fPEV8OIrMBICs2cPoFVLDtfn\n7HCwLNCSH1reH1u7Du60grx0w2K88/1olCle1mcdi6UsC8C0KAElEHoEVICzfU8dOG4HbroWOV+t\nA6bvRPw4ug9FRiJC3IyYgMBfkcQBVcpWsyET/e2bW++bgkWA85p6Kjthh7BpueFozLkh7D1LreVc\n1CkIU7YBnNL1zq7CpuVcVH6h5EwxHG0XX2GnDytDgLpvpCjfWZxuYUy3xOocOuQJ+DH+Q4CZpyTg\nh1jGRpJI5EIRFyap/doyuQanBf7a9acV5K9+nmZDZtapWNdnIYsvsrhIaVECSiD/E1ABDsA9dMSi\nKt0E+NdnMBW+hfvlu5hMYEiGxFf8Sycv+AjPD3o1AD3J2SasW5MMSUtl8Q5hn9jxB4q7OYx9LAbO\nVrpFcfGXE8/hYM4p+4awS9UFijFVYRBdowyNePM4RXgVRfgNdnA6hXgYt9Wk29YVAwBWhxG3nLnz\nbRYqMCymjUktC7jqsX+5UGRaoH6VBrZe1eVanD5zGn9sW2MF+d2Zb2LnwR30TW7ms5AlcIgWJaAE\n8icBFeAA3Ddn82a4PhgN982ca1zxMd2QvoXzKINtZKDIKtl29TvYCEwZ2D1f7OIUprVbgpGiCtKq\nPNtj59QRn6XscY36lK5Re3PENco0p/COpRBz1Nx9HwW4J+tg1mKsFSty8dzVAKuzbRucOXPhHvk0\nD3B5xDi6O6cUOMGcS0XCX7asQ99iVimxcbFcXf27FeRvfv0ScafjfGIsUbokvKYWJaAE8gcBFeBs\n3yeugha/0784N/oLhzMfvI1BOJjtJ+6k35YlmINkPMpIyEm/jeXxHUwUA1OIW1QK1yiZV5ZKKzm5\na5RYyfRVlmAi2XWNkkid5jKKcDTrOM+wtLmF2zgq7Y0oKUJrbh4MsErAD2fuPOs+hpIlPUPU0RRj\nCnZuFkkQ0aVJN1ulH3sP78WKzcuwbNOveH/WOyhepIRPkCVSlySg0KIElEDeJKACHID7Ym4ahIT2\nXRgAg5nlt25AwpdjEDHuXb8tT5w3Hn1bXxK2VovHNaoRXaNYWcRaljnQc65Rm9J2jZJh76KZd40y\nJXgeWsEOb5X7f3ykVewazm2cQUhcJOCHVNxxG+Nrr/EMU9/B8evKXHTGxVs24Eei7FWJj83J55JC\nsU/rfrbKeTfv3mStY1lX8NIXz9lkHl53J8mFLCkatSgBJZA3COh/YwDug2ncCBHbNyGhxXVMr3cQ\nEePfZZJ5Wm/pFImctGT94oyHnEynrVB6K+OuUeO5svkwHLGOz1rJNuxmBl2jDPU7gvPC7rmsT1KA\nJYDK7axlUtI0zZpCqjPsTuD3FTYutfuDD4H6DPgRTTHu1iXHAn6k7F3SLXUq1YXUgZ2vQnxCPNZt\nW2sFefyc9yBhTkWEvYIs+2lRAkog9wioAAeIvalaFShSC65776f48rmf4g05qUOEfkCdfTtt1ygO\n/csQdmquUb4hbC7+iuSEbyrFJUPSDKLi0HfbfRMFmNPB5t+sqfxnGFl93LYNDKtz5gynHBjw40cO\nU3sDfkR397g3Md9xXihi7Tar1cLWQT1vwfGTx20wEMl/PGraU4g9cdTmPbaCXKcNw2dWyAvd1j4o\ngbAhkMrXTNhce+Av9NQhznGmYkIlO9ParWuwZe9mPHYVTS8tWSbgcY1qRtcoVhbD6iRxjeIQ9u4l\nVqCdghRgay3T9BW/ZQ5hmyIewZHUhjIf7HA+2P0WH2dwWPpubutgm031jw3kcUFnGFbJcOUsZsCP\nufPhvD7aCrT1Mc7hgB+pdjTRRvmx16nRBbbK5v1H9ttwmSLIH84dh8KRhX3pFlvUbgWZb9aiBJRA\n8AioAGeXrcxZ8qvfOc1YywyoYUoX8dvi2B/exk29hup8nF9Smd8hqWvUhVaUpRXn+C6G2fybYkxR\nFteo1Wddo0pxGNk7hE2L2fVUNWB5BNyjedD0s0LsJ9OghLg0vXoCrM6xY56AH1/y4BdePhfwg8PV\nsrI6LxVZMd27ZR9bpV8xe7fY4erZK2fitekv0je9qm+4ukn1ppAV2VqUgBIIHAEV4ECxZHAHuJge\nLyr9Bhf9sQBux+2LgpT+3vpuoAgYRuyC1CoMUXm2UY9rlAxhU5ht1iiPaxQka9Q9tJLX1WH6SFrK\nXVlvpMhmYGRZkj+Yfn0BVhvwY/5CuCdMRMGt25BwQSda2X3sfHKgriuQ7YhPsdQBHQfyt2QC1u9Y\nZy3kSfMnYPOeTZAgIOLqJEPW9SpzkZp3+XggO6FtKYEwIqACHKCb7ez9B4hKf/hZvtQ+4GKYe/on\nylMYoPNrM5kn4HGNon9teY+PrR3CtlmjOKcs88pNKcwVfgTWM6HGc+W4UppC3Kpuhl2jDFdJm8vp\n+8Qax6QcrnkU4zc4xn3kyFm3Ji7gkpXWebBItK3zazS19foegyEBY1bHrLQW8itfPc98yAchbk7e\nBV0SyUuLElACmSOQowI8a9YsvP766zjN4do333wTDRs29PX2p59+wv333+97LU8+++wzrFu3DiNH\njvRt//zzz+kJQksmzxQOQYslsJcWcKHS6fZKXEMqc1hPvri05E0CqbpG9eY9XrmdC7WYKWrtJs4N\nf8577s0aRVGWOeWz88ppukaVL4+EK69AxC2DPQE/OF/sfmYUx8bpRx7d3ePaVKNG3oTCXkk86vYN\nOtoqnRQfdpk7Xsn6ycKJiGBEMxFjr4Us8a61KAElkD6BHBPg2NhYPProo5g9eza2bt2KoUOHYuHC\nhb7edezYEQsWLLCv582bh9GjR6NatWoYM2YMHnroIfTp08e+FxXlZ4zX12IOPzlwmN9SaQuwWBDy\nRTXqxldyuGN6uuwSkKFW07I6wOqe2QMOo2qZjmz1hv0wDq1kSeFos0aNT8M1qlaSLtiAH4NvBFid\nP//yBPx48GHmcy5+LvpWLgf8SNLhVF5IxqaezXvbKm+LW50I8oK1cyEpFyuUquizjpvWbA7JCKVF\nCSiBpARyTIA3bNiAli1bolSpUrYe4TCcWMKRTFogRXKoirgeP37cCvWMGVyKyrJixQrUr18fb7/9\nNq699lpUqJC6q8S4ceOssNuDzv7Zv38/du7cicOHKY5BKi4mX489Gks/4F2I4ErbY2mc69PFk9Ck\najOUiiod1P4E6TIz1eypU6cYVvkoQjJpgKyM5qLrAp9EosDNpXDmqvOR0K8BM0edRRR/Aq7YLawx\ncO1cBteGaXAd3wlXoQpIKFYDx7joy128JmttoCCjVJUvB1x9pa2uP9YjYuFiWsm3w6lYAfH0L07o\n0hmQSGt5vBQvWAJdG/Sw1c3/iU17/sTqrasw8ccP7PyxJJRoWoMuUTWao27F+vb/XfaT74Bg/n/m\ncWypdi8+Pl6ZJCMjnxMx4kQnglF2796Nn3/+GZsZVjh5efzxx1GgQHCkMjitJr8Cvt6xYwfKJIoc\nJEJ84MCBFMPJEydOxIUXXoiKZy0A+RKX6EgivBdccIEV5GJc6JK8tG3b1gp14u0xMTH47rvvUCiI\nidjP0DqKFKv8SCwMv1RTO9c/xw5hzuof8PqQt1N9P3GfQ+G5/LPIj6lgfWhznRHdlnAX66UJiHqH\n9352FNx3JtBClhXxfLMY1wJU8swrS1/ddI06c2CjFeXIkztgti6HOboF1jWqRC2bZ1lyLTuNKcqt\nhwH3MJnHilWInLcA5q57gbp14HTvCkfEmFZyfijNalNsWYFBOHXmFBNKrMbKLSswbu672MfwmZJQ\noinFuF65+mhUJlkYsvxwgUHs44kTJ8LieyIzCOVHvXynBOtHfWH67jdp0gS9e/dO0a1gib6cKMcE\nuCTj6R6ji4a3xMXF4bzzmLYvWRk/fryd+/Vu/vbbb71P8fvvv+Obb77BNddc49vmfdKsmccX1Pta\nHqX9pUuXBvXDHG8FmEngj9L9hMNykamI/dRZn+DitpeiavlqibsXss9lFEP+WQrmYNL7XIEp66de\n5TTuTxTZ0fxXEk+jOzg87bWGE3Uqvkx9m54xMpGAelyj+IubC76c3T8CGzi2LVmjvK5Rg9rCuXMg\n8McuYN4iOOMncGHY+Z45Y/FBziMBPxJdZqpP5UdppyZdbJUdjhw/Yoerl2/6DV8smYoCBQskmT+W\n4e1wLvKFn9oP+XBmItoho6XB+k4Rg7A0R5q6dOmSo5hzTIDl14WY8mLNyvCkDD95h5+9V7x37177\ntMbZxSiyzyWXXIJp06ahSJEi2LhxIwYPHuzdPQ89chHWIa6CFssnWZG5MUm0/v6wicne0ZehQsDQ\nMHW1oxBPoRDfRgEewHotq2d2Jc3LPOcaxVCWZ/dK4hq151eq1Sc2axS60DWqTydgdzyDfnwOZ/T/\ngFbt4OrZA5CAH2enctI8WR56QxZodW8ajQsadcXhLodx2pyygiz/J+98Pxplipf1zR83q9nCLgDL\nQ93XriiBgBHIMQGWIeTrrrvOCuq+ffvwwgsv2IuQxVh9+/bFgAEDsH79epx//vm+i5NfgldffTWu\nuOIKnGS0oQYNGiR537djXnjyD1dBV0s5VycxeK9kXtdihVMOm+eFbmsfAkPAFKTgXk8Rvoj1HQrx\nDRRlho423TLXvl/XqEgu+ipFZW/hpjj/BPd8Ws4T4xj+lJPTF/SHad8dNmRm5k6bq3uLC5PUfm37\n2x/of+360wryVz9PsyEzZf7Yu8JafJGDNQyZqxD05GFJwNAilYmrHCsyPyhzg5kZVxdLWIasixbl\nopVMFBF0WU0tC7iCVY7NvB1F2w5DwiVcxXrBpyjw0rlIWBJy8qUvnsW44ZPCKurVwYMHUaJEiaAN\nFwXrXgayXWcNRZhGKjhlK9mWjpfjFAX/1YonGoLOzvkcBnNB7A6KsITb5MnWLYazZy2t5ZMwZRsA\nDWktM22hkZCbxfzHJs9OX7J6rHexUWpTUd42T585zfnjNVaQZZX1zoM77Pyx1/9YAoeEWtmzZ49v\nDUyoXVtWr0fWC8k0ZrCGoCdMmGADywwaNCirXczScTlmAXt7l3zY2bs9vUcR68yKb3rtBfQ9fqna\nwPzxbpii58RXzvH+rDEY1HNIWIlvQNnm48ZMUwovp3SdbyjEI5h5qVNBxF9/2gpyIC7LSILjEtVt\nNdWigXb32Gbd29cD879kkoj5wJwvgJpF4ZQtzDSKzc6F3BSfZS7+MhE02/N4kfCXLesw+harlNi4\nWPoe/24F+Ztfv0Tc6TjfcLX4IEt4TS1KIL8Q8CvA8stDXIH++OMPBvA5ghYtWqB169aoKtl/tHgI\nkAuKJg1DuXjdQpxJOIPoZr2UUpgS4Po8mP4UYU7TYgwQObQQ3EO57RJWvheM4qrWiP7JrHgEznYG\nD/lxHpyZc+jytJmZnOKB2rv5y+Br4NgOOAzNaWzGKAqyjYeddtaoYPQ1K21KgogutOylStnLFWYR\nx5oAAEAASURBVNUrNi/Dsk2/8gfvOyhepIRPkCXgjWYbywplPSanCKQpwCK2o0aNgrgFNW3a1AbF\nkKXaEhhDFkPJqrFXXnkF0dH89R3WhSP4XAGNIpz/jfKA8IacvLvffWFNRi/eQ8BwGDrhzjNIYCyZ\nAuMLwqH+uWiwmnPLHYKCyjCQjfEG/NjEoWoR47Hz+WOxKEwP+h43qstfBUc5jC2rsJd4HhNnjTqb\nztGbNSooncxmo5JCsU/rfrZKU5t3b7LWsUSde+mL51CjfE2fIEsuZEnRqEUJ5BUCqX4aFy1aZBdJ\n3XHHHXj66adTHXdfs2YNXnzxRXzyyScYO5ZjbeFcxAKWKFhnV71+//u3qFi6sm/YLJzR6LWfI+DU\nchDxOoek57E+RQFuzno7a9lz+wTrmalL65YVt93KcJp/eFIn/uc1Bvyo6HFr6nEV+1H2bNYoWssi\nyjHf8TFZ1iivxVyM4s7wk3mt1KlUF1IHdr4K8QnxWLdtrRVkWQy5dV8MRIS988eynxYlkJsEUhVg\nsXgT+99KB//55x/rPuR1EZJ9xDqWIeqwL0eO4nRUUSw48h1O/3wSkxd8hFGDXgl7LAogdQIuDkk7\nXCPlfEwhvpkCfBXrv1lzaErWnN+E1ncTOHffwVBzK60Yuz+axOFpzgv3jObKbbpFVUnbNcrZ+AkX\ne+2j33v1s0PYtT2xsDm3bApIlJK8UcTabVaLAUFYB/W8BcdPHscqBgORxVyjpj2F2BNHGbu6lUeQ\n67Rh+MwKeaPj2ouwIZCqAMvwsrds2bLFugItW7bMOofLMPRbb72Fq67itwZLeisYvW2E9qODE/v3\n4IM9X+NorX9h6Q+LsHTjT3in2Aehfdl6ddkiIGkrDcXXuZgi/BYfB3NY+m5ukxjTOVQMFzeidSsY\nVuc+LtX+9Tc7TO1+lyNaItL0MTY24EdJT8aoJFmjTlnr2GaNEit5O92hjjC6V+HzUs4r+0lSkkOX\na+eDOzW6AFKl7D+y3yaTEEH+cO44FI4s7EsmIcIs881alEAwCaQqwIlPeNNNN+Hyyy+3IR3FtWTJ\nkiXWn1cs4MaNGyfeNWyfz5z/KdpVvAJ1GgzDqt2/46Er/ouXvxyFZ294MWyZ6IVnjIBEzYp4mgK8\nnEL8Bo/5ikI8jEJcNWPHB2ovI7FuO3WEYXUY9s/5aYlnmPr10UCb1nBFdwc6dvAF/DAR/AVRhou9\npLLImrLErlF2CPuvaZ4hbMOhanGHshmj6toFX3nBNUpWTPdu2cdWuYaYvVusdTx75Uy8Nv1FVGHm\nMu9wdZPqTSErsrUogUAS8CvAYgH/3//9n/WRkhN369YN4islmYxUgD23otjJBDSu2hWTd3+KS9te\nhr5tLsV9798ZyPukbYU4AUMvG9d4itiXFGLGmTZ9WQexFs75CzcMI2qiOU7O6jCsqMMEEe5vOR/8\n8mu00CnCEn2Lopw84Edi1yjQNUpEWYoTt99jLUvWqB3zGVpzHEX+MGOn10JUZCU4x5p5hrBz2TVK\nfIqlDug4ELKQcv2OddZCnjR/gk0oIUFAvOkW61Wu7/tOtBepf5RAFgj4FWBxO5L4zCK6EkBDwkVK\ngoMPP/wwC6cLzUPK8VtyRuwCbDwWi0G1bsbsFd+jYD7wsQzNu5F/r0oMRcPQz04vVo4Cu6/na7ot\nuS7KvWsysmK6LzvA6jDTlzN/IdyTPgGee4FzxV3tAi40p49xOn5VpjB9c6VWbH9OlM8ch/vQn3Dv\nWg0c5KKwv7k0PIVrVB0rzCayWI4DkGhb59doauv1PQZD0omujllpLeRXvnqe+ZAP2rzeXgtZInlp\nUQKZJeBXgCVy1ZAhQzBixAjrirRu3To7F3zllXRjYJHg1eG+CrpJyeoYcvBNxLmYjGFhJLbti8H7\nwydm9l7o/krAEjBcgmEepAhvpAj/jy5M0ynC4rbUIHcBGa4NMZfRsZnVYapPZ+58uN9+lwJ60LOS\nmhazadQwQ500koqxbFOcieBqaiZNEWvZccfTpW8rreVNrLSWd/3E15xfzgOuUYWjCqN9g462ygUe\nij1kxXgl548lz3cEV4SLGHstZIl3rUUJ+CPgV4Cff/55PPXUU2m2I+HBwrkwlicKHo/D+Lo/4JmI\n59C7RR90btQFhSLzzmrQcL4/+fnaRXAj3qYI/8D6CAWY4Z7Nrazn1kjm2uWZcuW4evvfAKvDnNvO\nnLlwP/8ScOaMR4xlAVetWpnqn3Hx64hzxbbySBFlKUmyRvlco05yP7pW2Xllj6WMHHSNkoxNPZv3\ntlX6KElXZDHXgrVzMfrbV7miuqJv/rhpzeaIKhglu2lRAkkI+BXg5s2bJznA+0KSI2jKLNJgrlem\ndsLGMzG4sH4f3z+kl5M+KoHsEpAhaKcr64f8qMm88A2sA1gjsttyYI43VapwvpqdYnUk4IdYxg//\nl8POhc9axt3p1pT1Idp0s0ZxXhnMGpW6a1Rdz4KvHHCNqlauOqT2bz/AZnrbuHODnT+eungynpn6\nBOpXbuCzkBtUaZipWPiBuUvaSl4k4FeAf/zxRzz55JPWD1iCycvihEOHDtkEB5KlKOzLKcb3LVkC\n60+sRc9KF4Y9DgUQHAKyGEuCdjiXUIS5MFliTEuSB1m8lZeKL+DH0CFw/lhHMZ4H97D76MZU3uPW\n1IMJIlLJA57Za0g9a1Qy16htcziEHZPjrlESu75Rtca2XtPtBpw6cwprYlZZC1ms472H90DSLHrn\nj0W4tYQnAb8CLNGwbrzxRsjcr6QKLFasGD7++GObPjA8kSW9akOXDZQoiXUH1mJ4lfuTvqmvlECA\nCYh7UsQLFOClFOJX2XhtCrGsmq4Y4BMFoDnTpDGkOnfTI0ACfjAUpvtmriqTgB+cL0bnjgE4y7km\nMuUaJcPdjH+dOBZ2sFyjZPi5Tb12tkpvjxw/4ps//nzJFCRwFC3x/PG5K9JnoU4gXQEWi1diQj/6\n6KP46KOPIC5Jw4cPh6TLmjlzJi6++OJQ5+P/+rhI7VhkcRRzF0OZ0mX87697KIEAEJCAHa42FOLP\nKMS3UYD/xXodax6carQrpFu1hGF1RtzjCfjBYWq8MxaF6tSG+5K+MF0ugClSJABkkjbh3zWKQ+aJ\nXKMg0bxsYgqZi67L7FU1A541ShZodW8abav0dtfBnVaQl25YjHe+H43CBYqgU5MLrCiLpSwLwLSE\nJoF0BVj+cSQNoIiwzAVL6EkpZcqUwbZt20KTSCauyv3hRBT8/XfELzLoUe4yXyzoTDShuyqBLBOQ\n0JXmWoqwzBG/QyGWueE7KMw0LvNqsb7D4kvM6j5xAvGzZsNZzKAfo7najALt4uKtxAE/gnUdablG\n2cheh7kKOwddo8SFSWq/tlxdTqNn6eqfsP3oNnz18zQbMrNOxbo+C1l8kcVFSktoEEhXgOUSb7/9\ndjRr1gx///03YmJibAjKuXPn4ueffw4NAlm8Cjf9IN0ff4KEm2vgz2MFcNG3/BL54zeY6m2z2KIe\npgSyRkCSOZhHKcJrKcJetyWZH+bwdJ4ukZGIZ6jLiMv+5Qn4sYgBP2Z8D7z06rmAH23bpAj4Eaxr\nsq5R5zVjfF1WFsPq1zXKm5xChrOLZD+WtBg9tSvURafmF+CqLtfi9JnT+GPbGmshvzvzTew8uIO+\nyc1888cSOERL/iXgV4CHDRuGPn362CAcsiBLrOD77rsPdepwiCaMi3vKZ4j4/RfEv9kDfxQ+hUoN\nmX91+qcMWKACHMYfi1y9dElv6HqPovEthfgBCkg31ptZ80FIYxvwow9NeVaHI2424MfkKcCoF2G6\nMjFEdHegRfN0A34EA36arlHHdnqieyXJGnUy4K5REv6yZZ3WvsxqsXGxXF39uxXkb379EnGn43xi\nLD7IEl5TS/4h4FeAGzZsiNmzZ9srkkxIjz32WP65umD2lKs6X/vmZVxEd4Pfdp5EZUZNqAh3MM+o\nbSsBvwRoQMFcShHmSK7D0JbuG/n6Js82eS8/FMPYAuZfvAhWX8APzhcz9RrzGHMVNRdwmcaNcvVS\nTLEqgNQqqWSN8rlGTWbWKAYsSZI1qm62XKMkQUSXJt1sFQB7D+/Fis3LsGzTr3h/1jsoXqSET5Cb\n12ppE1DkKig9eboE/Apw1apVIbl/69evn25D4fbmF6VjUful91HpovLoU6k8Ci59Dr/d9Qo6hBsI\nvd48ScAweqPhMLRDHZMkDw4jPdpoWk3zZHfT7FSKgB9cvOV+8RWAcQhstibOGZvaeWOsPVOuUUUY\nyESCiNjK/pdkUJEsZI2SFIp9WvezVSBu3r3JWsczln2Nl754DjXK1/QJsuRClhSNWvIOAb93o0KF\nChg4cCDKMfKNVG959dVXcdFFHDIK0/K/GsexoPltOL15FNr/5eBglZcw9vhaFeAw/Tzk1cs2tei2\n9BoFeAGF+BmKMoepxZ/YnPtXzqtdT9EvG/DjhusAVodrUqxb0yOPgxGBPGIc3T1bAT9SnDAAG9J2\njdpuw22CC74cb9aos65RhXhznIRWVpytpZ2JftSpVBdSB3a+CvEJ8Vi3ba0V5PFz3sPWfTEQEfb6\nH8t+WnKXgF8Bvvvuu202pMTdlEAc4T4HXLJoKZy6fxgOPfUOjrQegH3fN+AHfnViTPpcCeQZAjIf\n7KLrksNRUfcQCvC/WZnSW1ZS58ciVq+1fG+9Bc669Z6AH8NHSIJyDlFTiKUmMhjy0jV6XKNqMH4A\na2pZo7Yu97hGrX0fzukjHiHOgmuUWLvNarWwdVDPW3D85HGs2rLCCvKoaU8h9sRRxq5u5RHkOm0Y\nPjP7i8jyEuf80Jc0BVhCTUq555578Ntvv/muxc2wizfffLNdmFW3bvj+grqu+yAMe3co/ptwxv6y\nfDXqcYy/bJKPkz5RAnmNgImk4A6mCPehCI/h4yCKsgTx6JzXepq5/sh8sFTnLvpgrVzlCYU5hGZ+\nzRoUYg5Rd2fWpnwQs97rGnUSNVCqYkULwWHWqFRdozj/fG4I2zOU7S9rVNFCRdGp0QW2SuP7j+y3\n4TIlhvWHc8ehcGRhXzIJEWaZb9YSXAJpCnC/fv0g7kZSCjOmq7fIMvkqjOuaXoIG776h/CgCXKpo\naRz/eAY2/fMXXnNNsPMtoXzNem2hQUCiZkU8SQH+nUI8mtc0nUJ8N4W4ev6+Phvwo2ULGFbn3mG+\ngB/useMAEeloWsUS8IOxDfJLSds1KsYnzCmyRvlcoxhUpEj5NC9VVkz3btnHVtkpZu8Wax3PXjkT\nr01/EVXKVvUNVzep3hSyIltLYAmkKcBz5syxcZ8lDKVEwfIWiXMqVQus4/z2L0uiZ/U+aLSiqSJR\nAvmKgOE0o+t9CvFXFGIu2DJc0mFoFZvAB6TKcS6JA344jFaHpT/DzVCYzps0/UWkoynGnTvB0Bc5\nvxWPaxRHH0Voa1wE7+J2J7lrFFdjOwkMlcv9MpI1SnyKpQ7oONB+96/fsc5ayJPmT8DmPZsgQUC8\n6RbrVa6f4y5h+e0+ZaS/aQqw/JosUKAAJk+ebANw1KxZ08aD/vbbb20ISokLrYUEHH5hJfBfIEpp\nKIH8R0AyKpkr+DHuxTqWQizRtG6lMHOYOlSKFdluXRHB6jD6lsOAH87MWXBeed0T8CO6OyABP/h9\nl59LplyjOP+cdAibc+qJskZJtK3zazS19foegxF3Kg6rY1ZaC/mVr55nPuSDEDcn74IuieSlJfME\n/H7iHnjgASxbtgw//PADoqOj0b59e7z11ltYvHgxqlWrlvkzhtoRxvEIcP77IR1qd0KvJxsETEkK\nL4N3OH9ShN8AEmRYmmGbTcNsNJoHD5V40+aiCwFWG/BjwSJIUB0wl7FhVC5xbbIWMg2QUCh+XaPE\nSt4225M1KrlrVKl6jC3uST4t8ajbN+hoq3A5FHvIivFKzh9/snAiIlwRVoy9FrLEu9bin4BfAZ4y\nZYq1fCUKVunSpTF9+nQ88sgjkCHqm266yf8ZQn0PWsA2/oYKcKjf6bC4PlOf88Nv8iPN72Q3Y+6Y\ntqxDWUuH3uXbgB/9LwFYHQb5cOYtgPs9zhfv2+cJ+NEzOtcDfgSDesZdoyjOLi6TT5I1ivPKXABW\npngZm/u8Z/Petovb92+zgrxg7VxIysUKpSr6rOOmNZtDMkJpSUkgXQGWwODx8fE2BeHXX38Nb/7f\n05xTKV5cV8h5cFKB3ZwT189Xyk+Xbsm3BFz8XnUuYJ3Ij/dgCvB1rByqliHrUCySo9j8mxfI6uza\n5fExZkxqxMV55ouju0NyHYdq8esaJf7KO+YDKVyjyKRUHVQtUxPVyg1A//YDIJ4yGxkhUKzjqYsn\n45mpT6B+5QY+C7lBlYa6jujsByldAZZ54A4dOuDSSy+1Q84//fQTxo0bZxdlSYpCLWcJyBywWsD6\ncQgxAobOD2L9Ov0owrSKJca0i4uLxSoO5WIqV4bxBvxgClYb8OPxp4CCBT1izGFqwwiB4VC8rlGo\n2P7cYi9xjZKMUYyDjYNrGRSF8xXHdsA56xolc8sNpXYcgGu63YBTZ05hTcwqayGLdbz38B5ImkXv\n/HG1cvl8+X02PgjpCrC0+/HHH2Pq1KkYOXIkmjRpYtMQ/s4UfDIcrcVDwMSbPJmHVe+PEggEAVOF\nw9KjKMA/U4j/xxZrUojFf7hSIFrP222YWrVghtQChtwMZ/0GT8CPezlZzpSsNhSmxKZmXPhwKtY1\nqlxzQCoLzY+zWaNikrpGSaIK5kovSDFuzZXYrZu1ALpcgaNOlG/++PMlU5DgTvBZxyLKMryduHz7\n23TM/G0GSnP7w1c+jiJRIbBM/+wF+hXgOA7BDB482Mejb9++nCLZh4MHD6Js2bK+7WH9xM2r1yHo\nsP4IhMPFmw4U3jb8suWaJTfjXJj+rDI0XSgcrp7X2aihrc6dvPhVqz0BP4beyWhW1TxiLAE/SnkW\nLYUHkXNXmRnXqOJ0jepKQe5Wuw5zQN+Kfe6iWLZ3D5ZuWIx3vh9NAS7rs44X/bEAe1aNx/1NWyI2\n4RAGPt0LEx78CuVLhsaPnjQF2BsJq3v37ikiYQ0fPtxGwkoszOduRbg94xxwAueAdQg63G58WF6v\n4TeGuYYifBHrOxTiG/maeuSKDh8cNuCHpEZkde5hBJNlDB1JH2P3++MBEeloDlF3zV8BP4J199J0\njTr8F63lv4E9v6AcLeW+zBrVt0INoF4P7HYXxup/YvHZgg9QcONE3FunDP4qcj66lIvENweexNuz\n/odh/342WF3O0XbTFGCNhJXB+yCroHUOOIOwdLdQIWA4SmgeoQj/QREWtyUG87BuSzRqwqnYgB/t\n28Gw+gJ+zJ3PgB9vJw34EaVDZN7PhXWNqsChFKksdghbAoaIIFOMK9M1qlLB7ehemiJdKwL/1OZQ\ny5nTcFo8hL8O7Ebj3b95m8r3j2kKcOJIWBMmTMDWrVshq58bNGhgA3Tk+ysP0AXIh0dXQQcIpjaT\n7wiYJhReWsLOd/w3eJBfpl1Yb2Etke8uJdsdThLwg1N3NuDHrDlwXv2fFWjrY9yubb4P+JFtUKk0\nkJprVNTR7Vg/sQd+3n0YA1t1scE/HvryTYwZwA9YiJQ0BdgbCevJJ59E27Zt8ccff6AoY6iKW5Kk\nIrzttttCBEF2L+NsIA79gZtdkHp8PiUgMStMP4pwN9YJFOJBfC1V5og5OxOOxTB+vrmQvlysztGj\nTAfJgB9Tp3kCfkg86ujuHgtZw/qm+fEwxaugXoNe+PWXb/GvjTEoE/U2vmweyVjfN6d5TH57I00B\n9l7I0KFDrRuSJGYoxQUGP//8M/7973+jS5cuaNy4sXe3sH2UEWjEs+occNh+BvTCPQRMMQoup0Sd\nSyjCo/n4Da3j4dzmWSwbtphMiRIwl/IXCqvDxas24Me4CZz/3MNMTVxFHd2deZo5lKAlCQHxTS7Y\n9WUM2v8bri1QFAUiXDDNJsHQJSpUil8BXrdunQ1DGXk2aHnnzp1tBKxFixapAPNTIEPQRgNxhMr/\ng15HAAiYmnRbeoUCvJBCPIr/H/ydbpgpkHnmw74Yeo6YgZcDrM7u3Z7FWxyixvHjPh9jRj4Ke05e\nAJJi0VyzHLGMVFaSKSUj6IsdSsXvAJEkXVi5cmWSa164cCHzXp+XZFv4vuAQtFrA4Xv79crTJGC6\n0gL+iG/XoBAPYZ1IUWZiIi0eAqZSJbiuvxYR49+D6wWu6mUyCPcTT6PYsPvgnvARnO3bFVWIE/Br\nAd9xxx3o3bs3xB2pevXq1hqWoej+/TnBo8VDIIEPOgStnwYlkIKA4f+FzAc7fSnAXBjs8LkN4nFB\nil3DeoOpWZOL124CWOMW/4Qiq9fAPeL/GOaxlMfHOLp72AX8CIcPhF8BHjhwIGrywzFz5kz8888/\neOihh3D99dczKltoDQVk62YnRGgkrGwB1INDnYApz2HpkRRgDqbZaFp0WwJjWCAMV0v7u9cJdevA\nxcxMzh1c6Eohtj7Gt3IMnwaQnS+WgB8aidAfxnzxvl8Blqto1aqVjXolbkj16tXTQNqJb62swtJ8\nwImJ6HMlkCYB04IW8DgKMcMHO/e6ENm5EBwu3DJF0zwkbN+wAT+aN+MitmaegB/Lf/dE3xo/AajP\nVIGSrUkCfuiccb79jPidA/7rr7/QsmVLK7zt2rWzWZDefffdfHvBQem4zgEHBas2GpoExDXJNYDX\n9oEbhvEX3Dew0o9YS9oEJOCHoQ+x66EH4fp8ClyX9Yfz629wX309Eh59HO658+CcPJl2A/pOniTg\n1wJWNyT/981IKEr1A/YPSvdQAokJMGf7qTtPotjhYnZYOoFWsY2mpd6NiSmleG4DftCXOILVkYAf\nnDN2Zv/oCfghgT6iuwMdmL2Ii7q05G0Cfu+QuiH5u4Ecg46nAOsiLH+g9H0lkCoBU5fzw/Qbds9h\nfYLD0a1Zh7ImTYqT6rHhvtEG/OjdC2B1YmM9AT++4AT7Cy8zKtnZgB+tWjIgit/BznBHmSvX7/eu\nqBuS//tidBW0f0i6hxLwQ8BFHXHRVQllKcRcEOyewnli+d/SkiECpnhxuC65GBGvvgTXh5xor10L\n7vEfwn3FVRxheBPOmrUZakd3yjkCfi1gdUPKwM3QRVgZgKS7KAH/BCS1obmVwnsxBfgtPnqjabXz\nf6zucY6AkXzF3oAfjLjlMEGE+3UOMzAsps1jLAu46nHoQUuuEvArwOqG5P/+mHiD0xxLWMbkHQ5H\npDvyc82oaVqUgBLIIgFThf9Dz/H/6VcKMbMtoTqt47soztyuJXMETMWKMNdeDbA627bBmTMX7pFP\nEyhDO/Zk6sTo7jB0cdKS8wT8CrB0qU2bNnYl9OLFi1GoUCH1AU5ynxxG93HhtslA5YrA/ljgjo+A\npY8BxcIkUXkSHPpCCQSQgKHl6/qQQjyNQky/YcM404arpsVS1pJ5AiK05ubBAKuz8U9axsxjfP9/\nwDiPHiGOphhTsLXkDIE07TQJvNG8eXO0b98ea9euxYUXXogrr7wSvXr1soE4stK9WbNm4eKLL7Zt\nbNiwIUkTP/30Ezp06JCkbk8Uiu25557DuHGc18iDZd8/QJ+2wHMDgbGcu7quI/DyzDzYUe2SEsiH\nBEwERfgq1g/Y+YMUYgqwLNjSkj0CpkF9uBjsI+KzT5g0g8ML+/bDfccwJNx1D9xcyOUcOpS9E+jR\nfgmkagHHcWn71Vdfjddeew2lGXGlZ8+eNiXhHs4lHOJNkSxIIqANGzb0ewLvDrFcoffoo49i9uzZ\nNrewuDdJTGlv6dixIxYsWGBfzps3D6NHj0a1atXs66VLl+Ltt9/GiBEjvLvnnUdZBA0XLm4GTFoC\nFI4EhnQD7pmUd7qoPVECoUBAVkWbh2gNr6MAM3+Bz22JUz5askfANGvKTENN4QzjMMPvKzzRtz74\n0BPwI5rD1N26aMCP7CFO9ehUBXjjxo1W/G66ieYcy/vvv48+ffpAIrOUZTYPCcixefPmTAmwCLYE\n9JA40lKPHDkCiazlzbLk4nxEVFQUk4Ict0I9Y8YMe+5jx47hqaeewgMPPAC32223pfZH9pNcxYnL\nUS44OHPmTLrHJd4/a88dFIg0+G6VG8dOAuMWGhw5zgQNZOV2U53DsDicCJd7ld79CjcswsTLJdyu\nPa3rlc9Hlpjwd78ZQyFm8I6EBw1MZ/6f3cJt9CsOlZJr/zv83kLrVp56Zjjwy2+eYeq33gGaU6R7\ndAc6d4S4P+V0ydJnJYOdFJ2Qevjw4RRHiF4Fq6QqwBLzWSxfb5E0UFK9ReJAnzhxwvsyQ487duxA\nGa7M8xa5qANMMVW5cmXvJvs4ceJEO9xd8ew8hFi9I0eOxOrVqyFWdFpl1KhREJ/lxEX2F1GX8wSt\n8H+/dHE3LvzAhS51T6F4pIMXviuAGXf9w/OGpwDLDyv5MSQ/qrR4CHh/HJ7UaEW+j4SIjHDJ8v9n\nOzbFNLpRUwqj4LWROHVlHM70ZbqlfP6xEyHIMhMf3QA9aVgfkHrzIBSgGBec8T0iXnoV8S2aI75r\nZ8TTx5iLggJ0srSbCfZ3yr59+/DFF1/YEdrkvZgyZYrPUEz+XnZfpyrA3ka9XxryyyMhIcFnYcrr\nzBYRcLFSvUWGuVNLaTh+/P+3dx5gUhRpH397NpGT5CCgmI6gIKAo4EoGkRVFkayS5BRUPNPhnaJ4\niGJEgpxyBAUV7/Q48BQOiYog8qGgoCCKAgKS2SVsmP7et3Z76NmZ2dmdntTT/3qenu7prqqu+tVM\n/7uq3qqaRQsXLlTePv30U9q0aZPqi5Y+4rNnz6o+ZH9N3888w8t5FXLbtm1TTdnVq1cvdCV8X/dy\nVKXLptBBtvB/4O00qs7vKTX53WXf6WrUyKGGhYd50fEKvAg5Fuw49zuT3778b8rzWE24fALyfJEa\nh7/nQIkYSbN0fxbiV3k6Ou7VUrNp8ZzTdnXS1RfJZ1bIXMRS+tZbSJff8qo1qmZMM9/kFohrlDU1\nyYQfPGVmJJy8kIiGROqZUqdOHRozZgwNGTIkEskPGGdAAV6zZo1XZhcsWEBGk7TE1r8//+JL4Bo3\nbkx//etf1UNImobl7ddofjaiOXDggDqsX7++2jdo0MDT71umTBlVoyocxggbq728i2gpGpXhvt9L\nahE1rcvW0CzAExcTtb6AqFTkXw5jlXXcFwTihoDG2pA0mYV4LfcPT+JkXcJCLFbTkXv3jpu8Rzsh\nsviDdkN3It7EUEtfuZrXL55H9MyzpKVfl29Nzf3JcMEJ+BXga665RhlKFRW8pG+tNWrUoAEDBlDP\nnj1JqvuTJsm/hEiMsbp37069e/cmqbHKzFuGu+CCC0g2cdI3LE3KxnfDTzzstSTuN2GXncetMUy0\nMY9VbM7vEPPXcctN+3hIIdIAAs4goLVl4eWmaf1dFuLhLMA389aPN35Bhgs/ATXhx803EfGmcwVK\nLZ34Ks+gwjY+Wod03tiAi62t4fwT8CvAYoQl/bV163J1rggnTcIyXCkjI6MIX+cuyaxaQ4cOpWSe\nJNzoH5w5c6bHQ3p6Osnmzw0fzv+mOHQaV4H15HwBzhEBLmiBGcrCO+IfPEUrv0/UO9f1HYc5QJJA\nILEIiNjKWGG9G29srOUeXFAbxstwRAta40qW14Qfy3mM8YSJXAhslNqBxbgji3FB62ZEE2KjyF3+\n0ipt7Q899BDde++9JJNvGH3B4lc6w6Wm+txzz6kxwmKwVRInTciG+JYkXDz71VLyMZoFuFKZ/PHA\n05bHc8qRNhBIXAJaNRbev/L2GIvwHLaYfpC14OfEzW885Uwm/HDdOYSS5v2Dy2CcCAe5H3qM8oaO\nJPf8d0jnfm44Ir81YOmDlT5fGacrY3c3btyorKJlFiyxZr744ovphhtuUNfF2MbpTiuYdzKHR0EZ\nNWBhciMbgny8hWjND0Tt0Arj9J8J8h8jAtrlLMJ/Z/FdxEL8ANeOO/J2B2/lYpQgh91Wu/giko3u\nHqEWhFDzUvOEH1SrVn6t+HruNzaNkHESHr8CbABo3769mhxDLKBl3K+M3ZU+2tIxGANmpCnu9soI\nKz9VqgZsIiqjcO7pxCuD8ZDmVg1hkBV3ZYcEOYaAxv9Fjbsq9Q68vZnfLK0N5XM9eMvvQXIMi1hm\nVGvahGTzmvBj9lwiXhhC9RfLhB+FRgroXHt27dhJbBpOdOEFsUx+2O9tkovAcSexabnUeuECECiw\ndDY3QRs+m7BB1uX1YJBl8MAeBGJJQOMGO41rwXovFuFX8mvFLp5vQuPxxHDRI6DWJ255JWm86Q/e\nT/TF+vwVm2awTZCIdId00tpeSzzhBLlHP0BpMtxk9Vpy33cvuR7mvoQEcfxeCGeZQHI+Rn8CLHGL\nQZY0Re85YvlOiAAEQCAMBLQLedjSqyy8PMe0ezxvf2Mxxv8zDGRLHoXGRrkittJX7Hr/HdI6d1RD\nm/JuuZ3y6nCNl42BT7/0PNHO78i9aDG5eTKQRHEQYKslKU3QBQKcXagP2Ii6clkeN80LNEz71DiD\nPQiAQDwQcHXg/uG5nJIaLMJ38raAhZj/x3CxIaCxnZGLhy4lPfMUuV56juiKZmw9l0ulJrIAy+iZ\np3guiXVfxCZxEbhrUAGWsbtz5szxmsUqAumwcZSswDwRh7jcPKLUJP9Z6cUGWUey8g2y/PvAWRAA\ngVgQkKUNXdwf7OLpjvVvWYTv4H3iPONjgTQs91TDmsqVI9e4R+nMA9xPwE7/8D+kmaZJDsuNYhhJ\nUAEeOHAgLV68mGRWqjvuuINWrlypZrOKYZrj7taaaRxwcgABFoOse9kga+ZKorM5cZcFJAgEHE9A\n45nskiawEN/HIjyNK148fEnf63gsMQOg8XoBGq/OlHdebUpZsZKIxxTrvEyiJksnJogLKsAyS5XM\nzbxz506SGbJk0YNGjRrR+PHjad++fQmCIbRs6Nyvq4mYbtVI59ptoD5gI3YxyGpWlw2y8HZtIMEe\nBOKOgNaKRfgf/N9uzkLM01m62S5IPx13yXREglwZN1LSxs/J9dPPRFXPo6Tvt/DUvwVWrwlAIKgA\nG3n8+eefaceOHUqIZQUjmRZS1vCV8cJOdPoqfkPuwjkXgrqL8nhMYRmek8Q8Dtgfl6HXEf33G6K9\nJZu/xF9UOAcCIBAhAhq3ZLlu420234D/q+5BvC2L0M0QbZEENF4e8azUenkcsVaWDWoSyAUV4Fde\neUWN/ZU5nGUWK5l6UhZqmDx5Ms2dO5defPHFBMJR/Kzk8R8yaTX7d+nkausi1yyem5yNrFKDDOyq\nwr+fflcTTV1e/HvBJwiAQGwIaJX5L/4Ib9w0rf+LX7rv5T1PrAMHAuEgEEQuiHbt2kUvvPACde7c\n2WcKSVnh6NVX2Zbfie4CbqLiyV1IrKBTeWtBVG46i3LQVxqiDG7akmFJa/mP3PZiJ8JDnkHAXgS0\nS/m/zf9v98e8cd+w1oa34bxVtFc+kNr4IhBULp5++mk1G5axBvDIkSNpw4YNKheyIpI0QzvRyfR2\neY8X5Jyn0smdSrSjYfFIwCCreJzgCwTijYCrG9eG53GquCXLPYS3f/I7eF68pRLpsQuBoAIsywXK\nFJSyfq+4Dh06UN++fekIrwPpZOd6hv94H/AbsIwZfJsFmI2rVrUrPhFZN7gJbwvWFz8MfIIACMSe\ngFaGRXgUb9z4p/P/1z2M95tiny6kwH4Eggrw+vXr6bXXXqOUAsszEd/BgwfTokWL7JfbMKZYJnJP\n2sp/PDbW0DI0Os2zowUaAxzotsPYIOujr2GQFYgPzoNAPBPQzudnAM8V4WIBdk/mFrEn+HmwP55T\njLTFG4GgAlyOB0J/+eWXXuletWoVYRUkFl6Zf0NjI6wqLjUEKZgBlhdE/mIYZGGGrMJk8B0E7ENA\nu5ZFeA4/CtgmxD2St9ksxNn2ST9SGjsCQQV4woQJ1KlTJ0pPT6dBgwZRvXr1lDV0r169YpfqeLuz\ni5uguR8o2BAkf8nuxQZZh04Sfb7T31WcAwEQsAMBLYVFeCBvb3Bqf2URHsQizEMV4UCgKAJBraAz\nMjLUesAy9CgrK4vEKEtmxYI7R0DWA5ZJOALNgnXOp++RWE3LDFnPf0R0ZX2iNP4jw4EACNiTgFaN\na8J/YfHlUQ6y2hJ9yKI8hs81tGd+kOrIEggqwHJ7WYqw8HKEZ86coVI8cTYcE+DFRgMtxFAcPoZB\n1jts0DGkbXFCwA8IgEA8E9CasvD+nYX4PyzEY/kRcT1vd/HGtiNwIGAQCNoEvXz5cmrfvj01bdpU\nTchx2WWXUY0aNWjJkiVGHI7ea5J7pig14JIaYZnBiUHWEjbI2sez7sCBAAjYn4DYiLi4p06ttqSz\nEA/mjQVZlraFAwEhEFSAR40aRV26dFEC3L9/f5Lv0gTdu3dvECwgIItLh9oHbEAUg6y+V2HJQoMH\n9iCQKAS08vygvY83tpTWl7MIj+A9j6CAA4EiBVgm35AxwOPGjaOuXbtSdnY2jRkzhjp27KimpAS+\nfAIaG2GF2gdsZngTz6Z1EAZZZiQ4BoGEIaBdwMOWXuZm6P4swk/xJnMJHE6Y7CEjIRAoUoA1bkMp\ny5NfiwhffvnltHbtWnWLKlWq0C+//BLC7RIxiE5aMvcBcxN0KFbQZiJikDW6I9EMnlNa+pThQAAE\nEo+Ai/uD1WxatViE7+JtPgtxTuLlEzkKTqBIAZbgd999NzVr1kz1/8qKSDIRx6RJk9Tc0MGjd4YP\n6etRfcDFMmkrmknTekSN6/AMWV8U7Q9XQQAE7EtAS2MRZvF1vc7iu41F+A7er7NvfpDy0AgEFeDR\no0fT4sWLKTk5mcQgS4yx/vOf/9CFF14Y2h0TMRRXXa32AZuxDE8nWswGWb8dM5/FMQiAQKIR0Gpy\ns/TTLMRsKe2ewbNpPcLH+4I+lhMNg2PzE7SkL730Us9wo/r169Pjjz9OV1/N6+nBFRDgJmg2wpIa\nsNUmaAOpMshqDYMsgwf2IJDoBLQrWXhncf9wK17n4bEKSoz104mea+QvqADXrVuXtmzZAlJFEUjS\nVJ9tKBNxBIq2N/8h9x8nWrczkA+cBwEQSCQCWhKLcB+izFf5j8/GmO6BvH2SSDlEXgoTCCrAMua3\nT58+VL16dZL1f43tk0/wy/DADGMfsBGnMsjiGbJmrIBBlsEEexBwAgG9Is8v/xCL8d+4X/jf3Cz9\nR95/74ScOy+PQc2GpMn54Ycf9iFTeGYsHw8OOuHiqm84m6ANdM3YIOvSWkTv8gxZg641zmIPAiDg\nBALaJdw/PC2/Fuz+MzdPc8+fNpy3Sk7IvTPyGFSAW7TgwalwgQnIrDYWFmMIHHH+lRHpRKPmEHVq\nTFQLf7xguHAdBBKOgKsr14Db88bPAfcQFuBBvPXmjZus4exNIGgTdLdu3eiKK67w2ZYtW2bvnIcx\n9TIRh5W5oItKynk8d+xtbJA1nZui4UAABJxJQCvN7/l38zaVhZhXh5Xxw/pXzmSRSLkOWgMeP368\nmgFLMi0zYW3dupXee+89atmyZSJxCDkvMgaYuMM2HBNxBEqEGGR9wlPXffEj0dUY/RUIE86DQMIT\n0Ory42YSiy+PGXa/yNm9gEX5Hq4N83AmOPsRCCrAV13FExSbnExDuWfPHjUmWIyz4PjHL8OQeCab\n1KA0Q6NlGGS98DFRi/qRu09oqUMoEACBaBPQ2rDwch1IX8hCPJKfQRm8DeAtLdopwf2sEAjaBF04\ncpkfevfu3Wp6ysLXnPldpqKksE7E4Y+jYZD13gZ/V3EOBEDAaQQ0XjvcxfNKy/hh+o2FmPuG3eiq\nstXPIGidrXPnznTgwAGVKRHfw4cPU0pKCk2dyp0RcIqAMRFHOMcB+0M7PJ3ojwUGWTUr+vOBcyAA\nAk4joJ3HNd9xXBvmbir3KzxsiYcuucbwOW6ehotvAkEFeOLEiXT27FlPLkqXLq3mhU5NTfWcc/qB\nCHCkjLDMbKuyQdatBTNkPcVWkHAgAAIgYBDQmrDwzmQhXsxC/CcW4Ot4Y2MtWQ4RLj4JBG2ClvG+\nS5YsUdNPXnvttfT666/T5s2b4zM3UUzV0cyj9NicBymHsumRhWPp5OmjlBqFYQE3s0HWvqNE69kg\nCw4EQAAEzATEKNR1I29z+SwfuwfztohFWTf7wnG8EAgqwCNGjFD9vW63W6W5Q4cOakWkI0eOxEse\nop6O7Jxsaja6EdWrVp9S9BS6oXkvWvLZIMrJzYx4WsQg695OPCzpU8yQFXHYuAEI2JSAxq1l0gzt\nYktpnfuF3TyBh77FpplJ4GQHFeD169fTa6+9pvp9hYMsRzh48GBatIhfqxzqPt++lm5r25/+2GMM\nv2RqdH3TTlStcmva+vOqqBC54nyii3nYAQyyooIbNwEB2xLQGvKwpZdYiMVAawJvT7MQ/27b7CRc\nwoMKcLly5ejLL3nkt8mtWrWKKlSoYDrjrEO37qY0vRTlPUZUNbsa0RNJlJ11lDQtv5UgGjTEIGvR\n/xEdOB6Nu+EeIAACdiYg/cGueZyDeizCw3h7i4WYh07CxZZAUAGeMGECderUidLT02nQoEFUr149\nEgOsXr16xTblMbz7NRe1o13zf6R3896ivJQ8WnjRu/TDT29S+oVdo5aqamxY0acVliyMGnDcCARs\nTkBju1nXHby9zuK7g0V4CO8/s3mmbJ78oAKckZFBGzduVOLbqlUrWrNmDS1dupSSk5NtnvXQk5/6\nWRrNvGAeLa29hI67jtJvtfbSqzk/U6X10bUMv6Ul0V4YZIVekAgJAg4kILNmJY1nIWZLafcbPGyJ\n19rRf3EgiDjIclABPnHiBM2ePZvuuOMOGjNmDMmwpA0bHD4bBFMrW7Mszb5/AVWsVInu7/0Qlc+p\nwi8l0S1RMci6p2P+PNGfbiNawdup7OimAXcDARCwJwGN19lxsQBrPNmhmw223NNZiE/ZMy92TXVQ\nAYYVtG/RyjRwtJV/sP9Ulv6kv8+rFS3j7+m+fiN9RgyyduwnenYxzxfNVo7VR/OkOMcifVfEDwIg\nkAgEZEUl1y28zeHcZPEzTIy1eMpbuOgQCCrAsIL2LQi1MslcfluczQJ8zMWLZWt07zM8RzP3y0bb\nvbyUKP1SokpliB7gLuh5I9gm7MNopwL3AwEQsDMBrWJ+k7RrIj/X+GU+bxTvt9s5R/ZIe9BGU8MK\nunVrnoKpwIkV9OWXX258deReYyPwpP8Q5TzppqQHNTrC07+l8NtktN2eI0R3ts9vfr6dm5Bk+cKN\nPxH142NeJZF4ki61l+Zq+a4G6vPe+G74STKfY7/iz8tP4e/sR8JoheKXMKez0qhMGY1S+NdlxKHu\nWxDGSJPc27hu7H3uGyCMkQ8jDiO8OT9yH8Of13XTfY20yHU4EHA6Ae1i/k++xrVgadF7nP8/bOip\n8Uu9VtnpZCKT/6ACbFhBt2jRQllAr1y5ki677DJHW0H7K4qcXK4Bx0CA6/AfY9EmokdvIBrKQrxy\nG9H2fWwdPZj/QHrB5jYd87k843vBXr7n8XkeXeUJ4/FTEIfnu+HH2JuuG35OcGRpqfynZVGTNBjn\njb2RLq/vBfF5zhX+XnAfmQ/GCC/Hkm7z3rifzPxj+PPE6cev+DOuK/H281JhnPcScc6bIfayN64Z\ne3MYeQnIy03lEeM6lS517qXIX7hYvYDIi4i8UBkvJOa0Fc6L4cecV+PY2Es+4OxLwNWZnwdteZvH\n/6M7+L88gDduqpYm62g7qVB88n+lqUpFF8nwy0jPuR/N/AUVYMMKWqyfs7Ky6Omnn6YGDRpEM43x\nfS95gvPTJpfFIBY/jLs78BrBTxHt4sH1TesSzeFhBR/eR1S5bOywHT6czePES/HkLbFLQyh3Nou7\nIco+Is7lbBZt8/XCYTzxcZjMU7mUx28LpUqn+bwYmOPzxMFhjJcJ4x6Gv5y8gpcL9uPvBcRzX3nh\nML1gqHhMYeS7EafnvgHCGGHVvnCcxveCNBvxGiIuYqxEvJDIa+TiF5Py6qVEhNvwZ4i4vzDGObUv\niFf8+wtjtM6IX6/r5u8c1ogz2AuI8eJh7M1xGseyN/Lhdd+C+xj+POn3c/5MDtFZ3sz3CeX3bDWM\ndLVJ7Vfnl3s314qladrFNiZSK46W++Arome4pXFMeh5t/JWo8TiiTePZCDYtWimI7H2CCrDcXuaD\nlk1WQ/rf//5HY8eOVcOSevfuHdnU2ST2XK79xqL5WfCU4Zrm/z1FtORrbg7nB/PHD7IhFjePw5Wc\ngHrglTxYsUJkZrrV/6d8DOwEipXACHjyiLqflwkR6exsNx09nkmVK6d5WiGKCmO8LBgvAeaWD+NF\nRF0zvQjId0+cfGwOI/GpdPD/xstPoTDSMuQVf6HrnnuY71tEGOO+nnua/Mp9Tp+uTCn8vzbn1yzq\nhjAbIi6i7iXsBaJu9ud1vdALiMSt4uB9wDDpRLW+55f8R/llshbRtpu4/KoVvLyY4pN4zGn13Lcg\nTZ7vHMa4r9eLiimurLNEo+YQ/ZNFvwzlUr9r3VR3WRK9sYrovi4R+MHGIMpiCbAsQShDkWbMmEG/\n//473X777SRjguHyCeS48/s7Y8VDftS9msfq7rgvCPgnIL9L1WIZoNkyl2sxyaw4VdkACO4cgf37\nj1LNmjxY1+R8RFteHgoJt3w3i7Z6GSn8slAQpnB3k+dlQOI1hVH3Ne7DSfrpGn7BX0bUcQqPtmhP\n9EtXXgudXxZUWtifv9YZczqMfJjv4S8fcv3k6fzKhNSCq3NNo0kDopYNiVbzi0CiuCIFeN26dTR9\n+nR6//33qVGjRvymWpm++eYbkiUJQ3EygcfLL7/Mb77Zan7pSy9l890C99lnn9GDD3L1zeQWLlxI\nBw8epEmTJqkFIUaPHk09e/Y0+YiPw1wR4AAPmfhIIVIBAiBgZwKqtlhQO4x5Plqy0I8kqj2DqMWr\nXJO9m2vCHcKfqlxumRgxm+9Rn6jLRWcoNy+Ner1MtPCe8N8rVjH6FeCdO3dSnz591DrA/fr1o+++\n+46OHj1KDz/8cMjie/LkSRo3bhwtW7aMdu/eTTK+ePXq1Z58t2nThsS6WtyKFStoypQpyuhLJgCZ\nM2cOValSRa1D3L17d0pKii+1y9EhwJ6CxAEIgEDCE9CqsPD+mYX4W679sgjn8dBHF9ueaBeGL+ti\nUzPpNqJLudm72x/KUVZuEr1wO1H3ZuG7R6xj8ivAMvvVvn37qEePHkr0ateurQTYSmK3b99OzZs3\np0o8c5Rsx48fVzVhmVdanIs7H9LS0pShlwi1rEEsbvny5Wq/du1akiFRgcT32WefpR9++EH5NT6O\nHTum7nHo0CHjVNj3Fdiy9dDhE+TOOUOHDmWGPX47Rnj27Fk2OMpTZWrH9EcizblsKCA2FMIGLp+A\nLHGak5PD/5vI/T/tyNpWTGow4QnclbAshVLH8AI1V+fQ2YH8Gy/PbchhcFzppy1/IfrhtzyqWDaJ\n6rHwR+LnsnfvXvr44489lUBz0l9//XXPaoDm8+E49ivAMuToxx95sYF336XJkyer2mq7du2UmIV6\n0z179qharBFeRFj+eCLuZjdv3jzq0qWLVx+I1JpFlDt27Kge7P5EeMiQIXTmzBlzVCQ1+bfffpsq\nVoxsJ1OpMmWpTOnUiN/HK3Nx/EVefORlycnzhRcunlOnTikBLls2hubphRMV4+/ykiYv+5H+f8Y4\nmyW+vQiw7Zjcytnszsaoc0tTqft5VqBB3CF8I4sw2wGEwyXznPvly5eN2DNFuldlxM8tt9zik9xI\nPsf8CrCkoDybaw4bNkxt27Zto1mzZpGIo1hDy6pId999N1WrVs0nsYFOyA8qM/NcDfH06dNUtWpV\nH+9yH+n7NbvOnTuTbGJ1Lc3UHTr4djjUqlXLHEQdiyCXKVMmYm8vchMeLcB14BRKS3HxfcL0a1Op\nt++HtGbIjzbFbuOQIohcXhqlBgwm5yBr3LEpvxUwOcdEjoSLLZnwnATEzdB6BjdLT+Fn4X9Zf8dw\nfi73zl8o3yL9TBGdkJfjhg3ZyiuKrliKIRNvPP/88yS12Oeee06tDyxNwiVxjRs3ps2bN6uHkDQ/\nS/OT0fxsxHPgwAF1WL8+97qzEz9SGxaxFidvzCURfRUo4h865fKLHoywIg4aNwABELABAa0BW7+/\nwOI7hJ/hE3l7ikX5dxskPAZJDFgD9pcWqdXcdNNNavN3vahzNWrUoAEDBigrZsOyWfyLMZYYVknt\nVmraTZo08UQjbz3StCwGYdI/LNeaNm3quR4vB2oYUnzZhcULGqQDBEDAoQQ0HqbkuprFdwGL8DCu\nCffhrS9v+WY/DqXine0SCbB30JJ/GzVqFA0dOlQ1T4q4ips5c6YnovT0dJLN7ES0xRJb+kVEhOPR\n5bi5GS2qJOORAtIEAiAAAt4ERGw1rgnr3D/snsZ7PnbxMCKNp7mEYxbRhiDNzob4Fvfe4j9exVfy\ngHHAxS1J+AMBEHAiAa06N0s/yYLzCAvxm9yd+CcW41+cSMI7z1EXYO/bJ8Y3GTCOPuDEKEvkAgRA\nIHIEtCtYhFmAtWtZiNlAyz2VhTgrcveL95ghwGEooew8TMQRBoyIAgRAwAEE1CIZvIyAaw5nlocM\nuwfx9pEDMu4nixBgP1BKeiqXZ8KKxVKEJU0n/IMACIBAvBDQeHoG11jenuNaMA9ZyhvJ++/iJXXR\nSQcEOAycs6UJGkZYYSCJKEAABJxGQGvE/cO8uIPGk3m4n+DtWRbiI86gAAG2XM46YRiSZYiIAARA\nwOEEXJ24NjyPIZzHInwnb+/yxku9ut/g5QiHlyfqy5PZ7EksSBBgq+Wp82xYWA3JKkWEBwEQAAHS\nSrEID+dNhizxGudunhbC/TrRmXFsqXW3m/J4MQb958QBBQG2WpaaTnn8lgYraKsgER4EQAAE8glo\ndViE7+fjbG6avoQXe1iTQnS9Tq57WYDfShxKEGCrZSk1YPQBW6WI8CAAAiDgQ0ANW2JraXcDXtxB\nnKxlkkCqlUBZUcUTkw80QccEO24KAiCQwARk8g5iAy03L+6Q25qXvWELaXcvrhH3S5xMJydOVmKX\nEwhw7NjjziAAAolLwPUMi+5gonIZPGapRhIlrWEBju6CRRGFCwEOA94cTMQRBoqIAgRAAAS8CWjc\n9Zu0gOjooeNqjWQtwZZ8RRO0d3mH9A014JCwIRAIgAAIOJoABNhy8fM4YNSALVNEBCAAAiDgNAIQ\n4DCUuLKCxnrAYSCJKEAABEDAOQQgwGEo67OyHjAEOAwkEQUIgAAIOIcABDgMZZ3HM2GlwpwtDCQR\nBQiAAAg4hwAEOAxlLU3QyagBh4EkogABEAAB5xCAAFsuayzGYBkhIgABEAABBxKAAIeh0LMxF3QY\nKCIKEAABEHAWAQhwGMpbmqBT0QQdBpKIAgRAAAScQwACHIayztbZChpGWGEgiShAAARAwDkEIMBh\nKGtMxBEGiIgCBEAABBxGAAJsocD1UwdJS86l0nm/YxywBY4ICgIgAAJOJAABDrHU9b1rSV8+nKhU\nNr2ScgWl7v0kxJgQDARAAARAwIkEIMAhlLp+YjfpH3Yh7fqppGeWpuGnvqGkTRNJP7YzhNgQBARA\nAARAwIkEIMChlPqR70i76knSytUl9/5KlKnVIK3RzUSHvgklNoQBARAAARBwIAEIcCiFXroq6Qe/\nIvff3yD9vznUZf0/SP/2TaLS1UKJDWFAAARAAAQcSAACHEKhazVakb50Kzc/P0rUykW31nuW9K9O\nE9W6NoTYEAQEQAAEQMCJBCDAIZS6e8VKoq/rkOuWd8hdPpVmNZpOlNmJ9I+XhhAbgoAACIAACDiR\nAAQ4lFI/dZq09Paknd+Jfhn4Jn2X1oOP6xGdOhVKbAgDAiAAAiDgQAIQ4BAKXbuqFbkXf0RSEz5V\nryFd+MtGcv9lPGnXtQshNgQBARAAARBwIgFMoBhCqWtVq1LKJ2laAAAaGklEQVTS/LmU164D1W3W\nkrodTaWk7zaTVg1GWCHgRBAQAAEQcCQBCHCIxa5d1IiS9/9CP2z5nd7fUo1aXhZiRAgGAiAAAiDg\nSAJogrZY7Ll5GqahtMgQwUEABEDAiQQgwBZLPddNEGCLDBEcBEAABJxIAAJssdSzUQO2SBDBQQAE\nQMCZBCDAFss9Jw81YIsIERwEQAAEHEkAAmyx2KUPOBWmbBYpIjgIgAAIOI8ABNhimaMP2CJABAcB\nEAABhxKAAFss+ByuAScnWYwEwUEABEAABBxHAAJsscjRB2wRIIKDAAiAgEMJQIAtFrzqA0YN2CJF\nBAcBEAAB5xGAAFss8xyMA7ZIEMFBAARAwJkEIMAWy11qwOgDtggRwUEABEDAgQQwgMZCoedx7Xfv\nMRcllbIQCYKCAAiAAAg4kgAEOMRizzxDdP98om170ujoVt7vI3p1AJELbQohEkUwEAABEHAWAchF\niOXd9QWi888j6t74DL3Qj+jgCaK31oUYGYKBAAiAAAg4jgAEOMQiL8VtB3/NIMpz58+E9cRNROt3\nhRgZgoEACIAACDiOQFQFeOnSpdSjRw/q1KkTbd++3Qv2Z599RldffbXX9uuvv9LGjRupf//+lJGR\nQbNmzfIKE8svFUoT/bCfSGbC0jSib34lKpcWyxTh3iAAAiAAAnYiELU+4JMnT9K4ceNo2bJltHv3\nbhoxYgStXr3aw6pNmza0atUq9X3FihU0ZcoUqlevnhLf+fPnU+3atalz585KvM8//3xPuFgdPNaT\nqMUTRF0uS6bjOUQ7DxItvCdWqcF9QQAEQAAE7EYgagIsNd7mzZtTpUqV1Hb8+HHKzs6m1NRUxczF\n1ktpaWmUlZWlhHrJkiXqvIivCLE4jaua+/fvJ38C/NNPP6mwymPBx65duygzM1Pdx3w+HMdX1CXa\n/CTRmLc0SnHl0Zy78iiFa8KcJce7vLw8ysnJIV3XHc/CAJCbm6sO5TcPl09Afidutzsi/087M5b/\nDX4n3iUov5NIPlNEJ0STtm5li9pCrnHjxkp7Cp0Oy9eoCfCePXuoSpUqnkSLEB86dEjVbD0n+WDe\nvHnUpUsXqlmzpjptiO/kyZOpcuXK1Lp1a7N3z/G///1v+vHHHz3f5eDIkSN04sQJJcJeF8L0pQo3\nOTernUTtLs6mJHcu3ydMEds8GhGbU6dOsUV4VHs44pqa8fCQBwlcPgHjoSoPP7hzBOTFBEzO8ZAj\n+f9E8pki4istr1LBK+xefPFFSklJKXw6LN+jJsAVK1b0+lGdPn2aqlat6pMJ6edduHCh1/nx48fT\nt99+S1IbDuTuv/9+n0vbtm1TTdlm4ffxZPWElkkVKpTjlwurESVO+MOHDzOTChH70dqRlDxQpWZT\nvnx5OyY/ImmWF7Vjx455vZhH5EY2i1RqvxF9ZtmMhyRXKmuiIZESwjp16tCgQYNoyJAhUaUTtSqK\nVOM3b96sHkLytiFvv0bzs5HjAwcOqMP69esbp0jE9+DBg/TOO+/4+Pd4iuGBNLK6uOkZDgRAAARA\nAARKQiBqAlyjRg0aMGAA9ezZUxlSTZo0SaVTjLE++OADdSw11iZNmnjSv2/fPpowYQKtXbuWrrzy\nStWHLEZc8eSkm1OsoOFAAARAAARAoCQEotYELYkaNWoUDR06lJKTkz39gzNnzvSkNz09nWQznFg+\nS9t/PDsRYNSA47mEkDYQAAEQiE8CURVgQVC42Tk+sRQ/VW6pARffO3yCAAiAAAiAgCIQtSboROaN\nJuhELl3kDQRAAAQiQwACbJGr1IDRBG0RIoKDAAiAgAMJQIAtFjrrL4ywLDJEcBAAARBwIgEIsMVS\n13UNNWCLDBEcBEAABJxIAAJssdQxDMkiQAQHARAAAYcSgABbLHjVBG0xDgQHARAAARBwHgEIsMUy\nV8OQMA7JIkUEBwEQAAHnEYAAWyxzNEFbBIjgIAACIOBQAhBgiwUPAbYIEMFBAARAwKEEIMAWC176\ngDEO2CJEBAcBEAABBxKAAFssdBmGhC5gixARHARAAAQcSAACbLHQMRGHRYAIDgIgAAIOJQABtljw\nmIrSIkAEBwEQAAGHEoAAWy14rgJjMQarEBEeBEAABJxHAAJsscxRA7YIEMFBAARAwKEEIMAWCx59\nwBYBIjgIgAAIOJQABNhiwatxwBbjQHAQAAEQAAHnEYAAWyxzTEVpESCCgwAIgIBDCUCALRa8zqOA\nMRGHRYgIDgIgAAIOJAABtljomIrSIkAEBwEQAAGHEoAAWyx4EWDUgC1CRHAQAAEQcCABCLDFQldW\n0BbjQHAQAAEQAAHnEYAAWyxzNEFbBIjgIAACIOBQAhBgiwWPiTgsAkRwEAABEHAoAQhwOAoeyyGF\ngyLiAAEQAAFHEYAAWyxuNy9HCCMsixARHARAAAQcSAACbLHQpQ8YDgRAAARAAARKSgACXFJihfxj\nGFIhIPgKAiAAAiBQLAIQ4GJhCuwJU1EGZoMrIAACIAACgQlAgAOzKfYV9AEXGxU8ggAIgAAIFBCA\nAFv8KaAGbBEggoMACICAQwlAgC0WPPqALQJEcBAAARBwKAEIsMWCx1SUFgEiOAiAAAg4lAAE2GLB\nYypKiwARHARAAAQcSgACbLHgMRGHRYAIDgIgAAIOJQABtlDwZ3KIzuYSyR4OBEAABEAABEpCAAJc\nElomvz/sJ7rzDaJdh5Kp2eNEW341XcQhCIAACIAACAQhAAEOAsjf5UOZRC2eIBrbjeji6rn0wRii\n4bOJ9h/35xvnQAAEQAAEQMCXAATYl0nQM1/uInrkBqJWDYkuYgFuXp+ob2uidTuDBoUHEAABEAAB\nEFAEIMAh/BDKpBHtPpQf8PHuJymJKS7/jqgcn4cDARAAARAAgeIQgAAXh1IhP9ddQpTnJrpuItGG\nn1PovreJXEyyc5NCHvEVBEAABEAABAIQSA5wHqeDEPjHMKL567jZ+ac0urIB0Yv9ggTAZRAAARAA\nARAwEYAAm2CU9LB/Gza8aphJNWuWK2lQ+AcBEAABEHA4ATRBO/wHgOyDAAiAAAjEhgAEODbccVcQ\nAAEQAAGHE4AAO/wHgOyDAAiAAAjEhgAEODbccVcQAAEQAAGHE4AAO/wHgOyDAAiAAAjEhgAEODbc\ncVcQAAEQAAGHE4iqAC9dupR69OhBnTp1ou3bt3uh/+yzz+jqq6/22n79NX+Fg+zsbOratSsdPXrU\nKwy+gAAIgAAIgIBdCURtHPDJkydp3LhxtGzZMtq9ezeNGDGCVq9e7eHWpk0bWrVqlfq+YsUKmjJl\nCtWrV4927NhBw4YNoy1btpDbzdNPwYEACIAACIBAAhCImgBLjbd58+ZUqVIltR0/fpykZpuamqow\nungux7S0NMrKylJCvWTJEnV+//79NGPGDBo+fHiRuMeOHUtbt2718pOZmUmVK1emAwcOeJ0P5xfJ\nQyTjD2daoxVXTk6OKlspU7h8Anl5eaTrOp06dQpICggID/mt4P/j/ZPAM8Wbh3yT34lskXqm7N27\nlxYsWEBvv83zChdyixcv9uhUoUuWv0ZNgPfs2UNVqlTxJFiE+NChQ1S7dm3POTmYN28edenShWeX\nqqnOt2vXzut6oC/PP/+8Tw1527ZtNG3aNKpevXqgYJbPy8MjkvFbTmAMIjh8+DBVqFCBUlJSYnD3\n+LylvFiK4JQrh1nTjBLKzc2lY8eOUdWqVY1T2DMBPFN8fwbyTKlYsSIlJ0dGsmrVqkUPPPAADR48\n2OfmkXyORSY3PlkgBU9qpIY7ffq03z/erFmzaOHChYa3Yu+TkpJINrMTcPLGpGma+XTYjyMdf9gT\nHOEIhYexRfhWtosev5VzRWb8RsDkHBPjCEwMEt77SHExdCKSYuudk/xvUWsjbNy4MW3evFnVAqT5\nWfpzjeZnI2FGU1T9+rzALhwIgAAIgAAIJDCBqAlwjRo1aMCAAdSzZ09lBT1p0iSFVYyxPvjgA3Us\nTcZNmmBNvwT+vSFrIAACIAACBQSi1gQt9xs1ahQNHTpUteMbnekzZ870FEZ6ejrJ5s+tXbvW32mc\nAwEQAAEQAAFbEoiqAAuhws3OtqSGRIMACIAACICARQJRa4K2mE4EBwEQAAEQAIGEIgABTqjiRGZA\nAARAAATsQiDqTdDRBCPjC6XvWMYVR8r9/PPP1KBBg0hFb8t4Zcz3eeedR6VLl7Zl+iORaBnHKJb/\n1apVi0T0tozz7NmzdPDgQTXjnS0zEKFE45niC1aeKfI8L1WqlO/FMJzZtGmTmqUxDFGVKAqNJwfQ\nSxQCnr0IiNHYypUrvc45/YvMWvbII49Qo0aNnI7Ck/+33nqLRHDECBEun4DM9S7T086dOxdITATw\nTDHBKDi866676C9/+Qs1bNjQ96KNz6AJ2saFh6SDAAiAAAjYlwAE2L5lh5SDAAiAAAjYmAAE2MaF\nh6SDAAiAAAjYlwAE2L5lh5SDAAiAAAjYmEBCW0FHo1xuvvnmaNzGVvfo0KGDWnLSVomOcGIvueQS\nktV/4M4RKF++PHXu3PncCRwpAnim+P4QOnbsqFZY871i7zOwgrZ3+SH1IAACIAACNiWAJmibFhyS\nDQIgAAIgYG8CEGB7lx9SDwIgAAIgYFMCEGCbFhySDQIgAAIgYG8CEGB7lx9SDwIgAAIgYFMCEOAg\nBffyyy+TWPX279+fTp486ePb3/Vdu3bRLbfcotY2/te//uUTxu4nli5dSj169KBOnTrR9u3bfbLj\n77rM+SvrQffs2ZP+/Oc/U3Z2tk84O58IVuZFXT9w4AC1adPGztn3m3Yp45EjR1L79u3pySef9PET\n6PrWrVtp9OjR1KtXL/r00099wtn9hL9nhjlP/q5v27aNBg4cSGIh/eGHH5q9J8Sxv2dG4YzJHNkZ\nGRme04F+Px4PdjiQuaDh/BP4/PPP9T59+ug5OTn6lClTdBYOL4+Brnfr1k3nyb31Q4cO6c2bN9eP\nHj3qFc7OX06cOKG3bNlS5Wnz5s16u3btvLIT6DrPDa0vWLBA+X3sscd0nhvZK5zdvwQr86Ku9+3b\nV69Vq5bdEfikf+LEifpLL72k84NSv/3223V+yHr58Xf99OnT+pVXXqn+O0eOHFH/P69ANv8S6Jlh\nZCvQdXkOffXVVzrPJ65ffvnlunBKFBfomWHO33//+1/1u2jSpInntL/fj+eiTQ5QAy7iLUlWUurd\nuzclJyerGvCKFSu8fAe6/ttvvxELr1oRqG3btrRhwwavcHb+IjVeyVulSpWIHwR0/Phxr9psoOv3\n3Xcf8UNEZV1WSdq7d6+dMfikPViZB7o+ffp0kjGOFStW9InT7ifWrFlDt912G6WkpNCtt95Khf8/\n/q5/8cUXxC94JHvZ3nvvPbtj8Ep/oGeG4SnQdfm/CY9vv/2WuEKgnklGGLvvAz0zzPnKzMykJUuW\nmE+Rv9+PlwcbfIEAF1FIsgRWlSpVlA/5A8iScmbn7zrXdr2WzKpcuTJxTdgczNbH5jxLRoSLOX+B\nrnMNTz00ZOWo999/XzVN2hqEKfHByjzQ9e+//16tpCWrRyWiM/8W/P0P/F3ft28fcW2Hvv76a1q1\napV68U0kNuY8F/eZIvmXpmduTVD/G+n+cbkS59FtZiJ5LfxMkXPy8i5LnJqdOZy/35fZb7weJ04p\nRoCw1ErkzUvcqVOnfNZy9XddZvcRv4bLysqi6tWrG19tvzfnWTLDTWFqnU4jY0Vd//jjj+mhhx6i\njz76KKFqfMHKPND1ESNGkMyQNXXqVBKRnjdvnoExIfbm34K//4G/62XLllUtK2In8Oyzz5K8pHAT\nZULwkEyY81zcZ4rMoHbvvffSli1bVGva7t271ctJokAxM5E8FX6mBMqnOZy/31egcPF0HgJcRGlI\nU+v69euVj3Xr1lGzZs28fPu7Ls3V0sQqtWXuhiDut6HLLrvMK5ydvzRu3Ji471flTZqfZZH51NRU\nT5YCXV+2bJl6oIqxRZ06dTz+E+EgWJkHuj527Fi69NJLSd7epUZToUKFRMDhyYO//4fnIh/4uy7d\nGsZ/Jy8vTx3L/ylRnL88m/MW6HqNGjUoKSlJeS1Tpox6xpjD2fk40DMjWJ4CsQoWLq6u26SvOibJ\n5DdPnS139RtvvFFv1aqVzv14Kh3cZKizdbMe6Do3s+pdu3bVr7vuOn3SpEkxSXskbzpt2jSdm8GU\nMdb//vc/dSteVF2///771bG/6/wSol9wwQX6FVdcoTYxoEgk56/M2WpTGY5IPv1dN+efhdj8NSGO\nf/31V52bTvXu3bvrPCpA55c1lS+u9eu///67Huj63//+d33IkCE6W4brb7zxRkKwMDIR6JkR7Jky\nf/58ZZDGfek6W4gb0SXM3t8zw/xMkYyKMazZCCvQ78dOUDAXdDFeh6RJpKi38EDXz5w549UfXIxb\n2caLDAGQml2gvqhg122T0RImNFiZB7tewtvZwnug/4eReH/XpfYrm7l1xfCfCHt/eTbny991FhZi\nK2jHPlPMfMzH/liZr8fzMQQ4nksHaQMBEAABEEhYAugDTtiiRcZAAARAAATimQAEOJ5LB2kDARAA\nARBIWAIQ4IQtWmQMBEAABEAgnglAgOO5dJA2EAABEACBhCUAAU7YokXGQAAEQAAE4pkABDieSwdp\nAwEQAAEQSFgCEOCELVpkDARAAARAIJ4JQIDjuXSQNhAAARAAgYQlAAFO2KJFxkAABEAABOKZAAQ4\nnksHabM9gS5dutBrr73myceuXbtI0zR6/PHHPedk8QGZ1lNWRArkZFEPWTkpmGvQoIFaNcefvyee\neMJr7WbDz4wZM9T9ZTEI2apWraqWv9u2bZvhBXsQAIEIEIAARwAqogQBg8D1119Pn3/+ufGVZDWo\n3r17kyzNaDhZhJ0XqVCrIhnnCu+bNm1KvKBD4dPF/i7zKj/11FNq9Sp/gTp06KCW/ZOl/2S5uxYt\nWhAvokAHDx705x3nQAAEwkAAAhwGiIgCBAIR8CfADzzwAPHKWh5xW7NmDXXs2FFFwasEqdqnLEou\nS/OtXr1and+xYwfdeeed6lgm5X/wwQepdu3axKt00bhx42jy5MmeJCxcuJAaNmxI559/Pr355pvq\n/O233672EuehQ4c8fv0dyJq8UkOXZRIXLFigvARKl1yUNF577bUqPX/84x9JFpwQN2fOHLUUZ7ly\n5ZSgf/nll2oxAVlGThZTN9yjjz5KvNqP8RV7EHAMAQiwY4oaGY0FgZYtW6o1bfft20eysPoXX3xB\nV111FfFSlfTJJ5+oJJkF+K677lKLtm/fvp14eUeP6Iqo/fTTT8q/NGmL6H366af02GOP0UsvvUQi\nkIaT+OQ6L4VJI0eOVILIS/ypy6tWraLzzjvP8FrkXoTyhx9+UH4CpWv//v3ESw3SsGHDVNM3LxFH\n0qQtLwz33HOPElY5JxxE1NPS0oiXpSRezlPFK0xmzZpF7du3LzItuAgCiUgAApyIpYo8xQ0B6dtt\n166daobesGEDyeLjssSe1Ix5LWXKysqib7/9ltq2bUtHjhyhjz76iB5++GGSRddF2KSW+80333jl\nR2q4Iqy8hrCqLYuYm52Er1evHvXr10/VYnldYipfvrzyIjVr6YMujqtVq5ZKU1HpEqGvWbOmelEQ\nYZ8+fTqlp6eTLCC/fv16EhGXJSv/8Ic/qFq/3Fdq4//85z9VEqRZXfq269atW5wkwQ8IJBSB5ITK\nDTIDAnFIwGiGFhGUY3EiUi+//LISKakdiuDu3LlTiaP0x5qd9CFLU7PhxJBLhM1wck3WiTWciLbh\nKlasSLJeaihOaq4ijNJcLKLtL11S827durUnevEvmzSTv/vuu2qTfuVGjRp5+p979uxJvAA9HThw\ngORlom/fvp7wOAABJxFADdhJpY28xoSAiK1YMUvzryFiF110EWVmZqpmZKP/V2q0IphbtmxRtUXp\nJ5barzT/mp0I3ubNmz2nvv76a8+xHEiN06oT0ZYa+jXXXKNq2oHSVaVKFfr+++89txPR/uCDD2ju\n3Ln0/vvvq5qu5OOhhx5SoiweS5cuTSLCixYtosWLF9Ott97qCY8DEHASAev/VCfRQl5BIAQCYlEs\nzcAiVFLbNZz0e86ePdtjgCVN0yLGU6dOVbVF6V+VplvpDza7Hj16qHAidiLq0owbzCUlJan+1+PH\nj/v1mpOTo5qbpUa7adMmGjJkCElzda9evVSTeaB0SY1e/BtDlp5//nmSFwJptpaXjCZNmijhlXzK\nPQwnzdAvvviiEndproYDAScSgAA7sdSR56gSEPFr1qyZajaWPmHDiXhJ86y5CVeMqt5++21lxSy1\nzz/96U8qrBFG9gMHDqSLL75YWRaPHTtWWSCLeAdzcj9pHpY+58JORFz6cEUMu3XrpkRThkpJ2sUF\nSpe8IPztb39TTeQiuGJ8NXr0aOrfv79quhara+n3lhcPqQmfOnVKxSfjo6UJGs3PCgc+HEpA474a\n3aF5R7ZBIG4JSE1UJsTwZzC1fPlyZUksQ43E9enTRzVtyxCgYE6MvmSYUaguULrEmlnilqZqs5NJ\nRmQ4U+FmcWniFsGW5na5DgcCTiRw7nXciblHnkEgTglUq1YtYMqkFpmRkaEMmX788UfVTzxt2rSA\n/s0XrIivxBMoXVKzLyy+4t/fkKe33nqL5s2bp/p+Ib5CCc6pBFADdmrJI9+2JiD9rDIOWJqMu3bt\n6lfo4jWDMhuYWHIPHTqUUlJS4jWZSBcIRJwABDjiiHEDEAABEAABEPAlACMsXyY4AwIgAAIgAAIR\nJwABjjhi3AAEQAAEQAAEfAlAgH2Z4AwIgAAIgAAIRJwABDjiiHEDEAABEAABEPAlAAH2ZYIzIAAC\nIAACIBBxAhDgiCPGDUAABEAABEDAlwAE2JcJzoAACIAACIBAxAlAgCOOGDcAARAAARAAAV8C/w9U\nxo3q85ClKQAAAABJRU5ErkJggg==\n"
}
],
"prompt_number": 143
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"plot(nnetFit, plotType=\"level\")"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAeAAAAHgCAYAAAB91L6VAAAEJGlDQ1BJQ0MgUHJvZmlsZQAAOBGF\nVd9v21QUPolvUqQWPyBYR4eKxa9VU1u5GxqtxgZJk6XtShal6dgqJOQ6N4mpGwfb6baqT3uBNwb8\nAUDZAw9IPCENBmJ72fbAtElThyqqSUh76MQPISbtBVXhu3ZiJ1PEXPX6yznfOec7517bRD1fabWa\nGVWIlquunc8klZOnFpSeTYrSs9RLA9Sr6U4tkcvNEi7BFffO6+EdigjL7ZHu/k72I796i9zRiSJP\nwG4VHX0Z+AxRzNRrtksUvwf7+Gm3BtzzHPDTNgQCqwKXfZwSeNHHJz1OIT8JjtAq6xWtCLwGPLzY\nZi+3YV8DGMiT4VVuG7oiZpGzrZJhcs/hL49xtzH/Dy6bdfTsXYNY+5yluWO4D4neK/ZUvok/17X0\nHPBLsF+vuUlhfwX4j/rSfAJ4H1H0qZJ9dN7nR19frRTeBt4Fe9FwpwtN+2p1MXscGLHR9SXrmMgj\nONd1ZxKzpBeA71b4tNhj6JGoyFNp4GHgwUp9qplfmnFW5oTdy7NamcwCI49kv6fN5IAHgD+0rbyo\nBc3SOjczohbyS1drbq6pQdqumllRC/0ymTtej8gpbbuVwpQfyw66dqEZyxZKxtHpJn+tZnpnEdrY\nBbueF9qQn93S7HQGGHnYP7w6L+YGHNtd1FJitqPAR+hERCNOFi1i1alKO6RQnjKUxL1GNjwlMsiE\nhcPLYTEiT9ISbN15OY/jx4SMshe9LaJRpTvHr3C/ybFYP1PZAfwfYrPsMBtnE6SwN9ib7AhLwTrB\nDgUKcm06FSrTfSj187xPdVQWOk5Q8vxAfSiIUc7Z7xr6zY/+hpqwSyv0I0/QMTRb7RMgBxNodTfS\nPqdraz/sDjzKBrv4zu2+a2t0/HHzjd2Lbcc2sG7GtsL42K+xLfxtUgI7YHqKlqHK8HbCCXgjHT1c\nAdMlDetv4FnQ2lLasaOl6vmB0CMmwT/IPszSueHQqv6i/qluqF+oF9TfO2qEGTumJH0qfSv9KH0n\nfS/9TIp0Wboi/SRdlb6RLgU5u++9nyXYe69fYRPdil1o1WufNSdTTsp75BfllPy8/LI8G7AUuV8e\nk6fkvfDsCfbNDP0dvRh0CrNqTbV7LfEEGDQPJQadBtfGVMWEq3QWWdufk6ZSNsjG2PQjp3ZcnOWW\ning6noonSInvi0/Ex+IzAreevPhe+CawpgP1/pMTMDo64G0sTCXIM+KdOnFWRfQKdJvQzV1+Bt8O\nokmrdtY2yhVX2a+qrykJfMq4Ml3VR4cVzTQVz+UoNne4vcKLoyS+gyKO6EHe+75Fdt0Mbe5bRIf/\nwjvrVmhbqBN97RD1vxrahvBOfOYzoosH9bq94uejSOQGkVM6sN/7HelL4t10t9F4gPdVzydEOx83\nGv+uNxo7XyL/FtFl8z9ZAHF4bBsrEwAAQABJREFUeAHt3QmYFNW58PEXGIZF9kUQ2S+gOGMEtwsK\nMhJkExcElEVFQVHUaEKMEicm4iV40ZhEERe8kqtwiQY3lEkIi6wj7hJRFokKYUTAUQQGBgakvnrP\nl2q7e3qZZmq6urv+53ma7tpOnfOrZt4+VafqVLPsJCQEEEAAAQQQSKpA9aTujZ0hgAACCCCAgBEg\nAPNFQAABBBBAwAMBArAH6OwSAQQQQAABAjDfAQQQQAABBDwQIAB7gM4uEUAAAQQQIADzHUAAAQQQ\nQMADAQKwB+jsEgEEEEAAAQIw3wEEEEAAAQQ8ECAAe4DOLhFAAAEEECAA8x1AAAEEEEDAAwECsAfo\n7BIBBBBAAAECMN8BBBBAAAEEPBAgAHuAzi4RQAABBBAgAPMdQAABBBBAwAMBArAH6OwSAQQQQAAB\nAjDfAQQQQAABBDwQIAB7gM4uEUAAAQQQIADzHUAAAQQQQMADAQKwB+jsEgEEEEAAAQIw3wEEEEAA\nAQQ8ECAAe4DOLhFAAAEEECAA8x1AAAEEEEDAAwECsAfo7BIBBBBAAAECMN8BBBBAAAEEPBAgAHuA\nzi4RQAABBBAgAPMdQAABBBBAwAMBArAH6OwSAQQQQAABArDL34GjR4/KsWPHXM41/bM7cuSIWJaV\n/hVxuQZlZWUu55gZ2eES+TjiEtklXecSgF0+clOnTpXVq1e7nGv6Z3fLLbfIZ599lv4VcbkGl19+\nuZSWlrqca/pn179///SvRBXUAJcqQPUwSwKwh/jsGgEEEEDAvwIEYP8ee2qOAAIIIOChAAHYQ3x2\njQACCCDgXwECsH+PPTVHAAEEEIghsHjxYhk8eLD069dPNm3aFLJmYWGh9OjRI+S1ZcuWkGldvmDB\ngpDtgieygidS+bP2op03b14qF9GUbd26dXL48GHZunVrypc1mQX89NNP5eWXX5YWLVokc7cpv6+i\noiKZO3euZGdnp3xZk1nAnTt3yrPPPpvMXabFvtLF5fzzz5dOnTpVienatWtF/55UJrVv31769OkT\nM4v9+/dLfn6+LFmyRLZt2yYTJkyQVatWBbbp2bOnrFy50kwvX75cZsyYIZ07dw7M+/rrr+Xiiy+W\n3r17B7YJ/5A2AXjmzJmybNkyGTZsWHgdUmq6e/fu0qhRI265CTsqvXr1kvr16+MS5qK9WmvUqIFL\nmIu2OrhtLQzFnkwHl+LiYrnqqqvk/fffL18BF+b0HzFCzrfvNqlMWj1ypPxs/Hhp2rRpIJuBAwdK\n165dA9Pa4nX+nuvf9L1794reBub8WK5evbrUqlVLDhw4YAJ1QUGB2VbnaZo0aZI89NBD0qRJEzMd\n6Z+0CcBZWVkyduxYGT58eKR6MA8BBBBAIAUEtOX39ttvV1lJTrJP6+Zcd12l8v/0pZekXbt2IWfk\ntIEQnPTsVHDw1CCsPy5atWoVvJrMmTNH9Id0y5YtA/M1eG/fvt3MD8yM8CFtAnCEsjMLAQQQQACB\nhAXqNm9urut26NAh6rYNGzaUkpKSwHK9X79Zs2aBaefD7NmzZf78+c6keX/66afl1ltvDZkXaYJO\nWJFUmIcAAggg4GuBnJwc0T49eilETz/rEw6d088OzK5du8xHbU0Hp0WLFok+ZCdeIgDHE2I5Aggg\ngIDvBLTD6JgxY2TIkCGmtTx9+nRjoJ2xXnnlFfN548aNkpubG2KjHYb1kcT16tULmR9pglPQkVSY\nhwACCCDge4GJEyfKeLuzlvZB0k5XmmbNmhVwycvLE30Fp5o1a8rmzZuDZ0X9TACOSsMCBBBAAAG/\nC4SfdnbTI2MC8LHo9zq76ZV2eU27LO2KnJQC70nKXtJvJxelX5GTUuJeSdlLeu0k/gnW9KqPF6Xl\nGrAX6uwTAQQQQMD3AgRg338FAEAAAQQQ8EKAAOyFOvtEAAEEEPC9AAHY918BABBAAAEEvBAgAHuh\nzj4RQAABBHwvQAD2/VcAAAQQQAABLwQIwF6os08EEEAAAd8LEIB9/xUAAAEEEEDACwECsBfq7BMB\nBBBAwPcCBGDffwUAQAABBBDwQoAA7IU6+0QAAQQQ8L0AAdj3XwEAEEAAAQS8ECAAe6HOPhFAAAEE\nfC9AAPb9VwAABBBAAAEvBAjAXqizTwQQQAAB3wsQgH3/FQAAAQQQQMALgSwvdso+EUAAAQQQOB6B\nmvZGjY9nw6BtsoM+e/mRFrCX+uwbAQQQQMC3AgRg3x56Ko4AAggg4KUAAdhLffaNAAIIIOBbAQKw\nbw89FUcAAQQQ8FKAAOylPvtGAAEEEPCtAAHYt4eeiiOAAAIIeClAAPZSn30jgAACCPhWgADs20NP\nxRFAAAEEvBQgAHupz74RQAABBHwrQAD27aGn4ggggAACXgoQgL3UZ98IIIAAAr4VIAD79tBTcQQQ\nQAABLwUIwF7qs28EEEAAAd8KEIB9e+ipOAIIIICAlwIEYC/12TcCCCCAgG8FCMC+PfRUHAEEEEDA\nS4GkBuBXXnlFLrnkEhkxYoR89tlnXtabfSOAAAIIIOCpQFay9r5//36ZMmWKrFq1Sr799lsZOXKk\nvPXWW8naPftBAAEEEEAgpQSSFoDfffddOeecc6RBgwbmtWfPHiktLZU6deqkFAiFQQABBBBAIBkC\nSQvA559/vtx2222mBbxt2zbR186dO6VDhw4h9SwuLpbhw4eHzNOJL7/8UsaOHVtuPjMQQAABBFJL\nYOXKlZKXl1euULfffrtcccUV5eb7dUbSAnCtWrXkpZdekqefflq6dOkivXr1klatWpVzb9asmaxY\nsaLc/Mcee0xatmxZbj4zEEAAAQRSS6BPnz4yf/781CpUCpYmaZ2w9Brwq6++Kr///e/lqquuMqef\nNSiTEEAAAQQQ8KNA0lrA9evXl6+++kpGjRolev330Ucf9aM3dUYAAQQQQMAIJC0A69406B48eFDq\n1q0LPwIIIIAAAgkL1LS3aJTwVqEbZIdOejaVtFPQTg0Jvo4E7wgggAACfhZIegD2MzZ1RwABBBBA\nwBEgADsSvCOAAAIIIJBEAQJwErHZFQIIIIAAAo4AAdiR4B0BBBBAAIEkChCAk4jNrhBAAAEEEHAE\nCMCOBO8IIIAAAggkUYAAnERsdoUAAggggIAjQAB2JHhHAAEEEEAgiQIE4CRisysEEEAAAQQcAQKw\nI8E7AggggAACSRQgACcRm10hgAACCKSPwOLFi2Xw4MHSr18/2bRpU0jBCwsLpUePHiGv7du3y9df\nfy333XefDBkyRB5//PGQbcInCMDhIkwjgAACCPheQIfQzc/Pl3nz5snDDz8sEyZMCDHp2bOnrFy5\n0rw04DZt2lTatGkjN998s/Tv318WLFggGqSLi4tDtgueSOpoSME75jMCCCCAAAKpKqAt3u7du0uj\nRo3Ma+/evVJWVibZ2f9/LKXq1auLjml/4MABE6gLCgrk+++/l82bN0vt2rXlhRdekKeffjrm6H+0\ngFP16FMuBBBAAIEqEdj+/vsycuRIycvLC7z0dHNwKioqkiZNmgRmaSCO1JqdM2eOafG2bNlSdu3a\nZV5PPPGEWVdbyUePHg3kEf6BFnC4CNMIIIAAAhkt0Oass+TP994rHTp0iFrPhg0bSklJSWB5aWmp\nNGvWLDDtfJg9e7bMnz/fTJ5wwgly7Ngx0QCclZVlWsNLly6VgQMHOquHvNMCDuFgAgEEEEAAAZGc\nnBxZt26dWJYlevpZA6tz+tnx0Ravpnbt2pl3DdonnXSS7Nu3z0zv2LFDGjRoYD5H+ocWcCQV5iGA\nAAII+FqgRYsWMmbMGNObeffu3TJ9+nTjoZ2xBg0aJEOHDpWNGzdKbm5uiJO2fidNmmR6Q5988smi\np6GjJQJwNBnmI4AAAgj4WmDixIkyfvx4czpZO11pmjVrVsDEuYYcmGF/6N27t3kdPHgwZgcs3YYA\nHCzHZwQQQAABBIIEwk87By2K+bFu3boxl+tCrgHHJWIFBBBAAAEE3BcgALtvSo4IIIAAAgjEFSAA\nxyViBQQQQAABBNwX4Bqw+6bkiAACCCBQRQK17HzL342b2M5qJ7Z6la1NC7jKaMkYAQQQQACB6AIE\n4Og2LEEAAQQQQKDKBAjAVUZLxggggAACCEQXIABHt2EJAggggAACVSZAAK4yWjJGAAEEEEAgugAB\nOLoNSxBAAAEEEKgyAQJwldGSMQIIIIAAAtEFCMDRbViCAAIIIIBAlQkQgKuMlowRQAABBBCILpA5\nT8L6Nnol/bzkWj9XPkbdN8RY5udF3/m58jHqXm9/jIV+XVTfrxV3r960gN2zJCcEEEAAAQQqLEAA\nrjAVKyKAAAIIIOCeAAHYPUtyQgABBBBAoMICBOAKU7EiAggggAAC7gkQgN2zJCcEEEAAAQQqLEAA\nrjAVKyKAAAIIIOCeAAHYPUtyQgABBBBAoMICBOAKU7EiAggggAAC7gkQgN2zJCcEEEAAAQQqLEAA\nrjAVKyKAAAIIIOCeAAHYPUtyQgABBBBAoMICBOAKU7EiAggggAAC7gkQgN2zJCcEEEAAAQQqLJA5\noyFVuMqsiAACCCCQrgI17YI3qmThsyu5vVub0wJ2S5J8EEAAAQQQSECAAJwAFqsigAACCCDglgAB\n2C1J8kEAAQQQQCABAQJwAlisigACCCCAgFsCBGC3JMkHAQQQQACBBAQIwAlgsSoCCCCAAAJuCRCA\n3ZIkHwQQQAABBBIQIAAngMWqCCCAAAIIuCVAAHZLknwQQAABBBBIQIAAnAAWqyKAAAIIIOCWAAHY\nLUnyQQABBBBAIAEBAnACWKyKAAIIIICAWwIEYLckyQcBBBBAAIEEBAjACWCxKgIIIIAAAm4JEIDd\nkiQfBBBAAAEEEhAgACeAxaoIIIAAAgi4JUAAdkuSfBBAAAEEEEhAgACcABarIoAAAggg4JYAAdgt\nSfJBAAEEEEAgAYGsBNat1KqFhYXy85//PCSP+fPnS5s2bULmMYEAAggggIAfBJIWgHv27CkrV640\npsuXL5cZM2YQfP3wDaOOCCCAAAIRBZIWgKtXry61atWSAwcOSH5+vhQUFEQs0HfffSeTJk0qt2zD\nhg0ybNiwcvOZgQACCCCQWgLvvfeejBs3rlyhRo8eLf369Ss3368zkhaAHeA5c+ZI//79pWXLls6s\nkPf69evLvffeGzJPJ5599llp1apVufnMQAABBBBILYGuXbtG/DvetGnT1Cqox6VJegCePXu26LXf\naKlGjRrSoUOHcoubNWtmWtDlFjADAQQQQCClBE444YSIf8dTqpApUJikBuBdu3aZKrdr1y4Fqk4R\nEEAAAQTSTaCWXeDmlSx07Upu79bmSb0NaePGjZKbm+tW2ckHAQQQQACBtBVIagDOy8sTPQVNQgAB\nBBBAINUFFi9eLIMHDzYdxzZt2hRSXL21tkePHiGv7du3y9///nfRu36c144dO0K2C55I6ino4B3z\nGQEEEEAAgVQV2L9/v7ljZ8mSJbJt2zaZMGGCrFq1KlDcaLfWPvHEEzJ58mQZOHCgWVfv/omWCMDR\nZJiPAAIIIJCRAt/a/ZH++te/SosWLQL1O/fcc6Vt27aBaW3xdu/eXRo1amRee/fulbKyMsnOzjbr\nRLu19sMPP5QuXbrI448/LnrbVfA+Apn/+0NST0GH75xpBBBAAAEEki1wxA6kxcXFoh2DnVdpaWlI\nMYqKiqRJkyaBeRqIdZvwFH5rrd7JY1mWCby9evWSkpKS8E0C07SAAxR8QAABBBDwg0AL+xHI1157\nbcxbpRo2bBgSPDVA6+2w4Sn81tqFCxcGVvnggw/k9ddfl1GjRgXmBX+gBRyswWcEEEAAAQRsgZyc\nHFm3bp1pzerp52PHjgVOPztA4bfW6jraaevgwYNmlc2bN8vpp5/urF7unRZwORJmIIAAAgj4XUCv\n3Y4ZM0aGDBkiu3fvlunTpxsS7Yw1aNAgGTp0qITfWqvXhUeOHGkem3zo0CE55ZRTYt56SwD2+7eM\n+iOAAAIIRBSYOHGijB8/XrKyskSDq6ZZs2YF1tVba/UVnPTU9tVXXy16ylqfCBYrEYBj6bAMAQQQ\nQMDXAk6v50QQNFjHC76aH9eAE1FlXQQQQAABBFwSIAC7BEk2CCCAAAIIJCJAAE5Ei3URQAABBBBw\nSYAA7BIk2SCAAAIIIJCIAAE4ES3WRQABBBBAwCUBArBLkGSDAAIIIIBAIgIE4ES0WBcBBBBAAAGX\nBAjALkGSDQIIIIAAAokIEIAT0WJdBBBAAAEEXBIgALsESTYIIIAAAggkIkAATkSLdRFAAAEEEHBJ\ngADsEiTZIIAAAgggkIgAATgRLdZFAAEEEEDAJQFGQ3IJkmwQQAABBKpeoJa9i+aV3E3tSm7v1ua0\ngN2SJB8EEEAAAQQSECAAJ4DFqggggAACCLglQAB2S5J8EEAAAQQQSECAAJwAFqsigAACCCDglgAB\n2C1J8kEAAQQQQCABAQJwAlisigACCCCAgFsCBGC3JMkHAQQQQACBBAQIwAlgsSoCCCCAAAJuCRCA\n3ZIkHwQQQAABBBIQIAAngMWqCCCAAAIIuCVQoUdRbt26Vdq3by8bNmyQhQsXyuDBgyU3N9etMriS\nT7U8V7IhE58IVPZRdpnK9F2mVqyS9fpX/UpmkIGbt83AOiW7SnFbwHfeeadcd911cvjwYenbt68U\nFhbKxRdfLNu3b092WdkfAggggAACGSMQNwC/8MIL8vrrr8uyZcukcePGsmDBAhkzZowsXbo0YxCo\nCAIIIIAAAskWiBmALcuSo0ePSr169eS1116TYcOGmfKVlZVJ/fqck0n2wWJ/CCCAAAKZIxDzGnC1\natWkR48ecskll8iaNWvM6ednnnlGnnvuOcnPz88cBWqCAAIIIIBAkgVitoC1LI8++qgMHz7cnHLO\nycmRVq1ayeLFi+XYsWNJLiq7QwABBBBAIHMEoraADx06ZGqpPZ7fffdd81nn9enTR8aNGycDBw40\nnbMyh4KaIIAAAgggkDyBqC1g7elcp04d+fjjj827ftaXXg/WntDnnXde8krJnhBAAAEEEMgwgagB\nWHs5HzlyREaNGmXe9bO+tFOW3oLUpUuXDKOgOggggAACCCRPIOopaO2AlZWVJfPmzUteadgTAggg\ngAACPhGI2AJ+++23pVu3boZAr/lqazf8tWjRIp8QUU0EEEAAAQTcF4jYAj7ttNPkT3/6k9nbjBkz\nzKnn8F137NgxfBbTCCCAAAIIIFBBgYgBWB+y0b17d5PFvn375N5775WdO3eG3Hr0yCOPmJ7QFdwP\nqyGAAAIIIIBAkEDEABy03NxqNH78eMnLyzPXhJ1lnTp1cj7yjgACCCCAQFIEsu29NKnknmpVcnu3\nNo8ZgPVRlNoCnjx5sminLBICCCCAAAIIuCMQsROWk7UG3QEDBsjs2bNFn/9MQgABBBBAAAF3BGIG\nYN3F/v375YYbbpCmTZvKqaeeGnjRC9qdA0AuCCCAAAL+FIh5ClpJpkyZEnHgBa4B+/MLQ60RQAAB\nBNwRiBuAzzjjDHf2RC4IIIAAAgggEBCIGIDXr18v99xzT2Al/VC9enU5+eSTRe8RnjBhgmRna180\nEgIIIIAAAggcj0DEANy4cWPp169fSH46/OA333wjc+fOlRdffFGWLVsmNWrUCFmHCQQQQAABBBCo\nmEDEANy6dWu54447IuZw3333SYsWLeTDDz+Us88+O+I6zEQAAQQQQACB2AJxe0GHb64DNAwaNEje\neeed8EVMI4AAAggggEAFBRIOwJqvnopu06ZNBXfBaggggAACCCAQLhDxFLSO+7t3796QdfWpWF99\n9ZX87W9/k7feekuee+65kOVMIIAAAggggEDFBSIG4DVr1kjfvn3L5dKoUSPp2rWr6YDVvHnzcsuZ\ngQACCCCAAAIVE4gYgC+44IJyLWC9DalevXoVy5W1EEAAAQQQQCCmQMQArLcXNWjQIOaGLEQAAQQQ\nQACB4xc4rk5Yx787tkQAAQQQQAABFSAA8z1AAAEEEEDAAwECsAfo7BIBBBBAIPUFFi9eLIMHDzZP\nhty0aVNIgQsLC6VHjx4hr+3btwfWmTZtmjzzzDOB6Ugf4gZg7RF94YUXmt7Pp5xyijgvhiOMxMk8\nBBBAAIFMENChePPz82XevHny8MMPmzEQguvVs2dPWblypXnpEyJ1yF7n+Rhr166Vxx9/vFxn5uDt\n9XPETljBK1133XUyfvx4ycvLE30KlpMYjtCR4B0BBBBAIJ0EPnz/fRk5cqTUqVMnUGwdgKh///6B\naW3xdu/eXfT2W33pszHKysoCAxHpnUG1atWSAwcOmEBdUFBgti0pKZH7779f7rzzTtExFGKlHyJq\nhLX04Rv79u2TyZMnS7Vq1SKswSwEEEAAAQTSS6D7WWfJ/ffeKx06dIha8KKiImnSpElguQbh4uJi\nadWqVWCefpgzZ44J3C1btjTzJ02aJNoi/uijj0Rb0bFSzFPQGnQHDBggs2fPNpE/VkYVWfbAAw+I\nNtv1NXTo0IpswjoIIIAAAggkXaBhw4airVknlZaWSrNmzZzJwLvGx5tvvtlMv/HGG/LBBx/Ie++9\nJ8uXLxe9Thx+7Tiwof0hZgDWFTWC33DDDeb89qmnnirO63iuAWsTfeHChbJixQp54YUXgsvBZwQQ\nQAABBFJGICcnR9atWyd6JlhPP+vp5Ozs7JDy7dq1y0y3a9fOvLdv3160BaxD+tatW9ec4g7fJjiD\nmKegdcUpU6aY89vBG+nnRK8Ba+G//fZb0SCsn6+66qrwLM30wYMHzZjD4Qv1l4Q+oYuEAAIIIJDa\nAl988YXMmjWrXCHPO+88yc3NLTc/FWfosLtjxoyRIUOGyO7du2X69OmmmBMmTDAjAupZ3I0bN4bU\np2PHjqIvTXptWBuwzrSZGfZP3AB8xhlnmE2OHj0q3333nbkYHdwZKyy/qJP6S0GfH62vjz/+WC6+\n+GLR5np40tPe9evXD59tLnbrRW8SAggggEBqC2iMiPR3PFZrsKI1yjoiUi/2pdW4WdW086hImjhx\noumErPVx4k/wDwvtnKyvSOnGG2+MNDtkXtwAvHXrVpk6daq89tpr8pOf/EQ0kLZu3dp0zArJKc7E\nSSedZLpr62o6nvBf/vIX2bFjR7kL2torbdSoUeVy0yEQtZs3CQEEEEAgtQX0dpxIf8dTu9SRS+fG\nj4bIOVfgGvC4ceNME1q7VWu66667zH1Rn376abQ8I87XUxLXXnutWaZdufXitjbxSQgggAACCPhR\nIOY5Xb34/Mknn8gvfvELqV27tvFp27atuX4b6fRxLEDt7q0t2OHDh8s555wjd999t+igDyQEEEAA\nAQT8KBDzFLRej9UhCNevXx+w0Q5U2pNZ7w1ONP3hD3+QQ4cOmQd6HM915ET3x/oIIIAAAgikqkDM\nAKyFfvDBB03vY23B1qxZU5566ik57bTTTM+w46mU05I+nm3ZBgEEEEAAgUwRiBuAhw0bZrpZ6+1D\nR44ckSuuuEI6d+6cKfWnHggggAACCHgiEDEA61M89F6nSMl5gIa2jPv16xdpFeYhgAACCCCAQByB\niAFYW7iPPPKI2VQfs/Xll1/K1VdfLf/xH/9hHq81d+5c80SsOHmzGAEEEEAAAQSiCEQMwPoMzN69\ne5tNrrnmGvNsS+eh1Oeff77oPblLly4VHSmJhAACCCCAAAKJC8S8DUmz01uFdu7cGZKz9oqO9FDq\nkJWYQAABBBBAAIGoAhFbwMFr//KXv5Q+ffpIr169zFOrlixZInovMNd/g5X4jAACCCCAQGICcQOw\njoR05plnmuc262AK06ZNk8svv9zcy5vYrlgbAQQQQAABBByBuAFYV9QArC8SAggggAACCLgjEDEA\nx7oNydkttyE5ErwjgAACCCCQuEDEAMxtSIlDsgUCCCCAAAKJCEQMwNyGlAgh6yKAAAIIIJC4ALch\nJW7GFggggAACCFRaIGILODhXbkMK1uAzAggggAAC7gjEDcDchuQONLkggAACCCAQLBA3AOvK3IYU\nTMZnBBBAAAEEKi8Q8Rrw22+/Ld26dTO561OwunTpUu61aNGiyu+dHBBAAAEEEPCpQMQW8GmnnSZ/\n+tOfDMmMGTPMOMDhPh07dgyfxTQCCCCAAAIIVFAgYgDeunWr/PrXv46ZxeTJk0VHRiIhgAACCCCA\nQOICEQNw48aNQwZbeOKJJyQvL0+6du0a2MOJJ54Y+MwHBBBAAAEEkiFglYlYxZXbk3Woctu7tXXE\nANy6dWu54447AvsoKCgwAzAMHDgwMI8PCCCAAAIIIHD8AhE7YR1/dmyJAAIIIIAAAhURIABXRIl1\nEEAAAQQQcFkg4inosrIy+eabbwK7Onz4sOhYwF999VVgnl4nrl27dmCaDwgggAACCCBQcYGIAbiw\nsFD69u0bksuqVatCpv/yl7/IiBEjQuYxgQACCCCAAAIVE4gYgPXhGwcPHoyZQ3Z2dszlLEQAAQQQ\nQACB6AIRrwFXr15d6tSpY14zZ86M+LlGjRrRc2UJAggggAACCMQUiBiA582bJ6effrqMHTtWfvvb\n38ratWultLRUNBiTEEAAAQQQQKDyAhED8OjRo0WvA19//fWiLd1HHnnEPBu6qKhIdHSkJ598UrZt\n21b5vZMDAggggAACPhWIGIC1t3NJSYl5+lX9+vXl+eefl82bN8vJJ58sV111lezZs0fWr1/vUzKq\njQACCCCAQOUFInbC2rRpk+Tn58vu3bvNrUdTpkyRc845R44ePSoXXXSReVV+1+SAAAIIIICAfwUi\ntoAvvPBCefPNN02rt3nz5tK2bVtZuHChuRe4c+fOcsUVV8jy5cv9q0bNEUAAAQQQqKRAxBawk6de\n/23fvr25FqzXg/W08xtvvGHeeQiHo5Ta7233p3b5vCrdhvpe7Tm191vJZ9ynduUqUbrWCyqxcaZu\nelmmVix59YoZgLUYq1evDpTG+XzmmWcG5vEBAQQQQAABBBIXiHgKOvFs2AIBBBBAAAEEEhEgACei\nxboIIIAAAgi4JEAAdgmSbBBAAAEEEEhEgACciBbrIoAAAggg4JIAAdglSLJBAAEEEEAgEQECcCJa\nrIsAAggggIBLAgRglyDJBgEEEEAAgUQECMCJaLEuAggggAACLgkQgF2CJBsEEEAAAQQSEYj7JKxE\nMmNdBBBAAAEEqlTgkJ37rkruobSS27u0OS1glyDJBgEEEEAAgUQECMCJaLEuAggggAACLgkQgF2C\nJBsEEEAAAQQSESAAJ6LFuggggAACCLgkQAB2CZJsEEAAAQQQSESAAJyIFusigAACCCDgkgAB2CVI\nskEAAQQQyCyBxYsXy+DBg6Vfv36yadOmkMoVFhZKjx49Ql7bt2+X999/X6688koZMGCALFy4MGSb\n8AnuAw4XYRoBBBBAwPcC+/fvl/z8fFmyZIls27ZNJkyYIKtWrQq49OzZU1auXGmmly9fLjNmzJA2\nbdrIddddJ88++6w0adJEcnNzZdCgQVKjRo3AdsEfCMDBGnxGAAEEEMh4gb0le+XDDz+UXbt+eKJH\np06dpFmzZoG6a4u3e/fu0qhRI/Pau3evlJWVSXZ2tlmnevXqUqtWLTlw4IAJ1AUFBWb+smXLzPua\nNWukXr16UYOvrkQANlT8gwACCCDgF4Gvv/vatGw1uDpJTxsHB+CioiLTinWW67rFxcXSqlUrZ5Z5\nnzNnjvTv319atmwZmK+tZm09//jHP5bvv/8+ahAmAAfI+IAAAggg4AeBTq07yV133SUdOnSIWt2G\nDRtKSUlJYHlpaWlIgHYWzJ49W+bPn+9MmveLLrpI9DV06FBzmrpv374hy50JOmE5ErwjgAACCCDw\nb4GcnBxZt26dWJYlevr52LFjgdPPDpJzCrtdu3Zmlq6jrWEN1pq09du8eXPzOdI/tIAjqTAPAQQQ\nQMDXAi1atJAxY8bIkCFDZPfu3TJ9+nTjoZ2xtGOVtm43btxoOlo5UHpdeOzYsTJ8+HBzfVg7YZ1+\n+unO4nLvBOByJMxAAAEEEEBAZOLEiTJ+/HjJysoSDa6aZs2aFaDJy8sTfQUnDdqjRo2SI0eOmCAc\nvCz8MwE4XIRpBBBAAAEE/i3g9HpOBMTpIR1vG64BxxNiOQIIIIAAAlUgQACuAlSyRAABBBBAIJ4A\nATieEMsRQAABBBCoAgECcBWgkiUCCCCAAALxBAjA8YRYjgACCCCAQBUIEICrAJUsEUAAAQQQiCdA\nAI4nxHIEEEAAAQSqQCCpAfj555+XSy+91DxZZMuWLVVQHbJEAAEEEEAgPQSS9iCOPXv2yMyZM2XF\nihXy7rvvyqRJk+T1119PDyVKiQACCCCQGgKHRawfRhE8vjL9/0c1H9+2Lm6VtADcuHFjWb16tXk8\n15tvvimtW7eOWI2jR4/Khg0byi378ssvpUGDBuXmMwMBBBBAILUEdPCCjz76qFyhTj75ZGnatGm5\n+X6dkbQA7ABrK/jxxx+XadOmObNC3nVw42eeeSZknk784x//iDmqRLkNmIEAAggg4InAF198EfHv\n+LBhw+SCCy7wpEypuNOkB+Cf/vSncsstt0jnzp3NteC6deuGuOgYjI888kjIPJ147LHHQgY8LrcC\nMxBAAAEEUkKgW7duEf+Op0ThUqgQSeuEpb+IdJQIJ2mgrVmzpjPJOwIIIIAAAr4SSFoLuEOHDtKq\nVSsZMWKEHDx4UO655x4CsK++alQWAQQQQCBYIGkBWHf60EMPSWlpqdSuXVuqVasWXA4+I4AAAggg\n4CuBpAZgla1Tp46vgKksAggggAACkQSSdg040s6ZhwACCCCAgF8FCMB+PfLUGwEEEEDAUwECsKf8\n7BwBBBBAwK8CBGC/HnnqjQACCCDgqQAB2FN+do4AAggg4FcBArBfjzz1RgABBBDwVIAA7Ck/O0cA\nAQQQ8KsAAdivR556I4AAAgh4KkAA9pSfnSOAAAII+FWAAOzXI0+9EUAAAQQ8FSAAe8rPzhFAAAEE\n/CpAAPbrkafeCCCAAAKeChCAPeVn5wgggAACfhUgAPv1yFNvBBBAAAFPBQjAnvKzcwQQQAABvwoQ\ngP165Kk3AggggICnAlme7p2dI4AAAgggkIhAmb3yt4lsEGFdzSMFEi3gFDgIFAEBBBBAwH8CBGD/\nHXNqjAACCCCQAgIE4BQ4CBQBAQQQQMB/AgRg/x1zaowAAgggkAICBOAUOAgUAQEEEEDAfwIEYP8d\nc2qMAAIIIJACAgTgFDgIFAEBBBBAwH8CBGD/HXNqjAACCCCQAgIE4BQ4CBQBAQQQQMB/AgRg/x1z\naowAAgggkAICBOAUOAgUAQEEEEDAfwIEYP8dc2qMAAIIIJACAgTgFDgIFAEBBBBAwH8CBGD/HXNq\njAACCCCQAgIZMxzhsftTQDMFi1DtghQsVAoUqdf1KVCIFCzCgLdSsFCpUKQWqVAIypBpArSAM+2I\nUh8EEEAAgbQQIACnxWGikAgggAACmSZAAM60I0p9EEAAAQTSQoAAnBaHiUIigAACCGSaAAE4044o\n9UEAAQQQSAsBAnBaHCYKiQACCCCQaQIE4Ew7otQHAQQQQMAVgcWLF8vgwYOlX79+smnTppA8CwsL\npUePHiGv7du3y3vvvSejR4+Wyy67TGbPnh2yTfhExtwHHF4xphFAAAEEEDhegf3790t+fr4sWbJE\ntm3bJhMmTJBVq1YFsuvZs6esXLnSTC9fvlxmzJghbdq0McF33rx50qpVK7noootM8G7btm1gu+AP\nBOBgDT4jgAACCGS8wPqi9XLbbbdJvXr1AnW99dZb5YILfnhykbZ4u3fvLo0aNTKvvXv3SllZmWRn\nZ5ttqlevLrVq1ZIDBw6YQF1QUGDma/DVQKypWrVqsnPnTiEAGw7+QQABBBBIa4HDdul3V64GpzQ6\nRX563x3Srl27QEYNGjQIfNYPRUVF0qRJk8A8DcTFxcWmZRuYaX+YM2eO9O/fX1q2bGlmO8H3d7/7\nnTRu3FjOPffc4NVDPtMCDuFgAgEEEEAg0wWya2RLs2bN5MQTT4xa1YYNG0pJSUlgeWlpqdkmMOPf\nH/Q67/z580NmT5kyRT755BPR1nCsRCesWDosQwABBBDwpUBOTo6sW7dOLMsSPf187NixwOlnB2TX\nrl3mY3BLWoPv7t275fnnny+3vrOd804AdiR4RwABBBBA4N8CLVq0kDFjxsiQIUNMR6rp06ebJdoZ\n65VXXjGfN27cKLm5uQGzHTt2yNSpU2XNmjVy1llnmWvI2okrWuIUdDQZ5iOAAAII+Fpg4sSJMn78\neMnKyhLtdKVp1qxZAZO8vDzRl5O05/ORI0ecybjvBOC4RKyAAAIIIOBXAafXc1XUn1PQVaFKnggg\ngAACCMQRIADHAWIxAggggAACVSFAAK4KVfJEAAEEEEAgjgABOA4QixFAAAEEEKgKAQJwVaiSJwII\nIIAAAnEECMBxgFiMAAIIIIBAVQgQgKtClTwRQAABBBCII0AAjgPEYgQQQAABBKpCgABcFarkiQAC\nCCCAQBwBAnAcIBYjgAACCCBQFQIE4KpQJU8EEEAAAQTiCBCA4wCxGAEEEEAAgaoQIABXhSp5IoAA\nAgggEEeAABwHiMUIIIAAAghUhQABuCpUyRMBBBBAAIE4AgTgOEAsRgABBBBAoCoECMBVoUqeCCCA\nAAIIxBEgAMcBYjECCCCAAAJVIZD0ALx161a57LLLqqIu5IkAAgggkOkCZSLWN5V8HU4NpKQG4EWL\nFsnw4cPl888/T43aUwoEEEAAAQQ8EkhqAC4pKZGCggKPqspuEUAAAQQQSB2BrGQWRVu/R48ejbnL\n4uJi00oOX+nLL7+UsWPHhs9mGgEEEEAgxQRWrlwpeXl55Up1++23yxVXXFFuvl9nJDUAVwS5WbNm\nsmLFinKrPvbYY9KyZcty85mBAAIIIJBaAn369JH58+enVqFSsDRJPQWdgvWnSAgggAACCHgiQAD2\nhJ2dIoAAAgj4XSDpATgrK0vWr1/vd3fqjwACCCDgc4GkB2Cfe1N9BBBAAAEEjAABmC8CAggggAAC\nHggQgD1AZ5cIIIAAAggQgPkOIIAAAggg4IEAAdgDdHaJAAIIIIAAAZjvAAIIIIAAAh4IEIA9QGeX\nCCCAAAIIEID5DiCAAAIIIOCBAAHYA3R2iQACCCCAAAGY7wACCCCAAAIeCBCAPUBnlwgggAACCBCA\n+Q4ggAACCCDggQAB2AN0dokAAggggAABmO8AAggggAACHggQgD1AZ5cIIIAAAggQgPkOIIAAAggg\n4IFAlgf7ZJcIIIAAAggcn8Bhe7Ovj2/TwFaHAp88/UAL2FN+do4AAggg4FcBArBfjzz1RgABBBDw\nVIAA7Ck/O0cAAQQQ8KsAAdivR556I4AAAgh4KkAA9pSfnSOAAAII+FWAAOzXI0+9EUAAAQQ8FSAA\ne8rPzhFAAAEE/CpAAPbrkafeCCCAAAKeChCAPeVn5wgggAACfhUgAPv1yFNvBBBAAAFPBQjAnvKz\ncwQQQACBVBVYvHixDB48WPr16yebNm0KKWZhYaH06NEj5LV9+3azTllZmQwYMED27NkTsk34BM+C\nDhdhGgEEEEDA9wL79++X/Px8WbJkiWzbtk0mTJggq1atCrj07NlTVq5caaaXL18uM2bMkDZt2siW\nLVvkhhtukPXr18uxY8cC60f6QACOpMI8BBBAAIGMFTj8/WHZuXOnZGdnB+rYpEkTqVOnTmBaW7zd\nu3eXRo0amdfevXtFW7bONtWrV5datWrJgQMHTKAuKCgw22q+Tz75pNx4442BvKJ9IABHk2E+Aggg\ngEBGCvxz3xaZPn261KtXL1C/m2++WXr16hWYLioqEg3KTtJAXFxcLK1atXJmmfc5c+ZI//79pWXL\nlma6d+/eIctjTRCAY+mwDAEEEEAg4wRyGufKb/5wr3To0CFq3Ro2bCglJSWB5aWlpdKsWbPAtPNh\n9uzZMn/+fGcyoXc6YSXExcoIIIAAAn4QyMnJkXXr1ollWaKnn/V6rnP62an/rl27zMd27do5sxJ6\nz5gWcI0/JVRvVva5wA8nnnwOEV79HuEzmEbAnwItWrSQMWPGyJAhQ2T37t3mlLVKaGesQYMGydCh\nQ2Xjxo2Sm5t73EAZE4CPW4ANEUAAAQQQiCAwceJEGT9+vGRlZYl2utI0a9aswJp5eXmir0hpzZo1\nkWaHzCMAh3AwgQACCCCAwA8C4aedf1hS+U9cA668ITkggAACCCCQsAABOGEyNkAAAQQQQKDyAgTg\nyhuSAwIIIIAAAgkLpM014GrVqpmL3/qUkVROW7duDTw5JZXLmeyybd68Wdq2bRvypJlklyEV9/fR\nRx+ZXpROB49ULKMXZdLbP7p16+bFrlN6n+ngcuTIEXGeiVwVmO8WvyszNz5WqazX7Fod6FRVqYwq\nuXHaBGDt+q3dwlM96bNC69evH3gqSqqXN1nle/XVV6VLly64hIE/88wz0qdPH/NIu7BFvp5cu3at\nDBw40NcGkSqfLi7PP/98pOK7Mu/VVa/I559/Xqm85raeI8d7726ldhy2cTX7JmMrbB6TlRC47777\n5MILLzR/VCuRTcZtqs9Fvfvuu6VTp04ZV7fKVEhHWnnppZc4MxCGqLd2rFixImwuk7hk1neAa8CZ\ndTypDQIIIIBAmggQgNPkQFFMBBBAAIHMEiAAZ9bxpDYIIIAAAmkiQAB2+UBpb1btsU0KFcAl1MOZ\nqlGjBt8XByPoXV1I5QVwKW+SznPohJXOR4+yI4AAAgikrQAt4LQ9dBQcAQQQQCCdBQjA6Xz0KDsC\nCCCAQNoKEIDT9tBRcAQQQACBdBYgAKfz0aPsCCCAAAJpK0AATttDR8ERQAABBNJZgADs4tH74x//\nKH379pXRo0fL/v37Xcw5dbPSwScuu+yyhAq4ePFi0Ucw9uvXTzZt2hSy7bRp00Sfj5zOSZ9TO2zY\nMNHHBr788svlqhJpeVlZmdx0001ywQUXiD7ONDgdj3Hw9qn4Od7/lWjL1WnAgAGyZ8+eVKyWa2WK\n9X0I3sk999wjBQUFwbP4nE4C+ixoUuUF3nzzTWv48OGWPRKINWPGDMv+j1H5TFM8h7/97W/WWWed\nZeXm5pYrqf0HpNw8nbFv3z7r7LPPtuw/oJY9sovVu3fvwHpqePLJJ1sPP/xwYF46frAHEbA++OAD\nq7i42Orevbupa3A9Ii1/4IEHrD/84Q+Wuo0cOdKyf6SYTWIZB+eZTp/j/V+JtvzTTz+17B8oVuPG\njY1tOtU50bJG+z44+dg/8K1rrrnGOumkk6wXX3zRmc17mgnQAnbp19KaNWtk6NChkpWVZVrAy5cv\ndynn1M2mpKSk3K/vzz77TK6++mqxg4hcf/315c4EaIvXDkpmyMYzzjhD9u7dK/prX/O6//775c47\n70zdClewZF999ZWpY9OmTaVXr17yzjvvhGwZafnq1avlyiuvlJo1a8qIESPE+f5EMg7JLA0n4v1f\nibZchyJ98skn5bTTTkvDWidW5GjfByeXb7/91vydGTdunDOL9zQUIAC7dNCKioqkSZMmJrdGjRrJ\nN99841LOqZuN3eIXDTLB6YknnhAdOlJH+NHg89prrwUvlmAnXaBWdktRJk2aZE69nnDCCSHrp9uE\nnhqtXbt2oNh2a83Uz5kRbXmwS/A2kYydvNL1Pbiukf6vRFtuny2Rrl27pmu1Eyp3sEHw98HJRMfW\nZrhGRyN93wnALh27hg0bmlacZnfw4EFp3ry5SzmnVzZLly6Vhx56yFwX1jGAd+zYIRMnTpRTTjnF\nXN8MdtKalZaWyvr168U+ZSvvvfeeafkVFhaWuzacLgo6FrQefycdOHBATjzxRGfSjBUdaXmwS/g2\ngY0z5ENwXSP9X4m3PEMYYlYj2CDTvw8xITJ8IQHYpQOsp1Xffvttk5sOmv2jH/3IpZzTKxttpfzs\nZz+TBQsWyC9+8QvR08zaKt68ebOsWrVKcnJyxL72K/alGnP6+dixY9K5c2fTAtZf+nXr1jVj42Zn\nZ6dXxf9dWr0EUadOHXMGROv4/vvvh7Taoi330/cnXl3jLU/LL0aChcYgQbA0XT0rTcudcsW+9NJL\nZcmSJaLveq0q/NRryhW4igp06623Sn5+vjz11FOi16nmzp0bsqcWLVrImDFjZMiQIbJ7926ZPn26\ndOzY0bx0Rf21rz3IdV66pgcffNDU8dChQ6a3t92xTObMmWNa+XZHK4m0XH+s3HHHHTJz5kzzI2Tq\n1KnpWv245Y72f0UvXQwaNMj8H/L7/6VI34dt27aZ3vV6poiUGQIMxuDycdRTqtoC8nuK56Adr7Q1\nqKMkZWrSABx8PTi8npGWx3MLzyOdp+PVNd7ydK57RcuOQUWl0nM9AnB6HjdKjQACCCCQ5gKZ2/xI\n8wND8RFAAAEEMluAAJzZx5faIYAAAgikqAABOEUPDMVCAAEEEMhsAQJwZh9faocAAgggkKICBOAU\nPTAUCwEEEEAgswUIwJl9fKkdAggggECKChCAU/TAUCwEEEAAgcwWIABn9vGldggggAACKSpAAE7R\nA0OxEEAAAQQyW4AAnNnHl9oFCfTv318ee+yxwJzPP/9cqlWrJr/61a8C83QYSX1Epg4bGC3pAAs6\nulO81L59ezPSU6T1fvOb35hxkMOX6Xi3uv8GDRqYV7NmzeSKK66QjRs3hq/KNAIIpLkAATjNDyDF\nr7jAhRdeKG+++WZgg8WLF8vQoUNl0aJFgXk6GHy3bt1ER2aKlk4//XRZsWJFtMVx53///fdy//33\ni44EFSn17dtX9u3bZ176AP4zzzzTDFKgg1eQEEAgcwQIwJlzLKlJHIFIAViHTvzqq6/MyEy6+erV\nq+XHP/6xyenrr782rU8dNF6HVdThFDVt2bJFrr/+evNZhxz8+c9/Lq1atZJzzjnHjAT1u9/9zizT\nf+bPny8dOnQQHUD9mWeeMfNHjhxp3jXP4uJi8znaPyeccIJpoesPgj//+c9mtWjl0oV79+6VESNG\nmDGIdcQpHfpR04YNG0Trr+PMtmvXTnRUJk2TJk2S//mf/zGf9R/9YXHttdcGpvmAAAJVJ0AArjpb\nck4xgbPPPtuM07tjxw45evSovPXWW/Kf//mf0qdPH/n73/9uShscgMeNG2cC1qZNm+SnP/1pIOjq\nKEZffPGFWV9PaWtgfuONN+SXv/ylCWwaIJ2k+elyHXbxpptuEt326aefNotXrlwpTZs2dVaN+a7j\nw3766admnWjl0oVjx441o3F99NFHptWsw0Nquvrqq83QiFp3Db463J0OF6n1/9///V+zjv4zb948\nOeusswLTfEAAgSoUsH/BkxDwjYA93qxlt0qtwsJCq1+/fqbes2bNsuxWn1VSUmLZLU7LHpPYsq8F\nW/ZQiZbdcrTsVqV59erVy/rHP/5h2eOxWl26dDHb9u7d27IDasBv4MCB1l133WWm7Zam9de//jWw\nzL6ea9nXci07+Fv2f2nLHmousMz58MQTT1gXXXSRMxl4v+eeeyy75RyzXIcPH7bs68dmH7qhfYrb\nsk+vm/29++675v3IkSOWfQ3bqlevnmX/sDB1rV+/vmUHZrP8xBNPtL788svAfvmAAAJVJ5BVhbGd\nrBFIOQHnNLQddMwpWS1gXl6e/PGPf5S3335btJVct25d+ec//2k6aOn12OCk15D1VLOTtCOXtk6d\npMvsQOhMmlPTzoSe/tXxXY8nbd++XVq3bi1FRUVRy1WrVi3T+j311FPNLrSD2YABA8xnbZXbPxZE\nW/N6jVuvQ+s1aK3rxRdfLK+++qp07txZdFs9nU5CAIGqFyAAV70xe0ghAQ22d955pwli//3f/21K\npoHHbv2a08jO9V8NRBow169fL9oTWZMGMWeemWH/c+6555rrrM5pW7uFbIKYs9xuRTsfj/tdg/bS\npUtl5syZJm+nDOHl+u6772T//v3mmvZJJ51k9jd79mxzTXvYsGEyZ84cE2w1UGvgtX/Xm3X0mvTj\njz9uAvBVV1113OVkQwQQSEyg8n8dEtsfayPgqYD2KN66dats3rzZtHadwlxwwQXmWqgTgLOzs03g\n0qCnLcWdO3fKaaedZlqQzjb6PnjwYLOdtlD1mq52YoqXatSoIRoEtcNUpGSfJjbXZzXgf/DBB+a6\nrnYEu/TSSyVWuezTx/KjH/3IBFoNrnr9+fe//31gF/Ypd6ldu7bpzKXXonU/muzT5qI/HLQ3+PDh\nwwPr8wEBBKpWgBZw1fqSe4oJaPDTIKWnYPV+WyfpqekFCxaYFq0zTztVaYtQW5G6nbacdVu9D9hJ\n2rlp7dq15lYh7el8/vnnmyDpLI/2rvvTU8raSzknJydkNQ3i2jlLTyFrK1c7iWlw1DJoilYuXaY9\nra+88kqxryWLnmbXAKy9nrVzlva61nz1h0SPHj1Mpy6dpz8G7Gvj5vS2BnESAggkR6CaXl5Ozq7Y\nCwLpKaAtUQ2EGhDD07Jly6Rjx47mViNdpi1IvW58yy23hK9abtru7CV6m9Hxpljl0tubnFPUTv66\nP62Dnn4OT3rrkT6oRH9QkBBAIDkCBODkOLOXDBV4/fXXzb2/N954o3z22Wdi93oWfZhHurQktQWu\n9wEvWbJE9NYlbQ2TEEAgOQJcA06OM3vJUIFLLrnEXHPV+4q1Q5aejk6X4KuHRE9J66lzvQ+a4Juh\nX1KqlbICtIBT9tBQMAQQQACBTBagBZzJR5e6ZayA3mv8r3/9K2PrF1wxHSBDn9pFQiDTBAjAmXZE\nqY98/PHHprOR3nITa1SjdKayn4wlt912m6mCPk5SO1c5L+393LNnT/nwww8rXUW9VUlvxapIXvpM\n7cmTJ1d6n+EZ6HX18847zzw+NHwZ0wikswABOJ2PHmWPKPDss8+aW3a0lajPNs60pE+zmjFjhowf\nPz5QtTp16shLL70kL774ojz00ENm+MJRo0YFlh/vB7XUQK8P+YiXrrvuupCBHeKtX9Hl2rNc78N+\n6qmnKroJ6yGQHgJ6GxIJgUwR0Ocst2zZ0rKHGbQ6depk2Q/eCKma3SK27FttrCZNmphldiALLH/n\nnXcsuzVp2U+asuzHM1r2YyfNMnsQBMt+MpZlBwAzbfd2NtP206Msu+ew+Tx16lSzXztYmXX0+dD2\nYykte1xfk6f9mMvAfh555BHLHiHJsh/5aNm9p81zpu1AZ/Kx7wE26+lzou1hD63bb789sJ3z4e67\n77aaN29u6XOdNdmdvyx9nnNwsu9Xtrp27RqYZZ+utuxxhU29df7//d//BZbZ90RbdsvVeKndT37y\nE/OcanvACVMn+y+Z1aZNG8sO8Jb9KExrwoQJpuz2/cuWPqNakz7D2r69ybLvVTb10Odp27djWRMn\nTrT0edl6LHReNBd7gAiznZZLbfRlPx4zUEZ1su+bDkzzAYFMENDH0ZEQyBgBHfxAA4Y9dJ+Vn59v\nPtu32gTqN3r0aBMk7AdTmMEY7NO2lj0qkgmCdo9gy+7BbNnDC1p2z2DLfkSlpQMc2I+jNPk88MAD\nJh8dUEH38V//9V+WBm39XLNmTct+ipZln6617KdsmWn7KVnWlClTzAAP9pO2zLYaVHR9DZoaXHXA\nB/sBH5YGO52vwU+TU4/nnnvOTAf/Y/e8NkHNmad56SAMGmAvv/xyy37Ws9n/yy+/bFbRwKfB0n6K\nlvnxoYNE6L50oAZN9shIZlrLqANU6DJ7xCXLbnVa9oNFzLQOYmE/WcuyR4UywVcHsLj55pst9bPH\nVbbs27HMfLsntdnWftKWpfvR+tnPyrbsVmxMF+dY6Q8AewQnS4+F/hByfmQ8+uijphz6A4qEQKYI\nEIAz5UhSDyNgPwXKsq/9WvYzkU3rVIPJHXfcYZZpMNWA4ARD/WOuf9h1VCD7VLX5A28PL2jWtV24\nXOwAAAXUSURBVO/ltexnJ1v79u2rUADW/TpJRyHSIKzbasv3lFNOMQFdl2vLXMukwU2TPRSgZd8C\nZD7b121N0NIJ+0EeJmDap37NsuB/tDWpIyM5SQOwBkL98WA/fMNspwH5t7/9rVnFCebaStekox1p\nGeyBGixt/Wor3X4illmm/2jQ1fx03xpodV17uEWzXM8e6IhR2mJ2frg4G+ooTho4naQBWFvmOsqU\nplguTgDWMwGa7HuTzX7toRzNtH1q3UzrPkkIZIoA14Dtvy6kzBDQ65SvvfaauZ9Vr39qRyV9fOPc\nuXOlrKzMPGpRn+tsn9o1FdbnK9stTrEDZKBHcW5urlmmj5TUp0JphyYn6baa9DGW4UkfUekkXW4H\nLrEDpXmetF6/1P1r0p7Lep9wixYtzLQ+IlKfQKVJB0XYtm2beSBGQUGBma8DLwQnLYPdWg5s7yyz\nhxeUXbt2mQEj9IlXl112mXlAyCeffGLy0/X0edeadLQjfXqXjvik+7N/KJiRksxC+x8dNcn+Ayc6\n0lN40k5Wer1ZB7LQx1nqc6TtMwLhqwWmdT/O075iuTgb6LO6NemoVJr0edaa7JaxedfykhDIFAEC\ncKYcSeohL7zwghnwXoOuPf6teWlg0ttYNDDb102NkhMwtJOW3So0wxCGL7PH/BW7dWyCmvPMaF1f\nkwas8KRByUn67OiHH37Y9AjWR0LqEIXOqEi6n927d5sy6fr2KWaxr3uaTfUZzrretGnTTGAcMWKE\nk2XgXZfrIyYPHjwYmBf+QcvrDJGoPcJ1tCdN+lmTll9/CGgg1udR6wM4nGW6XEeA0qTL7Zaw+ez8\n+NAfK/osbH1utn2a2jx4RIdy1KTrauAOThV1cbZx9r1lyxYzS4dO1OQMHOEEYjOTfxBIc4Efnkaf\n5hWh+Ahoj139g6+tJA28mrSVpwFIg6L2ptWWrY7p++CDD4qOYGSfcjbj4+rzm3WkIbuDlMlDb73Z\nao+apEFGW8EaXLRVqiMKaYAMT85ACTrfCY52Ry/TgtOnY9nXiM0m2mLUgRX0WdE6Vq+2wLVcY8aM\nMa08HS5Rf0hoWXT0o0hJg6AG8eCkPw50kAYNlDrKkvb+1jz0FiUNsPZpZpk+fbo5I6D10Cd3aQtf\ny6UjQNnXcU2LWbfRoQ91nrbS9VYuTfqkLB3i8KabbjKDOGgAvuaaa8zZBWfoQ11Xh0PUYQ/1x4Qm\n54eHfo7loss1qa0GcQ3qmp96aNJbnDRpi5qEQMYIZMq5dOrhbwG95mr/pzQdkcIl7FOlpuOV9uDd\nsGGDpT2EdV3tCa29dJ2k12P1eqgu017Pzz//vLPIdFTSHr56ffm+++4z6wR3wrIDRmBdOzha9vjA\nZh3tzDVkyBBzTVWvvep1aDtwmWvR2nFLewprBywnOddctRd2tKRl1uurTtJrwFpmfem1WzuImh7Q\n2hHNSYWFhaZTma6jHaXuuusuc/1Xl9sB27J/GJiOW7q9PVKTpb2mNWmP78aNG5u87Va9ua6u16r1\nGrP9I8d0+rJPfZt1n3zySbOeOmmdtIz2/btmmf4Ty8W5BmwPCmFsNH/7NHdgW/vHhen5rdesSQhk\nigCdsDLlSFKPhATsU8OW3rIUnvQPvD3KUPhsM62dqjSAVjTZp75Nx6NI69utQdNJK3yZ9rTWIKmd\nwqIle4xgs459jTbaKlHna72dnsXhK2mZNBiHJ61zuIl2cotkYT+xytJ8YqVILk4A1sCtzuF56I8M\n/cFDQiCTBHgWtP3XjoSA1wJ6OlxPb9v3HJtT5tp5yjltHalsdqvaDP7w61//OtLitJv3q1/9Suxe\n26aDWfv27UPKr9fs9VS6XlqwW+Mhy5hAIJ0FuAaczkePsmeMgF5v1TF5daxe+17lmMFXK629kJcv\nX54x9dfr4Hpt2+kMF1wx7d2tT8Ei+Aar8DkTBGgBZ8JRpA4IIIAAAmknwG1IaXfIKDACCCCAQCYI\nEIAz4ShSBwQQQACBtBP4f9cZ82ZURzaoAAAAAElFTkSuQmCC\n"
}
],
"prompt_number": 147
},
{
"cell_type": "heading",
"level": 1,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Questions"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Lab\n",
"========================================================\n",
"http://caret.r-forge.r-project.org/modelList.html"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"library(caret)\n",
"data(iris)\n",
"\n",
"irisTrain <- createDataPartition(y = iris$Species, p = 3/4, list = FALSE)\n",
"\n",
"trainX <- iris[irisTrain,1:4]\n",
"testX <- iris[-irisTrain,1:4]\n",
"\n",
"trainY <- iris$Species[irisTrain]\n",
"print(length(trainY))\n",
"testY <- iris$Species[-irisTrain]\n",
"print(length(testY))"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"[1] 114\n",
"[1] 36\n"
]
}
],
"prompt_number": 123
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"irisKN <- train(x = trainX, y = trainY, method='knn')\n",
"irisNB <- train(x = trainX, y = trainY, method='nb')\n",
"irisNN <- train(x = trainX, y = trainY, method='nnet', trace=FALSE)"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [],
"prompt_number": 135
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"irisProbValues <- extractProb(list(irisKN, irisNB, irisNN),\n",
" testX = testX,\n",
" testY = testY)\n",
"irisTestProbs <- subset(irisProbValues, dataType == \"Test\")\n",
"str(irisTestProbs)"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"'data.frame':\t108 obs. of 8 variables:\n",
" $ setosa : num 1 1 1 1 1 1 1 1 1 1 ...\n",
" $ versicolor: num 0 0 0 0 0 0 0 0 0 0 ...\n",
" $ virginica : num 0 0 0 0 0 0 0 0 0 0 ...\n",
" $ obs : Factor w/ 3 levels \"setosa\",\"versicolor\",..: 1 1 1 1 1 1 1 1 1 1 ...\n",
" $ pred : Factor w/ 3 levels \"setosa\",\"versicolor\",..: 1 1 1 1 1 1 1 1 1 1 ...\n",
" $ model : chr \"knn\" \"knn\" \"knn\" \"knn\" ...\n",
" $ dataType : chr \"Test\" \"Test\" \"Test\" \"Test\" ...\n",
" $ object : chr \"Object1\" \"Object1\" \"Object1\" \"Object1\" ...\n"
]
}
],
"prompt_number": 136
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"irisKNNPred <- subset(irisTestProbs, model == \"knn\")\n",
"confusionMatrix(irisKNNPred$pred, irisKNNPred$obs)"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"Confusion Matrix and Statistics\n",
"\n",
" Reference\n",
"Prediction setosa versicolor virginica\n",
" setosa 12 0 0\n",
" versicolor 0 9 0\n",
" virginica 0 3 12\n",
"\n",
"Overall Statistics\n",
" \n",
" Accuracy : 0.9167 \n",
" 95% CI : (0.7753, 0.9825)\n",
" No Information Rate : 0.3333 \n",
" P-Value [Acc > NIR] : 3.978e-13 \n",
" \n",
" Kappa : 0.875 \n",
" Mcnemar's Test P-Value : NA \n",
"\n",
"Statistics by Class:\n",
"\n",
" Class: setosa Class: versicolor Class: virginica\n",
"Sensitivity 1.0000 0.7500 1.0000\n",
"Specificity 1.0000 1.0000 0.8750\n",
"Pos Pred Value 1.0000 1.0000 0.8000\n",
"Neg Pred Value 1.0000 0.8889 1.0000\n",
"Prevalence 0.3333 0.3333 0.3333\n",
"Detection Rate 0.3333 0.2500 0.3333\n",
"Detection Prevalence 0.3333 0.2500 0.4167\n",
"Balanced Accuracy 1.0000 0.8750 0.9375\n"
]
}
],
"prompt_number": 140
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"irisNaiveBayesPred <- subset(irisTestProbs, model == \"nb\")\n",
"confusionMatrix(irisNaiveBayesPred$pred, irisNaiveBayesPred$obs)"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"Confusion Matrix and Statistics\n",
"\n",
" Reference\n",
"Prediction setosa versicolor virginica\n",
" setosa 12 0 0\n",
" versicolor 0 9 0\n",
" virginica 0 3 12\n",
"\n",
"Overall Statistics\n",
" \n",
" Accuracy : 0.9167 \n",
" 95% CI : (0.7753, 0.9825)\n",
" No Information Rate : 0.3333 \n",
" P-Value [Acc > NIR] : 3.978e-13 \n",
" \n",
" Kappa : 0.875 \n",
" Mcnemar's Test P-Value : NA \n",
"\n",
"Statistics by Class:\n",
"\n",
" Class: setosa Class: versicolor Class: virginica\n",
"Sensitivity 1.0000 0.7500 1.0000\n",
"Specificity 1.0000 1.0000 0.8750\n",
"Pos Pred Value 1.0000 1.0000 0.8000\n",
"Neg Pred Value 1.0000 0.8889 1.0000\n",
"Prevalence 0.3333 0.3333 0.3333\n",
"Detection Rate 0.3333 0.2500 0.3333\n",
"Detection Prevalence 0.3333 0.2500 0.4167\n",
"Balanced Accuracy 1.0000 0.8750 0.9375\n"
]
}
],
"prompt_number": 141
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%R\n",
"irisNNetPred <- subset(irisTestProbs, model == \"nnet\")\n",
"confusionMatrix(irisNNetPred$pred, irisNNetPred$obs)"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"text": [
"Confusion Matrix and Statistics\n",
"\n",
" Reference\n",
"Prediction setosa versicolor virginica\n",
" setosa 12 0 0\n",
" versicolor 0 10 0\n",
" virginica 0 2 12\n",
"\n",
"Overall Statistics\n",
" \n",
" Accuracy : 0.9444 \n",
" 95% CI : (0.8134, 0.9932)\n",
" No Information Rate : 0.3333 \n",
" P-Value [Acc > NIR] : 1.728e-14 \n",
" \n",
" Kappa : 0.9167 \n",
" Mcnemar's Test P-Value : NA \n",
"\n",
"Statistics by Class:\n",
"\n",
" Class: setosa Class: versicolor Class: virginica\n",
"Sensitivity 1.0000 0.8333 1.0000\n",
"Specificity 1.0000 1.0000 0.9167\n",
"Pos Pred Value 1.0000 1.0000 0.8571\n",
"Neg Pred Value 1.0000 0.9231 1.0000\n",
"Prevalence 0.3333 0.3333 0.3333\n",
"Detection Rate 0.3333 0.2778 0.3333\n",
"Detection Prevalence 0.3333 0.2778 0.3889\n",
"Balanced Accuracy 1.0000 0.9167 0.9583\n"
]
}
],
"prompt_number": 138
},
{
"cell_type": "heading",
"level": 1,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Discussion"
]
}
],
"metadata": {}
}
]
} | artistic-2.0 |
jguhlin/nn-replicon-identification | iristest.ipynb | 1 | 7014 | {
"cells": [
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from __future__ import absolute_import\n",
"from __future__ import division\n",
"from __future__ import print_function\n",
"\n",
"import os\n",
"import urllib\n",
"\n",
"from urllib.request import urlopen\n",
"import numpy as np\n",
"import tensorflow as tf"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Data sets\n",
"IRIS_TRAINING = \"iris_training.csv\"\n",
"IRIS_TRAINING_URL = \"http://download.tensorflow.org/data/iris_training.csv\"\n",
"\n",
"IRIS_TEST = \"iris_test.csv\"\n",
"IRIS_TEST_URL = \"http://download.tensorflow.org/data/iris_test.csv\""
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false,
"scrolled": true
},
"outputs": [
{
"ename": "TypeError",
"evalue": "load_csv_with_header() missing 1 required positional argument: 'features_dtype'",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mTypeError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m<ipython-input-9-78348fe7069a>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[1;32m 23\u001b[0m \u001b[1;33m\u001b[0m\u001b[0m\n\u001b[1;32m 24\u001b[0m training_set = tf.contrib.learn.datasets.base.load_csv_with_header(filename=IRIS_TRAINING,\n\u001b[0;32m---> 25\u001b[0;31m target_dtype=np.int)\n\u001b[0m\u001b[1;32m 26\u001b[0m test_set = tf.contrib.learn.datasets.base.load_csv_with_header(filename=IRIS_TEST,\n\u001b[1;32m 27\u001b[0m target_dtype=np.int)\n",
"\u001b[0;31mTypeError\u001b[0m: load_csv_with_header() missing 1 required positional argument: 'features_dtype'"
]
}
],
"source": [
"test_input_fn = ''\n",
"\n",
"# If the training and test sets aren't stored locally, download them. \n",
"if not os.path.exists(IRIS_TRAINING):\n",
" raw = urlopen(IRIS_TRAINING_URL).read()\n",
" with open(IRIS_TRAINING, \"wb\") as f:\n",
" f.write(raw)\n",
"\n",
"if not os.path.exists(IRIS_TEST):\n",
" raw = urlopen(IRIS_TEST_URL).read()\n",
" with open(IRIS_TEST, \"wb\") as f:\n",
" f.write(raw)\n",
"\n",
"# Load datasets.\n",
"# training_set = tf.contrib.learn.datasets.base.load_csv_with_header(\n",
"# filename=IRIS_TRAINING,\n",
"# target_dtype=np.int,\n",
"# features_dtype=np.float32)\n",
"#test_set = tf.contrib.learn.datasets.base.load_csv_with_header(\n",
"# filename=IRIS_TEST,\n",
"# target_dtype=np.int,\n",
"# features_dtype=np.float32)\n",
"\n",
"training_set = tf.contrib.learn.datasets.base.load_csv_with_header(filename=IRIS_TRAINING,\n",
" target_dtype=np.int)\n",
"test_set = tf.contrib.learn.datasets.base.load_csv_with_header(filename=IRIS_TEST,\n",
" target_dtype=np.int)\n",
"\n",
"# Specify that all features have real-value data\n",
"feature_columns = [tf.feature_column.numeric_column(\"x\", shape=[4])]\n",
"\n",
"# Build 3 layer DNN with 10, 20, 10 units respectively.\n",
"classifier = tf.estimator.DNNClassifier(feature_columns=feature_columns,\n",
" hidden_units=[10, 20, 10],\n",
" n_classes=3,\n",
" model_dir=\"/tmp/iris_model\")\n",
"# Define the training inputs\n",
"train_input_fn = tf.estimator.inputs.numpy_input_fn(\n",
" x={\"x\": np.array(training_set.data)},\n",
" y=np.array(training_set.target),\n",
" num_epochs=None,\n",
" shuffle=True)\n",
"\n",
"# Train model.\n",
"classifier.train(input_fn=train_input_fn, steps=2000)\n",
"\n",
"# Define the test inputs\n",
"test_input_fn = tf.estimator.inputs.numpy_input_fn(\n",
" x={\"x\": np.array(test_set.data)},\n",
" y=np.array(test_set.target),\n",
" num_epochs=1,\n",
" shuffle=False)\n",
"\n",
"# Evaluate accuracy.\n",
"accuracy_score = classifier.evaluate(input_fn=test_input_fn)[\"accuracy\"]\n",
"\n",
"print(\"\\nTest Accuracy: {0:f}\\n\".format(accuracy_score))\n",
"\n",
"# Classify two new flower samples.\n",
"new_samples = np.array(\n",
" [[6.4, 3.2, 4.5, 1.5],\n",
" [5.8, 3.1, 5.0, 1.7]], dtype=np.float32)\n",
"predict_input_fn = tf.estimator.inputs.numpy_input_fn(\n",
" x={\"x\": new_samples},\n",
" num_epochs=1,\n",
" shuffle=False)\n",
"\n",
"predictions = list(classifier.predict(input_fn=predict_input_fn))\n",
"predicted_classes = [p[\"classes\"] for p in predictions]\n",
"\n",
"print(\n",
" \"New Samples, Class Predictions: {}\\n\"\n",
" .format(predicted_classes))"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"test_set = np.random.rand(5,50)\n",
"test_target = [0,1,2,1,2]\n",
"\n",
"test_input_fn = tf.estimator.inputs.numpy_input_fn(\n",
" x={\"x\": np.array(test_set)},\n",
" y=np.array(test_target),\n",
" num_epochs=1,\n",
" shuffle=False)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"sess = tf.Session()\n",
"with sess.as_default():\n",
" test_input_fn()[0]['x'].eval()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Will have to change this to tf.data instead of tf.contrib.data in the next day or two..."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.0"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| epl-1.0 |
sophie63/FlyLFM | Notebooks/Utils/.ipynb_checkpoints/100106_for_turning_components-checkpoint.ipynb | 1 | 248238 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import matplotlib\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"from scipy import stats\n",
"from scipy import io\n",
"import scipy.io as sio\n",
"%matplotlib inline \n",
"import pylab\n",
"import csv\n",
"from Tkinter import Tk\n",
"from tkFileDialog import askopenfilename\n",
"from tkFileDialog import askdirectory\n",
"import nibabel as nb\n",
"from scipy import io\n",
"import nibabel as nb\n",
"from scipy.interpolate import interp1d\n",
"from scipy import ndimage"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from sklearn import linear_model"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Open data"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"/media/test5/FreeBehaviorPanNeuronalGCaMP6/100106/100106Final/100106ss2on500cregcdFF20sMpsfkfint169Smith0_4_60TS.mat\n"
]
}
],
"source": [
"# from http://stackoverflow.com/questions/3579568/choosing-a-file-in-python-with-simple-dialog\n",
"Tk().withdraw() # we don't want a full GUI, so keep the root window from appearing\n",
"filename = askopenfilename() # show an \"Open\" dialog box and return the path to the selected file\n",
"print(filename)"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"(10608, 169)"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Ua=sio.loadmat(filename)\n",
"DT=Ua['TSo']\n",
"DT.shape"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"/media/test5/FreeBehaviorPanNeuronalGCaMP6/100106/100106Final/100106ss2on500cregcdFF20sMpsfkfint169Smith0_4_60IC.nii\n"
]
}
],
"source": [
"# from http://stackoverflow.com/questions/3579568/choosing-a-file-in-python-with-simple-dialog\n",
"Tk().withdraw() # we don't want a full GUI, so keep the root window from appearing\n",
"filename2 = askopenfilename() # show an \"Open\" dialog box and return the path to the selected file\n",
"print(filename2)"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"(189, 125, 10, 169)"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"img1 = nb.load(filename2)\n",
"data = img1.get_data()\n",
"S=data.shape\n",
"S"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Z-score"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"Demean=np.zeros(S)\n",
"Dmaps=np.zeros(S)\n",
"Dvar=np.zeros(S)\n",
"Var=np.zeros(S[3])\n",
"D2=np.zeros([S[0],S[1],5,S[3]])\n",
"Tvar=np.zeros(S[3])"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"for i in range(S[3]):\n",
" Demean[:,:,:,i]=data[:,:,:,i]-np.mean(np.mean(np.mean(data[:,:,:,i],0),0),0)"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"for i in range(S[3]):\n",
" Dsq=np.reshape(Demean[:,:,:,i],S[0]*S[1]*S[2])\n",
" Var[i]=np.sqrt(np.var(Dsq))\n",
" Dvar=Demean[:,:,:,i]/Var[i]\n",
" Dmaps[:,:,:,i]=Dvar-2\n",
" Tvar[i]=np.var(DT[i,:])\n",
"Dmaps[Dmaps<0]=0"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"/media/test5/FreeBehaviorPanNeuronalGCaMP6/100106/100106Final/100106Xk.mat\n"
]
}
],
"source": [
"# from http://stackoverflow.com/questions/3579568/choosing-a-file-in-python-with-simple-dialog\n",
"Tk().withdraw() # we don't want a full GUI, so keep the root window from appearing\n",
"filename = askopenfilename() # show an \"Open\" dialog box and return the path to the selected file\n",
"print(filename)"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"Ua=sio.loadmat(filename)\n",
"Xk=Ua['Xk']"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"/media/test5/FreeBehaviorPanNeuronalGCaMP6/100106/100106Final/AVG_100106ss2on500cregcpsf.nii\n"
]
},
{
"data": {
"text/plain": [
"(189, 125, 10)"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# from http://stackoverflow.com/questions/3579568/choosing-a-file-in-python-with-simple-dialog\n",
"from Tkinter import Tk\n",
"from tkFileDialog import askopenfilename\n",
"\n",
"Tk().withdraw() # we don't want a full GUI, so keep the root window from appearing\n",
"filenamet = askopenfilename() # show an \"Open\" dialog box and return the path to the selected file\n",
"print(filenamet)\n",
"nimt=nb.load(filenamet)\n",
"Dtemp=np.squeeze(nimt.get_data())\n",
"Dtemp.shape"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Fit turns"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"application/javascript": [
"IPython.OutputArea.auto_scroll_threshold =4000;"
],
"text/plain": [
"<IPython.core.display.Javascript object>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%javascript\n",
"IPython.OutputArea.auto_scroll_threshold =4000;"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/usr/local/lib/python2.7/dist-packages/numpy/lib/shape_base.py:422: VisibleDeprecationWarning: using a non-integer number instead of an integer will result in an error in the future\n",
" sub_arys.append(_nx.swapaxes(sary[st:end], axis, 0))\n"
]
}
],
"source": [
"if S[2]>5:\n",
" Nstack=5\n",
" Int100=[(i+1)*100/Nstack for i in range(Nstack)]\n",
" Percs=np.percentile(range(S[2]),Int100)\n",
" Indices=np.split(range(S[2]),Percs)\n",
" D1=np.zeros([S[0],S[1],Nstack])\n",
" Dmean=np.squeeze(data[:,:,range(Nstack),2])\n",
" for i in range(Nstack):\n",
" Vmean=np.mean(Dtemp[:,:,Indices[i]],2)\n",
" Dmean[:,:,i]=Vmean\n",
"else:\n",
" Nstack=S[2]\n",
" D1=np.zeros([S[0],S[1],S[2]])\n",
" Dmean=data[:,:,range(S[2])] \n",
" Dmean=np.squeeze(Dtemp[:,:,:])"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"for j in range(S[3]):\n",
"\n",
" a=''\n",
" if S[2]>5:\n",
" for i in range(Nstack):\n",
" V=Dmaps[:,:,Indices[i],j]\n",
" D1[:,:,i]=np.max(V,2)\n",
" D2[:,:,:,j]=D1\n",
" D1[D1==0]=np.nan"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.image.AxesImage at 0x7fc3e524d1d0>"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAL0AAAEACAYAAADm9HcvAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztfVustdtZ1jPW6T92/62N3U33bneRIuCFNlyUJjWhSq0t\nEmpMqJWoPdyQCNEQo231ovHKQgIEVMRDRdAWykHoNnKoTfGCxJY2pVZg94DY04b9gwFKaNp/zbXW\n8GLNd61nPut5xxjzsP451/7nm8x83xzf+Mbxed/xvO83vjlLrRVb2cqDJDvrbsBWtnK/ZQv6rTxw\nsgX9Vh442YJ+Kw+cbEG/lQdOtqDfygMnlwb6UsqrSikfL6V8spTy5suqZytbmVfKZcTpSyk7AD4J\n4BsB/A6ADwF4Xa314yuvbCtbmVMuy9K/BMCnaq2fqbVOAPwEgNdcUl1b2cpcclmgfwTA5+j756dp\nW9nK2mXryG7lgZO9Syr3SQAvoO+PTtPOpJSy3fSzlZVKrbWM5Lss0H8IwItKKY8B+F0ArwPwtzTT\n7u4u9vf3oc50fB9xsl2eWitOTk6ws7NzIV+WX6WU9vjVWmfyaP7su97j0gFgMplgf3+/2cZa60z6\nyDmAs7HJxn0VMjI2boxb10KOjo5mxgYA7t27N9y2SwF9rfW4lPKdAN6LUwr1jlrrE5dR16qlB/ZW\n3myi3TkDPitLr68KlA5YqsSRtqq6su/rkMuy9Ki1/iKArx7Il16LAZp38Ocd2NH8ChJNy8Dt0lrX\n41yt8SLAd2DWukbv69W96HyNtmlVcmmgHxGmH6uWABaDkydydGIywOzs7My0X0HcAntPOQBgb2/v\nQl4FItMb7Zv2l/scbZ9HoTLlyaSnaPOsAHptd3d3uB1O1gr63d3dpZfQbLIuS6FiAnZ2doateA/o\nbsL39manxgHY3dey0JEe456V17vWk8u22MvO7VpBPyrOWrnrvWvO8o/UmYF0BOjOcR21cs6Ku2tx\nzIDrnPgRwKuy6BiOyry8ftkVpScbCfplufw81CVTFAdWrkPTsjyj11kcSHsRLo3kZHmcjEaAWko0\nKi2K49IyUC+zmmwk6Fsy4lxlDucoRRi14KNgb527PnG7e6FWBaYDba8MN16ZjxDtXcQ/CpkXsKum\nSxsN+pGltEd9WuW5SWtZZ/4wp29x9hHgz2vpR4A9ehyhTQzyzMhkCjUql0mBVDYa9MB8YTqXN+On\nIWrpeiBvWXouo7UKtADP7XLHVp44z5Qiu9Yqt1eHG9dlImOt9FXJ2kG/6BLZKm8eZzejNwxyB3hO\n03JGwT4yuS3wZxw+zlu8vwV45xQ7y99qx6LzedmABzYA9JskMeABaD5mll5Dl1qOpmerg96r4GpR\nGpYW2LOy1CDE8eTkJC1HLbsqRbR9GQW4LLkSoB/V/ozC9K5xPQxmB/oWzeHyW7SH87mVh+8L4LX6\npN8zy+7OteyWpc8UKlsReu3Vft8vuRKgH5V5wJ7RGgAzwN7d3bWgDyvuHlL1uH6rjQrAFhh6PF/B\n7Sy383GcpXcfV5bWf3JyMpdfFnKZSrAxoB91hOb1AeZxlpSyBOB3d3dTi8/38f1chyqF9jOOo7tC\nMwmQ6X1cvqMbjqPXWs/awwDOwK9tjvxuN2erXw8spx/p+LKD04u4MOAzqpN9Ym+IU4qMYnC+eXkw\nl8lAdddDKVplOW4fZZ+cnFwAv6vHKQDn683f6PwugoONBP084ixnj7e7747Pq6VXTh/pcT/fp2W2\nHD+2xGp1M5DqquD4vYK91ord3d0zyhHXeA+UWy3i3rhvZ2cHx8fHzXqVIoXCaF4nl23trzzoR2UE\n7MD5DkQGsHNgszBmKEp8D6umkRzHt5kyjSgw96VFh6KMAK9bebieaKsCNtp3fHw8Q5WU15dSZl7i\naQF/HbJW0I86OIsudT1OrdEUBuvu7u7ZhwGrNEe/8z1MNbiezEK2nFz3PaMWIWyxW041Kxp/HKcP\na8+W3oFfuTwDP6NF3JbLlLVb+nkd0+z+1jUH+ozWKKDdvnl3XVeH+HDfNMLBkoFeubCeB4CiXB5P\nBp6CTVc3Lsvx8KxtmZ8Q1l5X0tZK1EpbFB9O1g76RSWz6i4tA72jJw64GQVii65pe3t7M5w/s+7u\n3PWhZR2dU8npHOtXgLLjnQFeFSU4PStaKACXo5SOfYlsHDIZZQUjcuVAP0JhXF7N1+PkCnoOQ6pi\nBHAY/Ap6oE1HsoiNA33PedQ0pXBKJ9iBZsBylCbKZF7OSsTnGdePfLoi3Q9Kw7LxoM8GpMfXs2st\nR9QBXh1Z5f1q6Usp2NvbuxDaBDzv1iiHgpetMFtT7aez6uo/6Hd2PJX+sNPrHOBSCo6OjmZA62Ly\nXDYDXtuUSaYcy1j9jXFkR7g5n/dAn+XTJ6kZl9/d3T2z1hqrZwXR+wCcgV4tffZ0Up1GTmcQZtQg\ncz41H7eD07jt4axqJEnpzvHx8cxYc55shVCF0vtZnAFblcO78ZbeSY+rcxpbWqUyLT7vYvUtRWnR\nphb1Ymuq7Vcwq9XWPA6cXL9GUAJIzlFXJ5ZBywBUpXTUxY3DKjn6vLLxoB+x5C3A87l+HGWJcw1Z\n8q8TqNLowyulO659atF7VtxZR6YrPQcUyPfSqMOtK1LP38jaHHW6eVGa0ypz1bJ20CvfddfcsQX6\nEcArSAHYODvTFLboCnwXs3ecni2mA5P77vaw6Li5fAp6Xi0cJdJy40mtApf7Ef3V9vLYx8rhLL0e\nW45tZjTmlbWDPqTX0RbQFwG+ozduv40CP8rLNqHpvVyH+6nBlnMb5y3DwOm8L4bTlQrp3hltk9IZ\nVSS+zh9VLm0DfzJLr33W9q9CNsaR1XT9noFerVRPOTLOrWHIvb29GUeW99M4669K4+pSSw9cfGqq\niuBAyaJlhYOpIA2l4zZEft17o0rigO2uqfL1VtkW8HuyjCKs3dK3OJxa7zh3ll2vLUJvNM3F27MV\nQB1fVw9TBmA2aqObwOKoFjMDfWbVdTzV0muUhsdNHVpuczycio9SITcXrXkeAe/Tjt6oZKB2eeK8\npRCcx92rsfmw9PFx4UrH49X6a5til2OIWsmRc/6uihKWnlcNVQS2+jwuXAcbAmfNs3Ds7u7u2YY0\nTmder9b+fsvGgV5B6UCv1mMeC8/lKHA1zYUuGfQxmXFfazUJesQrCzt9vYhJz+ozoDg/W3T3gokb\nY6032xKs/VSF1rnK5mPEb1mlrJ3Tt9JbFIbPW+DOrrlIi3sIpfmyp7AaqXGrAHBu6Vv0A/BgU0Dy\n955ldtZcxzvzA4DZjW/sEzi+7xRH68r61aNCq5ArYelb5/OAXst13Lw16KwIep/er/lUiRjUzK3V\nimcvhut3dgrdm01ctnsi61YSLTvKCGVg8Lsx741jlueyrf3GWfqMtvB3PtfYeUsBQtRSq5UOiQnV\niEuUl1lzt5owvWHwhDh6kwk7wEpxos3OCqvV5/HQVYUjRm4LRAbyzMC4et3867joNXc+r2yMpW9R\nmXnpDCsCpwN97q3RDAWSvgroOD8Lh0EBnDl6znpGnXFsWUOnoOwsxnm2CzKOUU/kZ8UIZXcKxu3g\nejOaks2HlstlXJZsBOh7Fp/TMsA7MKsozWgpAHBxX0mE6bh9XH+vb6EYDDYHeq13ZGzi3gA6g1+B\nqFTI9YmjNI4q8ZhyXdFu1+ZsfjIFuCzZCHrjBmAeK98aUEd/mIYotcnAn330KauWwyFQrhvAzL38\nUIkjLg4EqiQMYFW+1jup3H/H41kp9BPpDHhnzZn3a93afr2mbVmVbATo+bwFvh5Ae+DlyVFlUGfW\nrQTAuTXVrbU6iY7qZArN15hiZCFGx235fh0npTMxlsr39R6lYQxOnhOlVFF2q/88Vpr3aU1vWkv3\niCVXqz16rzqxuqPShSUzvh/WLpQgrLrrCwDbXp58BqNaycjD+Z2DrZbV7a7kutmRZUuu9CebJwa+\nKvMiVtqtPL3VYB65kqDX66P3qQVngGdHVRIGi1KcDISRn9sYdEettgLURVUU9Gx91V/gjwtlRpnu\npRAdN8fpnTXntnNdq4q+LCsb4cgCfXrTsuR6n6MuPHnO2pdSZqy9e+ikdSrw1eopJ+b2aL8ZVBrB\n4VcGtQ3qC/D58fHxTASHFVOVkMsP66+A5/5kURpty+jcj+TXFWRR2RhLr+dqZVx6SxEyZ5VDh5kC\nZA+URsTxZ7bYHErkcqNdTCt0bBho0T8XTmQuzvtgGLhRT+vvKXV1U4uv9brvI7LIPTom88jGgD6+\nZ/RF0zRdQc7nmYKw85qFHENatMVFdLQ/kTfaExY6gMXX1AoraDl9hD6wY+wcVgWQozbO8XWSUaiW\njFr6VclGgT7SdMCZAvToD0+ooyn6ZNRZ8syqu7ZlsX9nJRXQwOxWAFY8tsKsDI7DR34GjnNkNZ9S\nL9d/R3EY+M4IrUJaStk6H5GN4PSZNXchSpcH6MfjXbm6CrgwZfbRVcLtyMyA7yZU+8d90nsc9285\ntSEa/dCx0BdaXFRGIz26ctxvudL0JrPg2fUM0Jym150ldpGcTBlc3vjOb1lFZEb34cdK4xSM++nA\nrquAcnP1AbJxbI2Zmx/n0LoQZyY9qpNdu8xIz9otfcuK64S7FaDl5Ma9aoEVfAFYzucUJbPmcc39\nggIrBoAZR9oBrrcaARe3Hbce+7ux5tUgPvoTHjqGAU71I6I8970FdD7eb9kYSx/fnRK46/pdaQSA\nC1aVwep+hk8VQ4Gf3cvWX9+nbYFPzx1NYQ7NSuDK0dBk7JtRsDta5agSO7DuIZVz4l00J/M7XP33\nQzYG9BklcXkcPeB7HYUJMO7v79uf+HCrAZcZtMXlcWXoyqBAVedZx6MVHdFxivyOs+uYMeB5r46O\ntSqOcv6sbaOyLisPbAC9AfqPlHsrgtIcBb2+87q/vz+zASxzPLk+3aag9MmBrGflub1RlkovRMhg\nZgvNdbtXEvkY9bCvkPVDKZZ7C2zekKX2Z577FlklNsLSOxDzebYCON7bsvIB/v39fWvxuWy1mu7n\nPVybXBuUhsUx0jU06cbGKRH/IkHcy3wdOKd4oQx8LZSF+5lZaw5z6iee/Ea+FuB7CryooswjGwv6\njNZkAFOgZ1xbwc/5uU3A7BLsuH7kdwpWyvn+Gi7XPSdwaSrumjqkGrLkNF4RdMxb/ebvys3Z0mfC\n7VClvJKObCnl0wC+AOAEwKTW+pJSyrMAvBvAYwA+DeC1tdYvNMq48L0H8Mw6K/j1HqUoutcGyP8e\nhvOwKNiZLjHoQ9wPQbkVK+rVcWIQRXv0fVU3jgw2R0nUejOw1RmN/C49s7qqYEqt7qcSLGvpTwC8\nvNb6h5T2FgDvq7V+TynlzQDeOk27IGox+cjXW5Shl55FY7i+yAPkoHeWMgCuVCkcXt5iHJOaWXoH\n+rNBTigH94e3GLSiQHHuwH18fHz24Txq0VkZ4rvWMa8sc++8sizoCwA1f68B8A3T8x8F8D+QgP5C\nYQnwszwuf2bl3UfpjlviM2sboOYyOD3awu2KI4OV+8J94nsDyFk8nkOaLb6s13UsdaxXAcJeu1RG\nwe9Ww1FZFvQVwC+VUiqAf1Nr/fcAHq613p026KlSynOym92g86QreN3TTGfpewBnoGs0RyeIOTG3\njX/rMtK0HbyDUSM0Wp4bAx0ntwq5fNx2O2mNMrJVwpWrER/exjxa1zpkWdC/rNb6u6WUPw3gvaWU\nT+BUEViaPZvHumf3O3BrGlMPBiwDnyMd+lF6FE4wA5vpivYtAOvonBuDUXEg5RDlZQDLKVdLSTJD\n4vLeD1kK9LXW350ef7+U8nMAXgLgbinl4Vrr3VLKcwH8Xnb/H//xHwM4HZTr16/jxo0bdskH+n+X\nkzmnka6/TZl92CFU0Ee7mA7pfvSWn+KU2Vn2TLQcDlk62uJCklpv+AO60oxY6Jaje9lydHQ087bX\nPLIw6EspNwHs1Fr/pJRyC8ArAfwzAI8DeAOA7wbwegDvycq4c+fOBVBPy06pT8txVcvOURS25hnF\niTSeTLWWjjoBs3vQo91s3Zl7O4tP42r5qo5HtI37n5UbeaNvTpwT7bi4WwVH6E9LKRbi5dN5i3sn\nk8n4vXPXdi4PA/jZKZ/fA/DOWut7SykfBvCTpZQ3AfgMgNf2CtKB7n0cf9drLiavjqejOgGM+EQk\ng9unOyxdX9xKxQqgPD7y9EAfUuv55i+26O6nNjiPi7SUUi789HZvBXJgVgqj6evi8CoLg77W+n8B\nvNik/wGAV4yU0eKzmXV31AWABXpYeQW8OqK6b2bajxnLzG3iVUlXKD5qBEavaT5W2mhDJhzNYVBl\n1jpi+dm7vG4OXJ1RVjyFdVbfhTi1PSwubVQWuXdjnsi2rse5s46anxVCLTtb/Yz/M+gcKJT3Ok6v\nkZpIZ/rh6ISuWu492TienJxgb2/vAsD4eiaOvmUfjdO7eD1fa9W7DLhXKRsDeuXCzspny28vPOmi\nOO4ab00AcEZv3FPOuO4sPVtu7qty7tbK4O5346NW19XJAA5RQLuHVS6dJaMtXMYiIFflcHQvG6cR\nWfsuy8xyZ+DIvo/E5TPr7zaiKaBc2wL02l5uGwPRgZKPWrajAfHhnZ7Kn3t8PGTE0jvK4nj6KLh1\npXTX5wH3Qk7w3HdcgqjVVis/ohQtsDOwedvA3t4eDg4OzsB+cHCAg4ODMwWpteLo6Mhau5gctc4s\nGlHpAYUnXOsK4RdFHN1yK6Ern8dO6VsGfG5Xy4kdFWcMdHwvQ9YO+sxC6sdN8jy0RuPxDHQGPDu9\npRRMJhMcHx/PgD/aGaB3UQvtC19zyz4DjhXMgZkls5ZaLrdZx05Xh6zdGY1ZVpwyzrNyXClH1olb\nwtyEZwrhIjx6rfVw6tq1a2fnpZxuDz4+Psbh4eGZAjAYHejVQjsa46hIz9KrA8niLLCOFTD7g6tq\nPFqrhLZL989znkUlo4GrtvhrBb1SA412ZEB3IUwXd+/ttwnrHp9r167h+vXrZ9Z+Z2cHR0dHODo6\nOgNGPAmMydbQnyqA8noVzp9FQVg5Ij870Foer0bRvsjvKJADv7Ypa3uLf7d4u4La5eX2rhL4a7f0\nzqqo1XEPo1wkxtEbVo7MyqsCsEMboGdhaxflR1/cJEU7sl2SPA5MP7jMbLx4jPhe9+sGkYfbzcoQ\nT213d3fPFGV3d3fmzyicLEtz1K+IMvlaC/ittjlZO+gB78gqLcnAzg+hdA9NTKA6qgcHB7h+/frZ\nJyz8tWvXZugN18t7zSOqE9f0lwKUfuiqpZOUATkT5+y1gOdWIK1f6WBGeUZWLHePOqsO3FnfFPjL\nrgBrB71autZyq+ls0TPnVUF/7do13LhxY+YTm90iT5TFbZxMJjNWEJilHcrLHYhbXD+jKsDsb1C6\n69mYjow9tyF7JqLObk8pnRJze3UFimuO8vA5p+l4zyMb9XBKn1I6BVA64wCvlp8t+61bt3Dr1i3c\nuHEDN2/ePAO9cvmgIzHQoUTsyPJremp1e0DWc/dAy4UGHfAZTAqkLC/PAd/vVlgGfmb9HcizdM2j\n7XDfOW1RCx+ydksfkoGdJ8ABveWwMpW5efMmbt68iYceegi3b9+esfLXr1/HwcHBWbkh/HAqVgyO\nk2e/A8ORmayvowoSfLpFT7Re9jk0zX1UmLZxWFONDjvd0X4XHXJ9zCx3S1z+1jhnsnZL72hA75Px\nfVWOAPzt27dx+/ZtPOMZz8CdO3dw69atGR4fzitPUq2nD6aCzsQ+lxhkfZdUJ5EnHph9esvRH+47\nH1VxdAXQtB7liDwZ92bnVneaxuoX7T4+Pj7b1qt7b5QuZX3o9YfTe/dcKXoDtKMRusT2gM/bCYK7\n3759G3fu3MEzn/lMPPTQQ7hz5w6uXbs282AqaFDUHxY+gBrlcvvigZWCPiyzblYDcGGVaFlbHRs3\nuUp9AoC8F8ftr3GbxzIaqRGquI//5UQ3obFyq7XnvkV+zqP9V3EKcuVAD1zkksoTW9zR8XwG/s2b\nN88s/J07d3D79m0cHBzMxPPVYeYJ5Pq5rrCAwLlV53g4h/mUyugq4cCvHJ9Xh4zjs4Vu7XZ04+/6\nx2VF36It3He3jZjBH/m0zji2uLyOoX7ntFHZGNDz+bz0RvfWcOz9xo0buHXr1pnTeuPGjZkIDZej\ngFKQMTCY7sTkBgWIPFxOnHNfAwj62lum5G4b8Yh1ZFFwanqIrrSRh1e+UPzoM696znCpE6rX3Rj1\nKM8isjGcPrPs2QrAy3AL+ExfAuQc3WFRy+b2qUddzIVjonQLslrvDKAZzeA8Thw/1/HLVk++3ymC\njnVcZ9DzAyxdDdgncVZdwd5TVkeRop4rZel71lwBr/dkT2V5GwIDi2kFR2qY40ae2G7ggM8rQ1AB\nvg54i8VKEXXzSsHX+cg0QRVKwcXRE76Py2dhhc3K1DZlhodXS75XH+A5yuKAuwqr7mQj6A1wkVdm\ng8qUJo7M0d2TWeAc9DGQ+gDKAV/fj412unMgj0K4fjqgajlcFita3K9cOktzvgCvZPyUmd8fyPbQ\nt+bLbWYL+uasukZ4eAycclx5ehPSoy468ZxPf78mlAE4n9zYPxMf3dDFeTX64drJ/JXTtbw4quXj\nvsS5On6Rzkd2krnNXL5bFVui1CybG213UBre6qHt5/JZsUMR5gXxqiz/2kGf8c24puDnQWdrn60K\nwPlDHrXgATTHc107gXOqwfw1hEHMEZ0R3srUwFk+5bRqrV20RUOLGmaMtOgPf9TKZtaeH1QF3eOx\n5IdY2o95QezuWaScjeL0LQvf4v0Z/++BgNvB57xcx4A63u0iIFG/oytRnot0KA3IHDS27j0qk602\n2arASst1swKrYx4P7pxT7Oq9LJ4+j6zd0qsw4BzIs0kDvHKEsAIwd+XJ5AmJ5VijKKwMTKPiWkyy\nWjxg9q9zouyMzzqr6vwNtfCq5I6Tu3HjfjPlUeV3jjPTF8frs/5pX12/9T4nPQqnsnbQj1gfZ8mz\nAeVyQ3SAGTgAZqy/cyL5nIGt1j+E25pRFkdXuI1qOaOdHFXi9jrF5f63LGzPUVyUirTq0vNWnctQ\nIidrpzf6vUdpemAHvKVUKz+ZTDCZTCwFcryRQawUxj2IUiUJyTh4i6OH8ArF3Nu1l9vE36MNvBJF\nvriWjWdLMmVprcQ6Tu7+rOxlZO2WHpjl0YCPS8d5Ji06FMLAPzo6wmQymQnPua0B3A5tD5erR3YQ\nud645lad1n4WADYfAyMDZ2ZcHP3jVYnrz9qlhiUDqIZl3bi6MeV8qwL/2i19Zt1bzizf35LMmkbo\ncjKZXLCKyuvVUjIlUYqi/eI8rm0jdErrU2dTKVQI+wzM0bOx1Haplc2ss5u/THQMSzkPv95P2QhL\nD/jH0vpR6hDnGjp0jpE6gfzCNz8d1aeiEXLTdjke7CZcKYtGkjJHznH7kY86sVx/y9HVVS4AmfkK\nvJLGOTu+GpnioAD3KVOSbIxXIWsHvbNuLYvuJqAFEg5TMuDj9T99QKRtc5a2NwHZ6sXWV/n4iK/S\n6qvSKFYsplqRX8vSOrQvSj2VVkV9DvCxHUTpjRqZeYDdG6eWrJ3exDFzZBYFQQvw/CsHYeX13dcM\nGK6+bOLUUmWrglIw/q7X9XlD1B95Mv+A29Pi3jzuvKqpAdCn3rHT0q0AnJfDvY7j69j1ZJEVYO2g\nb/FhTXeScWIGiXMQWRGcE+UAwmUGwNSCMTXge7Q9CkxtYxaHZyXOIkE9h9iNtZsHzcd9VUVTH8yV\n6Tae6cqwShqTyUbQmxbFUeeNxVlfBY4DmAKEdwg6J5Qng+91D6BalrzFuZlTuxAmcDHcqeVHvc7Z\n1bGN37PhcpgGsa+j98aYMFgzpzhrZ090zJ0sqiBrB31PYqCcRXJgys5byhAWqjfILL1JZisY9caD\nJX7A1HtQ5igP9wuY/YmQHl9nv0T7zX1fhcXt+Sls1JzycT7Xv0Vl7T/rl1mjELfMAhdBpUu7Ar61\nGugzAkdteFlWYTBqGq8y8Vwgdnoq8KMejZhwvRwJ4ZWJQcEcninJCJeOfMA5+Nw4ZMro2qzlxnU1\nZi0sOOW9kpZeLSNw8d8/ND+fO8fOWXe17OzUOqfNLcnRLq6HOT1bXgAzgFYL7xxNttrqeKq0LJ5r\nu9IjR6vUvyilnI0P90vHYR6fQR15pkhchoY2Iz8f1fLPIxtBb9zyGuc6SHqfW/JjEhVwEZff29ub\n+VFW9yJE1MlgjKOuErr/ni0uA9z5FQqYFoD0u4IoMxSZ4mY0ygExjm4rsmuzGpMWxXH5+VoL4IsA\nf+3Rm0XuyaI0DMZw1BjwAfQAq1p6t6edvzvF0jSmFHpva3Kcoxj9y/KxcPt0XFp9cG1zQHQKoJTO\ngTsDfmtFysaGzxelNsAG0BuVbDLdvTyBSlvYok8mk5m3qmL7gX40isNtzKiBAkitqYscuXCk7tVx\n1lMtLreJ06OcqNvVoW3m8Xeg1/pdu1pBBjePzihkK10mV47eZEtazwmK7+HQOcDrNgN+Asu/SMxv\n8quV5+0NPSvEjrCmO2e8R0VadXJZrXaFAgdHV4cYmHXQuV5HnRyQM79K82X9mQe0DhdXjt6E6ET3\naIGzODHAHIbMHFiNT2uZQO54hYQ1Z0oE5L+swODQ/7HKVo1ojwNlRp/c2DBoMyVsRXQU3OoAq9+i\nvyTRm89RWVZpQjYC9Cy9pY4nL7unNdgjkRGlOnwtjicnJ909JQ4s+uE8mTJHnY566VjxtXDKuXyN\nUmkfXZlKhbKoj/aBI1Gjwj5NbyVbVHnWTm9CnJUK+sJpvRWg9ekBUSlNlOmcJ3XysrLdCuMeQKky\n6uQ72tQCvQKQ98C4MXNtcf6Bgl7Brn3g9vKWA507B/JFQd2Tjbb0+r23PLac4EwJYgLVsmf1aDqX\nF0t7lO2eCwCzv0upUR8FNTD7/1KZlde+6p4WHZ+egehZ+tZcOPrE570Iz4gVX0YhNsbSA+1H4A5s\nLUc4i8y4p8CuTrXqfM4Trt/ZYmbA4GcBbs+PtsH109UZ526cM+V3eR0oR0XnQceR+6urqLP+Li27\nNiprB70Ae0IWAAAgAElEQVSb6CxaoE5jVl4vEhT1KB3J7mHerlY60jREqA6z0g+e7AxkI6uOOoyx\nmnB4NNoRq1C8Gxxt5zp6yuDGuDXWrdVW+9jL49rUup7JxtEbFbaoLWFrzn/A5n7UVf92060CKupE\n8uTzb2byj8IyD+d/6YvojSqO6xOPAx95bNQ/AC4+V9BVYB4r78DO9WdA1UhUFq/PhFcDPi4rGw16\nxy2zZdOBkcGc/Qqa2wfeEq7bUah4vTDKZBCGaIxcV7fouwI40nls9AGU3pNZ72izG1MHLgfqFp3L\nlFTLa8kqAO5ko0CfWY7WpAXYMpBnv2ys+TkPcP6/SwAu7CvXZZVXCEdJ4pkBK2+UpXm1j8p7M2vH\nZahFjlVGFZHbzq8xjs6LRpyy47KyavBvLOjZCjKfB/ySqw5qpgzKReNcrb0DEX937eZrbuVp9TcD\nfRx7ys/+jiqlAtmNZdauuN89X2i1O6NKl2W955GNAn2IA74OcAtcIxSGAaIf5Z7hLGYOplPWLG7P\n5Wm824kCNBsX/jgO7BxOza80JfMPdK54ThzV5PPMcLSwsGrpgr6U8g4A3wzgbq31z0/TngXg3QAe\nA/BpAK+ttX5heu0HAbwawBcBvKHW+tF5G6Ug0ocqzpIzp1Yq4z7s5IaDy2WrokX5LPo0szOOM2BU\nC60rT4yD7vxUMEZ+BqX6B9mLI87C63cGLe9V4vFgv8CttvMCt+UXrEIuPqK7KD8C4K9K2lsAvK/W\n+tUA3g/grQBQSnk1gK+stX4VgG8H8MO9wnUZ5A5mnXUUpnWd89R6McwX98R1fZoaOzUnk8nMD0Xp\n70pyXn5hxD217PXLKZkC3704o1up9Xf59WGZrjitsW+tpI5OZvOybula+lrrr5RSHpPk1wD4hun5\njwL4ZZwqwmsA/Nj0vg+WUu6UUh6utd5tlJ+mK51woMic0ew/p1ofpjAhJyfnL4DHNd4aUUqZic2r\n1WYnlq0mAzC+O4nyuW26YjiOrTRF6aHSMU3XOeDx13O1yFw2UyINn7oVbMToLSuLcvrnBJBrrU+V\nUh6epj8C4HOU78lpWgp6wC+zukRn3FQtvlqaUIJsRVHLmTl5PcunQAkwc32cx20RUG6v+dWRZGuv\nwFaQ69jpk+BQ5Jaz7/h4j4q4Njmgu89lyaoc2YVamNETwD+p5PucBVIQtRxZZ7Gy8rmMaBu3kX/6\nL3i4PmzKQM91hqIogBTw2St7DuQMbG1LtJX3HekYOnGAzcCb5W/lbYlbreaVRUF/N2hLKeW5AH5v\nmv4kgOdTvkenaVaeeuqps4F9xjOegYceesjmG+2cA6/jm24yM+vG5fDfzAStYIBzmrOq/ISWP5k1\nVFqgD6la4zJPH924cT+jDc5KK4VpAVzj+iEt4GfKMJlMcHh4aPvek1HQl+kn5HEAbwDw3dPjeyj9\nOwC8u5TyUgB/VBt8/pFHHmla8xC2eK0Bay3nWibf7ywWi+Ohjs+6MhQQrs21XvwBVQW99tH1ySkA\nW3vXdwcqXT0cF1cHepSiZABv3eeUIHy1yP/lL3/5Ql2ZjIQs3wXg5QCeXUr5LIC3AXg7gJ8qpbwJ\nwGcAvHbaoJ8vpXxTKeW3cBqyfONoQzhSoTyzBdqWYxvUg0OTOzs79q832VnlUCCHTPlPw/gahwQd\nxZqOzQxvDsksoVKNqIPzqxPLCsZKqYoR9zgrv6y0FE/zjVCdUeWZR0aiN9+WXHpFkv87522EoxT8\nvTUxreW9tdfG8Xx+eBRlqMVmwMR7t5PJ5MI7usq741wB4BxzBb06ytlKlI2P9ov7wWlcVrYKuNVT\nldi9RqltyiiQs+qrlo3YWqwWja/pXhq3IriymIfzA6idnZ2zpXF/f39mh2SILvVs/dXS6zVtS3zn\nI/9TuSqWOrSqBEqxnHOtfYjvCrYewDNalI0/5+85wS1rnvWlR+VGZeNAz+DPLLO7r7VMqvLwU9m4\nlx/QxL7zmMiwjBHLj2san1cL7frF/eZ2c1tYCUJ6VMDdG0qitMnd6xRU+6B5W/OqkrXd9TGTRemM\nytr33mSWXh82uSd/Ki6OzUt/1BPlxXd9KhlPKgP0wafZMjKPd5PhQN9yKvW+KJf7lQHGPdRx4B4B\nfKaoLBllycS1ne9pKeOIzJt/Y37AVQHNTqi+7OEsT295j3yqSJxfwc/l6MMmvsbp2Yqk+bSMLL0F\nYCc8Fs6BzKTlV0V9o3H2UQV01/U+Nx6aNq+s3dKHqLVRa8yAdeDLLISbQLa6AXJn8ZlDs3PLK4Tb\nUJV95xWIv0f5XL86wCN91LHiNM2vAOSVjVcSTdPXC1mYqqi4/JmytMDeKmNU1s7pHV8f4fIZxXFl\nu3sjj0vPnqhy2boqRR4Hskh3tCSL4bNwqJSvs8LxE1WmXk6cRWWA60Ow7AFUa9zd6498bw/kOiZ6\nbRlZO+jnyZtZeH0y2PoAs1GSuJ95u/oEvBow0Li8aA+HB9WR1AdQusq4/rIfwCsPi8bdVYFc/VF3\nOO3Rjlhl4n4+srLHGGp7I10ddV1BRh5ojVCaRRRh7aDXpVmtp55n9CaObqI0crO3t3fBWeQ2cVkO\nQEx9gIs/4w1g5qcFI41/qSCOGV2p9eLDLKVJmQPKQM/64H6OT7dZZPPFys9lZ0B3xkdXrvth4UM2\ngtM7zunSgTFNVyqigOdYv7uX63W8Vy04T56L3buJjbZlq52jTFGmOqgtK6pUxQFfAZwZHeDcUVfA\nqsJx+Q7wrk1u/tz88PgsIhsBepYW0FtLIedtWfwo31lnnZC4psu20gAXp8/65iw091ufHfA1pS/c\n5ixUyxSqRye4nTxeGuVi4KuBcErVojOtuc6uZddHZePojZ7Hd5aRzquVY0ukgM24OVtuBiFPOltJ\nXWGck5xZVB2XqEcdQqUxXGbr48Yqo5OuPaqwPM6OMjFtcqBflSxS1sZYejeBDDa2VJyf74nBjVf2\nDg8PcXh4ePaqXzz+V6CH9eJ9KKEcGqKLSddJnbev3F623kpH4phZaie6IjC4oyzd/hzpo31RCsXA\n1h+szRRwleCfRzYG9CEMck3vcT3lkwH8e/fune2zqbXO/Du4gr61UUrbpxPJaUp9ghJxGXoti87E\nPSPj4PI4wClNyuoLyWgnjzcfeRxGlLQ13j2qM6+sHfRs4djBDNBwRCEbPOWSbO0Z8MD5PmwNy8UP\nIml5LeqitIhBr9GbADbTq/ge+XQ1cw6rO1fJAKr3x1gxVXORIX0Al9GqHtjnpTdunlchawc90A5R\nufCYy+uct7D0X/rSl84UajKZYH9/f2ZiAZy9kJDRCF72tU18LdJ4i3G0Uff2RHtDsd24sAK4sdHv\nOjat8xZAOeqlBkLLcFSnNV/ZtfslG/NHa8wrGUgth5EHWq1sPHg5PDw8C1cCp+B2WwrUurqYcki0\nhSM7umL1QM9lOm7N45MdlaJlEZLWh8cx6mbAZ5EarVPDkq2IjdZ9v2XtoGegA7McOyy2Ap8HFcBM\n3JxpRVAc3kYcoNddm9EOrpedMXU6maPrD6jGNX7KG/m4j6r0+nAn8nJaKyyp0RIdJ7XYGi3jcQ4L\nn4UtnZI5wLcUkttyP2XtoHfinFgePLX6DBC1MMHv4yXiAEVMZqwCoWgx2Qwibqsqp2uHtl3Dgbqy\ncL8zC+zGwSmCa0eAml+JdO0KQ1BrPTMO7L9wHfqjUS5cye3L+tMSR+lWIWsHfSsGH5PjdkHykstL\nL1tptvgBcl5J+O80gdlJz6wlMPvmU7SPJ1LDn9yX1li4MJ+uIlynnjulZ3Ex/hg7pjGRl9sWxiP8\nkclkcpamgNfY/LLSG7t5Ze2gB/xebmf1GPBKJ/jIH/5fWR48Dl9GfaEIXF/wb1VGZ8niPm5z64Gb\nUgNuP7fBgX5klXGiD6KUUmldocBMF3lcHJ3J2unasiiYHXZGZSNAz5aWRePevNTqe6R6X1zf3d09\nA7z6DjpBvIc/LChPbvZkki2aA6cLceo92q5I11VkFOyqZJqm9zkFZIoXVl7Drb2tBq5dXGemdNzG\nFiVaRGnWHrJUsPBed87DE8JcE8AMMFQpwtLHJ0T9gigrFIRpUkwmg57L4q0CkY+ttPJiLjPaHPmc\ncxjC5yqZ1XTgV4Ax8DTaFOB3NEb7MurncNu4TXreAv0iFj5kIyw9nzNoAL/V11mlyMuA5aWZQe8A\non+EzKB31qXH1TmNqYvrC0dNtAzuf7ay6fg5AEY74uhAqStfGAD9dWO29C06kymAa7/SPW1bZuGv\nJL1RbY993SEBGLauCng+53BhHI+OjmYesrDTG4MXe91dHTzAurowmLmdCjT2O1zZo6LAd6sgW2ym\nS5oW+Tj8GnydV0ld9ZS/Z4rWoizOx9H+tEB/ZS19Jpk10zx6rsBn55Qd4BB2WjV8F+VlVlytpnst\nUZ1G3fSlqwRHk1yUJSQUiBXUUQUHPKVWnE/77KJD2fMLt7ksiyL1ZIQaLSNrt/QKOGe5gXNAMJjU\ncivtiA8/XdQJZkvoAOfoUzjITDl4JVLlymSUpvB3vZbxaS6Py2gZEwYwr5jO0jPoMyXTNO2niyK1\n7nFO8CKKsXbQ85EtoeZjXhxA5jR9GZq3GgS9ifsYnMpTY6JDWNH4KS4rZ7RR+xPnzgrryuJWFbea\ntZb+DFyuLF1BNNbPbeL0zNI7ytajKGo0XF8yZ7fl3/RkI0CvAMqiDRmHjzwu5Mm8nsGrqwBPoL5h\npT/9p/VyG+MebqtTUu533D8a9muJjl0LFAxSVfxaZx1ZtfS6OvIYZBafj2rcevdpn668pdfvvBdG\nwcbKEfe47cfAeciNgc5lc11s8TW8GXVHfe61Q24Pr0ja7gz0/NR5ZEL5+qi1U8vKljz6HgAPRQBw\nAfQ96hLX+Lxl8bUspyBZ2YvIxoCeJ0SdNj3nCeMnqxkP5P3qHBniNnC9Yf3Zd8iiDaqAoRQaddI0\nBl+2pDswa3tajnMcdUVRwGs4Urk952991ABwfQ70bNjcOGj+TOalOGsHvVr0sC5sTZmfM7C0HAW0\n7tR0dfK9bP0BWEXi70GfIj2Orbg7H1uiK5K7l6+1AO94cYtOaVoogxNtX0tGKc6oLEpx1gp6jVsD\nF3/Gmi01cPEPDeLoLHyUwRYrWwkCpKxQMajxPeLW7qUPVlJtk1p4FV4RGKg8Bi1Ht0UzND+D2D1Z\n5RVAxYUgW9Eb99G2aERtXuAvIhth6YFzi8FWna0Uc2+2zkqF+BP5Hcfm/HGuy26IriCRJ67pBPJ1\nR4uydqh1by3bWg6XEePFFIwtstIa7VOLkui5jokCWK+5ezKqx33NZBEFWbulB/Jl2uVz10MU9KxA\nTEMULK4dnFdpBl+PCAdLDzRcl7adv4/QoYzKsA+hVE7j7tpmVgrnD2ifHFhbVl7HKivjsmTtlj47\nV+vFwGSK4zids96uHmcdmd5wWXy/Lu+ZszjKOdXaaVsdcLIVo1VHtFc/TJ96Dqsbx6yuRSRbDYDl\nth6wbATo1ZIyxwXO3zvlZToks/7unVimIAwUR18cHeI2u1VBfRSlV1FuDzCqAAq6lqJzOc5yu/No\nH39UaV2bM2XTOVGjkOW7X7J20DMAgdkJZeey1jqzVyYmLO7h9JYw1dH64jtbQKU/DBT1FVxEiRWY\nAeT8CW2LA772JQO7c1aV1qil13Bli5pwm7ndGdhHFKMnq6I9a+f0akk0zBeA4703IRx1YSCHKDCV\nzjCI+eFQttceuBjyVCeR644yW8LK3MqTLftuNeCYe/YaH+eJcebrTnTsgNn54mADU0V1lt1cZHVe\nhmyEpQf8wx51SvU9TuBcGTSdAZldj6MCJtrBExuTFdd5Fydbc1YKDkFyna3x4PZllk0pC4M49r7z\nMc4z4Ed/lNpou3g8NFIV/WVFdysRz2mL2uhYrFLWbumBi9Ebl+YsPAM747CRRymNW1FYKTg/TzCD\nMfMzdOWahw/rNfV3uHzuZwZoTeP7tJxMyXTsgXNjw76XbvvQMVMaq/PaolOrlLVb+jiyteQ0TmdQ\nqlVV0OuEOouruyndW1KcX3l3rCDOmkV+boOzju5alJFRmgBbRmEyOqOg0vOs367/CmxOU2Om/XGc\n/37K2kGvliyjNy6Ck8WRM8A768qWyfkFnF9Bn/F2Bb32VS2fW+kUjEo3nJVnesObw9Sya1u1Xz3h\n8Ywyg/LoGLr+cvqisgz92Qh6A/iHN8qP2SKqw6nWnsvnAVYLG9f0z5S5HRry5DJjawLn55Uk2qCg\n5xVCwcCi1pTP1fnMrHoGdse9M+Pg7o+jUpkeoLMVwPX/MmTtlj6O2RLKVl1DlgzujFLEKsGiTigr\nUohbHbgsVkRdtrl/rIx6r3N0mTK5lYLLalnzZSlDi2u7spXmjYCXjYOjiZclGwF6FrfMKv1hQMSL\n5OpQKmVRwDpr7ICmsXdWEgYprz7RFlYq3qPPKwqnq5LwGDGP1xg6W3c3nrGSufZzaFEplHuvwfH6\nWA3dgz+1+rzScRSIy2qBfxX8f+0vho90goHuaAyXodadAckgjfucg8lWOQMCn/MxABZ16wsuPKFM\nldQ/4XMXmuxxdR3f1ji3QMrpjvsrzVEfSj/Rb11l7xfggQ2y9Bmn1/x6DwPXpUdZDHiNwbvQqSpV\ntIefF6i1Ylri2q9lKw1TmhdH90DJAb4F/gzIDFq26q4sbSOXqxacVzteMble9WuU5l2WbATodaJb\n+Rkkag1jEDMrn1l6N/EO9Fw+v1fLvoY+sVSAKJVShVMqoRQmCz9yHc4Sc9muLr7XldminTHWDuxK\nnVgx3Aqjc6Hzr7KIH7B2egO0LT6nO7C2KI97cAVc3EwWeXSJVX7K4I/r/Lc9kcZt1T5xe3SJ1wl0\nlCuLznBf4pzr1HNn+XsUqKUsvOqxJddnJLpC8jhzOvsoq6I1IRth6XvCINRQpXLljBKxBWK+zsDj\nqI6jK9EW91qiWiqeMJ7E+K6ObXz493kyJdC6szxKgfRHr7gvnI8BGkctV1c0LsO9WOOsuvYj+t96\nOqyyiELkf509lVLKO0opd0spH6O0t5VSPl9K+cj08yq69tZSyqdKKU+UUl65aIMdT3Vc2H0HLv49\nTNyvIb7WI/rMqrq4uHsyGr8iED9xHZ979+7N/N2nO/KeGW23maOUKrQ+nXlP78ks/d7eHvb29mb+\ntqdVPyvs7u4u9vf3z/4Ib6SNi8qIpf8RAP8CwI9J+vfVWr+PE0opXwvgtQC+FsCjAN5XSvmq2kC3\n47QhTF30uyqC8mDHvbn8GHAXZoz0bKK5POr72ZHrjzK53UqndGXRKFC2zLsxGFkdop2Og+u9bLlb\ncxNjGu8vcJs0WKDRG74fwMwvq62a2gADoK+1/kop5TFzyanhawD8RK31CMCnSymfAvASAB9Myrbn\nZxWUi5EQR2Uy4PO5c25bAHfRIAWVgjGOWaSCl3z9WcAQ9/BL+6Vc3o2h4+iZtXWgZ2rixpP5uJYd\nf1nK4VU1HurIAjh75pJZ+BZG5pFlOP13lFL+DoAPA/iHtdYvAHgEwP+kPE9O06zoJEWaO+fvOgma\nBsxacOBiJCfyKCg5r2una7N7uNSiEtwvBRa3V/vgaB2nq7iVyj2TYCXnsedffYg26HMNt4Iy6Pn/\nvBT8DHwuzz0jWaV0OX0iPwTgK2utLwbwFIDvXbYhrUnUayHKxzNunn3XdC3TfbieXr7so/1wY6Fx\nebdzsrUH3nF8jZzEn8zFp5fOZWg61xv8XPm9Ot3ctpOT2b3/o3H6RRRjIUtfa/19+vrvAPzX6fmT\nAJ5P1x6dpln54he/eHa+v7+Pg4MDS18yOhPnbB01n+PSHNOPdOX0qly6+mTLKsfyHUVycWx3XZd+\n7e88SqX+C4+Hrkau7jhna60rpirc7u4u9vb2zpz5Fkd3wYCW487jtYiMgr6AOHwp5bm11qemX/8G\ngF+fnj8O4J2llO/HKa15EYBfzQq9efPmkIeutIHTOA/TAV063eqhS7UqC1s2BQm3aUQycAMXge0o\nUUtcXvUHNL+jG26lcPeqzwPMAp8dcaY6TFtYuXVb9MiY6hhl28KddEFfSnkXgJcDeHYp5bMA3gbg\nL5VSXgzgBMCnAXz7tDO/WUr5SQC/CWAC4O/VTg/0Mg++A5WCG5h1HJmmOF6sfJ3f9mELxuBmJeKB\n5lVBP7rCxH26OY7LV4VVh7g3dpHXXWNlY0rE11t1sOV1Pgr3hR1apme11gtHpjbuR2IvQ8plFt6s\nuJT67Gc/u5fn7MiOj/JLFw/O8mT5AVwANpfjeHFYM/3texeZcO1RvhvlaR9cW7PlPdLcz2q735aP\n/JPJBABs/vgbTXZO+d1aBjK3/eTk5Oy5w717986eUzBfZ9DzswtHb1pYnbZhaHnc2CeymZWPI1tS\n5c+aV6mMyw/ApnMEgsvL/Au9rrzYTWR82LLHOcfwue/aRy0/W3la/gi3s/XdtcNRyGh/GIb4X6+Y\ngyibnXLnk6xaNmLvDZDHmHVglTYondHyNAQY50o91LHUstlpC9GHOxpx4DICuEyjMuFVQq2i+jHc\nJm6jA37kYUWKvM5nyoDnFF4jLjyuvBKqYkYfmXpdNvvYGNCztAbbDbgqQlzXAY50x+95ArJVI8Qt\nz3HO+V3sO+7PrLJGWLh/3E7g3HlzBkKBr/c6+sVtiGsZFWytxK4u5wfwOLj2ZvUsK2sHveuQm+xI\ndzSFgcr5XXrm2LIDxpZ9Z2f2t1xcvFnb5aiIAsCBPcpna8cW042TKjv3XXmxA5WjE9qmrN4RYUC3\nQq33y8oDGwD6RUUni4GryyiD3y3jaokZQGz12KrrxLMiKW92HJzbxquSe4agfdLytB+uLk5rKcOo\nA6lt0YBA0BpdOXR87zfggQ0CfcviAz4cyXnciuDucUqilpSjEFF33OMmLqRFS7gNGqNnJWGKxaB3\n1pzF0Qc3JmrtnfVt+QTZ3JRyvkEuzp3jroAfWTVWTXE2InrTGtDRe1kRnLWMvC5/XHMT4oCm4HUc\n39GRuJfvcQ++tH6N1/dAkFEnXaVGqccIKJXaOa6etZPLyfi/W90WlbVb+nkArg6d3q9WFZjduJVZ\nXkcL+Ls+veR8mVMb3+Oo4FbJnD4H8gxAqjAO9BwtUdBHnhbQR9seZXIoMus736t5mPqtStYOepbM\n4rtlsmXhQ1yI0tWplETbwuVwmgtTRhmO32dWjGlXBvoRS9cDfUZf3HeuKwO6toXnQUHv2qlpvEpc\nZsx+I+iNnrfyZ05cVo6GByNPFjPWshzX1jY44Dt6pb5DBngH+ihTx4PzcbpSuYy2tPi7AzVbbW0H\nH90DJxb1jTIamfV3GdkoS9+TbPAcZWE+zIPH74TG/a7MqM/RG03XyE1MunNCXYzeOcpRBpetYNNx\nyYDfArMqrrOwnCeu89NVp2QtmpT5Js4o6PVVAH/toM8ox+i9vft1UmKbq0Z2QhRUkS+Lk8fRgdWV\n2QIjKwNThaxtKmw1uW1s1Z1T7/K6/PzUVQEe55xP/QVtazwD0fa7yJUb50VlY+iN+67pTtMz0Dt+\nmz3M0nL5KaQOuLOqWo8DPpeRrQo80bpS8LVMHFVQCgPM0p0W9XH3u2gPg95db4nz17Q/q5a1W/qQ\nlsXOtDtb7tzDKLdUO/qh/LlFJ7QNbpnXyEbmyHJ5+lG6lomjBgrAUsqF38J0gOb283UNf3LZYbVb\nYVAnujJftmyUpc/SFWS9+xnIbgnn+xmIyqEzSpMpm7PyrLgahVEa4RREY/SsoJmoz8Ag5MgIj4nb\nbuz8Dx3LTFmylUHbyWPnzl2/lpUrYekz6YEPuPgKIQNad1sy9WHwKq1xVEcBHOl6T7TF7c9xm7tU\nafSpshsLVfYAHP/QU0Z1mH+7Fcw94MqsekZ9MrlfFGftln6RTmWTreUycLMYfs/Sn5yczPyZW9zD\ndbGi1FrTf0LUugP8jsfrytCiNi0LqpEUpRn8MgiX55SGy+L7HMDj6BRhlO44x3wVsnZLP6+Fz6wB\npyvA2aq5OLuWryFER2lUYRmw7rfalTJlyugse9yXWcrWKqRWXR3jFhg1j0ZvWvQmji1+74DvFFhX\nvWVl7aBn6Q0AMO7UMpiy8yjHOb2O5mTtctuN3UqStcVxegc43TLRGie+pnTIjbMDooL35OTkwsrg\nQpOO4ijoW5Jdd9GzRRRh7fRmNF0tmNN8Z41DAlgZ1XGbz5yVdPH3mFjm3Fm4ksvSSJFaeWdxF5ns\nDPRchzqwegzAM71hp1jvz1aOTPEycTRvWYt/pSx9C/AhLmLjylDgacRFJ0ofFimvZ4XitvB1PmcF\nUefXWTPm/D3RPD3Qt+gHcP6Suf4hBPtNbsxcuXo9W83VyLnrrq8jciUsPX/vWXtOZ2AzaDOnMHNk\nQ7KNYQreAGi2dZmVy1EbJ9Fmve4AkIE+4/QKTI3TK9gzq851xblTuJZR6s3p087Sq7Qs9TyD4BRF\nQcllu1i9cnS1Ug6savVbXN6BOdrEdXJeViQFs65EDGbtc2aR3cMmZ+kV0JkiOMs+D4CV4i0qGw36\neYQHVoEBzFpmBxClJxmIeMAz55hFeT+X7Xi9u5eP6nQ7hdb7oh/uV8DUYmuEJiy9u5aBWmP/UX62\nWoyu+Nn4zqsEV4LeLJoHON+bzaDOBoqtF1OJuNf9GhoAa7Uz6+0cM7daqXLFd/6L0B7v5bFyHJrP\nHaePPukK4e6L8yxEORrBcbzf9as1zj25Epa+Nak9fs/XHMePMpzF15WBr7NF1WtuZXDWfWTiOH1k\ncrPl39EQd70Fer4vewCVgVtXAa0za4OjkGqMrhzoWxZ70WsjopY5rHtGhzRv9j2jLQpevd6iR9ym\nZcYiAz1TOaYkLRByHrXujtNnER5u2wjgefzUwIzK2kE/r2TL3YjFz8pjusLHDPQZRdF0pUTcZl0l\nnMzTlx7F4TwKNn1RRQHKeVUhlL+7PO5cy20BnvvjxnxeuRKcftTiK89Vixz5HUBdegZqXhEAv1FM\nuQ6ujO0AAAdySURBVLArj8/VmreUYWTMuKxWnhbgnOPraE2khcPLdemDrtacjwK+1Z8RuXKWfkQY\nMG5lUEun4NentRnfj3uY/ztOr0qidbo2qzJnCuDCkNpfNgJOMk7t6ohr/JOCjptnxxaws/bz0bX7\naU9vQlyH56U4yt/1AZaCPa7xPcrlOaITbWOL2XphXFepqK/1Qgv3w0kLLDpeLd4eR5cW6e4a5xn5\naJvd/M7TfydrB/0odcnSepacvzsLy8IWW+nOPPSH69a28XlPYRkMIxbPSQ/0qqwtgMcYuTIyK+5W\ngVb+kTaP9j2TjeT0i+bTvMrxNV82uC0HtQd2p1R8Ta2Z22ymoNEyWn3WOp04AI2CvmXFWwrB92eA\nd+PkyltW1m7pQ+ZZupbtOCuCWvGQFuAVgO66UifOz+dKl+6XZODlNOXy2f0ZkLOyM6vdapveu4xs\ntKWfF/BqFXvUR+9VcI5Qmuw8Uw7Nz227X6AftfSaz/kuWsYIvdH7tF1afyst2jWPbLylz67Nmz/S\nFdCOVjiLrS9o91aFSJ/nOCrz8vosrwMop48aJV0ZMsvea2dGh1ydIS1DlsnGgP4yxYE9zoF84NjS\n60QwuLMVIePjjuY4ILNlde1Sxc36nqX1eHOr/Mxit2gOn6sTP7oarELWDvrL6BiXmVGdTGKSnaI4\nP0DryCiPO2Zp87RzpH+LAL93X1aWs/KLWndn1Ufa05O1gj5eoM6kRVN6aZmVGrGMaoXU2a31NFLB\nf0LQ4u2LgP7w8BAHBwdpO0fan43J4eEh9vf3L+RZFej1p0acdXf3tepgaW3lHpG1gn7ZxrfE0YJI\nZxl1bjXt6OjI/nZNz2ntncfx8PAQe3vj0zNi8SLP4eHhmcLqtR61yDg2H4+OjrC3t9e02PPyfp6n\nKw16ltFlqufY9PJn1oavK9d3HDqsvbsnji1er+1xVMmFDJdZ4hlkrT3yPUqiZel9XH5rfOe18KuS\njQH9pogCvpWPJ89FhRjISrdaUaRIz17vG0nr9TGzwstY+gzM2f3rADwAlPtZ2UzFpayn4q08baXW\nOhQNWBvot7KVdcnleJFb2coGyxb0W3ngZC2gL6W8qpTy8VLKJ0spb15BeY+WUt5fSvmNUsr/LqX8\n/Wn6s0op7y2lfKKU8kullDtL1LFTSvlIKeXx6fcXllI+MO3Dj5dSFg4KlFLulFJ+qpTyxLQPX7/i\ntn9XKeXXSykfK6W8s5RysEz7SynvKKXcLaV8jNLS9pZSfrCU8qlSykdLKS9eoOzvmY7NR0spP1NK\neYiuvXVa9hOllFcOdYDDTPfjg1NF+y0AjwHYB/BRAF+zZJnPBfDi6fltAJ8A8DUAvhvAP56mvxnA\n25eo47sA/GcAj0+/vxvAt07P/zWAb1+i7P8I4I3T8z0Ad1bVdgDPA/DbAA6o3a9fpv0A/iKAFwP4\nGKXZ9gJ4NYD/Nj3/egAfWKDsVwDYmZ6/HcA/n57/OQC/Nh2zF05xVbrtXwPoXwrgF+j7WwC8ecV1\n/Nx0oD4O4OFp2nMBfHzB8h4F8N8BvJxA//s0ES8F8IsLlv0QgP9j0lfV9ucB+AyAZ03B8TiAvwLg\n95ZpP06N1sca7X1iev7DAP4m5Xsi8o2WLdf+OoD/5LAD4BcAfH2v7eugN48A+Bx9//w0bSVSSnkh\nTi3FB3A6uHcBoNb6FIDnLFjs9wP4RwDqtI5nA/jDWmsE0j+PU3AtIl8B4P+VUn5kSp/+bSnl5qra\nXmv9HQDfC+CzAJ4E8AUAHwHwRytqf8hzpL0PT9N1vp/EcvP9JgA/v0zZTytHtpRyG8BPA/gHtdY/\nwRSkJHPHZ0spfw3A3VrrRwFwHHhVm9/3AHwdgH9Va/06AF/EqQVbuu0AUEp5JoDX4NR6Pg/ALQCv\nWri147LyWHgp5Z8CmNRaf3yZctYB+icBvIC+PzpNW0qmjthP43Tpe880+W4p5eHp9efidEmfV14G\n4FtKKb8N4McB/GUAPwDgTiklxm+ZPnwewOdqrR+efv8ZnCrBKtoOnNK83661/kGt9RjAz+K0T89c\nUftDsvY+CeD5lG+hukopbwDwTQC+jZIXKnsdoP8QgBeVUh4rpRwAeB1Oeeay8h8A/Gat9Qco7XEA\nb5ievx7Ae/SmntRa/0mt9QW11j+D07a+v9b6twH8MoBvXabsafl3AXyulPJnp0nfCOA3VtH2qXwW\nwEtLKdfL6R6HKH/Z9hfMrnbc3jdQeY8D+LsAUEp5KU5p1d15yi6lvAqn9PJbaq33pM7XTaNRXwHg\nRQB+tdvyZRzGRT84XV4/AeBTAN6ygvJeBuAYp5GgX8MpZ30VgD8F4H3Tut4L4JlL1vMNOHdkvwLA\nBwF8EqeRkP0lyv0LODUGHwXwX3AavVlZ2wG8DacO5McA/ChOo2YLtx/AuwD8DoB7OFWqN+LUUbbt\nBfAvcRpZ+V8Avm6Bsj+FU2f8I9PPD1H+t07LfgLAK0fav92GsJUHTp5WjuxWtjIiW9Bv5YGTLei3\n8sDJFvRbeeBkC/qtPHCyBf1WHjjZgn4rD5xsQb+VB07+P4aESELTAKvJAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fc419050090>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.imshow(Dmean[:,:,1],cmap=plt.cm.gray)"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"my_cmap=plt.cm.jet\n",
"my_cmap.set_bad(alpha=0)\n",
"Good_ICs=np.zeros(S[3])\n",
"Label_ICs=[]\n",
"pylab.rcParams['figure.figsize'] = (15, 2.5)"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"algorithm = linear_model.LinearRegression()"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"Sxk=Xk.shape"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"(10608, 8)"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Sxk"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"X=np.zeros((Sxk[0],2))"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"X[:,0]=(Xk[:,0]-np.mean(Xk[:,0]))/np.std(Xk[:,0])\n",
"X[:,1]=(Xk[:,1]-np.mean(Xk[:,1]))/np.std(Xk[:,1])\n",
"#X[:,2]=(Xk[:,3]-np.mean(Xk[:,3]))/np.std(Xk[:,3])\n",
"#X[:,3]=(Xk[:,4]-np.mean(Xk[:,4]))/np.std(Xk[:,4])\n",
"#X[:,4]=(Xk[:,6]-np.mean(Xk[:,6]))/np.std(Xk[:,6])\n",
"#X[:,5]=(Xk[:,7]-np.mean(Xk[:,7]))/np.std(Xk[:,7])"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"(46,)\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAApYAAADICAYAAABS6aGkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztnXmYHWWZ9u+n9+7TW5q0gRCSAAECqCyyKYz0CAjKBQgq\ngt8MoKACyqDjhzguF4kzo4Ab+uGOMMqwiOKCILKIrTMKhNWEJIQlmJCV7J2k9+73++M5L/We6jpr\n1TlVp/v+Xde5qk6dOlVv7Xc92yvGGBBCCCGEEBKWmrgbQAghhBBCJgcUloQQQgghJBIoLAkhhBBC\nSCRQWBJCCCGEkEigsCSEEEIIIZFAYUkIIYQQQiIhEmEpIp8SkedEZLGI3CYiDVEslxBCCCGEVA+h\nhaWIzARwBYAjjTFvBlAH4LywyyWEEEIIIdVFXUTLqQWQEpFxAC0A1kW0XEIIIYQQUiWEtlgaY9YB\n+DqA1QDWAthujHk47HIJIYQQQkh1EdpiKSKdAM4CMAfADgC/EJEPGmNu983HviMJIYQQQhKCMUai\nXmYUyTsnA1hpjNlqjBkD8EsAbwua0RjDT8I+11xzText4IfHppo+PC7J/PC4JPPD45LcT7mIQliu\nBnCciDSJiAA4CcDyCJZLCCGEEEKqiChiLBcB+AWAZwD8DYAA+GHY5RJCCCGEkOoikqxwY8xCAAuj\nWBapLD09PXE3gWSBxyaZ8LgkEx6XZMLjMvWQcvrZM1YkYiq1LkIIIYQQkh0RgUlo8g4hhBBCCCEU\nloQQQgghJBooLAkhhBBCSCRQWBJCCCGEkEigsCSEEEIIIZFAYUkIIYQQQiKBwpIQQgghhEQChSUh\nhBBCCIkECktCCCGEEBIJFJaEEEIIISQSKCwJIYQQQkgkRCIsRaRDRH4uIstFZKmIHBvFcgkhhBBC\nSPUQlcXyWwB+Z4w5GMBhAJZHtFwSwMsvA7t2xd0KQgghhJBMQgtLEWkH8A/GmFsAwBgzaozpC90y\nkpV584Crroq7FYQQQgghmURhsdwXwGYRuUVEnhaRH4pIcwTLJTnYtCnuFhBCCCGEZFIX0TKOBPBx\nY8yTInIDgM8CuMY/44IFC14f7+npQU9PTwSrn5qsWhV3CwghhBBSLfT29qK3t7fs6xFjTLgFiMwA\n8KgxZr/09xMAXG2MOcM3nwm7LqKI6JC7kxBCCCGlICIwxkjUyw3tCjfGbATwqogcmJ50EoBlYZc7\nlRgbA37wg7hbQQghhBASjtAWSwAQkcMA3ASgHsBKAB8yxuzwzUOLZRZeegk44IDCLZB1dSpGx8c9\n6yUhSccY4De/Ad7znrhbQgghpFwWy0iEZUErorDMyooVwPz5wOAg0NiYe96xMaC+HmhpAdatA9rb\nK9NGQsKyeTPQ3Q2MjgK1tXG3hhBCpjaJdYWT8NialMPD+efdvVtF5bRpwPbt5W0XIVGyc6cOt26N\ntx2EEELKB4VlArDCcmQk/7y7dwOtrcCaNcCcOeVtFyFRYl+EtmyJtx2EEELKB4VljMydq67t3bv1\neyHCsq8PaGsra7MIKQt96W4ThobibQchhJDyQWEZEyMjWouyr89zgRciLLdtA7q6gOeeK2/7CIka\ne34Xcp4TQgipTigsY2JgQId9fZ4Fp9AYy1QKOPRQzQ4v5D+EJIHR0cwhIYSQyQeFZUxYYTk87AnL\nQiw5/f2avAPocPduFadMuCdJxwpKWiwJIWTyQmEZE1ZYDg0V5wofGACa0z2xp1IqNDs6gGuvLU87\nCYkKe37TYkkIIZOXqhKW110H/OhHcbciGqyw/Pd/98qvlCIsbeLPihXRt5GQKKHFkhBCJj91cTeg\nGD77WRVTH/lI3C0JT3+/Du+6C9i0SceLdYW7wnJsLPo2EhIlTN4hhJDJT9VYLJcu1eFkKVViLZaA\nV4alWItlS4snUJnEQ5IOk3dIXIgAf/5z3K0gZGpQNcLyjW/U4WR5KLnCspis8IGBYIvl4GC07SMk\naugKJ3HCcCFCKkPVCMvJhrU0Ap4oLNQV7sZY2l57Josll0xemLxD4mR8PO4WEDI1iExYikiNiDwt\nIvdEtczJjGuxtOOluMJt4o8VmIQkFVosSZzw5ZuQyhClxfJKAMuiWtiDDwJnnRXV0pKHKyx37NBh\nocLSdYVv3qzjFJYk6TB5h8QJzztCKkMkwlJEZgF4N4CbolgeANx2G3BPCNvnSy9F1ZLy4ApLKwoL\nibH0u8KtxXLnzmjbR0jUWIslE81IHLByBiGVISqL5TcBXAUgsv5fwrgtXn0VOOCAZPdG48ZYWkqp\nY7lli36nxZIkHbrCSZwwtpeQyhC6jqWInA5gozHmWRHpASDZ5l2wYMHr4z09Pejp6cm63JoQktda\n8UZHgfr60pdTTlyLJQA0NhYmpl1XeEuLCsvubq8WJiFJxQpKWixJJbEGBlosyVSnt7cXvb29ZV9P\nFAXSjwdwpoi8G0AzgDYR+akx5gL/jK6wzEdDQ/bfjNG6ZNmw1sDBweoRlu3thQnLIFd4VxewZo0K\n6bqqKnlPphK0WJI4sIKSLzRkquM36C1cuLAs6wntCjfGfM4YM9sYsx+A8wA8EiQqi8UKwq1bJ7p5\n8wkwK9qSXNvRLyzb2oq3WLqu8PFxz1JLSBIZGdEXQj7gSSWxLzJJfh4QMplIbB1La7GcMwd417u8\n6W1t+RNVwgrLl18GFi8u7b+F4o+xLEZYuuWGNm8Gmpr0+7PPRttGQqJkdFTPWVosSSWhsCSkskQq\nLI0xfzLGnBnFsqzFcteuTJHX1ZU/USWXsHzgAa9ETxDf+AYwbx5w2GHFtbdYbI85lra24rPCW1vV\nYtnUBJx+emXrtP30p8B73lO59ZHqxwpLWixJJbEhGBSWhFSGxFos3V4SBgaAGTOAVavCWyxPO03F\nYza+973i21osO3ZoOaWODm9aKa7w9naNH2pqyuzesRLcdx/wm99Ubn2k+hkZocWSVB5aLAmpLIkV\nlu7Dxz6QZs9WAZbLYnnRRcAVV+j44CDwl7+oa9ulry/7/yuR7PPkkzr87neBa67R8UKTd1xXeHu7\nDpub1XpZSWGZK7mKkCBosSRxQGFJSGWpCmEJZLp/XYvlhg2ZFsif/MTryWZgADjhBODss4GnnvJc\n4LW12dcbpsxRoVjXzNy5wNFH63hbG/C1r3ltz0Z/v2extBZPa7FkLUuSZBhjSeKAwpKQylI1wrK1\nVYd+V/jttwOf/nTwMqwFcGwMOOoo4JJL9HuQsBTxMqwBrStZLgYHgcMPB976Vm99dnvXrcv+P2P0\nv36LZRyucEKKxXoeaLEklYQxloRUlqoRlm1tOmxtzbTM5XLJ2huJLZBr/+cXlvb3DRtUYDY3a5JQ\nuRgc1J6B7LoAFbVuG4MYHtY6ldaq6gpL/34pN0nu1aiSfOUrwCc+EXcrqgNaLEkc2PPNX+KNEFIe\nqkZYZrNY5hKW1mJpE4Hs0O/utjec3bv1P7/6VXl7aRgc9EoE2eGpp3ptyIYbX+n+t66OFsu4uOEG\n4DvfibsV1cHIiJ6/tFiSSkJXOCGVpeqEpd8ylysm0t5IrKC0QtNvbbNCdft2naezs7xvt0NDnii0\nQvH887VkUC6ro19YWqwlKKj/cVJemMRUOLRYkjgYGdGkTApLQipDooWlm6FtXeHZyg0FuWb9NxJr\n0fM/2KyYs8Kyq6u8Ii3IYplKqWjMJWizCUsbu1ZtwnJ0VMMBqrkP36R2GZpErLD89a+B9evjbg2Z\nKoyM6HODwpKQypBoYbnfft73adN06M8KtyIxKIvc3khsv+JWePldca7FcnBQRV5NTflcdoODXnJQ\ndzdwzjkqMPMJS1eQuoyOapurTVi6IQjVCoVl4dgXIAD4+tfjbQuZOoyO6nODwpKQypBYYTk6qnUr\nLVZY+utYWnHiF2QdHdmFpV+EWmG5Y4daLBsby2sBdAViKgXcfbeONzXlvvlls1jutVflLZZRJO/Y\n41Btgtilri7uFlQP1mIJVKasFyEALZaEVJrE3t5HRjTb9oYb9LsrLF2Lpb1ZnHWW1rC0BAlLKz6z\nCUvrCrfleyohLF2am7XWZrYuJ4P+t3Yt8NnPVl5Y2hIedlgK9jhUs8UyV01UkolN3gG430jlGBnR\nChoUloRUhkQLy+5ur5RLZ6cO/ck79mbxpz8BN9/sTc9nsXTd3G6MpXVTt7SUT/C4yTsuTU3A5z+v\n2x1EkMVy5kx1x5azvUHYRKgw4QKTQVjSYlk4o6NeshPLVZFKQYslIZUltLAUkVki8oiILBWRJSLy\nL1E0zCbvWMuGFVTZLJZApju8o8MTjDY5xM57222ZBdB37tR12VqSdXWVc4W7BLm5XbK5woHKx1ha\nQVlIN5TZsMIyzDLihsKycEZHtSesU07hQ55UjtFR774ZxsNCCCmMKCyWowD+1RhzKIC3Avi4iMwP\nu1B/Vri9MfgFnysmXYHS0QFs2zZxHpePf1xF586dwKxZwMaNmbGP5bKkZROWQdMK+R9QeVd4lBbL\nahYZdOkWzsiIvtCdc051H3NSXYyM6Atgvhh2Qkg0hBaWxpgNxphn0+O7ACwHsHfY5brCcsEC4Ljj\ndNwvoNwbhWvJ7OgAtm7VcVcgumL1u9/VG8727cA++2jPO9aSWW6LZVCXkWEslnEJy6lusaSwLJzR\nUb3++IAnlcQ+S3jeEVIZIo2xFJG5AA4H8HjYZbnC8pprvGzSlpZMC6RfWNquGNvbgUcf1fHt2715\nOjomruvllydaLONwhRdisUyasJzqFku6wgtndJSWI1J5KCwJqSyRPRZFpBXALwBcmbZcTmDBggWv\nj/f09KCnpyfr8qx1w09zc3ZX+M6dwIwZaqlMpbyYSdvzDqDC0p91vWoV8Na3qut87lydVk5XeLbk\nnUIsltnEp63bOT5emVIutFhm4g/dIBOhS5LEAYUlIUpvby96e3vLvp5IhKWI1EFF5a3GmN9km88V\nlvmw1g0/QRZLe8MYGlJB+MY3Aoccor8/9pjnRgc8i+W55wJ33aXjq1bpd6ByrvBSLJa5XOEiXoH1\nVCp8G/MxNBS+3+fJYLG02z8wQGGZD9cVXs4uUwlxsc+SbduA558HDjgA+Otf1ZhAyFTCb9BbuHBh\nWdYTlW3rZgDLjDHfimh5r1s3/FjxZMuVDA5mure7uoAlS7ySPfvsk/l/O69bfH31au+7jZlLYlZ4\nruQdoLLu8KEhzdCf6hZLKyw3bYq3HdWAa7GksCSVwlost24FzjhDpy1ZEm+bCJnMRFFu6HgA/wfA\nO0TkGRF5WkROC7vcbK7wmhqthWfFiF9s2RhL+983vCHz/7Yepo3ZtOy5pw5tzctyZ4UHJe+42+G6\n7y25LJaAbpt1/5eboSEV6VPdYmm34aqr4m1HNWCvab/XgZByEhSmMhmT7g45BHjiibhbQUg0WeF/\nMcbUGmMON8YcYYw50hjz+7DLzeYKBzItc34XpO2hxz7w/cuwFku/5c8KUFvAOZXKLMQeJYW4woPE\nlu1uMhvz5gEvvRS+fYUwOKgi/9FHNTmqFBEeRS3MuBkeBt72NuCgg+JuSfKx13SlE83I1MYKy/vu\nA97yFp02GYXl8uXaUQghcZPYnndyCUs3gWdwMHM+a9E78USNr7Tst58OrfD0C7QZM3RoheUee5TP\n+leIKzzowTs87LUviAMPBF54IXz7CmFwEFixQruTPPRQ4LQSbNSTwWI5PAwcfzxd4YVgXeEUlqSS\nWEv5vHnAjh06bTIKS2Bid8WExEFVCku3951duzIFmf1PfT1w7LHe9KOO0uH06Tr0Czu7DNeF/tpr\npbc/F7m6dARUPAY9ePNlHu+9N7BuXTRtzMbYGPDVr2ZaGdetA556qvhlTYYYS9v1qH1gkezQFU7i\nwL7QdHV5tY0na5kwCkuSBBIrLLMl7wDAXnt5AqqvLzMLOpvwsvO4rvCzzgIOPlizBN1lA+UVlvks\nlt3dwa7lfMJyzz21Fmc52bAB+MxnJvb1XMqNerJYLCksC4MWSxIH9r7Z2en1xjbZ+qq391J2WUmS\nQCKF5fi4XvjZ6jHuvTewdq3O09eXmaBjXd0us2ZpHByg7mJAXeG/+hWwbJm6dAFd5o9/rOPlFpZB\nsZLWzT19emmu8BkzVPiVk2wu31JK7UwGiyWFZeFYL0Rzs3ocgh7u731v+a47MjWxwrKuznumTDbL\nnvXgub3PERIXiRSW1mVmM7T9zJkDrFypD/XaWuDGGzWJ5Mkngauvnjj/6tXAJZeoG/eII3RaU5O3\nfDucOVPd7EA8Fss99tAanH/7m+e6d0mCxdIVlq44ziV4/axapcJ5slgsp0/XFxySHWP0+qur885h\n/7W6ezfwy18CL75Y+faRyYt737ReockmLO39h/chkgQSKyxzuVbf9CbguedUnLS0qPv6uOM04y/I\nEmiFY02Nd4PJV4y8s1PjN8OU0wliZEQfskECsaUld321fMKy0hbLjRuBU0/V8Xw1OF3mzgU+8Qlv\ne6rVYmmMxgrutVdmt6FkIqOj+hLoviwuWpQ5j008474kUeKWrrNl5qK+r8eNFZS8dkgSqEph2d2t\nQdgDAxPrUebD3mByle0BVIROnx691dLWosxmjc1FPlf49OkaQ1TOOBtXWHZ0eAXoi42xfOklFZZt\nbdVrsRwZ8c6TOG/ow8PAn/8c3/oLwV+X9tZb1ULvsmyZDm0cHCFR4Mbr2+fFZLVY/vKXwL/+a7xt\nIaQqhaUtXt7fX5ylDCjcYgkA++4LvPJKccvPRyli2JLPYmkzH8tZ+sa/bLsfi83y3bpVt6e1tXqF\npX1JaG7WuOC4tuMPf9DyWknGf03vvbeXoWt57jkd0upCosR9IW9t1eFkFJY2jOvRR+NtCyGJFJa5\nMsKBTGFZrEizyy0kJrAcdSFLEcOWfMISUHd4OeMsN23K3OfW6lRslu+mTZ7Fslpd4a71ubMzPkFU\nDQ9J/zXd2jqxAwLbzz0tliRKhoc9D9Xcud60yURfn76sAV7vcoTERSKFZaEWy3xdHAZhXdCFWCwP\nOih6YVmIxXL9+mABOTycX1juu295e9/ZtEmTpZYv1++f/CTwyCPFC8vXXps8FktAqxHEJSyroXSK\n3xXe2joxg9XGq1JYkihxeyy75RbtzKEaXsaK4ZFHvN6/Zs6Mty2EJFJYltNiabF9iufiTW8Cnn66\ntOVno5A2T5+uGbR+wTAykt/SevjhmlVeLjZt0l6M5s/X752d6oYdGgru3zwIW0t0zRq1WD7yCPCB\nD5SnveXEFZZujbxKcOONwJFH6virr+owrMAcHgYefjjcMrJRiMVycJCJUCR6hoYyS7kdf/zkE5ZP\nPQWccgrw3//NGrEkfhIpLPNZ9VIpYPNm4IEHSnMrr12rtS3z8Q//oN1CRmlR27kzs6B7ELbemv/m\nV4gr/PDDgWeeCdfGXGzapMlTLjU1agHOt5+2blWxvmuXt2+twL/rrvK0t1ieew74yEcKmzdOYXnv\nvXqch4eBK67QaWGTtu6/Xx9OYTAmOMbLLyzb2rILS1osSZS4rnBAReZkc4Xv2gX09OgLW1DnGoRU\nkkiEpYicJiLPi8gLIhJQSbI48ln1Uil9gF13XWkWy0JdBR0dWk/y3nuLX0c2XnnFi/PJRVPTxISY\nQlzhxxxT3uDtIGEJZPbfno2lS1W4jY1pwfq//U2FZpL4n/8BbrqpsHnjdIXb9boiLKwVZssWHZZi\n+Rwb0xCONWv02PqX4X+4p1L6MHTnGxjQa5PCkkSJa7EEJp+wXLJEQ7ZmzQr2BBBSaUILSxGpAXAj\ngFMBHArgfBGZH2aZu3fntuq5pXpKTYQplEsvVbdjVLz8MrD//vnna26eKCwLcYXPnKn/K0cPDKOj\n2sNMUBhBId30uRn21pXe0aGCs6ZGxUncFNOGOC2W7e06dNcZ9mFpew8qxZV299167tlELP/55xeW\nticU18o9OKjlq9jzDomS7dszE1oK8a5UE1/7mg7b270wMULipIQenidwDIAXjTGrAEBE7gRwFoDn\ns/1hfFwfNEND+mlq0jct+1DfutWLw8tHuWNlzjkHWLAAuPZa4MorM915NTX6GR31uqG0cYb19V5B\naCuEBwa0d6APfzj/erMJy3wWSxF9OK9eDRx6aMGbWRBbtqhlrrZ24m+FCMuVK73x6dN12NAAHHKI\nHu/t2yfWNjRG96/dF21twOOP6/9tv+41NZk9ugCaJblokYqdvfbS86uQbieLyVD3WyzXrCn8vy7G\naGiHiLaxqUn3iz1vtm1T9/z112t8K+Ct1xVhYa+F1at12N+fP1zDbfvIiBeLbI/Trl2e+AX0vPcL\nX5vAY7dlcFCt+YVUNRgY8La3qUnH7XUI6Dk6PKzTGht1v46N6aemxrsuRXReK3SBzH6X6+t1f9gC\n72NjemxSKW8+a3UV0WUMDel4U5P+5v+4XQvm2q/2MzqqH7t8F/cl2x1fuVL354wZXuUCu522vUFt\ns/cw26WuLWFTDCMjug9qa3Xf19R42zE46IVFuB8Rb522De69c3hY/9venrmd4+OZ+9Kue/du/Wzf\nrue12+1vY2PplSjcrkiD9n2uacXOX8gytm0D/vpX4L779Hu5LJb2+NXW5j93S11+odOLmRcovsYy\nCU8Uu3xvAK8639dAxeYEUim9Qdibc2OjDnft0ptGXZ2evJ2dwDXXFLbycpeqqa9XV/jllwNf/KKe\nvPYmaG+A9mKzH2N0O/3JLPX1mrVdSM3BIGFZiCscAObNA374Q7UKPvWUupy3btUHpN3PjY06HB/X\n4+EO/Rdofb137LKFERRrsbTudGvF6u7Wtn7qU9o15dCQunesRc7GD7a2qgitrVUx5j58W1q8JCIR\nYPZsnW/9eu8tvqVF9219vcYT3nJLZhutJcMe51y4wvLgg4ELLgDOPx9485tz/8/l0UdVNK5d64mh\noSF9QLa0aBvsg+KNb9SXHMATNS+95J0rYYXlDTfocPfu4HAHALj9di3AvHmzd67Y6xbwzgG/1eRD\nH5q4rPZ2fVB3d+t2DgxoyZS+vuCXqA0b9Bq87z49n+3vg4M67nYDa+8xdXW6T233r7W1meLJdjU5\nMuK92NoHUV2dTrfnixUx9oXYClRAh+PjnpA1xrs3uSLW3jvq6iYKuaDkNysm7fyuRd29Tv3X7NiY\nnpObN3v3EStQ7XKD2uaK7p071b2aSulL0+CgTs8Xy1tbq6J6dFT3e12dtkdE901jo9eW0dHg89a2\nz16H9p41OqrXtTGatDY4qG0cGtJ7xfi4rjuV8j6f/GRmTH0pwvKBB4DPfEa7G7XHwuIK9WzTip0/\n3zJceno0Zh3wQkyiYGgI+I//AH78Y732amq8e6ufYgRgsQStL9u9OWh6OTsMIcFUVMtfeeWC10XY\nP/5jD3p6egBkvp2uXKk3wkKtbZWIldl/f72xlIp9gLhv4PlYsUL3gXtxFmKxBIBPf1oF0xNPAEcf\nDVx8sT68Uynv5jw0lPkG6opjfzuHh1Uo7NqV+ebvUqiwPPlkzTx2LZaAioxTTwW+9CV9IDY0aDed\nnZ3apv5+r/blQQdN3I/GqHViyRJ9iB1yiLbVnW9kRM+t/n61ir3jHRPbaF24ftdtEK6wPP984Jvf\n1G0sVFiuWwecfTbw7W8D739/ZlvHxrz92dAAPPSQWiytsLQPxuefB846S60WYYSle5719+vy+/vV\nEmt56CE9t+6/X0Wue74Yo8fKWhsLcce1t+u5cOml+v/BQT2Purt1Oa4Y2L0bePvbgfe8R7d1zpzS\neq/Khb1O81lk7IOqVEuIFVOukPOL1Ki3rRRWrQL+/nf1Isyeree67Y620PbZl+za2tz7y31hd5ft\nvrwDek4uXqwvl7Nna/jGCy/oPaGrK/81C+g87gukjRtfs8brSczlkUeACy9UgfWud5XHYlcq/v0V\nVfLO+Ljek4wBenvVWGGFZTbBGFYAkvLT29uL3t7esq8nCmG5FsBs5/us9LQJfPnLCwIX4F6o1tVX\nKNUQhB3Vg6KQGEtABVOQaConhQjLv/8d+OMf1SJpH852ezo7gbe+FfjCF4L3VXt7pmvVj4iKoLe/\nPfs81qrV3q6ic8eOiWLdxhkODhYnLOvq9EXAdq1WCNdfD3zwg8C55078rbY20w154omZ81lhuWyZ\nPgzr671r4T//U5Ok7rij8Lb09elD6aCD9MF09dXAt77lPUTGx4HLLgP+67+AI46Y+H9bJN72VV+o\nsHzqKR23rs6mJrWKX365ng/vfa92VHD99cCxx+qwXBR6nYZ1rVkLZNKZM0c/YbBWykLmc4fudDf0\npqVFXzgtqVTxdRsbGzXWXUQT9S65RKtSnHvuRNFkDPB//y/w3e8Cp59e3HoqgX9/ReUK/+1v1SK8\naFHm/TFJopoUT0+PZ9ADgIULF5ZlPVGcJk8AmCcic0SkAcB5AO6JYLk5WbUK+NjH9KKfKhTqCo+D\nVEotjtni437+c71R7bOPzmtFon1o/Pa3mpFdqTfZmhovrtPFFZb58BfoL+amPj4O/OxnKqAKwcYg\nW7fm0JDuw+efV0FdX68ieXxcrZp33lnYci1bt6plqqVFReHixZm//+lPKnRPPTX7Mlav1mvSLs+l\nuVnDM1za270anBs3er1SNTXp+fC5z6nQNQb4yU+m1rVOykdTk3d+2xeh3/9eh/4Xomee0XvC2WdX\nrn1hcOONw3DzzRqWlNTnDUk2oYWlMWYMwCcAPAhgKYA7jTHLwy43H7NnA9//vvaiMBnxP4SBib2X\nJAlrgVm1Kvj359OpXNZCaQWkLb3U1BScFFROmpsnCkgrLAvp+3xgILMHp6DeZLKxeLEKtXnzCpvf\nWmRtzOnwsCYlvfxyprBctEgtfA0NxWW+btmiwjKVUoHntz7//vfFPVzPPDPze3s7cMYZmdOmTfN6\niZo9W0MDmpr0uOy5pzff88/r9hcTu0pINlwLqr1f3XyzDv29lt13n4ZfVIvrViR8ZvjYmL5ITtZn\nKyk/kRi2jTG/N8YcZIw5wBhzbRTLnOq8//2Zrl+bfZtUF9pll+kwm8Wuq8ubxzI2FuxWrRRBZUdy\nWSyvugpO1URqAAAbfUlEQVT46le9736LZVDR72wsWqQ9gBSDKyyHhrys+K4urzbfHXeo+7i7W2PH\nCuHVVzUWt6vLeyj5LY6PPab1KXNhXx4s/hqV/m5UZ8yY+CBvaQF+9SuNMb7tNt2nTzyhbvBqebiT\nZOMKS7dSxWmnqVXc9bo8+WSm670aCJvA88ILGgOfLZ6ekHwwYiKh+EWPzUhNaozLSSepRSrbDS2o\nX/e4tyUo837HDhUwQcLya18D3JCUMK7wxYuBww4rrr2ucHWF5axZnsXy/vuB972vuLasWOEts6VF\nSxi9+KL3+/i4xkIefXTu5di+ii1btmhGPhCceOZaJS3Nzdr29nbgvPPUcvroo/nXTUihuMLy5Zd1\neO65WpHg4Yc1bMfy1FPAW95S2faFpatLqwGUyrPPag9uhJRKQmUKaWzUh7G1+oyOJtdaaWlpyS5m\nwvTrXi6yWSxnzMjuCnetyEHCslBX+JIlxfc65IrFoSEva3r2bBVtQ0OaIHXggcW5w6x1cts2/d/V\n6b6z9t1Xh+vW6XYXWlv2ne/UNnV3a2KFzYL2C0srjC+5xHOzu1bJmhq10j7+uGb5ExIF9pqtrdXr\n5d57gVtv1ese8ITn9u16P7DXQbUwe7aWLysVCksSFgrLhCKSGSeXZDe4JShm0RJksYybbDGWM2bo\n9PXrvaxli9vrUCGu8B//eGKtTEBju4qtgNDWllkO6eSTVbwdcICeK+vX6zy2jl8xwjKVAr7xDS95\nZ+FCLwFg5criHq5tbZnVC9atC44Pttm8X/xicGY8oHGfzzwTPjuZEIstdWZL2u21l56vbkkjQK/R\ncpS1KjddXV73rKVAYUnCQmGZYBobtX7mhg3JTtyxBLmWLUkUlv7+2MfHvVqd73ynCp+jjsr8jxWW\nX/qSxgLmcoX/4AdqjfvoRzOXYfvVLrZMit9iOWeOuq1tr0OrVqk7DyheWF5xhRaMtz3uHHaYV9Lo\nlVeKE5a2Pqptx5YtXi9ULjZxa9YsFclf/OLEZdk6mhSWJCo6O7UOq/UY2Gva9vplK0WsWuWdo9XE\nHntMjJEuhHvv1Wt+2TLdP4SUCoVlgmlqUhfhxRdXhys8Vx+8SXSF24QXy86dXm8d/nIdVmS1turw\nmmvUupnLFX7ppTr0u5Bfe00fboXU93NxhaW/zqYVllasWstjIdhSQ4C3Pa6wLPYBOzoKfPnLWjD+\n0EPVxR5Uf3Xffb3Y4enTVaz7sT3NFNrFJCH5qKnRUBQb42vP/Y9+FLjookxhWY0vNF1dpQnLM84A\nHnxQXwSZuEPCQGGZYGwW7fBw9bjCq8li2diYKSx37FAR6M9eBrx6dyMjXkIKkCmWXVe4mxHtF5Zr\n1mT2KlMobW1ef+QDA5liq6FB48Vs3GIxPXBs2+a10T6Q3vAGT1i+9poXf1YIo6PAOedoV3qtrbr8\nbNb2fG7GQmNWCSkWe+3al8XmZuCEEzxhma0nnqRTisXSJvvY7mSTdq8m1QWFZYKxFinbDWPSXeG5\nLJZJFJYNDZl9Bm/dqq7XIGFpxeTQkPbNa3F7x3Etim7hdb+w3LEjs6vEQlmzRnvVASZagOvrtY22\nj+9iXOF9fV4b7fGz/Skbow8dG5dWCG5/1k1NKg5LPXfz9eZESKnYvtndl5vOTu1das899YXIjamu\nFkqJsbRVIFav1n1QbXGlJFlQWCYYK3BaWqrDFZ7LYplEV7jfYml7BnIFsN3n69frw2ZoSOu8Way1\nw47v2qX1I++915vu74qy1H3xla/ocGBgolC3wtIKwGLKDVlLLaC99ixe7PUdPzpavLB0C5k3NOj2\nlios77hDuwElJGqCeqfp7NThxo36cmi/VxOlWCx/9CMdWmFJSBgSLlWmNvZhbLvpSrqwzGaxHBhQ\n0ZN0i+Xq1SosraBfsQKYP18tcBs2aJzhwECmaPNbLHfunBif5I8PLFVY2gSalhZto1sHtL5eBa2N\nFyvEFT40pMs59FBP/O6xh7eMxkY9nps3e5bQfOzYkbltDQ3ajlKFZb6i7ISUysc/rqV5XFzvQrUK\nS2uxLMYY8eyzmkBHYUmigBbLBGPdgLbv16QLy2wWyw99SG9cSRSWrsXSxhK6luKWFj0O69apsBwa\nUsH10EM6j19Yuq7b971Ph65rGIgmLMAvTG1yjBWFhfS+YXvxWbo0+GFi3eHFWCzb2zPP07DCkpBy\nsc8+wOWXZ05zr4NqFZbt7foiX1+vpbpysXMn8Ic/qLfm0EM1Yakat5kkCwrLBONmAFdzjKUt1pt0\nV/imTWqZs6KvsdGzTq5dC+y/v25fX5+XfOMKy7q6zLI8J5ygQ9cqCkQTFuD/vz03inGFuy8BQVnf\nTU2esLSCtVgoLEk1YZPfgOoVlm1t3j3XdlGbjVtvVUvl5s1aV5cWSxIFFJYJxq1ZWA2u8GwWSyu+\n3HjEJOB3hVuXr72x2tJDu3d7wrKvT3/bf38tOeQvGeS6vf/5nzU+0C+2oxCWfounFW6uKzxfRrU9\nVo2NwRbUxkYvCalUC2tDg57HFJakGkil9D7Q0FDdwtKS7+XSjTOdNk23vdAetgjJRihhKSLXi8hy\nEXlWRO4Wkfb8/yKF4rdYJl1YZrNY2htd0moRBlksp0/3Mrabmz1huWKFuoq2btXtqa/XRBc/Vqgu\nWqSxTm1t0Vosf/ADHfoTD6wr3GaxplLAnXdqXbpsDAwARxyRPZO/sVFjtdwHVbE0NEyMuyQkyXR1\nafjKpk3VKbLcF/h8FstVq7xxu62lVKwgxCWsxfJBAIcaYw4H8CKAfwvfJGKx4mFoqDpc4dkslvZG\nVy0WS2udE1GBtmaNCkrbG0UuoTV/vorTo4/W79ad7BJGWNpefPyWCHtu2IeDjRPN1WdwvljPxkbd\nJ2GF5datyTv2hGRDxOs5qthODJKAm9SXS1j+7ndadcG6/20CXzVaaUmyCGUDM8Y87Hx9DMB7wzWH\nBDE4WB2u8GwWy/p64MQTkycurEXOsmWLupLXrfOmpVLAX/6iJXSsCMu1HbffnpnAYzOrXfr7va4X\nS8UvLG1NPvsgtAXN3ULtfgoRllu2hDtu9fUqLN3YNUKSjj/hrlqxoTtBnH66Dm+6CXj+eVosSXRE\nGWP5YQD3R7i8Kc/ixcA993gWy6QLy2wWy8FB4MILK9+efLhZ4c89p5mUXV3aT/iyZTq9tVUz2ufP\n94oGB3VPaGlqyiyqHGSxHBgI7xoeGcn8bsWrbeMRRwCXXZa9rqhtRyUslmHd6YRUmskiLPO5wgHg\nXe8CvvpVWixJdOSVKiLyEAC3QzcBYAB83hjz2/Q8nwcwYoy5PdeyFjhBaT09PehxuzAhE3jTm1SY\nLF0KnHkm8Pa3x92i3DQ3B1ssBweTV2oIyHSFX3edDm07Dz5Yh6mUluI46CDvf8WEJGSzWIYVlv4H\nX1BPG7kK1gOFC8swFku6wgmJjyBhuX59psfE9pluLZb771/+dpF46O3tRW9vb9nXk1dYGmNOyfW7\niFwE4N0A3pFvWQuCsh1ITqxrc2Ag+RbLpqbsFsugbhLjxk3emT0b+MhHJs6TSml9S1cI2virQtcR\ndbmhb3974v4MsjIkRVhu306LJak+irnOk8isWcHCctEiL0Tm4Ye9mEwrLG0sOZl8+A16CxcuLMt6\nwmaFnwbgKgBnGmOG8s1PiscNHk+6sMwmZAYGkiksXVf47t2eldIlldLsUDejvZgHTlDcaVhhecUV\nE0XwdddNjLu0x+Omm4AHHpho5bTF3rMRVVY4QIslqT5s3HI1smwZ8I1vBAvLlSu98ZNO8sbr61Vw\nJq16B6k+wkqV/wegAcBDosFdjxljLs/9F1IMriDLFduXBLIl7yTVFe5aE3ftChY/ra06T6kWy/p6\nfUC5MbL9/dHvj4aGiedHc7NaHK0I9ffGMzycW1i2tGhGfFDx9EKxy6ewJNXEWWfl7xI1yRx8sHpa\ngoTl1q3AcccBV15Z+XaRqUHYrPADomoICcZ98Cf9TbKaLZbZhKXd56UKSxF1MfX1eUk9UcRYFkJz\nc2aGuv9BOTSU+2Wlo0PLFYURhXY76Qon1cTdd8fdgvDY+46fvj7gAx8Azjuv8m0iUwP2vJNwXGGZ\n9CLTdXXqSvEX705qjKWbvJNPWLqivqbIq6az0+vBBogmK7wQUqlMYeknn8Wys1NLL4URhYWUaCIk\nadTWVn+MZXe3Wi399PV5GeCElAMKy4Rjy8cAyXQnu4gEWy2T7Ap3YyyDxI8VgHbY0wOcfXZx6xkc\nzMy0rJTF0vYa5OLWtRwezm2xtAlBYUQhhSUh8bDXXsC2bRNfLiksSbmhsKwiirWUxUFQnGXSXeE/\n/CHQ25tbWFqL5R//CFxeZBTx+vU6tIK7UsKypWWisHQfMvmSd2yh5DAWS7rCCYmHmhpgzpzMbhsB\nCktSfqpAqhCLvyh2EslmsUyisLTJOx/7mH4PEpbW4haFEFy9WoflSN4JIshi6X7PZ7G0veXQFU5I\ndTJrlibguVBYknJDYVlFVIOwDLJYJtUV7ibvAIVZLEvhO9/Rdf3978DPf54cYZnPYjlzpg6jsFhS\nWBJSefbeWxPwXHbupLAk5YXCsgq49FIdVkMweZDFMsmucLd4edDNNgqL5eWXAxdcALzyCnDuuTqt\nEscylZrYI08xFssohKXdf3vsUfoyCCGlMX36xHsALZak3FBYVgHf+x4wY0ZmMduk4rdYjo5qwkgS\ni7u7yTtAsICKwmIJaC3IX/wi3DKKpbXVi++0uMLy9ttzWyy7u3X4hjeU3gabAOT2n04IqQytrWqh\ndOnrY8wzKS8UllXChg3aX3jS8VssrRvczW5PCtYVbkVvUHKUPyu8VN78Zu1KrZJ0dqqwt7GS3d2e\nsBwa0vFcRaBraoD77wfmzSu9Dd3dWmopiS8WhEx22toyheX4ePYKGIREBYUliRS/xTKpbnDAS97p\n6Aiu9wZ4rtywFsujj55oOSg3ts22D2BXWNoeOd797tzLOO208C8Fdv2EkMriF5a7dulLcjWEVZHq\nhcKSREqQxTKpwtJaLHO5hvbcEzj++PDdacbhCraCcHQUuPhidYtbq/f27cABB4TrrpEQkmz8wpLx\nlaQSUFiSSGluzrRYJjUjHFCxuGuXxoBmizVsagL+93/DW+3i7Od9bAy46SYtlmzhA4aQyU+QsGR8\nJSk3FJYkUpqaMi2WSXaFW7HX1pbMGNAoOOUU4PDDdfz8873plSp5RAiJjyBhydAUUm4iEZYi8mkR\nGRcR5n5OcarJFW7FZCXbN20a8MILlVvfr3+t2d+A9jBkk5AGBigsCZns0BVO4iB0rqaIzAJwCoBV\n+eYlkx9/8k6SXeGWXCV3oqalRWMbK7k+d3xgQDNDKSwJmfxQWJI4iMJi+U0AV0WwHDIJ8Fssk+wK\nt1Qy/jFb9nklqKnR49PfT2FJyFSArnASB6EsliJyJoBXjTFLZLIGqZGiqEaLZaVquj3+ePxlPmw3\nj9Ug+Akh4fALyx07aLEk5SevsBSRhwDMcCcBMAC+AOBzUDe4+1tWFixY8Pp4T08Penp6Cm8pqQqa\nm7WUjaUaBEylhOUxx1RmPblIpTQTnsk7hEx+Uim9B4+N6Usts8KnNr29vejt7S37evIKS2PMKUHT\nReSNAOYC+JuouXIWgKdE5BhjTKDDzxWWZHISZLFMurA8+ui4W1A5WlvVYnnFFcCxx8bdGkJIOamp\n0djq/n4VlP39mkBIpiZ+g97ChQvLsp6SXeHGmOcA7Gm/i8grAI40xmzL/i8y2cnWpWNSeeUVYObM\nuFtROVIpr//wf/qneNtCCCk/qRSwdKnel/v7gb33jrtFZLITZR1LgzyucDL5qaYuHQHteSbO4uWV\nJpUCli8H5s8HPvGJuFtDCCk3LS3Apz4FvOMdKizdShGElIPQ5YYsxpj9oloWqV6qqY7lVKS1Fdi4\nkQH8hEwVUimvGkV/v34npJyw5x0SKVZY3nyz9lGddFf4VMM+ZPhwIWRq0NICjIzo+O7dtFiS8kNh\nSSKlsxPYsgW4+GJgyZLku8KnGlZY8uFCyNTAZoYDdIWTykBhSSJljz2Al1/W8S1b6ApPGrRYEjK1\nsFnhAIUlqQwUliRS9tgD2JauC7B5M13hScPGWFJYEjI1SKU8YUlXOKkEFJYkUjo7vfHNm+kKTxq0\nWBIytXCF5PbtvPZJ+aGwJJHidlloLZYUlsnBxlvx4ULI1MC91jdtosWSlB8KS1I2bIwlXeHJwXZf\nyYcLIVMD91ofGOC1T8oPhSUpGzt30hWeNKz1ghZLQqYG/mudwpKUGwpLUhbq6lRY0hWeLCgsCZla\n+IVkY2M87SBTBwpLEjlPPAF8//uesKQrPDlYVziFJSFTA/+1Lux4mZSZyLp0JMRy1FHA0BCwaxdd\n4UmDFktCphbWYtnQAAwPx9sWMjWgxZKUhbY2L8aSFsvk0N2tw46OeNtBCKkM9iWSLnBSKUILSxG5\nQkSWi8gSEbk2ikaR6mfaNM0K37XLc7+S+Jk5U4dtbfG2gxBSGazFkp4jUilCucJFpAfAGQDeZIwZ\nFZHpkbSKVD0zZ2ody5ERul2TREMDcPrpwAEHxN0SQkgloMWSVJqwMZaXAbjWGDMKAMaYzeGbRCYD\ntbUqKgGWt0ga994bdwsIIZXC3n8pLEmlCOsKPxDA20XkMRH5o4gcFUWjyOSgtxc45xyghpG8hBAS\nC1ZY8j5MKkVei6WIPARghjsJgAHwhfT/pxljjhORowHcBWC/bMtasGDB6+M9PT3o6ekpqdGkOjjx\nRP0QQgiJB2N0yBhL0tvbi97e3rKvR4w960r5s8jvAFxnjPlT+vtLAI41xmwJmNeEWRchhBBCiqOv\nD3jve4EbbwS2bQOOOy7uFpGkICIwxkRe2TSssPwogL2NMdeIyIEAHjLGzMkyL4UlIYQQQkgCKJew\nDJu8cwuAm0VkCYAhABeEbxIhhBBCCKlGQlksi1oRLZaEEEIIIYmgXBZL5okRQgghhJBIoLAkhBBC\nCCGRQGFJCCGEEEIigcKSEEIIIYREAoUlIYQQQgiJBApLQgghhBASCRSWhBBCCCEkEigsCSGEEEJI\nJFBYEkIIIYSQSKCwJIQQQgghkUBhSQghhBBCIoHCkhBCCCGEREIoYSkih4nIoyLyjIgsEpGjomoY\nqQy9vb1xN4FkgccmmfC4JBMel2TC4zL1CGuxvB7ANcaYIwBcA+Cr4ZtEKgkv+uTCY5NMeFySCY9L\nMuFxmXqEFZbjADrS450A1oZcHiGEEEIIqVLqQv7/UwAeEJGvAxAAbwvfJEIIIYQQUo2IMSb3DCIP\nAZjhTgJgAHwewMkA/miM+bWIvA/Ax4wxp2RZTu4VEUIIIYSQimGMkaiXmVdY5vyzyHZjTKfzfYcx\npiPXfwghhBBCyOQkbIzlWhE5EQBE5CQAL4RvEiGEEEIIqUbCxlh+BMC3RaQWwCCAj4ZvEiGEEEII\nqUZCucIJIYQQQgixlL3nHRE5TUSeF5EXROTqcq9vqiMis0TkERFZKiJLRORf0tOniciDIrJCRB4Q\nkQ7nP98WkRdF5FkROdyZfmH6uK0QkQvi2J7JhojUiMjTInJP+vtcEXksvZ/vEJG69PQGEbkzfVwe\nFZHZzjL+LT19uYi8M65tmUyISIeI/Dy9T5eKyLG8ZuJHRD4lIs+JyGIRuS19XfCaiQER+bGIbBSR\nxc60yK4RETkyfZxfEJEbKrdl1U2W43J9+lx/VkTuFpF257fAayGbVst2veXEGFO2D1S4vgRgDoB6\nAM8CmF/OdU71D4A9ARyeHm8FsALAfADXAfhMevrVAK5Nj78LwH3p8WMBPJYenwbgZWid0k47Hvf2\nVfsHWqLrvwHck/7+MwDvT49/D1pZAQAuA/Dd9PgHANyZHj8EwDPQMJa56etL4t6uav8A+C8AH0qP\n16XPe14z8R6TmQBWAmhIf/8ZgAt5zcR2PE4AcDiAxc60yK4RAI8DODo9/jsAp8a9zdXwyXJcTgZQ\nkx6/FsBX0uOB1wJyaLVs11uuT7ktlscAeNEYs8oYMwLgTgBnlXmdUxpjzAZjzLPp8V0AlgOYBd3v\nP0nP9hN4x+EsAD9Nz/84gA4RmQHgVAAPGmN2GGO2A3gQwGkV25BJiIjMAvBuADc5k98B4O70+E8A\nvCc97h6vX6TnA4AzoQ/MUWPM3wG8CL3OSImk3+b/wRhzCwCk9+0O8JpJArUAUmkrSTOAdQD+Ebxm\nKo4x5n8BbPNNjuQaEZE9AbQZY55I//+n8I4ryUHQcTHGPGyMGU9/fQyqAYDs10IureZ/Rp2dr03l\nFpZ7A3jV+b4mPY1UABGZC32TeQzADGPMRkDFJ7zapNmOkX/6WvDYheWbAK6C1oGFiOwBYJtzA3Cv\nj9f3vzFmDMAOEekCj0s52BfAZhG5JR2m8EMRaQGvmVgxxqwD8HUAq6H7cgeApwFs5zWTGN4Q0TWy\nd3oe//wkPB+GWoCB3Pt/wvHK8oyamW+FZY+xJPEgIq3Qt/Yr05ZLf5ZWtqytyIulEkBETgewMW1N\ndvdxofubx6V81AE4EsB3jDFHAtgN4LPgNRMrItIJtZrMgT7MUijOAszjUnl4jSQIEfk8gBFjzB1h\nFlPsH8otLNcCmO18nwX2J1520m6jXwC41Rjzm/TkjWlXBNJuh9fS09cC2Mf5uz1GPHbRcjyAM0Vk\nJYA7oO6Fb0FdRPY6dPfx68dFtJxXuzFmK7IfL1I6awC8aox5Mv39bqjQ5DUTLycDWGmM2Zq2QP4K\neh118ppJDFFdIzxGESMiF0FDrz7oTC7quBhjtiD79ZaVcgvLJwDME5E5ItIA4DwA95R5nQS4GcAy\nY8y3nGn3ALgoPX4RgN840y8AABE5Dupm2gjgAQCnpLNlpwE4JT2NlIAx5nPGmNnGmP2g18Ejxph/\nAvBHAO9Pz3YhMo/Lhenx9wN4xJl+XjoDdl8A8wAsqsQ2TFbS5/urInJgetJJAJaC10zcrAZwnIg0\niYjAOy68ZuJDkGnBiuQaSbvRd4jIMeljfYGzLJKfjOMiIqdBw67ONMYMOfNluxaCtJrd/48g+HrL\nTgUylk6DZia/COCzlcqUmqof6Bv9GDSr6xloTNJpALoAPJw+Fg8C6HT+cyM0I+xvAI50pl+UPm4v\nALgg7m2bLB8AJ8LLCt8Xmg35AjT7rj49vRHAXen9/xiAuc7//y19vJYDeGfc2zMZPgAOS99cnwXw\nS2jWKq+Z+I/LNenzfDE0caCe10xsx+J2aPLUEFT0fwia5R3JNQLgLQCWpH/7VtzbWy2fLMflRQCr\n0s//p5GulpCeP/BaQBatlu16y/VhgXRCCCGEEBIJTN4hhBBCCCGRQGFJCCGEEEIigcKSEEIIIYRE\nAoUlIYQQQgiJBApLQgghhBASCRSWhBBCCCEkEigsCSGEEEJIJPx/SQOxPrvFZOgAAAAASUVORK5C\nYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fc3e51cf3d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"pylab.rcParams['figure.figsize'] = (11, 3)\n",
"#plt.plot(X[:,0])\n",
"#plt.plot(X[:,1])\n",
"plt.plot(X[:,1]-X[:,0])\n",
"#plt.plot(X[:,2])\n",
"#plt.plot(X[:,3])\n",
"#plt.plot(X[:,4])\n",
"#plt.plot(X[:,5])\n",
"zero_crossings = np.where(np.diff(np.sign(X[:,1]-X[:,0])))[0]\n",
"print(zero_crossings.shape)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Plot all components for turning left, right, walking, and grooming"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"Rsq=np.zeros((1,S[3]))\n",
"Betas=np.zeros((2,S[3]))"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"(10608, 2)"
]
},
"execution_count": 25,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"X.shape"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"(10608, 169)"
]
},
"execution_count": 26,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"DT.shape"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"for j in range(S[3]):\n",
" model = algorithm.fit(X, DT[:,j])\n",
" Betas[:,j] = model.coef_\n",
" Rsq[:,j] = model.score(X,DT[:,j])"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"RsqUni=np.zeros((6,S[3]))\n",
"BetaUni=np.zeros((6,S[3]))"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"Sx=X.shape"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"for k in range(2):\n",
" for j in range(S[3]):\n",
" model = algorithm.fit(np.reshape(X[:,k],(Sx[0],1)), DT[:,j])\n",
" BetaUni[k,j] = model.coef_\n",
" RsqUni[k,j] = model.score(np.reshape(X[:,k],(Sx[0],1)),DT[:,j])\n",
" "
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[<matplotlib.lines.Line2D at 0x7fc3e50a3950>]"
]
},
"execution_count": 31,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAApcAAADICAYAAAC9K8qaAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvXmcXGWZ9n/d3Z1Opzt70glZSUIgJJEliQRRwcgiqCg4\nzjjgyysqo86LyKujI6LjQAYXhnEZMQLvvOP6kxFmRl4GdUDWlkUgCQECIStL9pBO0p1e0lm6+/n9\ncddjPXXqOec859Q5Vaer7u/nk0+6q2s5VXXqnKuu677vh5RSEARBEARBEIQkqKv0BgiCIAiCIAjV\ng4hLQRAEQRAEITFEXAqCIAiCIAiJIeJSEARBEARBSAwRl4IgCIIgCEJiiLgUBEEQBEEQEsNJXBLR\nRUS0gYg2EdF1lr9/hojWEtHzRPQ4EZ2cu/x4IjpERGty/25L+gkIgiAIgiAI2YHC5lwSUR2ATQDO\nA7ALwCoAlymlNhjXGamU6sn9/AEAVyul3ktExwP4jVLq1LSegCAIgiAIgpAdXJzLpQA2K6W2KqWO\nAbgLwCXmFbSwzDESwKDxO5W8lYIgCIIgCMKQwEVcTgOw3fh9R+6yAojoaiLaAuBmANcaf5pFRM8R\n0WNE9M6StlYQBEEQBEHINA1J3ZFS6jYAtxHRZQC+DuDjAHYDmKmU6iCixQDuJaIFHqcTRCRrUAqC\nIAiCIGQEpVTs5NnFudwJYKbx+/TcZX7cDeDS3IYdVUp15H5eA+BVACfZbqSUKsu/w4cVBgfL81il\n/Lvhhhsqvg1Z+ievh7we8nrI6yGvibwe8nqU51+puIjLVQDm5jq/GwFcBuA+8wpENNf49WJwAxCI\naGKuIQhENAfAXACvlbzVJfDe9wJr1lRyCwRBEARBEKqX0FhcKTVARNcAeBAsRn+slFpPRMsBrFJK\n/RbANUR0PoCjADoAXJm7+TkA/oGIjoKbfD6jlOpM44m40t7O/wRBEARBEITkcaq5VEo9AGCe57Ib\njJ8/73O7ewDcU8oGJk1vL//LOsuWLav0JmQKeT0KkdejEHk9CpHXoxh5TQqR16MQeT2SJXTOZVk2\ngkiVazsmTwZuuQW48srw6wqCIAiCINQaRASVckNPVTFUnEtBEARBEIShSE2JS6WAQ4dEXAqCIAiC\nIKRFTYnLvj4WmD094dcVBEEQBEEQolNT4lKLSnEuBUEQBEEQ0qGmxKUWleJcCoIgCIIgpENNiktx\nLgVBSJrt24F3vrPSWyEIglB5alJcinMpCELS7NgBbNlS6a0QBEGoPDUpLsW5FAQhaQ4cAA4erPRW\nCIIgVJ6aE5djx9aGuPzkJ4GtWyu9FYJQOxw4ABw+DBw9WuktEQRBqCw1JS57eniFnlqIxZ96imM6\nQRDKw4ED/H9XV2W3QxAEodLUlLjs7QUmTaoN57K7m+d6CoJQHjo6+H8Rl4Ig1Do1Jy5rxbkUcSkI\n5UU7l1J3KQhCrTNkxWV/P3DkSLTb1IpzOTjIz1HEpSCUD4nFBUEQmCErLn/2M+C666LdRovLQ4d4\nGchqRT+/Q4cqvSWCUDscOAA0NIhzKQiC4CQuiegiItpARJuIqEjSEdFniGgtET1PRI8T0cnG364n\nos1EtJ6I3pPUhu/alXcKXOntBUaPBoYNq25XT8f+1fwcBSFrdHQAM2eKuBQEQQgVl0RUB2AFgAsB\nLARwuSkec9yplDpVKbUIwD8B+H7utgsAfATAfADvBXAbEVESG37gQHRnrrcXGDmS/1VzNN7dzf+L\nuBTS5NgxoLOz0luRHQ4cAGbNklhcEATBxblcCmCzUmqrUuoYgLsAXGJeQSlltsiMBDCY+/mDAO5S\nSvUrpd4AsDl3fyUTR1z29AAtLfyvmpt6RFwK5eCee4DPfa7SW5EdtLgU51IQhFrHRVxOA7Dd+H1H\n7rICiOhqItoC4GYA1/rcdqfttnGI61y2tFS/cymxeLb4zneiN58NBTo7xaXTDA5yLC7OpSAIAtCQ\n1B0ppW4Dx96XAfg6gI9Huf2NN974p5+XLVuGZcuWBV6/o4NjuShocSnOpVAulAK+/nXgwguBU06p\n9NYkS0+P7GOa7m6guRmYMIHrwQXBxn33AWefDYwbV+ktEYRC2tra0NbWltj9uYjLnQBmGr9Pz13m\nx90A7jBuO8Pltqa4dOHAAaC+PtJNxLkUyk5vLy8J+Prr1ScuZdxVno4OYPx4YMwYcS4Ff779bT4H\nnXdepbdEEArxmnrLly8v6f5cYvFVAOYS0fFE1AjgMgD3mVcgornGrxcD2JT7+T4AlxFRIxHNBjAX\nwMqStjhHKbF4S0t1i8vubqCuTk78WWDfPv7/9dcrux1pIOIyz4ED7EaNHi01l4I/hw5VZ4mMIHgJ\ndS6VUgNEdA2AB8Fi9MdKqfVEtBzAKqXUbwFcQ0TnAzgKoAPAlbnbvkJE/w7gFQDHAFytVOkTJpXi\ng3nUvvNaisUnTpQTfxaodnEps1SZAwfyzqWIS8GP3l4Rl0Jt4FRzqZR6AMA8z2U3GD9/PuC23wbw\n7bgbaKOnBxgYiNctXgujiHp6eFi8iMvK097OX4KqVVzKPsaY4lJiccGPQ4eAo0crvRWCkD5DcoWe\njg5eIzzqSju15FyKuMwG+/YB8+eLuKx2dM2lxOJCEOJcCrXCkBSXBw6wuKyrc+8YHxzkE2Fzc/U7\nl93dQGurnPizwL59wNKlwGuvVd+SoyIu8+iaS3EuhSCk5lKoFYasuBw3joWiazTe1wc0NbEgrXbn\nUsfiUg9XedrbgblzeclRXX9ZLYi4zKNj8VGjWFxW2xcJoXSOHgX6+yUWF2qDISsux4+PJi51JA6I\ncymUj337uLlq9uzqi8Z7ezk5GBio9JZUHn1MGjYMGD5cvtgJxehzjjiXQi1Qk+Ky2kcRSUNPdtDi\ncs6c6hSXgOxnQL7mEpC6S8GOPleJuBRqgSEpLvWBPIq41OuKA9Ufiw+Vhh69klA1097OLnK1OpdA\n9vezcqC/8AJSdynY0Z8XicWFWmBIisu4zuXIkfyzxOLZYMmS6l8qr9pj8aam7O9n5UDXgQMy61Kw\nI86lUEsMWXEZtaHHG4tXs3NZ7lh82zZgZ9CCoD7s21f9Dk+1i0sZ1s+YzqXE4oINcS6FWmLIikvt\nXLo6kLXW0DNxIncmlqPZ4tZbgRUrot/u0CFed7taGRjIl3BUm7gcGGAHZtw4aV4BCmsuJRYXbIhz\nKdQSTiv0ZA1p6PFHqfxKRCNGsKukywHSorMzukjU4qSaxWVHBwuNhgZg1ixg+3Z+3vX1ld6y0jl0\niD9/LS3iXB4+zF/kmpv5d3EuBRvSLS7UEkPSuYzT0ON1Lqs1Fj9yhGd5NjbmxWXaHDzI0XgU9PtW\nzeJSR+IA1yaOH189Nab681SufSzLdHSwg0vEv4tzKdjQxzyJxYVaYEiKS3Eu/enu5kHOQPlO/J2d\nIi5ttLfnxSVQXeOIRFzmMestAXEuBTu9vXzOEudSqAWGrLiM2tBTK6OIdCQOlFdc7twZrb5Tv2/V\nLEz27eOufU2W6i63bgVWrYp/exGXecx6S0CcS8FOby+ft0RcCrVA5sTlv/xL8EnvyBH+N3Jk/FFE\nw4fzWuPVGE9Uwrk8eJBrzvbscb9NLTiXZiwOZEtc/va3wO23x7+9iMs84lwKLhw6xOKyGs87guAl\nc+LynnuABx/0/7t2CYjix+JE1RuN9/RUJhY//vho0bh+7atZXHpj8SyJy8OHS3NQRFzmMWdcAjLn\nUrAjzqVQSziJSyK6iIg2ENEmIrrO8vcvENE6InqBiB4iohnG3waIaA0RPU9E94Y91q5dwIYN/n83\nI6i44hKo/DiiF1/k55I03d2FsXjaY2KUYnF5yincDe1KrTiXWY3FRVwmh9e5lFhcsHHoEO8nIi6F\nWiBUXBJRHYAVAC4EsBDA5UR0sudqawAsUUqdDuDXAP7J+FuvUmqxUmqRUurSsMfbvTtYXJoH8lLE\nZaWdy7//e+CXv0z+fssdix8+zKN1TjwxmnNZK+LS61y+9lrltsekr0/EZVJ4ay4lFhdsaOdSYnGh\nFnBxLpcC2KyU2qqUOgbgLgCXmFdQSv1BKaVlwjMAphl/JteNOXqUD9QbN7IjZsOMoEoVl5Vs6unu\nLq2hwo9yN/R0drJTM3OmiEsv3lh8+nS+LAvORZLOZa0PURfnUnBB11xm4fMvCGnjIi6nATADzx0o\nFI9ergJwv/H7cCJaSUR/JKJL/G4EcEPIccfxTMDdu+3Xietcmt3iQOVj8Z4eYOXK5O+33M5lZycw\ndiwwY4bUXHrxxuL19Swwt26t3DZpkhKXzc3iXEpDj+BCby/vJ+JcCrVAoiv0ENEVAJYAeJdx8fFK\nqd1ENBvAo0S0VilVVHl24403YscO7uI+7rhl2LhxGaZOLX6MJGPxSjuXGzfySWjMmOTut9wNPQcP\nsricOVNqLr14Y3EgP+vypJMqs00aqblMDltDjziXghdxLoUs09bWhra2tsTuz0Vc7gQw0/h9eu6y\nAojofADXAzgnF58DAJRSu3P/v05EbQAWAbCKy3vv5dhw0iSuu3z3u4s3ppSGHnMZxCw4lzNnAs89\nB5x7bnL3azb0lMNVKiUWr6+vbnHpjcWB7DT1SM1lcnhrLlta8ktCNgzJBXaFNJBucSHLLFu2DMuW\nLfvT78uXLy/p/lxi8VUA5hLR8UTUCOAyAPeZVyCiRQDuAPBBpdR+4/KxuduAiCYCeDuAV/weaNcu\nYMoU4OST2dWzUU01l+eem3w0XqlYvLWVHzvK+zF+fPWKy74+4Nix/HuhmTED2LGjMttkIs5lcnhj\ncSJ+37u7K7dNQvaQhh6hlggVl0qpAQDXAHgQwDoAdyml1hPRciK6OHe1WwC0APgPz8ih+QBWE9Hz\nAB4B8G2llG8v+O7deXHp1zGeVCxeSedSKRa273538k095W7o0bF4XR3XE7oKJz2Wo1qFyf797FqS\np51twgTehyuNiMvk8IpLQGZdCsVILC7UEk6hjVLqAQDzPJfdYPx8gc/tngZwquvG7N4NnHkmMG9e\nsHM51EcRHT4MDBsGvP3twNe+lux9e53L9vZk79+LjsWBfDTuUk946BALrWp1Lm2ROMD7bhbEpcTi\nyTA4yPWV3rppaeoRvEgsLtQSmVqhR8fis2Zx57hNOMYRl4ODfAJsbs5fVslYXAvAE07gA06UZRPD\nKHdDj47FgWh1l9UuLr2d4pqsiEtxLpPh4EH+vNXXF14uTT2CF1n+UaglMiUudSze0MBdtZs3F18n\nTkPPoUM83qjOeLaVjMV1dE0EnHFGstG4d4WecsXiQDRxWe01l7ZOcUDEZbVhi8QBcS6FYnp7eb8A\nuNlLEKqZzIlLPX7Ir6nHbOhpauIT5OBg8P16I3EgG84lwOIyyaaeSjT06Ehwxgz3cUS65rJaxWXW\nY3EZop4MfuJSnEvBpL+f/w0fzv8kGheqncyIy/5+boKYNIl/tzX1DA4WOmV1dSwwwwSUdwwRUFnn\n0nQXly5N1rn0NvSkfeIvJRavZnGZdeeyr4/jubAvZn6Ic8mIcym4cOgQJ21ELC4lGheqncyIyzff\n5JOxrl2yNfUcPMjCyZwd5xKN+zmXlYzFTedy1Sr/5S6jUm7nspRYvBZrLseM4ede6VhMv+5xT3KV\nXqHnhReyIdI7OgoHqGvEuRRMDh3Kn4MaG8W5FKqfzIjLXbtQsCKPzbm0uQRxxeXIkZWNxbW7OGUK\ni8DXXkvmvivR0OONxV2EcrU7l36xOBGL8Y6O9LdBKf7SZkO/7nFPcpV2Lr/+deD++8OvlzZBsbg4\nl+7ccAPwiu8E5KFPb2++oVRicaEWyIy41M08mnnzgE2bCoWKdyUMYOg7l0By0Xh/Pw/ubmri38vd\nLT5yJD/2/v3BtwGqX1z6xeJA+aLxVauAD33I/rfDh/kzMFTFZXt7NuJ4icWT4ZFH+HhfrZjnIInF\nhVogs+JyzBgWKzuNhSa9a/gCbuKypye7DT1Ack092hHVg7vLHYsD7tF4rY4iAsonLru77dGsUvy6\njx4dT1wqla8hGz6cv9AMDJS+vVHYty8b4lJi8WTo6srG+5kW+vMCSCwu1AaZEZfeWBwo7hi3uQQt\nLfFj8Sw09ADAokXA2rWl36/ZzAOkLy6PHcs7YJqZM906xvUoomo9ofjF4kD5xOXhw/bPxpEjfIIb\nMSLeSa6vj0VlfT1/kWlqKv+XhKyIS9uxBRDnMipdXdU9dUCcS6HWyIy49DqXAEfjZt1lKTWX3m7x\nSjqX3li8tTUZseF1RNNutjh4kB0ac4nDGTPEuVSKSwMmTLD/vVzisq/P/tk4fJiFZdzaL6+gKnc0\nfvQo73tZEJemI2UizmU0xLkUonDNNdW9v1QDmRaX3qaeJGsus+Rcjh3LtYtJ3K8pLtM+6XsjccAt\nFtcz30aO5FE4le6cTpqDB/ORsY1yOpe297+vj93GoSoudU1vFk4ufX38/L2Ic+mOUtUvLr3OpYjL\n+AwMAHfcwemFkF0yIy79YvFnnsmLjyS7xbWrF3fOXyl4ncukxGW5Y3GzU1zjIi7NmW96EH41ERSJ\nA5WPxQ8fTl5cljPSbG/n/7MgRsS5LJ3Dh1kwVHMsbu4nEouXxt69vL9UY+pVTWRGXNqcy3PPZeH1\nqU+xCIzb0GMTl3V1lVtdxOtc6rElpQpdr3PZ1FTaoOwwzE5xjUvNpXmgrUS9XtoEdYoD5Y3F9QQB\nkzTEZTmFnnYssiAu/ZzLNEYRbdkC3HprsveZBbQIz8L7mRbmZ0Zi8dLQTb7VvL9UA5kRl+3twOTJ\nhZc1NgL33strjF97LcdhcZxLW7c4ULlxRF7nsqGBn0epNaDe+9WrQaQl3myx+KxZfBIMmnUp4rJ8\nziVQ/PkIq7l8/nngjTf879crLss9SD1L4tLPuRw9mkVTUosjAMCjjwL/9m/J3V9cBgeB9euTuz8t\nLqvduZRYPBm0uKy280a1kRlxOX48MGxY8eUtLcDvfsfx+AMPJBeL6/uuRFOP12EEWKSV6nR4HVEg\nXVfJFotPncpfCl591f925oG2GsVlV1fx62JSaXEZVnN5xx38pc6PSjuX7e3cLJUFcennXDY2cjd9\nkvv2xo3ZqDN78UXgwx9O7v5qxbmUWDwZdu3i/6vtvFFtOIlLIrqIiDYQ0SYius7y9y8Q0ToieoGI\nHiKiGcbfrszdbiMRfczvMbyRuMmYMSwszzsPOOGEwr+VIi4r1dRjE4FJ1F3aRGva4tLrXBIB55wD\nPP64/+3MA201iku//U1TzlgcsDuXQeKyry94n6m0uNy3j6cSZEGMHDpkF5dA8k09Gzfm600rSU9P\nsvtvlsTlgQPpHI8kFk8OicWHBqHikojqAKwAcCGAhQAuJ6KTPVdbA2CJUup0AL8G8E+5244D8PcA\nzgBwJoAbiMjq6QSJS4BjxvvvB6ZNK7w87igioHLOpTe+BpIRl96GHiDdulJbLA4AZ58NPPGE/+3S\nisUfeAC4/fZk7qsU/MowNJV2LsNi8aEgLmfOzMbJpa/PHosDyTf1bNzI91dpYdLbm0wDoqa7m//P\nQiz+N38D3H138vfrbeip9Hs4lJFYfGjg4lwuBbBZKbVVKXUMwF0ALjGvoJT6g1JKv9XPANAS8EIA\nDyqlDiqlOgE8COAi24N4O8VdEeey8H6TdC7XrMkf+G3YYnEg3LlMS1yuXQs89VQy91UKfl9mNOPH\nuy2RWSr6dfW+/y7OZdBnqtLisr299pzLo0e5Ua5c+04Qvb283yT1+nd1caNmFt7PXbuSFc4aGaKe\nHLt28XlOxGW2cRGX0wCY/b87kBePNq4CcL/PbXf63TbMufSj1JrLLDT0AG7icuVK4NRT/bu/bfdb\nyon/6quB64qKIPLYYnEAmD+f/2Yu3Wli1lwmKUx6eip/4gXCY/GxY/mEmvaSiX6xuK659BP24ly6\nUy7n8tVX+TlPnVr5aFzvT0mJsK4ubub0O44/80yyjVFBtLenc06QIerJsXMnl8dl4fMv+NOQ5J0R\n0RUAlgB4V9TbPv/8jbjxRv552bJlWLZsmdPtSukWHzmy/LG4XofZO2A7TFzu2gX82Z/xwe/NN+1i\nPOmGngMHgJ/9DLjqKmDJkuK/+8XidXX5aPyyy4r/nlbNZdK1YKVsR5ATX1/PXwIOHixuUEuSoFhc\nnMvSGRzk16+pyf73JI8vGzfyimW9vZUXl1p8dXbGNwVMwsTlBz8IPPssMHt26Y8VRnt7OucEcS6T\nY9cuHlMozmWytLW1oa2tLbH7cxGXOwHMNH6fnrusACI6H8D1AM7Jxef6tss8t33M9iB/9Vc34kMf\nctgaD0PNudQC0FwyEQgWl319wKWXAv/rfwG/+Q3w+uv+4jJJ5/LAAeCGG4DPfhb44x9ZNJr4xeJA\nsLhMKxbv7R0aziWQr7tMU1z29fF7lkbNpVn7XO55sVlp6NEi3ftZ1owaFVxWEgUtLrdvr3zHuD5m\ndnQkc39dXcBxxwHr1tn/rhOJtMWlUjygOy3nUhp6Skd/8Z02TcRl0nhNveXLl5d0fy6x+CoAc4no\neCJqBHAZgPvMKxDRIgB3APigUso8vf8ewAVENCbX3HNB7rIiKhWLl9u5tEXXgL+4VAr49KeBOXOA\nr36V50i+/rr/fSflXA4O8vZ84Qv8+09/Wnwdv1gcCK67TEtcZikWD6q5BMrT1HP4MD9O1FFEfstG\nairpXCqVHXEZVG8JpONcTpyYLecyCbq7/Z3LwUF+n8vxue7q4mQpLedSGnpKZ+dOToXKnZYI0QkV\nl0qpAQDXgJtx1gG4Sym1noiWE9HFuavdAqAFwH8Q0fNEdG/uth0AbgKwGsCzAJbnGnuKqJWGHlt0\nDbADaDtY33038PLLwE9+wg7J7Nn+A65tzmXcAdddXXzbxkbgtttY2HrFkF8sDgCLFgFbt9oFlPl+\nJC0uOzvTr2UMI4pzmSZ+4nIox+Ld3bxPZqEBJKjeEkhHXLa2Vl5cplVzaXs/9WOVw63Vr2vazqXE\n4vHRy0RX4wi7asNpzqVS6gGl1Dyl1IlKqZtzl92glPpt7ucLlFJTlFKLlVKLlFKXGrf9We52Jyml\nfuH3GMcdF+8JNDcHHwwGB3kntJ0E4sbir78e/5tnVOfy5ZeBD30ov/2zZwc7l0nF4h0d+ch28WIe\nmvzNbxZeJygWb2gA3vY24Mkni/+WpnOpt72ShI0iAsojLvv6eNh42nMuy7lCj179SO/X5Wr0sOE3\nQF2TRize2lqdsbifc6kfqxzOpRaXaTuXEovHZ+dOjsRHjBBxmXUys0JPY2O824U5lzq68tYLAvGd\nhUsvBR58MPrtAH/n0k9ctrcDkyblfw+KxZNs6PGu437VVYXPeXCQTwqjR/vfh9+8y7TFZaWjcZdY\nfMKEYnGZ9HKBQc5lWM1lVp3L9nYWl8OGsZPvXTe9nPgt/ahJyrncv5/XiJ80KTux+KRJyTqXxx1n\n34fKKS737k2vDt/b0CPiMh5aXIpzmX0yIy7jEiYugyLKODWXe/bwPMXdu6PdThPVudy7l90KTZBz\nmWRDj7fZ5NRTgddeyzsx2p1rCGgJ86u7TGv5R71Nle4YjxuLf/SjwHe/m9x2aHHpff/Dai6zPIpo\n377856HSdVdhzmVS4lK7lkTZiMV1Q1eSzmVra36ShvexgPI5l7Nnp+NceoeoSyweDzMWr3RZjBBM\n1YvLoIhy3Ljo374ffpj/37Mn2u00NgEIuDuXM2fyt7f+/sLrDQ4WijZNErE4wE7RaacBzz3HvwdF\n4pqlSznW9x6s0xpF1NsLHH98NpzLOOLyhReAH/wgOTeury96zWV/P//LqnOpY/FyP66NMOcyqVhc\ni0sgG+JSd+sm2dAzerRdMGhxWa6ay9mzk3cudWmW/iIisXh8JBYfOlSNuPSLE20d1JqJE6MftB56\nCFi4sDRx6ReL21bz8DqXw4fz794B5VqweeP/pJxLADjzTJ43BwR3ipuPffrpwKpVhZebJ+UkDxI9\nPSy+03Iuf/lLXoLUZTuiisvOTn7/TzgB+M//LG07NXEaevS+klXnsr29dp1LIDs1l0mKS11eY6vd\n7e1lx7ZczuWsWck7lzop0MdmicXjI7H40GHIi8uw2qs9e/ybhaKKS6VYXF5xBQ8yj4NfLD5mDIsL\nr0j2OpeAPRr3u9+4Mwi9NZcAO5ErV/LPQZ3iJnPm8Gw+E2/NZZIr9Lg4l0rxQWrXLr6u6+vzxBPF\nQtlGnFFE69bxykZf/CJH40nUXsapuezr48uzKi6jOpeDg8Uuf1K41Fwm7VzqWl2/VbrKQRqx+OjR\n9mNVby+PqStXzWUazqX38yKxeHwkFh86DHlxCQRH4zt2ANOn2/82YUI0cfnKKxxpvOMdyTuXw4bx\nQcc8sB09yoLJK+Js44j87jepWBxgcWk6l2GxOMDCeO/ewsvSGEV07BiLiKlTw09EL7/Mr+HixcDc\nufw8dNwfRFdXuFjQ2+FdgcmLTVwuXAi8//38OLZGqKj4dYsH1VyagtRP4A4lcfmv/8qf/1tvTd7p\ncOkWT9q5HDaMP+eVnIhw6BC/pkk4lwMD/Dq2tPg7lzNnlrfmMmlx6S1Xklg8HkrlxaXE4tmnJsTl\nNJ+V0MeNYwfOdS7iQw8BF1zATmhccennMALFdZf6ROqNum0d411d/s5lUrH4nDn8gd650y0WB+zi\nMo1uce0W2rqwvezZw81Ge/bwSfryy4EXXwx/jO7ucHGphZffqi2a8eMLT5haXNbV8eD6730vfHuC\n6O9nd2v06Oix+KhRvB22NEApu7gs1wo9UWPxffv4y+DDDwMnngj8wncYWnTKMUS9v58b6ebOzV9W\n6Wg8yVhc16AT2d/PctZR62VF9RfEpDBrzAFxLuOyfz/vI83NEosPBapeXO7c6e9cNjSwa+XqAjz8\ncF5cxo3F/Rp6gGJx6a231Nhi8Rdf5FjVS1KjiAA+Aeho3DUWL5e41LW1EyaEn4g6Ogqf27x57A6F\n4eJcukTigL9zCQAf+xjw1FPA5s3h9+OHXvO6pSW6uNQHcNtn6uhRFp7DhuUvy7JzeegQD/S/7z6u\nZf3kJ5Op/PjkAAAgAElEQVSLlF2GqJcai7/xBh9vTBFb6XFEScbi5pdiv1h88mTe79IWE/p4m/Ti\nGuJcJsOuXXmjSGLx7FP14jLIuQTc6y6PHuWo8rzz+OCjVLgrcdttwPe/X3iZX3wNFItLW70lYI/F\nn3iC50p6SdK5BLipZ+XK0mLxtJzLlhY359L73ObNAzZtCn8MV3EZ1swDsLjt6MgLnXXrgLe8hX9u\naeElP2+9Nfx+/AgSibrm0vba69v57Te251eJOZeuj2u6RmeeybdJarB5mHOZRCxuRuKaSneM6zrI\nrq7ShbruFAf8Y3H9uU7TvVQq74onvSywzbkUcRkd3cwDiHM5FKh6cRnkXALu4vKZZzhWmzCBHbzJ\nk8Oj8S1beLyMSZRY3M+5tMXiSYtLW80lkHcuXWPxyZPLU3OpnUtv3GzD61yedJKbc9ndzSfUIFzF\n5bBhvN92d7PY1XVsmgsu4HmqcdHupO2EHVRzaYpSV3FZ7hV6osTi3qYb3TiXBK7LP5bSnOUnLisV\niyvFr+mYMfn9txTMhRj8nMuWFj5Opyku9bKiI0Yk71xKQ08y6HXFAam5HApUvbgMcy5dm3p0vaXG\nJRo/eBDYtq3wsijO5d69dudy+nT+mxYGu3bx7ZKOxf3E5erV/PdqicVPPJHr2sLqrFycS5cxRBod\nja9bByxYUFinWWq9nikuo8biTU3+dZSVdC77+/n11+9dpcVlmHPZ0MBfIkrZv23ispKx+OHDLMLq\n6/1n80bBFJeVdC7NWt6knUvvPiixeDwkFh9aVLW47Ovjg4SO0Wy4fiO2icsw57Kzs1hcRnEuzQOe\nSUMDf8j0fT/5JDct2Ja4jOsq2WouAT7It7Zy17hLLN7ayuJSuzd6FQ693GcazmXUWHzECH4/t24N\nvl2SNZdAobjU9ZaaUsWlGW9HHUUU1blsamInJu3xOPv38z6p93NXcWlubzmdS6D093HHDu6WNoka\ni+/YkZwTZ0a8SYvLIOcy6mSPqJgpUdJLQNqcSxGX0TGdS4nFs09Vi0u9M9pEl8YlFj94kAXA29+e\nv8wlFj94kGc8mifdJJxLgKNxXXfpF4kD8Vylw4fZJfJz4JYu5bFMLs7liBEsJLUo0yd77dIlLS5H\njeIDd1Ds5HUugfCmHn2fSdVcAumKyyDn0iUWj+JcEvF9pX2wN5t5gHjO5ejR4aUNroQ5l0Dp76Nt\nEYiosfjf/m1yg/nN91/XDZeCt6Gnks6lPtYmNfxe4/2CI7F4PEznUmLx7FP14jKo3hJwE5evvsor\npzQ15S9zicU7O9mpM68XpVvcz7kECjvGn3wSeOc77deLIy51vaXfOJ0zz8xvrwtmNO492Sd1kNAn\nYaLwukubKxtWd6lrsoaquDTr/oJice1qRmnoAcoTjZvNPK6P6W2mKLdzWeoSkLbXO6pzefBgsqUA\nenuScC5dG3rSrrn0xuJJO5cSi5eO2dCjv8wmsdiEkA5VLS6DBqhrXOKWN98sXuXHNRYfM6Ywbo3a\n0OPnXGpxefAgj6xZssR+vTgnfb9IXLN0Kf/vEosD/By0wPaKy6RqZ8yTcFg0bmtWCnMuu7r4Pe/r\nC56LGrfm0isu9Qku7sFTO5DeFayU4hPb8OHxRhFVUlyazTyuj1nJmkug9C8Jttc7as2ly3zWONtT\n7li8XOKyHM6liMvomLF4Q4P/LF4hGziJSyK6iIg2ENEmIrrO8vezieg5IjpGRH/m+dsAEa0houeJ\n6N6kNtwkSFwGNfMAbs6lbQlJ11j81FPztZGDg8Fux5gx7s6ljsX/+EfgjDPyNYxe4opLWzOPZtEi\nFi1BAtQkyLlMOhYHwk9EfrF40Diiri5+f8KK/aPWXG7cyCcafdDUDBvGTRNxT0LanQQKPx9aWNbV\n5eM5U8DGGUUElGeQehKx+FCruUzCuUxaXOrnnFQsnoWGnrRrLr3O5bFj4rpF4dgx3tcmT85fJtF4\ntgkVl0RUB2AFgAsBLARwORGd7LnaVgBXArjTche9SqnFSqlFSqlLS91gG6XG4mEHLZu4DHMulWKh\naIpLfZDxqwGN41wGReJA/gMY5UDmN4ZI09TEI5b8ts2LKS69J8u0xGWQcxk3Fh89OjzmjBqLP/EE\nu5a2EoRShImfuNT1lgDvh/X1hd/+4zT0AOWLxeM4l96GnnLWXKYVi0epuXQZoRVne6qpocdbc5nm\nEHUi/vIodZfu7N7N7099ff4yaerJNi7O5VIAm5VSW5VSxwDcBeAS8wpKqW1KqZcB2CRMyEJ4pVMJ\n5zKs5rKvjw8gc+fmxWVQMw/AB2vtqhw+zP/8omctLoOaeYD8aipRPoRhziXAo3NcCXIuk6qdMcVl\nUM3lsWP83ugTmmbGDBbVfkJAnwSTFpcvvFAciWtKEZfmutemUDRFJ1Ac0cVp6AHKF4sn0dAz1J3L\n5ub8MpwuJOlcmkKpnM5luWsu0xyiDkhTT1TMSFwj44iyjYu4nAZgu/H7jtxlrgwnopVE9EciuiT8\n6tFJu6EnKBb3E0W63nLmzLy4DKq3BAqdAH2w82uqOe44Pkk+9xxw1lnB2x/1xB9WcxmVIHFZX8/1\nM6XWzrjG4nr4u/d1ravjeZd+Sy7qrtYwcWnr7vVj/HgulUhDXPo5ly7iUs+5jOJclmOQetYaelxr\nLuMKu4EBFiDexyCKFo1nuebSbHCsdLe4WXOZ5igioLSmngMH0h/7lTX27OFVoUwkFs82DWV4jOOV\nUruJaDaAR4lorVLqde+Vbrzxxj/9vGzZMixbtsz5AUpxLseOZeHQ388ix8aePYW1HkB++bzOTrsQ\n0yLGFJcuzqUpLoNi57o64Pjj8+N3gogqLsNi8ahMmsRrZQPFERGQjzf86kZd8DqXfrF4kCurm3oW\nLy7+Wxqx+IQJ/H+QuIx7kgsSl6ZY8XMugxp6bHXAWWzoUarQwQUq0y0e9wuCFsa2L5g6Gp81K/g+\njh3j9zzJWLwScy6HDStvzWWaQ9SB+E09R45w8+attwIf+EAy2zcU0DXvJhKLJ0tbWxva2toSuz8X\ncbkTgDnGd3ruMieUUrtz/79ORG0AFgEIFJdRsZ0I+/tZoHm/7XjRK00cOOAv5mzOJZCPxm3i8uBB\nu7gMEoK6oUcp/6UfTWbPBk72Vr9aiONc2lb7iYu35tJ7oNUHCW9UHQVT1E2YwCvu2LA182iC6i7T\nisWB/JriXko5yZmiyjxpmzWXQHAsbjuZ9/baBU0WY/HDh/n5mXVa5a65LMV9DtqXXDvG9b46FGNx\nvdRkczP/CzMB4mKuKw6kP0QdiB+L33EHN3LudD4DVwc2Y0Zi8WTxmnrLly8v6f5cYvFVAOYS0fFE\n1AjgMgD3BVz/T9+ziWhs7jYgookA3g7glRK214pNXO7ZwwfgYcPCbx9Wz2MbRQQEd4zrWLy1lQ8u\nvb3hsXhjI/87dCjcuQSAK64APvrR4OsA2Y7FgfBvoPff7y8WNa4NPUHiMqhjXMfiYUO4o4wiOu44\nFmpeV1xTjli8qalQXGpnM6sNPVHEpW1fS7rmMs1YPEhcusbiSYvLcjb0mEtN1tfz8bRUMWujp4cF\nq95X0h5FBMSLxbu6gG99C7jkkuIldasd27lTYvFsEyoulVIDAK4B8CCAdQDuUkqtJ6LlRHQxABDR\nW4loO4A/B3AHEb2Uu/l8AKuJ6HkAjwD4tlJqQ9JPwiYuzYGrYQTVXfb18T/bwPCgjnHtXBJxs8j2\n7eGxOJA/YLs4l1dckZ85GUQWYvEgcRl2kPjRj4Df/S74MVwbelxicRtRYnHXmssJE3hAv19dbZIN\nPVFqLtNo6Cl1rp9S0WNxm0ueVCw+OMjPyXwtbbjE4ps3837gJUxcunRPd3cn69amKS69X2i8zz+t\nph7vsTbtUURAvFj8u98FLrwQOP/88AU8qg1bLbvE4tnGKWBQSj0AYJ7nshuMn1cDmGG53dMATi1x\nG0OxiUuXAeqaIHGpXUubAAjqGNfOJZCPxsOcSyB/wHZxLl2J41wmKS4nTODn1N/vvzZ10EFi797o\nzqXfSSgsFt+0iYWM9/1OIxYHgpcmTaPm0uu2eZdtTGMU0Y4dvKrTtm2FEXUUenv5PfGu7hTVuUxK\nXOrIPej9A9y+INxxB2/nTTcVXp6Uczl1Kn+5TYLeXv6yDJQeiysV3NDjff5pNfV4j7XlcC6jxuJv\nvgmsWMENnCtXAn/4Q3LbNxTo7s7XqGskFs82VbFCT0uLXVy6OpdBM9T86i2B8Fhcu50zZ/IqPUk7\nl66YQmFwELj55uBVZpIWl/X1fCLav98/Fg86SLS3JxeLB0X+Y8fytu3aVfw3127xqOIyiCRj8XKM\nIvIbor5jB7+mq1bFey4Az7mzdYvGEZddXaWPvrLdtw2XOZft7fbrJFVzOWUKb28SHcamUBo5kven\nuJMejhxhca4b+bz7kE1cpjHr0js/1c+5/OEP44lbm3MZNRa/6SbgYx/Ll9FILC7OZdapCnHpF4tH\ncS79DhpB4tIlFge4q3vbtvCGHiB95/LRR4HrrwfWr/e/ftI1l0A+Go9TcxnVudSxuE1AhEX+fnWX\nrrF4lFFEYSTV0BM3FrcJt4MH7bNXg4SeFkH//d/Rn4fGlkS4iEtbrVtDQ+mOh0u9JeD2BWHvXvs+\nZdt+TZRYfPRo3geScONMwUdUvKpYFMxIHAiPxZNyLn/1Kz4Garzi0u89++EPgTVroj+en3PpKi73\n7wfuvBP42tf4d3M53VrBdlyVmstsU7XiMopzGRSL28YQadKMxZN0Ls2T8E9/yq/Xs8/arzs4yAd9\nW41pKcQVl729HB+99pq/26QHSusD+IgR7IjYnLSgWBzwr7tMKxYPopJzLv1GEcURl3v3AiecUJq4\ntH1ZjONcAsk09biMIQLc3sM4zmWUWFw3oiXR1OPdpnHjkhOXYc5lUjWXGzfyKB+dbrjWXO7bF71L\n2+x4N4kSi2/fzqUIupnNrGGvFfy6xUVcZpeqFZdRncuwmksbQbG46VxqcRk1Fk/auezo4MaYL3+Z\n63b8tnvkyOTHfegDYtSay717+UvCiBH+B9QjR3h7zW32m3UZ5sr6jSNyEZdekVsqaS3/6DLnMknn\ncu9e7nB99dXgJVODsH1ZjNPQAyRTd+kyhgjIRiyuyzmSaOrxvqalNPVUyrk8eJDrv//1X/l3W82l\nV1z29/Px01YyE8SRIzyxxFtrHCUW9zqr48bxcaGWVvjxi8Wl5jK7VK24LEfNZVAsnkRDT9LO5V13\nAe95D/De9/o7l0nXW2riOpf6dZgzxz8at0UmfieisFh81ix784PpAPmdpI8ezS+3mQSlNPSUGovb\nGnp0A4ZtHmnQCj36C8L55wMPPBDv+dhi8aYmfs396of9nMskuqeTci71jMU4zqVrLO5SK+yKN+It\npanHWyakx2Lp2tC0xGVnJ/CpT3HMfexY8bFWf17MGlX9RTWqc+n3BSeKc+ndvro69y8X1YLE4kOP\nqhCXTU38zVCLD6WSG0UUJC4nTeLb2QrlTedy+nQ+OWpXMIixY/nbcX9/uBB1RcdNP/0p8MlPAqed\nxuNPbMIlLDaOS1xxqR3cOXN4LXUbfuLS5lyGPT+/yMnFuUyy3hJIzrk048YwcannXNoadHp6+LY2\nVzus5nLSJOB974sfjdvEJVHwvuNXs1hO5zJszmVvL2+/7X0OEpfjxvH9hjXTpB2LJ+lc1tUVTi9I\nq6Hn4EHg3HP5mHLPPXbx5nXF9ONGdS793sNSnEug9qJxicWHHlUhLuvqgOuuA770Jf59/34WMK7x\nZNyGnsZGPnDbbmt2i48YwT9v2eLmXG7ZEryueFRGjOBO3V27gAsu4AP4KafwWAsvaTuXcWJxLS6j\nOJd+sy7Dnp/toG2OTAkSl0lG4kBpDT1JLP/oFYt+kTgQHotPmgRcdBHw0EPxuov9ylyCHjcLNZct\nLXxdv07tvXv5cx7VuayrY4F5++3A00/7P5+hFIsDhe9nWjWXOlX6/OeB73/fXt/u/WK3bx9/VqKK\ny85O+zE/SkOPTVxOnlxbTT0Siw89qkJcAsAXvwg8/zzwyCPRXEsgvnMJ+EfjZiwOcDS+eXO4szVm\nDHcrJ1VvCfAB+957gSuvzNf+nHmmPRqvRCweFG9o1yvJWDyqc9nXx1H3sGHlFZdpDFEPWv7x2DEW\nOg0NdueyFHHZ2sojcebMYTEUFb8yl6DHzULNZV1d8Jim9nZu1ogqLgEeqv3cc8C11/Isy1tuKb5O\n0rG4raEnbizuJy71a5VmzeXYscAHP8j75ksvFR9vvU09+/bxMq1RY/GnnwbOOKP48iixuHfxAKD2\nnEuJxYceVSMuR4zgg+3nP89rr7o28wB8oLFFTEoFd4sD/h3jZiwOsLgcGHBzLrduTa7eEuDXpr8f\n+MQn8pcFicusxeJhNZe2VXFssbh2kIJEga1Y3jwJDsVY3HXOpXc98qSdSyBeNH70KIsK25e8OM5l\nEuLS1bkEgqPx9nbet+OIy//5P4Gf/5xTiX/+Z/8RWi7LlrriLTVI2rk099U0ay7HjOEv2tdey8d9\nF+fyLW/hfTloRrCXRx7hCN6LxOLuDA7GW3xDqCxVIy4B4EMf4g/dP/xDNOdSR0xeMdLVxS5O0AHe\n1jF+7Bjv9ObtZs7k/13EpVLJOpcjRwJnnw3MnZu/zE9cJr30oyZMXIYJkzDn0vse2WJx/dyCyg1s\nxfI2cWkbi5SGc5n0Cj2u4nLYMH6O5heuMHFpc+e8yzbGEZe7d/PnzLa6T5i49Ku5LFVouTqXQPAS\nkO3tPAf32DH+AmgSZX/ym46QpHM5OFgsqseOTa6hByiOxc3H0uKy1AH45hf/T34S+MhHio9JNudy\n6lQ+T7iKusFB4LHH7OJSYnF39GfN+/mXWDzbVJW4JAJ+8APghReiOZeAPRoPGkOkscXiXV18AjNF\njBaXLg09QLLO5WWX8eBgkzlzWGh4a4iyVnOpY/Hp0/n9sB2QXRt6XJuVvK6AeRJsbGQBatveoRKL\n+9VcmpE5UbFwi+Ncdnbya6JXYVm6lPe5KMsRBo0Vy3rNJRD8PmrhYHM3o+xPfq5ekuKyr694ycsk\n51wChfuq9/k3NvL7XcoXA6UK9+PRo4G77y6+ns25nDiRBaZr3eVLL/HrM6NoYeTo3eJ6xqWmlpxL\nv0RIYvFsU1XiEuDo4pvfBM45J9rtbMXiYfWWgD0WN5t5NMcfz/+7issknctRo4qdXCI+0Xvdy7TE\n5ahR7M50d8eLxRsaWGBs3Vp8HdeGHtfI33vg9p4E/Tpvh0pDj+lc6vEvQLHw9Db1xBGX3maJ+npO\nGH78Y/fnEjRWLK1Y3Osi2u7b1bkMisX161OquAxyLkePTiYWtznB3lj8N78B/uZv3O4vakMPUHo0\nfugQi9SwcWE25zKquHz0UbtrCUgsHgW/le0kFs82VScuAeArX/H/UPthcy5dxKUtFvc28wDsXA4f\nHn5Q07dL0rn0wxaNpzWKiIgPiLY5kC7d4oB/NO7a0OMa+YeJSz8XKOmaS9u8PReUKj0WB4qj7rji\n0vtF6ctfBlascBc7tjFEYY8LlNbQc+653CDoh+vyj0B4LN7aat+nshaL27bHjMWVApYvB267DVi7\nNvz+ojb0AKWLS9sXfxvekhQtLqdNK27qUYobSr1lIY88Apx3nv3+XWPxgQHe5gkTCi+vpVjc77gq\n4jLbVKW4jENccTltGp/8TLzNPAAvf3fqqeHbMXw4H2CTdC79sInLtJxLgA+Izc3FNY9+Bwk9YFoL\n7ajiMqlYvKur8Juz34k6aeeyvj6409iPY8f4trpGKUxc6tfeO6YoiVjcJi5PPJHHEq1Y4fZ84orL\nUoao79wJbNjg/3e/+7YRFotPmlS6uPSrR4wiLh9+ONhRtm2PGYs//TT//K1vAX/3d+HbHLWhByh9\n1mXQPmziTQ2CnMtdu4DvfS+/4g/An8EnngCWLbPfv2ssvn8/n0u89Ya15FwGiUupucwuIi5z2A5a\nLuJy1qziqNbmXI4b57/kopexY8vjXJ5xBo8yMbsf0xSXkybZT5Z+4rKriw/CWgz5DVK3dYv7xeJx\nnEvvqjTlEpdAvKYer4A0BWpYzaU3Fnd1Lv1W6PEuraf52te4Ptol9i+l5jLuEPXOTp464UcU5zKs\nWzwJ53LECP7SZr4W5nxWl1j8178Gfvtb/7/bnGAzFv/BD4DPfQ64+mquew8bOeX90qafR5C4LHXW\npatz6ReL25zLV17hy2+5Jf9ZWr0amD3b/zjuGovbxhAB+bXlS21uGgr4xeJSc5ltnMQlEV1ERBuI\naBMRXWf5+9lE9BwRHSOiP/P87crc7TYS0ceS2vCkiVtzOWMGH2zMGi2bcxmFj38cmDcv/u1dGT+e\nn98rr+QvSysWB1hk2NweP3Hpdb2CnEtbt/jBg4XuQCnOpau4TDIWB+I19fiJS29cDoTH4q7Opa7d\n9J7sbAOqAWD+fHZ17rgj/PkkXXMZ1tCjVLi4jOJcusbi3utE/bLidesPH+Za5bD5rJpVq4Ibrfxq\nLjs6+D166CEed9bUBNxwA/DVrwaLH9tSokENPfo5liouXZzLKA0969fzzMxTT+VV0IDgekvA3bn0\nWwa4qYn3/bjNVEMJicWHJqHikojqAKwAcCGAhQAuJ6KTPVfbCuBKAHd6bjsOwN8DOAPAmQBuICKH\nj3b58YvFg2ZcAnyQaG0tPOC4fjv241vfKu32UTjrLD4g6pNA2s5lWuLSe/AZNowFuln75SouJ08O\nF5c2F8gmckslTlOPVyQOG8axmh6R5SouozT01NWxG+N9H22xuObv/o5n04bF/uWuuezp4TpXW/OY\nJqpz6fceavHt51y6Clig2K03HZ+w5R8PH+bPSpC49Jv0UF8PfOc7wBVX5D8nV17Jx8SHH/a/v0o0\n9Lh+8TedyyNH+PXRjZE2cblgAfD1rwM338yfs6B6S8DdufQTl0B4NN7WBtx/f/hjZB2JxYcmLs7l\nUgCblVJblVLHANwF4BLzCkqpbUqplwF4v6deCOBBpdRBpVQngAcBXJTAdidO3FFEAEfjpsvh+u04\nC3zjG8BTT3EH7+7dLDJdT5pR8YvF/eINb6SqxaXXDfE7+CxdWliKUEosXomaSyAZ5xLIO0JpNfQA\nfOI354MCweLylFP4y83//b/+9zk4yPvl1Kn2v6dRc6ndoCSdS7/9RSneZ7zXUco/1vfD29Rj7rdh\nyz++8AILpM5OfzfIb/8eO5bfw899Ln9ZQwNw003B7mXUUUS25xiVOM7l/v18fiDi/dAWi8+fz/vy\n3Llce7lyJc8W9sO1oacUcXnffcDvfhf+GFlHYvGhiYu4nAbA/D67I3eZC97b7oxw27ISt6EH4DFD\n5omo1Fi8nMyYATz+ODtDb31r+JDxUojjXJoH1nHj2CHznlz8xOWZZxaKyyixuNmJWalRREDy4tJ1\nzqW+jatzCQAnnQRs3Fh4WZC4BICrrgqu89u7l9+z4cPtf49Tc9nczJGk3xrnnZ35Wmo/YZSEc6mF\nA1GxuOzrY3fLNjjeD6+r5xWXQc7lypXA295mb1DU+Dmp48YB7343N2qZ/PmfA1u22BtwBgbs70+Y\nczl+fPyh7UA851JH4gD/39VVKAzXr2dxCbAb/8Uv8hcnr3A2KTUWB8I7xrdtK02IA8B//Re70pVE\nYvGhSUOlN0Bz4403/unnZcuWYZlfm11KeBt6Bgf9mxG8DGXnEuAD3YoVwDvewXFOWixaxAc8L37x\nhk2YzJ7N7qU5miPIufz+9/O/u865bG3lx1aKT/yVGkUExGvosQmfcjiX8+axuLzggvxlQSdHgJ0g\nr9tpElRvqbfRr+7Mz10kytddeodTAyxepk/n99MvvYjaLW7bX8zji3efivNFJcy57OnJ79NeVq7k\nGsENG/gzaq7mpfET6yefzMsoeqmrYwFka0rRJSR1HnvDfD/9utPL7Vya4rKuDpgyhd30WbP4b0eO\n8GUA8K53AUuW+HeJa6LE4rb3Agh3LrdtK73E6dln2Xz40pdKu59S6Onxn3MpsXhytLW1oa2tLbH7\ncxGXOwHMNH6fnrvMhZ0Alnlu+5jtiqa4rATehp79+/kEpFcWCWLWrMLOyKHkXJpcfjn/S4u3vIX/\nefH7BqrXXTbR0fgZZ+Qv82ukWbiQD7BaFLnOuWxu5jpF3XBgi8VtjsFQcC7TaugB8uLSJMy51F2v\nfgTVW+pt3L27+HIdK/u5i7ru0iYudc20di9t4jKJOZemMz9qVKFQSFpc1tfz++73WVm1iucDP/aY\nf92l3zbdc4//Nun3Vzt7tm0z0fupdvW8x99SY/GDB/MLWgTh51wC+Wh81qx8vaUW7ETAvfeG7xtR\nYvGzzrL/zUVclsqOHTzvdWAgmoueJN3d9rIYs4kwrbStlvCaesuXLy/p/lxi8VUA5hLR8UTUCOAy\nAPcFXN98m38P4AIiGpNr7rkgd1nmGDOGDya6Lsk1EgeKxxGV2tBTa7jG4oC9qcevkaahgd3S1av5\n9yid8OaBO0q3eBYaevzEZW8vH4zNiNk8yXnnXJqxuFL2GjkTr7js77cPgDYJG6niIi5t7sXhw8Gx\nclDdpf78estdTJKYc2m6ukk4l0GxuO0xNB0dLNDnz+cymajiMoiJE+1fHnQdoxf9fvo9VqmxeKnO\nJVDY1GNG4poJE8L3DddY3G8UERAcix85wn8rNRbfsYP3de+XxnLilwjpBTlcl9EUykuouFRKDQC4\nBtyMsw7AXUqp9US0nIguBgAieisRbQfw5wDuIKKXcrftAHATgNUAngWwPNfYkznq6oBPfYpHShw6\nFF1cDuVYvNK4dosD9lmXQXG0bupRqjziMgujiPxi8QMHiteGdo3Fe3vDV5jyisv9+/n1DnI89BxT\nv+7toBmXehtt4jJM/AV1jHd28nZ7P9cmScy5TFpcBjmXgP+sy9Wr+UtYfT2vJObneEUR1JrWVnvN\npVGZ+8kAACAASURBVJ+jrZ3LIHFZqnNZSs0lUNjUo5t5opJ2t/iOHbyPJyEuTz2V5yFXiqDju0Tj\n2cVpzqVS6gGl1Dyl1IlKqZtzl92glPpt7ufVSqkZSqlRSqlWpdQpxm1/lrvdSUqpX6TzNJJhxQo+\nuF56qX8cZmPmTP4Q6mHkQzUWrxRBsbhNXG7ZUniZi7js6WEh41LmABQeuG0OULlGESUxRB1gIXTg\nQPHlrqOIXFY2mTWLXzMtSMPqLTWTJvlH4y41l37iMui9CBOXZixuI4k5l+br4xWgaYhLvy9FK1fy\n5wQon3PpJy7DnEs9tD3qkqga1y/+YeLSdC4XLIi+HWl3i2/bxk1FXV2Fi2REQSn+/F1ySTLicmAA\neOYZniwQZfi7XwkFIB3jWUZW6DGoqwN+8hN2Lb74xfAZl5rhw/ngow844lxGI0osvnAh8PLL+YPT\nwEBxnGuixWXU4fDmrMtKxuJxnUtbLN7REU1cms6li7isr+dlTjdv5t/D6i01QXWXcWPxMPEXNEjd\nFJdJOZd+4jLJhh5vLO66bKlXXPo5l3G2Kapzqfc5v8dqaODL466T7vrFv5RY3AWXWFyp4sc28U61\nMNm2jZsfR40KX43Kj44O/jL+rneVJi63bAE+8hHe3k9/mkdWRVnCM8y5FHGZTURcemhoAH75S+Di\ni4HTTnO/na7P0rVpIi7daWzksTCmGzE4aK/LmjqVBaU+qGoR4e061cyaxQfxl16K1jmpXYHBQX4M\n8+CWdXFpE9vNzfx6ei/XRfFAsSg1hZvrmsxmNJ5lcRnkXHZ0BNdcDg7ya+YV6n74xeLehh7zfS5X\nLK5UobicOTPYuYwTi0dxLrVbHvT8S4nGk3Iud+7k13ffPrcGIS+2WPy//qvwGHjwIO/ffmO4vIs9\nmGzbxu+ld9WmKOjP3uLFPAc1rgN6/fX8mq1dy/90l70rIi6HJiIuLQwbBtx5J/CxCItVapejp4d3\n+IbMDHnKPkSFIgfgA+Lo0cU1fkQs+l98kX8Pq3Mk4hPn738fzbnUrkBPT7F4tc25HBzkk2LUk28Y\nSTb0xInFoziXQHxxaTtJKsUn8TixeJgQcm3osc26PHy4uHY1CJdYvBw1l7YvRTt38r47MzcPZMwY\nfr424R11qDtgnx8MxI/FgdLGEUWpudSjm/ycyw0beH+P00XtdS4HBnguqLkUb1hZydix/J7Y4vVt\n29iFLkWIa3E5bhy/V5s2Rb+PV1/llYK+8Y3859hvn/AjKBaXmsvsIuIyIXR9lnSKx8P7DTTowGqK\nS5fZknHF5d699g5p20m6r49PGEmP60gyFg8Sl0oFjyKKIi43bOCf/dYV9+LnbulYLuj9TbPmcvRo\nfr28J8KgEUc2mppYSPT3F16ehrjcvz8vhl3E5cqVPNbLHKXj19QTNxaP6lwGxeJAfMGklz91eQ6N\njfzl4ehRf+cybjOPvn9TFO7Zw/vHmjX5y8LEJZH/FzPtXCYhLgGe3RknGv/e9zgKNz/DfnW4fgQd\n46XmMruIuEwI7VxKM088vOIyyPU69dT8muEuTTRnnsnfuuPE4q7iMo1IHIjf0OPXLe4Vl/X1fJLq\n7y+9oQcodC5dFyHwa+gJi8SBdGsuAXs0HtWhJrJ/SUhaXI4Ywe+ndptdYnEzEtf4NfUk2dDz5pvx\nncu444h0uZLrTET9nu3bVzhOS7+mzz4bX1x6G3q0mDfFZVC9pcYvGs+CuNy3D/jVrwqXBQX863D9\nkFh8aCLiMiG0uJRmnnh4440gcRnVudQD1+M4l7ZIpqWFD2imE5WmuEwqFrfVXAL5E51XlEZt6AFY\nXG7axO5ZqTWXaYpLF+cSsDf1RGnm0Xij8UOH2EnT+9bw4RxP66g0TgQNFNbYuTqXNnHp51zGHUXk\nLS2I29ADxI/Fox6bW1ryM1jN503EEe8jj5QmLs1YfPt2fu9MAecybcHWMa4U318SsfiMGfxzHHH5\nox8BH/5w8dSVKM5lfz8fm/z2O4nFs4uIy4QQ57I0bLG4nzBZsIA7EI8ccROXEyZwF3NSsThRcS1k\nGks/AunH4kBeXCbhXI4bx4+xe3fp4jJsxiWQXs2l3lds44jizHv0NvXo/duMo03xF/fLio7GgfwK\nUxqbc7luHY+sMfFr6okjeJub+bmZ7nvQF480G3qiHptHjuRj+sSJxW7n1Kn8JSrOGCKAHebBwXyT\nzLZt3ET6wgv5ph5XcentGO/o4Fr10aML94eomF/udFOP6wioQ4eA227jqSteojiXej/wc5slFs8u\nIi4TQh+Q9+8X5zIOtljc78Da1MTzLtevdxd1b3+7+2gpgAVpZycfqG2r0iQRY7qQZLd4VHEZx7kE\n8tF4lJpLW7S3fXv5ncvBwUJRlpRz6X0fbcIhKXHp6lx2dfHjeJfWSzIWB4rFRG9v/gualzRj8TjO\n5dat9mh62jQWiH7rfodBVBiNb9sGnH46P5Ye5eUiLm2xuI7EgeRi8fHjedtcm3p+/nPgbW/jdee9\nRHEug5p5AInFs4yIy4RoamJBsmGDOJdxiFJzCeSjcddVcW6/HbjySvftqa/nA+rrr1dWXCbVLT5i\nBJ9co4rLqM4lkBeXpdZcbt0aPuZFb6M3do3b0NPVxbfTjVm2mss4zqU3Fk9LXJqzLsPE5ebNLI68\nrlCSDT1AsTMd9Nmur2fX7cCB5GPxqM5lS0veufQydSq/dq6LMtgwo/Ht2/l1X7w4X3cZNxZPQ1wC\n0aLxn/2suNZSE8W5DDMPosTiDz0EXHGF23WF0hFxmSDHH8+CR8RldKLE4kBeXLo6ly0twUsX2pg0\nieN32zdn7ziiNJZ+BOI19PjF4koF11x6bxdnFBHA4nLtWr6ty2fBb33xN94IF5cNDfzPO5A6bkOP\nd9pDks6lNxYvt3PpjcU3bwZOPLH4PmzO5cBAtNmeJl6nKuyL44gRfP2kY/GozuXIkcHOZdx6S43Z\nMa5HB8URl95YXN8XEP+16uriz6P5xdpVXCrFnfRvfav971Gcy7Dje5RY/Ec/4mhfKA8iLhNk1ize\neSUWj06UWBzId4ynseSiRotLF+cyre3wG2MThF8sru/PSxrO5ZNP8vvn0pnb1MQnWm+ziYtz6d1O\njUssbqu59IpL26zLtJxLU4CWKi713FXzPmzOpU1cTp/OrpVZX6f3DdfZniZepypMXDY38/WTjsXj\nOJd+4vKjHwW+/e3o22DijcXjOJfHH5+P0TVJOJfatTQ/v67icvdufg/9XusozmVSsfiePcDDD/O2\nCeVBxGWCzJrFw3XFuYxO3Fi8uzsdxxAIF5emOEkrFtdjbKK4l37d4kD6DT0Ai8uXX3art9R4o9P+\nfv4saQcmCJu4DGvo0WLP26DgFZdjx7Izap6gk6i5tO3fpgAtNRa3Df93FZcjRvB7bcatpezfcZzL\nMHFZLufSLxZvbbXXE0ZBx+J9ffy+tLbmxaVSbuLyrLO49twUa0mKS5PFi4Hnnw9fTnLjRj4G+JGk\nc+kai//iF7wEZU+P1GiWCxGXCTJrFv8vzmV0vPFGWCw+ZQr/v3lzuuJyxw77N+dy1VwC0Zt6/GJx\nwF9cdneziDKHwOtlOQcGoonLOXP4flzqLTXepp5du/j2LjVttmgsrOayvt6+RrVtEQRv3WVS3eJp\nxuI2x8c1FgeKo/FS9u+ozmVYLF7Omsvdu8NnTcZFx+K6ca2ujht0Wlq41ttlzuXw4cC7382LRGh0\n/SaQrLicMIFrFj/72eDbhonLlhYWz7rkJogkYnGlgB//GPirv+KxSHv2hD+uUDoiLhNEi0txLqNj\nOpf9/XwiCBp6TsTR+B//mK64BNwbetLajqhNPUGxuF/NZWdn8d+I8u5lFHE5bBiPfooiLr1NPa6R\nOBAvFgfsdZfmGCKNt+4yiTmXlRCXrs4lUDzrMo6g1kRp6AH4cbJSc6lUeuJSO5emGATYIXzySXbV\nXfaB978f+N3v8r+bzuW4cVxC4DpCSOM3Y/Y73+Fo/Fe/8r9tmLgkcncvk4jFn3qKH/Oss7gRa9eu\n8McVSkfEZYKIuIyPeZC4/nrgnHPC67tOO40PglkQl2nWfqYdizc1sciyCSY9jkivbuLKvHnRnUvz\nZOPSzGNuYxxxaau77Ogo/vx6Z13GdS7L2S0eJC6V4ud59Kj/e+SddVnuWPzIEf/Ha25mNz1qvBnH\nuQTSdy7NBhyAxeXvf+9es/y+9/H1+/s5adi7Nz9eatgwfr28Dn0YfuKyuRm4807gf//v4vmvmo0b\ngZNOCr5/17pLl1g8bD/4yU+Aq67i13LKFKm7LBdO4pKILiKiDUS0iYius/y9kYjuIqLNRPQ0Ec3M\nXX48ER0iojW5f7cl/QSyhP62KLF4dHTtzK23Ar/5DfAf/xF+m9NO4//TFpe1EIvbnEuAL9u/n09S\nUbrt3/a28BOMiVdclupcuqwmYxtHZIvFZ83imFJTarf44cN8giu3c6nfw76+vGvpJ14qGYvr983v\n8YjyjlwU4jiXQLrOpRaXXufywQfda5anTeP369ln8+UkDQ35v5urNrkStDrW4sU8HP1jH8sPgTcJ\ncy4Bd+ey1JrL7m7g//0/3lZAnMtyEiouiagOwAoAFwJYCOByIvKWMl8F4IBS6kQA/wzgFuNvW5RS\ni3P/rk5ouzPJiBG81GCUYd0C09TEB4Gbbwbuv99tHfBTT+X/0+wWB+zOZblGEQHh4tI75y5Ot7if\nuGxuZiEU9QvT9dcDf/3X7te3iUudBIRRinPpIi6XLOFoLcp9exk1CmhrA5Yt4xPrnDnFzUpJOZd+\n4tJ8jKBIHCiedVlu5xIIfrw40XjWnEu/WHzJEhbjURridDTuFapAvNcqbOnVL32Jo/Zf/rLw8iNH\neGWtOXOC79/VuQyLxcNqLu++mz9z+pw8ZYqIy3Lh4lwuBbBZKbVVKXUMwF0ALvFc5xIAP8/9/J8A\nzjP+5mDsVw8rV7oJI6GQpiYe4/Sb3wCzZ7vdZsEC/oaelqjTB6QsxOJ+4nLXLn69jh3LX+Y3RN38\n30SLS5vwHDGCC+DTduO9w6CTqLkMez/8ai69AuSsszim13FaHOfyHe8A/uIvgK98he/nsceKX2+9\nT+mZnXEGdI8b5x+L68fo6goXl17nstSay6gNPUC4uEzbudSPP2FCtMdxxS8WnzqVX58si8v6enYD\nH3648PJXX+XPbVjKMXFieWLxu+/Ou5YAv7YSi5cHF3E5DYA5UndH7jLrdZRSAwA6iUhLrFlE9BwR\nPUZE7yx1g4Xq5CMfAR55hL+1uzJ8OPCBD3AslAZhsXg5RhEBwQ09Tz7JJ/5XX81fZovF6+v5ZObn\nXHZ0JOtcRqUSNZe2ZSdt4rKhAbjgAuCBB/L3HVVczp4N3HQTcNFF/k6MFpel7EtNTXxi3707ePi/\ni7hMyrkcN44/K8eOsdu1f3+wGxgWi+v7TNu5HDmS/8UZHO+CXyxOxNFzFHF55pnsGD71VOnisreX\nP09hJsnZZwNPPFF4mUskDpQnFj92DHjmGXYuNaU6l4OD/Dq7cN99xQtD1BIN4VeJhXYrdwOYqZTq\nIKLFAO4logVKqaJT5Y033vinn5ctW4Zl5h4hVD0uByQb99yT7HaYtLTwer+2E5LpXP6f/wOsXg38\n8IfpbEdQQ8+TT/L/Gzbw3D2l2PmynRCbm/3F5a5d/jWX5XAuTXE5OFgcFQYRV1yecEKhKAfs4hLg\nponf/hb4xCf4seK6eEEkIS4Bdtq2bg2Pxa+5xv8+pkzh/ejxx7m5rpRtqqvLC5z6eha4Qc7WiBEs\nsIJEXVTBpFS0iQcAP9+0InEgLy63by8ukXjve+2JiR/19cCFF3JM7R3uHvW1sg1QtzFvHn/OzO13\nFZetrTwzM4xSYvEXX+TSGnP6Q6nO5QMPcMnPiy8GX2/3buCSS/j/446L/3jlpK2tDW1tbYndn4u4\n3AnAPMxPz11msgPADAC7iKgewGillN6djwKAUmoNEb0K4CQAa7wPYopLQcgCRP4HwFGjWIh84QvA\nf/83f4N3jfOjEhSLP/UU8Pa38yDlSy/lk1Vjo/3E0NwcHIvbRNWIEeV3Lvfu5efsKmbiNvTMncvr\nDZv4vQ4XXQR8/vPshsRxLl1ISlyOH8/O79KlxX/Tsy7DnMuGBuDf/g34y7/kcV8ur2cQ+v2tqwuf\nItDczM8/SNxEjcUPHeLPRZSmtKlT43/pdaGxkT9bjY3FAuraa6Pf3/vfz+9Zqc5lWCSuIQLe+U4+\n9n30o3zZxo1cAhJGks6ln7h88knePpNSncu2Nj7W9vcXNk15Wb2a/3/llaEjLr2m3vLly0u6P5dY\nfBWAubnO70YAlwG4z3Od3wC4MvfzXwB4FACIaGKuIQhENAfAXACvlbTFgpABRo3iA8jatRy9BJ2o\nS8VPXHZ388H8iivYuQTskbgmyLkMaugpp3OpVLRmHqBYXOoBzS7icsuWwss6OornXAJcf3vCCSy0\nsu5cjh8f7FzqzvewWsL3vAf42te49GTPntK2SYuJsHpLgN/PsMeKGotHrbcEeO1wXQqRBsOH8/7n\n6tCHceGFLN69Luj48VyK4IqruASKo3GXMURAsqOI/GLxJ54oFpcTJvBnTC+7GZXHH2dh+VqIijHF\nZa0SKi5zNZTXAHgQwDoAdyml1hPRciK6OHe1HwOYSESbAXwewFdyl58DYC0RrQHw7wA+o5TqTPpJ\nCEK5OekkYMUKPvnYxEiS+InLZ54BFi3ikUzr1/Nltk5xzfjxdldu+PDgOZflEJfNzRzt9fREq7cE\nisWldm/N1YZszJ7NIsxct93PuQQ4Gr///vScS/0+px2LP/dc8Bgik89+lgXEihWlbZMWE3v3hk/T\n0M5lEFHduKj1luVAi0uXJU5dmDCBZzouWFB4eVrOJWAXl0nWXMaNxZVi5/Lsswsvr6tjJzFONN7T\nA7z0Eq+IFCYaV6/m661bF/1xqgWnmkul1AMA5nkuu8H4+QiAj1hudw+AFKviBKEyDB8evgxaUrS0\n2Gsun3qKv5mffDI7l0rZO8U1jz5qP2mnMYooDtq9jNIpDhSLS9fO5qYmPtFs28ajU/r7+XX2O5m9\n733Apz+dX7koaZJ0Lv1OyqNH88BtPcYrDCKePevtaI6KFhODg8k4l1EFUxznMm0aG7k84X3vS+4+\nr7yy+LI44vItb3G77umn876hndGBAbfFE2zOpVLsqptjjOLG4lu28HHN5grrQepR0hEg/2V+yRIW\nl5dear+eUiwu//EfgZ/+NNpjVBOyQo8gZBw/51LXFI0fzyfkXbuCY3G/E7ZeW9zPuTxwYGiJyyj1\ngWY03tXF4stvZagzzuCT0htvZL/mUt+f7THWr49WxjFsGI+5+cu/jL9NpnOZlLj01lyuWuUftWbV\nubSNDkqaNJ3LhgZeMOGpp/KupYsjrt8/cwj7889z17vZYR1XXNoicY3LIHVvox+Qb25bsCDYudy+\nnV+D97xHYnFBEDKMTVz29/OKHGedxb/Pn8/uZVAs7sfw4fy/X4c5MLTEpcuMS40pLoMicSDfkdvV\nlY5z2djIwvbAgdJjccB/PuvAQLo1wjb0e+siLl1icVvN5ec/D9x1l/36WXUulUouFvcjqrjcvt1d\nXAL5aNw1EgdYlI4ZU/gF4fnn+cuBuaykSyxuq7m0NfNowpaA3LaNPx/eemxXcbl6NX8RnTKFj9Pe\ncWe1gohLQcg4NnH54osswLRLdfLJ7EgFOZd+aHHp51wC5TkxT5qUF5elNPREGfgdRVwC+QgzDecS\n4BNpqc0zQc6lFpzlFpdRGnqmTw/fPq9g6u9nceI33SGrziWQLefyyBFg0yY+nrgSR1wCxXWXerzP\nc8/x/0ePsvgOWkzAz7kMEpdhzuWzz/Lj3mYsVn3kCIvGd7yDX5uNG7nEw8bq1cBb38ru5cKFtete\nirgUhIxjE5feg6fpXA5VcamHmpfa0BNXXHZ0hAuQCy/kmDgN5xJIX1zqyyrhXLrG4mefDdx+e/B1\nvLG4Hg/jJy6z6FyWS1xql9eMmx98kD9nXtau5X0jyv63dCk3ujz/fDRx6a27fOEFPqbpTmsdiQfF\n7HoJTfO5vfkmi9aFC+23CXMuV64ErroK+PnP+VgCcMnF/Pn8+Rk9Oj+RwYYWl0C4y1nNiLgUhIxj\na+h58snCeXLauYwTi2sx6tfQA5RPXG7axNFwFJcpSecyrPN/wgRuwsiyuNSxuJ+4nDAh/QkHXrRL\n9eabbg0fYYwdy26kdo9WrwYuvpi/YOnlM02y6FzqebRTp6b7OHrVJvMYct11wC9+UXzdVas40o1C\nczM3iD38sNsYIo3pXCrFwvaqq/LOZVgkDvDr19hY6F4++STP/vWbFhHmXK5cyfXF73gHzw0F8pG4\nxk806mYevdLcggW12zEu4lIQMo7XuVQq3ymu0R3jQzkWb23lA3MU1xIoraHnhBO4Q3VgwC0WB6Jv\nXxTSdi5nzOAGjHITxbl0ob6ePxd6bfjVq/nkP3u2/WSeVedy6tRog93jMmFCPhrfv59dwscfL75e\nHHEJsNusVDRH3HQut27lff7CC1lcKhXezKPxjiMKisSBYOeyvx9Ys4Zfg89+FvjRj3hb/vAHN3H5\n2mv8PPTgdInFBUHILF5x+frr/I3drEucMYNPoG++may4LLdzuW5d9BEhM2dyDZSOxqI09DQ384l3\n5053cZkmSTmXDQ3599XklFN4GctyM3EiC8u+vuT2JTMa11Hk4sX2aDyLzqXfqJw0MOsu29q4EfDZ\nZ3nFKZOVK+OLy5kzo6UmEyfmxeWLL/JYoylT+HV54w13cemtuwwTl0HO5fr1wLRpvK9ccAFvw+OP\nA08/XVyGZBONuplHI7G4IAiZpaWFD3JaPN1/P0c2Zi1SXR3XO734Yvxu8Uo7l5MmsYMY1RmcN48d\nBx1vR4nFgXw0Xi3isrUV+O533UbClIumJv43aVJy26VrCY8eBV5+mcXJokV2cZlF53Lq1HxtXtqY\n4vKRR4APf5jnSa4xFmLu7mZRd8op0e//oov8O/X9MJd8feEFXgwC4NfkuefcYnGgcJWe7m4Wc0EC\neeJEnvhgW6Xn2Wfzy6bW1bF7+dnP8jHJXNFqwYL8whUmZr0lwO/xkSNuqxFVGyIuBSHj6BE1R4/y\nUN6bbgK+9KXi682fzyfWpJ3Lpqbgjs2kaG3l/6OKSyJ2GfQ64UNdXEbdfi/19fHWpk6b1tZkInGN\nFkzr1nEcPnKkv7jMonN5/vk8oL4cmOLy0UeBc88tXl1nzRqunYwT0w8bFr3cwutcanG5ZAmLyzix\n+IMP8hfvoGNgXR2vErVnT/HfVq7Mi0sA+PjHOSkyI3Eg71yajURAsbgkql33UsSlIAwBWlqAL38Z\n+MY3uP7HPABqTj6Zuzbjikvb7UaMKJ/jE1dcAtUjLvXJtBTnMqtMnJi8uOzoKDyhn346CxVzODdQ\nvoUAsooWlzt3slt42mksmMy6y7j1lnExnUsdiwN557Knx9251OLy3nv9V84x8au79IrLsWOBG24A\nLr+88HoTJvAxZufO/GWDg7zduplHI+JSEITMMnIk1/388Y/+4z7mz+cIJslYfOTI8nUWt7TwNsQR\nl+efz7VkegnHKOJMi0uXUURpo0+m1Sgu03IuTXE5bhw/jjkAe8sWbmKJ0slcbejX6rHHeM3rujp2\nLp98Mt9xX25xqZ3Lri6uFZ87ly9fsoTf0+5u95rLvj6uH/3d74APfjD8Nra6y95engShHVTNl79s\nr+H01l1u2sTPyYzPAW7qqcWOcRGXgjAEuPNOPjFMnux/HT34OMlYfOHC8jaAXHlltAHOmsmTualp\n1aqh7VxWs7hM2rnUNZfeKNIbjf/sZ8D/+B/lKe3IKuPHs8B+5BGOxAF27yZMyAufSojL9nYeQbRw\nYX500HHH8bHopZeixeJPPMHTH1xWF7I5l2vW8JrqtkY4G966y0cesdfQinMpCEJmOfvscMFx4ons\nSCQpLon4gF0ubr/dvmyhCzoajyouTziB1xLu6Cj//Ecv1SwuTzop2eHt48ezQFi/vtBtMsXlwAAP\nw/7kJ5N73KGIFpe63lKj6y7b21mol9Pd1aOIzHpLzVvfyuU/UWJx10gcsDuX3kg8DFM0rl8P3Hgj\n8JWv2K8nzqUgCEOW4cO5AzTJWHwoEVdcjhrF/7ZsEecyTb72NeAzn0nu/saPZwFy0kmF++6iRfku\n6IcfZicsTgd0NTF+PDu8x44VltXouks9+LuujIqgpYXF/9NP5+stNUuWsHCLEotHEZc25zKuuOzp\n4e77m2/mUVhepk/nY9L+/e73XQ2IuBSEKuLkk2tXXJ5zDjtWb74Zvdt67lzuxhdxOXQYN45HEHmj\nSD3rUimervCJT1Rm+7LE+PEcM597buEoKO1cljsSB3g7Wls5TrY5l4B7LP7001z2sGCB22NPmVK6\nczl/PjuSn/oUzw296ir79XTHuG10UTXjJC6J6CIi2kBEm4joOsvfG4noLiLaTERPE9FM42/X5y5f\nT0TvSXLjq5m2trZKb0KmkNejEL/X43vfAz70oWj3VQ3isq2tDc3NfHL4wx+ii7O5c9m1cTmZpUlS\n4rIWPi96JSKvuJwyhYfIr10LPPBAvtO3Fl4TP/Rrdd55+cva2towZw7/fPfd5ReXANdd7tnDI5BM\ndMe1ayx+993sWrrOUJ06tdC53LsXaG9vi1S2oevfN24EVqwIvu7ixcAXvgB885u8upptidJqI1Rc\nElEdgBUALgSwEMDlROQtub8KwAGl1IkA/hnALbnbLgDwEQDzAbwXwG1EWRrtm11q+UBoQ16PQvxe\njxNPjO6+NTRwN2TUWs0soV+PCy7g+qs4zuXYsZUfPD5qFG9DqUK/Fj4vfuIS4Gj8b/8WeN/78nW0\ntfCa+KFfK7Pesq2tDUTsXoYNHk+L1lauefaKyMmTeaUc11h85073SBwodi6ffRaYPLktUlkAH5mM\nvAAAB/NJREFUEfAP/wD8+tfhn9d/+ifg61/nutZrr+W1z6sdl5dyKYDNSqmtSqljAO4CcInnOpcA\n+Hnu5/8EoHfhDwK4SynVr5R6A8Dm3P0JgpARiDgaK2e9VVqcfz7/H1dcVppRo3jbKy1yhwLjx/Pw\nbls95aJFXH8rkThz3HHsmtnGfJ19dn7aQrmZOLE4Etd84QvcvR3GiBEsUs86y/1xW1t5OsSLLwJX\nX81TKhYudL+95ppreIB/GC0tPCLpu9/lWZhPPx39sYYaDQ7XmQZgu/H7DhQLxD9dRyk1QEQHiWh8\n7nLzZdyZu0wQBCFxFi9m0RE13l60qDiaqwTjxmVD5A4Fpk7liNE2OmbxYhZLplNXyzQ0AF/9qv1v\n2vGrxBeaqVPzrqqXL37R7T6am4EPfCA/ysiF+np2L9/zHuCv/5prd//lX9xvXypxVkEaapDyrl/k\nvQLRhwFcqJT6dO73KwAsVUpda1znpdx1duV+3wIWoMsBPK2U+rfc5f8K4L+VUvd4HiN4IwRBEARB\nEISyoZSK/ZXDxbncCWCm8fv03GUmOwDMALCLiOoBjFZKHSCinbnLg25b0hMQBEEQBEEQsoNLldUq\nAHOJ6HgiagRwGYD7PNf5DYArcz//BYBHcz/fB+CyXDf5bABzAawsfbMFQRAEQRCELBLqXOZqKK8B\n8CBYjP5YKbWeiJYDWKWU+i2AHwP4/4hoM4D9YAEKpdQrRPTvAF4BcAzA1SoshxcEQRAEQRCGLKE1\nl4IgCIIgCILgSsWHj4QNaK92iGg6ET1KROuI6CUiujZ3+TgiepCINhLR74loTKW3tZwQUR0RrSGi\n+3K/zyKiZ3L7ya+IyKVeuCogojFE9B+5hQjWEdGZsn/QF4joZSJaS0R35kpvamYfIaIfE9GbRLTW\nuMx3nyCiW3OLWbxARKfb73Xo4vN63JL7zLxARL8motHG36p+cQ/ba2L87YtENJib6qIvq7l9JHf5\n53L7wUtEdLNxeVXvIz6fmdNyC+E8T0QriegM42+R9o+KikvHAe3VTj+Av1FKLQRwFoDP5l6DrwB4\nWCk1D1zDen0Ft7ES/G9wOYXmHwF8Vyl1EoBO8OD+WuEH4CkL8wGcBmADanj/IKKpAD4HYLFS6lRw\nec/lqK195Kfg46aJdZ8govcCOCG3yMVnANxRzg0tE7bX40EAC5VSp4NnLOvXo1YW97C9JiCi6QAu\nALDVuKwm9xEiWgbgAwBOUUqdAuA7ucvno/r3Edv+cQuAG5RSi/D/t3c+IVZXURz/HBojM3A0GKWF\nOQZuK1dDUkMZMRiMyyAip3auokVRtmjboggXtYhQTEgiLZ1Fi5DcBCXJOGY19IcJZix6YplQC6nx\n2+LcX/Pz4Yv3hsfv5rvnAw9+7773hvM7fLlzfufcey68zPKBODvpUR+5M5fdNGgfaCT9Imk2Xf8B\nzOG76uuN6Q8CPZw/cGOTJr+dwNu14YeAo+n6INDjIYc3Jinbcr+kAwDpQILLFKyPxE3AmpSdXA38\nDDxIIRqR9ClwqW24XRO7auPvpN+dAtaa2YYm7GyK6/lD0glJV9Pbz/F5FQo53KODRgBeB55rGytS\nI8Ae4BVJf6fvXEzjuxhwjXTwx1WgqngMs9zdZ5Ie9ZE7uLxeg/Zim6yb2WbgHnwi3CCpBR6AAiP5\nLGucavITgJndDlyq/aM4D9yRybamGQUumtmBtEzgLTO7lYL1kfrpvgYs4JPfZWAG+L1QjVSMtGmi\nmvzb59kSD7N4GvgoXRfrDzObBBYlnWv7qFSfbAUeSMtpTppZOtW8WH88C7xqZgt41rKqiPXsj9zB\nZZAws9vwozOfSRnM9p1WRey8MrNHgVbK5tbLEINWkuiWIWAb8IakbcCfePmzSH0AmNkwnlm4Ew8g\n1wATWY36f1KMJv4LM3sJ+EvS4dy25MTMVgN78XJn4AwB6ySNAc8D72e2Jzd78BhkEx5o7l/pH8od\nXHbToH3gSaW9I8AhScfTcKtKO5vZRuBCLvsaZjswaWbzwGG8HL4PT8NXei1JJ+fxTMPp9P4oHmyW\nqg+Ah4F5Sb9JWgI+xHUzXKhGKjppoqvDLAYRM5vCl9g8Xhsu1R93AZuBs2b2I37fM2Y2Qrk+WQQ+\nAJD0BbCUKmWlxia7JR0DkHQEqDb09KyP3MFlNw3aS2A/8I2kfbWxaWAqXe8Gjrf/aBCRtFfSJklb\ncD18IukJ4CTeoB/K8kcLWDSzrWloB/A1heojsQCMmdktaZF95ZPSNGJcm9Gva2KK5fufBp4EMLMx\nfPlAqxkTG+Uaf5jZBL68ZlLSldr3Sjrc41+fSPpK0kZJWySN4g+u90q6QKEaAY7hCQzSHHuzpF9x\nfzxWgEba/fGTmY0DmNkOfK0prEQfkrK+8HLWt+kmXshtT4b73w4sAbPAGXzt2ASwHjiRfPMxMJzb\n1gy+GQem0/UocAr4DngPWJXbvgb9cDf+IDaLP2WvLV0feGlvDvgS37yyqiSNAO/im5iu4MH2U8C6\nTprAu3L8AJzFd9lnv4cG/PE9viN6Jr3erH3/xeSPOeCR3PY35ZO2z+eB9YVrZAg4BJwDTgPjpWik\ngz/uS344A3yGP3ysSB/RRD0IgiAIgiDoG7nL4kEQBEEQBMEAEcFlEARBEARB0DciuAyCIAiCIAj6\nRgSXQRAEQRAEQd+I4DIIgiAIgiDoGxFcBkEQBEEQBH0jgssgCIIgCIKgb/wD61QqSIIhKiQAAAAA\nSUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fc3e50fa910>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.plot(RsqUni[0,:])"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import random"
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {
"collapsed": false,
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1\n",
"[ 0.33634311]\n",
"2\n",
"[ 0.45706318]\n",
"3\n",
"[ 0.37326077]\n",
"4\n",
"[ 0.44584405]\n",
"5\n",
"[ 0.40448967]\n",
"1\n",
"[ 1. 1. 0.]\n",
"2\n",
"[ 1. 0. 0.]\n",
"3\n",
"[ 1. 0. 0.]\n",
"4\n",
"[ 1. -1. 0.]\n",
"6\n",
"[ 1. -1. 0.]\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABEYAAAFUCAYAAAApnjkiAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvema4zjOLghqsR1LZmVldXX319+ZOXMDc/+XMdcwZ87T\nS3V1VWbsthbODxE0BIEUKcuOiAq8f2RLFElRBEkBL0BjrQWFQqFQKBQKhUKhUCgUio+I4rUroFAo\nFAqFQqFQKBQKhULxWlDFiEKhUCgUCoVCoVAoFIoPC1WMKBQKhUKhUCgUCoVCofiwUMWIQqFQKBQK\nhUKhUCgUig8LVYwoFAqFQqFQKBQKhUKh+LCoYheNMbpljUKhUCgUCoVCoVAoFIp3D2utkc5HFSMA\nAJvNZv3aXBDGiM+ddJ6nWXItli61TqnXl4Bv1xzbvpleC/0OXUspJ7XsJddT06yZ11yavu+hLMvs\nfHOxRp5vYVvvtfr/OeSIY2l7vYV2zkVue16i/QEG+SoKmRT5Gu38Ht/tObD0/Wv7pWFp++beJ81f\nHKH5/xL4qP2Fv0faDip76+Nc81+OfOVeuyRy2uetPc+l1za530V/FFxqzqLo+z54bVYxorgcUADW\n/HAoiiLaATiMMUFBpNewjqlCy9NL5aSWnZL/0jRr5jVXZ8UfF7nycep97wnnGOdy8Rrt/BHebQyn\nvu+P3n7vCa/5jj5i/0g1xklrrpz8YwYxRRpOUVStaQC8FFLm+7emEHkthL6LAD5WO7w2NMaIQqFQ\nKBQKhUKhUCgUig8LZYw4xDTuoXTvAXNskTW0kRIbBP/nXJurz6WZHOdoG8UyrCF3udYxCZdigEh1\n0D70x0CM6v6eIc2h/Mh/p4DPHX3fj36H0of+K86Ht9D2KezU9wxjjChDOW7boXxDoC5Rb+EdfxTk\ntO1bfw9rurKfA2usD3PziuGtv8/XxLm/w2cVI/QD9j0hVbmRMpmskVeusiWkULgEcpQTMfeapdfo\nOUTqNZrmEgPLJZUsS/GelDNr0e3PVU7KfTG5mUuXW/ZrvtP3MC/EaOT0+mu343uQTQ5J6YH/U86l\nQFp/5CpZ6Dt+j+38XvDW3CzegmyfglC/p7IkGZp4enotZR0qvUdJhrhS8r2280fHmoagU/FW4ogs\nNY6fuiaS5PiPquDNwaXXmupKo1AoFAqFQqFQKBQKheLD4g/jSpNLb1pCh1qDHXJuLKVpL2Vt5LrL\nzF2LBV8NPVPo2qluOTTtGkFdU/I6J06xoJ3D+nYp95g1qY857KC59OdikSzJ54+E1PZPua4YI2a1\nznWliY37+L8oiixXmpCLJr/Gy3lveA9srbeC92hppfKFO2vRY64rzW63G507HA4AEO7/1HWGHvu+\nF+UR0/D0f0QsXU/EGNKXxkcbP5Yy9lPyeM22fO9ydk72zSlQxohCoVAoFAqFQqFQKBSKD4skxsgp\n20udE2vGE1jKBpljisTSp+BUa/eacQlyLS80fcxKGPOTTYnXMMcSWYM5sqaW/7Vl6BQL2qntsPTZ\n5+5bgxWypO9JSB0v18g/hHMxSS7F8lma53u1oLyF+ufMXxJjhKZJmfdy5+9TY16hxT2Unl/7CDiV\nTXGutpvrG0uZdZd+t6nrLy5LZVn6a7Tf8jxTZAMAoGmaYP2kd5jC3OWMllCMGZ7X3IYAbwHnnKPW\nLGMthulc+kvJzZrsrrk5Z+kclTOXnfJ+JPYVP/de56+3yhRBKGNEoVAoFAqFQqFQKBQKxYfFu4wx\nkqNRWkNruBRvQfMlIaaVndPY5ljoQunxf4qvuaRBTalzLK9TNKprsE/eAtZifqQybZbmf6lrS9On\nsj5OSZdTr3O9j7VwSvmhseRc+b8GLlWHVOYjt2RTKzHPg1q2Q2wSgKM1HI8Y74Dmgc9fliW0bTvK\nS4oxQi1pklWNpuW/Q+nfanyaWL8PsdVi8+qpY8J7YlGmsALXLCeVpcjZF1VVRfOQ2BoxZonE6uD/\naRyRnDrH4opI+dO6pJZ5SUiMtxhiz33ufj23nn6PWDIH5jI7Ur8BT11PnvIOUphcMTZJjPn11pDb\nzud+rnelGDm1I+YuBnIEZi7vNRbx51DarPFhHFN+hMoLKVRiC5eUaykuNGsoTVRBcrx/qUtIStq3\noCABiCvlUtKnKjNy65ZTjpT+UnirCuecceOSOFcdcuatoij8R4ykIMnJq6oqr+Doum50pOCLu7Is\noa5rAAB4enry6fBDKmXL0LkxOtSf5hZk0nz02mN+zrOsgdd43jXLDM1fa4GucbgyQ1JcUMVIzpwz\ndy72jJJiI2V9s1TJRNNxOaaKTi7bqQrBNRV1sTFAUrhKH66XUFCsqegM5X/qt4KEFCNsbjkpbRGb\nv075ljv3eJjiXhMzEvB7+LlTFYK5WPpdnDK2nSIH6kqjUCgUCoVCoVAoFAqF4sMimzGypoYvBWvQ\nlXKtx+dmiszVaY30ufmew2IaY2bMQaIDprjZxM7luimc4/nfKs5lEchJm6s9XjOvS2JNlkfKM6Uy\nUta2xL6VfFLaLyT3OQy23LIvjVSWB7Vsh6zcUl4xSOyQmIzises6HziS1oFbk/EaslKk/GNWtlA6\nnheWGxovuWtPLM9UvJVxC2D9Oe0tPds5QeWFupLxc/g/lTESYzbEgqJieW3bArhb7XY4Z0sD9m4/\nygv7ddd1kzFhlH/v1lzu2BcyEw2f8eXlZZQ/PfL8Uy3aazC5Yu06Vx4v+4+ClHX0qd81uYxt6X8K\n82MJY2SNb9GUdCltEJvLpO2zU+5PRey7KvcbK3YuFeeYQ5QxolAoFAqFQqFQKBQKheLD4l3FGOFY\n05osXctlh7xHpGh/59KkxBZJKW+u7BTr7VxcE/yfo/1ew9r3HiwH56zrqcysnHxTyzsnYm2ZIhOn\nxB3JuX/N+CZL83lrSHl3S8ax1xoLYiwPiR1Cr8WsaqH3nMrCiAHTf/r0Cb59+zY6R9kn3Eq2BqMh\nVXZTGC9r1isV0ryXY+Wdq+drs8HOxVpJba+UvCQgA2Kz2QAAwOfPn6GqhiX43d3dqA7U2svrR+uG\nzA9rrc8X80S8vLxM82idDLU92BL7qsu37SZleyZLWULROZmTntW4/AscV6ZMPJSJw+EABdJVGCOt\nKAoxsLIkV7xNfFVIWl72HGJzG28TKWYKr+cfCaeyQihy2bOx9V5s/oqxQVLSzCGaDq/tnFyWBuDg\n5O8QjrOVgrk4IintK405c2XOlSOle0/rwjepGDkXreacio0l+b2Fj+ZzKAhSPyxSFiS0XUPXlihI\nlrjZSLjkgvdSWKrMSslrbcXjW1WMnIpzjw2S61koTQjvpT2XtuVS5fpc+hz5WuMjjX5shHauKMsS\nbm5uAAC868r19TXc39+P0uOHmJSXtEDDwKnW2pGbC0VRFP4eTp+XAsBSOj/i8+fPAADw/fv38MdT\nb6F03yldeaxzaC6gZfz5z38GAIB//vOfk/rTdNxliP7nH3qxj6ZUZUauK1DKYjU2h66BU/M6RY5T\nFURLxozUjzrqSoLyhMoMaY3CZaLve3/fbrcDgEHJQBUO9D5TlmC+Xg2/G7fD0/2Qpjr00DhZMC/D\ntbqu4WDG/dg/mzFgTbgPGVcv2u9RYYP1ouMEKk68gsQhd60p7Ti1tJ+lflDG6rMWloz/KXU495r1\n3ONKrhJECnh8FsUIHp1bGlzV4Lt25ebLpgfYd1ixSV45ygljpm6lqWtsnpfU75f2E/p99x6hrjQK\nhUKhUCgUCoVCoVAoPixOZoxckvWw1IKXornK1bKlYE2N2bmsNzxPSQNJ06xBL+d5SSwSRIorTYhp\nssTaE3q+Uxk1qW30FlhEHLmsgpi1IKaxTy0z99oa8rKURZNy3yl9L1ZuzJqc8k7n2u0t9dEUvFUL\nxrlYZ9xCTd1lJHYHWnS3261Pz1khUp1j8yVajlMtSDwII7oY8Lry+qO7jXSN3tdiFYTmluY9PPfb\nb78Nt906BsxLA6aZl+XUdUVKeglLmUsp/e2tsiFT63UpeY/NYzQNsjwQbdv6e66uBkbHfn8Mesr7\nBGWaILB/0kCuE8ZE10H/MrDAusNwtCiX9bSuyBiLPMxwYKcp8wvZYTGmmDFmkhcGgIXnJsmCL6WR\n1oKxcU9C7loulJ6On2tZ4+fq9ZpIWX+dUs/QvSHGSIwVknQNgwlbgL5MWHficeME66oG0zimILqq\n7TvwPb4Y5ykx6WPlDayroY9JTCk+hswxeVLlI5RHbOvqGFLXnJeCMkYUCoVCoVAoFAqFQqFQfFhk\nM0ZC2qxzaAHn0qxhVY5pM8+t/XyL1hga9ErCmhYnybq2NMaIVK+Q9S6mlZ1jxYTqIpUnIbW/LGUo\nXBpzzxPSyofOhfKV7qvr2vsvPz4+nlzXj4xURtpcPJ9T8ZHe0blkOiZzMZYH3UYUYLBMI3uEMj+k\n+3l5PF1VVd5yLN0baouRVRZ/VAWUdsjDW6MxT5Je8ivnFm1jjLjtKL8Pn79oXJ/vDJhivn3xPmPM\nJP4IWubP7Y99Sj9bU8bXfMaleZ3jeWJWaCynqiofbwfnrKurK58O+yPKG8CYDUJB/2PfpXF3MK/R\nFsAH7Pd4o4sFYgEKZu2lzA+pnUOBTyk7gq4h+VbE1LrMLe1m6xhZdQXdw36Uf8zKL8XyQSxhYoau\nzY1d51i3xfrsucaNtfKNMTwA4mvznHznGCOx7ebFtaljdGCPNgYA3JwDjjlCAx/7Pod5vJC5Dn/3\n5P0ZN+fAdM7JZfXGYurMtf8cJDZJ7F46l8bk8K2v85QxolAoFAqFQqFQKBQKheLDYnGMkVM1Pkst\n50vSr8U2WbPOp2jPcv2xuA9aLM+QPyhHCkMjVsfQfTGNe+haSMsqaaND6XMt4Sla/HNZ0lOeY84i\ncm6EtPFUUx9KK12TznVdBy8vLwAAwVgI50Kq7C1hQPFrOeNDqjwu8f8M1fFUK9lbtx68J0hWshAj\nAtNz0DlA2hGG34tHtHYbY+D5+XmUJ7Vo5/RLymTxsQ9aO9kq1BxvCD4jtWJR67j38+7CMQD870Pv\ny0u16CH4GEXn5dcaq3PYO38EpDJE6XXpPorYjhd4rSxLLx/Yn/f7fZBNQe+NyS+NCYC/UUZRjikz\nA+McxOYhKX8gu8fE5lpMj+wYuubkz0Hb3uKOTXfOur6d7tiz3++jjDcE3654v99P3gev2+hZI5ib\nl3NiOuTGY0h9Z6dijfl46XfYKfdJa00um/R/6B2N/mO/b49bT3dmnI6+R7zTb9z0HPieisyFKYh9\nMy3tJyn9OQexcSuEHKbWOXHx7XqX0KRS7r2EMiMV4uCJ4/ErbGuespf6KQIac3HJve+1XGnmlDox\ngV1y7RRIC7CUaxSx586tQ+z6moqRlGdNeea5OqemJze6o/vfhxdPqUqKNSa3U99xDCGZ43X46FhD\ngZo6nuKRB2mUFOP8o2uz2fgPN1sNeZX9dGEpKc6xXpTSix9GFPyDitYnts0tPgdVznjXFmH7Yd7/\nivK4QBMXz0hrLqeyGlM844cbVbL437htae/qCca3nbT9Km/XS9LmQ+XQ53+NepwD/D3OyV6qzOGR\nu5VgH6l/vIHaRTql1/Beug02z0vqZ7wcKi/Ss6WsUaTnmERYjSB1HouOZ5ieKCmp21sunT9Wr1C6\nVGVhLH9JWRbLKxenymBqW14aud94qem5rNJA5NE83LEw4JXx5qchUHL/7BT1T1OlP70fz23c/EoD\nLEt1nfQr/w1pALrpt1xorS0+T0IaCXPrvZy+tKT/X3qNqa40CoVCoVAoFAqFQqFQKD4skhgja1gc\nT2GKhK4tYZCk1uWU9BQWA7R5xkhY87xEi8fvS3Gbecs41cKayhzJdUFZWq/FLIQzI8a+WCPPUxkj\nMXlPYcWsYalZOk6YKrzldaqFcqkrDc0n1vdSLaZL8Np9/NIWsFNYSnh/DpU61jeoJVRiUyB4oNX/\n8T/+h9+S9rAftu0FwoCggeZCdY713Zg8S0wOLNdaO9k+9Pb21p/jLjvS+OLtfpsCwLq2eU4bxyfj\nF57vAMBZ6WtnrLelhd6tqNA1AOf7XtgfmL4nzrqJWahpfSScSl2ek58lDLbXHhM4pL6X685Arc/8\nGrKcrm+uhzS311A+jd24rLUTphS/n+ZLGWC4tTbKQYwxIs0FNG8+Tmy3W2/Vvrm5AQCA+4eHyb2r\nvFP01HHV711cWdNbMILrTWjtIM23tN0wDxoMOTY2hZ4txiKjCAXOfUu49DwZ+85JORdb94XWnlxG\nY640sX7Q1ca71ZiD66zIaoqse3mZAHKfiLG7jv8NgOCeEnoOaV7l94TA+zZ190z9xspB7lhy6vp4\nDsoYUSgUCoVCoVAoFAqFQvFhkRVj5FxMi3OzO3LyT7FGU0gaMvSvbprm6BPWX0Y7m8oUWdOSk+J7\nlluHnGtSOfR9pGj4Uy1IazBa3pr1bAnmZCrGGInlkWoJSL0/dC3FZ/HcDLlTYQB8kC88ovTXDUDn\n1N5tdUyPFrrYcJTqz5nLulKsg9h4VxTFJKCjZF3ZXA3+zoXbHvPh4cFzGkqM6QFTWZNiICBivvZ1\nXY+CQdL09L4YYwK3Ob25ufH9mDNGxH6HAVdfLAC7XpblZLtD3259f7Rou60ai/54DaWix5gsYKAs\nx5ZJynbhsV9oubwOpzA+T53bY5bAU+v01iDNL3PPymXBxxGpa89IwDXgbrsDAICqKWF3O7BHsE8U\nReHTY9/Gsne73SQvZInQ2CS0TlgfZHtQa68UpyR0zVrr+yjW4Wq3m1zDcqQYO1g/GnRZutYbV6ab\nwMri2LY8iGrbtv6ZUoKtY9rtduvHHrrteGhso/fGmJWnsi5T5sk/4lwaYzABLGOKhNacKUyp5O9U\n/PE8ZnkZoS9KdQjFxeKIMjHZGEUZTDxmjrTtdqwtU77VaLrY+mIOl+jTp8w5yhhRKBQKhUKhUCgU\nCoVC8WExyxhZonU5F1NkTWZJCpb6S3GfaJoX4hQLdUzTl3otxdp3TsTqIqVLteKkMjlSWC7nYo68\nVesZx1I5XsoYkTT8+L+sSui7qWU3xh5JQYq2e03ZSO33qXkcMxsOlfN7LcH4k7i9nAXwZg+z8JGk\nMXEpe0qxHCG5KstyEg9EemftfpijdoWz/vbHSPlm6yzgP1yDuW9c+sMkr9A7lixi1NqbMt5LfRyt\nvr/88kt0m9NQnuWnLcDDYXLdWw7d/xLjHUABXUH8u8GLGVgw/g8yswahmu/3yACgu21wH3i6S01O\n7Itz+WqfW55zrJeXQGzuxvfHWRVt247kEOD4rik7JGYBxlg0tHzOtKLnaOwMzB+PlAESslJLc6jE\n4KLpkbkSuw9Bd/+IroFZ1zO9jcYNSRlz6FiF74PKFd8lKsY0oDFcUthc9B3zus3J3Gv3/TWQ+u2U\nswakv1PXnCnr0FBdkq9H8qJju1RXDsoAoef4b4kxwpkjdJtuqV7yoyTIKqtLiNWUsiZP+daay3vp\nd3oMq27Xm1OxSyk5cvOSaF4pLz2XTjRHJ5u7N1RObFA914C7RLGRS9eVhC9H4RHKa2nZKVh637kh\nPf+SPELnlk5IsQnQ9ja6gFm6wEh5/ku9x1A/jk1ifhJEmqaj/HeVhabEtjlPvfi51PQfCanPn9tO\nkkIEYKDkj1w5Ybyox/T4UeePJCCccX3o5ofPsPt5cLl5+F//BoCj60pZlsExVFKaSJRf+qHIafYU\n0scZzytpofTUeGHAa3VdTz70wDVF0VkfNL1ohjwr1zbPNYBxX3Ml1q+Yjl8SPR+fB9+T5M5DadA5\nY/W5x6rUj4dTFDRvHdI8hOf5Ftn0P/7G/lYUBRS8Hwsf87xtaCBEqW/wdyRtTSrNobGtf6+uhi1K\nHx8fg/0x9FEXUspIChhfBzP9OMn9cJWeA2WObpEdW9/ztsl1cZPaZA5rfv+8F6QoKsT1Hv4HuW+H\nZDWmnAjVYU6pkHpfatnYVzEtdRvFfkiVH7G1dqwtEbG+Gqvv0m/mufQxpMyJp3xjqyuNQqFQKBQK\nhUKhUCgUig+LVRkjKVjTQv2aWMrakCxbuZAsdGtiLevNmlag17YoxShmSxgzl0SKNn5JHvx8KmMk\nlldM613wa4IljCKnzVMt+rnpU5hS9H+OlXjU9mjR2rj7wXjrY0r9YhTOOWt8ikwslYNLsXVykVqv\npdbCGOtGkjm0LldV5X9zSv1ms5nQxwuSt2eTOEtV13bwrXfbdP5pYI6Yf6DLjQFTuzy6aT1j/Ytb\nhwEATOVcY2pH13girj2CnHALrsTMkMC3SqyqarSF57gc64MUW4MWOtdGFqB0dJIDOMszuZ2/K2PM\nxJVCqldqQMBLMDOkfhajWOeyZt8KUuZvyhxASy5nLf31r3+FB7etrcRe4H2CsoJ4f26aJhiYte97\nMYAxZzfQYIy8X0nX6Baz+Bvr8PT0JD7XcNI3lr++rYY67/f7IMtCYqv49gYDxrmF9oL5VhoT+bvi\n4x/AkcFjrZ0EqaXvggfWpeDpY4hZ9EPy8pbmu6X1WvM7L7bGMySNJKu8f11fDwGQD4fDJH3MdesU\n5ojEWpls4dsObduWx3Pb7dbXFWDM0qTI6Y85dZfuo+WkrgHn+jtH7jdWSr1yn1cZIwqFQqFQKBQK\nhUKhUCg+LE5mjKRqYnL9slLuO5dVIkfLlKuRWsOqslQTJ2fm7nPKUmsAeCCspci19sbS515bUjaA\nbO3MufeUNGviFNnIkbk1GCMxbfzIqkysSfi/cBZmZExY1Pp3aX6P7xmiRZdel+7Bo7Pyd2dQjc/J\nQSqjjp97a+/vnFbxubGdywdnHNBzksUUj5JcYrya7tsTlF8HC1v30xBjoHBb0xb/fAJojxZmmheN\ngUARen/WWoDeWb36KWtJYl/wdkj1OeasDclK6K+B9QLla7VxbXrooXLPb8vpvfw/7ffS9sD4Pnhb\nhp7pEowMyUf7lPWY9K5Ca5k5i+OlIMkZD76KsXystbBz29rifTuyzS1nZmA+AG4LagB4eXnx5SD7\nBBkjFFzuD4fDhClGWSF861saOBbrSoMBc7nAelHmE2dmUGBdyrKcxC6R7uuwbBy/rIXSoCyEGVYx\nOaayFNtGWEKo39MtiRFz/fJczO5LQGLk5MaPyEWUIcLXhS6uk7Fy7B+JPQUwZgrGWHAxlsccYyJU\n57IsvUwjKwSehjFk3zVga8YaxDqbAjpBFmKMkVDfCwUrjskTf57Yd+dcH4m1VywPKU1O30udQ87u\nSrNUIXLpPCUsUZDklJ3SOVLuj3W4ZLhAjVAAwHSey6rPUix1T0hFrvIjNgCcUodzLPCW9vdcWVqq\nGKETVKjMmIJEUqgURQEbt/BsMYAi8tmLsDsHQDolnCN1TFi6GErpX7HFytz9vjYYYBLr11voQJ4M\nl/T/lEXUayo6TlWaXcptYE6+cPG/ux4UF6WZyhdd5FCXG/pfKrPqDVRu4db8OtDO2+fhA6bc1IDa\n9Grndt7YD/+3V1u4r4Z03aP7oGqOdaAKFAR38ZGmIL64pXnQPsU/EKXyJPB+ST+CuMtDWRZgK3Ql\nOu50wV178LjdbuHu7i5YdmzRzXHueXIOOf19TqmTMp/w/5cYN/h7wA+Zuqwm7wo/btq2nSgc0d2q\nN/J4gc+CgRXpxxqmazBYqxOK2+0V7Jvh2n17dDkL1Z26//B+WRTFRKlalqWvD96HLgh3d3f+Gf0O\nLzj39BZap0KkOzOGlIX0Qwx4vzfGT1YmwVIXU+JRlyXE9fU13N/fi/WK9VmqxMT00i6UNE8+7sQC\nRr8HnDrfSevDlPJGa0BUHjDDbig9V/5JioHY+pO6V+XUfS4vVJxCMcjZ4dsd9M44YJwR4topTaHr\n4ckpKPeH/eQZYzszSXWJrRNC68q5c1JZKYq0SxqMU8pSVxqFQqFQKBQKhUKhUCgUHxbZjJFTrQWp\n1+csDWthLUoPpVqlbul1qtZMYkAshfWMEQO2d6aJ/v1osddCqkbxFDbJOS3Ma5SbInup7A5+pPRh\nKehhSBsvabgBAK42g7Wu3A4WcwxU9fT09GrtfG7ErKoxJoPct9Hkkm6Zk/IO1SGGc7Bp5spZ4qp3\nCqQxeomLH/1N5xq0ZFfF0erL2Q10y1C0DqMcSvJIWSTbZzeXPThLm5sayrIEsxnyvakca6sbLKfb\negPdYbjv2bo5sZiyx6il/fHxcfSMklU1Zcyl75Fb0EIWtVCZNHAiR1GWx/vsMV9sa2xXfC5pe2Mp\nb3yfkpU7hnOwKUJyk7Jue08W8Bi4DN1UOyiuh37bO4tueTg+K7dIt/1xjtt9uQUAgJfvDz49by9K\nZcfxuHb+jgbduGoDtRlkbuf62fPhBeB57EJD2WFfvnwBAPAsCfp+JLahZ6s4NgR1pfFMEbwfj+bo\nCkefJzZHRdkkkTWHT4drVAtgYVq2lC/AwNCJWcVD74WOval9POSeECrvPa5b1mKRxdaOo2ulk4kW\n30veOjRWZ3qeMqtyGCOx92mt9etU7y5Xuq15iyNbAeXMz9W2ANhjpPNpWbG5M/aMtF6hPHPn4VSk\n9Jula6dTylTGiEKhUCgUCoVCoVAoFIoPi4tv14t4j1rROaQyRd40OgvwSsaeZP+vRGbOa1mvLllu\nrlb41DQxJkdMU0+t1iE/zznmCC+7KArPaqq240B4tA6ocUct/SXAfUhxu8M5SH0nxnLgv9FK2DRN\nvP95gtjRuoCMgboc2vJlP1gJJSmbi81zzr6fI18xptNc2pT4Q6lIsVTN3Utl6f/41/COvv/PaewA\nPy66wHQV6RvcAk4DtFIZxfKevz2M0tUuzXa7hf3L4OdcPrk4HJ8HS/pL00DTTWWctydaoSmTRbJ6\n4X2UjYHPiGPJ1ddPAADw9PAI/fPY519igFC2Gg9WSeOE0HtpO7SHxgeKlKyKNCAnwDGGBACMgkfj\nc2Ed+Dug6aR25H0j5M+dGsiO37cUp67vzj13xvIvisK/h//7/x369D/+Lxc75IcNmBfXd74M166c\ntbfrOjHmDaJ9cP3dTC26vF/2fQ+tk6HOiXP/3W0LvSmGdRoAmALL6cGy+RTnva7rJlvTSuwp2o+3\nhQvO6mOFvuG8AAAgAElEQVShzsffuL6+hm/fvk2uxZhbXE5oTB9fV5ysymPZnsnhFquH5hAMtClB\nChgrPROCvlfpeVLW/vwZQ/GdUub+SyH2vlPTx9Isngux/7t1X3HoJ+99Lu/Y2kBa04YYI8YYz/TD\nIMq///57Urm4Jm2MW7dWpH85wcf5whrwVAZkStFA5z5fPNi0do4xpugx1q6pcUdCSL3vUt9WyhhR\nKBQKhUKhUCgUCoVC8WGRxBhJ1dKcw0KtmOIs7dOSiMTu+Bq66lBfK8vSW9/RyoDa1jkfNH5N0n6+\npgV8KZZq7lN8K0PnlzJGEE3TJDFFUupgjPFWZ7Qco2WMpqfbEIbKmfOhT7VCcKBlCi0KMSbHGnJN\nLWExX1DEyBfcJdu42A+H1lnzum5xbJFzavgvwUzJGSfOVQcuS2VZwk+HwRr81DpGg6tWfbDQOvEq\n++FauxnHHACAyW4r19fXExYGBVq5axJPA8fjn7dD/ILHqyGv+/t7eHZySZ8DLdjcei3F8qDtjemw\nXn3fT8aQ/bdHfLDsMYRbAuk2rGgBRF9wbKMeLBRCfAQ+/ojbAbvXYJ1FkLJ1YnGXUseg3BgIMaQy\nUtZGTPbWkMuYJbwsS/jpYeirL5uhj3f/p4vF82kDcD+sO2q3C1N9c9y+l7eX344TjnMA9uOqqibs\nAcqOwr6EaMojm8pWLp2LLdTZ3uePfQjLttb6axPmE9lJB7fp3hQVNG6r3Nb1VWytuivgeTNmZuB6\nrKoqXw7t/7QsTIf/fZwhZMrgVuFkzsGd0wxhcPGtyNu2ncRWobLEmWi8bUNI6Vc0ftCa/TClPqmy\nlyMnqevDpWyPWF6h9eTkHmSMdOFYOTSvufqEypF2U5SO2LeRGUzZWlL9rq6GmHg0dg9P17svsKfn\nIU8DBvb9UA6dCyfPhfFXACZzG4UUPyfUFrQtz70GitV1jbxSkOVKc8oEuFQhkiv4l8I563XKgLMm\nYh+PsbJPGXxjiz9KM+V5nUrlkuqWElxojY8zmvepC9BcGUq9ljKJ0GuhBbU0WcUG5FiexhjfF6gL\nTaxeiJwFxlwAuRj4B+jcZM3rkxvgjd4fC6on3Y/My4fHh0mesY+TpXVeA+cu89TF4NJy6Hm/4Hcf\nQT/sK7j/4j42rkt3zSlBygIK97twHwgb8lEQCgD4008/eRn67bffjtfdJ9GV49RvD8P/Diy8VMN4\n/HAYAjoWm0GJUO828Bk+A8A42CNXUEoLUDxHP2r4Ao4qS0hFjwfWltRFhrqaAQwfNZOtgolrDaf6\n061N+bad0geYpIDZfR7aCZU5hTFQPbhtWn84Kq/m5sjQuaVU5EuvoWKIPc/argb8g7osS3j4yfWZ\njXO/PLgP8V8e4PPnoW/3TGFnrYX6vwclYfHg+g0JRirJXsiVpGmao3uV+7baPA9pmuvefxD2m+mH\nG98yuO/7iTIS0fe9/zjzSr/aQuOU4tCh4tU9a2lhU44VPIimaSYuejSNpLDrMNC/03Oa/igv3L2O\nug1wV5iqqkbvj7ZD13WjPDj4NbqukMDdkajCObZ1b6jcOaz5UXgOZcYp9YoqPyL3+nTddI2SolhK\nVQKkrI9pmtgcR+/DPoOKd+pqPZnvDkOez13j+5ekGPFzTzdWXAIcZYFCUiRJ55Zi6Zo5J+9zrfvU\nlUahUCgUCoVCoVAoFArFh8UsYyRVg7f0emqat4BzMzneejtcgr0T0gRSmrKUNoXlEUv/GtZuWm7s\nd24+c3mccj5WTooloCgKT59FbbdEeZXyiZWDyA1aKCGFFSTVgVqQQlTd3G04Y/Vbc7yQnocHEuR1\nCMmMxMy5FLPjLbq8caRYoeh/bpk8lAaebly7fh33vaIoPI3XW44xCOtuA83WydC3scvH3d0d/OUv\nfxnldXd353/XLsBkde/o9v3RMoVbvT+5rWmfqx7a55dRnam1V7JexSy0/N3SIKf+bbvAr8VDA30z\nttpJgSZpO1MWCC2H/o5ZFSk7JDTuUSt0+zC23nd9D81muLaZCQrJ646grJiYZTc2dqSwzl4D55Bt\nia1E+wG6jjVXLlgxcUF5YW5iBRkvza8D2+7HLz8BAMCjc8GiDAfPzOj7SUBwOhf6/uLkt0ZWVFEc\nGVLCnMjZJ9T1jLtqdV03sT6XZekt09w9x5oe2sM0DwR1k6F50t+0r3pGZT9mYQBM2RfUZUUKgBrq\nq0VRHOsvuO9Ja83Y3EfT5UAaj85pVV+KubXkqcyRVLYGws9BdT3pv4blw8tJYaSkMEbm5uxQnY0x\nYF2dS0eesuboeiO5eXu5RYa8Y4wcuoMfL/rWuZzZafBVOp7R7d/xHK+jxDqJuSUt7bPSGHUqzjUv\nKWNEoVAoFAqFQqFQKBQKxYfFWbfrXYNNcs77z1XOa9YrV8N9Do34KTFG+PWUbdAky1ZufIRYHd6C\nFl9CjuU555x0LYfJIVlT6TEU9GlOU59yLVb3Od/8GFK05HiOBpiVrGpLEbPehjT9/FwoD4kBQgOE\nxer/luTkNS3bFCn1SLFe0a1sCxdUzRoD94MhCApnRu67qX+8f9cYPKa1UKK1lwUvfH5+9lsMYqDR\nuq6PcTRc2fvbIaubYgM9DNarvbNoH5xly750SWMChRR0FBHdhhH73N3R8i61If7nVrKyLCcBknmd\naB4//vgjAAxxWDA9Mma2Ze0tgDw+An3+nWPMPaElUbCEx1gusRgbkvUyFSlrgZzYTDmIjR3nCLxH\n+4T0rtAUjbGGOxIUlK9J6H+UF9yeGZmDlB1B8wrFGKGBWVFWnzcuzg0Zq2ndeWwNfMbD4XDsq4y1\nZa31QZQpy9EzTJxlunaxRiproCvH7eot+kUJz4e9LxOB84hk2fbrPDMes4qi8Hlgms1mE+x/bdtO\n5lpJXihzJNY/+BbetJ1T1iaxtbZ0f2ht+lqW9ZS1Yu46hKbJXU8CjFk+KSyPpZhb0+Lx+voaAAZZ\nj7EpcP7FWEFlZ+DlWo71BUDk1sn/wTrmyEsDrYv90/bHeIu8j/g+e70BcHJlWBytWN+lv1Ni40n9\neA5vac0oQRkjCoVCoVAoFAqFQqFQKD4sshkja1kIUhkD7wWn1DfVks+jblM/zqUWyjXSS5rdU8E1\nm7FnjMUMkc6dwiZJyePciL2X1L6Ueo6fX8MSzv13U7T+qRpuPFZVBeWXwVLlLU/3RytWSp/gaUP1\nyYk/EovNMYfYfbE4Oil5SvnSnQykvN6qtv+tI6VvSxZKH5OisGDAjbHPgwWpI+m5xZSyELh1nFpE\nH12MEMpW4EyBvnAW3dstlM6ucns9RNbv9kNdfn36DhYDIvz27POKbR3IGRI0tkGKvNBrfcQayesg\nyWNsu1tsIxof4lCgVS7MrJDqg++pbdvJzjg0zkFsTgsd+XOnxPpJGV/mkDLmpJQdq3PqHB2bH2i/\n5wwLGsNGkke+G5Hf7pbsevTsdpmg+fDtejEWEM0D86zrelI2ZYTgNcpywt+c+UT7OLJDMM1+vx/V\ng8NvyYvtV5ZQOlYI3zJ3t9tB5cKCPDiZgLr0lnWMzUJ3hsJ6IXOGxkWRtvkNySi1nPN3Xdf1hJFD\n45fEmAaprNaU/hhjg0npXwtz673Y/JVyLtSGKdekvELlhcpeWgd+DllhcoHuaAHKzSDb1XY4booK\n4JOLxeNiflX3Qx9vXvYjlhkAgHUxsw72OE9QxgiC99X+oQfYOXlhsUbo+ELH11A/pmNI6vo4Zc6R\nkJL/uXFWV5qlSO3kr4m3UAecOMSPOkd9htIAHLpJOo6lHz50sRkLXpdSHk2fIwxzQnhpxYVUr7Xy\ny7mWouhIPReaDGcnkY0L9tTJ94bui5UTe6bRIO/KLpDK++yiX3XrvZNUBQSvZw6W9F+p78WUMrGP\nrlOQ+1GzFDHF1qXlP3VhGZMhrsCYA31n/COAunhRFxIA8IGQad+Q3Az8Yt41YfewBzCDUN+9fBuV\n86newZMLvgrkY+2JfSxSujpXpuM1+tEWc+caKUYCinlJVul2vbztrbW+rlxx0ff9UbHhPrLqq6vJ\nXCgtJnlgZikgM1WM5ECSY9q/YkoWCXNK4bUhyarUNrF7+X+6RpEUI9I7S/k4Q9CPeezjWEcp2CFe\nu7299e5rmI4qy7wM2HGQY1pnlA9jjP/NZWe73frfUrBHruCh/ZF/xHdd56+hYhD/bzcbMPXwHF/K\nwefuqexGig3elpJ7DR75+MXv5c+BWwrvXb0qolCSFIihsqVrtK14+rZtk4wjb+GbAbHkG+uUtQv9\nLclXiotHbH04V7+cMS62lpAwkqXayYs7Fi89ACoqrt320aYEW7k50BkQrq+Hebje1HD41RnwcEvu\n1gVh7jq/vTUdc3i9R2Oom4aLyskCcfXk349S+4bkIAWv9d21BtSVRqFQKBQKhUKhUCgUCsWHxaqM\nkVzt2lKcosVaCzENcSqy7jHGa8R7Z6EStaXIFLlyr7bppmlWrp+neAsWvaVlprTvUpeYVGvZGjhV\na7qUPbUGKySWb0z7P0LjNNoCPT/Fmk7P4zm0cu/3+7AFwRjon50LzQ8DfRi2zvrcdGBdoMjJfQS5\nfYnsHQfQj9PH6PlrgG+TmEpvlBCyGoTSxfKUrBiXtCTk9O9T63OKrIao+6H0MZkLMX4o3ZyzSjab\njehSQO+lx7ZrBjYiAJhqbL2u69pbk92OvtDuDJR7eVtc+vwhSzV/Vv78fCtQgDjDBK3JG1tAx/Kg\nARpDfTtUZ96+dDyyX4Zxq/t+GJXXNI0vk1vhpedP7Wepc28oXarlNFWeL83Yov04ZJkeBTcW3B0l\nFhEvR2JAIOh/Pjb/9ttvk7UTdTPFfDuDfeqYr2Qx5qwTlOfNZuMDKnMmWtM0vg6UFUUDxAKM3Sp5\nXT0jrW2hAecm5NwHoCNjBmOOUPnk7n9SsFoLxy1M+Zbffd9D147ndHSpq+w0IHUqGyvGnpTWB6d+\nF7ymdT1nTZB6ThqzqTzmsEJm15oCYuN3yvPGyhbvR3Z+j3LdH+XKudJ0toMD9hfH6Hh4nMoCBn5u\nsas3R1ZUSr8EILL3PMhve3Wcq0MsOppHbM6NzVGv0Y/X1AcoY0ShUCgUCoVCoVAoFArFh0USY+Q1\nmRl/FKRaYaW0AM4YjUbEll0zxvux+ZgOyBxpjj5uucFvUmOMxM4tjWuSUgepnDUs0znskzUg1Tnn\nvtxzS+/LqVeov0vvJaaBp9diGu7JMwKAeXDMqs1gye7R/9NaKHpnAexODxTs4fw4YVP4oJgYk4E+\nc0ofz2FhAEwtaC2znuF9sTIxIB8GyTs3zmVdeI1YInPXYpYX2rdjsSly2C8SpPGFWlBTWBeY5qkk\nvvbdOEYBDUpXuK187UsHpZOPwoztMZIFkVrXOYuEBmTl22lSBgAGWKRxQbiclHUN5fPwTMh4oeVx\n5g6y1V5eXvxvfN7r6+tJYE1kgBRlAd1hHHQaMZrHiCU7FKRxbp6IMRlSxpw5Rl/OWiY1zRoyy58b\n24++cy5ndV2LcTdC9ZOen/YRzmCiz0VZF5gGt7LFvnR3d+frzNkknT1u5Su9xxAL4nA4+GfEvDAg\nalVVYnwTHouItim/hnJG5R7jopQAUO42o/pRdgjmy4PPQlVAfxjyLa9d4MjeAFSu7RkZTBpD/XgB\nxzZCeZSC+aeyQ6RNEELWdJpXjgyeC6lzyFpzm3SOvispTQ6bRELuemopYuOr2yUXrDkGXT48Desq\n2/We+YHpm0i9rHBJ6le8Xtbaicz5caACKMtxXef6xhrj/BKc+/tLgjJGFAqFQqFQKBQKhUKhUHxY\nnBxjJFUDt1Q7+dYxV/fQ9UXtFnaZ9uEN/I4bLaos5TgcKeWv8V5y88hJnxpjJMXC9Vq+cTlW4KVa\n/NSycq2QeIwxPiSE/LD7vg9aEijQ6jNXT3/vt0FTbwqal0sX2Ukpu+9iFvseAK3iZpwnzXdpX+Pb\nJAIQy3SERUPLlK5xP28pn1zZicklTfOavtW0HgDrxBqR2pCfk7bR5XWh6SQ5k6ykMfZJjDHCt8yk\nfYlbdKVo+Mg0MsZMrNe2O1poMdeO3O+31HZpaHtI1le+5Tctj9efpuGxE2h6tKZRaz+32tM0+Bvr\njnEcaJm+jK6H3jHYKratKq2LJfenjKtL2Bv8vhyW5tIYCnMyvtRCGZMF7LN0ZyN+zVrrf9NdU3jf\nofF3uKze3g47sDw8PEy2mKV9j8cp2Ww2/t3f3AxbXqMMbTYb3w95/KirqyufLzJOjJluB4xb87Zt\n69OhjNPdbPhuMV3X+bpinpQxwtsE67zdbv2z1eVwbf/8MmlzbyVvmsmz+e2BawDzdahz62LzlN/2\nYP/+fchj4+btw3TO4mNIURQjueLpcsZ7OibQcSZHdvjY9VZwyjdaaH1IGUmUxRpKH7sWGxNz5+wl\n7OzYNsuxeknr1djzcxYk7cc8fepz+77nGFf95w3YH4dxC57d/PPvp6y8LoklsnqKfL3J7XrfA86t\nWBA/XI8Xg2kNKkTQlaYoAAq3sOzPRyeTkLsQku5N+eiaKyuGnI+6uWvnVK6kKjJSzp2SVwqkCSyl\nn0jKrDklRagcSUHQ99N3hbJkwYLFPJh7Te4kSvPNQaicUH+SPjaoG0DoWqz8OaTKXK4snCo79H6+\nyDrVlU66FrtvTjHCj9LWebFAkFVVjba6lfKUzsXeHaXdSs8kfRCnLGARowCY7lnr/ujOgDR8bAf8\nkLu5uYHH7/cAANBVToHRd5My6Uckd//BPPf7/cT9Rfpopvfx56Af0Xgv/QDHfEPKGQAA87fPAABw\n+Da4TdR3dhIAlH6cxt7tOej4OWNd6tiYu4Bfc+0kfXTQa1L/jckVfxZ855IMSUFSaT54/tdffx2l\nq+saHh8fAeConKDKnAl1X5g7qRIQ88D8UQ7oxyrmv91uvQKFK0GsPfZVNDSU7pqkeLQFAJAAz7TM\n0oSV+OXNFrqfB8VOsUUlSA/wacjD3rrn+c/QRn1jwW6dwuqvn4Y0/xzeS9M0wS25KWLuCRSxTQYk\nuQy5qNF3Ro9rrh/n1k2hNDnfN5IMUfnB55HaPGVtekp6jpiBhqaJuVXlrG3n1h84h1BlPG/Dsj7O\nOdQtdBFcqAVbFcc1qgsKC7cbsPf7SX3wuFa/jLXJkvXaOaCuNAqFQqFQKBQKhUKhUCg+LGYZI6dq\n6FKwlJ757lEhq8NpHpuwxU6CqPVlR7MpvSbdPLqAkP1U+5dq9cl5N6naP6p55TTDFDaBlBeta+xZ\nU2n952SDxHBJVkiOdSFmLVgKiSovaciXljdKLbUF1kNoyyVUTbyXHgHCLiu8TMyHp5OsqrF3G9u2\nVOrXUl9aywo9l89azJE18oyNE3Nl8mtzVrXQds7SfbH3ScHZJxIVNzUPbqGiLjspFvfYeHx7e+ut\n4zzNw8ODDzrZ26MVi88T1MUlxBjpus7TmiWXGKwzvYb5Y+BMvNY0zYR9QNOHGAIAANYFZjaP7eSa\nhBQL5dKxd0m/XiKbuWPIElmdWFqRmVTXk/mE9k+JRSAFHcX/kjsOpgnJsSR7EqvRuFno+f4RrN+m\nN8wqQDeWT58+eZYHZ220bevTY/+nLCqEZ3KU5cS1jQaO9Xm4YMqH/TFPrAN1n0CrOJezw+FwvOZY\nzbjdKTwC9LVzY9u5dvr2BN29C2B567Y+/dGxUO6fvBc5tG5+3TpZfJiOCTFGB31ujhCzLsYwCGGO\nmbAUsfEhd72Xcl5KE5tz5sYc7iqcstZMnatzIbVXjouq9I7pXCg962T8IoxEPubQ/pj0TYfu5PsO\n4HcXLLlw495Tc6w/Bk1v48/BkfptlpL+NaGMEYVCoVAoFAqFQqFQKBQfFh8yxkgq+wCxht+rUAnP\nGOG5ShrIZOYI/sCtScvCx4G0u6NW3sciyapynv/fHMOEW2/wHnqMWc6la9Q6GApydW7tZK4WNPaM\nUrrQ/1PPxdKErJaSFj90bu6ahJhP6Fzfkqx2vA5SoMVxkNb8/pL7HteAlGeMtZLCTJCCpZ1bds6Z\n/ynMlxQZmuvjoe2maYyRSdDSgOWFW7RTrDhSzAzEHJtEYvLxsmiamFWc/7+/v5/EUaAWfv6sfUOC\nlRYwSc/bEOOVHA6HSb3quo6+F/5s1PqN+dJrKDP4HD4WTF0BuO0R64chzd5Zx0sSaJM+a2y8D8lj\njJnD02E+i/3VI/le6r6YRZf2PR7IULqPBsONtT2NA0P/U7mU1i/Stcm7csX0BUDnmA/I1qD3cybX\n9+/ffdwQCZwxw9kbAOMAs5Ntrcm66mjJHmShcdvqSn3v6upqMrZRxmSH59zxUDiZ+PYI9Yubfxw7\npLhvoHHrVrt3rK6NGxO2BcD3gU3SP38b0pD2kNYCKf2eP480h9KtzmN5SJDG7VPZifR/CsNi6VoF\n2U2FNUfWe2SeTCmnKIrJVucpjJFcpN6fyuSLfZvE+gZ/RimPsjgy37BtMLDy9+/fffoow6Z24x5+\nc3a9Z6TBYZAlSzwJrJNRaX28Bt4qUwRxVsVIaufL7eRrfFjkKB5OzTuYfzueDCWhjw5g6IpjwO9F\nDUKwN79DDZbXw6CYgXylT87HaexDRFoUnLI4wntTaOYpE9WlMDdBLZWhNZUmuYoO+pHF85QmkVhd\nECk0Vwq6uF26KMhWiGJ5AGAjk2HMbSJWds5CTso/lI6nX+o2lIrYpHjuCfMc+acuLEMyBBDuEyF6\nPv+QlqjL/GOQ7hDA26EAA6YcE0jpx0NIeUDziMlLbOcG2q/xg22UxlPkh3QNHF0DTD/k2WFwxaIY\nKfQAjjtxHA4H//GLH5td100+PPF+OpfwHXvatvXprq+vAWAIwsk//vzCsmmhdx+6rdO3SP1AWojm\nfDzNjW2SIiUHc/P/Uvlaugak/RHfLSoINmz3H/pbkin86KBKjJjCSlKWhdxGrLWTQItUkUYVD3iN\n7lBD09DdbKjyDp+b18sYM1HUUUo+Po+UJ6Lvxjvk0GejQYjxQw/r0jSN/43XMI/D4QD150G5CCiP\nTnTLzsAW0zkx7DoLJbbnr0PbdH8ZPhDLL9dgnWta5YJVYo+iPZEql7ibburcydP0fZ+Unvfxc7t8\nzClXU/MLXTumWbaDlgRr7STwb65i5NSxJHV9mFpmTn2qqpqMHdQlEGUJ5yw6hvCx15ijMab4YZAT\n49zf4NCBQWFzihcz3DTk0Y8Vr2sqz2NYUyZOyUtdaRQKhUKhUCgUCoVCoVB8WCQxRt467eW9wuD2\nobn0M7xWHBkj4GhRPjW+qt4CuKCu6D5D3+JS7Wqum0gMMTZAzJViLs9TrVdLyz4XljJKYvd9+jRs\nbffw8BBMH2N50PS5loqcviFZc1KDOKW2USiPJa4xNrLnfcgSPPc8OVu1xVg+PN9QvaRrsfvfE9aw\nbKcwQDyzwhgoHCOjMMUkDX+naCVummbCCqFlcUYHdZeh28ji/9AWsFVvoNgN6dAaNbI4BY4AUxmV\n3HKWMsWqqjpadCtX13Ya+BIcrR8KA8YxIxszZdWgxY1bu6Vnk5gc1LKP9+LYudlsvLUTr+H/25ub\nI+0ZXWrcO6bzi9QvT2VUrgFah5w55xx1luSsLEuo3LvBd4x9pCzL4PhF+yplXCAL6OnpyZ/DI+bL\n2VOxbbepuwUem6aZsBUoI4n3Q3pNYsbSoMG0Dh3Ji5aN/z2jxjVRDQV0jDWyK4b+XJsSfq/GZfv2\naHtxjsI25M9TliXAi2OwdE62wbF2vlTQ4/rYTue7Ht1x/vewlbfpe78ubp1I98/HZ8xhgMTmTmkO\njeVPx9CYbIf+zyF1PsphjmSv1RI/IVIYuDFWSCpjhN8zV58Y6LiXsm5LKVcC3QaeM0ZwLqFzjsTk\n8FtkE7e8Auc+95IMRii2FmDj+iW6jht5+2j+/K8JSYZy2zoFyhhRKBQKhUKhUCgUCoVC8WGRFWNk\nTjNzDs1Nav6SlR//n7teMSRZzo8Xw2mkZyABVIkee/jvglhBXQLuY2ZJ2lN1fznvIvf+UF4hNolU\npmSFk+7LxTnYJEv76pwvZMxCi9een5+D6WOWh1TNfY6lIvb8c22TwiyR+kus7amlLvgc1vr4Pn0h\nXGd1CeUfqvvcM4Yw1yeXWnQvZTU4p8U5p5wlLIeQXCJThDNAJEsYZShIcUTwHA/eVpal6PuPx1A/\n7gqATvDt5lbx2PPSI5e5vu/F2AWYhr8Hb+3uuol1vO977wON8eNaewzoaF08BNzmF/Pe7/e+Xen2\nuzzGCPVxp/Wg7UC3+aXbo9LnpWi7FuzOsVw2w3FbDu/n5fd7caxKCcQr4TXXO2si9BxSHJ2rq6tJ\nTJEUthIATN6xtdbnge8YWQ/W2kkcHPo/xubjTA7KIuFb7Mbev7U2uv2sxG5CeWm6cTyCvu8n8XPo\ntrs4Zu0PLqbBwcIehjEHZcHLCxg4NMM1ypjisXtwPGrbFgrCgqF17u9eoP+v2+Ga2w64Ncfttnm7\nARy3D273Q33aw/FZuexQlkdO/ASpnWNze6zvrcEOof9T1manMEVymBzSWiaVwRJj6yxdf0rpQoyP\n1OeJsfpymS2U7cWZi1IQcF5fmseI3Yd5PDtmqQuUbGoAsPi7xowmzyMxU97q/LLmWlEZIwqFQqFQ\nKBQKhUKhUCg+LP5w2/XmWKjXyH/ptaXa2blyPHAHGug9Y0TK45wWWYm1QS093FIjpY8xM87xDLE6\nnJov5hXSnKe+61TNe+wcgrIVMN4InkM2iTEGbm5uAOBoOYtp8ddEjLVyjnKk/CVL9+h9OvUy1TKH\n+iq9hr6dtsBtKiwYzGU/3RlDYqGk9NGY1SP0TCl4Cz6na2GJ3KdYthBFVQbjdBhjJn1MiidC60N3\nr6BpaBwRzhiZs3rFaIQ54wq1dqf0M/rsfLcQUW7AQIUcSSdDpZMbWxqAa/d77+YVd3/f95MtTbfb\n7aQeMesibVP8jXWuqgoqd45vOdl3PRQ+1tdgqXtqhvH1arc7WujJ86dsAXpqjII55Pjhr4lUS7Df\neWZ8jwEAACAASURBVOlmC5WdMqsAxrulYDvjVst4HWC8k9C3b99G5+h7kcZhBLewSnEo8EgZXNJ7\n9OVgv7fTa9KYIAGZIhLziefVNM2E3YGDQ2t62Owd28SFJsH4BW3fyXFEHPhW3NI7pmtBHw+hdtsj\nWwv281Co/f15eq/b9cn4+TUcK4j/punm1ho5TNS5fiytE2JrB465ddia3yuxZ4vlxeNihOqfkmdK\n+6Z+RyFisUJoGh7Pi/bj0HwX6z+xugBMd4m6ubnx45eUHsuS6lLi1soYawSMnzsx1gh0AJbFKaJ5\n5a67zzk30TErt5yU55hVjKROUOfCUsE+d9kpaaQFcspgslgZQoGdo5l+WFkAABfIDicR20ypUrEO\nRmleoa0mu64TFyn4n3+AS2VLCoXYZJLzoShhjlK/ltvMGveuqSABOAYRlNKhQmRJPVPTxya00MSc\nM7EuHctSxyD8JS6e6d8OJxt3H26TaiyULghdSbaYpAoqXjZfZEoTZfQjM9Kvzz2+vjWsIUMc3q2l\nrCbUWEkxgu+BUvm5G4vkSkD/SwFSMe8132nMtYtv0UkXltJHU2gBa8wxeKF3MwALDbi86EIPAMoO\nAPoh3cZt5fvcHV0FcGFJA9zxrXWlLYPpBxv+9y4IQNx+3L24fKUfmOjO0Lr6Ydr9fj/JX1KMxMZH\nidYtITZO8GupY8JacyPPPzS2l2XpP7awn12XG6irsSKQrjm42wu2983NjVf64zhLg6/iObrG4UpM\nWj++zS+CLuCpIg7TceUMvcZdg+hzUGUDD0hMlXN4DfssdWfhWwXTZ7wy7qO2QjcbA13n3GXMkObF\nVavZHtuZbsnLXdTo/9CWuRaO86lxk2dRld6YUKKyVzCq8X5YFIU/F1MIUfB3nCpfuUiZt6X0KWsh\n6b6cOs3lnyKrADBR+sbySv1mwiPNk2/FTvPi7qVFUfh0uS5VsbXTUmUAfUYeIJzmQbfL5tf4PDm6\n7pSLGGGhKAqAGww87p5j3wYVu7E6S2nquh7N/RynytApeaakU1cahUKhUCgUCoVCoVAoFB8WfzhX\nmhS8BtPkHNbIxMoQU7Y7VRqwjjGCAVxz6yNZKLlWfrPZTDS8lNbNLXScJjZX9pyWfU1LVm59Ts0r\ndj6FdZSaV8q5mBZ/jskh5RnLK7S1XWgLUGlrTf4/1SqRkkfoP4BscbAYDBn/lwaAM5673qfuDm47\nxRTrRWkAEpLFZGNU1wxrR25ffy23G2pJPDUf/j9k9SqKYsKQo+Mk30a3KArY7XYAcLR2UcZFaHtQ\nmhel+cbYF6E6UzbJ169fAQDgt99+C7ZDTDZ2u91ky0FqoeUyK+VFWS/8HOY9VHw4eIpwXUC1dwwO\nl67eunfw0MKV2w70W3lk5vC6Usszls0t+zQobmmO1ki01uH7e3l5OeaJ1vTtYNnszdHy6FljDjQI\nH2+b2Fi1Zl+fY0+mnF9iMY2VgdewffEdVOXRLYUHMqV5oZzR+qEc/u1vf/PncGtlHphXCsRN8+Ls\nI1pnzujYbrcT5gsyMymbgj9XCJwxQRkgfG1GZYqPL0Nw46H+BzZZ9WChr1193LbTlXHjWVEAHIb0\nTXVcHyLotqO0LrRs37YGoHNsZ3M/vIOi6aFsHJsL0wtueJyhQp8fAzLHGFnSukJqS34fXqeIzbmX\nWpcuSZ+7puO/qcshvgdkYUnsb0lWc8cElG0aPBvPcfdSyiJqWNBx+o5T2zDFHScGypjCsQDrend3\nBwBDG0mMkRCLZtS/XbXK2slLXQJs3Zj20GFmYrBVhLRmCCEUaJ3ft4YMnEOOlDGiUCgUCoVCoVAo\nFAqF4sPi1Rgjc5q4XEv4uVkgvIyldci11udicl9hAE9ZDGbVWwA0uvWnaTj3+/1EO0i1xdwHntYP\nNZuoITXGTLafXKoNpOVgHb58+QIAQyyNnJgZsfzPyRLh13IZDaHYLzQ9tYxwP98YK4TmI+WVy+AI\nlROz4oTKxmPIsjNn2VxD9oL9ojAAzoJtmnGwOBtgfwTrY6fXMIDuw8PDyMoVyue1mByXwtoxgWJj\ntcQYkZgP3H/XWisyLABcQE8WM4FaWnHspH7V3HpF2QtcXiRLF68nAExioNDxgo//Ly8v0T4XC74o\ngTMnaOBu7x+OJjFrocVYxs7uU7gYBX1Z+ACWSOEyh6NFXHov3IJGY1Tgb34EOMZWodZx357O6t1f\nu7gSDy107pwhrIKcbUQp3pJMS4ykWN+YYw8BjIOWcguqlL+01SSN24Gyc39/79P//vvvAHCUK2m7\nah4riP7mdaDzFw0AjEFgb29vR//v7u7g8fERAI59iI4RvK9SazK3vrdtO2GW0e100WJO5wtuRffb\n6RYlNK5vXxsXB8ltp7sxFXRuO9DOMbP23WESwwTRNM0kf4S1FuzLfnRf17bQ90frNn0eygDg817f\n9xMWEd1aW0IodleIMZIzx84xMWPMjJS1Uy5iazo67ofmQqlcGqcJr2Pf3m63kz5Nt8NOWWtK6z7M\ng8olZxnG2C20v8TWzDh2SGO7NIfkgLLOuAzS5+XsMwoaayQcp8oA3DuGfjud73i+dV1HGYT8eZEp\nOZd+ze+oNaGMEYVCoVAoFAqFQqFQKBQfFtmMkUtoeFJ82c5ZVsyHMCefU1gxS+E1cSVqUgHIdhnu\nOD0l1StVq8e1kj5af98f/bCFrRClbSRzkNsXsV5ozYvlmZPvJbCkjWIaXp6fpKmPsTVolG+u2U5l\nmEjaf+wn6BtKtwdeaiWJpUHtf2p8m2Tw9kUZ2XfAa4OMEeitvy+J3WGnFgQ87na7ydbKp/Tn9xJT\nJIY1LRWp1juJMSJd49Zn6gtNGXUAwzsO7fDS9/3EOiZF6ee9y8JxHP/73//u8+RWd6nduIU2Fuck\ndC6EUFvy3UV6tEA2DZSlkwW8z9WrLXs4uBUPxhpobT+xsKcw7MqyhOra7R5Ado3CcQTHFdzxpOu6\nYx7YNveOHVkcGTApLJHY+EqR6ye/RCZiFm6edyzfFGYWvSaxNWJWfh5HBPGf//zHMzMos4FvlUnl\nKxQHi/+maSjDCne6ubm58f2EbwV6dXXld4nj8ytlTCGkeB3SNc6+obGPKHg/xDSH5gC9RTabay8X\nt+AZetjglsn2+NyhMTe2TTetg38eaycMZ/ocdAtmgOPaoW2Pu220hB0jsXpG5UEaA4DKo2Rxl/pj\nDKeyVyVWxFJI7L7YmM6P9FlwHqIsJewDnz9/BoDhfeL6HNPTMmJrR4lFwuWKzlGcBUmvxWJs8P67\n2+38NWSdSZDeu9QnMKYIroFxDun73o9VsefAZ6VrwAl6C7B3rB5hi3he181m48uh7J7Ys6aM99Ic\n9RbWjkmKEamT5wrcqR+/l8ozN9+5hd8llTzjAoaDLQyYVpiY3ATja5GwgJU6r/QcVLgkChsCFyst\n2zt7rkwhkajh4dRKHHDmBPqSyF0QppxbkoamkyYdvqCifUlyl0p5Dmki4xNFTNmSOllL/2MDcwry\n78M6C2XjXr4kK7pY5RMelRO8hgsN7OMSfTz2cUInstCR/36PCPWJubktp39Qecntv+juhwqul5cX\nv+DHOuK4SUGpybyf0PHYl8nrQGjuMZe4GKWcyoT0McD7k/Rxy9uDLnjpNe6+4/u7MX5LT5SAsnHz\nwKaAAzadY/rubq/h6TcSIDUArriw1kL7NKb6X11d+YUrPhM1EvCPjL47bjksbe8aQ4ocpsh9bp6h\nMpamDckE7UM+wKqTie1265WFXCEs5UUVCf/6178AYPyxgemoUkty3wEY3jGWjWMt1k/aWhvvu7m5\n8eXgh9/nz5+96yP2G+o+w+WcuuJwF6K2bSdyResV2sqX1lFyDZjIpgE42CHdi0Gl5HCpBOPdxLZX\nzt3AbGDngrM+2rGbdNu2QWUcNaqFAtrytsF2pe8Wy5PkNwWxuVBCaLx8DSz9RgvNVaG5Mza30WvP\nRIHMFRX4rjebjVcWcrd6Y8wo+DW931obdV+VgvTzPBBVVU228qX3SmtgHgyazr05fYAqXrEO+H1E\nZdbcOmMJ1GDcPFQ8juf7ruuCyh9q0KSyEZIxuh041mMUWPyVcMqcFbtXXWkUCoVCoVAoFAqFQqFQ\nfFhkudKciyWyRr5rMTDmGAqStS+lTqdaVqTrSdoyA7K/zIlYamGXqHU0z9CzrUG1kuogPYdU9lLN\n5GsxUGIafp4udI5q3rmFStLAh2Rjrq4SUBs9l2fsesrzS9ukUdeDnDqPrvn3fmSKILi1O9WNJ0Y7\nzLVsIdC6dn9//ybYIGvX4ZS+ONe3JQsVwHgrVxpokVtvqGUXfyMVF1kinz59mrz329vbSZ/BNPv9\nfpI/lyVaV+z/V1dXk3SU5cHbhwY75HnSsYJar3g62l4xBlaIRUbPUVCWxnB07I3+4NOjFe7+/j7o\ngkGtfdyCTq1rtO3586LVk7ZXz/IMWbTXWtNcCilzaSi9NPfErNBS8GDe72PsJiqXaMlGS/Vms/F0\ncaSz4zUaVFDqG1hHvjXtw8PDxHX4cDhM5lopaCFnZNLAv9SCjs+R4qIsUfEpKEOG5lX3NRRufuxQ\nvpwhu216sM6bZetYkLs9QOW2xr4u3HhUT10WuOwZY7z7ae3isnZFCfXVUBg+K6Lve8+4/Pb921Af\nEhSZB0iOseFi6wQJsXXeEhnm4+8p48A5xpCcPH/88UffNjE3E+z3d3d3QXYylXtel1DAc2mdiuDv\nmzLMJdcuqT6Yhq8Z6f0hZqUEaS4wzmXNVgXYG/f7ysl410PlgvjbYuxyRxkjnD0qzaE0WCuv4+Fw\n8GMgjp0ogxIbNPa8knxdau2Z2neVMaJQKBQKhUKhUCgUCoXiw2KWMfIaVos56/AlygpdS7FCp6SX\nLG5zdQjlNcoH0+Cp9rwW2Dn2hZRuCWL3l4GtMHP9SV8LuX1QupbLnIidk47YhmhJur6+BoCxhStW\nB6mf5LKoJKu1lE76HbpGz6GlWco3Vk4SSier7TTWQKqlNSZ7sXMSMB0P5pWTRwySBXCtvM+NuTEd\nz0vMKrzGg6jSrSnxWOJ9ELZePjw8eKv1zz//DACDZQetbyiH2HebppkEjqTWYQQfG19eXmblKXQt\nxh6jlqSQ1dWYaZA8BI2dIJUtWaN4MNjORRspSKBJGt+EW8wl61fIWkh/06De3EK92WzI3DzOX4o/\nErM0pspqjIVzKczJvcQUwf/8XfH4AhQ0VgiNlYH/OZsEx722bb184Za5Dw8PPi9MJwVsx3OY56dP\nn3wdv3//DgBH+a+qahIr4O7ubiTnvJ14P0ZYa+XtbVn/wPodDgf/G6/RLUf5VrZlWU7iO9Dn59bn\nxjFCwPTQdcM49FA4VknRw9YtRg/dONgjDYrKGXCUrdW6+7q+g+5lvOWv1K8wvcQYSVmvUpZGynyV\nIoNr4xyyTWVRWgOG1lOxtWPbtn6OQlmisu2D+hJmXWislZ6V5oPxenBNKrHOYmsmesxhjNB0OJZQ\neeFl97YHDCtXwnGMwrQ1Mte2w/HLz1+HvH/+Af7+j38MeTw4tv2+Afs83dYXIDxOAozlTZqHeN0p\nq5XP0ZJMzZ3jSO3Ha7H555C9K00MuR86p6a7NMVsyYdoriIlpeykaz56tz0uyEj6EL2JDlqUYgUw\ndqnwUb7ZBE1BA/ysgZAA0IBFdPDie6UjpAFNwlIhPwdC/SY2eaRMZPRaisICnxtpdHM7UPCyJWpo\nTIZSJ+sleYbOSXks7Sf+I6hn5wN5SotgaeKeuxZKz5GyC4YE2vbUTeKtgY51a06iscUgvYYUW7rD\ni+8D7tjD1GUFx1mqGPjll198+TimYf50rMPflOqKkFw2sFzeNlIAX1z4UZcdXnc63kof+nysnlN8\n5HycUAWMd2txt3d9J/ZZvisNv5/+nqNI8/Yd1Q/rKNR5KZaugc4xj63xHLGPjliZUv+i/RJdBhHU\n3QSVEug28vz87PswV86UZQn/+c9/AGDseoPHULB5GpiVBkWNuRfwDzEqs3TXKgTKJlcCVFU1odTH\ngnuXZemfCdsJlUbUXcw/a4tKPQCLz2acDMHxI7BCJbEdK65om9B35oNDwvEd835L29nLezte9zVN\nE90tRkLufB/Lcy0ZS/0Aja1zUuuSsi5KUYw8Pj6Ogq7OpafXYq40PA3dqYy6np36jun/UL0ocAyR\n5k5/zhrot84l83k8XlxfX8NmN3bpbg5O8fHrHdjvzoXMKUOg78H2U1ngZfNr0lxFFcihdqD1kpRG\nMVedWP3emsFMXWkUCoVCoVAoFAqFQqFQfFisyhiJIcWyMcemCOVBNYl4jDEZltaPpku1NIfuyykz\nJW2uxg3z41u7Sfvac41vat3WZIvEYK2dWK3X1kAu1WzO3ZfCdDg1bar2P0WLn3ONQtIap8hJjKZf\nFIW3nOE57HNLZDCnfUVUrq7t0VpA6dwAR2sxAOkTWK/SQOkC1PXNmA4sgQav45DYJDHEqPuh9O8B\nqW4Hc4j1e04xLYrCByijfZUHMMb/X7588fRfvjWlMWZihfnpp5/g119/HaWPUX5pnnyLPbQMG2M8\ny7CHKesB86JBD2N9T6Lx8jaUGBkozzHLUyp8OXaaV8wKeaQ8W7/1b9FNrdwx+ZLGDv5M9N3lsmJC\nbJ05xOajJfKRWq7EFJS206SyhNfoNr145P1LouBLeeEzUiYX5ouMi6IoJkFQ6VaZ//3f/w0AR1mg\n9HnMnwctpb9/+uknAAD49ddfJ9voUvYGZ3LQNY7kGoJ15G4wfd/7a9yq3rbtROa2261Ph8+Gz3p7\nezthEgNxEcJ2RXbIwR6gc01XOrfuK8zz8DJ5NiobsXWEl0P3+IUFODCXIMr8SmFGxtYHErvtUtbu\nXBmnWOueOfZFSl6p60kpODfA2MVFkn98xxJjhLehtC6IsRykOktsFQzaTOvFx6OmacAcnLxjXjgO\nAMD+2QVBr4f0378NwYTtoYMCn+1Y0WNh7mflloxNAWCAjbnu2ArMSuq+xt9113Xw22+/jdJj2t1u\n592YcAtz+u0nzfdLITFfzgFljCgUCoVCoVAoFAqFQqH4sDiZMZJj4U5Nl8qqSLHKzGmUpLJDGq45\n63gKeyRmVZ+rX8zidiqoFjTUdrHgPKn5r2G1lfzg1rKALalTTBu9Rv6xcynyEevjS1khVFuewhih\niFlAQlu1hZ6LW5pSA0jG6ppyTnzH3fTcxNpnDFXbY2bDYVNB57Ze6yNxO7Au1LIXrRe5lmOZXitd\nbto1EXpvKePWXL/n1iuahvr34zken+m//uu/AMAFanTNU9txXmVZ+uB1aLUty9JbpHlQSFq2tG0p\nWnJoUEgsz6frjmM8tzRLbcPjF4T83nlbnjJmcws7vY8/N6Lv+4k1mbbXpF7WgrHy2CZZHKnFDdsw\nxvKQrq2J1HniNRGST2od5mn7vp+wr6QYPnT7aEzPGVbGGM/g+NOf/gQAYyYHBoyk8wyXbVo/jFfC\ng5TT94tW5f1+7/NFZgZtB+yjyMLA/zQt7Xt8HKL14oxaysbhbUPXeDxmCn0vnBVHf+N9XddBi/EH\nMJ0QY4THKJDqQ58R4ypg3FewAK0dxxahdZAQkzkpTg1/VnotlNfacp3KPA6di90b+9ZYki/AmD1I\nt7DG39JaPmXdyplD9BqfZ+fqzBmfcwG/6bPxcmIsQokNhoGIC5f3Yb8Ht7s81E7OezeXFHBkitA5\n1493yJhBxsjGgkEWiZvH2kg7bLdbzyDlzBdpe3rEfr/3jBFEjK1Dz6WyLfl9Uvo1ZU0ZIwqFQqFQ\nKBQKhUKhUCg+LLIZI2tZHpZYwnM1SXP35NQH/6doM8H5JUMf3oEjtx1p/lTzSo8UktVOAo8xQrWZ\nqHE/ZeeKUJTjufqdQwt4KeTWPYdpFDqXagHHYy5jJLaFWozlEWsDSaOcwvxIeW4pzRxbIEcmxXcs\naMEncXasRYMZOeXSPzUgtVZIux6LPzKniT832+OtxCcJjTOhcYn+Ho3pDFJf9WNoVUJVD1Mr3WIU\nx220ymAcg8PhABt3rXavtOqcBanvoPuPs95cD+f+/e9/T+pP+wj3HabyiRZsrBfdfQKt4/QZOSMr\nd/6i7JXYPSF2QEiOKXuAlkPzijEzRJaHwDCRfuN/Xs52u/Wsnh6mefLxh9Zdep8p1sdUnBKnYG2k\nWKbpvCIxIXi/pLu+cEtu3/eeZYEy9+OPPwLA4BOP8XpQPh8eHiZxOmgdeF+lLJQOt8N05SCrgtbr\nm4sZIG0jTOuO+eIcQneb4lsYt207SUdZGLzPUYs9Z4XRmAk0f7yP70pBmR18y3vKaEOWR9MOaXrC\nPpHi0UmMkQmDpXHttT1uMSwxXyTEZCh27znWq2vK5Ry7hf5PrYs0F6bOk1weaf+SYgvx9aTECpHK\n4UwmGvMn9py4YxXuvPTrr79O+jidczhC8woeJ+vPwgBgXi4ena/lrgZzO8jj7k8/AADA0+9D3A64\nOwC4tSO2V9d1ACV+dyI7+XDM032LIjOlhGNsFpT757th3n9pDp51xRmpdV1P4hrR949jGmXIpnz7\n5UJ6Byl9O1e+khQj5/jQi1079f7QudjH+FLFyGiSxwnTdUYjfOakftylUMxyP/7ofSFaL6VM8YV/\nqoIkVi8pTWqeoWczxkTrliOIocnkHEI+V/6S9KmKDv5uN5vNZKEzchswsvJDmsho/tLiPkRPleqc\n+uyx93HOD/FQv/Rl4rnajQ2HzitQaB54D+ZgybVQW4wUoqiMxTGokZWlIbmnoIH5/qiYGx/xyM/R\nBZykVAYAMBZ80DNJWYgfz+NFvusDbt3S4QdTa8G6WRqVGHSrXETKR7QxxueBwIUPzTN18cw/EKWt\nbGNzboryLDQeh+Y7aaz2230a8AFm6VgnKT0wLxowj17jZQKMA9PGnkn6H1OMpGDunZ1LITJXx1xF\nGpWXkDKeKv+oXEpKDMyTj2WoBKT1osoQSTEPIK+PqNIBKfEbohBBSGMInuOKHtoWqNSh4z3fpnu7\n3U6UEjSfWPtTij/WgStSaBrueuOVOmDBXLtIqy/H5+EGtt4eP864ghbfAX1f0oYK/h1cD+3cvLxE\nx0BEbM0Q+6A6RX7OtVakefPf0n9ahzWeJ3ZNSkMVI6G1aVmWXkGBR+xnT09Pvr9gP5n7Jom1Cf+u\n+fe//+3/04DKoXIkY4SkzONl220FZuvGKFwmuvm/+rSF9pNT0G7cGqAaFDdXX3+A/h/3o/uKmwps\n5xQW31zA6Cu3IUHT4LLCB/X3svrcwL53LmcGt7U/zoU4l8U2M5H6XiydFEQa32dso47QGoAjtW+n\n9H11pVEoFAqFQqFQKBQKhULxYZHlSrNEE7MmUySXNcIR04ifWsZIS++NxfNWSencnGY5h31BKWA0\n0F6IIk1/c4sopTJyDelcPZZqzVOYAJJVcim7KdXillvmqc8v1UFKl2oJ4OmqqvJ9GOnGyBKp+wJK\nixbtqSU85kojWWVCdUxljORaSVLOrWlBsXDU6G+QuuhkaA8dvXGSD7feWUI3jrkNlC6vg20neacw\nvmie3ErOr0v/3wNy6cP0PL8uWb1K5z7z5fMPXoZomroYM0v8Vp1d77eFbcAFUCvQ+gGwd5ajG/de\nrq+vfXA0Sb6krW7n2kBKOwoSFxlrU8bQkLtIqH4Sm4JaqPn8Ta2Rk20IMRAqcZuRtkPmRxokkAft\n7M1UniT2CS9Peu41ZCl1zXAO5kjunEMtiHyNQV3P8Dc9h0fuglLXdZjBReqHlmAaOBWvU0s1UsN5\nnbfbrSjbWB5nUdBr0jju3xsGWHTTQ1dPA6bS5+HsELrtrrSF94h6T/5TVxq63SleR7cEZKhcXV15\n1wO8D12RGtODrd1zOBeX7pdvE6szZcBg/sjgKd2aA3oDm2pI99i5LYCramKRx3pRcFkIsX8QsTVK\nCgNbKpOmiTHxcuUxNObStVMscP1cfWPlLVkzhb5zJOYxggfPpawNzsqTnrX2a64Kmj7sCoq/OUOa\nvjPsn9TVVJoTJ8z7jZP1w3HLd4us4Zsa4K/DWGNKt857cc98XUFxPbCn+p2rT+/ubw1YlO1H56LW\ndsNkBMdt6XG+o+2MjCy/Vi97aB+/j+ssPUckoDr9n8JAxuPT05NPl8IUkb4ZUpgjp0AZIwqFQqFQ\nKBQKhUKhUCg+LGYZI0st0HP35l5bakGW0lFNGiLFohJjeZxi2c+1cnMtXkwrLW0rOafVw+veokm0\nh9wScjgcvNYvRVM30uw6iwOCbz2ZmlfMV3sufW7+rwkaVApAZljQI/cFptp5nn6/30+09+gvbazx\nTBEfPyeSF62X1C+luAAAQ9+TfK0RueNCzn0xeZzTlnuLmNPYm7YDNFq0GHaoO1q0eX9Kjd2D8iLJ\nm7cuCrKAx81mM7GwSW3PLZUh32vu7/sWIY2NsbT0SPt2SpA4tHa2bStbMlB2GKOwAwsFZwG6Y7Hv\nAZwP8P394F+82+0Wz60IyXods0JKTAveJnik8UpiTAna3injNlq9KDMjFheAIxS3Y8Lg2Dlm5VMv\nboc8VKIHU06XTyE2iMTkkfpl6lyWgkvNW2uyUaR5Qsofx0KanrMhkAHy/Pzs02FQQRwHKcMImQ90\nbOP1koLuSkwD3ha3t7eTLTBH7xrzd4NDf+igg/F4TNdldNzG8lLeA5dVyWJrrfWyhkfK2nLkUbj9\nYdii829/+xsAAPzzl39B37hgjZ0bC+taDAINMDBTUb4w/9q1e90a2Lj4IVc3Qzn/+te/Jm1P56wc\n9jfNIyX9XNvGxpzUtCEs/Z5IYbScUmZKWqk+MXYLZV1h38A+WlWVl19kHWH/lPLc3zfBNW1hisla\nljLj+fzy8vIyeU4aM4OyLgAA7K2Tm2/tEFcOAMBNJaYq/ASP62pTFdhYSADxsUL6zVCvw74H+M3N\nhQc3R+1J/uwVF0Xh2+uHH37wzwEAcCgOUDbjLZOlQOTSO0PM9S8cQ2Pr1hTExrYYA/0U2VPGQv0d\nQAAAIABJREFUiEKhUCgUCoVCoVAoFIoPi7Ns13su9shSLaZ0jfqm0jSSz2Isz7lycvPIAfVV59o4\nafcE6oOKZaJWDzWwdV1P8qB+ndzi8PXrV6+F/P3330fpQxY6vB8ZEFxDHEIKgyOmJZQs/6/NBkl9\n91Rryq0muSjLUoysj9plbqGyxng/SYw7UjqdatkbcOEQwHqldzhWCN2+jD4blhfyB8611NBrvB9L\n982NM5KFDmD8PM6wD4UxR+KG2wXDb99alhMrXcw/k0KKXzC5tw9bxLfb7WR8o5YRbiWRrNf0GPMP\nfSvIZYfR37H+KO30gGXt9/tJnAMpPbVmVXDc0QYAoHZUo77pAIkJh8oxTMj4nfpM+D/ELAwxFUKM\nkbZtJ1t54rXNZuPnhBhjgpYhbTGK90mR8TmrsXGR+WFbQnFwsRKwflvXtm0HN2aYA3Hb4qenJx9P\nAp+aWqN5LC36PJ8/f/Z54Dluyeb1pc8mIXVeirEp3iKkOSF0jh4Bju9YigtDrbx4D45L378PPvSU\n3YWg74D3Y8oi4e3aNM3kHdGtbaU4GgDD2ojPHWVZTnaX8XLW9dB241gL0g4XdN3Ht91FUKsqlkPZ\nwJxZ2nXdyErPn/HwMtT54WWI93C7GdYNn374DPf//icAABwej7td8bGQPjPvv36nrqYB43YPb4tj\n2/A2xLzatj1ZrlLmCjoenUv2+FwU+2agx1hskXOvd2P1SjlHt3nlu5dQZuJPP/00So9xP56fn33f\n+fr1KwAM3zLYj7Hf4Bq3LEsvLzxeF2WM8C1qeTqaZoTaUYY3Jdj9mAVt9y2Y390OMiUumt2h2oHd\nurZwR+sYI13fgnFrAIxhsrnZQeN2lwHHUile3DPbKZsbv7mMMX6MWoNBz88VReHbPmVnn1h5UtlS\nH48xwHL7/arb9eYoRFKVBnP5hO6ThJAuJmJ0/ljwulC9Yh+DqXWl51M6DL2Pf/whxawsSz8Y0HZA\nAeHBeaRFKoIG6KRHPujg/XQRwReYXdcFaf1Yx5w2yYGUFx045rZdXBupcoMDTcrCEmDqQkMXR9JW\niNRFB4AoQfrCK0KQirhthuOmN9DXw+/D5vihlyL3KQuLnDGFXqNKgFg59FxI4STJGZ3Q/YIa5Yss\nrI+ZuzwswG47TEhNO1ZmWmsnk6z0PqVxjNe5FBQwL5EtDZdQ+JfK47kXaWuBypc07oWuzS0GeX8s\niiOtd7N3yk8S5Lh23Nq90F6SSyhXoCKouxR3q6QfTzE3FSlAHX8uquCOtQmtF/+9jWx3WlWVT4fK\n+Grr5i9rfaBj4xaUpnXPbAxsirFrAHV7wlqZxgWxK4zfRlGqO354S9ckOUt1meOQZJW3Yapy9Zwy\nJ308zF3jCje69ghtC0vvk65J6yk8x+c4Y47byfIPeAr6cYYuOrhmwm0+jTm64FC3L/zP5w4afBTX\nHP49Qng8pu+fXpOCrpJGGOp/5T6enN6uLMvRNuAAY3chBD7X58+ffbrD03BsnN/o7e4abndDYNam\nHp7r+vraB2tFZSm29/fv3yfumz4AcmXhpXcfj8/Hd8u3E6UBk1NcY2i75cxDdKzLSc/LzEVISRLr\n4/QoGTRC9Vtat9g6lF6L1ZW2b2ybbuwn2Jfw2DSNvw+VJVdXV5OPfzze3Nz47xUEHYukgKx8beaV\neMZ4+YKbcXgAKIW18EsL8OugjNlcDfVrXdB12NYALb4bdx9uMV8aH8C13aDrjgG7c/Lh9/B17fXU\n+oCsOE+iQaDrOnh4eBg941zvTFl30zZM6Xu5kPpLaH1/Sh9XVxqFQqFQKBQKhUKhUCgUHxYnb9eb\ny46g/1F7haCUppSyqIY/pI0K1U8KSIn/+fZwCMqAiFnqT2WMzIGnp9o51JDS4ETc+katAdw1hjI5\neP2qqprQol5eXvx74/fVdT3aIpje9/j4KNLUQs8Y08DHrJe5iG1RugbmLA6SnCwtJ3Ytptn3MgHI\nHDEALPhq744dGLBV2JrOj5JlJ5eSSvPktEtqjZu7n4PnRcEDESMNU9pysiYB51A2nl1QOtP3UNWD\nhQ5lFOWAB+fDusZcXGLPyNuCMoUKR+E87I/B70L5zslnCoUxVS4vxSZJGaOXWOj4NeruGLKAG2Og\nwO1K/zxYsZpnt0XlVQV9iwyQfpI/pSADyK5qEgOSu6xQN0mJPSS949C7GrmXRebH2LumdeGBIL9/\n/+5/4xrCOFe14usVbO+G9n0ohr59bYa0lS1g8zwOtNl1nc9rYhE0nWeRSFYvPn/F2k2kW7P2kNpm\nDczNN2vKWmz+irFNeT+mVHe+hqDbNdO8+DbYNG9+jdaJW6jpuo/LSVmWfg2E6x3sPzQoqu+X7D/F\nfr+fuEB3bnvRblsA/Oas4WaoD1qVQwGNQ1ugWmv9+GJ/cHV1DKvuX/cjpgg+I/ZXtMhjmt1u56/h\nOIb/r66u4K9//stQjrM///1//e/JfIrtR8fEiUtRYcC6Oaon1nveXilrx5AsheYtaS681LzEMccY\niY0XMUbpJRGTVYkdgows7Hs0LZ6Ttu3lLCf6LcfXbXVd+zK/fPkyKq9t28l4Td1rsA9KbCWLYweu\ne4T22Gw2UPRDXWv83EAmSNMNAVUBvPzbDQb87jyro0OWdm/Bftq4s2wefgZo3XhSF+Nxj7JH/SYY\nmUz5uTVgjHmaghSm97n6tTJGFAqFQqFQKBQKhUKhUHxYZG/Xm2LJSGVPoMUUtX+pjBSugaQWhNCW\nk/x+zmCgWknUMnJLRVVVQTZFiOUSeo65NoppxKS8UOvHt7O6urqabItLGTZSoCPuC03bmbdr0zRJ\nlmauIa7r2mtlY9a0VJyqQYz5Xp4SSyHl/c2dn7sWvIfdG7Noh84BwBB8FYNE4Xu0uEVpCdYFhDLC\nVqYxywbfMlDy+5XqLAXc4302FuQ1BG4xp32dWy9x+7PPnz9PrBhXV1eTcaVrBjZItdtA9zxYzNrn\nseVB6isxJocETBuSSy6HBwgHPI6Vu4amPnWMW4sNllIX+nvOQseZQvTIYw3Ude1/Y3+nwRLxXuxL\n1zfX/n7sh3vnEyzJAmWfoHWaB7M2xnj/awSdG8qNY7S4pjC9hW4v99GQhRIhBSgMvT8q91j3T58+\nTdoG57TD4XD0HXdWsqsfBivjf+6+wcEO88mncpgLn/vhGTZfruCpuxvuw2esCyjdWOb9vFvHsJk8\nIUzmTd4WfNyT1iGSZT/GrAmNCyHwuWxu3FtLrmJ9gs6F9MjrKFmV+TX6W2ovHstDslDTfCQGE59X\npPgjeA3XXNfX116efv75ZwAAuLsb+tvt7a0YPwrL8bLqd940YK+dbD66WAZijxznJz2jMQYszkfP\nroCde+arGmpTj+4ry9KzFykzEmCY/3gcO3yHv/zyC9x+HuR2Uw33ffr0yV+ngS8BBpYIHyfoWmDD\nAr8+PT0F58o1GFapsUN4ulCA7rUQY4Wkyhy/du76zM2h/ByVZx6fB+fSm5ubSYwZmg+XcfpdiKx5\nPNZ1Pel7OKfQ2IejOCIOUpuifMF3Fxfn0aWv5DbyG07gnO625q26LfQooz2md9vqkrJbZIdsCrCO\nUbq5HeTr0Lo5vjjmQQOj0zai1wzAJAC5NH/z9x7qU3wMlRiVKaDjcez+uTVJDrKCr+ami338U1oU\nHufKCzUOXaSGJgcA+QOcUqvwPr5TDf639hi0lEbpxvvw3NzuKvxZcgd1TE8pxhjgigev++GHHyZ1\nliiJNHAXdyGiiwNOn+RKF5oXDWKEiFE/+fUcrLWoo8E0Y8q13HxT65eiHIlNMOyGYD7SxIQLLwzM\nBo6uBwXZlQbprTjomcLvwU4npNCiNrZXupQe++Jms/Hp6UDLP1TokQejkz5WMD1VZvDAxFVVeVnD\na7fuw+3q9tpHSv/ll198/bhcmAdXNljor9y+9G444gEBKSRFHW1bTu8M3cvziKVJ7atLZC6kLJy7\nZ2l5SxBTIKbQgencQ10pqEKPHmk6Tvm9v78XdyOS5lOAQV4wD+5Cae10B4rRR33jZMkFH203ZjKP\nSoubnHmfnqPKI1wD8MXwbrfz17AdqGuEHxOckhEeDz497vRjceeKpgfrlJIb50pwe3Xjg9D5+0gb\nSe+dP4f0oR+TvTU+4lJwiXKWlCHJF+9LUqBVeoyt87hS2trpzkaSEiT2fmIfSNJuZ1jeX/7yF1+n\nH3/8EQAGmQYA+Pbt22Q9tS0GuX/89s0/x6Fzykl8vsM0qD2V7WiQXycLtdtKrjkcoAPnEubmcfPQ\nQteM17f4rL/99ttERnFuhJsafrfug/WX3317UBc4fh+XbQR1XcCP4LZtJ0FaY/K25nwR+6iT5ui1\n6kFlhOYf66uxtlhTmRFT5sbmScn9mF7DfiIZqrjLHS1XWmuiy9jVbmwwpnMIl8HD4TBZa9L+yI+j\n949Hp6wwHUDp5mEftPhwOK4Z8Oi6v71/gcLJoV+/u+ytMQB/GQwA3tfj92eA5/HuL7uvw25p3ct3\n6O7dt7ULzEqNdyiXaCwJKa95+3IYczTM0w0PUgzmsWtrfBcuXTuqK41CoVAoFAqFQqFQKBSKD4us\n4KsSllolrLWTADoxS5NUjteoHw4Tyh/VFEm0O0xHqVUAY8s0gubNaV6UYo9WW7qVGGrxUqzkqUC6\nMQYp2u12XhOKz4X1vL29nVgJqUsQf9bD4TDRsknB+2g7hLY3ppYUHqiOBvujMYNSNHxLr0kaSF5n\nanGl9T+XtTqmiZXqN5sfsj6s8YFSJQ2/5OrCt6YEooGfWAJQm18U3s2GWgFCllbKGJG2n0VwizC1\n7EnWRGpNBhj6J6ZHGaRBs7hlvq7riUygnG02G/8bmVnoSkPr8+c//3nIvzJ+y0/ME+9/eXk5jlvV\nzp/DeoUsaBLo2IbPjeMZLYeml5gl58SabA/JurymXMbYNDGrlyRL2K84k5GnAwD46aefvJUM3xmy\nGKR6USsc3ZYdYOjHvGxE3/cjdxSAsetp52zSHQZ57Q30ztKELSFZ2qX24jJNXTR5n91sNhOGFcoL\npTwjKKuPz/s/fvnRPxvOwz5wJNl+d7PZ+uf2Fm8MgOe29y2+XoH5Pg42LllCR5ZN1wTIrKMuqjw9\nzSvHQiu5esQsx0vXaFS+zsHaos+NoAFTeaBU+g5SGMI4FvZ9P1l/8KCvNA86bkouZL6/ONA+yAO/\nYpDfT58+wT/+8Y9JnbnlvN+6ee8RwHZOdvy2na4uQt+w1k5YYFLbeLaW2xa8tBXsnBta+d+DpXmz\n3YL5/wYXIOO2Cn04DLJUbDbgdueF6799HfJyVvm2sLC5cu4v/8/fh+PzHqofnXscWsLbIzMTxz0E\nZYfwQP/0vUjvn89tMTZJyvVUnJOtwueNEFMkJP+8HigTlNWewmSbY4yErkmMkbIs/fpRmldDz/b0\n9BR9/sm5soDCbU9dFsf5EWAs91zGKTuEzo9L3LisPQYPb6z7/vrhCvp7F5IBWVpbN4Z82kFxO7wj\n+9kxPt3RbguwPzkXUtyStyoB/u3WCt/d+tU9WvmnG7DdUOcduO/bm+H+rukmY6C0nqLzC/c8oGmx\nnXB9TF12Y3PHEvZIKk6Zv5QxolAoFAqFQqFQKBQKheLDYtXgqzH/taVpqIaQB3uiMUO4tphayyS/\nN8oQAZjGGqHlUC1jyMJhzHFrKBqjBOuFdUXrFfWXjFl7qGUQGSJoTcNtpm5ubnyZPDDW169ffR1p\nwCK0eGOeqEF+fHz0WnzqE8fvowGKuN8nZQKEAqsac4xbUd8OWszm6QVgPYNUErgGsWmaVYLBro2Q\n3ITksewN9NW8hl8KvmqRmUGucc0+DVAsxfmQrKJ4DGneu64LspReXl5EOeYsEs40odeohQjTYf+/\nubmZBINFGbq5uRkFMwY4Boesqspr0r2s2x56N/y8fHsY1aEsS6h2Q75P3+9HdWiaRmR5IIuEM2Ao\n8D6qzZe05GtZydZELvNDmh9SrQspFqc5ZlWoDGrZlBhPIb94+s6lPs7bhgZ3xXR0/pICrGF5lMFA\ny6Z+1XhXURSwcf32YMd9TmI00TzxOWLBR7G8l5eXUQBLClovau3H9DxWVr3dgKnG8u63B91uoCpd\nzATia43ydbMZ8nyxw//SABS78Va+OOf++uuvYtyK3e3Rhx1guq0kxVImB322GOYsmSl1WLJ+C+Uj\nzQU80D2OpVdXV8drBcZkGt413cqXygufC2i8NbyG/UViNyJofCpMR+OzIfAaxg6hrGEpgCRe+//Z\ne5MmS5IjTUx9fXusuVVmLVkABkBz2GBLy8gMORQKKSR/IvkH+si5UYQXnngYEQqbFGGjZxqNBtCo\nJatyjf1t/nydg+lnT13d3MMjMhMFslwP+SJ9MTc3N7VF9dNPURe51sS7psyBE3g+BZymM6yY445J\nqVJ/vz6RfU+PHa60w/Z5Yr6MSm6bG04PPK0IDvVRZL5HEBl9j2Zjysdcr18YhCRF/JxFSB57qKf8\nHcPzhCJmc96FzOVzbbzJu93Oepgxn3777beN+sr1hUb8SMHYoVEot8ldvcl9+/tdynzf50np4kO5\nD1IEv30QI11cXFLnAnXMtQ59H6QbERGVFVVrTkU9q/PvuNLvom3SNG3sfW7jt9E6LXkZ9Zp5Op/T\nas46zYgsD1w+D6dEJ0Yn6HOz1/L4Wn8aEh0xCq7i94gDojGjzRh9sluaOh89eEAp2nfNe7KZGZfG\nm8quO8F55NI5SFmWjT2265uhzO12a78t2m0kuFbuuse6C0rHdd1d0ZMDYmSQQQYZZJBBBhlkkEEG\nGWSQQQb50cp7Z6Xpe+6+SJG+z9LXdHF5eJ7X8CJrtIO8Xsa26vhS6f3SWQCklwBlIA2atEDqbDbS\nuwhP9fHxMR0cmBhQeMvw//F4XEuBRrS3zj18+NBaMRHvKlOuaf6R0Whky0V9JO+BtppGUdSIBXZ5\ncfS3k+ibgp8T+M10wC65rzW+TzybRC38OXnVibot/PYceEL89pRo0orf1+qvLfvSY+fy1LXFgEtP\ns/Yc9x1LpNVf34tfmQoQOgtdkmkV4WU6OTmx90IfoWdxHDes/rI9tE54VUXjgHkeDowFPT41v/Pr\njWX8H4emXufn57Z+2iq/Xq9bUTRdPA/ynKvffMy46NukC+XxMdjH7zJvyL+7eCFkH9foDZkm0OW1\nxTnct1wuG1wZUr+0d1SWr2OmXZwcXWOb65zUL41AlB7HLn4LzQsgr9F13m63jesQoxxFkdVRiYrS\n6EzUc7ndEO3yWp2jmJ83HdH1W6NrSCeaJAmlrHMZpzClDB7HkqqszoOEufDw8NDywMgxQadkluOG\nRiG4dFVmSmjrt11IQdmGd+Xied95VT6nD9JECt4bY+5kMmlkB5uIvqrnE8kNpt9D6rFeq0hdkmXq\n+QvfVb6HzgIzmUwaei/7LNZ+kDRNbT/R68QwCBvfIQt5HZr7jfVqEAS2vXRbS6RFY00wCq1+MAUC\nxUFIdMz65XM2ti23wyeHtJty+Z8ZjzZnu6b4Z6cUQBd+YpBSwdmW6A8XREQ0f2LWleFbw1+yfH1O\n2zPz926b1NqNyO0l1mOhXL+6shHhty+XwfvKh56/+nq47zqXusaQ29AhXejJNk65No6Rrqw0fdCZ\nrrrrY3L+smgzgdjXiELJRaczU7o4RlxjnebPCoLAzi8F8wcVpyMin3k9GDVPMf//kwV5D8xa0fvU\n6Avxr/ezEwofmbnQS3nN+YcLSn772lw3e2fa8JyRX0VA23N+xzMz9oAPaFeVNDtk1PM7vs+BGJF9\nCGOUnr/H43FjTXN4eNhYT+D+oijeG5V/W9/W19x1brsz+ep94U1d5fQ1kOi0lnKS69pQy3S7ukxN\nJOOC4GNDJSH4rkWxXqyFYdiAvUsIsIY1y/rBwIHrT09PLdwQ5QO2JAcfLNwA75RhNlJpUT7OyY6K\nMtCRLy9N6rWyLO3kjjZ5/fq1LQOwSLkotsYP9X3kt9MEtbJe0uDTFoLxPgYSDfdyQcS7oIkfS/pO\nDo3rQNTmMHS4ynIZsewk5fEmrQooJExkDHnmTX1Bpf2W6Kt5njc2Z53GnJ7QSW2olMck+SRRXVfR\nV2W4ATZbErqNv13Eyq6NC5HZ1OGYXJgGDOcPeAM2HqNesdW1TVSHW1dVRSM2qKTF3lgKOL5r0aTH\nNLnp0uOkDNXRG1EZXmgXE7ekHXctwHF/m4H6tsnqQxlIXP+/rQ/eZcEnF3famOHUJWFc1KFnRE2D\nmwwbdUH92+rlakupGzpcTC4Au0I79bmuDYzciMjFkR5b0b9chNeYZ+bzuX036Gye53Rzc1Mrw5vy\nPLbdEQGezDrn8aIzpoAenjwgon17bzYbW9bpxITJpGT07e3leQ3+K9tNzl8Ir1kul42wt672Qtu7\nwgL6yl0hwn2k7zjc55zT8E77a/SaAd9zOp02jBly/aLHCRdRutz46LFN1lPPj/I6rVfz+dz+jT6K\nvnF1dWWfo8fs7XZr+xnedbfb2WfqsbYoCtv31vyc0rFJk+uWtjm3qio7B+p1WL7a0qZY1eq6yEtK\nAp4DeE4vI3Y4TEpKvzDr0PiEx3uQqc48yitOO/yUDanjlPIrbss/mhCXOOLv8mRCy7Fpu/XvzRoz\nz3ntuQgoZ4tLsdm/o/7ucuxpI5+V8rENJG2Oitukz0avr9z1PVzzXtcx13ryLoYRuVfS59qeLa+R\n7+j61nLOseFrbNgDGaksSxsnpcESY7R0wul2c4WHy3nVx1pwYXRwG5VETApb8bzlHRo9o08PiJ5x\nCM1jo2f010/M/f/1Z1T8N7ym4/C0yX93QvG/57mP47dnD00dTssx5QcPiYjokr42dWWC1m2WUjbh\nNliwAfrGb+gXROqe/nZhGNq9qNwzo03g5JDOd8yTXdLXydX2XVwOgb66NITSDDLIIIMMMsgggwwy\nyCCDDDLIID9auTP56l2vvSuk8i73uazGLiujhv7I67UHVSIntBcjCIIGCZe0dGqLPe7R1xEZqxnK\nh2dAeg0tIRx7VEajUSNlKO6P49haOOEZgMcxz3N7DCEycRxbGDDaRkI5NeQX9auqqmFJDcOwtX2l\n9Vffl+d5zRor79NtAYEXRhOivY+g7mgjiUyRXqPbvOcfQvp66jot+w7ESB/rvyttIQjaQj+kiQcE\nD6Mu2KbqR0EDnuwiKYa4YOMuyGuXpbdrLJD6BR2A3kgECfq0vEYT5kmPo0afyL6nvQTj8dimhwPq\npky5T3leA/EFCSqP1kVgn0lEtJluaikMidz6oj3TRbFPx+bySuI9pGezrc1lSKCUNq+NC8nyp4L1\nu+ooy+rSsa7woi74LKRGsKvIJD3x3eW4DQHaSp9zpQ6Vz9dzjgyJcekZ+rYkAce5rraWoZNEZjy/\nCzrH1fbyu+hnS3SNnl/iOKbVhgkcGYI/nZp2np0eUsye5smp8bxtdqaPRxnRdMztzESWu2xP7poW\n7F1EKsRZSOlNfdzHtVIfgM7c7Xb2uCaRRb2J9qmY8c1937ffo4/n1KX3fw7St14lM6wHnmfHH6Bh\nXSGXEIxZRPU1CVEd8QTRqA+iZppX2fckGqwt9WtRFI21gByPXak/icw4i2+sQ6jldbJeliyfr3Gh\nO13jkavfaOJXeb1uy6j0aHxqUFA0YYLYz8z3Cf7lE0qemu8w+6nxZCeMEglOJ3Q0YhJlhunv1lu6\n/rVZd0a/MMiXm2/emKK3HpUvmfCYh8Lqn024t3+5omDcTDuu6y9D1mwYkiPNs25fV//6U0vXPPmx\npI+Oel4zZOk2JEcfxIiL8NgSkvJ4OR6PGygwuR/RZNauNS3ElabbFdqp0eIylEa2l2u9ivva2jIM\nQ4omnCIZqXJPZlQccodnMlT6mUl9Tc8OiJ6aeYseMgnrXxmUY/RvvqDqiBEmHC4zOj6i+b9lHf0H\no7NHb0zdj88q8kKD0oquOZSI0VebmxVdrM05b84pjUVYIcS1V8Y3ODk5sdfoJCYyfA/IOpTdhy6h\nTe6Lhrrr/QNiZJBBBhlkkEEGGWSQQQYZZJBBBvnRyg9GvtoHXSKP3RZbpK3ErthDWMajKKp5g+U1\nMpbMFS/WlrLJxachrZjaUyGtsrCWyjhYeKGkJ0WiQIjq3muddhdlHR4eNghjXSlW5Xtpa7FM/+h6\nb10veU5bamV8rbYIy2+mPTYyhlZb+9u80H2s8JqsdjweN1Iru5BAH0u6+nuv+0C+ag46y3RZ16uq\navDmWE6OMKJRyF4lTiGI9GKxg2shCIJWPhipJzpmUR5z9QlIV6ypTEntIkrF87RuS2SVPleWpT2n\n6xzEEVV5nZMEnmBZVlnu9U2nmkT90jSlFPHq74xXeTQa2bFAx7S7SAilYEyQ6Qs18gX1S5Kk4anp\n68VqQ/l8COmLMPkQz9EIizbiOFyvU41iHIzjuJEOXsZV4znynEYr4XlZltm/uxByLq+1C1WivTWu\na1zoHtuPq33ZbeTJrnlZepA014qsP64HKlK+t50vD+f05PmnRER088aQqc5OOI18UNIi2CMLiPYo\nkazMacYe7eUbQwi5mM1peW24H3LLrcPe9d2eKycEgSsjwdbrta2rRE/q9QF09fDw0J7TKV2Xy6Vz\n3O8zB9yVY+RDe6bv8lw93rm4BjB2zmYz2wdwTOqPbq/tdttAZMm+q8dJve6RIvmA9HWyzi6vum5X\nFweK5CRq82R3oVakJ9y1ntRrO3mdroOc9yu+JB/7VHC/DRfMhTBhotkHIyrBgXDKSEy+NpiElATs\nVR4zF8/xlOhfPzXve80I6f/IKUf/8YyijPlKMvYqM19J5VV0UJrnvF0a73iY7dcOGm2dJImT1Fi/\nuwvNrOfODznfuFAh+nzX/99HbuNoaKtXHMd2bOrignCtJ7vQJK7rtS4dHR3RYmbWLWOf0YnMCpzk\nqV3LgK9H1g9rGskfpVG2rnWS3ofIxBiyjXRqePmL95EpuHGuZF6TjAlgwyCgHOl6Wb8rrP2nAAAg\nAElEQVSI9Ys+OyTvX5o02N7/yOmwf/WYiIh2z6aWkLW4MOvc9HBKo+MZX2/0Jfq9QVP6/7Akf2Xe\nf/GZ4RqZ7Ew9x+fXVDFn6+6zT0z9VltKvk5sG+h31GOVHBPBI4JvMB6PG/sIfCtNQv2hpQsV1Ve/\nBsTIIIMMMsgggwwyyCCDDDLIIIMM8qOVO3OM3Bc98iGe0ScmzmWh1zGd0rOjGYnlc1xxnC5LIn61\nNbKLfVmmVwMqBGUfHx9bbwniuKRFHF4oWHV3u51FnehYUsnqL6UPKzSOScQJ6oy6LJdLex4earSN\nTDXqiv+1Xg9h2K7EeSI3l0OXJVxabvW3kt9Yl4E2ldd9CA6T2+Q2nemyyrtvMD+V5zVik+VvF1M4\nLLyShyOEd7sjvZrsQzpdoctToz3O0qvsyrIBkcdavTueR6utsUwHEfM9RPs4SFeMuuZRkF5D7fWI\n58aLOTqYUr5ij1lR2edYj3FmEFx+zEiDrKQx12OX1z0QZVlSRuzRHHEqNH+fwhdjgkxRqOPdJVcQ\nsklBXLHprmwOWu7DzeEaO3VZfXlH2uJE+6BJ2jzwd52rupj4derB6XRq/8Y3832/0ecksghldXEZ\nSTRVm2daIkZcnnMX2g51195xOadZ72ol7vfww99TlKnnHIkia7T9KCCffTTQ1XhqPE9ZntsxJz8w\nermb+hbdMXtg4qojoHdGAc0XxqsWML8P4rnDUUwZc5I8npvvstyubVlnnLYw9zktYRUQ+cw9xlWd\nTky91snGvs/bt2+JiOjTTz+1f+M74prT01P67rvviIjo2bNnRET0xz/+cd+U3CboE2matnphe88F\nPeRjI7JcXlX57DZErcz+AhQg1hcSwSeRJhItSFTPdqeRIi6klDym69OVFljqGZ6p+7/LUy3bQ19f\nVVWDs60izI0hUVK/z4XgkuOTRqI9fGg8yLW0pezs3k2IKuY3GD07JSKi5CHz4P3kAY2eM5fBqUEy\nhuyV9uKALsfm7+Qn5pr4p4/o1Dff6viFaZuXf2ne65v//ZzGIy7roblmOTPPmQYxjbamXqt3V6bM\nyz2ySs/RURRZj7TWPdnHXcc+tryvjvZFhfV5H5c33YUeb0MWErm5BNuQlVKX5DHwHUKPgSKoqoo+\nfWC4a5C96mpt0CGRN2rMkxLNj79dKJe2VLu4V/+6IgO62ldHIMi2KWN+JjJD7TKihFHDn/De6hOz\nB6z++glV/8q8P/0Lo3tAZtGuIIq4fU+Nfk5PHtDBLxjNPP6KiIgmsUFDBr98R9O/433x2tRrvOI1\n7rogL+YMapxdKvxJRV+d85qZvxX4sFxtB/TOZDKpZXwkMutQrEUD/o7Yo34IxMhd1ov6XB89uVMo\nzfsSn3wocZXblk7Q87yGEUBCEfVC1LV4lukrJcSZyJ2iUdbJtUAkMgMCFs2Y8PGco6Mjew6daTqd\nNuojDSNYUGkln8/njXNyw+8ipMXAIg1JRERVVlDM5JsBp0BcrVYNwwPuy7Kskb5QD5xERH7JbVpk\nlJKbFMs1MLlggXLC1IYNmbbUVT7evS0M5GPJXfVEvqN+F1uW125wdC2s5QSmwwDiOKZQ9HP5e9si\n3TV2tF1/2/16Ieoa5OTCesdzztrjRTGPdus0ITpkkmLe6JTjvbEU+jL/3Cwel28uKGJCR0zW2MAt\nDo/In3EdOLf8Yjyj1dpMKPOAIaMIk8tz4uqQl9UJMGezWWORcn19bb/HgweGhAvf/Pz8vLGAkSnN\npd4SEXmCpFlP4HL8wn0wFvY1PrgMFn3PtRk/up7nKv82aetzcRw3xgvX+CKP6c2Ti+RRQoV1KI3s\nz9qI60qjLr9V20LPZRiR17oIKfF/1zl9nccGjHIeUJUw3BbhdajnLicvYH1J+V0PxuRdbGpl2s3q\nfESTgsdmHv+zkblvtJhROGboPS8KC59odmRgw6cPzeIxYqPTKIxouVwSEdFuaZ43mzIhZDSmYGzm\n2ukjo/cvXrygmwcM2U/NAnzHBsXg0ZzKLesTf7ttwvq2GFGsNqc3NzdWZzBvyzbV30qmBcf37mMY\n6zrXBSO+rawuXbrvGhDSdp8r7SxR3RHkMrLbRTef2263jfaVRmIc0+T5MkRXhnq1hdzIOdd1Tq+/\npA62GSXls2VddJtXIetiVjj137djTj0lt9w0VqxDMJr7vk85z4sZ66w3nVF5DGOiKX/zqenPwZdT\nKp/yWmDL80Ni5rrNJqXNc04M8NzA/+kzn05YZbbfmI3UJuQwmAcLiq5NvWLu9kHMIXThljZrYxAJ\nM1OHk5OThvFLhjNC53AOa08YK6V0bZD+lEaT2+Q2p0Sf+6V0zWmyL7kMfNpRKo1NbeSrrrT2MvQC\nIhMqXKyubblSdkXWMIjI9a/eaxA194WuEG1XSH8bibK+V4vbecv12bIO3iREU97/8BwKgweNQyLo\nORsz6A231SQi2rLj+3M2Sj6IKGZHm8chNaPHpszoaEMTVj7/gbk+IqOzk6OCRjx/zXNjlFmsPSq/\nMLr89ddfmyqzvrkcaJKMFXoo95p2TOO1MtavURTRxYUx3rj2zChL95G+ctsc2EefhlCaQQYZZJBB\nBhlkkEEGGWSQQQYZ5EcrvRAjkLt6GW4ro49Hw+Xldol+votAT17bZr13PUd69rRFVHsP5PVpmjbS\nL8pwBZdnnshYT2H91mnsUA95fZIkjVAaWPhubm4aIS6S7A/1kaiVtnS468sb8jlcgIo9tFSnvJXe\n0jdv3jjbaT6f75EpAT9nVxFlt6fF7QqvkGmX2wg8JfTPdU2bJf1jiwt94eqXEj6oocGyLP239Gxr\nL7cL8ii9MS6rP8p0tZfLkw3p8tTov12eeldomH6f8XhMq9R4jr0Fp0vjIqoyp3xnLOPTKcMIZzPr\n8Y4Z1us/NXDP0SKgRcXpU5n0KmfPdvBgRlHB3u0162UU05NjJsliYtaiZAKxJCFiItaMIcjQn6Oj\nI6ce6xSrXRBxIM2Wy+U+Vey4Gf6hLfYuxJAMN7zL2PshxOXZ+hDSBkt2ochc98lfjbDQpM3yWFHs\niTx1OnQ55uJ76vS98m/pfdbjl9Q9jSaSyBSXuAgq9TxpU62mFZWHpo7VCZOdMjKpPFtbxAhFrMce\nEUXsJcMvE5p644gyEBBzqE7CXsPHzz6h5ITRFNyWh0cT2j0x89XyganD8WPjjXr86Wf0gMtY/bNh\nlwNCK14VNC0ZmVKasqbhiHKF/jw8NAiSsyil6djocYnwmp2Zs8psRxW/hjfez3+agPn83JDDXl9f\n1/qCvMbzvFqfwbH7eoq7UFr3lb73t13XdlyvgaQXEu0jCTaJTPu5EFV6LJSkvdpzLK91rQ/bwgwk\nmgTimo9c69Gu6/RziPahaRTy+B3vw8URembJkKPAEpfmaZ2suAp98rmz+nEdIZznOY0emXCWMmIC\n5OMZTX5hwr2KBZMOM9T/+PkTCr4w4d3TNY8FM+PZDfyUql/ynPkXn5t6nU4pxic6Ndcdsvf66PQT\nyl8ZHfX5mvzY6HHxNKR4ZtBgh+kedYe5D+SbchyEhxnf/ezszLalRpK7kBgSJXDftV8XQqNL+jyv\nL3qkD6LBdUyuoV3EwhDooVwvutaT+HUda2v7169f22M6kYTv+/bZCPFwhajJcI7GuYOJfdeCSX1d\nyEq9n+hav3ah2YMgIB9bmkuOUqAN+SDjZ8bj8KGZc/J//x15f8WhaUjly2tOWmcW6Tz6739uyv/r\ndxQUjH5+a9a7R/x/r4zodMRps484mQeTvO6iOW1LnlfXph1mFNl5CL9AX8q20O1QVZW9Dt/liy++\naOwjsD/cbrd2jkVYDXT3Pmjgu6Ci+sqAGBlkkEEGGWSQQQYZZJBBBhlkkEF+tHInxAhRuxXnNovM\nXfgEpGfTRcLYx/rjsvTJ+1yWxtvqLC2jmuw1z/OG1dTz9mStkshSl6/rOhqNGvwes9nM3ov7ZBok\neJo1L8CbN2/ss1Gvw8NDex28MrD45XlurXg6hWLo+fTmu1fmus3eo62RBjLVk66XTG2J8i1hrO/d\ny1Ivr5XPdll22865ynpf+VMgTbR+dCFF5K+OE+3iCnG1l8v75ZIu5EifMaG3oN9wEddlYpEiSIXG\nmcoovUrIS9hLsGaUxGxMMadOSyvTh9ZnJsY5KDwKmafAP2b0FTz70ynFW/P39MDcP3q4oAOknMvY\ne8kpQFerldWvMZcJ79e7d++sl0QScyLOEzqKX0m+6tI9eFegc5LQcTExyJJdvCdrbkuf3fZdJMeR\nFJfH7Tb+gi5deV8ekT7nnDH94lgXZ4hGU0kkj2wbzfEkUSIYoyEu0rM+7yW5LFzfQHKqEFEtltyF\norTvhGNj9iROIvIZrVFNQVKw7zfgMijZGxXsSvIOGMHEBIv+CfdxjyjPmBRuwgTJzGXlfXZIwZfG\nQz3m9po/OqHsgD3fxClaHxl9m/ziMZ3MjQc8/425bzcz77x9c03ptwYp9e6t8UyeBwmlPCWDpDXl\n7NbpYUizguvDHr4p85Hs/ILCEZ9jxMhkF1PB33bsMQrskfF6h15Ijx8b3oXPPvuMiPZ6H8fxfkxg\nr1qSJK3jt/77Y0kbGvC2e247bnWK9p5jybNEVE/rjnFMpjl3kTxKjhB9vUZKyTUaruuDBpMk5XoN\nKPVLj6Gyfq420YgRqYu27RlV4cXjvZebp+EqL8jjVNJlXH//siyJgDZhxG88je17pa9Mh/cs8qui\nhOmGq0+Np9n7udGlm+drCjNzXc5+VW9nvL1pWFEB3pEXzBOx3tEkZO6DhNe7X/G5350TvTTj3IxM\nfSYHBjES/OyY4rfmu382Ncfevn1rdQbvBuSjJNzUbSm/Sx/OiK69wX3mrzZx3fen0Gstem3mqtdd\n38+FdHa9G9Y2kgfy+++/J6LmvmgymTiTZeg61tCU4OuYMsKsSFFBCpj/DQgr2Q6YjzWRr+t5sm3w\nHq70wD4vBcJdQNkVo9+4Sfz/96Upa7mh6t8ZlGE1Zk6y10a/wvMd+c8MIov+ivXgv7qm6LHhwosu\nTV3TNSOYv1tS+op5V85NOy/GRp+PHzyiyzdMVhwZfZ5MJhbhiKQfQHZcXV01UvjKdsB6At/lm2++\nsW34/PlzIiL6+7//e9smbTom1yH3RQ1/iH3XnbPS3Hb8PuIqS3fy+yx2ZTlEdViznvC7QmnkgleT\nasmQDA0xkx9fb1LiOG5MguhUR0dHtn5XV2ZzFkWRNTKgE8qc0dhIYaCBbDYby4b/9OnTWh1kGZAs\n2xMc6Qw3YRRRNIIC7N9Vw1Tl4IVn6YwMeZ43FE1u2NEmXWR0LnlfyO/HgvDfV7omGM/zanB8fV8X\nvBHXywlJl99lzOjSWbkxdJWhBfUajUa2//bZDFa+Rx5PbjRjVmzOZlE9nBJ53Ca8GKx4cqxCzxpQ\nrgqzIfHOfQtFjnnBNz3gzdZiQeMjMyHFDP8vVnvDos97Wm9h9HP25WM62DBEnHhBeskT02JhdRq6\nh83AbrdrhMLJzbmebHe7ndUrbMBxvzRmyUUj2OARokd8zeXV1R6eumMop/jWru+HMQeLVBhsujZU\nbfp1X+jyh7pf3uvqxzp0RWangMhrXQz5OpRCkrHqkDg5Ruv6STJJiGucaFvEE9X7iTyu/7bHsMAE\nSdxBbIjiiPabLiZhLbcBFWxKKY44i1lGRCt+Jt9XMgFdsM4tyWnB53LPtNWbq3Oa7dipsGDj5MKj\ngCH+O+57q+fm3KtfxXTB2aiimWn7HRNIrm7e0vZbs+iOmUw5TolOSg6di817byZM7DmtyP/O6ITH\n7+3xWLJJthSy0WfEu9PqwSNKMYc/MgvQgNH8Tz9/Si9evCCivUFEzrM6PBahrTgvpW0u0Oe6rpfn\nXH+3Hbvvuk+ORzZEz8/J53FL93sZtqxDdJMkafTfMAxtG2JMlI4dmVVGiyazl/OjK2zGRSCPayNF\nUm4z7znaOY5j+75d8552fuR5vp/LoeL+vi6u9asuw7Ux8TdssD2aEI34PZ4ZI2P6U86Q8W8+o/LU\n6Nrmd8YoMeYsGtVv31L4zrzH9CET8RceTd4ZPRn/nVGG8h/M/Df7HdF6w3M/jGWJuX8Ujywx+uR4\nn70RmTC+/fZbItobkIMgqP1NtNevzWbTOCYdmW3tJtvptvXIffXiQ+2j+obZyOu1YD4fj8e1LDG3\nSVvfbquXq54uck/925XNRI4vNQoAEM+vuKwR5iyfco6xrDhUjbL9N9b7Tte4KseetixUeZ43HCfF\nVUr5O3ZIXPH4x2HY3osrIs4I5TFpaXRmriku1pacfPQrQygc/C85Rb/gUDa2ssQc9p1/c0nJP/M6\n9S07ptkg+uTJE1p8bsLdUD9p/MAcBX3zfd8SNrscZ3o8lo653/72t852kyLXLF26dleD3X3Xg0Mo\nzSCDDDLIIIMMMsgggwwyyCCDDPKjlY+arvdDS5e3uusejcxwWcvhldCwcKK6pX6nPBwSwu5K+4a/\npfWayFjgNCIDcn5+3qhPmqYNklbp4fA9JpEM+JN69fciIopDJtLyAyp9N/msRLI0vP0Vkc8W18XE\neJ5T4e3SHqEkSRoErpAkSexz+qQqdHmX0fa3ESe6RPcl7VH4oaSrj8MTJi22bfnmu5BPXR5HlEu0\n7zt5nremMG6DXfYJodFtL3WvzTpff/Y+dCYE0SiHzxRUkc38jOdVwmvA5MFAiWSXa/IittQzWjHf\nsUc32BGNObSNvSq7rbGob9OCKt+U/8mC0RjehA4W3HZnrO9cvyzLGtBttPPBwYGTVFOmZ5Zt4/v+\nnmBVeVw3m429D8RWEgEByKQkMcR4sgVsnPYII5dHAII6YGzrIviU8jHmFVe/cfVt/Wzf9+13kAg4\njbqS3p+ucDI9Fso6aA9Sl2fkNg+lTqEoxy+X/rchuCQKxYWYIXjQgwo3EDGxcLXj64EmiQPyMyAq\nTR3Gs5iSjfE+2SffcCrcix1FnAa3ujTeZJRND+a0AeH3Z8ZrvZlO6Om/MOjH0S9MeMrof/jE3P+z\nz2jLl2eHBp6crEy/nP7bmIL/yF7RzNTr9KfP6OoL4/F+cWW8cMnYIL+qYEPv/mD05OraoKHG0T4U\nNmAPY8DvuNvtGmkk4YVNN4nVNaC10N9k6Cyuj+PYflMgsY6OjPf+4uKi1xqoj+etCzbvQn61lSfv\naxMX+kKHl2EOcJEVy9A9XVZRFI31nfTo6tAYV2pt1/XS84trNfpEjudtqbJd7y9RCy6EpX6ODHXE\nMzHeZ3luycN1SmIZGqDbW47VJVLhfvWGysL8Peb4ne3/YeY7/1+tqforoy8+6+/NyvTP6GFI+VMz\nh27/n98REVF6uab1W6MLj/6D0cOTfzZlZ99cU/naeKG3c/NtF7HRvenpmCqMuUyQHmWRrffxsUFk\nwYtdlqVFVL969arWNjJsGzpXlqVFmLjWQm2IvLY+3gfh+iHv65K7zqvoS5A0TRsE4XJNp0XOsXod\n4lr/u66X525rY9d9nuc1wlhq6xAOhUR63MoP98fK5vNcaHYt8h10MgdIEARNNElRkAfy1SXvXVam\nH1fzkLyLBA8wZV4ySez5xqJb8nNzX7oJafOXph+HjIIMeP7yX65o+73RtcMnRmdzZkJO09SGyUBv\n5DyENaMMYyx2HA6e1Nd5rrXD+0iftb+89mOE2QyIkUEGGWSQQQYZZJBBBhlkkEEGGeRHK++drvcu\n5+U1feJZtbR52vqmk+wTc90lVVXZ61ypi1A/SXaKv3XdJWICVm9pZcV9p6en9hmIq9Tey6qqqOJU\nayli2kUbwUq+4fjN9XZjrYQ6Xmw0GlmvVSO2L/AoUFZZaS3V/Ahpmtpj0hOEd9TfxeWZdom2iEtk\njoyh1V5VVwyiJrT9IRAjfXTC8zxbN5dnQ1ulXd5uF5qky5soY6jbECBtnAZdXguZBpiozovTdp9T\nvyvP9vOSg60LIKHWOQzuhm9EllmURDvu99xsq2RL/ktDyJiuTX3Q3usypPEj03/Hf/HcPC819282\nG4qZd8fDJ7hMKGW4Slzy+FKYPpfnudUv7b07OTmx/R9tc3Z2ZnlBJNqMqB6jrtOsFUVhuUvQvp7n\nWU+A9oROp1N6+NCQeIH8THIm6RS+0turkS+bzWbvybwHmutjifRUaU9QURS2ffF9fN+n2dS0YZa3\nk73puH0XYsr1zC7dc3ntXTrnShHcxT8C6SIYdCFsrDLB45bkNo0oMQEqgZtmlZE3QlpQcyp9dU0j\nHlqDLfgH2AO+TKhkAlcLZORriu+uaRKxt/vGlH91sabF35pvlM8NyuNm9BtTvS//NxqdGH6O0PvK\nXHNi7s+nERWnjDL8jZlzZ+uSilfG4/1wYe67jE3Zh6FH5dNH5j02nDL2pblvnHlUMaplV5m2l22K\nNPUYQ8bjsdVDjSZ58OABvXxp0C2Y96+urmocNERU83C3If7axvauOP/3WZMR9fPCSZ2QHl3dj+X8\nq69H3LtrnnGloJc8cHqedPGEdKFIXO2lyarlWgji4opyoVa0Z12mT9ffx3VfFIY1tKC8PgiCBhpO\nolH0+JL+4zsKrsCfY/qjnWf+1zUVvzQ6AFJk/5S57v71F7T5mUFDBV8ZnfK/PqfDvzP99uE1l7Ux\nz5nO5zQzICiajXg9yiTlh+WIEgwGzEU03vmWe2d1bfoC5qw4ju3chl+sqw8PD2tk1kRGB7EGtn2P\nOYMqv70/u/idXGM8pM++5GPJbd50jWpEu0mC4a77XPMRfjEfuTh92ubHxnX49RwHldw2T8rriIjK\npLCoevsAcalrrm5Dm+Z53ti3SE5FF7LU6rLS6VHm0+6F0R3LfZLs11zguCqvTV/d/p9fUfyd+W7x\njNObn3Jq3l1AU8UpB1LV+Xxuvw3GhjRN6csvv7TnifbfMc9zux5EGmzwjxRF4UQJ3wf545LbdOhj\nII8HxMgggwwyyCCDDDLIIIMMMsgggwzyo5U7p+vVcpu1Rlt72iyI+p4uK7n2JNxmdXLFeWvpk75X\nluF6Xxc/gEYrwCMSRZG1uEHQNtvt1v6N+OKHDx/acv/pn/6JiIg+Z1bh8Xhsrd+6nkRNz3xVVdaa\n/vz5cyLaIyem06m9VzNTx3Fs64z3kOl6EfcJC+R2u22gNOT3d8UCuqy+beek10P3F+l50m2j212W\n9bGt+H3lNvQIfvt4AvuU77pWsoC7Uhr2EVe8oEZK3FaP9sKJKK/HjtLK35/jbBmI5wSvSLXJLbcI\nTdgz6BHdnBt+g5xjKSu+5tH0iK5igxwIf28yPPkxe8SzgkaceWb9neEjKMsJpTEQKftMCkTGKwM9\nQb+ELgZBYL3I8N4QUQMxgjFBpt+FyFhqPXZGUdRAd0HvR6ORfQ48AtDjLMsaGSLW67X14OKZEvnz\nPvw/H1O6YobRx/ENVqsVrdbG04hv5fJQuzzBOr2vPi+fJ9GGui4S+SZFo8BcWTR0vRaLRS1zkLze\n9/29Z67cexIb3lGUvauojPl/zMVTMcrD26QUnxh9Sbz93JtfmbYcszcq50w0s+nUokcCePvHe/Tl\nImXkxDkjB5aXdFYZhMj00JQFlEj2fy8peWq+3+P/8uemLX9mYqnj00MKOSX35AmPY+WSZiPTp5c3\nRr9mjBhZHoYUPjSetuqrK77e3JdtdxRzSuFYZEFJ2MM2Yr1CX3r27Jn9DvDGQd+Oj49tvPeDByY1\n6cXFRaM/SnSF9kJKlIRrbG/zdnZJ3/jtPmW2zUsaySH1RiMLcU4i2HAsjmOrAzJNL3417wbORVHk\nTFOtnynropFyLvSsaz2peU6kzutzrkwXkvdAe2il51RnxpHrUJ1N0eW9nS/mRB7z2L1jJNofzLgx\ne5FQypwhyb8zaC3viPvnf7uj0X9u+m/JWdiCowmFM3P9PDT9Pfqd0bPwckfHDwz3AeaVt29Nmeku\npWDGfD7clGVW0I7f+/DEzKHIfpWmqZ0zMb/KOQtzk+TBAjLS9kfmSAqKJlJWiuu7/7msG+8jXehG\n+duGGnZxTMi26YuMxP/t9UhFzRxOlJbkkXt9KPu4zNTXhobzqbKTGTRVfkGtS13pgV1tg+vzPLd9\nW2boRD/UyN3RaESzoI62Rfac2WzWRIj7HhXXnMnJY0RWYObV+cOHFimCuQZzTxiENAmMfoU8lMzn\nc/vemIcgo9GIfv3rXxNRPXsRkVm/Qr+6eDzfR0f6IK8+JHLkzoaRu0DdXcf0wNxXpPJ1QT/ts1sU\nqKtut0nfe9Ch0zRtTEiSrLUtL/R2u7VKJOGaKAOd/Q9/+AMRET169Mgew31Q6CRJLKQexoLRaGQH\njz/+8Y9ERPTzn//c3meVRxlUfN+3ZcmQIrwTyOEmo/3mCXnmXQsTlI/3D8OwEcaBDWVXiItcJLgM\nQnoxJFMMu0jIfshJrgsiLTeqRN2QtPsaSKSgbeR36TOJdknXIqJrAm29jjcq3pb1pOJwo1Fgz1Vn\nHEqCe5KcqgKGER4CA4+ICSMz3uhdvDUGgslpYI0FesIcjUZ7vbwxOvgy+47mjw1kMeLdZpHsw8z8\nwPTHlJ8DA8P5+bnt55rkmWg/IUEH4zi256FnkiwLOg59Ho/Htp9jYsaE6fu+hRu7dAN9T45nqCuM\nBqjXcrl0klgTdcOOfwiRfRfvIw1R0ZwXNX59LJGGEb0YLMuysXHxfd9JGElUXzzCUCWJue8SzuCC\neuM5Nzc3rXpsFndclsNI3NDx64Robb5xhXTY9r6SMh+QZU5LuN2HTup+5nme7dsQOe5lgNez8aDc\nrCn/Pc8rB0a3I04Pmqx3FPwD68T/ZELjdk/MN5w/PKbyjdngfflHEyLjvdsQZ0Wk15dGx6sLc01R\nBVTyovOIiZVfeUz2mBX0+Omnpg6sJ9IYacNiiz0ZqzZKYs5+/fq1DZnFsQcPHlh9Qply44djGJd0\nu+m/2+Suxo/7ShvkucC6SK2P5PpQG/g8z2uEmVTlfqOjjX6SfFMbIMMwtHoPozMW2iAAACAASURB\nVGEURft05izyeXrtivFiuVw25m29xpHvIccQGb6nz8l5WJfhImLXIViy7btCHFHH2XRGGTsHsq9M\n/5pfmf9HxzM6fcXk+ksOvTg2db/+ny9o9l8YUuTkM+67z+a0qzg989aMF0c35jmToyML7ZfONyIz\nrxZpncDZC30q+R2hG5iXzs/PLekq5kBs7oqiqDn+cP0RjycwykpnhJ7bUGaWZXd2Dn0oeZ89S1dd\noRvSGK9Fbv61gb+qmqTDrj2abLc+xOVexE4rOLHKijy/3gauUBeZItsVRt54n7A+LhPVSbCJzJx1\nFyePnNvQl+Qc3TDUiLkBOoo6yH2i3gNHUWR1ANfDMLiYzGz/1SnPi7KgisODC54A54dz+76Yj775\n5hsiMvqANSYc8tC3N2/e0O9+Z8iWpbOsrU/IttAixyrX9V3f8UMaSIZQmkEGGWSQQQYZZJBBBhlk\nkEEGGeRHK7ciRlxQ+PcRlzXyfb0RvQUeBb/dC+cRkVeJ/9wiXXVPkqRGREpUh0q2hfikadqAchZF\nYS2WsP49emS8Xtvt1v79+LFJXwj0hrSWo6zFYmG9HLACwoP86tUr+uUvf0lEzRSQ4/G4RrhDZGBU\nbZBXSXoGkdZP9AWJjoHVWiJe0EZ9+p7LM4N2Q1kSIt6G2mk79qeSLsi/7BN9QmL6PKfr/aVVtisd\noetel2iLbpeFtwtFIj0CAdt4yzWQRTFZhWeIPwhXaZPt04Fm7HHLC3t9ujX9JD7ilNRpahEQV1dX\ntbqMx2Pbf9G/vvjiC+t9zKp62rswCukxez22m23tvuVyafUQKC0Jm9cQ7KIo7L0QifbC9fC039zc\nNDyNkvRQI6xkeIb0psk6E1GD0JWo/fv/ELDjrrA8eQzeFen1iCac7nyNNH/NFLsudJcc5/Gr21dC\n/nXKRIy9Lu+a1HvtjXERJstrutJuo/97jrTeEIn4tP0D4wQmzMojb2N0zk/3/V/3Yzm2Y47Be0si\ncnwPiVIc5ZwOm1Fhlz7r8dUFncxMfz+/NHPb6rcMNf78lD79xZfm+ohDQa8vqVpx/z3g8Iy33P8v\nN3QcMEGjb563OzTz6ma5cqZbBtIA7YvQgLOzs4a3XqK2QL4qQ0Sgty9evCAioieccvHi4qKWipRo\n33evrq7uvZ7q42lz9ce++qx1rixLyoGM4mskIWAbEbuzX4Z7pBQQebLfa2J4e19Z2nPyeZKwWv5K\ntClEjoVdIQVdHlQIxuMkSRrf2LV2kr8jEdIl37UoilZSWFfbLJdL66VfED97bOa/aRlSxKGfJ08Z\nkXFh6rVIMtq8M6Gmn5xyKtD/63PaXXCo6R8MguuLyT5NqEYWYm2bJEmNDJSIaL3b7lNXz83cjO+0\n2+3sdToNb57n9hi86UdHR3atjDKhj0mS2HT2rnW7K/GCK7TpvnJX1NddyuyqF3TvNloBjeqSKMU+\n9AZSh7rm5ooRQ3bf5qg/+rxEz6LfyHFCj9XyHfU+TCLSoIOyr0Lf+4bQ6ee46oPnzOfzxn4NfVzO\n+8cLo0Ozgzkd8DyBtsA10zyg6c78PWI1K5am7v44poucy03M/HqQbq1O6L3TdDqlX/3qV7VjQJU8\ne/bMzntff/117VfKXcNrulBFbUgk1+9tz3E++05XDzLIIIMMMsgggwwyyCCDDDLIIIP8/0h6IUZc\nXAbv6/Wrkex8AGlHgHjkC4sjkTFAtr+HR9TBYeKKf+o6Byu/K/ZOW0ul1RHXw9Kd53mNuFWWLUkV\njw6M9RAkcbJ8WCIPDg6sZxllwMr68OFDmxZYx3FWVWWtkjJ2Vnr+iOppRXEvfmF1lfHusKRmWWbf\nW6ctlfF9+pu1oR3wrNs8YG3yofr6fcTVv/A+2rtM1LTid6Ev2rzdXfrY5glzea9dPAd9xKUTXeVE\nUVQjAa5dv8upAngkq5+rMpEq+oIJQ6uSqoCt6x63L3u7d/7OXo/nSZQT+ib05fr62nqcoC+LQ+Ph\n8qKAphMmA87rOp5lmUVwAdEVRZEtC+8I3b24uGjEB6MOR0dHFt0ivw/qjfLhIbi+vrb9S5NDZllm\nvfaQOI7t9dpD2SeWVF73MeYXWV5fpJkL+ZKcm/fG2DmmPQJEj+kuMmmXTrmIM7u8I65z2mN8V0+g\nawztix4jMuM5dAHjv72vqqjK93/j2WgXxELLlKioW4KUtoKYGffBcxbHMaUFIw0433Zxbr7d5OmJ\n5TrJXxtPcMCcIfPRgpLCxEWPZozseHVD/ornUf5U23THv1vaXhgdwjeAHsiYa0nQJ8mP5X1E+3kR\n6A7oz6effmrbDm1zcHBg9RdlSTSJJu3Tnu27yF3WYR9izSb7ku6/ksAZOqf1SiJRXX1Wl1lVVWPN\nJM9hTAQnhTyG95WcP23oC+kJ16gwySsQj82cQKFPyc26UX+IRoF1cRQQtfcByU2i51eJXIaURWER\nX3Rg+t7IY94Df8+/8pTMPBGNeb4sPQqY8iZcM6/PNKKr0HyPzc5c/5Of/ISIzFz1/XeGABWpr895\nLHn58mXjfZbLJZUbcyxd8JjDXGHrZNNYH0ukmSV1XZv+9fSLzxpE59CzOI5t37u8NjoI3rE0TWuc\ne7JNZbvKubBvYgd5f9ux1n3Oe6BMulC5rn6JdpZkyF1ee/3+km+pE2GiOIPkGlVfL5NASC4UjVLs\nk8TDld47CIIGP5FEN2o+Rslz4kLFuOqPtsH8gLWjJN/GnAHCb98PKKL62j/y9oTUQLwiCiK/MfU7\n//4NnWWMlNoZXVosFjbN/N/+7d8S0Z5jxPM8evbsWa2uWGseHx/bd8Q4eXZ21kiRDelah0yn0wYx\nre/7Fj2pSeZd+08X0v2u68oBMTLIIIMMMsgggwwyyCCDDDLIIIP8aOVWxMhoNGrEsRPd33PwPve5\nYrnbyq+x1gIrckuM+b6Qu9WrzzltqXJ51a2lSySOktlYNCcHLJaPHj3a82dwFoAizRr3SQvpu3fv\niGjvHZb8I/gbljvwlZRl2eAA2e121rKJukoPj461l1ltYP2Uqa1QBqyk0tOjM3XcxmnQZvX+c+IT\n0f26jTNEHndls9DfWLLa95U+yBptZb+PhxKi6ydRZH2+h4sh3qLCktx6jqlqejFs+ZxRYzQZURia\nvjaO6jHdEhUjUVdEpn/mKgO5jDm2sZrcr7NVRmvmLonyuncpyzLrtYK3WPJ7aPTZ5eWl1R3oCcq6\nvr62fEAy4wfKgNdPelI0Ezues16vnXH+uBd6ifHCxd5+V4v9h0Qm3vU8xqDFYlHz/MjfLMsafBiS\nY0mPky6OEemN0h5qGWeMvyX3i+aIkUg77QGTY7U+JxnztZfMla4X96dpas/pbAZlWdoyZDYy/Wx4\nxmSGIxenA+YX6dHFsYDqXsKLr9/S4VOTGeMngcl4kR+Zvn6+Tik/N/NeNTXz5XRF5HEKX/ATZZwu\n8cAbEbFOoPwvvviCiIz3WqO0ptNpLfMb6k9k0AhAfumMKkmSNObJg4MD672DXmEckG3fyM5SNTlA\nbvMmd66FHNe2lXcbOsy1fkPbQeTaRnqkibo5eaIoavRH/D8MwwYCVa6lUB98s6qqGhwD0puskXGy\nbBf/BN7HojRGPL+UBY2nPDaX9baTKGCIC1HsStOsv4Pv+3YMgci5TbdvUBBVzLczPjW6M+ZMgw/G\nRzQZ8zyxZZRTbNotmo0o5jKmU17nvU7o8cwcu7xk1GXJae1PE8ouuU/z+vX8rdHPi4uLxtyWpiml\nhdGv/IbHuw3zc6Ub4qymjQwc8/mcJj6Pw6N91q/Xrw3nCfQKHD5FnlvekZzX0eAmCcPQ6jHa9Orq\nqsFrIn81mvW2OamPHt6GLNHH+njOc4HSc0nbGrDv3syFInFljWmrswsphjrLfYjMEqXbwSU6Ja/c\nm0i0peTskb8y+2gfdEhbm+A98E4YG+W4h+sSRjWmeUYBf8p5YFAVSc7ZDsOM8pLT6K55rFqa/794\n94peX7yrPfv4+NhmmtHzy8OHDy1qA2MB9o5lWVr9AOoO/yciJ3JEj5NyrQnBGnW1WlkkDtri4cOH\nRGSyS3WhqBr7g557olsNIxpmd1/R4SIuiNl9IWB6sm5eWP/9EHDQLnFB6/S52uZMSbpLbbphGSKh\nJ0oJaYNSbzMmCMr2C009WMlvaiHi431nx3l0wksm25ITMtIESvIyTU4kJ109AB4dHdlyJbRYDnSy\nfr7vNyDhkqAP0mcjJdvxQ/XvvuKqn4b5ErkNDnoB15XC+H3EBYfUk6H8Fl3hO5CuiVJe0+f7dU3u\ntbp3wDv1vXEQUcFw3m1eh8pOJhOrHxCZQvGAieBGDJFer9cNXcD9BwcH5HPbra4M1BdGShleJgm+\n8J1h6JALcUyeuA96mSRJI9wiy7JGn8F3lIsIpFDEO7g2wTLduMsoB72V0HgtP5Qxsq/ItOm6LWX6\ndNeiU/c5SSytU5fLjZgeL6MosunP/dCcS9PUfke9mHWlyZPGDwn7R/l4Vw2HlWVAZOiGLkM+V6dB\nD4LAHsMvFlppmjaMadLgm6hFUZZldgzU43d6s6UXFyaN/el/ZtIKnjJh6mi9pPG1uT7GwjyMaOqb\nsl5cGrj9myuz8cnTjG7OzRyFRaD8LpYUcr0Ph4BxEf0e9by4uGhs5qG7MsRNGjqwUQORHeqwu1rR\n0ScPa+dkv5HkzCirbePS1xjf1wHUR1xhLKiznO/1OC+NzS4DRNd7aEOHNngSEYVoe9+vhS0R1cNX\n9Zgm38FF7qrfZ85Gg81mQ0VYrzPef7PZNNZrkgxfjzku0mWIPKfn6qqqqMyxcTe/J/MjCuemH4dj\n88x5wHPbakUZp6BeMZn5QWHaY7yb0jQ01y0LM3cswjGdztj5NmUS8HdGp7x0S1eJmXd2S2P8u74y\nc1wURbbtMDc9evSIvvvOkLtmvhkv4ompX+SPKOcUwxPP1AHzWBAE5H/ySa0tZ7MZ/c3f/A0REX3C\n5/7yL//SvNdqRY/Q17Be5Y3ew4cPbbnyu2Cu1KSVLsOhy6H3IR3NfY9p6QpruetczRGOzrWWXDO6\nHGwyTFnWRzpj9Jggz0ljZp9xS5Ouy3PQdTl/Od+3R/vYa3zPGkJdxia9rsL8IkEK+JXG2F2Z1+q8\n3W7tu6FNdjdM7l+m1mBhw70XC7vG1IYn2b4IIYXzLssyShPu/8IZA3JWfCNNpizf0bWmlwYVuRbF\nM1E2yoOxRIa2owz89t0zDaE0gwwyyCCDDDLIIIMMMsgggwwyyI9W/mSIEUifdE59rad9oP9/zqKt\nZLLOLpIZCP6GNXA2m+09IRV79MO9BwZeLOntlKkPZV2iKLJIDpQJb/e3337bIMSSEDOIhIhrsjNp\n1XVB5TSZJMRF8NRFPNj1/aUHpat/f8g+1Kc+0iLdBjWU1/cVWG5hSXYR2bq83LKd27x3LnG9K7yd\nq9WqF6zTJS6IZVtZt8EX9fnlctl4b5kmEW2GtocFezQaWThvxWmBfc+zVvjlyni7ZuOFvf/1t4Zw\nDogRlDmdTmveZ/yiD0APZUiG1ZOQwx/YA5mtthaCD/2XqBCN8irL0o4nGrUiyeiklxtWeA27nE6n\nFgYJBIsu84eQvvOFbHsdxgL55JNPrHcF7Ybf7Xbb8FCHYdjwQstffCP9rUdhTAcTozuAqSejjNbJ\npla+9HBp9IUcVyR6RP7K8Va2hZ4fZEpTHS4kkUlah6Su4r3RfyQaUo9tJycnDe9VWZa0ujF9+fTh\ng9qz5+GI5sQhLgzdL3wm4d5mFLKz/4tfGiK5l69f0Ya92/h+HhM17tbbWtga0X4ck2m64WmczWb2\nPI7hvoODg71XueJwqWCfChJhM5AkSejXv/51rU1smM3jUzuWAzYu0aMaFeEKY3of1GwbCvauUlWV\nbR+tG6PRqIF8ks/vQrW4Qoc1/L0L+RWG4R7BwuGVXtBEOruQuG0e0KIsKZwx6WrMKYlpQpfnF7Xr\nPB7HJSpEh2Lked54DxfCRpKuusKc8etzWtSSGRqTsKTdDa8BN0x+X5m651lG+Yg97dzX6YXRl1Hh\n02hmxrHJJxx6UhA9WZj1x+M5IxEDfvbZFSVk5oPr1IxnwYjDZrb70OlHjx7Z98b8+JTD5SRCI56M\nascA60/T1Hq3oRMXFxcWKYK5GgitLMvoK6DteG7//HODPluv1zY5ARBvs9nM/i3HNKI6WqkPUTbu\naTvepr93DWdxrZ1cz2+bF/Vv4xgQEeRGheg2kP/HHNMVEugSiVRHmW1RCbLOriQN+FsS7WrEiGy/\nrjZv7HkD36KZNapZ0gngfbBuG41Gdn+Xi7Af8vmdRkb3ssicu7p4RXRuyn085dCWJSOZg4IuWSew\nVjs/P7fva8cJJjteLpdW9xAmg3rKUDK00enpaQNthzkuCAIbjqbbrU030BcwFkDfDg4ObF2hx199\n9RURmbkX7yP3n33mvgExMsgggwwyyCCDDDLIIIMMMsggg/xo5VbEyF1STQ3SX1x8Ci5LrfT6wLIn\nY8KIjBcLFnTtLYiiyFrsZDpKxGPBAgfSndVq1Ur2WJalTXsGa6Yr7g7PTpLEvhOuA5HrZrOxVkDp\nzdBpCGWsZhe3yF0kz/NbrfZSPib6yPM8Z9xbl1UTSABXf5FeIumtledc5Ji3pVxrQ+t4nmf5cEL2\nhOZ+s800uqDvc+S1d0UGtT1H/o02kZwJEHgeNpuNtdrrlK6Xl5dW92BJj+KYJkHdw75gr//h4eHe\nI2KcvTVUFfoCvBjj8dh6ofEd8f3fvn1r3+Pxp8b7dTo3lvSLdO+9hP5j3JCC94miyOq0JsKcTqe2\nLWQstfbQSm8vzukUin9q6fKM6WOu83gnnab5zZs3dvxC35a8SJJQl6hOtq3bTXqAtXcxjVJLkTUr\nmQ/Ezykp6rG2EFkWRHqH23hhPK9JEiiv03WOoqjBZSF/XXwl+tm4XhLT4hqMXVmW1ZBLRMZ7ZVOs\nPjLzWLDjevmhjW+/CU0bHYVmnjxdHNH165dERPSbv/sPRET0andFm5Gp6yJlNBjzc+2SpDEPSX4J\n6JPkU9FeS/T76XS6T7vNnA7Bwuj1YrGw8yokS1Ob1hQeaiCULi4u7JiAsQBrAc/z7JyOVIsyva8k\n1sX/u1B3fcbXPsi/vggV6Nl6vW4Q2Lr6pYt81IVKdnFx4LiLPNmi8sDdEux9iEBzaQ6QIAj2yNuY\nyUsXTEIaEW1XPHcwuf6m2FkkAuYXfGOXyPeRfCOyHaRIzzvaUiK+iAzt3iRgcubQHEuzrOFp9Q7M\nvBJ6FWUZt+/OXJPszHsdTOeUl2YMPH9lUJGL+YKSS+YKmJnrb+bm/pPxgi63TDI+4fUqo6h2BdHY\nq6OIzs/PLQpE94k8y6wHHGtbtOXNzY3VE8jNzY2dr0Go/OLFC1MXQXh+szZ1B1Hr69evLcoJ3+zo\n6Gg/P8R19JxEa7n4Xd5XXFxBXegFqat9kCl9RK7N7H4RS3OBBuxqExfySYtcV2CulXWAyD0DElm4\nkFw4pjmDRqORLb+GzALIg95vHUppO9paps9GH0Tf3e12VMVMas6kwD75NH1mkFjZhFGjGae7PV/Z\ntPc71r1ZFaEytMp4vXfOfGVlQRUjRKaHZnGaXZs6zGczymamTYBShEgUMMal6XhCIyaWBjIL89LN\nzU1jbH/50szL4/HYtj2eM51O6fHjx0S05w2SCFOsv/DdUR/dRyB9vtWthpH7SF+lui+cs8ug4BJ8\nLLkxkOy396lTF/zMfQP/iqp3QVL14lESQOI+wK8lrNfFmCzZ/ImIfv7zn9tnoQxMOOv1usbOLMuK\nosg+G50WnZ1ov0HA9bKTQzCp3Nzc2IlFQkb1IkUu4PBMPaC1hXV0wfU+prHjLiIHaNekcFdyLTkB\noO1B7tmVd16SGHUZEpztxrDJ8p74M9dk/b7fx2VIkf93LRR1lhXnQpmvkX0Pf0MXjo+PbRmRb+6b\nM5P/4eHhnmB4xdkmmDRrs9nYbwSooAyXsZuukhfiYUAJL2arE1P+7lsDzS7L0uq2HEOkwZSoTmal\nCapwzWQysd9FEsDqja5sP932fUMyP6ZeyrJd/Uz3cRkKiPrju8iwJz3Jy42+bG89D0ld1SE7+HZB\nENCEN1fImjT3iEZqbJahKxhjUR/0G/nNNLHdwcGBLQOw8zRNG98Wc8lms3GGIKBMvWmUZWgDrYvY\nTob9YbMUx3vDG9oL7+bxxBqOYlrtTD8+2HH2jA3PIbFH40MmgoxNmY+nD+j1pQn3Wi/NfWsYcbOC\nnv/kSyIienHBoS6r1LazzuLk+75dxOpMB5vNphGOA2jxo0ePbOgNQs9k+J5ukziOG6FKaIftdtvI\nLCDHVRm2iv93bahum4+04bHNCNlGJq4zNMkxV+uEKyuNhGvrUC3XOZTpahuZZUpmhdLXS1i2/B2P\nx/Y+u7FKeC21yShlYvx0xHNJuV+H4tc1R7vIzRvZiIqSiqq++ZPfWGelwf+LoqDokA183L8mk4kz\n3I+IaLQYUYrx4dr09Zzno5sisQSoi4VZq92sl3TF2Z7WKROKZ+bbfV+8oZLtVN61qWvswdia08GB\nMfY95Hk1qnxapXVidOiEJzbgeH/pjNGb36IoGsTl0JvNZmN1b7017wjSVznuyWxsejyFuPRLjvv6\nPm2w+JAhb23nuhwH8poux1kfB/pdxhXXOelM7brPwzWizlonpKPC5ZTQ65DamrlAmFA/Y0ivjbgg\necccIsMjUfeCjZIweMTjEfkjGOPqhpcyzSnhsvDel/6+LtvAlDGqYCxOiDjbjb819Vnm5v7NNqfs\n0pQxYz2RbY/6Y330+dNP6cET1lseq0EUvl6v7Z4E6wmsK4uisAZ9mcEUcy0c65gvkySx6xXouzTq\ndu1lumQIpRlkkEEGGWSQQQYZZJBBBhlkkEF+tPJBESN3tW72sVTqa9uu7ypLWxld3sv7Wmb7WmVh\nXGwjNmoTWM1837deBXicYNVeLpfWyghUBaC1Et4praXa2yHTCmpSIjwnz3NruQMMUSITXNdrCCuu\nkV4MCVuTnlL5K8vC95Mea51+T7ZzH2/1bUiFjxV6I9thMpnYb+zqV7C8tnkn5LO7zknrtyQYbUOM\ndHkLyrK05tVq/0fju8OiLD03XdDtPrDuu4blyF+0pfQaaGJQmToa+gVkFe5L09R6gqETvu/v+3HE\n3nEBybcwQE6FuHphPMfr9do+E/qYJEkDwZXujCdhNp3RamkQItvXpg7XF3vECGR+aMaCMitqBKFE\n7jAbTb5cVZVN0QaPNtGe1BfvDY+bDEtypQ51Sdt3/xDSZ4x2ea/zPN+TevKYa703oj/qMBtZf5fH\nAtejzbuI3aTIcCQX+SKR6UNt3jsZNqHRHm/fvnWSA+rnwDvT5SF0hTUQNUMPZJ/Q7y/Hc5ve99h4\ni+bx3OoXvETQ3dl4SknJxMLnpq++emNg8OPxmA4ic5833aMDlmeXtfrZ3zi0qZJPY/P9z8o9mTDq\nAHjvZ5991kCM4P9VVdExpw2ORvVU1t/+4Sv73pjvJdwYOouQva+//tp62jAmoC55njfC1iR0HWEG\n0FU5F9xlPJbi9ASjDWeM8kgKijgFbHbTDAWF2PCyaVBLSy5/pRde1k/rr6t8HUojUZoSFajTCMv6\n6TApOZfo8dsiM9INRTNGeXBYTrnbr1sayIzRqEHC6KqzHV+JKE/q4xD60m63a00jPJlMGqizzWZj\n6431pCRQzBkFs+VwPolu3DDC4mZpPLq17xLy99ywru9y+vRnz4mI6PLK6OBmzfpDAR2wjo4ZVvLo\n4IS8rfEsjxmmjxC04+NjO0e9/tqgO6bHTEyc7ChiJEpa7ufh7ZVBLKOdMZaMj+b0jklxix2nGC8Y\n7bLa1tYMRPU+4hpDu9BTXelK2+53nXMhU267t+uarnAc1zqsT3iQq8w+ZXWhW2r/n/O457H+r5sh\n4/J6rXMypN8Vdq7DfnoARpzPlvXXY5tE32gkm0R9VWugNCOKOXa02LJOc8ht6o+oqBiltjRzzYrT\nXG93W6qY6PmIw7w3ux2FxOgvThpwzciMyWRi3x9rQIxxm82mgYKdLGZ2D4p1ok03v9vZdUQ0Nvf9\n4z//k3kv37PRFSDwhV4T7dcfQJjkeW4jDzBO9tkD3CYDYmSQQQYZZJBBBhlkkEEGGWSQQQb50cpH\n4Rj5U4uOy9PSBzHSJXdFk+D6KIqcRJe33efy2ElvH47BQvbixQtLTqNjjmXcM9rh+vraXoeYLZ1W\nV/4N79J8Pm/EVUuiQReSQ6cFls+R5HtExoMm207eVxRFa8o5+W64X7a7JPLT993X+v0hPdoy3VSD\n9Ez0PU1MGIZhr/Sn+n1kekygdW4jX+0qs+u694mRdT2vqx5EdQ+1K20jBBZneF4lskr3s7OzM+tV\ngBcOFnLpqYFlezKZWC6D8Zy9VhfGG7VcLmnsm76NVJCSSHG1qcecS4+5jrXP85xG7E3bXhirOWIv\nN5uN1e0q37833k3/BsHeQ4v70Dbb7baB+JA6hHZCvxyPx7aOsPB3eX/k8Y+JHJGi++Vt3gW8Iwg0\nNQFZ232uZ7r4HtBe+huXZVnTd5zTqUxd/V72EyLzrVGW5mcaj8eNOHxXrLV8l7Y4cVd6b9/3a3OZ\nvk97ziSBt0zJSUQUeYFFKeEY9DkKQkp2e74Nov23yrKMzrm/n7/Y66qtNwhzmdhuNBlb7xj0Ee13\nfX295zfh+3e7XWOMlnMViBmhX/B0vXv9lqYhowafnNjyNVky4rIXi0Ut/ppoj9r69ttvGwgzObZr\ncs+uMdv1jXsLyt3yfF9WdMi8ExervWfPpYdEROVqR2VU90J2peGU45FEbunr9VrFlebWhT6RaErd\nf2Vd9BoN82uepEQr5rMKmfvEC6ms6uS+ciyVPCBETeJv1JWoTkSP6+VaYu/l5vYV/QGIJJSR5znt\nkj2yl6jOSZUyIgv1g46EYWgRSZI/DnOMJTO/MXPho9MHFHEZK16jXnBZZSqMqAAAIABJREFUB/MF\nFSl77TemHxyMZ/RkZngLSk5LnyzNfefZpSV51Lq3ulla3cNaOM9z2ub19WrICM50k9CW+WCCCa8d\nLzkhwW7XIDB++/Ztg4tG9jc9d7rIgft6tLuQHB/jPimdaA0WzaO13W4b7zadTvd6oZDetyF99Tof\nqc8rn4hAClzt132uuZbIzHdANAAhCx2M49iZ6EHOZURuPdTPkeOSfEeN1Jf9R6LqZRtNp9M9gr4w\nx6LpmHyuRsBbnt3a6H2apjSfmbUl1qY5o6Ioz4iYyHU7YvL8bUkBp+7eMtIZJK9xHDfGVdTz5ubG\nrmGR8jqKosY6+hGPDdPZjFaMwEL64fONmZdWVzc0802bXO72CQ800b3cY+qIhdsQI33WlANiZJBB\nBhlkkEEGGWSQQQYZZJBBBvnRSi/EyMf23n1s0Qzmt6E4+lhXXdZSiPTsuVKxtt0n2xd1lczs+j3k\nfbCW4XnwFkhUAe775ptvbCpAyZpPZKxzqIeMd0WdYanD9cvlspGuUsbca0uf5UlwZDwoy7IRJyaR\nJngnHRMor3f1UZ2iziV90BF9zt/lHER6eFws5W1lSYSN67lt77QTXg/JxK2t2NIq20cnXOe09VvW\nRWdGkc+R76Hvc/3t+tWIEZfVGF64qqqsBwGoKHgSiPYWd7QNrpF8IjK9b/naPPsxW9BHXHYYhHQS\nGm/vmtM3ZhNz7i29peW1QXxI9AW8bzod2Xa7tV7uDbch3kum+cWxOI4bqZ5lOlLt2ZM8JxoNFgSB\n1UedxUd6auDZdqX37hs7/CFRJG2oDVeMtkRWod4yM5gLuabfR3qQdb2tpzIMG2Oh9CC50i67PJO6\nXpLpXtZFPluOr5L9nsh8Vz0eu75f23vJ8j2vmYFB3i9Ti8oyR6OR7bPob+PxmB4/M95h6Cz67k++\n/Al9++LbWhm47/DwsDYvEtUzQUmPIf6PMQB9HPHSBwcHNY4Y1FXOb7ItDg4O7PuCp8hmYvnpT22G\nGpt2mAL7bnh/oEJ/97vfWb3SyInZeEpZwesb/iyT3KfcgeAhIgq9gCq/XffeG/HHceJHR0e0ubyp\nle8SqzdZQWVQR0O5ECMulBKki2tBep4bXmjByaLXQjJbDvqQjP3X2WKA0ImDkAr2vgZjc99oNKLV\n2VWtLNkXoe+SWwV1cqU51e/hTMms3n80Gtm/kVXt7du35Pluz3eaprY+kseOyMyRQNTJdoMOYK4F\numlbZvTyneH/Ycc/Fby0zYKK/Mj8B2l0j4+P6Re/+AUR7fVqxLw1z08O7TypETNoT9leB7MFZbu6\nRxupSbdhScQ8MAV4bniIL0R/Qdptz/dqCAn5/kRNFIHUL62/fXWua//RR27b29ylXLme0uOeROJC\nsixrcFd18aO41m0Bd5hANF+Z8PfgbyczFenfoihsX9WolaIonHOmrlcXsk7O33ofFcex1QWrs6yZ\no9KnijlDEpUdMMsyW6+TY4MsDGdjCqe8Xr9h3jggO0T2NtRhjP97ns2uE5WMlL5e11LkEhGNjkf2\nPbD20WuBKIoaWcWm02kDvY9z4/GYKiDFbozO5kuzzrj67i1dIB12up/38UzouF3bVCWVEx4zl3Ud\nvw0F3CW9DCOSxEmTpN0mHwpKL0W/3G3P0BOFNIx0TaZ9ynSJhrK2iVZWudHXky/RXrEkiQ3RvhMT\nudM36lRt0gChcz77vm/L0wR3uFceWy6XjXzbmBxkX9HpHvM8t/0KcPsgCFohrzKdrJY2I4AmULrN\nwNHn3McUDWVvk7uQyUrpgpjJv7UxTy6suowMfYxG8v+p2swTuUMDusruqhcEbSFTjWrxPK9BmIcy\nrq+vbd+TqUyJTB/TENksyxrwPsDnP33ylGYLDrM5MP3/+sWesBF1tOl+Hcfk5IB30aFqnudZHXWl\nKYfe435JroVfGIOwgCDaL4ajKNqnD1aGFCJqwLNluJwr/KsrlOZDhdl06cRtsGaMhdKgpA3VMj2o\nJh2WIRt6ESG/sd4gSUJqubDQbYAxbjQa1ULz5POqak86rDf8V1dXNTI1/d4QF+mqDpHJsqxRLxmq\n5TLs6zaRDgGUBaj869evrSEBAoPFd99/Z+uM+QWpNt+8ebMPF8h44Z5W5M/Ms0GiKkPqZDpr+f55\nnjdCYq6vr+3fOIffLMusPmnjyZdffmnb8GJtNtL+KLTfQxrjUGbu8TzJ9Um2Rqci8mmL78EbhJ1f\nUZXWQzyswY7aw6XajuvNS5cRE3J1deU0TmjdwTdI07Rh2JXhZjr0TPZT9B0ZBiLJRonqBgWUL9da\nWg/Rl2QZuAbfqaqqmnFYPkcabrD539F+DEGZ2Ji8e/euEQIsHVTaYCPr0zUHasNYnucNo7dMb6yd\nUQcHB7aP681dFEX2eoz/sk20wcLzPKsT0N9HgTHOrFYr+97oEwcHB7WwQPnssizt3ITnyLAOzDly\n/Bsnps1fvnxpyih4/k4ymrCB8sGhefZqznOWR3T11tS5YgNXvK6IfJ7neGm2o/33b1sfueY2tIvr\nGnndbffdJl3GD9m/2uqkn637uys0BiI3ul3l63Ny7sl5K+Azqa5n/6nfp42F0CHpmHWFXLvqcJe1\nplzb4rxc0yFrLowgxCmvs5Ioh5MAxsKKU0dfL2mMsYbHo6jyKNuacs+XZm068nidEO33ftCNBwfG\nKJkWGcUlrwv4/RdPHljyZITElRzqskm2jTERbRvHsTV2Qlfxf6LmGiJNU1rfcMh4wqmJ2Sj58jdf\n0TdXnA443Bux9N4XkiQJlYV739K23+uzbhxCaQYZZJBBBhlkkEEGGWSQQQYZZJAfrdyKGJFog7ui\nRX5IkZZkTQLjIoe7K7Kly6Ioj3Xdr70X0uIFazmsjFJgjZfQfW3Fk+gDTWgXx3EDkiQ9STrdH645\nOzurkRHh2fAw6pCa3W7XgFNJL6arffR7SM+Oy3LcJZpQ9odCgvQVFxzYJV2pT29DiuBXH5PP1p5d\nF8mUSyS0UJfft176nOv/XcgU1ztCXzQ5k6xXEASN98XYN5/PG6gzeKDiOG5Anv3SIsgbBI1+HFIZ\nsbeO9R0wysViYT3MQGm8fv3a6io8x5L4E4SM2lqOa+X7eJ7XsPrjuslk0niPb775xt4v2wmivy30\nPwzDWqiR/L0r8fX7Shsi0HVcEz5LiGyqYK2yj2svmSRqwzGZ0g7SR/dkymAJs9eeXzl+g4xNhzPd\n3NzYb4v3gU6UZWmJe2WYjUaDuEJ2NGJIeqHlbxcaTI/V0ouHv+HZLYqCXr/ep+Al2qM2rq6u6OfP\nf0pERNFhWLsmSZJ9uGfGHj2q6JMDE9qiEYZhGFpd0/qVJInVUXkO/QOeLemFf/bsWa0MhFmcn583\nxpfdbmdJz6FLEiFaMNHgnL/tbG5+t8mWgqKOyJHt6YKna9FzfJf09sQdjiwRK0gSZb005DuKosaY\n0zXfyfFboo1Qlg5HkygRPSb5vk/BnNcpTEIYMzlu4AeN1N2usRECT60MVUW7Xl9fk6eOSbSDHo/Q\nD1yoS31c/l+unVyoW9e6Sl8PT7BET0JPoF8SASTXe9AhoLywNo3juBauSlRH7aAtgNJcrVZW7zGn\ny7Uq/sYcineI49jOTTLdOL6NJXrOzVz97NkzOuLU2gv+1t989TUREZ1dXVAWMxou5XFyFJBPPBYC\nCsBNWZalk2wV0mdNet89ym0Iyfuuh12oRld4Ca7teo5rHm4rS56z+wP7fzdhclsojay//j7j8djW\nGXub8Xhsr+tKeNDYA8YBhVQfF9I03Y8ZBd6NkS1lRRUjl3Ypr1eBHCl9ymKjO2smGJ/NZ3sk2YhR\nl0w0HHh7BL7Wl2y5JD829404Ze7jJ4+tfsgU3ERE4/Xa3gt0l0RT6uiC+Xxu64V1hUx+gXAZEDm/\n+dbM7Zf5it5szDk/2Y+FGs1dW2td7dcwRP33EV0yIEYGGWSQQQYZZJBBBhlkkEEGGWSQH63cihhJ\n0/ROKWffR+4bL+cqQ1q/ZerL+5TdZWXtinfvsk5FUdTwUEnBMcnvoXk6JHEqvEmaBCrLspoXhsh4\nHnTqWpQpSQJRJiykknhLxvhKAkf9PpqsVXoNca4rZayM6daETbfJnztCxCVd1vI+0vXOLg+1tJa3\necBdqUC7Yk5d8at99eOu36zP+0qC1bb7PM9r9FGITFUmuXhwrpFGl0oqPFP+ODIWbnjt4zimaMa6\nxo6EiNP2ehVRsWPdWRtr/Ga9tp5p6PYXX3xBRIYDRL8H6jKbzRqkV0VR1DyY8vrJZGLPaU9gmqY1\n4k9cg+txHTyCSZLY2HE9hvypUYd9+aeImmgNfzGm06nxnNykdV4aiUjSiDyiOhKHyLSDKzYX/29D\n6fm+30g/KfVLp/tbLBYND7b0GqE+8nrURSP+5FygiZIln4ArjbS+3vP2xN0SDSP/T7RHQ+H+3W5X\nqw+ep+chyWWz3Bp9D5ZxrUwXuXccx06eLZyD3uLZ0ouP8QLfZ71eWzSBRkiGYWjbAmVCr9+8eWP/\nliSXUpfRhqg7Ys0zLhPokyzLbB0kSXOXaI+0CznQZ5ztKpOuEqIp9/F0P09ojhA5Vun5XqI99Fwl\n+6rk9YHIfihFoqIgfhRQVPL6hglTCzLfOJ7EjX5v7xOICfkd8X+MiTIVNQT3oU8lSWLRFBpRLFEI\nEmnV5h2VXAuyrqiXfn+J0gJXAJCJ6/XaXq9Tlud53iCPlumhdf1ubm4aXnjpZQYZrNR1TYIsSZTx\nvTHfSxTO27dviWjPrfTJJ5/Y/oR3k6m2kfL7zVszp4EANooiGmNMF++W5aafuNZVXXxp+lzfta1L\n+qy5+uhzF/cIUZMzQpL561+JlOp6hlznal4QeY0+B5Jgz/MpYvRFwLwdZeg31s+u9a5+ThiGjb2Z\nJGTWde7at4Z+QD41UZ24J5ub63e87vOyYs9nVdV5pLKiovmMIzgwrF5dWT6QMY9Zj48NAvLo6KjB\n4yf13s5t6X7/hrkDCDHo8aNHj+z6APMdkCBybpNzj0TGyfeX6NRiy4g3RlFX8Z6sebdc1crEs+R7\nSHJnUm0/mUzsWHBXGRAjgwwyyCCDDDLIIIMMMsgggwwyyI9WemWl+RgirX/3tZJ2Wexc1sC+3ui2\nMvo+p+8ztKXe9Rz8LdNeWWZ9lXKRaO9VkGnTYI2HpXc0GlkrHH6lhRTPRFkylgx1xvWz2azxTOkB\n1HFfeAeZuQEWyDRNG54g+duHK6SPFff/C0iSLsbrj1G+tOz35fDArysNXRuS4bbv0sejoesky+ri\nK3Hxj8jr4I1yZa1BjKaOI5cWaWuVj0MacZ9+dPqwcb1Op+oxIUm63NLZuzMiIrq6Mt7FbZI00uiC\neyCKIutVg47Dqh8EgdOTr1Fn8Br4vm89FTqlqczIIMvEeKIzBci0013xuD+EtCKyfJ+8mDkDeFie\n+zEVzBbve3UfQlXtOaJ0xhKZIl1mCdLeLqkvepyUqXY1N47MhIRzMn2r7qPSU6XTuePcarWy/V7y\njui+CpH9WPJi4P96rnLxleCcRB1iLpAoRIlYxHugT0MvJW/Bu3OjQ0m6RyISGb3R89Dx8bH15Guv\n4nK5bIxb0K/JZNLw5O92O4vA0Skg4zhuZNKA18zzPOvJxvscHx8T4XtXew4iIvMt0NZ4Du7PsqyG\nFsX7u7hb8P+2c314CNpQeM5xfFNHxsrxXnP5SJ3Q/DZhGDaQCZJ/wLV20LwI8pzrvT2ua4D7JkGj\nLN034jhu8AG5UBty3nOhx4hMX9LoX3mPa83c9a1cqBAcd6EWUA94e2W/R/1RL9l+2tNeFAWdnRl9\nhGdbIrh1BjRwGzx69KiREUemNcdYJfnDME6Ah0R+J1wv+wH0D7wKWAuv1+uGfkl0tv62Uocwr7rS\n9natQ+6LZpfiQvN2raf6PMvF76Ez/LiysLl4ulxldfEGuVAo+j6pUyXS9AZNjhHXnNtWhyRJGhxp\nWZY1xnT526Z7RZpTg1XN8yxCIgWKouK5kQrKAu5XnNkIfFJFUJKXcMp6pLXOMotmQv+Vay8gPzQy\nbzGZ0dgzY8740Mwrk/mcYh5zoIeSN04iiOVzjo6O7PvLeVhzJNkoiOWKihWvFfg9CuZHyQOi1Tsz\nlyHTWlVVljdIIq+JzJx48IgzmS2Zp+u8yUt51z3fRzWMdHV6z/PsoKYHuzbRg0gfw4oL1n+btBk7\nXBs3Z9k41PEt5GCqU8LleW4HZjm4o0NiYyRhvroeMkUt7pOpqlAG4JASkukizsOvXtyOx+MGIY6s\nC5QJk6GcmFBHCZvWiyGZCq8Lhn9fBfjYclu92ow2rn7VZmy47Xl9DUNtUFzXZqutbH1cL/xkSJQr\nnKWr3LsabPC37Pd4H1e4jE6RjT5bFEUjNaMcoPEcLLDCMLTnk5mZdLBxSdO0EUJw9c4sCs9WV3Sz\nNRPRKtsvPjSU3i5Ii9JCeDF2StJmTIIy9E4ucKXIDRXGHkkuqUMq5MZFL4aImiEzOnzih5CuecAj\nIo8XIJ5v6ro7W9JuzosHbsMg3i8A0Z80GbaE4sqUvjLdpiyTqD7O4Xr8X4eLjEYjWwb6Bu5fLBaN\ntJ0SUo7r8Cs3cniO7Es4r1OnXl9f10JIZJ3zPG+MQ1EUNUK7IC7iY2xaoihypptHfWAsALT+7Oxs\nDy1WaW43m03jm81mswYxI86FYWjbzqYvFMYQlCU3BWgL6JJcrOI5aF9ce3BwYBeiaK+DgwO6ODfj\nQsE6fvTwdN8ma9PX/sCbTmtkFQt+SN9xtWueuOu82jW2Q3xvTwaNbyXHKj2HSJ1Cu+J7SJ3QRK5y\nA66JZeXmCRKGYW3TJ+vleV7DiAGRxi9X+A/CKiNOp5nGexJGbDalvmn4u9RjneZYrttc6wRtLJKb\nTRcpsg7VkWO8hufLNSH6MQwqMgxTEyUXRWHbUn9/OSbIlPcoH+ODJEHXIePoI2/evGmEL3311VdW\n3+3Yy11UbnS1oVo6DiEeEflI06uM2PdxzL6v9HlOVyiJPCZ1UBsZdF8iaqZudxkz7moY6Zq3ZR0q\nDl/WaXuJ6mtZ+X/5HNfasStUTc5xbXV0fQvf8ygolMGG+2xRElUc2lIVdQNJFXiUFBzKmvCcE4WU\n7cz1Z98bg+CSDQsXTy7o+fPntXe07eX5tIiZkJXT9i6CCY0OjM7ouWoymTRC1bD2kHsDOU5ysbQ4\nMTq7W7HDzQ8oD3jc4zTXaWjecbfZUrqrjy83Nzc2EQDmYcz3fuDT6IDfozK6vd6Y+qXJfq15Vz0c\nQmkGGWSQQQYZZJBBBhlkkEEGGWSQH638YKE0ZVk64WZauiyvEtr0vqEtsuw2L7/Lyur0zFfUOKav\ndxHBSa8hrpfwdk1QBmt7VVUN8ioJX9KeB9n2ktyVqO6N0KR/RETff/997TnSI6AJBGXoDb6V9IzA\nc4BfmZrSBVfVll1Zr7tY412w248lH8pLIPuE9FBqD7x8niTKbKvXbVBP/Ladk+3nQrDg++twA5dI\nnYXXVoYkdNVLewIWi4VtG5lOkMjoki5rtVpZK/SDBw9q9crzvIEmcXncJPQX18MrBcu7RA7olNyv\nX7+21nipU9APlK+RI7KdZPsml4wOOVnYstAWQLDIMUSG3xFRwzMon+15XgN9gm8mCUM1ceYPSb7q\n+lt6pew3ZShuEfoUKU+zRmoQOVIyi7AkHHOh+vCNJZxdI3Mmk4ktX3pQUZZGh4zHY/tsHWopvco6\n3GK5XNpj+JXjsQ6JkiE+kqAO9+FvmU5Uw/llaIn2Psu6uyDiuA4QfMh2u3WiE/Xz8ewXL15Qmde9\nnNITpvUKenx1dWXbCd8K6BV9HRHR8+fP7dwJPUEdXr58ad9XngtCU++Uw7mgs7PZjC5S847PPnlq\nynhtEKAu5ICrDfuM7X1CaeT1+m8pTg+10DlNVio9zZrcWKYAlYTGbanBZVkQ131yftWpy13hLxpF\nKcMX7Vpra3QjLjzKE9aP8b5NdFlyrYZ+iD7Uhfy57Tt2EVrqv13IEdd6wYUEgO7J8QLfQff/qqrs\nfOQKwdEouslkUruXaO+9nkwmjTaUpI/QVejldrtthJPa1NrbgiJGUmN80eO5lIqIqtAcnyiEtJSu\nPcqHQrXf5bq2viDXx7J/ygQN8pxLh7rO3YYYgWhdcvXjvs9xvbucf4nqayhXKKSeA7vGSVsHf38O\nJKxUVhTyVOQD3hLzfi+OKC352SXQSjx/RR5RaMpYcz7oRRxQwKSrFXe5jIN3Xrx40SANl+/1sjQ6\ndzg389ZfTCIaB/VxGP34+vraucZGWYg8kKi+UQz9NfWaTWdoODrb8VrDM/W5eWXWnm9fvW4g5Ij2\n+1Q9j/lhQNspNyvrYDXFu+46da5LBsTIIIMMMsgggwwyyCCDDDLIIIMM8qOVWxEjQRB8UK+6tNxo\nq9yHKvcu5z7G8+Q1+jpYwV1p0lwIGhknC6s1rHPw1FZVZa+THjrcp+N44zi2lvPf//73RLS3xB0c\nHNjy8Tx4LC4uLqzlDtZTyb+gvfxVVVmrvU7bm+e5jROVdYZl0+X11IgJiG7HNrnNO6LP/aliQrvE\nZZWWaa/a+p+MuYZIj4rLYu/yAOG361yXuNpSp/LsEh0TLsty6Rd0Yj6fN7xX+L/rm0vCOa1fkhdE\nEyjOZrNGP5EcCpLrh6hOhCjjV/E8oENkKly8G0jlpMdGomDkOaqIfBGjies1WgXvM5lM7HdBe0kE\niIzJ/0/svUlz5EiSNahYfSEjGJGR2dk1Ui0tIy3fZa4z//9ntMgcpmqquyqXyFgYpK/YbA5QNX+u\nUDOHk4zM6gl7BzrdARgMBlNbVJ+qyieyTYjOffsxPgs+K+L39r+2rJ1ooRX/dc/aqSvTMks0WlC0\nVdmybOH4rdP1CsqynMQMkLbE8RXbWZ+HcTjQykV03t+1lQwZetpHH61q+v3hmKvr3jSn2AnYb/Qc\niLKkg1Zi2ZpFiGl0dUrTPM8njEq0+kvf9ukC+34Sz0rKRPakTs272+18uRgwVMuQvLP1eu0D4Wk2\nVdM0vs8hWw2t51jWhw8fqF5yzKbj+Nw/1mPf/Wn/6cXWOZZM6t8s33sLVtrOPM8nDACc46xAqURj\nn9L90WKF4HpBx0HC/qbjSGCgYCuIqk7rjSyvgeMD0JGZkhxAcLV4Rc2OLc5HDuhYtN6qqgMY13Xt\n+6gV5FQHNMTf9KfFgsa2tNpeW2Zxra7f9xlLUfV7LF9b5pfL5YR1JumBV6uVl5M///nP/t4YsBix\nXq/9/Cjpd+W+GFtL7n1/f+/n2J6f7c1q/L6uajq4sc11Gm0rSD22yaXU2CHge5kjv3NlPDR+Yxm6\nLJQlHVQVf8O1gPymWe0oqxZrKcZk0Z+heCXyGftNwzk32WPgsTlrU5SpEwvOHxw/ypxIUgpLf9l3\nVHAAjpJTDLuO9yNElNF52+fMGOn6jrqOZa8az9l1DeVC1H/Fa4YVr0eoouM7mQPHcSbnuCX79/fU\ndDz/MKG8+vW/6dUXjteh1gnL5dLvA6XdRDaOx+MkUP/PP//s5ztd1rbZ0/sv47UDx0fZ8Lr344eP\nwVhJRFMmZlmWtN8z67tn5i6zalxv73Pm4NmuNP9Mm8g/GrE20JNvjFJeVZVfpEmnquvab9j0AsO5\nU2BS3alub2/9YI0bRNmAxeoq9xYB+Pz581nuaqmL3hjId8x0oDduGKBPgM8lx6zArDFa55x3QPT1\nXWj+aODmxKIWazyVyjmHRh06z4rgLvWQBRNeE6IK4/8ymWy320m2Cat++NzStyVoGwbO1Eo8dB/R\nC+U8zyduZVYgQK2cu729NV0WrElHjulArr49yFGvRnekFOuNO24Q8d66naQNb25uJhtceWf4DPo9\nntXxmXOGtUi3zsH/ZeOJNGsiovXN2v+GE7kO4ImbDrlWH3POTdrSouLjwlqPoRjwWm/AsDwt0/v9\n3gzMqKHnBAxMigvGUPuiPOo64Ngj7z/LsrPNmH5GHdxVrlsul5PAvQ8PD5NnwzLRzYno5Kp5e3s7\naTfs93p+QZco+U2i4x8OhzMlv9RVfpPz5fvf//73yaLu/fv3RDT2N3kPOEdLELqb2/Pn2e/3E5r5\n4Zblf28rL0Jj4LUyGNvIzC0LA3JLVi1pG5QbS7kov+vxHqGDQlr1spSYqECT33AO0Pez5H9oeTzm\nzU3Oiqv28ZGW2/H/m+/HdVxTnIJsa7e3/X4/6as49mgFBz6nXlviBlGve6z3ic9oGfRC64mmaSbZ\nLzabzSSAqyigsyzzY46sbeXz7u7OKy4wO48oP/zaYTeOY//4xz/8HC1jhyhDuq7z5UqZGJy8452h\nYzH70Gxo9Wr8Ips7WUuEEkSElHI4R/nfpDvm2az3cS2khKojqjj7SX+FsQsNLtjv9ZhjyZBWqGEW\nI1QeyW+v3o59Qd5Be2ym7hJwH/2b5UojGeRKd1KkWKt9Py5Ig4kCY5gG340pSs7emfzPbh1ZkVMu\n7dvL/XIqRfkhFetEnh2V7Mo7yOn8mVNGNUcIdkepX0cDi2u+4DXnig0bZU5txmPGYjxpuRrl5tg3\n1Mg870b5/OvjL7S6l3Q3rDhuT2t1aYNXP4zKS+ImORwOZ/P8+BzDRKHr3XM2Gzpu2bVtO8qTzIW4\ndohBjBe3t7fUPkpQ+tw/G9GogBJRM5VYESRXmoSEhISEhISEhISEhISEhG8WFxkjSHONYa6m8yXd\nWeYidk+xLukggV8LlqZf6ida8Lu7u0nASKR+aWoSBvbT9FNkk4jGDtNvavo0ph+V88WKtd/vvRYe\nLXY6SBZaIeV8scYKQtZIrS2Wz7IsJ9a7GGI0/Rj9d44V+qXxVJmYq/207neNu0wsuFaWndIXzgms\niTnvY0FhYy5O+B2tu3h90zQTdwO0dOmAlkVR+PKx/0qddV3F8vTdd99NaNDb7XbiJogpueXZxJKN\nLhK6Dn3fTxg2Z3URa1Q7tTxJEFF57uPxOLGEoBUylGoQ64DuI5q7lS4TAAAgAElEQVRSiwF2tYXF\nYvnoY5dgWaavsVY757y1Xlt7X799462P8oxI3dUWNEzJK+OfoKqqiXtGlmVn6Xn1MZ3yHGn9uvz1\neh10PVkul/587aYwDMMkUCpa6LUbIwbutujz2kJt0a1RPqXO2pUky7ITc0cFJu37fpIWF8cQYZrI\nPIPuLCKjVnBwuW673U5kVK7bbDaTtLA4/+lghM6dAp8KMwnZLpo9JfW5u7ubBHkdhoFuuHztsrVe\nr+nf/u3fiIjoP//zP8+ui43j+n/9Xb9ry9odm3Nicydalf/0pz8R0dj2mkmLrA39G7I30N1LztFr\nGpRdnT5XUFUndzks03IrE2gGh2+b4bTWumm4TH7lQ997ivfjduxD7WqaTjIUJJXo3PXSYqTpORPT\nh1uBKfEcfB50y5HzRGZvbm68tVb32bquJ0F01+v1hFkl193d3XkXMpEzTKtruZaLbPo5en9iGnn2\nJJfx9kdmB+4eieNR+vssFwviOJP0mt13fvs4pr6uFwvachpsSybmsL4Rk3dpyKM1pz0ZfH1bEHXd\nyc1Pf1rrPPnUDCmLRWKVpd2lkFGOZfm07F/YNYrZGtQNwb46t10KYGPk7KLSMe2iz8PrD8cUDZf5\nZZVnkzgiIk4xK32JZOrt4N0xQ0eCpFLnyPXsCrpnhtVhOLFHJCUvlz3URDlfmxXnzxva03iGHLM7\n3D3vk0qijMehnolO1f82sqRe393RjpkVruXxLHO0uR/HpjrnuSY/ueP6dbT0r+a0TtDps3F/Jx4H\nPuHH/QN9/nWUry/tWLG//vWv/nn0OoToNP7ohABfvnzx7fJv78Y58Z73mvXbm0lwdt12ISTGSEJC\nQkJCQkJCQkJCQkJCwjeLi4yRtm1Ni8PXsKrH/Fef8lvsd4H2R7WYHDGglSLGrNFW61hd0VKJFgsM\nyEd0bqHVPrFoXRELYixFnRVAS46Jlm6323nmB2qPMaUw0Sl44adPn7y2UAeatJ4brT4C1NTr9/E1\n4oT8T4iVY1n0NOZq1624LjFLY8ziaFkQdJ3RD9nyr53zPDELKFqatSUYLa5WbAKMjUN0koNXr15N\nmCly7OPHjxM/9LZtJylDRQbfvn07sTQJc6SqqgmToe/7CSNH7rdYLE5xG1gGb4ulfwbHgQBbsDyI\nRb5knfjjfuvrHIrhghZKeUaMc4DpXaWNdJBXnDf+KBlDZoLuz/vH7cQS+O///u/e4qAZNmhp1Vbl\nuq49OwDbRLeFZUHT93HOTdgXh8NhwtLAeB8iA7qfdV3n6yD9EwOAyvn4GRqPMUCj/kSGkRUDQZgW\nyIrScUcw5oLEApC6lmXpZULaXmS2rmtfvvR1eVZk3uAcKmXpgMT5sqaqHMuXeQ+fEWNlyG9yD6mr\nxQrRAVqJaMJM2W62tH/kerwdn6PntL2Pj4+TILI4/+s+/hKYy8jSwDWN9GMZ73744YcJG0hgpczF\ncdyKc6Bl2gp2rGWiqqqJ7GFwY/mU/lWWpWcZ63GyH3rq2Jz8uOA65Jyud8joyPGRj5yrs6HTGGLN\nl3qsuZRG17L8C5A9QjQNCo4oimISPwTTVVtsQylLtwmOIeUNB4DkwJP7w4HK16NsZxW3cy/MbUf9\nl1OKeyIOEL5a+HKJzgO5+jlK6sfz3yKvaMVBbuU95kVBxXLsX8I62W/Gz59//YXeMeNLykfrtYwr\nInv4vNb6SL8XPPclGeqTe+fxoPmh/mIxRqwYI1iWFVhZjum+elZHCaQh8TSMtSM+n94X+b5VFFQ4\nvif3pSHLTr8xY6SgUx383o9jklDO9cwLT+oZhAHSDURH7gNOpY+vMs8mEVbY6SbdidXLrJjSnWKL\nDPybpHum6pSeV+axUFwbaQcd30P6allUVL0e55UFz1ELN5Z99/0b+rwfx+Evn0YW7avVDeXvOEFH\nPz7HsjjtJ31g5QPLFdfv9vbWvw8/f223fl0o4/3m43ifD7+8p4/MGNlk52mBQ3sAkTkr9qDgv/7r\nv87aAcvCz8QYSUhISEhISEhISEhISEhISIjg6qw0T7X2XWO9eCr74ykQrda1fmwC7W8XOr5U/sLo\nhy/aVUxpq307l8vlxEqI90a/eDynrmufAk0ibN/d3XktnmWNwFgkRHRm/bSshNInpEzxQf348eMs\nP0x8Rm0lQYur1q5jX4z1S0szrv2XJfbAS8Dyx36ulTxUVqy/6ngFFvsGmRCadYTHYpaHkBU+9Fvo\nGD5jLFp7jHWlfaOJaBI7oyiKSSrP4/Hor5E+J5p3jM0hWnPp49iXsH5aDjHtp2Z14admh3RdN7Ew\nizy/ffvWy6hOi010skZgO2t//X/h6Ptd19HPf//H2E7iVwv9TFvoHx8fJ2n4ZIw7Ho8TucfMAr8n\n5o7nYkkkOo/voctBa7S2SKPFRr93jGFjjUchdlNRFKe0kmD11ZmQdEpb/A1ZHtKH9BiPDBD9zNZv\nsXEdLYjINNKsEMuib8VyEUgfur29ncRkke/IChGZkHkJU3RKX0XruJyHfV3aThgdkpXm8fHRlyER\n9fthoJ6zAHwvGeSqU0YpeSapozAPqqryFjOpQ1kWVCwXvlyiMWMD0chg+4//+A8iOskTWrRj7EyN\nl2RvWdY+7EM6LgzKiY6Z45zzTCE9diAjCZ8D+zneG1Py4vkCK1uSltHTeznJntwH/d/z5pyB3LSc\nXanNqS94DpFQBf1J3nRWGowNZ63R9LNax/AZNMtY0LZtdD6VOiDrSmebwDrocWi/39PAVvplzWzG\nj2NbFquK6nejPN0fORvTZvwsKafv16OsFouxfT98uqfPnEY325231/39/WQM9c+4P9CumjIxH/id\n+ngXh/EZB+e8TFvMHIsBEZOjGBPTYggiNBMqxIZC9qiVQcWae0JZZpAdgvOXTv9uZaURWEzk0PHY\n84agGU2OToyMM9mVZzNiq03WshxQJMszn1UmF0bH0BMT9vx5kPKEMmam5Jx+N+e4I12W+1gkGdNE\nsvLElDkxWaTMjPKB18C78T0ueJteZQVV9bj+koxlQzdQI+tnrpDMUYMbKJN4lJtxHPryMKayfvz8\nQNXbcf55U47j7Ipqqm5438ipblwkrTfuMQUyXrx//957C/z6669ERLT7MM7HRZ7Tr//334iIqOWQ\nT0M1yON7+PW6y/z+7JoYdZZ8zp3vnp2u94/ENS41X7sOuGlHupcOoiqDymKxmAxuuKCx0u/KQkEr\nVHDDI4sIue9qtfK/WQtQ7RrQtu1EAYFlSx1wYtZtrututRfRadC1FqLWwl+nbbwWuPHXbYIU6H8G\ndxprgrTomiEKJ2JOml683gqmqO9nDTRWHawFqZViMXa+fOpFdGzgsxa+QknERSQGJsYBHsvoum4i\nq7JQxECbgjzPPfVP5EWuRyqgKBkklSDSuqV8TAurXSRQKanTYjvnaGDKZ0HTDajUQ+RsuVxSzuJa\nckCwI8Qp1MFqUR51ivC+7yeyjzL7UsrCa3Ht3HB/fz+RL1QIa+pqbDFouXHIO8CNi1ZOotuIp8jC\n5kzXCzeBmrrtnAsqRnBTY6Uk1s+IClGt6MDAx3idVjjiBlbfB8uU+qPCVqd/RwWGbGI/cABFOWe1\nWtFPP/1ERESLNvPnv9+dB+RFZZEYE6Td0N1KZFTOXy6XtD9uz84fdtyWbTeZ20S52jSNp+XjYrNb\ncVBjDnLX8cr88PhIf/nLX4jo3A1P6hxSYiOszdYcXJLZkPKvKAqqb8exsF6zkSgrzPPkefT7wHNi\nSnVdZsydAe8ZU/ajO7JcK2M8Kgo6VozJGNrt2VWtzylbcGBRSIetAytbY2jIZU3KkPP1WhQDmYbS\nqaKSyZpPteL1cDhMNkZYpu+H3FddRuTYzWC7E8UDj39EtJQUo7xp3L0fZWLoemoqlvuWZe79R6rv\nx7FwzUrFnpcSXd9RXZ3P36KAa5pm0iaLxcK7SWrDkUW3x4CQ2rXBMtpYSrmYYuSpcyHOObGA9dan\npRCR75a7jKxl5D44B4UCpur/Y3UNXWeNVaasq2DzeZ5Tpt2roO9qZWTODhSuGyB9LvdtckRSN7V+\nybLMB1OVgL4FL3eyMvP3zEX5UWSU8dJalCD+qV1GBStXJF+v9IycBqIlGwLYpcz1g1e0VuyWtuB+\nv3/Y0qJkN09OySuKlS8f7qnejXPUO57j3ry9o+Mjr2vrsYIiQ1mWndLLL06GbKJz10M06IliROaq\nfj+O47erNe15sblnZbEEvpV74eeQPU0+5iouLSRXmoSEhISEhISEhISEhISEhG8WfyhjZI4bgPU9\ndmzu+XPuHbsOWSFE5/Q1OXZzc+OtCqLFRKu1dufAYG6WhUNbAuW6vu+DVngM7CcWLrRQ6rR0lgUc\ng7yKFhAp1br+cr8PHz5MaJdoZdD3Xi6Xvh3FkiLthZp3ubcOxBMCWv7leXTwMYt++HvgKQynGEtk\njnY9dAxT8hGd2v5SWVawN13XuRpbzSaIsWPQsqEDUBVFMXmn2Gelf/kUf0XhteMCpHJLHxUZEiDL\nAwMJSltqOrhcQzQNQoksBLn+06dPE2aG1FmsxXItPmOWZf555H673c5bwAWY5vTm3d1YLzZnbNqD\nrzsGYJYy5X2ItVvqiWk4dVtaKZotXEOZjCE0V8RkAlOGaqaQlTLWcmPUTDSkOlsUVB3AV/rGzc2N\nl0dMAS3vQVPqrSCvlkvQ3d34rmU8z/PctGhqtwycZ7SsYoBxPR9VVeX7kA4AWRSFZ01ZQRU1e/DV\nq1eT/o59UNquLM5ZlK9fvz7NR2zZ3x73VPF5t8V43mN3Yodg+kEiog3L/6bdewvgjuVkvV7TujhP\nlSwU4M1m49+ZyKC8M5xzpe7IsJK028Px5LqgU5laQWFjMmRZ0+bMRXPWXvi71GW1WlHNzDVJBWm5\naKK8aSYHupdZ/Uu746A7lu6/yCDQfQkD6VsMLr2ewPYrOHCiWKop4xTrjqjM+djxPJW71V74HnUb\nh9gu+j1abt66b+A7sFwx5Pwf/m1Msfz5598mdUWWiFtw2y+Ynu8cHQ8SUJWf+5afq86p/zzKRMmW\n7IJttXlG1LDLDWchJXc8nta8nHY1ux3bd7koqeZq67XtMAyTQL6r1WriQoVjoh7bLPe0OewIZN1p\nRo8u7xpo9tDxeDTXADGGRciVxpJLoqkbbIyRZZ2HLnHXrHuvZbexdwoVHZHjKVZaGcfLUNtn5v/Z\nRHbO6pKfMx96aYbBx3T1jNwM6iPHOtmJOyKpljyHnJMVGbHHDjHRhLoqI8ft2vCz9iWn0V0TFQOv\nFdmtFFlofm/F/ivlzZJ6Tu/cttzfWZ7X5cIHmG24TMdrx8+fP/u2kLHj06dPnhHpWaA85z40e9pV\nU/Ybkf2Oq/qUUl27xVuIMUXmyltijCQkJCQkJCQkJCQkJCQkJHyz+KePMXLJV00fu4ZpYl1naaxi\nGthLGmSB5dOtGSMYGFFbPeQaommqtbIsJxo7K2UfptUV655OBYnXaGYKBpq04nWIVVjO+fLli7fk\nIVtF7hdK/4X1Rw2v1oijdWUO0Fom7fRcH8/fC5dieVi4lo1iWcCs++P3qqpM1lQIGLzMOqb/x08d\n04BoqnG2/LB1mchysoLdoWWaaLR06DhAyK7RlnBMP6r9WIu8mAQy9cHfHh48g0M+P336dJamFMv8\n/Pmzl2kMTCl1kP9FLjebDX3PaQilDsIYeHh4OL1Hbl+5HscXuV9d196ajrEysJ2xXlKHh4eHF2OD\nzEHIyhRjPllju0DaBANRa6s99nGMb6Nj9uB4pvu7tpIT0Vn/lz6HLCi53qfVU2Xmee7flbCN8LrY\ne9HvFsdj/TxojZPPxWIxYV/I87x69cr3R+n3Yp1smsbLoQBZkPIcUvbf/vY3CMh3bu19fHw8tTkH\n1Wublhyb5g7sA13d1r7uYlXTbK2+732y1bI+MYB0nKIDW+CoG+j942hBe+RnFDbJarU6YynJfeSe\nOr4Jtk9s/YIsJ80ishDr9wKM5SH3mLN2WK1WE1ZULOgwsq70mqMsS5PJpVkhyJiYExzSCgasnwf7\nngDXUHptdhYDgpsNY5PoOc0KZKqDnJoW0SLzcREshkmMdaKZEzjXyrHVYRy/qcxp4HgKYtGmmtt5\nvSCxhUvwyTzPqX3FQYRbbgsOKkkPDT3+ujm7j7CjqMhpfTO2U8cxdtqypELm7XVxem4iWry+of2v\no3ztH06pP6UOGsjq1Iw33T4aui3LsoyyQvQxK1DuHMTOtRhGyHgUYD+OMUassnSfju13YmwoZGRZ\nzzaHyRKts9ynz6mPMJB1WZfeRShWDNGJAcIxS/2ckrsTU4SzVFNfZSQZgjOJsZHJsxMRpwiWmEQ3\nDcfv+LIn98CsK2amtcucstvxvN0N9z1me2SPR9o+PAafDdlGREQPn+/psB3nlepulL0DjWP2Jh+o\nqXl8lWfejnL84cOHyRro06dPfu+nx7bj8ejj38XgmZ9lGdxjXJqrEmMkISEhISEhISEhISEhISEh\n4Up8dcaIthLoWADPwRzrx9n//uM6i3vsPmiJ0edtNptJJgk8XzNFxJKAPrToQy7ly3nyHS3aWvu9\nXC4nlmnMLiNaOalX0zSTNL1ildvtdpPsCcvl0tdHIPd+9+7d5DlQS6ujzqMW2bLUaStpLAo3Wgms\nuAb/7AyRObAsQQKr/8eYT6iNF2skWtCsFL5E4/sXVgC2s+6rmBZ5jmXSYmZZz3GNfzyWLX1H+ipm\nI9IxIOq6nqaHA/aJsAgwPoBoy7U1Ei2bKHNE43ghDA6MMaBTv2KMBi0LKP8Y80E+pXyJ6YDpPqUe\n8pukBbayQD08PEyso2jRlLaY864R18rlpfMtayHWy7KuYTvr94djTij+yCVmoVUXjC9FRGdZs6xY\nAZo9h1YsPS62kAVD191iuVgyh3UlGt81ZmogOo8fJeehpSdk7cM0wjoWAGbgwVhZmiHl0+8eeio4\n08XDkTM1cdn7/d6XK3374dePtCdmda3G+i1VrCUi8tls8J1Lm++4/Pv7e8qYPfJly0wWtrK9e/Wa\n8my0ZLefxvPlXa/X60nMEJRty1IZYitZ51v+9NfGH4lhztiLLAR517gG0nKKjCydUQQZf9jP9JiO\nay09T2AcCh13BGOQyRpIysb7WO9Hsy7xXOud6RgWljxqK6n1rodhmLShNd/785lpMVA/ZuGAOmR5\nTq4+z4j04QPHlqsLGvgYSSrTkmPgvK58jIXhYXzHfddTv+JxQWLkyLPujv5/34YcUOT21SvK2Yy+\nYubI4XCgL5txXr3pJcvG+K7Lu4KWt7wObafxYYSJhjHJ9LiCY24s5bXOYoPsE535Dvv9nHXrpTWd\nnlesjIN4joxhWpaslLyX2CR6/I6tJ61jGIMNs0CG2sKqV6wOpwLGj7Z0p0wwjBjDPzaOzWXR+fO4\nqIEc9ZWMD3T65GRMWXd2OpXDmMaaiKjidO0ckoluioqIWSQlpwXvioyOHBMu4xTD+4L7dd1RtuB+\nKKmMO6avtJ1nXwl2nx/9+rD+wllNH0e5WSwXlB14HFZ8is1m49+jzGN///vfJ3HQUCZ0e1r9RWJR\nlVXt2Z+x9ZQ1xz2VMfJVFSPY0ea6Ozz1PnMGE1SMWC4k+nxrUThHiARIa7aojJgqlOi0icRAfUhz\nlLpiYD6icXDRShaBFXgPA/RJwCkcvKWTy6e4weBkYrmxaOorUnj1omu1WnkhwsFR/tfKkrZtzYVb\nDHoBI7h284ULq39W6GCiiDkKRCsFIiKkGMCgghYlURYkSOkMuQ1Y9bLOsRYB1nd9DK/Tz5NlmZdV\nURri8+h+LN/X6/UkCN16vZ4oC3DTjQEviU4bhS9fvni3AaHZv379+mxcIBrdBYjGtg257KxWqzPX\nOaJRpqRcvegehmGixMUUvXohZm228B3LvfUG49pN13NxaZzGPq8XWxjUWj8/Tro66DQG2sWAkFpB\niwtTvanBhaNeWB6Px8m8gmOo3kihy5OcL3MIvs/J5gl+iylNtGsMPiem/tYbXDlvs9lM3MTkc7Va\nTRS2+/3ey+htNX5uOWBqnZWU8cboyOkIb9z4Dh8Og0/v+fHX38Z/Ng31q/PnEJrvfr+nH3/88ayu\n6G6n5+22bWnL8iX9Rt7j/ZeGck5J2h3P3Wp3u52fY0XRc3t7O6Eg//nPfyYior/+9a/BcQ/7ccyd\n8KnQGzcMRmrR4VF+tCxZrjRaOY1l6XPxGP4fWwybLi7KlQTdWPQ6x3KlwQW/pYQkInrz5o2XUZkT\nLfdgrKteM1sbC0tWrTWtbpuelRtdeaLE+7nqZkH9ijelnH90uGNF993Cn1fX4iIzPvOqWlDNm7T7\nn3nebzsaPrKyYM9BxmUMjbiUtG1D2z0HOq/GurxZ39K7d++I6GSsK5bsEk4ZVRkrSViG8Jm/qOCT\n+K7kNzRKxNYoem3unJsoNp8aYPXazbnfRNb1xF3OUvCgksFSPMj1luFMyyF+Dx3T5+l7ayWTVQaO\nJSFlBo4lvr1oKiexNsTv1p5BKzbxnOA7zjLvZ5Oxe40j8r4zfmsq/9QlFexns+ApvW74HbucMp7a\nq+P428ERDY8sj2ueV1lR2a9rcrzpzTaj7HmdRpVR34x9Y99yWIFdd+YqTET05R/jPLnf733QcN1v\nsL1EzixXQHwHsXW7Bz/HsTlGE22ExvvkSpOQkJCQkJCQkJCQkJCQkJDwBHxVxghqZedYrWOIWYKt\n8+xzLt9nrjX62vpdomIRnbuN6GBvh8PBW6a86wrfBgNgaitD3/cTKwxq+MSaKFRAtOyIRctys8Fn\nFauY1OEA1GXRFspvQuHPsuwsGA+RzW5By0uMRqVhaQtfAlYdrqlXqLznwmRkXcGmqKrK9wFMCxqq\noxUwN3Yf1LKH2CCWZc+yUFtBKwXYh7QV3ir/LC2mslAI6rqeaL0FVVVNLOXr9XriXoR11+9KrPc/\n/PCD17jLfUSmiE7yiMFbtZzgWCJ1kPKbpvFy+OHDh7P6lWU5KQNTZS+rc7ccK8Cm3Od4PE7GCWzn\na7T4z5VhTCtsjQmW1QvZPdq9BgMnWukR5T7a6nXpObQc4fhvuSyFLGH4jFbdraDcco68PwzsaVka\nic6p+1ZQbP3cVjp5DH4ozyj9/dWfRstwkeXeot2J1R7e1SNblVdMox++7GngFIM9MSuK6cd3t9/R\nw+NIxfcMpnVJS3a9EXnBQOkij7q9jsejOb4Ik0WYmN6CljtvTdcjNVqopQ6Pj48Txsivv/7qr9H9\nS9ijwkbQ9Yqx854jY9Z4ThS3KiJ0H0VXKs0wsVL5apYq/o99TzP3BDp4LP6O5yPTSrMGcazTjCcp\nZ7/fB4Mi6/91HfR3K/g4ypwuE8cxL6tsLc4HInfLgVUbbqOqopYDrNLN+D6yGz7n1ZIKTjdcSBrS\nPY8R/3VPq4yDbf/Cc0jT057dyUru//vyNBfq55ZnWy1XNHDOU5Htqi8m773iFMhd007cRnDO0aw2\nzaxGxNY71jvr+z5qHQ/NdyHGwTX7IUyiYK3bdEB5PBZjX8xhkVhsDf2Jbsh4TMuj9fyW3Mf3dzQp\nK/ReYrg0RurxxWKz+/PdKRCxsBWpyr27lwRkzqVPHDsqOIJrxQyT8nA6JlSGnvP29s5RJ/LE23mR\niXqxpKEY5bfjC3ebcb50naOBZfv4ZVznVR1NwiIgI03embAb5XOxWPh+iOEOLFm4BGx7zzZfVsGy\nYvIVOjZHvhJjJCEhISEhISEhISEhISEh4ZvF1YyRl7JwP6XsmF9tSJN4Zr2G30PWPssK7cvIM5+i\nzLpfzHqutcRoodSpQ5ExgvXVVqKyGK+7vbudBLoRTfF+v/eWQLFmYT0s/13NMIlZfdDfW2AFPUPN\no35Gy+/3qYhpC69FjAnyHJZIqKy5wL6k3/eZRSziX6nbvGmaq9rfCriKZYfaZ67GVuOSFv8a1oFl\nUXDuFA9INOEiU7e3t96SKZpx7LvaKjEMg38PYn1HH2e5FtORSdk6rfdmszkL/IdlIptEB1dD5oyk\n6MUYE2Ixl2dGn1DdN7Iso3Y4t/rge5R66NhEiK/B3pqD0Hygx2Ps+1Zd5TexYmDbh6xleF3Xdf6a\nmNXLGiflPIwHE0uVGwoAiT7a1vXaTx7HUOtT9zWrbKyDvidaEnVdt5+YadEP1O7G/rTImAlSF97f\n+QvH9CgfxnHosGtp4HSgtTC5FuyD/aqgg2In9kNP+XDOVhA2lWVxxu84dsqzylwoY4hnCTQZbQYO\nMDuE5xNMP+wDyhrBd615WJ5L9/G54+RTEIr3occGXO9YMQM0Q6Oua1M2ic5T+VqBkq0gpBZDStff\nYmLotsTArHrthLKqGbybzca0wmsZwnFJr4+seR/HEnkWXT9kAPhnlG7gHOU9P+Oa69z05I48r3OY\nD7fj7/c7Gjid6O37USaWH/jY4KhuR/m6KTgQ+fFIPQd+PErAyci4l1fjXLh1jQ9kfMzGtnn3v/+J\nDo9j+TI3S1yQ5XLp42eJPMqzVlXlY3fJfe7v7/36KGfR7vIpY1l/x/kex6851vGnyl6M7YXMwliw\nUutzDvsCYTFF5LuWBWR+hfZa+H+MMWXtmfT1l8q6Bta+BedCi30SuqfLxvS8ROQDGlOdUya8QZbV\ngmVw0RAtmE2yYCGt75lN6XLqcmGi8PXdQAuOC9JyGfWB71dklL/iwMXcx4cty0/Wn9IHM7Py8Lj1\n6xuRF2Qp67hxOO5h2xFxSt4Iy0Of79vLWJtnXR8tKyRzoT3gnP7xoq40McVA7Bzrmthi8xqq2bV1\nwAX/5DoXXgQ/pX4W3VQ+ZbN0CnRV+4WSpjAfDge/IJOOjZ1WJhH57ebmxv+v3QAsiryc27atH/Aw\n4KYsymKZd3Rw0DzPPW1LKJBZlvmFoUAWls8J3vuSyouvscGzNpux+8T62lzlhlxnZX+Q94ETv+7n\nsvnFwJFfUy6fA0tWNb0TB1EdMNY55/svKhDlmPwmfTXP8xpNSW4AACAASURBVDM3AaKTYqRpmklZ\n6MKkJ5vdbuflXORfZA8zQlkUYaHzy3XDMPh7y8ZNsF6vzbFDPqWOUn5VVSaVXJ4/tIgILSZiyqsQ\n5lIzrT6nqby4GBLc3NxMMmHNWdxZyjKsh94MoSJNgBs/eQ9WkGqtNHFumhkDN1hagWrVGRUcsUVH\nKCgmBq3VQSyJplmWcGz392Zaf1WWlLEBoCK5X+ldMuXaz/ejm0lX9LQsx776ph3nxEfiIOKwOcX7\nSX2kDUVGrP6Jig852v3IgWD3Oe2ZqtzxxtKPCUVBObsvZAaNPyYf+tPKzoDnWHNITL7mHAuNzdoV\nRdcV53utGMAxVysBhmGYuDtYAVnlc7FY+Gt138M5SgfdtlxpkDaug1o3TTMZa1GJGdo04NiOzx+i\n+uMcJbDmKisorKWw1OfjOYMovTmQaT90/jfquQzeiA0PO3rFSo/q4/hs63uu8+BoxUNU043zXX4z\nUFtz29VqTBxIYlCelDpyX5fRwBlxMt5Qbg876n4dy5Wsb+hmqBX6qPRHd1J5ft/XssvBIbFt9dym\n/8eyYohtEOcC+4s1R1nKuND9YkqTs/luRr2wn4VcwrBcq70sRcw1a02rLLneSlIgCBkEQu84Nv4R\nETkOiuo4iDAtcqqIFbrtWK/l49iPlztHS5aBFaesWX4aP+usoJaVGD332faHkjJ2ORsc34fd4I67\nhjIWsHXB+y++77EZvHwN+1PQfT1+YUIBnd0UZSJkVNNtoaGP4VglekqZS/H8uYqRpyK50iQkJCQk\nJCQkJCQkJCQkJHyzeDZjZE4+av1/7LcYnss+sa6NWQCvOfYUxkisLEsLplNfojVTtHma8o8WEQym\nqi3/qF0Xa7Jo5cWSjEEVUVuIaRTxPpvN5uxaIjpjvcj/aHHXmkfpX2Ilx2dEa85LWZh/b4T6ylPZ\nFKEgc6EyUJOOlmJEXdf+PWBgRl3mHOq2ZY2RvoquHhaV+RpLjVUv67nxfG3lxMDHwr7QQThFbohO\nbbNcLj3VX2vekSml2+vx8XESoK8oCv+bWCiRHSaWc0mzhudKX/jtt998HUTmRC7ReqnTqCJbTaeh\nXK1W/nxkysinjCFzqIxzKKlPhWYAxuRIW5qbppmMR2gt0TKA52o3xL7vo/e2rNb6WIzqj/fWLA3L\nzcaiA8cCB2pLEDJGdKDJtm0nFnq0wmvLftd1phWKiMi1PbVirWZXGto19P79+/E3tnbVbHlbu4p6\nTg/abMbrDu84UOO6pod+On9JPUQmcBzQ9RHZfffuHf3yyy9ERPR9x5b25kiP9w9nbeGDSa5WVED7\n6LYXxMYty8Ks11/4/ucwP54rb+jCgrKGbA351GsUDLCK46Ocb7Ea9T2tdMBaNqzfYowvhO7/1loD\nn1lbXK305jHGCCLEGMH6ILNF2lDfx0odi9cLa8M9jvPX7QORK/hatnIPDyxnDdHrdpT3N814vx+6\n8bP99ZEWHChywxnLH//VkWP/816CSfJ7XK5qavpzlrHrRO5PLMXdLyNL5HjM6XY1yt8var/Rtu0k\nmL+gqip/Twxu7tuCprJhjavyPWShDv32XMyZN2KunaHrQoy0S5CzLrHJ5Jhma1h7H6ssfZ3FOsNz\nrTk09B5D58s5MWaCb4cIU8QfK3NynHbWlfJsGZXsJrZmObvluW31eKSKh4KaU2VXLctz11HpZG4f\nz3lbrGjf+Ry8RETULU5tmvOxjO+zX4wyNXzpqd8y0/94Wu9JG4icYJgEWedpRurd3d3EzeZaOUD5\n8mOnPzg9b+57sTBnL5UYIwkJCQkJCQkJCQkJCQkJCd8sns0YkXgENzc33kpoBWTUeKpPnXXtJfaF\ndV3s/KcyRi5pTonONZY6zS3GHNHxOohOcQEsi778pi2VqFlFX3VtqcCAkxJ8Tn4TS1rTNJOAkdvt\ndhKsUj7fv38/sXYjk0WnVdtut/5aHaNhsVicxbXAMruumzBZYlrDS2yCPwqXZOK5fRV/179ZcSHQ\n2ieWUumzGI8ipP1HxFgBMS3zpfcYZNzQSdHs68c/uGzaNhYjBS1vVpvIp9agPzw8+L4pQayk3Swm\nAMaH0IEWY76a6/V6Iu/I6Pn8+TMRndr3cDhMLLPIjtH+91IXlD2pw2azmWjvpY/gMV3358jbXF9V\nq2/LZyzWgA5yq9kmoftpaxeWhedptobF8tBlYrBe9IvW9Z8rOzEfbd3nrL5qpeu1PnW9cHzRfQ9T\nKnvWiQR9cwX10r5s9co7CJS841g5bGZbu5LcHVuwV+P5x1f87E1Lq2qUw0PXBOuK7AIt79JGGCto\nnY9z1b7sJ+2L33Usk0vriklqUmBKYj0Q2Gdj7Lk51t4QsF8tFguzv+jUodjOyBKRNsSgqwLdr4S1\nh+xRq4/iukDK1v0L62W1iWarWLE8dNpODICpURRFkMmFZehrdL30+VivUMyfPM8nayafHtvl1HHc\nAil9XRe0YNKF24/HvstHBuRq21O/GWXvhkXvDZt2693CxwWoF+M/m8LRtmamM/9WrTil72pFH96P\nbEYf14djmvTuxG4Tlojr+km8PGROiSwgi5NoXFfqmCQIa77Q88TvzRK5Fsh8myPTMcbIJTZJ7PzY\n2IN4yh7L6uOxeUxfS3TOdtDj/dw4Mtb7DgVDJ8rINRLdl9tmWVKx4X3NuFyj9XGs33LvaHlgpgjH\nCimPfL9+8Ol9Cw5SvPo/buiBU/Le78eDLc+TLcRWchLwmz/yPPcMxprnldZgyMrebrVa+d/0ng5j\n3cmxn3/+2beF9Y7mrOX8dW7ar2L98iWQGCMJCQkJCQkJCQkJCQkJCQnfLC4yRlar1UQDi0DfNm3l\ntyL/xjR8z2GRxPBU5sdLMkYsaK0karNjPuDap7+ua9/28j4wfoe2VD48PPjjWguIcUR0BHNkuWAm\nDTlfpyZFy7mcj5Yu7bO22+2CvmpoCROgtVyzT6xMB4J/Bg1/CJc07HPOvXQMteXCBOj7fuIDLkD/\nXSuricUOsKyvciyk/bVSTWofUet+oef2Wl/Wlg/WeV6RHmYcFEXhmXGoJSc6j78hbbTdbifWTsyo\nIO0r/V/kBdsZrZLi56mtV7e3txMLoHxHP2tkhVhMNLwf1tn7evb9JJPIbrebvGN5jljEd6z/74FL\nso/PEGIOWNfF5gTLOi6/6/Pku7b2yXhpxR7IsmzCGEELvVWf0HNgmRazzDrvEi5ZiHQdrLSSA0fP\nLyijTGzZfF3VZbT82zj+lBLzhlMUDllDj295XuQ0vCsOorBzB2qH8zGnKArPfit3bDFcnp4jNE8e\nDgdfV7FG73Y7M9OOnC8yqWNBWO2ELCK9nsI+IXOvFbcixmqagzlyimyEqqr8s+kMV0VR+LaUOWSx\nWPjz5TcZZ7LslAJVykdLpWZfICNHy3GWZRMGgGZ7IG5ubnx2PN1uZVlO2KmWjAosRqIVd0THR7lk\nldbsGJw7tNwjE9E/v5MxYSCXsbWa4xEsqopWH8e+ejsO6fTDkVPM/9rQ7WYsvxKZ5ZgjN78QdRwD\nofmB67fvqTzwe2Q6SdNxLLr9kcrfxndavB0tzne3I73ry25zlhGDaOzrGCOE6CQT9/f3wQw/bdtO\nnt9iAuBaQ+6NbE7B17ZWI/Q8E1sfxpjBc5kf8qn7NMqjlQlrDhNt7rotNH9d2pvp6/M8n6ydrHg7\nMQZn7BktTI7lmV9/UseMqcZRtRn74+vP47P9+JFl8ENO9X48fzkmWqO6GZ9nWa9oueRMaw8jc6r8\nf1oqmYHVMAvy8Z7XX0VD3R3H6eE02i2sC/Ua5ebmxsuTnlfyPPcy8e7NWyIi2ux3/nppZxnHf/vt\ntyhDLtheBrLMTp98TRlY1hxcVIxUVeUnJKvzykBFRJPNaawiT93UPeU867qYguOl7mdRHxGiSNAb\nHgySiBsdHYTMUsrojlPX9VlQPPnUEzLWT7eFFeBMjq1WqzM6I9H5QKZp4Og2ozdnWAe9OceNHuan\nl/bQqaSsAfCfHZZ84ffYb19TuZhlmV/8i2sI3i82sYY2ovp867j1Xd9b4+x8Oc5rwFxyuedwnhRh\ndBFcDOt0tdLX37x54/uaBEB9eHiYpPyUhTYqSKR86dvH49FThVHO5DztsnN7ezs5X+6LLhjoviYb\nFt1eOPHr++D/lwKUha6L4aqFxgyE+hC2pQ7eZinzcAzRAUaxj+tNsHPOVFxoJR8qTfT4henT5TpU\nFsvCRRsjrOe25FLPF9b5iDBVmLzsFEz9RbXYtfLrrxOZpYJydx5Quq97OnAKz2rLv3GAu84NlC34\n4sNYk1e3b4iI6LgdqO/PlZhd11EubaFWQ865ifsL9v9sNb6zT58+jXU1AljrzTAew75ojePSd2Qt\n8ObN+ByHw8H3x5A8h367ZszFsT30rrRCUcaySRBdY7ywAvLiMZ/Clfs9ypLe6KLMyTGpC465Wi71\n8xKN6zLdJvI8dV1P3IRw06U30lg/HZh1KIiotZUqLiM/N7nOVo5i+diWOo0w9i8/xjse47OBalYI\n1g2vGY+OVg9jWW9+G499f8/Kxvc9fe/GTVB75M3TjgMTbwZ6fM3txYqU7DBQzoqRuuR7c7DHrBko\nO/KegYOw7vm6tm19O8vaA/uaVhxjGmUrYKo2tOG4akH349i8dy0uyZRei1vrQisNr6VI0NdZ97E+\nrzEm1nUdDBQcqlfIpTPLsjOXQV2WVX7oN5Q5PX/HlEzXvtdL5xcdH2cFSdkNtOZt87vRk4y++wen\nvv6pp3XDCkpu0jW7yLwpKnqbj7L9M8vcT//5gfr/k5Nq/OtYflPwGPQq88GMu4LbQSlPsf5Zlnl3\nRTF8+nUsEbklBymHRB1yncxRgrdv39Kvv/56di9rz6CBfW/ue5hz/rX7ouRKk5CQkJCQkJCQkJCQ\nkJCQ8M3iImMELV1EU82LDv4VwrVMDEvL9BRr+HOs6jGt5JzrYr+hZsyiZOogiRgQSFuS1uu1/19b\ne8uy9Oej1UtTMdEiLhp6bR3Psuzsf6Jzzb4ck7osl8uJa4wAWUWo6dPp+7RFCa+VMjEAZozGb7Fi\nrGN/JCwNuv7dkolr++U1Vg8MUGcFL7MsjnNYBNpyYmmLr2Zp8W1yd0oP6O/t70veyi2lv3l9Rw+b\nkdWhLRWLxWLyjGjN1G2DGnGRJbEqF0XhZU0YJtLX27b1MvrDDz8Q0ShDP/30ExGdUqcJg6/ve5MO\nSUR0OB6oE0ICW84fHx+DgbFjbiP4PrVlSJ8XK8P6/WvDsn4RTeUKx0SLCWKxQmKyqtl2RFOWCiLk\nxmOlHIyljIzJ+DAME8uZ9d7PLIcsIRVblWnBKXazjiqmdVQcHK7umQFVdz6fYO+mjIGYy1LOtP7F\nltPcNkQDl7FkRspQEBXN2I9vOIhdX7LleOnIsTXtyFboDx/ZLNf01FTn77bv+xNbTH7jr8MweFnT\n6a2Hwjv4nFmT9fyD7g3a1SEW7A/LkjEBXfYstxr5bgXkfep4qq/XGIbhjAGl5QrXMcjAIzq3NGsW\nKK4dZNxDFp12IcNxOPQO8H+LOSC/YaBU613p+QHZXXr9hSyGCdPkOHX3jVk/kQGiXTSbppk8P75r\nzbRYMyX/y8fPVDAZN//IDMN9QctxKqTVAx/7wEG9G6JP5WhNftNxAMgtt9umI8esEGIZrO4dVf/K\n/YPdbFYrnjuPna9Hlo1rxv++/zg+Tz5l3xRFMWHdiJvN8XgMygQy5XBsC61DYuMrXvd7AGUK62ix\nMDSbe+6eyZon9P0sRiWyVKWfzwluGztm9W2U51CwcZxbTbaKjNZGsPUYzsZQfzNuk/6ye7fLM+ql\nanuWry6nasOBhX8ey3jzt/HY6weiJW+pl9yUb1gG/2XT0urA7LmC9zv/q6BmN76HR2mbmr0Aakd7\nrnV3GIV8fxwZxof2xE7G8AM65AHKVH/DcivjC7ffZrPxez7pE6vVarLGmLtXmbMvsGCdM2cvbiEx\nRhISEhISEhISEhISEhISEr5ZzGKMPBXPYWu8FMqypNevR8dHDDD6VPaJ/n+u9V5reNu2neXjZvn9\n6QCry+VywvwQbeBisTgLmEg0avN0sDP0WdQxTDAwmKQAlev3+/3EQiEWnrdv33oNsvisofbfsmwI\n5DpMbag12/I+n+L3GbK0hlgLlhbzJRDS6l/LogpZEhCW1RD/D6V7s5gJl9IiX9NO1jlzrAyWr6KD\nT11qwQr+snPUMZtEZKha1FQezi0UGOxYs6KECXI8HPx9RPYWi8WE1YRBBtEvGq/DtNu+XlXlj4vf\ns9z78+fPk6CoEgOm7/uJDD0+PpqWMw0t913XzZKvp8reU8qYe+6lvo7jsbZGdV03CdJo9XvdV4ui\nmKR5xXvp/oUWcF2/S6kDtcUdLdM6fpRl9ZPvdV1PUjIPw+AZHF0t9Ro/F4eM1i0zRDioYsc+yFVf\nUMlmMok74uqcWrKt8Hme+3SCBX+2fJ9sWVG+abjc8be26WjJftgVW9e4muSco5yDrbI4Uy+fRJ4B\nc24J5DoWNDlmpdYlIsp6R8P2ODlmWUDl91B6Y7QKxyzAuk5Y1zmMPH3eJTxFnkPjxDAMvt7ClMNn\nFGCf1XGdkFmH5V6qN6brvcTAlM8Q86Wu6+BawGITYLwPK6i1fm5khfn+wad11Vh2mRe0GMZjj8PY\nB+uqprrkOEVZhB3E8Q7Kx/FdfN8uacHpQb9r+BmHjN5yatElM7HoFVuQ+4Ha1xyknca5kPqRTbWs\nFlRw4OP1u/H8m8WBXvHE23P9d/w9KwfKeHw4fh7LqG64vYp8wu4pisIzKSW2oawrcU0fYvJhWRYT\nL7queEGWyDV7D80YCfXj1Wrl1wwSu/BaRrH1jFbf1v0X14c6VpZVLjJ4BDgmyDhheSPMYYrgGKJZ\nC3mEORdjE539VirWSmz827fkSh7bua8vdo7u2rGfv2LW5U0+1vmHoqbicdyn3TJrSxgjrx9aWj5w\nX12xLL12tPuJg/7/XyyPd+w9cNxRsx3LuhP2DQcp//K4pX4Yx9F6dYpLJ33HBwjn5+ppIOKgsAue\n21tuQyvZALJPNMvL2vPE+p41Vs9hjlx7DJEYIwkJCQkJCQkJCQkJCQkJCd8sLjJGYswGjaeyQb4m\ni8S5U2RiK5XltfW5pq7WuVo7jb8JnHOe3YEaT+2ja2WUkbJE4/fw8OA1d6KBraoq6BPYtq0Z1Zvo\nPN2n4Hg8TrR34veJddbpz/I8N1kk2gKKZctzCJAxIohpFGPH0Dp+DWJsEsvycC2ulQ3RvDvnJu1z\nSSNuZd7Q9RDGBEZ5j1kmY5aXazTC1nUY+2RSZkfkcq4D672HjPt1STTwb8vFyaJnxZEgOvdfllgD\naNnz/0sWmMXCZ6GRdyAycXNz42VAjmEmGR1bZ7PZTCKrIztAZwxDhopo//X1iDn9y9LwWwwugfWu\nLuGpzKI511j9WDOg+r6fWK9jTACEZofc3Nz4WC+YZUaOy3tBf16dXQYtb1b6UZ2BA7Nt6PpY2Sm0\nnAV9w/mxxUpWDGyV6zOSJhnY55oz7FLRZn5l4cSiV+Y+/o8vnwtfNhkt2JK1ZEv140KscQMte2H3\nMIPidUX9YTz+ZcV9m6eGbiBqJS1oLvPXaRywGD+eyWOwqXTKwVPdp4y0uf1FH8OsKVa9kMFENL5r\n/f5iKXrx/9gc+Fz5wus1I6soCp9VR8a7uq4n8wrGLdCZtvC7rB1ETpB9oi2UVrYg/B5jGOjrcA2k\nxwt8Xv1eMG6FdR8ri4/vl5kqy2XUcLaJfbP39/XrQe7vWX6q+2pgRjHH5pHc9Yudo1dsma5343WH\n24z2HIvHsRwepQ40UMc0rftsbId/eTdef/dItFly3AG+QbMgWnDckcKxrL7imzcd8WNQwynjukHm\najdh2B2PR/r4cYxBIvOwxabTCPVRi9Ukn3MYklY5L72XQcaIxUiSY03TTMaqaxkjgkuMCS1Dm81m\nEhdE5jNcU1kZ3QSYHjvEiomxqJGliSzP0DiJYwI+t66fuWZuWUZlBogxRrqeXCvn8V7ocJrLaM2Z\nNVfcRh86KnkOXPAniyIVnaNC1r7CsHxoqP5pHAtXv7EnAccfKR8fqC/HfWT/3XjsKPvK3lFen68P\nNpuNf2+yrsSMYDq+JD6rrGlwbR6SSWRPXmKeXzp2LeaWdVExgp3rWjxVwfCSg0vXdV7orInMgrVh\neynMHWh1mlsMVCYbK1GeNE0zUf5gsC1RBOHiW84XARB0XTeh+mOQHgw0JtfL4sTTr4wFvFbq5Hk+\n2QxkWTZJq4ZCqI89FdYGHicT697XuIY8tS44kelNzdxJ7gCptK6ZFK3ykR6HkyDR5cXAHKqcdUxP\nLDFlCy5g5KyygbKUYsT5ok7nPHLA1WybTRQjnnYPG6oPHz4QEdGf/vQnXz8doHG5XE7cxKSv4xgk\ni3t0edGpKZummSg0xFXt8fFx0q7oLmgpF/2zGe9ab9wtWAsFfcy6Z2yh+TUnRa001opaXNBZKUBx\nQ4Sw+qUsHND1St7VMAyTdOvSJ/b7vQ/OK3RoTLFsyZLc01IkW5uyOe1jybFXCPBp4qYy5ETszUId\nH6wkrWg30KEYf9sN4xyypgWJZsTfhXdFZZtRueeUnt1Y6KsNB2p0A9XsV3PkMh/LI735/l/GIh7G\nuWnPlOGiJaIlKwm5XgWn9s26gbLq3JhgKZ5iNHALMYowypemG+uA6Xi+c6eUzHosuVbhcQnPWe9g\ncH4ryKl8Hg4HH0T6xx9/JKKxHaQN5DyRl77vvXJRr9+6rpu0TczNLBb02FLmxBQjZVmaqV/1dbod\nUKFiGbtiCi7/XBLsse/oWEzn6KYNJ0I4+mjj3P9ZlqjMKK95LFmzAi4bqGAZOq7Ge74mpsXvempG\nHT+5nNd2X3htsHJ05A3enpWTQ0Z05HDG+VGUufLdUcEprxs+Z2hZQeKGSR/CtWnIiGEhtNHX117a\nGIeui9UjZhyz5hANXC/EFCNYlrVus+4ZKsNaC8aUvnqOJTo3gOrzYm1vAc+RdLKyRsFkDTpxg3Uf\ny33fly/rxDwjV/CccLSTRJx9v/A8Xrb5p6HMvNJeFJDbf4zHDpWjgT1iOBu2xDEmGoj2bAA4cLMO\nmaPHw7iO/Pz/jm2yZ3e2tt9T9mqs/5YL6W54nVA5n7q3NPqEZUSzXGLk+Q4qhW9ZlhM3VJwLQ8qv\nufPX19qPCZIrTUJCQkJCQkJCQkJCQkJCwjeLi4wRoudZFLT1WbR5mHprTtqkl8Dc53guU+QlGCcW\nzU8zRrB8oerroKqo/cbftMVR0HXdhK0i2lkMhiTvE4OvagZI27aTgH6ozdV0cOfcGXND3/MaemMM\n1vVPcaG5pi4xF5GYRctCrH9pq9Sl8+e2qUWfk0/rmULlXbKyhCw0ppWUyAdv81ZLfuzcOWKjFbEH\nDTkZZrKM2kLJVz/48z2zhD/zLjsdW51ruLuuo3sOSHzkvrperyep5uTzcDhMrJDCyOr73mRYSaA5\nbY3Bdo5ZceYwh5Ce79skYr20rHBzjv3euMT2wvkJAyXKb3r+ElhB3/C7dncsy3KSdlQs4uv12gfU\nRTcDovOgsCGrIH6iO6Kus/VeMPWidUz31T3LTV8PVAqjqmVWDVevoJ56phsfu3H8X+Y5ZeKOw2x+\nkd22cJSxBS3jYI89U/H7vKNBLM5M/T3Ujh7fjDc7DOwSym4DN8tXdKDRerXfi3uQDATT8QRdQS32\nRWzcthg5Wn6RyaOPIZNTz8c431speUPj8SXMOW/OfGF9R4q0QOb7/X7vj93f3xMR0XfffTdZf2Cb\nCAPPCkyqmV/o8i110oGTsXz5ra5rL2sW60TL3iWrfWiMDTG5YvNdqK1H9zR31jYWy+FMdiWwME+G\nJUcabsnRl5vx/Id6PPbqkNOWLdmtsMJ2HGj4hmg7euv6YJLDUuo80IYjJPfCBstyyqVePIk6fuf7\nvPdy/kgccJOEoXdKiyzuwejup9+j1U6CUDuHxsK5DJM5eO78F+tPCGSU47WxtWWIFRKSe91OsXpZ\nzx1LCIB1CrEJsizzLFstl0VReDlGd2RrTCcaXal7DhbOWd1paITl5J1k4uzBGbKKkPmycwNty/Gm\nv9ywnH0/nnNsie6YMcLeb3RgFlZbEHVv+DeeLz/ejvMhEdGBg6luOMDyserpKGnsWZ6PfG5XZpT1\n53OUDvQrvxGN7SftKsBwDNJOOJaGxkn8fy5jJDQnzZmjnoLEGElISEhISEhISEhISEhISPhmMYsx\n8hIQa5lo8Q+HQ1Tz+DXie8y9z1MYH5aF1g2OCjY/S+A5sWjP1Wkh+0IsxVYaRq2NRe23FdxVxx/A\ntJXCEBGtPH5qa9fxePSafM0AappmwhSR+7x69WqSfq+qqkkQQEkP/BwtYMw3O/T990Kojz1XNtDa\nKbjETIlZwvQ5luXlWu1tzNozWwbl3YrPpfzsMipYcy7pDhu2muUDeQaIxzD6QxOdZDPnH8rBUcEB\ntDp3Yn4QjX13mY39eNNu/TGpv7BBRJO+XC59Sl15H2IZzbLMZIVIGcJkGcQaB0EbtbXIwiWfZs2a\nwndh+VzPSf0bu99zzpsLLA9lyooZEuu/+lmxvaUsOfblyxfP/EA2nU5lKOcvFgt69+7d2fmWdQWt\nN3J/7U9dluWEMTKHMRSykk4CcbOEOXI+6OrA8Q4kLaHrMnLlWNeaZcOVORVM/iv8eDx+r/qThea4\n5tg67JCdLwpqWfbW+djfF81A9WZ8xgdOmSvsrofNIw21yC0zVLjsQwaW4/5y0DfE3LWAZvDIugfX\nOzo4LsYRsJgJc8bCp8pejEVlIRajAOP0YEBpovNgfBh8Ws7XaxtksMlvEo/ECpiK7C7NXMV7y7oF\nraQ6UCRarfVaqygKL3NSH2RD6/hMuJbCNKpEHJ9FZEj1x2EYTgFshZkBcUVmxZuR1O97Isdsq4KD\nPhac37qscmodtwVPoqv1HeUPHMOF5WuVj8+62W6oygxxIwAAIABJREFUENnm9J2DWKOpo6Y8jwvS\nZzn1/Gwt1/+4ZrbXqyU9HLf8/BzTQeR+OMXkwbVmjA0UYnlYLIQYI8uSPX2Pl0aMGTInLggy/uaU\ne+lYqC7W9xjDxop1d+3aFt+djBM6EGiR51QV5zG8iKZJHDBQvht43uZzB6l7QZ4F+SJ7Bj4t4yVD\nX2dEr0aG/2bJjOIfx8/mnuhf/3s8r+T1654Dkw8Z0YFJGzt+xA+vHG1/HMev3S3HulswE3lJtL9l\nmeOYQcSszSzPacGzbn1zGleFkSNrVGlnDL4q61FhuRKdxlwMOi9lWYixlf6ovRjixRQjl4RMFnzS\nsS3qtlXWnOA/L+Gy8pKKmLMXK0KhPikLnB+oC56D2WXkUyZpPWBgcDnZgHVdNxkoMNijBDuTiVwG\nF6SdCna73SRoI24edHR6i6YsdV4sFv6ZrEBlL4mvHbznuZijbMBBJHa+jhjetq05gWlquEUVn6tk\nik2ioetC502+gywN+nFFeZARuUquPf1GNCoYiu78/DZzXqkiEb9zmchyopbpjZwgw294iIgeH+4n\nddX1Rzc4TQPGsVH6vzmpDOfvuCzLM5c2jWv6uLW4weCgAhlnZCzB862F0j8DYnXBhWUsa5lW4iJN\n2Rrb5J3K+bhw1RmwDoeDX1DogINYLsqxVjjjdylXnsdy59DvDDeP1lxrtqG0HQtRxb40TXZS4tUZ\nLzHynDoWqFLmB5alfU0SE5JIaMRM882LjERVLgFdncvp1+PoXtavzweAxWNGy9342443Ygd2f3MN\nncaO4hScXJ5Ru6haNGozGxW0m1aciZxgwDmtbKqq6sydTo6FXNkuydacjeGc60Nzj1aw4jOjqzRi\nuVxOjCrDMPixRWcgqapqQs+WhTi2JW6CdBBdLFMrTXDBr7N9aco4AhUpIrNS9nK5nARw1q6U8ty+\nnuKiacij9NXBuM5ypZr0C/7adAN18k7Z9azkTWSb5T5bW8F1/sf2I70+jm13yy43X5qxf7bFQAtW\nVC5vx83dzo3HhiynfsHrdY7MPLQ9bdky8YUz1mw5eOuhP/rNaO/OZanv+8kYisrrOWsH7MdaptEI\n99zMGHjspQ26qCCLKUj2+/1krW2dZ2GO4vwSQm2P41isnUWWuq7z44OeV61A2f7T/zkfq3Uf8vLY\ndtRzsOKhOQ+m7DpHrjs3NF1at+o5elnwOOgyemx5/cSTYrPMvPtankt/HL/vFkSH/xjP2/w2/vbd\nmIiJPn9HxDpSallp8v7O0e71WNef3nCga84k1dVEJS96K55gF7IGqWq6uRkF8bEfFSpN0wRddHHN\nIe8R5VKPe7iG0v0Rx+OYYsSSK2tuCh17zho0udIkJCQkJCQkJCQkJCQkJCR8s/gqrjSW5hGDaIbO\nubbc51LBrDIsbfy1FFZ/fkbUy6Xeah3XPOo6WBCLhlg9bm9vPfVJtHli0X54eJhQBvu+P7PayG9E\no/VS3Fe0Be3u7s5rdqXum83GW300pRxT8grkPtvtdlJXDICoLULIcnkuLAsaBi+0LMZ/NC71iRi0\npS6UQi2U5tAKNGlp0K/V1M5hn0SvBzOBXOWvzzL/W8ej3OAPnfLBe/eUDMri8xZs7T64jigXZsF5\nm9R17S3fJZ36qqZ/4/OFxsJrXZEw6JUu6ymsDa2pR3ceHSj2fworBH+3gita6T6tsrSLX+xdYRBd\n+c0K8injHlqTkVEp12m3HLSYC9Cyo+UWLT3a5SoWONQKvooMPm+RZ4sze65Q0/fezC3W6JIG6gv+\nsRLrEnGdx4B0REQV22oyz45y5PhYw4yRruypZku20KfzDbtjHolE8pec+rd+Pcrgb8ejdy8gtrjl\nRT557pg12kKM4Ton3TrKsU7P+XviKfdD6x+mJJZ5H9kY2pr48PDg1zLym1WWxczSrrm4zrDcbATI\nMCEa5c2SCd3fBTgP6/TbeF2MRWcxMfX9nHOn9KFqjqN+ajnX/yMOCyIKuElSXlAnzJxB3NgGcky5\n33Pwxhue2467npbsVvOhHdlQjsmTrh+oKcWkfUoL+shl7Dj1b0snVtwcpsEcWIxHS96kTHRts95Z\nqF6/N7AuOIYInsr2iI1ZoWMxK/+cYxYjEfcRoWP4PfRehmGgll1jhva0ftFu/vLZ97132/ILPvkc\npu/a2jOcMRqYNXnDTKu7chyPio7I7ZmRwXLSVUTbdvytEGblSujMjpy4zHFA1mHcjtFuQ9Rz3Q58\n78+Lgb6sxud+WHN/ZpfWos8o5/9Z9Lx7+WbT0McvY5tvM26T3PlxWKc+xvHYWr9qFizu1zSDr6qq\nYCrfECss1Paxvclz3HISYyQhISEhISEhISEhISEhIeGbxVWMkedYrWOYW+Y1frLXIuaPe62v7tk5\nYpGWg9lJMzjHwo4WOrE+a99x9MvT1g8JEkl00gJiEFWBaFJ3u50vS35Di4ilQdeBzURruFgsJn64\naDXSgQarqvLlat9AxLUWPQuWj27ofhZe0oIQYx1hX9Iad0serf5pWUQtjbuOb4BaXCtlqL4nWrFC\n7XtJCxyy+lhltgTySFOrhLfCsUhI4Mi8J3LMAMkq7tvdSSYGToV25NGxax2JsTtnGZI4PLvd7ixt\nmdRPp6K2nlGYAMg0iPm3a6A8mlaMQN+wYB2zLHYx2ftnYpAgsO9qCwVao2N9PGbZsKDfR9/3fizW\nFmeLYYIsP23Z7Pt+VjwgzRTsus4si8hO89v3/dSnuz9dp8d0P5a44cSQhPt4OdF9tSPqOGfiIDm1\nuWnLDCzmfKx1PVE3ylq943uKr/3NQEwUoYqN5G1zin0lMQ2EuemG6XgUs+jjOfp8bAuLraPPx3FD\nj7nWPWPsADzna66PLGD/0mnK8Xotc3iejpVjBZNEVo2+rm3bYDwzhG5nnO/xfjpOj2U51VZVTHdp\nsRbM9yLHlzzuL4QxO5B7OI9F5eNp9cNE5ojIp792xXk7W+OLTwcO1t4jz3tV7+jAc+WO44FsWU6K\nzNF3i/HH7iPHaMjEit3Sllld9Jrr0g70sOK2KDmN6u4U20OvOfAz1Mfxf0sGrWN6XI2xD/DYHw1k\n5l0Kni/A57ZkThDbf1zLmg+t96w1ylPYKgLdT3CfoNfHTdP443pv0g9TmfDtcO1egojqA8vVYazD\nuuZ3lmVUNsxgYVZITwMdM0lBzwGG+RG3q5PMSbDi5l/G62/vHWVc1l4YI/VAD5zy98DXZRIEfcho\nxZOhJAHJWa73WUc9y2rDc297aM24PvidaLouHIbBM4kxiYdAyx6yWq0U09fAuWnikZdAYowkJCQk\nJCQkJCQkJCQkJCR8s7iKMfIcS8S1bA/L2jnHOq6PxcqcW0bMam35xJ2VxdXIfBoa+SHOPtFWxSzL\nJmnoJHPFdrul169fE9HUtxe18qLVIzpZO8RqLVaP9Xrt7y2xQ1BDKL/J5+FwOPMZxrLzPPdWUkzT\nTHTuc4/+hXJvK0r/HDz1vKdavWNWvJfEXEugZS2z/JGt8rVm12KMaO3stX58l9rrGlaDo7jVZ5mz\n/3rH8XRY9gZy1Aprg3XD+UDk8vPymw605ML8Yrn6+PHj6T7M5ELfS20VFjkrimKSaUnkuG1bf57E\nDCrLkj58+HBWL3yfoUjvoTFlzruKWdDmyMnXkoOnlKstj9pSEWM54f9aJrBcHR8g5Cet3wkyE9br\n0dyjM3u1bTups5WJQ4D9S6cV3W63wTYMMbkknahYoUmIAEZ26Jh13OqPkjI7r6bxJHx7O0c937vk\nMoohIwllUKpsQX1+is3QtMxIFDHu+pM1jU79WMuQ1PXm5sbLZqzfW2OtHnPnMowEof6oj83Fc1kk\nobpotgzGJSI6j8OhrZBo0ZZjyByx5hqi83S1AmRyaNadlQ4ZPzUDtyzLMxYr0Wn8xmxkOt4aZu2T\nMnFO0GuZpml83TxTasnrt7albHnOyBIMxZShlGUZiVAUfG9pD0yLLJ8Yy00zX7JmoJzXq85bvvmz\nHmjPdV3/+HasA2e6oeZAQ84ydzM+x+NhR/UwTUEuzy/tI+12f3/vz7X6rNRRr00tNiDOwbG5Y05s\ngkvsimvmJosJEYKee+dYx62x3IphM+f+c5nx1thJdB7LJTZ2WsyWGItEs3QtOW7bdtIXGp642jqj\n4XDOPomxj8z689fFkWjFW6vVnp/1yPuckmghex8fXxLeaXbebkNGtOWMNR0PW5IlsXnrKDsyO4uZ\nmx9Xjo6c7WlfC9uOx64mp5Kz0ZS8zu1l0i1yz9wkTpqD71E+MaZcjImn2f+x+ECaTYjXYb+Mrcdi\ne2YL164dv0rw1ZfASyos9HWI2IB37XWm4oZ/ck+gCOEnLoZFESGTStu2/n9ZYMsnLiJkAFitVpOF\nPi4edHpXmYSwDrio10FXrZSDImCiBLE24uj2gwKp2yT0HZ/npRUWTyljTh1CE9Q1G1j8HxcKk02G\nsWGzXE8Gfs14XWjzFxqMgmnVYu+TiIoAJRPbyXSXMdI6b/tTfxrLP5+MiE7Kj9yRn+icfqTspFRx\napHqnPPyIcrJ4/Ho5VFvlDC/u9QVF3lyTBaAu91u8tz4/Jg3Xs6XYxZim62YkmnO+9PlPeVYDHPG\n6ksI9V/sS4JL40tokxhKby0BRoV6XkBgSlngSb/BYGbaJcaihmPqX52GUvoUutLE3nEmi9MiI6p5\nMNjxhtcYQ6y+YbXvRDHEt8kjfWog5wOxSlC8ISdqWIkpKYAlgOSiKKnfjfMjx8Hz9ynq2gyiq8dJ\n2QRjWnON0JgdGx9Dbk9IA5+j9IzB2kQ85dq55+i+aCks5Dqd0jG24Qm5dsm50jbyrjDVuQ5ki8Gw\n9XonNLbp+Uv6TV3X/lpZr8iaZr/fT+QR3ZIt2rh2DXB77uO7qUJFYI3B2PcwwKjUQdoG3aLlU7+X\nt9+/pU8fP43HOZXpglNx53VNnzg9Lx3Z3YjdB46up46VOXTPxohsoHxxboTDwP9SZ1mviosq9iVc\nq+AaEZHnuX9GOSfmloMuitfAUgLo/61rrO+ha/T7NcfomWvG0BxVVZVX8unApNb5luIJ349W2GBC\nhjltY7XlHEMF/q77Rud66jkIcCduzhXLSE40LPj/jUrXa8ztMRQtUc3imnMTNi3v0WqiVhScvsyp\nEufsWfjzwKnrt+MSjwaXUTXanmnHZW0WzruO7pbjbytRpNREPRs2SlEac+FFdtoXWnvLkEINj13q\ng7H92nP3ZF9bQZJcaRISEhISEhISEhISEhISEr5ZfHXGyDUazkvsEIspcumYhWupcs/Rbvly6Trt\nmVyH6e5Es6dT7RKdrBb62O3t7SRlbp7nE5YGag0xiCTWBX+T8+u6nrjqyDlN0/jftBXDagukjV+j\nbcTvYjXQKaX+/4gsyyZuHLF2sqzd1m+uF23x1BKor7MswRYlz7J+XitrT9VAI20+hKHISB5DLNTC\nOuzycD2xTHkHh8NhYmlEq6d2l8AyRN7FmoOWVrGmCV6/fk3v3r07O4YBPi0L5TWskDnHQud/TVzD\nHNHsDc2+EFj0fLzHnOfW5RHRWTrSrOVUvEem/y5PVG/tLqXHf7xPWZb+OSwrechKiGl+o+wAea52\nIGH4W2Xq9xDrL9j3NJW2LEt/bEIVzzLvxpZLlTOiVT2a03YH5gHzZYeh9QHtnE/5Ox5rmibqaojB\nyeUZ5ZjIIzLB9FxmlWmlqLTGS8tKOsfyZY3jcyy01nt5CrRFWDMg5Pnruo7OBZph1/f9hMkgQMs2\nMkwwnbX8ht/xN+/CEmC8aqYflq0trTL2WuwuDIrfsPz7QOGrgpyU/8jPtOd0l23r3Vcs67i1Toqx\nJ2OWdmlPaZPNZuNd6PpGnufk8rN33F7sV5dzEMcDdVSMj0vrw3h9s3R0cO1ZW2B7H7mMn3/+eXJM\n6oPrUYuVJ8BUrKHnt75bx2JzzLVMLH0dfl4qH58Zx3ZrHWZBnyesneVy6fcFur9gH5k71+r3gWlf\nLfeKEIsmBpxXLHanH1ek77qBXHvaPxEROQgxMET6hIa1BxIMBVHPhPuOt1qOh5xjTXRkF5fO2G1r\nxtRut/NBF3wAc/6hK4gcu8vJCHhcOOokkDifJwzJQ0W07Hm+k3WCjJ155schK9GFJRMWeyT0PLjH\ntAJxx+RRcK03h+mx8UQkxkhCQkJCQkJCQkJCQkJCQsI3ixdL12tpWa/VrF5il4TKv/be1nNcY6lG\nxDSJzynXOhbyOcbvmu2BFhH5vLm5OQvEis/RNI0vQ7TLmILJ0kBrq6VoixE6nbClNey6bqKNnKP1\nK4rCWxd8GrqIf/hzMOcdX3Nf3Rfn9l+ic/aBnD8nrS5aKtCi6X9rWMNrpDkVXGKM6HvOtbhrOUZr\nRkzGQ5aUS4DaiKHcM0wGKCLEDsB+jIwpfb4cw5TUc/oJWgctP15hiqHPPBHR27dv6dOnT5O663vj\nmDKHMWI997WYY417Kdm1+idibh2smDlz3uOZtVNZr9CiohluaC3V9UeWnk6PdzgcfFky5spnWZYT\nBoNlVbWCFuq4EBaTBeNEWOyQkLUXrf3W/SaB3fqBmg3HERBaV3aqi/hy+4CW8HqsdyZtbTG59PnC\nHJEgkQjLoonPHwtQZ8ljKCjsH4GQZc5iLCCQcWFZGifWV8M6rtvLYj4hy0O3M7JPtFU8VH+dbh2f\nXa6RdY/cD2OMyDlnVtjhvF/2LiMquV5HFd/Bnc7TcuOcO2P4ym+WbOpn0AxGDM6P8UccM0WqnttQ\nGL994y3UBccWaTkYbE+O6iPHzeLJc5dlRKpbnL2Dzg6u75ybxDuwGCMoN6EYPnPnL2tt8lzEYnPo\n/6376gDFei2AZVpMIS1z8n2/3/vYU1awfby/Vc8Q9PnIHBDMZfjrsoqi8HHchKWFwVd9LKmcmWbH\nlnpgiFhl4/+x9WiWZZP6yDpxf4rHTG3LYxXXxS1zzyah7HRPPUZhAgpS5TfMEnHVQCWzT45yrCbq\npH+wXA7M4CqWGeWrcYy6Wb8Z7/s4rkN3hx1luzjbSGPOGhvH7zl7uTlydonV+NS1fwyJMZKQkJCQ\nkJCQkJCQkJCQkPDN4ndL1/vPCq2Jilna8fgcS+Nc/925jBTtt67ZIUTnadiIzlP0yjFJq0t0Hrmc\naGSMYHwSolO2DbTsoZVBW1UwErvUX1vjQs+vLYcWK0hbkPD+VqyNp+JrME4u3ee5LKuYld8CXhdi\nDKDVQl+HWmErgvkcxoj1PHPOxzrPaTdLds/anj/zjsuUGCPVPMZIjEEgv1lsKqyfTveI1hZJ4fvD\nDz8QEdFf/vKXiVVNcH9/b9YrZnGbwxj5GlY1xBzLwLXlWf3YstTpzBV4T/m0rN66LGRMnMnXMO07\n8qnfB7L8OmX1appmYuWTuaAsy4k1ClkYl3zS8fxLsSpCcyemTsU66PkLGQBz4mL4zzyjXlYubByX\nRFNZd3rfBYtOzcb4TUHkqvOynHNmlhR9b50JLnSulWVA7hNCVVUTK/9TMmaEEHsu/P8SyxC/Yz3x\n+jnz0Ry2IfYXq+0si3mINWkdw0/dHzFdr65fURSmJTt0nxjLpd13PotFr+I94HrHYtv61LqROW1O\nTAAEzj19xYwZLrbgrDSDa6kUkhan5nWcdabKc3Ils+C42er8slwTkY93IL8tl0sfd8nKoKPbF/vL\nHJYDMgAELzGfXTOOWffW4yrOJTiuWsyRWP2F/Y0Z8GL1ucRk0XXW5yOTMSSXugz5DGX2yvPcj79W\nDEGfcYbT8LbH0zkxpuScsRblUeC/Z0SHMUQIHf0pUvf4fGo9v15zSHaaoss9e0Rmi64kn5WmE7kv\n5Pqeiu/Girnvxr3csBsnzuq/vlDZnJikROdrU5RD+S59R9cdxza8PrQHCP0WQ2zf/TVwtSuN4H+K\nkiSkwAh11ksNfw21DDtMbIExR8ninJukYbQGTE2x3O/3Z3QzorGzy3nazQYHTBEUUa5IgCAsq6qq\nCY0fy9Y0zUsbH2vjaf2P33GQvFbg5mBuWZeUPk+5Z2wSid1nrmLEdKWJUKIndEI3TVFp9XtrA25B\nPxsuiuYoHmODr79uIB8c6/za8bPk4LNS0tC7SfBkvMec53lqH0KK8Pfff09Ep43l7e3taUPF95HF\nbdM0sxQcMVeaWP2+toLka2DOovXS75aSxUJsTLcWWKF+YikecVzVASpRaRJLHRsbL2ILZUv5EUsr\nayledVlz5j/8P8sy399JVRVTbTe8QOxZa9I551MDYz8WmdFKqdVq5eeWOQHJsa6xIJH6N3S3mJOi\n11qkz4U1hs45P/T9ErDPyhpAPi1lAQZO1YYPq33xu34PmK7XUsYR2W42OObqjRS67Mh7w8CsunxU\nUup323cducGWodgcHFonxfpObJ7UytUztxRx6ZNhqHPUs6utBFUdJFUpuE34d9Y7sw3lu+6PsUCr\nWK85z/811oKIufPJ3LmFaCrbul8H1zQX1oSyqcU5Ibb3QdnR5c9Zm6KyWSs48d7W+BKaJ/q+9+7B\nVpkSWFVU07H2uiQjc5RF5wftc7PsFOQ0tmYy5ws+pePrezeQ40QA3sbinE8OUGTn45hzjg73o4vO\nJjsFgSc6d23EwK+6fmh0DslR6LlCipG6ricGwrmyeu2a66lIrjQJCQkJCQkJCQkJCQkJCQnfLL56\nul6NOayT0Dkh1kWMwjnHuv61gKns5lr59f94nZVqTT7FIiKUObGCHQ4H7y4j5+92O3+efCKzQ1Mv\nMXifBJ8TihUGhBLtMtYFr7WeWf8m7gKi9ZQgS3OYI6HyteXUChx4Lb7WdXMteZfKm8sYQWvOHOrb\nnDpgf9R9z6pXzJJ96T6xYyHr++B6ijWNWJp9tWZY4PRv2uJiwbLY6JSD2+3Wy5po9IVivNvtqFqM\ncr4/jhahgoPe3dzc0JcvX87Ktyxuc6xR1/b1S7RejWve+bVAS6LUDcu9NOaG6pFlmR/TLKuXThmK\n8qXTSVrWbrS0WxZtnZoUXQh1+k3LxU23B1q0z6xdav5CC5Jmq6Bl36JPx6jr+nzrXVgsEl2/IXeU\n8TQpWbb7gs/p7UCIOvUxBscN0ayRMYNW7jmWXEvu57B0rllLXLrnnPlljhxr5lTICo0pmTWDgMgO\n7htjKWpWq3UerpcspoiUpe/d9/3kN2Q0aEYWymJoHYpsCqyDZ48YKYmlDM0Cxuexxi/9GUu/ijKu\nGR14Po49fc6uCtJGw5QVhmWExjYcm/WzWi6nl+aol1qTPWfOuYaVOOc+el0Wen4cj+bM6ZfkX7PM\nL83RoX1XbKy2fosdQ0aDT7U7813NYRpcqlds/A3drygKz8iQEAaX1o6nH8ePesfv+DB4poi4jtZ5\n6VNe67K6rvP7J+0Cisw3wXK5PGMvynn4ieXjnK1ZZ1mW+XWrQGR7v99fJXPWPDTnXTxnTEiMkYSE\nhISEhISEhISEhISEhG8WT2aMzNE8xjSJ194Hr7W0knM0lnNwrbUzBtT2xgJgPdUyi9froKUYMyRW\nvtbUV1U10TyjRRD9g+Uc0RLqgEh5nk/iouh6a1hWi+diDgNiLpNj7u9zytTnYBC+2LuyZOIl7m9Z\n5kLlnMkZVyGnU5+wmCLy+ZQ2C1lVY/Kuj6GFO9a+k9tk2cQyERt75B74W+z5xaKw2Wz8+xfryDAM\nXq7kmHxfLpenlJHNKGfCHMEgytgeuj6X2gSvtT5j5xLNt26/1JhrlYtjr+4TMUsVnm9Z3K6xYqBl\nWpeNTB5M4SvfdayFLMsmTCRkjOgxBOU6lLYQnwctupZ1H+uHddZl4v9oTbesULoM65i29mM9Ch6E\nhm6gQfKDHvk+HHC1H3pzfhGWop7HhmEwrbByTAdIxndsnR+KI4HWSCv+QowxIYixNmLHsD4Wrp1z\nQve26ox9Qp4R05pL8HeL+YRlyDErXalArJcyLyG7yWJf6D6HZeo1lu+DRRGcO7FvWIwJS/Z0XUKy\nKMfmxCmZyzrSMQ/8uNc7KpmlmCvG2OFwmDBzhmEIjnv4/FpucNw7Y6sYY0eozng/i63x3DnnqXua\nGPS8gvW05iUE9kMsb24dY/Me1mvOmGCVZQVf1fXDOD36GL7H7AXb/hq23lxgP5a0yHPOH7+MH8vD\n+E8p5Klu8EwZiStydCAnzpjbax47OcYMMvJkvpMxEfdvmgFijX8xxivGuNPso8PhMGs/FZs7rsW1\nsv5kxchLDgZfY4CJLWDxXs9VpGB5T90kW5sNi4oZoiKjcuL+/p6IzhcT+t5lWQZp4Di5WwsRFCyi\nkRYltEedeWYYBi90eqMs9cC6Ep2EM0RlvQbXKj/+aCB99veCpUiwFuKhDSUR0dBzv4zwz+ZsqOcc\nv+Y63ZaaJqjPyeXZeM+X82M1la38ICJ69+4dffz48ays2KLLOiYTJ9KtcXOraZDyfrbb7SSoYEwB\ng7/J+bJhOB6PQSVA6Hn+p8iXteDXG56iKPxGTOinlrIAy9SbJyxTb3SRnq9l6ebmZrLQR1ccGR+l\n/1r92NqAxzJjxDJ3WON9KBuChSzLJsfx+5x6YRvpss7qJ9H/+bMcHB15OhlYISKKW3xGLEvmJis7\nTWyzpQOyxsbSUP31+TInNk1jbuas/y/hqUoN61hM5kNjjlxv1TkUwNc5N3nv4h6MShCt9MYy5dhq\ntZq4tmHZ1iZI93M0HIUygensfPhcof6vA8ta78Bya9DvAzMGCrA/h+QeafCx+ct/Lx0VJa8t2/N1\nQl3X5nUhObH6Jbp0W+sRPRZiWdcYiWKKbayHvj50j2uVkTHEFCDWmjx0vTWmxwL4xsqy3FFDddZ1\niNU9NudYilTrOfA7XmeNlzHlj1V/vE67jsZgBU2PlX+qFFHO/jLssQaB/x0NEnyVh5q+JILDkzLd\nkQ3kxlxizau6XS3lB5Zh/U90riTVCphr14mX9tZPVV7FkFxpEhISEhISEhISEhISEhISvll89eCr\nIU1rjB0R0vyE2B0x7a+lXQ+dF/vtuZij6Y0h8WYEAAAgAElEQVRp4GIWW+uYDs6HsKxwSGnUGjg5\ndjgcJtdtt1tPf9UWi8Ph4K3hlgZeU8TRChvTys55P1ZbznmfvyejIXYs1sfn9O2YlTDGZsDPWNBG\nS5OOVr+YPIbkmChuCdB4jobYtNryp2jjRTuv63h2zRP6A1rYiE79H4OLWUFbrX6srZdzxxD5f7PZ\n+O8xi16ozNBv+phlEbq2LI0571/3xdC9kfIaqzN+t9h2+p6WTMinjHGbzcYzd/Q5RVGYwVpDTIZQ\nXUO4dEzPARal1vqc05csy2asDnhfXy5LLcd/JAdG+ywPvzMsE92Q9DH9m34X+v85shOT1Zi1GJ8j\nBHzGl1y/zL137JhloZRrJAi81Lmu6wnbQiyPVVVN5gcMJqiZXPv9fhL8HWVQt5c156D1c45riJYb\n671a7lLI6AiN31a/sQLKz7Gk4hrCGl/0OEZE5JS8WGNDzAXJGif0ug8t1LF6WWWF7odtEZsnQ+fF\nEOo71phzzf3mrkd1kFb5nDNGzyk/tp602BTYB2NrOA18jhgzJbYWjj2H9T3WDigbIVdzhGaYWe4p\ncTiSYiXNfJZL2ad5ruede5ZnPvjxnOfH/mKNE1pu54RACLVlKCXvUxB67y/JEkEkxkhCQkJCQkJC\nQkJCQkJCQsI3iz8sXe812j3BNdrCmKU9do+nIqYFJrIDD8XKmGsNDUGs0YvFwlsTUIOnNZtyzEoP\nKZYatGgLhmGYaAZFa4xpmWIaa7R6xyxuAomrgPd9qiU7duxrWNzmItbHL/Xt0PkCyxplBcJDbXlI\nQ2vVwUpbGKuXFRzT+j6X+aIRe36zjcT6bFyvy7q/v7/KOm4FRpN+bFnJrPLwe8iCFrpucn6ECRD6\nHvrtOXhKeXPGS20ZC71355x/D3r8s85HhCzbWFbMemf9hu9JxjsLMavanDgiFivGSjGsYy445ybs\nLgwOG4sxYrVvrO5Rxoh8yliVSbSRuBziZ8jai3G9dF0vMaD0czwF18iE9Y7nzn/W+Cif0XFSfY9Z\nF621l5UyEpk5soYRubT6Ho6dMSaHZuBhcHpdbwxEbcUA0WUh8zXUXlYKXAwwOne+x/shYgwTnI8t\ni6suzwqmaDHfNDvAqpdVHyv4rBV0VmDFboqtQ/QzWixo67kvreFjv83BnHn02jWrNUdZY4GV+vqa\n8eXSuToOzrV7Lauvxto+9qxz7nOpTk9tG2TXE53HRRHE5g7nHGUkbcEnlSI3OWUSK4lz0i8oI2Jm\nZJ9HWF4Ruce94DVrFOv55/w+F3PlMYTn7PcTYyQhISEhISEhISEhISEhIeGbxe/OGEGELBWXzrfO\ne4rl/Gsjdr9Llp3Ys865D1oXdFl1XQcjvjvnJumbMF2ovldVVRNLDUYMv0ZbfOl8OabTAn9tfM1+\ng/0T7xVjh1xTduh38em20upZ1oVQmZYVGi16eJ4cs84P4dK951jJQtfjbzELagxzrXeC5XLpj+mY\nFlb/Xy6XXp4sS2VIwx9iKEx+izzb17KqfA1Y1nrr2DVWD6vMmEVMsnJZEelRvuakocRjNzc3RHSK\nB9N13aQvIEsllD4XrUTa6osZkc6sVwEZxb5npRPVx4qiCN5bngnLwGOWRT90bHA260p/tyynsWxc\nc8YO5xzpzACW7FnWcc2+sRBjyM611FoMhdCcE6sDfrcsoHMs7fhdMzPyPI/2cYGV4UXHE0GmgUBY\nWJhWEp87xD4hmsZvm2NdRZmwWETW+aE+YT1PrCzMiCXXIQtNv/cYY8T6LRZbDNcCc+Yjq4/PZZjE\nZFVbx2PzhSVDc9cH1rr9mjWw9fucsrBtLBaFlXFL90dLjq95hqdAtxeye3RdrLWj9ayx/aH1PfbO\nLObfNftPq67Webg3a5gFJzFGhoLrsMypXfN41/BvXUciyS63nxV/w3rqZ8vzfJK9Kxbr8dKa6am4\nVr7mHLtWB/CHKkaeizkdGn9DhBoqtqmJCWYIenCfO2Ba9fv/2vuy7caRHVtQg52ZVdV9T/f/f18/\nne46OdqWSN4HExQEbiAQHCTlMfZambTImOcAdiBqaEQs3EDo+35ytZw8lsLXVXoTGUMuSPQVajpO\nCZkXFsp4aS7hXsKvNYDquGaxarlDEyU/NT356enJNFBXMoiFYBkbRpstdB0ftwlpGBHl0eurtQsS\nb2HFiPRLz393bqnt7eMvHJZc5EcMrKInogpHFgjITU2/8sbbqPu1UBo/0VGXyCYVCd4QPHq5XNzr\nRYocnzVN2UoPu9F9FV2xiwSXKP/oal39zfPnLcRkOr0jJ0s2FvKbtxGTKNHT2Q3c8HE6lICEaHps\nVZapFgxNwg1Cb6TQdx2mVSZRYXxkzWUJ3nVaZZnqMvEECvKbFMbxU7c5mRYd7ufPn0chp77e1zte\ndzgcJvMWmgdL/YT9WcevS8J4VJ+6LLktog2fFEChOZrfeddVa//onZyjkNCfv8n6ZHfyOnuZdp1+\n9s/uuD7/+OMP+r//+78rv1HhB3JTszavhbc+lG5QXelxi8tNHvtC/T4yhrBw7enpabJ2r53TZRqs\nvQLqQyWhgy4vrz2i8BklYaQXlgd2949//IOI3uuF22Xbvo8hfG3vad/QGx+rGY7P9Oc9UT/06eEA\nSD9c9yuFGlowJsceuebQAkcpIFlTWBYJK7KO3KoP5lGaRCKRSCQSiUQikUgkEh8WsxkjHgPAc49o\nUZabNcJCaaz9VisF9Px6Utkom8SLJxLW+XweJbws9WUpO6KWeprt4/Ho0q48DTXSZD4qIpp263cp\n3Np6R+1+rvSWJcSvr6+mhrkUNmrj3rW7XnhaI/Tlyxciem9n8mpZGR9ChE5Z+u6NL9KNZkx5YbZ9\nF2IAsL+3tzfTSBzSgJc0wvoauci4V0KtVrlGw7hkzNW/pYaSobXL2r01RnvtS8Zfuq5Su49oApHW\nWsaHjuqwW49FhjTUSAupEdG4ovlOjjO14VtukPtIP0Zxy9+aYfn8/Dz2oaujU/wHa+hoGrd+Wlqv\nSL5RHi03pXfITaT/oTUNyiNqjzzOawaDZGRp1gZqx5K5quccj5khw5drIA05TlgMjrZtIfNH/9Z9\nSv6N5knvGEhkHYIYWYitJtPqae09Fpz2VzLqrY8Qyvr0DLIiJoDXF3Qef/z4Ye4ZZFutnQO94yyR\ncp4Lay3gjavavcc6ROA++9dff437CK5H6/hvJB8MNI7L9iHdeGwy9K60/3TDPzBbY3BDdhlZ9cvl\n9V//9V9ERPTnn38S0fsFF+M4OcTTPQ3xPe2IXoby5GB3zXiH73DyZrzCXrYvr0/IcUUbRpffLAPk\nVp1Z8/AS1OxzLeZTpM89/o40kUgkEolEIpFIJBKJRGIjPKSNEUui40n4ItqkqPsaIGnYXAmZJ+Gu\n8VtKF9FUm8iSXinh9SSufJb206dPo1SRz+V6GmEZjrzWN5qv3w012nSi2Bm6ue0YsTckdPhIM639\nyvg9hgk624jSp79x2zidTm67QuXmjSORMDwmlHQbYTxxfDIfnjvZLy0NHdISldKgz2bX9q/a9swo\nabStcJeMiezfYzSUtEpWn0HX8HkMEFn2VjpLYXF8kr1g2QUqxeFptFF5IY22Rok54GmhvTPjei5D\nmiB2I6+A9TSOiK3ilblO+/l8dq+n1f2467qrK2LlU+bFu04zWrdzvs+FbiMWK0jO91Lrq8uJf5/P\n59GvNnaKykv2Vc0ckbYp5DjMYXEfQkbjtUFiFJa8ppvDQIxJpL3luHUeEbx+qctFukN9GzFTIqwj\nxKZA37Q/K1wr7ehb0zSTurXiIrqMjWh9iQzMynl+7roN9Vlr7TRHm23VlRwv0PxVw4CR47HXhphZ\n9evXr8m4XTPX6bgj7jTQ2OO1vcj6z3pHn97bFTM06MfJnE9lWXJ7/PLlC/3Hf/wHEdH45HGj6zo6\nfvlERERHrsfTe7t8ezsRNUO97Kbrbq/voXHZY6npdiNt0niGj1F8S/eyUbeo/sN1qpCMkUQikUgk\nEolEIpFIJBIfFiHGSFS6xmA2gaVVmQskvYykLyKhjEqIkSbM8o+kWZ7Wq8Q6sfKP4i/lS2tC5K00\nEU07Sz+JpnYharFW/dwCa6dDSzVrWA61jBGvLD2NLtJQoTbo2TJA56kZnsRaaieiNk8iiEiNvT4o\nf3vXR3tSbE9TV2IflNIstUVRrV0pTP1ujkZ7rkao5D6qlbDK0CpnrSWJaDZRPEjT6mkopRs9ViNt\nzKdP71qmnz9/mloflA+pqUbX21rzHMoPKgeZH1QmHA+6KtfzZ7EuSjYNUNyWJgy1cc2wlH+jdMnr\nlz1NO2PNc9hr9q8ILKYQEWZYab9EuE9o5p5ce8i86jAk44TD0Nr7ppne0Cb/1qwV1CZkH/LGFa2h\nbZpm0rdl+7FupUHjEnInoeuDbRwghjBKs2QU63xIN3qM8vqj/I76mf4mbzZCdpR0mXDeUJvy+qOV\nVkYN08Ork6Xzsg4r0k4i8y+y+eQx2F5fX+ncDv2jw+u3NeDtvyyGgpVHFJaEm+6nYfwZnDQ/L30I\npYv7Gj//+usv+uOPP4jo0od+/vpJRETff/6g08+Xq7SP45KTFwk5biC7dxYQo1IytLSdLTQGyW8e\ni8rKQ7QfRNaTtW1CoigYQR3Oc0uEjVetiUin8xYbXqV5qN2IrgGZ15pBBuVfvotQ6lGD5g4jrxxk\nqqKe5L3FsBV+KQ018Dagawlc1mgPkUl47bLRkAsx+Y6obNiqRshQ+oY2Z5EwtsAW8ckNQnQysPrQ\nmukrLdKi9Vcb11oojffofSksGaY+BnA6nSb1iK7a9QQJ0lCjtUGSY6hctGh3PAZ7izw5h6A6QHRb\n/U4bZ0OQ9GGZduuIC8cln6W6shZBXv69I3zWEwlS+LfeNKI69oQfJUHaWqhdbKJ3aO6U77V/XV7o\nKAnazMp4WMEW2bjI38hYq7y6Vz7lmkaGxeHp6+PRetjLI2r/6Ipc3UZlPF6/QcoI7V72Y/2NN2vy\nnRSIauHC6+vrGL8+1oIUY7IPIWhBh8yjPt4thRm84ZPGW70xVJcXOkojEVFeROGNVWv18+gm0Bvb\nUJ+w+r3EuWupexr6STMYMv71CuPX6dOYu5ZA+Ufr/KjwEAk4Gi6T3XTsscajpmkme62Xl5fJ2Pb2\n+r5nPr9NBRlorkXtUddnadyc5JHso/Jt214JpHXckeM1tXvA6B4j0ket/mEhj9IkEolEIpFIJBKJ\nRCKR+LBYzfhqVDonv1mS1Jo4I35RPFYaS5rRudpI7Q5JJaPS1RoNqEeBQ3GWtMVa63E6nSbGKaXG\nRkocZViS4lXSVm+JtZgjc1HSfCItjuVXul9Ds8FAlHqklfAMx0UZB0u1CbVjyK2BNJQl9xHtM0vz\n+RrukqbOikuGGfW/tA9t2fessUXH6RnSLIUrj45yWEgL7bEP9PXJckzV5Ss1p/oYo2dMFLUlD3K+\nKzFROG6ZL+3GGkOkthvF4Y2FnqYdaZA9dgB/Q9T7SFl6fW63213NmTLtMoxbA40lpXcaXh0jdoSM\nW19vK9cL+ugMYmIhQ8Q6zK7r6Pn5mYgu179L5oBuL7I9ajbE4XBwNaHW0a79fg+NI3rMBM260uOG\n9oe+63g08022S51mXU7sHjGlUFlYeZRurbzJYzkyDYiVbIXlpQth7jcPMv+6bdSsAyxENeGITWDl\nSZYlYjkxxjnr1FDz8h73X//4BxERdfvLvFRTdiUWjbX3sfIeYYgwPCZX01wu5W1+DONL27Nj059M\nM7fdf/7zn+Mc8NdffxHRpSw9JhOaX7w+1HUd7bgrD8+umZbteKU8Tdvm1VX0AcPKkT5X2u9579Ac\nUsMKiiIZI4lEIpFIJBKJRCKRSCQ+LB7qul4k8dlCq1IKx/pekrLqs61S6r0USHvnMQYi4aHfJWnt\n58+fiej6rLl17vzXr1/jO9bmsJHAw+FwdUUVh4+0EPp3rZTxVvDS7PlBbZyfrI2WkmQJqy3MOb9a\no9FAWsWoTRLvm1eGnmRYlxuS/ke0nij8JW0LSbgtrZeVD24DP3/+NN1r1lapv3jpRG0pElbtGc+t\n+qeV95L2kuFdbYg0oWxvSfYDbahMatO1ZgdpzuW5ZH3W/nQ6Qa24Tr+n4UH5io5XOiykqdJpQX6R\npl2nuaQJ1JotxFbx+lfJ1oCX9og/OWcjRkrJ/+8AlH7PBg2qdx2GvKacnzwOEuE5R5/ll/MZrz90\nHUh7eEibrtkR3vXpu90OXknM/ry5KcIMlu0ZMQAYHmNExysZM7IPaYbJlc2j/eD31HEEMFydD40S\nW4shmTO6n6O1RnQM2RIRZgZiAS8BYjnUrKNL45DHGtb1EDX6idZHEdSOmaj98zu5JyG6NvSP2HA7\nbvf8DRhdLqXl+/fvRDRlXXnjQLF+hiff5Ls/E+3PQ3/sh/48OGqpGf8+79h/I/ry+/MwiAjaXUfP\nf76z7rhuOQ/WmjbCGPHeLcWSMGcLRrzFc9S/5Qd1XtTJlwhN5izOS27RJFITbmRyrA3LKuc5ghGr\nDvSkJinlDKaysjXm19fXcfPAixN5M46XN+t3Kf2PugBFm3+GXLh5k4hHg0buPSABhLe4qRUk6FsG\nopM12tRExpAIom1pbrjehOF967pubAM1Ya2BSJtCcdbQVx8FtfUvN3UMtAmWmzPd3uWCX28CkSBJ\nLjb5bw5LUv0tIQM6imDljZ96g4iOrESFBkv7qnRn5RHdFiM3eXrDJzezKOxIX/XyIctIH6GpFRZu\nLVDU8UTrC7nz8uj5Q3WshYVENDEE2HXdRDDCbrquG48Y/s///A8RXfcFnY79fm/OnbJNRObj6FiI\n2hcaQ3Q8kfUxOnrGkN9Q24aCkcCGR7rRwpLSfEeEb8tBwjLr2J5+3mozVgtvzKiB3LjXrPeJfCEm\nShd6shHfr1+/EtH12Iv6CVpjro3SnlGmR36TxoqRYER45EDdsdLrtyxcYDfyqJ63tkN/d+xuEGrs\nOhqP+/AJGrYb2xGN50V6ebyG0zq464/cdxvqlCFmqRBHdRwZH2qB2ou1/1jSpvIoTSKRSCQSiUQi\nkUgkEokPi02P0lhsBQtSGxXRxkh/UamnFd5SbYyUTj6CJLoEzfKISPP6vqdv374R0XV56WvaUDmw\n9obje3l5Ga+YrGXYoHRt7WerOtV9xIrHkn5vkS6v70Wk/5Y7Rs2xD0sLpd8huvFcibEn4UeIaHnR\nNZ9RDVpEa1079ujyOhwOE8aWJ52vxSMwRWR5ISOcGvIdoqdrLacsU+1+B+i2ss4sg6lEU62tpOWj\nOrKuvC2104imUbrXfyM2CSoTdJ0oKkP+hoxDWu3eM1Jd0hp740ukn5XGYzRG8W/v2FOEaXFPeOME\nOvLgja+eJhsd9YhqDr1+j9qcLmPUp/R1tZIVhtq4FxZKn1fPurxKfQilQ0MybBjoeJKlmZWMLNR+\n5XEkdmMxvqTmXLJIEHON3et1qNRo63ygudPbA6zJ1vL6di08lgh65+2TSnso3YaYJdJ13eQ4KWJa\nRNljkTKJsLXQGhDVn2bkWmUZYZ8g1KyjvDVdLePi0BPtB+pHN5yv6UdGSMPkENrxIZzuwh7p+N1Q\n13sw7vF40ff9ZI1iHf3fEjX9uIRkjCQSiUQikUgkEolEIpH4sAgxRiJndiwpaI3fuawPKalG6fFQ\nqx3eQnJcKzWe649xOBxGaS9LS5GxJJRHT3Pq+ePwOb4fP35A95GwIu9qpau1mBtmKe3eWcUIPKl0\nSSPM39nInZSkW+3e0pIijVbNN/S7tsyX9hOkeYgwRyzmh/UtyhyoyUdE0y/dnU6nyXWXKKxa9gjS\nDN1akxCBVcfevFLDGEGMQsQiYlgGTImwAchIG9rv91V9ApWJfFoMiGj4SEuotZK73W5i1BwxRqR7\nS6ON8oPsrmiWl5V2Xc6ob5TO2qOyWIq1+ld0DPG0w/KpDeWiMkTGUJHdCa43ZCsE2eTQ7A4ZByp7\nywj84XBw6xHZCLLyI8vLYi+gNMj2LxkUVrrQ2CPd8riP4vTmKIbMg7dm1HXddfb1u8ieiBU+0Xvb\n0Nc7y7B0f0RGXufMZ0tRu0bx+lcNM6O05kZ7Mh2WZDBG5xMOx9Luz2Vm1O45kTvZLzWzylvjSjbo\n3L2cDEvXo3d9/HVg7w++ovdwuvzds3GRwdG+ay60CJlkNi7SXOdH2i5DczWPr3rtiPJ6T0TTkIyR\nRCKRSCQSiUQikUgkEh8WRcaIlqhHJGNLNbUW+KpY76q1WszVQjOiDJI1mCZeufKtL6ztZ/sdUlrO\n/k6n00QaGdXMe9Jlzy3XlaWJKaWh5H4L3ELCafUvBKQRmnOerqSpZAv++hxvJGx271nSt7TjUoNY\ny+TyEJFml+rAa+M1zA/LvY4DxeddaRhFTd+OIjK2rT0XRBEZm/S7ErOKf3v51eOcPDOvb0tB4cs+\n4l2Fp7WqUnuFGA2Wpg61S+kOaSPRFbkWrPB1/qN9yWNWWUBa1a7rXC1/JP/eeIr6xu44tU2BtOmM\n2n65dK2B+kFkvRf9dlWGg7ry3NuMKR1W3/eTsdC7Klfa30A3vWiWkmQyIO2tZr7IfFmMBKtt6TaE\nGDbeWsgr30h7RuHKPoHYg94YgsL0bGpplNghVvq7rhvLS99Y9Pr6Ooalb4aqRbRPeeVb+y0SPmKk\nIfaFBzT2oDjZnVwnWn1Cr291WlFb8spg7pp26Z7US9eccdbyY9npYej233fdcMXMhR1yHO7f3e+I\n+obHvcHNwAhpuo66IfjuMIx7TU8tM0XoOg0yXaMtotNwO02/ozPbIhE3TtbMzaX6s9yX6trar5dQ\nZXy11GhLfiVKdCrkjzusNpaj/aD4LEQWwZ6/aIUu3WSjspflxQ2Sj8jwt2/fvsG08qA2V+AQ2czJ\n3yyw4Yl2jlCrtoMtLfMtw7TC1/A2T6gPReIpDfA1C+vomDC33OQCdm4Y6JgYI9qPa8vEeudtEEth\n1xw1rC0vry1ZYc1d3DwCov1mzsIS+ZHXkzOQkUO08Ndp3O/3VzRm+YwKRlCatYBAbjaQwEK/Q2XJ\nyozSVexoc8q/vSt50ZEinQ5eyL29vU2+nU6nq6uOS3mU8cB+zun6NAg/vk+vHeUFJf/e7Xb05csX\nIrosLP/5z39Owpa4Rf+yxkRL+IPgfZO08Se6vsJd/q0FHU3TjGO63ARbgrpSH9b+0PEq7xrtyFgi\n20vkkgG05kDja+3ciwQwnuFEPXei/KMjgexPXn2MjK7r/CID01BY8jz0r5eLUVXLiL9sD9Igaw22\nWvfV1KMl/EDurO/eelKnjci/DhldN4/cRtqvt/6KlJGVL29Na7U9ZCh9K9SsAa3xomHBSHsdRnPY\nU9MPAqvz+35r33GfJepYhsUCkvGiXxnB8Ow62g1X/54GIfbxbYjnjejX8bpNIOFXFHOFGSicuWnI\nozSJRCKRSCQSiUQikUgkPiw2va53bTDLwcNS6dRcf3M02izN0tcflbRrCFqDqK8ns7BUA46+I/es\nOeR0/fjxI8RWQZJkbXgt0i4eFSXpaIkVVSMRjWoLIqhhqpTi87QGtWwdmS6kafTcW+kqxR3RpqNv\nKOxIPB7mSshRGHPDnatB3gLR8c+j9xLhNmSFLecCxMhgIMOcSLuq6cnSMKHW9sr2pcNE8cgnj6dS\nI6i1g0grjzR6nAY+0omuIZVPZJiT6H2+8MZIpF30ylJDGo6LjDkec+rq3d7WObF7ye5ETMpHwhrr\nJFSW2igq0uhrf6g+EbNIMkC8voo04ZaW2vsmw0JHZDRjRP6t/cl3aDzS37z+ZaXVyo9ka+j0IdYC\n18fpdJr0pePxODnKKsdEXZeItSLHyZFZN/Sv7ml6/OnQq6t8G6LTYdofo2tkmZ+159XIt1r3qM3V\nALGbrCuy2T06VqbdeiwSBNSXrPnLWjvq8NEROnR8u3Z9y4j6s+oFjWNFMMFNGVrtmoaOA/fhS/vO\n2P+8e99jvnRv9NK/t/9fA+WkH/8TZTG82PUNUTuU+RDPeYjn9NRQQ9fzt2S1ItyKkTMXyRhJJBKJ\nRCKRSCQSiUQi8WExmzGy1jmgSNiROOdqWiOSVw9rSJIZrEE6HA70/fv3sD+pjWSN08+fP8dvnhSz\nJt2W9idSX5YBLsu9Z2hSa0u9NDwKoumraeNRyTuKQ7fbT58+VTGVatknHmsDfbOM31lp8LTWWpth\nhaFRy2hCf9ecIa0tU1T/V785jOAYZY1lXjyRNMonejdXs1WK08Pc/HhhIUS0P0hrLb/pvoCun5S/\ntaFJqXlz24uRNi/d6LfFTJHaJBk3SldUA47yatmakNpxydLUBhkRkwfZrUB1u2ft5stQL0Db6bEJ\npBvPELXGkna85tqNgdoVYgDo9ErjfRbTR5a9ZCvo9i7HYMuOSNM0k+ugZb1ru0A6XJ3XGuPhiH3B\nbrqum7AvvPUb0uh7cSM7J97cWYpb54cvA5DfdXmha4fl07OfROep+9G+SaPiaXrqVH72+717hbOV\n1yVAdWCNoegdai9z1gzarceCKxkp5t+WjZHn52do480br6w+EWVhlMZVhp47pH9r/VaCOw4Pr3Y9\n0UBqgmw4K79WupjBwTXALI+u7agbWB6fzkO6eK57OdF+d22YtTkSsUXWZmRbDWloOzoMNkVa7oJD\nfOfj5Ydkfm4xr2ggVtAaSMZIIpFIJBKJRCKRSCQSiQ+L0HW9jFtIgCLpQO+stJUkfkslwV4aPGmo\n/MYsD765xTsTK/3K+H78+AHdIolyrZQZxY1+e2H9/fffRIQtvkfike9qtPBLENHCbc1UWdL/rLQh\nSbrU3qD4ajTsc9uXlP7W9CX5N9KuRNLw9PTk3l5jtbm+76nne8/6qdsaBlAtCwMxf65/c1zztB5W\nnPw70gaijJ97IZqfNeYJTxNUe2WsFZbU3iHGhKXt1n+zf6QdLH2zwrTilmWDbtJB5aHZJ7WMCW9c\nRSwX5A+dq9fXm3a7Sx1YeULaWKTZnJzlYTcAACAASURBVIu5bdsqe0+ja41paNxDfSLSLokwC8Gy\n14GuE0XX/I7XUIK27bGWEMvHW7/IuC3bDHJMQKwVi8kk8+iNr9KWi64DWY+ob3M5oSuJUT+0xiMZ\nN2KOIJaWNYZAmzRD9uVdG8zKJrrcnIMYyEuxxt6kNh79zmPKzgmXEbmhSfaz6FqRf1trBzT2lPLg\njSvSXekbGtsiaYFMq2b6vbS/nbxj9kl3uY2m5d38MFzs3nrqhrXp6TzkY1jiNn1P+yEMfjY9UcPX\n+XLUbCvruaHu/O756fX93Xlw+7rDdposBt/vgOrrehnexgUt3FFYVoHN2VixO02L9DY7pbAiqE2r\n54aFG4fDYdNGtCTsyGYOvdNXLNcKrKICmBo3UfelhaUXViSf0cG+Rjgh3Xlxchivr6/hPm3Fw98O\nh4O5QET5lb8RzZyf3uYRhYXyYbmJGj2EmzoqL+bRZgClx9sQWmFL91ffgFykph69zQBKYyTt1gJj\nzfHOCis6f20RP4rbu+5QliVvtiNX4fV9TxRYiCN/SDjhbfRqwpfQGyW0EfOuTixtkCIbEfR3rdDX\nW9QzkICD3fBxAzT2ok1NZF2FhGa36FuldKGNMtHFACaXhRQa1Gwa5CZbG3BFbVsKSrTgAV0BLKHH\nRdkGvXrRf6O5AEGWiUakzyFae2kzaPXHvu/HNXX0CAL/rdfinmCk1FdR+qx2v2t7evr1/vfbl0v9\n//nnn0RE9PXrVyJaVzAiUTPf6zZUWhuWxtk5yofS/InaP5rTiK6vSEfzV0TgiAQjc9dHXn7k+8g+\nJwK4hnbCLfXnSfsnGs99jGUzuD03PR2Hcy98lOxtGOoaImrVcZ7duaeW17KDQGXXDIqH/Y5O+7ch\nnm50T0S03/fEPRsJRtA48ejIozSJRCKRSCQSiUQikUgkPiw2v643okVcE9pQHUoLwlztylwtJNLs\naAOqlvva9K1Z9hHtjfet1n9tWmr9RaTL0XjWlCpH3NcyTWQcKIy5mlPt73Q6zW5zEVZIxL9HI5Wa\nlFFaXqCdRhggiDmyJWrHhKh7xBypYZjIv2vZPTWo7TdzxtCa8qqFpwlGYM3209PThIHHkJpTdD2m\n1t5JoLC0gUJU5jpM2b+k1kj3NUT591gYcp6c08eizCf0HpVXhFLutQ2+ylgyFpBxyFrW6xZMkShq\n4pQaejb8zWwNyeQosRuIsPFR+bTGeYvBppnH+uhWKSzNQtntduMxDnncSoeBriaV4eu/pfFl6wiN\nbEvaf2kt4K2ndVjWFbv8tzSsy9/G63dVflAaZFnpse18PtOnT5+I6NKvxnx1LR3eT6nT83Bd6euh\nJzpcs8rluvsWfUfW8dw1Xamv14TrrYu9tCIGo3cltUSEFRJljHh7DS8s7V6u6TyWHmSDbLC+kG4n\neaR+pIgwy2N00xC9DjaQ+bbq/TD0dE9Ez18+ExHR+fR+UqElonbM97u74xD4ueuoG96dBqnB2xBm\nu28ullgHNE3j1vu9EN0PJ2MkkUgkEolEIpFIJBKJxIfFJtf1RrTR1jsU9hxIqXwkvDXirJX+1UiL\nH+1c1lLmyNruI4hovRE86XJtfEv8oDRE0uX586TeqK/+LvA0iIfDYZRmS82T5T5y1lPD0/ZZsOrF\nCjvq3vKLfiO3UvqPtEoozEj+PY2TjmMuSpo0L31evaM8orBkGJ4hRwvSjTQWKLW00p1Xj9LWgHeV\nr/zGBsE5bmm/QYchNfzazgO6flbGjQzF8lPH4/VtGbdun4gpZmnMGbo8pYYblbl3nhqlxyobdF2x\nlaZbYE2tH+oTDMkOYPaILq++76E9CMke4TDYv2YfROd7yWDhJ6oj/m0ZTJV2S+RVtqgt8G/LMKvV\n/3U/iTBmLMO+1jjstXXkThpRRcZX9d9Ia4/86Lru+55+/vw5JIIdD3nuG+r7d3fn83v9v+06ak7X\n4xY/tQHlW6Kk0Y4yRUr+Im5L79Fc6M3zJQYHPy0jyl48so2X1mZWOmW+ImFoP6VwlwLlUf+tfzO7\no2UGCPcb6un17b2/nHfDu/5yrfXhNDCxBvZVuyfqB3enwVorj8Bd35O8ipi/WWuNOayaW7NOQoKR\nSKXv9/uQ9fQlDWhuQ18LkU1n1K9s5LWIbGqXpi+KNQQea6ZhzUWjLLu5nXpNRNpQzaQajS+6adwa\nkTrwJmt+Smo6mmitBWkpztq0RzdpF2rk8G4/PA87op9lo7Fe3BF/aOMWnaw8N3pDTYSN760FL/9W\nfqz+FRWyRsKU8yZKF5pXdVyyzXpjgnWMRc7fUqjBRxzQpl7f3KE3n9bfOu1oIeodiUP5Qe0ycqMM\nGuOle0sAhdKDhKuob2t/crMtj8+g/iHTUkqD9X0OrDa9tJ+iDTFR+cYWL32RMcRbM8jNmT7qgYwB\nS3/eGhht5nQa0MYH9RcP2h2aV2SY3pyD6sfqX7LNRuqjbVvT4KnV3kJlMTjvh+Sdjv2FGz9s6hq6\nHJfiIzh8+UHXdZsZYtWYuy9w1wnitzX/luKZs3nV6WF4R0V1e0RGO9E3tG5D+V9DSMJu5ox1S/al\nkfUEmqOuvg9PNrTafRredzQKDrm/NOeeDoNBVX7SmcuP6O15+HuYjtg7dZcwOpE8a/39OyCP0iQS\niUQikUgkEolEIpH4sCgyRqREypNcnc9nU1uC3Fvhare1VCYdxhqax6hkFeWxxl8prV55WX6l1NRK\np5e2CLZkiNQyUjwsoXJthbkMny3CntuHIswHbXgNxRulN8p3KG79DV0BPFfj7qGGORJ1f+WHtR8t\na726USOAtJFag1AqX0+75F3NiNx7WgL9TtKt56KWDTU3DI8psgSo/Vpu0DWMqB178aC+xJB1Z2l9\npPYuoqnz6leyYrT268uXL/T3339ffUNtFbU3T7ss2TERrSpa20TWORHGFJq/EYuEy9szxmr1ty3n\nMC8dtes3dMUuCluzlUphWppmGY9kNOmjY/J4lpU3mRZ9nMs6guPNXxFNu2R3WX3auvJa50GmAV3T\nq/PPYFbNy8vLaGCWjw7JsV3H2bbtxIiqPHKEru4209X11PX42263o56TLNqEPqrFzJFbMkaWwht7\n5Pc19kM1fiPrBJQ+CTT+eYwRL27rWUoXo3T1sfXNW6NG45bvI/uhiJv9cX8xNszp6vrxCl425No1\n78/zjsbV5liG5JehtXZYk3FYwtx1YTJGEolEIpFIJBKJRCKRSHxYbH5dr4c1tHylsG8ZRuQcGzoP\ntlSSGMXWLBovXJb0epL4WinuXNSe40Rxz01LbR5r+0ZJg2C58TRhpXR4bA3+5hk0i2jJLQaEV14R\n7S2K22OmWG6sdG+BMSWdb+cD5Z/fsQFANlhXKhvEGKjJ4xxty5bw2s1WdWeN86i/WH3USiO7adt2\nMscg7biG7EtSKxvR9tWWl9cu9bfv379P/En3tfF57BbtxvNnfdPpkhpOy1Dufr+fMH6QdjQCa6y6\nFWPEGnNrmSMozRZDyQoD1VGUwWMZgJTXCOu8yTpj5oTUeiPGiGUoWI6vnoFljw3FQGN11E6NZmh0\nXTfJm1zTsbFmZmOcz+fJmk8yRjj/h8E4Qbu/lIs2lIvYPfI3/82acFn2qJx0WuU36zr0rRBpn6hv\nozAkPEbSnPSV0uUxkWqZHLq/7Pf7kIFhhpy/POO+0bXtnDWDxWiJrM1r5qpSWMwKoSHe8/k8Lftd\nR4eBBdIMz5YNrSIKhcPakdA2Y0rrikdAMkYSiUQikUgkEolEIpFIfFgsZoxEpfM1mvCSZPR3gpbK\nSWm7tng+V/MW1fBHJMq1iDJHPNsSteF/JEQYIGuELyXikbYTbTeR85W17RJptnRYc8aeiBQfvfOk\n+Gto0y37C0T+9YseY+bl5QW6QWmWbpAtFu8WCO8scJSZUIN7zB3R8XcOrHC0plm69+pd+0Pji9TU\nWQyIvu/NK0nl+X35TV7FquPRWiXpRr9DGkrEFPPKAfVRqWHmfFjf+v5iF0W6t26vQSwEWX6edlQz\nFGrXWmvAYuKV5g3PXZT5wUBrCC+sKKPJYzChK3mt9oXswvBv2R8kQ0GzYFD/0jc0SfYlasfa/kq0\nvSBtOmJp8hqW5xB2+/nz5/Fvvs2q67rJOlfOY5zWt+7dzevPd3/H4/FqPOF4NFNE2i7T72R+EOtG\n35L15cuXMayvX7+Of98C0fki0tfm+l8yblh9O9rHvXkIzROoDyIGl3ebmE5DJJ1zUFNncxgj1voT\nsnbAmks+z4NNEZ6ZzkOS251dp9G26K0FS1ja7lFYHmZf1xt5F6UMaSDaUimM2gKbQ4uqnWCRe2Q4\nbW6le/mv3bBG/ZXSsSSstd3PGfCigp5abLFYLW0QInFGhAw6XCs+K406HisN8nvEGGd0UW6lqQae\nn7XaUIl2qfO62+0mR5RQfUp/cyc17V5e7+pNeLUL8S36SQTReGvps9F+qd/JskXlqzdL/K1tW3Nj\nhDb66Fpc2W40zRzVmQYyNCnD1xsedFWwTEtkLPAEJOg3Oqaixx4kZOL+9vb2djkGIIw4eld9IwEP\n/9abtN1uN4arja96fWkrWHNBTbxefdSGFxWuaDe6T8jNk3TD73S9NE1jCqqkoEOPy/KbjMcSjKCj\n1tKtbqtwEyT6hCVcR3OCFCQwZLr4eJs3l0ijqt44qdu0XB97R2n4KcvZ2lCjtU3TNKOxVj6byv3t\n06dPE6HUrealaDxrCEhq+tASROYOb10o24glsERrQdm/GBFjzaVvqNwi61uvzkoCEcuN5w+5u0oz\nPwdj/m1DtBu7xOB+Jxyr4L21OqorVI/3Wu+VkEdpEolEIpFIJBKJRCKRSHxYVF3Xy7+JsAY5qjGc\ni7WkS4/KCpjrP8qwQe6RQbOtmR63iqMmvFrJ6z2ANDS1/dEKs8QmsL6tXR5rjBOMiEa/5HaN+CxE\nWV6WO0/rU8pjDbVUakmlJhBdg2zlA/Uv7yjNo2gS5rTzUjlHNOdeWjxmgsUwsSC1OZE2JDWo+qiH\n1PCiPEbSpduGZJAg422IacPvWPvM1H8rvogmD12dirTJUWYcikP+LesYHT1aer31FojOOR6i/W3u\n+sGra9me//jjDyKaHqXo+34cAxFzxGIYeEwm9E4aUY5qmrWGVl+Fi9KFvrVtax7fkQZTtb/o/IWu\nZOZ3kqGmGSPSHYrb047DOWr43LUDO2h3qWseMzgNj3akZg3cYo61WA5em7bmiWgf8vLllS/X+dvb\nW4j54YWP1mjSTc1c4H1D7BvpxuoTV98adk/jFbzcy/i6XhlFpJ8hoHp9VOZIMkYSiUQikUgkEolE\nIpFIfFhUGV+do4XW7xgeC2WO5qFWY8pgKSGy/eH5eyTUlpfMz1xJ+Fasm7lhzdXoRtzNlR7fA9G+\nF+lznubbi8cKfw6iWrKaOuq6Dp5HtrQYnoQ/ClTOXr1IzGXrlDR5UVgaHq2hjGoQPI3DGrjXOITa\nPyM630Xrn995hgY9Y5VI64s0VFqjK+PhOZPj4esvUXwyzZEr25Fmi/0h2wzSP7pilJ/e+XAES2v/\n/Px8pUUvhRUePw6DrkpeZWrYGtFxV8f1wPDmr7Xj0cyn/X4/tm0ue2SDB52hl2HIb8iYrjQmqfuj\nDJ8hGSqoj2v7JDLNFtNCxiP7Opoz2a0uE9S/kF+GZLLospRlg+y06PEo8k3mTT45/To/T09P43X2\nqI9vjbX67z3GAW9d6LF71oxnLnR7s+JkLInbY3lY7yzGiOc+xBihy/PtOAYyvLsKmIiEbZICAwSt\nsfl56/2Ttba3kIyRRCKRSCQSiUQikUgkEh8Ws6/rjTA0Sv5rzrkvgRcWS4Y9xsia8DTbtX6XSCzX\nLHvP/S0kglH2SiQtt2aAlOIr1ZN3DtmSks7xF2EtRFkRKB/WtxLY76dPn4jock3gnDZcE/8SbUxE\nW4Ak+7VoWGN4GOripW6Mk/G23aAx+zRMGb/OrkbA01BuzRh5VHhnpvU7pF1B7/RZeKkBR0/v/LZ2\nX7Jjgdga+j2yJ+Ahwt5AcUk7HPomHXnDBLqxR2uDJRNAa98/f/5MRES/fv1ybYwgIFsh/By/tZex\nUGu0+Xk8Hsc0l7ScS1Cj1SQq112EKRVh9MwZLyLtStaLZ9/FClP+1v7Rdb1EU8YXh3E4HCYsEmnn\nSTMs0JgbhS5PeUuS7meIrSL7oM5H13WT/iUZJtbtL/L6XZnOiI0RjzEif/M77kNybOCre/lK4q3g\nrc3WCvMeKLEW5vThaNnM3WOVbmqy4vEYEKhPlPJeu5+KpFV/M+tFXT0z/u7lu2lYHrz1i3bzKGvB\n6ut6vc0WA018pXDR7yWIFvDcgW/NikSbx7mb+LlClrmYK4BYI55HCm8reOks9Uerj1ptpGZxWvIf\nGSd02NE6Qe5//foVTmcUnrAoIjwqoVS3Ne61v77vR+ojnZa19b7vL9a4fp7GeCzBSCnNaEKNCN4e\nAZE6Qxs+dHxLhmkZspXlLN3wu7e3tyv3cjOvNy7H49E0Dmkt4LzFj86P3ORo9+j60UiY6J0U8Hj9\nUG8sPcEQSg8S8PA4I+vAa6sy39rAZEkwtjteU/ylgITfofXL1n1m7qbG848Wyp4AZulYiwRj0tCo\nrlO9gSeiib+u68Y64n6JjshIQYEWjMj08oZd939pHBXlybvmVruV4SPBgh4v0HE0q79x2PrKYxmm\nTiuK2yojCSQYKc0h+v2JhrS07ZgulKc1scY6IoLIPqzkf2665gpGIhvv2jWUh7lrjto1bW26atdQ\npXf8G9XL+H1yN6+dPmuu1v3dm3ul/0dY8+VRmkQikUgkEolEIpFIJBIfFrOP0niIaI4t9zXhS8yV\nwvERmrka2lJalmpXtvK7VIK8pr9HC+sRJJZz4WkgSgyIuWwIRIeNhLUG+6KGkYLgjT01Y1fpnYeI\nZkSmI6KhuJK8A+bP0j6BtAQRf/JdNN+PikhZRrUkFrXU+maxdbxvsl9qWBoki0WB2BTSOKq+5nK/\n30MNOz/1kZWSdlFr0VH+taYalY0EG4+VLAyt7UKa+sjaQeYfjSsojO50zRjQzBwEr44fBdExaAvW\nGKp/3abbtjWPlXlHaUrfPCaDDh+xomRY3AbkEXCPwWSNL9INug7bChuFWZoLPa01YqboemmaxuyP\nv379Gt/po3QQTTPOi+M49Mu+ivzR4LHNSu8sN6i9LO17aF7xjGdH46xNl26/iMEYhZfmSHlHx2iv\nvyB3tayQSJziCzVDkQ03+FInsmCNL0TTMRTNw1u0vSVIxkgikUgkEolEIpFIJBKJD4siY0Rrfy1p\nTkkCFnE/l33x9PQ0nsfUEuVS+JFvyM2aYWksYZwsYd3MQbEchs+NctZvJJL7XbXPSxFlivB7j2FQ\nI8WVZ4jluzlhoTR7mr01zipGpNPoXPUajCtPil/LmPHK+x6IjI/R+rlFXjztasQP+l0DpJHmMDlc\nqWWT9gZ0mq02IY0d6nikhhYZTEXX9SKDidqfzIdOn0yndeUzKtPD4TBhX6B4/vrrLyIi+vbt25gH\nT2PIdiHkeys91rhkpSd6FaR8IsOdRJiZsGQMuRei/WypVhFpaFGdoXaP5iPNVkLX9Uau5m0a21By\niWGpWRFoTJBjCmJkyN/Sn25vEiUDr5YNI5l+zyCzzM/INjsMjNT2Mkbp8eLl5WVMN1+oINM0GV+e\n9tS84St4ZflyWv/1r3+Z+bolrD4zly2C3Ft5XLq2QH0ushbgb8/Pz3R6GcboIWs7bo4NUTuT3KP7\nc4lN4u1l12wfEcYIKkvv29w6oKahfqfy3dvsMXRV+JL2eGsWZDJGEolEIpFIJBKJRCKRSHxYrGpj\nBEm2vTPNjKXaV8tKd00Yc7FmPua4neN3a1bJraXq95bi3wueJozIZ3nU9FUZhsc+Qe88DStKp/bn\nnUusDYux3+9D40VJa6fjtNJk+YtoI+a6n9MnasaOWi1JRCP0u6GGRRQNS9uRQLdHIPf8PB6Pk9ss\npEYM1Z+Gxwrx2qDX90oaKm1/xIvnfD5Pzv4jjT4zReQ35M/SaKHyRm5lWjl8dKsF/81X/rItk/1+\n79oy4LCOgw2U3X5Pu+f3a5p3/7ouL3TN6b8L1jiPHmn30kaOZ68CtRetfWagq5+JLm2Cnxxf27Zj\nWLotnc/nyY0tiFmn0yDzgeaV6PrVGgtkGiLjhTe3Xd3+c54y0fTz8+fPLhtGj4n00r3bGTHi1mFp\nNk4NvDZ6a014BEsYvwgeW6EGLy8vl/7F5bYf0tL2sB0vHQtlXq2wInMiCtOKxwu/dn1oobZcSu69\nExponKhp9/foI9WCkcgGSbqpGXTnUmfQYLXm4iDa+LyJYu10aNSUV3Tjtka6mPI2txS2EBLVDuhr\nYG75lgRvXv+a21dRmmuELCju2jYXLa85why56Iz059qB3BIWleKx3nmToX5XWsBGwvLyuoT+bsU3\nN6x7w8tbbZq1oA5tlBHFFwlIkNFRflrpsa751YIKLw3y/ZqbALSwloZbkVv9NxE+gvP8/DwasKxp\nq9G5BZW9NJhJ9F7eo/DjeJzkccz3MIvudzva0fWxDF13j4yl65g56yrLPTI0KtOh24bsE7qfnc/n\nK8EG0XX9aEEHETYerNPLf3vGUSU4fD5S0vc9vb6+TvKtw4rME/I9Ehr88ccfRET048eP0b0eJ5Dg\nAo0v3BdQ//Q27LVKDyTg8sbXNTeVNXuG2k12CbeeV62NskyL5/6qvQxn80/9IKje+cKQmrHdW8eW\n/Jbi5XeR9WG03XhzkSecmFvvkfYVDbtmnXxL5FGaRCKRSCQSiUQikUgkEh8WIeOrjJJWOqK99sJi\nafv5fK4KqxQuwq0kU4hSvAVqpMxR/0vT6tYT4XQ9isQwiluygrw+hBgaljR2LpPLcoPYJzoMqe2K\nuEd5jKRxida+BiUNQqSuELxxIqLZQ++XMnOsOpg7pq2pvVgLa6bBKi/vvdZMjtT645HoP981v+0/\n37Wwsg9p6v7r66uphfbaoKU59gysaraC1ByjK7w1y0Nq3DXTQWqQ0TWnOiyZN51mqf3X7V1q0r1x\nyXKj30X6r77KWMbDx2xeX18n7JbuPDU4i45L3AtozinhVlprq24lM0vWnW5fqB3rspdjiGaVyLYh\nIa+bJaIrA6KarYX6MbMpmqaZpIfDlPnURoCfnp4mbBLUjr12LfPIx9dkWPpvxDpD35AxZM47lxOn\n3RuzrGNMDD1eyv0HWr/UttV7MTPWYH5K99aapmbNugTSiO6EFdQQebT0SDq8sf14PI7tnPtQZB1m\npcUrf82UKoVVk4ZoOufuB2W/iYwdSzGXhVrC48yqiUQikUgkEolEIpFIJBI3RpWNEU87jL5JIO21\nfiel39JdbRp1vGtJqpakZY00LNHq3gK1UtNbp2ENSX+N9n1rTXiUFYLSV8MU8PIfZYpJ7WhtnLeA\nV15EFyk+uiY0wmqLXAVXK6VHWshSGDXl67m1GAbSXylchHsyR9bSPlgaITRn6m+ayXA8HunwNX7+\nGsUtNc0eg1FrR9E32f5Zc6a1sVKrLv1pA6uSOaKZH7Kf6G9t207SqK8ole9kODIMnVbtT2qaI+lC\n35DWWrvf7XajO2SbAWnVpdFN+US4xxpgLnNka0TXh9bYhvoXuj4ZGd/1xlN9Xe/hcJgY8kV1Lb9p\nQ7HIloe0YcNungajvgzJ0pL51mGhskH+dJtABqURA8zzx5B2VPRYcDVG7AdWSPfuZr/fm3XMrC0Z\nxvfv3808RuEx0ErvLETWXuj70n3V0jC8+Uu3X5S3NZlyEaYgEVHXl+t9CSODoZlSDGtfvNb4vmS/\nUjOGbpWGNRESjEQ3QbVYGlZpc6LdzMWam+21/EbD2mrB8QiNl7F1HSPcmkZYiiNSz14/tjZzpfj6\nvp8IDUr+I4v46ES+VJAS9c8bVX10oeRXL9Y899ZkN0eAUsqPtxjw3qEFTA1q55BHGmdqgDZg3iZW\nf5PtRm+C94c9dYM1fnq73gRISr1uq6VFeEixwekEC9NSWHMEadH5C21OdTuTt/J4AgstIELf5Djm\nCZ5QmUTrRZcXcu+V8z0RrWPPndUerfYZGYe9evHSi4QMEQEJai/SHQszWDjBfb3v+4kAcTye1vfU\nDP3/CIRrKD2WoAO1M5l+NA97Bo9ZUKGP52h3/NvaBPd9Pzn2I/Oo07Xf7yc3z1zNVafr4w/eWqX5\nf5+o//v9xihkfPde8NZOteujrQWpUYENWld4AhENr+/K8lq61yzd9sX92DLkHcV+v68yoD133I8K\nuuYKv2TfRk9rvWO909hakJ5HaRKJRCKRSCQSiUQikUh8WISMr3oSuLnwNJRzwvYkprdgZtzC/xwJ\n2hwmxK3yeCupdc23JcyELb7NhSctr+3HFsOEf6MjcKW0WWFpN7UoMR+88L0+ZGkQS3mukcKX3Hoa\nt4h7Ly4v7hKTJTIueRqBaP3cCmuMXzVhIq2tDFv3r6ZpRkp4o1gEKCyvrdYyDpqLIzMe1C6lO/S0\nvi25TjTyzTOmaOXDQpR9o9NlMbN0uUqKtWWY81FRmldL7rYCOhaB5kf5ZO2wZnKcz+fRn+6zp9Np\ndMffdrudeSQKGZq8Oj7A15N203EVHSuz8nM8HicGTD1/paOgHlMEhaHdyHatjxCh/q/zTETUM7nt\nMJTfaztJg2eElU7deP0rs2G5nm5h7Lh2zKgJq3YNuFV/1G3Bu27cG/c9tp4Xr/QbTm9f7682bsRM\nqd0Xz3WH9n5z9+SltemjIxkjiUQikUgkEolEIpFIJD4sFtsYKX3ztNYM7x1Kh4c1NRARv1uHvzSs\nWunmLfOzpQSxVgpeo9kvfavB2uFEmFior3phRfsxwtaaTC+P2k0pXZHyWprO0rdIO6x1E4k7oo0v\nvZOoOSf6O2kSbp1mq69a9imk5gxdJ+p9i6CGCWK5t/yV0lFaM/B7Lwz97XA4zDamiMKOtHddB5ad\nBw3PsOyjM0YsWBpK9C0ajhembU0QBwAAIABJREFUhmRmyHrxzsBrBgcyGIqYIFpL3rbtJG3SWKvG\nVVqYKcLJarAdFPZn9Rd5JajHOov2aeTGattSqxyZo72xZ3fYj8Yx+/PQT57sskThjQaZv16u62WW\n1r36l1x76fcRWGVYGqu2WPvKuua2yuwrjymC+oQ1j5WwhJXsrTGt8diKo6Z8SyyhyHpNj1W1/Tna\nXiL9vibOqNu1kYyRRCKRSCQSiUQikUgkEh8Wi22MlL7VMkW0v1psLV16hHRFNeBz4l1DO35rlNK7\nBhtkjuT3HogyR2r66tx+LLH0XKYl6a9hpCH/KI1b16kVD4y374lYUdzoT347jbBIahkjSzVJj9Jf\n1hjHazTT0r3XHzWQjQ15O4PHCqnVwmoNndToav/yvb6a9Hw+j+mS9hS0zQCpZZOaaw5D+2Pt4vl8\nnlxlyvHJq3xlGETX7ABph0Fr+2T9oKuC5W/p3ruutxQWusqYNeCdo76aqzl9VETZQx4i7V8/9d+6\nTvmbx9ohwteys9vxVhkRprZTIsPx0npBz4mfpAHlS5dN3/cTxkzJ7g76W/uLaIt3u93kFg+ZV12G\n6OYdtgHy9OmZfjTvYXW/hjFn8N4dcdwcF98I9PLyMv7+9evX6I6I6OfPn1fp+10QGb9vlQYZN7/j\nMRqxQlDarb7g3Vh0EwzspKEJUt/GWIhoXLEQ3YMgd3reKsUXWUdH0+qNBV58KN5btdvNj9JYQBvw\nUmXU0G9qsbTA5/jfUlhyr3JYG0vSU+M3uuGLCE0erQyXwhOIonfIPWPJpBWNe2n4jMjGNYrRfy/i\n4VfexNETNa1agO5jAg7tpsad5TYiJPEmt0fpG1ukZ41NHQLaINWEH6FizxF+RcY9tCnjzYZ8Wps5\ntOD1No0oPn9jOY1Txqf9ouMv3jiBDFl69Sn7XMeL6+FoQPN8CVsf50Dp+t2xNB+RPoLq2BKWaPco\nnV6fQEIQLZSQYetvWrAiw0dCAxS3VyayjXsbJ2vORYJUnQ6J5+dn2g2TYPfr/cjK+XhJHwss+DiL\nPHqkx4vXXy/U74Z0cbzndhI//y2NXGqh7I8fP8YNe83VqVshsuG3ythrq3M3ujWw1k56bYGEhbp9\nScE28l8750aUajq95rvTEMbQbXZDszkDeXWt0KCEOULM0lztvfPWnHPXh1HcSuj176FmSCQSiUQi\nkUgkEolEIpGYgc2P0shwtHtG9F0Et9KWLJGg3gLReLaUwN1DcxWJs5YB8iiIUNGQ2yi7y2N5ROKO\nMgVqJPWeNtZLcynch8CQrFJ77HbLtfuW25LU3wurJu41sLQ+79kOavujF4Yse0+jja50tfrcHAaE\nvmpRPvWVoW3bTo62SG2sR/X1vukjK/IoDdJsoXdWmUc1exF3fd+bmlD5N6Kb66e8FtYyuHlvrJGe\nW2gHrbpDbAiGxeSQjAbd1q3jZcyGQEcJtAFX3a7lN7TWRowRL/8yDO3ea5fyG2rjuv9yvr5+/TqG\nseerddspwwqxAvTRs5eXF/M4mfSH2DaoDPnYnr6m91YaawRrDVTyI4Haya2AxmF0VE3XFWIy6XKw\n6j6y72x4HbajiRsPV/MkxzOwe/kYF2KMoPRZv4ns43meH/3ey5N3dHYuvPmrtJfYsl16871EMkYS\niUQikUgkEolEIpFIfFisZmOkhBrNMQo3qrXeGo+mmVmKiKZyLm553rmWKbLEjeVuC/ZJbXoi9Yg0\nYqW+bWkqLG13RFMRTauOJ4rIGIXSEvFXcuNdj1ZKi05XT33RnfXbch9lj5TiK4W5FGuOIfccj+6p\naYzYFYhqlySsdtI0zUS7jTR6UguLtLb6G0o3ekbyK586jaWxTee9xEjx3HvvGHoskcyER2WMrIE1\n+/1a+Pz5M72+vl6F681Rsl61jRHpVhswjs6lKC5tTFT6sbTxGjVlVhr/dd8fr8XtpRHOqVFj1LZ1\nupiZ46VDlr1nPBnlidk9XJYyvntgrfXkPecjBDSGIje6jj0bTvJvL99jbN2UMRZJswyDWSdyyRbZ\nFyA3PBYwe+n19XX2OhL95nGCDRgfDoexf/z48aMYjwwTzXc1TBGJrZnekXCTMZJIJBKJRCKRSCQS\niUTiw2I1GyORcLR7S0MNpXoFKU8Nm6RWcrUmbmX3QF9neC88qp2H2vR4Uuyl6Vjz3Gekn6F3Xt8u\nMUdqxgQkjUd5jsbjxWmd6S/ZU0Aautp6cfvdENR4neBwvNyS9Lttb/i2Hwzrnw8cBdZSzGGFlNIV\n0Qx45VdqX/fE3PhLfaDkHmmaPeYE+u31Y+1mv99XtQmdRhmP1OKxhrXrusntD1JLzt/Yr7zGUWvT\n27YdtWjedb36m+zj0gYEx3mkIfzmUt66H3u3J6Az4F49emFpv0QX7bW0V4E0p4k4SgwjBpfzjx8/\nJgwI1Pb0rUHWNdKy/3F6iIg+ffo0YSdE53a2W6LzSUS0G5773dDWqc52lzcmyOt63TXN8PvQNtQO\nd9G3SkXbNM2oyebn29vbGJZu/8fjceyr2r4L6vecXp1+jvtR161rIcqK2Cpub+1gsUJQX0V17LEH\nEVNQf+u7nnYDe2S8Kn0HyorXcW1PzdNwlTy9t69zYL7Uf+vfVv+XaT0ejyODDcUX6b/S5lHkNiqU\nnxrGyO/Qp0JHaSQ8YUZkQ1W7SVsDSxe3crJbq1JLjXApogKRWw2OtdS0ueHXbsoiKAndlgpNthgo\nPAGE1fcigsq5/RfFo1GiD9cIM1A+vG+1wo+IEAi5u1qk8cwKhgE0gU3yc5GL0PnQ86tQerwJ88IL\n5TB9IUtNPGacN8K9Frye8Ed/t9xIt3PbvRVfSVhTG19E+IPC17+bppkYPixd18sbKb2Jkob9ZJjj\nRpfD6Kd0fh1P6RphNP96aUbhe2VitY812/UcgbD0u3Z6bgmvrrQbz7/87dW7bktvb28TYYl3XS+K\nc/RPRKdRWPD+7jiQxfudf52qTjOKWwp3tGBTCpHkEZr3bwfqLpfrXsXfdd2Yfu7P+/2evn79ehWW\nd001Oooj3+nvcpPN6ecjNNqYdAmRtmGNkbfqM9E1zC3SgOYO9LTKv9S/POGfjrdp3/8R0eVMxV70\nszEJQz3uG+q66/bBayZrnRSZf7XgAn1D8wwK6/Pnz0RE9PPnz/Ed9y8WpErBI8MbG2oFI6U0PhLy\nKE0ikUgkEolEIpFIJBKJD4sq46tEtjYZabFKWmUvzFqJ0hZST30N4RpxPD8/j0+mQEkjWWvjntLg\nWrj0ywKWSiW3kGDeUvqPYGkELGm517c9RPqvxyZB15FF0uelBbnzxp6o+9qy0bhy3+B4tXtPu+AZ\nZtXvPCm+F2YkjehZwpL2VRMPSuvvDq9vW0DathLbQ9ep1Krq+ZGBruGVf+ujLlLTrN02zfSYiYwb\nHXVhDZjWCMsxRB51GOMeirLtLmFa5fz8/DzGg4xJehhd7C7UbV3O8riQPFbEbrT23VtzefCYgjq8\nOXgE5kh0fPXWq7LdWMdl+r6ftG3EAJJXwOrweU242+0mV8UilpNMg9cWdHp+gat/0XXA3jc0h4x9\n7m3o6/sdNcf3fHA7HtO5txkAfd/Tv/71LyK6rJllGHoskXlDY8LI0gRHaVAb5TD0cw1E5tJbIsIS\nmIsSs02XvXW1spVWGQ77+/TpExG9My2qGF9D0MfThcTLR2l6asbvez4CveP+RtSf69ZhpfyU4LFJ\npBvNMuO+hNKA1t+RfFz1+9+YJSKRjJFEIpFIJBKJRCKRSCQSHxZVxlet70RlGwDavXaHfst3kXRK\nbMGUWEPixRqBp6enUZq3BbaQ+t5S4vfomiaEW6c52k9Q3/DeeQyQKLvLPL8J3HtX6EmJd02aUVq8\nNHjjEoKlSS65n+PGZXdUfoswRsZ3jsWS30X6r+v6Vn106XzkaV5uodErAWm7UZjyb2QrhOiaMaLn\nRKkRRn/rMKXmkMHMC6lBhFcFDwwOtjGC0s7pfHt7M+2PEBUYHOrZNBe7KFLzhjR5OsxJ2AC1rBAU\n/iPMx1ugtL6NhoH+jsAqe4/5A1kufX+xi7AfwhB+2Ngqv7zqBzzWgDTVarnHcD+9t+em66nTbLN2\n6DdtN84xXpuWDDCvrqyrq9G8h+pJskM4Tm1jZA08el9akzFWExf/jthx6VWbkuM415lkcEWYI2wM\nn1oaO0MzPLuORoYft4QxlV1s7RbpQ7VtorRG1QZcpdFyzUSUbTzKFOFn9J0O+1GZJYuNr8r3NZR6\nFJa3mJi7sJzj9xb49u3b+HdkU7c1IvGskZYtGv2ag0k0vHttsKLuSoKSaP+t+RZJTyksDTlY16QZ\npcVLQykdc1ET5i0EI6W4avwtyZOEJVyb+y1CA30keJszlF65cNQUd1kmHjVehyWFDtK9voEDpU1v\nSNq2vfqb6H1Bpo/eyOMw8vYanS5WJkghqXXzDKJi8+/T6TQRcCChgQwT3S7Cv3W5yrjRYlCnRwqE\nvUWqvDWAv1nxWIgKr0qYuwaICrG3QlS5Z32T8ARi3o1Iui+hucc77iZ/T+bXnqjhTSAbheTNXUdE\nSgc3jhFNQ1ShVBn90PttHERE3bBh7GhaJn3TD7vKi79Dz0fCOmqHdHHZPD09EdF7+el2L//W/VKW\nCapPLRBFQlJ5tE8f+/HKQyLSPx5xDrKwVNBnrTUteMZ9kUAQ3Vjjje2eAL0V/eXQvX97GjrO6dTS\n4fN72/zevwvNmrYZ3fdDE90Pfa/thzmxqVuHHY9HeKuU5d5bO0j33JekEWE+csRzjnW7jQ4Lzfve\nOxROdK1bSgvRNnvkPEqTSCQSiUQikUgkEolE4sNiNeOr6J0nLYwwR6x3+ls0/Y/IHJHYKn2PlO9H\noxGukY5IG711fksS1Zp+eA9tXySetdPlMRPWDNNj00T8RZkQEW1XlDmC4rbCRxqBGoZKDR5pbIvC\n63saHmNG+ovULWI0yG8yTn5axzg8NmipX6K0stZKGhglejeWGGIzsrZPaAKRdhkxbBj87fA2sF0O\nU021ZOOgsrHKF+UfxS2111YYSNs5tw8hrXpp3F/CGrF+e/GsOdegtK81hpTm2cjRacRCQd8mZbkD\nV5PyQ6g/J+E2DY3HBsQn/nM/6E6ZFUIkGCPdMPbwbdc9HkM0U6YdrpbfnRraEWbfSFaUhKW19tha\nsp9KJojuv1Krzn/zcwlTZMs5KspyejREWCNojIswQKR/6/gmYkIy0+rc0XglLx/16vqeXn6+DH7f\nv52PwrM6X8NGWzvjOLKV/9fX10narOu5id7nS86bPjaD3Es38upeC7JMEYOHvyHjq1E2Y8RNzfpx\njf6WjJFEIpFIJBKJRCKRSCQSHxbVxldr2B2eVqnECvGYKTotCGtIUn9HbaTGGnnYSnMTCW9u3CUN\n6tK8rFUWt5DuR/uQ1ec87V1JqxjpoxGG2JJ4Hh3RturltZYxUsMeWcJk8VDLYFmDPfi7tJfacRtp\n/j14WhZZnzos70pteX5Za+/k30izp7W30uaGvppWXmU7aq1GzV43GjLVV3sizZtkZjyfB2Owp/ff\nh8OeXgatOPGzufjX7R4xRtCVxqi/6Dyez+dJGDJsfQ1jCR5bQ7+rbUtrAKVvzT4aWYdG3Mu/I+Ul\n3XB7RNfuSkPE/FtruWWY6F1NHV+FNTSh3dC4ux3R06/3/J8Gdsdgj5jaQzPaJvh5fteg06CEtuYs\nfe00f9t3DZ0HVTvbR2H7CrJ/SRaVbveeRhvZ5JGabf778+fPRHRtaFX3R4SlfWMJ+8rDPee4yFoT\nzTXyt+5Xsj4jjBEe/9u2nbQTbhPH43FsS8wKGtlKu7FJU9Nw+7+Yot8PfyB7vOOrwrDs1Q23Pba3\ng5ggEp7R4Zp4S2HXMkZ0nHP3X3PXlUv6VjJGEolEIpFIJBKJRCKRSHxYVNkY8Zgj6B2SiC7RDmt4\nEiEUTy0iZ5eWaC8fCZE0r32e8VaS7TWlk2tIYe+FUp+I9Dntv5a1sZUmsLbPrSFVLoW9VXhe+LWs\nkLXc6G8ei2QuW4VRo9FeWhdbjlFRJldNurz+heZVFKf0b91Kg+KRYWt/SAMuf3uaQO1+v9/D8Ino\n6upEdo+u65W53729a7uOg1H+ly/vzwP1tGNVOZuHEFlGmjNZPugpIb8h5odVvn0/vYYxqtm+Jyuk\nFr8Lu8uDTDu6zcbSwsp5Fd0cxbBYJRZkHyIias/teD11d+A0E709D+5Vs9ydic7fBqbI/ppNgtLT\nti397//+7/u74duXP/54j2/fUN9yUO/fnj6/s1G+f/8+loVknFiaaTnneH1JMrhYM//169cxfH7q\nW7IkIsycCNbod954vvZaay14+0IvzdHxVd72pdujbD/yBiTppu976sbwRJx84wxNPtWh7w3LI9dg\nBtMYPygbZrvgaOoZGt6c441V3jsUViRd92y7Vdf1lho0eldLrdLxeJu5qFBiy03QPSfvew7I0bCi\nm+WS2+gg/4gTwSPCE/pF+os3kUUFmxqPOpF72Cq9cwVwcycdz5/1rUZg42Fuv7/l5u5e47w359bC\nOuJSEy661jdyXEQaK9WbG7lJ4W+8MTkcDnjhKq76ld/kVb7sRtLztRHVruuoHZa6b4MxvX64qvHQ\nXuLZna+v9JTCjJGCDa7Rlb9lWRBdU7hluJwuq3+hYwMInkBkrb5zizF7jfZ/KwG4Na+iNa00nIj6\nixYIRtOC2qB+JwVrLXfp/hIWuzvy1b8cttjUjVE2F/8N33l6FPkehoVP56Ht/TntE+2wy2SDkNZG\n14MW+uj+JrHb7SZHeyJXjaL41hRwLPHvCV/vua4q7RGRW8u/Nb6isKR7dPSK618fWZH+xrDE/71o\n7yaGb4cT0U6565qeTkecZg+1dThnLWi5Q8KP0jGbyBzlYWnbtfpEBHmUJpFIJBKJRCKRSCQSicSH\nRRVjhCjG8kDvIhpq+a1GyojS58WzJXNkK6wR/j0oszXannsyBkrxepLUaBiPjBIbzNOEbYlSPN53\nr+3dKv01mifk7/n5mV5fX2fFp+OWWkhNwZzDGIm4r0kfeoe0N78jSsxHb56MvPPCQnOgZk5IIOZH\nrdYaaZCQu5pvjJKW0PpGdFFu75kP3Tf0OtxnetixRvCiCdZae6QlZo3jy8uL6c5j60S1a7JeLYN7\nZr4N7XZt33qEvuitHUvuo+n35gfEBiqFLccxFLZ3ZEP3VenPuwJYtl2P3QDf7Ye2enE0iZuvyN6z\no3NPHSfn/P7yud3R/o8/r9w1bNh131PHdJJBRSvZITpvXdfRf//3fxMR0bdv397DGOYx2b805FzH\n7LGnp6crJpmMWx7ZuWR/Wn6SibLmemKJhlymRWIt1uHaqNkXyneovCPjHmJw8fpKukH+Gu5/3hDC\nTJGBkHV4I9rxXDP4a/dEb+OxtRjjrwaRdVX0HRpzIlfzWu+seD3cY1+YjJFEIpFIJBKJRCKRSCQS\nHxbV1/XK90RlRkbkLFlUgxZhn0TSX5IyPhKWpm+O/1rt4JywH0GyfgvcKq65zAQvDCRdR25rNOA6\n3FJa57I8PCmzx4BBuGdbfX19rfLraQG8awg9fxG2lOcukkbGozCRtvB3by2d1y9Lc2IN80MyGjz2\niacxR1f5ovFIpwHZGLliWrA7oRJqumumCGsEe3ENoU6X1GZLew1Wn0HXFrfivkdt70Cmewz7aWAO\nnKY2ELyxGoWFNOCRNnHvNqxRmy5vjeq5l79rWIryfYTdJFki6ApfnQY2TCqNG3tp8eY5NoDa7Qrr\nds728OnQvv9x3nW0G7rC8Z2MQecd0dsTe+Z4ht9nonNzbViW+4S0LSSZHH///TcRTbX8Xr+XV19z\nPzudTvAacPnbwhZ7hjXDjDKYLH/3xJI1xFzGiC4vkzHC4QeS+Ma2wA+XTTbPOecDjUaH+apsZlr1\ntO5YG1m7RRmbHgPEWx/MZYpIWG15qzabjJFEIpFIJBKJRCKRSCQSHxZV1/US1Z3b96TypW9rsU9K\nqNEcr4214rrHOeGtNEj3YpREzhTPDXsr1KahRsMl3ZcYFl7/1e7nMkii2CqeiBYmGs7S8741Gs7S\nN09bsFa4Jf8IS8fxtd1r1DJASm5r2leJceMxM5D7mvBrGSM1TBOUrqaZ2vlA8z0674806OO3nXAj\nmBtE70wRIqKG7FsQZFjym9Z8I1sgukw6wUzx1lP9zwurxKojxEJA8PqsN+4/wry3Bkr9bYt8o37p\nMZ8s/5IdgrS22iaJbJefP38mosvtL1dxiqKwymV37keGCN+s0fK1vV1PnGzmUJ0ORMQ31Qx97jQY\nJ/H6F9H1rU38ZLsgaA7VDBMZDofPTBM0RqFbNlzmAMDSuX1t5khNeGuyZtdaL9WkIbKPLI3f+pv3\nTsZjpeFNMqYE9kMHYYYV943zE8gnd5+OqN9fvfLRXxgpfJdUB6gQ0Tndeof60q1Quw6Lotr4ag28\njhn9ViMgmeO+BrUDjYcl4dxDEFIT9pKGOtdvrRDkd17grZn2iFAxupn3Ni6/c3kTbVfma/uvFeLN\nFWrcQ4BYu8H38Lu0y5Iwc+m4h+ZGuQD02kKknaAFEx8NkMdSxmtxFR1eLrrkN017R8cMkJFTlEd0\n5MbKvzwihK7YRRtWfup3Uniiy0nGjTZuOk8lgYglLIsISPS3ue1vS6w9p6+dL2tNq9seY7fbTepd\nHq3R7+TGDRkM5ramhQ0obu9bt6PRCOXYu/rLox/uJm2PFz/Hp+NV3GP+iWi4KXvc8EnBoj62hgRC\nYxIKgkdP+FEaYy0gN7XCBWuzvRaQsGAO1uhf0X3YWn3P20ciAReqC+S+5hptCyyEPA078B1fBTyV\nh178jP+9CxWJiJr+IiTpG1Bu/XV8fTdv3Yb6iyc0sb5rePv8CNbck0vkUZpEIpFIJBKJRCKRSCQS\nHxarXddrfYu4Z3j+PK31rZkj98ASSe+tEdHGWhLoGk1uye3vohWOYut8RPqjhuXGKvut2Tq1Y4L+\nJr/XMiCi7Kk5UvF7frPczgl/q7qfG+6jjRE18yVyt7bW3GORWSwE+bfF0pDfpEY3oqmy0lNy4/mT\nqKHKW988xojH/JC/Ixo6hJpyekT2x1zM6ctIqxzxg+JdE97c07bthFnFRlj5O9HUaKuEpx330Oya\nCx0flQOXpWBr6eMvnNaubYlUlMgAKufxeDyOxlO1u9PpZLKhJCMLGUFmRBgdVhnVtAHpFtXNlrj1\nHqhWoz+3DyJ4a02ZLo/pjPoHKsO5DCNGO1I7Cv5GdtaQBskYAXllgkikvLwxx5vb5Vwl3UTWkbWM\nqQircw0kYySRSCQSiUQikUgkEonEh8VsGyP3YGtYYZQ0W4/EEKmVjG0V/tIwahgdlntPU+NJcbcM\na2tGQy3umRZUXp4b6XYNxs8SLBkT5qZnqcZxDW1J6VtNXJ5Ge430ROO+Beb0+3uxTVA9Lh33S3mY\n20ZrNU6Rb6UrgCN2CNB7j/mC3LL2Wto3QWm04vYYIF6ZRDFXS+jhkdZSUZTmschaVsJrXzVsI2/M\nsewc8FO/a9t2ZIhwmNwuPcPEtVpvogsTRRs5lfD6EDNG2rZ1+562vyJZITrutm3Hb+iKbWQM2mv7\nW7RzVP+3ilsjmvdbrc3uuYaI7letOVf2R405ZbkWC7Tkr6bM5zBGoumwMJe5uUabLQpG1hYsrCFQ\nWSp48SbKyGYwiq2EIFu7rwnzkYQIa+Ae+fkdyjCygPPcRtvLmu2qZsF7zwX/kkVBrd+acq31v8XG\nbY77OXW5pL1tQcX3+pD87glI1hxXaudtfTMGumWDgdLsCUaQu1K4NZg7b/e9bZ3fE9g0TTM5GjE3\nrWu0448Er148P9Zvr297QgAvXV786G8dvgxLtzMkNEFhyN+1AjcdBgsUdRq1P0+4yGF440ttmqU/\nS4ix5PhEdI9y7/Xg2vFvPTfNTUtNO5buvbYQEX7V1n90XF663kPuvbFt7rxcQkQggvbpa/avPEqT\nSCQSiUQikUgkEolE4sNi8XW9JU3SHDq7RbWytCNrskluiUdgfizFGscm5n5bMx7pZk1pdinOLSXn\nS8OuZV95/jwJr3zvMVNq8/PvwGqaq8Vc6s5yuyaTZ+1wl2Dtfr8F1tS81WpXIloZr16j1FcUD/8t\ntd21WiJ2GxlzIlp4/Teny/pWYoxEmTIoT2thrqbyd0fN+iXqPhIf0kLL+HT9e9pn2b70s+s6k5Ek\n+1KUAWFpzq1ysa4kbprpdcXyN2KMaIaIxxjxDJuifj9Hux/BrfrvvxuWrlUkIicD5rIrthonlzLZ\navxa7ucyRubCKkuLiYPqsZSWSH0lYySRSCQSiUQikUgkEonEh0WIMRLV+tRKziLapwjz49HYJLVn\nD+eGsaa/JVhLMz+XfbJE23sPFsktsLZmv6Zdlfx5/VijxABayjB5VFbJUibAmn5vyRxZA/eqyyWa\np7n9y4s7qkGZC2/uRBpciwHhae92ux00nKghbZp4TFTvXUQDVmLteHmMaI4RY+RWmNN+H3FuXHN9\nwFhjPPb649J1qGwvmskh+xBih6C4LUaW7F86TGsdjtwx2IhqLeNLX78rr/zW6ZNxltZ5+u9ofazJ\nen60/nQv1JRbqY/X7jWRG69PRBB1v5TBUvvNcxeZC2vCZ9SMc2vuhaPpTMZIIpFIJBKJRCKRSCQS\niQ+LKhsja7NCIm6WMj8sKfa9GCZrsElq3W2NtSTcUc30XMnlXM13SvDjmpaIv4h2JRLvEjwqU0Rj\nTa3BkjC27OOPglsz3yTW0Bhr/1v3r7U0oUjbzZCaYOvGl2gaLK2f9utdB8yI+pNPb83hMUYicc9F\n1K6C1y4fYSyNzvu12t2laUBlU7venauZlr81A8KrY28M8fx5/Vu682zxIKDwEWPEik++i7IKLHel\n8dVjE6B16xbspn83bM20YJTmYKtuUZ0hFpXHHqtJhw5rrW/oe2TsXKO9ovFuTdSmcbHxVRT5ErpS\nyU3J/RbCjH9HrLmYeYR17t/BAAACk0lEQVSFkYdHTde/CyKLp6j7GgFMrdDld0dNnu4tIFmLDnqr\nMXvt9rImHXbuMZslVFLLX+28GtnoIRq8dIsWpN7itbSw1e+QUEJ/8ww5ok0XWmBGBENbjFtWGdbg\n0ddQa+TRQ3RT4/nzNh01qJ1fkd/S5slyh4y1RtsuEnDqI3cybG/80gKR6FyF6nGNNl1Tt1u0iXui\nVpC2JJ65grQtERV6165zI+mfu0bbQkAyB2i+j6QngiXr1zxKk0gkEolEIpFIJBKJROLDopoxcgvN\ngSWBq9ESlTRcVj6QRLlWWzb3W6lM1yzzrbQpNW5qKV81UsxaiegSf48g5X+ENDBKaZlD50+KKcZa\nZbKEfjnXT9TN0nHvlpqj3yncUnwlxklU22OFEZmPS4yRCJtkLjtC+rOuHNX+IvNQtK95ebTCKtXZ\n0rZU0nTea4xeW6O59ni4BF4bqh0ba4ydljCX/S1ZHmgs4Cdiac1lVkX6SaRM1q7732lNEymfrRll\nNWP7PdhtW+yPl+6T1gh3TphrlcGS/MztX7MZI3Mnjq0yWVMA0Ul0zUVO5FtkU/47DaSJBMJWG+0t\n3CXujxz35mHLTTD6XtP3rDm4JPyWG6PItzWEIlZ6Iu+XwCsnz09tHInHQ3TtGG0Tc/tqKdxaN9H+\nxWm+pbDZepd95B0fpRxq5z30DrXzufPj74pIPubMcbdAU5C4PUYqE4lEIpFIJBKJRCKRSCQWoO97\nSGtxBSOJRCKRSCQSiUQikUgkEv/OSOOriUQikUgkEolEIpFIJD4sUjCSSCQSiUQikUgkEolE4sMi\nBSOJRCKRSCQSiUQikUgkPixSMJJIJBKJRCKRSCQSiUTiwyIFI4lEIpFIJBKJRCKRSCQ+LP4/V/jU\n8xLvTnAAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7fc3e4fd63d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"pylab.rcParams['figure.figsize'] = (11, 2.5)\n",
"\n",
"#del Final_map\n",
"#del Fmaps\n",
"\n",
"if S[2]>5:\n",
" Final_map=np.zeros([S[0],S[1],5,3])\n",
" Fmaps=np.zeros([S[0],S[1],5,3])\n",
"else:\n",
" Final_map=np.zeros([S[0],S[1],3]) \n",
" Fmaps=np.zeros([S[0],S[1],3]) \n",
"C=np.zeros([S[3],3])\n",
"C1=np.zeros([6,3])\n",
"C1[0][:]=(1,0,0)\n",
"C1[1][:]=(0,1,0)\n",
"C1[2][:]=(0,0,1)\n",
"C1[3][:]=(0.8,0.8,0)\n",
"C1[4][:]=(0,1,1)\n",
"C1[5][:]=(1,0,1)\n",
"S1=DT.shape\n",
"\n",
"C=np.zeros((S[3],3))\n",
"i=1\n",
"l=0\n",
"Betas2=Betas\n",
"for j in range(S[3]): \n",
" if Betas2[0,j]>0.6*np.max(Betas2[0,:]):\n",
" #if 1>0.1:\n",
" #C[j,:]=C1[i%6][:]\n",
" C[j,2]=1\n",
" C[j,1]=i/2\n",
" #C[j,2]=1\n",
" for k in range(3): \n",
" M=np.max(np.squeeze(np.reshape(D2[:,:,:,j],S[0]*S[1]*5)))\n",
" Fmaps[:,:,:,k]=0.75*D2[:,:,:,j]*C[j,k]/M\n",
" Final_map=Final_map+Fmaps\n",
" #Betas[0,j]=0\n",
" #print(Indexo[j])\n",
" i=i+1\n",
" l=l+1\n",
" print(j+1)\n",
" print(Rsq[:,j])\n",
" #if l==2:\n",
" #break\n",
" \n",
"\n",
"C=np.zeros((S[3],3))\n",
"i=1\n",
"l=0\n",
"Betas2=Betas\n",
"for j in range(S[3]): \n",
" if Betas2[1,j]>0.6*np.max(Betas2[1,:]):\n",
" #if 1>0.1:\n",
" #C[j,:]=C1[i%6][:]\n",
" C[j,0]=1\n",
" C[j,1]=1-i/2\n",
" #C[j,2]=1\n",
" for k in range(3): \n",
" M=np.max(np.squeeze(np.reshape(D2[:,:,:,j],S[0]*S[1]*5)))\n",
" Fmaps[:,:,:,k]=0.75*D2[:,:,:,j]*C[j,k]/M\n",
" Final_map=Final_map+Fmaps\n",
" #Betas2[1,j]=0\n",
" #print(Indexo[j])\n",
" i=i+1\n",
" l=l+1\n",
" print(j+1)\n",
" print(C[j,:])\n",
" #if l==2:\n",
" # break\n",
"\n",
"pylab.rcParams['figure.figsize'] = (15, 6)\n",
"C2=np.zeros(3)\n",
"\n",
"Df=np.zeros([S[0],S[1],5,3]) \n",
" \n",
"for i in range(3):\n",
" Df[:,:,:,i]=Final_map[:,:,:,i]+Dmean/15\n",
" #Df=Df/(np.max(np.max(np.max(Df),3)))\n",
"if S[2]>5:\n",
" N=Nstack\n",
"else:\n",
" N=S[2]\n",
"for i in range(N):\n",
" #if Good_ICs[j]:\n",
" plt.subplot(1,N,i+1)\n",
" plt.imshow(Df[:,:,i],cmap=plt.cm.gray)\n",
" plt.imshow(Df[:,:,i,:],cmap=my_cmap,interpolation='none')\n",
" frame1 = plt.gca()\n",
" frame1.axes.get_xaxis().set_visible(False)\n",
" frame1.axes.get_yaxis().set_visible(False)\n",
"plt.tight_layout(pad=0,w_pad=0,h_pad=0)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.12"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| bsd-2-clause |
wrobstory/sticky | examples/sticky_examples.ipynb | 2 | 27016 | {
"metadata": {
"name": "",
"signature": "sha256:ec3cfb790044436975aa4e3e830dafede7485be41677fcd59316a6fb326c55f9"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "code",
"collapsed": false,
"input": [
"import sticky\n",
"import pandas as pd\n",
"from IPython.core.display import display, Javascript\n",
"from IPython.html.widgets import interact\n",
"\n",
"sticky.initialize_notebook()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<script>\n",
"\n",
" function load_sticky_libs(){\n",
" console.log('Loading Sticky libraries...')\n",
" libs = {\n",
" 'd3plus': 'http://wrobstory.github.io/d3plus/d3plus.js',\n",
" 'micropolar': 'http://wrobstory.github.io/micropolar/micropolar.js',\n",
" 'c3': 'http://wrobstory.github.io/c3/c3.js'\n",
" }\n",
" lib_names = Object.keys(libs)\n",
" for (var i=0; i < lib_names.length; i++){\n",
" lib_name = lib_names[i];\n",
" if (window[lib_name] === undefined){\n",
" function getscript(lib_name){\n",
" $.getScript(libs[lib_name], function(){\n",
" console.log(lib_name + \" loaded...\")\n",
" })};\n",
" getscript(lib_name)\n",
" }\n",
" }\n",
" };\n",
"\n",
" if(typeof define === \"function\" && define.amd){\n",
" var load_paths = {\n",
" paths: {\n",
" d3: 'http://d3js.org/d3.v3.min'\n",
" }\n",
" };\n",
" var libs = ['d3'];\n",
" for (var i=0; i < libs.length; i++){\n",
" lib = libs[i]\n",
" if (window[lib] !== undefined){\n",
" delete load_paths.paths[lib]\n",
" };\n",
" };\n",
" if (Object.keys(load_paths.paths).length != 0){\n",
" require.config(load_paths);\n",
" require([\"d3\"], function(d3){\n",
" console.log('D3 Loaded...')\n",
" window.d3 = d3;\n",
" load_sticky_libs();\n",
" });\n",
" } else {\n",
" load_sticky_libs();\n",
" };\n",
"\n",
" }else{\n",
" console.log('Require.js not found!');\n",
" throw \"Require.js not found!\"\n",
" };\n",
"\n",
"</script>"
],
"metadata": {},
"output_type": "display_data",
"text": [
"<IPython.core.display.HTML at 0x10e717c90>"
]
},
{
"html": [
"<link rel=\"stylesheet\" href=\"http://alexandersimoes.github.io/d3plus/css/d3plus.css\" />"
],
"metadata": {},
"output_type": "display_data",
"text": [
"<IPython.core.display.HTML at 0x10e6f3050>"
]
}
],
"prompt_number": 33
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"mic = sticky.Micropolar(height=250, width=250)\n",
"mic.plot()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"javascript": [
"require([\"widgets/js/widget\"], function(WidgetManager){\n",
"\n",
" // Define the DOM Creation view for Sticky charts\n",
" var StickyDOMWidget = IPython.DOMWidgetView.extend({\n",
" render: function(){\n",
" var chart_id = this.model.get('chart_id');\n",
" var chart_elm = '<div class=\"' + chart_id + '\"></div>';\n",
" $(chart_elm).appendTo(this.$el);\n",
" },\n",
" });\n",
" // Register the DOM Renderer with the Widget Manager\n",
" WidgetManager.register_widget_view('StickyDOMWidget', StickyDOMWidget);\n",
"});"
],
"metadata": {},
"output_type": "display_data",
"text": [
"<IPython.core.display.Javascript at 0x10d340c90>"
]
},
{
"javascript": [
"//Micropolar Library DOM Creator and Renderer\n",
"\n",
"require([\"widgets/js/widget\"], function(WidgetManager){\n",
"\n",
" // Define the DOM Cration View For Micropolar\n",
" var MicropolarDOM = IPython.DOMWidgetView.extend({\n",
" render: function(){\n",
" var chart_id = this.model.get('chart_id');\n",
" var chart_elm = '<div class=\"' + chart_id + '\"></div>';\n",
" $(chart_elm).appendTo(this.$el);\n",
" },\n",
" });\n",
" // Register the DOM Renderer with the Widget Manager\n",
" WidgetManager.register_widget_view('MicropolarDOM', MicropolarDOM);\n",
"});\n",
"\n",
"require([\"widgets/js/widget\"], function(WidgetManager){\n",
"\n",
" // Define the DOM Rendering View\n",
" var MicropolarRender = IPython.DOMWidgetView.extend({\n",
" render: function(){\n",
" var chart_id = '.' + this.model.get('chart_id');\n",
" var polarPlot = micropolar.DotPlot();\n",
" this.$plot_config = {\n",
" geometry: polarPlot,\n",
" data: [[0, 500], [1, 1000], [3, 2000]],\n",
" height: this.model.get('height'),\n",
" width: this.model.get('width'),\n",
" angularDomain: [0, 2000],\n",
" angularTicksStep: 400,\n",
" minorTicks: 1,\n",
" flip: false,\n",
" originTheta: 0,\n",
" radialAxisTheta: -15,\n",
" containerSelector: chart_id\n",
" };\n",
" this.$micropolar_chart = micropolar.Axis().config(this.$plot_config);\n",
" this.$micropolar_chart();\n",
" },\n",
"\n",
" update: function(){\n",
" this.$plot_config.height = this.model.get('height');\n",
" this.$plot_config.width = this.model.get('width');\n",
" this.$micropolar_chart.config(this.$plot_config);\n",
" this.$micropolar_chart();\n",
" return MicropolarRender.__super__.update.apply(this);\n",
" }\n",
" });\n",
" // Register the DOM Rendering View\n",
" WidgetManager.register_widget_view('Micropolar', MicropolarRender);\n",
"});"
],
"metadata": {},
"output_type": "display_data",
"text": [
"<IPython.core.display.Javascript at 0x10e6f3850>"
]
},
{
"javascript": [
"require([\"widgets/js/widget\"], function(WidgetManager){\n",
"\n",
" // Define the DOM Creation view for Sticky charts\n",
" var StickyDOMWidget = IPython.DOMWidgetView.extend({\n",
" render: function(){\n",
" var chart_id = this.model.get('chart_id');\n",
" var chart_elm = '<div class=\"' + chart_id + '\"></div>';\n",
" $(chart_elm).appendTo(this.$el);\n",
" },\n",
" });\n",
" // Register the DOM Renderer with the Widget Manager\n",
" WidgetManager.register_widget_view('StickyDOMWidget', StickyDOMWidget);\n",
"});"
],
"metadata": {},
"output_type": "display_data",
"text": [
"<IPython.core.display.Javascript at 0x10e717a50>"
]
},
{
"javascript": [
"//Micropolar Library DOM Creator and Renderer\n",
"\n",
"require([\"widgets/js/widget\"], function(WidgetManager){\n",
"\n",
" // Define the DOM Cration View For Micropolar\n",
" var MicropolarDOM = IPython.DOMWidgetView.extend({\n",
" render: function(){\n",
" var chart_id = this.model.get('chart_id');\n",
" var chart_elm = '<div class=\"' + chart_id + '\"></div>';\n",
" $(chart_elm).appendTo(this.$el);\n",
" },\n",
" });\n",
" // Register the DOM Renderer with the Widget Manager\n",
" WidgetManager.register_widget_view('MicropolarDOM', MicropolarDOM);\n",
"});\n",
"\n",
"require([\"widgets/js/widget\"], function(WidgetManager){\n",
"\n",
" // Define the DOM Rendering View\n",
" var MicropolarRender = IPython.DOMWidgetView.extend({\n",
" render: function(){\n",
" var chart_id = '.' + this.model.get('chart_id');\n",
" var polarPlot = micropolar.DotPlot();\n",
" this.$plot_config = {\n",
" geometry: polarPlot,\n",
" data: [[0, 500], [1, 1000], [3, 2000]],\n",
" height: this.model.get('height'),\n",
" width: this.model.get('width'),\n",
" angularDomain: [0, 2000],\n",
" angularTicksStep: 400,\n",
" minorTicks: 1,\n",
" flip: false,\n",
" originTheta: 0,\n",
" radialAxisTheta: -15,\n",
" containerSelector: chart_id\n",
" };\n",
" this.$micropolar_chart = micropolar.Axis().config(this.$plot_config);\n",
" this.$micropolar_chart();\n",
" },\n",
"\n",
" update: function(){\n",
" this.$plot_config.height = this.model.get('height');\n",
" this.$plot_config.width = this.model.get('width');\n",
" this.$micropolar_chart.config(this.$plot_config);\n",
" this.$micropolar_chart();\n",
" return MicropolarRender.__super__.update.apply(this);\n",
" }\n",
" });\n",
" // Register the DOM Rendering View\n",
" WidgetManager.register_widget_view('Micropolar', MicropolarRender);\n",
"});"
],
"metadata": {},
"output_type": "display_data",
"text": [
"<IPython.core.display.Javascript at 0x10e717b10>"
]
}
],
"prompt_number": 34
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"dat = {\n",
"'data_1': [\n",
" {\"year\": 1991, \"name\":\"alpha\", \"value\": 15},\n",
" {\"year\": 1992, \"name\":\"alpha\", \"value\": 20},\n",
" {\"year\": 1994, \"name\":\"alpha\", \"value\": 30},\n",
" {\"year\": 1995, \"name\":\"alpha\", \"value\": 60},\n",
" {\"year\": 1993, \"name\":\"beta\", \"value\": 40},\n",
" {\"year\": 1994, \"name\":\"beta\", \"value\": 60},\n",
" {\"year\": 1995, \"name\":\"beta\", \"value\": 10},\n",
" {\"year\": 1994, \"name\":\"gamma\", \"value\": 35},\n",
" {\"year\": 1995, \"name\":\"gamma\", \"value\": 40}\n",
" ],\n",
"'data_2': [\n",
" {\"year\": 1991, \"name\":\"alpha\", \"value\": 30},\n",
" {\"year\": 1992, \"name\":\"alpha\", \"value\": 20},\n",
" {\"year\": 1994, \"name\":\"alpha\", \"value\": 50},\n",
" {\"year\": 1995, \"name\":\"alpha\", \"value\": 60},\n",
" {\"year\": 1993, \"name\":\"beta\", \"value\": 32},\n",
" {\"year\": 1994, \"name\":\"beta\", \"value\": 60},\n",
" {\"year\": 1995, \"name\":\"beta\", \"value\": 56},\n",
" {\"year\": 1994, \"name\":\"gamma\", \"value\": 19},\n",
" {\"year\": 1995, \"name\":\"gamma\", \"value\": 40}\n",
" ],\n",
"'data_3': [\n",
" {\"year\": 1991, \"name\":\"alpha\", \"value\": 20},\n",
" {\"year\": 1992, \"name\":\"alpha\", \"value\": 30},\n",
" {\"year\": 1994, \"name\":\"alpha\", \"value\": 40},\n",
" {\"year\": 1995, \"name\":\"alpha\", \"value\": 60},\n",
" {\"year\": 1993, \"name\":\"beta\", \"value\": 10},\n",
" {\"year\": 1994, \"name\":\"beta\", \"value\": 40},\n",
" {\"year\": 1995, \"name\":\"beta\", \"value\": 35},\n",
" {\"year\": 1994, \"name\":\"gamma\", \"value\": 45},\n",
" {\"year\": 1995, \"name\":\"gamma\", \"value\": 20}\n",
" ]\n",
"}\n",
"area_chart = (sticky.d3Plus()\n",
" .stacked_area(width=1000, height=500)\n",
" .data(dat['data_1'])\n",
" .key('name')\n",
" .x('year')\n",
" .y('value'))\n",
"area_chart.plot()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"javascript": [
"require([\"widgets/js/widget\"], function(WidgetManager){\n",
"\n",
" // Define the DOM Creation view for Sticky charts\n",
" var StickyDOMWidget = IPython.DOMWidgetView.extend({\n",
" render: function(){\n",
" var chart_id = this.model.get('chart_id');\n",
" var chart_elm = '<div class=\"' + chart_id + '\"></div>';\n",
" $(chart_elm).appendTo(this.$el);\n",
" },\n",
" });\n",
" // Register the DOM Renderer with the Widget Manager\n",
" WidgetManager.register_widget_view('StickyDOMWidget', StickyDOMWidget);\n",
"});"
],
"metadata": {},
"output_type": "display_data",
"text": [
"<IPython.core.display.Javascript at 0x10fa98a90>"
]
},
{
"javascript": [
"//D3 Plus Library Renderer\n",
"\n",
"require([\"widgets/js/widget\"], function(WidgetManager){\n",
"\n",
" var d3plus_charts = {};\n",
"\n",
" function build_chart(chart, model, chart_id){\n",
" var data = JSON.parse(model.get('model_data'));\n",
" chart.container(chart_id)\n",
" .height(model.get('model_height'))\n",
" .width(model.get('model_width'))\n",
" .data(data)\n",
" .type(model.get('chart_type'))\n",
" .id(model.get('model_key'))\n",
" .text(model.get('model_key'))\n",
" .y(model.get('model_y'))\n",
" .x(model.get('model_x'));\n",
" }\n",
"\n",
" var bounced_builder = _.debounce(build_chart, 300, true);\n",
"\n",
" // Define the DOM Rendering View\n",
" var D3PlusRenderer = IPython.DOMWidgetView.extend({\n",
" render: function(){\n",
" var chart_id = '.' + this.model.get('chart_id');\n",
" // Instantiate d3plus\n",
" d3plus_charts[chart_id] = d3plus.viz();\n",
" build_chart(d3plus_charts[chart_id], this.model, chart_id);\n",
" // Draw\n",
" d3plus_charts[chart_id].draw();\n",
" },\n",
"\n",
" update: function(){\n",
" var chart_id = '.' + this.model.get('chart_id');\n",
" var chart = d3plus_charts[chart_id];\n",
" // Something of a hack\n",
" bounced_builder(chart, this.model, chart_id);\n",
" chart.draw();\n",
" }\n",
" });\n",
" // Register the DOM Rendering View\n",
" WidgetManager.register_widget_view('D3Plus', D3PlusRenderer);\n",
"});"
],
"metadata": {},
"output_type": "display_data",
"text": [
"<IPython.core.display.Javascript at 0x10d340c90>"
]
}
],
"prompt_number": 35
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"line_chart = (sticky.d3Plus()\n",
" .line(width=1000, height=500)\n",
" .data(dat['data_1'])\n",
" .key('name')\n",
" .x('year')\n",
" .y('value'))\n",
"line_chart.plot()\n",
"@interact\n",
"def update_chart(data=['data_1', 'data_2', 'data_3']):\n",
" line_chart.update(data=dat[data])"
],
"language": "python",
"metadata": {},
"outputs": [
{
"javascript": [
"require([\"widgets/js/widget\"], function(WidgetManager){\n",
"\n",
" // Define the DOM Creation view for Sticky charts\n",
" var StickyDOMWidget = IPython.DOMWidgetView.extend({\n",
" render: function(){\n",
" var chart_id = this.model.get('chart_id');\n",
" var chart_elm = '<div class=\"' + chart_id + '\"></div>';\n",
" $(chart_elm).appendTo(this.$el);\n",
" },\n",
" });\n",
" // Register the DOM Renderer with the Widget Manager\n",
" WidgetManager.register_widget_view('StickyDOMWidget', StickyDOMWidget);\n",
"});"
],
"metadata": {},
"output_type": "display_data",
"text": [
"<IPython.core.display.Javascript at 0x10e6a1c90>"
]
},
{
"javascript": [
"//D3 Plus Library Renderer\n",
"\n",
"require([\"widgets/js/widget\"], function(WidgetManager){\n",
"\n",
" var d3plus_charts = {};\n",
"\n",
" function build_chart(chart, model, chart_id){\n",
" var data = JSON.parse(model.get('model_data'));\n",
" chart.container(chart_id)\n",
" .height(model.get('model_height'))\n",
" .width(model.get('model_width'))\n",
" .data(data)\n",
" .type(model.get('chart_type'))\n",
" .id(model.get('model_key'))\n",
" .text(model.get('model_key'))\n",
" .y(model.get('model_y'))\n",
" .x(model.get('model_x'));\n",
" }\n",
"\n",
" var bounced_builder = _.debounce(build_chart, 300, true);\n",
"\n",
" // Define the DOM Rendering View\n",
" var D3PlusRenderer = IPython.DOMWidgetView.extend({\n",
" render: function(){\n",
" var chart_id = '.' + this.model.get('chart_id');\n",
" // Instantiate d3plus\n",
" d3plus_charts[chart_id] = d3plus.viz();\n",
" build_chart(d3plus_charts[chart_id], this.model, chart_id);\n",
" // Draw\n",
" d3plus_charts[chart_id].draw();\n",
" },\n",
"\n",
" update: function(){\n",
" var chart_id = '.' + this.model.get('chart_id');\n",
" var chart = d3plus_charts[chart_id];\n",
" // Something of a hack\n",
" bounced_builder(chart, this.model, chart_id);\n",
" chart.draw();\n",
" }\n",
" });\n",
" // Register the DOM Rendering View\n",
" WidgetManager.register_widget_view('D3Plus', D3PlusRenderer);\n",
"});"
],
"metadata": {},
"output_type": "display_data",
"text": [
"<IPython.core.display.Javascript at 0x10e6a1c50>"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\r"
]
},
{
"output_type": "stream",
"stream": "stderr",
"text": [
"\r"
]
}
],
"prompt_number": 36
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"dat2 = {\n",
" 'data_1': [\n",
" {\"value\": 100, \"weight\": .45, \"name\": \"alpha\", \"group\": \"group 1\"},\n",
" {\"value\": 70, \"weight\": .60, \"name\": \"beta\", \"group\": \"group 2\"},\n",
" {\"value\": 40, \"weight\": -.2, \"name\": \"gamma\", \"group\": \"group 2\"},\n",
" {\"value\": 15, \"weight\": .1, \"name\": \"delta\", \"group\": \"group 2\"},\n",
" {\"value\": 5, \"weight\": -.43, \"name\": \"epsilon\", \"group\": \"group 1\"},\n",
" {\"value\": 1, \"weight\": 0, \"name\": \"zeta\", \"group\": \"group 1\"}\n",
" ],\n",
" 'data_2': [\n",
" {\"value\": 100, \"weight\": .45, \"name\": \"alpha\", \"group\": \"group 1\"},\n",
" {\"value\": 87, \"weight\": .60, \"name\": \"beta\", \"group\": \"group 1\"},\n",
" {\"value\": 79, \"weight\": -.2, \"name\": \"gamma\", \"group\": \"group 1\"},\n",
" {\"value\": 88, \"weight\": .1, \"name\": \"delta\", \"group\": \"group 1\"},\n",
" {\"value\": 5, \"weight\": -.43, \"name\": \"epsilon\", \"group\": \"group 2\"},\n",
" {\"value\": 1, \"weight\": 0, \"name\": \"zeta\", \"group\": \"group 2\"},\n",
" {\"value\": 15, \"weight\": .45, \"name\": \"alpha\", \"group\": \"group 2\"},\n",
" {\"value\": 7, \"weight\": .60, \"name\": \"beta\", \"group\": \"group 2\"},\n",
" {\"value\": 40, \"weight\": -.2, \"name\": \"gamma\", \"group\": \"group 3\"},\n",
" {\"value\": 45, \"weight\": .1, \"name\": \"delta\", \"group\": \"group 3\"},\n",
" {\"value\": 55, \"weight\": -.43, \"name\": \"epsilon\", \"group\": \"group 3\"},\n",
" {\"value\": 60, \"weight\": 0, \"name\": \"zeta\", \"group\": \"group 3\"}\n",
" ]\n",
"}\n",
"grouped_scatter = (sticky.d3Plus()\n",
" .grouped_scatter(groupby=\"group\", \n",
" width=1000, height=500)\n",
" .data(dat2['data_1'])\n",
" .key('name')\n",
" .x('value')\n",
" .y('weight'))\n",
"grouped_scatter.plot()\n",
"@interact\n",
"def update_chart(data=['data_1', 'data_2']):\n",
" grouped_scatter.update(data=dat2[data])"
],
"language": "python",
"metadata": {},
"outputs": [
{
"javascript": [
"require([\"widgets/js/widget\"], function(WidgetManager){\n",
"\n",
" // Define the DOM Creation view for Sticky charts\n",
" var StickyDOMWidget = IPython.DOMWidgetView.extend({\n",
" render: function(){\n",
" var chart_id = this.model.get('chart_id');\n",
" var chart_elm = '<div class=\"' + chart_id + '\"></div>';\n",
" $(chart_elm).appendTo(this.$el);\n",
" },\n",
" });\n",
" // Register the DOM Renderer with the Widget Manager\n",
" WidgetManager.register_widget_view('StickyDOMWidget', StickyDOMWidget);\n",
"});"
],
"metadata": {},
"output_type": "display_data",
"text": [
"<IPython.core.display.Javascript at 0x10e6fa8d0>"
]
},
{
"javascript": [
"//D3 Plus Library Renderer\n",
"\n",
"require([\"widgets/js/widget\"], function(WidgetManager){\n",
"\n",
" var d3plus_charts = {};\n",
"\n",
" function build_chart(chart, model, chart_id){\n",
" var data = JSON.parse(model.get('model_data'));\n",
" chart.container(chart_id)\n",
" .height(model.get('model_height'))\n",
" .width(model.get('model_width'))\n",
" .data(data)\n",
" .type(model.get('chart_type'))\n",
" .id(model.get('model_key'))\n",
" .text(model.get('model_key'))\n",
" .y(model.get('model_y'))\n",
" .x(model.get('model_x'));\n",
" }\n",
"\n",
" var bounced_builder = _.debounce(build_chart, 300, true);\n",
"\n",
" // Define the DOM Rendering View\n",
" var D3PlusRenderer = IPython.DOMWidgetView.extend({\n",
" render: function(){\n",
" var chart_id = '.' + this.model.get('chart_id');\n",
" // Instantiate d3plus\n",
" d3plus_charts[chart_id] = d3plus.viz();\n",
" build_chart(d3plus_charts[chart_id], this.model, chart_id);\n",
" // Draw\n",
" d3plus_charts[chart_id].draw();\n",
" },\n",
"\n",
" update: function(){\n",
" var chart_id = '.' + this.model.get('chart_id');\n",
" var chart = d3plus_charts[chart_id];\n",
" // Something of a hack\n",
" bounced_builder(chart, this.model, chart_id);\n",
" chart.draw();\n",
" }\n",
" });\n",
" // Register the DOM Rendering View\n",
" WidgetManager.register_widget_view('D3Plus', D3PlusRenderer);\n",
"});"
],
"metadata": {},
"output_type": "display_data",
"text": [
"<IPython.core.display.Javascript at 0x10e6a9e10>"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\r"
]
},
{
"output_type": "stream",
"stream": "stderr",
"text": [
"\r"
]
}
],
"prompt_number": 37
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"ws = pd.read_table('CO_WS_2011_2012.txt')\n",
"ws['Date & Time Stamp'] = pd.to_datetime(ws['Date & Time Stamp'])\n",
"subset = ws[['Date & Time Stamp', 'WS1_50mMean', \n",
" 'WS2_50mMean', 'WS3_30mMean', 'WS4_40mMean']][:10]\n",
"molten = pd.melt(subset, id_vars=['Date & Time Stamp'])\n",
"# I'm sure there's some nice chart I can create here..."
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 12
}
],
"metadata": {}
}
]
} | mit |
ny0011/dockerspawner-edit | DataSample.ipynb | 1 | 6640 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"이용할 column : 시도명, 자료수(도서),자료수(연속간행물),자료수(비도서)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"hypothesis : 수도권과 비수도권의 도서관당 보유한 자료수의 차이는 유의미하다."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Requirement already satisfied (use --upgrade to upgrade): xlrd in /opt/conda/lib/python3.5/site-packages\r\n",
"\u001b[33mYou are using pip version 8.1.1, however version 8.1.2 is available.\r\n",
"You should consider upgrading via the 'pip install --upgrade pip' command.\u001b[0m\r\n"
]
}
],
"source": [
"!pip install xlrd\n",
"import pandas as pd"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"xl = pd.read_excel(\"data.xls\")"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"city1 = xl['시도명'].tolist()\n",
"book1 = xl['자료수(도서)'].tolist()\n",
"book2 = xl['자료수(연속간행물)'].tolist()\n",
"book3 = xl['자료수(비도서)'].tolist()"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"\"\"\"\n",
"\n",
"0 서울특별시 02\n",
"1 경기도 031\n",
"2 인천광역시 032 \n",
"---- 위 세 곳이 수도권 ---- 수도권 : 1, 비수도권 : 2\n",
"3 강원도 033\n",
"4 충청남도 041\n",
"5 대전광역시 042\n",
"6 충청북도 043\n",
"7 세종특별자치시 044\n",
"8 부산광역시 051\n",
"9 울산광역시 052\n",
"10 대구광역시 053\n",
"11 경상북도 054\n",
"12 경상남도 055\n",
"13 전라남도 061\n",
"14 광주광역시 062\n",
"15 전라북도 063\n",
"16 제주특별자치도 064\n",
"\"\"\"\n",
"citys = [0]*len(city1)\n",
"\n",
"for j in range(len(city1)):\n",
" if(city1[j]=='서울특별시'): citys[j]=0\n",
" elif(city1[j]=='경기도'): citys[j]=1\n",
" elif(city1[j]=='인천광역시'): citys[j]=2\n",
" elif(city1[j]=='강원도'): citys[j]=3\n",
" elif(city1[j]=='충청남도'): citys[j]=4\n",
" elif(city1[j]=='대전광역시'): citys[j]=5\n",
" elif(city1[j]=='충청북도'): citys[j]=6\n",
" elif(city1[j]=='세종특별자치시'): citys[j]=7\n",
" elif(city1[j]=='부산광역시'): citys[j]=8\n",
" elif(city1[j]=='울산광역시'): citys[j]=9\n",
" elif(city1[j]=='대구광역시'): citys[j]=10\n",
" elif(city1[j]=='경상북도'): citys[j]=11\n",
" elif(city1[j]=='경상남도'): citys[j]=12\n",
" elif(city1[j]=='전라남도'): citys[j]=13\n",
" elif(city1[j]=='광주광역시'): citys[j]=14\n",
" elif(city1[j]=='전라북도'): citys[j]=15\n",
" elif(city1[j]=='제주특별자치도'): citys[j]=16"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"book1 = [float(b) for b in book1]\n",
"book2 = [float(c) for c in book2]\n",
"book3 = [float(d) for d in book3]\n",
"bookTmp = [0]*len(book1)\n",
"for i in range(len(book1)):\n",
" bookTmp[i] = book1[i]+book2[i]+book3[i]\n",
"\n",
"books = [0.0]*17\n",
"count_library = [0]*17\n",
"means = [0.0]*17\n",
"books_area = [0.0]*2\n",
"\n",
"#citys의 값이 1부터 17까지 중 하나면 그 값에 해당하는 books의 인덱스에 bookTmp의 합을 더함 \n",
"for i in range(len(city1)): #i=0 ~ len-1\n",
" for j in range(17):\n",
" if(citys[i]==j): \n",
" books[j] += bookTmp[i] \n",
" count_library[j] +=1"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"#수도권과 비수도권으로 나눔. 수도권 : index = 1 비수도권 : index = 2\n",
"#data1_index : data1의 도서관 개수\n",
"#data2_index : data2의 도서관 개수\n",
"index = [0]*(len(city1))\n",
"\n",
"data1_index = 0 \n",
"data2_index = 0\n",
"for i in range(len(city1)):\n",
" if(citys[i]<=2): \n",
" index[i]=1\n",
" data1_index+=1\n",
" else : \n",
" index[i]=2\n",
" data2_index+=1"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"#수도권은 수도권끼리 비수도권은 비수도권끼리 리스트 만듬\n",
"\n",
"data1 = [0]*(data1_index)\n",
"data2 = [0]*(data2_index)\n",
"j=0\n",
"k=0\n",
"for i in range(len(city1)):\n",
" if(index[i]==1) : \n",
" data1[j]=bookTmp[i]\n",
" j=j+1\n",
" else :\n",
" data2[k]=bookTmp[i]\n",
" k=k+1"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"#수도권과 비수도권의 개수가 달라서 비수도권 중 수도권의 개수만큼 다시 뽑기\n",
"import random",
"\n",
"for i in range(data1_index):\n",
" random.seed(i)\n",
" a=int((random.random())*data2_index)\n",
" group2[i]=data2[a]\n",
"\n",
"data = data1 + group2\n"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import json\n",
"with open('data1.json','w') as f:\n",
" json.dump(data1, f)\n",
"with open('data2.json','w') as f:\n",
" json.dump(data2, f)\n"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.1"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| bsd-3-clause |
JonasHarnau/apc | apc/vignettes/vignette_misspecification.ipynb | 1 | 62574 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Misspecification Tests for Log-Normal and Over-Dispersed Poisson Chain-Ladder Models\n",
"\n",
"We replicate the empirical applications in [Harnau (2018)](http://mdpi.com/2227-9091/6/2/25) in Section 5.\n",
"\n",
"*The work on this vignette was supported by the European Research Council, grant AdG 694262.*"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"First, we import the package"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"import apc"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"# Turn off future warnings\n",
"import warnings\n",
"warnings.simplefilter('ignore', FutureWarning)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 5.1 Log-Normal Chain-Ladder\n",
"\n",
"This corresponds to Section 5.1 in the paper. The data are taken from Verrall et al. (2010). Kuang et al. (2015) fitted a log-normal chain-ladder model to this data. The model is given by\n",
"$$ M^{LN}_{\\mu, \\sigma^2}: \\quad \\log(Y_{ij}) \\stackrel{D}{=} N(\\alpha_i + \\beta_j + \\delta, \\sigma^2). $$\n",
"They found that the largest residuals could be found within the first five accident years. Consequently, they raised the question whether the model is misspecified. Here, we investigate this question."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Full model\n",
"\n",
"We set up and estimate the full, most restrictive, model $M^{LN}_{\\mu, \\sigma^2}$."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We begin by setting up a model class."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [],
"source": [
"model_VNJ = apc.Model()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Next, we attach the data for the model. The data come pre-formatted in the package."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [],
"source": [
"model_VNJ.data_from_df(apc.loss_VNJ(), data_format='CL')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We fit a log-normal chain-ladder model to the full data."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [],
"source": [
"model_VNJ.fit('log_normal_response', 'AC')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"and confirm that we get the same result as in the paper for the log-data variance estimate $\\hat{\\sigma}^{2,LN}$ and the degrees of freedom $df$. This should correspond to the values for $\\mathcal{I}$ in Figure 2(b)."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"log-data variance full model: 0.075\n",
"degrees of freedom full model: 36\n"
]
}
],
"source": [
"print('log-data variance full model: {:.3f}'.format(model_VNJ.s2))\n",
"print('degrees of freedom full model: {:.0f}'.format(model_VNJ.df_resid))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This matches the results in the paper."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Sub-models"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We move on to split the data into sub-samples. The sub-samples $\\mathcal{I}_1$ and $\\mathcal{I}_2$ contain the first and the last five accident years, respectively. Accident years correspond to \"cohorts\" in age-period-cohort terminology. Rather than first splitting the sample and the generating a new model and fitting it, we make use of the \"sub_model\" functionality of the package which does all that for us. Combined, the sub-models correspond to $M^{LN}$."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [],
"source": [
"sub_model_VNJ_1 = model_VNJ.sub_model(coh_from_to=(1,5), fit=True)\n",
"sub_model_VNJ_2 = model_VNJ.sub_model(coh_from_to=(6,10), fit=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can check that this generated the estimates $\\hat{\\sigma}^{2, LN}_\\ell$ and degrees of freedom $df_\\ell$ from the paper."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"First five accident years (I_1)\n",
"-------------------------------\n",
"log-data variance: 0.095\n",
"degrees of freedom: 26\n",
"\n",
"Last five accident years (I_2)\n",
"------------------------------\n",
"log-data variance: 0.027\n",
"degrees of freedom: 6\n"
]
}
],
"source": [
"print('First five accident years (I_1)')\n",
"print('-------------------------------')\n",
"print('log-data variance: {:.3f}'.format(sub_model_VNJ_1.s2))\n",
"print('degrees of freedom: {:.0f}\\n'.format(sub_model_VNJ_1.df_resid))\n",
"\n",
"print('Last five accident years (I_2)')\n",
"print('------------------------------')\n",
"print('log-data variance: {:.3f}'.format(sub_model_VNJ_2.s2))\n",
"print('degrees of freedom: {:.0f}'.format(sub_model_VNJ_2.df_resid))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Reassuringly, it does. We can then also compute the weighted average predictor $\\bar{\\sigma}^{2,LN}$"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Weighted avg of log-data variance: 0.082\n"
]
}
],
"source": [
"s2_bar_VNJ = ((sub_model_VNJ_1.s2 * sub_model_VNJ_1.df_resid \n",
" + sub_model_VNJ_2.s2 * sub_model_VNJ_2.df_resid)\n",
" /(sub_model_VNJ_1.df_resid + sub_model_VNJ_2.df_resid))\n",
"print('Weighted avg of log-data variance: {:.3f}'.format(s2_bar_VNJ))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Check!"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Testing for common variances\n",
"\n",
"Now we can move on to test the hypothesis of common variances\n",
"$$ H_{\\sigma^2}: \\sigma^2_1 = \\sigma^2_2. $$\n",
"This corresponds to testing for a reduction from $M^{LN}$ to $M^{LN}_{\\sigma^2}$."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"First, we can conduct a Bartlett test. This functionality is pre-implemented in the package."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [],
"source": [
"bartlett_VNJ = apc.bartlett_test([sub_model_VNJ_1, sub_model_VNJ_2])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The test statistic $B^{LN}$ is computed as the ratio of $LR^{LN}$ to the Bartlett correction factor $C$. The p-value is computed by the $\\chi^2$ approximation to the distribution of $B^{LN}$. The number of sub-samples is given by $m$."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"B: 2.79\n",
"LR: 2.96\n",
"C: 1.06\n",
"m: 2.00\n",
"p_value: 0.09\n"
]
}
],
"source": [
"for key, value in bartlett_VNJ.items():\n",
" print('{}: {:.2f}'.format(key, value))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We get the same results as in the paper. Specifically, we get a p-value of $0.09$ for the hypothesis so that the Bartlett test does not arm us with strong evidence against the null hypothesis."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In the paper, we also conduct an $F$-test for the same hypothesis. The statistic is computed as\n",
"$$ F_{\\sigma^2}^{LN} = \\frac{\\hat\\sigma^{2,LN}_2}{\\hat\\sigma^{2,LN}_1} $$\n",
"which, under the null, is distributed as $\\mathrm{F}_{df_2, df_1}$. This is not directly implemented in the package but still easily computed. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"First we compute the test statistic"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"F statistic for common variances: 0.28\n"
]
}
],
"source": [
"F_VNJ_sigma2 = sub_model_VNJ_2.s2/sub_model_VNJ_1.s2\n",
"print('F statistic for common variances: {:.2f}'.format(F_VNJ_sigma2))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now we can compute p-values in one-sided and two-sided tests. \n",
"For an (equal-tailed) two-sided test, we first find the percentile $P(F_{\\sigma^2}^{LN} \\leq \\mathrm{F}_{df_2, df_1})$. This is given by"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Percentile of F statistic: 0.06\n"
]
}
],
"source": [
"from scipy import stats\n",
"F_VNJ_sigma2_percentile = stats.f.cdf(\n",
" F_VNJ_sigma2, dfn=sub_model_VNJ_2.df_resid, dfd=sub_model_VNJ_1.df_resid\n",
")\n",
"print('Percentile of F statistic: {:.2f}'.format(F_VNJ_sigma2_percentile))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"If this is below the 50th percentile, the p-value is simply twice the percentile, otherwise we subtract the percentile from unity and multiply that by two. For intuition, we can look at the plot below. The green areas in the lower and upper tail of the distribution contain the same probability mass, namely $P(F_{\\sigma^2}^{LN} \\leq \\mathrm{F}_{df_2, df_1})$. The two-sided p-value corresponds to the sum of the two areas."
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAEJCAYAAABv6GdPAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzt3Xl8VNX5+PHPmSwEQkICw74oOyJulUUEZZEdBCtyBPeV6let2oXKr9Zaba36tbXW0lbUti5VevwqisoiqIggImIV2RRlMQkQCAlr9pnz+2MmcRKyTMJM7izP+/WaV+bee+69z0ngmTvnnnuOstYihBAitricDkAIIUToSXIXQogYJMldCCFikCR3IYSIQZLchRAiBklyF0KIGCTJXcQcpdQtSqlj9ZTpp5SySqmBJ3mukBxHiFCT5C6C4k9gdb12OR1jgOeAHk4HUUEp9XAtv7O76thnjL9MhxDH0st/3PNCeVwReRKdDkBEjY4B7wcDb/h/ZvnXeZo8olpYa4uAIqfjqOYrYGS1dUcciEPECblyF0Gx1u6reAH5/tUHAtYfUErdrpT6pmIfpdRp/qvEZwLW3aqU+i5g+XSl1FKl1HGl1FGl1OtKqVPrikX5/FoptUspVaKU2q+UWqKUSvRvP6FZRil1pVJqh1KqWCn1IdC/huP2U0q9oZQ6rJTK98fVv6HHqUV54O/Q/yqspX79gOX+xb3+3+HSgO1XK6U2+mPYqZR6VCnVPGD7KKXUWqXUMaXUEaXUf/3rUoDt/mJr/cfdFmT8IspIcheh9B7QUyl1in95NHAAuCigzGh/OZRSLfElMQsM929zA4srEnUtZgF3Af8D9AbG830yPIFSaijwgv91FvAk8KdqZToDq4FdwDDgfGA38L5SKjPY44TIdkD735+J71vTLH8MtwCPAw/j+2C5AZgC/Nm/vRmwCPgAOBsYCPwWKLbWFgND/ced7D/u8DDELyKBtVZe8mrQC19CsMCpNWzbC9zgf/8qcC++JpIegMKX7K/xb78NX9NERsD+XYBSQNdx/rnAJiCxlu23AMcClv8PeLdamZ/56zDQv/wwsLJaGReQDdwS7HFqiedhfM1WxwJf9fyOx/iP2yFgnfL/fq+rVnYc4AVa4EvYFjivluP2qmu7vGLnJVfuItTeB0YrpRQwAlgMfITvqvxMfFfm7/nLng5stNYeqtjZWpsN7PBvQyn1rb954ZhSaoO/2MtAK2CXUuofSqkrlFKpdcTU3x9DoNXVlgcBwwLOdQzfB09HfN8Ogj1Obb7FdyUd+EIp1SzwnEqphXUcowvQAfhrtTgX4kv8Pa21e4EXgZVKqbeVUnOUUr2CjFHEELmhKkLtPeABfMnLBXzuX3cRkAZs9yfwCjUNS6oC1l/E9/9OSwGstbuUUr3xfWCM9p/vYaXUEH9yq+t4tXHh+yD6aQ3bKj58gjlObUqttd/UtB5/ovc7XscxKi7GbuHEDxnw39y21l6tlPpffFf0Y4HfKqVmW2v/1eCoRdSS5C5C7V3gaXxNLu9ba71KqfeAO4CWfH/VDrAZuEoplVFx9a6U6gJ092/DWrurppNYX/vxYnzt878CDuJre366huKb8bWjB6q+/ClwKfCdtba0lroFc5wGsdZaoLakD5AQsC4L2A/0sdY+X89xNwIbgceUUv8Cbgb+VctxRQySZhkRUtbanfhuSl7L94l8Pb724AlUTe7P4Wt/flkpdY5SahCwAF+yq7V5Qin1I6XUjUqpM/03b68BUoCttezyR2CUv4dNH6XUDODH1cr8Cd+Hz2tKqWFKqVOVUhf4+6gPbMBxQmWX/+dkpVQ7pVS6tdaL7x7Gz5RS9yil+vt7+FyqlJoH4F/3kL8OpyilhuG7ibrFf7x9QDEwXinVXimVEab4hdOcbvSXV/S9qOOGqn/7s/7tpwWsexvfTb+21cqeDizD1xxxFF//+RqPG7DP5cDH+JpLCoEv8N+k9W+vckPVv+4aYCdQgq9JYzrVboTiu+m7AMjzl9sFPA90bchxaoj3YWBTI37P9wJ7/L+3pQHrLwPW4btRfQT4DJjr39YVeB3I8ceYA/wNSAvY/yZ/3cqBbU7/e5JXeF7K/8cWQggRQ6RZRgghYpAkdyGEiEGS3IUQIgZJchdCiBjkZD93uZMrhBCNo+or4OhDTHv27GnUfm63m7y8vJM6d+fOncnJyTmpYzSlUNQ52kid44PUuWE6deoUVDlplhFCiBgkyV0IIWKQJHchhIhBMnCYEHHEWktxcTFerxffqMzOy83NpaSkxOkwmlR9dbbW4nK5SElJafTfSZK7EHGkuLiYpKQkEhMj579+YmIiCQnxNUhlMHUuLy+nuLiY5s2b11muNtIsI0Qc8Xq9EZXYRe0SExPxer2N3l+SuxBxJFKaYkRwTubvJR/hJ8keOoj9cgMcLoBMN+qMH6DSM50OSwgR5yS5N5ItL8MufBH77iLweL5fn5iIGj0FNfUKVLMUByMUQsQzSe6NYMvK8D75AGz9AjV8LGrcJeDuAPuyse8uwi5/A7vlc1y334tq087pcIWIOF27dqVfv36Ar+nh2WefpWvXro7F84c//IHU1FRuueWWkB1z6tSpLFq0iMOHD7Nw4UKuu+66kB07GJLcG8hai33uz77Efu0duIaP/X5j1+6o6+7EDhyO9+nH8P7v/8P189+j2rR1LmAhIlBKSgrLly8HfDcOy8vLHY4o9BYtWgTAkSNHeP7555s8ucsN1Qaya1Zg132AuuSqqok9gBpwLq6fPAiFx/E+cT+2uLCJoxRC1OeJJ57gggsu4PLLL+fbb7+tXP/qq68yefJkxo4dy5w5c/B4PGRlZTFixAh+/vOfM2rUKGbNmkVRUREAhYWFXH311YwZM4bRo0fzxhtvANC7d28AHnroIXbv3s3YsWN58MEHefTRR5k/f37l+R5++GGeffbZkNdPknsD2EP5WPMP6HM6auJldZZVp/TC9T9zITcH7z/+hD2JLk1CxJri4mLGjh3L2LFjm/yKFmDjxo0sWrSId955h2eeeYYvvvgCgO3bt7No0SJef/11li9fTkJCAq+99hoAO3fu5Nprr+X9998nPT2dxYsXA/D+++/ToUMHVqxYwXvvvceoUaOqnOv//b//xymnnMLy5cv51a9+xaxZszDGAL6uqYsWLeKHP/xhyOsozTINYN9cAKUluK6+HeWq/3NR9TsTNeN67H+exa5cjBo9pQmiFCI43gVPY7N2hvSYqmt3XDNvrrdcXc0yK1euJC8vj8suu4wnn3ySgoICrrjiCnr16lXnMRuy37p165gwYULlA0Jjx/q+ha9evZovv/ySSZMmAb4PIbfbzXnnnUfXrl0ZMGAAAGeeeSZZWVkA9OvXjwcffJDf/e53jBkzhiFDhtQZZ9euXcnMzGTTpk0cOHCA008/ndatW9f7O2soSe5Bsgf2YdcsR10wHtWhc9D7qYumYjf/F/vqc9gBP0C1C264TiHiSWlpKb/5zW9o2bIl//3vf3nooYf47LPPeOONN7jqqqtqTeyN3Q9q7kNurWXGjBnMnTu3yvqsrCyaNWtWuZyQkEBxcTEAPXv2ZMmSJbz33nv8/ve/Z8SIEdx999111vfKK6/EGMP+/fuZOXNmnWUbS5J7kOzSV0G5UJNmNGg/pRSua+7Ae//teJ/7C66f/U4eJBERIZgr7Kby/PPPM2PGDM4++2wuueQSevbsyeHDhxk6dGidzTaN3e+8887j7rvv5rbbbsPj8bB8+XKuvvpqhg8fzvXXX8/NN9+M2+2moKCA48eP1xn7vn37yMjIYPr06aSmplY2uVRITU3l2LFjVdZNmjSJRx55hPLycubNm1fv76cxpM09CPb4MezH76OGjkJltmnw/iqzDerSa+HrTdj1H4YhQiGi26ZNm+jXrx/Hjh2jdevWKKXYvHkz/fv3Z8WKFfzxj3/k1VdfbdB+H3/8MbfeemuN5zvjjDO4+OKLGTduHDfffHNlU0qfPn2YM2cOs2bNYsyYMcyaNYvc3Nw6Y9+2bRtTpkxh7Nix/PnPf+bOO++ssr1169YMGjSI0aNH8+CDDwKQnJzM+eefz8UXXxy2cXXkyj0Ids0KKC1FjZzU6GOoC8ZiVy3DvvJP7FmD5QEnEde2b99eZXnkyJHcc889NG/enB49egCwZcsWhgwZwplnnsnQoUN57rnnADhw4AArVqxg1qxZ9e736aef1hrDnXfeeUIiBpg2bRrTpk07Yf17771X+T6wP/zIkSMZOXJknXWsfnXu9Xr57LPPeOqpp2qN72RJcq+HtRa7ahn0Og3VrUejj6NcCbhmzcb7yC+wS19FTbsyhFEKEd0uueQSLrnkkirrbr7Z12zk9Xr529/+Vrm8adOmygee6tovUn399ddce+21TJgwofIDKRwkudfnux2Qm+N7CvUkqV6noQYO9z3BOmoyKj0jBAEKEdueeOIJDh8+zKeffspFF110QlfD2mzevJl169Zx+umnB71PU+jTpw/r168P+4NbQSV3rfUE4AkgAXjGGPNwte2PAxW/vRZAO2NMTGQu+8kqSEhA/WBoSI6npl2B3fARdsmrqMtvDMkxhYhl9fU8qc3pp5/OCy+8EOJooke9N1S11gnAPGAi0B+YpbXuH1jGGHO3MeZsY8zZwJPAa+EItqlZrxf76YfQ/xxUy/SQHFN16II6fxR25WJsfnzN+C6EaDrB9JYZDHxjjNlhjCkFFgAn3m343izg5VAE57gd2yA/DzX4wpAeVk2ZCdZi3zb1FxZCiEYIJrl3BrIClrP9606gtT4F6A68V9P2aGM//wQSElFnDQ7pcZW7PWr4GOxHK7CH8kN6bCGEgODa3Gt64sbWUnYm8H/GGE9NG7XWs4HZAMYY3G53UEFWl5iY2Oh9A9V3jIPbvsDV/ywyu3Y76XNVV375DRz88B1SPlpO2jW31Vs+VHWOJlLn0MvNzY3IafYiMaZwC6bOzZo1a3yeDKJMNhA40HIXYE8tZWcCtWYqY8x8oGI4NJuX17g2Z7fbTWP3DVTXMWz+Aby7v0Vddn1IznWCpBTUucMoXPIaxSMno1q0rLN4qOocTaTOoVdSUhJxk1HH6pC/dQm2ziUlJSf8e+jUKbghTIJpllkP9NZad9daJ+NL4IuqF9Ja9wUygbVBnTnC2U0bAFBnnBu2c6gJ06G4CPv+4rCdQwgRn+pN7saYcuB2YBmw1bfKbNZaP6C1nhpQdBawwBhTW5NNVLFfboA27aBj+GaHUd16wIBzse++iS0tCdt5hBDxJ6iGLmPMYmBxtXX3VVu+P3RhOct6PLBtI2rwhWEf5Ms14VK8j/0S+8kqVC2TfwghREPJwGE1yd4JxUXQZ0D4z9VnAHQ51Xf1bmPiS48QIgJIcq+B/WoTAKpv+JO7Uso3iUf2Lvh6c9jPJ0Qku/baa6ssDxw4kFWrVgEwe/ZsuQBqAEnuNbBfb4J2HVEZDR/etzHUkBGQmob3vTeb5HxCRKKsrKzKAcEAcnJyGDVqFCtWrAB8g/jJXAjBi7/OpfWwXi9s34I657wmO6dKboa6cBx26ULswf2oNu2a7NxCOOGFF17gj3/8I263G6UUffv2ZeLEiZxxxhmVZb788kuGDh3K2rVr2blzJ126dHEw4ugjV+7V7dkNhceapr09gBoxCRTSLVLEha1btzJnzhyWL1/Oe++9x5NPPsnGjRurJPeNGzdy5plnMmTIEObPn19lm6ifXLlXY7dvAUD17l9PydBSbdrCOedhP3wHe/EsVMB8jULEmm3btp0wd+imTZsoKCggMTGRKVOmsGPHDnr06EHbtm2ZO3cuN9xwg0PRRidJ7tXt/BrSM8DdvslP7Ro9Be+Gj7CffogaNqbJzy9EU/nqq6/4yU9+glKKNm3asGDBAl588cUqZYYO9Q2z3apVqxNmbhL1k+Rejd25Hbr3cebGTe/ToWNX7AdLQZK7iFE5OTm0a9eu8kZpbY/ir1ixgo0bN3LKKacwffr0pg4z6klyD2ALj8O+bF/vFQcopXw3Vv/zLDZrJ6prd0fiEPGjc+caB3g9KTk5OXVu37p1K3369Kn3OGPGjKkyd6poGEnugXb5vvqp7vX/wwsXNXQ09tXnsauWoa68pf4dhDgJ9SXicNi2bRt9+/att1z1uVNFw0hvmQB259e+N6f2diwGlZrmm2d13UpsSbFjcQgRLtu2baN376r/x4qKipgzZw6/+c1vOPvss1m4cGGVuVNFw8mVewC7azu074xKrXv43XBTF47Hfvy+b7yZC8Y5GosQofaXv/zlhHXPPfcckydPZsSIEWRnZ/PDH/7Qgchii1y5B9q5HXVqL6ejgF6n+W6srlrmdCRCNIlt27YxcOBAioqKSElJcTqcmCBX7n72yCE4nA/dejodiu/G6ogJ2AVPY7/7FhUBMQkRTpMmTWLu3Lm0aNGCO++80+lwYoIk9wrZOwEipoeKOm8U9tXnsB8sQ139P06HI0RYjRs3jnHjpAkylKRZxs9m7fK96RIhyT21JWrgMOy6D7DFRU6HI4SIMpLcK2TvhIzWqLR0pyOppC4cDyVF2E9XOx2KECLKBNUso7WeADwBJADPGGMerqGMBu4HLPCFMeaKEMYZdjZrZ8RctVfqeRp06IxdswIumeV0NEKIKFLvlbvWOgGYB0wE+gOztNb9q5XpDcwFhhljTgfuCkOsYWPLynxPpnY91elQqlBK+caY+WYr5Tm7nQ5HxACZ7CK6nMzfK5hmmcHAN8aYHcaYUmABMK1amZuBecaYAgBjzP5GR+SEvVng8UTelTu+J1ZxuSh69y2nQxExwOVy1TiOi4g85eXluFyNbzkPplmmM5AVsJwNDKlWpg+A1noNvqab+40xSxsdVROzlT1lejgcyYlUq0w4YyDF7y+BcdNRidLBSTReSkoKxcXFlJSURMysRs2aNaOkpMTpMJpUfXW21uJyuU6qz38wmaKmfwHVvyskAr2BkUAX4EOt9QBjzKHAQlrr2cBsAGMMbre7wQGDbxS5xu4bqOIYR/P2UZjcDHf/M1AJCSd93FArnngphx++h4ysb2g2aLjT4TSZUP2do0m81jnevk00RZ2DSe7ZQNeA5S7AnhrKfGyMKQN2aq2/wpfs1wcWMsbMB+b7F21eXl6jgna73TR230AVx/Bs3wodu3KwoOCkjxkO9pQ+uDJac2jxayR07+d0OE0mVH/naCJ1jg8nU+dOnToFVS6YBp31QG+tdXetdTIwE1hUrczrwCgArbUbXzPNjqCjddreLFSnbk5HUSuVmEjKyInw5Xrskcj8ABJCRJZ6k7sxphy4HVgGbPWtMpu11g9oraf6iy0DDmqttwDvAz83xhwMV9ChZAuPweEC6Ni1/sIOaj56Mng82LUrnQ5FCBEFgro7Z4xZDCyutu6+gPcW+In/FV32ZgOgOkV2ck/seir07IddswI77pKIuRkmhIhMcf+Eqt3r7wjUsYuzgQRBDRvj67a54yunQxFCRLi4T+7szYbEJEcmxG4oNWg4JDfzPbEqhBB1iPvkbvdmQftOKFfkdYGsTqW08M3S9MmHMkuTEKJOcZ/c2ZeNivCbqYHU8LG+wcQ2rHE6FCFEBIvr5G5LSyAvNyra2yv1Og3adcKuXu50JEKICBbXyZ19OWBtxHeDDKSUQg0fA9u3YPc1/cz1QojoENfJvaKnTDQ1y8D3g4nZj951OhQhRISK6+TOvmxQLmjf2elIGkRltIYB52I/eg/r8TgdjhAiAsV3cs/dA23aopKSnI6kwVzDx/om9N70mdOhCCEiUFwnd7t/L7QLbhCeiHPGQEjPwLv6HacjEUJEoLhO7uzfi2rf0ekoGkUlJqKGjoKN67GHZTAxIURV8Z3ci45Du+hM7gBq2FjwerFr33M6FCFEhInv5A6oaG2WAVTHLtCrP3b1CpkbUwhRRdwn92i+cgf/E6u5OfDNVqdDEUJEkPhO7soVFQOG1UUNHAYpzbEfyo1VIcT34ju5t2mLSoy+bpCBVLMU1KALsBvWYIsKnQ5HCBEh4ju5R3mTTAV1wTgoLcGuX+V0KEKICBGXyb3i5mM030yt4tTe0PkU7GoZ510I4RPUNHta6wnAE0AC8Iwx5uFq268D/heoGMnqL8aYZ0IYZ2gdO+r7GStX7v7BxOx/nsVm70J1OdXpkIQQDqv3yl1rnQDMAyYC/YFZWuv+NRT9jzHmbP8rchM7wP49AKgYSe4AasgoSEiUoYCFEEBwzTKDgW+MMTuMMaXAAmBaeMMKL3tgr+9NrDTLACotHXX2EOzHK7FlZU6HI4RwWDDNMp2BrIDlbGBIDeWma60vBL4G7jbGZFUvoLWeDcwGMMbgdrsbHjGQmJjY6H0Bjh09DIC7X39UUnKjj9OUgqlzyZTLOLRhDWk7tpAy7KImiix8TvbvHI2kzvGhKeocTHJXNayr/jjkm8DLxpgSrfUtwHPA6Oo7GWPmA/MrjpGXl9eQWCu53W4auy+Ad9e3ABw8fKTRx2hqwdTZduoOrdtyePFrHOt7VhNFFj4n+3eORlLn+HAyde7UKbgWh2CSezYQOJtFF2BPYAFjzMGAxaeBR4I6u0Ns3j6nQwgL5XKhhl2Efes/2IP7UW3aOR2SEMIhwbS5rwd6a627a62TgZnAosACWuvAO5NTgch+Fj4v1+kIwkYNGwOAXSPdIoWIZ/Umd2NMOXA7sAxf0jbGmM1a6we01lP9xX6std6stf4C+DFwXbgCPlm2tASOHHI6jLBRbdrBaWdh17yL9cosTULEq6D6uRtjFgOLq627L+D9XGBuaEMLk4P7nY4g7NTwcdj5j8Lmz+GMc50ORwjhgPh7QjUvDpL7OUMgrRXeVUudDkUI4ZC4S+42htvbK6jEJN9QwF+sx+YfcDocIYQD4i65k5eLNzHB6SjCTl04HrDYD+WJVSHiUdwld3swl5JWrZwOI+yUuz0MOBf74TvY8nKnwxFCNLG4S+7k7acoI83pKJqEa8QEOJwPGz9xOhQhRBOLv+R+MJfjrVKdjqJpnHEutHbj/UBurAoRb+IqudviQjh2lKPpLZwOpUkoV4JvIo8tn2P376l/ByFEzIir5F7RDbIwvaXDgTQdNXwcuFzYVcucDkUI0YTiLLn7ukHGTbMMoDJaw9nnYdeswJaVOh2OEKKJxFVyt/6nU8taZzocSdNyjZgAx45iN3zkdChCiCYSV8mdvFw8SUnY1PjoLVOp35nQrhNWbqwKETfiKrnbvP2UZLbC5Yr9h5gCKZcLNWI8fLMFm7XT6XCEEE0grpI7ebkUtYqzq3Y/NWwsJDfDvveW06EIIZpAfCX3gjyOx0k3yOpUakvU0FHYdR9gj0bPDFRCiMaJm+RuS0rg+FGOt2zudCiOUaOnQFkp9kPpFilErIub5E6Bb3TEorT4vHIHUJ26+SbyWLlExpsRIsbFUXL3TfNaGMfJHcB10cVQkAeff+x0KEKIMApqJiat9QTgCSABeMYY83At5S4DXgEGGWM+DVmUIWDzfTONl6WnOxyJw844F9p2wPvuWyQMHO50NEKIMKn3yl1rnQDMAyYC/YFZWuv+NZRLwzd/6rpQBxkS/mYZT0Z8PcBUnXIloEZN9nWL3P2t0+EIIcIkmGaZwcA3xpgdxphSYAEwrYZyDwKPAsUhjC908vMoS22BSkpyOhLHqWFjoFkK9t03nQ5FCBEmwTTLdAayApazgSGBBbTW5wBdjTFvaa1/VtuBtNazgdkAxhjcbnfDIwYSExMbvG/B8aMUZrYiPaBZprHnd0Jj6lw7N0dGT6Zo+SIyZ/+EhIzWITpuaIW2ztFB6hwfmqLOwSR3VcM6W/FGa+0CHgeuq+9Axpj5wPyKY+Tl5QVx+hO53W4auq8ndw/HUlM4cuT7Pt6NPb8TGlPnutjzL4Ilr3Lw1RdxTbsiZMcNpVDXORpInePDydS5U6dOQZULplkmG+gasNwFCBwcPA0YAKzUWu8CzgMWaa0HBhVBU8nP43ic95QJpDp0gbMGY1e+7XsGQAgRU4K5cl8P9NZadwdygJlA5aWeMeYwUPn9Qmu9EvhZJPWWscWFUHScwrT4fYCpJq5xP8T7v59gP1rhu8kqhIgZ9V65G2PKgduBZcBW3yqzWWv9gNZ6argDDAl/H/eilnLlXkXv/tCjL3b5G1ivx+lohBAhFFQ/d2PMYmBxtXX31VJ25MmHFWL+Pu5F6fEzSUcwlFK4xv8Q798ehs/WgvR7FyJmxMUTqjbf38e9VXz3ca/R2UOgXUe8yxZira2/vBAiKsRFcqfgIFZBeas4fzq1BsqVgBp7CezaDl9vdjocIUSIxElyz6MsNRUSg2qFijvq/NGQ1grvstecDkUIESJxkdxtfh7F6S2dDiNiqeRmvt4yX36KzfnO6XCEECEQF8mdgry4Huo3GGrUJN+QBItfcToUIUQIxE1yL4zjSTqCoVqmo0ZOxK7/EJu7p/4dhBARLeaTuy08DsVFcT+OezDUuEsgKVGu3oWIATGf3Cnw93GX5F4vlZ6JumA89uP3sQf2OR2OEOIkxE1yL05PcziQ6KDGXwouF3bpq06HIoQ4CTGf3CtmYPJkZDgcSXRQmW1Qw8di17xb+fCXECL6xHxypyAPqxSeeJ9erwHUhOmAxS6Vfu9CRKu4SO5lLVOxCQlORxI1VJt2qKGjsR++gz100OlwhBCNEPPJXR5gahw1aQZYr/ScESJKxXxypyBPukE2gmrbATVsLHbVO9i8XKfDEUI0UEwnd2stFByUB5gaSU25HJTCvrnA6VCEEA0U08mdwuNQUixX7o2kMtugRk/Grn0fuzer/h2EEBEjtpN7ga8rn0zS0XhqwmWQ3AzvG/92OhQhRAMENQau1noC8ASQADxjjHm42vZbgNsAD3AMmG2M2RLiWBvO38e9JE1uqDaWSktHjZuGfXMBdve3qFN6Oh2SECII9V65a60TgHnARKA/MEtr3b9asZeMMWcYY84GHgX+GPJIG8H6504tlweYTooaewmkpuFd+LzToQghghRMs8xg4BtjzA5jTCmwAJgWWMAYcyRgMRWIjPna8vOwLnmA6WSp5i18XSM3/xe75b9OhyOECEKg/T2mAAAfSElEQVQwzTKdgcC7adnAkOqFtNa3AT8BkoHRNR1Iaz0bmA1gjMHtdjc0XgASExOD2vdw4VGOpqeTXsuVe2PP74Rg6xwudsY1HFy1FPXa87QeNhrVBA+FOV1nJ0id40NT1DmY5K5qWHfClbkxZh4wT2t9BXAvcG0NZeYD8yuOkZeX14BQv+d2uwlmX8++HApbtuDIkSM1bm/s+Z0QbJ3Dyf7wajx/f4QDi/6D64JxYT9fJNS5qUmd48PJ1LlTp05BlQumWSYb6Bqw3AWoazaHBcAlQZ093PJlBqaQ+sH50Os07Bv/xhYXOh2NEKIOwST39UBvrXV3rXUyMBNYFFhAa907YHEysD10ITaO7wGmPI6nyQNMoaKUwjXjBjhcIIOKCRHh6k3uxphy4HZgGbDVt8ps1lo/oLWe6i92u9Z6s9b6c3zt7ic0yTS5Y0ehrJSilnLlHkqqR1/U4Auxy1+XIYGFiGBB9XM3xiwGFldbd1/A+ztDHNfJq5iBSR5gCjl16TXYz9ZiX30OdfPPnA5HCFGD2H1CtWIGJnmAKeRUm3aoCdOxn6zCbtvodDhCiBrEbHKvmIGpvFUrhyOJTWridHC3x/vSU9jyMqfDEUJUE7PJnYI8rMuFJ03mTg0HldwM18zZsDcL++6bTocjhKgmppN7aXrLJnnYJl6pswbBWYN9487kx1c/ZSEiXcwmd5ufR7FctYed6/KbwOvFmmedDkUIESBmkzsF8gBTU1BtO6AmzcBuWIP98lOnwxFC+MVkcpcHmJqWGn8pdOyK98W/YovkyVUhIkFMJneOHobycgoluTcJlZSE69o7oOAg9rXnnA5HCEGsJveKB5haygNMTUX17Ie6aCp25RLsV5ucDkeIuBfbyT1d2tybkrrkSmjbAe/zT2JLSpwOR4i4FpPJvfIBJpmBqUmpZim4rr4N9u/FLnrJ6XCEiGsxmdzJz8Ob4MLbUrpCNjV12lmoC8f7Bhb7WppnhHBKbCb3gjxK09NxueQBJieoGTf4hiZ49nFs4TGnwxEiLsVkcrcFeZTIgGGOUSnNcd30Uzh0EPvSU06HE5WWLFlC586d+eabb8J2joKCAmbOnMmwYcOYOXMmhw4dqrGcMYZhw4YxbNgwjDGV60tLS5kzZw7Dhw/nwgsv5O233w5brKLhYjK5k58nQ/06TPXoi5oyE7vuA7zrPnA6nKjz+uuvM3jwYN54440at3s8npM+x7x58xg+fDhr1qxh+PDhzJs374QyBQUFPP7447z11lu8/fbbPP7445UfAn/+859p06YNq1evZuXKlQwdOvSkYxKhE3PJ3Xq9cCif4y1TnA4l7qlJM6BnP+y//449uN/pcKLG8ePH+fTTT3nssceqJPePPvqIyy67jNtuu42LLroIgFdffZXJkyczduxY5syZU5n077nnHiZOnMioUaN47LHHajzPsmXLmDFjBgAzZsxg6dKlJ5T54IMPuOCCC8jMzCQjI4MLLriAlStXArBgwQLuuOMOAFwuF61btw7Z70CcvJhL7hw9DB55gCkSqIQEXDf+BKwX79OPYcvLnQ4pKixdupSRI0fSs2dPMjIy+PLLLyu3ff755/ziF79g5cqVbN++nUWLFvH666+zfPlyEhISeO013/SHv/jFL1iyZAkrVqzg448/ZsuWLSecJy8vj/bt2wPQvn17Dh48eEKZffv2VZmQuWPHjuzbt4/Dhw8D8OijjzJ+/Hhmz57NgQMyM1ckCWomJq31BOAJIAF4xhjzcLXtPwFuAsqBA8ANxpjdIY41OP5ukIVp0iwTCVTbDqhr7sDOf9Q3c9PlNzodUsR7/fXXufnmmwGYNm0ar7/+OmeccQYAZ599Nt26dQNg9erVfPnll0yaNAmA4uJi3G43AG+++Sb//ve/8Xg85Obmsn37dvr379/gWKy1Na73eDzs3buXQYMGcf/99/PUU0/xwAMP8OSTTzb4HCI86k3uWusEYB4wFsgG1mutFxljAi8F/gsMNMYUaq1vBR4FLg9HwPUq8F09yNypkcM1aDjeb7diV7yB7XUa6tzznQ4pYh08eJCPPvqIr776CqUUHo8HpRT33nsvAC1afP/v2lrLjBkzmDt3bpVjfPfddzz11FO8/fbbZGRkcNddd1FcXHzCudxuN7m5ubRv357c3FzatGlzQpmOHTvy0UcfVS7v3buX888/n8zMTJo3b87EiRMBmDJlCgsWLAjJ70CERjDNMoOBb4wxO4wxpcACYFpgAWPM+8aYihGjPga6hDbM4NkC31fL8kyZgSmSqMuug+598P7rCWzuHqfDiVivvfYa06dP55NPPmHdunV8+umndOvWjU8++eSEssOHD+ett94iL8/3bbWgoIDs7GyOHj1K8+bNSU9P58CBA7z//vs1nmvcuHG88sorALzyyiuMHz/+hDIjRoxg1apVHDp0iEOHDrFq1SpGjBiBUoqxY8dWJv7Vq1fTu3fvUP0aRAgE0yzTGcgKWM4GhtRR/kZgSU0btNazgdng615V8RWyoRITE2vd92jRcY4nJpLWsXO9/dwbe34n1FXnaOGZ+zAHf3Idrmceo/XD81HN6r7pHQt1bqhXXnmFn/70p1XqPWPGDJYsWcKMGTNITk6u3OZ2u/ntb3/L1VdfjdfrJSkpiSeeeIIRI0YwcOBAxowZQ/fu3Rk2bBhpaWkn/C7vu+8+rrjiCowxdO3alZdffpnWrVuzYcMGnn76af7+97/jdru59957ufjiiwH41a9+VZnEH3vsMW644QYefPBB3G43Tz/9dKP+XvH4d26KOqva2tQqaK1nAOONMTf5l68GBhtj7qih7FXA7cAIY0x9g4vYPXsadwXndrsrr1aq8z71KEU7NrPmf66s8xjXn389OTk5jTq/E+qqczSxmzbg/fMDqB+cj5r9c5Sr9i+PsVLnhpA6x4eTqbP/Breqr1wwzTLZQNeA5S7ACVlZaz0G+CUwNYjEHja2II/idHmAKVKpAeeipl/nm9zjLWmjFSJcgmmWWQ/01lp3B3KAmcAVgQW01ucATwETjDHOdmjOz6Ooa3x9xYs2atwlsPc77JsL8HbshmvQcKdDckxRURGfffYZHTt2pGvXrrX2ThGioeq9cjfGlONralkGbPWtMpu11g9oraf6i/0v0BJ4RWv9udZ6UdgiroP1ePwPMElPmUimlEJd+T/Qqz/2n3/C7trudEiOycrKQmvNyJEjufXWW9mwYYPTIYkYEVQ/d2PMYmBxtXX3BbwfE+K4GudQPlgvx9Pk6dRIp5KScN16D96Hfob3L7/F9YtHUG07OB1Wk6t4QMnj8bBkyRLuvPNOhyMSsSK2nlCt6OMewQ8wyYBQ31PpGbju/DWUleH906+xR2qOM1YdO3aMp576fmC1Ll26SHdCETIxldztQV9yL4zgGZhkQKiqVMeuuH58Hxw6iPfPD2CL42eC7d27d7N58+bK5R/96Ed07tzZwYhELImp5F4xvV6kzsAkA0LVTPXsh2v2LyBrB96/PYwtLwvr+SJF9fb1wYMHo1S9PdyECEpsJff8PDzNmqGaR2azzMkMCPXyyy8DsTsglDprEOqaO2DL53ExyFhBQQF///vfK5f79etXOWaMEKEQU8nd5h+gpFU6LhWZ1Xr99deZNs03ckPFgFAVahsQauzYsaxevZqdO3cCvgGhxo8fz/jx4/nqq6/Yvr1xPU2CGRBq2bJlnHvuuTzwwAONOkdDuYZdhLr8JvhsLfaZP2A9sZvgd+3axe7d34+td8stt5Cenu5gRCLWBNVbJmpE8ANM+fn5JzUglNvt5rPPPov5AaFcY6bi9Xqxr/yDw3/6Dfaq21EJsTdd4po1a6osn3nmmQ5FImJVZF7iNlZ+HkVpkXkz9e233z6pAaF2794dNwNCucZdgpp+LSWr38X+40++5xdiyIEDB3j22WcrlwcPHkzXrl3r2EOIhouZK3dbUgLHjnAsQibpKCwsJD8/ny5dfANkvvHGG9x2221VykyaNImFCxcyderUKuv79OnDnDlzmDVrFtZaEhMTmTdvHqeffjoDBgxg1KhRdOvWjUGDBtV47ttuu41bbrmFl19+mc6dO1d2t/viiy944YUXeOyxx8jMzOSuu+5i8uTJANx9991kZmYC8Mtf/pIf//jH3H///bRu3ZrHH388pL+bYLgmTKd58+Yce/Hv2NISXLN/hkpKbvI4wmHXrl3s3//9g9w33nhjlW9uQoRCvQOHhVFIBw6z+3Lw/upW/jv5AvLPOaveY4Rj4LD8/Hyys7PZunUrL774IgcOHGDJkiWVSfNkxOvgSvv/80/sgqeh7xm4bv8lKiW6k6C1loceeoi//vWvgK830gcffECPHj2A+P07S52DF+zAYTFz5V7RDbKwCYceqJjlZvfu3axdu5YFCxac8IGRnZ0dkuQer1wXXYw3tSX2n0/gfexeXHfej0qL3huP+/bt44UXXqhcHjNmTOW3OyFCKWaSu/VPr1fcKi2o8kopiouLSUlp2FAFRUVF7N27l507d/Lmm2+yePFijh8/Xmv5bdu2VU6RJhrHdd4obPOWeJ96BO8jv8D141+h2nWqf8cItGPHDo4ePVq5fOWVV5KcHBvNTSKyxExyJ9/XF7s8I6PeSikU999/P++++y5TpkypdyS+ihlutm3bxksvvcT69evr3adHjx5cffXVnHbaaQ2phaiFOmsQrrsfwPvX3+F96Oe4bp2L6jvA6bAaxOPxsHDhwsrl5ORkGW5AhE3sJPeCPMpSU0lMrvtK3KVcZBZm8pt//YaysjKGDh16whOYXq+X3NxcvvvuOz755BP+/e9/k5WVVcsRfRISEhg6dCizZs2iT58+dO7cmVatZKq/UFK9++Oa+xjeJx/E+/h9qKtvwzXsIqfDCtqePXuqJPdp06ZJk4wIm5hJ7vbgfkrqaZJJUAmkH03n1utvrWwbz8nJoXXr1hQXF7Nnzx527drF22+/zVtvvcWxY8fqPF5aWhpTp05l4sSJnHrqqXTq1IlmzZqFrE7iRKpdR1z3PIr3qUew/3oCb84u1KXXohIj/5/y9u3bqzyXMH36dBJisA+/iAyR/z8iWHn7KWxTe3JPciXRPL85N11zU5W71G+++Sbbt2/npZdeYt26dXi93jpP061bN6688koGDx5Mt27daN++vYwH0sRUaktcP/411jyLXf4Gdud2XD/6OSrjxIe1IkVZWVnlEBIALVu2pGfPng5GJGJdTCR36/VC/n6O96i5DTbZlUxSbhLXX309R44cqbKtphETA7lcLoYMGcKsWbPo27cvXbp0ISNCByaLJyoxEXXFj/D27Id9/i94H7gL14/moPpG5s3rrKwsli1bVrk8a9YsOnbs6GBEItbFRHLnUD6Ul3OshqF+m7maYbMs1193fZ29WgK1bNmSKVOmMHny5Mrmlob2qhFNwzVkBLZLd7x//z3eP/wKdfFM1KQZETdkwbZt26oM5zxx4kT5xifCKqjkrrWeADwBJADPGGMerrb9QuBPwJnATGPM/4U60Dod9D3td7xV1XFlUlwpFH1TxK033kpJSd1zdnfp0oWrrrqqSnOLyxVbozPEKtW5G65f/gH7wt+wi17CbtqA68a7I6a7ZFFREf/6178ql9u0aUP37t2dC0jEhXqzl9Y6AZgHTAT6A7O01v2rFfsOuA54KdQBBsPm5QJwvNX3Q/02V805tOkQN197c72J/fzzz2fFihXccccdDBkyhI4dO0pijzIqpQWum3+KuvlnsC8b7wN34V21LCImnM7KyqoySNsNN9xAu3btHIxIxINgMthg4BtjzA5jTCmwAJgWWMAYs8sYsxGo+25kuBz0JXdPpq9LY4uEFqQfSec39/4mqJmNPv/88yoPlojo5Rp8Ia5f/xm698G+MA/vn+7HHtjnaEybNm2q8iFz4YUXOhiNiBfBNMt0BgI7eWcDQxpzMq31bGA2+ObvdLvdjTkMiYmJVfY9fPQwx9LTyXC3QymFS7lITE/kn4v+SemxUg7nH+ZI/hG+3vY169asY+vWrVVurBYWFpKTkxPRw65Wr3M8aHSd3W7s7/5K0dKFHHvxb3jvv4OWM2+ixdTLUQlNe5vpwIEDVSbl6NKlC/3796+1XvJ3jg9NUedg/qXXdNenUd91jTHzgfkVx2jswDnVB93x5HxHUau0Klffh/BPtpwCdILUTqkMPXsoo2eNhiJYt2Qd5557LgcOHODzzz8nOzs7ogcvksGVGmHwCFSv07EvP8Wx5+dx7P3FuK74EapX9VbF8NmyZcsJ86SmpKTUWi/5O8eHEAwcVq9gkns2EDjYdBegccM5hkteLoUd6x+cq7i8mGKKIRF+//vfVz7ING3aNIqKirDWSg+GGKNau0m47ZfYz9bifXk+3kfugUEX4Jp+LapN+Nu9a5onVYimEExyXw/01lp3B3KAmcAVYY2qAazHAwV5HOvb+Me4rbXS1THGqR8MxXX6Oex+5U90WrMW+/nHuMb9EDVhOiolPHMAyDypwkn13lA1xpQDtwPLgK2+VWaz1voBrfVUAK31IK11NjADeEprvbn2I4ZYQR54vRytoY+7EIFUsxT2jxnN2luvJKd3V+zbBs/cm/G+sxBbWnePqsbYvXt3lXlSf/SjH8k8qaLJBHV3yRizGFhcbd19Ae/X42uuaXr+nhCB3SCFqEtJqzS+unQSOYP30n3lWtq98k+8yxbimqxRF4xHJSWF5DyrV6+usnzWWfVPIiNEqER9Z26b62s3L3LLhBiiYY516ciXV13K+qsvIb9VCvbl+Xjm3oR36avYwuCeZq5w8OBBPvzwQ7KysvB4POTl5ck8qcJR0T/8QO4evElJeNMziKwHzkW0OHJKFz6/ZjqtdnzHKR99SttXn8P7tsF14QTURRejWtffZS05OZlf/vKX7Nmzh+nTp9O3b1+ZJ1U4KuqTu83dQ1Gb1iQ0cf9lEWOU4nDPU9jY8xRS9+yjy9oNdF7+OqxYhOvc81EjJkCfAbX2pkpLS6NXr158++23vPjiiydsHzAguiYWEdEv+jNibg7H3XKTSoTO8U4d+Gr6ZHYVHKbTus/o+uUnJK3/ENp3Ro2cgBo6GpV64vDSZ555ZpWRHwNdeuml3HTTTZx//vmceuqpMrKoCLuoTu62vAzycjnaS4ZOFaFXktmKnRNGsfui4WRu2sop/91G5n+exfva87jOGoIaMgIG/ACV6LsBW9dgYLm5ufzud7+jefPmLFy4kFatWskzFSKsojq5k5cLXi9HMqWnjAgfb1ISB885k4PnnEmLffvpsGEjnbd8SvKnq7GpLXENHI46b2S90yq2bNmSBQsWMGBA7c07QoRKdCf3XN+Dskcz655eT4hQKezQjh2Tx7Bzgof0b3bSYdPXdFyzgoQPltJq3OW17peWloYxhjPOOEMSu2gSUZ3c7V7feGYlbdpEf59OEVVsQgKH+/bicN9efFNSSqutX9E8ueYnXTMyMjDG0L9/f0nsoslEdXInZzel6WmolnJDVTjH0yyZ/LPPoHVZa1JTU6vM+NWmTRsW/P4B+r75AnZLX+h/NvTuj0qWidRFeEV1crfZuzjWzi1XQyIi2GaWbt26sXXrVgDatWvH008/CdtXkV92iIx338D1zkJsYhKqZz9Uz9NQvU6Dnn1RLVrWc3QhGiZqk7stL4e92RweHJkTIov4403y0qNnD7Zu3UrHjh3567/+yuH0o+S3HUj2+QNxlZaRunMXbXZm0zZ7H2lLN6G8FqsUqlM3VK/TKDprELZ1O+jQJeLmgRXRJWqTO7k54CmnQPq4iwhRVF5E/wH92fjFRv7yj79wqOUhvPb7ycm8yUkc7dubo317swtIKC0l5bssMrL34c45QMba9zjywVIAbFIyqsupqFN6QbceqFN6QseuqKRkZyonok7UJnf73Q4ADreVMWVEZCj1lHLuwHO5YOwFFLQoqJLYa+JJTuZ4r54c79WTHACvlzZFxXi2bydjXz6t9xeQvnYFCStLseC7wm/XyZfkO3aBTl1RHbv5rvKbSRu+qCpqkzvfbMXTrBml7dpFcSVErEk/JZ39ZfsbNzG3y0VZxw4cSW3BIWAXgLUkH8ynec4e0g4eotXBo6Rlf02LjZ+gvN7vk37rttC2A6pthyo/adtB2vPjVNTmRfvtVo506UhionxNFZEjtyw3tAdUilJ3G0rdbTiMb1o0AOXxkJR3kGb795Oed4i0Q8doeWg/LbK+Iel4YdV5MFPToE07yGyDynRDZhvIdKMy20CG/71c+cecqEzu3uNHYc935F0w0OlQhHCETUigtH07Stu342i1baq4mKSD+TQ7VEBqwVFSDx8j9UghzfftoNnXG0kqKvYdI3CnFi2hVSakZ6DSWkFaK0hvBWkZqPSMKsukNJcealEgKpN76abPwFr2d2rjdChCRBybkkJp506Udu50QuIHUKWlJBw+TOLhQzQ/Wuh/Had5YQkphQdJzssm6XgRicU1fAgAuBIgtaXvA6FFKrRI9TX9VK7zrVepLaF5KqQ0972apfh/NpeeQE0gqOSutZ4APAEkAM8YYx6utr0Z8DxwLnAQuNwYsyu0oX6v5OMP8LRowbFuXaLz00kIB9nkZMrbtqW8bVuKgYLaCpaV4yo8RsLRoyQeLySlsJhmx4tILi6lWUkZycWlJJcUkVRwmMS9pSQWF5NYVIzy32+o865DUnJlsj+Y2hJPYtL3iT+lOSQnQ2Ky72dSwE//S1Wua+b/meR7X1EmMdH3SkhEueLz+fV6c6PWOgGYB4zF1+S3Xmu9yBizJaDYjUCBMaaX1nom8AhQ+0AbJ8EeKaB47UpyT+tBYrJMai1E2CQl4m2VgbdVBmVAUTD7WIsqKcFVWIirqJCE4mISSstILC0nsaycpNIyEkrLSSorI6nUQ2JZOc0tUHichEOH/GXLcJWX4yorx1VehvKe+DHRoNvVLhckfJ/sK39WvK9jWSUmQkKC79uKy1X1ffWfCTWtq6m8i/IfDIGk8OavYC58BwPfGGN2AGitFwDTgMDkPg243//+/4C/aK2VMaYRXQbqZt99G8pK2TbotFAfWghxspTCpqTgSUnBQ2vKgtglPT2dI0eO1LrdesqhtBRXeTmUlaLKynCVlaPKfT8Tyz24yj0klntxlZeTUO7B5fXi8nhRXi8JXi8ujyXB48XltZXbXB7v9++9JajyQlwlFpfHg/J6fT89XlxeD3gtyutFWf9PrzdgnbfGD6C6HL/5Lhg8ukH7NFQwyb0zkBWwnA0Mqa2MMaZca30YaAPkBRbSWs8GZvvL4XbXP31ZdfaaW9l7em/adUxBcXI3dRpzfqckJiZGVbyhEI4693b1JutwVv0FHZKYmEiLxPiaji9cda54ysAT8iOfyFoveH0v6/GA1+Nb9vh/ej3g8f30ess5q89A2of5/3Mwyb2mDFr9YyqYMhhj5gPzK7bn5eVVLxKUTudPJrmR+wZq7Pmd4Ha7oyreUAhHnTPJJDMtch98k79zfDiZOnfq1CmocsHcacgGAqdt7wLsqa2M1joRaAXkBxWBEEKIkAvmyn090Ftr3R3IAWYCV1Qrswi4FlgLXAa8F472diGEEMGp98rdGFMO3A4sA7b6VpnNWusHtNZT/cWeBdporb8BfgLcE66AhRBC1E81agyM0LB79lRv3QlOKNroOnfuTE5OzkkdoylJu2R8kDrHhxC0udfbmyQ+e/cLIUSMk+QuhBAxSJK7EELEIEnuQggRgxy9oerUiYUQIspF9A1V1diX1nrDyewfjS+pc3y8pM7x8QpBneslzTJCCBGDJLkLIUQMitbkPr/+IjFH6hwfpM7xIex1dvKGqhBCiDCJ1it3IYQQdZDkLoQQMSiq5peub6LuWKS1/gcwBdhvjBngdDzhprXuim+y9Q74JtOZb4x5wtmowktrnQKsAprh+z/5f8aYXzsbVdPwz9H8KZBjjJnidDzhprXeBRzFN0FUuTFmYLjOFTVX7gETdU8E+gOztNb9nY2qSfwLmOB0EE2oHPipMeY04Dzgtjj4O5cAo40xZwFnAxO01uc5HFNTuRPfUOLxZJQx5uxwJnaIouROwETdxphSoGKi7phmjFlFHM1qZYzZa4z5zP/+KL7/+J2djSq8jDHWGHPMv5jkf8V8TwetdRdgMvCM07HEomhqlglmom4RQ7TWpwLnAOscDiXs/N9MNwC9gHnGmJivM/AnYA6Q5nQgTcgC72itLfCUf17psIimK/eaHrmN+aubeKW1bgm8CtxljDnidDzhZozxGGPOxjdH8WCtdUzfX9FaV9xH2uB0LE1smDHmB/ial2/TWl8YrhNFU3IPZqJuEQO01kn4Evu/jTGvOR1PUzLGHAJWEvv3WYYBU/03GBcAo7XWLzobUvgZY/b4f+4HFuJrbg6LaGqWCWaibhHltNYK35y8W40xf3Q6nqagtW4LlBljDmmtmwNjgEccDiusjDFzgbkAWuuRwM+MMVc5GlSYaa1TAZcx5qj//TjggXCdL2qu3GubqNvZqMJPa/0ysBboq7XO1lrf6HRMYTYMuBrfldzn/tckp4MKs47A+1rrjfguYpYbY95yOCYReu2B1VrrL4BPgLeNMUvDdTIZfkAIIWJQ1Fy5CyGECJ4kdyGEiEGS3IUQIgZJchdCiBgkyV0IIWKQJHchhIhBktyFECIG/X+VfvRt/HxEuAAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"%matplotlib inline\n",
"\n",
"x = np.linspace(0.01,5,1000)\n",
"y = stats.f.pdf(x, \n",
" dfn=sub_model_VNJ_2.df_resid, \n",
" dfd=sub_model_VNJ_1.df_resid)\n",
"plt.figure()\n",
"plt.plot(x, y, label='$\\mathrm{F}_{df_2, df_1}$ density')\n",
"\n",
"plt.axvline(F_VNJ_sigma2, color='black', linewidth=1, label='$F^{LN}_{\\sigma^2}$')\n",
"tmp = stats.f.cdf(F_VNJ_sigma2, \n",
" dfn=sub_model_VNJ_2.df_resid, \n",
" dfd=sub_model_VNJ_1.df_resid)\n",
"plt.fill_between(x[x < F_VNJ_sigma2], y[x < F_VNJ_sigma2], color='green', alpha=0.3)\n",
"tmp = stats.f.ppf(1-tmp,\n",
" dfn=sub_model_VNJ_2.df_resid, \n",
" dfd=sub_model_VNJ_1.df_resid)\n",
"plt.fill_between(x[x > tmp], y[x > tmp], color='green', alpha=0.3)\n",
"plt.annotate('Area 0.06', xy=(0.15, 0.1), \n",
" xytext=(0.75, 0.15), arrowprops=dict(facecolor='black'))\n",
"plt.annotate('Area 0.06', xy=(2.75, 0.025), \n",
" xytext=(3, 0.2), arrowprops=dict(facecolor='black'))\n",
"plt.legend()\n",
"plt.title('Two-sided F-test')\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Since $F_{\\sigma^2}^{LN}$ is below the 50th percentile, the two-sided equal tailed p-value is in our case given by"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"F test two-sided p-value: 0.12\n"
]
}
],
"source": [
"print('F test two-sided p-value: {:.2f}'.format(\n",
" 2*np.min([F_VNJ_sigma2_percentile, 1-F_VNJ_sigma2_percentile])\n",
")\n",
" )"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The one-sided p-value for the hypothesis $H_{\\sigma^2}: \\sigma^2_1 \\leq \\sigma^2_2$ simply corresponds to the area in the lower tail of the distribution. This is because the statistic is $\\hat\\sigma^{2,LN}_2/\\hat\\sigma^{2,LN}_1$ so that smaller values work against our hypothesis. Thus, the rejection region is the lower tail.\n",
"\n",
"*Remark: in the paper, the one-sided hypothesis is given as $H_{\\sigma^2}: \\sigma^2_1 > \\sigma^2_2$. This is a mistake as this corresponds to the alternative.*"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"F statistic one-sided p-value: 0.06\n"
]
}
],
"source": [
"print('F statistic one-sided p-value: {:.2f}'.format(F_VNJ_sigma2_percentile))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Testing for common linear predictors\n",
"\n",
"We can move on to test for common linear predictors:\n",
"$$ H_{\\mu, \\sigma^2}: \\sigma^2_1 = \\sigma^2_2 \\quad \\text{and} \\quad \\alpha_{i,\\ell} + \\beta_{j,\\ell} + \\delta_\\ell = \\alpha_i + \\beta_j + \\delta $$\n",
"If we are happy to accept the hypothesis of common variances $H_{\\sigma^2}: \\sigma^2_1 = \\sigma^2_2$, we can test $H_{\\mu, \\sigma^2}: \\sigma^2_1$ with a simple $F$-test; corresponding to a reduction from $M^{LN}_{\\sigma^2}$ to $M^{LN}_{\\mu, \\sigma^2}$ The test is implemented in the package."
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [],
"source": [
"f_linpred_VNJ = apc.f_test(model_VNJ, [sub_model_VNJ_1, sub_model_VNJ_2])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This returns the test statistic $F_\\mu^{LN}$ along with the p-value."
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"F_stat: 0.24\n",
"p_value: 0.91\n"
]
}
],
"source": [
"for key, value in f_linpred_VNJ.items():\n",
" print('{}: {:.2f}'.format(key, value))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"These results, too, much those from the paper."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 5.2 Over-dispersed Poisson Chain-Ladder\n",
"\n",
"This corresponds to Section 5.2 in the paper. The data are taken from Taylor and Ashe (1983). For this data, the desired full model is an over-dispersed Poisson model given by\n",
"$$ M^{ODP}_{\\mu, \\sigma^2}: \\quad E(Y_{ij}) = \\exp(\\alpha_i + \\beta_j + \\delta), \\quad \\frac{\\mathrm{var}(Y_{ij})}{E(Y_{ij})} = \\sigma^2. $$\n",
"We proceed just as we did above. First, we set up and estimate the full model and the sub-models. Second, we compute the Bartlett test for common over-dispersion. Third, we test for common linear predictors.\n",
"\n",
"Finally, we repeat the testing procedure for different sub-sample structures."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Full model\n",
"\n",
"We set up and estimate the model $M^{ODP}_{\\mu, \\sigma^2}$ on the full data set."
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"log-data variance full model: 52862\n",
"degrees of freedom full model: 36\n"
]
}
],
"source": [
"model_TA = apc.Model()\n",
"\n",
"model_TA.data_from_df(apc.data.pre_formatted.loss_TA(), data_format='CL')\n",
"\n",
"model_TA.fit('od_poisson_response', 'AC')\n",
"\n",
"print('log-data variance full model: {:.0f}'.format(model_TA.s2))\n",
"print('degrees of freedom full model: {:.0f}'.format(model_TA.df_resid))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Sub-models\n",
"\n",
"We set up and estimate the models on the four sub-samples. Combined, these models correspond to $M^{ODP}$."
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Sub-sample I_1\n",
"--------------\n",
"over-dispersion: 31903\n",
"degrees of freedom: 6\n",
"\n",
"Sub-sample I_2\n",
"--------------\n",
"over-dispersion: 168293\n",
"degrees of freedom: 3\n",
"\n",
"Sub-sample I_3\n",
"--------------\n",
"over-dispersion: 104493\n",
"degrees of freedom: 6\n",
"\n",
"Sub-sample I_4\n",
"--------------\n",
"over-dispersion: 17592\n",
"degrees of freedom: 6\n",
"\n",
"Weighted avg of over-dispersion: 68038\n"
]
}
],
"source": [
"sub_model_TA_1 = model_TA.sub_model(per_from_to=(1,5), fit=True)\n",
"sub_model_TA_2 = model_TA.sub_model(coh_from_to=(1,5), age_from_to=(1,5),\n",
" per_from_to=(6,10), fit=True)\n",
"sub_model_TA_3 = model_TA.sub_model(age_from_to=(6,10), fit=True)\n",
"sub_model_TA_4 = model_TA.sub_model(coh_from_to=(6,10), fit=True)\n",
"\n",
"sub_models_TA = [sub_model_TA_1, sub_model_TA_2, \n",
" sub_model_TA_3, sub_model_TA_4]\n",
"\n",
"for i, sm in enumerate(sub_models_TA):\n",
" print('Sub-sample I_{}'.format(i+1))\n",
" print('--------------')\n",
" print('over-dispersion: {:.0f}'.format(sm.s2))\n",
" print('degrees of freedom: {:.0f}\\n'.format(sm.df_resid))\n",
" \n",
"s2_bar_TA = np.array([sm.s2 for sm in sub_models_TA]).dot(\n",
" np.array([sm.df_resid for sm in sub_models_TA])\n",
")/np.sum([sm.df_resid for sm in sub_models_TA])\n",
"print('Weighted avg of over-dispersion: {:.0f}'.format(s2_bar_TA))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Testing for common over-dispersion\n",
"\n",
"We perform a Bartlett test for the hypothesis of common over-dispersion across sub-samples $H_{\\sigma^2}: \\sigma^2_\\ell = \\sigma^2$. This corresponds to testing a reduction from $M^{ODP}$ to $M^{ODP}_{\\sigma^2}$."
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"B: 6.78\n",
"LR: 7.37\n",
"C: 1.09\n",
"m: 4.00\n",
"p_value: 0.08\n"
]
}
],
"source": [
"bartlett_TA = apc.bartlett_test(sub_models_TA)\n",
"\n",
"for key, value in bartlett_TA.items():\n",
" print('{}: {:.2f}'.format(key, value))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"These results match those in the paper. The Bartlett test yields a p-value of 0.08."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Testing for common linear predictors\n",
"\n",
"If we are happy to impose common over-dispersion, we can test for common linear predictors across sub-samples. Then, this corresponds to a reduction from $M^{ODP}_{\\sigma^2}$ to $M^{ODP}_{\\mu, \\sigma^2}$."
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"F_stat: 0.46\n",
"p_value: 0.93\n"
]
}
],
"source": [
"f_linpred_TA = apc.f_test(model_TA, sub_models_TA)\n",
"\n",
"for key, value in f_linpred_TA.items():\n",
" print('{}: {:.2f}'.format(key, value))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Repeated testing\n",
"\n",
"In the paper, we also suggest a procedure to repeat the tests for different sub-sample structures, using a Bonferroni correction for size-control."
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Two sub-samples\n",
"---------------\n",
"Bartlett\n",
"--------\n",
"B: 2.89\n",
"LR: 3.06\n",
"C: 1.06\n",
"m: 2.00\n",
"p_value: 0.09\n",
"\n",
"F-test\n",
"------\n",
"F_stat: 0.63\n",
"p_value: 0.64\n",
"\n",
"Three sub-samples\n",
"-----------------\n",
"Bartlett\n",
"--------\n",
"B: 1.27\n",
"LR: 1.40\n",
"C: 1.10\n",
"m: 3.00\n",
"p_value: 0.53\n",
"\n",
"F-test\n",
"------\n",
"F_stat: 1.84\n",
"p_value: 0.11\n"
]
}
],
"source": [
"sub_models_TA_2 = [model_TA.sub_model(coh_from_to=(1,5), fit=True),\n",
" model_TA.sub_model(coh_from_to=(6,10), fit=True)]\n",
"\n",
"sub_models_TA_3 = [model_TA.sub_model(per_from_to=(1,4), fit=True),\n",
" model_TA.sub_model(per_from_to=(5,7), fit=True),\n",
" model_TA.sub_model(per_from_to=(8,10), fit=True)]\n",
"\n",
"print('Two sub-samples')\n",
"print('---------------')\n",
"print('Bartlett')\n",
"print('--------')\n",
"for key, value in apc.bartlett_test(sub_models_TA_2).items():\n",
" print('{}: {:.2f}'.format(key, value))\n",
"\n",
"print('\\nF-test')\n",
"print('------')\n",
"for key, value in apc.f_test(model_TA, sub_models_TA_2).items():\n",
" print('{}: {:.2f}'.format(key, value))\n",
" \n",
"print('\\nThree sub-samples')\n",
"print('-----------------')\n",
"print('Bartlett')\n",
"print('--------')\n",
"for key, value in apc.bartlett_test(sub_models_TA_3).items():\n",
" print('{}: {:.2f}'.format(key, value))\n",
"\n",
"print('\\nF-test')\n",
"print('------')\n",
"for key, value in apc.f_test(model_TA, sub_models_TA_3).items():\n",
" print('{}: {:.2f}'.format(key, value))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The test results match those in the paper. \n",
"\n",
"*For a quick refresher on the Bonferroni correction we turn to [Wikipedia](https://en.wikipedia.org/wiki/Bonferroni_correction). The idea is to control the family wise error rate, the probability of rejecting at least one null hypothesis when the null is true.*\n",
"\n",
"*In our scenario, we repeat testing three times. Each individual repetition is comprised of two sequential tests: a Bartlett and an $F$-test. \n",
"Under the null hypothesis (so the true model is $M_{\\mu, \\sigma^2}^{ODP}$), the two tests are independent so*\n",
"$$P(\\text{reject $F$-test } | \\text{ not-reject Bartlett test}) = P(\\text{reject $F$-test}).$$\n",
"*Thus, if we test at level $\\alpha$, the probability to reject at least once within a repetition is not $\\alpha$ but $1-(1-\\alpha)^2 \\approx 2\\alpha$:*\n",
"$$ P(\\text{Reject Bartlett or F-test at level }\\alpha \\text{ for a given split}) \\approx 2 \\alpha .$$\n",
"*For thrice repeated testing, we replace $\\alpha$ by $\\alpha/3$. Then, we bound the probability to reject when the null is true with*\n",
"$$ P\\left\\{\\cup_{i=1}^3\\left(\\text{Reject Bartlett or F-test at level } \\frac{\\alpha}{3} \\text{ for split }i\\right)\\right\\} \\leq 2\\alpha \\quad \\text{(approximately)} .$$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 5.3 Log-Normal (Extended) Chain-Ladder\n",
"\n",
"This corresponds to Section 5.3 in the paper. The data are taken from Barnett and Zehnwirth (2000). These data are commonly modeled with a calendar effect. We consider misspecification tests both for a model without $M^{LN}$ and with $M^{LNe}$ a calendar effect $\\gamma$. The models are given by\n",
"$$ M^{LN}_{\\mu, \\sigma^2}: \\quad \\log(Y_{ij}) \\stackrel{D}{=} N(\\alpha_i + \\beta_j + \\delta, \\sigma^2)$$\n",
"and\n",
"$$ M^{LNe}_{\\mu, \\sigma^2}: \\quad \\log(Y_{ij}) \\stackrel{D}{=} N(\\alpha_i + \\beta_j + \\gamma_k + \\delta, \\sigma^2). $$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### No calendar effect\n",
"\n",
"We set up and estimate the model $M^{LN}_{\\mu, \\sigma^2}$ on the full data set."
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"log-data variance full model: 0.0068\n",
"degrees of freedom full model: 45\n"
]
}
],
"source": [
"model_BZ = apc.Model()\n",
"\n",
"model_BZ.data_from_df(apc.data.pre_formatted.loss_BZ(), time_adjust=1, data_format='CL')\n",
"\n",
"model_BZ.fit('log_normal_response', 'AC')\n",
"\n",
"print('log-data variance full model: {:.4f}'.format(model_BZ.s2))\n",
"print('degrees of freedom full model: {:.0f}'.format(model_BZ.df_resid))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Next, the models for the sub-samples."
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Sub-sample I_1\n",
"--------------\n",
"over-dispersion: 0.0002\n",
"degrees of freedom: 6\n",
"\n",
"Sub-sample I_2\n",
"--------------\n",
"over-dispersion: 0.0013\n",
"degrees of freedom: 6\n",
"\n",
"Sub-sample I_3\n",
"--------------\n",
"over-dispersion: 0.0015\n",
"degrees of freedom: 9\n",
"\n",
"Weighted avg of over-dispersion: 0.0011\n"
]
}
],
"source": [
"sub_models_BZ = [model_BZ.sub_model(per_from_to=(1977,1981), fit=True),\n",
" model_BZ.sub_model(per_from_to=(1982,1984), fit=True), \n",
" model_BZ.sub_model(per_from_to=(1985,1987), fit=True)]\n",
"\n",
"for i, sm in enumerate(sub_models_BZ):\n",
" print('Sub-sample I_{}'.format(i+1))\n",
" print('--------------')\n",
" print('over-dispersion: {:.4f}'.format(sm.s2))\n",
" print('degrees of freedom: {:.0f}\\n'.format(sm.df_resid))\n",
" \n",
"s2_bar_BZ = np.array([sm.s2 for sm in sub_models_BZ]).dot(\n",
" np.array([sm.df_resid for sm in sub_models_BZ])\n",
")/np.sum([sm.df_resid for sm in sub_models_BZ])\n",
"print('Weighted avg of over-dispersion: {:.4f}'.format(s2_bar_BZ))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We move on the Bartlett test for the hypothesis of common log-data variances across sub-samples $H_{\\sigma^2}: \\sigma^2_\\ell = \\sigma^2$."
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"B: 6.06\n",
"LR: 6.47\n",
"C: 1.07\n",
"m: 3.00\n",
"p_value: 0.05\n"
]
}
],
"source": [
"bartlett_BZ = apc.bartlett_test(sub_models_BZ)\n",
"\n",
"for key, value in bartlett_BZ.items():\n",
" print('{}: {:.2f}'.format(key, value))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The Bartlett test yields a p-value of 0.05 as in the paper."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We test for common linear predictors across sub-samples."
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"F_stat: 11.20\n",
"p_value: 0.00\n"
]
}
],
"source": [
"f_linpred_BZ = apc.f_test(model_BZ, sub_models_BZ)\n",
"\n",
"for key, value in f_linpred_BZ.items():\n",
" print('{}: {:.2f}'.format(key, value))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Calendar effect\n",
"\n",
"Now we redo the same for the model with calendar effect."
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"log-data variance full model: 0.0014\n",
"degrees of freedom full model: 36\n",
"Sub-sample I_1\n",
"--------------\n",
"over-dispersion: 0.0003\n",
"degrees of freedom: 3\n",
"\n",
"Sub-sample I_2\n",
"--------------\n",
"over-dispersion: 0.0013\n",
"degrees of freedom: 5\n",
"\n",
"Sub-sample I_3\n",
"--------------\n",
"over-dispersion: 0.0016\n",
"degrees of freedom: 8\n",
"\n",
"Weighted avg of log-data variances: 0.0013\n",
"\n",
"Bartlett test\n",
"-------------\n",
"B: 2.06\n",
"LR: 2.27\n",
"C: 1.10\n",
"m: 3.00\n",
"p_value: 0.36\n",
"\n",
"F-test\n",
"------\n",
"F_stat: 1.13\n",
"p_value: 0.41\n"
]
}
],
"source": [
"model_BZe = apc.Model()\n",
"\n",
"model_BZe.data_from_df(apc.data.pre_formatted.loss_BZ(), time_adjust=1, data_format='CL')\n",
"\n",
"model_BZe.fit('log_normal_response', 'APC') # The only change is in this line. \n",
"\n",
"print('log-data variance full model: {:.4f}'.format(model_BZe.s2))\n",
"print('degrees of freedom full model: {:.0f}'.format(model_BZe.df_resid))\n",
"\n",
"sub_models_BZe = [model_BZe.sub_model(per_from_to=(1977,1981), fit=True),\n",
" model_BZe.sub_model(per_from_to=(1982,1984), fit=True), \n",
" model_BZe.sub_model(per_from_to=(1985,1987), fit=True)]\n",
"\n",
"for i, sm in enumerate(sub_models_BZe):\n",
" print('Sub-sample I_{}'.format(i+1))\n",
" print('--------------')\n",
" print('over-dispersion: {:.4f}'.format(sm.s2))\n",
" print('degrees of freedom: {:.0f}\\n'.format(sm.df_resid))\n",
" \n",
"s2_bar_BZe = np.array([sm.s2 for sm in sub_models_BZe]).dot(\n",
" np.array([sm.df_resid for sm in sub_models_BZe])\n",
")/np.sum([sm.df_resid for sm in sub_models_BZe])\n",
"print('Weighted avg of log-data variances: {:.4f}'.format(s2_bar_BZe))\n",
"\n",
"bartlett_BZe = apc.bartlett_test(sub_models_BZe)\n",
"\n",
"print('\\nBartlett test')\n",
"print('-------------')\n",
"\n",
"for key, value in bartlett_BZe.items():\n",
" print('{}: {:.2f}'.format(key, value))\n",
"\n",
"print('\\nF-test')\n",
"print('------')\n",
" \n",
"f_linpred_BZe = apc.f_test(model_BZe, sub_models_BZe)\n",
"\n",
"for key, value in f_linpred_BZe.items():\n",
" print('{}: {:.2f}'.format(key, value))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"With this, we replicated Figure 4b."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Closer look at the effect of dropping the calendar effect \n",
"\n",
"In the paper, we move on to take a closer look at the effect of dropping the calendar effect. We do so in two ways starting with $$M^{LNe}_{\\sigma^2}: \\stackrel{D}{=} N(\\alpha_{i, \\ell} + \\beta_{j, \\ell} + \\gamma_{k, \\ell} + \\delta_\\ell, \\sigma^2).$$ \n",
"We want to test for a reduction to \n",
"$$M^{LN}_{\\mu, \\sigma^2}: \\stackrel{D}{=} N(\\alpha_i + \\beta_j + \\delta, \\sigma^2).$$ \n",
"In the figure below, we illustrate two different testing procedures that would get us to there. \n",
"\n",
"<center>\n",
" <img src=\"https://user-images.githubusercontent.com/25103918/41599423-27d94fec-73a1-11e8-9fe1-3f3a1a9e184a.png\" \n",
" alt=\"Two ways to test for reduction to the same model\"\n",
" width=\"400px\"/>\n",
"</center>\n",
"\n",
"\n",
"1. We can move down, testing $H^{LNe}_{\\sigma^2, \\mu}$, and then right, testing $H_\\gamma: \\gamma_k = 0$\n",
"2. We can move right, testing $H_{\\gamma_{k, \\ell}}: \\gamma_{k, \\ell} = 0$, and then down, testing $H^{LN}_{\\sigma^2, \\mu}$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Looking at the first way, we already saw that $H_{\\gamma_{k, \\ell}}: \\gamma_{k, \\ell} = 0$ cannot be rejected. To test for the absence of a calendar effect, we can do an (exact) $F$ test. "
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>-2logL</th>\n",
" <th>df_resid</th>\n",
" <th>LR_vs_APC</th>\n",
" <th>df_vs_APC</th>\n",
" <th>F_vs_APC</th>\n",
" <th>P>F</th>\n",
" <th>aic</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>AC</th>\n",
" <td>-166.967</td>\n",
" <td>45</td>\n",
" <td>120.492</td>\n",
" <td>9</td>\n",
" <td>20.8271</td>\n",
" <td>9.59281e-12</td>\n",
" <td>-124.967</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" -2logL df_resid LR_vs_APC df_vs_APC F_vs_APC P>F aic\n",
"AC -166.967 45 120.492 9 20.8271 9.59281e-12 -124.967"
]
},
"execution_count": 29,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"model_BZe.fit_table(attach_to_self=False).loc[['AC']]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We see that the p-value (```P>F```) is close to zero."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Next, we consider the second way. We first test $H_{\\gamma_{k, \\ell}}$. Since $\\sigma^2$ is common across the array from the outset, we can do this with a simple $F$-test:\n",
"$$ \\frac{(RSS_.^{LN} - RSS_.^{LNe})/(df_.^{LN} - df_.^{LNe})}{RSS_.^{LNe}/df_.^{LNe}} \\stackrel{D}{=} F_{df_.^{LN} - df_.^{LNe}, df_.^{LNe}} $$ "
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"p-value of F-test: 0.92\n"
]
}
],
"source": [
"rss_BZe_dot = np.sum([sub.rss for sub in sub_models_BZe])\n",
"rss_BZ_dot = np.sum([sub.rss for sub in sub_models_BZ])\n",
"df_BZe_dot = np.sum([sub.df_resid for sub in sub_models_BZe])\n",
"df_BZ_dot = np.sum([sub.df_resid for sub in sub_models_BZ])\n",
"\n",
"F_BZ = ((rss_BZ_dot - rss_BZe_dot)/(df_BZ_dot - df_BZe_dot)) / (rss_BZe_dot/df_BZe_dot)\n",
"p_F_BZ = stats.f.sf(F_BZ, dfn=df_BZ_dot - df_BZe_dot, dfd=df_BZe_dot)\n",
"print('p-value of F-test: {:.2f}'.format(p_F_BZ))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Thus this is not rejected. However, we already saw that a reduction from $M^{LN}_{\\sigma^2}$ to $M^{LN}_{\\mu, \\sigma^2}$ is rejected."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Repeated testing\n",
"\n",
"Just as for the Taylor and Ashe (1983) data, we repeat testing for different splits."
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Two sub-samples\n",
"---------------\n",
"Bartlett\n",
"--------\n",
"B: 5.678\n",
"LR: 6.013\n",
"C: 1.059\n",
"m: 2.000\n",
"p_value: 0.017\n",
"\n",
"F-test\n",
"------\n",
"F_stat: 3.663\n",
"p_value: 0.004\n",
"\n",
"Four sub-samples\n",
"----------------\n",
"Bartlett\n",
"--------\n",
"B: 8.66\n",
"LR: 9.72\n",
"C: 1.12\n",
"m: 4.00\n",
"p_value: 0.03\n",
"\n",
"F-test\n",
"------\n",
"F_stat: 2.28\n",
"p_value: 0.05\n"
]
}
],
"source": [
"sub_models_BZe_2 = [model_BZe.sub_model(coh_from_to=(1977,1981), fit=True),\n",
" model_BZe.sub_model(coh_from_to=(1982,1987), fit=True)]\n",
"\n",
"sub_models_BZe_4 = [model_BZe.sub_model(per_from_to=(1977,1981), fit=True), \n",
" model_BZe.sub_model(coh_from_to=(1977,1982), age_from_to=(1,5),\n",
" per_from_to=(1982,1987), fit=True),\n",
" model_BZe.sub_model(age_from_to=(6,11), fit=True),\n",
" model_BZe.sub_model(coh_from_to=(1983,19871), fit=True)]\n",
" \n",
"print('Two sub-samples')\n",
"print('---------------')\n",
"print('Bartlett')\n",
"print('--------')\n",
"for key, value in apc.bartlett_test(sub_models_BZe_2).items():\n",
" print('{}: {:.3f}'.format(key, value))\n",
"\n",
"print('\\nF-test')\n",
"print('------')\n",
"for key, value in apc.f_test(model_BZe, sub_models_BZe_2).items():\n",
" print('{}: {:.3f}'.format(key, value))\n",
" \n",
"print('\\nFour sub-samples')\n",
"print('----------------')\n",
"print('Bartlett')\n",
"print('--------')\n",
"for key, value in apc.bartlett_test(sub_models_BZe_4).items():\n",
" print('{}: {:.2f}'.format(key, value))\n",
"\n",
"print('\\nF-test')\n",
"print('------')\n",
"for key, value in apc.f_test(model_BZe, sub_models_BZe_4).items():\n",
" print('{}: {:.2f}'.format(key, value))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Again, we replicated the results from the paper."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## References\n",
"\n",
"* Barnett, G., & Zehnwirth, B. (2000). Best estimates for reserves. *Proceedings of the Casualty Actuarial Society*, 87(167), 245–321.\n",
"* Harnau, J. (2018). Misspecification Tests for Log-Normal and Over-Dispersed Poisson Chain-Ladder Models. *Risks*, 6(2), 25. \n",
"* Kuang, D., Nielsen, B., & Nielsen, J. P. (2015). The geometric chain-ladder. *Scandinavian Actuarial Journal*, 2015(3), 278–300.\n",
"* Taylor, G. C., & Ashe, F. R. (1983). Second moments of estimates of outstanding claims. *Journal of Econometrics*, 23(1), 37–61. \n",
"* Verrall, R., Nielsen, J. P., & Jessen, A. H. (2010). Prediction of RBNS and IBNR claims using claim amounts and claim counts. *ASTIN Bulletin*, 40(2), 871–887."
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.6"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| gpl-3.0 |
mramire8/active | other/sent_distribution.ipynb | 2 | 78711 | {
"metadata": {
"name": ""
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Sentence Distribution\n",
"\n",
"Sentence distribution for IMDB dataset \n",
"\n",
"* How many sentences per document in general\n",
"* How many sentences per document per class"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"__author__ = 'mramire8'\n",
"__copyright__ = \"Copyright 2013, ML Lab\"\n",
"__version__ = \"0.1\"\n",
"__status__ = \"Development\"\n",
"\n",
"import sys\n",
"import os\n",
"\n",
"sys.path.append(os.path.abspath(\".\"))\n",
"sys.path.append(os.path.abspath(\"../\"))\n",
"sys.path.append(os.path.abspath(\"../experiment/\"))\n",
"\n",
"from experiment.experiment_utils import clean_html\n",
"import numpy as np\n",
"from datautil.load_data import load_from_file\n",
"\n",
"from collections import Counter\n",
"from sklearn.feature_extraction.text import TfidfVectorizer\n",
"import nltk\n",
"from scipy.sparse import vstack\n",
"\n",
"import matplotlib.pyplot as plt\n",
"import matplotlib as mpl\n",
"\n",
"mpl.style.use('bmh')\n",
"\n",
"def print_features(coef, names):\n",
" \"\"\" Print sorted list of non-zero features/weights. \"\"\"\n",
" print \"\\n\".join('%s/%.2f' % (names[j], coef[j]) for j in np.argsort(coef)[::-1] if coef[j] != 0)\n",
"\n",
"def get_data(train, cats, vct, raw):\n",
"\n",
" min_size = None\n",
" fixk=None\n",
"\n",
" data, vct2 = load_from_file(train, cats, fixk, min_size, vct, raw=raw)\n",
"\n",
" print(\"Data %s\" % train)\n",
" print(\"Data size %s\" % len(data.train.data))\n",
"\n",
" ### SENTENCE TRANSFORMATION\n",
" sent_detector = nltk.data.load('tokenizers/punkt/english.pickle')\n",
"\n",
" ## delete <br> to \".\" to recognize as end of sentence\n",
" data.train.data = clean_html(data.train.data)\n",
" data.test.data = clean_html(data.test.data)\n",
"\n",
" print(\"Train:{}, Test:{}, {}\".format(len(data.train.data), len(data.test.data), data.test.target.shape[0]))\n",
"\n",
" ## convert document to matrix\n",
" data.train.bow = vct.fit_transform(data.train.data)\n",
" data.test.bow = vct.transform(data.test.data)\n",
" return data\n",
"\n",
"\n",
"####################### MAIN ####################\n",
"from scipy.sparse import diags\n",
"\n",
"def split_data_sentences(data, sent_detector, vct, limit=0):\n",
" sent_train = []\n",
" labels = []\n",
" tokenizer = vct.build_tokenizer()\n",
" size_per_doc = []\n",
" print (\"Spliting into sentences... Limit:\", limit)\n",
" ## Convert the documents into sentences: train\n",
" for t, sentences in zip(data.train.target, sent_detector.batch_tokenize(data.train.data)):\n",
"\n",
" if limit is None:\n",
" sents = [s for s in sentences if len(tokenizer(s)) > 1]\n",
" elif limit > 0:\n",
" sents = [s for s in sentences if len(s.strip()) > limit]\n",
" size_per_doc.append(len(sentences))\n",
" elif limit == 0:\n",
" sents = [s for s in sentences]\n",
" sent_train.extend(sents) # at the sentences separately as individual documents\n",
" labels.extend([t] * len(sents)) # Give the label of the document to all its sentences\n",
"\n",
" return labels, sent_train, size_per_doc\n",
"\n",
"def distribution_per_sentence(data_name, sent_per_doc):\n",
" \n",
"\n",
" print \"Sentence distribution\"\n",
"\n",
" sent_per_doc = np.array(sent_per_doc)\n",
" sents = Counter(sent_per_doc)\n",
" plt.figure(figsize=(9,4.5))\n",
" n, bins, patches = plt.hist(sents.keys(), weights=sents.values(), bins=range(100))\n",
" plt.title(\"Document Number of Sentence Distribution {0} (mean={1:.2f}) N={2}\".format(data_name, sent_per_doc.mean(),\n",
" len(sent_per_doc)),\n",
" fontsize=14, family='Arial')\n",
" plt.xlabel(\"Number of sentences\")\n",
" plt.ylabel(\"Frequency\")\n",
" plt.show()\n",
"# for b in n:\n",
"# print \"bin: %s\" % (n)\n",
" \n",
" \n",
"rand = np.random.mtrand.RandomState(987654)\n",
"\n",
"sent_detector = nltk.data.load('tokenizers/punkt/english.pickle')\n",
"\n",
"vct = TfidfVectorizer(encoding='latin1', min_df=5, max_df=1.0, binary=False, ngram_range=(1, 1),\n",
" token_pattern='\\\\b\\\\w+\\\\b') #, tokenizer=StemTokenizer())\n",
"\n",
"categories = [['alt.atheism', 'talk.religion.misc'],\n",
" ['comp.graphics', 'comp.windows.x'],\n",
" ['comp.os.ms-windows.misc', 'comp.sys.ibm.pc.hardware'],\n",
" ['rec.sport.baseball', 'sci.crypt']]\n",
"\n",
"\n"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 59
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"## Get training data\n",
"data = get_data(\"imdb\", [categories[0]], vct, True) # expert: classifier, data contains train and test"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Loading existing file... imdb \n",
"Data imdb"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Data size 25000\n",
"Cleaning text ... \n",
"Cleaning text ... "
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"Train:25000, Test:25000, 25000"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n"
]
}
],
"prompt_number": 7
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"#Get sentences, targets, and number of sentences per document\n",
"X, y, sent_per_doc = split_data_sentences(data, sent_detector, vct, limit=2)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"('Spliting into sentences... Limit:', 2)\n"
]
}
],
"prompt_number": 25
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Sentence Distribution per Document\n",
"\n",
"The following graph is the distribution of number of sentences per document in the training split fo the data. Size of the bin is one and there are 100 bins. \n",
"\n",
"**Note:**\n",
"\n",
"Most of the data has less than 20 sentences (average=18.7). Few documents have one, two and three sentences (~500 documents)"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"distribution_per_sentence(\"imdb\", sent_per_doc)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Sentence distribution\n"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAjoAAAE5CAYAAACZNIrzAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XlcVXX+P/DXRRbZ3RISVFRARJFxt0ZHDTG1NFOzNBW1\nsjQn00YlrEmbKah+aZqRk5lLllq51hipuEw2CqKCKCiLuLG1uEEqBL5/f/C9Z7hw0Ssg9+Px9Xw8\n7kPP55x77ufe97nw5nze53MMIiIgIiIi0iEba3eAiIiI6E5hokNERES6xUSHiIiIdIuJDhEREekW\nEx0iIiLSLSY6REREpFtMdKrJx8cHNjY2sLGxQb169eDq6opevXph+/bt1u5arRMRLF26FFXNRDBv\n3jzY29vj2LFjldb5+Phg+fLltd6nlStXws/Pr9b3ezsmTZoEJycn9O3b1+z6Xbt24S9/+QtcXFzg\n7u6Ohx56CLt376611//555/x1Vdf1dr+asuECRO074aNjQ0cHR3Rvn17LF682GS7fv364e9///st\n91dcXIx//etfVa4/ffo0bGxscOrUKQCAjY0N/vvf/1ar7xWP9QkTJmDcuHHV2tfNVOxzTfn6+mL1\n6tUAgL59++Ktt966ref/+uuv+NOf/oTi4uJa6Y817Nu3Dy1btqzU/u6778LHxwdubm4YOHAgMjMz\nb7mvoqIidOjQAbGxsVpbxePa+GjTpg0AYOnSpXjttdduul8fHx888MADldr37NkDGxsb3Lhx45Z9\nA4DCwkJMmzYN3t7eaNy4MUaMGIGcnBxt/dq1ayv1c/jw4dr6M2fOYMCAAXBxcUFgYCBiYmJM9r97\n92507NgRzs7O6NevX6XP7MMPP4S3tzfc3NwwadIkXL161aJ+W41Qtfj4+MjChQslPz9fcnNz5fjx\n4zJ79myxtbWVnTt3Wrt7tWrPnj1iMBiktLTU7Po33nhDDAaD9OrVq9I6Hx8fWb58ea33acWKFeLr\n61vr+7XUkSNHxGAwyA8//CD5+flm1zs5OcmSJUskIyNDUlNT5dVXXxV7e3tJSEiolT5MmDBBxo4d\nWyv7qk0TJkyQJ554QvLz8yU/P18yMzPlk08+EVdXV5k3b5623cWLF+X333+/5f5Wrlwp3t7eVa4v\nLS2V/Px87fg0GAzy008/VavvFY/1K1euyJUrV6q1r5up2Oea8vX1lVWrVomISN++feWtt966rec/\n88wz8sknn9RKX6zh6NGj4uHhIc2bNzdpX7dunbi4uMi3334raWlpMmLECGnfvv1N93Xt2jV5/PHH\nxWAwSGxsrNZ++fJl7ZjOz8+XpKQkcXNzk48++khEREpKSqRdu3aSlpZW5b5btmwpBoOh0me9e/fu\nm/6MreiZZ56RoKAg2b9/vxw7dkwGDRok3bp1kxs3boiIyNy5c2XEiBEm/b18+bKIiNy4cUOCg4Nl\nzJgxkpqaKlFRUeLk5CRZWVkiInL27FlxcXGR9957T1JTU+Wpp56S9u3ba/vesGGDuLu7y7fffisJ\nCQnSoUMHeeGFFyzqt7Uw0ammqn6Bjxs3ToKCgqzQozvH+CUsKSkxu/6NN94QLy8vsbOzk88++8xk\nnV4THeMvxD/++MPs+pkzZ8qQIUMqtffp00emTJlSK30ICwtTMtGpql/Lly8XBwcHycnJua39rVix\n4qaJTkU1SXRudayrqiaJztmzZ6VBgwZSVFR0p7p3Ry1dulRcXV0lODi4UqIzdepUGTZsmLZ89OhR\nMRgM8vPPP5vd1/HjxyU4OFiCg4MrJToVjRgxQgYMGGDS9s4778gzzzxT5XN8fHzEx8dHGjduLL/+\n+qvWfjuJTnFxsTg6Osr27du1tpycHDEYDHLy5EkREXn88cdl/vz5Zp8fGxsrjo6OUlhYqLX1799f\nXnvtNRERef3116V3797auqtXr4qbm5v2WfTu3Vtef/11bf2+ffukfv36Fv3RYi0cuqplkydPxrFj\nx7RT0hcvXsTkyZPh6ekJd3d3jB07FhcvXtS2P3LkCPr06QNnZ2e0adMGK1asAGD+VGb50+jz5s3D\nmDFj8NJLL8HV1RWtW7fGrl278OGHH8LT0xMeHh6Ijo7Wnnv58mWEhYWhQYMGuP/++/H888+jsLBQ\ney1vb28sW7YM3t7ecHFxwdixY3H9+nWcPn0aDz30EADAzs4O//nPf8y+71atWuHll1/GnDlzTN5f\neeaGAWxsbLBr1y4AZad1ly1bhm7dusHJyQkDBw7EmTNnMHz4cDg7O6Nz5844ceKE9lwRwezZs+Hm\n5gZvb28sWbLEZN+ffPIJWrduDVdXV/Tu3RsJCQnaOh8fH8yePRteXl5o37692VPG+/fvR69eveDi\n4oJWrVppn+fKlSvRr18/AIC9vb02ZFDxfR09ehT5+fkm7V9++SXmzZunLe/btw/du3eHk5MTOnTo\ngDVr1ph8XtOnT8fo0aPh4uKC5s2bY9WqVQDK4r969Wp88cUXaN26NYDqx9ho3bp1aN++PZydndGj\nRw8cOHBAW7d582ZtXZcuXfDDDz9Ues+3MmbMGNjZ2eH7778HUDbE8vrrrwMAzp07h0GDBsHd3R2N\nGzfGpEmT8Pvvv2PPnj2YNGkSsrOzUa9ePZw5cwZ9+/bFtGnT4OvrC29vbxw6dKjSMFBsbCx8fX3h\n4uKCJ598EpcuXdI+h6q+V2fOnDE51vfu3VvpmP3uu+/QuXNnODk5ITAwEN988422rm/fvvjnP/+J\ngQMHwsnJCX5+ftp7rcjccNv69evRrl07ODs7Y+zYscjKykK/fv3g7OyMvn37Ii8vT3v+smXL0LJl\nS7i7u2P+/PmV9n/mzBn07t0bjo6OePDBB5GcnFxlXD755BOEhobC3t4eQNnx3atXL7z99tto1KgR\n7r//fqxduxZfffUVWrRogUaNGmHu3Lna84uKivDyyy+jadOmaNKkCZ588kn8/PPP2vr9+/ejd+/e\ncHZ2houLCwYNGqQNsxhf680330TTpk3RoEEDvPzyy9rQYd++fc0OFxmPeQCIiYnB6tWrMWPGjErD\n6927d8e+ffuQmpqKkpISrF69Gj4+PmjcuLHZz+I///kPQkJCsH///io/L+N72rJlCxYuXGjSPmTI\nEKxduxZXrlyp8rkzZ86Eq6srZs+ebXa98dgw93jzzTcBAFu3bsWDDz5Y6bnG4zw1NRVt27Y1u/8D\nBw6gc+fOcHZ21tp69eqlvecDBw7gL3/5i7bO0dERnTt3xv79+1FaWoqEhAST9T169EBJSQmOHDlS\n5Xu2OisnWnetqs5U/Prrr2IwGOTbb78VkbK/4Hv06CEHDx6UgwcPSteuXeWRRx4REZFffvlFGjZs\nKFOmTJG0tDRZu3atODg4yL59+8xm+BMmTJBx48aJSNlZFAcHB5k7d66cOnVKRo4cKQ0bNpRhw4bJ\niRMn5PXXXxd7e3u5ePGiiIgMHz5cHn30UUlOTpZDhw5Jnz59ZMSIESJS9teEnZ2d9O/fX44dOyY/\n/PCDODk5yccffyylpaWyceNGMRgMkpOTI8XFxZXe8xtvvCG9evWSwsJCad68uUyePNns51S+/0bl\n/2pq2bKleHp6ys6dOyUhIUEaN24sjRo1kmXLlsmxY8eka9euWp9XrFghBoNBhg8fLikpKbJy5Upx\ncHCQXbt2iYjI1q1bxcPDQ7Zu3SoZGRny1ltviaurq+Tl5Wmv1axZM0lOTpakpKRK7yklJUXq168v\nc+fOlfT0dFm1apU4OzvL119/LdeuXTP5TK5du1bp+ampqeLq6ir169eXRx55RBYsWCCpqakm2+Tm\n5oqbm5ssXrxYMjMzZf369dKgQQPt2AkLCxN7e3t57733JCsrS15++WVxdHSUixcvSmFhoTz55JPy\nxBNPaH8ZVjfGIiI7d+4UOzs7+fjjjyUzM1PmzJkjjRo1ksLCQklMTBRXV1dZs2aNnDp1SpYuXSqO\njo6SmJhY6X0b+13VmaagoCB55ZVXRKTszIPxL8OhQ4fKY489Junp6XLo0CEJCAiQiIgIKS4ulkWL\nFkmzZs20oZ4+ffqIs7Oz/PTTT3Lo0CHJysoSg8EgmZmZ2jHVrFkz2b59uyQkJEjHjh1l/Pjx2udQ\n1feq/LGem5srxcXFJsdsbGys2Nvby6JFiyQ9PV0WLlwodnZ2Eh8fLyJl33UnJydZtWqVnDp1SkaN\nGiVeXl7aKf/yzPU5ICBA4uLiJDY2Vuzs7KRZs2ayceNGOXz4sLRs2VL73H744QdxcHCQVatWSWpq\nqjzxxBNiMBi0Mzp9+vQROzs7Wbp0qZw4cULGjBkjbdq0qfIsVZcuXUyGUlasWCEODg4yceJEyczM\nlJdeekmcnZ2lT58+cuzYMVm6dKkYDAY5duyYiJSdvezZs6fEx8fL8ePHZeTIkdKtWzcRKRv6a9iw\nobz55pty+vRp+emnn8Tf31+mTp2qvZa9vb2MHj1a0tLSZM2aNVKvXj35/vvvRaRseLP88IvxUf5s\nSPl+mzvzN3nyZDEYDGJrayvu7u5mv+/m3OyMziOPPCJPPfWU2XXe3t6yZcsWs+uMPw+3bNkiNjY2\n2pnH8selcVjT3KOqsyZz5syR++67T4qKiqSoqEhsbW3l6aefFl9fX2nTpo2Eh4drZ+ymTZsmI0eO\nNHl+dHS0tG3bVkTKvqPG4TijJ598Ul544QX57bffxGAwyPHjx03We3h4yLp168z2TQVMdKqpqkTn\njz/+EIPBIF9++aUkJSWJwWCQEydOaOtPnDihHShLliwRHx8fkx+ES5Yskb1795r9gRwWFmaS6Nx/\n//3auq1bt4rBYJDTp0+LiMiFCxfEYDBIQkKCZGRkiI2NjVy4cEHb/vTp02IwGOT8+fPaaxl/cImU\n/dKcNGmSiNz6tKox0REpG7+1sbGRuLi4Sp+TuV+A5X+Y+Pj4yJw5c7R1I0aMkL59+2rLCxcu1MbX\nV6xYIS4uLib1ExMnTtS+wL169ZKFCxeavFa/fv3kH//4h/Zas2bNMvt+RERmzJghPXv2NGkLDw/X\nfoBbcqr55MmTMmHCBGncuLEYDAYxGAwycOBA7Yf0a6+9Jo899pjJc+bNmychISEiUvZ5de3aVVt3\n5coVMRgM8uOPP2rrjZ9ndWNsPM0+cuRIkyT0xo0bMmfOHDl79qyMHTtWpk+fbtLPCRMmVHmK/maJ\nTq9evbREuHyiExwcLOPGjdMS6ZSUFO17U/EXWJ8+feSJJ57Qls0lDeWHUPfu3Su2trZy5cqVKr9X\nxv5WXF/+O/f4449X+uX21FNPaX3p06ePyS8Q4zDJuXPnKn0O5vpsTDpFypKPCRMmaMvTp0/X/kAa\nOXKkybrLly+Ls7OzSaJjTOxERAoKCsTV1VW+++67Sv0oKSkRW1tb7ZgSKfu8bW1ttaEN4/vYs2eP\nto27u7t888038vvvv4uDg4McOXJEW3f16lVxcnKSH3/8UfLy8uT99983ec3w8HDp06eP9lo2NjYm\n3+POnTtr39PbYS7RWbFihbi5ucnq1avl0KFDMn78eGnTpo3J96QqVSU6p0+flnr16mkJbkUDBgzQ\nhoEqKv/zcMiQIRIcHCwlJSW3XaNT3jfffCP16tWTlStXiojIsWPHxGAwyAsvvCBHjx6VjRs3SvPm\nzeXFF18UEZFJkybJ008/bbKP5cuXi4+Pj4iItGnTRj799FOT9ePHj5eJEyfKuXPnxGAwSEZGhsn6\nFi1aaMefijh0VcuMpyzd3NyQmpoKV1dXk1OIbdu2RcOGDZGamorU1FT86U9/gsFg0Na/+OKLJqcF\nb6b8FQaOjo4mbcbloqIipKamQkTQokULuLq6wtXVFR06dIDBYEBaWpq2D+PVAwDg6uqKkpKS2337\nGD58OB5++GFMmTLF4isIyit/Srp+/fom77F+/fooKirSltu2bQtXV1dtuVOnTkhNTQVQduo2IiJC\ne7+urq746aefkJ6erm3v4+NTZT9OnDiBHj16mLQ98MADJkNnt+Lv748VK1bg559/xv79+zFz5kzs\n3bsXzz33nNbH77//3qSPUVFRJn2sGBMA+OOPP7Q247FT3Rgb95WamoouXbqY7DcqKgrNmzdHamoq\nli5datLPtWvXmvTTUpcvX4abm1ul9vDwcHz11Vdo0qQJnnjiCSQlJcHf39/sPgwGw01jB5QNWRh1\n6tQJpaWlJp9DdVR1TBiPOeDW8bqZ8se+o6NjpWPfeEWU8eeGkZubm8kViAaDweT9u7i4wN/f3+yx\n+9tvv6G0tBRNmjQxaW/SpIk2tFHxZ4uxraioCKdOnUJxcTF69+6tHRtNmzZFUVER0tPT4eHhgfHj\nx2PBggUICwtDt27d8P7775v8bGjSpInJ99jNzU37zAYNGmRy3BkfQUFBlnykePvttxEeHo5x48ah\nc+fO+OyzzwBA+7c6vvnmG/j5+aFbt25m1zdu3Nhk6K4qH374IdLT0ytdjXj27Fm4uLiYfd9RUVEm\n265btw5jxozB3/72N4SFhQEA2rdvj0uXLuHjjz9GUFAQHn/8cXzwwQdYtmwZSktLK/0cBcp+Txjj\nbW799evX4eTkhPr162vbV3y+k5PTLd+ztdhauwN6c/ToUQBAhw4dkJSUZHab0tJSlJaWwt7evspL\ntssnP0YlJSWwsflfbmpra1n4SkpK4OLigsTERJN2EcH999+P+Ph4ANDG6I2qk6gAwJIlS9ChQ4dK\nNTMV35O5RKr8ezIYDGY/B6N69eqZLJeWlsLBwUH7/4IFCzBgwABtvYjAxcVFWzZ+ac1xdHSsFJvS\n0lKLk7+//e1vGDduHIKDg2FjY4MePXqgR48eaNWqFcLDwwGUvf8xY8ZodSrGPpZ/X3Z2dpX2be6Y\nqW6Mjfuq2F5eaWkpZs2ahYkTJ5o8z/hZW+r69etIT0/HK6+8UmndU089hf79+2Pz5s34/vvvMXHi\nRPzwww9azVpFN4sdYHpslJaWAih7j5Z8r6pi/IVfXmlpqcn3xNznWNV3vKKK3+eb9aniPiseJ+a+\nG+b6ZnwN42dUVV+q6o/x+/Cf//wH7u7uJv277777kJ2dja5du6JLly54+OGHMXnyZHz33XfYt2+f\ntu3NPrPly5eb1JEZmftemJOdnY3g4GBtuV69eggODkZWVpZFzzfn+++/N7lUu6IbN25U+vzNadmy\nJebOnYt58+bh448/1tq9vLy03yMVNWzYUPv/p59+ihdeeAEzZ86slABV/GMiICAAf/zxB3755Rez\n+8/Ly8P999+vvX5ubm6l9R07dkTjxo1Rv3595OXlITAwEEDZMfDbb79pz1cRz+jUss8++wxdu3ZF\ny5Yt0bZtWxQUFJj8JZWSkoIrV64gICAAfn5+SEpKMvmhNWnSJLzxxhvaL5HyRW3VnXOjbdu2KCws\nRElJCVq3bo3WrVvDYDBgxowZVRbNlU8ybpZsmNO6dWuEh4fj9ddfN9m/vb09CgoKtOWaziFy8uRJ\nk78s4uLi0K5dOwBl7/ns2bPa+23dujUWLFiAPXv2WLTvgIAAxMXFmbTt378fAQEBFj1/x44dZucP\nMv7Fa3yNtLQ0kz7u2LEDn376qUWvYTAYtGOnOjEuz8/PD4cPH9aWRQSBgYH44Ycf0LZtW2RmZpr0\nc82aNdi0aVOV/TJ3zHz55ZcwGAx49NFHTdpFBK+88grOnz+PZ599Fhs2bMCyZcuwfv16bX+3q3zC\nFxcXB3t7e7Rp00b7pVrV9+pmrxUQEGBSoA2UHRPGM7bV6Wd1dOjQQUtcAeD333+vdLaq/Pu/ePEi\n0tPTte9GeY0bN4atrS1+++23avXF19cX9erVwy+//KIdG/fddx9mzpyJM2fOYNOmTXB3d8d3332H\nv/71r/jzn/9s0Tw2Rs2aNTM57oyP5s2bW/T8Nm3a4Pjx49qyiCA1NdXkzNvtEBEcPHgQffr0qXKb\nX375BZ6enhbtb9asWWjWrBnmzp2rHT/16tUz+55bt26tJTqbNm3C888/j4iICLz77rsm+9y4cSOa\nNm1qcibxyJEjaNiwITw9PdGzZ08kJiaazH2zb98+9OzZEwDQs2dPk0T06tWrSExMRM+ePWEwGNCt\nWzf8+OOP2vr9+/fD1tYWnTp1sug9WwMTnRq4fPky8vLykJubi+TkZLz66qtYv3493n//fQBlv3we\nffRRhIWFISEhAQcPHkRYWBh69+6Njh074umnn0ZhYSFmzJiBtLQ0fPnll1i7di0GDRqE9u3bw9HR\nEZGRkcjKysKCBQsq/bVuqXbt2mHgwIEYN24c4uPjkZSUhLFjx970Cyll9VsAoJ0FOXToUKVTllUJ\nDw+Hh4eHyRVY3bt3x65du7Br1y4cP34cf/3rX296VuBWfwkXFhZi4sSJOH78OKKjo7FhwwbMnDkT\nQNmVDYsXL8bq1auRmZmJ+fPnY/ny5WZ/2JszdepUJCcnY+7cuUhLS8Pq1asRHR2NadOmWfT8v//9\n74iOjsasWbOQlJSE9PR0fPnll3j11Ve1qy2mTp2KI0eOICIiAunp6fjmm28wa9Ysi3+Iu7q64syZ\nM8jJyalWjIH/fcbTp0/H+vXrsXz5cmRkZCA8PByXLl3Cgw8+iBkzZuDrr7/GBx98gIyMDPzrX//C\nW2+9VeWEjSKCa9euIT8/H3l5ecjIyMCnn36KmTNn4vXXX9eueDG+tsFgQHJyMqZNm4bExEScPHkS\nGzZsQNeuXQGUHX+XL19Geno6SkpKTI7NqsyZMwd79+7F/v378dJLL+H555+Hk5PTLb9X5Y9145kE\n42vNnDkTGzduxKJFi5Ceno4PPvgAmzZtwosvvqhtZ+nZm1sxty/j8rRp07Bhwwb861//wokTJ/DC\nCy9oV9cZt1u1ahVWrlyJlJQUTJgwAX5+fujfv3+l1zEYDPjTn/5U5dnnW3FxccFzzz2HadOmYffu\n3Thx4gTGjx+P5ORk+Pv7o0mTJsjOzsbOnTtx6tQpvPPOO/juu+/MnqW52XuvrunTpyMyMhJbtmxB\neno6Zs6ciV9++UUb5rl8+TIuXLhg8f7OnDmDgoICtG/fvsptjh07ph27t2JnZ4ePPvoIZ86csbgP\nhYWFmDx5MoYMGYIXX3wReXl52uOPP/5Av379UK9ePUyePBnp6en497//jdmzZ2PWrFkAyq5ka9my\nJSZMmIDjx4/jnXfeQXx8vDakPmnSJMTFxeHtt99GSkoKnnnmGbRs2RIhISEAyn5uvf/++9i0aRMS\nEhIwdepUPPPMM0oPXbEYuZp8fHy0AlMbGxvx8PCQwYMHV5q/48KFC/L000+Lm5ubNGzYUCZOnCiX\nLl3S1sfFxUnPnj2lfv360rZtW1m7dq227osvvpCWLVuKk5OTjB07VsLDw7XCyHnz5pnMdbBjxw6x\nsbHRlq9du2Yyn8ivv/4qTz/9tLi7u0uDBg1k1KhR2kR3u3fvFhsbmyqv8CouLpaBAweKg4ODbNq0\nqdJnUbEvRtu3bxcbGxut+K6oqEgmTpwoLi4u4u3tLZ9++qn4+fmZFCOXL/AeO3asTJw4UVteunSp\n+Pn5iUjZJHJ//vOf5cUXXxRnZ2dp1aqVfPnllyav/+GHH0rr1q2lfv360qlTJ4mJidHWWTK/z+7d\nu6VLly7i4OAg/v7+JlemmPvMKvr3v/8tffv2lQYNGmh9MBYMGsXGxkq3bt3EwcFBfHx8TAo3b3WV\n2sGDB6VZs2Zy3333iUjNYiwismrVKmnTpo04OjpKr1695PDhw9q69evXS2BgoDg4OEhAQICsWbOm\nyvc9YcIE7bthMBjE3d1devToUalYsXwxcnZ2tjz++OPSsGFDcXFxkWHDhmlFvBcvXpRu3bqJo6Oj\nJCQkmDxPpKyw18bGxqSwd/HixdKiRQtxdXWV5557Tq5fv65tf7PvlfFYr1+/vmzcuLHSZ/T1119L\nu3btxMHBQYKDg02+D7fqV3nm+ly+8LVXr14m86CEh4dLaGiotrxu3Tpp06aNODs7y7Rp06RXr14m\n8+i8+uqr0q1bN6lfv770799fmwzOnL///e8mxd0rV640mY8mPT1dbGxs5MyZM1qbp6enfPHFFyJS\nVnz84osvyn333Seurq4ycOBASU9PF5GyiRGnTJkiDRs2lIYNG8rkyZNl69at4urqKtevX5cVK1ZU\nmvum4udoqYr9Nvroo4/E399f3Nzc5KGHHjIpyA8LC5N+/fqZ3Z+5YuQDBw6IjY2NXL161exzTpw4\nIY6OjmavxBSp+ufOmDFjbvnzxOjbb7/Vfu+U/57Z2Nho/U1KSpJ+/fqJi4uLeHl5VSruzsjIkD59\n+kj9+vWlQ4cOsmPHDpP133//vQQEBIiTk5OEhITIqVOnTNa/88474uHhIQ0aNJBJkyaZfL9UZBCp\npdT5JiZNmoR///vfaNq0aaX5HN5//33MmjULv/76Kxo1agQAiIyMxGeffYZ69eph8eLFWp3FoUOH\nMGHCBFy/fh2DBw/GokWL7nTXiYh07cyZM+jYsSNycnJM5lah2/fGG28gLy/vprcsobpXJ0NXEydO\nrHQvDaBskrAdO3aYVPOnpKRg/fr1SElJQUxMDKZOnaqdxpwyZQqWL1+O9PR0pKenm90nERFZrmXL\nlnj88ce1ySipeoqLi/HFF1/gb3/7m7W7QhXUSaLTu3dvk2pxo5kzZ1YqpNqyZQtGjx4NOzs7+Pj4\nwNfXF3FxccjNzUVBQYF22eT48eOxefPmuug+EZGuvfvuu1i6dOldfVNPa/v0008xatQoq99smCqz\n2uXlW7Zsgbe3Nzp27GjSnpOTo1V/A4C3tzeys7NhZ2cHb29vrd3LywvZ2dl11l8iIr1q2rRplZc0\nk2WmTp1q7S5QFayS6Fy9ehVvv/02duzYobXVQakQERER3WOskuhkZmbi9OnT2kRO58+fR5cuXRAX\nFwcvLy+cO3dO2/b8+fPw9vaGl5cXzp8/b9Lu5eVldv9Dhw7F9evXtctqnZ2d4evrq80maryclMt1\ns/zNN9/w81dsOSMjAyNHjlSmP/f6MuOh3rKxTZX+3GvLAJCUlKTdzLZNmzYmEyvejjq56goouyPr\nkCFDzN6BC+VpAAAgAElEQVRFt1WrVjh06BAaNWqElJQUjBkzBvHx8cjOzkb//v2RkZEBg8GAHj16\nYPHixejevTseeeQRvPTSSxg4cGCl/Y0fP55XZCkkKipKmw2Y1MCYqIXxUA9jopbp06dj9erV1Xpu\nnRQjjx49Gg8++CDS0tLQvHnzStO6l59RNDAwEKNGjUJgYCAGDRqE6OhobX10dDSeffZZ+Pn5wdfX\n12ySA0DLAEkNZ8+etXYXqALGRC2Mh3oYE/2ok6GrtWvX3nR9xVsBREREICIiotJ2Xbp0MXtGiIiI\niMgcXd4C4uGHH7Z2F6icMWPGWLsLVAFjohbGQz2MiVrK35z1dtVZjU5dio2NRefOna3dDSIiIqoF\nhw8f1u63dbt0eUanuje/tKa8giIk5RSYPPIKLLuBpurK3wmX1MCYqIXxUA9joh9WmzCQTOUXFGPW\ntgyTtvcG+8LTteq7exMREdHN6TLRMV6Pf7ezr2dAUk6BSZuHq/1dl/z06tXL2l2gChgTtTAe6mFM\n9EOXiY5eXLhWgvk7s0zaeJaHiIjIcqzRoTuOY93qYUzUwniohzHRD10mOkRERESAThMdvdTo6AXH\nutXDmKiF8VAPY6Ifukx0iIiIiACdJjqq1+iYmzOnuPSGtbt1x3CsWz2MiVoYD/UwJvrBq66swNyc\nOW/0b2Wl3hAREemXLs/osEZHLRzrVg9johbGQz2MiX7oMtEhIiIiAnSa6Kheo3Ov4Vi3ehgTtTAe\n6mFM9EOXiQ4RERERoNNEhzU6auFYt3oYE7UwHuphTPRDl4kOEREREaDTRIc1OmrhWLd6GBO1MB7q\nYUz0Q5eJDhERERGg00SHNTpq4Vi3ehgTtTAe6mFM9EOXiQ4RERERoNNER881Ovb1DJXuk5VXUGTt\nbt0Ux7rVw5iohfFQD2OiH7zX1V3mwrUSzN+ZZdL23mBfeLo6WKlHRERE6tLlGR3W6KiFY93qYUzU\nwniohzHRD10mOkRERESAThMdPdfo3I041q0exkQtjId6GBP9qJNEZ9KkSfDw8EBQUJDWNmvWLLRr\n1w7BwcEYPnw4Ll++rK2LjIyEn58fAgICsH37dq390KFDCAoKgp+fH6ZPn14XXSciIqK7WJ0kOhMn\nTkRMTIxJ24ABA3D8+HEkJSXB398fkZGRAICUlBSsX78eKSkpiImJwdSpUyEiAIApU6Zg+fLlSE9P\nR3p6eqV9GrFGRy0c61YPY6IWxkM9jIl+1Emi07t3bzRs2NCkLTQ0FDY2ZS/fo0cPnD9/HgCwZcsW\njB49GnZ2dvDx8YGvry/i4uKQm5uLgoICdO/eHQAwfvx4bN68uS66T0RERHcpJWp0PvvsMwwePBgA\nkJOTA29vb22dt7c3srOzK7V7eXkhOzvb7P5Yo6MWjnWrhzFRC+OhHsZEP6ye6Lz11luwt7fHmDFj\nrN0VIiIi0hmrThi4cuVKbNu2DbGxsVqbl5cXzp07py2fP38e3t7e8PLy0oa3jO1eXl5m95uRkYGp\nU6eiRYsWAAB3d3cEBQVpY67GTN1ay4nx+3ElMxtubcpqia5kJiK5QT4AD20ZANC/lcly+e3LLyfG\n70dBEydl3l/FZWObKv3hsulfqqr0515fNlKlP1zmsjWXjf8/e/YsAKBr164ICQlBdRjEWOl7h50+\nfRpDhgxBcnIyACAmJgavvPIK9u7diyZNmmjbpaSkYMyYMYiPj0d2djb69++PjIwMGAwG9OjRA4sX\nL0b37t3xyCOP4KWXXsLAgQMrvVZsbCw6d+5cF2/rlvIKipBfUGzSVlx6A3N/OGXS9kb/VpVmPLa0\n7b3Bvghu5lqLvSYiIlLH4cOHq53o1MnQ1ejRo/Hggw/i5MmTaN68OT777DP89a9/RWFhIUJDQ9Gp\nUydMnToVABAYGIhRo0YhMDAQgwYNQnR0NAwGAwAgOjoazz77LPz8/ODr62s2yQHUqtHJLyjGrG0Z\nJo/i0trNLVW//xXHutXDmKiF8VAPY6IfdTJ0tXbt2kptkyZNqnL7iIgIREREVGrv0qWLdkaI/of3\nvyIiIjLP6sXIdwLn0VEL56NQD2OiFsZDPYyJfugy0SEiIiICdJroqFSjQxzrVhFjohbGQz2MiX7o\nMtEhIiIiAnSa6LBGRy0c61YPY6IWxkM9jIl+6DLRISIiIgJ0muiwRkctHOtWD2OiFsZDPYyJfugy\n0SEiIiICdJrosEZHLRzrVg9johbGQz2MiX7oMtEhIiIiAnSa6LBGRy0c61YPY6IWxkM9jIl+6DLR\nISIiIgJ0muiwRkctHOtWD2OiFsZDPYyJfugy0SEiIiICdJrosEZHLRzrVg9johbGQz2MiX7YWrsD\nepJXUIT8gmKTtuLSG1bqDREREeky0bFWjU5+QTFmbcswaXujfyur9EUlHOtWD2OiFsZDPYyJfuhy\n6IqIiIgI0GmiwxodtXCsWz2MiVoYD/UwJvqhy0SHiIiICGCNjm7Z1zMgKafApM3D1R6erg513heO\ndauHMVEL46EexkQ/dJnoEHDhWgnm78wyaXtvsK9VEh0iIiJr0eXQFWt01MKxbvUwJmphPNTDmOiH\nLhMdIiIiIkCniQ5rdNTCsW71MCZqYTzUw5johy4THSIiIiJAp4kOa3TMM16JVf6RV1B0x1+XY93q\nYUzUwniohzHRjzpJdCZNmgQPDw8EBQVpbRcuXEBoaCj8/f0xYMAAXLp0SVsXGRkJPz8/BAQEYPv2\n7Vr7oUOHEBQUBD8/P0yfPr0uuq4rF66VYNa2DJNHxXtzERER6UmdJDoTJ05ETEyMSVtUVBRCQ0OR\nlpaGkJAQREVFAQBSUlKwfv16pKSkICYmBlOnToWIAACmTJmC5cuXIz09Henp6ZX2acQaHbVwrFs9\njIlaGA/1MCb6USeJTu/evdGwYUOTtq1btyIsLAwAEBYWhs2bNwMAtmzZgtGjR8POzg4+Pj7w9fVF\nXFwccnNzUVBQgO7duwMAxo8frz2HiIiIyByr1ejk5+fDw8MDAODh4YH8/HwAQE5ODry9vbXtvL29\nkZ2dXandy8sL2dnZZvfNGh21cKxbPYyJWhgP9TAm+qHEzMgGgwEGg6HW9rd3714kJCSgRYsWAAB3\nd3cEBQVppyKNB3BtL7u2DgYAXMksS7Tc2vzJ7HJywgFcycw1WZ/cIB+Ah8n26N+qTvZ3pz4P43Jy\ncvId3T+Xb385OTlZqf7c68uMh3rLRqr0515bNv7/7NmzAICuXbsiJCQE1WEQYwHMHXb69GkMGTJE\n+6UXEBCAPXv2wNPTE7m5uejXrx9OnDih1eqEh4cDAAYOHIj58+ejZcuW6NevH1JTUwEAa9euxd69\ne7F06dJKrxUbG4vOnTvXxdsykZRTgFnbMkza3ujfqtKtGFRqe2+wL4Kbud7inREREVnP4cOHq53o\nWG3oaujQoVi1ahUAYNWqVRg2bJjWvm7dOhQXFyMrKwvp6eno3r07PD094ebmhri4OIgIPv/8c+05\nRERERObUSaIzevRoPPjggzh58iSaN2+OFStWIDw8HDt27IC/vz927dqlncEJDAzEqFGjEBgYiEGD\nBiE6Olob1oqOjsazzz4LPz8/+Pr6YuDAgWZfjzU6auFYt3oYE7UwHuphTPSjTmp01q5da7Z9586d\nZtsjIiIQERFRqb1Lly7a0BcRERHRrehyZmTOo6MWzkehHsZELYyHehgT/dBlokNEREQE6DTRYY2O\nWjjWrR7GRC2Mh3oYE/3QZaJDREREBCgyYWBtY42O5Yx3NC/Pw9Uenq4OtfYaHOtWD2OiFsZDPYyJ\nfugy0SHLXbhWYnYSwdpMdIiIiKxFl0NXrNFRC8e61cOYqIXxUA9joh+6THSIiIiIAJ0mOqzRUQvH\nutXDmKiF8VAPY6Ifukx0iIiIiACdJjqs0VELx7rVw5iohfFQD2OiH7pMdIiIiIgAnSY6rNFRC8e6\n1cOYqIXxUA9joh+6THSIiIiIAJ0mOqzRUQvHutXDmKiF8VAPY6IfnBmZKqmL20IQERHVBV0mOqzR\nqZnavi0Ex7rVw5iohfFQD2OiH7ocuiIiIiICdJrosEZHLRzrVg9johbGQz2MiX7oMtEhIiIiAnSa\n6LBGRy0c61YPY6IWxkM9jIl+WJTobNmyBSUlJXe6L0RERES1yqJE5/XXX4enpyemTZuGuLi4O92n\nGmONjlo41q0exkQtjId6GBP9sOjy8qNHjyIpKQmff/45RowYAScnJ4wfPx5jx46Fj4/PHe6imvIK\nipBfUGzSVlx6w0q9ISIiInMsrtEJDg7G//t//w/nzp3DRx99hK+//hqtW7fGX/7yF6xZswY3bqjz\nS74uanTyC4oxa1uGyaO4VO74696NONatHsZELYyHehgT/bitCQMzMzPx+eef44svvoDBYMCbb76J\nli1bYsmSJdiwYQM2bdp0p/pJREREdNssOqOzZMkS9OzZE926dUNeXh5Wr16NtLQ0vPbaaxg3bhx2\n7dqFHTt23Om+Wow1OmrhWLd6GBO1MB7qYUz0w6JE5/vvv8crr7yCnJwcLF26FA888IDJeicnJ2zY\nsKFaHYiMjET79u0RFBSEMWPGoKioCBcuXEBoaCj8/f0xYMAAXLp0yWR7Pz8/BAQEYPv27dV6TSIi\nIro3WJTobNiwAY899hjq16+vtRUXF+P69eva8sMPP3zbL3769GksW7YMhw8fRnJyMkpLS7Fu3TpE\nRUUhNDQUaWlpCAkJQVRUFAAgJSUF69evR0pKCmJiYjB16lSztUGcR0ctHOtWD2OiFsZDPYyJfliU\n6AwYMACHDx82aTt06BAGDhxYoxd3c3ODnZ0drl69ipKSEly9ehXNmjXD1q1bERYWBgAICwvD5s2b\nAZTN5zN69GjY2dnBx8cHvr6+iI+Pr1EfiIiISL8sSnSOHj2K7t27m7R17969xrUwjRo1wiuvvIIW\nLVqgWbNmaNCgAUJDQ5Gfnw8PDw8AgIeHB/Lz8wEAOTk58Pb21p7v7e2N7OzsSvtljU7ts69nQFJO\ngckjr6DIoudyrFs9jIlaGA/1MCb6YdFVVw0aNEB+fj7uv/9+re3nn3+Gi4tLjV48MzMTH3zwAU6f\nPg13d3c88cQTWLNmjck2BoMBBoOhyn2YW7d3714kJCSgRYsWAAB3d3cEBQVppyKNB3BNljN/vQrg\nPgDAlcz/S6z6tzJZdmvzJ7PLyQkHcCUz12R9coN8AB7K7m/vj/nYeMl0f//660h4ujrc8vNKTk6u\n8efN5dpdTk5OVqo/9/oy46HespEq/bnXlo3/P3v2LACga9euCAkJQXUYROSWk7+88sorOHLkCBYt\nWoQ2bdogIyMDM2fORFBQEBYuXFitFwaA9evXY8eOHfj0008BAJ9//jkOHDiAXbt2Yffu3fD09ERu\nbi769euHEydOaLU64eHhAICBAwdi/vz56NGjh8l+Y2Nj0blz52r3yxJJOQWYtS3DpO2N/q0wf2fW\nPdP23mBfBDdzBRER0Z10+PDhaic6Fg1d/fOf/0S7du3Qo0cPuLi4oGfPnggICEBkZGS1XtQoICAA\nBw4cwLVr1yAi2LlzJwIDAzFkyBCsWrUKALBq1SoMGzYMADB06FCsW7cOxcXFyMrKQnp6eqUhNSIi\nIiIjixIdR0dHfPTRRygsLEReXh4KCwuxZMkSk6uwqiM4OBjjx49H165d0bFjRwDA5MmTER4ejh07\ndsDf3x+7du3SzuAEBgZi1KhRCAwMxKBBgxAdHW126Io1OmrhWLd6GBO1MB7qYUz0w+KZkS9fvoyT\nJ0+isLDQpP2hhx6qUQdmz56N2bNnm7Q1atQIO3fuNLt9REQEIiIiavSaREREdG+wKNFZuXIlXnzx\nRbi4uMDJyclkXVZWVhXPsh7Oo1M3jFdilefhag9PVweTNs5HoR7GRC2Mh3oYE/2wKNGJiIjAN998\ng0GDBt3p/tBd5MK1ErMFyhUTHSIiImuxqEantLQUAwYMuNN9qTWs0VELx7rVw5iohfFQD2OiHxYl\nOnPmzME//vEPs7dbICIiIlKVRUNXCxYsQH5+Pt599100btxYazcYDNpkPiphjY5aONatHsZELYyH\nehgT/bAo0ak4WzERERHR3cCiRKdv3753uBu1KzEx8Y7PjEyW27dvH/86UgxjohbGQz2MiX5YVKNz\n/fp1REREoHXr1nBzcwMAbN++HUuWLLmjnSMiIiKqCYsSnRkzZuDYsWP44osvYGNT9pT27dsjOjr6\njnauulijoxb+VaQexkQtjId6GBP9sGjoatOmTcjIyICLi4t2ywUvLy9kZ2ff0c4RERER1YRFZ3Qc\nHBxQUlJi0vbLL7+gSZMmd6RTNcV5dNTC+SjUw5iohfFQD2OiHxYlOk888QQmTJiAU6dOAQByc3Mx\nbdo0PPXUU3e0c0REREQ1YVGi89Zbb6FVq1bo2LEjLl++DF9fX9x///34+9//fqf7Vy2s0VELx7rV\nw5iohfFQD2OiHxbV6Dg4OGDhwoVYsGCBNmRlLEomIiIiUpVF2cqpU6dw6tQpZGVlobCwEKdPn9ba\nVMQaHbVwrFs9jIlaGA/1MCb6YdEZHV9fX7PtBoMBpaWltdohIiIiotpiUaJT8WaeeXl5mDdvHnr3\n7n1HOlVTrNFRC8e61cOYqIXxUA9joh/VKrTx9PTEBx98gIiIiNruDxEREVGtqXZF8cmTJ3H16tXa\n7EutYY2OWjjWrR7GRC2Mh3oYE/2waOiq4hDV1atXcfz4cWUvLyciIiICLEx0nnnmGZNlZ2dnBAcH\nw9/f/450qqZYo6MWjnWrhzFRC+OhHsZEPyxKdCZMmHCHu0F6YV/PgKScApM2t/q2uHLd9BYiHq72\n8HR1qMuuERHRPciiROf111/XbuZZnoho/zcYDHjzzTdrr2c1kJiYiM6dO1u7G/ekC9dKMH9nlknb\n8Ab52HjJw6TtvcG+THSsaN++ffyLVSGMh3oYE/2wKNFJT0/Hxo0b0a1bN7Rs2RJnzpzBwYMHMXz4\ncDg6OkJEzCZCRERERNZkUaIDAGvXrsWIESO05Y0bN+Krr77CihUr7kjHaqK2a3TyCoqQX1Bs0lZc\neqOKramioK49sbHCWR6yLv6lqhbGQz2MiX5YlOhs27YNX3zxhUnbkCFD7pnanfyCYszalmHS9kb/\nVlbqDREREVnKonl0fH19sWTJEpO2jz/+uMpbQ1gb59FRS3LCAWt3gSrgHCFqYTzUw5joh0WJzvLl\ny7FgwQJ4eXmhe/fu8PLywvvvv49ly5bVuAOXLl3CyJEj0a5dOwQGBiIuLg4XLlxAaGgo/P39MWDA\nAFy6dEnbPjIyEn5+fggICMD27dtr/PpERESkXxYlOp06dUJ6ejrWrl2LmTNn4ssvv0RGRga6dOlS\n4w5Mnz4dgwcPRmpqKo4ePYqAgABERUUhNDQUaWlpCAkJQVRUFAAgJSUF69evR0pKCmJiYjB16tRK\n9+ECOI+OaoK69rR2F6gC1h+ohfFQD2OiHxbfAsJ4VZXBYECfPn1QVFSEwsLCGr345cuX8eOPP2LS\npEkAAFtbW7i7u2Pr1q0ICwsDAISFhWHz5s0AgC1btmD06NGws7ODj48PfH19ER8fX6M+EBERkX5Z\nlOgkJyfD398fkydP1mZJ3rt3b6UZk29XVlYW7rvvPkycOBGdO3fGc889h99//x35+fnw8Cibd8XD\nwwP5+fkAgJycHHh7e2vP9/b2RnZ2dqX9skZHLazRUQ/rD9TCeKiHMdEPi666euGFFzB//nyMHz8e\nDRs2BAD07dsXzz33XI1evKSkBIcPH8aSJUvQrVs3vPzyy9owlZHBYLjpHD3m1u3duxcJCQlo0aIF\nAMDd3R1BQUHaqUjjAWzpcmL8flzJzIZbm7IhsSuZiUhukA/AQ1sGAPzflVjG5fLbl19OTjiAK5m5\n98z+Tp1MwZVC0/0lxv+C4GEDqhUPLtd8OTk5Wan+3OvLjId6y0aq9OdeWzb+/+zZswCArl27IiQk\nBNVhkPLTG1ehYcOGuHDhAgwGAxo2bIiLFy9CRNCoUSNcvHixWi8MAHl5eXjggQeQlVU2x8q+ffsQ\nGRmJU6dOYffu3fD09ERubi769euHEydOaElQeHg4AGDgwIGYP38+evToYbLf2NjYWp0ZOSmnwOzl\n5RVnAGab5W3vDfZFcDNXEBER3crhw4ernehYNHTVsmVLJCQkmLQdPHgQfn5+1XpRI09PTzRv3hxp\naWkAgJ07d6J9+/YYMmQIVq1aBQBYtWoVhg0bBgAYOnQo1q1bh+LiYmRlZSE9PR3du3evUR+IiIhI\nvywauvrnP/+JRx99FM8//zyKi4vx9ttvY+nSpbVyefmHH36Ip59+GsXFxWjTpg1WrFiB0tJSjBo1\nCsuXL4ePjw+++uorAEBgYCBGjRqFwMBA2NraIjo62uzQFe91pZayGh2PW25HdYf38VEL46EexkQ/\nLEp0Hn30UcTExOCTTz5Bnz59cPbsWWzatKlWLi8PDg7GwYMHK7Xv3LnT7PYRERGIiIio8esSERGR\n/t0y0SkpKUHbtm2RkpKCjz/+uC76VGOcR0ctvNeVeviXqloYD/UwJvpxyxodW1tb2NjY4Nq1a3XR\nHyIiIqJaY1Ex8owZM/Dkk09iz549yMzMxKlTp7SHijiPjlo4j456OEeIWhgP9TAm+nHToau8vDx4\nenpi2rRpAIAdO3aYrDcYDCgtLb1zvSMiIiKqgZue0fH39wcA3LhxAzdu3MBjjz2m/f/GjRvKJjms\n0VGLuXtd2dczICmnwOSRV1Bkhd7dm1h/oBbGQz2MiX7c9IxOxbkE9+zZcyf7QveQC9dKzE4i6Onq\nYKUeERGRHll8U8+7CWt01MIaHfWw/kAtjId6GBP9uOkZndLSUuzatQtA2dmdkpISbdnooYceunO9\nIyIiIqqBmyY6TZs2NblDeePGjSvdsdx4nyqVsEZHLZxHRz2sP1AL46EexkQ/bpronD59uo66QURE\nRFT7WKNDdxxrdNTD+gO1MB7qYUz0Q5eJDhERERGg00SHNTpqMTePDlkX6w/UwniohzHRD4vuXk5U\nF4yTCJbn4WrPuXWIiKjadHlGhzU6arG0RufCtRLM2pZh8sgvKL7Dvbs3sf5ALYyHehgT/dBlokNE\nREQE6DTRYY2OWlijox7WH6iF8VAPY6Ifukx0iIiIiACdJjqs0VEL59FRD+sP1MJ4qIcx0Q9edUVK\n45VYRERUE7pMdFijo5aa3OvqwrUSzK/w3PcG+zLRqSHWH6iF8VAPY6Ifuhy6IiIiIgJ0muiwRkct\nrNFRD+sP1MJ4qIcx0Q9dJjpEREREgE4THdboqIXz6KiH9QdqYTzUw5johy4THSIiIiJAp4kOa3TU\nwhod9bD+QC2Mh3oYE/1QItEpLS1Fp06dMGTIEADAhQsXEBoaCn9/fwwYMACXLl3Sto2MjISfnx8C\nAgKwfft2a3WZiIiI7gJKJDqLFi1CYGAgDAYDACAqKgqhoaFIS0tDSEgIoqKiAAApKSlYv349UlJS\nEBMTg6lTp+LGjRuV9scaHbXUdo2OcRLB8o+8gqJafQ29Y/2BWhgP9TAm+mH1ROf8+fPYtm0bnn32\nWYgIAGDr1q0ICwsDAISFhWHz5s0AgC1btmD06NGws7ODj48PfH19ER8fb7W+k3VcuFaCWdsyTB75\nBcXW7hYRESnI6onOjBkz8N5778HG5n9dyc/Ph4eHBwDAw8MD+fn5AICcnBx4e3tr23l7eyM7O7vS\nPlmjoxbW6KiH9QdqYTzUw5joh1VvAfHdd9+hadOm6NSpE/bs2WN2G4PBoA1pVbW+or179yIhIQEt\nWrQAALi7uyMoKEg7FWk8gC1dTozfjyuZ2XBrUzYkdiUzEckN8gF4aMsAgP6tTJbLb19+OTnhAK5k\n5t4z+zt1MgVXCu9s/xLjf0HwsAEAbj++9+JycnKyUv2515cZD/WWjVTpz722bPz/2bNnAQBdu3ZF\nSEgIqsMgxvEiK4iIiMDnn38OW1tbXL9+HVeuXMHw4cNx8OBB7NmzB56ensjNzUW/fv1w4sQJrVYn\nPDwcADBw4EDMnz8fPXr0MNlvbGwsOnfuXGv9TMopwKxtGSZtb/RvVekeTGyzXtt7g30R3MwVRESk\nP4cPH652omPVoau3334b586dQ1ZWFtatW4eHHnoIn3/+OYYOHYpVq1YBAFatWoVhw4YBAIYOHYp1\n69ahuLgYWVlZSE9PR/fu3a35FoiIiEhhVq/RKc84DBUeHo4dO3bA398fu3bt0s7gBAYGYtSoUQgM\nDMSgQYMQHR1tduiKNTpqqYsaHV6JdXtYf6AWxkM9jIl+WLVGp7w+ffqgT58+AIBGjRph586dZreL\niIhAREREXXaN7gIXrpWYHc7ydHWwUo+IiEgFSp3RqS2cR0ctvNeVejhHiFoYD/UwJvqhy0SHiIiI\nCNBposMaHbVwHh31sP5ALYyHehgT/dBlokNEREQE6DTRYY2OWlijox7WH6iF8VAPY6Ifylx1pYq8\ngqJK900qLq1841C6O5mLr4erPa/OIiLSKV0mOomJidWeGTm/oNjsLMhUfWU1Oh7W7gYA8/FdNMTv\nnkt+9u3bx79YFcJ4qIcx0Q9dJjpEt4Nz8BAR6ZcuEx3W6KglqGtPbKyQSNQF42zJ5XEYsgz/UlUL\n46EexkQ/dJnoEAHmz9RwGJKI6N6iy6uuOI+OWjiPjno4R4haGA/1MCb6octEh4iIiAjQaaLDGh21\ncB4d9bD+QC2Mh3oYE/3QZaJDREREBOg00WGNjlpYo6Me1h+ohfFQD2OiH7pMdIiIiIgAnV5ezhod\ntVhrHp2aMDcHj1t9W1y5XlJp27txFmXWH6iF8VAPY6Ifukx0iGqqqjl4KrYBnEWZiEhluhy6Yo2O\nWlijox7WH6iF8VAPY6Ifukx0iIiIiACdJjqs0VEL59FRD+sP1MJ4qIcx0Q9dJjpEREREgE4THdbo\nqM5KXjsAABSjSURBVOVerNHJKyhCUk6BySOvoMja3dKw/kAtjId6GBP94FVXRDVk7lL04tIbmPvD\nKZM2Xp1FRFT3dJnosEZHLXfjPDq3o6pL0VXG+gO1MB7qYUz0Q5dDV0RERESAlROdc+fOoV+/fmjf\nvj06dOiAxYsXAwAuXLiA0NBQ+Pv7Y8CAAbh06ZL2nMjISPj5+SEgIADbt283u1/W6KjlXqzRUR3r\nD9TCeKiHMdEPqyY6dnZ2WLhwIY4fP44DBw7go48+QmpqKqKiohAaGoq0tDSEhIQgKioKAJCSkoL1\n69cjJSUFMTExmDp1Km7cuGHNt0BEREQKs2qi4+npqdXTuLi4oF27dsjOzsbWrVsRFhYGAAgLC8Pm\nzZsBAFu2bMHo0aNhZ2cHHx8f+Pr6Ij4+vtJ+WaOjFs6jU8ZYtKzClVisP1AL46EexkQ/lClGPn36\nNI4cOYIePXogPz8fHh4eAAAPDw/k5+cDAHJyctCz5/9+aXp7eyM7O9sq/SW6XeaKls1diZVXUIT8\ngmKTtrvxxqFERCpQohi5sLAQI0aMwKJFi+Dq6mqyzmAwwGAwVPlcc+tYo6MW1ujcnvyCYszalmHy\nqJj41BTrD9TCeKiHMdEPq5/R+eOPPzBixAiMGzcOw4YNA1B2FicvLw+enp7Izc1F06ZNAQBeXl44\nd+6c9tzz58/Dy8ur0j737t2LhIQEtGjRAgDg7u6OoKAg7VSk8QCuavlKZlmi5NambAgsOeEArmTm\nastXMhOR3CAfgIfJ9vi/S4orPv9e39+pkym4Uqhu/2q6v5o+v+Lxlxi/H1cys032lxj/C4KHDTC7\nfXWWk5OTa/R8LtfuMuOh3rKRKv2515aN/z979iwAoGvXrggJCUF1GEREqvXMWiAiCAsLQ+PGjbFw\n4UKtffbs2WjcuDHmzJmDqKgoXLp0CVFRUUhJScGYMWMQHx+P7Oxs9O/fHxkZGZXO6sTGxqJz587V\n6lNSTgFmbcswaXujfyuz86SwjW01ff57g30R3Mz0LKa5Y9DcdkRE94rDhw9XO9Gx6hmdn376CWvW\nrEHHjh3RqVMnAGWXj4eHh2PUqFFYvnw5fHx88NVXXwEAAgMDMWrUKAQGBsLW1hbR0dE3HdYiUl1V\nsyoTEVHtsGqi06tXryovD9+5c6fZ9oiICERERNx0v4mJidU+o0O1r6xGx8Pa3VCStWZV3rdvH68q\nUQjjoR7GRD+UKEYmIiIiuhN0mehwHh21cB4d9fAvVbUwHuphTPRDl4kOEREREaDTRIfz6KiF8+jU\nXG3Pqsw5QtTCeKiHMdEPq8+jQ0S3ZumsykREZEqXiQ5rdNQS1LUnNpqZf4Zqxtyl6W71bXHleolJ\nm7nbR7D+QC2Mh3oYE/3QZaJDdC+o6tJ0nvkhIvof1ujQHccaHfWw/kAtjId6GBP94BkdIp0zN8R1\n4eofVuoNEVHd0mWiwxodtbBGx7rMFzJ3tVJvyBzWg6iHMdEPXQ5dEREREQE6TXQsrdHJKyiqNDcJ\nb6hY+1ijo57E+P3W7gKVw3oQ9TAm+qHLoStL5RcUY9a2DJO2urihIpG12dbg0nQioruJLhMd1uio\nhTU66vEJ6mY2yeel6dbBehD1MCb6octEh4hqR00mJcwrKEJ+QfEttyMiupN0megkJiaic+fO1u4G\n/Z+yGh0Pa3eDyrE0JpZOSrhoiF+lpKa49Abm/nDqltsx+SmrB+EZBLUwJvqhy0SHiOpWVQmRJdtx\neIyI7iRdXnXFGh21BHXtae0uUAWMiVp45kA9jIl+6DLRISIiIgJ0mujwXldq4Tw66lEpJsaC5/KP\nvIIia3erTnHOFvUwJvrBGh0isipL63YsvYqrtrcjorubLhMd1uiohfPoqOdujIm5CT4tvdrLXOJk\nbn/WKoxmPYh6GBP90GWiQ0R3N3Pz95i7PYulV3sR0b2LNTp0x6lUD0JlVI/JhWslmLUtw+RRXCrW\n7tYdw3oQ9TAm+sEzOkSke5aeISIi/dFlomOuRsdc4SF/0NWNu7EeRO/utZhYOsRl6S0vanIDVHM/\ni3yDu93yeVS3WKOjH7pMdMzhncqJ6FYsveWFpbfBMJf8WFoEzavHiGrHXZnoxMTE4OWXX0ZpaSme\nffZZzJkzx2Q973WlFt7rSj2MSe0zlyRVdVVYRccOHQDQs9J2tXn1GBOi28N7XenHXZfolJaWYtq0\nadi5cye8vLzQrVs3DB06FO3atdO2ycjIuMkeqK6dOpkCePCXqkoYk7ph6ZBZ0tFkrMpvcsvtLFVV\nTZIliVNN6CmZSk5OZqKjkMTERISEhFTruXddohMfHw9fX1/4+PgAAJ566ils2bLFJNH5/fffrdQ7\nMuf3gis8eaAYxkQtlsajti+7t7QmydIhs5rcsV61obrLly/X6v6oZpKSkqr93Lsu0cnOzkbz5s21\nZW9vb8TFxVmxR0REdaO25w2ytCbJ0okZLb1jfV1N9GguKbK0uLywuLTS/uqCagmfHtx1iY7BYLjl\nNnl5eXXQE7JUfs55wNfavaDyGBO1qB6PukqwKrL0DJa57YzbmkvGLEnu7jt9ptpX4NWkzdKzYpZu\nV9v9q+2zcTW5gtFSBhG5q2bhOnDgAObNm4eYmBgAQGRkJGxsbEwKkqdMmWIyfBUcHMzbQlhRYmIi\nP3/FMCZqYTzUw5hYV2JioslwlbOzMz7++ONq7euuS3RKSkrQtm1bxMbGolmzZujevTvWrl1rUqND\nREREBNyFQ1e2trZYsmQJHn74YZSWluKZZ55hkkNERERm3XVndIiIiIgspaubesbExCAgIAB+fn54\n5513rN2de9K5c+fQr18/tG/fHh06dMDixYsBABcuXEBoaCj8/f0xYMAAXLp0yco9vbeUlpaiU6dO\nGDJkCADGw9ouXbqEkSNHol27dggMDERcXBxjYkWRkZFo3749goKCMGbMGBQVFTEedWjSpEnw8PBA\nUFCQ1nazzz8yMhJ+fn4ICAjA9u3bb7l/3SQ6xokEY2JikJKSgrVr1yI1NdXa3brn2NnZYeHChTh+\n/DgOHDiAjz76CKmpqYiKikJoaCjS0tIQEhKCqKgoa3f1nrJo0SIEBgZqVy0yHtY1ffp0DB48GKmp\nqTh69CgCAgIYEys5ffo0li1bhsOHDyM5ORmlpaVYt24d41GHJk6cqF1gZFTV55+SkoL169cjJSUF\nMTExmDp1Km7cuMV9K0Un/vvf/8rDDz+sLUdGRkpkZKQVe0QiIo899pjs2LFD2rZtK3l5eSIikpub\nK23btrVyz+4d586dk5CQENm1a5c8+uijIiKMhxVdunRJWrVqVamdMbGO3377Tfz9/eX/t3e3MU2d\nbRzA/wexzEClL5ZCW5o6ZDoko3OACE6YDpdshbG6ly5M0TAyN83my764iRkmEp0zm9sXJ0IBycbi\nvmxhupGGmBHAtwDZEsNU1mJfHJuymRW2ttLr+bDH86wqFZ45Guv1S0g4b/d93edK26v3aU9HRkYo\nEAiQyWSi9vZ2zsc0s9vtlJmZKS5PdP5ra2tp9+7d4n5PPPEE9fT0hG07amZ0bnUjQbfbHcGImMPh\nQF9fHxYvXozh4WGo//uTA2q1GsPDwxGO7t6xefNm7N27FzEx/3u4cz4ix263Q6VSYd26dVi0aBGq\nqqowOjrKOYkQhUKBrVu3Qq/XQ6PRQCaTobi4mPMRYROdf4/HA51OJ+43mdf6qCl0JnMjQTZ9vF4v\nVq1ahf3790MqlYZsEwSB8zVN2trakJSUhIcffhg0wfcOOB/T69q1a+jt7cVrr72G3t5exMfH33RZ\nhHMyfQYHB/HBBx/A4XDA4/HA6/WipaUlZB/OR2Td7vzfLjdRU+hotVo4nU5x2el0hlR9bPoEAgGs\nWrUKq1evRllZGYC/KvLrd6y+dOkSkpKSIhniPaO7uxtffvkl5s6dixdffBEdHR1YvXo15yOCdDod\ndDodcnJyAADPPvssent7kZyczDmJgDNnziA/Px9KpRKxsbEwm83o6enhfETYRM9RN77Wu1wuaLXa\nsG1FTaGTnZ2N8+fPw+FwwO/347PPPkNpaWmkw7rnEBEqKyuRkZGBTZs2ietLS0vR1NQEAGhqahIL\nIPbvqq2thdPphN1uR2trK5YvX47Dhw9zPiIoOTkZqampOHfuHADAZrNh4cKFKCkp4ZxEwIIFC3Di\nxAn88ccfICLYbDZkZGRwPiJsoueo0tJStLa2wu/3w2634/z588jNzQ3f2J3+QFEkHT16lB544AFK\nS0uj2traSIdzT+rs7CRBECgrK4uMRiMZjUY6duwYXblyhVasWEHp6elUXFxMv/76a6RDveccP36c\nSkpKiIg4HxHW399P2dnZ9NBDD9EzzzxDv/32G+ckgvbs2UMZGRmUmZlJa9asIb/fz/mYRhaLhVJS\nUmjmzJmk0+mooaEh7PnftWsXpaWl0fz58+nrr7++bft8w0DGGGOMRa2ouXTFGGOMMXYjLnQYY4wx\nFrW40GGMMcZY1OJChzHGGGNRiwsdxhhjjEUtLnQYY4wxFrW40GGMTcnatWtRXV0dsf7XrVsHhUKB\nvLy8iMXAGLt7cKHD2F3OYDBArVZjbGxMXHfo0CE89thj/0p/kfzdn87OTthsNng8Hpw4cWLa+o2J\nicGPP/44bf0xxu4cLnQYiwLBYBD79++ftv7u1H1Gg8HglPYfGhqCwWDAfffdd0f6nwq+typjdycu\ndBi7ywmCgDfffBPvvfcerl69etN2h8OBmJiYkKKiqKgI9fX1AIDGxkYUFBRgy5YtkMvlmDdvHrq7\nu2G1WqHX66FWq9Hc3BzS5uXLl7Fy5UrMnj0bRUVFuHjxorhtYGAAxcXFUCqVWLBgAY4cOSJuW7t2\nLV599VU8+eSTSEhIwPHjx2+K1+PxoLS0FEqlEunp6Th06BAAoL6+HlVVVejp6YFUKkVNTc1Nx164\ncAGFhYWQyWRQqVSwWCyTjmvDhg0wmUyYPXs28vLyxBmcZcuWAQCysrIglUrF49ra2mA0GiGXy1FQ\nUIDvv/9ebM9gMGDfvn3IysqCTCaDxWKBz+cTt3/xxRcwGo1ITEzEvHnz8M033wAArl69isrKSmg0\nGuh0OlRXV4t5Czc2xlgY/9ZvVzDGpofBYCCbzUZms5m2b99ORER1dXVUVFRERER2u50EQaDx8XHx\nmKKiIqqvryciIqvVSrGxsdTY2EjBYJC2b99OWq2WNm7cSH6/n9rb20kqldLo6CgREVVUVJBUKqXO\nzk7y+Xz0xhtv0NKlS4mIyOv1kk6no8bGRhofH6e+vj6aM2cOnT17Vjw2MTGRuru7iYjozz//vGk8\njz76KG3YsIF8Ph/19/eTSqWijo4OIiJqbGwU+7oVi8Ui/s6dz+ejrq6uScelVCrp9OnTdO3aNSov\nLyeLxSK2KwgCDQ4Oisu9vb2UlJREp06domAwSE1NTWQwGMjv94s5Wbx4MV26dIlGRkbowQcfpAMH\nDhAR0cmTJykxMZFsNhsREbndbhoYGCAiorKyMlq/fj2NjY3Rzz//TLm5ufTxxx+HHRtjLDye0WEs\nCgiCgJ07d+Kjjz7C5cuXp3z83LlzUVFRAUEQ8Pzzz8Pj8WDHjh2YOXMmiouLIZFIcOHCBXF/k8mE\npUuXQiKRYNeuXejp6YHL5UJbW5vYVkxMDIxGI8xmc8jsSVlZGZYsWQIAiIuLC4nD6XSiu7sbe/bs\ngUQiQVZWFl5++WVxRoluc/lIIpHA4XDA7XZDIpEgPz8fACYVl9lsRnZ2NmbMmIHy8nL09/dP2M/B\ngwfxyiuvICcnB4IgYM2aNYiLiwv53NDrr7+O5ORkyOVylJSUiO3V19ejsrISK1asAABoNBrMnz8f\nw8PDOHbsGN5//33MmjULKpUKmzZtQmtra9ixMcbC40KHsSixcOFCmEwm7N69e8ofFlar1eL/s2bN\nAgCoVKqQdV6vF8BfRZVOpxO3xcfHQ6FQwOPxYGhoCCdPnoRcLhf/PvnkEwwPD4vHpqamThiHx+OB\nQqFAfHy8uE6v18Ptdk9qHO+++y6ICLm5ucjMzITVagWAScV14zm4Pt5bGRoawr59+0Lac7lc8Hg8\n4j7Jyckh7Y2OjgIAXC4X0tLSbtlmIBBASkqK2Ob69evxyy+/hB0bYyy82EgHwBi7c2pqarBo0SJs\n3bpVXHe9aBgbG0NCQgIA4Keffvq/+yAiOJ1Ocdnr9WJkZARarRZ6vR6FhYVob2//v9rWaDQYGRmB\n1+sVY7148WJIYRWOWq3GwYMHAQBdXV14/PHHsWzZsn8c1430ej3efvttvPXWW1M+NjU1NWR27O/r\n4+LicOXKFcTE3Pwe9FZjKywsxP333z/1ATB2D+EZHcaiSFpaGl544YWQb2CpVCpotVocPnwY4+Pj\naGhowODg4D/q5+jRo+jq6oLf70d1dTWWLFkCrVaLp556CufOnUNLSwsCgQACgQBOnz6NgYEBALe/\n9JSamor8/Hxs27YNPp8P3333HRoaGvDSSy9NKq4jR47A5XIBAGQyGQRBwIwZM2Aymf5RXGq1OuSc\nVVVV4cCBAzh16hSICKOjo/jqq6/CzgJd76OyshJWqxUdHR0IBoNwu9344YcfkJKSgpUrV2LLli34\n/fffEQwGMTg4iG+//XbCsd2qIGKMheJHCWNRZseOHRgbGwu5fFVXV4e9e/dizpw5OHv2LAoKCsRt\nt7ovTrhLX4IgoLy8HDU1NVAqlejr60NLSwsAQCqVor29Ha2trdBqtUhJScG2bdvg9/sn7OtGn376\nKRwOBzQaDcxmM3bu3Inly5dP6vgzZ84gLy8PUqkUTz/9ND788EMYDAYkJCRMOa6/L7/zzjuoqKiA\nXC7H559/jkceeQR1dXXYuHEjFAoF0tPT0dzcPGFsf28/JycHVqsVmzdvhkwmC/nWWnNzM/x+PzIy\nMqBQKPDcc8+Js28TjY0xFp5At3srwxhjjDF2l+IZHcYYY4xFLS50GGOMMRa1uNBhjDHGWNTiQocx\nxhhjUYsLHcYYY4xFLS50GGOMMRa1uNBhjDHGWNTiQocxxhhjUYsLHcYYY4xFrf8AJP19n103VkYA\nAAAASUVORK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x504e5b00>"
]
}
],
"prompt_number": 60
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Sentence Distribution per Class\n",
"\n",
"The graph shows the distributions of number of sentences per document per class (true class)\n",
"\n",
"**Note:**\n",
"\n",
"The documents of class y=1 seem to have less number of sentences ($\\bar{x_0}=18.9 > \\bar{x_1}=17.5 $), however the difference is only two sentences at the most. "
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"def sent_dist_per_class(data_name, sents, target):\n",
" c0 = sents[target ==0]\n",
" c1 = sents[target ==1]\n",
" plt.figure(figsize=(9,4.5))\n",
" n, bins, patches = plt.hist([c0,c1], bins=range(100), label=['y=0','y=1'], histtype='step', fill=True, alpha=0.5)\n",
" plt.title(\"Document Number of Sentence per class {0} (mean={1:.2f}, {2:.2f}) (N={3},{4})\".format(data_name, c0.mean(), c1.mean(),\n",
" len(c0), len(c1)),\n",
" fontsize=14, family='Arial')\n",
" plt.xlabel(\"Number of sentences\")\n",
" plt.ylabel(\"Frequency\")\n",
" plt.legend()\n",
" plt.show()\n",
"\n",
" "
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 57
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"sent_dist_per_class(\"imdb\", np.array(sent_per_doc), data.train.target)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAj0AAAE5CAYAAAB76JGKAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XdYFFf7N/DvUKQXQQGlLR2xIypGjQVRUyxRY1fsicT8\nLEkUzWMsSZQUzRNj1Cd2Y2yJPTF2TSRRUVFEASlSlKoiKCIg7P3+wbsTBhZcDGWQ+3Nde13MzM7M\nPXMPu2fPOXNGICICY4wxxthLTquuA2CMMcYYqw1c6GGMMcZYg8CFHsYYY4w1CFzoYYwxxliDwIUe\nxhhjjDUIXOhhjDHGWINQ54UehUIBLS0taGlpQVtbGyYmJujWrRuOHz9e16FVOyLCunXrUNEoAYsX\nL0ajRo1w48aNcssUCgU2btxY7TFt2bIFbm5u1b7dqpg0aRIMDQ3Rs2dPtctPnz6NV199FcbGxjAz\nM0Pv3r1x5syZatt/ZmYm9uzZU23bexnU1PVWkcTERGhpaeH27dvVsj1XV1ds27YNANCzZ098/vnn\nVVr//v37aNeuHQoLC6slnroQEhICR0fHcvO//PJLKBQKmJqaon///oiPj69wG+np6Rg6dCgaN24M\nOzs7zJ8/H0qlUlyempqKwYMHw9jYGI6Ojli7du0LxTp16lQsXLhQnN6yZYv4vVD2dffu3Uq3lZWV\nBRsbG2zdulXj4+7RoweioqKeG+emTZvw0UcfAaiZz2t1OSsuLsYnn3wCJycnmJmZwd/fH9HR0eLy\n8+fPlztH3t7e4vKsrCy8/fbbMDMzg5OTk/h/oRIeHo4uXbrAyMgIPj4+uHz5skaxls0ZAMTHx2PA\ngAGwsLCAvb09PvzwQxQUFIjL33nnnXKxrlq1Slx+5swZtGnTBkZGRujVq1e5a/O7776DnZ0dTE1N\nMWnSJOTl5QEACgoK0L59e9y7d+/5gVMdUygU9M0331BGRgalpaXRzZs3ae7cuaSjo0MnT56s6/Cq\n1dmzZ0kQBCouLla7fNGiRSQIAnXr1q3cMoVCQRs3bqz2mDZv3kyurq7Vvl1NXb16lQRBoGPHjlFG\nRoba5YaGhrR69WqKi4ujqKgomj9/PjVq1IguX75cLTFMmDCBxo4dWy3belnU1PVWkeLiYsrIyKjw\nf6OqXF1daevWrURE1LNnT/r888+rtP7kyZPphx9+qJZY6sL169fJ2tqa7O3tJfN37dpFxsbGdPjw\nYYqJiaGhQ4dSy5YtK9xO//79qVevXnTz5k06c+YMNWvWjL766isiKsmZt7c39e/fn6Kjo2nnzp2k\np6dHJ06cqFKsX3zxBQmCQAsXLhTnPX36lDIyMsRXamoqeXt709tvv/3c7Y0bN44EQRDzr8lxnz59\nmnr27FnpdrOyssjJyYmysrKIqPo/ryvK2aeffkp2dnZ04sQJunXrFk2YMIEcHR3pyZMnRES0fv16\n6tSpk+R8qWIkIhowYAD5+fnRjRs3aNOmTaSvr09///03ERHl5uZSs2bNaM6cORQdHU2zZs0iKysr\nevz4caWxqstZQUEBtWjRgt5++22Kjo6mP/74g1xcXOiDDz4Q39OtWzdasWKFJNa8vDwiIkpOTiZj\nY2P66quvKCoqikaOHEktW7YkpVJJRER79+4lMzMzOnz4MF2+fJlatWpF7777rrjtTZs20YQJE557\nnmVR6FF3cYwbN45at25dBxHVnDNnzpAgCFRUVKR2+aJFi8jW1pZ0dXVp06ZNkmUva6FHVRB89uyZ\n2uVz5syhAQMGlJvfo0cPmj59erXEEBAQwIWeMmq70FPd/k2hJzk5mczNzamgoKCmwqtR69atIxMT\nE2rbtm25L9DAwEAaPHiwOH39+nUSBIEyMzPVbsvIyIgOHjwoTs+ZM4dee+01IiL67bffyNTUlB4+\nfCguf/fdd2nx4sUaxZmTk0NDhw4lCwsLcnBwkHyBlvXdd99R06ZNKTs7u9JtHjlyhDw9PcnKykpS\n6NHkuFu0aEHnzp2rcNuff/45TZ06VZyuzs/rynLm6uoqKYAXFhaSsbExHTt2jIiIZs+eTRMnTlS7\n3bi4OBIEgeLj48V5U6ZMET/vNm7cSAqFQrKOm5sbbdiwQe32KsvZuXPnSE9PTyyMERHt2LGDbGxs\nxGlLS0v6448/1G574cKF1L17d3E6Ly+PTE1N6dSpU0RE1L17d8n+QkJCSF9fX9xfQUEBWVhYUFJS\nktrtq9R581ZFpk2bhhs3bojV3Q8fPsS0adNgY2MDMzMzjB07Fg8fPhTff/XqVfTo0QNGRkZwcXHB\n5s2bAQBnz56FlpaWpEp2woQJGDduHICSKsrRo0fj//7v/2BiYgJnZ2ecPn0a3333HWxsbGBtbY01\na9aI6+bk5CAgIADm5uZo1qwZ3nnnHeTm5or7srOzw/r162FnZwdjY2OMHTsW+fn5SExMRO/evQEA\nurq6+PPPP9Uet5OTE2bNmoV58+ZJjq+00vGraGlp4fTp0wBKqlbXr1+Pjh07wtDQEP3790dSUhKG\nDBkCIyMjeHt7S6pHiQhz586Fqakp7OzssHr1asm2f/jhBzg7O8PExATdu3eXVH8qFArMnTsXtra2\naNmypeQ8q5w/fx7dunWDsbExnJycxPO5ZcsW9OrVCwDQqFGjctWuquO6fv06MjIyJPN37NiBxYsX\ni9MhISHo1KkTDA0N0apVK2zfvl1yvmbOnIlRo0bB2NgY9vb2YtX34sWLsW3bNvz0009wdnYG8OI5\nVtm1axdatmwJIyMjdO7cGRcuXBCXHThwQFzWoUMHHDt2rNwxlz633377Ldq0aQNjY2O8/vrrSEtL\nE5ffvXtX0rQwf/58PHv2TDy3vr6+GDZsGMzNzbFp06Zy28/Ly8OMGTNgZWUFCwsLBAQEiMdZ2uPH\njzFlyhRYW1tDT08Pnp6e2Ldvn7j8l19+gZeXFwwMDODu7o4tW7ZotKy0ss1bWlpa2L17N1q0aAEj\nIyOMHTsWCQkJ6NWrF4yMjNCzZ0+kp6eL669fvx6Ojo4wMzPDkiVLym0/KSkJ3bt3h4GBAV555RVE\nRERUeN5/+OEH+Pv7o1GjRuK57NatG5YtWwYLCws0a9YMO3fuxJ49e+Dg4AALCwt8/PHH4voFBQWY\nNWsWrKys0KRJE4wYMQKZmZni8vPnz6N79+4wMjKCsbExXnvtNaSmpkr2tXTpUlhZWcHc3ByzZs0S\nm8R79uyptslHde0CwNGjR7Ft2zbMnj27XFN6p06dEBISgqioKBQVFWHbtm1QKBSwtLRUey46duyI\n7du34+nTp0hNTcWxY8fg4+MDoKTZuXfv3jA3Nxffv3btWixatKjCc1taQkICCgsLcfXqVUn8ZT1+\n/BhLlizBp59+CjMzs0rfN336dKxfv17MXVWOe+DAgRU2zxERfvjhBwwePFgyX5PP63+bs/Xr12PQ\noEHitCAIICJkZ2cDACIjI+Hh4aF23xcvXkSzZs0k++ratSvOnz8PALhw4QK6du0qWaf08rIqy5mn\npyeOHDkCQ0NDyXxVnOnp6cjKyoK7u7vabV+4cAGvvvqqOG1gYABvb2+cP38excXFuHz5smR5586d\nUVRUhKtXrwIo+Q7x9/fH//73P7XbF1VaJKoFFZWI79+/T4Ig0OHDh4mo5Jd9586d6dKlS3Tp0iXy\n8fGhN954g4iI7t27R40bN6bp06dTTEyMWM0aEhIi1q6UrjafMGECjRs3johKSut6enr08ccf0+3b\nt2nYsGHUuHFjGjx4MEVHR9PChQupUaNG4q+ZIUOG0JtvvkkRERF05coV6tGjBw0dOpSISmpydHV1\nqU+fPnTjxg06duwYGRoa0tq1a6m4uJj27dtHgiBQamoqFRYWljvmRYsWUbdu3Sg3N5fs7e1p2rRp\nas9T6fhVBEEQS8SOjo5kY2NDJ0+epMuXL5OlpSVZWFjQ+vXr6caNG+Tj4yPGvHnzZhIEgYYMGUKR\nkZG0ZcsW0tPTo9OnTxMR0aFDh8ja2poOHTpEcXFx9Pnnn5OJiQmlp6eL+2revDlFRERQeHh4uWOK\njIwkfX19+vjjjyk2Npa2bt1KRkZG9PPPP9PTp08l5+Tp06fl1o+KiiITExPS19enN954g1auXElR\nUVGS96SlpZGpqSmtWrWK4uPjaffu3WRubi5eOwEBAdSoUSP66quvKCEhgWbNmkUGBgb08OFDys3N\npREjRtDbb79N9+/f/1c5JiI6efIk6erq0tq1ayk+Pp7mzZtHFhYWlJubS9euXSMTExPavn073b59\nm9atW0cGBgZ07dq1csetOrfm5ua0Y8cOioiIoF69epGvry8RESmVSvLx8aFJkybRrVu36Ny5c9Sq\nVSuxKlmV1wULFlBMTIzapsOxY8eSl5cXhYSEUHh4OHl7e4u/ZEtfb5MnT6Zu3bpReHg4xcXF0dSp\nU8nCwoIKCwspIyODdHV1acOGDZScnEybN28mbW1tunXrVqXLykpISJD8IhUEgTw9PenixYt06tQp\n0tXVpebNm9O+ffsoLCyMHB0dxWM9duwY6enp0datWykqKorefvttSfNGjx49SFdXl9atW0fR0dE0\nevRocnFxqbDGtUOHDpJf1ps3byY9PT2aOHEixcfH0//93/+RkZER9ejRg27cuEHr1q0jQRDoxo0b\nRFRSG+Lr60uhoaF08+ZNGjZsGHXs2JGIiB49ekSNGzempUuXUmJiIv3111/k7u5OgYGB4r4aNWpE\no0aNopiYGNq+fTtpa2vT77//TkREDx8+lDQNqF6qa7e0zZs3k52dXbn506ZNI0EQSEdHh8zMzNT+\n36rcvXuXnJycSFtbmwRBoD59+oifpW+99Ra9//779PHHH5O9vT21bNnyhWsHe/bsWWFNz1dffUX2\n9vYV5kvl3XffFZs77OzsJDU9RM8/7hMnTpClpaXabUdERJC2trbkM0rTz+vqyFlpa9eupUaNGlFa\nWhoREdnb29OQIUOoVatW5ODgQO+88w7l5OQQEdHXX39NPj4+kvWPHDlCenp6RET05ptv0kcffSRZ\nPnfuXOrXr1+lMRBVnjOikubPV155RaypV/0fT5kyhWxtbalt27a0ZcsW8f2tW7em77//XrKNESNG\n0LvvvksPHjwgQRDo5s2bkuXW1ta0a9cucXrDhg3Uvn37SuOWbaHn2bNnJAgC7dixg8LDw0kQBIqO\njhaXR0dHiydh9erVpFAoxLY/IqLVq1fTH3/8obbQExAQICn0NGvWTFx26NAhEgSBEhMTiaikHVcQ\nBLp8+TLFxcWRlpaWpL00MTGRBEGgu3fvivtSffgRlXyBTpo0iYhIbSylqf6JiEraL7W0tOjixYvl\nzpO65pjShR6FQkHz5s0Tlw0dOlTSXv3NN9+I7dmbN28mY2NjevTokbh84sSJNGzYMCIqaYP95ptv\nJPvq1asXffrpp+K+yv7TlDZ79mzxi1olKChI/BJ43jkhIrEd29LSkgRBIEEQqH///uKHxn/+8x8a\nNGiQZJ3FixeTn58fEZWcr9L/+I8ePSJBEMSq7NLn80VzPHnyZCIiGjZsmKRAqlQqad68eZScnExj\nx46lmTNnSuKcMGGCuG5ZCoWC5s6dK06rCgbXrl2jkydPkqWlpeS8nT17lvT09KioqEgs9JSuai4t\nOzubdHV1xWuGiCg0NJS+/vprcd+q623Lli2S41X97yUmJlJYWBgJgkBHjhwRl585c4YePnxY6bKy\n1BV6VAVJopKCSOn2+pkzZ4o/eoYNGyZZlpOTQ0ZGRpJCz/jx48Xljx8/JhMTE/r111/LxVFUVEQ6\nOjqSZo7NmzeTjo4O5ebmEtE/TSNnz54V32NmZka//PILPXnyhPT09Ojq1avisry8PDI0NKRz585R\neno6rVixQrLPoKAg6tGjh7gvLS0tyf+jt7e3+P9WFeq+QDdv3kympqa0bds2unLlCo0fP55cXFwk\n17uKUqmknj17Urdu3ejvv/+m33//nVxcXGjWrFlEROTn50fm5uY0ZcoUCgsLo/Xr15O+vj4dOHCg\nyrFW9AWqVCrJ1dWVvvzyy0rXP3v2LNnb24vnrWyhR5PjTklJKdcUVHp9Z2dnyTxNP6+r4nmFnpCQ\nEDIyMhKbEB8/fiz+aA0LC6Pjx49Tq1atxP+NpUuXUteuXSXbOHXqFAmCQEREvXv3pv/85z+S5QsX\nLnxu/yai5xd6Zs6cSUZGRhQZGUlEJd/Jenp6tHr1aoqIiKBVq1aRnp4e/fzzz0RE5OLiUq5Zbfz4\n8TRx4kS6c+cOCYJAcXFxkuUODg6SPP/111+kra1dYXcJIiKdyuuB6s6jR48AAKampoiKioKJiYmk\nCs/DwwONGzdGVFQUoqKi0K5dOwiCIC5/7733AJQ0RzxP6d7yBgYGknmq6YKCAkRFRYGI4ODgIFlf\nEATExMSI+3dxcRGXmZiYoKioSOPjVhkyZAj69euH6dOn49KlS1Vev3TVo76+vuQY9fX1JT3qPTw8\nYGJiIk63b99erCKMiorCggULJL30CwsLYW9vL04rFIoK44iOjkbnzp0l87p06YLvv/9e42Nxd3fH\n5s2boVQqcenSJfz8889Ys2YNpk6din379iEqKgq///675BiKiopgZWUlTpfNCQCxKQiAmLsXzbFq\nW1FRUZg6dapkveDgYHHZjRs3JHd1PHv2rNz5Ka101bNCoYCFhQWioqJw//59ZGdnS6r7iQjPnj1D\ncnIyAMDS0rJcVbNKTEwMioqK0KFDB3Fex44d0bFjx3LvHT9+PPbv34///e9/uHXrFq5cuQKg5K6S\n9u3bY+DAgXjjjTfg4uKCAQMGYMKECTA3N690mSZKX8MGBgblrmHVnVVlz7mpqankjkRBENCpUydx\n2tjYGO7u7oiOjsYbb7wh2eeDBw9QXFyMJk2aSOY3adIERkZGYixA+c+NgoIC3L59G4WFhejevbtk\n/YKCAsTGxqJbt24YP348Vq5cifDwcERGRiI8PBy+vr6SfZW+lk1NTcXr67XXXkNISEi5c6VQKCpt\nslNZtmwZgoKCxObxTZs2wcPDA5s2bcIHH3wgee/58+fx559/4s6dO2jevDkAYMOGDfD398f8+fOh\no6ODxo0b44cffoAgCGjfvj3Cw8Oxdu1aSXPMvxEWFobbt2+Xa84v7enTp5gyZQpWrVolOW9UqplI\nk+NWNXVlZmaWa7rJzMwsd02UVtnn9b/NmcrZs2cxcOBADBw4UGxCNDY2xuPHj2FgYAAtrZLeKlu3\nboWPjw/u3LlT7rMeKLkWVdewgYGBpGletbyizw1NEBFmzZqFtWvXYu/evWjRogWAku/k8ePHizlq\n1aoVYmNjsXbtWgwbNkxtrPn5+WjatCn09fXF2CqL1dLSEkqlEvfv34eNjY3a+GRb6Ll+/TqAkhMT\nHh6u9j3FxcUoLi5Go0aNKrwNvHRBSKWoqEi8QABAR0ez01BUVARjY2Ncu3ZNMp+I0KxZM4SGhgJA\nufZkdf1cNLF69Wq0atWqXB+bssekrlBV+pgEQVB7HlS0tbUl08XFxdDT0xP/XrlyJfr27SsuJyIY\nGxuL06oLUh0DA4NyuSkuLta4IPjhhx9i3LhxaNu2LbS0tNC5c2d07twZTk5OCAoKAlBy/KNHj5YU\nzIhIcly6urrltq3umnnRHKu2VXZ+acXFxfjoo48wceJEyXqqc61O2WuzuLgYOjo6KC4uhpubG377\n7bdycdjZ2QGoPC+VxVnWuHHj8Pfff2P8+PEIDAyEjY0NunTpIi4/cOAArl27hoMHD+LQoUNYs2YN\nDh8+DH9//0qXPU/ZYy/9P1tW2VyWzbe6a1zdOVDto7i4uNJYKopHdV3/+eef5QqkTZs2RUpKCnx8\nfNChQwf069cP06ZNw6+//ir5UlQXl+r4Nm7cWO5LClB/fauTkpKCtm3bitPa2tpo27YtEhISyr33\n7t27sLCwEAs8AODt7Y3i4mIkJSXB1tYWSqVS8tni7u6OU6dOaRSLJn7//Xf4+vpW+AUGAKGhoYiP\nj5cUjPLy8vDuu+/i4sWLWLNmjUbHrfqcVpdXLS2tctdEWRV9Xv/bnAHAkSNHMHToULz11luS/ooA\nxMK4iqenJ4CS4QTs7Owkfd+Akr41qpza2tpWuryqlEolJk+ejB07dmDPnj0YMGCAZHnpQqkqVtXw\nNLa2tpI+i6pY2rRpA0tLS+jr6yM9PR1eXl4ASv7XHjx4gGbNmkn2D1T+WSHbjsybNm2Cj48PHB0d\n4eHhgcePH0s630ZGRuLRo0fw9PSEm5sbwsPDJR98kyZNwqJFi8QvFFXNEYAXHgvEw8MDubm5KCoq\ngrOzM5ydnSEIAmbPni3ZfmmlCxyVFTzUcXZ2RlBQEBYuXCjZfqNGjfD48WNx+t+ObXLr1i1JCfri\nxYti6dzDwwPJycni8To7O2PlypUa1aABJRf1xYsXJfPOnz8v/mM+z4kTJ9SOd2FiYiLW5Hh6eiIm\nJkYS44kTJ7BhwwaN9qHqGAi8WI5Lc3NzQ1hYmDhNRPDy8sKxY8fg4eGB+Ph4SZzbt2/H/v37K9xe\n6W3FxcUhJycHbdu2hYeHB+7cuQMLCwtxWxkZGeXGUamIs7MztLW1Jds/efIkPDw8JP9Hjx49ws6d\nO7Fz504sXrwYgwYNwoMHD8Rju3r1KmbNmoV27dph0aJFuHLlCrp37479+/fj2rVrFS6rTq1atRIL\nowDw5MkTxMTESN5TuhD78OFDxMbGitd4aZaWltDR0RGPsapcXV2hra2Ne/fuiXlp2rQp5syZg6Sk\nJOzfvx9mZmb49ddf8f7776Nr166VjpNTVvPmzSXXj+pVuua1Mi4uLrh586Y4TUSIioqS1FyWfu/D\nhw8lX4qqsWxcXFzQpUsXRERESH7AREZGwsnJSePjeZ4LFy6gR48elb6nc+fOiIuLQ3h4OMLDw3Ht\n2jVYW1vj008/xdKlS8V4n3fc9+/fBwC1BSxra+vnXhMVfV7/25xdvHgRQ4cOxciRI/HTTz9JvtAv\nX74MY2NjSWHh6tWr0NbWhpubGzp37oyUlBQkJSWJy0NCQsSaRV9fX/z999+S8/LXX39Jah6r4oMP\nPsCuXbuwf//+cp2+58yZgzfffFMy7+rVq+L/oa+vr6Twn5eXh2vXrsHX1xeCIKBjx444d+6cuPz8\n+fPQ0dFB+/btxXn379+HlpYWmjZtWmGMsij05OTkID09HWlpaYiIiMD8+fOxe/durFixAkDJF9Gb\nb76JgIAAXL58GZcuXUJAQAC6d++ONm3aYMyYMcjNzcXs2bMRExODHTt2YOfOnXjttdfQsmVLGBgY\nYPny5UhISMDKlSvL/YrXVIsWLdC/f3+MGzcOoaGhCA8Px9ixY3Hv3r0Kf4lQSb8pABBrR65cuVKu\nmq4iQUFBsLa2ltwZ0KlTJ5w+fRqnT5/GzZs38f7771daW1BRLZhKbm4uJk6ciJs3b2LNmjXYu3cv\n5syZA6DkQl21ahW2bduG+Ph4LFmyBBs3blT7haFOYGAgIiIi8PHHHyMmJgbbtm3DmjVrMGPGDI3W\n/+STT7BmzRp89NFHCA8PR2xsLHbs2IH58+dj7ty54j6uXr2KBQsWIDY2Fr/88gs++ugjjT9UTExM\nkJSUhNTU1BfKMfDPOZ45cyZ2796NjRs3Ii4uDkFBQcjOzsYrr7yC2bNn4+eff8Z///tfxMXF4X//\n+x8+//zzCgeHJCJ88803OHz4MK5fv45Jkyahb9++cHNzQ9++feHk5IQxY8bg+vXrOH/+PCZOnAht\nbe1Kr4XSxzxx4kTMnDkTFy9exNWrVzF37lz06dNHUgg0MDCAkZER9u7di8TERBw/fly8NgoKCmBm\nZoZ169ZhyZIlSEhIwJkzZ3D9+nX4+PhUuqyqSv8flT3nM2bMwN69e/G///0P0dHRePfddyV3oRER\ntm7dii1btiAyMhITJkyAm5sb+vTpU24/giCgXbt2FdYuP4+xsTGmTp2KGTNm4MyZM4iOjsb48eMR\nEREBd3d3NGnSBCkpKTh58iRu376NL774Ar/++qvamoDKjv1FzZw5E8uXL8fBgwcRGxuLOXPm4N69\newgICABQ8lmclZUFAOjQoQNeeeUVjBs3DhEREbhw4QKmTZuG8ePHw8LCAiNHjoSuri6mTJmCmJgY\nbN++HVu2bEFgYCCAkmbw9PR0jQrhFR3jjRs30LJlS7XrpKenIz8/H/r6+pLChIuLC7S1tcW75zQ5\nbqCkdaFp06blmraBkhqu5ORkyY9NddR9Xv8bRIRJkyahVatWWLZsGTIyMpCeni4ee7t27eDo6IjJ\nkycjMjISf/75J6ZMmYLJkyeLP4j69esnXoObN2/Gjh07xM/fYcOGITc3F++//z4iIyMxZ84cPHny\nBCNHjgRQ0nRYtiaodGylc3bhwgV8++23WLJkCby9vcU4VesPGTIEx44dw3fffYf4+HisXr0aP/74\nozjY46RJk3Dx4kUsW7YMkZGRmDx5MhwdHeHn5weg5HN+xYoV2L9/Py5fvozAwEBMnjxZ0rx1/fp1\neHt7V17BUGFvn1qiUCjEzqlaWlpkbW1Nr7/+Ov3111+S92VlZdGYMWPI1NSUGjduTBMnTpSM2XDx\n4kXy9fUlfX198vDwoJ07d4rLfvrpJ3J0dCRDQ0MaO3YsBQUFiZ1NFy9eLBkb4MSJE6SlpSVOP336\nlARBEOO5f/8+jRkzhszMzMjc3JyGDx8u3hlz5swZ0tLSqvBOscLCQurfvz/p6enR/v37y52LsrGo\nHD9+nLS0tMSOcQUFBTRx4kQyNjYmOzs72rBhA7m5uUk6MpfuRDd27FjJOA7r1q0jNzc3IirppNq1\na1d67733yMjIiJycnGjHjh2S/X/33Xfk7OxM+vr61L59ezp69Ki4TJMOe2fOnKEOHTqQnp4eubu7\nS+6MUXfOyvrtt9+oZ8+eZG5uLsZQutc/UUnnvI4dO5Kenh4pFApJZ9Hn3e126dIlat68OTVt2pSI\n/l2OiYi2bt1KLi4uZGBgQN26daOwsDBx2e7du8nLy4v09PTI09OTtm/fXuFxKxQKmjNnDnl5eZGx\nsTGNHDkXJ4v9AAAgAElEQVRScs0nJCTQgAEDyMjIiJo0aULTpk0TO9tu2bKl3HgfZeXm5tLkyZPJ\n3NycmjRpQu+88444UFjpvB48eJBcXV1JX1+funbtSn///Tc5OTmJsR86dIjatGlDBgYGZGdnR0uX\nLhX3Udmy0hISEkhLS0vSkbl0J+tu3brRkiVLxOmgoCDy9/cXp3ft2kUuLi5kZGREM2bMoG7duknG\n6Zk/fz517NiR9PX1qU+fPpSQkFDhefnkk08kg+CVPZexsbGkpaUlGQ/ExsaGfvrpJyIq6bj83nvv\nUdOmTcnExIT69+9PsbGxRFRyR8v06dOpcePG1LhxY5o2bRodOnSITExMKD8/nzZv3lwub8/rMFqR\niq6B77//ntzd3cnU1JR69+4t6aQeEBBAvXr1EqcfPHhAY8eOpaZNm1Lz5s1p5syZlJ+fLy6/desW\n9enTh/T19cnZ2VkyXs3+/ftJEITnjptS2TEaGBhIOsKXVnYAwtLU3b1V2XETlVxTlQ1u5+joSL/9\n9ps4renndVWUzVlERIT43aj6nlS9VNtPTEykQYMGif/Hs2bNktwdnJmZSQMHDiQDAwNydnYWr1OV\nS5cukbe3N+nr61Pnzp0ln1fffPON2Om5rLI5+/DDD8vFqIpd9Xn5yy+/UOvWrcnAwIBatmxZ7nvw\n999/J09PTzI0NCQ/Pz+6ffu2ZPkXX3xB1tbWZG5uTpMmTZJci0REI0eOfO44UbVW6Fm2bBl5eXlR\nq1ataNSoUZSfn08PHjygPn36kJubG/n7+0vu6li2bBm5urqSh4eHOAgTYw2JQqGo8EOd1ZzExEQy\nNTUVC5Dsxb311ltqh0uQG6VSSU5OTuJIxep89tln5X48NQRdunSp6xA08vjxYzI3N6fk5ORK31cr\nzVuJiYlYv349wsLCEBERgeLiYuzatQvBwcHw9/dHTEwM/Pz8xLtcIiMjsXv3bkRGRuLo0aMIDAx8\n4c7AjDFWFY6OjnjrrbfKPbuJVU14eHi5uyjl6ujRo3BwcJB00C8rMDAQp0+fFvv+NARHjhyRdACX\nsx9//BGDBg16breGWin0mJqaQldXF3l5eSgqKkJeXh6aN2+OQ4cOiW2qAQEBOHDgAADg4MGDGDVq\nFHR1daFQKODq6irpqMgYYzXpyy+/xLp16+r1A0frWuvWrXHw4MG6DkMjn3/++XOH0WjcuDEWL16M\n5cuX11JUda9v374v/BDZ2lRQUIC1a9fiyy+/fO57a+WWdQsLC3zwwQdwcHCAgYEB+vXrB39/f2Rk\nZMDa2hpASe941aMGUlNTJb3H7ezskJKSUhuhMiYb6m4jZrXDyspKHDaDvZjKbhuWG3Xj6KgzZcqU\nGo5EXjQdzqWu6enpafz/WitXZXx8PP773/8iMTERqampyM3NLTfWwPPGkqnq7d6MMcYYY6XVSjHu\n8uXLeOWVV8QRL4cMGYLz58/DxsYG6enpsLGxQVpamtj2a2trizt37ojr3717F7a2tuW2O3DgQOTn\n54u3EhsZGcHV1RXt2rUD8M/YHDxde9NxcXEYNmyYbOJp6NOcD3lNcz7kN62aJ5d4Gto0UNL/S3Vr\nu4uLS402qQlE1TQARCXCw8MxZswYXLp0Cfr6+pgwYQI6deqEpKQkWFpaYt68eQgODkZ2djaCg4MR\nGRmJ0aNHIzQ0FCkpKejTpw/i4uLK1faMHz8e3377bU2Hz6ogODhYHCmZ1T3Oh7xwPuSHcyIvM2fO\nxLZt22ps+7VS09O2bVuMHz8ePj4+0NLSgre3N6ZNm4bHjx9j+PDh2LhxIxQKBfbs2QMA8PLywvDh\nw+Hl5QUdHR2sWbNGbfNWRYMmsbqjeu4TkwfOh7xwPuSHc9Kw1Fovpblz54oj6KpYWFjg5MmTat+/\nYMECLFiwoDZCY4wxxlgDUH+616vRr1+/ug6BlTF69Oi6DoGVwvmQF86H/HBO5KWmxwWqlT49NeXU\nqVPw9vau6zAYY4wxVg3CwsLE523VhPpxE34Frl27xoUemQkJCUG3bt3qOgz2/3E+5IXzIT+1nRMi\nQmZmJoqLi2ttn3KjeiBsXQxFU68LPYwxxlh9kpmZCRMTE8nTwRuavLw8ZGZmioMT16Z63adHdb8/\nkw/+FSsvnA954XzIT23npLi4uEEXeADA0NCwzmq66nWhhzHGGGNMU/W60FN6REcmD5o+w4bVDs6H\nvHA+5Idz0rDU60IPY4wxxpim6nVHZu7TIz/cZ0FeOB/ywvmQn7rOSezJi3iY96zGtt/YUBdufTrX\n2PZL279/P9atW4ebN2/C29sbhw4dqpX9VkW9LvQwxhhj9dnDvGeItnWpse17psTX2LbLsrCwQGBg\nIGJiYnDu3Lla229V1OvmLe7TIz/cPi4vnA954XzID+ekxKpVqxAQECCZFxQUhPnz52u8jR49emDQ\noEF1ciu6primhzHGGGvgRowYga+++gqPHj2CqakpioqKsH//fvz888/48MMPsXfvXrXr2dvb488/\n/6zlaF9cvS70cJ8e+anr9nEmxfmQF86H/HBOSlhbW8PX1xcHDhzA+PHjcerUKVhaWqJNmzb4+uuv\n8fXXX9d1iNWiXjdvMcYYY6x6jBw5Ej///DMAYM+ePRgxYkQdR1T96nWhh/v0yA+3j8sL50NeOB/y\nwzn5x+uvv46bN28iMjISJ06cwLBhwwAAc+bMgYODg9pX165dy22nLp6ppal63bzFGGOMsephYGCA\nAQMGYNq0aejQoQNsbW0BACtXrsTKlSufu75SqURhYSGKioqgVCpRUFAALS0t6Orq1nToGqvXhR7u\n0yM/3D4uL5wPeeF8yE9d56SxoW6N3lbe2LBqBY5Ro0Zh+/bteO+996q8r127duH9998Xp5s3b45R\no0Zh9erVVd5WTanXhR7GGGOsPqutgQM1ZWdnJ9b4VNXo0aMxevToGoiq+nCfHlatuH1cXjgf8sL5\nkB/OyT+USiW+//57DBkyBMbGxnUdTo3gmp5aVpxfAJB0nqCtBa1G8mnzZIwx1rA8efIEnp6ecHBw\nEO/gehnV60JPfezTc2HHcTw0bSyZ56JPaPFm9zqKqHrVdfs4k+J8yAvnQ344JyWMjIxw586dug6j\nxtXrQk99VGhqiiwn6XNWFJmJdRMMY4wx1oBwnx5Wrbh9XF44H/LC+ZAfzknDUmuFnlu3bqF9+/bi\ny8zMDKtWrUJWVhb8/f3h7u6Ovn37Ijs7W1xn+fLlcHNzg6enJ44fP15boTLGGGPsJVRrhR4PDw9c\nvXoVV69exZUrV2BoaIi33noLwcHB8Pf3R0xMDPz8/BAcHAwAiIyMxO7duxEZGYmjR48iMDAQSqVS\nss362KfnZcft4/LC+ZAXzof8cE4aljpp3jp58iRcXV1hb2+PQ4cOiY+zDwgIwIEDBwAABw8exKhR\no6CrqwuFQgFXV1eEhobWRbiMMcYYewnUSaFn165dGDVqFAAgIyMD1tbWAEqe8pqRkQEASE1NhZ2d\nnbiOnZ0dUlJSJNuRe5+ewgfZKLz/UPKCkp6/Yj3G7ePywvmQF86H/HBOGpZav3ursLAQhw8fxhdf\nfFFumSAIlT6orOyyP/74A5cvX4aDgwMAwMzMDK1btxarK1UXc11N/7BiPXLMGsOjRVsAwK2ocDzT\n14eziwcAIDa8pObK2sAED/edQ0R0BACgtWdrNDfTQ5peYZ3G/yLTERERsoqnoU9zPuQ1zfmQ37RK\nbe3P2dlZst+L1xJRmJmFmtLIygKd2ylqbPulFRQU4IMPPsDhw4dhaGiI999/H4GBgWrfm5OTg9u3\nbwMoOTfJyckAAB8fH/j5+dVYjAIR1WrVw8GDB7F27VocPXoUAODp6YmzZ8/CxsYGaWlp6NWrF6Kj\no8W+PUFBQQCA/v37Y8mSJejc+Z8hu0+dOgVvb+/aDL9KTv38B1Kc3V9o3XYZCWjz+ivVHBFjjLG6\nlJqaiubNm4vT546HwSY8rMb2l97WG9371s735NKlSxEaGoodO3YgPT0dgwYNwurVq9UWYsqeB5Ww\nsLAaLfTUevPWzp07xaYtABg4cCC2bt0KANi6dSsGDx4szt+1axcKCwuRkJCA2NhYdOrUqbbDZYwx\nxl56q1atEvvXqgQFBWH+/Pkab2P37t348MMPYWpqCnd3d4wfPx47d+6s7lD/lVot9Dx58gQnT57E\nkCFDxHlBQUE4ceIE3N3dcfr0abFmx8vLC8OHD4eXlxdee+01rFmzplzzltz79DRE3D4uL5wPeeF8\nyA/npMSIESNw+vRpPHr0CABQVFSE/fv3Y9SoUfjwww/h5OSk9vXqq68CALKzs5Geno5WrVqJ22zZ\nsiWio6Pr5HgqUqt9eoyMjHD//n3JPAsLC5w8eVLt+xcsWIAFCxbURmiMMcZYg2VtbQ1fX18cOHAA\n48ePx6lTp2BpaYk2bdrg66+/xtdff13p+rm5uQAAU1NTcZ6JiYk4Xy7q9YjMPE6P/PCYF/LC+ZAX\nzof8cE7+MXLkSPFho3v27MGIESM0Xlf1VPbHjx+L8x49eiS7p7XX60IPY4wxxqrH66+/jps3byIy\nMhInTpzAsGHDAABz5syBg4OD2lfXrl0BAObm5rCxsUFERIS4vRs3bqBFixZ1ciwVqdeFHu7TIz/c\nPi4vnA954XzID+fkHwYGBhgwYACmTZuGDh06wNbWFgCwcuVKJCcnq3399ddf4vojRozAihUrkJOT\ng1u3bmH79u2SG5fkgJ+yzhhjjNWRRlYWSG9bc7eUN7KyqNL7R40ahe3bt+O9996r8r6CgoLwwQcf\noE2bNjAwMMDMmTPRu3fvKm+nJtX6OD3VicfpYYwxVp9UND6NXNy9exe+vr6Ijo6u0f44DWacHsYY\nY4zJj1KpxPfff48hQ4bIrgNydanXhR7u0yM/3D4uL5wPeeF8yA/npMSTJ0/g6OiIP//8Uxwv72XE\nfXpk6kGhEsn3peMbGOrpoImJfh1FxBhj7GVlZGSEO3fu1HUYNa5eF3pe5nF67sakwDguXjLvaccO\neLVHqwrWkAce80JeOB/ywvmQH85Jw1KvCz0vi/TbKdDJfSKZZ5v7COYm0sduPKv4AfSMMcYYew7u\n0yMDjTLuwTHiquRlm363rsN6Idw+Li+cD3nhfMhPbedEW1sbeXl5tbpPucnLy4O2tnad7Jtrehhj\njLFaYmVlhczMTGRnZ9d1KHVGW1sbVlZWdbLvel3oeZn79NRX3D4uL5wPeeF8yE9t50QQBFhbW9fq\nPtk/6nWhpz5KT0yH9tOnknk6eU8qeDdjjDHGqgv36alljVJToQgLlbzs6mn/HXW4z4K8cD7khfMh\nP5yThqVeF3oYY4wxxjRVr5u35NSnJ+nsZRQWFUvmFRYW1VE0dYf7LMgL50NeOB/ywzlpWOp1oUdO\nYjJzkebiIZ3ZuG5iYYwxxlh59bp5qz726XnZcfu4vHA+5IXzIT+ck4aFa3rqkUf5z3Ar+YFknomR\nHppbvpxPw2WMMcaqU70u9MipT486WfcfQVlUpl9P2ekqaB5+FfnXpbVbmT4d0bynfJ7Hxe3j8sL5\nkBfOh/xwThqWel3okTtldCyaJ9+WzNMieuHtGUAJlFk9l5/HxRhjjGmkVvv0ZGdnY9iwYWjRogW8\nvLxw8eJFZGVlwd/fH+7u7ujbt69kaO7ly5fDzc0Nnp6eOH78eLnt1VWfnkvbjuDcvnOS12N9o3Lv\n0wKgS0rJS7tsqeUlw+3j8sL5kBfOh/xwThqWWi30zJw5E6+//jqioqJw/fp1eHp6Ijg4GP7+/oiJ\niYGfnx+Cg4MBAJGRkdi9ezciIyNx9OhRBAYGQqlU1ma4FXqob4gER1fJK9fWrq7DYowxxlglaq3Q\nk5OTg3PnzmHSpEkAAB0dHZiZmeHQoUMICAgAAAQEBODAgQMAgIMHD2LUqFHQ1dWFQqGAq6srQkND\nJduUe5+ehojbx+WF8yEvnA/54Zw0LLVW6ElISEDTpk0xceJEeHt7Y+rUqXjy5AkyMjLEh69ZW1sj\nIyMDAJCamgo7u39qT+zs7JCSklJb4TLGGGPsJVNrHZmLiooQFhaG1atXo2PHjpg1a5bYlKUiCAIE\noeKeuWWXffvttzAyMoKDgwMAwMzMDK1btxZL7qq22uqeVokNL6l5cmvbSe10YmIU8tJT4NFMAQC4\nlZYIABpPX0mKBwB0cHSpcDrbUA9de7Sq0eOtynRERASmT58um3ga+jTnQ17TnA/5TavmySWehjat\n+js5ORkA4OPjAz8/P9QUgehf3E5UBenp6ejSpQsSEhIAlBzk8uXLcfv2bZw5cwY2NjZIS0tDr169\nEB0dLRaIgoKCAAD9+/fHkiVL0LlzZ3GbK1asEJvLatPxPWeRXnb0ZTWyQq7APinuhfZh9OAedHW0\nJfNM9LTR2MlWMi+zk69Y6JGDkJAQri6WEc6HvHA+5IdzIi9hYWE1WuipteYtGxsb2NvbIyYmBgBw\n8uRJtGzZEgMGDMDWrVsBAFu3bsXgwYMBAAMHDsSuXbtQWFiIhIQExMbGolOnTpJtvsx9ep5YNkW2\nmYXkVVgkj47cleEPD3nhfMgL50N+OCcNS62O0/Pdd99hzJgxKCwshIuLCzZv3ozi4mIMHz4cGzdu\nhEKhwJ49ewAAXl5eGD58OLy8vKCjo4M1a9ZU2vTFGGOMMVaZWi30tG3bFpcuXSo3/+TJk2rfv2DB\nAixYsKDC7V27dg3e3t7VFh/797iqWF44H/LC+ZAfzknDUq8fOMoYY4wxpql6Xeh5mfv01Ff8i0le\nOB/ywvmQH85Jw1KvCz2MMcYYY5qq14Weunr2FqsYP8dGXjgf8sL5kB/OScNSrws9jDHGGGOaqtW7\nt6pbQ+vTk5f/DKkxdyTzcixsARkNTsjt4/LC+ZAXzof8cE4alnpd6JGT/CIlUGZs6+oe6vpxEys8\nLjPvWX5hNe+FMcYYeznV6+YtOfXpybocAfx+QvKyTL3z/BVfMtw+Li+cD3nhfMgP56Rh4ZqeaqL/\nrBCWj7PrOgzGGGOMVaBe1/Q0tD499QG3j8sL50NeOB/ywzlpWOp1oYcxxhhjTFP1utAjpz49rAS3\nj8sL50NeOB/ywzlpWOp1oYcxxhhjTFP1uiMz9+kBlJn3cXa/9JeKrn0zdPVxqZN4uH1cXjgf8sL5\nkB/OScNSrws9DLBPS4aNsXREoDtZ2Th1O1kyT9veFj27uNdmaIwxxpis1OvmLe7To559VjockuIl\nL528vFrZN7ePywvnQ144H/LDOWlY6nWhhzHGGGNMU/W60MN9euSH28flhfMhL5wP+eGcNCz1utDD\nGGOMMaapel3o4T498sPt4/LC+ZAXzof8cE4aFr57q54rzi9EXsYDyTxtvUbQMzepo4gYY4wxearX\nhR7u0wM8MG2MB0+lt6w3zX6IZnVU6OH2cXnhfMgL50N+OCcNS602bykUCrRp0wbt27dHp06dAABZ\nWVnw9/eHu7s7+vbti+zsf55Uvnz5cri5ucHT0xPHjx+vzVDrj0aNAD096UsQ6joqxhhjTHZqtdAj\nCALOnj2Lq1evIjQ0FAAQHBwMf39/xMTEwM/PD8HBwQCAyMhI7N69G5GRkTh69CgCAwOhVCol2+M+\nPfLD7ePywvmQF86H/HBOGpZa78hMJG2KOXToEAICAgAAAQEBOHDgAADg4MGDGDVqFHR1daFQKODq\n6ioWlBhjjDHGqqpW+/QIgoA+ffpAW1sb77zzDqZOnYqMjAxYW1sDAKytrZGRkQEASE1Nha+vr7iu\nnZ0dUlJSJNvjPj2ay32Qg7/P3ZTMM2xijnYtbKt1P9w+Li+cD3nhfMgP56RhqdVCz19//YVmzZrh\n3r178Pf3h6enp2S5IAgQKumPUtkyVjmXpFggKVYyL71dB6CaCz2MMcaYXNVqoadZs2YAgKZNm+Kt\nt95CaGgorK2tkZ6eDhsbG6SlpcHKygoAYGtrizt37ojr3r17F7a20i/ob7/9FkZGRnBwcAAAmJmZ\noXXr1mLJXdVWW93TKrHhJc1tbm1LOmXfSksEAHg0U9TpdFNjMwDAlaR4AEAHRxe10xE3r0EweFKt\n5yciIgLTp0+vtu3xNOfjZZrmfMhvWjVPLvE0tGnV38nJJQ/J9vHxgZ+fH2qKQGU72dSQvLw8FBcX\nw8TEBE+ePEHfvn2xaNEinDx5EpaWlpg3bx6Cg4ORnZ2N4OBgREZGYvTo0QgNDUVKSgr69OmDuLg4\nSW3PihUrMGnSpNoIX+L4nrNId/GQzMs6dwn2ybdrPRZ1mj5+iGbu9s99X3q7Duju375a9x0SEsLV\nxTLC+ZAXzof8cE7kJSwsrEYLPbVW05ORkYG33noLAFBUVIQxY8agb9++8PHxwfDhw7Fx40YoFArs\n2bMHAODl5YXhw4fDy8sLOjo6WLNmTbnmLe7To17uMyWSopIk84x0BDRxc6jxffOHh7xwPuSF8yE/\nnJOGRaNCz8GDB/HGG29AR+fFy0hOTk5qbzG3sLDAyZMn1a6zYMECLFiw4IX3+W8REW79GoJnOtqS\n+QUyf3rHUwtLPC0zT/fxwzqJhTHGGJMLjb69Fy5cCBsbG8yYMQMXL16s6Zg0Vhvj9CTmFeOqlZPk\n9dDFrcb3W1/xmBfywvmQF86H/HBOGhaNCj3Xr1/HqVOnoK+vj6FDh8Ld3R2fffYZEhMTazg8xhhj\njLHqoXE7Tdu2bfH111/jzp07+P777/Hzzz/D2dkZr776KrZv315utOTawH165Ifbx+WF8yEvnA/5\n4Zw0LFXqpBMfH48ff/wRP/30EwRBwNKlS+Ho6IjVq1dj79692L9/f03FKSt3btyG4ZNcyTzDnOwK\n3s0YY4wxOdCopmf16tXw9fVFx44dkZ6ejm3btiEmJgb/+c9/MG7cOJw+fRonTpyo6VjLqatnbxk9\nuA+HuCjJq0lOVp3EIjfcPi4vnA954XzID+ekYdGopuf333/HBx98gAEDBkBfX7/cckNDQ+zdu7fa\ng2OMMcYYqy4aFXr27t0LLS0tNGrUSJxXWFgIpVIpFoL69etXMxFWgvv0/DtPnhbiZlyGZJ6RkT4U\nzcxeeJvcPi4vnA954XzID+ekYdGoeatv374ICwuTzLty5Qr69+9fI0Gx2mF/6waU+3+TvBKvxz5/\nRcYYY6we0viW9U6dOknmderUqc761KjU9f7ru0Yg6EMpeWk/f7VKcfu4vHA+5IXzIT+ck4ZFo0KP\nubk5MjKkzSCZmZkwNjaukaAYY4wxxqqbRoWeoUOHYsyYMYiIiEBeXh6uX7+OcePG4e23367p+CrF\nfXrkh9vH5YXzIS+cD/nhnDQsGnVk/uyzz/Dhhx+ic+fOyM/Ph76+PiZNmoTly5fXdHysmuQXPENa\nzB3JPAM9bZg7Nq+jiBhjjLHapVFNj4GBAb7//nvk5uYiPT0dubm5WL16tdrb12sT9+nRXG4TK9wz\naSx55RUUVft+uH1cXjgf8sL5kB/OScOi8YjMOTk5uHXrFnJzpSMR9+7du9qDYowxxhirbhoVerZs\n2YL33nsPxsbGMDQ0lCxLSEiokcA0wX165Ifbx+WF8yEvnA/54Zw0LBoVehYsWIBffvkFr732Wk3H\nwxhjjDFWIzTq01NcXIy+ffvWdCxVxn165Ifbx+WF8yEvnA/54Zw0LBoVeubNm4dPP/0USqWypuNh\njDHGGKsRGjVvrVy5EhkZGfjyyy9haWkpzhcEAcnJyTUW3PNwn57qVwQg++kzyTxtLQEmepr1eef2\ncXnhfMgL50N+OCcNi0bfZNu3b6/pOFgdeFJESI6SFloL7jzEjfhEybynLi7w79e+FiNjjDHGqp9G\nhZ6ePXvWcBgv5tq1a/D29q7rMOqtp40t8bTMPMtHWbB+ki2ZF5+djfMXbknm6ZsZo30L23LbDAkJ\n4V9OMsL5kBfOh/xwThoWjQo9+fn5WLp0KXbt2oX79+/j0aNHOH78OGJiYjBjxoyajpHVMZfkeCA5\nXjIvtWVrQE2hhzHGGJMrjToyz549Gzdu3MBPP/0ELa2SVVq2bIk1a9bUaHDPw3165Id/MckL50Ne\nOB/ywzlpWDQq9Ozfvx87duxAly5dIAgCAMDW1hYpKSlV2llxcTHat2+PAQMGAACysrLg7+8Pd3d3\n9O3bF9nZ/zSrLF++HG5ubvD09MTx48ertB/GGGOMsbI0KvTo6emhqEj6nKZ79+6hSZMmVdrZt99+\nCy8vL7HgFBwcDH9/f8TExMDPzw/BwcEAgMjISOzevRuRkZE4evQoAgMD1d4uz+P0yA+PeSEvnA95\n4XzID+ekYdGo0PP2229jwoQJuH37NgAgLS0NM2bMwMiRIzXe0d27d3HkyBFMmTIFRAQAOHToEAIC\nAgAAAQEBOHDgAADg4MGDGDVqFHR1daFQKODq6orQ0NAqHRhjjDHGWGkaFXo+//xzODk5oU2bNsjJ\nyYGrqyuaNWuGTz75ROMdzZ49G1999ZXYJwgAMjIyYG1tDQCwtrZGRkYGACA1NRV2dnbi++zs7NQ2\npXGfHvnh9nF54XzIC+dDfjgnDYtGd2/p6enhm2++wcqVK8VmrdKFl+f59ddfYWVlhfbt2+Ps2bNq\n3yMIgtjsVdHysn755Rds2LABDg4OAAAzMzO0bt1avIhV1Zb/Zjoy5gaauHoAAGLDS2qbVMMz3kpL\nBAB4NFO8NNOmeY9g61FyPq8kldyx1cHRRe10dZxfnuZpnuZpnm6406q/VQMd+/j4wM/PDzVFIFVb\nUyVUzVrqODs7P3cnCxYswI8//ggdHR3k5+fj0aNHGDJkCC5duoSzZ8/CxsYGaWlp6NWrF6Kjo8W+\nPUFBQQCA/v37Y8mSJejcubNkuytWrMCkSZOeu/8XRUQ4tucPZP7/Qo9K1h+hsL9bd0+Xr0mWj7LE\nQk9lUlu2Ro/XO5ebz2NeyAvnQ144H/LDOZGXsLCwGi30aFRd4+rqqvbl5uam0U6WLVuGO3fuICEh\nAUfMdjkAACAASURBVLt27ULv3r3x448/YuDAgdi6dSsAYOvWrRg8eDAAYODAgdi1axcKCwuRkJCA\n2NhYdOrU6QUPkTHGGGNMw+atsndOpaenY/HixejevfsL7VTVVBUUFIThw4dj48aNUCgU2LNnDwDA\ny8sLw4cPh5eXF3R0dLBmzRq1zVvcp0d++BeTvHA+5IXzIT+ck4ZFo+YtdfLz8+Hh4YGkpKTqjklj\np06dqtHHUHDzVsUqat5ijDHGXpQsmrfUuXXrFvLy8qozlirjcXrkh8e8kBfOh7xwPuSHc9KwaNS8\nVbYZKy8vDzdv3qzSLeusfsh/pkRqzB3JPH0dARbOdhWswRhjjNUPGhV6Jk+eLJk2MjJC27Zt4e7u\nXiNBaYr79FS/J5ZN8KTMPIucLFhouD63j8sL50NeOB/ywzlpWDQq9EyYMKGGw2CMMcYYq1kaFXoW\nLlyo9u6p0n2gBUHA0qVLqy8yDVy7dq1GOzKzquMxL+SF8yEvnA/54Zw0LBoVemJjY7Fv3z507NgR\njo6OSEpKwqVLlzBkyBAYGBiAiCodTbk+ICKg7I1sL3ZjG2OMMcZkSKNCDwDs3LkTQ4cOFaf37duH\nPXv2YPPmzTUSmCaqtU+PUolzPxxAnqX0yfE55pr2ZmEAt4/LDedDXjgf8sM5aVg0KvQcOXIEP/30\nk2TegAEDXrq+Pk8sm+Kei2ajTDPGGGOsftH4MRSrV6+WzFu7di1cXV1rJChN1fQ4PUSEzNQHyExK\nl7xQ9KxG91uf8ZgX8sL5kBfOh/xwThoWjWp6Nm7ciMGDB+PLL7+Era0tUlJSoKOjg3379tV0fHVO\nJyYW9il1N+q0LCiL8SwnVzKr6HHZG9sZY4wxedOo0NO+fXvExsbiwoULSE1NRbNmzfDKK69AV1e3\npuOrFI/TUzse6hvjYaa00JMdl4akzMeSebo62tw+LjOcD3nhfMgP56Rh0bgjs+ruLEEQ0KNHD+Tm\n5qKgoADGxsY1FhyTBzIwKDfPOvk27m3bK5n30N0TzQf61lZYjDHGWJVo1KcnIiIC7u7umDZtmjg6\n8x9//FFupObaxs/eqjsGRc9gRkWSVyOB28flhvMhL5wP+eGcNCwaFXreffddLFmyBNHR0WKTVs+e\nPXHu3LkaDY4xxhhjrLpoVOiJjIzEuHHjJPMMDQ3x9OnTGglKU9ynR364fVxeOB/ywvmQH85Jw6JR\nnx5HR0dcvnwZHTt2FOddunQJbm48pg37x6OUDNw8el4yz1BfF049feooIsYYY+wfGtX0fPbZZ3jz\nzTfxySefoLCwEMuWLcOwYcPw6aef1nR8leI+PfKSm5uPXamZuNJUIb7uZtVtbWBDx/0V5IXzIT+c\nk4ZFo0LPm2++iaNHj+LevXvo0aMHkpOTsX//fvTr16+m42OMMcYYqxbPbd4qKiqCh4cHIiMjsXbt\n2tqISWPcp0d+3Np2qusQWCncX0FeOB/ywzlpWJ5b6NHR0YGWlhaePn0KPT292oiJ1VPFEJD3rFgy\nL1cp1FE0jDHGmJRGzVuzZ8/GiBEjcPbsWcTHx+P27dviqy5xnx55sUi8jaR130Pn8FHxded2al2H\n1aBxfwV54XzID+ekYam0pic9PR02NjaYMWMGAODEiROS5YIgoLi4WN2qrAEyKXwKk4KnaPz0n0dW\nPDY2rMOIGGOMsX9UWtPj7u4OAFAqlVAqlRg0aJD4t1Kp1LjAk5+fj86dO6Ndu3bw8vLC/PnzAQBZ\nWVnw9/eHu7s7+vbti+zsbHGd5cuXw83NDZ6enjh+/Lja7XKfHvnxaKao6xBYKdxfQV44H/LDOWlY\nKi30EJFk+uzZsy+0E319fZw5cwbXrl3D9evXcebMGYSEhCA4OBj+/v6IiYmBn58fgoODAZQMhrh7\n925ERkbi6NGjCAwMhFKpfKF9s5pRXPgMOXfSJa9nefl1HRZjjDFWIY369FQHQ8OSZo7CwkIUFxej\ncePGOHToEAICAgAAAQEBOHDgAADg4MGDGDVqFHR1daFQKODq6orQ0NBy2+Q+PXXnkUUTJAkGktdD\nSyvcSkus69BYKdxfQV44H/LDOWlYKu3TU1xcjNOnTwMoqfUpKioSp1V69+6t0Y6USiW8vb0RHx+P\n6dOno2XLlsjIyIC1tTUAwNraGhkZGQCA1NRU+Pr+87RuOzs7pKSkaH5UrOZpa9d1BIwxxliVVFro\nsbKykjxJ3dLSstyT1RMSEjTakZaWFq5du4acnBz069cPZ86ckSwXBAGCUPHtzeqWcZ8e+eE+PfLC\n/RXkhfMhP5yThqXSQk9iYmK179DMzAxvvPEGrly5Amtra/EOsbS0NFhZWQEAbG1tcefOHXGdu3fv\nwtbWtty2fvnlF2zYsAEODg7itlu3bi1exKpqS02nI29FIDv3oTjAXlx4KB4nRcNexwAAxKYb1Rc7\nTz9/Ou/pP53Tq5oPnuZpnuZpnn65p1V/JycnAwB8fHzg5+eHmiJQ2d7KNeD+/fvQ0dGBubk5nj59\nin79+mHRokU4duwYLC0tMW/ePAQHByM7OxvBwcGIjIzE6NGjERoaipSUFPTp0wdxcXHlantWrFiB\nSZMmVUuMVFyMo3v/wj2Xfx6iSkR4+MdF2KckVcs+GoJbaYmS2p7HTa0wYf7oOounoQsJCeFfsjLC\n+ZAfzom8hIWF1WihR6OnrP9baWlpCAgIEG91HzduHPz8/NC+fXsMHz4cGzduhEKhwJ49ewAAXl5e\nGD58OLy8vKCjo4M1a9ZU2vTF/l97dx4cRZnGD/zbM5ncdwgTchmOQAg3cgkeYDagLkREF2FdRURr\nXbRW1K1addVarFJwXcuFXS1X5FJKQPe3P+HnEWNAFDnFEGUJJCRkck0OcmeSzNnv7w9kkk4CCbmm\nJ/P9VE0V/aR7+h0eSJ68/fTbRERE1J1BmekZKAcOHMD06dP75b040zMwONNDREQ9NdAzPYN2yzoR\nERGRK7l10cN1etSH6/SoC9cgURfmQ32YE88yKD095MkEHB1XapYkaP18XDMcIiLyWG5d9PTnOj0O\nWSC/vAG2pvOKuL/JdJUjqCsd1+mpl3TY+tFhRSzc1or7/pA2iKPyXLwrRV2YD/VhTjyLWxc9/c23\nqhLRRQWuHsaQElNlhKgqV8QaI4a5aDREROTJ2NND/apjT48GgBZC8eLiA4OH/QrqwnyoD3PiWdy6\n6CEiIiLqKbcuevjsLfXhs7fUhf0K6sJ8qA9z4lnY00ODTgBotjo6xQO8+eR2IiIaOG4908OeHvXp\nyTo9IcYy/Ljz/yle36T/OOBj80TsV1AX5kN9mBPPwpkeGnQhrU0YUV+tiDnCI1w0GiIi8hRuPdPD\nnh71YU+PurBfQV2YD/VhTjwLZ3po0NlkgYoLJYpYteznotEQEZGncOuZHvb0qE9PenpawoehKjBM\n8TLZ5AEfmydiv4K6MB/qw5x4FrcueoiIiIh6yq0vb7GnR31629Pj3dCAQ/uPKWLW4GAsnD+hH0bl\nudivoC7Mh/owJ57FrYseGjqG11QiJvesIlY6cqyLRkNEREORW1/eYk+P+vSkp6dLAoAQipcQ7PPp\nK/YrqAvzoT7MiWfhTA+pQqvOGwU5RYpYVYMAfjPfNQMiIqIhx62LHvb0qE9ve3psgUGwIUgRs/v4\n9sOIPBv7FdSF+VAf5sSzuHXRQ0ObgITaFpsiJgEI89e5ZkBEROTW3Lroyc7OxvTp06/7ONlqw8mP\nvoIlKLgtJgRsXt79OTyPlFtu6LdVmcONxTi/7b+KWE1UDJbcx9/Meur777/nb7IqwnyoD3PiWdy6\n6OmLmsAQ1CSMcW7LQsBeWA001bpwVNReoMWMyNYmRcws2100GiIicneDdvdWSUkJFixYgAkTJmDi\nxInYvHkzAKC2thapqakYO3YsFi5ciPr6eucxGzZsQGJiIpKSkpCRkdHpPdnToz589pa68DdYdWE+\n1Ic58SyDVvTodDq89dZbOHv2LI4fP463334b586dw8aNG5Gamoq8vDykpKRg48aNAICcnBzs3bsX\nOTk5SE9Px9q1ayHLvIWZiIiIemfQip6oqCjnzExgYCDGjx+PsrIy7N+/H6tWrQIArFq1Cp9++ikA\nYN++fVi5ciV0Oh0SEhIwZswYnDx5UvGeXKdHfXq9Tg8NCK5Boi7Mh/owJ57FJT09BoMBp0+fxuzZ\ns1FZWQm9Xg8A0Ov1qKysBAAYjUbMmTPHeUxsbCzKyspcMVxSEQGgymRVxCQJiAxgEzoREV3boBc9\nJpMJ9957LzZt2oSgIOW6LJIkQZKkqx7b8Wv5+flYu3Yt4uPjAQAhISGYNGmS8xrtlQq+4/bcWbMB\nABd+ujxzlDhlFgCgsCgXppoqZ1/KlVkLbl/f9hV9fb//VZWgQm7AtOgbAACnjUUw5+TA/5fi92fD\nBQBA9E3zsWTF/Kvm29O3r1DLeDx9+wq1jIfb3Hbl9pU/FxcXAwBmzJiBlJQUDBRJCCEG7N07sNls\nWLx4Me68806sW7cOAJCUlIRDhw4hKioK5eXlWLBgAc6fP+/s7XnuuecAAHfccQfWr1+P2bNnO9/v\nwIEDvb5l/cv9x1EzUnn3VuM3xxBTXtKXj0j9yWKF5FDerRVgasSoKWMUseK4UUhZcftgjoyIiAZA\nVlbWgBY9g9bTI4TAmjVrkJyc7Cx4ACAtLQ07d+4EAOzcuRNLly51xvfs2QOr1YrCwkJcuHABs2bN\nUrwne3rUp197eny8Ifz9FS9Jx4UJrwf7FdSF+VAf5sSzDNrlrSNHjmDXrl2YPHkypk2bBuDyLenP\nPfccli9fjq1btyIhIQEff/wxACA5ORnLly9HcnIyvLy88M4771zz0hcRERHRtQzq5a3+xstbnieo\nrgYjk29QxHh5i4hoaBjoy1seuyIzuSeLlw6Gc8qnsVfWOwAWPURE1A23Lnp6++wtGjj9+eytrliD\ngmHtEDNrO9+uXvW/fFQUVyli3nYbxi251aMuk/K5QurCfKgPc+JZ3LroIbqa+vIaZOtHKmLD83Mx\nzkXjISIi13ProofP3lIfNT97q6rZhsNfZ0FC20yP2ccHt9+SDK1maM7+8DdYdWE+1Ic58SxuXfQQ\nAYDscOBEtkERq6xuAcKV+1ksdkT9dBrty5tifSxwS/KAj5GIiFzPrYse9vSoz0D39HQlvsyAsK8z\nFbEimw9MCYmKWKuPL4p+KFIUPRVVFsh2O7TeQ3P9H/YrqAvzoT7MiWdx66KHCACkX17tDTOWwLTv\nc0XMF0BDaIRiXxuAEyfzoNG0rdMpe+lw04zRQ/aSFxGRp3Lrooc9Perjip4eu6RBxQXl+kqiuRUh\n3v7dHht1qQLDjxyB1K7oKR0eA/nGUdB2KqXcD3+DVRfmQ32YE8/i1kUPEQCYw8Jh7hgMDHPFUIiI\nSMUG7dlbA4HP3lKffn32lovINjtOny3FqTPFzlfWuTLYZfdbvJzPFVIX5kN9mBPPwpkeog5i6yoh\nvspQxMqHjYAjcQS82OdDROS23LroYU+P+qh5nZ6e6mr6011LHfYrqAvzoT7MiWdx68tbRERERD3l\n1kUPe3rUZyj09Awl7FdQF+ZDfZgTz+LWl7eIXMlql2G2y53igT5aaDzooaZERO7CrYse9vSoz1Do\n6empPMMlVGUehRfa7upq8A/G7SsWIMBb68KRtWG/growH+rDnHgWty56iAaCua4RpppGRfdyXaMM\n2WoDvHzagkIgsqkOvmib7RFat75iTEQ0pLn1d2j29KjPUOjpMTe2wOgbBKN/qPNVaxMQjs6XstSO\n/QrqwnyoD3PiWTxypschC1xqsaOhptEZEwLQyO73Q436Tjjky/8AnIHO/w4Cmupx5L/fQtJq2x1n\nRyzcb8FCIiJP5dZFT297emQhYM69iMifzyriWuHoj2F5NHfr6TH7+aPgglERkwWAUGUjcnBrM24w\nFkHyUkevTk+xX0FdmA/1YU48i1sXPX3hJcvwke2uHga5mOznh1Y/vx7t62hp7VT0aP18Ad6pRUTk\nFtjTQ/1qKPT0dMXsF4AL5Y3IK6lzvgpyy1CdX4LqglLnq85ghMNscfVwndivoC7Mh/owJ55l0GZ6\nHnnkEXz++ecYPnw4zpw5AwCora3F/fffj6KiIiQkJODjjz9GaGgoAGDDhg3Ytm0btFotNm/ejIUL\nFw7WUIk6ET4+sPn4KGK24GAYO+xXDR98/+VJ+GrbZn+8mppw0z23Qhca7IwVVjQi97tseEttPUEt\nWi/Mu3MWwvx0A/IZiIg83aDN9KxevRrp6emK2MaNG5Gamoq8vDykpKRg48aNAICcnBzs3bsXOTk5\nSE9Px9q1ayF30WTMdXrUx916evqb7OsL48hElI4c63xVh0Uq+qQBwOFwQF9cgDjDBecrzFiG/u6L\nZr+CujAf6sOceJZBK3puueUWhIWFKWL79+/HqlWrAACrVq3Cp59+CgDYt28fVq5cCZ1Oh4SEBIwZ\nMwYnT54crKES9SuHAFrtMlptDufL6uBdX0REg82lPT2VlZXQ6/UAAL1ej8rKSgCA0WhEbGysc7/Y\n2FiUlZV1Op49PeozVHt6rseVx1NceVW12HDs44M4ufML56sq4zC8u7g1vr+xX0FdmA/1YU48i2ru\n3pIkCdI17oLp6mvffvstTp06hfj4eABASEgIJk2a5JyuvPKPueP2zBtnAmj7AX3lkgy3+75dXFuh\nqvEM9ralqhTRdjsEgIul+Ze/HjIcMWFanK0sAQDceMNoAMCPRQWK7TOFuWg8egR3/mo+gKv/+72e\n7TNnzvTpeG737zbzob7tK9QyHk/bvvLn4uJiAMCMGTOQkpKCgSIJ0bHbYOAYDAYsWbLE2ciclJSE\nQ4cOISoqCuXl5ViwYAHOnz/v7O157rnnAAB33HEH1q9fj9mzZyve78CBA5g+ffp1j8PSasGHr3yA\nMEtzHz8RUfe8GxqQmDAMWt+2RmjZaoO9uVWxX1VACCY/sRIRof6DPUQiIlXIysoa0KLHpZe30tLS\nsHPnTgDAzp07sXTpUmd8z549sFqtKCwsxIULFzBr1ixXDpWoX5nrm5Bb0Yjcmlbny2Csg62JhTgR\n0UAZtKJn5cqVmDt3LnJzcxEXF4ft27fjueeew9dff42xY8fi4MGDzpmd5ORkLF++HMnJybjzzjvx\nzjvvdHl5iz096sOenp4Tvn4QAQHOF3y8+/0c7FdQF+ZDfZgTzzJoPT27d+/uMp6Zmdll/IUXXsAL\nL7wwkEMiUhVZo8XZ4zkoOt226rNktmJqynR4R4S6cGREREODahqZe4Pr9KiPp6/TczWOFjPQ7int\nssUKQLkIoeznj/y40fDTtRU9PuXlmGyz9fq8XINEXZgP9WFOPItbFz1E7sDq54f86mYAbf06AgD8\nu//v12qXceJMKXxK6p0xGRImT05AoA//+xIRXQ+3/q6ZnZ3dq7u3aODklhs429ORtzfs3r3r17E6\nZPgcPYWIdgVSrdYXP1hs8GnXkScLYNKNiQjxVf6X/v777/mbrIowH+rDnHgWty56iIYSrcOGujwD\nTO2DDY3QdHg2RbjDjPBjRxSxao03WieP6lT0EBFRG7f+DsmeHvXhLE/vhZhbEJJ9ShHTtLSgxdqC\nVq32KkddVqf1QUxNPRCkV8T5G6y6MB/qw5x4FrcuenrCYbYg67/fwOYf4IzZZQGblxdgceHAiHpA\n9vdHjX/3ixW2mq049p9vcKrdbe82SLjlnpsRHRs5kEMkInIbLl2csK96tE6PACp9ApEfN8b5Kogb\nA3tg4MAP0ANxnR7X8PPRwavUCFFgcL7MuRfx3aFDrh4atcM1YdSHOfEsQ36mh8gjSNLllyLm6LRb\nTYsNx788Af92Dzu1CiB5wXTEDbv+XwSarQ588+UPCLBZnTG7AG6YMxFj48Kv+/2IiAaSWxc97OlR\nH/b0qIe3w45gkw4Hdh9QxGOMJQiQ7c7tBskLDkfv/i8JIRBcWYERDdXOmBka2Kcn9W7QQxz7R9SH\nOfEsbl30ENHV+TjsiDydBa2/nyLuGxHS6ZEXJRX1aDGZFbHY6FAE+/XiVnshYDdbOj1QVeOtg0bH\nbzlE5Dpu/R2I6/SoD9fpUQ/h54evjeUY532DMya1mjHWtxXadkVPkLDDJyMT7S+GNdpk5EfHQx/W\n1kQtbHYkTRmF0MT4a55Xttvx08EfURQzvC1ot2N6fChi5kzu8+dyZ1wTRn2YE8/i1kUPEV2DRgNo\nvQBdu8dddPFICw0AX8iKmNlhx3mzBnn2gHbBVtiO/g9RhnJnqMUhYDN1fjK8JTgEdTeMbHesBbJo\n7PVHISLqD25d9PSkp8fqkHGh8BKk8iZnTAAINjVd/SDqNc7yqEvHfAitF8rLa4HK+q4PuEIWSDTW\nQfZruzRmkzQ4ecNoaJtq297PasXUSzVAePe31RP7R9SIOfEsbl309IQQQHB1FUKtrd3vTDTU+Xij\n0ad36/bohIwEwwVl0GpFqLcDQFvRIwFoqm1CY66hbT+bHRXRfojr1ZmJiPqHWxc97OlRH/b0qMuA\n50OrRUVNI6Ra5SWukX61kEvazRI5ZNSHzIHVrryMptVI0Go63GrfQ7klNRAd3i8iPBCRIcrG7Qul\ntXDYlLfvh4UGKPqVBgv7R9SHOfEsbl30EJGLabVoiRjW7W4aIdBy5jyO1LV/WjwwbN40TBk7olen\nLvwuGyPKixWxggW3IfLGUYrYxSM/IarEoIzdMg/62WN7dV4icl9uXfRwnR714SyPuqglH1oIhOee\nh7exxBmzSxo0j44H2hU9NqsNH2z+FDpZOTOji4vGmOQbFDGNzQp/odzP3MWkkZeETvu56mI3ZxTU\nhznxLG5d9BCRm9BqURWpnNFxCIFggxGtIyOcMZvdAbm2HgHmtstlQggEnvkJ9V8rv135mM2oDg5Q\nxFrGXwKmK2d6iIiucOuip2NPj2y3o+liqWIfs9na8TAaQOzpURfV5KPjIzJ+iZ2HH2p+rnCGZAGY\nAwKBdkWPJElojtR3Pr4L2pqGTrHaglL4GpTfF5pHVQIuuLzF/hH1YU48i1sXPR3JFiu+PX4BjVHR\nzphdFpe/ifLuLSJVkQCgogqXqmsV8ZCWzuv+9JQMCTaHsrm50eKAJiBUEbOVXkLVT7mKmH9EKAJj\ne1Zc9aeSS00wm5XrJ/n5eSO2F89CI6Jrc+uip8uenoAAyBFtDzqUZQF4ufXHdCuqmFUgJzXnQwMg\nrqKk2/2uR9NP5/BJQZEi5lvXAOi0ilhJaCQ+q1aEoDv+IwL8fbo9R9zwIMxcNKvb/XLzK2BuUT7a\nIyZ2XKf98n/MRej/zihipZOmIHaR8s5Us12+/P2sHUkC/Dp8Nro+nOXxLKwGiGjICIQMmEzKYBdF\nQVBhIcwlyoJLbm2Fztz9LNPR4dG4UFqniMVFBuGWtLmK2Ik9GQgqUhZgzcnjEf6HpZ3H3aHR2tTF\n1cCj3+fAK/+iImaOj8fChbyhg6inVF30pKenY926dXA4HHj00Ufx5z//WfH1jj09NoeM0hoTWtG2\nTL4sAH+78hsKDRzV9JAQAObjaiIba7vf6SqiK0uBSmUsVz8COq8TipgZGgQEBSlihu8y8V1FhSKm\ns1lQ06Is1BrCo9FR3Zk8hGZnK2KNhWU4ZO7+0r2ICMOCeUnd7tdThvJ6VJYr/w7tXl4YOzpKEZMA\nDAvoxUNrBxF7ejyLaoseh8OBJ598EpmZmYiJicHMmTORlpaG8ePHO/fJz89XHGOXAZ/8i9Cfzxns\n4dIvimsr+ENWRZiP/qfpIqatrcPZ75XPFvN12DvtV9pSj/E2ZdwKLZr9Q5Sxi8X45v98p4xVXEJ9\nSLgiFl5RjphcnSLWZLwEc4tFEatKngh0KHqOZRXCXKic7bKGhWHR7ZMUsbpmK1qsyjEXFFQg/tj3\niphJo0P+QeWPlEtRMUhbMV8RazDbYGrt/Ay46FA/SO0a3hvNNjR1sV9UiF+vF7TsypkzZ1j0qEh2\ndjZSUlIG7P1VW/ScPHkSY8aMQUJCAgBgxYoV2Ldvn6LoaW7ufcMjDYxWq7n7nWjQMB+DI9hmBjr/\nfO6kp/kILymG7lK5IhZhtqFp2HBFrBkaXDxrUMTskgbmMGVxZGyV8dHOA8qxlFdhRo2y6KkJG4YD\nVZcUMVN1PULLlPuJxmZU2pSFlVYIDBsbrxyfbIe9Q5GXffwc8NU3itglfQzu+eMyaNsVPSc+O466\njO/QvrypDw7F79Y/Ar+AtlW3cwovofTEGbS/iNkkeSFUHw5dFxVq+8LKrtGiurab59ANgEazHdk/\n5MELbT1aDgGMnzYaw4J8nbFmqwM/nsyFl2jbTwaQOGkk9KFD83l3P/3004C+v2qLnrKyMsTFtT2p\nJzY2FidOnLjGEUREQ4Np2HCYOga7uJnLGhKKnizKEVFdCblGWcz42mzItyrvdPOrKEBgobIPyb/V\ngupg5d1vgBYNgWGKSEDNJfgYleewFFRie4eiTFisiGhRXpKrl2vQ0tgCjaatSjFbbYC/PzTtZnW8\nHQ4cP/QzvLRtJU6VsRqhx45D166ACGk1o1XSorXdflqzGTdMHAmNT9vltmrfQJQVV+H7g20/aM2Q\nEB6nh6+2bSwmiw2mskvwbldENbdYoNFI8NW0ndfebIZks8Onm4b4RosDfnl5iGx35a/WIiM934hA\nn7YxW+wCkcWFiNK2FY4tkhbZjc0I8Gs7h5BloEMbh10AuuERCPNXzgRCq4XU7uYeuyzDWFCOANF2\nDhlAzPgEjLmhbbV1IQQsDmUjPQB4aSR4dZh5yy2ugaPDI2JsZRUI9lHuFzI8HOEJnS/lDiTVFj1S\nV+t6dFBRUYHjh352btusduiCA+Cr462erlLnMMNX3/1jCWhwMB/q4qp8+Ha/CwBAAGjq5fGOYaEo\n77BcAABEe3fs6fEFEKyIhFgd2PfufuVYHA6ERkVAI7VVGv4tLZAPHVUUeiEQMI8aCbPm2nexB0Ib\nTQAADfBJREFUSY0NqG9ogaRtm23TohG12VnwDotrF5NgkjSdik5/4VBc2pRsdlT6haDJt634sEpa\nmCKGQWrsphRttWBUfSPq2g1ZdjgQaC2EHNj280tnt8PWaEJJu4JO2OwIzjgAbfuix+ZAs9UG4ds2\nAyYAtGq0UFx0dTjga7PCy78to0KWoW02w+rXFnMI4NuiauSNaCtsZVmgzlCGaC9ljhti4xEdqnze\nXeGRnxBjUvZ8FfqHwR6mLJRjo+uxiEXPZTExMShpd3dFSUkJYmNjFfuMHj0au//vVuf2lClTMPUu\n3sngSksjl2PE1GRXD4N+wXyoC/OhPneMDYVXu+VPvAB0v3DB5f0S+nTmOMWWF4D4rnfskY5zcX3V\nVWkeHT+yU+xyGaO8hDnuzgmd9pvUKXLZtm3bFJe0AgICrrJn/5CEEJ3nq1TAbrdj3LhxOHDgAKKj\nozFr1izs3r1b0dNDRERE1FOqnenx8vLCv/71LyxatAgOhwNr1qxhwUNERES9ptqZHiIiIqL+1NWS\nE24hPT0dSUlJSExMxOuvv+7q4XickpISLFiwABMmTMDEiROxefNmAEBtbS1SU1MxduxYLFy4EPX1\ng387qCdzOByYNm0alixZAoD5cLX6+nrcd999GD9+PJKTk3HixAnmxIU2bNiACRMmYNKkSfjtb38L\ni8XCfAyyRx55BHq9HpMmtXX5XCsHGzZsQGJiIpKSkpCRkdHn87tl0XNl4cL09HTk5ORg9+7dOHfu\nnKuH5VF0Oh3eeustnD17FsePH8fbb7+Nc+fOYePGjUhNTUVeXh5SUlKwceNGVw/Vo2zatAnJycnO\nux+ZD9d66qmncNddd+HcuXP4+eefkZSUxJy4iMFgwJYtW5CVlYUzZ87A4XBgz549zMcgW716NdLT\n0xWxq+UgJycHe/fuRU5ODtLT07F27VrIcuc7BK+LcENHjx4VixYtcm5v2LBBbNiwwYUjorvvvlt8\n/fXXYty4caKiokIIIUR5ebkYN26ci0fmOUpKSkRKSoo4ePCgWLx4sRBCMB8uVF9fL0aOHNkpzpy4\nRk1NjRg7dqyora0VNptNLF68WGRkZDAfLlBYWCgmTpzo3L5aDl577TWxceNG536LFi0Sx44d69O5\n3XKmp6uFC8vKylw4Is9mMBhw+vRpzJ49G5WVldDr9QAAvV6PysrKbo6m/vL000/jjTfeUCzwxny4\nTmFhISIjI7F69WpMnz4djz32GJqbm5kTFwkPD8ezzz6L+Ph4REdHIzQ0FKmpqcyHClwtB0ajUbFU\nTX/8rHfLoqcnCxfS4DCZTLj33nuxadMmBHV4uKIkSczVIPnss88wfPhwTJs2DeIq9yYwH4PLbrcj\nKysLa9euRVZWFgICAjpdOmFOBk9BQQH+8Y9/wGAwwGg0wmQyYdeuXYp9mA/X6y4Hfc2PWxY9PVm4\nkAaezWbDvffeiwcffBBLly4FcLlKr/jlKdLl5eUYPnz4td6C+snRo0exf/9+jBw5EitXrsTBgwfx\n4IMPMh8uFBsbi9jYWMycORMAcN999yErKwtRUVHMiQucOnUKc+fORUREBLy8vLBs2TIcO3aM+VCB\nq32f6vizvrS0FDExMX06l1sWPTNmzMCFCxdgMBhgtVqxd+9epKWluXpYHkUIgTVr1iA5ORnr1q1z\nxtPS0rBz504AwM6dO53FEA2s1157DSUlJSgsLMSePXtw++2348MPP2Q+XCgqKgpxcXHIy8sDAGRm\nZmLChAlYsmQJc+ICSUlJOH78OFpbWyGEQGZmJpKTk5kPFbja96m0tDTs2bMHVqsVhYWFuHDhAmbN\nmtW3k/WpI8iFvvjiCzF27FgxevRo8dprr7l6OB7n8OHDQpIkMWXKFDF16lQxdepU8eWXX4qamhqR\nkpIiEhMTRWpqqqirq3P1UD3OoUOHxJIlS4QQgvlwsezsbDFjxgwxefJkcc8994j6+nrmxIVef/11\nkZycLCZOnCgeeughYbVamY9BtmLFCjFixAih0+lEbGys2LZt2zVz8Oqrr4rRo0eLcePGifT09D6f\nn4sTEhERkUdwy8tbRERERNeLRQ8RERF5BBY9RERE5BFY9BAREZFHYNFDREREHoFFDxEREXkEFj1E\n1KWHH34YL730ksvOv3r1aoSHh2POnDkuGwMRDS0seojcREJCAvR6PVpaWpyx999/HwsWLBiQ87ny\nOUSHDx9GZmYmjEYjjh8/Pmjn1Wg0uHjx4qCdj4gGF4seIjciyzI2bdo0aOfrr7VLZVm+rv2LioqQ\nkJAAX1/ffjn/9eB6rURDF4seIjchSRL+9Kc/4e9//zsaGho6fd1gMECj0SgKjPnz52Pr1q0AgB07\ndmDevHl45plnEBYWhjFjxuDo0aPYvn074uPjodfr8cEHHyjes7q6GgsXLkRwcDDmz5+P4uJi59fO\nnz+P1NRUREREICkpCZ988onzaw8//DD+8Ic/4K677kJgYCAOHTrUabxGoxFpaWmIiIhAYmIi3n//\nfQDA1q1b8dhjj+HYsWMICgrC+vXrOx2bn5+P2267DaGhoYiMjMSKFSt6PK4nnngCixcvRnBwMObM\nmeOc2bn11lsBAFOmTEFQUJDzuM8++wxTp05FWFgY5s2bhzNnzjjfLyEhAW+++SamTJmC0NBQrFix\nAhaLxfn1ffv2YerUqQgJCcGYMWPw1VdfAQAaGhqwZs0aREdHIzY2Fi+99JIzb9f6bETUR31+kAUR\nDYqEhASRmZkpli1bJl588UUhhBBbtmwR8+fPF0IIUVhYKCRJEg6Hw3nM/PnzxdatW4UQQmzfvl14\neXmJHTt2CFmWxYsvvihiYmLEk08+KaxWq8jIyBBBQUGiublZCCHEqlWrRFBQkDh8+LCwWCziqaee\nEjfffLMQQgiTySRiY2PFjh07hMPhEKdPnxbDhg0TOTk5zmNDQkLE0aNHhRBCmM3mTp/nlltuEU88\n8YSwWCwiOztbREZGioMHDwohhNixY4fzXF1ZsWKF85l7FotFHDlypMfjioiIED/88IOw2+3igQce\nECtWrHC+ryRJoqCgwLmdlZUlhg8fLk6ePClkWRY7d+4UCQkJwmq1OnMye/ZsUV5eLmpra8X48ePF\nu+++K4QQ4sSJEyIkJERkZmYKIYQoKysT58+fF0IIsXTpUvH444+LlpYWUVVVJWbNmiX+/e9/X/Oz\nEVHfcaaHyI1IkoRXXnkF//znP1FdXX3dx48cORKrVq2CJElYvnw5jEYjXn75Zeh0OqSmpsLb2xv5\n+fnO/RcvXoybb74Z3t7eePXVV3Hs2DGUlpbis88+c76XRqPB1KlTsWzZMsWsytKlS3HTTTcBAHx8\nfBTjKCkpwdGjR/H666/D29sbU6ZMwaOPPuqcaRLdXGLy9vaGwWBAWVkZvL29MXfuXADo0biWLVuG\nGTNmQKvV4oEHHkB2dvZVz/Pee+/h97//PWbOnAlJkvDQQw/Bx8dH0Wf0xz/+EVFRUQgLC8OSJUuc\n77d161asWbMGKSkpAIDo6GiMGzcOlZWV+PLLL/HWW2/Bz88PkZGRWLduHfbs2XPNz0ZEfceih8jN\nTJgwAYsXL8bGjRuvu9FYr9c7/+zn5wcAiIyMVMRMJhOAywVWbGys82sBAQEIDw+H0WhEUVERTpw4\ngbCwMOfro48+QmVlpfPYuLi4q47DaDQiPDwcAQEBzlh8fDzKysp69Dn+9re/QQiBWbNmYeLEidi+\nfTsA9GhcHf8OrnzerhQVFeHNN99UvF9paSmMRqNzn6ioKMX7NTc3AwBKS0sxevToLt/TZrNhxIgR\nzvd8/PHHcenSpWt+NiLqOy9XD4CIrt/69esxffp0PPvss87YlQKipaUFgYGBAICKiopen0MIgZKS\nEue2yWRCbW0tYmJiEB8fj9tuuw0ZGRm9eu/o6GjU1tbCZDI5x1pcXKwosq5Fr9fjvffeAwAcOXIE\nv/rVr3Drrbf2eVwdxcfH4y9/+QteeOGF6z42Li5OMWvWPu7j44OamhpoNJ1/7+zqs912220YNWrU\n9X8AIlLgTA+RGxo9ejTuv/9+xZ1ckZGRiImJwYcffgiHw4Ft27ahoKCgT+f54osvcOTIEVitVrz0\n0ku46aabEBMTg1//+tfIy8vDrl27YLPZYLPZ8MMPP+D8+fMAur88FRcXh7lz5+L555+HxWLBzz//\njG3btuF3v/tdj8b1ySefoLS0FAAQGhoKSZKg1WqxePHiPo1Lr9cr/s4ee+wxvPvuuzh58iSEEGhu\nbsbnn39+zdmhK+dYs2YNtm/fjoMHD0KWZZSVlSE3NxcjRozAwoUL8cwzz6CpqQmyLKOgoADffffd\nVT9bV8UREV0//k8iclMvv/wyWlpaFJe4tmzZgjfeeAPDhg1DTk4O5s2b5/xaV+vuXOvymCRJeOCB\nB7B+/XpERETg9OnT2LVrFwAgKCgIGRkZ2LNnD2JiYjBixAg8//zzsFqtVz1XR7t374bBYEB0dDSW\nLVuGV155BbfffnuPjj916hTmzJmDoKAg3H333di8eTMSEhIQGBh43eNqv/3Xv/4Vq1atQlhYGP7z\nn//gxhtvxJYtW/Dkk08iPDwciYmJ+OCDD646tvbvP3PmTGzfvh1PP/00QkNDFXe/ffDBB7BarUhO\nTkZ4eDh+85vfOGflrvbZiKjvJNHdrz5EREREQwBneoiIiMgjsOghIiIij8Cih4iIiDwCix4iIiLy\nCCx6iIiIyCOw6CEiIiKPwKKHiIiIPAKLHiIiIvIILHqIiIjII/x/x+DgJ1JDGH4AAAAASUVORK5C\nYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x43baabe0>"
]
}
],
"prompt_number": 58
},
{
"cell_type": "code",
"collapsed": false,
"input": [],
"language": "python",
"metadata": {},
"outputs": []
}
],
"metadata": {}
}
]
} | apache-2.0 |
AaronCWong/phys202-2015-work | days/day20/MoviePy.ipynb | 11 | 702523 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Making Animations using MoviePy"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This notebook shows how to make animations using MoviePy and Matplotlib. Here are links to the MoviePy documentation and a short tutorial:\n",
"\n",
"* http://zulko.github.io/moviepy/\n",
"* http://zulko.github.io/blog/2014/11/29/data-animations-with-python-and-moviepy/\n",
"\n",
"Let's start by importing everything we need:"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"from moviepy.video.io.bindings import mplfig_to_npimage\n",
"import moviepy.editor as mpy"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To create an animation we need to do two things:\n",
"\n",
"1. Create the initial visualization, with handles on the figure and axes object.\n",
"2. Write a function that will get called for each frame that updates the data and returns the next frame."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"duration = 10.0 # this is the total time\n",
"\n",
"N = 500\n",
"\n",
"# Make the initial plot outside the animation function\n",
"fig_mpl, ax = plt.subplots(1,figsize=(5,3), facecolor='white')\n",
"x = np.random.normal(0.0, 1.0, size=N)\n",
"y = np.random.normal(0.0, 1.0, size=N)\n",
"plt.sca(ax)\n",
"plt.xlim(-3,3)\n",
"plt.ylim(-3,3)\n",
"scat = ax.scatter(x, y)\n",
"\n",
"def make_frame_mpl(t):\n",
" # t is the current time between [0,duration]\n",
" newy = y*np.cos(4.0*t/duration)\n",
" # Just update the data on each frame\n",
" # set_offset takes a Nx2 dimensional array of positions\n",
" scat.set_offsets(np.transpose(np.vstack([x, newy])))\n",
" # The mplfig_to_npimage convert the matplotlib figure to an image that\n",
" # moviepy can work with:\n",
" return mplfig_to_npimage(fig_mpl)\n",
"\n",
"animation = mpy.VideoClip(make_frame_mpl, duration=duration)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Use the following call to generate and display the animation in the notebook:"
]
},
{
"cell_type": "code",
"execution_count": 50,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": []
},
{
"data": {
"text/html": [
"<div align=middle><video src='data:video/mp4;base64,AAAAIGZ0eXBpc29tAAACAGlzb21pc28yYXZjMW1wNDEAAAAIZnJlZQAH+NZtZGF0AAACUwYF//9P3EXpvebZSLeWLNgg2SPu73gyNjQgLSBjb3JlIDE0MiByNTAgZGQ3OWE2MSAtIEguMjY0L01QRUctNCBBVkMgY29kZWMgLSBDb3B5bGVmdCAyMDAzLTIwMTQgLSBodHRwOi8vd3d3LnZpZGVvbGFuLm9yZy94MjY0Lmh0bWwgLSBvcHRpb25zOiBjYWJhYz0wIHJlZj0xIGRlYmxvY2s9MDowOjAgYW5hbHlzZT0wOjAgbWU9ZGlhIHN1Ym1lPTAgcHN5PTEgcHN5X3JkPTEuMDA6MC4wMCBtaXhlZF9yZWY9MCBtZV9yYW5nZT0xNiBjaHJvbWFfbWU9MSB0cmVsbGlzPTAgOHg4ZGN0PTAgY3FtPTAgZGVhZHpvbmU9MjEsMTEgZmFzdF9wc2tpcD0xIGNocm9tYV9xcF9vZmZzZXQ9MCB0aHJlYWRzPTQ4IGxvb2thaGVhZF90aHJlYWRzPTEgc2xpY2VkX3RocmVhZHM9MCBucj0wIGRlY2ltYXRlPTEgaW50ZXJsYWNlZD0wIGJsdXJheV9jb21wYXQ9MCBjb25zdHJhaW5lZF9pbnRyYT0wIGJmcmFtZXM9MCB3ZWlnaHRwPTAga2V5aW50PTI1MCBrZXlpbnRfbWluPTEwIHNjZW5lY3V0PTAgaW50cmFfcmVmcmVzaD0wIHJjPWNyZiBtYnRyZWU9MCBjcmY9MjMuMCBxY29tcD0wLjYwIHFwbWluPTAgcXBtYXg9NjkgcXBzdGVwPTQgaXBfcmF0aW89MS40MCBhcT0wAIAAAFubZYiEOiYoAAj2ScnJycnJycnJycnJycnJycnJycnJycnJ11x2AAgGMXRSlhc7X8S+PP/AAfGjmOBCH4o8PEsOSaDMQKq0nPMJ42SQAAgAAFEyjNFbzGgAYOcozYpQRiUQq//v4QE/OCAX2ttbOMc4DOwAhH2cEOe35k2GGO/AjCnNUBvVl11ho63EIcZd+r7TCpeUVLKKl8IZBGqSQWAWJcX6kRAAAgCgACAGACZZAAAgXgACAMDLmHAAEAUAAQAwATLDgACAKAAIAYAJl+++PwAERGNVVHZmRnf/gAOjBDfdasLavbSHjjHpYi7dYHDvvj8ABGRCVFV3Z0Zn//AAdmDH+qxYU1a2kQ+KIWtqJv1ob74XwAEAwAI5gEtD/a+1d6+IPCH/gAPYAjqUgAUj2kgzQUh6cREAAg79YFBZt2wCtgx/qsWFNWxpH+KIWtqJv1oU2TgS3eeBmHiiBQxtcf4e5s/waaDtNb74/AARmQkVUZ3ZGd/8AB2YMf6zFhTVraRD4oha2om/Wh+++PwAERGNVVHZmRnf/gAPEQmRDGCi/W0T98W8z2PqocO++PwAsAAQAAChBImRKE4R77/gEvrxszcuEdJpRVwoAAIAgAoDRw2OdsQAAIAgAAgBAAiWQAAIAoAAgBgAm5rrrrrr113x2AAgMRrGNY1rGsY1jf4AsQhQgVqJEHV/8LYACAEGBx88ePBheUlJSUFIlZQBYhAEaoDQoNqflrkALIQgSK1EqDq/gCyEAVigNCo2p//wgCYxgHQBUKM4Kecbav+B6fffC2AIAAEDEAAQFAAkEDEwMDFB1fwAOMY5pg+VOeLAt074GUMcw0fOnPlgX6d8QBJLgAjEjDWoIhayBTJkGlQVClkI9yYtwLOAIAAEAAAgQRIkCJFB1YExAQd0Kvmg6gkTv3/pmBBnSquaD6CZO/f/yUCr+6dx+41VKo/8LqABwAMALwBrIDiA0GFgrHMUf36ALEIAjVAaFBtTAA54vC4AwCa2oGh9sPUd4YghCBIrUSoOrxAARdG3wAkg6sbgtS/5Mp//AWMhFZxF4khbWc1sIUWvqOHzYzuDw4gABQGiLhKxkiBpLN3aDB2FnFQ1Zi/V7wjKuXiXOz3tyUC+AIAAECkAAQDABAFSkSMjK/P/wAMNgGEFUjUm2Sa7iwCCC6QqSbJNsAAJSAYDsAgg6mAAJSgcDsAig6ggCc5gEeAcRAx54XTwOpJJeP/BkIUpSEIQpSkIUP//AAq5hCiltww+bGNgtgAIACDiWEhd42z5ybvXjZv//ERiKzCq1JC2NDwAOMY5pg+VOeLAt04CYgIO6FXzQdQSJ34ImZPAApMh90IruYfOEjG8e4dy3/8SWkkThfAAQMUa46NOjbxYsNzY3GbmAA+RDK7CKxJK2M5PQQgpfccPGxjdgAIujb4ASQdTAJh97tQdQf4CxkIrOIvEkLazmthCi19Rw+bGdwww+EATGMA6ADmH2EQ9R6/V7/gR9We/76yMLrrrjsABAGEhkmGnt/nHPAcP+ABwIrgQHq7x65B7jAaDHclidyx0yBH+ASSrZDGwoTt559wzAIBDrkwxVksEifgKA3CzTQZclIl5YZwoG+AIEMW+wizu0H47AHbTEzbZ2d3/xkQ3dDGQovqVTghG7RR4zqffw//XXC2AAgAQOeccAkYcb77OXLhw5//wAOMY5pg+VOeLAt04CYgIO6FXzQdQSJ34ImZPAApMh90IruYfOEjG9PC+AAgyAUEMb0AJqeOagyliUJfgAPkQyuwisSStjOT0EIKX3HDxsY35hhvqsSab1SYAARjMS5XO9CKSb9ZKCP2hyhb/GwWfakQAY+2MVKe02Cr4CLsIUUt2GHTYxtxEYisgqtSQtjRAACYaXAAdM+MWIhWoVNmAMBy1HDanCXG0M245hd+AABAJegFBAAbKg2vOVgWavzTcZEMrwwnLJ1DGAAij54mAgNqfSwIm5wcUbefXGGATOPwXUbUwL0kgEExgIUSYQGTAs5DiylmFCgMrB1gIDruVqAC5X7TYEGdKs5oPJiZS/CuvdDiuiuwALwNKMV9rwH7DDJ/wYABagSItUthkG5j2n7tCAIi0vPYg6gwZtvlef4I3pB1Gy0HV/hZwBAAEAQBQ0OeenXhOxVKzsUIxF/+ABiAAJ+VAMQLJ1aJe4AAS9iAcgWSq2SwJgNYMX9LwHdCzN/wgQhQgVqJEHUALEIAjVAaFBtTDLXIAWQhAkVqJUHUEBFSox/pAy/XOcf4OhRloKecm3fcDKNUFuwAAQGgABANADwXKQnmMroyzRbcYAASgZCAOBAbUwG4ABL2qBiRZKrRNgACUDpQBwIjamxAAEAMqAAOAfk31hxAACUDIQBwIDamA3AAIe1QMSLJVaJ+A0AAJexAOQLJVbJeGwABKB0oA4ERtT7IABPyKByRZOrZPwwwCYGQLUgEF884nIApoxm46nq3a8HdkI3GU5W7QHpmRr+ebvwLk+BAACAYDtlz2wEBLvQt4kZnEZQw8MkRAEExQZxZaATAwdKTgRvyPcjxSYDRYBBBdIVJMkmw8BpwKUWzHGJAA1wsEQGU8BXBBWD5z88BusAgoqsakmybTAAEpQOB2ARQdX9qwDCi6wqTbJthhB4hw12xLcJ61qPQO/BsH0yFY6BFnwO4vzMYRTvV6N15fJ87jdzYLYAgAAQYQBAwADIQ374kvwADhqCvyh6hb3GgWfAZNAR+WPVLf40C74CYCSDF9asB3Quyf9pgS0YrqVgP6F2b/v///ABbYAY+D1C3kGgYegQ0AEPw9Usj5oGXoIAAgiBDgALAjJae9g2p+GALINRlqeNqYE1WNqf+ETRzCygAJgCzB12HZAIg6019CjWgAYgACflQDECydWiXuAAEvYgHIFkqtkuYDtHIQKl0ySaOD9jAEUOWEpTD/8/C/0AAEoHSsLFjE7LndkAAn5FA+gCSdWxb1MDJ4cGFG38LDH8RkIrKYXlkJa6AJkGWG2oDZc7oQETQwM8AEvYWIa3N3AwAfIsAGtrDAX6rjxg7dVtegguAUIAonBAg/nnE5eAHVDFf6lpq9HNB8npYgac/8CzgCGAAca4C8hEkNlgyEtQVH4MfgAVcwhRS24YfNjGwbATDZ3Yg6uIjEVmFVqSFsaGwACLgy+AE0HV4YEFIIQWtqGHjYzt4eMM4Ci81N+ar4NfvgIsgAgsd41UpvDwMgOBotrIAwCo0qHuoJVldAHAVClQ+EAAac4DBswA5Mg+QELNqvGQGI2XXg0AIAspjmFWRt+DTJIXcABAABAOABwcFF65auJSQlJGJeSPfsBMNndiDqgQUghBa2oYeNjOwzpdGTTTRdGdaaaaCASFIAT4AVSMLkBSjar38C/Rt4X9AABAVAAUwUDXRroaiZaIzMRrMAAi4MvwBNB1H1xmYyuARq9SSBgYtIAAEAYAAQAgA6XrRgMENGzpz5oF+nYBYhg5gTDBEgSd98QAAIAwAAgBAB0vGhjmED5058C3Xf8H/+EAAuwDh6BlVIkVV7n5gPMBkprtc/w8DGvm6+FnAEABAKNm4CJgYEJDGM1HZsbwJiAg7oVfNB1BInfg9MwIM6VVzQfQTJ37//4AH5IiAIJigzSy0A0YFvMYWUsxwwCoCALuY4M05MkHV/gAqJagnrWg9A78CbryCzgAIgABADAIEjqF09eOzZ4bG5sM+ALEIUIFaiRB1ACxCAI1QGhQbU/LXIAWQhAkVqJUHV/4AshAFYoDQqNqf/CAExzAEwBUKM4Kecbav+B6ffrrjsABDd2dmZmZ2d34AFeaYAkWZQHBFMPD/XXXXfXXXC6gAIAAIFoAAgIAPQCEUd2JUVgcT52YKfgZQxzDR86c+WBfp3DBjOEItEr6mHUsi/2AmGzuxB1AAWIgVBKh7+lE1AoSAEiKEQQoc/tRJQKEoBIyBEELHvaUSUCpIaDKFQSsc9tRNQKkp4EFIIQWtqGHjYzt+mBpRivteA/oWZP+CAANzgIJYevY6JhaYGaj8DgAFgc8lb7b+S2SIPasB1IleFn8AAEAYAZS1BxbWxNnXVWzZ8RGIrMKrUkLY0NgAEXBl8AJoOr/4zMZXcVepJW1oekBrBi/peA7oWZv+/xKs6uRsqr37366dx/wuoACADBDQ1QadmyRKkNjc3GTn7ATDZ3Yg6mAARcGXwAmg6gIKQQgtbUMPGxnbjMxldxV6klbW+GGABhsAwgqkak2yTXcWAQQXSFSTZJsIATHMATByD7ipeo5Xq9+IO/PfC6gCAAIBgAAgHgcwAuMHyDknKCkgFPCCCAuRDK7CKxJPsZyfBCCldxw4ZGN3AAixo2+gEqupRKOSwyYEIAjVASFBtTwJQR+0OUKd8yCh5hcc4QhgkVqhJaWAWMhFZxF4khbWc14QotXUcOmxnfQRAqCWD39KJqBYkNBFCIIYOf2okoFiUYIQBWKA0KjamGMGSGQgEGgKBKgcw+giHqE79XtrJCcwqA2W8OEEGoy1PG1MNrbVr0ZK69SaOfhn8AAEAEAdIPDpCRBnNR6358+FJd1EgK+bHKlvcuH3xwAASasJAAEkkWAAEmrAFkIB2KA0RmRpEgACSSAekQghGKDNHHp1DAu5yiylnEAoCJCgJNiSVh/gNOBSiWY4xYAGuFgIhNRWy8F/Mmev8JBjDwZXVCSRDIQbFKLZLUE9a1HoHeA/tyntEVXc2jdeX4WwAcEABWrAjSm1dKdVELmPD/+ABeBpRivteA/oWZP+gCxCFCBWokQdQCkP+FG7z7QCEQ8vDMr/77b+V4DL9c7j/f4XUABgAAgWgACAsAYgFQEEiSXUbknp8j/DAFiEARqgNCg2pgMgACK6oBiBZGrRIOwAAlAyEAcCA2pgNwACXtUDEiyVWiZaAAICMuoQTJgwX8EUSPtCALIQBWKA0Kjano0BhnSvfaD6CBM/MAASgdKFABI2p9kAAn5HA5IsmfbJ62IcwwdKvPlgW7cGECPYwEK8HNGM3HU9W7QDMGY/SwCUQVfwHYE2cOO/96zX8Aot5RC2ZBdQAEAAEA0AoABwpiTC+sSYnYdExksAefm5hCiltww+ZGNqAqHhkioKpuK/sCRkCIckeQ0sgoFSQf5QrVh6YACKNrioCQ2p8CHWi5UDSVLuZD/jATDZ2Yg6uAGRQEXmwGkiO4EvgRBC0FSTzhJEkiOvHAEyj9OejT+T4U/Lckv60Bk9MDizb9lxnrQGT0wKLNv4ZGQwgADo9gQHIGtTIHDoWJKTr6c/fwEpAdFhTdWI3bLQI4RQRBhV0sCjXDXoCHO7mRu/gWwBAAEBkAAQNAJAIqL02CkmFZfREM0iCAobdThPINnR+gWX6BBxlKUXwiu3MIOCAETX9eJsuWI1AOImiVF7riuz61iZLxFVDMpD/+wEQmpzgA5YL+ZD3WqEOaaMnNDxQFcXYZIiAIIH0KaWAEIGBogJe40stJrhgFBBAyF1Ea0FfMmPzsI0ZAGEsgP0x+cA3MJaCgJwI1SK4AZcDzEcGIjGwBdgmQdLQt3UAHlEeAAIAQQAEFvhGIEthJt8eOFS57bMugHbLhFd0dum1abjdhHhqccRqHtz/f5m0Rzbo+viAfuvoZJAFAACAIAAIAgcRPgRBBoOcZFVpBPneAww1UDRgXcphJCRSCAHxxgaUYpdrnAf0SQd9YBBxVZ1JNi9W6sAw4utSbYurf9xAawYtdLvAd0SIzsAAmPWaUZGgDCeoP5IytaMAIf6HJFu8OhR9gNeBHFM9hqwABABPl2gACfnQDOFk62SwCLw6lyELuEcCfv6gGYB5qUx4AFIpYSAImEOYQcyFH08Hga8r2wILgZIFLCuxxLiTvs7100gR9QzHwVxU+MSN7BwAsj4NyiNV/2uxfb/wBr/aVgs/gZzAigAKAkI6lWqRGMiEUgh/4EwGsGL+l4DuhZm/78RF1VTC1vR+/gbGjIAwmqDdLLz+EAAjucAL8CYsDF6H86IH0f+/oKfscLqAIAAEBkAAgCBly4cOX5//gAWIgVBKh7+lE1AoSAEiKMhyhz+1ElAoSgRMyeALCdRlqeNqfBL4a5hdQAEAxnvcFESHv+JESJAj4GjTgUotmOMWABrhYCITUVsvBfzJnr/9zJzOcycyAsqgP7cp7RFdCBhfgSCJ+uuuuuuuOwAENqBYMNaIfeS4mLN/AAeBqFaaFLuMfTOUHNxpIx6YoQAAIAgABQBVwgQxbngBBJCGErYlZ4yK7UIRApIuxN0q3u0H47AHbTEzbZ2d3+AEkdewi15if7FUJgDAVk0g5jU+/h/+uFsABABggAlQMJUglqpCTkZMrIy/gATMDJ4cGFG38LDDATIN3YNqf8RkIrKYXlkJaxgAEUZTFwExtTD8IFjmLgBccpUBEHl/ahoo4yJ/agMdXOFnAEAAQDgHAx5k8+KMQtbr1niRXDsFAcQETQwMLMvYWGwWBklBH7Q7Vf8bu+kAIAKADbnGZjK6nF1JKWvBQdYcBABQAfchwEAFABtwJUb4KY0sU0HxT/f5BGJc8JmNuFn8AAECcAgH2CrkeMssYu6Y/7BUNeokBX7Y7dfcbs+8gCACgAy5gAPkQyuhhOWSljGAAija4uAkNqfSwImpwcUbewuMc3MXqPs8iABFzCFFLb4RfNjA24iMRWYVWpIWxrATDEBdgKIOpgAEXBl8AJoOoPSAkgQvrVgO6F2T/gHmBk8ODCjb+FhhgJkG7sG1MIB444YIWoSSIaDYp/vA2Nw2EnHNeJv9LQswhJ6z3ru7wAZRYqClGmvjdzYRtKeCbLzxo6TYF8BIAAgIgHAcBoKBbTked40O361qAWIxFQEW7VkKABvWBCAAjVDyo2p42AFWHH4/9hJPZKTOBOAABKNwoW+FahVaAACUZIsW+FqjVYDWQA4GJAhJMFdbZT/3IA5BXqFyhIm0Wb0CIgdQTAio4RqDCJ7BgSmAAO54sQm3FCDOEAjBBH42JNlQ5uSy6BEwdVwEqOEUxNE9p5JAACAOM7EBlAD3C4GwxvoAT+3spJAUv0YgSWzY9Ug8iKo2wEQmHa2XgsiPqegwAgOIiXAnQNC5nMhsA7QDJZUFWfR7kct7kKkBq+zbWR+J2ATjNtb5k1zH/6A6uaGlfw4bsrkOqR3S+/tBdfAAGAAsgPALHdqdTALH4IfmqU9BkCIIWPe0okkFSQ5BuAWmtDhqSNvYpQ6BVlBxKG76WHaPznwBJQNgJQ+SA2zRMAAJQMhAGAgNqYhD4ADAfsWG1PgTCqtJpn/QJRAJpMBnwAuYQC26ui9u/Y4xILcawlW2MAPAcypjZoAMGoKselRj3UGncRmAMDQiqBYTXT9wakIc1I6dee0Ee3cyKIhyBxHKiigYKQYQQABm5A/qgy0aCUzoKgnwEYE77AdE/wT73G2FjAfZxHfpvJkmY6L1r8uYOjG1Mr8vSi35MaLBsoXcAUAAIAQAAgAgHgWMVgr2Y41srpvL0IAASgGQgAU2NqYEjfgsqm6UBDQuyGAAJQFSgACARG1PQFOHMk/0hMHgb8fASNsC0iL1gEtC7MAWIxFQRbPWRwAP7QwFFhyUACJlPtPMayYr1gATH/+QAhgAHSyAEMAA6X5ACGAAdL1jTgXiWY47KHMAEXMIUUtuGHzY1txEYiswqtSQtzQoAAgBYAgg65YLunOg6vH0tYZRJflqz0meQc71u4niQd4TTHNf4WfwAAQCACAwGTqNgKqj0ONlStloHEMCXgVmhAilzqWA2HnQOVrA/Sy8o9SwAEErW/259gAGAAC5AAYcnALhwoFUxyf4a0GlepkLdSggGwpkMLAVUAWgMRmonUjUYDfgQopmuNWAB7pbIF6pwEQkIi0JsGBLBOBWPJ6ASRaDLVtOAAEA2uwQEEjcv7uuhIWzJISNeARAgq9Y3ZNAjXBwUM1M2tUEBpwACAoATEzAr1oQSh+13WkBWhqyKmIpleQJyNQn11xccKwErr7BpsrofDX+GwTvoX8Iv1fgXJ8AAEBEIOmCVJSZklcQMrccTHogIQABsviMDDujl17QcsAESbiIxFYAO1WpIAOLdIAAEBEAAQGBEviANjkVwEbjhbgC+GHqgABAB9sDMnvQARAJ5awNbSVWvRAAEBe+8AAQGB1b9zRnNGFEVMXiAES5gUpK93gADFdAwOqDqM7d8LOkn/5MoZZLCCZIMI1p7CjAjqoe6fttAoruCuwiwMsF27+2GRjGNxwSoy4wQABMZqgvHWm6cBK+/HAEgQ5T6VO9axCkP3PAN8+37CBiqTV7lvKSfusC73b/kiXDH2DuX8DJPgABAACAQP4dPqgCElpapdE3aKwZSYVUvBX2iv4JgAOk4IVKETDkBlz6LwZ5hSFAckRWONIg9iTAB0gAfIhlfGE5ZKSH/9pEYithVakhaX/90sCJucHFG3sFxzjQQdPLeQrzCA29cW8sNq9iBt4FKWUF4smXEiA8EHuFkkZiKt9hkMoP9EMDEUQI//jgAEUfPFwKRI0sYANgFtguyvCDSG9PFLLAGu7wMJGKuuh/XpLuj/ABeoiXQhQiFuCsLlhsndvCCIL8Hxn/Z/kl0oeF8AQABAyHBNAQuAns8UxTndk1pWQIgEfZwAU1OTQOGNMbEOYOlXnw5932wO8SpXKIGgtEexIgDBVjI10hp3v9oCHvtQLasyzpsWf7TAX2ACgHzuxdHYq/3WIC3lNILWYaAUBTDJEgDC6oMZC280QMUTZi/UGHFgmVKxAaFKAxch4sSo/3WAycJ6A1FwpZMr7ayHVNqF8SbWystMOZRCwKwF4uHeiYCYM7hgGRtT5BmAQTaFjv2IaUDKgAIoymAMjRSEAAcAw6oa29UA0RJxtSPzJ2mbFyMxh8etZQmYThCaLsvfZx/kQMGSzhOYbCIxFzO9UL6tochxvVD+CxPsAAQCAABAXAAWR0AqHjRix8+BMBRGQGPuAAEvYgHPCiVWxEBciDK6GEpJKWMgACKNqZDU4yVS50AAEoHTDAOBGkudogFnGUJpmCJ8FeX+4iMRWQ4l+Qlh4gbByAAQbJADRzI314ATKOCQxNKalzgFzMZXU4qUkpa0gAAQCQABAEADbkCAAYbYACx3KlPngSIigiYhpT/8BEAzIgGbwnEW1xhtwIAq/YSVJBX0SmQ0AECxGzNnEWvtQ0hGEUQVd5JFYVgVArP2tyACxRFTi955893sQ7uQW53oLE+DAQEUhI4GXGCEdOZuDANWg2LdaYUcY+bJP/YDXgQopmmGrAA0qRAABwJdwQjh/4COBScxQzpqbdQ89wEnApZTdMMWABhUp3AAINl2lfmmYBJKKJ20thl08AB8iGV0MJyyUsZ/IGpgayqC3icWyQLBAAOCiBiGzJ6bbIEK/5kh0wyMHfA2Nkne/icHTbqoyOTIYUABAABAYAY8ADgFw2kEKNR0k7whv6OABhsAwgqkak2yTXcWAQQXSFSTZJtgABKQDAdgEEHVrLkHYLxXzaTCLaDIEQQse9pRJQKkhwwbCsak4tRT3FkaRAQd0Kvmg6gkTv2kBJBi+tWA7oXZP+5hWhSAe1uNCRMPdagjkAoxE7iEGgzU/6Rlvsut3WgMnpgcWbfwuM6ZgQZ0qrmg+gmTvwYcIABEIBQGcYAQHdsihJL6hteQNFC1DF7C8KXo6KAgfk4LrHztxqVKKA0RGYOcNeg3L3R1hb8AAQAAgAA0VLaVIhe4/zWg2B5DzQeOg93PdCqAyaAj8seqW/xoF3zAARBk73AVG1PTAloxXYrAf0LsX/B/+BuSIgCCYoM0stAAOMY5pg+VOeLAt07iYEKoSle3IBSVipA0YFvMYWUsxwwCo/ARCaitl4L+ZM9eECKUcAI8OG2535nQFKYHuSB4UpyaNsl/+Ab290k4oNem3kjynfx4WcABAgFAV0F/Vhv47NvBltVnPgATMDJ4cGFG38LDGwEyDd2DamA4gImhgYWbewsM+IyEVlMLyyEtZDYABFGUxcBMbU+MzGV1OL6yUtb4YQLHMXAC0VpFBUHlfaDDeiyIl9qA3r5ws4AgAAQDAAQAAo6AktGbm/PUagr8oeoW9xoFnwGTQEflj1S3+NAu+/6QEkGL61YDuhdk/7TAloxXUrAf0Ls3/f/8ILGMeUAaDFoPG1P2E0bIhtT8MbUc/rjsABDd2dmZmZ2d34ADxeyAAEAtfNwGKzDw/111111wtgAIAEAAU84BC4xs53cbuXGzn/4AF5AYZ0rv2g+gkTP2BliHMMHSrz5YFu3eFNk4AI2/5XgFUmYSxBULUcJfw3StrC6gCIAAQPQDBGjM4OxXIcChfvrwSQIKQQgtbUMPGxnbjMxldxV6klbWhh6gyIoIFN4jsVVJntIasD8FdQqgiBW1/4QEw2d2IOpgAEXBl8AJoOqABVzCFFLbhh82MbWAmGzuxB1YIFSAxaBExBupo99xmYyu4q9SStrWAARcGXwAmg6gwgACsUDCWHgjgRlES8miecACkyD5AQs2q9A05Gy694T6vXgKsjbwuvhAjTgQC4cKEK76c6J4bNPGZjK4KtvrJQABHdICSDF7asB1igk/4EgS0wJaMVtKwH2KCb/iAAEMAA6WCUQNt4AFXMIUYtuGHzIttxEYiswqtSQlTWAmGzuxB1cBo4zZwgtChuRA3CAIdeAI5vm6Zjp/txjVSMcAbw3CyURL0i9e/gQXAoE2XnguoATAACAIAAIEIAYV3AALCpUyp6iZg8ouJAGI+pnbcBuDox0jAw7oXXtB1hMmfsoDuUwCFhRNY7f+AXIDDOmF37QbYSJtSEOaaOnXniwL9u0mBh3QvPaDKCJM/AmCZAABUAYBMsAOEYLxPjXdKKjlhMAnqZgBj5Q1Qp7jgKPtAijcRox3KSg1kSmIqJZLIzgIG6D/wRQDAYY7lpkwhcY9VKg0xRC4I/fq/ZvRTffsEPLU6KEmxP+2TSj4VeSwQgX/AABA1AMQaAeEiYCK6R1CFxnkda1sQ5iB0q8/WbbgIfCwNqZ7AAP/OleK9gBwAVC9q2BsqgAoARSvQBMcTODQbkqtAACKvBlyINjOq3JBYEcSGcfNvBv5bxmYyvBV6kkDQxa7W0Voa5fW2nJXoXnKb4nJKHrUvm/aUcOByNYFpFG24iMIqMcT1kaY2/IdseyfnabMfzp3K07/+CAAIACWQImgQMWZNQqkJPUFKD6ipeo5Xq9QW1FuC8+Fe9o2FjQpVEVAnD8Ak/y/dA789ocbvrpsGXAEMQAemGnsA24Lmii0vJFFQBkAAT86AZgsnXGOQDQYujGNQsccLS0JVCTBTXAm6cxJ7GiPgZWMgKG6keslgYD5IABClSNNTXmI8YEAF9Hk+Gm06BVoMMWzgpeqCMNtzAQFvPWQesxwPDQ0yUY0TrilBX/tCoP/mBTML32ICd6QJhJrJyY44QTkF8RxC/0S4lZgzAYKcPlTnigLcGgH7XO9rFoiYfUm33/wgVAGFCC/VtzAFjLgun6kmtCdQrHIf/tqC7tQP00oS//tRpyphii/WJk/8Lfr1VX7RT93SMI3SLfws/gDAAxgaMy0j/RjsIZeiaqFkGBkzQjCOk7PebKwyDTQAAJSUIzpmnq+He6AXXqeJeQAHH8wU9XtAMJrZ0ZSoV89Q/v3B11PwDNWXRoGBAQcMCUNhFDiPAXy8KCvkkAAIA4I5ojSwFWFKYpTLln3DABgQUsx9JOg2V4yHfEAA/MHIy7IAhc+X4NDDvQ0lUKKMEg9gbNeqlABTIWABvzjG5xV+SSfgnqYMaj4K/KH4v7TE3wQABKl46NB9yia7lD8zkg7DkePYP6n97rGxo/GKLlRA/0sAAoUPj0EENoMD6tF3Q9PNlXuqENf2oGV8AwAugEi/UAghFFAkZ5BnIVhdbitUKxXf7hICDsyVSDg6ugYSNhwfGpWCrN/S5YL/+4y3g+NS0ZALApyRTJMxMG1JtAJ6iAKJKORfPrBAMf729Ej/O238kbK1GO6lX50p+96u/TY4rjYmwzs66GDTjBOMT0bRNDbuQsFNZQkwy6YncEmFfljUuEYAGCQ0owaeEZ7cEYQCADcQBgG3FgkqlOi4DsP2tAyC+v7VOsHFEAguamLNK5fzupSBCP76aGoKVO3hi3N/1RM9ZiPNE2B4LfhBg/YCG4YRV43MfBo6LR/4YF6MR1KDAizvKeuBEfumCwaWd50acRCgzAYMpMPBY1dYAAQCQABADuaAF3OOgKS4on/CHgi1EXVeIKGZZoCh+wjRkAYTXBull5WuAAIAwAAgG3fAHU0AZcwAgalgmM877Clanwp+UAwBNJBp//XnYAAgGgACATd4AN+abAYY1bhJoMnX/zp3A9w0FGRJuALgMuNEOALsYHEH16oIP2gME+NHolkZiyEkyf8EAAZFOGBUz1qMaER2kHJbSIGdscwSOwThsdg2BOLJYm8v9aLj5uR9Te6lNWo0/X/eKmuld4CC6+ACUYAobGxxzV68Y3RQi2rfZsAwgqkak2yTXcWAQQXSFSTZJuAABKUgGA5sGzCq3SAgr4XIrLRMiPrdIMDLmcEIGkbKgwQOolzo20RMAIbighUd2XCDGUSwtxok80JjHvYhorC1SU3P7yxjV3FuELuP3mkB+gNiqSYtVhr2BsoFHp8pxYKGPhWMkGuO3kf/+/qJAV7dGLlMWIg2+wEQmAAdbZeCwlqp6IAAEBMAAQFiJYQABsaxwfNKCEDHp0XTwAxdjMQkSjJLJMINTAj1DanTWTFWMzWh61WkUPK4y+IIzlTL6hb4BgACB+HIAAz2yE9kEDFllkJW/cDE5ErzzXjDEiq/DLMACQAwqJg6HXNqbQI74drco0AeZo09oiQptgAwCdWsEjiIxFZhVakhLGwAeYStG4BO96wYGBJqEBayMHgK39yUghBa2quvGxknksDhgH+vAAEAp5e4ni0daAMBcsRGgNEBbzWlGrMcNASGGSIwDChQikq3TTQZQqCVjntqJqBUlCAEAcAH3NBECoJUPf0omoFCQ0EUIhyhz6qKSgUBKBAAHwC+UESnQdIq3CCqQX/PgZ00YlRgWot9hjKxQmcTd0afuQtl1YGrUEb1sRY5PN8J5f7w3fxWwX/AABArAUABZkbKAMON1bHiWrBeJ5l46JEwDC2oM06vodBu44LZremRose0zBuUBhu2h/F8TNnkYAAgDcAAwAdAmBsaMgDCaoN4gvHh3QweO4GMEl92GJiF4gAAQBgABACADpfGRDK6DKxJK2O4DN0AxCwXiEah/ZNowwO2I4SgaS0kDBhmSRhv0yHP/+tkAYIYMlXnygKduD1IgGCnjp15wsC/btzIYsAAQCkMHktkEZiADZadZWNzpiCLUYVQDuBpfh+rnzMEFpRZyDqnp38l98UZHJQ84VBdfACAoABYCfLcO+9l2n91haQR/1oY5ho+dOfLAv07TMCDOlVc0H0Eyd+BNgQgDNUBYWG1MPxgAVcwhRS24YfMjGwAsQhQgVqJEHUWuXgCyEAVigLCo2pgPIIQJFaiVB1MBMNndiDq8CCkEILW1DDxkZ2CgNgEBL57MeZCq7COwEnYUdgU4821BVIwuQFKNqvUXN+Ra4F9oILOAAgAAgegAwh54HV3HD4Jb16x+IvxEYiswqtSQtjQ4AGGwDCCqRqTbJNWAAEpAMB2AQQdTAAIuDL4ATQdX8ZmMruKvUkra0OA3WAQUVWNSTZNrqNQV+UPULe40Cz4NGIMHYXx1MMt/q8MqpEiqvWYkjn5BMWsehHjbM8bBZ/AABAWBkggyCg0oOHOhx4O5RFfuLAIILpCpJsk3gJeBCy2441YAGOEwABKUDgdgEUHVhGjMAguKDdLrQDRlJoKyXgr5gz1+AwJe6wopZrhoFR/asAwousKk2ybYes0BH5Y9Ut/jQLvv/hARCDheuSmeEITR0rP/srU+TeWOMsR0ILi2HgxMMq6+bv209ddddcdgCBIyAAECwAAQDwBQbj3gAWGOEq8q1koaFKb4wEMwAYOTAJKPJwEf/PgJCHCFe0awWOCtN0ZYiABgxMggo8lAR/8+//x2AO2mJm2zs7v8BTMuYVS9xPdqqGwBAIyKSc1qffw//C6gAIAGAAQ88BCwzs43cbOXOzmBMYGHdC69oOoJkz9/UhDmmjp154sC/bv//hJMkCn7udZuCRBJEEQpR/zd+cLOAAhAAKFjZhtozbm3RvIBY5DT/AFiCFCBWokQdUAC8DSjFfa8B/Qsyf9AySgj9ocoW/xsFnwEBnOBD99Qor6YEJGAmQTuwbU+FAjgXl854ohIyF2AARRlMXATG1MIAgVZwHz+ABWSGuIrmZ1Hwg3Gutco0/PNwRtRuELpIa4WcABAjAAMEiyRMZITc3emDsZuoAsQgCNUBoUG1Py1yAFkIQJFaiVB1fwICQQyh/Czb7xs6Mh8ZmMrqcX1kpa0PwgCYxgHQBUKM4KecbavDgen38LqAA4QAAgCAlmw/zUkLACzV7jB9/oCyIDQINcLJIzEfXnuAAEvYgHIFkqtktMANXD+U2dJBQStf+AVgODKIStzzVkgAVxgACUDpQBwIjanoJ8Cxc1SgJsLsgADxAS9xpZazXDAKDCNGQBhNUG6WXgGjhRh3G4TNBXpR1yOqoGKIZrC1gAa6H4cIAA+igMJYeAugWdcdR1cPvYAC4yCxWcw/vY0DwJPkg7gEvrhfBhknwIAOCA+XAyUE8kraerU/g27OIDWDF7S7wHdBApOQILWakgAx7sYua1xMC745AgtYApYGTULJGZnyBMMYZImAMF/g7CJ2cMgMM6YXa2g+g4w1sQ5hwyV+fKAQZui+88tAg9YBogJe40stZrhgFBiPOgV3uBPHjc0jAw7oXS2g6hcQftUQDBTR0788WDrFxpBA9YaQgWsCAFwIcDLOSbGmKrGdyg1mRBxziE2V/7vWhr1EQtSBcR3LRHiUqO5hIaWptNhud1Q/rP7rYwsT4YDFFABAcNsuDd+jhmMQr4yIMroYTFkpYzgthLSvRD6pLLjepmAGLkD1iXvNA0+xPIW/KABQPwCv/5Z6+AAEAYAAszAAYPaASCTwl3TdT2TjT+wBYEQMzm4Iq5V4RfzOWRYDD1Jv32gBEVAFdx2WKZGSA4wS0IUBEtHRNeX2BGwAEXRt8AJIOpaAAEA0AAQAZANWVaeSFghQKNltLAWWkaZgn1HXdD3/6vMAAIBAAB5zQBiIPABjzcC4BBHzRYsFAdLjCbFmt76x52GDMOuFb21GVeSMQOyjbbRIKhU4lK9v1PSWlbCDv1xBbhxdia0e8DK+AAGAAQK/UCIO0h2vG3wWWuaAiTP3WJ1udCfOWZhMAQClANBc318oeFEZ1S/xRPrYq3jWKq2POFZ7//K+AAIBNtgAAgBgBMDrBAAanwB2KnvAA0xzYSFsySEjP/9gAEWhl8AJoOrjwBiWoSaQxtBELkvGZjKVRV6klbVhgYEvAhZLcYasADnmBdMgDS0QTxRfC6gEIACQBxBltgv1qGZIAnNqoHfnF3LFQewhHo9v9fMFIbcTaoDj8gjLLrg7UsAt5oDtxbpQLE+AwABAEOAStAb5nlnnWqnJ0yTAgFoQNmZgyQMHybLPoATKOx/aILncYAZJHBiuPFyoAiprGkYt/P/hwYB8xLgwaS931P+EBF45x5qVIJBwK6aAxaAUpVZFoKvZt0T7DFkwQohYdpgSmPGyGpR3dzbaBiYxZ5SCZZ5NP+skxxjqLOv/dtEzFd0TdMpYY9Y6rEnljQsNqAzBdMqnSBFx0he0hO46sNeM/fYg/8EQDESV6fYAkSFxQ6lOxlBoba20XPH2kwIdFGkkstdpf2iyDSi63MJr38JaX0l5uOoymur60mGdfBn8AAEDwAcGOGunQD4lcUfnOh7QlYRAE2CCOLKa0wfaiwK/bHKlvcKgq+ngpMgefrOZYCvvMWkPFb98yYAyTgLYK7ZsFKM06JiDWfHF8ZtLHDgIdO4CU2MBDTnwP1cEoNUIU1w6s+cZ2u7gTCQTXHhvqqVEjCOrL2frvhbNghxOPZJOCPMTd5GX+/mmAR65AZpIlA/pe2IbfsIAAQBUvAXQv1VAKv4IAAQBhEWI42MOFVQOttIEfrWab5xgnosleEwRSIt3/WhynMItRdNpBjxJrY1Nttd7cGPq33oLfkAAII4ucNBuIezmy+2EXANU4KRkYGd9oCKcfVlA7ElqnQm//tADdCAKKrelj3T4qSdWvwH+3AiPxeh+EBBL6w4sB1CrKiGMXgG4hTnhFIKbXgRNqJAV+2MRJe42D77CBkejGoOG0bSBFjuayUEftDlDn+Nh59MVh6q5VmQCHJ9hgEWESP/nMFEFCWkp1lpPauAIautFC0WWWx//AwACA/QU8SAiHvBUyd+9/2iIED5z/zdfT3/7HCNbhMMIV//biIXT0Vtr3yCIxnIb6r1S90N8fltom9Kgs/hAAIQAmAw/CVJoW73O6sC9ugEKIdrx1soa22gakOGNCY8gQcJvva0Mcw0fPnflgXVO0MMrF4IQQVCMqN2tMAIczZo0SQZkyJKsE1ctHB8YzDDA1hU8kRQBpVrANYy4wPUYr9XxoP6FiLEMbSUzZNgQEnXv7R4FZoQAQVuNQKNEtEXJz9aAAMiSMWVALD15ORK1qi4ARgQRlHBcyoyF+T+gAAlA6YYBwI0lzgKAAEAEYQvaEG2i0F+1jG+5oEYyopwLTJsvAdgTpVAmG0ansMyx0NlmFFmH/8Ot1bpo+0vfC70NcxLvT74X/AGDA8yZJgAcELXq3k/0I3EyRm7DpbccAZK0CAtO1ODBvYRSL9f0fbmMD6UgEPCC81jcBIB4hAEaoCwoNqYChEIgXuC27ZcmGCSerT+vqtAYKmEuHpPib6hToa2wh1Csy8yWbQbljAHLgqQEy0mTBphzDSAUqRm606Pi6u5AAUrcJUn3A7KTg0XnacuuQDkHeYLhCRFEAx3qQAiIIgRhJh8BLRBAAcBSgfmCIDUVeUtn2QdZe2KKyB07nE5gHrQJbSSJJwdAGUoJquVHH9A897snHGuidIH5+4Lr4wABAHHABwoMvrFzpKogCWFN3FTn2WLFjKcNVp6CEPXKBjP/7xlw/ekzgIi0wiW0tqZABYH0Osh8wDYgfVyAAeyABgFzvzAQFvNWUWsxwSBQcNBK9jsl0e8i+EDD70pQ6XcTxMYECzaM/eCeBX3t+6Rd7m4YIo7FkHlJKfziSBDkvuAAEvegHIFkvsktBFCIIIHP7US8PEpzcwhQhbcMPiLTYIAAuABGEhTyv0hV15083MHDnaCRadSEL6IDFRMLlEQc9TsfMmJ4hQBu/ftloDGh2UafrWHAobDH4B4AAoA/XAtf37AsdCBEC3xAXAqms7ytAMgZEeDGT5Rmc60AtEOr7IDSHKMaGkDj///NB+HA5AmkLIGgY0MMkRAEExQZpZaaQAxbWKNJ42iiGCVWZQ4jCKruXkXwyyWmAEjh/NZWEgwJ2P/YkeGhbs9379p5ERAIJyA7izSTohBqfCIGBk5aGE+Nw+1FqubLvvAM4UX+2LdV/ryFNOFmUOTqg7S67BAACAmAOFjgRUPQbk/Py1IDF4aFsgvy03yvfJigHShDGbDJb77pDdlIN1PiU3KtDrGZKuir+CPyP5Nt6QvkLOAIAMBQADJAwoXxCNpuXSsfrIbwFiMRWYVWpIWxofAaOM2cILQobkQNw4IYAFXMIUUtuGHTYxtxEYiswqrWQtjcMkRgDD6oK0yzAHBAS9xpZbTXDAKcZEGV0MJiy0qZgMGT4/SMKmlQwo6nYrPaXMwAAi0OvgBNB1cI2QAwBDGFJnBYPo+MzGV3FXayVtaHADARCdToZDitQNsa+8jIIwbmY/7jzQ1U9TGKGM/rubyD+MC6+aAAEAYABw1Pws2Ojs1dmQ2eQ4JpwJgJIMX1qwHdC7J/yYJ/BtsAB8iGV0MJyyVsYwAEUbXFwEhtT6WBE1ODijb2mRhgEyj93jamEAR2uBSeBT87nWAwqWw2G5j2n7tfAjaU8Cz+G4FsTe7MwBgOIdmGWi1xgS0YrqUHDq+0nyDIAAEAgAAQBwDrn4CxGIrIcQID+FNjYPrQGT0wOwAB7+F+B+IAAbAWM9xpQDAWogLPIAAIgOG3MeUJcoVx2AAhu7OzMzM7O78AB8+ZgACAUumwDF5h4f666647AAQRSkIUhClIUpCF//wAKDuGkVBWPomxaANdcLqAAgAMCCGQDvPHHHB1ydccBb+ABYiBUEqHv6UTUChIB+BIihEEKHP7USUChKfAkZAiCFj3tKJKBUkP6DKFQSsc9tRNQKkp/gAeICXuNLLWa4YBQAGAB/LaJMb9CI789MmxPkKjtzmyaG3QqM/YAsk0hBuqFSLgRYadNYWfwAAQMgABAaFgJatI3IeQNlZzSVs6ghgAfkiIAgmKDNLLRwNGnApRbMcYsADXCA0YFvMYWUsxwwCoECEKECtRIg6sBEJqK2Xgv5kz0GVgPCNGQBhLYG6WZn/w4CDRr3oIlEy1LWo8Ab290pxW7wixgXiyADI3XOKew3hYnwAAQHRwAJfQNwuHwOGRpaiymZSQAAgI+8wQhB4jUQoOoAXAanFeSMplHoQms0BH5Y9U1/jQJvv+ABw1BX5Q9Qt7jQLPgFgJIMX1qgNPdC7DTAloxXUpAP6F1r/hQAAgFvJVc8CYCSDF9asB3Quyf9+EABBiBgHd3BnUoN5ZiDvd8BnEkqnUg2LWCE0bIhtT3fnc6wkZ7dOp42/DBIAsAAQJAABAwAAaCzLWc6LWQV3/wgNIGjIXUx4OCvmTHWjGC0cZgYo2KwlvBrNAR+WPVLf40C77iMhFZTC8shLWMBMg3dg2pgOICJoYGFm3sLDPMAc/FAQteCT4m52gAEPAuO1VW6vWmBLRiupWA/oXZv+DA0RS6CMh4L+YMdAaJOBSym64xYAGOkwEw2d2IOrTwCPyHArmvIDEW4GAa4KYJ/lKyRckHG2DHj28IAAgUAFAwCgryxeeYfsJRuUSYZR/U9hW7VkWsWrNe7YCo879f7REP3/1pTrR7w6qiZxpqBhfAwABAYID7jU5oOPKszQLYb27SiAwDC5s6lNcFlTtaIgAwChs5x8fwQdhGjYBBcUG6XWmIA6gSu2KlO/5qMZEakX1JryLK0EQlRTnUcFomzL7QZR0PWOIbURUCZKB4pDQ83C902JrJU+iuk9duA3AQqF5osSyn3ITMEIQJFaiVB1eGABeQGGdK79oPoJEz8EAAXAAYMoHZvTAkuIjB70X2ZiGpSNbCCKEH/2DxFqnAjPToKP/++y/kQACov6lLbS/uvNCHhu/kWmQyugAAgMAYgAOGjxp82EhPRY4Ln/uEF/GkSAIJSg7SCUAA4zADHqh6hb3EgQfWMQI9Fj1SDxcz5/AaMC3mKJIWY4wABYsUB3woGA7UQ95/sEAhtv6gSO8of/5oLIcEHKscyaH5Gz4CYC0GL61YDuh9Y/7jAloxXUqcB/Q+3foAAgFTgACAIAYcKfEHuqANlcAoNV/9cBIwVdUWX6BlzQKLCwOjasRGE9Kviz/mJ7VWc7fggAC1oABg2GtyAATZxBk79jlc0dhzoRQmpYkgBkHqXfBbcOsYS45CffB5q0o+kv0SWMInLymqCxPgQDgAQPKhf7M2Ei8TC9mOQD9FICD7dkJxHmMol/FaKQCB49n17QPkKDOUHK34iGWppsCDOlVBap2gmwfsI0ZgEFSkP0vKEAACAaoAAgeXGBCFIAF6EEHVyAJRi6PWyA144M29kAAn5FA7zwurbOmZjK6nFQFo56//xIUCAABANcAAQPLg8ABBYLXAAgzADCz3DVXtYeAAU0wRgPrKePo7A4BFBAAEECg0Bg0wDgX+59dS7VJRgqQKggTKnmRBKIpUbtQ2AVFotJc5DdlSs5aCvuPkSQv+AACAWAAIBgh8HSJqzaGsp+Oiloc4GVJIM0/4XgbhRSaP1UxBpfNNRgACAfKvOGCYKbzUnY/jRN4+7MLvjz7IIAn1ZbwV/2AdfRTtAACAeiKbgyByFZqF+HbF6BGIIQBWKA0JjanyzAmnFPFG3LLizAARQNrhwWG1PiIxFYKtnrIFHesAInt7pG1PQZQvPSOc6gqoFSs4yIZXHYzEkiDvNMAQlqoFp52glwKIHBYL4ZirZDYq0rk0HnKKqvWj9k5/+rQssyNbtX/IagRxSnfTtpxGPc0fvzx7+MM/hQAcGOOV4FRupBallWmpkwAXkJgALyaYGlGKTa8B/RZQ/7hAawYtNJnAZ0WdwBNRq7nzVaw2wPUSoG6MBF+rQTYwNzArEPD2p8hqe4zB1vtaYAQ/0OULd4bDj7SQDOFYcKbMKqyCLYWlDQ8Hy1/6UOeAzqJgB0mOACAuCwo3dxn9ogCyhoenEh74Ir3/oATUf+57araZAwzpTaWg+hIefggADdFDhJgxNkyMbU7BFWlcS1n0jf87QI6iAPiddNW2eEwVDeeY/QbZ5Zx+wYbOVGac5gsT4ARQFAPsngFfH64puGQFIa9ZKCP2h1J943t9wVGGv4/w5CVZ/I6CIFQSoeRmqmoEvTAXCEIBhFRtLQSkOgAASgbhQk2MGxc7vgAEvaoGJGkqtE7aI4GCAVqkzXlxhwOo7Vh/1wRzVXaDIEQQse9NNJQK+mMAcUM8RGjeG3P215AMEOGSVd+WBYfuYCYTkcpB1VxwACAGq+AdTWRPWmEZ3VL/04gAIAap8CCsMZExwFAMNuaXCJ8BgASgEBAA9abAOPeBYKqX9ZkRgDV9R9OaxvYGzAe+OSTv9poaasA3xpilPmLJQvU/BL3KchYz84GCfMQAGaA2A8ER0IKOjrLO5lDSmjH3DIEHCAg//cMFIYdgZVx2wjKtj9jid1mLKMwKY5BYv7mApRyEi4wkSaOt6CPXNDAXk3AAD1n/MAASlA4HYBFB1B6oA3joAgko3Fo2ug0FEb5bPxRLrYwCZR+7RtT60Bk9MDizb+FxnnC4onO6W+KpdbeT0EIKX3HDxsY3YAAi2NvgBJB1K/4lioKAQEIB1+PCxFRw5OqftYTBkE5NMtihR2UREEZ6J5IZ/9WTHKwiGsNT7vRtyD+tf99yM7/Hf9Jt9WeC6+AAIAAoPWcACAaizzQlVaCQr5KGpCHNaOnXnr0bdoMgyHWEvaUQXWCR/6DKFQTY57aia6wVIAmYbODQckqsBoil0EZDwX8wY6wAoTHABwRNgUbqpT+LstbLAYoRyArtofhheACbzCIpRf/PAQFvEtKLWYQEgUGGSIYUnVBnm150ICJoYGFm3pLDIAoIEbVZ5rwU2GlVcitIVgi6Mhn0gkdO5CqDt0iVReWvgdk4n3gpN35Vx1ROOZBf8AAEA8DgTmAZANkdmVujCy1R896CylcHI50gVgJuX9QOnwtIqZQduMzGVyCt1JIAK53Qi4FpFxHASApq2JX/RV17gx5WPtrH/xNsBBiwQCTgACBYKk6NJ9gUsqAACBgMg4gCAOACpfEZCK0EXiSAJDlngIpdBGQ8F9MGOuLAELayQWhnaIvkSYZIkAYXVBzIS3mBM3A70lrCkAaTX9hGjIAwmqDeLLwIQMArRN034OAkazlqJfaMaklGgj4X6EGA+VW38MXYifzj3RqW2sZeNuWgs/gAAgMAMAFZzvXhgCkpkVsEtQvahqMZQ7pfDxs5B/zgJlFhnajW0YABkASwPioDDgA+gYfm/FmEH3WgMlpgeZG4XqCLWaAj8sfAEL7OkL4EUBCAKwSKNSduXO4gWgxfaiEAzoZZEAAGQAgH3BRfxgS0YrqUcDj/QvACIgAAwAEAq5CDAAKAIUg16xgCRGCrWgb7di1w0tQ7GFxajut3HNIC3GpSUoC3q12/0TTNvfAWp6DvjW9Q2ZeZr6+8NdddddcfgAXsAAQBwClhJAqQQTC+BPYAEXgACANvJwADgCpACobkEUORRvxQ+OY+HKWYAAgBifvgILvA0InDpwD+98oJKv94BTHylC11LV3xDSv+HjsABNtMTNtnZ3f4jITspjoUT1qpQYrcos8b1Pv4f/rhdQAERkAAIHCoqAACA2AHAubSm5sb/Aky8FvLmOAjgk2IGUMcw0fOnPlgX6d/8IBIUgBIbIENaiT0HV+GPKFXDP4AAIBYELCBFmEGVrciC8atQrfdANAeFIcxCghFMJg/AAg1ZxmBBnTCqU0H0ZEzMACDVgATkQyuQwiFkpDCFAI4FnYVWgACAh5LZYCJhTxhkpy4WfmATKP3aNqZmABBqxsixCOBAGIgwYfwAPEvAhZbccasADHCCAAEAE4AqQsVelJISIR+8DmwyDcx7T92vArU2+JGzsCNpTz4WcAQAEAFFEQZb4ODIjPBgboa2EEBYjEVkOJ6yEsfxkQyuwisSStjMIHg7A77oiR41ejqAXCkEBNGdkvkgW5PQQgpfccPGxjcNgEw+92oOrxAACUgGA7AIIOrSMAJg/bTTQYh0Jv/2gZ04zWZZoA43Tr3asAwousKk2ybfNbCFFr6jh82M7hhwwACeBgoRkdEzNPSkiDQgKWZVeUMMHNOGikEPwK5mwGU7T4ZUAQIAwAG5sWAAmhoVBFhsIpH9AaIC3mtINWY4aCwwyRGAYX1B2ly8fAAWNTMBgpg+UucLAtU7CNGYBBaUG6ZtNGAG/IBQUJZIe8UrlaRAQd0KvGg6ggbv2mME2FeWfmeYABT4SAAsWsA1QoCmBRNdh98JAAWAJgLQYvrVgO6F0T/tkEA2xZpIKR0kBt8wEw1d3oOrjAloxXUqcB/QuQ6lIIQWtrDxsZmf8EBnAAgLAVZgk45ubBSDVSwFAqdUxyPAhihKYeGFj7Bs0NxoMboi5gtacygP+ZL8izjYLk+AACAXTAIBoZJuwtm7ySqxaZYYeAAEATgACAIA0cNPBvBAGlQq8xp+N/GJ3giC/nocIIonD0lA8sQdf+IAAEAAAAwEAADZfIMoOI2OVTyx3bLRBzBDwUziPcakEA9XkKjScK734BcIF+IWgo7qk8AB+2QAlRZ2jPwbAw+4zMZXAI1epJAwMW4DIXACKbDwYeOGOsWOemVh4j9QAAijIUtMBOAu1lwGKQAUQYkXLf/7uTDwIwAov14288AILAgAkAKIAsvlpEsADKWEOpNMQWNmYREMNLUfAPNTHKvdomHwuYpGuQJ139pqkui/SJL9mC6+AACCQKDmBm1mjQAJZDXFSvYWOI9CEBa/Y2JGup8MAiUVoGpWpFEKP5HATQfeI2rqcAAnnAXzAACqurhkAxUOl4GovljdUcBrwIkpmuN4ACXScBNB94jauoUBNbeAEL5s2UPC44sriMhFICsXiSlAA7hNAAEBGOcIVECRX8lq6sAKlxgABADBMmBX0OIh/YDKTCtZLwVgAWU9YRoxhCcUGvsrTAYEvfYUUs0W6BUBARUFAKNBJieAy6UQnYSamBowF+SqhhaOC+PWTa0yILZyHH081gTt+LKp9UH6Y41WzgsvgAAgLAACACFgXTFxS6YmhEfPxkPeoP1fr1Qf8+4ngESUcTKDWFdAKgJIMX0oBIuwvK/+GCWjFdCGNAn4Z1AZAAE/KgGIEk6tEmAAEoGQgDgQG1PuAAEvYgHIEkqtkuMAJHD+ayukkGBOzDDmUOBREArFEyf3tEiFNkMXJgBjhAo4HUPofFTnHcoFOmGQLAd9DC6nQM6AQAjrHAY2TTliDBgp+kDamgCCceeTkAvBtoca0a36XwIEpXqailcin6k+YLr4AAIGIAAgRgpYAM4Bx3X9eIWl40sMNgE2H4eCw2p9aAydjA4s2+6EnPGRBldDCcklbGaQuqAF2YrbAAEACzoAAio0bd0HBlVZqA8AOADMIRcQA8wfCiLyHAoMWaMsAAQAAUSvyJ0sKud3tJib/r2K/z/+kXDWR9K40OkdQMSkhoSs4Yf9hkiAAEAcKTqgxIHt5jQhCT33wVhdEuyAAT86gckWT26TIAAEAFAABA6lkAACACgAAgeSwgAC4zgoK89odSJPQMwhzY4KFQdDS8Z+1iGnHc3jtyPf+8ABISMCCKIACq3siLW8/pLv+3rfjguvgARgYC9KhTV+zfhChCAQREVbxrFQCgiqcL3nMVwIRGS+QAAg4A8eiABC0Jd2QACPjqBXiyvgSS81sIUWvqOHzYzvpGBh3QuvaDqCZM/EAIIAARLIAQQAAiWDCBhehULDAAjWAd7Uh2IoqV9sGNmkV1ngskH9Cz0/M/C6+AACAWAc8AAQCRF6HSzjrsw4HYuL416kIc1I6deerZt3JUEI85UIGAyi24yIZXYRWJJSxnJ6CEFL7jh42Mb4YByAAoCJ0U+BlUw7tAQ1daHC7sshcgbv8wEw2d2IOpgABPgE9QABaDq4mJnurgHnc4AA7qbF87WFzSAAE2AX4+QADqVBHkE3t/0l7kpBCC1uQw8ZGduMzGV1FXqSUtaGGEAAbcgDB8zCpEE0QSJQfcZ5MighSfkf4BWJMqHXiH2jCwSrv9TNh4inQtrqC68gABA2AAECIAkCf3AOC/qtEfo/ATf/9zcwhRi24YfOjW3ERiKzCq1JC3NYCYbOrEHUwAAi4MvQBNB1cQ2MKryCeaI+ilzHY6gE2o6PAAEAGQCgFclQQgtbkMOGxnjQ1We6KgalOfgwMjTgUolWMOWAAl5sI0aAMJqg/SzMAi7CFFLbhh02MbYMYLhxmBiTYqW8H/0mVKo//9BAAGBbDg1NW8KIIl7ZPV5jv4gnmKRXQudahiy2YKCO3X/39ovAJ6YIBNT54WfwAAQEgACDmiircyEAFxbJcxCBG4Os6gZySK0N8DaTDFkUKXrA7TLswyREAQRRQZpZSahgW8xRJSTGDAOnGZhldTijhLGm0mDIAAEAYAAQAgA659OBCkiiLFNFlwXswEQmorZaC/mT/SgACLQVgBVYyFDAgAAQBgABACADrmHAAEAYAAQAgA65hAARg0mBZECQAnmigKWdEHg9ebRQ1WpGXgWpvr6PVRRhdQAEwABAY6gAMBwG2zaVs2FbX2a4GiAt5rSi1mOGgUH9OIiMAwusDtMrtgNeBCima41YAGul//4QJnMdABmFaOTOZKFkRkGUc7z/m47Hhb8AE4AAgIgDQCCxyrCCYla4sUyD6GAB4gJe40stZrhgFhA0ZC6iNh4K+ZNdYRoyAMJrA3Sy8/A3UCFFM1x6wANbIQIQBGqA0KDan+AB4il0EZDwX8wa6ECEKECdRMg6i1ywJlApZTdccsADGyYIQBWKA0KjamFwAYGEv2lrVpuPfAmMXKUxajgMBfioNO0A9EE4I++Qr7KCzgAWABgAHHtAVQOnXwkIF/2Q/vvRSAB+SIgCCYoM0stMDRgW8xhZSzHDAKjwHkIQJFaiVB1YDTgUotmOMWABrhf+AiE1FbLwX8yZ6/4UTG9qsMtYE4skAxFyOaOZu0ajRM/wYhHoN/11x2AAhu7OzMzM7O78AClJIAaJMgDgmmHh/rrrrjsABBFKQgcopKUFllFF//4AFwL07AAH/IkEGoP/gIRgRUwpiyxm1mVwtgCAABAMABQACzpwBIZOaDq/AA4xjmmD5U54sC3TgJiAg7oVfNB1BInfvAyhjmGj5058sC/TtMwIM6VVzQfQTJ37/EAE0uABSZD7oRXcw+eezHmQquxhshIxvmLm9cLqAIAAgLAAOBws3bN2zds3bN27Zv/gbGjMAguKDdLrT/+ECzsATBW4MlYF4okPwIz8G+F/wwAP4ABImZgLFPA44sI2QsMKIrJAa82mWAAIAorBE2l5YIAu+A0acClFsxxiwANcLgJIMyrEk2Bu2MhuEABFF1xEDA2pgLEYishxPWRdNYBMo/do2p9aAyemBxZt/C4z4f4eEAjJYATyQuauqlFQ1zqcgiD+17Tt2g/bPe4jac8/wx+AACACAQIHULds2ePHpm3MjIzD8OH/8AWIIUIFaiRB1AATMDJ4cGFG38LDDATIJ3YNqYQSnMAiH8ALjlKgIg8v7X8Bjq4Fn8iACAAEGwAcKi+hmd8zxOO4eyfgICXuNLLSa4YBYYRoyAMJbA3SysA0cKMO43CJoK9KOuR1VAxRDNcWsADW2AAItgW9gYQdW08K48C5fBz/9r4WpeI/O0oRgAP4ASKhbJghCDxOojQdQEBIIZQ/hZt142dFwUgAAqAMB9wLIQBWPUBoVUFzg4ABUAYD7hYACAEYCAAKg1A4K8YExkFis4hPvY0zCdgZjkwC9/0IFX9BDjE24XYAl9cL5J5HxRbVcIMk+CADzAU+AHmYZ0GIueiYcjO4EgCuQBp/CNIkAASJIFkKCDxWrR3VZYAAUNWcYHqMVtrjAb0HH2iA/Bi9peA7oOJ3/a0YAQ9wMWLd9cCD7BEAGPcjlSyXlQTPJsAAoTeAFwNKMVtpjATkEG36yUEftDlC3+Ngs+0gPwYv8XgO6Fmb/g9RICv2xypb3GwXfeEAIcJJAaRiCfcARuYe8vUaQARkhriK5mc4LyRsaYqoZ3FR8NUhtTARPSaXW+BdfAABATAAEAIFAM/6xFQFVL5AVVEnC+CCymAAIAiQBcC+zaAp+dCAWMDDui117QdYRJl44Q0J7aAyUwOLNu4VGX7UhDmiXp154sCvbgYUP8ACrmEKKW3DD5sY2sBMNndiDqCSABgYHuOMWmdXVZGNTG/QYgc/eBhBSaD5AQk+q98tbYywqpGwWfwMAAQBgASED9H81dszULj1eFJLIAALgDAfcIAgCgAq4HAALgDAfcADwCjlDAtPy88AsGz2AEXMIUUtuGHzYxsBIihEEKHP7USUChKMBMNndiDqsiBszAKqjyGf79RgQAtgAyKmAARcodgANoOoLIQBWIEipKeFztLAZX4YFJ4noZN3uSkEILW1DDxsZ2DDCAAL0PwdZnP4GEyL4Y7QcYKQrBPb+qoS+hhaVfV7cGkokkgu3yVVWNldTuwu/gQAAgSMPAYQAHQ9QKHbDpcBI38RGIrAFarUkAYGbdRqCvCZPqFvBx2bPmAARcGX8Amg6uQBGVAOzhFqtIjJABLBCCbt2R+0RCS0pQEHoIRZ65QOSdXsAhOu8+5uEf/tbTYujpY+M//+MzGVwGavUkgUFrelgRMAIs8UbeDD5wGGwCYAj+AOBAbU+tMXAN2xCQCA9D/JSCEFrahh42M7BAWAUCgLgwFmhu3JOM34TiDe8W3OZpPfuDA/DJzEKSEACScI2p86A/D6+fa28+uwyT40AAIDAAwOB8X4f2KR7qq8T3xGBh3RK61oOoMmGpCHNPHTn7RYG83cRGIrIKq0kJ6yQhU+j+3AAToAno0ABNLMCFTjMxldxV2klZdkhCoWIXlBCojD4KABVBHXLRD7KXO5gRIh/HTIgoaeLP6o2j64WUABBAAKBSBMawCUz+RyNipePO/0oAGIAAn5UAxA0nVokAsZCKymFHimFNpL0YA124HODHaviEAACUDIDww2MDMudqgRIxgJzArSTQAA+RDK6GE5ZKWM5gKBCbE0IoIktgsi6WBE1ODijb2FxhgEyj52janxABKwfjW0DR7BYRiGyWAwMvZrQAC+a7rQGT0wOAWk/hcA6Vm4GAAXHBgHhngaT74dCyPceXvgAc2GQbmPafu1xxnQJN4wxnYT1bAjZXzXxpws/gGPABMP/gEcsiGAh001mgI/NHkxq+zjZ8HxhFDqreQodbO4h/wEQmorX0C/mQp15AAIYAB1z8MLVzxm5jVZmywgZAmO59HZCnhdQAEAAYAAgKDXQQ8MfDD0w8MTHwxgaIC3mtKLWY4aBQfwyRGAYXVBml14H//CEJSHQAZhWjkzlqoIkYE4ogP+Jx/DfC+AAjAAEAIAgQOoHb167NnpsbGwz/AFiEARqgNCg2p/AFiEKECtRIg6vlrkALIQgSK1EqDqAFkIArFAaFRtT8IAnOYWMPAFAVdwQ4421fgdb5PXXXXXXH4ACELxrRq7vlfILhXAlAA5egABAt9koABgyTgFGE7GmgNQvfmjzyPh6IBh3DsRTRmrIkYf+0lAc0ApI0nF0y/gFQiDK0BWUOcRIBG3hAWpAYwrbStyS/DDx2AMkkN32zu7uAuRDd0MZCi+pVOCEbtFHjOp8H///S11wsoAgAAQDQAQGnAEhm5Oce8ADjGOaYPlTniwLdOAmICDuhV80HUEid+AyhjmGj5058sC/TtMwIM6VVzQfQTJ37//CAExzAEwBYERa3nsQdX4E2Wg6vhdQBABAUQwy8+8ywy8++8///EZCKymF5ZHtYwACKKpioCY2ph//gfp4g0UcYk/2v/VhL/7/4AAgPAACABMyAQEOMzGV1OKOFMabSQEMgAAQBgABACADLkH8OAAIAwAAgBABlyDDgACAMAAIAQAZcg/AdQuoACADABcAB44deDey4SMcEVPw5//gAPkQyuwisSStjOT0EIKX7HDxsY3gCxCAI1QGhQbUwBYhChArUSIOotcoAAneAdaoAAOp6Dr1nm+0AsMRUq8IRZCfEObFgABFGSxcBMbUwYAAyBEJaDDAFAVZgQ8821AZawnGnJa1x6/A6lwl2p4FnAAYAYYRGCaUAAC4FViDAGsSMPAgpBCC1tby8bGYJAAIc24A4gImhgYWbewsMh8ZmMrqcX1kpa0OHABDm3IcAEObcEAAEAQAeIDsgIcGXPDhDg65Hjh4PHAL/gBAUSO5ZJOWzZ69Mh12jcZmMrgEavUkgYGLSAABAGAAEAIAOlh4cAAQBgABACADpYcAAQBgABACADpf/wAOGoK/KHqFvcaBZ9AmAkgxfWrAd0Lsn/Bw3ZP/gAU0xpyI5ndB/wR6jcFnABwAwc4BCy66ww5buNnDlv+MvleBk0BH5Y9Ut/jQLvv0wJaMV1KwH9C7N/3yvleEJkT4PntDXlRjM6DAh/ILcbsMP4ABgYCSQhhjGjcOQ4hFk3G8PwAsagr8oeoW9xoFn3Bwbh+/eztY3EQIQJQFoMX2qwGdC7J/2npitJ8j53///gQUghBa2oYeNjO0MIAAmGNKCufgAdBYa9k/WlNk1vcAvnIanfDJPgAIGEKtPC2X9/t6ZRB/xEYiswqtSQspIhXcABFwZfFAP0sWVxCuOVxyuOV+MzGV1FXqSV+kQriG+U3fAzhRjQyZkaeBvrb4/DGADghQZ06dOAJ2LViwZbXJz/gAfkiIAgmKDNLLQDRgW8xhZSzHDAKjwNGnApRbMcYsADXCwEQmorZeC/mTPX+EJBmIOAColqCetaD0DoD+3Ke0RUCbry+nhbAAQGI0GcOnDp04dASWDNyc/AA8RS6CMh4L+YMdAaJOBSym64xYAGOkBogLea0otZjhoFBhkiMAwuqDNLrz//CAExzAEwALzMLkZjD89rT8AneqF98z7so7T1x2AAhMzM7uzM7u7wAK80wBIsygOCKQw//rrrrjsABAECkkGEnEGkmEnnEH//AAdhLCHIfoVCc3wEHh+iBCjyjNeuiQL3dWXXXHYACbTSTaSab/+AD2ALQUlibZxz+uuPwAebSaTabSf//AB6AHqKQxFs8549QBBCMYxrWsYxrWtb4AshAFYoDQqNqfw//9qGPUABNJtpJNtJ///gA9AD1FIYi2ecIvpb4WUABBgARAECOCnEX8XDTqdtTv/wAPEBL3GllrNcMAoAAegB6ikMRbPOYDIXURsPBXzJjoDY0ZAGE1QbpZefgNeBCima41YAGul4QTuYWqGABiWtWm498CNRcpSlqOOCPvieuPwAE2mkm0k03/8AHRdRPaVbCTn9dddddcdgAQvd3ffwAHGN9KNc/+WhXuh/4/4YMBQfrGWSyvstNFf/4gAIiZeA1nAIaOlhVHTN/sBYbEORxG8shbWcYAiiilQzemuz3LZXHXRMAAQJUylQAKFb40ZicBVo3mg0brDh/Ah/tRj39y0q5xAAAgXgACAAHSw8IfgZRUk8AW18oYaMlwiW4jQBRjrrgiiQUuPfiAABAvAAEAYGSwFQf7CJTmJ/sVwGEZ5okR+sgl18aVBwABAvAAEAYGSw4AAgXgACAMDJac/1+go/oBwS1aCDyTb/cBACq8a815DyNXlxgBTMqMOpaUNZySOBBVYWKPPbhNJoTopzYlcnYpz9+//v896cyw/AAhtPr6n//AAcQ/2ox7+5aVc6GPwALgAYCDpkzGT4xDPkt/voIRgB/BDyFSSrzQFQ6+I/MwraUR/QYZVmjTpDU02BSZ/3kAAidL0FH9AOYKtBD+W3+wFGNqEFua1RJCGncAZgCUvAClxWiZgr1TV8AAQILbQAKExH7m2MpQABAAJfrRZQb11VJL/tuH4ODKf/8ktZL1ktZLC+AAgEO5z3Eue57nkuf8AF4BqOkdSghQ9Yfuf/6wBl86zP+F3AUHQDgT8TPJbv7woKliZ/gRAGg6K3AJSHGP7hAABtgABA+l/ghmAFgcg4hfAAI35iAADbAACB9LAgOxgY19TpbChWmHqgKXyFh1Cht/wADn00AMGtwrFFxBogAAQMQABAADpYfwML1MEqpWv3iGkyAigH3NYVYBRS9YX4l1Z2gh0S1AGQnYi8Lo38owaVRn/8fg4CY5pb//kAAETklhwACJyS8OAAROSWHAAInJLeUiPwAEADBu79oTdptlpoOFfwWzAC2CHELJX6vAAViBlXGCIaakgrjABRAKJLsYvGqA1D7BHAIBMASQdTJQAAgCAAPYAhB1AQyBFRTBUNMSSVxAA4oFEFmM3jRAbhHYBbYAAgXyWwAAQCwD4h0gAAQLwABAGBksOAAIF4AAgDAyWHhwABAvAAEAYGSw4AAgXgACAMDJflKGfDoOrw/vYQR+ACwYkQ1TGxLGnv3fwAWaMAgtOsVUFnF9/4ADxWgABABAYTOM/LfYHKAYgBJAABALwpLSgCxWszBDMALAACAaQJ/sIdUeYwAAQL4AAIAwMrejDNB2wcA0dUQItWBDMAAEC+gACAMDK2HAAEC8AAQBgZLo8gAAQJwABAXAbcg9CB6aewHVH0Kfpnm/gQ2Ox374/AAUAx3kEKeDDiWEgmRwREDTBVkmySf5gAHQPugy/Uh5OMM0YC2FCTJSsvqCUT/f+GBkEAniaJkYIDUEnD8AA5iWrjSFlsNEYVe4xqU5QABAAe/1nhwrn8O++PwAHADbFFCjeTIcUrF0imhMxtAFnUSAMPXv9ZBj/QATjY5hQCkkWz64mQkpAAAgXAACAODZfATiqcEsuM3Utg0iHAUxNpBLG7ieRrOiTgABABAMfW04QqwuAYMeIwS4Uq+Le3Uyh8BmFWQELOMXSvY2iGvXXXfeGuu+/Xffvvrrvv9dd4a67668AAAB7EGaIIgK+JDMAWAARgDcGIkzRGATym4jG0Y5RAARVwKNkDRG+PHIW4lemIoEYJGSzn/wxx/AmcEGABXRWZsgs7o9vzXOTQADWHKSKxYVu/vATajWNHJHI/GApII9PzpyFG/+h+lZCyfqu5VDJcAi1+rX/4ZxR+Oi/5eHUCD+fTx//BtxvgALR6Y5qzHVs9IsX/0SaGlQqM6Q7bMIw1mEHEFG7X/FtgiZ2P4/hbgAPj1MGaSnN4pR//aPEHe64jkMaWtIgXtCSn4fHPasH/AkJ6HzzwMACwtQW4p7j+pCINEFOKc4fEKCJmNc8ETKINzv/C/gAWSKrzu0GY1v+6B228OAsNRzeoJ2MZe68Q9ti/RZLgFFNQ38v8EGAMX+sc/m3pTYF4pUQquh2Nu/8EkhJEIjMgcAFpm4hZX7IumUh6gy9zT5ZYYC+/8LQdaClOrEcffrk14cBIWnr+/S2AAwLC5bAKPQReAM0ajJmLs6uIu6J8bU0ANFjHtzKeUA0ZGo98FQcXLw/643wAGpxDZ/Oidl8UoSS/z1+775ZG8AC0w4TouElr3f22LBjpFU3wjEl/zXQziuyViH7Ld94cM/YBEzuGwJeS7q+Hfv5vXLwAH7Flzkf9lJ7HkaF2fodqCvcPTAJ1AQOeNqYP4HOAAABZZBmkKB1ifEnqAv13z/83N3dc3isKd4dnj1RbeFuABc2wMKoJv1A1Ax/wCaAWEu0a7WFGf2BAv3AYbfbJLBv//u54oZeJVphDV//3hiCZQAgu+pf+veEbfyKD/83AAtBEMPRu6bwrrneAlhFMNBmaYgVxzvLhyCR7Bk2OAHCFi0zKL6je/7ZiRSYlO9Zvf68BwNPRXTwvw1CxjWsjDf1nmJXIVB2ap7GL78MAhzC33hYqWSbuWAGEUmTer5//D3gmIZXiWBJIIdwaY5PT4ADzbAw6gm8OpGoGv++Ewv/0qTkrZJpcMYJd4AJe0k+aTLS55/jfxQCwkz2yRrCjP4MAYLQQSgrqFrYX875heiCEFNRtfC/3Qwzxu/+kEPdWOr4mHkNqfTD2r7OHN8I8NwALoxBX9PmDC/3kAnTJsJ8h2KRgMtNKBQCQ5SL+1ANNsdaJRXICi4Alc1Qj393/4bgAWGQJuF9sm4QkzAFgSwJFqQnvRJH+ASBwnBmks5RIiGiPgYtQh7WI/VKxbVwB4kQuUaI/1w94ABP4JCiyhiTgAEyiY2xVISuKj3pk8T5joUjOQ8R33NqbcGkkSST/B8QOjg0+VNqYP5rAB/flMjR+f/w1gAPgToRaQeUFySI/4AMxt8szGtACgBca6TBb/d4wPgDMy1Mv//ycNWgAuA8FsOhS2HlcE9762kXLuj/+4B+zbGXqVXdQw4Q4ZgZHCgcc7CFVHZGd9oIhEImnCyWWT/P+KBXev5Kff/33gBl851bfXBRGgft4AAWDwgcGheVcRgAcgVJ1pzlyG+++B6BmVOY5cpn59/1w3AAThFWfsyohVbT4hHW4SP/n2kAS/ILsNspCTU2TUCoFlzPv7DgAyDN1wX7//8M8fARpGmE+UzlIvF5Bh39OFjSv3QYYeBC3/9iAM42RoSmPSCqh+FuAOBLxK9GTBBo/zPpLEyEvftzuwAAVoAyAaqYNEbPv1cp3v8QkUEItXVgVTZvo/x/C+ACEgzBKs8s4ol/oExgW+BKUmSZS9AXBrRRCKm73yt9r/oawBGbSesfl0R/4WgMUEYLUScScSWD0iA9+CWpEkwl7+IGkFEoq7vbK3nP+DDkKYRSdvj93z349fl4b4BEuvT+b1wEN3n/+f/+F+ABhHkrNom9TIaZ27mUhXDocPrVV3q/+3M71Rz8vDMuP1wxgCEQIng08VNqYACZOyHnNykc4IfK6/m1N8FjsHvTYf+leAxcAQoqPYdf/iPCLzGdYBwcfxPDiGsKc9oPMP0C8b4AF9ICDJCMeTNxN/8wJ8B8WKTz8aWb/bEH2BOsHeyGE3HKX2tnw/4Y4F4TuKpEyQKstjfK2wZGJTU9+/PfimH+N+AA5KpWcNdwI6ygrqBaBkwVdn6o/ReyL+GRExDxChUquKvN7FfwCUTM0ERFO5CLp8IgZ/8UNLfff5segN1LNqG9UH6hCy3r0HuGLWksX/8tNBqmIYNcF1cF/HxO9NDCTk6rHBoBuFVqEAf8M2/ukO1g6Cxjl+KhFlI1jAqhabQrLHP6f//Lx0CApoQUuSAiREkJsxEYjBh1wx4AFjJROklfy7Cjf3YIHu4BBltMksm//+7wDuAj17YU+NNC7whwz0gDXdBNhll8k1tEnA6BJer7+AkRSYqWYeCiSP5rFCAce7CdV3JFt8oCuNvCRHvf/+bhiAAkeaI2JCnhBl+gAetYAmMmpDk6lfpQfhqpoWiqYAAjvoIFVBojUXkzFUdzP+Hh6HqGpaIoNcAbE0NSXef/eIPX7Gev4RxAYgAM2RExv0IjuzAAIwKq+6aNEa6HYNXlkI89XnI8R3ym1MAnRk2Q8xUdkDpCkGvzCE7q96zVARxsz3eenrn/ywAsBsHvTX/vPvARJEkJsxEZkDLiDzFgkbFz/wKkAAACvBBmmCoE3DGABWAr8xRUP8phO+miGymLnGStSdJvhNCg/kHE8/2vEcHLRPCS4nqpDAzqOBLrGdAbpnRxTzwrwTd231IVYk9eAYzlvf+J8SerSMnz8DapqNY/X/C3JAAfBrQp7AmsE2haNl/7AIwxE12lSQYY/PaSf53Sn/9sDe61NIiu/3ssQeUpyKOEme9f4JuEuiwxYbSpV9ngF2Pm4wBwKCFv8EnABSMchUIpEP39QGAIzu+F9TVEGUW+ahjjhDa9njHsEOG4ACYA+ZAGJOIS08fD5ryAHjoAUk8hDTh8PGNAQtHtodjztSXjL+0BCWeyh+fOVJfMv5cAeCrGQ40R/rku+XgipEFIzg9YAPkhlVDEzi6pCTA8SNgCwQ0/UnJiTjTX/vXlp0f/AA8Nc4AUMzxw9uIv/mABcwBYLNLSZxIpv+0BQZoMuTHomS+EtfgFkzAIHaC9RTXFYG//acyAYMQCcQUdQn/3vAcEnQ4gzicUVW1HsMiXjsNqh/8H7wAtvq3L/2COBy+ZPfvQmefOdr0BytObfv7/h/2l7eeVhw8ggJEGuiswxo8Ma6F4R4I4ag1K8W7Lch74uMjDQr7mBVeGPAAeMLKxlXCtcpt+miGymLnEWtSfC3AAtgAaAxAxendIkamu+/U0jROA1RLfv4vEcHLRPCS4jmpBhvNASP2/143Ezh5H9X/4KvHxcCHVLcV0BigUzWAAy0MwOWifEFBPNN70YlUxcw6FqQY/w1htf8KDEkWiWP4wF64Y8ABMomGiFcRlrJd+YAAgCLGKAFe/l0DVkDAYH28AaMLss5f4ZgAJDbnMUbL7141GAJ0IAFDc9eP6iLf5Rb0j0tf002yAEDMBPUFRSJv/xQSw/2+iIX/3DD/4cgAMxUWrdHstsEspIRkQMwpzh9yAEUwoJcUlRda5tT//eYAAgFNgOU/dX3nTSTF0FAFpJxobU/8LR8QH4A4WziqRtoR/tVyB2mAMCCsq2dKwEv8Hsg5ZQ1eJS1l/8Bvzg53O4r9ev94k9YGsp6oDPX++7jO4y433wrhMwLP+s0VNhqCJJe1f2kAGyZB/siBGOACjiOA4KdtTUCD+jrQIRnMyos2zzz/4sAPwq+o/33v//DkABOIao50TiMLW4OzY5l6JJN0GZ93/8l/AFQJVm1Ptq/wQYZgdYAHCJxY+bjUTWHyCKDqFNy0+YAgBmGY1TC72rVSQwY50wBM2tMXdAv/wrVgCX0yX/a/wwCDfYZ/c/Wti8P//v4ZQ3L+GtvABzAqEKMtP34vmjq1nKcz7gv/ieAvNrS6Zz+hhqFPoX8MYAHgQqfg5VQfZ4h6+gxslnpZ/AaEuMAFDc/eO8iLf5+m2QBAzAXtJcUgb/8/XD2JAJiRGGj//v7xIWgARFgQx9RIxl5dkPkhBcuxE+civLvwfiBpg49dv8M428kUD0AxKPbY/Pn7k/m394oaAI5PnI3x4dfG9LDdH+L5uqvhfgBtnz4f8fkGMmOWr5XrvAf2BHYnIOlRZHoZGwEbRZl70j3P8XDwAHdiODFLjhZcSyTv0mQ2Q5OUZLFpD8F+Q23bvRUiaWv99/gAJDq4xVMwraQQ0MwMqz6G1P/l4+NkwaOCJf4T4fwtIh6/5bsOD/wxwAEjzQl5CCtpRDfIAAQA5aQAJzpqwKXuI/mONnXGcV0IJaGB1JwA1s4SOv2v8TzcV3w5gANSMboYmcdKlJ6QAb7oE+iLE62LwIWsfv1/hv6fCMDFplAguJapw9Z5t4PY6Kft394sHHEiHHyP6v/wvh5bKaOD4HXCQ5izAgwEf+o7/DM2cAO+IID1DMQrzhwP6431F2/o9hMVf7v6BI+cBDzq3vLQSYtMAJ+qjIomxO+n6Bit9v3NGQccI/n/YwADAVCafPQDx+Bm/fPmVu9P6vAagDpBxSINe8jR2uhKtN3l/+DCm86tNyCXKO7bwAMQgYx2TY1l5ZluRAQh9aMZeZXf7nDCZcCJe3Fee/tLIAGRjuAJErOE/+g/CB11Z1F+ALESRVo2p/43AAc+RAxZiqYcEidym5ohk0E1a2N4ql5jd91H6i/df4BBgKnsPArOlC//v8QAAZgAGYApsXNEYAc4WdcZxXUotv+BswznU1NGvPrAjQIVvMy5s2Tjj/5YIvAKGuW4Q4u2btAoJACLub6GMBXk1T9/zGcaOnarg9kp//55Uwl/PXD2AA2HBNomUNhlkN+Q4vIuM4jbUS5gAAoGJwFhNqaIwCIVNsNPttkktsGOXzqZx+tIvvZ1u6qZhGaohnppgbzuAH4gHcEtLKW93f8sAURvjIQ28+a1ep/huALwxrU2UPd7ls/gBzhYqoRx3UotrgABIOXUAoJtDam9Q6LlPnmW2yHACvwBJjd7ejt7f/i9yhZ6LD6DufhXyUx8UHhYCPXLH076df/hXzhC7RE+6myS7mAACgKTQKCLQ0Rg/9Q6LVPnnW2SmBhwHZZqyMu1f/xnJgDZBd2P2oqiFoh+GeoALAhY1efeokLmO+/4vaM4+28Hv//hbsMMwTJg2ABAAeZIDDGXdD3zTBG4JUdEOZVGSxaSh6eC9cDR/8K+Mh80qGJgBgmvHKUyJvcICnQzf/G+PiCQ/FI1aDTbkx0Xjw4X0GNQBqH/iA7AFoHYQg7bxGS//+7zGmMco3X/MxawFM/ARiBbdNR2UQM4PQYjdYmpsyzzj/4BgHRQgwUjKzheYnvv/zAEri+An7d9phWi9N5FmxJzsI3UkMYAAJhiLBYQamiNzxCbbo9tMh7eBskIAQt5d0d8GjJ9///+bBYpzdpNWMtV/hfedfdH87TQQ9wzWYuy3d4ATOVxxy7V61z9xEl4Q6OsfJtWkrD5xhX0gpLQ+eKgnq+w8dquWrf997mNlxTKQXkL7AASAmgTOl9F3OHr5f4A8APDvHqkS+9/8bcAAJByagFBNobU3qHRcp88y2yQ4tOKf4Do0wA2TqN1kUJzo00Q1l6J03//vmTMJ0ObsOpS0euhmBilx4ooIZJg1QZ9wewDrts7/QP4gmkbZw3uxY0eX8FY38ME//764OjgT/dVzif5dxkOFoE8b8OAArkgGGOu6HkTDBH9JkNkOTuMti0h9JAiW4uBYbu9+gRABUEKFrThviJChjgwAS4mFqyGkNffrMSOLEuxtS5P3//mXQlAOLJfP3wR+Vio7hm89jmX5VowAnVVG6iZE76AQBSmAMCSka2dKTEv9oGKvV/c0ZBhx38wgHiw0WGa3s//rhmmdgaEJK+GE6v+IDMBOjEqmOhBeWpAdQFA2pEKZu+nvXHIxiBimWqGrZar+ICuNDp7DXDxo1+8UEu3V7YZBLfDVQx5eREvt/mfvn/iAvgAVByCBZgpGdXS8xL/dZZk1EsImp/d/QEVBGBylRwguI6KYeHoMAWWZkEV9ucm1FZ/98EEBMzEuKRSC8haOmQGOlEIIW4gjwdwzA1OH1pLzwGZ2iH8D2i2MVgKVLgEB7G79qVY+aYcuCfNfejggQ/rW4PP8LQ4KGywltR4b39+gYrdX9zhlHHHfz+fU07n7+EMQesBCPuR/z/7xIYhq5dNq2NRu0AAPLuyn/ieAA3IxLyFRheSjg/VBSbBNSdBCfDBgvnr4EzcOHL/EHrz9DOX9d6v89YdhpKN/8I4jxBuAIAtyu+Ig6vCPJivJzYr3ECQ1gAIw1zi+nsRW93QwFsADXu1p0z/+GeiQyWgiyO8nid7/gBQYNSlJH+//gpgAAAPcUGagOgd89Wcf782JPXgDjrTG1P0I/l4ACZkMjuIvEEqaxQbxJ5CgJ8nuz/+N4X4ACQnMLs85K/xuKacczf98jKC1mD6e9NqffvPIBNJQdJi9Kwnb2AhxVZkGybTe/dwQGOLrCZFkm22NLwBM93n06LAmLzhud/EheABbAHqAHBGdRaEsZG+/gFAQJK66Cm5JEHn/+BTXz9Gv8/UM0V43Rn86/4ACMBooYMZfRljfCShkhW5U/vGyW9D/Oi3JL7xj+JDf8QDVAway8jPGtElTIJr8Q+m7E9p08/wzAFgAHKAA7QHvDRojADCr0iKUgz7WU4QAAXBirB4acmiN9qBLQ0JfDILeoAniIh2OjvPrw2BesSHOAAgAQaXtBqyu8eaNZQO+ADDQQ0GLKbz5s1lE6AdBwuMcAcWJc42p/xAIIALAmBFrdyNLgnbwAsBPwwUw4lHWdE0y/hwAGYqLlkUl1totwfjFWxW5yDuppTXAAC4KZsA4NOjamATjgu2TSHU2iiOC1Ju3UvIjqkWNSnpTvggkWIWjaIbU/AnlBMXzOVe7+JDkACwMfRPpkscIXMoHX8BIGNQn9Su+E7mUTr+B5AzlUT0Vgj73kQIROt9NcI+9wu0VHWv2MHQwBYBU/dMNqf8SesAXa+55//xIagAXoyAGAjwJ0owOwOv+ASiCUmV1KVRnfu/wCFzgzgFfYJJov/Vv/8MwFBj2QmYPcmS0jHv/B8SABoHvWKgRZR1/+DVp35+HL//4kNd2zFgLlp3z1/eM4XwAHWhiC19Ry4aF91TrNFTQJQZJZDV/QMgcFDzxmUsuG6C++gCgE+DhrDyEc66RXLFLAHZDdsN/KH2a0GiF+v8SpCrjdlAAZoT6sLi3a1iwBAhAEagCwo1NqbQmBt3R0//kzLTzgJ1FWvUm1NqHg7D33oBLWi6Bxda0aTVvsAAEgQBuDpocNEbyIhEZDGQgyFKR4Y0JyE+T3YCOyghYnY799tlhhXGzP7X+GfIigu3gyX/Qbnr4P+qAQwikZEGCDTQfaiJQpEn7/ec/fb/+cNvZUf9+g+nV/5sAEwOwG1A2K27PMABkH9TSPX3kZCKymFxJCWsTxI3wAEh18R1E55NMKfsAAHYAARgDnxs0RgBx5M7oYo7qYa//cFBboq0uptmuBgINgAAsCm0Dg24NEbyQdFqi7Q622URwwxBRYBKoyGl3gAkE3OkPybJFZZs6/iAQQwbjwDEMABwAg5tlNOQyyHkmnf4AAj8wyGmy4pp5wCLTFpzzam7x+cmnXFmO6AU0gJqR0Ft5wa/hiRkEHKxnPv/QIN8f8McAC2gA+Gi2IP8oa5/aBIIWS0Qe5MFeMd/cBO0QAwM4HbUYHIXX/KLT04BK9ACglqyjSzbbfQyPRfcLASPZ/3SCT2QlWFUv/v/jeAA4ISiVVJxKIK4W7/8GAgAXOgByhCefsEYonPYAkMgBihKePskY+NDQAAQz2N3XAGAAkPrmVTEHfTDH4AFjwgQ63mcvpMME16QqE7ip9+usl74HzR/9ehzTiCzQINQpVj5vMenhncwWZOvZNpd/ef4bgCgGqBg1l5GeNaJKmQ8UAdVhlzkrp/f/rXhZxoWaw92//xEdw18jKC5mD6e9Nqffv/WAgoqsZkmybC5iwoKMjKPfv1f/w95mQEzNHz9+bUu/B/qwGFF1hMm2TZZDAASbIScp1INy1ocAAJgwDrwOmxw2ptoH5QbEj4LazrkkHp2rst/32ZhlH2yyT3k33yNCoszM40/fqB58DkQT4/djBnibhwr40ZtfhmAOyGy8guIfzVIDPit6w9Y16/VUz/xAfgAWBC0JRoSwgTuYQOv4CQIbT3YG58QuY+ff1XjJThDAKpYFBVobUwBW3NChWf/9c4EyCKVnG1MAjIhopDoUZLVJtsAQji3rwt598BYC0oNiBkVtY1+gEUDwL+vGD76N1t/vAikAfzPCF0wwt7AoQVN3z+VTCuLrhqadC/hZSQJilUn8/xa2AFLb609vX/8PcAC9AAlD1rFnoMGP/2/5gEpnYYfiaLnUMphhwgw5/8BSnxbsI4/RaLvv/8O+EHkIArFAaFWptTAAIZEinZF5A0kmleg7SAMAhmkM7PqqFgaAASbISKU6kG5q0B7QPyg2JHwW1fWrBKhnKgrSFPtO/I2hH9rAGNCdlEXiXJWxPG8YqzVz41N1dPhenNm1NNl/3+FSwosiq/f3ZR1djN/C3UADUG4Do2zs2R8Ib4PRQc3NSx06rc2AiIhHDlsxB40yi+GHUcPglI9fnD6BQjZ3P/xAXtx7mDBD8h+ggQ+WD3vgwG6v/835fP/D/AEPZaIPIWUkY+//YCASIcAHBOkSglY9//7v84DJ+hwPgAJBKgsporX24+CAtTles02QXLxr/8LQAIzAIKLrChBom21+6AMKKrGhNom0xowgXcsfP/pNU09yDILKJLp/udasAKASYMGsPoQxjhNQzhCjEYnqdVfug/GpQDgSlxA3OwDrUbqn3/6560HDGffH8KwwJSbbaypH/9v2VtHdzN93f7AssRnn38mA0Sb4/L//5MwYEgapeGOAAhwwW2Em4yxjBNdoMxIABgC1QADB8sxm2L6RtmAvdMb5tu7pKLHDgA+0PdWR4vucJWCX8F+cuQD0tAMWylyeQmS0jHv3fwkAGwe7hiDkFDXf/AxKhTDlvcfy9L/h2GDGALF+Vmubhwyh4Th5h25obebUEP1JUmtPPA17ITaRGm5/+H7gqAAmZDIVTC5z0NYgACwfHC8F7zmi4PStl6kkSEkyIm3+AEUJKxLiM7xUUTafh+bMbrznUo/tX4YcHdIA1dVI0/CDBMvu3f6//C0ACMoAgousKEmibbH7oAwoqsaE2ibTGjCBdqxs/+gxLj3M3BLqh8v9kxXnwG4lrFR9uyv/+aQkjERr06v/n+I5QQJ3hA3O8DWeiG1P/8F/tmzpg1BFGvc/p9YHBQ88ZhLLxuQvvmijr5gYAWrFdHvdI5j/+CH8CQQzOcjKsTFllv+fB8L+AAxaDEEq6jlwwL6qus0VNAlBklkMX9AyBwUPPGZSy4boL77LwBIIF2O9vZ/hb+ZkMjuIvEEqaxQekABsiIFTZlDNaP0BDO5nVFiYtts/z15uvztV/8M0TAJAk8EAVCPjk/+L5vAATIhldDCYklLGJ8N9gAAoDgPscODZojAIjE6IcT0uSpqQGuAMolmjX2v9c9bA4eX+PrhnZa7tbe/0BQ1KJVb9/g6yIAwpw1f/aBlwD/fG+ABYQr+Yi5sTFhpn+YGhPwBwSQhbjyDLrX3wRGAxWR0965P+7/6Mgle5KSV988BIO8LhShcU+PGtPBiKL4AMzNOc1+wIbhv6aAoRON/L3wz0QyAso0MHRJQj/wR8E/y/uAN43k8kFKD6gZFfdnm/4ZuAmUVSt42pssHaC0gbFfWHmAS2MpgxS7ScMLJPBnKOoiEhucfl0fnCf+GJA0/gAWCAOJTSo5fSxKKp3PF3Gc6BKKatf5eAl/a9/v+F+ABYId/M67sTFhhn+AKLmUAoFubzyhhxE6AHRhpLCKm7yggMGCjfpAAiLtWk9/Nk1JP+amQqABmEibaq3/+5bRHk9Oj//eKj4hvT2T+HPAAeYASB7qWpO4sY//5cJ+TY53+GPpTMAQHJB/FWR2B3/z+G0MGA19iEAS1xmRfzdDhlmn+E4APN7qmiO7/r0AMn/zVVsBT+Yw4vMcPJNprPehsvMLii+a5UAEuGQarNeY5++8fhvwOU+zYYGtva/+vfeARyNIZiD1gCtq3P/f/8QGYADhSBLLSdBSx5m74MP3ODOVIxNZBGp+v+FoACMcbFfCJeRTC3h+RD4uUXaHW2THDYOBhNMgAsBDN6xW6LSbbPdyxBdSXhMu4PPTjZZfgggLoyAGBng/UFGh2J1/3DYAJQ1UtMicpuPfxamA4AFBmW3E9VHkvjAa8OFMvIzzvpBUxqgAHOoEShkm4t7cKeQDbBw1l9GGddIKFhsDB0YlMQn5JLH/t4BZ5LFUwRS/afv/+Jz8f6h8fvQB8AUErPgt9tvncQMHSYFaAPiIRsDTPgo+BVV/C/FBLal5ZY93+jIPxKSevvXwbTOeia/nP21H6iS+6GXxNJLQOHLAHgJ2uMNFWg5zUPpcNcNegMaiEyc9EloGvfu+uCHbD5/+FuAG6kABgRvxUTvhdf54Egh38zrmxM2mmf4BkFBQ8+YnLLxyYvvgDjdp4R0nXLgkPXFnEutP/gQoFKfnHLVbMcXnffXeFk/YViOP+fGDG0ID8EEADuu1o5OPGAF4EWAu+Zfofawa4GGgI+zEcAC4CooQK/wSSqPLlfeQN0vZWBs0U+jIHAGogspUve/+HaYxtzGCl/QMdnsTdWImw2v/P5QABb/Ay0tg/EQamGbMq3OQ4/+PxB60uev/EAwguEgqLEb4n1PaMAG6I4XqMkZvoAhUIQStqGHDIvor8zMZSqc6uOlrU4ADFoMQWvqOXDAvuo8zIwnUReIJQ1iBQ0DFLP9ppOYEYmvAMX6tY7/ioeAAmRDK6GExJKWMTyQUoPqBkV94eb3xAdgAWgAJ1Rh00bYrXTiGrLoNNhc1kN3kaINuInEkJexfNeI4FNUgeZF9Vf/coAAv9gVfPkRjdaZiKS4+b/3+XQCI0gDDAA0BSUGpA6K2ra8TUAA7o7syffwWYaS71D95JSVPA/9wETE+xxNS5KlpDqwdBcQNXxZ9PeuF8ACgFaKCDpmEqPGpC/+6j7r4PQbJdDF/ML3+GKIV3G7pgW3VQ1QDADjAUjnSregH/+N6Ax3ez7ixE2m1/5+kABMqoETZtDdeP4APrjci/37/kRCIzCKxBCnMQGHgpj4iaPY0phnoCXsMUUruOXTAtqqMVqu7/8wq1f1f9/+SAsVoN/L+IDMACwQtlqg8hcFeMf/dgCZCgA4J58oJWQPf8D8PV2r03NkLnlgzMmjn/jfAATQ4JdE2htOkx6XGwAAWBC6B4bdmiN+h2FyHhDsYUED/jAAEAmbFABkFbuAe3cS8Y+1K6mYR2sKcMAiGGClTClXjqkLsHK2cNyru1JUJdfXj9xjJAdCfDEABshlXEExJPqUlgAAoCgPscNDZojXIKUF1A5feD1ecEEoqkXhtTAImJ9jm5RvU3wYd2DtBa4avrB6veuAHG4BOLyO8+U4f5Zd7xB4sTgP7job2v/4g9ZD4z1D//JZRWwEsQGsgQGfrAdSGWq/hEQvmxAb2AgBABbnd0ZB1eUzCX8gOvSUn+vB3AAAASa0GaoEoE3DFQALyAMZ182Y1qo+/8BQwj/cmpnxU33n/4FzEU+CMJSh//b9AXEAfHBQougjmmRMZSHBgH+ANFb84PAwiHJS1Py4acoKYnxJ6gDVcuOPjzekjr6/WJPKWBCPINDa+cufP4kLcuR0bG/K/maq3/EnqZS3LR3nDEIrIsQ/L/lxMdia4X4ESrHwCGWt2ATDASJmBmOJr3y/+wgR1qm3Iy73+AFgNVAoIbJJz7v5hc94gGyA4JdJpy3pEoseLcImH2mAWcavoiSuX8QF4AFoAF8ABAfrsHRvKcg38BIAweGX57tg2RDX7gPjVsqMm2/1iI8dkIR3P+66D+AAhDbh4JcJJT3r5dc9FcXKv4BHV1fev4gN/wxs08EOE0pZ30useDg/HW123cD/wtAFgAFgKAfgUYE5ojADEYiohxNWQljVh4CN5LGbxtTd8ABtoPiB8WeY/B4gwBHtAYHnxtTB/Hg4AKyIDw9Uh+Qfc8ji254IXKKnhEWevhnlFDZldUnBc9pfRe+vbxbs+/r/hzgAsdxEpVeZDf4CxKRaVHnRv8ARfwB0oNuQbU/8bgAIxZlKzCrIItp5XyMOjZZtKJsijifCAN0yNIr/rDQjlsq8guXiIt6CC7eY5gAA2BDtA8FCU0RvMwoNtmUsmiKPJjIAA+ZD5cAoGrAoUpgBbrCMwqHt/5/6cJ/fWzfDkACwENgz9C+UStjiYo/gJAQWxiFDGkS1jyAo/geICEVj0JvRH3vIQGOrHIVfiPvcD085EfgCxBaMXjan4eiuS4agAfMjACAcgBHV3woSv//uAljOxehEIZgpf7v8JWmAD5W3mhb7e//EhaAoMK73fcVoqbj7v+D5oAAmV2DJ02gnXgfkRCIRhmYgphDmBh2Ye8fv1/gQu0f9+vG4gEEAC0YnBh6Axfv+TQk//AFLAXhMaw9hrChEr/7wQMZFi4MBMuM5UGGdZaY9UEpxcAFLj3mhb1+6DkZgYbiYP8Qesry/uvof/EnrGEH91Pz/+N8ABsxt4UT2E4xqgBBDAFcsBQffG1NoZQLmYF0S9NqfXnAImOYzONqbWFwQkUhKgY/rVZm+3Mtp6fYAALgUA7IoxKTRG8zMZXU4urJS1qfDFb/hZZ4DDZPufw02FIlPz/DPQyA2VoTND8Xpde/9WAwo2sJlXS7r4ZBZazH1ix+/V4af+CTAATQcCbRtqJp1nE/EOOpnQRLn240jvEDfAATFG5WQVJBWvPI2AABAAoAAgCvAElAoaIwAwXfkZRVEE684gEB8sMbLNpBMug4ngw2AADIEOsDwUJTRG42ENdmUkmnUaT3goZPUfMUxKR7vIleJkur+JBBB4NJd2K5B/Fy8Bgi+cNUTzhPyH0u9AWgyAHMSCXrZskL5OsDAAQJwpzkscSWos0YguABDCSxv0IjunEyIPdHzs6f/+DAHErkdjieglDGq0Q2kEfMl8TcgYY1h4L1g5mq8Zf/vAHVY7Pc//3swuKKnn+H4e+gH8PGRzQwAWgYhZoRk2SPkiRu0ADrDM30P9a2XlGZyClFuI8vQGcc3UAEZEaH/mv7+v/C8AcADwnhyrqmkHS0EhXyAAai+HquKbScMQTFQw4AFhccNIPYlNBV10sjI6+bRf/9fCFcdMDKig3Qg2p+ErQo6zT/3t/w3AExs08EOE0pb30useDt4ApnCqjVWf376Br8HbFaTqyr//f/4n4anCAJxAdbeykf9+v+M6pSuCCH0Pl84RHh4KwCJwopBd0IAHmFx8sqkkWTR5TgABkCiKwFjYiNqYD02cGuBCXjYl/qs433jY1G6oXmABQyA/5YTVNCTlPfczODfmBckfyer77gACEYQBpR2lXHsDMHrwwAG+yg4iUhHmxuHnSiHgZQBzDgXdPpRFPo4rwDET5y0HmLUN8smkuNvJeIGUjXSlnHVE6AUtGlDORLKZ/+k1wLcHzSYOABLAFUJSg/L/tgt7TaI1zSDFsuELf0Q+RWIzYNwWYYPjY2EASgTwjPyjKb/M9esUCPAAvIRX7N9iq30AogEmBBMi3Xbh+3xr+Xd72uB6BxcNXjIAEoFq5cuBOFiBPRmNgYcgM38ek0BP/wZFxuggFzHCVIIlqPJmEgS36VmtRuNhL/r1AY2sbn+N4YIPAH6CBijFwm+AwAkJyBUkPHzdy8KSrO0p/fEAlUUCj/US49cVv//uICBTmH58Hzm/BJ08K/8bwAXAwW8Jqncqze/w+AgBMnUI1Qn1fE0FE0vAIwSCEthV0Mm049Bb1j/P7s0OsYIs9Kgph9tR/gJCPwAoS5ScVCSDpPQYbAwFEKqn0pNaVZJBP7hsc8MJCh2kHEvwcWXaWm54XWgBc4xOk9fv1Ag3ur2VPP/9sECCQ9xLxewfz/D8MrwBzIZncZuILY9jA+IAPFD0KVrlEUKK3X94w3wrUtxDOXhDPAQCJt7wTrukKMJbZD0WwMdIuGsI0cSv2gIECQNmoAIDyMcqkmCBO/3vojZW5TYnTuGeCBHxSdDU/+7wQhbbpH70f7/Gy3KDeKNeHIua0QGinuLQm7l6kABIxkMynF9RCnvY4AAZAwB3YCrMoNqbBmF4dochvj+ovZw+kjv/zhMs3n8I0gC7nzXqL3v8O2oVzwYC4C0BhH+QmpsVN953+cQBzjgwUXSyTImMpD/gwwE5DM7iN5RfPYoPgSK4aYdDyLdgj/BgpacIQIatrc9JnqnQ/8L0U0bEPJlCAARoI6kOLiNKIPe5Q6j5exB/hb4oITPSTyMLJE/TLIHCHlPxqbAIonQfDKk/8QHZBeQAAKAYAFQCC0NToY0kVueSFf94RimDuUJUz9pNRX4YaIeEbhDHMAR5nmSHXo8CI//V1dU5GcNfGLshyKKokinnFsAACABgABADeAIKBc0Rg/A/LlKjDODYz/a/Q8b+FfiChUMRB0kl48Sj5gAPDaCF31uJOmJJC4YfkAA+PoJXeW6k4YkmLgjDiZPdVzJo4j7FUikURBh//hzgR/uo9QS8EP3tf+GqUKUdWn1xhw5PX/BJYBIAzIXAHvhSHYGAAkPVTOm7KudPBgLyOzAAEAcAUXKckHUHHg8M4UD7Xh8QgP0Ox8bg6kfsBWIUsEDeMtF2rZBkz6DBIBH+oAG3euGioj/N0YAHgcl6oKQ5YEznBtxrg8zgi0CP+GfBAW22HqkFsqPHFxf/+LFBoIAwDWcaVV+nAFelzf+C+Q5JJ27oRX/6GAIGDNowaovWnee6omdgYAk+wMcAUDHboXo97oLxkskM9r/GwNDNrMVYVcp/+0G/DCfogs0SUnzvDLJ8NBoHLwzEjSo6o9QqOOl/f3/b8LZBsHVGSVC8bgAW0ABqDVrlCdrPlP7MYYCsxIDjEBa2Db4mjJv+D0AgAg1Ve7+OLGpKCufHg5UKEUPKHY+Ia/pC9qgBvEb8Hy2KgfAbptDhpXBHIIYy6/L4mNkzvJR8MzIvAOfkve+tfN42mPD/AATIhnKwzMWWtzm+nwQg5nsdEBEg7a6IABlRSAiaO0J980w0IiwPYImyl+/uAQ5HEo2KoXR51z+5gK4YGiq+KWlKyiIP9y4dcALKDsd+GR//v+HF89cPZQ3BM2PEBG9aMoeT7/gYXgADDmuJUYpBhVkLSWGGPgW8XpAZBV9dfuv0f+Kwz1/WOgq/h6pHKgiffVP+n4clelAZzTvb7+4aTAgHtR0v8NyL2w45GU9Iq9t64A+LxJfk89/XQL/BFAATH8daPeSJ2uqqGHi+G8cJjAFOaNDNNge9cF0fedPzU4vgg3vHi30OjgDlrvfZyuyYMAZmrt/yfJ0B+bh7C8ZzYJdgbT7THwlqCQuYs956rgtL8MxpADDJPPf6Zu7/hmkgMZA34Jw3Hx5o1/v/DHAFG+WamA6ABvQhhLoa9jZ+AA6YAEwPePbArC5In/CcVqBoY7dBtTh77t/jcquOhAfjAFssthIB/pNggoS3yOHxd/qvLkOEvSOj4WNTaIwOaHzKY6sUlg2qYOAheMbhBKaI8y80kkyANFNGv9xs9a2CNfDvwxABvGTMh5DoVMH5EQiMhhMUQhjlAo2A1QNEiZFBrx99OSugv+H7V7j/8RM8OsvkfR9mMNAY+Gc6IABMTOUrDMxZbSHLaM8TAH9zCEqKWeQfr0XouX7BsB70K/f4INgcAB9KmDPzAZQllb3OOAEBB85QLGRT9TcgbmAMNfpTO2PLN7RzMRRJkpK1b75k/OA3914YuUot7s1KFY9vEGjBVWbhNkCJqfBhgdSFKhqK2gMQIkynzf52cInD2z/BVogw/L4jQxUKAkcBkfQ0cEPaNnkq8PwAeCIgRSnRKU880uQBeRmqX1z1s877Je0PTerbKM5NmloHwQbAS8NswALrfETNkm/3dXTHoAXMHF2yEj/8XRHHyFYy9fwxAQ+CGGM/jggJkHLMED842hOTrBPSj66BSKiy++GB+tRc3AA/Sxm50lm/+v/w9HwWIAbLGUapXFvT9+h+MAGNxD1POmzhsCBZhfXD//h8l0x++CLvsHZO3RN/EAKYAHga8pqJFZXfJcIhKDjURayDnwljJv+DDEBQoAZgL/HxIr4+RUHD3rwNnPamkHP73+CKqAAL+ET3dcndSL7/jbYAFggpKHdt6Nm88//GB+TAYV1TKIgiT08BkBQKCxVdHJSiZSkO+/TCZ2Wh8BFG1dX95gAB8xOUzsO71Eqc9RQSNr+nIGIOY7DZAQfcMgw6gCZ1bkXbhsMA8QXo/6f/+HtlKdKCgAFQAwwzOkU51rbDz9AfHDKmXEdoqr//ihARpGgC5EvibeZaEI9Bsyeg/G5QGRK9sH/k411X93cBt1f83wnin6f8DQJfLc0hPtYaKwDNdpsX+AwGAInEIXfa1i0qd7MAhVxMqq6xNH/4aFuAQcjiUbFYLk8+5/sODYjhbFW3aL/tkFfgIKoIJjbGlOnMEiJvnMBTDg0XXRyTomE5D/hDlA2bA3I16ZJTQrEpvrNG0NNQN5diZSBov3v8O7uq73mfwMBdontLZQfQI4qMCyFF7MN3tm2P/7C3AwQHT/8E/YOABJm0lGeRNhr5do7/kYAkLlpIeztYtaiXFvjYwEyh8EPtkCkiNq+NhyMl/2gAAgAsWAACAAQRqrAQR+MslkIeolgNUTPGgatvo7MqX/+cCvkrKbb/CRKgAUDSsax8fWcMB63pRRyAHqOKIdRm2LhaBBqu1ZS3/rMQlVB9OpZXxsGBAKBmOMqkzrlmnGiv/0gkGPuX4AEGYBhh1o1Lvlnn/+JgEGH2hUs+WffDy9BIeNiFWP//8LZQEddoIBRI03AADrAFR95ZrqItRP+xGMuBdPyxVj+8LkqQQPAN30iPr6f/jYAFwBUcFCq+KShIwkId9oDCkJcm60VN593+ATBu7rA9AmTanL+1sCCEXSpLk1Hfu8AHI+UoRqkepaVFuzg4EMBL2GKMZ/Hb4k+7ZfiSkSRERIFGgAAjY8gE1RAlABxYKFW4dG+79eIerUX+IDcABAY9lLmBaW4zXyQJB8BMAVQvqKWLUuQ3P//Bh1tDxMVv3Rt/hwqe3u/P/1SD4c2BhqIZgbjBN8f961n/VOxWIPMWAR7J32dwwPvghjIcBUk5gw3LxAX8ABGFGU7IKlzreaR4jDDZpsKfZFGE84ZAeALVqPnn+HY6NAEGWQMC0QIEcAAQAdvwZSSIF51U0QyF4m/X9vh+HABuDsAurCWe5PT7yJzOHytzRlEx/++g/Gn8K0Y2SO3T8p71RrMX/wxsNtaNeHU72caw73LXxAegAIBhbMXMCUsxivkgSD0RAAaA865QjShEn/bwQeAGk/8pf++ApxQwX49uElSIWgIUMSygKmPNygHNoMya2zdvCpqjISl6AY26NfhnoBjQY2RCeor2fKfuwA3UwAGB3UC47fCTf4H4Hdt6tJEMuX7ywUEC/4LLANBj7osQ3AtaBj8XI4eqcvEBy7eUsZ6EgUSp+eN5LsN/EBm01rlfvn/8Dh4gMQAEwoylZhUkEa08hgAAQAKAAIArwBJIKGiN5GHRus2kE6RRxLAABkDCKjJsSmiMAMLupGcVBBOvOcH5mFht0ykvwijSw4MqMAfYZBGm7S0zZK7z4bzS/eI+fBhHk0AxnnNW/z/PwmXNg8waVJUf7/9dViD3MAbS42j/n4C9wQVaO/zcAQAEiipTyEHV/E518TJiA3wBAASKc5WMg6u8sdwCJqPeAUp/n8fyb1WJDWAAlCNv3ZmVV/hrABFPNdy3fh2i/hn5owaT5nZFdFDDgBQGGpVKkGHTqL4KYAAASy0GawOgTcMYAE4DhDHEcnS8aR/vAIWy1RB5CaKSMf/9o1AxEiI4r+S/L9+AIiHABwTpEoJWQPf89cAYWtfX/uGqJnU6nr/38KYnxJ5yjPYE1JKu8/zYk9eA9uFcvNiT1ASM9H/fr2p1o/79f43EhfgAWsAJAW6ak5Box/+wEyZgCAUkCeKsjsD3/gq+u39+9GOmKxnEJ9RpC4EGEJc+AGNKaQfshYbnlyw3e38SF4AFwBLBww+ThB4xYV/4AoMdyXL2rqSjDTf/xnf/+mFYrYlvjv9/gX59TeiX/23FJUURI8AjYDGEUjMiySYZitIonz8GbXzeueWuxkP/JgAMzEyKcXUO5bUdoHZQTEjYLazrwtYAAJggDMnTY0aIwCdDZVMdCD8tSHAi4xa602pqgFAS/GKbu+ng+EAViALCrM2pg/qAPcCcb1Y//WJDnAA9xazG0iK/3eA1RzZDazK/3eUAeKKeNEfgj2NEf+eYsA9cKdLC/zDYkfjtZ5/EhyAAkAEh1AOULTt5ghFA75gBcTQpJpPPmyUfnaJAQvf6VfT/+3pwGJ3ISv8f/24GeTb8N/WsM4b+gHgY99w2p/xJ6wOkZVf/xIagAcNVVcFoNkv7V/AZwIZlwiGyX3fsAr8YopXccumBbdU/BSkpFJXU6WqALcxbxhJ/t3Ke8/wtAkIZvN6poTJlpj+fzYAG+RQvUVYzfYPzMxu6ir33pa1IYdWMVX/+JPWAau0r6wXqR19eE8QF4PMOeOzOP4uXgQdGtFJoWv7vdf1+hOAhaApmtq/PfEcgI0J0Ux0cb1qTDMWAiCTMLPT+eB/4YhgAWDEkpFnkpsrhT/7oCpgBoGuoao7yxrn/gNBpygAwIwgTErYHf+bIdCc1BywrcCpIyw1ftEQKApYTqJMiXZbvwqENG703/c7qk2KF/tCN6Hb3aYwqI3LqX68H6fEB/gAODFshMwe5Ml+Kc/+DP112GAAmKJ3RDlEday3ftjgXdJrHYTTnJzQLPaXNvbBlH39B1JT5n3f4/EnrAe2p6g6mp6/xPAAbjgu2TSGU2jHB+Qo+I2FS8mmmvDDrjagCCGAVSQKCrQ2pgAcB2A28NW7bV5wImMUqsNqbUJQOgLag1IHLaw8/vAGMhFZTHQoyVq/gg+WaeFJ5rpZ1Iv/4MPQgWZBqZc/BfrliH77wJAZVgCD24fZQxxl/AKBi0UiYOIVJSRb//holAFYRT0kOPy8xAxkTVoGYxC+6q//f/jcABGLNysgq3EWs13yY6JVk0h9ugx7AABygAFaA8gNGiMHgASjCXssvG1N4YVGkYpu1Ap08uR0KLQzIXhulIN/3oYYAFsS8BMvyBPboKP8H4ChjzmrS9FIfimf8GBu2AHugiILi0d5xmMx9ELy6ftyh7NL/Ejf/AAZ6JMa3MiqgACZEMroYyFCpYpIf6JrI0YT1F8CD68X8lutbbef6K/MjGR0OZSD8xaIbgABIEAfaB00OG1NrjIAYGeDeKLDsD7/n9CAQUrZFjO3qZk72f3/eGAc5s2fr/hbAA5k/k/XX/7RsTAozwhfp08jdf8sGVc9qI0jmhgTkNS1psEGCnf/YMOImUFebryI/v76wVQsyB/+CCAAmVGGyX7LX2lHPAAEDLTgACAGHwHP+AlPBSR+I78+ABQLoF3eIttqJd//g4xnS9iPT8BXiLpVTEWdfwxTAGQR1G+d9AARmr1dv/pCGRbZJ3W/GzRcU8bAkEM/m9U0Jgy0x/P0Ygc3LrHqZts3AIfBCLNXKBija6n5mQyOoi8QSprEB6uFri57pf6Bq5Ly6rLD3PgIh2OA4HM0xo4yob/7RAAbIiB02ZQzXD9AhmcxFRYmbLbP885byswsFVOvy1z9Nvc3LHF/wvAkGMz2pqKEQbZY/nEA7RAQeMynh03IW/wBkABOqMFTRtiud0hqypAlhs2EN394RRqNYsIvOnGc1l7A7zi6fkqGyQX54MQbflYYI4OsTshxgAA5AAHeAx4bNEZfClh10w3t97+DGALJLRtTev4kL160L5RHv7v/AASHXxHUzDk0wp+ASYEBFRCi7kjhe/5wSYKaYDIbw6Zell5ACzg5FjWLdWQI5UHQn1gUHkqWiJNsYvcuePZMgdMhc/+FoAkZqQRDN1Po1qQw/3wvkfsaQctRXJP7r1+GFWPJZ/93/+N8AB4DlKAwtS1kU/Lqf9AARgTnGag8pahPlP84Bj2QmYPcmS0jHv/eYAPCaFJtpa82Sh4/4HOIF6NZlRN8ekbofEgAaB71ioEWUdf/gw4uRQAJ63L+sBlRG1HhLa/4IaXUZH77FjQdBoqSjr+JP1Hswy1WyTKp479Yk9QH7Qrlg7pCuX47h7AVmAIKd7k1bIIHr/oZ+hj/xw4wBeBfYGrh0FuYPgtSGt1GjddhgO+CQbOvf+H8oUCbhEDqpZJhn+f5fl558If2cPZww4ulP7t36gBWuPXPV2HPWnK54K+ju1//31wrwzAAcmB0KYZaffvwxn0AUCdxrDSiMPwT/19Q/V9n/eWcKuXLv//CvVlhgAIlEEC3YEv+9wBl4Zf0a5cnpFEP/e48q8DetkBcEg3KAS11/XvwFh0Ji3wh8kcQ28hR8RkFS99LNeG7cuMiFNkLvnFAQk1cm3///+N+AA7AxtzoYQQnFrbgw+IGLt9LHkIpam4PizBtFCaounFu+02RADAzgI2o0PRuv+cACZ3oeQuVM0BD2WiD3LgrxT/7vAL/0AKCXI4iw8kuRjD9QafBhhsSDEzLnJlbpS4WM3//XTCLZzZBdb/LDgAJkjGYOWykiHDKbxfCDeNgCBAXbUIRTxbf/aQ/wILelng2DWYCxkxV//8EC827oIkIAnFHO8zIZHcReIJQtig+ZnrIRzqEYUwiDn9SfDgAJgA+NgYmwln7ZOCJ7yAB4XAtNlLH2CcEDgHM8gv9GDfkMi625Bh+x/fJUw0VhtT/ywAEjYmZRV3xCGtV8MmAwUVKsypA60S6ZfbT5X/+rbE+tf08MwALmRgCA7gI6qyOQvf+ATIAGge9Yo7ihr/9v8KkkAw9vaFvd7/jYwfOjGcL+AAwfQbBmV5oYOjkq0ACmBSWg+JGQX5nOAnUVa982pvNGGz44mofymocAAJAwD7QOmhw2pl4AvYGURCxH/ywJhpIQeZL592f5JCZMQyEG5SkBrhuAAmRGG6GMhQqWKX6fBCCl9zw4bGN1ekABuisGTRljefNZozeBbDJrobv4BrgA55MJJy39/V/+CDAkDHXz69lCYsrs/b8ACgK0oDAevXGzjChn/oYcIWF2aZrNvYALbc5UEXlrX+uEnG+gSFYFMDI3Kulln/fenzwGYWJIjSocef8GHgAsFTnljEaC6+gI2hauvRNVn9YO20HrhsV9aXg2SAHEnRo3fMuNLOAKifEpnT/wf+9abnX5/gIRCIyGNiDIUhHgwLwv4EPj59i0HSpWngw/AA4BUUOOmZSs4aoL74bvih98nDuw0T4k2D3Dk8D4mCBgKIHRBtKVOFUJ87/ofhGFjcQHMABwYzPamoqjqEsrf7oCYEF9jSvbtbkg9FAJP1m+3jzfZvt/pOGb/fD8CQQ7uf1xQmTDbH80wLCAk+ZlW75qgtvv/AAcGJZSpEo5hFTDj/7QGinABgRpCJUStgev9Rzv/sDXwp+XoyL/+hi5oDVpy6bg7fepog+AFjTha8vyPBx7WIEWCvDuAAUjIHYKpyVNff0TQMoYyVYa013e8M64o6W1iO/FI8PC+rvk/u+KRwPs2OaO68v//hjgAMdDGaYmPFKtpJ0e9s89r+gACAxSWJ2XEdLCsGvh8eME+ZIJX9PQ7+DX428AHX60n+/+TwASgtQfUDor7w83haYl+7F6y5lSpg3BGAzUgUFGRtTaCB/0AHM0jk013n7mfrEDYAFQEPQn8iWkCdyyB3/cAIIWL1Yil9iWQh6jB+mRBspjoURK1JcCJzlKzDamAsBWQExAyK2sb3uUDAU7zZWyD+f5IY7cwkTCD/WaSAAdTGKJW1DLZgX0UA+kuq6jUGyW/r/g4bXff/LQTOr1Z0SW//RiUQr3/KtA4VOJo3H1KJf3/gySSNAepWyHUwIdIwy+xS+B8MSJzZfDgFfelEWP1INTJR0EH434ADjpiAEGrzzBFRJp1oEyoiMQ74sL/+tNQI8BlmrQSgr8sA2BFqJ9GlSTt79EGC7tDpf9JuvHvDAoEBjCaSJtEm2H+//6MAhhFIyIMEmmAw8WhGbApi+Q9DiYez5Ye4IBbiH/hrAwaqvgWg2C6Gr+gK/GKKV3HLpgY3VMvigFnlJi/6v/8P8MApzGFS9Brirv8iIRGQRmIIU5igwxsPMAJBiWUqRKOYTSw4/+/h/7gCAQxCUFSDa5EPKSa4b+7xgeV52Bl85GjI+/xfgAJkQyugisSSljk/p8EIKX3HDhsY1VhjsQHYADccFuyY51NgxngIWC0xBxCJgvxrnkLPiNjlFfSy28WBHFiCJ0uHHG/YASoQAHBO0SQnZC6/z9NmQAgM4H9WZHIHP/PDDAAsRAlEalWnacKY/t5UgCpb6z7tzpJgyscoh6ljYf/h75MAHg11C0SIyq69wkRgDA7wI1BVgdhdf8GCIMARUwS2kG6zRbBJVpLgGcKr1wQ5BBVDXf/eNGQAwEJAnkFmB+B1/0MMH8tl3paQ9/r012yRurng+1+Uaj3VGWzxsMABBJxZvYaU7qZ7dHBBHntlQhZtFBbCBsg+KNh5jvgYAFQAFAOIbfjHSWj2xPAlBS0FrxiusvP6vr/3P/7r42AEoaMlqZE1TaeD0CHfjEXNiZtNM/wCIFMKHnzE5XcNVF/8AzPGmjSaeQF3ARAB9VMdRLjGSwP2goPtFWl0Nk1gjCh2axxMj69A1ZzJSeOd/+xtfRyHyv2Umdu4gaAoxuB+FvmCkcBxilY28j1VDyCXnEUT9d7dYoMPyADQgnAO89bSgarwV+Y4md0MUcimFvYAALAptA4NuDRG8kOi5RM862yU4B1XHY1z+IRu5nER3n+g1RqxF4YgAJocE2ibQ+nSY1wAAsCF1IPDbs2pvEPOpHQxRH2osjxAACATXhAAJoq3URvHRQAiFRMoqUvt1mkh+MAAQCe1OADaKxzwxjkp8x5sV0MUd1KNeBnnAE0Iqi4xHecJb1jZ23aw4zTD8b4AFUEVOI2vK8li1HpifmHHowiMl8Dv/mhcxWGsVZNXGDf/vpmy3voBhFbNiO0gvJtrf7AG6kABgRlAqJ2wvP8wQGsCAGSxsdTwunvnjH2V3UxBnWwogMMMDbXADWvRmKfYCoo/1kSaLfH3UXKYyPjD/DOgEIAAP8ABmAPfGjRGAFj7KV1MQYi2GOA76GompERs68P/jYYADXsM4GNXKRZoY1UMz6nuaQBHABAaVlS3CAhMzzQGOz2JuLOsU2z/NRqq+BaDZLoav7RAASKrBE2bA3XAABGiDWesn2W715JMx1GyrvEwhPvP9HpQz0cTYnQXp4lDGoe3sZwMa2UjzAtuq8iIRGQRWIIQxigw18LsUVcP197pf/wQcABw5Q2GJEwQ0+YyRBhgFHSwN/dwBI+pQjWVvevGo0x5k+HsMiulu/v9hRmAFAsne3YEyHBAOL0DYkYQCpgWYyUuxKjB3S+XgAI2EdszlMxDjJWHxAa4ZaNHqaN+4BoHRQ48YnKzhuYvff6+FKlStu+P/xB+f4A3alJ/oyNBxsLL/iAzsrxRieU8vZkBZNP43gwgjzYEXAVTSmN4CUABMqsETZtC9cAEvxiiF9xy6YFt1XqQmZDGRgiGMRgANcwjgYxcIGmRbZT5EZBsgqtSQljUnaD3zhaNb/9X/9cMwJwANkVQnWZAvfDWSOnoWgyS/9X8AORmE6Cq1BKGNRydBmAhi0jDQtso/4XtC2eJbCHv7g//4gMwBhd1IynIM+2lMD5sITbIhL6ZRreDXwB5R7hojAGJXfP353+P8ffz/xB7y6DPXw/teHRKVX+IDWABYJFIADAnX4ExG6B0/0CZowBAcgHbVZHIXP/Fbj8f9tMrCUhz5ynVHU/PdV/wv4AnVU9P+uBJVBwjZvEUnB+Fs/3wfN8AGkzekvCDLZflMu+/iAz0DGf7Pq7OkWwz/NQHRQ48YnKzxuovvg/WK6h9b+GOJP8QFcOZ4YAK4ZR7st5ZL775i4gZsb8oDYmtxt5z2Lt/+f+veJjcQesAMK76Xrv/7xIYgAJDr4iqZh30op7AAB2AAEYAx8bNEbjQhdgiUup8ls5gAAoCm0DA24NEYAcebFdDFHdTDXh+odFqi5Qy2yU4Nf8ATxOx3MjvP+CXd8+TnrATANye49/z/1ic7+IPWAgBtyP5/+PxB68CbuH79fxAc4AgC3O7oRB1evEdQ/fr/DGJJgAIJG+VfV882h+/g0fIipU98+DDgpgAAATaUGa4OgTcMYACAhaLTEHEKmC/GvfGgAlBauWLg/ihz+gE6EABw/KMCQjZG6f7+NmQAQGcBPYrMjkD3/gbXAGS7VvfzjEBZFFpdf+/B6qF8SetOAba3P1/iT1zdx86/4kOW61yd4CEAm8sl75/lxJ68CLdX/vEnnLgIn0vvf/F4k9eBFur/1wvwAL4ANQSrYg/yhrn9gJ2iAGAhAEdUYHIXX/Jv0/WkKHZzsKRyzHr8K7YAP6m+xb7e3Us7/C8AC8A0owaeJRi+ZuKf8AUEM9D1ZdXBZphn/6hoN1Hw5KszP+/6ADEV+lM3/9q+tnmbV54BZQCHE1hIgwTZYXxmboG1X/hzNrAWvwHXKev8LdBjBuXhAXyghKkyd3n/wBoJuccfP/hzJmcq7vnhBB2XavfFVstV/hzgAes5xCe1Uf7vAh5JGJ5eh97xG+AO05obU/XDkABMANTIAYsUlfrJGCJzyADwuBabaWPtE4eNU8DE/uQvtf/29LAhf9KFdr/+3CVbwBYADhoyZG1P1iQrAAcEJBKok4lEGcNf/8H48AEoaslqZPSWKcDynyYYoE+5B7ko7Ihx9/i6ELtv+JPWS3Hv+n8biQvjKd7AcACDYBhBFIzJskmm6xSO+Ul3gF65jam2fQ38/4kv7IgIYXSEyDJJtsHxJ6wemMtV/8/UJGej/v1LBLPu2HG19Pn+UKpX1/z8oTr/P+/RNUpHz/EGJO9/4g2AAkxUXLIhLJbBrvmWLFTnIK6llP4kMQ4YAFgh28zrvRM2Gmf5gRApBQSfMTpdw1MX/wYln+Qm9gMBcTRMJqX/l/Eggg+hWsseDi53ggq0kClU9U3XkkvgWyca9Fr68k/8IsIAvPOIAAvSIAQGeBHFGR2F3/wAWwA1D1UNRB/GjXQJCAKIVSu1jqxGaxrG2/nT2HwQKgXbEkY5TUPKmu8MwfB+NxexXf7gig6frDZO76ciO1FzXzpVJTbDXhiGABYIWC0wcQiC/FvfugK0AEoeLliT+KGO/+A0EuIADgnKJITqhdf59hkOCGBNihEsy2btevmEBaf2hfqCnEiODQtX9/Eh/gAWGKz1fdWdIhln+eAtCIl5E163/wZYzABsjGqEMhR/UpMACDYDGEUjMmyQaZ8w4mKVBPeymEvxphLjVurq/P9fKjPJDam0gB38OHmcGMc15wzv8N/4sAggmkJkGSTLYfkkA2voE8pXm4SGvwRep8tkv/f/EeJPiwJBkne//G4hwAM6wEFFVmSbJtM/9+rAYUXWEybZNtsGAQ+IDmAAhgWcWHIr8hhUtZQvDXgETOsT+IC2ZwAD4gdqsMbR5FjKFPwfAMHu+EptJZgooiR//gYIOLkjSXgwZKikj3AP+IDMAC2GC5mD6e9NqfXgJYQJWWNn7s2JdeAbiAQ4isZkmybTLlzAYUXOEybZFtvg9JFgTH5w3O/h6Kq/43wAG020RTH0RQAGMxEZTnVhkNXwf9U4yyGk+tCiDc4rGFMc+tCKnIdCja1SYbAABMFAdc0bHTRGGQQH9Ywu1lv3547SSSn5/jf4Ae03uI9vfhAt2VSl1STpGovAvu7V//m1Dci7BLDYsIZv5AQEVswhGqINSspn90IoDFoCma2n898TzgkBFuJeaa4pi4tzfhirPX41NldP/tAAeBUIq8IfjCc/s+OvP8MIOYAUVyU3qAc0w2dt+n1OaHcjfl6qqnCZP9cQQ2ezzWn3EAgzx6mh/3y8DWCVJAaOCkPWP/dQcBEYTzFE9ZGqasMDWYyuKuTbaal+tR8upsMegGsSohRtW4khaQifPQwpPMyQVfv5eDkDXpqrTf/f/w7ARkIrch0KNrWJcAAJgoDLxOGx02pg/AHMxldTi6klK2pDD/BAwij6IWmShbD/9PIWcKbIm3eBnPSn/jYACMLZx2I/VKSl7OIB2iBx43CeHzchj/Id8XnahqypAlhsVkN38DbGCUAJwEYGn0698vyjO4BgG9xQNctHExODezuAIFquMeJS0mlBJ//3DYK2cIl5TTHreRZmCZRUOfbSiAz0v65UgslWV5EE0/vBsLAlN2nQ8/t5IEOyZqSqVNNPiAvLYLEPwALGtFPOG5muYFr1D/QN0zC0U6klemX5T7csAkmaIwuVf/7/4kP7AIwdOiUcq2ccPdz/gDkRjdBFUklLFJ9PhCCF9xw4ZFt1bp7J6HauaDZDVA82OdQ3/+DAATRDK+MZCj+piQ9C6gk4QWnC8Y/34XNm3Ns5u+u+Utyc3d1v8IcLwAHWgzAc1UpGGhndU8zIZHcRuIJU1itZoqaBKDJLIYv7SAA2RECpsyhmvAEQdwoJOG5Su8doM/7QEM7mdUWJi22z/A/E5YP5mPaGt39UCuMp/IpeuGsADwQtEpg4hBqRrz/9kCeABKHrVLPQUMf/ssARrq0Pz+gv8LQNAnQgAFBO/khOyF5/n1wvW6ddt/wI24fdIIofTdR/X7KDIwmTvHv/Aw+b05o3z6hw97gg/D0ABGLMpUQ5RnWst3jAAEAZ4QoAOSXy8AlpA1iYvj1CtTPv7k/kYs5axF/q63Pq+3UwRKFE0uS83SP7TCBELFZXr2jVSN7SG7dMEsLmshu/gBmRBkUReJKW1Sfa2IUWrqNnTYvurDDDXCOAJOTFhfk7E04T12/+L/ja/fHssP8Ah9xnv6N9lOfh0P4YYAT96Waf/T5kU2t8eqTX0s+n6CIIxUIRi7alv54xF+L+G3gAFUNFJbl8z8vMu7/C2waZgAVrLLCHC///s6AvDE71Et/4oybqq+u89xf//wtDDAE7J8nPntG6A+xDZkcBv4p4W/wP/7yDZv84NQtyHJUj/57w8khnlx98//XG/DgAv4un1fufAUJQVCYhDi2fqSMHAFhZx2oMYhJ5JTGw+QEJYlChPKBK5hE7/gw4XpB2WblX///wS9a2WmYKtpk7qvT1pJFVeDCcmnRMvG0YACFhXSsk7F6NYJqNAAbA7ICbw+K3ca0UgtkaIRGj/8HAhNGkZYJSf/8GAMaE6KQWkke1SXAACcBwHXPHR07EYGX+8xlXnF9L/W1IYcRZR2EUtaHH5Bn/fx7RCmyTu8D9cL4AEZQBBRdYUJME22OjCBdyx8/+k1TD0AUAkwYNYfQhrHCaxmHBgBxZJmU+PyhlbumO/wt7xAYUROMibBFpgHzYYbcofLv5MT18H4wE/DBjD3o4zomqXDD4QqrRsi3//L5xqVTff47huABYIdvMRc2fIhhn+ARDjAONYpHOFtJp4CcADZFUIizKG74NuK8XrXABVwU3nFRG3v/wzOXPN/4upSUzf9H52jd+cftLoPc9/4vAA0laVs9/UI4t1NL3ujv4Fh/gvwxAAoHyAMLZpC+1NKJ94MKb9/pwRdBjVVzoerAMRhKBmk75dMf96nvdf997w0Bgu3p8AwAWvy3MfT/3ce/4/k4Y8ABEDYw6knEqac8ty/QDEoSjMnnxG5dE6/vEZP+AE1z0n+rwa5ybS69/hzQBAAQCIGOI9aSCGNJJ9oa/8EPr1PWIDWAAiASIGDWH0JY1omoZaDXCa2yyRia/ywAEY42K+ES8imFkh+SHRcom0OttlODGYgPQAGgDygiuLupOEnkyfGxDbZUe2mQS/gwwwAEgE+DhbDiEc46RXLdGGHqqG05yLU+vQF/YCHFVjMgyTYbQwiVIAR8vFsiwbHjMiP//eg8cw/8L8ADgFRQ4+ZlLDxqgvvgBAbhn0+HM5vNBHSoGDVV8C0GyXQ1f2hIscgIlSmi+M3ATANCA7h9F4tEItfUa1UH/5MLiHgAYS9yb0dliwJpkjtVv4gb8ASMMhSdLfB74GVcDwIPNo9ERrMS9v3AX8Dio3wipj/u90WBjn7FhLJFlm8gAai6FpsJZQYIQ+dD/wWL+TW+73+gFyAWHqVyazqU3/4GwAEjMhMoq94hDWoD+GABMqKFRZsCt8EFlhFViHs+/cF7NJm9x/LA5lJyRZM3/v7/LH+v8L+AAxvISvt/sipBgAXwivObeZ0/vwHMIlKPJVLqfth/4AaqVO2df4fsBfLOrm4fEfAHHJiqm/2jqAOAAIA5IZwAIUQltA11M55j7KV1MwzrUY4MMNBgBl9V7uehewNrkJInIAd15mk276yuhq6m+4/8OwArva7H//dkUlRJKACw425V+ZHu2hA+mGjpQ2/w2oU7eAEQAA/wRaHG0k/n3gCjBCJvLWhOoVvFwYgJfCX6CCZInVKun/kmmH/D//gg4ALQNPQWdHr72+9Kbl8zSACGtJKefv951nQ/mgKQAafIACQtHDRPSZQUbQMdvtTc0dQhpj+ayR0WhaDpLp6v4MWjgCT8aldAApNM3Bd9///6lYBtNgsSqf4cgj3PIAV001WTN/wIljmX5VQiwC60a5a/795f+ADpyZDfLf//n/hyABYId/ORdyfIppf+ALgscBwPanG1jSyJngI4AB7fgyvZB+oo66J4cHogNAfgA60FEWi9O+z/Cv5ABcXAtJpPP2isfnIfmACw2BiTKePsk4oHARhxFqIQc5ltD1/W9ntjwf/4Xr37O4AOISKCu1bIY5LJdY2ZMT80NNJQ74/vkAD5EY3QRWJJSxSfT4IQQruOHDItup14GziITjFlsfbTGjIsC2GTXQ7fwglnwA8EnxXu6olIWsjE0pT39zBgTekfs2Iokdw54AF6RABAYkCOKMjsL3/gGeeAReIzK7Uo53hvgSNwsk4heCZLss/29ffor/43AAbrEKIWzDD5kW0V9QlZfQths10d396RiKyCs3yEsakPiDKASvrYKEo3y//g4A4SBpZZAZXdtZUa/igGEFyhIm0SbY0QMH/6HS6hBmPnugf9YBBBUoyIMEmmgxycgBxGxLH5f9R5QvYTa31r9xBiSFYh79xp9OK578b/1OMAxhVo1Jskmm+uAcUgiauF1Hn8WAggm0KkGyjLeOU0bInN75xRAMnoE8hWn8/5hv3DsdwBZhipiqaleIdSoYIH4ADgxLKVMiUcxSw47/6wGynABgRpAmIXu//+4QSsvM0U9+/VReKepfde8MDvvUyQdIyQ0s28QNgThdgOMVrfy12P98BJAvGlAMQjSZovkV77xCdjkYK71mNIe0PzMzDdTnUoqVrSGHYAALgpWgwMODRGATjgt2THMp8FOYAAOQAAqwGEBk0RvIUXETHcV9NLeGwF3SBBRc4UIME2WnaIDCiKxkTYJsNYEWjW60jfM2MNxXNIMpS3ecL7zoyH3/4XgDEMRM7Dlr/n4zmhCpuXKX3P1n3CC/BznkI0DUBCvBoAFxyAetqdCwaLNv27QAHWA+8MivvHvejF6yxF1SL/QDHXA9haFYTgjo4OTLAqoYAx3Im/+XghNNp9lfu964ViEsxLP84AjhqBLUWwTdOOJseH6cgxBSm4ZcMC2iwMP0LXsk3FdDcf/4agQApRAQfMRnh05EW/2gMdvtTc0Kk0wx/A/FIwgHatv29+LSD+N/gAIPGtACAknGNKtPJGfMmYnQVV8SpjVfEkoSRGzM3hi5CCWqzfQjmrD6Q1dVgXAmTaGr+gID0D6V58ErHGskNyyptpNgMgDXcAAoRHhAaxhe/8yQKUH1A6Ku8PNxuazjiDbk//8GarGWoNgfaaOvoVkxIdTF/7mHcdRfDcCQQlEqg4lEGcNf/d/HgCgnckltvtDv8GuTPUOHL//DUDY7TV80/cwBQwA4PMynd01IWvv9YJt1Tvv3f+MxB5iwBmq+b1z8h8P/WI8QGYCnOMP4azCCbo9A3cKADQLdwpR3EC3f/BhiigOu6KwUE3OL8///EHqH8AaiSnnHz/4ZgAW0AFw9WpJ/EDHf7ALtkAIDOB/YKMjkDv/3ggIPTQAijOZkWMngsPmjKlPX/xLgDjzYroYo7qYW0PkgxaomUOttmM4PiArgAUQAErogdMGyK598jIRWcReJIW1ifFPtgmhQPIpb/kKPmZDlHfSyyfa2EKLV1HDpkX3VhgfyHYp/FrehI/6WO3Xz/3/wX4AHg3QoAOCM+JCF8Lv/IE6ZABgYkH6UWHYHH/AAHbADUPVQ1Qmyrr//g+AISSVxJ5KYL4Y9/4NfAEIlRDqR/7mR6o/fqH/EB7xgAWwwXKofT3JsT68GAXFgIcVWMyDL7DIG7AKRxURsKt/f//+Jtmew1d1hLvKgz/OGAoF64AGD77hB0UygboYq8GMV123v/A9HhYqJnLrt4xA0PRQe9cbhwAGB9BsFXXmhg6NTr/uBEGqjHGOdfB+ABqC1oLyRkF9X04CdRVr3TamATMbLiiah/KahgAAkDAPwdNDRojAbDaGFmy+fcnv9JCZMQTFO5jEBr9AgBG4DKMi7z/wy4+TEHvgNXIr6g9JT143nrAkYk73/8ILXc1ua/ifxB/YD9qegB0nfF+cep09euevgTfh+/WkwZ6/z1bv0f9+g5Ghv6/4gNQALAh8E/kS14jcsgbfwQWf3X/u/+AtgBRuHXad+f/iD1f7/n/fr//4g9YD0xlqv4RxB68Ak/Xf2/+HOAHgFvTldCGevXiPfvf/eJzrnXP+IDfAEAFud3RkHV6wFlqG/qClJDf14RiRJMABEQIMi71Tu/1+uHxIZ8wFDEwpLDf9ySP4MOA6gn/b2O9T3/8FMAABaHQZsA6BNwxgAODEd7fqIgRBttj/dEABOuQKnD5Ga+aQDowccNwnZ83IY3wAzWwABADABBMJw8SVYJ6hq3SBLDZsJbv4NcAo9b7cSQLuJ8e/+X4gSdhmM3f9GtSGHCeJ8SecoS/mA9cpU8/1iT14GIlLVfxPiTwdnCnuX3EAi3XrXP4P1ibEd4k9QStBYCJbvl6v/8biT8voBwBB1/b/P88WpAe3T0JuTd7mimjr66/8L+ABVDMuC3zYZJj++IOPzPjOI+1Fuh9/jPf4W7AABYELoHhlyaIwCIVEzCrS+2WW9QAA6AAzAHkRouN5jqc7qYgxEsKdhiERQIQGO2l8IBrvpMAuJr/C3AAa7CFFKbhh02MbK/IjINmOZSjLYtfQXZVoWw2a6O/+54Ar+5jEC+e0ncQFKYAIDzEZ2fNTFv95h9lO6mYR1sIYe488As+NWdmJf9uYVX74/X/DnAAl0qbWyn91zVuUy38VIBeuY2p+mHjn/55iwBmHJ7BX/dyaUbNGr/EhzgAbNFmaktv/gL0jyNrU3/wtH5MzSn7h7RSpDtv8SesAepX3z//xIX8ABwarUBCwZapBk/o7/7gDZCAAUEa8UE7YHX+fEEiK0gRT8AXUzb4X7mydLMlXrEnlLRwCaklXeeM4X8ACwJlIADAnSMCYndA8f6BKZDDC0BC3fl5C7/5AbkAgomsJElibLWEmWALrNiYNMzQ0Uv5o2MGq7iTz38DK/tf/4isQFcABIx0TLLpD7ZRj0BhsAAFQQzQeGnZojADmKCfZVJfTKNf0IMBSwHu8TJ2r8bs6/NgAJDq4jqZhX0wp/6KC3RUpZTbLZxAYhwwALDGZrfqMEQZbY/mBAHaICDxmU7Om5C3+Di/8AMV+WXPfxAIMixxZmtHDq8GEVxIlRLN+U7NPwH+sumc21ptUGSlAT3Hk+AAXNmAMDuAnarA5A6/4AqQAWDXcsSdpQpz/wEjAIJUTs3nS5CCpvDxvsMBRgyRV7zShhBM+ob7DXACvD9RlvOCMAdm+VS///cGH/hiGABYQ7+Z2zp8iGGf5AnABtlcJ1lUL7wAyCgoefLRllw1MX33AHzoyyHuZbnDfg0WH+IPox6rD5+gLyowaRsiFq6PvZ/xAf4AFhCN5fVdHwJYY/n8eMqzF9mSb+DG5YAEZQCHE1hIkwRbY2mg0PHjIh+n4WpD++inEA+2iZqfH5fxAb94gMKIrGRFgmw0D+8BPJALxK8M1wa4VZNiur9+b/4k8t/BD6VPx3DXyYQLuWPr3kmpa++IBJgwWw+hDGOE1jKwuhwnR/f2//8SHMAC2AGwYwfKOXNG1S3YABEePMqmYV9MKewAAbgABHAMfGTRGNW+P59/UEUmj54K6Pv6GUHgkLS+/xsCVrNFXwEEjEbGMjBOYrgwAKgQ1CEaE8/J2MfPf7kBD2IQoS0iQwY8c/3mAHhtCk2UtIMkIIHdYAZ+fIGJcpiz9/9wEBfrziRCW4qqouf/3MAGXHZwznsauTtzAh6EoyJYQI5MIHf94EYrB0KPISkR1JH4fhgAWGI3XJqbOkSw3/Fa3r9cJAWIJ7RojYAXIaoKNp98ORCPBsMKoL38SN6IMEy6GU92bc+vAaEINjWhyUd9QX+3sZ4BwUmlXKslTxNzgguFFhLbpeJjuMCH/hAABQFAfY4cGzRGDwIVQhP7CZtTcOwr8WMpLs0mIqFAfeYsJzi8fvAkGAA89wAgKiklWQsv95mZhmBCl6k4cYSeD8IX8ICWXEY41okqZDFz4Hh8pDDRGApEW4XKnQcfORBove0C28cfRSUMUXiAr8ABMAHxMDE2Es/ZJwROfxEABhF3ZBY68kot/94gAeFwLTbSx1onBA8HSuHbJc+r/xWkFbUazFH//+4fJiRbz8OQG+j/xuABTEC7VjZo8ktTn3Sol4plvv77gEAquHqX9+bciTpT/tAGFRdC9RlBuKzGzFVUf4+e3qz9lX5lwFDG6k01cahmkPwM6YDo0Kj0pY+/bB/mnQwGbiCtHYVz+P8A7G9hV+Vb3/+C47ZMr0+GQbVBfdF434EIACdUQKmjbGc6/yMiDZxF4khbWL0mHxIlKJJRkf+/QOeMbuc5Q5OrF/VTRDOZ0wANgbQOlfPjJP4pvBiO77e/+qP5DlDg9R9r8P+Dl/HiOmQqaduv8GKstp16x+U2jd5nl39VrtEYOxN//3J5gwaxl+DAKtAvGw8ABjMgiOOnUFIe9XtWGKLU1DLpgZ2VQQtvG0MATA7Aa0DYsbw82yiMh3FQTcv5t88f4oCQYzbZ8Tp1nnG/1yFUAYY1WObrZRT3gDGQnbmOxQiWsSGGp5X+sHHgvksF3fb/rhEYtr/DsAGi3H0XhSCOzQ3MsD9SIlBNkTRIH4CFktEQJQzCCmXH8ATYoAOCdIkhKqB3/gf6DD6WYGcrJFplUn379BmGDYIBXozLL/36vNnNkFxxTEkp4H/hfraDrgAIxROVkO4zraay7YBhS656iCN5yxiVZNc22QY/uQBqMcvlGtZJI5n//QQ8YIHSLqf8P9D4jiFKcj1NeXb/gDGZCZRV2ghDVo4VjOBTlR40wL7KD6fmd4T6SVV3CUFwY/j/gwAEmxETnOpBsW1Aeh5A8W8hFkWtnvwe2mDUr6eC6571I/X/xI3wALgdIAgtmV9raUT76AAgwT6UJSRzjfvb90BQYrPZ9xViJrMs/7gDEsR6pOGfkLF/nAMBZQ3GuaNU0hEDAT+GOKX3PLpgW3Uc4ACRVYImy6G64D9JEJkEVXEKYxQcUCqsN1A5M2Vni33cBPEtJcd+Lg0NwvrEnlLeATUkq7zxvDMADwTqcAGBO/lRKyF7/gEgxaKVIj2opXdf/d/haSB+5T2iCwD+NodXXDHgI2u7221TkGvX/ADC/V8BF87u27/DGAHGX3B/uWMKTH9/AZHMFCOGszQaHG3/e4CD4et/uAbvs83x/hXABTYqVio33/p+EnNi9P804JdMdWP2ACgQhxH6s4hzVmpLeKSWb/oWD0qCdchX/vr+DNVcDb/GyHhgg97sUvVwD0AB7g/rdBmI5QLxi2Lm3/fdBEQkD0pBpZ+p9fxY4AGEvXnkmzA7ywIvAFGr0gg75Zx58AKAmwQNYfShrGiKhd8VWffUD/MAiJaL7FJecM4BCRLyS2e/gyWxBOtHqLjL//9o0Ih1o/SLvf/8b8PwAE8IEuI15D1073YYADhjO9v1FUdQtlj/Z01dj45v4CgOndSQI0pSG4W7QAB6/YHTzzuT/+DGwKI7Yi0s9ZbUGZXOuy1SyUiVr+xxOHy2oF43AJt/hl9nCT2EQt2pU3/9Ce0vDvdbUfsCV+/odIqRXzW7/v7xsjbfhd5b/FBGRyi51PaaskMOOqFAW0e/Rv76Dqy8L9Pv/3ni7vu/cCG1GE7htdAm2uHf8COTCwj40i3ub+AAcMZ3tTURQiTLa3+DDK9PwL776qtUAAvdAVPPO5N/68+99DNuwqwIt8kfzAPq2f9kH/hmBKY6nQTQnPEkf2GxzjC7iJorXQSbBPwIA1psMpbK9ifB/ET6PCPD2avyw7qA0gOjRYcb1F9RPA2jKn53+HYm6Akfrg/7HtaTD5zCEHZFKq3+mOKX0d5y/wzADJ+rn//vn9bkjaAGMiDZRF4lyVqTyigGCiZSgTInWycKGgjjK6bX+7Bh/8P8ACILaIUV1Zl8iMRWQ5lKMly04KLQZygL5IlF/218zYdruq9/gBgc5QGGsUjjq+lUPDebcptVSxf/gmXv1nRNKv/3Niw84z3lRxa8IpI0PXAHD6zLGCRO3jCLRDo+JyqjDvhiwICZrLpPous7Pp4ZNnFUrf7k+1AhRcOGhMBbOZMwuzq+hBv3rKH/Y1n65yl/qL8zdqkfnhZsDFurlP/l/hzgAUB8gDC25UvlTSSu0Bjs9ibjRE2m2f4Ad/j8AArt0/R/f/31r4YgAMDuDWZx8lNHmtEQ8FFYxVicprovzvCVQdcgG2/dCH7ARPc3HX3gRrgDv0YQz2WDK5pcAaSedX+QGphbPrSukP+0GHF2xvDmABYIdvMRd2Jmwwv/IEg3BRHITlyzeoovLwN+dX/DcDIFhQ8+YnS7hqYzvv1iR29C0HQXR1f3rgHRoB6Mdu+/4D9eNrhzgAIGJdhWpsPX1O5dU2Ga8BNm0fhl/hKUVAFsZVQhldQjjGOh4Ens/Vz/h/+bAYwikak2SDTP5tQ0vZWdeaDBMvB1PfmzPf1hBF7PsiEck39/4wG/BQpl5GO99KKluEADbFAPw0jDATFFSX/4PAyz48LH8WBwNjLCeQrPod4oEAeAkpOUb7sA6FcyQXbdddBjQNHWAgdfEDc23Z+P/qxg2GMyUif//qC9kH6LzEo//7ggG/WvMuvwFmMbLLjn2yCn8BrAAEAFQg/YhTgkSWvX//3e2xu/KdSj+tqfDDDD0AIwATpAV4PqouTMTm0jZz3pcasdX+Nth7P01DDAB/oLOesZzP3DAYdO/TWktagYA5Cgt4VaXY2yyAHgAFgY3AeHXZojeoKjZRUpfbpNJYAAMA5dA4NuDRGAFAvyjKXvd6dYjgGJZCJkSjuKmHn//WAyoAEBTllWl23TdoN5RznsGums7Rf5+AafG7d8t46hJ6g6X8OlbAcZP43gA8ACwuhqTaePNEooH/GAC4lhSTSufMkoonbMH/QWuCUeWfe4oRE/Nt6t/8vWl3JMYdHcgMSTqwmkkqSSK//3gc7Mipc9WfBhhgA+SGUqGMjjpcxPmgAMqKgROGWP50IRFKDidCjanIsxGRLu+/qRxM4XSuRsfvkETRzeXxFCxF4IOAAx+hO8i9My+MONjlQziupRL+HoRgIeueGGRbVSD1jyJ4FsMmv7d/dIPQ7iaIxXqo396AKOGrOgiXE2wtxg/nSgNQsWPkf1I6w/2SH42Dr4YgSkFbAqHkLLIW8AMgqJVEX7bZJbWAAD/AAIwBpEcNEbzH25XUxBiLYY49usAFeAIO2LSQpxLvsqtuKM0fx4Swu0DAC2PnPva0JUuXu+w0BCDX/167xAdgAeCZDgA4J0iUErIHv+ADATYMGsP+hjGiahfw+GAn4YKWc9jOiapf/tJowCApAO2qyOQuf+B+AoeUgBAIfpTMSZPR4HA3bdGphqYiLv84hJIAYCkiIWT4JJ6mQlW9RqgTxY9/M2nSP+/R6o3JfwrsBnwAwLIWRI+beN2gGwb4LMRjN/+8MMOAJmWmw4XuduxJepe98CQf/haAHQACwOA2xw1EdD7QAMRidkOJqSEqWlwETWqVuG1NrwO+0Fzhq+sb/g8QwGakCgo0NqYsBI/ggCPIBsL13n/dEgwP41+MxB6wFfzllc//EBzAAYuDEFr6jlw0L6qvM0VNhpoMkshqUGDAG5Nbjj54fTDubv/f/EB+MJUgA0BCUc/A2O0SdiyJzwIjnDMUOlC5ThBYl4YCoyBTfbeYNnNvEfIAHx9DU2kt+YJSRO4MDRhPX7lFKYYEYcAQQwCsSBQVaG1N1Bi9QDyZzJSN8yEalVMg3KpErXVBOuef4a4A0QgAOCNIFBO2B1/gGgAR5wChLup5SOan+FabhAWUTMOrf/+N1FKqrdgAiTDx/y0t/WrmACyCHTX6hXoU31L3Y2wcAYQBppa+RXf7wwA+APJSiKSUg95SAAcGJZSpkSjuaWHH//aY4LIYIeR0OX1bH++0xIqLQtBklU9X8BFBjbRsofDJMb3JyDEFKby4aGNlH/eQefmVDFEJthLgx02tY2aTxT8ArMyRkIt8TAWJa089ssg9gZ43ASAAX4CSD61r+5FypiH5ERCRDEQgiFKQGHYAALAheA0NuTRGAhCEqiJ9tskt/KAAHQACMAaRGC43mOpyrzEEdbCnB+0IDGESjMiySYbd0QEEE0hMkySZZwvoRFdac/vfGwEqGQyO8//8QF4AcQjXl4OtR/pZIv3uBiMh5WBOaPdLKl/8AOULlZDuI7Wmu1AArgABAB1cTICSEBjXph0TLLhDbZBT9AGgJJ1v1DAWOVr0H4wSme4AervYsbqgqruQPP3MaUv9w0j4gbD9MyEzirtBCFrRuMF0y3R//y8V7AAEAdE3cAAgAug0+ps4Sbl6N8WnBkuFz4v/aWgAnasxgAZKBH/vn379/XnujPiFOVcnAkMRus+rsRFlhn+cgcooceMTpZ43MX/2EHjmAAEAxk8BxeA2/eeZsbrynUo/rWkMMNOa53V8qrQIVvNb9a6yTClzz972WpVz/gg+AQ7uf1xVCZMMsf6GHgAIwNOCBTL6MMZ4SWM/iA1wIFsvIxxjhJcyGZIZu4bggZtvkvP9nfrncf5S++prwt4wFYMHnzcJ3dNSFv8DLgGJZSpkT/MVMOP/+1g25wAICtIExK+B3/w9oUWT/0tji8wAuAAaywETzD+Sf+tsJMCx4Uj65v3oIWmZ0Mf/vPoQ/lEqqXvv/fyGdZL+IG9hkM4qAA4OQgAYPYvKD5PWz14APGQisoi8SQt7F+MGucKteV2J5iA+hFAQnhzNbV6e6I5+hWPsSOVjAND/DgmgjPfwQQOv8AGY6Jll0h9sop+GyhpSgjRDKLhylOx6IM+9xwFFAVN1lWf/C3wKmsAewTiuHVRu1rwgAKQONbXpZotTwj/BhgSkAEwa7Yk7zBjn9v4P0bkYwhm4tL/Bh1NA7RBez+a+Bn9x/1iArgAKIACd0QOmjbGc/9MhFI4i8S5bWJ6Rqi6BLDZrId/4PhbEKJV1GzpkX3VgwToR+pAM6G80R3+z1IYANs6WfOjM3WRPieAAjHmx3QxRyKYa8PyIOj5Rd8y3yQ4EAQ43hmBpXDhGzeIpOD7b/uAl4AShqpqT9LGOf2/wHFAb+VS48MP/EHrwaFxNfxAa+F8PPo1hLOxqnzpta/fB+QpiWmFXHx4FkZbpD+N6f/z8caoAI++LRpgEzO0LlHnlTi5fxIVwAK4ANGXhkSZAvfnzIxkdhVaglCmo89XQN6QDQJV55jrd1UxBnWop3pyDEFKbhlwwLbKgwM20nDPcGnzMd/q//8QFoYYADTRWK4i6Q9DWID0gANsjBUyVQrXDwJCGZzuqNPkS2z/PKCy7SaPnawNvix529/ljgH/h6ABbYAah6pqD+LGu/20QQJt2On/sGZceAUEJJK6k8lMFoGOf+1SAYwmUJEWCDLBSgDqCJyUw/Xf/4JJEUgszJDrodoZ/nDAUD0YADh1tRi4K5wtkMNszR8Q1kTTf0wJJttbm/P+8R8XVA38QHPAARBlMMpJZfsEeTT9+ne/u/gCL6+Rvv/jeAAkZiIynOrDclaPIAA/QMgDLzlWZcrQUD/u/TpzoHtB2UErxcFNZ04QNBFrrzam9sjE7iNznoexDhCAKxQFhNqbU1gUkBNSKgtvIvBnEFlAiOZi3akEsCsvWuvebJqzRs6B/89QgZSlX//3//rEHrrvyasb/hHEHjo9Pcaloju84Dl7i+8DjRpb/+fh8AkHr66f/z09qO7ve4f/4kNQALAxLOdYXn5Cxf5p/R/d7m5/8tg96hNfbe3/WIPfAQg+5H/P/rEHrAZGb5Pfz/8fiD14ImxnL/hzgCALcpXQiDq9cgPjOX94nOt4gN8AQAWUpXQiDq+KBI9LzsT2nef+EYkSGsAB0GjhHsy0eulo6Gsh+9v/Ehn4gGyBwtd1GG7bIJFgw4DqBXH9+9s/4YovgpgAAAF+5BmyDoE3DGAAkzITKKu0FKa1X4wAEysofrNodvnNYxRKmpbbMDOyreiIgYQiWynkZ0JLhHxYld9Q0B8lkcf8GAcw4CM20f9+gIc0wZG+ORh+HeNiYb+zCoWaW4rPCEGjZcMOu2KrPf8J4nxJ64A0E3OOPn/CD3z1iT14A6qnv8/8SevK+N/X/EnnX8boANwJ5LTPj/rEnrwGNqOfmxJ6pwEANuR/z/xZ+uHJgOllL4ETqylAGQlp/93/wvwALgJIEFdKWSdHZmv/AJBnCyTV/hsFnn/eAltVLnvX/2sRXG3mJj/W39Dw8gIX7P++zDbJd3j/ZSP+/X8QK8ACjCFqyK9ktg13fMVTFTnYV1LKfD4gLdgAAuClWDgw4NEYBOOC3ZNc6m0U5QAA4AA7QGPDZcbyFFxGQ5R3wst+GIJlBqyIbGWAb0WJGT7X/xIYoEABY1IQAg1muVVlGn3/EDHzSARZeBElrw3iABQDXBg1l5GOsaILmQ9EGC7tDpf9JuvHvz+HAANLZ5eGl/0EmahxZP35/nkOgGDomNEeWUnDc4f/PWAf2Oe6F/86IGtSZ4QPqd6LiQ5AAU5gMYRaMybJBhv+LAQQTSEyDJBlnhAw1RdDJe7FmfXJBAtbY6fuTblv4GdtPcw7+csrggBZsq0bU/8SeYsAiXJ5Xb6Lc/iT2fALFY+P36zRTQ39fxJ4CL/BF7T/8/LCX8wHrlKnnjMSF/AA4BcUEHTMpUcNUF99AcGqr8FoNkuhr/vv8MUQruOXTAxuoMWAKR+61G9gDB0TGiMOKDnJoPn8R89bYeNo/5//zxHUQTOKdrEAIl6L73GaWkr7X8SFbDAA1ClgLfDIq7tokww8ETWqRuG1MBeDtoLXDYq6toPBKARqQMCjQ2pgTKHGpstUAZwiNYhEuveDC7/pW9//G/RIBhBdISItEmWkPtkBBBVIyJNEGmgYfgANRGG6CKxL1sYv9ehCCldxs4ZFt1YYttp2qfdzIBsS95x840E3OOPn/wvTOaYLgAIZEzjsRuo7/X0OL4AslD/w3/YL6JO/lfokJiahxE92IOIGwAGtDZ3EXiHqapHkZCK3MdChEtYnzzA6xBE/bGEKUHpmQHUPqpN1f/AXAAPaQFX7juRf+ASuINns8Sp9AQjuZ1Voma7Lf8BwALDGdrfqKOgSyt/IEwAJ+jBfouxWumoHTADA4vCdnTcBbfB6vI4xfH3R/+84tXh1omCi2HZhs81bMJVgvHItO7/jfwBiMhsgqr8hLGpD28+n0q/tkyc70k/8/f/WAr6cwnPSa8vBgwPkRAAcA+cbRU5EEy6z++MkMffCYIX6FLdX7AkaZty2/n+G+BIMSBP6k8+I3M/Nv718kGPTbf/EKYvnnFgDC7/pW9/xmJPKWsAhtpd3n+Gv0Bj2J9UlDHiFzKB35ABcXAtJhPP2CMUTi6LDiyZDQ/Dl//4gOcABGULuiHcR1tLcoAAcAAK0BrwwXGAQX6QBEcas3a/xvAAQw1u8I8wnvzJKKZ8GAgAEgAkFsLQZTx5glHx3zAC4lhSTCefMkoondAMSznWE5+9Yv84/tMBloEvHOb61nf77gYBfByDtP8mbQmYt1gGwItD/7SpL29ohAl7Yyf+yZlp7EG8qGVusvvB/wAgAeAwk9NiLyguyw/9uUBEPLu9YUA2wtFZE+SlAI19VH6nz4M1uev6zDE48vHrxA3owgXasbP/JNQ48CAxRkKTNz1xFb/1ehGoGBaScrJTUPkneDCaWYENOFoGeZyI/+EAAFQYB1zpsaNEYPAQiRKXmUjamwWHNyV8/+/7XDIpAGr2qCMZvFnMMOAhEQRw5asUJfMpvgnoAwn2UwkiH2fgq/4N1UAGsL40RxxAq4n33u2P7/7BMOT11f8b8ABGA04YKXf/DGdEFDP80ECXtjJ//BmWPvEA1wYLZc/HGtElTIemRtgnhwGSeUX0AiFRMwi0ttVlt4BCu59RR+CmWH/z8gABugAEhkALdgNLsD9sclGQEgo/r9e+qNDkVLbc/+pC3W3wxs0bl/jcACgGLIlCpLHiGS6Bv/AwdrB1yu0Rk/GABAAtWlYCfG7FYD7/2ASGKzWJ2LOkUyv/JNfX4/7/TxKbgItGRAyVwiWNX1Dd1XB4DYMoav7QyEoqeVnal7P8BB8AB8CCKWm/eXL1ad/P79X5Go46ZGI/DlBX03ipJf92epLKq9SzDqadL+///G/0QAN0Vgn0ZIvnzAUEKzm9cVQmDDLH+1miJ8FsMmuhu/v8YB9hRarNLYsjj3g/seUaxllYeydGploYm69L+98aJkwvHYvSly8Mfd21fIe3Cp50rXaEYVPNvUNLGkMJS//d+qIzD2khqmb2I+/I3FZQB+NoBFBAGa+AA1Dg20XfNp0lPAASyQ7EFhJ0lmEwgABAJslAAEAkALGwr25DCSTVI6afmX/+r0AAQOJAABABB8xp1/gE7ADUPFNQfxYt3+3kOPyOhiiPtRbvARuFXEnkpmC+FPBmFaG9LHr8jYGWQ5MuvCt7Wndeym0z4gbgDGRDIoi8SQlrkhh+CWBkJEm9wwmmLrdfaWGKLU1LLZgX2UaYAEiooVFmwM3w1EqrqEoNksjq/htDABUCJQERYqNkHvHgKAwI3i2U1agRczTPcgVCh1zHZ0s/ust6Y6Jllwh8uop7AABcGKsGhp2aIwf24PqMh+CRf/quSSgSsmDETMWpXy6FEqox6afC+aPZvfcABMkN1xDIUf1M/TAH9wAChEeEBrGF3/zpCsuBd4ZFXdtpuc40Qbcn3/Okm7WlonvVf/7l7JrccfPNthIUrV/7/8QDDoMqATC/O0tcDHf/cBgasqQJYbNZLt/ADGQis4i8SQt6k814QotXWHTIvur/6jnOihsByIaSlPf3eH/xvgAXgoUBRTE7aX2ql30ABAgXrWITQxnX/4/oCQQjeb1XAmTLC380AhaE/oSx4nct46/oJRMPUWYtRKZARUEIJW1DDhkX2U88ADVM4dEFWM32D9tmN1FXfvW1qQzlCJg2kALxVJ91re/9gC2ZMVq+7+ZfvDcF/hvQIACgFaKCD5mUsOGqDP+t6tMC5jin5lD/xbZ2PPxh5yzf/87CKdfxHiTzlMtAHRj0htT/xnDXyYdE6y6Q+XUY9gAAuCFWDw07NEYGAeAYSuzHJ0NH75fhprn+FfthQTbKpL6dBZPsBC4LRkSjjxO5hA6GHyAQmi0JE8+JXMInf8GHEpM+S0c6r0v6kpVXv9NSmdE/wrgAbxqNVr/qBOgAXD17Em4QOI/26hBvWiDbYiTyv/wMBabMgBARgG/ig2MP/+8HUGGAFicy2Rzvp65MlkM+H4AFQKQUEnTE5XeNTF/8H8xMnDlEuY3Pp0ew3r//2p+9dDm+TJvoDzzA+v0vx//5HP/B//98DQHqoAEDqag2JXt/974WqOa/ucAMuOsaC5ExMfvyRZl/UC3Tfy9XvQI5/Imc3b/EBvgAPIAEgJdyxJ3lDHv/Br/APD3/EBf/wAEQB9zUNKufxP24fBL4JyxpNaFnHJ/AA8ZCdnEXnkLepf4DAGCi5UgTInXSYll7Atly+8pQRxojK4O/u9/h2GA9ssNrjs334MM/qsAElXYClDkbaZLjVyuxmQcMAez5AXzeoZlBoH3PU4d39H73of+FegISxfJE8oEqmkRF/AKZYJkIY96dWh38DIGfBFouShRD0ev3fwYIcoNLQsBAqX/h7sIABMUZXZDlGday3ejYFuM0fXqFFocxnX0F+UVHPXYWDOKJlbismPL6myueO1332AKmZCVr0VUn/ljSY94eBlN8DACkgWemKu5eilf73H3n/DU6IAIMMoF8kuZVIxol+QBsBPzgAwL2iTELHv//cvgB4lcWbA3//ghhhgKAYW+yhWITgxFln4EcvuHgh+MxAXwAEjMRGU51IMha0AAJGYiMpzqQblr7yAANzgCKApHFLsuq6EOoHPKCZ42CmL5wJ0EWvPNqYHDyEAViALCrU2phCywEQTZF3gGJMtUHVkeHui8e+L5xCdjAECEARqANCjU2puv174d/4AHAKigg+ZlLDhqgzvgJDFdrE7UnWIbZ/ngC1X6A8w7/A06W1V/Hu7P/2kABMqsETZtC+cARBGCkDcFXjD7xu16REEyCKxBCGMQDZIHTXutp/98nmnarv9wsWaC0xj39wfrgghhgANFECBHTWISSdHYHPjMANQ9ZDVQJsm6/owACnNeWj7Btq+An6f4QKWxmOWznXwq3D/wzgBIYxCk68n5YZo538Chq+nrf5//8MQAEgASD6GpMp680Sigd9l5ADBDE4TVYTXX0GNBFU2iSV6gh/526VYH+soYACY/FKUs2jzbwxsXAEAB1Ke1kfpw64f/O/wxDwAKwYm4XPPh0lP74wAlUERpWacJPpFf/cSkkv3bfAZaf+ASGxqyO1e+F+ABwCoocfMylZw1QX3wEgx3ez7qxEWmWf54EoACZVYImzaG68AARRTRiuKjOnkRCIzCKxBCmMQLhgAaafL9OfRiXep/6347hfAAfAacMFMuo4zogoX/7ogg13Yyfewblp6AwgMYXSEiLBJlhDWAE1jrZX3/7f/8QHvkaEVlMdHGS1ifa2IUWvqOHTIvqrDDDgAWCRSAAwJ1+BMRsgdP8AIAHCEAq8NdtGEhMBYCVYR3Akpx2Cf37y0E/ldLY1wC4eXJAk4FSY9q42J9I7bKl/8HOa0m/Pv+gk27kQF6/W9tP754U9ni6wyf73+NwAHM4/rRRTjHSNo7/wdhhopPJnG6g99d4aJl3XvronD8wAsJgUkunj7JGPjgYf0HLVks1vAFjAdGuFQY1NrZ/8GAAmRGNUMZHHSxSQ+aAA3RUCJoyReuxQQU9xNkOJ//9wP6jcil/8Q5kgul8tesfl/je4wQ34ADgYlkImT3pshQwj/7gPRDgBApSNEzS65f/GAACAMAAIAYAUEZYAMzo1i6fv8/hRUBs0wX9ax+z4hGvT0LVX6Mmefuzp1kKo/wKpDAKqT54NSJ8+R/VAH45Huif9VoxppfwlgAQylt8SZqHiHJh0MNokpx3h/D0aDD/xbZnsfVfDDJKABxAAOWgi+KgnvcRB4AAQWUUl5J+nm6BxaiAvNGDSeGuleLU4kAeW1lW+P5z/m+l/ggwALgGFM+ms9mGjH3/AFf8s5TsJVbfu/sCz0AKHloQaIfNv3AEAixgDiE60z5b6iqb5dTx8yGWaGMKnveEbdginfqUo1aQwYBgMF8AFuWR8Zlb+wAffON1j2f8WBw/4YwAEIWY8uedcmEYaJ6aMgBgZ4E6UYHYHX/A4C9p6OjTSBqf5yfCqRkg1aH50Fjffh74hvyPjFEJlhbND8QABraBRiXJQwZRTJeYa5zuVkMR2EQCAIcADmiNqbonkwtXBjeC88RhThq6rtI+gv8NwJCqOAUCXq1wQJbEX/vfdL0ExQczd/nX4AVGwNqkk+3/43wAEAjjw71T8UImuywGU9XgLnMCmhVybxlhx/tcAocAC7ABIHumrOQaMf/tkHj/EUAMCj6QkRLnWSIYwTE5EAJf5rIa5wE+9XrK0uR7XmYkCh/XvEBWAAjAAEAjtCgA+i8fQGcMlHkAAIBFekAB9F28iMZZK2AACoIZoNDTk0RuNiMvDV7aZBLe8Qo+I2F976aW8MOMlCIFAT0fP3/cfHfJ/otme4n8bw5gAO7COBDExw02LaK3UJUX0ew2a6O7+XgC0bNFr/V/h/gAWAxZPdoVjxC5fx1/ACMqECrWPnGxXpFUn4QCJ2RbWr/ZNHcPkPMALCYFJNp4+yTigcwQEqnQyDrLW0wYcAQIQBGoAsKNTam8QooFgu4XTh9YmUsRpf/EDcYDFAZf3V6aYHBQScMyldwzIZ33EACVgGRUFPCeom6/uEHR8lCiiUa1JH8CA4EgQtHk4FW8RuWQNv7/oCGsShQnHPiFyyJ0MGCg7JGEUU+a/ynlPyVl8ZlI07204NCmQz+IGw/EghuvfQpG+nUgAIDMZHYXdX0ozEunlOXn8AwEGAzMH69Ya19/+BCBhgCeDaXVyxMCcJOOgAO4ANQ1XCkH+UNe/9psiAGBCAI6owOQuP+aZsgBAQgH7WbGoHf/MQOyAmoGxW7agwEZEGimdCm4VWhBvnniG10j92pC/RNDrf+a3TjbTJfu+9ooRE+rf4egaI/ghd5Ep+Hv/8MvyhWr7EKShigJAwB+SFc8tgR11jdf8DD8AB3MQohbcLOmRbZW9IxFZBVakhbGr1CVF9C2HzXR3f3JgATurhkUbI3v4DAFRAQdNTrZ81MW32gMdvtTd0Ikwwt/A3xdgCWRt0/0f5bYMBRY2+E5HvdntjaH4X4ACQ6+I/Mwr6YU+2ADnAAEAClQAgjEZPXXNBC7RUpZTZLd3IBKCwbTsS8FDtS7BhiKLgA2+6SN7u8HPpymq3/G4ADUjG7CMpJKWMTgDar7kf/93sAAIAyrcQAAoAyo6/dLM3BZX2O1iLFN2t/7TmAGzx3OADo8T/701xz8BmEox3ETrPwAcIVmL66oTBhlj+cwKwQEnzMp3fMSFv9hhcxwABANbHgeWiNP3nkSEyYhkINylIDDDDbb6GBKhQsXP9UDTnCj45U/Xm3n5/EB2zJ7i/n8G6jTWUwojcT7QwwwAEjIRWUx0cZLVJhhwAEzIZHUReIJQ1iBgAHst3vVv2r065Xwa8N+/8bDvJ6w7T3GCEwBuhQAcEbQKCVsbv/ABBCUWiJOJREFIFv8ZGQAYGJAnUFGh2B1/3GwAXBKpaZP8sY9/ADsAaiFLVhKXfMopzuIZhJrnp/DL4/g+QvQYALkyYPvEcz/ebMV4HhI8OrC/GwRQwALBUoAcOZtOLxLej9QByMZHQVF8ShjUACgW7BFK2/9GtSHAkyAKRoSxS8tH+CGfcEWcrEePAaLYMHVEJruSGF3/gEYQt0VaXQ2S3dYkZGggVQthA5EFOKnpnGw2AjkmaB4y//3/4W8Bw9Aag7NMtKDFjTtGAB0MMaWndsvX57uD8CdgBqHimoP4sa7/b+C0H9OtJbmqQ7wYS/QV61qMOD7261Dhy//EAi/r2na2vheIUWrqNnTIvurBhnTxIVhgAXgAbJ1CdZVDd8ICYxs6Cq1D0MagDJIqehaDJL/1f38OQzAQxceKMC2yoGdKOfyAaSITdY/L/+IC3AATY4deHhDqbBjg/EKPmTHcd9NLeGHUWpTvqgRTufxWIPWASB7eX/v/1BAEPhmBwF6oAGDa7fFMnL//7gNBiwUqTiOK0a6//Z/gikCu1P5CgOrlK7zzD9yf/9fxPw1AAQ9xo78aQ39Yt0dzutsH6/K+pT/8QFYFgLSgmIGRW1jXgJZjdeU6lH9a0hgQYYfMwbT3ptT79owgSq0bX3YtS69z9gIKIrGZJkm02/VgMKLrCZNsm22DsLqiCQ6vw2pgDEuuruvrGVVLvf/iAr8AC2gAXBa1ST+IGP/2D8DcaoMMWEb8s3j1//9wCdjdeU6lH9bU+GuFAZ3tJ8bPG/40hfr/hWGGaOABeNHZMEoMgshq/oGQOCh5wzKV3jdBffR8baXuOlVnFaYWZ7xa/bA/8PdIAGyZAv2VQrXAEA9AhGczqjRM2W2f4GgQIvGw0BMpYvz++UDIOCgk8ZhK7hmQvvvi1ydph1wGbRAJbZa3f/+qm4Ef4cvAAoAx7E+qUx4lcygd/3DGBNBLckUojuucD3/wB0PgHYSuF0/43gANkMq4xkcf1KT5gAFoB0gfaU5SLFLiof7pmvWve+kCkBb4YvvDc+cECUVSrw2pvSZBswrN9yXNS4IYBGpAoKNDamoB2gucNivqxbw4yUCMo+eDaQOYbFpMjvl/8QGfMglPqW2exFKb/8HwDFohEwc7pK8W7/4MjRgqSiqvf4SMb/n/EAlwAEjIRWUReJIS1iYfteEKLX1HDpsZ3Vhhy3zzFgEqTTrvPfjcQeszsqnx+f/hFZE9CYX86/Pw5OKNp7/IRAskj56Lc9c9cAh/LNd3a7T/PgtDfJ8333N/4g+DAmLU839T//89YDCu6T1+//nf56wJXSd8/+PxB68AZFqvfvz/4c4AgAtzu6Mg6vXDC6v///7/3ic651z/w3wBABbnK6EQdXcfADEa3OV8135871iY4QviXABDICGEUkSYJONP9/wUwAABUHQZtA6BNwx4ADtAA1BK1ipE3Sde/jTAB1DMooifl+tnGxIHFICFsGnD6N5/1iIBAU5GBBkV4U3y402AENDbWbkFWcN7jw3AhAO6FKEQR5zzcH5mYyuoq9SSlrVhgNePpDOj/hPE+JPXBgLia/WJPXgBRvlPj3HteJPXvra/+JPXNMob+gB3o1n39f9CObEnrgOpDLVfjcSeUvgSnWO/F/njpKg2ceMpfNd9Ldcl97/55botzxF7tf885bixZmpJV3g2JPecfP/nq1OtH/fr7VLnyPf72hvk+bDk7PxJ7wH7Qrlj1pCuX/EnrAHlHtDRHA6FCSJn8SHJzssglcdGa04u1u+oCo71pr/5/xJ6wGqXs/tr/EnlBEPtu5kl7zf5/FLTrG7+JPX9DP1f/PXgDQTc44+fhB75jMSG+ABQDHsT6ZLHiVy/jv+5gY1CUak8+J3Lonf8BxV4B68ZaqA0Lx45hmPzlq+f/z+27Fmfhy5D7T/8/KncaMjpPfHmGS+4nrrs2UqeZVJ6+GfMoUwqv3x+q2yJj0hhCD7kf8/4jxAzABPgIcVWZBsiw2f3wGggMKJrCZNki22DD8ABjMhMoq74hDWo/dMYolTUMumBfZUHxAXgAIBBjIIEyM3399A985wBhjyBEjF9fIICFyzvABgsuaDF19YQdNY8fva3yqP/58MASKvYRa8xP9ivh9wA8BjMJPrg3R6HCNg3A/xsNAYAhlHlvKlNWJguuuGAGR19/v6gJwDwuYghlstZN+BAkSKQ2IJHf/+ngEbhUxJ70zBfDHk+MHzgANRDK6CKr3pUxPogAbsrBPoqxvOnD4QgpfcbNGRbVSBvjTrCLCgZJJz+BBAwzauflAvpk6S+vgC3/pSb/zucC0Xoj52cdPby3EDf/MyMTqIuuJQ1iAwALoBC9M6uVfkf9/DgGN04laemX/sAFAJsGDWH0Ia1omoZ8YCfhgxh5COM6Jrl+gByQxxfcgxxWDBAZwUGGAA1kYTqY6ECoapGsCxh8FymRSLLvb4xQygBqUXRtTKpv8+aQxiraT6e/iA3wJAhZEekSx8lQx40/vX5lPpMve/51+enWARJ+43/n/xuIDWABUBDUI/Qnn5Gxj5z/fMAPCaFJtpY8yQggdXBWkzSMXX//7//wxwAPBuhQAcEb8SErYXv+AKCGolFHEoiCuGu/k/miG64hkKP6lJYAAKAoD7HDQ6aIwDFVWy1QPbU9ACEPy9kOD6B4ufu/iBvAARADw+BP10tdYIwSPBgAJgB8SgpFhLP2ScPmuIAPC0FpspY+wTQOf/2gCFo99BFvEbluG39xAIkAta97EKVB/+wAjAVCBeMuVYTIu/eNiC/hsDAA8BBY+oE2jFZhl/71lM9ZokHkMgo0Rz3xv6trS/iAxAAQx5katJxee5ICU6wPkJjgBQfytcKCHFbHtNUAMCfaC6JUR6wJEImGuUvF6tzP88hQb8BdoIX7pHx0FktfBBwADGkcb2F4QSw8AnHBd0mkMpdFMgAJirYrKKh7qaU+G4AAcgADtkBhAZNqYP4MyxvW/gI9FiRk3a/xuABYCEoQjInn5Gxb5p/BhMFGIzq6/ngNAMAEukKAR81cpEcf+wCQhG4tFTR8CWFv4//UB/pan+U9wF5kZgixgqGsU6xIibhJDIsI7v7QilgiNX/4hzf8D8AC4FPr8gjObJQtBs719AXaAKym0R5M/+8Da9pGOPb/31xPiF+n0s8ybrrf43+mABIqOF6S4Fb4YEgxG6z6mxEWWGf5qJVXUJQbBb+r+/xAFnEFKLVvm6GUfh/iDkx+FPp/B2l0IAODa/03zm+HvPuDFI4OqVT17jI4DpW7qmX7/z/BB4ADMVFyyo9ltgt0ABq2EOw9U8LUaVSBGjpy2TP99fiCtKAwCU54RMOKGf+0oAJA02xJ3lCnP7eYq2KynIKRSyn6AxaIVMHEIK8W//4GvAFDl9i6m/WMe/zf5/4kbgKEKzGomKo+hDK3+GMDsCJwBw8jfxHzjhu14EpgAkCzS0ncWKd/sBiZgEBSQfpVkbgd/8DKaAAQtnDVRT5uVINFh+AMMhBaaCJ+2i6p9SxGYMAGLWIJ1cj//37IKWAtoGRX3bTgImtQreNqYRRgdnEx8OC/Njr+FdWzmFJp6veSzIFrB5Z+2bIM3IvD2AAQdkBLQNitu1eAjIRU5DsUZLWJ+KRRKITTJFK0no+wwAAVBwHZOGxs0RvbMN1U51KOlrU/xAKXACAby80zbnzH/XhVtIcYNtwDBs5gOL3qe3eFKMjGTPX/v/hboAfKOS6FIURyzTw+gGPZS7PIXJaRT37ujljX2p+/WBvcfy7v8BsnIqRUUo++14szzT/3ff/h3gAJgB8bAxNpLf2ycETnBAXVB/19QyoZwkWwAFsIFvLHz7yTEtPAK3gi6A6i08Z5X7xAJEBAtgihDWOE1i/gQIi3CFFM37n10f6MAi0C37iHJUw//fclDTHRaRyf7wxBGUAdKGikG1M4AGsco0Rhe8bxIa5g/4gN8ACoOQQEnjE53dNzFv9ZT5oDxzGPzd4AIzV8mW/7/89YS/kB65Sp5x/uIjOrK4ehgRQFm1Bp0Mikjm+EgjOndUpCUt1b7G/P/3rw8ACoENQj8id0SNi3zn+4pI2qOtr/hKaNwu0fo/q3U+AB+kx5Lr6nf3+FvABAyVFShOsU6Dfz1AfbDvIX4OXq//9/y//DuAkLqGovhE1NPmcPgAONCFXrmoZBpJH1rRQ/Evh33AwwIMMTLLhBNsgp/eHpAATrkC/RtjOdLk3EiVqJ6j//7gDGRBkcRdJKS1iffttjW8vdVUc67jPpjKsph6lG/u//CvmGgDt1oJ2zGusw/AwPyQRidVE5V+21hjZdAKAMeVGkGnwwJwjc3/vLGijewuHFu8OKALkSX0tv+/PsQb+HofC2tD/D/G5t2iHmf7oGBMqvZrmwfrsF2JI8BMCA6nlT14rwASIOkgsO5GEVG12SHe2Q2dTC0onls5ic2OGubibETqSWkIl4HKEFqF/klTa/oMNHjw5GAqqAUcTT+3h9DL+Pm7xssghwA/AAygX2koxbTRP95oIB+EImwjMQUhjFYEM+LXZLmQhu/gw4fjEsz7/fapfasP6Gjq+3ddkm494ITJQ5SLv09rUhhwh0SDmu13e/7X7lJBzVXpwNlhuD/4IMDUCdh/R5LjEuNAECB91AhFPVu/Qwh+AA4SbFhBV9tVnf+4AlcoAMC9olRKyF3/j4PqA3+NcbIBEmAqSk6dhP9wBhXYxoFYpN6Z2Izv1YDCi6wmTZItshfseCqiZpDbr//9wA0TEjm5f/95DyUtK/6IA9+4f6pVf+GfmBMK1KBSWvs9U9/TACMClBc66IdNJme3kAD4vhqLSWfNEoInRsIIGyYQenF37cV34f/hXAAsEPBK4OIRJfjXv3vgSCdCAA4JyjAoJ3QvH+8BQx6sM5Rt+2rmFD//wa3SFcAOBbWlz2PfT/wz6xIyJQmhlVk9/9ywAN0zheoyxnfvSoQglbkLOGxnhX5mY3dxW6klbWrADi0lkwa3nn//q//rEhbgANAxKE/qThnxG5dE2HxgBYSgxJlPH2Sfjn/8HoAxqE/mVz4jcyiff3gBQAyLrQ4OotDsWjK8bXkUyVi+L8ABrsIUUtuGHTYxsr/IjEVkFVqSEsakN8OYADisIA4xW8LoIfSRf4DgCAo2Uqkih1l5fTZAAFz00UH2/7/8MbrT503//8/jwAuGrJWkTdNwh/7SAVFBB0zKmHjlBffQR7oAkMd2sTcWImwyz/ISppB1/xvl4HBfqZwUqr7AeJLHtbn7/T/Dem4Ahci2orPiSbhr8FxOMSLPP/+f8OIdv+GPAAt4RwMYuOHmRbZWsI37rz9+4BfAPC5yDHW61k/6tAznyM3H0/wRQC7vf5mbMMPL4f+0YyGDlMtBw8yk+GHwALQQ92lbnIxXv3vwA8QgCNVIFhJqmnvrsMMCJvO9vu7j1w3AAsLTAFHM1mg0iw2/4AcALiaGJMI58ySiid/xgyFGWk4vmHuNIUqCgBUN2UqtX/o/x2IDmABYIWiVwcQiiUi3P3QFJU71LlRLF/+KkBD70Lk0M+T5rXaD3+E/4gF8GAgAGY6Jll0h9sgx8MDAJUIADgnaJIRshdf8/WNzATiy7pIpoj+++OkzHQzn4ZwLd3GctPc9cL8ADw1QoAOCN+JCFsLv/AJBCUWqDiUUVwt39wAjEjQvlXXrdjgusYM1ingbRAREiwAd/SbIOF9BbdUibe7164egz4iB0WKX9yT/x///u2Idx6pQPUaXU0gAEzqwRNmwN1w08BiJiOQtHzH/PISMRkEVSCFMcjhg14V0uJttHaZ/96gQYysIV0vwse/vXSs9L3eYYIszqLKk0ixMymmJHT0egyi6er+EWCORsXtkf1XsA6fWtH+/wQ2kaF4po/1/gwqvJAbns7c/34yACABUC1oPXjIL8zWHMVRUr/54Zjn/G4EyAmy/J1//6gfLE4SafS3Pfk4FpNkOe3p97+58Sre9/rDAECEARqANCjU2pi2LguAi69q982pgWB2A/pHwX3kr4CrACQPdNXB3FjH/6wmMHPCbFSZdts3aERJABz60+X6vw4mKVGx//8PYIhafHH5UW1FPHfPoeQ3YiJWOfggwR+u3ABhMUCpgoqL6RrZKEbFPYbUVnsT97/JsQnHbKCENSgAHMCxJY5yK1LNmM8EQ+JEYAwOSBGoLtD8Lr/g18qsHrXFnb1dhRMzICUlPzvUDL74gEHzgsACjmJ0lyrF3eZhwf9LrlY+iGAAUB2iBx4zKdHTdBb/aFwrbE7lCFUFmM0hqy6DWGzWQ3f2AJ1KADAnfyYlZC7/wEB+OHT9DEEhcdCwN6Npcp++9aIacx0KN7VJHlEA9JEUbTgxnOfIU7/oNIAS0PJ69TzCttv/z/8PwACkkkzmZv3I2sDw/+AY3c0Sp6+fa/lH3iBLTiIJvlavXKBjBw4ADgxLKVIlHMIpWcd/cQHO4BgEIWoiadTL/9oJwLQie9TUmiu184c0ZhLGcjyIIxenqq95fBIAHZkUOFVTf//ctEoJ9vOq4X4Ayf6h/98hd9csPw/AGhgSM04nNFskpH/7m/JgAIa8Bqrl4QdFWV5/6WskVPQtBkF0dX8AiwUdigFDhCWUPNL9WA4N5l6yjOeuCy1Xz//DmABUHIYAcGGIzu+bmLf7xiZESjRYdNZHcuAqxy9y+8w54PkZ//3/iAtABFICHE1kQYIssP8BnkAxxFZE2CLDD/AQNg91Y2f+SYlz7TYDJIQFn0yRnv+4AQDerhLxH3uoDbC//vGAl4YKYe9HG9EVTLtf/Ab+fB44fA4+huj9Mqt3P86jPCsb+P/G+OiIgAWShiamXo5HuL6ACWFBthKySPxiCf4OAHAxLOI0Lv8hYuicf39AMehCNSWPkbGUDj+/4H+9BzW3twES00nzDB/e53v8b+AAgI51ZxOxXwndQxt9rP4wF6eFo0celf/+DDAlMANA101Ai6brn9gAHWAEgealaTuLGP/+1TMAQHJB/FWR2B3/zCSMAYHJB2l2Bt0//+4HQUoLnjF9Z1eDATGYSodlIfBF0GDEalRT8A60bFU79+cIbqRod/16yqiTw7fft/EB6AAkYVH7yqq/fOJ8xKonj+oT58Rf1seAMAHxtoBHp0ecXqL4MGwwALByCB5wxOd3zMxZ/AKEI/m9U3QmDLDH+APEiJqNFhk1Ed/WABuiOF7DJGd7yUEIJW1CzhkX2V7zMxlKoq796WtSHOfJVg6c+jW+89EGlfZ2uUV3mqpn/xlO/iAvAFjqFbxlbVXuWFVOvZGkU9+AIYqLlkV7JfBbLYB0Loi8BAmgbH748xVsVlOQV1LKfoABI9AAVzdRAEObPsHwMHb8nAD+NMdWkbZnzNkrvO54oev+tKMRsz+ID0MAWFs47FfqEJ96tKqu7H+PshqQwAAgHPvAFlxw/f7veIetsiHSGykQni9wiTn7W/9cAtgTUjlM5PT4BmcAAQBe1RwACgC6jIGYajtXQDOfecYhcrFX/uH5UqWfB75f/Eh+yEpb/n8EmHi9lpZOajmBh4ACRGIrIKrUkJY1IeAAjEjldBGZ5KWMX6fBCCldxw4bFt1a4SSY6ki2d8GCBGNf4gOwIrwjgc9XDTIvqp/4MGBwMZmAMDuB/V2ByJ1/zxIATBruWLk7yhTgEgn5QAYE7/EmJWQuX+4BnwRUnEIiSki3fzRDgMuC3tE/veXRRkYMt/e5lDU2X/uH/EDYcMABwSI4KUC7ygRWObOd4fpEQmQRVc7mMR6uGIJV1HLhgX1UeGABXhxS687MmKdE/6GMIpeIoUqXV9AMRZ10w6YgD9D6MM0t102yIGgqa3a2jf4gLQAEaGfIUyPhmkqfrAA+DmBDUuIIE7G++8zQyFURdIJQ1yA9EABsiIF+yKFa4f4kEJl7qEclLfWGoLqj/azu82th8//kgN/Nc5OuHQxBCm4XcMDGyoGHxAVhgAO0AC4eLYmD0FCnf6HxsyAEBiAfuKjI5A5/4MOB/IylgIz0CSbnjXD5+7r27vz/E8ABJCpkwaUvtkmvD8Y63deZhnWopwYcViA1e9YD0xlqv6xPiAzBnXtvbb/9P++sAmrSV3z4xyN3vD7j4+IPUP/AG5Nbjj5/+GoACNBi9V8hfIS3khh1FG5mu3I7aF6V6/1/+GoMBlsNvwxvw/fqWz48k/dzo8N/640N/X+fBBh0MN/D4Flpc8/xId4AFhjs9ibqxE2G2f58ADhKy+hbDYro5v6BgCogIPmJzs+amLb4CKABM6sE/S6G84D8iRCIhjIQZDGIDXrAjCBxzI+HvIqG/oP+ICsGBAAIwA8JoUmylhBkhBA6GHgBnWLSNETlf7uBA/g5SQj/U5e7AmiIL2Tae//3Wn/z9Rr8AQ6X8jTPjiT4ckY8EA9uV9ToRh6Q9TU9f/z4uB5eQEA/O/iD1+nASM9H/fr+IPWAOZzp59d+eN+fz/z+gtejr6Gokp5x84OrU9f65/LwArtq/fv8//5/Q59X74/P+/+esTanR9//nrI1Hv//PiwJGJO9//O/z1mJ1qfH5/8fiD14GJMtV/hzgCALc5XQiDq9camy1X7xOfzrn/EC7FAAkCO37gpObSivjd0tjbpYbdLTvWJg4gAAFq9Bm2DoE3DHgAWAgOJrRhDkGkSIy6ChYAB2DQCt8P1TSSulNPkcBtwDUYRPAj7ANOHg1AvUBqcjoJdyDX/hLTgBn1vkOA1SB82voGNef/uBVqA3hv4oAAQABzltLS/1DfcQD0AIDCJSY9ybfioy5PXDGNG22v/9/+E8I+EaxJ68Aqq92fxPhEN8ABJgxuvOStC0uQthMsrfm7wH0II2DXH8RiT1wCZKnm/8/8biQzAEEIArEAaFWZtTf9eAHoVsLt3x/n/C/AAdgNKMFniU4xdM5FP+4BDPQ9XbFwWaYZ/+rGqqe+v2edHSxU9X4ByV+le3//s+7ebbd+ywkY3lSa3F+cYXfSe/nx0zrXPOyoJfzAeuUqeDTOd3mepK+enhE+l97/S5JH5/v+Ay/X2v/9/4k85cqM9IbU/wynD+JPKWALDLCyuyisie0/xJ6/GJGWqAfN9Y28/4k9YC30N/XgUU6G/n/EnrgBmVLevdt4oWo7H2/ifnrwYC4mvGYkN8eH/rAJJW8984D20K5Cbrd/f+evzdwz1/55hbXWR/e/r/wQQ/AEIgCNQBYUam1NrkABWEupDocbVqTrp45NGOAnUVa982pgTg7YC6kazvLz+YAAJAgD7GzQ4aI3kREJEIZCDcpXdDaly0/6gIJzkP842sEZiI7z/8NWsihTFvs3840E3OOPnP6iH0xlqiVDLNNYVXhzwxBUSgh135//n4RgS6QAupzp4wIxNf4agAIEEtNhqSu8UWIXSL+AwlIsOSU3mipK6ZeQcpiV4w+bgEGvgDgKTWn37ALVKtuq9RyE8tc/6/8/JViF0Hi0QsiH39IbrfyX3u1AAbJhz4/w1lKPQEvqmYrlFBLZ9xlpVbP3+44Shp6/qAKrnrAeTGWq/jMSesIzcgPvcuef57xa1oNwRkXVvj9f/+IC0ABIAPC8FospY+wRggcD5AQ2nuwLz4lcwif/wYNwAPBMpAAYE4+TEbIHX+AKDFkhMnkJmS/GOfgttBycSjHF9/7+GRdIxUb/4gbwAExZuVMcohGrLcwAAc4ABWgPIDhojLAGF1UjcVRD7WY72SKUwKWyvOHGU3vMBWqHdHYtEEyjCH2YkKDlilEXzRjBcqhsvci1Pb2MJrFOj5LPe02Qwl2wgkkgoP/97gRKUpVcbUwwZBAnTvTVzbn//kGCvRCAFeixqRPtWl+sMgABGKTKJvv611+mAsxV//722EGE8qwz8MQJMBXjlppSwia3Y/n8SG4HJHaplcoN1Lt7ptxEmNWRXRfwcBBBMpTIMkGWQ1LIxiYnJpo7zhKydhF1n04nW+v+b/ggtwAHyDG/i55eOshveY82K6GKO7FFtgANhQfaIv2U2S3Q2AACwKXQODbg0Rg/ZiHSGtr4jvruBnnz0ntbkJ/SjTP9+f4gbsA6gOiBx43CeHzchjfaeCjSKV6VG/3kBI5cMMAImQgHQQbErkYyS/ATBuRdA1h81kN39WGr3r9+9laYUWvyOHTYzutDAWNojOvUnygABMYWtmR8+yENYJC0NUu9r0153F+holCDnZGmv128h7EZY8R/UChFI6z5rVDnuBhxer8P8OS8gcOn8ZCDDZzuQjRqdKj5AjGzB21+/yRlzDAdWyFJdMd9/wQTsYACR44RVMw76UU2AA0KxgFFK1hfiXVEwB/S27Vn/ntSxjDVeZaNCuabvtARsHVRz0QUga7+73Cgu0RaWU+S2eYNMAA2BRE7WUSbxJugAFQShdZSMht7v/cUWIXRrrng4HqYcl7G9i2s0v4gPYAFhiN1iYmzrEsM/wPwBB4oJIUaOZrgitTYnwmfcEQoHSQIR/7rA4QxxHJsvGkf7jqDMcCSj30J9/vAQskoiDSExBXin+eJIB6vXnKSQf/wYYBkvVQC8KIQrbm3v9eDKrdtC5fxAe8gOUUOOGJ0s4bmM/4GBhwA7cplh/8pALip/m2532+/gWw1DbKS9g6OzLwADGxMnKdSDctqMFYAgy9pr1kEd7KB2UEzxqmrvP7yTmkZZk0bBFeFlEkuyAEXc6Y30dWB4f2EGHBv4bgKDHZ7k7FadIhln/B7CCZe2Sv1++bVOjf9YcMBTVK9/y8F3O+6X/7enTsf8QN8ABh/EEWeuUDkm11IACBhuwkWopfPMfun73kMhVEXiHoaxHibAzWQHQYjyvLAAYjIM4cpmpEvGUHIz7sN8zgRMcpGcbU2gYR4aeOra8o0mgfXKAA0RmCpkyhmuP+sBDiKxmSZJtN6AhmcxFRoubLLP8DVmAC3BSl8qJx/+AC6MGUNcVF7fn+5+sfq2Pg0gxiv+GIYAFwC4oIPmYUs4akL74ABvYhRS3YYdNi2ivQkHfCd+y9XkdASDHZ7E3FiJsNs/z/mAAmdWCfZtDdcDIUYjXxrr/3FwU56/9mkaef9+o4e5XxHiTzlCJo54D+3yG1P/E4m+H4CzQwwvwhbDvu+hd/9xIANA92xEHIKGv/wYcABi0GILV1HLhgX1VdZoqaBKDJLIav7zHlZ1EXiC1NYgPSAA2RECpsyhmuHhykgir2eaFv9e8mI3aDfyEt6Q39Bt9/3ALrAQURWdSTJNhvxhlOKvyy0tF/TTRDD4gLwZAAODGd7/yKoRJllr/eUABOqIFThtiudfTIRU4jaS5K1ffrXmXWuI6Mx3rP957m6/8LeQHaICDhmU7Pm5C3+DwzR2KwWp4/+9McH3B57Z2/+o4oF1It73D3r/xvybEycouoI5rUcEAKk44GQtS6p1nghsY0hxoknnVJ7uC9IpmHv//UJClll29fsr9EiQ/+F+AwKLe3r1EJUtZB0ntgfdAJqBMls23fp2mnZbLX9BsHOtq/gFUM8/1wA8rgGBQhLDVCiawMQHy+afJfvwY1aGUABtmMsXkAADdixfz7984cAgOyem7yLB+iYEkE0YeID0AUEQw3vWZzmnjcru57iwHzwYQA4pFKie7ergBA1LsBEgzlLPIi9DnQNmUL+UkTnGE/24zUgABAEABBs57KoqPf4bUnxFonMgA7IM5M6CerFvxYMlCECRqZLX7s9LXllhmPu6/43wY1olpUzrk1e/7wEI9C1Vc7xuDVGlA+RoXp7ZlePfmab4oWOqxuCx705G/9wcDmCKJJWYQvnGwhNsqEvpkGk8JGx6Gnst9i/l+gpHf9X2g/hieQo8xNZJkv+2tMERN6kf+pbuiFtfcH9mGepy5QQD+Hv9AC2AAgbLM5si+UrhgE/ZtyS5L9MCUL2kZqrbBrMASoQAHBO0SgnZC8/zRwAJwWrYk/iBTv9tGQOAxQXqJQiYbbv3gKBCyWqD3JiCkin/hCGYjG1a/L4yMmYWX7wekuOZb1cOQn5kaOmeHeAoENQj9Ccd/J4MfOOAEPYj1CkcfJWLePP8YTlE56iPY4SR0yGH5CMIpyjCkEGGGMZ4GqqiuQjwktLwBNjgA4J1+ESQlZA7BhiOuImzFEF0+Ac2AoRRfTP//X2Uy0Ff4djCoBRiQjY9+JIQkwvyHomYw41ARr12eQPP+BgAISsNv4l6P9TNQAoTBIdvquBFVGmv5utsD/irQ/4HXT4JUgi4us4SZ0IZx83l1bz4YW0/4Z40YGhkylRF9+9tjKvOflFS1qfEAD3D8x1agRRtJ0ODi/oftWw/wf/+H4fkEgBEMArFgUF2htTAAmB2A2oGxW3h5nAmQRSs42pgBjIRWUwuJI9rEsAAEwUB1zh0dNEYCwFdAbOGRW1be6AfMzGV1OLqSfa1Ia5mXgLdYCYf7vPwGxsJVX1xfPUcPIMyS3v/8R83gAIh18R+Ih5NMMf4dwMgcHDzheVMuG5C++/wSGI1rxA6TSS//Bh9gAA/AACMAcRGzRGAFmhYr4xR3UwtoOSOEIY1Gk1+LALZjOGjt2vxv2uF8RufL/yAAg1MFyu1LO5ZFrK4L+ihXUpygL7xKP7O/16xbDANHyfzxihAYjbjluEo/8jZp//z0GZEUYTfhm3g78CY8CQ+7gGAh6ldFCexF/7xR0LcZar/Xs8P/wX/AAsBDut+ZfwceYf9+/gAJoOCfxt8vHWQ0NcMAh9+/79/1w7oCgEe77YAM7//ffX4eBk2OJR8clKxS1/eRS38CKnDPLoP/DkAN+76a+6HgATGUuXm1MAMHn5HQzjE6wtzAAB3gAEcA8iNGiMvjgCFBFUXGG3n/4YgLCQhQQGQ2mV29Q33pMRRFGstYpFZVHg+UGjU2GJEpdvz//8UARbSgkIRBMf4OCBAARwAVtKP6X+t65fiwBITnDc5Il6v+XZLzw7HPQfhiAAhHfkEWusT/YpOjIL4kV4RSqy7bHeZM5GEoB58SuZjl5944rrj///flwAX4jFa93284V+dRu/3/DHAAbBwS6JtD6ZJj/EAJkCatvVAt8+uTsfGcQbpP8mdeDCeT8qqE79q/gdrsZw5gAeDNwipPJSVwp1/+yApouSLOi+Xf/KwElCVpuf8F/7hQ/wa0uhsmuhggGilABgRhAmIWu//+7+RMUC/BRUSgW2Q//BrgKpjXMrF/7//EAgwAKgB8TApNhLP2Sfzn/94AhaPJwKjjxG5ZA2wAEzIZHUx0YdC1I8jMgmcVdoIU1aIftTDFFqahd00L6KgyPIgUgtKN/yO0aMSn4cvmR12PP+CDwALBCt5iNmxMWGGf4AA1EYbsIrPJS5ifT4IQUruOHDYtur0QADKyoE+jLG86ahoyLAth010Nv9yA+wEdA+q02SEGfuOGdt2WSvL/chdOtCxoXNn+6wQqaUY0ueZN8DqT5RIHPJi0pf+/qCaFfqWWe/iBtBgAe8YuF+/lOxnoMDWBKImv6Kbi3725wYTFlHwvs0w3+95jd+c6lCpa1PmBPwwUs4hHGdEVS4YfhQe/bxz/oAKDw9/UqLYqvQ0MaJIcDqAFnQHPUW99qvzz/v/3phBEn2G1VNcM9f8EGwDAATLkNF8WJ24AXE4HASxWOMHGFTOAaAUoeQCYUmIJonP+OtMi1jl+toWrr0RKs8OkHIF5h5LmL33i5w+EQALB0Qv2eY+wQ0UTSHiBuHuPoOxGAkl/ZCZwHkownh/av0FkDaWkRJDb5nJECQhHczqjT7Fss/wCTAxo5uC98NlqfP4HwQARxCbZUe+nQW/gw8ABIxszKc6kG5beCFgZ612DlgbEjVtX/vByJcQAvl3p2GoYbUaJp9nUWBLrwun/BhOJWwOpvJggAF6Hk2JoGB95/+uAEYEmlB3k+wyqXyoWgAOBiSUqZEo5ilhx//19N//2gO+giFVpX8hL+9vBAQETefOT+IBBABaAi0G1tIo1q8AqazcGYwOow8j/qvCF7AERBdny7godFonfB6ptH7/QAwqpAqBOo2dWcVUbkmhtr4gBlAwrv/1ovQkwR7TZIAYCOAjcFmBx1/3gQB0CRCgAUE6/EoIXQO3+G4RSjrTG1MHzbRMWjf2gUYNX02rxuctB8pXRvf/DEACoKQUEnzEZXcNVF/8HpiR96PQZJdHV/fAAZ9JmOoZHWfczEuOZSD8xaF/xAwHGFx9vT9dtSb4gbrBpSS53pog2Ux8Ub0qSAIMZNKPKLShvOS4nxAt2GUj9SvkvTwgB6gp4QjeelnUCv/vezGvKdSi+tfhhggQM+FwxBa+o3cNC+6h7ZGE7iJxD0LYoAB2gA1DVbESJqk25/aNQMIKYzVg4KZJn+0AgpfZJZTcdpgnf7memO+qtG//xxQCkvMk0/94/q6rwzf0IcOWWsohYr397/xAVhgAJATIGDWH0IY1omoZh+MBOoYKYcQnjeiapvyyGGF+ELYYd+XkL0MGDDFJdobtG9ggnxatl17Nt9c/f/D/wrGA+AKEVqwWZN79bv/AFAC3DY116kVVhJ5S/tf7ev2gJM4BmK6gehTIY7vlpx/38/wkeE//G/IcekfGKITbCyGAADtAAZwDXxg0Rg+AfmOtyvzMM62FODD8ABwMSyFTZ5KZM4Y//7sBtzgAwI0gVErXf//d4gm2v8sXKm7Xy22fUAbenQ8+Rc+fTG8OYAHAVFBB0zCVnjUhffQJhqqrB6DZL+xf1fwBDwFHOj/3/iA70kBTQE1IyCm765YAEnRwuWbgrfGcOAfDM+IdOfHDQ8wvSE7vqGoPksjq/v5AcooIPGo0s8dqM/4MZRDejCKJQA4M6SN8f5gWwc5bB43KzNHKjWkV9f4aggIC6AFaKQ1MOSz56XVkx987QPHobj5j87MyI0fw9DDAAQCOR3c3x2xFYoMD4ADGYmZTnVhkLWhvUDnlBK8XBTV18WNKhSaToDqH09sQ/DG1xuLqyXzFL6/fv/jYDQUxLFbqyteDCPNGw6Xr5uHpgAAqBAGXOnRw0RuAMhRTHoXFdQeW/+0hK66hKDZLI6v7+IBynACAwxOVnDtRf/BuEDQRa682psgFICX4yC27vIPIIArEAaE2ptTBlsFRgYPGiYyN9gna3/gJdsHdSzXuhCb44lac53CiG931YiZtGPEgggEErLFz2Zv8kBQiRVW4T+cAmHBNom+bTpKfiAUCYJhaIiTwt37yABkfSm2k/3QTgkFzr0M5pBfzgQIkLUHYcJctUDStPsIAGdmAAMLaT4M3on+7yvQuamxh20HzhsV9WvS+AYSwpsot+y441uHIWwg8ZuplLA2N8PfAAQi/sMtfYlPIcv0GXF4+xiQooAv0rjCZ6fv93qGEusfL4DJxIyx0sb3Gzy/9TB+guIHq6xp8A0GAAEATPFQAAgAqQwDDAAoBWigg+ZlKzxqgz/jXCJwPaA8x0f+4YpH5GwPfxAMLNJ5ZnqeJBCdd2piP1dpDDwAEYsnOyHKI62lsxAxA44ZhPDpuQs7wjglux4Zs9Xr/oC+JkaHcitv8NwAHJcP6LUSrsWh/tEUDZzscJjSnoGAw4oQ27p/nnwnuWPzYHJcNebg/4kbDDgAOB9WDFgq04kFzujveH7zG7qKu/elrU++xCiFNws6ZFtFPhAAcgYWwtK7BmuhL+hhuOzx1au2BIsqvSsiNuv+4Pwxll7P2AYWZQCmXA5Wn1z/C0ABLEbqx+3HYQtmoACgMaEtz6iiSua77yIxFZBUWkhLGpD0wAJ1VQnUTYvfT9YMQueXyzHfxff3iLKDecuRuHfmsuTmi/1iAvyQ4C4YBVJAoKtDamADQOyA28PitvGnAiYxSsw2pgEZENFMdCjJaxLAABMHAdk4dHTRGD9+DlwqVAl0v/wNJaqU8HLdT6h1gXA+IC34DgKyUExAyK2sYPzMxuvKdSj+taQw6qIlLVJ0tV/8ViD1gDEn86v/f/oQvzztgP7MPpKevAGZlfzt7/Py5nueA5e5feca7zz0qVxsv84zNld3gN+HNzbX/EhWBeDtoLXC4r6tr/gAUAxrOdoXn5CxdE1/vYDFoR+pSGPkbF0DgYYXmhiVCSKLp5/xB/fOS9GfqCiuG/r/PigVBTWmjzYTdyGW/+NPVqX+Gsqud2I+vn3MycNPi5H3l4TXRhGHOyPD6L/P8PSmv56nhFP/AEA1Jrasfn/iD4cBiXJP+0xawa4/7WXhg+gxmWn8Qf0/s2eAhdyP+/X1z1/gJ2RP73/z1gDYk95x8/9cJtfPjeeuypP/HrOmLi/zr4g9QCJNJ93jIXE1+G+O5F1z1gYky1X/z1GpstV//PWSN0N/1/1z1mdlU+Pz/68fhAXwNulht0tjbpYbOluIDHMhIMsNtSzFACgI7fuCvzcUZ8btSy/j+N4nP3w3wBAFucroRB1eodin4D19dP3/8HcAAAFElBm4DoE3DHgAJNkJlOfmDIe1UACrGbYAAxpDA8K70iK4VjFFpall0wL8KnJgVAxpwMlXzYLalP/LswAKoyF0D/EnMfPDfHxEN/ELl5mKKpz9Wc4PQMJ8yoQcQIeaD5yeves6Ocu/4TxPiT1wCVTJ13n+sI+EfEgvgwL0UzCCVNQw4ZF9lcPCLhHiRnT3KCZsb+na3XP/cCEGInzoP/CM+EYz/PPevAf8L3f5/aZULiaCEH3I/5/5sABqDgl0TfPhkmP+Q4vIuM4j7UW7iAzAAdIAGge9YiDuKGv/wYdQQGoqwGgm5xx85lSZOu8/wzADIAEnlB1e870X/sSMPoSi7Ea3YCQYz/Z+ToiLbTP81AdFDjxicrOG6i++JQcyjK4H13f9x5UmvHHNaG/r/PUEPpU8Tb5C6f/EgggAIgEuDhrDyEd42TVLeMBJw4Yw+hDedk1C2hlBcqh8veixHb2jCBKyx9ffmxLb0iK1+i0xLlZXRfmTAYUTOUyLJFlkMMtgD0PGIUaI4DRZoyOPnmUxo14k9eOqXPf+9lFN/4k9fALM0p+/8SfjwBD6tN/70NDsb2rZn7/xJ6/jv59/X/568AbEnvOPn/iYvEhzAAtohBhXxKzbl7C9/5AkGiEABwVhKBQRvgeP9FgBmZLbvfzIhBGkFnpz5lMl8R89YKjwjt8oTspH/fr/DcAB1gBIHupak5Box//3iUNgO8J1XCpUfpY8AYkFLk4lEyaga9+5ANawAGDr8g+K5wOP/P9utWscYRSDdRBw5ZgTenTPJUbatp8OQAWBqhQAcEb8SErXv//cAoISC0QcSiIK4a/+AnjIAMDEg/ijA7A6/5w2AEoaqlqT0minv/Q4wnu7rmAXE0DIApMvMyBmX/+8iLLvqZvni9JIu8b2sjQ39NqTTu85Uk95fnw7x1jy89L8AW8X42qmczXD5Jlrhzg///DnIECAA9oMRhqpSMVaXTLxte0j/KoPPPq5fb24ADWw/fv/hylgAWHhAh1u85fSYYIoxgGCADTWBucD/X9970806Zvv3+IxK/PXwBkl2+v/f/jeGYAFgQuCf0JW8RuYQOv4CQISxPqE8+IXMInX9wIMAKAezGwXT/GUl1fxIWgAIgG+DBa7yMca0SVLh8kMF3cGS7yDc+fB9OgCCCKRkQaINMA9QFRQ46ZhLDxigvvgJDFZ7PuLERYbZ/igBBBUOTyfvPb32690wKzRI7z/43gANSG64xkKP6lJYAAJA4DbHDg6aI2AhMhohRPS71LSHziEcpAb5guEf/2r4WqrUIj//2xwDJGBOTROn+r3hUj0Vxqp5ZhC3eODOYuBT2aJ0y9XjAC6hlJIqzhJ9In/4FwIq+kmSqWv99xtcCPfPGHRcxtTsOYpi5ekjfQJAlS08Td3+IGwwzgcABIxcWrIpJGto12wAAXBTLBwcdGiMHgIC/w52xA2ptCARw9eSccpG9XPZ4xVoVlFQ8imlP4eJgM4J3XCxUarX4PQAhkrNFuXxpzzrfvqFw0KauZzABoZFUpkdR3FqYGHPWOAh1cUJe0E0k4PPB+hZRQsPl6IorX4X+HAAac5BRSm4YdMjGy3iFGV0hCBWw3/cAYBSiBx0xGNbOnqjXTHzy3x8bnV13v/QpSvqK1/pP7ebfb4gbgAJgA+JgYmwltFknJM8Hgw48zEbUvb7YAIAdYx1MzES9tjfP3gWAmOBBeoNtO/3aX1AZy4eYGQg3/bHEIZ7woBW+xLRG/6Bjlpqzf9H9EzQIyHA/qY9YfY4vGCFLd3qMe5SzeeGMQQRrUZMxT///cFCnSZa+/+98I0ZGVx5d67ZvY73///9/xAMIgAAqDgOucOjpojAJzGVVKdSjpW1IYY4c0E1ClccTAvwokp+A2GAHiRb1aH8//hbgAOCGotEScSiDEDXf/Az4BgalVHi0cxck8//70HqUBgEJWjREw+mXyjTHYS41NP//t6cyAGOM3DTqzKCBB4hkceZ6ifflIyS34dlr+xjeuH//aOGkuH+F4AEyB+KTeR/v75yRbDuEqbzQQEvNNJ3BaxKEzRaIwAGNWgtJq0QAUwA8GuoWiTvLFvcRkbAPANbpSskz/tACQLS7QLkxFqbPfwY6F+rpH4+8ELKn91CRJ/53ScQSz+9J2zC8sRnf//+F8yDM6Dvdo62XYXngD5hEHqynlPffAAlCloLiRiusvP5/v+6wqrrFKp/NgaFsy2/z/cTC4mmG9fP1/gm8KADcxu/OdSj+taQa4BDN5qKmaPgS0x/g+thvMX+ZIn8HE74kMTowAGHoUZpy48YqyomAAwAWQEX5dVJ4k6iT5BiFA8wtTaaxVdct3GwA+HrIWg9BYt3/xaBv8BDWSmJEo5jBOzTgYjlBD6VMA2Ay+z3//cBiBsBpCTxvDqP20/4b5gwQAGuYhRSm4WdNjGyvlrrWyabQQ7/smj7P7v9Hhvf/nrwBoJuccfP/ERnD8Bw1VfgtBsl0Nf9zgAJFVAnyXQ3XHD8MUUvuOXTAtuqeREJmQRWcQhjEBhwAL0iAEBCQdpRkbhc/8lXAXYAfDxULUfxY13/wYa0uB/nEXQLU/0aTNLP8IwYzDP/aj8fL/BhAFgb8OFMvIxznpBUt4GHXBIlFWVta7hLwYfAAsDEVz75dCYsKN/Y7blTCqX2r1YHVXH3wbXtP73/iArDwASFv8mtVfv6kAlDuJTRHuXnCdFK9/+PEWlevDPRLc3Km++P//C3ICQAwltaJv7/W+IITzl3ZLSPnb/4PdH9cbAj/oOemcfggNhBCPTLyX0hz8+xDrN30XpHv7gp0NGLCidpoBBC48wKXszpDZv7vNhQbbIhL4ZBLQwFGdgZJyTcHXe3F3/g/MVmKz2LkrLwjeZCJnArTji/B/DdIY5RO9fIp7eAgnESla/PlqOMBiSEAHpkNFe5vf8rR7cR/+wHrPQ721/Xym6bkvngmYZ0VkFt/h4Y3iA7ldn/w439aYcoT2HkPYvfdPoCAgkiUQshNG///Hi6bLUxlW//wMD4SQRgOcyEDjIvsrc493jl68oNPv+l+//7NE0PRxdT/p/H1Ha6G0EIJdP7U/4gb5BkAiXWwCYeXgwT/7gmzkEwlZL1NLf7sCAwousJk2ybbc7vLs/El++xKAWQgCsUBoVam1MOqtnn+fYYYGRbio7am5uN9CamQr/HdTgDExBIGGvtILwEaMv/AzyiG/SZpdMt/394BrhB1JyrrJvfrM0Py2/Xv+FSQNCLHwxsBhYf/8lo4lAMqWdPoF4agKBDUc+g2OUSNjHzjhAJIJWoielGK/66FWMRa6v8DAJQ4gFK5lT//+Nh4Aqyvv/swJHBl7yXY3l2z998PXafL0oBItMjjCV2XRggTM0bX35sS69+8EBhRNZk2ybbb/eU6nXv0BHtZw/UAiNMmXP/f1UbZmY5Fn7+pBsw5mVgS4gbDG1gAEmKi5JUJdLYLZwGK96cQ76HMFHGP8CAp+0vzFWztzmHdTTH+wABAE0pwAdBc1gHNXEww/IUfETHcUmGlvDDhg+KFcbcZF73o1741zSvDzoR/tBlGCSqOP4gPQ/pnAEHFSnIoTOtE4fmZjK7ir1JK2tWGGOxpGAAmZmAGByAJ3BVoeief8djWCdTgAwJ78mJWQvf+KCeAMICjKJq6/9+GqPxIc2AYAFgMexPqkteIXM+Ov4Vt1WDPW6ICl5+lbP+FuABYCFsR6hLHyFiyBx/fxAB8XQ1NhLPmCSJ3/+DDjUoBmXepPzfuDSVEkj/G8NQALAxVobONZQtddf/dGN/v/X+sF7alOVu/PQf+uXw5gAeDdDgAUEZQJCFcL3/GwBhC0TUNilenzigDseNMA+1TcwO/wYQAK3rmkaTv+BINuAA8IMjKhxHPstpb4w+iirSjkI3FdWAL4Amvuk3v/wvD0AfGMLR6B3Urxb/b/AARGDCdNYtqE+rEgLfBmZrjk5qOB7lcYf/h7Hx5U/6v/4SsUfJrugGJ211/aAcYJf298eT+AEEF71jFVtZ9f+O80Bjt9qbmhEGGFv4QXYlUVSoos634AWgbl01SNkf9Vw6i4LwrmHG0f+fp9wEbhSI6Q35ZNqfE+4faQ//w5gBYbKqTXj/lpjDs/04Pj2Lr4AFo3kWyjlv+/wxAlgP0W+TMeu1/7vnFJvY+P1/joGCALBuhwAcEd8UErYXv+CCS/+BO6IzFJEiP/hhFoWdQe4cXRLtfDHhNZ0//x4ZQAnA0cGIkJoxBkhNn7D/oQG3B3X43hzwAEwBnIO3mFVRR0DXzJR4AbW8kbnz/DH1kVJnbTp/ffgAJohuqGMhR0sYlgAAoDgPscODpojCpOucV/AqpNzz/F8BExOmKZXGSpqfcRjdhFUklLFJ9NBGAxq54YbFtVa/w5jYxh9DhQFAIVLfPHENaiV6ul/8vABfpCVeuyf7LogjYbu/DfqGokbdoAOwuNXTCymrvksK3Fhddg3OoC/xA3AARAUflCBVIdI/W0zD0kADwW7Yo5BAt3+3Jhh8qhskPTWn37gurdpaTc/gALF4wCgLTvVAy8kWf4HQAXAAEAGlyAkhEWeugrR3HYrfegB2gbirPp1hYpEnDK27o/AQLXhCbZEe2mFt7/hgIIkIoAUByVIuV3bSNiWaS3fMDw2iXtau67J3Ypvn75/8MQAKQxcouedb5KdwYfHgMyLufoWgzxnwxoGj/jd4AB4tTo9aGfe0WBjotXVq3/9uo9LaE4FneGU/yzc+PJACh5+R0ES59sNd4fmADRxfAdxqmUQzjYw8AMXy3qKGxpQIbk0MfNAAb7oE+jLG66bhShxIWpgAfZpac/X6wUeRkmGF3/2NtCsJNi8MYe/U09oAccQ4RIjcKuKupKttNMba+MARAOL971JrVJskOwozAEArwJ0qyOu3//3fgGqkAAgIz4qI2wuv89f0MgSzQSay/3V08AVRDYlf+//gg4AFVobLZ8lT95EFRuwqfXrpJbAAs4GVQjU4xoiq3kEA2QgAOCNeJCdrr//uiWuav9pwrtngff/HAJUDgiojNdwRwOP84eAEoJWS1Im6rj3/jFZJBGAr9C4kb8B0jJh1YhSf97Ctl3wx/w7EcCGLjhpkW2UvSMhswqtS5KlpAAdMALAt01MHYWKf/tE8EFFs6oydFcU7/YAYQrdKLZr8NEPb3IlvM1iPX0/yoEDAvAB6SceGuIv/9/8NWjDpzIAYGeBOlGB2B1/z5QQZg+1+oyj24gP/8QHtmGcIWMyWdMuPm7QC7JVDM4Ce49//foAEVqG0e1ieGVjf3FaLwEXgFx4wGlWsykgw4yRwWHYRpz9Mf/9GIpWqRQyS3F/e0h7qgk2dpJT/3cI9xb8Pl46WW0b/AQUvJ3nTx/XjEZJnt/+/4gbAAZoTtzFzjetSXYABUHAdc0bGwPRGBLogE5jdeU/KP7WpDDh8AC2gA1DVrEH+UNc/tgTskAMBHARtRgahdf88PdDbtDWV+/DSq8/79DQUDYTXKc88ZiD1kjdDfz//EHi1/2oFkufkhIyq/iA/BsOWYADo20AAIA4AMOlHRVNkh/tAQz0NRV0fQlpj+Y6IgMigRbDWtes4ABg7FNMILHE//X/h4ABcFK2AcGnBtTAJY4LdlxzqbBTg1TRYokw3BBPkpP9AnZHQoqHn3TIjSRIrOgjYNwVZXoKH4X/gEI8buFc8mgWjT5dAPihu6/BaDYLoa/77ewxRSu53dMC26yHh8Q4KKVH2/5sf8bDD4AbHAiqeRlklt4d/+D4ADUQ3dDGRx/UpPgEUoxxVMZFbwIMd1gsKHnzE5XcOVF99pgAbMqhOkyBu+GjEjotC0GSZR1fwEhDv5yLmxM2Gl/57BQI8NPml78UcSRP5YADlBlJRJd82uQ9umIuVj6//gM8tfXHDj8BA7xIjsDbfdwQeiM9VLX/eHLFLEyguIC0DA1Z9glh81ks38CWgQDKCkuKTwj0+uZ7BgwEPpgPvBHmNZNvol9BNVKh/m4FEXeeLBklJUXc7TYySuIBfAHrFFyslVT/f1WPGmZG3in3t0PziBT8KF6K+gc/10v39Y1vRf6rv3H2/9f4gOwshAFYiANCbVNPbmvgwEAMYdEqya58sop44WYYSsHREC8EHltOL5+/KPg1DtW+pr17X//29dq7vN/iAYWAADIIRIPDTk0RvMwoJulUl9Og1/h4bi2DAMCN31xIjug4p6nr1BPY/43/huAC9AQjZtMWjj/33Axjc3HVK6RVfcAIGJRCZk4lUyXw1zQGqmABgRtCBUTthdP93gXgiRaB11xI/z/4g8jQBhXtU9/O+S1xlnh+09NH8v8M4AFhQJpfnQQseZy+33mo7hnnlKVR88vSlp89dcfn/iQv7AEIQBFoAsKNTamAA1BS0Hzx0F9Z04CLrVr3TamATGYlxTKQdCm8wAASBgH2Omho0Rg/MXxqCxIfnH5RmVozX2o2/7c4g94m7dfOvBnD/jeHIAFAK0UOPmZSs4coM/7QGOz2JuLETabZ/moaqvgWg2S6Gr+0QAEyqwb7Nobrgz/wApxRfh0N97/4g8VprO8RCySPn/z1Sgxy8cgrq+f/+FYwmPkgnyjJfX/9I70tn/m///PwhlXp9z/+fq3QMvQ54i1RRv5+v/89UxioQH9GH3h/33//nvP6Wq8AWBl+9f5/88TtAFq1HzyNjpFO8in77wH/hmNoP5Q8BHTT+9/nfxB6X+AMau5vX9f89YMBcTX/jRC51zr88h4A6pT+wNya+OPnmPbP9c9YBGe+c/n//nq3r/P+/X//1FtXDHgAWCHbzEXNiZsNM/zAyBQUEnzE6VeOVF99/fXBM3fP8/89c3+t/x+EBfAdTUsDqalsHU1LDbUtxAvlFeG2pY43AB6BHa9SgpObSjDdqWeJz94gXwAJBHb9wUnLpRnxu6WxtqWG2pad6xMHEAABYGQZug6BNw5gALQ6MaJlSZAkI9pEFrYXTYNGBiiGL/wCLwArIw7SXT6/w38zIbOoi8QSh7FB80ABsiMF+TKGa5BrzFQ/fL8J4R8I1iTy3hG3d/E+EQ1YLQGiEABwRj0CQjbA6f74bdYCHPi7sFv/xM+JPPcAkZ63x+f+M/iAzAFgAFQQzQeHHZojADmKCfZVJfToNJ8MOqcAJQMZNL/AD58xS18eb/PXMYJJPR3nHyYy1X+HMABGKN3THKMRbS3eIxiVJdc22UU/kuAnvnI1+//8SH4AFWABOquERRtjd9B8Ax3+1NzNHUIYY/wYcGYACQ66M/EQ8nGFE7AAB2AAMwBj42aIwA442d0M47qYW8DLlTR1fAIw4aFTtfxAVgR+jK5FProPne+i7AHMUE+yqS+nUWSGHlAE55b7/m+PHacLv/ifEhfj4FAwCYCAe2YsAweJjRHBI49J5fxJ5heBE6nlcbBvvp/8I+EfCPz0vgDTOO7z/PVqdaP+/Xh/F4k8WqYE3Ju9w2ThopRjLr/PX6dLVf+elzoxohojhN0l97wynDq0Pw3YZ4Tt6GRHhv6HpEMtVCYPjv9f+f0itDf0A2JPecfPA1D9+p5l77/8/+evo0kV9f/5+8ZvXbVuMFVV/bj1ynocqc7vP8McAC9IgBAZ4EaUZHYXf/ABQGAFK2XKCc+K3gifYBhgAIRU7iLVmo1OL4JcnwAoPF66XDnbh7EjRpRl977EmW/DEABzGXboaxVDHTqxP/vIgqJlEX77ZJr1AADoABGAPfGi43mPk5XUxBnWwxgYAFAVo4cfLwpZ41QX/wekNXX4PQfBdLF/DFvgHnY3ssRf/AaqPHLehL7+uMOptR8u/f4Y6Bis9X3VnSIZZ/n8UIifk0vW/+DtAAIwiHHagorniepJf2cBDCaQmQbIMso49MtxEZoNzloeSt2EU+qbt/X8Qevbm7jf6xB+GAM1Xzeufou2/+edP135/i8SHN7lLwBuTW44+f/C1AGmeJAzvC8jQS3oLpDA316vn4u/iA/AARgJuHCmH0IZzsmoWD0YgTMsbPnYsQ694DRAYUTWEyLZFtkGH4ACIBJgwWw76GMaJqF8sHLC/T39v+gggDVq3X6v8P8ABiMTpjmUo3qWkNNsFLxmAACMJjit4ormifqJfAASAN2AkugJqtVkhBsOxIsZyg63nln1gFKcrCpZC2FCcpAnpNhR1pjamEwyukskt6eBvB2b60YhA0HvZF42gLgAIh1cyqYg76YU/YAAOwAAjAHPjJojB4ACwoh2zD5tTAAXAALgU8exXnUilDvffQoLtET7KbJbOZdUdbuNn/UHwEYdidSRXhKxNpr/1OHOTs529/UH4iiiRRTxojFKWZDRWlCOIt3uoKIhVb+fxAIOAAjCjUVGL9jtWWy1MgABABLhAKCtLb9rwAUH8NzS7cU1z8AReYlPRqaWkdhEy8CYVVPweQgCsQBoVam1NrA6KHnC8KVcO0G+8H5IfRYAXWYduOjX83+F9jAASDZjiLMJxZxJpj/Abjy1CpTFiYLqqtxax/u5m/8n/ACmQvNykqBac1X4EWoIlYz0iLesbl0I7U8qnRTHDVX8fj/DnBK0Mq0hU0bFdR795dH0x0v8vPK25YV55Ule80xKHEWx4gO/DAAsGLZSZPITJfjHP3eAA7AAEAHoArQKvTXCj/j/+95jdVOdSj+1qQxhEBIID2u+EIag7F9z7wCReEAcBKd4V8XeSKZKeEp50J3//24WjAEIL1HbS7CPxxW41rTNFJKeWkHcaJSD1vwP/xsMYCQAFgBID6B8o1xowQ6IoYNauJqZOkAlzEtZ4yypAYfgZShMpAhit3nHrz8YAn4TFq6aHPm2H4AKYZBqstpTn33lCIMiHCYrsebuy4CLrVp3TamEEkr24zXfJMqyvegB0kxJKwkpzyMElWeBG5A/INsY+CDAnSi8OxdirJY/ym5ugNfa8AUOriKoiCX0wp7AAB2AAEcAwiNmiN5wRxfgwX+TO2yNGAACwKbgODbg0RvGONiuhijkUwt/DTEKKW3DDpsW2VvIg6PVE2hkvsxkJZj5+567QKEvOJRJI/NLPNBX/ro//OKsIpzXeesgpKbNdymNCjciZ/DfyIxFZDmVwiWNSHoaKCcWgXRS8GyP/uBANlOABAVhAmIWvf/+4F218Pqof7/v4Tcp90v/43gAYhAYwqkZkWSDDLsiAQwmkJkGSTLJOGAAiDQg7EmEoaI+n7uiDBK3BlPdmzPr2sKlG8qWIaTTfoDQHXDqU/08ZZH3uMdjncskWZP9/kAFxcDUmE8/YJxROBhhsmwAXpF7Is2sAF4BvzFYlu/yN9bXkwwlHb4gEcOAAxaGYDmqnxhgZ3Vd36cjTSRwsSeuAPKPcNEfhNg3OxuIDMABEBNgwaw+hDGNE1C/gQZUkCEFJ33nmU/hhw4hcekNqYf/+NjdAAO42PeKpy4i/+QFAMo5ROobqgbeWS/8BLGhK4f8cr2sb9Q+ypglhsWEN39oGD8jIRWcReJIS1iYfteEKLX1HDpsZ3VhhyJAcQXYr/2BumseWOufoLmRDxDvDfEh+AA74IQQruOHDIxqrB8aOrCKUDJeIR/6kqF67fvfbrCvizWlszqyFTsvf/coOmLgffLAqMtHhv2cATA8SWOeilTTJSPBcG4BVMyr/0BqMDOHCxLetQthdv//gZccEWxRZPay+fgeej/mGqYa+v3X1II9kr5u/9t/xA3AARAAPUHPCG7R4ikVubhr9e3UCA5cEQ0vVEEi/gAQzJmegkKqdHp4aC3a1OXET/zzNDIVzC0olT2I1gcEDzxic7um6i2+0wdRjOdRGFKcHhI8BHbVzuZJpGjTcLoZCK86Sv6r8B6+wlntilyaYu8Y+NgKMmIBh2q5R+h9P9Jml49Rf/PwZaNtcohycXpP8HwAl4oPIJwtZoQlmb2itERCdXlf/1gmYAAgBgEFSggyi21fYsAQDgUlCthH/BE/etAQjUNRU4Jk2wt/AzjyKWv48kBjtqLXEkQV6atO9y3PfevXH7H3zqvelbvAAwd6Eow5CkMQ+RfFsnDT4uR8AH7GUlkWrb6B+skjfaykTHiFus/7ViqqX+7B+O6bk17g8btY3NKKhqOP//uCNwTm082zAKyAA2NnIM+3xbv9QwcABIzEQiir1BCGrQHL9f8Jv2TXGflNP+AMAjAvr1pUOzC+tMACZUcOizaFb8BgC0GP1fil8pLULO2bsyONP8v4DtZy0ca//PAvT6kTSr+/xA2HwJHW9Z22Rf//c0c2RqDQ6M82Yfky+5MiaOAQiYv0rRkR/wPyaF7K6dcngceeQ6HeJTFqnD/vCAB5LabrLQp/hy3gMS05b//+ji825n390hQnL5XX/+oEX+IC/0xM6cwuJclavwAN6Wk9Li0f+sSRGP2zSP1eYCY5ykAxTGntOc0Edd06//z9HvdxLf7ud/lDBeiEqKLkz7/2PUHiNK63Sy7+IDuBe3itD/9q2GYTjfclrsfq8FAjB5TbpGuA9XFSz7gIBjiawmTbJssvAAeACM4itWf7Rd2iX/J3g6dpMjACA5AEdiqyOO/+9pgASOih+02Bm+AYD2dyaTOfwIIDZNgFKNl5M3dv94xDwoquZs71mmNhAQO+Df0vEh++7r7qL9PCA7XlCIYIaRJq8uh4AY6VUUKapiN3kXWfcKC3RF+ymyWzgACnAW38qLSHD8jBoAwtnkaGY8SyZ8df2kLBzwmUoEyp1cickMXKJnmS2SGcGHy5/9MJq8RV4ZtvIIuzxipnyZBO8v+Ges0VNAlBkmENX9qQIKyqTDpKRn7AZA8KHnDMpXeOyGd9oCGdzOqLExZbZ/igH0E6Xipvd//4/hiABYId+M65sXNppn+AZAsKHnzE5XcOTGd8BOABsiqERZlDd8MDQR6LyzNTcPx8QAASBQH2OGh00RgBiMRWxxNSQljUipRwAqMKN+OhvvcwijI0m8xaR+HOE4JPO0CX4CABkRItsWTv71xuCNmh2vKtvvv9/77aAjkaxPORXZfDyqMIXI5AHCG4xLbyS0+oVJpMGFgngArRpuKb79xpE8LfbMZXUVepela1hhwGPO1Cue4rOv+5znv4v+C82mb6v//3//hjACgA9yEZFez6BABjWI9Unn5CxdE5/v+BjJxg1Ttcf57vN+ABM9DTQ52Oq4YTMlF4XgBFZLPSfYFp7hd4ij//rhmABnZzFdyJ//+WAsXFT+QH117ggnaABfpRLsdLX/B//wxYIABGExx1oKIQ0T9JL/1DJf835d4n8WAhhdITJNlG2w+SCBa3R1UOTbl34EAcvwAtIjOLTfv7gpbJDnj9+r/D3wIdNJ2WZP9D4bxitNXPjU21VQYcABAbhD2YhJJTGPKS8NvfSx2+v/gkG5+7/G+AAmRDK6CKxJKWMT/GmkPWkUzuH+4ADdOwRNFaN50sI9dOFn90kBsdf8QACQCCSLdZ/+mUuc4MT2NC6Et1/+gXIREkRtTnjMQHPAA4bnAqzSZtApp798VcBKKrPv6g5fq////vw4if2SO/P8NwALpjDC/n+LsjsT3/n+gAylGVyiqkkXBsgHlxPXCRmLQyEg/f/hrAAeABYXQtJtPHmCXjv/90AxLOdYXn5CxdE0/lgApzZZEPp//9//xAcjgABj3eABYgELPEvfhcg4T92/o9BbjLVwligorGAmSVGe/9gFibUvVDidElFxAWgATmjokCYGSWQ1/2PITE+IxkRfuLWwAaAe5t5un//l+/2bQyZuNoCMZNZlfP03XOzb35iKKjJ5S0ItNJIzoHnCFTU38/3Fa+xnywBMrW0bfVxO6Dsv9rwbfwxAAcergIApK0ZfMPpl1oAHgABAAtUSAgjAXOemXFLNRf/98gE5g6WqMS1pw3ikbfvX8ACeAKFmVJyS3wxwuDEUvUgEAQcosdM6qFXBN6405Pv4gbAGxbnHZ7BVZlPd4BFWNcSKV7v+2AUkBtSMgt3OgJCEZzOqrFxZbZ/ntKMbJa2/fB+MVbFRRUPIppj9CDccUSQyaDQrK77+D/DACfr12+73inN6g7M8pQAPOltyXdn3YYHgwLN6mMhAPovD9fvneN8OALAAJAoD7HDQ+aIwAxGIqIcT0uSxqXARNapG8bU2PA/wfOHxZ1Z5gwAETACwe6lqYO4sU/59EFYWe+v/fD+kA2HRd52r3n3tMJvfOH4INjAyQHxlpsxi9prigjlBElmE/tSYIV9Fut+X3/kHXKFaLzW7a7qKYY2GPAUDNwypk8ldmIGEf/IfiYAaBrqFok7yxbwuZ/gsOJNlz+7/9DBSURftOlOuf79f4gbAFg0GfSJZwjPN3X8I5wLs5oyqmVpabD0rHFpnjHpH+4kzaIpjLE7IBaQG1IxbeXn8e10HaElQyCFYxzngYH1nlRAk0ESW9z+D5g7BQ84ZlK7hugv/jezLSiNoATDl64hvmEAL/gAECekRrCF2//xoDFohEiPYiplt39wHNIWDaadUhf/APN76dbaAU1IB+jyRSSHOKm/vf/DkkQAXmEcMnxCbaSd8ABLOytbjXaB7UAAQDMqbgBZWo0y4waP4I2r5/8b+YG6hwpl78c52QVLQ/IBpg4ay6jDONkFDAYcEC4IG3O2j9kJv/fcCwAQbRdJTMhmB/fPBqxcACBxXlKzVM8EPGldjFnhlkV0ABiFRMoq0vt0mkggvMdbndTMM62FODDbrcp87M++//++DVQS7cM//5h/4e0UABwDCT2zYi8pMwZY/+vtL8A4NOgwo3iMUWX1iFhwld7jRa7/6IwiLF6B0FPK+9rXEYHsD4QW793+MbsFAd6HrZF/06Bt9aqNo/3+GP4AFrACQPeNSdxYx3+2BMjMAQHeBOlWRuB3/zxtIMH8vce4DlcZknzeLxB68JGN/8T4gK9AYtFKkQhiKWXXf3f8ABIx0TLJpD7ZRRLAABcGM0Hhp2aIwfgLZGo9gH+HGXSx21fd+/8SGIAFgPimgwmRzAqYjEd78BIMd3s+6s6RDLP8A2RthHYBeeIQf9rLAAQMtLCySh5D/1/4gAAsCF4Dw25NEYCCEJVFT77ZJb+AP/hU4p6hyX97nOZiur/DVFwBEBrrjT5k1cDCH7pMjAEByAI2qyNQu/+FXjAXkH7xMgHeMd/VtO16L/C1NMXkh4CAL6V8IwQjJM37vAkELBK6OIRBfjXP3AaCXEABwTtGBIRsdf7wE6ACUPVsSfxQx/+2GzIAQGIAnqzY87f//cV8oBkthf7DxutM/79iFsJEOOHK4NEDVeffxx6JYZ88iWpKFkOzRmCgnJnSqR8wt0RhuBOiHzLouJG8ABsHBtouVPp0mEsAAFgQvAeHXJojAa49MhrLkf7vcSCte2HKpJP3EhCZRF++2SW/mHl+s/fkOPyOhijP1hbvEAAIBK3GABvKrdA92wkGHTUEjGjGJjxA9VGarvQlKCWdCDCCkqBqoTv2oRWU2NqZlDiUqdot/5qvxAVhgHYyeCsvjUOar04xUf4Q6kGnCHPyuocCFC7jB2go82hZhkXZw82GC1DgHzvgaTRO3vnkKPiMhyjvpZr+xJW8cO6Q2g+Vy//vTcekEql7sZViL+GcJqbjHOAg/TypXzIuXvj/I6ZmJ4f//h/hacIAglgAcwAFvuCo1p2ov/AdB9cCXwWh+37wChiN9iam7OkS0v/uIByihx4xOVnDdRf/PD3TFoqx+6Ni+ka5+LyjJUD9P+D/iA7AAvCRE1CWGTWR3fwEggdaw0w9eqjOW3r+AQqCEEqchhw2L7K+NlVDMUDeYWT/3iBLXCMbud6dYgMMoeD4FaGwvjpIUPM4fQxDM6A6tGx29E//FR9ObfwC0rD1tr9+r/C0PgO0LhXHySocYw8AAsCEotUmEoopA1/7wYEhTAm0J3if0rZveBswADlBEeVJO529Ybd3J7490nBx4cOP/rEH9yiSPy/Adin4hfTp+3+CGAAkRiKiHMpRkqWkPrB32gucLivrGD6KxB6wGFf0nrr/+d86+IPOn2iBgHp4y11/nrgLW0dfWDqdPX+f0oJucX5i13//DnJoANwBB2o9pCHPOeKDCdYzuQ/1ZyHml/96Lt7x/h3AAYyEVlEXiSEtYmH7XhCi19Rw6bGd1YYfARGQ0xTKUb1L8OKGAgn4p6fdFuf58sWTXuQ/3fGVI/m/J3+f+X0knBSXfZ1SX/+HMABAgVOuEJq2tvfrJfHxO6JPwi4gC8Sc7in9FP/ACoZ6l5Uff7/4b6Ax2exN1oibDbP8/SAAmXoE+zaG68eoA4JKeX543KgkP9O+9zWP1DHpp+38QfqHgBGZV8/ff6xB6/wCZKnm/8/4g98AaCbnHHz//hDEEgAONgazZhS6L4gQ3+/JaRkzC5FUMPiPnrAY93b38v/56trKkLn//8R4ED58HSeCOBKruL/79ePxB6wAzb69f9P/4Y5s4AgAspyujIOr08Mjd3Lrf3+fz/ic/n8/4gN8APA1ucroQ+6vWSZUN/1/wdwAAF/xBm8DoEwcwAEAMMUEppoJECBEiiQIEf/4ADswY/1WLCmrW0jwgSAxpuqKE/B7jgB3gAzUzcSNn+/ESw4Chngt2Juw1xdBC34MJn/EnnuEv5+j+f4kIgvhKwPGA/wBAhAEagDQo1NqZTxBBEv/hGfCMZifnkFA1cld5f4CJ6z6+v8ImgAOgEsHCj5OEIOGMCv/cAx3JcvampKMNN//P9/9vwYvLxh+HdebwADBS8FzxkF9Zrw3AECEAy1AWEmptTa64CdR1r3zamAyHLYD6kbBfd0A1OGDAEMIhaXHH5f/EBjgAeCTkABgXj5URugdf4AoDCu1jQL1eT0jcBjf7oAwoisZEWCLTQYRLeQBRMK2U+eXhR7qYVT/G9tn+euJFFNjRH/wiCS76XxJ64DVL2dYDb/EnlvgYiUtV/EnlLNrw2A/mYtBwb/xPz14CVJp3efjX+Ji8SesCF3H/fpEHXEllpf+v89f2EU//88pYu3ILlgILu6L3/v/EB6AAzITopjoUb1sSwAAVBwHXOGx80Rg/zokAAIAJuIBYToav9r22YbqKvUkpa1PhoBNoacEStc89uhnjfzD2Qni0z/f8QHKQei0JQQX0wuAOZx08MFVV/bv2tjQ6r/Egwh4ABQEAfaB00NG1N5IhMyGMhAnKYjw+AAmRDdcYyFH9TEgOs5XG2/tbBgQ/8SGOwAASBQH2OHB00RgFEKioQPxBlSmKMtwAAsCG5IPDbs2pgEIKiZRUpbbJLeBhydh/OHoAW5MjU8KVjdO1DZW+SvEBfgAWIRjjcH5u/osmW7wEjEa4yh1quaLJFu8FgOfVKjhv6wGB+gEx6wHtoVyaXcj/v0UE8Vx9Gv+CCAIIQBWIA0JtTam6fygNgsACyUpEydw6zCifvUgJykYxq0/SCif3BpeAQrO89/mRYxNGcZ8aL/n/BfAAqBCYI/Ynn5OxZE1/vQELYhChKOPkrFkDmUFKxGWupfLYcjHZKXO5gAWBjK59oXgmLCjf28FDesECUmOF0yjx2+URrH7D/jcMt886dp2v/zxanAm5N3vx4/zxSP5+/4zhuAA8ghMoiUvtkmv4PzHW7vzEEItRTA1AHlHuGiOef1P//f//DngAOQaJKDxLTuHI9ea2/+KHbT9o9vT3JrbMB99uQd/+IG8ABrRi/IfEF5aEOEMB2JAoKtDam6T76oCtA7IDagWx22fzgTIIpGcbUwYAk/GVaBrtYGmicJgJAJEAtNsBGuklr4JB4DKdXX3tiEf/+QCvglMwsoWWcgsemjX0hhFVgK4r3/aG4qFbP8/wxAAQzpCDpZlpzsWuQQQBHyqALCTNc/ZvpjhK+f/69wEW2rXem1MNXq5fAFAYFqAnTSlFEWr8K/3kYANw3xQbDc6mzKmkkMON+IWa7PYXX/ALN5wcxop3wIQJC2vLV8C8yFjedTb+3MppjYtfBBQBwAExIpXQRGJelTElkBCGAArpWZ6CRX3+ZMZHQ5lIPylo1yNE4xLUV961gNFYBbNl42q7AABIEAfY+aHDRGfe7A9x+L0mb9Z78zZb0Pc1XykLT/2QbYoiK4ef4QG4AG8AgomsJEmibbSXCB8TIAyygXyWcZzvgGdAMcRWRFgmw1/3rDomWXSG26Cn84xDsNRPBKii6HaAiDMSuOmBCyy3f4GNRPyIf+YEkWKAcaxSKTnGX/fAwbYDqAz1pjlPACkUmPCFihLexf4MRmhxZEx1Hx+4EeibFbUv77Roa7H3LjLfRBhx28D8MQAYmQ2YVV+Qti0gi4wC7DSJSpTh0fsY/2EAOcwAAgAX0WAQVH3+9wAHIJzSEFJRMx/waW67/U9ICwMVwZaM+IUrVoc5D+tDFVjgciVOlUo8Z6WV8OdQBrIxlmt5JN/n35B/wtOIFgmoChB2oKzY3Rc3mn//cwoUBQEsTjbBxZMvsTGiVcNW/jfkaWSebtYSdxJj/vqTVKR89kPbE9g9XvwtNf8bgRYAG2VwnWVQ3fAACEf9gi19iU8hzfDBLuwJLuazxkwMYremRohoomzn/hkYbGGcMUMyYeMOEDdr1bax/udZI6ehaDJKo6v6AXkGiCyiSabLipYDAvhuI1FZrVdyXasGAQ7mh3muW4V0sA7BJnKju4HUjx2DVS/5VwmfRf32/xvTCR8vC0GQXR1fwCUhldDERx0qV4CuhmAhi48YYFtFTZC1gPvDIq7xrdAkxVW6d7wyec913SCBLB1R38u3sYC1H8XiExQtdP//uBgRdz4eIYBFrAoKNDamGBiAOg4JtE2h9Osx9wxi/ZrzSSTPAZRs3RUFO1ZgKekkmrtO+eRJTzj52hPN/eITOLjDgfh/0AwBQJeoiF7iP/VcGHAEAYjuWQJ/X+Noa4m3FfZ+AAkOuhHUxBSaYY8oo6OdIz/efrn0dn/iBvAAykBDiawkQYIssO8QGOInGRFgmwwwwAEYSlGbxpC2HuKezRiBbqxs/8gxLj1gZBeJhvsdKtWMCYMtbuRpsFvb2opUIhLUv/+38YAeEsKRZSxxkl47//eGK2wAt6U3KveAEQF6x3iN5e+1OTfb/PVtXLOH5+6ryFZ/thKv/Dl70vwYC4mv4iM4ZgAdJETUJYZFZHd/ATgAaoihegqxm+gCqgjAcxUIGGRfZW8zMbupzq4VLVpAjIBSkw/aWfv6gQP/+FfWCLplOidLX/QBQCbBg1h9CGMcIqGeBiFkEDWE0Yb9FJX/7wBEBHURLFob7QT0r4wEvBAxh5COt6JrmQwfJCmOF0ft/b4bHyu9vsnz//iBvheIUWrqNnTYzqrBhwwBjMgmUVuoIQ96umABMqKFRZtDN8OAA+ABqNgYmwln7ZNE5//QB4Z8xTIXDNLY/yAA8Lgamylj7BOCBwMG6ORgk174/79ADMZnpFZppl5Jn/3/D/hWGKJU1DLpgZ0VA7JljIQDocJ8fmAn9vquk1fy1U9/7z0htnwwAmAAKjBLdEZ7SM4ycwYMmQjgxwExVOe/UHJlUlKuYBgxU/cz/xsGbfV99gBYBEUClklHQ1oUOyLgVDlCeoTBL+nNSSJIhbERv/7bA0FhKb4ikHuQPabtNPfX8AEBDfL9aJKU6jiS8Vbj5Nb/9e4A3w+sCjrv+Zsbryi6kn2rSGHCf0JkYfnbaedAA3PDFP//7BCwkX+IC9feKPASwjgRrUN6iEDGV6tDEklai1CJ5QN6//a4FVWRMp7FP/gAEMy4gVi7z0I9i9B0vACAotKU3G0S/vAUpDBEX3ocZR/sLBVoTIdb+3m8My8Xh/poPG+OWmYt/93qoIZRyoQKSYUUlr2pNL/3+Bpgl4u1lqulY9XUKmppg8o7H15ZVmFbLIe/h3m3MDTeApV+OQV2JeeYpvuEwAkD3UrSdxIp3/3ppB6o+cjxroYoFkL1wJ0L76O0P7gd2xY5jmr+PaHbTn5v88gDlaI1gR7/9tyC3lr/t//+IGwALDCFoONKSavECFf+7jCgT1kQlsEIJXACZn4IGLPejruirJnwyvDnKPWdy+Yj1iZ25h8W72qW4AATBQHXicOjptTB+H5D/ROsy2TXw/DOmIOtWb+IpaQw4yvRljzv3yH982MeaTni52XwD/iBsAczGVVOLqSUtakPzAB8bApFhLP2ScET3BAfXDVy9JVNM5kLYMxC1OC/NJMAhlpji0vOMcGMAr62nDao+RURhtv+P8mBwZsiru5J2wCJcpgHGL0uoku4//7xgJeGCmHkI43omuZDTbIKshopBrmDL41cn3wd5Jjasz3/0yrPHpFvDs9rCAMMWCqkmcX6EHG4YfgbFYgj8tifT2qwN8+776XkTSAr7nTbKDDIh8Tush/39pMJzzmMFTU3/yVNuI2fgVDMLdH++v/wtb3v/sh8YAjMO32mzRBwoj//BhwALJgNylwJzdX6zn/6C9K54fXUHLSEqR820nwYj5lIZ0//iArgAOLmgAUEF5RlJx1Iz6HoCGdzOqLEzbbZ/n/ADkIgx0cn3wJ/Dk6v/DngAWAhqEfoTz0jYx80/l0oAzNblVe/iQtwAEwAVE0KSYTz5slFE6H7AxaOJ0Khj5GhdA4GDAchQAt0+ydXL7havxWt9/i+GPAA4BcUOPmZSs4aoL77AkGO72fMWIm023/PFlwAjHfEm2+/1wvMMwALTABIHvGpO4sY//YCZGYAgO8H8VXHYnf/AJBjUQmTnokvhr37tAaqQAGBG/RKidsLp/3+GCleYABb7StDv95AYRhS0jDw7/D/4arvmkbVP/4YAugFBHpSShfEEG8ZZgACAGABhcow8QdcIuEwAeBLpaJO8sa9/dgBCniqRm+YPrPYMofBEAHMS99nJ8tx7CAWpD8FMkhwsVxH+8Sq6PzTGRBUzPnhj7hkAFgy4oAOCNoFBK17//3YCghKLREnEogpA1//2HNCr/ab//QDF8MAyC3wkdZPBodTEDGKrzuR+N8ABrmEKKU3DDpkW2V/r4kAAIAivUQABwBFRcOyYdaoZ5WbWjf9gDEWJE3/XYt5MR50XOi3fcZjX1xfST62reAxBepKFUOSmuj5kl2NKokkigl2sVeBuTQBmqWzXvwOHV2SoTL//fCyDPV42wDgAJD7ozqYg5NKMeH9EiILeoeuv3st3zFZjk/n26f0guN2FX7ddZbw+GEDfgcZL5z1Jpx3/wyLgCXUaWeJN5dK25gw2hgimZkyGl33mgFtSP+s93XN3z/XDGABZq6XEjZl6/7AAPQOltSmISOX/7RimUsT/Ld/8lNsUqPyAAReAPgCU6W9Nwwkd8kYnZDiakj2NSuzACVpopuP/BrxosKqgZggkjF8EEMMABGADeFC4YzEKFTVbnTd2J7+n6mRkQGauGS5rbIyCXCphiF///v1tEmGvzIv2wPRh0MLp7mXuWkcyHlZ0//9rzfn46tuh0ODmK3L9UX9XgtuER9Y9+/ZgwKxFgDIfxn48GECQxG6xNTYibbTP80gHxQQeMTlZw3UX3wf56GBBGQe0Xzc9Fhh//GwJgGYgDC3fWXasoV97hA/QBx60oxUaQTb38aIQGJCOUwoVHamOD2ppDqld3PV7wAHYACwFOCW5x1xItU/2WjZIhWJHm57M9h9Tra5pYjQ+tredB/Vdn93l0AAsIiycGx9j3psudpAE8yLMPEef9z287pCj0FvCUEuGsAcANBLDE20sINlIJHYYsTAt7mtHIz/8SG4ACMcbFfCJeRTDXh+RD4uUTaHW2zCA1XGp+f/FcOeAB6EYCKMKiEi2yP3wuvAsTO5fxAd+wAG1jHFrahdswL6KgwwAEyxYrc5ByKaU+H0iV3ShIDZLI8/4PxAB7h8UqN46haD4eFAYnvBhocw3Ex3r5Vxnbl95/4gO+VYIoUyV0Yo8n/e/NtmPqVXdQwwwALAhqEfoTz8nYt84/oA4AeE0KTbSxxklBA3nA5EyNARwpFES/fsDlPiMX6//3D1/+GMwxYEAEpMYrDEQkam0smid+kYiswqt9yXNToBkAFOCuK3tFlFyH9+w/5agCXQfTP+Vf4YgiXPG0AH4T+XonSf5A4/hJvCrIcFKKeV4eqKWdh/4LAQwmkJkGyTLfmAAIAUwDlHi5z4tY18/B/CgOv3ZUOcAv/G4AsB1sQOF1jwh5fbEPg4Ai0WpVpBKczCH+44CEkggex1J9RdX/vAEY4HJr4RLgV2FzsWymoO/FIAHRMBxSdYV4l1RPAIU0SJzLZ/+9PiIw1uRlXc0NvzC1xqCWKcUPBbndT7WzH/7dtbul/7cADYsBYoc/uV1lS3/aAbuQAGBW0IFRO2F0/wYM6Qdrv0y77SCE5LH8/e+vTtNNRG1hJvtf8bZLLo7y6sDej6+/y+ImHUI0u/ZYO2gucNV1h5/cBit9v3MwIgwwt/vT9CVZPdE4fiHF5FQxRH2otnsPuFSI2zVP5gWtUBhwC1vjf98QddMchByeUU/+AmIF741p99v//GExQtwRnqcnxPgQ2yQKCdNxn5++4YYA8FiVCjRV/iBtT6cPawXTF2KxYsT797hgJ6GCmHkMZ4RTL/9kBAgBdgIXb9CO+Zf/oNiHkAl43hK+SBLmk2Q2CEMEDIAAE1dcAU5TiJJ4p5W6gR8RCiOALlBfyK/3/alM0pc+6iQjE0Iah+i6fxA3/25hCtOTXC1G1lAwAORgSMdRS601ugM4l1NUK06VoOH92XTX3zt//gwYZQuZ4AO0AGoarhiJP8oW96AhbJRB7kwV4p/9xRSqWLwbfYLHXtJJkv//IKsuM3vzGToq7y/xvxBKK6/hficb1RTxgjA2RuC6K2VjlgOBEkOzmKm+bTaKZnoTLH/6WADwWuFr6wJnje3YBaaxTqKX7SXvBgcXRVC2FzX/1vXgQBSiBx0xOdnTExb/JD0BceZaYBuMVjyWfcOgx2gnkJGG2qSYCAtfon96sMkpH/4N+sjiTuNqc/CEkiRu+crBxSINe+iPNgaW2E0P8QHqrueG+/pzw9wiGApgRIzdZpQwomI7K+2ZAjh/wQkumhffACWcy2swDRx+AAIBkxWAcVoM3wgtIPNYpJa/1ycT3ZyfvbhSJHzxz+t/xA4L8fM6/BBAAaiMN0MZCjrc5fG0EMKV3HDhkY3VvtAAbsqBk0ZY3neoaIngWw6a6G/+wFDsDWZx8kLHlsPhmPAId3NRcRQmTDLH+5gVggefMynd81IW/wYYjF6QAW5GEk57d/VwDCEy0maWmMTsx8QHugMWiEScQqSvGv/uLYDYYAcGM3Vfk2dIlhn+Az1neuAC2xLFb46dn/7wDxQSwo0a3Wz60tifFvjIKFAVqDC/2aV2TNMdfXTkZzvDA/TOOrU1b5ZaMeljv+S72N/THL8x95/WIPXCPc/FYhQEX/nr4lLcr54ErOWVyWstfPFQgaGyrUHscpVsUlxyxOhTb2mzHSHHxAVw4wD2CAwY80iFq9tFLojPv6/p/xAXhtp7HefQF4ZQ/ToOUWfqdPa/6AulBayzL/6ipoOVBlYf5f99TkEwxniA90M9AZ3D37ayYSO7/ccAEoerliT+MGP/+4GCD6mCIAEWAJjkUui1x/73kMjqIukEqexHHjR0SBoDILe1/2kAA2RGD/ZlDOcNYHhQSeMwpdw3IX32gIR3MRUaJmyyz/OBghByJeW5JQsm9Zw+rJMgmD/4v87BtjWH//PPg+NroXhr4Y+Ibgi1ad9JjVT0d54n49EZmO2I/4v+FYAFGIfNIpLrbRZHcYA2B5Mp/JcCBypdg3DDlkQ29wwA1emsV+73+DOcFNqrh+O/M1ucj5k+5RsyAuk0Wv/wzcCjK7K5tTAzu2zzN3f+EH9aWWqAdXc/27/DOGAAWAVQ4VSbIQ3oC18QEwpuuKbthD2JY5L3DcYk73fA+tC6AxoWGuv42ggmYqRELPH/7+MABwGOHO2j1BUnc5welgYl1dfxcIjv/gRNacHEO3myYGL1H/QBjIgyKIvEkJaxcP2V5BxK/I4dMi/KlPuCuIeJQoP+k9U7u9SgrOKz8vz2ldkcP1ph3L/wtD8JABICXcqSd5Qhz/wdwFIQhOvf/vfoIDdCq7+kX/DL5Vf1iRvgAJkRhugisSSljk/p6CEEL9jZwyLbqw+iAAyoqDfRkjedIEgh3c3pqj6EMsfzWNGRYFsOmqhu/v1gUEDz5mE8umpC2+9bBgGN1HuJgsQzR70o+e+IDMABIXfkRTkGfaynB+8KCbZUe2HQS8OKAr+csrnDDCX8Gu+K56wJGJO9//O+dfEEgCCEAVigNCrU2pv/xBMADuGkONFl87Lff8LfgAWhtIQebL5u2eAMRCIyCKxDkMUgMOQeNVyiNvOeXH/H+/xAY8AQQwCsSBQTaG1N4pwAjGgvYaUYSieA+bwC4AzEEIXNF27/DmSOvnVT5+fun/hzwAEgAWF0NSbT15olFA7BMIfazf5Fh6eAM2/lNn+/w3/MAFxNDEmk9+bJRROhmB8Hri0si//9gy/nO4/wf+fBBMNzhwF42npY7PhLw25895ULiajGUdfLof/89x+AkDz0f8/WIPTH4Qs4f/nrA1cou8//hDhqAHAwhW/BBKpfwlrf7yXsSLZuvRPDUAmCa3I7zmKanr/1iPEY1b518RCOEBfA26WG3S1Axt0sNtS3EAopxRQgYbalmKACgR2vVwV+bSjDdqWPXhHP51zr8XIZgASBHb9wUnNpRXxu6Wxt0sNtS0/WJg4gAAFpZBm+DoEwUwAERmNEVWZ3Rmf/+AA7MGP9Viwpq1tI+KIWtqJv1uCDCh+TCIa+LMwAwOQBO4KsDkTr/tgJVKADAnPyYlY7//7lgCokmCUr/3//DJ630tV/ziOMwj4RVO+JDkABloMQWrqN2jAvqo9tGJ1MfMOhrEdEiQRMwRDnKeeMW4rkr9XOQpcDHU9BHsn97/xJ6wBVS57/3//89+AGfAlUydd5/+CPgAO5iFFKbhZ0yLbK3pMTsgqr8hLmpccQeuALdFzG1P/4k8pYEjcNqcF35kexRd7v4R8I+EQ54ADj5ShiwqV4lnS6xHwB3gBdNaLMdtcEuoziT15Lce//hHwjF4k8Tn04C5Ymnz/iPhrAAlGJlkwh9sox/Q+wB5yM4d9cIQfcj/n/hro25xUkWf/20RJIiWcN3/z/FnnFelfXKOMJfS6f6oOmuOyr/TEyXjf4ACRiovaVCXW2DXbgABcFMuAcGnRtTALmGL+lwh0Ngp3fGFUx2U7CkUsp7BBsAAHIAAVoDnhs0RvIWdCMhyik00t/hiEZ643gGomVEmzoz6qKqvxS4mTV3+eel/gGgm7jj5/+GWaf58EIC9l2v//uqtlqrvHRar5f8L80qWAAmRDd0MZCipUrxqmg8c2R8ATA3J5j3+vDSdz4ILARRggla7AKfw3IthLf1aneAAsIKtxoZyM0m12SXfADmQ2VTHzD8tnOBOgiU5ptTZAKSA2+MY7l5/ahIsIJC1zU/72iQANAW7Yg5Bg1/+wegcCJ8xkkL3q3/7An2m4UjoXP9nwKO97bSSInCBYnxAVwALmjAEB3AR1Vkahe/8D8CUgAaB513HcYNd/t/wNpMphxF9pGo+gMxK6UNB/WIcABMzG5VFXvkpW1IYfwzGwgn34BC7rfH529lI/79Wp9GYk9eDQuJr+ICWAA9QhBKmoWcMi+ilDAArhi7ZMIdTYKdwfkKLmbHKKTSy2h+FocACoGNQlGpHPiNzPzv+D8YAWEwKSZRx9knFA0H7dhCilNww6ZFtlfkRiKyCq1JCWNSJRQBDORtZ951237AN5kzRx8/+GIADUPCXRMobjrKawAAUBDaB4bcmiN/RTjJoaI6cXYM4xlow1JpH+AWIQlUVaX26yyeD0A0XAEppQMa51l3/vfnx9tCuQOrmCPacn//ba3Mwks+//5/huAA0OUNhiT4KYEmtkQ8N5GBFcEaSQ9n3YgzXlaRyHQYz9KehHJI7dXjr7SR/+9/4cjaEADiD3olElO0lsEk5F1gZcEZADAzQJ4ssOwPv8A7bbMBltAGOf0iX/+4WUVVp8dn/jfAAoBi2eRoVrxDJfxv/TuwQaOHaPi+yTVZfugYGHRjslsT51X4GozEHWKi+oTWcfvA5w3/ic9uXAUIXb62Inkpx7sGMJQGRcp/7GQaPL32Oh+WfFu7qLxOts/Vu/wvxoADAHAABAGltAAEAEAIgP6RIpkCRL+PXP3REeJ/k3khMHMy8lX/OZsXEn/9javov91E4alixHV5/h/QYCExOzCqvyFsasPngC68ojOL89pOBAQIbAeAA2QyqhjIUL6mJYAAKA4D7Gjg6aIw58GNaCtlk+5+FJXeTkyk5tZtMmvDZ0q/k/xsPIQBWIA0KtTamLpV/XG1GADGMlmyJn906qbWyn9gCEQ8Fq9ZFkaQS/gQPGvCmdRlQkqw74CUABuysE+jLG8+ahsyLAuhkV0Nv95ADYJX63oEzWJM34wrGKXxZVT/gcFEVHsmeWx1E53/sC/nDKiVff5lRzGsxo/fsbdZD7UXh/QEWgwF4oGZVyQQmUVaWyyyyeDICApMIACxbDHHjsSYNjNit/rwjsP+WJ///bhlBSQ/4+FdT7gquIN5WVumh5q+G+AoGB0rK9Ou8LQzs64wKQUEnzEaXeOTF/8Twxp6Oz//+fzwZ1Df7X//DcaEM4CeLAJyU9m66BwxyMF3qa56/vn+ecvH4py4LP4b//CCy8SeuDhcY/Gcb8oLo/o8WGzZR78sACdVcZFG2N33kBSiBx8xGdnTFRb/aAx2+1NzR1CGGP4fk3lGXjTh9BQALchBhXxCzbl7C9/5wB8AGoLFQ1ECcIuvhhtUAlz2jIIy//3Zk1NI+uMBiqGjFlfeX8QGfsA8Amgj7przEiDTxXwDB6pglNLmdocwin72N1U51KOlbUggILSWEcK6MNqYMD//jYEijIAUC370yVJaPP/AgD7DpGDYAeYASB5pqTuLFP/24ACYDbggUy/+Gs6IKF4AoE3C7tnmOxxS3+QBrgwWu8jHGNElTPEFQnUqUkyR5rYHW4hV+8NbPi281dvEOMGt5Mr///5/EDf0CATEyPA89UAIgcggJPGJzu+bmLf7gIZvPRk3QmDLDH+w8ColVUdxCH///7RgAN0RwvUZYzvyNHmoPw9OjaPyjvf+6OOtwfvC3zaOA9wvyFsYQStyFnjYrsp82Zhuoq7SSlrVhh5YTy+3/fktQ6yKIlvveAABlhpNTf3gydaHBikCUfjYYAEm2iKYasygF0MTaJlD6ZJT+0AFSgQ3TPYWCRnVS9rAOWslaCfK/oVOvUn/fwIRojs74SR+n79sRlsrD/nXXXtXHS92/zAKEJBKqOLREFcNI/sMbNBSFs+5S/9PGP7v3E5jJIII9uwjgIIzCzJca4U6AGoCqxBuJ+w/JlsGGOs9cpCU1WUYGB6L0ucOMzur1AAk3lR8XdgdqDi5q/ffpKGVJ5Lrz/EDYCNQIFPKi1qKUeXD1E2g4bXhlgmUqXPevU86d9cwN76/AcMKCDZNHGsqFkD/rM5MxXtVP39nlMAlCmnCN/y83ZTQMRMqepOsxbl/5qECqJ0xsCE2JEf3zS/4Djg/xX+17234DAwBCF7V67cSimfiwwPrOmGSwInZpERL/qPzn4pl++ojuz1pV/X9z9mevwImh/3/TJvEDYGzC55TNDuR///sCcA+HBZo/OCKwnC/75xFGl9N/0h8EhGaq+QKkt5P/gw0I4+OGpjHk+wNI5bBvq6Q2FAAqEAIbyGmsNHYTmY/56w3S28AqXY1LpC/778Av4gbD8bE+kqpGqKoAHQODB54xOd2zdRbfYEJFy29m6Rz/O0YYJtYLp/smo+eB8BhmbjHodeiUnngIAdowceNwjh83IW/wYMVdRy3+vwMF+0AxGltFZSrh4v/3uWNF3JYfboAQxMUjmFz3JWxfhXDUs8NrSTbIml5EjKBfPqrMt+ozW2/DRf9vnVO1p//5YWIitkZdl/B2qNO8DTRX/ODfxA2DGAIIQBWKA0KszamD8BRi+cgRtKhHL+4Nf9ZxZ7Lln/+msw3kQzVu5rvHfEaD66AMKIrGT7BFhhf4AOgyGFR5RaHiPppfhipxBBAs12Z5sZV/e/zvOsxYmv/G1++vfW6AAIWUHvhSu8f3ugHKvLTOFf3/wAEDYiKQVPr6VViQD51bUmKqfEWa8mAEge6lqYO40U/PtH2I9P0aAhFzKZ7n/3vgIW2EzU/8RDz1lAAHKCLQUT3/rwbgAB8QCwijkJlh8/MAYBrgwWy8jHGNElS99itfw6kfsGJ+VvnpOOO+6Vu/nC2xMzX/7/xA2oKsaG/KAEcIbbKhL6ZBb+A0aGtG8koKRk+/3f8AIZC7LGt1zCz6DjQcZfAUMX6tY+8F1Yboy4AB3AJTvXdIDx6ViDD1sITbIj3wwlvf9/w1yRhCBVaZJ+jbyJS4xLdXjKY/xIMI420PwAPDVCgA4I34oJWwu/8gLoyAMDPB/IKMDsDr/nhoXDl8u/34JkmJoBRsLFK1f7/xAX8ABGAHxsDE2kt/bJwRPdAIehP6EseI1MIHX96MpYAQ8rPRLeGPrjT9Xv8LfyAB4XAtNlLH2icPHA9AISzyMC8+IVLInX94c5Qw2ta1be3DJR7/F8EngAPoMa6LtD6dJj+w+G/wABXgJb/ZNLDwjSzeSCo1UZKXy6S3hLlD/AFcsbsbav/yck/l4ADTlIKKW7LDpkW0V+RGIrIcylGSpafPy2RFR9/8F+2kdsmW46Sz/z3+AAmKyFT+fbpwYxcf229JDqY2ncB/4IIeAA7AiSgKKbrlB7rDv/oRdpBL25bAYBZuGshsOABhLHYy7DqpThVsoCwbW3W1P4tACnCFO3W+9hXkMG1M9FMx4EgrO0diSAbpFJLr6Ejx/WkvDv/IAInIrB2uapEH4MABIUrCKVupSj3tjuzs+gMAcFcwDimby3pTKCfsBj0I/UlDHyNjPjgYcQxamTpzRwF0cCWxi89/nP223p4P/hmDkWXep/9+P0kkSW+2++/V/v+n2B//8b3DGAietB/8BBwCeAe+TyNMJeGORCuStFV//48BQYlELkR/EZq4be/cgBShwhhmkk9qqMf+DmBIM5DFZf4w8V4/V641I9OlzhxdIAed/Rm+YhPa/NgjF6RZ9F3//4oiJCTSy/v91aOPUH4L/+xHHQ9R5SXGkFPZratZo//+vACGQkqlsNHXQYpSGB8QSrsLkzH/JhnPINhEVDoMzi3gw5YEYSCMKlwhR/9e3jUB7d/gL737oCVdtEG1UC9eB/w9TY0oDO3AtNSe/+ypkXd54AF5BbsfrryR//+sQGsABMAGg1hibKmPMkoIH4esCn7XHLI3JrccfP/lgAUghqoq0vt0mk8H5j7cquYgztUY4MVwv4ACZEMroYyOFSxifGDMAWuqrKEK10R/3oErKtCyHzXT3/wB23ACpBk11/db38QFcAC5owAgOQDuqsjkLv/gMBBgKkAGgLuwxR3FD3//Bhx/gDitiLLVDHx+aoYYlyT/tG+avEBn4PpkRPH/t01iBVu4xtCUGpEv33mADw2hSbaWuNkoIHfIAHxdDU2ks+aJQROvKgGEpyjamHG13vj9RgYTZ1Df1/EDcABIw6JVlxz7ZBT2DD0A5WJR2PKSK+q/wA7Cgm2VCX06C39DG0h0jwAGlJQByARmfL5bm8EPsgGqZ6QUV+n/7oEM/m9V0Jkywt/PBsFE6xvSSvLIo0+Dk2jd+s+fsF/SRpEEvtBlilU6IX2XIX0inz+1zIovG9RKi+hbDZro7v61mxylOqlH3HtmY3q8Vd2ix/xRw+bQOQaIwtBEvQs//+/wJUvPL/OCXFIPTvIalBLvB6UCa30rvEbv7yIhEZDGQgRCmI0WAEge6akRhNx/+3mRDKqGE5b0sUnRmAFDgKR7C8UYNv/4RpYAWg+6jM+omooOAXg69Xi/w6o3F5r8GRbagtviA9gAdAZeAg9uHW/W4z7mYYCgAYRFrwR7lFFiYvDeDbwKGEE54Q6j/nuAIgNOVRYucUftEP/4PCgxKG69S62U20BiM8RJzqmr4CQxG6z4uzrEsL/zkDlFDjxqcrPG6i/+CPyADpXeT9OPwUUNGxMvzIIOWBebtEU1inC3/xs+M2Mi0QPcACDYBhBFIzItkmm/4LAIYTSESDJJtnxj7KV1MwjrYUQGH4aYIm4Moz9N8v+4LQVE2I2li6dkf7iQxE3Dlt9D8Z9xoQqblyl9z9Z8ahyXrtHVNxhDAFiyH8QbU/8bB2aFxvUcUjksqz7vALAaQOFrvo7t0gkU/7wNwVkjlZ0Zz/wYB4HoPwQxgiT7tBgMMMABMkYbsIrPetjF9WAdhjCod5ZBe7xGYiMAR7dUUBIQvah6g74d9yTb3pFaTvb/3sNBunr/h//i0GIo9U+MVaXVAwKq+qUn/9r/wAEAzHYhBe9SbX3qgAWmAEge6ak7ixT/9gwJBiUQmTnokvhb37jNBuAXSKiSQPB73XIXV/wQYACMA24YMbfTlreiShnQgJymN4X3ngJkxgg34jZvy9ge/8/QG6kABgRv0ConfC8f7TICwAQY9KlExlygW1EeDAlOkAEWYWV9e9w1mZECQzv/cEc58bgMC8bBBdGAuHAlofKiaISQu8Y4mK+MUKRSjSfAB0DTlCNVlo9eLQCDsjBkDdolFZJO+cAALApuQDg24NqbyIfFyibQ632U4DQb44AKHb8SEq4Xv+cAhKJVEiP4gpZ1//wNffRWjk4cBoq2AAEA2JvQNKVGL4UNy0zJe044ZFQS3STDYLJ/ky09f8QHoYAGcQEOIrGZBki0y8GHwMw1knrP3EngNFYf/aDeAACA5QG/hNtBuUz4gAJ1RAv4bYzX8RqyoNYbFZDbevI0IrKIvEuS1ieF4QolXUbOmRfVWBAYYixhXHhMAUbZBkgl6f0JSc0tgw/+CCnlf9cjWhzm+d/+ACGA4lKQZLkGvK2nLRh0gCKSeV2DAAsGJZSrPJTZSBz/7oCpgBoGnIWg7zRr3/uD/gBgIUpCTZRN132KX3pkU393oW4ULyaxCKLg/A4DLeOxDpRpmJvI+wBL64/frb5szFDKR/vVhQwlL4gKwZadltO4AQwFTgvjWp4lPzOSIYNebMbqpxd9/rWkMOQOFLH7ela/FU2WqDII9eQyzgfkr5/f2dPxWEPnrotz/54rT5/AOzS7/8/KByntDRGaaQ39NI9yPziok9uQ/P8K+KAU0BtSEIfr+9MzM5znHmDfZ18jbfwIM/oODcql01f1YPbueg//w7AAIGgDCVYZ+t5RF33Ngg5SfIXzkEDX//eWT15YiezqyqiffwFtEKd+yOGDNUMVVx4Z+r5V3WnQwf/z3e5inNZ78OFhktlM+j/gw8rnRplkz/4bBwcibLHnM4CLVPK/x0SSy+/dPvY5AaUqv4gOwAGNiZOc6kG5a0OAAFQQB2YGzY4bU2yDnlBK8atq7/5wIuMWuvNqb2yGyqYXEP5rO0nPTJM53/MIJKQSbK51ye5Q3+EZXkpYxYMBIvRtG3Uihk6Nyr4cOOLQZCFu87PUOoN3A6JQ/Cmqlb4gOwBRA+MGiOMM1uC3q5UH1oQg5Pc7ICpFSxsE3AiQoC+QI++BgAM0J8pDoUZK2J8PyMhFZTHQoy3qT7WwhRa+o2dMi+6sMMPSQNNovNbnwW/3S1ylKjx+wgaihW+78zELPHDzxAZuAAEQoBUZCSFqbU3vMxrzn5R/WtPhqeNx4nsvN/UB8fPJD/RjdMMIvb4W/AAclXtUkRV9n/3GVGHifpVqf/aMADZFUIiyqG74aYkVPQtBkl0dX8AIGUg5xMLVMdgIM/9OgxBCm4XcMC2yohQ0f6u/v39GjYS2U2Xe7/+IDX+BnUVLHZI/7/nTD6l/nwFkdxdin++cYPNYafPU2skz551zeff//xC/DXIaaOmBfjtRkPibgGU/z/55GkjNTvexO69v8ViM751+fB/4EjJO9/89YAxgkpvbvP64azv+eQWOHRVOgX//DHAATIhldDGRx0qV7gABIHAbaJo0Om1NgDExFZDiel3qakO8Bx07z7+oVe39v//qHvnkdxomj+P/n/+MRKWq//z4LXHdv/Of1J+BZ1aD3/56+SaFn9MNPTu4Dv0lfiA94SADQPewxR3GDX//Bh+AAiDKQRXlk+wRxNPn8hNRrGb7r5gdgoeeMwld43QX/wqSMK0A4AoIXj30z/POkAbk1uOPnPLAZ/in3/4hwAGsxu7ir1JKWtSGHi+/z17exwGRm+T38/+eYuAkCkqfn/H/8IYgNfRoxWcITzTlllNYAAKg4BFzhsdNEYPzi+VmZJzz/mxB64aS1TwwfnfOsfhAXwHU1LA6mpbB1NSw21LeL5VJkNtSywAegR2vUoKTm0oo3alp+sTIFFAASTTSabTTf/gA9AD1FIYi2ec/5+DqAAAWf0GaAOgf4R8IwnhHwibgAJkRhugis8lbGJ9PghBCu42cMi26viQ5wALiRow1tVG3vgJZomNLUeIT0B83UASsrLSP4R/eEfEr3iT14DqXj/xIc8ABAO9IAED3I2gy6gu8Ai6gqgCnIkx+J3X8I+JP7w3uf8SenIBKGp5f+//GF+LxJ5Swmb7wEo7yKM9/4g9fJbj3/8NfDOg2dUsNau/UyRt9pz91+YCFo99BmPEbmEDv+0AhpEoUJ58QuWROv4JXMADgc1JWn+/fR8mMtV/hqArjBAUwduFFzIxUraBEDwbN6jjjDT//Qfgk/GZtLu8nw5qEhhO0Td7wnMUWVze4yaX1/EBfAASMdEyyYQ+2UU9hhs34PjPB19/b4/UOPkgpD+z+IDNgAAqCGWDQ05NEYBdkCXhI99Mgt/eGBG4lAxm0mAXE0H/xAZgAUzMAYCuAncFWByJ1/3igAkDT8qXJ3lDHNAlUoAMCe/iVErIXb/e2FhP0qktp1FvKkAdSWWWwM+/u0m/Pv68Pv+IDMABMAHhNCk20tebJQQO+QAPi6FptJb80SgidDDDNNKijaENqc3w1zle08Fq3HrLXa/wrgAJGHRss2kPt1GPhuADnGJkhptTADmFBtsqkvpkGv8MJtfABvJfKQhho3TP/9OCk2+3f7/58DgJ/NX9QODkng0Jn1geHRv0su0NdAHtrhr0mjAIDuAjarI5C7/584uVw4nDf/wzAVIAGge9hyhGEnX//BhylwHuPATeS+9/89YCVcpSbz/8XiT0vgDUSU84+fhHr5ee8HC4xnfH7/+Im4fv1/w5AAbDgl0TKG0ySnsAAFgQ3AeG3JojeIPPzOhnEfbDXcb4DMENhVmrMI/yxW4b+vyND9/wFSEW2FIm7vDTc/DcASMnIIhG6tPatINaG0xUddCZF7/sRkTOqP8naCKUblgQVdLtbXzfBjFp6Fffzv+N0CAAoAx7E+qSx4hcugd/3MBjUJRqT3wrkv87/twQgCNQBYUam1Nb6vkAC4uBaTCeftE4/OewCwCcHIOm0GZEW3CQID9xjZccTUEoUtDggairXvm1MBbrQwAsicF7s/vuAEYaVCX/0ysqo05/7tlzWmk0EAwqIFYWOe/aESY7+mErMWtERnp/TU0afhbgLEIAjUAaFG5tTbW4CLrVr3zamAuDl8Bd8avu7/5gAAoDAPwdNDhojeohMiCMxRHMUr/xWyqz3gMY5hRjCf793FSk44U2EK3ZXhh8P+XsBhO1we0qFLloG83nM6ZdwIpAM/oymsQv1faYaNKKQlW7P/4dsR6G9urw37cU8UVT76wRLjFFzVf/+3+NoBIAuAA8wAkD3UtWdxYp//3pIzAEByQJ0quOwO/+f4BiUQmTnomTUDXPwIAAZyh/AhuCJY6P//51mBYfwC8SmILCE/f7uIX9Iy2J+u//7K+uZ5nCh3wyXupRb47n2bXwxJJAcE36Zf/QzEKxWpDejrcNL7VEi29t66zMNrhaC8EGZ5Ax2970HHAfNMDN4EWxXp5f3ByFEacmPFKtqJsABsHBNgu0NhkmP42AHwWqaqD+NGv/3kPPyOgiXPthrifJvHN9Hv/V5bSi/k67uGfvGVz6Pp/wQST/oAooJB8u1DQWP2rw9PwYjj6R5qzCO90AmEQTNiVF/U1h+2C/4by1x9yFUmDyJSN37ooj0N/X+GMQAgQgCNUBYUam1MABKCktBcSMgrrOcBOo6175tTdCgIHQesTP0JP0zZnDogEGK3yPeS94C6Tgu0V5wA1o+mr45oaiSkbNdqfn+u++f/DFKAIlHKUlTnvQWScw0b/AAbEN3QxkKP6mJGShTtHc3vufrvx8S/8NwAEgAsLoWoynbzRKKB3gwJiQzy244VLZVL7gFpA4uGMoqaQR71P1ld7+6eLn4AietcjSABdwK8WKuJfpayb83/hjwAWDdDgA4I34oJWu//+7AUEJRaokQjqCmHX//BhJ0UKKnW/GwP5Epr9rc4mErun/PXwBsSe84+f/PXEiinjRH+MxAZgAdGitoNQZJZDV/ASgANkRAqZKoZrgBEDsFBJ4zCV3DMhf/aAhmcxFRZ9iWWf4oB+FV3FTfe4f/8QGoACBDr1wxX9Mf77iHbAABABgWB2WlGLHQif/twfixZ8FXyjbkh///+ID0EY+CAMUjg4bgOm7MhCkIrkhVfu3/6OYWk4TDeebz/a8IUSrqOHTIvurDDgAIGUoRxHsVYn685kmC0w4F+1wggnimX/CU18VCY/+tgxeALSQ0+P2wP4gbDDgAPgAUigACADS5mAEkojHmAU7/Vd0e18D316ngYNdC43a09e0EJQjTLzCpPf/vfQyp8ZzNTAcLVBuYVTimHgWpMtHkrvA4Mkt+d/oFHsx3TTb3/+ICuAIj3AGfgwjnUtmFzcPg2LpFrW8ip/g/AyhD2VySSGKaV6/1dpzLawIyMp1GR3fM+CpR/36D/+ID0BUIUpMTZTSVcv//wfJAGPOo1zJVHk8GMggCB/EIVXmFnEtfeABiAAIDiayINE2Wj+4CYIRwE0xkoi0GbLP9Eez/5/lkvtk3LggQZioRSFP34N4ErUFBelH+9QKXPI3Bu+0v8bwm8gOP05Dv+sIANRiQd5KjJP6z39oyc1//nmYAfBcil9QmiL7vhAD00TlyNE+aY3bYYZwsrHxQ1Me4uiCLiHZZ7v37d67gNXNgAOsAEge6lqzkFjH//d6QCLGOILKTmszPv8GD8MgKr3hXeu+qQpgMvtVGveA3aZNiuRp/7yD7Hs8t3+/8QNgKAILIhTvVPdmhxrOwbCihkvIaYSvnCADp+AcsYplBgkif//gwBZYSFbioJIxZBLAAByAAFeA54bNEYPow5ftjnAAoAgA6DMqyqRYUiDEiSTjnkmaY4nv/OSeDRjruQ3pp08PsPiQg3Hp8QN+IUfEZBUvfTTXhhwQQzDfOEP9AAvHs09VZD3vpbz5cOP3YACBhVoaLV7bCHv+9zM1v8l/9a8yACAzgf1Jcaid/80tGAIDuAjqq49C9/5I2nu4f/litz61m+3cIgA8Hu2IgRhJt/+DEUkaWB0zEXp+y9YB5IEPqnjamvAUp8eEun8DpsfXxA2eJe8Abg5QavFpayb97wKo07ix3+/f4E5VQoiMR8LvUAY1+vaOJ+TbB2q+Grh/VwNyaDZ94id+71ngAFYCqSWRvfrwfjAS8EDFnkI4zomqbBAHOHUt6Mz7mF9DOoIoyfrzkEcBtL+/m/P+Ns+pI13xg7aC4gbFXlrwCYhl7GbHFtyr8ARB7SeE8piKjCjbvxmPQYVuN3zfYB0OEP73PmFfixlbb/+4ATICrPQlKDiDIG//7g+47DCmp8wYSWccmYEIKRdoxYuWm7g9MaMngWwya6G7+8Ff3rgImuyVH/i0a4ShvC6/iWf/72UfGbl+/iKxIW4ACIBvgwWy8jHWNEEzIeiGHu6GU/6Tc9PeALAAnNQAEDBS+3SZ99NmGc6QnpZYD4UScyFu0aq97+KxAXwAGbEycouoI5bUAAJMxMnOLqHc1qvIAAQAXKAIoCk8Wyy+rwSygdlBuWNW5l5/OBOgi155tTeHkIArFAWFWptTBk9RgDLWZhb7QCJXZ/36w/tByd8v+vXC3AAsEK3mIubEzaab/gEQUwoefMTldw1MX/wE4ADZFcJ0mUN3w0wmdloWgyTKOr+AO9OMtHI706DGEKdhlw0LaKBKKABfX3rie/7wc42EvhJ+/q9qEjZfXBfgDxvAhuXKS0PPJh8ABp5RI6yaZjSraYGYt3P5uQStr1sbK/4eyOunWv6+R8+kp+/fwJRiAOENwnHzCLDqD3UgZSEAYIalFFpNlvfB+ANu9Zv+iDw27/z738Ysg2DrKsl/90+ymfAJr66v3/T/DvgAnTU1TJv/Pxx7GG768/oF8T0OD/kaHV2vhPY/+5//G+AAglOIiexq0el2L/HFafXn9NMCNARRifL8n8gScM4DDVK2TTYbcf8eL+nErTXJ/PAEaIEuPlJbk0pDy2AYrvXeoAFb00aNL//71WvtVv//pA2OlbR+Hv5zLgBCXEFlq0nv/8MmIfYBAAQwSoL1LL1B8DkCOoYyGlUnuge4YD/haAPOFyFyosXb7+lAAsDHsShUljxC5lA+/gE8RgGFGzhEm6RZXwmDWYpXNkbv6Fq/Yf/isHqVT+pRJu88FhQvePeyK/v/8MQAEYG1DBTL6MMZ4SUM6MANgw1NSc+aSVZ76iBGykzv1/u7CYAHbAMhZBvo9+4AQAGJkNkORXG9S0/qPd1b8XF5V+w/gB0ADYtOkL+Ri30j2f8MbWjl1vP3PgPDELV/NKI1Bb8+DAEECfrRCiO7c/vaHvggMAC9IgBAZ4EcUZH4Xv/AM6eBeC2k7HbCe/nhfa4jMv5v8PwYC4GBoz1+19KEQQf/6Gh1H7x1feOHwA9kZToNnQ/fUv/sFR0x/hi4ACZiKxgxK8UIfNJkQPBSUH7xkF+Zu0fjt5a6v+//BwUiMLQRLULP//v+HAOMGQkLO1/HAF4zEBf+AA4YjPb8RFHUJbW/3wMcoqtUhOpGw+k1+yRE1CRYZNZHaqKZapWvcsTYFAazK73GiqgevhzAECEARqgLCjU2pgAWCktB+SMX5kf84CLrVr3zamFSf4BUFiF518v4gK9nAQbmysljTSXB/gAWwgfc0fXvpNS09AFAJMGDWH0Ia1wmoZFLRBU5w38wS0axSLb/kR6HZ7j52ndz/hjwAKDsACEgnEu0w1J/AAXkEN3GR/qWNVv4DXxWw6jb//vAYCnCBlJVhBC8a0boO8ABcACJHxSEWcUVEKD64Nk4ejB2t8k2XwIVGB1VYyJ/ufxA2AAmYWG/yqiuImuR3GGCm2WbHzUBlMOxGjuqXf+AB4xEKjmOjiNepoNUgpATUjFO50+AGMyEyir1BCGtQ2jSH4J+RkJ0chUcRb0NDGODLTAAmVHC9ZtCt8AAfFkUrIcohFtLd9Bjys9KPYYJitAjQJpGCP+q4SZf+BnJiUSTj9AjU0evpQy49/G8EgBAhAEaoDQo1NqbxgKGK9i9cR0sK4a7+DBAMCXBzoeFi/deQ/UbrovkT8AACAAJLFhf9p3kihxBx8jMIMlb3D+Kfa8igy2GRfH3gAuJxC1hbWNO5TyvrBQwAUHmZTq+akLb4NULDi+x/PFRcGpNf+exRlG0NHZvmCaG5aREU8GG8OuAEQl4F/q4QzuWC65oAOAFyAc3TEtKBA3moe9QfFqibQ632Y4AkFa8P99MCSPhJQTfNd5xL/wEvFbFavi5P3uBH6qjiGfj6PM//BA2ug8CjxfzeN/T9CDAFgSF6FQbUx8OD+HZyuID0AHMqum2//r8QNSA3qUJz7qbVlQsAAraCgMuaOj7+I3YQMc/YsJZJtswdED7YhH7o77qDAlIADAUX7EXDDTr+3zLpIi/F3uT7+gghQ0NUdt7yn/PgCSJLl//J0J81F+IzHlqWPvjBuGPEB38CQucBhTc5WyrtJJcYAPhuLy1kruf/b4NVXxwGjVUAAjV2aFuRK/7tAGFlGUK1KMGmV/v4uif4ACGhztlQRfIWvFhrhBDqF9c86/AhmcgVj/739OjF7zvwlsZJ9uqBa3h4fQ+ID3gs0J6oMVflyT/2A0PQ2mUjDVCX/fAloFQMPaIapv8n/7AEwPTjBi5xZN9VOhVoEVjAFkHJYvyMW4gGALFWQqKcgrqWU2GLhaPjT6mOwFHNYe/ZsBiFEPZantjlqT//80jmOQe8bVtdhMYo2DAPgKHMFsjxME9vGsvAAHCFbzOuZsTNhhn/aYFjgFA9yNrGmETPfBwAH0Qgwr4hZDtu/hd/942AGoeshqoE2RdI4YAB7fgyPYf6D/z7SJ6D15kZhOgrNQSpzVepIlCaYmZkCZFt/GntKe+zi77SP/vs+pJtmv9etOHW9hJP3Y6JiLtriA79rYQotXUcOmxndXx7YCHEVjMkyTabcB52AIBT9rZmTK8EAf6sBjiawmTZIstjYQBBgTBezi5PuncHcWRd/56qIAYKLtChMmfbK+YARGHX6zbooRFomGtNdXaudaOhqb//eU8G01rfug/8PQNBCWSk8lMF8Mcf93hgAWEOzF9cUfAhlj+JYaYPgIxaAHD3aXjgqsQYtlSm1tTu1sBsoiE45ZaibaxsyeB9DJr+zfwEzTRlT5rvuMBXDAk+blPL5yQx/jpjv8rB1lkyN8crwRkj4P3mJv7/42DH3Ry77eBAZGius5lecvrYeDD8kRCRDGzDcpXBh/AAsEO/mIubEzYYZ/gYE4ADbdQ3SZQ3fACIFMKCT5iNLuHJjP+D0xI7LQtB0mUdX94vrJRG1PPbLLH79A70D0YqQvvF4g9eAE9yW4/fz/4nxAZgANZmN3FXaSVtasMOtuL01j9M0bhv6/wxQwAGw4JdFyh8Mswn5Dj8j4ziE2wtzgABYGLqQaG3ZtTADIKiVRUpfbJNewAAd4ADMAa+NGiN4x1ud1EQ51sKcZ98iOxF5qg4wr6KeuDiMphDdpKpwyzT57xDc5T93f05J/v//8K4An3Oz/U4CghbLREHkLgzxT//mBISRGA73/MANAaTrfvMB49at2AJkOABQTpEkIWQPf8G1QTNFCWN6fNO1UxR7ofygwgM96arvf5L5YvP+IDN/N2B6OMP47Xok9s4+eeFCtW3/5xlweGZasqHYeX46CB+Nt3DyteNH0KBh4AyAAH7QZaFH4l/56AoQ7ub1xVCZMMrf6tPyve7f/WCggefMwnd01IW3wCXYQopTcLOmxbZWMUjUSU2cfO432s/zAKMAG1G1B3/h+PDj1IeFogP4CH6oUE4kypLFGXkKXXlPTg7xKqMwSTDh1ng+OojvljRpSr54Fyyh/GTRHjfyQeJ1Mi8OeADstVn7XvlMd7yGmK3DP1BukztIS77/bHtfDc6VQBbADUPWQ1EH8aNfDUfQdFOMfZSnx+ddVzXL6g/+ed9Ru8/tEOzTj3P5zPcMwbmzv7f89WuVSHn88W1/WIDP8PN0L7cAKLafPNJNKQ/P+ICtMAC5oYIL8e6qyOQu/+HIQwJUAGgLdsUdxg9/+3/ADg0GE4Qg1Z7zVaR19eKxB67K/l/nfOviPnpcGhcTX/z1H0lPX//DkACwY0kIs96bKQMI/uA1ADncABhkvPjmL9//9wAkcHwRKM/6i1FV15wETWqZfG1MZIBH7txcm/VDOc4uXfOGooFOdOzr/ELLxBIAOkIiOU6NgrzWvDD8QFcABmQnTmOhRvWxMNgAAqDgOucNjpojb929jq/vv8XD7YUiU/BgGf/+HugISSU0e9cF8Ke/d/+AAgQdNuEJr0p3PrId8SfsIsIB+JOd7w/DFEK7jd0wLbqAbaS+igx0TGiPAdPDyav8v8LUBeAY7vYm4ixE2m2/4PRAAJFVAybNgbrh/pIgiMIqkEKYxQYpEkZy7XTS3W2wakOP/+fB8eQ4BJ7eor1b1zyl/ASvknb/89YPUp6/8dhA9eCR4b+v4QPXEj0P36/+JDUEMPEMAjVgUFGhtTfUEU1XzbX6ef/E/xC4hbxEIxIkEGABZgBGI0tQwhGxd/6/gbalhtqWxtqWG2pZYCKXO1fv9//4fgKBjwIRqUhhEjYugcBh8XFARDbUsxQAUCO16lBSc2lGG7Use3je3b5/f5/PwIEAAAX4EGaIOgf4R8IwnhHwj4RNwAF51bVMt7kzXkybXCPy8AQIQBGoAsKMzam7eERfmjgAuYRh8sos55N987+EfCJvABcGYOQMuXfMOOm7XE5/wjF4RrEBqAAjgAfDVcKRIm6Db3G0QAwEIAjcFFhyN1/wfGQsVlFQ91NKfgCWAM+Kgcd9aElLWbj+TKYyvEBXzgO3QGvhs1t2zgTIMpWcbU3rQnRTHQo3tUlgAAqDgOyaOjpojPGULHDrtG4cz6atb7beGovzr1lteuv/28f6//ooVcjAsLct3jSvkfhyvxnZ/32YtiP/jhl5R3iD8vgmbbBqbLVHFyIv01IOtM+GYeCdxWr3zamBUH6D6kfBnucwgAAoCAPsdODRojeSRCTGMhBuUxCgPXARBELEf//xA3AAbpoAhxdYSIME22kA6DEnPaykbPrrvQGOIrGhFgi0wD5mUNdUPl/smp8+DgCgJkDBrD6ENY4TWMw/GAl4YMYcQjreiapkMOXwAUbQSQ9nn//QO2TxfpV//vJ+NyjYySPcjhWsV/w5AAsYrXmaEYs90ukX7wCzABCjyMtpQuM95t//8Hge3WOwF9Z5uMXqLEPqiP/xgCVSnZf6/iBvgAJMVFyyKS630W7wAESEZHKL3U8ktZLgA9QhEOYbU3mw4L9k0h1NgpwfmKtipzmHdTSngkCDkDIttqIv/vP33/e28CIHIIHnC0Z3fN1Fv8MbAGMATszN27wXnw/xVxAtHiJ26GWcvScSetLlqtAgQv1w1gcVbo+w9bDd/QMAqYAYGlozs6amLb6WAOwecie9//xIZgQYAE6q4RFG2N72D0DHf7fu8EQYYY/npwJNV73/xsHbxmJPXgF+p95/4gNYAHrRgCAVwO6uuOPX//3fK0AeKKeNEYG4cbhvDH53S//3DcVyZT+DCAqgA0D3cMQdxQ1//wYIKgC6CAAYJUHn6Kt+sJpnVmbXfBlKu3VC8Jn/hiAAgKixxayDYKyB2SIdoG8uMqdb/u70QAKYZBqs15hD74ABGXIbOu6J2/aI90XOz7//wnLpNHMBeexZz/vUQWaNMb2n/DHLG/mG7+lHXKy7XbYAAD8gADOAY/EbT8BDxKABOA0cCOkLoxJkhFv4ARqS1T4GskrsNTpoGJEynYEfxXv8Ipc0HxHb5HaqL8we37QJ/f2WTeHJrl/+fv8b4AEGwGMIpGZFkk03QF2UAggukJkmyTbYMPRBgmbQyXOzZn97wFADZ8Hoc/HNNqKmP3oSnAyaPMmnYeKJ+Y42KqGKK6lFvkAAKAWz7iQYGXi/9wa+EjxJ3cH9rGXdnv/V2FpDUhwp56kP0/DEPAAZNGRAydxkuavLUdWOkq8lQdWi+afuvjQikkPvK/w5KaQBSOCBidLAXK5CoTUVF/mZpHBkApafv6/wxY4APYkddhYSdJphek2CCjWdWZPi+Kd/r2oHkAeIQBHqA0JQtU0gfUH7m2X3/5RAjt3iH+1Ge6nQNT/gl/gg+PEjIlDWHRWRz/1N9UFAvQe/bZU/8AjPAQX2QstjDiZAX6Q2KiHE1JHqakMRj1aI//UsTrrat+AcXw6pnR0PFqTDamQMGLiA/48wa7F/2bb+DT7vrvjOOyH7kCHRALrFLeqLnCQev1PgS2iif3g5lKRfjBhhC8yf4g/oB+1+Wfuf5+f+593/4gEHgAIwmOK3iCEPPaUU8wDAAarGKo5UJGpuLKznsvyIyDZBVakhLGp9QzW/N+XeJowAJ1VwiKNsb354wG6hwpl78c52SVMLAe2hXIAVUFIXn2OA7M1DSK2nvYTaAKRj4QDEOGACwTcgAMCcfJidjr//uwNBiyUmTyEl+Mcf/s8V3xzQ+iD1xOJ/iD18AaZx3ef56fiXSjGiP8Vz10Ruf1iA1AAeYQuWVCXW2C3cwAAXBTLBgacGiNxibFIoqGkU0pu8gABAGt5gAVJMVoHNYE18CMAWQznR3n/D3GwXh74gmMIxBRSHCPKJeBmMAALFLa9nWXwaPmh5Gryz/2ID8PgAXpEAIDPAjijI7C9/4ALYAah6yGog/jRr4XaYGDmfynr4tNspN4kf/PGQ7cPLFBSMHLtOi4gb5ExQAoN1WuFhLatj2FDRFOjCyrP3gwIgQKUmSlolkGD23gEUg6ifeyBqTc5Eg3kVZZreAngA1DRbEH6ULe/tG8D+AK4DhxEqJQjnuLhhBjTNRGFIYkyuUUSd2nzxbdM59j0f8P4fAQADQFKFkB8pQhE4YgNyPT9c3/mq1snIk6/3tDxZ/9ylP3S35vAEgCfI1FtLckF9PaMh8SXMS58LubUFfQFA7w1/C9d/gAyruufmSto/s4LRlQC/vb/2+71Y7Ee/7d/EDYADStIKJX1PDpsZ3WqVueOWIXJIhLrbBbuwADIBSsN5pQIGNFFgNAYz6Qnvf6Fof+A72FbuH79Nm8K0/n4BjEYaRZ84YfD3+k31XPjf+w8DQgMl7MJaH4lgR+rGJUAgF2TQu0XP9Xv6BBpjcaqEutuIvua08D85EOlr/l3uMoydHbn+/GDDc5egPiBsAfWhM8SMcbfbxHKOaWm5GEJPC9fnAO4gop7cYEyZ5gj255Btbsr/ftEiAFFCkIwnWt++0BD7ivb1+6HL35c7U0DUNXxJa6AKFRX01Qjnawv1T+4UZsTJHU5JznndXfLm4IeEG8/SjNZ/eAACAAwHslR55CPMUFdM8ANpgHGrUnlJLiKYVDof0cxd61qP/WrZ/x689cBFY7okvX7S2aMWaMpUf8YuP9Wiz6sIfEDdmlGBJlhTH/TGAJBSAf9OrBLzL39lf7n6PJACwJs2j5O0gc54YAluOQNhVTuWcXwGHG3E+CSHAFgAW4ANQ0WpBvlC3P7QBF8FnetRbO5aHghFiuFCH7phsFm1S9dqP7lH8PTXZ8/X/EDfhnGEACyIiiKaUUSl/ZvuYAAgBhzu+3qB8rLJcnAAC4IVcg8OOzamswczHZq6KwPxKVCmyMIhEVc/rc/UjwADbmoZ8+eVEd3VvEgzK5RsTZJBbHB6DQEWligTO0LLkN+AU+SgBgQXlGdXXUDHgcDWvlv0PvAKVith6i+3SwZgi6mdfu5YeheItluP/8lBoGZeOXwQYAYAIwpZuSX/+gXtbVp7r//QAEDHRjBKa1s/shT/X6pb/z8NEsM7AZBJ5D/txJ/gixgOgk4j537cgNnfwEF6yxCq2N8r/SetWAqAOEFLZn0rs8/9zACwmBijKePrkUjn/8GNpTTRsGyK1LlZvIAAkwvQJ4OQOI9u2x+/4gOwA8ZnSUGdzgCkQ+qQaIC5PJ68CBftQpNHGu/5pDuiAAEA8Z4u7mNlmuwP9+DABeZQbQ6N47v/hwAahotiJP8oW9/AjlgDGK2fPee6FBkAYiQatXNdnSfmvQnPD87n/hmUU/ZruDgKQE1IxTd9XjGbba+eBtQcuBi3M3O/+oP//EhiAAkOviOoiGvphT2AADcAAIwBz42aI3uFBdoifZTZLcwAAUBTaBwbcGiMAOONiuhijuphbRgGekOi5RN8622U4GGRIqiWX09fxA1ewdzCKcl3nZqVN/uZXD3Vci4gF8AQQgCsUBoVam1N0H8ABwY9lJs8hcyakY9+D4SADQPdwxQiyjr//g1/YUac2z8OX/9wAN8BBRVYzJMk2mUA0EAxxNYTJsk223hisQF+AAmiMa4wle/1MTwwABAAmAVoF2vrRR5E7/rQKWAu8MV3Yr+cBMoqkXhtTeHiGAzUgUFGRtTCMWAhFI+fkkAWKbHXy/wxBQOQLyhME0OOfmNVVW/+BoN0OADgjviglbC9/zAUEJRaokR/UksOv/+DDZX4QE3oSOoDL53HbDXFrgggDlgFfiFHUSkxhekGrLsEsNishu/s0NpkzJvfNWacnRnN7MfABR8JCnrEdz/EgAHQACMAc+NlxgAdjhMVcIkkimGvEEXwhEaWK8rfzjKJMaFb7UyFhFPJ4Y/GAAsDnD26x4ggUqd6AkHDOQrjqABNGRiWVnVOAk7iJ+9YiLH/7kMpgAUEFM4lJcr01hFDAOgwftHeRv7tge4UPpLRJL/h/qADcXawg+gISS1weSuTeHOfvahgaKAA/CLOnds0q//u8WgUqMHfoHPib5f7/f/D/ACDaa03tjOWCIc4erARZmP0/4szfkxg/380bhfLjtun34ykqKSWAPb7AzyBAYJCckYeT+/X/t+Lrvg8Q7kqakd34VsMyWTu/+6EUICauG7fh/rwy3Qq0k2+/3MZgRWqDa6onJR3xzu8eEhhlX+sUr1t1YNyS6ez0n/g4fcr0b6gJAVdwA4YjCiRZVIvv3uICkoGwLtCpdff38HIsxrNO/eVcGyf/h7AATLkGz2dErLDnG/8d/0BENHrz9+oEozYkKfReS//ngKCFJWjJIK5pfDXv/ACTb3Xy8D584jsnqeh7yQZWfB/clpG+n+C80pM4Pfz6PvOxnxvyQSZYF3o7+8NTfZv/7U44dC/GAAMMAHOQkKLyvXPsAcAAQCfO4AN5WZQHN4E/GONDvhEvIhhrwYGtXXtCJjO+YYB22TDQrfapxrQWVw4/DG/NihzsJ7Xco1++TZFIZ+grzlE66bkfmF/7yjmPw3DEPXS+GMABBAv64QmvbG8+wl/5pAR9aDJLXxaCvEA1wYLXeRjjXCS5kPkgwXdodL/pNx58DAK/AOBpW1Vdfu4OaHIWIXL//fRCHYKss/DEACtTnzS096FKjTL16v639539bj48rWP39rC3OKyaZS0n3MAyr9o6je1hLkhGwafo2RAR39a/79o+53NirBn7wz4Wh+ABYQrlpp5HvM4Y/+7emkiMAMBXgRxVYdhdf8GjnkH0CYKyrP2jY5OvDIWk47i+FMlsaq67YBtw9xiPmYzhf+ABYQreYi5s+RDS/8gCEMSXdLSjOGR8m31Gqr4FgNgqhq/l/AEooKOVC/9/4gEEMABIyE6KY6FCe1iYYwGZeBwcABjMRGU51IMha0MAAEwQB1zpkaNEbaBzwExI2Cms7zgRcYteebUylGdb/AbqlKk/BqoMhC3ef/hv8AWA04YKZfRhjeiShnQcKYAo9iuElFHXX/CyknKOmmNqf/xAegAWwwTaobL/YMT48NjEAWAn4YMYe9PGeE1TIfggEABTX8ntHKBgHWNF2gagqS3uX9byMUU+ZnP/3+gZBwUEnDNIXeMyFd9wEMUMxiEfrIk7ld//s8AA8zeOyvZ3x0QQZ+PkHT/wOKEvLe83/u/xAdhtrdgejPqsTp5iBGv418iEIMTI/gweZ2rl/2gL5D2qpt0v+D6JL5XvfxFwNrcwLXXT/vnBVJF++ocxIX2+q+yit6O9X+IG/AAQIOnWClU8Y7/2kO8AHA0AETrGQinjcX7gGLRSJEIYhFLLr/4PjwMObuvXrtIGPf+DhJvS/v/c6EAKCYw2t8pDmnjcs+0PBVtMvlW47Qniz7hGcB9KMb/3ataeTZP/va8IUSvqNnTIvqrDAanuAbrnUyxt2UemQb8yYRawfNwPWgunl/nf+Oggbh+lQfEB6NG8BAEPNNSJxxR5Q+7/gAEgABAEenYAClk8ywY0gb8ih5mxyivhZbwBzYyuoqd8lLVpBhBjY8LQAoDtgJaBsVN4vMYCGQnRSHRxvWpIItkJSQ4vv/86+9LIMBZT81I0f8QN9KOrVy/sAWQwCsSBQXaG1N6Y6Nmkwh9ugx5kLxpAz/OBaHJEKTUrLcwAAXBDLB4admiN4Z9GFSpGpQimpcCJjFKzDam2AUlBM4ZFbWNMAAFQUB1zh0dNEbAHBTcJq0iVat/94NBgCGGvKHjstcEdzVBM00LKUavSpBaRGPfwgkfA+9oVf8kCD3bGRotT//ylZmB3i03fNeifaYne5tgxkynxv+geMA4tqVb4U0mqgBDCJxgtJO9v69tL4IxMZyGGRUT/6J9ynvggZUD2GI1wwjXbHYAIJ+2LzGEWWFnr+FVFbYb9tw3i50hjC+hfWnBLKmsp++bQCBkw25D/q814pfwJ6IQ4ZmIT3ztNX3yZDFnqrb76UiV/69zf+/kP+IGwAchhGnK5R1edVbyl4MIWkikjMSlR+/dcAACALiMAAICQgK6WVZxKdpnhnkruRLcjddMKUXtuu2Pjd4gq/MRReYTqSnRytyDf8nyLdgf79HI1ZdBpsNmshuD9rxCiVdRs6ZGd1YYG7I50sXV/ygsq2xkV39cuAXg4747C5HQ5l90thGTz+H9hWAvp0Q7hgV+FGvbR4pCtN3EAggDuEUJdmPNIffAIaIMjiLpLlvUkAQQtFpiDnImC/FucYFYwBwEo3qgZeQLf8Ai4MQSvqN3DAvuq8zRidzHRh0NcrWNnTQJQZJhDV/agD2xBW6RxjCloyAAuDwhtF0QYJ+cWmLHSqxdaDBmGG1Mgv1cyuv549oKL/+MXHsqMJaf9GRjhUx7/4dh9ggMYTKEibBJtpwFWcAoFvVvaBIp0RB7uAhhFIEmCDDT/B/mXt13/8yjmZ3+cCfMAgYReMyRI80SXkAGVxlcoyJJEwbJACrX+p+xfB9p0J0X6T11//EBWBIQzOZ1RZ9i2Wf54sMkchlfDtIU//TQispj5wiWsTNOp9PXokoxov9bEIwUsbYu+XdfN2iyEA1pMGegsYx58TG/0WgzkyziHeD/xAfhgAIgiGG1qTOcs8btfDnUR0vBsHg+hrG01Scdtb1/n/fouFcqvHogw8OMmfEHr827hv6gfxWIPS+BIHeN/PjFf/DXsPCQA7FAaFWptTdAuvkrpOfv//D0MAcKshyKKhrqaU+DBagPihx4xOVnjdRnfeHj4zMHqdZkQ0RgNNSVfcgG7Xyv7e7XKV3n+HsABNiKmndNun/xAJsGC2H0IY1omoZxeAAIAFwKhLzNQ/z4PxgJeGDGHkI4zomqZDDwAEgOhCOFZOwsYNlIDIlJHHpZ1+qWtg5rpd1g//w7AAQCOJqfdtL7Efiw8AYkkKk8lJXDH3/7ANBopQAYEaQKiFsDv/EAwAqcNSGc7CT7wcxWFR2MX39QCwYLgyZRvGFhtd7v/aUTADA7wdxVgbhdf8cBF1q175tTbYO2AupGwX7fQerivTK0R5+iBMw5Ke/kCNOAnnldm/zWTLZ19WIg6Hl1fxsAUAAIBSVBgXxOd7iu1a7yFX5mU5Bn2sxzAABcGM0Ghp2aI3mxQTbKpL6dRrwYIsC9DoC3Hw4ACQALC6GpNq48wSigd/MALiaGJMJ782Sj8+GMExlxNbR5eu73on4OrD2vi3ym0nKaH9r79mVYioXnqyFxNB87avc87kpXzMiGYv+N/KaHT36jXGGHfrAZLonf/PeKCXZUJfTILf1BwAHEBLWHoK7hhItdQzjsAwLzABcTQxJhPPmSUUTofoYKpmwUqhKM25EgxpDwE4PefOL5tyQmlaNPWb/tW/mO6Ok/9n/DkAB+IE9QLyzLeU/7iTMAQHeD9QVZG4Hf/gwwiNZy2lolIt/N1y92tk2TLakvtv88UPhoxuxW7+oGyyEF/+H4GQPCh5wzKl3jshffP9/xv6sABI8eZVEQ8mmGE+QAAgDtTkABiCvZYOZRO0HeleubHeSx/Ed82whySO++imzIjO7xwSwLyqfP3/hmB4J+cACB+/lRCx2//+7gGLRSpEIYhFTLrv7YQhgRm70T2kKD77waqq77/i10q88eZELX73FA3DSd79Lf/8MeACmBag/JGL8yerwAgQgCNQBoUam1N7gg1FWvfNqYFcD9B/SPX7k9XgDqwzhv64H4AZAk9my3a8V8751+fh8ZmS5vfz88v+I8R4g9f/zMlr4bgAMgqNVFWl9sk0kPzHW5X5iCEWopwawxaWz/+IDMAB1AB4PdwpB3EC3f/OEIArEAaFWZtTB/LK0w9g+cJ/4bgAVAxME/mTz4jcyif/wfmACwmBSTaePskYoGg++yuWAKqNiIx+HL/8QHoACbZjdRV75KXtSGH4ACGYpRmqNI1h7iiWcASqUAGBO/kxCyF3/nxLLgSPQxaKlQ4igd/EBaGCAWiQASBrtiTvMGPf2D0DFgpEmOVZSRbv7v/lLrR9DOaf8Rn/EeIjuev8c4MhRQAERkRkZGRkZkfwAM6wCCiqxqSbJtQ//xfBYVLDbUsMBwDgDQI7XqUFJzaUUbtS0/n/CMH8AABacQZpA6B/hk9eBoionv+GT106Kf/hPCPhHO/hH/iArgAOCFstEHkJiCkjH/0PQEyFABwTxGJQSsgev91/BOhPxJhRoWRAO/9Yk9eAOOsjG1P1iT14SNfT/CJeAAxMg2QVW+QljUhxL1hGLxJ68CQDuo/2f8R8LzggYADxAC42y2y3pxDP/rzRXJR+595gA8NoUm2pjzJSCB3yAB8XQ1NpTPmCUET4YYEqLgA9PeuvX3dBbhxPVrRXf/xNdzggCUIUN5vxvgAPgRJQHFN1yg59p3/35gBUTQpJhPPmSEUToaPkBiWcRYXlEhgyia/0PmBj4I/MlhEjYv45/gw48oAMx29FGzwYlc5o9jCN2jT0cfefXv4gOQAEDC0ig5VTWaqk6JlvAQW00Hqr6xdQjZItIGPbnRnHz/LwyFOM1B5HsPcUSqUSUe4aI8MAPBSSy2F/8B6K5eUK+NwAGMKj5ZUJZb4LZ8YVbFbioeVDSn8ZuyETEBiBCnvuIX5GW5OvTcwEJpboaa5vEFHxCIKl5NNLaGWiz8BGGpiW0i4ERWYYDg7t/74fw0crVGv/2qI3nokADQPesQIwk+7/YTgwfpByOcv3fcaQLx2M2sTe7d/jYYAFQOQQEnjEZ3fNzFv8HrEjIlCWGTYR3f2gIZ/N6poTJtpj+fqgYrYiUw4z//9eGAhUEILW1DDxsZ2V+H5mYyupxdSSlrUhh1Dng+Ri//vB9irwxak4N1/56+A7enJP9/4134kM9DAn7ukIw+xvengSGK/2pmaESYaW/nqc1Ue7Vf/xIZgAOkAFg03LFneYMe/8HoDFopBxCIsrxb/z1ATv/e9/8B6Yy1X+elwBsSe2cfP/4zgv27RUkAAwdsBdSNgrvNeoAt0uY2pwSa0eVBcczLusqv89bFtcZWqqqhqJKebef/DnAAcMBlWJw7tFiyTEyf/FrMYn6DvrDGWTV/v5rZSQvslv7zYQTcN2+IDsACkABOqMFTRtitdtnwZBnaF9UU+/3pkIpHMLnkJa5ei8IUWrizpsZ3Wv8HhOgi15ptTAZFQRoz1+hDeuxGOEIArFAWFWZtTBggIEGAHMBSQhiaUMKnN0P4GCgpACNyjneZcSJtNJN47GNlJFkm9hyTvd/JTLeEomo+IGwCXAMcTWEybJNtsMOAB00dkgSgySyGr+AlAAbIjBU2ZQrXACIHYKHnjMJXeO0Gf9wEM7mIyIs+xLLP+YCHQpcP27CFFKbhh02MbLeIUZVSEIOuG/7EaX4ABRZnfgfhgo2m7Dfv9qArP6fsf8QGPp6CMBD1ygYZGN1YfHBoiLAthk10N/8CCAASDZjiLMfSxH1UkdAZR28qUxYlddfv8HHfk+0MZWy7bRAQohQt3sZ7B76Miz94v/DkBMU+DXQYLwO8Hrgn/qL97hdOknsv1jIJtOR3nitf9iWSIK9H131x59QHnHvDsADwScgAMCdIkxOyB1/gAgxbKXMHkJmS/GOACIWcCv0aI55LJZc3I/1K670HwYGk0c7BWuHS2OiPcMEAg/ICBPw22gjCjJ54sFX/7wwPReit81NOOgDIlYidv4fvjS7f8f8ABMJ8YVBP1/M1jcAbOcAGDsIFRK2B7/idYOp9EsMVAqOpfqz6/fAarkrbSdi2OGQpchHtho2/U9W//27zApKf9igQjKRPDF6H2cGYrbEL/7BgziB/h+Pn33gDIxOmOJa3epqQ+AB6AXOAQD3ZTNOeNv3MpP1s/6qFBTh3Wt/SWl2X5uUriI7zX/DfAkGOz2J2LETYZZ/nqMu503t3xpbJdWeRXPvw5kCofS4XmNMAQ1qmg/cHjbl6V/2/+GPAA4C4ocdMylZw1IX32AoYrvZ9xGnSIbX/wa8LXQ11qPs3/5+vAnC00fPw7x+IjOC+gElS58KVSxlqhSksj037gt9Df1Ft0ruf4X8ZmbeH6Lc37gIKSU5qEL3sAnJ7/eMRRWLQWQlx7ji3eREIjIIrOIUxigwzBBAAQXOIi85q0JSzFnTTTfH99/+UPujSzbVA4yO+3x5/8QN+Ia9iFFjF+imL0ziZwldmL/fwfgSMESsxWTqSh6j/34DAPigg4YnKzh2YzvgJwh8siEultGsYGcABwQtlqiDyFwZ4x3/wYdgIiHABwTpEoJWPf/+7oC+CSdqdpmvW4HW09FpcbiU4KiQkly8YfnpxAf/gRNxreYLBifnvf3a3lrAFwAHgY4IbpHqCZOpzg004x6AD5BQYKEcI578VvmKwMzrf3i8+3sr13b/BpC3Lp/1/iBtO8vsQBeJiRnDSGLI9b9sBcBdwZ8DqrSZJwZ+ASQFDXJWo91KOa3lMK85wvsX7sXvxqRk3OWvAAI4A8ZlNQz7fSyLOmQrYkp7u+AAA2tgAOFJojT5/MGAvAiBDlX6SiHLaX7/T4IZZ6ZQOSZXS4GQvMsKTB8c9n/aUEIo5UcOSSY8hDNEJDZ73+M0yTmKf5HQAq1tNf5VojPyku5/jfAIAB+JkwvFYr6i7AFEKTvNefgCr0t7++v/BIQqHF3Xr7+zuJt2pJv7/4/Idgh1R0O1Pa0gMIxqmpi7Qpt9HvilNeuCERCjSu7BhM+gXuBAciB/4N1sv0brY/7QCBRG52l+PPF9kreYZhVPSYXxBpBrGCY+zZhP9MiL5+dmb+PvvZC8YkzH1X20gKJuWuj//T/D8AHzdi5WMdf83slTo1gEgCQobBTscTssuZ6LAaDw4a7zPoqx/q0Fuyd+99l1+A/a84RfOubpv9wDEshFnkpiSuFO/tMXnwtLOJFqf80ABBHiVsYcTc/Yun/9EBYLqyM+cElQ4e64aMdSzJvV+gp++XeSNhhlda5L420IEOAAhJtdg6CSXEq2/AOihSuo2I3LeQ/lVwET3oVuG1NdBtEIv7sfuecEMAjUgYEmhtTWIpASdUK9PuzD/+hynsGwywCXO6k9/9XD8CQAWAre86nBd90OgGoGKgo4J4efeLqvehBmz8VscRv59YWILE93v/3MBXn+1u/6UVTFLdl3X+ID3xirYrKdh3Ysp6gABoAB2gOeHS4wwAfACUTAxmV6Xj/RT//gwwIjzA/CgCMIuCBayddfxzPsgANdIAAQAgCiZTqiwgwz6AD4uhqbCWfMEoInQzIZyTg0I/2qW0s7r9/UCIHPa0rf/+8/w/AVivIQOIxQs+fWJ/9pCfhD3g/Dao/A9/54gNyCMSe9bBHk/68EAPbxV4FMWoZmrcU4AzcIqzyUxJSBTv6Pyt74joBKXOYf///6e4zcbv/PgajABHUfnkd6Hv17/MALCYFIMp4+yTj44GLRpWAqx+psv7L0JWxNDuWp4v//5y2j0Ks9/OcYY1Afw3wAEgASC6FpNp480Uikd880wABAGABBEKQVJLqkQdmjkG8thnnT4WvXX/vdOH0d0975Dtf3QOEHgXHxBbHrxIYgAWDHd7P2LOkQyz/PAmAAmVUCfZdC9cPmTgAJAAsLoWkynjzRKaB0pdFz8BHu1j9QU+TeqP93v+FpRgwAEYCbhwph9CGc7IqGA9GINVWPr78WJbe/qmAwomsJkWSbLYM5gBF+X/7fT8zZ01+/q/xfXDxAewALGBpNGNr3w2Yt8T7vgShMRqyb11f6//AAg2AwgqkZk2yTTYAUBDnRohqejGqr0/w12l/wXwAECMHWlEuJRJJVjXX5Ss7HoBj3AACABYMSylSe9clcOf/cCAbKcAGBHPFRS17//3eWAODMMP9WgKJ8GYvBWFHLEmkJVbeGZmWw8Hc4kxJsvtABKiQ8V3EX/+4cohATNX97/4IOABYEY5TopxqEKLr/7qi5XAD1PpbDtega2N7y9Rd3z/5Y6QG9/nf9Ehf+4PKGC5lrcdbnwAyPU/4gBWsaSx8+lGODop2bfBBieWvgP/4vj0FAAfREAIDPAjkVGR+F7/0AC+IgBAISDuKMjsL3/njYANw9ZDVQegsa/wZWr9xOc72FEYQUkOr37sNmuJjddnfQ5vSf8EEMCQAwEpEFoH7vRphn/2gCamH6s1auQtnpzgAQGTOEN9/zTWF5d/vY2Z+O89V/8aEAeSkY1uh3P1gI4BS0xh0vQaQZuxVJRSS/6L1wmu4C2W2Jpy7f/VWBX/fu1/EAw3FZmB84qz6wYZQxgAIfMF6q1akI9XpNHgqBO+1seVKF4b+UYGf8PLe/xAf+B/kAIO/0q5zX7nwwBheV447gMAYALj4FpMJ5RaJzROfPKGwZVmt3d4YMct26W+uIrTywHj7xv2rfJSAoBiN5TjaeaGZfHCH/3CJw9Flbsq/8HzWDBjkE+eE4fJt+DhgAsMNsYyITi7d/gB4RVl7N0n88ASD8+2wMmvZ47kgVxj8yMbOhzKQdDFocAAKAQB9omzQ0bWwgBjRXaazL/qlrWRzFHgqyj5p7rdxVB2lEn/dzBnhBNReCCGGQMRqYAHwbQg8m827e3F6iCbYxkIMhiupIg1wiVLT//3ACMjHUaOt2/7FGpk2xLX99y2isx9GZZ//aZBxRH0h+Ncp4pf1R+AFbCQLG9L3Z/EAv68wAOSAdDCDPT7+ANQX8VU6onSE9jAGOekoDfq/j4m9zj/R0Y6Y8YGoUu6zxbP7AuSRESUX79B/8PQ+ao0+5ZPQ/StBM1/qVfYGTADAt/KJLzTZu0DEGP0aW1fRj91u/3hHnhWjE/G16tLYgYm/wEpIYAYW6ASSdUf/8Hdsk0RmN/wtAkGO72fcWIi02z/A+KERKpNv3v/g1xo96MPLbPt8aoz/L/GYg9QBidd7//qJfbh99+NJx0/4gK4AFgnUoAMCeoxKiVkL1/vgCDFwpUwcQiJKSNf8jIRUUh0KN62JDDFCwAuchtu9YDWxFOxqJU2cfOUjjb94gLeKBB+YQfa05ppv9zYYJeUPl/smJ6+8QCTBgth9CGNaJrGfGAn4YMYeQjjeiapkMMsN4BCAp5rC2J9GexwyQ+sN1jB5zo8PA0ZyV4gPQ/GKtiooqHkU0wmCAqEJTJxFvVH//aAoAyCQW4mCV0sC0S3wGEMROnb6FIFp39hIEVY6XEsb3Uu+jwAMCOZPHkrXUmMMNhBmS/GlIeYF+oRolRvf/quTbiv1yiVZni13/m8GEltk1FxAdyATcYj7+bHFz5gXyy27rPw4/kH16NB2QIp5KyiFvcaaNiWI6O2B+2FBNsqlvp1GvGhVbfZR/hPgu/loLIVXqbhg1DpIaOJy9iFbDFgF9xkGstXv8Cuc5e/vEd3/gZBAeIGwAKMIF2rH1/6DUufesMk+jrC/R/EAmwIFrPoSxjRFQv4YTbMDGHkJ4zomqZ4AhYJTRxCJg1I1z95AaEUAo9v1kMM4Q829ZqoMNejZg2wAggAJ1RgqaLsZzsAoDCkIEOL6r+Ca9HOPSH0HSD7KkCWGzWQ3fweUQQKrqcb9VL0DTN5d/7OSILxoj+ucBIZze94YYlJvNMV8QHsfHSpx5/AQBJEpp1bxxYlJQ72wIg0DfsFQpEF8BELIuprGwTfuez8dTwgh4DRMOvY7aHBsALKpPlZrOr/d7A6+yEbTxX3hlOBQiS/XxP+mJtNMbUwxBgSw9HYj/iA9xio9QxNtRfvzgBBgZECXLkd78tcQzXuQQBWKAsKtTamT7gOyuGPx6N//PbDDVTatuo03v/yMxEZRW6ghDWo0OA6EaBCl0jpIM5ff/RgATKihes2hm+C5F4lAKNilSdooZJpBP/vYanUBgKa5f1yzqJsPQgX7fm/YVf/Y+CZNNvpf0bB4pG73o8KlJK/p/TY+XbNaW/EB34fAYACYTnEagsj2CfJJ8AI2xC29WWx//bgLcoiCxwFeYcTaAWYQJWbtOyHUFX9wICcK1WSEcKpn1zfbBgPA+QRE2Sly9GcZBggEE3N+QvZL5/59APTY7XH5ol/1n98Ng0hv+v/EDYI8pSDQpq5HaAgGBJN+2dd/W2/aYrMqLPkS/73kABBJGV471F8Tq4S+TxfFbv/OAbA0GzvPQvnML+KP4AnU4AMH7+TErIXv+f4YGSjHtKlJGMPf/qAToCvYkqRjbvv/A9BMMAbJG5hY98WPzrYDoWGPt9vnhUxGruVc7OSQGHlBRb4gO+4C2BJHFtFT+0WYp1zAM0KbI9YTYvlbs6L/+6xcM051UAQ7ssic2ECZlj5+/NqXfvTRBsoi8SQlrF+usBhRdYTJtk22Q3AACoOARmJw6Om1N7zG/5zqUL7Vp6xs6CM6BRmxuNM6qf/dpF43k0yv5X6SWS/3+p1adb/2FprAo2+ICv2vCFFq6nh0yM7qww8AByuwA5AJ3Dt7N0fMGGrceh2Kg9LvOr15dcaxR7/MH/EB7oCGZzEVGiZtst/wBYAIpQrksNijThZP/+8EAo4arC7eGAIAhbFy+pBKctTVhGWARBuosxKJji/6yraW8lv+7hsyAEAjgJ3FRkcge/94YYfEhhtRoXT6idil5de+sSKOnyQVNtP8OcABsQyuhhMS/1MS4AASBwCbRNHB02plD+AVFI3PP4g9cauk/chPb7fxWIPXgPJjLVeueWXwlPGcsP8G/4W0BAAXsyACBx1KkC59h+/3DwA3BayFqE2Tdf/8BIGmQADgi3IvC+cLh/uAISyU1IlPME7NPf+8MQOOARo1LPIcWP7AUVk8fSGwOkp/P/n9ZKdx88ksHwfMg3V/4donIEAwAwAdxSlzsZ/f1Q9F2OxWjxiNAcZDAYIpu5Nfz82js1sk9/hwk5un+K52i+X/CsBAAC2ATGqdWOCx2pj4sC2EkI/FfkP1bcAAP0ABmQA18YNqbzPJjfmYYi1FO4bwxWmrnxabaqoMPnskMpjU0ZVpPfNK/syfrv7ez/o7FIv4biemMo/G+EevtAHBoobxXG6KfMi1ikPToHPnhULu//AbgdsB78bBnOarQcD8LWg8lxbn++vUQmTEExDuUxXhiKPG5O7OPinLIT1bl/+5dtTj1EUzqe//9mEOT+G4Y6Orq9PSkfyaKpDPzegU0t/87sT1ZHv617Sx1PhjAAWs3ESY+yL9wUP4Ev2U2S3QOouHHHprsEzYAALApuAwNuDRGAm9T6fokre/D9+2xXyH3laejMaBEK90LWdvvzh6U/zxMWKcnip79S6flDbO4f9P/4IPDqIDAAag4JeF2h9Msp+fDc3XvjAABYGLwHh12aIwLDqhUtLtpbzPGAAIBLQhwAYgjV0BLaJyzh0GAatY6agOH+8EUKuGzvKhDGlqd+BCKT5+UuMGtJhsvkbmw3x8M74bgKoZFtjKvy7//B6Biv9v3NHQIaW/n6t9/P20/GMuz36v/i1pVxB8e5IfGg+e99x4ij/DHjThKCAODKUygv4A6Se8vz8MdMbiD1+i5a6/+euAQ2yXd5+GXH6xAewAEQCZAQNYfQhjXCaheH4wE/BAxh5CON8JrmQ9AQ8Epg5yIL8a9+4CWAsgBwJRvdA2wge34CTYEk2ULouiBDf52hSMtiVnV4ajK11na8apShdAtQ3/wtwEIxOmOZSjexqQ+fgP2g9IHxZ1bwbY1af9QzRuG/r/566I/gJnnIX6/5+fBfFahw5f/4XwAExEKOviiuaJ+ol9hf4Eno4g90TyBSiAg+YjWzpqYt/oYtT4A0P8ND39GUvLNA9/hb5EZBkYVlpIWxqw+eABOquE6i7F76D0DFb7fuaEQYYW/n/6Xhg/nRP/iMX+8RH4iIxGfhAR4UUABJtJpNptJ//4APQA9RSGItnnPeJg/gAAAFQtBmmDoH+GQx4ADYjDVBFV5KWKX+nwQghfccOGxjdWGvAHFamM5/4ZhPCPhGsI/8QGoYADFQQgtTULOGxnZXDijSfsn/4nwjR/P3hk9cB0kMtV+LxJ68AN8tznO94gPaAx0TOAB7aJE4P9kfnAYjI0uzMhf+giBh6mV6bu7mgDkQpxEISxLYBCkEILU5DDhcX2U+ZsZXU51KOtrUhhlaAX6n3nBvo6IjCP//98Rk/r6WO3/EBrAASMyCZTn5BuWvtoDsoNyR63M5/L8xN939uNiT3m3n/iAtcAAKggDswOmxw2pgEshs6mOhB+WxDgToIteebU2QFIDb4yC3cvIPIQBWIA0KszamGwV+CAIagikLd59KhgJqRK7zkrj/eFuAB4N0OADgjfiQlbC9/wBQQlFqiRH9QSs2//4CeMgBgZ4E6WYHYHX/LQaMPzjcJKc5/iBY4ABd/LZocD8/kpON+2gx/4cgAuMQ5QqZV8w0+btAjIYQgXQo6YbfN2gBQSAjN+TGOJSWlvhHCiXmmUWqwpCrjYEs8ALAEzW2LbLv8P7chr/BgvQcawxs4EhSNz/8NCM4YCCF+cgGMABe+giuaf67/y0H0IAxuz7+oyj/EhfgALxkAgousJEmCLbHegMKInGRFgm000Eb/xQ8tp0df+42wE8wHQSvDtZ/eGJdAKulu9xtncsPr4gSIoxjamqM/OOcT4R8I/i8SevAQgonz8/zx4QBwdZMbU3gamc/7GFhjPXzv/cNzhrEf8Qfnz3xv64bv63P+yep/Y/4IIAHgnU4AMCd/KiV0L3/AJAxaIVJxCJM8a/+7/gCBCAI1QGhRqbUwAKBLB0NIt5RLkgJ1HXC5lK5UuUz9sHLYD+karvO/7QCCCQMAEdle0RQEONGs//7xQOviz9f8M+hoDPnqxnM0/83gTaccfNDvEM/mBlii2vj8/8OTAegyqsoYuTHS1Mdsix04ecdZ72vxx/wxmBQ+WHaAAQwbKJ1rLtBtDECPEWdlfcTY1veX8LtGnc78B60b3Oeu3/iA3DaAkw/HGsKbeBYUnd9/FkBceEyGOcm8JAYWVGEt/ZA8aMSazN39P4gMU8ADg6wCC16X6ppRXvsCQY7PYm40RFptn+dMAVBfpVtcvrVUiHotvfeuMZ/94N/42CDAC0AAvZAVONO5N/5g8MABaygqPaZ6D/27BxCYsTXCm/ARZLxiao+EGqePKAtAYz/YupsRFlpn+UYdgZcAMCiGPkPuum7X+wCQOD/0eqb/z09YZTXWf7+R2LfvGsHmCkTOL8/8PwAENBH/m6pSeQ31AwtkndUCUF0a/z+gwNAfFBBw1GVnDdRe+//AA+YRBaiSGmPJgpEIoA1vPlnfMFHk8/76tGkugoDbLu+kaerAwP4g85UzYb94fkvSXhz/+IPKWETRzADjesmX/zDk9k9Hv+f4gNQAHVBCC1NQw4ZF9lb2zGV1FXvkpa1IYffNQcWJ/+EPEnrgDg60xtT/CJo54rqASrEBWAB4EykAAgJ0iTE7IHn+ACDFkpNwJQzGKd3HgNmjAEByAI6uuOPX//3cKABoC3sMUcgoe//4GgAEgSYYH8O4hSsxuZyGGoL8mgoR0FX/+6+bYy3S//EBX4ECIkgQglOu9+2j8MEBsgRIlIWEqs//WAUAwMc1ri1zXJARo//+AFDII1SSCUNOeaU/3mN3UVe+SlrUiZdVqhWgRQWR+9Kz//9vyq26fjYM4Z6HDkAJhljPxOa+lFNwcAC0wA0DXjUHeaLc/tAFgbKCBTL6MMb0SWM4SIwBgK8COKsDrp//93+IA1gYNZeRjjWiipnzHGxXwnvdSi3iZsjXcKVf+Olf0Zb0FOrQVorZM3dn+H+ABrtCSd1ZlQBG6a8XRb0Axlc9Bn+cEqvDsoCQe4TCvEwS0+YyRD3IQYGfHnHlnEwCAEY7ADA2/47FuoX//hoJim2euMDu7e/Xh4U2uT/3W/iXtd/vP4gbACwDooIPGpys8bqM74C0BcigTECJMYtuAHJEYaIcoztaa7yvAYKeCayoi/OkAFAAEAIALz2+gjNEXX5f/yz6eNEK++Yd+N2kGdiOLHNSxTe/69f7r/90j9DOoYBxObiSF/7wFbFAiWV74Io0n9USlS/f/NwJhqI31bQiazDX8GIo5wYVymEq8tWd/UBRVbZsSKv+1tqKz1/3+vtXlL/vA661O7p45VxA2GAELOHi6o5Ev//xRDXDuQDXXMEhRLM83yUu899vgfKTmGrHKvk2nzFJQQpS71pmvLzFaD93Rcun+hlKcEL/dEkjyZS3DCemGIKRhgw14l/wKCO8tUiM4cFSpVYnV54nwgwtCZiJ717D/QgX0SVUfu8LTR1GkfK6Ss2ll/iBsHnsh2SD+LThaMAhheI7aXaRRV1fu3XtABq0D6NczC66xb7uIwhasqPZL4NdzgABUFM2AUGHRtOD8MCbIX1+9TJ9/mQpOxvnRroN3ABsbazd9/tQ4xVVf9Xwzzxg1EVNMgV/fDJ4s0R0H58vN05G/BtJs1UXxAVgKwGHt4lNWcspxjP/va2F4qVnarPEMhBUJIL54j6an+ISqohCnpeQs8//tAKhDzkgxJvSbRJ78cIGgi11ptTVIT1z7IV/dU4QgCsQBoTam1NfRnJgqwu0flaAC40z86u4H4bvZUHA/EDYCrDMNxIiTLCDFm/zgABUGK2QaHHZtTAz8BToRPQ2kSaUEJk///OHker716yAZe0Avloo6nVOp+37/50GBALl2fAn1QZKUDe49/xk8tgZXw0rbna23YgHUOcRBCymm3Lt8BEFkXaGMS9qHAWO1bmf2ATzRWD+6N3//ABann9hfg1zoQP4gPwFQ5iuGE5mXeEN0H/aY2wU5gOy0oPQvP+eMExxVoOcpon6Xt8GANThdiua1MSUoK/gdsA9H+LBKHSSQjv2f+9SUSsl90AayABmQb3E7yXP17/IAPi6FpsJZ8wSgidDWQBr3USIXd/v8giRctlz12wUvyTZs///v/EBWc0ABYJ3AAgLzGmlRLipmyBgwIBQYtFKk4hESV41/8GHBGxwUKjIbGpeew//iQ5cADgFRQQdMylZw5IZ30DBq6rAtB8mUNX8JjxDxEaH/F2KfjgpRvL/AotApyy9z1iQtIByAsADCICCCaQqQZINtg+SEHrbGT56bcu/B6FAwmsyt6dUelV7wdn6D73gFdCVtK2/W//i+bwANQKWg+JHQZ1nXhuAA4fw2Crpx9o6NUrQIoARdauV36aeAU1IBcxCRsK76yz//CbuALUEQpcdfL8ONy/DHRAAa4pTxHrGfv+OjuAAFgY3JB4bdm1MAMgqNVFWt9ukskCVTwCnG7dq/iAQQ0w8CXAA2CxZfzkZH/+gBQchTBSl0sY22wnwcGlj0LclfueVrOAIMmJ9aewn4MaBL3UgBJ8TOYU3bSSthH+lYMM329A8pA1WKhKu9hq6P/4mAoTcOoX4fhEfm/Dd3yOAgJ0QAHcvJLCnIlf/7QCGgtUHEogrhb/7tDY9BiwvUChIy21fvNgAuCRUrTIm6rj35LAYwikZkWSTDJdAAgYAdzivD/c7Ba95lE93/1h1tsqzQV8Hpfwci9aRZv/VQXOX8p/b8KyhoSwYMC8bgZ9odWrNbf7541W8AB7AFzqxwrqZaif98Kt5+bHHb/robV/bBfUF3DR5akV+6RUGrrt9Xb/7Dyheip/6GF5fjaAO5jHLVsp139LiIAGEXduNCL2Sm//0a1MvDsAUw1cf2n6SW/zAix//nF3IRnPui71I2sYLE1jB2ucsdVpoy3hDbez6K7u0chz5cPA3SwdeO+HuYd+uU/7wYf2AQBW3KzPrbmkwP/yjPcZR667sAkGetNPQR8AfRk9BzD1Gf/3ggpWLyTQi2mfXSPlFZ4ko3fwXNdvkdfQYDB4g2EmJyZdeg+nPTw2DaEB8MfAAZCJP7k1cvUPpKl2aKz9yf/Aj26wsQ0IRi5Z3XGeqB3GL1N5J79fUr/xuAMSQQgtbksPGRfZXD8zMZSuc6lDpatIYcABAiGDtL5rYEIMQgTgxz04P7/3FojTZCvr8uMwGYMhtJiU9V//vSforkb/1Vw3UgMf/QEAXC+QdOxT/1zF1f2McBeRL9vh+AoIWy0RB5C4M8Y//7AEyHABwTr5ISsge/4H44IHgLxJ4MWeGWRZQ+DgANdiFFLbhh82MaK/FBKyrQuhs10+/8GUlgFZpnNkF1g7+SNQui5+HEbEj9H9QcW1cEO4TVErwx1HoH/ENMQos2/v45DCC38SiQKHWSHNH+AfnCTkpYnfQHkn1woLM6Iwvf4566Pw7bDWidYf8EH4ADgPxQAOHVxCTQtrE3cAhKLVEiP4glh9//wADYhuuMJiX+xifAEwW1nhPqaiosk67iEsIPNGJbdHa+MjZDiFRP/785Isa+GyqmmwAXBIpaT/LHPf25IDgQotKkINI9IMD+dx4MKt6HFUCmrQFZxef9201rdaaYdo1xnC/lyAAQECEcYpDaLCXfugSBshAAcFaQgUE74HT/dmKwAdJbpT4kR/EB2WwAPBOpwAYE7+VErIXv+ABOyECivHtwUYHIXX/BgKDFopUwcQiykjX//Bh9AxiFL15KXGeOf/d4d4AVh3XkYs7UMbJ9h/JZComhlr5kXEBXnDmHVgAUYYLWYPpzk2p9+/9YCCiKxmSZItNmBC8f/ZnYCkp1r5uHZ6kz7t2Kfvn7/4gGHmwgSs0fX3ZtQ78Mhg9MwGFE1lUm2TZbwcAMQJTIx5/PXgEIy4I/bdWi7+mgx5F9flVxMn5fv/k+z5CXi3/EDfCKyQTPV9Pf/59Llgfexh7wAEEUod5esZIhBicyYYMYACAhaLTEHEKmC/GvCRoU5cbyX6R+iv6CdFWsipLP/dON8O/uHU/ijOJZ8rf6saVJLvlDKNPGr3dqIYjVuL/2j0mmM8QHYYAOGCJ5wlJfNu4Quh2eIAAgc3AACACChi/53P5vNU5L/tAQjOYiqs+xbq/8hh9njUP+8kGHg6WR0N73Z1RPg0h7/38mIuxxL8pLnrcHLiCeJhmvLMI/4HDWmVTIK3piPTYVwZN6nXd+xqkBSyabv6uqEvlq//+/4gPV1NHFwAQhMkYV5lZeBpgC4hpYO1RQU7fv//u82Y3dTnUo/rWkMAB8BK4MTA6rEmScGfuYCEo4nAvPyNDCJz/cgELYhChLHyFjCBz/F/wMVTQYZTEIxmGeojvCURIF0pvcCu4/U/f5/4gPfNWNYTbldovAGAyBLFX9541UQzX8H4xdkKyiqeRTSnpvg7QB+7sp620wAAegADtAc8MmiNoCF8chTlpbf8bSf/dDPiV3AB2F8xyFdCkRxlgk+KRPOJnzqIKER7HVD/Z6aESHYjsmcaF/1CTLxFEGHxAdgRAhqEfoTz8jYsic/3ICHkR6hLHSFi3jn+8RBCMYwUlj3kFEOTL8qhF8i4AcMB/8PSieHDfPw+QfKz3qRXotNgArAABAJj+gCiEBe+8QSdiMRVKVCjrEB5QNxpw01ER+3+WFNM62fX//XtKrf7X6/FgG4dhjD/EBWAB+QADnAvrIkzO5w4Aip4FcSuFewBEAIgEG+Z5iVqOoP7QkzESa9qq99XBKLElff+fIZg5BUylaX//+5ym2lCL/DfawP9tCvyYEeTx1un4G2YZLbFtl4Om1Rb+G5CggZ/4gPYfvWi/1ni2KbJ+98D4BAi4AH2QMwdHC0mFUr8AB2yOOaTJ970FbYAAIBe7GSAopIb8MDB0cPN5M2wkn1GOSFXzzzwo9vr/D4wipejQf4d8OhiClNwy4YGNlAM+IYIBRamrX7vBy8AYkEajq12pvPDwDOEVLcZDzLfbDoJR04I51PTXgFoLsv4XQ+a6O/+wBuDC+Vt+7Wpoejprg/W7/1yOnTcPlBtLAibmaX/9A9yIPLrviA9BgYEhgNHj1k+bPtKTHf+f4YjoDGD6YgSfMOvz5BORAbesH4EUfhZA9VzUOJx+jg7iR/vPMaktRI/zP/EAwuBOgi15ptTYgWkBtSOgtu9B5CAKxAGhVqbUwNaNw8l72IazzpvPm6yhw5V08fNKAKzFOv8QevwFG9Tyuf4rCFc9cB6l3z9+tf8/r+pZn4crNdrR88Hf75iaqr5/8OYACaHBtwu0PplmEgAJkHBtwu0Pp1mP4ABc4DWSk5LDQ0ZzUgM8jQs0apFnxgMddL/BBtFR66AqwpM9D7ef2ACvA2k+yaWHhOlnxEENlFSl9skt/eMAAQCyYwoMSS32x1lUx5jqcrqYgzrUY73Cgu0RKWQ2TXMAAFgU3AcG3BojB+HR23666ephi0Ew3XhIzyCSpNz5gSPiaZ1PYQM9rqi8LQ4AsebO6GccimFvBAXqHRcouUMtslODD1VrUmM9Jbx2zT38+8N8r1+f8m0h/P/C8oIAwCj4mVABrsQohTsMPmxjZb5CVlWjxYbNdHcCYwrc5fYpQltV9QwC8yKXnbn+CDDgAeDdCgAUEb8UErYXv+cBDoqFBOJMqQ1ZtxC0vc9OCki1Ue0QdGbDZHKF8/I/99gAA7wAGYA98YNEZNOHwDRoyADAzwJ4s0OwOv+ACZ1xR1trO7+YgMNtILa4mKTb9/qY55Rmfk1CenpI9cSpk3E6ef4f+GAoISi1RJz1QUga//4H8eAEobMlaZP8sY4DAQZQgYAOxZLzba++BED2QADh1NRcF84W3/g6dd/cmjfMMvudb7cuPjP61ngfSlUk9e/iAtACgFVxyNFET0CpWFqFJCOv7/+XxMZK3nksz+H/wxAATIhuuMJiX+xifMAAQAMwCrAu0b68WcRP9IK6wH3h0Wd4zgCJr1K3DamBjgoHIHxQmCfuOfn3mDYPdAvEiW78AOJkCnFqWdRLalOpbHDKn4bmygvZ8W6bfv2+H/F9KvPOCRWj7/1QvT296v/P7ZcfwYC4mvG89fAiT5xv8//4jxHiA9gAZ1gIcVWZJkm03/0PawGFF1hMiyTbbWxLrAFOGwqONKMJU+8AA+tHPnTJ9jACcAAQA9TEUAgpQVcD8QmXjC6dnELrTCTGhFu8/iBPATjgu2TCGUuCnB+IUfGZDuO+llvDD8R89U8U/DgC+sR89OoAyS7fX/v/53+esB1IZar+PxB68AmZ13s/iD1xRlVX9v/zrnXPyYQPUdBnA63dfP/z8CnAAAFUBBmoDoH+EfCMJ4R8I1hH/iQQYAD6MgDAR4P5BRgdgdf+hwBAhAEaoDQo1NqYABExgaJpQ2Nddi0zZgai49N38fffA/A/QfUj4M9y83jb40DOBCAXs+L/wA3EhSLf3QcO7vQPR+bCMXhGuHIAFWAcHqGQUztS3/5/g783jvCAG0n6F9TrkhM1vfADQJhQrzKelSq2UP/lmUwA8AD1Fq5yj1+v81x0Ajj89f4d4/vw8u7XN4ACGQhx0oKK5onqiX+ERvgANQ4JsEyhtMkp/hEmMtKDvEq/fAFzkNUn+SOvfIcXkdDFGfai3ekxFZBVakhLmrDYBDwU+WGubzHW5XUxBnWop3ReNgHhYpFGOt1reIJFgDmhqgzNGFNGN3+1ThBucIhyABeAjOA4h3+FmrqFfeAHAC4mhSTCefMkIomzA38H//9G11ff1/fgD//gCAo86rkb5+B3gbuEfCPiQtwALUACQEm1LEXSce/t4Egz4MqRCGopZdf/d/8oez1mG/QTdN3v/ExeJPXgPfT1/ggsgAPAucAOCGcVIFO6Ps/QJ4yAGAhIE6WYHYHX/EJwAEw82K6GKORTDXhwBgAWF0NSZTx5olFA75AYliPVJ5+QsXROf58AN0jEh1JX/vECnbWiHU//+/8Qfr0OPdstUIQYmj58YKp1eIDHDUm1oIDSbmLbrkvvcYlyT/tKCisxonKpNWguIBfgAWBC0J/IpjxOphA6/uw9h5IUAEj+CYMuvNDR0clXha+PSQy1QBsA7xV3MElHtDRHAyVvkP9DxVQNwQGPiArAkCE0T6RPPiVS3z7+AGMgipzC4khK2JDDcAAKg4BGYnDo2bUwA7Y3XnOpx0rb/QIaeKPGA0pIw2ikG+BPEi857vUBTne3/wnQh6dj4g8Wp5X7Cg/fwdXOzr/r+ID2AAk2Jk5zqQZC2o5QPwExI2CnMvM4AAVBAHXgdNjhtTADmRiXmOhB+WrnAi4xa882pqAKQG1IyDHclAnEUa50x5rnwG+AYAeyZ6mn/N0BOFk6fgepIIpC3edOOGNDKArrZv/nDpqyugfEAvgAIAMPbngxdfWPOmseO3tb0pR/8/DAEzPiCqXefnaxKAcAUYYiNhC1oTaMSWgexO+3WudgLZi0X/pk/6ru45euLt9s/iAYfBDop8semJGtGlyHmw4Lulwh1NopjAAByAAFeA54bNEbyCxUMyHKOTTTXjMoIevfgAuAANZYCLxx/LP/UYJMCx4Uj66/eC9IHxQoundcf6NAAN0euL1xTOiM/+3JyFJLI+v/8QCCAMAmwYNYf9DGuE1jPjATqGDFnkI6zwmqZDD+AlEN1QxkKF9TEsAAFAcB+DRwdNEbAGRiKiHE1LkqakPHE+7HzSZLaofHg0RddPQO+2rfd/vn/xB4vboIGFMkytPf5//z32IA9uQbggDwMnssU9/v/PIL9YX+FKtR3P+HNP8QevAdcp6/z1wftCuX4nEnlTwF/fP89YKKaOvr/XD8ADgFRQQdMwpZw1QX3wChiu9ibiLOkQyz/gMGqr8FoLguhq/ucABMqoETZdC9cAK/DFFL7jl0wLaqnpEQTIIzEEIYxAeAN0OADgjaBQSthd/4GhgCCEotUScSiKKQNfDJ4AmUR/wPQz34p984aZmiDdf+0JWOzw383/Bhhb8ACwbscACgjaESglfC9f4CQAmLQTBzuq4WVM/cIKsAGN7EsN06UUe46a/nGagm90zaHB/jYBW04ZFl3/qAE/HTLZWmngEozE6HJ2F5S+sLmrPsdoj34BFDyJi9xaSnwYe4D+Ekvv9/2gIVvKRc6Jiwwz/AwFAQzLI/q+REUFEvv8YDbhgpl1GWt6JKGQwNmBiqmuRDdl//93CAa4MGsuI61woqZ/7QfBnenAylJ1dJ78GVL3xDWyo33ZqTa3e1VOeKvlPQDYcstcXCDGUWwg8QHoAghAOxQFhVqbUwCGiDRSC4tyWqTirM9CzvhmldHNR5gAAqDgOucNjpojAYAlUoAMH97AqKWEP/eD4A8JrutoCBOggw6urIkb/fqXMP+ID0DAERBQJM4+WEroHf/AfvKm0314fTAUGIDPnVFYcnbn++//Vy5Zud1KJT/tfnuFmwjOmWpkX+AUAMc0YjjykmG7IQI/7Uwb4sQJY1pDf/byZEGjiLzyEtYv2/GK01c+LVZVTDOkwyRRCYlSotEGbm1T73+C37UhrMv/+o+gVzOoBN43wbBjUmi5Q4SPnHevQD/Vx6aP4IGEMNiq9L1FYDDbHMql42bOgPNC9qeOANwAFQ9FEAfT7/l0f/z+WKdCl4AY948sBitsc0cfSO6DGzBBT169JI/I797QuLj/MpZAh3amzpL/q//oPsWRzSZ9wthsuard7f/btCTVRa6YyZh//PDeRmfv/43S31lz/u7285I3w0CQYqvV9xoibDLP8AARDq5l5mFfCinsAAHYAARgDGxs0Rg/W2UbDYSBmoIkqln0W9Su5ciYz6a9T4CpArMgVDylmlNcAEGg1CqONRJGDyP/gNy9EFCTWVJ996O5SuH/8pBQ0t3Jr6qKgXqdEtg+ikPnScQNgKI0F0oiSdS8tKf/xfSvAMZJBhZh4XGkqYYJ+JIMzwBG1B7iYzgBqDJWqIBF1U55c//2teLxSVnRf/7pMAhi1Esey0ov8YAAKg4DrnDo6aI3Axd1ZYt3tW1+9//zpqhUDf980Bh0oEGc/wJGjYnabqzLP/9gQ9SK/JXm7/9wbZFqd4ejIb+CrmChIbSV/y2W0AVuOX/r7bGN2RMTN9+p72Yd3v7/nMiHHB+N5IKUF1AyK+cPM4CZR0K3jamG4h4hgEakDAk0Nqbngd9oLnDYr8ti2IvMw629BzqEcXsT//K2nM79qJaDACMyNocwtTXGY0ygNRE1MqXrdvFQh54Q4ZVe//nMBj0cT4RZEnQyge/w4hhYyB8yI7zuJdP0/7kA6p/r7a9Lrx2JHtz/DHcEgFW1nb3V0AwpWbO/9ZSsWtu8d3vgaDQN6EvIb2c97P4Bj8UE4HJpsyXGVVg/iwEEE0hMg2SbbFKXYtrmfdzxv+UH9KjeX/+BULD2qX9v/hj6BjZi+em8Zbm78BIkyNv15PytgKRIAhKQtqlq9P+EcGF+4ls3j6ELjSxJqD9KaPANqXTJiD+ID1gwAH85qEZgE4gx3/eAhJgPLEYXhx5Nh+5kBe7OJ+zKFa5B8AhncxFTWiZtts/wYYAHQOCAk4YnO7puYtvoGSRk1GsMmsju/lqmCtiHe6DO7/Pf7DKQOsRRr3/56+DaSi/Pphxk698/v+IC0ABMAGgmhibaWvNkoIHfIAHx9C02ks+YJQ+d3gABEKIrGRFgi00gwJYwS8obLv5MR494EvAMCZQVafFSM5PeFVJUGO+INqfqCGevVirKMMZncTz49x16VJ/r/8QL8ADDYDCCKVJskmm/+/4sBBBNITJNkm2Q+IDGygAbRACAzwI4ouOwvf+YC+ADUPVNVB/GjX/4MNlKsAUZwldPmhfle/iA54ACMBpwwUy+jDG+EljN//4ARP8p6/fxAb/iAboCBrLiMcY4SXMggS/CKrp2g//C0ABExmRyCb9EvMY8+Ivg80GCVuDKc3N2Pfg9B11OiAsk0gwj9/dQCkBZosa0tOzRaqIj/VQZSTEjvegO0h1VLc+PiDBxOLzQcUf/gggS5CXH+1xC3LHsAWa8AAQBwAYbOHCiaxH/eEbdhFI/Ur73rgAVOchwMY3hpsW2V/8nokVhnpQOl4lHryIyDZBWWkhLlrD0wAJ+qhEUbY3vzzB4B4UJ0r2XsACiNCSPVn1Eqnci/VHSuNFY4t4e/DAAoFSgMB7c4WyYWSL4MPxg9mHWrPSjsWkHbGof7sMQtW0/n+AtDd/cFoNoqlr/iJArbP5JsBBpnQHAJG4Eilaa8fLeeS4gEEPoDAGR/U1zfGb0cVn2qFuRbfFrAkN0JGNCVR7XTMfYWNc1DP/uISm//n7FrsoIMIw3U1/5ATER0UY9HVo+FASER8Wf1wxoDgAvYtSo9Qz+72AgACyAJRPOrFB4RoY8kEJ1FT77dJb+AOy31AHTADkvPNdqAsOYrxAY/kRYIxBL9eo16yyhIQAK3ybJD+f2BI2wVySRSdGD8S3fGFwFp+bgs0OC/xCv8bAUMimCrYEUwT6SUJ/9oxI4ZgTGJBkkm33g/DhE46HMeIOYLAm3gfviALUEverX2z/bOMoxbL8qTjvOgKg1BC8DdQr1CmKgykYF8asF0n0pMR7YyYDspnHsF//0MpPhmaXjb8ABwQr+Z0xeiZtNM/0BCoIQWtqFnDYzsr4zqBuafklf/4PoF7hlaeMqbrF8YABJAHWBtpVpQsUyL5q16ZPGmkCKOmMOc0lTdXGBqUHhwTVeTBKDH8GGqINqBvzXzl3/+Ux8NPLvyYkQol7v/P8QFfmZjK6ir1JK2tWGHgAIzDDD0t2SUIDvSpEewYCAX/DrExHI957xy9y+8jqLbXiQ3AA4EFdBglFkig2RZe8DIFLcBCBRCDRJpetYypUv+v8P8ViD54EynDhyxcocLHtrck/3/iAzHLIdeC09OHs6YMGANya3HHz/xAVgAUGUFTfhtNVVkm/7mwgSs0fVDs2od+9/sBBRFYzINkWG+4IDCi5wmTZJttgy2HgEPBq8AWFHvfDam/mdXvdhdLY2+TaNS1RFjKzKYHxA2DCAASMhOnMdCjetiQALAhaLTAhDEE7uvfuwBOhAAcE7RKCdkLz/NKGosc9sLnY/94AgCDsbi7Yhv4DaZPYE41c31m5576p1ySr/9zAK4AJQ9XLFn8UMf/9zCdJSBYSy8hP/BhggvAASYBcWaTRboZaGhhgz41FS8gWX/cA3iio5Nr/qRMpzxUH9T/hepPv+u2YMDKr4gO+Z+U5Vmyom/6BrmVu/dFUO3QN+VggYbEvQTJCCGs8BIFxTTU4gI4leTv7f5Cj4iY5RX0014fgvwmild8z+6oAB4DrAIJVpDP0vKK7zMKCf5le+nQW+O643oEz796/4GlSkqVz4AfHqx52O3TP9+/xA2ABRgwXKofT3ItT79x6BEkB0lJWRxf9/1gEFETnN5l9hniAD0B0oNboasUdc/7QDHVzK5di5MqNfZr64/+/6xUzNIQgkqq//l0DwPwQETq3hNO65ZhDK8EHpSC4vqQk0XlV/gwYKYWEGD381hfzNsO8f5TKoXkqd12RI4oyuSJ53WRFxAehNRVTb13gBGAf6H8YSxJBTRHhvww/Jh0SrLpD9dBzzhhDAAfZAZNR1M73a37ljEREPWr0uxv337AQUROcyDJFhn3tm8x3v1dQ71w/N95x7gaCeTgJQfcJHvv+ID3zAPQbxUrxlIRJo3L9LrA7vYID6HWQT9Ip1/v42QBEnB1kJ8yiftTHyhERzj4inknvfDhpI4Ho8sdUhJo9Bol1H/3rD2iId/p9BbKr5v4gbDYYYA230B97vAB7Cwl6xSmR//2gSwYGZAa7K1tiVzPPIZqP3lZF+TNfwOgKtFrbSQSnQ2l/oAmJsIJUvcTyLQnD1A6cAYHGIys4bqL77QELZKKNITBXin/3f4u8QHL5KNqwQhZnLJ3a770/e+n/qrYyQ2p/xA3NG+P9/3TQ6KO0KRyzeYMomUDD4nAZfAKkvkEcR/MBeAnYe/Rai2dDUPwBMhwAcE6RJCFkD3/P9MAn7ew/1qyRESUZsz/nv8QWUKFgetRFV3nQ4Dk6//NkUgTIXbNVw6disOTwtB59/EB75N5BdZnVJn8ZDQ4C2BkISbgcgMhgwfiCaDiIidt/DSDj9H7pjFFqahl0wM7LPhgATOhQ6NNoV3kbUbeetaAwj0uXl1ZRph//rSVoJm/7f//XgbAXOAQD3ZTMNeNv3CBwnRHcHVr/WkcbKIgJG/5qKM8/6nKavMVf/4iUH0IPS1X8QHYeX8f48Ak3etZ/fAAd0MxwZMeMTZUTeDFJ77rH/fxwG5AZ1vJ3GyMUbYbr5guI1b9YMXLhXdG1///rQDbkfz1yK2/Vfdg/+HoYC4AzMM/lmTZR4wh//Q2sedvtfwS8wNvWAIlEtPq2GoxH8vEwI8AvNjPMez2OtonP575gDdSAAwI34qJ2wuv8/wwdWxXyzQ2o6DiQnWc94K9ycTHh3+ICsuhoHRhgtVQ2XPTYr94MAusBDiKxqQZJtN6MIEzNHz92bUuvf2rAY4msybZFtv/gwRWKnyClkT33vf/mqTUNCBfwLQmP89nSvBrIvnvD8Qpc+fvQ4+f/FYg9acBN4i+9/XPWoiUtV/4gMwAHgjQYCA20hjTEdnn3+4DHkx5bwLxepU+bl//tAaUMCaCE8OPJBC9f7hIANA92xEHcULf/lB7poJlx7/5+n//D2AAkAFxcDUGE8/YJzROQ/YAkEwMSZTx9snHxwMPIGKdgzqJqppplS8+qwHVan95/heAB5mNKUq9CDEn+AHMCoUOENLI4v1WcrUAVgD4150GPhtpYGWAG54QruZ+KLXH5rGUQJ59d/38e20rvkWu/iA7YAALgxWg0NOTRGATigl2RCX06i3gWApKCUgVFTVtB6RiKBFnFxSBDZH98BaAynOMQjCseb3v/3sbvznVx/Wvww0YhEu1rEydqCA+9xL/Xv//PgxoHZL7jaW9fg/Kqn7/A2ZwPMk8PaBQAEEBptYf5fsNKFrqGf5gAuJoYk0nnzJKKJ8aAnoYOpnwYqhKc26Ei0KCCDw1TQUpV9LX/q/2cyD9/PfIdtIf6Vw2L8/8O4ACMBtwwYy6jDG+ElDLfMiAm7Yyv/wblz7xANcCBrLyMca4SVLh6afgTwoCJNMN6AmjGGF/EbN+X8D3/n4sRuUwv9ryDFugyA9rzVuCl79++5EcR2Tovf/69Zx9WtHLh/tn/BhNsAYfAASABYfQ1JtXHmikUD9gwCUaIcPCuWED0/fgrax0jjH79f4A4ORkMbU/8b4ACIdfEdTEHJpRj47bZUj+dgAA/AACOAcRGzRG48k2Sx1E/8wdaVrvf396AMRiKyCs3yEuakPgAFWA8F+V6SA4bxVPEEvchgt8peyxw2FgwxW4axBGFIVkhTXf7jIXE1fcCkjmf9vs4QFJ5riA34Bi0UiYEIYildt//wYfCHsdr/F/vEBqAAkaIaKY+cT1qSwAATBQHXOGx00Rg/AWxSo3E//Og7/iHAHMxu6nOpR0tWkMONxHzy3UbZv/CHz1+G+P+I8R4jxEJ4QPS4ENpjhy9Ef+esDvGfr/X+fz+fz8CvAAAW20GaoOgfiPEcJ4R8I1CIRN4ADhw3wojDK2m/fr/3DPwxwAEQ+6EdTEHJphj3AADsAAI6QGPjptTYA44THdBFvIphrwxqVhgWBTh82AlBIjPvDTJDf1/DJ6kd8b+v/nwjF4lermmTzCA+F+AC0mZuC2dT9YBuyZN2RGN//9DqKlRojbcjCTdoU1PobyoBL2MUQruOXTAtqq8QoTODByEJf+IKLxFFgAYT/L9OYUjmgtIa3f1fxAX9TAQGNMB0q+dBbMp76BNggxg/VUhBCT0f36CYH4DYsfBbm3m5BlCSchgAzgXSXOrHLjHrSnr+IDMCLAA3RFC9hljN/g/MzG7uKvUkra1Ictdw3a/QP+IDGAA4+QwBB7NcwTUWadeMkCPKCLNSgviP7xANcCBbLyMca0SXMh6EUFvcHU7yTc9Pex/AChzwopdf9uCnDkLoi5/3YKHSWqo/DnAAQBlCLIBD5VOnKoFFDvgCcOpwLfLJ15RIoqdF1/AF2yZGNqf8IhjQQYAGoFLQfEjoM8zoARHmVyObU3uAi21q782pgMjsnC+0uXlvIP4AtQRClh18v4R8I+EfCP4vE/C+AA4uWQAKCCkpyddRMf96yZE3GsMmsjv/vCUEILW1DDhkX2VoeJDc4YDWZghLf+4D+3yG1OeLr9+/l/EBboCEfzUVdCYMsMfz+TAAyplCowyxnfg/MzGV3FbqSUtekMOtV3NeMm/3P+xd9X1/iA1AA/Gjpg0Bklvab1yQAGyIgf7MoZrgCIHYKCThmUruG6DP+0BDO5nVFiZstr/yPgAFCqrLafwwHty75oHUv4u2/xvQGM73pqsESZZY/gKAfGBBw3PzYi6P3+7SAAi9GCpo2xXPmLw2GZ4X1Rb/eYAAKgwDrnTY0aI3toZFUgvIJQtSHAnQRa8SbU1oFpAb0jlN7z+AQ0J2UReJIS1ieF4hRauo4bNjOqsGG4QgCsQBYVam1MNoe9QdmemRBHX/+8tiCgqvm+oIFxiGRLmuPRtHDSYY0Pzw2hMz0pxdQI6QtLrP3qJteRn69utT8+H/8QGOwYBbuRv782dRv/aXc3/bBrz/fcS52aPR/EBfw8kxt6eE/B/AxTVVseb/O05/OjRU/QpHM/0X5/8QN8ABJiouWVSXW+iyA/GCKcZqjSvUe4h6mAAC4KZYMDTg0RuAwRYWwRTTksyxqhHoIGAD5Iw3QxkKFWxi+T4IQUruzhsW3V/8AsAAIAzi8BKf8eiecUN95Cz5mQVLyaWW8MMatGFfXP3+6QzjfEoqEzOPik1OHB6oWbd5Ao1MYOQ/xAe+BEEh3thFwIisssDDjGrzv9fvPwiAVA3BFNqlxRkja1FDemNHTQJQZBZDV/RlPNW3c/2MTEHuq2/feT6wBqs19/cbHhe3fjs6Hsx+HOIH6MeQ1cD4gb8zIZCqIvEEoaxAMBerAe0Ea1LuKcZ7AhqEIyJxz8nYx84ABUCHoX+RLSBO5ZA7/uQENYn0iefELlkT/+0Ah9EIUJa+SsWQOP4GJsfYF/R4GUwR5mtZQhFicifhw1+qg+a//hu2hxSfqc/rCeehlxr96p+6Y4n3WnULJIl/97/iD14cGcPkpDk778Pzq/EBvgAJAAsLYak2rrzBKKB/wwNGLDPLdnhctlMuLm4AueJco2pjIBtj2vbP4gNQALWhhhfhC3fl5C9/4AqgA0D78MQcgwa//7wwhu8AHPj2oWsajcZtzh/xClovnrAQzZK7z/9YgOwAOgcEBJwxGd3TdRbfASEM/GoqaPgSwx/AJxIiahLDIqI7v7TAA3yKFRRVit9ABYXZCs4qGkU0x+iAARVBR5KdIuOJld/B+AqoIwHMVCBhkZ0VvbMw3UVepelrUhhhNyFsOpuJ997hgFHDzPu1sq6AhMQI5OWGuICsAUBKYVSD3LJOaQ8nSDoRGtQ+SkENv3mAHhNCk21MeZJQQO+BgqKYLTQxvvuaR+AoqFPnHjdp3h7CEidhjefggrfYKV/TCP/c93AAA8FgZmDCjGDoTf//cFlewHE5HEj5mV/cDWtDVmtp3L4IX/BBwAHUAAIAWCrzRnm534Z/4EGjAAtCC1aeQsyjViLoAjLDgIKRO1ik6sJUe6aE3JVC0ENo+/7bPU2m1H9WEC3yDYAx0wLHh//9+OwIkgIwr0l+X+gugi3MxPfk8vjt/dU1WsdZHNfU3T9/h/L0/uCsjmJeipax21V4nblGrQ/x0xvRUIv2gB2Qekqtt26h24YZMSYl5jUAUWPwCAa3u2rmHkDoMTvTvmsq90d62zFE0j6+AXeymaS3/9/43MLupw3yCJKy6ZhkIFWQxvVN0/4CD8GI89legprnLJ5N5lPtZ/u/2DmgMd3s+6s6xTLP8rYqVPe/9/gAMKdXOU8hpc2TxFHjIJv+hS3/9vwBBFRcINRZIKWJ/91WQyLOhyxQo+RF4UyTM/f86krC5Gt1z/qTiQ/Zr7vUi5nhIqvZ3+NsBAAfG0EUunbd7+vDO1srX/6Ananq1JvvgZ+UMJd7zGp9DUKD6GJ+hSzuQwBeTKOGxw/NUz/+GQnoUoBQhus4+c+064AQYCQpYZZpHPGT1Uz+eEjDhiHKz/aeHUTRt4jJoqMxXc+/c+wLiFaP31sVGjdMt//SJlpGDlu/xIZB8OGMXjdvyMKmKdn3p/CRKA2abvcBsPdoA/Q4ST1SUkeMabeYCHqfS8YAIo5GF8I76n3ZKyve2TEf2tgZSHDRGY/1p/7L82KzjugIP03BaqtZkizwKjtMBQyg9jlbq03SDzIbkdimUgrHLVh4AB6cCKSwu+b3hDrNmJPfHnIbfvt2PXyVZexp+x2Q+5/1CGdsNGRPLukq2exEw/GwJmmli5Fzrf38AMEVJZrFWgxLzSP9ohKqNbDrTbvgAEYzDortapHJZqQQeqQDRQZJCll0X8D8MBcUaFup5pdCzmGPt5mwZVcHSstLj35NCuTwcV8Q/cUtVxdbf/6B4zgW+xElqIL/9ASZh5KKHw0UdKOv3+EWVwkeFHx+zJ9Sg6cfPT4lAd9X9/kWH9pK5/9/8EGABQSYQQu9iTBsXsU/8gFBmqJ7ndAAWTgXg9yXkBrnOF//wDAAMSy9aCdCcfMT//nNoibBrBquca4yNwcw9Tj/+5QhEcZPtt2mk94gZTDKSeWlgjyaPKZQf5clDefd8xZDBDBTArHV+5d+9LEe6um+fMAAXgubQ2pywD0vXSvf9S1IbMEXhXiAvgAIwsynZDlGdbTSPEAEQoRXtNskTFgl/xfkowAgFIAjarI49f//d6BB/aGGuLwCPTqeRp9/iA74rwZQ5sKo1RhH+w2IrSlImtf+/WGkGlNB+gSARA80hWZJkTgdgEGABuiOFRRkjO/dewEOIrGZBkmw297MbqKvUkpa1IfgIgsN1MoixElmWQ9Ah9tXs6tXD1b8Au3GGqxk8Tf4gII4YTkRe3Pr+f7/H/fh6fvt/IEH/hiAAmSMN0IZHH9TEsAAFAcB9jhofNEbpArLAfUDor7tnATKOpV8bUwCEYipjmUoRKlp9uwhRC24WdMi2yvLA/aBc4evqzz+1CVFXhbDZro7v4XWKdivVz+fcdB4mQKRRYncGoopPOeGSx6aniArgAJGHRM02kPt0GEw2AACoIVYPDTs0RgBzCgm2ZSX06DX+GAvwB1eJm7V//xIbgAWBiQJ/UnnxG5dE6/vAgVDCKyK0r1d6cvg1KjPRDan4LzsPJNW9d99FP/FYgb4AGmAwgqkZk2SDTKwHNgIIJpKpBsk22DgSgwTNwdT35sz69AFgN+ChTJBGed9JKltIIFzbGVQ9NuXXv8QDbAoWyR/DetklCwcWwMAQsRcra97hZQoTIyX3v/gkwAEyIZXQwmJJSxiUeSC1B94ZFfdnmw+G/AgiSSw3kpQQaaXL8Hzcwv0LGdGn/9oAg9v+AuSm8+y/YycAKluAeIfN/b/hmdX8NwAHsAJg91L0nILGP/+2MwBAd4E8VZH4Hf/MAYkFJkQjhPDrz/9nmMWyA48nyVXzaNBKVnABWRaD5XY3//3wvrDDZVoxOIBB/0W7ERP1sqrGQvwAXf+pUzf/bCdxYdoiwRgoodLiGFks85AiqAAgShfElz/NnODZN6rh3kBC8nmngXmmZ5JEr+/8QFp+Q/sKP67r72BXzzeAx00sochTGptb2qAiMT3xl9yxAQ+ADAf24IdIo+54eYX/9GnuYb/9gakguzxae//8+Dg00TWf3z4f8QN/8AC0jfm0kt/3B2ZJPZ0s/vAFyeBqY2LcSlvIjEVkOZ3G9S/hYl3qY/4Jd7XDaQuVemMXx69Ba8vaNfJ6/t7/2rhgACAEYZJh5ceB6GqDAMNLTwEOfa42AAFcX7Om3ryOCZmlR/w1/iBsMABGKsgva1DyKeYSHoB0RRCyz5MoVZ/v7zG5TncKT7T3llvDTeA/7ioWdnp/uwBEjdUpevn852wL5KacJ14AG6NWaTLP74BCF89TfxQAD1wz3ILQs74Py8cB5Trnj0jpcOrNNl36pI2SnGveYci9FopxAe+ABRsgnXbqmReh+BnIgYs13Leghz1g0HwAyistPXsAsQZQImCzIRQ1gv/xqGBPu0hbIiI/7QYW9vIv4gP+LqAAZaYDGFUnMiyQYZ/gsAhhNITJMkG2eOYCJcBEGL83SflWVAYz6gBOnQMt7ZJ5V4vAZfVGcT1LWrxhms/4AYoDGESnMmyQYb6KfpY/A8chYSHsQ3/2H49NYdf4fhgCCcgdz9WqjyBdaFEDGhmXPVaSvNpm7oI/OSEuU/KAGZ7r31zgFmCmyhUkOQaSx4gl5zEFvEanXKDdNgtR2XDx1bPRJsA7Mhvlky//+f8P8NKs44kN2WAuASqYBRCcKsJIsK/4EPQMAWuSJG5oVk6GB537zABKJoUk0nvzZKKJ0GBcwMehCNSmkSODPjn+DUIWGQw8IxU6WSlxv/cD/TNsUbt/34Inx++sB+DDeWVogGXAymtpMjEHf2/AAds0gttrv191yW3ok9D9Br409cBP6vgdon/4Yh/AM7pb34ASC4vFrKEwSlJy7vB1/0d0oBkbprm21HypGcNQQwAEyIwyoIzEkpYxfkwDupGHQQk1xeXzI1e+Z3/4gbDAAqB2Ch54zKV3DtBn/LxUN0B6BDM5iKqxM222f4H8AIQB3Q5xkEJMeXg/bMZXUVe+Sl7Uh8AB3MIUUtuGHTItsrEFB/ovh6v/ujtiu4Z6HL3L7z+IDsPZvAAsCFo9uBWPE7mEDr+/+kZBshzKUIljVjPIlmM9IbUxvaaPPoQMm1/c/TYX10/etsYBAviBvkBCWJ9QnnxK5hE//vIyE6cwvJd62JGyEOm+GpSuV1+8AqG75UuLyu8/gPMXfLjlPwxm/rFZ6hK/3//tlX8APnADB7OZkynNH2fvAANRbOrwghfmIEUT+4YCGCSfKqakil7Wp2D8JOu+m0Ms/7a747IS26Sf8QN69jereX0tufmqAue8EBAfgCSBS2NljFtgIMPcIApBg2KGZF70pvGCAXQjru2+i/f0JTcz8DRs5fBumcPdgBaPDFVMT/Tv+8tOqTdWknvmDak9jvfcM3+eDIGDxAehgChmMOpJRaGiuqpfh8NicWzRNkys7O2pHnTFOrvL0ZDr9zC3/pEyuJk//gCOazAucRb82oDooccMTphw3UX3wGQ2QoSZWy9n/OGwA1D1TUQegsa7/Bnji3MCobDAIL+aWJyrr+0ph2n37zRZvm1/95VSbC8BcQH+mVmQI2/7f7+thXhPaZbjXuaECcIQTS5ORUKzu+/gw/uOAvgtofTLMewAAUBC6B4bdmiMNBggAYvks2Sf/ADEKiZRFpfbLLeyeXj/fgcoawCb46+6GxhbYGOq2BRby5J7/r/EB2AHQcM67V0TfPAQCoWeBNVlJ4wW5sV/yaE7cx0KEStiSV7lVDH96AAcoCqAzFYymUL5FfMzMaqc6uF9aU+nwQgpXscNGRbVSHxoatrs+Zdf/4MHiSHuT2xU/yBZXUWYm4/9nLCilXHMemEt6x/t6JwbHImhcQHYAOnAy2UHWWjikFeAMbDBK6yxGFYVw2SBHHNVBtf7ZFktLNkd78vg3B0OCvkYXGW1Czdr/aICdotk6/v/d5qdo72yD9BvUb0cB4Fqr8QN8mDBayhsvcixPf0ClfOfP8eQ0Q4izF0sQiyojwzVQM1KBkkCUfg7v3m2zZv7e7uWmvzdwxlCdJMqbLMMJB8KQQwtTUMOGRnZWh+zVziyW3Vm68lviIEJ17qFd/r9IYYUWx1aQqvLci3vre8GiTklz4RditPv2svOfz/EAw4YUKfepcue7rBGcIxvKLe5B6vQAAF4CGXINDjlHU3mxQa7KhL6ZBr0TUgZH2AeEJ9bCOw0FJM6TzoX99f+zPHI0PT/iAX9GABMqKF6zYGb4ADDNQuaRlX75xIEgxm+xNXYibLTf81A+KCDhiNLOHai++Q0bTGgJWe6Z/2vFiipJYf0wdpx+z3+w/8QHvmZmGVRW2klLWp8YAfwX2PjECaMquhgwz2sIdosKyF+AAqgFfnFZ/oZ6rIPrASeC0O0fex2mvrW/c0gOihx4xGVnDdRfff4XtNmtYgPVNAyKf/u8UZUpHfP+ICsQAAXBDLBocdmiMAPigm6VSXwzC3hhlsHz4RkuDvdxIEh40ZUg9y66ypoLXdb/EHsfqIlLVJ0tV4rCFYj4MOpATqdCIOstb7AmBn2ZuU5LvAgeABekQAgM8COLMjsL3/gCtgA3D1UNUJwq6//4CW4Xi6jr256JPecfP4itsPZ5wxDm62V4gRgAR1gEOInGZBsmw3D3ggMKJrMiyTbbf7q9AfEAggZgYzJtMNkj+/bhAyMuR0qrPP4AWhgWq3hUa9zJhdwIuMWvPNqaNAEWPBhh5CAKxAGhVqbU39eBg9UQjlbFfvz//xsECS0kACGwDCCqRmTbINN+wDIwzeaVNkHwKe0UBitSl6UJcwrXOswEMJtMgyQbb/4P9EGCZdDqIdm3Pr0AWA14cKZe/HO9klTHJAg9bYyfuTbh34PyAaYOFsvowzrpJQwGAQqlSq+JBIilmHZQBPqzQ0Rf/71UXkQtl//v/EBrZYWrUnJ9r+4C5BJF5OSYQPk5EwPdhX8k4h/y9sxlVTnUovrb50l42AalDU8t57R//xAejZiABlICHE1hIgwRbYB+w/xYRRdvxRFM65AGFETjImwTYYawPCAk8YnO7puYtvtDKG2qG0/+DU+PaYkZE4SwybCO7+AUHB54pTjIKsbl3/96UghBampWcMi+ikMMR0v4vlf+V2X6+sNs99//8b9C8ABsm2iFFXonOAAFJ3K4cNmwRwUrSb974L7QodcElLsbJrobgABYHNqAcG3RtTaBLA4dc/aHmgnE8f7+kEJJlK7Dtf1QNjGk/q/Zf/vHbQKGU/4NsMYB4G81xAZgATAF7iCt5/mOL3Fm04Qmj7oLI/95GRBsojcSQlal8LwhRKuo2dMjO6sKEy+SDSlr9+oMP/xvgAMDVgThXW6pIFxa1XhgARwBX1xdWT62rAAlBSWg/JGQX5naN47+9dV9f/vBBJFpThqcsdcWOqsAAEgYB+D5wcNEYC+ZYTwqF2/bgVdgDAWQve8SpLYk9RCZMYzECcxiAwEXhjCiqzxfwADspjoqkRu5PfzOB6jG//EBmAB4QuFRqjGthLP7f4R8F1OSo1ys9Tw1tX5E9v//+/h/n/hzgAODEspUiUcwiphx/9oDZTgAwI0hEmJWwPX+AOxk7RQz9IMI3rkef7/Pf8fgJpJK7z+NxEXiI/wLkAABZXQZrA6Apn8/R/P+EQQYAD4HIICTxiM7um5i3+6xIyahJDJsI7v7gCCGAViwKCrQ2poCqQhBa2oYaMi+it4awBfA6Qju9+op/DM+EYs/4Z8IhmAICZBkKzjamAxAKSg1cOmtrGhAABUHAdc8dHzRG95jdec6lC+1qYoAc3gbi+jvP//4RrhjTQCAALAtQWkjoL628wAgQgCNUBYUam1N7gg1Ha3fNqYDwdsB/SNgv3NAHR80+AWAkKXHXy/wrABOPUT2Fw4lnjgRMcruw2pv1DgFoKygmcMitqz7/eY3dTi6kn2tSGL6ASgayqna8P/rl4ZDGAA2DgmwXKiaZJhNwCO8p4gi0B9sO0sHZwqySVmltfWUMZQAAal4sSHgjuLeIJNAfbDilgY8K5QB5SQVcVUVW/d/CIc4CYdX+Gn234VP6DAHaNNDan/CPhHwibgANdhCiltww6bGNlfkRiKzCq1JCWNX8XiTy3gMeuf4agAdGitsEoMkshq/gJQAGiIgX9MoZrgBEDsFBJ4zKWXjdBn/VhzA+cVL8xxYAchOe0rnrrA5R7hojjntNx/LHCuVSu14g/uAqtq7mhc+1f+IDUABILIJf6VRGrJtfgPHpAiiDoKmBd3RsKA46sBIPnLfzJyg6yxtT/iA7DY1wAHAQ2CP0Jxz8jYt84+MAGg2hirKmvMkpIHQAEgCVA4a0QQjnXSapbzAm4KGMOoQ3npNQpyYYLVUNp7k2p9+0YQJmWPn7s2JdeE6R1+if3uGlsF5C3/dVEHjEONEcaHTtHef/DGwQAsAA7AACOAY+NmiMBkAGWB8aCNCUPcb3/iBeIABmoeXgvkBOHmB//2TQwCItoFhahq30BxhO6Q4ZB1MV++PDQQ2uc0/X8QCD/wAGMxMnKdSDctaPwAc61S9fPcQOyg2JHwW5mv7KDvuOO/S8++Y5K8+ff8bYNEGAAkeaCVTEFfSim7AAB2AAEUA58bNEYAWOJiqhijkUot/6CLyUNK+NLOxPyBHAAbMqhkWdA3fLzCmUsJ/plWeoOj5RN8yXyUzUkGix9xrj7/3tfAACAIADnbUtABiTYNhttgEAMqWNHT7UM/IceQUPF1yv/1v4gEEABGHwdtZB62kKKQrxDYEbOSWx71OW7wCMEY4FuFUKeogVUO17ElW6/6BgAICOGEI1xtFD/UFL68Yq2KinYcimlPYAAOQAArwHEBs0Ri8IYBDITopjoUb2qWAMLOhGQ7jvpZbwwxq8YAOka+yw877gNtvEJcWjZ7/n4FKp+Ug0k9vrxA340RhmCmsxJww2mQ8AYIqfLVbWeHYMzx7maOG3TpPLKgABAKVFGdIEKH/n8EljRrE/lvgABAB0gFWlRld/ezYCg2LPlBzX80BDM5mRViZrsr/xgAAqDgOucOjpojebMZVU4upelq19BAxrae6A9QnwgpDn90pF//88nwjNWsv+UfDyKT/OwDVX2nX4G0Pp/L+IC+g4KhF3y+rGPpAA5iJW5qDSEsEoJI8/qQBBBVIyIMEGGIq77f8KV/dT2eODVzUE3yxZgjp7vl/vfBaiKIqf/3Yyklqn7riD+VcOjnVG+e7//EBjnAQADVMMdRyoSNTcWX/IjIbIc3KESxqQ12IAPHik5n/9PDUVt4g+sAYV/SeueDt9WLzbwcZTMfxB6/gK+9n/PAFcMV0c/xXPMWCW13L/4Zj6V/v1mNv/wxYJ4AHg3QoAOCNoEhK2F7/gAFmQBCkhTFbU+I3scAURF/vipkiv/9oCMKcDyxLECzs22r9wCEslcSeSmC+GPf+EUHHXc0Zn5xcOE5OQRu9EjbfSRxSwrE1f+o2cmov7wvAAeAxYLtVEZyiCRf/91XZGmmab0MoiHJPekgwgtquAB0EjTHPS4l43BTgwwAPBuhwAcEbQJCVsLv/AFACRaCYOfjquFlTfwlBgHgDN0eTev/1x6GkfLErzDDG5PpeyHHyJE/WGX/h74UkYOeXNJ4GgzkW8tJgMKJnUmyRbb/7zG8IAEB25UymJ81MAwxkAHgA1EMpWEVXkpYxPqAPpSGF4jzXFh2X6mAAqTKAyEUTZ4vWt4OQ1b9/vEUy6N/+XSu6T/eJH5Rl85E068488QNiAADkAAdoDCA2aI2gAIhQauPI2zSAsZv/wfywACoEo6pBYaejn/NpsqMmGAiTDzfPAVUEIJU5DDhkZ2Vu2XGtDRFRCkqIituQ+mH80Vdj+uA4xexF9z5Pg6R4esPQ4tQ+yQYHCiOdYpxECn1Js7LKaqphXw8ul/f+q8OuKfePqgNp6rw//iG5gEYIg9WY8p7x8AAiYwJV4gXOetxaZt+G5XvF2f/3NAMdASpG90NZPF9//llzasls9/vgJ5psjkDQqYPgAAgkEHPY+CHAY9I2h+c6DO7Qeq6Z0o+9rFScP2DxPILOssy/dBPc2xPjds2GOFY1V42ygAAnAAEAeZQBRIXTfMAVVeP5xYBwa7+7xgX0webz2KUR37haroUqfx4AFQFsd+nF9pybUshO7bF9d+gFAQMT5qxdM64laqf/2gAxjViC+n53ukS13/4ePcsO8fmYXFE/mK+FGdL3fakI7ciWR7/S4KUueTX//dkR7SfQLf39/w/G0mcH4RNw/FwEIyDIwqt8hbFpfg7Mjba8gYIp/wSqxH7M3KyzdC9o/TNnSH4aQwALCFbzOu9PsQ0z/AJwcDJp/PgxJC794AYcgEsd3hj3SUIEUVfyxrjv+0HV/eljdS4sLr99FY+TfyK/rjBVNLcQNgAeatTHKl/JH//+gIRED/McZcT//2AUBAq4IMaukm8QcX/tHhWFG9pyyDVvgFAEQX0oewlhJQJPQ+tL4PFM5le+02wF2B+LWoqyPgfIAIoEGeW1mWZOov7kpEgREYGQohEGwJ0rdzQ7870af+xMC7YjwvY1fvCIpDoFsWhzPEIZf//Zad+LV00k1liio/fmZp46o/Y0OivobQgYvGwBY4zFXGKORijSQQC8iHR8ou+dbZKcH/gAWBYYs1PpCNJWi7+xLvjfT8IhRHqQWQlor6iaP0jPRJMNWZ+Z5E/PcNU3jmjI9B7D1MYgNtehh2e/kZt++e6fDF1pwcetsJDuDKNjj0kHsAT3ZNbsvyoPolt8VcwAVymfjanIAfMvWVL++v/ggwAGohu+IZCj+pifBBoPQ+09g6KWyuAEEO/mdcxOiYrMM6M4g3b/JnfvWA1NM6ZViuPi+j7l/wbuvwWYC4LoaARcwDGEWjUmyQaZ02YOAAgE17LgNMbN+MLBzy6Z6n+4kUUTP7+QfpDluzreGyi3hhKg4gb8H3z5NmSy30po+TW98+DAUGM7W/URQiDbK3+GRkABIBIgYLWfQhjWiaxnkA7xA44blWz5uQt/g/QITD9J1+oYRBAkMMAFx/dT0f7/XEGrKkCT4XNj3YPhyQYixEcV/Jnn+DGXoArsx6H7cUWg2slZVk4DSiED6WAv7d944IvNXdTuWofjYMYAFiXgAKOR1epYxmQnkBQ+R6GLC4WJPF13P/ASCEolEHPRBHDX/3f48AJwSMlqZP8sY4HBCGxB4YADWmEKKU7DDpkW2Vj4muQlb+jxYbNlHsG9YkFTIVcnveftY7awolo2ASsi6baff4gK4AEwOWUG5I+DHM6G4E6CLX3m1MBYCkgN6R0Fu53B5CAKxAGhVqbUwMIBc4C8GUtPjj8v+GWc0PwzAgwwXMwfL3JtT79owgTM0bX3ZtS69x7MBDiJxmSZJsNt4IDHF1mTZJttv8KOBYSPyhud/4rEBjwAEMfLMDGX0YYzokoX/CH2ig1l5OOMaKKlwzJwAjf6tvYZDzuub+IDGAA1zEKKU7CzpsW2V+gSsq0LobNlPf/eRGIrIKrUkJY1IfPAAiqqhEUbY3vQZk4aI2JY/u/qN/y2C/iA54ACQAJBdC0m09eaJRQOmT/4AGOrZtFM/8QGL/MAFxPCkmlc8bIRTO4YmhRasjn5JwAgQgCNQBYWbm1NcRTWQE/HTL5ha5AgHZQutPkklo4RSKv3pTkc0OC1BEFhcQh+f4dwAEbMH5sq1s2kMakHZ8D0IgMo4qki3SL/9ZvF1ooG82qwfoOhgtlNFsfTfPaVoQcpywU8PQHT5qgP/vekol0vfv2/w84gIADgwkR6LMFycMhbYz//IC6BKhbQtgma/+/8AA1IwyoYTPJWxi/CG8yyneETiWuUzUFi0H7eT8m/75Kt3LpgFiEcnizV1zSjb64gO//dN3rvveGCjgI6xURFO+fVvey7trKH9z2ORyGY/Ozt8HyeJLT/vUPaUj/aO8QH9qUVW2z/9oEX4AF2YWnWdWj/QCt8B0Uo09Xv/XvgAIExSqr4oysztXbh9CuPge0YsFcaGXYYBNeUntf/+6WCff8bwh86NSAwd8KvpYEC4cMAC8GESTsFQxVFGP/gAQ2AwgqkZk2yTDPhnVQcDL03H7BcLM7FZZyf7wAc1IL1ZvoxHs9fETNosOILbK//oweqt2wz3z/+wQQLvyPW7/f2CPF2yLs6//+bjY9V0XxuHolt+QB/v/J6hoTyV///G0BWE4Gv7esVtvFT9ODYEAJqQ5InF5WJZadJhiMvCfRvUv+4ADwHQNJ2BbFSZyRO/L2piN6dDnxY+e69ENIQWbL5s38HaSHcNFrZz+ehlA4YSPil//uGOkgi9YcfMgZkakGhNtfniBsvmAwBowKuUTvlbHoZphYrKqciffAEohlXEExL0qUtwAAkCgPtE4aHTam4ISuGLMbrvvv/T49LL3GVIWRMyl3wHqeMfrj6l/pa24sh0kevWWI/9f+AAzMgTKO2ech60A8bbJklNmp7+1mjmEqJ1u3/PDnE7+7MPvf97mTWFdwYfD/OWvFd1MGDDPQE3lPz0C4kJQ4tEQsh16ewuv/DZcgeAA4BU4AwPMylZ41QZ3wAPkRhugisSStTE+RA6P3F7N+TF+Fm8nxF2/FTrIjvbDggsp0tM7YaTp+NwMeiN26J99DJ7NTadU9/Ek174ChEDU7Uq2BE1mmP7fpH+x63f8uDS2OA/Ea0ylzCpfu89jvFTtz+CpSYAFBBTlby+d2Jc5gqcixD9ckek1fTWLy/oWyt6QHYbFGIJkdF5/faIlg0eyRCVxeEEhO5b+ETxdj/D9O+v8BZCAKxAGhVqbU3+AAkePEXmIKTTCn+ADFSiihjlsRu8m634gABAJJTiApRLPqnGUzchCKzo/Zx/39PyBNwEtzDVZk3yYMJ1IJdBgHUJhUTJPX3/FlOp4QnKaKhmIPUMTO613kYlSj79eSLVuyzhlx+IDkzOQBlPZlZ8/xtXQUCGzJG3n8MuPxAWgAVAhcE9kSx4ncsgf/3ICEsT6hPPiVS3zv+DDwAGbJAGCCpzkRJiHSXyJidkOZShEsakLVwGgvGjm2hrHzwPDXhtlXkoZy/xAa9B+gw9D8CPLGGUW+NvIG2r9ZW//NWTrGe5GkeG0zqjggZkXEBX+MZNSCIADgPhaRXCpLTZmz394ZQxWGm1Gt1yxFqw4yVFHfsCOdCn7yf/4/xAVgAfgjh09qjCs8l+fAKLBlBvE7Lzg9tor/+DD8zY3dRV75KVtSN8GCwiouA/kG+w2pwJgnll6/nQLGXWeHfk/6Jaf60wlRfhhnP4gPfAA4BIQGfIVRhkjFv77/gAJkxIVFFQ8inlE7AO3QE3hq28D/oAxkJ0Ux0KN62JAAYAAIBF4AtAmNZJXeYoZ3TGvLJt9fNv/Vfn4i2tMbU2FanzwP+coz/fzmUmpHxAd8QABanYAAQJcvZAAcTnP/J7lqhwImOUrONqYBwFdqDZw6K3MYREk0r8wERAi24avTioGTK/gYQbgABUHAdDJo2Om3m82YyupzuUKlbfDDMLehYC0g0xr9cTM+d/7tXXJV3//MbE86f8QC/gCyww0SlNwn3+0EATcHo9zs8SSgO/8wC/BAUABpKo0JorWY82iYYHPZh9Dtuf/3TGibk/3+cz+6H/xAVjcE0OXu8ycM+SNyeaq6fJ1sYRP0qCkQuXyTw0OFRW0haOW3FjyjgVtSwpSD7eRdd/yC3mVjp786lUzP+/WQHdaKBcQN8ZODRfPN8/cgyMAAnvVVBpqsBnwMEH5AA+PoWm0pnzBKCJ0GCDQCj4JCYL9Y/3IAeAAVBzx7VeIpErG++DyghaupR5E+/f/zfmQ8BzK+U/zBEmmzv4or3elf6tPwwHGWNfuYiXwPYl4g+LPHvm//8XzfJD+y02O9f4Qf/EBWHwAQevyKE4jNiLDP/0ED8LCqgHmXu31pYt87h40IQTFluMf38HqeEUYP160+6Di4iRCu3t+4gf8QHoJASAhaPfgZhAjct46/v9AIaxPpE8+IVLInX9/XxkoMTJvxk0yTH21T0pJJHwQLamfofr0Ufm+IP78RdfT984M/xWIDnN4CLADMyrn7/31HzUcRdJc9ZxtLe//xAV5HTWTTd+9MVFyyIS620a7/MXbFZTsO6mlPYAALgpVgwNODRGAHY4Ldl1zqbBjmAADkAAK0Bzw2aI3iFFQiIco76aa9fFUJnOo6O8/QGQk2z/iCbUAHQ5QnsPIJUvfeC+EXIQDxikOmjOADUFB9oq0shslsYAALAptA4NuDRGAA7MVI8h0Lo+4BADEQmZDCYgjlMQGIUKOTTzJB/cNwq7pDyraxf/h6ALHGxVxiikUwt4fkh06YPamW+SnA4AHwGcFQjmFEb5L8+AgGGU/zWWI/BuZP8AqABKLgeg0rn7RNE5//eYALCcFJNp4+yVj44DAgwALBDt5iLnRcWHGf4BLAkCmgEuamyYHLi3vhglBmFgZD09NTd4AGJd9a66I8Qra+McBevviA7BEABYnBDEnvxA8y+m+/gwJBjP9n1NiIstM/zNtW+s8WzHEByigg8ajKzhuYz/g/gDJiKmKZXG9S0hkSNjBBz6Oz0u5/5/b4gbAB4yE7OYWvIS9SeN4ECh9aT4I8l8+9tA/ICWgbFTdtcKgtEaMyVIDMEBLF6AgEMgnTkOhRvWpLAABUFAZk0bHTRGD8AdmN1Uoupf62pDDAARgNOCBjL6MMb0SUMi5d2cJ3rHD/TR7j50GG2l3eLr9T+IG4AFDIC3VjZ/5JqXPugBcJicWImxFmTPf2jYRZgdRvoK8jem+tMGAeuvLZt66I/EA1wYNZeRjjXCS5kOBkDhwAoOLyldw3IX33x0oQp2WRv//7grtiKWqvv+7Rpu4bTDONTnz/BhZpA/+AA1WGKw5UJHquML0z/WQDg/hmUX1/DAC2xSxbZ6GUfh6eviAr5zoch7YA4q2KynYcillP8oSpsy31n6h6IZgHMFZppciNVMZH+HzTTTP+yugT6/8QGerMAArIBULLK3vv38CAKn49AiOiErLmQa1fjr9X//7f/8O0eL7niArgAO4AJQWrliz+KFO/+h8eyAEBnAT2KjI5E7/4MOCdBN9voZxokRfzeh3xrXiAQ+Xsjf4jwh8NQYv8U3O3p8LVXrIkWaoXBDAIvwKCTQ2pgCXykbFJDr5f/iPEHr4ES7o92//4g9YxlUf+OH/3iA1AA6B4UEnjcpXeN0Gd8BIIZ3M6osTNltn+f6wTNDRGYdVRqWq/O/hDnrAFf3Vdv//PUwVVX9v//n8/n4FiAAAFPFBmuDoCxhk/LD3wIWx+/KBN19P8MnryBqPf85+Mwj4R8I+Efm7AR/xAWnECzAATQB4St6yny2kulpReRYv/30AhbLVAn2YJXcf/dgCZDgA4J18oJWQO/8D4YQukBKomjR3/Pwls5tCo3+sI+EfCPhHwj4R8Mnp4EoZ438//4o/4RBBQMo8cNrwdgAHgAWF0NSbTx5gkgf//vMAFxNDEmld+bJRRP6AY1iPVJ5+QsZROP7QDFoR+pLHydi6Bx/B0C8ACwGLYn1SWvEqmfHX8Af4AsCznjmG1MaOlvXv4gLcAODFkhMnlJk3xj37v8SADQPe0xEHIMGkQw4jCjI2MpVJIOqS1s/wQTixZv4Ss5UBYhAEWgCwo1NqawYAwALC6GpNp440Sj4/5gBcTQpJhPPmSUUToBl8AccJ0cbU/4gbMTAEEIArFAaFWptTAAOBCwSuIOIVBfjXv/chKQAKDd1plQR6sYdvkPw0ACUPlyxJ6Chj//uDqBAjRvcZIOj0LcDAgQEMgnnqIAqeAJnTxRIEbGlo7xm3R/Gxb+s7pUufkdHsMkdD4gK4ADMVFzSqS620a74xVsVFOQd1NKewAAXBTNBwcdGiMAnHh90uEMpsFOwEELS64egRb688Qo+I2FS8mmlvgjnS/Pv6tEG53u869eGfuKWSH+Z5ESbVXEBW4QgCsUBoVam1MALF0x2cXnuppTww2AAD0AAK8BxAbNEYAULLiMh3HfTS3+GAt8AmkRC13jZdd/GfrbR2ff+GIAgAAsCG5IPDbs2pgIQQmUVaX2yyyeEAAHaAARgDyI0aI3jHU5V5iDEWoxwMO/HlgTuQIh0gAHWBkf3CT0/f7mIcPsMqGYQ287dyn/5Y3E1+CDgAJ4j4Qg30YKZJJshwAHABghhRaidP9itFO/+AGIY24guW0GViRhICZRVSrZ5cnARba1N+bUwEsInOYMb+JNfnv7RAACABgo7QnVmlR2QvP+ekQmRDCYh3MYg9tiuF45WHviHgJhkLOfHDleZ8QNgAJmRhFURdIJQ1iNQOWUGxI2C2rr3mB0hBv+2OIQ4ti8hOPGuYAgVRCkJmTSH5HBlkHAQAngDgnaghtvpbP8H4BC2WiIE+3CSWWndGgxGui0ennob/C39AHB7E5SUeYZf/akbptSYxaBEMs70wf8b2MfhvA60vWv/7S9gn2K93b/TDm6+NhnMQALDFZ7PuLERWZX/n5sBjCKRmRbIMMlBgcQeT+LAIYTSEyDJBlkHAwgk/Jte999zQwStwZLnZtz78C6AYfHfATJPVvXetwAh/JFLKquRtTLBP/7k9AACAGAUVCE+MeZZ6PA+fh+/zhmTrEowgY9UDST5MQgJtETQ9+VJqa8WvEBv5AA8Lgam2lr7BOCBwPgjUpTEAqIClSjLf+DXA2h3NfVh7v3/4gNYADqhCCVNQs4ZF9FaGUXCJo5gKD1qN8/n/hvgCAADkAAI+QHPjpxtgBwAXE0MSaT35slFE6ELlCoKx9LYhY0/xmJPWANya3HHz/h3PX9cvh/gAXpEAIDPAjizI7C7/4ArYAah6qGoP4sa7/4DQbIQAHBWvEhG2B1/ngISSV1Jr0zBfDHvDB7SAYZCryOc3DmBUR/7VD8DfqPHbzOU0OeV+v/C8vPfNBFlMPyyEvYkkSZ+BAVOoaEW1j9F18pRBwAHg+g0oovWSSYT//iFCwZZV3xv/dM5KbKVN/9pzr61juYWqqf/Gf4gPeAwacUIWpDRRJJJL7QMAAj5CFE8TtOb+f/+wpwFA+MdDn0D03Y9PfHDvwBAxTjyo7yyGIaR66wM7r3/YGAhsgiKc/YIhrUekAp4U4nv4xpT0gGtlCvJVzEMha2ybMAiqvxU9dMqlaRYMRPEth/vz/jfhO4EfD4Vo4AB53DRbPt0Xt0Uv+20q3wBk/x283jg4CFBDCUm6WrjiqCtjiYAQAAgAn8DDUR8/3gRevOzSEkvcgrvtI+nvgLG18qb3SZx7Jz+6H2t/jaDAJ/1Pv7/+AA+gui4fEkW1STf9ofqAAiYYTpqmr7dVi4lMtpp/qaAY6AtSOapaueL7//M0C0oi3PfIe7NYdvq8mZwSq0WI2/mACTYDD1ifIdWKFU7GIvEaRsVbj//95RXCO4vTn39Y8CDttR/SxHSSr4n87SgHwseCS/75jILcBuHFJRcIDYA41xxVv6uQ3GI4YzwEgBVvpiTszQbf8wN1ofPc2ukdj42tMxYiqm6J3/78FVn0/4XDBSSy8N+5SgHX6+//+twZUfgP9j2Ffrf87QDoxhfRvDMoXd/7wfiQIbpuUMR/t1fAAEBzpwewRal1sXz5/434XSXCcy3rR2Jj2tYv+LMEa0p/Ul//+7AAvpZTruZQb4uhq33v/42DCAXBVgFGJ1hfyX1Fe/2FlD8asRJXBAzd7QEJRaIkR/SGG3//PQ+gTBl14+0dHJ1/BEJpaBYeUtIjf9ACLOtX6dT9MWzPwnDWTOLglkEXzeKLb63V5W+KGpvuaeJdnRUSkxqESly0Q/+9ngY4iL15qYxItgp1E3yPdYOT+yyb7oJY/962mRWmHLnqUMtSQaI+8ippFI+H4MQIgK7/s/bf4GBhgAIksQyirv/R5KQQHLGryOn9Wd53t3679IU3ZVw+q5frhCVYFoy9CfPvOwBJZJXfjgPgl1NrH2ZEdj7e1+0/4IICYjG+MZCj+pS+zBBwN4lbxMXvKf+5yayHuRVTgwAEQALC6GqMp480Sigd4YACQccwUrGhljExnBh+3Cgq8V7SOUa8YEGObVn4wE0DLeDML7jfK3gkytJhcTQ4nLej+sWQivw3CC3JrNRsjIseBsWlD4fjbI2evAATAI+MByjU8kgpZRIyfdd9/jGmHof+TgAAhHs2wxuOrpILmeBv0EKWl6BxSCqKtlt8U8AhhNITJNlG2Q1JVId33O7/5+QSYH0STt/egpcZBz5/+z/423gAJkRjdDGRwq2MSc/9PgjAQ9c8MMi2qsNAfGMuZzI8GaSptwwMnDBTL6PM6IKF/+1jxHKSfpq+/2s0RFwWwyLKG7+/mtC4FIqwWk5aMGCa4Bskn9O+vWl0Zjm+EvR/MFLwUmhowv4gP/DAA8DVCgA4I34oJXwvf8BvO7rz/94BOmQAYGeD+KMDsDr/njDBrGSLRbzhkdYdZgZApLwfEjIL8ynARde1e+bUyZxXdgXg7YD34+C+864CDyXwkbIKe1FksIp/Rt4ETSO67uZup9oo7CfbJ1eIC/HQsNXgAOzCptFByq8ySf+XAUE2zr61TlNrHf+FqFKLjIRSAvQuWGWIDlX5RP/e+UHKNiuWQKGVSdLVDhK2DGKwgN8ABEBOgcLYIIR3rZFUtAAZsTJynUg3NWjxgTKHCmH0IZz0ioW/opoxfHRlnkxh6yh9Pem1Xv3ntgIcRWMyTJNptzMgbMsfX3ZtS78MggOkmAxz9iwlkm22BjieADC6VvSPg4o05ZfWETI9M+byGId8kzv6sauNI8QWAAkQ6dMFtDrbJTgw/EBbAAQIe6CuyaI51C5hU6AA4MSylTIn+4pWcf/9YGynABgRxAqIWvf/+7gzLt9088VvtCMA5aQpit6+P/EMDA0Axyi0TyR3VLPt+8EFJsBDJ4pU5R/wwuDkbmJIWb7OJY6J9Pw1AAuMRwIk4uoQKfI/vq+ylere6vMD4PKPY0mRvyYP/8b+egACambSCiuqI+s/p2++7fVzo15ZNhgASkH+JdsZjYn6PeFIHCkCAoNvOrqDAglcG8EAeEXz9E6ZfvBMjwc1ep3nqYULRtS+XgCsh9P7TJb/GjuN9r+ID9sUo39QRecQHAA4BcUOOmZSo4coM77yABYXQtJlXHmiUUDvN4dqv+POzsBIMdns+YsRNhtn+Abf2VN+960QAEj9g32fQvnAEgk1QxNkd/M2wLrB8Rm/Nr+3uTWuZn3f8b/xlmB1qXPkZheTsA9/cIZxsuvb2rd3/wNLQrbep3/eAIw63+mzmGYcaL/ppJ3Lv5zYewO33/DgmZWmw4VWTABGJFhfLtkMbngyscBzuB8TOCM8yCi8lv7gI3rtJb/99o5kZKDVF33uOI1IIL42GgZ9nMgDoCObhBMk2KJn+/qAFiGKp+S7DxtF2vvGNzjrWWX7xf01f0QZTlcFJLLbPcaR2JZ27o4KK+uxPvmmY169eVX9ZtNwFhzJ68f7vXKtiNoCHVmof7Nt0LvBkzyKl/W1Aa7TI+KWK/8AtGBBD6T2y7cZbM0zuudkZkeU+/x4QSuG+fEB+sNa9gy38Bt//6D9YAgSrKGUVElEQw4AsBpwwUy+jDGeEljfiAb4MGsvIxxjRJUzAAYNUGlEF66yTKJpp4u5GO699w00sI8KBFmnG/Etm4Um6d3//+4bJZMmNqaDLe9f4gbAqm3rB0YAD4n01VtnJXvHhIB0FDb12G17LloDYaxAIdUa1KL6Tf/v4cAyCb6JmG+iP/+AH1D2FtFStPccBE1qlXxtTTKZWV/+7Awfwix0rHfxYRRnn/iLBD10ZvC4+OyBy8x6U1/vujkNB9mkSu+5KWg0z1xA2AyknYSPd/oEQPCgs8bhSV3DdhfAEbrW1zYP4II7FV3RnhOU03zZ2Pgxv07H4ETYZIzZ/+ihRyoP9dugYUkvEe4IXwRl16Bfn/Bn9WzZhr/Xf03EAbvtOof95lBXOb4Cfk32zV/3jKDbcit/AgWzDRkeR/gr+ZrBDCSA4SRCJUaVh5Innu+X+lgAblUvyP/XbMIhfZPLO5eWV5AeVwN/EB/wBe3NdV//1t7Uv/T/vWqU894AFgh34zrmxM2mm/4BFyDdp/Girxkl539wikZLD/vprV3fU/8QHOAOOrxwuwTCqD80z2mEvJf/dQAkEraH/r+IBB8ADoHhQ88ZlSrxugzvv4CgAuUDST5nqLDR3Na48J999muVf78BscM8rFLsUitKJEMNMJH+Dtzo0sfgP0hf/XFx9S5HRzRz/EAhgSCGdzOqLEzZbZ/n/qLxB6yfDf0kGQzrgUbob+f+ICuAAxUEILU5DDhsZ2Vw/bMwyqK3UvS1qww2BqJ3Nn39G1tHX15CBLPtL+IGzkwb8ABMAHhLDE21MebJQQOsAhnCBsQ8A6gUBYhAEagCwozNqb9WHV0Nlwnvrid2DwpVt1R/DxkqDz/EBX5ABqPoam0pnzBSCJ0ECGkWABsKThLSIjpPd4CHD4jS69ZAjKGi/1hMv3YF2qUNAomSTMeB4d189qO/6o4ru/7ryemaP1/xAe50HToev/79C1eITO63d5qqr4/yMgio5DsUZb0Nxhe8b2mS415wYMB8ACpkJKV1i5hnuMwQUKEtJJ6tVnN6vgy9+jPDpbUd1/97Jr4Z83H/5Hf351mRh7eT/+ICsaNh2wFN3A/ySbNokY0SDRDoH/HSSTVn//hfBYi56gCJMXBqFt2vz3RNSV5SvtbyIKWSyd4o8qM49xAVgAcAfAkGE8h4NHLGO8BIhlB11fEo2y+ubf+D/xgA+JgYmsllFkjBM94gAPHQAUsShj7RWCBwGxhEMjsD7+S/eYdC2cbU52CSp7d88pWxSe3f8/8QN6ZOCKxdU+/+3gwzWiCiTy10L0MonQy0chgaAgrfoRqUF5ttPXwAPjRyGDErxBw80i+sN41+wGBtdib9eDbX8djgDiMLQRLVL//7gjwBB2VS2qJIvvUhMmMZGCcpSJ+eYp5rj/Rayamb8+RmjHS2u/yfi5OX/wjyIi5xAf+Ax088av+2Pe/zngQCBhGCA8PDAARgNlDBjL/4Y3wgsX/EA3wYLZeRjrHCC5kOHx+ONFUt33/oGzT43xdVWrmefUS3/EAv6khtWwWAAkwAkBbyWpgRZNx/xRjDDfidkEOvL2B3Aqc5wfv/NE/hruXv/vcBisOYFbTsJzZgVkiO/+oG00D9n6TmbjETvf/EB70YFcc35ttnOIYZM6DhQIeZE8sthpTABb5NptRPftDnYAkbFaB4akcvahgOOYTD1JTzHku+ABTRDLCI643tFCb+1/9DgshNpxfncUuh2m4OsXSvsZJpjg38v+IC3yBPTABwbutrpCe1zAPRIYRh6rWMXYVTXjYxcAYNzGWMOtH6qlh77W1avN+Z+vpO3tsZQ/3SH/EBXAAeCRBJXZGMkk8v//Qz+sg0DWGmBnvWGrBS+q33vb3/tr+IDGwFAAeYASB7xq4O40Y//fhWuMSeC0JydIjMrUMXeru9Yh8By4+stLajCAbHV0fN/EBuwbZQQDVlkteavzQzlh412KwhXPWBRvhv6//iAzAAcGlBA+wlPDDfyRQvXEgA0D3cOUZxgt//wYYEU2q9vaFv9eD//EfDsABxBElmh/pSgg00uV4Pk2QtVfoyLP/7bB20HxA+K+ra8mAPiXXQU+F2lwYfgx1hMXiL8pqtCEzwMCEOMlBemgh5jejXj2Wtxx87f/w6DDjdP+IGwAKCERQ+JKiTwurqV4P3sbqpyqUX1rSCAIAFsMPWUNl7k2q9eAkyBsyxs+di1Lr22wEOIrGZBki0yu4IBhRNYVIskWWwcABsQ3XGExL/YxLgABQHAfaJw4Om1NwBBgDJkGiFMpxvUtYY2CGLCYtKG5wAouSNh10GMIE0V2/iAr8ELZ2EPAEEDns9QkveAGFnxGQ5RyaWW/wQGLWl2JBGyIm8iKG//xAVhgAeQNhR4+eX9Gkyz9YwWD5AIexCFimvkLGEDn+48aOiYJQZJhDX/eBOcO0vXKs5wqdSusDgoJPGYUy4doM74X1LLjaUDCPYOuZu6eb/MlijSL42HoggS9sZXu5Ny494AkphkzmtQn0K1HmjHpci5OusS9JZruhgpjUT6E66lwz0MACoGNglGpPfidy6J3/BwFfjFEL7jlswLaqkMRhhDUY5dEXbgtEiAjbLsvuge05HMjF7/e51LCQKL4j4L4CZmJUOZSD8pfSEohRCJL2BgQNjABwdilboH1fiHAAOCNg6ok4lEFIHv//B6NgBcEymrP80Y9/b4JKpPngLZax7rp76R5OQewf8RiybniAzjLGvgMf+IjsIHrwBgb1df+/8QevzFt2a/f/4gNdAYzfcmrsRFlhn+ATBpDmAAEAxmzQCC47/3v8iWoWlz8mtXz/+bEHrh7jgNNKg8+fhD/PW+o3/AtwAABZlQZsA6AsYZPXgSjgqP36/hmE8M+GQ5wALBDv5iNuz5FMM/wCIKYUEnzE5XeNTF/8oDrSnrB6qehHrW9/4RDnAA7jqrbWRib9wEpEX3iiI3eCZb+AEF/lF/t7+GQ5pQAEh18R1MQUmmFPKWOd4MZ1vf+IC3AAcGLJC7PITMlpFPfg/FABoHvYYiDkGDyIYdRE16t8jTTf+FuHafASs1tWADIAAftBF8g3Ev/PcZolsO4SpnAAiBSKmzDl44Dy4JQ46ACckAcPF6rZlLqdQ/w1oCR7r3asZIb+hkBRmRT38B/xHhEMeAAzCouSRCXW2C3enApMEQ5yiiFPca8AKsXpzfo/hHwj4R8I+EfDJ6gJGej/v17U60f9+v8XiQ3AASAS4OGsPIRzjZFUx5gJOChjD6Es56RULaMYLWUNl7k2p9e0YQas0bP3YsS28sAZlSfPd6ANAcYhRojqZGdO++7+ED+9LGvj/v//+HOAAjAacEDF30Ya3oksZ8QDXBgtl5GONcJLmQvz/AHFpoxtT/xvAATJDd0MbFHSxieT0IQQruzhsW1V/8BIXcAYC+3hRM81w22gDDy7Pkx3YUab/7B/zgAN8rDJoyxuu3N6EqXwbfy7gBMG0sX5lPihZa6f/3jAAEAZQmSJ2nXBORjdg0G4IQDNUBoUam1NfWoESBjMDtEFjQVpAa5eGf99hyqiyr4gbAbEAwoisZE2CbTQPmwwS6wfL/5MT58MKfmKtis5zCuppjwAIZJMx/ER3T2yMJ3EXXPU1XeMBOoIFMPIRxvhVcyGDPpjRU2CUGSWQ1f2iAAbIjBfsyhmuAEQO4UEnDMKZeN0Gf9oEIzmIqtEzZZZ/g1SCtk8VtSv99HRC9kq6/2jUq+5pUTMeotr//n/hj/wAHgAWF0NSbTx5gkgd//oACQ++IqmIK+lFP8BgNnNBWFO10yev87pmCwMobUh4+Wd/0NpDMwDlN8U2OArDc6NNP38QN9ZIiJQlhk2Ed/9o4wNBFvhLpM9//+lQhBamoWcMi+yvUVIACkA2U6wP2E9/ARYYa8ofL/YNT58H4wE/BAph70cZ0RVLhg4YaGHaAA7yAY4isiLBNph/gNlwXFh72480/gZwXjsq2d+JAqJp6ASyyI/l/EDYACIBNgQLYfQhjXCaxnxgJ+CBTDyEcb4TXMhhh4ACAgXvWIVQ1f3e6R5AAphC5ZEJZL4LZ3lh08MAbnHVhn4KSLJOf7wLUqDiHFbebLiVivkAAIARToABSX8ywY4kZ7yKNBIwvvbTSyRMHjD0NqYe6hf5G+kVQ5LXw58KlA9cFTfiZaMGvjfxiqYrc7DuhZTz/BwIGpSyZucALCeEaHcV8NJfogSBEAAiYYmXmenEpZyfaE7ugisSStjF8MYO4wofSlBJL0l7e6zMgTRx0sYkGK+7WWT9fwffMthwQYvtlSu8lmx3uhThflY/fP/hiAA4GMjnzfLo+RCjf+LYdtZI7fhcDIMo4v4GEADsJiirQYUh4vqSSLhGARiQNCzc2pjG4WKCBeEiiK1af//PB3DxoDCmOyMnvAthKuSR7d2v4gNYADFQQgtTUMOGRfZXDM3g8hn7X//DngAIgH+YBjz8xKylFFrwAYzX/X/+f4b7gABUGAfmBw4Pm1MAKAa4EDWXkY41okqZCdJwZV1eQ5b/GYk9Lg0Lia/+GYBdYCCiKxqQbIsN/qwGOJrCZFkiyyDAQa+1N0sfz//BBnGwAEQ66EfmIO+FFE4NArDTlblXfxxVAOABQFeKCD5mEqOHJDP+4CALAtVSzWeLEprm+4DEc9PJeiBzBd1j/eAGdqoIWBepREMkO6LzYALhoqVpkTlN54QUVltRH6+g9CLNPy9A91ci+2thGJ4da3ZH/h8cTi9S4WvCAegAWBB2ivSa9H1hiF4/weEyDIRmG1NxjmK6S9NHXvmJrIeVuqfjwMCbihFvIWxzn2wHMKxLiYMerdLylCsEfvlwAYGMa1xabzvARo//+AFDIYVSSiUNOeaQ/2zG7uKvUkpW1IYIYb4hRYjXxz19voiNAxc60ozZf8HXcP/hiEaKn/GwYQNBpe0AAIfew8ACCWAxhUo1ItkmGcAC0wAsHulrO4sU7/b+LAQQXSEyDJJtvpAMQXbmuU9Ky6/8b3H2BWxD+QJ+yk1fuhuumI8hkW+TX/2f8EEPwAGuxCiFtww6ZFtFfkRkGRBVWkhLmpAkX4QPyb1BF0fjav8BgAO2AAEVEaA4jQb7tyORKWzf/fgZHt+/4X4ku8MtKB0vEo82ABOquERhtjd/UjuT3Re+/9+ADB1+aumNWCLFqY4DqF73P7kJ/3cKUlx/xPNCDQ32i7tqjx/k9pmR/8QSZhtstXjcEQYAJgOeAXUjU95++Dluz/7wBABgznNxq2v6HUwsP2hwTaLlDadZj/QUrEje+qv5ZKwvCOf4OSAKyfFqZp+7wAgAwpOtU9JpbjiAONU81xA2qyxFajieYLHDpPM/tb/i0+LK93+37KvT2Sfr//wQURfBzmTqZVS+35YQwWgBQY0ZZDc04QV39+GUqRDHgCQXYYJvWcEKFXEId9UX6Fj//fwpcjqinZ9/N2Gv56ff6s5aY6iWf+1RGxJtOt32jDoei9g6VXH43QHEBF9WhW8HDAAQDARSD+F5rtCK2pKxKlTYcefCpenF14BcMKJtCyep9kyuX5RVCpqYhkIkEAgJTCFhJnv0gvFPwAleFqLn8jX//q0AwUQT1fqCFTkemf/YdDA6FI/l3lrUm3xHv9268iDXFn//dSXAf9aN/p6LSKQeEBvkiFtiJETJv/7GZWrjRZ/d3v/Fi/mw//a1wvNhpAACmDvUuyEPyBYWzy9x+/sDtwTlmyQ5ozgRactuebU3gCFdhuW59eMuqorYbuKW8XGH8SP3/IOpplwdFqpzfbhCAKxQFhVqbUwl/oD/K8VW6Hlg9xv3//58ckQN7UR731RbuLS/+Zikvz5yjMwj4ziH8bDAARiqY7Kcg7qaU/w3AAD0AAO8BjkBs2jMFIm1m37tR4ew/HrfnEAA2Q3fGNijpYpIADRlFS9J5KSTyy3t1xC5vlZ3nd4a5oFuFJednFvoVKuHJv+4p32BnjwgdWvEKtWvze6J8DGgoPsEp52POMgWaIh34kAJihskFcFv9P9B+zmxpJYIeIGwEAAICxb9F1nUiyDfHeoD4oIPGIys4bmL77xBsYLZDROEfqOZYD9g4ABj043sLhxbDwJgCVSvk/9DbVY/4ahv3iof//2gKHBG7yWY3oXavwPh4BGjh45cEe/v95Lc1O8Sf+vxGuJKt11/eB20F508X7v4gEEABMANBNDEWUreZJQQO+MBzEAcSpiefIeTTDDACwWIUqJ9x/3+gCMD3ksDGMSlUkuuRAEAwD9Z5D3gmfueBDq5y7sXL+xu/zc4/Q2fie1nloQOVf7wIZACwNiuS+y+/Vven7Qrt9TyjAudY+7KibW07XhwkMjlMjgPiAxMGBAAaPcbRmE4IbOjVC8AAwpaD4sZBfWacBOoq175tTDS0G4O0H9Y1fuT1eAXSEGFIiF0O3L2F7/wbF84OTE0f7n/C/bETxr//ROxDUm3+IDH4eAGoeqh6hOE33//BwAEgAsLoak2njzBCKB34wGBFjKYR3WdFbSgsGAuJqN+zwMS7JNr/5/EBmABYCGoR+hXPyNjCJx/AQAQ9iPUKY+QsYQOf4AcAHhtDEW0scbIQQP+QAPi2GotKZ8wSgidqBwFmM4o0R4fxeEA/AFgAEwQB2TpsaNEYAcyGR1MdCDoWpAEaY/EJHdUv/9sAtICakZBbudaCDcIQTS5GhUKyue/huHVnIKEUOagCGkEUxbvP5PU9/mpcN/Qd4+5J8MQAHDAu4QELYlDJRVcn71NNRkzC6OvNEDlwdDiWFkM+0TAAgi8eQOzROTv3B/AAoBi6J9UlhAlcygf/w2v0DDAHo2DLyRRJq/+FPPibqvcZHWoQeGNPjAY2Cf1J38TuXRO/62FOH9R0EkqcAFgAEgcB9jhodNEYBCMTtjiakhLGpnuHZDCP++0DMB/1V+yyxqTd/+G08bNNlzwYQAdahdFxdtpd9cQNw4EesD61a07poyP37NpvmaEtFSiItmY/6ZxLMg478YbOaG4XHU8wv//HiWVxIu8MrgdZItP/mpjZAe//xZzhLgz/O078f8c8OCge1OS6iUlq/3jBrHHW2sRycYgQYIGrBtTZGhxMqxdr6nishlrz//ydgliJKn2RwOq4U7C/EAg9vpvljgwhja577/49EG7GT27PvoAAsEFbzkbeiYrMM/zwMKrmCU1MX/T3EUTChh7kdehf90gRqNpVtfv18bK7BjxA2ApB1MPZZqHpOFXS+rQyePVv/3hgZF0LFXfJr3/F0IYMN0e0N/VeCxWx+9/31tdhaz7u04rA3pAGw813pr/4G2NfwAhJJXB5KS+GOP/2eArnNglqh1Sg8UroE8Uj9Kq/ZJ0cPvEY7NfeKAuIG/AAowYmWJhr+UqId6DAPiABQoEGQet2NLmamQbDAAqwwtRxTSkaXRPoAhurwN0gSMx1va3qA38n+mAgtj2Ht2Sb22137+gQapOTl5adZ9XFelv1eltyvN/73eadkzQ88IDE0JKUHh+N7jTAf1Rrr8DY5gYC/zABYTApJlPH2ycUDwYfACb6++/z4Nvxrn/9n/3gYDy/37PNjZn/higMaN0AXpJpj82r//cABzZodC0lUuMQ/5PTtlp7sKTtd/P8gAoFaFpFW6aQavgRAyaj/gR7zkAvLIZVdMq//68PS2/jdeVoaLs/eGdc4qV5SM3FdxB69gEOIrGpBkmw2u4IDHF3hEi2TbZdMPyRkNkKTuJ6kpDcd7HVX5ZwCCRp9YAPoFAv4VKXY/S1eMP5RfT2IV/MUH+sHtREIzW1GX/t4Lltt1X+5//jesCFUttP7yOcW3nGIRXm7P+pA5fw/Zq5RVmv1Y1FddMMECAAZtJMx/ERVSAAiDxBWJOehYhFVD4fBAT0B6C3a9WL3TMbmBjUJRqTz4ncz87/uYx5sDTy7lcKDVrP/+8wAWGwMSZRx9snFA5phq1or0Ky47/A9J06pzn5Ng9I80L9o80f8FiawMgkOfF+W4+F0Y9YcQN+WYkuzqnVMofrRD1RUVHqL72NfXF1JOravQABhgBlFdlzdv+FQW7IiJMmB6BlCSRiE+fp4hz+wCpP8IsMAuEiEPBKxeu5YsynF1BXa/Msbl74aMqmBUbQN9RE7cOd/+VP9Lr+/5gRy93S7fuT9gVx+/0Rr14DHc6sQFfAIZ3MRU1ombbbP8GH8wELh78CteJ1MIHf9D18ylxl++wgWSR8/+JhwAGRiKyHE1JCWNSHjB20Hzh8V9Wr6GD4/E4Q8SF85+ABSAIMUgxiLbRY939wBohAAcEY8UEb4Hn+fESLAjkbGLTI5MyG38QDCAEtkQAwMQBHYKNDULr/g+AYhCk68tMsM0Y7+DgANdiFFLdhZ82LbK+oSsvo9hs2Ue38OshV9savXXH0tJ3ecMJWRcTbT4iI2xzuIC0Pui8hKxWY4lpISxqQ+JBG4vmYxol/6raAyiKYQjyteb3ghakuAhyZ6xv5g7T9ta9w61Vp+f+IP1e+VmsfugfIWuiL9GG3XPIX1Nau3+IGxk1iNuheIgQyp/XK70r1YYekAA6YASB7p6YEYTcf/tAJ0QOWDbSJrn8ne/QBj31tspcN0rAMHJUV/f+oF5qaH9Fae/npl3N0f5XQ+qUJy2z9f//Vt510HxA2ABaE2XsyOvX3ccN4sIXEfp/tQbyYizHE1JXuasXABSoXjhqYMSLbk8EuI6OSmV/LeY4yFXGKORTDX+QABKgD89ZG+4KHbV3KDouUShkvkh3+D4LFA1lKYhE79/ACwLjNzYekRnWqLjwgKAlne6uaUMGPourh7US0kxdqv/zEUsulk99v8QHvqMS6FE1JHsasMGVpN8ffWAtwjkY7HCLWz/wG8NJPsT+/vrPIp6H9f8+AiB/gGdAXMlAmQgT+DljW5qX18FpkE8Oz6L2G/e6SUcfOLBao8cyZGJoHjQr+ty/l/iBv2A7wsgETjOFTxeYz0j42WTHP1RRf/8H4gf7BGt6kpRzF+GFRpXc+6oQTMNl8APi+xyys5+F+tM6QMpte3//0CGwJW2sf7nwAKEBjCJRm+uSYbUJZjuJIpf/nE1rgMBAVWsujlh1Hc3IFeKHHzMqWcNUGf8ErmYC1liw/1QfiyWSIr9TTu2urTgUaVjd9sPj3gDw+7fEDfAgIx6AtzwBQaqQZbcrUqxX6Ysi8wl10XH/cAuAA6DnDGqQ5zxugj2AIiHABwTr5QSsge/4Hh6Bjs9n3GiJtMs/zQEPwAEQfVBE6jGk4wp+sFhQSdMTld45UZ30GWDJU9tf+qB7QfOcr/3OqFeQ7+u0bt/4gK+AlTMjnM2PYf/8XAlg7kX/U3kQUpeRqBA/gOs9nCHaiJRrtehouR+X5p/jafjKS0x+GKmfdl/v6p+uUp//z/xA22MPm5kAsBQxAApgPchhZdQz/+tmGY4l6eNeffeZsbupxdS/2tT4wEvBAxh5COt8IrlwYEGgXhx3EAB8B/KAKBX9QSNO+N/8AWhAEfKoAsJNVz8fEAdBM9koMp9Fez70GrU0b/O4/pUf9g7I+DmldP3ww//GZfhaAA4aQoAYFYpWyYhrazLaWn+/WyY5cjifWLDKQzlQGc8tTPutmP1X6nVX//uIMgBN/KksSpfBD/cgIMEb4Rznwn8yvw95ERBMgiq4hDGKw7A0jyS98z/4aRa35oXzU1R8HFWrGF8QGsIxvjvrz5aYWuz3+5Q9UBrL/y/4Mwgf8PRAABUHAdc4dHTRGAVgAHhRjJe0qG2syGd4fEAD4uhaLSmfMFET//8GGAIEIAjVAWFGptTAAqBSg9eMgrrOjgJ1FWvdNqYC71MkaTX3MAAEgQB9jpoaNEYSkgysu0Rf3wKVIkpJf/+rKiwYsHwqMu/ekw4WvPw3A8HbAXUj4L7ur/IiEyIQyEG5TEBnL0/FTTSwOsTp/FYQPWMh9x/O/iPEBWGAMx0bNLpDdZBRMNgAAqDGaDw47NEYBdhCbZUJfDINJ7sMD3fxC3kJu1eKP9ap4jxAVh9IPoQOxQADtAxei6U1Ha3PDDr/56tRfEAqgiBKUMcwH4I+AAgGNZCLk8lMSUgY/ogH1AMBSFpInGUT+/aE4LB0JRZWkiWvz/JPI5GjIjXwXwkh5Lnuc/XpEQkQxmINyld4YAyMTpjiel3sakPrB32g9cNivi2DVcaQaSc6Ub/70W5/EBboCGfzUVdCYMsNfwMCDAA3RFDogyxW+i+NPmZjK6ir1JKWtSGHWenvu/7cHDa/xAZ+ABYDohRaI1AzaF3f+99QGzOX7BhL1f8QGYACRkQbKIvEkLaxPC8IUSrqOHTIvurBhrlxwtL+IDXwAjihoWJiUz/mHxUEIJUxCzhkX2VovAEBuvuu9/f3/8QGfgXQA/zia0Q9PkyYfmZmG6irtJKWtSGKE4qqUlIh/j4Svz/iBGAAkZCKziLxJC2sTD9rwhxK+o2dMjO6sMP56+UBcTX8diA5mDUtF4AYlOvv3+/8Qee4dd/c5/P/nxB7lAYClW5xXN9xRnvO+fjzrAuQAAAUvUGbIOgLGCHwQwnhHwiev4/3wipU8I/8IB3AApgAJlZwvWbQ7fHQGM/1fV2Imy0z/OLCVV1DUHyWR1/3M6D9QH/lI2CHcQ3tID4oIPGI0s4dmL74NDDYDUJI0WENl/UAPvOAB5AWcS7zBfrhhgT/DPQBAYRSjCHJt+JjLk/6tGq9n//wjnfwz4RLwAEDFkpNwa5MyX4xwPhHO/hE9cN21/F4RDfAAoBi2JQmUx4hcygd/3MDEoT+5PPiNy/zf+Aa4DYlULpgfrEBeAAg1QAnRiYs8bDkyGrCflihKHtJ6/7WYOFxDNcpTfXsIgAQH5Z8uKowLft90F5r9gBYAyETTrbbTRpb5/8F+7VhFHAAHB8xgyyT7KmBWH+9D6CX2F67VupobzfKEwH3poxtT//DkADhpgLdY8RyyKr/ASEJRKDHqiCkC3fgC6ZADAR4E8gowNwOv+4eAEoaqlaT/LGOf+XTAB8mTH1RzL//f/F/hjuWADwfQSUUTrLedBI2k8bzC5TFu6/AAdDORLk7h0mEF/+s9K2eKV5Er/B1R2IAZHu5r/7/gg8ABGExxU8UUh57yimwAGxDdUMbOP6lJ+MEUoTiWFewoaV0z4EN+kiXUtWrxBpUjDbR1BvnvT0KdX6ESLOYqHwcI/fww+paHX/+MLh+fJvXgO05QAObkT/n8QNwAfjUm46GqV//3DBKzC3HRC2If//7EsKnpuCgBACCOa+COqdS0mdM8chqVhMCEUStnqcUfjwIYACZUcKiy6Fd5Aw9NM1E5Zp/MSM2hbnXP9+1EYkhCMqFHJf93EWIs6b7g3m0AteUtzIGbh0sHuQ3Fu5l+8rxgsuJDEBQAmegk0OfxWyypv/vGA24IGLvowxnhJY31MgSeBdCJvod/7QiBr2x0//g3DT3iAN8CBq7yMcY0SVLgg9TAxmiLy2QVXUVzUAOh5NrYgFh2F7v8DCSKvga8VWpIpdv2Cs0HCP+vp/wX4AFzQwwvwhbry8he/8/gRAYkCUZk8+I3Lonf8GGOQUwBPdGhl/MMVyNqq8H/gw8JABoHu4Ug7iBr//gw+AAjAacMGMv/hjfCChfUdrAAK0DowRqOPf/cAd0pgDiyZGNqf+Xh5DAIxIGhRqbUwBRYCCC6QmSbJNtjMSesAaiSnnHz//iArDLoNB+ABRhh8yhsuem1Hv3/rAIcRWMyDJNhnDhSQBT0677z//D/RhBqyxs+fm1Lr3/qYDHF1hUiyTbbDDwAKArRQQdNypZw1QZ/3h6mswLiNW/GIQ4s8I4vktTeVI4TJrLIVP9bBroJ1lf+zf4MLOzGQvsEUAAIAFAK8UOPmYSs4aoM/7gGK72J2K06xDLP+GLyAOlVyprbPfZ0WPe4+91HRV3XXT1r0/73/EB+GDafYQYAEGwGMKlGZNsk03OQejYCCCaQiQZIMstAA2B+VJSudnHjQgN+TU7wv/fh686Rrxzj5fefv0Rac1Qwpbr/EDcAChkD3lj595JqWvmtALGMHUWdZlC8O9/eg4QeUSXTfY61BzylXi/+rwAg9CV5OqRH3Po2rcpvhoOAwGWxAn6rfEAGuxDilOww6bFtlZaD7I8PXFfv90PzZ9Dv7unyC3M/7C3nn6Zb/BqOi0uIG4AqM/RV6IknncQFuL8DeJQP4F90aBgQcv3Nc7rQaQbAQhOW+zRYAZyYUMTczW6b/pfTwW0HzzvA3mxJF64zvQBRjokRWfYQY2UZf/p2CuixxXceciEsV9PozB4bGsn/nVJsr/a/VrEUgcepbl/GNsB4xAeIGwEBdIwFaInBAfb2vz+lGO1e/P/5AJR0GT2K2XUZDd85+B9hu9wSf9LK0NTcLwM/z8KBHCIMXGyjBK/6auWP8X/v4AY4i7FTHNzdF23CP/3nkaAIEFzlAkRONk5oG7WSD+LnpoN2lyPm6f/0YQ4Vxsom+tSUS+uX/zoAUs66FX/vRPcFJ1X/fX/xsABoK8NhaBE1NPmcERsMQ4YaRjY0AEABAyINeLlpLNxXPBJk01jjrUKw/DdYBxp9NtOXwIQdKJfRN3J7+dwDAUUjFe9VOaMUcn//s9UlQzac8pXOjKyF9VX9X6jA380J/Wf42ONoyhMXKWPomDNIZ37P66gRwjxAmopaD9/QBSWBfRbC2djWE+nO7vt3BK6p2kZYvn/942ogDOZOURGFpWNTJXgEpeUy/+xsps7/uBpu+wD9ACXtOMmaZh4NSO9l1tSh6Ydsi2ugPYX0VH/tgW5rWX/1IfZH4gEHoECAwAEJTiKnKatHpViwQDAARgGnBApt9GWM6JLGfEA3QEDWSH46xwoqZ9PNgGKN3Hb67aaeHwJRptjX4lnuHYIkoMor0kpL/lxraGxEAWhFWWonTL0A4wvNt8h8/qSlfIpvdoQYdJywtqQO3Ijrt7/4TjSS0IA8QN6NABcLVqSJso4//YDW2IMK8I37cvnr//7vAg6PesdnGUKKfwuH+NnwYI940Q2K+uyiPQv/1HjqODvw+AA4a2pMmfwfmCYAVbUFBlY5Rs8zxWwEMJpCZJkky2C0vPQGdcyrX8Poa7rbpI5y96R0DKk+AvEBigQACARxIf6ITdiJLsN6RmiTbzEi/+jat5GkmYAgO8CeLsjsDv/nsAAIohFoqsdsO8OcFgDQm02ffzudle0XvqRbIVsVLfuaAX22zTxgh5ShtS+PEBjaTQCz8AC9EIEFIiFm3L2N3/wE0eD2bcLJWPUWh25ZvxIg/sq8J3D5f/VjGs7iAxwB8ANwWKhqoP4sa+HeQMBXAGxJ7zj57PMHduTP+/X/PeJFFPGiPKdiXn/a7CKf+KwgF8ABmwmRSi+ojmtUAAkYqLlkV7LfBbtYB4H0Ru18HglYw3vMKtis5yDkUkx7AAByAAFaAwgMmiMH4hGYj2gBkJu9Ja+A6jlrFVil0owmo/aDH73EeID2WXDAHcVxc5KYprt4AYiUWUParqGSKTrXkKvyIp2GfqzHMAAFwQqweGnZoje8UEuyqS+nUW//zYDCCqRmTbJNN+aBglbg6nvzbn36svZ99chCI0hUPC9g9UZokbfv1IDBP5nPpcQNh/MSOUqCKpJKWMT6fBCCl9zw4bGOVYfSSuqUNgTRz/P+8aDFzP7k8pbeX65DZTPHCJexesQCtMQWIuNfyWqb/e4c06HhQE8swngCKBG/ydHTU3FXH/7gWMgBwLd7jti7iBwCCDzQmK6tP2/fAUARQ6UNppCCYDuG/jJBDblc0f9gigNGH2tQiF+wSbYe1je99wRfl8MHuIGwSca3Uhng4/5C+vCObCkWyJ5MMepM9/YeXqr6lwD+WQcQF3ppYHnr8GKNwC0GVfARRqEGpI3zEwDBBcZRJkDzZINk9Xex2wwuQvXr0rjik32j/nbnaHlTX/do5EtNS8IDYOUlTJG93eGjylE/7uBKClmTf0Sr/+3BlRAOBi9sxQeZed4yVE0euuUNa/r/yspLAAEDL8AAQAg+I+fvzgrRnKCuxmVaJ1q4HtOAMDWZ3VIMMEf/YEIiIQrLxLyT/B8GCOxQCTAnpGLX2bnyNqPmzP2hNF8CruFjNbVXH/7ahX9LOLDf/KQON32lfNDKZrtx/NQLTRTt/EDYfhgHST5phgI2imZ5CRVwi/D/dpeFw/6ggEbGyAoMwRqcWXHBCxV1z/0DWk2g3vIuVACCAPcDvofUtkg3vwgHu5gs3yW4uLW/g92pAnfQS00x8j///xA3YImeO7LMhvvriYyaZXj/Z/p8TmTd9rwAN1gSIHEI4lhNM3wBj/Egp6ekiL5zgz3godYjHPiAY0cq/kvGt7xf77oJuVzIQV56S0oajqnf+5+Qljpm3M+x4hdOh/jwxVhaUc156n9KV0cFlEw42+jlturd9yGokGkUNNSKLv7/lRGTRi8W/v+UNSS/ff/SwHOxNLL/78PThdAjl+IG79fe1nQ/Qd4bN9DuX49NX4MLanNoewyt1//+gQFAWABIPoWk2nrzBJA7//aDAaoNEOHoiuWED3/QbiK7ZbX+7zABJh7936gXBxJ+xucZqij3/9aWghNkuSFv+/uHAQ03psom/928ZstXZY0Jf8ycT5xtTwQpnfTU8veDEIHM3J5CHc6fpnEDYhakc5OqdX7HnEjrLx1NIt/AEpnBwmk6raPRgb/x2jkvss6ebbHza546/KvVSveDxBGyk2K/q+T/WV3916UDr+Gakzv+qZeWKiZfXrAaPsniW+v//d8M4gIEBnsyzdMyC/7v2Qv9YhuVv9tLAB0XNPH/+1vjtymP3GFHxAIIAXxLBELet6+YbY+ABBumtrRsMGGAB8PfsxXzzd8AiLTw1/GQi2fslJO3/+8YSIUKxnzyF6tAtEPwrm0U9+/UCEK2k1kl//8f4gPz8gAgCaZjxiRQqWMWA2m+Rv/WkFYsAsqFSX3gi+xn0HeT7QN1IABgRtCBMTtheP96SIEIw5lKGIMKJfQDEkpUiUdxSs47+4ECRahDQosf//6BmNmGKfVpx9MPE1Y7riIv9ghOpxD4v4gbBUGX5/SJt/f1rIo9Dup7n0L2/NSbAz0WW6u8BFjPw7DvhhAf/e9fBRKgqam4aNAACAMACjoyj8ugyQ5x7yS/ndIABMkxuxmzi+hHmZX0jffCQ2uLlN0c/+lBYVY9k9LlX+fU/pAHcfqroc+eBD1Mr7DSf4QD0ABAw8Ck6T3CO/PrmknAAEUZK1QExmbUzfqx2VBgDmY3VRW6klLWp1geOAFBxmUruG6C++08Y4xnsdunBbNQtEgBMEu2JEXSce/sAMHawDC1aQz9LiyvAMWiFWc5ESYka/+LocIZmVAulp5kQ/WV2eTFr78hqQF/1P/ysaJ4kL3tqHr1KpM8QGsACjBgtZg2iHJtR79/6wEOKrGZJsm02RIYUYyMU/fv1f8c0/iQtBP5JidscylG9TVh4wO2gXED4r6xXyNdtX60khfp//icR884O2vPD6wG6Tv8Qe9BdldQHq1Hzz24Ojb/n/iA/AARAJMCBrD6EsY0TWM+MBLwQMYeQnjeia5kMNgqAIACaHhNouUNplmPKxYAALAheA8NuzRGAGIVGzCrS+3Wa8RS8cBmQe92Zejrlnw4l9Sx+myAOKmlHDSGU0ugfEBrdSjE3wxabHoWAAng0Yy0p+m3w0k/ee/zoH1SNKuX7pO6+bNdpDLf/43L7Y9QBmGTeR3j9Jw/BwVuZPMSzvXSQ9HAB8Eq1IE3Sdc/sCBHq7sADgcKAglaVtq6VS77xh1FOVTGGI1hDNYAxzzfWXgNHzGOolpmuT/3A8AAvwxDUQTqMg1dhq+P1CPxwpw82ktv/9iO+HbOtK1Jv+9YfT30Fv3/f42ApbIMQI1DTjDSSAOsJjt0R3/X3BhVGu4ACRGQNmOZShEsakEDwPUF6ZSxjl/vbCBAAboxfo+Qu+3NgARVVQ3UbY3f3ELdEEq4O4wgj9171N8kr4Xji3tGew+v/HNDipDhnvAm+M4+8Eo8fJ3x6UQ7bq4gbvGD4AgQgCNQBYUam1NAQeMCAQAl5oAh19iVq4hq2CloPiRy+st/OCBuK1d+bU3mRjZ0OZWCoYtHgIwMvDwlPk4uI4YIAow8D6SlIn6bk9OnU/9/Th+Vf3zmB3gWTJC2akDkSX/bHx4OaiuI0sM5jXecHhnQgsXEf/tlCZarBN8QNgPRpiXcilRWQAxxM4TIsk2Wzfx+SmbJGHxkIr2onSP0/tQqSi3Px+Tm8CPQGUSTOR4a1Bko7/3hoAgCb6vPvfwRUqmfNyByDSv/3CAAEAj4AAQEx4RtkiqoRdWdjDsMv8YALiWGKNJ582Siid0cRACAzwI4syOwu/+B2N9IAJaXhUHXQyXJnXv/XFv9lCSFOURlCLdOYiVjjeIFHSfEAggbiuKzypUr928QElIEYy7/0a1fhwAMNgMIKpMiySab/4BdgBqHrIaoThN9//3NDDVeDqc7Nuf/uyIBBBNITIMkmWQehIdlcBEuRJvF71HgRIBvdJLtn/Bbj7dpfg+cTk1s/vnDmr0sfo/+IDsMBzTJBm9InX/8cI6wcFBJ4zCV3DchnfXkW+pI774AtACw+amXqt1IfuZKe229/wYAaqt9D/n/vqgpqvhv/69JgB4NeLQd5Y1z+2iSMAYHeBGFWBuF1/wTphDmpB2v3SBmXNMkrvVGUvsNIUGMFk8ID+IGw9ZuALBkQAICSMr/IJOPtfaMACZUcP2l0I3wjajN5614APFUDDa4tnLmO2I6RTQTEtUl//1AGRv8I8IBUFnEfQOQLZXiYI9eNZeDHNtWHAQCA/JNxPIfb/BMXN/HLks/1hHlOpgdp/5MuC9WGbKRnn/iAtDGtAnNEmGTLoW/9mTf5o0+AFl8AHBTULOPosuf+0BCSWmpPJWXwx7/znEAAcloMlRBuf/+DAFbNZGkbu/vRp10+PznjIjYe/4f+FYYAxkQbKI2kkJaxcEB8UpADBRdqESZ9kv/1q6GhSOZ3fg/ynpLVMlNjg++f/+FfjAnf5cKVYfx2Jh9e3weKgZypHY8d/f+IDlAoAgQgCNUBYUZm1N6m3cN/UDNG4b+v8VzzFgSMSd7/+d/qW8Q4ADFQQgtbUMPGxnZX5mZhu4rbSStrVhh+fhxqJKecfP//DUAUHlUj4jjEy49zgAB2gAEdADXxo2pg/CtPWsYld5N0DXbS//4gNeDDeYLSVlCOtKrN94wE/DBTTyEcb4TXMhhnFDELjZENqY6Jqtg1v+IPUO+mb/8QFe0DsoNnjYLczqAMFxi257iprCUQHkIArFAaFWptTeJGIrIUTfI9jUhhxMl7AuSF5x+SYwSf/4gNeAgB2JAbcGWwtpnoCqhCCVNQw4ZF9FYiQw9xKSPUf1f/hAPdJAAMOLrNKh6QkpX/A/MzGV1FbqSUtasPgAOvCHYJ1GzqjSqToAvwAED65hJsWyibt8gMfauK7gePZPTrW8HLjIjk0+/iA1AAsAOFAxnG8o0EjWSt7zHszlErU4qnr8MClIZVeRLtX//CAZ6AYtEKk53WQseT/d/1DAQu5H/fqZ2VT48/zv4jxEdhA9YJHhv6kHw39fxB6iR6H79fA1D9+v8DpAAAAV10GbQOgLB/PwnhnwyeuASBJttHef/n/DJ68AONtTyucc7hn55ggjAOFKvtqANF1NYp77i/hk9SO+ff///hmj/hk9eH7Z/P1hk9cAlDU8v/f/F4RDHAASABYXQ1JtXHmiU0D/mACUSwpJpXfmyUUT8ADwdNAAgJJ368k0+/2gwBkPr6wscPompwJNJwBwWE6FG1MaCBRTscHv/CB69Bwz1/xJLMwQjwmfiA7AASYqLllUl2totzgABcFMuAcHHBtTeMVbFZRVEkU0p7AAByAAFeA54ZNEYBWAz0ONSdlih4FMCb/cAQxDTolwnZqxwsc/3hAyf8DC8Pwg+ENJSPQAYKcq4CFOQcyVL7/A/bPBAEL4EQp7vOFSiRic52+95oYxv6Zh3n4z9jxqzY/iA7DgUUBDCaTJMkm23++AAykEILU1CzhkZ4VwwJQQLV2On7k2Ybe8AUA2wcLZf/DOOklCwbH+wvFCyNr+34F/iAn8zMZSqKvUkpa1IYaFwAGwcG2ibQ+nSY/iA/AAsMZvsTV2Imywz/AJgHRQQeMTlZw7UX33+VgYCa4AAWBDckGhtybUwAxBEMmBD5FpaVi+AsQgCLUBoUam1N04AT8dMPlaaeBUHaD6kfBfucwPKhC695L/28GIpWNW7UOwjHPMcfBTUtC5xAWgANAQ1CP0Jxz8jYsic9AIexHqEo4+QsWQOeYAeG0KTZS0gySggf8gA+PoWmwltBglBE+GGBOkQAgM8CNKMjsLv/gAgZRZahkrqxMmV2QOpIA8BYgntGiPBXpS3j3+vcEG4rlxv4IMAD2QAEOnXlhGLKPv/b3oHAAcaDR3tW3PUow/cNBwllI69n/vWeUXW6fvrQa0J78Uk6LvN/4EEcWAOK+88AY3x80hVwy2SR3///wiF+AA4jlKM87dgORJuEdzAMaDzfH5QIzLpn/9xpAR5QZZqeL4r+4pgy2gyjUIL8r+7BAYwu0JFWCDK3aAVqjQInwkWMMcfwjF8C1sLp6CAPAZTkqQh/t6AcP6n4bhwEohlKgjMST7GL9PghBSu44cNjG6tcNunsIP/wvAAvEiJuEsMisju/gI4yro7rkTJ8AhUEILU1DDhkX2VgwYcACDYDCCKRmTZJNN9kQCCC6QmSbJNtjU3eEAuS0xr3n//l9f8SGfCgAkBLti5EXUce/g+AYtFKk4hUWUka/+Dyt4/9734/AkZTvf+Jij/iTzEpgDfqf3miNyOd/PUx0hXJqVrP+/X//w/xl6eg4AFAXFBB0zGVMOHKC+AAQwCZQ3zae6qLcIdMjYYHoOnpVVTrev7jYBT0gj0vQa4rBjVDr7pznnmoLIp19BqOeStj1piqbPSpP//EpcqtQc+F6GdVQBpgAcBcUOPmZSs4coM77QGK72JuLETabZ/l4Dyzi4b+A8DK9uqP+kA7tqzeWGzP1eu7+/43wAO0jTuWnvgBwARRxlo6Q7qCrMGx8IC47q8M4/xB7qYpGUxVQdWBKi3H2FqcP/wYCgACAATwBDSAqcfEXlEv9wCLrlODI99YYb7QGJZSpPJTJXDH/3aQmcCrMKi1CW3v30stbXIfFfgcUZ0CL/vl6/Sdscs/X9fbyF+lXSD/RSoV3KpqWrPiAQQAHVBCC1tQs4bF9lLzGru6ir1JKWrWGGAgBp1AAwZLUYNi2sbfgBSh5AfCEJTOGoDql5rUTa/r8hcST0n7/UOKRsrj9/kGsMBkW0CwpU1N2gnVzLwZaoJ2fn/DMFOGvpOjzfviO+PRfz/iAQSpOCA00ULZXrVgzTol/AQPc9wIEAAkPqhH5iDvpRj9GgviRSwilVvSZBsxzK4RLGrkzPknq7m2ZsDa6RL9wHTngdKSjJ/qKPI97ClEu3/+/ujmtzT/cK/co7nrayDTy16P/pAL1RbiYmqv4gMYUDR02RRpbba5/nwyHUP0T/5wAMAgMIKtGJFkkwzvIErBWILO0k5pRLZT0i7f9wudgXeA9WXNHR0OCiFpq4/XhVkwfiIj/v0PRoKw6LBB1OudvEDYAkf9hFr7E+jGJkAAKgkGRsg8MPV/8wfgaMA9IaWDtWSFu3r//7gB2Y3XnF1b0tWnwYlGr5GABylFhrULchHEPNFj4o0y+bVQCCgU5N3qvfgKQrTZZNvgqUxTyGyoXaMGSNOKRIt/frCRyw/6e/M1YyMmfEDYIBAQM5rCkWIhRiUPwt14AoEtRlBQgw2/i/IjatG///wHqCgAGqYxWGMjxqbCyelpxl4unV9XuXzT68LZZADkRjKhjYoVLmL9fBCCF9xs4ZFtVfGWPKlRW67sfCUReiu/U614NyocjiWrXxxsqSKUEmQ/2uJhtE/+sVhWDTEXEzeX+IGwQCTHAAoN0mQELHv//cAICo00nFiqsRivBnw4DyiluP2sMRbmTflMrv/f4MmPgGAAkZENOQuKMlakgAJINlEh6t0jVLW7nqs39xx7M8zzA7aulP2l7+qEpobXRBSKtS3Mf3Z/deYB1kWDSYBZo9w2T/EB/wgqUpjAXqCFyjLf+DGhB+AAkfkJ32XpkXjZskcBtXmgGFIWR83gq5B13+3QeCIAD3oGSwg3E+/eJXQbU5KgttvdgS3yc+7QGL9Jyz0/v8EEYX8wuoj1CeXw2owih4MC4kMRX5TTJSiRnQAHBARsibvwtjzCCLv+AA4wCFcQS1VlopNkfRDcp9bwDzm7EYoAgRJ09qNgLSQ6h5dV/32Bwho+kLO1v7PnlMmPTX4fwAAFAQyokGBp0mtgIAQsnOwKx8hYt45/tYAAgB9hRq0NNpAtsKd+8Dd+zuYzw0tOBglZ/Qths10939xIZFuZfcs3wCgCegIEGVI2V10x4s8YAn4bFuRMDnTbREP6QqJmFWl+skt4OAxQlbRDnKL/+3DgsP/iO0/7Y5+U/UMSZ6OxviA5gAIwGnDBjL6MMb0SUL7IQGmRGdpp2t9+x4A0zju8wbRuKjH/3ukrMk4gLQAEIb8LC2HkJ710muY8YCZQ4Uw+hDeekVjGjDBazB9EOTaj17RggTM0fX3ZtS693xAQUVeMyTJFht3BAYUXWEybZNtsGGpwAGkGSNEeDFAx44fxOJDO92QRNHz6B1udfP/8QbwAEyIbugisSSljE8IBaAIAAJggDswPmxw2pgE6Gy8guKJ5bFATTHYiZSu1f/tgFJAb0jILdzoCRBkCEE0vTkTCs7vv4bFw6gCtQRyHu8/h7FIcrszi1DvH2DHxAbgAOEIQ5GpaqR7Zd9v/eMwQqK7Vq7ls9fgsFw+OTVKSskwjhCBandHVQ5NunRk6/oCAHi61D9kpm///X/8QCD7a2ufzAAGIP8kbXY2L8tMJlCxZ2f39/wAmq/lvDAwB0FBdoi0sx8lkcBAAruXwFelBkIR9of7w2hggFiqWqfWblxemnKl/D4/T4BmUMi7Eo5khgg7/8Ad8PnowS0/f2MBQgvRgfywT6H/rChxPG4gb8GAbTUgIwZYqn95bugGoWaITJkbJ4fgIR7fr20rBUVmWWSpeKNGZj9P+PMzpGFZSP7mu3FAo9YH92gBJcWkFwhJD0oJI38CGOqghgkw1fwgoYRx+p/P7bnr7T//3kiBOpF6S3394X8iixW37/iBuRm6Ktfv26egMrcohwNJF69eibu//2gf/AARC/dIfagnmFlgKKrAAHAcJURR1vZoJPWGctOfopBHPdogw2XQyiHZtz+9hCLPW1JOnf9+DsDXguIFr2w/z4EACMQA610BEqYGz83jAanKUoOSt5/if7DnDAAU2tXQ9uxszYOQSKvohev/YIcNFuli937+IG/Ghl2UmeBFlseGHTjAB20JSE8FajPK7h+z+ypLr+8Pvipp//2AqABOwDnlDJo04d6Y/MD/ZwDGESjMi2SabYBqICGF0hUk2SZZl3C4bTiTNu7cD0Mnd95r/7AQkGZWGpf9yviBtxa5eB9iQYYACBEY45tLuSBi2qmwMneChHYSw19BvvvAgyNcKUUvfd0Lo9b38CekHfFdgbz3R1d7k/9d+GZjguL8Vr9kF6oBgAWB4InrS8j8Vxe8MB3wyBC07SilP+0KsTJk09Cn52gbuJZ3YDuWoeXT/uOW6Tj//r/xA2DPvW1/M+ft/T+/7/xgAPqBHnBlm/xaCP7gnAqA9qXkoDm+cL//uAw3GhOh2SfQlwjV5gRMAtjNjv+djYoYZx3v/XgE/kxLM8hcz6Z3b4/xA2GAxDLPhF/JAYCiRVXvKmjRf/8fkDQfG9p9w6k+AMK5Vjn+4XQrA2KA2YNdilcmzd/cQTLiV9bNWgQQtXl1efUn94GU+tPGqnj0VZT+cAGPYvFyUteJZKpHQgcDOz0ab1zNpVj7YxE8rzywi/79kngbrdLPd9/EDYAWkY4XKJMou7geqgAYJR3WpUtiQnrSIGrTd3/77cAMrCBJS10hTGBm915gJeGClnEI4zwmqZDDwwATWgRSttJJq9J7lKrr0oCz3R+5f77z777wIv4/+gAcTOV0EZiSUqUnxgAnoQiHE2TwAJASj1DKU7B5hTNWGkHnxko7KYM7B2P4TT+5dtL+kBO/bl+g4HItdwgN+gBm6AwFLy3L767zmHGQFgq4VHw/9305Q555ffvY8AkKHjnu4hu/uQZAAOtvjRuivOr/P/7ZMFOCbwiTKHGXswCAMxPpESw/RY379geoGMLuYBYcldtfYFlfNK7kT+vIXQ4ij2SkUmsqjyBynACAwxGmHDcxn/Bgg+pGxjiWbDzexFb4wghKi7q5USv/fiDXiiZmuGkxnzMYh+Lh1q4PiBsMAGpBlKwQrGjfrLJ/iqv6e3//+pfHXgigB7/PeZvBgaBBF7Gie1Zow09+ASZAFKSGsWzLx3whgJm1XYArTNLptP3eRbg71BhRW5nIop7vvExm1O1LMLd7H+dPYIDUlx+IBBBgYALBOpwAICe/KiVj3//uAAeoQwtbUMNGxfJS0bADUPVNQfxY13+3AIJusAJiDNf83r77//cB4RsCSXE8JLOu4//tAQlkrg96ZN4Y9+9yIgLm2Or70W5d+DCSaeIM1GQez/rAFiKV9If9/MU/Flme7/rDtG34ZgKBi0UqYOIVZiRr//gw6jBpVHYMP8VhD4VwAEQCTBg1h9CGMaJqGYfjAS8MGMPIRxnRNUyCIMaAEKZMAxJUM9//wYTw+AA7kIMKRELIdt3sL3/uANmIADgjSBITtief4RowaUp1waiSnnHz+OkcQ5J36cpaWvCA35EYNwMkovEEDxFdToMwSyRO2a0uuOtf/f7woJtlUl9Mgt+AkO7akKWmh//AgDtEDjxmU7Pm5C3+/6wEFFVjMkyTab0g+ypAlhs1kt38GDAYAxkIrKIvFkJWxfh+02IUWryOHTIvutDDkBbw8h+OypBcon+9z2iHfaHjOKPhAb8vAALA6QtnFxneVTXomvDNSAKph5HzQMZvs+p0RNlpn+cmjFqT8SYn2mZ4Dqi3aaTf+5oDotLp9ALDXgaYfr4ki47/rSIpZ7ANx3t+7+BnLzrhUz5a2t//Qz2gAIeYuIMUDfAjHul3eCgDd1JCLd/99zZ6vnb7+2y0s+fwgN2VNvWLX/8aGYoQgSrZmDkjxP5pYYrBGoZdXaS+rZdRkvKtxZLn5AAI+RQKSJJzZIs8ADcY5zGpx4mVqkvgxgMQBwlUSF0RrqefRIYcARbraA/3IBWWIwlKhESiu/8ApOwF+6GZh2EnHf5wgeMc+c2pgsk3SFDCUllb7p093H39hdFoCHNEYcrMX37gn8zNxG3iA/DATZi8dqi6LAAH1Jsh8hrRY/vADFehZAjkvYylv6b+eo2pi+VZYAdAB2BpwQMZd/DGeEljIArMizNFT/+gFTDQisCyVflQT+4AwojCzavPblaCqf/ckGC3dDJf5JmfPgn9VgMIWi1oCSXOi/nR8Tyo/c9MOsSLu9/Xb+IGwMgAaA+gIhS3Dj/BHe8zMbqpxdSSlrV8ECQad7u4hEBdNEcz0Wn/xdN2GOBAQAWAAWANJMhjREy6v/m54RIpTqwIx5KAGujYLXRS9vv9DHqjyiFCOnwoq532e2GVPgr/cNfulTT9TX3JDGGvRGzdx/iA/cTMNVK5tTB+MCaIJl3u+zcXwgAWATi6ER9MqLyp+4oww4lr0rtmhfJNrOMZJUV1xrtgKl4YsVBeblGX69xugIwQyU6Y0sn/YwAPEWzFDCKVmVOGXR43+koS8j33fltNApVRnX20Z9Nl/CCYI2zxA2GDUAG+RhURL0LN2scKADAVAQVvaMtcKt7VRD0BiN9n1NiIttM/yAsAEgthaTauPNEkDv/94zAAQ/VTyh9qpwc/7gwEx4pgxecjbGpjO9PQhBS+44cMjG6vqmTI5i6orjjnASxwG08x/gpsmVkOSWP18p6CqLre+1ZwtHXXdsIZdFqzN//v2Y0VTAvxAW8SMzkFuLcVoZEB0ZoDAGBhCdaYKGQj3/rCeWPqlYp/cGQXuCB4BDUSipOLVBXDXf/AgwbNqx4Vczswr5IVedze/1ysPWWyfceVJ/43gNxAQUROMyDZNhvU2MU9+uTAMcTWFSbJFtsEH4YHiSxzUVqWbLXQEbIwiBakp5RJN8wYATmQRFHXfFIe1QABNEN1xjIUKljE6GAbVNJAndYrC3D3/vcCVVCiVrUv84EaGHq+//9PYABK4DetpW88LG7WMRJSWH/fpD9Ln4UVij7/1XEycHk++xINPQZRhYyei9seYrYZEpHbHXXw33RompuwN/N+JiqKKs3DsIhaVKdbfrf//iD1ygzh7Mftxva//8QNgCCEAVigLCrU2pg/gynO4ACWAEge6lqYO4sY/0BiUQmznoktAtz93BVxCTw9CcnSIzK1wIBcwbqYAGBG/QKidcLr/g+noS1TtmD9pn4Ar7j5yzgAb0NjN37/wgCbgAJsOD7ZscynwQwPxCz5kQpRXws14YforEZ3k5IYfBAFYgDQmzNqb/CAe/zAh6PfgVjhG5bx3/Q/QENYn1Csc+IXMInw+DwfSotSJP8oa9/aQeOCHCr1YLC2CzvtAIKTmSSQuneIb3+83RDXa/JFXwyLja0ZfnrwOpC2ww5e5feJ3Xz/iBPgDjzYqoYoUilFkh+oOi1RcoI19mEBh+IC8AOBiyohRBxVwN2/f3pSCEFrahZwyM7K/4gAkF0NSbTwg0SSP//3QDGsR6pO/yVjKJx/fGy+CWU3kSzvRluaaXXv4gO/MzG7uKvfJS1q/MXbFZRUPdTSm8YALiaGJNK5QZJIn//4NwAA5AACtkBzw2bU2YDF7yNu/7/4AY8CP1KQx8jYz44DDhh+5ubTkc0PV+ixIRN2pzvbb1zB/4jxAajC+4lr96cT/4gMeABYId/MRc6Jm00z/MDIFhQSfMTld45UZ33wQ2UAIzrjRpfvnfxEfiD1gEi6t8fr//PUYVX+/fn//zrnXP51zrn/EHvCJodxgySh8/+fgbIAAAS3kGbYOgNmGfDJ64Brd3z/rDPhnwQhjQEAAiH1Qj8RDyaYY9wAA/AADKoBDI+bTsAc4iDdDFFdCjSQxc2kA3b5BfwQ5+z94ZPXASM9H/fr/F4R8QTAARi7IdlOQcimmPh+GagABwAArwHPDpcYAHihwiYVLyaaaThhZI4AG9FiRk+1wvMHP8bDvGAWQwHYsCgq0NqYAIwHfIDagfFjds4ETHKRnG1Nd63oaYd+TIRUUx0cJ7WJYAAKg4DrnDo6aIwIC8BOzGqlP3F9q0gwCHGpQBCginNccfHmGZpND81QDM1D2HxAIMAC7IwBAVwO+quNRu/+fJWwFwAXlAnGrfhvm++ARAdFRyLdy3LLPhBL4Abl0ho8+0M2X8fn//EBmAsAcFSlWOxRCjT4MNgnwNWteH/hAK9EABOqMFTRdjOfOJjssYzgL5AhH/gBjRBsoi8SQlrF+02EKLX1GzpkZ5V+RQ8yIco78aa8MOFlcAdTFn0tL/3e//+GPAAcIFfwiVPxkuiaYL/1lqQCQQydfZCTWs2VcZPAO7YAJObLho6e9/CIYgANHONoyyskNmxyhaHyaRrEXKi7//2jwctwFToSnnr/5mz3bKt6WuA1d4GLDIXKOmVn//Aykwk5b1A8WSRN5v391FtT0Taf7+EQQcACxQpwCjmJYSVTdcf8ALATcOGMPoS3nZNQt6ADMcA8IbPAXSlRnsAMAFh9DUG1dIMEooHRW99B3n68mQvZ1TrmusGAaDThQgzuuien78gIwCSxIHhRqm+YNq4EjNDamCOrNqQ6PZNtcnGh/CJYcAosAhhdIVJMkm2w+ET1hK/3x/wj/xJ6mJ1qfH5//xWJPWAQgyJ864u/w7oDAAZC4mUVKX2yy3hwALAUFXL3sMRzvJfoCAMSziNC4Z+9Quia8Y+yldTEGdbCnBh4/ogAU7ZZIfT//7/jKS0d/EBaANCNnc+JgrS1tDwPsKKY3hsyMbK78AMRiKzCq1JC2NSBgSs/4Ww2K6O7+0YAE69wnYbY3fwCYBUQEHzUZ2fNTGN9oDHelf3OHQKaY/j16y1Qapb2kAas/EuIJD/MPsLpLf5f7+IDUer/0CIErtz/yFh3W72j5KGHt7I/dzbySvpfxA2AB+BEDJTrS39xT8+AERVtaAb+aO6yh0BRUiaK5ER/X//aYZcsZ2b9Pc4AAVBwHZiaOjZtTADmY3dTncoX1tSGGH8ALA9lkVFIJ/rAALAlAir+llGbBJ//e6dYN/u/e8ApE4/z6SnIxiSf4VWBoLp3p/eBhRbzar//dEFpCoEtn9mn29/EBiAA2m3CScvZF+ONIaVWVnWsj0rf/z8lxROKfvywBuxQAcEbQKCFsLv/AJBGQOqTCUQQga/95xacTZvZvPAFQ0h1t9iVHVybUzQe1cKr3/+OYbU83//TajOyh/38+vCTMx4qf//cclwCYNLCq4gEEAB8AvBKNhNLf0u/+8jHRssukE2yinhh9L4KCQJlpXzNFIWm3atmDmvtPWAJd8B9D/4AAwKIikg8rKebP2n//4q8rYcbQh0guORrtPvvDwd1ssR/DG2nGtTQB/tv3/bkUpxg7DfEDbAABcEKsHhp2aIwGmroBoaOwRlR1//7eAHXwTUL/gf/HfWHtMi8F5LCnhNX1+8ASJPCMhTjk00lozANXFDAUztGK+ZShCDyf/x4n/MAHCIYQr2+YpmmiZ/wJMj9WSnKrfvBnJcZFsREZ/+IHpnZPt/5uiPiL2l//zyvtFw3q3/iBvQigIagMbva/z3RHH+9SH9X+GAgpCCHnKhAwuK6KUAg4ACE5xkXmNWrVsxPR8NGamg9FWL/eDMOapDWMJQQWJ0iDLNtW+u4CcBCFsLU2yvKeXuEkHDgwa5k12kdKFZueJhWF+DcAzz7/XIKsMtuKcQN8G2OHRy/6ltN7uD5rAAwcVlWbrqRb/mPXax7sDVupLBeiaPSyvPed/bsy0rdfv3U2tJ0+f26Fa2W09+8MI95/eBk6m+d38qejB+/Wn7/mRBufCI7ydUpPqaaRlsJWdccOKRc4l1u/2mhzMWOAiSTi/g4CSrFN4X0+Lr+dO7PP9jyCzhL++VfSF4IsnVWfoxnGOzHEAg1eTXIbHVcBg8AE4AAgEV0AY/ARXL8lgMIIpGZFsk03/FgIIJpCZBkky35ABEgECEkEISZoTXI8C6iE5JnsIsbpcGH9rUzf1pkd3cAKDKYIpZpKWCEEUeBDouo+4jbrICu2luv/VSHDdO+R/3/Opnlf37oMjirVA0NFxA2MqN91kLgAJpDKuMZCj+pSWk28D7Yd0C4DXEIcURPZdYi4x/5s/t/L4EAeKH95xK+HnM9E94aMjCBxiJ3UGFB19/7ocRR0y+z/YuRjtS7vYVhsj+Kfw6uk6WJIofEDf4a5oUfCEkuQol5ZFgR4Id4N0neuFTT4CxkTGjF7mbXAYCp4OgcUvcRRy/ff82unJ74CUmN0I0cKlSlhh/8APHS5WbrYVDIvy3v3/ToEzQiRb939fsz+7+IDEqjOHsqQADwbocAHBHUCglbC7/wYngav5Csq2f8954yzIf5g5L9CT8fv4gMcCQQlFqg4lEFIGv/u/gIHrDRjMBOFp0/Kf+6ZWPnP+G5QQBHQOAMpuR/qcHSY0R4mWjxeT1PisQGMADmSo9bFPdAkigmXQynuzbn14BfTVmpNZ/B6EQFy7HT96LdNvASCHfzOm7Ezaab/gjJwGADtM0XP/f1A+m0Q5O/f3fxAb4EQUwoefMTld41UX/wZhcxnNNTz/4gPfA3EjIgSwyqyO29DwArTATuBCR1WJMk4N/QEmK2Six09lny7z9/gEsxldRW35KXtSGCA4ACMBpwwUy+jDGeEljPRBAl7Y6f/yblp6UqRtHr/UXxd+AUs+Cyvl//v/EAggAP4SMmoSQ6ayO/+ba/Avu/wmMIi/1yFasm2g1yDUQJbavKXkGGyOD0CoHb5QK0vGu7SfAI9BCCldxw4bFt1YffGMUsf+7+AkGhWDoyVFedp/78a+D5Iw/aXXf1BiAGF0Rcv+3a60aNzkaHkU1j4gb8BU4DLYDrLRx3Ef08oKN6HkHnLLp+qK1gYf+AlqPA/1XgKSgVyJpxg/NU5uf95izu7CMryUsYkRYMGNbWr/lf3//92ne+t+7d9nU+5mDRjgnupxA3/wAPHgCBLdKxTY803nhgKPyAHCWKSj5pBtsHAUG61gxoMxUkyd0d/9wXziMLZKRS7yq7wGBEYWGkCEb2m/iMfHgA1BayGog/ixr4fgnFWLzDcKwSp6VU2sdN3z1vvd/U2PZ899Hi1+LCVXlGnPUlL//7/xA2H8AT09TL8D/wAOMA5cMW5EkobeYDa1k5b0w0BBkZAw1znzsI8BCGy3k/uXJ/DYIHwBgP68FOv/j7nh5hb4gMohwaq0/thzyRts9BleVvS359+tD7SWkgelyV3dtWWL+eMmlpriBvTZ3Lk+d2oPymMQc+znLgfQLwxepgTOmL7SUlVU9t4B8CAewL5uO7qfz+v26wOrypJNH/OGwdt/VEZ6UnlRHi/+fgjrUI/JjgpBhf/4QkXZ7mWmiNmxlHeUO+tNPr7GywZfPb3/sO7sVg9xIYv9xA2AY0p+Sz914EP/eJjpOPGqdEO/mIA1oheluNrW/4DCoxQtNjGe09j6fgQdOuEJr6t3fsIIgBksrh9v/79UYnA7qsFsELV9gqTSSkye+/ZiIUVddCV8f/gDMbAt6VpH/zhPxkqdu+9mFkOaDt+yFzAZFni//rhmV6XFjqc4gbbGscc4fjDJjHcbL/lY1IewkHAlbp7xmJgwQJQGDPcwkRVL/l2X+vIAMIqS1z+fwAxNpkx/CvyAATiBPfNZR7pe3v1VU1pS/p5rCEyaOUQvy/PCVaWgdh78/WGY6jTv3/O0FOUJkVqa/9PaAkbhv1cQNnnZdeqnzZTeC1xc/vbetENlEXiSt12uAAnGzmes2pmt36oMJp1Xz+jzHZ3VZEi5M1fof5/INqocy/jjICHqbOafuE4RmxnZr6Q+tkyfyfgACBSXyU/gzb6lH//6tC5soYAEkEkoDzhT/3gKpksdTRKr7/yrl/FNd36JY34SIXXv/prjQDR8RSZe/OB24S+MeW+HEDYMmpV//2B61T5D1YOApBuMFJLSjPek1W+DD4/rLu9/+7fwwABAAkUAAQFwAXKlWZg9FP/zgABIFAbSBgQITadgIjCKiHMpQiVLSGawJk1rk/dzjUqr60UJ+Rsv4D/4gMeACKPJZtE9+OCQAUfCRS1iO4uB83ZGE5mvUEtef/0POVTAQGXVI5fxA2AAmWLFZTsO6mmPYAAOQAB2gMeGzRGDAUxCaUQbrKGMklW4AUKOjMgqXvpppIYbgKMARglE/Dc5OGlri+0/H6r93V6//OAia1Sr42psgew/MPh5TvK79+HBiXIScdhoRTcG4AewLOumrgZ3//9glbDLh+IJ70/EemAAxUEILU1DDhsZ2VsYfmZjK6ir1JKWtSGHE4QPXhD7+f4QEYBdYBBRVYzJNk2m4frpgGFFzhMm2TZbDD8QGcD335u+XgCCEstMSeSmYL4Y4GNUt7uZ/WjoGlkTPAZWnLj38QGYAFf2AgoicyDJNpv/vXRgMcTOEybJNtsb40yoDM5XN++q5X/weKVnGN9zALia/iBvgFG7yTR/qwWOMF5hteUgxddyJh7uQ/9cVD/d/BvvTeQkP/W3w4AEwD8qAQgSRm0Sbc8BDA2sXr6IAlbmKf8BIqaUY9rZ5r90qPbp3frwXMnrBIdTdASFHv8QNhLn8oq/eMgO6ixMMNkABTTUazCVFUADvBD0xxvsoYyQXZD69jtVequv//vemTYniOiogAHkV96yOmeH/7R5jTRk+Qs//fIAhj/5jYrdQJYmAACgKbQODLg0RhGHwUSUqv/ZBfzW3/wmlcK399/v2nQwVK5Hvt/+IGw5P9Xeat4q+ek5v9sAwrhX40+YrUTs/lvlKz1E/4GByl6UL0X/v4foAC5gHolZiWnBwvqq9IdFyi5Q632U7lBj5Rd8y2yUzuQGPon0yWkCVzKB3/AwXwM7uHT55KUjdqopggQxEuF9FojX8trQ6/StZn/seiFvdmctsspN5PahSjBDdGeN8QGNAUABwYkEJk4lEyXw1z8hHAHgB/oAAgdXUIuit8DpYDdCgAoI34oJVvf/+5lEu75gjFrM/mt//8zU6qeV5Hbxs1d9swTgx4vEDfgDGQiophe93rUuHwMKmCTAzlZfcZZK/+BkHPMADgAyggdUzW2tiUDHfwAgRpzJwQEoXILd+Z5+x/q/cqrf/4AUA1QMHtvfjjGiSpnAG6FABwRtAoJWwvf85E4Pe8Il+0na6+00aAGBngTpRgdgdf8CaLwWO6axN5jXoSWWTftWwRNd1/ryABliOOiR8gOGoGCwY8QCDlCCe2ZjdTnUoVLWpxgOACCEotVScSiIMQNfD4bABKGrJWs9JYx7/3l6JMx3EzrgAPxOJvHobjCC37vYA2UoAMCtcKnswH/8Zv4sa5s7/ODln/QXNCmyP2j/9quMrbwnT1pz/nYNMk39e/+9/hAK9CKfGT20sE//dyEQtBwdqC6MVpkf1iCMFLH4Lvl3Xzdr+t3c4upwitK8v9xoYQfeMLRmxB9pvmlkYAgO4COqsjkL3/nCQANA93DECLJOv/+DML5I1p13Pnf75M5eRy+QIC//xAIP/AAqB/KAKBn8QUNN8N/9AATIjGqEMjj+piQAFhwa4JlT6ZZhOoAuGw9m8sHhGtjveMAApgP4G0lWlCRa4rTzSRH/7pxPgtVfsjPP/6w5KELPQCA7A6P94EDInbwFpz76VsE3+8MdCh3s6yMVJHnFzP91QbVRPFxAdgj6AcPmnOpt/+r+AYzUsTUzYibbTP9xAc4oIOGp0s4dqM/4MPyMAuPsPg10otTQQuAAPhCBSGFcIl//8e/gx57ipC8i8ZwyN/0v7fT0Z5Fr9cD/iDyv+3dkR//5//iAz8AXDPmKZFwzy2Ph/rp8+aqxBxrL0S21Dr1FRXaVHH9eIDFrABKBbg+JHQZ1l5gBAhAEagCwo1Nqb3BBqKte+bUwJwP0H1I+C/dvMAfgdSn3ziHeffDBGHSR+bSteM8KELn86+I8IBzwAEYDTggYy+jDGeElDK0tor6omBH+GH0INwhJND0aFQrK77+Bl/hAPQ/EAmwYNYfQhrXCaxlCD8YEqhgpp5COs6Ksl7LAGGYnmE+S7vapvkTHU3f72ph+I0dX6XobhCAKxAFhVqbU3yLLeAxLzX5Su0HBEJ3/76U9FxOr+I8Qev/41c/ljnfWI8QGMABMiMMqCKryUsYvpAAbp2CJoyxvPnp6CEFL9jhwyMbqw9MeZFgWwya6Hb+8AzPwBq1+j/IOImeR8X/V8/4QPXGAG93Pn/8RHYiIxB50/fcb/P5+BrgAAFI9Bm4DoDYfz9H8/4ZPgVQ1xBFwz9EKrHgn+GZ8IxeEfEl4ADhis9n7EaIiwyz/g+EQzAEBMgykVxtTAQgFdKBMQOity2EAAFQcB2Th0fNEbzMxu6nOpR/W1KgBe8B1R/j7X+z/hEbzqWeAB6FPuVeqER/uASzlj3ueI3q7AQACIa9jFKzFKzDLAU04glR7cKLmRipW4BGDwXN2joMKNP//KAAHQACMAYRGy43mPJiuhijupRrwgJ/iqAAfVtJGKlBEjMjbZYLnGUx4rQFAARizKdsL7CJaWz5MOiVZcIfLIMfBviQYQALeAPh6pqD+LFv/2/gmHv0tW3eWwozBuxWWUAbvKz5y9sKJU/Cgm5xfn/iBsABZjb5xNQ/mPQ4EyDK5GG1MGBGoybtFkeAIgAbJwSuGRWxYP2zGVec6lH9q0hwYEAIEEARqgNCjU2pgEohlVCCYsn3KSHYAAKA4D7HDQ+aIwCExFRDiakj2NSNWgNeRmg88MATqzRqdf4Y/tzCFFLdhh82MbK/IjIMiCqvyEsamkGAAiDYgrlnE4sUiqgiZP0EBK1zufwyGMALeEjnYxffcIAPj7gDN1u2KM7yv/sAakAkFwPtZzr7/1CxhZxuUArYu5qQ74vpCs+WU15wGIKgYLlULeZagkdgxqwA6NlVv5uAorsyHm2reWfyTa/7+EfDJ6wSLhv6kHw39fwyeuAMrTXf2ZxavZ/CIW4AFgxZKTIlDMU7uPfveAqQAaB7uGIOQUNf/8GHWab9uRpqoF/xeJPWBj09QYrUr5/xAXgAOqCEFrahhwyL7K2onEXoid7W42vfwfA5pccgco9w0RgGyucm65//xAf6bB482xiIpf/rwasC7sQAD9hHAxTYQNMjGysABYx1Bl1Pk4W2QUNv/CMX7M3vyRNNjPXAfSz38ABCvSJWcQlGzbLJDopySo+ZIQgxPn4BEn7jf+djaArv1WE+x4D321rRxAIIAHDYAoA8NU4RwXGON9/ACQDHVoMed9T5VEdlsA4MLuPrGYi5bOWIlndKXap72fjH25VURDiLYY7hAAikAHcc/WmB91TGDr/n5Jrf+ZoGGgoQaZpETNVi6Hu8kyDZBVakhbGrGCkN75X1sDweWNGJdd/lZCdmyXrtREjemr79f8QN5IRZ8dqiFfn9xsggiTZm04wwkHbHlG9hcOLY44QwCqSBgTZG1N1+AQ4q8ZkGSrTegCJOMUrMT9N5FYE2QDSdrBl1vm+Z1hgA7gi9inRlGcWt3AfZQLbEMonEOP/4PTEistC0GQbR5fwB8apmkjJmDcQ8BjS9qg3WOdYKwaZ38p0fFal/+TDisRL//ooTPUTD+IG/VQDHAtmkOkWAL88DFXAmwilVhtTAlCmBsQOitzHYABxWGAdQGTrd1ESgZ3CQAaB72GIOQUPf/8GGDwACYOA68YmjcB9cuMGqqBli7w+PtKyHwfrpzIe6KqcHYIMAB3YQ4pTcLPmRbZWCBl3BTh8llE23eBCX0byS/zzqJPJC/6Q2UJVr4/I6IbQmE41xAII/ZgXRM/IjEVkFVqSFsakGFYYTtDtNF+E662rhn6zg4YEU2lSPv2DiQV1lc36/xAf9GDzowI2sf6p0IBRwTEp4xLTlMWko1tSI7ELtdFsP9fonX7PTjCgVFIUHCKHbQq0fFqvVE2lH//nUMuYf1s9/9jbS0MGg2nuIGxsAAfCKRgvlNJ5pIwplYABDIsIOxt4nkexbgAExHOSqbU2lMdyJld2r/9rwXqhPaVbCS32hAiBCSKXJyLhWd338XzeH4ux1BJhPXmLYXN9rk37+zNBSm0CISqRjx5IfvwMUIPBdecJeRff/cwJvRoTOpA7WziXRZwiSyCxP3nRn68YUXEDesAKxQABAD1sQAohAX97hCLQiM4kvz/JL//Htd7nemwXFUl+dpNTY08uk//dEnJ8c2vv8HX1AEBj0KQ+SRbfvnu6z39xoQQ+oAUJncRn9/owZjfg1VnEwJqTDGYAANnIaL4s1ThSc1bcmgpPfLVe5lkaU/OwVhatOHqxCRspG/9/xA2AshlXUEigmTn+XIzh6qh8vemxPv2oHxQQeMTlhw7UX32g2CtKvUfCHlF/fuMsCHcJxPBNJZFLsZSEANKuA4KQLn/tewADSgS3Q/MeGhCRvqA5GF6PlSLX9f/oWrAGGKRjtNT6avhk+YdC9xOI1S9AFhCzVxPjsewR/7z6Ep5///G0w1HW0TXavfkK6ip/dYBHgimn2hlmf+CNC/hIhVTfanObJBki/30CRi8Wz/+iTDLbhrhAPwFgX5AMAiEIuXORHP3AJUIADgnP4wJCdkLpwGU3BxZNpSFSxSA7/2jbECCvCNu3LyB7/yUPZU8c/1s11oDrppfNa+/+feK/YGsf4R8vGASjAAiCpsTi6n2X//0CQikhVD9MscLf/5h2gXm9DzlZ/v0ITTk2r/g1dvcESK/G8ABERhFRimVxFuS3RNMAAQBwAQTOSBBlgj3mAQAGllOKox2LGosKJ6QjCkZhS9Zh4n/qUl8j5+/Tm9h+q/d3X//3BqQpNFLJbF//2gAgVjySitaSwb5K2kAFgZBeEMkHm8l++0AQ05cBOVsvhixy+8YDXhwpl78c52SVLaNBahAuMxC3+7HQdQBlDY8i3/dMGiM4vL/v/oRAzgxkUVt/fan0aB1h6//OwSri/RFxAYjYQGABETaIWV1Zl4ED1ZYQzicMFE1iPkBfMcbFdDFHdTDX6A3Q4AOCNoRKCVsL1/hBJMyVWblv340yIZ5JVKf4IlvhZVX7Dk9x1eIDHAkEJRajiVRRSBr/z4AGIQGEFUjUm2SabeaDBKvh1PfqvH/ywNZT1dswLV4iWdz/R/hj9WYBBBNITIMkm2/bmEOKW3DDpkW2V6EwfL8dXyE15fe1CVn/C2HzXR3f3pGIrMKrUkLY1IfywAJ3VwyKNsb3oYHaQftCuWGEARLqLmf0tCD4rCB8UEjw39Cvvhd/OcNmsfOJQorR88v4QBhjAHZQAA8AAgdsBNQLitu16AjQnRTHQo3rYlSstvL8/ogpOF706KdfxAWwwAHTACQPuNTB3FjH/7whYSl6Rtb1bRb6uCAtEAAIAI4zXvT0qXWZQ72mgR9QZZf8Wgje9IYLc7Q6X/QbnwQCQ5Bc/Smh/+vB2bYUypjzPduNsWDGa/CA35AA8PgWi2lj7BOHjQfICE091Bt/ELlkTv+DAiJGTcaNDpsJ9uE0byDIwHg493/aQRgCZ+0UJVph//NLNoyBOA6SDCf28wGZ6A4l/0LrO0SJB8gIaxPqFb8JXMfO/4EMBo2naM03teEKJV1HDZkV3VggCMhgQdjhyZIbrHFy4oSrVfekiwH/RMMqWv/cwV4tt/EAg+iRbjaH+Azh1JTDiEFFUEu/+VX2zst6ztprJ9ZSvb7muAWFPE8xc6bQIdvMRc6Jm003/DNDKP3H6fgBZEDwtxsZH4//n46tDlmBFeGl/hq4gbAH687w56f+yM/Tg+878H2b+ie+bXwwYwNZv6Kx92gAIwGnBApd/8Lb0SULvPu++nBhSCijxukJ7h5VX/+8h88MemYdfMc/3IZXQRWJLSxS/CRzBVIeVrRCfle+cM8YpmLgiyVPsuatbr3BBkw24zov/m/x/0/ik8AVtPLvf/KiNkTav/f4xbDBqDarlHCA3gzG8irYw0Nv+D66odlfzQA6SvtE2KQ00r/mD2bEvlqZ//n9WwU8rpSpf79CGF6uv/XiH9UG/e2FfqM9JoSfIcS6blmAcnMnYldluABhkWKZMo0tBIpoT8H72YZVFXaXpetYIGBbNN2wBIFmp//ihtcFovnv69jDfeWe696W758T/+2JkjGO3xA2DAfTCDZlcSP9/3hAAIAQCG3X8BOb41Es1Yv4GHRzBaqGM99zSPWBlxxozBlQ/zcC+vZnzf6QXTsc6WPf/PgAICloKbyCCaBZh//+a7AuQBUFlVXNyVHbZt5Y/3LBAGE/iU82nEE7/ghnMbpzRv/PJm8Sy8mv/ryrT9X/upZROThr+WPhoawcnEDYIzOylvjqfyqSVev/m00YaVlTVZfr/ApCAwgilSbZJpt/gCiYBDC7QqSZIMs+ECIoQS9j0JI4IukfGAJeBhvldRk1Z1gmGAFkcV9WZx/fqetPMxH/vvAkOI1aRC2et6TQSDFXQIUUffsBEP4lSdfP//mXbRxGtF2BoEjU/3xA24odtSAPqgwOg1lcjGRS9/CrU7Pe8BE3cfM6KUA/WH8hdvy4Rvr0/XVe/u9eBhWIQeLY5f8tUR/T2z59+//8yn7w+fsGVuvd+hp4HSL+JM3/9Baju02BxEngkvv56ljpjTtJDdf/fWIHc5OOoGRYWC+gQC0QHhAbmE21Svt/ADcUwknuPGocZ7+AEAhG+9ZfLKZyla8aHeAMkIADi6bEL1wsu1Uf/uBhrewQqQSRaLpr1/+j/a0Hb+cP36Qft/Pv9+b2bM2MPBhgBX8qVr3wEaZjaNK6N//21GCYKrzGiF/395GRDZTHQoyWs/ioIQWpiFnDIzstBZF9BfMiLuN/Kt1Ed6FBor3WkR9val02kS/Yc6v/ei8k1QF4gb0NGzxarpIv/1onnWLOLTL/voyK5NH9dKakee/Lw3v/jaJMz0EjqjzHlEas5tIFpLpekgBgAMEci6OWvR3z0AABugAJDrAKfHV/u8yIbugis8lLFJD4xkC3LVDk9lO3f//etokxvUJuuDVEYYBtweJhx+6CsT+EdeIw9pWcsWv/EAg/Alex+FIQynOan8AnHn7d/lkTAMEFzlEqSONkuAIA6XDnXIenw7Zwh/wW19ca99qMdNZl892lOznrEd/uMsvn89oVHmDwcbh1E6dX9gq2xWzdt++zXHK68Z/4gMfADtvq1/zeAukCPKDJLSgviv4BA+g19huu1ZFPDwsDH6a5Sm7b//7vC3oP4qJjTfPj8g4wy7LD+94HhM4feWIuEArAUDFopUnEIiSvGv/gQMP5YYLWYNl7k2J9+/9wEOIrGZJki0yRFkDX1IrxPLvf/eBlFfRfn/xMP/McbFVBEtIhhrw/UHx6ou0Ot9mODDicIfPXHb5yT/f/+F8OABaGkA9xzxXLJrv9AXIaBxiIjVBpw7gdf9DEGLuDwGaJ7urf8oQgSO5ab38QDCAoBqAlAhFg5WsCrExZoYqIHuu0ug/5pz33gbj2/4lMSXqy38BDW+NWvzqUjD050ADwbocAHBHfFBK+F3/mgISi1QcSiCkDX/3B220w56YkkL/634IEADE8TbIOHlQJPnzwYRsYPMEAjpTADiB0iEvJ9lIqFJnffwAXBSXguJGQX1ld8Q/Vfq7vf/4A/HE5fH29Q+g5LOcf5DCGmlIzP/aoHD1VwgNgz0K6o1j/e/gyL2V2qeRd+AEIGfnh/G4W2WY5E7wehOEIVeDbMtk//aQSqQDYBEHNnpjn/PAxS1p5BkpgIULNNP7tpb62CjtEaOpffA6IMGBj4D4EUAAQhJJo+uj6ZH4n/gYGHEoWCEyafxH6NJmYRUN6iwr//D0D9Agjxapgbb4gbs1cuY0h+/r8GWEMGE5pQg+eZJ89GoKgP+vgwjeZuWdEAdWJb7Xb9bXBsggltk3SxYoMWDWnxpK1/uBsBWAAIAPQBWgVm2OFCKB//eZsxqpxd9/rWkMMYC8HgIB9xtjaSIn7v40O9y/FXP34VS0ldwGf/iA982xldTi+slLWrBhh/MbB3RlluIctyX8aQnRfvc5PvDYc12fxD2IeWh8LNt7f+4MAY0Q2URee5K1LgyUMFQs0P/5Z++zC7/hAO4Qonw8H3n+IAAQCpQZQJorFuJFarlTrs/T+6fvlok8Gmvt4UEdTXm4qhbJFVneAP6YheyL/wGfkZBOnMdjjeti9C9IKJZ1Z0yL7q3+DBCcUH4FYqPCddidBhYYR0/8IBXEzJuw37P4IGbZIwZ/hkqjTKLmbAABUHAdc4dHzRG8zMMqqK30k+1q8ATIUACgnXyglZA9/zhwASh6uWLE2Scf/8GDiES4LnT35Sn9EUiQsNv6JvrjosHxsuxkRvOxVAF8HeaKXjhnxHEr4Iaa5+gICGAAgEJRKIk4lEUUga+Hw2AFw1ZK0npLFOf+DwAEgAWF0NSbT15glFA7gwBQoADGVoBJpxYE3tgi+ZGlSVO7JF1E979+cVPOo3+eUvJxDsu/4gbx7Jg1KfOV7de/b2833nmLs8CAClhTRAV2rrygW5VbQSPgABAxE0jkkBinPFUg8Z0cg/Q7/dTEikE1/vIAKwnRTC15HtYsBQY7PZ9xFiJtMs/wf/FtjWq6ldT0l4AQBADjiOAcCCNraJE9CL/wJjOsklP/z1CuGo5lX7wQY7yps+Tv4gPw+oAUYMRW0ha0J1VJGAtjmAAIANgMhJRf4/vwffHo9yJF8HgANdhCilNww6bGNlfkRiKyCq1JCWNSUF2Zaev/8ZS5ESQpYkvfBjwtd63iD1p6E7QpEjsZ//4gK2tIACdUYKmjbGa6QEZCdnMfFCJaxfCYHRJtFwLh7FfwftbEKJX5HTpsX3VhgLmNHv3z4j4C718e/N//4gK4AFzMwBgdwE7VYHInX/IGgnU4AMCeoxKiVj3/eAVIAJASdliTvMGPf+D4Bi0UqTiERJSRr/4NQ4jRuZy1/vG/3m++f58bhA923sqP+/Xn+IDX3CEAVigNCrU2pvr/wCG+s13f8Qe/au+QuX/4al4AH3kMT/MLNIXvgAMQrrXzu8gA5YwAAgBUibkDytRJeoAVhFU6GNvP//cCEITIKlL7dJr+D8x9Fd1MQYi1GOD4gMwAEzZhuoq98lLWpDDrAIy75z+f/8QeoVbb63v/f//xAa+YAPCaGJtpY82Sggd0w5Dum7In/fg/MXw93GZEh1P/8QetiW+//wgC/1hIyahLDJrI9/7mwAG7I4VFGWM7+9JQhBK2oYeMjOyvzMzDdRV6klLWpjYODwF/wAOVZvbjU4NIfOwvrp+/z4YQ568Xf/U9n8/n8/nXPwN0AAATy0GboOgOOGQ5gAPgOQQEnjE53dNzFv8wegkZNRosMmsjsXgChMzCMf+34QtW/BDOfi8IhzwAWhmClDMl3zDz5u0vDScT+GS8AYjIMjCqtJC2NWHwyDDySAAQOjLzpS/mdKrbKWnd593JCGvKLI3Hoe//vaQDPPRmNZy/QKeQBypx95/rvfUB4NNqXDsNfwiCDgAMTQxBauo3cMDO6r2yGR3EbiCVNYr/mRGG6CKxZK2MT6eghBSvZ2cMjHKviiISGJmGQxiHnhj3Vc1aUc5CtG3OKmnj/mkJMiaSO7l/9L5Roq0L+EQvgAVByCAk8YnO7puot/usSMicJYZNhHd/QMKCEEqcw4ZFdFPfdkqwBNA+Qzy9ntWG+P/C3QIRvNRV4fQlhj+fowAb5HCooqxW+n98Xt7PbYMOpJ+0Hv//+CDAQpBCC1tQw4ZF9lcMABEAA7A41qC07OFr/EfCf8wYH9/TFXinBHTTIAYCPAnijA7A6/55op2JKoDuDXCHhD7RQay8jHGOEFzIfJBh72h0v+k3PXwagEa6Jm+3XBkN/QPi6z4Kqb6lxmocjyfvB5D9uoPwYfbZhuoq7SSlrUhh8ABAAg0kvB7C+8ecNZQO6AcpKAAICFzIeEI4H/7gDvElHuGiMBCHRxDqffwiF+AAmAD4nBibSGftk4fOeQAeFwNTZSwiwTggcD0aAAgv60sdjCkH/uS8Ph4fFdBTNZayQMrYA7hp2G1Pynvhy7/DIcgAKaYDGFUjUmyQaZ7IgEMJpCZBkk2y0xvNWJ0iv7/9gMl/BllYs9BIAzz9kKlUCOJXh5/hHwirHhHwyevBgLia/hk9QAzJVP1fP6/isSeWxzoEM2S7vOET+fw7wAEiMRUQompd7GpBBwE6Mj0OYWJrPkSyCoSrg6iCiOsDttB8QPizq2DLEb61ADdYcs7aj3/DdT+EA/+MnuL9HQejGCXmDaf7JqfHvAgAEUCDOMczKtHUSODBBgAO7CFFKdhZ0yLbK1jGU/UFdE2K1LP3gu3V9RMrjWwoYQZW7V9/+IG8ABGLIpUQ5RnW0tzgABygAFbAD3ho2ptJkMEF+ELdeX0Lv/niQAaAt3DFQcgoa74hUvIyioY/VlOGkQJW9WgeCAMBAANdhCiFtys6ZGNlvkmQ2Y5uUIlz0hieEFEcWwA6mfM4kvtDANT2yOPxBXmvi/94ZTSOFWIOID0bAVE3RYdaa7/lHW4EXnLXnm1N7AaAaw77JqVJFGJDIfEAVSANCbE2pk+4PbtYAJiMboYyFHSxiTJ8MGIH2xKE1nF42J/8BSu7ubkb54L4G6z7tB/xoAZBR7msitfgf4gb8gAai6FpsJZ4wSgid8jIg25jocb1qSNCAh7Z4sdupn5f37HAAHtgdOuO5De8B5Ix2OnT5XvbQIRnMRUWJmy2z/PXwhBCu42cMjG6sPnowCOGfGhX01v7RtgbqWq6rVd/gu/XOnfbwmrhLE1IgpvtwUIXe0v13kw+I06P/7GBbQpz9uD4+K4WFe+PxA34AG8AQUXWEiTRNtpeAqcDPcBWmo4xBH8BWIDCiJyIsE2mn+ARhUXLKhLLfBblt/HF5irYrcVDSIaY+idbhgAHGzAb40fuHoTcf/qHZi1W1////Lan7w2fOsDYjC8Uw/Ylhgz4mK+iEK5HM58U17KFEnv/eAHDZU1fHvb/wgNuAAFwUy4BgYcG1N7w3P+HMgYj1KTjAAByAAFeA54bNEbxCy4jIKt5NLLJgCJjFIyeTSAmArJQauGTWxZNncn8/MzGd1KdSjpWv+w+AQTeavggCAt6rwP7iRkSXtD4/SCPy5UgbnPd52Aoq9ae8pF1xZp/+zq3lpI/39Bgz4iCB4gbAmzMAYCkAT1Vgcidf8AEIgkM9sdcCJrLLeABkmDim9/zZli0SbKqtP+C+CA+CvPAc4cjTy5UayV6hIWpA/8AQACUakI9ZtTAAIxLiHILeL5WuX6ACVwJr/O9Tw0dzWglrMCflkGtvm514FrQPhZvPOLsXWLVsz2T//4zsPbGjznwkFjqj32/8QN2Jgdw0JhKE+34CwICfSpaKs9+v0HhIAVSALCrU2pk+OJM09tAbK4sTsVwf8+YUfn7YrSNO4FX554H+lnzo/GaFbrzn6B4AvWTQ85nI7/XgOxLTyedl3+EoDoHFsHbZEX21GJ8XTxl1/5sj8S/z/f8jsg5rHev5hhdJUlpATDPEDYCswOkYRPyphCGQa4dn8SAMDTDeYLQXhzC6TL95w42AAIAAAwY8tGGzarv/7JNra6HFwFMH0kqB0oYc2bSL9wAPKC5I2WbXU3R0pJYGW2zPY1r0G+GEJ5cDHd09mt1DxdS36X/8/DUt29bKT7aa3Pn+ID8EA/EYP8QjYri4iltJSuGwk71/HYt9AOAAgyl4tylM6XpL2hw4X3E6NP/59wAy6Lc/IrWN2/8QG4+aaQAU6q3bU/p401mzMQYEAD/q7o197g8uh9bM/38wtErnH7KYy8fiBubbDAA6DgoJPG4Su4doM74CQQzOZ1VombLbP8D/OCEAC4drNVi9Gv/cwP5jjY74ZLyKYa8OPBW/qydt4Z/9L+f0emCqyOv+9k+4Z7NsxD4QDngDl9OZB+8AZ8Ukm7zhK/n8N8bN3gLPOQBcHem8hSp9Sf9fisQHPAAcAIhuAWXtqgMxCgv8v4AX38k8P+IDHsmYAQHJAnibI2/N/+74AOgpQXPGL6vq8eAB+MJoduNVPmwQtVmW4XyJ74v86H/CAdgAJGYiMoq94hDWo4zBQROndUc6s//uNAKfFKMl/GNK3VNuIU5VR//7gGMv9nzv8GOl2iP/vBLEQACNy5eAHi7NLswAAXBCtB4admiNhguhQUDoO0OTH3/6AwvEAHOHxSo1B0C0nQxoFiMUAiZhP5tFP6wH98EhMzjav+DjzqJ8fpZNx6DcYghqFAnGGLiAxAAeAQvDmHvxsu5VUr4PgDoc4ORvr/SrT5zn/YAyKUAEBHPRJiV73/eAGszRM39QDRjCa4slDKbVlWuwkZy95W/c8YuUTiSBF+eZI8ZCekPiCc+qmnJ+/wF8WoUWv//T/CA2AAiBOgceo4hG+tk1zGgynBfs8vWeKaIP9Z4AAgAzBXY4y0m36tAnyXvf/HggrILOWRFoJtgn3KFExMmEnooWM2blePx7LIsDsERodaGgAWTbiFu/Zl9KNgQwuUIkGSC7Yfg1MOis9aO5LNSDguogHGaW0nu/zdgK18sLFqgrg5LT/zwt92befwgN10Gbg4r+v3pW751/9rCX41t2Sv3ewDBJGPkY76SUeJ99k8O+bfd/+QI2BoaqrJMen7A5wHCWYRwBTbQ937giMEKUVqSVmLEp9xA5S8TalFqv//833fveMD/GCAK9Uz8ugOM6v/6AzFdBMrlyPvY3fWMJs1NaCvp9paYltul/V3J2Tkf94awN5XCBwDp8QN8YZ+Qgmp0hhTGQIAhgDhz0hvv+nGe9Hz9j6KBjWzNbcsrQerqeyAVG0a0NGVABUMlKUTvtbnqYHyGWBRRrXmBib3xH+4AA8cBbSLhmYjRrI3B2bT6incX2P36CkIsLJK7/9ygrrCOR3f/Pw7SfEDYdTo7g7FTAWQ6+MmVXacGHqYihtPZf8VJL/7DYj7d8RKr/3XgaomYolq1boCV/wNtvLvnpYv+/7QAmDClcqxUTT6wKBzjODP89Fdd/b/+eNsFoixBdp7/emBLaQKhrpNMbFsjmcjIcv/3tLSHLrPPn//ZEfD3Z0T97sA40p1mrV+/6UdaqQIU/hAbBIrQ+7EmX7E9D0lnle/14Ag5cHDEbyhlXCSieIqkclU3Lb/wXJFQ3g+7TZg6RVfsRp9/j+rvls7QjRwKkowvwxt0wMYe9PG9E1TPBlPzqc9ULL2k/hs0GDfL9Ou3O3wEETazT0LUhwjFXw8j0Bu+SwRn5+jBMVVfXifd/0B5StI9knhp7LGrAQvHs7ww/4gbDAYFZHq9sCGJaR41Utt7P0Xg3tLXx7wYoqXAdx/Ahla4YohXP++6j2rrT73vr8n2ZNae/PA0DcEUl+IjSoJujPZJn+10ILzuhrC+//ssIcE8lrn8825q7u6WamyBzQqd/WcA2lNOso/6g8bSGjnEDc8faoTuB/AAMCeizaJUiVu+AEnMIt3nPQ0VtND/ggOIN6xD1a8UNTADi17/kb/rAAQ5LM+Imdtw3CLhAniqXl4ZCIr4qvENTC6/YAzgdKxa7KP3+H2W+qVPx/V7vql/MrhEVzr6tN+JJo//1jy2ZTwgN+BlGRKjAL7eIq5bxQYRpHSG3selFfG4vf+neYJYRd7lydH14AAgAFAMFRyrxqRcr8B6zc2l3/5aBAN36kZLBGVlDb3NaBgGG4vlLJT7f7CG/cRXn2YKRf5vGA9iAKJUxPPkOJo9WacnJmn8GDAQNyuDFkvgMitfE67L37kITqmFdEMTOW5eOaNJ9+hJJSk5/5Gw8CE79r3s7f4gb8zMZXU4vpJStaQQjygbABDsuocl9AAHZkYaVDx3/735dAAmB1GuH+YcP8F6bLwFDHf70zM0dQphr/cHoNidWWzacpvtAQgAJG9EZqbKJtsfl5lI0FJe9HfvgEt0xOWbJbr6PgP69R5U9YvGvv+3DlsOyRrPvsA6LB16JpziBv8ABJgAkDzktTB3FinwwALmjAEArgI6uyOQvf+em2YBjicxyyy2iiHxAGaw8yFQnq/+3K74r9/nAACwKbUA4Nujam4Q8jCDZTrN3bxLtkbZt3Z3T/f3FwaFSODViRPUsZ/BhgXlXX22BdPFELdfeYEuV6fQhRK/tTOyney3//7yiIZTH4gKwBSADQPdwxUHIKGvhh4JEtEttttfWBqyDDIIP/CvqzXEas5/aweFDzxmUruG6DO+BjDAkEM7mdEWJm223/P+AFBlLjSMiPfgw/icQeWzbADC7fS9/X/iD1ky0uef/+HMay4tZSCEANpnFm3q3aL+IDsABMECIDFYJ22iqoJYrMCMJOEDNrKCH3j/ZpESFE2jE0vaEHRr1QvhkWVm/gEwat0gSw2bCHb+/hbEKJV1OzpsX3Ug/EFuwikfqV972hhwxzbgD1ImaNBds89gu8fI/yD24wCBX+ICvgELZKog8hNGeOf/90MjLCvGuJ38Hobl53wqdLW9f/bQHewBBacNopaWTf1FbgqrSvv/IYB4GgTqcACAnaMSolc9/3hlMjDhFXLLuvuMDyPeT8f+//4gbCndv+voBFPExalESz0tAAblDcsEOTwgT6K9/gegy51oHcFMuV0mRVE5/7vhty8kyHhSms+GUTmAKGvMRxaxOopzWAAC4IVYPDDk0Rg/EJl3B5muGqP7DQHc8ac4sf+3lLhs/av4gbBdsc9TNHqAKCM5qAcJNdjpQxsT/+rrxGx09+9MhFRRE4kj1qXA0h36GZoACwQ0l6/SwR1wi/7AQ3pKr14qDSycfqmBtvjnhCbZEJbSoNfwYwiAECCAI1AFhRubU3+BIMayFSe9clIGEf3AKgHKoAgGexRM4yid/4UDLgpJCN6Jaxv1TV+/vGa7Dn8QCDhsVytVizP89V1yvbv8eBFibc4t8QhrUI6DB8kYnRDmUo3sakOgfAN0OADgjaEYlBK2F26NGQAwMSBOlGB2B1/wUi8iSnnHz4Qdi9G26f/v8OKwSHdq/3MiaOxw14gPRW4bM/bDh3zpoSv8aFBSjC/v3GK7ow9XfXSf/9WX0z939rQAQGvx7u4qacagX+7RA8UQAR6cMDCeB732sUFDj7tcir2Cth7cLSZGAIDuAjqrI5C7/56ARCQMjlJi1x82IPw6pwVeQgwc5Oo0f3t/8bUSPWbPIAPtDZeQ6EH5aucEMAjUgUFGhtTBhggCAQ7Wy5AJptxJMNzI4MEABDClmO42L8AAiANcCBrLyMca0SXM+0YyOgrPQ9DGoUH2U3NG09OJnAACgMA/EDpocNqayAUGBB85LjZ4aP3+4FAjAtV4lO/5HpaIj1apwVBLqVOMy/+3wyu3wgFegCV1AHBLWIsOKMv+7TBRkUaMhDqz/fh/NpHsV6/3aSEmmTXr3/P8TnF3kIlIzRNpLXjCBCrTqd/Mp4gb0eKJlE0Iz5VP9tJhhzh95RIljzJDAEKgjAcxUIGGxnRXwwAF+FFMr1syYp0T/sBgyTlM6gZTZbb87FGABAACBRv14OE8lO+o676u6k1cP7P/6y8Thk/WuHp4W2XNbj1X4ClA1RRDf/C/X+ZNmyWcn/OEDqenNd///UlkDcS/DEBYY0/quT5Ki2EQfpEIjIIzEEKYxAeAA+HzMFODHojXBbGOf+8IgUTekGH1IKubG34RM1hpmfr/CDbGofv0DdcJXfD56f4gNQBQb8xij9n6rGLwBEQ4AOCdfKCVkD3/A/AW+CkotbE11v/+EArD6wEchToLyyFGCeh8DJDWcp2tyL8wAAXBTNBgadGiNGlfdsYAAOQAArQGPDJojAfrrhuJte8DyaYN/4fQOQ842PhAKwE44Ltl0h1Nox2mNnRIGoOkshq/vIWfEbCpeTDS38wOCgk8ZhKWXDdBnAQgANkRA6bMoZrgPQIRnM7KsTNlln+eocHAvWO9Xcnc9nYev4/jf4gOYcgB3pfACE66+//+/8Qevwd/f137/f/4gNQKR2p9LziAOjYKreEpipNIz7wwFoAcvnL7UIBjLpf/mwwGvsHccAKDDMJUu4boM6AhnYzoqxM222/4DCDAW+Ed6PRX/tf+f8IH8/A6QAAAE3RBm8DoDjhle8MwlhHwj4RDnCTv+nX2p6lHOEQxAASNiZlKLqHc1qGAACYMA7J02PGiN1A55QbEjYMaznAnQRa882pmv9HJuhepkNMUncb2N8NcAR7AbDfd5/wH/Y9FwiF/AA8EzkABgThEqI3QPP8gKJ6AhaApuuK9EL2fQxCZYAmrH2QDoUSa4aK6vf4W4EgxZKTMHlJL8Y9/5+gyqi7Js1V/vv+crb631vXGl3TzmJK+NwAH0ADUErVKkTdJ17+AARB/sYpWQ5WYZegAB8uMADcKvgSRxvX/tNkQAYGcBHVGB6F1/zvkAWIFBJWW6nDikQj/wYYDY23xJmnRAGmBWGfQzbqjf7vSHTpgt8y1yU4PmBjUL/MntAnUyid/wYKD4DUS8JQCsD8F3ZFwBGizPgv/c5xnIzWfSIxwYN8QGYADyADQPewxByChpH/wYeDA1Z7w/8Inrwyo38I+GT14AtVz5+/8MhzAAdopgACAMADhNYbKJMEf8jw+GoyaE86pw/n9hFPwBwr8l3HiW9w7I9wj4R8MnqAkZ6P+/XtTrR/36/xWJPKWCNrqA+9y55/EBqABeEjJqEsMmsj2/gIcMFOH3hMiWPLvYBVQRgOYqOGGRfZW5Q34SlL8tmiVf+D94NrmLpgC6TaexHqcspw377j/v1/EBb5QASAl7LFyckoU8HSC0IYlVXXvv9gGAA7sIUUtuGnzItspDp+cq3UMBIUtR/xg83YG1SP/5/4gLwEjHrafzgBYRQrutBTXKWTxPQwYDwAKZQBggqc4EyJpojeRGQ2YVW+QljVmaE+UAiFJe+kn/++YD5Z4/1uwYkth/uf/GwQEHkIAqkAWE2ptTEQgDkhu6EMhQvqYkOoJgCDuexSALAhUQIVgisqu3gAEw3OcVJJfvE/VR7rkxfFhn+Lf7kA7cAAgZHknRnGF9/3FB4vENxgN0i4tp83Sx/+/5kcyOYlVPpPFRUV+KhX9eA8CJieafyiI5A0Gm0/IgQTlpqfgKKAwXmVdap/7sheEbezX/b2jGS4qxfcQNgAVYQaq0fVDs2pf+9YdEyS4U+3QYT+pgMcXWFSbZNtnzABqJgUmwln7JOHzy29AefEBg19jn+50wO7KUeeZco/7vGZDI6mOxB0NVwfsBC0J/QpHCBG5bx2OPLYZ3VxhWBEjaSpA6GYnv9qFKPksTC0Rv3coslitJSW70o2YZR9WG/XZbwzAxnzKCYN/3/6AYGRBX23kTE3vyilTRDTn8x3xTTE19UotKTJaDsJVN8QN+AAkyCKimFxLvaxIYbAABUHAdk4dHTRGAHZjKvKLqXpa1ICwOuAwlS0bdR4ulvGDfFHa1FYhfK4OBoZoEvySWdzC398Kpc5ufYGHoIJFWVdN24A/kV1GwEnTJfSYXNoj/t/DbYNCPEDehpwOUWjGFLAAtoCK4QABEhgAoURRRlkEUbf/8H44A8EjekwmVx7PGAAICD8YMfehHWxGHXDyFS8iKKhxNtMdPiIlWIOL9/IrQTJf1TuvjINU8jLE57//gAEiMRWQVWpI9jUxZzhWhn50G6j404EOHOpbDv8azpQlDjT2xE99uSPYGrMiWS2r3r2AzWOuvWBS2rLb01/v8QNghAAIDDO8TWceQmx422WGDsd12ajAxS7SvHY9BTGeCuu9prn9QBqCQI/TGT4SsX72sDEYgPObSwLdwv/+AAU2na2vBpwEhuKEA//t+P/qBtsuKj+nDfztXMEPkWHZQcvhf/AGuTBMi8qlu/QJTA8qpf+Ug9ZY7H+0THn2gouIGwBgDzhaOknfeDB6th7Y4PekwpnPg5WAtBrqLeybb/r0ERaQmC+SfWvJBQCdqbD/bKeM1qv8Lx4Dp942k8BIOrfgIQRg5Y3Bd8u+RN2g0hTLbYEjXye/1QdRSOmN1/1/PR4bkWIt+kDrTaVo7/k9tlxv/pwbYadCu/EDYAkHuyqU2MWdI1F72B0I4Cj4h9PLEXt5INY1ZUwaw2KyG3+4hA7l3Liwi9kou/9gAAwOsa+2RpSK85P3fATAQkmtTrTCKQT99KOaenP/Og0AleEKLV1GzpkX3Vh+xyIA4tqkb4Wwir6HagDC26QzlbSSYC4vEKz7zdH/zle6YbsEFROgRf+Kq/b7OO7HYA76AqmxyDyFkwtefgMCtfaj7PRb/nog8qUz/t2DZFxTL5jh5UlFAoC4QDEIsxLdK5/veAQbPzOc1cKxghdcVDlb9VuA+5BgAPANWBnQE1YiyQgz8AoGigjTlIX5hZkhP/9qErKtC2Ezb/+/iAtLZGfvBh6ju29siurgjCXTnLl2eqBo3xAX/AAsCEoR+hXKJGxZE0/gIQ6YADHgdKMeVGHn/+AVAYkDnXcVgm5xp/2mmQYAHEi0lsjiF3/wbMQxCDMTPLSTGs3yT3Nb0jDssl++m3mYmt+r/hiFjCQ5CiJcVMAIYRfMGrfvhH3u++HmBnKAcAWfA+2HTTG4Von/zcAQlFqg4lEQUga/+D1gUMYwr1+TrjL8BJLwMWWvGFrAAxoCqEUn4G4zFgak1ME9/9gv6Y4TXr+n8QC+AIIQBWKA0KtTam/+BIMdns+4sRNptn+eUsBX3s8Bjn5Kfr3/wx4ADjtMAywMpe7nxOBrfjwA1D1UNRB6DRpEMJclBujn3wTHYiVftUZrPFYgMYADkaj7K2uI7GJJ/voDGkQhMrDPyFjKJzgzQbYS0kj8ZxP95kQyuwisSSljF+wMWDn6GQwiRwXQOcDCm2vRTVbEsf+I/hW/8AGVtLPUf4HumOUSU3vX8IDYAgAA5wACvgBpAaNqYAYXdSM5zDE20xwEAD4JR0vzkg8JWL97YUG2yoS+mQaSHDAASbEzKc6sMhrUebMbupzq46VtWGDAXlA/KCYkapzLz+QB6Bi5oCsRIPK4TcBqg+LC7VQMEcidc3/EAggAcbaAi93ya/4BoMWClHEIkpI19/3f/wAEQlIKsxhSXkhp7hPQRxaQI03TNnRxr/3oAFAMexPqkseJVMoHf8BECkFBJ8xGV3jVRf/cIALi4GpNJ7+0TROf/wOJHxCmBXlD6zJAhgozJGoDbT3SCQodUfiAQQYCBgQADcTkIGLbijgk0mRGgpwNzHOcD3kBqpNl/etpJmegsq7QBAYx45hsr+bKohY/3BHFGEbjvEtSfFXO1WPDXnfrVuuAUCFTg5DFEav5KJG//V1vrbXcrbUP90IJJD6wWO5CoSc1X/eB2QXaE06QiiFGiPPN8QNh687p0+7gGvW/lVbjNKzMTjbZTSXNvsokQIhx1MOU2B+HgYxXuYBaZ8RIxqm4ABnpLM9CyrtbJAYoiMSKxFZjf3mExzsDNIQ1gaIVpdAAImgApb7kA7yiIf/oTFAnRNz6Se/8/jrke1RJz3k//r18B9aR/97/iBuDckpP/7y8VpItWbjsUZUmn/oD/oBDbVA/AHBlFat5JaSTTz3v5k8ys75Z0f/4ADwMgjBKtZR95wq9MIJGZKqvl7v+0IzTTz0V7U/9oGWTFKn/Ag79clPPv/vvxfRNQVr/MusX5hHkHtKX7H8VS5WW4fCA2Aoxy0oUxL9KMCOeqxqRtL96UPTNUPhD+C2sC/pBVxL4uUT/SBfCW2v7Xf0TgZbGg4vusnrlh1ahXYHnp5R5oLTqVtTYF2wNo+ARBYf65REiGF1//wMGHEstHDMyQXZvXMNpEWCk6rv/s6cLiUYdirH/trGhyvOq4QG46LLbfyd6SMwBmAyoaNXaSRjSr//68NYSECUyyZa/XsCripyIRyErd+wzJwfokZOv/44LpisNe95Zpx///dpF0VyNr3c1CBIamYDdSqkhvl2Gdjn/9Ew4oqtJSq9ZXxa1X++cEi2OpKQLp7RX6rcRoS52fLM0wKJ3JettkpvPY7kff/cPTmFo2Vh1A+EBu1a2m4KHv98LfJrTQvfgIdelDk94xvaGvfGlo9JFnd9/BlCi7y9JFHaSS2PAzCJtMt172yHMgmNPsgxt4MACxAWaGIq+kipRJvf3/XP0Ox1/rpBz4VWoJxD0MI4vMBpEHS6v9jMSsGZRkAVtEytqX3/qwkt0+yrd2YA9Z/R8lIWRpzcvsVBV3BdC4gbmVE9jwh/eHKBXXZHU882cPfNYykA+X+Dy6Xbm///MVvvHyj2ZR0k+LRyiz1FHcybtc3XBzc9I/rAXxFTdWydOv1Leriza+/nAHdzmGSYoSioGhDyLa+lfv91OOPQq9WL9E4JV3u9QfRe5rOi/+vANhBzZRDuH/4LiBsGQYAGzraS193gIDVgSyMH1YqySk3oLoqt10nb/Z8NNgbz5XrYF92uX5aQGGAA4AiA5ASt5uUyAnN30A+ayWxxKz7ksZjAqJ8Umwqn3BGA2vDGGa5u2281/zUrKF7xi+WJYCvSKtt5qBum1M6SsB2MfMioWc/0oQB6DVNHEB/wBMLfiSKmoeW8yz/gZHmFx9NIJRU3hGa2kAONHIYMW2kCHzCb/LEKxJBPLGZRQ/1A3rqcWHpTfe4yAxCNotc6zBC//wfkYAbgnxQXLdanTaWkiMAYCvAjSrA3C6/4HvCRuzjpvtDAIbBOkNtatXX4H5b5hIvnuugDxh4gbAA8KCLa/U+1v2+9FR2j/0w2Z2r//0uDKW0Hcojac77SWgPO4P8RDWPn/mAQgZAAIRSC2e2zhSynf5BXjZRpw4MNIUnkDP0EWPzuB37w/iBMWwCv5E19f/z/f/z0zsdSx3/EUuQIuRxgGt4bf+w0ycQNgIw6Jll0h8ugx7AABUGK0Hhx2aIwYAgEQe1iSPKYiswk2/xsIS7KhZNMo0ng0+7rMglnLdemwJziAADvAAZwDSI0aIwCsahv/YkRiqjFvdLoxPyFKIktihS7/eEVI6roT05B66bf87YKwvKLszyEb/tN1M0sZLMuH3uHxAIMADgE6V1bMWV70DQJgy5S7kebBd/uABYl4ELJXjDVgAc4BVewJGUmhzUUFdMGSvQY2D4aCK2Ra0/BELPiTa/Bwzf//hmBeDRGV8pZH+B+GN9lBSzyUdZ4RVMhxXHMd6y97f/4nCB6wjYPv//z1DNGcN/X/iArAAQAbvA0aOcjimF1TIYcABJh0bLLpD7dRj9Z6LCcrOYr7g+gMD+dIgDF32aFz3/8IB3ykLQlV6TlfsR+INyz7IKee1rRIOYT8Tt/uUAf2c4nFeI6jtMjJAJwHolDCj/+gwQcBCkEILU1DDhsX2V+ZmMruc6lCra1YYYhJHQHc80XjRz/+7WkJET5v//CAVgSDEf7Pq7ERZaZ/nHoUihPaInpfv7/BDIQcGqEUraxQ2of4wCCucLWTTpmWElf/5LTOtvDG3SAxh70cd0TXNhg2S4mLss6P4r4NPnL/rv4/8IB2CPgTD9KypSe5TV8t467ALMRnuLv4l39pM+wRigL5AhH9qU/jn7rkWwc7AyoAMCCGOkEXXTdoEGNbxASEAhMjrMRZIxb+hrZkDLv/SE7/vmU8GsU7z7xyvjvsAwyiw1rw/iBufwRIk4+PLQANQBwhiHrIGVoJCOADAACAQ9OYAHJL5Vg5pA74hZ8RkOUd9LLfNY/OQv/n8IFrSeY6tUIk2o+X3MMbYDAATQcG2jZQTTpMJYAALAxuA0NuzRGoIAAmGQaps15jiYAMhUaqItL5ZZb5oGW+dHvriQrR6hG0WX38/Hl8kpK3hqqEVTbVBw2JIXof1ONvExoYqfqeIBfAA6BmKNLlGJQ3y9hCk4iH/v/AEYF/DSwFdpbnDjah/Y1BUDlgPqRq/cl334QwUeZL8u9f3+ZEqRei4gPQ/836D1OAG21Y/rrQPuAwHOWni5xtM2kl9lY9wiRTq1H/sABjnoakFbcLPfH3//3e0xkMHKZqBD5lJ8bCwyCwAQ2AwgikZk2STTfRBglbQ6nvzdn14En9GjzE7+c9j/sXTGp7Pp/54O0zRc3+/qUTRA+M9P8QHYLKcAAQDbuwHGIj98A0EBHYKJbLa8+GSF//93/7WxCiVdRs6bGd1vAYz/YmpuxE2Wmf8GDBcVsBBBcoVJNkGWQN8kCBc3R1fem3LvwYzc+PP5K+hi5XMkcafv1f8eu/CAe4A4XADBxLCLn23X+1cMOWIsnJ+AVoAEoerYmD0FDH/7jbIAQGcBPYrMjkDv/sIyMAQDmAzaqowRv//u4LAuG3sIQdxA0n/4MMACwGLYn1SmECVzKB9/AKgAbBy4HyjYj06mX4AYAFxcC0mEc/YJxROYipGX51+zvwRSLhRLwTRBH/rrrLPM/79eDwL14LGImfP4ciYHCAV4LQwwnghXr62IX//3cjJZna0S823+QADlBzRzNI86gXqf4EUyH3lx7Dp/7jGvFE9I1i2iv9X/p/JSp788GBByxsSUw5bD3976k/yvSlnfQNekgZP4QBDBhACBBWaTUMtMDqvuOw68R4gOQAKgGBhFKro9m6gSGHNzFwLlgd6MjoIeRje0mAAYcZWiUz0xNSs+YQEBzTwZOXHgVzJt8q5g+cmADqsPkfB4KG5D0oKR/b9g4Jtx8+EAzAA0AtKDZw6LGraBgQCWxuqnOpQqWtWCDch/jXfxp18IHr8N0r+EPEBr6yEVlEXiSEtYn72bzNsaurhhri6y4//8IeI8ReIPUNJaoqJlV/z+IWAhIAABOHQZvg6A4n8/CR/wz4ZDnAAcBjQrrkTusVpNN//YA2U4AEBGkIlRC17/vAHcAhBNzkd5zL1N8v4ZDHAGPNBOonNfTCmsAAHYAARgDCI2aI3eT5YDXMSYkX3eQVyPv6/hk9fwFTxrHf8MhingANRDKqGE5JKWKTuAAFAcB9onDQ6bUwAxGJ2Q4mpISpqSi5DXHb9EZu+f/BBgAeCZSAAwJwiVEboHn+QJtDDCUBC3fl9C7/4wH8QAXUPi1ziDqGJvl4W6BhrgAHmFDqXmAsHZyYeA8CjpX+670y4Yl/DIZgSDFshdnkJktIx7938KABoCzcMQdxQ9//wawvscOX1FoVy/4ZDmgQEti5dN5U8APfUuzXH8I+EfCIc8AB1yYAYMPrQiWOLvf+FN4AOetTaL1e/hle8I+GT1wAwTu3K/f8ZzxWJPXgDcmtxx8/8SCDh2/W1SAAkgqJVFSl8uk14fjHU5X5iDOlhhAeAA+SAT+gRJa8Px33ipAMILpCRFgk20MVAMZEF6AwBlufOS7/v4QGwALCEfzUVdCZMtNfz9BnLpD25GkP4AghgFYkDAq0NqZPvssOACgOyAmoGrbxn96pCkRoxEqQAQQB4oamlpauHnLon6Nsp1hXd+HSIPs+bwxf1dqIy7u5IChBUfc7n2v4gEHXjLNivSTb3/cswBEkFapuoQn5qbt/p/v/PnaYNkcPIHzgzY2O/94LAAKASz6gFhl6n/NwbN70GSSa4bpaiFkvQf8f/VAuNmOvVqNJ/+vdyMnzlrvbzmlm/rcFRSolvtyjgubH8D84JgsC6F0ls65gcOBIm511/rl6rOUZD//+IGxn6gkAWYRyRFHUrvdqwwAcg36kMF564pMWn1DPgADAWSOTIxLFGouu/+DPi7vgEBCscY51rNU8s3/YstA2HOt5RvVgsHDcnKfaCMbz3mtGL1C7HTM//BCBM/TzH/2gDB+DePR/CqgjE939fHZLkZv7OC5xizR09yKkCri3gydkMG/TbIhYcB7AymidiKi5hGExOz2Q3P/StDKf7r4QG/QEPJzqCo6RIYLeOdQO2QG3h8Vt43kADUWwtFhTfmCUET/poRU5joUJ61JsUBKJhCJju33gBhKACb8kQo0HWVGocMaMq7ckKr97ueABuiOHRRlit9gw+aPQAAgCgg/f7WTQV/7laEmtvnvwC8msjmLqyvMzG7qc6uP61pK3QvghAlyFKCXOQ+71f/749B+9rY8P9exnMjRf+3Muao7CX+EBtgIfDwAGbAbNEbhAwqOk83QWVwvs3BjduAAFwYzZBocdm1N7xQa7Ihb6dBrwBQB+iaZHUuC127HAdgJqBsVt4eYOADsJ8QrC7i8RbFor4HhAQwg02W1vZwc4GJCXkWSLAmER9p7sUZrSku89Nv/ZooAf9vU//R6htVWjvEDZ/i9EDjcyB+I5pGteoMDIDERVmGrHNsljL/usQIkhB+oC1RDL/weB0fW49d38fvgQHbA+pFwV3kQCAALFHUBsqyoieIYGfAQh7ZLDfchRpTjpV7IrbF5114W8imu5FUpuDh0qKO1J/3dEMlJnrZwbXRn/0BpT9rmRlz/92sNdZj2Q+/31fhel429+9goUsdL4299mn5+TfEB+AAmAHhNCk21MeZKQQO+QAPi2FptJZ8wSgidGgl4CBe9rwjOr+ssjhcAQMxBkuX6SWJdinvSFI+A2Edx6YvQG7RtcTYfh5AKBQWRNCH7IMqimS/3DAAJgKsCZV2h4oSVP7wNhS2MaZz8KPH+++ltNedYYGkPIx4NczWtuAsMZKFy7mk51gWaV0J+/l9BhOVGoFF8QNgAIxrjjtfldzccrwJ1Hi+hhj81vshr6rd92U3p1j/v4cBeLnnf7wBAAQjGnAS0pX6aQvXiumsOWLBf99XKpE59vr1JESIWRNkga3uud/4dRIWNQQBCoK2ubfdqRkgSl9SLnQUzZm83rWVhkntuuffxA3oCGbj0VNHwLYY/gEhd3AAEAIBZdeUQ9n2hf5R2/XunQ2Bdyx8/+g5DTwAjCiuuJ9LIyh1xGEaEPhJx8tVL/u5MI7P6BvKuMBUGag8VNJvnE7ZOsr0FECbulYy0ky8AHAQleabSdspQyNnVdT377jADlAJJ3DWIkTkif/ONVPP+PIe6JQRHCh5aJW7uA2YAKH2y22DGs9BVffeolyUUdbyogdh5h1eGICqGRuwC+M7kpgj+4pjLBkV79cpqGPs2oOPncWSJocoTd6/BgAJkQzlYIRyz1lFN4AL0CGvBzM5QaeLjN4M0oGd4Q1m1sidrURSfguAzEtkVZ1gi+7nPe/iBsACwQzOYio0TNltn+f8ABioIQWpqGHDYzsr5joFzAN/CR0Eu4hrDYPDLR6ADEAMGGzlMiSOLvWDB05JJOsfd5x5AkiBMYVTinfA+iDKBkliJw5Blgq+BjB1HGCtBTmjJA8Jq/YHpKb+k739rN53van3+WpQWx3EDegCAwilFkOTd8TGXZ/wALxoraBqDJLIav4CYADZEYL9lUM1wAyDwoeeMypdw7QZ32gIZ3M6osTNttn+YyCovBr/wAvdNetNniMHaNJf9UDoVVZbRbgzqzlV/4XTw0G/iA98ABGLsh2U5ByKaY/w2AADkAAdoDnh00RgBQs6GZDlHJppr/D4ADABYXQ1JlPHmCUUD4jf4AhSQsRO8wRUxrbEtv/f4b/GACUTQxBhXPGSCJ3/+Bo5Q4UDCrJbJ3v+KxAYwAOB17dTNCK9/9AFABcfA1JhPaLROKJ4DIUedTtSRnvwEgh28rrnRM2Gm/54wAsNwUk2nr7ZOKBzWgjARBxUUka6T/fCWL8AD55NqbkWgR9B3Uk5/9q1BjGjiAQYcABshuqGMjj+xiQMgoKCT5icMvGqi++/zkQbegsYOk6jwPUgoD6gYruz6eAAZgahqsTZIjtLBh9xAAgDFS4ABoC5tTBEaoVfC1vdGnfvDg7QCQK26XAwO13EDYADFQQw1TUMOGRnZXwaivmU5tmajI7wAjC2sSR9TE1GEnXX77++AwBOHHpjzsXgxkioz4ftzBe4uZ2iTaBPKpydqz97kECWAiBD6rZjA5vf+8AMDYcMhtkzjt6NIf/gDZTgAwI0gVErYHv+buAlkHrYE8nVLOBgWAzfCb0zDp33wS5dB52BhsJGlclU3wgNjZQAuLAQ4qsakGyLTYAD4jiO3C2zrMOP/+wBtzgAwI0gVErYHv+aG4pO6XW6h9/3/eMOUBSEBDdaw4e6JcAMVfLlDZZQldln/9OK7bEdfrQ21fJ5lrpv3AlXou011Wf/uLAhW1MImXG9v/7DIdrK4BpPcS/Ou8aS7Lb7bzAAEAosF8amzZKAhVovp9b0K1+/5nAMntl/pgyiaBt9srSD5YZCyV3lK6f5gR1YydXIQt+/aJExU6yd4r+HAcCacpgzwcK8nT4gbGAP4hMY3Ko3K1pNtAX0cvVGKr5M6foGDcHvKJZunhk4UTWM9KA/kiUf0p71Gx/FrcNmJrT76ddfhSd90axAB8kY3QRVeWlTEgKBOM/Qmx+XGSgIYObwAYf7kQwaSviChXYmBlyu/R9dXenXfv/7BYBwpuRFht/5hxDq1olY//v5AqJGs7GeyniBudm6cI99UYePR9/Mzvv0lZ1zfzz9/7+AUvc2e12gBbCPmIdWwRpS3pnD/T4BGD8f2eVPiPrLs1fmtq3vo7bhSAbNPYGVZQN/snAbBlZ+0r5pb/2yZZ3fNpyY6o4/X+NIjMOowi7gwNNIEFm66J92wMWMVzwRO5E5/9DIcWFpDv+YeBuoIiPivy8nUcQNhgTaJkHYtf3B+jf3ijdWm3f6oZfRAB+sAAIA0dGgLfgOb+AUwu00xf4ZgDQ5Yr8AAjAacMFLv9hbuiixvTHqzqnSIV/85KCa1kQq9f9ZhKpPQ1rIWf/AZ9GEC2JrI049//sLO9jVuvtVT4ZAmalp9CX+EBtsjLOwIHHPzmBsFYbs6kh/xXVuDfoyjdabqffLYcDXvh+9KeMXumayZH/5AKABAMS8oAf/9ZfeLKP4ybSj/awBg6+MVxEPJhhj9fSAYuVPzW//2IMa/DP+8MN7cB4laNLV9JocL6e+xo2QNM2R91AIKINF5CPcxhjTbOnxA3A2s1yWi2CI/Rl5PCgBSAhuvdQrPW/VgeZl88yduBrxg9GAKLatHNlOJrznupt/nPhbJgbHXDdldub5M+5J28BHALsoz8ad7yl6aKcDOwCIaeR+3AAQGKN14TGNYOxYJfB1jOVMKZG2kfUT1wMuna755PvrDnh2E+IhH//6/4gEEJt1fLB+dujnUZgdaQcr4fhEOQdHPI1ojqiqIctn60hB/jGKZpYjrTQ9YG9/gX7yUz3v+E04eY4JweiLyE8K6m25/4MRVPhdmSbEh7/yBKbDzWJO+Q1Dd43lue5/IEUfM1s4d7Ew23LzdAH5D85oqZMoZZIMrSFLcpTLiR658AxjJHp2/gaymGidms/eg/5H/v8/GRNu/EZHRo0V7Sm6Qpwf5OoQanwQbnkWXpJYuXUrOiueXTnT2a0+vIAHZSd3uf/38ZdMTcwYgFo66CdKz8TXcxC1ZgOJiUPpS8/9zGaBXI2ySdju/aYZ3YWoQ5C7p/4SvxyVJguOC1jfcQH4fX3iBvUFDGAYctjqy7b/+rdn6j3n7+Z/hT0B1zteSjrq+IE5h3IPc1ohFT/Yju/DsVAME2t2B9O32Ju6mGVyxaPkO6k40ZYVI7/tDXqj3H6cMyHE0N3cMCLMzeDtHuZ8CoHaD8gfFnWMx8LGEEQNBdySs2Jd///nw21C2n7/hh6n6RXX0//wWQ093Pf/qxZeAVXxAfgDFcSvbmzBGGhaiUwBSWekgCgjSyX+U9ORoyvIiITMIrEEKcxVkwEKuLVSPg/97hjYfZ9jiP7AJaCnK9zbugHeKffAbDAQPuFppZ/GQGS+T3fxA2ALQHQAn4xYcbzQ/74HAFxqmQHnA3mlFhgjAAnFmRKNoZNhPf/JcKghBK2oYcMi+ylOFvz2/3hDlV/nbBgIAkFj0y896tYpgCnkRY712u3//B8S0BUwPaiXaY//5wAJwPaPAAKATNqYLmpC2VOch89xE7V53/Dka4vsPw+FDNWHIxF/fPmIjgbUex8QH+jAAyoihUUZYzvz/MzGV3FXqSUtakMOAMRiKiHE1ZCWNTgDVDgA4I74oJXwvf8wJBCUWqDnogpA1/93gdk13DPQdZF8JHcAxM53Htpo/iQtYBi+rwLff0DAUYnHKOQXY+7uouf8H5IfFyiZQ622U4MGAagv+D+k1/1PDhC9uficIeI8IPwCGdjEVEaJmy23/gw/CAe2d/Fzcfv+/GBMRaB2lkKMnn/dAfEYxMt9IfboKJ7HCQ/URbkxL//7eQq/Iyi859rKdYODWeQSMu8qzfYDOCedqliKMFyb/8AYN1XwPQfBf2r++UAAmVWDfZtDdcAS9hiildxy2aGNVXkREERhFYghTmKBwxIWt+xJ0RXKBEMko2473hVzQSQ1fv1Zu146sh8IBX6ZCdlEXiSEtYstvQPAGGxh1JKL5or6an9JowBAdwO6qyORu/+B7ggCD5IYzha9Ov8///wgFfgCGXJZYu09W4oomyDhlDwMcQ1yk38gA4IWCY9xKKQlxfg0CAkWX+yUf/Sxy716s9//+EA9aAEvin3yOAATmgJ6wS9LXyehX/9wCD9eC9VREvMs5reGAMAqrnju0okTWDwzMcdvHEIaJRU93kAhrE+oTz4hcwid/3EwAmDzUtSIsi4//7jF6IWeNxJsqN4rf+wAYQrfIJVb+EtPb3kvMiPibZEGuPmKlI5n/VBxYaBORdK+bBgdtlPtOvhAPdcBzyg2JHrczv+1LQ9Faqzr//QwBKGCU15+Mwa2TXZbFJLHujm/YU8GBOiEGFIiFm3L2F3/yBINmIADgjSECgjfA8f74OZrjhFaF5x+WOdpbiDff94Yj2Lqg7/CAd0WaFSuRnPkDcnyc3t5mAPg+RhKpfQlcmNs5wKCxwd4hhMuJAAgQU28hKaiojG5+DBl4CEstMSa9c0XwxwMOIHLK/J2/l+qiSzhfvx6wiT/hAK3BGAAIB1wAo2ETad5jU53ccn2ieqpo+GH6ZEGyiLxJC2sTDlLHA6ZOr/wgHuEIwcsbGxd0y++18CAeVWmIA8EqlAAgNz989gI//92gMWikSc5FlJHv/u8BVMY7BGIXfTcWVEDy8bTrgBMApRAQfNTnh05MY/w2VMNYy/0H+Ajkcqtov2/hAbwBOpwAICe/Kil0L3/MtGyfUbd70hoVmFVaSFsau9t3TshqxgNVV7AE1j8Zo6rU/lMT6FE1btY1ejAAnVXCIo2xvfgegY7fanZoRBppj+f6CmCYNspJDR0boWhhwAsjzekoyhrZhSkWH8jBqq9vGDP/8MBnwJR9MnATpuJqRQj/uBshABESEPURkIsSX/uAAUCkiUaqb8W5z5v+DCKr2MZcnFvYyh/x9pPpgRj6iNc9gewgduOIPOkbjXFut//4QEfjQM7ZWYrEKOhcPOtXbt/3B/4QCssA64AnU4AMCd/KiVkL3/PoC4BnwZUwc5ElJHkf/Bhw8vDEK4PMoJjNr/47EHrAxJlqv/EHqNWy1XwzOz/hDEcuIPUNTuoBlP8/9O4/n8/AQkAAAEntBmgDoBC4Z8MnrgC6jjp5/8Il8AQQwHYkCgq0Nqbhk9eAVeXP3/hktAcABFgxKaQZ7cGsklmQQFwQhjAAR4IfHOP1mDGSTLIADjZgNtaPzDkKuP/3jeYcjr1Fn5kP/hTYlmKipgxc44A1ck2h17/8EJZQ9AAxCAwgqkZk2yTTb+LAQQXSEyTZJtvhkEnABTCIPllEnPJvvMLO/CIRN4ADhw3w4jDK2m/fr/3DIJPAAVZIAwQVOcCZM80T7wjnfwyeuATldM1z/8ViT14NC4mv4kLcABGA04YMZfRhjfCSxnxANcCBrLyMca4SXM4MCAZLQZ8jC2/za2iDBb2h1P8gzXTwCoSlKCA2GlC+npmu7ZAQwikZEGCTDQZKALtppjan4sBK2MG51Av4QD/AARIAFgS9li5EXSceD08AAQAJEBVJfB2894GwshGa/dVfudKcGHSYtExKAqjvvWIvyEtqNX1/iA9AEEIArEAaFWptTf8ACyAGQ40kJgiT8lg9eAWIgA6rADZoBNBKWD+ASwTIbKEiwiDSPdABDkDU6XigJUx2M/ryEjDWmSKVbzbJBkHHS+ANQNQjjnC8wOLTmN8EWAf5Qz/+IG3EgAGuAAgDRAD7YcgABMAjIFg+sHCEOMQvSceV/uHQMbzlx4jaqSoAIERxEEmWkd1BXewCBSRpJCfFl9k1r+scNYcsKeF13mBhx98z2fnC6NlW12ZvGiUA9cpIl6+g/L5l3xAIKIrGbzJFhuwwlaOgQ08EO6Yht/vcBBcJ3737Lpww5mrfdUA8HYvp70CXXyYVpQHwgNgCwJuChSz6EN56TWNeMkLlbCpIItZpGjCBMzR8/dmxLr2rGJVkwp9uMJ7/mAADlAAK0B5AaNEYCRFAdriwdQ8M5kPhLtMrjiKEX5/igBcab3SyaXXM9+zeNbyq7qGWRhADM6vrbz9amlxEEREREj4VryJ1uGDOtpTVEZpr//eEGx8fO+9zoS2D+P/3cgvHbbme+6hi2qwFNaKSAuIG2x/A2iAIxUWpIhLrbRrA/GWLFbiqaRTSnsAAFwUrQcGnBojARwxbkuEOpsGO5gAA5AAHaAwgOmiN5Cj4jYVLyaae/QGynAAgKwhEqJXwPX+GhECQBDrt54O9cV4/8676mO0f2mkktXvgMaAICiKRgQKn2Ca4Y3enB0ylttWk715rRr5ohx1gZ167wWAD2gRHO50d56RuqklN2T/7UDhhN1MzA7Jo2RUc73CA2+d2BH2cmLLVRVNaRf+DGWBsEwJdltU/J9QvVaLfvGwgB8YQSrTAp9LpnlovF8pv0/2fAVLeP9ft2P2ivC12/8ALAZcUcAzsKawKI6msns1Sf/7Mus47y0aXtnEy9MpveJFa55YtjNEtLO36gjDfeRH9P95/iBsMGGiAAQiryGOdmOdGGb8ILhMQyUvkj3rj0kcdpZosD39DgMsqWBv5SOK1TV+7pFeaJh3iV4YRGkw1aKsY8bbc4BDkoELFUeKTEyDpX3OYIgc5V0FOifCHuNt/7Yzlc///BmP4AH02ZOIadOCAAW6C1SxjHGL1NY4f/91BDIgRTCA+CDwwAE0ABDpjWl2MthKDpABDs2Ql1WIqn7nvdve/byZW4aAhss+gAJN0MHSsTPBW5dMr/02LafAnv9xinwhZrQ2AakvSVZmEwGQluVP/xot0OA/GwwALxo6aBKDJLe1fxJYjAoLIGfoMFnZhu/wEEAe2IcKlyjHFYaCngINScMcwlbzUPPN8QDWmAwlmkt7SskiAOkY1QwmJb6lJ4BaQONli6KmkEf9wAfBllWkBd+TRx0V9nha5oU9+j6rsP9umFu3T+6/AAgBLa+xPUcJJQW2zFgyongZ+uJJHQBiQluESvQA19vDiePCxNbgKz8uP/1mni/4vo3/18Jt10MsuIBB4YEBjTAZKvHQWzKd9AQqCEFrahhw2M7K/9AYebuhgBwFQuca0osjDtF/9dAwwegUMQwwB/idNc6oVHVToEf/+sda7RvnjXNfEB2AsgADDi4VmlQ9QSVr/wftsxuoq78lLWpDAAeC52CHhj8RvYslHf/a4kgMa2hG1HV7FvfopiCC1OQw4ZGeFIMBmA9IJErFhleqkp/A1GispdQkefW11Ft9/7JO01+S//riEQNviQQRt9QNWD9QGAHgAFQU25gGht2mtgFNQIkPbl9KA3vjA//4MHK8d//rxkTfMONv8iMg2QVWpISxaw9GAAnXuGRRtjd/AEuYQopbcMOmxjZWBxRFHhwRyE4tsuoR//57qfy/iA7gCFAANcACANEAPth0AYyEVlMLiSEtYkeAAQEHaC8gF0AAkwAIA4QA+2HOAAnA1I0AAsBM2pvMzGV1OLqSUtamH5EZBsgrLSQljVhhK6YAPigyh5s3c3a1Bxk1hB75WIvDMAYyEVlEXiSEtYn2vCFFr6jh02M7qwwxSkODhjw4fwdhjE4k9RoWo1My1X/wgF4RMTUAHMMg8kspk6FBWd538AJgOwG1A2K3cPNxKQSTEiIyT/+AGMhFRTHRwntYvyAAPUBUAZas5VLFbioYY8SAyfr/+gOpyG9E2N/+HFOz56awFbFPll/CA2wAAcoABXgNIDRojeQu6sinIM+1mEcgDUEo6W8hYEhKxjueENclQl8Og1/BwwAExRuVkOUR1rLd7bDK6nKrjpatIYIH8sY2WXCH2yiG8XjIIc9nCYVsGjLxDHnw++kamlc+v/EDYGQPCh54zKl3DdBnfZi3mB8Vq34B5PxDRaaXnbf/zgKAItAoWpWErEim8C+D5atJ62U4MAHwgxb/rCuancV4ADsAYA4NhDRu3pkIPmXgId1A+dpJxs550of9PghBS+44cNjG6vRBhq2h1Pdq3Pr2EAwMWaDZ146C+RTvvGA1UOFLvIx3nZBcwDiAlwXvSN0SXPYW7/8ROfYSAdkEn4QTJsSNwRgWMXKv94ZKBXmRfDXOXtj0cQN+Y3OLxrC/aQFn+FeRSsAB1AfCMUaj73//aemltSyf3+BgWiFohEa3K6/4A3fb2bM3vAEwWViSPqaiowk66e03FhQSZshn2hZ/ewE5AXLDFFVdxO/+4A+AXxZMniWS3Y8POcWJRLjeT8WiqJPw37OBIAAgAwgAoIpDCCixVI69MJVsmO9qEZ7cm6uBR+PM1fcD+Xcn12hoiCRCLmEV7/9ZM4OH0yLt1XKTkF0DiBsMAC8+G484Lqmqj+7z0AXETO3OwpENKfl+rOigeAXFmxvVKrusnqj+c9DUhZbUX1wPapt/CoAcFlOIeSiknBhdVrgBByaIGmGoXqVhKn+8gHqrgMLpGEiSLz/ghkQRLSVRQ9s6uTE4spXZxYPi11DB5EPnqb99cJtwXTuHX994EH+nwgNjpKFLLb0Le9x/bzCCN7lD7+hoemODYY1nOMR/I2AdZj7f/DIwI4BgJTptU0k07/6cFK7f/3BeCL1CBG0YFmVn/bki2pVsdgea1xYpPe6IauQNguTXLLxo3+kEiTFVOt9Xu2Ce3Gf82Yrcms33//s/4YG/B0c1aEOS/SDgr3q8qCxZHNMPY9iuZefWCVLk3HJ769IxYpLqOO+ys1+ORr7k/n/CO9dyH77sAUAA6orAOnbW9iXPBP7AAEANVdwAImNS0DDewuAMA9gtMqczuThIP4MXqQv0ctvdjUgwYQnXgEmACveqb19sdStLry///rhWlDkRn5/yAkF4G7Ydpp0CAdgod8t/WSen/pOMhS29EyhlkpPJTV/D6MVHrU+drpvcufeSs7RzNr2j/m9KrHXmDT3KbdXKmcze/bOx4usGBzvOVBkF5aS5sIaVn0dFi9/RebmRcacQcUqRUyq8GLAUq0Q9xoucaSvGv/W8C6OY6pL7+ucQDallRaMmMLCicMioqDv0EmiZcOZkz+u+JOHDA2w6w0hjmqlu+R9rgg6cGFE89knR5wr/1oK0Il5nsPWVTwW0JMPhvUdYiyaX38+2TySSzcjiZshOqPdk//bwEBhRd6kVyLrL/LhbAwcDGAtxgMIIpGZFkkwylXLjsX/vf+rPl63IgIMLpEg2SbZf7wSCEIStrHcWWJ+qsAjZnE7cVyp0C0ZIb1vw2Vnz+SoTxdbIlVRu+zX27+gVfCA3C2kbj70Zcs2f2617som8/37rP3H75HfuR/ilYaqttes/AYuc4aitjvdeh/tKlqx2v/vDLNFj8VRQrtYb/6GpbSXgq/HCWdIWi2Xr7xhIyjqdtoVutUFS2wky92rFLf3K8OvSfq9jLoUppkDxGYbhGeJKRJ++Vzbub8JlqFeEBtbJ8LzOaaJtDtYC290gL4cwvRJ4diOpcuG+8N2GXxwPSNH//Fd5mPa2E9xyzrmNn8XKGOqo+/9zR4nmfdJ5QQ2TdsYr/XqWRiXmelT4pUMIu0wJUwQhXHUgHsW1Jsz30Yd3ctBOv82LjWNcs+7/5+Ef2dX7/dIkQSmDrhnhAbAkQmIZEVF1v/9QH4Vt74tbjXt6zclKUqevjAE76AgFubxM0Xv/653pv0zf/2cFAGdd2sEKcMz0b//ns9ioFHph8pKv/9NwEnGBtPYBBgpOX85k//8ZPu8FlbaZPfflgQmbSEQ/Vf8sTnL+PdWKtTTl/8eMIE72vOUH/EDYGnVYhNEZe7791ggwB+to3BABF5tB//vfwbvXnr5BPvP21++vdYMgiHShvwTZdLB9ZgkAODOAf0VcwWKUvd5xVdxz64oJOtqhn4tGyj1DO1fN9xytDPWAIxppn4DAYuV4FtlVC2ckaFP8/w87KethWsjiFNWB+jb3jQ3HKnzXCA2BEAAQI3CkFACw5NRj+YpFP3kANUDcQudkgCx613Yf3c0KyXPb0WYRpZrsUNdLqv+YZCAxZIdj6cSE+3szAoJiMEIZuf91B/T3nrXnGaAQKKlWRImfcKpb9AIQYdifckaH8KUjhgfvCeqNue+/WaFSJ7bDsaUflPn+9fqNv2lZ9n8IBXpgAZURwqKMsZ35/mZjK6ir1JK2tWCBwAKhLpFUjMs5TBAwjDAzvXF/1BxTEuWvjyZup9xe3PwP4kLcHefz+1vAEGhAZzKXdhs2ebUD4weC3YmyhDCdjRAGHcge4dXWyMuoGoMH/icIfP7w/wb/+evnSdYz9f+EAQ3T3PDBk2AOzG7qc/KOlq0h4eEA9D8AYBfo0Z0rKUjZashmHwgA+dQDliks8YIJiP/8NiofgAVIwdlgLK8a8IIFBv8DJCFGajUweM1JXwALKWN6hMr/8QHZm1vOrzeakP5/9AT2gDgtqOlHGGXb/KLLKNwX/0QMMzQFFetfEPlJu94ig4MCDSlCRGN3XNPI0Q87B/4gbAUAOFASDMNQw0EjGSt5mKCbpVJfTILeH7aGQwYtuIEPlkXw2MssgBmAALAq+1pHEPfeAA3ApaD8kZBnmXOAi61q902pgExjZcUykC8xqHAACgIA/EDpocNqYEYPcD/5tDUa6vXoLV/WZI89IhEyEExTkMYhwQwCNSBgUaG1MIZtGz/1pCm+5R67gfuAZRkXed1DIWkxx8yA4ZcdbNcQHYYIBADEYitjiekj1NSHBOTbpLQEwloq4q2IYtvvAfmIo22Y81z3fB28B/g9IHr6ser3hwlNZBkAXFiuWd0bv3//8QHvBA0SaSGy6hh5arv/BhgAJH6Er7fpm4AiVflbRPvbg/EAHx9C0WkM8YJQRO+MBpwwUy+jDG9ElDIfNCBL2xk+9g3Ln38UAxhMoSIsEm2g9WMYWZN1Zil8i/v+fgvTI0OVJ+/qfrwgZh3iAtAASJEEgDqdSnASE6ma/fj5+IBrgwWy9+OtcKLmQ+SDBd2hku8g3Pnwf9FAIIIlGRJgk00GQtK+6+L/ByiiJCqV+/V/D6dX4gK8YIFoGB4GQcFBJ4zCV3DdBnfaBCM5nVViYstt/z8QZzA9ECv9PpT3uQUf+ICsGA/czQAhFXPksSSTAg5yI7IkEXzw+gMMroImStqXYhEiopD5//xAfgA4YZOOFqK5x/SF0u6BDM5iKiz7Ess/wGg4ACZEMroIrEkpYxPSAA3TsETRljefPXwQghXccOGRjdaHrGjJ4FsMmuh2/vGQb+39Kei2DPD3jfyGoUeKiP6v9S3hAK4APkABBhcYWqnI7AQUL/kZCKyiLxJCWsTwZ8CCEC8YbmTDnReYCHw8ABmwGTRG9rwhxK+o2dMi/KsZC4QCZyAEmZu2X/Zupgah8ypxj///r/iArAGCj4jIKl5NNNfrA4KHnC8KZcN0Gd8H4CkhCNVeIHSaSX/4MNgxQmq5qOTL4P/jsIeEJ8QuWL5Wz8BCQAABEaQZog6AQuGfDOf8Mr3hnwyGOADPSmPonCXtYAHgkVgAICcIlRPCB5/mBNoYYX4Qt35eQu/+LnKACLCjsLCf64WwHghz9H8/n6wzFYR+CDwAL0pgACAMADj69KJMEf9HBAFgJsZD3ATwaLTD4ovLI79AYSRHpl4Z+9omiIAIsADHVt8rZNxzxtdfIm/YcRMF5nhAEGAAsGga6E5UI8S2aIwwYB+QNjDsWcTzxCKKHdGwAah6xqD+NGv/2YP4YBMgWg6zmqSSBLpkGCDXJPannWBUT3e/mBc7Hml83/5kGEaevEh+wAAVBCtB4admiMAOwoNulQsmnUaT4YADwdpAA5YKjKcBKlr/5gAAoDgPscND5oja2Psokwpr8S/nGx6eHZ7QJgr3Y8wG8g0v7wEhglUNnBSWCbyxf/tzOrae93p+v0CsKe2ofWAkJDwB1eJm7V9X3Alq3vuBYFNu+XV1//2P80caOUF43KCBAAdDKRsnWBfMIJ+hJqZLX+wALBAakwBB9FsZ6dH/+cBIAGB8ItNjUs0beIf+2TOL+a3f/6A4X9tCQhy/3kCCx7sJGfy8jxFPHT61k9+8h/1cZ6d1ZRJ/0D9g9w3FJEyU06YuRJErwN4844apLs6MqX/+A7SEfDdYBY6yBN4W/+fCHNTF9ZOvfqJnkNGyv//5QjwXLQ3uPEAgwAJyRk1GsKmsjv/ugh/DqK/KQtl9gy/8XQB/iszYknPEI79jQh9zAQyLI1/cJv71n7I8Wt8AVSGTKqP6g381W/65FXaW/iox7FAviBvgAMwqRC7iMp3bWZe7xBV+ZlF5j5aU5wAAqCGbIPDDs2pvNhQy8NSSYZRbw4IMNOVwD4QAFh/D1F08eWIKCP/8ABEW4imPo31IgC2DW1/sPf3/ehynAMAhK0bfKMqm/EAJQhJIWkTlhZTWhd15CkPuqrQ7PTl/QK8kEN6RFBsef7n4620Vu/+AgXws9WXG2/9/4gbAkDHRzq58iYMrMfYZMdaCzEUNoKyQVTv6GSDIUjvXgAFSEQHZX8SjjL65v/4MPACLrWwvfTT3PAdX0DpWGxd//WZNeGkk5+/+PAjAwhKU5c9ZVVP68X3JO/6oAiDf7TgGp7xzoh5kxgXZ5Wahk0az9UxRQBuZ4u6+MI7EewQ0TndD3AjQC8SLRY//3Cyx+aRQ4vh+AAmAHxOCk2Esotk4InPIAPC8Fpspa+0Tggc8ZDpRWDk/POrj1j/QCEsShYrtAlkwiff3EicxlpQOlolP9zCWAkiYtRSPn4m//pLikZXcnTWQsftyDgDByuBQ53EZIFFWiekAqGNore8EhW1jsBhxYAFguQScaNqfuEA/AaYQcPsgTRq3uJB14ymrFDT4RG4ACMKE52wqXEW0tyIEFxFsDOHNhFPwwz/H3rWWpma5uBgCRdq0daAEARh0rPFqV9ii2vpzOo14nP0dtkTDh2sMAKO7Ncv/eBIWFv7qcrKv/fnKsOem0FsAHHZisudd+ASzGjdPJz6v1jLyNTk///1/hEEEACMKAIcXWEiDBFljvEBjiKxkRYIsMJj3NYj698sgIu46m/jtV94AKYRB8sp5T33wAgBuYQZeExWnyytVM79tjV/S3lfKWdfux850y/GdvvXHiOmr5MqVfm8MbA7p5eGYIIIg0KxrVLprgdKohVqN/9/PISG47wQeOjd8dro0Bn8gNhtFFz/i2LZ7gSGc3bD8sHJnjZv7gBwFSADi8P2r4UIOJxaNphpJMF6huloic/TQ/9TRvnzHih+NsCpINpgAXZmAGArgJ6qwOQOv+ALAhMMHDO0kESdhA8/4DQTqUACAvaMSYhY7/3tAe4IH0EKYb+SCN6/wAOwGiggYu+jDG9ElDNkHSAAdYHTRuPPT9/u4ha3ueinvEro+lDLaLxJvIjEVEFVqXJUtPAksAKEM1jFJpNhtwPWDpjNsb32Gf9qA+YTRcokEi65DfBLkvTAC2CaiLqRLf+cFrUJaUtRfuwnMxXIX6f8h8upYcPhEP9AY8lJkShmKt3nv3fxIANA97DFHIKGv/+DkAAOSgAEfMAOfHW62AXAC4mhSTSefNkkT//9R9qcJb2/+QZBluScSgk4k1yw/DYANQ9ZDUHoLHv/+4cwhxS24YdNjGysEmi7Sbefhy/YbclOLN9df/67b7vLDTZhFy93wXjfDSmePpj+RGIrMKrUkJY1IaPgAPg0oxX2vAbsLMiX/ls/AGB/rP7/4kP3fgAQbAYQRSMyLZJhv+LAQQ/IsIZINt+BrQGUldAZe7V8HxPwF8AXlNsDsZXrg4Jh9BlJoc1FBXTBkr14F0eARPpf2fIANwlTdx9/fz/iebgANdhCiltww6bGNlfkRiKyCq1JCWNTwgF8ACGQAJO68DIAAvNwKgBUAMB88YvrLT3P2P1S1VX3/+ATMxLjmVh+Y1HAEAGrYeBb8qHkxKKL/Az0hq7/BaD5Loav4xYCMBZo5/vzDqAWso8e/fxA2Nm6VcGnaqfDgAIh18R+Ygr6UU/hCgDGrC2KWn83oV4PgQcmnWKcrd3feiXwYACaIbrjGRx0sYvmACYAfQEpUzyTxhM72MFZAe+GRX3i6HuoXTzwuvAvB8qlCzO+vBzrApzp9/Cxp60uEBvWB4UPOGZUu4doL76jZ5/lt/++w+CgzSG1ofPAChHKYFvWRmFJ5//weAAXBCtkHhx2bU2uMwMDTkUMs6R4GRS2tecPwDK8kbSb3zoIZDEFHrFndjO+8AiYnRDialnsX4QzRYPIftJV0f9/FjFQkXdp6Y+Z4YLSWa9/8dYh7v4/f+GBvwErAKUBtS8qkygueoF9BGCGAbyIu0IR6r7qE2fqpt/XgQBxZGIrdTTlbfsPEKIVPbgkVVi/e+BjAYOaCbwl92cIVgJToZreWEK//8vABtlwNHYzn7+oPgBBsduVwH/+7AAqh+fslRFuhmQcoF5xLM0J7+5oWmKXn0Zbr3QyipCrj5sn9Hmk/37DPGcG8qrhgb0QAiwoAPfCq/GT9f/79MGcLo9WeyafU6vbZj3LGzEs7vf5NN/7nC6Uy6mioVgwNXcpQsSmZf/9wYzMr++/6Gw0AHLcRTG+BTSub6XAAVQTAg/re1v4OLHd4AWigctBNac4MhA7IMWKmVrd+wMgiOY4VLEuZWZVPSNc/IHf2/TsMuqwmyV//SZkKzVHr+R5RtEFgh4YG3bxej+ejM/oyVsAb5KtX//SILc5uf5Xl+Osz//rAtPliyyrnYHHAMBK8ZIlmlia/R41Lf8j7zfszM2PqcuUYGQtPGoMgi/XLZ/+/mnoN/hKUZFxzVoT6M8M5psRQLfLKRPflpi2kdwrc/xROaHJHq++qnSZc9ffoeRWEK7DwWIuB8MDcwO+xW/7k1Shwa30d3cPT+3o22ow3/KZL0PJbq/R66UKZ3f85hhXrKL/rzK5SWL56MN7g//DToGrAEFqyhn6SSX2BAYfAz5CWATJ+DDS//6PhbZT41WQgm1vRXp+b35eXA4A2FVmWABXTuq1ewwPztuXtU/zFLxtGhNzUUEs1R9Vd4tBoBhvsqC4QG1++z2ht9/M/fwco2BtNGYzV3+t0sIc59VtYmr2X9afWJEddIozEf+dmgB8Vzt/5vv3w1nw4fhq4TKwi3LE7d8NLU4zwdKZtf1fTAqVYCXHeuc7oAZDLya39y8GMWbQx4YG5baMN6y+qOPUafgDANQwcv+tO4UWf39zZCPyS9Li3op/MiDLrR8jqN3xZ4zpar+ukdSe2SO/+cMPiGyg6BhbK7oM/kAEhD7FOTGPTrhj/+4MxQOB4iilllR0JqyvAbi+3JAHX9GnUP2kh9SppsIqH+ZJTo/2QCz3NNFdFLrViB/wwNupQvYtU/ihyobXhispRLyEe9zqJfLueZbu/e6ZDtixel1I27cR333vyPX+Fl3E4+//k+7Wj//+zinl8kxFZBVX5CWPWWBUc4AMGNX5U9/84AdJvCLCAfCTnc14FaYw6SUGuK0JnmhBIVB6mK39/bZiS/LO1vu8wnZ2Z/NGPTX7dP+7pIrqtGdg78MDc/WvPEdf1jS5j7XrbRAMK0KG/Nt4xn7bwwq+dO/9adduph9o5Z1hgBxP58LDKsiG3vHPZuA3/rBvLXPLaeHMb8B/e4FhPiWb3FStrWHro/9G///diRMP3ye7+zusxVT7/umpN2h8MDeE1mOSXSNf9XkKoSeL+uv/r28/9/KjkV+LV6+vIAnNeDAW52OZHCdLT03ZIS7bQV3iKZCi9n/3osvMZpPdCz1EQfPv3eVEz9g7/eLX93ijBVyjI2WuehXEQANxd9TiMZGv/wzocTDtoDQtZWtNP//PgGqDG1Vcxe976URYivel389mKaSRJk9tZRYMhnjvl/hgbrreYkvv+xJBv9btwWyVDf0OaSiNP74OjPhQMvt0QCGooUEfJIka6B5/x+i7lvkuhbF6645WwE4MQlBLFsKw4Sv+79m9WbvRUJpUoDzv3HAeY0YKjd95HT7/3sIm86yY+f7Lgm13wwdAVsM/v/wgN8AwDQJURo3fSpCCZ3mpEqU7egP/EgQ3X/qVy/elYwIQ0CDwRNaxH0bUwCeGT0wuMJxblB4hgM1IFBRsbU1oANgSMupfUG+9u0AA+IDMEk5tEnfzgiAM1QGhRqbU3rIg0pn32F73AAsBfWAkESM2pgwJYNVumVF/aBCp8FtFaqu6BTyAB4JHb6/eubA3gRwgCCAIIQBWKA0LtzamT7g+c/8ABrsIUUpuGHTItsrA4Q7ihaLJFB0i350F2VaPYbNlHf/eRMg2YVWpISxqQ/IZwCQWxUQ4Hk9UPhmD+GNRETL0f1XZ/H/v4gzGHUkotDxH1VPjYJBcThDwx4g9fxd/4gMxp05/ab7+Pp3+tYrKTf/rYMP/8IB7AAYqCEFqahhw2M7K4elYBji5wqRbJsth8SY/gAJAAsLoaoyrjzBKKB/6AxrEemThn5KxlE4viW7z/eoB9nEjMr+3/iA7/wAEYNUcVa+xCP5yg88aQhM2I38iOGZYCivWPiHyc3+D4GDklPWCHvPp6CtTgGZobaU2u8BuaH9HQxav//uHYYMxVfCAdgCzAPiGkgRqygt2/f//dzDwCv14L2zGfMw/cZZCZaPV0Ee1FJ//mIEYOtOtMdiCX59wNWwZznKZ/FrPgYzL+BwNh1R2wlladf/70/DVzz2r/uthAZT3TySgoPxAdgDMhFZTHY4ZK1LsABqgDimuUiIoH5+/7MYHPAfUj5L7zcHyGsMCGD9yWLjGK//gbDgISEyIYTkEcxigw4AWcM2lt3i/fPv/D//EB6Cf1cmHlaDee0CNhHG+yiTXE3wfgAVI4JV4Op7s259++MDdQ4UuQRnvPySpiGYoYL1GaFYt/f1Qg+9bQ/v8QFoACNiKjEP2QI8ppPoQOxeyY+jiYFUJ6IIFq9HV9ybcuvB+IDZA4WyRRlvHSShgMOJRcSexZ5NV//h599+9uf/CAZ2gAwAFcoJqIWSqin/VyFgL+Ad+MjwIewjWAS2Y3UVdpJS1qQwiSSBPEbRjTqwlhBxlz8/xAdgAWGKz2fcWIm0yz/AwDYABIqsG+zYG64GATxKoqvvvzdgdV/6fpIhMhjYgRTHKDDrObdOf97wsoibRd0//4QG/ACIwHD6zZwmWGKk2ZaGGAAmRGG6CKxJKWMX+lwxGGqlIxNhdMEH0gAbp2CJo6x/PkCQQ7ub11QmTDbH85jRt4FmwybKG4PWBUQPPmZTy6aoMd7wNV6VQsjRGOPyW9D/OL6971E2EhmJT+U4Tv91hAk/L+H6jn+EH/2CvDYXwiKWnzOH4Y4QuIUOdc651zrnXOsBDwAAELVBmkDoBCn8/R/P+CEOeAB4NUKADgjKBISthe/4Ad4Ayg8LKu9/DM5+KxJ68BEtE7vP/EhfgAPgOQQEnjE53fOzGP9wIIuCRSLcoQwWDL7//cxIiahIsMmsj2li6nioi+/PSoIQWpyGHDIvor5swxXmvS0/Wkr/BXbAEytRhI3bLC4xBEuB6+Hya62YYoF2vG/2yGxXEXiHoe5QcABsCKF3BXGTCKfBdR5sCJKKaIMuYXFlbkgD2hjipI4xxWDXL5FRePksa3MjqiGUHhzGv7Pe0Yktff+X+GRtgAA5QADrAe8NGiMAMLvyJzkGJtpTmAAC4MVoPDj00RveFBrsqkvpkGvD8AJEBWmqWlBRRUD//8+hrj/+9PKEocEEARqgLCjU2pgA4YyiRdBHWSmYluM3/sAFYwH5qfAsE4Cf3aOAPW0F1I1XO3/2kznC08/nv3oWoRzBk+p5Ui6roY3pcnLsBFxVoz/gQnC4A9IIg7zdpAXNkyORpaCuO8Y1WU6kgADKTZsXzocidFOSwIB4RG8AZiouWVSXW+i3MAAGQUqwcGnBojZl1UeW4vMwIfKq3q5SUW8shv9vwYrz/1oWm2qrCXYW/dPuHGV5TxD5gBCYRSj7FoW1n5eL4OLcRo+ZC75fAwUU5NTfcAavy0mK9bv8EGABYJlIABAThGEConc6f/0ARHuAM3hhPPIZLLnQAUwzDZZrznE3wEOYGMdk2PbJMN3LRDKQs6fIX7jRxTFEAV4S2T/Q60P2hn488AeHrOox0qvX2Vzqi7//26BitsokKjko2ZYI3+lgCQRK40L//cEGa0SZiievbpCBd4qv+/f5Qa0SPCigvD8CQMWSEzAlDKd3Hv/PnrUrv3vjBwAEYDRQwUy+nDW8EEjPEjGGGon/RVbHYHv/aBiFKe9Rltdg9d/9pl4AGgDMaL64gzfwCHwQwpfsbPGRbdXX0dl9z9W0cZiRWI8x3//wwAe0qDn683x7z4EUVPXg6GXnqDf/df+NgAk+XXu3gFALBrCXV9zzpVZJ7gBDHJUnZcQiWFcPdGCHpN2VIEkPmshv/hsg+ECIwZbMnIJXTK5fDlgLz7bwd/vAg2EjNy+vpf9L70PZxxq3jwABAZBy/8wOwaeYRXF8MMJ6m6hrpKNZ/ASMKoo8wVOMcmQ0/7/0owS/p5XTyEQhiAKYUooYIv7lYOJeAE+RU3yn1/AGlklTZ9Z60eGgk///2w8kgupdzl39QMbN7PxAfgAWDFopRxCokpI1/5+4YCxjCODxlPZ5M8rfuBV2+w7I/wp2Aj3CXojvsy4G9RBMvnLNS/uCLaYGoa9fIGdb0SV/3MAtmSQ3/hDC/wStNnCIIIACIBLg4aw8hHeOk1THjATKChjD6Et56TUMAgFzwgas0XXm5vS78AK7ymnwAIZQx7MQkspimme9rcUgH3qvzopflYfuNkAEDjpToQMm1iZj3WGXucHSFKx+/yF5sAJ7O1F/++dM3lMyVV/f1YmM0h9ZW/f6dd51gS4RGw4MwALmZgDA5AE7VYHonX/MBQqNBn0RdmPKFEv2jZcjE+/re9oMB7WPSQ/iBtpMd/92hFfmIQ7hWJFrv94ABUCsT6VGNLagvHag7I46Xk+816TOf+LZfx+9qc4MSiPI394S0dBfE+zkSfBap0yy5SHPXYVVaFJZEm57v+EQQYADFwYgtXUbuGBfdV1mjomCUGQWQxfwAkVaxn7Y4eCDC+MBSCh50xGV3DVRf/SOh3Mtgn0wRA8w3xMpRp/wYGQPDh54zCV3DchnfAMRAIILpCZJsk625AKihhsvGEqOHqDeDB2/wCwVK2G/kBrBZ4LXLurnfs7c6ZT36HGehwG7+EQ/8zIwiuIvEEqaxAeiAA2REC/ZlDNcP0BDO5nRFiZtst/z/N0BEEOiV6c00vT2AgcZasCRUywVsAAjAacEDGSKMMZ0QUM6B8QLdavKXkmGSawiWGWlAdJZp75CbTdv7/QOMu3fUf9+ugPFaMF6y770H8FHp9fT/4RBBwAKgcggJPGJzy6bmLf7QIZvNRV0Jgy01/P8AYACDCNxgtJGdv+9v3dZIyJQlhk2E+39zwAN0zhUUZYzv7wCDY0wgWenzRBU7cN+Zsbuoq7SSlrVgwyYAGYat0mWB6Vsask/FksjDttKj/d/DIYhwwAFQ+GqRNkn9pYMPvcEAEAQqWAANAXNqYCRMIawCvKlVbnPjoEF3bhgOuU9eAdpC52HV9rhI/m4ZDHAEIYuwJqtuGPAxRrYLeAxCqB9FsX8C9Gdov/35EYiswqtSQtjVhhAuiIOkhlqtuQR8Ov3P/ieHOABQ4BfsD/SkcBDyIb2gBAcRObH+Tc8UGXYETMvwAKTI8yCV3MPkaN1ch8QN8fE4AAxoTtzC4kj1sWwAAVBQHZOGx00RgQFnJEAJaQCLOBEkrw/Gf39iAwgmUJE2CTbTyIwG9sAyCew/XaGD+zSAQhfxSoq1+7+sAhhEoyJNEmmtMMxQ5wa9Aa3LZBxvwHPrDDiuHm6ta7uenLJ2LgBFzXgeCpHwRG9z8IDYCQAlc7gACAC0XfKIZwtXeQq6syiocTrTHch3eGJDgrRCSPXCC0MpSHKfv6gw/AASYVFqyIS6W0Wyj6+v1f0D6AIJCbsbmcptrMffwbAVq4ec1KYrkAfJk8T5HypCqR0gTcp6beQc6G9p1/1CGFX0Wz/iBsAWCdTgAwfv5USshe/4HMq/f3UH4iShfDsqB09/Ij125+arc+wMAWGik2P5AyTCS9GhkBEw8m3YcJ/69QRp/yJC31dUADWwMYWqk7z9gDblAAgI0gVELYHv+dCgveTIw/D1ADwsEmTuLG8Q0bJhlIQT+o9ohY9ZFMD3ny3v/kjNPVOkduigX+ZUNfuUJMBjYL7EXCA34wAeGsCLopa0+arYZwDUAoS1KEVGvLt4H+bQiy2yX/znKAAwYlMLcUsovAb6CEQR9nLPJfua5uFp3UmLYAH6r3pN/16A1fteEi+vTQDEohMnEqk3hb37sAgYmBPIyOoHThZ/+Ibxxkj11u9kuP/vfgYBCGjSrTzlk4ZT+1wgllaqlo6J3/4IlbRjkgqYroT6g0qTdCpzf/QuRxbIR+PS6H2Bz09NtYl/soKUY18m34YG+QfcBCDOtD2gALZAzrINMVRyb19lRYAoY/nvqtRo4lSvXzR5j/X+3+vW6r4m43/6hCfp8HYtf/Hq/g/3c/AewkULWL1lCl+0RQEBDjp8kok81/Qr6dv7+secLm/qM/JlC6FIM/n+pwhayIn1X7/nAb3kpD8F7eoK/6q+/8b+0Y1RcMDdT9MEuR3/JfIbgfN0QurZu5VF1SJq1OblzHD1J/Uv7qeABoNySh/bo2ykhpFo1aDkH4ENwtXeo0v///gdGWwxKw+hJWmmuhh4z+O+elpS/0xvPAkPCvSpK5hRA0nDEEDQmFZtN7M1HGbdrVOsfq2C6F956xrMda2//n4Gt2NFE7T0/0XDA27HqF7s6ZKSmX1SCu0c0tBvIBs8Q4a8/7HNB/8ZNXbQD/Kdi5JMRc5wjbqaHNSAgAArQLgCbyhMwYsM/+xYFKC7gya+7PN7ditR4hWjTxCUhyIKQl5iyCW3v36a/dpb7zf3t5k8vOrcHYboQRERNUmPNhj6Iipymm76o5iEq07/vmsFbvfWWd/cuHhQIk5YZZQR+GBuCp92h/8X5WXhFpv73NnduY+KrZrfRuFxI1TMO/FVIvP6qS/55qzmB7A0DZICHc8Hc1mH5sD5/ydc2/0C0rQ44m2UN3QwLRW0VbjEPNVaBk1bw3vpAze2GapRIul3Lf1neDreSX/f2CjVOe+sAFPYTF+724bgPHmjhgbZP48arV+/ha/zAvqd1DfXzXC5VG2a999NmYHuaYsK+pYG34guPsUC/7te7Avmn+CFM0lPa9wCYBiyX2cwp02T98EuTTcj3/v8HxiUKY9JCDiRX0+AgFZBfjIxkt4q07/2hMkAF8NtBlkZ1U3+Ay15KAzrTTSppQ7x2o1T/EZ974pqQ3vyqY9++FJYRowSkHg8MDc9MWChx/DvOtw5f7XhiqpT2kYklzqJJkU5sy3d+9jx/j5mutIz3xHv/e+Qz8180lOL3Yv/3T7QVzWVK2a5IAHzh0SZSlKJa1tEtj+Ey+f/k+/UHncoP+Dvo0YDDCKTJtkGmf+9y2AQQTSFSDZJlsC/thEJnwfIjU//59mQqqd+lf33Un499bP8MNXR9LEkKuC6PwwNzKFb+q2f+O9CJKjrF/+v9G967bLbXt9L9Kx1f/+dw/oxsg7jBrcGP2NO1tw4dnWCAQFHzTrv/280QyvjGRx0sYnYdRhVUR19/YBI/KfLt4r9/jC6N7ukZsrZ/ajdT4PvZAUzU8Y3tVV370Qimz9arsiujwyVJ/lRkOILN5m/6+gQYSTokrjwwN2X2jNJI//9qAd9woi+8d/N+vaYUieSH9aaAh2C8RwTUWTSyBL+p10suraRzP9/0gxovGgZ/uuNX7PYaO0f5p/oDAgz4CL4ro0/+hgRjqgPaKS3ERd98D6Nj6bFdv9Ykyc0t6uu3c01emoQEJO9Hh7+GBuYHNCaRyjwF51puMkdrXXSx1PQoRPrXF4zMxac/f5xiRgMADyloREivJQsrw72pI9P6MqjNh2+vAMHroDRCOy552Qv//u0SsgSLeS9ffv8GEJooqetgPwYsctsAQjNisnvznCztOlRILE59VfzOf3nn/GY7j4dJYv4QG+ATesoGu7bKtE/psKyqmtf794Ona2t71TgrQtp/VrT4GtElDNYIQpWCbfDzTkIRARZJb3/P0C80QvboCN4AFDiML+eTafv8n2Fo0WAEXbiPaaSxj/6A6YAnBdrYgiXe/4QM3wVD+ZBD95gAAkCgPscODpojSJPwrM1VcvQt1eo2i//8Mwli1Mwj77X///VlGgViGPcusNlXO30s//rAiURzJqGvquNDhyxAyn3dwUDfkQAYAKX3QaiACsB7//yMhFZTC4khLWJ0ExNRVy0F9MmSvQfkANWrAi/8wiAABAJ6BnxsMAXbywLhozAmog4oAA1wAIA08B9sO9AtvCYGq+us3xBd+YinYZ9rIcDBe2FBNsikvplGvBAgBjEjtxH8kj2sW4ACcBKRoABICZtTAwXgmkKu2znP36tGBcoM3ZmCDN4GnQWjmhftTVZfL/EhaNhAEHTrhb3AHH25XUxBnawpwYc493bLXP9YE4P+Jwh/xHhgK+YccBSD+hDHgALWAzvAsIi8+RMmW1xfteGHPx9/iT4PAWHigN3q/lT5W5H4cof/4QDXyMOidZdIfbKMfIAAVBDNmAeGoHq5B/qGDl321n3ox9zq/7f/EBavW+AA+AA/Ac4IctLyCRWx0AHgG+BA1l5GOtcJLmQ+SGC7eDpd5Juevg+6oBDCJSJMEmmv+DEosyaNkPP/voPKoiQqlfv1f/CAV+8xuvOdTj+1awQIOAsIFq41ZBSrcl9ryYiiWokghvGl2j7rLbmAFYoAAgB6mMgDiVhPwuEhIxNTsgqJtwzz/+I8R4g9f/DKdT/4jxHhAKwBYCfhgxoghHG+E1zYYaBgAdGipsEoMgshi/gIwAGyIwX9KoVrlxzoGQtikqL/9oCGdzOqLExbbb/g8sip+ulBKW291Xd/3h6wgFcAYyEVlEXiSEtYuH8QsOaNpKRUifbJg0HXzJfycXP/4CdgAAEHZBmmBKARR/PwjiT14B7a75/wiL4ACY8TFdBkklU48kOgQei3KsaHCIIPAAZhcfLKxZFvo0g4IGADgQOvSBi7OMI5S0ojoDCkJcna0ZN59/+fMKkxWcdRZWEnFgCgDdgEkqA27lXzEiPtchotiolR1wA49fMu3tW+O8S/wiNmywAAbAp0gcCxIaIwA5jg+2XjCsfQhL80I6sUXEWQQe0oNgAAQAMAAIAbwBRQKmiN4hQqEZBVll088vgYNCNA6nEb6bGr3v/9XVdq77vZqFXGQ9b2IVynbOzz/6+sOHKJk5UN++8J8WAFDitvyUINlioYJ8ogDqcJi9q+y3Bb/GQzYNQAPEuLfrUilp6jEnCIIOAA4MCskYXHFksMd61mTf/7gAQEE+bS1u2W4kSBL/3kK+QFKYAw5qseorfbbfrXmee5UiNyG04s5npePmqqcRxvvzaA/0KxJmVn/9+BhmkSgATzUm0kYuBvU/0p4wIxeHmu1EanXgSN44v4ZDEAcACcbw5RxfaDpiKIuDAXjgxHJQk04NewqYK8LAAEANw/DkE3DQ5KvG+AGtuRG/vwNDKEe5auRpDXv+QwZ5UKQMv/fKAAEAQhrQABAP5qoAMqPG4SZIqDAWtob+gPMa5XC4de+fYZGAL6j123Z/93Fyi0FwyGP/OBcB+0ByE6CYivQyXiAAEAMApiAyvBKe29+zowMMDIqx8sWocxe9wgAIbzA7ClXoqAdtGcDgCZdUL/1PIwePW4jccCHAnHlOIUv2+wIt/1qFuG3n43YzSXB2gAXMag49AXt38JICb/iVA7MAIrigYf6mZGroSf/AJG2Rpp6S3urTR+0H/W9f7wAIBGAbSbsT7XmqluvgKTgEk2VgISkbpYgF/vIhkOyCu9pSXPb5D2daj5xPTE6BgpLR5EIJda1xHWZ/8ECcZAFpJ6z/tYcBZlzCrLt9D4oPZWi++sEE070fchexoeN2UcSwaPCIfgTIAAQAAUItVWYpK6YNPn+IAjAGwJJBBRVjnEYnuPjAJlAoc0VSh3fy7B7UDBdnCax3MubtYIM0og2eB7I54ndcy30NP+elFos8PCL6sCcxCk8R5ZDFHm6kfTTCrgubeBNkw7dKtd4RZQq5GDTnl7v/ACgvSfEqiJ8/+A3MtlAHEZ9/vqQQPFe/qqNeERvgAJGYmbnF9RSHvV2DA+FAOhyBsIxlR+/eAGAA0CoBK7amkXDMFBZcDL7myaGnR0I6Nsujcd+AiBhCGd/Wa9tVe+wfwJWV1Tx2zVHBgFkmss0VAaLyuAQjqMLf4LTbxIqdf89egMUs9T/9pwgE2Y+cPhEMT41pwJBhyn6XnpAqE7jrS+yLNeAnB0n5ACZiDlpYUYos8sYgqfoqcNXrwQd+XCUmUdVs/ZvngGwAuERCLm7/kjsGBj54XDIIPHSy7IgCDD6QqWfLPvg+BBSCTbDeVSgTBmY/7STGBAlUXqg37emf/esCwAxGI5GHd6ylue3g5RHjmOy0TEyD5qDGsYCB+hwIJHfN8r1v3Hd85p/rNGHbKeGQ/1wIToH0QEpQUA/cpCTwqkDHQIldHwAAg7QAAQWz/1qwYEgB1RPAO1f4lcj5PW1gygcDSQrbHTg5gf7+CgHRBOuwR9DcGGycrBCs/eG1VjkETp9kMjVfCIf4AFgghPEozaFyfee/n8mAAZUZQVGCKkPog8YAOAcTWMoi5vAUvyAkIAerewaE7IGNSMr/9wfQ6eAPQDCu933HipuOv/wsjohAuiQWGnshqkj/U8/esZF3RCfQS8Ihj4ACQ66GK4iiS8ccWx2AABABwAAgCOAEEwqaIwE7BAKoMU6ymyLSM9BE2hY/ABzti5WK27Xjq8EIYsH4QAXXgQBe4WtYCzYPdoYNV0IGLZpZBN3L+/YAxGI5GHZqyluesMITInBxcGokrU//1v/ieHIADXMEOOY7DRETIOmfkRiORh2aspbnrwQCAIcJFI5cUIjrq++8zAAEAEECZxrJagnE5YtwiN0MLTDgAPh7Mgm5v23+oFCDp3CAIIADNgAJNVADoLA6h1ZHTMmMAAQGlBcYhB/CS9+04B/UCYsfBj29epppDaui5VDGh2B59QrWP/NsfVffvwlOyBLrPmcBVBWuM2qlpHWDFXg9uTV2hL911iJwwHvIAAQAFDtOACVhfVCL8MeF/94lsG5QBTWMASVF56+B1US9mKVzCevJv/eenwYASgEkDGo1mAV0E3Bj/2UefkBqwNwz7tVvCL69iABYABKWgflhUm/Z9wdp6qlp1LVV7jDIqHG9RfMerTCdA4U2L4RaaE5R/3gZ7IkBGerB7XYV81/nJ/DqQqMxi8p/yc2q/H8G8YvDA3wwARBeKFuHUPnigqJf+8sQknji8uUfIGiLwIWAdlQMh5uuMLHwSM2Q2QaMjtg7Y9+jpf/1IAAbAxUTADQ9AVrs4N0T0BMj4FQff2gTOXuZU0hX++w1edTd/bpNguiEYYd828o8A2HBHpX13OayL/FE65NXqMRWQ43rISx7ZGGm+nt3P8EhQdKUyJS1GSbP/4MtfoF0r8RabR1EPpAPbPbytdf0gpj171T172TWG/a+Z/+CR/7GmCecgLWN1cMDfAANuoGeSM5NtrixlsMAAQCRwD1iWXws6+EL/e42Roe6KyOlkhoP2CecV8Z7iEs+VurFNxf2jCzOlfORm+/9hnhnP1H+d1Z0aJbO85F0lPg0r/2BgaIk4AUKYmkVRbJP9x/Gzq+pH2qj+r+AwCP4cUWEb7vcfa2H0h0QpY9HxVQYYjxpEwcXi2/TlWShC/GT2TvRB1WkP+sgD73hWEg/ekvjneavojB3H4IBvQjAENNKKNHncBUtKzJ1abGy5764YGoZZa0iknCiRhL/9QS7x4VE6+fp9EsIzjko2IWJsGZVFUTGpH8qm/jrU77qx7UfhzLmfTFXVD/i8DYnxZWRiXmc5C76cVw7RHvgBQGMZJ8biPPo44b/7DQeE3L1Xas/8EAMmholjOUw0I9A679qHwYXDlIa2i9d//2G5SlzqrJf/Owx3GPpasS/xDdt85hc+/UQd/wQDcoXNkZQn7UtvsP8R7+bQM1fb4up1ErfvKUukKavPrdzprn/+9ljneuHN0WKk08PwNaBBbbQjheb0H//mAEYcWsXhyhqkXFkjo+YU1f/9M0dmoj091RJOab1/7vxMANcrAEUJfmQKEYBrpioS/voqW9jUZAmymr/K/IBLY5MyPv60BzGi/sVf/bq3DdZroet68AfBAN3gHbygJD98/RzMmpO3//8grtGtLaBuoc536q8SpUhM+vr78bPMdZ076Bif7KdL4qneQYwJyaEch6ik3/+vIjCOzCu9JCWEr8aELqEtxVucW0j0kZCRjnBX4sWqv9gT+HtFbbhbrtRqU4/m2DmFHeBorCEKSijJz/mHiCUqXSj3Xv/R2jHLX5bsL/1Nb99Pun5nXvePXFtnDA3D1pEw/ZNP9lDoib0Bz1HZ+ucD7Ho0fFNdHJpdbP8rqvsNrzf9U3i4ti/6q0py+f391Te0BM42+3Ssv20AhT7IpjLR5ZLv4w+2Ke5r0C/0lHrs29Y+uvjQRVlubohe3SHpUD04brbHoEqdWCRtzNIde/7A8pUC7911R+qI7A/dCb9/1zCYTJpSTfsxRKR4o2P+hcEA3UWXDCzltW8bQTV/anoAcljAUfrytqYU3+Wf+hbKZI380Jm2ErBfNV3REOd39qEX5fvol0tEfCLtc9A8ivkwqt/2gR1RqMFoS/7D/7e2NzlKO+0lra1fHywJw8S1HIT/7CSPx26bfv4fAGCQACAXgQRFDyfYwwnKx9wiDV/6i4oMYmlCMpbb9++tTHS+11hv3/MdKV3O2zofBwFwQDdnGiBZO7dvq8cgJDyq88BBsW4Ut7u/1t99OQXGmD1gvfA/oB+e33nSvgdz7vv6UapJK23New/7Rip0r84DJ9FWwDUBQXIjRRVZifh//7Bi2r+wkQ7+9aRDPu4lq09v7mAwi8CFyc6baWeO/7wwe6NS4mMULo+uT4BCIgCTRu1MSWE7HcDAPYp4IEEOH07iVsI9/7+GAu2H70xbk/9fTD8LZ+/VXBIiZCX//Vjno7+HVz19N6B8MDdCnaeb1/VvwXC1ivP3z9S8j93sO83j2SnJabYjtfLPSbOEP3oCrdB491T/XvXncMEfxZcbj/e/4IVgkxZXC6FzDxQfJZ4JFjke+lA/2zPu5rf2M/NdaG+UHEZhUOxala0GA2soUUZmim2i0V3Qt62/n6bGUCaR7/ldQDWW1Rb/d6CSRHyijBjwQDdOMihrqi/Mre3gFbJ7y5uP/JSSbxEmvs5wAoCmBN8TF0ij9JaJCiGiZEIYT/fqEoycnXQpeDYB/u2zuN7tGxrxIwGe2AZR6kG+cCQAhnUNfMwg4rcal4fEDwD/oDUpSEBFehEm5gCAUde7ifpuKFgiRgwA/L4CCxf5j5+UI/esDeoCzdQ19f66iJmg5V1/cuyBW1iV6I3qnHmTLDceAqt84YG7avtmBZL+n4Bv0/vdnGPLKPwVZ9fKJX/vW6JM0tGfv+rBgphsAXPMQRL3r//vJkceeDAiGhQDgOftLWhL3ZjuABAz1nUO7qP3pkyPgw7LQdmRJaaeATFeBirlgVr7qACSVzFYd2qJU5rPTkDGHMdlsgJEHDIISBc3BmiEhKhmQxp2glakd3/O4mceiOy3AX2aC9f132yZJ3g+GBuyLiCxFXKe/9uyxiW3zPPCAVSeQa7FPY+xpeAMDkmSLDCLpJtUlTrcuGxyQhsYBlEClPKNVDpf4AsYC2HiTO2SpF1FY9iXtj9fu82NoYbpjr6/WHwXAuHb0NUKyqRKf+5pDTsqOTnIrmAFaCSLnGtRs9lK/9wCcVkFiy25HShlwh/rGE4+Y5T2xH//eDDhdBoztyKRqOB5MQaKy9vrP3R587jWqMBHK0Wia//Kx8WXEzmnvp4YG9IABkRmBfs6gjnjoAXsQBSh5Sb5Z9oCCEcxGV42bb7/8DYAg+CwHrQvNEbxoMDpjtDWSpGSL7OioP0gqNlGWkm3WaSNseY6RSqoiCCNYcRy0Sxr0MhV2AB0wMNhJAi/6EXSzT4IPyaQ92fFYtRcsD9A/tCYN/28wSjFxW+5zn+VPgktBGYo3mLX3PMGdVzx9O/sd7dC/C3wEDp9wxdXWP/9pL4emmTxPjsVI/3T9IhERDDcopDHMDDrj99m5F+tBAh/E4QvEeEA18jII7KI/llLe5bgABEcIpq4BMKTamD4AgFlPhhEjjQlP1+hn2fhAMwFvFQAtovvAJBeclH9qZfBh9Q/yA2sVf+EA1A0yAaxPNyVsk4Tf88k0yQbVSOR38OPagWS5+PIzS3y//4gRx4DvA+ICYu8w8wcDUO0/jef+GofMiATf0Kqj+T8vfewQDCDaQkXeLPvaXwJ0eJcWStI/+/gD2749/4V8hFB9+gqiKEHZ8+D/qgEEGSjQs4YeIBzU+0SISIS1r+/qD/fT+X/DUPjRBgg9/l9uCT/Vdo04VN8CrmntJk/7/8IBWfpMdVBw8IgehwdL35tTH9xv1TDWIP/wgF4MBDKIqLD0hNNpa5Sqdpoj5Y/P6P6xHiIWOsafgeYAAADhhBmoBKATmJUt4RLwAEiMRUQVnrIS5qxh3Egg8ABjMREU4/sKQ8lgADWRhFcRuKNYS5gfGYA6xAi1+4gxxUHcSAAEAN8AAwBosB9sOgDGQikcRqGlJeQ0TpwJHsa6cf8Mhj0DS5H8ALQyksoFwEvRbrAFRx8a4hkApCFuuAAQA+BGsOWJZopSD0Ca5eZ14o8AYf3lweJT80gGXoBjEGh9WHm0DsuZLAYBDfzdr/qJMbcNG/+EQxAB2LMp2QVZBFvEpOAACAFwABADJgASUCxtTeAJ1egAoaQlSSxpIibDj6lmzQRmqY9MNFTkfN0Ks1A4agp+iKT7QI4T/VE8v/7zDTKaDuEQQeAAxaDGHt8nsgIEPLT0RJesaOyIGwEScW9/yC4QDAbmsSA3yKioQVE//8v4AWNgXhCloPccPHCIf/vQzO4zcQWwlzA/ABgyfgc2eXvuS5zY15BdVMziqKJ1pxWhzD6KUgqTu4s63gCoMT7/R6yjAV5sbBgzC09pGTb95wCgxJxFjby3Zqay/xhcEGepNc7BZ/7Aq4XKuZq/7WiIQaYsFqcEIYgAIBIBjQmFkXfJBKfSEx0IhoBzw3Ey5k++/fuJGZjHL00LTMk2V+kFvf3//eALNkSja2LL8H4wIVIRGHcSiYmNuifhCEWI0XYZi2wAtCHf/hBJRwIFREwmvmy+xlnqWzRDr+tNFq6uEQ/AATMjCdxG4gtj3MD4RAACAAChELVVuJRumDT8HoAIBB1LNJcq+kXCJGfqINnCq17tCaq7CXZNVf4BAvrJhHKACvRtXX+9fY4Es2JE2/++p12/hEMYbiz2kFqZ2G2wqAHogBgg+kJFSBh15AIAILIxKxiOkSljygoHI3ramIfyCRRzLBjItdIAcfqC865f+/hEMQwAPAmcgACA/iZkbugKP8yxHo0xHOAjHiVNYLkQFAYWGJmBvKwdi89/8HA+z9wfe9TD6+dhCazgkTIH5SEKxAitREfDnv9w0olkB4RDHAkYm0zaEzl1Zpn/6BAGRRQOEqskrikv//7vwAEyIZSsMzEmtIc0wvC9nSrjG1/hkMQALAhqLVAhPElsESf7v8MoG0cY0R72p0VPiApt6UAAICNtgAAgnAACA+fv/YwIUAgJYPcymC6Byowzd/819r51f/0IkvgGyOVMvB4FoUV/Nyz3/x/CIYgAWBj2UuYFpbZyQKf+fxsDhZtjGjKf/+9lOUdgrkNkWSDTZqNfkujXk02CBrjRU/P95f/hkMeAAmRDOVBGcslbHL2ACFIXbGmuYAYjEdkOJ6yFuet/AG1b828/8MhvQfGBpQxidXgE/BBwY/9wgHwhqcXPAR8EHJjwDVOFlwcRby/+v+J4cgAPB4Bf0BqEpCAgwQibcgBAKOrVpP03kDARJbWgGAU4WKyyXohHWVO+4ZgACAACBEZUVqKxu1zT8QHgApBFGnWvULY//+/BIrj34QG4ACEE/Dw9wolPevl2RD5mDLZs5eTaN4wEcjABhQIy5JdMCN1p1QAAgALkXjwitT2mEqooxBINo5ybryN87egb6vsBYH8fdvfaD+Ep3ACKU4zJP//7giFGtnBXIXk+VfZo8DmrnIDf2F/EDfgXEcKXMPmPJTNC8xvowMHdgBBrpDwwlWid6Ht6XAMBCkEMNa5DRATIemfADAC/wtxURgmib/bmP/+8yEUroI7mkrcxvjAAEASEAdoC6VygkeJLioAiJMAU1IcSrmfhW94H6REEQgzMUYwghgerAW8A+oCIt9xp3+CvNWGP1y4wAZGIAA4FYQLC9cBd/gGAAxMiBBoFaxw2pjcGQlc1RsZvvFksbFl5Ns/GDxzqyouGBvxtAYZTAR2/WUnTLfEfDAop3dHSwp6q/9pBbMIqqyfVG2ngaGg8c/oIf99yiBEEGJQwe00wsrxYyumZ1/u6MAEBNF2o2qxx4zfIAEcDZhj0ja+2KsY2Um8O+3pmAIlmFexqeQnwjJ2CKYn1/jWv+JW2ksb1Z0PIvF/z+AgRYYVJGZIMKUZ8OuCy+2kOQB0EilP+5IAAiKrAidPoJ8hBCjTwAuTxw4zM421KXBDRRkWXMrLmdhAAex9L3xcqIwJj20dGneAWvzbqC7UO9f0B5iy4YG8DReptrVY72/tQAkoKsjKC/lFnf2BnNnuay/UlRiuq51ZbZInEYpvDrWeZuxV71/CLt7gBD7Ayi26gAM4BWeAXUBEWe455YVdjwiok//gMHJ+UgyPd+UsZ9Fwar1r0Z2uZpOcsctI3kqWSf/4YICGU24cAfBAN+HkEYYQcKfOqLcCr3DnCiaVFb/88gmEY5BwjHnuaU1QS/S6pYv5/n3sRaTd//KJMf5qyEKlSniK+EVuhrabo+59rN/cuJ+fV3Xe3gdwyhCf56IGxzti4cjTCfObuzp60xzV/pfO2u+SIWDiX6UkXMi/6sthYQhTBfSDuDr7Mq0O19rzAAgPRHclZne/0+hLaRK+2kHG55cdPvoa77Q72Ib7vms5zhePBANigTHcFx9/MHLKgDnPtqtJ00E769+RcqFEgjfvBLscqIkEvxhRR5rPzPB2wim3QOnIAU6N/E8+zSF/us41GRGm386AeoGBASwMk5QZwtmiRYiAAI4RVnrIqMXpy0Q0rLikKi//wFRcDWGAE2zQ7OqmaZriAGoCDFPZena898w/tuUSX96XNE1jrreOA5aix6Bzfz61fX9AfBANx4cgBJQztU74RXbo35DDfvqZP6O8odwGzWE3ZzFEMRf/0uJmNxE8XeUHnTdK9Hd8zSsUgyb/v7VACAB0YHXTLAYlSjHv5ultjhG/wABGe4D+sJk33YeO9ly2t+v6CmRnNov+9QEBOjEBQhMXq48J4ib/gYABZiR06BwpAhxllS5I6b//0YAdMAZziyjvGai/54qkq7poyG8TyKLHU/6Le+P/+wlfpu9X3+sf3BANwGeaCRj/VZPGQmPf9nE45XoOSz/qtrNkL5/vUIBuWfwNkjrYbUPf1yZFZD606G3Kt/yUE1zDrhw6u3RWrpn//44AzA4VSMIs2VVMlFpetmI5xjqBOi1q7Nz+Jkmsy8RkCOQozUJIaSxuEBiXOKuU5ue/wGMNwYCGqKEUnjjOz//waK7Au/Sf1yPts/Aznrv///XICQ5qq6x10rfUnzH743Yz11cEA2QUAMJQaemMZDf/MD7xR5UTX7rTS9Xp+/czkVfZz69KjvjDMrvQ6FTHtDZaogdtn9f+/lwKFMDiCkNzMmxDz/2NglODLedZh5bZpEAAcloCLcYJtt/8HEgr5NU/rpHc/ntD4YMQ9kAISBpVPEa9s+/8BY6D8aoiUJKUTgRqmVb5SJrLZtEmfL/+C9LXwyBCXzq+dVwdrfwwN5LDtat7K3fnQKpDCQlLnlOscN/z0i1o8dQTf0C3lpeH7b5RZ8bjnus64klbPcnTW2QD9UwlrTY4T4aDgGjAYhEQSkJ39g5v2DJlPh1lI/eAJZMQVLG1hPeYrjBjZBS02J8LlBIb//uDRQAj4oCJ/dSKyS/KFeCYD7VBAZZiw8EenEqSq53uoJI8WhL+1bStFvbe/O1hzGgI6s4tEv/lVRfgrQS8zYN2uCAbBGtEF77189Iz0FHy3/SpPYomZO/j9IPZQ79LUn0wT9avV6JzBn+p/8qJNfMNN3qyOqMgne+92jKF3+rhBCO7/046m+/t3NAAEyuwInT6CeePnnP+G+/zGtfxv6A9RcJzG0jkO/ElP7mwQACKgAaV8b6Zb/72+YFJCIxt6p+9s3tPtqggnUGxdyD/BAN0b29IGfeu2jL8/gv0jUqejH0jprVg7fclh9/oCvBcOcP7TJ0wadMbkLMEcUiFCHHiGusMNiJexNstd9DnNhLv9F+VxgB2gCBESrNLdHLnv/z66ADAQZSrqfZvoGAgSnACDSaBFnUu5hwMoBL9giEDluByYgKM8Aq/4MmgQggAlRBGOAE5HZFCC/1hj/tgBloiAuNc6Rfl/yW1bUO//VPzvMERd3iQ1n50hmiN8nwPhcMDdVxZgfjbnZlZbJLb9UAN8lLO4b12P3ZIuj+Y0tpCua5jDQEzqGwpc2lf6Td7L737Hds43fLwQmShiM+1lwaJXf6x1QN6A/M9n0ASZNry+3XC++/DQVebIxx6eQkb3vboBcb4+ZIzXzRW47oq/d25fW/8MDeYHIhPqTP/e1ETS02ZKtIDbtLbK6+0ZngbKuMMApq2hQWkmICsjhl/3mAw7Q8vwdvjgt8KMC5PKD/fwJiKeKAAIBPvkAI4MGP/l4t2mAUBqPyRxRbkk2k3X/9hhl+wAA+AgHSjWmHEivFUWGjIBNOCj7DViXOrfgwLM8ZJcS8zVcxnv+BPlBrAETTkvl/269979/UPo34zmX/bhO9cwR6ubd4KBvyEDAWti0W9xDVJ0gRazEVDzxgj9Zy+ZvvDOCMGZqxf0QrcTkZKH7B8N0jqhHPpIWKFIN+kGACj42uCPqn2KGb/9zDCkRIlxB0qk4WfOAAEWAZDwDQaMTam7AAHSATVhEGO58Gn36UgPlsAEBYTACuYA0PwkKaX4QAmOYoBUcZ+r+X7KJiHvN8CCCX/uYEX2BQH1w0DoFxIdyuqz4c/tgi8gYFU7YOZQ9eZORgaGR8QLYV+kQRkQRyGFIIIUGCAXtGbD9+rX9GcGf8kQaGviRC3gw8IeEPEBWAAxkIrKYXmkJexLAABcCgHZFGJSaIwf+2YyqordaSl71l+oPIK1Olz8Xj2z/+DDxC94g85a7pg//hhe8HHhANQEObZtTADmYzlcdurLaS9vhikfJ17c8/6GLrELgJyAAADHNBmqBKATmJPAReBI6p5/CIb4ACMA2UGBTpVOWs+MLCPhBfo4Eukk4614syfAa4ibJkY2p8D/hkXwALAw5TTPneGZKPlf3fHwHIASO4JQVVeKGBkojduGQxejYCDAAaGihtCsMyS2Lk1Dn4YAAgChhcaOalkli9xnaQlcGE/GbtfyOEt/4YXAMpxsZwxVxx/CIYmBhiDoxHgQ4JtAwVEEKW/BgAJCcgqgtNCv2hYp3ceYbOI1JhPOFoLqIelBMYgIZihnPMa82Awf8Qws8ljBGkAlJ54gAPvNmWkJKf+2w2nZ4RDEP4xM53YZ2LLW5jfCcUhU9jXq9pGNgAPgOQIDRRdHLSlYykH+PrRgREiNmGrIol9dADQgfpCPK28Mu3wyGIIAwBGM2zKaR08OKnWDvgJSggZDzzrsEZrbL88aMVVcgBM4hJliML+Q2ZGKloFdw+pN/3bH9Mf+CEMQAEyIZysMzFltIc33poAQEG3hQsbGv1/gylxkUABgERQW8dPgbt1TtZJ7/DgJkDO6BDEFhf3HmXQAAgGXgACAaABUQ/NgOy+ALh8ism6v072u/iAiGIACEJT9IGu4NEAWVR/oPbIZCuI3EFqe5mAWwenkolfzD8//hoATBdKpxNuVWosRD8ACAyl48tfrg9BB33gMOe5ZRlchiSF6WFTbgAcmwNVqaplf/jjVrvj+GQx9GAkoVIA/EoRGGhb/3gEDcQhwxdfaDgmTcuSsm2DtkyWn8wAgQK3yBi7NuI7UwkiDe5ly6gCVOVF/b/hEMfyAAEAC0DnhblYeRSOWFwYDQ4AHoWgz+Cybhp0s//4AlgA6AEApfmEm1jAws4XyiBgMRx1JG+t/wiGP4gDfAwJdKIx1jxhcRBFAAYtBjD2eT2QEiHtl4w2dEgJNAiTSnIWN5Po+gD4nPWz/V/DIYh/UaMAYYdaNzLpZ4jcwAAgHS2gACAaADIBs2uKKTcALpAgQW96WnhN/oxwM7eS2sIwFsZCzuYX8Ihv+pzAGGGUjUq+Yef7IgEGG0hUoRMPkS9Rt9f8IhzgGcxdiM0EAQEXgBlKOIye7X8MhvgAYwpRtZlP4NcMbrVH7/3/xOEA9gAWIoCkQUwIuI+rjM86gLkgABAHSgOFOxk4iBQU/gJERAo1Ut2yyoCnYfP9+hYgHORnySAMBqIHL/+/rPLUAFaTNIZO///3BFmYCEe8N6Rg/z/gTSin7/4gLwAIoADLKBOWPgxzMGOR2aOrhgpvQVkL1Pt6ArRiBxyYvdBt8SwE3/RjAlTfBfyAIPc1Mb/tw0FfkZT7eDc/vwwHuhDMcjrQ5SETv/zgCjAKCU0YdHNlkkBL/rR2SS0uh/62BnohhzjwutPfOAT+B+wAjB7L3ljjMKAumJkoNw/HBnQhxkLwosT5UeKeTBqETwvSbHmfYCvYMUYz2OyIk+7ZAgECa4RasZMQ1kw3+2/8BPmA6SUscGHZf5cfOrbJQ+yP9Sa6GFVzLq4KBujCJgZPRKX+qAiY7WghNPO9iRRa+PbZn9znmt2+5wJSEFs76WCBYq6JP5zjr2J11Z3Lewlc//+NQwYaao8brrCA2U/cekvKAonnsKn1JM/4MNM43aIBYMb2owCvgi6L++/A4K+QJUBa4czK65h/8BKYQQI1MvbsVasv+X+0y5nNLk1+NnK+QNcqX8r2G+CAbDRgrutHD3qaeZoNHu+rBmEshWRT939/L7491mWSmDwh82HCs8UnrGf643HwAUiCvo2F4AT6hCiBKEJi+Bb6K/MB6GAKPWpHKCnGVww+AGCKIawamum0QtHv/0jZXSNr63mRhkdBXewlDns94GCeWTYiXLRsswEAKXZ0mBHGauF0t1y/sEFZwKXBu45P1hKVKklH+0aTA3NFLmjP/Tc1+6BbfC5dW4g8EA34MFRRA363N7lri/5w2CrI+np4ef7xXsXHtee/5r6MNH6T/9UTlmNaQ3/kyqnj4+zz20uze9TRKpXs4H0WAQ6Zz2MZ8R/wPoMOHP5YfjbfDNUCR4YXKfEcbrTUzgOhStieSqV45OkL1SMvq/1/zJJri/AhXfe/Ro6zupxl//BQNsxYSFQCt+tuIQTapXWVf1ZTUOKrur70WE2y++qBrIMzcw6FF2r7/YNa7YPIc77+DxwiEVHROrxi5gywmJvLhJYC2o50JWbJSu+c50HwBcMStMikIykf3JIaWF3ETaE3gmGIVe+xikrf6wwsRboLqAaFsGV5/satYMHMK5KqQiM9f7lQSeZGyyJpGziEmYDRt8ZfYn9473fQ+vgoG46C8xEN+e6i26kMr3APXV+n9JzJRA1XjVonMOeIStfV/Ay9Dq+OKP7sMqZf/uzqjKgWW3/2hAB024HcrdMMIbTnexgBoAhjdYYAkevcvUALB8iip1iiCrccQHXFI1P/4hOaikGe7/wOSR+A3OYgRHskj0fWGAAIAeIMKhiiWYw/fpfE7XFq//1AI462elyN3fzAH/e4d5r0CvBANw+O7NF8pyMkDhR8Ik9ND6Fa5/H39uFWbJdrTob6f0+SW0Nl7rmIipodPb+ZgZK9H/dUBsSH7nZjv/lTh+2xH3NsGD+JuI5GYo79ftMORiqYlbFL/7eAKAAuF4EqNL5RcMzTFgwDPzoGcgluMRdik/0fWbAdHpstM5PmW3Y163abGyyq93+vmsZqO3PI873HA1jiOCAbZGEFi7VSU67smdeApfmewRse7fqk/p+36u7L2M2J6q2bwSvXz3zz2jN76twTv+WI/0D9IAIFs0h1NhRpPxmFAyfEW2jZKSqfjAAsNwIWdX0m6bmoLBy4k02qq7w3X4QABFHxThAEbKoA6WLNib/aIHYHcsZS6Htcf+pne1U5mG7f3wnmz6wCxu0/0GJn36v2zmnB3BANy016D+bfuLrHZbRo9/Yf5Dk3UtOrQY+D77/+tKhQ5U0R3t1TD8y5D6foNQKb818rdgv//nYaPNXB+8J1O6Zj653/4gE3GCFFr5/tyKap4SnA6EIWnQBscBDW3V4uq9//cYBVjC507AVHcO6qaLSMct8QTJmzTz/GquP3enEVr9efcEA3LJUKLK+/+A47XoYf3+qf6hIn7m/SCuUjUIf+1XrwEnivvS9FgrRb/T/t5sgoyA+i7bdUWvMeAAMIQw8gn2mkJEcsmeUOED+wMrhM8w3u9N/oCFQIYexyGiAmQ8MxAAToi4iBzi9UXCO+8CAi+BFqcxBPcv6zdRWKRD/nd6e0NWQyuoC239L8R9Ph8MDdkzajwqWm//eAJzzLnnw/bMX6R/kOH/+/olU6/r/BCyoOmQjTa5IBT8XNPSPCYyICM720ZkDSE5Ggk3++g2i8Hg+f18YSBX19kIaxifRoEUqYR1EgSiePG+vGwzqQwnp0ggR5KLAAEBsRYIieCYfh3XiAAyBqFrICENUyJq9F/gCIcH0sTxNpTnElX/8AclAdumAxAmyt4IwIL1aTpNma5PoSKApw2AACYInv4+z1vgEZxi06TKH5IQowlREXe6sQIp+FilLM7xH9D8N1HFfucd9B9HDA2QYAYSoNaoXD8G8CTn+1WWXV//XY/ZLUWP/fH20O7Wyz/Y39g7N9X77nPeuQfZA9zOI/tclQQw9jmCAiQ9M/+9vxjtPTPjVW11wwxoACd7Xzir8FaDcD1Maur/qRV2XdmLvt4MXhbcwF0v/ggG7crwejrv8+oqQkiHsX29oxWHmBM+GsX/fuKPDSF7htnb/wCmO3RTbFdxLFSrD9wJCFAUgGzlM6QeItTDfg3AuG7hi8eFePSaXnAACI46mrgEwpNqbhQIaCyQmHjLp18v/7w5VVM2a/9B/A4EjC/gEeoMTd7zJrvgFDKJ/pwEM92lGNBnpEkm7y/rPw+rgbOL1BYaa8+/hgb4SAAkBt1y5FZYIFP71jFVlknGBbvljhPgDC0KxGCzlL2UPn//4ujN5AA1YEQc3fkwBYavI/AEIK64/5F98u2YDnLryEBYClfyJfUCpXXseuBHxj28k2pvSDoXKNtBFkycR+yRMb1CI5WBAfmRhmVBXeotDnq4miHqzorOi//2gsUEgLxOyomIYqG/mAACwGAP0KsCY0RvIhMRkEdyiEOcoIEnwqcXx2X3f1sTEtOcLZmq//8lhTQ39YMd/Zb0IyiBgJNPu+jfcfiQtfDZoD79MGzOaOGVz/1twCKB8xpjMNLwJkQ/B+pBEZBGcopDnMDDnLRwa/JWdFfvfS1Qf/jcR89c9j/+JWYQoYCfgAAALeUGawFoOcVxgfB7R4MuS6A2UCcf8I+GV7wyHOAAwDuAmiMPxY+ZFKlYzEqcZ6i/hkOcwBAAZNDDmDqRqdImiREqcCR1Txp3bl/CIc2AoAHgEQpgABAAAnSp0J5QGH+BKTfwAa8RRh8hE/hkMezI8E+7AudWHiCACEsANBQlNqZtPeMe8hu4/4ZDm0kAA6Y3A4WkO3wd/FkBZ/wSk3KGwAX6h2dWRl9/DIYjV30LAbhVZ+29tYkY/t+AC4ZAU4KqfMiSJSbtDwABAQAAEBcABAKywArzaxuB/wiL4APCVjkIFZqznkEt8jMIzcV/sKQ0lX4ML0OFHlZTymXbYNB8MhzgAuGQFOCLnS4kiTm7QIZDBBBGhwuJIVJu0uBI9Sn/wyf3gJv13n8IhjgAWAghaC0ZfD5ESRD+fwAKg0IAFAKetPvBdDu2wCL8MAEQflIzJP/fwiG/oAghaC0ZeD5PkCH89en3I/4ZPAReAUU055/DMTwvQFAAI6hinkUiK/foCQAgChF7vK+mSUNBcrAMkFC2mxmWTNMK7C933jMAAQBAIGRjSS9xuV+ydAK9gwoQ32OyosTeunkQmMRhmYoxhBDAgBNvmAHmH29YpunwFYNYdgnRXWxPxoh0KK5cQHsh/2QALYADMOCK6F6lFtTgPAIk8UxlyQv5awBb9e2V7t5eFmKHe1XufzhQdgAh3Qbd/+cO+wzTAdtT1t/DA2Bgxco5P2AhgLLGkAkIGGCKdVcvillw7VP/rezSE6j9B33/DXTSFGlIVtB9sBQICXKAxUQ5iK1BdcEf/cBg6IEXtTPwxy2ISH+8aAwA9jE1vy0GGOeRHzeYb473i6vf/2oIH0UxggS16HCwuS+N4fmNXOdwr/Wa0klugw+YCx7KqfZ2h3eb8H4QABMR6AvMDQZnMCMTNXYmf74DUBC2obzP52Rxf/jdT78Eb0j94a2mru7f98FA38qGOKJo0ibMDXqbwQ1fxQX7Oe34AetDSJ7I5h//K1jar6s6n8/vYZYHC0ncS40ODDMzaBJgmM6J6uZT1U7zIgbLXACRTiRihskI463/+jjO+728AAEAEIPutZ7yUOJeO8GfD4BdAUGbEaoY9FRjKSPBlAizBHXmUc6NhUkkDDCAAIl448AgmHwnIysp6/+CMyACBkHqaSF1//VAms3kRdvw30RROD/sl6n2DRVE8r2BgeCgbBhkoNHNGe8AiXx1+sLoFjtY0poh8JbWJ/v1vulBKlN/W+KIiASIQNFdmuyMgeVA8z3f6TGXkgOv/HSSrJ8x/z745GAMFH3hU2TNkSbzAdhwBQDiNIY0Oe7Nww+YkYAMDCEJRVIMky+0gzLSE9FpM9cGBEhzydAEH/k0h9MzGHwMBncIGFOZpCN5DiN/4CSBm4wL5OlYVzF9dTjSMiffasGKrrS61qVz/wCR+2zfVCFeuH/7PXBaxwfOIBANgeYIKJdnASTEHiJAkze8DIjv/LqiFb6tW7//2VIWf5qStcCi5bg9Kf//E5UsAys/1VLb0P0t/17yLQ1EqEF9/4Q7TGGEktL4TFJ4jrfsAAQCwAGGwSPMvHf88UGCiUUz/b44bQFGwfhr24ABgUepijJRM+T0p4DGbNoI1zb/B+GjFcOMVUwZarEJzzDvB0FJFQ36Gq/jWuBoaC/PZFZJ/9pIqKlIRIo9qG+8C876r7llHr18EA2BNMKsPGozK5/4COG4YUU/G4gsTZKk2OsPnl3PW5N0EmiPbOFmaA6rLfpA2lf7LP3qJUXy2rvpLX5HN7tcQSGZsDksKUJJ21A6E+SXOTFetBh4IoIR6EjQkNqbwCA7fCMw0r72kCuTHvTJmCfIqCowMMMAp0c2AQOphYU1JSnUfz/0MDr5/2WpCP7X/9SSMS1iKbdixIkvggVKNunN8xrl8h39vn8FA2GSPCp2JvngbjmvUQIV/lZIk163ESLQ54v0oiWSodxF+7WYP/XHe+XNYEHcPQnZVzzftb9z0MqY3/XSK3lC3a/6+gC2AaheC0iGj4/QxXtmn6D/GLxCs/y5Oz6i7EZutYvPvg/CmQBkWBjtK962zmC0v3wEsAAQAUGsimeihZOD/nnpuDl4FdkY8NCyxwsCPckO8n/HwUDdRYWVZkf/p4QgeoBMSm/61FQ5dEY//+3Ztoaz8yo9wL1yCtmv/v3R0ctZz/V/EhaRJaWa/6nwVS2Xv8/cED55ciMXSktmSf82xMbn3sH/ClAAYEJ2ElGEnC05N797v0H1ghToYXAxnLGp5wnW7/qsEuFMlLK/f7Y9wubUyq1/k64VyNRviX43Ktk13p8EA3DMSwEUqaeAXIZKjjTm9U5n2LARkNvPCkbts61gLQRWdSNc6fvYSRrDhlmt9RFili9WVabFtycI9/z4DBE4wakzvSevdSVtSZhwOst5Ju0H/k/Iga6e90F9g5CAHCWLRygt5tkMMIF+LcQspA5OV4usT4CcA+BD6rKYli4f/Z8ffv8+rAJjjldd2iNkxbBjXDunB8fBAN0qcjM8b7+1wmQVuLWOH3M//Wa+Jb5n3a9kFrY7HPv3o7Cqw9s/9zhBjWLqhz03LZXoFkiLf/9a4K11dlbGhkdzOyopBWP/9aBFY/SLRKap/fv/gMAWHo5IBqaZfAIrfP/2h/MgAHmLkAKAzGVd4PwwAYChAAkGEEoantBOEkd7f+BGBc0AqNGTVl/+h/0VSQCxmofLQRDyj/5k3d0h8f3dJ4KBsBoABClC0J4KqEHUNmALbZCGII//++nDiJEjxe/rVaKPI0V1TbTCSnb99i+LTZxg3+71Br70qaMf//xT5UUq8EBw5OyZxWr/k1BFxFX/O2d4H8/JIiW9+YslB+EBPgcZWmCKMk3u3cwTF/4EAgn2Qplxp4n//85pHPOWP8UYqrf9+k35f/mfSPtPj+HFAEMIAUGCekbaUmLOyyocVcAWBmIFWc8Xj6LhhPAXMHKF4qgXUebNIqPEUhJUpHOkIwaL9oCEHCABpCKyqy4AW/5RIJGI2hlDTI7ysTBnq7svpbsCr3AKYvU40AIQxfeAurx4AjAMXXDCPPuvgVhJhkyMmdGyCBBRH8eOBEm/OAa5gQwgDKRRuA7ixGTIyZHF4IRgBdBk+8PckP7m9HAgqvMNGiFdXGroNTf/TGqlfP1ETCnwHei49wJbSOBjsoqSHPQdUoRGtpBa3IvYh2hetuJopH3+BriGDiCdamRJx6f6DtvBCSVUyM2cJG76wb6d+Vr/UqZl5ofr2dCzwkprVcdtECbzqeYmNwjCGbtU9kI3CKczdr/XD98uGEU4y1Fle4agkvhhAAHQZ6hDnCgSVj0pALqO9pMGFURTM300W+D+YrTcEL0r6b/4IBvhGQBHuUeLjtz/9sDAox+NJkyQ16klghZqyoWkyC7+0PoFKKC9RFE6hOl9wEEkLJEgkKkr/2rgMHGFa4KiTLdRv6rqaP5/6fl24YSJk2cCYAK5gBYKk5tTegkMMJRf5jDpUZzY+H4AQpdFLVLegdUmVc0LKBw+4tRBH2uLSh//B+EApHdAVJ0KVcoSC4eAnQAnc4EF7+pmSD7dayOMPOipT/79ukKSAR11O8zwPXggGwFUAASAbdc2R22Chj+8YWB7T2BXFRGNN1r4NVDSpXOEIZt/64IC4Fcuym5WcqncAEAx3BT5GsV22g5uRfuACD8Xi+JAQiKS2lJT//v4If2JDnKJjT/AxAA4xuxJbmJSxSUvZhuAAHAFE0gOHpcbU3kQPheo+1GeTYpLYQQxBCJ03APi2uzAojKC6/7Pe7/YEYL95ETRn+/NEoBtKbEOfC3jGUD/EJLaxRnZ9wZDFBlnDbIlFekPvAABABAEZaiRAv3FB5dpc58RWIzE/dW5XXGh1ch90DMEJhWpR5ZULfdDD/G/GYaWKEcDn3CbADL4KYAAACU1BmuBaATp/P5/P5/P5/P5/P5/P5/P5+J4XgAJpMa4jZTuQj+QlIcjBXasxpBLQ+MYBTg2N6MUGZHrN7+AAeCwDfoBCk5jArwQSxcwAwDj83fTRkSVNBYqBggwgFkWEAD5trUuf/vQISE1dTMQpwu2OE2NuID0MABAMC05AFNsc7t87xMQD8RB6ekLCXk7+BB1HtAWrBxU5gL9MRRcaAAEBXxCAACCxAAAgPHfXDYYMUsPn790ECRFj45DS3UCf/wYCAS9hhRzfY5JihJ62hhWEVC0iGkcjuL9QNJOHnSiNQWE6/wMZfptA8RSAOPIvev+HFAEMhwiAYVOIoJ6M71k46yGioAfulW+///bV08f96qsr30Hy//9oDIfChYa/qio0aKfHASrwDAAEBpcXLgBAjItEYIVgejqqqASPbThnGTZB5AvJoPQ1liWCPhgAE6Hj4G7Ekheembf6A2gJXAqG5Ejt/Yvyy/L4MCXOT4Jumw5gCAZiDElAxlP+GwIGGCABRCdrjAA/m65yPtL3QAAgk68AAQFQCoOy4pUtjdystxGGT3QoAAIJdwAAgJgOjPBqAAIItgAAgLgFST+L3vbG5apr6KjB338BozlL+UiJAACAexMxgABAPABuOMaucrjv1ZrSXhhhAAFQQ0oK0wWHxFa6jxKNFz4DfCMw20Wk8TT77/hqUNqbe0lfN/8OKAMAAIAYBQmDw3PFJ/H3SiWiAACZwABAQUgAwVG1MOT+TZWcYkdY/yFwTJrLNuCfzgFwH4cA4DHZS4sLJeuIA9TgGAY5SfFxZL3jvckWglmL58yRC0XrKVME+TfSfdOUiJAACAazZjAACAaAC7eGEEbCDoFAnK5XFYwfpv/CxAqweG1Jbf5k3rrn8hK/hxfEDIwADKtwGS7gFRHCl8GJ+MPcSnEsYt3EZZggABAgzppYAgZhrIMWf//u2st5SWtcZuMMAAQHJqMgAUK0cAgMiyngET/tOQonmrh204KvVwva0FXtczJjbodCO/KwABAKtAAEA4ACJU/2AABAKtoAAgIAAVG4wETCGMKG1P/CBDaVkDEBmik4y7NV7gFWDHmqmDo8/a8MRtNB1pGi6v8OL4IQa+iY1helpICSJVzJYgAwC3KwmyTcXQIAAgl8AAQCQMgjgeotEhYDk5IVVKqgCwACJweOdesiXARA/CgHC27Qwkqs1I1ILLPtJ7WLq3789gAGrYACAIRp/KREgbNkMCi7eGwCco7XljanzmZMGrdDgo2/hgcDTDvCDCpqZQQq22YE4cJw1Ntg+Rv8IH6rP0lRz/hxfAAHADhc1gtvH7BvpxsTaQOFQXutH7FuGoAAgfrUAAEA0GJ++ufa8KvXunt+HQHgdOPfQyk5OwwyAAEEGAACAaDK3/i3dIl+Y1u6RL8xq6AAIAFkoADAERH7iMhFMDELxJwceQ8PGthDieRwRiz++xKghhGoYIRY/ff4gABgGR0IgNhRXURtTB6BCdQmXUbttdfijHKC+i6Xw5gSAEEaufLTZzAA0BNb/9gFwH4cAoBjtJcUEPeHgAAQQrAABAOAmM/Md7ki5nJyzbY3nYBYDlOAwBy1I4REPedMDpQCgGN0hhI42w52WUh41qqtp6B/y4zMwygCPbqSwHBy/lIiSE2YzMwYfasAwYXWFSpgS95FMYZwjkMEmHGgwwhAJQh0BrBEo2STGD2d3ALyRwr1airjwxPSllMmf8OKAMANDBQgxeus/uk0EgFCBEaosN7W6eG0Pcy8QAYDXJwqmdefWlsCGhOLVpozL1BNwA4Ek6sFViG7Ud9c7rLNthP50FopaD1nBAGCDazLlhb0/3P2YAgYZeNSxoa+8OuvcyY/4vS/wgRvcGz8NCbthbXSb0qxiGROJ09hu7+g/An1XOm+uX3P/w5gCGOLL4cAljVrfjIj8eATA46HRKTru4BTG/GFgD93p2guguf6hfXvrXO2sJvOfh8cOKgJZZAACAYAAUZOVUS6xN1UvKkSX+VnNvCfzgFxq5ygCNfqywCAQtIAAEAwAAQDgAdLDwI7ZgCAg68bmDgt9V//VbwPwgACYELOAysCDGUnM2GXR5/6qGVkXjOG/6B+Y3kr60FVPH/DigaAIDRJk0UEDZnlm/bhj9zX9vAXAfhQDgFOyhxQ821d1oUuveqy1GmGq3ACEZ7DwCP57vB5tLA6sACAUQjRkgi/76tvxJhKtI3ILR19cY1c5QDNfqyQGB61gJkGYogbUw/YCZAjEOG1PkUxhlHMhAQo4x4YYAAgC0A8iBAeGVfybRhU/+cBKEe8rjoKQM5N9/0zjukJP7Wv/w4oCjoBA5nw9L3HH+Q5df/NL23/oG8tO49vnPML7TehLTFCQ2eA1A/RJiK1fz/sBEH4KGhDuiCjhkr0hLTFCQ2ejzmQS1rtEwBgYfeFTZoaQ8IbEOwAjH8sgBgIWBhg0AuNynKAM9/rNAcCl8MQF0gtYZmVnBTK9uBEgDI5HCNCykW9/tTxf3O1PCV/v/4c5AXAwUwwScaaX+cICI5gQAN9eedjrS9GAAIIoAAgIgOhcbUUqXs2Ohh2vTWgAnA7DgFCW7Qwkq41gqwBj7O57le+dDH4+a1XL2jYVeGDPAvHLmr7+nhAAFwY8wDMwJbIiBdHfg5aHwEoxlSEYwixaO3/3+rXQBG8q338OKBIBgcoc1Hla3HjjhoAKQnawwAGoZrno+uvZgACCfZAABAPA4XvjGko+/pdVKLZPQDIH3AHD15S4or5ZwCkIj2HAA/2Z5yOrMZTNMsSLnrVSlNkOwf4Cw2IKhLn80p5buZfmChLfp6Ki5L6GGEAOOgBIG3BlI3MbCtP8AsBN1pKHS7Glz4bS+p8VFBPv8OL4AAICoxYDE0DfxzoQLk9SIHTAM5kAAI91lgc2BFn0BIKOoDDl/4QbXXLHSGATf9xxxIlgRH/FZkNQQTjBtY+UEAAIUAO5oIJxtTBRbRO9373G7hVWHMtHmNHp8SJS1wVbPEBED0PD5eNqZKpf4QABEAckPA2LRTzBouMgBB23wE6Sd5rBGz9/WCd9i/xIWgSBhC3Du9Y2LzNmZB9gIAZIDgjxaFOigkrrn+8YBQKJT4oxhcj9hpP1YQdjBPK9EMUV/P9SAEGHWjQ0QNECQYcITMcgbAG40QR24a1F61Ff8+fgjaWf3wFpAAACndBmwBaAT/N4AEGYAYIEWjU2TNECfl/8TACBAm0KmiZoiTDPxfgAJiQpysEdizWkEN/R/GCBDf46KDJN65DG4gPYADgIej2wMU5GDeSpj90aAATgXPcsbhYkZ/tgw8AAICsgXOkDUBSFr+AUCGo90SMV1JrRUz/6gyYAMATOYWhYwL+e0bAAJQNmPWPyySMf2yjFD/QEg2s/DlBcQ2SDyv79/P/v/D0MABAEDW3QJYb7rDBy6wn9B1rFYsKR/11eAYJBFgUssn/yIlb+t5gauAFAFNwlxQ8+0L94pjKVAgjDK96JT5XByfVYpb//y9W4QQA7mAFgmRm1N+a+ABTJ4nFiax23D+HF8EAA4poL/NlpDUxXnwiuetQ8HCDL2J8RTQIuAgCtOAIAPfrDXQLpuLOxXL1Jq9zBx52q72gxWGwAm4hg3oFcmK8ArB+c51TJPjU6lMTF9jlcywdWue2YAjAN86CklCHLowAxAm8Km1FiIYfMOMoBQFL+sk0YF0XBDV6jqKSl++CehhhgAG1BdoYCLidiiqjXwDJDmbNolNQp7/+3NceZuSbaIoJeWmgONx1b4ZvHDj+AMCiUxDYi8XV96Yu8NtIvAYVczBCY5AKAwj0KOC0t82mvrsynRGRO3+P4SIj6mhbCCDbXpaLCpPoASwlKcBSxc1/s9VekZkePIp2k/ikpEO/zb74pvPcY3Kc4AxL/WaAUDGPhugABAOlwAAgJAAIgHl4yopJb/CBAAngUBgY4SgAKLAfRtaXANzAlIyMDrsXvv/D6Y9SjTBfKVV/DigCCAKFGLEh3SzLvazBIzAUwRuGFB6G9J/JvbjfKI16YrsYFG1OvP57PngabidMKa+1IRmAB+7EIAGh2BqqVEjBlOXhdirnI2YAAJhQAiWgshG1NIeDO/+IUqABw4nOd1CCJLiAe5wBAHOYnxMW9/DDBzUCLYQVMiJXSTcbposd5nARJNhyNWr5RZCTbtAkBINrv582a9/38OL4VBws3mRE7GZMCAslyuabFWduYtT1UAAIDC+0AAQCAAIip9Kc0x/3+44o9mM1WgJOyjBmoSn8eEkVAzGAAEBa2QAAQCgAIjvpSzTFZu8cUbjGaohf2n3f/MAAI4ARbgQXjan/8DD7hI0NdzTWVPk+3AIBEec0Aje9qwEkcwYYFCJBOdlEM9ngup+A2Yyi2awxhoE0+95VaaR3rYKtk10Bp3xe7/w4oA0AAICAAMMOdZYlFUBM7YWDFtti7QECTGwAHVVZwAWCtWeJ8+My/vpGpBZ0+3CGQwL4lNnH+i73PmT8nAAu5eFgBYNx06dCfsi8lCSNFlGaMEtEDhvqSD1b4nf9z2zAIAAQExmY5MGwIfeGwAARHP5hcjanzA7hQ0m7SWPO4a8MDAAGoEGqAXH4wfLagqPmN4CAASc6O4dFPuxVpSRtVldNvT4l24bv4W1KO/4cXwAGCgQJW6H11PON0cGgi5BylYGrJRYOC0/GHY/Bk5HYBQSiUUxQy1XvPbEYtRAAAgAWYAAwDIzoEFjAgzktEIxaXU7USYiKpTwkoLFo4gcpWPkpFLH1zaIAAQPyWhADxyx/g/YAARSeY+htTZAACCLKAAIDIKjPP8HAAJIsgstzDFycsauuf4GsQzJUuz+Ep7v8yGgyyeECDLLAvcld5nrq+r/hzAEAAhkItgsvVzj4AJBNURwFYNVKoAMW/1lgGBzGgKBKlyocqVzp0MiNO/nVlVtkP+7HQABAUoAAgLAAyNwAEfYwYIIXnUwcFvpZrKVL6qOVrpmdcYD8OAKAY7aXEBj/zgQ/6oQCls0lc4ox0gw9CahxqRKd0kACUqE1k4cYgTnZL4BKdE7/A4ATgMChgaPjI9WNqDzW+4Gyigbuyn9/fFpPW1si5gqCJCDV29rZKOylrl+nUn43wMF3i2FwhAF1CK8l+1DigCgY7Gixh9w73gQHA1nGkfyAEyLBAIo963mXwEUIp4SQECBLiEsFh0vwUi8X9dB+KEW3vBzQBLBBylVRBUa1D3ASGBiKqgG3D5CY38H9hJQA4FE5sGGyxs3awNUgAIBhSiJxciZb6/ww00oArPRqp79wGAcOUQlB0DdvRf+GNvDfelt/4CH6aP+v8OfwACENAyM2bxmONmkPDYZSuAGJLlIkLHVqgAAgJegACA4AAye8iHRAc99phTwHDIAAPm2ACAMEVjc0IECJgG4OXfwmtmVxFwHMOnNtgGR3jFeWGX/av3c/vw4AAgheQAAQFgXL3txlxAACAYAECIwqqS+R8MIAAyBBLQGFMDA4dVwZSXLE5fwHQzsTqEgktpB0NwwtyjCCyny/4c+AACAEn5Cit3ChcCRZDVuGDUpygAEJXr3gGBzGkQxVul1OI6/5o/lYnr7xDI5jNgHtgACA9IoAAgKAAZG9gFXgACBBLMgAAgMAAyaiXRJiNis9pCrX/814Q7BPI4IrON8YDuOAcA5vFOKDX6AMPgAhmJYeAYnfvdCyPLAa6ABgKJUiqYbJ34PwgAC4ENFAZmBlABbuiqFpQ3b//Akt3D1nYR49GL/B+Ja1KpwflGn8OKAoVACh4YitsIrp6mLGn//DGrjBa7rc22wAIHGXnM4RXcx/pWJuVTpOphdz7a7kAAID6WaAACAuAFt/4GQA6cCiD9r3Lk/H3/pYUKeiZBL/ve/VZowAMuBHNAKwnKM1B5XuCUmGYZAAAgHAACAoAAqXzDjKAUA5f1kmAhiiwxdGqAw8Aa4oaLwKXggOsAsK9LigKTpngNVGh6x0RTEGhzCT44F/9EcOOAl0IAAjoKnIALBlxOIfgMkugFGJsKPY/+SjLIofIy9AuMyGhsGNNvg0XZgABAaycuwHFb8BB+t4wKcUT3ZtEe7oYdQJZrVcmeFglV7ghstRwAehWu8hvy/L8AAQS5fYAAIDoIhcH/GA7BQ0m7SWkH6OUJYBhX3T4Ru0H4YAAgEcACRBGgL8LEIjlOKLo+AlGDU0JDFMHF9fx44/VtNGtGQu36lt8xtpVR/+N+MAAQAXQDngFfSotwQ/sb+QLXABwYRrGbDzLTsfBljx16dM+WB6VeExCKABjAQrJm9n4m+BlLKAcHHWmG7AftHf/b8+Kc0F+v07Fj/mXteENmqMHoXv24TF89hluAAICdtAAEBMADQ/fWwf8GpfAAccdYi1EDtg3/+4BYarIGaff+SQTt/wYYdheCCVC5xMlvT/u8CWYAwQTe9mJRip1//njj89s5I9oiWGKBXbl4j/8b43I8lmlDXuQBlYcBYlblCuIM4y3/wL4DCV4P9ciY1+vBHp1SABAGkuoAJBuEve/8AEjEURyiP96WaS1UD6LhqbdNa1r3+D8hsY5FEJ5piWuXDYAAMgcAVcWempojeY3Kd1HJ9pq3kt8MJF2FIBVBE5NcL6rAJUfDcJeyRCH/weA04ytMn3L/C3gBOcOeKFJoKqGtbVlsQAEoAoDf0hgEdmBc+athNcguoXn//axqgewtpih/eAYxPqiyvlYCmRts35BqoBBC3qpN/AdRhHgwwO0gaAIcLlGqU6YcXiP5aR6ZpsTcMC32l7f9FoC0gAAA34QZsgSgE3hgMeAAkZiMzjt1RTCXq/8KZiXIdiswMArwBop3n/+f65vAAac5hxzHYaIiZB0z4QDHGh4ABFhmzFF9OOINWR1xpzUYAfZAEHH3hQs8XfeXgR7ht7/hAMfyDcgTxfFboInBmxZxcYBgUZaNSpoZ+WIAD3GAMMOtGpd8s8+8YRBSeJaYokoYX+Q8DArWaIiWc8YYZD9hKF3PxgAPkpjbPyEVT/wgGPFZgCDD7QqWfLPvg/AgVi0i4k3kSzbII1kduZGDgiiVsN2vbAAKbRIx9CZ3b8ELJPxFvIsaEPXEDx3T4YDH4QB8oRwAzOq/CKnIm/3kdjIdEqeq43yAOIAKWL5HaAnd4q51OTdVowuAEouPEkZLS+DxEhXQjo90w7gRBcIBjgPAQuguJpEy4NN0KTDSDAAhlWY+hM7pHrmqC+ul3+EAxwB4h+dURWYqt5DtQjl2Xtmf0QGsCFgbDdBJti5/74CACYPQCbVK+eiEka7sRScCOnzwCfRWw6yI6n8IBj+wE4bAOtYz16AUTr9/U4wDAo6kalzAv8s04M4bEUnAbCTyHkKjtHRmnXefwgGOAAjBEOHhdiMK0Udqt4hlIMxJpfuEeVVQ/Z7iPeI/DT7RVhx9Pd9vMn1D4AYh1yen38IBjgCwiCk8W05BZQ438kHgCAAIoAuuhxI9NqYZG5ye4Xymgi+2fwgGOAxBAEBR9IVLGBf9Y4CUQw0T9xFn4gUkkH/uzAE4YBInRT2Zwk5+6ACEBlDZ2+pBD+D3y/wpsnCEUt+2A5OHEvVDp+cZ5YQF8AQE4ArmgOD742pgBaCOrHF7tIKE9U4364/3l3wgGPAAaCyg+HpGSX4UP7KYw4xxcNcUXiuGvoFKQAhYi8+qiYjvrvtgAYAGP/4EcgG6DtGl8xScrJ+iLzt5IBg5cQ3UsAi4sZGAQkyzAnbAaEwqb4wxDfgIzb+5f8PQwAWJRfqEci58vAwFGCkFCJmYbySSOpnOBA0O2pHJ45eAThIgwd8Swg2/L3//u8IdtsGxEKLsVtSPpEyNQOm3vIyEVlEfyyltctgAAuBwDsijMpNEYPwKEkFOZk0Q1b//7gg1lICtVVO/314YBTmQvu1iKoBLX/D5/DmALAAEAEQFFxr1aa7FpeMDVYsATRxwAwTXB5AoTYDDGHErE6U8gNCi46Hn7ACpf2cIGKwhxJYnaCDF2QJgmAHHSioYCeHx1e+kxUoFZX01gBASAojJljYzi09NbOBvyxMQiP/2mAeIQAoFpU5Aw4OPaBnCqLFlCXWFRRYWn/hDRw5huMBZgCHU0jCOIBaPL94DDLE/wgRh4gGocDTwhKKxSc0en3/gaAzUQ2JxF7Y8QAyHYK1Tj/U8cMLF9dvswM/+4rKQ3uWdL7ZB3jamsTafCI2Bk5BAnkIfCYhpqd/uAEFEdZyzK+sCIhmK/SJZPhzi7Z/g7bG4bMGD+aTbQ91Vv77CAbtt5xxB5YSm3Jq0Ruv7UeXP77v4wZGGLAGc1G9gaS4nPAIIQhysitGzddd/wYfApjGA5jKQOOj/TN4QLZMuAFdSQfKglemFIYYQhcY6B8AG+DzIpScusYDsMq9AbuEyoiJTxqdFzwKdwRh/lV/Di+CYBAEMC2trjfe4SpNTvohISEA7hck/MpP/6YAAEBOT4AAQFwAXcvR/aId3dcjt1wvP3EAAQE7tgABARABev5VYAAgLrcAAICoAbd9u9tcTAMvr13e8swA9qRgBUAoZAmApj0RhYOs0m+Q+HU4DwmAHIYA8ERtTBvCMgzBicKBOZPFhEQRg5PmAjMny6+sIEF5QMdAUwQGR3MNpkLf9oTNlH8rS8B14vqKMMvcNpR27SiwZfpUxE7n3KqRk+lFuVhSYcXwAAQBCAK8vgm5fTx80FlhnKHOdlnujc1hNVavXnwCXd1CU6HdX+8UcRkIpNfna/u9lU8+YXe+m1ptwi9pnEAAIAwYfaM1+7edSM1wVGBIFIu6BP86HC3lAA4AHTv+5pBnQkInwA4AGTAVBMQZgWolbzgyT8cYblHas0v3i01VQgxwAgDAPANjEdGPTBajl8eKrJwQizsruIyE9TlR3ME/Asj5XXlcBI/+Ne6O82L3TiR3E+pMU9hxfAABAFUARjg4cYoqU5KZpSZ9W3m+FXo2DpAL/tH4V05/fSNqEiqnn3HhXkWhNXPIEj7+meB70Y/tqc37V6vuwCJwLsVrAEIBNyfcBL3DEvB9JJyTARVAkMbIICR8K6Snz77tMJSPlIL/+34gIFsYYexyGiAi/6CCAbTgcdaID5qUgKpCqmH/aesXaAXV4Rz/sKISYbGKh6j2pthcm7OvFZqP+hXVHPjQ6/9uUdqntDhPgAAgImAAEAAA6Gt40KyXXDuETuYH1ALbkhc39nhCep2O1p7rk7WscRd2m5vyAiruppQDnlt9+RaH4j8v+Ur5KMC591VolCs5nExxCfvSGJH0IHyxlbX9d9YBOB/9xmYylAEe3UlgMD15AAAgGAACAcABEuQBGjaaqHJn38GPmKLFYtXtFgHcSAABAMAAEA4AHSyAABAMAAEA4ACJYQgACAAOBggKrBhNeITZRqz2ncwZGMa+h6zz22WPWPGY2fLVkbLUQXt/EyqSvhvQ//w5164cJ4AANADB4jyonURMfgPPg/+hka3Uavk1WgBQe8rORDQS1zMs4CKhFHRLPE4W9Qv94Jff0m2bIgKXXIGk0QvrZRkBgAHFI+J0A10/56gACAjQ4AAgGYvi4hoxyOM3FmNJdwYm0osb+tM2HxXOmgABAJ+rnAAEESjdhC9VADpipeAAIAn+/qG6gIYYzSD2gAGkW1oYc4STrTyJ4CfzggACgORwbA1o8EEV7JlOOgt//4z2OPFuv14ewyCjOxTHUNu/7r2AMq7cG4JpGO3Lw5o7a4jO3YLzLmnhEIjfGOnvYWGyJ/O/YVoAAQDbcgAAgJgA+IVv0psNL4l5VMRDeK7vHFSADAobSFiZkZQo3jEUcpD2OtSgtuyuOuc2lpaTckQz8TRgxhBDjeN7MgU6E+9xgSBFBKbt6EiAEPQj3hlMEU4sFRortcCbEZ/qYBhx94VLvmXyPhIXFKBBU52PgcdJgW8xYXCgCSsJmCwPejX/BhhOwABAIHHQCD8tpZCWKUnYGZhpNkJ9lJqF1Av6UocnWqX3fakQlykEO5QCLl36cOsu36+3NYv5i3Yc/QMgZTvJ0TQK1oCR7PR4hIOzvvXhC91U4xwoI/u3W1rH2SvWSKEQ0Rjo+1N6Z8ELJ+yANwkQxOy8fDaubmFI6onpMcXeEB0ejADpteffCe6oMG5tAAEAr+AACAuADoTrkdQgQQ32enhVt6BCSJAACAazZDAACAWAC8cujAGHH3hUu+ZfCAECNMAwO+BBLidvEPU+T/7XIGLUfvUlK3cWk9bXia0SolBMNyfRm4fHZOplvt9HDi+AICLWSUWSaQYaEa8XmKmgGW3SFOcHe72pZfqCLPdzOrqTIzmfLrnAbH/6r+lAOl+yNrEmdPPyNJ4kFy+9YEg55gVOvtPokzYQ04AxROEAkbaIIDW+8EgpDVjPIbymJusrZPQQofQsVNE99De76EIANw484QRqKJv22MLQ9tBQrmHkRDkWlKM2vc5mncTbwm36zuxR3mhz6+uHPgAAQCACgaH3itpwYEhCTqcfv/oNsLe6xCa16T1Vm9ilm36/6OgHstqefmzNtEfeaICEgs4LhyBc4cJq6L0lRLJ/7a9wVsXk+37gQKnXGgzHLfsur3AmHNCCkaoeV6RMCfHy5GAMAw+8KlwLsP4AIgHetYdOpKrAmBAtjDD2OQ0QE3/QRACGoRNaxRiqeBrKpuP+42hlgRxaahPqqsrkEbKvU8Sw3MDmCVP6YPDRKYVVf3N9T2jaHHAVgMBBwQW28exJcR6vI2AlXAYrZuEPYhALAeYqKM1HnEtIg3OGHkto1O2jZshGAAIAosxCwCwzbYDmjAAEAMOVrgWNvfRLFf5jv+T0H8Sy620CjlOBTMIsBWg6/f14UAAIB19wAAgox/63GNXOUAz26ssBgevIAAEAoAAQDgAIl82LtfvMKz4vLpmaI/1ci2MMoRyGiCzzXGNXOUAz26ssBgevCAIESAcB2B6F3k4bp0tYuj4FANBMqeWe1O71v+pCQzfljB70+FhvBWQbKkcziOqQN1wOdpcIjYxXgMP8tBjAtBJtIQ1Ef+HTatHKqS3Oxfvv6fzCdxPDd8rbo2V1ueWQMjgYmCRxNlzuno8kjFeS61smYiffBuBXeCyzXKnA1AhEf9cKWAAIH3oAAgHAsMn//OD/BARxhDJ52A78dBa997gDOAVi2CQgisiIkKEY//vDBwQNGMKzCbvVr/f5BwEkHSriAz8/p8iqYgjX/OocG5WYE7x0GEY3jfYDvy4gb4ZgwI2dUDzpeJ+CH5NO4vhEAAIAIKFwvNawlE2Xtf3ujY8hIp1MigU1FNL1ff7EG58LfwW3SXu/iQBggOUgYAhm8WB4ayb37zMxnK47dWW1728YxlRLxLwmgq5IGYMNwAArQBAuIafAITam9tADQY0HESIzJmS/mvhgwJj2TLBW57VGCoABVVAEmJKm37DEMwWEVpORgwWJr1/cSFoAiOKogPfKdvbShJs6G5zHPIf+mChf4nxRe/8AMRyhMr+bsdqKMm/+4GfAYYobjDdTYNfHryMhFIozcWU17l+1sEOPZ5HRETIe2YQ4THgoYkWpKURuv3+9eMnEgeXOpSOGbd2/adcLwFpAAAOQkGbQOgE3hA9eGnH/iD18ELXn8QHPAAsB9wAOHV1CDgpjA7ZfAGRfLf77+EAxzF9qDh7mAIBPB3Hp/KJcJlJoABrsIUUtuGHTYtsr9JiciCq3yEsandIbip0T3qffe9+ACpAcJ1rHFB9TQITFw6YNr2hcgV0SCt9Lv3e/ECAxD+4RVZxa6SHGtdGnpaL64ADgajrFsLI+WJMBlw9ACACcFXhvmUZ6KoveJIlYoQiQJJcM2f3r/tAiGh+nhoKr//9eEbOY4QDHmAxMEozJ78TuZRP/4OSpJnnN+eAFA07jNZ14lOJR6CUQJF8ZYqcFP2SZsYOwY5Mo4IZpD7aZCfv0MgrJiUHv8MBjgA5k42lj4l/ESVQe6NH4ukVAALMNx5ckIuXAu5bv4BYmxM/ideidrcPpRZbDGZ3/szi+Vz9YS04YwQkcIvG60CxVXJJLFXVhLscuBU4QDH1MTohxNS5LFpD0MExY1FHEV3AZhIv8AkAAlSgAFJby6BrHhJsV7fSW4FXbZkQ4x7/3BdzzWl36BIvSGn3f+EAxwBhHoSD2epsnsWc/lNJ+QAEYDThgxl9GGM6JKGQPpjiXx6j9+eIFifQuIQpT6BW04Kz5pYou78DtvxS27/2/hAMfEA1wYNZeRnrXCSpkPgxt/RLTm/IEfo8/3kBXlAYQzOVuq9WW5WPT9HmgeEUnBu5DVCPt5+CjUzhpedglbtVHwgGOAB5HXxuSY4qn//9AaGSeqNMbPkPfgAGIQGEFUjMmySabNQAAgDUAAQAQAgfH1toBOgRCXGBC6beKueM0SA/84AYGsVYFEZtJkQfAdOMS1D9f0fwgGIAxGQbMKq0kLY1IeGwFSoEYW0l57yDRW3KVMEWm7Wv95P2OqZgcESHW6TLa9gdkTnxxv//CAYwAEBiWUqZEp5hFKzj9PhgDKwDYCKyRsbduKf7kA9wAEDqYnJsY1lc8H92mxLM6Oye6bAQOJpKZIoJ9pgDvBL4vzgZ+zbotJ/38R4QDHAEEMA7EgUFWhtTAKQpErJMpti2CqjkAAmRDK7CMxJK2MT6fBCCl9xw4bFt1fGYOIcbF8xJ7F2u2IVX+c3zn98FbThH4dAA8bxHEZV+u6f7+EBcOAKFXrJxUOJlpjA9ggAEgSsH4X1q6vjAzaqFYRDUABoB9KOCBGODJU3ayCDQRAYiSVj6m2TIYKuvc8mhpUdEdPJEIjIIrEEKYxQRZDTqQA3sgtkI7D27Xfn8SHvgAWMVrzNCMWIdMoGe8GFge3fLWDfPASCBUetLQTqp+7ov/3gJkWsM7gL5J5P3YDqTCbFky0x/k41CkUxABxVsVOcg5FNMJcAAOQAB3yA54bNqYPwra/TKzQNBEHvhTo4NCP9qN/q/8IjYCQj0YSuXpLcHQX2MeMOmIHODHojXBbGOf+d7oVN5bgJYGPFV3eAha1UuO8QEAv5WUAssvw4XZBnDDOcFfLx7aq/RwEIwNksyLyKbN7lITf/7QDVkAMNnXC4XjfCD7zadSHpAy/1mjokCYGSWQ1/0skqhWCLecwOwUEnjcJXeN0Gf9oIIggUi1KMcFwy/7/wQH7cE8YBXko6RVPfYPISn0ofAqXkDjj+5DdPuSkLdVHv99kjLkiaeCi4RG8RV1eUC76fv3CoDIKUxKAQ6VeM+rFvJEJf89Xnzm5/3FO3n0CV/fm8I2AFF3YRMp4PRETzdca20dadh+GXAZDBbPBEE7JEC+C///8AQSF7EiczhBWjTnmZjK6ir1JKWtWGWGwARcpCDSJTqghxNFT8yA3DfgvTRv6mhZWEFEJ9eyAGhAX/x1Y/+wTWC+AmGfkb/zfaj/kZ20ajKPvkCd0Vd2/AwBEbsYHKFn55GMq3trMOp0z0ZZlN/wnav9Qq2fWN4nGypMSv2v+5/i5i9Bt2G0aABtnofm0y/Z+JvlgA8ak2cX2yze0PRCh/ngcsRdJc9OQYwpbcOuFhjYCWAghAkThqJ2Zl53kOi7tmT5AiGv3oMDqaowF2tQKXtC3f7wgyNugaKV3wRMMmLcMEEdP6Adi8KEYhONq6EwzcrUjc21ir/a2g4JZaSR+EdNYP9KI88F5hN/vCjxPFQ5eSBuXdVwN+4ZG7P5tkbd//4qw0cSGby/37Wrjll27nGnw3N52zwui0E+c8z7ZTdgiwixv/fZfmdDlmvy42PlebA2ZfvK/32gbpmo3a6gXsQCuEkJtkGdABC0bIAHIxAdTQe4JlrIBQQCWmQIOpxm6ObSv/7AAGF/HA1ySzAlu/f//cECqjfglNYLBJL8rkXTALGRN3DMX/9dNeKyx3+v1DC203p6vvcJtecb3nED5oFwQjegXKMJva8ExcnrWvR9IKU4Z3K2/KEWq9/KMCLwkPs5KFiqCQqV3F5mlAVpzpm3TNmu+zoNn36/CTak7AOsOAhEzctS3kMB+/TPj8TM3lQB/fgbMhhhfj3VWx52//+4IOXF2gDoRbDpSOwp7fsABmwrOxMIYog/pRoXERvv/U8KqeO0nv74xPPZfXQm8ftvMk6q+GRvgA8I2GcCOFnsg34XqGwyyrX7+//aYNY0u30K0V9qNgnypJ5fvu8esS278PPHJftIaUXuWku2BfxnwAkArtl0J1yx5Li+jYAQCttvUHA9hCPb/OEeAAUDbirU2pp/T+IR9/ujMRyUCN5EgkUT/35gIfDwAGZAZNEbYB/cDvFkatkW9wIAALId2MFrH2LRqd7ANPWkP/aQ//64oLEKiv6j/2CFmIJ9Td2g/7rGgZU09is5TxDfwQC0FSP9LxOYOHalNK2ckn20UrvNDqnEkRoDv1yZQGWShKns9k1dYrb96HXKs1p57JV+VJVKfh3fmoS2NH2cMChwFQ1ZCsDVAykiF5ZfNGdMgZV6TaiOmvMWPLTdgtw/WDGFNMHywlwoCnBggAELrAAHB4jEhsVAa//36MUO+hIxjv2pgxUfmQkhOW/uPDO0vH9iRW5Ee54cmju7JPl+sw7nXn/BCN+DMpGcxAdQ0l8iQI6/DAJh1KJHgb7EPfVobgOTXj75xm/VoOj7qUq0m/W8BLMYVIvcKk/p9ZUjtw8me8qwRTsq5f2rHbdFA5/27Z9m3Qrk7vsACwGzKZigiLjS3tGGR0OZSDoU1EDP8sQGjM+u/9wT2AIQAFIY4aMGcokLenUoVCwQoBtg1+QMlY//6IIyHdexSlUqx/QX9NCMVUesBFT4da+L9GfuCEb4AhSNhOGaKaIgrcQ94Y3wg81K+WwEgzoTsv7QG835jXnw8/W1CaBpRbwL6OtW/zMI40mWdxgjrT1ZadLGKiIAoaZL55x8GvMCBDOn/qXvz0GWSgeVYELjAMIKlEi2QYb/7kAhrEoUJ58SqWRO/4ICbBhqrCCQ2KXdcRrf7nLAMLBHVDko6Lf/Y/+EaNoixX7pMi9ExeYT7QgeCEb4CHdKYgqShRMEdCXqMzBqKnW377pSHwVm8X56nbKyCkz2m0OLAX8369/rKQAAgG/SgACACAJiNlecEioLLL21NpHTxY5OSf8rMpQtotR+74MEAnU4AEBO0SYlY9//7oaO1ekC5pZrF7aPjzaAMLPddGIuRTa//d4xO4y1ElawSkwqkEiwIO7AkDpSZUwoZD2+0Izs6Aizl44j3/YmZvjLHD77DbF1Ejs+e7EojlCYb8/zznouERsB1oBAUM1GRB8iwRYFgxZYnUSJMuy210ANvJZsn/4UTZ8AansCtQ1Tq4SWOV5FgA2AKObwvZ5QuSMwvSqDvsw584e/59N2dkjBt++LAf8BQnDkvTq6axBntlgZeD4zFwcrvBggCdzgAwJ38mJWPf/+4MCRm0LwaI0UTF//XpIg7IxCCtasuqhTarHjgshocW306gR6h5PTeJG31+kH1gRBcIonhU+cIm6P5gZLLK7Iq6+fdankNqY4qErtAZnMJ4UGWJWV4GIUVufv4AYS1Aou7mcPuEGCNAuwABAxgAAgABg+H7EbkAgMIpRj3IuoExlyDA0qqNfmUqJv+ouMiETeF/4EGw+HMsbKAVbfAz//2oQxR8nTIweXwg70EBHSUVBW3qod/Ohahn04t5FekJD/tGyBC84zVpo01//8fiAXZJnnwyN0sAFQGgqSgAPAde/+bwBuKTwxgUypsoua6uWW1of8dxXNsyE8r1qrS+2m/7uRndgKVGjwIuDGnqCCRsm1/rmsS3LsLU1zgbCStgqtZNsiHCHsEYxiBtJPLlm27+0AIDCKUY9ybfiYy5A+lMphXjXE60HhVAoqU7SBEwmW39rA8KCTxmUrvHaDO+0BDO5iKjRM222f4IARJ4Ih98bpV4n/+vgaog6l1mKI/3pA3IsqCVdSkkJ5WH/l/I5CES759cXjdGNyjwX5OQvYPMDFWFhtiB9sODAiAooyRH75/QCCMVeAkEdx30cBmH6BGkg3+u08JDCIYo9XvQA2EE0U9vVXDgQ4ZdcPbOViZdf///IIUmYELUy+mtzL/4AAQ9iAcgWSm2SbYACWiLdZopaEEsoe0MqI1k9dDX3zgAEoHSgDgRBebU35AAI+RQOSLJzbJshAAEA+wG0wcJ0BYnyupPgkROFooXfODD2CMdThjj8gffjrKaZnziQtAEypCCpVmp5GNSGnTZXzICz3tKOeQwSm05A/jBwiWbCValuw/7QnBnwSobY2wYDBj1oT4IJTI7qkkBTQJ3+ErxgHaE8d2sJXtGOnWazXOG++8OOIX19P40KL4DFa1rWta1rWta1ghAFYoDQqNqYf/D/+IUOIXEL/CL+0zE6HJyBUMWr1SSiJIJGRAw8SJewBhDDfzUElFG/vuH/hDELKFFAEmZmFa3u5rWtaAsZCKziLxJC2s5rYQotfUcPmxncMMP/4CbgAAAPd0GbYOgE3hDxAc8ADwbocAHBXfFBK2F7/kHgBkW4kbT7+IDHAFAk5AjnfepRrV+lwYglXUcuGBndVAAdzCFFKblh0yLbK2IHB3N52hfiU3/r2iKaBvSgWxav6C7nJ85dSFXcTN/2v4QDEOD9v9Uvr4CgYgmHMXpnn7pbQ//DYsCYMHbMZMQBIb8NC1iCEc46RVLFTgmks+el2DRV+la38IAg8ABEQYcenyyajw5wrSHv0AvVDhhCKUfnXx7/vAKGBW2LbyjmCUnmnv/AAJDr4z8xByaUY/SAzEEK159GWtJp+oIdkpaz+/yIB9qaOKmECrmADtMfYkcpwqWsURuL8QRSVAtT9TUmRcIB/+Mggg9Ll01Xh/pWjPQ/Bg3lM42iyhPd+6wep249XcH+7sUNOtLfbfADSAQ/q8Wl74MlJBxpDyFjkOfIDY5edXU3SUsfvkWlxIpbhAP+AIEIAjUAaFGptTAAbgpOD4sZBnl36QGi61crv26estcWKsJvr/48Wr0TuVaEZAKJw3iYQm2vuJOhn/9/xbzPMauvjBlKD7+vwYysJLcIvtLCN2UgBXAHYV7DxeM/fwKDyvlN2H7DQ+EAxBAvggX0lHAKRlrKZ0m0JP+j4Mwe6S89P/rhzv1M33UbTjkdaVU5A64k+3+5//CAYkHexBAHf7ICHJEOghgD8DRjOItxtFGuijO6l+CeirDUZchr92a9zMZ/CAY8O9HMVfGqAEwqaae8lilOeohnMCHJ4kHf9XAMIx7hkTkTC4wWReW+wDv4QDEABIzEzKKvUEIa1XtJhii1tQy2aF9FXEINe172f6HJRbBwpxrQL5T/NwYAFpCCCWtSw0bGclKAHA/ihXjbY5jaSHuFB8A4ctj12mW3SmKLgeiY0K+uEv/vAw8JMVv+5ldm0JGgHCAYgD4Abh6qGogThV18PgE5hBfU37IzsYo1+frLlldAAJozF6VjszXNYK6AeG1v+MJxcHe45ASF/7oCsH0ejTTsxYLJYK/hgb4ACAxLKVMnkpiSkDH/AG3OABARrxUStge/54E4sUABFAJpFKgRhIO+5DCjNz8v6loFemu1wIdwnEbPrJIpZqAhoYeOVvWAHrxl78HAVgS4AK8Z1ymFQ/YKP/aIBQDCH167KBlbeNOgwA9aCFp7/AGYcnIaOhSQvYlc2f62cNfjEWK3JVtlr4gMfwAEhKwspojW242CONl3QcYK2nTgA7/wBW3ZGdlf+IDH8ZFmAAjEEEXrJl9WCjmRwh4g4dghwW9Ed2K4h3/06P3Q/79ULWox1ZuQQFSoAj8YAHlMx6Xe5CncJGvdwgGIbWAKoAOIWsC0aNkcdlgsoaoFSvr6lf0FkcAKxYFBdsn6YLPcIx+ziJvmwbc/5visSGoADiq4CEkN1paAAKbAo0N38MaCAjhgwW6D8K1xgAaRJ6kzNvvwt1/Eh74ADuwRJQZRn+bpP9LyJ4qBktgMsrkm8Xps2DUp1tF3f/15ihOVkOUR1rLcwFVhJjXnLDEyS4Q+3QU/mAAC4MVoNDTs0Rg/CPqW0uv2WE7MOQqr/Of28kYbP2p6kNJb/PDI3wF0MCni40/wmDfRu4w6Ygc4KeiNbFsY5/7g7NPz1MjdnMYbyCREa39ID9Is/vIBB0fHCAX0gYdEb1/5gFg5/jbUx0qQGdlngmGBPMQfmXYGebtjrRADBEhhDtcyBc0yDjXLwADfMAF/0sUILfAhhwQLAmMtDcRqSdfZgXEEAeynHB5BgExqJS8Kp76xgiUoCzMjkEH1Mp+bb3l0N72BHkdbgtb2IRdD4RG6m6HF2f/wo6cq3u7zGwPCx3Qn1dqPj9JP/wFSBiajYah5bx2AAIABr2AAxwOWnJywavrzP3wEC6gQ0r2918EGm//WAMdXQI1JabLZ7ucwEBBVJMIai3wqMu4MAUDosOXpzjxtFiTPsc2UAnVe8A8OTuQa9iGttjSCi57IIv1t4MCZfBG7AN8JCLj/tjTTFdqmvfU3F9REX6vABOTFKQXdowcN9qlZBNGuWBYBCN1GHO1yIP6Gyh6pevVtdsxx/rVZYduzO6+zwyhQr/3TQxyWJiQtvpGom1sQ/dZpY1283Pd5fBtUgPn7+HVrLEBu+PQWgcsC2dwo+TBBCKvCc/AOUk8xQHbJrKDUWFd8tnVcXiX1L7ZsECOwxtnuQ/l/QqC+iEYf/rgQAHCeI42AzVUGZMYiBaXB4qKpzxiP/+zY2IWj+5gltomasRsAVbssCNy0zwcx16VM0vghG9ulStBrr/0S0Equ/7jwMKnmifq6t606KWwr+rtp/vAikpwJn59fnYKSISHOtDWcHko961KmKXeG/+uwz3YH7TBAuBkcVxAdSN2lBJJ14teDmTNNG16MLIvPWgtosp55utzVD0spv+7GgJjoqAAyCkpslTJ1/+4KAZpEMSn0yik58Ht5hNf37FYDP/azXX/Ab62bh+LeotWcYfZc8EI25PBKJERR0Qvpwy8zYZSNhr2uf4zSA8snkEmMQqnV5nIteH/9Jv3k6ujt4X3QemDzyzv32xkjMFwdC8R/rxDz8RPMS59sLdwDY7QIc1jylB2in584Kw/9anSZe5b4/m47AkKGMClBMbEXiy7XvgwkKXWkAqwEVDShlJGBDoggRqTnp0r/34Qrxpn2TUV/9YoUDRKJuK7+qz/sKrw32ylctxzhkb8YlVDgDtI1CQLDNbGpha2Fej/Nmq0RQqEudCL4Ew9l1h630GClS/dtK8bxpa71UTSK5r/gDUQnCt1Q7zbKw9sSmVTHYw6ksVzBM5FZg0XSsr/vSgC7TAACAEhoImENL5/ulXdsG4E6DLTnm1MCBW8b2mS4skYDCy+MRaNqtjVqYfWwDhVa+ncb/8/kBpeySOCT+/yGRIgxLw3BM9c66RscnvO3lNeGRsDs1LJrbX5up7A17t9/S57lt47AH5zsshe4/+PcS8Qc0rtGu7rUwHL+uvNxjyJMLyxFVFU/+q3SYr+3/jTjaRAfUyAJBR6diyiqvP+8ULDJGOW2vpQDqs4AoRkGRbFS2Fe+3UdGA/aib39WsEbWlX+NxH/rFPhs7hSId+kpCbcPnMJnwQjejQYjTiaWUN2ki2DMDHaJnNlNddG+hGcG+gfYWtve6cddUcWC6rM4FumioaKd6B3WJi/PTMnqHxT/Co05Dv//UZs5k47fwGDobAtO+0nJVkQW5ZgUqI/z1P//mxkh9bQOv1MOPmBALwwAmocZBB0Oxz9M5vv3QCMJLMFrzYv//rwQRkcqvVyr/mH+SewtGsAxpw+jaZ4O5Jo6fBCN8ZMaS/+CXMf//C0PUTYr69++ULtMaXdcrJKftoOLeYynK7gr0nnkpemYDasQiiPv6oj2gpVtOzwsZyQD7FaKvAfp4fFYldfWvsBQgZS1Hjd1TqTS8p/mY/HAC+/yQVp//w3PU8jXj9ecsRB2V4wQ2sTBU+gq6jEKBdgM1KHtUP/qPEgtpmcj/vWaAu/nTqL/vif2P2KQf4dPOjDwQjc/AbVDTjppHbUQ/N9WhAVl+r6VNKYqsJP1+9BWoSrf9pXvYJIn5/j6USGG/VYoBr6JkJU23Vpz/tf9zIPIsykXbgwLMlCmFq3ZLz6Kf3RVIqIiSp3TmLiO8Ow2cne5fl5Lcpi71/vWMTpyHtVvuxoHDIyAAIssHRljXv+foCEULnDFmYX3/dnYvl6//lFwAg0+m0RS32I5PtRvmuArfc8Ijc4UYDS/n9bIzMdSLZ/zR41lh9d7Y1Afx5w0eAAZNgeSXUlf/cGb0T7yNA7o6sa/8kNepW2SFVphgUMAPJtoTZXuRdAYEbIpYkxaFvCr3/3cQDlFBB4xOVnDcxn/aBMKBCuM0suZ1kxnjNkHQBXou8DgvIQBuDgQiAoOMAPthwQACkQVqmY+v/Z3E/9uwxtKPKoVv5/fyheRSNP09YhZQ9xKGPoMAskq9bsxb78IjfkzBlBwFT3PeR5jqZ6gFwGDLPJVx0ZvZ7/RxVKDevUZPRJ/PbZ6GiwZL+S3a0xcwuPHIkyCstO6fK/e0yOLW7i//p70y2Q4j5USA9znH+6OsAAQFeAmiDMah7vbju/VgMKJrCZNsmy27ntSP+F9Hsk92S72xYJFBoQOopzHLPVIqCfn/3oAgAjsHgxpW/KlvflYtJllKN/34OwsokxM1nf/oWWDUX8RDNt/y51LRh7pVpZcIjYHgokA/w+QaCpS/b9bAFAjkFALiMvXJfTlekpfl6W09Ic+9WLbtQ7K1oBkHSVFK4CojL0gd8RjEFuwhdwkI+ohgIBbPSgHxIQAWqWNxJj5TqP4PwD/TABAS1HEG3VGSHAMWSkzBpSZL8YQ/9pNDDC+CF+/bqF7/zhIAGge9hijkFDX//BEYk6BePoRSpPA0P/a6C8LrwlNUrtD+iUjS9LMgUJxar/0rPLLDFX5p7oPEjftgygu6J+0aTV+LKtcBgcw8Fzp9wFcijvgwF3jHFK7jd00MbqnCAB4wBsFIeIgTzotHX3sAA4NlgdQx5YgEo0HukgTEgEZBDnQV7+5FbpS4ioUmwfkZiIinF1DkLXwe0HZQTEjYKazpqVHGub0CgdQJ0YIxvZv9RZwIuMaukm1NsBSQG3xkFt50HBuoyglYs4kontuAA7KkTDtW//gwzBICvMrbtJE/kksb0jo8LQ/gIF73ilUMX93uEeeZ8xuu2RcyaICH5qdKaY8VJ//tgYCIkbRu9oNbg//+7gRQeHQQwZc2yYC5Z9zEzBRKZDtFEwLahJ/wVGaIadX79/jBafD29NbRyA+gbZxmGfhmwAAVBDLBoadmiN5sKDfZUJJp0Gk+GFSSVXiZu1B//4kNehAIkkAxhdIUJsEG2Iawfyx6t7eN4///EQ1ASjGy44mofymo5gE/BALfzKXzzTB3gwwP0hgUy4yyDzOf/xIZ6MAAQBWMcFBXLQUFu3v/u95jdecXUv9bU+GAFj1JKu8D//wiFfgAh7wBVYblPYW3o2EHGmh8zxlIsh++4CPbzMxuYEKbqRDxpQhagyD5hbjCXXx4/B4S3oxL5o3/f6H//iQr4SABIGvZd4i6Tj3/gT4Bi0QqYOIRJni3//BgAoiAMMLoVeMOvG7QIzMBAgypR4w08btf50x/tBvPrY//8SGv4DXqGGu7qf+t//yQG4gIcRWNSDJNpt+uAwomcJkWSbbIYfCPiQr4CGZzEVMaJiy2z/Bh/AkPOA4GN2ljBhtI2vkToj3rc1Gk3/f/iRL+EZKwRjNtPo1qQw/E+GQzGUwfV+uluz//ATcAAAP9kGbgOgE3hA1gOQmMg28QeLrwF6fs/iA5jRZWghKLg3brdADUtyn91/CAIOABwFxQ4+bhKzxqgvvgJBjs9ibjREWG2/4ADsNYcdLcxGLpym03Dlryhp74i+5ZtgrYq66WX/c9jX0t49zetKgABAAloEWlZtI/vdDM1BRRbqNaMGM/AFFPt9PumQaeBzrwAMJ9y/I41nR8CeGOVVQRFWnM7TCNwocQCDAAcdB0uWaGrGhBRO6Cd9IAUAMSCOxZJnA7D+y8ABMeUSEWTiqeVbwJFyOAw5mV011Wnn/aMzDUVc6an2+sYLWg/JHQX1uvbbbwz/usX+ZGyDQdlofzG85qpSzzGDhgAfGg1ZWEL10/8stGyliV3/aSSNvInfsjQ23Ur4QD/xkEEHpcummQHeFaM9D8YihBynLfSfG+1aA6DDAAvJGZF08y7ycSQ+5Ov3x3j4BQgLCQQez6U/je8Tr2meYzqkyVBO/0+3jkvdOvOdcvKJYejY7iOUfhy/V3LmX/vAXosRwi+vf94jYV3WE+sOGA/xlB0YAWcAAQA9ngFtBR9c8AohEr7J2FEweYI6+NQ06qfa8GKl74YgJ2rpZKSSmjxHz6AX5Joue7aBjw49ziHofFvn8OTYKxJFXg82gFVJ88BlUztL7+oGRgsQma7Vz+0zEIuUO6V1KnbDoSvM44QG8ABM4WK6GKFIphpIfAAa7CFFKbhh02LbK9EBopgHJgRqqNGrwCjC8UUHdnOKr67BTtGAAIAxRlgt+9umSGBbv53Xmd29TGENK5L1PY1zSRN4Z1AqSxPfesknvySXrVlgrf5v/56+2FLDS9DPc/gTomYmVEC1mv+zNq3Sy0fCA3+RGQbIKrUkJY1IfAARABYWw1JtPXmCUUDvghdmPQk4MndV9uocD6bajyNsm4DbymxWsd2shvqD+zQ0hxznH04sD/U4LKYAJ622iTZ4LLLBJCLf1clDZt9Ba/+7Mj+tNe1fCAf/mACUbQxJpXPmyUUz4fmHxyGLbQz5Txsucvvnc7/2+8ujrJn+/s8iEQIjCiuQcQU5X6eIlq63NMH27rA/1rCJegVT85HNH2Sb9naP//IDcNOnlks372uBAkC8XCAIOAAmA24YKZfRhjeiShnzA0hgFErSnfCWk0wAH0mbiUTG7f+0TMtfC6qTv3h1XdIne4iTFwEnQkAmpsIuijorRJ6o/V9P6//xQUIG5AQo0l6/cgxTwpU1XPabOfGvBq0wA+2R6cXIF9Ovpq32k+Dkt7I3f+6IMp0+EAxAiCRwd8hFmZME5tfMlJ5f5sNaAIbGDvFGPLnCq3y2GQ+j3Pu9Eo+chhGGtpvi3GIz8Cf4XXSk4hLAhCuKn/N897Q6h4X4QG4AFhDt5nXdiZsMM/yBLAA2RXDdZ0Dd8AFwFMKCT5idLuHJjP+D9cRrIeU3qcMABIwxGK8ktLhHlVUJBBhCZggLUWE/dj7867b5A0cLhxe+8GD1rL+GFKD4QAZwg+EhCu2VD7IVfcYAXbAAHCUayIDNEpJ/A51kAhHlM//6DrhyPErio5nTFP/brKbkrmJ+/jJCKMFow8QG/5sjE7iLrnoaxQIGUX/GBKMmd63/hAMcAQBgSDwAN+A8diMBO4Agjog8BsxN8698BM3H5wCqRA1ITqVi03QSNAaa+Kx3YkdXmoQmLgrJs0SQZv//7BZTmgeppGq9/bDjBriAx6gAGw4J9Eyp9OsxoYbgABYELyQeHXJtTAIgqJlEWl9ss14EgEP6zRTlrcdRdc994w6nKqiIY61GOy5I8t9uFBDLZiGy698ViSQ4///C8ABmLi5ZEJdbaLZZtNkhGYiHq95hKDctCw+uhKZPfVqAqgD2mKkDg3IQZYMB2FgRj4RuZaXuMAgwQsfBh2aIwAxkIrKYXEkJaxLgAJwEpGgAFgKm1MGBPWYgjPH3/gvG8EqdLRy32HozHBqPWcflHTORVV+XDIdgQEw9LHJ1yQTb99wyEIaYMQjtrgEewrSAMZQqIRSHqdxgIOcwS91FmhMEew8vAUOQAXvBjchDmBuEOPkAMLvHWEKKlYAmuONxuAAEAP0DjWYQZ4Ch1+8QDCQH6WKJ7tJQJdlnkAFqGYXybfqgAFZA55JCIiGMhAiGMYNCBDCAKscwaNw8AThvIr1KQf9k0A2qKBEeR36IWzMa3eAwGBxtH20jZrxfCI3k1VhVyJeuwWPzdXHo//TabgZhD4VZLTiN9Gk2qD/vU6AwozqSkfFf+VU3oEoDId1AZhJS9K/TGcNZ43/UVO751wcuX8H+3fYGfABAWQx0n51w3aAkL4A/82xDE8VK/YPm9m2qjlcCDDG8AcfaFEDKhAi5i9Yis2P+PN/vg3E4P6Nft0fRVrHx+Zi95OGwTeW4RG5AmvMZCndfz0SCkgrJDHWAUA4nTFq8XVdIb9gD4ABjtMWgEm71GKjc/BkDbv4mABr0hGFMWobtgqP9VL6/PZD3sGCCyGA7FyBQXaJp7U4KF/UbudpO7PfSBOE+U40UqyIpcHmF3QjO1vMzOlsEDSq87AJCFYL1o1zsGYOlIaUqiZ9/VPebZNX0zAslu9PIj7NmU3cFQXDI2D6SbxO1cbsD5b9V1/9/AGdA0boUksW3wQQfka7D0t71+DemfXXyjLzP6Td1yMdzyGvBPbRqm/tP7pp0e40Jvv8BuOMvTGO1W3K0F5H0ntV1I5rtx6b3CPr10f7wNFjKqryt9n3/AYFitCDOu7oQa186yA2U5yyj7t0kS7mrRGeU4ISPTEdV/tSNGFq9+nqryfq4ZG53pBda4h5Kag7xvc2ar/S+Ud6gGChqiaxp/zSPMWv3ffzwetiuP0nbqCvPf2BtuM1uEu/v3x/wNuuWMkuzri/f//amziJGPs3I+HN2GdCdOHVj8SbQEzACAEZAOWAaPV4VVstCe/YYKZREwzbcu7c1PARMP30ukrbVhUio1b18+ukGXsI3d5/l3lxm59vnFpX7mnDI3bzG6/+/v38O7Df0L8TkV9RqyDlRjSJQVREYyMl6nxFb+e+Z8rMmB9iqsDXJNf9YBwuVZkTi3F//6UWojE6CP7PyAqFBGTXZ2k32NNwAGRgKdyU8HMpZSrn8jyw/8wbsZCSd+ASUP2GoTrN7NX/3g8x2nAArTeCL5S1g5emrV3JH/YTLDV1XIPv/1Qw1dSra3X/+rzCeoQDQaCrQOcMjer1ZKPe70B9e7Pv3e/HMDbCdYDil3y//slN9izCJIMyut/GOX3NJHmfVr0fru8BPXc75Pf5TGWwPOsgtVZxNz3AQhnlJJ0t+F1xn0f+3vq8NBfU8uMW0zveuvU/16gcTFNqN1f63w2AsbLSd3x+gKY/VkRvMFHCFpePP4ZG4t9CxQ4Mg5XOEj7vXGt0TzOv54UvOE/cqRyfy7T148jIj0bcduVpaDWl+gOtgALOIQoUjPajmpf+40GrwgyEtW5i49Zr0gwA6f7cjQGA2ffgACJBsy+m9tAS8xqhHF05ABIzY8vy/5+A9KrEWwl/+kc9vrVBkaCA8MjdJbLohV130ER1UbD9/+SKSa5N7vsEHXJD6Yldde2mKXIsaF+/+tRYb3ZySD3+ewFKc9TNF6pqqjAaR+svbdf6Ql3rJN55GirA3WzRu637m1VIJ8vqF3DM1lLif1/9RCsEI6Kq191iRiitfY6e+4RyhSDxUo3R4uHc/QNYNnhkbVmQqamDzascTtgmjScqX/Oqop/Efv7wxnsjD/f3EiR0s+/uf9S8cdzzpfKxw+qiMck2/j++iU2qa+7eGW0CEcEu0tLZzgjoPj1gu6D2VbmiAX7nFHHlwf9+oAmZHDrYUYpp5ZTGiFnz9AqEiqb/30TWAfV+VT1X+oPa0kX/e/9YTjYFb5Pz/3/CI3UcOrunb6Wp/Y/opv/+cNsrWH23aP4U1k3uWGbDhwE8Q6IyL3/ncNRgAQc5MJHdXURZ587H7Hv2e5sWq3rACBhE/d2dfuYBNw5EBNdPbOKl/9HEkq7NAakEoDP+q6fomc/yNu/w1//hgRFQJlAZ+MzoI9wjaDAAJsjKOIBunuLm6n/6wYaKdmk8JO9gVtgTNyZvPfqUyoMKmM0DAKhg4b9V4VcOnCI3obnpTgTM4oADVAO/3sIBIGZV+DVwi3Yv3IZ4pODO4YrhJxxZXefYArTKNDblJ9/hoPT1D5/nZTeKW70v7B39RyAYGE0oz7smfkxpwBAoDUBuzbeAgQRWMyBA4wSQC4GJYiSkM1NplRJp/6AGJvfoHD5BAAJnkHg0TeSnXTa2LKpDtcrH/+yNkYvNU71YeXNZEgVz/ukYrX1mI8SNh+FfGpyfvcGYSTanvzAFRJw2qOiLvIABagIgC7UjOpcpkU8JijJnaYtOoXSA680/P/91V72jc/m3geMEOeBhlpvMpHzm8YrTAAZQHSQuPkL//7vCgct5ZXXyQEUGXJJgJi8x4IC+GzBR+PBl+LscG1ICMlO5egABAVMYAUGDgH2w4QNsvNpO3/Wp7sjNb6g3T+Wgs2n7qPD69GVWiMxQG+jDRRpfjfqQm2IJiHcpisAbIQAHBGPEhG+J5/gYCGYmbit9DkLerQCNQqaPJTJqBT37wcgACJAyWbAIwDRfyAHZBs/MLyiUNcj5ZAAfwAIAs9GA4uXh4ABABQ5Fx8u4g6mACyBs5BoqOANAAlgr7IQouRIF2C0YAAXBloahwAAiBw9Bx0s4g6gxQMr04u7Dpuj0ZDXYGBqWADBzYiIJ4mx6EzAU3XxxIWgAeDFZrNjRFXG3X/z9BdaDIWeaGEjO4/7sRUYMxFjlaM8V/394mNt5lfL034IhAEFoG5RUcYE5vdYYJfqOAxwyMHsR/+3EobFuXx330LQCW388X/7/QtxM+LxPhERAkGO32puaOg4Ux/P/dOnwiFekvgKADBzqzJCXKuT+ke/5vewPa5D/J0oI6TMQC6apRsd//EghjIlsdyC8SGupLBmBj/12dauh+IC4DuFBJ4zKV3DtBn/LxBY2BWodx+/8VUfy/Ehm3BqWc4egQzMZ1RomLbbP88iSuJz//4RD1uWiRtTN17XhPgFoAAICgYrxUqQJTo39IuIPUQiNhFcohDFMD4mYw4vwjbBvw8gdf9wBOpQAYE7RJiVkL3/PjxEK2vst+nWVIQlVEoR/994bo5HmX5nc5Bo+JDvzNGJ3EXSCVPYo+T+HiQACBRUIUmnU9MSULAwAeJITEEVHEKIYwMPoAgMIlRhDk20CYy5P+ctetrp/v3J9w7zvGqqh4P/E+JCsMCZkYAgFIBm21QhK5/5/QTD0+0s4VZZln+w2DPgYxIZEtA4xR0Y0qs+/wmY2/xIa9ZIyJQmhk2E+39AQqCEFqahhw2M7K1DMoF2q09/L//CIax/1y4uN+s5R+/3+Ar8MUQvuN3TAtuqKMRBSbRjtI0//N/+EfCJ8WZqRFXef/wiepikMtV/4CbgAAAEilBm6DoBDYYPXgkeG/r+GD1xI9D9+v8+CCNwh8OYADXMIUUpuGHTYxsr6i7L6FsNmynu/oPAGoLNH6P6v4gMQ/QYAFQOQYPOGp1u+bmLf6ABfIgBAZ4EcUZHYXv/NAQz+aipoTBlpj+BiFi4QWKx3J3zcJaDutcX8EHAAvSCCCvnuLMjcb3/gA+ADUFrIaqD0EjXwD8xrynUo/teuQNg/NEJ+374E/dApsvyPP4LEBe9MGktvHFf/gy+64z1EIiYhkINzGKDU3MAZQ5uHl4FQbmt3j9c9YWUtl3ejiSUIN8SCDAAYBiSIQqThn5Cxf5yDAXkbEQiit3iFNarRAAkOYxzgsEliGv/bw1EIoNZKzpmCZTQlOdb0OO8gBQyiKZ5pa2CuKqoc1ORg0Q+KY39CTdSwznKB8trFUECnwEJ7U0gDEYq6L+JV2/2CWfuKie3/D/2BjwI/UpDCJGxlA4GMQAAYF0D6bwiafSBvBB1n9nZ6d1MgGzAdTjWd8DJFZLJu/SHUtFL/78aDSALIT9Dh5yAUsdJlOuJ8HsqOm4RdvFW977/dB6eYZpdYx5H/mT3M/afwwN4ALWMAsI/QMDMTrXX+WgNBABMGC7cIaSX1OQ6njc7Fd/QHSlAZPptoKCm7h7wBgPgYzTTIKYRZUNUBM21GBgfUOknw77beym+4Fct/44YQkISJThRBhddhS67M4vdXF4I5g5F8CUlE0AX3wAd5XQ5V1wGvEVGWSLKXJCojfidhZSbwBGOhlbHHV6D+SGnkEjTvF3jgdwgH4ADEYnRDmUoRLGpD2wO2g+IHxX1jXniJ8/GkBDvHwJ4XJfBrARQABLRvVLUJ+ssYAwXfmbnIMTaymN29G+qFJm+2B1n0JUc374Daz4WW+Q+/+EAQYACMBpwQMZfRhjeiSxnjEGzSLt/rqGyARG/g1fzRo3b7MnZ20r/4AKYVFpZkLZLePUnhWygHnaIT4txR89bi+8wMAK8daKub+3C+2JN+ju1Qo8CIuuf/fko6ry/CAf+IBrgway8jHWNElTIehOD7dDpf9BuvHv8Co6ZGmHL2is39kttoGcI2FC0m2FlP1LHO9Q6x083btRGCCKm8gPKHoP+QGoUYAOCyd8NlPGnvgePkHOHIXI+3/7/aceD0SGu+8DwSdUffJPvIivkOnnhAEGAA1zCFFKbhh02MbK2A2N8bH4UgAIWHK1K3Kf5pQnygNvux2rehvr8//FgAF23WQcY+85pAACAIADjJyn8mgySriQrJ+/u5tDEjOWg9Aaw8+9/obLAGQWijb9+oE9o2FOTr/1IawHb2n/3/8b8iMRWQVW+QtjVh8QZQl01Y5LZVGj//6AAA/AACMgBxGI2mjAbXq3Ub4EHwGCrS9eRaCpFJPfAgag8LU3XCeufMn1dj7f/iVsus4YXjHaI+kEaLAPvIeaF9fL3HIzFehuYBWiZodtlN9/jcAmAAEBcRYYcGw//YdBBFbioYCeGDZQ/MBLFCOCHwkGJprK/ABiMg2YVWpIWxq8CpqTo3JiCHtGAAnVVDdBujd9IAtEYzBzWYkQ8bVJdHqcaML50y5cgKUYEHzEZ2fNTGP9oDFf7fuaOo4U1/NBg4YhKNBi2vGqQmv/YY8g4hIUtu0fOn//3BApFgAMYXD6S//OCdAIYx1XvZ3f/N9q6q/0CadVaeVf3IfbpRQLiAx+AgvijCV9Ru4YF91XADHIojYdqQmxFwh/7LYtADUkdjku/nE4v2x2oPBH1wz/E/8QCCAAmRDK6CKxJKWMT6fBCCl9xw4bGN1fEYACDi4SgnQ9IRUL/2EAwMaeDZ146CuhTvkgALWACQFumpOQWMf/t03W3OA3898ARwirJNDZYgK97qb/YAi0goGk7S0ROilpc4qVPQ/zLQHAIYCatgAUe0wsmfO6mMVHTh++LgfYbaMT+VMZhvC+EAx8Qu/IinIM+1mOD94UEuSIS+mUa8GHjQgQB5DAKxMgUFWSaeUPofDspfxfC+DwDgTuOQQ5wO9AwAGYqfcNXsttFsYAALgplg4OODRG8Yq2K3FUSRTTCVAADgABWgMeGy4xSxmS0bU+RSjZBPajvPHTKqevEjYCsa0EShEqJSwsyDDgJRjZcUykHQpqPMAAimAMsDU72uw6pwSD8yZiVCiep/KagAYIfAk2lpSkONuxGPGAm4cMYfSlnPSKhiwlAdCGIBc+Mtm//zRhBqyx9fdm1DbwfmAHxMDF2EL9XdimIATBCpKElX4De5ZION+8xqE1s+MSeKSWMMBCghTVl/TDMpM0d+KgAawiRojshs6qmahJpiO0tHYe4RG8JCaSyJTx///oAIQrDSVNIKSo9JRauBFwELYJ9DKQI0qDTolcEkYM/O8wAn8YAAQBwNYlM2VDEDbTEAGroaBlLrp9Z36aEUyJa1+/Tc8z2AGVV/QfthlD/g7wBYBZQHMkS9b9dG0i0FVO435gYXhjp/gT2sqiRVDIarzCv50Dxuv1KaE3z6Uv7WPHLEIltv+hK7z6WrsJIuIu5qG+GRuyRFokR5n8/V4dx9L/80JHA7SCIsjzRJR9oDdSAAQEZ9AqI3xvH+u2vzJFmuscuhX73O/rFHCRiVmMN62pZmyCRenjwz9iGUqhHFOcDEGw8gQFq1MRZjjKT3vgAgT8xlOxgtvMI2g0MF04W6pxMle3/3EEwhogWNAkq+qlHP/YGouajKma2PkAG++96a51g9UT3Ie5BO3jhY1DeQECVAhuGRvg0OYdJR+KC/ZQ4gDelTSznGBEA1EUYCoqJTeKf890qkP1ubbDsA95Q/60x1v//U0k65X92qdUYHWftMwjkB3WoX5hNSMaVLo21323nMiuL3++j/CiQJkkLERmI0j/Y3/euBV///roAUFr0rrJlGR/3BrNEOGA1pmWLDE9rYZOWnc0Dpv/6bJEQ+ln2f/sIb56Q27rr/BtKWgt7wNUJrghG5kqkhlXSVSvaY+//6N+pbxb5nczbJHMRpmNlA8Ckqd9+5hTMTsaL31YXWGn/vJHLWm5vfUpmBUVj4puwyQklg41LBzh9hPx9OxHUknwPJwcI4QkJ0WeMsvP9oMMWd8SFSiV0SW9Au9gD41IHy7df91/1kKGYga2e3n7qBEY9TLR37f8Pc2+GahvU30oKvQ/g+GRukV8SprHrvSt2PfV+LyFzUyE0QOYduQQt175iv7/oJTY1PDa6W4/X0tz1Z2KKiquGEXwEGAVi4AoLtE09ggcBOI9XPHDKAkAdG2iFuVWZwujZfCCPy85v790ZYAmooimOxlAhC0DpYtfmn4aT3WcilbzEQs6h70RajDwyNwTmdPDsX3JoaSzUf1fDa8c4cH86JZXO0PprKzCIOP/dRTcdkr93ceF3//8oTUfQcM83ebAXe8CKSqh868wxy4EkoPa7BFnbeIxeTff1nc5ZUNnwAZaNIyzErKoA/hj9li0sVf/ThAFhJUyFvfRNgMJFR9xP9ZGtOvHP32YynSatPxcMjdQuVMjafTtMke05mVWI0Rk+JN/OVLGp0OdhiTWqDvzyVFEHL0pl7/Yn73By7dhev9zw1XiaMoMn4kwmR9lyRmo6ZgwoeuP1sAomuO6pMG1jmQ1McsTqxERiqH3/8GGvuC/c9Ui2NOjpJ8Xf31GeaOb9A3U/+RzrdF2h9XXwyN+BDet5hH+oxaSUKzp/W8k/6e0x1Cn/B9dSLJ5szf++8PQuBsNTMArb8dj/PTbTpT31kfZj2P9rxCjmG67d/IO8h2zbfz/tilnl4Vua9Ay67XtngYGJ2daIASxBZN3/i0utlrkNo6r++1MdjX63L5sQPSKSRNC++CTBdhcCpqG1QKnCI3BrhW1yk7u1pf7B+sSlPTn9Vs365+Faz8QAgHQnJRlgdsRjoY0MKfVceQ/vAlYq1BCsSBuTGt6IgAZNAQfFVB+s7+a1fgbH8h3834OPT/t4Sv3D2YH1hhiRaL74tli2Ii4yTJ76wCcWlIeiJlCf97mGyhN2ExEO/Xlh0KyNLc0mvFwiNkzMZh8PvYA+JUnh/75hyRrPQYDBaDTmNwIwrXmyT9YkgR88fLe1/RjHOQen9xku9sjvZAAz0kxrcyKuBSZArHcRG52oas6YJobNhLN/cwAYTTBZKcfP9rUl7wt/b0FjhdlVFA/IDRAeXWPkvNwlVwIBmQoYgaDUuXdyY376gNxegi8vJ5/QAd5vjOfj9RVVd/9xEi1qGF13YsH/CI3Y9gQHRFg8GZSc+874IGcCtlIttVv9FHlC5/ucl1Qrrfrm7V77Yr+PavXd3O17v7Cb6FstXt+wJnV/gHmGAHdMAAQBgAcTOSZJZgnfly8OzjmAGX8GxUtDeAglNv+94UG/zK9+EUW2xhQ6kisekP04MMadYOhVyT9SQrMLhM/rbP3/v9qg7qyC3fdg4mFPIR1JYx4Vmni0CDJeabiRvQEAgv43Mdlfbe8CVZz4CRdf7fM20w6JiGRCGa8xFOjocb+ShzUOIYDNWBQWbG1MzykheB6SSBZs3IQSv3+/JC8WLXwLLQFC9WikZeCSoz+4wkBwJ0VhHQQZJtxP10AAcwFWlhlIN890D8AQEddDESr8Igr6w3PPDKEEWrFl5WKjuhp4IACIO4Gm2xfJjb7/kikIktz9+NFJgzDI3/s+X/as95g0IjielYQHuP06npxiF8bXGpPAkS4CElL1paAAMdAkv9A6H7c3lAQ4WHtO/MAAFgY2gaHXZojACh5+R0ESx9qNdwg6FxD5U63pIZQAGMXPuEpLrbBbg/oxmXBImESHGaTcAALgplwDg46NqbzMcF2y6Q6m0Y5wACIJzcLF7Y2pvUIdVQQLjMjxusxBwQVyYvKirkw9CKVbHRF0GFYEI2Nbts6MlDjPusmuJC0BRlAiRkkJ3VUssIq/g/JIDa1QZZ3NL4sPwGdjhGtINQgXhPyQYwGww68hQgm2keLz++ixXe1avfdQxar+LwiGYAsBvw4Yy8jHOeklTHiAaYOGsvoy3jpJQwGGdID6ZJmNqYf/8SHs1ouZ+OJiAJgf0Br4etuzz+gDGQisphcS5LWJhrQ4Z8D/+JDsBZGAViQKCrQ2pshcLgETHKVnG1MBCAVmoNiB0VtY0OOfxI+f7tp2s1dq0AgmYawsqCMNwTf8uNMfTAABUHAdc4dHTRG8zMbqpxdST7Wp8MRylEMpDc6+TIApFuGoMxSRK7wM0bv6A/xIV+2AAYLUqcnBPJ4m5MrZRHif/OH5YAfw0ApVcRUz8v/feA5IBiCbSoTYIOsH2TzCSSLf9+x2wSPLZJ93+H94dBfiQr4E4LKaWFSzdSqrjxMI3Ugu9pJBi3dsgIYRSMiDBJpoHXyaKGmvnBAGk41wai2+b8cyErwUXjZRJIUml//b1Q++YirlPfjM9DgT+EQr0cGMKW3DLhoY0WLgM8WYoXCQ1YJJXkDAgYoAmuMRhmJ+m8IfLeISajWGigSideGsttm8fff7sAuuXSef/+ERumd+m3Wvf+/jglRtSTtvgEhjkMRryEsN4Y9+4PRiwX1M1bm2WVf9oGFXZIlZmsMmg0Rf94ATALlDOMK6qmp1/5YGD8ACsAV8IcVD0mOL3yMiDZxF4khbWJ1GrKkCWGzYQ3fwIuFsIUSrqdnTIvurAjELOLCqWvd6q/7us248xQjt/+3Mu7++6vw5I+3dHBFEmew1xIW2woRDlL+jG+vaCHsogatru3/Nkn8AIwF7oFN9sgwdPbeI8IAHxdC1Wkt+YJInf/76gAGiIgX7MoZrgegQzOYiqsTNltn+etAcJCW5zxAwEAx99vfH5//xIV+AAjF2Q7Ocg7sWY/wAHoDoAoIUpyrTL75K0CA0zoWmKRw8zOHv/e4AQmiUKE478QuWTPiJuSlyE4uNAyd3f/4kK/EEqlCOb9clPqQCDDYQ+0z/YAhB0WSUeRyWebzXYOYEvlFPBxxdL+s//4kM/IDSBwtl3sM42QULBhzi39b97wGQwP/8IhWAAgIbHuay1qweeODMO9ICGFUkQaJNNb9w2AEoaqlaT/LGOf+D4wfo5SYXoP4FGJJ/3Bi+kXxe0NcMA5sZcGGCVM8zU9yFSIUHXH/V/i+JH+EQr4SACwJdypJyTBTn/g+AYtFKmDnIszxr//gwQQ3+LW2T36//3D//8ST6Yzuv4RDMCgEBhBNJPsEm2n+/qgCCCKRkQaJNNeDJSjlQxfv//ATcAAAE2NBm8DoBDYIPBB4QN0GAIEIAjUAWFGptTLDHhi8MHrwA5rp5X743CBvD0Hj4gMfANVbufgO+5p1/oDMirABm23K8/wqBjeWnf9f4gL+ABwC4oIPmZSs4coM75ALHmPuW86qv3+iAJ1bbkjcI0uAML1eDzDNAMMGbyeb99/EAggAsG6HABwR1AoKWvf/+4CQhKLVBxKKKQNf/cBP7jHJE+nfvHgFjIxYHfb9UQMf7o+dBcAQIYsrfNJT5tFCPsEHzXcir6I3eDGxXUEBACICGo4nA3PyNjCJz/Bl/PgAopoZ3vbf/6ARlsULpxNQuvntxEvqjNQHb+0MDwyF4ACZEMqoYTEkpYxPHHgAMMGy/A7QAGmqv/oJgAEigA4DBGAPw5fAc974DxuzuaAHIxkdDmcwVDGq00QBJAGIwI85pC/hkMBDBmvgAfbTIAEu8B59/ozhc/75SA3Pku9++f8b9E6cGMYR+gV4QswDj772j54Hym9FNo9gDTJgMFFSnMqQOuEg21+HrS5G17+Dng/Hkb6bMB2jyz/v59tnr8rB75WEli/84AQs2BISqnjkbTsZ5vcAQafloyMZkyQr0m4Yi9MEf7MBrIGiKVyNJj//gS9aqBYtOz/pHGYNQ8vBBABCOo2Wa/25NB7o8dnyXbDNvACDu5C38SzvGWXHB2PWAIGBVYZwiuOpxV3RRvI5D8Ub98+bsMBQIdesqFygIo+65/5qe4Df/BQwM1hbDb2YXAEmwNxOfxHBgAaT3VrKwaCVb0nu339HQVWijBfxvTA5bgfUj4L7yv8iITJjGYg3McjgBBZTcUIxKTMWWP/vRgLIAcC0b1QOtIHN+ax5384vMgTAwA8VAN2zgOD0L7vvYLRwOB61Z4wCqLMut6i1vMv/35g+8ve7pwRgWhcE5+a//ZQp+rAvbIXf6gGLMz4wl4coBI3BGrnUzFodoWWIIle7yDNQOKVEY3i/jiRtAUBcJHFTJWNhxsu+/qThpc6I6QAKoGGq6HU9+bc//cAQ9nOoIjjpChZA88w+48dRuvxRFOuZ7W55+5+Wh1yJL8lJW/BHNUtujf9+3h4ItR5DCSDcc3mG6zJFjJ0mLiEl+40mgSEEKmgQAJ/Fa+7Jf+WLx2uuUWH/eyOeAepD5d3f/D/kgQLW6Mr7k25d+D4BcRJbST5NixVnu8BucM4jWK094mdSnmKzAEBqk6V+TYXKeAZeRzAlxmav8Q3bp3Rl9eP/2rcC4f+O573XwEgxme/4ijqFrsfzTTMK50uDoz/9cAEYhfRGntB3h5U48IDhQQooEkuRIO6KprkxXn0BPicyY7NdM/mphglUcIB/ozmtBk0AEBBGOfk/uOX+GNjwc84uvg8lPua+gAFxmYAYBzgXtVAcgff8AGQAKAzCxtLyHLL4HVOdQ93vuOKBQdw26EzKxgiQBKm0IDFiqCJmJ7bNMNkE1dZ/zkv/6EW1YwicAfjaChmaYTDXWnuM5rr0DHX39P/feiZsAMDsAncU3BR9/3skKZohtibxUaD5qbQ+REyF3+Xf/qlf8Z+7+1I1dGjHXfFAfEs3ZXzZ7UuYPbQG7fADI+SmNP/3kgG1CKFz7f/8YZAzqpUsKhT//TjxfkC4dhniRuABUAgMJpVZHkG/khlxAKEEjcYh37qre//hlPQQ8WH2COkVk8/SB//ASCEwtUHEooxA9/92mjIAMBHgTxRodidf84eAEoaqlaT/NGOf+DYDxDqxtCeN0gAO0AHwSrUiT/MGvf2mZEAYEMAzaCQ9A8/4DhLWq13r1kabAz3qFWP/qaFtrpr+/+20sfus0/9kJNDlQKj4gMcABwQ7+Yi5vRMWGmf8AJGWuYnXED28wrnGGmWMVJSz//6BVnAOBZC99FCWxN/74kTopBnmbhXJ+AYWRV8HLrNW1P8C0ewRdi9t9bwS73HCAIJjZQAAlFoFABKHYQz6FUj1BYABUHKi4AoJECb5uCwlwaWC0Y6JoFi3+BLoIodAQp19Foh2MP+ADmRhOpha5/NYgP4xkcwXHQbkdMm/8DMqd9v/9f4gb4ADYcG2i5Q+nSY/YAAKAheA8OvTRGARBUSqIlL7ZJrwAEkFRKoi0vtklt5bTQ06FzLnjHUpVUxBnWoxweggLelhS2qaKqrkvfeY+ildTEGdajCMpukhgOyEgUFYGi5wYJKinAhAY7aSUNUtXBfuBr/9UZ4yKGLxIewD9f/Bwu49Dn3r4R3yA2APArrNe0Ua6Ufnf4ACYsiuyHKM61mkMAAHOAAV4DyA0aI3EwxqsukPt0GP5gAAuDFWDw47NEZeOQ2btMA/MMiiY1Hefg1oniRsDIFhA8+XlG7pyQtvgQkBnvKoFf2H7teAl7DFEL9nl0wLcqgJgAJl6BkyfQvXj0ew9DLLyRwcHJl3pEQTIIqkEIc5AYCxDoE8enpRJQTlWbagGOKrGRNgq00vaAAEAQUKVsq2yf+0FkajgQFIMcoOf8+hoKWOAYADwJRy+xk6DNBdiSdoaYClFKtpSAALbAovEhgOecjQfON5IGDAaEOjINAcef7z31VLhuKYAAnF1TOG1MEcZEeK8ybfDT/0iK5PZ4kbDAE0KpPnGvi0KawACi4MwFNYsYYF91X/B+uQxBC24ZcMDGyrmY0FVjaJeved/8yjtqDefjSg0qjW3CYd/9427UISMHW8slQIpJipk5l/3/AxDQQo6sq7+F6acJ6AhnczqrT7Ess/zxAH0AYuDh9UKbNIldGJfPVSo5l//fkY6Nlk0h9ugx+DA0pjgMydASHnb//7gw+tf2rv6JB1Qqp4/f5YxYbdrbv9k/YKRj39olb7/5jRw8uieERuhtbItbf++sErQqKmVXKn/uuCMFHym4QraGbnRS4w+DdoGoQmfBHqAbWM9UW5OhTP/v4ChtJ5Q1z77Wz/sNEAmAYjAjzXEG7ctqRnhEQqz9lAQwiUYEFiDDQDDtW+pf8gABACnAjxK+a/V2U6YAc56T2jS+DA44ZFaBYjjan8dH/6WOYFooiMtf//+ZZf+O9VzbDM0NuHkUpIbS814tq8MjfUBp6YCqKCbfc8zXXojLf48wwRhDtCWkyLHh+kk240BXIdFSfMMahCwiVyhUyom19ozYzws5etv5R8g9IpL9xsu2Bvr/YgMYXaEibRJtruFIQijmUgco0so54jyaukIqL//l+2e+NuyZiQqLD31uMyYM6mYQjWGEaaxfxvf/28CY7IZjuRggBhfNGPzEFzIrX3wLUfF0+qlXfc4C8Svs4lo61s5Xr/uyagd0UA+GRt1mP9WrbZ6sxe/+psGp+cWnn4EFTKHjMcp2zqPWHdQPXgfNRFbLQf81W2tfP4/Ag3ggT/iSjA5otbrN71vqH/j7iXp5/80EPbIFxbbsPv19dh5mAWFr5ps/egWt2W4/btoWJvkf3/15QaDXQ+eHwyN7heaWLZP/c2UuGSR4FxoyUg5HLA15XdVvKXvzo+O9Oq/LfjMl39qIShWWv0AICEjzCxvbz/pvmHK0DSub6QMBgC2J9N1bbt+duUbpEMAC4bbRV3Xa3BBSJ7SwINBeShCt/fHGALFa7qmPr4diVZ3///vBJMci73/9/LUW6CkijhkbkB0tlll/XXEdv8i8vZto8Dbv30ZUfnSM9kWf7WBumZriFnz/dSxtxWh//PPy9X6wRFO527+BAgYCAAuY2aR1S9P9/qZw/j6GGATZWg/7uD6BaUDrTVJ9V374LktJRKuOybsrUblP//tRjSaLEf/vq/hkbkDLtK9Qccfn4+LWN08oKaueeLdysN0Vh/NpuuvyOTctQj1fI7qLW6edd+4Db2fUGH4l+CtcAwT8ACzDVJgJcrDJdh8pvwCghW9YEYtS6ZEqgJcGCijIIIh3yUe7/1qCdXXj5kJ39MKDjZrOnnv/ijcyloYTf/DMVawTViYel4RG/BhU488s/kO4uiGBh9+Nlwm5fY64AdLOKVAHqsV3qbL8eIs7P//N4DcYWlbWfqakn6Ob9uAGYMeahz/npLRyZHr5YXFPxxm34cu/fb882zvduMp+DGISTW9CEfv3tYpTlElHNrUP/9inNHL80abnhEbBX1GpDUo/YSOHJtbNgZCtTW3tI9ntHtfXmGhNfB/H5TeRsNaxR5UvD7coNfOaZyYwg4PKcUDh4xnf+vAS2C34RJLvKJa5p/W2Dle+23/2grp/5D4f7A4Ap3REo54GlHhb/+0vDZnE+qfHP6iEuONyMnPf/9hH4qkfEb7lCJiG1jf7QgPEjfgB6t8Z573R3T0zvFL7uNLP54KBbVSI1Xv/3YN2//gb+/+I/Roe37TaJRgfk+bB7dLX17/2wmJTtAzGz0v//u4EQuOkKRQ3ue//tG1RhdwZZh5PgIuBgRchHZ3W1pEygX/4Ti24dTuS3X/26TFBJcif3fAcgmlquYmbvn1+w8am9NaWfwiN6QjMBWMVzAJCszM15gZwdtpHrsr/KGL3K+Vmkq8oftgaPtEBPyBkY7nc+qTyUj9uv9jMrsJWh0WHCR+/gibw/9oYK1oLh2MjYSVcHXcBOEsylJGqVXK1vz+/DCiQW7NPMgef4b//PsxETz+r55/5imKp61esIWLX0yY83hmN2EXrR8IjdHyFZNa/f7pbMPVVw+H/vAKcF14w1BVVAjQltDRjXmEhVVOP9wBgxdmBay9pbchCf/2gJsHHLEcbkGjD3TzgnMOM+ux/aRwJ1uFkrr9yP/3r0iISMMrFEcxTDwhogJdfX/U/vwGAtoYwlXkcuGBfdU8zRhOoi6Q9DWKBw2fgNNmFvp5VXu7ETexVMqeojbv//9bflDsl1v8GkLypwD8SNjCUACrYY4pXccumBjdVvD4C5Aakah2lCMEpoAACwIXkA0NwOU1PEPOpHQxRn2o0jhB8Lin2giSVkKpWQ2MMYXxqK/nTSW3fAwx+vzxuG9EnvNvO1QJv3dH+JGwBkKiVRUpfbJNeGnmAXIAQBWihx0zKVnDVBf/egMV3sTcWIm02z/P/rbM2w7xbnf/4hnxhFFYtBZS2CUFE/aIABIqsE+zaF64f6RCZkMZGGUxigxQ177kaHU/sOkUh5FWRv/aDVI9v0oI/DR7xeEQrLA4RsH8OBfmfM/t0AbIsAwQXOkyZA42U7xAuRkHrUkT3/+P+NAx+q8UtHevEhhw/gARQACW8UCkiiEmybXmMd0SaKQZI+aINofCIegAUbYAAgAwC5PMCAKdHWkACYD2mOAAMgAouQ0CAPB2aIAIEUGVuw1w/f3gKE5CYPZqEgfAJMXwBTWgRaf0IrCEXnP/RttW/lvyYiK5Dq3HYUtwYcNG6ZYRrc8FtgKa4g+wqAi0q5Ln40Rlxwx+JCv1wBzUohHkILeU5tintWrrTSGjfD8vzTcAl4zBirxjHpWQIe4twCD7KYxmsSv36i+L0P/xIe884AgqlWglbjyrmOwoAYkFVlSJ64l/4sB9Df6///tsQhCSheC7hh8gbteAoYBJFKK3bx9cjJQ13SZDDC/CFu/LyF7/z4GBtIxiLsz39tv18pmxM/7w76jIyu38SHYEDhRhSnYZcMDGyzP/LquG7+OnoCQEqQAAgBAAoqMI9KrKlFwG8QHP+LEaZhVr/BggPhIANA+3DECMJOv/+DDvbQx4+bVxof/JMZteORK2Z/hEb1UZYNDObm3rgAAQCxWklS8AuUsXHKKrhRv8gGwDqJIM/6Y2q9/f+YH4QSE3iLuvvuBBkFkCBvrmOH9XYQf/70RQWU0kMluakU3iwJrxmDHTnctaUKdygw0/PGfsQTU6Q4xhHq4YgtXUcuGBnVUWSF1miokDUHSWQ1/wntjKEGZG38/n9QTa77aL7740Xd3/FH4h7z0f2a6YvGDzxIW6aYg4z4jZp0/gdf8/NAY52zQWwVac5GwPuWPr/kmpa+0YwTeofLv5NT494BASccErJyks+0HSCHxgE/BAph5CON8JrmXoAAQFRFBpocA+2HBhCbbbWB/RKNc/kHba5if8m//X+N7FYnjDwXxIexnrXw/Qv9jAAsQe2fy0Hw1WnPAAIYHmkhyK/IaTLWWM+QAPi6GptKZ8wSgifDDAM+e0utPdtcCQYzRH+p+25VPCIVgDAjEAKt47U4uIBn0g6hBOQpBV1nGEf+4cgxBCm4ZeMDHCw+mXJSjy+FosPzwEK1BCEvLSowoSj4EGCARX7NGWKxCdf2UTAETV0tRVhhH6u8O4wfwiGfsGcQgXISvhkjjI9S7iDoqSjgx6A7uWxjj/ixHAoQKq7gi4UnkQ8sqdJx7//4kOwAF0wQFQveUBZJTpZ4AAEAiQAAQAAAgeWabmgANERgv6ZQrnIP1EQREMbMEQpSNZ5wCBLlIIsoMtb4P+AQjOYjIrRM2WV/8GHFtfqrkfxKbmlz26/r/iQzhAAEwcAnMTpgcD7TgBQDRAULZfRhvGyCxjcNhgd9rwv2Y7fQf/4RCuAAmjGR8cykH5TVRhS4AEQXXNAEBobUwAxEIjYxmINzGI8bUgEsTYHxbbJu/P4RDPjA/RyvhdgvgUYkn/cQHoOWm12DOBRkSf8DQYS24xAalZ1N1sMZL7k9df/hGIEhrS4A4g4sSxhkg0Tf+L0NfBj7udM+//hHOufzrn865+Ag4AAAVH0Gb4OgELhDwQBzgAJGYiIpxdQQhrUOAAmASv4AAsBA2pgEXgDIKIzJf/n8EBeAOaGy8ReIehrFB8MBzgAF7XS2577gEAOUfhVKxnMUJJWACLgIQUT5+BsTP1JnX8IeED14dinX8IcIBAOcABLMWcgl7T2lKfgAlCuBcaSMrCix/fxk8ADHVt8k/+GPDB64ROPnQEYtppF+f1hiLwh4gMeA2+xWBhKM5FTqMnACab5TzgccFV911NRw18EHlhmGgAPAmUgAEBOvlRO6B5/gADYcEuibQ/GWUTAFJLY7p774GCofmkjFeIsysIZwAA7wACQQA18aNvMJNMCT8O/0FWrHczotrCLr/21+pto0zxI3gAPoggMSFcpZYqO1L9wzABsF6A1C9NHfmf4AB6F9aovj7oro/9owAJ17hEYbI3vxqBlpQH92BqoLji12RjHP758PUv/309zXHJzzD6Kd1MQQiXGOBuh1hch2OQ970kEyYhmMEQxSMRlwBDUc/AuO/k7GETgHAxZB3qvZrz8DnjmWkRF/2SrR3Xd7sJ9hl2q29/6Y2h8D4RBBGj2otAAeAAfBjwpiUOoplcHO58QDHEVjIqwTaaB8CCrYooM3eohd9M0cIXOH5lywcj0u8AAQIKjXiE1MZ53+k+cCyTORpiRkZR9awi2vrm0vYjF9FShW0EBncw+EViWbJd8BwPDNhk7Ounf6wsL9/SIdaf3zBLu+cNoraQ8hcSNh41c6B6dCGwHyMXMRpLzoPWj+PUi9ZrnrLs6W//lXUvhU9p++AGI6IphqjdBpUb3D+WgwimtAY/L6A7J2s24AYqx44Sb7TV63GNPGDD1mXGAvm2wEBSsRx/qHXv32H3ZMkQep21AZqGjCs7MOLxIegAVCUPUnILHbT0becOGUgxL2DFcvlntgPycKl5cvLaOQGNYhCpO/SVi/z3+4GwAtRTgrTC2I1v//8MBIdgpMBhIRQoH7zTxL2+QXJissgIf5xKkKujf/uj/zRu+RhBE/CXsT9K9HuMlto79YSbDiBbDekTzKpH6gcKY7XkqKf5hZFO/8pN4NtnW/28af9CYQ8SNgDIPi5hOodbbMcGGAA4I4kN1HzoiC7DP9ABYN8cAHBG/EhK17//3YMCWkOA7ZkBYfcv/+9QGdEyo9SP/f4CEGH++mv9MBYAAQCMwAdpBP+QButinAdgjLZu7kkX2h/i+BAjeE2jHUZr8LtEgYQQhX504AOawWsC7g/8FLyyZgv/+rAYs793Njh0WsPw/9gEDbOaJaMyfu9wGWw4gKP+6tAB1Wn6Sn+7wwIuilC5Z93KPLqSmuAA0OqcAjwi0aTmplyOGvMPkvIG+QxT2zMtgihjmBA+kCMSkW5a833gWc8KXU1v+52zLEwcX78P8OJNaH7Y3FeEJ7rX4wSTruAgIRAircrXY2QaJf9I+FavqDi/eOBXcitvYAikGalxcWUfI0h4IF4TGtS1PWRyz05XD/6T3/v8DcV63Md5PlGCOJAco3CxEiJ9R0fbQFxbwhKXZZaH0M570tauBE8SNgAWDHd7E3ViIsNs/zwJQAEyqwT7LoXrx/BgUgtyQQ8g8lsK2O3s9yjpF1jN1dH/9EDDt0BRXraAj8nOHtSQwh4F9iKuyCMfP95EQmRDGxAiGMUGu2p+yAP+gQ2bgGNu+tuAJQB9rOG/+sv1vKCzJgqD/nOxX3n290R8Ubk/+9wLWwrOhQXEh/8oABMqsG+zaG64HpAoYEL8RA8JKZ3HvgCwiOcEXHC/MpJaMayGM0MAxRxH36WVSUUIu/xkPscNveAgYiTtPb/lqLymAfLfK/n/+gOUO7zevf+uJgYP1EEntIIKUM9XN51PUBI8kmSh+/vAfASqgSi6uYfExpgzOLHMnYVOvUNxwsyB8/bfjbEgIABEMphFJLLS4VxNX3maMTqIvEPU1iAAJBuq+BcDZMoa/7RAAJlVg32bQ3XDRsYopXc7umBjdUvUQmZhFUghTmKTQxcvg3UXxVyV7wg5V7/95GYRicHb6jmNPIt2mLyCzn/vehR8ELEyYhRujXb2rGKJU5C7poX2WeYgYZ6mn4ol1/6oKcTJ1gaEALhxrv+DKB7gq2ZBayGv79AbkLWVO49I99CIHHMuZz3WNiicIL1XEhiGXOYaMAUDGrRzg22ma3AQCVeHC+zr0jBp78gJmuWlhQTKaLYITEw/GubFLSB77NqjX//P/BBAD3AAEBemFDDQ2H78OECBCJCw0xAuw4CSKTw5qMC/FjJLrgpsByS140pAAGNAULEAAFQUqwcGnRojACw1xSuLnK5OOV4bb/J6wOkM5jAAvIg3yvYUGZQEMsesaf95A6U3J8eeEgtt2viBvwAGohlVDCYl/sYkEsMBawC6gdFntqYAAKA4D7HDg+aIwAxGIqIcTUuSxqXATKOhV4bU22B+0C4gfFnVtMvYjICCAkf49jLrzR2cGqVhYFGXkIBcMB2LAoKtDamDbT4AdkQPC1CH4O3Xz/3WhzMdtfi8SHsA4ANKd0IzMvf8yMCEuC1mCY8pyvsABdQG9ryN4sLG71/kOL2dDHGfai3egADLSQABHkYmQJf4e9ZiZOcX1Ec1qHAACYMA7MDpscNqbaA7KDYkfBjWdOBOwjV55tTLqiBGkyH6fGu/If7AbDJu8+BQzcPiRvgsSAQKKI1XSEmU33BhwwMYCusAu8OX3jf8iX+h8MAnQbKpDoYdC1ID8wB8DcHItGEWYPtOkvQAeFwLTZSx9onBA9aGBLygA0INYQ3JX86iNnErwDW0vvMYDBK4NlINqZj/0+LN/xI3x2FejxCpNGmgIpAe1NlmlLPABmLB1MBi86tUNVGo4GW9P+saBAQxlDM6l/gCogyP0y0Og0gj7iY1BRaB/cF2B6J5/3GMiEtUikKgzv/eAgrfYMT3S3U0tJZ4Bi0UqYEexNLL7//uNqoMlKAiXCU/uAh+fZBK4ka0YdLdxgIHZBLgEUk6Vu0f3BfeZW6spXUBnoggGz4JaJhEf+9T4ydz99KjGiNmrqP/6fQBUQWrOOKZgbgRPH+6eZYJcNrimnhkbsbF5dtbz/389NkhXl8Gqcf/tAlB3oXwZGcrukN+8wKwQEnzMJTy6ckMaHqYsRYyxSP//zAwZAWln25ZOwEOU3DkBAxAKtGvHOVjYTchuyIV8/za9AIYRSMiTBRpoBoPxESIkUgWhJ9xAACABwzxJG8epqkpiWoqt7q/9z3ll2rP+9xEwm0KZzF9+b/9vhwLZzar3m/SAOktvWzyQrbhKLdfMbOHfjsh0CAY+JG9bAyYHlDtToj1PG/0L+jyi7A6t28z3htreL/fAL+YBXIAA4bH8HBe6F9/10Sq6My3fvv5AVEWpAnmfvbSR3CxLdh89gytW6kBoM2oAwcTr19Fh5vqNnjq7MGho08D6jtIXjADNLN1Tf8l53pJsqxx/3+4IxKtWyQIt/v1BDsGR4QPiRsEWcCTiKZzP9QOUqu5/er/A0ADBkshI7OnaOvP95Wnunr//++lx+b8a4CM8mmTQ2+//uFAWc4PmQULxG/ApPSMAoKKXABQx6NEH0WyH/qfbvx939ujDFzK74IIsetWP5X/R8QocBMcPDWPiQNQCU8W3L//8wIdoQEVBcIjctHpfEn39yt5NIMV6CpqYNatDeH3sNRhg/UTOly74aPMZgPth0/ZmS7+1Jmk4p/f+AAIE5cNH73CT8GiX0Qpq0e/X/W5rjk0G339G+Q/YBFDyA5YIJRcTEZ234QBMCxfIr/2QyoHLVcO7RBJvZV//aCbzFDfnQtG+9FwvCI2z0qO92r3w7zw6KJHUJab/P5iVzOwrrUSpTUagCm+/2hGUHXMMA9tqMmZvACwaHE9ZRvKG86h4RvWfg0zv9CmZvEgRQPtXSh9c9vdzjwnqHh5M7Mzg3u/6wmkwkwpeLfyyCBSv+dy4K//3wBuDK4EIGNZd1wiN8gABACiECjC09FKsQEP+whWkRU3yo/2+p4ay3Wy2X4ii8XWV+HTV9P+mgSHeNG3ff91L6Orn//rg2zrg7+yvQVNTRX5fg6cq0ck0/Ak7fxTGpT5tO//YxKuw2/++pm0Qor9E40QhzOdz5CVuV/gwdK2f3Neex+NGGISiIr/8srHBJxl9XtyhiwNZp5BfeS4kb8hEEYjiClMEcUS8ybahx1S7faTFdnluJgUe4D3rZ4Hm5hwbpKjXr6yrc3O6upbhy+a+/fgS+ice8+NqjNn31y6pU5vz2JrYPw2sVfYe+7ONQ9YbQIIyRy3Dz2KI/7+YHHT3vb+3wCy/r11EqDsjx7yUnXv+Mu/UoufCOK7FPOERsMAys/vvwfhbeh96vxqNrZw55+5+2Of63xqX325qx2nuzy2iLGvht3gARstiWI6OyNPIox9El8faCgoCrWfpE+dvMNb/cpoNO3dDxf9hsm0ckOa/0Br7OP1XhthETcIh3IffWda/Is3ANhtiHejvbb/9+WGeI88nS+1hxHAc3EyJ9YAklcl60L1FchQGgQGqwUabsXr4RG2u6gPoym/9616rWXbo8QsLJeqffw7Gvf0oARFpEYlFXX79MrPHk4jV/wBh3w88klGMxqGOD89jXTOqpkTBt1rA388CMKnIgvsI1pbN4CDqt4pNa2eZRsjzTH1KV5Iubd+BgPxhJiiqRtoz9agDAb82PZoGo11Ef+38HYg3osjahEXNh66Uua6/CQpdtNfCQ3QE6/FsqTr8+JG2WWoCtMx2xQ1zV3HN0r7HrbQk/+f3hVr2g5/N5h5Ro6S6djSNbRslZy2/u/uISAAP80BBRNYUIME2WgJDCPRqB/Ir2ef937kjwECCqxuUJGGCEEwUaSTDkVk25Pb7/z6mxC3FzG/PsLyg++Qm3fy21xLgauO4kbsIm7awT1n1lJH+wBzMZTBil6k4INIPWSpfY7H/gYIA4ypPVeVoJt5Xv4bo5s7yWiTGFYMxt1lpJF/gFGo14h7H7rWmCMHoiABoC3rFCMIOu/28RZhoSmRZfLNc+lrbZ+b9/uySEFu/3ES/7usr8+fqnhq4HclYYLiRugEAA4ENBaIOJVEGcNd/AxABOg4JsFyh9MMf//OAAFgQmpBobdm1N5DjqR0MUYnVGu4g6FxT7URZKSGXDYAXDRUrSf5Ypz/wYcGePeSfl01/fFVPfYAvKEPfYsJ1IbnKcawkXr/CYcZpvLcSFoEIIaqKtL7dJZPB8RgAQybp5g69E5N/8HkJRN2fP9+uvoOJXR25DqZ99MdvvVvf//pwD+KxJ4pGsbF/8IhniCEGQpQ1PXUFn/6tEGC7tDJf5JmfHgGBAYwmkJE2CjbT+qAQQRSMiTBJpoX0WCdsYNzuAq/8SP8TAPmubBmrv3f/BhxrfTsxKm6fxUhwAEYsynZDlGdazSPkY6Jmlwom2QYTxI3pDzgA6wJjGCMh593/geAAUBAH4jA2cgPLm//SITJiGQgTnMV3xAQ6EXxKyDzPAwINgAA5QACtAe8NGiMAMKvyNzkGfbTHOAAFwYq5Boadm1N7woJdkQt9Mg0kaYGQSg8B2Dc8zdvLYYEdiZDoc28/0CD2afhkPfAxXAyXZ5PJwa3YefdOPXlbizm9/7AGIQmTC+stA0g9vdGAwGSVVmGn0Ja0qpaYPX/beDCiLGChNeqKa4ZcbruCXg5yiZw5ZvlEXAGcR3veeFJe51hr/+BAfRIBjC6SoTYINtIYGAHFiE6ZBwpaTf/vigHxV5iaILzf/agWlz8uek9Ku+QtgkV1NW+nEh7ogAD/AopDUuGUUSnvsASuADoK+QUXtAc7wfute9fq9DhaAICSV83deXNe94A4WRSshyjEW013wQsYF/s2Rx2WDCxrgCdTgAwJ2iVErIXv+AcTG2lvabGLI7b3+e/eBhgExM5lOv/99mWKcDWsfiQ75gVggefNyrl81IW/3oAYSTjPHwv8pIuiecAAOUAArwHkIDRtHkLupGc5BibWY7RlGAAIC+ABl2p+ASc3/3GM4gQJbwTW7q97mHBl8rfARxVO/ipTI9cs437xQS7KhL6dRr+AYtFKk4hESUkaR/Bhgn6Icv8Nd8WPuPYx65LtER+DXxOSv/wiNnYcGheACZQABAFETmleQvxJVYUAogAxySCEeUQdfeZg1hhjgqRRbl8ddA6Ey1Fv0YNBvFRaRfNA6lPPf3DCge3EWl2Nski8x1udVMQZksKI0S0Mvl3z9/u7hj5gBYbApJlHCLJOPjgegQBBCqtm99WIyXNYAi0GYDmslIwwM7rAYgdpQ3dvQjp++2EFU/r7KUS/wK8grPluyr+x3o48YDlddVDk54kOy9GADWrOVx76i0MX2OuLozv59+cCFrLk5Byo8VlS//1sfUPrzZaS1zxmxVxbcohi0OcuNCNEDD0Ey+mPBAXwuYJdBgLYbNZUi/GG2ogLXobd/6f/oH/wiNvprgP9vPgAxWIQIc7ZG/U/+Q8M8J5gekS7jPURi6NwAkxxkzuOWnVN5UABJjomWXCHyyDHw+MD1gn9KzkiF0+5sYEnMGy/2jldfeIAkwIGsPoQxrRNYz4wEvDBjDyEdb0TXMgWDJtZcTSM0tQvmVDt/W3g7myREOz/s/4kK+2ea40Tn2GE1q5MhVThRgM/Y1ceOw3X0gimMj0kf4m63NZ/8VhmeMvLumZ//17LqY5gpGsEpNKqAOLALFXS6X36o8Bdo0+bX+NKPQrmqvma/iQzsQYumY/lP12oaAX9YBBBFI0INEmmg2NlKSXil/dg/Ye+8lOEQ98YN+ODOiFccs0Dqd5Z7xgACArFwASUHj/3uGhb9MABkgSmgvQlB3A8/5pswIABTgMrGPajbzv/ARA5BgSeMRnd03MY/3EAFvAADBMuwIjN0Dr/uYkZNQkWGTWR7foEgMBiF1jwNCVC/0qCEFrahhw2M7K/bMbu4q9SSt7VhAELHjZikzrUMViyFZ8XLggWlwP1S676k3sZTPCIVwEAEAQureAA0BhNbWx8AgVDWAf7rH3//cMbgjtBlf4RkMBXCxgp1uEwQDgwgF3LHCaMkT/AHe/p+1uN+p4IPerIsr+JCuAAmjMSoUykHxTUQ2AACgIA3B00PGiMAhEJkQhkIJimI8MAhQzGMbP7X/4RDPmRwrdAUV6z4R+Um32hGDP0BZXjfxH5MbPDUwwhMzgyDRFasbU/Moanl/7/4Rwi6GADnSj25x2tsYwSWYh8IwETAAABYMQZoA6AQuGD14BHtO+z+GA5wAExRuVkOUR1rLY4AAeoABXwA0gNG1MEybASLrP+/XyQSE3L+GA3SgCIE+BKSKPpVgUCczoOK0qnn/frzj92z/hgMeAB4CIHax3pnjZKuIGI4ZcMBJw4Us+hnOyahb/gxLTgAxsFpeVMQLr2LVlv7538IFgA8RiKyHE1JCWNSHjA/aD0gbFnWK/hAOYACMBpwwYy+jDW9ElDPmRAa9sdPvZNy58vACvHSbrm/t/4QDfxAN8GDWXkY41okuZD5IMHvaHS/6Dc+fBrg5x0PZ8v/9//hA3D0JSgS5OEPDAcgAUUGILT1G7hgZ3Wb2yGxXMLiCVNYjjGipoEnAyDCGr6QANkRAv2ZQrnPCAs6Q39IED/PC1Gu/vf1hCLwgbw9B4/BB4ADuYQopTcMOmxjZW8Fmdd1wEAhR4MjXroL5lPfBF14c4ARZAAI3M1IAgnJYGv4qcEjUegDsXB0PYVPecMuPxA3+RGIrIKrUkLY1YcABrsIUUpuGHTYtsr+KFd+5a4D6We/hRAnKP3Q15K2+Db7KA9+mwglCQeAAmKNysh3GdaySAVTABqaJbMvVCQLyIfKxqn0aM/+EQ7wgC4UGHT8ocYEHr97wCgx3ez7itERaZb/o2P7Yd/+dQjEtJtVLbd50IcXtHElmv2ee8EIwulYPTZzsnEQcBgyA+XYtUao/1+4pk+Tejl96Y3AVPvNmVeOaIceYCLMBUPXhWlfwYB3EKxRFvFq7+rD0EZ2icp/qzZGDi1GI//o9c8kh/qkE+vGG5j/CIIOyClgPvDIr7trXzCWo+ZUb/+50nQgXjSiCGzocFJXXfyBQAEYWbnIgqWOtpbuBw+AIBTusduZdQOAAdBsYVyzCUNOJJIWDA4waqM28O8eMJVNA+bT/eAoJZFqFrSMK5Nn+d4dXDHSL/EjYcAQYPXcgUnqu4v780/W6Qu2ABYyCNXKkajHpd+fx7GGEOVnF4weWeyeYCPVTdVcu9Q+rXhnmBIyBzFbhM9//+q0jte01/vrgYMyjROe5QilzCP1x0caJsv24HKDjlRD2PWGl9uUdwACOxgBwwXTQ1TF61gw4R0rnrVwBXk+8Uj7wIARCix6cylR/n6hpMRJmNtd0HBN8/qkzfPjepg+OAckcff5gFDGZr0xEQdQttr/eEPC7KbhxYgnNp9jxAAaPgHILUw0IUBDYVQPVGmGev5oAsPUtk13Uhv/0DpLKwz+bwMXUl05xqXlCCXGOTQ0ODoT1URU//+BFpYqRG/q7aY5D81gMzAciTjXrDnSn+eBc4Zi0OS/DSxHFZN4/bUd/2jItaezjS/qoHYsJxOnV//vphI4uZFSnU4/6UCK3K+rR8+YjnmjiFgR42eNTwQaDABoAYI7+U/y2Z4CN3o6NNIIfcOfqrJIRGyIyMXYCADoagCp7hSIivkIu9tDZVIdGHQ1ip2E3pzbbQADUBQ6rydb14OVsFol7MO3uW+/5/83gbGnwAwALDrOwAk5yS3gmu//2A4ZCs7Y+IzP+DDC3owAjotLxPnICTXTJGrv8j0sAAhBI1ZaOOWjHj+QtIfjYcCWPh0FMFp4IGJOd8SjSzvMvYgMIJpCRFokyxgN4bBzrZZqhaC+0IGSLxmaF0VhHRZ31YWDtxM+/3OBBUqKRBqyPNFY/9MFexWjj6vxAbqD6YsNm/cocqSbKObvLiiTEWahVZqqCaTLHTcaIBh3DkkSu/PKxh/wDgDagjUZT5hVdOSmh7u/zSCTkfxJ0MjUADkzhUZro3/9Rt6xLxooYVnw/7ZAQQRSMCTRBpoHQ8Ep2jC2r0gB2jE7iJpBamsVLeoo8Rdu4GoqVhCad+tiTzFcwwANAEAsiUXhr5Sr9/lk0vRx8/njZEAGBnARuMFGhyN94gEAelUl3ZgAvDvg5e1txBJ38llrC63iK/gIFEdPohl+QAJpXqKLF/eAaUK7Qd+ZP2f/ihAM2YPgKC/fxthog9uIH4ADQcggJPGITnl03MY0BDP5qKmhMG2mP5oOOcEMCLwLECzDXumU+S6/p/gwqMQLT9a6OsId3KBntnS0/uJIoFW2EQiKvNYAxRpByMKsd26UYaM5DmpTKouEfeoLbUQAyfqp/oMQtAj6HD3/f0C8GzZ3Pj27YMQ5OLxI2AAgEbqVKBwTPZBP5pRwEXWrXvm1N5ow2dCmUg/IajCZEAAIAoB6IoIUtB77AH4a/uP6Sfa9PINygDgr8qaUEt7GPLjRgPWB7Or/T4YC6RjDGjZWIEjq5D/34VaeZ6if++vbRidRF5xaHsZOBna3v9rdupheCwjUUK0wOlIRWeAmWzdVj//wDiIr7RD/Z5DDX5DsgzxeZ/PHfG+AACGezdDHY4qokuZ4PghSSXDF0fQzqSif/2gYrPZ9xYibDLP8wBohAAcFYSJCd8Dz/NAQ1lpg8lcG8Oe/cH872yt3+p50un/vQN2/pV2wwP9AehgAyMt/pP//vBIXoLkcOLp5/+2isnh9Iww78jKiyQ/6S2yhRa9f/f4Y4EjBbRIaIRWQ3P93n/uAVT8gJViUqJ//MpvwacDSRYsA/1GIPwc+r0y/+7BDcWGlpdN+fxAYgCCGA6lgUFWhtTALCUARKbqaNNdYz/+gCSpAjFKT/0cbAOzDauwOQOECjkXPEzZR7rIA36B8DQYT4bGj0it6e2jE7mKhB0NYoIz5mEwJIorkQ3N+LdT/+kENow64qn/95gizXs1bbwgCDjgUMaFBghxI4AMZiZFKdSDYtvMAAEwYBmTZ0cNEYtp8YBEfaXa+KxIa1AHCxTFCHP1QXtd8++v+HuAQDCbjqhvLte/4AsBuocMZIIx3nZJUx0CD3Ma6YZyc//4fiAbYFC2X/wzjpJQwGCAgBEMArEgUF2xtTAAmB+A2oGxW3Z5nAmQRSsw2pgEUVke6SXsoooUsbU93h6sIpTY7HkjfsqLiRvASwA+jIAMDEgTxRgdgdf8/AFsAEoJFStMibquPBh4P7fz/xAJQj3ooKlAPULUpd7CSjkdao8G6C7AkogwAEYAPmYAxYhLKLZGCJ4RHs4FeRlX8y8fY1GBJGRkNqcEdIHA9tJr4kEGAAiCUdl/C0icd1ZaGAB4JnIADAnCJURsgdf4AIGLJSZg8hMyb4x7zCMOknjClEnlnOf4oANAW7hioOQUNIhlD+VDsNyFpWfuyAtBYblGIIYFRtOybIA/EqGNbcXn5kdmoUsZQBNm4/iRuygERa5+sY/Px8dd+BoQz2eSYkakVeef+oDQwp8qTL1lCqqNfXoA2GAAhBloPDViSl92uXROeIBfnAYQ3WmMo9QUqTsWxLH+7x0T46t9vsKRQCjGqz1hXKKTAAAgCACwogA0JGiNZhM5KsUn7VMrbGvvPwJ04X9Z+fmPUJJVe9W+3IABWdCXdlqsYH8iO8Jt/+6UHugbBlIudwiNhg9tXTh8fq/FUJJzbAiz+Dv8bA4DowIOG5w86fGn77gJjGK3T75C1DFL+scoK17pHVm8vmycX6B0cG9BsEEq2eAEQDq0WySzLRMwRWQo9LihSu/z9kyjue8//54HPwfn/XhxB1FxRnLViEQTXYudv0hRoNfG939W1NL3KkqeERu7jzgZRU+etVxLORb+/9s1uUB5sD8BDhiVVMfvXZXbXxR6btHvnD9vresb4ZO5yprIGhRLdM5En7/48AxfQwwLR8mqXCtEJY2z+A/u+AliOEJGxxEs8bIvWwdHBEwmMzrpHfsU0HzaCpNtl5dVjQn77Ry5xua7hGOvcRSnGo9ZmUwnKaJ3TAeoFGvG3wiNt/WB+/OZfpslv//r5YpGBZ4u7D+ApZTjiWOQyRLCfSgzLccN4sCUYnsyzbRsPxTJ1ES8Rz/dvgiHnSo9/84xGFPo/3TUbxqd42ItE+PWtZZDJfbK69lweH01hD/J3iVRP/9rBlYJMXEK2ffHH14plpG0K8MjZUq6Avr2bBt1ko/hebC7O3zlp99QjvmjImVMO/GmwAwGeKfadlasVj9//68TO00ntis/H8+/EXhJ7k9rbBh2hJqZ0djpIAHZCH9LBNFKMfKxc4XT5Bf//NKNDJJ4/fXRYrs88b399El6ihVcIjfjAa8OGLkEY3v0kqY8Bgq6LEopyprHcIemz9mp3XgYwwKStWnGu/gEWTnbg0HxxpgPsvsB1L3B0O/JpT5Q4eCbnhPVBn6SADok0Y718XbeDCdpYcOsYop5iLOKPmAdYCGaf7CA0YxX/C60aFtdcX6/a+bWM8cAXKKa3Pojf/urU2PlefvzMleacvdMRcSN1rVav99UL0ug728dLXcZ/pDfd+n+ZyT7eBO3Dnwa/Yhb9L3TDunVXZoDftBmBRNT392REnAb+2IbTNDsrsASHd/jc1h+/3KeMHTYcQ4tM9i5Oqb//SgHQ/FtP33VFzzlL75hrghyZqOme/8g1AHBgzzfCI2AlwfQCmvO1FBeCP7eAalnY9A+pNfusM7bzMN+3C10K25F+mnJQCIel6k3+YTFO64yOsZpGpF+AFHqDBy7SyZZNYJanf/ABwYCu4xhloWTB7aMhgy3L6X+8cEtggttqp2vXX7+2YNY/n7hJ9fUSW1CNqn06BThE73ogiqyRBE7qviRtJaLxgOIlT1fxPHX1X3J1v1//2gKBK4qeSodW8Zstf+T/mO4kDxiA0rkFKFihDBz7PNT29z4eksc/crLuVw9f//P5MeDEJDcwj5Ktp+Bhl04WkrfG8euh2yIRGa3V+d4GAJC7qinv7FpVxDw7k6MUadP/WIj/6AgtqSMrn+VgP56JPTMQ/7J4kG81ITZRRPfwiN2WkstR5///NWLwoamBf8pR/z/15a03Pd7i+vDqkZncOa/8zBRzRC/ag5Kkh3Wrn7g4VdkXqyIm9EEob3hx54Yeul+n+8ZmWeHY+eAYVdli0G65LBp8//+7QoU4BRzFMJKpuvP+5mrUAAQCOlEyGjsL7//BoEjFbspsbReZoOkAUYhYp4V/6/0HpDcurLVdrWSzC3FrP2D6GxdFCxW1cMjdO61GH/9+2NgnrFmlJL/eBFVSrQAYCp9V6ZLgtoB47gmBiO1OCEDTvtaQBYogtJ0gVLP/3vEEFE3pJh9SCbmRt7wmjAIABj3WkV8CfIkcACBOExo62jG7sDgh+9RCYjCKziFOcoPBg+VdJFbI54Mgx8cuGA98aEJFvL003/+Z1Yav4ol99ZERkB/65x+bC1IWfIJ9Ztn6z4kPQQJcgD9QwhEmifMkEGSDb5wALAVLQFgiRm1MBkDkqgQkURk0TaWhcf/E4455+BghXgYBsvzZ1R8j/0AWA14cMZeRjvOySpgNWyD4Fwoij7dPcR6kaH/1UTjVtMuciBI82avC0FQO2A/pHr9zn94cAYzEYZZ77UKQZXS+5p5HINHbaLAI/hQePRJWe/7DAMiTsLcp9Df/PfiwnLjBudtpQp4LFYk/Lxd/4RCv2fRXdzEEZbDHBggkAh9NxEbVW0dXrd//sezK67cVr5roEjPW0/iQYZL8vu++gwJSADQPdsQdxQ1/+3wn++oAXEFfJgr7BNFoiw8vEqkqqpGKanoP/8IjYChhkcBELo22yIw2NM3xf//Yf+agR5aDLNTxKCuQkOB00cRpGiWyH/Qk0r5P/RwDRAHLIpCCRzEpPf1VgAAuCmWDg04NEYBOOC7JNIdjaMIBKA2odhDNclr0xoO/AloC1N6b3uAMISsj4rZFXIuP/3EA5RQ44WnKjh+43/gw/hgkran7m0gAOPW3ZUr/wOJ0UJVadASV7Dn31/4RCvwwqcaeSXyHIfxTvNCgu0VPspskuDBqA8nbSfpsDuwGARCPRn+N496/oEBlOl8VQO9RyY4eugL/+EQ9cAALAptQDA24Nqb0h0fsJlDtbZjtQghpthmNyHsAKDLQjdYX5nbdAYcACoFig75CKMwYIxa+6YbOmwSg6CyGr+Dc0xRKOM02kyMND4EwFT0mPfqWmtAsEn7++JG8AbqYAGBWUC4njC8/zxgSBprFBl869tZz/J4IzkAH22EhSxktRLS573v+MAk4LZY57t+HTT973oAHIIwAFKKwu5HiwGvNkYl5hcQ9C2ILQ+HKB2A2eNgxzLzdZHSIdElb/+G0DgT4Ra882psQKSA2pHQW3mg8hAFYgDQq1NqYGQgAum+rOPYdWprdjVF6/65/C+j8PYyjKc6HXyhQuBhjPXEjYETv78JJG2qWe82ZjMCGfeiiB5goDXkazCVJUVcunp3rV/54CiKxyAc0j2jDg7mqcZKjGXmBiBK6HvUPi5RdodrbKItLjbLGsM9ILCPOAHYDGZF02/Qf//fVODYOxASgkyhfw0Gw/eHB90mkMxsHEBhThxjL7bQ/KMc19NCX/++AO8KtJj38hgYpDYIzTXwiHdkkon58f7+oZNgiWB78ZhnVEJ34jjFEcGMofB4g7G6jQtK4DQBDAAqAhqEfkVz8jYwic/3ICHsR6RLHyFiyBz/eYAPCaFJtqaQZJQQP+QAPj6FptJb8wSgifPce9v8/ZH9qagChBPeNEf8NiIEbQ0R/xI3QK+SXNJ7feBMOY17TFE6WcL14BG0KV36IlXYcDtoH7BqeuffcREQl7tp19//zmY5JTfug+fY/x7GXVn/ZwcnWAiDsRRCNzkQbtukwJ0xLKjLn/9hHOJSFYnb+L/iRsAQUygRJY0tFhdMjV/j+DEcbSPNWcR/uIAM5RkYoyyRcmSn/aJBjCV+Ry4YGdVSP27yr+kab7zYnM6mF5BalqVwwrGj7xVlb/4EtY0dNglBklkOX9AyBwUPPG5Sy4doM77GLkRNSEMaN/2HwCGZikVEWJm22z/gzi2VthZDeE/umSn/T+rw9sFSFd/7x8f/P/H/iQ9pHTsV6QZD7p6zBbAtaEQ/yrzhBo4ia61F2QeV3MCuEBJ8zCd3zUhb/fHmp1fyD1rAAexqHF+Ea4N+HkDz/3AE/OADAnfyolZC9/w+ZdHm8CZv7cMMANEyFzKev/dWZ+PGvEjYCEIhGYwmIYohDOJ+gABAHABhEppEV2SX+DD9IGoVHF7irbJTgwRLokAEgJdsWd5gx7+38AxaKVMHEKkpI0j/4MADwTOYAGD8IlRO6B5/gCfmbOkmigJTQwwlAQt35eQvf+cCQLT/SrJFUUZb/so6NDXIjfRvv6fqNle89/rd4ujZnwv//3ceoDwjoa14kK+EAAgQVGrEKqYzyqNv8UPQGO31puaOg4Qx/OP/amJ0c7/9/hjYTD8P8/4RCuAAzBcLVncWO2jYy9DcEAGAYqHgANAWNqb3g8F2z+KHaRwYIbIgwiNlFrxFJAzi9qzgm3F+cTYhB758Mhn4SECjk+XRVfHuVaM68NChAhLmEVHx/lWiPAxoIBCEzHEWoEIsLp2xno/79eUYk/RRmEfEnqVpSkfOH/1ifE+JD37MA1hBgAMWgxBKup5cMDO6r1mjpoGoMkshr/usDw4JPGZUu4doM774xLkKAAmmAO3ZYX2GH060+gfxp/CM/PVqdaP+/X/8BBQAAAFw1BmiDoDbgg8EEKYi8IeEQ1gCoAQA0rAY6KgffB0AcGtHK/FzoN4FmZJ2ABeh0yoPk6rIf94v8Mw4AGAB0gMcgLh/9n/hA9By/tegzQWYEn/BnSBMigTYbJxWS/7wYX+EBvAATIhlVDCYklLGJYAAKA4D7HDg6aI2AhGIqY5lOE9TUh6WBawH1AyK+8ahgImtUjeD7U1hcMPEMBnrAgKNDamywP2gucPX1h5/eeIQeMZKAVSRueeUjY5sdfLgFgPvx4FwgHPAAtohBhXz3Flx+N7/wA7wBMriM3fN/CAb4CtgBqHrIao9Bo1//wIa9NtKhfwh4YDfAAcGLZSZPIXMl+Mc/A0e4aWcDgzaKM/X8IBuAA4ISi1RJz1QUga//4PxsAJQSqlq5P80Y8CA1yOqG+H/wwNwAHBiWUqZEo5ilhx//3xMANAS6hqJOSaNcsBspwAYEa8VFL3v//d+kiMAYCkgVxVYdhcf8+DIACwIIWovorxtn2nP3Ahn6WFCoTGVZAK75B7hu+HiFJd/vKbb7Upw6sVSIowZLCHhCKxB+9DAGF21J/uf/8QCDxkoOAB80zJfuX32hgNBZRpZPX/6AjAKyUgUFWia2X4A7zVn39BdcLlSPny/wX4AHgyocAHBG0CQlbC9/xBAjGW0XOjVd7vdnWsXDAB/YUsd2oFNtR89XTPMlP944ZFRtvw/AGcYwOQP7XK5QctWaJABIG3Ved5Qpz+1jqDyHjsw6MVXv79ASJuAHKApTbfIPm2F4wEyhQpgihDuek1DAA4/LEIaGBHCFkNMI3ZwdeMIWSY/4MABCE/Cwth5CO9dIqmOj5MMFrKGy5yLU+/CAloQOonjun2NNuKJRv2B6isdRl//3/xIIIACIefkVDFCPtRpGEAAIAp0E4CmZcNnRp//9wIMBdIgAgM8GcioyNxu//DIQMtAzAA8xU6KNHut8Furw+p/BgBwyDN5ar0XBRhfuKUBbuG/oStoBDtdkRWT+SP2ji0S/Pn+/xI2BHJk8h5lbJ//eftvMf7qr/QAMHGotsGFN1JQjX/wPQaMBvjYF55Nx3/0Hgi61bb02pswAEJd/1NegTv8ma/fgCBgHQQCiIK5cwhOr56GfAAPpQDELMvrfwlT/XDbAAEC6QAAQAw+AQP3+A5TQdzCTCXWUv/9weZIx042f/vxw6vQ1v1/+5Ovu0/7+WGWxkWtHxI2DoO0P7RKaPV77kAxrEeqV38hYz85/iwFCDAbgABcIWDCqRd4+fmBEDEoT+pPPiNzPzv+B2nXl73/98MKjV0tMau+Sz+BgcBRCJlKunaQWWYR/+GjfAQYA/deu6P72Amqz/5U+HVs7oLz2p/64DgUTwvXxLpmhqkqF/yBW5tLo8/XmNAbD8LiRsMAB5gBICzEtWcgsc//4MPDEtBA+J3H1wu5f//d4MPhUjUHzV+hzN/eJgBEQVzfapjUvOPU4tFhAA8A7AwDpzjQ+XmNe4BdDZeQ6ECoaxCl0+Te5bQAGoHDquK1zPg5SwQMCACORLG/QiOueADKSDoeBLEJtSNyGvMTlMUg7vYapj2BgUOlua/vKJowNdwb1Hv1v7CT+Sf3OTfqQe+BZuE34kb4IwM2KpoNXiTbFiL/yMoKjUgwH6/jc0AByID1uiJ+xN+W3gJgnZV4ew2a6O7+8g8gs9ZdP1jrdoClEBB8xGeHzExh/QNy7X/zYMAAQCcAmgjGk7skSj971Y0qt//cBh+hgkaA64B/PaTGj2uE3deCxF37KIwv/eARvY7Wd6llavWzvFqG/ldQLiRsCGABOquG6jbF77ezB1tyClUKSg3IjoDFb713dCIMNMfzxAASi0FpMJ5+0TmieVmhU1MAzlzkrq/gCbQADKJ2QWV0EP97BgEoQFmz8kVxSEgfvPtSMR8cgi0G7UAIKkhY5HrOh++eDAEkFM9K3Kb5pQvyXCLYHAIbdA1pyZFeFT/AjQ5mssDK/e+A+/ufB+A/4dkfH76wuy8C8b4BCwWmDiETBvjXP2AJ2IABQTlEoJ3Quv8wKuI8kdsy4ZeIP9pxSmdAeeYCyAMYTKEibRJtpgKcBBBEpEGCTDT/P2jy+H5+rbQcjo9h/z58QRX+G9EI2q7/+AEQJ3qOOO9b2sklrC1sVXtqXbLhX/v7OIMtwCC3oUTd46Q/9Do+tBnfRgWoU4H33YZM81W2CrJir//ele5ZHfeWQ1rUWJF1t37BAvCZIvd5/6erinOEyfjYwCgAaBZQeCdFUVo0Vm1+PREBEQEYQQ5rwMOAyNt6JNq/wKPIcxc7ZgB98IhuNdAiA4Hi3NUsbZcf5pMBF1P+C3/+fphlFehg3avEEvff7gAEcEYMat3dw7cx+dK2JQ5/VzaDrBeUbG7vLEbvEFeUBhWawwn3KyggF1BE6gtpgIBwbAhFEkz2xVVThhL86J+V//Ph6e8Y8/VxI2AIuAzvTY302k5uzJh6QjVOrO6RZd4AFdhiil9xu6aGN1m8iRBMwis4hTGKDDDGgU+GAqnA5ArNOL3bU/7RB7gBgpO1VS/0i2/uBkDMUBxLvrrN0UKe94VY0G9jeMkSe+Vh1X6r/gTtJsBI/c9G5VrZcYEnf/36hgSh7wxYzHAxFuCAW2XHcv4AInnU10G8N/rB+KRdT/v2DMirjCJTh7jI1uv/z1VY9tNFe7+JG4ADgxLKVJ5aYspAwj+6QBiJQi2Jc1ZoitMcFkOPOTwMvKWP98AhyGYDFLhIwwMbKrCc9RiLnKh6fAkoc+5py2N4oAM9CEWau+GKOsqe9DZ1MLiCUNYroFd8g9wK7GA2sCfEqUijVVsvuqI1UnP7I2e3vw9DAAMFrALqB0Wd4rtw8EyjqVfG1MB4HbQfED4s6xQeIYBFpAwKNDamGGPgAMzEROU7mG5q0MAAFQYB2TpkcNEYCrTbuG/oA66QEglS3eLDOG/qeKIfZP/zCN3Dom1F4kPYG7bpvkpt/v9KLt3pd8GHsYACTFxcsqku1tFkMAAFwUywcGnRojBMm/8AUvzIXfL+JG8ADwbIQAHBGECgjfA8/z4CghLLTR5a5g1Ax795oKC7RUpdj5LIDDYBgJw4Ptk0h1NgogaAAHgAJASwcnsVOgzQVZkgT7R22FXYmb7ve0GCTfJM9I/w73vwiN+CYVUpaV/oBJAqUc0hGcgHSQXbpM+eADM8FQwCF41aocqNeSPwhLmMm0xDgABQHAJtE4cGzam42GFBjPDKLah0EPUHtTQpVeoyLN/7qEi13ZQAWAL8t/wYwB+6FsjiDR2QGeJTOxAMYTSECLRJlpqIMNzTgedCBrVt9C/+UYJ8yzkB+1vq8B6W1Lt/Sqh3U8f78h4uE1UWyrYXYMHhEO9AIOoe2Vf7kw7JQt73B7sRyirKB1mW1O0QwC3sgZWiupGTV2hbAUstdNKUABjgFFwEISz3kWmB7D7hD7wAMA5IllAh9bOnxji7MaCclzdcx/z+f6MAQQVSMiTRBhoPxJOZ+bnSDCHNsgABdgdeytWWBQmgm4kTEr/+lODXS++9voY5XxPn+gSq4dqxa4CY+ERvhtINQBe4QgzQQQfrlRvz62aAYSTGWE3+SkXRPP7m0cMqXIddP/zusk8Cf6XwCJIoGt/6uTTovL36D/m1h3+VjNye3hAnWVmqvUnQOUe4GCB+BiL11y90oHwQbS4RGAIvQgv/jeV+bntFf1kQ8MdL+Qcr8EAyvCjgW6kVe+62kWZecuCj+jcuzL/3ss0wOX3qv/f4kbn5a+Y5/757t47ef6QHocyuhaAQ0vaZiKw6tQWpzVfFEoiiEiNgw4705h/+HGcOdqH/J/eAAuAAICWl12A8RmdXALFAU0ACD1+IJmAL1SYL1u1//MBuYJnhXhahn40RmBkovy1czD/aAsIqnlBeDbhZl7/QQSdzmk2BVnQuu/5B6QneEdY5DhkgdGCN26uf+gzL+Yl0xx14DdxIIIc+PyscXq7BAgPYAUuHLcm2IX+a71DMvMxEBx3BbGCHzRxA02RLB0TaPy/eAUmT7rav+2/+XPgB/4zVrD/arPmSI0I/tYIFPh21MSx3+gR2WD0LDX3ewzgsroXJOf7/Ejcoy/lvz0Dli0lvj/q20GpPziANIFGKrVjvqyrX/gnRS/HXPv8EKpBKPKJ5ZzzSH6NphGFiLWlCO+wQreRC3FZH//5AJYjjNSQbSj0PMcCccznB976FE0Kqp63oK+Csn85yW2BH5Ht9M3ch7z5h9/B0yRwizXtd2sTG6lVZXR/dpnSTfEE6v+liSDJXJV/pgxgdFpzeJG+AMbjQnA/JPkT4SrcXoshBFGOxgxJhZIGQbXZi4E/UAUPPxks70N3Go8PwSLlkoKtgHkGcUT73f3oA8ZWFJVIAREDf3aXr9s/CiuNwJwhy7oLdEuP3CTWsmYJ0LfgzNsdDEolzzmdmPfRAw++xultgd2pi2yIPv/8poW+ERu+q0PKzL4MSJCryet1dQhThqDQuX+irXk3L3w7fTquq+i1TU/7qS4h/W9//m8CL9wA2aAa74NVtIf//47ok4y0YlT/+Duq+2fMVOTjxxnX2aFttFVXlF5//zQXLJrFdspCPA8FY/+JG9D6ZMm9vk/vgReZl/Kjzf3YTcOyPt4ECAtiMlNM0bTaPfzztP7+v6O+AjBCKEqbNFCkb+7/2EaIwVMCkCFUHymcOXARRhDsPVOBayy/u0wEUAOss0HYRQJrHO/oyAfiXI/jSn+X44Qndl66Zl/2CMAdZ36N7qmUJFpClv78/8IjdtXnpOv/PSqJTrfPaEjiNNOT4JYNtNe+pPJ73ytvABCnn8hNgVmAjN5bhhjWK5XjUgj//2/A6B/s5wIQwwUeUQtG1mXHrXh8UmXOKSuwhogsw/FdgbYWRNAhgxtar/n/wMN2NFpIZzrndo8sQVJrY6kx66Bh4HyDTug0aTqbOhid+1gmI5oT9meNAACRPb35d2tOKYsirv9ofRhM96F3YA90fCI3hZJFp3z/2kHxZpoHko3pb4RuyTPjvvhlV+//vktr0UhFtOs9cBnlrTbQ/Lf3OAkFUnYn2neQYKzY/gbrYfQFjh6jRqKTvb/sBhV2WLQbrksGiB//93+GAGXl0D/nMlXzkBzZdeWv/XZBchZn57/X3CVJINZ/93jQaI83uDB4kbGwAEBPyfyf+jUCe238b1QZf0DAEEJJ1bxtUnJQ5gBuiWNbiZXQCQgl3qmVM/tx/3o7Iuz+15tGIqmPmCqWpQfNAAbIjBU2ZAzXIMGtL4dzO8lf3/////6sZlASFT1O/3tweh+/X/DFpAKAAkxcWrIhLrbRboALIPVtuUaqKcYAALgplg4OOjRG9CqYAKYBKWmuRfNLmKH/AYAUWYo1Qvc/iQ/AB0H6C6sev3er3gQGCMf5qpFIwZiT/B4SBJu5HLlbv7pgoxOadd3kPAIhkbKz72HGe/nYa5wZ/FYk9Y9Tp6/8SGfhAJJJY9Y+uo8klUs34wASiWGJNJ58ySj87wAxNEeqVhn5CxlE44AY9CP1KQx8jYz44UBYUc8jiI1sbCewTwSNyp//G8GAZGnIPK/6G/f8BTQDlZMRrlP2H4NhAASbcRTDVN0PQIZ3M7IsTFttn+f+3AAZsTJzi+p3Nap4PTxv517v976Foufn//xvjAEbhyh866eyYTM/hgYINbAc37gAJgNScAAJAUNqYBLQbLxG8olDXKAA/lSHbdI/9fASAwMshWmH9LCR5L7+4ABwIQJQutjxfnEDv9ozMgCBmA/bSo9E9/4HjbfaylV/3sReLyy9LP9gopHBKy/at+JGvneerCRw3UHY9hjxIegAIEIn2iEu30h3/UkHY088D//6cIFAvSlpZKNYgj+rD3XLel713VfXASOO17hkF8kDciHA2GAAhhcpg8a8ilnhWo6WXABAxrDyEJzYEtuNf/tITkYK60iu6TyvGwges5JblKSYloBCuHG621bnSBu/y7o/2oEEFVDqJxEt97wIEj6qbXDZ4RD0PmgwTNoZL3Ysz78vDAb8OGLvI5z0kqY/6o7VEt3tuMSFAzQ3VdsPD9LLSXM4OWX7WjAAnfuERR9i+7Bya44z3NMMf4VZ5IpKE1P3eAKAAEAE6gGJGc9D7+WbHDhYHIPTtr3fDaQLCVF5Ef9gwXW0vZCXzdvHs6jhEb0kRgBgKSBGlWh+F1/zQdTq4qkMI4pz/4EENIp98tY4/16MInOdkxqd0/sBK0AAIAgAOIjCKJVRco3Bgf3DbwibiJYbVNv/OAAFQYB2YHTY4bUwCWJ2fmOhgvLUjnTHZmyurX/+yAWgJaRkFt5eQJDYT8wKDHPbwFC/9dfvSgfX+qpznBXgTiJu84MNhoSZcX4RG7EwAMmoSfeiC/e4ACYnFBpGyNyRsogogBE18qRvJrbwPLJDwAcRUnXsGL+p8aW98x/rA6VDC0vvy/e95jdwGW3UvAoKWtA8RgM1IFBJobU3EAESAhI+M9v6NImP2gV0CA80MRbtC7kOK99xAEWAavIc1C1Sd/g+IAHx9D02kMoMEkTf/8GC3cHeFT2sFiD/aBuqWpLKRyP/gVpY9lTv//97S3qMx9///uOPJChwL+EQ7B4DNHsJ+J/t7yvpE2b/5/kj28I8IA/EnO1gSQFkXJxE0IwJv+tAjcD0H7v9XgxawrBgALhB2xGvVIhufP//uD2P8PwxRSuY5dMC26x6REIjGEziEMYoGBBgcc2wqYsRFo8T//RWoY0e/8IjejjAvljVrkeii7EsD/hJJCSmYhqRdrBhikEDI5KOGHnmvvYMcblNXNVYlJmjhy/MT48z3/uGEEAS0fiyB7DwAsAbAyGnlEN99BAZcAMCyVvkfNuG7QGrQcRSV2Vf/3hkAAxei3PgbyrD3/+F9oQUglTUOjdvUM2gV7FXT94SlyF8VTefkq0vwsiA8SN6HcQFfbEDFk9Of97xAJ8PbVdNjXjbDz9FXrztD8IEUgr0rEcSuizP9OvpfP+OjT1x7/6yaAQKLi8QKqtHfOAx3+37maESaYY/wIBhsC6FwGOArqCTNtYSeKffZgmRpxWwW94viRBBBpntogdCH8GHZV0uANBwAHwOQQPOGJzy+ZmLf7rFiNqEsMmwju/sMF0OylP3uH4AaXBqRnr/3YGDwhb7+H446YH9AhnoajJoTBlpj+fowAN0Rw/UZYz/zwAGWhmApqp8YYF91XMqDdgGIxidBH2EbXGNlZIEmA6DCGr9EEOIenGTJc4o6AilHb5DuoKUf258Pr93veSGxeWBDjb632CwlGbfhEOwckvUlv7v3wAwQokSliMdLZVTQ4PAAJgoD8xOnBw2pvEA0wcNZf/DeOklDGAISyUweWsvhjz/9nQIPoCGby0VdH0LYY/gfNgAZURwvUZIzvYMDjt0hNZTLqY0QX7sJV+ce/Rf4kK2AvNCwu0RaXY3TXQ2AACwKXQODbg0RvUPi1RdodbbMdicQwvN8dqOM56//hvgAeZG9OcQFcMmSj84CTXAQotWNNUABrgFEBC0xaQrl4AblqemYof4zCPiQ18yMxOgqtQSpj0enQxBC24XcMDGyoMNSQTbjr5h//xIZhgCBDAI1YFBRobU3zpAi7p4N7//EnrHfzkn+//4nxI2ABlAAP6egRSUF2j/9BmjClp/a3QxrjSMm0EVVzab2cn3wwG/Ay0BykBTN8y8e+IYtMvAEELJKog9yYgpIx2HgBMhwAKCdIlBK6B3/gfxCZKgoMPStq/RNA9p5rPqrvvCKJSCw2/wtRQA4IRvN6LwTBlpj+eBBgAbsjhUUZYzvwfmZjKVRW6klLWpDWwtpt4u5Y5X/xJ64f4+j1//CHifhqDC80zQBAoqU5EiZ9orDX8vv/icQvhk9Rgne6v/f/+AgoAABZuQZpA6A24YPXgQ9Y4cv8MHrwv44cv+fDEbhA9eEbBv694QLwAEzIwnURec9C2KD4kNYACMBrw4Uy8jHd+klTEGMg7CMzstpP/4MPhD5RYWy6jLeOkFjAYfAARhJnORnchHcdDAABygAFaA8gMGiMGzTn3/2/L9g2AMtY1I32v4QBBwALBiSQqTSU2YgcR/cCyHuiADrZHlLt9/OZswBQq/IinIM+1mOD0TADQJkLUIym6Q+9hgSUpwCsiwFB90//72QQYYgiOYBKDBIV+10Y6rFHTtfwgH+ALHGxXwiySKYaSH6g6PkF2h1tkxwYYAFhjM9qaihEmWVv5MbAmAfCAgwdnHi4rA874bRL/gwj9R/CAX8AB4AEg9hqTauvMFEjv/95AY1nEaF7RIWM/Of5KwCZTAAwJx8qI3PP/+4IStgAHVt6JMxhQVR7gUdNRBvM8IBb8YAXGsKSaT35koif//g/YGPQj9SkNfI4M+OB4AYskJk8hJejHn/7ANALhZ+uEUXXmw/fgdbwDL05HNH3wslvN87np17/+EPhznEQBqqvN/1KLowP/v8O4AFcABsiuG6zIG74+ZMxOxzcgVDGq0xMqeh6DpLo6v7/TkMQQtuGXDAxwqDhgSGMveS7m9S7Ze8oIEQ2h+/Q5Exo3R/M2tXe9Ah+sMBjwALNm9FXLAVwyZKdWAgIDXAYglVNNUABrQEsMgwY2ESm5kUg+mQ7qRa+P4QisIeIDHgAJCcx17DJanm4r8xMc6coyFoxuschgOxYFBVobUwtTBIuG/oAOmZotvj91ET4Jb9P35/higwAGLgxBa+o5cMC+6rNnrNFTYJQVJhLV/e2Q2dRm4glDWKD5wAGzIwVNlUM1y9YuLlkYl2to13cBYLynXDDPGeoSz9YsDZLev8SN4kkZjx3Uvb6AlgACAB6rlYIpIPbuuMMPBMoqkbhtTAXg7aD5w+K/MaBSGQfKNIMe6+GBYwKQuTQKTBlOIYQQr7jCRx06Vi8YbJX3gAIgJcHC2HkJ7x0muWD5YYeqwbT3ItT38GFo0Afvd5oWj0IdIAgkLHnITCdNcvd9dUxcNUR1//vOiHS+UpfEjfgAIwGihgxl9GGM8IKF8m+r//tvEBvgYNZe/PVvFFy+hAqBKCCX5zJBad1395wy7fIuTvlXzyg4YCbhwxh9DOek1i3/Aj4GAlkolH45K2CUHiIHQgWJ4xzW5LerliaYdWGtzYgGAcABONPIZ6xzfMBg/yV/TGdQFHb8lh58w1JCFmk5Wdr/y+fe3R7Viv4kbAUAM4niFn0Izy2y0Q7ho5QRY4Ce8Qj+qNHBsQqa5xc4DCviYTHd/7gKii4Fy5L2fLOInf/4ZEBfQxbQ2pjwH+eGvd7f9EAIsoZdziPX7vwgEC8g0YCmEobSWwOTe8m+AAEAcAMMhSPCqa5IQWBBBRIJ1UtOR//drqHMHiIqP35AD/Lra/5q6HktW/5Uo2pYAoB8SN+YAAgDvCnABnlcygc2gd8DAtw0QRKV23TIgt2ZDmbv8/BQ2APCDXuK00CO/94Bh7QSJRXxbEkcLesRgAOwDcsg30ffoVjlswZ2zRlQG6b3z7pfNAgRtHolEmqDWCX7F25Vqp7969B4gA1Ap4XsZWXsh8QACr0gqek389IO6eTMvvrWjsirff/2kIMIiyBAFgYDxIIPgAIIZPjbPlUaSOgwbQwmBALfPR/90xDQBEAauVwHWf7mWGADglQgOfgJT5HeCWjBhRqJK84+cHnzy0gN9/9ttFN/tfvqx5NuPCTJQknDC/eJG/EJpRQEnkLksCDbm3AGqlq5Miqm//OnkX12lTyh/ugFAMLwzbjk8ZVEUVVYPHawnyiX03/gLWD1cfSz2tL9/B+5FIOASAgcSozJ61426u8Odd3VvZiUrA3b8b4wZ3Sb9G/+GCc9ec2/veAKG5hFeSWlwjiafBBYoVFiPBF/39lJUIix5v37tGb4ilmFkf/1iDJx93dXM/7uDFw9KpRJKv4kbwiKmXALXALEvZXNqai4XxACPhTFH8gyhKOvYYCQKBZq0LrBmB0/WBL+gS0WPAILxYTselm0J8IlWLwg20WyD+mRnXE2aAgEvtAbuZi5qYD8zhZ4rVWL/AwJOV1o6nF3oFeErqmV5/+VgO2krV9O9/wdhyI2Tc//iQ/AkARAjR8ZMvqtd2Mf+8CZMwBAK8H6VbHYHP/BLXbHvi5Clqhw+fzOyuR96Ag9O1lvsPv8c3lTA+/3QXTafad+8CcA4QwrnekviSr8+Cekd4LQNc0xJPS2f+wyCCpRUL3sz/uXkP4ZHhW8is91sECWmQX5uZpokLIeBe4kbAATRjZcUT1P5jVeGAATOtQAJTvCzj4WgoBgJ0+zPA3/rIe9Ug/785cKEGCy46QCQB4UwTGUyZI02Ukat/TT/A9+U3Hy/URCZDGQgRDGIDbKmhwjASMEiiihsrp9M+Lf94aNALfBaznbnBsQLT2X7MVINaVoth/qE7uYPRP8ZKwlLsyfhjgLi0fk1TF7k/3iAJacBBDM5Y2rlRAABwQtFpiDiEQX417/2AJUIADgnKJQTshef5pYEcWIdpdOON+603H1KRP/h52b70knv/L5aods8v7uFgN6NY6H9L/DHwAGgsoLBNjJKyaJzcAWBCcYOG+JIZkq6F5/7Rj8jGaEAQo4j78CBADF+RkI+pmNR8aPhDwlf2ufAZNhhgE3vj/0wSOQ7ZU0/aTV2iR3bQ+MPiRvoFIADjQauS9bc9jCjcGALAAKA4D8HDQ6aI2DQFBYpNRfa//s4CJrWK3jamDwACoMA7MDp0cNqbBmYAlUZpT1oIb+l+jzvfEiUJJmZk3QTipQVWctYlb/nEMAjVgUFGhtTevQhFnrlA5JldT3oZHUReIJQ1iAkVuaTj5xhIGNEemkOegEUpGVHcdnhcEmlr588aeSKFJ6D8PQBiMTohTKUZKmp8Q4/I6GOM+1GkdYO+0HzhsV9WwbAABvgAEcA8iNGiMAOOtyvxFOdbDCPDwAGZiZOUXUEctqnAACoMA68DpkcNqYGIdJXSc/eAANd10DZiONW3ayUfF4kGGfYXl8ACYClnArxBCDJNjOBDYfQADcgNG1MEIkXf+AFSZBcVLlfa4SC2lxJeA4B6TAUgURkySYAj4kGEMtAfeABYBFCqEkPTsoqm6934ABI/ITvJ/oiq4pSm72vT9gwAduNNJxe/4kEEABxg9YQFL6rHJVVYl78GSIURkZEDDAHaGRVMLiHoWxXiATwOGsEPRzjZNMxwAIIgdvDtL7X4IUsnILEGYMxDBBJhJLcgATgUdxvWJ3m/4hgYtEaADEG6jxthZdZSAACAQAQFw1H41A8XYDQavmMcaq/cBa6xlTJl/b8IK1WkrpN8/iRvgCMY5kc2PwMcIY//O2esQEvcGMVeSqcDTjFvR09kALADTBtY6PSfolRwDR6Bw7BzMNNBB9/vakQkmJsNUc//LgaM/gStuQvv2i50taryk+aARzggNLk8wMO0YavwEPmwrpHZd7f//JIaHI4YV68hqX/uCOIHKrKpteD1qa1bVu8SNpxhhASCgoJKNS5NhllcpqjnrP9u+NAQ1lpg8lMGoFPfuwQffKLD9JyPcH4OVUqp/f7loHT2AUgcJBvCKGG48S62aTQBHCpiAogRXaIwAHDUJfIex/+1pR2sSIwTDLfHwf+92gBqrAGDyFNMtpNkvfBo6nKVDi2ek96tA8+b/W+y3CMl5fN5FpCvuN01xua89xI3ODfvb5hnDnRYn/u+bdws8A2JlieKns4YYCXfgf794eAIfKYAMGwEc5OyJ/3IfSRea19B8fLAB7ZMlHX/z7XvfXIu3/SPrlwxXvra3JE3fzgIB7LTzHS1b37b26bOrb6hY6YjmHYtXWkAaw6E4kpvkP//hKxsIfY/zriRvowJ1m1PND2OLjSmNjf6vU//g3i06A3frxBelGYu67U2pGDRQUK5aqEf+va9glUS0lSotvyVqkfVveQiGGRxhXMOYUUqe5Ict/aRvsP9850auz/wLWKkWr5G/fYB3nqHTaGJGO0jeoWtsf/zbvRpnYGAhYqhw5QQeh4tSeJ//rqyY69h5ogeJGwQfgmG4qKKqV3RIlELrCttye1V6dRLdd0vtgf5AKOLxUdHPnhFKs//N/tStUpVB01M/B6z/8gzWhWoTUVJDtS9//yPsf+30wAAwWRVluJbz2X3+/3XaTj/hzLzltwh0DAp2YdZ6VHYil8j/qFnsTXe/6WFwKQeZk2I/dIKQHVxHnzgEL9H+2/uFyVJ64kbDbGqQ7r/QGnW/MP/Gr/52dwW6I7Ld3gArdbQH/+2Gj6HbRH7dYB4JC8JU5Maf9vcQ5VI26VEWfh0LcU0ff0/n6Xj2OZzKOf8rIzES6OLKH8YWpglzdxI20apflAYH//AC+GokLQ9Tdbf/Q8pApNN8cont7/vARACIcBgtxnF4CMk/W6gAECBe9ohVDWfd7pHmAEBBO0PcPvGcXZfvek8umaXfwqbRoJbhoxFhqRO0FSmPSrnv4oCaZSpivBw8SNt3duziNEWDVcyLdvD4AY9CP3JQx8nYv44BgixCtF+DOagFEs4zPzvnHOTj4oQ9ZPcfrAOXuIkwNcy+AA5tcAAw33aYLm6RFMHoIUI/Rpu+o3OJn8LQ/McfZCeVq9ubU0kmB7XiJe9usiRDW9P+JGw/ASL0gPsFyPgdF/4SuH23ABh7MLStZBAqs6R//H+DQWRqDppWAkbk00dP+RP/oATYqWo7Ujv14PSjCX9nXPE/uAe0Ahxc4SINE22rDw4qvM15Q2OamMp3IsWoJjnz7z73X+JGwDGeu+PX88QBOgXWo6ZCSRlYl6ZiZFOdSDc1quAgDs7kAKzKjJn7IMf0Cz/VE8CAPDAOKAKP/PCVezIPeD8QAAgAnUAxIznoffuzY5xWOxGiv6lcZgQbdIjKQyYztpscKlZ239/+4ADJAS/GKbz7+/xIALAl7Kkyd5gx4MJzOg/wbT2Mv+rDdFleiX7/zwe4jyOqU1MHoUhWxgSNL6/ggh9HAAfAJqBN973+1kHf7gAIyQldEOUZ1rNd00Cm/IRH6u/+cAAOcAAr4Ae8NG1N5C61mU5Bn20xgFE3wr+tpR/YKzsR41M/vVBQ77wtYF0Ah7EeoQt96xbxp/fjwa/MVidH7+/RgwzeAQW6z8+RMgo8AIx6aXjgPMKJ8MlSQeCozRmU1Td6+9AAcTHNFCfvf+jFPcVhFe8Ih6GQaGAK864ADoAFhdDUm07eYJeO//39BIAa4xRzK4t/g6x6CGhOIEiRdlr/Sw1DVtgBQQi2SVXXUIl3MmXu9/Ehnxk0IAGDT0oUVKXEP/aBit9v7NHQIYY/gIGGE+0HNnSY3ojL6aQ8YM5/CIV4yfEUWFMbvf0gi1oraBA5SgBywXGc4iFDL/zAABQGAfg6aHjRG4Y9vWWQudk71uElf3M1VPUQmRCCYh3KYj3GMjocTUEoY1QHc2vFbEnT3/3EKOa//m/i/hEb8YyCof5RaCDSDXMcOKpfD78ehhLIR7PNxaeEPemGuM4io4lbBbDDtdI+VsKnZYQoT7N/9qAQBwNJMyxJaYAAgA9wDx+1TAGSHPnhgAMxU6cakutsFuYAALgpVg4NODRG/wBYa4oqV1nd+KQCAwux2QDro54r3/32JlsD/jCIj9HLGyMZBrCkSLqgfwiFbAABYELwFhlyaI3EGqnBJAyMHLGZjv/MAAHaAARgDXxo0RsAT+AAVRHgwviA9/nN4fpf6db7qtshnQ+TXNEBVZiHlYeVf/yzYQhH2UIIcavmNieOUeOpBn//3oZ6PIhMn+/f/JWAtJfhEKwwJL0fKLtTktOY//eAgBjWI9MvDf3sF0zyp1Z+L7iy3Wu/9xi3ABUAZePN6OwPbxAl5QjF/XLXqlAZjaMuNW6/fMwAdESsO/fr///hEO8MBJBfF2qJFcJA//5gDojDAIZ38uq85/QIDAWAaibiIKfj9WRVpvNcv/1Fe2oP+CusgCaXTx29zIAAQMZQABAFDh5/MAA9oMQWvqOXCwzqqezysVRl5z0NYrWaKyQJQZRZDV/bTRCa4iGRr+BxOgftmFCfzp/2poB3++G3/70C7bD0hrV3ZTVXI6DwRgULRThEb4kA3YpxmNMKLJKYZRMZ+glJi/9YzbVAJBnOPzJ7eewAyAwU2tuJsrEeNe7iAAEAUUpwKV1TODJXwl2AATA0mu5DgeP3Lb3AWKCSjEE2adwXNsAAEAUHlcRKM9S089gACYAPiYFJsJb+2Tgic8QANB8D020sfaJwQOeKDoWlPtREvWUpPZ2wHAGB41Flg5AJKY/zdcJJvZgbDB6UNqqI0+xSMzbGt/3sVa3ChDMNj+ERt+D9H+LB6wATAiQEztfhkh4Q3wNZtLjs/+sAIEwQNR0kK1xxKlq6COVvheUcOVzuxtEkP//mjoL49H/MMFgB1QjkootbieG+XRZ+OsGBGSopf4AJMcZc7Tlr9T8VrHASkki7enenlmL3ZHW+3/wdJUCNbLP30VhBVRp9eDPxI2NhZ977ZRwd1fYAAIBkGC8KzVMqZMefMmmo30XUWajU4f1QAcBjyjMFYlODC7P38AhaDMBTVSkYaGd1QIFxhsqaBJwMkshq0AZqBLTxMWWso6/9wEPbnDSX8MkjbfqsDINVsFYdTFPv3+zQEbgdkBOfFqmvnX8JmwpB2dqrvsOMWfykLx/rIkw7KhPgw7ArM1tcU//4TVDl1ZrsMPCIe4gA8GwCrcTgZbMP3vcjdYRyEwK9QtT/gwwwBEB1QP9Cyc6roCXrBkHY4AFgmcgAMCcIwKid0Dx/hBGEHK4kzRvn4YAnrDrINv8SGOAJlCHd8iXFYqO6GiAO2AA+FwaqAxOMzoJ9xja9GXgUJ0L0wSY6PpnwQiQuQcVZ85/v5QdJUc+OzXew9lGjUvbIJJ/8wGlDK4nhEK+GNeX1fVKX/7yDOMpyxKeUFkle8gAANYAAj4kBr44mtvMAFBODEm08fdIxQPeNgBcEqpamRN1XnAw4SzMnAyQmKew0bf2nO/965g/AhavR/N/2C4kEHgw10OABsD8gNvDYrbtoAQRgFckDAq0NqbgDcCZBFKzDamAsBSUEzh0VtY0LR+IGKR88KMZguJct3n+EX8NTEEZhEmEbk8/xIV0x4THACQAMR7csMdjmyKCpjrAN3QAIGd8VE633//cH4XmgDlTj7zlORMY2p135/+FfjCrY5OdhXQsp7gABzAAPLQHPDZt5g/nGu8c/q4C+FUkJJo4aMu7VyKf//xIasQADxzCdpU6506CS4Aqq57/3//hnhCdnZf8qI/50CAWQAaAu7DFHIKGv/+DUcJX2n+///iQ94D0QA2BRSak492omx35sEYAoBtg4ay+jDONklCwYNYAFQcwgeeMTrd83UW/3TCzIlCSGTWR3fw1SGammQ3X/+9fH/eZyH7Pv6jgIHzZ7+3ihQga2vEhvoCEfzeq6PgW0x/P0YAG6ZwqKMsd358ezb0htTDbjz97//4kK4ADUKC3RFpZDZLdDxyB4OhhJC3EP4324cfj/f4IyhNutsvtv/WJPWcWr2f+JDUEHxyMwAgKPlQgWOquf+h9sTpULh//JMut/94k8hQCIdKN/HL++/COJ8TA4QAAAXQEGaYOgNuCDwQT4YPXgClW5p/v43CFYQ+fXGwZ1R6/hH4YsHh9K8cAOCPwsc5yY9LSvPXhtPJ/hAbAARDr5nURRL6YYSwAAdgABHAOfHTRG80FB9oq0up8mucAALApdQDg64NqYAWZKBqYJ5aIIeX7AUoWwC6ShK4gkkb+RB0WqJviJfZTqOJ6kK3YH0DAASBKwfhO2pp+MCtaotDCGwQQREGQLkGsMeRfUPcFYQA9aCKx3ER3nCjaAq4uN3vxTGthJ7nR56ib+EBPyIxOiHMpRvU1IfWB32guIHxX1bBtjUW6//CAIMABGA04IGMvow1vhJYz0IgJu2Or38m4cezhEdNYDlAYwuUJE2CDbTDWAE0zwsr7/9ug8YoYbnnYLhAP/EA1wYNZeRjjXCS5kPkRQW9wdTvpNz58H/VAQwiUZEmCTTQYbDgDEztRt4ag0cOQ+R9//9/GwgR0bP+EPhzAAYuDEEq6jlwwL7qum3pCvEzkVf4jdmARFvJOfzfxAfwwio/oJn9MeDAvhkwU6/wcAKTisFJwbSsQkUDIHjBgOO23jtHXngzFtNyn3gbjHdYQPWgGgY7l/CEVhDxIc42cwGB84QDHSdtwGKmWug2f86/5v4kEGABcNVX4PQfJlDV/QEzNGjF86MqWAiMNCqYelhaHwDeA4M/Ghu2VnHnzpmNnpnfEjYAvThyLm7FbciIhQhNWPebWzD/9wgw1BSy/J1EsOY237gz5jCpERyVWKtOf+YAAO0AAigHvjRojACx1uV+YwR0qMcGH5gA+ZgDFiEN/bJwRPeQAeF4NTZS19onJA4HyCEJlf60qCqwvgxgWENWFiCQUg0FJHmVOv9EVoGdTXVgm44W1hZ3z9Bts+/GtKFZZVCdj4kbDAAsRCw7cdGmKe3/tAiaqt5fxbmdVHBLABYN8UACgjaBIQrjd/4hlRePUE6MgPtjt9kjXMAEowIcnrKdGNsSt/9wkDCBYnnPNXwr4uWd+GV4Rvy0guCVf/oEVhqZLRd78/7JI4mHHJN+yhph8/3uhhqdUYKPgXEjYAgQwSzybgcxgz02VT1aJ9mGNLWLzv9Tnf8/619C/5ToTl46dPKeaBoMjymswKFV0tARwW25aL8pQf/7cFtaRskf6vEbuG3xduwAdlVBmrgJ7hP38N2hU/nbQBBDsuBzRJhjCQTDZMGMKIdPI7YladF+dLGQAAgAgOJlHzaDDXfBPGgo8Zdo8dvdZI7U1tYLHf9pmMyx2my9H/9Fq/Wj6/Ul662h+lxI3WKqVL774gYBYEAAmkwFBDrS+GaW32BKJWfDznrtC3B6KAYr0relSXOK14AFG4ljdCZSp/wG4BFA7cxiBFc3fn1lU48tZ/+m6tbTkOfYHwAEcY8isP2WHFBX/9Yw0pDlEues//+4HaXJdzR9s4IFrls+/R76QABpsR28av/uw7dVltt/fynhHw3f8SN+0PCXRNofTpKfwEIQ5Fpb0hLJV9n/eIcfkdBEsfbC3OAAH6AAR0ANIjRtTReqFUfLAJ22eY7T8q/zAAdYA6VaNx9BgW0YAgYIEBMBKwOSEXXi0Vg19bgHgr2DsE6jh1ZhPwMI2D+FgAEugDD2ELRPER5///p4IWMC/0dI47LRZY0Byh6dhFOIbtIAvQdqDRMIqf1QrUNZ4m/+aw55qtzNn/A4zSrE01IrMuJG+JixbkLCghZhf/7AhctqbvVpTD/3YEH4AoDbAoWy+jDeNlFi1gNmMABQRpAsI2uv/+4PcYgLtxfG/qAQLBwxytP+TM9kaq9La7d7vD4DOO1OKZ8BDBZxj/a0D/VCdp61wMXglKIQrTRPfKYRT8DEzQvzbsaP38CNZxtzB721n48RNJd+1wstsXqc860yJaEynEjYCghrJTB5KZg3hj37kBiWI9MrvpCxdE5/g/GBJHCuZuoxOt72Bj0I/MpC338FUhD62mjLQbMraQDogIEFMUdHquJtvgYB6BthnH/3PeIDCiqxoRaJtMPAgLdWKVYSvFFGaJL6Zkcwvh6ie8YNc4VbcxCk8pBZAFBhxqkLD1vusO4BChaokVMv/92M/E11l179rdh+6aSwj4uKAat34kb0WwCNhjGGVxWP8B6IaI+US6T9+xHGsqxlKRv6wK0BQV+KCPmbEj38QM4Rv0fkg/glB0B7nOFdkcFtAXpgJDAVCBmFNw71FFj/7DUEPjriXqj78o60hWn/fcSZLFDd6s0H017qjD/f8SNwAGozIaHMpB0MWjwR6GJfOqaxFZHf+oGhzRYnt3gMYhZKaqqgiDSzNKDc4PFKUeowzIAHNfI9o0V2YBCHpoCGbcLmWld/76PyM1HrQGzWYTxNVZ//+nAeH3A1s+80bMkU0f+DI6kPdKpnz910D1VDh9/1dTLVXqTT//6UBfp5lVcu36Q4MbAbwgHw/4gw9kbDIKam1s/+DD/9nsFBXCl4VQaHom2kAEQELCZzy/g0ia7IDIHOBEc4IpQ6WSXCSxT/gw+dlEp/PLvkJqbsie75g8eEWW7vd2cqIOTzPDGADCA5LJ+u3w8KIEGsaF0KAgJXocPeWwEi1xw/UELsHEvlj+qLkBb9Nf1n+JG4AF4ADZFUJ1mUL3wTtaNaNJ0AXgXPunI4Sfn//gx6Wl216V9/gQCgCG5QjitYqxKa84kgE6abI4g8qJPBFbrRxRgAxUSohRfJakq9+gjpiAKtJAQk6mh2ATobOoi8QShrlCE0qzRaoSaACST8+DbN8RbbluoiYmqr//XIqGcOfEAwgAVxi7ZMc6mwU7g/EKLjNjuK+FltDowAEyRGGyHKM7VluYAAOUAArQGkBo0RgPTdAPgwCQ4aka2uGVVxEVwvzpYACRjomaXCH2yjHkBAEGAgAGNhMynF9RHNepwABMBoTgABYCRtTBCVoDMztX/+9Yl0i1//nhsosNSJ9r+JDsAVHZx0tNt5bTuIClEBB81OeHzUxb/Bh8AxX+9OzdCJMNMf7yHlUjoYoz7Ua4MP2yC1Ta007Jmgf7/2/sP/4kb8ADOEhZgh3kZ1ZZaIcOOtAccBPJOf9oCHZz0XFCZNNtfzkDxBx7LuKUR8gx/hmgAkAxhMoSJsEm2gWdQYBAQmgzAU9UpGGBndZ5mQ2dxF0gtTWI0xo+2CUGSWS1f2kAA0RGD/ZkDNcNAkIQOYG2gVeMLkPdwgABACKNxp5UaB3uyGngMA1WPSR8nWxFzXxHzvLmCqc1Vg1jGyIS+i7De9/2LQ/QWmbHpKaru8CuhMI3Lpsf/oaM6ZsIEsK3iRvuiQCGEUkSYJNMf8CGHAARgAK4BEgbmkJyKlMC3kRCIyGMhBuUxAYadYaWABsBDiawkSYKttNMAGDICFXikY1fSHt/9wwAG6go1FPs3JvLEv++egGOIrGRFgm00HwgA2gOEJ8RivMgyQ/5wAAQE8BDIANuPG1MBjA6Now4s42b7QONgtXOmb9/1roTF56Rf9vhiNKnD3S8SCDBvenGY3XUP+8mBSek/nzYuvoT/ygAeBB+0tBRBMi6uN+gMgKzAAKG/k8M4Qvv6yxRgmMFU4txq4wBFYZvuLsg+xZL/uMxAuRCXI5LP/+trgXQpyEKf//f2ME+wYWO+vH6q5JYMAqsWQYDBQblaVLddv4FeImDtRE979zUQT3P/f5jI3mHYfCI3yIQiV+Qhzxbf2XAARCrQAHAUMRTRzs7Iv/9CcsUkRvXtBn2tzpVWfgEEPaUQBe81KCKqKLYw74HjBs2UsWjGlQf//fza3M9vdgwwRADUkm8+6vWOhqQ7YtQIk4l/3gFU/eCOwHQ8Qh/2gglIForRz4sHb2QtEAVWfEtb86XOzRg9/9lhSXR/5o/aRwhPidyV9n/hEbgrINS13Hq6vIOSaV1zyPBcaNNsvTHd9+CIwSvlaLOfRf+mHzzR4XC1qmg2UiQsn0m/3zgBMLaV8o2ppaW1rQv/f7aMJVETnEqe5AwZ8YY1McY/Fpa33GPyVkBRfweg2CHizZj7MHbe9///+h5kCXro3u2piuy2oq//v7Ednhql7X/uDFzrd/RwQXnuJGwwjxfMKa/M8eAOpjWzqlt8DAwOYCDi4Qi4SOslIAJlIcZflFocL8mohIDpJPfhP9Z4AmFXSz3kqQwh6CHTtpEW950FpgbX0/32wL6uAAGJNbMGd/9bCFLdp93CWLPVlad3/FDb8ha2f/+7BM5eLLUnf60HLSNcfqtCgDRIpuAfEgghACLVQNvWArEqLgsVAmyiaXC9pj8EDAXh3lRTr4+BocVGNe3Xd//644LvFTY8AhMg1FQy0rMG2UhPSHoH/+G4bDVdN3Vtp//CTDAYKRLGuwsX+6Bc+VNjJ/uvj2gBZbaJdd9Twhgdzn+n58SN4PIFEYpS1mf68idIG40POmA9vFfGw/jjmNr599AVNP4waDACi87e/31hds7BgNtK+QHv2baLBARTAIVSCyTGfrUe4KQFOaZ8KsbLaAIZNxjQ/Gqpm4rv9GGrnC3o3MtuJ//+URgRejJ7FYLVA8pVJk6jhEbABwygCQEe9uX8y7ZDiA4Wo2thlpco31QA4AKIcBShU86Szn/I8vHYH7DaGyPuDpoAEHXApwWT1wVfs3X/upMVLAvIfz3/zUM5R+JKIpCREwyAfCLq4iWVaN/FqhkJTEKKsPtTaAQHvFAmvGSYgwhw7cRBi9xdqdb7KZyW0AMwxzvBD7Ce6siU7FWM+G7y0bX+1BxLEl7RW1YRJe8i68EnH0uqXr+JG209DW9NFgya0taAYnsgL1AYALLwB1coUjTzR6AAdhkFYvyiUMPcWY4NfevqDEvZXP/T4aP5ThHt+PtjlDh7rbBkkY7v0v+7qvBujwAAxXszAxyOrKIrmeaPPA392EXewAonlkp13rcti7outhAkwePy4qJ/+5aHX87/+3rBM8ZXg0THQr4kbX7s/XQWyugqj25xtrUuChavMv9GkUXo2smVqXEAUAxSJwwYr6P1U7Mf/J7DmmAeoLTpoAkEEbWzvR+REf8ARMo2wfIJN/wethmAjDTbhohon++6GHOGDEBmWyvn7IAc6k/0Pf3WIjGYyfLC+dNUgpGRf/yMGw7LaqeK47kHiRvyYmW7qn+boDGHDDgAdBwQPOGI1y+bmLb5AdDAAsN8AGBLEcSXfWZasGL59YkRNQ1hkVkd/9wDFkpdwJQ3FO7z3/3pSCEFrahhwyM7Kw+xG7CCxLbJN8CvyUx3IF1iVpc8Vf1ARSFk54RBBkngAJFABQGQPj+OcwAAicBVheQCZjZ0OJqiUMarxAACARhcDbsr4owYA9gSBwyTDsgROUqy1GNMw+oY3wHUpoADvigTo+nWyk7/fko5np8SFoB1AAN+ADyA0RhHF3P+YACBKBTBasWqnNRI4PDDjcxH9qs23/IXO/Tncf73VkSwz7/rOVXxWJPWTk046+f/4kEGjgAO2kQxpuD6JII/KZLgAWCZTAAwLx+BUTuidP+1REUgpBKrn/4CZowBAdwFdXZHIXv/MIAAQAeCsPHagPa5v/+4TlODomNEYBWmZFnX78UpIIZYWxIflVfv4kLSwAGGQDhJk09xpP+B6YADdEcKiDJGd6f7bMN1FbqSUtasPLEpJ/nvzrYXRTr6X7Qzx/+JBh8M3gAWmYw4tARr14dQOv+ACoAEga7liZO8wY4BEt0II1JJaEkt/vGAIFFNQvh/FHOpiKwJVtI3mss07fSAMjS2azngskkVZu6r+3qytgDw4iefGwIy21V/3/xws/3pjBazBdPam1Hr2sINsa24XTIm9hqfHHpL9+BAYIEgDtZzXTc/oEBetiZOcXVO5rVOAAEwYBmYHTY8bU0ABMAGomBSbSWfsk4InABGHyCg8SWRyw5oWsRJoBADBqB/j0lAnHI0p+wwFND0cSQrF//jgtB9UpnZCrw6ZDHXUPHkCXk91EVKtGK1X42YF6hWD/dstDb4rM6bEEQIqECuLLJLxD9QAHDD0YQqqVye8TAGYBVGT0EBfjaUvIAHhcC020tfYJyQOeTYiMpzqQIhrUcgEJZ7sC8+IXLInf9lA7ATEj4Lay81BYhE2ImRe/deAA1moOrnGev/9IBFinJhsJX89xMwAkTi08EUkRj/4IjlTLwy1QG12elAaezqyRjU/Dl5XWYraqLP8EEbBBPhmgwAAVBAHZOmx40RgNGIm/HZaVrmrXuxAABcFKsHBp0aIwCWOC7ZNIdTaKcITSot3X84i6uc/cxOYlT3eTIjSZIrOv4kbDAFoR+xT5uMwlbmHqgAF7IHTzTuTf+DyA0Ih85kfDwtyAAEDW0AAwIGQ+bbuEcAJFIADAnCJUTugef55hIxAPIC5Ri3c9Achr8sAgPQCHsV6RLCJCxpA4/gwwK/l9EdhF/l0lkcPTrv7rJ2hXpJjfv7i200Z89X+ERsLJyUtHmn4lpI2/gQjJTBL0LL4RtSowuYfGxs0/v9PHAAMEYSgDqaXqVfbDHoAWKBbJoRjqJQd2WaCGVBRjhVI4WtH/3eIeVSKhiiPtxrgwBAgdPuaEY1b9l08rD4pww+D7YENGet5YqM3K74MN2LGrJZrr3+p+CDdW0JLU1ICVb/KhElrHv5Tu9fO2v5WWHk77k9jfoB8SHdK1727f/yMkFEsD/dNgAAYvFcBDsI+LnRz++0CU7ApoZeBd4us97vDIIpA61y6F3XVSwkj4uNhFh8tDJQC91Dx3q9/6/oH5CdTiKJ+u9usUfolgCx3Q6VMU9WziQ/9IdAYmzF0v//hs5//EjYhbAAEA8wAOcX+bgJ1HWm9Nqb2mNuhRNQ9DFq8MAl8O+I0wzW2JftFnAA3H9xjgAXOPyppn/0fFGDqX/vocefPFbvqoQs/nB/1DZYOABUDkGDTxic7vm5jH+AEwkQkawpWeuI7VSgAANQABlzABLo4mnvEF35iKKhz7WU4MJFawbgZROi7zBIPIUhZZb/+gyrks2Rb9KZWLrDr+JD1MYSzCCH6LDAwDRAdg+TMWCEWPr/AAdcGYCmslIwsL7qhU07tSiGv/+YZWjDAM+rfIP+EQr0SDlwdBBKjSlPYUE0dMhV9f9/gCgAXFwLSaTz9onFE5jBYAAQCkxsSEhGF48/3AagguPIVp27GooBoE8GdynXpjBpIOK4MBxoIBRIqrDsyr+LApw4A/8SFYAcsBCgJe9CbwiyyMqn7OZJ7uvwBYijqSgkpLBPllUNIACZVQIvTaG68B+kiERhFZxCnMUGEJs42oRij8r7XftzYrhv8/4TNB1/wx4AEUAAhvFA5Ip6TJVrcIAsDwAA3YDRtTAEAACOkQCkCiNGSTQQiy76K0ntMA40aBKIv7U9Z6+fBElHuGiPw/jMI+EQ10bACIg/PJj0od2e+uwPcL69xheXgfvVKdPsAkCiVPwPh9x/iSVxUdq6AcOZ7mD8OuACWAa0cLPE4wi8Z0K/9wCGchysyKks003/9xIX4gQEazAAuZmAMDkAT1Vgcicf8gSCdSgAwJ2jEmJWQvX++IWX6OT7OIk+hrOhoig9/Ehb/EAqAFBErTTdY9RR0HwDFopUnEIiSkjX/wYfCeFF8DUG/+JGwJhqq+BcDZLpcv7xAPoYgr+1ZQQN1sAFDkD6UkTJPbxjLwGC5gMWDidDMfI2MoHP8CEHDABGNs0SNp/oEGAAmVHD9ptDN8AJVjFFqchlssL6Kg+LErruEoNksnr/uYOQQPPGIzu+bmMf4FAJoOeeS0AFF/72Kkkven3/RBdIfrVPAU59MP3+G7P9AMDH5QlD8m0SI04DUZCfjX6Xn3/4VhgC4awgkwXrrg9ARoTpyHQo3rUnF4AI6zNizE7GbcE0KQanpJehJLfF8AmLAA+rbH9Fm+7/8SGumCPQOIIZsk/tt7vwA4AUNACOGq4+2Vige8MAnXfjlp8MuJOo2p//kwiesSuUr5//CJ4vbHAFs/Sd7/4Rwj4RzrA3wAAAFhJBmoDoDbhg9YBN30e/3xDb/hg9Wk/ddv+cbf/DAc6AgBBDAKxIFBNkbUxU6YEj1PPNhg9cCZvG/qJX3Xz+NwhWIPXgLdob+v8EEABrsIUUtuGHTYxsr8iMRWQVWpISxqcEBAYo8HTr90F9SnfeZgAMMLjGclKHaCatfaIG4YECgE2wM9OJoEfIRpcwDAomtWUfwY+SGHAMMQASEpgAVdJBfK/d0E3Td72i0rZDqFsepxzXiTUBUwAKJDEEp6jlwwK7qtxIbnSgAPASsDySOqzNgnBr+wHBly41RuaRl+4WW3DIwD8Qa7/l4AeSaDdWh7+VpFYf8PQAOYFLAfUDor7xoPATKOpW8bU1ZjQejAItIFBRobUwF4HbQfOHxX1bQZ415QMAHBgjKJPIK3VIast3jATKChTD6EM56RUMcbDR1EfSEqapjDQACkoF9RJWf78NQoApGQ9Njj5i4DgegYHABqQ3j3/hAPwzdN8OAjYmRSnUg3LWjwBlGhRwztcwXXTeYxoYQAHArAeD7CptyJHZkgArwEyk2Su8SNQm/hAEGNoWn+GRo52RaQNJJpXjHowAMGH5xhRUvY9QiyjoZUzCYAlqvvVcC/wgevhI7/r4/CAIMACgFaKCD5mUrPGpC/+YEctH1ggAHaABqGq1Ik/yhr39psiAGBnA7qjQ5C6/4UECAD4rWFYeqeHpNLrBhhl+EAPmFp1npgAP65/zK7/B/4f6Bjs9n3GiJsNs/z+cAAmVUDJs2BuuA/SQiMgiqQQpjlBggMABoLUPRfiII6cM5IRoiXVh9iQp2PE5a+h8fkrXdZw7f//1dWEAx4ADtABuGrYYo/zBr3/vTZEAMBHAR1Rgchcf8DwuAVSwKCbQ2pgPnCoePgDYetEc+38IRQhfhfAAa7CHFLbhZ0yLbK+olZ1oWw2a6O7+gSAjGKJSVNsUswx/u+YsASgo1j8v+rF3DPN/EjfkRiKyCq1JCWNSHzYBf05huJSeSbg0EAA/mgwM4CY8WZtCn/AAGCktB88cvrN/zgJ1FSm/NqZ/tUbpf8BKY2VDiagnlLQwAAUBgH4Omhw0Rg/B+ZyJ4GzgMbpicTcGMGUr7HfIjNd5KXPn4IKDGBcDwBzE5nch0YVj0MBdUgpsTMzab/3iAB/gmMXneIiyi5hjIOCNa4BkS+qv/CWBbd8+BRYYrjTc/H/4iVstVSx0vviRvAAsoQTbOx2pJ0l7+oiAubI6vuNy79+GRBamejkvgAMbEyKU7kG5rUTp5cGljs3xr8nsLMJLM/vmovpefWxAfE1y7vp++8SEBKvfFQnrMF2QZKgK98vcd6DIFiSTN34cHHKNHmxJERhy86///r/EjYcdFKc/40wMOQI4+0UQWWV3xgFZVbBzeqf8sHOLDuV6j//XDSPwQmxR27Khf9+jY/JeAv9XAB8EQirBUsqSuoY8DAeEDciiWgbphVJwEfQgABATqAFmoDx++gSo2upSdnf/RaUCjRN75UaQo10Ll9vM1OyHb5JZ0ZiNBcSH7blSM8BeD9oPiB8V+Wt+Aq0FgKAY+YtxIHoQJYE4Xn/tO56caan+gCrKff/R1ACTKWmJxeIXpJThDAg8fRBIRMv/HD5XyHtoYAYTxJ1/tjuK+dP9j5ePeJBBADwABANBoDlG32Wk/TQvEpIOHfPg8MLDKQpzX3UBIA3AuCL7v3ZwaxZIAcx4W7LjnY2CiK5NRvn/efxM4PFnRTE8cAIWBKdCUceI3MIHXgwDOULioTZvwJS2YreAAS6AEGsIWjM8/Ac//gwzNLK9r7yBDFvl0LHf3bQrlNv+lex/+ypkbdlP79DU3A8GH+JG7rrWWkfv5+KkznBrK83kAaILa/isTbPZxgACAP4JYO2hL5tmxr/4GGAA1+MUQvuOXTAxusBMbFXQGT3QD3MuAAhVknDtRk73668vuAnxXy8VAbH2AAw6xjHBX2ocgyukAwunZIwMaopTpf9CB3foq1++AUJr00XX4gYVjxxfNKu9YO03GuJG/SRCZhGZxSnMR4wN1DhS7yMe56QXMBgz0h0oAKSDZzvEQmZb+AQ6DEEKdhlwwMaKi4bA/rkAwoisZEWCbTTxgAfMwAhohLPV3YpiD9AAcARooIaW1/+IdsW//2Pc9qJlv/82lsewmJE3SWT+4OzSFBtRw8fcE/P9t761BWNv55V//lFNqiAvPrf4kPwQMMAC4yRrXGJ2/9ASyMrqHUVu5dHmTo09q+lgrpItWSn/8SD+OX6iO23cKKk85Ltg0+kUr/9xiLBdu1Of8iNB5sqCk8/JP11DyePR+i//1nGEMIrh4kbqnrH+5Q7iET1jpGW0pBtmL/1XmCLI9T7+6QACwMaEt16mmSyc7723jFEK7jdswLaqCGQAlgAbMAEeY7VngmyJrAVA2PfxF/75DFmOndMBiePbfQus7RQp7x7ntcWByUVyXF8wkpiAcAUW6navBSxk9vCE6AWqS4c7X+AppJ0IRVf+ywySdEWMif+3aQvV2r0qav+n1eaIfjYAgJwykgSYK7h3RLaSPAISi1RIhHUFMOv/+p2t5dr/4xaxVPFvR/t4OAMTHyM5yCPtpTg/EH+QRK8xPoxnyAAFwSDrgGhiF2v48jWxK26dc6caFjAAcSLyQw3yuHX/+82KDbZUJfDoLavlzFLQCH0R6hTHyFiyBx/atGSYrRLn3/4h4HIPV38Wfn/75PIFa6Gb/zgj4FhZj6zd95FORHC08MQAfaGzqY6ECqaxXEAA6DHjnKQ6iqTsc7UfFCEf3uiJPrWRyFkydkyMJkf/j3D7gL2npkMa73ff/KSwfusEX+4GDXyNFUBIvy38z2kywON7k///qwnl5rfvP38/xIf0xwXm4gAA5QACtAaQGjRGAFBVezKcghNrKItgeGbbvuk0e//9BDDgAIQF+RGMJzhEhAm2U96GzqI3EEoaxAlpxAzmgASVRuN3VDEydlc//8cTDsLFpLBjRcUE6XhywOAAmSIw2Q5RnWs1zgABzgAO2AGkBo2pglJ5GIlLVUF4BRHWbS+L4ItOABWELtET7qbJbu7xAdgAUoqEmzIjI9KQhBamoWeMi+ikEAg/M2G7uKu/JS1qfTQnZSC57vWpIYbAo+btWAXE1//iQ/DBjbAAsMAwhJO7eOqlZLGsRaTIwAgO4COqsjULv/gADxmYAwOQBPYKtDkDz/uJAAkBJti5EXUee/gN326pe//dVcDfQMAHBHGUn0Ez0BLBJ1oBxsQHIpTgDB52Ho1MdfXBW9XIUfNrGiD8SNgAPYAaAl5DeEXRbe/9pJDDi/nuLtDsbz/gfIYIwAEIZy2Iskn5eXI55NmL7HKK+Zh4W7JpDqbRjtIAIgIWEzr0jo4iY7aTIwAgFcBHV2RqF3/zwEQeG+uUVYiDDLOAYBrpXih6tRWgeP//uYAAEAQAemEAGhA0RgM5oInek0h79vZoZeiMn96atW0p3rZKi+LU4z/f/Eh+ADmpwv11Jb+MdiixHBmeCcDACQD4NB4pFthBA07vv/wEwDowIOHZwjx0+Nd/7j2fT+lL7AIAL9Cv8o1gz3z13TswdNKLkv5X//7ATJhiiVOQy6YF+FQAWT3ac366hsMYTQerOd/4VqXDscf4kbBALQN1QAAgCeZg5OZ0KX+k3dn/z/AwpNrEqsVra71xRsDA4+7/D//PPQPlDwhgPYz1H3fdIAC0QZH7ZQ6DSCPvAT6qDM4GSw8n9vrAA3TOF6jJFd6OJiDVO5l5cX7d2qL3aV//+1eZse3M///3BI2JaFsXEjfhwCAI/ejj5wwAUnPpHMrs4weLILyuy/J0+8PtOc/t56ikHRACAJgHYWeaYZLZFfrRuK4f/tDIgho1m6r/eBNtdEaJa89/vuctbEvnfUubTLv+frXuQpfIP/UI9JZcSNgp5u/Ti/vBQwAEGJmJJYz/Ry/agEJKvmoFG/5eUhH7/9eIhkXlIi8dxrCA9y4YAggm+8xh/8xL/MIVO/AfoLQOZuw3MAEleoAcGOQlPxNVkhYC6mX6X7evw8rW5uG/k5S0iQdOV/efb/fLGy8//xI2GCDCIYkyVgd4GDcRKC61DliF7+SoPRv6kkvZ//9YWyVCnXXSE46+0KyQ20BIQWlqQj9bhaGYFSVDk0r/q4N0BN9wmllYT1aUZ44wm4KQqkwVLSDhnlvgzXKjadsoaUfmS/v0DshMJCfuP9mk3aGNE+qFP+oIfHunXC4RG+NAJTDPIaSh7P2hPcXh2qtIzA5h163W+oNVa3aWOvyVL/Zoc9z06DQruSf/9Y9yUbWLsn/8k76obEGMskNtYMEMTOuVp0pc0B1j80qvOLA7AEdtMrW5oTLMsHOZfSR7uaQA5Q/J7Xb//qWGYfau4fufoWSImsnLIzR40YtxgNdC8SN49mGt7qvvj6ncf2gwMHq5FJ4sVP9nPZVLEUVqag/98/GA1xwOJZlSmE8IJLtoDyl/+2hkVSD4glDVK4YBeCntRhvAMDdSjzghscpBEG1MAIYZGPEpKXvzH7o+8Nwnlbrrn0KQeSeYAKg0h0lip5l//vpkoCVIluSP/8YMYLs5Dh95bS2wdou/j4kP6jbpSb/+1h+NEN5ameJamlkjeDVBpbz/70XEWFOLw3BVdFxx9N0byoDZtpR620jiWx3Mzlv//gAdA8MHnDE51dO1Gt9wD0xEbJRrCJuJ7v49oUKCdc7Ud+B0JJhDxdZK5xOOiMu3Tp6etPo+JDEBSAnjdTmlDK6Qjwq4ECwJmKvVK9N23/AWBLhU4ideUN418AA70ETjrvisa1QPpGrKmCWHxYS3/w2Cwy8eALgQUZaLI/rA22KzVuiZuPG3iRsHuLseEO2ACAY6FWUMbtuF303GrEEW5DAKpIFBVobUx8iHQ7cVowAiCgc2CdAjKLiKpr/oYTIIxFcH2puPDZ02DUHUWS5/2gACKh3AAEAUAUlmJS5WH/eBIBSA1cOitrDzdPQRAU+FrToLqZ1zsGID8gfu0mkZo5sag7GSq/KBqqPv/3GSPmA7+5+L8CR+OzLAg8hgFYsCgm0Nqawi1nEhaADoHQfOHxX1bR4A4AJRtDEnEcoMkoonQ5BAYitZ6bwR97+BEBj0K/Upj5HBnx7/BkKADM85OaLw+mKovPstYRT/xWJDUPSW/lg0Lia/8IhmADscbHfCJeRSi3h+SDouQXaHW2THBr9U40VvCIV8aMgBgI8CdQUYHYHn/cNgBKGqmrk/yxj38GHoGMgNqp4nG+nlzT/zLKkB5nPgPyWZ6CRVwDrcARviSXD/cuPHQv/+JD30hEltZMfrPDXpilP1aek4ZJqpgf9Aw0i1YAFQOQYEnDEZ5fNzGP9wCEbzUZN0Jg201/tIgUZgJaR1Vu5e8ZYAMFydzHqZtuCRatoNR96pyKz9/YYstJzn/rwRnqhaMq///qMg10PJXhEbBWBOEf47aqX89fnIaSOh7/+egReFHvo695PiXu9wAxiqx/mrc6Vks3MACRM53H1c5Vf//wF4owvY71DUR04o9bDwm0TCI70a/2gDB54Ow9BGqorC6/5wgXHVftSbzVYZ/WUFepFdnb78H7ghgEX4GBJobUy40bKPoYpTvg4KiQvsun+0cQbKF+5v2SzRSZn1zBn/EjfDoYgpTcMuGhjRU4AoKstRR1GxIm73B6MMPVUNp7k2K7ed2u77sBgfIdYJKC7Z7WUv+DADUAxxFYyIsE2Gl3xAQURWMyDJNplowwTcwfL/5NT495GLi5ZFJdraLd7NecVZrb8WmumiHpmmeLMSMZNAkw5Do1OZn7vDW4fKIDeynt/ZAq1/n/n9AnsX7Xpb/x1GeWVH9BydcGC5GgzPxI2oBUAKg8C8g2mudjAHxPpurI1T2k81hp1g8oAGZkRGDF1DMWvviAJkDBrD6EMY0TUL6362Jk5RfQ7mtRZYAAgIAgFdlv1DJ0f/aeYA3Px0Fg++E/+8wAAVBgGbOmx40RuGhsvILyieaxAHpuCHKyn81v3624hlZniz9o9NxWinBcnP0MGSqB++vCI2wPaPGvsDW5IzB1jWf++mBLRvALvSMRNQ+/93kYAsC6Cpo5ikEnnSDREU6XTdf0bYUlD/8HsMU7WjdvpIxze2x+/rh+D3Gjk00hv2xLgwYHFSj3G+U5AAEAi0AAQAAB0Rz/z+MJzMg6hRha24tDJ5qBdBevavo/9MXijBebM/ccn/JE65YLtuxeN9DDxlbQKgJtm5PYABgSkD8L61dVAwL2qvWOiVb4Q23QY3wAGyZtELcvbX6ZCdFMdCjetidFsVzp0dK7//wyBGCBQjpYnUROn//ziIQsIYTr095b/7zEnCvUcznj/pe+BlbIqDea6q5HGOtF+UH38kfvPqCSCpWmYq2w/5h/wxP8+N8APALmA0BJOt+ocCRy1fg6QY4EAsBAHH83mU0n//2BiAAfCELn5H/faYT7HEvyPc9JpwBY7OLZbiOf/9dskxq6oaun/4OOFj0ofPAKCO2z5EVv/3xltiXYCteWe+O2p0f83pycfP+9qIngE02mX/9o8Ff0RMHxIIIyAC9GCY+BvzgiBzEchqxEP9/6/LUAHwtzjsOZSRKaiicgABSBzIyAWHHrd83MBDUIRkTz0rYt85/uAEPYr0iUdfJYMeOFD1GU2i/ns2WYL0uyf/xPUHM6FbDrdDddwplxJ6mriQtAFhMcLhKzEPYcPywDD4YGaAKLbpeKDvmnOD0AQ0ifUJ58SuYRNv7wYNFlkR9LUSLIHGAyKXvvVlFr0v4kGHz9DsSBAGA7KbMIem0REj/v7VZt9Hn6/COX/EhzIbAAtMzAGByAJ6qsOQOv+cJABIGm2Jk5JQx7+E6YsyjTNdfjviUsAUvZ3Ir7+/56wBIJuakPz//z+iEYx/xfrk+GOgzKwFPCsoADXnOAAwFqwAwE6zGqZ1zZrQAw8Mvz3JouTDv3a8Ss83ZWL/+cEiltWSEpFfl6gAX5NBRo6Cv+/zIg/dB/CIV+YALCYFJMp46yRigc80LC7RV+6myW4MNgAAsCm0Dg24NEblDOiB7Q612U7vDEWu1rberOyJpU5fzedtbn6/8SFYeSFJQfPGL6u9vkCAHRjZcUzkH5TecBF9qV75tTbQfsBd8bBXd3MAAFAQB9jpocNEbyRCZEMZGGQpiOjYk95t53tYRCGu87e/6x+Yf+H/8AxmetNRQhttp//cBgDpgAgOMwnh83IY3wFIAA97gKtCzM/+9AOWWOw/vkEWTybJ+tgGM71piMOHurP/7vgQB2iBx4zKeHzdBj/BjRCAMdc7av6DBGKzQs96f/3glo7Jk0+DTVfD9FxPiQ90gDD/+AA+QAGOiNYWPtdSLn/AAJgA8JoYq2ljzJKCB3xAA+PYamwpvzBKCJ0MMK3T4nu5rkDRhuhBtT/ifCJ6+AGjep8+aLcx3vwiGZEtDxbq9WNlxTv/P+v/EhmAB4MWSkyeUkvxzz/9ngDQAaB7umKg5BQ98NRzq/Pw5Q//xPhE/uA6kMtV+EcSevQNAHJHgj/4k9UEPn/8/n8651z+dYGqAAAWJUGaoOgNuGD/mBimWq8aKrfDB/RqbLVfUFVsp4QNwALBBXoIVs3pZhhv/oBc5BlbVYm69wh4Q8IXhgOWBQAHXBiC1+Ru4aGd1T20YnURtcShrFFsBZ0hv6gOUqSr9vjcIHr/GE9YQ+C+VQMxLAegUBGMrP3+wJPE5UcELri5I/aLYgA9ST3RuX/xIY8ABMAHxODF2EL9XdiqIMBeIAGguBqrKGOrEUjn/9zA5Bg84YnW75uYx/g87wBmp7Fge/wxsXAIRvNREzQmTLTX+vi+v4/+4YPwFArlgA4JdzBh1JZ7/aMhK9RPoXt8DzvaiuwCvmRi8czjY72z8F8CcADRFcIizIG78d6s3xTcASmYnQVWoJQxauHIMQUpmF3DQxooDR7+AAPqB7I9t6kEBKdo9scF2y651NgpwWbY6C+FruUjA9YQlv+GMACwQtEpg4hVFpHkP3DQHg0GCBOAK5AAHGxRg8P4PP+8AOaGzqQ7EH5bEKhTZmyvBObhEiPT1Cvt+5fgAp34FK5F37/8EHAARIMiuUzOoVxrHBh9BKYA4GqzhdAy4kYYBWABEAwWwvalrRd83ubDBrrBdO9k1H3wfmAS8MGMOejrOiapcMTi0g0FLIyHdIPTPZ6pn+N8ABjYiJznUgTltRuAAFQYB2YHTY4bUwF3aORoyT3QAcHIESghNtf9SX98UCaAQtCf0JY8RuW8bfzIexw28HyAhpE+gVzx7JJM//gZHSkAHacTJ9oF6SNNii+/97IoMvt/+z9/CALPGA60BjgAWniddtevhjwAEQPcoR7OvErxqIAW8u3z37/Ig6MFieMM1eS3rBZB+JbSf3gIKwHgAexWKnn3Ivvf4bgSFw6EwhxbP1JG7/BsAntONBs98KFiaKHmZGE7iLziUNYpfRA4pxFGb//+v+sMBjAAsMZntTVUIk22x/H5QAEqowX6NsVrsBsAxAQeMwnh03QYd7gtJgNAi5axORufHAhuEwA3SODamCEiGwIAZw38wIWv3uGkgCXgWkV3XE0fCAvgDmho6kOQw+LcrhODEFq6jlwwL7qFgL20YnUx0YKhrFBi8QGPAAdhqM7OYkTvu7Lf3gILp0LhoqbKpB6weAATBgHZgdNjxtTAcx5gNUnP0ABTnrSmOpqvLHvym/+7/iQXwAEQddDOoiHk0wx/IHhgRYx6NcOanHvNCwu0RaXY3S3MAAFgU2gcG3RojYA5kMjqYXkE81igZAT1oXABesjAXvHrB/QAKTH+bywDPE0Q/N/EjfAGC+jTWlbYZIhCn8H5IOj5RNodb5KIGqjS/0AQ1CP0K36TsY+cf3ACHsR6hSOESVjCBx/hAD6WihWUK4eoZ7YMACoCGo4nAvKJPBj5z/AnxgA0EsKTbS0gyU8b//gs3MG2/s9QQmMqgW0SJCd/juByR8JUVV//v/Ehv6Ah5EIUKR0iSsYQOFkRdADAprB7LRDkFlDv3+8OUihBDyNsuFBi5YFJ+AEVJy/3/8WM1C+ks36/40xopVqOqb/pX6+n+7GI5UMJ2HxI37RmJ2FVvEqc1FjGKQUOyWeLOOG7QfhgOSSEkzIyIgzACATb8l+8Gv7pfADwQKQuTFolVFDW2/rHCVwoqSLzjf1AF00gABAGABxEKqvsMkP8GLm0dyRdj9/fIxkK6TP3/evBRiTSLtGo2uqHU//S/xIII0WIAPsALhqyVrk/zRj1AbMxeM3/cABAwyMeJSUvnmEbo80AMXMS4kD0CmBOF9/zQykUns+Njr/64BCP5vRM0Jku0x/k6Lfy6MAG7IofqOsZ3p5Fj5GcVDidWYRFZjse5/vYUTw62sf/6KZG5Xgk3vXoEUmTyuO/NAg/NxQHxI37hQXaKtLsbJrmAACwKbQODbg0RvbQ2WmOjD81igwNFw8oSniD0uM39HHSo+v+As2Q0FRfFqc9ScapQib4AmAfoCOMJ2mip0n0w2ytm/vDD0wEjgUkIovBgjNr6AAcAijyo8clGyS6bb3/uNncETEAyHCEPg3GUYQRPkubvNTS2Q5P0r//vDKDWzf///3wilKumJX//RESqT1xI3utmaFuu3506v15+wwBI+7hGqRqEpQSzGtYixTclv/AePzjpabby3ntAqbgDgsjuHCvmnPcoy6HPYgVx0Z6NbEA4SvSMeNoMMcgKudZdfTfDn0oTtMuVzgndxMs/o+SDCf/6Hn40gX7/m4AiDNFu7UWU6nwG7XeYqaG3mw7ThNKIij//Rjjy6Ku9dUxHxCSVp7/Doizx0HbiQx8DCoxw1f1t/97X+h94gMcRWdCLBVpp5gA6JwYqsln7L8UxKwIYXACeTnyaR68rDqnD/uMNvWN+PUUIm9ZIkR//sNCSw0eE68Hd5/iRtA3ocR+vZX5osWPgPbrtPAaGM72/FCKNutP/gBufYDvdrR5u0FHkdzl3IRL5x5zPO95O3mb7+1qwVzCpZMM2/f1WkviFe/+gQADOHMq9rORG8od4JElQRrhMPsVM//5AiFvy6++e72JQWLS3K33+t+gay2j5/7uU0Q60zFxI3+2PreX09/UCUYPKWo1KhEbhBJByhd/WE/vsVECgfQwhBee9ZRT3niiRAWCOhTOK52B1wCXs34HBqVxaAbsekT4tqREZv43++p2JVK1TO/SA8hZLA4X+r1odd/EBqgQKfJ3nJ6NL/+dMrc6eEVIFXzxMVbrCECYN2tBEXAcnytxO/IFoftltJhyElYn//zCNA7OSu81/4dK2pWViKX68PwwwEKSIiFEZEbAlwAicOB4ZQRRw0nn9E4EAtINO5xJ4TJZlD14YWaSNZVtKyCPlEEBww9B/hyFjZj8H/b79HtaJI4hJX5PMzi3/3ogrfvwxGggJggQIImAMCD6wiRKGmyEwTtipfnAG2fQHy0BszTErFrFZ5k8MXjddBrFqEsfaD/VQ2wgVkM//XA2I0N4ay2f91n8ZXgfj/I0MMaK2LiRvoCHdz0XVCYMNtfz/MJiACgS/e24EyGhDBh/OLgDhI4pJoxCWzJQ64UTQOz8AHMAesCkFG4X65k2ue96GR1EXSCUNYoFIzlrvu/3lqw+deqvMZczhYucudNfnHKip33Y4OMeFd+DCNqA94ACYsilRDlCO1ZrmAADlAAdoDSA0aIwSk9E3fXzp0U6DEIA1m0visSf2As9Df1AplQ39f4nxIJYIYADXsZwIauUjTAtqoh+khMyCKriEMYj3MbLjmVh+UtAYevEh/4AiBLUeEo23BRlJxxMYvWh+AB4JnIADAnSJUTugef4BIMWyk2JQzFXLj37wACAf6QAICXI4gy6oy9gDPwyZPISWkY8//Z4I/wBn4MJ59DJhc29P0l+LQ7PIQR35vefBgjqzSRhcAJbCuJksdCwIOTxAn98nEgggAIhgmD5lIt5ysOMPNOIjMAICvB/oJsjcTv/2KBWU5iqlb97rziWCdBaX3/74AoBPg4aw4hHOPkVTHiAX4oxhmdMbT2kl0g/EGcRiEllpYI8qmg4AIZ55Bw1Y2phgt8DlNBu+6Ip/wcErNac3zXzZ//jjoJvq/HYdsrY4kP5dy50P+/xoXIIDbew/jozARsYolTULtmhvZZvRlOB1wabdqoU8Qwm4LGsZdL54EYAS+GFXxemOJwkxa00u3f3G6TJ9NizPYNWxLLn/79wIAsBLXq1/Ejf+BJ+O/zQe03dz31nv0a5+f4QVTqcfv7w9FjCsOZCQlVRj6BCBqQgDJ0Cw5A7P3+AR7nbgE6MIqiLpBKmqRyyMkYuolxvvqAA2ZkD/ZlDtcDVCDjyRqv9z+ru7r15TjYrOzxPnObGkIsfuc3qa4kbGKABwHSbVQvv/P67oPAAQGQrMhcpi90Vg9oPoIhpsuKe4Ggyc9N0wALPNeWcz7H/hMtmvDc4damELasUookhg4jMiH85We/gK2UzF2ix+/Mf0V3nQnEQ1+0CoFS19Np/3wxHYkKN8SN+AEShDpBtWTwtJr+D8JcEncJXUeYo04EQftw2dRFxj1LYoMAfgZGjEC3qSP9vRykOU9au8XRio6Y8OjGxxEf39MEh3CJNpZYp7qgeiUQwMD269JKMP/6A3ABwN/dSdm6fvQH7cdxzrWt/iwDPAlAxqtcI91BVUK9Xl98xStBkVp5u0viQQQDzKHPf+g7nk2iyz2JdqwXQYADgEQDiZd2st1JDaNEAUDj81Rqa9+94F00FkQ4AmkdfWwiWQxDcatd5/iRvzMhsqmOhB0LV2pDa25ezzf3LFUOpB8WQlu7t/kb//BhoAhwAEQbkEV5JPsMcSSy+DTX1732BdHAB5DgB2JAoKtE/TRWr3D3putQ4d75K2v/metL+JG9xPwCt3d83vwChBY3XWR157SVf/3BhjM/ECAgEgIWjyaDI6QJ1LJHdAEJYv0iefELlvm38A++6A/qYCA3Edyyy0uGa+v5h4twD9c4FHitHxzwhdRsdLXm0v//MMDqDCVwukFAHJmWatff3/xI3/gwTIWLSQvnSH8/5D8YALDYGJMp4+2Tige1AUGDjpiNcOmpi3eTz2uD+dEAxxFZ0JsE2mnwC+R+PToxvFG9C1rdrv+1hX9myupu9/AKCEgVbDWsReo0g9uFwYglXEcuGBndU4ABQK8X+6m/FueRO/2ng25MEgKg17n9CEMMAxB6HLrP30C4x1XKX9vQ6mIWMFjKy3/6QvFCusev/ceHNQlOHGJ8SNv9/gP99wPwBxV+ZnuFwQFuGB+ByiWvCYZ5BvECd+8A+WHYDMC5L4UMSIcDB3PETsnjmlXtq/zjGun3iwwJi8l1balPwOzIyHvDbvvqMKo/Yq2mSo66B8SNlgABPzODDgAXIYglXU8uGhndYgS/Az51EQJI4DloC27Xr4QuYZ4DKE2iGhNJTLLHWSxhTTGyskCUHSYQ1f3maMJ3MLXFoa5XMDgoJOGYSpdw3QZwVM7okoYngDZft6oV/vQhwVIdb9n/D/ATkYTqIvEPU1iAa5wAGiIwVOmQM1yD0CGZzEVFn2JZZ/nwAHYODZSFFk/60O/hr3sCHoSjIpHSBO5ZA3lv568b+gEQU3E367f4b8EWj9KFEE960kfwfICEsT6hXPiFy3zv+DlwUtVxzvPv8ViQ1GqfWANRJTzj5/w9x98SF512KYYYZitgAFgmUgAMCcIwKidkDx/tjTu/1fuDZlxZhNvl/+gH9vkNqeF8PeZOnP3+JDv+kTHHfMhQ/wS0up8mu1F6lPjFzmm4GBB/CITEuozkgrODBkdEfIfiKlD55Ke6OilPXz/iQYfGOxXVdk3jYvBWDpn2ABczMAYHcBO1WByB1/wBUgAWBLuWLEXUce/8ByvMAbXSrYe/7hhWFSWuf/wwcm2PTNf3/L/4kEEBTIdRLSiaJpjWfgQMMxYABHBH6OLiNIUW12iADcG5RNaOi62Q72kACdUYKmjbGa6bPgyDM8J6op9/hAABMCAOudNjxojAJ0NvzHQw/LYhwIuOWvPNqbIBSAm+Mgtu/bqsNrw/36VahX+P3FDTDrKmGSv/94akQMg8n6IE0PBCwbre14kMQyiD0BgAzMJtzi6gjmtQAA40uAAYehulC5u0xDcAxZKXMHkLkvxj3/sKIZswzV3MP//rpA+c5xiGYVjzf8BzGy2l/Dv+3oP6WSWr+/e9P+1nq0dCN2iqq+8jTw9sOJBh0PcNDxl6o4BdYSs+fw7Uc/M+J/3O2/tnwZUsfr/xI2i9h6vwAgAE4JwHyjfPTZD4hrxkiiS20LcnAMGGjDAzXY+xoU5CAMY6Jll0h9ugx4TIMys8Kj+WAGFXUicVTn60pzgABUEK2AaGHJtbe2FBLsqEvpkFvAtnM9uUi+/reshW+bft+oD/Zb71FARNFOi//1/iRsEOj9uOkobixUpa29sAOsFZSBUlFJJC3PQP8IgAVPMMVEWcD5XTeB7lD1bid/5/MyDIqkF5BPLUgtG7QnAU1AW3bNfHvCGMfmsfa7AE6lABgXv5MQuhe/54AB8fRULkil/ao+iI/FIoSRGRkT0XxTA57JSOLC+6qpununb+6Yalty/iVVfvggblbFivjx3Dc97Rzjbae/esyJKZDO9f5ThDpmqmIOCHZEQ4OfEjczXd17uBvwAIdWz0Kf4AIDBVK2DGUJ+vYp/+BDwQyUKSMuVeMvEm+r6HtOAAEwYB2YHzo4bU3BqgIm+N5ATS1ELnEH/iSK/T//2iYW2AidCIpZ6+rj0b2/9XW6Jv9LO+Z3r1u79wCYVUknBWZmXyjTf+ExYDE9st/TwX2BLvLP3VW1wp8L/+3t3GWDsdf92/xI2MBCMWADUsMUWtqF3TAzsskOPsaFOTANAId4is/zZW7Mg3vnx/zfV+gABAMpRIBc67gmdLKj2lDHaTFKQSg46ay5VRQSYDWP8f/cQgIR028sfe6UHP+0AEcoB7QyaAqlbjPbzAB4TQxNlTHGyUEDsr0VUPjqw+CA++HorIVssUomZwMYGBys6pIHLbzPMZFR339cU+OQN//19im0NbHs9v/8SFoYGUmR4B4AlC0eX8AInoPNoQMlb+aGzXIuQArUD4XCU5NkKPWQasNjTdIKe5xsyAEBnAT2KzI1A7/7wwwEtUKuNm+Ap7cDcv/aBVdd/8SFYfixE7kO7cVhS2Qa5AAsDHj26x79Mlc1wYIUUiC4dtSXLPfXSmzHa6t968QtcobTKgUmJY/iTxTaH2yYul//51++ff+Xxo3FF/Enr7ALia/+JCsuAMIANexiiF9xy6YFt1mCD9REEzCKziEMcoMvA7/YAZpY6wun/DEQX8XiSfBCEQKQNwVeMPvG7X+EQQ+Dd74Y0EBXCxYl8GH7xIbgCAACoIA7MDp0cNqYAc0Mj8h2IF5bkB4TsIteebU2oFJIDakZBbeUu5fWAIV4E4ybvP+HeP8SN5Ta5GA7EgUFWhtTABoH5ATUD4rbxpwJkGUrONqYZv0AxrFeqThn5Cxn5wBEiEmIZGE5SuDAQyE7KY6FGS1SWAACoOA7Jw6PmiMH72//tuC+BxtZxFOaHXyiHtaNPBxTjImrQaRnqA/xIZ+wGPQhGpSGESODKBwMYlF9zOn7m9B+xtVzV4kK4ACYsndEOUZ2rNd4mOm3Cxz7UU//+YAAOUAArQGkBo0RgEF35Ec5Bn2sxzAABcEM0Hhp2aI3vFDfhIS+mQa9eBjsTIdBTbz/DUbK/iQxgAdqZkWk2v+4ABsQb+MJySdY5bgT4ZPo02pgB2jCVTHYg/LYoPYBSQG1YyDG868bB/wEKLP3+f/CIagSQkjKy8QzdSKjH73AGBnNGr81ikXm3XP/wGxCHKF0gVeMOvNdZmMYoVUo4YcIG7QBCj+4VycEB4txIjTgRaUG6//xIVlgDvwlMR7l6UOgwkgMOcr9+v98P1UZDhnf/P/b8Af8SGuKE1VExV/f3+AihvJcy4nq//6oMq40wShiwBUlQNzv/Ek8dFfxJM+sL8LQAG5GEqjLxBKmsUHzgAGyIgf7MoZzkHoCGZzEVGiZsts/z/qEjrSx+sxSl5//xPiT1/DZbXG4k9b7jf/P3iT1l/G+EDhW+DOCM+vr4HGAAAYQ0GawOgKmGPDEL4Q+esAY+7q/7f/+epg1Vf2///hgOQAGMxM3OXsMhrUe+02RyHnRNkAFvKHR7xF8X/g1waRiaAStqPTefwx4YPXgQ9Y4cv8MHryHxnL/wh4Q8MBzgAsEikAAgLwiVEbnn//cAIMWTE3BpC5kvRxAIUnkErR9/4Np7n64COnJZGa9YQi8IViD14DVJz9f4YgAWDXhw+wjPBfwRQOn+AGQAWBL2VJkRdJx4CSwVzVkLJRjiV/WgguCod1ya0yLLG4OAqsYotbksulhfRUDCrbYGAQexIbs5+v/30vYoyNsZMn14RC8ABshuuIZCj+pSWAACgOA+xw4OmiNUgUB9QOX7h9Pc9MXrFjOiT/+tVzyBswfhWm6KoGBaxRQGDIH6YAUYyBU+rd4s42Vw0YzIpfwiH4AxGIqIUTUu9S0h89m2NfyqqqBAMNRwNTwQcgICAGQV129/Up1a0r6poxAkonIfmFjL45G/z/xI3HxwAAJmhkVTHQgVDWIDPiDAYBDACBWI5pPEunoD/SE1phJkrnXJuBX09xq2AQ2JmUVeoIQ9qgAhp7SbZGlB6NuYjZgIpxxnwFBB0STd9bK/v4gvh3rJu7U3yZBTzUKm/8/4kPwBkhM2IJyHcxiAw0BwAEKHCW1p2LsawRWaAuB+QGtA2K27a5KQtETMRGn/8DAg/e44JGTF6ZWe28wBnKHWIR/XapwezXCTT8dhOWkxx+Qyn5yX/tQIaM0yV04RGwAHDHdrE3EWIiw23/B6QAEyqgb7PobrR0UAC0DDt0BRfrfhH5OcPAAIBUWOJW42CogZl0P0iIJmEVXEIY5HoXQWfoq26p+MBgftGYQqjWWoWkwqlyQMPe0Ml/kG56+D7qgEMIpIgwQaY/4Eg8MwAVOdDf9hJkaMmxHITDlqZz50IrkSOv8u0jX42AKA2QFC2SKcN46SWMB6AhH83quhMG2mP5/AAc/woXo7uMU3B6FsAjgAboiheoyxm+wIB+ZmYbuKnUkpe3z4n4gANptoWiv2T2RwEkKA+nGPMvTIRScReJcl7k8LwjgU1UoGmRfdWDIdZFXx9/s4C5yfuIu8f4/5/36lzy4yN/3r/C38LAmGXcsTJ3mDHg2AADaAAQMURGz35gaBOhgAUE7+UE7oXn+Jpgf6QNE+HA+fuCUaXNuyPMCSok+83H/EjYAFoABIqsG/TYF84B4hAEaoDQo1NqYBaQARDYxRAK5dqH/nATqKte+bU3wMj8nC+82XlvAFCjuAYCyN6YiUJaEXtMbLjiegnlNR5gACABWARoG1njqBdxI4Gnu7mCDt/E5MyW32D+mpp7f+4RXZAEiImtVf4YXqx9wVU7JmS7VkOzVJMbe+8ySegbRI+IDfZFAUFD2gDhxKFuPptvf+4CEbzeqZwTBlpj/ACv+DMNbpr++/6xAXgAWwANk6husyhu+AGSRUWhaDJMo6v4BKMwnYdm8ShjVcOQYghTcMuGBjRULCQDIAcfCznrEdwQAAdgABGAOfGzRGDvbAAOh1Fs4lQf4JcPn8WF5oXppfwgGP4AFQOYYPOGJ1u+ZmMf70CEfz+icEwbaY/ngCvxVWeSA7ofi8QGPAATAD4nBibCWUWScET34QHnXD2StKVNM5gMQAAE6DAMzA6bHEdTBKRo0aAOyj5xgDqsrG2qvVaNE9gUXz0yIdRSdRfDGAB4EzkABgXhEqI3QPP8ATkGy8x2IF57kcTIwBAdwO3FNcahd/8AoMeSkyJS3Gad3Hv3psTbnO5hkNajhQA0D3sKUcgoa//7ZBy0ExI2Cmrvuga92M84qJr3Jve0CJTHHDlXD4zl/4Y+E3emEslDmrSQ5uvQEawtD07dSK//74MA/QO40niqa3yPTHww41cFwTp6JHtyq+5/5gtHCgibttL/vH2deff1apog+X6/wQQALBFtAChxCFOPpsvX+sk9MgHhWKPzADtEWyCqmjO7876fzMMABMWZSsxyjOt5ZAAS0AGoJVw5Am6Trn/vByk4wppPHXCwtgqfLdgf74PwGQaW43OmRslGlfIAA+wDcxr75wWNWr9MFAo8xyrLIwzg4oIDfZHBrXnz9A9YvkZz31QJg1+2y61fhDTq5z/dU5opxMzR42HClmvS1//PIOpAP8ABwEI62amU6r1KZ/i7A4BhgRMtd8ABAAnQ4DT5N6aKuvs4fUj2tPBOak6F+//PItoEIIlGBBgow4GNgrIUmvMkO7XkkfsdNBS6za/7+Kf1jm19/b/xI2Dd2JWKx2/XvJITMhDIQblMUGGH4aQxloKAHqAQvTKUo/j//7gKaOmR0qdf0//vCG6jAth9CGtaIqF4xqr/7fBBCaXFHC82I450Rmqzapvx5GhFZxF55C2sX4NylHb7TfaNTRT+Ed5wAldX8njr5wnwPXn/47ToF//Bb/fPoFIpLZYiv3lKkVLwWfBB3BpbE1wil2jnf+ABvSmZtBIV2vA18cR+vePFTWbj3kMhVEXSHqa5HkYqLVmUlmvgt3pYDmgi2pcgxxgwFhek9JcY4DJSWn/frlGGxspZdpnQ2i9/HQlroheN0MGFAASY2ZFOdyDIWtAfQYfijA7s5ousrFO/cB8NtQ1EhlYzEfuADAzYOwv1JakxYj+gzvrP6e/XuQMvnYEuoEjFRNY2GzDp69T41LRGIMsTmWCjD7LQHjrQRK0WM0A5QiVOb8Wkv9mG/b6zmO/a4//79QmCJsXEjYYANFlFj7IpuONkiNgEMOAA1oxFcRdcSp7kASsGSwHUUjykl72noCNAdZSUlYX+OCwABADAAy7APFj5+euwGFG3lMiqXdVYVV5rO7bkA6ApnCFb5ggamc0GKRWj+3cBjZpKWsp9HGwj4J68gMTe2X137zdrfX8RaEjqt7Wew1SNEvvuqRWPER4n42ALBHBTJzU8YWac/fWgTcOP+YtFEkOxMn/B8ICYSsvoXQuK6Ob+AnAAnXqERhtjd9DxeZt5u/pS+DIN7LOTp44f7/8AWDbX6ssISz/ODAzxrde+sg3IS9UfQ/738QAAgFE5hAaonn9TrCZoJj/buCW1GeO/Ab7OKZogt3rZ1E7+379f6eQtYfwT0MkUEHFqPBBCXj55pAUhgGA9yszLXzX+fQDJ88VAB4AJoGNDa7bwcTNfrFGQnmKi7NkFp1bD/h/AKggegphTcKimXETb962QTKcW0EKetHPHPik+jZWuiCIxBK52OIR+DodSAXob/rwkphZ9+rATUWFVE1G0esRDo91F7N/9/gTqqyvAXEjeuYvUfIXIz/94AyGAhO/KoYC+yofwZ4P2upS9baah7ws411b/8HARC5kwS/bbJLaDWIA74AAgV6D4zi+f/56AAA/wADKgBLMB5NAfB+Y6ilfiIc6VFMDDhkt4sTB3sQs2v/ten0f5/8QGIAFhDP5vVNH0LYY/gCjAJaRiiv8wPtrQHP/CF9OH//IGAuHsxhjhk5vEjjBL/RoBeSoHD13+K1HYlQCFUwW0qD//9kM7o0DOBjkcZuOICD9xDRUkWYr7FW3/QYzRxrxvgARkgEFF1hQg0TbaB2HqZWcre/qYAAMAptA4NuDRG4+QBhRE4wfYJsNAYC4HxNAZ7AdJqkEcZ/AKiGO08cpLpsgfaLJVrlC6/++huCblDaf/Jqeng8AAMA/wO4YoYhB8u///fgBEh6YjbqrVJmIe5qZiek4TsKmUS/f1dozwu6wyIjo6KNiLwYQEQ6LlE2h1tkpwYfAATFk5WQ5RnastzgABzgAO2AGkBo2pglJwh/Tllc0VhghAWRuSPn43EhjgAdBwQPPGozu+bmMb4BQQjef2TdCZMtMf7DAAsAxvQYNcrbL6DrXvhLV/wAL7Um6RlgzFY+iA9/iQxwFiDoE8ejpJBQRlVbAYD1BRw04K54wPn//MBYAHheC020sfaJoHv/4MS1P+Mm2yRAyt67Of4kEHoECcBVls9sABIasQiirtBCmtQwfAghUKwa3S5PKXhD9wphji1NSy2aF9FThjDJdbttbu4s39pMSqWKCQPaR9/28iCERe2xCtW21hbeNggDatoKqx9GA4EKI7FZ99/3+JG9EaNo6A0WEOGMEJLKHytMTRcJ+jU8xmiuX2lgXkREEyCKxDkMcjhoNCoQPWa1Yxb/gxkMDMv8f3tma3PPL38q+v7dMKITGy92ReTn3hT48bSSf6/DqNxn+qkWrhI3/3za696w5YT/Wcv+6V3HJp+6ooQHHCHQHxI2G0Ok55bXkunk+wx8MQ2npr5/glwZhOmmylHcAB0BiKWqGJ8viTKDAEnQLe5bi3VS0NvCZ+Uo/f7wAPFVq5ck3t/pN0fExHf360JbleLyEz/+wjZBLoqIzt7jpg8NJ5z3uy2hOvmn1ZDszbVVn/t0hnmgHIzffWAxgpIBq53iRtfsj9h+eM517dCo9vNxtyKX0ggYPgmKUsirjUZKf/Ai0Bi02H/omZeC8P/c9JJtG/qgAeGHJiVavzB1WG+gBQIhhiEGFc44gpyvILsK4auhXbRwZ1VcAJHxQOLYhNskRYa/8G0NYylKX1himB1v7dLFv7/hbOYsmf3/n/EhjL3HYuOP8wVdfyn65INmQmjaMJUNNZ+lY34EUBu1sk/dASAFAPablTrMceX++9l+TxW7Ol8wwEYBqNckwswc0/bBiUIeg+CGmkBM6qy/7vBRYHxoicRn33MbCJyZ+ERsATVk2b5VVdtQFz3iLpSc989lmdw69H9TX/fvEMgM9JDVkJeUI+lYJd+nVUrH/v6vAuhYz69Bvdf1JEcs//jJ9ioG0UtJ2hDDARN931AqUKSpVw6v6iyilQcfOBB+H+gZDk8J76Ss/7TMCSB0Qrb6HP/+yRBcsylv26SaIqZz6sG0Tq2zByEL/G/QLD5vy8t6NQhjqqfgebm+7nG1N9RsAgUXKUSRA+6SDGAwfMyMTuIvFEqaxQfpkZkaFUL6WcbOdCMwG5xzv+8CCd6hSzGc9uhf/8NOgyH+7K///8ccwcKAibk0EClab/cgEPIhSz1kSkiyBz/Rzr8174KuPaPp8YpsLJXSRV8XgQDYIA1dh1jamCJg761ueL+0N4wQ3KfBBwAKEEsjZbJb/pTv/gQOyf3V8f/+4/3GGhU6PkhSHD8AgeqwUiylqCqkEH/BAWLWHoqenhQxhcuCMEQdpLxoAUF07NNG1n//V2MO9G+t/xI2BfG8oTfJtOH4L2mwlCp0zQjv7dCTgBc5OoEM1+0ycwTngwuoIFU1Jz6FJtSI/voxPNQfPzz7ZORfBgTeeQEgomelN/PA5A74BJ4el2ze9wgxDrYAZpFVBT1/zbUl/ashYNWyPSjgCeQfvkHmDQy+uJBfyEIAOwAIqqoRGG2N78ACAUrAIAliudnWEzX/aBiv96buhUmGGP5gAeBNzAAwfhEmI2ROv8AUNxtQh7G/q2lHYIraCBDg/RRm7C2ORDJ9B/+F4fwAEwAfEwMTYQz9kjL57oId92ySHSqve3xOXwBBeVZ5Ihmbus5LSvEhaAAYHbQLiB8WeYrxg18RhkJUgqVb7KWHyQYfdoZL/JNz58GvxEWxKx+3vOi+KxJ5iwBv1P7zKe6/hEbKjgAGDloPvj4L9ze+cNQAEYDRQQMZfRhjPCShcAZITJjGQg3MYgMEfzIgJu2Or38m5a+hmL2AGB9U8fuAgtLI0NI+Py/iQXwAHgHmB3WE0Xi0Qm18WAWIeHAApAANmRg6ZMgZrgNay79S9/XgDKfVr7pGSEharF38SGoJGVZCuwA/dbT9jw5C3San+253bOc6rkNEf8SHrgeDJpAIbBHgIdnN7YjD4FMsf6hBtYACIBKgcNYeSjvmyKpgRhWYCi1cj53doKLEf4HQbZYRF/f1hSUs279/EjdsBcICzZ+SLIg8P3+7sVSkVS/aAD5kZhOhzKw/MWig0QAH5QzJIFxd+/qA0EJJaYNJ8vhjz/9kgaJksUhHPXzUpKKhJNfuH4wE3DhTD6EN56TWMBgbIAwiUx5CiTizcZjdeU6lH9q0uCDCJwZgluO0sP7bW+ySTIN9U6Jro73aCRK07uozJV+JD33GZGgZlIPzFosSOCQjKjEGD+JbScO+jzrtLYY/dbX7w+mAAmSFyogqXEast31jomWTSH26DHrAloL/xw8ZALJJTP1by3r8IGDVU27/+JD+/u89n/+A+gIACwYjPemqwRJtlj+MAAHKAAVoDXhg0RsCIGXTIHqFb+IPffYAALghVg8OOzRG9sFDVQaPJQiXlgTHtEYs54Jf990n395fu4hdXtuZLxywApZ5LX/F7uE0FlZtnvQP2mQuk2gEONLf42QGgP03xsM6sQiqojCEMw/A2GNWp5KGeYcLRQGhb3GYlwqtQ9DFo8wAF4AiQPvKVaFS1haPISAwBwfQZDS5IKe54wABABjAZYFUlfqBd1E97yMT8wuIfy2I5JwejtVI9f//+YhqOChHqCeu1CgpZA4XxldJKDj9+pUAyOjfcDQpOtP1tRuJBQfrpd1/42AlesD6H+qSpFEUktwVEkSST/Ag+NDE2i5Q+HWQ3nAACwIbUg8NuTamnjcu1KAbEkqqOfrjYgxSAAF4DmTIKDkDxu4A0wWffxWUbThGwLKV8tydCqOxfFiKhnBtJ+Y3+SLv/63JNJppGgGCrM5FQheirhr+NOsELNRO5Gug7zKmi/VhugyrYi23+afDuYjoiB6/rxIe8QjBEmbHpDSzh/HdOgEEEUjIgwQYYeMfbldTEGIthThkBDIxFKrW3P1vr+AB2aAQ4u9CSxFth/gI8gGOInGhNom00GqZwClRt3/uyGFCz7Ow47Fpm3Cw5t5+iHz9kSoqtNTStfEhXBXWduPVAKh+eKl3Qj4MrXaHCsCF5EQiMwiqQQpzFaEA4hFC7WvqEZoHsD8HWkFnxclM7VSueTzNJxvPyN/8+gTmaWpn4kPQwAEbMZTBim6s4YYQIQw4ACIBLg4aw96OddIrmPEAlooxhmstbTyoloww+Zg2nvTant7Q+wnQb7vWRjXgC6wCHEVjUgyRYb3ggMKJrUi2Tbbf4MK1cDazG8t3Wb0okmPXVXqguOdsVSrfH+/fv/iQ94D0YZYCFhGYkiZlhu/BgQAREoChDUfNf31b/AC2ANQ9ZDVQJsm26HoCGstMHlpg3hj37v+AA60MQSrqN2jAzuseZoxFUReILU1yiNgFkHkKQ3/7nXlDOWdMUVv34rX6mjv8NN16m/CuMHDQ17wAAiAxhdJUIrEGWmGW4yBL25u9f/+GfbICCCKRgSYIMNAw56oumMaKd4mDxz/xeJPXRcN+X/iTeAAjFGUrIUozrWW7iQXwACNVVQuBdGfab0CxBOt13uvhe/gD9uSb0iSD2AADnAAK8BpAaNEYAULvyM5yDE2sogKm3AvFkg38wAo04JWf7Qc5oe74kPQJBjUQmziUSXw179wGADvwACBUeERnGF1/zoGMggRIAB0AAjAGvjRcbzHWUqqZhHWopwE7UkXs2hfziJkZLs8aN/4DCMSFJ3CJc1K+yHqq9LOV7ktAQqCEFqahhwyM7K/MzGV1FbqSUtakQF1Gu00jDw147OGrrvr+hfxIXgAfPAEDItBWGIKeQEhjv9v3NHQIYY/nIdqAA8zMAYHIAncFWByB5/wl9DAxS21TM2QKdfWcRO/iQR/hIAFg16pMiLqOPfwfeJG+AXuMbKhzcg/KaiG4AASBAFxwdNDht5gEIhMmIZCDcpXcEGAAxmQmUVdoIU1qOFMYotTUMumBnZU5YAEyo4XrLwV3lxMm8YkoH2QZS/DSX5C6qyOcgz9WY4MSwfFC22bu8AB6Q4X2UkXd4P/Egl8PYxRSu45bMDG6p6JEZmGViCEMUoMMbNhsEOgS5eJC8GDAU8XwAIHlJzq64iY/6HAAcBUQ8pO9A/it4ufgAKgQuCf0KaQJ3MIHf9oAhLE+kTygSqYRPv4Sy+Gtem0doKO2QV+LP/O8EbY0V8SI6Ax2+1NzQiDDTX8AsgGMLpCRFgg20v6C4vQCGEWjQgwQYYDYCGwH8T4RGzRgAJEYnZBVX5CWNSDYfRwALgFRQQfMylZw1QX33JgATqrhOo2xu+wegY7ff9zR0CGGP58COZnmHef3qSshGClC8F3DT5A3aw5hevHwCDV73gA/DxN1A93DidTxPifCMZiSZdp+JDPKEBA31bCiVPz//WJPWaNw39f+J8SHJAmABczGCi0BGvXh9E8/5A0E6nABgTtEqJWQvf8Wi0/IY6ivrAhCBUyqeveZHB3R8Iz4k9QJXSd7//wNMAABdGQZrg6AqYYPXgIfrQv1/hg9cYtu6rn+fDB68O8fwhhDiRIawAEQaUoRrKtHrxqIZQeP//iPCAcsBMFLVfy1Mi4Q8IeEPCH/EH3jwxRu0qT/WM+S5v9z+sIReIPWAj2T+9/X6wgGOAAmZDZ1EXiCULYgOcAAgAJGyCTnOpBuWvnAACcBAGXOmRo/CMAi8BMEzJT8/iQ7wAHcxCiltww6ZFtFbyIyDZBVb7lsakAC9MgBgZ4E6UYHYHX/AJbABKCVS0ibquOf2BIPa2G4Vvj0U1/v9zwATqrhOouxe/vAQGlMYSW+bgJo0Q88M/zGcqjMKY4K5sAFfaKpE/36Ba2DroqCIX/+7uqKKf74cRWKviQvAArDEui5Q+mSY/nAACwIbkg8Ouzam8Q4/I6GKEfLDSPEAAIBJ4EYDmcWzIuV8IB+ZGNlQ4moJ5jUQ18AdhFgrDRq+h3T9f4f44ThsBBgAQ6Wb0SNoADwCxgQFknORNGYhB+93gycbnOfc2G36ge+MmAwUVKsypA+4Ubf52uCUkfXTBY4lX94wABAEeEcABTSUNwGtIGgOYb1lLkR0N/oN5GYKquR/3RyrDKPiRuAAkACQXQ1JtPHmCUUDoACY4md0M47qUa/QDGsR6pPPyVi/zj+8MBE9AxjVfsHTmnyPDoMQUp2GWjQxosYAYoi+XN4fsz5534O3n4PM8I3uwKCAw/ALOejFaQAu3ZIa7//cF6fj0Z0P726BZVO36lsaFfo9+2261z6WD74kbDwALBCt5nXdiZtMM/zAyBQUPPmJyu4amK774KYMVU1iKSs//+/5w1987gFqFIAa+ADK4VktsODYU6Xn46PjVIvHp/4fgAIoASAl3LEyZ5Qx4PwGLBCJgxyIkrxroeAwiCRKLkslAzA+fvAJgOiBxwzCdnzchbfAuyP47b+6fx5tMjFHMZd/1mHCfENscYIQnCQ0XRuv+54cP1DxzsWUR//BnPYX8b+n6TqDpPSf/+oZhdqI+6/w/QOiAAsAqFtOIFUZgzFrv5BaMMPlUPp7k2J9eUAAEAXcAAwASOWm744CCirzILlWmf+AnYI0wOspPlIJ3tQl61YDHF1hMm2TbbDEZIJOmfVgvJaMmKLX79QEftt0rS/wxOlHRMgA+8rs5P//1DR+W5/+v4IBIpgAQG6+TEbnX//cBIMeSE2eQmS/GOfuCUtQFaBtMZ0wms6jFxv8EGhQALjBgOYLzXa5IYrZRgIABoWofC/EQT08Zy9xgOQQEnjEZ5dNzFv95s7kI0IBEFHFBglaSh2qtb+gwIj1MHOHZgmdEsFf/B/EN8sBy/qf5ZrkbqXu+oQ4nv2/9c/iQ1AAoLA22BnpzPAj5CNrkAYFE3muj2TSJIYcQYIYRNDeMFJeLMri+OXaqh+sIBjKG4ADGYiM4q9QVzWoYMAQQwCsSBgVaG1NoiBjtFkGqiKBXkuf5wJkMYyMbUwCLwBMFy2NEP5v4g8qYA+pzvn2rLfZx4vggwAL0hBhXxC7bd7C9/5AUBuBKhJYiMVOxaIfuAAkAFhdDUGU7eWIRQO+AhWc3riKEyabY/3mAFxLCkGE8+ZIR+dDMmAFCbLDxqD4AEPb+KbfV2TpmS/ff4YhnFQAG5BsvMLyCUNYo+L5VAAYzCZOcXVEIa1TAniBy0Nni4KazcMnhV++51x1e4vvEEvHC99LVf42DhovAAzMAgomciDBNtr/vCbvSCW9BTVpIYeVPumHp2qkWrXhgH6B3GE8VTU6R+W+RkB9qx8/8k1LnwfiAJMCBbBH0ua4VUL6oCnILjD3SokH0BjVQEVeLlUXMaxWLb+8z8Od3Q/G/9mAMKIrGhFgm00CAsAEzImDRBZVj3eG/X4H0/ubDBNyhsv/g1Pn3mLMpUQ5RHW00jhgJ+GCmHvY3wiuZ/6uN323/0kJeSeHh/PvhAHzupuGII97f69AAPsAnKWTvEBY5av4wVwUeY9VlcWZwcQMy4PtMXnStf5ZU0wJU1///mj4A1S1T/+m3whK/ZTWa/3+N+HsAAgAOgqFxboW6SUEsgw/IXdSMpyDP1ZTATudz+KR335LIr2ocvbwIwdaVS56LLK0e7KrWRPseRjIZCuKlDmPaxPN38yvJc5OjpF//9kpGAAIBHlAAEAAAIHD9/WCGF3BHoNdp1yb/pNne7//2wyCJJl1R5/+09m8lF/Pii+OifR+GMQACBAqNaKVStfn+8R4CAFjAgLKENGDcBw/f7eAIhYgcoHdjIRz+2Q8AY8lLmDyk2WkY1/4ZDnkgAaB9uFIg5BA13nmBqoeEMxtFEdq5UCl1R/6kXFnS3v6t8jgsMuN/bUV1nz9ef+H7AjUAA/AAaA2gIrnh0j8Qe57ZDIvMLyH8tSEm8Zl4CADcIV6p2PViKFTnP0Df8BrbQRBgAIIA/2M6wpiiavyPDAAFgBieooa5em3fNte+wSEkzIhsjH/wbjITTcJZW5lR48aI6bZY9LZXsyHQyzERd//+JD/w2DHCY5lW+PvnRKm4kxDOOiZCGijDWjL34fsuqPOwOf5aSLhai/+cY/X1lWRP0inX+/w4BLswkN/tYkWbToAKyZBLfbfuMIoSyod1anoFJFuGtzZp/q/+v4kMdQe/TIBjiKxoTYJsNbjAQ0CvyK5+/okmIf4JRgTOAC2SMlQeYu/QIfAMAyIE3RTtvxpPm/8LUwyL/exFqYlb4X6xN5DWrk17YbxxpVz2e+OHoYd1FxI2BhkmTTjE7f+sGmKXyOys/fQGsWUqNN+7P3D0gke+AcTyPemXiIGN83il//N5C4fXTy1vP+Ee/8tIDHXrPzEQf/t0ilMj3D/4lxjOqL6iNI2YE7M8u6EqP/MHqMQFaTaBrGGhq3fvEAAIA0uIABeL3dA1y4oGw1AK/Aqszt3/1PzQt4Te/32vN6bIpreEERd5aNDGNHNKTavdPjYZ5gQ/WAHgAFgY8Jdr1FMlc53x/70PAE7JfTAFost3CjGN/uIgg5DLE85meeS9AurHaHbuAwwAGgtwtE+dBKhxvJAJad3yve5s8KNFqIIjPCftqeZl4pP9ql7ZvYNffFEE1OL17df+nQC8Vt7L1/w/RQT+9BgwCABGUAgousJEGCbbUDx8nI/nwMoscXpKGEY690yAYUVWMiLRFprB6MYJuUNp/8GJ8e8PaYLeiTT+P1i1qGgUPZ9/v0D0oPEWkt3+wblP0jAFby8EEAD9JmSrZp+4BAHaICDxmU7Pm6C3+BYrnXW6crZMpK40SbnZ9/wAE5GwECi6SmSIH2yhYuOhlp4E32Hj2FrTYZWx2722/IjUBcMeapmi9L2v0SWqAF3Mdx0qLP/QbAkdssv/77MtqHN/v/+pU1ZfN/jYYYeQwCsSBgVaG1NuGD+iQof3AiYxSq42pgUFoE5giCCGnOCAeNG+Epp6rUn+K//B9JgIABMC0cBRS1Y24rtlTgIRvNRUzh8CWmP8B21rNMr97jY2Tld1C5sA9T+/fG4yId4T/nyj1qx6GJjwy2ivr+IisQF+oHPKDYkfBTmUBC4eik6s73/+1D+hhvOJLLZGB4Vkd9/IIGDDSTmRYoQfw39bdQukt396//4lwzRp1/xI2HnDtok2j+gDracZaB5lQQAAVBgHXOnRw0RveRhPyHQg6FqVZMdmaK6pv+6oBSQGtIyC286hx0GoDIAMXhKw5RWgckcVj/uAhH4/qm4FwbaY/3WJmROEsOmsnv/vAhRO5KkkEZRWT6ySAQWU+svAN4FVE+734LOF8EpaLg/mPGbGhlq+JG9AxIKTIhHUVbOvfu0BupgAYEZQgVE74Xj/B+CIEAQAEBsVEIL1o/UoSrGR2UN7LbRrt4P5tDZVILiGoapXiAS4OFsEPRzjpNUwGAuAERgq/aXRAqbBX/vMBMoKFLPoQznpFQwGDp7R3LSY8MT3dxfJW+Vq6Zfkf35ym/jyDiRsPffAEZvqt9nFDlWt+H72I/8pXKX+2/531b5GmTw233gf5y/wEc2H6nLhJxJhP/5d7Z2hgCgzEsL51bt78PCm+MeYY30EmLlE71HffCPIbpIfPPhHymtrx7cSGInbjG/oHG1z8+zwBfXNGuoFRdRkvKtxLXAvs1Obm7PFABYNeypcneUMeMKDA/EPDeY+/oEVcMvurf/6//EjfgNmRhv740WTLitYAPG8hK8n+2/+U20Jp3VkUb9LIYYASAEEMkh5e14rLTjn/vJuJbeiRmVdCacwVyKWkvA9V8n8SNhnkKX3u/7vzMSsvEXSCULUp+TrA+uPUAA+BCLQLj8hjmTzhdwrTeP8DKKteI793FdWcGFiODRDCSO5X3eu/7gWWMyAqzVhdyQh/gNFTcWZsiebL//7z9BA+YarOZ3s2yIbcL2KVQCcybmUx+qyHru03CyGO4RSsyK5Bht4BjFEmiIFUubOV8R2DCm38BLymepF+pItWDWT+MNtpY7Y27/42lz3C8GRwuNtGXKuJGww46fU3/V+BOI4w/F4erqRv6AratTuvixMvbNSN/VtWqGAL2J0yoyp+/+47XqgIudNbLRviBzqTsnaZZ/9yAAw/HhEVpXgfT8JeCVcJSnZb7/v3TYPKhJF23f6ERRI0U+7thNFV/9xe//89A0AlwuCgZ3xIf4gYhSk808nUFPz7QZu5xs/XkFoYB+Xx4O/b7Xv6MK7ViPfcAHDpDzpTF/tCh+VBxtN/zA2qwxE2QVEiFHF0y0NNSs6rfPgP0jmjxJ/X/iQQfTGEt4aNtMm1zADszDXlP1O5SqBKYM1gFUV3lJJ3tAdYEI9ZOoJELOv/qYEw/ymfQp7n7AFhswuoyWma4t7nhkKcI1B5CWCUEkeBqjf8RNkZDG1MN1cnT7638SNti4u/9OB3mONxJPIc/tlENiIX8K92N01zPBgAN9jFEK7nl0wMbrNqh4fr2q9b8QBdxIMBEJ1MWeQNSN1TmOb3gCDAuXolNtTEVE4IPB+GgCPSqhf5tIVcmT4TMMFGoG7wXWHIH3/hrQhDJ0zX//9Fg6oeQT7u0ff/oEVoFHpdZ7t4TZ/0GXeL4kb3GSUURJ8HwD4nzU/VE9fbv5SugCAlgrbtqZS6Y0Jd3FocnSqy1aIpnhy/vIInemrO/wD+Ljxas37ubquXk//EjejIB0J9/hWLqfgAgCwY1hIWyhSpb8eCQCgYjedaZVYmTC7X3surOhxNQSpTVZVd9EW//ew+SoIZRyOFJNKKf8H5MXFzSqS62wa5gAAuCmWBAcdGiN4xVsVuKh7oWU3yAAEAb2mAB0kxWgcxgR94cFuy4Q6n0Y4PyFi4jMcor6aa8NxbnyFIJXf/rrIkREK1Jf3aUwyaCa1f+8MPu0oZBeVq7IuJC8ABsFBboi0up9lucAALAptQDg64NqYP4ACIgzHq4RKdQ2ldGGC1lD6e9NqfXgpr3wNVkNu1QP4lj8yen+/wtARB0fKLlDrbJjgw/jIRyxaIhec20B82ECZljZ+7NqHfgzl+BWS8uZOf9/isSGqxNnlTAQgonz83bF/EhzTgAeCZSAAQE6RKidkTz/AEF+BxRTxojAYzlgyI9cyojjza8SFoAFBKyrQsWGzX/u0YAE6q4TKLsXvp6ApRAQfMQjPDpqotwGO/2pubo6BDTH+DDAUGPZS5PcuZL8Y9+D6ADTZ6YiCT/7L5INZPLv7N1RIcOUxTU9f4kPRqAIP8DCL5g1T9cI+93ndAEElNWKvCbEGV/vtPAILOjOq50vpS+d067/2ASxh6yhtPcm1Hb3DaAjSA6zkpI4n+AxgwGBspV6ELD2C5vY2+AonaNpCtrOu+HdgcvlqP6YIhm+UtI+W/syCisSvPnRfz8wwriOH2h8IjYIwCg4LOmpdaPDJ+/3AKkNVoU/WgvqLK+3hAiil4M4yrx/tHYUKx0umI/3AgYJM1iSHIIab5065oNgRAiDtrND5A1r1oBfACl0NIrrQ84h8840kxCx4RdNT/vMzAgwiMYkiBxwl4gMgxds0TpO6TVVAYENBZNMHB4CARlFaPyu/VdKLn/eGACyDEABhmxXs//94UQVIaZXX3/F+XImOZUtzdJU+lhJiJUcfEjZ4T2wAkCtCSATOEYzPmojhgAA5QACvAeQGjRG8Qq6kTnYYm1lOGxYFDYBYAALghmg8NOzRG94sJ9lUl8Oot/UDYMJkABczMAGApAE9VYHIHX/PEgASBr2VJk7yhjwYAuqIXG8Xy9jtuol/haW7mSBZf7UrMpIWvW/4kbGwQD6b6boD9+rjVaYEvb/soY3kYNwAaXUaF0VrKebDxkIIIRZW12oHXBJIlL//Un4+djrZ/H7/H8SNpjAmT8gAqA2oAAgCT3wBpMUO+8XweRg5okxxDqiWm3f4sDrXUN4AKQ7idMU7e717LTmnb9B8nPJiVixjp/e8cF2yaQ6mwY45ZB8KLKsd76QnGHJFt38z9DJtD/TTZsfn7Zf/8zEWGpA9xI2Hd0eEpgn3mrV9odavDDDGwOAV4eBAARhJHHUzdRidahgAA5wACtAaQGjRGBEAJCvcZbuE7Qyu1JMAULqpEU5BH20pwYYwJwUtYbSbG+24hSfaz4kHvJkBxv9UU5Guu86DTHTXiRsBbxCqPVaBqTS6j8FURJEiJAwCH5kYyOgrL4lTlo9OQYgpTMLuGBbZQCBBwALBjOS34qhEm2WP5HRoCEba43kP/f3w2SAAEAYAGHwnP5VNgh3Om0vV5rnShYsUD38OlufFLa8GNcB0VJacfPDcysfRv9wuXQsh9eQNuM0da/e4NBIciqXODiQQTvXv8yjvPN/7/kD9GDjxmU7Pm5C3+8NDDrjdcpOIfqvnMEugabH1e930ZgXZyx8/+k1LkVp8kfGAwAGPx2bd6Dg1C2zTIDCuEWpsiqskrlMAKBzIqAWHnb7v2EsZmm6R5+1i+O+7ftKGIK9ixv7KA/8ekpip+/0zpkxVNPEgvhn0g6MAHhx+RUM4z7YW4BcDNIA4tu10nUGnP/B6AISRPpE7+JXMIn39wGrLqNH3GU618YRfCseH//9w//EhWobD8N1tAYEzEUDt1zHZ3H794oOheU+VES9JDA8AZeQAGBGUCojfC8/zr+H2m0vMDPu5v//u3nXjv79YdaF5bb1r/8CHzNwWE2Da/iQz4oauvwWg2TKWv+4oRGtrIlVV//2jwxRCu45bMDG6pBhvqFvDiCTEZ0t+zi1daokdnn//xJ/ccy87v1Rf+fxIVjIDAAoClEDjpic7Pmqi3+Qg9AxX+37mhEGGmv5/wW1gFYqHzts6JhSfxfDWAosVoHMCo3KvllH//Qzi4Vo5GyO5v/xNcRODus0/iRvAATJDdcQyFH9Sk8kCngPvDF92ef1ow5LCHo4p5996RidkKZSjepaXARNepW8bU2WDvBcQPivzDzcJx4ehgEakCgo0NqZMYbtf+9Qd9AbCoR3n9P+JJDAAbGNlQ5lIPyloh8SHbAABIGAfY2cHDRG9IhMiGMhBuQpHhgyGB/xgAYvBpF8kYU5s2u0H/+JCsAIAU4wcfMTrZ81UW/2jADFeWulLK4OsY+/B+Ar8GYMJjLUVdpe2hEYm0bIWW/3+x4qjkfPkP9VwAgeJeYWMQvLfVUv/4QTSClekmzx1gqJqW/Db7W/f8HazOYY/EhXyZim5bUSLP/7bB20FxA2K+ra0MF881hba0KCUjrv4FBB5h2c7ZFvSUKv38g/Yf/EiIIZYAU5dHz/4RDMAqoBDCKRkQYJMMBh9Z76x34A6qnv8/8SGIADgxbITMHuTJPinP/B8SADYPdqRBnGDX/4OMg7aCX8kr8+cuQIn/E+JPhGp7/Gk3Izy4kKwAnsAA5LQZSVG33/7mkNOhZxrmveIeVWXEcQm2GugAAO+AACAAqAPbHk/O9QqbYJKX2qTXh+MdTlfiIc61GOBsR1wAow0is0fo+U2fPQ0RpPf8SeuIHtB7/58MnqA6SGWq/4R8CxAAAAWskGbAOgKmGD14BGXXuf9/wweuDv7fXfv9/8+EIQwh4lWVhAI8ABqIxuhiZx0sYn8lpGWwuyrKDUBxdwAA7ZYCJ5wm2f/wfAQ7uai4ij4ENsf7TAlog0V9lkT/ZLv84Q8IeEPCH7whF4Q8QevDXF/n9hriwN9mhnc/4f4AFwAp8AAwXL74zhA6/4AoMWSEzB7kyWkU5/4BdBmgmk4pwlzqrpB0pzmCIwjHl/6wx2liZUI9bpJz1glHR5Waq2waQCAOwCdiAA4J2iUEbnn//d4QDZ0AT1M6Ri5Yxi1hbzwt/uQyDMmRg82nXwxoMABIzEQiirtBCmtVhhipk+FEbhTt/MHDn5VG+d5ReYmeqvwMdPvl3r+JD8ABMAAQBz0KsGN4piZgvoR8xxsV8Yo7qYW/hACdAutdli3DqxL/3mfMNXk2WJvIjINmOZShEsamyfJMD5jHPzc8BW05hEPSaSXupg0ik+nff+AUs8oAUEloyo44mZ/4aA+CIcZ5RtmNPDaBQA/7DY4kXeGJNL7vISt0su5AMxFmXOed/h+OYwBIFJQTOFKaw8/uh+wAGrgP7ml6kkMHLV3vHBdsmkOp9GOxoyAlpTjKmH//28AJUA+q4ZKH//VE7gzAADjGVI469Q6ef//oWo0S08BIQG6hEfTnKtsESjWRp68gM6oxqLiQQYAEglZfQths10d/8AC7IPtPSRSv94gBdEABgS5rPWC4xisHhsJEHB+cHgp69ZCfb/tCO4pCzd7x9Ur+/gNA6BzLC4t1IHpkrEOhTrACeMbWlIRc/xqJKNnHzxbCMxufvNLVhp268SHfCDca6asclkr2z//5gAA7AACMAYRGTRG4AyrwO0i2mDNqSMfuIK29jwwFIEqe4ATOmIKlWalCMasGCPuufQYJfQGicVdjzaB7/zQGnOADAjXokRK2By/2mglfX5lbL//Qw1EcFckmFO5K/gZHdkOD9gaWmUusPr3o6fc67f/haAA3RidRF4glT2ILoeD9QAGyIgf7MoZrgMLgEM7GIqIsTNttn/AjYRAACAdYCzIQNEYAcyDIVRieYewsxiiGtqH79emD3KP+JCsABwISiVQc9EQVwt38Ho2AEoJFNSf5op7+3AYACQALj4GpNJ7+0TiicsGASzDhh0VzwhfH78D8MSeIJRUvAAySKYcrYZB+1v11Pl3I/79f4INAUAC/vTo06UABxADxrJIBHKsuv1Gv+AA8CZyAAwJ0iVEboHn+fBbJMJFKqqyyQGcMFie9SlY6P//m8ilKJIhZE2hlAQpAWzK1PnPH81AFfwAGHx+RGroXf/BCYvoEFGGsxNffgXcBGW5R9VfmrMJsFjiQtAASErFIhzKUIli1h+DRgG+NXNiH59mRD0GPJF0yiCV6kh/7wyAABIUAGZ7rnF8EuWvc8f9YgLwAGxmE6Cq1BKHNVw6DMBDF0kYYGNlQMOYGlAAOLbAI608/NyKRI3BS/v+EAxAATZDZeYXEE81SBmuIFJAbUjILbvWiZmAMDkAT1Vgcidf8YNC8kAEga9liZO8wY8GH3fGxNAIxfnIl3MoNUiIbMsXwx4AFgQlHE0F5+RsWRNP7AWCD0EKLdhUSu4gbfmAACYMAzJ82OGiMEqNGklr8sPAB3ysc6SP8qojBS0mX/a/wxgAPMzAGApAE9gqwPQOv+ATkGyqY7EC81itATqcAGBO/xJiVkLt/uEQAJA13LFneYMe/8H4DFopVwc5USUka+vGzvHaiKr6bzTNpXeeULglYpb3j/f+97xszHjX4kLQBYDXhwpl5GOd9JKmNB0pwHHszygqo04/7xAJUDhrDyE946TXMeMBJw4Yw6hDO9k1jHnjdZMq9oyJoxAlZo2fuzah16uPq+3N5ABhHBSDBNK08ERO1EEsbrMA2CSlB9sjUq5Y2SISxypN6fv7T6njT0x2A/jfDQAahquGIP8wa9/4EegI9DqoShmCmXnf3WATIUACgnSJIQsd//91uJPACQQyPdGsbYqCjCn+DBggBjMIjKK3VOQ9qOEmGKLW5DL5gX2VOTAAmVHCo02hneOLBQW6qO8men//BoXrMTM4q94pD2o4UwzgUxUJGlhfZUBuNrJiaWOq50gGVU7O+dckmP7Y13OlshXrI9fg4hLggVehULxtP5/uL2GoaTRlJxwP9oFwTv07TEX+7/6ldWV6/wAB2QAGOiNYWNxVKL3/As8iW/oPj5wI5jOAR6da0CgpWyBhltXkb6Cy//5yUlVU296aLB+22frvb9BZ1W2e+Kx8aBLgfIHxIegZkMiIuVCpX/3gB8W+DHntUp1p1kmAtxgGBRlIxImD6xC4YAiKLySUSKaOrlP+zl65ZN//n/UhMzCKxBCGOV5uMjyDiPu2YK8fhoO4AEQ9ANaFzoOrS41+8YNjmO4IWhgni6WAxh4KEb8OesGEnfqwtSNLGNVd4EEM5mmOX0m7TarYp8EHwALPMtGk0Qg5Pxbpv1zgTqmGQ3+L0/+gevdKod/vfOfIPXAQj0NRU3QmDLTX+8IA/yO6spaiq/SaBbwAGYLSTjxn4T2ysyUsKMmbIZMz34JpqdZ/CFhsfh3ysOFsZX6Sf7uxWTRj2Zl3/7gmMByVIvh/w6DMBDFwkYYFtlAMGK2huNxEAIRyDF6hJ7G+QZZEC91/fWSA2SS/wcffoMCQGPawgYAI5AORTmMim7/Bra7MAbT2taUdTGl7//7kiT1rLn3762INZrL++wiIyNeD20p439keDEVVN1aDdrqIH4AD5RhsS3R793CABOAqt0yEmlASwc6AAiDYgqklFoaM6ql0F9gQSBH5F45+/ogiJUyZ9JEldVu/aAxv4vHPZVkuJ5p3/76QJwfdKp7nC6WuBCLgZat8Xj9imXw5d/OUD7ntjP3XoxxIzMq//+t/jaSgwIA3fFb4Aw201p794AJoHx1b0ufL69wYBHJzNVv72wLdJD/kjvufIfIKxNRxX0hyh1dAz/PoAIehO8FNIE7lkjr+0DCZMIs1cMITX/u4IAaPUBNHc/RGcM1Xg27KTXpAdnfwJoE1X5324HvbQjuvxKCIrXH4Sgazno7E+GIcT5ETC78EShSbJtlsECIBaEJP4sj+T//d8HOaWKQ4s5ueAFhQlFRzUudrS2cDDM0stJHVQwfrbf+dfh2P3t+iQkoTld1/gNmw4ktuw+6Phs/O+WECSvT80FuP/VW0V0i/38qHEQG3iTcQHw/QEADwxHEsShKpJk4SwAMfrscb7MxzPaiT//7+QHaYAIDi8p4dOyGP8MgziZkaMKw+ZY8QkwjmHMpAxRhJAaIQAobKg6t5sQh/uwYA2RgCA7gd2MVWRyN2EY3mzHdETdbn9mxno/79Uaqh9u/7siBBFiY6H1/8b4ADGZCIoq9QQp71JdFngDCjMXJvCPSjvgVVYasZys78AoBj1i2PA1CJLAnC+/7QRQHLUFs0vNA4gIZhoOVvTLFU84PYSWmwiT7Xh9/7npS4SCL/eBrKlG7+2cJBcIWyZk/97wq21eGegHRsshp/2HxkUnff/hht/H+NzWn+N/IACIBPgULYIIRzjZNUxYLxgJlBQph9CW89JrGA/1sw5sfptk98AgHR1Ag8ZS0j8iuoY4XD07dSPfWjCBKrR9ffm1Lb38AQACFMODf+vHA3H6g/7gIRvNRkzgmDLTH+BYKQo8r2L+fz1LwVT+f4JofrpRqi/va/We1BKSv+bZhAO5TS8ObQACTFxc0ikka2jSGAAC4KVYODTo0RgPmtCuhv5+GAGQI1tTJu14ZdIZiSQwi9x6b/Eh/7ZjKYMU30iHjSRAMPgAWkMwHNVKRhgZ3VIAdkYRXEXSCVNYrDAAaiDKYOSzlinjapDvQfhLhylxB/xIII2CEMABDD1hWsdGpE1bUcP9lcd98m/mA2UAgomciTBVtr/usSMiUJYZNhHf/aMR2IKnKY0hbbaogIAOBFocn8HWV+3mZmG6it3yUvakGdvg9I0y1bdOg5VMb3l//92qQw8fBB9dNPfoI/jlQrJVvDj1XwwAHAGV8AaGKvQN3GYx8rE1+HkQAMBjAZtRYaIH//3AbAzWaGev2Z/wIFIYW00fE+P3DGG20utHZsqP/5/+N/w6h8fgB6qf8H7E5g+IjeZ7m+aVFs/38n3bUB+yGjfR+xzwVfApQ5HHFzYxgtuMAyUAxru/CxPEVO0BnoZNnkJk1Ix794RhdygX21Wzf+wKw8eFOkd//WmhS5ooyfrMHA0NT4RGwQmZnsaa7XQ0hmS9Hz+qiShU1NxNpoyaDzOh+ALyIBr++i856b/XdP22V39rQAYSgqycF4R6xCPv6lta8mJ7/Aw4ES3L+aFUnrfVlkoVj/ceTCMrkOrKFcYsjiOYTkl1eLuBTdM2MxHtuiM1MOmT9Hm7qEPVKcf+aEDWTpzEveL4hoT1CK5eJGw/8ABqMMi4plYdDGoeGA40QEoTCPW+2vVuoAYdvcwniHe9wNSUISxqG6kpYi/kzh4qVuZrA2Uroo0y59/l5BIwQY2QpKVOkJkvAw6caNTRxj3u8Q54GcRpnM01xGGiJ/15AoQLqvLMxu8F7S+FcFTqe7cSr3cBshumedv4KNB2tow8r/5bawWiG9zxIfgKVcMp56iRxbR/8MG3zmz4ccbtuj+bqveGBq2/3fBgQECUzFqkX5UX/7A5qdz6+954RdkAGJoMQSvyO3jAzuqEcuiLvwk0QjP/8OGJfQoiPgrj5Smv9D56hdQ26OJDH9tGEKs5tIGoLrJBgAvVvQCQVqj8xR127eBpYXey+WllQf+0mfYIhQOkg5/7Zf/oEABqVfrrMJ8vv+JBBqm2pks14Ht4ABIYBPMkXpOC9H9Rc6/qVfx/v17LcYP5nzAAEAQAU6op4nzbXCABwXA1VlLX1iKR7/+jS9rD//X3gQLWvEJpa3xPtk9Btj4MQA2x8zWn/eFAO51RUZ/6bGiEZSZPG3EjdP7rXv9/P4IP2tFKqUvrP8I88aCKqKXE4RhbyNI9kIfaEUTVQ/d4gG2Dhq5FGW9dILGOcGZUD2h9Mkp/Bh6CMWyl3qJcecZi8VvjydKAgC2UeNPi2eLx/fne+02RpBo6ICUEQAFgiKwAMCcIwgTEanz/+Gg7ZHdB2vJ69P3b3z5jTpHMRd/6XoMk2iIpXggvxIf8iVEkVVflL8HQCF2aRyZ/n32ACx9HFT/YhX8xXhgSDAFlBQapbfiqfBDbrwALyCHR5l8lbBal/cGDdOBa/rMhISe4GCrXWuafRlJzmVpOh5i9F4kEEEQc5ewMADoHBgScMRrd07MW32gmOQvacOgsgj70AC5mYAYHIAnarQ5A8/5qAOsE6nAAgJ6iVErIXv/ABZ/WgG9pbqNZ6sCZCUynX/+/IbzJjPQn8NwBSABICTcsXIi6jjwfAMWikTAhDU0suv/+DX4Y2ve1//v//EhaAAyHxcom0MttlEB+IA1wIGtvfjrXCSpkPXDAszAi2fJ1t9+8DYgAO8G9DoLz+eSmLQAUUgtZM1/b/AJzxWJPwwMenqGKaK+o6v4k8wvAvXMbUwY21e637/EhqABUAC4EOCXKw/5UlQ5zY1JMH1AZtAhB+cX/uDlIOZy2q6r7/Xfv930LS5+Njj6tRcSHp4v1B/gj5KaQBzBiytGKUAFJLT7hXvIe5/2ExgU9aO8yAcsUNy/8SG5MQFwY6zCM7T1ce1S27B0Mth5T0+Ri0cecoszHCi/DMBGsxK0u6x20e23VOUwfUcspkqtV/7tuiR27tsGiP1jbxlEf6f/4c7gAMxcWrIpLrbRrosE5PxVx9lDHOhxnP+20iaH/fOBe9vb4/c0qQzlviRsAcitnP/2IwStpeWAsgBmA+Rg9You4OAG4KkUoaWmwWU45D3wNJPs+n+wAAXBTLBwadGiMAlh4XbLjiMbRToblp/S/+YGfTDDOmWvK/nf81cFNkc+9okRtNFX+RIha1un/xydA78SNz8v1Ic3xoCGkn6k96TeFOf+Oi1FI/vkGgWL0aMDLQD8Q2GTsJar/xHqD0QYCmoC2aZqge4IYJ3cOw7wTPXIOtZqdaojXX5Ak/sbCjPD8sRf/6QWuvqO01IqviQ70AQPaEA2WkT4g2n07ASM5MBSWVwiPPY3ly0dzQ3MKf2G+cCAXoCzFAFSGAViwKCrQPtTXUNhEFqIBU9rKhbkOJ4OQ9XjThUuRCr+d0JhS/Hz9kkQi3QuJD0AHYDdQUKZIfnnP3lTHEBtAUNZI/zjpJQ1/wMMPmEwZGKCq7shdRzza3m7jxGCGXfa1SfQz1U9kOYuzaf4YCW8YopXcctmhjdZDBk1EIJmxJoV/vovxpmb1f/9qeTjrJuNaneX3H/Eh2H4gDyjiE1KZ1v/E0AJAQUnmHnCkla3IlP+8HoDCkrJ+b0ZZ5xz+wfjo8PkSERmEZXEIYxAY2m502hSay1FnvvX787udhk2bv+3DoDh6dT8SDCB9zLjkaACiCcQWH7hOaT6yxLgw0AbI4IAgOtitP4JXjupVIUmkXfBa1oNwTyGyrT69v+JPWyvcnky/fcsAzz0G1FLuf/4VgmMnHvQAAIwN+HClyCMc56QXLQy3wActi8sdLfbK0f4Z+IDTBw1l9GGcdILGBodDi+3sd/57/YGzFpCuX4vEhWAAjAaqHCmXk45zskuY8QDZA4Wy+jLeNkFDAYYYAD0WnjO4BfLNf/3AGeADAkhGnXUGXmvhe0pyTMbU4Z4HnIhf+//HUfWJdtbH4YgAJiiKVsKtzrWaQwAAc4ABWgPeGjRG5Y6JVlqJtkGE/5wAAuDFXIPDTs2pgMAFvgAGC+wfG8oHn9ACBjyUmYEobjFW7xDjasjFSgZ5wlHvKgH5DuEUUkR9V4ZPP5f/52ONKkG9qJsMgjTdpD0kKMoqF+uNvMFWmnj4kOwAEQDXBg1lz8ca0SVLjS+iDBb3BlP+k3Pjw0bAAuH3XwLQbJdDF/AQQAEy9gn2bQ3XLi2mjLQaMqPIiIJmGRXOUxiP6oBBBFIyJMEmmjzmAHloNOHIXI+//+8tzQSSGfv7i+5+xEdFkpxPiQr6DyQpQX0DIr7w83pB4ImtUjcNqYE4O2guIGr6x38HoYDNSBQUaG1MWAAQLbwIqiYhOdfL50Cd22C+JD0MAOAMBr7oPEfiVo2W/6/AVACcg7bMTQtQys9/reP06M8Inu1wKWpJ1p7+6cbqdVuAEZznHDGyG61z95ct4I5iDhbb+7Tsi8oWDDAyji9bXLNoNiuOGtVv3Nf+JGwwB/ARjz0vZj//75RR8BiQQuZMJVJqBb3/gRZmCqhVNij//7gaRDodNafmZ//5Q6p7y63BuDPNIGytMVScJegfkZhMilOpBkNajgDllBs8bBbmQ1KmjXNgMqg9kCa1Qgkk/zuVoPTkqsq3/+/BJIhTGzIh0qdOj5kgh6EFT0/GQ+/+DNNhWK3h/kEMvOvN3EhWAogpNMsQ9W7+d9EvvQGNZxGhcM/IWM/OeRIgmQRFIIUxig+BAHuUcJGpoIVsqF5//nAACYcBsMmzg8beYPxBGmYrnHX56Ir8dQ6wfw03X8SGYAwGiAoWu/+GcdJLGAw+WLX72N9//8T4nxMbhHxJ5QQCmc+8/x3+ef6xJ8uAPVX3z6/4kMwA8QwCLWBgUgbJpfuQxeIDR22z0f/+JPKkAelc1vXWooERuHDX/H+CPgAWCGehvVdCYMsMfz++GvjMZTu5xdS9b0tDDrBpS6v//P//iyZaXEwjiT1xsuHKn+v/xOfgVoAAAXukGbIOgKmGD3wSPDf1ETcP36/hg9PIrQ39cjQ39fnwweuGop2A7T97/38IYQ8TWEBsABMiGVUMZCjpYpLgABQHAfiJw4Om1NbApAfUDos7tk4CZR1K3jamAGJiKmOZyjepqQ8sH7wfOHr8s8/vq49B4hgEesDAo2NqbAHAD4mBibCWfsk4fPJjAlZ+QAPC8GpspY60TggcDBy1kAQ3ATjou8/QhWVty9gxFr1Mf9/CHhAXxgCEBZDAKxYFBNobU3y3wgL8emMBZDAKpIGBdobU20OEPEhuAAmwA1D1kNRB6CxpEPgCGktNHkpmDeGPfg1wEz0j8OX/4gPYADZjZ0FZfEoc1SGH6cgxBCm4ZcMDGywEAgYCpyiE1G99Elrh4fWEDcdHWwd4QisQesB6Yy1X/iF7xAY4ADgxZITMHkJknxj3/g5xBAAZi4tSRXstsGuYAALhzLAgOODRGA9PM4TBHsPDvziIvXGzHEh3gAWCSBg6p7EfMhGF2/wCtgB8PVQ1AnCrbv/hyrD6GHdYhacYq7faIfXFQGK1KSUoS5xXi6D4NBISIoAoduHgZAzvnscURVmHV6OC789+X+JBBAASOGpHYxxibUa7xAACASeBGAxvVryLl+CAfuMbLjmcgVDGogFllN4gZgPeg++Ew72r9iCFD4obLeRV+eJ/BgTPcAsljbSHFXf37sDXPn7f42GH0m4EAvYMABHADwkWiTCbbSXAgIADwxZITJrkk+Mef/sAVGGqZDaldBSPwFgjcFKCcF3DjbX+qAcSHgDKHPPGeBsKuCDAqGYFnijTXEBBkh5kEUWkMsBl3H//9EyYdGmfWUr99sQJGZERKk3BUfjhoBApMo3Cu/nwIag2g/2tF79x7xkquJDMABIjEVMcyuIlTUh5YftBcQNX1h5/eYpkGu/to4GJLO/3XUMp/38cSMOV//1/w9gAJGYmZTn7DIa1HTABI6KF6zYGb8e6wzgc5lJGmBfRUCAu2QZA6pQNUYX5uNjF2y6Qym0U7rAABAOo4bVWSRZixXz7UwNPh6SPpJuD/gBATB1PBLxRSv5Ik0znMSAryrNMculFu//wGZvgDrxEfavB7kRGhCIutqsMJ32nEjYAO8ALgkVLVyf5ox49oQoMAJMHwo6B8o5e0bVMcADgyHDPIxi9OeKlUryArRQQdMwlZ45IZ/3sBj0c/QyGvkbGUD3QNXX4LQbBdDX/cAbn84s/eEay1nH9hVEkkHPRk8S5lyb/+GBXh7GKIV7HLpoW3VAwwUpEB6V7p7w0B+ZBeuv/ME3eX0Dn++6xHmRf4HmBMXERTxI3oGKz2fdWdIhlf+B6QAJFVA32bAvXD/ABofH/RO+p9M9GK7Tnv3fIiERkEVnEIYxAYKNBBBsYXwUHLeTij0dRsAXGxFV9lTXf0ptfxg2MnqA6/h6BBgAIqq4ZFGyN7+D4DHb7U3N0Ig041/gwAIFAGMJlCRFgk25swCGESjIk0SYYQf5HsCHSmSqkj3uU6vG1MSLBWQZ5xum73/wxgAWgAHQ4thatmDFeiPcAA7IiAEBiQdyKjI3C7/7Q2PwQsJxIoQNtuX7wQPgbRACcjEVxF4glT2IwgLCBAr5HKp6vVP3BFCvmbSu84InSx2R7776dxFmH9d9KWJSz1Hf9UiKOPPw3AHBkeEv6PP7++z3pICxhFH5vghke3cu8+urtsnff/6xJ63CZnNQEwiaJL/+v4gMQAEQuqkZzmGfqzHcWhiCVdRy4YGd1j2xQS7KpL4ZBb9MbKmgTAyCyGr+9tGJ3EXSCVNcoEHogAGyIwVNlUM1wDAFcN5GHYTXfubi9I/79eLxIXwALg3d/gtB8lUNX9AiYBVsVwmOXoTVOfQwAGpDdcYzFH9TEsAAEgcBtjhodNEYpYAaAs8tTT7rSKJufkIn+6DXic4kO9AI4NcaSMnJFBon3/fpIhhxfxKyDPp28/73+4WFuiLS6m2aQ4AAWBzagHB1wbUwf8BwETE6IUyuN6lpDAIV1zQSsfXu8qKMjbAfxN/8EHgAIgJ0BQth5COcfJrmAAHw4F1ZMIdBKCFReFD4wDZQmKbsQKdOLkfIrITJ+v3dfkwYLmYPl7k2p9+BP/rAQURWMyTZNpscTEtAxhBolbSd/AC/jCMW8+s3q2rl79/u/iQ9AAtMALB7pqTuLGO/20J9U6N8Lc179oDEgpcnEok3hrn7rAN1IABARnxMRtdf/93gDOFXpBoZK8BbvVNb4AAZQCtLIUgTFNG1Vb8bIgJRmTCoyY+q+qf6/r20kZQWYSFY/+8AE4nlw1a1y9IdUQ8MMcx2CUg/PrcmOMDtWr3LdCdwYQLNpYa794QubKpnYi8PwTAUE9D9uIKarVpZ/SnjCouLrxse84hC6if+LwbX9UATBdwn2PrEC6MqtpnzUABzTEpRML8hiUlu9tGJVIdiC81SoAvfOsw+/CFQoh+FSJI0y8fhP3DkOE1yGXf0i1CxukVw91cp3X3wzcU4Wk2/y9rwI8PG2gAEG45bUKU16SCjmOHq9Bg0UUEr7nkogkT98GCe0wmuxRhw0Ompg/AkBYwICyRDUSxmUB7vwEhDP5qIuhNGWGP4AHBDyWiDXJorxj/7vAwqMUL/6WUeKaR+CPQ1wspNpTl8Ux/4TtC0dnQ/UfIBIQTbmLc/r0abyIPTU3HI5ZbKev8bWiPgQhJswmII5zFAww4ADMxMinF1Dua1EHi2lubnAEwt6F804/nuYGvnHbo4WA+23OeW3WbQIR/P7LwTBtpj+c5snGSDRlT/vAAzDwk48Z+FcsqLkly0ZYHJrJK646+pDyTYyD8RS5LP96zAtEarfv9/xv/Q5guCsKwR0aGplkAABMEAdmEDZ0eTT3CZYNQ4IykV0Rke/wMf0ABzALTEJreBQ1U24QA0C4EotoY6sTQPf/06H9pj/nu8I+GN1SR+k6pKVQYfL5C+1BauA1zq28cb1/RgPS30C3nQ+lIKT65wAmAKJOuLYio119W2A7Gs1sg07z2TLMPL4iv8ohNP0i9P38U8wzqn/Rf++a1g6OA/G+NHgEI3YH/jmAA7QANQ1bDFH+YNe/9lTOgQp6KFpVjRb7C+4AWADwlhibKWPNkoIHfIAPi6GpsKZ80Ugid8YCZQUKWfQhnPSahicvJ6niZYFn3DzmKH9//9H611X+6MADAg/yU2K/SwK5d/8bH2QKvL7JJ+34oSH7Xf/E8tk1DL1MjPdaibQ5n3nBUgxSrixcSN+ZGMjoKzUEqY1XpyDEFKbhlo0MbKgzGurwwyA+w7EHcpDz+BAAIJ42vVaM4sof//evma5p7/36FQTV3WksdfN/28Aaspc3ozvBWp/N+e+7PI5QuBP9dADJxmaBNbkIl6ij+tz0FilIx/v3jAAEAnylAAnkVlAc3QT1b3pf4AGEsTh72Mm9f/+GlOz0U/v+XvB+kCv7+v8SN6YAxMGnk8IFB33Q037wCIAi0LOAS/uI/B90fBh+KkBCUhnUxxBWaB+0AAQCv6sgBRWgywLpxAih0zwpJtVJExzNAOeC9jt9W/qMGGUCWJTevX3ov/93wsgdsI6Eip/7wFDsCaVwmKG3TWHweKUzNBuVVb6CBd1mz1Ysz8ffI8MIxg/dW1+qf968+Ls/4V8QTYhAyqnkTE/+8wIckolheJkiBLzesCwKC6nJQh1gJvO/9bAFQ9E9IMD8Lo/fHjOFivhEvIphpIfkg6PlF2h1vsxwYTtumSFRfiKvUW+4Ycu0IcgPEDcAC8ACZUcOizaGb4MtAYz/YnL0VFthn+AwALDo4XryvGff4arKAIBD0JQ6UTbIjJoACwMKr5oTq8F5sNb/DAYh0fVcGfcB73CnM/MCNoQR/aAuQA2Q7LEX5HNled49BLWP3yAOg/vJRbar4A98sArnq3//fbKseyezfb/h/gCAACYMA7MDp0cNqYBLRiVTHxAvNYoBVwc3JXQs/YohEaQiE085jOAYISGeobJykRxZQGAdQQBgA5AAmSwJuozfqB+yp7QIRvNRl0fAlhj+BjMhXiOTcnr5lspS3zKB4qesUnv+y0Il96N4aYTp+HMeqAASYVOihKS7W0a5wAAuDlXAODDo2pg1MQb/wA2JnskTOvF8NbYKWA98MV3jP7TsVqPEdEj/94CA0YLwrjdFfGBaxUsPw2ekhx83/+/Pz8zzGqqoMP4f82AA2TuERZmDd+tZMqLQuBkl0dX95kZhOgqrQSpjVaCAD6YBhqNncOKFAU6DAfEjIlGsMmwnv/hos/VQQgtbUsOGxnhXpBCrIPCYcEPP0+2/gEsjE6mPiBVPYqw3HenPszVUfn/yQAGyIgX7MoZrwMG1QBThuaVUiftgxuFWj9H9QURqfSQl3/8NPvZgyXKxI3dBWHMWkUhvfYMXUjVWld3f//+VtL5N6XAxh+AAhYUj5/FN/1E0yAMmf0P+fVuiunO8M+GbSLYg5LF6aItyCmmriG+WD8AF8oNHkuX/P5NaaOlVPfEgvx1Wtxv+j4dKlYoH//LgBkgPAusN2ud/5SPn0lP37jyydj9DlWj/EwAA6QS5uDfuAgX+JD0bf9hNdbjPWAMIUx+VDC1l4JSaB+Uopq/XtAQr0oRNo9TWkffgd1E3Mj/vS/GNiuBFOFbn+rusxWcw+xU4fv31DB1+V4K4vyBA/0kQyrn8SH5YcwBiHx+wu0M1+lODDACTQCCaTvRCfKTvjwfACMG+oVAm6u4qz//Lts8WAAQCIRSFF2fTje5gYOXOwtKXF9YOyHl8t9s3d/+H4YRv9VNfAGUPR3Xz8FqHfw4Phw1MaqoV+eAAgT8eNRDin9qfUADrCoeluhJFkoJVoEGWJ9mEUC8rCFr4MdMoggzPrpz+sAFppmLrye59ZcJ10b6q/42YGASzEkiZ+r5P7vr7TzauqZ3qPjhDt6Bw+f/IVimGLRKRjKzP2HdLAcaALvqwP9rhBAcqrESH8/gQYbYrfsb+lxFo+mNniRiLzUnfOmZV8sfHqiRcbw/4NRbLizaTkmMGfn+v2ff3h7BhAXSg0Em0RMtr7CZjDi/CNu/Dpw//+7QDBSihKOo7Wwomn3sJjuMhwH0Uki/zACBcShV4S9ObH0mCR6i4H1ZZJivJd1DBrVjBdbP9bDYAIuLqyxtTHXr87cmA6QisP4YgMe7687wJaACcPWsSfxQp3+wENHRi/IqLXVdXdu/6bzCoBYTPlbgf+JGwIVJRKUlf8GGAA/1ZvRTaKgyB/4SeJdio6IHLh2ACIAA3A28LipvHtyUhbZohEqf//UxFPqIglNTP/OLk0bIABBZ4GKu3pBjFP+AFeCKWtI1/BqIBi2b6WHGemIuJC0GAQAEOik2xxlt0YwSWah4ADFoMQSryOXDAzuq82RhFcRdILU9iFn6O/lwFN0zc//w5gAdptkjiPX1AgwgW8sfX/oNS18VP4AfeRGZT4/L/DcEnNy2jJ/72/2xhrjKGy72TEeBrhVRGxXV+/V+F0jxWJPKWHqqBDbS7vP4kNx0XmAHAQlCEaE8/I2MInH8BIEPYhChTHyVi3jj+AEXiCZsihtTUSZar+JDUAY3kJ3mX6MvhhP0rGsyYFOnViPiHlUjoIlj7Ua7xgAHtQIMR5GGzKKRQP6iPkxlqgX6E8kFlW7vVTZap1ecX3g4VS55qCq+JCvkhCZRE+23SW3vQGLZ5GhUMeIXMoHfMfbldREOIthTPGKSlZPc3/nMDGo9+hefEbl/nf8GGgwFoXDv2IWOPtQWb79JNN5/OS1aSLeoHz1Z+v+JG0gRAAM0JdyC4l3vYtWve8KARghdoi0uptmu7RGAHgS8aoRdVt7+3vsno0h5WQYHdvrJo4jrvGAAXgCLA29JToXKWFPD2KkqJJKB/DzSNSapm3/ON58j7bga/UlZBlx/0Tx15Hx+k5By9B8SHvJEYAYDvAjUFVh2N1/1IADtAAS2SAS+PPf+4PwBkf+EXEAVDxCXKAAkVWCJ02huuXs73FFK9nl80MarPSIgmYRVIIUpigwwAHWgxBauo3cMDO6p7yMTqIvEEqexQaY0yWiIvjr/tBnBRFyBJT/pLvw6uf/87N731Yv8/s2xmXXxIV+0LC7RG+6lyW7ST8EeEByiRCXwPz/E1szIbXFRvHAAkAGDPYrGsW5JNNd/8DhP6HAFnsSwemYCsRoVOnpKpTrinK4fbfxIegwCOgk0y1HnwF2oSlWoxH8ALYAwKWaxYmSowSeoP/W2IBHbZgMHMGF9VU/1t+/9z9DMwH2Zn4d57V//gRDSKhicGhI3Eg7JrwHGd7UZ/d9s7x9TWZ4YSouoin/3+JG3vV5s2AEbFDKQ2yXfE40zpBjQ/wdZAQ0Z63GDIzcrgAHBgZaBGG7X4irqan/1aBLpNPf/zQqAQc3YH4AOwADjAZYGWlnqBdtM570MjqYXkE8tiA0jTQ5mP3WHXffBscTk2pGU/6tp8U386Bo4mR9pMP9H4kPdMA0UAqxt/4dd6V/fLlsD/Mci/ZFXR3+Tg/R5eM3lJYTbC2awKCB50zKt3zEhjfaAMQwxH/A3adovXg/w7EsBXbR6g0uuq//+y7k4Lud/d4c0xtr0HN3SfWf23/xI2N1BgEABNDgm0XKH0yzHsAAFgY3AeHXZojOc1Lz76weaKsO1+3nKFRMoq0k2wt//8je4E/EHH5HQRLibYS5wAA7QACS4BpEaNvMWIgBQUFhJKiDoNsbdz/7xjrcr8xBiLUU4ONjdaN9fhkKrMdwoV9qAVpF6yfr/9qpw6a1xN/7cCi76LL2/rqsBnSJYcF4kO+Rw4yxWZZJLroK7zA6vQ4XsaNhbSOjIWpxfQcgtajRCbhT3g7TawRjff8290b1FJ4CYZX64XAmDvtX8GBgDxAdwTRmaxCbX0AoGMz3pqKwRBllr/cgdogceMwrh83QY/2ISHVtSFKaN/30jVvoEsNmshv/lpAokqFuG/f7mJe7fDmoyNu0gIVf/7hh5FYfQQPiQr0Yn7WXhJ9yf2DDNAti2ooklcIE2aZn4J0leB17eov/nKBk20vfv9p2aKHkCA8SeoPo9uJ8+7rceHcsOzNuwNI9YOqeJPWLWtX3Qekp6/iQrGgOAB4NkIADgjSBIRvgef58CQQllrg8tcG8Oe/d/whPOLIdbISnvh46M0hoj+ChlOHi8T4n4XmBtAM4WAAMEYET+tNJxBT8+9QAD4M7VCY/JU5k8AIfUAmxyIoQ/PkiOrDVDxA0hLSG/+wtT4CMyrn7/3hsBlU0cdr/n/EhmABAkAxhNISJsEmWt2QCCCqSINEmGn+D9SyVXV/+JJBgEY7BNAHw3AEEMB1LAoKtDamt6kHhExyFZxtTAiApKCdwxbls/tfwA4mYLiXKH4wComv4kKwBAJlFUrcNqYCcxs4ULtj+COsXg9DAItIFBRsbU3tMxKhRPU/mLVy6HqyxWVL//e+A5/gW/GwX3dgAAgDAPwfNDxojekhMyEE5DuYxB0lUTEJzr5MCwJhOlbP86IfM/xIe8Q1Vfgs0GyXQ1eABAUmHElFHQemwuxL29hiildxy6YGN1npEIhGEVSCEMYgPgKO4BgJI5tyJJ7x8WABH3mbzeM/vX8YjiuWgkpLBvEk/Qwh3tmzITWIyxv07BBSvu9s6Cygq/4kO4AADsAAZkAMdiOpoAkYtFEuZwtTdiMH3GAWYezyN9wMCNbD+5QfFyi0Ot9lO/wGkL/FTaqbZbi4zcYbvJo6b/+L5oGAt6SExGEVSCFOYoMMwqNU2Ik2zYlaf7kd2tvj4w//iQr5wCCm3TGc7zR7n/gwYbAwBBgmY0WkhnPubyn6AAA1cAAywHvwHnFAfgZtTD18Q8oseNS+gf+JDPzACgmBiTKePtk4oHAw4LSaN+9nmY7//xIihxkBXABAgMIJpQisQbaf4Cb0AhhFKEGCTTD/f/gvpNnF4AwAG6GzqI3EEoe5QeiAAbIiBU2ZQzXD18BC7kf9+gBkdfd3+7/ZSP+/X+JjcTXJlp+TN6JcPziBKJYbi3BqwAEBC0SmIOcqaLSNc9AToQAHBO0YEhOyF4/3UB81g4cugAODYqijvEYRPOUngET6X9n+EcSfhVFUiRaX09f8Se8gfPnv/4FeAAAZKEGbQOgKmGD1gBkXXf+/3//DB6jCq/378/9/PhgMeNgcAsO5qGdKYRexIQDZ5KQuXjcIXhDxJrApQACAMrV8o4kEcABIjE7IcylESpaQTwzHSvady/nf3hA9h4cZp9h8IeEAvgAIwGnDBjL6MMb4SWM9CIDXujq//JuXHoDAgMYXKEiLBJtgY4GsAG1niyrr/+m7Mv4QD/xAN8CBrLyMca0SXMh6EUHu6HS/yDc+Pf2yAhhFIyJMEmmgYfYYAFgW6AAQE03F8VyjcP8HToaJw9lz92/7pgCXY+2Kb+EAxwJAxbKTJrkyX4xz9356nAAxep/qP/PX8ft3hDxEVhDxB68Ba2hv6/z1gGOlx74hBImj5/4kO3AASHVxFUxB30ox/2hQXYIn3Q+zXMAAH4AARgDCI2aIwAscbFVDFHIxhb2AADAKbQODbo0RvUHRaou0O19mOjYPINRjxwEZlfP39cP/gyHJd53QG+P79pbtO+dMZMzDH8NQ1DmgBgaEC8cwXRVAwLVKsMYg+Aly+f7g0SW1f0Yqhy1+Z6TIvBBSgAmAAfoM1CoNz3qMj6Wff+jIOwAO2EKiM17EZqtS4AG2Qk7rlWu5P11Za9IDhhVH5uMCYQEnUU7Z4fW4Ie0kDPaDKN7i0u3hmQGpodclZCN32nI4Wp18SV/D/0oWxUyrU+OqMi0/GwAEzHBbsmEOpcGOD8Qo+I2OUV8NJaCAMwTAARgB7BvYyN8+xKjXigzd3MheOwtTI151gCMxEZxV6ghT2oAWa8Qqp4bTi6n3ghliLznL+IhHznog8xkw3+VlZzppHNgAN0RwvQZIzfaQjY5CiN/R8fm0eGHPC7RRPuBWb6/AlTgAZlSzqMsFPF3b81n7yYhHHy7l+/u/iQrgAWEO3mdd2fYhhn+Bg1BnNchkOU//+4GgUFDzpicruGJit8BAClGDjpqNbPmqjH+nXvv+AQzCt4+3/UFdHj13cz/ELOVz2dp3N397+JDvQYV9N3z0sA6Hin94BLTCtzxipEg0f8waqKDOntzviAxK60QQPW+Kn6035de4XiA2wKFsvow3jZBYwfUU6jQLQ0CF1AOKGgkB2qRGd8I3eFt9//9533oaP/x2dPbL/ZUR0pd+JG2BAAWBhqcmwmKWL+s7Z6eiCDbdjK97JmWnmZ1CprmP8JbwJCgVNGFRbpLFklgN1IADAjKBUTtef/90BhQBjCaSItEGWP+AENojcb+r4hHGTNwxP/i+R/WAQwqkZEGCTTQYcPMQVkPxJK9/e6AhwhoQaD9lAqRy0eel+/G6G0pf4kLQ4ClQTDZxaYOQaMf/tJGYAgOSBOlWR2B3/yUAaUj9ul57bcJKRSCwnL/3CLALwZU0UmyQ6ke6UpA+cHu3VbPw5aqRlPEjYACQ8XkVDFGfbDXcQAAgEnCKBjerZkXK8EOD8yMbPjmUg/MajVyHqj5WVv/6CDqwDCUI0Mhl6fv9zgABQGAfiB0wPG1Nwamc5XGUxVuMZgAGLQYgtXUctGBfdQNgAHjGjpoEmgqSyGqQCUmdM1a+v8Amtk5xoCAPSA6bQJQNdNID17MFKjBJ/dbnGNpKS/+7yhx6eNU9/wtAUMB0fPKFx0TldcyD0jAAOywDcso3UP/vXGh9t8GwG8FJmkOTLP3v+PSrz9+v/568ETez/G6HAAdMALAt1K1nILFO/+s9JGYAgFeBPF2R2B3/wNLgDGohMyIRxFWzrn/odgN1MADArqBUTtdf/939A4OGrjRViIGMg0rzVBlQrXVVL6SsVD8N1OCAlMwDw+BIUkj5xQ21M1+4M/F8EGxQALBC2SqjXJopIp/91YADgIahH5FY5RJ2MInn9YAI8BMYCOiUXULz/ggAA5QAHaA14aNEYDmNBI8N/Q2Guzj+QArqzptSNlSxS3wkPf4fgAMwEELy2NRDdMHuB4AkQoAOCdfJCVkDv/P4CgDC68jKdhG20pwMDYdosiCg5yHY7rk/F2ypa3Xz13DPX+FuAAmAHRuDE2lN/bJwROeQAeF4NTZS0i0RggcBC8aAAgqY15cjsWSg6AHyIb1Euiqn1oQGkoe2vXLRmnxDuB0eUAFGkcbzCssxqpI3sGzdfsbhxJ4nw9aRIEkBHnD7GuylAjC+gJXBCHrPvcuEoiiZ5JIiyOAn9mh2vr6/2gQxE4nPV5YXN2/4BGZCZRV6ghT2q4UwxRKmoZdMC+yoGKkjJ5+T//TAA3lNEq32VqUol/rve5+/Nf73/xsGJc5H+JsCE/g2s+KlkC5aL09x+naF62UlZ2qx7HkAggqUiDRBxpfqcBmN8LaUP/vfxEMCbfqGRlr0GmNAxn6xNXYiLLTP874tmexq7rsm+bRPn7zDQGIqLpcWlD///bHTni93AOQMvSMBMaRs2S/7CcBjnXQSwVaaa9LC9/Wa9yx763VH73wamOmVghphMb2w/+htuP/9SSYPCzFY3++QdJmhWuvhx/GC1o/G568z2/0pXUup/701vYAAgCAAQVCXzCbJHvjwkewD+iJrfXR//7gftgIKZusb0s4wa6GCAgAfBFOI1B5CWCUFEeAaEVQBw4lHHiKLbjX3AQCHiRhLbfHI9bW7Ie4kAEgJtyxIjKTzn/gQD4Bi0UqTnKizEjXfzeZR+lkVwE6zludKSq3Z/35ra/EQ+xC9//UvxdbP/32xgsnBAFyfxI3gAVxr+4upJ1rUgRABwrodr7+gKMWoekhiuOm68StOmYMIdKoEQbk5CTzzDGtx0XAEglUFdy69blomfHQ/JbeffSjLbUH/CXwGKz2fcVYiLDLP93BTI5iVU7lECS9k1/X/wYqoYsABo1wG5wIhkp+2irv3vXex7f/D//QDkF23uWd/D3+lIffjldvA//nIMAFwOtEM73kN9YPVYpeS8AERxxp1p5pHClTvVA2yD0u0L/9XQ3sr8+BqtdNxLNSagOo0VP3/7/Ejf8FSiJqyvYrRvGwACAhk+0Ut2+Pf7v3PIG4jFJPJSQI4mj4MAC0wAWD3jUnYaKf/t3T6OTRpNAMSilzJxKC+Fuf+eQALi0GpMI560Tj815gBYyAGKEp2+yTigcDfDqYcD/pkmBC2QbNBUstv0uzs/3uxVwFN3WNhgl/gggH0pQBdXb1pJ/4oVpfsAAdgcGzscSSnVoI/vIDoufUMcSi2pIkBukRfoOP9cIvKph//lIeAoGApVogIUijQirkx/ewAP8BbI9d2kEBCVkEkh5FzBzDMGGhwO/Xu/+o75sUN+ynAAI83V9bvkHlhbNFPN+H/MHYcAKDDMqVcNyF/9wCEZzOqI0TNlln/B4710adIABdx6IV6La//sEjZNLm777AMKSt+iXfMP43/7YxE97pX23394ACQAa4I8I9qKc134lpxmZ+5Gib2kPjquGRbES/6PX4wqs5B+62JjJ95v6VoIIllk/f4sm/Hy/8bYgANbnccnMAAjCXEFUvcT3az3AADkAALKwGODZt5gE44LdkxzqbBTg/EKPiIgqWvppbwz/FNAFgEuDhrD3s26TVMf8HNFIoPvHcRQEM45FIClFkFO8YCZQ4Y0+hDOek1ixbDpoZA1VY2fuzYl14ZHw9WirOo81/kfE3e9DFTr4mXVQj0Bfujv1/43oYADmDcN3WSEcrKCOqrrfAZGgAwIIxvD5FNp6fwpy7AAclW4A4MehCfCqLJDhs5wRowCIYIQ/Z55Onz7w2ciY7JY4V2pM3IU5/nf/hTlPw73/cQZIFEberGWuzj//xXluvV7AiMBpK2vu+sz4wLzTF//3ZFSQGl+e/5f4YhEf5btfgFEbLKv/pW2/+8IFTYo8YH4qs4r0/CbgM4R6sU1FjmSjrf+/wp5GiGjsgfiAAEAxuIE5WX31A7hk1wEI3moybw+BLTH+CaNfi6//Maki1UyCo2TJV33cGDPISm/MzohKbcN+HNoABmKi5ZFJdraLc4AAXByrgHBp0bUwTThRbmGAGQJnsot2vHYkGEACwh3c/tqhMGG2P4BkCggJPm4Tu+akLb7/xoGhsXtAx9OLSM4D+Of/wiNgKgTULviVtS4pn/9oYkWv1M6bvb/9+gGEkx1j9/KULonn97xfLSPm7KmwIhUPtaLbMf/+VEnU6cd/4VQbi0t7f1vrDiFJdLfXJTTOr0SEIRBkdxHKYrwSwAgqdIIZamvNIe37REkhZMJmZjvAkYTWclCT6WvDHhBMEHhqp0ux2/r2x1ELorLmzaZ93Pl89Ix2/vb/jY2hDjIyvR//Ckpz0n/MMIAHwo4A5QKkmIYt5Tz++zZkiMJGIhu0fovg4wQOB25S3O64vwAHEBP4kBbiF4yYivL//cBCP5/ZN0Jgy0x/gwM42+d9x//3PDMmLt2JUUYohZ9+tOE3fI8g/5qPQCC8bbfoDb4m4yevGiH/3wP2dUo02Snl8//33vtlbv/sbAASwBCGD/V5nmLXMzVwLYMpDchPpyv//1getz/nbV3+TGC6m49OwEaV3ry+/5UqHjwhvGxxZ27/2cxhlsQeqRKEW5kv3jR0+zzQYD+1586FO05/1AAQCKVyBxHJWvhXfVA7euufXu4DOlTa2lvBvV7fLI4rDYbtTmyLZr/94Dvl0ZHIdASGVxdvjY7FBRswG4ptvLeWYC/EszyCRXR+06HkVCozngDlvUA/TLtYMwERuXbvdKjUDNlQJDrsvn+DSscjjoezGsf73mGVecXUk61aYuouASc++//WwdOprsiT/XWmZUNy/0t7/RkWEbE0sE1xI3/wBhZJtToOLRTRab54Im9zSnG77V/yaxN/P+gQ69I8DY6gx1m6/8+xiZhbjfqrcf637ilQuSM5XfdbBkZ9674pvz1vGhRFRf3i/6uAwVqOu/t6Oe9cb/vuNG3xH8SN6BMquKRvQRjX++fg2cBv5bGNfOP7FhsNnteI/NzZb/Dr2rXusPWAjEDBlIrFKJUIeCAACgKbgMDbo0RgaAFQiYpRc6iXlrfDD+AAgYZFEiUlL35hGqfg6zNhp7n6WWf/lgiQkjX+Nu8HB0x+HX/Eh/qgDA22o5fkr7/AHtTp+3xgJuHDGCKEM72RWLRpl+HBPgA5jdZoUs+hLOek1CweDQABWUHSgkrP7+AXA4MHnjEZzu6bqMZS6JvweCiZ79L/zgdsXhu+i//21DjtOJG/AEA2pJ3N+dQFED/B1KTGlWJ+5/nhU9fAcgkOKSibt/fQ4NHD/sgANWVH3qfyfOnVf27wINOB6W8WsjWw6mQde9mexq69rugyPdyb//WgQjOYiqsTFttn+B/qDvkGSx/D9QBSqXWZxe6eYd4wK4uUe6T//GorgX6AuJDEAcWZSsgq3OtZrmAAD1AAK8B7w0aI3rHRMsuOfbqMewAAZBitB4acmiMAMKqrMpzDPtZjg/NhQTbKpL4dBbw1D8UIyOJjUd5/+uGJ32wAHTMwBgdwE7gqwOQOv++EgAmDXqkyd5Qxz+DA33ACafZxEn2cGB8ViT4MN8eAu+csOv4kNWIVFlTB9lIAV267fv9/xIVgAODfHABQRv0YlBC2N24CEotEGEqiCkDXf2jQ0DikT+lGB+B1/zhsALglUtMibquPf3BAeoKHtLWy0Zr4Q/tMxu8dfsiJ9AzG0wrTwADky2ZoMi//3B3haZTrdkZN/ufzvZO3HHzpBuTn+FoGLAMIKpGpFckw2gBQTmFUg0r2iPpJ/8yMBNLAIgpfm+9pxcP68cG7n8/825/0v/m/iI+CzkiZClsXehmFu+v/uMdESGmyz/3sRybkWTy/+yOJat6xCeF/3hXAAUAgxSoMR1rgse3wpSYUzeR//9K23stAgWgDEIKR65Cdp2i5eBxA4ThRzELMRPavvaB/23v/hEWV6OLnSPMh23P17/4kPcoGoAuADkwABFXoDSdRp+1/GKqnDfBgfgAMAvRQ46ZjKlnD1hnaPFVaUorZN/9uBAHIC2UkSn1wxl7/gdxjwbFpe7PkWpH4zmXhlqmlx2H/3P/EjeAQQc9FJ8cQ1zACj2ox4sku7/7oErKtC6FxXRz/zDRrh/KD1Lo+n4/l8m57jPZuAesH5JCZMQTFO5TEAoyQQwhAl0js79eDDpfLKYZJMV++ihMfpbm3XP6RUHJNM7+fhFBRLLvdoehCtLgN5TiQ7hgC51YiEOeBuB+v8y//Gn+aCICwUJ/BFKRrN6Co/P27v/ceQn5zGH2u9euQCAwYbAgt5woiUHJLb/uq5ZpREY7/5nyz8PHDtl6Xn04DYIGmqHPiQ9YKOnmi3wzACUNFLTJqTRzn9Nt37b/qgyQVCo0bzhngtF59CaUTkAGRTKH1RmNLKuhgm46kJwPtTeHiGARqwKCjI2pvjRSr45ztrlpEAra2V0FajkV26PDAv/iRvhgkIADDRSaSSi9lK23CELhpTg+0tM2xL/vbIZHUwuIehrEI3FBqXCA3rFEV7iZ4sjcwKwQPOmZTy+aoLf73zJ5DkPipgwQYBDrCVjsdj3oEgxne36jDqEttfz1EJkxhOQ7mMQHwBxWEBxJe3UxOu5d/rCOzgnsttGuXgYh3SI0DSyXcvepcTacI6v9ccPWHQ57qCrFurfVPiEJqkNMOcSN8IAKi4GpMJ7+0TROf/3BganDGCtZVNt4oLYMPXgY3mpkrmScV/3SYr0/a/7AkBh8YmgmCurIZcs7f/++3AgDtEBB4zCdnzchj/AiASjGyocykC8xatHWAMO3KY1hBT/AwQYLAaO9kUNP+eks1BqlJP3/07CPXJ+9n0FOaH+k0RmZalj4kK/MSuQqCq1BKGNR7ACEzRbDEaoLbnlIMPQAgkL2xO5wZk0198MA/yDE6ZgDajL0//EtvZLLEa9j//iQrtdiVixisWeAMOq5ENFUJZsmZ4e/2mMjsKreJUxqNMSPl4XA6C/+X90vTUMwEOXCRhoW2VBhv4hb04hkPLoNBZG1HwPObe0n/Vi5ETQ/y7OPHniQr40iAEBng7kVmR2F3/3HgBqFqmog3iRrv9gDRiAAoIwgUEb4Hn+Y97/6k//aBfftEdg+U0aq+Yz2YMwy1XX/iQrImRBnQAAJABcXA1JhPf2iM/nIYBCY4A9TFcHoE1JKu84fcfiQz8wAWMgAhQlPH2yc0DgMIOEt5Bvwpm29j/walvkLp/xfCtASEY0yTImaBw4BozJDRG8qWmZ/vGS+SgeDKcNqv+f1NcN//jdP8SSABAoBhBNISItEm2t2QEMItIk0QYYf4PoPwQbDgAJgB8zAGLEJZ+yTgicwAExZlKyCpIdrTXMAAHOAAVoDXho0RkuYELgn9CWPEbmEDv+A4AouAAYL++N4QPH/+OAMWSkzAlDMVcvPf/A0aod6lG//53SLVjWJiCA1k0plvFTO32yWPY4kNQAKA1QoAOCM+iSELYXf/cAjYOiJOeqCuGv/+40ZADAQkCeQWYH4nn/cNgAlDRTVyJuq49/EFDBcjJh92URf/7/8dIblHxIJYYAECgGMJpCRNgk20CGHw6DEFKdldwwMbLGMKXgtJGQV1mgwExjZccysPymo+PDvwAEjCo/aVSWW2i3DAID5lkhspyCupZTdAdUtHZDjUCvqMAnHDrwtc6m0U5gAA5AACtAY8NmiN5FDxExyivppbwAGJwzAc1V+MMDO6r2yGR1EXiCUNYjWaKiYNgZJZDV/WxKRkxCGNjf/bKHEriVfIH6gdOc9+4AOrg17SGX//83yqef9+qDgdF+CDAAYVxTAU1kpGFhXdUAD0xz6Mrs/7+VhutWQJHOQf9MABEAnQOGsPIT3jpFUx4wEyhwxh9CWc9IrGAE5AbTUVCs92r4MQkoQ2wirGFrLM/+76AgoisZkGSLDO6pgGOJrCZNki22DOxc++SXjOFCxn+kivGZjRiG1Nm3pDamvrUvuv4kbD1OdDAFwAD88BF4wTbJ/5tK3M2NMSteTx/v/tZRAPHBrSY3zjjIAYCPAnkFmB2B1/wYAgIHZHkLtjEgmxieA/cFBdoi0up9mulnjmHYv/S6bGmbgB6ByoJYbUwCIfFyibQzW2Y4Gvls6x9/WFbAKbUpUx/2WE0tsGU6F39/mErlvzQZ68P8Ru3QNY+rXut6/w0KOjP5S0IS/khhwwAHmYwUb4Rrg14eQOv+AS6pechj3XWf3ANEBLWwIU4iiJLq/+0AQlieSK58SuY+dfwYb2qZPzrqFi2c/nz+d+CZ3lE3zDxBzjLn/+DCbSGfgAOuDEEq6jlwwM7qhwVxo7f/8AZtvovf4Y/townUx8wVT2ID4ADgTKQAGBOkYQJiNkDoDzH6Dxz17YnkSt/ifE439GYR8SGoADjAf0RiBMckI3XMNKRgBgFNBWIrrDrz/vB7BggZtgDB2lnf91AIQTc5HecPyYkb8ByQBjCaQkTaINtIezAIIIpGRJgk0035xNYADabaIkYfZOeo/IyEVuQ6FCe1SWAACYOA7Jw6NmiMBgFZOCZwyKmrL/NsbvynUo/tX4YHZP7owGhhXJy/1iQr9IUloLiRkFdZ3zIxs6Cq3noUtCibPI2Vxn5RfaXLSWnvDftSi27iHJQ5gJhtJwleJKqNOf/QeOf+J8TJhGEcSf1ElqgnOHesfzminDf1Fh/ghlfJvUCvAAAX1UGbYOgd4Y8MQxz1gEzzs1+v/56jM9Snr/n//whNhCNxF4QBJwA8hgOxIFBWFomlkcOHhEOcjwjqbleDQuJr/BHAAbjgt2TSGU2CnBx93/O97/NwAToBDiZyIME22r8AToBhRFYyJsE2muIC0ABMcbFdDFHIphpIfqHRcom0OttmEBjacE68A6ld9f4gL4AFAMexPqkteJVMoHf98QAXH4LSYVz9onNE9DSAAa5hCilOws6ZFtlL4AomTEVj8OUMOcGev/hAPwanlD2/hgAJMVFyyqS7WwW5UBMAAFwUywcHHRojAJ+b+knEghllOAbfAEATjZCW7cdXj9fCAucGIQ0k+RjwxOH9DAQtf914AoAAQBkpDAAVxPr0HtfOSRwFAYtc6bHBHecEpNx18gKK5DN7a/y8CQhm81FTQmDLTH89YQVhwhFYg9YEjEne//4g9fwCrpN3v/nmLAlU+frREuJzTNWavnqHsot6x5ygm7RfnElHvGiIc1tyf6/wX4AOh5+R0ES59qNdDsaCOXg+atHOIkcf9TGp1aR/z/iQ94QAAgD+EABvKjdA9vAl3jH25y8xBCLYU4MPHBfBUNKt5T2wPBF1a135tTdCDys6HDfm9IICxBMUBERSK5XV2B2kD3+TreiwanniH5Rb7SXf/tpUpktPw7AvB2wF1I2C+76AIYBjCaQkTYJNteSITJiGRhOQrg/6KAQwikZEmCTjQYMkCGGLAlFaTCK/k38A89jvWW7/HPiNJFj8SpI9pSfMMpk5dyfh7HibaaAF3ofSekytf4BCMhohRNS7WNTo+CnpaTE+f/sk3xRYL99V7gFA7QLJVhcW6kD0yQOw8RLXd9ELwDSUi2R0fVF8GoYveHyE/osT/mMNzJf2rijYaLWr3S4fWK/C8eAoeQuyrQsSHzZR3fEBTjAg+YjOz5qYx/oYAHsTO6J9n6P+ACCDXohMnXcGdE1KEAxmmUDSwzAWbGjkI/95Hs1LJr99dBesbaydSzak4kO+bAATr3CIo2xu/gQ+Ax3+1OzNCINNNf5MMGJfWknWc9/73AgD0EHgmAAjEiix9lU+mGyR0TFJcnvoyNYVnn3j/+TX1+H/iQtAUEJJK4PeuYLQMe/AkGiGgO+AOH+jV1tn4aPC/I6HD3+YhkhVR+/X8SHoSbcgEA0IF45guSaBgWsVYYfgANhwTaLtD6dJRNsfUVLS7eStyfNO63bOAgEEJryUkEPebhAdlwAAgC9qqAAMAJqMML2gWz0jE+KSQqfhmMmm4ud3HJEhmpx8zMraQ+G/PRsQrTGwgeo2skvKle5arGAIrKs//9//1AReJD/jrd4AFtAA1DRrECbpOuf2wJbRABgYgCOrNDkLr/ngfNbAGmz5P9BKwZsbwAW8c+en+FcABIcdSOhihCbYaRDcAAO0AAjIAe+NG1MAOOspXUxBnWwx3hhWnHwIgGuukJUr756XDf/U1cXiQQYACBikM5dEuTBBdDnOgMSCEyc9El8Nc/dwAKAYtifTKW8SuZQO/7/MBiYJ/UnnxG5dE7/gwYU9h2a1sisAInS2VejXnka5v4kK9IBhyNotCVQaOdf9+ANeQAGBG/ExO2F1/mkAAGxjZcUykC8xqGAACgMA/B00PGiMCAPgZtC0byEjUrhmSIzK7wP/4kOwBiITJjGQg3KYjQId3P64oTJhtj+eQAWF0LSbTxxglHx3jAC4mhiTCefNkETf/8BECsGBJ0zKuXTUhb/Bhw9JgAY3Y4obe6cXPu+Gaa8CxPiodTr6/Ntj83dcg7A/4kPQAK4AGyKobrMobvlrJFT8PQZJdPV/e0YyOwqt4lTGq4chiClOwy4YFtlQCWHfeD1g+CfrALCgn2rrev929hB70FnQmH+1PuFmeYwZC2KG7W+A2kTFI1ml+wDHJ1G8vCgqTjX7gH4b5CExsS0z4/mQB2INcJjm75/aF1nD6h0fFoIBp/h/23XDXnJfd9Nh+C48JGTcJYdNZHv/PC/OA/yrAE4IK7KnMt7mj6jamez714ADE0MgDtReuAoK1tChHfW/no93W3P/7/AZcJDkZ1SLef+PiVowkTcA3WJd/q6iBELZJv38VDu2Cpj/h/gAdBCQYtOrLJziPvgJgEcE9WsJp+aV14YCo6BTe7eaOnsvEZ2/KhH+r8BY4LAWaObrl5mWxLgIRvPRU3h9C2mv90MACyhv1719cnv8Nk+UYKJwTFBElMY+ETomYGiMNCcmMG0/9a962eWyIfGv//1aPVC2xL/d+gkWbkSJZ4F43gS+pgCwC7A74HVZi0Rk18HtlbgPKuV6PnDn+sMAWLJ3ZDlEday3SPezXv7f0sqwNjALghNDvqKhTfaX3km0nmsd/XAUGLZCZg9yZL0U5/4NLaDqIAd5vOErb//UH+2teXGTWuVjMiGiORmBx2hY19ZlOLz7hzkcEiY00d4kbDwETWsVfG1MDoHwXOHxX5bRAIYBFpkCgo2TT1IVg6FiE0Mr33A7hsGXVn7BsalVg4AaLr1p3UdTADmY3dSi6l+rT9Vym4NcPDu8/xhRZytGiO3QAj8OyEuAeCI6YSwtPoSVg04WaIhjU6+UOJnq/IfhneenfVUTuHrvewbXDVF1qWnxufkEu4IwR7hTCH455FNP/7ljJPo651z//7RAvxAJMGDWH/QxjhFQvwYl6cBVpY4sWC7G3/vGAmUOFLPoQ3npNYxxBoFXDA2t56sg57CjYeFmulnP/emlukPrmSFVXHbDvAAG7IKc6wiX4+IxQBjNBaYA4tkjZd+g+zHrIce1h3IdvbajJEjb1lff7zRjwnxZ3iQ7AA6bMi4PYZNdDd/AToiACAzwI4oyOwu/+AShIwAOFn5TuqWwId+4SFk0REJEIn/AJ8Ny8KTqxe9r70gzIziimosxw/v/P39hkfGfoO8+miBC39tId2I9+9pgQl5bXuXiObvKB6puBbvdu+4D02wELRxJiaDM2/VbBSZAUu+ykVuKkW3/1sMfQ6v8SFYEAOjAjBjk50e1Oe4AYOny10paQRYtLHcwpFfMvafz/7yQ+LlF2h1vkwjgnAlCYS32ikkVm/uHmzMP1VKvrgDGopcyIR1FWzb3/3IP1gCAIRpVEy+kW/46bRVDi/lUnN9+iRNB0vxl//v//4kbYbXSzsAySKlz6hJq3/7xB7uYpGUhVQVEAAB/gAGhQCWYDybwBEKiZRE++2SW8PzHU5VUxBHWwpwYYC4DTggYy//GdEFC//dMwMdonMck010U88gGuDBbLn44xwkqXD0Qw93QyX+QZjp7zloRk55kV+q8FxnibWrT34GnHQ9n3//3/xvgAJCVBZTRWtsg+CvXIArxXLbjvI9AWnMonsNxxrtAAsAoQEBZIhowbkPH7/dw87QjQgDKUcV+BGPIqsT5nP3/ay0O82m5fLxwLaYvIsQCGtdaeRrhHoCLtSfMDk51iaDYM6GE+YiEz/1ZTRupFL/46iv1c6auJ8QHOH4uJUsPgQgotHz/xEViA19YdEqya5tsop/AAdYCQZpfuKBI1mpB+MXZCspSCkU0wkai8MWhxn5413XDkb/AMAPMzADAVwF9VWHIHX/OJABYNNsXJ3lDnv4CrdNwACvbcShfu9Yk9f4GdhOvJ/iQ/DBkAO/+MzACblOOxznpWQKe0l7Z/Hb/GRCm+5eHyxwAKacjLYuiqGYQVXtO7v5e8xv1OdyhfavwHUF6remV/XgQNuqm/PBcvc+aL//+N+BKIMINd5XLRwTzTL/DQLoHk4txrD1Ef94TLSiIbeK1MuUHafomp6c4DEd7/qIw6BLbH+LZY6UAAXsgOtDTuTf+rfs2p/UwAvxSvGTz2088fz+n/oNUIKrE0Q09TW7cnAMDWgrRrdrXn9Najs/USOVkzdbowVxeWW73T/jYYSuT5/Bbeqsdt8LE1/4AHQ0ncZJAmiiPIAsQAIIqbJLH3qhBz/phXOcL4AEAAQBQ7HLE+/7NEDN9GuQXOAwp2NrZXyopmG+kP+HYWObyfFsf/+0DTS2muyylmNar2/7NU5B7ixSIt//5CY8+qGX/uQNJFP65C8EHwwAGshkVTHYg/LUgNtqcdc3vJpB07czGEIWAlgA+IIF1hW8XpISl+oASbQhRsJS5yVvZ7zGQaSZYFz0djZLKh+C1kGdLmv1wHtlGau/799w8GFz/D8AHQALi8GpMJ7+0Tj857JNQBAxucZKsprLBhpHhn5cQnqPAASMwiMpxdQ5DW9YgzBzRVy7hlx43a8MnZrVrU+McTlD67E3HuK8IOCOHFW5Ua39+s5E3f7cDsjh/o1/f1jwy+oQBDKed4cgAJF7AAEAUAwqMJeb+yx4wJlDhjD/pZ3smoYbA9H+O6ITe50/Ii6+BvfwA/zy0rXv+HYCIV2fvfaMFxPUajA3zTbHff/bICGFSjIkwSaaAjD8cjfonT18DHyQAIqog6aNsVro/RM4jlCyp2bi/oXxwPs3M4Lf/43/gAUCUcLccxSfk2W3tpi1cAQIfhllNRr/gATs3Qn/IiZKHpM/r2D/RmAB7YC8wiTNW8xlHw/qgQGUZ4RhFLT6NR//rB3FdV0RJv/nwFwADwEMCGZR35MvU5wY41hU0ZDanhbQ5PIvh4FhQkFm9T3K4/vLr8v+HIyTQA4JnIADAnSMCondA6f6j4tGAIBSAI7Fdkche/8v/AGABZVExdf+7Kao0i8IgvgAzBcLVncWEbRwbIOCADAIVDwAFgLG1MCAOQeD8YlCC7PGFu1MEcT/qsIp8Dnybuv3+8NCq4H4WgDj7cqqYgR1qMcH4wEnBQph/0M56RUMB6MIGyrG192bFNveBwIUpKPUaTnkPz7xrZW7a8Z+K7rrvv+//iuuXiQtVCSQgAVB+g+pGwX7nN4AyITJjCYgjlMUGUXBL4a5iH2OHL/EhaQY2Ax9KDtTg/OgJJb1j84+ISS09+T482fd8kwuJqc+jci4kK4ACIAEgthqTaePNEo+OnD/iBlMMpJpaWHONJZxgBcSwpJpPKDJRE7//BjaiJg4P4Odmq3//sFDz/3SxN+gt2h7RXz/UDaiZZv5v4kK4AD8N0uZUlWL9BgeUBXQC6gYrvH3wEsADZFcIjSqG94X4gntMZHYVW8Shj1GUW1Vx2fUHNQpZmi7pUPEBDfCo5Yp7fPf/VhtlGKx58SN+NK7DPSAbiRKWpbJPr0u/tOgxBCm8uGBjZY/weQEZV1IwX4fv60YAIq9w3UbIvfQCAKUQOPmJzw+cqLf7QGO/2pucEQaaY/ngAIZljCqX/f3axMOAAAsDGxgNDcLtN5G9fn+2AkGcQ6e43zzGe0APC8fhFGc8rBSEdxnEhQSp//KWY70fEMv/95Grgqvf/85AostubPX6PY2iuNNEDxI3bFqFSw6CSWOYcxf55nyf/vI1w1ognWa85//+tQIgTKKcY5194EghHJW9DEGmi/o+ZAqFTxkeqSYarQnfpUTp3Vv4DHYwSJQWPCk/XfeD5gKwQEnzMK5fNSFv9oI6WK+zKloAlGYnQ5lIPyloBgF21OwN8F+Bbxs12OWN97eYOg1TD8NOJ8FnmojM/95Fwi6XR+6aBkPq4rh/xtwAsZFdXjzCS/G/v5Dw63wifC9ACiDG29xS/Sh/K+TKCWWI9FBGZnFqs/LbLHf3M6DrkXX/tAHGmMco2X/KxqfIdNjHULNCJK1o4QwCsWBQVaG1NpgATLlDos+hW/HjM0NV6TJe0svy6ffr+45MNdEij5G//sN8yAAEDOUAAQAAVEdf/8IDdRGP2RqP/sHBV59r1T/+yuqfT0yhg8xc7+/s/xI3eXnZX73eE4LbrxFEPh+6Qgqoop5AAeod4KvyalnFbOh+IZ6OGiF8U1mCz3BTpsTtFyaor/UNLOJwZ/nD4fBDNPXPClGVUnQIPRsAJQ2UtYm6bj39i0FD+ILFsmTKGs69/zaP5Wktuo6yiKWdFw2NDaDelPvxI3xAAFmAiDhfcMtS+V9yjQYRht0v3mFf7R9hVlh4ub7wNcmOLmQz6O7YZVe4cEuidQ/GWU9gAAsCF0DQ27NEYYynYWPvCUh4Q5LYMg4hFJSqVN7YJAww0tZjYDo0Ur3kkyJlA3evGsGQsP8NKUXkDuuZqPGRAouJGwAEQAXHwNSYRyi0Riie8MDTjhjBW8qm28SGPUFRMoiffbJLeH5nkwGcpGEd6jCI55rM+xsZoDwJeY63K7mYYi1FODGwxAASYVFyyqS62wWQRB7gABcFkzQcGnRvxgE/bbUlxQYsaiqSYjIHN5Ew5ek/3xgUelt3lHOPoW+/1/EjfBSFJaCLKR5PF/1dLn/b/5N9/71gwGBIVEVvpfjfVbP3wDgS57Q8hMW0e/8H7AAR0AM4Xr8vvXYse6cMof+0Y2VDmUg/KWiGKRsHs12SbZ/3DcG3lkoEG59R7/Yf8SHfAKagyWi2kMsk6Hf+GlmF/ixrmCoANB98aru7LwMB9hgof6wGHSqFEPYcUGDBQ9vw9ZJCP/wVrkhnKFCWG7vVd/lOh+ayf317A2w5PIgLxsPxWMBaGAR6wKCjI2psAR8rwELDIXiWfLrP8AwY/PADUPVQ1UH8WNfBC8CWYABR3tWsWN5iKaHoCEklMHkrktAx794P4MdIBkP6Cd/+cnWcxJ4V6KVmpH9SiLjeRd7j88p/zC4+7uAqu1K7X+GYCAA+dQDliEL+YJQROhhxQ3cGpSUkeH8XwvwAHXDMBTVSkYYF91Tq16Ojjk0xsraBKDpLIav7SQIdlRSXSZ3f8AyB4UEnjcpXcO0Gd9oCGdzEVFiZsss/wVNAf2+Q2phEOdCtuXgpRY/KLsP9f56n9bXw/+HOAA4ENRz8C45RI2MfOOECBaHLMdhUSw4icfhLv2ERqAWcPxZCNXb/8McsiGAWQwHUkCgq2NqawIBbQzAUtE+KMDOqx7yGzuMukEoexAlrIY1Ko/1Z8c3B7Re85S6zunW431/wvAiByCB5wxGd3Tcxb/cAhG81FTeCYMtMf7WSMiUawyaye7+5MADdEcL1FWK38AikIYWtqGHDIvor8xqru4qb8lLWpBAIvGSn5OqDfR0kYR///u3WUOHKSExNIo40buJJAUYGboqt0bRi6QXJf/vQVYGpF87TBGiUQ/EPKpHQxRn6o0jwQQQLEHgN4IYAJ4AgousiTBNtq/AAeBMpAAQF4RKid0Dz/PQ1cCps0mdI0Q0QAZyAY4qciLRNpj/g+bGCbVDZf7JqfPgwpMaKBP5yH72ZJtsvzgTZild9myd13E8V6e/vP8PQAcQ8YF/o2Rx2WDDBqprvqf1dYAlUoAMCd/JiF0Lv/OAxaKRMHOVJXjXf/f/ygEFEzhAgwTbaLw6PtmAzzQVbVIQhEedjtf3VgTSLnZvFdv3tB16iIRpFj+8JgcaEiH2pV9PUclg7JFXf4YWGiTc1KT3+w9LVwPOFfG+oACoDglaiSG22kuvbQG1BtZP0azvbhLoC8AQf0ldYTL+kGleKh4gflBMSNgtq9VieaZTv7duhcCLTFrrzamBUvxvaVbi2uAHaL067teOMYDuSrG0WR8hdIgFW+N8f8b/MmsjRi6ssNMYFxgg3ggGH+AA+ByCAk4YjXLpmo1/gAKgQ1CP0J7+RsY+c/3oCHsR6hKOPkrGEDnARPCjR/8wT1T3/6z/M1xUf77xCaWi1Gf9VUXHpe8b/VY+mCEFLoX3yMidG+TTh+e91lCkOyPD/+HPAAdcGYCmqlIwwL7rBb+FJgI2t6g/xIIYAgiAIpAFBRsbUwBUSAIIIpGRJgk014feJjcT4nxPiQ1AEIYBGrAwLNDamAHIeE2iZU3HSY3/EOPyPhEsfKjXL4NffYh0SlV/w3AAtIAFgS7YsRdRxz+3gSDFopUnEKkpI1/93roIBha973/r/8SuHifEhXAXIMTaLlD6dJT++IedSOhijP1hroACiDyXL1prbyQVEyipS23SW/jfA2CG0qzVnEf71SRIhZGyMkXA2vDOktMhvf/wL+JDXmHhQhtq9J/TYZIbxANsHC2X/wzjJJQsGGK0hlLU2Nqf/+J+4egdv3hGEeF7PAAYuGILV1PLhgX5VdMxOmgag6SyGr+gZA4KHnjMpXcOyGd9Bh1cfAwQKsdUHvTjzy4k9e3v2ff1/8/nXO8CpAAAZjUGbgOgd4Q8IHrh2K5fhj1hCsQevHO/iLwwe8JcPn4DtP3v/f78bhC8QGPLFA0SwLci1MCbk3e+k+zf5vABQdg3NPkghbnEhuAFgNo/tNJJb77w64A5U5959q/4egAJDjqRcIlz7YaQwAAboABGANIjRojB+ArHB120VBQxVEhD+9Og9UeOzxLoEO7mo2sEwYbY/mjCWiJAE/pCYymff97/GgG6gh80AW2Ku2kNLDOY13nUSZao3FnLHMd5Sa0OLiBdLAAY2QRFFXqCENWj90xii1tQy6aGdlQfEBfAAtjD1lDae5NqfXoDcQEOIrGZBkm0zoYADSBVs6Sm0eRIqhTAE3IACAnXyYjZA6/wJU2AcYyZT379TYdUmbFht/hj6SAA1BS0FxIyC+s6AEAkAI1AFhRqbU2gYuAi61a982pgZ33v23tg/tbWqQuXhgEkJeucXj+EA3AAsEM/moq6EwZaY/n/WABqmUL1GWK78NclrWvJ//wxAASMKi5ZULdbYLcwAAXBTNBwacGiN4xVsVlOw5ELKb7AAEAQkKUACkEpVQMaRNgJxwe7LrmU2CnB199/6hrN8ni4AlQyIZzo7zjIPpN12fxIb4CghKJVBxKIgrhr/4PDASB56P+d+2mrvWIPx4AxqXRvXPyng6OJOPiD1/gClRx3efFYQ8QevAHG14zl/hyAAk2Jk5TqYbFtQwAAVBgHZOmx40Rv6AAyygleNgtzMAToIleTqaSwB6lffPqVDR0GYh43ef4WgANKIMEZNahBR0fgc6NgB8FrGqPw0WR/t4S+4AcHMUpFIiyu9gCGstMCf7Tw08//Z70Nn5hcQ/msQHQCkBLSMgpu5WwYCoA+OzwcTjQvztcpXeKH80N8ETT/v5hRQ31go/DGAAZjpPhBEXhTNoLNVQddpfP/v6YBmwNBmMCA4mSwXbo2030AIANRLNhISQt/U30BAT/Eehv61dYgdTaaW/tOVqIgEf6/f8PwAEoAoKlC9XimJKN0kZgAgFeD/JsjsTv/mgMSiEyIRxNOzrn7tAN1MABA7foFRG+F0/3FwkAuJf2S+F1zPg+EBmtAYa3a6L3Gm//BoD8gA+LoWqwlnzRCCJsGBgd7g+KFrlprVwLLQye7ufys5MSXpbfP/SR4k2WJ/vQSM6S0v9od8L+YMExMcBMwpwbtjhyaPnBxbxz1N+/5xTE89z+Zh2JrTf//xIXggNIgIAwWwQACYondkOUR1rLco+2p6GCOEzFq6vmMA/ZV/c/+NgAJkY2dDieh+KajnJAMFWyGEEqMMAwQZ43gDAedTsAAHOAAVoDyA4aIwAwu/IynIM+1mMogwAR/NTRNX8IJ0BVcmvS96wZaiL9/zh+goJ6tMnGsg3/aHN0F4L4h1H8+ZMZ/N/AEIq6Mdjam6AgwAKLRbRQAhE64WtR1R/v5w4hqr+W+n/5F7H3pvNzbzpmF20+JDHNIABi4MQWrqOXDArqq9BnamcIvhckVvfsApEOYsjF58Oxn4YKWHmKKP368d3bEf5tA+xRfNjpzyVsiLwrD8g4/I6GKM/WGuhsAAHeAARgDSI0aI3KDH7i5Q63yUzuhgwEGo74LhyJ/uUv++QW1C89P97iq1JVV/nilKNNw+cfKazMfv17xwTX4c4AF6TNLp5rvAQB2jBxwzKtnzdBj/AfN4AOpGLrFTK33+F+AAmiMa4hmKL6lJYAAKA4D7HDQ6aI2sFdYD7wyK+8JwETXqVuG1Nda9DxDAI1IFBRsbUwjFCVh9/OmONj4gwwpHC2lGhn2/wtwBkyGiFMpQnqWkPbB20FxA2K+sa8E69d+EIlKqu5al4vhjAAn0AhxNYSJME22N0YQe8sXP/KMU49+6AY4isZEWCLTQeDMABFKYgAe4YJcb+hAABzgAO0BpAaNEYDlGgJB667duncNvAFOSx+5PH/Z4OwvRaqu/f4IIIg8hAFcgCwq1Nqb+AKF3UjOUgz7aU4OAAzFRc0ikuttGuQ/MVJioovPIppT1G46lHz8Bv1mtP9cMPqLep8SHoYADUzCdDiWotTmqh8OQYghTsMuGBjhYDDAASABILoWkynjzBKKB36AxLEeuThn5CxdE5DMXAGbs+UZnoZBvVruv8bDvIMJA+CBK4aPXDMPaWC2WsCxZH/39wx4aAC4eLlST+KGO/+4DGd701EYdAltj/ag3IAYCCdsbKk+CG/3JAATrmC/RsitduQ1Z9Ak2GzU9uBgQfpsRGUVeoIU9quFMYolTUsumBfRUVBnEH3oLfIU7K4vrKtliQRbfe+6n31klYQ8h1+NhmR2ZNf/7WOAEtHIa2mLU2cXMoNKrOn4/IHcOADhwaUlKJETVnF2zgYYDC9xY/i7Q/8C4TD49UyhK3HkcQKlOAnh+KNLCd67/OQ7b2z/euzml4QK7tEQ6aWucvr3rVr0TXv1EP2SRJ/fw7IIjpuj/aOS3fOT8b2EAAiGURivLLSwR5NXwT4usAVD/7uwffn8fAmFsw/yg2VHM4HZLJZXm/vveRiK4i84lD3I+NGUYqpvOvKwHoY46yEHMK9pgPCgk4ZlK7h2QvvuWEHdJg+fS1fNQ97ZsMdpbdWPRfVR0CEZjOqLEzbZX/lICuBs4YtrG94GVLsVvhWm0fbCWYDItXS2/o0CCkda/c1rPZuMHVDJfuSfEh3+r8dQQAHk5PWf0hdm1gxPajXEL82gBYDdQUMZe/HOeklS3iAbIChrL6cM46QUMRrLpHn/e1vdf+vgZmvp7vt7blMbU6IqSVV//7w/8SNhh6Q/UIr7tsv+wAiHSg4NTJL35KRroiAA8AOCehGs1j0mmXEmMKJe1OZModWIcNkvAIChiTcIp8i4bpEjkTnWPEunx/kcAHYnVEKxedqZBuq3EBZyOVHY/zwMC8SwYTLl5eqWemVGvXQPRrfPOz/3XnPU66ffxI3Va3aLb/9mPV4/DvgzhXPGso+hjsEkv/ucEWy1E7at//gMjRE+C2HTXQ3fwEcADZO4brMofvlgkkADUBcokzzH728yMZHYVV8SpjVeMDXhwxl5GOc9IKlvEA0wcLZf/DOtklCwYI9tQXEi/iV798nHDe5UDMirYcAIAhMPok2y+pFkXYrMYGFpV9HRFze/00dCjCId/7supsbU9SMzYORY1j/xQifYYTxfGwYC6zRUSDUFSW9r/g2wfx75PjTl+VcmQY/OlbNfRJH4NPPFQAchiJtsvfGxRDcIA8CV6PYuJtJjJBLlVMz53/f20aeLvi593/B0YAhgDnXWGcOjXBnORZwAAvQczQcGnB2IwSFrm6ZGFqm876DZW6cfYoFZBZyK+F944oGe1mf9v/h+4AAXoKZYMDTg7EYBLHBdsmkMptFOASKwjy+KmmviFHxmQ7ik00t4fXKZnoLO6AE4cH2y6Q6l0U6yZ0tvUf89xqgxHmWjS1Hlf6wIoUdWUEFU4LF963xuuMre+usjNBt2xv0Gxpl0kBqd/f8PwHaR2Z8Y75TSfon/bV5ICN0nv7//IiKpGwWXl+JD0AKiVnynr7Al3im9rf/gKgKjB503LrYk8P3+5gAAoDAPwdNDxojAK0QAbnwyZLAm+U//96bhCCldxw4bFt1OkEOySgiPi0vtTd1DRk+C2GRXQ3/wCgh2Ib2xVHwIbY/3s7OAFLBOpevdyTwYYYNo2dcK7GmQFPyYtOW//+oGgHvpy5G7/EjYYAFpgBoGumoO8sa9/YMBJookIkmmQ8ySfKGnDiXpTiTKHWHg9nAOYQlTNagn0CpVDoKZrzGlBkM8ULz9xdH3RV7/0bxN8veB18DcXy61BpCl6292QlB5W3HxfPrYT/hucYwAKAdogccMynh83IY/wYG5pinxaPp2KtzQe9nZEUxLuP5U90/X+JisSflwiaHYFMkp+/8TJiQ/AA+Azh0I5hjtSW/PhA5t+/PAEExQ7iaYuzyBMqlAUPAAsMZ3tTVUIk22x/IARjd+r/++BAHaICDxuU8OnaC3+wwI4f0awpmeS/PlByMc9+k/9UCC6BgA/JqyG0X//l/jfije8IsYDoeIQ0gAEzqgb7NwXrxxbEKo1k8PSaXUekRBMgyqQQpjEArY1p8eWkYAMEHzlEiWPLvfCE2gjKQUhzFT5uvHPSDhY+Tgv+/QV/A+3zeG6lxpY9AKXxRBLOo5IGhfdU8zQ2KojcQSh6kCLSFXNCSEr9+rCTf7iifvyokvPnnBntxR7r/7MmhIhkHXwxoKMhsAZPX1+mAIgqBsZzKU9bu1+mNDVlAB2p2TApuJR/+AQdD7j4AQcemYsH/BB4AFgFQupxQqzc4Lrd/71CQBH+7/3AA2mOwzHKQn2CgBnesPNI7H/v4M4TroUvxnbcd+6VWNe5LTF0vr9/L/Du23K7And/ACZForPeqDXvoy7/M3i4xrwZ78g+XfsrZ/n/99jZVSf+7pH8/bb/+sP/EhiAMiLWvG/3fC9aTcfeg/26wNYoADYg1dEZu1OUwL2CMpTvIj+WLowg2YQAQLwACmGvRl+id8CLuNbFK9+/w/8TETlId247jGsBGH8pqAMRC7QZ6xPsAJlMADAnSMConY6/3vII4i3IEoZRWRU/3iR4eEyt1KIsAIBlhAsyLWjWH/rFAYHA/1WHG6ACTuIxXklpcK8in4M53CUIbICIbnPG1MYVd2/rYz4xnQ1kB/D/AASZkIiittDkParhTGKLU1C7pgX0VOWABMuKFRZeCu+aJk/DMQDocJS/bWbBSRk62fULvKVkeSvFLm/fAJ0AxxE4yJsEWmg9GGDXlD4f/JqPHgFtBiC1dRy4YGd1QS0jgtQwWsMzFmfz98Aja0Ptfd//7pQI/SHnxvLwWwAtFe5GZt3+/i/mZDZ3GXiCVPYgPXwrDAARMANA15D0SdpY16Hw0yAM4CJhQ1ZdLz5gAEyqgb7NofrnD8YopXcbtmhjVU9JEERhGYghTGKC83gQG00U/ZZ1/xmJP7TgDcmtxx894S6+vEnr+AM19fd0/4WgAXgOCAk4YnXLpuotvgJCEbzeyaPoSwt/AJwkRNQlhk1kd39pgAaojhUUZYzfQCaICoAKBEuT+DrK/fvM2YyuKu0kpa1IEsMEvKHy/+DU+PB9AD1DqJxPvvf6N2R4ql//6v/iRsABkYTpjib7vYvwQ6AdtBc4avyxf3kAiYACBhG8wap+uEfe77uAABcLIzEWFWcHAi//+4AQxU+SlJr0rPaSWSDfjAFhsCPMp66yTikcD8B5IBUEi3Id4kdsaVvixqYMAF84AgqlWglbjyha0AVMbrP+wkOWmWzf9+g8GXxprq/98pMsyIDCRe/jBUgeKElXvG4CgEMVsZJYuCO4NNf+AFhbKchHcxFcVUhXBb14OO98LA7KBKSNUxnv7SAAn+YL9FyK10wm9uYmkrf69ZCKyiLryErYnVyfT6Tz0AB/AJhGtnEB49Kz9gIShH5E47+RsYRPcgELYhCRLXyFiyBr/ZELQnesV37vBhwlvQdQMkW79DfTm+22vnyUN4nomxg/8SHYYAHsAoObyJkCA7K4fnwyCCHb/f1Ufv6DBXQQHAFgAFAUB9jhodNEYBEYitjiat3sWsPBE1qlbxtTZYO+gtcNV1Z7fDU+ExrJJ8toyD84v/cG0hC3OLiPvnK57Z3iZSrTgweviQ9AB0whNmtSr0oZ6GSbxwz1A9AlB+JPw+9P44jDfYStevFJAEyEC/F6xCVIbPVgi+/9f87Z21xomgH94zEEdZK3/8QAAavfeQ+5QE3B3eOfzsLB2WHy3/EjdQJqp1dGf11NkVdA4Ilod0AIQRmuJHo1zuzvNKaCpCEAvN14n2fP95RAFv3EV3rb6w0BAYc2E5J8/3/12LY/N7rkT9zwygAIeYsDpxMx/NtZt34Pf+YHul2K6b6BS+fnuX8SNiVqMZu6AGDBVO+iGUJ3V3BIBzuXH79HEGZjHAUCFJKOOdn/3rkHKjx2eJeAhVSSq7ffg/B23/7xgAiBS8LSK5+nnYqDAAQXxDLCEK7HyXnMi8R+0AOTMJ0FVfEqY1WjhmAxi48YYGNliLYhgAdB14R+ZhyaYU8P2goLsFSl1PktwFiNwSjFOntFk/geI/G/MlP2w0h/W2kbH/LjR09fxI36Aa1QABAHdGZQ4XplaUmRGZCq7X9BgMAVELWqiR+vukRAZWBPaRRJKn/6wG6kABgRtAqJ3uv/+7lBg+7Qqn9UZj74bbqghMwr126Xt7wfIAlB4NojEtBQ/YwwMBeMZx11mNWnkOxQYZkgKHrsw8vU/trIrC3RGdP92BG2YTyt9W+WgTWjfVMO49HZ3UvxIXgte3SL3bfSPeV29/WAIRDh3F8xdi0GZTITkN7cO/oGBAS4U4S7aaxoZtUf8MaH80BtjAmV9RdlkOVPbyZf9+KW5dxWAY3C6K81GCtbXjej8IsBVF/xHkfkZ9Wn/oPGp/wHBV5yHazJXTf3WGlaQNARBhDX/B+gAGRQCvFb9PztGanwQUAHAFT4DiFMOXqRdFbDCwE6GABwTlEoJ2PP/+76yE6KY6FG9ak+GBo1mW7zeZt/btwDEp9Lu8tjNd2w//iRu2g8adq5W9fgBIInH21nTY146w8H4IFIrbMObigEkwSjxxh7JwWwqrKG29dHoAJyIA4eL2WzK3U6x/gwQPiiJ44kF/fv3iA4UBBrUo22vpdLuTAAn6uERRtjd/g9AYrfam7o6BTTH88B1CjgPr2VHf8DMCygka+/cVgF8e5b2OU+yJC+pSCzDidT8SHYAHgyocACgjaBISrjc/4AoJsHgYsR1mQYLvdPAToyADAzwJ4owOxOv+WIrr3qP9/oEMAB34YopfcbumBbdU8PIEDLgzuDHEdIKYs6vSHSD/Df25LIsNk6L3uH/EhX6iEzIIrEEIYxANh4AFAMaznaG5+SsZROf6DIAl8AA7mj7Vd/0oJucX5/4kK+YDPgZ+hWPkaGUDn+00YgUUiI2bcPYnX/A+GALYAJQ1VLUyf5owgGHCX6DyWFf41n34TJQo9w0R/4vEhfwAHmZgDA7gJ7Bdgcgdf8w9APwoAYPXzMiS5o7f5ww70gDyj3DRHVJneok9g4uD0W7l9/hbuGPyQAJA13LFyIqo88H4Bi0QqYOciJKSNfDDnSX8f/4kPSxX8ABIALj4FqMJ56wTmic8wAWGwKQZVx9knNA4GHgAIwNuGCmXfwxnRJIv4gGsDBrL3441okqXCnb5yE3KNc4DjstNH6f+JCv0AxtEeqThn5CxdE5xgwWwplj0qiuHcDj8CAQInAAJgFtPAAEAJG1MHgEIoUok0obU3+GOeLDohRxtTCSZnGY/u0DAeqL/D9wQwCNSBQUaG1MCH8ACgEPZzsCsfJWLeOf71sTJznUgyFtR5AB8WwtNhLPmCEETuMDsoNnjYMaypwAAuCAOvA6dGjamATicn5BcQShqkOBFpi155tTWgWkBt8Yt3OfwbsVyL16Aq/Wn94FrOGq9b+3hskEcgqO8+jjpr43K3IPgAJijKVEO4zrWW76w6JVlxz7ZBTw/gAMbCZOUX0O5q0Q3AACoMA7MD5scNqYBOQ2XmFxBPNYgCvrabh+/TRVSP/QYxThKy/a/4fsAAHKAAV4DSA0aIwAwu/IiioIfbSiGAACoIVYPDTk0RvNhQy8JXvhlFv8MMABMAOjYHJsJZ+2Vkie/IAPBcDVWVMfaJy8eDELWWGESitNHpdBRqnneQmW2SsVtW7hiHIl5bXiRvjAAEAoYw8wlqGAMSeQN/0AMO46177iptQ1dVg9Bsl0NX94AAxjRClFUpQVZrmRIHR0L7TZLJbgZQhgAIRVpBFtzE+jFJAV+MUQruN2zAtuoeRIhMgisQQhjFBh+CDSvQ9RXOLLEM+JxnL0j9XhstRiWLM/3WCx7oz2P8/zEbRMVaoCzbv//qCAgRACwNZyqw/CMHyPjwNHxsNCGoQUE7Yx9IYgT40Pecwyai/+AK8Qvc1PQxpC2+D9tjd1FXaSVtWnyYuLlkUl2totxiHwBgLZgk2IEeEsFMzVFuwPYWpoP8SAHR5vpKdSs9pkiVk+vkBvwijzExUTYLd3ST7+dryOhRNffKGXDzjPjaqb/PEdJqXbVrwwneo7NUYR8rhHp8AQwyacJSVvbuPXS64AAUBAHYgcOjptTaAhmczsixMWWWf54ZbD3BYBNv4P9+IL/9eH/7PBIumZHYdtj53/ysChNWyWLv//7LBoUGKeNEf+FcgIuY1s2inX2DB+MBKoYMYe9HGdE1S4dpCTIWGsNS/x8dr4cMzo/56+JWrho9f/nncn8cfwCQPby/9/iSY3E/DW1AAK8EWksvs+/c4byXM8bqv/+jNw+smtqUt6LHAB6m0p/wy/GwXzb8QFYwwwPcB4ADAt0AGAvGY1VOudMYAGHpl6a76LMOf/tueQ2XeVFYv/aJGHb5IQjr3+VkLiaAekgmcUcOX//Ek89AMj+JPX+PPuDZX8MwAOCVF/C2GxXR3f1oaHd+Vznpv/tgLAKUQEHzE52dNTGP9wGK32puZwRJppj/KFHDifDc33uCX/WJBLDLowfrwYkMwUfxIatKk12RjUr/P8wNYgTjZENqf/4nxPiQRQAHewxRC+45dMC26h6RCIyGMhAiGMQGH3hHwjGeXEhWAAkOPyKhnEfai2MAAG6AARwDXxo0Rg94gDmyY35mGdainBhxHaCYtTy6GBKYSGfr/Ewxw54ALQA9xSGItiVuLsuP/JhCDuAAABdSQZug6B3hg9eACtW1d///3/hg9cYVX+/f7/wwIXEL4QF8seABYEFL3rKIZJPnit/gIvxus23yJ3CHhDwgeuCVob+v3hBejcQevAE+S5uLn94QDfAAqDmEBJwxGd3Tcxj/cBDP5fZN0fQlhj/ACuACMNLdTJ//6S9cMcACxoQr94gRBbyPvAQA7RA44XhOzpuQt/v0wqLmkR7JXBZDAABUFM0HBp0aIwhNOADHk+ZlfQqvOISHr/BBAVoAJQ8TKkn8UMd/9xD8MGOF5owVFsVv/Bh4CceF2ya5mNopwMBYADQA+JgUq0lnrJOCJ7yAB4fA1NlLH2ickjgSpwh/bvA0w2Ug2p/xIf+ofFyibU622Y4MPhgAWEO3mImbEzYYZ/mBkFhQSfMTld41UX33lLhvj+B1NDw0L/iQQYAFgYknEaF7+QsXROP7+ScABGxFzEOrIM8xpIeiCBa2xU+am3Lr3QNcAZBvqd/uBgKJ4X5Gd09f4MICQGPQj9SUMffsZ8cDDw1I9zg0qkl6f793npK5gSMCtK+P5/iAX4AF6RACAzwI4syPwvf+QBBgiKaLUQ3fnu7R01FKHYiiwA8cVhC7mv1Q4+dSPjXONAl3R4gMdBgBYA0Jyz5IcvwAB2AAIAaIAjwKxffCr6Jz/VKAAEAM8EAoK0tF2nAi4pKc82ptRqZkZ6DURUMAgv6wAsaMsME2v6f8NwEsjE7iLxBKGsUH6WA5oQo6SEGMIBDX/GUPSWEPCEViDy3S8FX9YgEGABeiIAIDPAjizI7C9/4wWANGMABQRpAoJ2wPP8AAsIZ/N7LoTBthj+eArzDfIVVmSb+DGAYw6MwNFfwDSZAzDOUBA9NPcUElPL8/8SHe3vZ7Ntt97QoPuESl0Pst2gCGbsWJ7ODMmmt/g3AACwObUA4NujamARDotUTaHW2zHbIg9oV4COLbGxmojX7iskWW0PyKGvSPXzNo1LVfxIYxgTIAFuADUEq1IPSUNe/tpgkSmGhDKqc95wfgpggghSM2/u//ziqcN/QDaMR5ZZP3tS7PsaTf9fGi/V/4kMacAC/BNIuKV6jd/erFZhffIv+yn3GfqpC0qq6xsruP98/+GKCoEAAhARWqePvvfaMoaW9FAGdQI6dWgbEhgGgnxAAcE5RKCN0Lr/BAKrJSnO7BUGW0g1934RvZ3WfvdRzh3d9Lt/hXA3WAAcoEUlh+of+emRnXZ/rm19/LohgJwMTHkwMS/2FOP6D76S1woH1iqLuZURTdrwrwAEYG/DhjLyMd56SXLQ/EA2QFDWX0Yb10goYDBBxFpC28uaL/0K2HffX/RzSsKHbnfYKRVfN/gggANQLBf4rfVTZLIwA3UgAEBGUCYnbC6/wP+AAhmTFCsZuo5OtR8gO0QEHjMq4fM0Fv9wCFglcHEImDUjXvwhOnK3FvmEzKI0+Vgvvv49TTwU0xcHrOb+GPgBKhAAcE7RJCd0Lr/MpaYA9tKJtsiP3oBCNGSa88bEBI1GhwtT+/W6cBL//mGJP5qv/f+JC/2lmpedc41wh4ADgwjkkpzKyCCzTP/2kK3kQvmfb/6Aq0N56B7Yj+Z+/chNRnrDK1JIj7Vf6HJ8RwTX+H/JAwfboZRFCTNdfB9ezp7iJF8GGwGCm+6T4//3wAuGQgHVJhcSkY2Q//fvIbLzHQg/LYgMCFoSRJCkSfv9/kUsH7dH9/n/8+XGiqAr3Tvb+JC9jh5Dt9jHUNJaoB1mHLTPzZUUYANvSx9ZFhx2L4Z42cP/47avn/vfRT/4vhrAASaAOblIMspBryvtGNnQVWoJU5apYRaPXpkSsV8SHusmdvQ8BkmUdX9/rkMQQpuGXDAtssDgCEMAjUgUEmhtTfgANhwS6Jnmwyym/IcfkVDOM+1FuBakUEhXty/6g9CKf+N9BSLlCA8ACwEJQj9CefkbFkTj+DY+AnHvVOYz+a0s7aASoQAHBO0YkhGyN0/6AuADwmhSbaWOMkvHf/7wwgy/JQdaxtTBjrd9LvggAj/Su2b16Z062+/iQ1ABbBowflS3TlLwPUcwfJUb+t8CZgBoGmloO8sa5/ZQRApK4yD2++v//iRsYQOvWZ+9y2AegxLGStS3OO0eJZnZdAfgAImAHg21C0Sd5YtwABwVFQWsg+iogZd3gwwA7q94dj3//OMelTOiL9w1BFJFnOqnihNBo61dWhle+vbVsDvmXTj/KQlpmSgn+/f8SHsbAAEA+QAAQBgB40G95qLWRmjSX9OLgww4DNpcoffnAApwB7uQTyONeV6A33Fv+JPaY2dhVbxKGNV6UhCKMVCBiTSygYYgtMKV5syu1nmE5JldJ94P/8P/tg27/6OhJDwcWAZCn+Vn7/QAtMmwi9HLu//v5Ny3hoJvvAUGLJCZPIXMm+MIfvAhYoL/Rsjj8tFljWgQrnL9BfD1Czbn+tbzNjvL49eDo+sKRb1jcnqJiA1EWBpXJpd3/0QqUyxFW+3f43gAXDpF2+X6pgAggF3SAbXvKbUPw8egAJIZOriZ+vcapwNc2GCbmCad3RiPvm4G4C+o48mlGSEqf/5qJbhx16DM5kFrIiV/ff+XXpHac2kRaJz/fMdUOndNwgEqBw1h5DOtkVTX/AMoNuEsS7TZg4nkQaWT//uN61/osr0A0JV30Rfv8bDTCx/1LAnOgvLDVl0Gmw2KiWeGgAlDxcqSegoU7/7cHMw4coVP/6BgQYAGWAgomcJEGCLbTxgJuHCliKEs56TWMcQaB2woNrmerJPex+WzCzCKx//uC2uL3ai4dz/eAgEAEtGlnmU+Fn64Hm1AB2lDcFY2szaqX++SlQ5a3v3zSJUN/Yvlf+/iRsGGAFi6L6FsLmuju/tdg96f7q1/WkYhvfCH06yHvvsTaXCCgWekl42ivBgG0PVly61L/0cLZVKWOd8CxazHqrap+q3BayJV3upIapJ9Ku/oICaYQ4DQq4niRsQAAWBC6BobcmiMBBBCZRFpbbLLfwGBylaSp1v/f/jHW5XUzCEWopwIgQwZAAWvCFQajBaDCaj/f0fxFMfRO+RrYlbXfx04vwjjG1+GJMJ/1gZAw2U4opIRVL73jForon+17z8rFJdqq7RbljdrGYm14PwALpxjVbidqlcXxwsvGwDoNVzCZ5OsUuQCLqm1rI9eiwASHkIArEAWFWptTWgWkBtSMW3kr+1MRsMGAMMDTAeoKOGnhXPGB0//4GAuKnHUItC5FVZBPeQAeHwNTbSx1gnDxwYEHQEJYn1CefELlkTb+GkIoaB3Xa7T/9RQqMb/rQ5souzc1iYf+hEwpy9XFbtJGmLeFY18btnCQAOwB7BvY6N8TVlJwABDxBdrd5HoQ/0evRCUVM4QhrUYRCfVWX7M2/3VmQR0ueo6fRWIhRmkE6Me/ACeDKNdHuLYRflWh01Mgne49M0GxZ9oOWsB7xU+xx/790A0o2qF00vz0IO+Mxm2iB2EO2OSeK3/95FiE1dXFvv/iRV4i25//1yeK5pjxIVhgAWCHdzUXVCZMNsfwPODhAiBWCAk6ZhPLpiQx/gw4rSfkRUI47ebbX7q/4/hfgAIWFI2/xDf9T6UmdmazRWTBoDoLIYv7zZA22pU27XgRA7DgBQYZlLLx2Qz/tAhGczqjRM222f4awAyLXX/8oPCiUs6n//P2OH5fj4VoYAFAeOAw1ikcdXwql2H8AMELVBqlwuyxzULfcjQH6tPu37UOakR+//kHjBEEEEMyXUU+GIAQ8mp6P//uGa35c/v3hFeVuz9/Polmt8y//3fgCwDRwEOg8bZCuzCBkEAw3r8AUDsejRNzEf75kGOa9v8SN/8BNJ6DngKDUGuoJd7YJWo79/kwQnzXpV6UMSoABmyCZTn5AimtVd8/URkf/6vTAAmVFC9ZtDN8L6C1oPW//9gVmqdX//s808Xxdc7J9oCEZykVVn2JbZ/no/TAAZexDRZC0nx4TCOSPHxr047NWZFA8VLE///62ajNRkY774nHAaFYCVxIfxOZrw7xPwwaU5VE5zrYURnhZ+z778PxmEjeqRaZ0GID8AAwfwxr1Sz1GVZ7IyBAMABGQI586iITyn2oOdPqsf/NfIcT00u3v84dpyTOR3f6t75/8MQBlK5nCH/b0fgF37G3RgSCKLTIlcEILJI/bZKv+AdWfKSfpqzD71/h78JG+r2v48zbAboAEBbWFXVm3DdosCB/PA0Cp8vMVTSHf/wODAQdnqAAtwAahqtyD/KGuf20Nz0GMCswKEDDTV+DYxB7opj+xiTQsqGAWkvNrE911yuiKOrQRvC8OR7+a7+bweAFWrfT/54N5z7Jx/7s7gUutPXp/3jgkJZ8fan/xIemDb8/5B/0GcAB8DwmdTC3r1KCP4EuAEPQlGRSOPEblkDrkBDWJ9InnxK5hE//gQgbDm3Ov9vb2/f+s2tW41/+4GJzMbD5T/4fmLy0Bg/hgARVca0cmtV6+5v/7GGBI1MNCGVXP93v0CADSoGvnbIrBLvDP+vqCLMGjUcfyjGBZ+6vX/vjI60Einv8MQAGbEyc51INzWqcAAKgwDswOmx42ptkHLwbkj4Lay+cCLzFrzzamAS0GR+QXEE8tig+gCkkBt8dBbucGuwMPPYGwybvP+c0G/iZ/XDHOQgAeCZSAAwJ0iVEbIHn+YCgxZKXYlLcYq3ce/Bgb7gB7JY1ZAOiqsPsNthisSevBoXE1/En/0WCR4b+v4kOwAOtiFFKds6ZFtFO/ADJiKRDmVxksakBYSsq0LFh810d3PABOvcbqNsXvrTTIAYCPB/FGBuJ1/wCcAhuQnW616zDqBIPkClEBB0xOdnzFRb/aBit9v3dCJMMLfwEQYRU0ADvUXb25gX7CmkZ+uVFJnTZ59PKiRs4+f+JPyyRodjaKrHzsKDhu09z9/3RzzE6Wb//rZ4/DKSx4kbUABwCMOWXSXaoFXncv/AANkY1QxEKL6lfiPlqr1K/du/azyIuHsMiylu/gNmBCrrVTCvh/7u0Q2eOGTj1IWpuAhWc1FxVCYLMrf50yZiUD7YdICbjolkyhctpAIGmHoVReSODg1Mu/ILSYOIeuRAw4paANdkSsaKv1EoU2bMnfJVOHTNm78pXJrP/9+/+JDvpZC15fhKnv/7OJHJppbcwKjB503CE8vnJC3B+DvIgY8d62miozcr82AGoeshqIPQWNfwBshAAcEYQKCdsDz/NARqFTB5K4NQMe/cHj4hjlpaRqIJr/qOTYb1BELuc9V/aM//0ZlXf35h/8FQMwYeJG8NEsN8ZC/H89bO/q3uMMi4plIF5jUQHEAcesYq0H4c/GQYeIn3+T55Jv7EBXWA+8MT3g/8mjDvWfkAuBgICYHx+pKiJf5TL8wJRHd2Au+PAhXavcXT0ZvJ/+DdUrNgfbDvGi2aAlf6NVd98hPxV+1wj7K/p9/ORDm5dJH76f/Eh7qgOWK5sRKV/9Af8/SloJGXd+/8if7F9lh0gABALAwVFZXZFZ7wAQYCWpgZhn+Psn7oHKxqqjf+gQQp0+kh72j7QB4AW/D4H8kETMTMb/UsSJkgWOv+fP/1XWkhw2/0r7+Yxc0ZQpxI2oDU703W6z0vNwQCACQhXc1FxFCYNMsf5wZegMr2gsABIeVSOhiiE2w10gAB+8AAjpAa7AaboD8QTCDKbNsbxhQA+9P037yPNj/+e/9W8BqoLyNNAzAb4kboMCwB7EcPBHV8+v3ActhFxAHUWIScAEIOuyDiS85rWKMJ+UYCQYi2kydZP+6GsvRFIlWB6si+XEKz+fwwyFCvX2IhNI7ey0s5T0wEYeewakH5IdFqi751tkxwMIOCVIKrLA2TodfbpClEFqmf754RmwIttRFSSkyHelrrP+JCsABycCcHOQRSiNbZwPv+4gAM/Ca0EaiIxdwvv+PTswRcR4MxA84zX6Y54RyGHYkwlDRH0fdDd2p0B/n6EvNEAJdbFG07oAHonKx+Gq9k1uOPnnZdxbPP4kK+AgHGaL12RqoOx2q8f9oOc4CLAuVKEPCrTf/HtNMPgAHwhAj1lcfL9+kc/tNEQAgMSDtKMjsLv/gYAsAZmGTSyplwmjBI9BU2r1NzdPb6O9g4VxamWlX2gY0CCsp+JDsBQDXgLDiF6o1Yk/fuAhHuTqWJgJYKvMf4NPsDaFfPDttov1JWJYjlBdM12stfJsTaTVPgeA2I20Q/8wPTfI/33/xIVjF9AVoEGAA78YohfccumBjdUhht16qPSPw218/yA/qMK3W54lqnDGHkk/iQr9REJsIrOIQ5igw8ABgGNZztC4ZRIWM/OQxbfACLac5L93tgFxNfxIZ8AMWjn6GQx8jYz44DGJKLxvCovMX//vJjFroQLjH/i+HIAFQOYYPPGJzu+bqMf6yT00Bw4iD82mEjInGsMmsju/tGAA3RHCooyx3fhTwcLjFtbqu3g7plCKJ8r+wwxQcF+2/Pe+NWsfgNcaj3/+F7GYv4AGUgIKfsUOYIssP3QDCiKxkRYItMd8etIVygKxT+Fh6+f/ngzqJUZ6IbTn8bk/XS3YZQi0kc2FGKzo/DlrGMxHa2n3p+su71/v3xkr/c/ndtirVfk/+FcAJAY1nEaGwz8hYz84h6Q1IHaOjB9gqk137oXxqmnc0+S/futUlL7/3YP/8N2pzUTpj1GuReHNhRPvvFy4Xfcr/D0ABIxUXNKhLtfRbmAAC4OZYODTg0RgwBAAwRzFoJWt7NchTwE44Ldkwh1Ngpwb/X/tgBmyEinOpBuWtAAkInnhrBDU70+6iSjCu8v+2nj0ixpX39XDKejaRr09gXCVFFhdTtya6fllOGFoNIboXl9P+FuwAAVBgGXNmxw0RgB2QbKpjoQVDWI5yMfiNl/1//sQLSA3pGQW3mvZK5hCyGag4eZQJgwMJPcZ4DRD3f2mLgSq4/fqimze/t33RumTSl+/3/xuAAjhH7HF5GkEHtd0YQLuWNr/kmJceLQISj4jDNLo/hej//4MifiASYEC2H/SxjRNQzD4YF3BgMxTXliwXZ1/9+6AYURWMiLBNpryaAy2UHSarisI82YCLJAdBaeK0gdDDUQP7w92WZhRPiW6f//muPDRNwh+bCSjfMiZw3Gyi8M2HHXx59dGZ71+/38P/z3+HWfFRcv/4cgAWtDEFq6y4YGd1T/AJyGzqIvEFoe5QGTZ02DUHSWQ1f2iAAbIjBfsyhmuA1BL4wfwAc48yWBdf/7+CfzT43l6MxPifEhenGdb9wnL8Q2cL6mLABmgDkpSDLI415XHCRU9C0GQZRx/3mjMToKq+JQxqvTkMQQtuF3DAtwqDDAJYTcjWYop7qv/EgioMADAQDGE0hIm0SZaQYffC/XAA2B2YE3hsVt21AGaINlIdCjetX9JmYAYHIAnqrA5A6/4DXftqqAbEz9Snn8SFaMABscAvgtobDLMeH4hxeRcIlz7YW5wAAsCG1INDbk2pgEQqJlEWl9sk17AAB2gAEYA98aNEbzHW7vzEGIthjlwBRGVDIY28//DLNP4kKxokABbsESgiikpL8v6DAkeIcAg9iuE1VHXn/AQQQLl2Mn7k2Zd+D8gGyAoWyRRhnXSChgPoW4qWdNf240Isia97//+JEUTJkZEAIxVreFNkN3rn7ypbwRzEHDW392rj7yhYMPxsNFAA2B2QE1A+K28aAEJGGiFY2puANwJsIhWcbUwKApATOFRU1jNAQyIach0KMlqkw+vwIExcrLY00uDDr4sfAIIV9QFkp1pH8/+GuhQW62nsyGSv+vPIBERoD+UmRFEQE/mAhxFY1JNkWm/XTAYUTWEybZFtkTtHVXe/93A6e2qj9Yf/8OZ4a+At3Df1Aozob+f8SFuABYISCUQcSiCkDXf3fxsAJQ0UtMn+aMe/gw7hqPn7/ifEnrAGxJ7zj5//wyee/AQN87f/jPLwQw4iw+heiMSeoyX/J65//8I83gAtAD1FIV1u9rhMRB3AAAYjkGbwOgd4Q8IT4QhPCHhDwh4Q8QevDVF/+IPX4fdr1hCLwhWIPXhHufxAagAPpEAIDEg7kVmR2F3/3DwAah6xqoP40a//YA0QgAOCNIFBG2B5/nAISy1weWuYN4Y9+WALmw3YQcOVTxlU067z+IPMc+AhFJ8/Pu1X+DDj5t0gBAhAEegDQkzNqYABEYYEy6QNnPW4sMuCBqKte+bUwrb8GJ7SvmAagppP+zr/G9ggAEYAfGwMTYS39sjBM4gymPkADw+BqbKWEWickDgfQLQCFgT+hLHiNy3jb+0Nh6AIbRPqFb+JXMInX9/Q44lACGymeSHgTdNbLJiO9NPr0bMil158Mp4Lwx4AFtAB8NVq43yBr39sDWPIKOWPdUSHHT//7gE6Gy8h0IPy1Ii+vTACra+W/+1/wxwwALQAThzxk4af6aUL9gAEBOQKwnVqo9x94FB8gISxPqE8+IZLInf8HlY2KDW/TAu6Rxxyuv8MYADGFRcsqEst9Fs8qNMjmF1RZwAAuCmbAODTg2pgK4t1Lks8xa31NO9M30WfATQoH8o5/F9BiAB7RRgseLR9/5/EAvoYAEAkoihG02QH4gyEFUkovmiOppd+AMZiIyittBCGtR7VjHFrahdswL7KtYDflPQvPdS+n/xIWjAagqlURSj2GxbGBDbS7vBcX9vn/EBuAA4Qj+eipuhMGWmv8Hw0AD7IEWw2rV5X4MUpwVaMPfrCAu1gAMbIJlFXfEKa1H7VjFFrall0wL7Kg+IPfwCEE3NI7z+KEL4g9eAOqp7/P/hunAAcMQlSNcSiGF6Pc/BgCsBW+csrjQ2mn4TC4mpazIvPIKUHoKDbOmVtISLqhv2IW66fuUYrAGVL560GA3zy0P4xrNosz/KWx+y5uP8bKiRTK/vAAaIrhOsqhvfaGZravQJa3q/z3GNnQVXoepjUaQbcMc4vQ48IXMN+AAavCHYaqeGqMLpWhIw3MMwghzg0DgbCiEb11c3gfC8ACoADHlciMalWyOf/wdMY6LUVKfZH4q0/NBbhnX9Q2H59XD5fxId+SITJjCcojmMQH1a2nI5lAwAEgAXHwNSYT2isTj855gAsNgYkynhFsnFA4GGH41uCu6KIj4+0QmTCKpBSHOUAEK9EnvOPnn1Arqd67sJYD8kzv+tOTBl01v66HHlspgTD/EhyAAgjHIOFtParfH3VSngzGOOGNP6tXPX1CkN19QduqKbVp0opP1H3nYfPIv/VdPdD0piYP8SCCGABwFxAQfMTnZ81UW33w/hi6HOIGCNGJ+hlzYSnHom1PJnS4RnGLmiPPQotFXu5NmW6LiQrAkMVvtTd0Ik00x/PQGNYj1ScMokLGUTnh8AMWjn6GQx0jYv44DDjjQizjd3+/cnRS/6/5QPfrz/2Z8RAv8EGxAAOtDEFr8jlwwM7qntkMjqI3OLU9isYBn9Zo6JAlBkFkNX9zgAGyIwf9MoZrkAObhlo95Im6av/EQIjXvkgdJpJY8I+g4KcgGL9TWOUTEHw2VJh+Wl7/eQxltBeHOAC7cXqM1f8BIU2AAEA3NnZASUqMMD2sr1o7xQvw5ree/1nSfo1X/umcVr/DfAUk3wAoPZnNAis0S/8HhjElW+PLwavHL0bVe/+JDnAA7aTjaWv/gGg0UoAMCNIExC+B3/gB3gA2/ckRvb3+CCHAAeYhcsiPZLYJdzAABUFM0HBpwaI0cKzo6H4yxYrc7DuppT2AADUAAK0BhAbNEYPxCZR0GcBoAJZMk/R9h844F4WJ9r/C3ATjgu2THOpsFOD8QouI2FS19NLeGCt5ZLXgbazX360r4vEjcACDYBhBVIzJskmm/MigmbQyXvzZn37+LAIYXSEyTJBtnw1FJ+upK/xTqZogg+bYyvvTbl14P4wDXhwxtxGOc7JKmIfiAaIHDWX0YZx0goYDDjygDIJxT379ThbRD8WPyCL12uX/X93t/pjaJB8SFZ4iHPxwIH1jGqht4f+JC/gAWAxbE+qSx4hcugdf0BYAFxcC0mk89YJ/Of/0MRRc3purQBEbTsto/xuYK9BAA8zERFOLqHc1qEtsgzHluX5bjr4AW0YlURuIJ5akB4YaUo0WXjsk5g+hOBFxi15ptTbAKSA2+MgtvOgIYg3B+4TUQLgranuKYYolLUMumBfZQDm0jL7mr/imUmPMVnXdP5Keh/nZUP++OyX+hIxMb8b9AIIGPAhegIWSUQeQuCvFO/uABwRSBXF6tUCUG4yIB+NBH7OfE4zi1ssOwIQmLbeceso0BCNvV2jn/3u/nHIfgQMEABYfJAGD8VuwgN2tPQlTyU/V8t2smLck1VJLekpvOnLmNw6R20Gm/ukDJVLZM7/6NHaNdC/G22AAIG4ABgUNjvtvinopX/8/gPYNACgKyZEA9/UAJaACUPFyhJvEDH//cwUKEQayVikSCqPAJ0YnURuILQ9igYuB4pwAYPKbreap7Ih7QGLJS7PKTJqRzn7g7YMtQq1kif39u8F9PFZFr7v6BEVq4Ac0jZh6lsaEioWX7oZj4TL/2C5z+JBBFfXOT+5wg4VcUxRCfYWR/eCPwBKqp4Z/rAnRqDaxURZ/v5HZyheDq/AkEJBKIOJRBXC3/3Bphg6vToKSPoYhfhtTAA56xHRntnf/7N26P93/xI2wAAd4ABGAPfGjRGAHHW5XURTiJYYQBOKFRV1RPPngMBs4kGU1uulT0UT/AQruejYqhMGm2v94XDPoe+frGRATSXVB4IQLl6IrzU2f+/xiGqw/vbihotsj/6z//ji5J6VvlC4UwTW0yZA42QDA2SbM5u5u+D8OxiCVexor0X7+pPJXQ/vf1CQ2sZ+zN4rkmOIbTx3iRunKayanv9wtfwetDAB2JzjLUWZ7BPElfAB8JHT0LAZBVHF/ASsANA00tB3ljXP7elQQijGRwxJpRIP+0gMYRSMyLJBpl80wJp4BEEL0/Xhsj5ObmbikQrKm0n/40ETVBv7tKvS9T2AgG8XadT8MQEZvnIEJFhqzV1YYDYILU2+7d6obv+bu3vEe+sCr05HNJ7/xShJEJkTBgFUQDq15wLgKyer+sAQAUnU98Tr/972fBEptOeeaPGCb74kOwBAJ3FavfNqYDwO2AupHwX3mgBJcWmDwUly940iwiGGdXFKd2Oc8ABsyuG6yqG95TwsxTcR1v9oxkdhVaglDGo4cgzAYxceMNDGip1HvyC4h6FsUPGA+UEJVFT7ZZJLeDDJQ2RBqkEjCKr95Ao2F4aHv1Mt6p/MP/G+eEm7i3xGLWpIAiYlV4ucXoEg8QwCLSBQUaG1MCoO2g+IGr6sV/eHgDABYWwtJtPHmCEUDvxA3MMrzSVqOILezzAC4mhSTCOeMko/Oh6AYtCPzJY+RsZ8cf3nLjtrTq188FNGyaEt3//3BX5tshdP//v/jfAARAC/D4185wijCboCgRwfiFkMuJs3o//3CFw5fBlq26jS8mGY2sR0y123+7QTDMs7RWX7Y2OqW0XZ178PGat8UNTGcp7PzldhlrAbnifATTjGS05js3vvLS9etomgItAIWV48VZIOXtzPAMSoP/2SGuNiLSP//NhFLmTwZ+GNpB2GVnpye7ACwAGU4H6ENTbCgyznjFyY6KKh5FLMf4AIRKaJGuVxGzyTrfNhwL+l0hkNMd//B+wAOlAFCLsM573AhuqwBiyUmzyEl+Mef/sDDl5K2sjWLNOjvFY+AGUhzn0+C+M1vkNP4dG1Hsi+JjeNnBDgAOFOFwtIiSfHjNyBhy1G6BaYaKiQNAdBZDF/QMg8KHnjMKXcOyF99oiAhWTKY71RH3fwCAQ4QMJbMYoyFrXui7QGLJSbEoZirdx794IUmaNC9DAUGAqx3tdAnzHtit14UYMyIfu8SGYADUzCdjmUgVTmq4chiClNwy0YGNlQMNW3dn7NIYf/EhjwAGMyCZRV6ghDWq+KYxRamoZdMC+ywCOX/hM3f/wvgLAKUQOPmI1s+aqLf7B2tTg/79YAtkNJv0RvPWAuKgQgtbkMOGRfZWD+3wA91xbhex1Iwp+j+r/G6tjouI1nP7qrViRZilIx6vB+G8NQAEaBCprfUxPIXquJAOpDlGUV5jy8D+2ZjdR22klLWrD+5mQbHJ2HQxaAALADAbEiUMxkSwXzj32iAXAAwgn2FpRIxY0YWOCr3VsGXIwAM6un2af//+H5plSODo9Sebr/54CQFxCzl6gfxOs3v2swGDXCH+clxpvvrxMVH6SIW7zee7zLRDR7lydPGFCvpu38ARgveMs/2KEm6Of/uHMIdpy4QNUbWUPtd4Fz6UTKO5s3/+5iKFACdpAs29a1GDci4rd5CN9g2RkP2Qk/d8dKTBCNrEtrhX+H8OACsEUf6KYW918XA0MDXN0WwWPTFL00F4FnwT7AvcwYDoAC3lB1eTAi+oV3goG51OTJkfdMFw39f+N+AM4A5uUgyyEGvK+ZGYToKreJQxqjiQh4nQ0PqkEIo5lIHKOMLAwxE9fE8qPCQCf6jYICK+mZQZ+1wS49xATmvkgpf3g41gDMDawg46JYp/EMtFlVCkeU0njoYccTBHob276QkEuYq/e+FqmA2kr4/XGVlJ77Sf9pywmFE8WB8P6FwkY0IQhX/BuNGr2AAG6aAIcTWEiTBNlragGOInGRFgm00eErM91XLUSzRmwEWA6iU4d5H0CHQ5orUqYRiypDqd4IYG34b/A4YREExKbZNeUmBVJk/4wuum90/gJDIILlnDXjYAFlzWjSNOKIkyCjNdsDDfGqP7/Xak09Hq/BBmOCFj8FCRdto3awAEZQudkFS51tNI0EBK0kJZ3PBVJgh774GdPJxDR2y8LboN+uufv95ocmJn7b/gVtFjVk+0DOhrj0hR/4Z6i3RQWOCLN/0/DYQOhgGQhHiYbIwqoYeDAdX9TWcfUH//hzwAEwA+NgYqwln7ZOSJwWN4AOelM9I5/hv+IAPC4Gpspa+0TggeDFY4Jumtlpj/FYk9eAVElM6+v8SSxCoviQ9YDDn5YACfY9QmjMKw906MTLQBUFLQfEjIL6vTgIutWu/NqYBMYbKhzKYLzGocAAKAwD44Omhw28wfg4a1r2n971tMJrEXf/8Y0AlgVFpsMpdWNDF4kbPEm4AENgGEFWjEm2SYZAUwqCzghtszE37FhP/3ADHwoUuqs9ClNsk//u4sBBBdJkmyTLf/B8KgZLQIszkl8X/B+iDEKqMEcxSUtU4AEBVtMWI1O0VbLpb3Npw2uLkVExsRfD/QFqIYAwzXhXG1xt+6QOaWaW0p/pQgMjpWbu5/Tb/I2aX//uyRJ4Nob4kPdONNkoj/vrwFW71W39+ARMCHXWomlef+/sHADUIx/UX5DeaBCuQ9F1gmDTbH8AE1KL9chafQx3MDDjEEkVrHDlD9q7PwTvEdnS7pyhJsXvjX4zqYC8d4kKwQ0LK9xk7PfgRDJVYokEeg773MCsGBJ03KeXTUhj/QDBgEakCgo2cVMBENygeih81YLPUa/gwyBYDvxBcZUOIQTP/28TP8O3t1bzsXn/sUZXnTSUilUnxI3weKCIQmS3LqiSv/yhFutnP7jGy44nqJQxqvMAAqwEWBtZ42gXcSOcACBDTy2rwTrPNvu/+kOStp6/90DFclOOdw3CKllS7t7gcGHAFq7TH+OAoYQ7hf9JTh2/oy/7mjE/xZhauuNu1jh7uJ3hHbdKX7/+AtcAbwRelRZs/6STKM4ee+5MkV9iFmtb1gNL03+7wmZ7e4YqCran43jwKXMfusJ38w1KyXYGrp42bS9//60fC+Fr/98k2Jn83dU3aEBbvmLWIUaVrPveCxnZxfslcNzFfMgMOSTNVjSmODAk/YZ/O8SV/BgKGMz2/UVR0CW2P95g04j5M3Mb2qwbN6REQtDbCRHP/wMINu2mbYmqyp/7dSLvva9Je/s7suHE4ZGJ7taS37mhLrHR8eJG4Fca7T3QCZBlvBHG0o+SttDzkfb7l3ZvAxyYWudJWYDLYsY1KCuCoJcsshfnMJQJ440jWpFsUidtYc+uRdnO3/70oJG9+RH6//2fdz4fxZwwJYCHM7+4ldzrvd4CgcgHgyguDNCByRRMTJPpf4H4b445oiNTF51kNgf3ply7+o/jB2Kn/2WaT/79/7HSiaSaZo+JG+dsAQwmkolnSC7eLwFP4AAdfwESQjz8L0P0mmYyfu/v6zBI4VLDKJJY4BMiMAYCvAjSrQ3C8/5QEHufVKsXC/t4JaY1d1eTdGbvAh/AkBYNK7SLmzJiTXfwfwYZxpRFaEtv9vSmbFExH76Vkp47VJb/2gYa368eUrKiZTiRvxCYRSOIIQwR5RLxeGkGUciXRZWI7UqThc/tgERgi3ZB7rF6XuW//Zw66FJX9gAE0HBLou0Ph1mPcAALAxeA8NwOzaPEPLyOgnuJthbmAADtAAI4BpEaNEbhCMJ0FCf1Y42TnTk91V13jH053UTnOlhBFkgRBqgphjiL4apUEGd5BrmFgtSmT4h/vlRQRTiG7TGnjLd/og4auW3VMTw+JG/GEQ46VFFIaJ6kl30Jc5BC1WsIVUVRh747P/LsIomma7mvpurAGgJyEuLb+JIeymwPygwAc0YL9f7lJpC7R4AIK9KHnEU5ajXtIcT3/f/QCL/80LC7RG+yGyaRDDJYwADNI72n7InTN60+YK1L7/eB/+JDvxgAsgX2kT6D+EJOh8g5umIsUgtX/+4ANEAmtSOmjz6wnh/wAiEigrs2XrahcyodBvAG6mAAgI2gVE7YXn+fpF5kDhgcoSsh5hh2CpmMish/twEoIE27HV/2TMuPexRx4TJVNQx+sDJNM0mHl03/QQJ2JrOYFmZjN569T/n9fSx3LUh6nPwPiQrAAbMbKhTKQfmNQwAASBAH2Omho0Rg/AGIhMyGMhBuQpGjxiiFdxy6YFt1SD8Du4gV1QtbOVnNKvgs8ANy61exYRf8NegEPQn9CVvEbmPHX99falOYb3/8SFYMwAJDV18C4GwZS1/32/GKKV3G7pgY3VaQACZVYMnTaF84f5EQmZhFVxSnOQGdNIqjy0yZPoFUN/MQKK3jan4eTlaOK5YvnwQB4op40RgMftGr//XNhRlPnHUXV5/TBpUb7dMtwF//PxFMjcZs9IbU8yB7eX/vGpKLF54jNXIJQ6wXPd+U15vk9/PED+KQv6//DfjQOp0tn+N/RI0ffq+t+h/K1pMKHDs/8M0+jmksUZyHbZaVHf1Q//43DQYACYs3KyHKMRay3XEVmAL9+gABAz1gAAgChg4//7zAAB7gAFaA94aNEbxC78jKcgz9WY76Y6Jmlxz7ZBRMNgAAuCGaDQ07NEb3hQTbKhL4ZRr/DDAK1MdUydd5FI5Qm4d7+9G5FGS0iVabRr+8M+AY7fem5vDqEMMf4MNIosdsyzf/CUal3zBsA2AUpNdXf/OPjZVeGOGYALM3djsMJlI1094b9P7swXWqLN378F03DpW6Ebqlq61LFlT8OSADZDAQEYr5A72n++lAABq2D5++fWj/kDzd1Lu/3/56ujlvM/3n4f/CsAykAwguUJE2CTbWltAEMKpIkwSaaf4PvUD3gALBi8YJtjanLP++J9/z//89VwGI6+vwI1yH79fEkxnxP8EFCDE1AAGY21kdU/SfuAANswJaBqW8f/qAgBBDAKxIFBVsbUzf7qX+AxG+z6m7Os8Qv/uQOU4AwMMRlR4zUV/wYY6sNMbUfd/oCHrnk9u+rp//EhfAARgbqHCmXvxznpJcwABYPxwBwK3iiRx3hl/tACDS2uMb1mQab+4DEaMuzIxT92GyFNbXdEfn7/EEihh8zI0Db7XAMDf7kks/+9/gwgywyobCgAdA4IHnDUZ5fNzGN8E00voEaSK+gwEelj6IP38SHcwAQBYAB2AAEYA58ZNEYAccZHdDFHIpRrzl0g2CDwACwKbkA4Oujam9IdFyi7Q62yUQGGIFCgK/IaFS7zdEyqMx9q86JGSnxPw1CNwM5C8fuP8o4k4UkGs0hoj//EhqYNUt/gKSYf06slvepTvbiEMpx9B450ksiMPq8/xIagCA+KtTAXHvEg58qAW7wFwEdwHFOfjdZuqpT3GAFhMCkmUcIskUDn/8AS7pR4XSibp/8SrjiQv4AFAaoUAHBGfRJCFsL3/vAfI4Y0NhaBR4yu96CBiCiwBhB4WVQeIHgdprtGXd7/PX49SH79f/8Inr/h3j+d4zCMuJCsABFgD405kGE0u/ZEuKI9DP8/kPOpHYxRn2otzAABugAEcA18aNEYBEFRMgi/bLJJaH4zZGN1MQZ1sMcGBboAOPUuMl2+/MnAUx8M8vjeWZHwjCOGQ54ALQA9RSGIt3tcXjAt43zf/iT1nvDf//vCEHcAAABZZQZvg6B3hDwhPhCEMQevDtH94gOQAEAg5aCnJTN6fBghtgAA7AACMAc+NmiNzwAPIvCdJkC++bgAJQ7ZQMWbX8jlCPcwMvcu8424RSku8+wMOOPwh4Q8IeEA5wAIygEFE1hIgwTZYTbD8GvCZg7e//w5KPoYAFzMwAwFIAnarA5A8/5xIAEgJOqTJ3mDHv4JU3gAFe7SoX56xEXiD1pwCJPnG/z+sQoCL4c8+6wGFbpT1wAhHcj/v0xU508lUyV4kOeRpwfAFVan958T90f4b5R9LDV/MUuNE0N+DUSIzr6whfL0PwX/NGMjsKq0EoY1HDoYgpTcMuGBbZUDDjYOA/LO+P3/qsM/5ib6PfnbAxLWfz/xIcmyhoBCODgFGT3x9LB27/iQ1l3ymt1OLTNjwRBEjP+y/iRskdngCBCAI1AGhJqbU2pDACoAYHxIxXV2nmA/cBF1q175tTAzrfv2w1CU8C4qlgNBCvRVDXEAxU+tv7cHHmTBSGb/9v/EhqGADoGUgzEmk+oR5FHkPtIBYU99kR/xKVTL/4kM9D4JplUtInKbj39v6D5YAfIfv149TU9AETpY7Hvv/dq0MGfnrb2Uj/v0Mjr7u/3D+sQfFgFnyTvfMb8/iD8vhKfmB1ylfP4vEHrwVJlqv8McZBfrYEQURVdgLLlfO8uZgmtyO8/+eH9HANwZNWsa6jGfsiylhu1KVHv8OY0GMIHqsAQAMCPdXFueQmj0NcOjg21Z89B8o+mn+9T5Gsv9cw9SUvPI/+/wxBGiYmhZCZROmikuoASLx8+oUU9FpWqEAF63d33oPpCWK77XpY+YLuWi2y//+5KUA7CltW9CVPpv7NoD6NaB+FuAA8AugK+hlVasFZOfB8WJVXcJgXJRPn/DaIODOo1qHLCyl9Comod//nIxg1ti2fFkSJK8yIk4EdX4cgAWs5wjUvqt7/gJPtUjkLr63vN2L15bZ6PgN+WD9I1ElPOPnFpIid18A8TQrs8LnGRDYx7lPh+lQYA8WoWN2vmWJDtzkHdSyn6AAJn4ACuf6IAhzp9g/AkaGK/fIGQaSV94BUAMw9gw11CPxHeBx/wEoACdUYKmDbGa6N0TocCHqMRXH93brauGezKtbsPWnqUbiFhExv+NObfBB2SxeADh+AJn3YEBaBpfgPAYIW1vlbGmGf+QatE8/2vQcYdUnoW+hnWn7+koJRP1KH9aLbIfa3xa8TooN/X+GPABYJlIADAvSJMRuef/9xAkwIAWBlo57S4hBGsOZYChMCPasmBTB/7/wOTRyNGN5LH7ojd9TMZw5GdTCJtmD3mZv+//DewIQAATBgHZOmRw0RgBzQ2XmOhB+WxANaZe99KyUF//l3kJfguTmNFJvvc2UjiKp/PF6V++scuUvZLie/3//hzgBayZHJ17AM5EAMBHA7qjQ1C6/5h0YAKyxW9Uu/bf4a7AiMGKVW3AuIR/nvVELTj4Tw27eB+HOr5fwMZpdyxfv8XxuAAiASoHDWHvRzjpFUx5MMPVUNp7k2J9+8YEihwxZ/0M52RULB8zYNVWNnzs2pd+D98EBBRE4zIMkWGUEF2hAY4msJkWSbLOBgIEAzCC8AJZcbJNf/7zCUmZO/vemcMKxkP6Z+/NNAceZ+GONi9ezAA2B2QE3hsVN20ZPyNCdOQWkke1SVJMqM/MNqbSn74Cv/xvABVBlE2i3HuIvvgARlAIKJrCRBgiyx0YQfcsbP/pNS09ypC0QkZkSf/1NkDXioYtX//fSAAMDqAzFYyqUL5Fc8zZhqpzqUf0tT4AoBJgwaw76GNaJqFww1AZg5c+fa9yWOxL//9wXEwYsxadhbi6Y/iRvgId3NRcVQmDDbH+5gVwwJPm5Ty+aoLf4P3EY1xjIUf1K/0U7JBM2DuKKIDtGHa4h6OKebfADJkNMcylG9S/DtErDzBGvuHPuAiW1Stw2psYdtBc4bFXVqB44YDNlIFBRk9WwwYiLB3ZmrUziCpuG8T/kDAg9YTGhKcfN/EhfAAsGJBCZOJRJfDXP3fgATqAYIInOBMicaIkAT2iqcodkuP8CQXKb4/d/iRsVAACBpJQADg0aL/cBsAGvIAAIAnTNgNJjT3fv8CYnsIWuPQWcV0DokqydfXvr4CRgHSiEIExy9CKprUDIF85sIFoE1EM9IyGyCq3yEsWkPTYC9KQZBKTXl68ME4IbI1kr/af+39M90wOA9UnWxijamC/iAIt3Tb/fjLd7j6qAkGlHz3/G/mNluD1YAcAB6AQ4IdpP/ky9zxzu4Dcf5HhsBArusr64m0Gjp0UhLgYxb1Fu/tpF/B+9B8fvuEgAsGu2JkRdJp7+BLQIUh3+h+BKxR1z/Wnpt4JGIhib/gWKQrIm86XaPDacARtPKytO3/tWROB6S//2mFh9D9FJacSNgLAAJAwDcQOmhw2pgNLmGnBHp6YJVd/ADAFuE4XLE4RESmNzS9dtbe//2wAAfgABGAOfGzRGAkDHQOTvy8svdNqP/nZFflgD89d9ASuV+vH+vuu75yWP4l7w5SepE2L/3h/DZJnAPQ1K8f6hwDHiazt//xZ//T3PVkpq2b//78cGKZO/0cLxtcL25vMJjnFQUVzxP0ku+H6mQaIU3cZKl+DBhj2cABEBOgcLYeQjnGyapYABGAm4cMWIoQ3vpNYxjYx0mF4lXsIf5g8OrOtZuAMAQif+m+xqjBFAga6DJL6Z8wPBSkSSWt2qdlkO03/32YIEv9WPERP/v/EhWAB4N1MABARn0Soje6/7gw42XB+9zVDi//AB2rVXP+9npDovcbfM19kMAdXY+Pq4WR/x7GH/xI2GDAPgMZOOEpfvjvPZQ/4Sqoo6gpDFF1EtgcgAOmADQEumqkRdV17+qMYA+QAQCMbr369gYlCUak4Z8TqXRNjA/ivV8ZkT97WAzCucxfGpWUvf/CxNWVUd9Pvgw4pEozFV7VJ55Yis/9oDbk5l6XZ9bN7e9/D5qultgwt430AjQaB/wAHuDEFq6jdwwM7qgAH7IgAwM4CuoNDD5//9wEgQ1CP0J5+RoW+cfwOznN3r5+8CBUywQmnbW+oY90CQIWznYFY69Qx44/vs0dEgSaDoMIa8gAfF0LTYQz5gpD53WBwUEnjMKVcNwF98BK1I0G4IBFleHIX1GZDOufnv7/MsaXLZR0yMaE0QmwY8SFcABwhXIejYihMGG2P8GH4WS4AcGvzjPhdJggGH7ZXqd++/23oP/8SSSvGcNWCARB7tz+6qAOKtisoqHkU0x6rEwLU+vr/+Jczju4Pv7jw/hmAqYAaAk1C0CLpuvf+0kJQUWie0qwPxvP+B+B1uAHd+lqNf3g//4X/AAcSj76HMYnmtLEbRBth6Y3iGrFqP8GBOAwhnW9vt4wY+/74V2wwXpmLDbKST/DWAHjWYJyfV/v97/vjD+3F7//GwQ2AoAFSRApAmVIEWCTLmRwFxEyAIIIlOBBgk05g6fwrsgIA4ipbgzjT2/XfHwA5UfsMFU+V8hM36P9AVb3VPf3v+bKIjSFAD4JIACIgYn3/IT6VE8wGV4BEeCoUnv2v74IN5BHYzRk4ewqbfvt6XBfjA9vR3XAAeeTQydCoioloT9UlEQURDMl//4xZVRPU36p3HOBDNPhOnKMf/vEJOwiGJ1u4trV8EOrd2K/9/CRx49Q3QmtPy+/3sBMDDCH1/hvgD50Lt0Scl/sIW4b3I2HD5TLiZFKdRAweRTq8Ve9+rUR/1i+H4EzSanfd+96PILfWXj9YVrPD4AD5ZMg90KRPsPAAX9AQ9nOwMjj5DBjxwMBRRTa42erYZnKbkZeGUb0jqveuHMAC8BwYEnjUZ5fNzGN8gXWJGTUJYZNhPf/KlgDUgfYyrD3QFh1Or4bgSEI1DUZNCZMtMfz+bAA3bOFRRljN/g+8BdoPf/+GOgMAB8DkGBJ41GeXzcxb/egQz+ajLoTBtpr+eBvuAGOlmyk+tRdHxWJPfwC/U+8/8Sf1/jnf4IMABgvB6G3Uj/RwbnWAA4DsBN4atu2nzgRKYpVcbU2AAjATKHCmn0Jbz0moWDARkJUUh8UJrVfwg1QAcHh5dBDLOuE8X//7QPyAm8Nitu2vSkFojRmS6DEGAYEpSRXyARc0uZ/HdMD4lHHz2lKi4kbBCQHvB4gNMABGIxxVocQh4n6SiPkRkGyCq1JCWNSMIABqMgTLNeY599KEguKliEv/b8tI5kOOzpf/7nMj0D0FqY5wEFcUStCWZ2g/R//aDAJqx2HVn387s9/3gwdkgTGbkf+7xGsovSO93/sBazY8x7YRX/7+JG2wAWYBPWrz0BFVDP+2BwHUDRbQWfC0Ub//gFkZgCA7wJ5FNkbgd/95MRlVhd63uKa7kaqR8E9zdYazDV8SMIDkhPK4VKjtbHaUSYtI1iZaGA7ghiSU8pnd5EMD4zbGt/9zI3/4MNAMSlwFVLUZj3gXcPSNUT56RoBtDORKtSPHL31/qWYzL/D/VMzkKU9jv/29zWyaPNQHRQQeMRlZw3MX3wfMAWAAXBTNBwYcGiMBIBlArFZpIx13Uhz/gAghgOxYFBNobU3QPSsBfUbs5U8/3FkamswlR+ClmwxB+qXz3ByObJJ4I/2BqQafyW5F+/v4kbAAQ0UaEfjSn/7EkTdBIvWX/IPwOYDxCDqI8thbyAeGjIuCyFRZQz/3H4Yj9KLcJtCN0rQiABaM0EAcJcjxRJl3/XQYcABwMZaMjVJVsNWr/+BALVO00yzIzENeUeUrm49/cGLjgBuTEk5Yz3goHo1WX5v7/YRXtHP23yGeFovV72fxI3lghFUlCd+Jf/oI0RHf6VngIbIvvT8n/ve7DLI9fP+AY+dwgoj7/4u7ohyA3oSCsRjXt1n/3gsV1OLmkKzkWnQikx8QvG97l/txAK9ImH6jN7HgwrdknDyzf2D4oRc8A8QP5Rs2rf/thqqtob3f7RQ1ss0yZ8AtYjvG7+JG1C8XpusBxAt64h6sf7GzCNojHFWZ37vAkDAfAGJRS7k4lEl8Ne/9BAgeJoJD1hVXkBKoIILW5po2K4J3+8CcFHAcUpW3k/rpd8ApoWAeGDL0Wr0zf/9CAALAp+QDA26D7U2gISy0weSmC+GPfuDCGnCjXXaan6lKt5OX/+nB5GOW9CscmhkX/G+XQBimbMB7hFZrB8hlAiFa0CY+UkyQ/7ACIHxWnoSnRCjz2DwENnNpcqi93f4oAijTLm5Brn9nFYfiNHd6leSkFpiJo2246AwISCpxtx3t4XAD4LyIwFTwpW6pnwYMKDOMMR3bvH/PkQyPSH79YHURkCumL2P99MYqX/gggAJIxe+Z6uXYPkIFU3zGwK/BiRP9ZfS6jjf/9AAEmFRasqkultFuYAALgpVgwNODRG8xVMVudhyKaU1QAA4AA7QGPDZcbTGcXyxHqM7aISvH1qvkSNBMh3HfDSX28MosyW01774VXwAq1E8552AP7DIxnFR3nGB/CfbP+NgAJDKYRCSSUsEcTT5wNKzilLpQSoqogZPrh/i7DILheP9TrZq0BLQ/pQ8pnagn83GIYACF3CZeY1fX6K8AQDGYj3Gvt6klMUSqyp/7DgX6x8TLJrmyqDHww2NuAF6/6olJYf6sSKIq39e9v9L9YH/EhWAAgAhpyq0YRjJpRMv/m5hXo+R0Sf/wfgAZiw5BgYvObEjlxrgiQAhOhLFrX2J4MeD0BqpAAYEbQgVEbYXj/eG+kNOCHvuh+sDqZtBVq/3DOMQpdv3/Z8Xuv8F/oqEIJU1hwyL6K3++goAWAAduAAK6JAe8ON1sAMADwuBabKWPtE4IHAqbf8AfqXtRguN5fm/iQ1gAWhAm3Yyf+yblx6AQKAYQTSFCLBJtpfABt5OHLU///cbEnvOPn4c3XiQz0JwXdodT/pNz08WQS/6wCCCKRkSYJNNAgEsKREhJ0XZw2HS5jan/xXPXRbn/z4IL1MaI5toZymDxzGrDSVY/3/n5X89R+HKfbEn2DPf/4egJjGR8cykC8panAACgIA/EDpocNqYP/IiEyYxkIMhjEAkHAAdaDEEr6nlwwL7qnm0NiqIvFEqaxWmGiokCUGQWQ1f2iAA2RGC/ZlDNeA1s4zKxK6faY7fIbU/A7h1Ukolyf58t+DCHHlQwV21AAqBCUIRkVz8jYx85/pVCR7Q0RvdVRx874BtyP66J9hvLt7/pFwy3Hgg/6ByAtkeJkjtw1khD+AEPYhChKOPkMGEDj1mJm5zqQbltVuAAFQYB2YHzo4bUwA7IbKpheQ9DWIBA2G9KFEf8cmVVK//tz1tfK+9Cd4ubm2NHnnr4a6hLyADO4yqUVFvFyZKAAJBogtosmm24ySAzpbztjh6H6xSWfIP/8Mw0pRBAJV2Co+7Q65o7L8DaSK+hC5Sp5/jYADUQ3VCCYl6VMS4AAUBwH2icNDZtTfotYlit3Rd2a/Su/e8iMTpjmVxvUtIMH/xPxvedX/DP0W4Pgihjl6hJZT2uK92GGgGADxyZkr9SP/1zgGJh+R44JETP33/DFaPal1a77h/fBJlj9SllnR8SCCAA5oNfJc13+1RYjesN8J7GRxLeGqBhwAHEo++hjHfz1liN8aABKCxsqTB6Chj/ODbC4xeFLSLU/4OrifM0nvt4CgxZKXB5C5k1Ixz4QnX3es+3kDXRkLTnb31K3Pj7v97XAtXwsza/IRkrgwXEuJCsMAGwcEuiZQ+mWU9C4Q1pnQRLCbUS7MAAFAQ3AeG3ZojcS5Je3ZveZuMbrIkWJgQw1bKDvbXDA9cYe9Nm7uz5c62ul40qVf/neMijvn58Wthi5jq/7fy+b//nnFoLjmFhta/3H/9P8N3w/w5yBU4qRsLdREj7P/lh/175+tB45/8Xz129lI/79f+J/Ehf/wAEQ68I/EQ99KKaABaYAaBrxqDvLFuf20kmAYHeDtLsDcLj/n+B631wCKlHPuaPIel4X/MAPCWFJspY8ySh46ABUHDAFApyEbwMt9ObgEM9D1ZdXBJphX/6ToyxWr/X7scleS6nrvAGSv0rZ578d/m22h0xycHRJGKmVPaah0ufmquZ/80///+JNh6HNfwtwBYABUGAdc2bHDRGAToxfmOhB+Wrg8IuMWuvNqbEFJAbfGSW3eg8JADsQBoVam1MXwCwx9IBFMjF7vDmc75xwTaaIvyu/P8N8ACwYzvamqo6BbbH8AgB2iAg8ZhOz5ugx/gq3kdzZTP3g4yq/fH+gb1JrNJ7gw7ft6XiQ1A14rnZ5FiP8wCwBlEehYy9m0tLqPDAyjQxLoSONFJQn/+HoYzu0v3v3igDou+ghlMpJP+8GoACUGblOJ329xrHAAugEL0z6eTx//9+bGCblD5f7JivPuhjLQ6u93+QeQfLrhJidqDhlPBee9F+n6QAElkC41zcN/X/4nxIcgAUArzgBAebhKzhqQv/l03E/UNVXwLQbJdDV/awBb8wi/Jw9hCXYQAKJikL8KqN+f4W4ADhCP56Km6EwbaY/wejAA3RHCooyxm/n+ZmYZVFXfkpa1IeEOPgm8l97t/UM6gf+evgGrWlfWBtKUj5/G4RkxP38MeMNEYn8Tn6CCzpb6/3z05AJ+U8//n//COEQT48aKsH7wAWgB6ikKRbEtceTCEHcAAAX40GaAOgd4YPWBE6xn68Xfwwepi27Nfv+fvz4QhDCB68Novf7wgF/AEEMArEgUFWhtTAAIMgP4icJ+1FuazrjgRKYxWcbU2gIWSUUa5NEJGO/uswCigAONh94euenv/cqB4A3gUYXzjb/xHiD+8AHO119+/3/iA3x7PXCMv7u9+//xAc4ACMDThgpd1GGs6JKF20N33avAQvrQfX/+IrCEXiDxWmBP71JhW6Ti5/WIPXgLdob+v4kNQAH0PAopERqg04ewOv+4bAC4aslqz/NGPf+GCCGBm2AK+0SqJ/fwR7T+93ok95x8/8SK8AHqxqQkKLxkBGHRKsuEPtkFEw+JBhAARjjYroIt7qYaSHbx+nRnhm92+OhEcanjPYDfWQX99axK9YvP/G4AEGwGMIpGZFsgw30QYaroZT3Ytz692RAQQTSEyDZJlsHyQQfN0ZXnpsy78HgCwN+HCmXEY5z0kqYYGHwgG2DhbL/842SULf8GHHJQAZRV9f5mVLr+32cadk9H2B23W39Vp3+fH+AlVPDy3FK2l1s/4ef8/DtTxSptLr8Jxehn39f54xL5GWv9rP6hRyBJckb7NmG1/fw15oIEvbGT/+TctfcSYGewGQWpBvlfuwQGEE0hIiwSbYYtAIIKpIk0SaYvwfaYLcB6LMaRV6hg+6hwynD/iAYeAhmcxFTFnyJbZ/gw53ACVRL5P/QAAzYiIpzqYblrR4hctMRRUOXryHCofwAc2RN/P9/+f8NwByCCpyfYxKMXqg9GECZVj5+/NiW3vXBWy8XnTv+/+sQGoAHgxKKTJxKC+GvP/2AaBq5AAYEbQJiN8Lz/P8CZ7AGEPLHmx4/4Qi8QHNg4AHk79kmZVuf+9v+AOk58M8/+G+BOMhAKgwmpSKbJfvvFYxEKcP3pDrDXTdz+Zi9y55/n9UdFmNFPcE3jX1KaSrn+HIAF4DwgJOGozu6bqLb4CQQzeairoTBlhj+AZFkTBIsKmx/d9w2Y3mhVWIm//wbZApcAR0+mt/UfMKH/gR9imkpC+++RSOl+4h8F9gYyPr+AAo091/OT/3QHl3eeN/JnVZmiHXPMpRqGF639kOY1fWWv/hFkh3q/xvjoDEAJDEd7fqKoRBltj/fIvwAhAL3DlruyIYP9AJAIPqjTV0UyCfFmA4n3Wjf90JxyITX0XiKnsAmmM4HOVCRpoZ2VcgEGKHLvl9SVN3zj/3FrbGJPBOPKpfg2drILa0Yte+cR5j5e8k5CthvHf5kj7n0zaYRo9HGLRg+F4ADGYmRSnUgyFrRgADUGwDo2zsyR8IX1EB2g2JHrazp9wuDkU1Ll17EILxGINgJzCqnjoI1q4Atq/6E292QACMVAbki4rYr/YWQuJoK3xIRlv/nDEiivGiP/hiwAAXBAHbPnRo0RgEtDZVMdDBUNUhwIuMWvPNqbEFJATUjILbzcXgzgCmmrnppwP4+ASwv5e4vmh2n934QikPd5wt0q3nqP8MQ+RCRCMbUwA/221S0RcXEYyOwqrwlSl8DAAY2IjOKvUEIa1GmyIAYCEAR1Rgchdf85YACRUcKizaGb5ApHW77tQddV337/iBJjlzcv93/DH2phii1uQy6YGdlQIC1CVfuEwNksjq/gYVGACff+kJEf8B5IiWJmYfDkIcOGzk7Fbv6tKswu1Iv2chQRVFlaa4kbgAPAAPgxo5iUO9RK0PcgWMoTI2w2ZDd/BjQv7OCMZwhI65Z0y8RN2v4DAHGrldRV75KWtWDWg2AuiI61VWaS7XzhIkSBJEYjSBakAjYramWkVUfus6RPBwdpxttL9//f4YgAI4R+xSoyjOLW7TAAcBjghunUEyuTnfKi44f9l9Nkcwrhaq+/7Y4deFpDqbRhAZ6zTPtDz/IxmLQTav6Pw2ul/PXDcV/BijmNwf+CCVmPDLwAEaABqGq4YqRN1HXmLgELZaoPITEFeKd/abIgAwM4CtrMDkLr/n6AmxQAcE6/AkJWQO3/eLXwT7bBZoSb3Cb0HuG6h9znn/T/P6C3aG/rWG4b+ofi8SNwAEYDRQwUy/+GM8JKGeiCDXdjp/7BmHHvEBrgway9+OMaIKmQ9EMPd0Ml3km48e+BZAMYTKEibBBlhf/rAIYRSMCDBBhgMOoAV54W65v7fI4cj6Z9/3/0/4k2ACUFKC54yCurvNATMbLiiagnlLRxI3gAphEFyyHnPfffAAxIBhBFIzIskGGbogw2XQyXPzZnt7T2O1Xruq1/+BxMLQRK0L//78YACoCJA29ITkVLWFO8iRCRDGRhuQrvAFgNeHDGXvxzvZJUsGH3KD0FczRb37+QD2gJhOR8554v4kO/MVLmBgShGnuiSm/h0GIIU3DLhoY2VNCIC5tjq+5NuXXhnNZMIrjM1akjU7+5yBlS1ksL5/9pCTgfZ5wruEFH+4AAiFAqtPf8GkhUBa8QDZAUNZfRlvHSChgMOHsQQnso6hx/usmHz70zMjvr+v971wf+JDueXklV1tEgXuCoeQ0shb2g8UA5obS2I9Ww4sZyXpZusf//eAiFRMoq0vtklt0CFch6NqhMGGWv5wMygyTkFaOu9iTf/B9AgMgbQYje97047770hXbZCKXWTjuu/1dUamZL35rdO/WDDqev/EgwxIAAgZ2gACASFRHF+Y3s25OSfuf8AAo/ZKpm9UYgblw5dwDrT2zbMzNPg/AGIuq3fbEi8hb+JDvAUa9oAJgAFwKeEtVh76BSx3o+5wi1Y8PPO7vmjWh5U67gHbTTLIaMsPScUTJABt91T93MJzaIbU7Pe6pX/5B/xIIIADUZglQVW8SpjUcMEC9eACDMvGuAhT94ZSWQDH6YxSk/Jv/30FAAQix3M4JPwGJlWmwJG2THvXQADsBFJcbqjz8jcUGpcdzxPIXLsFohgizSJ8df9wCdrcfUcwIz2a3X//EhXwCeuAQUnelk0+pKPIbmEYksv3CEE09Bh+9GJeYuYdDVIDDQBAdXl3vVgw2B/xI2ALANlDBi7/4azogkX4Ax4qiVzEdVVP/c0ECbtjp/7JuWvtRVzqNjTEC02vxkXQ8M/PQJwaTd8nlIawv5RQyk+kVfc/9AMTTiNC4Z+QsZ+cw5PRpnBT9+69uU21Ev/8CYYS6ZVN5Mv+/2hqR/8sMtGPwxzxC0ChfgtYWwG9PAY1Zbck/CAAe2JuP3lGCI4URn9ToXxI2BhtClUvRkf/+48D9B84bFfVnm8yG5HIUysKxyUFiJD5ihQKcZN8olppXWCO+CyekWf7/84YCg19rSXJxHN/gIAYmikJk9/IYMomv9oBiiL5c3aJGjKD2AgIABwgLVBP1uS0447wT/wfiEtOYgu8rU2xQRm8UcNSG0iX9/UWggEECkJCvNS5+/jzfND8M3KbtYUXxI3xhuQAYGbpa6YnzYy4MOHgAP2IUUpuFnTItspaSZgBAd4E8VXHYHf/OGnuOcYCRaiVl9HsNiv/d/QMAVEBB8tGdnTExTfCLMZa2KHB5zJQsnthMHCmaPf/jeGAA8AIiiM9psyWeKe//kDHBarLcvdAY2q+ffdANBugAwLajZVtRtxr6QroUV6OP/TxSMCA5IMj1dq8b/7laDyp1Zat/Fx33EGgvIFLImyLd/9fg46RCORBgdWj553qgshC9U1dx1C1sLyS/+95FY/BfEhiAD2KU+doYquwAwAEQwG2UsRSyw27YAw4/IuM4j7UWzwMHioICl8TjcqqsS1QhMoiUtlhbe/7+iSQkmIjIgNRlHoExkAup0NW7z/HcOcACoOYQEnjEZ3fN1Fv9oEI/noq6EwbaY/gTW/wAMwqTcpl/65fDkfHkAPNCwjAlDmPef2VS+DKCwm0hdNVRou+KX0HAB+NGW2b9d3f4f4BK1cZuNW591E1fl213o+/bD/m9ejwB1rl5f3/gCUofz/NKvgBgsuMyHcV9NJeJgwAJ3rJ/ey6GA2oVqNEW7P9Z8kTTcf+//4iGAL2pS3tk//9b7X+jvHH+AJgXjfQCw5Zi68bpPEHP2/BkVh+I9unGqp/7b/4ADgoOkthB1GxI27nB4ACIwQjZy39+qI1QYbbgZB7aMa/rGvn0//4Mu1av6uD/4INoI2ClAB0bIAxButOrMJoP9wJl0fdMAEARMgiKQUpzFcAA2BLEMp/3y+lsK9xwnq9GdE/ntBGEYqORi7etv4IWXwAffamcvr4AMKq/l1/pXINP2f76nKlLMSeH4AsBuocMZIIx3vpBcx6OVQDhL8Iy83xhiTEkUSr2B0VSpb3/9jgBDAS74DfVABeltkBQ4qj8wCgCP3C34ctPs3fnP+8AqNWg0u7mcUGXFiQYxpYrJNjan7YyjfWCNFZ62KDv+GIEAO0QOOF4Ts6dkLf7mByCB5wxGeXzcxj/cmyNMLwWonHJIikFsNURzgEM/m9E3R9C2Gv8HjM7pF6xsjb4yf6PffRf8eABKGWcMw5al/wvIiGxjAJchfH+1wBBhk4oSszvHaIX9+GvgHExN11j9/dgTzZdk12//kw3Ff6qnjZfAogiAXyBpEKm33v95hI49fZWNhxskWIAGAx57Mmw/8EZKxGxecPDzyf6A5ccS0Foc9XhkFwz8NftDPMwnzAAEAFwIDAJZRzQ6wvccOD+ZicjuI3OehqkBh7Sv2j5sx53J0+tWuibJb/wPiKw9L+GICT9Hfiw8hgFYkCgq0NqYEwH5AbeGrbw8/nAJkGQruNqa4zXBIBSUGzhzGrPP7wSiHAEKCKemxx+X/4c8ABEAnwKGsPIR3jpNUwvABjZVvUXDqi8N/xgTKChTD6EN76RUMB9wo3ady78178PF4kvAA3B+wF9I+C/c6/iQ9OnYJGHqeAAqgxNoueXDrIb3AAFMBsJ5UUoPCMzN5HD7KhnEJtRbvQAHYo4AhpSMyIMxceB+iyCSmyqda3y0MSlwI1yH7wrj9+Fv/fDPV0e/XXGcKvvy/wQcABEGURSkkkpYc4st3mZGE6iLxBKGsQGADYTj3Rji3uvsaMOUhIKtEf73O2XGKo7LP/7loysK01lVwGM8lyv5u/gMyc/2ggHxA/LSrzmNXd/7wYsb4Et0P/kBRCUtjdPvJMsyhvP+r+JG4NUIYMAMIWqaW+/4DPJzVbAEU5BXqwrWF97zQi+epqmepoDEopMycSo3hr3/njEuIUg94vkWxeKcQ1d65VebgbPu4yYYXS6YYAAO8AAjgGkRo0RuAAEFQ4hpfv8aqKbT//tYKCgk+YjK7xyovvvDUtjn4NRRn4cjBoCFr8kVH95PwIWGDVScs7ps08/+6IFCPV7RNltkyL8Dlb7+JG4m3OIOHZNgpUzADVSAAQEZ8TE74XX+XEkopJacDvC4UgTNXTxrBAGHD/kACsGJuEyh8MkpvMBWAACgIbQNDLk0RqVh1yIWLpxMa+apBLHd7N6VFwaIU9Y4VK5v8EHgAJDTlMUTPR6cagAD8iYwDBDvVU2HH//B0Up9/5Bh67xTLf0AkuCC1bLuSvhhWn7+D6jIVB3awbryKGxhJiDQhUVPP7hc34xkm5N+/UCPV5GxbfvP8bsoDF+UfPZx/+75QxaFg6U77tsi+7/xyf5W+PAIIm2mhOM6xpRLKYfgPkigRYN5O7yArW24GiqNu1HHoQl35pz818YLNkJo/K3v/sAAbA+gIjbGjRHgjfebMZVU4vpf62p5Q48VrTLuv7PU7fV+3mbMaqc/cf1p+TvXenu7g7KILQrSsn6791wfpQTIHtZZKzmN/++1mCTFnkXz37/4fwPYAWwpLk67GtmGSmyEiXo//7gW3ThxxNQv8+Ai8Y4pfsctmhTNNuDIZCspeOjM5P/2EDYBBadK/Q4sq77RMIDS0baa9OGKd/hAABcEO0Ghh2aI2AMWiESc5BXjX3/7PWKj5pVJZb6NcJxX5dPyDgqiJDd8f5CUrZVs49/jbBBz+04O91wLhS5WIR3V9/3GzAMWlIgs2Cik/abMgBAI4CdqMjUDv/mMe0zFZnyn/nCGAVSQKCrQ2pgBM6Rh1qzU92NSH4zdxAiYwGcIUSBgEC4OyA2oGxW7bTgROYpWYbU22AyGOIQvy8eV3tOEh6QZap2Z/4Gi6Qc1PLt/+/6xt41dSvvn09b0R1XqNZGAvsffe6GGFR0U+xfiQ9wOGPQI030FoKer0JnAqYIKjXaeNJfFIAwgmUJEWCTbH9UAggikZEmiTTVo8wvKP4swjSI/rg7DjmhBt2xU/9gzTn0a/ph2bbigCxxhaOKxaxtCPGjzTGRcUykH5jew7AMK2oU1Dnb4NM1FQQfjUa5gvK9Q7r/vx5ElPOPnmJ1b/u7/EjYCgY1FLsQjqMVbOvfsBf2FjAVB4hBp4R0MOrzHoac8tzeQAGQBQlgZnngf9WK4OAEXAV3LsV6TKMnYEBqXpEJmYRWIIQxiny14G/uij7v+1/0fBn5/2sPwwBTEBLmvEylrE2VoymAQoX0Mjw8OtQdST5P+9nSeUv/X8M1DXc8L8SH/kGrDSiC9dLzoLDwxLSkWFAQk578/ADEYl2KZShPYtLgI2tYy+NqbgKh3hwir5ou18wwWgBzZhmDELtIh4wk8cq12gY7PYm4sRNp1n+deiAATOrBk2bQ3XAMTfJ0xL7Jf8SpmN/QPUwcwJiNe/8o150X/ix5qjkMfocv4kK9QPlCK4MwAKApRA46YjOz5qYt/kwxJhgb1o0+oZT5M0Dz347WfBfBn/xIZ8Biv9/3M0dAhhj/BhoPWu59bzcOHL40zju8/4Z6MQJlWPn7s2Jbe8AlwGOJrCZFkiyyGstbZnufvzeH+L4MICIhETGE5BHMYgGDD4AFQOQQPOGJ1y6bmMf7QEI3n9V4Jgy0x/A86AODrJjamONrs/79YUkGXJyQNucG5w/Mi89Zbt9c7/3MVqei+LD/+HoAgXEhJKyTbJiR2Hgw4EUGCVtDqIdm3Pf2kAhbWwShTLXPoX94wG/BQpl5GOc9JLmPEA2wcNZfRlnHSSxgMMmQWpru/DosOLD5mivmYXct8fn/h6WH54ctXvYGrg8OgJqzJYlBjBAfDKXw9EIxiFU0Lppm6Q9SGWqODY4nt/hqAOQKD/hUpdjdLZoAaD8fhFHc8rBCBAQYezY5REP+BzX5V33fhRAw83xy//3/iQrAyAoMCT5uU8vmpDG+D9sMAVGBUpxkfbXEoYAAjE7iLQW7VC/KKoekJiMwiq4hDGIETTa5x7Ma/9pm7M8/74B//Ehf0IhRsSYiEn/8NrB5G2Bht0+J0b5aA8mX3oJApKn48CbnHHzyJD2gz1xIa9Y2AAeDB+0vR/k2fc8kaT0qB6IB9jTF7//hnyYibnFvikPey0kRgDAUkCOKsDsLr/gfIbtFCi0K/Qn3zSgdaujV//jUaTzfuwlAUJrTf7/8Lz0xIGDASJdPD/77vAEECskkQmlK+u/0n7UPuAce3OHl0GGN93SAgomcJEGirbDagGFEVjIiwTaYAeYq3LmPRITHrbv3+80j/33e9VUXRI5f77/PguOmk5D/Hp928w3ft4P4VgzABpXkFYeqUD0HF1ofpEQmQxsQIpjFBhsBi+0WMMYeZ7je3//Pj46PUSbr/4Iuot/55m678/xmJxP8L0WAAzMTMpTqw3LXwACZYCvhChUPSYwvkfRUgSZC5sIZvIyIMiiLpJCWsT7XiFFq8jZsyL7qRq2IBk1avucEZNIctWX9z+JD2kG0oAcmDXtjJ9/JmXHoDAIBhBNISIsEmWjYaCHABZS+Adsmjyn79X9f+eppqWO2Qm5xfn//4kNwBYABYELwHhtyaIwCIsEkCT77ZJbxAABugAEYA0iNGiN4w61K6mII6VGMX4A1BdDIY28/QF/E/DUgIBKB0uD4em7lIn4OFxj/+CC+ygAMwuLVlUl1to0j5i5MVOKh5FNMe4AAXBTLgGBp0bUwCceF2yaQ6n0Y7wt0Y4KIptGLFkd8BC4eg9JdBOH8zc/4Jkb1hY4m9tq/+4LlUDdji2f3/xPz18AQpc/Dz/DkAB1wxBK+o3cMC+qgHpjRUSDYGSWQ1fwICK0j7btX35fADOAcRlJuT26z/DdgWi4MFe+BCt0nFzz3x99B/xMbhG8QesAWq75+//4jxJ6+PEXvE/ic/WJcABiRCIwisQQpjEBh41ciVhGEcIm04ALQA9RyGdbPW4TEQdwAABbbQZog6B3hDwhPhCEMQevAm5G73+d6wh4Q8IeEPCAcsHAAqBCUc+gvPyNC3zn+efdnv+RaPAGOZWu1v/xIY0MYTOkmgNgNeASB7eX/v6xB6VcAY3Spvfz+LxB5S04EjJO9+P/WIPXgIR0m/9/8+fmPkWCNUvjvPEgXE1/EHvwBuTW44+f+HM1/n5UVyK+sBmAyWa1d4gbCLKdvA/xJ5UgJFyz/v0YVT98f6PLLCw2lsOX8SGsADwb44AOCuoFBKuN3/kCdGQAYGeBPFGB2B5/xfADjYLFKSv90jPQZlu5y//P4kMwJBCQSqjiVQUga7+7/HgAlBKyWrk/yxjwcFuE6jP98ca30/nOOo9J8e/n/EnrBHGh/2QhmdM7YUWFYiB+//iQ1GwcALEc4y0FlJYJ8kmhDlxa7g3BAfdofv1/+DD6SIJkMZCBEMYgMPZxpFD+kBqJKecfO7s/AeIlbIx88/89fgjklx8+f6xB/c77OuBZ1Y38v4g9cAlSZOu86XXDvH4vm8ABzZss9rppP/9xIL8ADwaIQACgjXiQjbA8/z/qJygRJpEwgS0R/feDKexPFVbwDFqV/8SGYCiBLTIcIyWw2v9oH3/uAx3+1NzdCINNMf4MMX28fU2e94P5lOevggwAKgcwgeeMTnd03UY/yBcYkZk4SNDIrI7gALBCwWuBCWop3de/eA01ZwAK1dmBTsS3+4AWgAuFq5YmBNknH+G2QAgMQD9wUZGoHf/uh6BAEKTaVu0wn0DX/3Fa2ynuZf/7gQpTF+haIGtEnXP8HugBxiPVvnzjPGVSIV+7cQmYTMOOHLA5IKFsfH5IYZwJXQHYN+N6AhG83qmhMmWGP5/ABsFlSeJxt+yyPDQIBZQBsg6btCnIfueAHAOwL4qN4TkJE0zQM68B6IPyo/94EAAYgjWZd9XUNqtABYuyFZTkHdTSn64CHaL1i21GmZ+/wID5IACdUYL9GyK12CvGs5c//IEdw1lnqZ/0oNe69Gfq7KOm4rXeUhmcovwt++m3UnFcHwyTYCluQ9VO8QL9QjG/SFpS5kD32aP/KO2F3g6n1a5Ex6QYBP/mszoiZBtpG1S5iSSSd8/4cgAOIZkkG4E5u/wwmW/3AxmwQVgRi72iyBb/AwG2/YHkL7Mmtxfnc/pvP9wGcuPGiP/G+AfN5e4AAbTeAAIAuSKoADADaDQMPE44ZKh8WX/gLAUlBsQOitrGgwAdgvmHYtPJRySF+HgILzxAQ4hiYI527928zMbupyq4/rb/C4mYSXF+v2/9BUcc9lmD7YK8nf+4WkTvNq94SLaJ4i56DHTUcZ0F4f29BAe+yP2yjf/vA0BhItSxV2aWbabv6NCW4z/Z8JYeOkOYZKF9p4yyhHPGb8DWOTJm9zJv/Hfp23pzjBNvhiNZPFoBgB5sYcWgI169PInX/GLuDJSUknwAsUTnZDlEItZbhS0HdhC24Qu5H/foKwv6rdO5b9oUlu/73/4fyCYAHgTKQAGBOESYjdA8/zSmnWv1f+wEzIwAgO4COrsjkL3/miQAaAt2xB3GDX/7MAAHKAAV4DXho0RvImPkZTkEfaynbIQANGgABAF7VUAAYAXMYX9bmtGk1Hf1h+8dhPuALt7kTJ7h7sf8R/PCHzYIJaeme2xWO0aCDPWriQ/ABewMZsUqUbB/73eBIMd/t+5w6hDC38/xYzR2N3w7SFN0gAFQc8e1XX0CljffK2yx/2XNIy0HKJcxr/KEZIEv22yy38Gqm8MPFEmHLe8//DkACI/JTek/T0EIKX3GzhkW1UshcXD/cuo0ZFgWQya6G/+g8AF29MJNH///m/w3DhlkswoTa18+e7FPyq+c/zR+bxcSCGAAxGJ0xzK4yVNSHth22gucNX1bf9+EXw16AxKKTMnEoL4a9/59YEP7h//DOwGqkABgRlAqI3vP/+7/QDCW9EPjqqG//rEgn+fvpP0iSDDIA8ABqIw3YxkKFSxSePghBCuY4cMi26sx4kP/DAAsdIEgKhXNJJ/bwFF/3fn/IAQQC6w4NJYQjPQvV0g8BGdRRpulaash6e9MADZlcJ1lYN74bYZMXvDAAQLO9HLZqMQxTS9HG2hcQMqXBG6pPzv9eDBViEiYzS53YS+87NHE48PjH42gAAIA4AAgAgBI+LsDO7ee377/7MABDO4zMRDPNStvGcBCNxqKmaPo8Qt/g/AOj34MKuXlNNl5choDFkpNnkJk3xj37kAfA13TwInFG0liA+eJkNlCRYQ0jv/8EduQsHTSLcX/js5Y23c1xrOLhf0hZ0K8un8SHoABj846Xmy8t53giRgAJABcXA1RpPP2CcUTnGABYyACGCUcfdJoHv/4O2CloLyRi+r5/fAAcGYdqMSRHhSpNx3/24Mv9bbCFlxAoIVnHPwJL25Nu/xsEvSAAvnoEfYfWLd/OiYADAQX/kHTT7pDD4Oqlqwz/PZAQqaT2Z8Qb7AISfm404BPULimnGtrdnRJD6y/3MggVZymEuX3+Qhs0ygv9/DQAsdSqFdLoU35U+OG60iPViuYlH//UVCC63K3P9v7EOeC7OTk///uAvkO7uPsWUQsaStIv7/Eh2HEfjsaP3EEAWDqsAAIBhIJUjFXJLNWAADoDJjgMFT5x2YP+gtcPX1p95MaDgHAFAN8GDV3vx1jhJUyHKDgiVh+lou3kHHTdw+BsEmlXVoJuJDsBcBWCB4irijp9WSNv8HlpTabKfoE2k1TL/Q5ltZUqA6U7ozEfZ4PwJQwStodT3Yt129wqBktBGmd5fP/gJ826b6V9/gwcZt3+/Nm1+1USz5b9/4QmjMiG1MNlFUghviBvTQdkCIa9JTlve8UE2yoS2mUW8AWI4qmoLKS41xxLuEgk2MJyiuc5QMCRVAKcTceopZhbDII+myERxV7xCmtVhLKL2YXv77mQWCMlklNTSVf/AJAHgNoci2Y8xAkw4R4Bg93wlFpLMklPv//wfBPsO/iRqcVjkS3/cYLFAcUxWeNL9VU7gIaHiEJLwgrJm0vAaKbJC/l+Ij87PnfLxkDwaTbWKt3z6Q7Wp1XL//9/8K/EHuon93qT/PVAAAf4ABmQAtuA8mgP/MdbldREOIthhAYc5TpvYf/G+AA+AM6CtQoyIKOGkf/4BUMhHi9KHQcSV9plohj1guySaH7j7Kbbb392AAsEigDgpu6jSrDZu1ImfJVjrQEmYByvHsUrLx/ghgIHZRSfgASXNbJp/4MMMogB3vJGZXKP00TI3vu4GEmj8zBWZ/0fXunx/CMSyIfiA//4ACQTmHtqDEkrOH6YABQ1jCQX7rp7OEEgilZhtTAQFRIBJ92VxR3BQy/tAAGPazAQliKajbrb+BIFKGzhUVNWeX8wA+A4dMgnW8/DF7DcAY8lJkShmMU7uPfhCatccTe3e/x8m/Pv52/kG07C/+91U2X0mn7/EH6/8Ab9R/efxEbw10QAG+7BPoyxfOmmNGywLYZNlDt/AKCHZzeuKo+BDbH+4wFcMHnTMp3dNQFv92AFaHFXjIb73+gMJHLQ/4fjCsdf5R2+QID9sACjGHrqG0Q5Fqu/vH7AIKIvGZJkmwy0bCNoDtMT5nE739wEAwomsKk2SbbIMRSQ/AA52mVrc3Ab97crkf3/wxANWk1/+whKPZ3+YBjaT4f+0Z82z3X+BNPMgEygXyCn99bbZG0/4eGKW0lQ5oIz3OaX4oxZnVMCA+CDoAA0JQAGcz0wBLexBvDL85zlZiEdhmeX68AHOA+lRsMRInKT72sTamGhDKie94CP2P+3AlF5dVSXPV4CfQxTALKyjDhsb+ynU4FEehVs0L8KhghYFAr0k974Hte9FPdZDAA62vUoaYlopHDHwr+tkyGnQqMreRIgmQRWIIQxigwwwsI16xk/bv+cAhgDGE0lAiwQba6GD1NGh1M/fq4D//C3kgwW7oZL/oMz58HxJIkRJBIiIBgJdl083gHS41GjHP51Jx2pGtkqRIV1fv1eCK+HKit329gPDTs/wx4ADNkVmPom66AAx7QneT9Ii+2hsVTFzDoapAa/BA0K1/8b5MA7qYw6HJLIL2kaElPVxk+3/y68B/xNExFgXtw3GEoXPxLTdI7LNgwQfiPQAAgBgFOipIOIPP4MGQYgtyBDzaABBAMIJpCRFogyw0AQ9nEcEYRIUMIHn8MVkDXojmOO0330Qtn+4PQGp31h9u1JXpggh1OU+Phv/CdgUXl9gcXd3ff/h74AUT2P1ewgSFXYAwGvXrsqS6JP/T53fjj6X3a8WQzEY9Xv+V89pag5eTbtkWUG/L/+JWLxIXgANjGy4omofzGocAAKAgDcQOmh42pgwL4BBRNYQJNEW2lAlhAu5Y+v+SYlx6AKATICBrDqEMa0TULlsPbJGZd5DzDJc/ve/8SH4FwFrgIQKegwSafeH/2RAQQTSEyDLzLb25hCilNww6ZFtFP6TE5EFVfuSxqw1+3r/P+/H+KxJ+XgIQUT5+cN8fifgg4AFMIXLKj2S2CWd7AA7wPrvXNrDghOyQCKEE8vzLFnRTkFIpZT9AAKVBgBLacCAMQ8/v8GAk+osdBdvpTqYJZUAgBo5xF2ooBldiX1/Ehj1RoaQYACQzCLck4nnmEmub5mAGoeshqIP4se7oEAc4srRVupEZpGMDO/MfG/4mej7+oYWf2SubVqON4+2vvtjwNzVfEja8AxLKVYn+YTUw4/+QfEQAQQ7iEZbYJHr/tAbKcAGBWvRKiV8Dt/gJB0VJSyDy5kVdrvuIKD3jp0iG2W4GHpxEZQJGGhWP/oA5EYboYyFC+pn6IU8jveronv90PgAiBbWeNQphRRJtv/3dXEptpcHKS2yRjj1s9Or2Ecn/+tLYvgfzHQO7481jNJUIrI+Ns1LmBMaF+/QCASIUACgnHyQhY7//7g+ApgmmpEQS2+Zu+DD/DAAZip04SkutsFsgAMWgxBavI5cNDO6pgAAqCmWDAw4NEbjbqEkIAiDDivBDTcJmLe2O4sHFgvwYIA/x4syorP8SNh+wMACHSZvQkdU8DcMJ5LV00va6lf4IM/RYwAPB9UMUrMUrIIsNuCrfkGFRLSO4R72AkBYUVOMdI+RjdTvB8DCPLEXv68lprsM/gxGKYxFr45/O3Q3jvM47r707/jIaG6jY9xrTD3P42Hr6AC/m7K1/ntoZFVhc56msQn8BWATzRsS5HRUwMdkEkJVcnOq/gJADOQCMLMlYXf9jm+kMpdJXt8GQAsNsYVJHX6GY1voWw1DbKSQwdHZluQcVQU208vrWGGFXJ6GV9FK3o56sOD/QTE0EKWGi+dN+/6O+kaqHXAEzNMugiz7+/xI32AE8RuNoJan3/+owJq4julMv7/fgAJjUFqBbd65YUOf94OBdOnlxC8Y0wngA0QDa3xk0fIqCd3/IBtM43LHx+px/Tuk8CrVaUn25h0oDgcrSGPFnUi/e0gMs9GQtHL9HJ8IZpq+FJMqpf94SQLXpU1mcphZoejYAShqxaT/LFPf2AWGuI/MQd9KMfgl9N0dS7SCV//9weZDtvyNXyT+Jmhc3/TUZ0R/qf8SN8Fragm1U6lEf6Ni62H//7YYGwqy8756ifXDMZCFHZRXrC/o/caK4M9YDcSJQ/cYIXSJz1VBqDXf/vTkMQQpuF3CwtooYX+PoIwx0WnzEmknmHM+4cEuib5tOsprAABQENoHhtyaI3iHH5HQziPtRrtQ6Oah0OUJv9TvhenCORB2SLbv+BGPZS2YTq//FnyRisW797p4QTyHGf72/4e2JgyA6jOSV5J7OPgiSA6ykpK4v+z4ABIKInMgyTaZP7YwGFE1hMi2TbZOK16T9OvlbXj3Lkxh8yhsuci1Xfz9aaA3rbrAfMKKQvSDedfoyM1MPv5eshOnIdCjetX4gC/4ABAuPyIxg7f//cISSwFlveDanMC4to672GGiZCUilr/3048a+N0GAEtqoMlcDaUe/8ALBKcZfGuWw9xT1awAJwGCGRiaaF93Wo7//NA8mK5kGSUt8DH7bMbuc/KOlq0huVdKXjygfeq3xncAYsFImBCGoqXdf/8GGAFABoTlnlOXee/XCmjIONaTl1yXjZbNnuneHYqv4C+H7BQAf8SLOO//9ACchsvIdCD8tSHAi4xa602puA4EcGiCrae/LvG9YAGJEI4clmIEvmU3z4Ou0CEby+qaPoS0x/P0YAG6I4VFFWM30+UBEedd1OAIEkG4e5mpnITd373eMvPfDcACbQCCiawkQYJstXeIDCiKxkRaIsNOTCBbyxtf+k1Ln2hlBNrBsv/kxPjy/AOBOXGDc78V1AJfPeAe3INwQPZMtUDrSFchKru/v/DUABMhQXaKlLKbJboAAC1gKXQODrx/EYPiAm0amy1QaCJbEqM6sIp/4wVSsy/wzAFAv3GUv870+xAYc6XFP+w70B0OWLD17fx/8KyBgdkFLAXeHRX3jX3AEziqVvG1NsSRAACATAboD6MXg8QwCNWBQUbG1MeKsCnqgop40R0uJAtEJV3uFfKnm/84qXM5D/ZUDRejcqheFYeCZRVK3jam9wabvEMBAbURkhD0MBmrAwLNjam8YDfhwxl78c32UVNc4RZ+yUmWp4GvEA2wcPZfRhvXSShgMapBVtCyJQiJf5b5T0lP//7FtINFjLVBtcOj0vCvSaFvb4/o5/9ATBAOtKOFbF81a22eP2+/d+D//hr0AnWux8d+ldnCFWglkfS54qtSuwSBcTX+Hr41S3OBgsAxYAg/MhQ64NaXU+S3MQeABNoBDiZwkSaJssE2xLS1ouivPQYau7VX36CEpmPxL//+zVoQye/DPiACcHg2ncl4IHbF2GWQ4b7QkivYp1vKl4XWKr/q9p//+dEAGXE0aKMcShviQ9gCBDAItYFBRkbU3wR+YIBADOyV//7nOKAKAvUAOIYzCKRP65BDDZiBffFZQU+j3yX+/YYFJj7htvm+y2vc/7+ZkYS8x0IF5bEAkH4kK/EAFx8DUmFc/aJx+c4YAEhgAjj10k0E5ULYMMMAB3MCNKDKMSkny/74EHRpIpVSmeX/hHwQ7ZBHkVKkwOP8kytXl/7f/8GEOGOCIwAGLhiC1eT24aGd1XvIxOoi84lDWKLfw7d36xKnBF89cCBPnHvn/64c0GWECvgCUbgtDaRL14+jX+f0G5rMZ+2QuJoZJdvr/5/4cwAEYo3KyHKM61nu+TDomWXSH26jHvb2qPnJgFxNB/+G7AABygAFaA94YNEYAYs2EnOwz5WU5gAAqCFaDQ05NEbniE2yIS2mQa3s/cA2JhWm7TECiSPn/zzliPQ3vMR6H79A/7/kV9z2xqH79fxIayDnpEJ3H8XLwGGRjRaiGc853afABBBKXgeopvOVCt0y3gMNaMDlFd2uuTukWFtDDinl5bv//jYIY6bgwBcB+QG3hsVt4oAxPcnq++TFSUm3fcFMjDamdvf7QEZCdOYXPd61fDcAAJg4DMxNGRs2pveY3XnOpR0rWnoCBkcU8rTBCJBj9MzdT3/4qCSy6L+X+GoYh4FAP9BMp6eNpxF27nldg35/xPifCJ60aVyOGv/PXwBoJuaOPn8b/nqAurSvr4JSlfX9Yk9fhntfxPiBtgUBHXzrDI8p4+P3OAMKvyJzkGbKynBgIx0TLJrn2yCnsAAFwQzQaGnJojB/zxCXZVe+mQW3gwRwxOaMwi0qy7/YMcuHiPaX/xPz1ie3w0U/5+XEwjiQv4AD4HMMHnjE53dNzFv96yREShLDJsI7/76Qh2MFpRSWLHzPBkTl6gAc2lZtJPobhdrK/nvfxOd6whB3AAAFz5BmkDoHeIPWADnadffv9//xB6hV9/W/f7//nwhCGIPXgDNV83rn/56/hHuesQGupwX0AcElPL86FtFfXmuvn/EeIPWBN+H79YTcP36/iD1iPQ/fr5Ghv6/4g9eALwfTcfh5/z176dP/iKxB68BKGno/n8XiD1gIXcj/v1b2Uj/v16xB68AUV69P9cc7zxbecziB/G/mNBNzjj5/+HMaTOgPXAcvcX3n//hmH2B3x4W8LTp+UzcGZKpu7/2/G3p/0HTXcZb8NSjsin+MUy1S9ZarSoD+TZodiMyIiLD0Vi8/XAEXV8HvmtRjfc4/8YcUfj88ThgziaXubF61En3+j+4KdSJ/TR8fzqfCvjKDzyMXwEg4nl9CiWWqBenaN8f//9/zzr0Wh3qpf40n97//nqVC4mgjXaP99cQxKk/8/8/v74lqv1iDyn/CPQ7Bv097/xB4tXgD6nO+fI6/Z4vEBzY4AP0BiKil2lD/+3hGEe5AZi3q7vz/DcACpZR0yVTaINl3weoXVdQ1BcFkdX94rTtP+7+RRYVav875tkrvPtoZNPnqwMlNjsRrS1Df0CAZplDf1/iQQYAHAKihx8zCVnDUhffQJhq6/BaDYLoav4ADwYklKk8lJXCn3/7AQSKwAMxVFhbhX//2ACmADwa6hqJO8sW5pJGAMDvB2lWB2F1/zwJDAKSiEKbRbs8Y/+Bt09WjN93cDELWrkqTIxsi47/lwB6CzlSPcAiaJB51cRf/7zsar6/5WGHE9f43yAAjIAHw1bDESf5QshyBxQGPKiUPNKPI72YppKfN/4Z5QxzhsiAGBiAI3BRgehef8NZ4tgKH7DzfbDl+5tOMsh5lR034cNb2sgsDSSaGfPOuP++lZV+x8cR+QTPxgJ+GDGHkI4zomqZxgAEgVQ9GqFXOPv2/B7Egk9syBfwnlXOgZvDWnR9nrYA/7xMf6Y2qhv6P+H/5ERBMwisQQhilAgwQwAHAAEAHoAkA6tI9sTbqYNJaLDswkfO1VrwDIGfpMsbzEMD+kNQOjBx43CeHzdBjvaJMaMCpW5wRxi7G2BIfdCp09+DFJpnixJD+yGJp8S7vstIJ7UYsb6TvMEjNnv/IfM8MCXRK+f4IIyC2AEGNvjiXxKCHqVYT2ltGLV//9uAcAcyMJ1MdCD8tiAwAXIU7leNEP9VwM3T9hDfwizzP/wEME6auqbkW//cjBcK9Mwm0MEJ/CkxFXuWm8UZY6sThgYcU5RtTbWLMp4kb1sGzmYXHLLU+wEsL1zPDgaSzierYk46XFU8tznvQ96b5lSpgMaQAAgBVeiAAOAMuN7fTRCLFNyXT8DoOwFtI9XOdPhqWggXjzGGNnQoKSuu/g/wGE9wkI7xRsUUzR+7eSILEw2dRVc7P44g1nJvMt38PKCCWyqRb63/+u+wKFeIf5AgYbr8zeqyTUmlxIW4fNCVSObU3TexJR6HngCBUPMNnB8ls5Um63S0h/+Th8LmWmKL3r5f8DCJlmx6Ve//v/iQ/AB+gIxfz9iP/vcEpuRimFRUy//TgXT4AF8iAEBng7SjI7C7/5hHf379sAMOriLyMKTSinhp6QU5otIZZbwk1ctmt7gH/gw0DYQ6HoABI2IiKKvUEIe9XtrJ4nmdCo3SAAk+oOr3wd6KH+Z+4escCF8j/v+LHHkv5npEP3yBch/yzGVc/2G2dE+/DEZBaBhja3XvnYvMBQBIFKCZwyKmrPLd5PglC44+fsJC9fofj/8OQADptKvafuAYB0wAwMMwnZ83IW3wGMCdjOXCtIU+2o1Z0g1hs1vZv47cZE0AIQjsOlqQr///xvgAMZkIjir1BCmtR80xiiVNSy6YGdFWD/kwAEyo4VFm0M3y/QMZvs+psRFlpn+dJO66hsD5LI6/4PSA6KCDxicrOHZi++86cCKoOc78bfesflAtg5X8Hn+GeGKZx5K6XP3szqjNfxeJD2AAkAEguhaTKuPMEooHegGNIhCpXfyGDPzj+8wAlG0MSaVz5klFE6DPQDHgQjUlhEjYz44/g8A0/ygBCFk0QfT//723pmbQXT//7/50oyVf8b5AcpwAgMMRlhw3UX/wYdLAAYzISc51Yblr7AAbhwXbJpDqbBRAfaB+UEzxsFNZ1o8FblZHSp+AQZI3w39f/4kLQAEYDThgxl9GGN8JLGfEA1QMFsvIxxjhJUzZ4EJ0QlHp8//+/JBgt7g6neSbnz4GAfNjP2MJv24gxhGHFAG4AYtF5Yqf7CcNxXKCaZ+ID/xgJuHCmH0IZz0ioYD5sINlWPn7s2pb+BPuCAwomsJk2SLbIEENhOqhAAWGIz2/VUdAllj+agdEDjhmE8Om6C2+AQUNdEzR//7yrzHkkf7wPUjLVA71CTysv/+uNiBJV8SHYG6xcvwTvTzP3LkHuhc7Kl//gJpBDMOVw5RpZR/sACtCSuavWa7/MYHbAf0j4M9zXuMZHY5uQKpz1eizMyGMhBkMVwYYd76sPtTfV7qQi7hKEjfVwSpP+DjJt8dz3k6XP+JD0wAAQBgABAAACB6W3GpRSU/34fwAEIyCtv5bxyFK03pAqblpXl6Nd8ai7xCJ9xTY/kAjil6xP/43zAAEAMp1AAxZHMoGOpG+8ZoWK6CJaRSi32yniSWeHv9/jew1WTZc24MMMABgOoGsrhc0tvmME445O0f654Wofon/z+AtJC5mTYk0//gFeAHw8UtEH8WLf/uKCdl9HsNmujv/o2/+/nfySQjQZUcRSFcNpBKh45/NW39Fkk0Y+xTrLOvt4VEw05kN9uOCi1BbtvxvBIAD6mDJ6Ji1PbzoCHdze2qEyYZa/gcvcfBn+cNPMP8/gdJaBHjZSu80I5pl+aAnEEdXJS9t7/399GAEIVtc8cpmzn85utzx8YgN06Hf0q2bezeP//4e6CKocLIq69xPnvd7wMIpDxqXL3Q8j1HwAwALi4FpNK5+0Tmic8YAWGwMUZTx9snFA94gS9xkN3EenVI4g1YRFF663nQ/4PjTrEXFAnlnF+RDUsJb2mVpacLN1//vabhhMGB/+N+QALC2GpNq68wQigdwBDIjEIZNd1P//d5BjaQhKEiYd3ZT7ADdGAhSBPWYzS02xOgO8sG2F0YjVXd/56xAPwNscmbg9/6kAQrjyZERINDi/uDAtJzwojE2iZ/5kqgJU/QAC7APjVkakgMH613qHRcwuedb5Kd/xbzHeXqvDCAdbDEskA4LdJ7N+BE5BlI3xt/voDHM+K7c//54aOM12hiBLR3/xI2BswpQqXOUWSrwBEOi5RMoZbbKd4hmEaryieec80h/Gxr+U6nD+16wzoEnFAh5VTyy1FlMH9m790ZI9/8my9HxN//AAeB0gDC2ZQvtbSifeY8mO6GcV1KJaL7b++Xm//sGGBG1nXj/436yIachUKJ61JYAAKg4DrnDY6aI3tWM4HMVCRpgX2VAwvbZhqpzq4/tWkGIMACoOQQPPGIzu6bqKf7iZfmFSAOpxpX7wEGTZIpJW9uZ/dDkCyj975uXj4EaSg6yP8riQYf2SImoSLDJrI5D5KghhamsOGRfRT/wwSks8j+0C+VjdsTgcDTq5U+L//ngFw5FnL/y2ETh8A+JDlqAAgAMO5jGGJUW3Wp5Qa//gT6xnLwhwS4xpw/K/DHhnABWLAYMJnKZMkcbJQ1x//6435h4gBQEIWnlAu+iW6H4RFU4zH/XJb6kBhz1ABRg0FvOmWcaf0DWNag69S+J//ZO8DzsAHQ9eR9rl6LsAMKzpgRqTE223vzgOcQNwYzKSL49E1CtoRfHYny/4/uODlhtlidVffJ6IxoX3960zo0MkvjeABKLWcf2GU8tiXhasz8TNFJvub/9wGJVJSIWYD4YxWE/ZLJxtiFv/n3vlmXBYFw3bhiBFEnX//T5pE4R/a62XGRkh9oY6AYKNj6eUb7YeuxbQGncGKBmZvMHMHO/AUWb4PGITZf1X/sBt+I39l1/97Ood8saf1/w5oCgAXgHhO/in6+luvy/8JGmV/wtgBWZ/Ir+ISJ8gQfA1IWv5bqH98AYludLl/+NgIzU1775nYwL1dEFmgZQm4J59DV9OSuq/rgBY1UWFUXraIMghcaJYAZQS3DzSvv8eF738PAAcZO2z9P+n38MDg2KAB9PbWoVnf2PHLkStYv/s2FIlPxUqtdYUYnLHRfhaGHjESAAmgAaglXDESJuk+95siADAQgCNxgowORupLAziUyE+P+d+TJNhs8U1S//wAtPSLM8QI2aYW2R3f7//+H+ABGEgCHF1lQkwRbY7xAY4qsZEWCbDCxYAhY82EodR/fqyOIc1Piof/tASAoNnHuNKIw/Bf/Xh4aPc26+FsYQSBI1RQAK1dyUFOxKP/38NmQAQGcD+wUZHInf/gzl+APgKsKkbkwGICyKfHr/3GzLGtCo1jSuuXwx2BAAMWgxBauo5aMC+qr9tDZ1EXXPQ1iA9cN0n+M4f4AHgm5AAICdfKidkTr/AJBnoZMnuTJvjHv3ATNGAIDuAjq7I5C7/54kAGge9hiIO4oW/wIMGCOAIACYs3KzHKEI1pbsBAaJoJRE5eZXTp//9wQD90AZAaTFTXhAdntC3+vBj8g+yf7xkgmy08McCQIQRjDWsRco0g9ngAJiOKp6DyvcaUY9mkgAsGu2JO8oY5/bQGAY8ouhd9JkIJm8DKlHCMu+r7wHIpFimte///wx/AASNkEylPyDctffADKNCjhiM7qqptOf+zlvlNx6X8ASNrmB3+H6AckQARx2/Pe93xAABUGAZk+bHDRGAEDIDP9tqXzuYCelugABegAHh8gLcgPXzjEtZxlrIxdu8CbvSya/cg5dMx43+ABEW0RTH0RQBCYKcu08US1bC+YGDWs30ygYFf2gG82g6B8WVdalpffngvx/rPfqwIUgwbLSNE0n3H/uvCGj5UZkxb1xUy/VFBv/C44R7JXPtAjkEPUXCOl/v/xI3ogw2XgyXvzZn159jRZvzgDsMpY0FWlCGQolUXgRSPAC+r0kAcE72FojMgBijIwfWKrOd+wzOgxaJ1dQf3AGNqClllwRHHcJvezH64urXrWpDXTd/MAJgBYZAC6ZijM61c52eqiG4qfNLNe2eGBvPWH5uCg6UqDTc1H/ycB/JjXVTos7m13/YcjbWr2///AkYdceGvjfgBalf/CE6iA3kYV/wh//+/wDPAitoxipkpYkmBKCoeluhLieJVf9wAlUD4rhsvd8qIW/8gNBoNynhDMcNcQHHiQhX/XoKUgDAelWOfl2ky3DYES6DpUv1clzVjHUYrxarCif/cGoTeQ1jd9bSjMHokADQFvVIO4oW//YAcUTlTHcZ1rNYMlFOOzrv9gvpAQmRUT7+1JF4i1lnekNNhmkZGZ4+vLf8P/M6gZZLURPww/xWwzjn0ji+MI/3iADvCcxsYkRNtVoABmKn3CQl1tgtjAABUHMsHBpwaI3mKtitzsK6FlNsEMYl9vSItxO+CrbJlKqj3/ukW7tTsoKUMiGUVHec5ZodM6H43AAoxiZZMc22QY/oenywZOUCJMNJ+B9wJGKjfG5gwpPNGnhAABMCAOydNjhojeQUB8xFIkSIyUS9uBOwzV95tTASMROpHZmwnXdVngFgBsMJ3ba/ux80t//vYqCVqJRAkQkom7wvIAwpG8Qosl7yL6hCD7sBsIm7z3F1PDfH/GwFBD2WqIPITBXjH//i0COGAHIpUEr04RT2s/bb8I8U0Nh7F9WENUdMEsLaQ237eRiZWUZeeQl6l+14QotfUcOmRndX4AO0MXIvkJxSXoaGGE6Lp5n/SErW3vgm4mpr/fwH/Eh3oGFdjt83ngdDpP+84CfirXum1N7jGRWFRqm4Q2vACMNajx/8bgsyo01Zh/j+0uXktc6IsCPqJt5GyuMO2Au+Lgvu9ABKAFqCHhaeJ6XcSKf+9RCIiENiCIUpBWhkPBqxL/+IdHt8PgKezHqxt3+H9m//wxgAWBNnBTAfmRFY9k534AQIQBVoAoKtDam4CeqAQBfF4wDJZnx+AWgAkDXbEyd5Qx7+D0Bi0QiTnIkrxbv7vg9CgJUSKZ3//cY9/93+6c1+JCsABwx2+37u6EQYaY/wYeABUigmbQyXvzbnv74wMqgoUyQRnvPSSpjKegAO7KzIaIv/9/bwtOn5Mrm3wrLoeHTDRWSBMDpLJav4MCIHYKHnjMJXeMyF/9zQAGyIwVNmUM16D4BDO5XVFWJiyyv/g4s8BBWMd29vM7798fqH5kVUQ8XiQrAARj7KV1MQZ2qKcGHgAPABILoak2nhBgkgf//ugDGsR6pXKJCxlE8/so4kgFbOxI65f/7gaz0htTfSU9Pj+JDPzABcTQpJhPPlyEfnQY9AMehH6ksfJ2MoHH8GtPn40RUX/+75nkrvONq//iQrAjBD7RWpdD7LdzgABYFNyAIDbo2pgS/gIVOygfaDCc8UYeMAJcDCCaWJQ2u4mWBECAwOw2sgkfE1u1LDKlYXcPr4nsEqIOk4/xId8YAMlYACJH0ggKHS6D94gGqBg1l5OOtcIKmdEECbtjq//JmXHuSDBd2h0u8kzXnxfDQfBAMqDkjepxbyqtN4EAgQYDAgMYTKEiLBJtjv6oAhhVIyJMEmmgwQyCVB4gt7R5Rp2Scq6eEqH/5tyhmjlYqc6eOGIQO64NXSvEhr4AFobCBJ5C/1D7aIh3jJhkFcvx6IfsaYE2/1PjdAzJLnm/8//hmBoG7mAAgIygVEcYXX+eegLTUhVWlyeGBa2yrU22NXeeEtvPvbD8cMKD3/jfoEO3Gdd2Jmwwz/IEWABoiqGRZlDd+WZog1a9Pz9/VSb73W6ruNFdhlIBkPEpf8yAAEAaQAAQAAAgeRbfMjMJ2FVqCVMaqH6cgxBSm4XcNDGyoMOMa+WnLH5zsRMdERv/IaCenHHz1cj8zPn7YNIYM+JDPRzBGHixCZdLLn/u05DEFKbu0aGNFT/eREQRGEZnOUxiAwHfLZH8ev/kG5R7+R/nEODUfv1/xIX6YADZFcJ1mUN3w1iR0XhaDJLo6v4CwBFFU96KM1xfe0XghUC4Zp6bH79Kb3/8gvXAIKTnpFP6SH/YY2UL0u0I/eu9ADWLrhL/e503azjz5pgNk+b799/iTw31BMl12JN87+dRdFJX7/TCO25zv//sGH3IwN+eQ+Rt1I++/PZZVje1//DUdhvHR3HBHrSFcgoO1L977r0Fxz/z1YfHfDr5h//zyg8/fxnDWQICw21Ft8RVwdQ4//WJDUAC4JUX0LYbFdHd/ATgASr3CdRtjd/AJgFRA4+YnOz5qYxvtAY7fb+3QiTDDH8WFrHGXCdfe//8OQAJMnojehzfq2dDyog+zPvXfaReOZ7mH8ddlX32Zw43NtvjzAYJKeX549U43FzsoZS64bPnqHX2+3x+scCT3o7zh/Dm6/55S+CXzOcAcqc+851aUxl/z8uwgewdsmz/Xv+cwVVX9v/z184Hz8b+jg6WNEf2CDc4f4cx8x9+MiMaWs/7Zw3ItaljOrBQJ98+bz1DHiRGK5KIlLVB7mvpYvP/89f+At3Df1/nr8AS90WP8/w1Da3LEnWAMku31/7//+ev4MBcTXjcTWJCuAIEMAjUgUFGhtTfwSRMrBeMj89ps2Zv9CRP/X+UHhg0r1Wze///8/vgFu+G/6mjNDf1/n9vs0/wP/Egg5/AAhkrG9xEf5uXfxvNMxLjmUg/KXzgABQEAfiB00NG1MCoOwH3xsFc5y/0iISYwlIdylcGBvv+AKAyyk0fv9YkK4ADYxs+OZSD8paIfCACTgx4Wniel3Ein/vIkQTIYyMNylIDDFtjq4zZh1//Fkh5fPWQbQ39f/PXMK5qcd6f94RhHEhzAAfSQAgM8HaioyNwu/+6AzHEBpjEEOHBeVY//L7A4AoRrj4j/3/iD1zO/c+fP/o6+Ig7gAAAWukGaYOgRcOeAA+B6jFfa8BvQsyJf+XgAzbfK8/3+G/xAfgxf0vAZ0LMyX/g1wZfrncf7/DGEPCE+IPWAs6Q39MM0yQ39eEMQevAkDzG/6/iTwEX8c71iD8IHROJoCJMk+7z0NmRDRn+IPKn8ELXn+EC8ACwhGoaipoTJdhj+fwgr+EAv4ADFwYgtXUbuGBfdUweDPgRsQBOKEIPjEAIYRNOEpK3t3HrodLeAKIujrKZ/nrz3h9B/+G9HUoMg+lPAhX0nFz+sIReIPMS4COtP739fvhuAAy9pPr9IEWtAbIdzMEaQ1tgxiXScnIAPl9n1MOrlK7yxmGL6+fFwiFpc/P+HVj/w5AAQl48ejlEN72rIbar39dGgAlD1bkibJOO/28HqI4gQbbvww6eRMhnlgpTndjahU2HagwDuGJfVMVf86Q9APD+OAx2Ar7AAB6gAO0B7w0aIwAwu6kZzmGfbTHfGA5BA84anO75uox/tAQjeb1TQmDLTX8BiNZAGM9du/8Dq/pp3728BrPpVlHJqarz/hjYwEMxMinOpBua1HkAAfoCIA6s5TqXL2Fvun05NGkBAgIXPgP/Nc/Q0ONWxqS0RXnXWpa/EhvgAOGI7WpyIw6BLLH+1AfEDjxmVbPm6C2+CNtKqlPufaIydoyX84wFWSfFP/EnnDpgSAfevFlqOqP9/MtRtn+9/9f4L4AGkAwgmkKE2CTbTdsgIIIpGhBog008Mw/RMKXoHBK2NqYY3Vx/v5B/4Y2BwAGNkIiir3iFNaiw9AlB/GmPVoVaE4HRw30gTYgEUcYV4JVpOTWzr6hj0eEs//jjBE6YX9lv//mHnk7cxB8NyhjGZ3/465vs+/6/1iD10BgCTc3Fdv4g9YBYk3nXz//F4g8pmOdCIdW/z+JC3AAsMdmq+4sRFhtn+eBEMgYVydZ8u3qH/g9Y8ieBZDIqobv75eOQmWeHz1f/haAlsxuoq9SSlq1h+Qu6kZTkGfbTHB8bEJdlQl9Mg1/AwCHOCdA2xVj0V7TpT//DEAC3ABqGq2KP0oW9/YCciIABQAGQUdQREp7wEghbLRBpCYK8U7+7AEmKADh+PkhKyB3/ngAIcMPanl4zRTBFVoAd0Q6JO0Lt9D3JMyywVx4u//h5briA6/Ixv6ARwwkY54v7MOC6QWYz4n91scM1gmvGyAgneg4QfEYdGzS4Q+WEP//q8bHf3BgICO6H3Fn2bmKy//92g0YDf7ICcVg+x/54AOJaPHohjl1K1uAHMhs6mOhB+WxHnABKHrZYmDeMGOhk+to8mn/SaQds3t9zZ0GRCvQk7/T1dz3+2M1A8K88/Eh+GGAD5mM5XCv9Zq3vaGGAA4AAgATgLIPlOHqkGpGQfD4UvPWiXxwAnDspy1e32h3CP7WBQUPOmIyu4amL77h/CVwyFPeP2z9hEgNTWci5ffgvyH4oeCUqHvzhaitPO//f/D3UDnlBM8bBbV04BFxi195tTdAw8hAFYgCwq1NqbIBSATfGQW3l5vG2aZB1gsPQhuTKZo2dV7O92//cMeBLKJi/xt12ul7+8xeovKlRTLv/wAxjomWTCGyyDH8wDQEk6yfQ4Ejlq/F4u8EYAMHPJRtLgwZxoDVh7BsBZDAKxIFBVobUwDwFfDCvQT5hBeI82J2HvN5f39Urt33JCMTQYi9xxrvP8LcPCrdH5DamALN6cjjV/AI5zt2qDeQWSV/+sm5d7SP/0mG1cP8OZOv8DrFXj7xcf4Pq3OSz/D8AFwAqopDV0QtzQKOME4huONYWf8ABi0MQWriN3DAvqq/ZoraDTQZJb3M7+49L/bwwAHWoB5QTFo1JJX/8E3oWkrg7Kc17T+94oIsxmwvo1RXKOH6MMTaRLQvG6V4P8JA3pHSwLD3GIS+cn/fXKAYUi0EIJJO89gAfgOcEOUhxBIrY2GjpMAAFwUywcGnBojAJxwW7JpDqbRhElvRIzWAaPNwABAMibwDytRq+BLwMT0CoxqvTmmwR4jfmOp2JqiOfzXtWrk/P//hiAoHehgAMM/a64rXcw/2hlAUpAUzO9OHuns4W0jQWUXUdv/txZv8pX/fo6aP0zCZnFTqCkLej2kwxRamoXdMC+yoGLTXDXzlPfi8KVtPxYv4YP3o3/h6aPiQ5ABT0TfyZ+/YDIFDgDg0xGV3jUxffAZgGinYnEYSt1tZI7ehYDJL/xfy/gA9xaF5zsf7/4agAMwqLlkUl1to1zAABcFMsHBp0aI3mWSGynIORjTGsAAHIAA7wHPDZojFKG+UC/aLwQq7NwMY3aSk+aOevV+GYA7HBdsmuZTYMcH4hZ8RsdxyaWW8MhRQ3p5r9effr+L4awALCHdzeuqFyYbY/n13JuP/hnzArDABQaZhO7pqQt/gw/Q3c9758//8SF8ABGBpwwYy+jDG+FFjPmggTdsdPvYNy197BAYwmUJEWCTbSGsAG1jsNO+//++a/Hz/iQt8QDXBgtl5GOMcIKmQ9EGH26HS/yDcdPf24CGEUjIkwQaYBh1qOODmXf/txoQg1C/8b/4AHoB6C1nRzcW//7A4YCgY2HvsJhlAjcv82DgDAFFNR5X78WjlQ8EgrAqCSFlkL8AEjJ2MQzq7kUVIt/3DFg1Ahszk/LdV6Z3J6qvBJpzJsjmLM8a2/a/3v+HqTghgEWkDAs0Nqb/AY5DkaSQmiDaGPfmfoVNcwc6pc6AEiZ8fFJXCa5q/3SGrquHoNgz7V/AIoNAhZA2Pfdb33mOjNIv8/iRsBdvM2N+XlVf+DXJt4IAOYCmjmosWw2Wv4RwABGBuocMZeRnvPSS5jyAbIHC2SKMM46SWMBhl0IGGHsOAg8sD7/1BkowFHbRFH/dxFMkzG1MaFzI9WX138SC//gNjhnlY5eiEWKXK/IwDolwqimwm1qCUz+7hDXqSee/3eUHhgymuPmv/0JbJsnNeDaj+JBBAAtAALAho9uvUUyVznfADkZhFYVWoJQxqABrgbQfr0y+WuGx/w0f7+AAjA24YKZfRhjOiShdAeGEGzWbK7bENmm2zeHaLc6//eCDk0yLFOXq/vuxLxhFHYtBZSXHkGEu8iIRGQxswRDmKE+CfZ4JCwL91qqqL5B9lW+m6zMGjTJJUbwciuyhjoUs3iQr9NQZgMYuEjjQtsqDDsHrwYFjGGsZbVJ8YF5ABcXg1BhPP2icUTnRtUBscjas0KZ//8SF4ADhDu5qNiqPgQyx/uMFSAOAluMK0OsIGuDDgR3Q/abgplxZ133jpX7Z862etWozjD0WV9Kf9+ChguwRC/h37jMXxTKwvKWhgAAoDAPsdNDhojB/6REJEMZGG5SkBhxxrTw58YaXB//X8R69KTa7wNgitZKfv+PQF/w9gAJkhuVhFZ5KWMT8cMsQomfhDSVN+gAI58AQHxrg5kl8T4W8EKgTLNPTW//oXtVC+gU1z4P+Omyj8JLSiA65ir/Km/9eH/EjYYACQAJB9DUmU8eaJRQO/6AYkiPVJwz8hYyic8wAlE0KSaTz5slFE6HoAxaEfmSx8nYygcf3sCDgAeMiZb+sZHf+9YHP8gFIBBsW1IaiqJyKQYjJCEtNIPp//97vWbZC6f//fHh1uNpPm8fw5AAbgGHLTJa00yTBzkx++r/76wE/OADB+0SolY9//7uAYtFKkQhqE0ruv/hvGzgAWeJMTycvWn+uvgiwEvxiiFezu6aFt1kOXywAO00+5aef6BeCDwAEYhGprdYr+U3UQAJNAMIhdoIW88zwAHQPCPFoYnBy/fQ/oeV7ZDZ1EbiCeaxGjCBdqx8/+kxTT12EUk17KQ57BCmBEkmYolB7/9wAV4BUwGuoTkAWUcF4i3/r/8MR2/P1+pZx4mMR7QfeV84CQWcLm+VjcQXLhgHFTxeCxvT2+Kt39sDE07uz/f8N8ANXJ4Wgn/zjrK+A+8/i7UOjSG+f/4XwRNLXdx//8IvxouEx2AxLDrX3F9ZgcpsXT/w/wYHxfvfuFYp+9v/4AFodI6S5VSzMAYAPD8FptpaRaJwQOBiWmvu//9c/MvJbcj/BCWWyyN564VwJBiUQmTiVSXw179zIPlG8ESxCq83+DD5pCVvywPf7H1W+j9EMXCosZiT14DHq+v8SIqhLYhUX4X4ACZQuVEOUZ2rNIYAAOcAB3gPeGjRG9YdEyS4Q+3QYSwAAXBCrB4YdmiN6zEyKcX0O5rVcpoCDJbDCSWmFAyOqLQA04akbahUycPmX9p/HRi8SH5AwFD//wEDXnCEGE8wTUj98bVgAIGEXzBqna2/z3fd0CEglVHEogrhbv7uAxqsN5Vkhbdi6Rr/4MYl/xWAH3FuT64DCErbr+11f8di4ZOHuJDVggAHAM4nhDdiPc9oapiQHwmAGgacWqRF03Xv7PCPX1AI6NUx2L/mVdgXP95jPpZ7t/4kbgdl72j9cFafm1pm//fpJGAMBXgRpVgbhdf8lre4kQ5/IBYABYGPCW6x/9Mlc1wYOgL/gANRDdUMZijpYpKBWAACgOA/Bo0OmiNsIPQUbw0uh8oGZrZuOqg41Zxz8/wQeAA0o1dMKljrWW5oACyKApaA1ul6oHvCGAB9kIFFICF+3T6F1/zkhwxGF95ONNJwCgAcBOTV8TDbYR/9L19qHPetGEQMmRCsll06y/cMg4Ix8+MiMFp5RgVpW+FdG+t03+NgSwg+1Y2f/QYlp4bZ8kIhKtMQyuLaQQGBKRgMQRScSLJJhtYMiMAjAeBypRd1+8LoksAIevLYUUTp+iG/XEiFIw2KZjGIBhgAPgD4VICq2h6hxux3oMF5CERxhRjmT0c/8G83BDDZiB0pbysz/7120uYhoTALpnOFfP/j/GwwFKl28yqn0X/4mfv698PHHRW4xaO9tJ8sTez9u+ToGGAA+QIIHCOEdNuqvrFR1sVivyM7sV/cQKuAwpmsLXXyklgNhdUJadzMq/S2lt1e2DlXF52L/5/8GEntk5DSS5b/+2m12DVMv8y5gdVUyGX/vsnNzTV/z/GwerX7Riv2uNL3rxADwtBabamPtFYJCFvAxNrEJR9H/7e0VRAdgQu7Ho5Wy//+/YQ+ABBZk8xqjHsskgTjRoFJgyHFMMIU9gPuixkbWq//9NBg1EBbeYwuQUYf1w0ABDpjXljsSUg3/wfAwYh/qxdrQgPP2+xWAICppBGFpc8stWbpFWJt9cHGaLX/SQGlNmxC37tmwlyKYTf42gRjK3LwvCUbZH/4WAIDBK4k8g5PowlZrgRICHVrfjtQf/u9Eyovrdf/8AKAmwQLWdQhrGiahfjAKiiEK4Q37Kcmf/hhTzHuIecOzJcyMXK/+AlnwA6CdBk7EQiLh94O8YlLzN93f/iRvRMANAS6ag7yxb39vejJsRZi59BsEHSAqEDjZyd5ExCFh36833zj/090LQMVet+5o6BDC38PUWzDBjAAyg9eKV1l/n3hF3cItWahaeWrmBWCB50vCd3TUhb/BgA4bFRCHIpnp0cwYYiO2tqRxiiP5ONcrn9bOTrbW0Q9dp/haAAgQz+b1TM0fAlhgONdHJWV8W4qSVGbKgoC0oJXDFtWz+ABoAAgG0R4UYYxv7NjKPeGBq5QrX7tv37/4TFDCrjTi++ZwhU9JL/vvrDKj6wr/hagUAC5mMONQEbdeHkDr/gApABYNeyxMneUKeA0EqnABg/aJMSshd/5oIxJCM0VijvMxkGICpgACl+2qJ/teDuptkQoN/8SFYADhjt9v3M4Igwwx/gw8ACqDDVdDqe7NmvfvjAb8FClyCMd56QVMcsCd/1YJ8rGj5F//v49cp6/w3lNAANAhoOJwNjlEjYx85wAh7EIUJR0iQsY8cBGbfglmJAun8Vz1gopo6+v/EB6AAiFHxGx3FfSy3hh4AFQB8SgxNhLP2SPzn/90AQtHvoMx4jcx46/oCLhiC1dRy0YF91nTGjokDUHQYQ1fxwcAFbkaZii///eVkYbYb+X8Se8wqv3x/pS3LuE93gf/8K/IMHYzYKZglGLdCgIYfxABYfwtJlPCDBKKBvSABEUysHe5bEG7/7kAxpEITJ5RIWMonP9zAx6EfqU18nYygc/x01gv2KX5zkFzw7RGj//wr6ZzIMl4sLAY0Y8pRL1mNFLGM2jOvqAotVDpOjqTTrvP8K/SRpkPdv2UYCBF62iLNshJelo9hecXRJDHPMjGZUOZSBUMaoN5SzOGdvWWD8kTJGvQYzVfN656QyLHH4V4AmQ4AFBOPkhC6B3/nFMH7XbJCdf7wy2ND4yLEaFkYnBh/+N9Axma36qhEGWWP5AmAAlVEC/BditfLImYSPMuh+/qDzdL0HbwmfBEcDpYcS/7MwABAHtAAEAEAJHUW0BDIg2URdeQlqkw/a2I4HNVPCzYvupBgYcHYRINaHHm4wl/V3Vz+AX8SFfkNCHWOKhP4q1cytYdRquGoNKqf8GD+REJmQxkYIhjFZIKWA+oGL7s8/g5fiKCfa/1+z/d0HDhWg/ci/OJJPffP/EhX7ZD1reMuqTTDRk8C6GRXQ3f2hB0CVOJbnUgEpXnf3GBWCAk+ZlO75qgx/gQB8aREs48HxMk/CKm+pLzQ/Uz9+tZVxg1lNjWJK/c4fGGwexl58QN0AgAHVhji1tQy2aGdlQOMMAPer3PiqASAHeC0c/2kggIWrn7SEpVThqD5Lf5f2iIAQCOYCk5lrhgK3Oh8aOgCDMRQ6UGEKWe0oomgAIKZGRALDkLuvB9DAz0chdA8El0j2EbuAd8brVdZ3yDbzyaNr/En9j50vF3ytKqmrd/+FegEPQn8iWPEblvG39owATBTAmc8PdNKl+3/4AFgQlCP2J5+TsWROP6AIQL9sFJp413/te6FSkXY3YLpAH6RG0jFV//+//+JPUxmGWq+Ihg/z1gvSR19f+JPeLWpBud/xeJP7JDtz/Hrh6ev+vfDNbHKWAGHn80v/94dAyltlfzsjKHcE/DGAIIYBWJAoKtDamAA4B3yA28NixuycCbCKVnG1N8AyEmxBMU7mMUCAIBjxmKimWqCvIweEuG7wx7Tvs4b4/54po1NlqqAI3tPkV/r+JPl0wJztOnQ0E3OOPnw7x0GevDUAQIYBGpAoJMjam/jitIQN/wGM/bwGINnWd9839Qzl/z1DAWJYvvUf9B/aFcv/wxvAAYwqLlkQl1tgt24AAXByrgGBpwbUwCWOC7ZMIdT6McWr6DogV5EFIlk/eYW7YJDJbvP+GMAB8DkEBJwxOuXzdRj/B6YSMiUawyayPb+wCGbjejBMmWGH/8/lgAbojh+oqxnegR9DHqsTBDTwfIz1/70WCt/6nB8/vAGjpe+n+fjYAzVfN659HwnXD8U/iVeN/zzp4/gDQTc44+f/8MwBjIRUUx0cZK2JcAAJg4DLxOHR02pg/ILFa54Mw//iSYACI42E6GKMTbC2Q/C0EDOFgALBDPQ1FTQmTbTX8DAnAAypnC9RljO/PAHMxldRV6klLWpDF7ZLtiV6bMX/4YgDC1fPfqmtmdwBxVEKinYV1LKawAAcgABWgMeGTRGABuHB9suuZT4IcH5Ci5kQ7jvpZbQxZWxno/79Bgxgiay5f8//PUHWkK5f/wr+ZYsVOcg5FNKfD4IBNmDxqHZaLeTJ/+4hPCJjuK+lltwYYH8wMv0gtK0yP/f/ifnrALM0p+//89aGh2Emf6dJ9//r3ifnrgOkhlqvwjw5gAsEikABg/XyYjY6//7oAppgEB3ARuMV1xqNytm/WCfX98CgkwRxw5f4lWM/n/EZ/OviIOIAAABc3QZqA6BFEQ54ADgairErKI+WJMBds9BW08AHUsNWJHKc4aovDf8yEGHpcumq8N9K0Z6GEtJwc1BoxcUhz9AosMYQ8IeEJsILFCGIPXgPJjLVfxJ6+Ay2ivr+J8QCCQJ0mPgAIgJUDhrDyEd62TVLfmBIocKYfQhnfSKhYMqaCAGY29QIIVr12H8QCaAAkRiKyHE1JCWNSHtg/aD1w2LOsa+Rrdf5eIP7AGRddv3+yV4f8Qf9MKr9x/r//4gOUByhAQylNLAGbf0ZEB8n8bfwm8v8//9TWx/88pZAQDATeJfe/rEH5YbtnATZtxOLn8XiDzFgBmZXO9/Gi8b+sQevAHqV98/+G9gMsPLU8Avz9yHecQKJI+f/P7g6mp6p42y6f4csaGWGoDYl7zbzoXor6ME6bN/1BF8xWxZf3P8+C+/OPw5X6qUhZka0ivoqxosbQxHmw1aH4czgIgDABoW4+i8KQ/s0NzLip8AcbS7mTgwFPh6b63/PK0kSJZn6iVHljQc+w9UkZ8N/X/G+ABlgIcTWEiDBFliQC++ZNkPYqKiDIQfIyAu5o+qPJMS598QCTBg1h/0Ma0TUL0bAOZh12qn+/5/4wE/DBjDiEcb0TVLh5QK75G6jAwK17f/zBrGsKRbf3IBw1L56e77HJbDYO+euAGfzZKY39f/EjYABgpLQXEjl9Zv+DwRdate+bUwCYxsqHMpB+Y1HjAAL4BFgfekq0LlrCgHh2wPqRsF93r+xpKSkrAoYcABsjG6CKryUsYkPoHgbBhn9KkmRKF2ALK/BvygVZ5pfngLrgNxkXef/HQRwy4/3iD1+NAzgPp7dP2/iD1gwFxNf+M4W4ADgxbKXJ5HzJfjHvwesABnMQMvmSYNXU7/eBMNWdINobNZDd/ecpVBS+tHzgA0lBWOyxvximp6/iRMABkiEyCKxDkMUgPzOFivjFHdSjWh8SGLVFyhltkpnBh/C+AA82wBgcgH9gqwOQOv+YtAEwFu+KPii1DX/34AC5mYAYHcD+rsDkTz/nFAwASmvGdq5HAxFgB49EIDFz4LSdnNtHcBDsCa8hEAtZVj3gQOgVhnX/28ZAbs7v1iF52Lkx3c/mRkUcl8SNhgAPjIAXOipKEI3w//v5wAtFURE7Kbj3GNkT4LNhU10O2mhC7RUpZDSXd/3CLA1KpQMh+EtK/+PcWeH+AkAwgukJEVijqwmqZm/N6QHrMMWQq1qW7ZAIYRSNCDBBpp4eg058teq4Qp4elgBoGumoO8sa5/aWmtmknr3/vZQWRJWZpyABjbLLS7e3hnDfyU6tWC3+H4A40cxXGfyjVPcwMEGwMGIABMAAQBtBNBdE4/gZWmWDxAOhMFVhERKIG73bwABQpQfqOIyDWhsRbACfEABwTv5IRshdf5jYGyWHc0N2f/oClX3zpN/7wkWq/A4VldjSXihr2x1tHwSlu/tJ+hoTX1c/9/xIVgA6ClBd4Yvu2rweCZRVK3jam8PEMAjUgUFGhtTAnB20Hzhq+sPP56ZPj9g4YGOad3p3e1KRsU0OvknOPCB/8SHoNvq1yP/08CR7fYniodO/+1gRjOAKD8/wL8RvP+cgCUFg+iOS8EDti7fDACeUz0mV6GAIQgCNQBYSam1MA6BzUphkkcaSVjggb6FuEiarFX/4fgi8MqB80xMRfEhbDDwULlbFNqYITrZJv++8BQZiCfGxreJKIN//TX6vHw5LoeH+L3/AQUuRk/1n/xAYgAeBKhgAcE7RKCdkLz/LiG1AL5kAEAjgf2KjI1A7/4sjSAFgEnQABA2nYvi+Db/vASDFkpcwJQ2rdx7/yM5+gz8axEAq1/hzFWmPvBKtEU5j9+hmZLm9/OUhUrjjP1lhxKZVLauf4IIE8B8aJ1KHRcf766YCCE0l/kOO8AgABYGNHt1j1FMlc1wfxAABYENoHhtyaIwEIQlURKWyyS39FW9LjAaLvgABALuKsDilBu+D8NVa/HVgmBRjJHuyrMy7VdTpf4YgKBTKcADjfXssKUWs/9oTAIWkLYlafT/j+ecjyMdSmR1z0SntD5/gJiG7oY2cKlTE+noIwGNXPDDItqpCXJ4AvRQ8p/M3/9f/EByABznlkt3f8AkEqGABwTv8CgjZC6f4CTNlEetee7lNv3DuCMUCwnXUI7/n4eRX8AUew0qVFXe+4bxfhnzc68GGcj1vl+5Kaj3aMqnn+JcACkITKIv22yTX8H4x1O68zCOlRTgxnFeAA2IxrjGQo/qV+2ClgLvDF94z+/4W0B9awMPzJWQxRpoETgImvYq8NqYE4HbQeuGr6w8/g9DAI1YFBRobUy41kMlACjpztA94hYRDEp18v/yQ7CCRIP8LQaxkFTlEQs3aL9gAaCVl9HiQ2a6O4Ft97D/jGoFRg4+anXD5qYxvuDKqnKrYgaSDiu8MSjgOqJBLSvj+QwYL1Wz7vcfcmuBfhWAA6ACwuhqjaePMFEDf/95gBcTQxJpXPGSUfndAGNYj0yefkrGUTj+sA4Yon9K7hRb9w0QfnpE+yp//g9Ah3c3rqhMmG2v4BJYkwAcNLxmyQ8c/6Am6JAoUXVDRHVU/1l/7uwz/+DCABYAowGN4zmFAsZwVvAIgqNlFWkm3Sa+COyX+h9e/lUkJMjIzIsKABOP+lH9LfW1KCCLPMaWkQm/f/gDVus/79BA72r1tAXjYAC0zaEmV+yLqFQzBaOOhDei1KRTKdh/7rwwu4TRF0IZ3d/5+cBF1a235tTSAnHeJ3AnJkR1dBgQCm0CTW+Wz8Upf8ZS1e4/WGH8JgHTYmDPhspI+hhnVABeOUiSeLf/btObFiTdmSPLh4/zwQFj5oQcPw95wGJDnDmuJPJLLf94QpTyxS6SE9R3RVbxgN1DhS7yM976SXMeIDbBwtl9GWcdJLGPGABi8WAW02pKxwpXQjwAQSV5YrMozYgyv9iMXuL5Vvsp28H8ABIMgyXJOJ55hZbG+NgBqHrIWqD+LGvgWMqwACJYbDW4AwzHffvt//oIEM5VExz/+9sHAxvr/D0EBABcFxGWVFlUY4zvvhgeLEV0jEOef/YAFNk4xdCojo8hIxGYRlIIQxSg3BCAI9QFhRqbUwAJgvA/NOkshvjgIutWvfNqYRbZpvXwPTp7uf18MagkJS84+ZhoNNnoXjfnBYLqHSt0EpJZ5j7KVXMQZ2sMcGGNxAA9YhVG9glBhNLfegO9ddgnB2gtpFwV3l5vgAeZFCOSQKQoufMv3vQBMvRRUp7kd/MQI6baMzSmP1QYYSMPwv/D3h0MwGMXHjDQxsqBh9IADVFYN+GWL500w0ZPAthk2Ut38BIIV3NRcUJkwyx/GAAD3AAECMANoDFB84/AwauvgWg2S6GL+gRfjFEK9u2YFt1H/HCc5DAG0dg3gSpf68axo7ZY/L+JG/gSGOzWJuLETYZZ/n+MFgiYOowRdtuGsp+/NJCIn5k36v/fjC6a0f1fI2Qmc51YJzVo98wlrLkdIkHP2WB7v3gMAsClFLNZ6qTmuc7SPElfIWuYiDEUUGzCPT0ewHHaApFK27f0QsrT6PlfP/f8bAFgAEgcB9jhobNEYAYjEVEOblG9S0uAia1Srw2ptBjokZErJJ0VVVKUHuIux6jETAwrJNwUWVKt5wQfFWvdNqYBKMbKhzKQfmLRoIMgo0P/KaDbSxLvwJwdsBbSPX3d5/eCDwWLQDYXliP7lYDriddb8i0gxqSGO4YwAHjNgBgdwP7BVgcief9wBOpwAYE9+VErIXv+aQAhvSul6wlRR1fwDKCQoTB6mWB4ja2b3kYTqY+IHU1inPDgBojRlE9Nf+41rfoX5Yd7VSh+uXwv4ci3sSCqHD1/L4YkswLPUfKj/C1qADvxOBiAjtMrFBqpcG1vUB5h3+gMNe4gGYXJlI/vfSqpJV7/20Df+F/gERDt3UKl1kOK/ocABwh3KJZ+b0lmGmf/gAHCC7jPeiP1lMfuM0QbtL8mVey8s7r9cNXJlTmjmjb7pv3+sFIlm4je/7f/wQfDwmQZWIw2pvwAlE98XpNd+AgoveG0VXSUBOh2zmIVq/J5GYiMoqd5ylrR4BgYdsvKz8ZsDUNivPwHjA0BRw7uWX16cEhFN8V9EzrvAAQQjY/uQlV2C2hJou+T/tDvUmCS10+FvokRmxhM4hClKDD+ylcUSpqGXTQrsoD8sn8GakAVDhKQZRfxDGYTcb+X/+fh+HFv//C0YEvxpVUQokPDSUUAHwpwujbLQ/s4M0LFbW11zB6iD/w5gAUSGILX1HLhgZ3VZnrNFZIEgOgshq/haPnJwA3icta679f8Mfehs6mPiBUNYoP6QADRGYKmzKGa4HwAMpAQ4ucKEmibbBcSzahv6eNf5fviAwoiciLBFph/vFYle8SveJC8MGBAANiMa4hkKP6mJYAAKA4DcGjg6aI2UCkBd4ZFfeOnARPapW8bU2IMEFQNgAz9aQFA1agvh0Np4kB91G3oBCvpOLnlTIOKZMzz/wx+AIMHq/EotpYikrDzwYACBBVa0Yryl/d7z/NAYskLk8hMl+Kc/dwEPcBnaMEb6uWTN//BgCvwyq9aZwDPloolkc/7/DVwAECFgtcQc5UwX4t7o0AFw8WpJ/FCnf7LbGaz8OX+AL/D+8D3rWffeFvcno/2vDbIAQGcBO1GRx2//+5sW/W3/AAYzEyc51YblrRsAAFQQBmTpscNEa4k+I3DIRqzzvumB9DAEnk051/EjYAFwBiJ7rcljVmnUDsDcaL6W96+dAfgwub8ZwIalIswLaqP+OAD7SG64hs4/qUmAA5AWaNGtLVs0Wv8R/gBZmwAgxicUXusuvPsGBsgeeZr7McWgdDCZTnRCeKTv7/9JD3R5zL85xAIVteor8C8uTkDFogB9sMSIi3P7QXii46eLPf7UsjLsyPnTy4W3e9eUuU+w3342XpsA27m6V31p7sxNMYwBeIsYh1bDPMW8EC0gmtIJMlc65A/AQERbFhOd7/RVDSwfIB9wmHF5zwaPWMf7wypjHcTtTyqa0DQN2AEBLkbJurOuNfAbn+ZyRRP389mJphfhmY16hW846Oyk/u0yQRkRTB/Wb9//ItSUPO9fuBsD8NpJ773f43wA75T4PnnfgB/X7kntuoBR2sIHhDCWbnpOn4//wHeRtB94lf/58ZAAPiAAEBioA9h7Gc8fNY4qHiwDCsof6pTfmXt/AIABqw/AKyvfCAo7tYhB74U5UIL3CL5Y1/fvDqkAkiS+z/G8DVPoP/9d9qbmB9+nwiEU5AjbL5QV5D7SZ9iIUBfcIR/b0NEFz1N5JnpcnhbCFEq6jZ0yL6qXgHo3g1IMaJJpu2x/z2JOLCbIptEFy7zCyKVEOUYiVluYAAOUAArwGkBo0RvCKLRzkhOYV4xuk9AHzC6ZkJGzQW6osirNJre/9MQlsJ17i7v9V09prO9MgJvYJS12/iKGlb78P/AQRHsELLbz+qF0fhhwBRM2CRxUOfbSnOEMArEgUFWhtTcYRxPkwV+rfGidZwJkEUjMNqbQLQSgUlBs4YtrHf3lFxSSpUq/fewoIpTY6+XEehgm1EuifG2CAAU0dGFeSp70wOBQ80dlSZIRgY9+TODpPoCEZjOiJPkS2z/KjB0dCYDoNeDVN4fTwACMF8g6l/iVcli+QHKKHHDEZWcNzF/8GADgnIvKYqHJDKxwwwURARPxbP//5CNqocPeFHpWbfrqGVf/GwBQHbIDagepvF/zgTYRSMw2puAxigtCZJ+36V59Z4Ayj0s4I9fUV2FW3QOFLBOYZDiGHeHbPtPQfgAOHeOG4N5nVN4elaEF8SACQNdypciLpOPBiI6B+3DEiVLm/u1SXovs5F32UEBDe68CReCDAyDgoecMyldw3IX33yj4AHgeMACB7F5EyfNnGfkYEzRgCAVwEdXZGoXf/AJBiyUuRKG4q3ce/d/iQANA+3DlQIsk6+GcVGMQ00sHgGABRVMha/93ybefhy4dbP8K+AQzOZ1TFiZsss/wYfyYQLdWPn3kmJa++IBJgwWs/6GMcIqGVDAGABhPl7f2///hbowwTcwbL/5NT09/jAT8MGLPIRxvRNcyGHAATAD43BibCW/tkYJnvEADwuBqLKWPtEZIHAMXyFuOuvf33v5Uwbcg2p+MFvq43Fc9YCGbIrvP//DM6/HQ0mjmBA/Wb7cB/b5Dam7v+0/5/4agDoKWg+eMX1fP72/D9713WLQExjZcUymH5jUOAAEgQBuIGzQ4bUxQYwzuKqFTDKQku8P6KV/LVfiQ9uQtQf+FM/serweCJrVKvjam9IiCTEEpTkMUpwQwDNWBQUaG1N6DwLfJhMiD873W8QAAgAraBRimpQ0ZRTJFgHgQQcosDMbKzIOqJTd76HoqxKVFXv8qII+G6tLiQ71gFhg02XlG7pygxvgInMoAhZPCZBIgySQfiHlUjoYoz7YW7wIwzlalsIkayXbZ4BgL8AjzGWHU0axa/5wAA7QACMgB5EaNqZwABccQQywQNqYfB4QQC4djScE1gxopBFGGVKg01WsAiM+r/f8zbKev8QHofTpxloeRUeH3BbiUY1y//3OQDdCAaz4eOqv3kaEVFMdCjJWxIfpODEEq6nlwwM7qvejCdRG4glTWK48bO2gagyCyGv+5wAGyIwX7ModrkYvhgdvb/982H8fKkMsfu/iQrBCA42XJ70eRsgR31N9KVHGdz+dfAGG1FkbWoin7z6KuElvn/7Bmt9Sn8SGodFwbtgAPGmE7a7rlTtv+AAEDPWAACAKHQHP+Km3gxQtA5bWjc8wIxNCanO+f/D3zEpTJWESjNXSfToYizFx4xNtRMMPzMxu6nOrhUtWmgHZQTEjVtXL+D/gANAcggacNQrPL5m4sLRD/ACLVZtLGOidWReJD8YIggaJlAASYASB5qWpgRZNx8PAGNRC5OJUXw15/+ywjEBTQnBUiXbbN2uAWgG6mABgRtCBETtjdP8MBiUEaA6T77njBOzjf+cb9acXc0ZeY8JjNV8/4kEHwAG/jOBDWykaaFt1REWAABq9AARbMQBDvj+/gAHkzAEB3g/UFWR2J3/4PwIV7VZLiEQ8vh7gY3AYz7sPz7wC8BzxpwBVOaWSD3b4RQAfJmqbPWImm/27z//4kM/ISMzMYyMEQxiA/GD2IKlmanEUtIatTNx9/X0dOqSl9X/xIVgAWhAm7Yyv+yZlp72KFFj5Ip/MfagCFAMIJpCRFggyx2yAggiUZEGCDTAMAB4AFhbC0m08cYJeO//wfiBqYZiTyUsOILew4oeINPDSI0BSxzsSrf/9/hSRkokc7n3iT1OjMkNEf/i+GcjeL4zAbr923vmf1v1z1gPTGWqgcz/n5/4Y46mXg3AA8JCADAXy9UTrmzW+AkAwWHbp7vo2TDv3AfOD6dcf9+hDZFR9Go+2p6FLSxdI/z+mFV++P1j4Zo6eB21i/z3/g60p6KAuJr/PFv5uvgCgxVnvnnCr7+5+/P/hqAHBDAM1IFBRsH2piw9fypxxZQ/z1r6Dxz1R7Zfnyxa+5P+ZqLkUe5PDVkntNZ1c9fPwhnB0mNEYNdJ73FmIOB+3kGEN8eBefOh8I9z/PX4De4M9fxJ5iwJum739Y/56/gEqmTrvOEv4NxPiQ1AAQGJRCZk4lUyXwtywG6kABgRvxURvdf/9wfQEBPYCHWlmvH/8NQTl2XVuha//TCRm3Qq3V+e78BajvV9Qx3tIWs//z1/gDtr7vP/nvBtJSvn9dwz1/54jl4BeAYhmsM8L/z1ANGZIaI//+eLWwC3iRaKn3aDxz9c98DfNYzl//DNnMAAGvGB5ND636/rr3z1wCUNTy/9/8I4kM2QAgQwCNWBQUZG1N5w9AgQPPPn+JvEQrhANYAFvBqB3PlY7YKpDN/3wFsAQy5rjSZ/+IcCRM2oq5aC/mS5Pr/glgAAAYJEGaoOgRcOYAEGwGMKpGZNkk030QMNV4Ml7sW49eAO8AHaZkWjf7+r/Df+LAQwukJkmSTbYehGBa3R1UOTbl17wGuDkzIjo1+/q/wxiPEKe8QeuOd+bEHqBK1n39CKf/P3//CGIPXgIQfcj/n/nr+ARLSfd564c4RsDw8qQLLS54yRia2h/xAZsci/D4Ba3Q38v4g98DEmWq//iD1GpstV/+IP7TgCApfbcj+f/PFdTyKl8B/4c5vWAhdyP+/UzspT4/P1iD4Ma1iV0ne/DKji8QesAZA9759//WIPXgYkZar/C3AAdcGIJX1HLhoX3UPbIbOpjoQKhrFWcJBFYK5xLje5wAGyIwVNmUM1yAWMtgACASADD6w0WVYI/7QIZnMRUSJmyyz/OgBC/VrHGLSnqlBVVlosrv2ZUp6/wxoOAAiAToHDWHkI51siqY/GAm4KFMPoQznZNYwCAIxT6UAm71ewYeuZarv4kGEABGAAIBPanABtFY8gMY6K/GONivjFHIphb3AACgKbQODcLo2jyIdFyi5Uy2yY4ABUBUXcTBLqdqntx+Nw90BiUQmTiUSXw1793sY8iDBwjzHXyKKBoJpoAkRu5nER3n8EwAeof9lRsgiK2343gANw8Ltl0gim0Y4PRAAIwAfEwMTaSz9kjJE95AA8LgamylhFonJA95FGQSIco76eW0MEH0Ah6Eo0Ja8RuWQPv7QBDWJQoT34hcwidf3QMMQmcADDd1z4MAZGKEv+6v8tOn5WQdw3Zv3/P+JBBgAXoaAor4jVpw9idf88XwAEjZoJVMwr6YQ/yAAEAfXkABuImrA5u4n2X4u5qQrjgFHcNgq6sfYNjU60IJN8MQK/IyXewZecJHXdoYCn+CDnHQALmZgBgcgCeqsDkTr/n4zSIAAQBgAYfCcelVWCQwE4EQTqUAGBPUYlRCyF3/0MI/8W0RlvkATxG+ZEr9gXRrMmKKr7Q2OD2XuMNodS4H4W2CAlIAJA12pJ3mCnP7DIM8BiwQqYOciLK8a6DAg2jlneLuQDkc/0Lbv9miqRm5p4wYU/iQtAAcEJRaok4lEFcNd/8Hw2AFw0ZLUn+WMe/8GGgEAAhKcydEc7FKJyfcmY0M2UdLFJVve5H84dxLF/8NR83fiiIFkkfPEOjPmfw46m23H+P89f8zD1Tn9/9c1AKmAIEIAjUAaFGZtTevReIP7AW7hv6hsyx8//iQtwAPBCQWiDiUGcLff/s8DAABGOUOr2waMWX7/eBkWdFoWgyC6Or+9XKMQ0BofP8//4Wh+AA3HDrwtIdTYKYH5Cj4jY7ivhZbQw1iiynsNwQp1uZr94c9/wOREvXiQQQwAP5EAIDEg7ijI67f//dAkDcCVXlnTJTRj378ZEVDRgAXoiAEBng7izI7C9/5zwgA9scN5RuGRmHcRTZgAMJHApNyUpaawJGQQw2Cq6FQx/eAYLg+7XqzJn7+IG/AARhmA0wqYeSubwz/BtCHOYDRcBapBh/GZWqjRZ/dnv+DfICGkT6RXPntkkz/+WW5TwnmfzfGQh09PsV/Uu0QDFfdvyRPZ1ZV2qBgCoDEq+c22wljPBgKCFslVCfZhBLLjv4HLZ0GwDfNPV1Qd6nztU36Jal3i9/Hv/jYADwF0B30MmrVorRz70zIJlFXaCFParpJXXKEoNgsnr/tGAAmVHD9ZsDN+OawxRKmJXdMC+yrB8hK76hIwPkwjqD8a9YqnRxEbWBk4TjHSgOmQq/X0YAAEDewAAQAAYNh2Z2m5I2SSt/80CKcYSSKHvfiWGVf/26B6YdFitr0uVcX/tEQP817QqPmB1pmSZbBL3dkdAA2iTJfSUpcM7ydami8BJatzIaQ1pqXT0ngg+UIpwAEEI1Twtghq9dffVLeGYTyQ5hu1szTJsEsCSDJPILJZVhgTmdd/adQZ0lN4n7lB+Dd1aquoKar5QBsv3ymmse/OV/xvZNE81VH+//ofteEcCmslAsuL6qQ+ADCMWp7W8HgAJGYmZTnVhua1Wy3pgAAmCAOudMjRojASMDNTK0WoPQoaTvw9bG2OyzPth+g45L3jITc4vz2aVHxYS/ff8LcFm8Pdp6a+4FJud+SP3FHdWTtf2uBiFv6zBM17f9kl+9lIOogb6OVEWl05NTJe7v3kPdLJk7vPlEBV6j+NPFa97+f+JD/6YaSxl2V5/0WsjRiVU4ICDAA8GinABgRrxMStge/54G0RgDA7wdxVgbdP//u8AD0n+cpM3/9ASzTI+4iMf/rws4l9WJZ5Y4rB6oRRK/36/8P44GzEHkMArEgUE2htTcCcCJjFKrjamAYgAZKCYgVFTWPAAIBhikmv5FVRUniWLIAvRAGzzEIpHh7/3ckABP8wf6NsVztxewGYGZCQlNBZEQoAzGW7euu0UqdgOcZhTkX7uW4x3dIhDv97A2ZmHKfD9PAAoFYH0vjiUjjNnv+AEWI0ABQSX3SskTmhLxMv4M1YBUECfePkEBiBub4WKjVrFSSi56gIOBIYjvb9VB1CWVv4BgDogceMwnZ03IW3wwUuMoV6ofu/juInZjef8Aren2yQS+3698NQADBTUFxIyC+s3OAj61a982pgEozEuKZSD8paGAACQMA+xs0OGiNBgC9AZRELOf/8Qf0SpT75xDvPv6/8XwrgAUAxdE+mS0gSuZQP/75ABcfA1JhPKLROKJzmBjUJ/MntAnUyif/3tGYnQ5lIFU5qvGACw2BiTKOvtk4oHg1AB8ZxNieN7/3szimZEKJ//9/8ysfGz/DPhyGIIW7LLRgY2VAw6r9/H1Bj/hmAAkACQfQ1JtPXmCUUDvGACUTQpJpXaDJJE7//eBIn3Va667bUYKpiTGULRbgS/fQQAeKIeFtqkVf4fFD0V26mfhrqNVVYHoNguhq/tRg5x30q18C9in+4BTvKKKV3G7ZgW1VPIkIhEMJSCFMYoCbYK7NBJZCX97//xIe8RmIB5DNywvx/DW1OC35aRCXb/wYWDDsL6GIR1MBeD9oLiBsV9Y0GHKGEAB9KAAEAYAONjOHyiTBPwAWqdY7Rf+9xU+WmBLNk6UpgRfepFrg/ABeh0yevZMv4kb/YWQYAQAR0gCjm4fYQzpn/B/wBCUWipEI4gpZ1//wegYrNYm4s6xDa/8xxiDjPiNmnT10//+62IhL02Xl//fBlw2AEoaqlqT/LFOf+yziyRNlV/70GCL4719/+vDJSQwi9C3UG43A2XtH2Lo3+lLU+9+5DhRKTX+JDv4ETWb7iRoD7UgAaQDGE0hImwSbaPMkH2BAxClUEBBRgHaRD+GSxaY//7+Nokw/0ydcBlgohmC5QnyCvN9pEAVyi7spwwWa2Wpon/37AgP/Ehb6AXwWACawnKggmjcnuWaWRhgT+hKT0xwvLvye5PiMFRAs8hK+0DraZzDIUUCOzeG18MbcVunTof+C+AA0P0PRXHyWoIMYe8MEqidWy942hiBEEBetJpkOKTui8ABEXmCoXKk6yC34fvr0QTeHf9cBf43yAY9iUJlNeJXLpHf9pgB9wVp92Ly6mz+7yABcfAtJhPaLBOPz3sAqwQGcL50iXZp44O7hTIUhgAHjCsQsL8vXX/7yQqNlFX77dZbw/EOPyOhnEfrC3Q2AAD/AAZwDXxo0RvMfTldTGGdrDHeGIIjAPA3vTsIsXmEYyEaUSv//66CDR2hqV12g2oKwQLQR8SNgCZDCvWoohDT3mFP4w4QAELBs4wtAQoZ6nd7PdPe4Ll5QuItulp3wh9woLZeRjrHCSpcPkhgu7g6X/SZnz72iMZWEVnkpYxfp5GDHliiDFoKZxDCNNMD6IoPlnO67yAC4uB6TSe/rE5onOAQNVeIQZTxFNXz3/96kiSIWRkZkPl+gPDrc2NhVCN+738/4Bjg8j6/t7QUlFn4mp/9sfkIEsEGqPXAvwtBQ8QwCNSBQUaG1N6fCMBjUygUZGNVYemjqCO4CJJEI/t+I3YsIF6QMNqKJJK8//je4AFSYgGYcVEJkW2T/bb8z9hP8SnBIQSKZh99/vvt9/+GHVIAoNxGafMZWqzv9hqcjMg8TjBLM5kQTMI8jMSflhL+QEz0lGv15eF4AhnCMQunkJog2ghzhZkBmAqJQEoMLqAw4BKy+X5BGCPlPoR0/9/FLBoo9bGte0PjsItp/38/w3mNAS43+vescv1D8OtN1Pj8//wxwAEAhYLXUHEImC/GvUBqznPyDT37+lnYgguFW5+AQD2ZC///zUOAAgYi0K5ufybajVFsIH4flNWMblL1Kr+uEAH8BywrJgJ++knx32AAP4xus2ykRf/3et8QA3w2oZcwLdOLP+MNMYrjZq+Rj1kDAhuljP8AV58jBNoJmpc/+98cHGQPLn2uGMACiQYgtXU8uGhndVvDzuCNCAJxAhD95mRhOpjoQKprEB6QA5oY4vkKMcYvEtP4AqSGWkyP6orWdfL3wxwAGYVHySqS7X0a5wAAuCmXAODTo2prAwB2OC3ZdIdTaMcCMKTbgD55kV1f+sEbw54ALyGUbYLINYVfKgWG1z/8MQAEwAfEwMTaSz9snD57wDBbpolNP2se7byHAaKg8w6lNhlF/7gK7hxUM5QUyij7gYEAAkZiIyirviEPWr2yMSqIulPxKEeCOMYlLH+7yxTX/CWnAPBeiUy9ov/QrpY4ziWznh90cSHrYAFhDt5iLnRM2Gmf5A0hVxOxko7V//QEQKQUEnzEZXcNTF/9oEK3mdd2fZwhn+YgF2wF1AqSvaHtMADRO4TpKgbvgAouB+UmSlYaSfAV/+9pmErCqtBKmNQGCAIuaG+OCOenSD0z8C6414vff4pSch91jBuqp+DCuNL3rD8AFgSKQAED9fJitRB//3EaMBb4JVTS/43pgEL3/TeWxBR9XWCQea2Fefr5/hkpAAZmJk5T9huWtDBgAWYEkwc2vbLZe3hDeA0i8AUavKCDvGHHn1iAnUNrcZRr14DQg4icqVRpesrNf/pmLztcfbscYDMJfLL7QrDsIgaExTG/Fk7goBLtRoDA+S7fc+v8bsXIg0unU297c53/zfZ3a3G7BYnPkFRG//B728uNGk/wCjG5pKlTOK9b2dwwAPhC000wwIjek//p9kjWI60fEUoAQAAvC0ADlv5Vgc9oR4lgHEMcf3IMYd+8NS4db21zMaxiKw33bfI+WQJVQABzr+Vn+wbj0tFOpaGN8yjZ/f7LHC4umt99B5F2+hjQtfGzj4cNTEp7gN02ECfoNWYslEvftgQPRc+xBijBZFvbxkgqUaiUuclJLvbQyLzHQwVDWcybZxrmwkKM0xGbY7CYfNhchvIh/+v+zlIKs5dIGpNrKaZOCqpnkfftPXjm3u3smmbLpgww7DowanixdhnqVVvv715rNi23J3//ppQdL6kSx/pynNm/tGVQzQYtr/G+dZgkHzTGkPX/3uZiWdOj6ecKgRgKUyOGGRfZW8QWeGIgqWk40tvkREJEEVXOQxSAw2AeGATAolBSUZc2qy53nhwPq3woiCUFM0gDHtbTH4sV1D1/cIA3wS1M2hr5pp3/j4vR/MxQTdKjyadBZIdQw3Gh2GcBcJN40dLkMVT/FNCLQ3lvw9AATxOk3Vol1XExtui+C9r//deICTBg1h/0Ma4TUM+YEvDBTDyEcb4TVMphwbBYcABGFG52wvudLS3eMABCwg4bTOs7d5dzyY6Jkl0hssox+9CI6VQR5hJNB0nkE2wFZSWvf/dvu/foOlyun/D9jgAIGCKgs8gq/Up6TSPGAmUOGMPoSzvpNYtG9p4d+VwyXOHHx1ngBCkJWWI7T+MJb8mvx/HgA5tXXyu9gDi6IVlFQ91NMeelaNMhtT6gQCjP7/Vsa3SB1OZ/43wAE1gFbCHHQSkxhoACDAOiB2mEcTRS6T2YD0huy6BLD4rIdv7w4AxZoiB/2F8DpAeF75GGCdkKPIAAQEHQOFukJT3gQh3x4IZdmEa3Wly9v72vCFEq6nh0yM7qww4+gStMbThX4LuR4fgEeQhHXMZNzAI8PM6/CvzFWxUU5B3Usp6gABwAArwGPDJcYP8hR8REOUUmmlvDDgbEzmaDQjrtf8fr/4Y7DAATFk5UQ5RnWs12wAAeoABWgNIDRojADEzYTKcghNtKcEq3gEgwlZ+14zEh6ABODttB84bFfVsGCHgAYhAYwqkZkWSDDLzhhquhlPfmzPv3xgNVDhjL355z0kqW4A1xQAcEbQKCFsLv/FgAHbV9e8AHlHuGiOXTzgULV7/4agA4DsBt4etu2r3KkFpmjMiT/+ARkQ05DoUb2q9gAAmCgOuaNjZojL4B17AkF+W7z//iQr5IMFu6FU7qjsefB+NhnVCGVeEcYwgYBAH0DRgeSJH0Xmw9NgMPLKohSVEv+3jQkyRvn8/Q245/8LWUACgGPYn0yWvEsl0Dv+9gY1C/1Jwz4jcyid8gAuLgakwrn7ROaJ7zABYbAxRlXH2yc0DwYYZF0rwAuedyKfoPx8fmgFqpKfDC1JLh0vEhXABQXwvNKlpDXPhYJ1HSv41NLnstpyDTpsAKDi8xUM4j9USygIJKpEQSSaSv7GKG3c+Dfv90k2lEJk/3nIwu69+/BETdfD0MDyKnXTK1rZ0IFJXpXs33svrh/joZ+WfTzEjitUY7FifpJf8BEFhvrlEWIgsuuH4xRlKyHcZ2tNd9YdGqy4Q23UYSRIaF+1n1/xI2BIwXzz2GrjQgKSOu/gRBgAPMAJA91LVncWKd/8CID3oLfj+9q+9PZonw+PO0hq8Oeld/n94EAQ+AYkEJmTnqknhbn/gYCDwBupAAQEb8TEbYXH+f8H6W2ze/jS2PFE+ouIpDIEntpu9VpXg8f7dQ3fHJrdFxIe+MBKjM8KY7lRSag3AwlakbdT4qlgfgSDHb7fuaESYYW/g2Dug/gANRDdUIJi3+hSQd2vbt8jkdvmUuknO/9+lWfXy/+H/KkLRmyIib/+D0ADUF4DpQrbZh/oiv8AC9ABqGi1IP8oa5/YMDQQskog9ySvFPv/2AgylBDAi5IgWaaN2vwBNigA4J0iQEKoHf+eri8Oq61e/AzZXnUZCXRDWl5Vff/iRsABEPLTOhijPthbmAADtAAZwDXxo0Rg/8x1OV1MwzrUU7j2GcCGrvxpgW1VE74Ej481AHW/xw93gOJVvP8+g7qfZ9PgCCBWSSITSlXW+4TQYAAJgoD8nTQ4aIwbg0gSgaVtI6k6F/iR4dt171+pAxZr4Vnv9x3uBmBA+4eADoEtKIht4jU2pAfEhWWp30fxhnidxs8o2qk4EAU/hvFw2AEoaqamT0ljHv4EYf+xf53JJgeGe6WrHDx61CuX+JCsdeoAS9jFEK7jl0wLbqmH5ERBMgiqQQpjEBh+g8+i4a595/R/4k98zUiKu8/47hqenWEgeej/nDwYiSLUOp/542VqfJfe5lKcJH39jTBM04erz3Kv4Zk9ATNTF7ma56N0IP1Q3UfUp6/zz3tYAGxJ7zj5/8/L+9QjXIr3//91U2Wq48eWDvh6Nkmg+AAy7AYwiUZkWSjDIeigEa8ZDEpT635oJKj9YDWj0yDdLmf7vYKKbGUvuZ/u9/hqaesLBkyL357XmTRzKciYxtTkCAY8k+HYAFNolmPoief/3nkAAIBJc6fifoGsT8jIRThi20s8cYTe0CFYhaLjD6FNsfzTGiJ4PYZFdDd/ASDJjAAUEc9AkJ3wOn+5+mGUu2hdv/4MPmMiGGN547ZNJMRpbU2C3GVPX4MGjMckzz4aPf8M9AQlkpg8lcF8Mc/d0XzrkO0kLt/3l0Wvw39AxfjcXY+opvEBvgAOBnoZMweQmS/GPf+DKnGe/4k9eA61T143E/PWEL6/V//9wBypz7zh/4asc24ow3NL+1OV/yeu7//56/wMROWq/w3y0qATUiVd4HnFr/xIfgAUBSiBx0xOeHzUxj/cAxW+1OzdHUKYY/wMMPAA/RQ3sIhVx5oXWA5YHg7YC2kXBfea8HXiCSv6TM7/8Moos4Z8//56ge3xC6f//nmPhhFnLQvf/fCkw2nH/PVYZob+v//z1gC7r6fv//PTqu4+fgNYvlh9vX64TNB7/nrQ0O//89YPSU9f+ET1/j38bz1rvz/8R+uHPAAYAkdgAYF6TlImfQgNApG3wNP9RgJ2VhMV6/ic/nXxGdc6+I8IwjiA1+IFHQCMc9JJ/NHowwFsCr41oeZ2/DPF/DPwDdQ1uKUw5y2EkiQw6gUNJUpI//wSwAAF0VBmsDoEXDmABUjB2aAkrxjh4gWBf7wYEIMcsEkOvoaCtrovABqjByjIatH//34EbW2/w35EcMzQEFesdPEC4L/B8DArzCVgh7z6egrY6Brg6yB/iqYtS//3/gvbb/DAhcQofEH9wFraOvr82IPeGktUGo4paz/hDEHlPhE0c4CCv1K9W/z4P8AWrU+ef69894KKaOvoDS1uL84R74/79Nx6H79f7gAMgqJlFSt8uk0kPxjrcrqIhzrUY4PiA3TgAOkAEga7lyTvMFOf+BoUpgESu98fqGk/j/8QepmX9uP9f//hftgAWDXFABQRv0SghbC7f6AJFKQZyTS/YIQTR5DFiYAU5uJD4PZ7Vun+FuAoISiVRJxKKK4e//4PzwAlBKqWpk/yxjgYwEBMIMHVLtohn/iD4+AjrT+9/XHkPKxB/YCRno/79YTpH/frx2JC3AAt2IUQtuzZsW0Uv8AhMhshzK4yWNSC42Bl4FW0tae0wAJ1VQnUXY3fQCWnIAAQBgAUdLZVJkh/rQMdvtTc0Igwwx/F+AFBwcywTm+9//w54ADFoYglXkbuGBfdUW6LckR1bn/hj+2hkdRF0glTWIDOAAEwXRgDgOwEvhsVs4ywgOC/Mov4ggpaPnGRv8nv6rikOWU+fX/DEAP4YBWLAoKsnFTavcCJjFK7jamBEBaA2IHRW1jMUfQwJmZgDA5AP6qwOROv+cKACwJdyxJ3mDHv/DFLcbj7+hJ7iG/qUxmBcS5bvMk7ZZITWpwgId46sh+CDAA8E6lABgTtEmJWQu/8/+sVFyyIS6WwW70AB7AencurQHBCZl2s6DzPTN7twITv4AOznRkTH4Okz2UlaeBNzjj5/+H/AMWiFScQqJKSNd/Bh8ABxkCy7EqyBM1mWv7TZEAGBmAVlJwYhff8RS4uBjvLQFdZ/5hyUfJu/3o4tx8V//zgj/w9gAJGFRcsqksttGuMGD4xVsVuKhroaU1gAAuCmaDg04NEYC/f1XFNoCE+cq++Ud//89xGbQmyl6IoAmSthVe3nkU0p+oD4oceMTlZw7MX3wfnbduIAH6EpnFjdbf7wBmXuv/k6pURHZ5w4lPX4gN/QEAA4vxdRiCF9q0u9ziwbIVTCesl2KDPePn/iUlh5Yn/+NgAJMdMiha59sgx/oAH8BqI9t4gEhCdmGHZC0J3rU7r3AD/gAIIAeNZZAI5GrLr9RgABmyEinFtDuW1G1gIItNILS84q3iIB8GCxH2CKepGioYTn3e33QMOvID/DjPpA9SwVq2P1g90hhM4epJHn7/Pw4QYHDAaUq/f5/rEBygKAAkZiIynOrDIW1DAABMGAZk6bGjRGCa346VQBN68waY/X8QG+AloxPzHRh0LUgNYBCCbnI7z/8EDd8/GYgLcAC0gAsGvVLO8oU5/bwFABcYx60LRDht3XAem2QAgI4CdqMjkDv/nVFMWARJond5wDAtSuM5eH/Eif+ABSEZMEtL7ZJbeD8x1OV+ZhHSopgYfwv9Y0dNgkBkFva/4ABi0MQWrqOXDAzuqwAMKkxdDWheTWHt/m1mjokGoKkwhq/vYLunIgLp4VqhKAD6xYDk1QJTdtDo8K+g4PmDbEAsbOnvD4iXMezrjJbcnFz0FPC2ZBd389/EjYYAFoI4HhcuIVFab9eAonpRELFxkSUIsvf+xIJ4g8wZv77/jYh5gY9COxLW+7omke/x1ynrlt42+RhjI2Oavv1VJb47/u3zhl0uR8n84YBlCZW017gfhq6viaedQggW080v3oYZJf6Xeg/4kbAiDygjrGyUk2Sm397RGG6CIr3pYxOs8ifBbDIrpbv7RAAap0CfRUjdfOXCEEK5jZwyLaqcHrNGTwewya6G7+/9EyMjmgyxbCLgumvSGyI0P3W5ihQFEKVjTyfU0OxWyjf6T3zQbEFEEyp/voFxhV/9vyAhJup7mrh+/sDWYWxc9IrfeEyYdoJaWOf8maJCvkPyBez9jvvP/0dsjAfjv7/1FQiDigxxIIIKgtYC6gYvvGfwEWYVuWNW+2AEZzFGCmSOaU355Ir4gGLnB9mE7xgFhRZoYA5oWK+E97qUW8NA62VDmpqYH2rvoGUoYalsh1o/fy6B9Af+JCvaJVlsRW3//ofJ0GIIW7dwwLaKP+D8AGY5z6T3j1jCRk438v9r+JC3B4WNP7odduA/S9dRt+4H781odr4EcM5NFnQIvz9CPwdNlieB9vYDGcoZt6a1fAwceHMsiTf9v/8MQAL8iAGBiAd1Zgcjdf88BRNFAUBfVZSChZnz+9tGEKkxtKFoLpIAAtK2/dEf3gLY9X1ioz6tm4JehiwdlBmoF4sigsBymgMjP9Pf+oyS/fX+8VgVeOP4++1SjuA273aQelhcSF4YGwFhAgX8jjV9XrH7nwAHBDkoIVu3ZMmFG/+0zkQZSa9lv/1pgAbbuG6yqF74Tnsi+/tFB8JbLybQ/eC9BTe0XoO7/hmAoY7ff9zdCIMMMf4MPhP7t4aL+IDlBo0yhgMsJfxmAV4mLR9F/x/ExnDGAAjAbcEDFyP4YzwkoX80IE3bHT/+jcufeIBrgwWyQRjjXCSpcPRBgu7QyX+Sbnx71ZwAdsdjZV2//cLYw8j6Xs/iAQeAAjKJhoh3GdbS2YADccF2yaQ6l0Y4G/rHRMsuObbqKeRgOKBryfchPb7cYd/8SF8ABIAJB9DUm09IMEooHegGNIj1yu0SGDKJx/brdvXwAU02TQi9v//v+Eeh3/G+MALiaFJNJ58ySRO//wegGPAhGpTHyODPjj+AjDGui5Q+mSU/g+hwAAFgQupkGhl2mngBiComYVPtlklvLA8vEOPyPhEuJthbsNgAA7wACMAaRGjRG8x1FK6iIc7WGEeGIJHNv0z2InT//7tVGNjRl5hTDd1u8VGrkuTrheBIEMpKrQ2xEGEmPswfFdyx4EAYsn1RFIKZzxf/+4TBrsUqmyN396AV8Hbjh1lL+7dAYIjsSpbPf3v/4WloID698/c/76v1iS9u//6v+Rsk6j6fRmezZ+///77wxD//xuAEeltkjH6UeXD/dxM3ZjcAgwZTfg1VnFwLqTC2rRKPvXhkoSu2GkNXaGq3UPE8JZvB/3L/jihkX8n/jzf3+eDF+uxLUs4jEQR8LIA/EimT/XT32wd2Y7VWz/9+euHYejoOpTvWNWf4ABMBpwwUy6jDWdEEjPiAboGC2XkY4xokmXDBZCxGoYuU9/v5hgCwNeHDF3kZ7zskuWwRAAL8G9L4PpHPOMPb5nTdZ8lgMlD7aZORpSOJ9emn7BVmXq3ugYF/+N70l9pwEozCKgqtQ9Tno4dDEFKZhdw0MaKnkZkEcMUu0HjyyDpetwANQUtBa8ZBXV9QByMZHQVV89ClocBF1q175tTAJ2Gv7i6l/tanhgCWAggqlim13ky3/qKikKZEMPVNkyTTB6FQCx6AmERd57KPmfhuCAgAEDDopwlNSl+49ZHoaOr6f15orBloMovkF+R9LwqoKLK7X9P9IdG08/A/CuABYQreV1zombTTf8/4Bc4PIWbOarggtPYnxo5WQG4BNLOf/x+uaXLQ+eAktZGjsD2jNA7LiTf1Bf/w5wAGlZiov3ROz6AhIJRBz1QVwt39xr+EXJz8Zwr7EAxhcoSJsEm2l/neQCCCJSJNEmmv+DDrCb/by+eP/LwQeASHrg6/AJ6fTw43WBs+nn/qm53M/+PpL4VeAEjxOAUDHdY9Qw+gfGTqKDtWAPAA8WYgaEw2cL5/V/THQX0stfw3ACfINtSpt0q/B8AhncxFRViZtts/4NQ8/05X/4agAzPdO53/9KGy3oq/Pv78AsApRAQdNRnZ85MW/3AMd/tTczQiTDDX+AIWMYPSKb+r//h/8MABDQw/1/qV6FP9DD4TTcGakAqijzPrWrUB9So2FgAM0sx1GR1R7J+n8qD8AS+cch+7/8F8JGB/sAE72ZjX93Vew+BgacgoJW3LJVJch/7dm2iPYkQewoH++CHpd+gBsRJF3VdoP/DnAAtAZ8Agl6VvkfOvd+AVAA8PweqyhjqxFI9//FV/4Arn2SNb/7gTSAMYXSUiLRJlpb4AAgEEUjIg0QYaP9cNfQVwoZk3aM0HAjC24bABKCRTVyJum89/BhgEJggDP5SWb/7f8dwvwAGZkJOU6kG5bUMAAFQYBmTpscNEakDtBM8atjOnzgRcYteabU3gCgAlxQBfHPRhoIimrLAJYAtkzVPIbhc0lPWfb+JD8i7fwFYDRQwYy//GeElC//eBh1UQJRSlfeuaR/o4BElKCR6ZJz3/aEVxXFMr1nkIbYPhKwAJACBTLWkzUyKwRcZ/hGTEfmvXHaUjpprzpf36obpOEnv7j/D3gAvZUkfmj/74yjGPayu+14CngJ6eg1PmMOsJ//BhxYk28/oCCU79d4Hwf+Nwbo39XjKWBP9fAxSUv1t94BBWFEEr6jl4wK8qveRhOoi8QShrkYNgZ5ycCS5GP12iAA2REC/ZVCtcPwE+vC/gTgOCgk8ZhS7hugzvtAQzucjI0TNlln+OEYDsSBgVaG1MXX4I6XbXWg+dyzx41WPy8GcXL5Ff1Qbtt+GP8AEMo0nnV7+wBIL/q9Ec5aF7qgYJfh3bMlv/+gJnanems/wv2QAFjMltC6QWEJE5e/+BaAy2BXkspymbgAKMv5PZGlThHbZHu+8HcJsMmfAHbOJaNz24biG+N/AqUw9fkv/2xhAKH+AA4+bAOBj3M9sZdROFHz8c5gIWhmA5qJSMMDO6qjCXki6+v//cl1fNkYjqEbSn89SmNxNjjr8YoFZLoHwTLW8QjIAAewAB4bQCGID67AzsQbXlG1v//9hqkp6LrpYvzH3j9/bKBlUk/V/eQ2wYYfofjbA4fjATcOGLOoSzvZVgxwJFX/pUkSr/96GiIqfvJov+32MCJ9Cg6PK83/9XDxus3fpk2+8IjVm2dTh4LPJD5DgDM4sF7YhDl5/nAACoIA7MD5scNqbhCNDL3AGID74or/5wJ0GWvPNqbC56+kWhj933ddAn8nxfrHzeMPHKTH+ZEkB/2PxI2AAgIIv2ilu3wh//+cz1p1bT/d/yABc6ACkCEc9YJzROeYAWMgBihKNusk4+NTK2p+P+V4GXm1B3js+CG71JTfpXy4xFlVW7ef7/9BoP0vMiMboYyOL6FfwYNSCyB6cd2UUo7/9jClwLvDIq7tTzu7t8JM3IsAuFuwuoHgfBZ+YiL3uZbU9DOk9Lu+f/xsBmUAxxVaEWCbDH/B8NmAi7AdBK8M0j4OAAxcGIJV1G7hoX3VMtY0VtglBUmENX86qqgPPef0AO6HOMgjzHm4OAIwW6L1S4xB8D034YgzQtNEbFq+PyKTPFkfVGTVKq8H/v5shkKoi6QShrFB+NjP2YyvxmFKcDBcSFYADYUF2iJSymyW5gAAsCm4DAy4NEYPYEAgIQ6LkE2hltkp2ANsQAHBGkCgnbA6/wPxBNIAcEj9JK9oYc0GRLIV59F6xIWgAOBiQe/QuGfEbl/mwfmACw2BiDKePtkYoGgYDDgAJgaKCBS5H8Nb4SUL+IBrgQLXe/HWtEEy+UAHdM2RCVPf++47D9jan/i+F8ADLAQ4ucJEGCLbDoxB7qxs/8kxLT0AUAkwYNYf9DGuE1C+wEnIADAnCJURsdf/9wtTADjpM1Pj8odUsHSbq/iQ1AAbDgm0XaG0yym+ill7npQd4lVHyHF5FQxRn2wtjgAB2gAEZAD3xg2nKMvX3f9uziKU0NGQ3D/4gK+bCBqqxc+bq1DvwfkhGRSnRsO8tbwwAiBK4M+B1VpMkYM/Bh1e1v9Y/UbCv/8LcACwIajn0F5+TsW+cfwEAIWRHqFLfIWLeOf4AcAHhLDE2UseZJQQO+QAPi6FpsJZ80SgidDDEBUoA+xpEF1fA1g1RhtT//CuCo9xvYXDC2OfcCZBkI7DamAI3RlsXReArCTCo1fNdiyH7zMxuvOLqX+tvitMGlXmY1///P/xIe6xI7fhaDJLo6v6sv1U/+7ujgxBSm4ZcMC2ypUxxyro2ZZxwlTsLnke1i3o56AMSCNR1i7lXgZcUYJyid9tYSpngAExK5jkBXaoT5RP0gExgY5UQKadd4YHgpcC6gZFfdqBKmWB20w1X3lklgXsaqQV6lC+NEfIa0x/Ejegw/nmsNbGhQUmdd/cYdMaDVfbA/0AANLTlI1+3qpYlMAAQNLcAAIAYLkNH3ggAAoDgPscNDpojADIxOyHM5Rkqb7gImvQreNqbbB20HzhsWdW0WJsMOGzpKve7KiMHJVyLt4ZSQHj6N3iYCQ+1f8SFeDBYXxFdSRiug9tgHSAMApO1UTJFItvtAQklpg8lcG8Oe/cGDQA6HBNouUNpklPQLyHH5HQxRibYWwITba1icjrfg6PsV0q33/1MqTJ13n8QNpjAniAFTYgOgwuUiHXn/63iDfkEST1elmMXoCTFABwTr8SglZA7f4ME+E4l2U8tz78AIYjtf9RMUIky2x6A7RgQeLwlOzpuQsH0YAgAAmCAMzA6dHDamBAdDQuTyoMFqb72kyCW4u+S7+7VmRzCgtRfP97LU4otbUMtmhfZVpZjDjUxOmLlHnD/3gQIgjY4rZGc8f5Zy6cbFB/RFxGuda40J9N+XZyTdmLcSN+jBgYACQ6+I/MQcmlGPuxT0ESCYaoKYYx19AAAdgABHSAwjAbTS0wFqP4BdqRFFEL//gfskQKeYDId06ZelngXNBglXQ6nv1bn36xCeFEUueTJ//6qPKFbrICL1MhMt39x4hBAdEJimp6FiiA02KOmK2L7+nUAUZN/Hu++/8SGYMF9JkZIMTUu1S0h5dAwMKsbPkT33v/XEYADqhCCVNQs4bF9laH5mZhuoq7SSlrUhhxuJDVrOLLEOgUmeTCnbv8dR/z1sTq//4cgAIgE+BQ1gghHOOk1zHjATcOGMPoQvnpNYxj2AAIAMgOpBRH6/v3IINq0QfasnTTAtTwBQAFpzeIl/hiH9bITKc6kG5bVMAAFQYB2T5scNEbAnshqN+EqJU5/gZnTh5U1+FKftRNku84f8SHYAGEEBBBNJTINkmWweiCBc2xk/cm3Lb3AEABejIAYGJB/FGB2B5/wBWwAlBKqWpP8sY9/4MGBACgGyBwtd/8M62SULBhwwzmAAYSvr9YDvuKkn+/qDdfvbMj0klXeI2ofcfz4IfV/AMqc+8//CsPEMAjUgYFGhtTFgbv4ZTWdMcd88RpIr6CubKRz32PlV5/36/w1ogm4J8LQgJwXxv/P5gGdNat3/UGLRb/DPgXAa4AAXgMjZN90p7/Kldhr9p//8vmEzH31/h6QDeMBrw4Yy4jHedklzDYfiAbYOGsvpwzjpBYwH5AAsLoWoynjzBKKB3zABcTQpJhXPmSEUTuEC5Oc761iNtx4OEvMZ/arf7ogQGDuTeadrcPbsBq/V1h+DHQAUJFDcF6xJ+HhHufxJ6wELuR/3629lI/79fxK9G4nxIVun6yD8/NbPRgCVJk67wPDvH/DUHKePl711/t5RAKflMYjlF9YGoiJ1heNn57DNs3vIiJ//9KOXuX3gOZntDQhl//v/tjaL+JBFgAGC1oLnjIK6vUAdMNlxxNQ/lNV3w3AAsEI/m9F0Jg20x/PAlgAZURwqsMsZ3p4pEB67Up89d+UXh1//DVLU5Qb8A0p7W8L/z1AOUew3Bfwk4XH/z1gOWYfkPv6I9aQrl/nqTM0p+9DQ7//z+4GIlLVf/PMVOlqhDEs0OD7wf/vf1z1gJpIld5//xJ6/ASM9H/fr/Gf54DrRdpf/xHifE+JD0ABEHn5nQxRn2o1zAAB2gAM4BpEaNEYPwBYfTndTEGZajHBh+AA9g2CmGFqIEmR7Bngn2gWi7t0f02H5MRJiT1anWj/v1//COIDX6kiSEkzJm0NY13/iH42N1mjusyb//BhwSwAAFi9BmuDoEXDmAAQZw6OxRhF+S/PoAwAXFwLSYT2i0TmicXgA43CXs+b3/v/huB4Zg6PxZhF8S/Pv8wAWEwMSZTwiyTigcDXBe1G4hRPf+/+GsQfhwCJaR93lM3PWI8QeuM9+8Qeodin4D1unT9//CGIPFaYz0JvJfe/8Qe/+ANRJTzj5+Htz8+L1fz/4Y0A4AFgQkCP0J5RJ2MInH9gQAh7EIUJY+QsYQOf4MEt5CFcvvAAC+TdfLv+t9NqdP96/z1/4BjpO2/+G+ZCAIIYBWLAwKtDam1gTNw4colCdDeL/88WpitQ4cv+C+Yf4g/fAH25cfTAf2bobVf8+KqKLQWu+f/ni1MAIzK+d7rUfU/eIPXhL+eKxB/YD0xlqv6xB7+ALtW6fv/hnjsAbE4MypNOu8GfOoq7eDcO8cbRf8MbFAATAD4mBSbCWftk5InvyAB4Xg1NlLSLRGCBwawPO/4CL8g3iveuO/8EHAARoIX63UK9SH+oNgWAEACwQ8Fpg4hEF+Pe/dpAATqjBfo2xmugCrPuERwF0ox//eQVEgEiMHsk7R7BUw4thCjVeTw+ZF91ZQE7ciu7DZLv/5MN7RO36dyQcio5Hf4bGLTbGBeHcAcAHhNCk2UseZJQQOth+QAfF0NVYSz5olBM6GCAcaBYwAwQ4QsX3fmucmWVchSI2ffljNsemN1ZH9v/wQcAmdHLlijYADUmzQmin7J2FvBtNk2m/yrQ6bDAkApKCYgYtqzz+4DBUBqo5DjHpsgZ1pd5AXFXQB+VZ5VC+1rAxaLTGgZlPW01/xrBhW28yEzDvji11rGELOHUznh2AC4DkBPQPitu2HAiYxSs42pvWhO3MdCjetS8IAEfg+lAhERg8ev//uAkBDLEZixr5JHCB69oY8AQmi/SKx3whcsifBgi0S8EkuACg9mtVCLSxD/wMQN1mWMRhIVa1+A4uhPY99/FdctkmrfHxPqNTjFP8b4ACYAPjYGIsIXRZJw+cYSLADFyJ2U9n4h//9uj8wIehKMiWECdyyB3/Q9AIaxPqE8+JXLfPv4G/jU9sOOJnwG3bG7X5H7/Dfo08+fAZEXvkagDfxIWgAVYACdVcN2G2L6iD4DFelqdm6ESYaa/wYcABx7CYnVkq+lIf7kzgTqRBX4op+Uk1XvfwY//D2MhX+AA4+RAHApzl+0LuonHTwSehEtckglrhsMmBq6KRkRb+/9dhSjFeaq1exOUEU1XzAC8vGjzxfn+gHT8SrMbrv4kRQl05xNYg8twiYfPwOv6vj/PwwHrlKnn/jcSGYAFUGGrcGS9+bM9/ckEHq7HT9ybMt/eMBuocMZeRnneyS5bkGo4S27ec/JsNEMo8AEoyDh//xIXhgAcJUX0LYbFf+7+AAa5iFFKbhh0yMbK8ACCINhVjGxaXTp/+vaiVlWhbC4ro5v70DzLiqCYcF7qTmAowDeM4yhmiKHSHjHB5fKweKZEHvC3aEuI197mRMoRPbXxsMBUgAlIr0FbLcQz7+EDNAEFu4rBNrTDvZWFEHz6hGv3cMg7yAD4uhaLCWfMEpInUywf4UFTQ2t8Qaj59Qwpqt9LADIqVp5v/d4sKh8W6EuklD1BgGRXptPPeQu6kZSkGfrSnBgwFWtgAxop+HncYol2833rAezzEv9i/+2vZ/vpyXxA1fEjYACDRoAIWAPQ9XenRTNZ6REJEMJnM5jEAgMPADRDAA4K16BQTtdf7wCghpLTR70zBfDHv3hgx39zU973gSP0gCAKTtVEy+kWf7cIHBD8C7MwZNMQ5mZu7y8OpGYdWw5IzRQWan/Jvl3X8SFfkPPyPjFCE2w0hgAA7wACMAaRGjRGD/zHWUr8xBiNUU4MOB3NjocSunaD//43w0JAxwv9+NGRjFXBuEYBWLAoLtDam0FcABwxme38iKOoW21/uA8LAcIc3TV1q+7GAPAiYxSsw2pgLAKSgmcMitrGhAABMFAdk4bHTRG82YyrznVx/a1OiAAnVGDpo2xnOjdTocC9NEGymFzyFtYnQKA1iX/2mM2kN9+/Aynwtl0ImQ+YI0/WMmfA5MwfFuEPzHdGnMyf3x6pERKscSH+4ABGG0oLkrM2pgBhJTEYTfXqresbDGOjVa/9eCrygKsMpGLrwngmuHa/qP+7/AARMAJA81K1wdxYp3+AY0FJuTnoktA17/whIrcI3Y0ZBzL0zCrXyG/5yF+v/DHSjMAQHJB/F2R2B3/z8Aa8gAMCN+JiN8Lr/PlCsAAp6ABhrETrxVmXHAVRDIR/79D/iAvQQCFQhBamoWaMi+imGAA4CCwX/SUUrSdPEf/WGspyqjdt//f00AFw8WpJ/FCnf7aNoIIKZzRg6LYp3+UAKNUT9//1TFBnoTStscoeJ4o2Ohfr/iA/8zZhuoq78lLVpDDYXkPgChryEKLXJ1WMWwAAXBCpB4acmiMAAkLvyIpyBCbaUQHoBkAmvMrfFIKn8egIAdogceMynZ83QW/wgKDABobw5fc/ytptZbPAZtPmxQ964ajAh/4cSAsUH7uckU1UM/f+G9u2qiJS1SdLVf+P43/8TaEk7qyfYSssEvL378/31NgIYTKE3mSDLIeiBAtboyfuTbl174EgdFSQsg+i7GXc7++Xx//ig7JmRc/9/VhLaQ7J7u/hh9PveP6HxHocToLw7AkDH0T6pLCBK5lA6/uYGJQn9SeUCdTKJ3/ADAAuPgWgwnn7BOKJ7gJkRUIc7Usxv/3rgDm5SDLKQa0zziGuvzdt1nslcjoKq0Eoc9H3ngECCpxiSJGnCQYYADgWT0AOCHZXYcTWI/+0BCQSiDiUQUgW7+4RJ6wBUp2NRtAK3rtE5v4En8W2g8QYzAXV2H42HDBCpsRkaIBEZDZBVakhLGp5fJun0vigACAuTI2hxD6xnkkQjBFZzoQpH7mwAJ+rhEUbY3vwYcyWvdHHy4QMpaDs7T96BlD9+saqoLw7/6QnsMLMEe+4DDVdFgTWLd7McNQjAANw+dGjwhPr5W+C3MWSXS/drC/GDIiIycWT/w9BMBNsIVh7LQPSaXUxsb9REJmGZXO5zkLlWdxuHlAasN6zK41rZaEnFxHTef14wGrRg4XWOnkGercADMSAGpK48C6ykNfgwwlLSw9AeQ8rki7t/b4G591KQd/+f8Ow+IH+ggAK6SZm0Ejqi0NGFxx/EkEOB9AvMbHMkcXkd6rS/T3G92+0ECbF2Mr/8mZchPZLw7VEKGEjO3g64CiVYVPf/sGY4C4vKIy4XH/EhmAqHisLRHkPSol3vUQiJiCYhyGMQGGoPpfqv//+D/9cF+AMl/LyFGd9w+GAAs3OCGhFyhMyw2btAQppRsw45X8BIgFgoa0tSrRe/BLeBOrFAB+9odVMxv/8bMx09/jfwEZkJFKfkG5a1OAAFQQB14GzY0bUzUBLQ2XmOhB0LUgPCA55wTPGqazf9qXBzcj5f/+4DQJ0MADgnKJQTshdf5wJwxyzX1ih5d1V1wLGcoOcFTTgcfw8DwTIAzA7uHpJLoX4BUgAkDXcsWd5Qpz/wiYIAcaxjop+0t39c7/3BnJByWVi963a2FaS/fin/I6euJj+N8N3W4DJrWxHebjhH6wPvcv8YqiB49PLZzk//wYcO9OUcIyAuaQ7vmRRTiDlEQrmk71/h/poyADAxIP0owOxPP+cbABKCVTVyf5ox7+8QNlOZxuvvXzVaJUAAIBIAObdlBLDBDvwdWg7JvYVRuAEe9pFNgbb//+2FBPsivbjKJeBwSqQaNsUSVl//u/mrTWAE8yLXnv/+fXDnAAQj7uEa7L5K+arQCpgAUEr3jB4nzBqgK74AZCbTMWUMNhMEEXh/8OaA4ACF+PHqxRT0a1ZHf+CRcVs/4W7iAxhMpE2CTbT/f1QBDCrRkSYINNeHqP1T0tdBzMZus9/b/1w3wAHJeF9XKKajWrI8uHgDketwlYd2dBQ0tljsSevAY6ufxPwtYFAAYuDEEq6jlwwL7qveQ2VxG4glT2K1mytoGoMkshq/ucAA2RED/p1DNegMgeFBJ43KWXjtBffaAhmcxFRYmbLbP8UAZmvp/v8+CshV0t4/7f/txkyr8MaOAA1IZSBSVYk4cXRewYYAHmRdC9LVJX+v/bBGqANZorH9tff43AAsMZntTUUIkyyx/ICzIXurovyJ//gIAdogIPGYTs6bkLf4PGDywGrx8VubPuGiBh3+X5B9YASCFgtNCEMRgnd179oCdCAA4J2jAkI2Qun+B7Fo6FPCta99xEbgcddPTYsX+HsCD31WQQIKgAVUAAQAbbACCEBk+9cZhwW9LrmQ0p3/8DAOH1jUpa53HQD+ABUDkGDzhidbunajX+D00OqUmbHife5BqJ3/DH9AO0QOPG4Snh83IYDjXgANH+SaRtPamjKMK8S7S//AC54CFayNNPhsBdZUr+7NY8X3jcEo1Ig1ygErYrOTs7VcGAl4QkIkv3aWZi7QLUEzhkVuWyBhACGBUYQwIzbPau94kDFoiH/iSOvSv/3wxPoUT1ka5qwFCovh5Zqsp6Jqvse0k2k9PyXfceqgzU4G9wn/4GARcIAeChil3kX/Vh2p6zyftay8lmJbu0AzFOjy9gR4Z/+vjHjPxsPAGFq3c3RoAE4etUkTZJx3+3QOJ/dfTwBmOiZpNc+3QY0ABxsHt3JVEH6YJY/uEkQAhBmoacUYQQcAA+wCQR5vsIDxrFWDBAKIRjjzfsQeqvNkT/166W2JGNtX/DP1NMhFS9isqhgzYJTPqp294f/C8AIl/9R+f4Lt0V1u+7oAjH3Eo6MQjVTv2f+5cUf7/98jYmZTnVhOWvvAgF9YjK2pc7P6MFrQdlBM8apq+fyf7p8MAPABQySSwufbctV/hbo4AJQ8axYmyTjv9hgHBwUABEMSCal02rf40oAHQ15BkvzE+jHNsBMhwAKC8IkhCx7//3AXoV2r9wU81St/n3/8MeABQBZAAMH0zOrYvpK074BiyUmzyEzJvjHvwYnSg4AZirH8w1HN198N8ABICXAoWs96OcdJqlvGAk4KFLOoQ3nZFQsVOAO000Nqf+K5+GB7cu4/+Hp0UiTwAHAxZPdoVDHiFy6Bt8gAlFoNSYTz9gnFE5BgINU3AQjE37YHC4xDMea8gszDFsPBHDgAWEI3moyaEybaa/nwfCsAFAd0BPQNW3bP5wImMUrONqYAZkJ0Uh0KN7VJYAAKg4DrnDY6aIwA2GYREmiPTY0wQryAD6Bl4VdiWTiRP/3mZjK6nOrj+taQwkuQA69gTDpR3nbMbL2r/MiGsvxId+DAWZKGMQYrdkzfYowAASBgH4Pmh40RvEAFhdC0m08caJR8d8wAqJoYk0rnjZKPzvkREJMYTEEcxSAw2HoBiWI9Mnn5CxdE4/vYDFoR+pKGPkbF/GvDBhOgizjRZ2ANf/s60Etvk37xAPaJoNqSeHcN/iQ9SAATIcE2i75tKkp8NgAAsCG0Dw25NEYMCKEKnCp9lPslneMfZSupmEdaimAwGGebAY0lMhEtquL8weY2fISPXNnQ6/LQf4e6hqy6BLDZrIZv4za+D//jnheEKLV1GzpkX3VqQqxE9KrrOLGnjibxOMapzKYAKQCdw3ezciOBjDgAJMxMylOpBkNariB2UExI2C2r0KK9gq8eV+qUzo0mD3//w70EGw4xpTJwJCcrvv4P7Zf1kWYPUAh+hOun+iLALQAAgZ0AAQAgVEbD5hgAAqDAOudNjhojADtDZeY6EH5aucIHhEpzzampAoDb4yC27twAtDCoKazeqXgFgALievDh/8M7ED4mH8u3GPPfXaBaFAcBKV6IGHkyr/aAxYIRJxCJM8a7+4MLKbwKzm4W3+H/+JD0AC4qGUW0nvEqp9AagAMQSwRpK50UVTPz/gSAAIAJ2CcBDcIR8XNjT/+0kjAGB3gRpVgbhdf8AHJjI6HE1DUMWi0QZriHf5TzL73ENyoIrPJSxieHwQgpfccOGRbVS9eA6nMQXnJLcTxx1YR3AyXnE/8XxwaBQjwAcPJ54RQaa/0DLSACfElO0iCs/7wX6mKod0P1aRTrDSQ9FelxP/choyKVT438MABMUTlbHKM61lu8Af43HuzWmvffOAAGqAAVsANeGjamsgHRsAKvWAmpeH7/cHwa8IYWDY6y4YfngbNZ036MQLdWPn3kmpceww0pDlNFax//56fcLXbDaIdX6S/3AxgZIb0wP4Yk4BdtCryWfv4kAfqpJNnf/eRKPid8EMPwE6MS8guIfy1IDw8SGYAFoMNW4Mlz8WZ7ehKpdH0+ALAbqChTJBOO89JKmPIBpg4Wy/+GcdJKGMofD54QkRoaLlIdX4Wxx6UbpfxIVwAOAVEBB8xGdnzUxbffAkMVvt+7oRBZhj+f8a0IaorQae93TP40/6xIak/gkq+Q2p//xeJPi2oGajjz29lI/79fxPw5AA0wGMKpGpFkk02gFrYCGE0hMkySbZASgYJW0Ml782Z9e5Ewf4QFT1NGqTvlgDNVc3r94gRJu6jan/huHBgQAgQgCNUBoSam1MPPvjN3y938aTyUi+cP/8K8fjNNiXDmLu69hNyRP584zlVqK7H8SeUf/wE5ZOn5w7x+JCvwEwoLtFT7qbJbobAABYFLwHBt0aIwCEOi5RNoZbZMd0BBhs/Ib7YAbkiss2dA/z/l33XjXdxrj/EBfAATJjI+KbsPyloAAchmEG0Fxzl/xZEpzz689qw4hUrKmvN/lhVSrWRJFN/n+ITL4Avw0Si/jxC0NUYbU/4kbfvqu/7g/AZxrZyqTdC4rsMBtGwwAWLo5j6lEj/38AkCEolEHEogxAt39wYACQ6+I6mYd8MKf80KC7RUpdTbNdLAFZ9J8O/36eAWMzHwK8nmf/TAABYFLoGBlwaI3kh0XKJlDLbZTgwdUgur25z/2VLeHr1uv6GCtwcmZ27STEcaNeJD8AHJTDJvNWz0qZqgQCD/DAA4CooIOmZSs8aoL75A+gMdms+Y06xDLP88dMRqBbqGtrw8EgDTWwaKv/CGI/EnlONOAkeSdv8d/EBuwOAIAALg5lwDg06NqYAdjwu2XSHU2jHACL8AariIzbV/+FYAKgpqC4kUvy73zgIttWu/NqYBKMxfFMrD8pqGAACQMA2x00OGiMAfjW1z84+rakYKg1ACoBIWGUhkd54IO4b+f//EEwACB2QE3hsVN2qAM0J05joUb1qT4bgAMRidsKrfcljUh/LAAlVXCdRsjd9DM0AaCbnHHzl/sTRhA99P/z+itpdHv9jcA97Kesfn/+eoOFxj//hX9ocE2iZQ+mSU/5Dj8j4xRibYWxgAAsCFwDQy5NEb0hUSqIlLZZJbeGAAaSgwxHU9l/pEv/cY0pV5mEdainZYcQy2CSxNz51mkNEdS+b94jxJ6wBarvn7//zxamwin4CqjKc1/7+sP8/re/5/36D/6xKnozE/PUXSVfP/8RfDngApB3uZkZXPV5Ramq+easPv4Hr/vn4z6fzrnXxGdbxJ6gIn0vvf/+EeGsC9UITGCKeW5u+AS4A7rJ2Rmk//wzAhYBpDFHSQgxxXgw6hnf/9fev/4JYAABUdQZsA6BFw5gArgMxZCEdin//3gCwG6hwpkgnHOeklzC8APSHL0kpv8NwUwEcthSMxT//7/4gGyBw1kijLOOkFjAa4PxClyS/t/n4vwAEyIZXQRWJJSxif0+CEFL7jhwyMbqwwniA5wAEhuQhChSfYcwktjAABUGAZk+dHDRGCUtwBatT54YjjVE7WarmxB6oQBPlKK5+P9whiD1gIXcj/v1jskf9+ptteqRrEAv7IAEl1BUeWKvi/9RZ6ezregJDEb7PqdETbYZ/mkA8OCjRycNLCsL/vpvQDCbmYu2TRNTOaugLPLQe75P3Xb/xAZgWApIDX4yC2768GVf+AHG9TyufxAawALYwWsobLnpsT69AbiAhxFY1INk2mcVzABCV13zdJa2B/5uAIEIAzUAaFGZtTfxAb4ADghm83qmaEyZYY/wfYAwCnX1/MGFEHRp6ou1/hzhiD57ubsxJyfd5+G+P8TWIPwwE7Sf3v6/F4g9YAYefzl//v/yYgL4AEwOWUGzxsFtZ0OwFAAqDkGDzxidbvm6i3+DVjgBjK3y/3+4zAhSvkfdb+JBBwAETDE68xK+Wl3LDwwALBiWQiTSUyVwx/92mABtlcJ1lUL3wAVxXYysAmFms/7jHBZDhCHyORq8rY//3HQxBSm4XcMC2ygYfQCaWv9gG+zU9MEUhfxIVwAEgAXFwLSYTz9gnH5qH5gAsJgYkynj7ZGKBwMOdIRadraXXft7PbHAl/8SCDAAoClEBB8xOtnTVRb/AIbW+kHAAf5Jmegs65p21NTjsjcUGwgCoO0F1I1Xd9XvIAApQEQBtpTnUuUuKcwKmDaRuIEKUaj/4CZvhxK7Cf++MtIW4VrCZNnf4d+BhW439k2LARKBbzgJ+Ktd+bU3uY2XFMpB+UtFmADJgbCwT4Q9eH//1ASAx1HogTnhFC/zt7+AMWhH5lIa6RsVQOAw+dG9gACAQADHVhoQ2u/34M5YDM4MpCX/nDM+aLS//3o700aaH4Ef8QHYAFghH81FTQuTbTH88CWABlRHC9Rlju/OAPwBpkK5D5SKB/NcwA5mYbqKvfetrUgwYcXEBrXrN9uChz1Unk3++4TcP36XGhuF/wt5sADdkcKijLGb7B+8zDdxV770takMOABbAOCZvELttJdfgPQNFDarW0W7eVP4MnhpO7an7//Eh6AAiONidDFGfbC3eQAAgE25gAIkqt0D27CQYdOhZiRiM2AKWLwGAtvduVLOIHX6UD+gXmPQSQx0DSyLiuqpJn/ro6kcHNV1hjsTKHEpW7QGx9C8u8/+3hc3BUs1fn+IDfpcR3rsWoYkP9/47EBjwAMsBBRNYSIMEWWH3oDHEVjQiwRYaDIwxYA1dJ4eBC33Y6OOd+IDc4juY+U3OOAtXKeHSKeZarRbn/DMAC2GHqqH05ybE+vAK8BEsjgsd8Ef//gL9gEOIrUgyRaZf7qmAxxN4TJrkW2RHwsOvlVcX/zF0/vr9L+JD2AEB/nUazxgQMLLs7CCYbaSPgw2N0BQhUH9yh5xngGevup/b/DuCs5f3I/9/5/RPPYBVLadt8CD/hELmgL4V9Tja3/qPDNvrixLfGSPL/7wf+NwALBDtQ5FzZ8imGf5AlgANkVQnWdAvfACIKYUEnzU5XcNTF/8HrJnb0PQdJlHV/fAlgASgEW9IqCUXzpPv/IHhAA5UAAEAKlSAkjMYf7nguAbHuDCz6KogRffR6SZgBAKSD+LsjsDv/kmlyq/tW2rCVjodHvhW0aKtyw9xUgeiHZO3gviH0sLmT/8cuZmZwrfyMaNw3AVj74gOwAGaErch0KN62JYAAKg4DrnDY6aIwf6DFTiRt5Lp0vhl7WBwJYqF4QPhaFv338H8BdjOvCwhlNgpnAgEH6zWr53X5i9upOn4LASe4Lp/4kb4TGoKaKQt9kwM3KoNwRAM1AFhRmbU34AFhDtxnXNnyKYZ/gCCpOAUC3N59Ys4idDwRbatd6bUwJwdsBd8avvLz+EAAEgQB+DpocNEb1EJkxjIw3KUjRgAbIrhOkqhe+BL5e0zE6Cq1D0MaizGcIUKuUeMOPG7Qb41g15mffYGEZu5Hn+cegJhuu87jGL2EWLu/iQt3KM0vM8wA7BBerLapGerUhx+ZpBw7XhQiNyJrer/z9xgacRkrNpEiKJ//GM4vAcr6GU0e19nnAcRI3n/+nQ/8KwEcA4lOI5LlGvK80VrDPSAIgkT7zIxkdBVWglTmq9OQZgMYuEjDQtoqL8fhwHUOKNhLDPj93//wRYCX4xRSu43bMC2qiHB8P/SRCIgiq4hDFIDD4ACMSQpWEv0cnWqYAALApdA4NuDRGAATHmxVQzjuhhbw9AIoPTiZxA1FQ9f0BkCgoefMRldw1MX3wd48BCjrJ2ggv103v/wjw1gBIMSCl2IRxGKeH3v0NcH9Kf/w/4zBjBgljBRXmt9wWcGHAAcGNJCpPemJKQMd/egepwCAcpaNkTD65XywAaBrqFqkRdN17hzIAYorMNNqMpIBtEAAh87OMQyMxJCVkhnxEwxe2W7eGqqD3gbYtnh7VJT/jL3+/vkGMrSXQoAvJ8B+SzbQkVcglxA2WYuAbN2P0fzulabU/NAATKFypjlEdbS3AKEI/m9E3R9CWFv9MK6pr/mAmbkARM4H0wwnlsVUTVmThacQNT/XMYSY0Zf/bwIoKeo9sYkYYfTee9GJVMfMOhake7GTxdUdIu1CYhnEzDLIu2A6rgKkGXtrj9920QNY78Ls3NTB/1kcx3SDTO9wyPTYHGvDFzdXX2cBQm5weA6upM7PWEfenoII09coGLLpoaEV0UbbYbQ9bz1CcP6zS33tU1ehU1MAibMSOsxVVsIwv8Bg9L2hPK7eA38hFkmfXP8K+ZMCbdjp/7JmXPuRFB92hkv8ozXn2xAMYTSEiLBJtpY4BDCKRkSYJNNDTIiACAR4FcWXHYXf/ABBlHl6FT8WJguyzpsRyqZhHaop2gwxm4CAE7XGg2pgV189pCjwfhlFcjRx1y4A/Xq4Vgls3+8ADZlUMizqG751EyotC0HSXR1/3uMwnQ4loJU5qvTkMwEMbCRRgW2WAEvg9RsJbDS7+v/+HICN+gP1zAEgCfY3rK15JL8IeLgKACDELIWW2yVvQpn/2tEZaD3Euvf/jg/YGAB7w0SCTF/1/e9Yg9eANRJTzj5+G814iP4IMeFFwECeo/YlBS6LuSP3f4QfDbYNg/AMet9bWdMqHUxwDgoukW8+sRo/wzAwTcD7PECu2QWf7yI2DRA+4jSbId4YS3oKU9SZh0cGHTjsA/D0MAQHgsWrUC6MwgtFiHPR36J7/UH/AARFOA81tQWfYXgqBttDErl8P5qIkTIx0v/wScBEu77f8Xw3wBJDvqQ3zzA30H7dNcAD/tIL+PJ/17BIgdzm+GqecL2jAp1zmja6wf+sSCKCJ864gFiMBmpAoKNDam/5vvY1fxvDEABEBLg4Ww8hHONkVS3gQZdkiEE521v+UvWLAMtIC90Eaf6vcNkAmlB0kJ0rCfwcMACwMw7OX1QJms2x3LgMABYTw2GasE0/wQYADhiM1v1EUdQllb+6QAEq5gv0XYzXSACWDcbaNYWQ53wPE8AECCJGgw6EX5zgRMcpGcbU3gIaINlEXSSFtYkBwFdKDZw6K2sYFCpmwCIz7R/ZgB9lIDeWobVwf+HdHScu9rxMsWp6THZCEKB0uEI/cHqA6OHHC0aYcNzF98H6L2thCi1dRs6bF91YYI4+w7wVUn//cGDKkpWcD//G+AGB+Xx32AIBARi2JJest9NYoixeqKJcb/5oEgGoCBJhKFE99M+LMYP4gW0Br8dFbez7GByCQuEal3v/P0j7dpT33dmM5YX/MkN7+DFKfACipyGlamADuh+NnNuoBv9b8myd/xsABwIahH6E45+/QsicRiVKD7z+DeibCFOcnFpf/Bv79H/z0C3Sja2p/QFcQEOIrMk2TaZf7yHSZwcPRjL/xNPfOHV9/QHrnwpKfLioAoDrhuKgvkEgsJVL2kAQiUppvsego6umXZk+Wvm5qAtrgxHFB3SrLIf7/94CskxtFkIvb/U3Eaf4d+AH+4vzzd77CHaYuOFpNqJeBFw96jVFu7G83Q6Y8gOo1PFJI3vD6i6rqEoLk5/l/H6J6AUIKySYxE3RhpBv/4OCAHccXGf+2DOO/z93q77IMYKJgywf/GwXXL5ua70Cda9Pjn87XsDrSBIAuYV5NLWonmGHsr7QHXT4ADHkEYoK+1DEGV0uCTlMNZKCGpWQR7gqEbEwkuE1Jmf/7imH8iR3epx5i0HrFbVGS0yyC3nigZA2LuvTV//QRFOIozn//9wNtGyDLkE2/8X7w38f82AA+Uw2a1MvdOh+CDsYBPV8jf8DBuAAgAxGISUJ/f+Lpc4iHAENGZzD/rVSrI/ywxssukPl0GE8aw4hBgCD/v+mXv8LcBcAIXGN9xsWUeLIf/wdsKVbbqkPf+8AULvzMoqHP1pjtAAdAzqF7hAkmUbfXmYLhP8VOubpV7cRMoBo3i6KV4I1BEJJ26X7zUjsRrhjwAGbCZOUX1Ec1qNwAAqCAOzA6bHDamATkGy8guKfy2IAReAJaMjJ3ecd/6wRfC/gAWBDQI/Inn5GxZE4/oA4AeEsKTZSx5klBA7DE5YBL3JFVCEtaOTXfxIL7CAAsWQTbMpmtJtrxwABDDgAJEYikQ5lcIljUhxZrQ39AHG5N3d+NjUff0H/h76aIDMcM3PFKqrf+9t41vKqv/CI1YRDN1O9q1g/HaAQUTOECDBFlhxzJ5DmKitmhkBdzR9UfQYlx7Rhgm5Q+n/yYnp4AUAmQEDWH0IYxomoZ8YCdQQMYeQjjeiapcMMPyUjSYWBKWEDc7A1jaIbU/4kb9shs6mFznoarvNEN3xhM9/sYkYEDqwLWA9oHRX3bXgIQ9unhqHpSYS4yTwZAVC9faZqdf9/uAia1ir42puAHeC4xAAmcdNV0KA9wggAJkRhuxjIUKlik8PghBSvY4eMi2qkHiMAi0gUFGhtTHi4oeIsIF8bwBOT4weZiOjv8dGZQ0RoO98cx8bIf4V+AAxiouWVXstsFuDDYAALgplg4NODRG8CGMbtNjm26iG94hR8RsdxX0st4BL4ATVWOuu/8//xs4wRs2GAB+CzSFK97ZvvYTUjtDiU9vAsQBOgMhBf6lPIW20AWADwmhibKWvMkpIHYegCAHULfTMRiJfWwPe/eZmY3UdepetrU+GA579O5J81DqMh6z+5AVW7SOTf9mNKSkiGzw4YP8b8PwALBC0WujiFQX4tz93QLzADH6xLLNkFt0wl/gZBgK4AEoetYmD0FDHf75hZlKRjlEItZbNNmQAgM4CeqMjkDv/gbAAB6gAFeA94aNEYAULupGU5BibaY4NurzUvAMud4SouN1vQnK+nUAlG9P/8SFfAgrZEZ5LPGLruuf+wASUODz1IbYCsLr7aNgCUNVNSf5opz+wYEghJJXBpKYL4Y9+7h/CXtkzgrYna/nju/PT22KXv/epi5T1/EgggCAwiUFJgLijpNxTieCEpgAYtgiBOTUP+/hMAGgJdQ1R3mjXv/aSIwBgK8CNKsDcbr/kABwhW8xFzdnyKaZ/3mwANkVwiLMobvloEX0AKCSEbIEvNv3+Gwr4e0srlpANxIlDQCEWlua1lCllVf9wdtLDqg+jzge0SME9gWsv8ZH1N/8OwnYuWTH0P5IPJ0qoVPhiABwHRA44ZhWzpuQtvtR/UaoqQJoXVr3b+0AhqOfgXtEjYwicfwATX/1P13Bej/pw++gACPkAMFXgQSs44S/99AADlAAK6JAY9Ed3IQLi+ETjugD6WKKUkV7rA/Gcmlc3/35/xIW8Bjv96bmcOgQ01/gxsVgDmZhupT9x/WtIYcXprrJd/e3M/9b/vwwnU/hmBLCD3ljZ99BiGnnp9+vdYAoBJgwWs+hDWNEVDPjAS8MFMPejjPCKpdQuAryc60vp//rEnrErlK+f/HYkOcJ+P4i0OBfjcm73jg5ejRp9OG5w/DPmgAN0VgiaMsbrtdkon6I31LpntAQ7uajYwTBptj+aBRmAOBZGttlSHBJ/5QbSOZmYRv//u52NZYfPOHJ8N/SlFUzf/hbgAWBCyI9Qlj5CxhA4/vAWADUfQtFhDPGCSJ3/+DDiLKEYeXqfn994ySKkv3/XDv6x0SrJjm2yCmw2AAC4IVoPDTs0RvbFDLwlJbTINf4dBgAeCRSAAwJ0iVE7oHn+AJwaBf8nsZTYKcITb88JFdQAZFyRiUYP/D0bVN8ABGCXEFQva/EapIACBBpXoeorvFliV/FW1fG6vBsVzs8yzP82CxzsR7n6P838AxBRKA3wD48ifLC7UQJlJMbU/4gbLImwwFBEFhvrlFWIWZX//Ahh+ADxorFN4YXv3/4BIGLZCZPcmS/FOfuDAARijUqY7jOlZbvExiVJcc+2QY/pQBS726jv9+EAfK6moI4j2t/pgAAuCFWDQw7NEbzYoJdkQltMgt4YfFyiCEjI0yxd4G7xEb3uT6n4eZrxIegLsApeYw6XoNcZg/JEQTIIzOchjEB4h4fuAAvNVtKa3s6Vu2r+e0CDbF2Mr/cG5a5IMF26GU/yDNdfDtVeWN+nWrlX/JaNI8GUiT/xFYk8pYRNqcAk9vpXq3+eLG/wRK7HjcT88UphaXIclfH1DPf/wrekgZ1V21GxNbjbzj6Yy1X4dz3F+JPUPAapez/xIVoMABIcdWdDOM/WFuhsAAHaAAzAHkRo0RgBx9lK6mIM62GO8MK00GAuJoRANddK1Ob6Qx34gP/JkYBAdwO3GKrI5G74UANg83CkHcUNd/8GHgBher5ouJ/vAB0FX5G52EfbSnBhVXrDvNEv697Z+g8//EnqAPFFPGiP//njEskBsLEHziO3yG1P/hr0SAYQXSUibBJthvSAggikiDBJprvg/FIjM85dXA/qvnIP/4k8xfAFG5PT5tFuf567qwCg7Cp9/Xt7KR/369c9YHXSrj/xJ5C8OlJ/jP89QJqSVd5//4j9cPeGEBRU/PQy+bvsLACAADSmbEUp/XoIwMZkT//P4YAptzk+Pn865/xEmJPUBEt/L9V//CPCuAAkZCKziLxJCWsXD9rwhRa+o4dMi+63ANCgCqBNpLtC1K6+D8AlhJS5lluffh5xfEROBqf9P/AFKGWDtQdX/BLAAABUyQZsg6BFEw5gAWagFPrCICmIrIs9/0AcmMjoKq+JQxql4R6E/+G4ClKKu5OUahBfkfwf9YAggqkZEmijTQYArgEkpN6a7vf5+GPAAsEO/mdM2Jm003/MDIFhQ8+YnK7hqozvvMngBGHLjTS/eE+HOAAmJinKwQjGntIKawAAUBQG2OHB00Ril4EYU3PP4jxB68I8bfxF4g+KPGrLSSu//wjiD14NC4mv4g8VjoFV/4VogBBCAKxAFhVqbU3w/QDHRFwyVaL6ABkbr3rmjXvjXNLWRXxLgAnB2gtcNivrDy8PxIawALQg13YyffyZlp6BQAAIjCaQkRaJNsLsArMjR2V+/m//EBjwAEjYiMpxfQ5DWo3AACYMA7MDp0aNqYBsK05OavwFWhg0qUv/9/8AJadxipuH0X2/L9AYrPV8xYibDLP89Yg9YAyS7fX/v/1iD4sAY1XRvXPzHtH8QeAi/xnvGYg8pYQ76gHf05ce/w3DrbYA42o8RrkP36FG3HdqW/dSfqejf+fxIXwANQUsB74ZFXONf4AHAVFBB8zKVnDEhffFF/oMANuepufP8EHAAQl48ejGEN72pdGWvqrfgAO0AGoarhiD/KFvf+0aAC4eLYkTZJp3+2DbIAgMQD9rMjTl//93HkQAwEcDuwWYHIXX/BjwgMqkgpHvgUCLWRV/9qm1HvPfTacbEJ73+HKCPKgEp+pQQ9eY2qsyT3l+dsyYzb9f4gEGAAyoIQWtqFnDIvsrANwqpv+ftobPzHQg/LUiABfxPJGHEI6QDBBuBPjHLnNqa4BaAm+MU7k9XgECmGwbZaHtHRuRfoxt8Kq+LQ5qAE0mb1Z/bh2vr7/6PMp/ag7Deea7z/DvTzAG5+OgsH3sn/3gNtB7dq5F//6CIFcMo92WSa8m+pP+MGAf+AvtgBAw6dYkCxxZ6cVE4436gUNCdHLbXnDo1z3/NZDx82+l/fHpi/4kOwALBiu1SZixE2GWf4GBMABMqoE+y6G64f7fEc47KuyIAYiITIIjOchikBh1N25YnmYZPLJd/f//wt0gAJFVg32bA3XD/URBMgiq5yFMQGHAAuAKi7iSVUy0PvwHMEqB8XTLKfvLI0N/XAP/EDYADNCdFIdCje1SfIAA5QFQB1qxlUsVuKhh1e9vbzOC8AF6qHfJIb6uAA2MZHQdV8Spy0GgBsJtn+Ri/t/54OQwpRwIRlVx4YkZaHqIaIcvJc2LXKX+jwJVXPBBeDjw+jOm19wDWQDktrJX/iQzAAQEJRaIk4lEQVw18O1Lv/o/9bes94+fMP64c4ACYs3KyHOEdbTXMAAHKAAVoDSA0aIwFWzX8QgDvarAiVduDX7w3wELNhIpyDP1ZjgYDi4E0kSrvP/43hmABaCBLux1e9kzLT1igDLWBJ/icP9egSQDGE0kRYINsH906AQwikaEliDTBRYJWxA3O//4ewAJiEVB0pfPea/uANkIABQVhAoJ2wOv8qPbV+/9Z5Q1VfAs0HwXQ1oCEktMHkpg3hj37vD5wv11Jb/KdivDAAsIAolVTDWdLEIrm8DX13iT+EsoAqBe12yfszAAUepS/V4LW6bMjIYtSopQwfG/AMxUYg+WxMppLJbeu++/8VaHTU3iIGN93jF/aE93FpYdixRpV//4MMAHZvim1PAHQBmvaaD6NQGKLrSEuK+jlL38x+Nsbaw/AlgAJlRQvWbQzfCAoMZvsTU3YiLbDP9BB4UVRJmalXfYVotH+htjSxRZTLGm71j9+v4kPQAHAgA2n0YCH51IggfSw4YS8cJnZaFoMgujr/gaAAoApRA4+YnOzpqot/uAY7/enZuhEGmmP8DAIYACAiKLuppZDEYxLw+JHtiFhAuyqiHwZSiRA8guR7hAdqjPH/eVzuf8/4kK/czEuKZSD8pqGAACgIA+x00OGiMH+ghEWgZaayU7XYexAKhaExtE8GYGz95/iLSyZN08pevqNV3//hWDJrxevxvgCRU5Rmo7VLSh7AQssRZxLRI/8A+DlsB/SPgzvOsYnIcAAQDya8BZYcP3+7QUMZmYiAjEEU8paJQ2gWIZjg9/2DPZ0X4fggO4jV1Urm1MAitJX/Zn/jBKhgqm/XoR6EoEc9+egGynAAgI0hEqJWwO3+/QiAKWkKYrevj/xDOgYDX46DAgJxMyBKYv/f/G8wgILoEAB4NUOACgjaBQSvhd/4AoISiUUYSqIK4W7+AnRkAMDEgTpRgdgdf80bACcNVNSf5Yx7+3HGkDJJggVk5pB0fgb/84eADUPWQ1Amybb//lhIeAuP8BdrfylpajAy2wAfI1j7s5l//vsEAgiw/zsWGTP8hxOmgcC8PQYPgDXOGLBuJQKLH9nuDD8zIwncRdcShrFAjDgAOAwkld8FltwjDhP/1iLgRN3z//+/omAGgaaWg7Sxbn9tEmGFFtaqycF8Ez/AtSr81cxYeYYBCyUOP1Mv/9/rEBjM5j8ABwxne1NRGHQLZY/3EA7xAQeMwnh83QW/wKRNBMIvCACsKE9nNj3uE7v0cTHcMwAKAMWxPpksIErmUD/+5gMTBf6k8+J3Mon/97ACh0F/jSXseiBHmAFhuCkl08Isk4oHHgDwKlF5w0R/CThuB/4agLoaBxXxGyDTh7A6/7RsAEoJVNSf5Yx7+wep8CbsDd65Ksf/vf/xvmAJgFCDKsapa4W6X7GAUD7CLzn6h+tpDdVWB6D5Loav7EiGpJjsLmH8BCDouYbKGS8pn/8HsYZhOmySTHF5qjAS3hiiF+zy+aGN1HAUIJDs7qMcgrAYIB+mkHqi52eJ/GZjKqlFvydatJZE0GGJ+OJGKo/9MLl/8u9j96rS64HriQVZka/3CBv98bE75PjMGP+Zy1p5CsQGH8JYACQ6+IvMQV8KKf9O2JUl3WLo7KgI4+9vH3jcgAB3QABpVADnR1f/MAJC7RQWu8nHGOEFy8o1Z1vq8GHgAcYAqLXwSxUof98YnlxfmQVP+AI2UJVbCyn/bEuhh0p0AC/QSrZUdP2/q9rQb/P6VtB+uNwAuPmRfHISHt//gJRjI6Cq1D1MajDoE4VNCPbR1vg+KRSIkQSMyA0B8cDCWh8ofTvc/tsR/4Z4YdR33vMcbHdBEvdDC3h+25hu82yxkDKCAlbo/39QpEK0lL/cCPMmi03O/4f+FcABEACQ6gHKEp4QaJRQN/EHSkMUCyiQhQm214wASiaFJNJ782SiidTe3RpgGWgTec5qVrM/3wagic2TQi9P//vb9M2yFU//+/+HuyaM/iBvgAcB0QOPGYTs+bkLb7wAEaACUPVyxcG8UKf17IAQEcBO0mRqB3/wPwNjNBHNYXfe/ACGH3FiU0cW57ukOARVAMMIrGhMiYYI3oCEk8igmOfELlvmwzCAgycCCEDbOGLrTJp8F1m2hfugNhqmzSXPtooekpfZ/EjYMOAA4ISi1RIj+oJYdf/8GGiVugCfTO/2QJOE169BsuaCLxv/SaevggDdIz7Ku5pr9IfKYYy2TtP/cJ4zaU/D5Gx8Fd3cn22+EeHKBgANwGHL3SWphmlDHBkSHKHDGY7iv5ZpOLXDfwItxuC/4f8egg4BhgGtcooJWD1OKKJU0/9HmFQO16+v0BvzN9V//7f8RgKldv3ul/9DT2mR/wxzAAQA4uPKQZ/nwFARhtZvyv1WrlfwM1+AC7dJN9eKnLsHILR2P1w++7K1fxPj4NwACDEqPKD1bxtkggo/4gWpBEKvU72tSGCBeCDYwAHLPiqgNJt4XBH4PgAIMJmPEpKVvi38o+5MMFrKH0Q5Nqe/uG4EaQHWV/lIJ/uDMjgUDLT19YyF2Vn/dqwGFF1mRZKts/8Jy+EZr67/9uAGV5L7f21kFki94ff3ljhJwvb4bgoADkFVgnkdfnuTSb3/cAgu85L+i9ZTm7hCt4AoNanRAkoyT/8v/kGxF8fwvAAuZjDi0BG3Xh5A8/4AqQASAl2xcneYMe/gNBPygAwL2iTErIXf+cAxaIVMHEIkpI13/3hwAbAQUTWRBgq21fKjAB/ESC7O4q//39AUOTP/LwEtDMKkx9KFpLrIAz8P+ABYGFdTu6/kSiol9+gThMyahrDIpJ7v6AbJ2Q527soI4cnfbzm77f7bMb8Vd+9bVpDOUAMdW9JPgycKsvG/lX4fXTagnx8MxkXgm3LH+6wJiiVp/NFDiVz0i9oF//EjYAF4AGyKoTrKgbvgCZCWIPRn/r/2+DEzUaTW+btVteAA32M4ENbaRpgY3VACAgYlJbX15DlO5b8zSXx+/368CLEYUUg7VaZclJvAAUegRgMatAwyLaq/+1ErKtC6FxZT3f1DWX9K/32uN5dm/r4MVOFoj6+3ZOfThWf3/oO5IAbCYS2Gt3+waDl81XXA7ZoURV/eVwKkSZq8/xsFGYdnOu5gFYOBMpDCXp1vO/g1xte8P+IAILY/XUnu2tV/990DBCjxEABxEVVMESvmJbqlB9mS/Xd8crvlZDmWIr/nyv9N6o/bdXq9RkbLHpUX//egQZvx+NsDCPBhyRxjp6j1vAB4bkIylF1DGPSwsWeFsF4rVCtXikFIEQw4ghi98f0OG4LwAL9jHGM7y2cFs1D/MOFYnNEwPhIAFgTdYmRF1HHv4MU2DdjhahqLBn0iP391eXXxJ+PgIsx9cMcABMWZSshyjEWstzAABzgAFaA14cNEa0AMKl5GU5BCbWYyn3SI7d/aAxbcAiCxqzdoEeiY5Y1jeYDuMnrw7Q4Y/onPvsAARBlEYpJZaWCPJq+4CL3AIA3y8YBMq56RsNAAFNQdaCSu/34PQDFghUnEdZCx5H932te1y4/b/YZh+Nx6VEa7VrEVt3yWt1umMVSa/+wZKFk1OOb/nxb2zY7Fs/erMoBOllKu/IMaBX41oVy/Cv0wqLllR7rbBrmAAC4KZoEBp0aI3jFSIVFFQ8iGlP4AIZaaLFuVxZ5Jtv/wA5jh/w9IZTaKIDTL3sZ00WxkSUjl3d5nbrd+7i/1iQYQAHBCWWmD3pmC+GPfgwYHwBAhAGWgCwozNqb+sQGKZar/4ZgAWAhZOdgVb5Chbxx/eAMAD4uhqLCWfNEIInQ1AKTyTMfX3/v//F4kPQATg/YBdSPX7l5/eAMiCZkIZiDcxiA+AAkAFhbC0mU8eYJRQO9AMSxHqk89IWMomn94BGPgBkXynl8APFFPGiOnc13L9/V/gvwIj6i5RdtxhFK+h/AAayGzqY6MOhrEBr4JB4Uf/4Z4PAM0YFlPy7H+f3gCBwWUFMIMgrYH7fDygCf357f/84v/4I+AAkzIJlOdSDIatHCsMUWpqF3TAvood8OcACoHIMHiCiOOf9XG4/3AQj0PRU3QmDLTX+Fo8AE2puoyz3+HoYcBXdtaHb39RDgxS6zFs6fyw3ZQAdq7ICmyn//sBAIDJuQCILLr4GMFf232A4ARgHfIDbw+K27YpQ+cZGRn/fqx+YPFqZY/uD//BfACINQq5LuEI1ApACPmS0aualZeeW3AggFkMArEgUFWhtTbRcAic5CMw2pgOAtKCYgdFbWKKCGCdCiMrV1P/7gDUBKSG5x+QIWIdNafhXAgHawCDVaX+lxRP/mMPQGLBCpOciSvFv/u/6jbCjv/wQQAHBC0WmIOciC/Fuf+0BOhgAcE7/AkI3QvH+0cAEoLVsSfxQx/+2m2QAgM4H7UXGoHf/IADhiM9qamqEQZbY/uiAAlXMFTRtjNdLAyYAYEEb/IotOG7QPYmxEhQP5AhE+AJAxVIVeMbYtdRT/dLgBM9hdkY6//3AWeljW4mAraVPG3+N+sdEyyYQ22QU9wAAqCFbIPDTs2pg/94oJdlR76ZBb9MD4oWKewSSKO7lfeBh+hKg+C7qT/o0OzruE+gNHPwaxK52xfdOx0Wf/wg1oVCacIYDkpZXGJe1XOnc0tj+e7cw49MViX73f8T0CGZzEVFnyeLZ/gYfyREE2IbMNylIDDj8Sflx27a3+YjJO9/4k9a7hv///4c4AFgQ1CP0J5+TsWROP4BQIWxCFCUcfJWLeOAlW8AfY0iC6f+GejAAk6KF6zaGb4XBoL1CdcR0Z4CQYz/YmpsRFlhf+aB13AMBRCldEiPRF/5QAo4q2wvt97+H/iQtwAEYALiWFIMJ58uSiidD5gYtHPsKx8jYv45/gw5CgAzPOncU5f1E908HKSS+f79zwJuccfPG0XFxIasR6b76/8B1qnr/h+IAAJgoDrnDY2aI3tmN1U51OF9a1+HAAjCgCCiawkSYJttfJoDezgXy1YZhHboBhRE5EWCbTX/B6MME2qGy/2DE+PeMlbCkrvPBE8iY7Kk/foOqI2LV8fl/wvgAIg07iJVlo/8WgABAw8KwOVU1m65HHyjdVZursSHOzt0vP9VZwrnK3bKf6r/EJlgBuUGm6W6XpRMgun+JDssg4CCQCowVcomfbXPUqD6QMkDa8iRBMxjYgRCmIBhBsCBnbK9/H291HieyP51IMM+trtef4fgQgHdCnG5ySnm4PzZmG6irv3pW1IYNYAFqGIJX1G7hgX3UIACTX8t6d//uqf8uT77mHwOz5cCdMTtzH//0YQaqsbX3YsS28DMKfHGfINfenxAYOJUcbU/ILfKNP+JP1gd64fQkETdj/8LwAESf7tUSz0zIyfOITr/66mRsEfED89zHlDEub5TUr5/K9tsMUUvueXTAxuo8iIRCIIqkEKcxQYbyoXE0JA7xv5//4awAEh18R1MQV9MMb9wodcElLqbJblD+AW/Y38/4gOwwAEyyQ0U5B3UspoYagABwAB2gOeGy4wAPCj4jIdxX0stuHgAOkAFg03KknJKFOf+DB7bAN6LCRk+1sV/+JDPUaqqwLQbJdDV/c8At6Qwvk8ewjAJbxiildxy2aFt1HpEJmQRWcQhjFHTVuInIFl33L6K1qvPw6f/zxSuA90uMbU/oPHP/z+xkJGz9u8iSjzhojjku8K8SGo2BxoEB1UtfXzxynl9P//xJ7/AKuk5+//4kL4ALBuhwAcEbQKCVr3//uDEW4OgNcUMaDcSJMCNKzvzQSfYcP4ehy1MBRsLFKRf++3XJfe/rEnrAGgm5xx8//G4n56gPXKVPP//EeJPWaKaG/r//w54ASB0piIyu+XlbgnecPn8VrQe5r1zj/F9s65/xEK8K4AFhiN9nxdiJssM/z4GAfFDjRacrNG5iu+8a1AACAAAHOmreErMkvDInwHJRUuj/+/hn+cK1uYhCeUgMOCWAAABAqQZtA6BVwx4ADgxLKVMif7mlhx//3rBspwAYEc8VErYHv/PCtpwBgeV52CCKdDR2Fw44gniD34A1ElPOPnGy6X3z/xHiD14E34fv1/EHrxHofv1/vEHr5pqG/r/G4g9eEjG/3iD4zAI6077PX74YwAEQCdA4Ww8hPONk1zHRhh8yhsvcm1Pr3jATcOFMPoS3fpFQwHowQJlWNrz8Wpbe/f49unoAMQeMxIq//3vAlRGNF//+/+ev8AWpc+ft/hjtjpxwAegyK5zM6juNYQGUHJ8N/TV+kfV/+HPAAsBaoABg2m4ui+ULh/wSk2Rob+vASLxbH8QG+AoM9CJmD3JktIpz/wawB9tWNwnaYta4NwX+HOAAwLoPQ261UdHBulYGLToor/h1XFP7URWu8/+esB5MZar/11wi8QesCMX0jXX/58SCDAAb+GKIV3G7pgW3VAGOOIb/n6mJ0xTKUb1LTAA5ZqNiJXKy+4CbnMTsbU0AANBc4arrFPAJO8exl1Zo5ODU67RCfcRdeUl7EhbosNr0YDqIhIbnHzfxIW6UQATGwiSgItdL/vWbCtzxnTb/oYKQiDVRTjGEX3+BMkgAwUfKhEudXfv8IvOLN8IwhzhkWxkX9018d/lWQ2ZDqfewf+HoACAxbKTMHuTMk+MeD4SADQPNqRBiChbv8HBycudzXngGQe3g/eQGILfPa7LGyxJLuyL//70Qgjd+u/hbwkAHg93CkHcQLd/8GHwAOyAVpwjWwQlnwAbzjHyOI+DDWdgZX2nqLJtf/EjYADZjZUKbkH5i0eYABWAIkD7yhOhcpYUDDqJSSSjP8AFz/FNbab6uAAzIRUUZce5LVfA1mH8qq2yRtcCpRCzwT6MnXxmVngwd2jtpN0/H4mrR/P4SZSHOUivz/C3AgMaSbptFuRqH//B6AaGDFKhKRvVaOf97+nD2ltz7Pvv773tvt/rhzgAJD74jqYg76YY9QAA6AARgDHxsuMBLPAGWzEhVbvP8vAB8cTFXGKO6lGvDF8X4AIoABEIIpGJFkgwyYJQIYTSEyTJBtkuAb43gAWEO3mIu7ExYYZ/gEQKYUEnzUaXcNTF/9hgTCVn9uBLAAyIrhOsqBe+HUSKnoWgyS6Ov+ASjGzscysFUxquXQxBCm8uGBjZR/w28AQEdA7BJAukji5avvhlkIGIcUAEUZ6uJ6p6ygoo2Ethn7+7DOxKmy+LfzSJoxLxsAkfVmZ6t8UNTFVm5j4AQ5Wek76AAyXRr0e7QFYLBN61luXXKb/eGGBKAA3yoE+jLG66QJBDs5qJqj4ENrfxQDxmCI8sT/q+ALUt9el/uXMWq/w/RwFSwxWGIrxabSib1GQZEFZaXJY9LjWikvat793/mvHQAAga2AACASFRHp8aZ7Nuk4l33+MADxbfqjopSe4TlHGzGIgqhmr8gwvCnW7giIiI4xaj8JQwMqTcTv1/z+AshGTBJS22SW3g/CuzMGQMFCGtada6P//m5tGL0j5ujT/+sXo+g9h8FYVgjo0OTLAwRPj48BAYBqEqVjoUJrXJCFs4gasjNA7Sxf37gL4ckF/iQtAWIgCNUBoUam1NwNQR9V5uFAH4b2uLqyda9fxkML1wx6mSW4v+AGXfcrAYBA1SAHSR+OoPX8L/hjAAsDfFABwRlCJQSthdv8ABTmAwgi0Yk2yTDLRhdAFFeEep9uZJv+8BhSKX9t9943gACBkQa8Xry2fikPMmjQIAQiKiF7P/dXdN/hXfTa7///4YHmyhjUFp1dL5+IBhwJ6wMVvjV1A6n1f4WgAHEIEFfELNuXrt//9wAvABqHqoaiD+LFvgCEAtqEFymEIzwL1eIOBAI8SVPoI/hXAlxvuHGDSKTzVd/7nIy4OUa5rQaVSZxOJCN6Lscrq/r+Fk9mClrj/h/+HOABYQr+Yi7s+RDDP8AiCkFDzpiMruGpi/+FSeADCM+pPP+/iAxsYYAEZQBBRNYSINE22EXvEAwoisZEWCbDQMTpDU6o0G2KnHnfj9Nlx2O2z+IPTxN3186dFP//F4gMYACYAaiYGJsJZ62Rgic6AQsHvwKx4jcsgdf3IAaC4FpspY+wTQOf/wegEJJ7sC8+IXMInX96gJd2nzGVqov/cdo0YlPw5bUxRVnxb59/l4AFIQmURKX2yy38H6pz4YgAXMAJAW6ak7ixjv9gNkxhhaJ/i7Y27f//cBoMSikycSgvhrz/9lgN1IADAraBURvef/93oC0n5ePhAA+iaDpXYRf/7+UMC4yMQP8N4ACErf9rlSJ8vkuGMNX1lo4L5qP+1/AIjbox90v8NSYwPJ4zf1/l8F7TJsS9M9//PWRqKugL64IqIAB4ANnHVzSqJFSYK/9BFr4V6EUNW4Ol7s259ewQFZFcRVJ2P+vDH+ywxlxGOd7JJmPIBpg4au/+GcdJJFg+GkCLqCJLSgviP4PokAxhMoSJsEm2mU6ADHG4aIwqcmR5T9+r8KJRLyy/wt4C7+fZMuXz/+5XOTTLTf/WIu6aKJalz9dzvvqAkmSGxCYNTnO/brz6PdVf3hqDkIhutW3Wfnff9cNQNGdpYT5O/P/3MoWVnTiXsTeXpxZnRW6Of8/+NxAIvgA4g7DKxRUe/qQwBxVsVlOQd1NMf33x1wSMaEERbw66wfD2CUCX2ODmxQBDKHPfyEEltU4rmB+a5OPnLTL4/Q8hRga7776ugK8pVoN8vG+AB4IWQSYIQpp9Ft5r6wMASE2fUi/xRMknFBwE6RNkK0myrDyxnfP/kSP+/vARsgiKO3UFIa1FiGISWMuXcMuPG7Q7oAQVyRuT/NREP9z4PJ749d8ICOuF+EbQewD8GAViQMCrJHUwAmB/QG3h62cPP5wImOUrMNqYBDITsphcSR7WJYAAKgoDsnDY6aI2WNREBYtMBMP93n/wxAxAKyAmcOiprG9/mbG7qUXfJ9q/DAAd6EI09doHKOsqPbIxO4i6QShqkaZg8e87cE+o/9+gRQVEKYlKSDFCL/wHzfqUAA+Rxjck6af5sQbS8XhuHnaT+NfHaz9d//83YGABaQYglXkcuGBndYvLwEqYZwOUqEjTAvoqD8L3xse8AJJgIhSaE9ur+Cz3/+xRebpFn1oBQAPyIzSmtrvf4f4AXvFhc05Li138BCAH8jnE4rxHU95dGBHAz6SMRZUT8zMZXcVupel7V4EeLOSa1K////AwVcfrdp3gLMYmWXXPtlGP5gAAuDFaDQ47NEYM8IAaPLR1dr7UZlGzaf7s1mEVTbUwNAxoVzqeCDqALfFFYknDmkLAuXxiJx7yz/8ALCrQ7KKhrqWU3UDooccMTpZw7UZ30AF2Abh3kqpymG8ASwoJtkUl+Mot4eDMABWQD8skr0e/OEYBWJAwLtjamAkAYVcZygKJO1j/9/OBExylZxtTCdZ3JgpsKVkg/zvwBl7nZbsHsyBh7m6ut/FJBPpg1RpU3fXlz9HOnAmArJQakDorawvXG+AA9mJrIVUvb//4ABIBOQCyTARVeLBOTQfEEqqlDRQbJhHkH4DGf6k1M2Iiy0v/vGA5hgScMVrd03UW/2oD4occMRpZw3MZ338BCP5/ZN0Jky0x/gxWI6IKDBMi5+QAyrSUP7b+oqJJCiRXw1Toh49/EhWAAmhQXaItLqbJrnAACwObkA4NuDamDyGgAZD4uUTaHa2zCMAbIQACgjSBQTvidf4H4SHFiARZiezaobycKsbNI7Ihx92Z1Q63Rq0euXgAawCHEzhIk0TdaAGxAY4isZE2CbTQViT3wBuTW44+f8JffP+4AeAGA1cMU1invAHZjdVKdSj+1aQ1wr5MIXrKhLLfRbu5ABowOvC7o8QcTJf+8xdEKynIO7GlEuAAHIAAV8gOeGzam8gABALhwAKSUFtcUJx+wXcCLjFtrTam8QsXEZDlHJxZr/NGYRA5StQcPLpOge5AGMQ2Qzjv957GfgnEmPqd+f6aov/4egIRkNsUS/d7F/5GYmTlF3nc1fB0gdBK8bBbV9HAw/FGBn5zii2ysU71sTJznUg3LWhwIuMWmtNqZgkAAIBwegIRLpg8hAFUgCwqzNqYGvqmNfQAtvATifd54//xIegoACQ6+I6mYUmmFN8NwAA7AACKkBzoybUwYFotXH9hmEksfAQhi5RM8y2yU7vDAAd2EKKU3CzpkY0VvUxORBVb5CWNWGGyivK0Z/+MEMnGHbFyP8l9sUw/8M9IJ3XUNQfJZHV/DK32r6u9Ac4oIPGoTph47MZw8G8yEZr3fu0odHB+Odft//DEVygP+GsF8y6zW9P4ABabyEkUvZFoSewABAGwAAgBgBER1/fgH7YOrQ7MnUvvQv8LfMCZh89NvRKK5IfCgA0D3bEQdxQt3+DBCgAIIWKC/2dI47LBhY0+HqP3+RKK+KpUcCBgTRt9lLJvB8GMJz8LwBjIRW5joUZLVJcAAKg4DMxNGx02pg/AAtoANQ2WxAnKTr39gJbIgBgZwO2owOQuv+VuW+OgT8AOCWI4io4sy3YRihhhZzSeuoHbGnaNE5//f/xv2zDdVOdShfWtYYYADMxMnKdSBOa1DHYAAJgwDrnTY4aIwCchsqkOjDoWxGQGXUBzygmJGwWxdB6Bf1cahpVZd/eNVKvO9mrldxW6l6WtSGJ74CQFMn3nAQapnWeff9YkMwAGABi2F+YKbxIgaaSp7fmbD/ruv/kAEotBaDCefsEYonODAlKDvK7hdUvlIthfQsDKfntIX/vA8W5Z/fTw/t9JGn/8+DAr+I5HeOiTztTWr9Yk9QB5R7hoj+Horl8IYkEWAAkPLyOhiiPthboffDfAAqDkEDzhic7vm5i3+8Qq6mIovMfazHA3TgAd7pN0mT//+Pmo6UfxIehgJgsPtEWl1Nk0iMpsAAFgc2gcG3BojACLi3ZWj4epucCFABM5HGDGX+0tdBxImumwGO6JBe1qWV9/XlCZJi3jZ8Buk5p6WvXfF0fyKXwxreykf9+gy+CRlX//jwsQeiwkhdmE7bNYOeFox4CsgcZhd6GPIW2D8zZhupz8oVK2pDDZrPaPmwGg//C8OABlCAgomsJEGCbLTj5AMcRWdCLBNhpyYQfasbX/pMU59oww35QuX/yYnx7YkQ4u2/X/9cabIok1c//wnvU1AFgTFiF42p+8Se/Q4BCD84v/fwhxUAD21Up70//2wExNNXbGif+gHUyQZO4T3PW5kLUVq1IR7PXeqQQglTUMNGRfRT5sxldRV2l6WtSGHxPz9QBsSe84+czUkq7zv4/38Kw+DEbI1x69IpO7Ze6CLzABYTgxJlHX2ycUDwYcR01HuOyLv8KuzZ54Q/RN3v76r8R9ZXw1gAsEykABgThEqI2Ov/+6BIJOwcwGZmTZPYO9+WAHBI2CQtHz/8Sesr439B/0cmP56wCzNKfv//PWhoT//wx4ADpgBIHupakRhNp//3pJmAIDkgTxdkdgd/8CQOuZkZSvl4DPFokaKL9Zl26AYw47Bvi32nxJ6gQAzhv5//wjyflfny8E0AAAE+1Bm2BKBFEzYAFhgp7iK/UHOELr+///huAoDC0MTqYhpMvg+kKAxgQGBC3ABJ1Hs4x6/CZoVZ+euH0XlheE+L0Y8MfuiXXvrq+vkb1MK+HI7HM96x3P/xAc8ABGLEU5EFSQVrzyM48Abk1uOPn/wRwAEiCoTKMtZNuk8sGH5j7KcqiKIKtxxCa5G3+GNnDcHwp1gXNfxpFj8FcjNuh10cdFOf11d8N8JsHQayhUaQ4oS4NowF4LqVqnDSCd+Hw5Y05WZfh6Wq6xB74AbJVP589HJsr+IPX8A1aWr5+K7w/Ew+sQHMfB78JmjARDNJ/78NO14kP8ABMcmdU3+TfggDyYCruIhvkuPYRB+RCIYjDMxRTHOYGQQEh3FdQCQMwV/F/9//iAQfkYdCZZtIJsiDCYc5mAMryPXcaPKVpv5AkCZSAAID+IwLjd0BI/wTW/ACMX9XvBlOQOYl/Zsw6mbxsEOhj4Ahg88AHNECTy9ea5POUW/Hrlb8YADpgASA91L0irKvFf/aJgA0Bpp6hWVyJD+2CRDBx6YtZz4Skj//7tKMwAQDkgf5l0LwEv/A8LGCdtb+3k6kHnhWtR0K7milsqrz8P/CYlz5Ns3z4YyAgjDqoHD6F5HBLQ39UZBQKGBgD8e94dxkE1QEtr8B4A9SNCBr8qIZLqhfl3T+Fq4eX8Bj0U6ATBaxcocf3x+AD8o0OyN/3+/txuX+G/PRVKORlw/4IaA5K4qxJ+f/CFtn4gEGRSvgAJmHB9sukEU+DiPRfHEHr+nsgJEPLL9shkdxm8g1hLmBlTA2lKL84AzG21A8DL4vi/GwhGZ8alR+DDpKfGD2Hzpj8J/xAW6MEVQokUv0+c/Ik/74AQiMcFY4LhPBb5hkyBwFpgJqQiDG8qG96PAAykAg42sJEni77z9yAMOMrGhV4u88HU0oMG8Ig+aojctVEGaG1PxkoWIvxI3Drz+j7/o2AAn+MFQnQuHmFrSxZQMPiAK0KDBdjBFQiZSEP+8YAGpQBkzUnFh30j9XAALAzARcGvCBq6uC4CZOpcb15IIiW0jNeWv4gDYgCyVIbRuJAtF4GBxQZAo55zM0Pe/YIGfkRcKX/z/w7AAQBCs1aSPx6qV/Lcpxzl5/AYAtggqIzVqQhLvXtbgUbkCwtH97gYIDQmFnttZ34kIjWszdVq/eGZr0rprH7qf41ev7+/Gw/nSoMGf8GFBQ6gGDjl2CD6dJeDDCHh1BQ9D/8kwk8QlYen4MKsYtLtAMaw7QlEQJAYSCmyMT1FfBEp+8wYqYAo31Hz8Wz1q8EHgAJkJylYZmLLa5zYAgAU4y3Tv3NA7kAAQOThFsR3yWb95h1jBmje108wRXW1I80AAZ0VgRNHWE+ReZkMxXGbiC2PcrgEFK56NiqFwefe/wRT0Mouzg92Gm8J3XRXnKQ7MefOqILUvh2AElwLgitP6i5lciS/vJCcChKItdDBz8Twknp6CECGez08IkHbM8eBgimMDRoj3UNCIsBdBVW1P/8MkHWAsMDRVfBPSlYTEG+DCduQNmtqyoad3HnA0AWrCIk/7QaqjrS/GwAPAbocABQdtIwNXwk/+awjiXKl5nILLf9poaA45MXu4+J4Cb/nGwASg1ZL1i8rvFP/cA1DSyBoEPgANXI0+aWJcBQgA9dFcASCshLYvdzFDgKKWnG3FfrrdlAB6jJg1dHGX/++oY+EgxZUcKrjHTPxtgFsOIo9uKQEdrAjCQeJJ2MmT5Eq30CAfmG8MACAZ21rqjfdzoYIWK8IAkCBgj488KLJQkSl7XRmP1Jcf10x89flG//DUsafX+kcf4vhyG4PF9RoqpgDIR/xXgAIh18R1EQSTTjiSiPuFAu0ZKXUTZ5RkwQHxAd6GQF3NC5o+o9Lz2hlBNzAmSP4PV89YARAZbSEK0+D9veMAn4MGNEFI63wuuf8ABwENQxOhmO0SuDiYoD8YAHhNDl31tJOmIJCY1hYTMKhiig8NEtdVK9u/5g5R8ErKq//3C1VIK0bg/8O0+4UrwxwAMDQ/D16HQGH1r+BX/6BHkfYfgptxikAAEOL8TQZAtG0CDoaKJBqHz4Z0Axt3RItyvzhBKoOEB/Gw9Pi9Spg+kgZhAcbBGvBAVkFQDRABAU1z7+/EBIG5ggICPT8f42HkKZAOGgqAgQ4e24Ab5frxV+l4pIn//f1+Pg4DsVY3gnBuioDOkRmS+t//A0zjxGoKrwQQYBBgIcCA6JjYCno4CbxJpngVrPrD//BTBApwQjz1IFzGPfHh4V7uUHxtaEQMMBFwZVwACaUMgINFQx8aCA2AhWsiTov/gtsDhXfEwSUuSdL05fG4ADQ0cJSrNx0GiIqmR8glI68PFguba/YtntUL9ztT+3y/pJCRW0J8m75AMEOGL0ug/26OALUIHE4IBKALEj1z+qjcKijd8/ckd0fq4BE1bgtCgQ8VXgrrwhFEtCB03AAKGT5jgCmNguM3L4uhscGxsDnUoYrhyqaCZw/DU8X/J0DM/ySCzh/8GEAJAxoMbYpXkYs2JlP2gGVzAAIDtqQMjeMJQ/wIGNCEaEjqEuBBL3Qa3EyQzot19Z7HkXfP428AARqElBVG4SKD1g46CQDKyMAjPBLjjAgFc+oa/IjhJnD+H+siDh5aA3DSQ0WtAAFouzgBr50Y8OT3kvBhRsAmF2ihh4E7YGYMAHgFhnZMNKbMAWgYZh3D4djIRbqRLhgpl0wyFPGA9ACAMwiIGF3Z7h0gw0zyrRFe9G//4MaBoS1ReS6gCeIvIRGN9//Cn0BKRz6MwgR1JoBg0Q2HA2wTWh6YY8Xw/YGvJBA45h4IDoDHw+gAWf5Q5L7pyyDjn8DvK5/P/f8F4LEBQMfSJhBBTLQsk/0qAbCCZw/QoyGXahnV0Xh60vBw0htI2IDV0DQ8wIAkqvzKuGpcfggptCyexDADMGkhaUTezPg83/l9GMgnXkJqrw/YAkkHoTBb9JmzDC9x/rQIMxcWAP/gwo5ywfwwXdAl2F9EuajbyZlTRTxsyR4AJgW8Arx4ehJsBonVQ94AGgM4WWAUlKVClMxDWvi1F4L5BRwswEkQ8SR3ScQ059X+Ww5kiIZxtUBU4zm5TUg8ViziBgNeNDgzMrfBuM/G9BsgAG9oAQcbWEijxd16kn6+IAw468aF3C7jwYcb1wmQBn3AVJquO4z54gPgGDLg4WszW3dIbWT0M4E3MC6I/k5VB7KLzhBJGIzS/d1/4NUw3aYAOSDlJ2dd/+8gNLaXq///3/8buABgAal/Ej+vEf/Qg9BUJmRz6X/nwy8ED0wVACSA7yF2Iojq8ARggiG079prVui6+jiAO0IDBRjBLUlYxEH+EFGDlYBIM417cAgP6cbmNMfoyiYfh/QEjjgAMcxwaskBND6a7jLKIMeJAdo07p/xuOjpBG2dI9S2jGYigPyCqwdPaNQTDEt5hTdHIBrSyAEOurek7/G4aUACaayHlIrsphFBcdGAw4u8Kk3Srr4MABEBHEL8tQjKP3CvGj1Bpa6Bvqf13/+Wd3fNM//aGYWSjQmGDRQ6TKX+AftPTQ99v++HGUYXUnncYEBjDBcnNtZf//UC6ebLRf7/2Y/MhGSD43ucOKwAkNS4gA8K44w1lCeyQk/7ZA7wQaOiofjYN30SlUmqTOxE/S8c/mA9eaSZezxzgOobFaxamuv/G45L0AHWFAeQ/XAiSHqT9/tSokW2t/fQ2gAJbHVAfBlBJjOD6I/oQmgBgtHkUgEgky223gYBZT4oaEFvdf3ZxCu399TP/4egA4HJBIQ/k2ucllgCoyGI6WVSi37zAAeE0EKuqaQdMQSF/EAB8fQ9d5TaDRiCIr0KnnDowAHBjLSY3hKWfOpMJ++Dg3JINenlmKU//EAACCYhZQHgJCCe+RtAxKtpOr3gdtbJo5Z8jisTxg6AvDuwL0AQXRyVDEdIlsHEhYGAzggCcqod+z9+uLj/d7jEL+L3we3LZI6ftwX2CqlJJIYl/jY1b0BjYGLGvdeAAjATwYtRdSTdWHtWGEr/DNBE5qamaNAybAwH/i9YInja92sH/hmHIt57DPTh48glYNh/4vhewPAATAA+Ngcu4ptF0zBMUYC0AILQ1GhjCBXJ5IVf3wZ0wAY2SmeSEZlc0dV5lYIdReJCsraMEFeIQALYAGoOcFQhgh0R2W9vnE/JqAlEq9ofuDBlSpf9eHN9tS88/4er5pOgwRABxnRCDtZmrUjmrDBANBAAOAQTBiNC89plcHERJwgAiwBs8oglTWSI/3jAA0G0OVdW0k2agkL+QAGo+h6ry3UnDUFRcMMMLxLW3Q3CnMbEGinwHo8V2INqaGVVqnCB45+NsSg/hkAQz4m2z/Kif+8sGpl0CTYJiwh0bY4BTA2mpHSW6VEa04OiMyVIDPcbzwgXMWOlnPV364FxQlzvv/C9rjIHAeghsNT/9YNlYKL/G1oWKkCrAC+BawxyljsjgAkIVUFqSy0LSw0r/aA3dgAM9vmgkhGJt/tNl9Wqf3peP+r36BEAh8Ho0LaSL5PJCv+wQXAAwANmNlgBKMBCZREV/9oBDOQ5GRY2Lrr/8D8JzKQAxvpJm0ik7hm9IKv7YMfJo0fq9VXpRES+vMsbPKOnxI2NAv2PqH0IuzNPIoRUtPD4MriStxUpIZw9P8vU4DbO45gGNg2GvT3dj3VDb8eSP7PvgCwADAMfQHgqRmiMAMQKhOoy0vsizyfraNDS47I7NIAAgGAACAYADIhhDAIfAMNMmeMogXhHQrfsOr3/OKNhx05z0wXkW81Bkmvs+CC2AOLNzsgqyCNaeR9MOhMsukE26jiQBYWZSswqyiteeUwAAIAVAAEAUkASUCxojDIfAECCnilo2suv7P1rbAFC7qRlFUQTbTiA/EAAICBqI4C1ldo1F/t2XkLl5mcVRBevOKByaf8Da4Mi2wyHv/xVOE5H7TzVDgT+DD4IDVsGh7O5x0bSYLAwfMANANIiad8ICJJe3wICjwTLFjghhCLfFQ/r32RA3I9Laix4rfGzjaUPMEUSKbeY7IKgAlJgxR63obfECHpoPTo0hOVU4JgJk0ry/vGABqNwcu4ptNszBEUATmn5h37/BvJa3y//P8AACAGdFACgncCi2yZAtH/1gAKgeBEJQFzaEn98DANK8cApQAlGomRu5hv+AocO3+KncSJ8tawdrzgfdM7r/C0MItVHwJAFzDkk41qjUOOP5AIJY9ChnaRbJ5UV/waggXaU4iQy5f//v//DMABoBBKGI2MxyiVweTFuRRkxk0IzbbzAA0G0EKuraQbMQSFeBALbQWixyOFj2lT+lACgAsSjX67d2bIfHU8DtFU8ZzBHwRQQfA8f+RXr64RmJD0ACSQBhBtISLvFn3nToAgwykaFnjDzwMMGDAAfJCBhyYtdDt+Swkv/dAZGMAAoEcSgYG74CZ/iSDwM+gDnS2NqdPhLoejSrrwafufRe++p/VovEHqvPGt8P/xIc0BgAOgALC6HqPq6ScNJCv/9wwALjaCFHldoOmERX/+Cvm0u5H/fqG4DInhFa6//EhmAAiYAEgPeS1MCMLkCvorwgb0Rqhg1RlML/wDGoxdyKR1GKuCJLzBvBAYKWzTV8u+7GyiJIN1GHDlQBhYTyDAMfnTp/v/iQXwAKCUirQ8WCZtp9uTAAR1VwyKE1J9RvIBShAULsII5aEbCUi4BhX+9OzeDJOPPf7JGsMAGmZ7IaGE//+4YDSpS//3JAuJqNjDHz2xFxAI7dvLxIfh4AAgA0AAQBHACScQkbR5j7crqIggi2HEeMgLAAqdIKMY7DBERfbMd5EYiswrNSQlj1oFPUPDWEs2wgGuuk0rSjRlMeG/qI9D9+v+Hv1h0bLLhBNug4mGwAAbAh1geChKaI3thQa7KpJNOo0kARCLQSCXCnq3sqRVMN32A7ts2HpHhLqe/n6WRG0P6vs+A2bWmpnH67BXlWzz+EVQYIG6/aC5EX7xYExacNzqiq44Wnhj4wLiHQTC5S3Xffxs7/4kPQFowRepF/jxP4PQGO/3pu6FSccc/njYg90gAGAMexqFzEMJEsnUhPQBjUNRqZ2gTydTFX9qwOrMU5TJiP/sJASblESmtR38Bk7mYXOaLtqwZUq39bxAAFx5/qG1P989fnfLq69G8L9AwkGVT6NNbqin/rG0sUv1hvr79xBzt9g4PwiSLb+uJ//h70ZhBhUMACeNV5KZP//ZPTsmTe+vXrtTliUK1p69P91wCoAkgYOFU0EMCVdS+/7gDCkpLb/3sFHHCP/wYYtSYwSU9HeeruS53v4+B9+njktlfxCl/w1ZnYxYmREMjH/4Vh6EOwIIkcVgqQ44V4QYIMA+IAB8fwSq4ptBwxBEXBw0MTJAt12uaIzMaiRSI/3//uRIYQP4kPUIABMjGR0OJ6iUOaqDTgABYDAG4gKsiY2pgBiITIhhMQQhjFeNyhiLt4GCEYD/AfHvSiQNp7YyDcMW4Y+FYY8BBrTQC7p8W9UETlqr6L6//4k8twFrcN/UFFNDf1GzWrM+JC+ABQCtHBgqxikoRMJCH/IHokB0fU3I2aOqfGL5hcFEPzpMuaEkKiH3ADGJAtRck/IGGETTZS922OGWYubLEhq0hvWDASia8RRY3E/PUAaCPxYcfP/wxnr/EXw/QQci22gegwALaAA1BqtyheVHyX9sCdogAYCFAI+s4FIST/myAWpQONpYBsusiHPsH8DviMSegOgOkQZar4mMeEeFcCUAcHISolSkFkHz/ESwBiJXCzueKThsIIcJTSAIfnc6y8FKQSEYX/Cd+cE0AAAQK0GbgEoEUTDmAAgzbFDkO21IX70QwEXh2i/w38DA04wGJL9ltU7tgQDDkLgTu/8/z8MeAA6wAJge6e2BWlyRX+9FGMGHojN3PpPAT/88DOirCRZsAa00Ou1tcNKWE8QHNGAA4AgLB62aIY1FWpUp/6AAA2BZM2AEAoTJ+cE03BoSiaAOxO9qZGdZkQzNGxC54QxAa6AZ+YsAZmVze/nmHf/yhylf5vAARD74z8RBJNOOJ4gNwAKQCunAmICJsc1g/MzGd1FXqyUtakNcBq0ivr/wv4aAAlB622LE6UKF//YQ/gIDIC9OXJkTv//uD7ON5KwP6cKMdjRl3ADItXb9/uV0v/d/7/XWL4c6GAA4BrHAAcGX5CBAe1gIQEtKAWAGQXwkd0+/iDyrMASAMVtee/5/Ck/xIMIACAQ2GsiRSeoQWwRKh8NgASgSqeuReVyBT+DwAGhxQ2jrMyU2KkUzcECUZ3ddd/v//COID/AAa+ZmdKckDAuAiB6L1KskVRh1/+D8wANRuBC7y203TMExTyAAeH4ErurcRcNySFsFSCk2gCjyyf3u9EnvOPnETgUrM/DNpy7L4kn5oKD7RVrIomTyIfEhW4AAYA59QAgFSQ2pgBiDo+UbaCrfZxWmB+QfdDFURRJdOEJsAACAHgABAEIAEFQuaIzvy+/1QAYvurK4/WGObkBsVGNzbUBvWBCxUSnr3/dyWlM/+HoA44yHdBFkkYw0nsEAwwu0KF3jD5B6QdHzC7URZNnFB8GLnjBqmW3DpcZOL/+8QBugMHtkkY614suf0IgNu2EVR/J+XntCKD7tBVE/Sfnx4ByIAYYbSFCrhZ8g+vQBBBloyKPFnngQGDEp9Tpgv8BSlodEr+1wCuS0v8OwwAGohlKwjMWW1zm/pAAMqKwJ+HSE8ROHoIYcz2OnhF9yzB+MjqwRccAnlikwQCDAFGBBE3WvYtKHeyGApYKnj9gglyIcq9F3P//DVCAA8DdBQNPdSMDl8JP/hQgdMjEDjkxe7jwlgJv+L4ARxE7MdzT3xAP/8KwJAhqNVApPUFrESv7v0bABODRTVicrkCX9vYOWrdi8F/72P1Gz9SF+uudac1tP3//hmBLwAJQJWPWJyq8S/t/1vqt//w9YgAKsJrDj1ZiH1d9oxmfHE9RaGPU4CPr2t3zamA8NY4VZJtlmlnMAAGAMAJwLsig0RhhfgDAKe0nNp1+xghAgJcOIbI4i0JEN7D/uwBA9AIgZF3ngY1mRkKi6qH/o3Nx3SeG4AiShZ9fEnOznLJD82ABKBKyXtkXdcgSDXgLfxbu779/311F8L4ADXMEOOY7DRETIOmfSBKyrQWwXVtX9/QFwABAA4CCCr1YIpLmrCXQxBRzAGoLEj9H9UHNZPTMh+/iAx0M4ApiAQ7XNEBTNxngaBMwoGn+JmBzCIn/zzqWP70QA1ElPOPnCd0DWnOc/3DhHr5jBVfxL+RDIdGOJ6yEse0PLA7aBcQEs8w8/vfD/gCAAQIKItHRpebUyAwENEHqz4qL0VlwAL0GkAXWkY1GV0ZItg/QX3i4pp/c8vTfFLuAEy4Hoomd98vS7/wd9QvC/AA8UU7yMzWq9wCQbYFQx2WJjhBPoFsSQ7ruie51huNlsPwY+mh/ttQgHYIEJTlBgDgPI7FG1PgQslGcc/8bxAABgDgCcCzIpNEYAYjCOyHE1ZSWNSwF8AwlmKuRae4TW0QK+YzQOCBjSKm7Vp/q1cARvJYz+NqbXgHfaB8QFt8xv+DxDAEesBgefG1MmM1fiYAGgEvIayRWVyZKwRTAU8O2ZMHXCBu0HxA4Aa8hotZkaXaBXvJGhFUGFhEMJZ18rJz0WUd/rgkZ66PY3otcOYACaIM6oIzkkpYxfpiMjE/N3Rf+yoLCVw6Z/wX41LcAALAcA/ERRgUm1MAMJWOiCs1ZCWNXofxt3L2Znj/9jwH/QLyglvmnn8voYA6nQHYw/Rr34cbnhThqAEowANAachqBV1SZT/3Bd1BxZBDSLpwJ6MoYcXwegrWY+APu9LUd/55gXQX+FocAp89Se919ZWEDGCaFCpcdxJbng/6haXO6unfQerb/wt8AUyGxvDnCKa10Gnv/vNkBQlOwBgFkO5RydJKiiGIujC3df8wYr+txO/1xtAVgYAHMBS0C4sKgzzOgAajIEyzSTHE3yacbPcBF17W75tTAeB+wC6kJg33NQBYncxWHZqiVMWjojDI0dd6mf8gAALAIAfiImyhJk1PUQREQw3KKQ5yvAGC5QSoat6LXSycTIMYuFIBbCMLC6OP5ABj39f7+3NTNyA6PHdA1oT0yUNPhboZxThCZlSLpYlrL/vDFzEEtUj2uQol/eBnwcLFm/74ZP4jejlz3yTeiJFF4EoPi1gyqpf9rw9+Xb+lfG8ABqE5VQwmLJWxi3AACwHAE4gKMCk2tmBwEJhFbHE1bksasPVgLWAXUBEWe604CNpLFXxtTbcBQ4gXB2F5J6FCKho2wO+gXEBMW+a3vBKJI5AFLZEfPz2oASHNj/fL/HdT0nDkAQ2fLAnKAkxIq/wja+G9/4AoOsw5xK9U0RrCv+74CxAqJsd1L/cuwUALAB42Y1GUTd/ulbDUVt8MQBBBCeJVUzeDZPvOB6YABuiOHVh1hH/no4ACAh16z3ZyG0/7YCrwBMDGU+u7/8+EjYG9QcSl+GOAT5Hrs6BMA4yJkBrgCCf1enP/f/w7gKmAA0BryHqGZXfKf+h8E5qDnh0cyMljrhCDBDsGxuACvBKBlpq4+URZT22P1e/++GMABNUzRPp5pPiGNH8xK0PeYwu5AO0YGCjGKOpGzkIv8H0jVnSBtBM2lO/8HLgBD16v//QaEAu4nrD34JvR7+HMk2CADoxuBR6Qvbz4TRE3/AmW/8AH8R8ziEn3/DfAEsBMETrHm4tZWIFA4vaUp+P4Y4ACQbc5ijZ7PXhLLAMpuGcQI04ktfYA5hwL+n0oii4MKBgQVe0gBteNiG2r/8LxoHHABwtThSxQjrHKhSPp3nCQAEgEvXNkVlgkU/sAIqigYf6mZHLoSf/PAMejGTAxLkIrbJlfBEIFziAC5ftpIX/b0F7kbaILDTxjYwfBFD9KQQg1jkMPCJDwxh4fCvzMxlK47fWat72hh6+UnHL+zwEKQVWiQiUtlYMMxegMBOLHMuL/q//w/C4pLC2pKxIWIEyys0JuALwAUD8BEPFxUS+4AB4CDvTQzkpNzdcevvYNcUAUJVhDii6SigCE0DmUSf7YuaxpVS/88wTlAnj/vVWTEX9rMMM43iimNT3lv1zw1lB9uzfWwuY1qFzTog8gIMKbUyvCuADghSnN9RcogNYMESQS8RPGDJhmrKxK0OwlvhnfFCtb2KQnmMBwQOoAQ601u+eH/4X4ADmeBupTiyU+9BX8WB4PABB8Go0LRwkTucSFXsAAkFBeFUXNIoMf3bnAO3QCaoJix3G+JEohRGREwllPYBL+cf37h0x472ff+/4IMxiggA6ZjAoSkL3wc+ExN/3hgQIAFhiK+EE6pyUiVtecQbqgjOWWkghvGzEBAhQXvh29JICf/gT4gAI7h2awTRN6bZ3/gwwwdJXwwAcyfZxC54HJtLKHV+Pp5Y3+Ff5DRjkUZuJKa9ywJAQhBCVqmhkWnnO4PheEOPZ5PRERIe2YMOpcBB0MMuv/+GrA9YIqnAAQH7TLjl0JP/z4TNOGt0HmcHv/4LvAMejFSISxCK1yJP8GHwBBBgDsaAwPvjam+UZiQ9AAZBUJlGWl+kWaSH4x1uUriIII1hhAwJcABGAZFBg50mrLW/FmD/mRAbf0ImmjJ+XvvEpAGGG0hQu8WdeGFgTbwwAt0uMbUwbYvCytJ+898O/dyaPTSybAAAgBQAAQBXgCCgVNEbxAE6AUPcJJR3r5ds94YbtPDniqku9+XYPeILPjEQVJJeNPJDD6GUHzsCaIem9P73MzA2ZoXND83Jf+AT+wCBRl41KPl3H+4IAw42sJl3TLroHo0CkSYlXYoT3/7xYERetDc7DyeB3DH4c4ADrQYw1nUckBAh5ZPZo5iqMvFFqe5TlFwbI6j/mzugAMYKj5ZmLK0nDyvBfAQv0hq2gP6B+wAAZAp1gcCxIaIwA5hwLtmwginwcUFXsOJDgCVOFGVNr/8M/GhKXKg1LFxWYX0bQEGCHe2eFX2q9/hkEAg0FRJCLnNMV/3wP//jYAD5IzV8nmXcgHwgMFF8EEtCNjE+1qj63X//zpG7KmDWCZtJf/4EKCSYCGQjsUZuJIa9jdR4E0NM5W6TBNWlvwYEGAATOzgqNPoI6hWIMQ08KybJHSRQ3a/iIzOILcfYrwMBxQACEqyl1QZMX+8KNLfk9/9AjiMwUva9v4aGH4bYNeT6ZBFRRH8spLWLssAIGdutIaWb3g/4kO+AIaTV1ItPcV8ECn/wYMBbZGcADwIajWaKVwxZ8m/9zwBkwGW+AIg1SBN0g8wrudvAHE5i6yH3//n//WKsSesAYQTc6bvPwga+vGcKwAM4gEFGVjMo+XcfdwQDDjawqVfMuugww+JmMHHoC98G/xJASf95gRVOAAgP6jEyNXQk//L4aI2RRPX//v/+JXvhzgAJgAfE4OVeU2m6ZgmLeQADQfASq6ppFwzBIUCUm8AdKDZSDan/hnw0ABqDVrESJusRKf3s5goZwQrgh0QFEBBwBD2WqIFpbgtkgV/9xAiCg0Vslnq2ddWt+ygFcyYSMjjr//fw/+GusaOiQNQIgwly/tIABkRGBU6dQRxAAyBwKDRRjFJOiYxEe+0BBHc7qrRc3XXf4zACuFX3HS33v//J+YXbFZTmHIp5hMPwzYAAEAKAACAK8AUUCpojeQs+IyCpJJpp5PhhUpDeiwkI32v//kwAEMzY4VTt9XL16mIPiQ7BIMCVrH+9bhkMACQSkX8PYLmyn3/vIClGBguwhjoSspSL/AKDHf703F8Ik445/Bhyggv6pf///DshOOjI/jPmHOGLF7b5/W4lGH8TqyP4a6BBZNm2WYUzFlv/WVuHZrKb6+/4sNB7PJNf8/+sSecHgQuoL+JCuABKBXWAXUDos7xoMJwET3sZqDamAfA77wPih8W+YB4JwBnrAYHnxtTAghOHAFKjju8DqRAWGyUPxPvzyVOi/DdDRgAO0ABqBK1zJF5WIlP7TMTA4xIWv4+JIyb/gGvn4AOyR7TFvvb/4k8hQBwdZMbU/wpOG5w/8QFcABjIRWUwvLIS9i4bAABcDgHZFGZOaIwA7MZVUVupJS1q/DMDh9LIig69C/6wVwvgAVA5BgaKLo5aUbGMg/3TYFBsVUDIIbr8gHY8GEvSnAsZE0CmGsAdID7Ceg92XH/Ewjz0W4bXzlz5/1w9jL9f+5TrszDgBQ86mKgiyidcJSYAAEAGgACAE4AWVCxojABMQQ2UZKSbIs0vg/GNUU7uIgojXHFBh4ASB8oiMRqXy8E+dA5018OMn8/oGSvhnEBXAAQRW61vnab5YfmF4hUfou3bhhyI6CHm0jVj/BNAAAAMSEGboFoHvDnAAcAGBJEa7RtnMFqFjP/nAADwGg/AGg6Wm/GCtp2BADqoRX7VxzuI8QevACHrer//+/DVFxB64RT5bXb8/74Txub+2PmBvUqTcNeEYADQDTkNQK2qXMf+wxJwFAmIxRn0clj//7g/Cuew3l4Slb5yAf/8ObyAgV/AxE5ar/C+Nh66EmOAO194rgL2OGfrRX/iQtAB2AASBOBjD7PFSJ+ag4GHs5kAvbnx29m29vD/4LaDDMF17cgWQEw4gPwA5YDcInX23MsEjH9vAUBhaMdYxTUIsbJl/wYIKOg6gAjpNnokzX5gACAKkAEaAVis70E185J5mQZnUR/KLU9zAKtAnf0Hv4pBbRfUPwYicQyL9rDeencdz1+GVteuuXwRypZgKxufDGigEjspjnEb+reAZVnABp6reptGa0E3+H8wmAA5cDcLnSKPXtMlDP/tIjGBgtMdu9QlcRb/zQAwlHNkYvybOipj92gBu4wDBK3KBaR4wlz/B7KcAAEgdAcMJK8gAfP2USNB/399zaJkRg8t4TteNY1dGH4YqwEgMgiABcALhQKG2sUlChtIU74BQMKQshNxVhEyD5H/aQbldYC8D5Oqev75QAAgAEd2Bk6LoT8gowG6g5ABxMKFVAVEb7MI8G4KfGPEheiQZbAWAAmQOBE4fai6KkQrxAAnAShc1L6TFy29/hGloKn4AdGk02Zey+UU8PQAagUC/gie0qIzZU8gvb3ILThqz7SwfjAGVQKDnyys+7ROMinIjALGpCKpcuTp/4Pwg6MFnSJVeXeImmhYEwziBMOUwk3yF97UYnCQVxYWREv73D6G4+eYB64JLFHBn8vjYET3bjtvoPMC4FYbovwaKKnnjYcD8HVMwGFlEtIEBUpyc9DJxWpcggxLhSysFAAsMwAxyQ5yuMfHbyPAAGkeBPo+1G4RYhXhEvMGVTgO8a6z7bdsE5BYU9D1uDBDD8Sasw47wN0TnGGCOXzIPEfhG+xkereW9X/+N+NgANQPWQ9kDdLlTIN1fzfV/r/lEpwwMtBw5c7KuxNMCVNkEc+gP9YgMWGNAc6+AAkYLj5p1LK0uhKjAABsBRVRw8KjRGAq0nGeAJnur+3C2glpmRF+PGcOYAEgBCtYTJbOEXSX5gXADCQc+xivIxbwTMfotBwA46facX6/4b6CMAMekFvUxVEZyf5+gDdxAFCVeUK0hxhLn/epC8ORuyCYz/9//y8eA4K8J/GzmgQgGi0D2sFqp5feYDAgApQgFDbSOWhO2nKP9oDGXNwy7vExQNDegGFLWWnZwIoQIPfwNouO3GgwJQAEbBwP0KQHpXEyFB5nXYF8Mt9KnWtGi0d8PXYtIFV4FA7gGwTAjB6OMlD7yxgw6OWFn/h2gGADgMJpzpkaruEWNFDPhAA4GWpnuS41ol69gA0FFmgUrkhtMxxys0/ISMYzBGYw5hDnaIiGBwtUaw5QFcpZ/wvRYyGGmtAnggC1OtDP1poMrkgyVSp90P2jiPZ4AuIGxgyAICYAchgBYKkptTfn9C9eaZD3sun34AWkLK5XubI/zcBibW7xAnNlJtsf/mAoAHsAAQCUBAQiPWaLF+Jc//+4AcyDMVRH8wtDXKA82rXMhd1e37hAzlG8voXR0DGfgQCDEC4PiAq9TINqwAopGgnI/2l8yGiP/gwp7BUYMCYiQmDYACHzC8hT0oww0V9Nddap0L/+EMxwmJ0M6YE7S0RPUoY+agZUMAF0BlqUZSLSfr142YKcALcQDRD6qSJUvvveUvAAnwQ32swh/0hLfc4MNAG9XgAB9CQUZhIa9oTIqu3P//gjxsRlLu5DF8V226DMfXgP+LzhV4kouGDd04zhbIH5wABs4egiV/jI5X1hOLPhWcAMwOKHnCFp5fXOMlDZg434/8lALZFD/jdeS4AOYelaw0FXkmYXf8RoI4V4PgfxMrQR0/hkmX/8GPAV6AZGEAWJXaQLiPOIuf7wg0PACCWJ7J9XsYN4KGPwMYYYQpwZCqQAr2nCV3fzVWZgi8mYXKS/P8f/dmaYyID+CO3YDWH3xuAATyEq36Ir9xAQeqa6vuiS2ZRly/3+SBAL2+EXS9UnJH6eMyCvEfteCcQhv4l7Gr5XoLLpYFA1VEUvYG/YYfTQ8p4ARIDzBYq8s/O+h+6huf/tFfDMEBDgKxkACqD6v/WWNOh+NssYAvAATCkc5Cepn7p5CPQ6uFzwhdWayAIEDBMBVyB2RggX1gBnNdfv37F0L/BHHw5OEe48P6dNjVJgIoe6BTzUpoOyvRQew9/hugSAIBYIwIj/kAqaEa7e+WpkhhIovXCFOnTp0DbYTYrlyv/DkyhBtsax6n/xsOQU7zmgChmV6BlLkZ7M66sSa/Dku1B6LwW2Y2DxPSihHgX5UDXAC2fFUCQIijOOTC6B+GoANpsk+4/5+AXQaNqg6Qra7C//TvL/AVDG8vexzvhYuPFGAepsL4lPf5Lgka3/huOAQMBQAjRuUG+AJttF/rloaGUd/JQZw6YotK/myjpwgF4V8ENAaIeBjoBd8F+AFgAbAVDxjKn/fDw+eAkiBhIKaj8WqBNJNw9M3hW4AhfJe//NqYFdm8dLXp67wAhgiYEOH0KUiqTefPeJEEREGZzClMcr4wuUfUA2BuwyCkP95/84qELl4bRT/nqwGPB4xx+u5BSNw+LEL8b4R+e6gmSJuAHjG4HC1Bu/tEWRF3/OEQABMBt2XNHbaKFv/ASAiuKAwTt1hXkGEJe/3ADHw5lwMU5NjZUz/4OCEHEh1wAfoSYnIUoVf/79Bf4f8kwAIyQAQcfeVDhIyRJeMGYcolZwnCD6jLCXIZgP+eH1VQk9JD7GAzbMP6dRF+8NvMAAIIwA4AQPa9jAjEpEXyH/0VLBwBYBg64xg/DdfT64Ph4B9R9fDdfECKIBYzbLNXwQoLn3BhSbMoB4BoN4SkcroDnOrXr+uXz1h9gQw6A/8Es6KgQZgvsbdugOL4qcKMjgaUAiKGC/BfGBJeQAlrOQeXxyFcEBYMLQgD4qx0DO5CzjQwK/w7JXsmUoVWYRVhBGRl8pDUH6c/uykDF/BJyAAF4vgi1Yzg1zxIegAIYCW7QcsQX6k+cimNh8wDHwITqc0qbsI6Ov8DiKXxt68HUALUN50Mef/72IfP/4rq592Nsga/fsHMMfw90MCJEEVm6S9xtgj37kAVKBmS4pLPEzX/+8MPOAwbEg6Pr4WUh7jy9EWKn0XsX/Dvww9SGOWJuy5JccqflodY2MfYEzIH32MAD55JDMuAP//CuAAjChOciCpIM155UNgAAQBOAAIBLwAkwGjRG8EQGpAyCRd1FEXABzCgT7MpJOEUJTAIVAwAt0IiKjq9efORCJgs/8PUJggQx4D4ABNKZkTynmXoV6gAIYBf5IYyToaGDWkDKRUgJoLmSSTv6AOCUoal0dpVGjYLwYGdPQYALmuDXYln5v/8VRThekY+yqXNkGYACBMOUm/5T1+4vHeCC6dBgzeU0wGmhg2RXHAd2XWOhAIARXXO074GX+uHzXHQCe+CGDuBCAbcjOGY247QxqH0tV/1wYaMcFnoCGwcHr40LCxF/FaAZSakuF4BEBUAPhrHjjol4zT/DfAAYVhxh7fo7KCxH228zEUzuM/lGqe5jmTVoxHggtNr8VwAKyM/FlyP0+G17GeDsz1mh//qwGZXem1f4ARDMYYDXi/rW0kXaEfAxmtKBhAt6+OpF2xHw16YaFbYEoCJNKcv6BEB3BQLGGcEVaZrIU/7U4IIAkQFSC/J5h6f/hPw8QqKpeVE9O/wMWgEEI4hFRo+ZEiR/gZVQ8A6ms2+HKAmjAJQLfsOL4dB+P4Lc1fHquvioAGmT5G8hp+/gTXk4eXJvhj/X++ofhyPc0f93ICTD7JoNGFccKZnUT/84AQYpRjuysk8W27/+8PwSY8ABqkGVn1l8LdY2dkwJgEUcU9f2oBOGzIvlMIyH/wEQHcFAsYZwSUqGshT/uAEEKQQiorR833yP+BEDJgRBtQB+kCtOlcOvf34AujhNg359V89fGiqaNd89Q/Yv/7yMWhuJBFjQYqodf/EnqB4ZRNf9dWC4VgDHq9V+4SruMw4AWKthUa9RZVPEJsAACAFAABAJJACCwbNEYAHzDgX7PpRVE0IUD8Qs6GZh1ll488sMDZcANQEiRldWdfz8H8AAADMxBm8BqDvdY+aMby+H0M3NwjyBiscm0baQMhBhwwh1LXwRzoDJKD6L5JkrOhe+42+fPXhI7+574ItBhlB8O/zTtzEvBXzyMkI3XodBEpiYu+JkQo6bGUbQErFz4a8z1/gxiq8sagPmI+CishBsG0ZJV3z1hhF0WD1Dc7/9SPeID9SpSj/bAATMgxF+U/mCfJpeBaCci57AGIR2xdX/v/1wvoIaTDQgFWOi5XBuUrD0W+tGHxfBFLEg2gHpa5/Y8CCXiA/4WoFHCDwTBgAIgABAAQOkC2irfFCghDsQ+MAAQAOE8CGijf1iYlDuRhJpR0EALj5iscbU//wQ5oofB8I0cMolljh0taFjLgoDAByLToIvXMNPwgQr+MRsHTgifVKJzdW8bDyAFcASFA9IGmE7icD0I9gAAQCcAAICRgAIOgqaIwAsOEQVfELNOogaq4AAIAABRtIBIUqhtTeIR6H7BNdLVVm4oGPgNlx950jQpcA/MGc4RZCO8/AVICT2j596+FOYAsCNXBumMgAHQs5zwCgMMoUag4Y8Aw2hA18FkaGz/tD16aTQ74h4TkagQbiUNDbmY8E0fA6o4JhWGAB+YAOIEEoIVZ4r4BuhVh1FjLruKvRj4IpkKaHYeCGMjvSuFxFDYoPwOUM7x84r4YsErNs8bx2uhjtHOifEcnOwPpj37GZa4J8cD3SpdNQFvS74Kbq6HMkZ/HYfl8b9ADBNDFricFu7CpvuQeAzlEFfRNThsRyY+NAQwxoSmDAaDhi/PbtlwJZtEqgiFF/PAX/BPsGPAkbKIDYCfXxuAPgABAAaAYownRe09IEgeEeDDZK/myLhk0/4Dwh/9WT3fcNjbHWj/jwQL3DRNGr5ivuxYeOrpQfjI/z2DSDWjIVRIO+xAH4xSDCmjQAX4qWS9phwXixPUt9u1E+mVIWv4e8AwAWQ0kQySx4mJS+EeLYpuCuUctgZP1l7kVv8NA6yI6LnCaATIpxmUZXIMlzv/fcd07Djp/vGjQ8bRvyseDH5KnKMYj1tNpG+POI5VoobnDPWvwpWD/qagako0soQa9gYwAew2M7eHw7wAa7DJER7T98ACEQoPepo0UtS3NpsOjBIoOBePVZK3Rr72x/A98zwHq0VmAALRHDUqEWN6/7wNZ4r7yZPf/vpjBf7Av8bwCQLQQCrHXDoDYEMCRVEKinCBD8QzRPABanADqYQcAg1Dg/8Ek5oIGHheALvh+UEAh1CNEAsPpDo6IACELmpKaxSSHtQWQwAAIBPAAEBIwAEnQWNEYAHiBUE7BE+rzWm6uH4wfM4q0ucYd5QxYMKm0lYAPoIryqRmN9sCP+GJgwNNAds4IGGpXBxFukq315Ce/wvZsDMGmITAhg06vDSBKAeVYSv8MwxP3oD2lHCuvDBg/xfG6BqowCl0OrGpwqlaAFpWBTggENIsX/DmPAN61+MnPCQ/CthCcJM3B6mAHAGH0NWqJWaLq2+xG/sAUAAIACheAloo31coJw7kFYABPaEqkh8T/vHBXgjB2HlfL8bASAME4NVqJwW8L63PJCXmjxgACAEgZAFNFW/MlROPgiGwlszjlZ4gSXmnDz5qRVOABaDHhAqBucSG6ENiT/n+h/43W0ogEwNyZfOxjgTUAUaUGpAPXg0Og9AajYXemHpfiwQ46jpWz8RHR0YBZQke9wQIw/PG2bCxkTBgACjko5lDZHDAkLY/vDgJ6+PmewJIH4Kta7PADoBnNsUEOOC33wpIEpUAjcaBOMm/3Hnitg3ICCDBNHa+NwbE6FAJhlAAC9UNPqi60AG1ca9EydWxIj/8bjUDHgwOpcDAACrHLQNwgWAoEQpAjxUnaCLVQQgw6OaINbCP+C2NTD0GKKBGgJmwOyFDi+HuAA4AGBMUjQ/c6wKSKFfoMC0ADxW4AAgAAIKYfNOkz/+i6xP8W94BOJrhUhPifHQMD2leMQF8Gv2S5lPcjQ3AhlFEoGiQgrxugSOQDjYNB4V6p5qhKgBTilFh5xBXcYLRXUMvJLXn3E7LKeHNTBD9/x0x4I46VHSlSI77jcvzSX/JHyKoh9SLzwV6CSroBJzh7GQ4B2Hh/GR6mXMmHLFiowSinGihgYNU8vWpDRomg3/D1gPDlxWBpi8mjwxfaZx5xKFXILAY2VDw74dn1oAGAFwYY2OugbwxRVL1jggSiesCK1hrALw7YBJ2LjoMEgvQK2UYMNR6GoVGc4QIAh/ppUsrj8bcZ6GdcwAsCYNMVjYJCgDpfYTomCwHIEOncdoSx3UcFUqDgH/jdhx+NHDWB0CYFACAD4kcVwtlCnSBwb7WAAXkAO/AN7ATMgjrecAITinKZxtTT5/6H8ZUsChvEQiCVjCFOEYQSQBgMCFmVAcAX0RnuYWa3/4ZwBPAh1SwfqsO2GUpf+H6DKJEA8IwRoIPya7HnWUdD60M+ETD7IdBoK8V7iFcW/jabAwp6wHXDBtG6AQzDFKQYzDgE/1ED5gZA8KoLxk5Td0ngz/w/yEIbg4tqIAHAQehf5QIMejJ/pk9oAR2GALGb+YGRTlGcP9xwAKAvJaJSqpTy/+2zCOkLwnHVmle90BHSDYZXj4JC2Q6AHg/XGnLrKbDB4GPCYNF4Q2RMYCAae4NmkcECMBuNmD+L/hScBNDwRsU6vJa2As1d56wMHrcGBKAvRiUP8+HqdhjsYeSu/wjafxfsEDFQ/BHIAecpVwT83DNrsvDUwgxyBFfYJkHyWhej8f2h+Wwppgivxtn4UjibAHRBlDso2GBXgjwHgnUg3AgGg40++NrY2AFWkAB8edU1+2/xgIwZP8VigDa0Og0BvKUBOLUByobERFCl4/8boCVCyQPyDQ43IYKihsM4xaFYBvAAO6txwI6YIfz6umETFVPD3yDYwqEufzTHvIaNpRsABw8ABEM9DdommlaqSaXlw8pMAAKgmmVAiRYv/D9hIB8NrQJUq4VE2TD4yd4z1dAtAg0BDbhUTCkIRQFCQAf6UOI936fAwQ3rQZ/hSqCU0AaAwAc+Q7TdSIim7p/iYZkuRyoqkzjAV/CYwzL/SlO95evGRth+Gw5Lq/imux5eEjYkDAaCKdRfG2oUlAiaA2hugOjbYYwAqAKmNoBJEW0qgkaeKUFsIKZAuWtfhiwJY7DaYZFWr+a84X7qM9oUvl/wQVoH/4dStRAgMBqANdgAAUTLkEDpjQoo89fDsbdUAWcIUAigrJxoGpLIJoOUivZGg8HclHwWTyKigbp+GY4BKpTHBujA22CmnCVi1dcx7mjh9orcM5+TAHHWP77j75fDmZTCHAujX8egKJfq8F8q4YSmsjAHPxVh69SQ1/+CbAbAhwq+jyPf46wh8wxauMgecvQywvwVYYRMnwVgIbhCCxybckM4+CqwW/ziasAB1L7RtFnry+HcIPpQUAobQK530pVfQ7CMfjA0f8L1ImuBmNoE+KA3iilJIL94aweX+NqAvs/c/IDzhAkGmeQECqGeA6OuQVRQ7NcCl/gwvPPBGA1AFCBA3O0BoABlALAQzv6YQONyS9KVh1YqqX/bwQpNUiA+AB5Ot6X4l7XmBzjYZlU+Jos7wBGPtLNJehDmLQQwYHQX8RDKXfAWUzQHcICYIfDtpoYGG8RdrQQyF6B1sTx3OtWi/+I0AY8LgZ/jw7RnD0cEK0MD+QuPHusHwb0C/GuNOBLh2dQrp9iOLqAcT5sbn5RjDK3Pgq0h4NvexoBGlHwA/PfPUqwQ9/0jAQJ1QZpbf5N0P4asYYQVjqwFlkNmP8bxwXHqRhgA+AWUBcF7JSbSODd66gfhq8uwjKcCNLEllQElIa8AYGeg4Ned3pXjGWFYIDEs4gFuQnPSRLv1g1uanJt8wwkeDF4QD4fgh0DZNPQ/3r9AEGK4pWV4TMmVJ/zhhzgljKi5Tf6Et0ECOoCa5Fp+HIAFQAg2BitBO3dfU43IP96ACBdDFqCUNm6yptsQYaAJPzDKbqV9/YNgN/hHqZvN7+CUTR4ThYB4OA8AERmIfo2p/viLExDjROMAqMBH1TRHEWDd3QBuNgn93G3z5eGpx8gC1+ZsF898bQh4cNMnDWhoV4HB6OJ1w9x0FHz/UwICcPlFf/BbbpdtSHHgjlAo4A93fBPsYZQRTxgtADBxx+Jfglsh4H3Wj6BgsItqfh8E/jMAsvw+DDqR8HMACOpRI6/CR97/ghjIYOvAk/xvL44ZLnr4ck5/5uOGX56/DinP9e+C2zYz52hoIVqV0nLxwy3y+MGR+TGRcD/E80qKr/GXyrvXjVJhivCHGA6sANCXVctV/Cd+c4RaczfLSS3x+g08tH0Uj/0A2Nja8THBg/IbXvj9G5QgDnZnZnZnZvl2GOl/vj9Cjz7KIrDlBB1DkAAABA7QZvgIoOckaB6ViheeMGcf36ka98tg0cNQvlc1gwQvnea/mo2DDaF875rBo4bQvknDElw2hfLQslMGGyMMouPnlUGrZl75clo06HyvmjAIPoo3hzKfCFh2rgN4G2NpVoMOMyP8vzl/+HPD8qctOGk6fk4U7A4dptg+xQvffZH3MpqFFF802hpIYL5eF5ooBSpjoEbwnCW1JAgm2P83TMEf89KH946//PX9Cz1S8F9AgDWoMea0DHgvsuZ0EHYbstFQ5SweilfiaaH9bz9vOU8MbDUPIZimw4DHBMu/ogtf/56j4qHwxf6GEXxmb8EEoNHht14WJhMjLDcyQ4b4Fm6uJjD8NEeEP/xNH3/sBSoLEMgsy4PIWBj4IIxcNsH+pon6AcdCF25lLa+4zXcwuGrBtjhUsBBWwKG4v5D89z+GPBI8s/dSOSiX/hC18334YvXPz0phEwyt/rivHn3Y1jeG/G0N3AAdjyaETBR3GjJXJvCDQeqZ6/OJkRHVfgsjYnqgzV0HpFTYDqiyVAoGL42jgz6RLdZF2O92qAro6+FpPAALB5weBQSc5Q9bD5rgpZm47E/pwwEcnkgvBoMlPTHfGxwJNdDmBEYAgWAUEBRBFCIwGNwtqRh1UAYf91YOsOy93hfOCAQiYe05QeBMHBL3VzQQqwoTpQDRBlChJp/+PP51aD8bQpGzmlhx83cHsO9vHvRgAWAIDi/MevW52p48I/zjAApgKAeCpVHNe2LKRT/rcZpi+tp/625iIPElE55Xr6xcAwcvxaMJHsK4yJE0w1+BLnCla5QsW/+PS+GAw7PaHiq0Y8K7AJgEZuHzBgwjITPoBnpkODsJu9KgZgxOmm5Th/42u1eVeCAUsUT8PwByzwkYpnQxuF6NUBQFNFDcqwidaHA9DgR+j/vv/G3hi0AWgliQYBug8eAUyhhwxD7jAAK8hNGnAVS2HFsDNnQO/4frg5Q1ggOaOESizgCYEOidaxmTKBTQqSXFwwopmuNytjANcoGoUoCeHkvOaMKLBHUqy8EcIeF7NFGZQEr3j8O6WAeRJ4CbgCGgBi4FL9ZOvPOf1757Ec1AQI31fb3wvlURoMloAAYZRe6sMotiygoYYf34djhT4AWEP/oBYABoDTpXv4C6tBoJvseTA1uGB2MZfd+HaeFAOjQTz1d72BItoOotxVMiuF6LPafY2jf8bHgS1x7Xv5WHKaB5TKg+aPJd/UAtoArYJUKaglGCEiSuFDNfCQ48dQV58ZoJeCCPJMCAOAMBYGBaECuPmggXl3hgK3Og4M3wJfpeCnpKQBrCppKAKBYD3DhB0Xp5X/hAwCvEFLfBBYSkLhQSrDfMJRzTXh4vHHn1/lev42fYdMDBdhhPnTMPtFVQvUqG67EFwCgCaB3hSK4N5F2aLB82xBRYpwvUZBq8PzA1nWOlhMmmG+0MEcDCVQMAu1LglxXNpaUhf8baOukOA1LA9qgODhA4BWAMvPrAcC0MFipUL58ugIPLjYOG4Xx3WYv96BJ2Fo3P43QjBgGRULg7A+7K/PEnMsKKg0LB3EVUb0EA6CKElxGSsPzR2/+NqQaMBwJgOQBsBrjtjMm8EYErDgUMXw0BVlF3BAHJAuHkX4NmzvA6Xgg48XiuBKTI12j9A0wKvqmEj28KwfdS/+HcMQXi4MDQ2AABqcC9aBherYCOtRw7c8WwKYp/43GluiYLSoFgwJ5kzUMxYyqWLtUwa+CJ6fRv++/DlvRHDkeidwkgEvsjpCELBA+Fo8DwNA3CkDYTjIG6o7UOELelRf0ivH/79H/xsaACLsCkZ8N+VDC8zjE5Hw+lqoAoAxgOAtAdaAxTg1Qwii8Hz/8O7odAJ8ojAZ4QFHAHlQlKwAR0AyrQ3YHlQFQYhH8ZdMYXuk8V8bVAuKQpX0W49B9DHJsgIDQpMMtbI04QYtvrDGoSUjA/+NqQArRwZGgzJhqCVpkHCfbqeDwHOLh2JdAw8i1zAU0s4XOvgYfY2RINt4+NUAfgw6dBgK4EEYDLQErDNWqAQdSuDRAVZff8bDKWGxHQDBVOMA3vBALBDwkgQPsR9RFBFmGArNjWIbk/SwOrhpDCHwegPOQfG1oDH0MgVoVCVsJeW83ggHiM/MvUgv0D+uCArRMQGacbQyqiBlwkqKHxtqmAM2Yr6Ug2jpL4LOB3IJgaQahejAY4UrdeTVg5e0MKBftrPOs5XwRPhab8MUYKdSicYcgSdJppMMeDwhhazRA0KMSghNW8bPkGOBEVpjBcUnhNoMWAUCwDAHQdCDKDM9in61aTkKSXiwPs3HBFW6vG6BB1BdVA+OdvQJPLQQH2JSCk0caG6GPB/ooBhlBgdVIrCLo6PV4PP5DV1+HuQ4BK1Afb87BAJwRQlQGla8KVAPcZR4XhtBDbqIbB6UgsrxcH8EsJmtpFBMakDBzBivmBkBEckEHwA/STwAeEuN8eKPxlsrkfeNQBR6DUPWIx2qqg3cKag1xi95fUgvhegGOgS3qSC2GF1zRi4/UzDRPxtcAjQKI+kZWAGwBsCCEvs3jxiBvDATDsHAMPQyNKPjonFQa+AfjeODaDaDdZAIKeDsWCB4A9NLO6B7h5x4fA+VAcBeGBoNOlHytBM8xq8EtChaxmf420sPj4TrsSOA24AuBAaDcEJkwD+4EDkflH1+QtQmgQeW1qVeEyBLwRJCgQsJ89F4fooedSXa5sVgPtBjkbhNomNgA7QY0HNH5YlOTgcxH/8bUYBCmAAFwHoDGwl7wKZYnPObtAi8BPXiXti8QXNg9o2MDbICQnd4WGUMrr6Cz4d9ALgAAsAAFytAGBQAjzqaH+BDB7UbEM4FMC+0HK3TjBhVg4fBBUCFRINa8HY6DAtCrAAAoIF4J2o7BPcAAehtVL+8U0iL7o4bX42pDeiSeVA6O2Edo+zOcCzgB6Mwwf6mAgHC8Fwkk0PxoOpfgGxRAJoQB8P7Et5BqA0YtfU8GQCHCDqwMAq05Fv5C2vtmYIE0CdAvGzxgJEhUAjQObWMAYtnbA3QGgJg+QfgWXarxHcEA4w6f/G3jTwABQCQXCiRINwFiVIhGSKlYO+Z9dAaFBgViQpdFx+G0VVAniArL/jaBKKqCZwAsEExYTKq9BQSgDBokUVwrRP2DA6BF67qKHEUYu7Dg6Gi4MBaCBD+fVIxbjPnjaExwGPgZmAAN3HwChI3H7E+gPQMBXB2WikM8Dp3UqGEbBbFocf70Qcwn4fjQqOnhvPqH6kdTleHZvM4KVLw7ggSiP134cW9FcbXhN2AALAQw5dB0BhmEgeHaqOCeDN8BxaAI0DmsgfGRQtW/xtngnENBryhoTQwZOClgBrlkqHZOCiiBwDXBzPaOD/NUCH3MTTOeEUIg4om/BBPeagTu+pQ6ODVOBIRu5pwB4D1TIGF4TGp6FYBzBdYKWgfh/OC00MqgD2kiAABOEASI2KG1ipUS5kWFFgUQS6H71LAaDwDRJ4PxkwAuUDoEMBUZj8rAFkIsnh1iMEXAJlfD9ec1QDHQ8AqwIjfDoZstSFgRmveMrAe8IYSUMo0FUCNXL+ehY1wir6H+eNsBsGiAAGgJskqDbUTiRhWAJgCcIEZITBjUxB9GnRUpDRo00OdwFh9FF+D42wAtCCrKxMlG0Ak1yVwJgEgSWqwgtNhq1iFQAN6BeUJGDuGBp17NYZQlAjrA9sGHw7cAqA8dCC+sCimSntVU2bDX7htqWKB+NjQb2E6OAn+wrQWMmajbB9Txh7gmjFwfUTAyq5bzY/HEwii17z/46te0jCOBOGFeKTr1ca/Kb8O1APFoYMGwAuOtGtBt1IBsSwEvF0Mh5oP/wrWlD0PDMNMg1oDyKEghIh5WP+HfjRIXB6eNaB2oDFwaWe6xqAfoppgt7Xcnrso8ITTvbxg4rgih9LPgecQFFD8bKEq4HAqII4aYniBXBBnAKgY8N8AdbAkUQMA1joM6EhRN/+Px1QClDYBWOweTq7hAJrgTHsxpeNp5t4QOA6oIpJv+oXwg4FaCXw3LRPqufSsB9j3hFo4YtMa3RDCKpvxJ+0J+NuRQFlCAuRqo2An9DAcorZ1NCAYE8UaiYicrni4GvZWTGqGg0kTEyvheOm9xpg4vC7jH3DQaZJ3U4Sj6E0P/8EEEX1gvUFUNcHNCCVwvYMAo9BsBAKwDhXp6OC0MWBsdhq82GU6oyOec8+NsDDqATvEGhKTDAR8ZHm4HLCqUhtUjdqkjVwoRXn4i8MB2GeSE+Z4LTP+H6kPBgEp9o4ZSwOWYMs1cPxBkLTC/W4Mp3/WjZ9YDQru8bcN6rhyBfKQI4AWqIdAYLFLwpjIAZ4QFTHWrFatCgkw2niWpqy2Vm+H42cQVI8t4IqwPWibsS4beHoJcHASI0dkqAniWUBbX9Q7Glv8L7RE4YDCMFlQw/AqOGoahyHBwS5D6a/G5AAR8ACODcbSQmwfodEKa/1RNDHaFlYRQdhn/AJRmB0LUaG24QHKZ8EkmoTqW+6ARQgNL1I1d+Gr1y83HBg0InCteACHpIVadDWWEPVgmIIbi5H+Ih9FwOwLeRfxvxgbw6kdgfQap5QQtoBFCBDKWWwAVc3YshDan/h2EjgHXQLxtjAC8lQ5WmFBZwe/MDhVCC0bBiR2vv8GVPwUyAA08/nmG3V4FTwfgL4kbQ73LUqwVLx1K/Cc9Z+MZvRQBIIPL4dhpF+rUF+h/nmgKJJWKlw3cY4DewYnMog+x65D4e5C8BlzgHwGhh8RVKwJpgqZ4VtGAE9RhSoOIptGh024QP/ggjQelDNogqHW0ME5+gUWzoUDWty0SVfevF+sF3sn4eqS46A1geRIg1DBuLwR4qRSqh2tk36s/Xmbnpoqp8EFsyJgmjEhRkMha0ngiU6rAPgV0BQ3Fg6xwt4vo+I5NGETjr4EPD4jKLU3D1CEKnYeUg3FiwM4fngPsPYxD/8PXBgU2HYxoV7GVgMZvh6VcHg/1YfSoklGqFKEDl9njBej/BBMisCCXjxwdEj+uEtgLX4cZh/8O2AjggGgbQLQ3EHDF9FHjQWOesCIfViw4+PRf+fw7TQRFg9HawPf7cBHCNQQfYrA5hVKKgHpRZNGH7r9DL0RB78RHTy1aioD2NgRh/xtjGhe6gFmjvSsd60iBQDoweoL1m+HcG8l/qUXw5hhC/fBmDBhMxf2f4Xx0KIyPpNB/VIeswGH8o8PBSw19iL77EfXBLj71wHAzDCw6iyl94YvX5eL4uNia0SL4FKh1puIpDgSWG0b6EMjt9c9Zr2/P/hmnS0fQerbqkJP//jYyFJc6FgF6kIEeFL2b0HZjoP+tB9VACploQZqjocAhG0GO0UXziT6kTOsvdgEInDo4YAYc4kz8fvABhCwDmqHdhE3jCCbg/r4ncNQZKAJKlO68qnC74uYiEjz+rvAAR8POgT4rYMOoq+jTJ/lSiqBDokHO+F7CHDiDquAAMA8YAMRoLQr+E7zxfz1Anf23//8Rh9lvFeEzg3X4QuHefiZQ637bE2lXeVvicMp9iAKsSFeHAJJ74vDyJavDSkvt4XhyAAAKrEGaACaDvFxgHx5Bo85BOQeFPpp6af/iP5pyCcg8KfTT00//4YnIJyDuYf14aXp/4bhCwsNeQaBYArr0H/i5yCcg5yCcg8KfTT00//5ZyCcg5OqYTc1leN5YbgpMDePNBq56/w1LweG+G0Xm1Th1F0f74aoRj5E/FggfOtMvq6i+SkPCyMC4Zeevx0aDKl4cnGCjYEH4dEtBwze5/4uUDXpGAo1A7N8IbAg5BkfX6AZzaEG0F+oa4docOoZ9zq4ehW9MjqIzaMcj4/+EK4An1ZsBoJGHIPgFgY+6IJoYD5udM4Q+Lo2ODHAhggYMDKHlAJpcSH5jzBoBGJD5tgdNuk3/gOEhRy1T3C0quuSwENug4IBoGL4V2ChmB/hmTl+cAOvwy1nXFeMmi6ND8N0AUAwAEMAF8VoNJ2ijX1qSxIzrwQAKgXoMp2qbT9oTxIDwIi65YCMCwAd4LQKxZEe7WEaSOxtJ/DvTHAgNeESVoQoG8QFIesHRq/xdASBsEErOSgAIMTHeW5AlFwhdku5+IMLYrVytknatUMP+C/mKMoTgAAgNcAAQNRoDpBCNDaABEJrfKcs8ocRq2YegAAEBEAEBGYg6G0B1TS8YYShW7lKIv2aoZfUeBDsHgCxZAEEZInjLd++EVjkEBBepp/C1ShZAFwMnECcRcAAV+MJmKA/gvoMNpFHOrIcACwAYDDPtp2pYSkatWX8AWAAO8DABQOGsk9zs3oF3+BKhervZI/7+1DONJZG8ahSafBESrigNgwAPK6lsfoEnP9ujYEchCVh4X/hKwFhuA5dWMDRQ/w3HQGLBwALwgDQkWSXXwUXc8wjBw4GaIM6IGXnoVqDj0xB/4W2BBbiTc4W3HswzIiDYM+SxETKgonyzA+RVF82wSAZv4uywMiApZgT2GBgPjfAAAgBAPwFv4DEOnxLeYIDt4AIIwsPWYH5obirsmWlZ5RFjbgYj5kUbsNDfowiQkRIYUVrBop4c/+CmueP0AmRxVxWYDVT/DtBgC8AAQDy2ADi3WMFuPXsCIBOHMAJHms2aZYrdPf/ADYBgyphDfpa2ZbgySfT/48BgM3w4MMnyKXLXgnVmOEz4CJR0qzT+YQNNwkXZAB6gxJmKTenBAhlhniDq4PYqG0WhgK2LwYeABAACAJAECa+pjfqyJ6FJxhsa8D3wYQiJwyZ2/UMvwzhsgJD8q2AbGpgQilnoNlXzgC3DOdqODkgbwgHx0PobpAFnCHGgAp+zjwYi0NAPh3uAAQ6AygYMQEKgdDytMi1/5wwmOrhI+N2BgAmtAIW99FQ//wAIBiqCKY5doyRzlXzhwGThsDBaCLiLcVCtffHl1T/m3PBcLxvJg4CcgAebsQg3pyWxXfeCCaPkOpU3/z3QIJ9P3ecFWD8RBrCABvsGH4sFAPwvQx8UJi3KHR0HtwwV8ohUIpw6rFl4YtsGADhhkocJQT/5dT33FWAABAaQAAQNxoDhANTRGAARhhaF7uVok5Z2hh4PwQ2PQU5R5Y0jhsy+CQQmRfADGAAiIpC0t3a1LsSSK0X534b8dBIXIcGQeB/wYcbqqQDTKB9fszB11if5tKVKL4iqcJnG+PclHgUvF7VUASBMwYFEgC/DWABUAAQAAGQBhHQZz/J7jJCdf74MAHQMyGk7VRp81JpEB3OsgAXhZFORhXe3//7/MjCXFrJRb/Bh9AACAAAvgQQwGIckJJcZIjwGLwQAOkXsMqWijP5oTRIzsNBmCCgjPgr/CCELupmcV+t//+//NsGDbxAdL3Ypi7LyyiA6LwQR4OiZFMWDrwWUMFgc5vGhAmTgOvmFURxBXBBPCtYBItqgdbiRh3uPio6GGVOfJzhZtcOSLMQ0H9gAV+xo8DN+WwCPl00IP4VwAcAAQBgBdLTHAchTERONqyIDw+AAC5haADwTbw3rnqpo+/8GeFaoBCmR62AKWCNvVXKfn2EMDFbYJ+G5iYyMU0tKv+hn7FIKgaPggoBNIZdIoOoIoeoHhKoegNSvkYMJfiuTqMD+8K46Lf3gABOAAlDApEAUXzuIzFfh2hMDWAAjUAcegVJAoMYFojXBUUgdkZHUx65LTQwoE1fwjYMxc5buQQHjMuzpeSiODEAnC/k0gQaGXjheCCcPEBwyHzgAIgZRCjwQUZygIvTJI/AAuMABb8AOgsBUjqyOpAAECymR6v0dr/5hprCAFjKO/9LE9TI7ZdXBGEtJMMFEAB9vGxNcfl92yXCDsN4fwtHHaA2UYCB2R2dS/Qji3rhrRY8HgVRfqN2VI8LSn/wrYK0MCPgTyh0yYfxegNx8IMXcwUBsB+Es80A9AMp56A/LJTYC8F8cJiuApgCwCMG7X56KaYfvvVAaM4bygBjocC3zNOHEMyYrs8PyhCRhgLqZtAKWYSU0AwzAvCB/4cjAP20PqsBGO48Kj/j/GxEEQDwWniWOxPsD8OU48DvQN5QwIwCGRtBAmYDsXdYDo/HwBYRx3NUecsoeksugNhQYIWjEZASwHgmDhPQBMgSBe7ErouUbqXeowVBs/DPIr4yTYGxcyhmxnj9pKAC1ObYTtH//zuYzUOcui/xvYwAELCkfe8hqU83kMBMvBoYL8b6mJ5DdQDA/gYpIlOmsOpr6UcwogQfgRwwhOurupK7UcysGCBEBHWNBLD6K49frgvpHEFAVA0OcQtnOPQGeBwwH8OUDIkGz6g2HnHCKznHp+WgeHUSR4yvy8qqQClBriSVA4yNGAKkqMo/D0cOqHQbBjsf9AGNnrXxoXdHFPxEwABCZh/V6KWknCNtNyjzoCMGLZIDhuYYi8Nw9F1aODb+Ggggw78GqwOh9L8/irNzIf2xCjOHzl/wjHxJU3hdw2h4RMD7vYCJ1/DXcYGN3xkTC8frnqRs+ELI5RaF1clxRkGDnMUVAvCeZJOZQ0M6P8EFgE4ACcq0BFDBZI0AaBORFAA8Wwi0jAgp6YwM/7vRUKL5fhGmjYCWgZWwMoAA7hr4+pA6cNOJ5WOiYUYER4jIrmGrIxkDA+EY+PelvKCleMZghRR+SxAvA4CtBeFbwQFio0a4/4HUMoqrpfF8XjYwu0IBKE5A0uevx0d95/xXRj5TD7vHQtC8XYEQAAyAVAMx+J6TyWiisgT8JynGG6NbAbmDcAvC9mgRs1aGaa/GRbNDBzj3uU0Ogcbkvgg0Zh5wCQGQMBQnh4AIAACACAqQLIbDGnxJeYoD3/ewABABAZAFkdhmDX4lxMUZ3gSg6ewk8kpCnd/aEgNKM0kx5qFkP/giZlgxUh9BgPAAKBzfaYgbU7BNgWzDc4p1n4iYMEJXBrfzbaNwU1kX6BFjKaKRpHL4mMgMbqhmB/w/4engVd20DVFbCgSAKIoqwOt3+K/EZi5Unjgx/hDQp5TtQW0mcN/gtxlQoFxk48ovhyH55DCsAbGr8fabFfk2YXgMCXXLDd7XYFfhqMg0pkG1+mRSsf0/9UsbyeEjBXXv4+Jlc9fh3N/XE220SRDmNgJwHF9JHcRddgQ8F/+I7Nk7syB7XETUNTNQ1MnCNARLYUDQMYaPA5RI4r4yYkYlzEjEslCU5KEpwoos/9NNhMJNNhMLxtT772RQxJQlLuK2AkSQQk4yEYYJX/5qrviaIrqGTwbSG+5qTH75uViHIAAAJykGaIHoHvDnAAcAAgBaC+pXKEuRfqJtP/QAACAOAeR14BwdLyfpghInvAFCbBwxO1/E+JPrwEdfH/fr+JPXjDqPv6/wr1r4a8DYA3hMrxS+T48JNf/YQG+AEAIkG7eEY0YX//3B+EIlQzhALhwXmJ/2vQX+f38ASiS02v/f/DHAAQhdXxC0mOEs0UIMuAACAigAAgPHSABwmITameBIAwcRtrMYXLZNGzv54S0m2lzR/36CTFSwjC+vtB/xAZgAIQAvm+At8099gwNRdlYYcLJPYKoiRCyMGH9YkGEABAAgTBqFIlm0IQIcPiYfg1AMkIpSKqMS/XzwgHSAAaBo4G8HcJ0aRDIgmJb+/aFbYkAdXTkHv4wgllDrd5/hDrFXDHcAGm+kQ+gIKMTO6LvMnABGK2+KbBga7uP8LbIABzQA/hFLwUQL9IHxD/2jGQgBQY0HtUSoQQ2D/ngAQLY9CUC7iMJEOnhPQAIxAoA0J5dwujLSARv8HwxAE5iAC2UkZsjBJ/r325ph5XYbVugyHoZTp/hjsxgcYAD4AOYEALDRFHPaxJ5zr/cACBj1Huyd4E0NmjH+0YEQxG4G0BlSzad/cjACrQhY31CFziq5eAFQcLau8R1vvfgoxnfViuH6IABMBK4G8G9KVaRDIhmpcPZgAOCHkCXdCqeiunIsyNOAARDEs/tHU6xdeRFjhm0hBGYwEJFiRD2QVmOxwzSm+/YTwgOLavprzrr3g8vFAkWo0JCWvm/PeJDl4ACEfnYZflOEt0UIMsAACAegAAgQHAAYJn5ojBE2iOAMA2uy8aoMzB+QIrd+9oxuL6zIvhzAAvYADCFFnCv5fwu93oCgCB9HoSgXaRkQ6eE//LwCAVNM/fr/huAoMeAJe8MKZ65uCrku4PQAIxAoA0J5dwujLaARv91rhjEEYpQ/kr//f8OYE/q58K4GmE3qgMlwY86sP/QIgA7gUAkOEck1rAnmO/9oBB3VUk5VeydP4AEDCNLcpClTNTJk3/gyUMgCEuFEpn8zW3yDX/64VwAkAIFwejKBZpCRH58S/8x8MAAqDue9B6ixCBAveQAAgAOMFCovnR4E5sLKHgteMNzitSab7xqKqqOjG7AEBiwd1QKRBEX/+BqADtTW1P3/vVNBGMcOp/v/f9yDS8f+F9oACwIGOFE8C99bPQg/IO94AwY+BRCwpDZay0IPiAAQbmZGZ8dVdUbwEU7o7JiOi9W8MAXDkgKfMkEGjY1B4U+EAL56QFkTRBFg0NRdlYRM0+Hp5qIB4AKCIT6RtT2A4R4NzvN2AwAEEgpCVvMQ3xbBNRpcEngAXsAoJGwS1s8r75j4VteAA6sCgGBFTfLG1eZZF8PwMP2OFqqYv/SGFUQweFpYHGh5lHf/wh1cvq743bYIABBAT28SOF6odmvijNR+CQARARW8VPxLfIHhIPoAEdwoAwJ59wuzLaMRv9/gAMFwYlOBZr03unxH/wYcQQZ0AKML7lYjv5mtlf9oMQClx0MUKxqqjXrh7AAqowyNbsvdOwrj7z7/iRSEtzzr/f0McMzbB3C6djkWHpB04hliX9rwZBz3dqjCyHJepoH/v9s2ZwfwlOQ3qgApmAJXBJm6+j/Q5G3vz1w1AASD/YZa6r/Riv8wxKOakIt1XDFH1ww6wBN++P67/1zeBG3d0vLw8CFA1ZEFBeqG1N0l1cjOrq66rq6bgvwTgHqAjSg2DzajZ8ABwAwbRiE4lW0ZkOHhP/2gAYiSQBgSw6hdmW8Qhf7hYADoN6HDF6L1Ra/3QIFJgER2pDt31uXAA/CjBY2r3WTr8OMx/hm4AQRBxRSFG1MBClC0JBIREf8AIEA7JHkxzeeeDpYrTPfMbnF/yS0vPWWW9QBAZ6CtPXd59wx6OmEhiZ/j+G4ACMhEAIDGw9pDCkViOGw+DUAVITa0FUIF+ET4noAGYgQAaFMuoHRnrAIn+8AEDaPRlEq3+MiPDwl0soAPRhqo9NQoxf/7/hRgP4YgAMmjAAYGBWI3F1bZYr8EI0o8pw977Jhkg+zzEOEYvYQm45lVy6/YQAhbtJCGcua94EfwAEAAYCU5E+C/zvAxA0XBW4BwAEI7SQ3OWomEeDc78N/jAYhIBQYymruRmSnMv4MJNJoEAnD4Ly0Ad+Hk6v78ABIXqkRbk/6IuuVdcK5603LfdAnA+AL5MQFoAFAAQP4IawMYdtrCDoo/wfhAC+ekBpE099gwNRdlYYcABrmQACAUF3lQWVOVarybIQFFmrxsLqm6pUCFIAYQQORzh///z30tUIVNGQ2p/4rrq+DDwIAqgk4+SvOCaJAia72ABwQJTgmzr8cEJOBhu+A7ID4lZHcbU///wz8EBNoGlbnC00auAjaWBgsBxojZxnOP9AX/CuAAiA1Ogy0lMEt0SIMwYmAABARwAAgPHAAcJn5ojdghgJjgV5wVht1ZwAYQtno4bXzF16vMAe0wAfGGd7CORq9//C8ABI/IJV2XpmXzA5mAAEAcaEspda7F0rUPhgRjsXgLPAZY6ytfEA2MBZIsfZerRSbUMBb4ALaOCjKp5fx/1yWV/m8ABA3DC+S1f6nMJsXT8EHZmQbd1/a/HAcCALAAEAIgA0h7WkFgyJbCXeCH3N5rdtjjuEHrJQcAYvddvYEGzZduWZ9X+COAIQbtYcQQlL2sSa8MGBcq6tXViM61XVyuuHwR8ABo9xjQUUTl4+FThIS+IIoj2ILMS8V9RP9fC+AAwAaoATwjhebyYmRXNQAGZia6OqdSI/hM1no77eDetmW9CSG15JHPf/e8AgFKaNOEyCGUus2fYAEDDkvEjStljTTfyyRvvAIOUQJG1bPOim7lkieCCjlEAH4wZBIXp79UGmmnltD+h/d38OwfDvaphvf9/RARTFfgLoD5lXUb+gLAAooMAQGyKWWxmSTnn+4AMHNWa3Zvg6Rg0Y/wYc9gjTZ4IaIPULKRH/cH+B8zX+CHwoGEXvu/bpOd/B8ADBz1nt2b4OoaNGP8Hq+rgfz1w03X/x/RkYAAfyHpurbKR//9yuaQ05FZ3/7e9OnOrtC2Em5VEbK79/wAiAyKFDRW6ighiZkV5twAGBxP2083neDxIkS//Bh+rq4Z6QEUxXUBfAbUu6nf2sAZgf/2ltJN2X/wCwAKcGAIDZFLPYxJJzr/cADBz2nv2b4EUNGDH+UAKA8WFfwjzfe//Da4f/VldWfWKuuo7EeIPUBoAlWLDj5//7618KwARjuvpNgVo11dnqwAkfHcItBTxDdUn2GAABAR4AAgPHAAaJiA0RgBhCWcjhlfr1WqRZD8M/Mo60mOEMVUINBgdboAMwAEX4uE8juf/wfwAAA8iQZpAWgRREOYAD4ckABAe/Karyzz//Q14CZneff4b+BAPFtAlVj0dMCVHbMMOcuYNSvb/Pwx4ADngP4qVYe47lgqW/96NiYDhSQ5j4gKoSz/ngfNw1RAE7dMUR+e8J4kOcABACAp6hSWcxjduThAm4AAIAuAAEAh0gBRcNm1MHbfwBwFtPS/OGUs4SOu7XmxJ65pSQ39fwhiTzFgE3ycLu4IB94kNdMAA2Z+GRoqRVFI0ogI4FfKgpx9tJADkYzHIO7VGsIJZ6PY4QIa/DpQWJOmwGZvhhAWW5qm7QAyN6e9fqM7fOLl6xIL8ACgAw1hClTvVTWhPV1/oYAFgYchJC9rR03nyP88CSAZH+g5ei5E/IHik8ADto0+5acAJVTdHvwH/hzwAGAEnIAAIAQE2/GZUK7RlASk9/AGYrDVmB7+JPj4A8m1Y3CfB1pCuX8QDCAAgDC2Y2YGqbjFnJIwH4kAA2At7DlQMwwTLh4ADAugLgXlqavBoppdA1PASa+y/9/9/CPC1hQAGB9QcF8F64Yd0hdCUeFgNwqdY+3FzKxQtwNNFAAgC363ZOPOG//eAMLRzrgYpyE2MlTIYYgLlAA+X7M5IX/vBgX7lD7xCQ/1w1AARhYiiox6yiteJUYAAEATgACAWSAElg4aI1aU+1+/UADUk9Kzj90HuwAWuAY03MI+u/23w/iQxAFgAGAFAG6GGxeaIwAxGEVkFZ7Slue0PAQnkudqDam14D9oC4oNi77WvZzkChDXYaKi5J038iGQ5GCs1ZjSCW6hOR14LoPm6qjf3JgACAAV3KCIwXUn1ODeqab6C12vPLtg7EwuPqEPzvSRMvw3n8QNwAEhuxiOFfqjGPJZ+GAAIABHZwVWi5FOoe1MGFCWvQ2VFiXxsH4jL+Bm4gXhZ9QMPw0FLVW4x6kJfzQww4ACRhUL2mUsqyYEqcYAGwC2KorbaQsWXPsDkdmtDPIBEBMXyZV3Awmr2ml6vfxIfgCiIIRXEOxRzCHODDgAJiYpysM7FmtIc30dxggQ7+OiguSet/yAJBw9f08KhMxtf8MJZzifDQyK7i/wf16FAA1pvEACQenLwwlku6FGaXPxFDihvXRMyxJ5HV84P+ICsABwGFs5tjVNxi3skY/B+FgPwudYe1BzDBMyHuZycPWF+fvAgK3bn59J32mjSb9//4ZgCWA+C51ghqDmliZkMOtDG3//CuAB8DemCXgnaVZHQEMgjsoj+aUt5DXAITCGMzjamBYmoHEO3GjyAsdfjgABkBwBm4jTUvNqbkg4MxD0lmoeJVwBCwAXaTA7ODm9/nv/4ZgKkAAmA26Q2R2WCRb+DhZS/Prb1puEc/76vF4kMeAA84wAww6kamyZogTQAHOBocStpbGqIIE7iswBAgTaVTRMwRJtEYADQCbhLB2WSZj+z4A1dE8PNbv3X8SG/hgPViyhCLlMERKfJ6HoiE4FC0xq71AVwln/PMfKbnHAdVqP7wNxbB4xyXf7pluf7gAIzEUhVEfzDUPcoPVAFpAN6wyDn9698P/+AIAAIAKNJOiD1gbU0BMzEuKTsrRcwXoAOQD0AEUnCFB5jEU2gUgIhwyCiXnPBgOcvhgBCBAvKwvz+M93/C/xhciHI46jSsJEK6gAClQAAQEcJiQBRiYZ94MAYxmM3FfrDFNeziAc+oCcsNa5u/7sIhKd4GJfPWNCKv/8bDDYAAMgIAM2Nty40RgBzEUzqI/lFqe5gfgBD0e2BinIwb2TMfvEIWTAaO7x1Y8O0GzhwCF4h7cSbU2qALSAbVhkHP70HkCACkMALBUlNqYPg8BtFyrH3X8MEjP/rBmFFNGdHjoghSm7QfSGAAmM6JxGT+0CtJHozBZYPoGcWW0cfljunGjxX362MTWuCTAASMwiMor9YYp71fNZkZBk+FxG4/w3cAAMgIAM3AZbmBtTADmQZHUR/MLU9yvZbn+QmKV612AFpANqwyDn96j8AHD1GifI+du/wn1f4agAI0AAnA+bJDYH6YKF+B4iAYYTT2gQFSTVzBhhNr+AP7jjjy/v7/+FocALVqe1Dq+tVgGYDeEDIJF3UWRfB/JR2euzt2fft5/8LfABWZDPhmErcbtQqrSqQj32wEBoJ4JHkdlWVDBPs7hjNMjy7//8Mqzlyn/XG+ABWAO+QDeoNi13WABegRw+4ISXTSvhgVcAhOIc7EG1MCQC0oG5QY9zTz++RkI5FGfyyktcvgyCKVk+jqz/jAABsBwBmRpuXmiN7ZhndRX+01L3t8AQJ+hS5/P4NoG1IHAwQIwBHBnNBNOPyDPahuRa0I6e3pTUfRfC3RAhhLaxpWBI6X7p/3hCbqymPXzHrWQ7FLKxErWvfOtGrNKZb++IltpTM2YYde+/v//DD/fG8ABIxkMRR3+opT3qYAANgMAM2NtS40RsAcyDI6iPxhqnuYHrgD8oG5YbBz29OAQvEPfyTam8BIX4bQvLU1OjZTS72AFtAN6wyDnd68OImUASKRmSTeeHrBHEhunH5f/q8d174agCik9QG/noA2JV+cJKAvDDK1pDAqESRrPUgwAxENLHkXef9cOQAu/VThxv8A0QW67S8tEs978AUFCuMJS5Tvm95W/2KEUoJ8BPk0OL8vgBYAUC7ql7JF3+/+GIEgMOR5C9jx03n3/5/ygABACM7sCJ0TQr5APAAQDCIx/F761azseGvw9506r3//DfAGQbMprl4ruABmGp9Jlh/4VwBPAbxcqxQ7B/TBIvD0MgsCmDOpnDYh+jv3/B8lUigbvt6kRF/e/++GMAB56F1k/0Re8yCzyWoYkogT9K5gFIFAkZZRyVpmkpT/g9YTFZeC4DqOq8v7pa4Ej1qCoYA8Qfr734acfw54AFtCYCBSo1d0hLYS3/gVtP/AEgrQnc1zf8N8AT4H8TKkEdQf0yTMh5fMifj+GOAAhkfGFUTqG8zyn2AIh4HJNE7fTbvsAYgVDZh1rJkqTywwhaW4AtNQiv2r/8L8ABA/DBjholpFMiUksxHw2AA3AuY9kD8MkzP9gAyIIAsSs0WEeMBd/ngCCWe2JGq9jBvRQt4YgCQsAD91SWbD396CJbZRGM/D/JDASd5wo5v8dlRYk9cQ/CvyEjCI5zsUYwhzAw8ZWi2fevBD8NBZWp0K/zvBKnwAkRCvqVU+//h+JR+khqZfGgckcOm4L+ACoKUHS4ZBdXzm7u8BTnEvabCty8hf3/f733kA0IBUDvEbNqChJc2DCSTbrhIbTG373f4AbhZp27s6/wrgAIAxDXsQ0ykyCGzpIqETDGeCETZLlF/zFvSQzwQmaghjP9aUe9oYdQAtnNHLYeH/wvwALIwf5a8wxXOWbvZARgFAMNo5KpuHVTGBHN09AACAGowMysgR2km2hzOyAtaBeWGQd5vX3mbY36v1XhqmwCVXzvrcPHIUR6t2f4IPAAdoTAYKVGroekJXCX/8GAA4IeG9KSMaWpQpn3rMIiKKT7DlElu4SE4HDVRrCDtAVwln/B8MABiKMbzxE0iMnj3/BhhgVt8AA6zVwqr98E8tzxZfkfa+Rj/EfmJXMdh2eo1hBLPADFJklDJXVhMnSJEP0exxghrsNlBYk8bBh/DWBIDIwgDRKzSBYR4wFj/fCtNim8JSsB3/8GHwBBLPbUjVexg3okYDD4AgQIAISwAsFCU2puFrHX+tf/xmID0ADQBaUDcoMi5zWvAHMZSuor/Wat72h8ABGAA1CcDmSC21SJ2Co15gEHwJVoc0ob2JaO/9DEssATZnosAHg5p+NEaiSGnaaiKE1qK+Hfrs0xT6rFRgAAQBeAAIBBAASXDhojeMA2UCA58urLnUDTQr4QdOCDr5ZWPOIGmxXxh8inK4yijNcISDD8yMBv3QyqqciNEPtCOBf3AyiaUiNUHvxQAwQJtChskafJe5sgAgwRaNDRA0QJCJ0DbZobJ1IH4/+8WAIqqYG52asMorl+bgAO5ggoQ1+GiouSeOXkJ2ORh3asxpD2rkgT6wNnx/1wtAAuNkLrL9k/fAZAKBwJF2UM1aRpGU74JfK3Lf/+50wmKy8FoHSdV9fwA5GMx2Hd6jWOJZ6aQMIENfhsoLEnjgMPoAKjzQyxR0Tt79SP/BFAHIwzOgrvYapz1anYAMHfmOLcYd3wfv4gLeAEGKQQrIrR83yJH/Bg1AAREAAIAUBvbpX2EbWeLB6AEEsJUsd2kayJau3950tH6+wMLDaSnFiTfb/7xB5WwBa4oqef/1eL4VgAMpEAMME2hQ2QNESX9FACBAi0aGiRogSDDDAAdoTAQKVGroekJXGW/90AZEEAaJWaQLCPGAuf5ag3hO7D8pf/v//EH9vor///DnAARAAJAvg1YivpIgcioN+MAAlCeDlnmdpPnIqjYVtR4A4LBFQ42p/6v8NdIE7OvBdB83Vf39owABACK7lBEYJmT+mALAClCAUNso5aE7SUo/2gGHJSSvbwdJ4gQ/iwAosHCLgym+9//699e+CLAAQQv2whr8xqVcQ2G/iA7L4JQASAwxKSF5N6Om+QI/4AHOsPClPSiiCzHkh8QBzhQKGmEclCZrGT/7jwTMyUE0HVcV//wfpSBDBLXoYKC5L458xq5yuO3VmrJJaGHBkvAD1G5Y4hzwqAAzIVqd+vA/dJ+y1X8SvQlw10DCQdWPo81/qMf+wbkwpV1sbb/7B3Kioa3V7/rEKW8QFcABIwfDdp9KLsqhCsNgAA6Agio6eFpojADmFA26dSy8KoSn4YSTSAOhb1aX54oBhG0ur/8N8ABEwAEwHvJe2BmlyRnRENwIFpjuHqErgLf+BLSfgAXP5lJGh9/+/+IPIeALdFxjan8HPG1P/4kK4ACZDKZ0Fd6jUOeqG4AAYAYAbiA22LjamAGIgjMgjuYUpzleGASw0W4zN/a//q/174XwAKAFeFAoZZxSVJmkhP/vCIB0LOt2QmKerfvlkLgoojWkzpwYRroawBoICxR+OD36pf4g9bEPn/4R56wCwzSn7//z+2MGv/4e/UY7CEnFSjLfrar5zyMgisoj+aUl7msAAGQHAGbGm5eaIwEIBXSgbFBkWvawfmZhndRX+0tL3tDDwBAASKKtOKQdQofDcLiRD51nX+AWFpY38/i3tDHCuAAgyOiZZ2erqkPxB6qRW3ZfHwYc6SUz9/BNAAADUNBmmBaAqYk9eB0RRNfxKiuvrlNiTzFgBDdK1H7v9R9T/iTy3+GFV4zEnlLAkep5Ct9HLj38QNwAEjGQzKK/1GKe9gACRPZEbkbyWOANZQExoa97bz+cAAMgIAM3AbalxtTADmQZiuI/mFqe5jgELxD34k2pugBTSAbVhkHP73MgsIQ9LEFEiPqxZFF5jdzlKO/2nveS0MPCICUOBU1JTamBr+XwBAp4BHDLu84Z3+Vfv2Dh3jlU/hzwAHgCvCgUMs4pKEzSQp/z/xt/gHqfRPLl/iA9AEAAHQEEViOnhabUwA5hQJ+nUsvCoEp8Aww4ACCVQ8LVzBCer/6pet8vj31vDwG8XKsfdg/hgoZwbGQCBSg7j4hKC1//9wfiAFg4A1TxEY21N36Q75DBGnI+bF/28fjb77619YvhvgkXs94BfhvZuwi+uQuAD0bJi1r79/v/+HMAIym1omf72gRDThhrhbcnRkkwa/8Kk2KAC5oho7jYuX+RgzqT34bgCN8CQhXkHlpS9hgfBYD8LnX3IPaYKmf4NcL8q3m/9f/eJDfAARjxEOVhllmY4SqGsJpIWu8//G4kLeZGA374dVX8n6IfaFgVcygRPeoq29/2oGwFIGpzqCKSxfseabIAIMEWjQ0QMECAAxCIZkGdyilOcoMOcEOoB0iwanP0xNPffP//EB7ACmV7+x8ASFotNqlxpiueo8PjAOYIBY0yjnrTt5yj/cIABIQAKqNEqG0FRKb/aYJGRKBNBlXlUb+8bDK80d3iNEAFgCcoDQXAdd6BM3IiGvguyS0iYR9/CkxrK9nfP8LQAEAMZvKQSj3LtfewMMABCQUhO/zHrSp/Kq5LJEk//t/GwyvNCu+ZonhrwBfdbH+uF+ADxoJ1r9NRzf4CBRxNtPfF8b/ARDfwxEu6+7qCZ8d9ERfc7/CndgC0kDZSDanKgxayDanDQpX+HMJbDqOAHAILZ7IGrdg1soZ/cUvAfoQAhp35+HD/gg8ABIbkMRx26oxhL2cDQSqAAcGqRg8LcatV+/yYAAgAEdig6NFyJfSdAMMWkheXo6ZEgR/gS0nBSxN/F/bzxxXNY7/wtACTwG8TKvuwfwwSM/2jMxAYKSG7+kJZAX/89pMGFCWvQ2VFiXpsHqCcrpwTAfRxX1/fyAc4UCBhlHJQoaylP+DCokgbpyfH4X9vixwHyjpvvfamGJ1fwYQAPARFEAUK2aryPCAu/wDRjPiGq/fSUcf4CZicDBaQ1f2hLIS3/nhYD4JrWHuQcwwVLgAM7ZNJptGWA+cANv3qQDgcnKLBgQDpgGGtyhn7Hmm+6AD3i+NiOQdf/7h8AYTMbDsXei+G4EmK2RTRa8DxoQSJr9/kBEo4Gi9lNNHBB5iRhmb8BtbH379/8fxXgAIwsRTsg6yiteJS+Rg6E7T6UXZVCFYfhb+EAJlyPJro1h4V02XeILlURGvUUbbzinAADoCCqxHTwtNqbzMKBv0yll0VQlXVGGIAlJCAGUocM5H3a8QmeEzdq/3z1hhFuP/w54Ax2tWON+l/gSLlnv8NwIXkP8f64A+3pt+/r8woeSF+CEbMTfzWP/n+XhjAB7c6Svd/978HJbbXT/3z/85cCbp6sE6qJKvd/4R6989eNa/4bgAIAEK1cjzTkvR8Vbfc5+zZ0pxLgwws2/AG0bHoVyq7v9cOQALFkMCOIqXqJEsv4Lp/Vh//fHgSAhqNlJZrcSwgR4JzPBG8PlPm6yjuN8ACCWAGCBFI1NkzRAn/UzACDBNIVNEzREmH8ZDDIi4HaY7lvK/wBAV1iSC7Fr+6npdTkRgPm6GVUSmRoj8Hgw3OdyzLmZ+564AOPCsPnbL//cLKChMxNf2+wQfTq+HvAA/Q037aVl+/sVC0rafx4KAAa0GILZQm6WrwBeGLqlEenyjDnFBgZtBK00wCf5aYgfA/rhzwBktQ7m/8hW3zK4AV3cRt983+GIACMDMOZxSxelPPlNvhuxTWpCuQMTdO6OABZHGNOCtny4gkUm7QBG6Mtk0b95MS1DphcnODM2xgj1yR8d//+QL8pEfjn7+v/BB/AAaOcQkIa/LRcXJPHIcACwBhpcqx/Zzck8R++AkC3MAEClp9XYTXXf7wkCZv3xEK7//+94I2zw39QQRJtGEMgJ4SOj/+tgoxFIWbkj5+Yco4EbFtXhb8ABYowBxH1o7FCsRacTjNs2ciTiLtEIHjfBF0vVJyReD0UZvAbjxTqde/oAML7qV/7e6ypVdv//D0ADwCtCpclFO2GtvwGgHIOlqfhuy1t+AFAAEoXgaw8v1UgfiqNeMAAkCcDGCK/EyJ2Kg18MABAQVij2JFK4+8mysr4Kj+o04hHqPa0r/QYCDVpAHgFzjocNEYBe58m6r0YE3LiNGTMn4OImD6fhb8wBhMCU6m+qG8iObv/B2SXJzOZv+94H8SihhKcja9Xv1/+z8f/P/1grrlGcL+AAiAASBfB7BFfShA5FQb6AGG0ISqd2qa0J6un98RRYAI22+JMxCvt22TX+7fxAL8ABMGrh4Rh+l8QZjkAwRfAATMRTFKEbijWEuYH1u/R/36HQNsPZGjBqpz/qH/hmcPgGADkJ9pIY3+UlfuUGA61jV2/36D//11WICsAB7BFKVODYD5NK+/7CB3371Mub77kAOcKBQ00lmqUNZSn/YeBlkYRSJ1b92AgZNU8qH87f9gG7OAAIAJLdEGisRD/cGBEZzAMo8TGW4Enj/4QkPAC5nAz5R5d/vgB9PGI6OdaTcN/S40N/QxNMBf4gNfeBlB12JnDmr6ILUcycmNK9P7TAsLrlFJ88NRb//LCT1QAJUgBoFIS8/fodCe1X04TGcg+VKSff8Hs9GL1+dESRWPBLqfmOmv8QHfhhEIL5a5LZbMU3yA7TACBbNIZTYQab8LAfhM6wQ5B7TBUuHwAwtHOsYpyEWskzP4MOHAAQEFrAenYmZ0nLgl04detSF9wkiwVCmbZD2TBv0AmQ/e4mRExb/I1pFfX/4fgSGA94cCHOS6Ib9r/fbj4AwAKuAtDZKW6iLF9z4EIYsAHyIZykCO5ZrSHN/aAAEAErKwIvBVSfkbDMKccG4EFLJKpN2v0x5kql7DZaH/7gDqC+w1VKZzK/f36MrPv7gXY0Z5iyLuwWf+RF4YgAMP4wQIb/HhIXJO3IfHA2Iy4F0CKuqf/7xAAEgXQaw+zpIgcmoNgA033ST//3P0AAEAYy4AMDMRMs6KEzf/vAiPEBSQitYGyBt4lgga0fBBMEg+z3bpv+CJEwVwuKTP/731wzAAoAMLYSlU1xQ1kRyd/7hjrvxd2UpTe7xAAEoXges8ztMgfiqNeDAaeYBCTv5bbFa+GR2gCAC5wtcqEaP/47EBrAAvDYrJgSgZJxb1/QFwDuCgWNM4pKUzeQp/2fB4owK5D3g9K7hZ3v/E+IDnAAsAglDk6G9pm8CGrp/ASAILoQpQ1pUxYQydP4ISnmAj2T+946F3rND7U/4gL+AAjAAahOBjJBbapE/BUa8wBBcHp0OcUN5ENHf+hiWVoI4sQ/zBJmO6L1ZLBhmSaORnP4kMQwAEyBwJtH2ovCrEJ/EHiqYqDLKL0gSowAAcAQTQdPS00RgBiCoTMOtZtlSJVYAAEAWgACAUUAElw4aI3jD5FOVxlFGW4QkvjNjwD+YM7BEEI7zz7CFdz8STAARB4qmKwyyjdcJUh+G+ABUA5AgFjDKOWlO1lJv94RuVRle9BRevOKAgdz8K8SJV3gAvyUN5m6cq463cu8/xIehgDoFg/0ZayqLkSlDYAAOAKJoOHpYaIwAxA+F6j7YVpNiFABDHYswHETKNsZUKLH4h05wZ/34RQEv7U88f/5/IG8qTkRZ++AhpHY8vRun2m2Zx5pCyfQk9DAFaHpE50F3fvFgCOqGBud/hWHwAg5CCVXFYPk8RIf7w+MArAgFjLGKOlO0iJv8GGgEASnuSGfHZ+NVXfv9JJlvxAe8oAP6CtIUU0Qm3g/Mxucrjv1ZrSXtD8MABvaAECj7woaIGyJL16IAMFCLxobIG3iXIzAX8sLqqhR6iH3MzgT8wLoqnR6aH2qREcNMn///XOZkUJPt4v/4Y1PAsdvnDKdk/+cYgACgsV9jan8JcNQFwHQn9xBhi+as3+y9tlcKV/vwP4MHHun1e+wBI3feB/4XgAO2pRc3nl//tERkZJpjdif+ulGJBWWk5ZRL3mwguVntIUxZS3+kkCCBLXpaKCpL018xq4qfe31mtJe0MNWQlE0Kpdtl/7/+uuvhWHwMZ8h5Qpu0VifyJj0PxgAEgTgcs+vpUifioNBhxBaQKVojTF1R+t/s9j6qPf/rEBXHB2cBZAgApDACwVJTam/6wBsFvVpx88WFHqhuC/zy0SWt1846vp5f8//+IPi+ANXSeHnn+IDWABYCZxAFCNmcC0hwgLH+gKBEcgFEC1McKn9xY76DRaHYEAAsoyZcXLC2polD56xB6wCEBX7xHef/jcR88h4pXFFJvP//E3ySKrcRiD1ACFhyy+P+//8G8AAAEZ1BmoBKBFEQ5gAIwysHC7e5TDp04cRhgHKuAIYmTR89/hvoAQTRqEi+0i2Tyou/v+A1xqUiQue/z8MeAAgEPRragUpqMGckSnoBFYQDT/U4GBvCMmf7wlJuAk/WfBoK8SkcPHuCeJPMLgCqtR/eZO/ifEr3iV68SeuIqjmSUe//Gn7xJ6wELuR/36mcZSnx+fvggsCjYHBoKABBJgGGGWjUu+Yef8yODZtBVEvzdr/7imYAgw2kKlHSz74PkRgfN0Kql6b9P/BiMmi3BgY2S334AF62l6vbtV6T5fp3+fB/4ASa+U9T3+GOAAmRDK+MNyyVsYtgAAsBwBOhRkUmiNgDEYisgrPWQlj1h4YAa+dqu/3lX2A/8OeABQCtHBgqvikoRMJCH/KMBlVX/b/4Cjk52n+F8ACoDkGBoowjlpRsZSD/fUhMkRoQyRE+IGQQlizDUEjEV1k4YrTABtLD9xPvbv/4k9enAGiaJ8/P/z3wEgeej/n/xuJPWARJ843+f/l4Y8ABGgAGoNWw5Ui8rESnpsTA45IWv4+JoSb/ng13DdKAIwumRD77esQN8EflMoADCkMMPY5DBATIemYBGoVsryX3eZkMj8wuKJQ1yoAM84jwkKeMImG4EfHPbnm1NqgFpAJqwiDXd6AQEiBMCdMSUwLkdDfkZSLh3Wg9RBLA3Q4lvmvSZuH+F0GK2VxiH5/EBb5mYzlcdtpLW9rQw+hnpszACAgVO5Q4JdJL/B6UTHIb8Xfh1jiMSvm6f/Eh2ABYMK5JCdixU3HX/54EUAAmVWBE2fQTxAHkX7846+6nXqbm8iIRGYZmIKY5zAw4taBWcOuYHexD9MRPZ/9iRuPv6PEV+/wtAigACIrsCJs2gniAPyIhEIwjMUUpzlBhwAHWAKi7zS3QRbC/9aGI1+PgRNZP1dKaVf+fg/SDtllf2//iBsABIyCKyiP5ZC3uX4gABAD3AOoBmJzpU4dyEQw9+Ob89vff4AH8pIfvkj/19wAGw3M7BWXxbCGqgLQREXozFXrfvB6EHKFHlZXeKD0zwMGzRQozInd4D++Kbv/99jEHuQ61xjr+ylHC4fC3AkILRla6zC240p/79AJRTT2oVIV5i5X9/f8RZYyrbb+waiUiSIP64c4ACYoylZBUkEW08hgAAQAOAAIArwBJIKGiMEpN4AcYsNzN2v8vAGF35GUVBBNtOKDF8FHgAZSAQUbWFCzxd158fEAYcZWMi7xdx4HFfG8ACwYQj3pyqFSdde/gEAHaMDBRjFHQjYyEH+wwJCau9YEEAARVRgVNH2EcRtINWdMCaC5tJdv7yGjHI4zcWU17m+08EONZ5HBERIe2cH8jIAQDMoZ4wycXQzg/ZFIZEBBmGLmgAh1pPTMn/+ZfXofOB2YsVJRZ/f1aKJho9vTdnjIqQy9PGwEeen5T15Opr70qKg6amTGJq8tJg/C4oSLYsMMAEas3Cyrn+YAGrS7Hq0ASF0uk1DDiWalrvDDAgwACI6OCo0+gjvroDCP9ycvRU33n/4VoecQ/9eHD91laEjXNo/qgdrkkTEy/t0w2u///f/h/gK9Ahni+x0QYfZWeZichXEXiC2EuYx5jvHNSbKVU/8tNAACCBLAABAUBMAz2tIkRJe02fffxxIAQGvS4ikdhF5sPAoVHA7HHTHOA/q6Y6iH+wZiH+CyHpPaJmTJI/+f/Mw4Ptm0oiiYOIDbfIL4V4IgEKeCRvqxgygJ3//z1ND0Kyuix/0P2F1DeE5Wip0VJaWoZYhgANjGywonqLxxLAqSQNPOjc2xOyd+/4bSqf8QH4AggwBXLAYHXhtTe4RZE1ptTAIiCbYg3KI5hDP1GYIlHvKSSKTY/vABRvqtXtxBOcFYM1Tb7ZBhff8iMR2YdmpKa57QwhP4BjBG0jZ92gzEPEe626F/hjAA8CIpgAEB+kzI7hATf4AA/NACCjbwoWeMvvNEDRwBBqYt/Rz9LP/3gI+zN1XJcGGAAgIrhc9VOMJ7WrKi/ADQBI6mxZPgYWr6X9mGe1/CuvS9X+/hAJFHhZGLNMPHsIDYYcD3LYoNBIyAd//8LQALmYwcekL37/E0BN/wAUgAJAa9li5FZWIEgBBgG5400b2nCWwhahT+BgFggYYFs8roZK3vfnFiM9Q+tzdP7kas+5vh6i+Ah1lrZ51wi7iMhINU0tqY3vA02szHttu/7vCfP5eAL4c4AFgwhHvTVYKk669/AFgDtGBgsvijmRs4iD/AV3gAS8tT0zK/iT8MZAeMLW7kGSUpDf1/iT+kInKqh/8XiQxgAIYXtODnSacub8YYEfMiA27oVVP8n6e+8QBvgICXSSc+a8YZEQ+RFB9/AqifpPz98G8AKNrXz9+cOvt9vj9QMyx/Ekryv+k8NhYq4v+3/y8ABNhwfdNpRVE0cQH4b0EAA7QAGoNmw5QvKxEl/7RshA45AYv4+Joyb/gVNuAAdU9tMLe/vNc/+G4AFtAAagStcoXlYiS/sBrYmBxyAxfx8SEj//7gFAh7NZAtLcILZIFf2gERDgAKD+JxMDl0BO/y/4AP2aYWIzjr//f/rhqRdgcMYKNBWGgflb4ItGQ0ztl+9//nrfcn/XJDAATAAjsEXrD40gfN01B/CvQyA+5oXVH0nqeeoMLOcS+0VPrrxACZAYPcJpQ5rhlYR8MJ+nAhwkpHnfF2T/8R4GJcC+MYypdX+D74IAg4ysalCJd58pwAAhSBUjRHJOMjFPX79X6acNo7/C3waG3y1VbpEuvXkaQ8qZWHFu67r3cpxqjVt3/eASw3FtfxZullk9uhEvSTb394ZyhYhlFzuiK9vwS/1xuAAkE7BZXRmk2UJgp5hs7bBpwESYU5YwjFsPuqNv37Q+a4rLhaRcDpk9S8+gffgOP731/X4xv8P+6/4jFAFYnLSZH9UZjj3OLKq19xnf/9vG8NfGF2Q7OKgsjHnF+MAAQDtlOAA6DbzACHsjoYYSmjrw0UcGhH+1//eh+GpRZS1Zn/8M+AIezWRAtLcFskCv/sAIiCgaf0mYGroCf/A/CpJBtrczETrf/1w94RcEIekAQRgQUlfO1FPb+vlEPVzJq1s13/f8alADC19Qagj3+usV8b4AFgYkQDD5eNflFHit/sARi9CFppGtMgoSqHAQjMaI5Zi9USHaCM3Im7vf7+8BKIZ3YZmLLW5zbGEKYYE6NFTxMqbtD6ACetvSTM2xi1Llz8oYPW+EMQeVPBCq2euF+MyALEEAI9gDQ8/NqYAVApaBcSEQb5unAR/Ja3fNqYAcjGR0OJ6iUMepgAAsBgBOhdkTGiNh4Ag3ANwiLvP/hiB4H7AL6wuDfd1/kRBGTCO5RCGMUHh6QcAJGxMXH8emmX/y/GARFyu/nf4Y6acjPAAsEHJ5yLvRc3nHf4BEBTDg0VXQxUpGEpH/gv08H2VgEZfeVoj/83gAOcphRi34aIiJB0zeCP+juMMOZ7PRARIO2YdfD3gANmycNuhUZUQD/W0AQQZSdCjhRxwGYYADm4CpayxnMMIRbK//7ZWzXEn//njJ4AFw+zKsVPkrv8P8AEsNwn8L0mt5nwEcALLyCPSfwtBLcaxDuG+np9RxdjeREIxGEZiilOcyxgVaoVZnh//v4O+qrdZvfeAlAoF3DLWRT7PKcAANAU/AOBeAmNoCAbvAAIypGoxf/5/49EZlES138ZPhka/1MFD6bX4IPUAPpTCP4rxvlWseNq7rgmbV/+8QedRF85ZBOuPdxgFYEBouxilpRspCD/QAP4AmgIQU3Xre9gCIPhcw20EW+zig7IQCzIzPEF7b+/OCCAEeoB4efm1MBIAQZl/7QEmXqQQQv5wBH97W6k2pgx1fAOlBx14RDfe4FM81zSZhURgQJUZtXv6fWqH5fwLwO2AX1hMG+51643wAE0Iqz1mWItQABMA2KAkFSG2ak+Wi+Hxg8yLAWdDqtofg+gEFIQ9G1QuTj7n8gQAV44MFV8UkyJhIQ/7mArBgaKr4paUrCQg/wegGFd7k7WjJuOv/zxxCAj3yG9kSQ3n6CIduJG1+v47ebNr9/EBWAAjF2xWUdRJWNOJYAAEAKAACAKSAKJBU0Rg+BgChZ0IyCrJJp55fGAdwUGii+KSlExkIf8GGM+AaKOMgnXaMTNWPi2WQp8w/XLwAMQgGGGUjMq+YeffxYBBhtIVKPln3xWIPiwE17lpvP/7gAnA/QLqQmDfdvN4CEQiJhHYohDmKD9cvEBX5hjlNIWOMwXUZqxv3tm2N+pVd18GInTApgglPXdF2xEPgQAVAX9xXFVk/F+n+DDg+SAFu3B95H7wyHawIb2/wpP+NgA1kMjuYXFFoepHmRBldBHcklbHLLAw9WAp4BfUERZ7rXgEML/VkyohKTSiDpnQ2GLhG952r2OnAEbXuZqDam0AO8C4QoALn4hXQ4/7uyb8Bh4gwBntAYHnxtTFgy/FI7ysYqoh8x1op7QuqETwb/xAe+AAxhUfLMhJFvo8jw2AADYFO0DgUJDRGDAGMOhEebSCdIox/kLOhGYVJJONNJDDAAqByBAaKLoY6Uq+Ug/2gII/n9V4Lk645/AadC2kJbVcX5jhTD784MrvBGDPmdQ0+3/DPWNmb4PYImyl2/gqzqvbPcwCsGBouxilpSsJCD/SgCSqcpUIIrqUdwFmE5Ht/BgX/DVgMU3NCUPl3AAnkTG/QjO7KDXTAAtgDAdgJn9+AM2wadilV8g/uh7/C3xAMrhNUiCFwm0qD8eABKDVkvXIvK5AkGHAAQMa9BSFSBTKEdn2RNm3+OHuEWVPr9WjIGtLrj2av/B/8LwByMZHQ4nqJQxqnAADAGAPxATZExtTB+AAiYAEgFvJemBWF3iukjGDD0Re7n0lgJ/+Jvk7uAOkwAMDn4bkyTbcIeELKGMwlkZr7UFUhfLyqgn//3mrKp8GHyIhEZBGcohDGKDDwAgi6Sv/++gQAc4xHhMplmD7Zb/BNe/8AD0ZM0yI+L/n+G4EAA0KIUVbGLM9p4PQBj0MRqY0iVsfSFH964O6ZtiJ09/7//EBmABZkB9zQmaPpOU89V97O9/6fAFAEyAQEuFUoa1wuwf8YBPwYENEkI634uyfIKCCoSbvptMy3zxmlIdX4WjkWzYu3/55DwxqVY57/p6fcpn+sQeoAvt8Q2p//xvWXwv4ACQAFh9D1n1cJOGIpCvQAxrGIVM7RLWOpij++IosAEPZvRTb6Yhmsir3+Fv5gALjaCFHl9pOmIpi4egBhaGI1NaTK4PpCj+6P4lF7yvRyNNBzOezZ1Xv/iA1gAMYmKiiNxZCWsXDXgOtKev8N8ACgCtHBgqvikmRMJCH/eGeMgq8YkkjGGkiwcAKNfy9kcCBfxAehgCxdsVlFUSVTzCYbAAAgAQAAQA3gCCQVNEYAQXIfgbSrL0bWpe4AgwWFcDF1uby2Z0iart2r/+dYkOdit2qn+qw0Fc5Wnbd/m/wMu/WAGZEQrGEg/tFoaxo5/4WglAFRgKlKMhNvILY4P0SMRmGViClOcoMOL60dzPm4H//C+GACTAMMMpUu6WefvwDEQCDDaQqWdLOvgIkcGy6CJJfq7P/2hGB8uwiaSE3Zfe17ZliX+bf/rlyM8zT1l/+C+nxQBYAnJXNhtT94g8pcBC1zt8YV/Seuf4Q4qABaT3npRR/34CWZMja4TOX/0BhkbBHxA6CSGHlDG2b5T1rQShgCXsMcYv2OyIg+5YekhGZhGYohTnKDD4g9fwFraG/r/PUDxuJo7Skr68X/4Vh6C5RAsk3LaTC5Am/74AsAn4MCHCiUeb4ZZPhhyPm4kPWYb7hGJLZ+HT/8TJw1gAsDdDgAKDtoGBq8n//7oEgboUENAvEijgrW078sAOolbC+r/9+wgf4isQeuBE9Mv8fz1gUU+G/r/1wYTw/ADwAkUVMJxRl5Qe3EOS1++v7SdIBr2nOzxGIPIUIjPfxe+//+EeFcABzlGcSpZTVpIJM9D49mAIVSrUelw1LwYcDM0BM3fCRY+GruB3/4JoAABVPQZqgSgRcOYACI2DN9AO4RbbGVf/TAIOOrGpR8y8RAOYeAA870yWm4+EzG3hvw3AjbAd4jO2MK/wf6mAYcfeFSr5l8iGBdPr5s3STk35u5tnCmABwAOhjnodpeJEM//b/AAc1OFTWY0OetjiYfEiEl/RE/X8Ykc5WGZiy1ud8j+MMOZ7HRARIOwSCfDnAASG5hFeSWlxzizSHAAC4GAOzAVYkxtTAIujAGUlmZL7XzvLiT1OIQBV5Sk/P+EcSevAHBJTy/P/EnlB0enz/iQrAATIbkdBWeolDGqcAALAYA/EBdgUG1MH/khMRkEZzCkMIUGGzCFvIQBmEsSlT7TK9l95GQevvZGlfd/bmqWtH4IYAGgFpAJqwiDXd68GD5fDHAAZmJm5xdQ5DWqYAALgYA7IqzJjRGwEshkdRG8glDXKDAFcAtNkp5/+HPAAqByDA0UXRyzo2MpB/hTUeAENlZtIf38SF8ABzlIKMY7DBERfcM3yIueBloo/KbaPwEDqssUuxjPtp2VQhmLACgkmk8492COHI8+0y71iTxamAGZlLj9/7zBv/z1iTxamAnxPdnF38SeLU/wRN7PG4kLcADENNbJk8G6Vr4Dfzx4Cgx3+9OzeCpOOOf4MXiGHwnCyaPnBtNEL896fxAXwAKwDnlAnJCYMc3oMD4AF4DgwNFF0cc6NjGRb6X/AR7s/7BhBGVtpN9/gg4ACJgxu3OS3lrIQ0P8ACwMSzGSLT3FbBAn+7mwAGyK4IjTqCeoPGinYZ6QAmHiUOMcHkFDEKCWh2VWuf/70exxhzXZbICD7pgIwoHXRK5gxSYvS+hZJ/eAT8/T1gTmd/nmD7xDg9vIy5+xVm6fJ/HI52RklY+JBBgAcAXGBQquhjoRspSDfAEDMV9cHp+gAQykxvUIjrv9U5rQ9vlF+KGwwDYABvgPqQmDP8+8gABAC3AIoBtqTrU6ayPaAVEEXQrTTTVCEX/ASTfADIKbC/y3oIKJo+e15jT1CN9ff4kLdAYV/kp26GScec/gYcOArfMAAQCgAEGSsqWfbK/+jjMtmpGLXH/NP3bBfyNp569WfPTQ9UX5H+Ua7/EB2ABYII/iUVNC5OuPfzwJYABuiOCoo6wjqJ9ykoVRDfKc37cwA5mMruO3Ulre9YYdST9oPeBmEXWU9/d//4WgSwADdEcFRRlhHUT/MzGUqit1Ja3vaGHAAvAHBM9RT5JpZV+BBC9pnusmjyF7VF/n6DWd/xI2AAkPOpHQRZBOuNI8gABAL9xAAE8qv0Al+w4GDANCoFiCQhSDP7ABkFp9Ft/vzgAIwSoYK5/16GexcBRIzpTlqu0m//eYzcOChbayORCy1ne3e8g8fRv3fA4toCwa6NgC7g5S0+utguDtgaCTH3nfb+IDMABwMezGyNS3GLOSRT8G7eVYGwfHnLIdz3gYIF9cOcABMkMqoYTEk+xi2AACwFAP0KMik0Ril4I/H3/gXEy9/l/hvgIRiKyHM5wnsesMrYD1ykp5/+N4Z8mGD5mBckPTcr/7BsARIUHpCYK9/f7/rAIOMrGpR8u4/8yYAwo28Kl3yr7oAeCATF5w3O//4ewAKHB22PlhCGcLIRhHQCdTgAMD+pxMjV0JO/1vUUn0j/1zjCQjJwSNBUWle3gGFoxkwMS1CK2SJPwTDEIv9YxHvJ14YIQADgwBpHMM3dx9czJoS6vN86fH8GlNBFgyS3N1rGOAuTOZ+7wStE2UJUXYI9f0ubtaGj434AxFctD/1qNZ3Nt3Ld/H/rIN8HZE0FgHD4jsf4aLRc21AYcLAZZFz1/FIBYGoAzPjKwYnmrf/+vaOveth/v5/GhnTdELk6pwwALgBDpQnSUMIWYJoMAQY1FLmRCeoxZwRKCh+lsK1Fnw6IBNpXr516E8XyoP//vrvs9x+HL/xA2AA4DAAvDpsnyUqFAKiuJCw2z5YNSLsGnQTNhLYwKgAVA7BwaKL4pKUTGQj/2gII7nIqtFzfff/gfjYtAYZ2AAEBlYN2Klxr/1qig+Ni2mcIkdlhdP/gwFwdEBeuJqLf3xck9oiQwFGOTXOz+ICsAYyCKyiP5ZCWuWwAAXA4B2RRmUmiMH/AYVeSsL3J9WmbPuYAcBtGQvOEBkyhI+DBmISXdKMyJz8krtHiUvg//wrBjFJt3P5/4AmJuIJY38apSSngbHHBkqC4mL/wDEAAhpwJygiLHNesQNhXABiU8BRaUn7/dwPnPXKUqg60m6U8uUErwH4Uf41b//cvVbkJDMQzG1MAn7bakWiXjdPT9losfAFgRFMAAgP4mZG7oCb/AFAx7MXItLcYr5IEvwEzIYMPQFr9/SSMn/54kABoBb2HKgVhYiVsHDSK48YDLQcNQO5gmWC0bj/2gEIZAiNaYywss1/6hl6yHgumG3ciRJN///4FqcAF+RoLErsO/7oDBYWM403a1yKnHoF4eh6ATOYHOArMy7YpY578HrDyErHIw6tWYtzWjdhwAEAIFg/+k451ybo17mN5xV3HdfVX+0PATT6tyxeFiBX+2hrhDhz+6OC77Va/wIpMp5pm/yBQwAW0Y6SkRhZf59YkOcABMiGcqCMxJK3Mb6Owgg5vc8PCb7lj2Ev5AM4fKRq/efxEdwzAAqAglDE6GdplcHkxT/cgCC2MQoY0mUweSFP9pAAMyiYk4ghrli9/9wgANQvh6rim0miyIr//dAHgCxhktGiP4e2P/hrpMTgw9AYv59JoSX/niQAGgFvYcqBWFiJXwwlNMDau29oW/vf/43oADKAYNPLSsv359A82oAMGqZTVakjF4BkSMycNoIm0n2/ttmJi3mcT/v4CLCCbpkJfBEGk8HZkEKTuGFC0VL7hgIVAhBrHIaICJDwz4GpVLge2ysSzdv//h+2mEHCHOw0+JvtmPtNheO1YpK88iIRGQw2IIQ5iAww4tcNkHlZIK6fv8DEJeKw+BxWZg4pX3/v/yfCQYhW/6nKSsn2hh/CWAAjCzKUiCpIK155X2XiFZ/lydl4AIGiUSJJ/vG5AABACWgACAHTZAFkgwv/mAEwmWJLNFVIbyiXYEJF9xfP6eBoPAAvECwRqrMJJhZH3zUd2/P/AERUC7aJYeR1NUTDDW6AC0nA0S5SP//fxjbBg3Vv/gwH/XG0AwBQJBf6pQtbqb/uAMZCKRRm4khb2L3KDIERYv/Eu+8H72zbMfUru6h+JgQemlQsizce7tA6JFNhDSG7+28QVdTEUdRBNvOID8hSoRm/fp3UMJtIEZ5n39TYjd7C67/kC6Iad8sy+/h/8K2GAAjAA+Nwcu4ttF0zBMWQLwzYhRVDIbgXbMPEfIADw+Ald9TSbhmCQsHwgBEgD15JJCGMgb/g1BGtRpmFn//+9pTRERh5///vgNAf8SHeAAw7DDDmfxwQESDlmGABVgAGRFcERp1BPULjgkdloegVJtPn/eYlchWHZqi2Oez05AxhzHZbICT7hlxoe2Y8OAZrxC/7wGDqowauxjP9JYV/REdikSb+64SwZ/QMwTjSuVP4Rm9AwADodR7eJkH/AA9MIiGk5t3kDnjlmO/3jZmdLA+IGw/AGPZTZgWpuLOSBL/wYcetOQ8AD9burv/8QuWsRFC7Wt38v2h39/2V7j4YAX6C/OLaost4qgdwxq1t6t9aASghZmpcXnLAO4DsXzazSfwjw5gAMgCDCLUQ9iP7LkSPmxUVfsQQV7DisrggDzAD2vctw8/wxDhgDA3fc/wj4fG8te39L/5vGIqdsfqv1BJZJe//+7/iMAW3OVKy84a42/1+ufrgheD/9csABBBbvjwUtaV9FV1y3hneHHW2sVy8YoMPwvwALNScTvErUytFX9vAkjA27oVVH8n5eeAVLBntAzD0IPSZ/AIkkAMMPtChV4s6Q/qgCDDKRoUeMPPBNb4MP6+776B47TklSEs+v8sMACzCN0Z36EtTfUJ/toDDZr1EJzn2WRv3BukwAQDH5VTMsuGv/D+bwAHtMAwwykZl3yzj7wx/QlYUhwlCuyCrjKoYADUmGOwRyGyLZBpvyIxHIw7NSUtz14kBcamJo1H2/93+bgBVecwRhaRKK4GdOoAVSIgl5a/fr/w/4ADgIMTZcJTSBkEm1//B6QN3dcC4CZMqcv4MBM2TQ2qFRnYGEDbifp8/32/yIhGIwiqQQpzlBjJQBhHkjYPBydDYspNd/VIbGSsNZ9/DMBFvln2s87h/j+MAs8zxz+6obR3VE797QYf+IGwALwAh0JTj0NIYcLoCeOBMFvExDv+/vGVlbqb4AgCAZzSElktLLolzDNFNyFLpLvtAkAGUAwWeWlZfqJ1A8wADwB2jAwUYxS0JV8hB/sEBJsBLSFRa/0+xgPQamwzUkJf+fpHzdZE9/94MwBixOp5kTzeuhkNIpOon6n/+DAsqQBqCRfEM+mColhdLn1+4FVsJ9HJJ3+1/i720w0Q5hGCZYPvwtIT8Eahf1LSiEcxJf8DemAAw1Bm48XK+zu378GHAFRo32f/+f1dSJf+r3f+Nwm4fAoCI+SPtcAB2JilchhOW95Smh+mkD1R8UjxrQDtB0tFxVT+Z0NMIAIJQQYJc5p4Vf6Mf+UkHiw3BAfh8C6JlSH9QZsuRJgwYb2IDrXUh9yFSgIy2vWv6giDXqfr+PwWxOXGAsX9cMcABEHysR1MYKXjji2AABADgAAgCEACCoVNEbAFhxkKVDHClYw0us/zyf/t4S4nAGITgkK/2gbUY0Jc///9WOdQ/DuCC8DawABGEYUlqCjlEjU1FEfYZswBwDEWITDx3t2mDD0AEGb8WN7WDdHnt/vsjku3f/LBHCed5SHl4TqwgzFfEVYXI2+hrf/f/YIJlAD0jZbQXeweEfgDIs8Ii/XvGCj/CsBMHBtou1E0RZxLgABoDH5IHguSm1N4g8VSOgiyCbYeVwAGFYrTAh/G7lV3iH/gBkFRuwzUk26RKYZRELkSAD+IIr07CTu4GL9+k+6F/rhrAAcAx7GpVMQ0gUyfSFXxAASj8CVnFdouGZpiiwAUe0RmQeb//7//wz0AMahqNTO0iuTqYq/v8wAEg2AhZ1XSLpmKQsGoI3KNoRMn//3/i+LxAegAXQFpAJqx0GO5d+cj+ABUAglDE6GdplcHExT/fGAB4bQ5V9bSTpiSQrDFIwAU+TfqX7gOEoxBjta4cQ///4L/yCRAkpszCNeXbYYcABiMRWYdmpKW5qw4vgBieutdb//wr0UAI9cGpCINj/PAkBDJLWSJmrKJDRKvAUYARIV51TNF0ulOHODDqDAFRSJKP9WPz//1P//BHwAExI5SsMzFltIYv0dxhhzPZ6ICJByzM3w5wAKAVoUGCq+CKZEwiIf9oDCu933GipuOv/yDwAYh5fkdd/h6DDBeEk+hfK7e7sMcaHYuvJsr//uwCZUAARysPDyEDv+4MDSMcBUmHRKgl0199+ABqBa0C4kIg3zeg22haWJ2Wo+P3UijE5H7X9+wf/4L4AFASBkQZFtT3j0QML0OtA+pchx38cQGAIEEAI9QDw8/NqbhOAhde1upNqYC8D9gF9YTBvu9CyhgAkx9XR6yCf94ArCIenQ4/IEChlPdHJr/CtgXMKFAKOWrGyCv2Vuh6AQ0mtgWnuDNiBT9wf8pfJMd/D7//4XgAIBhLKZMjU9wmxp4noBspwAEB3EomRq+Alf7hMADQCXj1SIyuRJf2khKDj0xazfwljJv+B/AAsBDNS/PeyhzTbf+7OPAAOZEQPFjlG/70Yiz18/IIdqeeriAQQQQI2DKF2zSTyS77wBAAUAd4wMFFsUtCNjEQf4PUbsqAk6H1cQ/fARAQ1DkaGcolcHExT/ACn/ke+oMC/fX6/0AAEAA6IAMHZgWWwQIFv/fQAAIAM4AAgCy6JAFFAvu7gwDVcqKeq+e5vX323gvoFFdui8/BjI25DR23/7f/E+AMKT703M4Kk445/gw4AsaudVFbqSUtasMOP4awAOCdlWh7BM2U+39AgBSjAwXXRxzI2UZB/oMqQHHMyD3/LdviPhzgAWAx7GoVMaSKZPpCr+AUBhKHpzLwygXybRFwVmo8AeoT1xdP/DPRAAGVHYMnDrCeImPxOMnRXfqfZ8BIEFIQSi6oXJx97+cAoRgBwElb23A2W8NFACtBx3UIpvvfw/8QFuABYCFschQxpEpY4gKP7wBQAD4+h6rim0HDEERUGGHGpQAO9Nq+rc/jpC/5wKGkqSScwuUVPP4g/X/gDKlsjvtcO8fiA78AYw6Nmm0gu3QcXDcAANgQ7ZASCxKbUwA5hQbbMpZNEUeXwMPAA8CZTAAID+Jlxu6Am/wBLA0D/5uYynwYUDw3Md/nhXhYjaVac0Koq6163TnKk9Wq/wvcABDMsIOxacWhHuWAAgIElfg1ZfusNGNoG50q+n/NY2K5yPniH+qsmHOxHz1D/Vf4gkXwAsjsI9RdLvFqIjC6f4gPX0393/ADDRjkUZuJKW9zfARgsEpbKKsZBptsP2thDj2eTw+Iv+WIYfkkQEH1dTk+idsDtStfgYh8ISYPvhfxIfgZwBSmMFSSo8gRuDAQiIERhmYgpTmKDDwAGnOQccx+GCIiQcMwAN4ymSmTf4BtsiZrNTf85AWAQlBYEbflft4fuSDBf2gqiPJP198E1sY1W+PyDDAFosVlINqfkxB68JT88biPEHjEPAPS0hyV8fUM9/+GoAFpF2fttF/9gQbzcusdiH+tgJwNgQekazFciFJCHv2gEIXBt2jjoMPF/eUbk1uOPnHyYy1X/+GsABjCo/WZSyLJg8j4xVkOyiqJIx5xbw/gIR0m/9/4kOwwAEh5+Z0GSUTbjyAw2AABABoAAgBOAFkwoaIwA463K6iIIItxxHh4ADtgAag9ZDVC8LkSf/gwpk2MKcGpX+1Efveg/8QFuiZGACAcoDusuhSEn/5wUAvH3tMYKwoRK/+8O84uEUprcdVI2sG0QzCLSrLv9v/z+gDwc09GiP64biuX/PFaZoA2HWPUB/Z8Q2p/xB8EBW+csrhaLYP/iD8OAHFep5XMp7z+IDWABaZmAGA5QH/ZcCkBN/yBoHzgAwNd3Mqa9oVZ+XrAC8P0S0auv/f29lI/79esQeYsBVdqK7X/G/56hIFEqfn/D7j/4nxH/hzsQAgAJFFSnkIOpWoEyLn5/DADWrc6rnxb9XiYV4VwALBBSEEousFycde/n/MArAgLFVsEEdKFhA+8TLYAAgDgAINhWSBhlwyGGASgEnuz97cvbN7MzZv+GOL+/iBJSBnO20pV7VhhwSwAAFJpBmsDoEXDmAC6AQ6LlKUfx//94AoCTAgWw/6GNaJqGQDvAC5l9H/H+G4I4DGRE8lP8f//f/GBLwQKYeQjjeia5kNcLTHZKup+/zhTAARmQkXozu2Z3/wAHZgx/rMWFNWtpEPiiFraib9aH4TxIc48MoCxCAZqALCjU2plwEIonz8/1iT14538SeuZc2/eJPUPIr+A9brp+//hDEnitNOAm8S+9/eJDUAJEcCcJlLuYNSXcd/OAi61a782ptAY0EJswlFloGkP3YQA+gADDIoQfH8Xz33v7tUEAhnIa7zkR4b+orcN/X/DMFcD9B/SPX7k9Xv8iIRGxhMQ5ClID1/4DqXj/56wmbtC5GTzG//w54ADuwhRS24YdMi2isrfqk+b/R/xIb/kRiKzCq1JCWNSGsAxcuPpAf2+htV/z1QS1WLtrvn/xFYk9YCRno/79Wp1o/79f6yisSesB5MZar+sSevAH2vr5/4gTwAMp9OjTUDXTQ/z8AOEIzGIqLExZZZ/n+GPAATAD4mBibSW/sk4InPxAA8LgWm2lj7ROCBwMYpwAhtW9IeCH1tNNr/BBwAE4IXav0K1CH+oPgAWCFgtcHEIgvxrn7tIACVUYL9F2M10AVZ64gnAeyjG/9pCogeIwexTtH9TD3+9rYQotXUcPmRfdSthzWomA20R9NAZDm/iArgAJgA8JoYmypjzJKCB2H5AA+LoamwlnzBKCJ0MORIFPzWnJmYyKRJI+D/+IBBgAdBwUPPGYSu4bkL74C01YwcADILaIXL2S/9zSuybmEWPGjADQFICVwxbVj1e8wADsAVIGVnKUihewvgDhwXn1aRKs2/+8HUPg2cGxmuAfsOKLtXU/iA7AEII7WZlGTQHziX+4ETGKVXG1N6ZCduQ6FCetSe2ICDc2Vvc00sAMSEzIY2YblK4MblDDAlKgABAHABxM6pEWFnu/eUEEfEwUiHWD/WU7C9deWjAP/DsABiMRWQVW+QljVh6MAE6q4TqNsbvp+4Zgb8HW0tpnrQMnG/qgSDFf7fuaOoQwt/P+AtVNABEzGL0TVbX4Jlu7+M6yUpHun+FujAAlVXCIo2xu+n6Bjt9qbujoEMMfz/gAOew2Jtb2fTFP9pnAiqZjhcUU9LY7fiRiWNf3X/EB6AAmLtnTnIO6llN8wABAGkpQAfibygOauJhhyhh9zlOUSvf4AMZTV50/35AUfVFhGiItv//XVipKtXaISDACRTHmW7wdzNEz/v14M4Uwdkb0/38SGYAFgx3ez9ixEWG2f5+wRmpNqr3/PWHvH79fOMpVd+f47EnrAW7hv6hsyx8//zzFwhBRPn4CFf31xd/iewagAaAroCUgdFblt7wB2Y3XnOpR/W1IYfw9x9qoP+Hd/WQSH79ludiCfvv/wEv6QdpfwJ8Bhar7v3f4dwc7ddb/68/4y4pAHY+kM4YfDIpc03f3b5WxW4/30qOpRz4ZpLJmuP8D/xuABYMRiWpqsOgW2x/IEoAE65g/4bIzXQCQO0wAwONynZ07IWf36hqypAlhs1kO398Al7R2Wy4fhkAvjrvqtWsKs0bOvTZEAMDOAjqjA5C6/4neV/pJwaOZTKvfAIoFnloPcTAu5lj38ArzSSLGf3nGI6er0nEjYACQ4/IqGKM+1FuYAAO0ABmANIjRojB/7DoJurlNCD1c2W4dhX48ap5mjRcmYyTJ/+9os4PgJhs2BwaWf974A5wsV8YopEMLaGHnRmNJa5KBuykngnPjjXUTjKqXYGn0Fg10bKSnw/TTf+4MWAA8a8Dc7/EDfhyMgIYNRvxgyNYqw3IYBWJAoLtDamzlVgBwxna38ihEm2Vv4AkcPgCAU7q37mX0DTgRMcpGYbUwFgFpQauHRW1bTAABMHAdk0dHTRG8zMZV5xdST7Wp0QAE6owVNG2M50bouhwL0yEVlEbiSEvYmxCMFLH4KvmX3zdoMpGL+P0KsnfAO8un21QbwNx/i7yWWUPSlfv7h36hGg4+wQHiA/3QkTOX+YAUgY33dMX/8vES9XE2I/tfIGKWUl0pj9Ulm4gEqCvhhlrgXNL/5ldkwL/94AnQwAOC9olBO6F1/n6GUBDEBbNLU6e8fzwqew1Tnpy2DsiWBPfau//2xgAoynQ93+//Bh5wBfwxx0PSYQbuJjlhCQoHS44nvJkQbOIvEkJexPteEKLX1HDpsZ3VgAWku2fuQv/AJY9vX3sdie/00VKH0jWRE2VXT8JTQCtkg0lPf39XhgBbard3/x/kwIKghBa2sOGRfZX/0Pw/9mrlK4q78tLVpDD2QACIa8hinyHUyCLYAALghWg8NOzRGAASFV5EU5Bn2sxwegGQG15UasYguIzegIAdogceMwnZ03IW/wY6b8BMwnXvkAz2p9mV4R4awJAhbJVB5CYM8Y7+78W1t8hXz//D/hEEOGieUdNWSzrFXwYcABwIWiU0cQqYN8W5+9hLCAOAtW8L+MvJFOGgAlBa2VJPQUMd/9omjAIQXjLC7CKL/BgAISCbzSWz+oJQwjy2C8DGeYRUhIyAPAlxvC5JYx4CPes//xj564/k4CybcJJ3Vk6HxI2HABfW33rN9ekqbEbAHJDdUMJiX+pSQAYjEVmFVvkJY1OKOCWUzvueA6ESHW7OuX+1pkeh7C1WP/wEFRDIPlCeIJ8/7yEmMGw7qpWZmaMABOquE6jbF76B8GEXrKezsGOnWCP/ZAd4X3k60lryDL2gB/Mf3iXc2E9AS2B+8r5ZCK//uXpXE9rimMMJTX4bgDr28f/tgKB0iFGGpT3iBOhb9zSYYVhyEjV2Ekf+0MjKg9Q0RNxnry/9COtNie+53/8K+TDBcqh8vem1Pv3NhAmVY+vvzYl37/rAQ4isZkmybDPcEBjiawmRZJtttJmYAwFcBPV1hyB1/wAQRBIcltImhUVmGNSGYiHcV+NNfoMOWIsCYvOG50xap4a3//74agTAAT/IF+jbFa6aQ1RUgSw2KyG7+AGNEGyiLpLktUv3eEKLV1HDpsX3V4eByckPSlt39X/8OQA7/rg+54ARgHyBnmlcTTW2T+WAEAMOWotRSqKVLkpbqZkcwvj6s//C6/gAeoLvT65n33vWJPXgC1anzz+Jj+G4Ah5X5vTh7522b2/QIOfX2d3ahmevAPPxtuP9S//DPTGuA1VrxPLorv94zJAS8EzU4RRb/DCykI2e0goAf/+NhgSAXCUnEiqsRXgv3++Ekkqvvvf/gCblG8M/z4CgBh3oJMhNKUSV4v//BkFGEa65sav4oBWk3pX/w/0X+bgEDXdfv/w3wBiWFNFEf87b6z/54VuAD6bMc1b/v+fD9cMeAAggu2wQmrSmb+t7/4gG+BA1l5GOscJLmQ1wAYyr31//gZldrlbe8QTAEEIArEAWFWptTfG8NQAL0RABAZ4EcWZHYXf/AFbADUPVNRB/FjX/4DQbYgAFBGkCQnbA8/zQEJZa4PJTBqBjn7lgA+zbDzsxl//v+UzGzPwxAAQwvaUGNvpwxnhJQz4DDqooSmpS+9cwmjhwBGhQSE/JOP8/uJGA3sAnEo43yPg4YADgjjQ31JmxEF2Gf5fgDoAGxxeG/Hs7/ggwALBDv5iLuz5EMM/yBOABsiqE6zKG74fCQ2Arwnl8Llxutfg4A5GYToKq0Eqc1EMBrAFGrdV7gBhK+My77B/4W1l2tc/vzw/NFdhnpAMh4lAPhyGIKU3DLhgY2VAw/YGQPIXUfP//gg4ADjC/i8V2IVidT/9Z147LbTfX0ACoAFgc4JbrHiCRKp3uGD/4LXD4L8wfQ/PF6HzeMSt+Z69gRGtJt1e/f4MbTAGQYvTb92AGOK6ln7UgHNlqZHr//v8bAAYBj2J9UlLCBCpXxvfWmq2X72hEHyVte9GsQ7eBgnS3/HZWAen+lpPvgFqQDCCaQkRaJNtPMLFVgICEIT9wQTXPx9Tr4dprPwz+fYVAkAmD+XJWpKBQVrXLWAYqORrOaxJYmtA3Q4dRC0sRCX4kuwwaSK3DgzDqW4ZCwqXI5caD1G0JalLou+pQLRWsnv++jU/hsF4dhgCxuZw/Hj0uGIw1U+MTaVT8GRQlcumkN/Ve7hSBktBlld5aC/4MPphomUebCps87fB6AYZpE/8VJphJnf7zUBaWOdJXbgwGqikj/Rg/WXXg/8bD3TpYE5TlPuZ/2HeStWB1kBIB4oziJUxZHrNPVtTA604ADUjDFQU7Fi0WFk/DfEhRYISS5CC38OAMSaniJRsG7//vT0Fqr1mSLCwEnsh7DoYXTynOeA60HOnzJPVf8EZrNtFle+Aa5kjCJ1Fyv8LAZf82AAkb0Eq6LdmWH43hbmdP7ttTTg5hMAA5YDKSUX+d/f/xdRvkSKDf1dvw8oYvwAcAQr0oJEct7eEe9QDDAEJSlQV3cxdLu0fcFBdoq0uptluFIiBF4up/342SkLJPdP3vrYMclrv8LcAYAMzju5pk0adAoiHSHUmni19fvAFjjYroYorqYW3gACsA77FajEmkXaceIR4HVwuFsUTpqwhIoxlw0VAe8ETDKX2oVFrxmLsP1wx4ADYgyuhhOSSljE7AABIHAfY4cHTRGAGIxFRDial3saleAHXWaNTrxnC/gAWAx7E+mSx4hcugdf0AYALi4FoMJ5+wRiichiMWAiUm0+aDD05ltD+IDcOABYQzeb1XQmTLDH8+CYv3XsOk04vzL9z/+GYCSrmFUWzUC0ll/fElIiRCyMnjBrijrbWdycYoM6abiDf/8P9BgOQOYklHapvdz2eAMAEguhaTKePNEooHfMAFxtDEmlc+ZJTTO8AY1iPVKwz8lYyicaAY9CEaksfI2M+OP4GQJfAECEARqgNCjU2pvCK/AOPPE/g9p94h0JI42p7kgh0FPS+FcACsGJtEzz6ZZT+hsAAFgQugeG3JojeAmFB/wq/Zj7JZ5jqd3UzDOtRTA1oYALr92KNv9z/+N9BhDAB6Dr1iMj933UNhAECXef+EW2oFkAEookpS7vtrCVMgDAAuLgak0nn7BOKJyHgAwBlinEjMBP26N4/eekRCZhFZzkOYjwwNnl9sv56Q8TF5cuoMJcy2jk/H3tmHsfeP8b/wwALBiWUiTyUyVwx/9wDBq/H/fIPiACE+hCy00WdVur/gwwFWADQNeLRJ3lj3P75DroR1MQcmlFP0kRgDA7wI4qwOwuv+ewAAdgABGAOfGzRGAHHGQroYo7qYa8D9LZ3+2r5dGRkI82KcB/AbCvH//EBWBIID0uuFobg1Nxv7wE4ALagACACPj14eygd/8AEGLRSpg4hESV418MCQhHczqjRMWW2f5/wsl6iyayCm+b5HsV09e/9Y5aaPn/iAQQBaAGobLhSJPSULc05EMDPAjSzN40/zQELZKKNITBXjHf3YAmQoAOH6+SELIHv+TAgEAQQYBWJAwKtDam3DEGBfQwAECMEWhUkv+CS7HNDtDdpuDj/+YGviuTY7///eeK52/vKNTVj7b38f4YgAVApBQ86YnLLhqYv/g8ZIu4egqTPdN6AkDFsT6ZK3iFzKB1/AGtee0gJ6r3xXdAAGT8AoXaJFW7rpP/3uAAHLAACNAe+NHYjCCQ78MrDqM9v3AgWdD+xizef7+IDPzMxu6ir1JKWtSH7aGyqQ6EH5KuDOWPDrNvROPl//hnohglXQyXOxZnt6M6XB3u0AWA14cMZeRjnOyCpbxANoHDV3/wzjpBQso6AAwsMkRZ/wynD+sQeszSRKu8/4zEBrAAvEiJqEsMmsju/oCqhCC1tQs4bF9FYWthRQ0k86va3spH/fr+J8QHOOAYgAz0JFOXkCIe1UWAM1L43rnzKVPZrr/xAZgAKIACVUYKmjbGa7yaRoo4Buze8jIRWUx0cZLWL5rYhRKurOmRfdX/wwl12o7nmt0ZHyUv66b3Nlf+FuABYGJQn9SefEbl/nX94A4ALCUFIMp46yRj44GHEooxXTaqveGcX72zn+uHf3Ch1wa/dDZLdDYAALAptA4NuDRG9Q6fYLaGW2SneHgAeDdCgA4I2gSELYXv+AQgXCdhW6m2Fk//wgibi6MzuQAQXlsh5fg/8L2GAAmjMTocysLyl8AA5DOcbgXHN3fFvkufe7P+Dmg8VKypKrf5YV7rWRJFN/n+HPSuvyphZGqfW0u3YhaNkQ2p/xI2vdKfwCUxkdBVXz0MagDQZRncpM0JXWWft4Ph0MQUpuF2jQtooB2BKlUx9Sjf///wAQIai1RJxKIgrhr4YACQ6+I6mIOTTCn/NCgu0VKXQ+S3SwFddt4O/34YBYzMfApL+Y3+nAACgKXUAwNuDam4iGLlFzzLbZTuDBSpT73eOO03Dfz/BEhlLpmKnx/EAwgSkAGgebUo5BQt3+wYcAHRWMd+6MvfAoO1iOkfo4BECFo8mgy3CdzHjf+9AQliUKE458SuYROhl7SwMQGIMAWADxM+LG1P4vvWIPh6cCRiTvf/UBFG4jxIL4ANNTnTMOleYzFLbvN/7D8AWAAfgABGAOIjZojADjzYroYo5FKNeE8mOe+0GgAxLLGjtu0H/EHvHL3L7wYk/nV/7//+TAArDE2iZQ+GSU/vkcbCXGKI+2Fu4gOwwAGNENOQ6FG9bPDDYAAJg4Drmjo6aIwCdmNeU6lH9a0+GAA3RidRF4glDWID0gANkRAvyZQrXD1AHBNzi/PAyp5MVD98v/iQ/00ZADAzwJ0owOwOv+aPACUNVLSf5Yx7+3/gSDL3oZHutf9WALHmxVQxR3Uw14YS/c+1KTP7/fUcNL/iD1BwuMf/88pYaCb6aZ75VnkhtTkLxsh+fKYhmrHxMZ+vD/8QeuAPUp98+H/n4TLhv/AVYyTtf+/1/56z3xv6//+esBIFEqfn/4hQBUZiPnqPqU9f/ibxAc0HAEAFudyoRB1Klz1iFrH79Hae5+vzvnXOvic65/xPiD1Alck73//hHhXAAajMJ0FVaCUOaiH6cgxBSm5ZcMDHCzQVcgAiwVWLDYvUvfwfr4B7u4cXn3/9wBBnFleIlMaJgu2yGHBLAAABWDQZrg6BFw5gAdBGgIv9WWTnO++gDgBoNoUm2ppBkpBI6vABWkzRGLr//9+ETQ6+G4GAQslJR6iyc9333+QAaj6FptKbQYJQROhrgpbyRmPv//9/0Ha4axJ64D26ev0I8R3iT1DSWqGo1LVf4QxJ4qbBI2FAYVvpPXP/iT1/gCqtT+8//ggjYKnQGguAAkAFhdC0mU8eYJRQP/mAC4mhSDSefMkoonwzJBimpXzAbFrcbecAZO3xTy3v5yc0fxJ6/8Bb8N/X+esAONrvfH6//xJ7zOt/Pj8///EnrALdyG/rCw1L7bj3+f+vfPMWAm+Tdv9fs7xWJPWASS95v8//WJPXgYiUtV/n4QS+e9oLrvmFP+5T/0jKlPX+GPAARgaKGDGXfwxvRBQv+IBvgwWy9+OMaJKlw16LcSONiNH+CDhKwc38ACwh38xFzZ8iGGf4AF4AB/eBl8w/l3/gQyIN7jZ/HMBDKFviaqhCgJv/W+awUEDz5mVaumKCm+DbSAkF/mkP/ZiWk+7xsvkfhxyKg57kZ19f4V+QGJYj1Sd/kKF0Tn+h8wGLQhGpLHyNi/jn+DD5ZfTT5P36pQZtalr7iOqydd4sjxHb5ZtKMfDGHGyQC2xdDsVvfAmxqNygA8hUTKIv226yW+GAVG68DEnof2EbZFGiMIOAN+hbiR4WyWvFT4CinVY+jUUL9A08Z/ayLv2/w7AAbDgm0TfPp2lPYAALAhuA8MuTRG8hx+RcYoz7UW7n8BkGLhGltKI/4AUC3YRCt3/7WpDDggg+EnsAAQBwAcZKGiiS5H/BxR2E9clNuQfKPpp/u77i47KDan+IDsABrIZHURecShrEeRiouWRSXW2i3aQAGyIwX7MoZrh4wqmKnOQUimlPYAALgplg4NODRGAnbsIkIBkOOI+eBBL2qvtqZVidQLX0wEghHczqiz7Esr/wP4KbmHsAHONuNEbXtbD/v/4gLQJgANEzBfkyhWuH6BDM5iKqxMWWWf5/wAHL8fUUpzetq3e0iwZEOphtWW5FBb1/o/7D23/jYyRP8BvcM/fAA6ABQHMHt11xAtU/30AO2EmiKl7rP/70Gy5pw5qUAYbml/aB7QVl659bvCtBpbJ3f9g11C0D4hwALBDP5vVNCYMtMfz6DO8LfEaL396xJ/cdKoGp44sT/xJ6wBoJuccfP/43hbgAJEKiZRUpbbJLaCAXmOtyqpiCOtRTgw8USUe4aIw5rc4rnXfn8QF4IYAE5s6aBKDILIa/4AB1oZgOayUijQzuoYADDpObQ1wZk1h7f5tMaOiYJQZBhDV/ewSunIgP4klqxKQAiAP0j+sJ2mgrwj0uHF8A2bBch1a/3wXS81MG5/fHjW4MHxsMDYI4HXUuKZnlv794EhOcRSxcaFFCLb2/qSCdh4M/d/t/yN6E7yL0yPzAxaEfmWx13BVQ9/qp+LP0n72XrRt3+IwxlbCFrR9opIB39D79//fcsGHxRJ0L/KML/gwEAegLDLPh7xRzpL0jE6IcylG9TUhmbFgNRIsX/8yWQLapsz3wA0Su2Lg3fDd/NP8QN4APgegCJ5hIwfkM7+ATsZV5RdS32tSGCAsATqUACAnf4kxCx3/vAKDFopUwcQiykjX//eG7q5v5wAoAGlAVBGHy+wgSjTARFIUBQFpXsgYeTL/9bABTgACADbYAUQgLnrrjMMX9LpDofBTuDhv7b0VLGLCGkSZrLIkp6o6jbRCgoDswR64U/1NdeOfg6KAYc2Oi4gb8xVsVFOQd1LKewAAcgADtAY8NmiMH/kKLiNjlHfTS2h2LNohP78fe8BrZaRiLqqP93ttIeM0QltrkAZ+j3Wz4m/cxfv4GEV0oxoRe8bgpobU/EABgsxcDan/EjfHC76+J2Tz/+Bg+DmcQUpuWXDAxsoB0wAGohu6CKz3pYxPEGsEIMF5k0VGMV//MAAFAQ2geG3JojADIKiZBE+22SW0QAAdoABGANfGDRG8x1u6qYgjrUU77QAG6KwT8MsXz/HGatEaF9f/7QId3N66oTBhlj+WBE4A4Jfv4ig04btHtGoiApNL76MiZVKkZTGN2kK0jZkC7/vP4kP+QLGnW6HXbgJ2ieXqm+8+005b1wBAVynePcp762UjfqEcAreOhGzjfRfbWCgoefMTpdw1MX32iLWJHT0LQZJdHV/BjUpp6luU8ZdT//ICxSHMWQfP4gPxkmCabgB9kQAwMQBG1GByN5/wMDQREKADgvCJQSsgd/57NE4APcwAIPgulurJTlAoY0iMwfOv/99lP8SHsCZAdPeVQLJKM/dANiwDBBc6RJkjjZIMCYChgGA9yNamWPmO+8iRCIgis5yGMQHwCHJUQjbvZLMMN//aZ0g3JL29/+ueABsncJ1kUJ3yjAmRPPWilADYu2KynK4mqDIiVTj7zg7iqayni79/xIfgSGO/2pu6OoQwt/P/wEwEAbi2rnUg2NaiAEzioR84mkAAyZDTFIrjepqQ9OQAynxCkAB2+K/94CvghBSu42cMi2qsegNj7PT+f6dU4b6e/z/XP34Eg/E03gbnVOaS3v/nqIUu+fvgBn/8d1w+HerHzyJjfoyKu6GldKLX1iJp7j0gDHFTnB9giwwD5sME3KH0/2TU+fBwFBYRBqiTLKiBeHehmehRZEzyn79UsURstb9+ozK6+4WEH+HfMCGoR+hPPydjCJz/aAQ9iPUJY+SsYQOP7zAB4TQxNlLHmSUEDvgaqqKUhnhJafmsAvCFHQSk5xfvLMW8RVz2J/IyE7OIukkJaxPxFAGCi5SgVInWyYYYADgf6QAICXI4ZdSXe/9wDFshMnkJmS/GPfhCblQBRhNaNEYLmp2zWu9ArpZxRhdYNUCTXX8bDhhA3d9MAGshkdRF5xKFsRsZy+v5oAtxqZNgv1P/kYEfYzhU3r59af2kABsiMF+TKFa4BhsouWX4BG0xSx7E9Hd4/fv+IG/xjaFEiy+dVntgghpwFvLPit5tw5kCVt94A+YgipWtxDTz39fuIDNba0CrJknZ8d94GlT4cNTAJ5I2JryIy8YlweeH1+WPv6kypuOK+MwrbyWf4ehgAxpBiLOXXjlW2FbD9sxldRV35KWrSH6odGrW442/MU1N0BZl4gFn5QwRaHX0WNL6JABoC3qkHcUNf/sH4RPsBgrHRMSLFf0GCJXt7Qp/r3+C+AA2mbQmilVmW2JVE9p3kEvcD8AYTmF2UO9f82lQld1p7r5MMFzKHy96bE+/K+fHtMwIYELevfweYB+IRVi8w/4gMwFNuxRNegliFkP95mY3XlO5R0rakMNQ6vRtyPr4P/rgvwAY99T5/2jZvWB57AAWRDApgTgqQMMtG7QH6zyRBIRnu8AowEmSxjbNaNmKdE/4OCYPwAfEiZSbGb///h//wBAhAM9QFhJmbUwAGoUtBc8ZBfWdOAi61a982pgBYAXXgA4Jc1njJYWxX6AAQ1MLBae4IKtOOP4DcDlsBbSLX7m/79AAsAgfImlS0vjNzFAKCEotUScSiDOGv/+AzpCUJY6cPOqtlqhgBD8OJX9vMWOGho/iI/jfAR7tD+3MK46DP5fGRTvhxvb/kHlcNKEJY34agMOG0mo5b/gpavj2X3gJd3FftvmZjnW33r/D/RMjAEB3ARtVkchd/80SADQPdsQdxQ1/+wAsJ0MKh/1/K1i9G9gACAQADHVhoQyu/34OC9j/50OL6nH//+FAGmpGN/kEXdeodFyibQ612UwDESNqR58NJP9vene5YAfc20u/5f618Lxd5YP4ACDEvOJc3c/lepOgOYoAYOWtAiS7k734Inzvl95zyCn+lpD47/DngAOaINydaWz8Yp/l//CLR3/hbvxAQUVWZBki02/3zJgMKJrCpNkmy34e+G/fnQCvQHAcdVfft/rgj4ADnoNydaSz8Uh/i5qSjsQfLxzv4j4W4ADXYhRSm4YdNjGyv0mJ2QVWpISxq+gSsvoWw2a6O/+0wAJ1VwiKNsbvpyApRA4+YjPD5qYx/uAx3+37m6ESaaY/y4AUcON8Mhvvf/8MeAAkbIQpBTb48eYSfzzA1ABIjp6Sx5EPv4A7sBAAXpyzdCyqv4gb4ACBGCNQqSXph5djmoACAChheCWLktW5U3XNbW1aS///OGgAuHi5Yk/ihTv/gAHVjFFqahdswL7KGkiHgujqftpNX/riFO7LE4+d9QfMIaz3UE3QIVMfO/4MOEvuT3pPi2vgnsv/73uZqYI5nbRoalF/O/w9D8MAAgA4gAAgAUqZASRmMPvcgBMAgSXTjVPvTHy3B0lBIxoxmWf+ABwC4oYdLypRo9Qb3wHW2KLbkSbybf/+QPKaP8b4Id7WADjKqWZkbdurhwAhoxOk6f59wEQKQUEnTU5XeMTF/8HqCtFi1R8qej+/QG4cLYDuV09bJ//7BGR6HMdMx/8Oj+A1uwARRXGnLeoswkv//T9/jbgDRu9PB03AT0PXPFZYj//BC5JBjykzn0QbrP7GDngLvjYK7vcWNABCBv8to/E8ek1zapZBT9Mwtu/7NKu4yGi8guKJ5rFPAcEyAQVblOWyihBnzOkbU2lN8JP2EeEA+EnEfgYILrQDyM5Gs9X/Xi39OU1vWfHR5Daf/pIco/INv7eMl/5d8bD4BN3rC590TABoGvFoEZTdc/t7b7xgwEoKH6BJS6myW4ABxOEx/8ubOws4/+5PZgGKLzttdtFH/uAALFAWy+M5ZocN5LAYI4Qxe+QPNgPvdJG3/r1sTGvav8M/emhu10KR9gRglPWlf6beH/wvADG5V+/984L68++d93QBEEz1LTPpTi6xGElajW+f/7nuIbvjGQo6VKTwGAnKPQJ3XvIIJM//6zAUsBd4cr3Gf0Z7uN27LAEABU62pUatxg8H/C3hMANA101EneWNc/gYBDSDAAdiFsq3xi+R5xv4AcSQo6nXqOXr2aAbqQAGBG/RJidsLx/wJRsLeMGQn7tJa//DHgAVAaqAAodXEqOC2sjXvQEJRaoEI4glh9/93gMXADCL4kZinjwxrGkSGuuvhvgAJgNuGCmX/wxvhJQz4gGuDBrLyMda4SVMgNcAXbJoxtT/xXPWIgWSR8//8PR9MfgARhQCHE1hQkwRZY6MQLuWNn/kmpcegCgEmDBaz6EMY0TULwQLvgBDksdiX//7gDyj3DRGmhodf8sOABYMdmsTcWImwyz/P4gKwAKsIGzLF19mrku/B8SWAxz7iwlkm23BgBOAlcGJgIqxJkjJn4MOPPAEj1Zd+wOy1rL/5/J+NEf+FujAANQc4IYl7iRWR3vvAkCEo5+BefkbFvmn8BIELYj0iWPkrFkDj+AFgA8JoUi2ljzJKCB3yAD4thabCWeMEpfOggwwxemhHDlTaRPnf0PxY/NmMP4g2pgj/iArgAbj143uLpxLnvhYROYqFZiae4tNRivbovADirY5FOwrqaU/zNmNVKdSj+tf/h2tzg3x+oWRSOv9fDPa19rHn/w944JlZeFoOkujr/py1Xj5LhyDEFKdllw0MbLGrB2xyu0Jme9aF9WHxJXtcvg5+AEJBWo8xdypADCDgANRDdUMJiX+xieLAWoPfDor7w8x0sUJmJxv5V06abS7wPpf4d6GC+eawtsaFBSR138CAvlgtDBg6YACcW7s3+37p2CVsAAQMrMAAIAYNgOP9jAABIHAbY4cHTRGAGRhOiHMpQiVNS4Aie9SN42prMDvoPnD1eWz+BnSf26A0jseRFeAG3kBsPz/ecOMxA0auR+GejBTC+IrHVEVefv3AfpAGAQraF0S76RZwCEstMSeSmC+GPf+DCX7L6Lkxm/w/S/4Y4AgQgGagDQk1Nqb+AAgZQqkrhzukgqh7YB48ANuOpl8+f43wAEQ++I6mIO+mFP8FIJhsgphTnXzAAB2AAEcAx8dNEbWBaj6AbakZiih//3vuFBdoqUuptmubSvu8EAbQ0YLxBeFuY4hlW36SC6wJRqYNHEeMgnfs+bgFq7vb9//SmVGuDg+4fgITE6IUylG9S/D4gMwAKMMPWUNl7kWp9+5DYSegu3e11N3/WAQ4isZkGSLDPVMBjiawmRZIstgA8LClW1fi/+bMM90P++Xj3SFcv8QFcABioIQWtqGHDIzsrh+ZmMrqKvUkpa1YYfoX6Fb6i/P++/WIPUqM8kNqf/8XiDxYnGzFC/HUf89SBqPf//DkABEAnQOFsPITzjZNUt4wE3BQxh9CG87JqFsMwAOTAXlEGen37WEZbOWUqZH/8E1sCQPbzX7wsYyClRTdP/wxDgDGYmZSi6h3NWhwAAqDAOvA6dHDamwYUgABABLDAAYA3Ip/QCWQyO4i8QSprFDk5frpbsGUrhJH1vntZmJPtPxk5Zb/58GQ+M5Rnqq7vy+oxmkkq7z+IPKP/V/Agud3n8QFfgDlixW52HdSynw2AADkAAK0BjwyaIwAwo+Zscor6aW3ww3j+ANpERKfge02oz94OF9X74/1/wvgAJMhOymOjietXgAOY73maFQxRz5fxPm63H0OaC5FjotiN/lB5kjqtqN/n+IkXwLBVQ9T4D6xIrjan/EDa5eX83A0BhZRkCMQmwyu/96+GAB8CVYQeELiuf7fAKkACQEu5Yk7yhTn/gwAGYqLlkV7LbBbvmTFipzsKRTSHywVvtTUc9v8OqNaFQop3w32sAACAEoAAgOrAAKKzNCbyFHxEQ7ik00t4mFAIr7qS9/tSTmDexJ//1hhmSEW3v+/7/iBvwAEQCTAgaw+hDWNE1jIYfjAJ+CBjDyE9Z4TVMhggGgMOGABYJlMADAnSMCYjZA8f5mz0Bj2UuTyvkvxjn7gwN/tj0Np1P0ho9JIKMbCBi542O/P/P74R7n+esBC7kf9+szsqnx+fjv8NWjb1ucv38fmbmNn2vAJUmnXeB/xJIFiv0rbd/+kFs+G7uPhyAlgD2ADgjHIMCeMbbf3ABBoXfQavZLgw7/3nr/ADRvU+rn+e8B1cUrvD+jD/88B1Lf+AHSn19fP//PUAeUe4aI//+FfXAdkBtQNitu2oCGhOimOhRvWxLgRMYpWcbU2wC0oJiBkVtY14wA1wOIJJZpHazqZfzMxu6nOpR0rWlYOSZhn7+fvyPWkK5fxPiD+wMRKWq/8SFYAFghKLVBxKIK4a/+7wJeAFwSqak/yxj39vgAXCVl9HsNmyju/oCnnsACAkpGs3XETH/KBO9cd/uVg85kQe//HUf4isQeuAkZ6P+/X+M988t0W5/XDngB4Bb0X05xnpfjpVA6eZ1fEYg9Wp1x/36//hHEhqjBSMM7iia/X6ePhM5wBlLmkZEfff/iQzAjgK+lYZBPmvLwYdZGvb/glgAABROQZsA6BFEw5gAIsIcl7gzFKYI9NmOmgBAWSrCgoviZUCvcAd4AGUCnyn6DYv/8N+GCDrjAElON8Ef0xsD4EBCC3IBL/3kshSt6DXtRDJsIt6l///f8OdrhjCPhHxM2JPeNAzgPp/8/f/whiT32BwEIPOR/P/EHr+AiWid3n4b4656gDDcyX9pkLia+CDLjuRf3AAbhwfbLrmU+CmB+IUfERDlHfSy3h8SG+AA4ISi1RIhHEEsOv/+DWBiTLVDWn/xJ6jU2Wq//hfwAPBJyAAwLx8mI3QOv8gCwRCjtQYVyxKKCHYYV2wBXY+iBa3N3r3+FuBIGLJSZPIXJvjHv3fwoAGge7hijuKGv/+DDrl05FJ5x/xJ6wELuj/v1b2VH/fr1iTyl4CJ9L738fzx28XY/+HKK4AFYMa6LlDYZJTeOCUBKJoHtqeggBtyP54D6PuDIipN+GO4AAWBC8kHht2bUwCIVEqipS+2SaT4A3Q4AOCN+KCVsL3/AFBCUWqJOeiCkDX//CAouBH30f+OKMpSPc9sgMdNKnDsv5vD1/ggwAL0yAGBngTpRgdgdf8/Y/IffEdTEHJphT/EAAIBOvIABEFbmgY3kT6dhdzVjus4AQOlvgCQSPSRf7hiTiIz+0+Mzjh+f+FvGwAnBKqWpE3Tcc/8DQN8ABwGMzpsXusYLSYb2gNlKABARpCJUStgev8IwMokzt8gDNbrTl4EvepqPJWz5X1/wrgAJDqoRVMQd9KKf9woLdFT7IbJbmAADuAAZgDHxk0RgLo2rcptuEAnQunsdCsn+LIYlmPW6gESxqu4jcX9vJK5GbdvKoY2/iQtzu/8ABEwxMvM9OJSzk8SZjQxIo6WMWXdF8UM8b+f/42AAYK6A+8MivvFweCJrVK3Dam4MBA9h8GWVkjg4NTLARhqUWIL99U54Zqw4ACELsoc1tV/o5iWYAu8Iw/WU8p7d9oKgmhIr9/DB8kqdv/73tvZmzH//vAUsgfNoh+NlaM/3P4Oej7Q77qKiTp+flk7ab3a+qPn3f7xJ6wYC4mv47jcZTHcFgAOxEAQEJB2lmR2F3/yAoDKBIrzTpsxsjHv3MuABekQAgISDuKMjsLv/nPBAB7YwbyjcMi8e4imzAAYSOBSb0pS+2ALlAFGG1lWPeDgHxI5n/1gA2xv+sJeGsv8be/v4gb8AD8MwGVMPJXeFP78GBo2IKtQqpNUg0+96B1hs40m5mf2/5lTGzW6L1bkBCWJ9Ivnjmyip//TJh9stfeya4258ZCFXkpUpPUm+JNJfdviZBezq3VEsDAyBcEbB0uYJN8K9B+LWrKpt7jIAls9l3yhg22Jou9B/xA3wEBEwE8jlbv0DaRb/vTMhM4695ymtRpCd1ThKD4MI4v7kwAJFRwvWbAzfLhTDFFqYhd00L6KgfFiVXShKDZMf1/wfmtkYSp8pidMDbhMMdPB03qv19hBsBhadL9S4oq77jco2SkrP/2ginEEkih7n5lhlX/9vw8GPFbH+5Uv39gSiD/JVaHQuYR0ynJhpTV+/U9AqSk6P6ggGUSpP91FpGQCSs2//TR0U5/iAXwNgHLATEj4LazeA1ED1SrnlW2MRuKiQAAgC4kZAACgC5C7AGLHyNzkGJtpTg4oYPY0jKHX7+X//EBXsnk+q5/r+/B8LYhRauo4dMi+6kHwAK09L1PNdPn4mY4+fv1B//iBPcBUsR0Q2pgOvSOvSfu90EBIzD0i2aQkmHlffAES6sWBAvD/6Y0liOmV5+NRrI0YXVOBAIEAwAPDRSgAwI14mIWwO/88CZIYcWie4qwNwuP+eAB6X+cpMb/+gJzTT1xEY//XgQwAwwrPO9rWeGmf/0Ua45yx+YZmq5r//cPTg4Z0f+9crrNq+/+ID3hsChoTA0EJt/3QI5wBAoqVYEiZ1onB4YHTgOBztJGGfGX7nmbMbqKvfelrUh6AxiFkpyowo0sz/0BMXsJi2Z9P/oCYACdcwX6JsRro/6NpYtZEk9p5n5Vm6cmnwyCwWsO9LIZzv//BDAkIZ2MRUWfIllf+f+LxJ64din4D3HJnH3n43hjAARAJcHC2HEI5xsmqY6MYLVUPl7k2J9e8wJOChTD6EM56TUMB82IEzLGz92LUN/BrgB1hF+Tn97hfLC6t773/iRsABjkGIKU3C7hoW0VBh+AA1IbriCYl/qYnAATOFiuhijkUwtoe2ClgLvDF94z++egCZP28rt7Qz4b+v/xAawAEwAfEwMTYSz9snBE55gIehP6EseJ3MIHf8sAF61GmYsv//3/DOFf434gAeHwNTZS19onBA4HyAQ1ifUJ58SuYRO/7yYqLllUl1tgtwdsAAFwUywcGnBojADscF2y6Q6G0U4PzLFitzsKRSyGw2AADkAAK8Bzw2aI3iFnxGQ5R300t/hhhettU4kjHF//+7NcJn7V4zEsSET7TKlIU31XC8BQMdaHziVULiyq3/nBqD1hsAwIghqOvS7SWtLhX/+4aBJ+QzF6v399fCgrIkGhH7bwr0ZHKfv8/8LQ6xVmA/R7dcUu//+x6myo/bsiKRRVL///f/xuACNTPiRtP9mPD/ctTzRqeAXEDrZxi6EoRaoS/DC8x2iPpeEWD7tSwtyqSpdalcHvyUkm/3Q/DV7vVAwAuH0F3Km3v/kcKwLySqn/P8Cuw3/3ovC8fnTFg7EED3HH/AGpj8xIpVzn/3gSBDo9tIXgiLKzP2+vgAvhSI61ZP//5/AX/C0MAH2LwjFPC+tACQ20WGsOJR3rZFUt4wE3DhjDqEN56TULY2AA5gfkOk6U88WJvYqp1ydPDOlnmmQ2pgwgcWs1z/f1/SIaMFfwQQBhojsoi8SQtrE+14QolfUcPmxndX7RGGIWWykiHi6LwcAFAfgNaBsVN2zQBmQispjoUZK1JcCJjlKzDamAMhNowmIdjGI8QAacFPCk8zjpZ1Irn1vZ7bPL8AoAjeA3H+7zjLr8YM/DcaAIACBBk28Qkre2s/uhx/X0f/P+NwRJAdZXpK4n+q3MIDUjKf6f/+FcACwxma1NRQiTbLH8+AIPGBoCDR3tLkV6aEvLJvhmpAHwo9x6Q/BX3x/KC8bggqyc2+71f3OOBBhMwZ9tReHOAA6NYlTVOufdoDFshMweQkvxTn/i/w13PxnEYBdYCCiqxmQbJtNw+4IDHE1hMi2TZbBhy8EHgIv8Bv5sAd7r2Nvn9ge1bpeaT6l0vv/LPCl4ASFz4AgFubz25l5E8AAXTxgA8ABgkTI0LFJHO2idn+G4APIbLfCKtzxA9AY7/am5oRJhpj+fFD0eTV/4ex8QTgMz3fXAA7INJK6JOl4EQOwUEnjMpXeN0F/9oCEdzEVViYsss/wP3MAAgLcHvRWeb/2//8Pw/gAISnGRfYtaPSzk+NHWI8KBElnF/WMnef6bDAAkzcRJjVkV83d36/7tfgBNbT4v9/V/+C+gwAGSREQk2Rm2h8CAtWWFL6nCxRNYj6q9bSN6vB+GlfxgDrLctIAMQI1+6Y/Qf+HOABY2Zc/+rSfvcJf+EXHeD/uBPsAgoisZkGSLTK/VgMKJrCZFkiyz4a4a8BziBujGYSRdCETdooANA82xB3FDXf7B+AtgB5Xve7Ke/4zrhXC/AAbEY1QwnJf6mJcAAKA4D7ROGhs2ptkFrAe+HRX3bTgCJr1K3DamuybgFYAaKQATh78MhAVVpX/hssAbLJN95AmqGQWZiGTCntpEz1xAYgDgA+JgYmwln7JOCJzwDBbhIlNXmse7ZBDQNOw9MpT4ZRf24Fdw4qF9oKb+jzgwAGH0Izir3iFPar20Yn4i8Q/FqR4I4xSUsb7tLENf8AK/BA/lEhkpm6b8DsiBTpcm//lrizWlX4e8AFxP35JM//3xjFS/b9/x4ClwLyEmI41snwO/BhzqIIWqsAjD3V94HwC/xAelOSRHYPo1m1BwegJ2yAEBnA/ajY5A5/5YBhYAdCcJHDcBu+AkqRig5oRBIy7d9/4Ovp57edv+wwALAk7ABg/nYkxOqB4/wZVbZXGR5y9f1/jxrm7/fuV2n9/wx/ABkFk3Re/37wBYCYxSPSjqSjENDr8BQck3p8f6ArKPJzuf9/h7RX4AFiP5IG4koJTJT9/8BegCaUMQ5eta3+AA2dbStbvWfxVL/b/WWvgBNoa7tL+X+N/Bcx43lVY6/escno8ABwoVQDAa/u3KmHEDpoyoD/FgJaxDiluww2bFtFdEGmL2eaP//cp/wJ+SMhmw7LW73JW/hjSRuvBB0I2mjEi+fk3/+fkAAO8AAQAJVICW4jy7AxUQBzPItr8/Bp3knn5aRVEFEs//9LMK5C2ebf3ihgnGR8TbEfjf4gN0DBbL3445oouZ4Y0yJlj++J/8hcCVenzN6qP//W/igMu9MDT/SXn/+8oRNf0bLf14N3jv6yGDEHEf/g+YXAduuBWm4z3iH5gAAkDgPscODpojcYz0rYgA5IdbNVP/OAmUdSt42plVbszJm2vsgpX1lzA5JQgT0qn3+Y+WIXbgz4gPQAHEMQ8gYwgjHPIpq//YsZJ0Vcdu//3XiATYMFsPoS1jRNQv4wEvDBjDno4zoiqXdfU8Dc83fbP9uPISEM9cTlbrbS0ZUfvs+YonK2O4jrWWzxgAR4wILpvV9u8u56w+Jll1zbZRTbtCFyzGmPeT4OqggRp7w3BAsFUpbZfV2Rpck7vnjKlbRfn/42AUcBBBNJTJNkG2Q+SIBtaBkkI8vif4NgEABrsIUUpuGHTIxsrRdBKyrwthsWUd/8/3/A88v48AUWmMP7+NcVgYF8IEqzMWydWdIxJ6GIW0HLaQ5Fn7+oSJCi++qp5/+11+GUrAY9ODJW/v6RidmHVqSksWsPxQRo7nRsO0lLw+ICsABMVbFTioeRDTCXAADkAAK2QHPDZtTB+AMSHiNhUvJppr+YHcKCTxmUruHaDP+DDA2SAMC2Mjd74GJrlg8N3Elix/tNcN//rEBaABbGCblDZf/BqenvAFgJeGCmHkI4zwmqXDDgAJgA+JQUmwhn7JOHznoANBcDU2UsfYJw8cCr0AN0x+q8fr2zgzoApUjn/i+F8AEAQGMIpMmyQYZ36BKGCZdDJe7NmfXoAsBrw4Uy8jHOdklS0OLACuZot79/KMu19X0/wtAKLAQQTSEyTJJtsPRBAtbY6fuTbl17/EA2wKGsvow3rZJYwGHIUHJtI6d+/qBnX1ve9W3/8KwJhgt7QyndSbjx4MAWxnViGd+EcYxwfEA0YHdITRmbBCbHwYesAyQ/fo8oc7//4WoOABYGLJ7tCseIXM+Nv4CQMShP5k8+J3LonX8AMAC4uBaTCefsE4onPMALCUFJMp46yTj44GGIRFDZGYXTgYcSco2p//hXABQXw/NKt5T3Ph4J1FWndNqbq08jkPKmAChx+YqGcR9sLd5EiEmMZCDcpXETAHf0hRGbb5/+ID3jbIAQGIAnsFGxyB3/7WRdOumVr7gwKAb0l7f3+joo5Zu3gayDEWV6RyrayN+8wmc5yAzsSJRUS/4CYWGpXKKsRBZdkPzFG7shyjOtZbvrHRMkmEN1kFPEpNHcdBbb95RUUsm+/5zfcb+IDsAc2Y3cVdpetq1gww4dhJqAAmXIaP58lRcKVYAAgZegACAEGxH3//GAADlAAdoDXhg0RgBRMfIyi859rKcwAAXBDNB4YdmiN7xQTbKr20yi3gf36xFjGuZMvIFgJCnN2ltUaO7z/xAV+DJCiLR5KNO1JhfIOlAQDmJRtk4umZ2gQjOYios+RLLP8DDBMDsgNqBq28PP6AhkJ25heS72sTlkZv3qr6ByNRI51//qcxtXy/4V8kkLRmiJkn/8DAegAag+AIlCuNmCPRFBjIb4GzThw641s50V/XiaOkfwKhsQKA7or7TDXFFh+N8ABJiouWRSWW2C3Ag/YAAKgpmgwMOjRGBeAFHAAEAX+AWUiNPrj5lkg05yCupZj4IXtlAJ3CV76dj3jCIOFMjS1whMuFJ4FvDvsri/WAylo0+PX/EBmHAFAl5REL3EanVIDWabdW7/2+RrdSr/1/+uFcABv4YohXccumBbdVD8iIRGQRWIIQxiAw+sp4+T/4/hyAAjAbcMFMvowxnRJQv4gGuDBrLyMdY0SVLzAABwESksvsfPaxhcUuzqbvGGv/iA8AVADXh5UWf4YhwExGNUIJiX+xSWAACQOA+xw0OmiNgNlMAAQAm8KAAoAqwz/3olIcxA7vWc8gl6/aVI3Pz/4gOwAEYCbhwph9CGc9IqFg9GINWWNnz82pbe8ACwSqUAGBO/xJiVkLt/gJBiwQqTnIkrxbv7uoMBemAxxNYTIskWWQYcNccAIAqiY0X//7gzjk/gkh94+pT1/nr+gVQGknvL8/+fL9MG/Ir93f5VNlqv8/vgLG0ntY25k0c6Dxz/w3socW6FjRW/ST/k89FyRJf/t40Ex4tOPmbH0diLwvwAGgIahH5E45+RsWROcgIexHpEtfIWLeOf7VoEn7EYv5ff2Gw/cxWJ0fv7gD8AhQw8mO1EiN8za+G/pfhE/rELF8vAAcMd3sTcRoibDLP+D4g9eAVWlnXy8biPEH4bU60f9+gBdbnTQf+fFfQLJc/BhW+ieuv/hlx6/56/wDqU76/4bh9Fq/wQkKSp+Byvjf1h9x/+ecxkfe78DaDsp89H/56gftyGiP//niKJcOLNaKL+d0WhlPB/z1VN0M8///z1gCt18/9//4Zjo8O8OxanODOBYuZDj75r+j/PWRpYn//56xNKq+f/xB68BO0T+9/8YI/nnSbv+z/8TiFxC+ID+AIIQBWIAsKtTam/gbalhHehiWNPaqYAHgFh+Bx3jN6vn1rBI4P4Apt6IHyYnOuf8T4iEcSGtD48zNjeqXq/QyJjLd1n5+Gcr8SGflCIl9IydXqhh1DBqqlfv//glgAABaXQZsg6BFw5gATcAhxM5UJME22nRiBdyx8/+k1LTy8AKLImOpH79XCRodfDfj6AY4icZEWCrTQPQygn5Q+Xewarx71w6ojYtXx+X/DGJ8T4k8qcI9z82JPiowCDzcV2z3/PCGJPXgPJjLVf56+Ae3d8/XPKkD3uV84DUSVs4+dqPH7+JUt4k9YBIurfH6//iT1aVXn/fr//xJ6wmaYTAeGzrK2f5+vq6w/88pbgwMAZvxKN71iT8sCN6zQyM3xfv48XiTzFgDMyXN7+fIfDvWJP7wB1Ve/z/5+XGI83mOx6M0klXeaQ+Z+GPAAw2AwgqkybZJpv/vsiAQQTSEyTZJtsGsMU0V9f/4gGEABEAAIBEeEAB8F5+iM4ZqvEKvyMpyDPtpjmAAC4IZoPDTs0RveFBNsqFvp0FvAATgDgmeiSm2+luvjy74/f1cAhbJREHuTBXjHf/ehBMEmzr3c8IEvImylANyIiC8uG7z9XAAc+wppYqq7/G5A+AAjHGxVQxRyKYa8PAARgNuCBTL6MMZ0SWM+IBugYNZeRjjXCSpnyIOi5RdodbZMcGD9EECbdjq//JmXHuSDBdvBlP+k3PnwCykAxhNISJtEmWH9FAIYVSMiTBJpgHzQEyu0LlDFS/5oLWr6iBA08Mg2plqzTKMeIBBgAfNGAIDuAjarI47f//d8P5ijcrIcoxFtLd5gACAN5igAXy6vAPasJcCHmLCkaACRThbG2Sl/ZoboWCE2+AL9GjnMMtY+yfaPWiNGMXggoOODZAFg3Q4AOCNoFBK2F3/n5tGgCBBdZQJEzzZMEAsCdGQAwMSBPFGB2B1/z4iikiJNTP1B6nuQl8uyh+ByMj3LSfUM22vC2wIBQQkFqiTiUQUga//4PxsAJQ1VK0yf5YxwMOtvtAJGCr1H+22g6z/fagozcO/1jkugiv3EBaABYGLJS5PITJvjHv3eAqQAaB72GIOQUNf/8GHAARoIXaveRqEN9HG0QlOWoMhrVFGHX29fuGDB//G0DmDYAHMTUosSZz8l8AA0eUJozC8kNnRqZeCUAIs61a79P0wKn1H9pdtLe5AHRjZcUykH5TUQ2AACQMA+x84OGiMHshHzMQRHIDl5xfeBkAMLbVRX68DUdZDWdVX/X+f3/HXN9n3/X+sSevxoGcD1t183+vReJPy1gIh1b/P88zYm+u+cNKrTp4sKaOvr/PUWBsWwnaztb/3/f/4gLwwAOZmAMDuB+1WByB1/yBIEQCzfFCYST46/+/AAfNmAMDuB/V2Bx0//+7oDADQ1oztWo4FosAufIgAEFnQWo7OcungJGL4AMHMiYXLP+QPKYizaK61/jYGRAG9S/EZIQooa+73DNUKnH5Yrvbq3yTd/2hlwM0AV/SOD4j0k3soHZQTPGrcy8/rjTTm9n/7+oDD0GjALQAuNe+S+GxjP8Fr58eX/nhsjUo0PS5iUluDBXBlHuS3mvffe2Q2VTHRh+WxAeWugFixUVd3dbJfSyQy7d0oUCV2pIpAz/iRvyRkNmObuMljVh6EJA7933La2ZSN7/ALMAWC3UrSdxYp3/wYIfEmYAgOSD9RVZHYHf/B4Gb8jhl56Lh//92mAiEQECFbf/Yjj98GNAAEA3SgACAMAPGm//dRa0znJfZgBrzAAgdtAmI1wuP8/rIEyZKchOvS/+2GxwiOXIRdhwCTqnJPWRolbybLFfgZATHOw+++ei6MffnqDJbS+C/9aG1Pn9/ngc4ydPmn7mAiMjIgZlKN6lpDGQZzcyX9oHt3bt+sDIAloLgZcfzBPxufbSUI61/oWZAHAtvdu0LteNB8AMxs9LMDRtJ6fBxwAIEIAjVAaFmptTAMgACcxzCJIQW8r8oYiYWjIT317Ffvn7sAuJoRds4X7nSw1Jm3fC3DwULumc2pghCtlpsboCAUGZjFizi8SYQb/+ur+q8/7p4b1gb+HKL+Dir5Nf70H1c3Jbf4gP/LIXsqp7ms4trjJocRYBoslkACwSoQACgnPyQjY6//7gwN2xBhSB/qjI05f//dwwAP3VL20T/+gJic1dmZC/9eAJoMamt/CtQj/rCg4TREjg0P338CMii38MfsAAFAQugaG3ZojAQhGTBLS+2SW/gAEyIM7sEI5ZrSiH2QFxUAG5lAQWPz9/u44AB/LgRfOk/kzjWSkvaGlcALb2lzfr3VDSU24yeDhU8tfZKmb9/UI3rRK/4YgKCm5QAFGoVwsKVWsf9oRAEL8LWpavz/j+ecjYlftTYrpn2IqbPf//f8AckMrsYiFCpYpfD4QwhXccOGRbdWA6lw7lKca/P0ylkGddLFf+/64agAEDsgJqBsVt2oPCJjFKzjamARkJ0Ux0KN7VJYAAKg4DrnDY6aIy4TIEg/3efwHGprT4k+K1Onp/resp7z/i+GMADEIDCCKRqRZINNvNBhK2h1Odm3Pf3ZEBDCaQqSZJNtg8EIDoQtIKlHrTrf0IAAPwABmAOIjZojAYdIGKZapVbLVABerdfW3/9S8g7poVW//xDgANWxCiVdRs6bF9VYYdcNdZIyJQmhk1ke397IEEr2j2EtViY0JgIVCEFrahhw2L7KfbMZXcVepetq0gKegYOUTBraWfv5/D/w95pDASA3VcqdIZb2Fh3QkfvPf+DDyEpiFFSbU2QBSAm+Mgtu7y8OQUAARN8AAIA4AIMhKfiqLJIANVzZUJ/87p1fJoKknLyA2kjH25/gAtMUKshJbl/EDf/AA6AbKAg9qPm0bdY9wfgKDFspcnkJmTUjHPwegIZvN6po+hbTH80mQwwvwhbry8hd/8sDK+jr0ho+/DYg+KADQPewxUHIKGv1CWx/7P66gwX1r51//3DE9QFWxqjAcvtp6kUmo5DtyzJM5S1fvRaDqKOaUB8QHYcAGNtXfP/77O3AAR1gIcRWMyDZNpvxDpsUHDU5yR+fLoh09hai81CP/+/umNcTZeuTlgJOj8xFG2xH0Uuv8DQDUSvZ3vm5PSQKTT+/Pv9v/xAf+wPKEsAikZTuIpZHBYJhdvm1YGLDQ90OYT1RKxrg2OOFCOMc1mKzrJb2HPd5Xf+0BeR0mLtq3/v3gCoEJ276FctJPrwgp5RTZf6xc2apzVikVjvM/8EEABgpgmmpOgpI03l/hAB/hqUuM8weiQ//B+7NGjFcXMs+GAAjNRBwJdwfRZREZgHX5GhvEjPX/xI2GAAYVMahJMgxxj9z82AYwikZkVyDDPZEAggmUJkGSTLLoWIWJ1SMQpY3/fF5aMtBoy55ERCZDGzDKYxHNBhqvB1PfmrH/2AKh1cTodCd1ib32wYDE+K5ULRst+/E+pIN31+RMg0QomrYlS0uCEARqALCjU2pvBAzVC9lZCMVVF0tTFwEXXrXvm1MGA+WjSa9A1ifAhNWwe1t//zgUOd6RPZv/+97RGn93x/EDfiGcZykklpYIQVT95jR2dzC5xKGsROfIkx37uURUEkzIRMD8MABjMgmU51IMpq0cZRoIZqyTUJLb/cwjoGrWGNlsLd/vMAHhLDE20seZJQQO8AwLd8JTaSzBRT7//8G2Go63IMF4a5uEjx1fcmT/9DoDsgkddXCvtup/w7DDyEAViALCrU2pvasMUWpqF3TAzoqDL5WB/yyb4GSsB+cJ8CGeUAGUgBXZLAKbZ+bM59/+NxsH9QAYblA64NLm1QKcIQEjfPqQrn/7z08alP6LcOeaqxd+/6AxBZQA1/ZonXYMP7+7YYhkPJweTbhNfGYg/LjRVApSr5/LwvAEEYKv1S4lEvKsJd4OI4ixF5Xe+yoqDDgCmephyBwZvcT0qfe/wtbA/Nwp5m2P6HoqVLYffh/hvJ8BZztjSOf96gwXiKXeM/3gC/4b4ACAxLIVMiUdwilhx2wJHrGNijx///oLm/AEiTkbKr/XD/ZEJiTERNHPzgABADZIPS2Dn/mjdP7AALSEQyVVQqmu/ygG+MAJlC4luRIxw6u94gl5zEFvlem3MFokB6xicnR8jAidjd4ZWv+z/XD4YwAGuwhRCmZYdMjGyvwkX4Z6UDpeJR95EZBsgqtSQljUh4SAIAUcVpiXC+j/fgFwAXG8MSYR3xkgif//g3V+AKI0JH6P6g4tpZxt574Y4ADYcE2ibQ+mSU9gAAsCF0Dw27NEbARComUVKX26S3hhPL4BfCd+1f47m8AFMIw+WQ855N94YgAPAAsLoakynjzBBA7//eAQJUqEJKd3n/Loo4BKjjS2WuXJT/13gcsgYXG2EVce90MABqRjdBFV5KWKX6TIaY5FcT1LT5wz5imR8M0lTcuAFgUh+dKnnz/4gbgAOCFolcQIQxBO7r3/uKmv89J///1gCdCAA4J2iUE7IXX+aAhYJTAj2oJ5be/dzHQnW2EPl3GNeOACUFq5YuBOEnnxgAIZ93T+ALqCrL9CPMcZcjww4jNAQvW/95Gy37DX3sHF7ArP5/uZ9Mk0e3/wYa2//7d9eGh8ADoP44AKHb9AkJVv//co2CA/QwRfib/G9QDE/kWz1NWWdWFoNRovplePz+//wAE0RhrjGQoX1MXAAsgFg0a4tfDBavxHeA0ZMAIMYrFN7rL7z7qYDZg88622Y7gNGEEyrWiV8Wnlr/9Ih7o8Uz/FPaAQr6SopPBeXpyDCF2tVWZ7+fRBUL65anjgW43OScu9f43KM2GO/EUQ5m+T582LVl+UQVtNNGzYBRDrhTlpjW4xj/+8QACgUrrYeaEwha8myCtDmjym9AyAA0MABineuANf6IdbYCvOI5D/Nafu8JG4RTlT6/Y1aZpnTW+588p6CTHAAcb1ej++4UqFBehOR/1wPYEZSWePX+2HAv+Yy8W8bOnoI2VKNrx9GGBpuPd2wj4e/bQ6DWR0NSas0UQ+9wS92HshD2oQQ33kjE6IcylCepvu/0Lm1Nb2MpaV1/N7caCxfDLKN6Z///C4YijVT4pVpVVZDQsZe3Jz91pbUyShHvTP6JdTBhh5fpA7yCHoIkWaJr//ROJB+2FlsjeFCaL7//6p+URESbvDmTBtOhm/43p8QbjfhbCSGP8A7EaQ4rLZ/3B2lFONbfjTAtuqeGWk5yqIhjtUY72zMNVOdSj+tqQw/BBfKEIqxhXuFGG+8UCoalESl8kLJXowEJCmGulQ3n+39wwCbhaa3pHPG23v+LwD1+oOj5hd8622Y4OKs8V274ekglZZ3ObNh/Piwd3m3segPw9AASht7UR1dFyY4Rbumpnz//deMBvw4Uu8jHOdklS3iAaYOGsu/hnGyChZfabV119vj/1YPwAEh1cR+ZhXwop/iAAzVwUVPW7ac7Z33Cgt0RfsptlsuGMTcNYaQQT4FrQLZAcueZpH/oxpV74Orxr3/D/4ACAQKuyhCasrZzzCSPiAaoCBrLyMdY4SVLzwf2oR/U3QnrFT/5x4AYhKFEHu1y0kqaY2NJ/jwBi/yxz+rwBjhqRUMUZ+sNIBqoi8tGNqfg4D7k001/XrWxgrdgX8QNgAWIZttzDEsA+GiX98HhExylZxtTAKDEKC0JkiOO0rz6zwBlHpZw7lcRVWTbdBQWw3MMhxDHPBvGlfYJ9S4IYAcPihuDOZzReHo2igD8KAEga7lSRF0nHv/BjQaAGdQMaM+//cwuv7kD+sGW3R3/hffH/CvyHF5FxiiPlhbmAADtAAIwBr4waIwf+ZsmG/MQZ1qKYGHCfaN0hKVLef/+ICsABwhGcxFRVn2JZZ/wYeABbEH3LFz/6TUtPQBQCbBgth/0MY4RUL1gA1jWKxbf3k1ZbHn4zEB6AA1hQTbKpL6dBrww8ABEAlQOFsPIT3rpFct5MMPWUNp7k2p7+98QEFEVjMgyTYbQSOeETRzAQjxsW6//3Af2+Q2po/wZ6/iAt8YEihwph/0N52RWLB82EGrLH192bUu/B9UwDCiawmRZIttgw5XwwmiY8q//3HL3L7wP/8KwFxAi38WuznQIqT/Bh/GLtitzsKRTSn+GAlVBw1PtY7MIJFQwwfJbNkSx5ghyTCWR8r/r8KSfTnvwt8QmUQdPe5zYJGS/u8QGOIrGRFgi0w0Yg91Y2f+Salp7RhhtzBsv9k1PTwAoBJgwWw+hDGNEVDPjAS8MFLPejjOiapkMEDEdKhBriKNEYfjN0zj7ipvykX6zFpT1/EBXAAiinGWh5H0P3WZxFMb5F9ygG6EA1mw8ZVfyMhFZTHQoyWqSHqUszHDt9hq5vd36vDffk4D/D0EB4jJ8lvR5myBfn1vpX3+XSsddxCGx88eQbsYxQV+oEIJp+4BuIzlQm4ExXWY4PyHVzOpiDvpRT/OELcESllNkt3CkQ1FRHP/4gbAHMzG6ir3yVtan0zERlFXqHIe1QejAAmVHC9ZsCt8PMZoE/ysrMddcySOr/61YlPuIp6amf+BhgKDEf7E1M2Imy0z/gSPCHucgOUUEHC06WcNzF/8GNiTZ2zBpbC4IsmAyerLr/igLiaZEktd4ynyIm/iA98xKKrJ5iUd7ab6dDMKYuEjE21lQZB+2Y3dRV6klLWpGpB+AAhkTFFQrdRibagRwS5APChLQdurX4KorL1Q/75h0ci+H+v2Pu9Vet/fgwNACQG0BMaZ0ZIcEL7/AAeYASB7qWpOQaMf/8DA/AYlFJmRCOoxTs65gVMQOeF2KkTLbb/a/AG6mABgRlAmJ2xuv84JXiFMRL3uHG/2nF+oPVGyIJiV/7/8QNgAMyEVFIdChEtYlgAAqDgOycNjpojB/5mYyrznU4/tb4ba3AaeQeuS+/9h5HBIAT5Bts6Ju3X+BAEFx8nq93vlB0yYVVJRu7eAGDIYVSSi0PFfTS+4jAK1IGhVubUwLD4I69gLYrdKqLttHQAfosRedgWlT22l19v4lw/AFg0xBUqzU4ilpD4gKyBg+g7WAINXtC/0vKKw+AMWiFScQiJK8a/+DDjyh1vyLLsC6HWSSnr3/VSMpKsr/56j2wy1X/+esEqq+f8ZzzF8AzIrrbvr/5j+n+ue+D0zLVQPn3P1/wzMfeL8rU60f9+g9si6Pt7KLpc+cP/PKkOdX+5/2w+TRo+f8/Q7x/5/fg1aWr5lAXE1/zzre+4AODFLM/3mGdf137/f/C8ABBGKw4a0Q1W9vupklz+fxs2HpFjWU9/P5sJTcbt/34B7a4mpnP7cFals9/QfidvhYhymUi8vpkSf/4VgKQq4dbGJoe+cYJ/9zwIDYsV1PP8ELu/g/IyE7OI2vIS1ick3JucwVFQ//+4DIHhQScMyld47QX33/HNmbY1KqhiFL1b+z4l/fYF7hps+f581WkbtP+GegIZ3K6osTFtln+B/UMoPZMbUwMdJ+oFmQ5Laet/+fL/wQtef56+At2hv6/z8MCY6bveB9f+ev4CVTJ3efh3jjf89dAYA2Je84+f8JtfP89Raur5hI8Sdv//iCYACZZINOcgrqaU+H4bgAX4AfD1TUH8WNd/t4AgQlkriTyUzBvDHA1BKlXz8StQ4cv/4b0EP2IjmFJ5rDAXtztY+x/+eoGjPJDan/wynD/54sTAF/8RL0KH/7I+Nc/9e+esD+a7y8a7+eqhFEwllsvXhfXPXn7/4QjRC+Jz+IUPwx5vwAGoiACAxIO1OKjY3C5Cvn0w8ubAQPoJOo3B3viBfTjs8balsbalhtqWnXOviZBCwjiQ1+MH2UHa13EHewd6GAS4xBeLqx2//hn4BEYPRJbXmvU0hxwYdY7/rX/8EsAAABZ0QZtA6BFCMOeAA0DMZAZPBLIhfuun3XgBAX8rw/w3YL5GGFHJ7wgoRHOVSI6DCptwnvErkYq/ff4Ywj4Rz82ERFtdVwhiT14BJL3m/z/xFYk+PALk046+ZVWp95/lPUfxJ8X+Ee5/EnlTAIG6zfz+XX+JP61d2hc/9P/EnwZFEAOAySaq5/3/n967hv6/88pYdpOAwrfRPXP9Yk9acBBOch/n4vEn4YBN8nC71+sSevAGAb0+v/X+eUuY30PkxlqhK1KuP8NYAGF5KZtJuMFrAXeGRX3ilwCG2l3ef/4W+QABegKgDaylKpYtYV8kZDRCmUo3qalwETWqRvG1NrB22h84bFXVkHiGARaQKCTQ2pg/iceHZEDx9EPzkdP4dteAU4wX1sl+9/hygKABQCvHBB8zKlnjkhf/aBhWexO1YibTK/8FbQA42ne+P1du/cf75gjBy5nNq/98/89/gL/esPqa0KIgS83/X+CDgAUGDIb5rNOJgbUn+DgAIIDRaAT5TccqF7qmIfmACwmBiTKePslYoHAYYZpAxayIaU+cZkSIppb2FQ/j339/ggpAAMBXigg+ZjKVnDVBfb/e/HP/+6gAOBj6e6wqFkHql/HXyABcXA1JpPP2CcUTlgbqL9wuf1J+ZNFWN4wAsJgYkynj7JOKBwPfgD0Ro7y3B/sVjOz/frzaF3/muhLYY+eXiB8LdAxXez9jTpEMs/z9IAEyqgT7Nobrh/kSIJmEVnOUpSAw6iPeP36Df6qaH8v/4X5AQCAAiMOiholjBNZgu9uWoekDoVFLlTn+Uy/6BON/WTlciTX/wgkUBuTtxx84yD0It/l4XOCXxa+fCRtsHxFYk9fowBTc5p8/+JPWANiT3nHz//jMQTAAdUEILU1DDhkX2VofEP5mzGVRW6klLWpDB/hfAAsGqHABwRv0SQhfC7f6AsBhC0QSxMNsscwABYNUKADgjfiQla7//7tQAuwbPOB6nvSGf/eBL0DMYHhGk6c6/j8idRQkfgB7sxR3Y3e4IooMtVBSNM9oNI93+NgSCEotEHEqgrhb/7v8MxR+xOMXmWTyxoIMALEKAElqALCTVf/MAD8TFFkrmxa9tb8frvVXv//WfoVNKwAklHnfh5DKpHrDdf8SHPzeZEN3YhmKKtyF+ZGNnQ5uw6FLR2oAwrcilP4h3gww0tsbB2qff1rcGky+++W/JQF9MkicZvbZ/+b/xv4E7883m23+24A8UG6r4FoPkuhr/uUABMqoG+zaG65c3sMUUr3LpgW3Vf96kQmYxkIEQxiAwAEwABACnAWwfacvXJOSMsA+vhbqWtEt3gBFBXU6EqS1LQzhHWCgoefLTldw1UX32h3MrgiFPaP6zdhEgNRLjUXW+/B+SZ4oSQ/skXnBeDVf3zcOCJO8Rt8DCiEt9/+x81eioTx3iArxA7KDYkfBbWaDwnQZrc82phk+HkIArEAaFWptTAkBaAnpGQW3l5hr7s/fpL80ButGvrTfuEOGsLkPzr5YR7h/8QHoJa/t3v/z8BJf7qVKywy7UBir4OOW9kU5ie/89gHEBJOsn1OBY9avBgsMAMI8U3GfAEEMAqkgYFWhtTAmAVIcVBKSnFvIUNAm5m4B71T1/g/AQP3/+gZwR/xAfww8Pb5extTBFuRzSG8BQR3OSpcJ5BrzP/zVvgN/U07w/xFkXB/gNfDDKXZka32f/w/ABLgGhh1It6Gv4CZZA0OG15DXp/gAVApBQ8+YjS7hqYv/g9YkdPx6CoLo4v7wAHgK0cEHzMJWcNSF/9oDFd7E3VnWIbZ/kfTx7n91QBw27DrWH4fuFyRI5IdX9MCb5OFwCqUBxFi/55FZRHgcv/8/4gbgJH7X42d8AmwLC3GIS+cn/fWWQDCuviEElnecYAHwU4IcpDiChOx3g/iAACoKVYMDTg0RgI4xdsmkOpsFM6o3pTaMAkeZQABAKqJ3APK3GECAYwCgIW4nxCr4HVKs7wdaKIw6bu5Bn+GICg78QABBn6ZXFa7GH+0MoClcFL1vLh757PLaho2eH5G8ZBNJTjz/gDGyEjnOrBENWjhWMUSpqGXTAvsqAb78BbPFUNrPXQP+JDkADm0Td9E++AyBQUEnzEZXeNTF98BmAbKKhGuYW11uMSO34WKDJLo6lw0lqgDoDUu4Wptt/nlLFvB8tS8B15Sk+P4hwAG4cH2y45kNgpgfkKPiMhyjvpZrwxnFeAAxsTJyi6h3LajIADYCZ41bWevf4kEGAAmA04YKZf/DGdEFC/mTBtvRU+9k3LX3wALBiSUqT3pkrhjv7gNBspwAYEa8VErYHf+fVSAMIJpCRFggyx4YT0gCBQrItRvYJo3ClW/v9gafj0rJ378Yp/EeIC0FbEpcIhq0G7Q1EBfGypoEoOgshj/qJLX0p/8rTAcHBJ4zKV3DshffcEZGMTLyhYJNL7wwdmg+zYaaEt39QYO76bkW+7+BnyhOrHVA/J/4AEIuZDnZVRfBhAAsAOlA5WmpaaCBrNQ8AOxwXbJpDqbRjpZr9KHHef37Nsz2H3X8ACQWmYTEO7ldmIAWohMsdSt37/0MAQ135/39DkmNyL4dgAM2iWZ6FnVNMHA7RXr8CO1diInQ71w/7rsg2YPh/EoVx/62cCJjFMrjamkCQYiRGiUWBHfVGQnPfOaiRnRv+ww4i1EAPhV+lSPiOoWZg7Fd6XgYD8OwgdQZwP8K+IwIeSXj29quprq/94ZgpBAtZFOW4amkv4gEmDBqz6EMY4TWL+MBLwwUw56OM6JqmfEAAhEmAFNsKzufM06ewAYXtwXqcINsLPX9YQn6V7YdRb14MQoWCAVpqdaX0CMkFIny+7//DW0G4JOlfP8PQwACBw54FguTWmv3PhgmGpUb1ymI////AAZBsjmErp3tmY3U5+46WtSWi0cIYDsSBQVaG1MAJRyhPYfBD1eOBExilZhtTCxr6XW/xs7xx7vGwXKa44+P+N8LDobFkofJHEL/3gQNdtFkC0ts1uIq9g5BAbIcXEVDrrxgJuChiz/pbz0msWsYzClfopNlJW+5sINVaNn78WIb+Tz3Tp9x/vbAQ4is6kGX2GQOArpQbEDFtWv+D/4tsa/l7v8CfBSUPEp1YPFn73gwBhZ0EQhPrT3vWS9DxNq/5BIiXYmVW9v2DYZkHRzIIFk9pHbaE/wr4XiOBzVSgabGdVYMPywAEio4frNoZ3l0kqvqEoPgsjr/tAYzdZ9TYqbbTP89A5xQQeMQnKzxuYyowIEALHFO2w///7/+DcZp/EAg+GA/m9cAWy6QVk0r/d8Cbfb8QFeaKgAckMroYTPJ9ik8XB6Kldlq0HWXHQf8u6BAEEqq3ZtpYhJQ3nvijaC6tEOUMGGUfDrU2pH4ABMVko8Tit/78M8j7Jib/6WvjEP0Thfw//AEEMB2LAoJsjamBsDsBN4atux6fOBExilZhtTAI0Iqcwue71sTwML5JgZ6soItMrleBQFJQSkDFtWz+8GB10SfP1YEw/v95+AfjuGMAC9EQAQGeDuKMjsbv/kDQbIQAHBGkCQnbA8/wCIDoqEI1mLcks+D0CYFlIh+9mwiQNq94BCMg2QVWpISxqV+AMwF1Q6Gr/3bWVIX79cL+EjPY4QnrOz9/r6OCRsffX/C3AB5RhAUkJ5XCpMdpXhyul/4+cfwDICQNpADCb42Xrt9/ffv3+fhmLxVeF/gM7ifSOIU2iXl/0OAA4Yz2kL7e+CDTDf/wAFhhM1qHfXNslm/eQreRl+Rf2Su9x8f+HOAAgQqPXrN70QpOJBAl8dz9cEHwsE/HXGp1NPfgAfw0mtRFtqBE0RudajMtmA6xTHcztjv++ASiGV0MZHHSpSfAQHG6LVuQhRcdgtWZeAuUHkLOmtVsQWnsTAgZISGQVtJ33gAL5ick9eM3rHWP1PP//81AwH93b+FvmbG7qc6lH9a0hh+T4IwGNXww2Lbq/+D4aOoI8KBkkiEfwIDFl/HETFj5H9X/89cJeXTp/4Wh79f/mOqfx4fwAMH8Ngy6s/YOjU61QyPd8v6AgLYH/rm8ADEIDGFUjMmySabeX9kQEMLpCZJsk22DFYg9eAy2ivr+I8QF/lsQ4ACZRMaIcozrWWxgAA5QAHeA14YNEb1jo2WXHNtkFNcAALghlyDw05Nqb0zEyKcXUO5a0atAIN7YUS9phQDDp8MK72Cb9dAJvJVe7ybBiSd7X+GPfwCBtrhSDCu4KpTTfDAAQMZvMFqfrhHnu+7oCEotECEdQSw2/+7gMaJC+TbJY/gyoa/+8wndJ5HmOXUbX+CbXNI7VwGEg4q8tIuK/7IeDsuJ4awALBiSQiT3pkjhT/7oArADQNdQ1EneWNcVAZP5w35Syif/xurp0zp69GVanhwetKRgDA7wdpVgdhcf8jz0pLe3v0A/+AA1EN1xjIUf2KTsAAFAcB+DhodNEac+fr4jtshud2uZcvb/AGJcyObvP8QNgAOSj1vNU3uUso/bFm4NHElWv/g/DDgAJiid0QX3OtZLoADkWAKSoLZpevD3BDAC2RkAIQZJ5Yow4/eelnAiMdxX401/AAPAnJq8fDbYRv9D87oP9paMJgi7OLww8u6/cGUUASrJenP/IhtPh8yxHZH3lZ93+cjiKsr/1/jYQtqoDODcW6+fbh+Apk4SGt+ExTDrLcQtbxj+FA9WN5Cj0T7ah/v8DAv0tgRjGuVW/lUPjALEC2JQrfxwdrZf3kJecRDdxGr1zAJBUigBQQ3C6DSrTvvgMJJEK3rK/f9wR0ByuC8SpxGlqITKR+/u0EIgbNzyCT7r//vFL9t/t7MDt9Ewvf/GClos3NxVf3g4h2vhFx8p8b4Ab1/Lb/M7+AHXvtr+rpgSLOOCB/OSfjtMm53/wGqNTCjfy/oEgFYAAgN8BqBDOMdeN56pgfHAEEXYR+hfn2Ht/CAACQMA/B04OGiMEDE8PQIFyxtrq8/fvCSbAcr+77r/gg6wbiVdx/Kltv//zRXYZ6QBEEiUAExhkKhxNQ/lNR6cgxBSnYZcMC2yrAREEyIQTEOxiu5H0ERBNstpUP+8QdXEdTEHfSinsAAHYAARwDnxs0RvGCG0T3RC0adZxWnAFccbD/lAySa/ABLrAHjGYXsNLv6uAwt0E6HUyO8+EHDfkkkcfw/8DHTzRKq+sesnT3AwQKALHkx3YRJLqcWS4IQBGoA0KNTam8UGY7YFE+k1tshRwEXXtXvm1NxQLwfsBd8bBft9eNS7ez9nt+//vZIyMVTr5f/43AAboyeQcx8unRAqEDDpyd6ExCFh36c33w/4pfwDHelqbm6ESaaY/zH+8dlUCmAAQmoPSRi+s/3gAEQPdQjVZqlpQ9nGArBgSdMynd05QW/wYAhsdEMKjWJtueoMMRHoAl+Wa1l/5C/H33A7L3opfqz6e4Pb/GwBqFqC54xnWT0+cBF1q135tTcBClhSMib1+Vp3irwBEGtQl/tMwUXSacBUf4/tNl5LXPDvpnxXgfgAWLCBWTGISQfH4mqwJeAGoeqWg/ixr/9vBBEF1Yj2Cspf27MZTIrls51XZtf4YwAPAuUAOCF7TIEu6Ps/QF0yAGBiQJ5BRgdgdf8BIISi1QcSiCuGv/u/hsAJQ1ZLUn+WKc/8GvAR0jIgak9/7x2sfef+GvRDDVdDJe7FuO3oAsBrw4Uy9+Oc9IKllgB7ir5U1/b//8QFZbEOAETRU0CTQZJZDUHzA7hQSeMyldw7QX/2iAA2RGD/ZlDNcP0BDO5nVViYtts/z3huxgsxa7/dHd4/fofbQrl/iuesDq+r5//Eh6AAyHRaou0OlslODDwAEYDThgpl9GGM8IKF+iCBLuxlf9k3LT0BgQGEE0hIiwSZaecRACAQkCORWZHYXf/AHcAK88KKsb+3jjOEqp838QGu0DsoNiRsFtZ04EXGLXXm1N4eQgCsUBYVam1ME3MZVfuP/MMmVmjVopT3/8QFfBC1TIGoSX5RCzM4AAXBjNkHhp2bUwMP/MxQTbKj34yi3hhwqUytcPEX/kIFxj6f+ICsABgKYNpfiJIbfN5f5wHbIDagfFTeMDAvE0E6KQXEuS1n8qQtkaIyJP/7RgAMqgHcO8WitaZH/6YAAJg4DsnDY6aIzgAhViU0WUzamAXwXqMaIwFDZsD5Uf+pjHUjN3u/VNO7zmUkLJuR8SHv/otZHMXVP4fL4iN6E1VP37QEiuB8Mlw2i3mRjI6HMpB0MWgP27EKKU7DD5sY2V+RGQbIKq0kJY1OkF2VaPYbNdPd/aYAE6q4RGG6N78Be8MKvJSU1/N4K9JBLaWf/+r+IDMZDnlMHbY7ImJ1h5WeIqP80TlX/v3dh//EBqCIE66uW9//54AGQUyOYurKhgACAPbYAAIAYASOy/BKa40rzYgjWxZLuAGgm5xx870SNnnHz/8PfIaGOscdCdxlq4WxHENVPDUml0gYfpEJmQRWIIQxiAw/AAYArRQ42ZjKmHjFBcGdo2CA/0wAaW/kjw/iBv0mQ9nbqiz0PgV4mjapR9k2NzrXpmQTKKu+IU1qAw7IZgpYy5d4y84bteHowAJvnC9ZdDN8AwJDGb7PqdERZYZ/n1ZuIkYPzOHyA5RQ48WnTDh2Yv/gYYmDgA7ePyVJfamoyM9F+/0aWQZvEiGLcXLnt2+anEDYdpdcAA1WM4FMVCRpgX2VbQPyA2oHxW3bThDAKxIGBVobU2V9SECSDKnkcu3gOAcg+CsTgKFzp//92olKqUNQbJZHV/eRkIrcx0KMlak6AQ6kvpC8ERXUZ+wfn7N7HVXr3fGrOe4PYLBTg4txJ71wGvXTLmFP/dyzew7XzuPDktq+n8QGYYYAsH84q15iO/FID/n/4ngB1jJSrfbv/iArAAqBD0J/IprxO5hA7/tDAmFlBNZ4e2cTL9g/BmABUBDUI/Qnn5OxhE5/vgQL9qFJp413/te6BpJRAXjRzA+Q7ktqUt//0Hjn7xB6gi1Qbr/4vEH9tgduR/H/XPO5gDCD8dT5CoHUtstf3t/hzgANogQMaO1CixkZsV+BnDybFalEHwaaeBh4qBsorfoMMSaJ93ldrbh6z/DNKPB7zCqrZapjUZ3cg77j/56/AZVbJ32hoJuccfPjxmgbn565MUncyB2ys5ji//3brUOHL/z8OHisX3qP+g/tCuXXBH4aPf8M3G2KA1rlDvUDrohSJ5+/n0QMJCZ/+fhDHqsTBAcb1af76BBj0BNX9TF89fAKulz9/4g8WpgBPcr5+/nyHljtMub/88p/8AXU5088b/nipvfQYC4mv/DXRnJoGkyqye9ohTwq+96jev8DM3birJ46kf/zyl8z3IG3zQz9f9e8QGICPfG/kd9ZmDAFi7IVlOQcilmPYAAOQAArwHPDZojAA3DwtyTSHU2CnB+ILOhmQVLyaaaSGA12NeAFASJKiqqd/+eoHddDRH//z1gcUgpBv//8/Kh+5//z3wCzaU/f/8QFYAFqADwe7Yg7ihrv9v/AAcu0oAUEFYSk46gZ/6GRNDNoYmNonX+f/698/um7h//nrwHSQy1X4RxAY4G2pYg2hc1GF7VzAMt91/RfQcBFvy+1/EC/SFFbDbUtjbUsNtS06518Tn86+JhLCIa4EVAkAj2QoXgFEpl/6GASwKgpk5kzR+O98MSwBShnwq0HV/4jgkgAAAWLEGbYOgRRM3gAIwSQoVjNvuXbUeG/4wEihwxZ9KW89IrGA1wBhG051t+H6LDGJPWAM37qv/f/8Serdahw5f/8+JPy0wS+WOxpklB54QxJ68AIzJfO92/zyp/CM3PWEfCPhHwieuGIrz/xIcgATaAQ4msJEGCbbRsvwH+K0YQLuWNn/kmJce4jDJLM/hei//5eAD1AOOSRFq71wH/Hc/8//+AJE/nF/7+sIxeJPWAhdyP+/UzspT4/P3w3AAxDTXk08Gvfj/PxSfK+nyAJJds3/68CbnHHz/5+PgPvcuef/+HIACTDEy85K+SlnLD0wANkVwnWZQvfACTIZT+bCT66/0KGiKnOnlvjipVGbL+gL6VeeJf/7/xAbsOwAAUBwH2OHB00RgETE6IcTUu9TUvGJMtUFx2Wul83fOJJNmhojKOpQw2PiA34ADB/DYMqrNDB8anWlFwB21uf53DsZbj9y/xAb4ADUQyugis96XMX6eghBSu44cNjGqsThxmWPb1+sqNbQtcOSWlmaDRp8yvzzF8AK418h/92P5MtUE00b7P3//f4agCgE2DBrD6EsY0TUL+MBPwwYw8hHWeE1TIYePzGehtTM42T/tB/8MY4Pf6AYACQ++M6mIO+lGPw0EIw606V5pbPKyFxNCJcjvvWHEqtVXv/PX/Tsy1X9Yk9cELbzmBGdrh8/iTzHwBpnO7z6788XiTylhHuQDMW6ctvv8NYAHgVEDj5iM8Ompi198DNuAMp9PIHms65/j5tpXef/DPQMdft+5wRBhpb+f7C6wKW3jbCt1YzzLZWklKhv5hqKj/4YgAODEshUnkpiyuGP/sCTsADMVRYW1Ar/u0TADwaaao7yxbn9tJEYAwOSBHFWBuF1/z0gTORmpaNt/gFGIW1XLYuRjZFx3/EPAcSPVnzzlUcno3l5WhVFvOSfdRcnybZvv8EEAdGNnY5lIFQxqOIeCJIOOC4jibyhl/4NsPx3v84cYdsKc3/IEQAQp60W5uNlRwtAGwY3X1L/EpUhYN82ABsiuGRZlDe8gGFeS5ecZ0iezUzl9jiz1EkLzPkq9Z8/8QNhhgDCQhiIM7EGKcQwMAC8JETUJYZFZHd/ATgAboiheoqxm+gE1BCC1NYaMi+yt/vezG6irvyUtakMABgAAgA3AJQMrKf6E3ZmA+dY7MR75P/3gDICPt8qXyuYG9IagdEDjxmE7Om5C2+0VjRg6VucO0tdjbAkFqaTV178GKmhgLxGP0qx+4P2DqEV/votZtai//+/+FYGMFrQXEjIK8zpwEXWrXem1N7RjI6HE1D+UtDgABIGAfiB00NG1MBsNIQWbJ592cAahFTiNpJC3sX6kIjIQyEG5TO1ytonPd/yeNLDKQl3nbiO1BgYvOw3Bf4f9JsKPR1OyImQ1sWmL0plhwEkswnrBmDMGCBDWlOrhdP//nvmTxLk6VNoj9D2HwZZOCOjQ1MqhgjABl962vfQDiKu9bXZag85CwulFjnS4/J1s5yfA6HWr4X8IKHaWH/D/AETRMwnNqbY4GAAiGKrNqnrxrUQ0aRaf5GF6Y4qE+4MACwh34zruxMWGGf54EcAGyKoRFmUL3yXD3jpKl5wzoIi9H7Cf8Px1W+gH5gUwoefMTld41cZ/weskVFoXAyC6Or+AnSIAQCEg7SjI7C7/4wLhvzfntsADD64j8RDSaUUSEnRUZQ1Nl/7tLuR/36quQGhi+95j+0KS3X/7/xuAAzIRWcRteQtrFz2l4PBeFw4l1C/HTIverumYF8HYaQQvvDAsyUMagpW7ZfPzxaEXsAAG4AAzAGPjJojADjjYqoYo7qYW0tBCgB+ywABAEzsoADgCKDL/bxtPXpv9Gv3B//30FbDWWP38lg/pGwkx525GJUWGNqnjUf4bgKHCQAlB+Z4aVGLWvvGAByhxjEVKWbLV8IsKvocKmW5WT4+A+rTQrBfng25C9WLf//y/+IDkAA5M0q80/cAwB0QEHDMJ2dNyFt8BjASoJ6caspj7aQ1RdAkhs1kN38vABQqtfW4T9v/+ICuAA4Yz/Z9TdiIstM/6HpAOigg8anKzxuYvvv0BANaYwSikp8/gL+JDMABMcbOuE9pFKLaHyhi1RModbbKZwcE68ve9Bi11pTr8XiCYADhjN9iam9ERZYZ/0PiAz0gHTgBAYYnSzxuozvv/KElJRESnwf/4gL4ACQCXBwth70c42RVLdGMPlUNlzk2p7egN3AIcRWZBkiwz/0PLQMLYUL0T39v/+IC3xgJuHDGCKEN76RUMB6GQNWaPqh2bUuvf3BAYUTWFSbZNtkGHWCxUnVlv7ctiCfQP/G/DgAewC9Gnfn2ap//2QGGAoEPpxFBUcIkLFvHAcBcA0PhoRjtUnW6HxsHJOEWQSwoljxg1jjpXmIQmlIXBUBNY/pOIS7TKbaRV7PC6+p6CNa5pY6iRQSTJ+v/unIKBtmM8SNgFgABAGoAAgBABQ8ZptwGRSJEk90B8g+YBhbcJXupxJPAwLoHoGKz2J2rOkQyz/PEBIOvflvHIUrTfImIrIciuEWxqdRq6rgtBsl0NX94D5ASQo6d1Kz609CfAMFQujTDVtsOBBjd/3OAAm6oE+y6G640Ijs5f+lk13pIhMgiq4hSmIhNTrD/sLOLAAye1X5dqqif6TP+rV3B6uRP3ujB1edT+ID0ADkkiFMZGyL3614Hv6QJIDSYPbZvlozb4h3AAIgEmDBqzvoY1wmoZ8YCfhgxhxCOt6JrmRsiHwDNyGi0IGrUL0mzZfdyqjNENqYd5fr/iAQUPwE5grCdarBKDc6EskBDppfdniPvcEjw7B2GS5+U13vgC0AKHnOod0sriYYuaDCAef6z9sEAb9Gka14Lb6/iBsO3DwP8ALgA6CnDnKcQSJ2N98HwAwwAEQCdAUNYeQjvXSapjqDD3PPikYyZvWISlIy9e2P35/CZkAMQbqOm1mE0GiQASAl6xJ3mDHP7BqaQwwBqRJCAWyPlXvaiJxy0vx/EBr+KBAb2mNbSmofyALAB4zgGLFoW82SggfUMENWaThd/ff/AX8QHoYMhhL8BjN9n5F2dItpn+4gcOAwHOQjS5xlEzwICDgEbXwepK2y8/tQmSuHhn4Adk+3ei/gI/k9lfH+f8b9aI0wjoUb1qWwAAVBwGXNHR00Rg/ATmN35zqUL62+GGABUDkEBJ41Od3TtRb/DHmuQrPjze2/nu/rEjIlDWGRWR3f0BCoIQWpqGHDIvsrD0LzbROfgMbErbUTCOQrw/78XaJWjqj+r/Dv4CEfzeqZoTJthj/BgTgOGMUQhel48q/aNIMxQJaNfQlC/bBKE81LD7w42Mq7FXzNE/gw0ARU3Ek3eStJjg19FPQ/4kMQAE0OCbRcobTLKawAAWBC6BobcmiNwW4caKrqq8ueHHKlwMHrCghfEY5KprEvAIhUTKIv36yy2h2LgjUiYxBj39eBIMdnsTdWdZwln+PDbkvbe7+TCq/fH6hviA6FyHv5K3uGev8RHcOQAGQCBCkQYhEto0e3I9d/1/LQGyGABwRpCBITvgeP9wCEktcHkpmC0CnPwCLwAPTHy63NEh3rhqGAqoQgtbkLOGxfZWhr9XXPeG/8NwAObTK59rP4dfyq6Y6DQ+CDwAEJTjIvsavvWqlwAKzwCCpRSSVOOLgAHsAucQZ/Mpt45+BAfkRidkOJqSPY1PMigmXQ6Xvzbn36mDIe/I6HL2jHaDogo3VlJO/+C5PQKsBP1tY/IOOQadsf3v/wQZsv9ddzLjanr/GTRU/6rENZ/TTa3rA6/3gSH0GusJ1VpIe//v11sFc+KNKn9BYWJtYiIn8ba6u93+G+AE01cNa1945/7A//kV+IUTa237I/8L4G89O77f//z6Ao2LAmLzAMWGX11j9k+lT/w/0gWM0I0tOovff/wALYsVn+7J98wFwAuNoYk0nnzJJE7//BjaaxqUpfcDxavekm7gYnRyOMhwRNiFcPQ9AIWy0QeQmCvGP/u/hmUgMu7Zlf/94P8AB3YQopbcMPmxjZWOi6BKy+hdDZrp7/4fZTYpgOVSJJUhheY2JC89+r/DfyIxFZhVakhbGpD0YAE6q4RFG2N709f2EU//G8L8ABI80JeYg76UU1gAA7AAGcA58ZNEb3Cgu0RKWU2S3OAAFgUuoBwZcG1N7RDdcYTEv9Sk7cwGH5SyHMNLf4QSLAGJcJHf7UHH9woXH8/iAx6ugEIIxhrmIvWYQezwAExHFQ9BpCXGlFNVokAEga7Us7zBjn9tAwDCUk6N34mSgmdwNajhv/f36P+/WGoVPbZpe6yiSTKWH/73/EDfAAdjBXia/zWXooPLfoAFjB0uMNFUtPBPsL/8vngPe/QELZKoPITBSRjv7v2WyHTq4tt9/8EbwEHob3SkTSMr/vwfQ4DqFES+3RHWB1sfvr4+OfCK1fGv55yHUVtvakORXV4gbFZLvaewyAN72hnbtAkQoAOCcIxKCFkDt/u+vb2bNsAgKIE0vxEkMvmdkww/hwAExZuVGO4jtWW6gTAABygAO0BrwwaI2wJB+kFb0GtKvn6wyS76v/C19tYkf3L/BB4AJNolm0nvoAFjIAhSQpitqdP/EcAA9GRgDFGxIrlWXX7zRipyuZhHawxyA0JltVckR1f+fB6INQ6KPK084qr/d4K3gUID2hxFTMFzlODTf43zQYbNodL3Ztz78WAgvjMMpc2FWvkOhAYGNkAhxM5EGCrLm/tEZkAMUZGD6xVZzv3gSBhNQY00uCMO4Tf972N/XOpQvtesMOHa3isxir8008trviFsCdsv4D8kF55pH6S/vaYec4YBYkWWcTb/H/GwwFHCe69Gfep/9L882eCUwybz2qWlDNR5wypLkXJ/uGGAAkMtHDxDGSirJZ7grxHYiYqwhCruYcYBRbFJ5sxpNPZZ5lfGY7o3x82i1+VBw1ZotBn+fwByIN1xhMS9LGJBy2gjtk7tX//dmMvQJOv7YTgKIizqdD//RpTTT7wNj4vJIyV6eFuIGwXgHggNMV2uFHb+7d5E0ZENL2XfluV5mYyupzq46VtTxMg1iBMSXLCG/abZACAzgf1Rkcgd/8D8AYjIaIc3cb1JSGn3BekAHQAfoTlPjEiIsqtAAPGI6cJCWW2C3cwAAXBStBgadGiN5irYrKcg7qWU/WIYpL7l6RFvJ4IHtpaQl0knv+QI3G92xXz+u0iFbytH3PKgRCuvOf/C8A61R9iPT/gCBb8gQivi25oaU+CuDGTksR9JP//vIo/OtiL//AVgN1BQxlz+87JKlv+0AyAp6C096XDMvIMCAngpwl3E2Dgzeo/4Jlw8AXjajqyZ+cn7eGhDY2OXM98o7Hj1xA3oCHstUHkJgzxT/7uGyqDNSgJpB7+GSmhdWBCBfOHCoXk9/zmQsdi9RjllLfDQV8zZjdRV771talkuuT9PwfuPtINUdMNoXFhDd/aMMWCCRUNknS7T9/va8QolXUcOmRfdWGBLJgDnGITT7U/34MAZkQ05joUb1qSJFOnDhtbuseUnpaXut0237TfeB/+FoAFhjs1idrREWGWf54f+sAIvOqh3MYxR+/+AWCkMyf10WrwKj7QAXHcR7lku//DvAAvREAIBCQI0oyOwu/+AK2AGoLWQ1B/GjX//IuQFKYAIDzE52dNVFv8GGBoNkIABQRpAoJ2wOv80M5/TutRWGIOmCBBgdVkAD/pJN+Pe09PrcDwNKekzH3uD/iA1gAUYYesobL3ItV39/6wEOIrGZBkiwzr4AKemrX/f9MqTJ13nGe8N8ACwGLYn1SWPELmfHX8BEDEoT+pPPiNy/zv+Aut+LUJXC6cyKsScXiArAASFnxExyjk0st4YeAAmADUTApNhLP2SMPmugELR5OBWvEbmPHX8OlHEkB2jTEp+HKDRmSGiOaX3lhlOGs7wr8gAeF4NTZS19onJA8HyAhLE+kTz4lUwid/wYJl0IC+o5ZIw1Pw5W0CyXefcQP/4kPdGBfijEZrbn+614QAAUBzaBwbdGiN/8BCpuUD7QWVnayzhgBLAQ4LQtLa7iZT/wYeAA7sIUUpuGHTYxsreSMg2QVWpISxaxBaYlXkNE3yjyRM1d5//56qCinjRG/QZS/8gI2VG4u5ZY508/4agiDVhOaXriGuAIA5QbiaVZtiNXZ8Mh5jTUU47Kzb97/X///Qx3F70fz/7ggPj0CkpHVeXJ9D8bgAWEO/mdd2fIhhn+I9GABonUIizKG74cZog1JKsSf9MD26x8OWnEnBnYBOJEofswAAIAklAAEAAAIHI+gJRjI6Cq3noYtEPh0GIIW3C7hgW0UAw2MAhQBkerb9/uLCFlF1U58d/D7+IBhn7//ZBh+ABZgaTBza9MtlbeEN4NtLXbs0eYY1m3pD/McGzGmjf8LQEFl/Nf/zajVlSBLDZrIbv4AYyIbKIvEkJaxPmWxCiV9Tw2ZGeVIYMBtP7q//waqFaJknid/1uhPhT0kJrNOR2G4AC0w/YfGSqLbS3h+cUAEBIAVigLC7M2piDB8wQEABoCGo5+BccokbGETiLzADw2hibaWvMlIIHeBJISYiYkTJ/4PyAB8XQ1NpLPmCUEToZyxm5t6sztjzBSU0Lk9n/spmq4vr377v/55DiBm6kz9z+2NY3tf/wrAkBjWI9Mrn5CxlE4/tEADcMaOlLL/DaRbt/+ABYDHsT6ZK3iVzKB1/QBDBOpYtJLO+e/v/Anek8hRRtTA2PcWxR5v/f//iD1gez5yO8///z15+/+Ii+eQXA9cHFib/rnwYCNPiNu5jVp8j/zEKmRbwxAAbEN1QxkKP7GJcAAJA4D7ROHB02ptWAtYD7w6K+7acBMo6lbhtTAIjE6IUyuJ7FrDr7//76eOlbX4ExM298eaEmQLi1KH5Xqvnerf5/TOv7fH6vRJ7Zx84ff8Qfn+Ev4ALqc6eDq5Su8/z8lSW1O8Ar02et7/gwVVHu3/w1gCZiHHao4hDRKKSHYMEYP4dA2brP7FB1oxtTD/xvgCIO9K5RFioLMr8GHDsPj8oYzvgA1BSgueOX1c9XgBAhAEagCwo1Nqb3ARdate+bUwNwfoLqRq+8nq8H5LY1etidFo/7fwNAktqF6pxgx9/+GMADwbocAHBG0CQhbC9/zwF0ZADAzwJ5BRgdgdf8BoITCUQcTxSBbr/9n6NgBKGqmpE3Vce/t7wxYkUYbgg42Filav9w9x7yZYs//Pf/wFu0N/X+e/wBL3F4+3+esAkD28v/fn/89fwBsSe84+fxuI8R8M9gyHiGARqQKCjQ2pvnS1K+Dp8b/zv//PX1gEQzVj5/ni9Mt22eeJ1f/DEAA5Qb3ER1x5HPfyAExjZUKZSD8pqGAACgMA+x04NGiMAKg7YC6kbBfea/1EIjYxkINylIDC3rf5N28MKkfllyJ/v9cK4CUzEqHMpB+U1EPxACSgwkmnisNLuJFvIiEzIYyEGQpXBhgELCgbfFF/T6/9c9YFGfDf1//hmOB1+vjCu5T3ev+usvnrgEAN7i/9/8I8MefaKAM2/ofF2RfAQdzT/eJS8djfTksmJg7gAAAFU5Bm4DoEQjwpgAIyISoqu7OjM//4ADswY/1mLCmrW0iHxRC1tRN+tDDGEfCM+EYQxJ+XgI9p/fP3iT4IAqrKP7zjotwCGbSzvw1cMuPxPiT38AT93V/b/xJ6oUMGlVL//f/4k/vAFzarG83/PXg7z7+v/iaxJ6XwBjUum9c/xeJPg8BN4l97+sSevANdL3v/ni2+sBmquN6/dgFxNYetqxFxB6wBuTW44+f//Dc4IEjGplU067zzObjzXIQOEWSmf5DvH1Q2XF/P6BIurfH6uur8+/qM2QcMqv+evgYiUtUkZ6GZNzTv/z/56htun6218n6NvOOWVdP+f+F/AAc7xwnRvMYpuD0LZiruLD5+dgXi2+AEPB29pv3EU5jOuhL8iWXeSn+Hf4oAJAS7lSZM8oY8G5D/wGLBCJMciJKSLd/Bh1re+QtdoNwUG7ko983/54d6RqJKecfPdMB+AeIqrJEZxfmZFj5n568c+S8/79f9Yk8pduOCz0N/X8SeYuAnCydPzz9DvH4vEhzwAEGzZct7pU2604A+7+/L/Df1E5QJ5pUwga0T/feIzaQz4Aq9xmiuwi9y55/n9Ng2qLq8Zr1D9eGmSUHn+IBBgAdA8YAcGGJzu+bqLb5HpizJqEsMmojm/gALBCwSuDiEQX4179wGmucAHWuyApuJT/cBLgAuHi2JP4oU7/bTzIAQGcBPVGRyB3/zwJCAI77SllmP3h7/4DGvS9pyubrcBvtRrAE5A/GI6J3CbbF2RhV//vfb6U3qkIU1wgvEDYAgTOIeRLFxe+Hlue1sIcWrqNnTIvqr8AMgeYQnn02dVJAfrITs5joUIlrE8y4VBJ4klAdT+0s//BnxJ+Gwyk1eaSAgADEOQmHqtkLNFIAO4IX620dfcv0B6IACdUQL8F2K101XA6WO8Y5LRT7yyy+2WnpY3f+H4ZwwgA5CdajHEf60s8loYIIAPABoIcNWKiCVHUwYCGkPVHy73UAciGV0MZChUsUn0+CEFK7jZwyLaqeGGCmm9Tt7YBexH/cccliF0I39RH/hBJcGriJj0jAn867/cP4JtLU/ToWTESn/fk/SOcofhyADyUr5Ea1W/wCQ01C8hVSehj/vwPPm+RYjf9PPgFY+B/QIovuxSjcmtxx88H+t758BiCRvHhtT/w/Dq7SNfw+IAAKA4D8GjQ6aIwAxGJUxzcoT2LS4CJr1K3jamqwdB8QNX1h9PcHhqQtrW97GFH7DDGQeHHGswKGRd//+bhMAHgS6hqDvLGuf+sIpAU0IuVJF2mjdoi6iOT2OY711gGUJA5YgsRa1oU+flbv8QcZMnDHiA/wBCTHkKxtTfMEdv6Sv94CgYJUqjx117WVo5VE4ubnX+2FY8XQ5BPQvgwALDGdrfqqEQZZY/ngTAAnVECpo2xWuguT1BgZN4saN7mR//TVaxz/iA/ABTAxUTVMpPn//3BQkK5jjL2K/9Og/5AdogceMynZ83IW/weo1RUg1hcVkN38BM2wBgK4H7VYHIHX/GaLMZUVKvwA5IXK2OUQi1muEJFBlVu2QqX3KJgrRWTXfaZ/hzRAAWjAAsDwteGYWcL+abPHyq6le9/g13gD/3n8VF8c/hf+8RSJ3vA5I1Duf8MfGPeAPAAZComURaX2yzXhq3xlofn6CYSUPnf/DkADC8lM9FvT4IQQruNnDIturhD2vj/w5miIsCzodNlDcK38NRT8A/vFn9fyn+esQgFJj5+5zY39Dq+dP8/z+k3dDf19YZob+oH4vEBXAATAB8TApNpDf2ScPnPMCHoSjQljxO5hA7/vIAPC4Gptqa+wTggcD5AIaxPpE8+IXMInf8GoAOyjWYWf3/vSnEox5ff+/A+/8PwFBupAAYEbQjAmI3wugYfAATOFiqgiXkUw0kOABzAtaC4kVBfV9QB0Y2VDmUg/KagDvrbB24vONpb3QTq/xHiRsBzYCGF0hMgySZbAlyQQerkZP3Isy78Hz26v5KUGDBDIDB8QDTBwtl9GGddIKFiwNkGD/AATIjDdBFYklLGL9PQQghXccOGRbdWPCCL1ffzvRnjuU//qD3bXmbvsfhRKn5/iA7BTHibhf5W99zWwvOSo6LP/72/DFWamfGpsrp2AHIHRV1jab/s1QFdqDYgYtq2/7yMhFZxF4khLWL9sxu/OdSj+taQwwo6q+H3+BreeaBFOGePl1iB7o/4EKOvU6fvDM9r2XEB6gAAIAtAAEAEALH6dl+357bu/DDgAOwajKrmeela8K/vHBwtxDNdFf/QylwF0Mxm9JRjGZrVf3v/EDYACQAAgDEonASojfszriJrxExqRnOQZ+tKdAOs+aR+vxCmZE/W7uvBggMMABoUUPhaRUE9PGdkJw9G0P/+tbL4lbXngLszODV156v//gFSABYNdsXJyTBj39rNHTQJQZJZDV/K9aAl+82zGejrlJN+vwS0KgtxGZfy3/IvNNotSmMllj+9BNBW46l9eC7Pd68U6orfG+rhhgA1tGhonxrwMBQxmpcmpuxE22mf8FWS8U4v/3DMPTt/xxjza2H3emxfnfphybbfKe/19A/AAyn05HNUUUZJBGcvXPyCLbv7f/NqSIiklTY6F2GnX58SNh2UtRgQATh/oAAIBhIJUinclev/aAxWaxNxZ0iG1/5hga+0PGDVdYP/JjAPCABtgMYRScyLJJhs8QDfAgay8jHWuElTOjIwE0AiCmrfZvzpmSMti6LwegVQwBxScrpJfSRfwCgCZ6Gwc/HFbKKmfhFLqgyRRoqB0rmxXOv3/qjrOLv/f9aISr57LP07/iBvxgNSDHA+T3bi5ezTwUBj/6ffO/b+/d0CC4TqloOlDNPe5gRndQddugxTh/0cMXsPnhfNXrwofVZ9sloPfeGIlKJTVkM9b3YM9IsbzNGE6mFxD0LUgPlJJEFMRCZMGCC2zjMBUarVtt8CL8gnW9Vf77rRWbmv///H+dobBeQThwquIGwBbgdwZBJKyiF+AJxQTbKpL6ZBrwBNjnMKgspLjXGEkeUQiJjCcornEKGgAOBIBRCc4V0l1JWB/pK5Qrair/3P/XgbYi//gAPgWOA4xic7cX6qh3iCrqIj2oY+1lMD12iTq+Re+0MGgwTPDvc/8b8Q9XM5GUxXQdTAAB2gAMwBr40aIwJf5nkw15iCEWwxw0UDAAd2IUUtuFnTItorAAPIzAIBXgTyKrI7E7/7xCKYVXEle85pRb6f2mf8dRP5ejVk6f/4PoJ2X0LobNdHf/B6gVEDj5aM7PmKi2+EEZVCapDaGWqBDofJJrEb842B580/3/iA9gAMzERlOfkCKa9Q2J+LETuQXet7iluwWGYKaMuZcMuEH+0HFtP9db8IsDgA4AIMStbzUJIVzFJaGATHoEEYLa+T/d7zn7v/eEe8AFs4AgUVKcCRM64ThrjZ2eQqUAgCU6ysiWcSL9D8w2xh1uzUoVzVgwCHgAf6gnGq9hev/fIIIjRxmYh0d//6JNA8/ACWLzHZf2y7/9gBDL+RPayZg009fcBXChmTeJzQeCMbQJnkC3tZOOJgxEHcJ+k6aKfAr3shPST/2Nrhnfaud8b8AFB3Dc0u3FNc+IuWaNFJ8aJLx7gC77f5mH3BD4hCPIzClxrMEr//J7iC4bAC4aMlqT0ljnv/ObzJyD12ho1sjIzB4AIGGdhZCmFyNmWgCgnzApYNtKL653JvgJS/g8sbrkuRXAJ6jB7TzLH//JbLljrb5iYRR9n4c7BAAWgC4u4st1M1T79lD/gMI/Mz/wtgBMIkv+bV370Pnj8ztbaGQ9Diqsb+X/42AFGfbsRn7zA/lh33/tYTBcsRvieb50vrzn+ADCRBJTZWOt5tkhg5kaLFX71/c4YfwQKAAgRctUlT6b7nxABZWgA9qJG+O136SLszH9//5GMZt/aR3xdR/huAAiYASB7qWpg5BYx/SRmAIDvAni7I7A9/5QyAQjZtc8h/978aMyglSofLP/4DtIIF4A+SMg1/7M/3//h/gAQSYBhBFIzJskGmf4sBBBdITINkm27HAGaMCWhJPn+vWmKuTy6GpF/7ASAx98xphck+dYi/7gSjoWyt61NaWRwGiZUABlMosLcgV/3fpERgBgd4O4qwOxvP+erfgD0BvREDW4DKCZkBKav/fGyGYvDq+L8ABrmEKKU3DDpsW2V/pMRWQVVpISxqQxWIPg8AiWk+7zj3+I8QF4AF4kZNQmhk1kd38BBgAb5HCooyxW+gFoLhBpj1WGBdrB33sAB9wH9iyd94UOWrPMVbFTnIK6mlPYAAOYAB3gMeGTRGD8A/AQu5H/foFyoDe/oRd+R6kP36YjnInSX+GPwAPAxROcs7y7VlMi79wGAAkMwi3JMJQ8wsti9GwA+HiloP4sa7/bQIA4hNKrVupE4pGsDzH5zTz56ALTzMfzX/5v8P+ABaEGcdjkVbXjVf33gmSMgswkKz96AORDd8YyFHSpSQQhRY6+vkP9bfwARAtrEv+phRZJtv/wYmKANmiZnzNuCnLLI3BwPd+caFz/4f8AMFSko7fgAeEO/nZdn6Kabf/MHgAHYAASWUApuI6uzUEAito+VvjegBr7c03m/wQfDgAJB92MUpGFT3OWkAO26bgAWI7gZNluRZ4pv/HEySjwN52gKBFHtVqlHstKUf6paV0bevfoYV3JkpKEb7Gmhj2iFm/OOVMf7wiheg+ILQrSVeRz8gXTDGlUX9e/nf8QN4ZgAewPyGSdqeTlN2THHa3txhL2OzDoW7i8Fh8BJSqgAAgF+tDmgIcUN4E/AONWlHzXF3XnrULQndqV/dtABnMDMJMlYTdGxrfXjVKp/fGwkH8HypU7XaItbi7zgyB5WixWyv5eMSihNfpW87W7/1IherSa5/vN/xvsBGusDf4pZgRK4hXRKZP3/ZwBGoVuSW9MGqEEP/AS4MNaHofDllN73ABsgG1aRk0eIrCt3/KH8JTcFj79Tj97xOZ4ClbrSk+0wZQCgcnaGPFnUjOe5AMs/CIarl+jh8EMs9c8MUbXSeEkC56WNZiFMNPD4bAC4aKlqz/NGPf+8h18y8xByaYY8XtC/PLhHv/QXeDF29iYvfSkaKkdK11P9io/yUYfw134f+S3hEtmfqmDD/G5AjDGWnyknl/7xgBSBdWyd4TBhRsACqGZcFlDaZJT+YAALAhdA0NuTRG8hx6R0MUR9qLdYMctDocgTf6V8Eumbf/8v98iRnrIPNrCqJ1FxSO8/+IGwALDODy3SQTCnV2yb/8Au4CNICpKSkji/4AusBDiKxqQZIsN/qwGFE1hMiyRbZZvps/mwBCB1WkQmhjPk/07zkbharBtOeqtH/3tsTOYQ3WFnisLhg+IGj98QEOInObzJFhm22NyvetflfAgXEBXqAIBvcyTNOeM/8JJHQgKLesG1MDcCqf2ddn/72Qkp5fnmHglI6//7/43gDEgpMnEoL4W4//YDMMABzITn5CTj25zf08AwFv6npAaliv0xIqfj4FQZRxf1iEYKQL0TcLNvG7XDoZgIYuPGGBbZU8AOjQArhyUW6ls9+DAHRmJccykH5S0AgUth/PoPRaLIVlQrkUf/EBX4AY8Xd4NchF1VQtzS0HMqVWda//A14UMNTXm4yhbJNVvokoTTERkwMOPTzKAGdd3yT5zeffyCyY/LtS/rkmNH/higMABAbrWBDQZasSTJ/R0AQQwCMSBYWbm1N7DbIA4CvrQmGC3LdB48ANQWqhqoPQWNfD0BCSWmjyVybw579716bQDMEasLiK/924eSPw5UcF/CvxAVgAJmYyuoq9SSlrUhh4AFGGC1mD6e5Nqf/vfEAgoisakmSbTY0uABTvTV3z9l3Omv8Kw9RKi+hbDZro7v4MDAFxAQfMRnZ01MW32mABOvcJ1G2L30/QMV/t+5oRBppb+erMg85kGvc01LHf/iv89QHtoVyGKZaoDrWoaIyiqej5/89VVstUUV9I+ewin//xAVgDirYrKcgrqWU1gAA5AACtAc8MmiMH/kSGhEQ7jvpZr/aZhGDkMtBw0yk6GGRohjHkWeKFHuGiP/+ICvhgA+JQYqwlv7pNE5//eQAOD8Fptpa+wRkgc5gQ9CfyJYQJ3MIHf9oAhLE+kTz4hcsiffwyoAAYAsoEtugI5wmvmxUMum5R4CwjxMFDK2cJQ09H/MbS2ccfMG4mDXmNcQHrgRcYtdebU2wCkgJqRkFt50HkEA7FAaFWptTAyBhABJAvY1oZ9KCzTdCv/0NxwXqAoAwtSC7bDXXpvXifw+VjNB8mMtUUzxwqvCsEGDcbzEZr3P1b5eHCGsChoC6Jss9Yrdrx204cb//4VwAHBCwSmDHImC/GvfvGgAuHq5Uk9BQp3/2mP6nXxN03/fkK8AAQCMAAIAYAREbHz4020AQGIAnqjI1A7/4GENy/Trz5zT9CJgua3+cVXJXeRIRiah7PdiLiAz4SADQPNwxQjCTrv/gw6xouha/rhhjG/VKf0JDfH396o9YzN+F/WAoUxxyVaVTi/9wc+IIsTDNUKMf/2EAUU5xkkoMJMu8mX8GSsAqCBKE3wH+s5CjAMKavHOVMpp9hj/gHRD/T5SHFeyiZPfwyFdp//7wq4CkyO+X/POCCDDwzyLOf76ZYFIffqZxf2+P1hyHOnLQPz4sDk0Vs3/T5fGj/88Xi8qQCwak1ntr/2//nkbHF9E4ucP5a/5/dd+fxnPfjDz+d//v/rhygEABwY10TKn0yynsAAgGJBC5k4lEyXwt7QG6kAAgK2hAmJ2wun+ARYCQYinZBR8cdkFv/L/DHo5aowEAQALk9tqSs/4BOZMj7iEV//XVk2CPiB0Pcx5QY23fKb6UPQpQYHNvGcioa5NTJLnm/85KGRfnq2tKQuTALiaD/+eUuM8AkCT2dj1bCiVPz/POk7TobhMZ6Pv6D/v0S8ca40N/X+ewDDoal9sfH5gilMLj+vBoTKfw5wAG02aIpjVmX+LAQQTKEXmSDbOp4S6IPqMHr53f++NiR55x8//P6GJznjRGIunqfvnBv/z1/gGuk97/5/cxaHYGKXMv9/56wHpjLVSvjf1/8RG/5+EtPAkCiSPn/+DDxHiPEDeAm3w0o+Z4eADoVfmIp2EfbSmBgDGeCThaQ22QU9gAAuCGaDw07NEYP/eKGXhKS+GQW8MOEuu3b7v28kYbL2r/8/oZtxz//EfXq55xcZD6VA9/3hCEcQL4G2pYhDoSY21LABKQE5qqqFbX8Z//eL5u1LDbUtjbUsNtS0/WJg7gAABamQZug6B3hHwjPhGEMSevAIXct8fn7wiaAA5ODUfEJXBWEiG/33tvM8w1L30AxqKTZz0Sbw9792iAP4AwFI2qmdZQPb9wj4R8I+EQ5wAEwNuGCl3fw1nhBQu2m77tXgBCHl9z3f/iD1bwA38pxvfz+sSevAT4nuzxeJPFaYJGwoDCv6T1z/WJPXgFv2N/P/PW31KWPzEPWm73eiT3nHz/xAX8AH1j7GhSsZARjomWTXNtkFPhr4NC4mv/4gLcAYAAQBt8QAC8TeyB7VxLxFmwkU7DPtZTnAAC4IVcg8NOTam94UEuyq99Mot/hiAueC4aztmAt+CbJ9DXZPWPzbnth8QfFAIG6zfzjF53VUWWokZbxob/wQaduAA1EY3QRVeSlTE+cAA3Z0DfRVjefenoQgpXcbOGxjdWHw90gTwoCSLW/3mONivjFHIhhrwrc/MuGegDtvszF/9U1b8QNgAWCGbjUVNCZMsMfz+TAA3yOOiipFb6DwAEoZFcomfr3GqcH7ZmG6ir1L0tasMMABEAkwYLYf9DGuEVC/NjBLyhdN7k1HnwfjAS8MFMPIRxnRNUyGOlASd1/bfRW13Jn4GcAbbKLH7538QeJZYipMTes/fqYwgkuyPs/Da/jxAL4YAhhk04Wore3dIXS/DHwcD84rIqzyIbTwNSxJ//DPQIZ3MRVaLi22z/P+PHJ+U+8+KXRbhOPJI7v+f3zy79F/rhqAA4MZ/sTUzYiLLTP+5AcooIPGp0s8bqM/4MMx8Mjdpa/m//Enr4Gsp6gvUjr68XwSeABZKtS7Iq27+7vEAvwAPBKpQAYE7+TErIXf+fwMmxAKgwuJSKbIfvvEtsYhoOMoPATqTPmQctZa8QGYEjBa6A0Qlqsebwvf+ASEMzmIqtEzbZZ/n+HpN/FL5FPcH//BBgANdhCiFNws6ZFtFfoJUVQsWGzXR3/AAWEK/ndd2Jiwwz/AMnAApIIxPt7OVI4BHABsnUJ1lQL3x1EjotHoMkujr/v8AQjhuJVt6SZSUuFA8rmuHk8AjGA2+QC7YpYt8+AEYlJLLSoX/wPClyo+Zv8P/IjE7MKrUkJU1IfABoYGXTycootqR//4MG9PjK0AJMmCX1rLYuuQ/+wwAOoABrPAyeYbyb/2Vs/h+AfIGPbf/mi2G76yVX0qqo6aw1P6kLfhiAAtN5IkzGbF8hKjswrNSQli1wMrRUfpU+87//9zB/HQcBEGaGgmdoyZ73KOg5aYxIWmpnnjY5EVX+3/D2D2vaIbrjCYlqWKTgACQH0D4Vxo0Q6I327AAIXAtoGRZ3j84cwr0PCdPsAEIJabBKi+8YUKXQL+AxKQ8MFtO6YdTh9nUXgP221gf2UrIXE0GoOY0vz9dfhY5Kh2G7DIkaU3cMfG/DBAMCrQc/B4AXJaYcJ/KIyXwO/+AIhUTKKtL7ZJrywWQA4mwr1EfqOb71efUtT4EC7+DhyWyCPNqhkZeY6TnLzEGKlRTAabfsd5yIkWASwv5e4vm0xx0DPW80X8puXthrdKgy0jnw3VzOJb3gA7MEOiItbEd7LTGTSHHXoLqMmTksZYvjL46Rgl0wRmhTWVb/20UdY34/+GPAA8GuKADgjaBISthd/5guiS+33gCYhlfGMhR0oYkCa0NnJ2Xd/VwpMfyIHQZESwi1c1TOi4gPYACQaKUZrOnkpxaJ7iz/EgPgwWI+wRT0I0FC6WzSLbEft2hlAQpAWzS0vnvH80YDo4LOHZwh1oRd9/7/AAtkADoNKFaXZBoj4BMiiQWRiJI/wbaTLBnwMIHBE7r5XeeGT5tZf+uw5l2/w/BEgIdk2ulok/97v0BDM5nRGn2JbZ/ngC4RexT5uMwlruYAHgY4c3SPfIlbmugp87j/w5NkaYrhai8B/eOC7ZMIdTaMYGet9/Q/X3CZtBeXvP/4cgAZtt8U3PasMUSpqF3TAvsqV6eP+01F1XUJQbJZHF/LwAdlozYVn7+P4kK4AFzADQNdLQd5Ytz+3wJkRgDA5IO0qwOwuv+foi/nLABAwWsR1/ctJapWnDqxPH4tiLiHAAayMS8h0Yflq4PEFJMCakYpu9/3i+GsBQQtlqiDyEwUkc//6GawEGdo03/8M8ATIUAHBOESQhZA7/z/gB84NEiIHv6DQP/C0ABEBOgcLYIIT3jpNcx4wE3DhTD6Et56TUMWUAxfmUJQhB//9+bCBMrRs0Ozal37/EhGzlFzqJJNa+HhADKADGkE+d+38X+IC8ADiv6tn4DD9AKggAGMyCZTnUgRDWo9qYYolTULumBfZQvCX/FaghyTL8QH+GABZQ4eQ2MsXqhxrAXnV10/97eAwExoksTz+Eti1fqHwGKjHDDVbV7lH8NaIACdUYKnDbGa+Rzs1GdBgAIGqEgxDeTqXrcV6lX4/1gYvThW250ifv4OxDPPKqBoweG37j//EpwwL9VAvGxIAAgY2gACAOFDVztft7q5LvvpfwAHNW5tlBSq8qX/95IyDZDiWkhLGrBAPwDUgNYUbO4pYipPAnoDFZ7PuNERabZ/iArQJkdmyv3/vx8gAnDgD1rgvpH0X3UDu0F7dzHS1Po8Ael1Rf1qNPKO/vfbtGtWr37kictD+ID0AFwWwnMKgghznl+E4ATgA0EsMRbUx5kkkd//uIAHxdC02kN+aJIn//4O3AdgNaBq28Hp8x+ABYIUhi7UTwSwWba/0B/tt1an73CCi5airGaIbUwaDjtSWlehhOTgXjYf0gAhAkbSa/eMBASEcNJbQQZ0hBEsXf/4rlW4M+50QDFzOQn5l3sAxcGlZN9elEia15meEWO5nBp+ApMq46gqjgausAA4CK9xtoP58rfFDU3+FPIexUXIBdqwuZ7PayNx2fd9Q3OnTa//ThgiRfFny/xAIIADoLZQABANcHKwQsRtT/mAADgComwLFD5x2QJNA06MU3l94GF/xgJuChjD/obz0moYDz9/UEBgj5CkaDZGBibTuXB/42BADooIOGITlZ47UXwfOm3pcR6+9TCt97oRB/VDFLT3wYi3eH/eCwYU3OSWJa///bABCNOIEwIth+HdcmIPdSPr/UGqa+4xlJmCmmBe1lsQ/apXkl5vuDcAALgxWyDw05Np3vFBL0iEvxkFv8MMD4YqJKiSh+09juS+pW7/hEmRGMbU3txVk7X8SNgS9Cn5ajJFf/4F4O2g9cNivq2tAGCPEPtNwhVylK9/eERqYxAm6nVW9YMC1koFOKmcUSssrA/wU8S2aLp794YlO1Gy0ty8UhoCsAAhRnKTx0zrTq6TQNfBsqMW2PR/sWQ0IASEB4wf1b0tONP8Ef97UxiqOVSRqrSyvAiC0eY43qhBtR//gYckJDpGhDJ/344zrZLP7mgMn0dF/d36mP2O7/0zLKl4V+ML5jkK6HIzjLgAAOYAAsrkBDA+m9wf+Io0EmOUUmmmvDDkq4GY1rD/43wAHgBGUZnvNmyxLhD/+ADsgyt2zhvPKL+9xHMbUa9EXRSR/8g27emadV9z/9oAFg3QAICXMKurMuG7WEXRX5899wEkUBiUBDNaV+IWs8XLawpn71Sr//j53OdUcjTUAwx9oAps2RDqmaazS/T8Cc9MUSYWrt/Pj3p+DqLhO3Qa2N8SGIAUsLU8R6SGL3iAAiGA3ylyKWWH5f4RGAYCgaIVX6c8OO07zAAEAHjYUFLy3DpnrjWqCGyirS+XFv7/v5gACADlAAhiRmObGI9le0Bju9ibjRU2m2f4QF9ArI14sxi33V/F2oQsbENz3+1oWsefH8HjPS57ZUfw10YAEyo4XrNoZvhpBK66hKDZLI6v4BQxn+xNTdiJssM/7UD4oIOGJyw4bmL75YAUWFW2H9vvf/+H4Zh293S/4AFSYE3bHTR3B2mvv4oBhBNISJtEm2vC1Oe+Ayi+4tJQf9FAIIIpGRBok00GJ0jAID0BgBBvnWkCBUv4/3e/4YgDp3rM/QMzPVj//oHdzSA38W26kBvl+kCaEo/8Ix9XjPvBrRzwB+IAejSuOwsZBWsmD2Mg7tS+CCAkABPHgADtbyJAhrR/xC3YxGdznZx2hh3AASwAkD7ktXB3FjH+IGqwoWYS2dj/AlHhe4ArY9LE91f84BkvOQ4CKNNPGQx/vR/IYCCfxo0bFuVIgkDArjy3kinzXTeftxCABs8aeur/Dv9WmJZyK6L5j7ndxV6klLWrDDDoYDiIc8xN39wD/wEOKrOZBl9pnUQFwZdkvhqBc0ZMuP/f1cAfQf+FujCBMrRs/fi1Lb3AD7828b3uquoaa/LALGyPaaX+8b+j/cRmy1szHFj9+rwX8soyGi/4/D6Wqab8MeAA2jPiImeicABMlMNmt2WrvJGJ2xzKUT1L8GBr/gDC/Twff/jYYC5ZnAsld2i6HyUNMffs7VcDMGfmpgACAIAQ+bgkSis1wY0TZFSQA+zAIcRWcSTJFhtAJAY1Hk6Fwz4ncyifAOhxZNduD0PkiUjTzDggJjpN7h2f4b4YI9nvav7dtfDi6F+FfgFaKQpE2DsAKHEcA4FEbWxAoT0Joxi6D/safpdDVyuV9XvIUOIVmf8tl+L1hn9Bf1wvocADEIDCCKRmTZJNNvNBgmbQyXPzbn374wG/DhS7347z0kqYWw4AhxFnbXvf/C37IgIIJpCZBsgy2D0QQLm6Or70WZde/xANsCha76Mt42SULBrheFGyNr+3/xWIP14AtWp88/iPhfSAAahwS6Lnm0yTH8AAUwGp/KiEB4RmZvIcfkXGKI+1FuYAAO0ABnANfGDRGD8QRHMCaRj7VDP1iUqbtSo40aeIBBwAEQZRFKSSWlhzjSXe2jE6iLxBKGsQAk8phVmPxgtBdRIPR4AzRAWd+yo71/EZGSYX4lxPuVgPRijpI4xhXuCAF4b1hG00kdEdl+BgIwpmM3R/7sZhJHLf9/9VcNZCf/deDIOWC2i9vQjZsI8QN9QgDoUvhGyMLLmvuDA1gukgJXBHvWP/cbIgBgI4COwUYHIXX/eOGVGKJn04k1TeMSYrcVD2Y0x+DDA324fry+36ALFGpWx3EdbS2aREiVUZmf/r+ABCcmTRbdb2dQaY/8MhIFCNqTDsub4KO9+Oqq+pB4xjr1XQ1iXdOKjJWL4gbBAMDJFickPRVVuHBAFwhAFYoDQq1NqbhkAsDBgn5PPWjRUsv9gDFspMnkJL8Y8//ZomRgBAdwEdVZGoXv/PEgA0D3cKRB3FDXfwALAXC6ukCqMxgut3/vDDXO3y/+bULBh2RwoT3snhcf8wkhM4o4cuR+q/KPrU11tHf93+IGwaBgIMlQw4ACQ0pyFEzVb9NUwQGMvjPcQCDguYpYHb2AkJQhr6osROiXYf9+bX0kl9vtpe4csn51hqrCp1L4n/3YJeiqGTKxyK5KAGSNbY/9vcqj0Zbb5wvIIWJr/z/jaEAFcq5y/53pMRUxTO4yVN9MOM5AIuNQ9e3ZVGJ28fpchYZvdgJACMcHaQbCgi3rm99H3/77f4Zgj4Wn/60vcADYhlQcl85pre8CDAlUg8WE6J4qs/8OoIYBWJ8djZf/97YeRbHiBsL88u389vDPBEmB2mas6i/2BiRjXTEKi4f6/+AhHcpFRNabY1VvR4clCJcSop6ngJAyA+tLjFDEVz2fShjyEbgqfenyYx5xN5dz3PxjjF+xy2aFNU2AXBEQXNTrWZ2L/+1B1gEEr0v9LiiffcQBQT0pxuqego6GwVoDFghVnOVJXjXf3cYqLVkV7LbRbgdJoT6fXL388IBg5J/31aTiJDtdf3vfo7e/9/+IGwJSKIJLVNH/eddq8Da8GBkLVFIRljqWcZmAMWIUiDTSjF//uNmIEFeEbYOO3kDv/2oe2zHI0LnjhDAKxIFBVkbUzAQfmbuQRMQGYcYQCGAmgO+QE3hcVN4cCJjFKzjam8jQnRTHRxvapNsw7nkvRxbj74Gb2QNzWH3GAJZ8w/XnPSP/9mQdTKdCw78RSXOv/5GXSOiiWPj4e6OCPKDLNTxeEb2kgZbQRRaEF+RvWoBjCZSIsEGWl9/WAQwikZEGCDTGuNWaU731RfbXO89ohBruxle7g3LTzjVsmvDYBwCxxBaNqxYx31A61vQfPV7RjZUFZ/P5jUYwD2wABQjxAbvidP/8CJpUBdJmGiqLxqZG6eGKiZoHif/v/4d9BASk/CLCALxIj3bwEvYYopXMcvmBjVUBAxJ21YnXoLU6D8iRCZBFZzkMUgMz33n+5h6AQkkrgSnmCeGnP3cAIOuSFLR0mp86TNf+fN5//DGAA4UdwBALJ5tqJIh4RW8u/1WgMdnsTdWImwyz/P0QAEyqgT5Pgbrh4suAJRCnWW9hiuuL/398NwAMQgMIIpGZNkk02/iwEEE0hMkySbb0IoJm0Op7s2Z9e0QQLm6Mr7k25deOX4BwExOcNzvxXPOmh3c/+eVcDHWmNqZiV3vj9dVJqYcWKw3OH6XhW9HAATC7IVlOQcimmEsAAHMAAVoDHhs0Rg/A/u3j9n39YSjjIS9q+lqv/4Z+GJ9lBCz3o23oqubDD7y1wnt6GinCF3I/79f8K/rD42WTSH26jHphuAAFwYy5B4ccm1MBFiEuyoS+mUW/vDCU7lhcYjfijNaQ9SGWqUBjk9GGLMeKpqTwrB+TDBayhsucq1X/3viAQUVOMyTJNpt5tARpKDpKT5XFh9wQDCi6wmRZJstgwbJv4RS6RKux9v5TlvgTGHnzr/8/+edLpc28++ZWtuPv1D/8/LMbjH+oH6cPyCQKJU/GQm5xfn/4a/5irYqKcg5FLKfDKCx5pM7ehO/gVaWlXeS+9wtu96dmevhnoAAkegAO5vogCnNiLDIM+RIG3UqkLT2sa81WL1+6Ael/vizxoAMaem/3frSMby3EBevnmAa0EGAPj1+g++4ZX9c/rsAQYI2iBKStabx7aSLgABQGAdiBw6Om1MDfSBxI5ltlx//WQAJY5Zd1bd8D/3Z9+lF0hDM/+CH6mQ0xzKUZKlpDDweICsABEAmwIGsPoQxjhNQz4wJeGCmHvRtnhNUuGGGAA3GWyZ/ybRPiDIYVSSi+eI6ml95u9DXPl2l01hy4fvEHqQu5U/+L56wGFb6T1z/+uF+ABYGPYn1SWvErmUD7+AiBjYJ/MnnxO5lE7/gFQSB8+1mtZaFO/qiK/bf7+4MvCV3hnGUJUf9/zgjLiQ9uv//zv894YDH3dX/bjYmtxt5zJMZar/hzAAbBwbaLtD4ZJj/kcPkVDOI+2FueMGVVd/uyE3OL8/+zDGev4bsAAFgQ3AeG3ZojAIQqNWEWl9ukslwAA7QACMgB740bU3jHW5XUxBiLUY5fAVWkdfQBiGURhu0j6Snrhlmmh+fhCje5W1bp7X3X7DI6VC4P+IDUABGNAdkZJrCCFle3wzBRDzrCLtZTlZ5+zMwCDiqlHTLj5u1ZEIKWNoVfMuvm7QC0MCQrTV7La8oUYh/54baQbGcfdzREcOUtT3f5+FcteEAS0Fwb+a0Lkl3BL/EeIBHq9jxAbgAPsAGoLWQ1R6Cxr//g/AISS0xJ71zBfDHg/4AxJ/Or/3ATPUfhyh/56+HePA1cUXefxuI8Ri15eI8R8MwAE0AGoaNhiJP8oW5psiAGBnAR1Zgchdf88EqD3/WwtnYtD5hMfSbX/PAcUF5kxIlKqLvn9B/XPWVZ5Q2p/+dZcRCPBRwNtSwXdTkpwbalgAegjkvUoK/NhBjnxfN2pYbalsbalhtqWeEYO4AABaJQZvA6B3hHwjPhGEMI3iQ5AAsCCk/0kEKt/iWt/gBz5jVZNlyIApoCaTFyxJ/FDH//cQfhgxw29GCoxit/5U4CGbJXedkjE1/E+JPXgYky1X8SeuNTZarwwnS+JPXgD1W8b///iawjF4k9ARpwCEH5xf+/rE+IDUADokZNQlhk1kd38BDAA3RHCooqxm+gEFIQQSpqFnDYvsr9tjKVRV6klLWrB2C4AFK5n/xpAELup8f6dVOd3kqmSvEBzDsm7pmGANRJTzj5/+G89fzzmF3j4EKPbQ94JQUS86/P/Pe2D1124577rtwYgt0nx5cv8MeMiA7h1Ix/gDrpfc6KxFO/8Nzy5wQBOSo1upxe2d2f/SMI5Z74+PbGCH4cx0PAeJZjgkWmWxiLde11rRrvdKmnvP/PK3Af98htTqqDef/43gAJMVFyyIS63wWxwAAuCmbAODTo2psBOHBdsukOp9GOD8YqyFZTkHdTSn+YAAgDNClAByC9VgENInQw4++3g/8QTKKgr6myH55hsyI7vAsnQH/lc/7/iQ3AAsEJBKok56CuGu/+eBBgC49w2jWdqm//Biz7AZndPRrm/1hEMeABYIdvM67sTNphn+YGQKCgk+anS7hqYzvvNZowAm9OaaT7+EYvEhzwAPsxJHVOk7/zl4HRKVX+G+AMAGRx2YsyYJEQaIh3wBszSw8Ew3Tx7JraOPn/zyCcIYMksJV9eYzeyTTn0ZWlKq5/hyAA12EOKW3DD5kW2U+RGIrIKy/IWxqeglRVo9hsWUd/9zcAvykGUSk1pfhFLg21Z89AFIp9T+enYk0W3r8vxQtf1T3d/huHv+ddx7f4Et4KZiMsfv7av0V6WPnOGFf0b/9qgG+UVFLlv1f9z/G7AUABMiG7oIqvJSxifRQxFGqlIxVxdVYQL+kABunYJ+GWN18T8gEhgRLWlIc88f9fTDRk+C2GTXQ3fwIB8AEAgi8jptV+EVCUr//tJGMML+I2b8vYHf/BAUXYBcTQcy1mf/7grDe2yJ6lzPEScRF9/xERlSCXo/DkwZQQSOS4AC3gFpQLXjFeZ/vC18UpKT0P5zcpEvdQwFvyjl5l/wQVsoAgQgCNQBoUZm1NmBccBF16175tTAPg5bAfUjZL9zntAAe3pZz6L/wYYKzxiNe6v/S9VDf1nYi21euNWZSl+7n/DFwLE6pym1MB/JtfI2/d7gDAFglQg6m7W8j0J/gDZTgAwI0gVErYHv+ACmAEge6lqYO4sU+DO+C5xoiXTmP8yGVTTQ8n3+GPpIzAEByQJ4qyOwO/+fgAWz1yKizH/4CCb/N5Wdz/WwBHjjG8VR/VV5kaYcVkmA6/Y5akn/X+HOABYGEK76JLXhGGCd/gMIuBNlfPb/mtFoPYQaC8v8b8yd5EONWp21NDp33+H4IDjIleABYdCYUkTBDT5i7qAnYGiid9OaSx9uOOrCOUDJJEI/9/zNCxXQxR3UotoYS66/fWOXKHYknkff3//PXYgArsvTn7Th3L8QGMACwYlkIk8lMlIGP/ugKmAGga8hqDvLGuf+A0GylAAgK14mJWwPf870SIwBgd4EcVYHYXX/AzFAlbkO2sYRFt1Xvo9wevDSGK0B6e8qPz8vKM0u5A1Pt/F4gbgAIgE6AoWw8lHeOkVzHkwwWswfT3ptT794wJFDhjD6EN56TUMB+2EGqM0fX3ZtS6H74gIcVWMyTZFptB+4IDHF1hMm2TbbBh1AEDCP0b3vcLsVbq3v7f9CZqkrQfEGwATA7ICagatuzz+gDMhOimOhRvWxPEDbBQAVgzjfhZB7CL74AIpAQUXORJgm20/0CBsC3lj599JqWvvSkLRGiEStLtkH+Opi0H//38gADlAVAFWrGlSxe4v5mYyqpyqUf2rT/iATYMGrPoQ1rRNYyGGOlMWDvtJbImOpn79QC94DcX7vO3hrlCjiDGJr4gOwBhwiqDghGVf8EVF3tbEKLV1HDpkZ3V6MMEuqGy/2DEePB6RjOdQe+QtQxK/vLYERZCrLyagSw1wGqNeL5lFd/uAAMpAIvjndZhAbEZvGAl4YMYeQjjOiKpkMOE3MAqPLLPfqwYiQnTU6vzpxqq/tgx8WrLer+IDuMsbeHG1z2D04RZBLCCVfegqrAGKCrzzDi93bItJr9CP3/f2xwXbJpDsfRhGgMRvs+p0RNtpn+cCFw9B6y6H2f3Nz/gwwOAnHfX85XW1+ffG3tkYGc1fKP+X+ngpsiP34b+7QPBhifqd6L4gGEwAAQMgABAGCxuWxUlL7e/c+gcAB/ipI29pf2uhrd70pZilFJR4PwAfqzX3e/t/8QHeAn3xVgFwADQCHBDdI/8mVuc4Bl18z1H3//8D854U7ibTjFUVE+fommh7sqtz+vdiLSACWTl/qv8ytJsbU6JFX7a/9IPCfj+C+IBBAASMiDZRF0khbWJ4QMN8aAJMRRM7BGb/weGAhNid9KMiG/JRSAA5krIVgWOC0ijbX/gE1PXRegAD1BV88ykn8+VaHTU3TajFaRU/AzUMNrbUW/79AF/16aA2gYuTLj/v+ICvQNGAKNSxWqCWk128wmFa9BRnNE/SS+GH5CViohzcoT1LSGHExX5pSdYMP/EB2AKAS4OGtEEI5x0muW0BDXtuRV2m7n/v6GUFyqGy96bFevczjESj+wvxSDP89sxLD544DYHgye4j2pY0j7LQlstXJdtAEPQn9CWECdzCB1/Aygq00J6//3VqT4ps93+AwEFyZ182z0Vf/583vxHvrEJLgugdpNRr1V2u+IAh7ulXD+DgAc/LZHx7p/Z6C6lB24GvBNT4gbssOzNFVU3/QaApATfGLbuer3kyEVHIdnMK9SxsMEEB8jqAQ8uI1ZCii+w6LaTUdP+/QBUB0XPxhD1an3fwEBB1N8xtCPwYgR/YBJqPdzqlZ7//1BgAOGBpsdxXs9utvdEP9/mZQRSiZ6cRjUhqhhUGf2qi/9DBY6U015PFXzT1xx8v8QN+hNTgBwfq97KCG17MMOHgAWuGILXxdowM6qn+09EAMDOAjqjA5C4/5hC+fds/gZGj7QJQZJRDF/QMg4KHnjMJXeNyF98GS2t1JK0cuPs9n7A4Ngqh1r/f/G/oCAARABdQuLfOIEUaVbKB0BHxiRF2YCsDJgBgS/fpBBp03asbDrv1K/d79pI/ELCD0GnEdIJ4oNSPEpvgwFo7MZLDmFR3+DBmaEfvpgBdrbZSoCmQMhZd975kj6ToNcpc2cQGIAKIdhO0c7e7wAsADc4HykNTaiAyzgA4u2KinIORSzH8CAl6SEqZlCxZJcn7Xhj7ZccyGkM7/v+9t5nmH3VQ1BvxxGRjKc28/QHhrAfxJ4rb/wCJNJ93n8TGcOcAB4BXihx83CVnjkhn/aBjs1nzFiJsNt/wA7/wANZ7l+nH1w5gAcFyUqgthMW/9v5AvYmBJ6EBldyQqo8LU+xQAskYyb/S79v8MSvdxv+/jPl6NMdbWv/hgC9I8LXbljffADj7d3UhBGaop0X5hzTZv8wLptmmkX+/+/xEMAOiPe7SSP/7fredv+N8AHxDD0XwzqF33/69+UmdoWo5+cf0J//AAQDo0qMWSJmpGDVnQ8ABMgYqo3Hf3LfiwwJy1XTHTiSJbfvwYT6t/xGH/ggy0gAO0jAIUVuG2l2UEXALNrA8zQADfMxqc/cKl7W8AATh8FsIIY7jq+1O4TGSJnVn6J/uBnFe2YSvVY5Sv4Ri+ACJ+nom3/4AkevN0U9ZhPMVvvr/D/xAJMGC2H0IY1oqoZ5lYwBgpyUftfZX/1vzN57b/sHb9n/VH/deGHn6AEupgfMYr8wASAM2YbEBq8vQe4f/7wDg98CizmJSRYfXIhnQsLjMiG1P1++N1gBqM3EnQ++5SobnF8P+oBbwpxkvQYSVk+OXXF0BBAVyGahE15mtcsBECmFDzpadLtGoi/+1AVFBB8zKlnDlBnfc4jFcWcS5r3PMx/lvFub8BIMd3sTdaIm02z/PxIEz1Mleq2+KrukP6FyQRJlykO/8+DQAATUFVHNaRmVUYTwX4X6XclAXvzTQ7XAEEFR7RCq2s+qjb/oa+DsQ3yfW/v6qMEZJ2jTp/8/xsEWAMhmX+EX+fb0PsJKIJtlvMok+yFgSKqvoH/BneOcvbGDOMI//YJphC15nkuaPIMTTUacyrG/YnLUAAIATUHAkCecU+jzC//1wH8iMRWxTK4yVNSGIwKGvDNgG2RfeTr/3ovt8mz+B/4YwBAhAEeoDQo1NqYAE4KcHxIyDPM9OAncVq982pvgXActB9SNgv3L92ZIISBACLDISF5x+X7Y2/2l+IC8ABIyEVlMLiXe1iXAACoKA68TRsdNqYPgB4ACMBsoYMbfThjeiShkClMa2ZE+8jZq+k/wtAHMxldTi6klLWpDBAv4gGqBg1l5GONaJKlw5fhhVzuL7/F83gAQbAYwikZkWSDDPEB7kHQ+uAvkH0K4eht1I/wcG6VgKA5AS+GxU3jDgTIMpWcbUwCMhOnIdCjetSWAACoOA65o2OmiMH4fhAmOm73nYcOoEr//bcMBOAytU6kxVSovBBwAEYiCrWggpDT3mEP9JkNkOZShEsakBBdCiINdqxSKyqdkYZBsk0kwh99pEC5FgdGGMG3/73LRD1RcrOn//uaZG0HILUxzgIdxDU97M6wfo7/uBgE9o7TajsXd5s5//gx0vsEAfWbBY8fH5g7tyPCar+1jwLTVPjcACowDetXiYYIRqoZ+BvBA8toLPhaP7n/sKMwBAd4P4qyOu3//3eWInch1ThXGLZyNVI8E9zbUWzB8KMQHJCeVsqVHa1+spLFok0320MB3DmJJT2md3c9niHXhH5mFfDCm4Ztt/kRE//8v0AGLqChTVLZc+2374D3cFnPSGLQwIcAQmQrH7/qjOgmR1tegFJISE3ivjrHl3rjDZo26fiBvSRmdApR9jX/6QJ6gy4Sj1/PATAOjhx4xGVnDsxffOEIArEAWFWptTWpFCYjNN/6Bho//qAA/D0Ub2Gw4tx4AQQwCsSBgVaG1N7gRMchHYbUwOaI8CKZ3V4DFNlOZjjiy925CnjLVzC1fT+w0B26NXf0f4IPAATEsMcgu4vOtiwAEYPQgVrKv+RzVq+7M9AYBzfUbfu/AA48CilKrOxtllKf7+gqvbP7frhopiocG9bGqgkRxkYh09+/sBSmnC0pmRafH5A08E5RJu4/3v/EB6GALapZ02eIEvcxCuxHdxkFiLunAAEAoDhcV1NPM/6AkEAuGvC8vEIyOLD//uo7GqlpRfJwAhiqyCgle7O0NGP+lXTjH9cUAjAvgakDueov3gxHXBU19Sbks//+gorj8aPXdUxuhuDpcOuS1qv/+f+H/gcQLeuIain6xs0hr8ivFXIv+8MByRaF2Fz2XPATQhhq3IYaNiuSdACRTqZ0Jhkxe+jmFHAUQpWNvI7VS4CcAxeQjWUtiSz6/AEJJK4Pekvhjj/9gCYcEuiZ5tMkp+FttrlgQFTeZsUqX70TPUOHL/jciDY5XAFB2dHK7JmX/aSQBCTK/KMJLR/21RGAMDvAji7A7C6/5rF/65CrW7RwQgCNQBYUZm1N/iJewy8oFaeaT4MC0FLQfPGQX1nTgJ1FWnfNqYBwBU5SCko4jXG/7CzMCjhVLjIf//eDAxRBt63d3/79klEREJl2fNqbKPUWyA9F5vz/f4gPeAIWBKNCUcIEblkDbTABEwfGAnolD1A9/4H0PCCIcUVjqMFv7X/gwFhB1P8xtHEwIkR/Poz4DXO1wOygmeLgprOl/my3lHxBNjKPclklvfvhCSUEN40cwqA6KJ1bT/3wTC4mg2+rs/Ziw2W5kVfEB6ABYYj0sTl2dJ4hn+AKhtxj3A7MGVx6N7/4MEFwABQckT+qWfFuc+b/hoRDAARYxq3kJT3pV309wn7hnvB2PMy2n/3adSFk2f66nzDf/8b8AIaaqtGPxg0omX/pzCvR4jokf/qKPOWV+/5vNAG5wxiOLaDPHre29vMdL39f7w/HYvWfI6RI1RmDTBfSvZv/mmAxrUwQhTDXOIX9BdS5H0//gYACMBsoYMZfRhjPCihkFrcKrBossaf+9+dIHQ6YR3RsR+/5zq+Xt1Yx8iIemfiAr2l7GQM+AAxSCEFqYhZwyL7K4fQzFL9rnviHUcx9uC/xAZ+ZmMrqK3fJS1qQw6xla6+tGxJt5x8/+GfIigt7QynfSbnz4P+sAhhFIyINEGGAzlkpJEWW/fq8P4vEBzgAWDdDgA4I2hEoJWwvX+AkEJRapMeqCuGv/fB+EAe6UxojC1p4qYPHMGzhslqxR//Rwynv89RmdKp64BtPsGff/EBryYYLmUNl702p7+5sIEzLG192LEu/d8QEFEVjMgyTabfqwGOJnCZNsiy2DsNR9nYKNmcNqeY9p32Yyk4fnqoUe4aI3uqo2874BtyP+cHsayxz+f/4agLhJBeSvmkYsp+8Y3OdgdhPvICxGxKCAw5a/leS3/XhaqSr/5f36P+/TbHQhxqn3b8K/a2EKLX5HDpsZ3WhhwBwmcVqDHYsSiokjwQDSgemj/MDTSUB//wYYC+uz5+3aJ4nu//8NQ75q7q4ehvVKKh71FvmtI/jg9SnodXKK7z+IG/JmIiKc6kG5reYAAKgwDsnTY4aI39U0ZNBoz7K31e/bv73oZF5BcQ/msQCAsJFBNIZm0PeGAIbBz3clBRbFPNQ+GGAA+AAWBzh7d4+8kQub4ABAg0p8EqK7xZglnxPTeHVX8Wdm7g4+yrC4420QTyx4VT/ZUf9+g/hwZEwh31/h35BlUwi35XpVjF4AmQ4AOCdfKCVkD3/A+BAz6G8OANDNXKN321j1MDCpaBSPM5sib6fAkL36v8le/j7d5WB8WsT/4c4ACMBtwwUy+jDGdEljPiAboGDWXvxxrRJUvFF2u5RnbDluu/7yVu322KStKSd77/PWpVF2Orvf5fPeHp0/+etB45yHLfa6/2//4c4AFAVooIPmYSs4aoL/7QGO72JuNERYZZ/kMQtVCRG+f/ADE9fa/u/rr0XiM/89YlyWx8lpUPT/iAvgAJgA8JoYm2ljzJKCB0AEE/0+a/+2eHTjmVfgY/fd+1n51Hoo/39QE4B+hQ0QSwwIFNTf/rgEEchyuyKkss03/8LW+EJa0cjXf/56rjQ39ClcpSbz/+IC3AFgAFQQB1zp0aNEYBLQ2VSC4h/LUgPCdBFrzzam2AUkBN8ZBbt9B5CAKxAGhVqbUwYizBoEmTn5qIEaAJS0+OPy+YhCD3y/iFc+GtniuVnizH+q4QDcQlCxl6MoaXSeGAS+HgqkmsRgAeUe4aI//iA1ABAy/7/AJgD4u+op1OpZN+/0sMiv97yIobbPiPnr4GIlLVf55TiG+OvE0FsRZrzTfxAW4AFghm83qnD6EsMfzwI4AG6I4VFGWK32D8zZjdznUoVLWrDVT3t7/n/fr/4hejcIXiT1gYkZar/xJ630tV//EOQMGm0XrK8QeQoAldKm4uf99+EeCDAA4BUUOPmZSs8aoL76BAauqwLNBsmUNWBtqWNxQES8PwxRSu57dNC2qwNtS3qCOS9SgpObCDiqEANWAsp0v9jLV/+H4Ehjs9ibixEWG2f5/JAATOrBPs2huuQfpIhMgiq4hTGIDN2pYbalsbalhtqWUlabH79f/5+sTB3AAAUxkGb4Ogd4ZPXgDjrWff1/DJ64dfb7fH6/58IwgfvCPhHwj4R8I/+HOABwCooIPmZSs4akL74CQY7vYm40RNhln+CtvABLfX6OPesSfLwwnneLxJ68B5MZar1iT14R7n+frAQg+5H9cbeWTp+fxBsAFcW50ekM/u9AFDj8ioIlz7YW7iAtwAJAV0oNiB0VtYwe/dvz22+8P3AME20r5gYrky/b/hilABOB2AupGwX3l5fgAUAx7E+mSwgSuZQO/7mBiUJ/UntAncyid/wVufMJoDshKo+U8HdVxB8sAt+xv55M3X/n/EBfAAzrAIcVWZBki0z/0Mgi/l+MgFdbL//hST5nv1/iA/7ggMcTWEybJNtsGHgAMxUXJKpLrbRbv6tZD3IrsrgABcFMuAYGnRtTAJ+23SXEnOt8R+909pve5p+M/QA/FOylju/35/hv48ANQ9VDUQfxY18PgEJJaYPJTMF8Mc/BpTKOi19Bmn/8bYHAATSGVcQyOP6le4AASBQH2icNDptTYCIxO2KZSjepqQ9kFLAXeGRX3jXDsK/FjK12Yzb5AaIH4RpuSfjApUo55n43vOr/gwwAXWd8l/73DJQBdtJ888pGxTY6+QUeRGfv//sfxqTVqTiA3AAcIZvN6pnD6EtLf4Ph5jWR38zTfg1iGuJO92lXdfqD9Yk9mAiX3L9W2VG/iT19PAIQTc5HefxeJPXgNUnP1/nswFb6ayuxg4Z6ZC4mo7rci88PYjUaFohsGRARIuqG/oQt10/f/hzHroEn8DPsAkADBDOE6XRx/XMI/w5QjzxADufrR/zHSest/7MMzxczj/4YgAwcnGaI3DLir637Y1cf3m6817kmvhW9rjgueMsIDn1dlK///huLPDchnxXJC/c6W5J7Aom4bys5N++fAPutjz9aRkROFfDcAORoAQnx7lsbMqHd/tf7mZNDb59lwZhTpJvL8xmZF5vf3MoWBzJEjqqV4a6a1d9f4cgAS5Km02Uf3G5qzSRlv6lCSpM/r7r3HD1msb6vX8KqOq1P7x0+eSv/VMjcDwUbXr0a3/h/wBAxVxm3v7hQfaIlLqfJbOQBKDwbBHJeCh2xdgwYuy8lZsluCH+SBHn60QIhCVv/7QgL/bxH0ZYvnTjQ1TXZc3S//wd7X05Olh/2vC46nMSzlr1ibTpf38Nsa+9X4bwAAFwABAG7pAh+AupACZUzHdmU5kIFbWTeZOd964CHKd9HiJKXQ7gr+A6pbfOP+/TKlWN7Wm7abTu34+orh/iAx4AHALihx83KVnDlBnfTBggKMfsNScqUqIg9+4BGU97iJZjMWT/8DMlWgw+eMHHf0F79YH5hz2rKr3+C+1vBlQLcEIAj0AWFG5tTcKK2+s7FRRcOJZYq73tkHmN/Utuv/nnK2JFH/fnxQ+eicfr9uNjH+HOAB21NG5a/+AaDRSgAwI14mIXwO/8AO4cccB2bQnp2U/wvYcABMhwbaNlD6ZZT2AACwIbQPDbk0RvI0ZhOhnGJthrmAADtAAIwBpEaNEYGH4gLHJqgIr0C3VfWo8PvUV8jDbrWcv8LcAZFgSYJPttklvD8x1uV+YgxFqKYGHw09zw3/OXVzgH4vjcACDYDCCKRqRZINN9EGGq6HS92LdevfxYCCCaQmQZIMtgguSCD1tjJ+5FuXfg4AsBrw4Yu8jHOekFS0PxAaYOFsv/hnXSChYMHjkoAMopfXvIPJ3x37CmsxLHFyj47x9xdX/DmAA2HBLouUPpllP+Q4/I6GKM+1FuUoVRK58P85ZXOP/BB4AFgYsifVJY8QuXQNv7UrMZ6UFeJVR8AHOkN01+0deIAAQB7iAAnlRdge3YS7xj7Ur8TmEWopgYAwAXFwLQYTz9gjH5wMMQ6QY6TGiMlYm9WDAhlkJTf7nsm01nv4gbAAsGI3WJq7ERbaZ/gGAdOAMDjE5WcN1Gd8GAjMTJyi+h3Naj29BvxdyTfLLJDtkCEPLcny3HXwA7RidTHQgvLUgP5w0lKJFl86rhuEDQZa882pugFNIDakdBbucHkIArFAWFWZtTAxiYHXL7c2ix2SxVv3gZIAuc+Ovl/EBfAAQEfh1RB7lxBSRj8OABWPAIOLlKJIgdbJVdDaawhymxWvEiahv5fxA20AACBvgABAABg6BocC8ALQoAAgC/QDiQ6+/nf4GWUhiT5yShKfQWAxYkTRxx4CBAEUmVpEQw/GSxvmBQ4RAnkduJklUe82RhOpj4g6GsQHqWAeIUdJCDCCvXh0QGPs4tXZLvvfbf3sChZuxRKCGdPorMA2ny/f78rzP6xMJ5afPUfgLCNF+N/DAAcOcNhXiYJcfNZfIWmW/bWt7X/sPom397Mp0AlKAliUvv7pGclkfd/XIsfkjWDq/AUEJBKqOeqIKQLf/eGJehHLtEM8nkuqb4AIdC8LGNyvYgi03/7HixFhBGdEP//vAzpeav/+5IvBawFEeujW/W/9PhQNi7X/z/xA2IAAKg4DrnDY2aIwGjgr409+NFkaO/gBYD8HSKreE5CRNI2pq6Tlvf2nAAD3AAK2AHkBg2tuAQyRqEu2nh+PDiqJR2VKHznrnYuYMLVd3+39G6vdX2f8K7rOsWI2/DssBCTV/O/+m5qP31Wb6VJV/H6kxxofjcnprI5791PYKOGADsJyiLQWR7hPEleQ2L0kJkQxkYZClcHysAxhFJkWyDDZ/AAYRAIYTSEyDJJttpowJEAyCFpL034DPKXLW4Q6wClh61Llu7mONPw+4miCqUm0n/44yopFap1tFzf7+q0rZstt+/144H1D+IGwAPBIxwAKCdIlBKyB3/geycEFA9XeH4f0AAXyb+rfueZhQT9Mj246iWnuH8/JuOBGXWRERDk2cfqQ//EDYfwEFRrxCqFr82jhFDw0ZhB9RWKOPuFdC4AAtwAJQWrYkTZJ5/+wI+IQA3yASCUTv/+uQEPYj1CWESFiyBr/A1j5N20jb93WARzDtarzOUWvf/HDLFyKjf5fgw42HFKrHGcRwhoxkc3CAV7ZOcmPbiklSKT/hkYjvQvw/4j1wAPBpzgAwI14mJWwO/8AGABILoao2njzRKKB0Ijn23/+f+EdzDM88lbBHk0deYALiaGJNK58ySj87w0iAIDEgRqKjI7C5/7mBj0I/Ulj5GxdA5/tAbYgAOCNIQKCdsDp/gXfPkIyBMlTzf+evErqdCb2Z/6r2g1N1G/f75lQcls2DHiArgAWDGb7E5dnSLaZ/n+GzYAAgCAAw6UJdLJskeDDxdkQFkpKpSm//G8NUCAQvTGgDoKC7RUpdTbNcvmIGZLnX/4hwYDX9+73h/DPhoAEofNYuD0FDH/7jZiDCvH+xUZHoHv/BhhUkcArm0bF3l4P5ay1+F/wAHGg2cl7X5rFGCdyMjqJbWaWzhSv/B+4BBzdpyuhnmjXkQYQroQjOSZIPhZyJ/hqcMQIrINn88Sp+hr4Mv7uvd//jZfuUDNXhYAHbGCPERnEo2+s+vACBE84UkTOUSLJNtvBhJnwF3Sc+VJ/vX/E+m0ze7fpauWcsdCmjV38118btgrvWGs0mfSsr/33345PTQ/XzRgO7wAAsGP5uAICpDFOzvzMLXxsP4bapuFMYlVUDYE0a/79MBbqtKn89IAJ0mmJ9yOqK09yjnq2eZh9XOVf//6byEq7L0iLonBnGOtGHrPd3vDKsUf1oxnapjsPhj5O0PffgRvx/f8ljfSGxF2/OjaMff34b4BQztVy+o9/ugnN7JpB6pMXkgdp4cHgrZmuTPfq/64fgenlzubf//9ey6iR8Ga6mlw/w+AAk6MmF92dZ/QDEoT+pPaBO5lE+/vBEQ9aO0SNbDMQ6t9eDXNTaXXq+NFdcOYAHALigg+ZlKzhqQzvkFpBqrrAtBsmUNX8vAFBgKOdKvf/DcCQY7vZ9xYibTbf8/5QACRVYN9m0N1wNcNF06b9/v/8MdwAOAVFBB8zKVnjlBnfYEhis9n3FiJtNt/zxcnADItxI2n3+KxB68AaiSnnHz/xHiA7AAYuGILV1HLhgX3Ve2hs6iNxBKGsVrNHTYagySyGL+0gANkRAqbMoZrhomjACA7gd9Vcajd/8ANAcFSlFM5hCCzxsMQwMgcFDzxmErvG5DO+0CGZzOqLEzZZZ/n+EMaLADEA1UlE1f/7g03HmLaazc6kjPp4JvaWmc1eIBBwAEBjI5olRTOfURv/ngEwd1kS1fs1gJ0SKLAAU1AMIpM85rTSIAGoHYDYkapjP684EXGLXnm1Ngbm5l8QmKV//5YODUjipWUIyhfvYCVAam4B2/EF73JhmbBuhv1hRUjSd/9sJTQqzmM/X/XxL4OQ338QNwAHAGcYojUN5YLpKxT+4Uxii1NQu6aF9lTGRGrDTZmZvv/0kqqlGoLgwjr/tGAAmVHCosuBneGjE7VAve5foW2gYz9Z9XYibbDP81KMaPqPiPq/Lp9g4BWAA+BTAhikOcSK0O8Hf1vNtu+D1DGDroQuQdppX+8Fy7m2frxUCv7390tbCvvmvCo8PTqfG/ADwTLR0d+Jvm8PEYBFpAoKMjamCdjeld/V7eH+ALAALAhuA8NuTRGAkAmAzU7RA1p7cx3/gAgQgCNQBoUam1N+HwD1g/36f/3grbIDYrJX4EIcy4KPi0Hge2opvXA8As+TzWK6f+nQOJV+PiBsABGgx8reQvkJfy2ciizPUD4BADZBLZSotyXbIHPKDZ41LGX/x6Sjek2+cymC4paAACMPxwrV5XYvGIBAw4AcZDiolC862qb+AllArzpAuWg+8QFNLNznR0l23V3tbaxyyX98/iBsDfAYiaQiE9sv/18LekhTr52g+VPGzaer/szvCSP8/gyjwWMMWpxDKn5o8ED3N8xLRCzStZ/7wsZ2KKvSWw2sR0xO2j4u+BiAga3GL4r5Nf9BHzdI8Wu09/4MOOmIIw19Zv9d/+uCh7oi/rW92tMhcahD3JbEt98BHwwY6xsGHiBu2tZz0ke/93jIASC16ZJdbKxtrIw9TEO7H//30XBmA5qkijAruof4PQMZ+s+p0VNlpn+AzCjkaNK4MNVZMyGOVLlvHgA0KwgCiF5wvpLaifKABoiMF+yqFa4D4CEZzOqI0+RLa/+LUStdFIU7J/7e6AGrZan87+EP1z8OpRe/G4z/43zngCGNqNDnSC7uL4GB1hEAvtxgEdViwR/5gDKEtfHLQjDzXnuCgg+pdcKpMm9/eBIgfBPtN0txnFKP9o+ClV+zMsf/uvD/UqrX6/aLwIHKBdIX+9y1//4ALAn/dguWVaYULeDPGOcQq0iaWRUS///wD9pOud/74C3deEJiay/99/u/R7ViDV3sD8EHQCAS/4D38YAFYMTaJvnwyyieYAALAhuA0NuzRG8Q4/I+E9z7YW5wAA7QACMgBr4wbUwA0IgnQUJ/dbjJGp5tb5j7c7qIhzrYU61CINUFOKY6+XoKOwiuLijbz9Dw4zT+N7L0av1////4X4A0DIR7CW/yXPZiGXwAdoQW632KTSPvAAcAhyUoJOYhy+JW0oFBf3BQXaItLqfJpEMAlBE1GnX3//rn4LZt7dX8A//xAVgBICTAaXksxJiBB7HcBiuajENRI5ko2z/gxhCu/6r+CLTGOPZfoPd89B4MRmkqP/sa+H7HDf9WC/+C/Ai9hiilc3bMC26r/oeAIAAOUAAjZAc6Om1sAuAC4mhiDSufMkkz//8EtKPwwouLYj716cagfxAawAGgQtCf0JRx4nUsgfhi1vgCHXGnn1gFxNfxAZ6AQ0nuwLz4hcsidfwfwAtZSqQsOwGYkUU8aI/8V/nlEsAWKK3jamYmnR75/NhRinz/zygzjKqr/3Xj2wP/wr4QeQgCsUBoVam1N8/osRA5X6hlWeRDanBmZS/nv//4X8sIAGIQDGEUjMmySaZdEDBMvB1Pdm3Prwln0QRB1BTL3yzjP7l7+g40tjQvvf+G/cWAhhNJkGSTLP/B8kEHq7GV96bMt/Bmfff/WfKMaqcfN3Kl9fpn90l97/8NQAYNUGlUF2q3mYSDAIdZ8udf/SFqqkfew//zxDgztUZOZ4/BOLXjd7iFJI+cO8fp/w9HyuHsBJhgJ5/SGTYADzpbMzRyv+urUQYL9syM///VFcivoGwEwKE11c9z/iAXwA5ocrds4ZJ5Bf3gFjTG1GuxF01Ef/eG8MBvAAM4rf/ylFqSdn6/3Mt8z/ecQm8GvfH6MYRsCgfEBWMkQOA/IDWgfFjeKgDGQnTmOhRvWpMhBJBGSjuXb2oA4LgrUYwEiyF137vp+Y1fvV/5MUXrgrTWMxT0/36CDtpbLo5f3vbPob/pQ3SGfrYhDML16Lwz8YfzipT2I7+UgMOocLL/N8/vw//POL4VP++T7/n//nq2akdv1/gDC7lz9+Pwitz+NP4hYvr2f8QCKAA6UIQWtqGHDYzsrebMZXUVu+SlrVhgwEw8L4AsBrw4Yy8jHO+klSwALre9Smf7ttM009ciGv/oDORmEXMPzWKXlDEu7xTfTz0KAS/DOBjVz40wLaqvIkQTMIrOIQxiClQtor6DEp5fD8GKaK+m4xJ3v/EBWGAAzHRKsmOfbIKf4bAABcEM0Ghp2aIwCcUEuyK9tMgtvjCkJXIZVeQk7V//4WhwB4AB0ABmAOfGS4wAPjiYroZx3Uot4DwACgKXgODbg0RvIh0XKLtCpfJTABiMRWYVWpISxqQxKPG6jIen4VJPeX5w6SKy2rQf+G+AA4YllKs0lMSVwx39gDRSgAwI14mJWwO/8FlCMMiXne+G02WqDCLKodXPBhudywd/EBqBqymjE1nV+97A6t2QjaK7/d7/K3ELT5Dan//DmAA4KioLaQfRVQKu/wAFSICbtjp/7JuWvtEGC7tDpf9JmfHilDDkzOa0PyDp0mInit+/3/z49pdJu97Sf2Df/EeIPWgcELyxz/wtwAHBCUSqTH9EFcNf+D42AFw0VLUn+WKc/8GHUe5vZSP+/WF4//nr4CVJk7vP78bhC+evxrvxFiFxa6zriFzrWEIR4Y4G2pYa6kxtqWAB6BHa9Sh35sIMWHYRXS/xewZu1LDbUswbBjbUsNtS0/nWDyAAAWn0GaAOgd4R8IziOE8Im4AHgYQjPJJXTsENvbwAxWhJrf06rwj4R8I5/P+EaEcXhGj/hEEHGAda8AC3hCiltww6bGNFaA0qXhCxEl6tUbfr3EAAHYAARgDCIyaIwA48yFdDFHdSi3hXp4Af9Y0Kna/iT3wD213z8MU0V9f4c4ADMKi1ZVe7Wwa5wAAuCmXAODTg2pgPm8DB+DiXYqJnkiQ/P4gF/X3Qghpe+Q5zTvED/AHY4LtlxzKbBDAzZgBfQ5FyKX00uGcsZTSUb+b/DHgAWEO/mIudEzaaZ/mBOAoKCT5idLuGqjO+9f+AS+ai7d/hyAAniKiEF3qIeY14ehMC1tiq61N2HXvX4GAhVPP+/X8QH4ADABqLYWi0lnzBKCJ0MPQMAB1ABIGu5Yk7yhj3/gQCMiYFQJ4nQAQKVFJLvX/hnuAPZRhZ+//3w7Lc8SC+kABeiIAQGJAjizI3C9/4h+BgnYsSolm/Pd2jwABwRsHVAhHUIJYdf/B+NgBcNWStcn+WMeDK2AFc8g43PwF/f8tL//cP/EBudFk+WePD9zxCnLvOZTOc5s/iQX2mvAAsMB+/lCZ4IwuqZe9Y8M7c925/rCPiT2eDAXE14rCNYkNwALBjs9ibizrENs/zwBGGIK3Uo70DaoJOh48A9r76jxWDUSV5x8/+eoEK3xOLuUdJFfTMaaQ28yEzKpuMlCxF4Y4ADrACQPdS1YjCbj//tINVhQsrbNwn3qL3AahN+1j821ukfzA1yOU4dH/qXZ9mlv+vlPFvwvPTwWGPLMkTe78oAEABmkyZHMXdH+MAD4xFmbCdk+VMg1gd/LU9WAGy5Ui7fsYJKsWM7jOLs//c/w/8hR8REOUd9LLeGH8/35vzbbBAWDLsBLuhUr92AGCTmEQ77T7Neu2GcQEjXVTnd4zGwrBrLfY3kvv/b9LBqjKv8QHIAFLYDCCKRmTZJMM9/FgIY/IsIZJMt8ogInozGb5Ot+5xg28GWrPfjfhOKZk4np7HVhrLFnz6UGAH0xd+7mVEMzdsvBB8ADwSqcAGBO0SYhZC7/wfLhDDgjIa5tBG2AxYHVDi9dzv4dxxYjh4xpYUO8O9qiKf1rIkqovD/gGLRCJOciJK8a7+DDv9D4AFgxLKVJ5K7KQOf/dOnNKGiOFqqkV9h+ffodVNK4Ef8MbBgSDZTgAwI0hEqJWwPX+DAAfREAQGJB2oqMjsLv/uGwA1D1S1Qegsa7/aYSQXWs4pqhSj/cFgt+klr/5rCjsI5UdDhanjopwaIXbDhbDdhj8OVKMo2mfDnABFdKx3J7wGipcAAIBtxVgcWoN3wtTT98wihDtl3v6hMozlhm8Zcv/7hyfEcKr/DFg4EojYAAgDgA4yEPFEmyfeAXfCVZr0m79IxOiHMpRvY1IctRVVUu7/u68Haf/v//xAc4AHOeslud/wDQSoQAHBOfkhOyF1/gsbwAdpbmyRn+FcABGgA1DVcMRJ/lC3OgIWyUUeQmCkinf3cNogBgZwEbgswOQuv+DsBNigA4LwiSELnf//dwNLBF9YnAVSwPupf/3BiFAbVSx1n+ev4u1u+qdFP/G4gL+ABYCGoR+hPPyNiyJp/QBwA8JoUiyhjjJKHjsMSy+Aje3JK6RAxNrnJl/xvwGJRCZk4lEyXw17QGqkABgRv0CYnfC6f4P98wAUwiC5ZTynk33YMBAAlClD4kVBXWXmgO65rmk0cATqKte6bUwF4duBd8bBXedMAAEgQBuDpgaNEbyRCZkMZCDcpSAxey675UPL/rLgA3v/b5KlnZnG6wmYl3n/iBsAKqLueL54ARcJx8eiZUlbjyANYbUxx1baqp//977PjwHj++QuqkRzkGfazHB+RLISJav1VQ9CKAhfBDc8T6e+I5NgAlIjYqu/AQC/ywqHxJFJdJKiVeIF+UZDd7t/VITm2sMMXMhA6DoZ7amPTOgQqFWb+FP68EtBMkTMv//4AaNdd/vot6vI+NtYAAgGwAAQBgAkYAuM1uy02nL/04X0eCogeDppKjxf14AWwHq5BPI48krUB3wvejcBwAeAfOCgoq/kqaHX9/sAkGKz2JmtETYbZ/gCUZidjmVgqlNR44NkDFDEpILLLJIAhVGnW3L/+0YlB5SkzAqsekTeFFdJdxOSaTdX/qG+Za037fxAIJinH+/MVZFNTkHdzSCcMMAESnv8r74BYyzBPOi9PP9BkWxyh764EgxZIXJ7kyX4pz9wAiPEAK/BZHG5WLKGl/WOu+jawauenVdeBDfuIjIQQEyukmrv7Up4JvejrG/iBtgAA5AAHeA54dNEYAUKPiEQVb30014EwdIqbx1TpngIB90gH17yn1j8kD2gMZ+s+LsRNtpf+caAMbQggctMmJJba/+D5sMGusF0/2jU/fPyUsD71PjwSpsrIn3v+eiXOQe/zjNAIFEUrQgTOsES0WOPaiLJabd8H4KiCPHsR8mE711so/stTXYwmEtS7+G61Dv3B9xPDlD+ICuPlzWn/aIr7x/+UMAYZDDq8ovniOpqfAmGrOmCWGzWQzfwI+HsYrT1z41VtVMGa29s9///589gq8XI/qD//G9JEYAwO8HcVYHYXX/Ofjal9bterAJ1Xl++0PMPyjceQxxmAB/NqVmKFbeAA+DpeQjSVVbbRkgcy5ctSvg9gggaTjIenDdIWgTpgAAsCG4Dw25NEYGY8BFEvN1KZiKPEk/cHhzrc1j3f/sjs34JXP2/xAdg8DBMYqVVz1PAwgAENAbOHLaw/17RliKEfz0Z5T/awynCvvzWvTrnKAAn+YKnDbFa+nzLNq/uv1kQyOM3ElJaxPtbCHFr6jh82L7q8BfYo2pISp7Qn3L1g3DxBMYAvMEy8WyZn9+U0yg0lL/39U0/W/veGsKpw9/D+PDdyN//U72ora8D+AAmAHxMDE2Es/ZJwROMF4wkOO3jiFNPeU5fEADwtBqLaWPsEfGv/4GegENYn1CefELlvnX8MB9dLS9bmVP/vA3skaY6k//uGGLZXi+/9/8bs4ACMAPYJqnRviaspNcAMgN5Lntyaoz5//3DDwIR4bmVeIXtN5Yme6qi9JW1ZiIclz9nR4bHZYiFEJIJkY9/FGvIsOjUkE+3L+Jn2ESFAX3CE/wG+WQi0RbE+/2c86amkznBOZcAQpRtQeKlzBFXXFiCNm5P9+IL56QyRb//5z6OP9hrwxpcLFLWM7YAIYAv5aikEIzwjt3fNCh/g1pdTZLZwEYdibSpMD2CrjX+8xxoV8J7SIUS0PxgACAWsHDNKra4ieuod0Bjs9ibqxE2G2f4H4Rjx8W/9PHXmbP36sChG7mWI89Ux58fn8RG8OcAFg3xwAcEbQKCFrv//uAUEJRaok4lVFIGv/+CtpKIIcAGFaWzEXFw/bPwQwAEjIg2cRee5LWJ4XhCi19Rw6bGd1YMOL4Y8ABMSK5UMJnkrYxP69BCCldxw8bGN1Ya/8Ow4J/hfAyDwoJPGZUu8doM75goGT+WH/DcQBUYltTfvrp9tsMcQvuN3TAxqqDbT4Zp0aWd2D/kZDS6//H+N8osUhqr1jv//U+MachDlfXMH4fAoACEopCLzGtQlLOT7eAp+QgVJPGsKD8iEzMgisQUpjEB/WkYnM8UZLVJAAsAIBdQIRxKZXZbG/fWMB4ACiSHLxgQbPXeEwdqeVdi27JlxSAKguepE9/7/D9pfbWc4ECsr3dFf/74EgPCmGqxIzaFJO/tggCB6lLkCcdio2/cODCfBMofhmub3kOXs6Tp/l0y8zKxHWuABhRivl1JazTZr5n96TQYij2Skcq4yrHlJ0HC/mjjK1xb+kITExA5Mx9+zzv/0DPDsdwipxPyf/wNmaMSS0tneWNldWKXw/4AKYbDVZbSnNvgxN9Y6GDzcPzGosopDjQHAcANAAaxYDJ5x/Jv/VYDgddryMmX0laDf/rNfxvY5xlgF4Q4/E+Y43zBeQ0YrOY+cIlrFuOtHy86g/b8Mdpq7SPVbZXDAYru995XixSP69/7wSDAM0R23/t5kYFopQVLHUSWzgJ9QHWHWjN1wTwTXBkJBl2LQ7XaV+fDBsNLSNlW5Ye8fBGWLD36gu8gE9sfH7qD1LNdC5fPIBjMyUKJJfD4YhxoFFOiTgAIPAMIKpGZFsk03/FgEEF0hMkySbZ8ZDdp4n0dZ9ERAMlAiSusTRP6EZFQc385UwmM3rFT/8Nw4IEH+3XGc2rcr8W8X+ghzfd9b5/xsASaXMm013v2P5Xqvv/4Z/Ueuh+cv9zYIIpAUwIuVJlmmzdqxgAIh18QqiKe+FFN4GBbogIU1KFyya5P3/yWkNqpFZ1DCdJDT9/N//WVkjQ3ZF//AqpnBMV12g8cHsCBqPP8M9D+VKCToTdr3QPmIA6Ur4VHRCNFTPwZLGB+0i/UH//hzwAHgAsLoWkynhBgkgd//hd/AA3lbPRI2f4b/GAEo2hSDSe0GSSJ3/+DAvODe05Gmlv8ViD/+DQuJr/LAARh5kO6GKORjDXh8oMXKLnmS2SmcHxAIIAxmQTOc6sIhK+8YAByAIkDMTjORUrkU6gc84NXj4LaznAi45a802pkCbAARAA4Lgam2lhFgrBA4GeYg0PIQB2IA0KtTamo+AYAqAM+U5v9zw3xOYRJv85jDrj3NIknnXzMpQri/iA78zIZHUwuIehakeICVA4aw8hHetk1THsA+AnByLRr7MiLDpTwDApNvPe+KQIz5BLxgJuChjD6EN76TULB+TET2d075OgxDg0lLcTY/0f/3AEO7DUKJjxnVWE/wzwSCQ5SoMpFVF7o//dgdXKT3f/dOwRo6xHv6su2J0mj9+FaXDUl+tf/EBXt5Uj84j/54we1OZ4H1Tqv79BwDJ/C26IxJJ/9/eDsSGqKWrrPQG1IpUoSb9GPxBI/lyvJrPf79f8QHpQAIABAHAmkT8AsOQO37w4YEMNNd+v9B/w4g07CEGl4ayfIVf7SMg/uL/9zw36H//7o2ur+/6fxA340MC1VoGTnvMGmcU4NiE6iXL//cGt8wJXDeJ61VREyK2qeAAgIR5Xr8tLrMII/1K6L0k/u78Q1Mki9CqSf7RtoORrFjZ//Q2wAfDv1qbV1W8AMCayjWQXVlW2Y8zURjyVW1e0fddPf+d3BTJphO7KEMUQ4IsvH38SRVkUtl7XE7HrdOpclNxjTz4vuYxccJYYTpYQXvG8gOzuZGyl7+c358antCxFlfr7In+ypQfs8/mckNSa9EyroYNFatCjzRaVJd7wfOzsIjCFSy7Xx7AghRUXeuNe+DAC5JKcmRKvn+BgSEK3mIu7PsQwz/PILwV0G5es/l6Hz2Zj/LeLN7//AiD9aaJJDfX//9lA8y6QkLB6MAsVXc2PIbZbI8n3f+IG2BruNdgCRAi39Za7Eas1cnx6Huyx5yo7gMdNWsJvBlWG6Mva2FZ25HarLAwRAWJJPOk9cDzfNAADwGsRAjVKzJ7JVOa4jaHa6buvP/3/IMDQnAdCIooV3V3fz+gUTtrbvj3qBXK1m8AsLFo+zFSumkfPGqrH7/VePbKxl5lM/EDYAsCZwoUs6hDO+lVjG5L9N87+/WxZY4ufSJ/3f55h3ROvRNpy2MhHBeUTJDk//2AJMUAHBOvlBKyB7/nBsCVGaLr7dWIfA/37bM2Y1V1Bgg0/EQIRV7qlI9bbSGCCTDXHcY0bJn7J8KSRTmYie/4jsJdzcZ1oEjvL+9zUTzQ0W/xA2DsAAwBBDAKxIGBVobU2olv5Lpd/++hdHzg+9Xp6JNmREP5/l08ffEAAgfkBLQNitu1OBMgilZhtTADGiGnIdCietSWAACoKA65w2NmiN5YZjNQUR6q2miFbkmFyynlEvX3tsbqpxd9/rWkEGcsfN9F/6oH9os9SJ/psmCmP6zpk3F3P4gbGnjRTrN/7/gBAUMdedCnazpXS5q36f/hgCDIZCof8VW51eAIBCuSskxuEoQUthYIEH+Yq2dlOQd1LKfDK2WNnpHPfabK7PVoWq6LtB/xAd8YAjsM1LDYso8WQ//uJjZLI669F//zj0LSmw0AyA9vLjEDkVz2fWkEq9A0YG0Y/y+/UB0UEHDEZYcNzF99/BZUY4KKpn7FP7/+1s2Gr9e/W79zAQtCf0JY8RuYQO/7hgAiBzJHzjh7pxUzwYPiKnJvnGZtgtbDlLYPAWH0Iw0xEwp9Prbl399P8QGcAQQgCsUBoVam1N15yeMku3V/7fB/UYVu69DFquNf/DXoBjWI9MnnpChdE4/vywgN2rS9//EBWGABc0YAgFcBHVWRyN3/z4CpABoHvYUg7ihrv/gw4G16waRoj1qxRFhcY/i8QGsACoELgtGRTCBO5hI7/oOLqDhcYgDKHRxZkbF2aQf9/wz5AITRPpE8+JVMInf8GHliMiksDXGo9/+IC8ABMAHhNCk21MeZJQQO+QAai2FptKZ80QgidDDowARgACQUTWEiDBNlhdcgDCiqxkRaJsMAlah5UYN8QbU//+HMfCw8YldjPSkaE+u+UVyTvdtCLTH2z/4Y3gAPoMTYJtD6dZj+LlgAAsCG4Dw27NEYBEFRKoqUvt1mvBhbiu+2KdZd2v/fhhVP3x+uf8lmRl/rh3j+FcCIELQn8iWPEblkDf+h6MJigigmEXmSirffg/kS99NHn0YMiRe+D//4ap9wYkAdAAEAeW2AACACAFj+/38O1c0y9eMLJRJ/+qr+cfVT1/hn5mzDK5zq4VbWpDDYGVnCztEv865/hNOn42H8FwWi96OsOGbkeZT43wAMjuJY+if/vpylZzZJ/B+cABuisETRki9feBOCGxCmIsEzLb53mjVYRYUDJeIR8iMg2Q5OUZLGplBp/Kso5vt5MACde4ZFF6N3+Edq9xn486AK2rZd/g1XxR2cWbQSpkqI373/88rX8Yf68flwcoKSH/FAyg60Y2p/58fehmf+T/f4f/PXx1nqkaX/8874N8Aj3p/b/Dyh8Zz8ukuHP/xHw1AlggXasbP/pMS4943gjyQHUalBXlADEEMj59iu+16mYyq9f/MF5sAKgTPZi+O7SH/8QaH0H9YB/xAr6/fF+cAUB2QE1A2KnbVARkQ05jo43rZ8PiAtAWQwCsSBQTZG1N7gTIIpVcbUwHApKCUgZFbVqYAAKgoDLnDY6aI3vY3VSnUo/rWmwhSAxqUAqIZCc6+XDbCkkX5/8QHcAB04DLYDrNQgjiv7oLnMAUIbllBRdx1/2hlBtqh8v/k1Pj3+MBKoYMYeQjjfCapkNAMN2NQD5wXqP67cPTw+r+u33h/+epltCuWEoQRaoN1//EAww47QABB9Nsnirf9tYgVbOMbQlBqBD995gA8JoYm2ljjJKCB3yAB8XQ1VhLPmCUETq/onAEAKEJYpUaf/EBqABZHVCoPDMh0pvgF8gERGAqSl2dhP8Av7AQUROdSC5Npl+rAMKLrCpFsm22KqwYgNT3qPw3f/8R4gL4ADFoYgtXUbtGhfVV485ogowDcUYz90BQ3ACggnC/Hk2iPvvlLAFxK9bP9UGO500mf6Nmuvzyg1GfuvB//EHr8PZ6/ERnlxAegAMw6Nll1z7ZBhMgABcGIm5AsKQv12B+BHCE2yoS+HQa/gw/AAsEymABgTr8CYjZA6f4QpoEs0ZfL6TD5+AxitsJnVeI56+Nd8I8FHA21LCdeQD2TKVbUsAD0CF6b1JpObCDk3xdg5u1LDbUtjbUsNtS0/n/CMHcAAABd/QZog6B3hHwjDHrCIc4AEn8iTNom9gFOFkAmUIQqJIpG5RdhgFVI+efxPifEnrjmv7wjG4k9eAR7Tvs94kMeAAzYiJznUgyFrRYBYAAKgwDrnTY0aIwCchsvILiH8tiAlWwCalxuLnTCFOpDyjRnv5vHbHhigLjBKwAfSMa4xkKP6mJcAAKAoD7RNGhs2phW3ZgRlNzz/BfLcCgS9SLS38FIMg9UWwprr6gGAMTE6Y5u43qakNYcw2PWyL/LCJr/8/vpwDbnz8v89YIvR9hODaaH+nKDT/hjwAE0I/IUXEaQ41boAFQcggeeMTnd03UY/wcGSkK4/8oU0YNVX/X/Ie3uARkglW5Hh3v4kF+AB4JFMADAnXyYjZA6/xEALCIcdqjCOaJRSQ7oEI3m9U4Jgy0x/P0wAN8jheoqRW+nywAqY3ix494o+E4yp/iQxo4AY/3LfXzDOWAgAFiAJBaDOUUHjOCugV9AUBHBz2F67/ARMy/QK1EAHae5Aaa70jbxAb7f7p13rAemMtV/6xJ6wBmSqbr/3//CMVifEnrwBRXqaf7/4cgANiG6oYyFH9jEuAAFAcB9onDQ6bU2SClgPqBy+7PP5wEyiqVvG1NBgYkZarQuAomQLi1aH5/h2MAWZQPygmJHray8/vUxcIGgjU55tTZALQG1Y6C3cvMHkIArEAaFWptTA4CEYnRCmUoyVNSHjB20Hzh8WdYrwx44CXvZkb/zrIJvRot2oZv3p8fSxT/5+/8QGMADhDKg6VkznltZg8BESOEViHTHf7N3fofpfoBHFPB5QrmJZybTt+AEACQejrQFE78zB5ERGJjpwSPW5hLhH066H3quGn7pavX8QNgAOL8bRt1I+2dG514MP44A4NV9JT5bCXB6Aj0KqDyE0UkY794AUQKBw0Rytjk+WYTtYADswDx82DMlkpf8DD8wJywAopxFKyj9SKQYfmACQbApJlPH2ScUDgYaW+cnNDPMFoyGS7ev39TyrHEnfUcoKWolO/JIG4+afBBAAthguZQ+nuTYj14CLCBMyxs/fm1D/wDcQEFEVjMkyTaZdqwGOJrMmyTbb/6YFQAEEDb5bx+q45JhDLIYI6J8jB8Ri35gIgpBQ8+ajK7hqoz/g7vbVMnd5wcFZSyrZ+/5zxRG3vf4gWYksnT/zGvrAXNWX/nvQXK/oc03Sz4QU0V9NAvFF+T/+eL2p44rSNG5ZWGQ6oTn87w4/Isf7/iRsACiAAmVWCJs2heuQfkRCIyGMhAiGMQGAYqexVBF3BCAI1QGhRmbU3ggOhdlba9t77QCgmHL0nih8jaa1xX/36eghBS+44cNjG6vQIdvM65sTNppn+AdkrKDrq4tv/X//YOUcy2177hbKH+ID/3sxupz9wqWtSGGgP6CAAa5hHAhi4QNMjGysiFH6uMIg/TpDyGtvE1k0/PT2uxRR+/XmS+W4uAvkfQcve/8LwYHLVD+vgdRyp+uhAAJkRjdBFYklLGJ9Wmoy2JWdRb8Pj3Zbz/vhiwva/41eMlJ2f4WgfgAFZAdCSytzv7/Gh8yVAaTM8uCQw0Bw89do1sAgAMinGoki8WMis+ToK+zbt9+5+K6xyz/n+//P7wEg65D/T/hqNiwdxrlDUU/AfXvp+1xxzj42VtyVlvw1AEEIArEAWFWptTf//4xEpapOlqvF8EG4+FTlNwALAxdE+qUx4lcz42/nu8YMEkJXX5GQnj3G3/MAAFAcB+DhwdNEYy4CR673vXenfL+6OMR7TSmzpof1//EAwgAPYbs+gTQ2qyHf+D5rwhRauLOmxfdX/wcABmKi1ZEJdLYLd8xVs7Kcg7qWU8AKOo1LHyP6gw/+NyNJr0XAASABILoWkynjzBKPjY0DIXBKUjWEqh0mEE/+1gUFDz5iNMtGpi++8gMSznWF56QsX+c/3h4R9tCuQRu3U23wBVMOSy2ri+2n137n8QGYAFghZJRB7kwV4x/92AJEKABQTr5ISsgd/4H4Wpvrb8guvwYI/8QNgosQVrgBLKFIa2GNY+9C4YAD8AEoerliz+KGP/+AAsHhElMJOs2xtnO/wcAH031L3++z/kxN7OqdcnQN6jv6AT55Laf+GL0h/sWdUPc63mvTXfA42TW3x/NDOaI3jv+/f/EB6/AABAMoAAgDgBAyBcZpGbRa3ez/GRjLDLfZ0HH84AGwF4hReJ8xxunBqxzHZmAQ0QbKY6OMlbE+94xWnrlI9NtdUMMQpd29JE/msog0LajLfvB//xvoc778bpwAEh98R1MQd9MKe+JdH5vDALqX934Cxm0Bi1GxERfn8srQegFDFZ7PuIs6RDLP9oEA4lVKzWeKEoqm88ACFdfHnD+RphhVgnwx/KrvtpI3//FbLhK6+R7/gSBdJM4SRf//0AxI90a11k/xu3LAAO4AAkogBzo6Ob5gBIf0HBaZJe/oUOfEYaQBhRNa56wIGCKXpqrOJgXUn+RY4ebZCn7Avr1DPn6wFgDbpyHqSv/+AxOUn10pQFHI5c7fnnPw/MS3IABMIKlOpNkkw6gIrohJUJgF9oVlk67tbZt17Cv//2ohSCTF9dJ4bHF50XjYadYf/AYEsL3WaMngWwybKHb+D0kkADUBcmnmeZ3+/2iIBRYBDCZQmSZINsz77U6qy1AuJGphvv/eg63T81dQo5dUUNv7vABCYJoivVOlMVSnUG68Ajvs2r47MFORsJKxCb+6rfCZQi8wdXSe/4/iBsAC9sgBAZwP6oyOQO/+B9Dxj28/x/rRgDTjS1mtgshI9tuGF64ntO1j3nvABLX/IdRt8GBdsVdOn3n78H4EmkHS5FmY9HnPCAAC4KZoODTg0RhCnmvr6RF++aissazrPf/JwSIf3lf3LCZExl/EDcAABegplwDg04R1MAnHB9sukOp9GO8wvDPP8+Sa+Qo+I2OUcmmlvPcW4luGLQHAIAvhmOCfopNtJO/B+tpJmO4mV0AThwfdLhDqbBjuaaDR7Oidl7hpQYjzrRp6jSP9gCpQoysIJKpwUe97iHbkX7L8l//ceog/F8Tdf4BxbpCZ5SuddePK84MAN2QSNuXPkOCahY++vG231of1Ol5LwJ+cP9xAW/wAEYG3DBi76MMZ0SUMnpL38Y6cd4nM8k02UU+8QDfBgtd5GONaIKlwfRBgt7Qyn/Qbnx4MFRsjv5al/72MaqnvXGGRj+ySrbf9Jx6SYWrvnf8b4ACYaKJCLJpkPMkkvBM2NKtnAOYR6Fe3n+rksPyzkpIL+J8UTTYxfH3RV7/xjkmuQ7Iv8ZuU2aKjXolsdwmWh/+ju6g7P3cQaghqA3Eq7QlaoBv8UavI/f5B3cgOakX320k0xypfPb+ID3AAsGI31JqdOkS0z/P8CAHKKCDxicrPG6jP+DD7I7Bg9+VmDlSokpPv/x3D8P4ADh1A2lIEzS2RNYIvQJWVaFsNmuj3/vIFKMCDpqM8Pmpi3+wbAZh4hH825f+z+Ax369NzNCKMMLf4NcJehgaQPOZEHuaannaxk1/C/AAQfEf1dq2IxZFrXe4tcQSsv48WHxXT3aown9N7Y+/v3IClEDjpqc7Pmpi3+4DFf7f2boRBhpr/FsJWLQ8AcN1JbENo8pQQvrw/hXAATArDAFGMzlfSm1E8P7AgUhMmLRKqKHtzT9Kd/fIPyJCLd3WEl7OSSX4HoihlaWsFV4YgBXHdJj5+sLrSnYf76zFPVh96pVpqmyP3f/AFAE6AFNkQ5dG2jKJYGEHnh8AFhTpBbiouX98ynZJi/dNFOqC4gEEPgEwPWy4lDJdyz/3xoMXovkNQhbeaAAmRGG6CMxJKWMSNP0gANW7Bk0ZY3nR2y+R/97+RpDZSPOR1T8C9qgMABUZNsEEazeGy+qbtYEOytnI28FPRNocae+W2EMkfEB/xGRhsrNCrF3/BvclFgT9T9EQaqiFR2cd/7u/AAIG4Pd/Iq7dZKXCEz8v6AAIjDMbsgvotZFNDXx8Dfxwhcmcizqa//6HbW2hX6y/1kZ6/4YgI1XgU5+Z59AgKG6G344EgzDW+6RL1kEP/aj4eyX8AfJZc3v//sL9Qb/P8bgCPqiwmjJUtXYCIoAUFN3UaXabN2m+2+r8XqBKE7iP1dskskPdgtfhwAHWAEgealvnYSKb/9oiCgKWE4iVJl23b8AIeEB3okzCaF8PS2uDBabok1H7n/+Htp8w+4qVp1+D+G6VztDdf2BwArv5eP/qwopXzQjf/tfBlLmpq++8LI4tapy/+dWfVQkeID0zspR/MCC+GzAAeAqPv28ohXIS/+Gw3wBjWc7QuGUSVi6JxoAx4EfqUx8nYv48/g+BAc27gykpKT/2kmn9fpv/8NGJnC6XmhgmYNxnw/AGR58+fuG0gfwAGcmtOybJo6NI5Xd/6XINVkOPC2zcJ/wfAYAekgwgejfy4T6x0/4NRjfvxPADIAvsTNX/v/wxAAaiGV0MJiSUsYtgAAoDgPwcODpojZIFvAe0Dl94efzgJlHUjeNqYAYjE6IcTUkJY1Ie2D9oPnD4s6troEuHGcAij8jvPx4miHDL1gi8QevAG5Nbjj5/4g/v4CPfH/fr/BB8yIxuhjZx/Qr+IAAqB0AbeUITKFLCvZIWsB74cvuzz+cBEtqFXhtTYACYAXMoBihCefMkoonQ/DxDAItIFBRkbU318BbcBKL13nCEp0c0PFk1/xAfhsBcAxgzAECMRAykHFKUcwoooPxABqPoSiwpvjBKCZ8He3KUOmN1bj47FG9x/zgHi8d09e//3FCmmKufm/xA3AAQAQxnxUli4RR3JpwABGFs5yEdzGdx1URMW9LLXzmEwdlAlLGqaz38BJAT/ziU0bY7nzC2zHujSVv9emhFZRG4khLWL1eibRuRPfeQABqwDcxb95waPVsfxA5aDYkbBbWbuAAxxUmEFpJ/Rqjbn+2q29FNw4E6CLT2m1Np3tmAAIBFAvh1W/3wYg6yoHw2RanrF8H6ubL/uYbmJvX6ukQracizy42Q1ox8QHfkz7giQoHS4Qnr0jMtyTfe9rYRwOeqUDTYzurD42DotRcJ8ien//aQADREQP9mUM1w1geHBJ43KV3DtBnfaAhHczsrRMWW2f4wAATBgHXNmxo0RgE5GJVMLiCeWxDgToI1eebU2wBaSA2+MW7ff8CKYFj6yxC/ylFmdgfi71VZIVjmF/u9yufs7xPSS2zh8QN0g/AiGiUkOr33KyHsrdSK///hpPheBgpoNrKmW0aSvwYkJJDIRExYYmWWh8sIa/d6DzdUf/IP5EQOGbD+9NNLfbv4Bf3xMgBFlHYtuclHwyF3xqv93xU2nyAhYucvf6YANntUdjWiOjHZvf/TpF+w3k7/9eHc50B6B8QHtmCbOdV8zGmdas2bbQEIIkW5N/6vwYHeAAIBYGC5RYQ28z3wAmEak4OUeUrrODap+6m9t5CERxRhxCjnjPkvA84RGqYAbJvGVF3yFTDtrzP08z3UMtnZL56xyv4gbYWvUaKuoAA07Z4hPShufALAq4DCm7yxdfaSGDABjITs4i8SQt7E+5Z8JIpVZFPS/uByMyFaVzI5/P4s6XteRoRWcxUKGStSfaeEKLV1HDpkZ3V+RoRU5joUb1qX5geYDpAEUVvzxgZ1Wh+sdEyyaQ+2QY8IT6Fk1CYu/k3p4X2Jf++3ORy8y/9fbBkjvW/4gb0wA/QoLKH5w+oLkP/uAwSmO4En8YoSq/3gEHiWlPKctjX8aRg0CmDIIKUUQzz2UJdXcrWkZwxoz8NQunvaN3SV2b0hpqBGHNhelKOJ33GANASTJfqHAserY4PyKNBMhyjvpprww0BBjy4I0tH5Ghf5/wigpZNNdyitgV4sTf9xBRgqG/r+IDsABGADwmhSbaWPMkoIHeCA+tGslLTkaazEZwNAwFwyxBiq9ry6JJXLpWPX3gGUwQkjVsgUitORN7clSP8glYm9Hw1SKAPTUNbCSXagaRpJ7F9eUty7idA39X3z/4gKwAiOBjVWwNQdtSlP/3g0toAEFp5vUucpIXfGq+7Q+AAGO9WUGOT1ZJFUz2saOmwagqDCGr+DAUwW6L1S6pB41Mj/+IUFR2xY/9v//IwG04vniwDH/8QN4Dx7QiCTRyUnn/t/gAhl/RI9q9sPKNt/+BF5E0GMLX5HJAwL7qBkz8zQyOoi6QTzVID49pBVROxFNfED2mBUgDjGZ34ttRXvuaAA2REC/plDNcg/CcgIYDvtJXVE0+qvTwGC/zRaaOse93SHA66GyA/qLWV++3xfD9+zJVA+e582sNpdWWISmGJ58QGYIBNyAAQE6RJiNzr//u4Bi2QuTyEzJfjHvwEzIwBAK4COrsjkLv/mm++qp/7hc2QShJ2qj1//PxsDZcqb9//xAawAEYAPCWGIspY4ySh47DWADL505Pfo0E3OOPnoOGM9cQHfEAD4uhqbSmfNEkTv/95NGAIDuAjsYrtjkL0MGvEgAbB72HIg5BQ18MO0H0Eo8KkSElRFoF9Wkab6KFHuGiP26REwcXiA5AA8G6HABwRtAoJXwvf8A0jm9IVEQg5J/gJaMgBgISBPFmB2B1/zhsAEoJVS1J/ljHP/KAPKPcNEas0WqwDlhcqo5r/tyGioo4VXnqmMWp+H/4cooACYDRQwUy6jLWdEFC/kBvgwWy8jPGuElS5S/gKUD8dtGe7/DUPIQBXIA0KtTamP60v1NhsR2+SJaQv0YnWp8fmPZCP//+H4eQgCsQBYVam1MXxwfkBVEOjB6N94MQh/aN+eNWy1QzFRw43ef88U1c+G/pcaG/oM1/P8bjonIAqC1oLiRkFdZoBYhAGagCwo1Nqb3ARfete+bUwKg7YD741fec/oA6MbLjmUg/Maj4wG3DBTL/4YzwgoZYAAKAwD8HTQ0aI3kSEyYgmIdylI8If6MDWXkZ6xwkqZDEEjkbEnvNvPOAAktta+1fHYFC8ff3eGPj49/4Xw4ACEd6QRK8xP9jEgAIECSvQ9RfeMMEsoFb0q53f/f4bLRieZYj/NYmdiZ49x/qoqjQuo/5SlZ6nsGGoAb1flav/f/haDVgAA7AACOAY+NmiMAOHGxXQxR3UwsnwxlW+mvRFjHDrJLyIdFyi5Qy22YQCBgkMnvYasdA6B7aMHZKv/1IO5Ki392mdElDbMwxie1QXhyAAjAbcMFMvow1nRJQz4gGuDBbLyM8a0UXN4gTIrNle1/MQN0Zioj2P4KjwOO+y13+8BiFrPHzfJfSQ8Qt1p6jTmJnDul56jrNnI/eD8P/EhqH4EH7XiE1KX5n9keQ18Mg07Uv+8//EO4IYBVpA0KtTamAqCAxxNZk2SbLb/f8WTeMEL4jxAaggD8hUfLIpLrbRbgAEBCySqIPITEFeMfwBMhQAcE6RiSErHf+8E3eAObmKLl991//C8ABICvKAQDX6ytEs5w7wBhXJIXtTklHGm//oFkPF0aq/ZQUtxLYp7/7gH56k20hRNiUSkLIiIP45ZCSnl+cFYURbYfRvvGB6//u/8QCKAIIQBWIA0KtTamzhK+HrxAVqggQAcB+cGzxq3L5/egTDwnQRq882pgSApgbUjILdz0HkIArEAaFWptTBi1qAwGgCUtLjj8v/xAZgZGitoNQZJZDl/YxKZm1YhDZv+wJwOCh5wzKV3DchffaBDM5iKixM222f5PCuCrpx/b73D//EeICuAAmLtnRTkHIppT4bAQ0kkQ01zADCj4iIKl5ONNJ8ECApT4qliRmnX/8NQFE6FDISExu94iyW/7gDFgR2ZSGvv4KpHgJBi2kIlKoSI0sw0bv/zzFwFWXfPbX+IDsABrIZHURuIJQ1ig+UABoiIH+zKGa4DlGqWgIZnMRUWJmyyz/P+oTfUf9+sqL/6xB6wYIxNf+EIzy8OYADuYQohTcLOmRbZST1ErP6PYbNdHd/FKngDUFiR7/6v4jOufzrJz1DyKf/8IhRQAEJxOb3s9jeb7G/AgpBCC1tQw8bGdof8AHoAeopDEWzzmAgAi/mZjK6ir1JKWtSGHn8/4Rg7gAAAXGkGaQOgd4ZPXhHjb+GT10Ci/DHPWEzzkL9f/56x6oZy//8I53z+fvDJ6wFnSG/qCmUN/XjcSevAQu5H/fr3hHwgevAG5Nbjj5/4g8wuZVMnXeZO/iQQUBsIpCtHVAARgNOGCl30YY3wksZRaEQE27HT/2TMtPeIBvgQLZeRnjWiS5kPkhgu3Q6X/QZjr4NZBAgFLPgsrov/9wex0HEff/7/7kW38McABsHBNouUPpklPYAALAxeA8NuzRGwBITL5ikfv+jWp9uxCilNyw+bFtlYS0ihDSHzgF8Q37V0P+EQx/IjINkFVfkLc1I2CAeAA0phB2zWIQSdH4G4B3wA4r4jZV7+EQ3+HgDcPmQ1R6Cxrv/g8PdUr/4YgAJojGuMJiX+piWAACQOA/Bw4OmiNsgUsB9QOivvGtHYrcWN22f/gETE6Y4mpI9TUh68x0pbzq/73AJcAQ3ATj9d5+hf6uVhHxJ7+AlSad3n4S/grEnrj1Ifv1/+JPX8AqpPdn8SGOAA+wAah6yGqE2Tdf/8GggBCEARqgNCTU2pgAOgUl4PiR0F9ZTgJ1HWvfNqYXXzooDiGxIfnH5cc7iA7AApbJPreVxcE1rQNkF1mOaU19gQFona8zYyu4q9SStq0hjYb1AD5bs+pjgm3F+bgcvs8Rq4xG5uq7f8OUBlGDABWAHRiGop6XfwYg/GbnaMJxqWrSP+f+HYADhOPuocxW8tpp20AnQwAKCdoxKCdkbp/3DQAJQ8WxMCbKOP/2jbEGFeEbduXkDv/mGB42GAnMfAGYzFIPur60dzQYINgI48PTYTTDoXcmS7TO/4iwallh35J+ckW/f7/iArOoDoCgiZDYYDAEqC0u+bB0eaH4RocRoH38OSTypXP4gPYACaADUEq4UiT/KGvfAnw83lsJZlLQTwOQcK4azCKTQ5A4BgwbDTYDgAJkQ3+MZChdYxIi0vRAQAsittVfQmG2l3eTwdzt56pBlx3CHiBsGEBJA3mmjpw0/s0oZ7f0AhrE+kTz4lcwiffwN+1sAAEgKATY0aHTRGARGIqIcS1u9jU4IAgAJro581aYgwednX3/9BkLIkKV/KjdjaSSbujYKw6cfSbEXEB2GAArI1kOK3VPDZXxI0JgZf3E2NVOU2pgFRtAEJwm+s9Qir8qU2WqhYkeFtI/iLU3/+IDnAAXjq2pMs+w07yaZ7sNUz9sHwvyOhw9/mZJc83/n/EB34CGOiZZcIfbIKfDYAALghVg8NOTRGBULqMl5luJeWcD8AB4BWihx83CVnDVBf/P/36dBqqrgtBsmUNf91gFvyCL8nj3EYXDtgTWCI38wVkkfg0u/rUjkyTbz1SaQ+GYA+YazZ1XIkQMPqndlrraCKz3/6//BJwAMLyVnpb0+CEFK7jZw2LaqSp8+CZWAJK49Fdo3Bryc9x/n5f6x1Vz3/vYRT/h7jYvhjYBgAWBi6J9MlrxC5dA+/sBcGCSFqs6rYVv7jc/nAACgKA+0ThwdNqYGFJCVgz1NPD5gAQjzbSWZami5ZDz5/h+HOo4AyMTohzKUb1NSHAASHXxH4iHvpRT/uCgt0RKWU2y3ZURbc/Uh6wxavp+9dw3//4gPYADGQnZRF55CWsTD4WwhRauo4dMi+6sGGAAmAD4lBSbCWfsk4fNdAIWj30FY4RuW8df3yl8INFb0mttzT7m/wX7X6in3wByIZXYRWJJWxS/T0EMKV7GzxkW1V84ADdFYJ9GWN51xoDEib/YEQ/avBikMafS/tUH5UyS3b/+8LLEm31tyMAj8WIvzjKTAFRDD68b8ABIwCot0ui3QiVLhjNmRAAI8IuYh1bBHlLeGgIAON06fzr/wF6FVxNh0KwuwR/7yTE6IUyuN6lpeBdBT/fxscDHjoTkSKm2CMH48vIx6/vr0HWQYP2NP97gNRUQvOyyn/f8EGAH3uWmn/oAAfiGtqJ0xanyvQuamDAASBkEexJhKGiEU0O8NgA1D1kNUJwm6//7AGyEABwVhAoJ2wOv88gDeAHZENZgP1IXl0DxwFEswlTiflFlwCEstNSJRzBPDjn/uIgoNVEe21WaT/hSIIhzaCMFrGcmveXXlBxakh40X/EAMxZInNf2UyNPiWsC4gO/kJrGACzZ5FZCkXm+dgTk0V9SkytoAUAmwYLYfQhrWiahfwMGuHCiBSm2JWEVe7dX4/xftBJRDvw+w7VfZ3b/3SkeC6bN+f//+/w/kHxsr+NuAmUVCt42pusHfaC5w+a/MZwQYBGpAwKMjamtCsHQsVFFDbnodw2DKpz9g6NTrwYFAAi69Mpv008ALbMNVOLvv9a0j9t3IJAKBk9tl9/ACsimjfkqf/34cCWXlZkR37tJv8dmX1aGQoARaArRMV5+2i94Idl5+SAsZq3eBXGEz35v/Y1P6R+7RHCq50qf/B0Sx56ZZnjf2eyGTiLahJu0GAIYZGNEqJZz7n9p86C6IAEegOKXltr1dN94BQgAkvtoduMlWiFR3cIGfcWAQQTSZBkk23/3oDHsXyZSGOPbJpCO2b2lmJimTv+0jwoRYOVHxH/Bo54YJdFats4k+RybwyshOHrL60PvwhJj1ss3s3Tvm1CEmj1FS77r/xtAEsA9bHD9P3X/9vhLGTCvEKVZvHDeRtXrzPgCYCH39eQ5WKS/eAlgQm9rSXJxCH70gZ6uqLRxfswcQ3XKilZXkNpM5nwABsOGYpBPEM7EImZgAA7AACMAY+NmiMNCHigAZpth98l+PPEGb77YC8sii58nwy2o/+7DcTVkP+N+wABAD/UUAKXhHLoGNtbcZCKKOuwrzVZ+cYUnXItSS3//8Qij9gmFMQRhzXfBgMM5ky+mZyT/tx+v2/aAiWjHXoRpi88IyTIOk/RXngAjPAIKlFJJUwwuwEpcCJEoI2ggm/3evw5TIr3kdc22H//6wk5OJcZhyY6S/Pic0h/nAnz0CQ+38ShMy2xl1///hiBECkFBJ8xOV3Dkxn/eMBsoYMZfRhjeiShm0TkY8rFTvfa2DHaLzPJNVlNXPIDfBg1lxGeNYJLmcAnRAAdi6LDHIlf92iDBb2hku+gzPT2mjIAMDPAnijA7A6/4E6R8nr7W//4b/E3b6MjGsiZ7v/9ycGjRR0Q1ptoYHwsGPEDcAB+ABKHrZYk/jBj//ukJUFTRFtlxpH3+88jgAgIPrKRIucZfD2oArxSFtxnu9AlOKJ6jccW548BfOahGYBuIMZ/3hxz/V99A7aIDxavbQCKAzJJkU0OxVF8Hxu5Q+ev+G+AA70EIIV7HDxsW3VgYWGKNaFgkSKoKOYJtJL7yhoTzog2lO/ERWIP7AWdIb+oKaQ39fxF4g12XxAfgAGCMGSnWmk8gh+fBzL0pf9oAg3IGeVbVUc8ROhUEQeABYId/MRc6Ji003/IAYV+r//bwMgoKCT5idLvGqjO+xAxCkJ5pb/QU/PsIO6LVN//qj1D+HKLUEQ967SF7f+u/xvxspUGSuBkuEo6MADdMoVFGWM789dBiNOXSRSrKyvs1crqKvUkpe1Yab68ObIAIFGSmQLnVn//fbDLecXUl+9q1y0X8Q4blsuX7/1ByyTeLv2ux8B58BXMIcQtuFny4tspeoxFZBVakhLGpB6WysTDWlj9/LDaVUzzL35xdM6P+81iSJM8p///9/4f/DAIO1PphIivzRv6uxsQEH+ZcOI174lT1j/t/gAOA5SbkNmrEpw8a/gJugAMxVFhbUCv+4MXWPGekPn6s8Ko8lqR//hB5TIJa7cwwR8SXEDYG5ZBs8sbd+73iCi4xEO4r8aa/ww/gAOAcCUrVi7sQitBnvgMdjAAdZBSipQhI/aMAjNM4kT6fm//eY3lyKIp1ulhHPPK//hvtw9bkVkZDlz9/d/xAdhghR+7sv+ngQ1vQZ+qJepYcN8v+dtdT/u9DgMQaST5W76O/nyBi2/TRvyoVFXJfv3w/4gMQBrH4lN/U8HP6ZyTu/fMbO/vAAYzCQjqr4uMYUAWk2+0pG/f4DCKKH4AF7F02vkq1//T/jRl/EB/40MuYpkeDEmseGH88ngEcpMUFQwQjYDLjgA4I74oJWu//+7zDMKglYhHCCqCvNYbIXOvTM87/gJAI3cIKXhSfEGSvzuFv7g5zgBYTHHXxRHPGooJIiJJ/wOAjlfrJUwC3lvtP75sCjcEf4f8MMABMiGV0EVnkpYxfp6CEFL7jhw2Lbq9EADdOwRNGWN5840dYRYUDJeKR+5FCjEC4Uq8uWdXqcb6M7Xd/eoBDC6TILkG2b+/RAgXN0ZP3Jty68AnmEcDGJhA0yMbKwGPwA8HwWxQ5Tesl3/APzMkPev36+ETQQ/BfAB/Mfm3W5E2DGwwP8iMg2YVWpcty1hr9Nwof/4VhgAI4AFw9XLlwegoY/D9rIwCMAqLWOVYV/yYAGXZQqMMsZ370qCEFrahhw2M7LfMzMN3FXvkra1IfVLozgjrNUTRXoF/1wx4AHgy44AFBG/FBK2F7/mBoISi1CEcQSw6+/7vA7IqwBKtCzqLhka5xni8QG4AGgKSg2cOipq2vAHMzGvOflH9a0hxcImjmAzZ6u/7f+IDUAB2ACWDhRGr+eInlzv/94wABAAgiCgtaOpdM8bY9Y6Jll0h9sop7AABUEMsGhpyaIwbJcAklzzf+YDMB7iRcy6rilfc7i+JkYmrCHNXIuID3yLMwmU5Bn20wjzAB8TAxNpLf2ycET3PCE2yoS+HQW/vDIQoVqDCkNEopId8gAeFwNTbS19onBA8H7EcVT0CUMoJpJI+wAAEAAOrzt4YowdQHn//3eAw2wLQI5Tj5clqpvnJj+RM7un//g7sRRtsp5rib4MCWoqhmN5IbjzwsLKqcWIfD0Fvoe0V8/1TbEmtkvb38QNwNk57z1E9/AIEpgAoPze10hHixhwMA1qtSr3AYEkJg11e1niyhFmf7AYB8QOPGZTs6bkMb7jGgYdovmMFGwhC5wIj+1EflkCe6n3sa7iYGJMX2wJhy0+P6Fo4gEjAQmQii02SM2/gcGKId6pkaFkCha9BMq8lLsoFJPlGnBVL1/+ffxA3sFQAVACtAAK2sAc9QZPtB/X3//ng/YGCSAQYfREQIno/XfgCwS5h3N2v5GqSAHqtEJetvt+JC6sCrgqvfHncClul5+9Z9mNID4gOzhgJn7ex4ADRI4tJsqn0wu3B+BnHE/pbCqPUPe1rg2YpzEKrblHRvAAwYxD+f9ksapyiXMqrN/4YID66g04Gofof+3CeoHRQQeMTlZ43MX3wY6ermlnrShAWd5fVqf+D7xjzE/b63wOQ5LI56aknsEPwHxA3ngDKxmVVd/3y2FHhnpDAJ6vT5/fkAEgjAJjT9FRk38Rjr3kjYFimEjFCX6IsxdHD//kNDkBGppkcxd2WCefW/PbwH8TC2SJbDsa/31KP1a7/uac5bnLLIB2e17/P/iBtv3Id4UAQC46z/yRV/OcoqIgm0KnsVhFv/3XrkaZHMJXZVJ+PGpgAsAIhgAMAkplGwjpAkf7wGARWNUPjvqF0NUZiFFmsM/z5hDFkfwAPkgyriGQo/sYlgAAoDgPwcODpojB6BBAGTE6Y4mpd6lrBgENo8nK+ord8GkHKvIqo76VitBS33h4YEoMbaGP4gPeQAAgEitAHqB26i+i9rhfuEF2sw3+utmP9Ykw4duQiufroPgxqn+J1xZ2PIT2oHxQQeMTlZ47MX32gAAgBBz+Tj0gRSrCfRwAAuCmbAODTo2pgfw0KalMXzBML90LGQi73+QWZGQdNbf8UooF5TIn+kiDIcdFkzJyYqr2aiDrAZAwfiBsGFlE6AOY4Pek0h1PopwNAqd7TRUtP2+gT5lUvr/MLNJh9/LyFHQjIKl5NNNeGDAmIpiAsAv1AGA3uYKnGvG/+ET2P9ywAB2AACABKoqwEEaC+Aw7UyzfFI2679NudGZ6Xd5VRzNQRf/3r0AxrqvG+FIGS0GSUhJPE/zMtP//o/p7P+Coir+Vv5vwrVYE7L6FkLiyjs/gwFEEg5DaXthEkuEuBOAoAOIEIkLr3pSwhSS/sAaKcAGBGkIlRK97/vfMmYlxTKQflLR4YPQ0SVEURZ/K+hyuku517HKaIdHB/4gPeDQMbCCgvyNpcv64AQI+jxJRGdrqFvn/B+RkIrKIulkLexPEG7KmGnQ+anuwfBekFEq6jh02M6qQYcACwGPYlCpLHiFzPjr+AFgynHak0v2ifp/2DKODMfLmAef/eDdMxxZLvwPJD9/6N7XwXROO99gbhiU6CGih4gbMaGQdoAcJCEDmBuIFXiy7nu4EqACQEu2JO8oY5/b4EmnAAQJ/uty5rEBXAQYMCwBiwUiTiEFeNdf/s/4iZQ2Cil9qXfuqsG/+T8E+edvvRYRf8QGsABMAHhNDEW1MIMkoJHYeuADK0a7J/fsdXKK7z+IDPyAB8fQtNpLKDBSCJ8GAw8t4CVKQs9BsdvkNqf+L4XwAHdhCiltyw6ZFtlbqErKtC2HzXR3f0BTQtgAYElpzm64mY/6GNlA/bkNEd9BJcnn32Hgxez3DkJZ6cQGfjASqCBjDyEcb0TXNhhyJjGqQ33h/8QF4AEdYBDiKxmQZJtN/qwGFE1hMm2TbZDBgsACoEJQj9CefkaFvmv9yAhbEeoSx8lYt45/gPt/4CqNmHWn+IG/EAmwYNWfQljGiaxnxgJ+CBjDiEcZ4VXMh0W2sUdL+/rcjAKxIFBVkbUwbgRMYpWcbUwJAUgNiB0VtYeaAjRDRTHQo3tYkMNgAAqDgOycNjpojebMZVU4upJS1qfGwhDPNKqbSG1OdACU0pK3fN4zVoiX2kw7x748QF4AHQOCB54xGuXzcxbfcBDN5qIm6EyZYY/wB4kZNRosMmsjvRgAbojhUUZYzvT0pBCC1NQw4ZF9lfmZmMrnOpwqXtSGGoYdUNNxvR73/Zj/hiHgAIh18R1MQd9MMfsAAHYAARgDnxs0RgBx5kO6GcUimFvFbQ/gEqjIaXef4IJhBwnYmv5AVooIPmYSs8akL/7TAAzwPDwVqEBLt7/+mB/MBjUJ/UnnxO5lE7/gxGSUEYmhsSe84+cJb3JG16elIzXniIjl5K8QHvghYwN/R0jjsLGFjUL31Gu3oCdSgAwJ3+JUSuhdv9wDFohUwcQqTEi3//B/8oBDiawkQYIsseZGYnxRN56EL7RsDLoOtauVyHn878//pghZNGJrOp972Dz0iCbTq/3eIDoyC2J9uVX4MhsMANgA2kp1ruxcLViLOFfG9vDWhenADhHw689AyjM5UfdC2WGO/xYPQYAZBS0HxIyC+r6G3mTf8wC7ADULmU1BqCxr//mb+SNc3BZgXkrg0ld04r/8JbLCGecvv///V5B/xJffRIfCyllAtvbnr9f8bgAIEQgV5vNbQhBiEiaAPIDEs4iw3fyFjKJz/QqR1jD///aNN9v7+6MwANwBhsPJDu2cLz/ndICGFUjQgwSaawMGGGAA1zEKKU3Cz5sW2V4n8CB+RGIrIcTUuSpaQyhi3M8yKMaP99GMtfWTVc/Bj6bFclx6aMOi89ZGt1JX/r//+I+ev8B5MZar+Ijf8NeDLwl9SjHNr1v/qP3yVfvwPyJgDh12W2JJ6v+8R9wSGwgDrEBXARiouWVXuttFu+YqmKinIO6mlPcAB6hCIco2pvNhwXbJhDqbRTtKQEUKZa6MUaT3vvbbM8w1VeuCOgiPZDuXX///EBryCUQJaZtWXkG2CO8wE6hgpZ708b0TXMhhlb4GqPSG1P/lwgeuAShqeX/v/jD8vDlBgAO1EAICPAj0Vlx2F//3QGyGABwRpCBQTtgdP8tBwAf/CV0Ohl//v/EHr30U//OIWEQooACaTbSSbaT///AB6AHqKQxFs85Ern8/4Rg7gAABVQQZpg6B2fxHDGGT06gDItV73+f/8MnqGF1f///z//z82ET1/j/DcI3hHxFYR8SGYACRY+RlOQZ9rKcH7woNtlQkmmQa8NngCjeU0/3/hEMQAEiMgyIKrfcli1h6MAE69w3UbYvfzvAARsIuYgu9RTzGkhrLUT1PG/r/4RDHgANiMboYyFH9Sk7gABIHAfiJw0Om1MEIWmWm/7C68AYlpo5u8/hH5uAA0NnBPEebop8uLWKw3hHwjFYR8SevAW/Df1/hzYyqNmAVdJz9+KJI+8/8QH4AFQOQQEnDE55dO1Fv9oCGbzUVdCYMsMfxilELD/6zkwANURwqKMsZv4A7Hgh4qlZEiZ9grAIDDvgsLTTDfXAQQGQnFzarNU2pf/AK9BCCldzw4ZGN1YPWaMnwewya6G7+8Gd8HdHJC5Cr//dgFxNGHHT5A1SfTeSEqREYYw+IBfgAMYfE7S6Q23QYTDmWkX7zglbY/QiKDiFn/iBv0AB3AbHJbNKDwhOz9sKDXZUJfToLeCAYfrCouWVSWW2jXMAAFwUqwcGHBojH2CShYYsuaxN4yP/A8ACwF0BNcaOPfEXuAA8KULqhEEUdGX5XOkj/9/QwOggAl/UsFsm/BRYVjFWXKPgq46//cJnI8tQHf94FXbbkWl42Auxi7pcIZT4Kd3iATYMFsPoQxjhFQv5Cj4jY5RyaaW8PxgJ+CBjT3o4zwiuXDBAO/fX31+GAAkTIZEFVqSEsanLYcA46ev8AAUAySR9XvxwDbCSu2zK2R+q99/h7QBmkACmpvRHkb7OghzVD5qeAwFZKCZwyK2rIDIAAgDwA9gqkELPN2M73ffN+bNsBJxqncraJX97Ao8XoVrsr/d4RkyjsZ+gHXMxtZKi5i9y55Rryauv3/OHeOvxAe+THxMkukPtkFP4w5IjkpwYkQqjwYIljeOpAB7NgDA7gJ2qwOQOv+eBIJ+UAGBO0YkxKyF6/yAYYAR9f1jgFIEXjSQT5GKzy0yf/w8MIezgvgbJhchS1ro+h0ND8I88cpzf/+KowsM278QFYCpABYNesXJ3mDHP4YBfAGLRSpg4hEleNd/8H4ctOOYZ2/5WLYdvXtufnsrYmn1zf6/TjBt8OAgytH4gMwFoANA93DEHIKGv/+DBhxMeZVRFj9/NdDO1UJjdnznerpJ8QHoADGQisphcS5K2J8QAAgAooCsArEr66Ud+fDBiBjgAIxZuVkOUZ1vLd5sOD/pNcyn0Qys+6u97OhELlnNOJJZ9+9LwJRlzwKnHrK0d8oHKtud2mTjlxf6/56jnS/Pv6/HAq+Nfr/88wvCZXn/iAx4AFgzcMg8lcSUgY/8YC4AbOcAGBGkColbA7/zxdQ0nTBt3WLqiCaG1kL9P9MjjU34VwAEjDomWXSH26jHw2AACoIVoNDTs0RgBzCgn6VSX06jX+GE2nAlAxk0g0b1Pq4DfxeIBBgAOCELX6rc/iytHt/+R8Aj8OiDyExRXjH/3AAsCEo59BefkbFvnH9DAkBC6I9Qlj5KhZA4/uwctsBEBWmkfeABmdW5Kf09a0nV2/iAr4YCDF9ZSehdmD2geAJscAHBOkSQlZA7/zwAGZCdOQ6FG9bEsAAFQUB1zhsdNEYPzFCgFrYXvI+alpOeB//EBaAnYyrzi6kn2tWDH5gB8bAxVpLP2ycET3kADwvBqbKWPsE4IHhkMD4yAAgqYt5cjMUUg7DCX8Sphp2G1MNtP2ae/+ID0AC0ABFfMFTRtjOdNIPsqQaw2bCW7+AQyIbKIvEkLapPC2IUWrqOHTYzurAZQU0Bp8dFL9bwCoAYjBM9L8RmspVD+swX0BKwIQ9Z97RiSMQHSxbRnF7gN9jxVryr99wEMVPJz2JksLm/eDAQoXAK2kGm5b+/qoKL649T3//+n70Vy/xsGEaZdCAq9MBEgiBKoxxRDr7/FCU0xjjou3//30uU3gaAAhFILV7bOGLLb/RAtw/Az/OYOFWZWbkX+/AXIiBAO5FKcBoVqawqbLOgUslfu3h+uf3uBtmGWF3Zrf8V+JlbP8P/nw+/b/+cAFgEVxyXFIxySdXAAqR0Lg7SEqZhYBQMaznWFwz8hYv84r6p3791YwABABQO8Q52A/noQ/73kRiKRh1b5SWNT1gAOBTq/6Yk0//wIDwSARAJa3yzSydB1PMyAJ6kW93e3Wu8/2iAF0JI35d9kmxLdZXr/8g9Gyp/BBCv/NWIuZ9tqA39fB7U5Y//aIb9BHZ69Iclx8+2b10ARDZQV3b71uWiZ8ftUSHrItPu/nL3ig/4l6AxWez7jRU2G2f51TTI5hd0V0EZOpE1/6/1V6bSN6vBNyu2jr6YAAaNNxA2p89IZ62s7zvDlRn31/xA2HhOgi15ptTA0BQE3x0Fu5PQ4QgCsQBYVZm1NIAyjeoSgjj33ApRdG0Uh/ZobkVA4AiYxEIrE08AMSISYglc7lI5PZ+uDQeoOlo0Wn5fGEAtqK2XLMCChyYtAJTlx18oTGNknR3hzK1aFqt6+sVnX4iIbIeAPiA9AJGLM3D3gTMZBWCcYfSYVQf5Mv5vBB164Qmnqne+0h0CdogBgIQBHVGByFx/wCWABMqOF6zaGb4KAAFRBa2ZHz7wAMDljrqFbVucJiqLrgCiFIRXYq+/qpbUWOpNd/wB42rpyZzOkDYSVlWdYt/3wO2EylkUXZAfpIq90tHxAdgYJXXcJAfJZHV/AKmzAGB3A/cFWByB1/3DMxgAwYenCNFC+T/cbPP2Pve6/9+ACjYI7FCtaU1zEWlYwHEwYhDL2G4piy8xpgxsymEvTaUM3tEBi1+Mc9W/7N5QGJ/gLd8qpd2Oe/kYg0WfDehX5r1dLbswdmfgNx6KSr0mn3+NkFmuHvxAd+gABACmQwAAgLmTCBgGd9LMRitLPqgv7dJeYQdzddFsz9++mMg36dOpIl6+/gFNgezplDNNsg8R9pJQsTZEIkf//AIWy1QeQmIM8Y/+4wLYoBwEoXokYeTL/8FtxFtn9uGRhAS2Zj5TqUf1tWGe0fAiaV8+7vs2aYoyOev8CAOdJmNv/DRjhmxUHxA20s/luAgzRxi+C1F08YS5jkO7HIzjLoAALUAA8tkBTUR++e8cF231zKbBTg/EKPiMgqXk000kMMAUAlwcLYeQjnGyKZZHqQIZgi0sElFkEs8wJuHDGHUIZ3sioWD0YQaqsbPnYsQ295C2MXl12X3894H5FY38ml/8H8gXVPe9/+CDgAPYBU6oUKymWh/+xGZ2D8unWU3eAA8AhN1TSAMRJ5En7//7gMkxAZRhUQkS2/++AfmC9zwXpyv/OFcGshsF8+O6Qc18ebADx8s7ZRPfgwYhAaRQmtA6lSe/+wXncFzpP///EDJA9b3P9v8R4k/tFueBjqev4mKxIagTMBbwHvhkV+41zcxXoXIVGn/9/BjKCYPEH4zUYEJXRZPhv6uKmIvEqP/+fxv/XDnAAtoiAEBngRyKzI65/9wAvADUPVQ1UH8WNfC+n8AI2ImbNf697xAY8E3j/4gQ7sAAmFPIcxc6IDkg9kpbnPd5EhMiGExDuYpEXGSvAm90V0CjdWRa2///h74EtiDimtwwybFMkq98JhooSDynlLMaT/3mNMY7jVqaVjVh4tU2vSbYAB9G4VX76Wf+a17/QBsJlKY6kUKwRnle8u9u4ElTV3KPTT6dj+SS68GC4HPGxPP7/b/GwY0yp+DzT/Qov7ee+sN/+MNAgBYF+iCoJO00haAiwAYVcU4odaiMW/+noFZZrfzgBAAEAQI96hH/d1dEtbZnmDQwDi2pVvZTSaeVf4dOZZa4rxF0g1kigvWxXWjbEiTNJ9yzWL4SbTMN/+HjzKTxTon7kGwYT5z4yxbr4Yp3hZq3bdhQ1vQ38f1kABEwYyLrGtR/s5YCoddhbIQS9CiH+wQYVhY6HSk/sw6Pfgs5OYy6rv37gkjyJv/ffoDHY/+H4AOwAaDaFJspYQZJQQO8hr4AcLYlNJhBln/gw2/XgPy9O2zgkdcB/ugABMkMqoYyOOljE4MR4EKG2KPmHX2+vCe8eoREo6Hof84kT8twlXeBhiLAhOBujDan9FqJG2h7//gDTvJ2a51sP+AZ+jIa4vUaK0eGPxm4AFXEAAIAgBRMIz+15hvvEBvgway9+OMaJLl33X4H2B8DUspFTFVO2gM8/8AWlDlqvf8OwBRu7fd6IPC8sxehiLbi/fdMPuCAY4usJk2SbbYMPs6pmtpP53zwAaN3CI06hfeE32+SFHFlxI+1sYUJSkOU9X+Nh+ABYNBAp1u9ZfSWYfQCoaxgBR7044WSVb/8AHkRMabP163TAv0VXcwfgakAAXtA3rJL5Hv0bbKw7y2BYEQVwTdBXbyUt//iBcjIn6r69/PgTAAEoFNHsV59AtI733jD5R00Y2p8uTy2vFqCg6U0kQiv6n6rtH84wSXHlYINS//Dk4gIALBuhwAKCO+KCVr3//ugLoyADAxIP1BRgdief8ofbQA3SMSC6iv/eXMNJ1PCAagAZAACXqAUgWQmyQb/MBBcPAAVsBs0Rg9wSEoymASTIeFQxO7W46ISPiaDqhC3M1aE3haAMKPiNhUkk000kPxANcGDWXEY41wouZD5EUF3aHS/yDc+fB4wZgVScWYVqCX595OhCdc5w/vsiSCRP08/efwa85Y54rEHlLCPcgOXuL7z+IPFY/IkiJvGcv4gN0CmX5QHpjLVGInpMwxbpuU/nsmtxx8/8QHM0aDO0A9jRJvN3zCrNu3X/3E8KNWnv6sIGci71z/oNldQLGBI4mHxA3YxwADYAFMGJllwh9qox/aaACUPWuWJso8//Y/ocDGBFCh2BgDgGgJYKaF3mZIDid/HmM7va2v5VdFuRyUj2g7dXu9f+N+AOAByAAEVegNfqMH2vtjVvYP4AsAA7AAGcAx8bNEYBSgiVj6xngk5z4n+DwACgKbkA4NuDamwgaKYGATF6p2A4//TdNfO7fpuz9d8IAG4Y2B0pZf4dUKd4gerjNZl96cXwiwce6VxbrwdiZD9FmqWV//9wRm03j23//+sMLt/EB2AAzD42aXHPtkGE42kGauCFkCU348yLGAYIdhCHV11nhhEWxogawRB1Q/ElNYl5/AAtDfxjIULrHLGwgQSxvyUAHVtL2R91Rczfq1v9Z2j7kr9f3wSKj/sM/xtwBc7oyNHkQPSz1D19foO0IeascSAF4Q+Vn+pHJclvnCYFoo98ElYCs5cCllkt7JYK9bp5/WAGE/OIp+13t9ivGFC85GCRYmalJuCEARqALCjM2ptEABlRWDJo6xuvnkSYkTeq+xfh1Z3pO3/uLaCy9+g2zn/6xVzAAEDCAACACDZDR//BwbK8eaSrH/bBMHGS+RFv389Pbzh2eQfOEi4iO797/iBu6m7WXHecALirE5o1fz3JKiP8CAfoPYP5ixMldkjFXg9kWhnTbdFvqN98H0BcQOsAgtWkL/S8sr19KzD4BngZEwIQxFLLr//gwYN8MQzzFD9t355Ba6f/8Y04VR+R4mX8QFeIaIEkZcMpifWzySd+oMGB3Uf5pIz9eg+5UyZ5o579/h1zijT95uAwsOhh0kHLOfO7/xAegAIgEiAgWw+hDGtFVjPjAS8IGMPIRxnRVUyGH79mG46b0lb3tSbwYLoxKXcRTVq//7ghgDMiGnMLiXetSdd4AgzLtblkl+8GBNe76K9//kKT3lDezDAkDs6f/f+K75X1tLS23/xAd+TE3+7p32rIveIG8ACCtqTY7/tMTMiUJYVNj/b+DA2E1MUAyhKM/Pv/MHA0DOMx0sR5SXll4DT6tN8h3d2QV98oS+mQdr/zDGFYw/iA/YUK1YaJvmyGy8guIJQtnaWh6K1cjr3/67RArROYpB//9wRsM4v2WSe0m+D/GRCYEQPIuiLJlfokZfcRf8hfuHbkRbPf8/+e85Gtw0e31+73uYMwy1XhI8Gj1Amvzyl/hwJApJHz/8MwBwAWEwKSbTx9knFA4GHOUI6372x7w/xfC+G0FggAUArRQ46ZlKzhqQz/qfaMC4jVvzaQ3dVweg+C6Gr+5QACZVQJ9m4L1yAS/DFEK7jd0wMbqvIiIJmEViCFOYoHz4GjPJDamGi4Vqxf+vCOA7NZDZ/3aYcbKrz3tx/f4DD/8OQAINgMYRSMyLJJhnuiAQwmkJkGSTbe0QYJV4Kl782Z9e4Fw7O/wqNKzu4TwM7fhrofv1CwG6EkXnv+f+NwAqqz0n4mAbkSwxdQ7FtQIAAJAoDcHDQ2aIwCExOiHE1LkqWlwETWqRuG1NrwfvBc4bFXWNBjSv2iGVUMZCj+xSWAACQOA/Bw4OmiMHiGARqwKCTQ2phgEDixIdLwjSmvnYFI14ui/CMLB1U3j5L5EDgtQ3eP1V/eOc6e313+F/AN0KADgjKEYkhK+F28BCUSiJOJREFcNf05kAMDEg/SzA3A6/5xsALhoqWpN8sU5/7oQcABsQ3VDGQoX1KTlBkFLJmZAyX97kmqQe6oTbi/P/EAqhgAZxAIcRWMyDZNhsGH1TAYUXWEybZNtsGHSzr18LQ8EXWrXum1Ntg/YC6kfBfOdCAACgIA+x00OGiN6RCRMYyEGxikeGAB+kIMK+IWbcvXr//7gVH3H9puvNe4EmSFKFK2CMQiO87oBt5bYwV9PgcXXRrz41zD5qxE4QP4IMkAAEMpCjBTZHtrXQaSJt5uf9uABiEAwgikZk2yTDb+LAIIJpCZBsk23hKFbalex//+uUJpMk5s+6ZdnPi19vxc3yJL6B8+542+Q/zJBGtx8+gwsQeiw0hdn+N+4iABsABrPARfMP5d/4CJXzAHMjF2qm8L/t6BiC4sRXK3fNNMQcZ8Rs26ewOv+agvQEO7mousEyaZY/gfwGs2b3H6oYfNCdSObU2wuQ5JttmnpslkQWjqmz5MLLp4fsyIx3////4gK8Q3boGsLq577egIMIPuWNn30mKa+8NDjoreYvkJbifEAkwYNWf9LGNE1DPACAr6cI/2WV8eSV/2B8Ao9iUp+Y827nhjfZQUw8hHG+EVS4IEYPSQ+nth10/6Z967237++H1/4Z8AY9CEakoYRI2LoHAYcag1ikuf+/j//4gkACOsBBRFYzJMk2m+4IDCiawmTbJtsgw+I8RG4jxHiA1C8ZYrVqv1Y5O8lR9f3AMiv1Wz3l+35s25F8HFJh+0s/f1f/1YrEAl+A/sAhxVY1IMkWmUPl0wGOJrMmyTbb/4MPXiPk+OW82EIRxB6jpVEUAbVfPDFcGev4iBXgAAASMbW9vdgAAAGxtdmhkAAAAAAAAAAAAAAAAAAAD6AAAJxAAAQAAAQAAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAAAAAABAAAAAAAAAAAAAAAAAABAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAgAAA7d0cmFrAAAAXHRraGQAAAADAAAAAAAAAAAAAAABAAAAAAAAJxAAAAAAAAAAAAAAAAAAAAAAAAEAAAAAAAAAAAAAAAAAAAABAAAAAAAAAAAAAAAAAABAAAAAAZAAAADwAAAAAAAkZWR0cwAAABxlbHN0AAAAAAAAAAEAACcQAAAAAAABAAAAAAMvbWRpYQAAACBtZGhkAAAAAAAAAAAAAAAAAAAoAAABkABVxAAAAAAALWhkbHIAAAAAAAAAAHZpZGUAAAAAAAAAAAAAAABWaWRlb0hhbmRsZXIAAAAC2m1pbmYAAAAUdm1oZAAAAAEAAAAAAAAAAAAAACRkaW5mAAAAHGRyZWYAAAAAAAAAAQAAAAx1cmwgAAAAAQAAAppzdGJsAAAAknN0c2QAAAAAAAAAAQAAAIJhdmMxAAAAAAAAAAEAAAAAAAAAAAAAAAAAAAAAAZAA8ABIAAAASAAAAAAAAAABAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAGP//AAAALGF2Y0MBQsAM/+EAFWdCwAzaBkfoQAAAAwBAAAAFA8UKqAEABGjOD8gAAAAYc3R0cwAAAAAAAAABAAAAZAAABAAAAAAUc3RzcwAAAAAAAAABAAAAAQAAABxzdHNjAAAAAAAAAAEAAAABAAAAZAAAAAEAAAGkc3RzegAAAAAAAAAAAAAAZAAAXfYAAAHwAAAFmgAACvQAAA91AAASbwAAEs8AABNtAAAWiwAAF/IAABULAAAWswAAFE0AABYKAAAYAAAAFpoAABaDAAAX5AAAFqAAABUPAAAVRAAAFt8AABZbAAAU9QAAFmkAABTBAAAV2wAAEuIAABSTAAATzwAAE3gAABOLAAASfwAAER4AABC5AAAQegAADhwAAAx3AAALfQAACVEAAAp7AAAN/AAADkYAAA97AAAP+gAAEi0AABNnAAAVIwAAFhAAABcRAAAWcgAAF0QAABYWAAAWKQAAGEcAABdKAAAWtgAAF74AABksAAAX2QAAGZEAABdWAAAYkgAAFl0AABfnAAAW3wAAF0IAABa+AAAXOwAAGCgAABdJAAAWMwAAFSEAABU2AAAQLgAAE/EAABAvAAAMTAAADNAAABA/AAAKsAAACc4AAA8mAAANRwAAEaEAABVTAAAUngAAFYcAABRSAAAWmwAAFngAABYwAAAVUgAAFqoAABaNAAAUygAAFqMAABeDAAAXHgAAFVQAAAAUc3RjbwAAAAAAAAABAAAAMAAAAGF1ZHRhAAAAWW1ldGEAAAAAAAAAIWhkbHIAAAAAAAAAAG1kaXJhcHBsAAAAAAAAAAAAAAAALGlsc3QAAAAkqXRvbwAAABxkYXRhAAAAAQAAAABMYXZmNTYuNC4xMDE=' controls>Sorry, seems like your browser doesn't support HTML5 audio/video</video></div>"
],
"text/plain": [
"<moviepy.video.io.html_tools.HTML2 object>"
]
},
"execution_count": 50,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"animation.ipython_display(fps=24)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Use the following to save the animation to a file that can be uploaded you YouTube:"
]
},
{
"cell_type": "code",
"execution_count": 51,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[MoviePy] >>>> Building video scatter_animation.mp4\n",
"[MoviePy] Writing video scatter_animation.mp4\n",
"[MoviePy] Done.\n",
"[MoviePy] >>>> Video ready: scatter_animation.mp4 \n",
"\n"
]
}
],
"source": [
"animation.write_videofile(\"scatter_animation.mp4\", fps=20)"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.4.0"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
anshbansal/anshbansal.github.io | udacity_data_science_notes/statistics/lesson_01/lesson_01.ipynb | 1 | 3163 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"# Lesson 01 - Research Methods\n",
"\n",
"To believe any results of any study we need to ensure\n",
"- Good sample size\n",
"- Representative sample\n",
"- Sound Methodology\n",
"\n",
"Constructs\n",
"- We have constructs i.e. things that are difficult to measure. e.g. Intelligence, Effort, Hunger. \n",
"- To properly measure them we need a operational definition i.e. a definition that allows us to properly measure them\n",
"\n",
"Lurking variables\n",
"- Whenever analyzing data we should think about externeous factors that we may not have thought about. These are called lurking variables. \n",
"- If we hold more things constant then our confidence in results becomes more as we are bringing down lurking variables\n",
"\n",
"Population and Samples\n",
"- All possible people taken together is a population\n",
" - Metrics related to population -> population parameter\n",
" - $\\mu$ is the average of population\n",
"- A subset of people from population is a sample\n",
" - Metrics related to sample -> sample statistics\n",
" - $\\bar{x}$ is average of sample\n",
"- sampling error = $\\bar{x}$ - $\\mu$\n",
"- Although $\\bar{x}$ is not the same as $\\mu$ it can give us an interval in which $\\mu$ lies as long as we have large enough random unbiased sample. It is our best estimate of $\\mu$\n",
"\n",
"Correlation does not mean causation\n",
"- McDonald's example of world peace\n",
"- Observational studies are good enough for showing relationships\n",
"- For showing causation we need to do controlled experiments\n",
"\n",
"Surveys\n",
"- easy to conduct, inexpensive\n",
"- important to word it properly, cannot rely on it\n",
"\n",
"Controlled Experiments\n",
"- People receive actual/placebo treatment\n",
"- People are not told which of these groups they are in (blind)\n",
"- Researchers measuring the effects are not told either (double blind)\n",
"\n",
"\n",
"\n",
"[Why Sleeping May Be More Important Than Studying](https://ww2.kqed.org/mindshift/2013/01/11/why-sleeping-may-be-more-important-than-studying/)\n",
"\n",
"## Summary\n",
"We discuss that for doing any research there are certain points that must be taken care of. Then we go and discuss some terminology related to research methods including constructs, lurking variables and statistical definitions. We conclude by going over few research methods - surveys and controlled experiments."
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [default]",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
minesh1291/Practicing-Kaggle | Sberbank2017/test_vx3_lr.ipynb | 1 | 132755 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:18:23.076458Z",
"start_time": "2017-05-05T21:18:23.069128Z"
},
"code_folding": [],
"collapsed": true
},
"outputs": [],
"source": [
"#version vx3\n",
"\n",
"## new to this version\n",
"# optimize lr\n",
"\n",
"## already incode\n",
"# selected features 11\n",
"# STD>3 train entry removed\n",
"# keras.layers.merge.Concatenate(axis=-1)\n",
"\n",
"## already tried\n",
"# \n",
"\n",
"## other options\n",
"# optimizers, batch size, \n",
"# dropout layer, batchnorm, dense (layers/nuron per) numbers\n",
"\n",
"## future\n",
"# remove column with <.2 variance\n",
"# try individual feature then try combinations"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:18:23.875544Z",
"start_time": "2017-05-05T21:18:23.868917Z"
},
"collapsed": true
},
"outputs": [],
"source": [
"#0.40094 <- \n",
"#0.39138 <- # real,elim std>3, # 12-300-30-10-1 # test_vx1 #epoch 60/200 0s - loss: 0.3677 - val_loss: 0.2493\n",
"#0.40566 <- # real,elim std>3, # 12-300-30-10-1 # test_v1_ext #epoch 72/200 0s - loss: 0.5543 - val_loss: 0.2496\n",
"#0.48500 <- elim std>3, 12-300-30-10-1\n",
"#0.52512 <- Epoch 11/200 16s - loss: 0.4993 - val_loss: 0.3509\n",
"#0.38798 <- 12-300-30-5-1\n",
"#0.41785<- 9col grp1 loss: 0.3123 - acc: 0.0000e+00 - val_loss: 0.2602\n",
"#0.43247 <-3col \n",
"#0.53085 <- adadelta\n",
"#0.50647 <-decay\n",
"#0.48978 <-rmsle\n",
"\n",
"#task\n",
"# feature extraction\n",
"# feature selection\n",
"# optimizaer selection , lr , decay"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:18:27.633249Z",
"start_time": "2017-05-05T21:18:25.108180Z"
},
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"Using TensorFlow backend.\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"20170505-211827\n"
]
}
],
"source": [
"### importing libraries\n",
"%matplotlib inline\n",
"from keras.layers.convolutional import Convolution2D, MaxPooling2D, Convolution1D\n",
"from keras.layers.core import Dense, Activation, Dropout, Flatten\n",
"from keras.models import Sequential\n",
"from keras.optimizers import SGD,RMSprop\n",
"from keras.datasets import mnist\n",
"from keras.layers import Concatenate,Merge\n",
"from keras.layers.normalization import BatchNormalization\n",
"from keras.callbacks import EarlyStopping\n",
"\n",
"import numpy as np\n",
"import pandas as pd\n",
"from keras.wrappers.scikit_learn import KerasRegressor\n",
"from sklearn.model_selection import cross_val_score\n",
"from sklearn.model_selection import KFold\n",
"from sklearn.preprocessing import StandardScaler\n",
"from sklearn.pipeline import Pipeline\n",
"from sklearn import preprocessing\n",
"\n",
"import matplotlib as mpl\n",
"\n",
"#mpl.use('Agg')\n",
"import matplotlib.pyplot as plt\n",
"import time\n",
"timestr = time.strftime(\"%Y%m%d-%H%M%S\")\n",
"print(timestr)"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:18:27.647452Z",
"start_time": "2017-05-05T21:18:27.643526Z"
},
"collapsed": false
},
"outputs": [],
"source": [
"def load_data():\n",
" df_train = pd.read_csv(\"../input/train.csv\", parse_dates=['timestamp'])\n",
" df_test = pd.read_csv(\"../input/test.csv\", parse_dates=['timestamp'])\n",
" df_macro = pd.read_csv(\"../input/macro.csv\", parse_dates=['timestamp'])\n",
" return [df_train,df_test,df_macro]\n",
"#df_train.head()"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:18:28.487346Z",
"start_time": "2017-05-05T21:18:28.483813Z"
},
"collapsed": false
},
"outputs": [],
"source": [
"#print( df_train.shape)"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:18:29.656605Z",
"start_time": "2017-05-05T21:18:29.306375Z"
},
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1\n"
]
},
{
"ename": "NameError",
"evalue": "name 'df_train' is not defined",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mNameError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m<ipython-input-6-9711c9ffc3dd>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[1;32m 15\u001b[0m \u001b[0mprint\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mlen\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mgr1\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 16\u001b[0m \u001b[0;32mfor\u001b[0m \u001b[0mc\u001b[0m \u001b[0;32min\u001b[0m \u001b[0mgr1\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m---> 17\u001b[0;31m \u001b[0mprint\u001b[0m \u001b[0;34m(\u001b[0m\u001b[0mc\u001b[0m\u001b[0;34m+\u001b[0m\u001b[0;34m\"\\t\"\u001b[0m\u001b[0;34m+\u001b[0m\u001b[0mstr\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mdf_train\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0mc\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mdtype\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m",
"\u001b[0;31mNameError\u001b[0m: name 'df_train' is not defined"
]
}
],
"source": [
"#selected features\n",
"\n",
"#gr1=[\"full_sq\", \"life_sq\", \"floor\", \"max_floor\", \"material\", \n",
"#\"build_year\",\"num_room\", \"kitch_sq\",\"state\",\"radiation_km\",\n",
"#\"green_zone_km\",\"railroad_km\", \"public_transport_station_km\",\"metro_min_avto\" ] \n",
"#\"kindergarden_km\" \n",
"#\"sub_area\" = object, str\n",
"\n",
"#gr1=[\"full_sq\"] #elbo 10 epo 26/200 0s - loss: 0.3472 - val_loss: 0.2767\n",
"#gr1=[\"life_sq\"] # 20 epo 163/200 0s - loss: 0.4144 - val_loss: 0.3150\n",
"#gr1=[\"floor\"] # 55 epo 83/200 0s - loss: 0.4261 - val_loss: 0.3554\n",
"\n",
"\n",
"#gr1 = list(set(gr1))\n",
"#print(len(gr1))\n",
"#for c in gr1:\n",
"# print (c+\"\\t\"+str(df_train[c].dtype))"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:18:54.775895Z",
"start_time": "2017-05-05T21:18:54.765433Z"
},
"collapsed": false,
"scrolled": true
},
"outputs": [],
"source": [
"# This section added: drop crazy data point\n",
"def drop_crazy_data_point(clist,df_train):\n",
" '''drop_crazy_data_point, STD>3\n",
" clist = columnlist to use\n",
" df_train = pandas dataframe\n",
" '''\n",
" \n",
" #clist = gr1#['life_sq','floor']\n",
" for cname in clist:\n",
" df_train.drop(df_train[ np.abs((df_train[cname]-df_train[cname].mean())/df_train[cname].std())>3].index, inplace=True)\n",
" print('shape after drop_crazy_data_point:')\n",
" print( df_train.shape)\n",
" return df_train\n",
" "
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:18:56.333201Z",
"start_time": "2017-05-05T21:18:56.287526Z"
},
"code_folding": [],
"collapsed": false
},
"outputs": [],
"source": [
"def take_ytrain_testid_traincnt(df_train,df_test):\n",
" y_train = df_train['price_doc'].values\n",
" id_test = df_test['id']\n",
"\n",
" df_train.drop(['id', 'price_doc'], axis=1, inplace=True)\n",
" df_test.drop(['id'], axis=1, inplace=True)\n",
"\n",
" num_train = len(df_train)\n",
" df_all = pd.concat([df_train, df_test])\n",
" df_all = df_all.join(df_macro, on='timestamp', rsuffix='_macro')\n",
" print(df_all.shape)\n",
" \n",
"\n",
" # Add month-year\n",
" month_year = (df_all.timestamp.dt.month + df_all.timestamp.dt.year * 100)\n",
" month_year_cnt_map = month_year.value_counts().to_dict()\n",
" df_all['month_year_cnt'] = month_year.map(month_year_cnt_map)\n",
"\n",
" # Add week-year count\n",
" week_year = (df_all.timestamp.dt.weekofyear + df_all.timestamp.dt.year * 100)\n",
" week_year_cnt_map = week_year.value_counts().to_dict()\n",
" df_all['week_year_cnt'] = week_year.map(week_year_cnt_map)\n",
"\n",
" # Add month and day-of-week\n",
" df_all['month'] = df_all.timestamp.dt.month\n",
" df_all['dow'] = df_all.timestamp.dt.dayofweek\n",
"\n",
" # Other feature engineering\n",
" #df_all['rel_floor'] = df_all['floor'] / df_all['max_floor'].astype(float)\n",
" #df_all['rel_kitch_sq'] = df_all['kitch_sq'] / df_all['full_sq'].astype(float)\n",
"\n",
" # Remove timestamp column (may overfit the model in train)\n",
" df_all.drop(['timestamp', 'timestamp_macro'], axis=1, inplace=True)\n",
"\n",
" return [y_train,id_test,num_train,df_all]\n"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:18:57.758652Z",
"start_time": "2017-05-05T21:18:57.696349Z"
},
"collapsed": false
},
"outputs": [],
"source": [
"def factor(df_all,num_train,gr1,gr2):\n",
" factorize = lambda t: pd.factorize(t[1])[0]\n",
"\n",
" df_obj = df_all.select_dtypes(include=['object'])\n",
"\n",
" X_all = np.c_[\n",
" df_all.select_dtypes(exclude=['object']).values,\n",
" np.array(list(map(factorize, df_obj.iteritems()))).T\n",
" ]\n",
" print(X_all.shape)\n",
"\n",
" X_train = X_all[:num_train]\n",
" X_test = X_all[num_train:]\n",
"\n",
" # Deal with categorical values\n",
" df_numeric = df_all.select_dtypes(exclude=['object'])\n",
" df_obj = df_all.select_dtypes(include=['object']).copy()\n",
"\n",
" for c in df_obj:\n",
" df_obj[c] = pd.factorize(df_obj[c])[0]\n",
"\n",
" df_values = pd.concat([df_numeric, df_obj], axis=1)\n",
"\n",
" df_values=df_values.fillna(df_values.mean())\n",
" df_values=df_values.dropna(axis=\"columns\", how='all')\n",
"\n",
" #df_values.drop(['area_m','ID_metro'], axis=1, inplace=True)\n",
"\n",
" \n",
" df_values1=df_values[gr1]\n",
" df_values2=df_values[gr2]\n",
" \n",
" #df_values.mean()\n",
" #df_values.shape\n",
" \n",
" # Convert to numpy values\n",
" X_all1 = df_values1.values\n",
" X_all2 = df_values2.values\n",
" #print(X_all1.shape)\n",
"\n",
" X_train1 = X_all1[:num_train]\n",
" X_train2 = X_all2[:num_train]\n",
" \n",
" X_test1 = X_all1[num_train:]\n",
" X_test2 = X_all2[num_train:]\n",
"\n",
" #df_columns = df_values.columns.tolist\n",
" #df_columns\n",
"\n",
" return [X_train1,X_train2,X_test1,X_test2]"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:18:59.235972Z",
"start_time": "2017-05-05T21:18:59.231593Z"
},
"code_folding": [
0
],
"collapsed": false
},
"outputs": [],
"source": [
"#for c in df_values.columns:\n",
"# if df_values[c].dtype == 'object':\n",
"# lbl = preprocessing.LabelEncoder()\n",
"# lbl.fit(list(df_values[c].values)) \n",
"# df_values[c] = lbl.transform(list(df_values[c].values))"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:18:59.995918Z",
"start_time": "2017-05-05T21:18:59.993521Z"
},
"code_folding": [
0
],
"collapsed": false
},
"outputs": [],
"source": [
"#c = df_values.columns[4]\n",
"#df_values[c]\n",
"#c"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:19:00.672944Z",
"start_time": "2017-05-05T21:19:00.669354Z"
},
"collapsed": true
},
"outputs": [],
"source": [
"#X_all.tofile(\"x_all.csv\",format=\"%s\",sep=\",\")"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:19:01.309313Z",
"start_time": "2017-05-05T21:19:01.305639Z"
},
"collapsed": false
},
"outputs": [],
"source": [
"#df_valuesclean=df_values.dropna(axis=\"columns\", how='any')\n",
"#df_valuesclean.shape"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:19:11.590062Z",
"start_time": "2017-05-05T21:19:11.548377Z"
},
"code_folding": [],
"collapsed": true
},
"outputs": [],
"source": [
"from keras.layers.merge import Concatenate\n",
"# define base model\n",
"def baseline_model(df_values1_cols,df_values2_cols):\n",
" \n",
" model1 = Sequential()\n",
" model1.add(Dense(30, input_dim=df_values1_cols, activation='relu'))\n",
" #model1.add(BatchNormalization())\n",
" #model1.add(Dropout(0.5))\n",
" #model1.add(Dense(60,activation=\"relu\"))\n",
" #model1.add(Dropout(0.25))\n",
" model1.add(Dense(15,activation=\"relu\"))\n",
" #model1.add(Dropout(0.25))\n",
" \n",
" model2 = Sequential()\n",
" model2.add(Dense(30, input_dim=df_values2_cols, activation='relu'))\n",
" #model1.add(BatchNormalization())\n",
" #model2.add(Dropout(0.5))\n",
" #model2.add(Dense(60,activation=\"relu\"))\n",
" #model2.add(Dropout(0.5))\n",
" model2.add(Dense(15,activation=\"relu\"))\n",
" #model2.add(Dropout(0.25))\n",
" \n",
" model = Sequential()\n",
" #model.add(Concatenate([model1, model2],input_shape=(120,1)))\n",
" model.add(Merge([model1, model2], mode='concat'))\n",
" model.add(Dense(100,activation=\"relu\"))\n",
" #model.add(Dropout(0.25))\n",
" model.add(Dense(30,activation=\"relu\"))\n",
" model.add(Dense(1,activation=\"relu\"))\n",
" # Compile model\n",
" #sgd=SGD(lr=0.01, momentum=0.0, decay=0.0, nesterov=False)\n",
" \n",
" \n",
" \n",
"# RMSProp optimizer.\n",
"\n",
"# It is recommended to leave the parameters of this optimizer at their default values (except the learning rate, which can be freely tuned).\n",
"\n",
"# This optimizer is usually a good choice for recurrent neural networks.\n",
"\n",
"# Arguments\n",
"\n",
"# lr: float >= 0. Learning rate.\n",
"# rho: float >= 0.\n",
"# epsilon: float >= 0. Fuzz factor.\n",
"# decay: float >= 0. Learning rate decay over each update\n",
" \n",
" #default optimizer\n",
" #model.compile(loss='mean_squared_logarithmic_error', \\\n",
" # optimizer=RMSprop(lr=0.001, rho=0.9, epsilon=1e-08, decay=0.0))\n",
" \n",
" #lowering lr\n",
" model.compile(loss='mean_squared_logarithmic_error', \\\n",
" optimizer=RMSprop(lr=0.00001, rho=0.9, epsilon=1e-08, decay=0.0))\n",
" \n",
" #my model\n",
" #model.compile(loss='mean_squared_logarithmic_error', optimizer=RMSprop(decay=0.0001))\n",
" #Adadelta\n",
" #sgd\n",
" return [model1,model2,model]"
]
},
{
"cell_type": "code",
"execution_count": 35,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:06:01.686174Z",
"start_time": "2017-05-05T21:06:00.379348Z"
},
"collapsed": true
},
"outputs": [],
"source": [
"[df_train,df_test,df_macro]=load_data()"
]
},
{
"cell_type": "code",
"execution_count": 36,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:06:01.988976Z",
"start_time": "2017-05-05T21:06:01.900523Z"
},
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"_________________________________________________________________\n",
"Layer (type) Output Shape Param # \n",
"=================================================================\n",
"dense_15 (Dense) (None, 30) 480 \n",
"_________________________________________________________________\n",
"dense_16 (Dense) (None, 15) 465 \n",
"=================================================================\n",
"Total params: 945\n",
"Trainable params: 945\n",
"Non-trainable params: 0\n",
"_________________________________________________________________\n",
"_________________________________________________________________\n",
"Layer (type) Output Shape Param # \n",
"=================================================================\n",
"dense_17 (Dense) (None, 30) 480 \n",
"_________________________________________________________________\n",
"dense_18 (Dense) (None, 15) 465 \n",
"=================================================================\n",
"Total params: 945\n",
"Trainable params: 945\n",
"Non-trainable params: 0\n",
"_________________________________________________________________\n",
"_________________________________________________________________\n",
"Layer (type) Output Shape Param # \n",
"=================================================================\n",
"merge_3 (Merge) (None, 30) 0 \n",
"_________________________________________________________________\n",
"dense_19 (Dense) (None, 100) 3100 \n",
"_________________________________________________________________\n",
"dense_20 (Dense) (None, 30) 3030 \n",
"_________________________________________________________________\n",
"dense_21 (Dense) (None, 1) 31 \n",
"=================================================================\n",
"Total params: 8,051\n",
"Trainable params: 8,051\n",
"Non-trainable params: 0\n",
"_________________________________________________________________\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"/home/minesh/anaconda3/lib/python3.6/site-packages/ipykernel/__main__.py:25: UserWarning: The `Merge` layer is deprecated and will be removed after 08/2017. Use instead layers from `keras.layers.merge`, e.g. `add`, `concatenate`, etc.\n"
]
}
],
"source": [
"[model1,model2,model]=baseline_model(15,15)\n",
"model1.summary()\n",
"model2.summary()\n",
"model.summary()\n"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:34:47.630759Z",
"start_time": "2017-05-05T21:34:47.625299Z"
},
"collapsed": false
},
"outputs": [],
"source": [
"def trainKeras(model,X_train1,X_train2,y_train,epo):\n",
"#model.compile(loss='mean_squared_error', optimizer='sgd', metrics=['accuracy'])\n",
" print (\"^^^INFO: Fit Model^^^\")\n",
"#X_train = X_train.reshape(X_train.shape[0],244,1)\n",
"\n",
" callbacks = [\n",
" EarlyStopping(monitor='val_loss', patience=50, verbose=2)\n",
" ]\n",
"\n",
" history = model.fit(x=[X_train1,X_train2],y= y_train, epochs=epo, batch_size=780, validation_split=0.3, verbose=2)#,callbacks=callbacks) #verbose=2 )#\n",
" return [model,history]"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:30:28.429886Z",
"start_time": "2017-05-05T21:30:28.197307Z"
},
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYUAAAEWCAYAAACJ0YulAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xt4HfV95/H3V7LuV+viiyTbssEE21yMsQ2EQEkJBEgD\npKRAE2iSZkN4tkk228IGNiRptrtbut2m2RQCgcYpuUG5hKzbmGBIIAnLzbIxxAYbGyOQ5Iss2bKt\n++27f8xofCRkW7J1NNLR5/U85zlzZubM+Z55JH30m9/Mb8zdERERAUiLuwAREZk4FAoiIhJRKIiI\nSEShICIiEYWCiIhEFAoiIhJRKIiMkJn9i5n99xGuW2tmHzrR7YiMN4WCiIhEFAoiIhJRKEhKCQ/b\n3Gpmr5lZm5l938xmmtkTZnbIzJ42s+kJ619pZpvNrMXMnjWzRQnLzjKzDeH7/hXIHvJZf2RmG8P3\nPm9mZxxnzZ8zs+1mts/MVptZRTjfzOwfzazRzA6a2e/N7LRw2RVm9npYW4OZ3XJcO0xkCIWCpKJr\ngEuAU4CPAk8A/xUoJ/iZ/xKAmZ0CPAh8OVy2Bvg3M8s0s0zg58CPgBLgkXC7hO89C1gFfB4oBb4H\nrDazrNEUamZ/CPwtcC0wG3gHeChcfClwYfg9isJ1msNl3wc+7+4FwGnAr0fzuSJHolCQVPRP7r7H\n3RuA3wEvufsr7t4JPA6cFa53HfALd3/K3XuA/w3kAO8HzgUygG+7e4+7PwqsS/iMm4DvuftL7t7n\n7g8AXeH7RuOTwCp33+DuXcDtwHlmVg30AAXAqYC5+xvuvit8Xw+w2MwK3X2/u28Y5eeKDEuhIKlo\nT8J0xzCv88PpCoL/zAFw936gDqgMlzX44BEj30mYngf8VXjoqMXMWoA54ftGY2gNrQStgUp3/zVw\nF3A30Ghm95lZYbjqNcAVwDtm9hszO2+UnysyLIWCTGU7Cf64A8ExfII/7A3ALqAynDdgbsJ0HfA/\n3L044ZHr7g+eYA15BIejGgDc/TvufjawmOAw0q3h/HXufhUwg+Aw18Oj/FyRYSkUZCp7GPiImV1s\nZhnAXxEcAnoeeAHoBb5kZhlm9sfAyoT33g/cbGbnhB3CeWb2ETMrGGUNDwKfMbOlYX/E/yQ43FVr\nZivC7WcAbUAn0B/2eXzSzIrCw14Hgf4T2A8iEYWCTFnuvhW4AfgnoImgU/qj7t7t7t3AHwOfBvYR\n9D/8LOG9NcDnCA7v7Ae2h+uOtoanga8BjxG0Tk4Crg8XFxKEz36CQ0zNwN+Hy24Eas3sIHAzQd+E\nyAkz3WRHREQGqKUgIiIRhYKIiEQUCiIiElEoiIhIZFrcBYxWWVmZV1dXx12GxOBgRw/v7Gvn5PJ8\ncjLTw5k7oW0vzD4z3uJEJrj169c3uXv5sdabdKFQXV1NTU1N3GVIDNa/s59r7nmeuz69gg+eOiOY\n+cJ34cnb4StPQc70o29AZAozs3eOvZYOH8kkUp4fjDW3t7Xr8Mz8MBxaG2OoSCT1KBRk0igryASg\naVAozAyeD+2OoSKR1KNQkEkjN3MauZnpNB3qPjxzIBTUUhAZE5OuT2E4PT091NfX09nZGXcpSZed\nnU1VVRUZGRlxlxKLsvysIS2FgcNHe4Z/g4iMSkqEQn19PQUFBVRXVzN4UMvU4u40NzdTX1/P/Pnz\n4y4nFmX5mYNDIbsIpmVDqw4fiYyFlDh81NnZSWlpaUoHAoCZUVpaOiVaREfynpaCGRTMgoO7jvwm\nERmxlAgFIOUDYcBU+Z5HUlaQRVNr9+CZhVVwsCGegkRSTMqEgkwNZflZ7G/vprcv4fYBRVVwoD6+\nokRSiEJhDLS0tPDd73531O+74ooraGlpSUJFqas8PxN32NeW0FooqgyubO7vi68wkRShUBgDRwqF\n3t7eo75vzZo1FBcXJ6uslFReEFzA1ngooV+hqAq8T9cqiIwBhcIYuO2223jrrbdYunQpK1as4IIL\nLuDKK69k8eLFAFx99dWcffbZLFmyhPvuuy96X3V1NU1NTdTW1rJo0SI+97nPsWTJEi699FI6Ojri\n+joT2szCbAAaDyV0thdWBc/qVxA5YSlxSmqib/7bZl7feXBMt7m4opBvfHTJEZffeeedbNq0iY0b\nN/Lss8/ykY98hE2bNkWnja5atYqSkhI6OjpYsWIF11xzDaWlpYO2sW3bNh588EHuv/9+rr32Wh57\n7DFuuOGGMf0eqWB2UQ4Auw4khEJRGAoH6mDOymHeJSIjlXKhMBGsXLly0HUE3/nOd3j88ccBqKur\nY9u2be8Jhfnz57N06VIAzj77bGpra8et3smkLD+TNIPdg0KhMng+oJaCyIlKuVA42n/04yUvLy+a\nfvbZZ3n66ad54YUXyM3N5aKLLhr2OoOsrKxoOj09XYePjmBaehozCrIHtxSyiyCrUGcgiYwB9SmM\ngYKCAg4dOjTssgMHDjB9+nRyc3PZsmULL7744jhXl3pmFWWz5+CQYC2sVJ+CyBhIuZZCHEpLSzn/\n/PM57bTTyMnJYebMmdGyyy67jHvvvZdFixbxvve9j3PPPTfGSlPDrMJstu9tHTyzqApa3o2nIJEU\nolAYIz/96U+HnZ+VlcUTTzwx7LKBfoOysjI2bdoUzb/lllvGvL5UMqsom+e2Nw2eOb0a6l4C92Do\nCxE5Ljp8JJPO7KJsWrt6OdTZc3hm6UnQdRDam+MrTCQFKBRk0plVFFyrMKhfoeSk4Ln5rRgqEkkd\nCgWZdGaFF7ANOgOpZEHwvG9HDBWJpA6Fgkw60QVsLQmhMH0eWDrsU0tB5EQoFGTSmVWUTZpB/f72\nwzPTM6B4rg4fiZwghYJMOpnT0phdlMO7+9oHLyh/HzS+EU9RIilCoTAGjnfobIBvf/vbtLe3H3tF\nGWRuSe57Q2HWGdC0Fbq1P0WOl0JhDCgUxt+ckhzq9g8ZCmT2GeD90Ph6PEWJpABdvDYGEofOvuSS\nS5gxYwYPP/wwXV1dfOxjH+Ob3/wmbW1tXHvttdTX19PX18fXvvY19uzZw86dO/ngBz9IWVkZzzzz\nTNxfZdKYW5LL3kNddHT3kZOZHsycfWbw3LAeqpbHV5zIJJZ6ofDEbbD792O7zVmnw+V3HnFx4tDZ\na9eu5dFHH+Xll1/G3bnyyiv57W9/y969e6moqOAXv/gFEIyJVFRUxLe+9S2eeeYZysrKxrbmFDen\nJBeAuv3tnDKzIJhZNCc4NXXbWjjn8zFWJzJ5JfXwkZldZmZbzWy7md12lPVWmFmvmX08mfWMh7Vr\n17J27VrOOussli1bxpYtW9i2bRunn346Tz31FF/5ylf43e9+R1FRUdylTmpzw1B4tznh0JsZLPoo\n7HgW9m6NpzCRSS5pLQUzSwfuBi4B6oF1Zrba3V8fZr2/A9aOyQcf5T/68eDu3H777Xz+8+/9T3XD\nhg2sWbOGO+64g4svvpivf/3rMVSYGqJQGNrZfN4XoeYH8Ohn4U/+BcpOHv/iRCaxZLYUVgLb3X2H\nu3cDDwFXDbPeF4HHgMYk1pJUiUNnf/jDH2bVqlW0tgajeDY0NNDY2MjOnTvJzc3lhhtu4NZbb2XD\nhg3vea+MXEleJvlZ06htbhu8IL8cPr4K9r8Nd50ND1wJmx+H3u54ChWZZJLZp1AJ1CW8rgfOSVzB\nzCqBjwEfBFYcaUNmdhNwE8DcuXPHvNATlTh09uWXX84nPvEJzjvvPADy8/P58Y9/zPbt27n11ltJ\nS0sjIyODe+65B4CbbrqJyy67jIqKCnU0j4KZcfKMfLY3tr534cJL4IvrYcOPYMMD8MinIW8GnPVJ\nOOvGYPA8ERmWuXtyNhz0D1zm7v8hfH0jcI67fyFhnUeAf3D3F83sX4B/d/dHj7bd5cuXe01NzaB5\nb7zxBosWLRrrrzBhTbXveyS3PvIqz765l3Vf/dCRV+rvg+2/gvU/gDd/GZyyWrEMTvtjWHxVcBW0\nyBRgZuvd/Zin5SWzpdAAzEl4XRXOS7QceMiC8e/LgCvMrNfdf57EuiRFLJyZzyPr62lp76Y4N3P4\nldLS4ZRLg8fBnbDpMfj9I7D2juBRuRyWXA2Lr4biOcNvQ2QKSWafwjpgoZnNN7NM4HpgdeIK7j7f\n3avdvRp4FPiPCgQZqYUzglNRhz2ENJzCCnj/F+Hzv4UvvQIXfwP6e4Jw+PZpcP/F8Pxd0FJ37G2J\npKikhYK79wJfAJ4E3gAedvfNZnazmd2chM8b601OSFPle47Ewpn5ALy5Z4ShkKhkAVzwl8MExFeD\ngLj3A/DsnbB7U3A3N5EpIqkXr7n7GmDNkHn3HmHdTx/v52RnZ9Pc3ExpaSmWwrdidHeam5vJzs6O\nu5QJoaIoh/ysaWzZffDENjQQEBf8ZTDK6hurYesvg1B49m+hsApO/kM4+UOw4CLI1jUmkrpS4orm\nqqoq6uvr2bt3b9ylJF12djZVVVVxlzEhpKUZp1UW8mr9gbHbaOlJ8IH/HDxaG2HrE7D9Kdj8c9jw\nQ0ibBnPOgYWXBo8Zi3RPaEkpKREKGRkZzJ8/P+4yJAZnzinmB8/V0tXbR9a09LHdeP4MOPtTwaOv\nB+peDgJi29Pw9DeCR9FcqP4AzD0naEVMrx7bGkTGWUqEgkxdZ1YV093Xz5ZdhzhzTnHyPig9A6rP\nDx4f+uvgTKY3fwlv/Rq2PQmv/jRYr+yU4DDT/Auh+gLIyk9eTSJJoFCQSW0gCF55d39yQ2GowgpY\n/ufBwz0Ya2nHs0FA1KyCF78LaRkw99ywJXEeVC6DrILxq1HkOCgUZFKrKMpmTkkOz21v5tPnx3QI\n0QxmnBo8zr0Zejqh7qXgUNOO3wQd1jhYWjC897zzg7CYc24wLIfIBKJQkEnNzLhwYTk/f6WB7t5+\nMqdNgPtGZWTDgj8IHgCdB4L+iLqXofY5ePl+eOGuYFnpwiAg5p0PVSuCjm51XEuMFAoy6V14Sjk/\neeld1tXu4/yTJ+B9KbKLgvGYFl4SvO7tgp0b4d0X4N0X4Y1/g1d+FCwrrAo6ratWBI9Zp8O0rPhq\nlylHoSCT3oULyynInsaj6+snZigMNS0r+MM/Nxwfsr8fGjdDfU3QL/HuS8FwHADpmcEhp4GQqFoB\nRVVqTUjSKBRk0svJTOfqpZX8a00dt374fVQU58Rd0uikpQUtglmnw/LPBPMO7gxCon5d8Fzzg6Dz\nGiB/VnC70YGQqFgKmXnx1S8pJWmjpCbLcKOkitTta+dD3/oNy6un84/XLWVGQYpd9d3XA3s2JQTF\nOti3I1hmaVC+CCrPgsqzg1FgZy4JTqMVCY10lFSFgqSMh2vquO2x1+j34Kykk2bkM78sj/lleVSX\n5bGgLI/K4hympU+Azuix0NYUhETDeti5IXju2B8sS8+C2WcEAVG5LAiLkpOCVolMSQoFmZK2N7by\nqzf28Pqug7zd1Mbbe9s41NUbLc9IN+aU5DK/9HBYDATHrMJs0tIm8bF6d9hfG4bEK9CwAXZthJ7w\nlqVZhcGhpoHWROUyKKxU/8QUoVAQIRxEsK2b2qY2djS1UdvUFoRFUxu1zW109vRH62ZnpFFdmkd1\naR5zSnKoLM6hcnouVdNzqJyeQ2H2JDwc09cLTVuDgBhoTezZDP1hUObPTGhNLAumc0virVmSQqEg\ncgz9/c7ug53vDYzmNhr2d9DV2z9o/YLsaVRNz6WyOIeq6cEjCI7guSQvc3KM0tvTGfRPNKw/HBZN\nbx5ePr16cGti9pnqyE4BCgWRE+DuNLV209DSQcP+Dur3tydMd9DQ0kFrwmEpgJyM9CggBloXwXTQ\n2ijPz5q4h6c6DwTXTgy0JhpegYP1wbLEjuyKsH9CHdmTjkJBJIncnYMdvdQlhEVDy+Dw2N/eM+g9\nmelpVBRnDwqLgZZG1fQcZhVmT6xO8EN7wpDYMHxH9qzTg4AYOOxUerI6sicwhYJIzNq6eg+3LgYC\nIwqPDvYe6hq0fnqaMaswm9lF2VQU5zC7OJvK4hxmF+UwuyiYLs7NiO8Q1UBH9kBQHKkje6A1oY7s\nCUWhIDLBdfb0setA56CwaNjfwc4DHexs6WT3gU66+wb3a2RnpFFRlBOERlE2s4tzqCwOQ6Qoh4ri\nbHIzx/Ga1GN1ZOfNGNyaqFRHdlwUCiKTXH9/cObUzpYOdoVBEUx3hsHRQeOhrvfcQnp6bkYUElFg\nJITHjIJs0pPZtzGSjuzE1oQ6sseFQkFkCujp62f3gc4gKFo6orAYCJCdLR0c7BzcIT5wmKoiDImK\n4hwqig5PJ+X021F1ZC+DGUtgWubY1jDFKRREBIBDnT3sOtBJQ0sHuxLCoiFsdew60EFP3+C/A0U5\nGdFpt1XTc5kTPleVBM/5WWNwiKq1MeybWH+4n6JjX7As6shedvj0WHVknxCFgoiMSH+/09TaRUPY\nwmhoaaduX9AxXh+egtvR0zfoPdNzM6JTbaPgKDl8RlXe8YTGsB3Zr0JPW7B8UEd2GBbqyB4xhYKI\njImBq8Lr9x8Oirp97YNeD73QryQv83DrYiA4SoIWR2VxLjmZ6SP78P6+4Fania2JPZuGdGQvG3yx\nnTqyh6VQEJFx4e7sbe2KWhWJgTFwsd/Qs6jK8jMTAiN4nlOSG10lnp1xlNCIOrITznhq2gaEf8ui\njuwwLNSRDSgURGSC6O8fCI2hrYzDF/sN7dMoL8ga0tI4fHiqojibrGlDQqPzYHDNRHTG0ytwoC5Y\nZmlQfirMXgoVZ8GclVPyimyFgohMCn39TuOhzigkhvZn7GzpoLf/8N8pM6goymFeaW4wym1pHvNK\nc5lflsecktzDrYyBjuyBw067X4PWPcGyaTmHR4ytWhHctCjF+ycUCiKSEnr7+tlzqIv6sIXx7r52\n3t3XHo1025IwnMhAYFSX5UYj3gbDo+dSNT2X7LYGqHs5aFHUrws6svu6gzdHd7QL72o3eylk5cf0\nrceeQkFEpoSW9m5qm9upDUOitqmNt5vbeecYgTG/LI/q4gzeRy2zWjeRsXNDEBT73w7fkAYzFh8O\niXnnB/0Vk7Q1oVAQkSmvpb2bt5vaeKf5cMtiIEAOdLw3MOaX5bG4uJtl6Ts4pWcrsw5tIqfxFazr\nYLBiQUV4FfbSoG9izjmQMTlu/apQEBE5iv1t3WFItPF2U9CyGLinRuJV4OnWz3mF+/hQ7jbO8jeY\n172N4vZ3APBpOdicFUE4zDknaFXkTI/rKx2VQkFE5Di4Oy3tPbzd3MY7YWDUNg1MB4FRQDvL07Zy\nYdprvD9jGwu9ljSC025bC0+mv2oluQvOY9q8c6Fs4YQ45KRQEBEZY+7O/vaeqO8i6MdoZ3dTE/nN\nr7GoZwtnp73JsrRtFFtwJXZrWgG7Ck6nbeZyMqvPpezUcymfXjLuQ6ArFERExtFAYLzd1Ebt3kMc\nqHudzF3rKG95lZO7NnOS7QSg19PYSjU7cpawv2QpvRUrKa86iQUz8plflpe0oc8VCiIiE0R/v7Nr\nz072bXme/ndfpGDvBirbNpPlwY2Wdvt01vcvZEP/KdTmnkbPjNOZV17MgvI8FpTnc1J5HhVFOSd0\nO1eFgojIRNbXC3s20V37Ih1vPU/Grhpy2xsA6CKTLT6P/9e3iBf6F/Nq/wK6Mwr5i4tO5osXLzyu\nj1MoiIhMNgd3Qd1LUL8Or18HDeuxcPC/5qwqGhd/hkVX3XJcmx5pKIzjfftEROSoCmfDkqthydUY\nQFcrNNRAw3pKd26kdO7spJeQ1FAws8uA/wOkA//s7ncOWX4V8DdAP9ALfNndn0tmTSIik0ZWPiy4\nKHiMk6SFgpmlA3cDlwD1wDozW+3uryes9itgtbu7mZ0BPAycmqyaRETk6JJ5b7uVwHZ33+Hu3cBD\nwFWJK7h7qx/u1MgjGhBdRETikMxQqATqEl7Xh/MGMbOPmdkW4BfAnyexHhEROYbY74Lt7o+7+6nA\n1QT9C+9hZjeZWY2Z1ezdu3d8CxQRmUKSGQoNwJyE11XhvGG5+2+BBWZWNsyy+9x9ubsvLy8vH/tK\nRUQESG4orAMWmtl8M8sErgdWJ65gZidbOACImS0DsoDmJNYkIiJHkbSzj9y918y+ADxJcErqKnff\nbGY3h8vvBa4B/szMeoAO4DqfbFfTiYikEF3RLCIyBYz0iubYO5pFRGTiUCiIiEhEoSAiIhGFgoiI\nRBQKIiISUSiIiEhEoSAiIhGFgoiIRBQKIiISUSiIiEhEoSAiIhGFgoiIRBQKIiISUSiIiEhEoSAi\nIhGFgoiIRBQKIiISUSiIiEhEoSAiIpERhYKZ/SczK7TA981sg5ldmuziRERkfI20pfDn7n4QuBSY\nDtwI3Jm0qkREJBYjDQULn68AfuTumxPmiYhIihhpKKw3s7UEofCkmRUA/ckrS0RE4jBthOt9FlgK\n7HD3djMrAT6TvLJERCQOI20pnAdsdfcWM7sBuAM4kLyyREQkDiMNhXuAdjM7E/gr4C3gh0mrSkRE\nYjHSUOh1dweuAu5y97uBguSVJSIicRhpn8IhM7ud4FTUC8wsDchIXlkiIhKHkbYUrgO6CK5X2A1U\nAX+ftKpERCQWIwqFMAh+AhSZ2R8Bne6uPgURkRQz0mEurgVeBv4EuBZ4ycw+nszCRERk/I20T+Gr\nwAp3bwQws3LgaeDRZBUmIiLjb6R9CmkDgRBqHsV7RURkkhhpS+GXZvYk8GD4+jpgTXJKEhGRuIwo\nFNz9VjO7Bjg/nHWfuz+evLJERCQOI20p4O6PAY8lsRYREYnZUUPBzA4BPtwiwN29MClViYhILI4a\nCu6uoSxERKaQpJ5BZGaXmdlWM9tuZrcNs/yTZvaamf3ezJ4PB9wTEZGYJC0UzCwduBu4HFgM/KmZ\nLR6y2tvAH7j76cDfAPclqx4RETm2ZLYUVgLb3X2Hu3cDDxGMshpx9+fdfX/48kWCMZVERCQmyQyF\nSqAu4XV9OO9IPgs8MdwCM7vJzGrMrGbv3r1jWKKIiCSaEFclm9kHCULhK8Mtd/f73H25uy8vLy8f\n3+JERKaQEV+ncBwagDkJr6vCeYOY2RnAPwOXu3tzEusREZFjSGZLYR2w0Mzmm1kmcD2wOnEFM5sL\n/Ay40d3fTGItIiIyAklrKbh7r5l9AXgSSAdWuftmM7s5XH4v8HWgFPiumUFw28/lyapJRESOzoJb\nL08ey5cv95qamrjLEBGZVMxs/Uj+6Z4QHc0iIjIxKBRERCSiUBARkYhCQUREIgoFERGJKBRERCSi\nUBARkYhCQUREIgoFERGJKBRERCSiUBARkYhCQUREIgoFERGJKBRERCSiUBARkYhCQUREIgoFERGJ\nKBRERCSiUBARkYhCQUREIgoFERGJKBRERCSiUBARkYhCQUREIgoFERGJKBRERCSiUBARkYhCQURE\nIgoFERGJKBRERCSiUBARkYhCQUREIgoFERGJKBRERCSiUBARkYhCQUREIgoFERGJJDUUzOwyM9tq\nZtvN7LZhlp9qZi+YWZeZ3ZLMWkRE5NimJWvDZpYO3A1cAtQD68xstbu/nrDaPuBLwNXJqkNEREYu\nmS2FlcB2d9/h7t3AQ8BViSu4e6O7rwN6kliHiIiMUDJDoRKoS3hdH84bNTO7ycxqzKxm7969Y1Kc\niIi816ToaHb3+9x9ubsvLy8vj7scEZGUlcxQaADmJLyuCueJiMgElcxQWAcsNLP5ZpYJXA+sTuLn\niYjICUra2Ufu3mtmXwCeBNKBVe6+2cxuDpffa2azgBqgEOg3sy8Di939YLLqEhGRI0taKAC4+xpg\nzZB59yZM7yY4rCQiIhPApOhoFhGR8aFQEBGRiEJBREQiCgUREYkoFEREJKJQEBGRiEJBREQiCgUR\nEYkoFEREJKJQEBGRiEJBREQiCgUREYkoFEREJKJQEBGRiEJBREQiCgUREYkoFEREJKJQEBGRiEJB\nREQiCgUREYkoFEREJKJQEBGRiEJBREQiCgUREYkoFEREJKJQEBGRiEJBREQiCgUREYkoFEREJKJQ\nEBGRiEJBREQiCgUREYkoFEREJKJQEBGRiEJBREQiCgUREYkoFEREJKJQEBGRSFJDwcwuM7OtZrbd\nzG4bZrmZ2XfC5a+Z2bJk1iMiIkeXtFAws3TgbuByYDHwp2a2eMhqlwMLw8dNwD3JqkdERI4tmS2F\nlcB2d9/h7t3AQ8BVQ9a5CvihB14Eis1sdhJrEhGRo5iWxG1XAnUJr+uBc0awTiWwK3ElM7uJoCUB\n0GpmW4+zpjKg6Tjfm0wTtS6YuLWprtFRXaOTinXNG8lKyQyFMePu9wH3neh2zKzG3ZePQUljaqLW\nBRO3NtU1OqprdKZyXck8fNQAzEl4XRXOG+06IiIyTpIZCuuAhWY238wygeuB1UPWWQ38WXgW0rnA\nAXffNXRDIiIyPpJ2+Mjde83sC8CTQDqwyt03m9nN4fJ7gTXAFcB2oB34TLLqCZ3wIagkmah1wcSt\nTXWNjuoanSlbl7l7sj9DREQmCV3RLCIiEYWCiIhEpkwoHGvIjXH4/Foz+72ZbTSzmnBeiZk9ZWbb\nwufpCevfHta61cw+PIZ1rDKzRjPblDBv1HWY2dnh99keDlViSajrr82sIdxnG83sihjqmmNmz5jZ\n62a22cz+Uzg/1n12lLpi3Wdmlm1mL5vZq2Fd3wznx72/jlRX7D9j4TbTzewVM/v38HV8+8vdU/5B\n0NH9FrAAyAReBRaPcw21QNmQef8LuC2cvg34u3B6cVhjFjA/rD19jOq4EFgGbDqROoCXgXMBA54A\nLk9CXX8N3DLMuuNZ12xgWThdALwZfn6s++wodcW6z8Jt5IfTGcBL4bbj3l9Hqiv2n7Fwm38J/BT4\n97h/J6dKS2EkQ27E4SrggXD6AeDqhPkPuXuXu79NcHbWyrH4QHf/LbDvROqwYCiSQnd/0YOfxh8m\nvGcs6zqS8axrl7tvCKcPAW8QXHUf6z47Sl1HMl51ubu3hi8zwocT//46Ul1HMm4/Y2ZWBXwE+Och\nnx/L/poqoXCk4TTGkwNPm9l6C4btAJjph6/L2A3MDKfHu97R1lEZTo9HfV+0YATdVQlN6FjqMrNq\n4CyC/zL0dBKhAAADzklEQVQnzD4bUhfEvM/CQyEbgUbgKXefEPvrCHVB/D9j3wb+C9CfMC+2/TVV\nQmEi+IC7LyUYGfYvzOzCxIVhusd+fvBEqSN0D8Ehv6UE42H9Q1yFmFk+8BjwZXc/mLgszn02TF2x\n7zN37wt/1qsI/os9bcjyWPbXEeqKdX+Z2R8Bje6+/kjrjPf+miqhEPtwGu7eED43Ao8THA7aEzb7\nCJ8bw9XHu97R1tEQTie1PnffE/4i9wP3c/gQ2rjWZWYZBH94f+LuPwtnx77PhqtrouyzsJYW4Bng\nMibA/hqurgmwv84HrjSzWoLD2n9oZj8mxv01VUJhJENuJI2Z5ZlZwcA0cCmwKazhU+FqnwL+bzi9\nGrjezLLMbD7B/SZeTmKJo6ojbNYeNLNzwzMc/izhPWPGBg+j/jGCfTaudYXb+T7whrt/K2FRrPvs\nSHXFvc/MrNzMisPpHOASYAvx769h64p7f7n77e5e5e7VBH+Xfu3uNxDn/jqe3unJ+CAYTuNNgt76\nr47zZy8gOGPgVWDzwOcDpcCvgG3A00BJwnu+Gta6lTE4uyFhuw8SNJN7CI47fvZ46gCWE/wCvQXc\nRXh1/BjX9SPg98Br4S/D7Bjq+gBB0/01YGP4uCLufXaUumLdZ8AZwCvh528Cvn68P+vjVFfsP2MJ\n272Iw2cfxba/NMyFiIhEpsrhIxERGQGFgoiIRBQKIiISUSiIiEhEoSAiIhGFgsg4MrOLBkbCFJmI\nFAoiIhJRKIgMw8xusGD8/Y1m9r1wMLVWM/tHC8bj/5WZlYfrLjWzF8NB1R4fGFTNzE42s6ctGMN/\ng5mdFG4+38weNbMtZvaT4x73XiQJFAoiQ5jZIuA64HwPBlDrAz4J5AE17r4E+A3wjfAtPwS+4u5n\nEFwdOzD/J8Dd7n4m8H6CK7YhGNH0ywRj4y8gGP9GZEKYFncBIhPQxcDZwLrwn/gcggHJ+oF/Ddf5\nMfAzMysCit39N+H8B4BHwrGuKt39cQB37wQIt/eyu9eHrzcC1cBzyf9aIsemUBB5LwMecPfbB800\n+9qQ9Y53jJiuhOk+9HsoE4gOH4m816+Aj5vZDIjulzuP4Pfl4+E6nwCec/cDwH4zuyCcfyPwGw/u\nhlZvZleH28gys9xx/RYix0H/oYgM4e6vm9kdwFozSyMYufUvgDaCm7PcQXA46brwLZ8C7g3/6O8A\nPhPOvxH4npn9t3AbfzKOX0PkuGiUVJERMrNWd8+Puw6RZNLhIxERiailICIiEbUUREQkolAQEZGI\nQkFERCIKBRERiSgUREQk8v8B3A++lrzvCYQAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7eff4c53b668>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# list all data in history\n",
"'''\n",
"print(history.history.keys())\n",
"# summarize history for accuracy\n",
"plt.plot(history.history['acc'])\n",
"plt.plot(history.history['val_acc'])\n",
"plt.title('model accuracy')\n",
"plt.ylabel('accuracy')\n",
"plt.xlabel('epoch')\n",
"plt.legend(['train', 'test'], loc='upper left')\n",
"# axes = plt.gca()\n",
"# axes.set_xlim([0,120])\n",
"# axes.set_ylim([90,100])\n",
"#plt.savefig('acc.png') # save the figure to file\n",
"plt.show()\n",
"#plt.close()\n",
"'''\n",
"\n",
"\n",
"# summarize history for loss\n",
"plt.plot(history.history['loss'])\n",
"plt.plot(history.history['val_loss'])\n",
"plt.title('model loss')\n",
"plt.ylabel('loss')\n",
"plt.xlabel('epoch')\n",
"plt.legend(['train', 'test'], loc='upper left')\n",
"#plt.savefig('loss.png')\n",
"#plt.show()\n",
"\n",
"plt.ylim([0, \\\n",
" min(history.history['loss'])+min(history.history['loss'])/2])\n",
"plt.show()\n",
"\n",
"#plt.fig()\n",
"#plt.close()"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-04T22:42:51.225714Z",
"start_time": "2017-05-04T22:42:51.184883Z"
},
"collapsed": false
},
"outputs": [
{
"ename": "NameError",
"evalue": "name 'history' is not defined",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mNameError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m<ipython-input-30-4788bc045bd5>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[1;32m 4\u001b[0m \u001b[0;31m# summarize history for loss\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 5\u001b[0m \u001b[0mplt\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mfigure\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m----> 6\u001b[0;31m \u001b[0mplt\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mplot\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mhistory\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mhistory\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m'loss'\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 7\u001b[0m \u001b[0mplt\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mplot\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mhistory\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mhistory\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m'val_loss'\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 8\u001b[0m \u001b[0mplt\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mtitle\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m'model loss'\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mNameError\u001b[0m: name 'history' is not defined"
]
},
{
"data": {
"text/plain": [
"<matplotlib.figure.Figure at 0x7f6c3b2c44e0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"from matplotlib.backends.backend_pdf import PdfPages\n",
"with PdfPages('multipage_pdf.pdf') as pdf:\n",
" for i in range(0,10):\n",
" # summarize history for loss\n",
" plt.figure()\n",
" plt.plot(history.history['loss'])\n",
" plt.plot(history.history['val_loss'])\n",
" plt.title('model loss')\n",
" plt.ylabel('loss')\n",
" plt.xlabel('epoch')\n",
" plt.legend(['train', 'test'], loc='upper left')\n",
"\n",
" plt.ylim([0, 2])\n",
" #plt.show()\n",
" pdf.savefig() # saves the current figure into a pdf page\n",
" plt.close()"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:31:10.503507Z",
"start_time": "2017-05-05T21:31:10.313678Z"
},
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYwAAAEWCAYAAAB1xKBvAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XuYXHWd5/H3t6qrq7qrb0l359qJCRiFcAsSEEZU0BEC\njqCjizCiM65jZB91nV1lhR0v6+zOrLOz6/ioCMYxjzoqDCMyww5BLjMgulwDBgg3CRBId0I69/T9\nUv3dP86vuiud7lCddPWp7v68nqeec+p3zqn6dj3pfPp3zu/8ytwdERGR15OIuwAREZkeFBgiIlIU\nBYaIiBRFgSEiIkVRYIiISFEUGCIiUhQFhsgkMLMfmtn/KHLfrWb2+8f6OiJTTYEhIiJFUWCIiEhR\nFBgya4RTQVeb2ZNm1mVmPzCz+WZ2h5l1mNk9ZjanYP9LzOxpM9tvZveZ2YkF2043s8fDcf8AZEa9\n1x+Y2aZw7ANmdupR1vxJM9tiZnvN7DYzWxTazcz+1szazeygmT1lZieHbReb2TOhtjYz+8JRfWAi\noygwZLb5IPAe4E3A+4A7gP8KNBP9PvxHADN7E3Aj8Gdh2wbg/5pZpZlVAv8E/D0wF/jH8LqEY08H\n1gOfAhqB7wG3mVl6IoWa2buA/wlcBiwEXgFuCpsvAN4Rfo76sM+esO0HwKfcvRY4Gfi3ibyvyHgU\nGDLbfNvdd7p7G/Br4GF3/6279wK3AqeH/T4M3O7ud7v7APC/gSrg94CzgRTwTXcfcPefA48WvMda\n4Hvu/rC759z9R0BfOG4iPgKsd/fH3b0PuBY4x8yWAQNALXACYO7+rLvvCMcNACvNrM7d97n74xN8\nX5ExKTBkttlZsN4zxvOasL6I6C96ANx9CNgGLA7b2vzQmTtfKVh/A/D5cDpqv5ntB5aE4yZidA2d\nRL2Ixe7+b8B3gOuAdjNbZ2Z1YdcPAhcDr5jZr8zsnAm+r8iYFBgiY9tO9B8/EF0zIPpPvw3YASwO\nbXlLC9a3AX/p7g0Fj2p3v/EYa8gSneJqA3D3b7n7GcBKolNTV4f2R939UmAe0amzmyf4viJjUmCI\njO1m4L1m9m4zSwGfJzqt9ADwIDAI/EczS5nZHwJnFRz7feAqM3truDidNbP3mlntBGu4Efi4ma0K\n1z/+iugU2lYzOzO8fgroAnqBoXCN5SNmVh9OpR0Eho7hcxAZpsAQGYO7Pw9cCXwb2E10gfx97t7v\n7v3AHwJ/Auwlut7xi4JjNwKfJDpltA/YEvadaA33AF8GbiHq1RwPXB421xEF0z6i01Z7gL8J2z4K\nbDWzg8BVRNdCRI6Z6QuURESkGOphiIhIUUoWGGa2xMzuDTcQPW1mnxtjHzOzb4Ubk540s7cUbFtj\nZs+HbdeUqk4RESlOKXsYg8Dn3X0l0fjzT5vZylH7XASsCI+1wPUAZpYkGi54EdEIkCvGOFZERKZQ\nyQLD3Xfkbxhy9w7gWaIx7IUuBX7skYeABjNbSDTiZIu7vxQuMN4U9hURkZhUTMWbhDtTTwceHrVp\nMdGY9bzW0DZW+1vHee21RL0TstnsGSeccMKk1CyTr7t/kBd3dbG8MUtNpgIOtELPXlhwVNMsicgk\neOyxx3a7e3Mx+5Y8MMyshmhY4J+5+8HJfn13XwesA1i9erVv3Lhxst9CJsmW9g5+/xv389eXr+LS\nVYvhvr+G+/4KvvwgJFNxlycyK5nZK6+/V6Sko6TCTUW3AD9191+MsUsb0d2zeS2hbbx2mcYaqisB\n2N89EDVUz42WPftiqkhEJqKUo6SMaNbMZ939G+PsdhvwsTBa6mzgQJhA7VFghZktDzODXh72lWms\noSrqRezr7o8a8oHRvTemikRkIkp5SuptRHecPmVmm0LbfyXMuePuNxBNGX0x0Z2w3cDHw7ZBM/sM\ncCeQJJqx8+kS1ipToCKZoDZTMdLDqMoHxp7xDxKRslGywHD33wD2Ovs48Olxtm0gCpRjMjAwQGtr\nK729vcf6UmUtk8nQ0tJCKlXe1wLmVFcW9DAao6UCQ2RamJJRUnFqbW2ltraWZcuWcejkojOHu7Nn\nzx5aW1tZvnx53OUc0ZzqFPuGr2HkA2N3fAWJSNFm/NQgvb29NDY2ztiwADAzGhsbp0UvqqG6kn1d\noYeRbYqWXephiEwHMz4wgBkdFnnT5WdszFayNx8YFWlI16uHITJNzIrAkPIxtzAwALKN0LUrvoJE\npGgKjBLbv38/3/3udyd83MUXX8z+/ftLUFG85tZU0jOQo6c/FzVkmxUYItOEAqPExguMwcHBIx63\nYcMGGhoaSlVWbBqz0c17e7r6ooZsM3TplJTIdKDAKLFrrrmGF198kVWrVnHmmWfy9re/nUsuuYSV\nK6PJd9///vdzxhlncNJJJ7Fu3brh45YtW8bu3bvZunUrJ554Ip/85Cc56aSTuOCCC+jp6Ynrxzlm\nc7NpgJHTUtkmBYbINDHjh9UW+tr/fZpntk/udFYrF9Xx1fedNO72r3/962zevJlNmzZx33338d73\nvpfNmzcPD39dv349c+fOpaenhzPPPJMPfvCDNDY2HvIaL7zwAjfeeCPf//73ueyyy7jlllu48sor\nJ/XnmCpzh3sY+XsxmqKL3kNDkNDfLyLlTL+hU+yss8465F6Jb33rW5x22mmcffbZbNu2jRdeeOGw\nY5YvX86qVasAOOOMM9i6detUlTvp8qek9nbmexjN4EOaT0pkGphVPYwj9QSmSjabHV6/7777uOee\ne3jwwQeprq7mvPPOG/NeinQ6PbyeTCan9ympmhAYo+/F6N4djZgSkbKlHkaJ1dbW0tHRMea2AwcO\nMGfOHKqrq3nuued46KGHpri6qVebriCVtJFTUsM372mklEi5m1U9jDg0Njbytre9jZNPPpmqqirm\nz58/vG3NmjXccMMNnHjiibz5zW/m7LPPjrHSqWFm4V6MglFSoMAQmQYUGFPgZz/72Zjt6XSaO+64\nY8xt+esUTU1NbN68ebj9C1/4wqTXN9XmZtMFp6TygaGRUiLlTqekZMo1ZitHTklVzQVMgSEyDSgw\nZMrNzVayJz9KKlkBVXN0SkpkGlBgyJQ7fD4pTQ8iMh0oMGTKNWYr6ewbpG+wYD4pfYmSSNlTYMiU\nG/NeDPUwRMpeyQLDzNabWbuZbR5n+9Vmtik8NptZzszmhm1bzeypsG1jqWqUeAxPQNipwBCZTkrZ\nw/ghsGa8je7+N+6+yt1XAdcCv3L3vQW7nB+2ry5hjSV3tNObA3zzm9+ku7t7kiuK3+ETEDZHU4Pk\nBmKsSkReT8kCw93vB/a+7o6RK4AbS1VLnBQYh8tPQHj49CDF/nMRkTjEfuOemVUT9UQ+U9DswD1m\nlgO+5+7rxjx4Giic3vw973kP8+bN4+abb6avr48PfOADfO1rX6Orq4vLLruM1tZWcrkcX/7yl9m5\ncyfbt2/n/PPPp6mpiXvvvTfuH2XSNI6esbbwbu/a+eMcJSJxiz0wgPcB/2/U6ahz3b3NzOYBd5vZ\nc6HHchgzWwusBVi6dOmR3+mOa+C1pyan6rwFp8BFXx93c+H05nfddRc///nPeeSRR3B3LrnkEu6/\n/3527drFokWLuP3224Fojqn6+nq+8Y1vcO+999LU1DS5NcesvipFMmEj04NUaz4pkemgHEZJXc6o\n01Hu3haW7cCtwFnjHezu69x9tbuvbm5uLmmhx+quu+7irrvu4vTTT+ctb3kLzz33HC+88AKnnHIK\nd999N1/84hf59a9/TX19fdylllQiYcypTh0+PYiG1oqUtVh7GGZWD7wTuLKgLQsk3L0jrF8A/MWk\nvOERegJTwd259tpr+dSnPnXYtscff5wNGzbwpS99iXe/+9185StfiaHCqXPI3d6asVZkWijlsNob\ngQeBN5tZq5l9wsyuMrOrCnb7AHCXu3cVtM0HfmNmTwCPALe7+y9LVWepFU5vfuGFF7J+/Xo6OzsB\naGtro729ne3bt1NdXc2VV17J1VdfzeOPP37YsTPNIXd7ZxogUaHAEClzJethuPsVRezzQ6Lht4Vt\nLwGnlaaqqVc4vflFF13EH/3RH3HOOecAUFNTw09+8hO2bNnC1VdfTSKRIJVKcf311wOwdu1a1qxZ\nw6JFi2bURW+AxmyaZ3eEr8tNJKC6URMQipS5crjoPeONnt78c5/73CHPjz/+eC688MLDjvvsZz/L\nZz/72ZLWFpe5hTPWAmTnQWd7fAWJyOsqh4veMgs11lRyoGeAgdxQ1FAzD7oUGCLlTIEhsWiqGXW3\nd8189TBEytysCAx3j7uEkptuP2M+MHZ1hHsxauZB506YZj+HyGwy4wMjk8mwZ8+eafcf6kS4O3v2\n7CGTycRdStGaa0NgdOYDYz7k+qM5pUSkLM34i94tLS20traya9fMHrKZyWRoaWmJu4yiNY/Vw4Do\ntFT13JiqEpEjmfGBkUqlWL58edxlyChNtdF8UrsLexgQnZaad0JMVYnIkcz4U1JSnqorK8hWJtnd\nES561y6IlrrwLVK2FBgSm6badME1jPwpqZ3xFSQiR6TAkNg016TZnb+Gka6DiowCQ6SMKTAkNk01\nBT0MszC0VqekRMqVAkNi01ybHrnoDeHmPfUwRMqVAkNi01STZn/3AP2D+elBFBgi5UyBIbHJ37y3\np2vU3d4iUpYUGBKbpppwL0ZHwXxS3XsgNxBjVSIyHgWGxKZpeHqQ3qghP7RWX6QkUpYUGBKb/PQg\nIz2M/M17Oi0lUo4UGBKbMScgBA2tFSlTCgyJTSaVpDZdMcYEhOphiJSjkgWGma03s3Yz2zzO9vPM\n7ICZbQqPrxRsW2Nmz5vZFjO7plQ1SvyaCu/FUGCIlLVS9jB+CKx5nX1+7e6rwuMvAMwsCVwHXASs\nBK4ws5UlrFNi1FyTHulhVKQh0wAdCgyRclSywHD3+4G9R3HoWcAWd3/J3fuBm4BLJ7U4KRtNtZW6\n21tkmoj7GsbvmdmTZnaHmZ0U2hYD2wr2aQ1tYzKztWa20cw2zvQvSZqJmmrS7O7sH2nQzXsiZSvO\nwHgcWOrupwLfBv7paF7E3de5+2p3X93c3DypBUrpNdekOdAzQN9gLmqoXQgdO+ItSkTGFFtguPtB\nd+8M6xuAlJk1AW3AkoJdW0KbzED5m/eGexl1C6HjNZjB38EuMl3FFhhmtsDMLKyfFWrZAzwKrDCz\n5WZWCVwO3BZXnVJa8+uiwGg/GO72rl0IuX7oPprLXyJSSiX7Tm8zuxE4D2gys1bgq0AKwN1vAD4E\n/AczGwR6gMvd3YFBM/sMcCeQBNa7+9OlqlPiNa82A8DOg+HCd+3CaNmxHbKNMVUlImMpWWC4+xWv\ns/07wHfG2bYB2FCKuqS8zK+LAqO9I/Qw6hZFy4M7YMEpMVUlImOJe5SUzHKN2UqSCWNn4SkpiHoY\nIlJWFBgSq0TCmFebLjgltQCwqIchImVFgSGxm1eXGelhJFOQbVYPQ6QMKTAkdvNr07QfLLjbu26h\nehgiZUiBIbGbX5fhtXwPA6B2kW7eEylDCgyJ3YL6DAd6BugdCHd71y2EgzolJVJuFBgSu3m1+Zv3\nCu7F6NkLA71HOEpEppoCQ2KXvxdjZ8foobU6LSVSThQYErvhwMhfx6hTYIiUIwWGxC4/n9TIvRjh\nbm8FhkhZUWBI7OqrUlRWJEYmIMz3MDS0VqSsKDAkdmbG/Lr0yCmpTANUVKmHIVJmFBhSFubXFtyL\nYaahtSJlSIEhZWF+XebQu711855I2VFgSFmYV3hKCtTDEClDCgwpCwvqMnT15+jsG4wa6kIPY2go\n3sJEZJgCQ8pC/l6M1w6EXkb9kuirWrt2xViViBRSYEhZODwwWqLlgdaYKhKR0UoWGGa23szazWzz\nONs/YmZPmtlTZvaAmZ1WsG1raN9kZhtLVaOUj0UNUWBsP9ATNQwHxraYKhKR0UrZw/ghsOYI218G\n3unupwD/HVg3avv57r7K3VeXqD4pIwvqo8DYsb/glBQoMETKSEWpXtjd7zezZUfY/kDB04eAllLV\nIuUvXZGkqSbNjnwPI1MPlbU6JSVSRsrlGsYngDsKnjtwj5k9ZmZrj3Sgma01s41mtnHXLl0gnc4W\nNWRo2x8Cwyw6LaXAECkbJethFMvMzicKjHMLms919zYzmwfcbWbPufv9Yx3v7usIp7NWr17tJS9Y\nSmZRfRVbdnWONNS36JSUSBmJtYdhZqcCfwdc6u578u3u3haW7cCtwFnxVChTaWFDhh37e3APua8e\nhkhZiS0wzGwp8Avgo+7+u4L2rJnV5teBC4AxR1rJzLKovoqu/hwHe8LNe/Ut0L0H+rvjLUxEgBKe\nkjKzG4HzgCYzawW+CqQA3P0G4CtAI/BdMwMYDCOi5gO3hrYK4Gfu/stS1SnlY1FDFRANra2vTo2M\nlDrYBk0rYqxMRKC0o6SueJ3tfwr86RjtLwGnHX6EzHQLw70YOw70cOLCukPvxVBgiMSuXEZJibCo\nPvQw8vdiNOTvxdB1DJFyoMCQstFcm6YiYWzPD62tXQiWUGCIlAkFhpSNZMKYX5dhR34+qWQqCo39\nGlorUg4UGFJWFjVkRnoYoHsxRMqIAkPKysL6qpEeBuheDJEyosCQsrKooYodB3oYGiq4ee9gm75I\nSaQMKDCkrCxqyDCQc3Z3he/3zn+RUufOeAsTEQWGlJeFo4fWzlkeLfe/ElNFIpKnwJCysjjc7d22\nL1z4nrMsWu7bGks9IjJCgSFlZcncKDC27QvzRzUsAUyBIVIGFBhSVmozKRqqU2zbGwKjIg11ixQY\nImVAgSFlZ8mcarbtK7gXY84yBYZIGVBgSNlZMreK1r0FU5rPWQb7dNFbJG4KDCk7S+ZU07qv4F6M\nOcugYzsM9B7xOBEpLQWGlJ2WudX054Zo7wj3YuRHSu1/NbaaRKTIwDCzz5lZnUV+YGaPm9kFpS5O\nZqclc0aNlNLQWpGyUGwP49+7+0Gir0udA3wU+HrJqpJZbcncaoCRkVIKDJGyUGxgWFheDPy9uz9d\n0CYyqfI3723bG0ZKZZshVa3AEIlZsYHxmJndRRQYd5pZLXDE2eDMbL2ZtZvZ5nG2m5l9y8y2mNmT\nZvaWgm1rzOz5sO2aYn8YmRkyqSTz69Ijp6TMoOENmh5EJGbFBsYngGuAM929G0gBH3+dY34IrDnC\n9ouAFeGxFrgewMySwHVh+0rgCjNbWWSdMkMsmVM9ckoKdC+GSBkoNjDOAZ539/1mdiXwJeDAkQ5w\n9/uBvUfY5VLgxx55CGgws4XAWcAWd3/J3fuBm8K+MossmRsNrR2WDwz3uEoSmfWKDYzrgW4zOw34\nPPAi8ONjfO/FQOFXqbWGtvHax2Rma81so5lt3LVr1zGWJOViyZzoezEGcuHM59zl0N8Jne3xFiYy\nixUbGIPu7kR/6X/H3a8DaktXVvHcfZ27r3b31c3NzXGXI5OkZW41Qw478tOcNx4fLfe+GF9RIrNc\nsYHRYWbXEg2nvd3MEkTXMY5FG7Ck4HlLaBuvXWaRpWFo7St7u6KGxjdGyz1bYqpIRIoNjA8DfUT3\nY7xG9J/43xzje98GfCyMljobOODuO4BHgRVmttzMKoHLw74yiyxvygKwdXcIjPolkKxUYIjEqKKY\nndz9NTP7KXCmmf0B8Ii7H/EahpndCJwHNJlZK/BVQq/E3W8ANhAN090CdBNGXbn7oJl9BrgTSALr\nw30fMovMq01TXZnk5d1hpFQiCXOPgz06JSUSl6ICw8wuI+pR3Ed0w963zexqd//5eMe4+xVHes1w\nTeTT42zbQBQoMkuZGW9ozPLy7s6RxsY3qochEqOiAgP4c6J7MNoBzKwZuAcYNzBEjtXypmqe3dEx\n0tB4PLxwFwzloh6HiEypYq9hJPJhEeyZwLEiR2V5U5Zte7tHhtY2roBcv2atFYlJsf/p/9LM7jSz\nPzGzPwFuR6eMpMSWNWYZHPKRG/iGR0rpOoZIHIoKDHe/GlgHnBoe69z9i6UsTOSwkVIaWisSq2Kv\nYeDutwC3lLAWkUMsC4Hx8u4uzgfINkG6XoEhEpMjBoaZdQBjTd5jRAOd6kpSlQjQmK2kNl3B1j2h\nh2EWXfhWYIjE4oiB4e5lMf2HzE5mxvLmLC/nT0lBdFrq1QfjK0pkFtNIJylryxpHBUbTm+DANujr\nHP8gESkJBYaUtWVNWbbv76FvMBc1zDshWu5+Pr6iRGYpBYaUteOasgw5vLInTBHSfGK0bH8uvqJE\nZikFhpS1N86rAeCFneEU1NzlkEzDrmdjrEpkdlJgSFl747wazOCF9jBFSCIZXcdQD0NkyikwpKxl\nUkmWzq0e6WFAdB1jlwJDZKopMKTsrZhXM9LDAGg+IYyU6hj/IBGZdAoMKXsr5tfy8u6ukUkI54UL\n37s0UkpkKikwpOytmFfDQM55JX/Hd3MYWtuuC98iU0mBIWVvxbxowoHh6xhzlkFFRtcxRKaYAkPK\n3shIqRAYwyOlnom3MJFZpqSBYWZrzOx5M9tiZteMsf1qM9sUHpvNLGdmc8O2rWb2VNi2sZR1Snmr\nqkzSMqeK3+0suMg9/2R4bXN8RYnMQiULDDNLAtcBFwErgSvMbGXhPu7+N+6+yt1XAdcCv3L3vQW7\nnB+2ry5VnTI9vGleLVvaC4bWLjwVutqh47X4ihKZZUrZwzgL2OLuL7l7P3ATcOkR9r8CuLGE9cg0\ntmJ+LS/u6qR/MIyUWnBqtNzxZHxFicwypQyMxcC2guetoe0wZlYNrOHQL2hy4B4ze8zM1o73Jma2\n1sw2mtnGXbt2TULZUo5OXFjLQM55cVfoZSw4JVq+9kR8RYnMMuVy0ft9wP8bdTrq3HCq6iLg02b2\njrEOdPd17r7a3Vc3NzdPRa0Sg5MW1QPw9PaDUUOmDuYsh9eeirEqkdmllIHRBiwpeN4S2sZyOaNO\nR7l7W1i2A7cSneKSWWp5U5ZMKsEz+cCA6DqGTkmJTJlSBsajwAozW25mlUShcNvoncysHngn8M8F\nbVkzq82vAxcAGhIziyUTxgkL6nhmx4GRxgWnwL6XoffA+AeKyKQpWWC4+yDwGeBO4FngZnd/2syu\nMrOrCnb9AHCXuxd8rRrzgd+Y2RPAI8Dt7v7LUtUq08NJi+p4ZvtB3MPXzC84LVpqeK3IlDjid3of\nK3ffAGwY1XbDqOc/BH44qu0l4LRS1ibTz8pFdfz04Vdp3dfDkrnV0SkpgNeehGVvi7c4kVmgXC56\ni7yulQvrAHhmR7iOUbsAahdC2+MxViUyeygwZNo4YUEdCSsYKQXQshpaH42vKJFZRIEh00ZVZZLj\nmmt4uq3gInfLmdGF767d8RUmMksoMGRaOa2lgSda949c+G45M1q2aroxkVJTYMi0smppA7s7+2nd\n1xM1LFwFltRpKZEpoMCQaeX0JQ0A/Hbb/qihshoWnKzAEJkCCgyZVk5YUEsmlWDTq/tHGlvOjEZK\nDeXiK0xkFlBgyLRSkUxw6uIGfrtt30hjy5nQ36Fv4BMpMQWGTDurljbw9PaD9A2GHsWSt0bLVx6I\nryiRWUCBIdPO6Usa6B8c4tkd4Rv45iyDuhbY+utY6xKZ6RQYMu2cvnQOABu3htnwzWD522Hrb2Bo\nKMbKRGY2BYZMOwvqMyxrrOahlwq+PmXZ26F7D+x6Nr7CRGY4BYZMS2cf18jDL+8hNxRu4Fv+9mj5\nsk5LiZSKAkOmpXOOb6Sjd3DkC5UalkLDG3QdQ6SEFBgyLZ19XCMAD720Z6Rx+TuiHkZuIKaqRGY2\nBYZMS/PrMhzXlOXBwsBYcQH0HYBtD8dXmMgMpsCQaeutxzXyyMt7GciFkVHHnw+JFPzuzngLE5mh\nFBgybb3zTc109g2ycWu46ztdG33zngJDpCRKGhhmtsbMnjezLWZ2zRjbzzOzA2a2KTy+UuyxIueu\naKIymeDfnts50rjiQtj9POx9Ob7CRGaokgWGmSWB64CLgJXAFWa2coxdf+3uq8LjLyZ4rMxiNekK\n3nrcXP71ufaRxjddGC2f3zD2QSJy1ErZwzgL2OLuL7l7P3ATcOkUHCuzyLtOmMdLu7rYursramg8\nHhacCptvibcwkRmolIGxGNhW8Lw1tI32e2b2pJndYWYnTfBYzGytmW00s427du2ajLplGnnXCfMA\nuOfZgtNSp3wI2h6DvS/FVJXIzBT3Re/HgaXufirwbeCfJvoC7r7O3Ve7++rm5uZJL1DK2xsas5y4\nsI7bn9ox0njSH0ZL9TJEJlUpA6MNWFLwvCW0DXP3g+7eGdY3ACkzayrmWJG8S1ct4rev7ufVPd1R\nQ8MSWHoOPHkz5L/7W0SOWSkD41FghZktN7NK4HLgtsIdzGyBmVlYPyvUs6eYY0Xy3nfaIgBue6Lg\nb4rTPwq7fxfNYCsik6JkgeHug8BngDuBZ4Gb3f1pM7vKzK4Ku30I2GxmTwDfAi73yJjHlqpWmd4W\nN1Rx1rK53PrbNjzfozj5DyHTABt/EG9xIjNIRSlfPJxm2jCq7YaC9e8A3yn2WJHxfOiMFv7LLU/y\n0Et7Oef4RkhVwelXwsM3wIE2qB9zzISITEDcF71FJsUlqxbRUJ3iRw9sHWl866cAg9/8bVxlicwo\nCgyZETKpJB8+cwl3PfMarfvyF7+Xwukfgcd/BPtfjbdAkRlAgSEzxsfOWUYyYVx/34sjjW//AiQq\n4F/+k0ZMiRwjBYbMGIsbqrj8zKX8w6PbeGVPuPO7YQn8/tdgyz3wwLfjLVBkmivpRW+RqfbZd72R\nf3xsG//9X57h+x9bjZnBmX8KL/8K7v5ydG/GotOgrgWyTZBtLlg2RyOrEvo7SmQsCgyZUebVZfj8\ne97MX254ln/etJ33n744CoDLfgwb18Mz/wy/uwu6dgFjnKKy5EiAVDdG69VN0XrVnFGPBqieC+l6\nhYzMCuYz6Lzu6tWrfePGjXGXITHLDTmXfe9Bntl+kJs/dQ6ntNSPsdMg9OyNgqNrF3TtHrW+G7ra\noXtP9Og9cIR3NMjURwGSaRgJk3Rd9B0dmfpoPVMPmbrDn6frIJEs2echciRm9pi7ry5qXwWGzETt\nHb184LqQHndLAAANJ0lEQVQHONg7wDc/vIp3nzj/2F4wNwi9+6Fn3+GP7r1hW9ieX+87CL0HYbDn\n9V+/sjaER21B0NSNrA8vayFdEy0rC55XhrZk6th+Tpl1FBgiQOu+bv70Rxt57rUOVi6s46RFddRX\npaiqTJJJJUlXJEinkmQqEmRSI23RelhWJEmnEsPLdEWCMJtN8XIDUXD0HYh6Kr0Ho2U+UArX+w5C\nX8eo550w0FXceyXTUJkNIVJbsJ4PlZqo7bDntWNvq8jARH9emVYUGCJB32COGx9+lTs2v8are7s5\n0DNA70COoWP4Z1+ZjIKjsvCRHFmPtiUP3S9ZuO3Q49LDxyUPe63880xyiPRQL+lcJ+lcN6lcF6nB\nLioGOrH+jihU+sOjb9SyvxP6uw59PjRY5E9rkKoeJ3hCwKRrR4KmsH04fEaFULJSIVRGFBgiR+Du\nDOSc3sEcvQM5+gaGouVgtOwNz6Pth27rG8jRlxuif7DgUfC8L78cbsuNuX3wWBKrgBmHhtGosEmH\n4DqkLWFUJXPUJXrJWh9Zeqimj2p6qPYequghM9RDxntID/WQ8l4qcz2kcj1UDEZBlRzsJjHQRWKg\nk8RAF/R3YWMNIhiz6GRB2ORPr4XnqepRp9wKA6r20P3zy4q0AugYTCQwNEpKZh0zo7LCqKxIUJeJ\n55z/0JDTnxsJkENDJTeyPkY49Q2MCqFR+4z1mvt7BoYD7PDtCQaHMkAGmHNUP48xRBX91CX7mFMx\nQF2yn4ZkH3WJPmoTfdQleqmxXmqsj2rrGwmo/h6q+nqoGtpHpe8gPdRDZa6bylwXqaHeot7bExV4\n6MFYuhYbfV2nsOeTvw40OoQK99WIt3EpMERikEgYmUR03aQc5IacgdwQfQND9OVyh/eYhkMm6pH1\nD+97aMj1jRF6OwaHeGVU7ysfevnXyh/TNzg0fEN+khxZeqOH9VBTsKyh55C2bH8IJHqosW5qbS81\nFo6lh2p6SDJU1GcxkKxiIJkll8qSq8gylMoyVFkbhVJ6JJSSmRqSmToqquuoqKqjoiqE1Qzu/Sgw\nRIRkwkgOB1h8I63cncEhHyOwojDJP+8djIKrLyx7B3PsGxhiRziVmG+LlkP09Q8yNNBDor8TG+yi\nor+Tilw3qYFOUrlu0rkuKoe6qaaH7GAUMvkAyloHNbQPB1eWXqqsv6ifZ4AKeqyKXquiL1lNX6Ka\ngWQ1AxVZBiqy5CpqyKWyeGUWD6Fk6RoSmTqSmdookKpqSVXXUVldSzqVIpNKRgM3KhJUJKe2N6TA\nEJGyYWakkkYqmSCbnvr3H8yFgBnIjSxDMB0My96BIfr7+8j1djDU24H3duJh4IH1d5Lo7yAx2EVy\noGv4mk8+lNK5bjIDB6j116jy6JpRlh6SVtz1ny5P00kVO72KLjJ0U0WPVdFV2cQf/PnNJf50FBgi\nIsMqkglqkglq0lP3X6MPDdHf20Vv1wEGug/S332Qwd6DDPZ0MNRzkKHeDob6OvC+Dqy/i0R/J4mB\nTuoGOpkz2EVq8CCDFQNTUqsCQ0QkRpZIUFldS2V1bdylvC4NBxARkaKUNDDMbI2ZPW9mW8zsmjG2\nf8TMnjSzp8zsATM7rWDb1tC+ycx0c4WISMxKdkrKzJLAdcB7gFbgUTO7zd2fKdjtZeCd7r7PzC4C\n1gFvLdh+vrvvLlWNIiJSvFL2MM4Ctrj7S+7eD9wEXFq4g7s/4O77wtOHgJYS1iMiIseglIGxGNhW\n8Lw1tI3nE8AdBc8duMfMHjOztSWoT0REJqAsRkmZ2flEgXFuQfO57t5mZvOAu83sOXe/f4xj1wJr\nAZYuXTol9YqIzEal7GG0AUsKnreEtkOY2anA3wGXuvuefLu7t4VlO3Ar0Smuw7j7Ondf7e6rm5ub\nJ7F8EREpVMrAeBRYYWbLzawSuBy4rXAHM1sK/AL4qLv/rqA9a2a1+XXgAmBzCWsVEZHXUbJTUu4+\naGafAe4EksB6d3/azK4K228AvgI0At8NX0ozGKbZnQ/cGtoqgJ+5+y9LVauIiLw+fR+GiMgsNpHv\nw9Cd3iIiUhQFhoiIFEWBISIiRVFgiIhIURQYIiJSFAWGiIgURYEhIiJFUWCIiEhRFBgiIlIUBYaI\niBRFgSEiIkVRYIiISFEUGCIiUhQFhoiIFEWBISIiRVFgiIhIURQYIiJSFAWGiIgURYEhIiJFKWlg\nmNkaM3vezLaY2TVjbDcz+1bY/qSZvaXYY0VEZGqVLDDMLAlcB1wErASuMLOVo3a7CFgRHmuB6ydw\nrIiITKFS9jDOAra4+0vu3g/cBFw6ap9LgR975CGgwcwWFnmsiIhMoYoSvvZiYFvB81bgrUXss7jI\nYwEws7VEvROATjN7/ijrbQJ2H+WxpaS6JkZ1TYzqmpiZWNcbit2xlIExJdx9HbDuWF/HzDa6++pJ\nKGlSqa6JUV0To7omZrbXVcrAaAOWFDxvCW3F7JMq4lgREZlCpbyG8SiwwsyWm1klcDlw26h9bgM+\nFkZLnQ0ccPcdRR4rIiJTqGQ9DHcfNLPPAHcCSWC9uz9tZleF7TcAG4CLgS1AN/DxIx1bqlqDYz6t\nVSKqa2JU18SoromZ1XWZu0/F+4iIyDSnO71FRKQoCgwRESnKrA+MuKcgMbOtZvaUmW0ys42hba6Z\n3W1mL4TlnIL9rw21Pm9mF05iHevNrN3MNhe0TbgOMzsj/DxbwrQvVoK6/puZtYXPbJOZXRxDXUvM\n7F4ze8bMnjazz4X2WD+zI9QV62dmZhkze8TMngh1fS20x/15jVdX7P/Gwmsmzey3ZvYv4Xm8v5Pu\nPmsfRBfUXwSOAyqBJ4CVU1zDVqBpVNv/Aq4J69cAfx3WV4Ya08DyUHtykup4B/AWYPOx1AE8ApwN\nGHAHcFEJ6vpvwBfG2Hcq61oIvCWs1wK/C+8f62d2hLpi/czCa9SE9RTwcHjtuD+v8eqK/d9YeM3/\nDPwM+Jdy+J2c7T2Mcp2C5FLgR2H9R8D7C9pvcvc+d3+ZaHTZWZPxhu5+P7D3WOqwaFqXOnd/yKN/\nqT8uOGYy6xrPVNa1w90fD+sdwLNEMxTE+pkdoa7xTFVd7u6d4WkqPJz4P6/x6hrPlP0bM7MW4L3A\n3416/9g+r9keGONNTTKVHLjHzB6zaJoTgPke3Y8C8BowP6xPdb0TrWNxWJ+K+j5r0QzH6wu65bHU\nZWbLgNOJ/jotm89sVF0Q82cWTq9sAtqBu929LD6vceqC+P+NfRP4L8BQQVusn9dsD4xycK67ryKa\nmffTZvaOwo3hr4LYxz6XSx3B9USnEVcBO4D/E1chZlYD3AL8mbsfLNwW52c2Rl2xf2bungv/1luI\n/vo9edT2WD6vceqK9fMysz8A2t39sfH2iePzmu2BUcz0JSXl7m1h2Q7cSnSKaWfoShKW7WH3qa53\nonW0hfWS1ufuO8Mv+RDwfUZOy01pXWaWIvpP+afu/ovQHPtnNlZd5fKZhVr2A/cCayiDz2ususrg\n83obcImZbSU6Vf4uM/sJMX9esz0wYp2CxMyyZlabXwcuADaHGv447PbHwD+H9duAy80sbWbLib5H\n5JESljihOkJX+aCZnR1GYnys4JhJk/+FCT5A9JlNaV3hdX4APOvu3yjYFOtnNl5dcX9mZtZsZg1h\nvQp4D/Ac8X9eY9YV9+fl7te6e4u7LyP6f+nf3P1K4v6dPNqr5TPlQTQ1ye+IRhX8+RS/93FEIxue\nAJ7Ovz/QCPwr8AJwDzC34Jg/D7U+zySMwih43RuJut4DROc5P3E0dQCriX65XgS+Q5hNYJLr+nvg\nKeDJ8IuyMIa6ziU6HfAksCk8Lo77MztCXbF+ZsCpwG/D+28GvnK0/9anqK7Y/40VvO55jIySivXz\n0tQgIiJSlNl+SkpERIqkwBARkaIoMEREpCgKDBERKYoCQ0REiqLAECkDZnZefkZSkXKlwBARkaIo\nMEQmwMyutOj7EzaZ2ffCxHWdZva3Fn2fwr+aWXPYd5WZPRQmsLs1P4Gdmb3RzO6x6DsYHjez48PL\n15jZz83sOTP76TF9b4FICSgwRIpkZicCHwbe5tFkdTngI0AW2OjuJwG/Ar4aDvkx8EV3P5XoruF8\n+0+B69z9NOD3iO5kh2hm2T8j+m6D44jmExIpGxVxFyAyjbwbOAN4NPzxX0U0+dsQ8A9hn58AvzCz\neqDB3X8V2n8E/GOYO2yxu98K4O69AOH1HnH31vB8E7AM+E3pfyyR4igwRIpnwI/c/dpDGs2+PGq/\no51vp69gPYd+P6XM6JSUSPH+FfiQmc2D4e9XfgPR79GHwj5/BPzG3Q8A+8zs7aH9o8CvPPoWvFYz\ne394jbSZVU/pTyFylPQXjEiR3P0ZM/sScJeZJYhm0P000EX0xTtfIjpF9eFwyB8DN4RAeAn4eGj/\nKPA9M/uL8Br/bgp/DJGjptlqRY6RmXW6e03cdYiUmk5JiYhIUdTDEBGRoqiHISIiRVFgiIhIURQY\nIiJSFAWGiIgURYEhIiJF+f/R7kMdpa0UVwAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7eff4c53c2b0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# summarize history for loss\n",
"plt.plot(history.history['loss'])\n",
"plt.plot(history.history['val_loss'])\n",
"plt.title('model loss')\n",
"plt.ylabel('loss')\n",
"plt.xlabel('epoch')\n",
"plt.legend(['train', 'test'], loc='upper left')\n",
"\n",
"plt.ylim([0, 2])\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-04T22:42:56.880710Z",
"start_time": "2017-05-04T22:42:56.876740Z"
},
"collapsed": true
},
"outputs": [],
"source": [
"filePath=\"myfile.txt\""
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:19:36.478009Z",
"start_time": "2017-05-05T21:19:36.460288Z"
},
"collapsed": false
},
"outputs": [],
"source": [
"def writeToFile(history,filePath,columns):\n",
" fh=open(filePath,'a')\n",
" loss=history.history['loss']\n",
" loss_diff=np.diff(loss)\n",
" val_loss=history.history['val_loss']\n",
" val_loss_diff=np.diff(val_loss)\n",
"\n",
" loss_Elbow=min(list((x for x in range(0,len(loss_diff.tolist())) if loss_diff.tolist()[x] > -0.01)))+1\n",
" val_loss_Elbow=min(list((x for x in range(0,len(val_loss_diff.tolist())) if val_loss_diff.tolist()[x] > -0.01)))+1\n",
"\n",
" print(','.join(columns),\"\\tlE\",loss_Elbow,\"\\tvlE\",val_loss_Elbow,\"\\ttepo\",len(history.history['loss']),end='',file=fh)\n",
" print(\"\\tloss\\t{0:0.5f}\".format(history.history['loss'][-1]),\"\\tval_loss\\t{0:0.5f}\".format(history.history['val_loss'][-1]),file=fh)\n"
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-04T22:43:03.008451Z",
"start_time": "2017-05-04T22:43:02.986797Z"
},
"collapsed": false
},
"outputs": [
{
"ename": "NameError",
"evalue": "name 'history' is not defined",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mNameError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m<ipython-input-34-04bf8de6f0a9>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[0;32m----> 1\u001b[0;31m \u001b[0mwriteToFile\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mhistory\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0mfilePath\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0mcolumns\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m'1'\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m'2'\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m",
"\u001b[0;31mNameError\u001b[0m: name 'history' is not defined"
]
}
],
"source": [
"writeToFile(history,filePath,columns=['1','2'])"
]
},
{
"cell_type": "code",
"execution_count": 35,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-04T22:43:07.208900Z",
"start_time": "2017-05-04T22:43:07.204533Z"
},
"collapsed": false
},
"outputs": [],
"source": [
"\n",
"#print(\"loss\\t{0:0.5f}\".format(history.history['loss'][-1]),\"\\tval_loss\\t{0:0.5f}\".format(history.history['val_loss'][-1]))\n",
"\n",
"#print(\"%0.3f \\tval_loss\\t %0.5f \" % history.history['loss'][-1],history.history['val_loss'][-1])"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"ExecuteTime": {
"start_time": "2017-05-05T12:38:31.406Z"
},
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"---------> ['num_room', 'life_sq', 'metro_min_walk', 'nuclear_reactor_km', 'ttk_km', 'zd_vokzaly_avto_km', 'sadovoe_km', 'bulvar_ring_km', 'kremlin_km', 'stadium_km', 'basketball_km', 'ID_railroad_station_walk', 'build_count_slag', 'build_count_panel', 'prom_part_3000', 'build_count_frame', 'build_count_before_1920', 'indust_part', 'raion_build_count_with_material_info', 'build_count_1971-1995', 'green_zone_km', 'railroad_km', 'public_transport_station_km', 'metro_min_avto', 'full_sq', 'life_sq', 'floor', 'max_floor', 'material', 'build_year', 'num_room', 'kitch_sq', 'state', 'radiation_km', 'life_sq', 'big_church_km', 'metro_km_walk', 'public_healthcare_km', 'kremlin_km', 'fitness_km', 'market_shop_km', 'basketball_km', 'zd_vokzaly_avto_km', 'green_part_1500']\n",
"=> loading data:\n",
"=> drop_crazy_data_point:\n",
"shape after drop_crazy_data_point:\n",
"(21836, 292)\n",
"=> prepare data:\n",
"(29498, 390)\n",
"=> handle factors\n",
"(29498, 392)\n",
"=> model arch\n",
"=> train\n",
"^^^INFO: Fit Model^^^\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"/home/minesh/anaconda3/lib/python3.6/site-packages/ipykernel/__main__.py:25: UserWarning: The `Merge` layer is deprecated and will be removed after 08/2017. Use instead layers from `keras.layers.merge`, e.g. `add`, `concatenate`, etc.\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Train on 15285 samples, validate on 6551 samples\n",
"Epoch 1/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 2/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 3/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 4/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 5/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 6/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 7/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 8/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 9/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 10/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 11/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 12/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 13/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 14/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 15/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 16/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 17/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 18/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 19/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 20/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 21/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 22/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 23/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 24/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 25/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 26/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 27/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 28/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 29/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 30/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 31/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 32/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 33/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 34/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 35/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 36/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 37/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 38/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 39/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 40/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 41/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 42/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 43/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 44/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 45/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 46/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 47/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 48/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 49/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 50/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 51/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 52/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 53/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 54/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 55/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 56/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 57/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 58/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 59/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 60/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 61/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 62/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 63/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 64/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 65/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 66/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 67/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 68/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 69/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 70/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 71/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 72/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 73/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 74/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 75/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 76/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 77/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 78/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 79/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 80/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 81/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 82/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 83/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 84/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 85/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 86/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 87/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 88/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 89/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 90/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 91/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 92/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 93/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 94/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 95/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 96/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 97/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 98/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 99/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 100/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 101/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 102/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 103/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 104/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 105/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 106/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 107/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 108/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 109/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 110/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 111/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 112/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 113/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 114/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 115/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 116/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 117/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 118/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 119/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 120/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 121/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 122/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 123/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 124/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 125/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 126/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 127/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 128/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 129/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 130/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 131/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 132/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 133/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 134/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 135/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 136/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 137/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 138/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 139/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 140/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 141/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 142/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 143/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 144/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 145/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 146/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 147/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 148/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 149/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 150/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 151/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 152/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 153/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 154/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 155/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 156/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 157/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 158/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 159/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 160/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 161/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 162/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 163/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 164/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 165/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 166/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 167/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 168/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 169/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 170/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 171/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 172/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 173/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 174/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 175/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 176/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 177/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 178/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 179/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 180/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 181/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 182/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 183/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 184/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 185/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 186/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 187/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 188/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 189/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 190/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 191/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 192/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 193/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 194/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 195/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 196/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 197/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 198/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 199/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 200/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 201/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 202/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 203/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 204/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 205/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 206/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 207/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 208/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 209/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 210/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 211/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 212/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 213/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 214/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 215/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 216/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 217/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 218/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 219/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 220/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 221/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 222/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 223/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 224/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 225/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 226/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 227/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 228/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 229/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 230/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 231/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 232/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 233/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 234/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 235/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 236/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 237/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 238/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 239/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 240/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 241/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 242/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 243/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 244/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 245/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 246/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 247/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 248/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 249/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 250/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 251/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 252/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 253/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 254/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 255/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 256/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 257/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 258/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 259/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 260/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 261/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 262/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 263/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 264/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 265/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 266/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 267/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 268/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 269/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 270/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 271/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 272/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 273/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 274/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 275/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 276/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 277/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 278/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 279/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 280/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 281/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 282/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 283/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 284/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 285/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 286/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 287/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 288/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 289/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 290/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 291/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 292/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 293/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 294/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 295/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 296/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 297/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 298/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 299/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 300/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 301/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 302/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 303/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 304/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 305/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 306/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 307/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 308/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 309/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 310/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 311/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 312/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 313/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 314/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 315/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 316/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 317/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 318/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 319/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 320/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 321/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 322/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 323/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 324/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 325/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 326/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 327/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 328/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 329/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 330/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 331/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 332/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 333/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 334/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 335/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 336/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 337/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 338/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 339/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 340/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 341/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 342/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 343/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 344/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 345/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 346/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 347/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 348/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 349/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 350/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 351/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 352/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 353/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 354/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 355/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 356/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 357/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 358/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 359/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 360/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 361/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 362/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 363/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 364/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 365/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 366/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 367/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 368/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 369/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 370/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 371/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 372/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 373/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 374/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 375/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 376/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 377/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 378/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 379/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 380/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 381/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 382/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 383/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 384/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 385/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 386/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 387/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 388/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 389/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 390/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 391/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 392/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 393/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 394/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 395/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 396/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 397/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 398/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 399/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 400/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 401/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 402/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 403/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 404/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 405/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 406/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 407/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 408/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 409/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 410/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 411/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 412/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 413/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 414/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 415/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 416/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 417/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 418/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 419/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 420/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 421/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 422/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 423/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 424/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 425/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 426/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 427/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 428/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 429/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 430/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 431/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 432/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 433/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 434/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 435/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 436/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 437/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 438/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 439/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 440/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 441/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 442/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 443/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 444/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 445/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 446/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 447/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 448/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 449/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 450/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 451/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 452/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 453/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 454/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 455/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 456/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 457/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 458/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 459/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 460/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 461/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 462/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 463/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 464/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 465/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 466/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 467/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 468/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 469/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 470/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 471/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 472/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 473/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 474/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 475/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 476/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 477/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 478/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 479/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 480/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 481/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 482/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 483/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 484/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 485/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 486/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 487/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 488/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 489/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 490/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 491/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 492/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 493/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 494/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 495/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 496/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 497/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 498/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 499/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 500/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 501/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 502/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 503/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 504/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 505/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 506/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 507/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 508/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 509/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 510/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 511/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 512/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 513/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 514/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 515/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 516/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 517/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 518/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 519/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 520/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 521/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 522/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 523/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 524/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 525/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 526/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 527/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 528/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 529/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 530/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 531/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 532/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 533/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 534/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 535/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 536/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 537/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 538/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 539/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 540/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 541/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 542/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 543/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 544/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 545/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 546/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 547/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 548/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 549/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 550/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 551/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 552/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 553/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 554/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 555/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 556/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 557/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 558/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 559/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 560/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 561/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 562/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 563/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 564/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 565/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 566/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 567/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 568/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 569/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 570/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 571/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 572/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 573/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 574/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 575/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 576/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 577/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 578/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 579/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 580/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 581/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 582/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 583/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 584/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 585/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 586/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 587/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 588/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 589/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 590/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 591/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 592/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 593/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 594/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 595/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 596/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 597/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 598/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 599/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 600/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 601/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 602/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 603/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 604/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 605/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 606/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 607/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 608/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 609/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 610/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 611/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 612/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 613/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 614/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 615/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 616/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 617/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 618/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 619/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 620/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 621/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 622/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 623/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 624/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 625/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 626/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 627/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 628/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 629/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 630/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 631/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 632/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 633/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 634/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 635/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 636/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 637/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 638/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 639/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 640/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 641/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 642/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 643/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 644/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 645/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 646/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 647/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 648/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 649/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 650/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 651/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 652/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 653/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 654/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 655/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 656/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 657/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 658/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 659/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 660/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 661/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 662/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 663/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 664/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 665/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 666/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 667/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 668/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 669/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 670/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 671/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 672/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 673/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 674/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 675/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 676/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 677/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 678/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 679/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 680/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 681/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 682/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 683/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 684/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 685/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 686/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 687/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 688/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 689/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 690/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 691/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 692/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 693/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 694/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 695/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 696/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 697/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 698/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 699/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 700/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 701/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 702/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 703/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 704/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 705/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 706/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 707/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 708/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 709/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 710/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 711/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 712/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 713/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 714/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 715/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 716/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 717/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 718/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 719/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 720/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 721/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 722/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 723/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 724/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 725/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 726/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 727/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 728/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 729/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 730/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 731/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 732/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 733/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 734/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 735/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 736/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 737/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 738/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 739/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 740/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 741/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 742/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 743/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 744/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 745/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 746/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 747/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 748/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 749/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 750/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 751/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 752/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 753/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 754/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 755/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 756/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 757/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 758/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 759/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 760/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 761/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 762/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 763/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 764/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 765/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 766/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 767/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 768/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 769/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 770/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 771/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 772/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 773/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 774/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 775/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 776/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 777/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 778/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 779/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 780/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 781/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 782/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 783/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 784/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 785/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 786/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 787/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 788/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 789/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 790/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 791/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 792/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 793/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 794/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 795/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 796/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 797/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 798/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 799/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 800/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 801/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 802/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 803/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 804/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 805/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 806/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 807/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 808/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 809/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 810/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 811/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 812/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 813/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 814/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 815/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 816/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 817/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 818/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 819/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 820/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 821/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 822/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 823/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 824/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 825/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 826/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 827/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 828/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 829/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 830/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 831/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 832/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 833/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 834/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 835/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 836/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 837/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 838/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 839/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 840/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 841/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 842/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 843/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 844/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 845/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 846/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 847/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 848/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 849/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 850/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 851/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 852/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 853/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 854/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 855/7000\n",
"0s - loss: 243.4148 - val_loss: 248.3149\n",
"Epoch 856/7000\n"
]
}
],
"source": [
"#looping for features\n",
"gr4=[\"full_sq\", \"life_sq\", \"floor\", \"max_floor\", \"material\", \n",
"\"build_year\",\"num_room\", \"kitch_sq\",\"state\",\"radiation_km\"]\n",
"gr3 =[\"green_zone_km\",\"railroad_km\", \"public_transport_station_km\",\"metro_min_avto\" ] \n",
"\n",
"gr1=[\"num_room\", \"life_sq\", \"metro_min_walk\", \"nuclear_reactor_km\", \"ttk_km\", \"zd_vokzaly_avto_km\", \"sadovoe_km\", \"bulvar_ring_km\", \"kremlin_km\", \"stadium_km\"]\n",
"gr2=[\"basketball_km\", \"ID_railroad_station_walk\", \"build_count_slag\", \"build_count_panel\", \"prom_part_3000\", \"build_count_frame\",\n",
" \"build_count_before_1920\", \"indust_part\", \"raion_build_count_with_material_info\",\n",
" \"build_count_1971-1995\"]\n",
"\n",
"gr1=gr1+gr2+gr3+gr4\n",
"gr2=[\"life_sq\", \"big_church_km\", \"metro_km_walk\", \"public_healthcare_km\", \"kremlin_km\",\n",
" \"fitness_km\", \"market_shop_km\", \"basketball_km\", \"zd_vokzaly_avto_km\", \n",
" \"green_part_1500\"]\n",
"\n",
"clist=gr1+gr2\n",
"print(\"--------->\",clist)\n",
"print(\"=> loading data:\")\n",
"[df_train,df_test,df_macro]=load_data()\n",
"print(\"=> drop_crazy_data_point:\")\n",
"df_train=drop_crazy_data_point(clist,df_train)\n",
"print(\"=> prepare data:\")\n",
"[y_train,id_test,num_train,df_all]=take_ytrain_testid_traincnt(df_train,df_test)\n",
"print('=> handle factors')\n",
"[X_train1,X_train2,X_test1,X_test2]=factor(df_all,num_train,gr1,gr2)\n",
"print('=> model arch')\n",
"[model1,model2,model]=baseline_model(X_train1.shape[1],X_train2.shape[1])\n",
"print('=> train')\n",
"[model,history]=trainKeras(model,X_train1,X_train2,y_train,epo=7000)\n",
"print('=>print to file')\n",
"writeToFile(history,filePath=\"try1_concat_lr.txt\",columns=clist)\n",
" "
]
},
{
"cell_type": "code",
"execution_count": 48,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-04T22:58:32.320089Z",
"start_time": "2017-05-04T22:58:32.314386Z"
},
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array([[ 43. , 27. , 4. , ..., 1.30515949,\n",
" 0.27498514, 2.5902411 ],\n",
" [ 34. , 19. , 3. , ..., 0.69453573,\n",
" 0.06526334, 0.93669973],\n",
" [ 43. , 29. , 2. , ..., 0.70069112,\n",
" 0.32875604, 2.1209989 ],\n",
" ..., \n",
" [ 45. , 32.99267568, 10. , ..., 1.72722333,\n",
" 0.63001355, 2.15279162],\n",
" [ 64. , 32. , 5. , ..., 4.89804719,\n",
" 0.26152751, 3.37781368],\n",
" [ 43. , 28. , 1. , ..., 0.7349489 ,\n",
" 0.25015115, 0.58463601]])"
]
},
"execution_count": 48,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"X_train"
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-03T01:53:15.725201Z",
"start_time": "2017-05-03T01:53:15.721230Z"
},
"collapsed": false
},
"outputs": [],
"source": [
"#X_test = X_test.reshape(X_test.shape[0],244,1)"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:31:29.537437Z",
"start_time": "2017-05-05T21:31:29.353190Z"
},
"collapsed": true
},
"outputs": [],
"source": [
"y_test=model.predict([X_test1,X_test2])"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:31:33.708778Z",
"start_time": "2017-05-05T21:31:33.702379Z"
},
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"(7662,)"
]
},
"execution_count": 22,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"y_test[:,0].shape"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"ExecuteTime": {
"end_time": "2017-05-05T21:32:00.604353Z",
"start_time": "2017-05-05T21:32:00.564063Z"
},
"collapsed": false
},
"outputs": [],
"source": [
"df_sub = pd.DataFrame({'id': id_test, 'price_doc': y_test[:,0]})\n",
"\n",
"df_sub.to_csv('sub 2017-04-30_rmsle_vx3_lr_4000epo.csv', index=False) \n",
"\n",
"# 0.49433\n",
"# Epoch 4000/4000\n",
"# 0s - loss: 0.3124 - val_loss: 0.3100\n",
"\n",
"\n",
"#0.40908\n",
"#120/120\n",
"#0s - loss: 0.2793 - val_loss: 0.2215\n",
"\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"submitreal 12 elimstd>3 #0.40566"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.0"
},
"notify_time": "5",
"varInspector": {
"cols": {
"lenName": 16,
"lenType": 16,
"lenVar": 40
},
"kernels_config": {
"python": {
"delete_cmd_postfix": "",
"delete_cmd_prefix": "del ",
"library": "var_list.py",
"varRefreshCmd": "print(var_dic_list())"
},
"r": {
"delete_cmd_postfix": ") ",
"delete_cmd_prefix": "rm(",
"library": "var_list.r",
"varRefreshCmd": "cat(var_dic_list()) "
}
},
"oldHeight": 516,
"position": {
"height": "538px",
"left": "1166px",
"right": "20px",
"top": "120px",
"width": "335px"
},
"types_to_exclude": [
"module",
"function",
"builtin_function_or_method",
"instance",
"_Feature"
],
"varInspector_section_display": "block",
"window_display": false
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| gpl-3.0 |
LSSTC-DSFP/LSSTC-DSFP-Sessions | Sessions/Session05/Day5/MultiwavelengthPhotometry.ipynb | 1 | 26194 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Matched wavelength photometry\n",
"\n",
"**Version 0.1**\n",
"\n",
"For today's problem, we will perform matched-aperture photometry in 3 bands on multiple galaxies within a rich galaxy cluster. Ultimately, we will be looking for trends in galaxy colors and other properties as a function of cluster radius.\n",
"\n",
"Note - we will use `astropy` for these tasks, though the use of [`Source Extractor`](https://www.astromatic.net/software/sextractor) is more standard within the galaxy community.\n",
"\n",
"\n",
"* * *\n",
"\n",
"By M Alpaslan (NYU) & AA Miller (CIERA/Northwestern & Adler)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Problem 0) Install photutils\n",
"\n",
"If you have not already done so, install the [`photutils`](http://photutils.readthedocs.io/en/stable/index.html) package from the `astropy` conda channel *within your DSFP environment*. You will also need the [`scikit-image`](http://scikit-image.org) package.\n",
"\n",
" conda install -c astropy photutils\n",
" conda install scikit-image"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import numpy as np\n",
"import pandas as pd\n",
"import astropy\n",
"from astropy.io import fits\n",
"from photutils.aperture import CircularAperture, CircularAnnulus, EllipticalAperture, EllipticalAnnulus\n",
"from photutils.segmentation import detect_sources, source_properties\n",
"from photutils.detection import detect_threshold\n",
"from photutils.centroids import centroid_com\n",
"from photutils import aperture_photometry\n",
"from photutils.utils import calc_total_error\n",
"import matplotlib.pyplot as plt\n",
"\n",
"%matplotlib notebook"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Problem 1) Download and Examine the Data\n",
"\n",
"The images for this exercise can be downloaded from here: https://northwestern.box.com/s/x6nzuqtdys3jo1nufvswkx62o44ifa11. Be sure to place the images in the same directory as this notebook (but do not add them to your git repo!).\n",
"\n",
"Before we dive in, here is some background information on the images we will be analyzing: the imaging data and the group information all come from the [Galaxy And Mass Assembly (GAMA) survey](http://gama-psi.icrar.org/); and more specifically, its [panchromatic data release](https://arxiv.org/abs/1508.02076). \n",
"\n",
"Many of the difficult steps associated with multiband galaxy photometry have already been done for you: GAMA constructs large mosaics of co-added FITS images in 20 bands to measure photometry. The images we will use today are from the g, r, and i mosaics that I (MA) built $\\sim$7 years ago. They are built from SDSS observations in those bands, and have all been convolved to a seeing of approximately 2”, background subtracted, and renormalized to a common zeropoint of 30 magnitudes. The group catalogue was done by Aaron Robotham (see https://arxiv.org/abs/1106.1994).\n",
"\n",
"In the downloaded directory there are g, r, and i images of 36 galaxies that all belong to the same cluster. These image cutouts have been centered on the galaxy position, are $\\sim$80.7\" on a side, and have a pixel scale of 0.339\"/pix.\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To begin we will focus on a single galaxy, before eventually working on the entire cluster. \n",
"\n",
"**Problem 1a**\n",
"\n",
"Display the $r$-band image of the galaxy 85698. Use a asinh stretch."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"r_filename = \"galaxy_images/85698_sdss_r.fits\"\n",
"r_data = fits.getdata( # complete\n",
"\n",
"plt.imshow( # complete\n",
"\n",
"plt.colorbar()\n",
"plt.tight_layout()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Problem 1b**\n",
"\n",
"Roughly how many sources are present in the image?\n",
"\n",
"*Hint* - an exact count is not required here."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Solution 1b**\n",
"\n",
"*Write your answer here*"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"## Problem 2) Source Detection\n",
"\n",
"Prior to measuring any properties of sources in the image, we must first determine the number of sources present in the image. Source detection is challenging, and there are many different thresholding approaches. \n",
"\n",
"Today, we will streamline this step in order to spend more time focusing on the issues associated with matching photometric measurements across different images. We will use the [`detect_sources`](http://photutils.readthedocs.io/en/stable/api/photutils.segmentation.detect_sources.html#photutils.segmentation.detect_sources) function in `photutils` to identify objects in our image."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The simplest model assumes that the background is constant over the entire image. Once the background is determined, it can be subtracted from the image to determine high significance \"peaks\" corresponding to sources. After this week, we have learned that the background isn't so simple, nevertheless we will use the [`detect_threshold`](http://photutils.readthedocs.io/en/stable/api/photutils.detection.detect_threshold.html#photutils.detection.detect_threshold) convenience function to estimate *a constant* background for our images. `detect_threshold` produces a \"detection image\" that can be used to estimate the significance of the flux detected in any individual pixel.\n",
"\n",
"**Problem 2a** \n",
"\n",
"Create a detection threshold image using the `detect_threshold` function, set the `snr` parameter to 3."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"threshold = detect_threshold( # complete"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Problem 2b**\n",
"\n",
"Develop better intuition for the detection image by plotting it side-by-side with the actual image of the field.\n",
"\n",
"Do you notice anything interesting about the threshold image?"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(7,4))\n",
"\n",
"ax1.imshow( # complete\n",
"ax2.imshow( # complete\n",
"fig.tight_layout()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Following this measurement of the background, we can find sources using the `detect_sources` function. Briefly, this function uses image segmentation to define and assign pixels to sources, which are defined as objects with $N$ connected pixels that are $s$ times brighter than the background (we already set $s = 3$). [Read the docs](http://photutils.readthedocs.io/en/stable/api/photutils.segmentation.detect_sources.html#photutils.segmentation.detect_sources) for further details.\n",
"\n",
"**Problem 2c**\n",
"\n",
"Generate a segmentation image using `detect_sources`. Keep only sources with $N = 7$ pixels, which is keyword arg `npixels` in detect_sources.\n",
"\n",
"*If you have extra time* Come back to this problem and see how changing $N$ affects your results."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"segm = detect_sources( # complete"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Problem 2d**\n",
"\n",
"Plot the segmentation image side-by-side with the actual image of the field.\n",
"\n",
"Are you concerned or happy with the results?\n",
"\n",
"*Hint* - no stretch should be applied to the segmentation image."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(7,4))\n",
"\n",
"ax1.imshow(# complete\n",
"ax2.imshow(# complete\n",
"fig.tight_layout()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Problem 3) Source Centroids and Shapes\n",
"\n",
"Now that we have defined all of the sources in the image, we must determine the centroid for each source (in order to ultimately make some form of photometric measurement). As Dora mentioned earlier in the week, there are many ways to determine the centroid of a given source (e.g., fitting a model, finding the max of the marginalized 1-d distribution, etc). Today we will use the [`centroid_com`](http://photutils.readthedocs.io/en/stable/api/photutils.centroids.centroid_com.html#photutils.centroids.centroid_com) function, which calculates the \"center of mass\" of the 2d image moments to determine the source centroids.\n",
"\n",
"To measure the centroid we want to isolate the source in question, thus we have generated a convenience function to return the extent of each source from its corresponding segmentation image."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def get_source_extent(segm_data, source_num):\n",
" \"\"\"\n",
" Determine extent of sources for centroid measurements\n",
" \n",
" Parameters\n",
" ----------\n",
" segm_data : array-like\n",
" Segementation image produced by photutils.segmentation.detect_sources\n",
" \n",
" source_num : int\n",
" The source number from the segmentation image\n",
" \n",
" Returns\n",
" -------\n",
" source_extent : list\n",
" The minimum y, maximum y, minimum x, and maximum x pixel values \n",
" over which a source is detected\n",
" \"\"\"\n",
" source_pix = np.where(segm_data == source_num)\n",
" source_extent = [np.min(source_pix[0]), np.max(source_pix[0]), \n",
" np.min(source_pix[1]), np.max(source_pix[1])]\n",
"\n",
" return source_extent"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Problem 3a** \n",
"\n",
"Measure the centroid for each source detected in the image using the `centroid_com` function.\n",
"\n",
"*Hint* - you'll want to start with a subset of pixels containing the source.\n",
"\n",
"*Hint 2* - centroids are measured relative to the provided data, you'll need to convert back to \"global\" pixel values. "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"xcentroid = np.zeros_like(np.unique(segm.data)[1:], dtype=\"float\")\n",
"ycentroid = np.zeros_like(np.unique(segm.data)[1:], dtype=\"float\")\n",
"\n",
"for source_num in np.unique(segm.data)[1:]:\n",
" source_extent = get_source_extent( # complete\n",
" xc, yc = centroid_com( # complete\n",
" xcentroid[source_num-1], ycentroid[source_num-1] = # complete"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"**Problem 3b**\n",
"\n",
"Overplot the derived centroids on the image data as a sanity check for your methodology."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"fig, ax1 = plt.subplots()\n",
"\n",
"ax1.imshow( # complete\n",
"ax1.plot( # complete\n",
"fig.tight_layout()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"With an estimate of the centroid of every source in hand, we now need to determine the ellipse that best describes the galaxies in order to measure their flux. Fortunately, this can be done using the [`source_properties`](http://photutils.readthedocs.io/en/stable/api/photutils.segmentation.source_properties.html#photutils.segmentation.source_properties) function within [`photutils.morphology`](http://photutils.readthedocs.io/en/stable/morphology.html) package.\n",
"\n",
"Briefly, `source_properties` takes both the data array, and the segmentation image as inputs, and then calculates properties for every source. The list of properties is long (see the attributes list), and for now we only care about the semi-major and semi-minor axes as well as the orientation of the source, all of which are needed to measure the flux in an elliptical aperture [this is a lot easier than trying to fit concentric ellipses, no?].\n",
"\n",
"**Problem 3c**\n",
"\n",
"Using `source_properties` to determine $a$, $b$, and the orientation of each source."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"cat = source_properties( # complete\n",
"tbl = cat.to_table(columns=['id', 'semimajor_axis_sigma','semiminor_axis_sigma', 'orientation'])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Problem 4) Photometry\n",
"\n",
"We now have all the necessary information to measure the flux in elliptical apertures. The [`EllipticalAperture`](http://photutils.readthedocs.io/en/stable/api/photutils.EllipticalAperture.html#) function in `photutils` defines apertures on an image based on input centroids, $a$, $b$, and orientation values. \n",
"\n",
"**Problem 4a**\n",
"\n",
"Define apertures for the sources that are detected in the image.\n",
"\n",
"*Note* - the `semimajor_axis_sigma` reported by `source_properties()` is the \"The 1-sigma standard deviation along the semimajor axis of the 2D Gaussian function that has the same second-order central moments as the source\" [according to the docs](http://photutils.readthedocs.io/en/stable/api/photutils.segmentation.SourceProperties.html#photutils.segmentation.SourceProperties.semimajor_axis_sigma). Thus, be sure to multiple $a$ and $b$ by a factor of 3 in order to capture $\\sim$3$\\sigma$ of the source flux.\n",
"\n",
"*Note to the note* - this isn't well motivated, but for the sake of argument assume that this adjustment creates a reasonable aperture."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"positions = # complete\n",
"\n",
"apertures = [EllipticalAperture( # complete\n",
" # complete\n",
" # complete\n",
" # complete"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Problem 4b** \n",
"\n",
"Overplot your apertures on the sources that have been detected.\n",
"\n",
"*Hint* - each aperture object has a [`plot()`](http://photutils.readthedocs.io/en/stable/api/photutils.EllipticalAperture.html#photutils.EllipticalAperture.plot) attribute that can be used to show the aperture for each source."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"fig, ax1 = plt.subplots()\n",
"\n",
"ax1.imshow( # complete\n",
"# complete\n",
"# complete\n",
"fig.tight_layout()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"With apertures now defined, we can *finally* measure the flux of each source. The [`aperture_photometry`](http://photutils.readthedocs.io/en/stable/api/photutils.aperture_photometry.html#photutils.aperture_photometry) function returns the flux (actually counts) in an image for the provided apertures. It takes the image, apertures, and bakground image as arguments.\n",
"\n",
"*Note* - the background has already been subtracted from these images so we currently do not have an estimate of the **full** background for these sources.\n",
"\n",
"We will create a background image that is approximately correct (we know this because we know the properties of the SDSS survey and detector). In this case what we are doing is not only incorrect, it's entirely made up and should not be repeated in your own work. Nevertheless, this (bad) approximation is necessary to produce uncertainty estimates.\n",
"\n",
"Execute the cell below to create an uncertainty image to use with the `aperture_photometry` function."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"bkg = np.random.normal(100, 35, r_data.shape)\n",
"uncertainty_img = calc_total_error(r_data, bkg - np.mean(bkg), 1)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Problem 4c**\n",
"\n",
"Measure the counts and uncertainty detected from each source within the apertures defined in 4a. \n",
"\n",
"*Hint* - you will need to loop over each aperture as `aperture_photometry` does not take multiple apertures of different shapes as a single argument. "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"source_cnts = # complete\n",
"source_cnts_unc = # complete\n",
"for source_num, ap in enumerate(apertures):\n",
" phot = # complete\n",
" source_cnts[source_num] = # complete\n",
" source_cnts_unc[source_num] = # complete"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The images have been normalized to a zero point of 30. Thus, we can convert from counts to magnitudes via the following equation: \n",
"\n",
"$$m = 30 - 2.5 \\log (\\mathrm{counts}).$$\n",
"\n",
"Recall from Dora's talk that the uncertainty of the magnitude measurements can be calculated as: \n",
"\n",
"$$\\frac{2.5}{\\ln(10)} \\frac{\\sigma_\\mathrm{counts}}{\\mathrm{counts}}.$$\n",
"\n",
"**Problem 4d**\n",
"\n",
"Calculate the magnitude of each source in the image."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"source_mag = # complete\n",
"source_mag_unc = # complete\n",
"\n",
"for source_num, (mag, mag_unc) in enumerate(zip(source_mag, source_mag_unc)):\n",
" print(\"Source {:d} has m = {:.3f} +/- {:.3f} mag\".format( # complete"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"That's it! You've measured the magnitude for every source in the image.\n",
"\n",
"As previously noted, the images provided for this dataset are centered are galaxies within a cluster, and ultimately, these galaxies are all that we care about. For this first image, that means we care about the galaxy centered at $(x,y) \\approx (118, 118)$. \n",
"\n",
"**Problem 4e**\n",
"\n",
"What is the magnitude of the galaxy we care about for this image? [We will need this moving forward]"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# complete"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Problem 5) Multiwavelength Photometry\n",
"\n",
"Ultimately we want to measure colors for these galaxies. We now know the $r$-band magnitude for galaxy 85698, we need to measure the $g$ and $i$ band magnitudes as well. \n",
"\n",
"**Problem 5a** Using the various pieces described above, write a function to measure the magnitude of the galaxy at the center of the image. You should create a new background image for every field. \n",
"\n",
"*Hint* - creating an actual function is essential as we will eventually run this on every image. \n",
"\n",
"*Hint 2* - `source_properties` directly measures source centroids, use this it will be faster."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def cluster_galaxy_photometry(data):\n",
" '''\n",
" Determine the magnitude of the galaxy at the center of the image\n",
" \n",
" Parameters\n",
" ----------\n",
" data : array-like\n",
" Background subtracted 2D image centered on the galaxy\n",
" of interest\n",
" \n",
" Returns\n",
" -------\n",
" mag : float\n",
" Magnitude of the galaxy\n",
" \n",
" mag_unc : float\n",
" Uncertainty of the magnitude measurement\n",
" '''\n",
"\n",
" # complete\n",
" # complete\n",
" # complete\n",
" # complete\n",
" # complete\n",
" # complete\n",
" # complete\n",
" # complete\n",
" # complete\n",
" # complete\n",
" # complete\n",
" # complete\n",
" # complete\n",
" \n",
" \n",
" return mag, mag_unc"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Problem 5b**\n",
"\n",
"Confirm that the function calculates the same $r$-band mag that was calculated in **Problem 4**."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# complete\n",
"\n",
"print(\"\"\"Previously, we found m = {:.3f} mag. \n",
"This new function finds m = {:.3f} mag.\"\"\".format( # complete"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Problem 5c** \n",
"\n",
"Use this new function to calculate the galaxy magnitude in the $g$ and the $i$ band, and determine the $g - r$ and $r - i$ colors of the galaxy."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"g_data = fits.getdata( # complete\n",
"i_data = fits.getdata( # complete\n",
"\n",
"# complete\n",
"# complete\n",
"# complete\n",
"print(\"\"\"The g-r color = {:.3f} +/- {:.3f} mag.\n",
"The r-i color = {:.3f} +/- {:.3f} mag\"\"\".format(g_mag - r_mag, np.hypot(g_mag_unc, r_mag_unc), \n",
" r_mag - i_mag, np.hypot(r_mag_unc, i_mag_unc)))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"But wait!\n",
"\n",
"**Problem 5d**\n",
"\n",
"Was this calculation \"fair\"?\n",
"\n",
"*Hint* - this is a relatively red galaxy."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Solution 5d**\n",
"\n",
"This calculation was not \"fair\" because identical apertures were not used in all 3 filters. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Problem 5e** \n",
"\n",
"[Assuming your calculation was not fair] Calculate the $g - r$ and $r - i$ colors of the galaxy in a consistent fashion.\n",
"\n",
"*Hint* - split your initial function into two functions, one to determine an aperture and another to measure photometry. Use the $r$-band image (where the signal-to-noise ratio of the data is highest) to define the aperture for all 3 images."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def cluster_galaxy_aperture(data):\n",
"# complete\n",
"# complete\n",
"# complete\n",
"# complete\n",
"# complete\n",
"# complete\n",
"# complete\n",
"# complete\n",
"# complete\n",
"# complete\n",
"# complete\n",
" return aperture\n",
"\n",
"def cluster_galaxy_phot(data, aperture):\n",
"# complete\n",
"# complete\n",
"# complete\n",
"# complete\n",
"# complete\n",
" return mag, mag_unc"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"r_ap = # complete\n",
"\n",
"# complete\n",
"# complete\n",
"# complete\n",
"\n",
"print(\"\"\"The g-r color = {:.3f} +/- {:.3f} mag.\n",
"The r-i color = {:.3f} +/- {:.3f} mag\"\"\".format(g_mag - r_mag, np.hypot(g_mag_unc, r_mag_unc), \n",
" r_mag - i_mag, np.hypot(r_mag_unc, i_mag_unc)))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Challenge Problem) Colors as a Function of Radius\n",
"\n",
"Each of the provided FITS images corresponds to a single galaxy in the galaxy cluster. Measure the colors for each galaxy, and plot these colors as a function of cluster radius.\n",
"\n",
"*Hint* - the file `galsAngSep.txt` has the galaxy names and separation from the center of the cluster."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.2"
},
"livereveal": {
"height": 768,
"scroll": true,
"start_slideshow_at": "selected",
"theme": "solarized",
"width": 1024
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
gregoryg/cdh-projects | notebooks/jupyter/datascience/K Means Cluster Visualization.ipynb | 1 | 7540 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Visualizing clusters in Python\n",
"\n",
"I am wanting to see the results of clustering methods such as K-Means; this is my playground.\n",
"\n",
"Initial examples are taken from [K Means Clustering in Python](http://stamfordresearch.com/k-means-clustering-in-python/)\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import matplotlib.pyplot as plt\n",
"from sklearn import datasets\n",
"from sklearn.cluster import KMeans\n",
"import sklearn.metrics as sm\n",
"\n",
"import pandas as pd\n",
"import numpy as np\n",
"\n",
"# Only needed if you want to display your plots inline if using Notebook\n",
"# change inline to auto if you have Spyder installed\n",
"%matplotlib inline"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Using Iris Dataset\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# import some data to play with\n",
"iris = datasets.load_iris()\n",
"# look at individual aspects by uncommenting the below\n",
"#iris.data\n",
"#iris.feature_names\n",
"#iris.target\n",
"#iris.target_names"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Original author converted the data to Pandas Dataframes. Note that we have separated out the inputs (x) and the outputs/labels (y)."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Store the inputs as a Pandas Dataframe and set the column names\n",
"x = pd.DataFrame(iris.data)\n",
"x.columns = ['Sepal_Length','Sepal_Width','Petal_Length','Petal_Width']\n",
"\n",
"y = pd.DataFrame(iris.target)\n",
"y.columns = ['Targets']"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Visualise the data\n",
"\n",
"It is always important to have a look at the data. We will do this by plotting two scatter plots. One looking at the Sepal values and another looking at Petal. We will also set it to use some colours so it is clearer."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Set the size of the plot\n",
"plt.figure(figsize=(14,7))\n",
"\n",
"# Create a colormap\n",
"colormap = np.array(['red', 'lime', 'black'])\n",
"\n",
"# Plot Sepal\n",
"plt.subplot(1, 2, 1)\n",
"plt.scatter(x.Sepal_Length, x.Sepal_Width, c=colormap[y.Targets], s=40)\n",
"plt.title('Sepal')\n",
"\n",
"plt.subplot(1, 2, 2)\n",
"plt.scatter(x.Petal_Length, x.Petal_Width, c=colormap[y.Targets], s=40)\n",
"plt.title('Petal');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Build the K Means Model - non-Spark example\n",
"This is the easy part, providing you have the data in the correct format (which we do). Here we only need two lines. First we create the model and specify the number of clusters the model should find (n_clusters=3) next we fit the model to the data."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# K Means Cluster\n",
"model = KMeans(n_clusters=3)\n",
"model.fit(x)\n",
"1\n",
"2\n",
"3\n",
"# K Means Cluster\n",
"model = KMeans(n_clusters=3)\n",
"model.fit(x)\n",
"\n",
"# This is what KMeans thought\n",
"model.labels_"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Visualise the classifier results\n",
"Let's plot the actual classes against the predicted classes from the K Means model.\n",
"\n",
"Here we are plotting the Petal Length and Width, however each plot changes the colors of the points using either c=colormap[y.Targets] for the original class and c=colormap[model.labels_] for the predicted classess."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# View the results\n",
"# Set the size of the plot\n",
"plt.figure(figsize=(14,7))\n",
"\n",
"# Create a colormap\n",
"colormap = np.array(['red', 'lime', 'black'])\n",
"\n",
"# Plot the Original Classifications\n",
"plt.subplot(1, 2, 1)\n",
"plt.scatter(x.Petal_Length, x.Petal_Width, c=colormap[y.Targets], s=40)\n",
"plt.title('Real Classification')\n",
"\n",
"# Plot the Models Classifications\n",
"plt.subplot(1, 2, 2)\n",
"plt.scatter(x.Petal_Length, x.Petal_Width, c=colormap[model.labels_], s=40)\n",
"plt.title('K Mean Classification');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Fixing the coloring\n",
"\n",
"Here we are going to change the class labels, we are not changing the any of the classification groups we are simply giving each group the correct number. We need to do this for measuring the performance.\n",
"\n",
"Using this code below we using the np.choose() to assign new values, basically we are changing the 1’s in the predicted values to 0’s and the 0’s to 1’s. Class 2 matched so we can leave. By running the two print functions you can see that all we have done is swap the values.\n",
"\n",
"NOTE: your results might be different to mine, if so you will have to figure out which class matches which and adjust the order of the values in the np.choose() function."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# The fix, we convert all the 1s to 0s and 0s to 1s.\n",
"predY = np.choose(model.labels_, [1, 0, 2]).astype(np.int64)\n",
"print (model.labels_)\n",
"print (predY)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Re-plot\n",
"\n",
"Now we can re plot the data as before but using predY instead of model.labels_."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# View the results\n",
"# Set the size of the plot\n",
"plt.figure(figsize=(14,7))\n",
"\n",
"# Create a colormap\n",
"colormap = np.array(['red', 'lime', 'black'])\n",
"\n",
"# Plot Orginal\n",
"plt.subplot(1, 2, 1)\n",
"plt.scatter(x.Petal_Length, x.Petal_Width, c=colormap[y.Targets], s=40)\n",
"plt.title('Real Classification')\n",
"\n",
"# Plot Predicted with corrected values\n",
"plt.subplot(1, 2, 2)\n",
"plt.scatter(x.Petal_Length, x.Petal_Width, c=colormap[predY], s=40)\n",
"plt.title('K Mean Classification');"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.13"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| apache-2.0 |
evanmiltenburg/python-for-text-analysis | Assignments/ASSIGNMENT-1.ipynb | 1 | 23090 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Assignment 1: Calculation, Strings, Boolean Expressions and Conditions\n",
"\n",
"**Deadline: Friday, September 9, 2021 before 3pm (submit via Canvas: Block I/Assignment 1)** \n",
"\n",
"\n",
"This assignment is **not graded**, but it is mandatory to submit a version that shows you have given it a serious try. We will check your assignments to monitor the progress and get an impression of how the course is going so far. You will receive feedback and solutions on Monday September 13. **Please note that the material taught in this block is essential for all subsequent blocks.** \n",
"\n",
"- Please name your notebook with the following naming convention: ASSIGNMENT_1_FIRSTNAME_LASTNAME.ipynb\n",
"- If you have **questions** about this topic, please contact **[email protected]**.\n",
"\n",
"\n",
"In this block, we covered the following chapters:\n",
"\n",
"- Chapter 1 - Getting Started with Variables and Values\n",
"- Chapter 2 - Basic Data Types (Integers and Floats)\n",
"- Chapter 3 - Strings\n",
"- Chapter 4 - Boolean Expressions and Conditions\n",
"\n",
"In this assignment, you will be asked to show what you have learned from the topics above! \n",
"\n",
"**Looking things up**\n",
"\n",
"Don't worry - you do not have to know things by heart yet - feel free to have all Chapters of block 1 open while you work on this. This also goes for all future assignments. \n",
"\n",
"**Finding solutions online**\n",
"\n",
"Very often, you can find good solutions online. We encourage you to use online resources when you get stuck. However, please always try to understand the code you find and indicate that it is not your own. Use the following format to mark code written by someone else:\n",
"\n",
"###Taken from [link] [date]\n",
"\n",
"[code]\n",
"\n",
"\\###\n",
"\n",
"Please use a similar format to indicate that you have worked with a classmate (e.g. mention the name instead of the link). \n",
"\n",
"*Indicating online resources and collaboration is mandatory! Please stick to this strategy for all course assignments.*\n",
"\n",
"**Being stuck and getting help**\n",
"\n",
"It is very normal to get stuck every now and then. Sometimes you find what is wrong within minutes, sometimes this takes longer. If you get stuck, please apply the strategies described in the readme. If none of them work, please contact us ([email protected]). "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Exercise 1: Calculation\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 1a. Average \n",
"Define three variables `var1`, `var2` and `var3`. Calculate the average of these variables and assign it to the variable `average`. Print the outcome of your program as follows (use casting or an f-string):\n",
"\n",
"`The average of [...], [...] and [...] is: [...]`"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# average code"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 1b. Book prices\n",
"\n",
"\n",
"Calculate book prices for the following scenarios:\n",
"\n",
"Suppose the price of a book is 24.95 EUR, but if the book is bought by a bookstore, they get a 30 percent discount (as opposed to customers buying from an online stores). Shipping costs 3 EUR for the first copy and 75 cents for each additional copy. Shipping costs always apply (the books also have to be shipped to the bookstore). \n",
"\n",
"Write a program that can calculate the total costs for any number of copies for both bookstores and other customers. Use variables with clear names for your calculations and print the result using a full sentence.\n",
"\n",
"The program should use variables which indicate whether the customer is a bookstore or not and how many books are bought. You can simply assign values to the variables in you code or use the input function (both is accepted).\n",
"\n",
"\n",
"**Tip**\n",
"\n",
"Start small and add things in steps. For instance, start by calculating the price minus the discount. Then add the additional steps. Also, it helps to a start by simply assuming a specific number of books (start with 1 and make sure it works with any other number). Do not forget to test your program! "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# complete the code below\n",
"\n",
"n_books = \n",
"customer_is_bookstore = \n",
"\n",
"# you bookprice calculations here"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 1c. The modulus operator \n",
"\n",
"There is one operator (like the ones for multiplication and subtraction) that we did not discuss yet, namely the modulus operator %. Could you figure out by yourself what it does when you place it between two numbers (e.g. 113 % 9)? (PS: Try to figure it out by yourself first, by trying multiple combinations of numbers. If you do not manage, it's OK to use online resources...) \n",
"\n",
"You don't need this operator all that often, but when you do, it comes in really handy! Also, it is important to learn how to figure out what operators/methods/functions you have never seen before do by playing with code, googling or reading documentation. \n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# try out the modulus operator!\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Help the cashier**\n",
"\n",
"Can you use the modulus operator you just learned about to solve the following task? Imagine you want to help cashiers to return the change in a convenient way. This means you do not want to return hands full of small coins, but rather use bills and as few coins as possible. \n",
"\n",
"Write code that classifies a given amount of money into smaller monetary units. Given a specific amout of dollars, your program should report the maximum number of dollar bills, quarters, dimes, nickels, and pennies. \n",
"\n",
"Set the amount variable to 11.67. You code should output a report listing the monetary equivalent in dollars, quarters, dimes, nickels, and pennies (one quarter is equivalent to 25 cents; one dime to 10 cents; one nickle to 5 cents and a pennie to 1 cent). Your program should report the maximum number of dollars, then the number of quarters, dimes, nickels, and pennies, in this order, to result in the minimum number of coins. Here are the steps in developing the program:\n",
"\n",
"1. Convert the amount (11.67) into cents (1167).\n",
"2. First get the amount of cents that you would get after subtracting the maximum amount of dollars (100 cents) using the modulus operator (67 cents).\n",
"3. Then subtract the remainder (67 cents) from the total amount of cents (1167 cents) and divide this by 100 to find the number of dollars.\n",
"4. Use the modulus operator again to find out the remainder after subtracting the maximum amount of quarters (17 cents).\n",
"5. Subtract this remainder (17 cents) from the previous remainder (67 cents) and divide this by 25 to find out the number of quarters.\n",
"6. Follow the same steps for the dimes, nickels and pennies.\n",
"7. Display the result for your cashier! (the amount of dollars, quarters, dimes, nickels and pennies that (s)he would have to give back)`"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# cashier code"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Exercise 2: Printing and user input\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 2a. Difference between \",\" and \"+\"\n",
"\n",
"What is the difference between using **+** and **,** in a print statement? Illustrate by using both in each of the following:\n",
"\n",
"* calling the `print()` fuction with multiple strings\n",
"* printing combinations of strings and integers\n",
"* concatenating multiple strings and assign to one single variable\n",
"* concatenating strings and integers and assign to one single variable"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 2b. Small Talk\n",
"Write a program to have a little conversation with someone. First ask them for their name and their age, and then say something about your own age compared to theirs. Your code should result in a conversation following this example:\n",
"\n",
"> `Hello there! What is your name?`\n",
"\n",
"> -- Emily.\n",
"\n",
"> `Nice to meet you, Emily. How old are you?`\n",
"\n",
"> -- 23\n",
"\n",
"> `I'm 25 years old, so I'm 2 years older than you.`\n",
"\n",
"Also account for situations where the other person is older or the same age. You will need to use `if-else`-statements!"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"name = input(\"Hello there! What is your name? \")\n",
"# finish this code"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Exercise 3: String Art"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 3a. Drawing figures\n",
"We start with some repetition of the theory about strings:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"| Topic | Explanation |\n",
"|-----------|--------|\n",
"| `quotes` |\tA string is delimited by single quotes ('...') or double quotes (\"...\") |\n",
"| `special characters` |\tCertain special characters can be used, such as \"\\n\" (for newline) and \"\\t\" (for a tab) \t| \t \n",
"| `printing special characters` |\tTo print the special characters, they must be preceded by a backslash (\\\\)\t |\n",
"| `continue on next line` |\tA backslash (\\\\) at the end of a line is used to continue a string on the next line\t \t |\n",
"| `multi-line strings` |\tA multi-line print statement should be enclosed by three double or three single quotes (\"\"\"...\"\"\" of '''...''')\t | "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Please run the code snippet below and observe what happens:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"print('hello\\n')\n",
"print('To print a newline use \\\\n')\n",
"print('She said: \\'hello\\'')\n",
"print('\\tThis is indented')\n",
"print('This is a very, very, very, very, very, very \\\n",
"long print statement')\n",
"print('''\n",
"This is a multi-line print statement\n",
"First line\n",
"Second line\n",
"''')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now write a Python script that prints the following figure using **only one line of code**! (so don't use triple quotes)\n",
"\n",
" | | |\n",
" @ @\n",
" u\n",
" |\"\"\"|\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# your code here"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 3b. Colors\n",
"We start again with some repetition of the theory:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"| Topic | Explanation |\n",
"|-----------|--------|\n",
"| a = b + c\t| if b and c are strings: concatenate b and c to form a new string a| \n",
"| a = b * c\t| if b is an integer and c is a string: c is repeated b times to form a new string a |\n",
"| a[0] |\t the first character of string a |\n",
"| len(a) |\t the number of characters in string a |\n",
"| min(a) |\t the smallest element in string a (alphabetically first) |\n",
"| max(a) |\t the largest element in string a (alphabetically last) |"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Please run the code snippet below and observe what happens:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"b = 'the'\n",
"c = 'cat'\n",
"d = ' is on the mat'\n",
"a = b + ' ' + c + d\n",
"print(a)\n",
"a = b * 5\n",
"print(a)\n",
"print('The first character of', c, 'is' , c[0])\n",
"print('The word c has,', len(c) ,'characters')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now write a program that asks users for their favorite color. Create the following output (assuming \"red\" is the chosen color). Use \"+\" and \"\\*\".\n",
"It should work with any color name though.\n",
"\n",
"```xml\n",
"red red red red red red red red red red \n",
"red red\n",
"red red\n",
"red red red red red red red red red red\n",
"```"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"color = input('what is your favorite color? ')\n",
"\n",
"print(color)\n",
"print(color)\n",
"print(color)\n",
"print(color)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Exercise 4: String methods \n",
"\n",
"Remember that you can see all methods of the class `str` by using `dir()`. You can ignore all methods that start with one or two underscores. "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"dir(str)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To see the explanation for a method of this class, you can use `help(str.method)`. For example:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"help(str.upper)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 4a. Counting vowels\n",
"Count how many of each vowel (a,e,i,o,u) there are in the text string in the next cell. Print the count for each vowel with a single formatted string. Remember that vowels can be both lower and uppercase."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"text = \"\"\"But I must explain to you how all this mistaken idea of denouncing pleasure and praising pain was born \n",
"and I will give you a complete account of the system, and expound the actual teachings of the great explorer of the \n",
"truth, the master-builder of human happiness. No one rejects, dislikes, or avoids pleasure itself, because it is \n",
"pleasure, but because those who do not know how to pursue pleasure rationally encounter consequences that are \n",
"extremely painful. Nor again is there anyone who loves or pursues or desires to obtain pain of itself, because it is \n",
"pain, but because occasionally circumstances occur in which toil and pain can procure him some great pleasure. \n",
"To take a trivial example, which of us ever undertakes laborious physical exercise, except to obtain some advantage \n",
"from it? But who has any right to find fault with a man who chooses to enjoy a pleasure that has no annoying \n",
"consequences, or one who avoids a pain that produces no resultant pleasure? On the other hand, we denounce with \n",
"righteous indignation and dislike men who are so beguiled and demoralized by the charms of pleasure of the moment, \n",
"so blinded by desire, that they cannot foresee the pain and trouble that are bound to ensue; and equal blame belongs \n",
"to those who fail in their duty through weakness of will, which is the same as saying through shrinking from toil \n",
"and pain.\"\"\"\n",
"\n",
"# your code here"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 4b. Printing the lexicon\n",
"Have a good look at the internal representation of the string below. Use a combination of string methods (you will need at least 3 different ones and some will have to be used multiple times) in the correct order to remove punctuation and redundant whitespaces, and print each word in lowercase characters on a new line. The result should look like:\n",
"\n",
"`the \n",
"quick \n",
"brown \n",
"fox \n",
"jumps \n",
"etc.`"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"text = \"\"\" The quick, brown fox jumps over a lazy dog.\\tDJs flock by when MTV ax quiz prog. \n",
"Junk MTV quiz graced by fox whelps.\\tBawds jog, flick quartz, vex nymphs. \n",
"Waltz, bad nymph, for quick jigs vex!\\tFox nymphs grab quick-jived waltz. \n",
"Brick quiz whangs jumpy veldt fox. \"\"\"\n",
"\n",
"print(text)\n",
"print()\n",
"print(repr(text))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"text = # your code here\n",
"\n",
"print(text)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 4c. Passwords\n",
"\n",
"Write a program that asks a user for a password and checks some simple requirements of a password. If necessary, print out the following warnings (use if-statements):\n",
"\n",
"1. Your password should contain at least 6 characters.\n",
"2. Your password should contain no more than 12 characters.\n",
"3. Your password only contains alphabetic characters! Please also use digits and/or special characters.\n",
"4. Your password only contains digits! Please also use alphabetic and/or special characters.\n",
"5. Your password should contain at least one special character.\n",
"6. Your password contains only lowercase letters! Please also use uppercase letters.\n",
"7. Your password contains only uppercase letters! Please also use lowercase letters."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# your code here"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Exercise 5: Boolean Logic and Conditions"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 5a. Speeding\n",
"\n",
"Write code to solve the following scenario:\n",
"\n",
"You are driving a little too fast, and a police officer stops you. Write code to compute and print the result, encoded as a string: 'no ticket', 'small ticket', 'big ticket'. If speed is 60 or less, the result is 'no ticket'. If speed is between 61 and 80 inclusive, the result is 'small ticket'. If speed is 81 or more, the result is 'big ticket'. Unless it is your birthday -- on that day, your speed can be 5 higher in all cases.\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# your code here"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 5b. Alarm clock\n",
"\n",
"Write code to set you alarm clock! Given the day of the week and information about whether you are currently on vacation or not, your code should print the time you want to be woken up following these constraints: \n",
"\n",
"Weekdays, the alarm should be \"7:00\" and on the weekend it should be \"10:00\". Unless we are on vacation -- then on weekdays it should be \"10:00\" and weekends it should be \"off\".\n",
"\n",
"\n",
"Encode the weeks days as ints in the following way: 0=Sun, 1=Mon, 2=Tue, ...6=Sat. Encode the vacation infromation as boolean. Your code should assign the correct time to a variable as a string (following this format: \"7:00\") and print it.\n",
"\n",
"Note: Encoding the days as an integer helps you with defining conditions. You can check whether the week day is in a certain interval (instead of writing code for every single day). "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# your code here"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### 5c. Parcel delivery\n",
"The required postage for an international parcel delivery service is calculated based on item weight and country of destination:\n",
"\n",
"\n",
"| Tariff zone | 0 - 2 kg | 2 - 5 kg | 5 - 10 kg | 10 - 20 kg | 20 - 30 kg |\n",
"|-------------|----------|----------|-----------|------------|------------|\n",
"|EUR 1 | € 13.00 | € 19.50 | € 25.00 | € 34.00 | € 45.00 | \n",
"|EUR 2 | € 18.50 | € 25.00 | € 31.00 | € 40.00 | € 55.00 | \n",
"|World | € 24.30 | € 34.30 | € 58.30 | € 105.30 | - | \n",
"\n",
"Ask a user for the `weight` and `zone`. Use (nested) `if`-statements to find the required postage based on these variables. Assign the result to a variable `postage` and print the result using a full sentence:\n",
"\n",
"`The price of sending a [...] kg parcel to the [...] zone is € [...].`"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# your code here"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.3"
}
},
"nbformat": 4,
"nbformat_minor": 4
}
| apache-2.0 |
chengsoonong/crowdastro | notebooks/107_features.ipynb | 1 | 344544 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Features\n",
"\n",
"Feature distributions for each subset."
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [],
"source": [
"import pickle, h5py, astropy.io.ascii as asc, numpy, matplotlib.pyplot as plt\n",
"%matplotlib inline\n",
"\n",
"with open('/Users/alger/data/Crowdastro/sets_atlas.pkl', 'rb') as f:\n",
" atlas_sets = pickle.load(f)\n",
"with open('/Users/alger/data/Crowdastro/sets_swire.pkl', 'rb') as f:\n",
" swire_sets = pickle.load(f)\n",
"with h5py.File('/Users/alger/data/Crowdastro/swire.h5') as f:\n",
" swire_features = f['features'].value\n",
"with h5py.File('/Users/alger/data/Crowdastro/crowdastro-swire.h5') as f:\n",
" swire_names = [i.decode('ascii') for i in f['/swire/cdfs/string'].value]\n",
" swire_coords = f['/swire/cdfs/numeric'][:, :2]\n",
"swire_labels = {i['swire']: i['norris_label'] for i in asc.read('/Users/alger/data/SWIRE/all_labels.csv')}\n",
"table = asc.read('/Users/alger/data/Crowdastro/one-table-to-rule-them-all.tbl')"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA2gAAANuCAYAAABjTyogAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xd8m+d57/8PFgGS4Ca4SVHz1h6WbEu2PGTH207sLKdp\nktap02a0TevT02acnPa0ado09a9Jk7hJGidtnGbZibctb9nWntQkb4kU994AN9bvD4AyLUsiSAIE\nHuh6v1582SDABxfJr0Bcz3MPUzAYRAghhBBCCCFE/JnjXYAQQgghhBBCiBBp0IQQQgghhBAiQUiD\nJoQQQgghhBAJQho0IYQQQgghhEgQ0qAJIYQQQgghRIKQBk0IIYQQQgghEoQ13gUIIYSYX0qpIHAC\n8ANBIA1wA5/TWh8MPyYN+ApwX/gx6cBO4K+11u1KqRLghfMO7QIKtdbv+duilMoHfgEUAh7gfq11\n60XqawB2aq0/MeVzm4AntNaVs/uuzx3nx8CvtNavzuBr7gK+ATiAp7TWfzOXGuJNKbUQ+Fet9Yfi\nXYsQQoj3kitoQghxedqmtV6vtd6gtVbAr4HvAiilLMB2IA+4Smu9GlhMqKl7USll0lq3hb9+vdZ6\nPXA7MAH85UWe78+Aeq31OuAU8Llp6vuwUuoT0zxmxrTWD86kOQt7BPgssA74rFJqSbTrmmcLABXv\nIoQQQlyYXEETQojLnFLKClQAfeFP3QtkAV/QWgcAwv/9plLKBDgJXQWb/Ho78BTwstb6uxd5muPA\n/UqpZcAm4K+nKeurwHeVUru01vUXqPlrwO8BPuA08Kda6w6l1I7w97Ec+A/gQxe4/b1wvd8FthJq\nLM8CD2ithy5S+wfCP5N2oOViRSulvgz8QbiuM8Afaq0Hp6n3EHATUAB8h9BVxhsIXbX8qNb6ePhx\np8I/u3zgMa3134af8yuEfmeO8Nf8ldb6yfDv9V+Au8PPuxv4AvBjoFQp9ZLW+raLfS9CCCHiQ66g\nCSHE5ekNpdRRpVQboYYB4IHwf68DXp1szqbSWv+z1tpz3qf/ExgF/vQSz7eP0FDKGuBvI7iK9Sah\nK1e/CDca5yilHgDuAK7UWq8ldGXvv6Y8pF9rvXJKs3j+bYAtwI3AWq31RkIN2tqL1PI48DfAt4Gt\nWuuxCz1IKfV+4A+BLeGrjvXAn0ZQb6XWegPwQeCbwA6t9SZCVzH/bMrjFgDXAlcQanbvVkotAN4H\n3BA+9leBvw8//vPARkJX/lYDGcBHgQeBOmnOhBAiMckVNCGEuDxt01r3KKU2AC8Cu7XWXeH7TITm\nnQGglNoG/Fv4Zi7wea31c+H7/jdwDXC11tp7oSdSSq0k1Gx8mdCctofCjeEfaa0/f4ka/xa4Gfg7\nQle8Jt0B/FRrPRy+/R3gq0qplPDtt887zvm3IXRVzA/sU0q9BPxWa73/ArV/mdDVqTuAnwH3hefn\ntWqtnzjv4e8DHtda9wNorR8KH+M309T7u/B/68L/3T7l9o1Tjv/D8M94QCn1OHCb1vo5pdQfAL8f\nHnq5mdAVzsl6HtNaj4Zv3x+uZ+oxhRBCJBi5giaEEJcxrfURQvPGfqyUqgx/ejehIXaTj3ljylyz\ns4SG0qGUuoNQ0/V+rXXvJZ7mj4H/0Vr/D/D7hP72vMI0Jwm11j7g44SG5V0/5a7z/3aZw8cyhW+f\nP0zxPcMWtdYDhK4s/RWhRu3XSqkLzZ/7G+BTWuvtwF3At4B/IDTU8Xw+3t3YZod/ptPVO35ebRds\ndMPHn3oMv1LqCkK/r0zgZUJX4ExTHj+1nkKlVPFFji2EECJBSIMmhBCXOa31L4E9hIbwAfwWGFZK\nfVspNXk1BqXU1cAiQo3BcuDnwCe01qemeYrTwHVKKQeh+V5vEJrPlTHlKtLFajsL/DmhVRQnvQQ8\noJRKD9/+c+AtrfX4+V9/MUqpu4HXCF05/DtCV8fWXaT2W8L/f5bQVa0UQvPEzvcq8EGlVGb49t8B\nD0Wj3rBPKKXMSqkcQkMVnyXUuB7UWv9/hIaF3gtYptTzcaWUXSllJjQHb3IenG2Gzy2EEGKeyBBH\nIYQQEJo/dkwpdZvW+iWl1O3A/wbeCi8Mkgo0hz/3FKGFJuzAN5RS3zjvWPdorZun3P4hUA4cINTc\nHAVWhD9/B/D0pQrTWj+mlLqN0IIeAI+Gj7c/3HjUEroyNxMvhp/7hFJqCOgHPnOBx30MeEQp9SCh\nK4f/CRwG/i28yMbksEW01i+Eh3PuUkoBnAwfczgK9ULod7Cf0FyyR7TWrymlTgAfUkqdItT8vgbk\nKqUyCP18KwktQmICdgD/Hv56v1JqP6GhqcHzn0gIIUT8mIJBeV0WQgghEll4FcfvXWDemxBCiCQj\nQxyFEEIIIYQQIkHIFTQhhBBCCCGESBARXUFTSl0dHl5x/ufvUUodUErtUUpdaOy+EHEhmRVGJLkV\nRiOZFUYjmRVGMG2DppT6a0KTwR3nfd5GaF+cWwktx/zHSqkLrWolxLySzAojktwKo5HMCqORzAqj\niOQKWh3wwQt8fgVQq7Xu11pPADt59z41F+Tz+YOE9mWRD/mYzUckJLPykWgfkYhabiWz8hGFj0jI\na618JNJHJCSz8pFIHxc17TL7WuvfTtm8dKpMYHDKbQ+hfW0uqb9/ZLqHzInLlUF3tyemzxFLUv/0\nx5+OZHZ+Gb1+SL7cSmanZ/TvIdkyC5Lb6Uj90x9/OpLZ+SX1T3/8i5nLKo5uQnupTMoABuZwPCFi\nTTIrjEhyK4xGMiuMRjIrEspcNqquBpYqpXKBIUKXgv81KlUJERuSWWFEklthNJJZYTSSWZFQZtyg\nKaU+Dji11j9SSj0EvEToStxPtNat0S5QiLmSzAojktwKo5HMCqORzIpENe/7oHV3e2L6hDLeNb7m\nYbyuKWYHvwjJ7KUZvX5IvtxKZqc3H9/Djqr3vr+7cX1pVI6dbJkFye10pP5pjy+ZTTBS/7THv2hm\n5zIHTQghhBBCCCFEFEmDJoQQQgghhBAJQho0IYQQQgghhEgQ0qAJIYQQQgghRIKQBk0IIYQQQggh\nEoQ0aEIIIYQQQgiRIKRBE0IIIYQQQogEIQ2aEEIIIYQQQiQIadCEEEIIIYQQIkFIgyaEEEIIIYQQ\nCUIaNCGEEEIIIYRIENKgCSGEEEIIIUSCkAZNCCGEEEIIIRKEdboHKKXMwCPAOmAceFBrXTvl/v8F\nfBwIAN/QWj8Zo1qFiIhkVhiNZFYYjWRWGI1kVhhJJFfQ7gUcWustwJeAhyfvUEplA18EtgC3At+O\nRZFCzJBkVhiNZFYYjWRWGI1kVhhGJA3aVmA7gNZ6L7Bpyn3DQCOQHv4IRLtAIWZBMiuMRjIrjEYy\nK4xGMisMY9ohjkAmMDjltl8pZdVa+8K3m4FTgAX4p+kOlpOThtVqmXGhM+FyZcT0+LEm9c+ZZHae\nGb1+iPv3IJmNg1h/DxlOR0yfM5kyC5LbSEj9cyKZjQOpf3YiadDcwNTqzFPCfAdQDCwM335JKbVL\na73/Ygfr7x+ZVaGRcrky6O72xPQ5Yknqn/74EZDMziOj1w8JkVvJ7Dybj+/BMzT2ns9F6zmTLbMg\nuZ2O1D/98achmZ1nUv/0x7+YSIY47gLuBFBKbQaOT7mvHxgFxrXWY8AAkD3rSoWIDsmsMBrJrDAa\nyawwGsmsMIxIrqA9CdyilNoNmIAHlFIPAbVa62eUUu8D9iqlAsBO4JXYlStERCSzwmgks8JoJLPC\naCSzwjBMwWBwXp+wu9sT0yeUy6nxNQ+Xg00xO/hFSGYvzej1Q/LlVjI7vfn4HnZUtb7nczeuL43K\nsZMtsyC5nY7UP+3xJbMJRuqf9vgXzaxsVC2EEEIIIYQQCUIaNCGEEEIIIYRIENKgCSGEEEIIIUSC\nkAZNCCGEEEIIIRKENGhCCCGEEEIIkSCkQRNCCCGEEEKIBCENmhBCCCGEEEIkCGnQhBBCCCGEECJB\nSIMmhBBCCCGEEAlCGjQhhBBCCCGESBDSoAkhhBBCCCFEgpAGTQghhBBCCCEShDXeBQghhEguO6pa\n33X7xvWlcapECCGEMB65giaEEEJE2fGzvew92cHouC/epQghhDCYaa+gKaXMwCPAOmAceFBrXTvl\n/juAvwVMwCHgC1rrYGzKFWJ6kllhNJLZ5LL3ZAc/evYUAANDE9x6ZTlmsynOVUWXZFYYjWRWGEkk\nV9DuBRxa6y3Al4CHJ+9QSmUA3wLu1lpfDTQA+TGoU4iZkMwKo5HMJolAIMhTO+uxmE04U2109Y/S\n0j0U77JiQTIrjEYyKwwjkgZtK7AdQGu9F9g05b5rgOPAw0qpt4FOrXV31KsUYmYks8JoJLNJ4siZ\nbrr6R9m6tpjr1hYD0NI9HOeqYkIyK4xGMisMI5JFQjKBwSm3/Uopq9baR+jswjZgPTAEvK2U2qO1\nPn2xg+XkpGG1WuZS87RcroyYHj/WpP45k8zOM6PXD3H/HpIqsxlOR8SPjadY1HX0xRoAPnTzMqob\n+nAcaaW9Zxhnuh2TyRTV50ymzEL8c2sEUv+cSGbjQOqfnUgaNDcwtTpzOMwAvcABrXUHgFLqLULh\nvmig+/tHZllqZFyuDLq7PTF9jliS+qc/fgQks/PI6PVDQuQ2qTLrGRp71+1EzEcsfucTXj8HTnVS\nkJNKutXE8PA4JfnpnG1z09zhJifDHrXnTLbMQvxzm+ik/umPPw3J7DyT+qc//sVEMsRxF3AngFJq\nM6FLwJMOA6uVUvlKKSuwGTg1+1KFiArJrDAayWwSONnQx7jXz0blwmQKLQriyg5dTexzj13qS40o\nqTK7o6r13IdIWkmVWZHcIrmC9iRwi1JqN6GVbR5QSj0E1Gqtn1FKfRl4KfzY32itT8SoViEiJZkV\nRiOZTQLHz/YBsH7JO2sL5GSEGrR+z3hcaoohyawwGsmsMIxpGzStdQD47Hmfrply/6+AX0W5LiFm\nTTIrjEYya3zBYJATZ3tJtVtZVJJ57vPZGSlA8jVokllhNJJZYSSyUbUQQggxR539o/QMjrGyMgeL\n+Z0/rSlWC85UG/2ecYJB2VJJCCHE9CIZ4iiEEEKISzhZHxreaLOa3zOPKSfDTnPXEKPj/niUJoQQ\nwmDkCpoQQggxR5MNWkle+nvuy3KGhjm6hyfmtSYhhBDGJA2aEEIIMQc+f4Capn4y0mw402zvuT8j\nLdSgeUalQRNCCDE9adCEEEKIOahvdzM24af4AlfPADLCTZtnxDufZQkhhDAoadCEEEKIOTgRXl6/\nJD/tgvdLgyaEEGImpEETQggh5uBEfR8Ws4mivAs3aGl2KxazCc+IDHEUQggxPVnFUQghhJiloVEv\nDe1ulpZlkWK1XPAxJpMJZ5oNz4iXYDCIyWSa5yrF5eD81UNvXF8ap0qEEHMlV9CEEEKIWTpxtpcg\nsGpR3iUfl5Fqw+sLMDzmm5/ChBBCGJY0aEIIIcQsHa3rBWD9kvxLPm5ydceewdGY1ySEEMLYpEET\nQgghZsEfCHC8rpfcTDtlrguv4DjJ6Qg1aL2D4/NRmhBCCAOTBk0IIYSYBd00wMi4j3VL8qedV5ae\nGm7Q3GPzUZoQQggDkwZNCCGEmIWDuhuATapg2semp4bW5OqTBk1EWTAYZGQstACNECI5yCqOQggh\nxAwFAkEO6y4y0myo8uxpH59+boijNGgiOjr6Rnh2VwOHT3cz7vXjSLGwojKHVZW5mM2yUqgQRjZt\ng6aUMgOPAOuAceBBrXXtBR7zPPC01voHsShUiEhJZoXRSGaN51RDH+4RLzduKI3ozbAjxYLZbEqa\nIY6S2fjYUdVKMBikuqGfI2d68AeC5Gc5WJqXxenmAY6c7qGrf5QbN8gS++eTzAojiWSI472AQ2u9\nBfgS8PAFHvN1ICeahQkxB5JZYTSSWYPZebwdgFS7hR1Vre/Zg+p8JpOJdIc1aRo0JLNxEQwG2Xuy\nk4O6G2eqjc/fu5pvfnYLD310Pfddv4jivDRau4fZd6oz3qUmIsmsMIxIhjhuBbYDaK33KqU2Tb1T\nKfVhIDD5GDG/gsEgg8MTtPYM09YzzOHT3QyNePGMehmb8JGf5aAkP52S/HQ+cO3Cy2WDVMmsMBrJ\nrIEMjXo5fLqHrPQU8rMcEX+dM9VGe+8I414/dtuFN7U2EMnsPJja+Gc4HRys6eZMyyA5GXa+9geb\nyHbaz91vt1nYdkUp2/c1UdsyyCHdxcYI5kdeRiSzwjAiadAygcEpt/1KKavW2qeUWg18HPgw8H8j\necKcnDSs1tj+YXK5MmJ6/Fibrv7hUS8HqzvZc6KdY2e68Yx43/MYR4oFR4qVtp4R2npGgG7OtLj5\n+z/ZgiMltlMPE+DnL5mdZ0avH+L+PSRVZjOc725aEjUfs63rzdfP4PMHWL04n8yM1Ii/LivDTnvv\nCCabFZfLOavnniqZMgvxze3UzCZSXqfWpRv7qW7sJyfDzge3LWHpwvwLPvb2zZX8+tXT/PK1M1y/\nqYK08PzHRCCZnblEyuNsSP2zE8k7dTcwtTqz1toX/v9PAaXA60AlMKGUatBaX/TsQ3//yCxLjYzL\nlUF3tyemzxFLl6q/vXeYJ3bUcayuF38gtFpTusNKeYGTbGcK2U47mekpZKTZSAmfnR0Z89LWM8LZ\nNjfVDX08/PODfObulTG7khbrn3+E/1Aks/PI6PVDQuQ2qTLrGQoN42vvHeZobS+7qlr55G2KnAz7\nRb9mvs32d+7zB3j27TrsNgvlrrRz32skUiyhWQW1Db2kMLcV95ItsxDf3E79PSbS69lkXSNjPt6q\nasFmMXPD+hK8E7731Dn5WKsZVi/K5WhtLz995gQf3bZk3uu+EMnszBn976vUP/3xLyaSBm0XcA/w\nG6XUZuD45B1a67+e/H+l1N8BHdOFWczcuNfPc7sb2L6vCX8gSJnLSV6WnYrCDLKdKZdsttIcNpaU\nZbGwJIO9JzrZe7KThUWZ3HJl+Tx+B/NOMiuMJuky6xmZYMeRNry+AF39o7T3DvN///BKUu3GXjx4\n57F2+tzjvG9T2bkTYZF6Z6n9pNisOukym8gO1HQx4Q2weVUhmekp0z5+1cJcWrqGefVgMzdtKCU/\nO/IrvUlMMisMI5K/lE8CtyildgMm4AGl1ENArdb6mZhWd5nbUdV6brLv0KiXNIeVq1YUUF7gnPEV\nMIvZzIZlLlp7hvnV62fo9YxRlJsGwI3rk261J8msMJqky+zxs314fQGuWV1EusPGKwebeW53Ax9J\nkLP5szE+4efZ3Q2kWM3ctXkBR2p7ZvT1k0vtJ8leaEmX2UTVPTBKY4eHgpxUlpZlRfQ1VouZFZU5\n7DzWziNPn+D6dSXJ+Ld+piSzwjCmbdC01gHgs+d9uuYCj/u7KNUkAK/Pz4HqLqob+zGZQmfD1i7O\nw2ad/d7iaQ4rN2wo4eX9zbxV1cZdWxaQnpo4Y9OjRTIrjCbZMuv1BWhs95DmsLK4NJNrVxdz+HQ3\nLx9oZtsVpeRnJf7Z/PNXZbxxfSnP7K6n3zPOXVsWkOWc+XDNNEf4CprH+A1asmU2kVWdCZ0IuGZt\nyYxOzi4szqC6oZ+Gdg8rF4xGtaYL/ftIdJJZYSTGHmuSpFp7hvnRMydp7hoiMz2F69YWkzeDlcIu\npTAnjSuXF7C/uouq2h6uXVMcleOK5DU67qOxw0N77zBdA6P0DI4xPuE/Nw+ytCADp8NCmcvJ8oqc\nc29CxeWruWsIrz/A8socTCYTKTYL9163kEefr2b7viY+cauKd4kzdrp5gO37msjLdHD3NZWzOsY7\nV9CSYoijmAc9g2O0945QlJtGqcv5rrlykWztsHG5i5f3N3OgposP3rAY8+WxkrNIcF5fgLaeYdp7\nh+l1j+EZ8TI24cfnDxAMT881m0IZNptN2CxmUlLMOFNt5GTYKcxJozgvLeaL3sVT8n5nBhQIBHnq\nzToee+EUE74AS8uy2LS8YE5XzS5EVWRT3dhPfbuHjcoV1WMLYwsGg7T3jnCmZYDalkFq29x09l16\nEnR1Y/+5/zeZYElpFuuX5LNRuSjISYt1ySIBtfUMA1BZ9M5KhVevLOTpnfW8dbSde66pnNUVqHgZ\nGvXyg6dPAPCZe1bOeol8m9VMmt1Kn0catETkDwQ50zxAXcsgW9cWoyrivx3Wyfo+ILTox2wU5aZR\nUeikqXOI3cc72LpWTsqK+TU67qOzf4SWrmHqO9ycbXPT0jV07iTvbJmAkvx0lpZlYTKbKMlPw2I2\nG+JqbiSkQUsQ7b3D/OSFaupa3ThTbXzmnpV4Rt+7fH40mEwmllfkcKCmizPNg9x+VUyeRhhEz8Ao\nT+6sp6N3mI6+EUbH/efus1nNFOWmkZflICcjhYzUFJxpNmxWM2aziWAgSNBsprNniO6BMdp6hqlt\nGeRMyyCP76gjJ8NOSX4at11VwdLSbOwpM39je6GzxMnyApyMgsEgHX0j2G2Wd+3RZLWYuePqCh57\n+TSvHmrhQzcsjmOVkRsZ8/LqwRbcwxPcf9MSlpVnz+l4uZkOegajO9xMRMch3UVN4wAAu0908Om7\nVsR1lEmfe4ymTg85GXaK82Z/suvK5QW09Qzz69fPsGphbkKtpiqSw/N7G+jsG6XPPYYjxcrA0Pi5\nPXlHx33veqzZZCI3005upp1spx1nqg2H3YLNYsFs5tww3mD4UlogAIFgAK8vyLjXz/CoF/fwBP2e\ncTr7R2gNnxB0pFhYuTCXrWuKsVqie2EjHqRBi7PXDjdzqr6fo3W9BAJBlpRlc8WyvJg1Z5MWl2Vy\n5Ew3umkAnz+QFGEWkRkd93GqoZ8T9b2crO+jZ/CdITOOFAuVxRkU5qRRkJM67SqhWExkOB1YTVDq\ncrJ+aT5jE35auoZo7PTQ3jNCv2eck/Whq2zOVBvZzhTSU20sr8ghMz2FNLuVNIeVVLsVh82CPcUS\n3sfPIrk0oK7+UUbGfCwoynhPdq5dU8zTO+t5/XALd1ydWPszXcjA0DivHWxheMzHHVdXcGsUVr/N\nzbTT0j3EyJg34b//y0n3wCg1jQNkpqfwR3et4AdPn+SxlzWLSjIpzkuPS01vHGklGIQVC3LmtDVO\neqqNjcrFvlNd/OezJ3no/vXy2irmrK1nmIM1XRzU3bR0D73rPovZhDPNRmFuGl6vH2da6G9/XqaD\nnEw7FnN08hcIBOkZHKOxw0Nd6yCHdTf/9PNDfPEj68hMm36100QmDVocHa3t4ZmdDXhGvDhSLGxe\nVciqxa4Z7aszWylWC0tKs6hpGuDw6W6uWlEY8+cU8dU9MMqL+5p462gbgfDQghSrmYpCJ0W5aRTl\nppE1XUMWAUeKhSVlWSwpy8LnDy2x3tYTGmc+ODRBS3fobJduGpj2WCk2M67sVMoLnJQXOA2/RPvl\noKYp1IwX5b53IZAUm4Vbr6rgiR11vHqohfdfu3C+y4tYW88wb1aFtglYvzSf/GwHbx5tm/Nx8zJD\n84l73ePSoCWQydejq1cW0OseY9NyF28fbee7vzvOPz54dcz2Dr0Yr8/Pm1Vt2G2hk2Zztaw8G58v\nyKHT3fz4uVP80V0rLzl9YnLkQjAYZGjUy5pFeRRkp0pmY2zqiJFEGyni8weobRnk2Nlejtb20N4b\nmv5gtZgoyU+nJC802iYzPQVHigWTKXQCN5bvac1mEwU5qRTkpLJ2cR77qzupb/fwL784wlc/udHQ\n7xmMW7mBtXQP8dsddRyt68VkguULslm/JH/Ge+rM1fIFOdQ0DfDqoRZp0JLYa4dCE8TPtAwSDIau\nYi0qyaQ0P528bEdMJ41bLebQC3f+O2egxyb8jI77WFaejWd4gpFxHyNjPkbHfZxtd+P1BfD5A3h9\nAUbGfLR2D9PaPcwh3c37NpXhkv18Elp9uxvgor+nbRtKeXFvIy/vb+amK8pwJuBKsjuqWnntUAsm\nTGxdW8yiksyoHXtywade9xjlBc5pHi3mw9iEj6ZODxlptnPbz1QWZVDXOkhbzwhVtT1sWDq/87X3\nV3cxNOpl1cLcqFztMplMPHjPSgZ/VcX+6i66B0b52M1LWVKa9a7m0x8I0No9THVDP229w3T1jeL1\nB3jyrXoAFpVkcuWKglnPwxTGMuH1U1Xbw8GaLo7W9uL1B4DQyd0NS/PZtLyA9Uvy2VfdGedKwZ5i\nYevaYhYWZ/L64VYee1nzmbtXvufEWqI1vhcjDdo8auhw89zuRg6f7gZgeUU2S8uz4zYePDM9hVJX\nOrUtgzR0uKksit6bEJEYBobGeWl/Mz2DY2Slp7BmcR6VRRmYzfFbyWty+GL3QGgejjk8FMKZZsOV\n89439Z6RCRraPVTV9vDqwRbet6lsvksWM1Df7sFiNr1r/tlUqXYrd22p5Ddv1PLc7gY+dvPSea7w\n4oLBIE+9Xc+zuxuw2yxsu6KUggtkci5yM0M/lyTZCy0pHDndg88fZGFx5rlmxWQysWl5Ac/uauDx\nN+pYuzgvasOyIvH64VZMwLLyyPY9i8Sekx1ctbIAfyBAfbuHf/r5YbKcKRTlpGE2m/CMeOnqH2HC\nFzj3NRlpNsqy0rHbLHT0jXC2zY17eILbri6f15+HmF8DQ+M8+vwpzjQPnsuDM9XGIlcmpa50inLT\nsFrMjHv9CdGcTTKZQlfz8rMc7D3ZSbrDSqnLmCfCpEGLsT73GFW1PRzS3edWu1tUksnd11SybnFe\nVIbMzMXyihxau4d59WALD969Mq61iOhq6vTwnSeO0e8ZZ1FJJltWFWIx4LyDjLRQY+lMs7HzWDuv\nHmjhimUuFpdE742LiI5xr5/W7mHysuzvOglw/kIvNquJ/CwHrx1qYeuaYsoS4EpSIBDk56+cZseR\nVlzZDq5dU0xmevTnMJwb4jgoDVqiOHa2FwhdNZsq22lnaVkWp5sHeauqjW1XzM/JobNtburb3axf\nkk9GlOfRWC1mrltXwrLyEQaHJtDNA+jmgfB9JjLSUqjIdFCQk0pxXtq79koNBILsPN5OQ7uHI6d7\n2LS8IKq1ifgbGfPy3J5GXjvUgtcXwJFiYdXCXBaVZE4/Jz1BmM0mtqwu4tldDRw+3UNJfroh6j6f\nNGhRNjhM1pU6AAAgAElEQVQ8QV3rILWtg1Q39NPY6Tl3X2FuaIxsUW4aA0PjcW/OAEryQ3OP9ld3\ncv9NS6L+x0DER1f/CA//uoqhES9XKBerKuc2yTwRLCzOxAS8faydHz1zkq8/eDU2qwyzSSTNnUME\ngsFpN6K2WMx84tZlfPvxY/zkhWq+8smNcV20wOcP8OPnTrG/uovyAicPfXQdR2p7YvJc78xBkwYt\nEQSDQaob+ki1W8hyvvfv37ol+TR2DvHk2/VcuaJwXobkvnaoGYCbN5bRHaMVPwtz07j/ptDV60Ag\nSCAYar4uxWw2cc3qInoGxqhpHGDFgpx3NXDCuALBIG8fbeNXr9Uy7vWT5rCycZmLxaWZhjyxm5Nh\nZ1FJJmfb3DR3DVFROPd5nPNNGrQ58vkDnG4e4GhtL/tOdeAeeWf1RbMJivPSzi1wkIgvZCaTievX\nlfCbN2rZX93FzRtl+JjReUYm+LffHMUz4uWTty7DFMfhjNFWWZxJ98AY1Y39vLS/edYbBovYmDwh\nlZc1/bDttYvz2bKqiD0nO/jtm3Xn3izOt9FxH488eZyTDf0sLcviix9eF9PN1rOddswmkzRoCaK1\nexj3iJdFJZkXPImVarfy/msrefyNOn73Zh2fun15TOvpc4+xv7qL4rw0Vlbm8ObR2G/JYDabMBPZ\n3wmrxczaxXnsPtHBifo+rl4p89eNrrlriJ9tr6GuzY3VYmLDsnxWLsgxZGM21epFuZxtc6ObBqRB\nu5x09I2wfV8TB2o6z+0bZbWYKM1Px5WTiivbQX5WatQ3mY6FLasKeWJHHbuOt0uDZnATXj///sQx\nOvtHuXPzArZdUXbBfcSMbN2SPFq7h3huTwPXrC4iN3xFQsRfU7hBy82I7HfyiVuXcbZtkJf2N1Ne\n4OSa1fO751Sfe4zvPHGM5q4h1i/J508+sCrmix+YzSZyMuz0uWWz6kRwqnFy1dGL7zN2y6Zydh/v\nYEdVG1coF6sX5sWsnpcPNOMPBLn96oqEHfWwqCSTqtoezra52ahcsmS/Qfn8AZ7b3cDzexrxB4Jc\ntaKAisKMmJ6gmk/ZTjuFOam0947gHp6IyZD1WJJ/VTNU3+7m//10P1/50V7eOtqG2WRieUU279tU\nxv03L+HmTWWsXZxHcV66IZozgCynndWLcmno8Jzb8E8YTzAY5Ju/OExdm5tFJZnkZdmTrjmD0FLt\nH7phMRPeAI/vqIt3OWKKpq4hrBZzRH8Id1S1sq+6k82rCkmxmvnpCzUcq4vNsMILOXm2l7//74M0\ndw2xrDyL1Yty2XOygx1VrTH/d5OXaWfAM47PH5j+wSKmzrSE5l8VXmBbiElWi5kH716JxWzix8+e\nitkCL4ND47xZ1Ua2M4XNK4ti8hzRYDabWFSSidcXoLlraPovEAmns2+Ef3zsEM/saiDLmcJffGQd\nn/3A6qRpziYtK88GoK51MM6VzJwxOogE0NTp4TuPH+Uf/vsgjZ1D5GXauWF9CffdsIirVhZSkp9u\n6BWNrlkd+mOw+8Slx6CLxPXS/mbq2z3kZznYsrowYc++RsO1a4upLMpg36lOTjdPv5+aiD2fP0Br\n9xBlrvQZrRKa5bSzbWMpFrOJ7/3uRMybtEAwyAt7G/nKf+xiaMTL771vKVevLJzXlU1d2akEkYVC\n4i0YDFLXOkhWesol55btqGqlviN0tcg94uXfHj+KZ2Qi6vU8s7uBca+fe65dOC8neCdPRszmpMTk\n1hNn29yxKE3E0H9vr+Frj+6jscPD4pJMbr2qnD7PWFKe0C0vdGK1mGjo8BAMBuNdzowkV6scA609\nwzy9s56DNV0ALCvLoqIog+K8tKR6A7xhaT6pdit7TnTwoesXx3UZdjFzJ+v7eHxHLal2CzduKDX0\nyYJIvHW0jeULcmjo8PDo89X8859sTqp/j0bU0TuCzx+konDmKzIW5qTxZx9ey78/cYzv/vY4n75r\nBVtWRecKwtQ3HZ6RCXaf6KCzb5TcTAefuXsFqiJn3t+YTO4R1z0wSuElhtaJ2Op1jzEwNMEVy1wR\nvX6oimzcIxPUNA7wz/9zmL/4yLqo7cvY2OHhzSNtZKTZCAaDCf9mOdtpJyfDTnvPCF6fXAk2gkAw\nyFNvn+XNqjaslujv8ZiIrBYzZS4nDR0e+jzj5xZpMoJpGzSllBl4BFgHjAMPaq1rp9z/l8DHwjdf\n0Fr/v1gUOt/Otrl5fk8DR86EzuYuLM7gvusXsaoyNyFWX4w2m9XCVSsKeLOqjerGflYtzI13SbN2\nuWW2s2+EHzx9AovZxI0bSpNuiMLFFOSkUl7gpLlriGN1vaxbkh/vkmYtGTLb1BWaf1ZeMLvJ2Ksq\nc/lf96/nO08c4z+fPUV77zD3bl0UlZNFgUCQmqZ+qs6E9rsqK3By69ULaO8bob1vZM7Hn6mpDZpR\nJUNm61pDV3+WlEa2ZYfJZOLK5QWYTSZONfTztUf3cc3qIj5129wWDvH6/Pz0xWoCweC8X82dizJX\nOv2ecdp7jTE1IhkyO1vjXj8/fvYUh053k5FmY9uGUrLjtAfvfKsszqChw0Nju8dQDVokp9nvBRxa\n6y3Al4CHJ+9QSi0Cfh+4BtgM3KqUWhuLQudLS/cQ3/rlEb7+s4McOdNDfpaDbVeUsnVtMT2DY0nZ\nnE26NjxBf5fxhzleNpkdGfPynSeOMTzm45O3qaidzTWK9UtDTdlv3zxLwGDDF85j+Mw2dYbmoszm\nChqErnS19Q5zy5VlOFNtPLe7ka/+516e3V0/63lhwWCQtp5hntvdwMGabsxmE9euKWLbhhJS7fE7\nkfFOg2boIY6Gz+zkvJTFpZFfRZjcwHrLqkL8/iA7jrTxo2dP4h6e3ZDHQDDIf71YQ1PnENevK6Yk\nP31Wx4mHyf0LW7qM0aCRBJmdjYGhcb75P4c5dLqb5RXZ3LF5wWXTnAHhKUgmWrqNNV8ykr9QW4Ht\nAFrrvUqpTVPuawZu11r7AZRSNuCSf3FyctKwxnjvIpdr5mdwg8Egrx1o4j9+d5wJr5/yAidXLC+k\n1DX/G9xlOOe3wz9UG9qkMxgMkuVM4WBNF2uWuEixWbh9S+WMjzebn3+UXRaZ9fsDfPfHe+noG+G+\nG5fwwZsV2/c0RL22SMx3Zqc+r1qQg27sp7rFzY1z2Eg2zrk1fGY7+kNXg9avKMJ9ZPbDszKcDu6/\nJZ3XDzZT3+bmmZ0NrFuaz9olroh/Rz5/gAOnOnn6rTpOhjchXlGZy5Y1xe9qzOKRW5crA6s9NN9p\ncNQ7p9wlU2Zh/nPb3D2MxWxi4+oS3AebZ3ScK1YUsaAkm9cPNrH3ZCfH63r52K2KO69ZSEqEK4GO\njfv43uNH2XOyk2UV2Xzx9zby+jR1xOu19kKc6XZS7W209Q6Tn++M6L2SZPbSpv5+J39Wc/mZ1bUM\n8I3HDtEzOMbNV5bzhQ+v57UDTXOucyYSIbPlhRk0tLsJmkwz/nnGK7ORNGiZwNTlT/xKKavW2qe1\n9gI9SikT8C3giNb69KUO1t8f2+EkLlcG3d2e6R/IO3MTvL4A+051crbNjc1q5sYNJef2TBgant+l\nkDOcDjxD8TururAog6raXk7U9bC0LCvin+Wkmfz8ZyPCfyhJm9lJwWCQf/nlEXTTAGWudNLtZh5/\npSZGFV5avDO7akEOtc0D/Oz5kywrzpjV5PoEyK2hMxsMBqlrGaAgJ5Vhz1hU8rB1TRGl+ekc0t0c\n1t0cOd3NvhPtqPJsivLSyEhLISX8u/b6AgyNeukZHKOhw82phn6GRkN7Upa60lm/NJ+8TAc+rw+P\n1wfEL7fd3aHJ6ilWM62dnlnnLtkyC/ObW68vQF3rAGUFTtwDI7PKQooFbr2qnIA/yFNv1/PoMyf5\n7etneN+mcq5ZXUS288JXKcYn/Byo6eLZ3fV0D4yxuCSTP71vDYPT1BHv19oLKcpNpb7dQ1V1B2Wu\nS189l8xOb+rvt7vbM6ef2Z6THfz3izVM+AJsWJZPSW4qT70x7bcUVYmS2aKcVBra3eiGvhn9POOZ\n2UgaNDcw9QhmrbVv8oZSygH8BPAAn59ljXEzNuHj5f3NDAxNkJfl4Pp1xWSkGWuvhGhaVJJFVW0v\np5sGWDKDYR8JJqkzC7B9fxO6aYBsZwpb1xVjvowXyHCm2bjpijJeOdjM9n2N3HPtwniXNBuGzmy/\nZ5zhMR8rFuRE7ZgmU2gp74pCJ3WtbmpbBqlu7Kc6vG/VpWQ7U7h5Yxk3rCuhti3xllc2mUy4slPp\nGhglGAwadYEbQ2e2uWsInz8450USzCYTN20qY/OqIl7Y28gbh1t5YkcdT+yoIzfTzsoFuWQ5Q+8p\nPCNeOnqHqe/w4PUFsJhN3H51BfddtxBbjK8cxkpJfjr17R5O1fdN26AlAENnNlITXj+/eu0MO6ra\nSLVb2La2lPKChP/dxFRpQTqcwlDbQkTSoO0C7gF+o5TaDByfvCN8puFp4HWt9TdjU2LseH0BXj/U\nysDQBEvLsrhqZSEWg0zOjRVnmo2KQidNnUN09Rt2AnvSZhZg36lOHn+jjjS7lZs3lZFi0D/s0XTv\ndQvZX9PJc3sauXpVEQXGm4tn6Mw2doQXCCmM/lAQq8WMqshGVWRzxVIXDR1uuvpHGRr1Uhde4tti\nNpFiM5PusHH7VRUU5KSea3oSsUGD0MbIrT3DDAxNkGPM+SCGzuzZcC4WFUfnRKQz1cZHty3hri0L\neOwlTWOHh+6BMXYef++c7pwMO2UFTpaWZXH3LKYRJJLivNAqpCcb+rn1qoo4VzMtQ2c2Ek2dHr79\n+NFzrys3rC8x3AbNsZDusJGTYaezf5Rxrx97hMOQ4ymSBu1J4Bal1G7ABDyglHoIqAUswA2AXSl1\nR/jxX9Za74lJtVHk8wd4q6qNnsExFpVksnlVcu8bNRMrK3No6hziZMP0Z6oTVFJmFqCmsZ9Hnz9F\nqt3CzZvKSHdcfO+ey0mq3crHblrKD585yS9eOc0XP7zWaP+eDZ3ZhnCDtrAotmP1M9NTWLv4ndU6\nL7RwSHVTP9VNif/aVZyfBqehvXfYqA2aoTM7uX9XtJcZT3fYWL4gh+ULcggEgnhGvIyFh9XabRac\nqTaslneGYSf6cvrTSXPYyHKmoJv78foC87J/2xwYOrOXEggEeelAE7978yz+QBBVkc1G5XpX1i53\nJfmhVUdrGvsNserztA2a1joAfPa8T0+d7BL/2X8zFAgG+ekLNbT2DFOan841q4uM9mYuplzZqeRn\nOWjpGqK9d5jiPOOsKgXJmVmAlq4hvvu74wSD8Kf3raHTwEt0x8JVKwp462gbx+p6OXy6h43KFe+S\nImb0zE42aAti3KAZ/c3sVJOvq+29I6ysNN62JkbPbG3rIOkOa1T2obtYLs1mE1nOFLJI7isYJXnp\nVDf2c7ZtEFURvWHO0Wb0zF5M7+AY//qrI3T2j+JIsXDDmiIjDDedd6X56Zys7+P4WWNsy3NZttZP\n7Khjz8kO8rMcXL++xDB7jswXk8l0bh+0Vw7MbGUrERvP7Wngn/7nMKPjPq5ZXSTN2Xl2VLXy5tE2\nVEU2ZpOJR58/Rb9nfhf4uVwFg0EaOtzkZzku6/m7M1USbtDaDLKHVDLp94zTMzjGktKsy3r+brRM\nHeYo5qa+3c1Tb53l16/V8sNnTtLSdekFKg7UdPF/f7Kfzv5RygucvH9rpTRnF1GQk4rNYub42V6C\nBtiW57Jr0F7c18j2fU0U56Vx08bSRL8cHzflhU6cqTZ2nejAPTK7/V1EdAyNenntUAuj4z42KhcL\nozwkJ5lkpqewUbkYm/Dzw2dO4g8E4l1S0utzj+MZ8VIZ46tnyaYofOWmvUcatPk2uf/ZkrLINqgW\nl1aYmxbevLsv3qUY2isHmnn7aDvDYz4sFhP7TnXyxYd38Prhlvc0FNv3N/H1nx3kP546gdfnZ8uq\nQm7cUIIjJX77OyY6s9lESX4a3QNjdPTFdsXYaLisupOdx9p5/I06cjLsPPTR9RLkSzCbTKyozMHr\nC/DG4eQZVmQ04xN+vvP4UQaHJlixIIeVlYk7fCRRLF+QTUWhk9PNAzz1dn28y0l6deHFFhZGabGF\ny4U9xUJepoO2nmFDnM1NJrWTDVqpNGjRYLOaWVSaSX27+9z2FmJmmjo9/OaNWhwpFu6+ppIP3bCI\nz927GnuKhZ+/fJpv/fIIR850U9c6yLO76nn67XrOtrnJy3Rw15ZKlpZny1SdCExurn40vP9vIrts\nGrQjZ7r5rxdrSHdYeej+9eRlGXKo8bxaUppFusPK64dbGPf6413OZcfnD/D9p45T1+ZmUUkmm5a7\n5AU4AiaTiWtWF+HKdvD8nkYO6a54l5TUTjcPALC0PDvOlRjPgqIM3CNeGY47z2qa+rFaTFTKSYWo\nWbMoj2AQTtbLVbSZCgaDPPayxh8Icu2aIrKcKZhMJq5cXsB3/2obaxfnUdM0wHd/e5x/fOwQT75d\nTyAYZKNyccfminPbOIjpleSnYwKO1vbEu5RpXRYN2k9frOb7T57AbIbr15dwpmUgqSabx4rNauam\nK8rwjHj59Wtn4l3OZcXnD/CjZ09x4mwfaxfnyUI2M5Ris/D5e9dgt1n4wdMnOX428c+WGdWZlkFs\nVrMMcZyFhcWhn1l9e+w2QhXv5hmZoLlziCWlWYZYatso1i7KA5DX2lk4WttLXaubDUvzKT1v/lhe\nVip/8ZF1fPWTG3n/tZXcsqmcT9+5gg/duIhVC3NlDYUZSrVbWVSSyZmWQTwJPn0nqRu0QDDI7946\ny9tH27GYTNy4oRSX8fZHiqu7r1lAmcvJjqo29ld3xrucy4LX5+f7vzvOwZoulpVn87l7V8uL8CzU\nd7i5YX0JAP/+xDF+9bqcZIi2kTEvLV1DLCrOlOWcZ2HyCk5DhzvOlVw+apoGCIIhV85MZOWFTjLT\nUzhxtpdAQIbsRioYDPLUzrOYgA9ev+iij1tcmsW91y3i9963lK1ri2X/0znYqAoIBIMcPt0d71Iu\nKWn/oo5N+HjkyRM8t7sBZ6qNO7ZUUJJvrOXiE4HNauFz967CbrPwXy/W0NWf+BMrjWx03Me3Hz/G\n0bpeVi3M5S8/uk7O8s5BUV4aN2woIRgM8vqhFvadkpMM0VTd2E8QUBUyvHE2JveNq2+XBm2+TC5k\nsULm80aV2WRi/ZJ83CNezrQMxLscwzhR30dT5xBXrih4z9Wz8+2oaj33IWZv0/LQFjwHaxJ7+kPS\nNWjBcFf8tz/Zz+HT3SyvyObOLQvIdhpyI9CEUJyXzqduU4xN+PmPp0/i9cnKeLHQ2j3EP/z3Qaob\n+ykvcLJ+aR57TnbIi/Eclbmc3LChFODcRtY+v2Q4GiYnWk/dPFpELs1hozgvjbpWt7yuzgN/IEjV\nmR6cqTYZkhsDVy4vAEJLv4vIPL+nEYA7Ny94z307qlrZvqdBmrIoy89KZWFxJtWNAwwOJ+4wx6Rq\n0Fq6h/jaD3fzvd8dp889zu1XVfDQ/etxpMgViLnasrqIrWuKaezw8NMXqxmb8MW7pKQRDAbZfaKd\nf/jZQTr6RlhZmcMN60uwmJPqn2dclRc4uWtLJSX56bx6qIW//68DMpl9jgLBIMfqeshMs1FZLG92\nZ2v1wjzGvX656jAPqut7GRye4IplLnl9jYHlC7Jxpto4qLtli5MI6KZ+TjcPsHZxHhWF8ho6n65Z\nXUQgGGTnsbZ4l3JRSbHOfHvvMI8+X019m5sgoVVarlzuIstpZ+fx9niXZ2hTz9qUFzrJbbSz92Qn\nJ8728bl7V7NigQwTmYuugVG+/9QJDtV04Uix8IX7VuORZYpjIsuZwg3rSzhQ00VtyyAP/7qK0vx0\nHrhzBS6X/HGcqdNNA7hHvGxdWyyb/c7BmsW5vHKwmWN1vTIvKsZ2Hg29GZu80iOiy2I2c/WKQl47\n3ELVmR42Kvk5X8ozuxoAuOeayrjWcTnasqqIx3fU8mZVG3dcvSAh5/kb+hRSS/cQP3rmJP/nx/s4\n2+Ymy5nCXdcu5H2bysiSIY1RZ7OauePqClYtzGV41Mu3fnmEx17SskT0LIyMeXnq7bN89Ud7OVTT\nRXFeGndsrpDmLMZsVjPXrC7irmsWUJSbRmvPMF//2UG+9P2dHDkjZ31n4q3wm92ta4rjXImxqfJs\nUmxmDp/uJiD7ocXM6LiPHYeayUxPYfkCmTMZK9uuCA0nf+1QS5wrSWzH6nqpbuxn1cJcFst+fPMu\nzWHl6hWF9AyOJexiIYa7gjY24eNAdRdvHWujrjU0sbq8wMmikkwqCp1kZqTiGRqLc5XJy2Ixs1G5\nWFDopKq2lzeOhMZGr1mUx3Vri7k5RxZiuZTB4QneONzCKwdbGB334UixcNP6UopyHLKM/jzKy3Rw\ny5VldPSN0N47womzvZw820tOhp1r1xRz7eoiCnPT4l1mwuodHOWg7qY4L42lZfLmYi5sVgtXrShk\n57H2c9tqiOh7s6qN4TEf912/SIY3xlBJfjorK3M41dCPbupHVcgom/P5/AF+/foZTCb46LYl8S7n\nsnXH5gXsOt7Bb9+sY/3S/IRbiTjhG7QJr5+GDg9nWgY40zLIqYY+fP7QWcaS/HRURTZlrnR5czvP\n8rNT2XZFCXUtbmpbBzlW18uxul5+/Hw1V68o4MoVhSyvyJY/hMC418+phj52He/gaG0P/kAQZ6qN\nj9y4GKvVTG52mpxUiAOTyURxXjrFeemsXpzP4Zou6tvdPLe7ged2N1DqSmfDUherF+aysDgTm1Wy\nPOnnL9bg8we47aoKee2NgpuvKGPnsXa272tkzaJc+ZlG2eDwBC/sbcSRYmFbeMEgETv3Xb+IUw2H\n+MWrZ/jaH2xKuDe+8fbr12tp7x3hpitKKS+49MqNInaKckOrPL9xuJUX9jby/msXxrukd5m2QVNK\nmYFHgHXAOPCg1rp2yv2fAf4E8AFf11o/N5tCAsEgPYNjtPUM09o9REv3MM1dQ3T0jrxr2EdGmo1F\nJZksLs3CmWqbzVOJKLGYzSyryGZZRTb9nnFqWwZp7PTw1tF23jraTkaajVWVuSwrz2ZZeTbFeWnz\n8sZjvjJ7MeNeP40dHs62ualu7Kemqf/cCm05GXaWlGWxpDRL3vAnkLysVDavKmTTcheNHR6GR32c\nqO8716zZrGYWl2RSWZRJZXEGZS4nBTmpUXvjEe/MzsT+6k5ePdBEmcspwxujZEFRBmsX53Gsrpcd\nVW2GaCKMklmvz8+jz51iaNTLZz6wWt43zIPFJVlsXVPMzuPt/OwlzR/esTwh5qnGO7PBYJDt+5t4\n7VALpfnpfORGuXoWb/ddt4ijtT08/XY9RblpXLWiMN4lnRPJFbR7AYfWeotSajPwMPABAKVUEfDn\nwCbAAexUSr2itb7opKS9pzoYHvXhGZlgYGicfs8E/Z5xuvpHmDhvmWGrxURelp28LAeFOWkU5KSS\nak/4i36XpZwMO1euKODGTeVk2i3sr+7i0Olu9p7qZG9476lUu5WCnFQKslMpyEklMz2FdIeVdIeN\nVLsVm9Uc+rCYsVrMWC0mLOH/Wi1mLJFP4oxqZv2BAOMTAca9fsYmfIxN+Bkd9zE67mNo1It7eAL3\nsJeugVE6+0foGRh710mFbGcKpS4nC4oyyMu0y9nxBGa1mM/NB1hRmUN77zCdfaN09I2gmwaoaXpn\npT2zyUR+toO8TAc5GXaynXacqTbSU8OZTrHgsFux2yyRLEIS1czGQp97jNcPt7J9XxOpdit/fM/K\nhJxYbVSfuk3xtUf38/OXNAOecW7eWEZmekq8y7qUhM6sPxBANw3wu7fOcrbNzeqFudy9dRG9vUPz\nVcJl7fdvWUZz9xA7j7XTOzjG+6+tJCc37lMg4pJZnz9AXesg2/c1cbQuNJT+Cx9cg11WGI87Z6qN\nL9y3hn/5xRF+8PRJqhv72bahlLICZ9xPKkTS7WwFtgNorfcqpTZNue8qYFc4wONKqVpgLXDgYgf7\n0TOn3luExURmegpZ6SlkOe1kO1PIyQi92ZE3s8ZiNplo7xuhvNBJWUE67uEJOvtH6ewboc89Tmv3\nMI0dnlkd2wQ88/AHInloVDP7mX/ZEXGNGWk2FpeGrrSMeX24slPljK1B2axmKgozzi1/POHz0+ce\np29wjIGhCQaHJxgcmqCrf3TaYz07fW6jmtloenZXPa8easEzElrAJifDzpf/4CrynZLraMrNdPDX\nv7eBbz9+lGd3N/Ds7gZyM+08cOcKViXm6o4JmdlgMMi/P3GMk1OmQ1y9spBP37lcTijMI3uKhYc+\nuo5Hn68+tyCG7TdHyXHayXKm8Ok7V8Rjnu+8ZvaxlzXH63rp94zjD4SyuKw8m8/cvZK8LMesvwkR\nXQuLM/nKJzfyyFMneLOqjTer2kixmclx2ikrzODBu1Zgt81/Mx1Jg5YJDE657VdKWbXWvgvc5wEu\nOWP82Yc/IK+QItYks8JooppZlysjapn99L1r+fS9a2f0NR+5ZXm0nv6y4nJl8PM1JTN6fBxFNbMQ\nvdx+/fNbL/UcF/y8ZDb6XMA/XuJ3EQfzmtmHfn/Txe66KMlhfLhcGfx4VWIN2Y9kAoUbmPqKZg6H\n+UL3ZQCy26aIN8msMBrJrDAayawwGsmsMIxIGrRdwJ0A4TG7x6fctx+4TinlUEplASuAE1GvUoiZ\nkcwKo5HMCqORzAqjkcwKwzAFp9kYc8qqN2sJTQN6gFDAa7XWz4RXvfljQs3eN7TWv41tyUJcmmRW\nGI1kVhiNZFYYjWRWGMm0DZoQQgghhBBCiPkhGzEJIYQQQgghRIKQBk0IIYQQQgghEoQ0aEIIIYQQ\nQgiRICLZB81Qwqvv/JzQnhYpwENa6z3xrWp6UyavrgPGgQe11rXxrSpySikb8BOgErADX9daPxPX\nogxCMhsfktnZk8zGh2R29iSz8SGZnRvJbXwkQm6T8QraQ8BrWusbgD8Evh/fciJ2L+DQWm8BvgQ8\nHJtiYr4AACAASURBVOd6ZuoTQK/W+jrgduB7ca7HSCSz8SGZnT3JbHxIZmdPMhsfktm5kdzGR9xz\nm3RX0IB/I9StQ+j7G4tjLTOxFdgOoLXeq5Sa+Rb08fU48ET4/02A7xKPFe8mmY0PyezsSWbjQzI7\ne5LZ+JDMzo3kNj7inltDN2hKqT8C/vK8Tz+gtT6glCoidFn4L+a/slnJBAan3PYrpaxTdrlPaFrr\nIQClVAahUP+f+FaUmCSziUMyGxnJbOKQzEZGMps4JLORk9wmjkTIraEbNK31o8Cj539eKbUG+BXw\nV1rrN+e9sNlxAxlTbpuNEuRJSqly4EngEa31L+JdTyKSzCYWyez0JLOJRTI7PclsYpHMRkZym1ji\nndukm4OmlFpJ6NLkx7XWL8a7nhnYRWhHe5RSm4Hj8S1nZpRShcDLwN9orX8S73qMRDIbH5LZ2ZPM\nxodkdvYks/EhmZ0byW18JEJuTcFgMB7PGzNKqacJrRrTEP7UoNb6A/GrKDJTVrxZS2i86wNa65r4\nVhU5pdR3gPuBqTXfobUejVNJhiGZjQ/J7OxJZuNDMjt7ktn4kMzOjeQ2PhIht0nXoAkhhBBCCCGE\nUSXdEEchhBBCCCGEMCpp0IQQQgghhBAiQUiDJoQQQgghhBAJQho0IYQQQgghhEgQht4HTQghxMwo\npYLACcAPBIE0QnvWfE5rfTD8mDTgK8B94cekAzvh/2fvvuPbuu67j38uAIIkCHDvKUqUjvawhiVZ\nnvEesTOdOH7SuHHTtOl46j4ZXUm6krZp0rQZTRPHSZrhPeJ4yEOWZEvWlihR60jce+9NAvf5A5RM\nS6LABQIX+r1fL75sAuDFj+BXJH73nHsOX9JaNyilsoFXLjh0GpChtb7o74pSKhX4DZAB9AD3a63r\nJqivEtiltX5w3G3rgGe01vOm912fP86jwBNa6zen8DV3Ad8AYoAXtNZfnkkN0zX2c0vTWrfOwrFe\nwv96/nzGhQkhhJh1MoImhBBXnhu11qu11mu01gp4EvgegFLKDmwFUoANWuvlwAL8Td2rSilDa10/\n9vWrtdargduBYeAvJni+PwUqtNargJPAHwWo76NKqQcDPGbKtNYPT6U5G/ND4PP4l7r+vFKqaLbr\nEkIIIcaTETQhhLiCKaUcQD7QPnbTfUAC8AWttQ9g7L//qpQyADf+UbBzXx8NvAC8rrX+3gRPUwLc\nr5RaBKwDvhSgrL8BvqeU2q21rrhEzX8HfBIYBc4Af6K1blRK7Rj7PhYD/w185BKff3+s3u8BW/A3\nluX49+npnaD2e8dekwag9lIFK6U+A3wW/2hjl9b6RqXUZ4E/xn8ytG2sztNKqS3AdwA7/hHKb2qt\nn1VKJQA/AFaP3f4q8Nda69Fxz/Mu8B2t9TNjn/8LYGitv3yZ58sGfgFkA1VA+iVfdSGEEGFBRtCE\nEOLKs10pdVQpVY+/wQF4aOy/1wJvnmvOxtNa/4vWuueCm38CDAB/cpnn24d/KuVp4GuTGMXaiX/k\n6jdjDeR5SqmHgDuA9VrrlfhH9n4+7iEdWuul45rFCz8H2ATcAKzUWq/F36CtnKCWp4EvA98Ftmit\nBy9T9zLghrHm7Hrg94BrtdZrgH8Dnht73N/jb7LWAr8P3DR2+3/hb6xW4G9kVwH/74Ln+AnwmbHX\nwg48CDwa4Pl+AOzVWi8D/gx/wyqEECJMSYMmhBBXnhvHphvehb9xeldr3Tx2n4F/9AYApdSNSqni\nsY9qpdTd4+77IrAZ+KjWeuRST6SUWgrsBv4Kf8PwiFJqrVLqhwFq/NpYLV+/4PY7gJ9prfvGPv9P\n4ANKKefY5+9c8PgLPwf/qJgX2KeU+kfgWa31u5eo/a/wj0jdASQDH1JK/blS6qMT1HxMa9099v93\nAUXAu0qpYvwNU7JSKhl4CviBUurXwFr81/ud+96+r7U2tdZDwI/GbhvvKWCTUioTuA0o1VqfDfB8\nNzPWxGqtS4G3JqhfCCFEGJAGTQghrlBa6yP4rxt7VCk1b+zmd4Hrxz1m+7hrzcrxL5aBUuoO/E3X\nB7XWbZd5ms8Bv9Za/xr4FP6/O28QYIr92LS+B4AvANeNu+vCv1u2sWMZY59fOE3xommLWutO3hud\n8gJPKqUudf3cl4FPa6234m+AvgX8I/6pjpcy/rnswC/HvXZX4R8V69Ba/w/+UbI38DdZx8amN17q\ne4u6oPY+/KN6D+Af9fxJoOfD33Ab4w4zihBCiLAlDZoQQlzBtNaPA3vwT+EDeBboU0p9VynlPvc4\npdTVwHzAq5RaDPwKeFBrfTLAU5wBrlVKxeC/3ms7/uu5PONGvSaqrRz/lLxvjLv5NeAhpVTc2Od/\nBrw9NuI0KWOjgNvwjxx+Hfhf/A3bpWq/Zez/y4EywIl/NcpAXgc+qZTKGvv882PPee46sjVjqyh+\nDkgEksa+ty8opYyxa/s+h7+Ju9C5aY6b8f+8Lvt8+Bd9+dzYc+cDN06ifiGEECEiDZoQQog/Ae5Q\nSt02NnJ1O/5rod5WSh1RSp0G/gn4Iv4FNr4IRAPfGDf98dxH3gXH/h/80wwP4L8GbSmwBMjk4ul7\nF9Fa/xJ4ZtxNPwXeBPYrpU7hHyn61BS/31eBE8BxpdRB/I3O1y/xuE8Ad49NGdyNf6uAO4CvjmsQ\nJ6r7NeBfgTeUUsfwj3h9WGtt4l8k5R+UUkfwN6x/r7WuxN9spuOfglkCaOCfL3HsQ/hHwZ49d01c\ngOf7ArB07PX6KVA8mRdJCCFEaBimaQZ+lBBCCCGEEEKIoJMRNCGEEEIIIYQIE5Nq0JRSV4/tL3Ph\n7fcopQ4opfYopf5g1qsTYpoks8KKJLfCaiSzwmoks8IKAjZoSqkvAY8ytnLXuNujgP8AbsW/4tfn\nlFKTuXBaiKCSzAorktwKq5HMCquRzAqrmMwIWhnw4UvcvgT//isdWuthYBfvXwpZiFCRzAorktwK\nq5HMCquRzApLCNigaa2fBS61AWk80DXu8x78Sydf1uio18S/J4t8yMd0PgKSzMpHGH4ENJu5lczK\nxyx8BCS/a+UjzD4CkszKR5h9TOiyG4UG0A14xn3uAToDfVFHR/8MnjKwtDQPLS09QX2OYJL6Ax9/\nBiSzQWD1+iHyciuZDczq30OkZRYkt4FI/YGPPwOS2SCQ+gMffyIzadBOAQuVUslAL/6h4H+fwfGE\nCDbJrLAiya2wGsmssBrJrAgrU27QlFIPAG6t9Y+VUo8Ar+GfKvmY1rputgsUYqYks8KKJLfCaiSz\nwmoksyJczflG1S0tPUF9QhlODa05GA42gnbwCUhmL8/q9UPk5VYyG5jVv4dIyyxIbgOR+gMeXzIb\nZqT+gMefMLOyUbUQQgghhBBChAlp0IQQQgghhBAiTEiDJoQQQgghhBBhQho0IYQQQgghhAgT0qAJ\nIYQQQgghRJiQBk0IIYQQQgghwoQ0aEIIIYQQQggRJqRBE0IIIYQQQogwIQ2aEEIIIYQQQoQJadCE\nEEIIIYQQIkxIgyaEEEIIIYQQYUIaNCGEEEIIIYQIE9KgCSGEEEIIIUSYkAZNCCGEEEIIIcKEI9AD\nlFI24IfAKmAIeFhrXTru/r8EHgB8wDe01s8HqVYhJkUyK6xGMiusRjIrrEYyK6xkMiNo9wExWutN\nwFeAb5+7QymVCPw5sAm4FfhuMIoUYooks8JqJLPCaiSzwmoks8IyAo6gAVuArQBa671KqXXj7usD\nqoC4sQ9foIMlJblwOOzTKHXy0tI8QT1+sEn9MyaZnWNWrx9C/j1IZkMgmN/D1j2Vl7z99k3zZu05\nIimzILmdDKl/RiSzISD1T89kGrR4oGvc516llENrPTr2eQ1wErAD3wx0sI6O/ikXORVpaR5aWnqC\n+hzBJPUHPv4kSGbnkNXrh7DIrWR2jgX7e+jpHbzk7bP1nJGWWZDcBiL1Bz5+AJLZOSb1Bz7+RCYz\nxbEbGH8E27gw3wFkAYVAPnCfUmrDNOsUYrZIZoXVSGaF1UhmhdVIZoVlTKZB2w3cCaCU2giUjLuv\nAxgAhrTWg0AnkDjbRQoxRZJZYTWSWWE1kllhNZJZYRmTmeL4PHCLUupdwAAeUko9ApRqrV9USt0M\n7FVK+YBdwBvBK1eISZHMCquRzAqrkcwKq5HMCsswTNOc0ydsaekJ6hPKfNfQmoP5ukbQDj4Byezl\nWb1+iLzcSmYDC/b3sKO47pK337A6Z1aOH2mZBcltIFJ/wONLZsOM1B/w+BNmVjaqFkIIIYQQQogw\nIQ2aEEIIIYQQQoQJadCEEEIIIYQQIkxIgyaEEEIIIYQQYUIaNCGEEEIIIYQIE9KgCSGEEEIIIUSY\nkAZNCCGEEEIIIcKENGhCCCGEEEIIESakQRNCCCGEEEKIMCENmhBCCCGEEEKECWnQhBBCCCGEECJM\nSIMmhBBCCCGEEGFCGjQhhBBCCCGECBPSoAkhhBBCCCFEmHAEeoBSygb8EFgFDAEPa61Lx91/B/A1\nwAAOAV/QWpvBKVeIwCSzwmoks8JqJLPCaiSzwkomM4J2HxCjtd4EfAX49rk7lFIe4FvA3Vrrq4FK\nIDUIdQoxFZJZYTWSWWE1kllhNZJZYRkBR9CALcBWAK31XqXUunH3bQZKgG8rpeYDj2qtWy53sKQk\nFw6Hfbr1Tkpamieoxw82qX/GJLNzzOr1Q8i/h4jK7NY9lRfddvumeUGrZbqC+TP3uGOC/pyRlFkI\nfW6tQOqfEclsCEj90zOZBi0e6Br3uVcp5dBaj+I/u3AjsBroBd5RSu3RWp+Z6GAdHf0zqTegtDQP\nLS09QX2OYJL6Ax9/EiSzc8jq9UNY5DaiMtvTO3jRbeGWkWD/zC/1GsDsvQ6RllkIbW53FNe97/Mb\nVucEtZbpsPrvWsns1MnPPLRCmdnJTHHsBsYfwTYWZoA24IDWulFr3Qu8jT/cQoSSZFZYjWRWWI1k\nVliNZFZYxmQatN3AnQBKqY34h4DPOQwsV0qlKqUcwEbg5KxXKcTUSGaF1UhmhdVIZoXVSGaFZUxm\niuPzwC1KqXfxr2zzkFLqEaBUa/2iUuqvgNfGHvuU1vp4kGoVYrIks8JqJLMRwmeabDtUyxsHaliQ\nE4/KTwp1ScEimRVWI5kVlhGwQdNa+4DPX3Dz6XH3PwE8Mct1CTFtkllhNZLZyPHavmqe3lEGQGuX\n/zq0SGzSJLPCaiSzwkpko2ohhBBiFjS29/Pc2+UkxDm5Y2M+DrtBSXk7Pp9spSSEEGLypEETQggh\nZsEre6rw+kw+efNC0hJjWZCTQP/gKNVN1l3FTAghxNyTBk0IIYSYgR3Fdby8t5LdxxtIiHPSNzgC\ngMpLBKCqqTeU5QkhhLAYadCEEEKIGTpb04VpwpJ5SRiGAUCC24krxkFjWz+mKdMchRBCTI40aEII\nIcQM+HwmpbVdRNltFGbFn7/dMAyyU+IYGvHS3j0UwgqFEEJYiTRoQgghxAzUt/bRPzRKYbaHKMf7\n/6xmpboAaGjrC0VpQgghLEgaNCGEEGIGSuu6ACjKTbzovvSkWOC9JfeFEEKIQKRBE0IIIaapp3+Y\n2uZeEt1OUuKjL7rfFe0gxmmnTRo0IYQQkyQNmhBCCDFNe0404TOhKDfh/OIg4xmGQUp8DH2DowwO\nj4agQiGEEFbjCHUBQgghhBWZpsk7R+uxGTA/O37Cx6UkxFDX2kdblywUImZmR3HdRbfdsDonBJUI\nIYJJRtCEEEKIaSit66KutY+8DA8xzonPdyaPTX1s75ZpjkIIIQKTBk0IIYSYhm2HaoH3NqSeSJLH\n36B19MoImhBCiMCkQRNCCCGmqKNniEO6hZy0ODKSYy/7WHdsFA67QVfv8BxVJ64EvQMj1Lf2UdnY\nzcioL9TlCCFmUcBr0JRSNuCHwCpgCHhYa116ice8DPxWa/2jYBQqxGRJZoXVSGat57X91Xh9Jres\ny8Nnmpd9rGEYJMRF09EzhNfnw26z/rlRyWzodPUOs+9UE41t/QC8ebAWZ5SNxflJLJ+fzM1r80Jc\nYXiSzAormcwiIfcBMVrrTUqpjcC3gXsveMw/AUmzXZyYGp/PpL6tj5rmXopLW/F6fbhdTpI90Xhc\nUe9bYSzCLyqWzAqrkcxaSHffMDuK60jyRLN5eSa7ShoCfk2i20lb9yAtnYNkJrvmoMqgk8yGQGN7\nP9sP1THi9ZGZ7CI9KZbB4VGqm3o5VtZGVVMPqxakkpZ4+VHdK5RkVljGZBq0LcBWAK31XqXUuvF3\nKqU+CvjOPUbMLZ9poqs62FXSyJGzLQwOey/5uIykWNYvSSc5PmaOKwwJyaywGsmshfx2dwXDIz4+\ndkMBDvvkRsMS3E4A6lr6IqVBk8zOsZqmHrYfrsPr83HtyiwKx60culb5OHymBV3dydd/tp/br87H\n43Kevz/CT8pOlmRWWMZkGrR4oGvc516llENrPaqUWg48AHwU+OpknjApyYXDYZ96pVOQluYJ6vGD\nLVD9W/dUAtDU3s87xXU0tfunOXhcTuZlxZOW5MIV48Bu81/zUNPUQ3VTDy+9W8WmFVlcpdKD+hqF\nwesvmZ1jVq8fQv49RFRmPe6LTwSFY0amU1NFfRc7i+vJSYvjo7coHHbbJb/fC2WleeBMK10DI7P2\nWkRSZiG0ub3wZxhueR31+vjL/3ybkVEfN6/PRxVcPMhz84YCUhNd7D5Wz7ZDdXzsAwvPry4aLt+P\nZHbqwuVnN11S//RMpkHrBsZXZ9Nan9tt89NADvAWMA8YVkpVaq0nPPvQ0dE/zVInJy3NQ0tLT1Cf\nI5gmU39n9wCHdQunqjoAKMhws3heEumJsRdtlJoaH82CbA/1rX28e7yRPSUN2DBZW5QSsvpnevxJ\nkMzOIavXD2GR24jKbE/vxcvJh1tGpvMzH/X6+PavDuHzmXz8xiI62vuAS3+/F3KOvYcrq+mYldci\n0jILoc3thT/DcMvry3sqKa/rYkFOPNkpsRNmbkG2h67eZI6Xt7N1TyU3XZWDYRhh8f1IZqfO6n9f\npf7Ax5/IZBq03cA9wFNjc3ZLzt2htf7Suf9XSn0daAwUZjEzHT1DvL6/mpbOQRLinFy9LGNS02Wy\nU+O4eV0uW/dW8+7xRjYty2TpvOQ5qDgkJLPCaiSzFvDUW6VUNfWwZUUWK+ZP7SRXXGwUNsOgsT24\nb+jmkGR2jnT1DfPSnioS3E7WL04P+PjVC1Np6xqkrqUPXd3J4kuMtl2hJLPCMibToD0P3KKUehcw\ngIeUUo8ApVrrF4NanXif2uZe/uPpo3T0DDEv08Om5ZlEOSa/GliiO5obr8rhjQM1/OyV0/zzH1yN\nMyq4Q/MhIpkNIzuK6y66Ta6HuEhEZrata5DDZ1oYGfURFxM1qTeX4eqtw7W8eaiWBLeTvAz3JXN9\nOTbDwBMXRWN7P6ZpXjTbwYIiMrPh6He7Kxga9vLQ3cvo7w+8l57NMNiyMovf7qo4vxWEACSzlnUl\nvo8I2KBprX3A5y+4+fQlHvf1WapJXMKpqg6+/9wxBoa8XLUolWWFydP6A5+R7GLJvGROVLTzoxdP\nsHLBe2eBIyXskllhNZGY2cHhUd48WMvQiBcD+O8XjuP74DKuXpoR6tKmbHdJA79+/QwxTjs3rsmZ\n0omx8RLinFQ39dLdN0yCO3qWq5xbkZjZcNTRM8TbR+tJS4zhto0FPP/WmUl9XWy0g6uXZvDO0Qb2\nnGji7k3zIuGkwIxIZoWVTGYETYTY7pIGfv6q/3fI5z64dMKVGidrxYJkyuq6OF7eRlFOAq4YiYEQ\nYnYd0i0MjXhZq9LISnGx7VAtP3v1FAty4klNsM4S4NsP1/Kr18/ginFw41U5xMc5A3/RBOLHVtVr\nbO+3fIMWyQLtazeXtu6rZtRrctemeZNeMfSceZkeyuu7qWvxX4N+zYqsIFUpxMwNDI3S1NFPTVMv\nlU091Db30to1yNCwF5vNICUhhnmZHvLS3dhskX+yQd6ZhzGfz+SFXRW89G4lToeNG9bkzLg5A3A6\n7KxemMreE00Ul7ayeXnmLFQrxMR8PhPD4Io/g3ulGBwepaK+mwS3kyXzkrAZBp+6ZRGPvnSK37xx\nlj/76MpQlxiQaZq8vKeK594uJ94VxSP3r6a8oXtGxzzX3DW096Py5bqgcNM3MMLu4400tfdz5Ewr\nv3/nEpI8oWukewdG2Hn0vf32psowDK5emsGLuyp48q1SVhWl4o6NCkKlQkysq3eI8vpuapp7aezo\np7NniL7BUYZHfXi9PkZGfQwM+T8fzzAgLiYKZ5SNgSEvVY09VDX24I6NYq1Ki5Sp4hOSBi1MdfQM\n8ZPfneB0dSfu2ChuWptD4iyecS3KTeBkZQfldd2sWZhKbLREQczcyKiP+tY+qpr8v0irmnqob+1j\ncNiLYfhPDiTHR9PdO8zKohQKMjwR/Qv2SlVe343PhIW5CdjGfr6blmXy9tEGiktbOV3VEdYLF5im\nyTM7y3h1bzUp8dH85SfWkJnsmnGDljDWoDW2RcxCIRHDNE12HKmjrXsId2wUJyra+c+nj/KVB686\nv1T9XPvZK6cYHvGxYn48u0oa8FR0TPkY7tgoVhalcli38OS2s3z27qVBqFSI93T1DaOrOzhV1cHZ\n2i7qW/suekyU3YbdbmC3Gbhjo0h0RxMf5yQ9MZa+wRGSE2JIcjuxj40am6ZJZ+8wurqT0tpOdhbX\n09U7zP+5TYX0JEowybvyMDM04uXlPZW8vKeKwWEvVy1KY2FeAtGzvJiHzTBYXJDI/pPN6OpOVi9M\nndXji/D15qEaWjsHaekaoLtvmL6BUUZGfYz6fBiA3WYjKsqG02EjOsqOM8qGw25jUW4iGP7RsKER\nH0PDXgaGRhnxmbR1DtDeM0hH9xDjJwfZbQauGAcJcU58psngsJeGtn5e2FXBC7sqSImPZuWCVJbP\nT2Z+VrxM+4oQ5fXd2AyYP24jXcMwuP+mIv7xFwd5ekcZf/vptWHZnJumyePbzvLmwVriXVHcsCaH\n09UdnK6e+pvjC50bQWuKnJUcI0ZZXTdt3UPMy/Jw7cosqpt62VlczwvvVPCJDyyc83pGRn2cquog\nymFjYV7CjI61tCCJts5Bdh9vZP2SjPddey5EIJdboMNnmrR0DlBe383O4jqaOgbo6h0+/7goh42c\n1DjSkmJJifc3YXExUVOeomgYBkmeaDYuy2DpvKTzM8DO1HTyqVsWsXFZRlj+PZkJadBCzDRNuvqG\nqW7qpbi0lcNnWujuGyY6ys7GpRkszEsIWugWZCdQfMYf8BULInbJfYE/ZyerOth1rIGDp5vx+t5/\njYXDbmC32TBNE6/PvOh+gKOlbRMe3zD8F6UvzEskOzWO/Aw38zI95KS62X284X2PHRweJTU+lsNn\nWzhW2sb2I3VsP+L/AxDjtOOOjcIdG0V8nJPk+GiyU+POX3sRKQvZRLKu3iHau4fISnFdNPJQmBXP\nusXpHDzdzOEzLaxV4bWqo2maPLGtlDcP1pLodnLL+rxZnV0QPZbvxo6BWTummDnTNCkpb8NuM1ir\n0jAMgwduXsjJyna2HarlulXZZKfO7UqIe080MjjsZVlhEs4ZboRssxk8dOdi/vEXB3nslVP8w+9v\nmNG1lOLKNDzqpbVzkI6eIcrrumlo66NubIbMOQ67QVaKi8wUF1nJLgqyE+mbxMqjUxEf5+SW9blg\nwlPby/jJSyc5dKaFT9+mIirX0qDNoaERL0++dZa27iE6eoboGxhhaNhL/9Do+cckeqJZMT+ZZYXJ\nQV8C/9yZuRMVHVQ2WHcjQXF5lY3dPLmtFF3TCYDHFUVeupv0pFgS3dHExTqw295/8bnXZzI84mV4\nxMfwqJdRr4+lBf4m3mYzcDpsxDgdHCtvJTnRxfDQyEUnEiobe6hsvDhXMU4H6xans25xOl6fj7K6\nbl7dV0V79xCdvUO0dw/S2vXeJqwOu8H87HiuWpQ22y+NCIKS8nYAciZ4Q/vh6+ZzWLfwzM5yVhWl\nTnnhg2AxTZOnd5TxxsEaslPjuGZFZlCmfmckx1LZ0MOo1xc23/uVrqy+m57+EQqzPMTF+K/RinLY\nuf+mhXz/uRJe2FXBH9+3fM7q8Zkmrx2owTCYtanA+RkePnL9Ap7aXsqPfnucR+5fPe38XYlLnl+p\n+gdHOF3VQWVjDy2dA4xfP8duM8hIdpGf7j8h29U/TEp8zPtGx4K1mIdhGNywJodl81N47OVTHD7T\nQmldF39wz1KWRcgev9KgBdmO4jo6e4Y4XtFOdVMPo9730h1lt5GWFIvKTyQv3Y3KS+Satfk8t03P\nWX0qP4mTlf65wsL6xv/hNE2TkVGTp94qxWearFqQwl2b51HT3BNwVNZuM4iNdhA7bsbhqqKLp8FW\nNHYT43QwMjx60X2TYbfZWJSXSH3be3PUTdOkf3CUrr5hGtv7qWzo4UxNF3UtfczLjGdRXuK0nkvM\njWPl/pHWifZeykx2cd3qbHYcqWPHkTpuXpc3l+Vd0vYjtRSfbaWkvJ34OGfQmjOAzCQXZXXdtHYN\nkpnsCspziKnZc7wRgPnZ759KuGZhKvMyPRw83Uxtcy+56e45qedoaSv1rX3Mz44/3zDOhls35FFW\n18WhMy38+MUT/ME9y6a9ZYSIbK1dA7y2v4Z3jtUzPOJfvCMtMYaMZBcp8THcsi6P9KTY9zX5U90b\ncjakJ8bypQfW8Pr+Gp7dWcZ/PHmUB29bdP6EgZVPJkiDFkRdvUPsPtZAWb3/wnJ3bBSFWR4ykl0k\neaKJjXZcFBT7HC8d6o6NIifNTW1zL9VNPeRneOb0+UVw+EyTPccbKavrJsZpZ8vKLLJT46ht6Z32\nlNnZ/OV7uWMZhkFcbBRxsVFkp8axuiiVY2VtlJS18a3Hj3Dr+jzSkvzLtFvlF+2VwjRNTld14Ipx\nXHaqyX3XFrLvZCO/3VXBhiUZIZ2WYpomR0vbKClvx+OK4tZZntZ4ocwUf1PW2N4vDVoY8JkmcTh6\n7gAAIABJREFUB3UzMU47WSnv/TzO/Y6anx1PZWMPj71yiq9+Zn3Q6zFNk1f2VAGwvHB2RwJshsHD\n9yyl58liDuoW2roP8cmbF7EgO/7834WBoVFqmnupb+sbu6bYJDUhlhXzUyJ2MQbxnhfeKedERTvl\nDd2YJsTFOFhemMz87PdvyXSmtpMztZ0hrPT97yNiou3cuj6P7Ufq+N+tmrO1nSzMtfbJXGnQgsA0\nTXYda+DJt0rpHxol0e1kzaI0ctPiLnpzfOEbVY87Zi5LBaAoJ57a5l52HWvggVukQbM60zTZf7KJ\nsrpuUhJiuHFNNq5ZPAs712w2g9ULU0lNiGH7kTreOlzHHRvzI2queaRoaOund8A/VexyJwLiXU7u\nu3Y+j795lt+8eYbP3zt308fGM02T594u51hZ2/nmLNj7QmYkjTVobf1QFNSnEpNQ3dRDT/8IC3Li\nLzkdKyctjuT4aCobe+akqT5R0U5ZvX915cRZbIjGv9dYtySdUZ9JeX033/jlIRLinHhcTvoGR+jo\nufT1QjbD4PrV2Xz8RgltpPGZJsfL23nzUA3Hx6aoJ8Q5WT4/mcKsS/+7CEdpSbHcuiGP1/bVsPd4\nEwlxTtKTrHsSTBq0WdbcOcAvXj3NqaoOop12NixJZ1F+4vmlpsNRbpqbGKedPSca+diNRTLlweKO\nlrZxpqaLJE80t6zLDfq1jHMlN93NxqUZ7DnRxPbDddy1uSDUJYkLnBm7zjHjEn8ULzwZZbcbpCbE\nsP9UM6uLGtm4bG73Y/T6TH79xhneOlznb8425M3qdLKJjB9BE6EX6JpJwzBYMT+FncX1vPxuZVCX\nqT93wgDg3i2FM97WYSIOu40tK7P4yPUL2FlcN7aC5SCuaDuZyS6S46NJdEef3zOts3cIXd3J9iN1\nHCtv49b1efI+IQKMen3sOd7Iq/uqz/8+Sk+KZem8JPLS3ZZcFTHRHc0Na7J5fX8N7xxt4J4t82a8\nyE6oSIM2S0ZGfbxxsIYXd1cwPOJj5YIUPn2bOn89Rjiz2QwW5MRzoqKD4tJW1i8Or5XVxOTVNPee\nHw24OYKas3MW5iXS3uN/s3C0tI2b14b++iXxnnNTXtKTYwM+1mYYbFmZxUvvVvLYK6doaO8/P4Uq\n2FNXh0e8fOuXB9l9rJ7cNDeblmfM2V6QGUmxGAY0tl28N5CYe8fL2zAMyEqZeJXG/Aw3iW4ne040\ncffmeWQEaRRt78kmKht7WL84nfwMT9AatHOaOvpZXJAUcCGSzBQXC3MT2HOiifL6bt4+Ws9NV+VY\n8g288DtW1sbjb56hqWMAu83gmuWZ3Lwuj4rG4GZuLmQku1i+IIWSsjZKytpZq6y5wJg0aDNkmiaH\nz7Tw9I4ymjsGcMdG8ZnbF3P1UmvtybAgx7+a4ztH66VBs6jWzgF2H2vAbvOvbhSpm49ftSiN+tY+\nTla0U1bXxYKcme0RJGbP2Zou3LFR5zdkDsS/IEcWO4vreetQLbdvzA/6KFZX7xDfe66E8vpuFuUl\n8mcfWcH+081Bfc7xohx20hJiaZARtJAbHB6lrK6bwqx4op0Tn8wyDIOVRam8XVzPb3dV8LkPLpv1\nWgaGRnl6eylRDhsfu2HBrB9/pux2G5uXZzIwNEpdSx+ldV2Wv8bnSrOjuI5Rr4/9J5sprevCMODG\nNTnctamA5Hj/5TWR0KABrJifTFldF6eqOlB5ibhd1rvMQ8aop8k0/dNjvvTfe/jB88dp6Rzg5nW5\nfPMPN7JxWaalmjPwDwv7R9Haae8eDPwFIqx4fT5+9OIJhkd9bFiaEdEXc0c5/G8UTODnr55m1OsL\ndUkC/zSotu7B9y04MBkFmR7WLEylb3CUN/bX0D84ErQan91Zxt88us/fnOUnsX5J2pw2Z+dkprjo\n6R+hdyB436sIrLS2C59psjg/8FL2BRluCjI87D3pH0WabY+/eZbO3mHu3FhAamLgEehQsNkMNq/I\nJMph49DpFoZHvIG/SISN3oERXtlTRWldF8nx0dy9uYC8DDfHytvYUVwXklUYg8Vht7FmYSo+n8nx\nivZQlzMt0qBNw+mqDr75q8NsO1RLW/cg8zI9fPCaQrJT4zhwuvl80K0W9mtXZmMCu0saAj5WhJeX\n362ivL6bwiwPRTnxoS4n6DKS/VNu6lr72H7YWv/OIlVZXRfAtEY0l4/t/djdP8LWfTU0BGH6357j\njWzdV03/4ChrFqZy8/q8i/b/myvnVgtsbJNRtFA6tzekyg88EmQYBp/4gH+BjF+/cQafzwzwFZO3\nu6SBXSUNFGR6uGtTeF9bGxcTxYr5yQyP+jhZKdvzWEVVYw+v7Kmis3eYRXkJ3LExnyTP3C9KN5cK\ns+Jxx0ZRVtfF4DS3AgqlgHOglFI24IfAKmAIeFhrXTru/r8APjH26Sta678PRqHh4Le7yjmkW6ht\n8b95yEt3s3phSsSEfP3idH7z5hl2lTRw1+Z5Yb2wyeVcaZmtaOjmxd2VJHmiLTe1dibWLEqlrqWP\nF3aVs2FpxqSn1YWjSMjsue1EFuQk0NQxtcbDMAyuWpSKw25wtLSNb/zyEJ+/dznLZmGZ8VGvjyff\nKmXboVqiHDauX51NbogvgD93vVNDWx9FudacohsJmT1d3YHNMCjKSaBtEjNHVH4SVy/NYN/JJl47\nUM0dV8+8mTpW1sbPXz2NK9rBmoWp7LLACdLz+6dWdrC0MMkyizBEQman41RlO//1XAlDw17WL0ln\nySxtfh7ubDaDJQVJHDjdzJnqTlZeYi/XcDaZ04f3ATFa603AV4Bvn7tDKTUf+BSwGdgI3KqUWhmM\nQkNpaMTLMzvKeHF3JbUtfWQkxXLnpnxuvConYpozgNhoB+tVOi2dg5ypDu3+FjN0xWR2aNjLj393\nEp9p8tm7lkTcoiCXE+N08KHr5jMw5OWZHaWBvyC8WT6zZWPXNBRmTW+rDsMwWFWUyublmQyNePnO\nk8W88E75jKawtnYN8K+/9s92yE6N465NBXO22fDlZI81aHWtll4oxNKZHRrxUtnQQ0GmZ9LX6+4o\nrqMg07/q8TM7ynjyrbPTfn7TNNlRXMf3nj2GzWbwhQ+vsMzWIVEOG0sKkhjx+iivs9Q1S2Gf2fEz\nsGZjFtYh3cJ/PH0Ur9fHdauzr5jm7Jyi3AQcdoOzY9OZrWQyDdoWYCuA1novsG7cfTXA7Vprr9ba\nBKKAiLqA6URlO3/36D5e2VuFK9rBDWuyuXVDHqkJ4TlHfKa2rMwC4J1j4X8W7zKumMw++dZZmtr7\nuXV9Hkvnze6mplZww5ps8tLd7C5ppHRsip1FWTqzo14fFQ095KW5iXHObHGaotwEvvKptSTHx/Di\n7kr++ZeHqJziheumabL3RCNfe+wAZfXdbFyawd9+em3YvAHOTo2IBs3SmS2v68LrM1F5U1voIsbp\n4LrV2QBsP1w3rd87Nc29fPfpY/zvVk2M084jH19luTfORbkJ2AyD09WdmNZ542vpzE7V9sO1/PCF\nEuw2G3/+sVXMy7zy9rmNctiYlxVP3+Co5aaUT+YvaTww/jeQVynl0FqPaq1HgFallAF8CziitT5z\nuYMlJblwBHk4PC1t5iHs7R/mpy+e4M0D1dhsBh+5sYiUhBii5mAoPxSbVQMcKm3DNE0S3E72n2ri\nT+5fM603NLPx+s/QFZHZvccb2FFcz7yseP7wI6twRtlDlp1QPW9mRgJ/8vHVfPn7u3hiWynf+Yvr\nsU9zU80Q59bSmT1T3cGo18eyolTS0jwzzsPVq3JYtiidn7xQwlsHa/jHXxzk+qtyuf/mReSmX/7n\nVNfSy6MvnuDgqSZinHb+9OOruWVDPoZhcKL6/W+mQ5Hbc69bamIsDW19M8pdJGUW5ja3b4xdu7p+\nedaUM+txx2Bi8OaBar71+BE+ddti7tpSOOHJCdM0aWrv57Bu5p3iOo6X+bffWb0wjT+9f/X5zXQn\nU0OoftdeyOOGorxEzlR30DvonXQWJbOXd6mf71RfM6/Xx9d+soejZ1uJjXZw9zWFDI6aV9z7g3NW\nLUyjtLaLisYe1LyUKb+eocrsZBq0bmB8dTat9fmr7ZRSMcBjQA/wx4EO1jHFaxOmKi3NQ0tLz4yO\ncUi38NgrJxkY8pLkiWbzikziou0MDo4wSHBX3fK4Y+jpDe1Jm4U5CRzULbzw1hnu2Di1Ofaz8foH\nOv4kRHxmWzoH+O7jh3HYbfz+nYvp6vTXGIrshDKzLS09pLmdXLMik90ljTz12iluXjf1vdHCILeW\nzuzB4/4R95zkWFpaemach3PHfvDmhaxdmMoT286y41AtOw7VsqQgifVL0lmcn0RaYgw2w6B3YITS\n2i72nGzikG7GNGFJQRK/d7siPclFa2sv8P5/H6HK7bnvLTvFxbGyNiqq289vCDwVkZZZmNvcFmv/\n6p1pHue0MpuVHMtNV+Vw4FQzP3/5JE9vO8OSeclkJbuIibYzMuqjq2+Y5o4Byuu7GBh6b8XDzGQX\nywqTyE6NY+fB6kk/Zzi8PxhvXoabM9UdlJS2TiqLktnALvXzncpr1tEzxE9+d4LT1Z0kxDm5aW0O\nsU5byHITDpl1OW0kxDmpqO+mraNvSq9nKDM7mQZtN3AP8JRSaiNQcu6OsTMNvwXe0lr/6wzrDLmu\nvmF+/cYZDp5uxmYzWLMwlWWFydimeUbeqopyEygubeWtw7XcuiF0K53NQERndnjEyw+eL6FvcJRN\nyzMpreuy+vS+aTs3Rz87NQ5nlI2ntpeysiiV9DBdpvoyLJ3Zsvrpr+AYyJKCJL720HqOjO03eaqq\ng1NV760eZzNg/IJ6SZ5oVi5IIT/DzcmqDk5WhedKczmpcRwra6OupRc1iWXew5BlMzvq9VFW10VO\nWty0muNzctLcfPCaQt44WMPukkYOTrBlgyvGQX6Gm8xkF7np7hk9ZzjJSI4lLsZBZWM3Q8Pey+4l\nFyYsm9lATNNk36kmfvPGWXoHRsjPcLN5RaZlFnAJJsMwKMyOp/hsK9VNvaEuZ9Im06A9D9yilHoX\nMICHlFKPAKWAHbgeiFZK3TH2+L/SWu8JSrVBtP9UE798TdM3OEpRTgLLCpNIcEfuXlKX44yysyAn\nAV3dSfHZVtYqy21cHbGZNU2TX2zVVDf1UpSbwEKLrgA322KjHWxYksGuYw387OVTfPGBNVZbhdSy\nmTVNk7O1XXhcUbPWGE90cfztV+fT0z9MXUsfrV2D9A2M4PWZxDjtJMfHkJMWR2pCjCVWMs1N8y9W\nUtvSZ9UGzbKZrWzoYXjUx6IpXn92KYfOtJAcH8PdmwvoHRihKDuBoREfUQ4bHlcUaYmx7DvVNAtV\nhx/DMFiQk8CxsjaOnG1h47LMUJcUiGUzezkNbX08/uZZjle043TY+NQti7DZsMTvwblSmOWh+Gwr\n5Q3WWdQmYIOmtfYBn7/g5tPj/j88JkRPU9/gCL98TbP/VDN2m8H6xemogkSrvbmbdYvzE9HVnbxx\nsNZyDVokZ/bF3ZXsOdFIYVY8Vy+x1s8l2AqzPFQ19qBrOnnjQA23bcgPdUmTZuXMtnYN0tEzxNpF\naXPyhsDjcrK4IDwW+5iJvAx/g1bVGLzpM8Fk5cyeqvaPqi6ZxcbYMAw8LidNnQPnb2vpGrDUG8Lp\nKMzycKysjb0nm8K+QbNyZi+lrWuQl/dU8vbRBnymSVaKi43LMrDbr+z3r5ficTlJS4yhsa2fzt4h\nEi0wADOz5bYs7mxtJz9+8QRt3UOkJcZwzYqssFnlK9QS3NEsn5/M8fJ2dHWHVc/wRpR3jtbz210V\npCbE8OcfXcnhsy2hLimsGIbBxmUZdPUN8/T2MuZleiS3c+DM2Ga/C2dhNOJKkp3in5ZbMcUVKsXM\n6bEGbdEkNqgWl5fgjiY5PpoTFe309A/jccl7qGAaGBrlmZ1llNd3U93Ug2lCvCuKq1QaeSHe3zHc\nFWbF09I5yP5Tzdy6furXqs+1K7JB85kmP3y+hCNnW8GEVUUprFiQcsWPml3oQ9fO53h5O0/vKONv\n/s9a+YcfQo+9copdxxpwRtm4ZkWmNGcTiI128Mf3Ledbjx/hv184zlc/s57keEudFLWcs7X+Bm1R\nnky3nQqbzaAgw0NpXZdVrt+JCCOjPkpr/defxUszMSsKs+I5pFs4eLqZG6/KDXU5EcHr81Hb3Mdj\nvztBTUMXPf0jdPQO0dI5wLldDRLdTpYVJlOYFX/FrZUwHQWZHg6cbmbfySZLNGiWW/1hpnoHRvj+\nsyUcPtNKrNPBrRvyWFWUKs3ZJRRmxbNOpVFe383hM9IQhMqeE43sPtaA02HjlvV5V+y1kZO1KC+R\nj99URHf/CN9+spju/uFQlxTRTld1EuO0kxcGG0BbTWFWPKYJVU3WnOZoReX1XQyP+lgso+uzpjDL\ngwHsORmZ19rNtarGHp7dUc7O4nqe31HKQd2CrulkYMi/RsLywmTu3JTPPdfMY0FOgjRnkxQb7SAz\n2UVFQzdN7eG/J9oVNYJWVt/Fj144QVv3IFkpLraszCI2+op6Cabsw9cv4PCZVp7ZWc7KBalEOa64\nnj6kXj9QwxPbzhLlsHHzulxSZDRoUm5em0t79yCv7a/hO08U88UH1hAXExkrp4WTls4BmjsHWLMw\n1YqrvYbcuY1jy+u7Z2XBChHYsXL/HmTLC5NDXEnkcMVEofITOV3dSWvnAKnWW0U3bBwra6P4bCt2\nm8HSeUl8+q5lRBsmblfU+d+xEy2iJAKbnx1PQ1s/e040ct+180NdzmVdEX9RfT6TV/dW8S+/Okx7\n9yD3binkA+typTmbhMxkFzesyaapvZ9nd5aFupwrxqjXx6/fOMMT286S4HZy+9V58kdvknYU17Hz\naD3pSbEsykugurmXb4792xez60RlOwBL58mb3elYmOtvys5dxyeCr6SsHYfdxuICGUGbTZvGFgh5\n90RjiCuxrm2Haik+24o7Noq7NhewbnE6y+ankOCOlhNgsyQ/w0N0lJ09JxoxTTPwF4RQxP/EmzsH\n+LfHj/D0jjLcsVH85SdWc++WQpnSOAUfvWEBmckuXj9Qw7GytlCXE/E6eob49yeK2XaolpzUOP76\nwbUkeWTkbKoMw+DqpRksKUiivrWPf/7lISplQYZZdaLC36DJaMT0pCTEkJ4Yi67pwOvzhbqciNfW\nNUBtSy+L8xOJjpJr/mbTusXpOKNs7C7xrygopqasrosntp0lxmnnlvW551cZ3Lqnkh3Fde/7ENMX\n5bBx1aI0WjoHw/7EWMQ2aKNeH6/sreKrj+7jTE0n+Rlubrs6j+bOAQn4JJ37ZbD3ZBPrFqfhsBs8\n+tJJGi0wd9eqDpxu5qs/9We2IMPNdauzz49SiKkzDIN1i9P4+I1FdPYM8Y1fHuado/WhLisiDI94\nOV7eTnpSLOlJMro7XYsLkhgY8lpqA1Wr2lPSAMDKBSkhriTyxEY7WKfS/W98q8P7jW+4GRwe5X9e\nPIHPZ3LtqixZCTPIrl2ZBcDO4vB+LxBxDZppmhzSzfzdo/t4ZkcZMU47W1Zmcf3qbGKcMqVxupLj\nY3jg5kX0DozwL78+TG2zvJmYTe3dg3zv2WP89wvHGRn1cfXSdK5bnS3X/M0CwzCIibZz49ocbAb8\n7NXT/Ph3J+gfHA11aZZ2vKKdoREv61S6rPA6A0vGptodr5ATMcH29pE6DMM/2iNm37k3vm8dkZPg\nU/HMjjJauwa5fWM+WSlxoS4n4qn8RLJSXBzUzWG9iFjEvPvzmSaHz7TwyHd38oPnj9PcOYDKT+SO\njQXMz46XNxCz4IY1OTx46yK6+4b5198c5ogs9T5jQyNe/umxfXzlf/Zw5Gwr6Umx3LGxAJWfJJmd\nZblpbu7aXEBqQgx7TzTx9Z/t53RVR6jLsqwDp5sBWLc4LcSVWNuK+cnYbQaHxl5PERytXQOcqmxn\ncX6SJTaptaJFeYnkpbs5rFvkmt9J0tUdvHW4jqwUF/dtKQx1OVcEwzC4YU0Oo16THWF8MsHyDdrA\n0CjbDtXytz/Zx/efK6GsrouCTA/3bink6qUZsrfMLLvpqlw+e9cShka8fO/ZEh596SRdvUOhLsty\nRr0+dhbX8dc/3su+E4047DY2L8/ktg15JLhlekOweFxObr86n7s3F9DWPci/PX6EX79+hv7BkVCX\nZildvUMc0i1kJLsoyPCEuhxLc8VEsbwwmermXpk+HkRvH/VPb7x6aUaIK4lchmFw87pcfKbJ6wdq\nQl1O2Bsa8fLzV09jGPD7dy0hyiHvV+fKlhVZxMU4eONADQND4TmbxpJz/nymSWltF7tKGjhwqpmh\nES8Ou8E1yzP51J1L2XssfDtiKxt/7d6dGwvYXdLAu8cbOXi6mZvW5nLLujzS0uTN2uWMjPrYfbyB\nrXurae4c8F+wqtJZlBePU345zwmbzSA5Pobbr87n3ZJGth2uZd+pJj5zx2LWLEyVkctJeHN/NaNe\nHzetyZHXaxasX5LO0bI2dpc08JHrF4S6nIgzNOJlx5E6PC6nNGhBtnFpJi/uquStw3Xcuj6PZNka\nZkJPvVVKU8cAt23IY0F2QqjLuaLERju4ZX0eL7xTwZuHarln87xQl3QRyzRoPtM8v2HygVNNtHX7\nR21SE2JYkp7EwtwEYqMdnCiXVQbnQqInmjs2FnC2touSsja27qvmtf3VXLMymw2L01hSkCTLwo7T\n0TPEzuI6dhbX09U3jMNucONVOdy9aR7lTb309Mp0kLmWlhjL3ZsLKClv53h5O99/roRl85K4/6aF\n5MqmyxMaGBrlhZ1lREfZuWZFZqjLiQhrVTpPbCtl++E67txYIFvAzLIdR+roHRjh/lsWyeqNQRbl\nsHHvlkIee+UUT+8o4w8/uCzUJYWlQ7qZ7UfqyEmL48PXhfd+XJHq5rV5bDtUy8vvVrJpaUbYbWUU\ntn8FTNOkuXOAszVdnKxq52RFO939/mlIUXYbC3LimZ8dT2ayS87ghojNZqDyEynKiaesvpvTVR3s\nOlrPrqP1JMQ5WbMojdVFKaj8pCvyj2L/4ChHy1rZc6KRExXtmKb/j9fSeUksnZeMK8bB0bJWPG45\nwxgqdruN1QtTWb4glWOlLRwvb+drj+1n3eJ07tpUQL5M37vIS3sq6ewd4r4thbhk8+9ZER1l5+Z1\nubzwTgVb91XzIXnDNmvauwd5YVcFcTEO7tkyn+GB8F0UIFJsXp7J9iN17DvZxFWL0lgvi7K8T1Vj\nD4++dIroKDt/eM8ymdoYIq4YB5/4wEJ+8ruTPPbKKR65fzUOe/gMLIRFg2aaJp29w1Q19VDV2ENF\nQzeVDd3nGzKAhDgnW1ZkERVlIzvFhT2MXsQrnd1uY1FeIgtzE1ixMINXd5ez/1QTO47UseNIHXab\nQWF2PEU5CczPiqcg00NqQkzENdYjoz5qmnvRNR2crGhH13Qy6vXvB5OaEENRbgKFWfGyMmMYSoqP\n4apFaWQkxVJ8tpUDp5s5cLqZBdnxbF6RxaoFKTJVBzhytoWte6tJT4rltg35oS4notyyLo+3j9bz\nyt4qVsxPoShXpjzN1ODwKD984ThDw14+ecdiEtzRtEiDFnQ2m8HDdy/h7392gJ++dJJ4VxQqXzYG\nB/+m9P/1zDGGR7z88YeWy2yNENu4NIPDuoVDZ1r42SuneOjOJWHTpAVs0JRSNuCHwCpgCHhYa106\n7v4/AP4QGAX+SWv90uWO19EzRHNHP00dA9S19FHb0ktNcy+9A++/SN8V46Ag00N6UiyZybEkuqMj\n7g19pDEMg6rGbvIy3OSkxdHSOUBtSx+N7f2U1XZRWtt1/rGx0XZyUt1kp8aRneIiPclFamIMyZ5o\nYqMdM/pZz3Zmxxv1+ujpH6G9e5C27kGaOgZoau+ntqWX+ta+8w0ZQH66m+T4aAoyPSTIqmGWkJPm\nz2Rdax+6upPy+m7K6rv5JZCV4mJ+Vjy56W4yklykJMSQ6HYSFxs1443vg5nZ2TAy6uXNQ7U8t7Mc\nh8PGX31mgyzANMtiox08dOcSvvNkMd95qphP367YsCRjxtkKlnDPbHl9N/+79TTVzb1sXp55fgl4\nMTeyUuL4o/uW8/3nSvj3J4r54DXz+MTtS0JaUygz2949yNb91Ww7VIuBwcP3LGWtkpHFUDMMg4fv\nXkr740fYc6KJ5s4BPn5jEUU5CSHvOSYzgnYfEKO13qSU2gh8G7gXQCmVCfwZsA6IAXYppd7QWk+4\nrN9f/mD3Rbe5Y6PIz3CTHO9/g56SECNz8C3OZjPISHaRkewC/KNLbV2DtHYN0N49REfPEGX1XZTW\ndV30tVEOG+7YKFwxDmKi7Dij7EQ5bEQ5bHz9c5sn8/Szmtl/+PkB+gdH6RscoW+CvbPsNoNEt5PU\nxFjSEmPJSnFJhi3KMAxy09zkprnpGxihprmX2pZeWjoGaWi7eJU9w4C4mChio+3EOh1EO+1Ej2U2\nOsqOw2Hjy7+3IdDTzmpmZ0NtSy9vH62nuWOAMzWdDA57ccdG8YUPLacoN5GWlp5gPv0Vadm8ZP7o\n3uX8+Hcn+fGLJ3l6exkLcxPITHZx6/q8cJtSGnaZ3X+qiaOlbVQ2dp//t3rdqmwevHVRyN9sXYlW\nFaXyfz+2ip+8dJLn36ngpT1VzM+KJyvFhcflJMkTzTUrsuZyVsmcZLa9e5A9JxrpHxyls3eImmb/\nYAT4Z9M8fPdSFuUlztb3JGYo2mnni59czc9fPc3+U81881eHSYmPoTDLQ25mPPh8LMpNZHHB3I4C\nT+Yd5BZgK4DWeq9Sat24+zYAu8cCPKSUKgVWAgcmOtjvvn2v/JYUwTarmf3eF2+SzIpgm9XMpqV5\nZpzZtDQPa5ZOPOpwuRVbP3bL4pk+/RXrjjQPd1w7uZUcQ7xq7qxmFmae27vSPNx1XdFlHzPRayaZ\nDY4b0jzcsKEg1GWcMyeZTUvzoBZMb39IyWHo/N3Dm0JdwvtM5rRFPDB+mMOrlHJMcF/vJtSpAAAg\nAElEQVQPIBPnRahJZoXVSGaF1UhmhdVIZoVlTKZB6wbGn3Kyaa1HJ7jPA3TOUm1CTJdkVliNZFZY\njWRWWI1kVljGZBq03cCdAGNzdkvG3bcfuFYpFaOUSgCWAMdnvUohpkYyK6xGMiusRjIrrEYyKyzD\nME3zsg8Yt+rNSsAAHsIf8FKt9Ytjq958Dn+z9w2t9bPBLVmIy5PMCquRzAqrkcwKq5HMCisJ2KAJ\nIYQQQgghhJgb4bEbmxBCCCGEEEIIadCEEEIIIYQQIlxE3E66Yxd3/gr/kqlO4BGt9Z7QVhVYoB3u\nw51SKgp4DJgHRAP/pLV+MaRFWYRkNjQks9MnmQ0Nyez0SWZDQzI7M5Lb0AiH3EbiCNojwDat9fXA\nZ4AfhLacSTu/wz3wFfw73FvJg0Cb1vpa4Hbg+yGux0oks6EhmZ0+yWxoSGanTzIbGpLZmZHchkbI\ncxtxI2jAf+Dv1sH//Q2GsJapuNwO91bwNPDM2P8bwOhlHiveTzIbGpLZ6ZPMhoZkdvoks6EhmZ0Z\nyW1ohDy3lm7QlFKfBf7igpsf0lofUEpl4h8W/r9zX9m0XHKH+3GbKIY1rXUvgFLKgz/UfxvaisKT\nZDZ8SGYnRzIbPiSzkyOZDR+S2cmT3IaPcMitpRs0rfVPgZ9eeLtSagXwBPD/tNY757yw6bncDveW\noJTKA54Hfqi1/k2o6wlHktnwIpkNTDIbXiSzgUlmw4tkdnIkt+El1LmNuGvQlFJL8Q9NPqC1fjXU\n9UzB5Xa4D3tKqQzgdeDLWuvHQl2PlUhmQ0MyO32S2dCQzE6fZDY0JLMzI7kNjXDIbcRtVK2U+i3+\nVWMqx27q0lrfG7qKJudSO9xrrU+HtqrJU0r9J3A/ML7mO7TWAyEqyTIks6EhmZ0+yWxoSGanTzIb\nGpLZmZHchkY45DbiGjQhhBBCCCGEsKqIm+IohBBCCCGEEFYlDZoQQgghhBBChAlp0IQQQgghhBAi\nTEiDJoQQQgghhBBhwtL7oAkhhLAOpZQJHAe8gAm48O+X80da64Njj3EBfw18aOwxccAu4Eta6wal\nVDbwygWHTgMytNYX/U1TSqUCvwEygB7gfq113QT1VQK7tNYPjrttHfCM1nre9L7r88d5FHhCa/3m\nTI4jhBAi8skImhBCiLl0o9Z6tdZ6jdZaAU8C3wNQStmBrUAKsEFrvRxYgL+pe1UpZWit68e+frXW\nejVwOzAM/MUEz/enQIXWehVwEvijAPV9VCn1YIDHTJnW+mFpzoQQQkyGjKAJIYQICaWUA8j//+zd\nd3zb53nv/Q8WAYIESZAEt0Rq3trDki3JU05iyyOOndEmTZO0btI2o02f5mlz2tOcpM2TJunTuCuJ\nT072cNIMbycesmPLtmTtLY6borg3OAFuYpw/ACq0LIngAIEfdL1fL75kDAIXya8BXL/fPYC+6FUP\nANnAp7TWIYDov/+ilDIBmUTOgk19vx14Etirtf76FZ7mLPB+pdRqYDvw2RnK+gfg60qpA1rrhsvU\n/L+APwACQC3wF1rrTqXUvujPsQb438B7L3P5G9F6vw7cTKSxrCeyR9DQDHUJIYS4RsgZNCGEEIvp\nFaXUaaVUO5EGB+DB6L+3AC9NNWfTaa2/qrX2X3L1d4BR4C+u8nyHiQylrAG+EMNZrFeJbLD6s2gD\neZFS6kHgbuB6rfUmImf2fjjtLv1a63XTmsVLLwPsAnYDm7TW24g0aJtmqEkIIcQ1RBo0IYQQi+n2\n6HDDe4k0Tm9orbujt5mIzDsDQCl1u1LqVPSrWSn1zmm3/S1wI/A+rfXk5Z5IKbUOOAD8PfA48Bml\n1Dal1MMz1PiFaC3/eMn1dwM/0FoPRy//J/B2pVRa9PLrl9z/0ssQOaMXBA4rpf4/4DGt9Rsz1COE\nEOIaIg2aEEKIRae1Pklk3th3lVIV0avfAG6bdp9Xps01qwccAEqpu4k0Xe/SWvde5Wn+DPip1vqn\nwB8Sec97kRmG92utA8AHgU8Bt0676dL3THP0sUzRy5cOU3zLsEWt9QCwGfgbIo3aL5RSV5o/J4QQ\n4hokDZoQQoiE0Fr/N3AQ+I/oVY8Bw0qp/1BKZU7dTym1A1gOBJVSa4BHgA9pratmeIpa4BallIPI\nfK9XiMxxc00763Wl2uqBTwNfnnb1C8CDSqmM6OVPA69prcdn/mkv/izvBH5L5MzhPwI/JtKwCSGE\nEIAsEiKEECKx/gI4o5Tao7V+QSl1F/C3wGvRhUHSgZbodU8C3wXswJeVUl++5LHu01q3TLv8f4Al\nwFEgDTgNrI1efzfw1NUK01r/RCm1h8iCHgDfiz7eEaWUGagjcmZuNp6LPvc5pdQQ0A/86SwfQwgh\nRAozhcPhme8lhBBCCCGEECLuZIijEEIIIYQQQiSJmBo0pdSO6B4vl15/n1LqqFLqoFJKhmiIpCGZ\nFUYkuRVGI5kVRiOZFUYwY4OmlPoskTH/jkuutwH/DtxJZNWtP1NKFcajSCFmQzIrjEhyK4xGMiuM\nRjIrjCKWM2gXgPdc5vq1QJ3Wul9rPQHs583LEQuRKJJZYUSSW2E0kllhNJJZYQgzNmha68eAy20C\nmgUMTrvsJ7J88VUFAsEwkY1I5Uu+5vI1I8msfCXh14wWMreSWflagK8ZyWutfCXZ14wks/KVZF9X\nNJ9l9n2Aa9plFzAw0zf194/M4yln5vG48Hr9cX2OeJL6Z378eZDMxoHR64fUy61kdmZG/xlSLbMg\nuZ2J1D/z48+DZDYOpP6ZH/9K5tOgVQOrlFK5wBCRU8Ffm8fjCRFvkllhRJJbYTSSWWE0klmRVGbd\noCmlPghkaq2/rZT6DPACkaGS39daty10gULMl2RWGJHkVhiNZFYYjWRWJKtF36ja6/XH9QnldGpi\nLcLpYFPcHvwKJLNXZ/T6IfVyK5mdmdF/hlTLLEhuZyL1z/j4ktkkI/XP+PhXzKxsVC2EEEIIIYQQ\nSUIaNCGEEEIIIYRIEtKgCSGEEEIIIUSSkAZNCCGEEEIIIZLEfJbZF0IIIcRV7Dv15oXgdm8pTVAl\nQgghjELOoAkhhBBCCCFEkpAGTQghhBBCCCGShDRoQgghhBBCCJEkpEETQgghhBBCiCQhDZoQQggh\nhBBCJAlp0IQQQgghhBAiSUiDJoQQQgghhBBJQho0IYQQQgghhEgS0qAJIYQQQgghRJKwznQHpZQZ\neBjYDIwDH9Na1027/f8FPgiEgC9rrZ+IU61CxEQyK4xGMiuMRjIrjEYyK4wkljNoDwAOrfUu4O+A\nh6ZuUErlAH8F7ALuBP4jHkUKMUuSWWE0kllhNJJZYTSSWWEYsTRoNwPPA2itDwHbp902DDQBGdGv\n0EIXKMQcSGaF0UhmhdFIZoXRSGaFYcw4xBHIAganXQ4qpaxa60D0cgtQBViAr8z0YG63E6vVMutC\nZ8PjccX18eNN6p83yewiM3r9kPCfQTKbAIvxM7gyHXF7zlTKLEhuYyH1z4tkNgGk/rmJpUHzAdOr\nM08L891AMbAsevkFpdQBrfWRKz1Yf//InAqNlcfjwuv1x/U54knqn/nxYyCZXURGrx+SIreS2UW2\nWD+Df2jsTZcX6jlTLbMguZ2J1D/z489AMrvIpP6ZH/9KYhnieAC4B0AptRM4O+22fmAUGNdajwED\nQM6cKxViYUhmhdFIZoXRSGaF0UhmhWHEcgbtCeAOpdQbgAl4UCn1GaBOa/20UuodwCGlVAjYD7wY\nv3KFiIlkVhiNZFYYjWRWGI1kVhiGKRwOL+oTer3+uD6hnE5NrEU4HWyK24NfgWT26oxeP6RebiWz\nM1usn2HfqbY3Xd69pXRBHjfVMguS25lI/TM+vmQ2yUj9Mz7+FTMrG1ULIYQQQgghRJKQBk0IIYQQ\nQgghkoQ0aEIIIYQQQgiRJKRBE0IIIYQQQogkIQ2aEEIIIYQQQiQJadCEEEIIIYQQIklIgyaEEEII\nIYQQSSKWjaqFEEIIIVLW9P3qFmqvOiGEmCs5gyaEEEIIIYQQSULOoAkhhFhQ089GgJyREEIIIWZD\nzqAJIYQQQgghRJKQM2hCCCHEArn07KEQQggxW9KgCSGEEAsoHA5z5kIvTZ1+lpdksWF5XqJLEkII\nYSAyxFEIIYRYQJ19I5yu62VgaILTdb2MjAUSXZIQQggDmfEMmlLKDDwMbAbGgY9preum3X438AXA\nBBwHPqW1DsenXCFmJpkVRiOZTS2n63oBWFWWzfnWQaqb+tmmPAmuamFJZoXRSGaFkcRyBu0BwKG1\n3gX8HfDQ1A1KKRfwr8A7tdY7gEYgPw51CjEbkllhNJLZFDE0Mkl3/yjFeU5uWFuA2Wyio3c40WXF\ng2RWGI1kVhhGLA3azcDzAFrrQ8D2abfdCJwFHlJKvQ50aa29C16lELMjmRVGI5lNEc3dfgDKi1xY\nLGbysuz0+8eZDIQSXNmCk8wKo5HMCsOIZZGQLGBw2uWgUsqqtQ4QObpwO7AFGAJeV0od1FrXXunB\n3G4nVqtlPjXPyONxxfXx403qnzfJ7CIzev2Q8J8hpTLrynTEfN9Eikddbd4RANYuy8PpsFHqceEd\nGGN0IkRujnNBnzOVMguJze30zCZrXiG5a4uFZHb25G+eWImqP5YGzQdMr84cDTNAL3BUa90JoJR6\njUi4rxjo/v6ROZYaG4/Hhdfrj+tzxJPUP/Pjx0Ayu4iMXj8kRW5TKrP+obE3XU7GfMTjbz4yFqCz\nb5j8bAfBQBD/UJDsDBsATR2DZDmtC/acqZZZSGxup2c2GfMKxn+tlczOnvzNEyuRmY1liOMB4B4A\npdROIqeAp5wANiil8pVSVmAnUDX3UoVYEJJZYTSS2RSgW/oJh6EkP+PidXnZkTMz/f7xRJUVL5JZ\nYTSSWWEYsZxBewK4Qyn1BpGVbR5USn0GqNNaP62U+nvgheh9f6m1PhenWoWIlWRWGI1kNgVUNfQD\nUJznvHhdhsOKxWzCNzKRqLLiRTIrjEYyKwxjxgZNax0CPn7J1TXTbv858PMFrkuIOZPMCqORzKaG\nqqY+rBYT+TnpF68zmUxkZaThG54gHE6dFbsls8JoJLPCSGSjaiGEEGKeBobG6egdocCdjsVsetNt\nWU4bgWCY0fFggqoTQghhJNKgCSGEEPNU0xwZ3liU63zLba6MNIBUHOYohBAiDqRBE0IIIeappmkA\ngKK8jLfcluWMNmjD0qAJIYSYmTRoQgghxDxVN/WRbreSm2V/y21Z0aX2/XIGTQghRAykQRNCCCHm\noXtgFO/AGGvL3ZhNprfcnpkeadCGRwNvuU0IIYS4lDRoQgghxDxUN/YBsK7CfdnbHXYrJhMMj00u\nZllCCCEMSho0IYQQYh4qGyMLhKwtv3yDZjaZyHDY5AyaEEKImEiDJoQQQsxRIBiisqGP/GzHZVdw\nnJLhsDIyHiAQDC1idUIIIYxIGjQhhBBiji60DTI6HmDjijxMl5l/NiUjOg+t3z++WKUJIYQwKGnQ\nhBBCiDk6c6EXgE3L8656vwyHFYA+31jcaxJCCGFs0qAJIYQQcxAOhzlR6yXNZmbNFeafTZk6g9Yr\nDZoQQogZWBNdgBBCCGFEbd5huvpH2a482G2Wq943wzHVoMkQRxE/+061Xfzv3VtKE1iJEGI+pEET\nQggh5uCY7gZgmyqY8b7O6BDHAZmDJhbI2ESAMxd6aezwEwiGWFacRTAUwmKWwVFCGJ00aEIIIcQs\nhcNhDlZ2YrdZ2Lzy6vPPAJz2yNutLBIi5isQDPHCkWaeO9TMyPibt25wOW3s3lqC2+VIUHVCiIUw\nY4OmlDIDDwObgXHgY1rrusvc5zfAU1rrb8WjUCFiJZkVRiOZNZ7zrYN4B8a4cUMRjrSZj3Wm2cxY\nzKaUadAks4nhG5ngG4+fpa51kMx0GxtX5FGS78RsMtHQ7qOmeYC9R1q5a8eSRJeadCSzwkhiOYP2\nAODQWu9SSu0EHgLuv+Q+XwKuPkNaxE0oHKarb4SmTj8HKzvxjUziG55gZCxAVoYNT046npx03nvb\nCjKjE9VTnGRWGE3KZjYUChMOh6+6BL0RvRqd65ORbn3TvJ8rMZlMOB1W+odSo0EjhTObjPadasPu\nsPHYy+fp841zw9oCPrJHcaSm++J9PDnp5LjsHKrs4rXTHdyzswKbVYY7TiOZFYYRS4N2M/A8gNb6\nkFJq+/QblVLvA0JT95mJ2+3Ear36ZOr58nhccX38eIul/mAwxOun2th7uJm61gFGLxnmYLWYcTqs\n9AyO4R0YA/o5Uevla5++lRJPZpwqj0iC379kdpEZvX5I+M+QUpl1ZToIh8P89lgL55sHONfYz+c/\nugNbnGuarbn+zft8Yxyt6WZJYSarlubG3Hy6nGl09A7jzs3Aapn/B+dUyiwkNreuTMeM90kkV6aD\nF4800ecb544blvKXv78Fk8lEdavvTffbtrYI38gkVQ197DvTwQf3rIlLPc8fbHzT5bt2VcT0fZLZ\n2UvGPM6G1D83sTRoWcDgtMtBpZRVax1QSm0APgi8D/h8LE/Y3z8y+ypnweNx4fX64/oc8TRT/YFg\niIOVnTy67wL+kUkAsjPSKM7LIi/LgdtlJyvDRrrdislkYjIQotc3Rpt3mMqGPv7pu4f4hw9vI90e\nn+mH8f79x/g/imR2ERm9fkiK3KZUZv1DYzR0+NBN/QCcqvXyjV+c5EN3qrjWNRvz+Zv/al8dgWCY\n3VtKGRqO/YyY3WYmHIa6hl7ysuc3RyjVMguJza1/6HfbHyTj61l1fQ+1zQPkZzsozHHw6Ev6ivfd\nvCKPhvZBHn35PFtX5JKfnb7g9Uz/fUFsvzPJ7OwZ/f1V6p/58a8klk/pPmD6I5i11lOnaz4ClAIv\nAxXAhFKqUWsd89EHEbvW7iEefvIcnX0jmE2wekk2G5blkem88rBFm9VMUa6TolwnxXlOXjrWynd/\nXcWn3rMRc4oNOZpGMiuMJqUyGw6HOVPXi9kE77yxgsPV3bx6qp27diyNy4fFxfTc4SZePNpCut1K\nKBTCMoszYVMrOfb7x+fdoCWBlMpsspk+bDYUCnO0phuzCW7cUITZfPX3bpvVzHWrPRw428kTrzXw\np/eti3e5RiGZFYYRS4N2ALgP+GV0zO7ZqRu01p+d+m+l1D8CnRLm+DhU1ckPn6thYjLE7q2l5GXb\nL+6rE6upRu3k+R6+8dgZNq3MB1JyrxTJrDCalMqsb3iSweEJlhZmkuOy864bK/jOr6t4/nBzUp1F\nm4sTtV4CwTDbVO6smjMApz3ymp0i89BSKrPJrL7dh39kkvXL88hx2WP6nuUlWTR1DnGospN7dpVT\nmp8R5yoNQTIrDCOWd5cngDGl1BvAvwN/rZT6jFLqXfEtTUBkSOPPXqrl209XYTaZ+NS7N/KRPWrW\nzRmA2Wzi1i3FZDisnKrrpc07HIeKk4JkVhhNSmW2zTsEQGl0vusN6wpwu+y8ca6TsYnA1b41qZ2r\n7+VCmw+3y86qspxZf//0M2gpIKUyO2VodJLOvvgOW5uNcDjMuYY+zCYT29fMvN/eFJPJxLtvXUYY\neOr1+vgVaCwpmVmRmmY8g6a1DgEfv+Tqmsvc7x8XqCYR9eyhJl473U53/yjZGWns3lqCf3QiphXD\nrsSRZmX31lJ+c7CJ03U9lHpS76iaZFYYTapltq0ncvCnLPr6YjGbuWVTMU8faORIdTe3bi5JZHlz\n4h0Y5dvPVMU8zOxypvZCS4XNqlMtswDVjf0c19089XoDv7d7BXfesDTRJdHeM4xveIIVJVlkOtPe\nMvfraraszGdZsYtj2ktL9xBLCuK7QFiyS8XMGt34ZJDBoXGGxwKMjQcYHgswODxB7+AYnX0jdPWP\nMDA0zthEEJvFTFZGGttVAdcpDytKslJudeDpZKPqJKWb+/n1G42MTQQpL8zkxo3FC7Zcbl62g1JP\nBm3eYXoHY3+xF9e2YChEn2+cnsExRscDjE8GCYXCLFsyhiUcIi/LsSAr0wljC4XCeAdGyc5Me9Ni\nRLduLuGZNxp59VSb4Rq0nsFRHvr5KYZGJ9mxrnDO88cunkFLjSGOKWV4dJJjuhu7zYI9zcLPX65j\neUk2K8uyE1pXTdMAAGsqZr/y+6un21lekk1Dh5/HX73AX/3e5oUuT4iYhUJhGjp9VDf2U9c2SHOX\nn4Ghiat+j81qJsNhJTPdxkQgRJ9vjOePNPP8kWaynDbuvGEpu9YX4Y5x6K+RSIOWZILBEM8dbuKx\nffWECbNdeVhb4V7wowRrlubQ5h1GNw8s6OMK4wqFwxePWvX6xuj3jdPnG6PXN0bP4Bh9vnFC4fAV\nv99qMVGan8nSwkyKcp0X99/LyUzD5Uyb0xkHYTwdvcMEgmHys37XxEyd9S/Jz6Chw09zl5+lhcm5\n9PKlIxTKC13812NnGBya4F03VcQ8B+hy0u1WTKTMEMeUUtXYTzgM1632cNuWEr7yyAke2av5/IPX\nJ2xBraHRSdp6hsnPdpCXNbeDAiX5Tgrd6Zy+0MsvXj5PYa4TSMm55yLJjE8EqW3u52R1JzXNA1Q3\n9jE89rsh7k6HleI8J06HlTSrhVVl2WQ4bGRlpNHU5Scrw4bdZnnT599AMERn7wj1HT6au4Z4dN8F\nHtt3AbU0B3eWg2XFLqwWc0rkWxq0JHK2vpdHf3CUli4/2Rlp7FxfePHFdKGV5GeQmW6jocPH8Njk\nnOa0CWPr842hWwaob/Nx6kIPA/5xgqHLN2Dpdit52XZczjQy0m3YbeaLZ8sCIegfHGVgaIIW7xBN\nXW9dktYEZKTbyM2y43bZ8eSk855bl+NIm/kl6HJDelPhxTdVNXRE/v55OW/9QLmqLJs27zD7TrXz\nkT3Jv1jIhbZB/vul8wQCIT7wtpXcecPSeQ0xN5tNZGWkpcQQx1QSDIW40DZIut3CspIsVpXlsHNd\nIYequjhzoZct0QW1Fltda2RF+FVLZj/fcYrJZOI65eG5Q80cqe7m3l3lcrBMLLjB4Qkee/UC3oFR\nBvzjjE8G33J2LDfLzjblAZOJQnf6Fbd7Gp0IUOC+/Gq/VouZsoJMygoyGZ8MkmYxc7Cyi5royYbj\nupstK/O5dVOJ4XMuDVqChcNh6tt9PLm/gcqGPkwmuGVTMe+5bQUnz3vj9rwmkwm1NIfj2sv+Mx3s\nSYKx9iL+Gjt9vH6mg8qGPrr7Ry9ebzZBdqad7Mw0cjLSyHTacNptOB1WMtKtWMxXHrroynRcnBcR\nCoXxDU/gG5lgaGSSodFJRscDjIwH8Q1P0Nw1RHNXZAGJl4+3saQgkzJPBiWeDNwuO3abhTSbhWAw\nxPhkCBOR+TqujDQsBn+xvVY0dEY2zs2/zDDAMk8mGQ4rb5zr4H23LceZpAeGwuEwJ2t7ONfQR7rd\nyqfevZFNK/IW5LFzXHbae4YJh8MpPX/CSBra/UwEQqwuzr74OnPPznIOVXXx/KGmhDRooXCYurZB\nbBYzFUXzO9vsyUlnRWkWF9p8VDX2sWH5wmRZLLzpB4CS/UBkv3+cE7VejlR3Udc6yPTDuxkOK0V5\nkZE0mek2Ct3puJy2BX3Ns9ss7N5Syu3XldEzMMpPXqxFN/VzpLqbrr4Rbt5cgsVsSvrf45VIg5Yg\nI2OTHKzs4tlDTReHuxTnObl1axl2qymuzdmUFaXZnDrfwysn27jj+iWpvC/aNW3fqTaau/ycq++j\nJzrn0GY1U+bJuDgUMTfLPuslwy/HbDaR47JfdhhYOBxmdDxIn2+Mrv5RxieCNHb6LnvG7VImU2So\n2Y0bi2SeW5Jr6vRjMnHZOQFmc+TA0InaHvadaueeneUJqPDqQqEwb5zrpL7dh8tp4+8/tI2iBRzJ\n4M6009TpZ3gsQGZ6cjao15pzDb1AZGTJlLKCTDYsz+VcfR8NHT6WFWctak0dPSOMjAVYVZa9IPPP\ntykPbd5hTp7vwZMT+16E4XCYfv84Q6OTuJxpKTnXR8RmdDxAbcsAumWA6sb+N713F7jTKSvIpNCd\njttlv/g+Pf0Abjzl56SzdVU+a5bm8Nqpdpq6hrBVdnHjxqK3jHowSsMmDdoiCofDXGj38eqpNo5W\ndzMRCEU/eGayemkORblOslzpixJmAEeahYpiV+SoWoMcVUtFk4Eghyo7qW2JDJUp82SgluZQnJex\n6Kf/TSYTTocVpyMyPGH3llKCoRDd/aO094zgG5mgqrGPYDCE2WzCajETDIUZHJ7AOzBKY6efkfEA\nt19njBfXa1EoHKbNO0x2RtoVz7quXpJDddMAzx9u5u3XlWFPsyxylVcWCIZ4/UwHTZ1+8rMdvG1b\n6YI2Z/C7xrXfPy4NWpI4Fx29MvW3nvpAV+h2co4+XjrWuuibPde1RV6zF2qREkealdu2lLD3aAsv\nH29j/bJcNix763t+OByme2CUyoY+Khv6qGrsZ3wyePH2FSVZfPSdsvH1tWIyEORIdTfPHmqis2+E\nqWnoFrOJteVuMp02ygtdFxdAWmyXNl/pditv317G84ebqWsbpKwgI2nnO89EGrRFMDQ6yU9e0Jxv\nHbg4Jjcz3cb65bmsLM2+4jjcxaCW5nChzcfLJ9qkQUsxPQOjfOPxszR3D+F22bllczE5mclz9PPS\nF1aTCdYvy73sfYOhMAfOdNDY6eeFw83sXFdEdkbaYpQpZqF3cIzxySDF+VduatJsFu7YXsbTBxp5\n7nATD9yyfBErvLJAMMS3n66kqdNPoTudt20rw2Y1z2vO2eXkTGvQrvVlz5PB+GSQxg4/eVkO0mxv\nPlhQku+kOM/Jkeou3rd7xaKdPfKNTNDS5ScnM+2yQ4XnqjDXya2bS3jtdDv/9ovTbFyex7oKN440\nC/6RyIIkda0D9Pp+N0cyw2GlKDeTdLsVi8VMZUMfX/rRMfbsWILLKa/BqWoyEOSVE208e6gJ38gk\nEFkBvCTPSWF05M1CrSy+0KwWMzdvKubXB5o4VuOlzJNpyPlo0qDFSTgcprZlgAxKfx4AACAASURB\nVNdOt3O0xksgGMJsgvIiF6uXZFOU60yK+Qf52eksK3Zx+kIPfb4xcue4UpRILkOjkzz0i1N09Y+y\nqiyb69cWGHpooMVs4pbNxdjTLOjmAX66V/PJd29MdFniEq3RDardMxwI2HPDUl493c6zh5rZtb4o\nboshxWqqOTumvW9qzuIh92KDJlucJIOmTj+hcPiyw/5MJhN3Xr+EHz2veel4C7+3e+Wi1PTG2U5C\nYVhVlrPgnxPKi1zck15OTXM/Z+t7OVvf+6bbM9NtbFvtYf2yXNYty6Wqse/ibbu3lPLKyTZ+8oLm\nwNlO9tywJCk+x4iFEw6HOaa9/OqVOnoGx3CkWbh7x1IcdouhGvKcTDsry7KpbRmgsdPH8pLEbpcx\nF9KgLbC2nmEOVXZyuKrr4nyfwlwnpZ4MVpRkJfRs2ZXcvKmEhg7Nkepu7tohi4UY3WQgyNcfO0NX\n/yh371w6q/kGycxkMnHD2gJ6B8c4pr3o5n7U0tnvDSTip9Ub2aB6pqXo0+1WPviO1fzvJ8/xracr\n+YcPb0vYAYTJQJBvPVXJyfM9qCU5XKc8cT0yPHUQrM8nKzkmg4aO6KI2l1l1FCKbkj/xegP7TrZx\n787yuC9sEwqF2XeyDYvZxPKS+Mx7y8t28A8f3k5X/wgtXUNMBkJkpFsvzkme3nRVXfK9u7eUUNXQ\nx/HayObXRh0+Jt7qV/vqOFbjxTswitkE6yrcbFyel1TD0Gdjw7JczrcOUNnQz7Ji421qnXzdggF5\nB0Y5Ut3F0epumrsjR5DtaRZu3FDELZuKWb0kh1dPtye4yivbrjz87MVaDld1SYNmcK+cbOX105Gh\ngBVFrgUdHpMMppq0Zw81898vnefzf3y9IYcupKq26Bm0nMyZj7Rev6aAMxuLOHC2kx89V8Of3Lt2\n0d9AR8YCfOPxM9Q0D7C23M2n37uJg1WdcX3OvKxI89rnkzNoyeBig3aF10qb1cKeG5bwq1cu8PyR\nZt5z64q41nO6rofugVFWlmXH/YNxodtJodvJvlNtjPuD9PnHoan/qt9jMpl44NblHK/1Ut3YLw1a\nCmjrGeaJ1+o5URtZnG5JQSbblIcsg08jyHTaWFKQSXPXEP3+ccONEJMGbY4mAyEOVXWy72T7xRd4\nsymyCMOykiyWFGRitZjp6Buho28kwdVencuZxvpluZy50EtH7zDFeRkzf5NIStVN/TR2+vHkpHPT\nxiLDHTGKRX5OOrvWF3GwspP9Zzu4dXNJoksSUe09w9htlpgXv/jQnYr2nmEOnOtkYHiC61bnYzIt\nzrLIXX0jfOWR47T1DLN1VT4fv389Nmv8jxS7XdEzaLIXWlKob/eRmW67ambfdl0Ze4+2sPdoC7u3\nlMbtg144HOaFI80ArCtPvtEB0+djFuc56egdod8/Lis7GtTg8ASPv3qB/Wc7CIcjBym2KU/Ch5wv\npOUlWTR3DVHf7pMGLdWNjE3y/WerqW7qZ3Q8iMkUeaGqKM5iaWEmdpsxTwXvXFfImQu9HK7qSppJ\n+2J2mjr9nNBeHGkWdm8tWZBl85PV+3av4HhtN4+/eoHr1xQk5dDha00wFKKzb4QyT2bMBwbsNgt/\n9b7NfP77RyL7QAJbV8d3z6l9p9po7xlm/5kOxiaCrFmaw/rluRw4F98zZ1NsVjNZGWn0yhm0hBsa\nnaRncIwNy3KvmNmppmRdRS4Hz3Xys5fO8xfvic/816rGfmpbB9m0Im/GYcLzNd/Fb1aWZdPRO0JT\np18aNIN55WQrF9p8HK3pZjIQojQ/g/fetoL+obGUO6hb6skgzWamocPHNuUx1M8nn2piNBkI8dvj\nrfz6jUZGxgPYLGbWVbhZW+4mIwWWSt6yKp80m5lDVV3cf/MyQ4VYwNhEgG89XUkoDDdtLE75huX0\nhR7Wlrs5XdfLd39dxV++d1OiS7rmeQfGCATDlObPfAb+0g+Hd15fxt4jLZxr6GMyGOK2LaVx2Zcx\nFApzuq6HM3W9mEwmdq4rZPXSnAV/npnkuuy0emWz6kRriU5JiGWY3srSLOrbBjlR6+W10+0LfuY+\nFArz6L4LALz7luUXN3xPVlMr4zV1+dmyavE38hZzMzYRuDgNwmYxc8PaAlYvyWFgeDwlX4ssZjNL\nCjK50Oaj1zdGfrZx5uTP+ClOKWUGHgY2A+PAx7TWddNu/2vgA9GLz2qt/ykehSZKOBzmuPbyq311\neAfGyHBYuW51PquX5LxlSV4jc6RZ2brKw+GqLho7/Yu+KedCuhYz+7MXz9PVN8K6CjelnmtjiOra\nCjfVTf1UNvYxMhZI2D4sCyEVMtsWXSCkJIYG7VJOh409O5by4tEWdPMA33ryHB9757oFeY2dagaH\nxybZf6aDrr5RMhxW7tpVQYY9Ma/heVkOGjv9+EcmDTvPIxUy2xzdaHdpYSYj44Gr3tdkMnHjxiL2\nHmnhkb21eLIdrK24/LYgc/HS8VaauvzsXF9IeZEr6Rs0m9VMaX4GLd1DDEa3D0p2qZDZ+egZHOW/\nHj1Dq3cYT46DWzaXXBN7MZZ5Ig1aa/ewoRq0WMZAPQA4tNa7gL8DHpq6QSm1HPhD4EZgJ3CnUipl\nDmVXNfbx5Z8c5+Enz9HnG+eO7Uv4yp/vYsPyvJRqzqbsWFcIwKHKrgRXMm/XVGbfONfB/rMdlBe6\n4j48LJmkWS2sr8hlYjLES8daEl3OfBk+s+29kQateA4NGkRWdtyzYymF7nSOaS9f+ekJegZHF6S2\nxk4/zxxopKtvlCUFmbzzxgqKEjjX1j21UIixl9o3fGabu2I/gwaR+doff2ADEOY/HzvDyeiiChA5\nEDD9azbq2308uu8Cmek2PvD2VbP63kQqi+7j194znOBKYmb4zM5VY6ePf/7xcVq9w6ilOey5Yek1\n0ZxB5KCh2fS7bWCMIpYG7WbgeQCt9SFg+7TbWoC7tNZBrXUYsAGGfscBqGsb5H9++xBf+/kpLrT7\nWFqYyX03VVCc7+SY7k50eXGzYVkuGQ4rR6q7CIXCiS5nPq6ZzLb3DPPjFzTpdgufeGA9FnPqzju7\nnDXlbuw2Cy8cbWF4bDLR5cyH4TM79SFtLmfQpthtFt5xfRk3byymqdPPF75/lP1nOgiH5/Z65B+Z\n4LXT7bx2qp1QKMzOdYXs3lqS8GWj86OT1XsGku7POBuGz2xztx+7zUKBO/aj6usrcvlUdA/Grz9+\nlkf2akbm8drT2OnjPx89TTAU4mPvXEeWgfaaKsmLLCYxdXDGAAyf2bk4XdfDV396At/wBH/wjlXs\nWFd4Ta1+bLOaKcx10ucbZ2Ts6mfKk0ksY4KygMFpl4NKKavWOqC1ngR6lFIm4F+Bk1rr2qs9mNvt\nxBrnlbI8nrkt+zo2EeBHv67i1wcagMhRtR0biihwL+6KNq7MxV1p5njd7zaqrCjJprK+l6cPNrGk\n0MVduypm/Xhz/f0voGsis2MTAb7zw6NMTIb4Hx/ZzvrVhbT0LswZh9la7MxOd92aAg6e7WD/uS4+\ndPfaOT9OgnNr+Mx29Y/iSLOwdoWHlp75rVz7/jvXct2RZr7z1Fm+/2w1+8918IE7FNvWxPbBIhAM\n8eLhJn7yXA3+kQkKc5284/qlb1l4IRG59XhcrCiPDI0bmQzNK3eplFlY3NxOTAbp6B1BLXVTWJCF\nK7Nvhu/83fe/w+Ni+dJcvvbTY7x8oo2jNV7WVuSyfnnuxX3SZvrbjI0HeGZ/PT/fq5kMhvjU+zYz\nGf7d+/GVspnI19pLuTId5LjsdPWNkuPOiGn/QMns1U3/+079rub6OwuHwzyzv57vPXUOk8nEXbsq\nyM1Z/BUakyGzy0oji9oMDE/O+veZqMzG0qD5gOnVmbXWF1tQpZQD+D7gBz4504P198d3yXmPx4XX\n64/pvtOHIXgHRjlwpgPfyCTZGWnsXF94calR/9DiHURxZToW9fkuVZbvpLK+l8oLPeRk2GL+XU6Z\nze9/LmL8HyVlMzslHA7zpR8fo6nTj1qaQ0e3n1+9WBOnCq8u0ZmtKMyksj6NJ/bVsW1V3pzGmCdB\nbg2d2UAwREuXn6WFLnp7h+adh56eIbYsz+WLf7KDX75Sx9Gabr74vcNkOKyUF7m48/qllBe5yHLa\nLk5sD4XCtPcOc7quh1dPtdMzOIY9zcL2NR7WlLsxm8JvqitRufV6/dijn2Mb2gbmnLtUyywsbm4b\nOnyEQmGKc9Pxev0xZ2H66+znPryNvUdbeO5QM0eqOjla3UlRrpOS/Awy08x4ctLJiDZsI+MB+nxj\ntHqHqG0Z4FRdL6PjAVxOGx+/ewNbVuTNODQy0a+1l1PkTqfGP87h062opVffGkAyO7Ppf1+v1z/n\n39n4ZJBH9moOnO0kKyONmzcWkZ9tX/T8JEtmc6N7c9bP8jU3kZmNpUE7ANwH/FIptRM4O3VD9EjD\nU8DLWut/mWedCVPZ0McJ7SUMrC13s3V1PtYUXqL8agrc6bicNho6/VynPIkuZ65SPrNPH2ikocOP\nJ8fBduP+nRaEzWrm93av4Hu/qeYXv63jU3FaAjvODJ3Zrv5RgqHwgi1QM/2D6toKN0V56VQ19tPU\n6aeqsZ+qxshmumk2c3RYb5jxiSBTI7PTrGbedl0p77yxglN1PQtS00Ly5EQOInT3J+aM9wIxdGab\nLi4QMvej4zarhXt3VfC268r40fM1XGj30dE7QkfvCMe196rf63bZuWN7Ge/YvsTQc4GK8pzUNA9Q\n0zwwY4OWBAyd2Vi1eof49tOVtHqHyctysHtrSUqsNj4fbpcdR5qFjt4Rw6yeG0uD9gRwh1LqDcAE\nPKiU+gxQB1iA2wC7Uuru6P3/Xmt9MC7VxsG5aHPmtFu5eVMxRXmps0HfXJhMJtaWuzlS3c35lgHu\n3lGe6JLmIqUze6iqk6f2N5CZbmP31tKU3u8sVjduKOLV0+0cr/VyrqGXDcvyEl3SbBk6s23Ryddl\n85h/djVul4ObNhazc10hnX2jpNuttHmH6PWN0eeLLA+dkWUjOzON3VtK2boq/+JQs2Rkt1nIzkzD\nO2DoBs3QmZ1aIKR8Hg3a9AMJa8rdrCl3MzI2SVffKJnpNnp9Y4yOB+nzjWGzmnE6rGRlpOHJSScn\nMw2TyWT4ee2F0SkgurkfWJbYYmZm6MzOJBgKsfdIC0+83kAgGGL1khyuX+ORzwhEPtsW5Tpp7PTT\n3jsS03YwiTZjg6a1DgEfv+Tq6WOpEj+4dI6qppozh5U9NyzBZaDJufG0ojSbk+d70C0DBIIhw51N\nTOXM6uZ+vv+bGtLtFt52XWnK73cWK5PJxIfuWM0//fAoP33xPF/8E3dM8yGShdEzO7XEfqknM67P\nY7GYKfVksHtL6cXrLh0WdtPG4rjWsFAKctKpaxs05GssGD+zzV1+LGbTvBa1uRynw8aykug8tFks\nPmJU9jQLbpedujYfk4EgtjjPIZwPo2f2apq7/PzguRqaOv040izcsrmUJQXxfT02muL8SINW3diX\nGg1aqnrxWAvHtJd0u5U7r5fmbDqb1cyqsmyqGvs5Wt3Nrg1FiS5JAK3dQ/zXY2cJh8N84oGN9Awm\nflx3Mlla6OJtW8v47YlWnj7QwHtvW5Hokq4ZUxv+li3SHnxXm6sz2yXOE6UgJ53zrYP0Do5dnO8s\nFkcwFKK1e4iS/NgWthBXV5TrpN/fT327zwjDHJPe2ESA0fFgTKtpTwZCPH2ggecONRMKh1leksX2\nNQU4ErxSbTIqjm6tUtXYzzu2L0lwNTO7Jhu0fSfb+O+XzpNut7DnhiWG3Sg0ntYsdVPd2M/eoy3s\nXF9oiPG6qezXbzTy3OEmRseD3LypWJqzS0x9KPe4HWSm2/jNwSZWleWwaYXhhjoaUlOXn5zMNLIz\n7TPfWQBQEG3KOnpHpEFbZG3eYSYCIZYVJ3zF4ZRQlOekuqmf6qZ+adDmIRwOc6ymm5qmfkJheP10\nO59472ZWXSGnDR0+vvebatp7InPN/uguRY9PPhtcSWa6DZfThm7pJxgKJf22RMldXRwcONvBj1/Q\nuJw27rxemrMryXTaWFKYSVOXn/OtgzN/g4ibwaFxXjzWwuh4kO1rPCwvyUp0SUkrzWbhti0lmM0m\nvvNMJb3SyMbd4PAE/f7xec3luRZNzddr6zHW5qmpoL7dB8DykuwEV5IaCt3pmExQ09Sf6FIM7TcH\nm6hq7Ccj3cbykiyGxwJ85UdH+eFz1YxN/G7/rr3Hmvnaz0/ypR8do70nsvH0nTcskeYsBsV5TkbH\ngzR0xG9lxoVyTZ1BO1LdxfefrSbDYeVvPrCVC+3SeFzN2nI3zV1DvHishdVLchJdzjXJPzLB135+\nCv/IJBuW57KuIjfRJSW9vGwHN6wp4FBVFw8/eY7PfnArdpsM94iX5uhqeOVF0qDNRml0fsjU/D2x\neC42aMVysGshpNkslBe6uNDuY3wimPCN4I2ovWeYJ16vx+mwcteOpaTbraglOXzvNzW8drqD03W9\nXKc8TEwGOVrdzUQgRGa6jV0bCi8O3RMzK87LoLZlkHP1vawsTe4DNNfMGbQTtV6+80wVjjQLn3n/\nFpk8GYMCdzrlhS5O1Hpp65EPEYtteGySh35+irae4cj2D6vyE12SYaxaks2NG4po6PDxjcfOMBkI\nJrqklNXYOf/lyq9F+dkO7DYLrV45g7bY6jt82NMsC75AyLVsbbmbYCjM+daBRJdiSI/uu0A4DDvW\nFV5c/Ks4L4N//fQt3H/zMsYmgrxyoo0DZzuxWExsXZXPu26ukOZslorznFjMJs7Wx7YxfSKl/Bm0\ncDjMN584y4naHqwWE7dtKaGpy39xDxRxZSaTiXfdVMHXHz/Lt546x+c+sl3ORCySPt8Y//7L07T1\nDHPblhKWFmbKPMBZMJlM/PHdaxgZC3CqroevP36Wv3zPJlkQIA6mPpCtSPKjkcnGbIqsINjc5Tfs\nSo5GNDw2SUd0WJjZLK+pC2XdslyeO9zM2fo+NiyXub+z0djp41RdD6vKst+y0FKazcL9Ny/jnp3l\ntHqHSLOa0S0Dkt05SrNZWFmaTW3LAL6RCbKSeIHAlH5HGJ8I8n+eruREbQ/O6GqNBW6ZjD0bW1d7\nuH1rKW3eYf77pdpEl3NNaO7y86UfH6OtZ5i3byvjw3uUNGdzsP9sB+uXuynNz+BcfR//+IMj+Ecm\nEl1WSgmFwtS1DlKY6yRb5vPOWpkng2AoTEfvSKJLuWbUNPUTJrIQllg4q8tysNssnKnvTXQphvP8\n4WYA7rup4orv9TarmWXFWZR6MqU5m6eNK/IIA+eSPKsp26A1d/n58iPHOVLdjScnnXtvLCc/J/X3\nJImHD7x9JUsLMnntdAcHz3UmupyUdrCyk3/+8XEGhibYrjyU5Dt57XR7ossyLIvZzO6tJZR5Mujo\nHeGLPzxKQ4cv0WWljJbuIcYmgqwuk7NnczF11lGGhS2eqsbIQhYyn3dh2axm1lW46eoboatfDjjE\nqmdglGM1Xso8may/JJP7TrXx/MFGw2wdYhRbVkamixyr8Sa4kqtLuQat3zfGD56t5p9+cJSW7iF2\nbynhzhuWyIa+82CzWvjEAxtwpFn48Quajl6Zj7bQRscDfOeZSr7zTBVhwty6uZh1y3LlzNkCsFjM\n3H5dKVtW5dPnG+crjxznmQMNMi9tAdQ0Rz7syiJCc6Oiv7faFmnQFktVYx+ONAsVssT+gpva1uRk\nbU+CKzGOF4+1EgqH2XPDkqu+3+871XbxS8xPSX4GZZ4MzjX0MjI2mehyrihlGrSh0Ume3t/An3/1\nJV4/00FJfgaf+f3NfOSuNVjkdPCcTb0gVDf3c/3aAsYng3zpx8f40fM1iS4tJYTDYd44087nvnuY\ng5VdLC/J4r6bKqiQ1cUWlMlkYtOKPN6+vQyb1cwTrzfwNw+/wU9f1ITDM28GKi7vZK0XE8ickzkq\ncKeTnZFGbcuA5HARtHb76eofZc1St8z5i4PrVnuwmE0cqpSRNrEYGZvktTPtuF12dqwrTHQ515Tr\n1xYSCIY5kcQHEwx/Wql3cIy9R1t45WQrgWCYdLuVHesKWVWWTY9vTI42LKBlxVmMjgU4UdvDq6fa\nGRqZ5A/vXE2ObE47Jx29wzz85DnavMOYow3EphV5Mr48jkryM7j/5mWcruulprmf3x5vo807zEcf\n2Eie05bo8gxlcHiC862DrCzLlvlnc2QymVi9JIejNd20eYcpk9WF42rfiVYArl9bkOBKUpPLmcbG\n5XmcquuhzTtEqUfyfDUvHmtlfCLIu26qkAMGi2zHukKefK2eV0+1cfOm4kSXc1mGbNCCoRBn6/vY\nf6aD03U9BENhnHYrW1a62bqmkPHx5D1laXTrluVS6sngYGUXx2u9VDX1c8umYm7ZXEKpLFkck+7+\nEZ4+0MjByk7CYSgryGTbag/ZmfIhdzGk2Sxcv7aAlWXZnKj1UtM8wN/+1+tsWpHHPTvLZbhejI5U\ndxEmctRczN025eFoTTeHqrp4nzRocRMOh9l3vBW7zcJ1qySz8XLjhiJO1fXw2xNtfGSPSnQ5SWto\ndJK9R5txOW3cvrU00eVccwpy0tm8Mp9TdT3UtQ0m5Z5ohmnQxiYCnG8dpLKhj8PVXQwORVZjW1KQ\nyZ3XL2FsMojFbCLNZpEGLc6yM+3suWEJhOGJ1xvYe7SFvUdbWFGaxV27lrGqxJXUS5cmQjAU4uyF\nPl491caZ+t5IY+bJYGVZNuuW5zM0PJ7oEq85bpedt28ro6tvhLP1fZy50MuZC714ctJ54JZlXLfa\nI9tKXEEwGOLFoy3YrGZ2bShKdDmGtmVlPo40C4erOnnPrcvlDHqcHNdeuvpGuGlDkWykHEdbV+dT\nkJPO/jPt3HdjBW6XjLC5nMdfq2d0PMj737YMR5phPoqnlD03LOFUXQ9P7W/gM7+/Oenm/CdlKoKh\nEJ29IzR3DdHU5ae+3UdDh49gKDJGP81qRi3NYWVpNrlZdiaDIZlntshMJhOY4P5bltHaPcT51gEu\ntPn45qOnMZtMqKU5bF9TwNpyN4Xu9KQL/mIYHQ9Q09zPyfM9nK7rwT8SOXCQn+1gbYWbiiIXJpPp\nmvzdJJPCXCcrl+ZS19JHZX0frd7hi5vab1vtYcPyPNZWuOWgwzR7DzfRMzjG7VtL5fcyT2k2CzvX\nFbLvVDuvn2nnti1yNH2hTQZCPP5aPWaziXtvrEh0OSnNYjZzz65yfvhcDT97qZZPPrBB3uMuceZC\nL/tOtlHqyeBt15Ulupxr1uolOaxflktlQx+HKruS7mDjjA2aUsoMPAxsBsaBj2mt66bd/qfAnwMB\n4Eta61/H+uTBUIg+3zjdA6N09AzT0j108WuqGQMwAXnZDopynRTlOSl0p2OR8bpJwWI2UV7korzI\nxdDoJJ39o3T2DFPd1E91U2SFtwyHlRWl2VQUuSjMdVLodlLgTifDYY3LC3c8M3s54XCY4bEA3f2j\ntPUM0do9zPnWAZo6/UylON1uQS3NYVVZNrlZjvk8nYiTQreTwm1OfMMTBIJh3jjXwYFznRyIbi1R\nkp9BeaGLiiIXxflOitxOcrMcC3LGY7EzOx/17T6+90wlTruVd8qH3QVx303LOFjZxWOv1rN6SQ7F\neck/XNwomQ2GQvzwuWo6+0a4+8YKinJlL9R4u3ljMW+c7eC49vL0gUbedZX9vRZTMmS2sqGPh588\ni9Vi4mP3rsNmlc+yiWIymfjIHsX/+t5hfvh8DS6nLakWvIrlDNoDgENrvUsptRN4CLgfQClVBHwa\n2A44gP1KqRe11lccr/XNx88yODKBb2iCXt/YmxoxAKvFRFZGGrlZdnKzHJF/XQ4JsQFkptvY6nHh\nLxljy6p8WruH8A6M4h0Yuzh8bDq7zUKOy447M42sjDQcaRYcaVYcaRbSbBasFjM2iwmrxRz5spq5\nxxPT0sgLmtn9ZzoYnwwyOh5gZCzA8NgkQ6OT+Ecn8Q1PMOAfZyIQetP3WMwm8nMiBxXKCjLJz3Yk\nxRuUmFlWdMGLe3eV0+sbp6NnmI7eEbr7R2jvGebgtBXKLGYT2ZlpZGfYcTltOB1WMuw27GmWyJfN\nQprNzO/dsWamp13QzC4038gEjR0+ztb38drpdoLBEB+9f4MMX1ogbpedD7x9JT96XvPlnxznju1L\nUEtzWF6SnczvfUmd2baeYWpbBnj1VBvNXUMsL8nio+/agG9A9uiKN7PZxJ/et56v/vQET+1voLqx\njxs3FrNhlYfgRCCR74eLntmh0Um8A6N09A5zoraHE7VeLGYTn3z3BsqLZKuHRPPkpPPJBzbyjcfP\n8m+/PM32NQVctyqfwlwnbpcdT2yfOeMilgbtZuB5AK31IaXU9mm33QAciAZ4XClVB2wCjl7pwY5H\nl2V22C24XZEPNS5n5AO622UnOyNNxuCngMx0G2vK3awpdwOR4X79/nF8IxP4hyfxjUwwMhZgcGic\nrr7Y3zDvuWVFLHdb0Mx+/9nqy15vAuxpFjKdNpwOG5npVnIy7eRkppGb5ZBVmQzOZDKRn+0gP9vB\nxhV5hMNhfMMT9PkiOfYNT+AfmWR0PECT30foKqukx9CgLWhmF1I4HOYL3zvC4HBk3q/bZefT799K\neb6ciVhIt20pxWQy8YuX63hyfwMAN20s4qP3rktwZVeUtJlt7xnmf3338MXLu9YX8cE7Vsmc0kWU\nl+3gcx/Zxg+fq+H0hV5qWwfhucj2PO+9bTn37qpIRFmLmtmRsQB/880DbzqAW17o4sN7FMtLZCud\nZLFpRR6f/YOtPLJXc6ymm2M13UDkM94/f/ImirIScyAylgYtCxicdjmolLJqrQOXuc0PXHUplGce\nul+6LxFvkllhNAuaWY/HtaCZfeSLd8/q/jE0pOIy3vsOxXvfEfvKd4k8ussCZxYWLrcej4tnHrr/\nirddjmR24Xk8Lr70yZsTXcZ0i57Zx/7lvlkVKDlMDI/Hxa6tyTUfMJZDYwIeAgAAIABJREFU/D5g\n+iuaORrmy93mAgYWqDYh5koyK4xGMiuMRjIrjEYyKwwjlgbtAHAPQHTM7tlptx0BblFKOZRS2cBa\n4NyCVynE7EhmhdFIZoXRSGaF0UhmhWGYwuGrTJzgTavebCIyJPNBIgGv01o/HV315s+INHtf1lo/\nFt+Shbg6yawwGsmsMBrJrDAayawwkhkbNCGEEEIIIYQQi0OWmRNCCCGEEEKIJCENmhBCCCGEEEIk\nCWnQhBBCCCGEECJJxLIPmqFEV995hMieFmnAZ7TWBxNb1cymTV7dDIwDH9Na1yW2qtgppWzA94EK\nwA58SWv9dEKLMgjJbGJIZudOMpsYktm5k8wmhmR2fiS3iZEMuU3FM2ifAX6rtb4N+GPgm4ktJ2YP\nAA6t9S7g74CHElzPbH0I6NVa3wLcBXwjwfUYiWQ2MSSzcyeZTQzJ7NxJZhNDMjs/ktvESHhuU+4M\nGvDvRLp1iPx8YwmsZTZuBp4H0FofUkptT3A9s/Ur4NHof5uAwFXuK95MMpsYktm5k8wmhmR27iSz\niSGZnR/JbWIkPLeGbtCUUh8F/vqSqx/UWh9VShUROS38/yx+ZXOSBQxOuxxUSlmn7XKf1LTWQwBK\nKReRUH8usRUlJ8ls8pDMxkYymzwks7GRzCYPyWzsJLfJIxlya+gGTWv9PeB7l16vlNoI/Bz4G631\nq4te2Nz4ANe0y2ajBHmKUmoJ8ATwsNb6Z4muJxlJZpOLZHZmktnkIpmdmWQ2uUhmYyO5TS6Jzm3K\nzUFTSq0jcmryg1rr5xJdzywcILKjPUqpncDZxJYzO0qpQmAv8D+01t9PdD1GIplNDMns3ElmE0My\nO3eS2cSQzM6P5DYxkiG3pnA4nIjnjRul1FNEVo1pjF41qLW+P3EVxWbaijebiIx3fVBrXZPYqmKn\nlPpP4P3A9Jrv1lqPJqgkw5DMJoZkdu4ks4khmZ07yWxiSGbnR3KbGMmQ25Rr0IQQQgghhBDCqFJu\niKMQQgghhBBCGJU0aEIIIYQQQgiRJKRBE0IIIYQQQogkYehl9oUQQiQXpVQYOAcEgTDgJLLk8ie0\n1sei93EC/xN4d/Q+GcB+4LNa6w6lVAnw7CUP7QEKtdZved9SSuUDPwMKAT/wfq11Wxx+vEWjlPoO\n8C2t9fFE1yKEEGJxyRk0IYQQC+12rfUWrfVWrbUCfgF8HUApZQGeB/KAG7TWG4AVRJq655RSJq11\ne/T7t2ittwB3ARO8dRPXKX8JNGitNwNVwCfi+tMtjjuIrH4mhBDiGiNn0IQQQsSNUsoKLAX6olc9\nAGQDn9JahwCi//6LUsoEZBI5Czb1/XbgSWCv1vrrV3ias8D7lVKrge3AZ69Szw7gv4ictZsgsvnr\ny0qpW4B/JXLGbwL4nNb6eaXUHwPvBdKBCqAZ+CbwF8Bq4N+01g9F7/cHRA58lgJtwB9prduj+wD9\n/4AdKAZe1Fp/NFrPO4EvRb9vGPg48PtACfBTpdRHtNaHr/gLFkIIkXLkDJoQQoiF9opS6rRSqh2o\njV73YPTfW4CXppqz6bTWX9Va+y+5+jvAKJGG6EoOE2msaoAvaK1futydlFI2Is3eF6Nn7v4U+E+l\nVB7wKPBXWutNwB8Bjyillk2r+UEiDVkh8AHg7UQ2Yv1SdM8fgJuINJ7rgONEGkGAvwI+r7XeAawD\n3qWU2hbdDPUR4I+jz/uvwFe11v8AtAN/KM2ZEEJce6RBE0IIsdBujw43vJdI4/SG1ro7epuJyLwz\nAJRStyulTkW/mqNnlKZu+1vgRuB9WuvJyz2RUmodcAD4e+Bx4DPR5ufhy9x9IxDUWv8GQGt9XGu9\nEdgB1E01Q1rryuhj7o5+31GtdUu0qWwgcjYvBFwAHNGfkej1Uw3pd4A9/5e9O49v67wOvP/DSpAE\nuIOkSIoitT3aJUveLcdb3MRJHLtL2mbpkmkmbd62M5PMpJPMZNpp37SdNsnbdNJ60iZ1miYZZ/O+\nxLtla7VWStTCR6LERdx3EiQIkgDu+8cFaVqWSJAECFzofD8ffEQCF/cegEfAPffZYj//DlCglPpv\nmIu35mC2FN4BnNZa18WO+4TW+oFrvalCCCGuD1KgCSGESAqt9QnMcWPfVUrVxO4+ANw1a5s3Zo01\nu4RZ8KCUegCz6Pqo1rp/jsN8FviR1vpHwCcxv9de4epd+MPMKg5jx9nC1b8L7YAr9vPEFY9dtViM\n7X/28yOxn/ditrY1AH8BtGEWqu+KRyllU0ptu8a+hRBCXCekQBNCCJE0WuvHgIPAN2N3PQ6MKaW+\nqZTyTm8XGxu2GogopTZgdv37lNb67DyHOA/cqZTyYI4dewNzjJtPKeW+MhzAUErdHzvmTuB14LD5\nq7o5dv9m4H3AngW+3PuUUpWxn/8AeFYpVYg5Lu6/aq2fwByfthZwYHbN3Bg7HsBDsdcNZvHmQggh\nxHVHCjQhhBDJ9kfAA0qpD2itw5izMvYDbymlTiilGjAnyvgi5hixL2JOqPFXs7o/Tt9WXrHvf8Js\noTqC2UK1CdgIlAPv6i6otZ4AfgX4M6VUHfBt4Fdi3S8/BnxLKVWPOWX/p2d1V4xXG/ADpdQ5zAlF\n/pPWehD4a+C4UuooZqvgfmCt1robs9Xv+7F4voA5vo3Y+/ATpdQvLTAGIYQQFmczDGP+rYQQQghx\nTbFZHH9Na/2R+bYVQggh5iItaEIIIYQQQgiRJqQFTQghhBBCCCHSRFwtaEqpW5RSe65y/4NKqSNK\nqYNKqX+f8OiEWCTJWWFFkrfCaiRnhdVIzgormLdAU0r9CfBdYlMfz7rfBfwd8EuYUyZ/NrbophAp\nJTkrrEjyVliN5KywGslZYRXxtKBdxJz16kobMRf2HNRaTwL7MKclnlM4HDEw132Rm9wWc4uH5Kzc\n0u0Wj4TlreSs3BJwi4d81sotnW7xkJyVWzrdrulqC3m+i9b68VkLjM6WBwzP+j2AufbMnAYHg/Nt\nsiR+v4/e3kBSj5FMEv/8+5+P5Ozysnr8kHl5Kzk7P6u/hkzLWZC8nY/EP//+5yM5u7wk/vn3fy1L\nmcVxBJi9Zx8wtIT9CZFskrPCiiRvhdVIzgqrkZwVaWXeFrQ5nAPWKaWKgFHMpuCvJyQqIZJDclZY\nkeStsBrJWWE1krMirSy4QFNKfQLwaq3/WSn1BeAlzJa4R7XW7YkOUIilkpwVViR5K6xGclZYjeSs\nSFfLvg5ab28gqQeU/q6ptQz9dW1J2/k1SM7OzerxQ+blreTs/Kz+GjItZ0Hydj4S/7z7l5xNMxL/\nvPu/Zs4uZQyaEEIIIYQQQogEkgJNCCGEEEIIIdKEFGhCCCGEEEIIkSakQBNCCCGEEEKINCEFmhBC\nCCGEEEKkiaWsgyaEEEKIeeype2e27rt3VKYwEiGEEFYgLWhCCCGEEEIIkSakQBNCCCGEEEKINCEF\nmhBCCCGEEEKkCSnQhBBCCCGEECJNSIEmhBBCCCGEEGlCCjQhhBBCCCGESBNSoAkhhBBCCCFEmph3\nHTSllB14BNgOTACf0Vo3znr8PwOfAKLAX2mtn0xSrELERXJWWI3krLAayVlhNZKzwkriaUF7GPBo\nrW8DvgR8Y/oBpVQB8B+B24BfAr6ZjCCFWCDJWWE1krPCaiRnhdVIzgrLiKdA2w28CKC1PgTcOOux\nMaAFyI3dookOUIhFkJwVViM5K6xGclZYjeSssIx5uzgCecDwrN8jSimn1joc+/0ycBZwAH89384K\nC3NwOh0LDnQh/H5fUvefbBL/kknOLjOrxw8pfw2SsymQzNfw4sHmmZ99Xk9SjplJOQuSt/GQ+JdE\ncjYFJP7FiadAGwFmR2eflcwPACuA2tjvLyml9mutD19rZ4ODwUUFGi+/30dvbyCpx0gmiX/+/cdB\ncnYZWT1+SIu8lZxdZsl+DYHR0FXvT9QxMy1nQfJ2PhL//Pufh+TsMpP459//tcTTxXE/8CEApdSt\nQP2sxwaBcWBCax0ChoCCRUcqRGJIzgqrkZwVViM5K6xGclZYRjwtaE8C9yulDgA24NNKqS8AjVrr\nZ5RS7wcOKaWiwD7gleSFK0RcJGeF1UjOCquRnBVWIzkrLMNmGMayHrC3N5DUA0pzamotQ3OwLWk7\nvwbJ2blZPX7IvLyVnJ1fsl/Dnrr2q95/947KhOw/03IWJG/nI/HPu3/J2TQj8c+7/2vmrCxULYQQ\nQgghhBBpQgo0IYQQQgghhEgTUqAJIYQQQgghRJqQAk0IIYRIgsFAiM7+sVSHIYQQwmKkQBNCCCES\nLBCc5Nn9LbxypI1AcDLV4QghhLAQKdCEEEKIBDt+vm/m5zNNgymMRAghhNVIgSaEEEIkUCQapbNv\njByPk+wsJy1d1p1mWgghxPKTAk0IIYRIoObOAJPhKJUluRTne5iYihCaDKc6LCGEEBYhBZoQQgiR\nQGeaBwCoKMmlINcNwNCojEMTQggRHynQhBBCiAS61DECQGlhNvles0AblgJNCCFEnJypDkAIIURm\n2VPXPvPz3TsqUxjJ8jMMg+bOEXJj488KvFkADI9OpDgyIYQQViEtaEIIIUSCDAYmGAlOUZzvASBv\nuovjmLSgCSGEiI8UaEIIIUSCNHWaMzYW55kFmstpx+N2EByfSmVYQgghLEQKNCGEECJBWrrN8WfT\nLWgA2VlOghMyi6MQQoj4zDsGTSllBx4BtgMTwGe01o2zHn8A+DPABhwD/lBrbSQnXCHmJzkrrEZy\nNnO0do8CUJSXNXNfjsfJYGCCqXA0VWElXKbl7PS4yettzOT1JNNyVmS2eFrQHgY8WuvbgC8B35h+\nQCnlA74GfERrfQvQDJQkIU4hFkJyVliN5GyGuNA2TE6WE4/7neuf2Vnmz8FQRrWiSc4Kq5GcFZYR\nT4G2G3gRQGt9CLhx1mO3A/XAN5RSe4FurXVvwqMUYmEkZ4XVSM5mgJGxScYnwu9qPQPIiRVo45nV\nzVFyVliN5KywjHim2c8Dhmf9HlFKObXWYcyrC/cAO4BRYK9S6qDW+vy1dlZYmIPT6VhKzPPy+31J\n3X+ySfxLJjm7zKweP6T8NWRUzvq8nri2S7VEx3a5vweA8uLcd70HhfnZAERttoQeM5NyFlKbt9N/\nr3TOV0j/+OYjObtw8jdPrVTFH0+BNgLMjs4eS2aAfuCI1roLQCn1FmZyXzOhBweDiww1Pn6/j97e\nQFKPkUwS//z7j4Pk7DKyevyQFnmbUTkbGA3N/JyuuZGMv/mp890AeLOd73oP7JjDWAaGggk7Zqbl\nLKQ2b6f/Xumar2D9z1rJ2YWTv3lqpTJn4+niuB/4EIBS6lbMJuBpx4EtSqkSpZQTuBU4u/hQhUgI\nyVlhNZKzGaC5y/wiL8rzvOv+d7o4RpY9piSSnBVWIzkrLCOeFrQngfuVUgcwZ7b5tFLqC0Cj1voZ\npdSXgZdi2/5Ua306SbEKES/JWWE1krMZoKUrQJbLQa7n3V+tM5OEZNYYNMlZYTWSs8Iy5i3QtNZR\n4A+uuLth1uM/Bn6c4LiEWDTJWWE1krPWNzo+Rd9wiIqSHGw227se87jNMSoTk5nTgiY5K6xGclZY\niSxULYQQQixRc1dsgeorujcC2O023E47ocmMakETQgiRJFKgCSGEEEt0qd0s0EoKsq/6eJbbQSiD\nWtCEEEIkjxRoQgghxBI1dpizd/sL3tuCBmY3x4mpCIZhLGdYQgghLEgKNCGEEGIJooZBU8cIpQXZ\neNxXH9qd5XZiGBk3UYgQQogkkAJNCCGEWILO/iBjoTCrK/OuuY3HZU4UMhqcWq6whBBCWJQUaEII\nIcQSnG8dBECtLLjmNlmxmRwDUqAJIYSYhxRoQgghxBKcax0CYEN14TW3mZ5qPzA+uSwxievPnrp2\n9tS1pzoMIUQCSIEmhBBCLJJhGJy+1E9OlpOzLQPX3M4jLWhCCCHiJAWaEEIIsUit3aOEJiOUF793\ngerZslzTBZq0oKUzaYUSQqQDKdCEEEKIRaq/1A9ApT93zu2kBU0IIUS8rj4fsBBCCCHmdepSPzag\nonjuAm16kpCxcSnQROJNhSMEgpPkZDnf1QJ4947KFEYlhFgsKdCEEEKIRRgem+Ri2zD+wuyZAuxa\nprs4jkqBJhIoGjV46XArLxxqYSwUxuN2cOvmMqrLfKkOTQixBNLFUQghhFiE4+d7MYDqMu+827qc\ndmw2GA1JgSYSYzAwwd8+doKf7blIOGJQU+5jKhzlzboO+obHUx2eEGIJpAVNCCFEUvQPh+gdGsdf\nkJ3qUJLiaEMPQFytFTabjSyXg9HxcLLDEteBow09/NtLmtHxKarLvNy2uZwst4OOvjFePdrGvlNd\nfPSOmlSHKYRYpHkLNKWUHXgE2A5MAJ/RWjdeZZvngae11t9ORqBCxEtyVlhNJuZs7+A4v3i7lecP\ntnDH1nJ+78ObUh1SQj1/sJlzLYP4Czx4s11xPSfL5ciYMWiZmLNWMDo+xb+9pDna0IPDbuPmjaWo\n6oKZGUQrSnJZV5XPhbZhmjpHUhxtepGcFVYSTxfHhwGP1vo24EvAN66yzVeBa6/QKZZdJBplYCSE\nYRipDiUVJGeF1WRczk7Pbghw4kIf4Ug0hdEk3qUO8+R3TWV+3M/JcjsYC00RzYzP5YzL2XTX1T/G\nf//OIY429OAvyOYjt9ewYVXhe5Z32LqmGLsNTl8auF7PAa5FclZYRjwF2m7gRQCt9SHgxtkPKqV+\nDYhObyNSp6UrwPMHm/n/flrHH39zL//lkQP8xfePcrShh2j0uvqQlpwVVpNRORuaDNPWO0ZJvoeN\nqwoJhsIz3QEzQTRqcKFtGIfdRk15/JMxZLkcGAYEQxnRzTGjcjbdjU+E+bN/PkggOMWW1UV84JaV\n5HvdV93Wm+2iZkUew2OTNLQOLXOkaU1yVlhGPGPQ8oDhWb9HlFJOrXVYKbUF+ATwa8CfxnPAwsIc\nnM65Z7taKr/f2rMXLST+SCTKgfpOnt17iXPNAzP3V/q92G1m0fbIU6fJ97q5ZfMK1q0sAOCDt9Uk\nOuwZafD+S84uM6vHDyl/DRmVs2Mhs7VsdWU+a6sKONcySH3zIA/evS6pMS3UYv/mb5/uZHR8ik21\nRRQXzj29/mzeHPOE2p3txu+ff2KR+WRSzkJq89bn9dAzEKSpY5gNNUWpfm/f45s/Pk5H3xg71vu5\nY1vFvNvvWF/KpY4RDpzt5n03Vi9DhPGRnF24dMvFhZL4FyeeAm0EmB2dXWs9ffnvt4FK4HWgBphU\nSjVrra959WFwMLjIUOPj9/vo7Q0k9RjJFE/84xNhzl8e4lzLIPvqO2euxlb6c1lTkUdZUQ7ZWeaf\ndmRsktNNA1xqH+blt1swohFWFOcm7T1K9vsf538UydllZPX4IS3yNqNytrXLPAfyZbtw2iE/182x\nc920tQ/NOx39clns39wwDH7yigZgTUUegdFQ3M+128yeDK3tQ7hZWq+GTMtZSG3eNrcP8fzBFvPn\nzhHu3r4C+xVdB5fb9HpmAyMhXj9ymdqKPLbUFMaVc7lZdgq8bg7Vd3KppR9fztVb25aT5OzCWf37\nVeKff//XEk+Bth94EPipUupWoH76Aa31n0z/rJT6n0DXfMksFicYCnOkoZtDZ7ppbB8mEuuy6HTY\nUNUFbKguvGp3h7xcN7dvKWddVT4vvt3KvlOdPJj5MztJzgqryaic7Rs2TyBLCjyAOQ19/aUBTjcN\nsEv5UxnakunWIS60DVPlz6XQl7Wg52bYWmgZlbON7e80rPQNhzh8tptbN5enMKJ3nGzsxwB+9yOb\nudg6MO/2YM4aurYyn6O6l0Nnu7n/xpXJDdIaMipnryfDY5N09I0xOj5FQ+sg3mwXD95eg9ORuauF\nxVOgPQncr5Q6ANiATyulvgA0aq2fSWp0gosdw/zo5fNc7hmdKcqK8z1UFOdQXpxDaUE2jjgS1F+Q\nzY51JZw438eB+i4+cFP1ewYWZxDJWWE1GZOzhmHQPxzCl+OaKUhWlpoF2snGPksXaFHD4Gd7LgKw\nbU3xgp8/3XqYITM5ZkzORqJRWroCZLkcfPCWap7e18TeU51pUaCNjk/R1jNK7QofN6z3x12gAdRW\n5HHiQh/7TnXy/l1VmfydH6+MydlMFolGae8d42L7MBfah6m/2M/YVcbtvnS4ldryPCpKcsnxODEM\naOkO4HE7eHh3LZV+70wr9N07Kpf7ZSzZvAWa1joK/MEVdzdcZbv/maCYBBAMTfHzNy/x5ol2DMyW\nsDUVedRW5MU9pfOVttQW0dkXpK13jDdOtHPvzqrEBp0mJGeF1WRSzo4Ep5gMRykvzpm5rzjfQ36u\nm1MX+4gaRsq7ji3WgfoumjpHuHljKSWLWNttumANBK1foGVSzjZ1BghNRlhXlU++101JvoeG1kGG\nxybJz01t18Dzl4cwgHt3LrzAys5yUunPpbV7lOauALUr8pITpEVkUs5mCsMw6Bkc52LHME0dAZq7\nRmjtGWUq/M6sv1kux0yPBU+Wk0jUYGRskvGQOdxHX37vRDjHdC+ba4u4YX2JZb9vZKHqNGMYBofO\ndvHj1xoZGZuksiSXzbVFlBVlL/nql81mY/e2FTy7v5kfv9bI+pUFVCVgoLqwvtBkmMb2YZo7A7R0\nBegdGmckOEkgODVzQu2w28j2OMn1uMj1OPHluPFmu6itKqDE66a6zJsW4xxEanUPmGMyZueCzWZj\n25pi9p7q5GL7MOuqClIV3qINjIT4wcsap8NGVeniPjdnWtBC1i/QMklLlznGpLTQLLprVvjoGw5x\nXPdwTwovZBqGwaWOEVxOOzdtKF3UPtZW5dPaPcpbJzsSXqBNt06ANVsoRGoMjIQ4dbGfs81mt/fQ\nZGTmMZsNCrxZFOd78Od78Bdmk5/rvur57907KglNhukdCjE+EcZus3GisZdAcIqTjX2caRogy2Vn\ny+piS+aqFGhp5NkDTRzTfbR2B3DYbdywroRNtUU47Imr/nM8Tm7bUsaeEx08va+JP/zlrQnbt7CW\ncCTK8fO9HGnooe5C30wXWjDHNnrcTgp9WbEPRoNo1GAyHKVveJyOvneubr11smPm55J8D7Ur8vjE\n/etTfuVZpEZXrEDLu+Lvv0uVsvdUJ0cbei1XoE1ORfjHJ08zFY5y6+ayRfdi8GRQC1omae02C7Si\nvOkxkz6ONvRyorEvpQVaz+A4wVCYtZX5uF2Lm1xnuvvXoTPd/Nrda8j1LC53hViKYGiKw+d6OHCm\ni8a2d8Z75mQ5qSn34S/IpqTAQ6EvK+5xZbOLrmn+gmz8BdlUlOTwzL5m6hr7qS7zvef7yAqkQEsD\n4UiUl49c5pl9zUSiBiuKc7h1c1nSWiNWlnqp8udSd6GPkeAkedLqcV2ZCkfYe6qTXxxqoX9kAjBP\npqtLvZQUeCjJ95Cd5ZyzxTZqGExORQhNRpiKQFuP2erW3R+kbzjEUd3D6oo8tq0uZlNNEVV+b9rM\n3ieSa7pAy89994ngpppCcrKcHNU9/MZ9ay3T7WS6OGvqHGF1RR7rquJfmPpKWW7zKzcQnExUeCIB\nWrtHsdttMxeVvNkuqvxeGloGCU2G8bhTc6rU1Gkuhl6zYvHTfNttNjauKuSY7mXPiXY+nMQldoSY\nZhgG/SMh6luG2Hv8Micv9s90WywvymFlmZfKklx8Oa6kjI30uJ3ctMG8KNjQMsjNm8oSfoxkkwIt\nhUbHp9hf38kbx9vpGRrH43Zw745Kygs9SR3Ma7PZuHNbBY+9doGDp7v4wM3ps0aKSK5jupfv/eIc\nwVAYh93GhlUFrKsqoMB79S4E12K3mS1sHrcTn9eDP9+czW58IkxzZ4Ch0Qka24e52D7Ck3ubsGF2\nH6qtyEOtNGcdLS2cv9tu1DAIBKfIS9KHuEi87mu0oDkddnau97OvvpNzLYNsrilKRXgLMjAS4pGn\nTnOpY4Stq4vZtrZ4SXnodtmx2TJmFseMEI5Eae8bpdCbhX1Wb5Ud64p57sAoZ5sH2bl++Se2iUYN\nWrtH8bgd7xrPuRjrqvI50zTAy0cuc+/OqplleOIx3UoRmoyQn+umfzjE6PhUQoZdiPey6qQWrx2/\nTGdfkM7+oPl/qneM4MQ7E3vk5brZUpvHmso8cpapFXdVuY+juodLHSPsVH7LzfgoBdoyixoGjW3D\n7D3VweFzPUyFo7icdu65oZLSwmxKinIXtK7OYt22pZyf7WnkrZMd/NJNK+WDNsMNBib44cuaExf6\nsNtsbKopZHNt0YK+qOORneVkY00hADuVn46+MXqHxhkcmSAQnOLQGXOpCDA/sNdV5rO6Io98rxtf\njptI1KBnIEj34DhtvaNc7hklNBlhZamXD95SzU0bSi33IXu96R4cx+W0z0yIMdtdOyrYV9/JnhPt\naV2gGYbB22e7+eHL5wlOhLltczmf/tAG9tV3Lmm/dpuNXI9LCrQ0Yp5QGhTlvXvJhO1rS3juQAsn\nLvSmpEC70DY0M3HJUlub3S4HD9xSzZN7m3juYDMfu3ttXM+LGgbtvaOcvzxMW+8oxqyl+zbXFrJL\nLW5cnMgcPYNBXj/ezp66dianzBYyG+DLdbOqwEtlmY9iX9aCLwIngt1uY01FPqebBrjcM2q5SXKk\nQFsm3YNBDtR38caJ9pkvZ1+Oi21rillTmY9nmbt/ebNd7Fzv5/C5Hi52jLC2cvHddkR6O395iH94\nop7R8SnWryxg46qrr5mXaFkuB7Ur8mY+FA3DYHh0kq7BIN0D4/QMjnPsfC/Hzvde9fk2m7nAcaEv\ni7beUb7z7Fkee/UCH7hl5cw4CqtdZcx0hmHQNzR+1W4re+raMQyDQl8Wx8/30tE3RkVJbooivbo9\nde1MTEY4dLablq4AToeNWzeX8ZmPbEzYyYUvxyVj0NLITJfcKz4Ta1fkUeB1U3ehj3AkuuwXho5q\n83NxVfniuzfO9ks3V/PWyQ5efLuVrbXFbFhVeM1tDcPgh6+c58T906xqAAAgAElEQVT5XoZGze64\nhb4s7ttVRVlhNj94SXOmaZDKEu+SW/eE9YQjUeov9vPmyQ7qL5pr9HncDjbVFFJV6qUk3zPz/8Xn\n9SxLo8O11Fb4ON00QHvvmBRo4h2RaJS6C/28caKNs82DgDn5wuqKPFZX5LGiOCelLVd3bq/g8Lke\n3jrZIQVahnr0hbMcqO/GwODmjaWo6oKU5ZzNZqPAl0WBL4sN1YUYhsHYeJiBQIjQZISJ2ExOeblu\nfDku8nLdMx/yo8EpTl3qp7FtmKPnerjrBinM0tHI2CST4eg1J9Gw2WxsX1vMnhMdPP7mRf7oV7am\nVet9/3CIPSfaGQuFKS3M5o6t5fhyEnvl15ftoqs/SDRqvKtLnUiNmS65V4zFfutkB2VFOejWIc5f\nHmLTMrb4Rg2DY7oHt8tOeVFiCqAsl4Pf/+gW/ub/HudbT9Tzh7+85aqv6VLHCD/f00hD6xA2YHVF\nHhtXFVKcb06gEhifYve2FbxwqJX6S/1SoF0nDMPgUucIP99zkebOABNT5vd1Sb6HDasKWVXuS+iE\ndolS4M3C43bQ2T+GYRhp9X0zHynQEixqGDR1jHD8Qi+HznQzGDAnYVi/soC7tlcwGprC5Ux9F63p\nq9nebBeHznSxstSLy2mXFokM8uLbrew71WX+XW+oZEVxerVW2Gw2vDkuvDnz90f35ri4bXMZw6MT\ntHSPpmXri4C+YfNK6VyzHK4s9bKuKp8TF/o4dKab27akfjFgMMdnvvh2K5GowbY15nizZExk4s1x\nY2BOtS/LUqTetcZMAqwq86Fbhzh0pntZC7SL7cMMjU6ypjJvpojfU9eOz+tZ9D6nxzbdvrWcA/Vd\nfP3HdWxbU8yW2iK82S76R0KcvNg/M8NepT+XXcpPgTfrPfsqKcimJN9DV3+Q8YlwwrvKi/QxFY5y\n6EwXrxxto613FDBbyzauKmRNZd7MzKfpymazsaI4h6bOAEOjkxT63pvP6Ur+Vy1R1DDo6g9yqWOE\nxvYhTjb2MzxmdglwOmyo6gLWryyg0JfFRDiSFsXZNJvNxtrKPOoa+2nuHGHdSmtNfS2u7eCZLn76\nRiM5Hifvv7Hqql+yVmOz2bhlUxnPH2jh7bPdfHR3TapDElfoHR4H5i7QbDYbW1YX0dQ5wqMvnMNf\nkM3aJcyMmAjffvo0h8/14HTYuGdnJSsXuc5ZPKbfm0BQCrR00D04jt1mu2rOlhVl4812cbihm4+/\nf92yFSJHGnqAxHVvnK12RR7ebBdHzvVw6mI/py72v+vxFcU5bF1dPG/LWG1FHn3DIZo7AzPjjkXm\niBoG33vhHHUX+hiLTSq2S/nJ97qpKM61VOt/RUkuTZ0BOvvHpEC7HvQMBnl6XzN1jb2MT7yzyJ43\n28Wayjyqy3ysKM5J+wkN1lTmc7Kxnwttw1KgZYhzzQM8+vw5srOcvH9XZhRn04ryPKhVBTS0DHG2\naZD7dq5MdUhilr6hWAvaPK2ivhw379tRwRvH2/naYye498ZKygpzlr0F3zAMnt7XxOFzPXjcDu7b\nVTXTlStZfLH3RiYKSQ/dg0FKCjxXPeG02Wysrcqn7kIfB053cd+u5K+JFolGOXyuh1yPM2m9HvwF\n2XzotlWMjE3SPxxiKhwly+3AX5BNjie+08JVZT6OnOuho39MCrQM09Q5wg9e0jR3BbDbzWUaNtUW\nWnYNvbJC82JD71DqxsIthhRoCzQYmODZA83sPdlBJGp2EVxdkUtJvoeSgmyKfFmWurKQm+2iwp9L\ne+8YQ6MTqQ5HLFF77yj/8GQ9Nhv88a9spWswmOqQEm7H2hKaOwPUX+pndHxq0YsGi8Tri6MFbVqV\n38ud2yvYe7KDV4+0cfcyjyuMRA1+9Mp5Xj/ejjfbxf03VV2zRetqC6Iulm+mBU3WQku1YGiKQHBq\nzskD1lXlc7Z5gOcPNnPnthWLXjA6XmebBxkZm2T9yoKkj+nJy3UvegHfHI8TX46L3sFxjNnTOwrL\nCobCPPnWJV4/3oaBuf7ervV+ci3+HZub7cTjdtA3NJ7qUBZECrQ4TUxF+MWhFl58u5XJcJSyohzU\nynxWlfssNejwalavyKO9d4zmzkCqQxFL8NKRVl442ML4RIQ7t63IyOIMzCmjt6wu4mhDL68fa+Oj\nu2tTHZKIiWcM2mw15T6c9krerOvgjeNtrF9ZwE0bkj9191Q4wtd/eJR9Jzuo8udy6+byuFsOlsoX\nOyEekZkcU6570DxhKy3MvuY22VlO7ttVxS8OtfL8wRZ++X2rkxrTvlPmUg5rKtJ/xrnSwmwuto/I\nxV2LMwyDIw09PPbaBYZHJ8nLdXPLptK0G7e+WDabjeJ8D+29Y4zPWpst3aV3/7s0YBgGRxt6+Mp3\nDvHM/mayPU5+94ENfPUzN1OzIs/yxRlAVakXp8NGU+eIXAmzqGjUYO/JTgLBKbasLqLWAl/uS7Gu\nqgC3y86rx9pmZn8Uqdc3FHrX7JvxqCr18v4bq3DY7Xz76dMzJ6jJMjo+xTd+cpJ9JzsoLcxm97YV\ny1acARTECrRhOalNuZ5YgTbdBepaPnzrKorzsnjuYDOnm/rn3HYpBkZCHNO9FHjdlBSk9+QLAKWx\n9617wFotE+Id/cMhvvmzU3z76TMEglPsWFvMg3esypjibFpJrOv69EVEK5ACbQ7tvaP89++8zSNP\nnWYwMMHm2iI+dOsqoobB3iSfRCwnl9NOld9LIDhFc5e0olnRE29doqNvjMqSXHasK0l1OEnnctrZ\nUF3I6PgUe091pDocgXmRoH8khH8RY7jKinK4/+YqXE47j75wjpcOtyblYtEz+5v4yncOcf7yEGuq\n8rn/xqqkd1m7Ul5sTOj0ZFIidXpivQz8BdduQQM43NDDTRvLcNjtfOvxeo5fY+3GpXrteBtRw2Dj\nqkJLXPwtjb1vVjrpFSbDMHjrZAf/41/epv5SPyuKc3hodw3b1pbgsGdeaVCSH8tVC3VznPeyoVLK\nDjwCbAcmgM9orRtnPf554Ddjv76gtf7zZAS6nIKhKZ7a28Trx9uJGgaV/lxu2lC66L7aVlBbkUdz\nV4C3z3ZbbjG/K11vOXv4XDcvHGrBl+Pizu0rkjI1eDrasKqAhpZBXjp8mbtvqEz7CXnmkgk5OzQ6\nQSRqLHqSjZL8bD5wczWvHm3jJ6830j04zsfvW5ewmW916yAvHGphcirK5tpC7tq5ktGx5W/Fyp9p\nQbN2gZYJOdsz9E4Xx4HA3EVGaWE2d+2oYM+Jdv7hiXo2VBewU/l5/67ETFQ0GJjgtaNt5HvdlukB\nkZfrwumwMTBijQItE3I2EYKhKb722AlaukdxOe3cvqWcNZWZ0SPsWorzzQtjAwHr9FyI55vvYcCj\ntb4N+BLwjekHlFKrgU8CtwO3Ar+klNqWjECXy4kLvXzpnw7x6rE2Sgo83Luzkvt2VWV0cQZQUZKD\n22nnSEMPUet3c7xucralK8Cjz5/D43Zwz87KZW8NSCWP28md2yroHwlx5FxPqsNZKsvnbG/sZHe+\n1oi5FPqyeODWaqr8XvacaOcvf3CUlgS06u850c7Xf1zHVDjKbZvL2KVKU3Yykutx4nTYMqEFzfo5\nOziOzfZO96f5VPpz+dBt1eTnumloHeK5/c1caBtachyGYfDYq+eZDEf55TtXW+Zik81moyjPw/Do\n5MzCxWnO8jm7VK3dAf78X4/Q0j1KaWE2D95Rw9qq/IwuzsA8X8jxOC1zMQHimyRkN/AigNb6kFLq\nxlmPXQY+qLWOACilXMCcr76wMAenM7knkX7/4tYOeWbvRb779GncLge/8+FNPPS+1bx25HKCo5vf\nUhajXIo1VQWcax6gJzDJ1jWL7ya32Pc/ga6LnB0MhPjHp04zFYnyld++JaUfPKnK2Y/vquaNunae\nP9TCA3euWVJrS4rz1vI5W98yCEBN5dKW6/B5Pfzd5zfyz0/V88rhVv7i+0e4fVsFH7q9hs2rSxY0\ns10wNMWf/fNBGloG8bgdfPDWGipnrXGWirwtLc2jMM/DaGhqyTmXSTkLy5+3fSMT+AtzWFGej69p\nMK7n+7wefrM0j0OnOzl5oY//9aPjPLh7NZ96YOOi10l7ck8jR3Uvm2qLePje9bzydsucx08nZcW5\n9AyOMzYVpapi/v/7krNzm/77zn6fEvWevXHsMv/w0zomw1F2bSjl5k3lyzLreLrkbGlhDs2dIzg9\nLgp98ceUqpyN59MkDxie9XtEKeXUWoe11lNAn1LKBnwNOKG1Pj/XzgaTPLOc3++jt3dhV1zfONHG\n0YZezrUMkp3l4N6dVRiRCE+9cSFJUV6bz+shMJqaE+0qfw7nmgd4+WAz5XmLWztrMe//Qvcfh4zP\n2alwlK/9+AR9Q+P86l2rqS3NpaVj6VdyFyOVOWuPRLh7RwWvH2/nZ680cP+Ni+tulAZ5a/mcvXTZ\nzD+PwzazYPViBUbG+fi9a9m+uohHXzjH/pMd7D/ZQZbLgb8wmxvX+6n051JenEtZYfZ7WhzCkShH\nGnp44s2L9I9MUJzn4a4dFXhznDO5mqq87e0N4PW4uNwToKdnZNFXrjMtZ2F583ZiKsLASIiNqwrp\n7Q0sOBe2rymmvCibuvN9PLP3Envr2nl4dy23bSmPuwUsNBnmqb1NvHzkMnm5bjauKuCJ1/Q1t0/l\nZ+21+GIT7JzUPRTNs/6h5Oz8pv++0+9TIt6zcCTKT15r5LXjbbicdu7ZWcnKUi9jweR390unnM2L\n5Wfd2S62rC6O6zmpzNl4CrQRYPYe7FrrmXkqlVIe4FEgAPw/i4wxZabCUd6q66Cle5T8XDf37aqa\nd5HVTFVWlENerpujDT184v3rLNPN4ioyOmcNw+BvHzvOxfYRasp95HicCV2nyUr21LVTUuDB5bTz\n+JsXiUYNPnBzdarDWgzL5+z04OuSfM+SC7Rpm2qK+PBtq+geHKepY4SOvjHaekZp6xmd2cZmM9cW\n8+a4qPJ7CU6EaeoYYSwUxmG3sXV1UWzge/p04SnwumnqNBgLha28jp+lc7Z3aP4p9udTVpjDfTdW\ncfrSAKebBvjeLxp4al8Tu7eu4Ib1Jaws9b5rwoWoYdA/HKKpc4SzzYMcbeghOBGmtDCbz39sO+da\n42vFSydFsYu5ieiKvAwsnbOL0Ts0zj89c4ZLHSNUluRy08bMnk9hLjO52h2Iu0BLpXgKtP3Ag8BP\nlVK3AvXTD8SuNDwNvK61/pvkhJg8U+EI//jkaVq6RykrzObunZVkXUdjeK5kt9m4aUMprx1r42zz\nINvWpH8CX0PG5izAS4cvc7F9hOJ8D7dvLc/4vuPz8bidbF1TzHHdy6mL/VYt0Cyfs92D49hj680k\nks1mo7woh/Iic0rvYGiKgcAEw6OT5m1sgpGxKUb6gnT0mVezczxO3r+rivfftJKzzQMJjScRZiYK\nGZu0coFm6Zzt6jdzZTqvFsvpsLNjXQnrVuZz5tIAje3DPHugmWcPNON22inO9+B2OghNRRgMhJic\nis48NzvLwfa1xWyuLbJkcQaQ783CboPLsy6apDFL5+xCGLHZxn/82gVCkxFWV+Rxy6ayhE26ZEVF\nsW6Nrd2WyNW4CrQngfuVUgcAG/BppdQXgEbAAdwFZCmlHoht/2Wt9cGkRJtAU+EI//DEaeov9VNR\nkmP5WeAS5ZZNZbx2rI2DZ7qsXKBlZM4CnGzs42dvNJKT5eQeydkZG6sLON86hG4dpHsgSNkST7pS\nwPI52zMYpCTfk/SczPG4yPG4qPK/+/6pcJSpcBSn04bb6eDuHZUAnE1qNIuTH5tqfygwQWWJZdcb\nsnTOdg2YBVqiPityPS5u3lTGDev9tPeO0tEXZCAQon8kRCRi4HTYyfW4qCh2U5SXRVlhDsUFHsvP\nuuuw28j3ZtHeO0o0aizLmKYlSPucHZ8Ic/x8L3tOtLOhupA//s2dC95H90CQf3tJc65lEJfTzh1b\ny1ldkdmzNMYjN9uJ22WntdsSrb3zF2ha6yjwB1fc3TDr5/QY/bcAU+EI33q8ntNNA2xdXcy2NUU4\n5EQXgDUVeVT6czlyroeH76yddwHPdJSJOQvQ1jvKt585M9OHfDkX1013DoedXcrPm3Ud/POzZ/jy\np3ZZqni1es6OT4QZCU5RXZ6YwdSL6bLrctotc3V4etbAfgvNKHYlq+fsdIG2IsEXc1xOOzUr8qix\n+HI1C1Hoy2IwMEH3YDCtFzhO95wNR6K8Wdcxs4B6W+8Yu2+ooqoovm64E5MRnj/UwgsHW2aWiLpl\nU5mVW+kTymazUeTz0DUQZHwivOhJfZaLNb7NEig0Gebvf36K000DbFtTzB/9ylYpzmax2Wx89I5a\noobBs/ubUx2OiBkJTvK/f36KickIv/eRTQnvRpYJqsu8rK7Io6kzwE9fb5z/CSJhumMD5a14QScV\npgu0XgstmpppugaCOOw2Sgrks3Spinxmi7BFujmmrb2nOukZHGdVuY/7dlUB8LUfHmVwnrW7oobB\nwTNd/OdH9vPcgWY8WQ7u2lHBvTsrpTi7wvQ4NCvkanqXjwm0p66diakIrx1to284xMpSL1vXFLH/\ndGeqQ0s7u5Q5Q9rBM108eHuNFbuLZZRwJMojT9TTNxzio3fUcNOG0ut2UpC52Gw2btlURmgywqvH\n2li/soAbN5SmOqzrQveAWWiULWHChURL5/8j0xdY+oet24JmZYZh0NUfpLQw+12TeIjFKYyd9LZ2\nj3LzxrIUR2NNhmHw+vE2bDa4aUMpOR4nN27wc/hsD99++jRf/PgN7+kVYhgGJxv7eWrvJVp7RrHb\nbWxZXcTW1cWW6U2w3IrzzM/elq4A61cubUmYZLtu/oLjE2FePnyZvuEQqyvyuGtHhXwwX4PdZuOh\nO2oxDHj2QHOqw7muvXGijb/50XHOtw2zqtxHvted1ieeqeZy2vncw1twu+w8+sI5q8wsZnnTLWil\n0oIWl0JfFg770pcjEIsTCE4RnAhLi2+CFM2c9I6kOBLrutA2THvvGKvKfDPDF9TKAu7YVsGFtmG+\n/4sGwhFzgplwJMrhc938+feO8L8fP0VrzyirK/J4eHctO9f7pTibw0yuWmAc2nXRgtYzGOTFt1sJ\nBKdQ1QXcvLH0uh8sOZ+d0oqWFk5fGuBixwjFeR7ukBkb43KhbYhbNpWx92Qnf/2jY9x/00p+9X1r\nUh1WRmvvHQOgokQ+J+LhsNsp9GXRJy1oKdHea3ZvqrDuBC1pJcvloLQwm+auAIZhyPfUIhw60wXA\nupX5M/fZbDb+42/eQFt3gP2nu7jQPkxFcS4XO4YJBKcAqCn3sW1tMQXexa1de73Jy3XhcTto6kz/\niwkZX2afax7g//3+UQLBKbauLpLibB576trZU9fOWyc7WFuZj2HAd547K602KXD4XDcnLvSR43Fy\nz06ZsXEhalfkccfWcianorxy5LK0pCXZ5Z5RsrOcM91HxPxK8j0Mj04yFY6kOpTrTktsmu3qMm+K\nI8kcNeU+xkJhGVe5CNGowbHzveTluN5zMTw7y8mXPrmT3dtWMBSYoK6xj6lwlA2rCnj4zlret6NC\nirMFsNlsrKnIo7M/yOj4VKrDmVPGnvEZhsFrx9r4xk9OEpqMcNuWcm5Y75fibAGqy7zmgqodIzJW\nYpmdutjHd587h8th575dVTJj4yKsqcyfKdL+9rHjnLjQm+qQMtLEVITuwSAr/bny+boA/gJzvN70\njG1i+UxPs70qQbOOCqgpN2etbJaLYQt2/vIQgeAUO1XpVZddyHI7WF2Rx8fuWcOv37uWj92zhps3\nll23C04v1doqc+xZY/twiiOZW0YWaMFQmO+90MCPXjlPbraTL378BtZV5c//RPEuNpuNXcqPAbx6\ntG2mW4hIrmO6h289Xo/dBnfdUEGhT66OLdaaynzu3L6CSMTgW4/X89TeS0QNI9VhZZSOvjEMA1aW\nysnuQlSVmq03VphNLNO0dAfwuB0zRbJYutoV5v//i+3p33Us3RzRPYA5QdtcHA47HrdDLoQt0dpK\nsx64KAXa8nr7dCdf+e4h9tV3Ul3q5U9/56a0n6klnVX6vdy2uYyJqQhf+3HdzNoxIjn213fyf546\ng9Np5/O/vl3GSCRA7Yo8/ttv7aIk38Mz+5v5+mMn6JY8Tpjp1oiqUsnVhaiWAi0lJqYidA0EqS71\nWn6R6HSyuiIPp8NOQ+tgqkOxlGjU4JjuxZvtYkP1e89VXzzYLENMEmx1RR42zJbLdJYxBdpgYIL/\n89Rpvvq9w4yMTbJ9bTF37qigvqlfknuJ1q00J1YZGZvka4+doEf6mCfc+ESYv/zBUf7l+XM4HDbu\n3VlJpxQRCXOpc4T7dlWxstRLQ+sQX/nu2zx/sHlmViyxeDr2JbemUnopLMTKWIHWKgXasrrYPoxh\ncF0tJL0cXE4H66ryudwzSiA4mepwLONC2xAjY5PsXO+XmcWXSXaWk9qKPC62jzAWSt9xaJbPhmAo\nzONvXuTL/3SQIw09lBfl8JE7ati+tgSHXa6OJcqGVYX8+j1rGQxM8NXvH+XNunaiUekqlghnLvXz\n5/96hIvtIxTnZfHh21ZJ15skyHI7uPuGCt63owKX087jb17iK999m6MNPRjS7XFRDMOgoWUQX46L\nSmntXZAcj4uSfA+t3QHJv2V0umkAgM21RSmOJPNsWFUIgG5N75aJdPL22W7AXPtMLJ8da0uIGgb1\nF/tTHco1WXbmgfGJMG/WdfD8wWbGQmEKvG4+cedqsnPcjI3Nveq6WJwP3lKN22XnZ29c5PsvavbU\ndfCp+9fLlfNF6hkM8rM9FzmmzckrNtcWsmOdXy4sJJHNZqOm3MeK4hz6BkPsqWvnkadO89qJdt6/\ns4ob1pVgl/c/bt2D4wyNTnLTBpkddzFqVuRxtKGHzv6gdGdeJqcvDeB02GXoQxJsriniybcucfx8\nLzdKwTGv8YkwB892U5SXxcZYcSuWx451JTzx1iXqGvu4dXN5qsO5KssVaF0DQf7txQYa24cJRwxc\nTjs3rC9h46pCooYhfcqTaE9dO3a7jQfvWMUx3UtTZ4C//MExVhTn8NDuWm5YN/cAV2G2OOjWIX76\nRiMt3QEMA8qKcti5rgR/obSaLZcsl4PK0lwevKOG4+d70S2D6JZB/AUe7rmhils2lcnkLHE4Fhvc\nLq0Ri7N9TTFHG3o4caFXCrRl0DMYpK13lM01hWS5HKkOJ+PUrvBRWpjN8fO9jE+Eyc6y3Cnmsnr7\nbDcTkxEeuKVaLgwus8qSXEoLsqm70EcgOIkvJ/1mxEz7/z0jwUka24Y5f3kIfXloZj2jnCwnW1cX\nsG5lAR63fNAupxyPizu3V7C+OsiJ83109gf59tNnyPU4uWtnFWsr8thQXYDHnfbptSwMw6ClO8Ax\n3cvRhh66Y9NqF3jdbF1TzNa1fkal1Tcl8nLd3H1DJZMROHaui+auAD99o5GfvdGIqi5glypl25pi\n6XJ6FVHD4M26DtwuOzcquVq+GNvXlmCzwfHzfXz4tppUh5PxntvXBMDNm8pSHElmstls3LF1BU++\ndYlDZ7q4Z2dVqkNKWxOTEZ472IzTYePObRWpDue6Y7PZuG9XFY+9doHXjrXx8J2rUx3Se8x7Bq2U\nsgOPANuBCeAzWuvGWY//e+D3gTDwVa31c4sJJByJ0tVvXt263DtKW88Ybb2jDAbeOXF1OmxsqC7A\nX5jNqjKfXHFIsbLCHD54SzXDoxNMTEU5UN/JCweaAXDYbayrymdNZT5Vfi9VpV7Ki7KXZRDscuXs\nXIKhKc5fHubUxT4ON/QQDIUBM4drV/hYX11AaUE2NptNuoalgeJ8z8xaiS1dAZo6R2hoHaKhdYgf\nvQIrinNYU5lP7Yo8VpX5KC/KJsfjStjx0yFnF2p/fSd9wyF2b10h6/QtkjfbxebaIk5fGuBM8wCb\na6zTEmm1nB0aneClQ83k57q5dVN6dmnKBLu3ruCFgy08ubeJmzaW4c1O3OfkUqVTzj617xIDIxN8\n6NZV0lsjRd63vYJn9jfxytE2bt9STmlhzvxPWkbxfKs+DHi01rcppW4FvgE8BKCUKgf+A3Aj4AH2\nKaVe0Vpfszng4JkuQhNhRoJTDAYmGBqdoH8kRFd/kMgVk07keJxUluTiL/BQWpRDSb4Hp8Py85pk\nnPzYKvYf3V3L6ESExsuDdPSNzZzgTnPYbRTlZVGSn01xvocCrxuvx0Vutotcj4sst4MslwO3y27+\n67Tjcpq/O+wLKmQSmrNgthZMTkWYmIoyMRWJ/RwhNBlhYjLCSHCSwZEJ+oZDNHeN0Nn/zgyMbped\n2hU+qst8VPpzJYfTmMftQFUXoKoLGBufoq13jPbeUboGgnT2B9l3qnNmW2+2OclDUZ6HIl8W+V43\nvhw3vhwX3mzzluNxkZMVVwt/wnM2WaKGwcH6Th579QIet4OP7q5JRRgZ41fft4Yzlwb4/i8a+A+/\num1mfTQLsEzOdg0E+aenzxAMhfnk/etxOeUzOFkKfVk8tLuWn77RyN/99CSffXATZUVpc+Kb8pwd\nC03x3IFmXjp8mZJ8Dx+5fVUidy8WIMvt4NfvXcv3Xmjg7352it/78EbWVOSlzUXzeAq03cCLAFrr\nQ0qpG2c9djOwP5bAE0qpRmAbcORaO/vOs2ffG4TDRqEviwJfFoW+LAq95r9Z0nXRUux2G5V+L3nZ\nTnau9xOajDAYCJmFeGCSodEJRsen6B0KLWr/DruNp7720Xg2TWjO/sHX9zAZjn86dqfDRnlRDv4C\nDxX+XPz52dLaa0G52a6ZYi0aNRgem6RvOMRQYIKR4CSBsUlae0ZpjnW7nsuz33hovk0SmrPJ8vLh\nVp49YE7M5HTY+eyDmyjJl+6fS7Gq3MfD71vNk29d4k8fPUxpYTaf+cimmcVU01ja56xhGPzNj45z\nvs1ckPb+m6u5d2flcoZwXbr/piraekc5cLqLL//zIfPCbF4a4nQAACAASURBVJ6H//SJXXhSWxun\nLGf/7cUGzrYM0js0jmFAcZ6HL378BhkKkmJ3bquge2CcFw618Fc/OIYvx0WV38vnHt6S8tbfeDIj\nD5i93HZEKeXUWoev8lgAmPNb5dlvPCRnqiLZEpqzj//Ng5KzItkSmrN+vy8pOfvJD2/mkx/ePO92\nH7t/QzIOn7H+3UNb+XcPbV3w8/x+XxKiiVtCcxaSk7ff+PzdcW0nOZtYX/70LakO4WpSlrP/+bdu\niitAycPl97mP7eBzH9txzcdT9Tkbz7WMEWB2dPZYMl/tMR8gC2CIVJOcFVYjOSusRnJWWI3krLCM\neAq0/cCHAGJ9dutnPXYYuFMp5VFK5QMbgdMJj1KIhZGcFVYjOSusRnJWWI3krLAMm2EYc24wa9ab\nbYAN+DRmgjdqrZ+JzXrzWcxi76+01o8nN2Qh5iY5K6xGclZYjeSssBrJWWEl8xZoQgghhBBCCCGW\nh8w1K4QQQgghhBBpQgo0IYQQQgghhEgTUqAJIYQQQgghRJrIuBXyYrPv/BBzTQs38AWt9cHURjW/\nWYNXtwMTwGe01o2pjSp+SikX8ChQA2QBX9VaP5PSoCxCcjY1JGcXT3I2NSRnF09yNjUkZ5dG8jY1\n0iFvM7EF7QvAa1rru4DfBf4xteHE7WHAo7W+DfgS8I0Ux7NQnwL6tdZ3Ah8E/iHF8ViJ5GxqSM4u\nnuRsakjOLp7kbGpIzi6N5G1qpDxvM64FDfg7zGodzNcXSmEsC7EbeBFAa31IKXVjiuNZqJ8BP4/9\nbAPCc2wr3k1yNjUkZxdPcjY1JGcXT3I2NSRnl0byNjVSnreWLtCUUr8HfP6Kuz+ttT6ilCrHbBb+\nT8sf2aLkAcOzfo8opZyzVrlPa1rrUQCllA8zqb+S2ojSk+Rs+pCcjY/kbPqQnI2P5Gz6kJyNn+Rt\n+kiHvLV0gaa1/hfgX668Xym1Ffgx8F+01m8ue2CLMwL4Zv1ut0oiT1NKrQSeBB7RWv/fVMeTjiRn\n04vk7PwkZ9OL5Oz8JGfTi+RsfCRv00uq8zbjxqAppTZhNk1+Qmv9i1THswD7MVe0Ryl1K1Cf2nAW\nRilVBrwM/Fet9aOpjsdKJGdTQ3J28SRnU0NydvEkZ1NDcnZpJG9TIx3y1mYYRiqOmzRKqacxZ41p\njt01rLV+KHURxWfWjDfbMPu7flpr3ZDaqOKnlPp74DeA2TE/oLUeT1FIliE5mxqSs4snOZsakrOL\nJzmbGpKzSyN5mxrpkLcZV6AJIYQQQgghhFVlXBdHIYQQQgghhLAqKdCEEEIIIYQQIk1IgSaEEEII\nIYQQaUIKNCGEEEIIIYRIE5ZeB00IIUR6UUoZwGkgAhhADuaaOJ/TWh+NbZMD/Dfgl2Pb5AL7gD/R\nWncqpSqAF67YtR8o01q/53tLKVUC/F+gDAgAv6G1bk/Cy5uTUupfgdNa668nYF+/BvyR1vrupe5L\nCCGEtUgLmhBCiES7R2u9Q2t9g9ZaAT8BvgWglHIALwLFwM1a6y3AGsyi7hdKKZvWuiP2/B1a6x3A\nB4FJ4PPXON4fA01a6+3AWeBzSX11QgghRBJJC5oQQoikUUo5gWpgIHbXw0A+8Ida6yhA7N+/UUrZ\nAC9mK9j087OAp4CXtdbfusZh6oHfUEqtB24E/mSOeCaA6bWFPgmMAX+PWTA6gP+ttX5UKeUFvges\nA6LAMeD3tdZRpdRngf+A2UrYjdnSdX7WMT4LfFRr/ZHY7xuA12Lvw/qrHS+23V/EYuoHLlzrNQgh\nhMhsUqAJIYRItDeUUlHMbokh4Dng07HH7gRenS7OZtNa/6+r7Os7wDjwR3Mc723MrpQNwENa61fn\n2NYNPKu1/vVY8XgS+C2t9XGlVD5wUCl1FrMw82mtd8Ra/b4NrFZKVWMWgLdprXuVUr8LPKWU2jzr\nGI8Bf6uUKtdad8Ve+/cwF2z9+TWOVwb8KrAj9nqfmuM1CCGEyGDSxVEIIUSi3RPrbvhhzMLpgNa6\nJ/aYDXPcGQBKqXuUUnWxW6tS6iOzHvsicDvwa1rrqasdSCm1CdgPfBl4AviCUmqXUuqROeLbG/t3\nPWb3ykeVUnXAm0A2cAPmmLjNSqk9wJeAb2qtGzG7W/5Ea90LoLX+V6ASqJneudY6gFmIfSpW3H0K\n+Jd5jvd+4AmtdUBrHQYenSN+IYQQGUwKNCGEEEmhtT6BOW7su0qpmtjdB4C7Zm3zxqyxZpcAD4BS\n6gHMouujWuv+OQ7zWeBHWusfYXYPtAOvMHcPkdHYvw5g6IrxbrcC39NaNwFrgb8G8oBXYxN3XO17\n0wa4rrjvu8BvYxZ0Z2P7u+bxMItW26znh+eIXwghRAaTAk0IIUTSaK0fAw4C34zd9TgwppT6Zmyc\nFwBKqVuA1UAkNmbrh8CntNZn5znEeeBOpZQHcyKRNzDHuPmUUu75wgNCSqlPxWJYiTlZyS6l1Ocw\nC6eXtdb/FXgJ2BL79zeUUv7Ycz6NOWas8YrXfQiz4PpTzG6acx4Pc+KUjymlCpRSduC35oldCCFE\nhpICTQghRLL9EfCAUuoDse57H8Qsat5SSp1QSjUAXwW+iDn26otAFvBXs7o/Tt9WXrHvf8LssngE\ncwzaJmAjUA48MFdQWutJ4CHgM0qpU8DLwP/QWu8H/g2zxeusUuooZiva32utXwH+DnhdKXUG+B3g\nI1cbU4dZmK2OvaY5j6e1fgGzW+NRzDF1w/O9qUIIITKTzTCM+bcSQgghhBBCCJF00oImhBBCCCGE\nEGkirgJNKXVLbCarK+9/UCn1/7N33/Fxnfed7z9TMSiDPigEicJ22JuoQlnVkizLlmzZ6xbFm6w3\nTvFu7s1G6ffmJpuyiVO8cTaJneIeK7Yl22q2RHVaEimKvROH6L23waBPuX8MSEEUyRmUwcwZft+v\n17xEYAZnfgN8BczvPM95nsOGYbxlGMYvL3l1IgukzIoVKbdiNcqsWI0yK1YQs0EzDON3ia5G5bns\n8y6i8/A/QHRFrl8xDKM0EUWKzIcyK1ak3IrVKLNiNcqsWEU8I2gNwMev8PmNQL1pmkOzFz6/Cdyx\nlMWJLJAyK1ak3IrVKLNiNcqsWELMBs00zR8BV9ogNJd3rzI1SnRp42sKBkMRovu96KbbQm4xKbO6\npeAtpqXMrTKr2xLcYtLvWt1S7BaTMqtbit2u6lobecbiB7xzPvYCw7G+aGhofBFPGZvP56WvbzSh\nz5FIqj/28RdBmU0Aq9cP6ZdbZTY2q7+GdMssKLexqP7Yx18EZTYBVH/s41/NYhq088A6wzAKgQDR\noeC/XcTxRBJNmRUrUm7FapRZsRplVlLKvBs0wzAeAXJM0/xXwzAeBV4gOlXyG6Zpdix1gSKLpcyK\nFSm3YjXKrFiNMiupatk3qu7rG03oE2o4NbmWYTjYlrCDX4Uye21Wrx/SL7fKbGxWfw3plllQbmNR\n/TGPr8ymGNUf8/hXzaw2qhYREREREUkRatBERERERERShBo0ERERERGRFKEGTUREREREJEWoQRMR\nEREREUkRatBERERERERShBo0ERERERGRFKEGTUREREREJEWoQRMREREREUkRatBERERERERShBo0\nERERERGRFKEGTUREREREJEWoQRMREREREUkRatBERERERERShDPWAwzDsANfAbYDU8DnTdOsn3P/\nbwGPAGHgL0zTfDJBtYrERZkVq1Fm09O+Ex3v+dxdOyqSUMnSU2bFapRZsZJ4RtAeBjymae4Bfh/4\n0sU7DMPIB34D2AN8APhyIooUmSdlVqxGmRWrUWbFapRZsYyYI2jAbcBeANM0DxqGsXvOfWNAC5A9\newvHOlhBQRZOp2MBpcbP5/Mm9PiJpvoXTZldZlavH5L+GpTZJEj0a/DmeBL6nOmUWVBu46H6F0WZ\nTQLVvzDxNGi5wMicj0OGYThN0wzOftwGnAMcwF/GOtjQ0Pi8i5wPn89LX99oQp8jkVR/7OPHQZld\nRlavH1Iit8rsMluO1zAamHzP55bqOdMts6DcxqL6Yx8/BmV2man+2Me/mnimOPqBuUewzwnzA0A5\nUANUAg8bhnHTAusUWSrKrFiNMitWo8yK1SizYhnxNGj7gQ8BGIZxC3B6zn1DwAQwZZrmJDAM5C91\nkSLzpMyK1SizYjXKrFiNMiuWEc8UxyeB+wzDOADYgM8ZhvEoUG+a5jOGYdwLHDQMIwy8CbyUuHJF\n4qLMitUos2I1yqxYjTIrlmGLRCLL+oR9faMJfULNd02uZZiva0vYwa9Cmb02q9cP6ZdbZTa25XgN\niVxmP90yC8ptLKo/5vGV2RSj+mMe/6qZ1UbVIiIiIiIiKUINmoiIiIiISIpQgyYiIiIiIpIi1KCJ\niIiIiIikCDVoIiIiIiIiKUINmoiIiIiISIpQgyYiIiIiIpIi4tmoWkRERCRtXb5n3VLtVycishAa\nQRMREREREUkRatBERERERERShBo0ERERERGRFKEGTUREREREJEVokRAREVlSly+4AFp0QUREJF4a\nQRMREREREUkRMUfQDMOwA18BtgNTwOdN06yfc/8DwB8DNuAo8N9N04wkplyR2JRZsRplVqxGmRWr\nUWbFSuIZQXsY8JimuQf4feBLF+8wDMML/A3woGmaNwPNQHEC6hSZD2VWrEaZFatRZsVqlFmxjHiu\nQbsN2AtgmuZBwzB2z7nvVuA08CXDMFYDXzNNs+9aBysoyMLpdCy03rj4fN6EHj/RVP+iKbPLzOr1\nQ9JfQ1pl1pvjmdfjkyXRNSX6+5BOmYXk5vbyn1Uq5hVSt654KbPzp595ciWr/ngatFxgZM7HIcMw\nnKZpBomeXbgb2AEEgDcMw3jLNM0LVzvY0ND4YuqNyefz0tc3mtDnSCTVH/v4cVBml5HV64eUyG1a\nZXY0MPmez6VaRhL5M+8dGudrPz1PJBxh94YSMtzvvIFbqudMt8xCcnN7eWZTLa9g/d+1yuz86Wee\nXMnMbDxTHP3A3CPYZ8MMMAAcNk2z2zTNAPA60XCLJJMyK1ajzKaJiakgf/ndY9S3j9DQ6efAme5k\nl5QoyqxYjTIrlhHPCNp+4CHgccMwbiE6BHzRMWCLYRjFwDBwC/BvS16lyPwos2I1yqzFXdxa4FTD\nACNj02ypKaRrcJy23gCB8RlyslxJrnDJKbNiNcqsWEY8DdqTwH2GYRwgurLN5wzDeBSoN03zGcMw\n/gB4Yfaxj5umeSZBtYrES5kVq1Fm00AoFOZc8yBul50tawrJy3Gz/3Q3de3D7FzvS3Z5S02ZFatR\nZsUyYjZopmmGgV+77NO1c+7/PvD9Ja5LZMGUWbEaZTY9tPeNMT0TZnNNIW6ng6oyL2+d6aGzfyzt\nGjRlVqxGmRUr0UbVIiIiS6ChI7r+wJoVuQA4HXaK8jwM+qeYCYaTWZqIiFiIGjQREZFFmpoJ0dE/\nRmFuBvnejEufLynIJAL0DU8krzgREbGUeK5BExERkWto7w0QiUBV2buXTS4tyORsE/QMTbCiODtJ\n1Um6ubgozUV37ahIUiUikggaQRMREVmklu7oXjlVpe9u0IrzMwEY9L93bzgREZErUYMmIiKyCBNT\nQToHxsnPcZOb7X7XfR63g8wMB8OjU0mqTkRErEYNmoiIyCKcbhwgHI5Qedno2UX5ORmMTQaZDoaW\nuTIREbEiNWgiIiKLcOxCHwBVZTlXvD8/J7poyEhgetlqEhER61KDJiIiskDTMyFO1g/gzXJdasQu\nl++NTnscDmiao4iIxKYGTUREZIFONw4wNROiqtSLzWa74mMuNm7DoxpBExGR2NSgiYiILNDh2l4A\nqsqvfP0ZcGnhEP+4GjQREYlNDZqIiMgCTEwFOVHXT2lBJoXeK09vBMhwOchwORgdU4MmIiKxqUET\nERFZgMO1vUwHw9y6peyq0xsv8ma5CEzMEAqHl6k6ERGxKmeyCxAREbGiN093YQNu3VLO6aaBaz42\nN9tN/8gkA/4pSmY3rxZZqKHRSc41DdE7PAHAhbZh7tu9ipry3CRXJiJLIWaDZhiGHfgKsB2YAj5v\nmmb9FR7zU+Bp0zT/ORGFypXtO9Hxro/v2lGRpEpShzIrVqPMWk9rzyj17SNsqSmkKM8T8/HeLBcA\nvUPjadGgKbPJEYlEeO5gC8/ubwHA7bJjw8bBsz0cPNvDtjVFbF9bxN07Vya50tSjzIqVxDPF8WHA\nY5rmHuD3gS9d4TF/DhQsZWEii6DMitUosxbz7y+aAJQUZL7nRNmVeLOiC4X0DE4ktK5lpMwmwdNv\nNvGjnzWS5XFyzw0VfPr9a/nU+9dw340rycl0caphgKNmX7LLTFXKrFhGPA3abcBeANM0DwK7595p\nGMYngPDFx8jyCocjBCZm6B+eoG94gqYuPz2D4wQmZohEIskuL1mUWbEaZdZC+kcmaOz0k5vlosKX\nHdfX5F4aQUubBk2ZXWZvne7imf3NFOd5+NAtVVT4crDZbNhsNsqLsnnglkryst2cax7i4NnuZJeb\nipRZsYx4rkHLBUbmfBwyDMNpmmbQMIwtwCPAJ4A/iucJCwqycDod8690Hny+qy93bAWx6u8ZHOf1\n4+0cOtuN2TrE3D7s+YOtl/7tzXLhzXKzuiKPDdWFZLgcfHBPdYKqfkcKfP+V2WVm9foh6a8hrTLr\nzXnvlL9UzMhCa/r+aw1EInDT5nJyvfFNV3S6on9u/RMzS/a9SKfMQnJze3lmUy2vgfFpvvKj/bid\ndv74l/dQ2zz4nsd4c+DDt9XwxCt1PPbSBW7duZKivNSaTqvMzl+qZXG+VP/CxNOg+YG51dlN0wzO\n/vsXgArgVaAamDYMo9k0zauefRgaGl9gqfHx+bz09Y0m9DkS6Vr1dw2M8ZMDLRw8100kAjagKM+D\nN8tFZoYTmw0qinMYnwoSGJ+ha2CMrv4xOvvHOHimi53rfOxaUxhztbFE1b9Ux4+DMruMrF4/pERu\n0yqzo4FJAIZHp7jQPow3083O1YXY7Yn73TNfC/2Zt3SP8tLbLeTluCkr8Fx6rbFEIhGcDhsdvYEl\nyVq6ZRaSm9vLf46p9jvtsRcvMDw6xX+6czXZTttVc+e0wQ3rfRw818Mf/8sB7twZvS49Fa5PV2bn\nz+p/X1V/7ONfTTwN2n7gIeBxwzBuAU5fvMM0zd+9+G/DMP4n0B0rzDJ/k9NBnt3fzIuH2wiFI+Tn\nuNlYXciqkhw87nefubn8l/DeQy3UtY1wvmWIw7W95Ga5+bl716XUG6UEUGbFatIusxNTQZ5/u5WZ\nYHRZebvdxq9+ZHOSq1qcYCjMt56vJQLctLFkXr9HbTYbOZku+kYmiEQiCT1RtkzSLrOpqm94gn0n\nOigvyub+mypjPn7dqjwaOkdo6QnQMzhOaWHWMlRpCcqsWEY8DdqTwH2GYRwgOmjzOcMwHgXqTdN8\nJqHVCfXtI/zrs2fpH5mkKNfDp9+/ltGJ6av+cb/8YnWP28nWNUWsXpHLK0fbeeVYO809ft63tTwl\nzqgliDIrVpN2mT12oY+ZYJgda4to7xvj7XM97DZ83GCUJLu0BfvhvgZaeka5bWs55UXxXXs2lzfL\nzXAgQGBi5tKiIRaWdplNVc8eaCYUjvDIBzfgdMReOsBms7F7QwnPH2zlqNnHA7fEbuquE8qsWEbM\nBs00zTDwa5d9uvYKj/ufS1STEF3849kDzTyzvwkisKWmkG1riwhMzizozGt2posP3lzJS4fbaejw\nU1GcDWnaoCmzYjXpltmpmRCNnX7yctxsWVNEVVkuP32rmR+8Ws/2tcVxvclMNftOdPDi4TbKCrN4\n5L51HDzXM+9j5GRGFwrpH5m0fIOWbpm9aHI6yPRM6mwmPjQ6xVtnuiktzOL2HRUMDgTi+jpffiZV\npTm09ARo643va9JdumY23V2v20lpo+oUtPdQC2+c7KJrYJxsj5PbtpUvyRQFt8vB7dvL+cmBZg6e\n6+Gjt62mwJuxBBWLiLyjrSdAJAKrV+Rit9nIy3Fz+/YVvHasg7fP9fC+reXJLnFe9p/u4t/3muRk\nuviNT27D417Yn86LDVrf8IQ2FE5BHX1jvHGqk+mZMC3do/zaR7fgcib3ZMIrR9sJhSPUlHt56e2W\nuK95BNixrpjWngAn6vr57H2RdL+0QVJUMBTmpSNtBENhbNhwuex8YPeqdJjmnVBq0FJMbfMgPznQ\nwvhkkApfNrdtLSfDvXQrBOVmu7nBKOHtcz18Z28tv/HJ7Ut2bLm+hMMRZoJhRgJTDPonmQ6GGR2f\npmdwgp6hcXqHJugdnqB/eAK3y4Evz4OvIJMda31sX1tkyVEUiU9zd/Si6uqydy6A/tDNVbx+opPn\nDrawZ0sZdgv8cY5EIrx4uI0fvFpPtsfJb316B6UFCz9ZlpP1ToMmqWV6JsQbJzsJhiMU5mZwvK6f\nJ/bV88i965NW09RMiJ+d6MCb5WLNivk39Hk5GayuyKWhw8/b53rYs6Xsqo+9XkcpZGnMzc9MMIw3\ny8XZxkGaewJ09Y8Rvmzbpx/tayA/J4P8nAy8WS6yMpw4HDaCoQgTU0HGJmYYmwoyMxNmOhgi2+Oi\nKM9DZWnOcr+0pFGDliLC4QgvHG7lxz9rJByOsGNdMVtXJ2bFxfWr8mju8nOyYYAn9tXjy48uw6tf\nyHK5qekQ7X0BWntGaesNYLYNE5iYYXwySCgce589u92GN9PF1EyIC+0jXGgfYf/pbjIzHKxdmc8v\n3m9QmPveJdnFumaCYXoGx8nPcb9rGl9RnodbNpWy/0w3p+oH2LGuOIlVxhYOR/j+K3W8fLSdvBw3\nv/WpHawsWdybA++cKY6SWmpbhpgOhtm5rpgNVQXsO97By0fa2bO5LGmjnYfO9TA2GeTBW6twLPCE\n1va1xTR1+nnyjUZ2byhZshFBNXRyuQH/JLUtQzR3jV56f5DlcbJ6RS4zoTBOh41IJHoyxOV0MByY\norHT/57mDaIXCGZ5nLicdsanggwHpunoH+NUwwDnW4Z4cE8129YUpfUonBq0FNDaM8q395o0dfkp\n8GZw44YSyooSt+qSzWZj+7piXjzUxsn6Ae7dvTJhzyXWMRMM0doToLl7lOYuP83do3QOjHH5706P\n20F+jhun047Tbicjw0kkHMbpsON22fFmucnNcpObfXH7h+gv0FA4wnBgiob2ERo6/ZxuGOB3vnqA\nnet83LljBetX5ZPhSux+MpJ4zd1+QuHIFadl339TJfvPdPPc2y0p26DtO9FBMBTmjZNdtPUGyM9x\n8//+590U5S3+REL2xQZNI2gpJRyOUNs6jNtlZ0NVAS6nnc/et56/+f4JnnyjkUc/tWPZa4pEIrxy\nrB27zcZdOyo41TiwoOPkZLowKgs43zLEy0fbeODmqiWuVK5nkUiEs02DvHi4je6B6JYD3iwXq1fk\nsqokh8ryPAJjU1f9+nAkwvRMiJlgOLp9lA1cTgdul/1dsyympkN0D45T3zFCQ4efv//hKVavyOXh\n22vYXJ3Y7aOSRQ1aEnX0j/HcW828fa6XcCTCzZtK+fVP7eSlg00Jf+6ywixKCzPp7B+jb3ji0iia\nXB/C4Qhdg+M0dfpp6vJzsqGfodGpdzVjTocNX34mhbkZFHo9FOZm4M1yv+cMrDcnvr2gHHYbRbke\nijZ52LneR3O3n46+MY5d6OPYhT4cdhtVZV5qynLxFWTiy/ewekUeednWXkzhemO2DgPR3zGXW1mS\nw/Y1RZxsGMBsHcKoLFju8mKamg7x6rF2+oYnKSvK4q4dK5akOQNwOe3kZrno0whaSqnvGGFyOsS6\nlXmXfr9trC5kQ2U+ZxoHaez0s3oBUwwX44l9DbT2BKgszVlwc3bRtrVFtPUGeHZ/MzdtKF2yPMv1\na2RsmrfPdrPvRCfdg9HGrKwwi001BVQUZ19qmGI1TnabDY/biSfGn/kMt4OqMi9VZV7Wrsjj6f1N\nHDX7+N8/OElNuZcP3lzFrvXFOOzpc+mEGrRlFgqHOVE3wJNvNNDZHw11hS+bT9+9li2ri8hfxkU7\ntq8p5sXBNk7VD3CPRtHSWjgcoaVnlDNNg5xvHqSpe5Sp6dCl++2zzVNxnoei2Vtutjth1wm5nHbW\nrcxnbUUe/SOTtHSP0js0QVOXn8ZO/zt12WxsWV1IXo6bqlLvey5y17Sa1HOhLdqglRRc+aTPh2+t\n5mTDAE+/2cTv/Fx+Sp35HAlM8cKhVoYD09SUe7l1azkOu+0907kWozg/k5buUcJhLdqQKo7X9QGw\n6rLrWx68tZra1hO8cKiVLzy8ZVlrMluHADAq8xd9rAyXg0/evYZvPlfLN58/z6Of2qHsybzsO9HB\nxFSQtp4AzT2j9A5OEI5EcDps7NlcSmGuZ9ka//rOETbXFFJWlMXphgGau0b56lNnKM7z8OCt1dy2\nrdwS1zjHogZtmew91MKF1mEutI0wPhXduN6Xn8nmmgJWleTQ759k34kOvDnLd2arrCiLkoJMOvrH\n8I9NL9vzyvJ57Xg7jZ1+jtf1Mz4ZzZ2N6M++pjyXmvJcVq/IpbHLjyMJf7Bttugo3cUR3JlgGP/Y\nNKMTM4yOTdPaE+BUQ/TscV3hCHfvqkj6qmpydZFIhMZOP96s6PTWueY2ORW+bGpbhzndOMC2Nakx\n1XFodIq//t5xhgPTGJX53LSxJCHNoy8/k8ZOP0OjUxrJSBEn6vpxOmyUzxn13Xeig0gkQoE3gyO1\nvfQPT1C8TDNNhgNTtHSPkpftvuJI9ELctrWco2YfpxoG+P6rdfzcPeuumu/J6SDnmwcZDkwTnv0e\ntPcHcDs1Bf16MxKY4tiFPl460k7P4DgXJ9msXpHLzZtKuWVTKd4s95KexIpXUa6Hu3ZW4B+b5nzL\nEPXtI3zr+VrePNXFFx7ecmmVcqteL6kGLcFGAlM8/3brpaVyXQ47RmU+61flp8QS90ZlPr1DE5fO\nekv6aOz089zBVgZGJnHYbaypyKWiOJuyomw8c1YGkQ4dQAAAIABJREFUbekZTUpzdiUup/3SCB7A\n1jVFDAemOGb20d43xqtH23n/DSvVpKWo3uEJxqeCVJd7r/m4Xet9dPaP8R8v1WFUFiTt2sOLf7jH\nJ4O8cKiV0fEZNtcUsGu9L2Eje8Wz2e4fmVCDlgIG/ZP0DE2w0pf9noU4bDYbm6oL2H+6m5ePtvOZ\ne9YtS02vHesgHIGNVQVLlkObzcYvP7SJv/zuMV4+0s7Q6BQffV8NZUVZjI7P0NozStfAOF39Y/jH\nZ97z9Q67jdUrcrnB8OHWtcJpa2IqSEPnCGbrMOeaB2nqGr10X3Geh+oyL5VlXh7cU528Ii+Tm+3m\n5k2lbF1dxOHaXuo7RvjjbxziAzeturS1iRWpQUuQiakgz7/dyouHW5meCZPlcbK5ppC1FXkp9eay\nsjQHj9tBfccI0zMh/eJNE2ebB/n7J04RDIWpLvOyy/BZ9hdVfk4Gd+2s4I1TXbR0j/LykTbu3b0q\npf4/kqjm2T/mxTEajwJvBvffWMneQ6088Vo9n/2AsRzlXdHEVJAXD7fNNmeF7FpfnNBplxdHi/uG\nJzEqE/Y0EqeLJyevttdodXkuxy708/rJTj7yvhqyPIl92zQ1HeK14x24XXZWVyztdW/ZHhe//Zkd\n/PNTZzhq9nHU7HvPY5wOGyuKs9m1vpjCXA92m42+4QleP9lJXfsIXQPjln/jK1FzT1A1do7gH5t5\n16qKDruNDZX57Fzniy51P+dnnowRs1iyPE7u2F7OyWw3pxoGeP1EJ/ffXJkyJ6DnSw3aEpsJhtl3\nooNn9zcTmJghL8fNZ95fQygSScmQOOx21lbkcaZpkMO1vZbbQFbey2wd4h9+eAqI8P5dFYteGjwV\n2O02bt9Wjs0WbQIO1/Zy6zX29JHkaOqKXj9YFMfWCR+9vYbTTQO8eqyDylIvd2xfkejy3mNiKsiL\nh9rwj02zqbog4c0ZgG+2ee3VSo4p4Z0G7crTFx12Gxur8jl2oZ/Xjrfz4QSPHPzsZCeBiRm2rUnM\nXpH5ORn8ziM7OX6hn2MX+hgOTJGd6SIUClNamIUvPxO73faeaWAF3gxO1PdzpnGQl4+08+E9VTpJ\nZnFTMyFO1PVT1zZCOBLBBhTneygtyKKkMJPSgqxLP2OXyxo/a5vNxva1RQQmos3m6YbU39LlatSg\nLZGpmRCvn+zkhUOtDPqncDns7FhXzMaqArCBI4UvWFy3Ktqg7TveoQbNwvad6KBvaIKXjrQRDke4\na2d6NGcX2e02bttazkhgmvr2EWpiTKOT5dfcPYrNRlx722W4HPz6x7by5985wrf31uJ22bll0/I1\n3QMjE7x4qI2R2ebsBiNx0xrn8hVcHEFTg5YKzLZhMlwOCr1Xz+z6ynxqW4Z54VAb996wigx3Ymaa\nTM2E2Pt2CxkuBxuqlnaF0ytdh7N7Q8lV77+c3W5j13ofoVCE8y1DnKjr58aNJdf8GkldZ5oGePqN\nJianQ+RkuthUU0B1We67Ln+wKpvNxs2bSukaGONc8yDrV+UnfOQ7EazREqewtt4Aj710gd/+p/18\n7+U6AuMzfODGVXzszhq2rSmyxBkmb5abiuJsGjr9tPcFkl2OLNDEVJDXjncQCke4Y8eKtGrOLrLb\nbezZUoYNOHi2h6mZUMyvkeURjkRo7RmlrDAr7t97pYVZPPrpHXjcDv7tmXO8dLgtwVVG9Q5P8Af/\ntH/ZmzOAQq8Hp8NG75AatGQLTMzQNTDOmorca65q6HY6uHf3SgITM7x0JHEZvbiC6L27V6bsG+Vd\n64vJzXJxvmWI4cDV97eS1BSJRPjpW8383Q9OMj0TYue6Yh6+vYYNlQUpm7mFcDntbF9bTDAU4fQi\nt6lIltTvHlJQdOGPFv7o64f4428c4pWj7TgcdrauKeLhO6IX3Xrc1urW167MA+DNU11JrkQWIhyJ\n8OapLianQ9yw3kdlafqOLhXnedhYXcDo+AzPvJn4PQMlPn3DE0xOh6iaZ/ZqynP5vUd2kZvt5nuv\n1PHvL5qEwuEEVRmdhvkX/36UroExtq0pWtbmDKInGYrzMukdGl+255Qruzgld/WKvJiP/cCNleRk\nunjuYEtCVj3uG57g+YOt5Ga5+NAtyd9Met+JjnfdLnI47OwyfACcaRxMVnmyAMFQmG89X8uPftZI\nvjeDD95SydY1RWm75cLaijyyPU4aZtdYsBprdRFJFIlEePy1es63DNHWGyASic5N37mumFu3lLN9\nbRFvnrZuc7OyJIecTBcHznTzibvWJGTuuyTOc2+10DUwzkpfNhurU2/z36W2fW0xrT0BXjjUxs2b\nStO6IbWK1p7o6Hu8P4vLp1Tds3slrx5t57VjHZxvGeLO7SvIcDuWdEnkg2e7+dbztcwEw/zKw1uZ\nnEzO9iIlBZl0D44zNjlDtkeLLSTLxT0XV6/IjTkalOVx8tHbanjspQt875U6fvUjm5esjlA4zNd/\nep6pmRD/+f7179miItWsKskhP8dNU5efHeuKtWCIBUxMBfnq02c40zhIVamX3/jkNk7U9ye7rISy\n220YldHrR+s7RthUXZjskuYl5m8BwzDswFeA7cAU8HnTNOvn3P+bwGdmP3zONM0/SUShyXSueZCn\n3miivmMEiF4su25lHjXluWS4HYxOTFu6OYNos3nrljJePNzGibr+d81Nt5rrLbMX2oZ58o1GsjxO\nbt1anlIb/yaKy2nnls2lvHykne++dIE/+Pldln7d6ZDZ1p7oCo6VpTkLWgAjJ9PFA7dU8capLtp7\nAzx3sIW7di5NczY1E+IHr9az73gHmRkOfu3hbdy3p4YnXqpdkuPPV8nsSo69QxPUlFvzzW06ZLah\nM/o3ffWKXI5deO+Khpe7e2cFB8928/a5HravKeKWze9cM7nQvZYikQiPvXiBC23D3GD42LM59Rc/\nstlsbKwu4K0zPTR2jLBtrTUWYUiHzC5Ez9A4//jj03T0jVHhy+bWrWVp35xdtHZlPifrB7jQOryk\n21Ysh3iGSR4GPKZp7gF+H/jSxTsMw1gN/DxwK3AL8AHDMLYlotBkaO8N8KUfnOBvv3+C+o4RVpbk\n8MGbV/HQ+6rZUFWQsAuFk+W2bdEFQqzebHIdZXZscoZ/ffYsALdvK0+rOeSxrCjO5ob1PurbR3jr\nbHeyy1ksy2e25VKDtvDRTJfTzl07V7B1dSGj4zM8f7CFN051EolEYn/xVTR2+vnTbx1m3/EOVvpy\n+P9+8UZ2JPkNZUnBOw2ahVk6s5FIhKZOP8V5HnKz3HF9jd1u45ce3ITH7eAbz9Vitg4tqoapmRBf\n/+l59p3opLIkh//6oY2WeQNZXZaL02GjvsO/qP8/l5mlMztfkUiEt85086ffOkxH3xgbKvO5e2eF\nJdZGWCoet4OVJTn4x2cY8Fvrmsl4xtFvA/YCmKZ50DCM3XPuawM+aJpmCMAwDBcwueRVLrPxySBP\nvdnIK0fbiUSgvCiLXet9ab+p6EpfDjXluZxuHGDQPxnXSmwp6rrIbCQS4Tt7TQb9U3z0thrycuJ7\nk5FOPn3PWk41DvD4aw3sXOdL+alB12DpzEYiEVq6RynK9Sx6upPdZmPneh+FuR4OnOnmm8/VctTs\n4+fuXUdpwZX3qrqSFw63crKuH7N1mAiwoSqf//GJ7Smx1+PFPbd6rH0dmqUz2zs8wdhkkM0185v2\nVFaYxRce3sL/+eEpvvSDkzxy37p5bxERCoc5UtvHk6830js8QU15Lrs3+Hj7fM+8jpNMLqedqlIv\nDZ1+K51oSPnMXj4S+8n7NizoOC3dozyxr55zzUNkuB380oc3MhNK3LW9qWz1ilxaukcvnZCxinje\nzeQCI3M+DhmG4TRNM2ia5gzQbxiGDfgb4LhpmheudbCCgiyczsT+gfT5Fn4G9ys/Osnrx9oZmwyS\nl+Pmtu0VVJcv7WaRsXhzkhMgn8/Lg7ev5h8eP8Hhun4++8GNCz5Okl0XmX35UAuHa3vZWF3I5z6y\nhZcOtSagsvgkK7Mb15bwqXvX89jeWl461sEvfWTLgo+V5NxaOrMDIxOMjs+wZ2sxPp93SfKwZa2H\nyvI8Ttb1caq+n7NNg9yxs4L7b6lmQ3XhVfeVHB6dYu/BZp56vYmpmVB0o/NdK6koyeF0y/A7D6wf\nSEpufT4vmx3Rn81gYHpRuUunzMLy5vZsazQL29aXxJXZud/r9/u85Odn8VffOcx39prsO9FJhS+H\nCl8OBbkZuJ2O9/xsRgJTmK1DHK/t5cDpTgb9U9jtNh6+cw2ffWAjr8W5OuRSZfby+hZy3E2ri2no\n9NM5MB53FpXZa7vSzyHe79nzB5ro6Atw4kIfLd3RGQ27NpTwhY9vo6wom71vNS9ZnfORrPcHFxlZ\nbg6c7qalZ5S7dq+adwaTldl4GjQ/MLc6u2mawYsfGIbhAb4BjAL/LdbBhhJ8xtDn89LXNzrvrwtM\nzPDdF00One/FPrvR3ZbVhTjsdkYDy3cSxZvjWdbnm+uJl2oJhsK4nHaeeb2Be3asmPdiIQv9/s/n\n+HFI+8x2DYzxzz8+TWaGg8990GBwcCxpuUl2ZgmFycl08fTrDUxPB/nEnWvmfZwUyK2lM3uiLno9\nQ1m+h76+0SXLgw3YvqaQ/GwXJ+sHeO1oO68dbScn08XaijzKi7MuTU8bCUzT2OWnvj266arbZWfX\n+mI2Vhdc8fd4snLb1zcKkQhup53mjpEF5y7dMgvLm9uTZi8AJbkZcWX28u/1qsJM/vS/3sQPf9bA\n4fO9tHa/c7/baeeJVy7gctoJhSKMjk8zNhl8536XHaMyn03VBXgznTyzry6u+pcys0tx/WVelhO3\ny059+zA9vX7sMaZnKrOxXennG+t7Nj0T4sDZbp55s4nhQHThI19+JtvXFlFelMUbx5Zn+5IrSeb7\ng7lWleZQ3z5CU/sQfX3xT3FPZmbjadD2Aw8BjxuGcQtw+uIds2cangZeNU3zrxZZZ9Kcax7k6z89\nz9DoFL58D3u2lJGfk5HsspLC6bCztiKP8y1DHK/r50ZrLhaS1pmdmg7xN987ztRMiNu3l3Om+fpe\n6tjhsLNnSykvHW5n/6kuPnJrdUpMY5snS2f24vVnVWVLf6bRZrNRXZ5LVZmX7sFxmrpGGfRPcqK+\nnxP17318cZ6HmhW5rKnIxZ3g0ZiFsttslBVm0T04TjgSifnGNkVZOrONXX4cdhtVpfHtF3mlRUAK\ncz38ykOb+cz71/HEvnr6Rybxj00zMRVkaibE2MQMdruN3Gw3+d4MinI9lBVmUVKQmRZLm9vtNipL\nvNR3jFDfPsL6VfnJLikWS2f2cpPTQV491sGLh1rxj89gs0F1mZeN1QX4ZhcikqjK2Qatpds6e/3G\n06A9CdxnGMYBoic0P2cYxqNAPeAA7gQyDMN4YPbxf2Ca5lsJqXaJhSMRfnKgmaffaMJut/GxO1aT\n7XGmxS/OxVi/Kp/zLUO8dqzdqg1a2mY2Eonw7b21DAemMSrzqVnm6bepqrwomw1V+dS2DPPDnzXw\nyL3rk13SfFk6sxen0yRyuwObzUZ5UTblRdnctaOCkbFpegbHCUzMcKZpAI/bSX6O2zLNeXlxNq29\nAQZGJq36ZsqymZ0JhmntGWVlSQ6uBTbxlzdsayryWFMRez+1dFNZlkN9xwjH6/qs0KBZNrNzTc2E\neO1YB88dbCEwMUNmhoMP3VJFlsdBlrbtuKLyoixcTjutPaNEIhFLLMYTs0EzTTMM/Npln547Nm6d\nK+7mGJ8M8q/PnuVUwwBZHid37liBN0vBBsjLcVNWmEVt6zDtvQFWlsR3hjFVpGtmAV491sHBcz34\n8j2W3gohEXat99HVP87LR9rZsbbYUnueWDmzkUiExi4/Bd6MZZ15kJftJi87Or3RP56c/cwWo3x2\noZCugTFLNmhWzmxr7yjBUITVK3SCa7HKC7NwOmwcr+vnU3evTek3vlbOLEQXPqprG+Zc8xCT0yFc\nTjvb1xaxsarAMiemksVht7PSl01T1yitPYGEzPZYatfPWptz9A6N87/+/QinGgYoL8riwVurLfkH\nMpE2zW52/OyB5uQWIpecbx7k+6/UkZvl4o4dK666SML1yumw875tZdhtNv7tJ+cY9Cd/3vv1YMAf\nnda1nG92953oeNfNilYUZwPQ0TeW5EquP3Vt0XUi1l2HI15LzeGws6I4m96hCToHLL0qaUqamglx\npLaXrzx1hidea+DYhX5CoQhbVxfy8TtWs31tsZqzOF2c4XE0jj0PU4Fl16ReqMdfq+e1Yx1MzYTY\nWFXADYbvup/SeCUVvmyqyrwcqe2lo3+Mitk3E5IcrT2j/OOTp7HZ4AsPb6FrUH8Ir6Q4L5NP3b2G\n779az5efOMkffPYGKy+9bwmNnX4AjUbMU+XsGdyL1+/J8qnviDZoa1eqQVsKlaU5tPYEOH6hT+8V\nlshMMMyZxgF+9LNGxiZmgOisgbUr81i3Mk9N2QKsKM7Gbrdx/EIfH79jdbLLiem6GkE7XNvLi4fb\nmA6GuGVzKTduLFFzdhU2m42Pvq+GCPDs/qZkl3NdGxiZ5MtPnGRiKsTnH9yEUVmQ7JJS2n03ruLu\nXRW0943x1afOELxO935ZLpcaNF0POS++PA+ZGU5aeqxz0Xo6iEQi1LcPUzC7aIcsXoUvB7vNxvE6\na4xMpLpB/yTP7m/mdOMgLoedB26p5I//y4185LZqNtcUqjlbIJfTzoqiLDr6x+ixwEnu66JBi0Qi\nPH+wha8+dQaHzcb7d620wsWsSbd9bRFVpV4On++lvVdvIpLhp28182ffOcJwYJrdG3yMTwUtO6Vr\nufzsZCcVxdlU+LI50zTIFx87RiisJi1R6tpHcNhtVJepQZsPmy26gmDP4DgTU8HYXyBLomdoAv/4\nDOtW5qX09VJWkuFyYFTmX1phVRZu0D/Ji4fbCEzMsKWmkK/94X188q61VJV5ldclcHGa45HZbTZS\nWdo3aMFQmG/vreWJfQ0UeDO4/+ZVVPg0BB8Pm83Gx+9cTQT45vPn9SZ3mXX0BXj+7Vb8Y9Nsrim0\n1KIXyWa327hj+wqK8zw0dvr5ypNnmAmGkl1W2pmYCtLSPUpNeS4Zbp3Vna+LF6q36QTYsjk/uy2J\nZiIsrV3rfQAcn90TUeYvMDHDa8c6mJ4Jc+uWMnYZPjI0WrakVpXm4LDbOHxeDVpSjYxN84dfe5vX\nT3ZRmJvBPTespFBTGuK270QHA/5JVq/IpalrlBcOJW+zw+uN2TrEX373GOOTQXYZPnatj39jRYly\nOe3cd+MqyoqyOF7Xz989flIjFUvsQtsw4UiEDVWakbAQF0cdGzpHklzJ9eNMU7RB21KjE15Ladd6\nHzbg8PmeZJdiSZFIhG8+d56xySDb1xZduj5y71vNll4MKdVkuBxsqSmktTdAd4pPc0zbBq2ufZg/\n/dZheocmqCrzcv9NlWR5tFjAQty4oQSP28FTbzTSqgvaE2omGOZHP2vgr2c3on7f1jK21BRqasMC\nuZx27rmhghvW+6htHeZPvnX40p5dsni1rUMAbNBoxIIYldHGtrZlOMmVXB+CoTDnW4YoKcjUys1L\nrMCbwbpV+VxoH9E0xwU4XNvL8bp+Sgsy2bqmKNnlpLUbN0a3KDp4tjvJlVxb2jVooVCYZ/Y38cXH\njjEcmGLnumLu2F6Oy5l2L3XZZLgd7NlSRjAU4X8/ftISF1daUVOXnz/79hF++lYLRbkefvszO67L\njU+XmsNuZ2N1AZtrCukdmuDPvn2Yrz51hnAkkuzSLC0SiXCifgC3085a5XRB8nMyKCvM4kL7sBaz\nWQbnmweZnA6xWdPFE+Lm2Te+hywwfSyVjE/O8B8v1+Fy2tmzJbpVjCTODetLyHA72H+6i3A4dd8H\npFXX0tjp59Evv85TbzSRmeHkAzeuYuuaIo0+LIFVJTn8/H3r8Y9N87ffP07v8ESyS0ob/cMT/Nuz\n5/izbx+hvS/AupV53HfjKi2lv4Tsdhs3GD7uuWElbpeDw7W9fPGxYxoRXoTOgXF6BsfZurpIq4ot\nwoaqAqamQzRrZDfh3jgenSa2y/AluZL0dOPGUpwOOz872UlEJ8Di9uPXG/GPTfOR91WTm+1Odjlp\nL8Pt4OaNJQz4pzjXMpjscq4qLRq07sFx/vXZs/yv7xyhsXOENRW5PHRrNaWFWckuLa04HDZ2ritm\nwD/Fn3zzEIc013xR/OPTPP5aPb/6xVd462w3Bd4MPnDjKvZsKdOIb4JU+LJ58NZqqkpzqG8f4U++\ndZjHXrrASGAq2aVZzrHZVbD0ZndxLl4Ldcwim6daVTAU5s2TneRmu9moKbkJkZPp4sYNPnoGx6lt\n1bTdeDR2+nntWAflRVncf1Nlssu5bty+bQUALx9pT3IlV2fZi7IikQgX2oZ55Wg7Ry/0EYlER3m+\n8Int1DZqFaFE2bqmiCyPkyO1ffzz02c5dL6Xj9+xmhXanDJuQ6NTfOO585itQwRDEbI9TnYbZayu\nyNXUhmWQ5XFy584KOvvHePtcD68cbeeNk51srinkVx7arNUI4xAKR3jjVBdup53tul5iUbauLiQz\nw8nb53r4xF1r9DsgQU7WDzA6Ps09N6zU/qcJdNfOCt4628MLh1rZWKVG+FqCoTDfer6WCPAL9xs4\nHToxu1zWVEQ3/D7VMEBrz+il5fdTieUatN6hcQ6e6+Gtsz2XroWqLMnhofdVs3O9j9KSXDVoCbam\nIo8P76nm6z89x7ELfRyv62O3UcI9N6ykuDgn2eWlpEgkQn3HCK8e6+BIbS+hcITMDAc71xexa0Mp\nExPTyS7xurOiOJuP3FbNhdYRTjcOcLyun9/7l7f44E2V3L2zQo3aNRw+103/yCR37lhBlseV7HIs\nzeV0cIPh481TXZxvHmKzVhdccpFIhOcONgPRBkISZ21FHsaqfE41DFDfMaLrU6/hqTeaaO8LcMf2\ncm37kAQP3lrN3z1+kh+/3shvfGJbyl0OlfINWigcprHTz5nGQY7X9dPeF90vxmG3UV3uZUNlPr78\nTEYnZnj9ZCfenNSdT5pOaluHuHVLGZWlXk7U9XO4tpfDtb2sermOGw0fuzeUUFqQmXKBX06RSCQ6\nSnO+l7fPddM3HF3ZqqI4m1UlOayuyMXpsOusWRJdXEBkh1HC22e6uNA2zOOv1fPcwRbuvWElt29f\nQYE3I9llppRQOMxje2sBuGfXyiRXkx7u3lnBm6e6eHp/E5uqC67r35uJcLJ+gKauUfZsLadCsz0S\nymaz8bE7VvPFx47x3RdN/vAXdutv3BWcqOvn+YMtlORn8un3r0t2OdelLTWFbKiMnkw4XNvLTRtL\nk13Su6Rcg+Yfn6a5a5TmLj917cPUd/qZmo5uMGu32ajwZVNV6qWyLAe3U2e4k8lms7GqJIeVvmx6\nBicwW4do6wvQ1jPKj19vpDjPw8aqAqrLc6kszaG8MCvtz7ZPTAWp7xjhbNMgJ+r6Ly2m4nTYqCn3\nsnZlHmWFWXoDlmLcLgc71hWzsaqA8y1DnG8Z4qk3m3h6fxM71hZz08ZSNtcUkpOZ3vmNx7P7m2nu\n8nP7tnJWlmjEfCnUlOeyY20xJ+r72X+6m9u2lSe7pLQxEpjiW3trcdhtPHL/hmSXc11Yvyqf27aW\n8+bpLr73Sh2fvW+9/ubNcbZpkK8+fQaXy86vPbyZzIyUeyt+XbDZbPziAxv4o68f4tt7ayktyKKq\nLHWmOsZMhWEYduArwHZgCvi8aZr1c+7/ZeBXgSDw56Zp/iTWMUPhMCOBafqGJ+gZmqBrYIzO/nHa\nekcZDrx7qldetpuqUi8rirMoK8pSU5aCbDYbZUWzPx+3i3ON0ZHOroFx3jjVxRunui491pvlojgv\nE1++B19+dC+aojwPxbke8nMylmRaWSIyO1cwFGZ0fIbhwBRDo1N0D47TNTBGW2+Att4AFxevynA7\n2D27h9yqkhwt/GEBGe5oo7a5ppCmLj8X2oY5XtfP8bp+bEB1uZeqUi/lxdmUF2WRl51BbpaL7EwX\nDrttwW9CEp3ZpTATDPOTA808e6CZ4vxMPnHXmuUuIa19+p61mG3DfOcFE7sd9mwuS+k3tVbIbFOX\nn3955iz+sWk+dfdaqstz6evTapnL4efuXUdTV3QBjPHJIJ+5Zx2+JK8nlOzMBiZmeP7tFva+3Yrd\nZuP/+k/bLm1WL8lRWpDFL314I//y9Fn++nvH+cw9a9mzuSwlRn3jadsfBjymae4xDOMW4EvARwEM\nwygD/m9gN+AB3jQM4yXTNK+6JNpv/uOb+MemudIKrFkeJxW+bIpyPRTneSjO9+Bx68yClWS4Haxd\nmcfalXmEwxFGxqYYGIk2Mv7xafxj07R0+2nq8l/x6z1uB9keJ5kZTlxOB06H7dIbX7vdxhd//fZ4\nyljSzP7VY8eYmA4yPhlkbHKGianQFR/ndNjw5WdSWpBJaWEWpYWZOOzJ/59c5s/ltLN+VT7rVuYx\nNDpFR98Ynf1jNHeP0tR15Td4dpsNt8uO22nH5bTjdDpwO+1kuBz83aN3xXrKJc3sUpmYCvLS4Tba\n+wKcbxlibDJIgTeDP/vVPWSkbu9gSaUFWfy3j23hn358mq/95DzP7G9m/ap81lbkccf2Fcku70pS\nMrPtfQFePdpOU/fopU3pH7y1ivtvWpXop5Y5MjOc/M7P7eTvf3iSt8/1cKS2l001RZTkefBmu1hd\nnsuW1cu+wNCyZXYmGGb/mS6GR6fwj8/Q2RegodNPKByhwJvBFx7eouvzUsRNG0sJhyN8+wWTbz5X\ny4/2NbBuZT6+gkxKirLZtCqPkoLlXxU+nu7nNmAvgGmaBw3D2D3nvpuA/bMBnjIMox7YBhy+2sG+\n+ycP6M+6JNqSZvZv/8edyqwk2pJm1ufzLllmf2nl/C9e/+R9mkq2EHf5vNx1Y1Xcj/f5kjodZ0kz\nC0uTW5/Py85NV58ierXvmTK79Hw++D+//f519F6QAAAgAElEQVRklzHXsmb2k+Xzb8CUw+R46C4v\nD92VWtcCxnN6PxcYmfNxyDAM51XuGwV0SkCSTZkVq1FmxWqUWbEaZVYsI54GzQ/MPeVkN00zeJX7\nvIB2J5RkU2bFapRZsRplVqxGmRXLiKdB2w98CGB2zu7pOfcdAm43DMNjGEYesBE4s+RVisyPMitW\no8yK1SizYjXKrFiGLXKl1TrmmLPqzTbABnyOaMDrTdN8ZnbVm18h2uz9hWmaP0psySLXpsyK1Siz\nYjXKrFiNMitWErNBExERERERkeWhNcBFRERERERShBo0ERERERGRFJF2u0DPXtz5XaJLprqBR03T\nfCu5VcUWa4f7VGcYhgv4BlANZAB/bprmM0ktyiKU2eRQZhdOmU0OZXbhlNnkUGYXR7lNjlTIbTqO\noD0KvGKa5p3AfwH+KbnlxO3SDvfA7xPd4d5KPgsMmKZ5O/BB4B+TXI+VKLPJocwunDKbHMrswimz\nyaHMLo5ymxxJz23ajaABf0e0W4fo65tMYi3zca0d7q3gCeCHs/+2AcFrPFbeTZlNDmV24ZTZ5FBm\nF06ZTQ5ldnGU2+RIem4t3aAZhvFLwG9e9unPmaZ52DCMMqLDwv9j+StbkCvucD9nE8WUZppmAMAw\nDC/RUP9hcitKTcps6lBm46PMpg5lNj7KbOpQZuOn3KaOVMitpRs00zS/Dnz98s8bhrEV+D7w26Zp\n/mzZC1uYa+1wbwmGYawCngS+YprmfyS7nlSkzKYWZTY2ZTa1KLOxKbOpRZmNj3KbWpKd27S7Bs0w\njE1EhyYfMU3z+WTXMw/X2uE+5RmGUQq8CPyeaZrfSHY9VqLMJocyu3DKbHIoswunzCaHMrs4ym1y\npEJu026jasMwnia6akzz7KdGTNP8aPIqis+Vdrg3TbM2uVXFzzCMvwc+Dcyt+QHTNCeSVJJlKLPJ\nocwunDKbHMrswimzyaHMLo5ymxypkNu0a9BERERERESsKu2mOIqIiIiIiFiVGjQREREREZEUoQZN\nREREREQkRahBExERERERSRGW3gdNREQEwDCMCHAGCAERIIvoXjxfME3zyOxjsoD/B/jY7GOygTeB\n3zVNs8swjBXAc5cd2geUmqapv5ciIrIs9AdHRETSxd2mafZf/MAwjN8G/gHYYxiGA9gLnAVuMk1z\nbHYp6N8BnjcMY6dpmp3AjjlfXwa8Bfzmcr4IERG5vqlBExGRtGMYhhOoBAZnP/UwkAf8d9M0wwCz\n//0rwzBsQA4wOufrM4CngBdN0/yH5axdRESub2rQREQkXbxmGEaY6LTESeAnwOdm77sdePliczaX\naZpfvMKx/g2YAH49QbWKiIhckRo0ERFJF3ebptlvGMZO4HnggGmavbP32YhedwaAYRh3A383+2Eh\n8N9M0/zJ7H2/A9wK3Gya5syyVS8iIoJWcRQRkTRjmuZxoteNfc0wjOrZTx8A7pzzmNdM09xhmuYO\noBHwABiG8QDwB8BHTNMcWNbCRUREUIMmIiJpyDTN7xFd4OPLs5/6ETBmGMaXDcPIufg4wzBuBlYD\nIcMwNgDfBT5rmua55a5ZREQEwBaJRGI/SkREJIXNLrPvu2wVRwM4RXQ07AXDMDxEV238GNEpj5lA\nG/A14PHZ/34aqL/CUzxkmmZbYl+FiIiIGjQREREREZGUoSmOIiIiIiIiKSKuBs0wjJsNw9h3hc8/\nZBjGYcMw3jIM45eXvDqRBVJmxYqUW7EaZVasRpkVK4jZoBmG8btE5+V7Lvu8i+gSxR8gujLWrxiG\nUZqIIkXmQ5kVK1JuxWqUWbEaZVasIp4RtAbg41f4/Eag3jTNIdM0p4E3gTuWsjiRBVJmxYqUW7Ea\nZVasRpkVS4jZoJmm+SPgSht15gIjcz4eBfJiHS8YDEWIbhaqm24LucWkzOqWgreYljK3yqxuS3CL\nSb9rdUuxW0zKrG4pdrsq57XujMEPeOd87AWGY33R0ND4Ip4yNp/PS1/faEKfI5FUf+zjL4IymwBW\nrx/SL7fKbGxWfw3plllQbmNR/bGPvwjKbAKo/tjHv5rFNGjngXWGYRQCAaJDwX+7iOOJJJoyK1ak\n3IrVKLNiNcqspJR5N2iGYTwC5Jim+a+GYTwKvEB0quQ3TNPsWOoCRRZLmRUrUm7FapRZsRplVlLV\nsm9U3dc3mtAn1HBqci3DcLAtYQe/CmX22qxeP6RfbpXZ2Kz+GtIts6DcxqL6Yx5fmU0xqj/m8a+a\nWW1ULSIiIiIikiLUoImIiIiIiKQINWgiIiIiIiIpYjGrOIqIiEgM+068s9bAXTsqkliJiIhYgUbQ\nREREREREUoQaNBERERERkRShBk1ERERERCRFqEETERERERFJEWrQREREREREUoQaNBERERERkRSh\nBk1ERERERCRFqEETERERERFJEWrQREREREREUoQaNBERERERkRThjPUAwzDswFeA7cAU8HnTNOvn\n3P9bwCNAGPgL0zSfTFCtInFRZsVqlNn0tO9ER7JLSBhlVqxGmRUriWcE7WHAY5rmHuD3gS9dvMMw\njHzgN4A9wAeALyeiSJF5UmbFapRZsRplVqxGmRXLiKdBuw3YC2Ca5kFg95z7xoAWIHv2Fl7qAkUW\nQJkVq1FmxWqUWbEaZVYsI+YURyAXGJnzccgwDKdpmsHZj9uAc4AD+MtYBysoyMLpdMy70Pnw+bwJ\nPX6iqf5FU2aXmdXrh6S/BmU2CRL9Grw5noQ+ZzplFpTbeKj+RVFmk0D1L0w8DZofmFudfU6YHwDK\ngZrZj18wDGO/aZqHrnawoaHxBRUaL5/PS1/faEKfI5FUf+zjx0GZXUZWrx9SIrfK7DJbjtcwGph8\nz+eW6jnTLbOg3Mai+mMfPwZldpmp/tjHv5p4pjjuBz4EYBjGLcDpOfcNARPAlGmak8AwkL/gSkWW\nhjIrVqPMitUos2I1yqxYRjwjaE8C9xmGcQCwAZ8zDONRoN40zWcMw7gXOGgYRhh4E3gpceWKxEWZ\nFatRZsVqlFmxGmVWLMMWiUSW9Qn7+kYT+oQaTk2uZRgOtiXs4FehzF6b1euH9MutMhvbcryGKy2z\nf9eOiiU5drplFpTbWFR/zOMrsylG9cc8/lUzq42qRUREREREUoQaNBERERERkRShBk1ERERERCRF\nqEETERFJgKNmH8cv9CW7DBERsZh4VnEUERGReTBbhzjbNAhAYa6HqjJrb9YqIiLLRyNoIiIiS+zZ\nA82X/n2ueTB5hYiIiOVoBE1ERJbUxeXll2pJeauZnglxoW2YwtwMwuEIQ6NTRCIRbLZlXwVcREQs\nSCNoIiIiS6ix008wFKG0IIvCXA/BUITR8ZlklyUiIhahBk1ERGQJ1bYOAVBamEm+NwOAodGpZJYk\nIiIWogZNRERkCTV0jABQWpBFQY4aNBERmR81aCIiIkskEonQ0hPAl+8hw+0g3+sGYGRsOsmViYiI\nVahBExGR/5+9+w5v8zwP/f/FBgiAAPemSK1HkjVtWcOWbcXxTOKR1Wa1jk/SJm1z0tM0J036S9Mk\nv7RN67ppOtI004ljx7FTO048ZVmWhyxZe1J8SA3uBZLgAgGQIHD+eAGKorhJEEPP57p0iSRe4L0J\n3ATe+5nKAunqCzDgH2ZJgbasvs1iRKeDwYCag6YoiqLMjCrQFEVRFGWBvHCgHoCRSAQAvU6HzWxk\nMBBKZFjKNPYebx5dfVRRFCXRVIGmKIqiKAukq0+ba5aTaR39WYbViD8YIhIt2hRFURRlKtPugyaE\n0APfAzYAQeDTUspzY26/G/hbQAccAf5MSqk+hZSEUTmrpBqVs+mjuy8AQHamZfRnGVYjnb0QGBpJ\nVFgLTuWskmpUziqpZCY9aPcDVinlduDLwMOxG4QQTuAh4H1Syq1AHZAbhzgVZTZUziqpRuVsmvD2\nBcmwGLGaL7V/2iza14PBtBrmqHJWSTUqZ5WUMZMCbQfwEoCU8gCwecxtNwCngIeFEG8C7VJKz4JH\nqSizo3JWSTUqZ9NA3+AQg8EQWWN6z0DrQQPwp9c8NJWzSqpROaukjGmHOAKZQO+Y70eEEEYpZQit\ndeFdwEZgAHhTCLFfSlkz2YNlZWVgNBrmE/O08vKccX38eFPxz5vK2UWW6vFDwn+HtMpZp8M67THJ\nYKHja5IdABTl2EefA4Aclw2AEXQLes50yllIbN5erTm72FTOzp56zRMrUfHPpEDrA8ZGp48mM0AX\ncEhK2QYghHgDLbknTWivd3COoc5MXp4Tj6c/rueIJxX/9I8/AypnF1Gqxw9JkbdplbP9A9o8rGTO\ni3i85qdqtALNbjWOPgcAOrRpLN5e/4KdM91yFhKbt1drzi4mlbOzp17zxEpkzs5kiOM+4D0AQoht\naF3AMUeBtUKIXCGEEdgGVM09VEVZECpnlVSjcjYNXGzTPsjHruAIYIvORwsMpdUQR5WzSqpROauk\njJn0oD0D3C6EeBttZZsHhRBfAM5JKX8rhPgK8HL02CellKfjFKuizJTKWSXVqJxNA/VtfVhMBuy2\nyz9aLWZtCFQ6reKIylkl9aicVVLGtAWalDIMfHbcj6vH3P4E8MQCx6Uoc6ZyVkk1KmdT34B/GE9P\ngOLcDHQ63WW3WUxagRZMowJN5aySalTOKqlEbVStKIqiKPNUP8nwRgC9XofZpCcwnD4FmqIoihI/\nqkBTFEVRlHm60KItDpfjurJAA7CajWnVg6YoiqLEjyrQFEVRFGWezjX3AZDntk14u9VsIDg0QjgS\nWcywFEVRlBSkCjRFURRFmYdwJML55l7ys2zYLBNP7baYDESAwfTarFpRFEWJA1WgKYqiKMo8tHb6\nGAyGWFbsmvQYa3Qlx/7BocUKS7kK7T3ezN7jzYkOQ1GUeVIFmqIoiqLMg2zsAWBF2UwKtOFFiUlR\nFEVJXapAUxRFUZR5OFvnBWDNkqxJj7GoAi0lqB4oRVGSgSrQFEVRFGWOwpEI1Q1ecjKtky4QAmN6\n0PxqiKOiKIoyNVWgKYqiKMoc1bf14wuEWL0k64oNqseKbVbt86seNEVRFGVqqkBTFEVRlDk6ca4T\ngPXLcqY8LlagDagCTVEURZnGxOsBK4qiKIoyrRPnuzDodVxTmT3lcbE5aKpAUxbaSDjM0ZpOGjsG\n6PMFWVLovGwe3c6NJQmMTlGUuVAFmqIoihIX6X6R2NUboL6tnzUVWZPufxZzaYij2gdNWTj1bf38\n6Pkqmj2+0Z+Vtvazc1Mx+imG3CqKktxUgaYoiqIsuEgkQlWdF7vVSEVRZqLDiYsn9tQCsHlV/rTH\nmox6dDoYCKgeNGV2Yg0dH7591ej34XCEqrpujtd2Eo7AjnVFbFmTz2O7amjqGOD0he5ph90qipK8\nVIGmKIqiLLj69gGOSA8A/uBIWvag1bX1o9PBdSvzpj1Wp9NhNhrUIiHKnL20v47+gQAer58DVe14\n+4NYzQZuXFfEx29fCcDOTSX8bl8dp853sbzERYZVXeYpSiqa9i9XCKEHvgdsAILAp6WU5yY45nng\nWSnl9+MRqKLMlMpZJdWkY84eq/GMfn3mYjfhcAS9Pn2GXDV7BujqDVCSa8eZYZ7RfSxmQ9rMQUvH\nnE12kUiEI9LDmYvdACwrzuS6VfmjWziAlmPrl+dw4Ew7Zy52c/3q6Xt3rxYqZ5VUMpNVHO8HrFLK\n7cCXgYcnOOZbwOQ7dCqLxh8MUdPYwyuHG3ni1Vqq671EIpFEh7XYVM4qqSatctbnH6Z/cJiyfAcr\ny1wMBkOcutCV6LAW1JsnWwFYXuqa8X0sJj0+fyhd3pPTKmeTXSQSYc+RRs5c7MaZYeLOrWXcuL7o\nsuIsZlm056y2qYfhUDgB0SYtlbNKyphJ3/cO4CUAKeUBIcTmsTcKIT4EhGPHTCcrKwOj8co3lIWU\nl+eM6+PH22zj9wdD7D3axEv767jQ3HvZbbsONbK81MX7dy7nxvXFGAzx31khCZ5/lbOLLNXjh4T/\nDmmVs/0BbSGMsgInxXkOahp7OVXn5bbtlXGNabbm+pr7gyH2nW7DZjGyemnOZY/jdFgnvZ/dZsbT\nEyDDacNhM83p3GOlU85CYvPW6bBS2+hlYHCYZaWuRD+3l3E6rJy50EV1nZf8LBv33LQUq/nyy7dY\nvLH8W7s0h4NV7bR5/Un1u6icnb1kev3mQsU/NzMp0DKBsVf9I0IIo5QyJIRYC3wM+BDwtZmc0Osd\nnH2Us5CX58Tj6Y/rOeJppvGHIxEutvbx673nudDcx/BIGJ0OCrMzyM60kJ1pxWo2UNPYw7mmXh76\nxRF+5DzNXVvLMRn1cZsPEu/nf4Z/KCpnF1Gqxw9JkbdplbMNrX0AZGaYsJl0WM0GDle10d7RlzQr\ny83nNX/1SBM+/zDrl+UwODjEU69Uz+h+sfax+sZu8rMy5nTumHTLWUhs3ta39LDrnQYAahq87Fxf\nNOXG44up0+vj7ZMtWEwGdqwvYngoxPDQ5auBxn6v/oEAAGX5dg5VwalznUnz/qxydvZS/fNVxT/9\n409mJgVaHzD2EfRSytg7wx8CJcAeoAIYEkLUSSln3PqgzFw4EqGmoYfDsoNjtZ14+4MA2CxG1lRm\nsaLUfcWE4OJcO/2DQxyt6aS+rZ8DZ9rYsb4oEeEvJpWzSqpJq5z19AbQ6yAn04JOp6Mkz8755j7q\n2/qpTPEVHYdDYV56px6jQY8od8/qvpc2qw6Rn/qDqNIqZ2ubLl23d/YGqKrzTru33WI5c7GboVCY\n7euKZtzzareaKMq109Lpo7XLR1GOPc5RpoS0ytmrjT8Y4rVjzZhNem67rizR4cTdTAq0fcA9wJNC\niG3AqdgNUsovxb4WQnwdaFPJvPC8/UH2nWrlzZMteHq01jG71ciNawsxmw2U5NqnnHzvzDBz0/oi\nfP5hLrb2U5Rj512bFiv6hFA5q6SatMnZSCRC38AQmXbz6JDq0jwH55v7OHm+K+ULtB89X0VXX3BG\ne5+Nd6lAS4uFQtImZ0MjYS609GGzGHjXphJeONDAq0eakqJAGxoeoaaxB6vZwPrlufj9QzO+77Li\nTFo6few/08YHbl4WxyhTRtrk7NWg1zfEyfOdnL7QTW1TDz0Dl3J/9+EmVpS6WF7ioiArA6NBz4B/\nmP7BIfR6HUsKnZTmOUa3qEjFVYRn8unyDHC7EOJtQAc8KIT4AnBOSvnbuEZ3lRsMhHjytVrePNlK\nJAJGg45lJZksLc6kICtjViui6fU6btpQxHNv13PwbDvv3b4knVvUVM4qqSZtcrbXN8TwSJhM+6WV\nDYtyMtDrdJy+0MV9O5JrHtps9PmGOFHbicmon9PFu8Uc26w6LQq0tMnZJs8Aw6EwlUUuct023A4z\nZ+q6CQ6NjL5miXJYdjA0HGZtZTbGWc4hLytwYDLo2X+6jftvWhqX4cUpdgGcNjmbbiKRCN7+IBda\n+jjX3Et1g5eG9oHR210OM2srs+n3DxMcGqG7L8C+U23sO9U26WMuLc5k+9oCDPr4r70QD9MWaFLK\nMPDZcT++YsC9lPLrCxSTApy+0MVPX6zG2x/E5TCzqjyLyiInZtPcPyycGWZuWFvI68db+K/fnOGr\nf3jdvB4vWamcXRjhcIT+wSGGQ2HCkQgRwGw0YDUbsJgMabVkeqKlU862d2tzMsYWaGaTgWUlmZxr\n7mXAP7wgC2QstkgkwqO7JEOhMNevyp917xmkVw9aOuVsfZs2xyQnU1tgoyzfwakL3Zy+2MV1IrHL\n1L8VXS10RdnMVwuNMRr0LClycq6pl+p6L2sqEt8jmEjplLOpLhKJ0OzxUVXv5e3TrXh6/PiDI6O3\n63U6CrMzKMmzU5Jnx2U3XzYnNFbQ5WRa6eoLUtfah9mkx2o2Eg5HqG3q4UJLHyajnq1rCkYbEiBl\nGhPURtXJxucf5pEXz/LGiVYMeh337ajEmWFasIvhJYVOVpa5qGns5fn99bz/5qUL8rhKauv1DSEb\nvFxo6aOurZ8O7yC9viEmWw1cB9htJjLtZkrznRRmWSkvcCLK3ditqXfxrSyc1liBNm5vsHVLc6ht\n6uXU+S62ry1MRGjzsvtwE0ekh/wsG2LJ7OaexcR6Y/rToEBLJ/XRlvrsWIFW4OTUhW6O1XYmtEDr\nGQgiG3rIc9tmvNfeeMtKMjnX1Mtbp1qv+gJNSazYOgoHz7Zz/FznZUMWbRYj5QUOcl1Wct02cl3W\nKXuMdTod2ZlWIhBdGC/vstsrizN58UA9sqGHyiLnvBdlSgRVoCWRX+ySvHO2A59/mCynhRvXFeJy\nzO1NeSqbV+XT1OHjjRMt3LujImW7f5X56fUNsf90G0drPZwbM0E+VnzlumxkWI0Y9DpiDVcjIxFC\nI2GGQmECQyN09vpp6fRduq8O8rNs3LKhhBWlLsoLnJiMKr+uJhP1oAFsWpnH029c4GiNJ6kLtIla\nWvefbuOJV2tx2bX5vHMdKmY1pdUQx7RR39aPXgdup5azOZkWXA4zpy50EY5EErby6OHqDiJARdHc\nl/nOd9sozM7gcHUHH7l1xRV/l4oSb7F1FHYdahwdPWAxGagsclKUY6cwOwO7zbigq6aajHq2rClg\n18FGztb3qAJNmZsB/zC/3F3L/jNt6HU6NizPYe3SHAxxGkJmNOjZfk0hrx5t4uT5LjatyJv+Tkra\naPIMsOtgIweq2giNRNDpoCDLRkmenTy3jexM66yKKoPRQENrH529fpo9Ptq7/Tz52jntNr2O0jwH\nxbkZFOfaWVHqZnmJSw2PTGPt3X4AMu2X96SW5Nopysng1IWupJjbMxOvHWvi9IVujtd2YrMY+T8f\n3sDFtr45P57qQUs+I+EwjR0DuJ2W0cZKnU7HuqU5vHWyNaErjx6WHnTAkoK5F2g6nY5bry3h8d21\nvH68mXtunP0c0BSbZ6YkWK9viPq2fupa+6ht6aPqQhcR5reOwlwUZGnzSRva+xkMDJORYqN7VIGW\nQBdb+3j9eDMHqtoZGg6Tk2nl9q3lmA3xv3i9aUMRrx5t4s0TrapAu0r0+Yb4n9fP82Z0ToMzw8Tq\nJVlUFDmv2PR0NjKsptFx4huW5+IPhmjt8uHpCdDZG6DJM0B9+6V9RJwZJjYsz2Xj8lzWVGRNeu7B\nwDDnW/po7fSxpjKb0jzHnGNUFk9nrx+TQT863ypm7/Fm8tw2WrsGOSw7uHFdcm/3MRgI8fbpNlo6\nfWQ5Lfz5h9ZTXuCcX4EWm4M2OPOV+JT46uwJEBoJ43ZYLvv5+miBduJcZ0IKtL7BIWqbelhW6rpi\n+5yJjO35HS9MBJNRz+4jTdy2uWxO8yeHQiMcr+2kwztIZ1+AopyMpNknLp2kajH8mzcvUNvUS5Nn\ngP7BSw1QOh0sK3GxfW0hw6GRRV33QKfTsbLMzcGzHTR0DLCqPLX2NlEF2iLr8w1x8Gw7+061jV60\n5rqs3La5DKNBhyvTNrrRZDyVFzipKHRy4ry2n1qW0zL9nZSUFIlEeP1EC0+9dh5/MITbYWbTyjxK\n8+xx+YC1WYwsLXaxtFib1B6ORBgYHKZnIEhLp4/GjgHeOtnKWydbMRp0LC9xkeuy4XZaCIcjtHb5\naO0apK378g1AC7JsrKnMpiz/UqGWah9i6S4SidDZG5h0uMryUhcnz3fx2rHmpC7QGtr72X+6neDw\nCMW5Gfzfj16LawGGhun1OmwWIwP+0PQHK4ui3Rvr8b389e3u1/byO17byf03Lf5c7RO1nUQicO0C\nNKCajQauqcji+LkuXnyngQ/MYO753uPNDA2PcKG1j4a2Adq9g5fNSV5Z5mLrmgJVpF3lzrf08rt9\ndZw83wWAyaCnJM9OTqaVHJeVyhI3oWHt/S4Ri9KV5NnhLLR0DqoCTblSaCTMEenh7dNtnL7YRSSi\nzfMpy3ewssxFUa49IWPcb95QzM9fluw71cr7bqhY9PMr8TccCvOLXZI3T7aSYTHysdtWoNfrFnWI\noV6nI9NuJtNuprzAydY12kV8U8cAPQNDVDf0AD2X3cds1FOYnUGe24ojw0xdax+tXYO0e5u59boS\n1ZuWpAaDIQJDI+S6rBPe7rCZKM2zc6Glj7N13axOskULRsJhDld3UFXnxaDXsWV1PqLcvSDFWYzD\nZmRgFntZKfHV7tUagpwZlw9/MpsMFObYaegYwNPjJ89tW9S4jtZ4ANi0Mpez9d55P97qimzq2vp5\n8UA9G5bnsKx48lUhBwPDHK3xUF3vJTSiVWU5Lis3ri2kMCeDp147T01jL/lZGSwtTu19DZXZC4cj\nnLzQxSuHGkdzMz/LxuolWZTmOy6bnmOzGOkfTlyDlDPDjDPDRFuXj5FwJG5Th+JBFWhxNOAfZu+x\nZvYcbRpdrSYn08rS4kwqipxzGmawUPYeb2YoNIJBr2PXocbRFm/VI5E+en1D/P2jh/H0BMjJtLBz\nUwnGJFiwQ6fTkee2jV7wDIfC+IMhBgMh0IHLbsZqNlzWMrui1IWnx89L7zRwsKqDoh0Zo5sgK8mj\ns0fr/bdPsYz++uW5NHl8PPnaeb76gDtpFil65XAjb5xoodnjw2U3c8vGYtxxGFngsJlp7BggEomo\n3ock0BGbMznBKonlBQ5aOn0ckR7u2lq+aDH5gyFOXejG7TAvSHEG2qIJ16/O55VDTXz3qZP82fvX\nIsb1KPgC2jXLS+804AuEsFkMrFuWxbLizNH5O4GhEXZuKuY3b1ykut6rCrSriKfHzy9eqeF8c6/2\neY22x+W6pTkU5iTvIhzFuXZkQw+eHj+F2ckb53iqQFtg/mCIX+2ppaF9gMaOAUbCEUwGPauXZLGy\nzB2XVRnnymwyUFHo5HxLH23dg+m8cfVVZzAQ4uEnjuPpCVBR6OSGdYWz3uR0sZiMekxG87Sri+W5\ntRa6qjovpy92s2F57iJFqMxUZ69WoE21z1muy8r2awrYf6adZ9+qm9Fwq3gb8A/zyqFGOnsDFOdm\ncPPGYszG+AzHcdhMhEbCBIdH5jX3U1fqqoIAACAASURBVFkYsR60id5/yvIdHDrbwf4zbdy5pWzR\nCurY6pHl81gcZCJFOXa2ry3gwOl2/vHxYywvcY0OGT9b76XD6ycciWA26rl2ZS6rlmRN+LnhzDBT\nnGen2ePD2x8gyzlxj7mSHmoae3jpnQZOnOskgjaMcUWpC1HuHt2aIpkV5WRoBZpXFWhXjUgkQs9A\ndLWatj4utvZztt5LaCQMaEMmRLmb5aWuuH3Yz9fyMhfnW/o419SrCrQ0ERoJ85/PnKLJM8DKMjdb\n1+SnTUv9+uU5XGzt4/SFbtVym4S6erXeiOk2ov747Supberlubfr6Oz1s7LMnbDe+z7fEA//6jid\nvQGWFmdyw9rCK4YAT7UAw2zFnpsB/7Aq0JJAu3eQTLt5wpVrbRYjG5bncrTGQ317PxWFi/Oec7i6\nA9B68BbailI3bruFY7WdnG/p5VzzpS1WspwWlhZnsqLUNe18oeUlLpo9PurbBlSBlqYutvbx673n\nR3txc11WRLmbJYXOpG3wnUhsyH2sATFVqE+HOTpb181PX6y+4gV3O7R5NksKHbgdlqS/MM5328i0\nm6lvH2DL8Mj0d1CSWiQS4acvVHO23svG5bmsXZad9Dk4G2ajgc0inzdPtnKo2sM9N8x+yWglfmLv\nh1MNcQRt5c+/+L0NfPORwxw4004oFE5IgebtD/LPTxyjtWtw0RozYnOd+geHyXUt7rwm5XKhkTCd\nvQGWl0w+H+vmDcUcrfGw+3ATn37fmrjHNBgIcfxcFy67OW6Ld+Vl2bhjSxlbVxfQFf2brWronlVD\nclF0SFv7uMWclNTn7Q/y673n2X+mDYDi3AzWL8tJyb3EQPu8sVmMqkBLd3VtffzP3vOcqdNaFIpz\n7eRn2cjOtJCTaU3ovLK50Om0fSmO1XTSMGYpdCU1vXCgnv1n2lhanMln7rtm9A02nVQUOZGNPTR1\nDNDQ3r/gw4CUuevqiw1xnP59sCjHzp1bynjlcBOHpYd/fuIY14m8RZsL2949yD8+dpSOHj93XF9G\nQbZtURozYkPp+nxqoZBE6+oLEIloCxxMZu3SbEry7Ow/08Z7ti2hODe+I02O1HQQGglTWZwZ93y0\nWYyURoc4nmvpneboy5lNBrIzLXii2xQoqW84NMKuQ40893Y9weERsjMtbBb5ST2/bKZyXVYaOwYY\nDKTOHpSpVU0k0IB/mKdeOze6h9Q1FVksKcqcdLWyVFJR6ORYTSd1rapAS2WP767h1cNNZFiNXCfy\n0rI4A61RYe3SbPYcaealgw388T3XJDokJaqrN4DZdOUeaJNxOy3cva2cVw83UVXnJTA0wg1rC+Ma\n497jzXj7A+w50owvEOJ9N1Tw/psqef1ES1zPGxNbjEIVaInn6dGG5E61QuMbJ1pYUaoN5/vFLskX\nP7Iprqvgxq4xKouSv+GpMDuD7r7g6OJASmqKRCIcrenkV3tq6ewN4Mwwce3KXJaVuhKywng8xAq0\nVOpFUwXaNCKRCG+dauWp184z4B+mNM/OR969gjUV2Qs6LyGRnBlmcl1W2roG6fMNTbtYg5J8Onv9\nvHmiFZ1Oxy0bi1OuJ3e2SnLtuB1mDlZ18IGbl6qhYkmiszdATqZ1Vi3/DpuJO7eWsedIMxda+hga\nHmHHuqK47ZnT0unj9eMtDIfCfOTW5dyxZfFW54MxPWhqs+qE80QLizy3jeAUQ/zL8h2U5Tuobujh\nmTcv8MFblsUlnro2bT74uqU5OCdYVTLZ5GfZqKrz0hEtdJXU0+Ed5NFdNZy52I1OB2sqsli/LCch\ne5bFU060M6WrL5jgSGZu2qs4IYQe+B6wAQgCn5ZSnhtz+18AH4l++4KU8hvxCDQR6tv6+a9nT9Ph\n9WM06LhO5LF6SRYdPX460qQ4i6koctLZG+Cw7ODWa0sTHc68XG05Oxwa4XvPnCY4PMK2NQWLvl9P\nIuh0Oq6pzGbfqTZeOdTER29bkeiQ5iUdctYfDDEYDLG0ZPYLKVjNRm6/voy9x5pp8vj45yeO87kP\nrptw6fO52nu8GdnQw8Gz7ejQccfW8kUvzoDRPdV6B1K7QEuHnB3bg9bkGZj0OJ1Ox/a1BXj3B3l+\nfz06Hdx/09IF71148UADAO++rpTu/uRv6Y9d9Hb3JX+skB45u1DCkQivHmnif/aeZygUpigngy2r\nC5JqpfGFFJvP6U2RXAWYyTIs9wNWKeV24MvAw7EbhBBLgY8DNwDbgDuEEOvjEehi6vMN8ciLZ/nm\nI4fo8PopL3Bw345KrqnMXtQNfhdTRaE2nOJgVXuCI1kQV03ORiIRfv6SpK6tn2Ulmawom3yye7qp\nKMoky2nhjRMtDPhTZ1z5JFI+Z2OLDeTOYNnlvcebrxiBYDLqufW6UiqLnJxr7uX/f+QQ55tnNy9m\nMiPhMAfPtvNOVTsWk4E7tpSxoixr+jvGQRr1oKV8zs5kiGOM1WzkjuvLcNhMPPd2PV//yUH6F/A1\nPN/Sy6HqDnIyrXT1pUaPVIbFiNVsoDt1eiVSPmcXQu9AkO/86ji/3F2LTqfjpg1F3La5NG2LM9Dm\nW1rNBrz9KZOrMyrQdgAvAUgpDwCbx9zWCNwlpRyRUkYAE5A65ekE3qlq5ys/2M8bJ1opzrVz2+ZS\ndm4qmXZVslSXYTVRkGWjtqk3ZVrDpnDV5OyrR5rYd7qNyiIn29YUpNWKjdMx6HXcvrmM4PAIe442\nJTqc+Ur5nO2Mvm/kzGNerkGvY8f6It5/UyXdfUH+/tEj/PMTx3j5UMOcH3PAP8y/PnmC6voe3A4z\nd28rn3JRiHiLreKYBnPQUj5nPT1+zCY9mRkz+3x3ZJh4z/ZyinIyaPL4+JsfH+RYjWfecQSGQvzk\n+bMAXLcqL2Xex3U6HdmZVgb8w6nSSJbyOTtfZy5285UfHOBMnZeSPDv37qigsij+C9IkgyynBV8g\nlDILhcxkokomMLYZc0QIYZRShqSUw0CnEEIHPAQck1LWTPVgWVkZGOO8J1he3uwn14bDER57uZon\nd9dgsxj5zPvXcff2Cl45OPcLg7lyOhKz8Miqimzavc2cberj/lvy5vw4c3n+F9hVkbOnznfyxJ5z\nuB0Wvvbp7Rw+m7jez0Tl7HtvKuHFdxrYdaiRD90mcDnmvix1gvM25XN2SGoXqhWlWQSCoXk99u/d\nsZrr1xXz7Z8doqrOS21TLz2+YW5YV8yaymz2Rgvyu7ZXTPk41XXdPPTYETq6B6koyuT2LeWXza04\ncq5r9OvFyuGiQhfODDMDgdC8cy6dchYWN28jkQidvQGKcuzk52fidHTP6P5O4P07l3OsxsOhqnb+\n/elTbFtbyIP3XENx7uz3LRvwD/OvjxyktWuQe29aStk0q9IuZJ6OzZ+5Pm5Rrp2WTh99gREqy7Nn\ndc4ESPqcjb0OY5+nhXjORsIRntgl+dVuiQ4dOzYUs3557qIUZom6PhivMMdOa9cg/UNhlpTN/DlN\nVM7OpEDrQ3tPitFLKUc/fYUQVuAnQD/wp9M9mNcb3z0z8vKceDyzW43wlcONvHWylcaOAZwZJt51\nbQl+/xBP75n2b3PBOR1W+gcS02iT77ai1+nYc6iBG9fkz+kx5vL8z/bxZyDtc/a5t+t4fn89kUiE\nrWvyee1QfZyim14ic9bXH+CeG5bw+O5afvzsKf7gDjGnx0mCvE35nL3Y3AOARQeeeeaDx9NPYaaF\ne25Ygmzooarey8sH6nn5QD06wOXQ9ojq6BqgPN9JWb7jssWNWrt8vHywkTdPtIAO7ttRSabdRDA4\nTDCotZ4mKm89nn6cGSa8fYF55Vy65Swsbt72Dw4xGAiR5bDg8fTPOhdWlGTy3q3l/Pylag6cbuOd\nM21UFmXy0dtWsHSaHonXjjXROzCEwaDn1cON9A0Os2lFLu/bVs5bp1onvd9C5+xTr1TP+zEcVu0y\n8mRNB8VZU1+Iq5ydXuz1jT1PC/GcefuD/PB3Z6hu6MFuNXLLxmJy3TYGfPEf7pfI64Px7FatkD5V\n00FB5swacxOZszMp0PYB9wBPCiG2AadiN0RbGp4F9kgp/3GecSZEr2+Il95pwNsfpDA7g5s3FmM1\np9fqNTNlsxhZvcTNmTovnh5/Ki82kdY56w+G2HO0aXRRkILs1N+jZK72Hm9Gr9fhzDCx91gzmRkm\n7tuxNNFhzUXK52yHNzqfJ8tGU+fkCy7MhsGgZ01lNqsqsmjvHqSl00eHN4C3P0DPwBAXx2wNYrca\ncWSY6R0IEhjSVuQrysnggbtWsbLMnVSr7mZmmGjp9DEcCmMyzmSmQVJK6Zxtj+ZrQfbcP+eKc+38\n1cev5VB1B7/cXcuFlj7+7udHcNhMXL8qn4pCJ1nRC8HegSFaunw0tPVT29zL0LC2d5jRoGPTilz+\n7P3rUnKOe2zxhcaOhfmbj7OUztnZikQivHO2ncd21eALhCgvcLB9beGMt0FJN1lOrQEhRXJ1RgXa\nM8DtQoi3AR3woBDiC8A5wADcAliEEHdHj/+KlHJ/XKJdYN7+IA/98hje/iArSl1sXVOQkm+QC2nL\n6gLO1Hk5eLad904zfCiJpW3OhiMRfvRcFT0DQ4hyNyvL3YkOKeH0em2F1b3HWjgiPalaoKV8znp6\n/FhMhhnP55nK+GJKr9NRlGOnKEfbJDgSidA/OExxjp2Gjn6aOnxcbO2jdyCI0aCnvMDGkkInf3in\nwKBPvgLIHR2K2+sLpvIWESmds+3dWs9HQdb8Grh0Oh1bVhfgCwzT2jXIueZemjoGeO3Y5A0CzgwT\npXkOinIyKMt3YDYZUvbaw5FhwmjQpcpFb0rn7Gx09vp5/JVajp/rxGjQsXVNASvLXFfFXLPJuOxm\n9LqUydXpCzQpZRj47Lgfj+0XT47BpbPU2evnoV8ew9MT4JrKbK5duThjcZPdtSKPR3fV8PrxFu7c\nUo7RkHwXN9NJ15wFeOaNCxyr7aQwJ4PrV81tGGo6Kst3UJBlo8nj4+T5LtYvy0l0SLOS6jkbiUTw\n9ATIc9sW5X1Up9ORaTezeVU+m6N/BxP1kCVjcQaQHV3psqs3kLIFWqrn7GgP2gItGKPT6SjOtVOc\nayccjtDVF8Dbf6k312o2kJlhJivTklY9GHqdDrfDQmuXj9BIOKmvGVIhZ0fCEc7WdXO8tpOlxZl8\n6v7ZLSQZGgmz61Ajv913kaHhMIXZGWxfW5AS++rFm16vw+Uw09zpYyQcTtrPh5j03s12Eh3eQR76\n5TG6+oLce2MFLodZFWdRdquJmzcUsedoMwfOtLNjfVGiQ1KiDpxp4/n99eRn2bhlQ3HKtrjGg06n\n4/rV+bywv54fP1/F1x/cMjr0Rom/vsFhgsMjCV0dMZVc2jQ1OeZmXI06onOH8ufZgzYRvV5HntuW\nytMEZiXLaaGzN0Br1yBl+bNfKEXRhCMR3jrZSn2bNnRbNvRw+7YKbIaZfdafudjN47traO0axGo2\ncOO6QpYWXx0rNM5UttOCtz9Ie7ef4lx7osOZUnKXj3HQ5BngHx47SldfkA/espT7b1qqknec92xb\ngtGg47m36xgJhxMdjgJcaOnjJy9UY7MY+PMPrcdylc6TnEp2ppXNq/LpHxzm+8+eVrm7iDzR3oj8\nRb4gje2nNtn8suluT5ScMT1oSmK0e/2YjPrROWLK3F2ahxa/xRSuBsdrO6lv6yc/y8ZmkUdweIRv\n/OgAvmmWhW/2DPBvvz7Jw786Tlv3IKLczX03VbKs5Ooe0jiR2N/7VBvTJ4urpgdt7/FmOnv97D7c\nxNBwmOtX5WO3mZLugzsZZGda2bG+mL3Hmnmnqp0b1qpetETq7gvw70+fZCQc5nP3bqAox45s7El0\nWElJlLsJR+BwdQdPv36BD79reaJDuiq0R3sj8twJHyGUElQPWmJFIhE6vIPku23ok+QCNpWvRWJD\ndhvaB7hhbYKDSWG7ots6bbumALfDwlAozMnzXfz4ubN87gNXLiLT1DHA8wfqOVjVTgRtuO7m1fmj\nDUDKlbKdl3J1y+qCBEcztaumQGvrHuS1I82ERsLcsLaQ5aWuRIeU1N67bQlvnmjhd2/Xs21NoRpO\nlyCvHG7kpXca6B0YYrPIo7s/kNIf5PGm0+l48O5VNLT38+I7DWQ5Ldy2uSzRYaW9li4fQNIPGUkW\nubEetL74L3OtXMnbH8QfHKGwYn7DG9V7sSbLaUEH1LWpHrS5amjvp6apl+Jc++giQuuX56DT6zhe\n28lPXzzLJ24XmIx6qhu8PPFqLU0e7X23PN/BslIXpXl21WM2jexoD9rF1r4ERzK9q6JAO3i2nVcP\nNxGJRLh5YzFLChO+kXLSy3FZuXFdEW+caOHg2Xa2XVOY6JCuOiPhMG8cb8HbH2RlmYvVFVmJDikl\nvHO2ne3XFLLrUAOP766ltqmXP7lfNevGU4tHFWizYTEbcNhMaohjgsSGN6n5UgvDZNRTmJNBQ3s/\n4UgkaXolU8k7Ve0ArCy71Hmg1+n4ygNb+NK/v8G+U20cqu5Ar9ONLjyT57aybmkOJaowmzGzyUBh\ndgZ1bX1Jn6tpXaCFIxF+8+ZFnnu7DpNBz82bSijJUxcQUxnbIpjrsqLTwa/2nGNwKMStm0oTGNnV\nJRKJ8NgrtTR3+ijOtbNldYF6A54Fl8PMHdeXs+tQA4eqO6h8p4E7t5Sp5zBOmjt9ZNrNaqWwWchx\nWWnp9CX9RUI6ii2zXZanCrSFUlHopLVrEI/Xf1XvzTkXkUiEQ9UdWM0GSsY1ctltJr7yiet4YX89\nx2o76R8coizfwfJS11WzCM1CqyzKZP+ZNtq7B0e3bklGabtISGAoxPeeOc1zb9eR57Zy97ZyVZzN\nkiPDxLJiF72+IY7XdiY6nKtGOBzh5y9L9h5rJstp4eaNRWqI6RzEijSbxcCTr53jh89VEYy2PCoL\nJzAUorM3cMWFhTK14pwMhkNhPD3+RIdy1Rkt0FQP2oJZUqCNTEqFoWPJpq6tn87eAJtW5GKYYJsC\ni8nA+29eyjc/tYX7bqpk+9pCVZzNw9LiTEBbfC2ZpWWBVtPYwzceOczRGg+ryt38zQPX41ZLbs/J\nppW5ODNMnL7Qze/erkt0OGkvNBLmv397htePt1Be4OC2zaWYjWrFxrlyOcy8Z/sSlhVncuBMO996\n9DAtnb5Eh5VWmqPPpyrQZqc02nvTlCKbpqaTJo8Pq9kwuliLMn/LovP6a5p6ExxJ6jlU3QEwuqfj\nWC/tr0va1WhTVaxAO68KtMXjD4b46++9xbcfO0p79yBrKrLYvCqfw7Ij0aGlLJvFyO3Xl2G3Gnnm\njQvsOtSY6JDSVndfgIefOM6h6g5Wlrr40kevxWZJ61HIi8JuNbFtbSGi3E2zx8fXfnyQ7/76BKER\ntQz/QrjQrH3Iqbm9s1Ma7b2JTfRXFoc/GKItul+XGvK8cJYUOLGYDMgGb6JDSSmRSITD0eGNayuz\nEx3OVaEs34HVbKCqrjvRoUwpLQq0cCTCgTNt/M2P3+HU+S5cdjN3by1n86p8NTRsAThsJu7YUobb\nYeaJV2vZdaiRcCSS6LDSyoGqNr7ygwPIxh7KCxxsXp3Pwer2RIeVNgx6HVvXFLBzUzEWs4ET57r4\n+k8PcSbJ36BTQU2TtuXDyjJ3giNJLaoHLTFkYw/hSARRrvJ1IRkNepaXumjtGqTPN5TocFJGbHjj\nxhW5mNRomUVhNOhZvSSLDq9/dMP6ZJTSBVokEuFYjYe//clBfvC7Km0p8tUFvO/GJeRlqfG5C8mZ\nYeaLH9mEM8PEE6/W8u1fHKWhXS2pO19t3YN888cH+MFvq4hEImxfW8AtG4sxTjAOXZm/8gIn9+2o\nYGWZm9ZOHw8/cZzvPHmC+rbkHuqQrCKRCLWNPWQ5LeSq4WKz4naYcdhM1Lf3E1ENXoumul7r4Vm9\nRPVWLDQRbaSpqlcNXzO171QrAFtWJfeeXOlm3dIcAE5fTN5cTcnxU6GRMIeqO3jlUCN1bf3odHDj\nukLuu7GS+s5B+gfU0sXxUJxr52sPXM8Te2o5Ij1845FD7NxUwvu2V5Cl5vjNSndfgJcPNrLnaBMj\n4Qiryt2sWpJFpl2tghdvZpOBbdcUsKLMxZFqD6cudPG5h16jNN/Bx29bwcoytxr6NEPNnT76BofZ\nsjpfPWezpNPpWFnm5miNh7YkX00snVTVebXenpLMRIeSdjatyOXpNy5wsKqDbWvU1jzTCQ6PsP9M\nG26HmXXLVIPBYooNJz1W4+HWa5NzhfKUKdAikQgtXYMcru5g16EG/EFtNbbyAgcbV+Tidlg4XdeN\n06FaceMlNkH1mspsspwWDp7t4LWjzew92syG5bncsrGYd+WoVbEmMxIOU93Qw+vHmjlS4yES0YaP\n7thYTF6mRV3gLrKcTCu3X19Ks8fHmTovTR0D/OPjxyjPd3Dj+iK2rSlQy8ZPY//pNgA2iysntyvT\n27Ash6M1Hk6e71IF2iKob+2jyTPA2qXZajhZHJTkOSjNc3DqQhcD/mEcNlOiQ0pq+8+04Q+OcNt1\nZRj0atTMYsp121hR6uJMnZfWLl9Svv8mbYHmD4Zo9vho6OinprGH6oae0XHNJqOeNRVZiHK3uoBK\nkOJcO/fcWMH55l5qG3s5fq6T4+c6+fnLkmsqslm3LIc1FVnYrVf3G3RgKMTZOi/HarXnZ8A/DECW\n08KqcjdLizNxuzJUr2+C6HQ6SvMdrF6ay/lGL1V13TR2DPDL3bX86tVaCnMyePe1pWxckad6iccZ\nDoXZf6aNDIuRDctzEh1OSlq/THveDp7t4I7r1T598fb8vosAvGtjSYIjSV/b1xbw1Gvn2XOkiXt3\nVCY6nKTlD4Z49s2LmI16dm5S+ZgI776ulNqmXnYfbuIP7hSJDucK0xZoQgg98D1gAxAEPi2lPDfm\n9j8CPgOEgG9JKZ+bTQDB4RG6egO0dPpo7BigyaP98/RcfsFqsxioLHJSlGNnSaETk1G1NiSaQa8N\n0VlZ5qarN0BtUw+NHT7eOtXKW6da0ekg025mRYmL4lw7hTkZ5GbayHFZcTnMcducNd45O5Xg0AgX\nWvs416Q1KtQ09jAS1uaX2CwGVpa5qSx2ku+2qYuxJJOfZSM/qwR/MMTF1j4utPTR0jnIo7tqeHRX\nDTmZViqLM1lS4CA/K4N8t41ct5UMi3Her2Uic3aunt9fR8/AEHdcX6Z6I+bI5bCwaUUux2o7OVbb\nybUr8xId0oylWs7Wt/Wz+1ADOZlWNizPTWQoaW3nxhJePtjICwfq2bKmgMIk2rQ6WXI2HInw6C5J\nr2+I+3ZUqsa/BLl2ZR55bit7jzWzWeSxuiK5hpnOpAftfsAqpdwuhNgGPAzcByCEKAQ+D2wGrMBb\nQohXpJTByR7sP585RSAYotc3jLc/gC8QuuIYh81EYXYGWU4LWU4LeW4bmXaTuqBNYjkuKzmuQm7b\nYqGupZcWzwAtXYN4+4Mclh6QnsuON+h1uBxmnDYzTrsJp82E1WzEYjZgMWn/TEY9JqMes1GPwaBH\nr9NxV96MlvJe0Jw9WuMhODxCcGiEwNAIweERAkMhgkMj+IdG8AdD9PmG6O4L0Dc4fNl9lxQ4yXSY\nKc21k+u2qhxOATaLkTUV2aypyGbAP0xjxwAtnT66egMcru7gcPXl23aYjXrcTguZdjNOmwmHzYTd\naiLDatT+WYzcs3PavF3QnI2XcCTChZY+ntlXx+/21ZHltHCfaiWflw/esowT57r44XNVfOiWZaxb\nmk1+VvJc1E4hJXK2f3CIw9UdPPvWRYZDYT5xx0q1unMc2SxGfv9dy/nhc1V8+7Gj3HNDBStKXeS4\nrCRB80PCcnYkHKa9209rl489R5s5W++lsiiTu7aWL8TDK3NgNOj543uv4du/OMp3f32Su7ctYW1l\nNsW59qTY4mgmEewAXgKQUh4QQmwec9sWYF80gYNCiHPAeuDQZA92JHqhbjTosFtNFOVkYLeacDnM\nZDktuB0WbBaDupBNUTqdjlyXlVyXlfXLtbmD/mCInoEh+nxDDPiH8QVC+PzD+IMhegcGGGmf+Qpm\nd+1YOpPDFjRn/+PpU9OeUK/XYbcaKczJINtpIT/LRp7blhR/5MrcOWwmVi/JYvWSLCKRCD5/iJ6B\nIH2DQ/QPDuPzDzMYLdA9PX4mW4zvnp0rpjvVguZsvLywv56n37gAQK7Lyuc/tF7l+DwV59r57H3X\n8IPfVfHYKzXogK8+sJnKoqRfxCIlcvZfnzrBxdZ+TEY9n/3AetV7tgi2ry1kMBjiiVdreeyVGkC7\n5vuvv3o3Ce5rT1jOfv83ZzhSc6mheu3SbD577zVYTGr0QSItK3bxJ/ev5ZEXq3n2rYs8+9ZFnBkm\nvvO5HQlvyJnJJ2smMHZr+BEhhFFKGZrgtn7ANdWD/e7h+1TlpcSbylkl1SxozublOeOSsw/et44H\n71s37XEfvn1VPE6ftu7Oc3L3Tctmfb+8mY0oiJcFzVmIT97+2xdvndFxKmcX1kfuWs1H7lqd6DDG\nS1jOfv0zN8woQJWHi+/OPCd33jh543+i3mdnMpGrDxgbnT6azBPd5gR6Fig2RZkrlbNKqlE5q6Qa\nlbNKqlE5q6SMmRRo+4D3AETH7I4d73UQuEkIYRVCuIDVwOkFj1JRZkflrJJqVM4qqUblrJJqVM4q\nKUMXmWzSRNSYVW/WAzrgQbQEPyel/G101Zs/Riv2/l5K+T/xDVlRpqZyVkk1KmeVVKNyVkk1KmeV\nVDJtgaYoiqIoiqIoiqIsDrWZmKIoiqIoiqIoSpJQBZqiKIqiKIqiKEqSUAWaoiiKoiiKoihKkki7\nHUajq+/8Am1PCzPwBSnl/sRGNb0xk1c3AEHg01LKc4mNauaEECbgJ0AFYAG+JaX8bUKDShEqZxND\n5ezcqZxNDJWzc6dyNjFUzs6PytvESIa8TccetC8Ar0opbwE+CfxnYsOZsfsBq5RyO/Bl4OEExzNb\nnwC6pJQ3AXcB/5HgeFKJytnED2ETcAAAD15JREFUUDk7dypnE0Pl7NypnE0MlbPzo/I2MRKet2nX\ngwZ8B61aB+33CyQwltnYAbwEIKU8IITYnOB4Zusp4NfRr3VAaIpjlcupnE0MlbNzp3I2MVTOzp3K\n2cRQOTs/Km8TI+F5m9IFmhDiU8BfjPvxg1LKQ0KIQrRu4f+z+JHNSSbQO+b7ESGEccwu90lNSjkA\nIIRwoiX1VxMbUXJSOZs8VM7OjMrZ5KFydmZUziYPlbMzp/I2eSRD3qZ0gSal/DHw4/E/F0KsA54A\nviilfH3RA5ubPsA55nt9qiRyjBCiDHgG+J6U8vFEx5OMVM4mF5Wz01M5m1xUzk5P5WxyUTk7Mypv\nk0ui8zbt5qAJIdagdU1+TEr5YqLjmYV9aDvaI4TYBpxKbDizI4QoAHYBfyWl/Emi40klKmcTQ+Xs\n3KmcTQyVs3OncjYxVM7Oj8rbxEiGvNVFIpFEnDduhBDPoq0aUxf9Ua+U8r7ERTQzY1a8WY823vVB\nKWV1YqOaOSHEd4HfB8bGfLeU0p+gkFKGytnEUDk7dypnE0Pl7NypnE0MlbPzo/I2MZIhb9OuQFMU\nRVEURVEURUlVaTfEUVEURVEURVEUJVWpAk1RFEVRFEVRFCVJqAJNURRFURRFURQlSagCTVEURVEU\nRVEUJUmoAk1RFEVRFEVRFCVJqAJNURRFURRFUeJACPGIEOKTQohiIcQLUxznEkL8ZjFjG3Punwgh\naoQQH03E+ReLEKJSCHHFZuDzeLy9QoidQojNQogfLdTjAhgX8sEURVEURVEURbmclLKF6ObNk8gC\nNi5SOON9ErBKKYcSdP7FsgRYttAPKqU8DHx6IR/zqtwHTQixE3gOOCClvE0I8U3gQ0AE+LGU8l8m\nuM89wNcBO/CylPLPFy/iy+J4CMiTUn5ygtv2AAXAcPRHn5FSvjPP8z0G3A18QUr5yHweS5m78Tk7\n5ueLmg+zMZPzCyE+AXwl+u2LUsovLsB5Vc4qiqIoCSGE0AEPA+8DWgAD8GNgL7BXSlkhhPgY8CVg\nBLgIfAJ4ErgLeF5K+X4hxN8B7waygU7gA1LKNiFEK/BrYAcQAn5PSnlRCHFb9Lx6oB74GOADHgJ2\nRuN4REr5nXHx/ha4BzgB/DHw8+j5AsAdwL9G44gAj0op/zF6TfL/oW1CvSwaTy9wf/Rn75FSto87\nz2RxXw98B8iInvcz0Z/fAvxd9OdZwJeklE8JIR4BcoDl0eewbZL7fwF4AAgDB6WUnxFCnASWAj+T\nUv7ZmNh2Av8UfY5OA38dfc3cQBHwSynll4UQFuBHwGa0zcPLgM9FH+brUsqdQoiVwA+ir5sP+LyU\n8hCzdDUPcTwcLc5uAW5F2+18M/C/hRBi7IFCiKXA94H7gHXAtUKIuxc7YCHEu9FaOSa6TQesAjZI\nKTdG/837YlxK+XHgt/N9HGVBHB5XnC16PszUTM4vhMgA/g24BdgA3BT9gJkXlbPJRwjxTSFElRDi\nTPRDc6Jj7hFCHBFCVAshvruIsU07rCg6hCU2lGXvLB57dNhLIocvKXMnhHgoekE40W17ojl9PPpv\n6yLFpHI2uX0Q2ARcA3wYrZAY71vAHVLK64BqtM/LzwMt0eJsefRnN0gpVwLngI9H71sIvCql3AS8\nAXwuWjg8BjwgpVwHnEQrTv4IQEp5LbAFuE8IcdPYQKSU90b/3wh0AAL4RPR647NoRcj66P0/KIR4\nb/SuW4EHo7/nnwAeKeXm6Lk/MsHvPFHcZrSC52PRGB8Gfhg9/n8Dn47+/FPA18Y8VpeUcjXw8kT3\nF0IY0Rp/NwPXAWEhREn0OT48tjgbYyVwq5TyAeCjaEXZtujv/qdCiNxoTETP/Xkm7o37BfBvUsr1\nwF8Av46+PrNy1Q9xlFK+LoR4l5QyFH3xjGgV71jvB34lpWwCEEL8PlrLAkKInwO7pZQ/j37/n8AZ\noIpZti5MRQiRjdaS8PdoF7NXHILWuvGiECIf+KGU8j8WM0Zl8aRAPkx6/jEMaI1EdrS/ORPgX8QY\nlUUwrhHMBFQJIZ6XUsoxx8QawbYC7cAeIcTdUsoXFyHEuA0rGjfsJZHDl5Q5GNMI9vwEt8Uaocql\nlKFFDk3lbHLbCTwtpRwGPJPMO/sdsC9aAP+PlPK4EKIidqOU8pwQ4i+BT0c7DbYD58fc/6Xo/6eB\nm9E6D5qllMej9/9rACHEr4GNQohbo8c7ose+OUX8HVLKuujXt6L1uo0Ag9ERKu9GawQ9LaVsjJ6n\nE3g1ep96tNyZyPi4V6J9lv92TN9IZvT/TwDvE0J8GNgWjT0m1uA74f2j1/RvA4eAZ4H/lFI2CyFW\nTPF7Syllb/SLfxZCvEsI8UVgLWBGu1bZCfx39Jja6DlGCSEcwHIp5dPRYw4IIbrRrolOTnHuK1z1\nBRqAlHJYCPEN4IvAU0DzuEOWA0NCiJfRWgB+B/xN9LbrgG+POfY64GdoXa1b0VoWutBaJf5SSrlZ\nCPFTtNaF2bQS/zfahWnZJLdnof1x/AlgA/YKIaSU8pVFjFFZPMmeD1OdHwApZb8Q4m/QWg/9aMM/\nYm92KmfTRLI0ggkhStFamO1oQ14+L6U8gNaLWyyEeCbacv1l4PfQGhBeBv5qot8r2kL7X2gf3gWA\nBD6Alp+xoTK5wEUp5c6x5wEGgDellD+IPtZrwJcXs5dbmVoyNIKpnE1ZES4foXZFAS+l/HOhLVbx\nXuAXQoivA2/FbhdCXAf8EvgXtDwZQcuR2P0DY86l49JUgtj9XYAT7TX9UqxgiPYCjX//Hc8/5uvx\nI+10XKodxs9Xm7ahYoK4DcCFaO8dQggDWm6CVkS+hnZt8Crw+AQxTnX/+9EKu7uBl4QQH2dqo7+3\nEOJhtKGQjwO/AW6Lxjvda6tnzOsUNfY5m7GreYjjZaSUfwvkoV3w/tG4m41oL84n0F7sLcADQgg7\nUIp2gRlLjNVcqpJPSykbpZSDaONiZ9K6cAUhxKeBRinlq5MdI6XcL6X8QymlT0rZiTZ29j2LFaOy\neFIhHyY7/7jfYz3wv9Am7RahfQB9UeVs+hnTCFaF9npN1AhmEEK8LIQ4Afwp4I3edh1weMyxY7+f\nzRCbTwHPRW//Eto8CLh8WNFd0ce/Hm2IUgmXhhWNdwMwJKXcHo3fxqUcX4nW8vzAmONHzwP8BO3z\nBCHEEiBfXegmnVgjmHeS22ONUPej9Sh8Vghxe/Q2lbNXt93Ah4UQFiFEFtq8slFCCKMQohbolFL+\nA9qcr01oF/uxC/lb0OarfR/tffMOtGJkMhLIE0KsiX7/JbThiXuAPxJCmKK9O2+h5eBM7UG73jUI\nbVrCx9GKpoVSDWSPGXb5v4DHow0kK4GvSSlfYPLff7L75wFngVNSyq8Bu9BGcYx9jqdyO/CQlPIp\ntLqgJHr+3cDHhBD66N/BDWPvJKXsA84LIT4AIITYhtaxc3oG57zMVV+gCSFWCSE2AkQv+J5GexHH\nakNrDfNIKf1o1fQWtD+oU1LKcPS4jWgtT7EWghm3LghtjkZsHPu9427+feAOIcRx4JvAvUKI8ZM8\nd0SHY8TEWlQWLEYlaSRFPkyVs1Ocf6w70cajd0gpg8AjaMMHVM6moSRoBNuN1gDwONqH7fght0Rj\n2AocAY6izV+4ZpLf5w3ge0KIP0PrtV3BpSE4o0NlJrEXrWeiAvhDtAs0JUkkUSOYytkUJKV8Fu35\nOo02FLBq3O0htPlUu4UQh9GG+v0L2vDuhmjv5K+ADUJb1GIPWv5UTnHOANr758+j91mDNgrl+0At\ncAytkeCnUsq9s/h1/htoQltA5BjwWynlM7O4/5Sin/0fBh6Oxv0A8CkpZTfa3LIzQohjQD6QEf37\nmsn9PdHYDwkhjqD9bT2CVrS5hRCPThPaPwCPRu/7f9Geu0rge0Bf9HF+yMSF1yeAzwshTqH9zX5A\nzmF1TDXEUevC/IYQYgda1+V9aC1FYz0H/EwI4Qb60bpLf4P2RmgRQujR5lb8NXB8LkFEK/yvTXJb\nrFUOIcQngZ1Syr8Yd5gb+KYQ4oZoLA+gtZ5sXagYleSQLPkwVc5Ocf6xTgD/FH3DHURbReoQC/h3\npSSeEGIV2vLNx6WUg0KIKRvBoveJNYKdY5JiXWjzDWZcrEsp90Vbl9+H1sjxSbRW0rEMwL/K6Eq+\n0ff8EFpOjv+97kVrIPku8FO0oWGxoS3+8cePiyUihPgZ2kT030NrrFCSx+8DRdFGsGzAIYT4ztj3\n2eg1g2VMETdtI5jK2auHlPKrwFcnuKkievsv0YYwjje2R2bCni4p5dihjo+gFR5IKV9ngtcdrSd0\nunh10f/rYjFGvx+e6P7RIm/nmO/H3ufrs4x7P9r7/fjj/xL4yzE/+tPo/58cd9xk9/8O2uqO462d\n4Ni9XP77TPb6wJUNjDE7o/etHvtYc3XV96BFu05fQGsZOAK8LaV8AiDaM1Ac7cb/J7Su4Sq0lq6f\nog0raES7eHwNuADcKrQJ74tiTIzPoU1kjv0eP4kmbcJjVBZPsuTDFOcfG+MutDfAI2itgya0Fj+V\ns+llKdqqWhahrdh1H2PmWkQ9B9wphHBHexzuRsuL0WJdaKtgzblYF0L8E/AHUsqfoS2LfG30prFD\nXvYAfyD+X3t37MtQFMVx/Jd0MdRk8hecpQmDWSLhD5AQq7V2I+bGaJSgqxAGsZgkBJNRzsCg/4LF\nZjiPvjyPaD166feztHlt3rtpzkt6zrv3XLO6xXqdY8UWLGVmJe27+64iwZzW51OQilNr9hRFi47H\n/khIhLvPuXvDY13LuuKpQVkRbNPMRsxsVFGEOhIxC6ACPEHT29SbjZLjk7n3Oyo8WTOzKUnzWbb8\najV7fVCP1YUvjnVPWdWhZIxr6jYvefXrY8TvSTkePrh+cYwtSa3854O4r/Bz3P3Uov34rWKd4WG+\nCKZojHCT/Rm9UCTqZ4oiWFvdZP1J0qWkpT6T9S3F2oTlbBzN7PjbtCJ3nzGzCUWHsJqi41hbsR6k\naDs736KkZ0nXiikw9yXffXcdd++Y2aNy9y/Sl4vZk1xc1xRd4q7MbEXELIBvYqPq3L5SPZ6jLulR\n0pi7J/kjVjFGY9PfJBCzPZ2DmP0nzOxO75P1P8+iRfu4pHNJjWwdBf4BYhZAFYYyQQMApO0vFBT6\nZWYLinbnTXc/GPR4UA1iFkBVSNAAAAAAIBFD3yQEAAAAAFJBggYAAAAAiSBBAwAAAIBEkKABAAAA\nQCJI0AAAAAAgESRoAAAAAJAIEjQAAAAASMQLpX2dc3nRM6UAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x119b86a58>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
"<matplotlib.figure.Figure at 0x11a35a470>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"import seaborn\n",
"\n",
"plt.figure(figsize=(15, 15))\n",
"for j, (subset_str, subset) in enumerate(swire_sets.items()):\n",
" swire_indices = sorted(set(numpy.concatenate(numpy.array(subset).ravel())))\n",
" features = swire_features[swire_indices]\n",
" for i in range(5):\n",
" plt.subplot(6, 5, i + 1 + j * 5)\n",
" if i == 2:\n",
" plt.title(subset_str)\n",
" plt.xlim((-3, 3))\n",
" plt.ylim((0, 1))\n",
" if j == 5:\n",
" plt.xlabel(['[3.6$\\\\mu$m - 4.5$\\\\mu$m]', '[4.5$\\\\mu$m - 5.8$\\\\mu$m]',\n",
" '3.6$\\\\mu$m stellarity', '4.5$\\\\mu$m stellarity',\n",
" 'distance from nearest radio'][i])\n",
" seaborn.distplot(features[:, i])\n",
"plt.subplots_adjust(hspace=0.3)\n",
"plt.show()\n",
"plt.savefig('/Users/alger/repos/crowdastro-projects/ATLAS-CDFS/distributions.pdf')"
]
},
{
"cell_type": "code",
"execution_count": 60,
"metadata": {
"scrolled": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"RGZ & Norris & compact\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAbQAAAGoCAYAAAAuIBCmAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvXvUNEdZL/qrqu6Z932/W26EhEv2BqINJkvUyDJCUBZb\ncBN1kXVAFAkIXsCjOeuIIAYh3PYhIIEIC8TlRqLIRUVD1tnqlqMHt6wNCC6TuAUWGU4EYgyQfEm+\ny3ubme6q5/xRVT3VPT0z3TPdMz3vW7+1kne+p+vy6+rqfqqeeuopRkTw8PDw8PBYd/BVE/Dw8PDw\n8KgDXqF5eHh4eBwIeIXm4eHh4XEg4BWah4eHh8eBgFdoHh4eHh4HAsGqCUzDyZPbS3PBPPfcLZw6\ntbes6lYKf68HF4fpfg/TvT7iEcfYqjmsA/wMzSAIxKopLA3+Xg8uDtP9HqZ79SgHr9A8PDw8PA4E\nWm1yPGj4+3++b+K1Z3zPo5fIxMPDw+PgwSu0lmCSsvOKzsPDw6McvMnRw8PDw+NAwCs0Dw8PD48D\nAa/QPDw8PDwOBLxC8/Dw8PA4EPAKzcPDw8PjQMArNA8PDw+PAwGv0Dw8PDw8DgS8QvPw8PDwOBDw\nCs3Dw8PD40DAKzQPDw8PjwMBr9A8PDw8PA4EvELz8PDw8DgQ8ArNw8PDw+NAwCs0Dw8PD48DAX98\nTMvhj5Xx8PDwKAc/Q/Pw8PDwOBDwCs3Dw8PD40DAKzQPDw8PjwMBr9A8PDw8PA4EvFNIA5jkyOHh\n4eHh0Rz8DM3Dw8PD40DAKzQPDw8PjwMBr9A8PDw8PA4EvELz8PDw8DgQ8ArNw8PDw+NAwCs0Dw8P\nD48DAa/QPDw8PDwOBLxC8/Dw8PA4EPAbq9cU0zZv+0j8Hh4ehxF+hubh4eHhcSDgFZqHh4eHx4GA\nV2geHh4eHgcCXqF5eHh4eBwIeIXm4eHh4XEg4BWah4eHh8eBgFdoHh4eHh4HAl6heXh4eHgcCPiN\n1XOizadST+LmN1x7eHgcZPgZmoeHh4fHgYBXaB4eHh4eBwLe5HiIYE2Rx45uYHunn7nmzZEeHh7r\nDj9D8/Dw8PA4EPAKzcPDw8PjQMArNA8PDw+PAwG/huYBYL5tCH7dzcPDo03wCs3Dw8OjJZg0sPzJ\nZz1xyUzWE16hecwNv4Hbw8OjTfAKbQbaHBHEw8PDw2MEr9A8lgo/q/Pw8GgKXqF51I55ZrXT8nhl\n5+HhUQZeoUF/TIuiZ3i0A4uYfcs+V680PTzWH4dKofn1MI9JOCh9oy0Ds2kDhLraepn36gc86wFG\nRKvm4OHh4eHhsTB8pBAPDw8PjwMBr9A8PDw8PA4EvELz8PDw8DgQ8ArNw8PDw+NAwCs0Dw8PD48D\nAa/QPDw8PDwOBLxC8/Dw8PA4EFhoY3UURT8A4Ld6vd4zcvKfAPAGAAmAW3q93geiKNoE8BEAFwLY\nBvCzvV7v5CL1e3h4eHh4WMw9Q4ui6DUAfh/ARk4eAvhtAM8G8MMAXh5F0SMB/O8Avtjr9Z4O4I8A\nvH7euj08PDw8PPJYxOT4rwD+twL5kwDc3ev1TvV6vSGAzwD4IQBXAfikSfPXAH5kgbo9PDw8PDwy\nmNvk2Ov1bo2i6D8WXDoO4Izz720AJ3JyK5sFH5frAEERAQRwzhYuR0oCY0Ag/DKwx6FA6ZcmSSQF\ngail0k/+wzdqKadO/Ocf/I8T26KJ4MRnARxz/n0MwOmc3MqmYplxJhljS61vlVjFvRIRYqOEQraY\nEmIAAsHScqemPUTPFThc93vY7rUsTp3aq63eNgS6roImhrdfAfAdURSdF0VRB9rc+A8APgvgapPm\nOQD+Z5nC3Adpf1eRlc1TV311y9rAoQ7+MH/5ku/JxWFu/7bxqoO/izZwLeJXd9ke01HbDC2Kop8B\ncLTX6/3XKIp+DcD/A60wb+n1evdFUfS7AD4URdFnAAwB/ExddU/Cuo/ePP/VgojW+mPi+XscNrT6\n+BhaIjnGDpf5YqUmxyWuex2m5wocrvs9ZPdaWrOfPLldW6O08ZzAn3zWEye2RatX1NtkPlhXkw4A\nxFJBqvE+vkz+jDF0Ag7BWeW8ACAVYRhLUC7dorxiqZBI1ei9T5M1ZZJqsv+sU/9ftkmwSa4es7E2\nJ1YvcyRWVFdZWdW0TSBfF2cM2mGUTU03TV4Hf8ZYqRFUUV0MAOMscweTOCmlP8CB4OkHYVJazhhQ\n87Npov8sE030n2Vind7VIqy6/nXG2ii0ItgH73aARWTLxrL461lR/SO9ZbY/5wy85D1IRSiYkI6B\niMbapq39pyqHtvWfuvuKXV9rW/u3tf8cFrTa5JhfFLYduAmTTpX66pbVwX+esteB/zyyScpsXfjP\ny7UJ/nXfZ538XbSx/avmKcPBYzpaP0NbxHyzqEmkqjmibq6LmkkmySa9IOvCfxLsNWsgm5Vu3rqa\n5t90XXVwrbvcg8i/qTI9JqP1Cs3FMl6YeWRt4LCIrM6yFVHhtJ+IQAS4unRSeQTMXCubxl8IhkQS\nFBGEU2Eb2rpINm85y/qIFnGdxf/OO+/EjTfeCCEEnva0p+G6664rTPeHf/iHePDBB/GqV70KAPDF\nL34Rb3/720FEuOCCC3DTTTeh2+3WNggt4r+3t4ef+7mfw1vf+lY8/vGPz1z/5je/ide85jUAgBMn\nTuCd73wnNjc3S9X31re+FbfffjuOHDkCAHj/+9+P7e1tvO51r0OSJCAivOUtb0nrnFaen6WVQ6tN\njouaK5YhawOHqjL32rQ8RMAw0Q4WZcqOE4VEUmF9tpxZvIaJgpqRblb7C84RCmacGcqVsyrZvOXE\niUI8oa3bwP9Nb3oT3vWud+FjH/sY/uVf/gVf+cpXMun6/T5e/epX42Mf+1iaj4hwww034MYbb8Qf\n//Ef4+lPfzruu+++xvgDwJe+9CVce+21uPfeewvzfOhDH8LVV1+Nj370o7j00ktx6623lq7vy1/+\nMj74wQ/iIx/5CD784Q/j+PHjeM973oMXvehF+MhHPoJXvOIV+O3f/u3SXD1mY21maNNGQmVHkLNk\nZeqaJZsnf5v5B4KBgUEpraw4Z1BECAUf4yA4g3RkRIREERj03jOVkRGk1LMpIoJSOi5jILjWpAbK\nuOt3Qj72ck/j735sZ93/qtr61ltvxac+9Sns7u7i1KlT+OVf/mX86I/+KL7whS/g3e9+N4QQeOxj\nH4s3v/nNGAwGeP3rX4/t7W088MADeOELX4gX/NRP48UvfjHOP/98nDlzBjfccANe97rXQQgBIsI7\n3/lOXHzxxXjb296GO+64AwDw4z/+43jJS16C66+/HmEY4r777sPJkyfxtre9DZdffjme+cxn4nGP\nexwuvfRSvPa1r025vvzlL8feng6pxBjDE57wBLzxjW8cuycA2N7exnA4xCWXXAIiwlVXXYXPfe5z\neNKTnpSmGQwGuOaaa/DUpz4VX//61wEAX//613HOOefgQx/6EL761a/iGc94Bh7/+MfjgQcewNve\n9jbcfPPNmXquvvpqXHHFFbj77rtx4sQJ3Hzzzdjc3Ezb+t3vfjfuuOOOTNt/8IMfRLfbTf89HA7x\nvve9D7/xG79R+Kye+MQn4v777wcRYWdnBxdffDEA4JOf/CT+4A/+AEIIXHHFFekM0+aVUuKee+7B\nG97wBjz44IN4/vOfj+c973m4/vrrcfTo0TRNp9Mp1Vc8yqHVCm3ZduVVmZ/qwiL1FaVjDLCO8rHU\nykgqYFJs4bwnoiKtm7T7PCAYQyIViIBEAgABSqch0vkZQ8Yu2R9KcIbSyikvK6sEq6KuPrC/v49b\nbrkFDz/8MF7wghfgmc98Jm644QZ87GMfw/nnn4/3vOc9uO2223DZZZfh6quvxrOf/Wzcf//9eMlL\nXoKf+RkdbOfHfuzH8KxnPQsf/ehH8d3f/d149atfjdtvvx3b29u46667cN999+FP//RPkSQJXvSi\nF+EHfuAHQER41KMehbe85S34+Mc/jo9//OO47LLL8K1vfQu33norzj333AzX3/u93yvdHjs7Ozh6\n9GgqO3LkSDoDsrITJ07gqquuwic+8Yk03+nTp3HnnXfihhtuwCWXXIJf+qVfwuWXX44rr7xyTJkR\nEfr9Pn7iJ34CT3nKU3DTTTfhT/7kT/Cyl70sTfOrv/qrM7l+3/d939TndNFFF+Hmm2/GX/7lX2I4\nHOK6667D6dOn8d73vhd//ud/js3NTbzmNa/BZz/7WTztaU9L8+7t7eHaa6/FS1/6Ukgp8bM/+7O4\n/PLLEUURAOBf//Vf8Y53vAPve9/7CnlNk3lMRqsVGjDy9HF/V5EBKJWnrvrqlpXlX0U2z30SAbAy\nPrJUT8s7SjMuM1fM/RWnS5VRzgRT5d6Lnu2q298t+ylPeQqEELjgggtw/PhxPPDAAzh58iRe+cpX\ngogwGAzw1Kc+FT/8wz+MP/qjP8Lf/u3f4ujRo4jjOC3vcY97HBhjeP7zn4/f//3fxy/+4i/i2LFj\neOUrX4mvfe1ruOKKK8A5RxiGePKTn4yvfe1rAIDv+q7vAgBcfPHFuPPOOwEA5557bqrMXK52hmZl\nl156aTpDY4zhwx/+MP7mb/4GRIS3v/3t2N3dTa/t7u7i2LFjM/vjOeecg0suuQSXXnopiAg/9EM/\nhC996Uu48sorC9swCAI85SlPAaAV06c//elMune/+924/fbbM7JbbrkFYRgW97OCvnLTTTfhxhtv\nxNOf/nR8+tOfxvXXX4/rrrsODz/8MF7+8peDMYadnR3ce++9eP3rX4977rkH5513Hm6++Wa8+MUv\nxtbWFogIV155Je666y5EUYQvfOELePOb34x3vOMd6fpZmb7iMRutV2h1m4Oq5ClbX92yefhXkeU/\n9mXyMmiHj1FeNjFvju34ltxMnsnl1CHLVtuO9nf/fvnLXwYR4cEHH8TOzg4uuugiXHTRRfid3/kd\nHDt2DH/3d3+Hra0t3HLLLfie7/kevPCFL8TnP/95fPrTn07L5Fybfz/1qU/hiiuuwHXXXYe/+Iu/\nwAc+8AE8+9nPxic+8Qm87GUvQxzHuPPOO3HNNdcAKJ71cmew4nKdNkMjIlx77bW49tprU1kYhvi3\nf/s3PPaxj8VnPvMZ/Mqv/MrMtn7MYx6Dvb093HPPPbjkkkvwT//0T3je855XmBYAkiTBXXfdhSc+\n8Ym4/fbbU0VoMWmGlucw7dkfP34cx47pQ0Ie8YhH4MyZM3j0ox+Niy++GLfccgs6nQ5uvfVWPOlJ\nT8JP//RPA9Dtevfdd+OVr3wlbrvtNiilcMcdd+Caa67B5z//edx44434wAc+gEc/+tFj9U3qK16p\nlUPrFdo8qPJxaiPayF8IBpJWsWmdpIjSUFYu0o8jAyQY4kSiE4g0vSJAcIJUdnQOANocmT/fLAwY\n4mTcQ3ISiHT9i5y5tsz2P3nyJF760pdie3sbb3zjGyGEwG/+5m/iFa94BZRSOHr0KH7rt34LgPaa\n+6u/+iscP34cQggMh8MMr8svvxzXX389fvd3fxdSSrz2ta/FZZddhn/8x3/EC17wAsRxjOc85zm4\n7LLLGrkXF29605vw67/+65BS4mlPexqe/OQn4/Tp07jhhhvw3ve+N03n8u90OnjrW9+KV73qVSAi\nfO/3fi+e8YxnpGt8ebMjAHzgAx/At771LVx88cVTFVgVuDxf//rX47/8l/8CKSUA4A1veAPOO+88\nvPSlL8WLX/xiKKXw6Ec/Gs95znMy9/SEJzwBz33uc/FTP/VTCIIA11xzDb7jO74Dr371qxHHMa6/\n/noAwOMe9zi85S1vqYW3B9odnBgA1W3mmSSb17w0T542yarwV0qBc546iBCATsCn5h0mKq1DcA6r\nrxhjGMQyTRcKljozTKq3DP9EKiga8cpfb1P733bbbfja176GV73qVel9MsZWzqtt/V9KiZtuugmv\nfe1rM+me+cxn4q//+q9Tx4qqdbSlDUvKSo/QDnNw4lbP0Fxla3+3XdYGDrNk0zhPK8d94QKhvR2n\n5R3JCd1QYJgokATCQCunbiggFaVnpM2qt8x9Cs7BnOvuR7fONqxbliQSkoBOMLkdysjy15Z9T02U\nrZTCz//8z68F1ybb1WM2Wj1DoyWSy380DzKWda9SEaQihIF2xY8lQTBA+ONjMiDTNgxa2S+Cdbjf\nunDI7tXP0AzW9vgYILtwbX9XkZXNU1d9dcvawGFeWfpvLbQXV8Jh3vJW3YaHuf/M4u+iDVyL+NVd\ntsd0tNrkCCzPJNJUfW00kzBW3ctxXq4AdFzFFphq2tL+E8smApbg9bnqPlwXfxer5tV0W3ulVg6t\nnqEt+yHOmrHVIWsSi3Bogr/eEA0oqZ0dBEO67mahiDIhsYhQGPpqHq5tbf+xGSxjOvJKibxN4rD0\n/3llRMgcBls3JrVXgf72mIBWKzQXyzAV5K+VkVXNfxD5A6PRZN5cFAqOIBAAgCAQCM36mU1HRCZ6\niM4fS1UYKf8gtr8Lzlm6frYI/6L62t5/Vtn+VfLn++ay+McNKtGDhlabHNtkPjhIJp1pnKuWTaRj\nMxJV99Aj0qG0GPRLLM2L6wYVXrT9XcW5yH3WLSPKOoIs49ketP6/qOm8ap5OwDMWhmW9q50FHYUO\nE9aqpZZhEplH1gYOi8gWLYcoG9+x/AhZy6zXoySAMf3fMvmvQma/WYJXn+W0QdY2DovkrcKB5+Rt\nunePNVBoyzKJLFL3PLzKypb5chxE/mXTLZ0/Y1qrzTEQaAP/ZX3I15l/U2V6TEarTY569L8ck8ik\ndEUcFpE1xb+KWaYsr+r8WSX+MCsS5OZRBIjq/CfJXLSp/UEKMLPbg9B/VsHfRRv513HPloNXbuXQ\n+hlaHu6DLRpt1SFrEm3lT9AbofNeiHnk62OMpY4e7otXhitjLHP+WSgYwFihJ5kiqsXDrC3tz5n2\n+sSM9s5jFoey6VY1I2iyrT1/j7VRaMt82MsyiTSFefkrZYMAj2ZaVsEVzXbsaJJzZs48q36PwuQd\n8SnmSqQVrvv5X/f2DwKReoBWze+2/yJY1CS26vZftP514e9RDq02OTZtPli2maEt/Is4M4zCLtmP\nZd570ZZNpD30OCv20JuXKwB0AlHIX3AGwcXU9i26Z1c5t6X9F+0/09ofKDbVt4n/smXzcG0bf49y\naP0MrYkRVNm0dZukptW/KP9psnn5E2HMqwvQx8eAskfHtJH/ovUvmr+p/rNO7d/EDOQw8/eYjtYr\ntEUwySSyLmgz/zLjxjbzL4M28z9o7T/pg77O/KfJPZpBq02OQL0eQ9OuN1XfsvgvajqZnpdlZMys\ncykiMKrGr652qFJf3eWtug+sU/s32f9drJpX023tFWM5tHqGVpepoElZGzhUlbnXrJwAJJKglH55\npHmv7MnPbjmcMQScgXOGROlDPGOp0rxF9SWKkMjRy7oIf8tVmvoSSYgTVbmcpmRSaT5Es82h89Tn\ntn8+XV11lJE1WbbnP87VYzZardA8lg9yfjCGzDqNC85N1ATKZ8xCe05SORvZAiAgE+R41aCGbzht\nfw8PjxStNjm2yXxwkEw6RZwZgECMTIv6NxtLmy97WjpF2lMy4Cwtuw7+ea6CA0pq5Sl4Np5kOgNd\nYlvP65FZh2wZdbShD9tnu878q3L1mI3Wz9CWZRKsq766ZW3gMK/Mvos8F69wVaaaw9b+B52/izZw\nLeJXd9ke0zH3DC2KIg7g/QCeDGAA4Bd6vd7d5tr3AHi3k/xKANcA+EcAXwXwJSO/rdfrvWdeDh4e\nTWLdF+M9f4/DhkVMjtcA2Oj1ej8YRdGVAN4F4LkA0Ov1/hnAMwAgiqKfBHBfr9f7ZBRFPwLgj3u9\n3v9RtpJlmUmaqq+NZh7G6omxR/ofE9PZb5FU2ixYZzvknx1j9vBQVnh9njqa4LpufaXN/F2smmvT\n7e8VezksYnK8CsAnAaDX630ewPfnE0RRdATAmwH8n0Z0BYAroij6dBRFfxZF0cXTKmiT+eAgmXTc\na/nriVQYGo/BaeUkiUo9CxUBsZRjXo6c6bUz61iiiBAnUrub19z+oeDputq897QKWZPPdh35r7tJ\nsEmuHrOxyAztOIAzzr9lFEVBr9dLHNnPA/izXq/3oPn3XQBu7/V6/28URS8C8F4Az59WSZs61bq/\nFGX4M8bAHQ89xnSwYM6yLvyMMzBnNMkZhy3SLU+4LyQRGOdgKFY8RNrdPQx4RpZINRYrsui64Hzs\neso3d091tqHvP6vhUAeXVfJvSqmde+5WYYzQeXDs6EYt5SwLiyi0swCOOf/mOWUGAC9CVmH9HYA9\n8/s2AG+ZVcm4aWk8/l8dcD+Qs+qrW1YX6uClZ1OjF0gqpd3hOcAom06YdDpLcfu54IylB4EWpRsM\nJQhA6Fx395eNTJkj/olUsN76RfcEIMN1FsdFsIy+Mqv/LNK/2sB/Eb7rxj+PafVVUWqnTu3NTlQS\n2zv92spaBhYxOX4WwNUAYNbQvuhejKLoBIBur9e71xH/PoDnmd//CcDt0yrIP8iihztrlFNltFe2\nvrpldfBftL5JeW27cNY8f0UFvJDqykKu7vs/if887TEP/8PSf9rC30Ub+Ze5v6r1eUzHIjO02wA8\nK4qiz0EP6V8WRdGvAbi71+v9NwDfCeAbuTzXA7gliqJfBrAL4BdmVTJtAXge2TT5vOmqltEE/yr5\nq4Bo/AOyTvybqL8p/nX3Fc9/tfybKtNjMlibG43mJDdtdF4lz6owD/9Fy58EIn1UCcPoeJlZ6Tmf\nfaRJEQaxhFLARkekszJrUuxMqFsf/Kk3eBdFzpin3aq1T3YGuWqMZq7t6MvzoGz7t+mdddEEL1Zh\nmnby5HZtlf/9P99XV1G14Sef9cSJbdHqjdVNTt2rlDdNVlc5y+TvXit1fzSKwzit7DhRiCVV4q+I\nMIglBrEEAGx0eCojAgLBEYrJG7MF19d5TW1Ttq0BYJioTLitNvQfoNh0Xmcdq+j/TfBvquwm+HuU\nQ6tDX7moOk13rxXJ5i13lmye/FIRpFIIBW8Ff6WUnvUEHAyAEByA9kAMAg6QCQycXtMQJlhxnKjU\nhT4x6bRyGskE56mDSCB0Pdadn0E7nbjejdP42w/rvO00q60nlRuI8ZnoPPUvmn9W+rb3/3nbfxVc\ni2TL4O9RDq2eoTXZAZbxcpeREWm3c4ZqI7G628ZNlygCgVJGgjMwbhQO9L4zRQDnPJOXc5ZRTIq0\nItN/TRR/cwq2HXhypvepcc4QGOVoZ1s6T733XufHgrNs8OZV9al50Jb+Py8OM3+PyWi1QgOWZxKp\nq775ZeMcmjLpzJLpd2hc5uZxZ0eZdBg/5TpvgrGlz+RQs6mmLSa1ZcrawKEp/i7awLWIX91le0xH\n602OTUzdp4165jEf1Gd6GFcEZflX4ZA34eXTMdgwUsUywL5kI86Z8rLExl/IElwZA0gt3tbZauvt\nP8vuK57/7LRt4l8nV6/UyqH1M7RZaIP5YFFwBrhHeTXNf/SiFF8PjBOGq8CEkUml0rWvWCoQUcYx\nIj3WBaMN11b1EYyJjrHMhuki2HRNn3G2bn0lj4PA3/YNV1aUro1Y9/Y/aGi1QmuT+aBJk04YCIQT\n4hA2ISNoD71JMRW58Rx0Q0nZ39nNz8x4I1ImnfU6ZIwhFAydUGRklsM0rjavXVc7jCa1RUxS68Sf\nCIjj8VigTfNvsuwmuHrMRqtNjm0wicxj4lrEpDArHZHeFyaY9jCcp14Gva/LlleUp8gs2Ql4OmMK\nhXavF5xDKlWY13KlJEF/KHFsKwRnDGHAoaSayTVbjkrrrdL+Zdu1LbJFy6m7vGXwZyCEgQBYtbxF\nfbRprqtsV4/ZaPUMzWMcWqFQxl2+KqaN7GdBpAGKR7/dmZwLay3sDyQYRnvFGFCJP5H+T/jR6oGE\nnumhop+vh8c4Wq/QlmUSqau+umXFXFfPq4zMgqAVYN7MWLocxrRGW4DDvPe06jZsg0mwrfxdtIFr\nEb+6y/aYjlabHIHlmUSaqq8p0wNp4VzlMFbPAZ9luWp9NNrXVr0cApgOVLyIqaYNJsFVy9rAoS7+\nLlbNq+m29kqtHFo9Q2vDQ5w1i6sqWxTCbl6W070EXRBlXe5dud7oTJl1MIuxmRbZ2IqEguKy5Uob\noR/Y7AgQdGgs5bji2/qngTGWHjtjX/BVtn9VtK3/VIXnvzy0gcO6o9UKzcWqzAf5a3lZ1ZdjXl52\nlMaYdqqwB/hNy6uVBhn3+jFKUKRd7oeJgqvPJvEfJlKfTj3FQ5IxhtgoPUA7cXRCgc1uoJWaHOXN\n85rW/mEgUo9HN/2y2n9e2SxOdfMvKmOd+Bf14UXuaRqnKmlX3Vc8yqHVJsc2mQ9WadKRUiFRhBCj\nUFCz8mpFpmMiao9GjEFw60qPdOY0qexEaqUXBkzHc5zCIRQMsdT1dwJNuBNor0jORkopz6uJ9s9/\nGNvUV5roP3WXt8r+b/sw54SAj3v0Lmo6b7IdmmhXj9lYmxkaUL/5oEnTQ5312QC/+aTT8lpTouDM\njKQn8dR/OWc5efbfdiO03ThdhoNbJGPjx7sU8Wpj+zchm4U2cV0Vf+3Qq5VZWQ5t4t+kzKMYrVdo\ni3aERTpI3aafeWTz5idaHX9yZE293GX5F2EZ7T9L1vb+M0u2DP6kO3GtZS6Tf1NlekxGq02Oi5oU\nqpgZJqUr4lBWtihX+5cBIFTMw7RSIy1cmD9ngDkSbXZbmt+KJm/cLitbtP1drMKk1ob+s678menE\n+p/zPdtV8q+jHMvLK7dyaP0MLY9ZI5myI7BljIjmGYkVcQ2DcZPLrHL0+ph+KZSiuWIipqYfk1dw\ns54nKZUpIkjH49LOCjizaVUa5cMtLy7w0mxr+wMjB5qqZS+Cukb369r/ORs3W1ctexHU3dbL5n8Y\nsTYKrakO0DaTziSOoRgpNXJmPqmSyMkY02eMgQiJ8yF2002rz9ajFGmPRTZyBkmMdyJjDIkkSBof\nNesy9PV8dfZMNIvivMWc8rJlmXRkwX0sWtcy+U9CG/jThD7JmI7lmV/fXaSuOvMvo/2JqHDLjUcx\nWq3Q6jRuTuAOAAAgAElEQVQfNGV6WJb5xsoUac8vqbIyO2vKyxIFgLRziFImneE9TPQMahL/QSwx\njPWp0ZwBiSRwzrHRERCCIUmkzYBYUoar4AzdkIOZUbZ7T2HA02DMw0SlCret7Q8AnVDf8zzlLZM/\nUGyqb2v/B7TDUZLrP/PyqsK/zP3N0151yhI5ahuP2Wi1QgNWOzWvaj4oY7qaJCsL5XgvujIg66ko\nHSVh5dK8KJyx9DxqzieF1wKUArg9DoYs91G6dE0NWdNQnkN+/5ity5bpRuHPp8nzWsSkU+baNEzL\n1RT/ZfX/VfIn6H61CNap/avMABs+PenAofUKrSwWNYmsGkvhP/ZylH9bZqX07b9aeP6rRRWTpkdz\naL1Cm9c8YP+WzVNXfXXL8tft+5FZM4OVjdLZB+uO8mxeIoCZ06aJJnNgcGZ/zPBx0rnhqFQB/xEv\nKrw/qyancVhU5qLJ/tNWWRs4lJEV9Z9Z/F2smv8kfouW49VhNbRaodVlKmhS1nR9UlK6qZkxfeim\njfCRygRPvRrzMn1Qp74gODMbrXWaUPC0HCK9ljGMtVciYwzdrkg3UgdCR/UYDCWGsTQHhFpTZJaP\nVIREKvC0Pn1NESFJ9CnXtu3CgGd4V2mjutt62bImyl5GHXWWM+oDrHLeNvBvWhYGPLO84DEdrd6H\n5gFQZgeahlUS7miuqMszGOXGRi+J/e2urdmRsHb6ABhpOWcMzBzkmfIhpLM0bhQrmbqU0vndAXSe\nKyFrvuSMgeYcVq27OWcZ/O0zaQJ18eeMgbV6aL066EHsqlmsD1qt0NpkPlimmcH96zpUTEonlYJU\nQMCMgsjIspHqXWTLIAiuvfnc61bRAdpk2Q0FCHrWyBkgTNxG66koYMNjsbF6OGPgARuru852y1+3\nH91V94tl9R/3miL9XAT0wGId+Fcyx7HF7mmZXBeVeZRD63X/skyCddVXt6xMHtvnXW9BlcrK1UcA\nuDOUT8s2FYzMhKP6RC7Gnp21zdP+TZqVFilv1fwXkY02xLNW8aqr/V20gWsRv7rL9piO1is0j3bi\nMLxifnS8Wvj296iK1iu0Rafu85hqFqmvioxq4m/XwuweNQAQ6Uyt2MMwf+8MUzwVnZEykT64E4yN\nlc0Yy3Co0v7LMNUcZJNUkSzdf6hm94E2yspcbwvXZfUfj+lotUJrk/mgLpMUkT7kcpjIjPfiIhw4\nYwgESz9gjOnf1kNxEKu0Lhcu/zDgCARDIhWGiY0eoo+u4UyfXQYAsdSmx0CMPBg7Jm/geFS2tf3b\nJmvKJOX2iyafSRvacF5ZGzhU4eoxG61WaG3CpFHhrFleETgbHay5CJ9hLCGlgpQqdXvWcRYprYex\nkau+m1cf2KkyXJUiMLDUnCgVYTCU6Us1jKXZv4a0vmEsoUiH3ZoU8cPWt8hIs2z764DIcu56FoF9\nJkVcEykhlRpLP0//mQT9TLN5Jz2Tqqiz/68CkzitC3+Pcmi1l6OLZZgZptW1KFITHrPmQDZ2rQrX\nwVAaxw+VOnPEJmiwC4Zxr8NholKXfltuLPUmziBgENDeY7v9ON1LttdPkEjCkY2RF+QwlpAKoESl\ns4AirkW8mmh/RTpQspigVCfJ6uo/g6EsjKhCRJAKC+0nmsVfB5EGOPSgpK39v0g2b/szNh7HclJd\ni2Ldvz+HBa2eodlOa2E7cBMmkSr1LSIrw6UMfzsQJ2glqetDZiY2vezZ6YhGH+FEkalnlM6dcEzj\nT4SME8nk+hZra90g5LRH9sPQZP+xz6SIl433wFDPfRZxIej+y9n8XqbL6P91tr+LNvIvc39V6/OY\njrlnaFEUcQDvB/BkAAMAv9Dr9e52rr8HwFUAto3ouQBCAB8DsAngmwBe1uv19qbVU3YEU2WkU3YE\nVMdIaVn8GxvpmSLY6OeoXEeoZeMDhMIim+Rf4uVfp/avUm7+zteJ/7q3fxNc/UytOhaZoV0DYKPX\n6/0ggOsBvCt3/QoAP9rr9Z5h/jsD4A0APtbr9Z4O4E4Ar6hSYd0PfZ6OVdWkUKbsee7BOnwwxnLx\nFrPpMqdGw47iURjFO7/GEwY8dSbZ6AgQ6VBc6XWz6ZsBUw8QZczWnZVXbX/C9LZ21/6W8dHI5w0E\nG1vD0ry0TFJ1r89ZXK3Mep5WOci1Lf2/TqwTf6/Y6sciCu0qAJ8EgF6v93kA328vmNnbdwD4r1EU\nfTaKop/L5wHw1wB+ZFoFTU7d5zH/FckWLWeYqLGTkMvw74QC3Q5PPQwBHVUkFCNOQ+ecKamMw0Iu\nHWMM/YFMFZU9Zw0AjmwEOLYVpvUd3wrBGFLOQcDR7XAIoc89c89js2XEiV4/Cx0vzHna2uU/qf0Z\n07ErU0W75P4TmvbIp2PMeILmvA3r6D/5e7cRQdal/xfJlsW/znZoij+A1OvYYzYWcQo5DuCM828Z\nRVHQ6/USAEcAvBfAzdDRkP5HFEX/lMuzDeDErEqa7nyLyhYtJxAcilTh9Vl5Bc9+uG2oI6akKXs0\nY7DKhkHPzuJEQXAt64QcidQHeUpFiEkiDLTzhxAMcaI9HQPBoRQhEEgdDwTXszgpgVBk1yEZYxCG\nw6JtzRghEDydhc36wLqo2q6LyETFvHVyyN/7OvT/RWR1cFkl/zIyIio8T3Aazj13C0EgZicsgWNH\nN2opZ1lYRKGdBXDM+Tc3ygwA9gC8x66PRVH0d9BrbTbPvvl7eloFy5xq21HUssEZwE1k1kXrjxMF\nEIEYSyPyc2E2QGPk4DEYWrd2SvevdbjQm6KRjftnvecCbpUVHMd+QClllGP2JRzdH3MOCZ3//riu\nuHI5q3quq8Jhut/Dcq9VnWNPnZrqllAJ2zv92spaBhYxOX4WwNUAEEXRlQC+6Fz7TgCfjaJIRFEU\nQpsa73DzAHgOgP85q5K6Rq3LGO01OeouPeJ0XvLRdQYYX7vxUbybF+lClysjyubNlFEz/yZmEIuU\nt2r+y+4/bZM1+WybljVRtsd0LDJDuw3As6Io+hz0p/BlURT9GoC7e73ef4ui6MMAPg8gBvBHvV7v\ny1EU/V8APhRF0S8CeBDAz8yqZNbibVG6abJp8jL11S2ri79bNsunIwKMdJTXyMhNB4Axo9cozWpf\nqCL+6atWQHVe/nXKZtVRJv0q+a+i/3j+9fCvknZWfV6plQNr85SdlkjuIJgvlDJraND6pRPoNTHO\nkDqHWM9Fe/YZZ/qARUC/OIkkgGkPRmX2nsVSl5E9ykav2QnO0g3Wm93qdnv3ZbW/XZk+1mb+l7np\n59q2j81B6MdlccjutXQnO3lyu7ZG+ft/vq+uomrDTz7riRPbotUbq9tkPlgHk44w3othoP9ab0Rm\nlJbrDQlklZm9l8B4CQ4TBWk+1qFgaR5bXyJH3pndToCNDp/Ia5LpRPNDJp09CXt0PW8+bUf7T+Jf\ntbymTFKHsf+3wSTYJFeP2Wh16KtFzQJ2xqEPouRLMUdU4cXMrMdNJ5WePbnu9/Z6nEgQ6VlWUR1S\nKjNDG83GpInXKJU+8FFJHd6qG3IkilKXYNeNHxjN7oDsS5UkEpLMDK7AJFKlvTpB/jRsfd+x1KGc\nLP9F2n8eXovwX7SORcupu7y6+CulEE/o1/PWl5+hLbutl92uHrPR6hnaolCkTW+8ZWeYW16Cj/NK\n5OgwTRdEJlbflAFbYjYUE/TRIQxAwDnI1CklQBh3A55kNsub+oh0rER9aOhisQltfTw3GrWvr8u/\njSji7zEZk/q1h0edaOfXwkEd03RWIk8d9VXhZUdeRem4I0vlzt9Z9eXLRiZwlVMeZT8yrTBJoV4O\nLg6bSa1N/KkB/i7acp9Nl+0xHa02OQL1TNNJC6fmqaO+KrzSFz2XjgEZU56TeYH6CFappTKijFKr\nUp4igkAx/zL3PjUP5r/PWaaaNpgEVy1bFYdJ/XoR/i5W3a5Nt7VXauXQ6hnaog+RM/MiyflDx8ya\nxVWVpbzYeOxEQEf34Gzce4sxZmIwZuX2LLLsWs4o5JTOZ0d6+t/DWIFAmbiDcUEbWf6JVOgPE8BE\nB5FSr8klC7Rrnr8FZ3qOZstuov2XiXXmT6TXZfOYh/+kft001rn9LZbcZGuNVis0F/OaK8KAp2Fg\nFpniT5JNS0vO7GeMl+BpeCm3DM45woCnZ5y51wMxHg8Q0MoofyK1sutppn6rRBkjKFIYxlmFQZTl\n6354hrFCf6hP2QYAUoTY8UYs0675UWaev3ud8xGnovSurOrHadnmp2mcJmER/kVlzDKLFfVRQD8X\nWfCM3TLK3uu0fr3K9l+H/lM02PQoRqtNjm0yH8xjZkik/uh3ArZw2URknD6y5XHG0AlFatLhjJsI\n+8AgVggDHQZLkVZyg1hhsytM9HwCoE+zHibaC83UCAAIoA8CFYJhkwt0Qx0eiwWjQ0LL8LfelyG0\nZ6d73eVvZYIzcC5yG7znM/NMMu2uWkY0OlTV9VpdtOz8tVkcEklmz+J4H3W9OFdhZpslswOlectb\nJtd5ZYB+Dh7lsFYtVbf5oGnTQ94rcaH6WPbATTedldjDHTlj2lRE1qNxZDoECN1wNDNkLPsiZWd1\no0MrO6GOIs/56HDRQPBS/O1m73zSPP9ZsipoU18pktlv1iRP0eX0YZaJ8VmUzj0wtApW9Q7W9f62\nqa/M+/05jGi9Qlu0IzT1cpQ1dWQ/zbPLzcvmvX89+TKzE/N//RGtaqopngE0zX+WrHz7l+daJGvs\n46QbFmDVTWVt4L+Iqe+w8G+qTI/JaLXJEWjWJDivqabI1DHR/JF6GC5oesjNombl4ZxBSavENIdx\nWXFeZj+2JhljLHO4JjNpNJfZ7cbmvOc62t9Fk/2nKn+QSmfddZjP5uE/rQ/M4l+3+W8+/iiVZ1X8\n6yon7TMeM9HqGdo8I5myI7CqZSuq5tXHmHb8yH/M0/KMY4UuG6nX4CTvPluCVNrDMDahp1xPSTdP\nIBgEz9bdDbmJAKKgTDk2X+BECuFaqJ01YBSSk9Y6bdjFasvfffFcLmHAwXKmtWWMUlfdf6TzjPPg\njEHozlEr/yLZJP6MZfvIQWv/SbKyWHf+hxGtVmgumnrYZcsl+9HOpZuWn3OWrjMVfezcspRSJjxV\nMU97ojSDdrLQfBSIRrM/98PEmHa24JxBSh3gNwy0Mwhjel3L5cqYdpdn0GHC0nuWSt+H8cjM12Nl\nmksx91S5O21ARMX77XLlzvrYumlVxQ9z0/1HOc+4KF0QiMKDGJfJPxBiLHLMKk2CVbHuJkGvxOpF\nq02O85oK6pYBeuFccJGRVTUzuGVrzzYz4wGBCY5YKuNeP75fpxMKKMoeDcO5SD/kiSQEfDxmpa0L\n0Ep0GOvDOPU9jdJqRcZwdjeGEAzdgCMQIzdrmy5OlPOR1n+VieXFOSvdrtYDFMbzMRTZvOk9CYzt\nXypq39go+by3nqvwlt1/7DPOc62j/0ySAeP9p47+vyz+Tb2/dZgEV8nfoxxaP0Nb5Qimqvlglmz8\n2kimSM+IxJS4k25Jbrl2YzKfYNazf605k3JpR9d1OYHZtMb5+Ajcvl5ElMZZzJdXBnYmSkSFnnTW\nHJq/NqldicbjQk5CE/1n8gymuf5TJ6b3U89/Vl2Loix/j+lovUIri0VNIm1E7fwbHOyte/t7/qvF\nQeQ/Sd5G/gcFrVdoi5g/3DWYWXnqqm9eGYMxFSmqzN8Y1UA0PZ2eRenfbrip1Kxq3jNZcC3/mzFm\nNnCb8iq2v32ntYmlgKuTtmwbKlJjMhdN9p+2ytrAoSn+LtrAtYhf3WV7TEerFVpdpoImZekaDbSj\nhVKTo9db78SicjjXHmeMM8SJQhxnvePiRKE/lBgMpb6eaI9IG4KKG/MWMPKuI9K84kRhGEvzYjAo\npeVSqRF/0mbAbsixEYrMhnCpVOpVCWQVH2M6vJjtSGXbMBTcnILNwBgVtgeANHpJUXnuM9CHl7LM\nPVVp/1XImih7GXW07R08yPyB7ADTYzpardDWDkRTrXqzBlqCc+MAMW4dtHm1IqLMX0Xai3GknMxh\nnkRQ5sBQqbJl6vLYWB1CcHDjwk+kAxGDAFJk1thIp3Gycsamrv0VQSshPjESBWNs6tlvNg3grCGy\n8XsCkLZFnQNdIkq3KsyLdTc9rTv/dYGfoJXHWnk5tlnGgNT9eVIeO4uYVXYnHFcOVqbMLMPNa5WC\nNdHYAZ1URiGB0hkP54DSEbAguHt2GhAG+rRoexij0nt/sdERUKRAihAK7enpunrP24ZEOp4hZwAX\n47EEy9QhTQDdUHDTvjmTFbSzi+Ao3f5lZNZL0w0b1QYzVd3ltcHMNklm+/w6cJ1XBiDt1x6z0foZ\nWl0mwTaZahbhr2jcpJn1Rizq/ONlF3k5EqBnmc4LZdONNmHX1/5AuXTTZKOI/8XpiAggSrdDVK1j\n0nUd4xKly1mVrA0cmuLvog1ci/jVXbbHdLReoXksG/7lsVj3xXjP3+OwofUKbdGp+7qYasryL9pr\nZr0NTcpUDmAs9JaVFXkysvR/I9j1KWtacz0b5+Gf/U1jZVZtL9sceiI2no7rqRskVW//adc503VW\n4bpsWRs4NMnfxaq5Lqv9Paaj1QqtTeaDIpkbq2+RchQBsZQZD0mpCIOhTBWPjvNIzunTDAFnCIU+\n7yyW2pNxmOj0gdCef0EADGLtHZmGwAoZONfyvuM1yZj+Siul16Q2OjyNMtIxR87o067raUPGGDoB\nT5XlPOUFgUDARx6e+euMmXYoOBh1Ef7uYauLlNeUSaoNJsG2y9rAoQpXj9lotVNIm1A8SioeOZUd\nURHpgMT2w+D2XTvjsjKtbLL59YGeJoJ+rm4pbV7tTejOWGy51mEkkQADYZhIdALtwWjX5ZhzL2HA\njaOJynhVKtKyfEzAMmCMlRpVTRuVW66TRrSu00xdYEwPCsqWO8sa0HYcRP7T5B7ribVRaMswM0yr\nqwiCc5T9hheVmZ5o7XjfWTOd9aCzMzI7i5E2fBURFLQyy0MpgNjIszEMOJQiBAEHY0Cc6Dq0xyOD\nUgr9WEJwhiMb4UT+gpsQXRh9yIlGnorufS6j/augjf1nHq5Fslnp14l/FdmkwcS68K9Sl0c5tNrk\naDuthe3ATZhEqtRXl8zdL5nhYn673ov2b76rW6WSzZp/8fVvUVDeiJcNVjydP1AcM7EOk1QTbe2i\nyf7TdF/x/Keb4drIv8z9Va3PYzpaP0OrOlqaJZsmnzdd1TKqyOq6/9LvRC7d5HLHBwPFsnEs+vwW\nRRP9pyn+88wW0sHPgvzrwLLe3zbyryO/RzW0eoaWxzIeelXzDRXIypQDIDVXunEQpRodEZOPeONG\nBBl9tMbvgYGlcqJRmjhWGQ66HMuFYZjImfwZG+dVJCuLfDV1mc9W9dFYNf9Fb7Eu81kb2r/t/Ofp\nKx7T0WqFtgozSdl6gcW9HAMTdcO6xu/ux9jeizGMJRj0GWEWZ3YG2N1PMEz0eWahYNgfJGOxCTsB\nx0ZXYKPDQUp/4KzC6ccJ9gYJlKK0bPuudEOBrW4wNRYlY/qgTpvXXs/LJrW1IsIwlqkCH8Qys32g\navtXNakVyar0FZd/Hf2nbv5xotIoMsvo/8tu/0W55mV1lNM0fwAYTjj13GMcrVZoLuYxvUyTudeI\nCHEiU8UyNZ1UaTrGUBhvUJlgvkUR6KVxr7eyQHCA6d/6hGsgCLgJ2aSw24+x34/RHyQQQs+ktndj\nDIYKgnMwaCcQpXQZiSTs9WPsDZLUm1GfFq3z9gcSUimtGI2sGwp9qGeoT7PO338iFRIze1OOErfp\nsjPG6aNd4ZxcHQhuDvLMvrBVnnXdJq0q/Ouoq07+2olo/Nqs/r+IrGxapWwg7XKzoKaea9NlNsHf\nh74qj1avoS3aWcuWLZXxKizoN/l0dsYDaOcInosfOEpHYzE3iAiDWGXi/3EGcKbd4YXg6HZEmi9O\nCHFCGAwTMMaw1Q2xux+jP5TmNGkGvW5lA+/q/Wh7A6lnTQFhoxOAoBVnnJjZBRhA+uNsJokQ9keO\nrzJtE5hYi3n++XufBr3JefRvltsE3sTHJT/aXaT/uPyX8cGtKuOcgZeM9LJsrsmEd2JS3jJlz/ts\nl6Us6yqHM6/QyqL1M7RlmUQApGeSTUrn9rdp6RTZ0ialKy4nfUnTcuxoD2kU/jSmIs+uo+XvxcYu\n1GKt9JQzESptljEzNobp/Odpf1e71WFCmmRWWqS8pngtS9YGDoB5d2rm76It99l02R7TMdcMLYoi\nDuD9AJ4MYADgF3q93t3O9VcC+Gnzz//e6/XeHEURA/DvAP4/I/+HXq/32ll11W06mSafWR8DqMAs\nmU/H4CqjonTFdTMAcGaAOWYAc1QAAe5wV5ftbC526zbX2Fj6CfeZ4zpuTixgN0/7F/Apz6ucrKje\nJs1UdfOv2v9nmUNXxX/SO1GGUxv4N8G1Cn+v1MphXpPjNQA2er3eD0ZRdCWAdwF4LgBEUfR4AC8C\n8AMAFIDPRFF0G4A9AHf0er2fWJz2CHWYCgTXG5SlUmYvVjYElTWxBZwhppGMHOVj8xDpDcukGJTS\n62IErQj1GhlDIildO+oEwjhiAGB6k7M9bywMOKSU2Ohw9IcKcSxxZDPE/lBCkQKHSCPkM6brE6YO\nqQhhwCCl5gNQWh5jZoM0aVMl5w7XnELlDJDQC9PdUKT8iazXZbZNdduMophMav/0nqHX6AQXTlr9\nd9I7PGrryWnKoklT0zKwLvyFYCA5/nFuI9dJWLap0qM65jU5XgXgkwDQ6/U+D+D7nWv3AvjPvV5P\n9no9AhAC6AO4AsCjoyj6H1EU/fcoiqJZlSzTLKNjCnIMzQnQgP6Ij45NsV5+OnrH/kCmJzabBBgm\nyuTRXoj20EspFRJTTifUHog7ezHO7sYYxBKJcbQQDGmeQHB0Ao7NrsBGN0C3I5BIXd8jztnAsa2O\nVpxERsHZWRjD0c0Q5xztYKPDTXQQBlJ6Te6cYx1sbYTY6HAkUq+JWQ4Dx4PPvWfQyFxp+Scy2zaA\n9rKTtpwp3ovDRLcHYzrslcqd9K1Ih+FyZ4eZEapp66KjdJruK3XLmjJJtY2/4NoTlnM+Nd26mwSb\n5OoxG/PO0I4DOOP8W0ZRFPR6vaTX68UAHjQmxpsA3Nnr9b4aRdFFAN7W6/X+LIqiqwB8BMBTplWS\nH8013YGICJ2ApwrNhoxyEUuC4IRuyJEo/eENUyXEMBgSGAgsGMVPdIuw9xQYb7lOKLC7P8QgVuBG\nYQ4l4ZwjHTNzAggMm90Aw1hiZz/GRkcA0OXY2eJWN0A/ltjZT7DVDSG5mcUkCfoDCWa+I1IBDBJC\nCAQgcEbggqXBibVDi0ydSBJ7AGd+JorRAr9r5mTQSm9oAh7b4Mb5F9P+UxjnFs5Hrs2cAyHTnpn5\nPjBMFAKunw0oe73MRysxXqp5Xv6j2jx/q8zapLwX5dBGpXbuuVsIgnEnr3lw7OhGLeUsC/MqtLMA\njjn/5r1eL7H/iKJoA8AtALYB/LIR/xOABAB6vd5noih6VBRFzMziJmJZ0/LMi2d+MoxiKJIxEYII\ngouxY1UYkM5iQufEaTuLcV1vbUDiIxsCpAj9oc4oiSAVpcGB40RHtufGhKcICPjokE8pFYiAzW4A\nzvW+NAYbY5EBIOwPzBYBpU+k1iZRYRSBMQXl7PfcBDOOEwJjWnXNuqeRzA2EjEy59t5tOt3u2bYn\nojHnHJvftj+35smC8vNgLHt/tn1n5VtXuPd70HHY7rUsTp3aq63e7Z1+bWUtA/OaHD8L4GoAMGto\nX7QXzMzs/wbwv3q93it6vZ4NP/FGAL9q0jwZwL2zlBmw+CinztGetupZbcfSxZ40DwOAcY/A8Y80\nS9e9Mn7MRKk83zAs5xFIzgISS2XIlDemKCq0R4arU4dbHsDGZSzbRpPaOl9euRn0qOx5RrVN9p+2\nytrAoSn+LtrAtYhf3WV7TMe8M7TbADwriqLPQX+bXhZF0a8BuBuAAPDDALpRFD3HpH8tgLcD+EgU\nRT8GPVN7aZmKmvB6K+vBNOapxZB6OboeCWkeAmB2V7kyq6BGZeu8Y/U75THkdB0K7sUx9RGZmUfB\nwZ266FF0/Gn3yRjTpjxkZVRUXrr/zaFPaUMAE+pLS6/4HO3gYFa68fqK0rGZeav0n3WRtYFDXfxd\nrJpX023tlVo5zKXQer2eAvBLOfFdzu9Jhtcfq1JPG0wKLgfBmTmMU0GYDqaUXoNyJg8YxgqbXWFG\nmAQQYThU6HQEpCLtLQntPNHtCISCpUewCMEQJ4T+IEG3I9AfSgwGCt0NbWaTisClwjBWCEMOpRQS\nySAlRyg4BolCnEi9HtcR6HaENl0qbX48ssGw20+w2RWpI4ZIvS+1OTA23pfa6UTPDePEeGSSXuuT\nAJJEoRMK0z5aSUilz0XjzGxWz7Wn9igF4kSiU8LOn29/klpn5yO0lOkrjDEIw2tRWKVo42tOqzPP\nq6ysDfD8V4u28morWr+x2qIuE8BotJ83Z00eDVmZa/qKzSGXofNRTowruvU+dMtUBOz3E0hzGKc1\n5O33E+2gITg2ugE2OgEEZzqyAoBhLNGPJfoDo6SE9pDc68d48HQfioCtboDdQZx6UsZSK0syH9tj\nm4FWWInC/kAiSRT6A4k40euCNl0n4KkpcJhIcM6w0RHpMTbDREKRMQXpxtP3CZYqatseYSAKHS/G\nTJklTSw2b5g74XpSWvc5uh+EYAKvaRwmyWKzhlmW/6R7mpR2EZNU3SauZfFvykQ3aYazTP7A5O/P\nLP4e5bA2oa8WnboTkQm/A3SCrKMAkT6k0qLDRr+TREKSltk8nOkPI9GoHin1LEjLtFJh0PvNdvva\nX4ZzjlhKDIYSnZBjMJR4eHuAR12wha1uqGdjQ4XBUC87bu/F2NoKEQz1FgHO9QxtfygRCIatjQBE\nhDM7Q3Q7ApwRtgKuZ49sFIIrltoJ4/jRDkDa4aQbcvSHEkrp2WFACsbaCIDQDUeOLzbmImc83Ryr\n92DHJt4AACAASURBVLQpnVcgnW3NeibpC93AM7aQSiEx98S5nf1SxmFl0foAoBOMzo+rk/+ivOos\nb5Vmtlmy/OylzVynfX/KcvWYjbWZoQHVRo4FQhAhYx6y6aSzLpbPKmlkSrTx6FwPPZ2N0pOcAcrI\nY7uvzR2Jca30zu4NITjDRidIj43pD+L0Yy+4ngkRmbiRjGF/EAMAwlCk/IXxNgwD7QJvgxtn7x+p\nY8lGRxiPTJauS3FjTgWQbingTltxMxp3N0vbMUA+1ty0ZyL1jm6EAS//7CpCGmL6nvRv93DTslzL\nyPLiukbXTXCdVzYPVsWrrfynfX9m5vUojdYrtMU/OOU7TV4JpCYAJ8Fsk8KE8lKdSaliIaMsySmX\nnAot/6JybI3p3/w90Yx2YuMyZrVnUfo5ZZNe7iplVjXz5J9j0XrJIvyrypow9Xn+7edfV5leyZVH\n6xXaotP+VG5lE/IApuMUlGNH+XY2M6m+tAxH5vbFfF4bospc1XvOGEtNfUrZs61GHGwkEWVtmxiF\nsQKQemG6XEHZ9SRCRp9llRhjAJVra11kufbPtzXR9LIXkXGHF8NoULBI/1mVCa+u/t82XnXwd9EG\nrkX8yn5/yso8pqPVCm2e0c2kERhjOjqH7VjudXuOVKBD1Gc6kD64MusAYEM8JVLpyBNk69F/lbGV\nK6XNd8I4iUhFkNIoKEU4shEiEBxn94aIE4X9QYJE6bL3+vqYmN39GLv7MYaxvn50M8RWN9DRQtIR\nrHbqEIZ/nLicGBhn5gw0qb0MFQEM6QZuZk1zWuwoLH1DUlF6kKjbboEx4ylFztE600fA7pldtq2S\ngrLLPu8imTUvEsyRKsxV9PP1n0myRbk2JVNk1lBbxmuR9m8b1yLZtO+P4Cj8/kwrG8ieaO8xHa1W\naO4IrUoHmATtnp695bSzmRBMoVk/cuvVH3knWjiQKjJF2hNRKffgT4Y40V6GDDqOnRA8TUcExFKm\nHorDROL0zhB7/RiDoUR/KLVSkoTt3aFWbP0YiVTgHDhxrJs6bXBulKbQH27tEKEDGVvlJMysS0pl\n1q6gnSYCrg/35CPFxdhoFmjb3yroPDjXHocEXe+kkfP4zJSP1ufYyHll2nOtYpLiXG9hsGt7geCF\noYDqMOW0waQ2CVKqudu1rKxJ/nWW26RJsCwC481ctVwpvUIri1Z7OdpZkfUKchUNgNpkOvL9aJYz\nTLTHX+g4WwBaocWJynygpSIM49FBY52Ap7Ot8453jYegxGCYYBhLnBkkJsgwsNkR2NoI8fB2H3Gi\ncPxIF3EsMUwUHnPh0dS7cJhISAX0hxInT+/j/BOb2N2PdagrFoBI6sDKcWK8DrWi6YQCg6HEIFbY\n6OgtAVqZ2RBePA2cHAi9F60/VFBKoRPyzKyUAWNtaD1AQ8EhHC9Hm46ITOxLjNoVoxBcjOngxN1w\nPK/7nNy/s2T5666ptan+M0u2CP+q9QEw7UrozGjXNvJfZvtXvb9V8AdG3x+P2Wh1SylFYx50QP2L\npG5cRtuXrFefW58bXd/+TRKrzEZch2Z21Al1hHxAB9XVMzv7sgDdTgBlFGIYCKMA9CyqEwgkacBg\nUwPpE6gBYLefZGYggN0qoNN1Qz3TVGTMitoamZHZe7L3O/JyZClHW68btzFtj5ypdaxdycwQ+cix\nxfWcdDFtpFqXSbDMtXnRFP86ZgZlsEz+TeCw8PeYjlYrtCpY1CRSClNm/mPWtpJVUPmko6It/xb1\n80VNOqvGUvpPg1gn/k2YNJeJJkyaHvWg1QqNMVYYw7CKyaBMHpbKAWByXrcfWpmdcWhTwSiSPJlF\neRs1JOAMoOw+t2EsUwcJaUL1c6bX3xTZAzd1SCxbnzV5ukfb2DUozliqIO2eOca0t+T4vds2NnKn\nHYrWtDKelPbeC9qjqF1dj8yyz6QumYum+k+bZW3g0BR/F23gWsSv7rI9pqPVCs2GYrK2ZaA+84Er\nE2bNyZrktHOF9r4bxNpBIzGhrgD9bbaejmHAEQim1/mgT5ze3NAxFPf6Mfb6Cfb6MYaJAsCw1Q1x\nZCOAUgr3n9rHqe0BAODYZmg6rjZBfuObZ3B6u4/dfoz+IDEc9KnaZ3eHkFJhayNAIHjqzLHZFQgF\nR2jOYrPeg4BWkgDS8Fi2KVJzpTkwU3DtFMKYDoVlz0LjTG8xGJq2sJ6URTEVbdtxziDYaKQdmudZ\n9EwSSaaNqpkTx83CqtAjs8n+40Iaj895+dfBoek6lt2unr9HWbTaKYSxca/EpmDDItnTk931OzKz\nE850AF+GkVIjwXWQ4UBgGEuEG4FWkuZwTqsQpS2TMwjz0VeKsL0XpwrowdP7EFyHxFIdfd/crOt1\nO1x/rBOO/mAIBqAb2g5vAh2HAp1QmDBVQH+QgAsGpVi6v02lM7dRNJF0JAiWrrfl258xBmkUjlWg\nQLFJyE7IlKJUOdr2Y44HpT6c1OSZZs+dgEl1z1FUbXAHX7Ow7h+rJvjn+4WHRxW0WqEt21QQm9OM\n9wcSYcBT7yIiQn9IGMQJpNIOF4IDp04PMEwkhrHCRldAcI4TRzvoDxLsDyQ6oTCHc2rPwiTRswcp\nyZzmrBXf2Z0B7ju5g6/+22k89sKjuOCcTWxuCO19yBiOH+lgoyNwz7e3cQZDfaAnA/qxxCPPPwJS\nhDP7MU4c7SAUHLGktL5OyME5B2cclChwpvfHDZWCIJa65Hc7evYUSwJMoOF8e+lI+VqZdQKBRKr0\nxOxsOiCW+sBSjuK4dXbbg80bOl+wRZ5nkCuHpYOS5vtPvv55yquDQ9P32ST/fL+YltcOlFbFddnt\n6jEbrR8HLTp1r2KqsbMKQLvsM2eGBoz2odmAt4S816IOWDwynY2u23KJnKgfnGszJQHbuzEUAceO\ndNLo9naGuNERmaj4FnqjOFITm450r68rx+yWMQuy7IfC3ptdf4OZ3U1rN8HtNgaMXXPrKPIUtb91\n1P7x/E2aag6ySeqg8Dd7/kvfX9v4N122x3S0XqGtJfygysPDw2PpaL1CW3TqXsVUYyJHAQCGCaUz\nGCtzD/W0ETdCZ3+WPfalE/J0LcBujnbNI+keMKnATHT+Y0dCMACnzvb1Zmep0liO+4Mk4zlpy7Gz\ntsCYRofDBIC+nsZ8VKMDLd32AOwMFmk6vSym1/6IaOyUavvbzjbtzC+fzk771JT2N06fU59J3aaa\ng2ySOij8OcuOB5t6tuva/h7T0eo1NFcJ2N91yQB9sjSY9qYEtN0+TvShlqFgGMZ6TW2jKxAGDIxx\ncKJUIZ13fANEwG4/RsAZBrHE9s4AxLTzyMPbfdz/0D66HY4jmyEEY+na3EPDPrb3YnSM+/1GJ8Bj\nLjwCAsPD20Oc3hnixNEOzj3WxdndIe751jb6wwTHj3QQBqFxJAEe3u4DBBzb6kARcHZ3CCE4tjYC\nJIleR9vsBum9a2XEzNoaM+0g0+go2hFE8yeM1ras2aMTjI5kCQQfKULnmeXTFbW/zVv0vKs8T2Ck\nfBOpT9O2Dj55803d/Ud7kbJ00/ki/Ovk5V5r4t6b5F+lXyx6n023TZ0yj3JotUKrC0TaScIu2CdS\nf7y1m7ruMEmi3cwDwdIZhxxt39LnkXHAnv2plF5LsjEclTm1WXECCDi1PdBRQBKJQZwAYDiyEQBE\nGMYSX/n6QwgDjkQSHnHO5ihAL3Skjv1BgofO9NEN9Qv+wKl9nHuso9fQSNffHyYIAo4ksfcWoD+U\n2Owy4xAiIKXMfNiJ9Cg4vxZnZ3v6BdIvkg0cLKUyp2qbtT3o2SXnWimS+bfrEGHTTQKz7TnhhdXt\nT1O9XPP5OGNL3WvOWG46URHr/qFqgv+sfjEvJpW17s/AI4u1UWiLmBncmITSRscnGJMhT/d4dU08\nw1gSbESrbkfHw+OcgRNBGmUCsxV5Z19HxQd0JPtOJ8D9D+9hey82h3cKPHCqb2IpCpzZGeCbJ3fw\n93fci0eedxTnHN3Q56MxQCrg/ONddDsC3354D5udANt7MU6eHoBxhnOObyAQeuazszPQHpcdAcaA\nnf0YiVII+Gj7wUY3ACDGZiv2nixcJxAiSt3+JbTX42CosNllCITOp5RuB2YaNZbZQ03LPJNp5hSr\nzMxZoGBs9oeHAc4+wcl9pUg2L1fBi9Vn2fonYRH+Rennaf8ysklYRvtPmplW5VqEZfGvUpdHObR6\nDS3/Ic6bOqzM/ZuXpTMOW6ZTNs99ALVXoZXByNyPvVuP5hIno2mcMLO7vX6Slpsk2iS32Q3SMh4+\nq82Em91Qc3DWk7odkZpcOjYeoyLtdYmR56DdC0Y0OjDU9SoUIuth6JowGJvcXvqvc89qZAqy5dgZ\nLHPq41Paf9rzcWUZM1Yqn55uVnku5u0/8/Bfpuyw8nfRRv5l7q9qfR7TsTYzNBeLjirnHgExjJuY\n3L5GGDd5GauUu3HYWqpSJQNX0Y7KcrlmqiUqYVpr9iXIl655sgLZOMo8q6KmrgtN9J+mRtWLcPX8\nF8eyuPpZWT1o9QwNKJ6mV4VIFcjo8Ec7cwOQWVuzn1E7KErkyFOP2xmKw+PIRpj+thFBzjnaSWXa\nvEc4dXYAQIeuuuSRx8EAPHRmH1IRdvZiMOiwTfc/vJt6UO7ux2CMYbMrtIMKkT7jCtaTcsQJsOZU\nPaIbxtJwhbkflo74BkM5mmk5bWtHgzZ0EwNgtpyleXQ76AZKnEVGVeLRlHl8aR1m9qxy7V3VpFNU\ndpPIcyBazCQ1qeymUJf5zPOfD2XNkh7FaPUMLW8qsx/cqrIgEOBKpWGkQpGtg3NgoysA0ud3abm+\nLpVCIPQxMHEsMTQf8W4o0uNkBNfrXwTgnm+fxfbOEEe2Quz3E9z972dwdCuE4Az/+u9ncXp3iDM7\nA5x/7hYGQ4V/f2AbD54ReMyFx/DNk7s4vT3A5U84H91Q4IITGzhxpIPNjcCEzdJhtgLB0QmF9pwU\nVrFpJXB0q6NjMJrzxzgDNjfCVPE9eKYPIuAE66SmjP4gAUFv4OZspOD1sS8cRzb5mLejnXP2h9rp\npBNkzZt5k98glsYDcXI6V8ahn9Mks2nGPDmlnHxfqqtPlZHZDfadYPzQ2LL8q8rqLm+WbNn1ubJp\n/aKMbNn9wp6nqN9PXpmrx2y0WqG5KDtimvTw853E/juOR5Ht7QfXrouFAU9dzwdxgiRRGMRKH4RJ\nhN39GDJR+PZDezi6FWIYK2zvDtAfynSN68TRDu69fxtn90Lc/9A+zjnWBWfAt775LWxsbOGy73wM\nzuwMIDjDyYfPQBHHfSd38JgLj+H09gBSKZxzbAMPnu7jkeduYG+Q4JKLjoMrwpmdIS48b9OEtjIn\nY3PtIUmkFVwYmuDFZqbVDQUkEULBsdOPzQxCK69Q8IzVcDR7g/F0HIUCs3/dmSygTxewkURc6P14\n2s297DN0n1OVZ121ryhFZuDCp46Kq8oCwdL1UBscOh+aqw7+dZexaP11lLlOXItkhfWRef7OQKvq\nc/WYjlYrtLo626TrimjkoUfakQJmhGRd2wWYiS5PiM2+NMn0jOPMzhBntgfYGyTm1GuFvb7+cA1i\n7fU4GEo8cGof3354HwzA8aNdPPTQKTx48kH80JXfjXOOdrC1EeDbD57F3v4A5544htic7NwfSgwl\n4YFTfQBaqVxwzgaICKd2hmDGYcK+HlubAaRU2O0n5gQAgY1OYBQP18GTBccxs0dtGOt9W5wBRzc7\n7nsGIsps4naDCo83J4FSx5Ss0rPQEfunf8ybkOUX1PPpyPSBooNkF+XAGdPBoYky8QmX9bFuquy2\n8J/1bFcpK7ruHm5bV9keWbR+DW1ejyH7d7oXUvaFYO7/2Xgkebdz2XWmxDlrTKlxZ4lBLFOlY//u\n9YcAA44d3Uzr6Q8SkCIEgRi5g6cmndFaWRjYk6gpNTfCKLY0HiNGXof26BdbDgyHzHvCSng+Or/J\naQs3DxGlXPJtuOhznFfmYnre4nT1cNAjJjZH3ib7/zrI6nm2q+t7dZftMR2tnqEBzZoZZnWTkflg\n/Bpz/nOF+aR23c6UZGS6TNepwh7bouwMiNn6mZMTIFVg1iA9R3LvylU6NhljSN3wM8e1FJhJpppO\nkDPh5rjYRpnHzDOLQ1VZtfonD2AW4W8fKM1IV7b9mzSz1d3+h5n/PPkncfBKrRxaP0NzUf/LQakX\nH5GO4GFVh52B6WgVujMJYWc9zBwNw7BlDuYcxnqxNww4gkCvnZzdHeK84xtQROgPYhPxYw8XP/JC\ncCHwv77yDShFePj0Li46/xg4F9jbGyCWCoOh3svGAIQmWgjnDA+d1U4dG50Aw1iZI20UGGNIYglr\nok8SPV3c68epd6Sd+e0NEuOoYGYmLOuxCNgZ32hmZs2P+pw4ADTuQckYS+NPzmp/pYrXxSblm5U0\nTVciTR6cZb006zYHMdOO+ZBOVbFsU1ndWCeuRVj39j8MaPUMrcjbp04ZoJ0kiAiDWEcQoUR/+IXx\nEtQfcQBEiBPC8SPas1BKhe1djmGs3egVEY5uhtjsCigC/uGL306Pjun3h3jg1B42uh19SOdwiEdc\n9FgoMHzys3fhyNYG/sOjzscjLzgH+0OZuv0f2wxSnhvHuggDjo2OwO5+DCE4uh2B3f0EUhIeeV4H\nQSCwvTc0QYbtKdN6o3cgHIcRaDf8bigQBjzjdeW2l+DakcN6Ptp4jyHXpk4iHZyZmxBgbrtOa//U\n+4+zUs9paJ9JruzUBEoEOOmqxnIMA5Hh30Q/C4PleTku491pin/Vdl2kvGVyXVTmUQ6tnqFNmn5X\nlUmlMExU+tFyr2uHD2U+0Fp52bWo/UGSxn0MhFYm+0OZekEKwXH8SAcXnruFjY5ALBUeOLWPk6f2\nceG5mzpyCBE6nQDnHN9AJxQY9Ps4u72DbqcDQOHs6YdwZCNAwIFvfONr6O+dwZHNDrZ3h+jdexrb\n+3oG1gk4zju+gQvP28KJo9qBY2dviDhR2N2P8W/3b+PU9j6A0YxJx4pUOLMz0PcpFbY2A3BuTp2G\n9k48tTPAfj8xIby088nZ3SFiqfee7Q8k+sMEYcBNlHzr3agdKoaJRCL1i6iMwrIztThRafBj2/6h\n4LCHFJR5nnZfXlG6NC1pz03Lr2pfySjHOfvZNJl9Lvl0yvRNKcf75jz1FdXb1D257b+s+uqUtYFD\nFa4es9FqhVYXEqmnE3k7tPU+c61tDHo9qz+QIHL2ZKVBi7XCG8ZGqXGGgAMb3QD7/QR75j/BGaQk\n9IfSuNPrDdZnt3ew0e2Ac47TD51EwBkedeG5+PYDD2J/fw//4VEXgEjh7F6MTqDDYB3b6qATCpx3\nfAMbHYFAcGzvDgFm97fokwOYE19joyPAGMN+P0m9qwLBwZk+HkYwM/uJJZTSbWE7g/ba1PdqT6UO\nhDDxErk2zzFm1gezR+zYjehauWG0edtpf8aQbgGYBcZGIb9mpmPrt4CemIZ2PeA8PDzmQ+sV2qLe\nQVOvF7iFMJ5dvNfp9cfdHStR+nf0NVeZkZX9S6n3SDqzYdbUpsCNeSxJ9Gwo7ARQlP04509+Tk0T\nhW2VS2d+Gx00aofcbCErc0QYKSG3DYvMJBZ55ZO/Ps9znFfmovb+U4fMPpiG6lhmWy+bv4s2cC3i\nV3fZHtMx9xpaFEUcwPsBPBnAAMAv9Hq9u53rvwj8/+y9fcg1W1Yn9lt7V9U5z9f7cft2325HdBSH\nUjAGYpCILRhGMW2GfJAIgyGIOGYwAYMmITKayZdEMJjBGDBkpoc4iEOI2IQIbSAZnNF2BgexiZLM\ncdRkMnS37W3vve/X8zznVO298sfau2pXnao6VedUnVPP+54F9z7nXbU/fnvXrlq11l57LfxlADmA\nn1itVr+SpunbAH4RwAWAzwP4vtVqddvVz5RmBtRcCIgIbC0ICqQIML4ddz0sW/wVwQSgEuy4lBvi\n5ShyjwrTppTRsEbCW0kke8JmkyOJYjCXyTyNM015MOz6slU/jkJbKn+zE8ZcuOrX54a8tK7wgjZR\nzkGb+ay0828L9nIOTm+qmaWZilB4pJzNbMPwh3RqXFPP9Vmo9aNDNLR/DcBytVp9M4AfBfDT/kKa\nph8F8EMAvgXAdwL4yTRNFwD+KoBfXK1W3wrgdyACbxISU5wsiEgBoDJGoaemRcIg5IaROJOYRN2Q\nQ8Y+EejdOgcRcLvO8PJ2g9ww7u4zLGIxEb66yyS1S6yKBJ4AIzcGcRxhs5HYjR/92MeQ5Tl+/w//\nCa6ur5AkC/x/n/8Scit7T+8/uwMz8OLVBq/uc3z+Sy9hLGAM4/oiQaQlzmOkxCPx2at1MS6f7NI7\nmChFEuvRimenteKxuIh1kXnaspgM/Z6VtVw4yOS5kbxn1haZvcn1RfBei+Ik4gVY4SUpoBpfROH9\n2rhoGiUPW96Xbfet64G37A+JC/5TU4g1KhxjTghoALXN4UN64Q5dP6ekueKaKx3i5fhxAL8KAKvV\n6h+kafrPB9e+CcBnVqvVGsA6TdM/APANrs5/5cp82v3+a20d9L2ZFW3DkXUvQ++FB5eIU2IelnJc\nE8E4933/Is5d/jT/8fzqPhdHBifQcsv44OUa7z9b44vv3eLqIirazAzjvRcbXGxEAKxzU0QQ+cIX\nvggdxbi+uoJSjCRZgIjwhT95D+++9wIfeedjSBYX+H+/8BxgIIoUFIlQ+aPPP8eXvX2Jtx8vi3iS\nX/mxRxKhJBeHDwAuR5rCxSJCEitoHeFyGRcC5/ZevBxBYobUmnB1ERdj9w4vi1gVY7pYVL0ctaJC\nuAN+nw2wbKGVwiIuPSaTuPubyZdbZy5nXVTex8wJ0aa1MOSlZF1uNQPRWHVH2WNRaE5KRjb8Tzm2\nTW7cXmq/ezI17dvn6yzUnj69RBTp3QV70M31cpR2jkWHCLRHAJ4F/zZpmkar1SpvuPYCwOMa3/Na\nqa+HT+6SdoYvWaLqv2OXuDMzjITKdpVLwkmEwkHCyzuvqSwTjdt7U5wjur/PsN4YfOStCzx9tEAc\naXzu3Rd4cSvmwyfXCV7e53j2co3nrzZ4+8kFsrtn+Nzv/yaevPM1ePm+xjt/5qvBbKB07MyRGqQT\nXCwifPk71/jjL70CEeH5bY4Xd5K9+uYyxmf/4E9xuYxxcxHh2csNvvwj11AkQYnBjItEY51ZPMs3\nePZqg2snrMhpVReLCJYlE7QxFllm8fIuw9VFVCTwNFYSniaxnNG6c/ErxfV/O7SVP1NmLIFh5SPB\nCZHwHjTd39wJ2mWiYQoTLxfzbxrMcUNIzLnKJS2lQmvft725U928OzaVFofTz+HUY50TDRFq77/f\nuYsziF68vB+trWPQId+GzwHchG05YdZ07QbABzW+5/Wm1i9wBkInMW8Gq1UGUM0yHL7ogaq3o39O\nRACI4PNa0CvnxRhphUUSAZCszl67WecS8Pj5qw2SWCPShP/r//yHAOTA9eLiGgzGsw+eASCQ1ri8\nuoZShI9+6BLMokX6pKDvP78XTYf84WV5OceRAsMJXkgqG0bpjVk+684cqERgxVEZOf/eHeDW7hwa\nM4tgYdEMvalOOdNYU5Zm3w0zQ5MPzbV9T7ZJTG2+zTApqae2rNBDyTvW1B1W+n6pH8Ibi46BtQ/+\nfT0yjzGvY83/qeZ6rlriQ6FDBNpnAHwXAKRp+i8A+N3g2m8B+NY0TZdpmj4G8HUAfi+sA+ATAH59\nVyeHLo4xFpe/0vYtWPFM8v/n6r+tNRW3etR/y0aTvHDZ7VFVMLk2wyq+iUrZJpTO8YOqrvNAKPRq\n/RVjHzh/hIqZcJT5D+d3IK+Jjr5+DsA/i/X/BuLft68x63fhOlMzHSLQPgXgPk3T34Tsg/1wmqY/\nkqbpv7Jarf4YwH8LEVh/B8CPrVarewA/AeAvpmn6GQDfDOC/29VJf0+g7Tpe4wgLcEc7De/zSrv+\nw1TRdn9KuXNZ8NqAC6nkzHHXN4/gX/XWHVhWytu5ueCtM1Mmt/SJNolceCsUXofWiiZFQR9N1hcu\npYs7W1adr9IzM9yLDBrw89AUQ7JpLr16WGuz2QtsPh5pbbw5YDjjb1s/aKwzF94UbZ+pm2jOk5Xl\nhqPaAdwmuzkzinxWnvzLW1F5ANhY5+xBspcSu70Vb8LL3XWtvHOIvNwjrcRBgYFX9xnW6xwv73Op\nY6Tf5682+JP3bsWER8DL2xwA45988QWsZXzw/Bb/8O//PTx6+yuQZRt86MNfBlIK77/3p4iTBATg\n6VtvIdYK/8yf+zCMsXj2clOkg3l8leCrvuwGF8sISRzhahlhkWg8vVnCWIvHVwsksYYmIHPejJYB\nHREeXSZgln9fL2Mxn+ZShgh4cZsVe4mxVtCasM5ssYe4ySzAjOUyKhJ9hmSsxIoESbJTf/jauntS\nv2fGiOMNKZm/JFKN5drudx+ev6/VNbHN69PemLim5vnfbwJ+oPqyf2j4h/BogJr27rsvRnup/9pn\nPzdWU6PRd3/H17bOxaxjOYZ3petmy/6O2ipnjAWJzz6Acp/IZ6X2ZCzDOpPfIi5frNYaF4XDOA0M\nsEYyR18uI9zeZW5fTbwkFUkg4UgpPLle4NVdhlf3OT737ktsDOEr02/Eep1BKwIpQhzHuLq6BgO4\nWC5BEC3q7ceSyFMR4b3nd8iNxdd8+WNcLCK89WSJxHkwvf1kCWtF8IqLPDu3e8m+vc4MiGXPjFm8\nBsnl8MycW79WIsCMEQ/HSBPiOIJhZ/aE38cqYyk23RMGECtyKW2cy74KrjMX8SJ99JE8L51NfJmw\n3NZ66PnxRUQweTWXTxtv10tl6hcmgEpItkPb7KKp8I/Z5jHxT9XmFPjP1I9mLdDCDfz6V88ungIj\niXXBAyAxG4u24cpJgOKm9haJdgGKpU7u6l9diHZ0e5Fgkxm8us+wSCI8vl7gC196BSJxJnn3g3so\nIlxdJFBEuLlMsMnEbf4P/58vYHlh8PjxI2R5DiIFBuMrP/oIT64TfOFLr8AMfPwbvgx36xxXfebM\ncQAAIABJREFUFzH+8T99hvderPF1f/YpFBHef77G1UUErQiv7sW5w1jGhx5JElDDgALhxasMUSRC\n4r1na9xcxlgmpVvvo6sExlgJ+bWx2LxYI7eMx1cxtFK4XWdQBKwzwiJRQX61cl4BFJpwfa79p0ns\n3OYXiZZ8bkpVzjQV3qpUvZ/1j5BIe6Es7cVaba0BL8RDXhJr1ON5dq0p369WqGSz7qob/u3Ds1Y8\nPSONrXntu9b7COW+vKH467xD8R/KGwvr3PCfqR/NOvSVVs2bwvsQ+//ci6pudgK2N1/rm7I+eO8y\n8Hzc5JLAUysqknkuYom4/+I2k7NbKNPRJHGEly/vABKtDACU0q4Pwtf92adYbwzuNwZvP1lCKTkn\ndr8xyIzFW48WDpNP+lnugxlbHor2B5IjLft5zAzrhELkkoSG49RaFSlUche4OI50kTHAextuhbWC\nmHxDb8T6XDP75JZlvTIBacm0XC1TaACovugleLTXutvDIxG139M+5CO1DPG0rGPYxfPrIgxv1lb3\nGDQU/xDeMeih4p8DhteBZi3Q2qjpBrfxhpQ9mBhF6hZwEGuRgLqzIKEbGxEVZQpeHWsLZOb2a2NQ\n37mafP73/Hod0v9R109Pmu3670lvCv6hZc90OM1eoB1qEin47q9fTKHHX1c7oRDxiT6tLfmFpkcu\n5xUAK/4R0Nrn5qpqMMuFhKPKssxXLehLz+5EqwLw8i4TzYolySizRPrwFB5w9bi956Mqxumj4VPR\nkdc86mOnYMzs5sgfMrdOFWNU58jPayWqWEXQcPD/an9Ncx0mwSxxVQUXs+NRGRuzqb06DV0/1Tkc\n1zRXjM3dk/q8jtXHmFhPwZvq3h6DN0XbZ+qmWe+hhTZm/3sfHuDMWShd7/2LxMf5IyKwM9kZW3rD\n+ZxillEcZPb1rZWoGMtEQykg20ioLWMs3nu+gVJy+Pljby1xc/kYf/j5Z1jEEV5dxnh6E+PqYoEv\nPVtjmUS42+RYxBrPXm7woUdLvPPWBYzLen2fGbz/fA2tgHfeusCjyxhJovH85QbrjSkEjzWMJzcS\nTuv6IsbdRhJ7eicSZnH+ePlqg5urBJlzzrhIIhhri1QzFwsxNebGIIk0FnHpWJMVDjJURA1ZJrow\ncfoPhjgiWGORGRFAcYTCy9SbCTPnpOE9JyNNyIw48/j0Mr49RW5P0JlPy7icoo76+22su1d626w6\ndP0oBWgOz+6Nsx7D39qly5YPF5ll71iz71ofC6uxZQzTNvxj9jeUd2i/x8Q6xlo5026atUAbk/xC\n0Xr7QWDmLc3ABgtK3PYl39gyicAsHoH+SMBFEuFunWOTG1wuY0l4+Vw8/a6WER5dxVjEGh/90BU2\nG4PHVwk2+SWUIiRJjLv7HJfLCERAEkkIqOUiwsUiQp5bWCteiY8uE3zFOzcwLmiw5GDLkBvGzSLG\nvTW4WEg7caRlL4yAq4tYBB8AZguwaHLWBTr2lOcWcaxBShXxBb1gtyzn3hhl9BCwF2KlBurnUjmP\nR+M8RWXfy+2p+SPmrmsfloqIoIiLDODh/pqYn1gEHcM5lZTZqX2/gmv42vCY66SD4wR+XezKzdaX\nvEmN/Ji9al+jMFfdMameNaFOXqicX7hnmgvNWqCNqabXnUD8de+6vsnkPJT/UvaHo/2LjIHCxHW3\nNmAwri9iLKUxfPG9DYgIH3v7Cq/uNkgihQ+uE+flGOODF/e4Xkb40Ds3YDD+6RdfwlrGk6vYJQw1\n+NPn9/iqL3uER9eJC2cl5+VuLhP8s1/zITx9tESWW/zR557hw08vcOGODjy+SvDVf+YxXtxuihfz\n7TqDtcCTm4WYK2NVuOwDLrEk4LQvQJHC9VWC+7XBemNcgGEqymW5xHdcusPguft690KAIM4phaei\n4yexlrruSz+8DXEk8TWNZShdOnlkhgHHCzUZ7Q+iU4nb35/cyD0KY0f6j5iutcIsnowe/85yhAqu\nsdYoAZXjC/Wxyfm+3V5x9WuH4ArPHPate+g8DOHVtZeh7R0T66G8M/Wj2e+h1c1GQ3l96hhnLhPt\nzZm4Au+5eipNrx3AlSYi3G8MFs4V/n5jir4j53X48k7iPyaxwv3aBHjkr0+d8uHHS9H8AoyXywhR\npJHEGs9dipiLRVR4LT65XriHO4j84bzTl4kW/ERuf40qL3nRQPy4BE6kql4szKWJz5eVF0r5u4hu\nwlXnFSLy0bm25r+Ya6ItXt97538zsKXR1amrvVA7a7ruB1tPttqn7UN4onFyccxkSN0pcR2D1+f6\nXLAea/7P1E2zF2ivC52X5JnOdKYzTUuzFmje5BL+O/zbh9enjndAkP0k4fn4iABAqLajCDC1Pbdl\norHeGBDJOTVATETGWBARbq5i51kJLBeiyZEoTkhiJY4lBLz3fF2c4/IfZuvMIM8NjGU8upZzaPeb\nHDpSUIrw/st7p22JYwsAuMApggkcaFEet/z1ud8AwFn9XAgw2Y/y446cuau611he93zxcSi9Ib0m\nFxpOynvh6lbu87B7F/62Pcs11m3wrqz85m2sxzA1kZgAanE4Xz+T2j74Qzo11mPN/5m6adZ7aLll\nxDUnjik8irSCC3mFwsOxiPlHQJazEypiavTei+wE1O06x/Wl5DVbb3KIRznh+lL2x5JE42p5jUdX\nC8Qx4YMXGzy9WcBYi3feusTNZYK7+wzvvVhDKzFfKgJuLpPCueKDlxvc3md4dL3AV3z0BtcXMS6W\nEYhlP+6tm/uKYNaaEEeE23UOIMKr+wx36xyPrxdQBGxyeVla69LJMGOTK1wsZHxgEXZZbnGx0BLq\n64N7vMwtkkRjGWvEscKruxxEhItF6Q0KSLgwZudVSuTMmP6a865caCQRVRxwABS8zAnb0MvO8wjl\nR4U3//o+SieOUjgD1OitF/bXtVbacFlml0hWFSG7hqw9ADuvh1FEdrXtaYznpGn+h+KfknfoOI+J\n9VDemfrRrDW0Y5B1gXW9NxsRQZG8JP3L0GtK5LQPQnm+jFm83qIg8zMp4PH1AsuFxluPli7gr8KT\nm0WRx+ytmwWuLxM8ukoQRSL8Pvz0AtcXCT785AJXFzGePlpKPjVFeHKzgLGM2/sMN1cJtFa4u88R\nxxo3V4nDLmGlPF4vdJ+/2gAk+0S39xmYS+3RGFt5YGKtXHxF0fZEMIlwSGJV7O95YQ6I0JJAzQxr\nfV646r5PqD15zVR+S3s+WHLI8y/xPMBYP1/n7w+hOU+Xx9pFRNt50rrKEVHLnuAwknnd/bKqRxE5\nFu2ak77450wPHf+ZqjRrDa3Ny6rO21edl69Qdi+98mtfKzlXZS2DlILWQKw1wGL2WyS68pJcxNqF\nu2IsYo3LZQytCE+xKBxOMmcyzHPGxSLCxaNIwlllBvcib6C1wtNHMeJI4eYqwb0LgfXkZoFYE27v\nMiSxxG784MUaxlh86MkFvvKjj6C1aCAMwDiBFWmFF7f3YAY+fH0BaxnPX2W4SOLCDJjESjwEWUyr\nYfzLu3Xuzpwp5FaOEmAhgsxaxiaz0IpwsYwKl/ksFy3t6iIuXvpZoLkBImjj4D7kzoNSa/lYCO+F\nz3ztyfMAOXunlWr1YPWCTrRwqlw7ZP1EIsEFA1HhoVkvv4vXRoes9aY29q0rz8L2vE2JfwivTXs5\n5fwfwtsH65mqNHsNre71E5o6wuttvG4vJH9tux1muUDBthMXbUqduvnDNxa251/GzCj2xvyBZGYO\nVBX5E2kFrUQTyl3Q38Qd9gbJ/huRuMcrpyWSCsbq+oucl2ZuuNAm11npzekfmUiVXo5KhctB9m2i\nAGtdS/DaKfn5Yi5iXIbzL8IynKLqXHvtrS2eYVPm6+JaRyzHKs79vMuG1Glam2Pzjo1/7HGOiT+k\nOc7/0Dp9MJypm2atobXRoV9lfcqKwOrG0afM6MQB1kAe1vE3wWp6LMaCz8xlW06ADZn/KSey/j44\nxvqZks74Hwb+IWXPWtk4NHsNrUlNH4v8i64pJmKYNdprY978UkTKCEIu5cYWL3FjyijzPjKJHJQW\nM6r3fKweApa/m8y4cFwWl0sx2726z5HEGkmk8OJ2A0AOLPu9JY/fYwWzS3vDWMQK600OYxlXS/l+\nud/ImTgCsM7K2JC5sRUPyyRW2LjEpn5+yrkrz5gZW45TKyoSaXpyPiat90+cb6iyVxb2F5ocvbbl\nMYRxKZvqyj5QWe6QNcQ1HM1lpjNJHeOldwyT2nafBwDeauv4+MekOWB4yDRrDe0Qr6C+PB8dxOfv\nSiLnGAIg1vIyfXmbg0he1oukdCDwySk/96VXsJZxcxFL/DuUsfmyXKJuLJIIL+8yLGKF+41FHBEu\nkgSv7m9lH2oRgRRVhOKjqxjrmwVyY5HnFu+8dQVrLZ69WGOTW3z4yQUYwN19jrceLaC1eDVmxiLL\nbDFmw8C770s/15fiULJIdJEN+3JRCvf1xjgvR9lP22QW9+sciySCUt5M4udQvCRf3WVYbyTsVhLL\nnpaPRyjzpLDJLTLDYJZM2DrwCFQKlTxr/t5snMk11iKQcmPFSSaIdbhrrfj6RGHsSNoq17VWAPnQ\nIBJnGY8rocPXI7C9H3TIuh67vanxy7yWUVKG1O267314U8/NmLwz9aNZC7SQmm5qX96ua0Tium+C\nLyJmSbyoyAfrFU9IrcT7L/Soe3q9wKv7DHGsgdyCrS1yimmtEMcaDPEYXCQaT5fi4p8biyfXCzAz\nHl0lyIy8tMvI+hle3mWItEQLYStJMe8zU4ZBIjkWsDEWETPu7nPBD9EySw0Tlaj995tctEpRYMp9\nQi7jO0rYrgjGMPLcIIo0lJJrPogzkcyR9660FtCxCKAiAosSQSDHCaou+FGoCasy3BggHwy5Ke+D\n1yq79hR8stE40H59ea2pOF9oLIv5lnY7HxV1mQHIEYRwrdTp0LU6xlofu9198EvyUls5slEvp3X1\nhT30+T3lXI/x/hnjvp6ppFkLtLEWVp86ShFUsMvkzYpKy4s0fEGi9oBeLDSiSMlLOVJYZwywC9Dr\n6r7/Yg1jWVzsXb0XtxmWicbja3HJ18bCWAVrJSDxs5cb3K9zfPjppZj4tCQRVUrhYiFaimRhFo3u\n5a245APieanIlXcmv0USFX1vMgvDwOUykhc7e9NP+YWoNQEkAYapiCNIhXCxLMIyjsXpxFp2MSC5\nSAwKePMkoKJy3ja5BZhBujy/VnMWdBqbAJMzdqVG0HQ/RYvj4l7VtTjvkWhDz0nLgN5qbnt9UKmZ\n19dKW5258E6BQT5Yqs44TeUU0fYmZ0/89Q+bOcx1E28qAXmmbZr9HtohXkZ+n2efdvw6qmsEu7ya\npG7wMvf7bsbKwx2Ut6aq6flf/rqxomlFuhp/Eai+CBjeNFFi8N5/wiOnhYbxKX250suxbkIqC1Y1\noyJeJG+PnRpeUEQtc1j7MBgy1+3zv/0SrZdjlFo4dvSx7/qZC+/UGDAh/pBOPc42fGO3faZumr1A\nO/TrZt+vHqLhG8hSr7b4Qlt4rfzWOm1Zt4VwpfJA79YI6mPipq/mgFdcY5SshnGWGeC2rrURBeW8\n+bOKY9g9DS/tvifU6YBSYAzmsqv/Mb6u+66fXbx9+j81/q11+cDwz8GkedbS+tPsBVpIxzQVeG3G\nH+KVl2StLEptRjnFhAAsE7HkSn2pd3URg7maf+xiIQeS7ze5S1xZYmCW+JBEwKu7TVEncWZD48IS\nMbtcAERYJj4VDLDJfUgqXfByYyramE/3QiS5uMIvYkD2+Py+lXVRU4xL98IQE2FdmHtPRa8lEcl5\nOmYuYjwCPjak1PfapPcO9VFAPFnmSqSR0IMyJO+F6vfR6lRqtwVgx28uNxZvLDqV+Wwf8s9E3UN1\nalzn+X+zadZ7aH4vJ/x9LB4gXo4+Pp8NvOx8ZBFbZPQlxJGGtmXWZu/Gbowt4hp+xTvXYJYDzsyy\nL7RxkTWICFkmyTC1lrBbz15u8PR64fp0LwmWPTtmcau3LIk5L5cRokUEpTIQiUkyUoR4mcCYNZaJ\nxsUywv1GBNgyEW/BSCs8eyUCc6FLM+LaeZ8RJOWNUoS7tXGxJanw+vPjBSTupo8nGWnv+CFCbO3K\nF16OWoFIPEuzXDJ9K1V6EDKXQsknIlWRXCfU0vsE9yzS5Uu0br6p31vPC/OgnWKdjdn2sZ+dLvxx\npCVp6UQYDh3nKe73IVjPtJtmLdDCG9mkfo/By3IDRrOnW7iYinxgECG1zqwzSwKIUDgkyD6QOGsY\nI16FlEkYrfXGwrJFlrOLs8h469GycO3/4nu3SGLC5SJBEim8/eQC1oqWdLmM8crFYby6SJC7IMHW\nWixiBWNFMHgh5bWV3FhEkYJh4G6dw1jRZNaZRRJpMEu4rtzYyviXiVxLYoXnrzIoBfeCkkzXcONc\nuCwDzIAhgI2tuGCLy72FjjSssYASz0W2pnDtjxQht4B2wu75qzXYAo+vkyIxqNfQYudEssntVjJP\nAC67dskLX7r1e+v/5rl8SMSROOT4RJ5gFPdpzLVXv3astk+Bv23+x+DVX/ZD8e+Lgdk964TiCMlY\nY2rjnakfPSiT49gkpqzdQVj9y9S/qNeZ2BGZUZxj86Y2htMeIFoKQC5Cv4KxFpu86p2llQQ1fnGb\nOU0lcoJEQztnkJurxD1I8kKX83AaBBSxF+H7JtHcfB+lxsMIZBa0Nzk6t/7Si9ObAMUkmucuozSJ\nX58/LuCFnZ8HwB8kry4p/9AT4ASYYFXam0fd3qKrm+ci8OUYACF2CUiLhKqErYSh1f7K+IN9iJlh\nuNzPzIpD8VvOrKPRQ39Jven43YmPIoTdmeZDs78jh3oHdV5Hv3bgDmpRyPNfh9Ru/nDFSreKgFfv\nw2sVirazJ4eY2rB6PKS2z18V5YIHmZQXJNV2fJHiy7psfqs9cpmw61h2zT+o4TxZbYy7M0N3z0d9\nznaVazJPYieG+fPmgGEq/CEdExfQrOk3lRsbw5m6adYmR2Aa1b24jr51Sp2g4HlzCu/C4BckV3iA\nE3YsbXuXfssoknQ2Yd/GWgoreRFb+O+UsF79obDWO5NU+ytlX2li9ZjrZh5mDn0fXWPlvHbNv9fK\nAmYVH+9KpNk2H9v99SkXzmU4zqlMSKfizQHDWPhDOjaGPqbUMTGchVo/mr2GNiXJYdlqrq6QmCVB\npC/no0MsYuW+3r1JrzwDRkRbcQyNtc5jUBWJRH2MQf/ifHyd4GIpoaMsJNSSN4W+usskXFWsJOki\nZJFbZtyvJSwXSMJ1gV10DRcv8mpZejkC8spWJN6b68xI5Ayg2Bfz44bDoLU/v7YtFNeZkX69ZEQ1\nNuT2fHIhMLPcAPD55QS/MbKHFkfkIp403xP5PKjyjG32bGzHgmKOxFtT+D5MFiGM2TkudWkYD4Ee\nEtYmOhS///gcuubOND3NWqAdw3wQR9rt01RNe8wSmsmvWV8OkL2gi4V23nqSYdoLMUXVuHREhNxl\nvE4ShctljOsLiYvorYPMUu6rPvYIH/3QFbLcurxi4lQCEueKJNbFHhYR4eVthvuNwd3aINKEONZl\njEYXMmu5iHG1jMVZRBGWiwiR2/e7W0td644SSJiswEOTgZd3OS4XEW4uE2gtcReDWRTB6zJ+i7Za\nnevwK9MyB8cWSk3PZyaPIhG+yyRyqXF4695lpkyp4+fX36c+ZiD/10cnYWZEkS6cP4gkaLR2+34M\n3loX+6yzNiE2tvmsfu3Q9vriDzX3OZgq++Dftx0ich9e+mj4z9SPZm1yPIVZg1k8mBhBHrKWurLX\nxTAGLsQV4X5jYa1BEuui3PWFaF7rjUWeZ9gYi8tFDEXigr/OTNGeMRYf/dAlNplBpBXuN5Ix+oOX\nG1hjYSzjchlhvZE6lxcRIlVmzwYk7uPFIkJuGMYYJ0zEnBhpwr2Lvu+C3BcxDgFvchTPx5d3GQBx\nMgm/RsnFsySSEFv3G4PcWCwTXWi7fi4zwwBb8a4M8rDJNRSCmoJ5TSLx1Azd6UPzX90smkRl8OMk\nqplEW0xDcSRZDzLDiF2OgcwwlOIiR1wc4GKWmJLM2OpjrLU3Rjtjt9eXlzlP0Snnps4Lheg+7U2F\nawremfrRrDW0OvU11RzCg4s04T3lujzmCHDZntm99GXx1TMoy4Mni3Od2yLSfByXX3iFm73TkpJY\nu+C/Zf3MMBbu0PbdWlLAJJFGqDN5DdHvQYk50b/Epb8sZ3jRIoJXRuOnw7si+7iIRFQ5EO6pzG4N\n55GJSngtK7bRwruy/nD6sVGFR5X5CCl3gYW7MlR3Uf1++yEReacchiZVYKJqZRlnzWFnVx9j0jHW\n/z74ww+mLjoGrjdx/s9U0uwF2qGLY4yHo8sswFzntZtdttrvhanOL51RiMq9n6I+Vb0XmYM3DYX9\nhGPaxlDi9702I+PgdzP8wx9uCkB03pMGr9VmSM3XnIJbKTfGy2kKU19f3lHx7/Aanj3+kef/0Pp9\n3iFnqtJeJsc0TS8A/AKAjwB4AeB7V6vVu7Uy/zWAj7s+/ofVavXX0zR9C8DvA/g9V+xTq9XqZ7r6\nOpZJJ+hxUNviLBLWJznb1lDO1rz/LHPxRWGZod0rwdY0jlBQ+n0fSQ1TCrXQBENwqWOMF37+LBqK\n64xQc3QYrE/ngcJTMTRF+j02L1RD/LvNJCItwoeUg0j3feY6FOCN5Rq8UXe2V/HwlA+FJi9NBHVP\nbX6arZlt4Pwfij+kU8/r1HN9Fmr9aF8N7QcB/O5qtfpWAH8LwI+HF9M0/RcBfM1qtfpmiFD7j9M0\nfQrgnwPwt1er1be5/zqF2Viq+9AvwjBG4a66/kBylkuOMkUSscOHyvKJKUHiTPLoMnGJQeWFzgCs\nsdhk8l8pQKhoz6egeXQZO6cQl/aFJCGnsRK1xP8npk+JpxhHBK0UNKHIT3bp9vSWsYJWYi703n25\nsbi9z5Dl7Dw0JY+bzwEX6dIcuN5IOCvJjVZ9GImo8KwUB5ggnxlcqhiqmjJLUyUXkUvCufbelvXX\nGREVDjseg7FceFK23btIURHxX5H76ODtfv26IHjPx+0XjLVcOKy09Xcq3tT9Nc3/mH3MYQ4P4R2q\n5bV5YZ9pm/Z1Cvk4gJ9yvz8N4D+pXf/7AD7rfjPkOzwD8I0AvjFN078L4E8A/NBqtfpCV0enWFTe\n266tnN+b8od/I10uOK0JxLLf4wr7VsQTEEAcJcXh6U0mobeMizTihQ8gcSRjl0PMZ4IGJEM1EWER\na1j2aWgEj3dkYRB05IMmczEmZokScnGZlOOBCFVAYiZaBu424n6fOGEFABcOPymCVbbgE5UJMHVg\nJlJKgawBQIVXop8/a63ThsJpcpqf90AEKgewiQhJyycYEZCo8r5tXB64pvtXb88LqErOu1o9hnNq\nMYDXQsLrxtrS/NrS37F4XSY0T+EaHtpfU936/B+Cv4m3y6TnNWdvpQivPWShxiyewXqA6vH06eXW\nO2xfurlejtLOsWinQEvT9PsB/HCN/UUAz9zvFwAehxdXq9U9gPs0TWMAPw8xOb5M0/QfAfjt1Wr1\nv6dp+m8B+FkA/2Zb3308fMIFfAiv6XobeZdvH0tQXL7lWqRVoZWFMRW9uW+TW7AFli4KfhJLkOBl\nIteUe7Fu8lJby3KDdWbw+Cp25kAUdb3zxyZjxJEtHghjLG7vLa6WERaxtOfNi94lPgu0I3Hdl5BT\nzE5IKSqEqH9hhPgL06l1gZoNEGlb8fCMA/d730bYr3ZZtdeZddokFQ4ahH5roE7WioCPGrSGJspy\nW3i1Attrwd/vWCskUfkCDcu1xXycmupYwxd8V7n6Gh5C+9Yd61mt80SjZ2fR4CIWZzxECpwQ/y6q\nf2jtovffvx1UvotevLwfra1j0E6BtlqtPgngkyEvTdNfBnDj/nkD4IN6PWdi/CUAv7ZarX7Ssf8O\nAD/bnwLwX+zqf1+hsy819VfnSfzHah2vXYj24c5zFUk2/YFi2feqe/ARodB2okjVDg2LxuTbynIT\naH0ozGBgRqR1Uceb7OJIFdH8vYCMdCk0yv2P8IvWaarufF5oYgvxFy/PAKvHUJ9TT95kB6CIGZm5\n7NWR9h6Xoqm2zf8unmmY//q9DUm0jS12QZa9pthexrc/FOs+vDGozStx3/XfB/9UZN2a0koV60cR\njT7/x6A2DGfqR/t+wnwGwHe5358A8OvhRec08n8A+Jur1eq/DC79DQD/hvv95wH89j6dD1Hf+5Yd\nk3Yt/yHd181erQ3sNab9HtS+XQ2a/xHvye75H3/9HPOlc8b/MPAPKXsWWuPQvntoPwfg59M0/Q0A\nGwDfAwBpmv4URCv7FgBfDeAH0jT9AVfn+wD8KIC/mabpvwvgFYC/1NVJ/euo6YtpLM+j4f2hgec0\nDyqDDTfVDUNjFV9jKLWocu8HhfnPx15URDBgd62sCzhPSaddKSXhrUxDe8xw59BEs+QAa91k1Re/\nnz9ry/BWTXVDM6K/7MdUhMECKslTh66BemLJPnW9l2lTe37e2vrravsQXt8+msq18Yp2sD2m3lgP\nqTvi8+upWDNOO/P/n+KeDME/dHxd/Z0FXj+iY6rTexBPbb6pL5hd5UIhEWa1tpYrtm6/h+bJ12eW\na/7Acti2T/Xis1crAu42BrlhLGKFJBaTSpZz0QfYJQQ1toj3KC79FuuN8CJdiokslxfAcqHdvhoX\nQk5woojQUfLFhOMdP/x5I+/m748SEIAoKpORhmvL2DLrtGSmFg/M8BB35FLFMIu34S6zY9i2vyeK\nykzcdZNpUzu5sYUQbiof3k+PzacDOnTthdSIi7nYB5rCfNa2RvvWDQ/RT/VcdvE8WSvexEW4soHr\n51T4B/J6S7R3330x2kv91z77ubGaGo2++zu+tnUuZn+wem7ktQgJzaRaHw7/cqyTUqU3HTMX9v+Q\nin0mIrcXICGmmJ3Hky5d4X1Nn0nbe54pUohj7YST79vdbqfxecHjcSpVWv58nrIs8DgQ1MQwAAAg\nAElEQVQUSOQSYbITZH7MTsCjeUx+rF6YFX2weMyJgEchXLRyfVjrPC9LgRjOczj/zOVeILlYkbZJ\nVavh8sKsjcL76fHuS+HchHPfhKuow9vzeSh1rdG+df36PzUVeIp1TL1zlc0B/5nGo3Msx4G8pszW\nbaGYdrVdeIspqsVA9AeoLS6XkQQrdgF4FcGFuwKSiHHvzoItE10pBwBaodB6MsOwzv2XUR4rIJJ4\nipmpmuy0E5Y6VuK1iKppkxQhDgSB9zTz58qSmpeFVlRolv5dE2JQWoIMs58PK7ETrYurqVmOIChN\nW3NZn/9NJlqtP8rQlXV6yL1TRFCR3lmujWesHHWI3UdKU7k6Lq+9alUmV+3qr629Y/GO2d+Y5su5\n887Uj2avoYVfUKF5oy+vb52x+hvCC5UH5nLx+iraawUBPhWYedgdU47coejgMZA2iJwWF+wNBXPC\nzFtmo3ofXquj4Do7dU0rVeGx0yT8iKsaiO+jOifMoUdaOXafqocbyu2aVxNM7CH3aZ86nfc7OLfX\nt66fa0Wnx39sXp/rc8F6rPk/UzfNXqCdaZ50/m4805nONDeavUA7VHXvW2es/obwqmd5tr/EfPSQ\nsFxlD8aJFR92SsxYvi/5n3hHbodr8v/2ecQowOWdPKS/ahxIj1X6tRVeqTmWfZTj56IdKV9+ffox\nhfjDhKRFOe43r+E5vzmZpDyscC531fWadt+xT4n/2Lw+1+eC9Vjzf6ZumrVAm5P54FCTZhPPJ90E\nyjBCRBIXb5koRM55xJsFtULBA4DbtQFDkmMCEpuQWUyGPqv2xljcriVXVentCNenT/viInRYFL+z\nXPbDjGW8usvw4jZDllvcrXPc3ucuCSkjyyUbd4g/CgRKbiw2uUQwWS60hPBSEjsyUmXGcGbx6Iuc\nh6LkayMsEoUkUogjVey97Zr/JNZIIlXkVTvkfnv8+97jkKfd+PzlXeuHWfYZ/Z5mn/7q1w4Zex/e\nHJ7BfXlTtm2ZXY44Hg3rmXbTrAXa3KmqgewumxtbKU9EhaeiMVbiIEIEklKq8hIr9rqYi+DHEuqn\nDLBLVAYP9s8Bszs3xtjKaWa51MCkvgfrNS7xNvS7WdZpUd6LjCCZuAvNKMBfPJwoBQNbLoIcK6Xc\nXxlD7kJz+fNzmQsDppRkBQ89OPvMvxfU+3oISnZtCwqSoniecS71+1BlD7QHNgrGXV8/x6CmdRte\nO2sP7URUzfV3punp7OV4oEmhL1bv0VivwxzGnqOtw72eFAEG4q3ILF/sy2Q7zJQ/EuAj64NL7zjj\nvCQrkgvuHJgtD2tbljN1MZz2FHz3LJNyydze58gN42opOHQDfq0ljY2xjMwJ4fC6IoIFI7OAZhnb\n3dogiVWBZ5/5D+fVJ1Rta6etriRLlTF5nidyQn/K9UMERIEwa1o/Q9rbh+fjXLa1PXZ/Q3hE8/Vy\nVERQmvaqu2utnKmdZq+hHcskMlZ/bbzwZdRUTu3A74WQX9/hl35jfy1jQlCOC02Mam10z01ojlO0\nXb6Ov3wmubE/r+2oIjCxS+0yxvzvSDrZuBY659+/sI5rKtu1fqYyCTKa4pYeb+x9zXDHxtWHN0Xb\nZ+qmWWtobbTrC7GL18WfkgioOEvUSXjUwNumIWMdg0Ls9b52j6neUgvWOm/CZ/jQtXLs+Qf6rp9+\nmE6Bf5/+Hzr+oWXPdDjNXkM75c0fYhao79XUy3mHhqbxELZjDzaKAi41HO+o0Ebl/purX9GUUAiQ\nPK/2REQumgeX/VJ138eTTzVj6uDr2APh5MuG7URaHFgkFJM4imw2YViuPmbC7bklQnBgvR1fkywl\nVGNW+iF4raFtzFOZs7rWz5hUx6DIedbuwNrnPh2DpjQnTklzwPA60KwF2pb5g/kkvCYs/i8R4X5j\nsMlsZ51Ia8RahMomt0WKE0D2vbynIhFhk5lyD8zR/cZUUn54oWO56pixyYyLayiehItY4jvGkTiK\niNMIACJkucXtOsc6k8zOsaaKJmAZWGcWBMl9Vce/TCIsE11zLKnOoXdgKaKcuNxsmSmPEijnzeg9\nEm+ukkqEFD+m+vx6D0SJDLI9/7EW78jcWBeFZPveStsNdSNV8QrNcpmH2GX39vuSU5rUmtbPrvUK\nYNS1rp1N2TbMv8fvPV13jfmYz2Uf3tA6p3jXAC690pl60YMxOY5h+jmkjS5erBUM251l/UJ1Ckmp\nBQULmFkC/tbbiCMl2a1ZQjkVL3iW/TcJ9SRf0j4WZKSV+7d4DEbaxU8kAhGDWUFRqYkRibALPfgk\nRh4KnEWAYctgNpJ5O3j+OLhuTOlQkMTKxY8kRKqMBJIb444LAOS8MwkoPDcNc+BpWSXlwuqTUuDg\nhWutFXd3RWD34UANLTTNddM9AcqM3OFLh5mRZQYWPlxY1ZEF8CHBbGVPsN5XE64mnhcg+36577PW\nya2bpq58Oe/4c0g/IS8ztjE559jP71RtttG+7eracZsztdOsBdpYi20qQeZJvPu2PQ4bzYsk7u1d\n5ZTYFWs8AC7Mlf8P8I4UoqkZG0TpdjYq0SwkErmXPF54LWKNXIm25b0jlSIoV87HTgxxhgk6rfP+\nS2rp3pkl/qCnxGUW8GZQ34e05+sA9ec2xNI0X6EnWei54DEaI9MYqS7v0e25biunah8elktPShDQ\nkNu0mH+i7RigXf2NyTv0Ba38V0ZLOYlxuXsO+/AylwEifJx2fSAe0t/YvC7T4T5tA9g6rnKmdpq1\nyRE43DtoqPfQlB5Kh+DHDm89oL9ZJmyXeX+sYX8VLLV5rY4DW2MqhPAeGJp4oqy5+djDy7Hv+qm8\n5YlGwz8mbw4YhvB4AP6Q5oJ/6rbP1E2z1tCA45kZusr1/QLbxRuKtVHD6yhbf82WGGrlKDCzEQpz\n3Vj4t/oPePu0OXSuCWWanyY6tpmqPv+78LfxTof/uOufO8odC/++fY1ZP8R1Fmr9aPYaWkinMinU\naVeOrTY6DIOkQ8lqexXMQcR8v+ip9MJThCKXWb195tIb0m88Wy5ziIXl2iJjMPOWxx9zNddanm9H\nmpA+Sq9Ncpj7zH+ToAjJRwkhogruPnPt40rW73Hzx4UzNzotN3TUKbAQGvf/9qE2/Fz/98Trf1/q\n058Pm1YvOvQj9FA61bumzpvyfryONGuBNifzgf/rPfw871gYiGTPa5mUt0ywyPVYU+GJmARek2G+\nMk/s6lpml0gTyA3j9j7H/dpgXXhsyvGATS75xbw3pXXRSkLTYx1rpEsMHFzzuHPnrBG7ct5zsM98\ngKjA33RdKzcPLqZj37nOHK67tansAbaZfjJTxpuMNUEpiXIShhiLombvxHCu+oy5i8cs3q3WNs/H\nQzJpau3n8mGaBKfg7Tqic6aSZm1yHMvUMSYv1gqW7Va5Jtzeg68rweQQHlAVInGksN4YGCsZrcPr\n5Uva4G5tcLHQYHZZiiFfwrllWGskUzUIkctE7bvz7uwyZoZheXl6b8QSV/kAep5314+dd6PHUio+\n22OSWImlg0rbfIT4mU1jkk5vVvV/d811oekwY5noiit/W12fuTu8J8tEVz4ejMu4HdNwM1XfdUFw\nc0bNHpD1ceYurJfWqncf+5jZ9l3rFZP4COX6YB0T/5g8AI0en2dqplkLtDkSEaBpt0uxmOKmU4GJ\nqBA+9Rd6SLf3xgkfFF+95O1kxf/FrR5AJf6cP/emFMHkXivd7qMexd+/NCMfVNi5xoswY4CBON52\nCRStaJiJRakS7yHkBW0caRB1zylQCmHdoEmEXqxNYxrb1Ddkf8VYBoOhmlwye9KxTZVj00PDP+D2\nvvE0e9F/LJPIWP1ttTMh/rLtdlMTN2BgdpKKq3nSGjF4T8QB+L3GFuL3GFgaOtgjsJDSu8qFqHaU\nk3kZ36TWFqdzCl4dc9v9OXT+j8Ub496eijdF22fqptlraGOr823Xp+qPAx+/sfGjKNdhlgnKbdUN\nhNou/AQUe1a757Jq4gqxFvwWXL3nwePfVS5EtaMc9WxvKNYmx5RTmbOKfwtzNrj2Wv/heGaO9VDe\nWaj1o9lraA+ViEg83LafvS0qvQpRCSHURcxcmNty097J5VK+WRQRDIuJMvcejYEnX+bykfmHSL6O\nS2EZec9BIHDLR0XAefxEcvA7jNsoD2TYn9nCKqbL7ge37ANFnMExyAc8qYccG3JPmki89sgdfB+G\nldnHSNy7+6IdAEXSVAJgDxjTmc40V5q1QJuT+WAfk0gU7fay8956QDXnVR8Mm9xK8ktVCo3611wS\na9xcxkhijVgr3G8MMsO435hKmwxgk/t4kQ6/8h6SgHKegz6QsLXyok0iBeXKhfiTWBf52jzWqrDa\nHpNWqogqAlTH5P8tMRmlXhxpxJHeaqfPfaxrZtKe2mqv657U57rOY5YILUmkCsHI6L9+AEJm2r05\nu0xSTWulnDeFaM95q/Pm8Azuy5sDhj68Jo30TM00a5PjnMwHU5kZkkgVAs17zfWpC6CoS5AYgnlu\nYBiIqTxUnGUiwC4WwrlYaBjDZWxCAEQuzqKLmVj2I/gY4q2XG0akpF/W2MLahr+ClVQlkn3bOEV4\nMWBMoakQJMJ/U8T+XaaaprYVuXiXHXPdNiZjxMU/nGs//wmVfWi2kllcERI39v4mtXL++66ppvYA\nd89muP4P4fUxf88F6748v6YWs1Y95kMPapp2fYlOxRuL2voLnQbqiTv71PWXDMu2UliyiDUYkA92\nqoIv7MIDsqFPMcVxtRyVB5hD6sKvqAxE1VbOU3jI2pvdvOdh6Fk4hHx/XuOSYMK757oJq8/wHXJl\nikrzHnOZoZsa2u2Ll2r/7sLaxavzp1zrTTTX57IvneJdI0dlzhpaX5q9QBv7IW4r29X3WOaDKfF3\n8cbAHz5SU+IvNarQhOceatrPrNRE9ZfEVPiHYJ3D+pnSfPam4d+nfl8MZ2qmWZscgeOZRKbq79gm\nHVguIpWPiYEIvWM+jmHmESHmhJr15qX9+qvzvLbEKA+R74W/Ya79/Hv8+4x9St4cMIyFP6RT45py\nrtEw3jM106w1tLHU+WOYCqbktX2hWS4zQBfefqrcV7DM0O7laq3k5TKWsd4YSZ4ZhNRhVz7LbZGs\nlBlFappIEUiRS9YpHnuZCcoFEUY8ntxIlIw2L8Est0Vy0fo4tYtGEik5mB05xxefX6xOHn/oIl+f\nN2MZWVZ6SLKVw9653W7Pz60XqnVKIgVS1T2cOFLF/GtFFaEWUr09iZCyjaGpXBPW13n9+3U0N1y7\neGO1E7t1dqZ+NGuBFtIYi2uKhdynbJsNfJ+Ho7Jh7Dz+ANnTASRMTul1yACocMgwloN4hfmWG3lu\nJMKH3/+xzhGE2Xs5yp5T7l4yXmNiiFDwmasLXs7OS695bB5Dk/mPSOI8Smw/hSSJXPZpRg229Mdc\nYG2b1yy3sPIPRFo8/XJjEdpTw7qSoLRZQHp8fq6Z2WW0Fl55vdt0RURbY2or68cX8trWVhOdav0f\nwjOWW9fPobwp2hzL1Fr8xv57xm8izdrk2Eclrz/Uh/L69tvGq19n7vaoG4LLa1SxS6a4iMu4gUlD\nvMgkUtjktojQT1TWIWh3TbIDkyuPyGkypmxLq7JtIhRHEXIjbUtwYYXMMExexn9cJNK/j7xff/k+\nukqwziQQcBztjkPox6qdFhRmHogUFbjCOv7lwFzGWfSvh9ydhQsD4fo6CozEhefadZ+sE6Zaldia\n8LfxvFv/rjp1T8XCqxVVx585rf9dvF24fBzUKfCPMeap3z+bTGK1Xi4fjO5xUpr9LPUxvU3d3yE8\nt0TLFC97Erv/VO1rLfxX/Ys5/M3MiJzmoIjgU19q2j5LFLqpa6Ua2wMQfDnLby/AKeAB7XERvTbV\nFFk9/O3/eo1SK8HvMQLbnohtX76hR6mXh4dmBPYpZ+r3eMhaIepbbhv/mI/F2Ot/jOd3SL054h9C\n9f7O59+H0V4aWpqmFwB+AcBHALwA8L2r1erdWpn/BcDbADIAd6vV6hNpmn4NgP8R8m7+PQD/3mq1\nGnzLmr7223jAtslvqKnmYKp1NQX+vcfU8IzuamVIX22CZS/8W5f3u4dTzf+xqAt/qJUeZf3sQbNa\n/3vQkP6HjPWo76TXlPbV0H4QwO+uVqtvBfC3APx4Q5k/B+Djq9Xq21ar1Scc778B8OOuHgH4V7s6\nGcPM0Nd8MKS/ITzXcKHB7IsfBW+g+SMcW6UOCy7LW3UVhXXa+wiVRUKpQXDAA0oNpj6+Qn/tOTd+\nOrn4P9XaGWYiCvEfsn4KFNzznozEGwv/MbB28fbFH9Ic8fcZ3+7+toZ6pg7aV6B9HMCvut+fBvDt\n4cU0Td8B8ATA/5qm6W+kafoX3KVvBPB32+p1UduXfv3aIbw+fQ3FqkhiOjaZtYaZpMjtdXFruab+\n40hBkY8pKA4fG5erzBhxEqm/HiItdWItZsnc2CDp53Y5QEx+2vUT8gBxWDGuv64xNeEHnGOAi0Po\nYy6q2hzX64demG3zFOKvl7PsnW6aw055XMZITE0XsrG1r33XzxD8xsiYTc0z8JTrvw/vGM/vEJoT\n/mWit9Iznamddpoc0zT9fgA/XGN/EcAz9/sFgMe16wmAnwbwMwDeAvCZNE1/CwCtVivuqLdFYy2W\nqXh9sPq4efuMSfaz2AkAQCndu66nOOh/4xwhGHAxIJvH5OsoJRvT4ZdjW9vi3Sf54uTruhyz1K9i\naxsTs4/GL/9jFm1SEVWSfyoCGC5pae1+NOEt2vZQmAsvxa059BgaMPv2/ZiIqAj6O8X62ZobLj8W\n4sracp6nFa1a5vCU638q3tB+2+qcCn9fXtKQO7CLnj693Hrn7Es318tR2jkW7RRoq9XqkwA+GfLS\nNP1lADfunzcAPqhV+2MA//1qtcoB/Emapr8DIAUQfuY31avQMW3K/mUxJyq95whjJa2NtSqNdcGa\n7xp7HKliobSVC7EqqnogCv7yAe3qi7nmvegDIjfUbeP7a1y7Vm/bXRUhWauvCFC66jVZJ9+/tYzc\nylk9NaGblcdPAOKGJLNaKyigNPVOsH7mRHN8ZqeiIVrn++/fjtbvi5f3o7V1DNp3mX8GwHe5358A\n8Ou1698O4H8GgDRNrwF8PYD/G8DvpGn6bR31tujQr5ypvvaOwfPP6iHec0082qPuLu3D7x8p8dFH\nSEPwo+69SAd4Drb2Ud2f6SrXpz9/nKDN03JsXpNXaNN9soFX6JzW9RCNaqjG9ZDw78M7Uzftew7t\n5wD8fJqmvwFgA+B7ACBN058C8Eur1erTaZp+Z5qm/wCilf2V1Wr1pTRN/wMAfz1N0wQi4H7p8CGc\naSidH5DXl8739kxvMtGcVXY+Irg5mi+qJqN5v6iqJkd0mhy7qMnkeMg5sfC+Npscy4Pi+1JhcjwQ\n6y6qmBxbMIfjfUjrZx+a4zM7FdGAL5V3330x2qT82mc/N1ZTo9F3f8fXts7FrC3rczIftPHq13NT\nxkg8tG1FhCh4GY2Fnx1O44L+5sZK1JDcYpObLfymYUy+TogVQNFmEilEigqvRx9WCwCyoK5lxiY3\nhTchkUtAqX3d9jGFc10fU1OdCi5NiPX2i36v+6R2Y921fobgr6+HNhPcVOuna/3v045liYJjO8Y+\nBW/KtqfAeqbdNGuB9hCJCGg6rLwv7cobtouYuXA/D3m2dCMMHiS3FwZU67SMqQ5LE1VOhvl9Kq6V\nJUhHWe7c4muN+7xplrkVf+GWHlalMnhySMbagucFkCKCUspFHUFjcOAu4gA/sN992tIuqD4T2+Tx\n96VD108XjakdEW2vpzOdaSg9+FiOc+NppQrnwTngajpnlkvWQGilwVyapKwTdMwMG7xam8bU5GGo\nNUGjIc4iqgFWI01YWzk3dRHpwgMvxG9dUFrbYCLc5HbL7EYQz8QcLssAlS7uxgJQJS/EXZjxSJw+\n+87rOjOwFoiDJ2jofQp/E/xZwcPud1cfY/PGaqfJo7RP3brJ8VT4jzXXZ9pNs9fQjmUSGau/sXmH\ntsOoRfRw19viJ6L2AO3Tb/1Tu8lT0dpmXIUZqoDDLeWaMYJdJunClCfCW1E3fjVw/nfhnwtvDhim\nwh/SHLA24Ru77TN106w1tCG06yu1D/+UNBv8RFtCrU//s8K/xdvdv/BoZ7ku/rFo1vPfg94U/EPL\nnulwmr2GdsoFMbb5oH5tCqx1niIXS7GBF5ZjLl/nhXbD27nKmvuu/pv8f+4Lu553DRCzo5g3m/GH\njgyN+IPiodkOqMaOFM2rGUOIt+NyI2mFTvwhb+z1MwW14Wc+4z8G9V0/Z+qmWQu0LfMZ80l4TVj8\n30HmvwEYLEvIKRvsFezTnnYHnX12aAaKw8+b3Lr/DHJjQSSef4nzMuzTn+Rr2o4bGEfK5UmjIkdY\nWDeOFBax2nJwkPZYwly5TNUgqgjgSEvb9fn3+P3+Xp3Xdm891r7z6vcl6/gPWT/s2u3ycvQv6LBc\nvT8Ao63/zOXL64N/7PW/73M5BH9XO8fAP2ScZ+pHD8bkOJWmc4j5Y4iZwVrJFB13hGuqk9aq4gG4\nDy4iQqSdRkautZAHgEiBAy9AoNz38m014bdWXuwS6FiyT0eRBhGK7Na+zbq2RyRhonJjwFw6mWjt\nMzNz4HjCaMoqneVGLpHUJ1RfANYyjLWtZ7DKL+Ay+3cUZJlmlqDK2sWo9OW1BJGEqiXz7HtP2nja\nRV7eVVY8F4ev/7oGkhmLqMELMhyn2cPScOjz00ZD292F/1CsU+M/03CatUDbZwEMNSkc2l9fXm6r\nwXrbypWmMhT7QYc+CIoIKojY7V/8IW8r7HwTfotK/Mfcucgzw0V4ZxA5AbIjTqQXcMZWPSDrZk/x\nlmTo2oeA98h0jC13d3lhVx1EmrD4ctbCCbSwDzEr1sO8KkVQDQ72h9wnAkCqWbBUypEcjxjSR9P1\nTS4Dpo4PrCnGecjzW6/TJog9zR3/vrwztdOsTY7A4d5BfeuM1V8bL1yXU+AfwgvbHYSfsMXzVZjl\nf01mwLa2gX68Jg9Ep8q4B74Df0N7bSYdruH3L5O6UJzinkzF67zeERNyLrxd92xOWJvwjd32mbpp\n1hoacDyTYFe5fTTA+jUCtqK/78I0lpmkjpVo9/mdofilkBMEo+NvKOelKTcngeyitnL19wYRAc6s\nGl46dP778Pbtaxdvn/pn/MfD2sRr0kbP1Eyz19BCOraZ8BCqt6M1NfLnhp9dG33w+/0XRSjygfkI\nHsxcOdAtbaJ2yFtMglUPRDEfep4mj6mu5fq/gqEeHcSTrb24bMP8lAkCqBKVxJt989z2mmsf2cTj\nPYTa+qvj33ddaGrGONX6n4LXt9996FTvGv+cnGk/mrVAm5P54FCToFbiSaeChFmnwh9eq183xhZR\nPphlr8U7RtTxa+dtuEg0Lhbyn/cYtAzcr03Fa4/ByALPTSLJWB16GBJRxeswirRrz8V8DMolkULi\nyoZ7bERUxIoM297kFrlhrLMqrkhLO8tEFdFHKqbH2lw2zatvGxBnFIlPOd768fhD4b/r3naV8/N6\nrPU/R94cMNTv3Sa3lY+Ws2Y2jGYt0PYxFYzNa8IS8sY29Y3FY5ZYgz6Ab1/8KghmyxCvRkXUij98\nMCMXOJdItDXv1u7rEJwXYa2dQnC0PMiiBVLhyWgtF0GJ/XUT8Ji9N2YZENnzFEl0fUUEa8u5CV/O\nIRZfZ9dcO67D47wug3fRPusnN2ZrTKqhzV3r9ZD1eAj+uT+/u8qeAn9cWzdnGkaz30M7NR3L1Dc2\nGVt6EdYNfU1Umtmo2DAamgol9KZsCqArQmNQk6UwpNK7LzN2a08rN1z7OmMA1f68oPGU5ey0xfbv\nunqdJjLuhHUSiz9kOIf7rh9/71QNv+7AOgU91PXv6SHhLz4OdxzVOVM7zVpDA45nEhyrv7F5+7bD\nYpsDM7fGKZwz/t08bPHQUA4dXo7cwNsXPyYaZ9OY5jH/p18/Ic0BaxO+sds+UzfNXkMbW8Vvuz5V\nf8fCX+cRAez2ieqOEUTHM33ui383Dy3laKtOW3uE0mnk8PUz5RzSAXX74X8ovPrvueCaeq7PQq0f\nzV5DO9N+5ENeOReHvdpg9rHwDsPiH8w2T8Stch0dcu0vIF+wWlV5XrPpasuH9wqFZD4wLxrgD4ZT\nkVOtqU/m3eMPiYhaPRHP1E1D51rqcOHhOyfyz+CZ+tGsBdqczAcPzaRDJDEM43jbm62JCjNc5ekh\nZMYWXomH4BLvre3+mspxrVz4hZq5XGhJVI1wEWld8IgkdiURKrx6f0qJd6P33MxNibHNhFRqwNW5\nTiIFrVUjfkCEXGbslpmzaw6jSHfiD3n1F/GxTGrH6q+upXTVLeaa+5sE4daM3VHnmDyvnd9vDM7U\nj2ZtcpyT+eChmXSYXZJNIw9DQtUXHnPpARhHqqiTGwaBEUXiJZhEqvLlug8uQARL3fRZL5cXgWTL\nellmkBnGxSLwlqQSv68dsa3EYEwitZVRYBfWOFKFW3y9HLPEdbQMJBG1tpe4uaz3oRQhIfHSHHv9\nZLkpcI3RXh9e0/qZqj9jXBxRKkOceQHXONdESFxM0b5zjeLezev51Qq4WNSDr52pjWatofWhXV+L\nQ3nHpqnwe887oNngyCwmujCOovU8Xf1S7JqlIVjrXpP1ciJLqk4sPh4j4ONhsouc70yM7uFv8qps\n4u3C6o8dNBSUuI5tiVHR/NVdXGvhj0GWm5ONNmHbxetLTetnH+qDK7dcpCTq12b1o2gIjq56Yz+r\nfZ7fQ+f3TaPZC7RdanpTuZA3dCEd28wwFv5tcwWAwlTTUFc+XwGqPczMvbz/psbfyONt/EOwnhz/\nBLxT4W9ePw8H/xRYm+jQ57er7TNt06xNjsDxTIJT9Xcqk2bxvqG2w9DsBF5odkHxEJ0KP3qMqQBL\n7sTOjv7GwN+Fax68fuMcq7+m9TPVOGnCtqfkHTTmYK2Xz+yZdtGsNbQpTSfHMP2unasAABboSURB\nVB+cEr92ObMi54FXf8ErkhiM5QNEkm6Dwjxpx8UvYaeqWJeJLl5ofkzMJX4CQIoaj4439cEsTgPG\ncpH8kRlFGpwuvLo2X336m5pH5BOadoBvoEMxNK2fMfsIKY5U5cPMWm70Ru3bNkPWgG0IIzYF/n3a\nCdf6mfrTrAVaSGObHvZtt86b6oU1hqkm1uJ5FweefCHFkUYcVTecI622eL5Nv1k9FX5FVMEqfTHi\nWHh+TH5vLI40klhLkOSWNpt4ueEioScgLzgflLgLfxTpxqgh9Y+FfdZPOLdD14pWtIXrGOu/af2M\n1U8dfyjUcsuN3qhD+vIORcd4fvdpo77Wz9SPZm1y7KOmt5nU9uX17beNN7TOKfB3YW6rU3ia6dDO\nPx1+y86L0b28LhbUWS7SZaiu8DrVeEQSsDjLuUx0ijJs1RCszC6JKIC4w/OxD88fGejyoGzi1XEB\n7WbmOZrZhmD1cS1DT9J9+iWUxzkOHfOx3jVn6kcPRkMDjrM5uusrqq8Gso9pYgyaCr/pMEOOSb59\n6zwaLVe9FetYjXMdVzVtuWsevDfnrhiNPdBK3x2ej3Ve2xe85bZEps3tjEFjr5Up1z+7//xc97GO\nzAl/E+27Vs7UTrMXaGOo7n3K9u17KB0L/1QPYKHh7Nn/vljbzEFT0dznf1/eMbE20ZuMf4z6ZxpG\nszY5TqW6t5nhxjafHRP/1FgVodi3OAZ+QilEO8sRwC24toSk4xHKNtrq9sHvETKPuQaGm3P3xT/3\ntV55Prk613U6Fv4hYxo65q7+zgKvH81eQ/PU9VUzlpmhq69D6aHjj2q5uIbgqvPC3GVt+LXzuFwk\nquJNVydfbheF/SglHotEZR61LqcQj9mbN/11Itm4r/tYDp1/IgmdRR3j7Lt+msrvM/9jU6HpM1zE\nlWHh1OpzPeX6H6pVPYTn902hByPQTk2HmkROTWOYdCRp5bCxWd5OAmmZG53MmblyZCDSClopJLFu\n9NIkkgzadVx9MGqXSNFYLty4W2RJga3pslLVbNlttGv+w/mdev20zX8Xjbn+d811G/Wd6yZqw9Rn\nrpvW8JnmSbM2OY5lrjgmbw4YdppvOjCP2Z/3QNRKNCl/LdZqqzxQevopNd78l5rBdh1/linMEtw2\nX3UHkrmunz7ttc3/MfATlf0f2t+U5lf/l90aVkrOdJ7yvXKm3TR7De1Qdf4QdX9sk8KU+OfI889i\nPT5iWx2JdI6d5YbwQqqXK88ytdc99RweOvZTY5gSf0iTrmFm6D2exSlwnamb9tLQ0jS9APALAD4C\n4AWA712tVu8G1/8lAD/q/kkAPg7g6wEsAfwKgH/srv3carX6n/aDfqYzTUsP/UVyxn+mN41oH5U2\nTdMfAfBotVr9Z2ma/kUA37xarf79lrL/EYCnq9Xqr6Rp+pcAPF6tVj/dpx8+or5dN1+8znSssZYm\nR+oVNdznsApznU1J5WHm2RsqetN5HY9LzD6NS781PBXRAOn+7rsvRpuUX/vs58ZqajT67u/42ta5\n2PdJ/jiAX3W/Pw3g25sKpWn65QD+bQD/uWN9I4B/OU3Tv5em6SfTNL3p6mRO5o/XySQYXhujbcsi\njLLcYpPbgmfc3oNWXXUZm9yAmSVUV+2lse/856aM1djWTrRHf2283JRj71s3d3O2T39tvPq1Q9t7\nHdf/0PFFmioHuo+JlRnYZMOzqL+ptNPkmKbp9wP44Rr7iwCeud8vADxuqf4jAP7aarVau3//FoC/\nsVqtfjtN0x8D8J8C+A+7+p/TA7DvQzFn3r7tGGNBykW3YAaBAGKE7nNEVNl7aGyPff6z8uXho4R4\nj7b98Jd7ePXrVaHWLgy6+mCWAMdauRdf5eRcv7lURDAD6/TFpUiirEQ95nDIOMfEeihvDCz+dznO\n7bWia30ec5zW2kpi3D709OklooYYm/vQzfVylHaORTsF2mq1+iSAT4a8NE1/GYDXrm4AfFCvl6ap\nAvAXAPxYwP7UarXyZT8F4Ge7+j6m6cQv6jeBDh2rZQkQqwEn1AClRSh5Knnd91ERVcp5E48igjoA\no1YEjd3970vePOq9N7Ue3p9SBDUyRm9GNUDn+b2+lOW2SOQ5t+djrGfWrznC/MZpbDWfYR96//3b\n0fp/8fJ+tLaOQfuaHD8D4Lvc708A+PWGMl8P4B+tVqu7gPe/pWn6Te73nwfw27s6OvQr55hfe1Pw\n5oChzmOWl4DqgW/4F7O/dvpxduHnCTwyR/mid+9i79Z+aNuM5mzYp57/Os1l/sduh1vGe6Zm2vcc\n2s8B+Pk0TX8DwAbA9wBAmqY/BeCXVqvVbwFIAfxRrd4PAvjZNE0zAH8M4N/Zs/8t2nUWpw//lPTQ\n8NcfsYeGv06vI/42/kPBf57/Mw2lvbwcj0V1L8cmE8NYPP+7qdxYNCX+Ll4fHH2IiMSeH5gF4yCV\nxxBczAyltusCwCa3IKoeAN6Xmu7xUKxNvDYPyVOvH2O5zIwAnzR1/HFOhX8KXh/q42F7Cvy5sbCW\nsUii3mra2ctxprRt5uGT8Jqw+L+DzAczwR9eG4J/kxnkxoKIEGtx4NgHV5ZbZIZbsSaRcpm25zv/\nkVaI9LbDy6nXj8fl789U45wK/6HP5ZD5D3/HbpzHxN+HpxUBDc/umZpp1qGvQppKde/b7qEmkWPj\nZ3ZeW1rcDsbAr50HInCYXV8rgnF9tGGotz+3+SciqAP7mgq/39vsM74+60e1tDWX9V9gVe0Bnndh\n9fezray1PsFtc9iwQ/B38YgIr9Exyclp1lO1z4Phf/fl7dNfXzolfhOkqd+X6n0oosakmEPxK0WN\n5sTXaf67eH1pLGE5l/XTh7fP/BdYG76xxpr/3LYHVJ5y/QDVBLJn6qZZCzSgnymji9e3zpD+DjGJ\nTIW/zvPPBh0wplPiH4q1DX9IDxH/HNfPXPDX6ZC1vgt/KGv64t93zF28M3XT7E2OxzLpDO171xfY\nGFgPMekQoTAP9q07J/xDsHbhH7v/Q+u/Lutn7vh38YbiJ6Ax4ewxsJ6pP81eQwvpGA/MWAvr1Fh9\nhHsfdSOkPpEHTo1/F28XzQnrVPjb8nRNvX760BS42nB4rKYF6xj4dUuQgLmunzeVZi3QplTdT23S\nOQauuCEG3Sa3ReblOeMfMs5TYzgFfsmyzVvl6uUPwdW0fsbCP4QHuHUbhDRswtoVM/RQk6BWys2H\nGlz3EB4zcLc2OFM/mrVAC6mvqWBsXv1anTe2qWNMXvjC8bxYK5B6GPj7YHpT8Ueaiggeu9oYc/2M\nhX8oL0zC2oa1T/9DsNZ5RMdP8AkCFsk4cRnfBJr1HtocVO2HbiqoYyACIprew3AsOnT+m7SXY9JU\n64eIGgMrj01zWP/+HtaDBPehOeA/hAjAiZfwg6LZa2jHMumM1d/YvDlgeMj4Q3qI+B/6/E+JP6Q5\nYG3CN3bbZ+qmWWtowPjqfNv1qfo7Fv4hPKLjm05O2d9Dxv/Q539K/CGdGtfUc30Wav1o9hramcYn\nZgbjOCYVZsCYYQkKmft5Yg7CcOgp4Qlozrhs7QU75v04U386xjP6OtGsBdqczAevk0mHIV5ylqfv\nLzcWzhmvd13LLHm4euDrg8FYWwbsncH8j4ErfNF1meCGtFeff2uFt3G/fZ8Pff3PCUMfns+Efqbd\nNGuBNifzQRtvDhiG8ggSADiM0TdVf3EQaLhvXUWEJNIgGmf+tR6O4Rg8HQTEHbrmMsPInebbZYIb\n1p64hyuS0GS5i9wfa4JlFMcEHvr6nxOGXbx8oHXjTadZC7Q+tOvrdCjv2HQK/OWX4F7Vd2Ko85Si\nQfiJxsFWtIf2eHinXD8EER5DyVspJRjv4fiNZYAluK/wy0PbksHZ9zf+8/KQntUmmnr9yK3Z/mA5\nUzPNXqDtUsmbyoW8oQvp2CaFsfCfyiQyd/y7+pg7/rYx1V9yB6//Wn8cmHudqjzJmMbCP8f1P6Ts\n0P7O1ExnL8eJ+5ujmYTo7OX4UPA38QjykuMR8QOQWIWF4Cp+ypU9+5ty/VSwv6bPqvuxNd4zNdOs\nNbQpzRFjmwqObboau+1j4rfMjXsD9Xb6ltvFC9uZw/xvj7PZE7RdawEUAWzbx7SLwjoSCxFA8N70\nPGYxiyoKBOoDXv+WedBc78vbReHabHIM8hRHzWblMzXTrAVaSFOp7ofypnq4Hwr+LtNX+AL0miEg\nzgV+H6irrz7ler3EWnJ7DZn/EH/fNnbxPOXGFvja9kvqeCKtEEXtIZGa1k9T+34OY60qcRvrvDjS\nW7nwHuL6D9fUWG028XqbDlnuP7dgUkSIzxk+e9OsTY5jmtSOZWYbo52p8XdhHtKOMS6LL2zxEPrr\nWW7BAJKIkOcGhoEYDCLxsOzTRxKprfNQu/DVr/uXf2m9GT7/dfxD5qiNxyyeheV8IOBJ7MJ9723b\nWsmc+3ccTefdOkY7fdf/Ps+En+sxx3wIVqUIC6V39nGmfvSgRP9Y6v7Q9nZ9bXXx9umvL50af95i\nKmH3n3eKM4ytmHR9v+5Vrdy++In2n/8m/G11+84/u/TKPvUJUWnx0wO8Qvuun+KeqGH3uA3/HNZ/\nE/XBX18LD+n5PVM3zV6gHar+H7JAxlhIx8I/1YPw0PE30XzwN3x9d5hw9+Gdev7fZPyH1j8LsuE0\na5PjFKa3tutD+hubNwb+Y2ENeYrQvPcT4GPmSrbfY+MPad/5nwI/2AKgwtQoPAaoyhtr/ZT3ZD7r\nZwj+XWa4OeIfOr6uts/CrR/NXkPz1PUFc4hJ5FhfRq8j/kgr1M/a+q/qOHAgiKNqOWO52M/pi99a\nRmZsk06zN/6+81rH31auq686+QPVoRenIoIEDtkeZV/8TeXDe0LgQXXHoiHzb2zVE3Gu6/9Yz+8c\n433OlR6MQDs1HWoSOTVNgZ9IHC6ayitFhVdcvZxlbhRMzAzb8vAyAK5d2wc/Mw8OtNs0To+176Z9\n4xzRNl/CYU2T0FEpgtbDHnk/zmOu/7b1cQi1YZrT89u0/pn5LNAG0KxNjoeYJk7FmwOGneanDszH\nwBBqb2E5776u1HZdrQi6pzdYk6mGWYSPj0eoDvT081gTRYPr+t9RyzxMdW/34WXOpbzpnky1fuKa\n0N3HRHcsrGPymtZ/7sKSnakfzV5DO1SdP0TdH9ukMCX+ufKG1JHo/9hZbggvJCJq9fRrq3tMrGPz\nxmiHGRVz65zwh3TquR5j/pvWFDOqzDN10uwF2pnOdCo6lenpEAq/+B8i/pAeOv4zHZ9mbXIEjmcS\nnKq/OZo0DzXVTIWfqGpdGau/Os9aLiLH74t/Cqynnv/GcQKVyBoPDf9Dwtq0pggYfT/xdaZZa2hz\nMh+8TibB8NqccMVabaUoGXP+iQhJVPbRp25ubJFgcSjWtrpTrZ8+/Q3lxVH3OOt1jLGNHqxzHKf/\nnZvS63ZsrEN4TWuqaf7P1E6zFmhnerOIiFqjZDRRkxZWv25sNRAtEbXmRmvEBEJT6X5Yu/vZhb+L\nrOUi43XFzLh3i83UNc4m/JbH0Sgst3u87jNKazvam4G88J6MQ9b/mbZp1ibHOZkPXieTSBfmuWHd\nd66ZXVxEHObRqDVBuzfe0LqSjbq97r7zYJmLsGNAmXhzCq/JIfPv3e3998K+bRf3jgCF7Xu3a17b\n2lOKoBquR4oqni/HXtfGWAmvRtWsBkAZE7UjDvWZApq9hnYsk+BY/Y3NmwOGM/554WIuX9T1a6fE\n78GFGcr3aQ/utxoJv4+bqSYce9t89Knj72L9XCIRnffPBtJBGlqapv86gO9erVbf03DtBwD8ZQA5\ngJ9YrVa/kqbp2wB+EcAFgM8D+L7VanV7CAZPuzSQPvxT0hn/aemh4SegMRxX+EI8Cf6Gj8Q+NATr\nHOa/TnNeK28S7a2hpWn6MwB+sqmNNE0/CuCHAHwLgO8E8JNpmi4A/FUAv7harb4VwO9ABF4nnXJB\nH8PUNzbWJt6p8fcpPwV+IjRGBXko8+81sTopAhBoL2MMZwz8XpSFEVT2WT9hO32pqx+v5xhuxnXs\n57de3+/pNkUJUYRxbvAbQoeYHH8TwA+2XPsmAJ9ZrVbr1Wr1DMAfAPgGAB8H8KuuzKcBfHtXB1vq\nN/NJeE1Y/N8hZoi54A+vTY0/yy0yw0effyKJXeiTI/q2mQWTsbz3mI6BP8st8v+/vfsLkaoM4zj+\nPTu764a7WpJ2FXSz/ZKCCIsSLEQSMyolCESyMIWim9CLwi2hi24KwqywUFzoD1FkSRsVFdlFu7UI\n/SE35AG7DMyK/mxlmkkX7znr7HFmdnf2zJmdM88HhN33PTvneebd8Z3zvmeePTv5zrvksUNu4Y7N\nzlJ03kVRs+JP4ioveVbv+ZLcZhpXpeOiKH6uOmrnUs9jZ9HWEUV0lsLNSunjSmEdEjc9Uy45StoC\nbEs1bzazNyStrPJjC4Dfy74fBxam2pO2WqJ6f/nyapsLMczl+Lu7Ju9m5x5/6txRBN0dpen9bBOf\n//Tzlj4u+bpU4T+7ZsYfpeJpZAxZnKMRcdXTlh7H8r55M7zsWLy4L7MZ8K7VV2T1ULmYckIzs/3A\n/hk+7h9AX9n3fcBvZe0ny9qcc865WWvUXY6HgRsl9UhaCCwFxoAR4Nb4mLXAZw06v3POuTaT6YQm\nabukO8zsOPAsYcI6BDxqZv8ATwAbJI0Ay4Hnszy/c8659hX5baXOOeeKYM5/sNo555ybDp/QnHPO\nFYJPaM455wphThcnbiRJFwCvAksIn4m718x+Sh3zDnAx8C9w0szW5h7oLEjqAPYAVwOngK1mdqys\n/7zyZE0JNAPTyHU34YP943HTuvhD/y1L0vXAk2a2MtV+O6Eqzxlg0Mz2NSG8TNXIdRuwFUheu/eb\nmeUcXmYkdQGDwGXAPMLrcqisv3Bjm6W2ndAIVU6OmNnjkjYAjwEPpY7pB640s1a9c2Y90GNmyyXd\nADwNrINJ5cmuBXqAYUkfm9mppkU7O1VzjS0D1pjZz02JLmOSHgY2AX+l2ruAXcB1cd+IpCEz+zH/\nKLNRLdfYMuAeM/sy36ga5m7gFzPbJGkR8A0wBMUc26y185JjzTJcki4BLgTelTQs6bac48vCRI5m\nNkqYvBLVypO1qqq5xldv/cBeSSOS7mtOiJn6HrizQvtS4JiZ/Wpmp4Fh4KZcI8tetVwhTGg74tfo\njhxjapQ3gZ3x1xHhSixRxLHNVFtMaJK2SBor/0cou1WrDFc34V3+esKLaZekJbkFnY10CbL/JHVW\n6ZtOKbK5rFau84HnCO9+bwEelNTKkzdm9hZhKTytaONaK1eA14EHgFXAihZ94znBzP40s3FJfcAB\nwspRonBjm7W2WHKsVL5L0tucK89VqQzXceBFMzsDnJD0NSDgRIPDzVK6BFlHnE+lvlYvRVYr17+B\n3cmfKpJ0iLDX9m2+IeaiaONalaQIeCbZC5X0HnAN0LJ7wQCSLgUOAnvM7LWyrrYZ23q1xRVaFVOV\n4bqZcPmPpF7gKuBobtFlYyLHeF/pSFlftfJkrapWrpcT9htK8T7ECuCr/EPMxVGgX9IiSd2EJakv\nmhxToywAxiT1xpPbKqCl99LirY6PgEfMbDDV3U5jW5e2uEKr4gXgJUnDwGlgI4Ckp4ADZvaBpDWS\nRoGzwEAL3lBwEFgt6XPCevxmSdsJ6/BDkpLyZB2cK0/WqqbK9RVglLB09bKZfdfEWDMnaSPQa2Z7\n47w/JIzroJn90NzospXKdQD4lHBn6ydm9n5zo5u1AeAiYKekZC9tHzC/HcZ2trz0lXPOuUJo5yVH\n55xzBeITmnPOuULwCc0551wh+ITmnHOuEHxCc845Vwg+oTnnnCsEn9Ccc84Vwv8h9po9Ct2wLwAA\nAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x112fd4dd8>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"RGZ & Norris & resolved\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAbQAAAGoCAYAAAAuIBCmAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xu4JFV97//3qurec2GGOYM3NCGJ14XBn3gEEoljvERQ\niXg5CUkcNciRaEzMBWMSFG/BSwxHJB7z6C8ixAsh0RjwGH+A/tRgBOThCcLvQSPLoIkxmMgQBtzD\nMLO7aq3fH1XVu7p3997Vl92X6s/reeaZ3V3d1dW9e9e3vuvyXSaEgIiIyLyLpn0AIiIi46CAJiIi\ntaCAJiIitaCAJiIitaCAJiIitdCY9gGsZ9++5bkYgrl793b27z847cOYOfpc+tNn05s+l94e8pCd\nZtrHMA+UoY1BoxFP+xBmkj6X/vTZ9KbPRUahgCYiIrUw002O67n21jt73v+MJ/3IhI9ERERmgTI0\nERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGp\nBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0\nERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGp\nBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGpBQU0ERGphca0\nD2Dcrr31zr7bnvGkH5ngkYiIyCQpQxMRkVpQQBMRkVpQQBMRkVpQQBMRkVpQQBMRkVpQQBMRkVpQ\nQBMRkVqo3Ty09fSbo6b5aSIi808ZmoiI1MJCZWj9qLqIiMj8m+mAtl6gERERKZvpgDYL1O8mIpPS\n73xzxinHTvhI5pMC2pDKX7ydO7ayfODQhs9REBQR2TwKaBM0j02o6wVhZa8iMktMCGHaxyAiIjIy\nDdsXEZFaUEATEZFaUEATEZFaUEATEZFaUEATEZFaUEATEZFaUEATEZFaGGlitbX2p4E/cc49o+v+\n04G3AAlwqXPuYmvtNuAy4KHAMnCmc27fKK8vIiJSGDpDs9b+AfBhYGvX/U3gIuBU4OnAq6y1DwNe\nA9zmnHsa8DHgTcO+toiISLdRmhy/DfyPHvc/HrjDObffObcCXAf8LLAHuCZ/zNXAs0d4bRERkQ5D\nNzk65/7WWvsTPTYdCdxXur0M7Oq6v7hvI6rLNaNSHzBAFJlpH4rIIqj8h5YkaWg04rG86DVf/dex\n7GecnnvyT/T9LDajOPEPgZ2l2zuBe7vuL+6TuRUwRsFMZNbs339wbPuqsorILNmMgPZN4LHW2qOA\nA2TNje8Bfhw4DbgJeB7wlU14bZmQSMFMRGbM2AKatXYvsMM59yFr7euAz5H10V3qnLvTWvtB4KPW\n2uuAFWDvuF5bJk/ZmYjMmllfPmamD05GE0IgBPXDiVRQ+Y9k377lsZ03Z3ENxzNOOXaifWgilRhj\nUKInIuOigDagEAKB7HJpWs1uRVatZj9ZJMXfnvpvpR+VvhqQD2GqwQyKzEZ/1LJYUh8UzGRdCmgV\nZf092VD11AeG7Xss9iMig4mMIfVefz/SlwJaRa3EY4whMoZGHA2dISWpV3YlMoQoMsTR8H97Un/q\nQ5tBRSYoMq9uvfVW3vnOdxLHMXv27OG1r31tz8d95CMf4e677+b1r389AJ/73Of40Ic+hDGG008/\nnTPPPHPTjnHfvn287nWva9/+5je/ye/93u/xkpe8ZM1j3/Wud/HIRz6y57b1fPe73+W1r30tf/d3\nfwfAO9/5Tm6//fb26x955JF88pOfHOFdSJkCWkXNxniS2Ua88X5WEs+W5nhK14hMw1vf+lbe//73\nc8wxx/CqV72Kf/qnf+Inf/In29sPHTrEeeedx2233capp54KQJqmXHjhhfzt3/4t27dv57TTTuP0\n00/nqKOO2pRjfMhDHsLHP/5xAG655RYuuugifumXfqnjMffccw9/8Ad/wL/+67/yyle+cqD9f/rT\nn+ZjH/sY99xzT/u+8847D4BWq8XevXt5+9vfPuK7kDIFtIrGlTFV2Y+Ss8VwxRVX8IUvfIH777+f\n/fv385u/+Zs85znP4aabbuKiiy4ijmOOOeYYzj//fA4fPsx5553H8vIyd911F3v37mXv3r28/OUv\n56ijjuK+++7jLW95C2984xtpNBp477nwwgt5+MMfzrvf/W5uvvlmAJ7//Odz5plncu6557K0tMSd\nd97JXXfdxbvf/W6OO+44nvnMZ/KoRz2KRz/60bzxjW9sH+urX/1qDh5cLan06Ec/mre97W0939eB\nAwdYWVnhx37sxwDYs2cPN9xwQ0dAO3z4MC9+8Yt56lOfyne+8x0A4jjmqquuotFo8F//9V9471la\nWmLfvn28613v4qKLLup4ndNOO40TTzyRf/7nf2bXrl28973vZfv27e3tF110EV/72tc6nnPJJZew\ntLTUcV8Igbe//e285z3vIY47LyTvv/9+fuu3fot/+Id/6Lj/4x//OJ/97GcxxnDaaafxq7/6q2s+\nh127dnHZZZdxyimnrNl22WWX8dSnPhVrbc/PUIajgDag7g7pXgEqTT3GDD8asRFHanZcEA888AB/\n8Rd/wT333MMZZ5zBs571LN785jdz+eWX86AHPYg//dM/5corr+S4447j53/+5zn11FP5wQ9+wMtf\n/nL27s2K7Tz/+c/nlFNO4S//8i954hOfyO///u/zj//4jywvL3P77bfz7//+73zyk58kSRL27t3L\nU57yFAAe8YhHcP755/PJT36ST3ziE5x//vn8x3/8B1dccQW7d+/uOM4///M/r/yeDhw4wI4dO9q3\njzjiCL73ve91PGbXrl3s2bOHK664ouP+RqPB5z//ec4//3ye/vSns23bNnbs2LEmmEGW5Z1++umc\ndNJJXHDBBXziE5/grLPOam8/55xzKh3vl770JR772MfyqEc9as22Y445hmOOOaYjoN1xxx1cddVV\nXH755QCcddZZ7NmzZ83zn/nMZ/Z8vZWVFf76r/+aT33qU5WOT6pTQBtQlSDjQ6AZD99kqKHJi+Ok\nk04iiiIe/OAHc+SRR3LXXXdx11138bu/+7tAdtL+mZ/5GZ7+9Kfz0Y9+lM9//vPs2LGDJEna+3jk\nIx8JwC/+4i9y8cUXc/bZZ7Nz507OOeccvv3tb3PiiSdijKHZbHL88cfz7W9/G4DHP/7xABx99NHt\nTGb37t1rghlsnKFddtllfO5znwPg3e9+N/fff3972/3338+RRx5Z+TM59dRTefazn825557Lpz/9\naX7hF36h5+MajQYnnXQSAE9+8pPXZFFVM7TPfOYzPTOsfr71rW/x/e9/n1e84hUA3HfffXz3u9/l\nT/7kTzh48CCPe9zjePOb39z3+V/96lc56aST2LlzZ9/HyHAU0DZBHEd474kiDSKV9X3jG98A4O67\n7+bAgQMcffTRHH300XzgAx9g586dfPGLX2T79u1ceumlPOlJT2Lv3r3ceOONfPnLX27vo7jI+uIX\nv8gJJ5zAa1/7Wj772c/y4Q9/mFNPPZUrrriCV7ziFbRaLW655RZe/OIXdzyvrN93dqMM7WUvexkv\ne9nL2rebzSb/9m//xjHHHMN1113Xd1BI2YEDB/j1X/91Lr30UpaWlti2bdu6f0NJknD77bdz7LHH\ncvPNN/OYxzymY3vVDO3rX/86T37ykys9FuBRj3oUj3nMY/jwhz+MMYaPfOQjWGsrZ7E33HADP/uz\nP1v59aQ6BbRNEGXtjdM+DJkDd999N2eeeSbLy8u89a1vJY5jzjvvPF71qlcRQuCII47gggsuwBjD\nO97xDq666ip27txJHMesrKx07OsJT3gCf/iHf8gHP/hBvPe84Q1v4LjjjuOmm27il3/5l2m1Wjz3\nuc/luOOO2/T39Ud/9Ee8/vWvJ01T9uzZw/HHH8+9997Lm970Jv7sz/6s53N27NjB6aefzktf+lIa\njQbWWl7wghf07UMDuPjii/n+97/PIx7xiMoBrOyee+5hx44dHcH9jjvu4LLLLuvbR3jsscdy8skn\n85KXvISVlRWe+MQn8rCHPazya/7Lv/wLL3rRiwY+VtmYihOLTMkVV1zBd77znfaQdektSRLe8573\ncO6553bc/6xnPYurr76aLVu2TOnIJkrFiXPrFSdWm5iIzLQQwsBD5mUxKUMbkgoEi8gEKUPLafmY\nTaBAJiIyW9TkKCIitaCANmUhBJK0egXxGW8iFhGZGgW0KQuBdlWRKtTUKSLSmwLakLwPQ63N1L0e\nWhafjDIvEZERaVDIkHwIlSrnd+vOsIwxxEq6RERGpgxtSHFkSAfo+xKZZ94HvPfTPgyRdSmgDckY\nQzzCytUi86SVqjapzD59Q2dEd9/apJ8vsp44Mnh9v6ZCf9fVKaDNgGzo/mjrn7VSr2xRNk0jjrSs\n0ZTo77o6BbQZEUas8mXQlZyILDaNcpwBxhiaQ4yYLGs2hl9QVESkDpShzQg1K4iIjEYBbUgahCEi\nMlvU5DgkZVQiIrNFGZqIiNSCApqIiNSCAlpFfoNCxOpTExGZrqH70Ky1EfAB4HjgMHC2c+6OfNuT\ngD8tPfwpwIuAm4BvAV/P77/SOfe+YY9hkhIfWGr0j//qUxMRma5RBoW8CNjqnDvZWvsU4ELghQDO\nuVuBZwBYa88A7nTOXWOtfTbwV8653xrtsDdXkWmVg1QxcVmBS/rp9b0RkckZpclxD3ANgHPuRuDE\n7gdYa48A/gj4nfyuE4ATrLVfttb+jbX24SO8/qbpVUaq2Yh1opJ1GWP0HRGZolEytCOB+0q3U2tt\nwzmXlO57JfA3zrm789u3Azc7575grX0p8H7gF0c4hs0x5a4wZYIiMqzdu7fTGFPloJ07to5lP5My\nSkD7IbCzdDvqCmYAL6UzYH0JOJj/fCVw/givv2ma6/SVTUIr8Sw1VcpKRAa3f//BjR9U0fKBQ2Pb\n1ySMcua+HjgNIO9Du6280Vq7C9jinPte6e4PA7+Q//xzwM0jvP6mUXYkIjJ/RsnQrgROsdbeQDZm\n4ixr7euAO5xznwEeB/xr13POBS611v4GcD9w9givX1vNRjTVZsdWktLQ4qUiM0FdENWZGZ87NdMH\nV1crScqSqveLzJLKEW3fvuWxnTevvfXOce1qbM445di+n4UmVue83/g74L3vuy1NfaV9ZIt5pmOf\nhD3O/TaiSJPERWbEeucd6aSAlouijS+Aoqj/x5X4UGkfAIHNGt49nv1GkYafi8yK9c470kmf1Jg0\nIoP3Ab9BZmOMgRAqZXODUvktkfrZjHNFXWn5mDGJB1hxejNWlzbGaNVqkRqq2vIjytBERKQmFNBE\nRKQWFNBERKQWFNBERKQWFNBERKQWFND60BB4EZH5omH7fWhisYjIfFGGNoNU6kZEZHAKaDNIpW5E\nRAanJscKir60AERqihQRmUkKaBUU/WkKZSIis0ttW1Om0ZQiIuOhgDZlrdRrRKWIyBgooE2bkjMR\nkbFQQKsg9X7Ddc6G1WzoVyAiMg46m1YQwuaNblRzo4jIeCigVRBHZqSBG8M8N4RAK0k7nqvBIyIi\n/WnYfgWjZlHDP990PFfZnIhIf8rQKggh4P1ksyNjDMZsTlY2jfcjIrLZlKFVUASXSWvEm3O9Ma33\nIyKymZShiYhILSigiYhILSigiYhILSigiYhILSigiYhILSigiYhILSigiYhILSig9RBCIEnT9uTj\nRSk5pbXZRGSeaWJ1D1kx4ogoyleqXpBZyIvyPkWknoYOaNbaCPgAcDxwGDjbOXdHafv7gD3Acn7X\nC4EmcDmwDfg+cJZz7uCwx7AZvM8W3ExSjzFR7U/y3nuiSIm6iMy/Uc5kLwK2OudOBs4FLuzafgLw\nHOfcM/J/9wFvAS53zj0NuAV49QivvymiKAtizUZc+2AGKJiJSG2McjbbA1wD4Jy7ETix2JBnb48F\nPmStvd5a+z+7nwNcDTx7hNcfmfqMRETqY5Q+tCOB+0q3U2ttwzmXAEcA7wfeC8TA31tr/7HrOcvA\nrhFef2RJ6mk24mkegojIWO3evZ3GmM5rO3dsHct+JmWUgPZDYGfpdpQHM4CDwPuK/jFr7ZfI+tqK\n5zyQ/3/vCK8/MmOyhTsn3bQ4jdcctzq8B5E62r9/fMMSlg8cGtu+JmGUJsfrgdMArLVPAW4rbXsc\ncL21NrbWNsmaGr9Wfg7wPOArI7z+yDZreZaN+MDcr0emYCYis2aUDO1K4BRr7Q2AAc6y1r4OuMM5\n9xlr7ceBG4EW8DHn3Deste8APmqt/TXgbmDviMc/sumcmANakExEZLzMjA+KmOrBDdOsVuU5xWeu\nLEdEKqp8sti3b3ls581rb71zXLsamzNOObbvZ6GJ1esYJuBUeY4CmYjI+GkSElnGVC5z5StkreU+\nsBACqfdDTQHw3g/8HBFZHEmSTvsQ5oYyNLKMqUiajDGVcvuiLBaAD4HImKEyL01sFpH1pEEn6qoW\n+mzanYlVycy6hRAgZJlW1QxNWZmIVBVH6qKoaqEDf9SVUXXfrsIYQxwP9jxlZSJS1bSmF82jhQpo\n3RnUuAdnbNboRY2KFBHZ2EKF/iIgJOn4q1yEEEj85uw33YT9iojUzcJkaJ3Z2SZNb9ukOX0zPldQ\nRGQmLEyGlvpAK83WOtuMNulZ3W/qw9yX2RIRqWJhAlo5y9ms5rvZ3G8YoMaAiMj8WpiA1ogjGpHp\n2XxXrIvWStLaNe9FFefViYjMu4XpQzPrTHwu7vehfiMJ6/Z+RET6WZgMrYpmI8rLYFWb+BxCIEmH\nK3klIiLjtTAZWhXFxOqqWU3IV4FRFiQiMn0Lm6F5HzqKEg9TXDiEQMj3IyIi07WwGVqSepaaMcYU\nFfYHr5kWqySNiMjMqP0ZuRjB2K0IZG0VMq1++xKZFn0f55POJZuj9gGt36TiZiNu930ZY2g24w37\nwtYbKSkyDfo+zh+vcnabpvYBDWP6VqTqvkLSFZOIbDaFsc1T+4AWR6uLd3qfrSxdSLuaGVup1ikT\nkc1ljNEaZ5uk9gENuptlVn8OoTPtV4ImIpOg5sbNsRABDWhPgDZ5pf1WkhJ3lcJayidWF7K27o2H\n8x9upZpgLSKbYiVJp30Ic2Nhhu2HEGg04tLttStHd181hRCyWogVrqaiSANGRGT8dJ1c3cJkaI04\n6ihp1Yi7srF8NGQ2Jy37OTKmPQE7e4xf83jI+ulCx+M6++rKfBjPci6hYvYoIvNtM5alqquFydC6\nh9xHXZ2yxW1Tqk5vjCGOy8+J1jwe1n7hUu9plrLBjtcxZizDnFIf9EUXWQAaQFLdQp0Ri+zL+9Us\nzPeZUF2e+Fj+v0pGFEdR3wxtXKLIkKrfTkSkbWEyNMiXh6Ezu+qXTZWzOTNg0eJs/5t7VRUZA7Gu\n3ERECguVoRmyzKwz4xpsQnVdS9bU9X2JyOJYqIAWRRGNOGpnWknqs8EiA5zIfajfqKNiXTeN0hSR\nebZQAa2bMYbAYNHJQM9nzHt2M99HLyKy4AEtjgxJGgbKuKLI0GvQUTLHZbOMMTQrjJjU5HERmWUL\nHdAGHezR/byyeT/PV/kMukuFiYjMktoHtGxVak+Spj2zi0ZsMAw/IKIYTNHsKptVR92T0UWkOg28\n2nxDDdu31kbAB4DjgcPA2c65O0rbzwF+Jb95lXPuj6y1Bvh34J/z+7/qnHvD0EdeUdZPBib0zkLi\naLSYvkgZyyK9V5Fx09/P5ht2HtqLgK3OuZOttU8BLgReCGCtfRTwUuCnAQ9cZ629EjgIfM05d/ro\nh72xkE+gjqKs8ocnK10VQrFaddYfFkJYU9NxVhTTCrqrmoiIyFrDnsn3ANcAOOduBE4sbfse8Fzn\nXOqcC0ATOAScAPyItfbvrbVXWWvtCMe9IR9Cu2CwMSZrLsNgIoMPEOfD92c1mAH58SmYiYhUMWyG\ndiRwX+l2aq1tOOcS51wLuDtvYvxfwC3OuW9Za48G/tg59zfW2j3AZcBJIx39BpI00IhpZ2GGQJoG\nIgNp6jeskO/zavtlIWQD/Q2DNSEU2eKkDXu843jN7s9ORDbf7t3bO1YWGcXOHVvHsp9JGTag/RDY\nWbodOeeS4oa1ditwKbAM/EZ+9z8CCYBz7jpr7SOstSbP4sYujiLSNMWY1YnUURSRpCnkmc9GJ/he\nJ+QiyA0aHKaVaQ17vKMoF3gWkcnav//g2Pa1fODQ2PY1CcO2t10PnAaQ96HdVmzIM7P/A/x/zrlX\nO+eK1eneCvxu/pjjge9tVjArZH1loeOfMRAIfYsSw9rndEvXee44jHM0lMF0lPsSEakrM8yJrjTK\n8YlkrVlnkQW4O4AY+CvgxtJT3gDcTtbMuIMsU/tN59ztG7zUSGfhrKRToBGbjuVWUu9ZWfFs29o7\nQV1ppSw1Y1IfOooZFyWi+i0NMy7F64uI5Co3euzbtzy2q9drb71zXLsamzNOObbvZzFUk6NzzgO/\n3nV3OTj1a3j9+WFeb1TjzE6G2ZMmJIuIbL7ZHeI3BsZkZapaaTZIIfWeJPVExrBlKXvrnatMZz83\nG9m2ODKU41DVElHl/QK0NiiLFUJgJUnbt4vXFxGR6mq/HloRVvIiV0Smc/Xq4v/A6ojGXmuh9bvd\nT8fjKqR15WEUyuZERAZXq4BWZEXlgBAZIMqHrecD2IvHJd7TiPL5aMa0l1AxZu0Ix1GCTCMvi9Vv\nH8YY4mh8TZO9phuIiNRdrQJar2AQRVHPdlUfAobOTC2Lc4FGPN4BGVWCyziH9SuYicgiqmVnjc8L\nEhc/p963b0PWlxZ8thRKK1ktWhznS8OUHytSF2nq8V7TN6S+ahnQsiog2VuLjCGOovbtoj5inGdh\nqV/N7OI4Io7jmS6HJTKsdErVakQmpXZn7mLydHY16kujGD0+/zmEsNrPFFYnWXcP71/vvkGnAmjp\nCJm2ohi3SF3Vqg8NyIfnQ2QCSRLYtqWBD4FWGtjSzOJ3e2J0bIjXGYbfq0/O5wM3Bu2nmsSEbJH1\nNCpOORGZV7X7hhdhJoSsudF7X7pv9eq0u7xV97b++197lVvlqtcY084QF52yBBHZDPULaPlk6jgy\nxLHJJlWHQBxloxjTfMDHSuJZSbKfi+H6RWmr9YbOR9Ha7KzKUPtGHKlgb26jieYiIsOoXUDrNRet\n0+jzy9qTsQfMNDRhOqNPQUQ2Q60CWgiBQytZCalAYKXlS9vIy15lj1tqRDTjLCtrxKsTn4vtVV6r\nV6Yxq81ps3Rc6ssRkc1Qq0Ehnetw5UPxs1pXGLM2c+s3Ebvqaw1y/7TN0nHN0rGISH3U4lI5SbPJ\n0an3xHEW1Lz3xPlq1T7NhuwXw5bLk0uLydWtfB/FtvIAjvLji9cC2pmdiIhM39wHtGyEommXrmo2\nYgLF0HxDs5FNlI6jbIK1yVerLvhQlIoyHdvKAz/K66EVr1U8RtmGiMhsmPuAVhQTTr3HEFhppYSQ\njaRrRPmwfZNlWb1KWrX7zCpMfC5eq5iYPY5h+EVWqExPRHpJVYqvslr0oTXiiMOtlC3NmFaa5E2B\nEJfWFes3qdkYQ2OACc/FgIZx5WUhZJPBVVBYRHpJ0oDGUVVTi4AG2eCPNB91mCQek/eXhcCaRTqh\n96i/7m39bo+q87UDwUMwRcX/ta/lfVbOS82bIotH5Terq03cb8QRPg9eAdrBLQ2BlcST+s61xlpJ\nsfbZ6r/2ttLk6mywyXjWKSv2l6Sh/ZpRFNFoRB3L2JRfq2jeVDATWUwqmVddbQIa5MEsZFc07YGJ\nw/RNdT2l1y5G6fMKVZawLr3GuPvX1F8nInVUmyZHKPq3spGIRzSzTKffJN71TunNUt9bto+u5+ZZ\n31Ips6rKGEOzYoN4se9xT0RWticidVSrgAYQmYi01EQ3SmmrfrdHNUwQFBGR9c1tQCv6yIo5Yknq\nacRRPkk6EBlIfKARGVZanmYj668qBlcsNaKOARjZBOtsiH8jjtrV8UO+KGK5Ty3L2tYGmTBDfV0r\nSUoz3jiDLPoI40hz6mS+1fW7PEvnlVk3vwHNB5aaq22B2YAQk0+UJh/amPdW5QNFyhOqe2VhxfD5\ncvCKuv442qtb9yiRNWtfuirHU4wCnbVjFxlUsWRU3b7LdXs/m2luA1ocG5IkzX/ZgQhoJSlp6oki\nw0orzQJYHpQik2UtjTxAeR/a5bCy+GeIo6zkVeo9FCMmxzxkf1IaUUSSpkQm6gjk3YqBNKNeBfoQ\n2p+jyDQYk30PQ9D3cFHN7ShH7wONRkyapxhxnAWqVhqIoygvgxWBMWxpxsRxjIG82dFgoiybi6Oo\nfV8URdkVHqtD6ott8yaKDN6zbjCDIpCP/h7reGUs82Vc32WZX3Mb0OI4IvXZcjDeB1ppVkKqERvI\nK+snSbZadSvx7Qwk9b69QrWB9m3IChoHH4CsTFbVZWSGtdkrWGdz8zREX0QWw9wGtCi/Ggshz0bS\nrPmwGUcQDM1GRCALfKsDOSLSfFJzHEUsNeOOK7ooijBRMdk5rnSlN8rV4GaXu+q1uraISF3NfEAr\nsql+24AsqzJACO1qIT7P3tLUt29ngW01K/OlbK1coHi9rGuj49mMScuzMBF6s96biMi4zHxAW0l8\n3yzogcMpSRpIAyw1ItIAUZRnTfmIxyQfxtvKM7OijEy5HFbxb2VltRxWPz70Lz6y0XOHNQt9Aq11\nfg8iIrNg5gNav3Nod7ZQrnS1ZltYfU62rbNW4uqL0XcZmfZox9JriYjI7Jj5gNavTFTqA1ua2aKe\ncT70fqkRkeSrUxeDPgBMZGjGhlbqaSUe7z3NfGJ0MWDkcCttj4osZGuohfbjgPYUgGH4ENoTwqsq\nJnxPW7kcmIjILJr5s9S6zVxdE567y10Vc5+L4fpQZFemfbu8sFkxxL09sZrQc+GzoZveAv1TznXM\nQkufmhtFZNYNPbHaWhsBHwCOBw4DZzvn7iht/zXg1UACvMM591lr7YOBy4FtwPeBs5xzB9d7nWy5\nFd8uR1UjpUi6AAAf+UlEQVTcl2VW2WTqEDxg2LIU04gNaRpoNlZj0eFWylIzzor8hqx6SAiBRhyx\nkniS1BPn1UTifB01Y8yaWOa9J01Dx3IvSerzOVjrn/SzJstQtGpWKkmVJJ5GI5sYPerE53mdIF5X\nvb7Xg1jJWxT0+xRZNUqG9iJgq3PuZOBc4MJig7X2aOC3gacCzwH+2Fq7BXgLcLlz7mnALWQBb11Z\nUtO9Rtjq9mxgR9Qenl48rtloEEVRHqCyIfJRPlm6GKpvTNZ8GIBGI25PDi4P428Pezerg0261yvr\nLo/Vy1ATtdvHOPpgk80asCIjGOF3ot+nyFqjlL7aA1wD4Jy70Vp7YmnbTwHXO+cOA4ettXcAT8yf\n8678MVfnP1+03osUZRmLDCVJPYas+PChVkKaelppSpJ4tvhsBGMcRTxwKMlGPEaGKMqG6hf1F4sV\noJN8SH9ENgm7qDbivV9tkiw+qPx2VEwJyG834gifFzAu/i/rta8qsgCowqSD6PX5z6rsQiUM/fsd\nR9Yu9bR793YaY1oUdOeOrWPZz6SMEtCOBO4r3U6ttQ3nXNJj2zKwq+v+4r51GWOIS02NIWTZVOpT\nDq140tRzxLYm9x9ssaXZIIoMS0sRBw8lxERsX4pZSdKOYsJRlFXSj4xpT7xOSqtS9wpAxYky7qqy\nb/LmxvJjOp83fBIcz8nJeVbMSzAr9CpwXf258/VeZXL271+3F2cgywcOjW1fkzBKQPshsLN0O8qD\nWa9tO4F7S/c/ULqvMu/zwsGtYgK059BKwvLB7I/7cCvJl0yBYnBkltGRj1bMZl0Xk6h9AOPzEYSl\n4fpF1f2Bjq2rOG/I++o2u1LHpF5HRGTWjdKHdj1wGoC19inAbaVtNwFPs9ZutdbuAh4PfL38HOB5\nwFcGecHEZxnaAyspBx5ocfe9h7hr/wPcfe8hDq0krLQ8JsqaJbcsNYGsSbAojxVFEQZYaWXNgM1G\nTOpD++eiSXOY4NA98bjo+9psk3odEZFZN0qGdiVwirX2BrKurrOsta8D7nDOfcZa+7/JAlYEnOec\nO2StfQfw0XwE5N3A3iov5L1vjzossiuTV+zwPrDSSjEGtjTjbJ6XMQSfZ2YhG3pfLnGV9Z8FGjHt\nEY+w2nyY+rBmrtlGfRXxEH0ag4w8LE/2Vr+JiMhaZsbr84UQAiuJZ0szZqWVcGjF873/XOaWb+3j\n2q/9Gz5N2b59G887+cf5yUcexbalBjt3LBECbF3Kh+rnDrdSIGueKyYKpz60h/BPWjFsuwofitUE\nZn7qoIiMX+Wr2H37lsd2Ur/21jvHtauxOeOUY/t+FnNzdiwH3iiGRiMbLJKmaamaRjbYo5gP3e4T\nWxO0S9kO/WszTkLVCwrlZOMx4xdwIjKCmV+x2hhDRJZdeR/497uW+Zrbxyc+/QVu/uJfkqYpJ592\nNuanf4xDhxPiqMl//Nf9PGjX1qyifsgmoW7b0lgthYVpD+OPouznosRVNvoxK0IcGdNeAbcRG9K8\n0HF3k5/3gUBoj1pLUt/zcd0GGalWrKgto8l+h/Vqtg0hkCp7F5mPDM2UTvwhwAOHEg4e+CGtw/cT\nNRps2bLE1qU4Hz4f8kESZvV5xUW5oZ3qlAdSZOMfQ6nEVNaXVtyXzYOjbzWQrNxx52TrqmupDXJi\nrdNJeFrqOHdLOadIZqYztFaSEuejFr3PgspRR27hxJ98KIdf8ByOOebH+eF993DC//UYWonn3gOH\nWWoaGnFMUioCvG1LgwcOJxxaSTjyiC14PFGI2wGsmc9Fa+WTq1tpVry46F+L86kAaRowpcDXnrdm\nVqv8FwuJjnLiLK64q2R5MphRfzezKDKmPfCpTu9LMvq9VjfTAa1Ij3yp2HxRomr7tq1s/29H89CH\n/yg/8aMPZdtSIx/s0WDrUva2GpEhjgyNRkTroIdgaESGgOmYhNvOlNJsAnbqU6IoIknT9nD+Qq/J\nu+XJ1cXtUayXDcpo6vqZztukcqmurt/ZzTDTAS34kC/QmfV9QPbzQ3Zv5QmPfhBH7WzywwOHeMju\nrezavsSWLQ1WWgkQ2LIUkwQDrSzT2boU8cDhlJUkJTKrQ+yLWo/kmVcrSSEUIxANSeLzOWxZVZGi\nlFW5zFK28nVRrmr1vmGrhBhDnpHqykxWzVNpL5FpmOmAZvL6iHEcEUdkTYGNbL7Z1h9t8ogH78jm\nixnDtqWY5YMt4tjk65hl66MRiqViAkdsK5aMyUte5eWuWklWjR+TNTsWa7BlRYfD6srW+XOLbYXQ\nfmw5kxu+ezJrttSJSzopmImsb6YDGnk5KR8CcT6+vhFHWRZFYNtSxEqSXbUm3rM1v50VGYbDhz2N\nBqysdGY8zdiw0kqzzCuErHhx6im61733rC72UpqUDaXlX8p9aKby6Llek6m1tIuIyOhmOqA1uypG\nb4uz22nqOerIbRxaSdiWFQZhqRGR+mzl6UMrKVuaWV9bK0mzPrE8K9vSiAjGkBxO2bKU9Y+lPhvY\nkQWliEYjYiVZnYQd55Ow28P+e1QRqZpRtVLPUtf7UiATERndXAzbL3jv876pvA+stC312ZyzuDRU\nP8kf69OQT7gOpH61lFa2z3zRzTwf8/nIRtN+zVLR4hDy/rLV+4r7q07YLfrvNMFXRKrQuaK6mc7Q\nuhWFhLcuNdojE7dvXc12WkmR/RgCAZIsyG3d0sgmnuZZXLGvlZbHmOz2lqWIJA+IPl+0s7y8R5p6\nkmLyaujsz+iVdfWTTUMI7dJbIiLrKUr/ycZqdVbNMq1VxWIw6zXorV79dD0qdG3PM7rxNA7qiktE\nZNzmKkPrLu1TZDntIfh5P9bWpfxxSzFpyFajXspHITbiwIFDCduW4vayMkuNfDh+3o+WpoFmw5Am\nKcHDlqU4b8rMBp80u44jjgxp6om77g8htLO3cjkslSgSkaqW1JpT2VwFtO7BE8Xtfv8D+NTnC35G\n2WjJKCIy2VD+NA3tddICngjwaTHiEAhZncdCZAyeXnPDzJqBIt3HmAXdqOf7EBHpR+eL6uYm9K/X\nMVpe6yyEkBcyzgZvRAaasWn/HAjtjMwYaK2sPtYHiA1EUTbM35jA0lKUz2vzrCRZcEtS33U8eTXI\nrmM0JlsRoFieZpDO3c0aOJKVEfMbP7CH1K8OihERmTVzk6Gtd5XSkZHlgz6Kic3t0YwhK2OVZUqr\nFRdCPvE6pD6fHB3h8yH7jTgu7Rcgz+i6igrH60yiHnYy7GZdlfkQOt7XQM/1fs1UChGRWTE3Aa0q\nX6xUXZSoyjOdyECSphTNg2m6OgE7SVNSD6SBRqMohZWNbAyhs9yQTwPBhHZ5qqLfzuRLzZSDnc/L\ndRlj2mWL+gWqkC9TM2gALKYjbFSZpDiWRql816DiEZ47T0K+mOp6vy8RmT21OzN5YKkZt0+6kcmG\n38dxjDFRezh+IzZsacZs29IkTbMTWNHHBtkaanEc0UqLYJGd2JrNbKCJD6Y9jaB4raKeY6GV+rx/\nLrNRljlMNpem1QJM0VdY9B8OY5TnzpOQ/1MwE5kvtTs7FROXC+WJ0ZHJC7yaLLNpT6I2WUYXG9Ne\ndqZYtiaOTLswMmR9UJEBQlaQOC31p2V9baWVtU0pY6Rzgnb3xOzyz4P0UcVR1DHZe9b7t+bhGIuJ\n9rN+nCLSqXZNjt1D4ruXiSlKVJWH2GdLxEQ0G1mdSGOyKQGNOOKwT9troi2ZQJIWFUkitjWzx8em\nXMx49bWz4f9Zn1Oz3B8XQscCo+WRkIOuPBzl0wlCyFYm6J5SMGvmIevJ6n2qr1Bk3sz22W/M1h0p\nSZGtmXbTYXdGlRUozjK8ol+s/LisH231tYoSXd0MWX9br2MaJYNRRiEii6x2Gdp61ssOQlgtMROZ\nrNbjSsuDybI+kzdHFhlQEcgaUcThVkojjvK11VaD21KfcjVRtDrwZM0xmeEGImRZxUJdn4iIdNAZ\nsIfywIdsubUeq1vTO0BWDUab0fQ2D815IiKbRQGNvG+t9EkUfVnNhqHZiNrNgP0mRxuyASCFtROv\nBzmO3s2URRktNSvKKJLUt5u7ZT7ob766hWpyXE8cxyQ+m1CdNSd6oooDA8qLfUJnmatB9Z+nll19\nKAuTUWRzMnUdO0/0N1/dQn6zy0Pry4psDLJ+rtT7vFRUaF/ZZiWysn9JmpKkaT5AxNNK0nYml1Ys\nL9Xr6qvXVbTJ2j47pgiU95GMsSTVoKWxkiRdyKv+kH8H5ukKetASbCLzZCEztH4TmMtD6YsJ1odb\nKY1mRJJ4GkVxYYr5aBGBbDJ2MZ+tuJqKR+hL8yG0X6v8uPKi2B3VSwJrynGNYtDJ04HOz26xzFc1\nkXk6VpFBLWSG1kuReXWLKCZjr6407X3IRzT6jonbkGUrrSTNV9fOs6nyRO981evi52J/5X10Tw7f\nSGSyVQWmdeVtBjzeOpmHieIii2IhM7RejDE9F+9MfKDZNESURzpm/8dxTLmXrREbDrfSbEJ1aSXt\ncvaSJL49nD/K57J1ZziDrpdmjKExxaLBi7q+mzFGxZpFZshinonW0T2ZOo5MR39VkWF19Kflt70P\n+TB/8ixt7dV71LU/WJuhlY+jfCwbHfM8UWYzv/R7myx93tUpoHUpzzErJkeX+6siY7KCxcZkRWx9\nIGAIPluHbakZs21LY83yNYVGHHXsL5BN2O63eGn5WDY65nmy0XuS2aXf22QV6zDKxhTQhlDEo6yI\nLeSFszqupIzpfWW15r4+JbBGpas6EVk0CmhDaJTKX8WRodXyeA/btqx2SUbGkPYZkl+W+sDWpXjs\nV70tXdWJ1MJSQ6fpqoYaFGKt3QZcBjwUWAbOdM7t63rM/wL25K/xIefcxdbao4BvAV/PH3alc+59\nwx78tHQ3B2bj9Ydsihn2eRX2KyLzT0281Q07yvE1wG3OubdZa38FeBPwO8VGa+0zgcc450621m4B\nvmGt/RTwZOCvnHO/NeqBz5JmI+tDW63WH2glnkZs2vcBHeWzivuaXberKBdAhmygSpp6Qr6/1Adi\nYwbe70avubrKd/9Vt8vHNYvm4RhFZDjDBrQ9wAX5z1cDb+7a/lXg1vznAMRACzgBOMFa+2XgLuC3\nnXP/MeQxzBBDFJuuASVrJyiPUsx4veeEfGK1Z7Vs17iH8QfYMJuchyAxD8coMordu7eP7e9/546t\nY9nPpGwY0Ky1rwTO6br7B8B9+c/LwK7yRufcIeCQtbYJfJSsyfGAtfZ24Gbn3BestS8F3g/84ojv\nYeqifABIIA8u+fIw3nuivIpImk/GrnpC9X51PbXUe+Io6vvcYlXsEMCbLAssnj8uxXSEcWZ9IjJ+\n+/cfHNu+lg8cGtu+JmHDgOacuwS4pHyftfYKYGd+cydwb/fzrLW7gU8B1zrn/ji/+0tA8WlfCZw/\n3GHPls4lZWj/X2RogbXL0GykMxhtHAjjOIJSEBt3zMlKbymQicjsGnb4zPXAafnPzwO+Ut6YDxr5\nInCpc+7tpU0fBn4h//nngJuHfP2ZZ0xW3DiEbLJ190TstFRMuHuScXc5rPKK2b0KBxf9dlUmK486\nodnnx61pASIya8wwJyZr7XaypsSHAyvAXufcf1prLyDLyp4KvJXVfjSAs/L/LyVLWO4Hzt6gD22u\nz5or+UTrbmnqidZpfszKYYV2geRCK0lVaklkMVVuHtm3b3ls581rb71zXLsamzNOObbvZzFUQJug\nmT64jSRF4KKzubEokxWZtRUzigws9VltSErPzSr8m46q/r1G7XnvK1Xi0Ig/kbmhgJZbL6Bpxt4m\nasRRz2VdImNIWh4f1i4M2koDURTRbERrglJRNmu9sljFPqoEqdRrgIeI1IcC2rTkcaRSeawhVN3H\njGfoIiKVKaBNyZaleM2yK8aYDcvceB/WrIZdvq/KPqAYHDLgQYuIzDCthzYl5UnYve7vJ5sC0Osx\nXeW4Kh2D+s9EpD6UoU1JVh4rHWi4PeSV/rtiUFFOchDGmPbE7WGs97zU917jTURkMylDm5LAYGuC\ndZTV6rFtmDwrGiE7W++4vfeaXiAiE6cMbUrKpaT66VzZunNSdDH5epYUx5OV3tLyNSIyWcrQpqRK\nKanuWoxrh+tvyqENbbXsllajFpHJU4a2jqJU1ST4AcpJdZTCGmMZqrHua8zZ47C/h3G+JxGZbQpo\n6zDGjNTPVFWx1tgg/WnGmKy6/xgnR7cSP7Z9jbPSPwzf3zfI5yoi800BbVb0ySTWGwGZFT2mo1+t\nu8jxIKIN+vSGNdVixsrQ5pZ+bzIoBbQZYIyh2Yx7ZhKHVtK+GYYxpl0iK4RA0pWNDJqZNBu9j2FU\n0+xT6/e5yuzT700GpYA244q/6WpXq7qiFZHFpYA247bky8+sJOsPgzfGrCmlJSKySHQGnHHtCdUD\nPFZEZBEpoM2Y8gCPsmYjGrmTvN/zy2W4NpM6+UVkM2li9YwZtmjxIPvus3XTMzxlkCKymZShSR5o\nNLxdUMkymWvK0ARAxYQFgCjSNa7ML317F1ivslAqFbVKS+CIzBcFtAVVVOsv92v1um+RJX58pcBE\nZPMpoE3AtEo/VVk0dJwZ2qxkM2P7vMPsvCcR2ZgC2gSsjLHo7yDWe82sbFa8plTW0gjlr2Ylm0nH\nVOl/SWWzROaKAposDGVbIvWmgDYBS43xfMxJ6vtW5K+7bPJ3tSHlcZ+la6o+X0Tmk4btT8C4mq1C\nCBizNjguQrNYYLVQ80YW4fMQkbWUoc2Y9QY0NOLRy1/NqyhfbHWU998YsHzYJMqBicj4KEObMRsN\n5Fhko66CPcyq14v+mYvME2VoC8yHMLZSR96Pb1/Dvv64mREzQlid2ycim08Z2gKLjKneMbWBJPUs\nNadXPmvU7K2Xcawvl63WPYaDEZENKUOrqUlP5o4jo8K2IjJVCmg11UonO5k7jiMVthWRqRqqydFa\nuw24DHgosAyc6Zzb1/WY/wM8GGgBDzjnnmetfQzwEbJR2F8HftM5p8v6zaBuGxFZMMNeUr8GuM05\n9zTgY8CbejzmscAe59wznHPPy+97L/Cm/HkGeOGQry8baI5pMreIyLwY9qy3B7gm//lq4Nnljdba\nhwH/Dfg7a+111trn55tOAL7c73kyPhpuLiKLZsMmR2vtK4Fzuu7+AXBf/vMysKtr+xJwIfA+4Cjg\nemvtTYBxzoV1nicLJoRA4gONyCgIy9Rl1Xjm+3u4e/d2GmNasHfnjq1j2c+kbBjQnHOXAJeU77PW\nXgHszG/uBO7tetp/Av+3cy4B7rLW3gJYoNxf1ut5smACWTPBvJ9EpB7q8D3cv//g2Pa1fODQ2PY1\nCcM2OV4PnJb//DzgK13bnw38DYC1dgfwBOCbwC3W2mes8zyZcX7MUwEMwBgmMIuIDDux+oPAR621\n1wErwF4Aa+0FwKecc1dba59jrb2RLCt7o3Pubmvt7wEXW2uXyALcp0Z/CzJJw5SPWo8xhnj+L4pF\nZAaYGb8ynumDm5RiknRWdWLzz/7ee80pE5ktlf/w9+1bHtt589pb7xzXrsbmjFOO7ftZ6Kw1B1If\niKJoYu37CmYiMo905poDkTGkvvfinoui33sfpcTXpMuDzfpxiMw7BbQ5EEWGeIIZ2izq996TEUp8\nTaoJdyOjvAcRWaWAJptiUhmHMWbsIy8nbRzL1IiIAppsklYymRKdjTiq3ls+o8axTI2IKKDJZplg\nlKlDc10d3oPItGmBT9kUzTjKBztkzY+RSlvNLR8Cwet3KLNPGZpsimLARUAnwnmnCxKZFwposqmi\nfMCDBj3ML/0OZV6oyVE21awMjZfh6Xco80IZmoiI1IICmoiI1IICmsiMU/+VSDXqQxOZceq/EqlG\nGZqIiNSCApqIiNSCApqIiNSCAprMpCT1eK/BENMUQiBJFnsdPpkvGhQiMymEQKQq9FMVAphIg1Jk\nfuiMIWPh/Xiv4htxNPZ9ymCKOKYMTeaFMjQZiyga71V8Vm5prLuUARljiPVLkDmiDE3GJoQwsdWj\nfQ0mG0/y85L5pZaK6hTQZGyMMUQTuKIPIZD6MPd9O5P6vGS+jbv1o84U0GQuzVo5qFk7HpFFpD40\nmTvGGJYa8bQPo8O8Z4sidaAMTYamjEREZokCmgytlfhpH8JAQggk6Xwds4hUp4AmQ5u3/GzejldE\nBqOAJkNbakRz1ewY5aMKNzrmeXpPG6nTexHZiAaFyNDmcSBElSHQ8/i++qnTexHZiDI0mUver98X\nlubFjUVkcSigyVyKovW/umkImpAqsmAU0KSWImNUVkpqYaPWCFk1VB+atXYbcBnwUGAZONM5t6+0\n/bnAuflNA+wBngBsBT4L/HO+7YPOuU8Md+gi/TW09IzUxEatEbJq2EEhrwFuc869zVr7K8CbgN8p\nNjrnrgGuAbDW/j5wvXPum9bas4H3OucuHPG4RSopRvlNY3BE1dee5jGK1MmwAW0PcEH+89XAm3s9\nyFr7o8DLgZPyu07I7rYvJMvSftc5tzzkMYhsKEk9zSmUyfIh4H2olCmmFR8nIuvbMKBZa18JnNN1\n9w+A+/Kfl4FdfZ7+OuAi59zh/PZNwIedczdba88D3gq8fuCjFqloWr1og+ZaIcz/6gEyG3bv3k5j\nTBdxO3dsHct+JmXDgOacuwS4pHyftfYKYGd+cydwb/fzrLUR8HzgvNLdVzrnisdeCbx/iGMWqaw5\npczHGEPVl443GI2pYCeD2L//4Nj2tXzg0Nj2NQnD/rVfD5yW//w84Cs9HvME4Hbn3AOl+z5nrf2p\n/OefA24e8vVFKplmIKj62tnq3P0fq2AmUs2wfWgfBD5qrb0OWAH2AlhrLwA+5Zy7CbDAd7qe9xrg\n/dbaFvCfwKuGfH2RuaDsSmRyzIzXepvpgxMRmZDKV0X79i2P7bx57a13jmtXY3PGKcf2/Sw0tEpk\nBCEETXydQXUqfabvV3UKaCIjMMZo4usMSn19Sp/p+1WdPikRqZ0oMrXJ0KQ6LR8jIrWjieqLSb91\nWXghBC2EuQ59NjIvFNBk4SWp19D6deizkXmhgCYLTydskXpQQJOFF0dGzWo1E0KglXj9XheMBoXI\nwlOGVk/G6He7aJShiUjtFPUxlaEtFmVoIlJLG61iIPWjDE1EpIeQL9I67SxPpa+qU0ATEekhMBur\nJaj0VXX6pEREejCAZ/oZmlSnPjQRkR6MMTTjeNqHIQNQhia1oStpkcWmgCa1Me2+DhGZLgU0ERGp\nBQU0kTFLfSCd4HBvNbXWm36/1SmgiYxZCIE4MhNrAlVTa73p91udApoIWRBK0/EUs421WrLIVGjY\nvgjgA5gxZVVZHcExHJSIDEQZmggQmazEUF36K0Z9L74mn4MsFgU0EbKsqhHHtemvSNLRSjZFNfkc\nZLEooInUkDEaHSeLR31oIjXUbKhkkyweZWgiIlILCmgiIlILCmgiIlILCmgiExaC1tgS2QwaFCIy\nYXWZGiAya5ShiZSEEEhrNMFaRpemXhPN54QCmkhJ6gNxFCmLkjYfgiaaz4mRmhyttS8GznDO7e2x\n7deAVwMJ8A7n3GettQ8GLge2Ad8HznLOHRzlGETGKY4MaeqJJlgtX2abMYYQRqu8MgrvA1Gk72IV\nQ2do1tr3AX/cax/W2qOB3waeCjwH+GNr7RbgLcDlzrmnAbeQBTyRmWGMIY6VocmqxpS/Dwpm1Y3S\n5HgD8Jo+234KuN45d9g5dx9wB/BEYA9wTf6Yq4Fnj/D6IiIibRs2OVprXwmc03X3Wc65T1hrn9Hn\naUcC95VuLwO7uu4v7luPLk1ERAbwkIfsHNt584xTjh3XriZiw4DmnLsEuGTA/f4Q2Fm6vRO4t3T/\nA6X7RERERrZZoxxvAp5mrd1qrd0FPB74OnA9cFr+mOcBX9mk1xcRkQUz1oBmrX2dtfYFzrn/BP43\nWcD6EnCec+4Q8A7gV6y11wMnA382ztcXEZHFZTSBVERE6kATq0VEpBYU0EREpBYU0EREpBZUbX8A\n1toI+ABwPHAYONs5d0dp+5pyX1M50Amr8Lm8j2xS/XJ+1wvzCfcLwVr708CfOOee0XX/6WTVcxLg\nUufcxVM4vKlZ53M5Bzgb2Jff9WrnnJvw4U2FtbYJXAr8BLCF7DzymdL2hf7ObEQBbTAvArY65062\n1j4FuBB4IXSU+zoR2ApcZ639f51zh6d2tJPT93PJnQA8xzl391SOboqstX8AvBy4v+v+JnARcFK+\n7Xpr7Weccz+Y/FFOXr/PJXcC8KvOuZsne1Qz4WXAfznnXm6tPQq4FfgM6DtThZocB9Mu3eWcu5Es\neBX6lftaBH0/lzx7eyzwIWvt9dba/zmdQ5yabwP/o8f9jwfucM7td86tANcBPzvRI5uufp8LZAHt\nDdba66y1b5jgMc2CvwHenP9syDKxwqJ/ZzakgDaY7pJeqbW20WdbldJedbHe53IE8H6yK8/nAr9h\nrV2UQI9z7m+BVo9Ni/x9We9zAfhr4NeBZwF7rLXPn9iBTZlz7oBzbtlauxP4FPCm0uaF/s5UoYA2\nmO6SXpFzLumzbZFKe633uRwE3uecO+icWyabaH/8pA9wBi3y96Uva60B/tQ5d3eehfw/wH+f8mFN\nlLX2GODvgY875y4vbdJ3ZgPqQxvM9cDpwCfzvqLbSttuAt5prd1K1plblPtaBOt9Lo8DPmGt/e9k\nF1B7gI9O/hBnzjeBx+b9JAfImo7eM91DmglHAl+31j6erJ/oWWSDJBaCtfZhwOeB1zrnvti1Wd+Z\nDSigDeZK4BRr7Q1k7dtnWWtfR9au/RlrbVHuK2K13Nci2Ohz+ThwI1kT08ecc9+Y4rFOlbV2L7DD\nOfeh/DP6HNn35VLn3J3TPbrp6fpc3kiWoRwGvuicu2q6RzdRbwR2A2+21hZ9aRcDR+g7szGVvhIR\nkVpQH5qIiNSCApqIiNSCApqIiNSCApqIiNSCApqIiNSCApqIiNSCApqIiNTC/w+94PYcJTqV5AAA\nAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x115444ef0>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"RGZ & Norris\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAbQAAAGoCAYAAAAuIBCmAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X2ULFV5L/7v3lU9M+dlzvEoGhQ1CWo2BJd4AyQajy9R\nUSESXxKW8SgiVwKaeBMxekV856dGuUFEfPkJQjAYDCaBXK8XkF9MNHIIixUUoyZsRHShqHAOHGDO\n20xX7f37Y9eurq7p6q5+r67+ftY668x0dVdX98zU0/upZz9bWGtBREQ06+S0D4CIiGgUGNCIiKgW\nGNCIiKgWGNCIiKgWGNCIiKgWwmkfQDe7dq1UtgRz27aN2LNn/7QPo5L43hTje1OM702xRz96WUz7\nGGYBR2gDCsNg2odQWXxvivG9Kcb3hobFgEZERLVQ6ZTjIL5+2z2F25739MMmeCRERDRJHKEREVEt\nMKAREVEtMKAREVEtMKAREVEtMKAREVEtMKAREVEtMKAREVEtMKAREVEtMKAREVEtMKAREVEtMKAR\nEVEtMKAREVEtMKAREVEtMKAREVEtMKAREVEtMKAREVEtMKAREVEtMKAREVEtMKAREVEtMKAREVEt\nMKAREVEtMKAREVEtMKAREVEtMKAREVEtMKAREVEtMKAREVEtMKAREVEtMKAREVEtMKAREVEtMKAR\nEVEtMKAREVEtMKAREVEtMKAREVEtMKAREVEtMKAREVEthNM+gEn6+m33dLz9eU8/bMJHQkREo8YR\nGhER1QIDGhER1QIDGhER1QIDGhER1QIDGhER1QIDGhER1QIDGhER1QIDGhER1QIDGhER1cLMdgop\n6vpBRETzaWYD2ih1C45si0VENBuYciQiolpgQCMiolpgyrGHonTkyccfMeEjISKibjhCIyKiWuAI\nbUDX/9uPsbL3YF+PYYEJEXXDjNBwKh3Q6laaX7fXU2SQPz5WmhLRsIS1dtrHQERENDReQyMiolpg\nQCMiolpgQCMiolpgQCMiolpgQCMiolpgQCMiolpgQCMioloYamK1Uuq3AHxUa/283O0nAXgvgAjA\nZVrrS5RSGwB8AcBjAKwAOFVrvWuY5yciIvIGHqEppf4ngM8BWMrd3gBwAYAXAXgugDOUUr8E4E0A\nvqu1fjaAvwbw7kGfm4iIKG+YlOMPAbyyw+1HArhTa71Ha70G4EYAzwGwHcD1yX2uA/DCIZ6biIio\nzcApR631PyilfqXDpi0AHsp8vwJga+52f1sv7MtFRASIsneMotiGYTCSJ73+3348kv2M0kue+SuF\n78U4mhM/DGA58/0ygAdzt/vbiEbGWgshSv/dE9XSnj37R7avflcUmbZxBLT/AvAUpdQjAeyFSzf+\nJYBfBnAigFsAnADgm2N4bppjDGZE821kAU0ptQPAZq31xUqptwL4Ktw1usu01vcopT4D4PNKqRsB\nrAHYMarnJiIiqvryMZU+uFHqJ10WGwMpBEckRPOj9B/7rl0rIztvVnENx5OPP6LwveDE6gooG8z8\nhw9jmF4jIspjQKuAKDZ93S8MGMyIiPIY0CpACoEyqd9ASlbyEREVGEeVI/UpCMp9rpCSgYxo3vBD\nbHkcoRERVdhaVO6SBHGENnEmSS0KsLCjyqy16Sdj/pz6d9ttt+FDH/oQgiDA9u3b8eY3v7nj/S6/\n/HLs3r0bb3vb2wAAX/3qV3HxxRdDCIGTTjoJp5566kSO9z3veQ+2bt2aHof3s5/9DOeccw7iOIa1\nFueeey4OP/zw0vs1xuCMM87AC17wArz61a/GxRdfjG9+003Bffjhh7F7927s3Lmz6z5CZmZK4wht\n0ixYcj8z+HMa1Pve9z6cf/75+OIXv4jvfOc7+M///M+27QcPHsSf//mf48orr0xvi+MY559/Pi6/\n/HJcddVVuPLKK/HAAw+M/Vj/9m//FnfccUfHbRdeeCFe+9rX4oorrsCZZ56Jj33sY33t++Mf/zge\nfvjh9PszzjgDV1xxBa644goceuih+OhHP9pzH2UvSRBHaBPH62CzwQWy8U6DvPrqq/FP//RP2Ldv\nH/bs2YM/+ZM/wYtf/GLccsstuOCCCxAEAZ7whCfg3HPPxerqKt71rndhZWUF9913H3bs2IEdO3bg\nlFNOwSMf+Ug89NBDeO9734tzzjkHYRjCGIPzzz8fj33sY/GRj3wEt956KwDgpS99KU499VScffbZ\nWFhYwD333IP77rsPH/nIR3DUUUfhd37nd3D44YfjSU96Es4555z0WM8880zs399qqfSkJz0J73//\n+zu+rr1792JtbQ1PfOITAQDbt2/HTTfdhF//9V9P77O6uopXvOIVeNaznoW77roLABAEAa699lqE\nYYj7778fxhgsLCxg165d+PCHP4wLLrig7XlOPPFEHHvssfjBD36ArVu34mMf+xg2btyYbr/gggvw\nrW99q+0xl156KRYWFtLvv/Wtb+E73/kOXvWqV6XHkfWOd7wDy8uuY18cx1hcXAQAXHfddbj88ssh\npcQxxxyzbmQHANdffz2EEHj2s5+9btsNN9yALVu2YPv27R3fQxoMAxpRgUmMzg4cOIC/+qu/wgMP\nPICTTz4Zz3/+8/Ge97wHV155JR71qEfh4x//OK655hocddRR+N3f/V286EUvwr333otTTjkFO3a4\nZjsvfelLcfzxx+Nv/uZv8LSnPQ1vf/vb8e///u9YWVnB7bffjp/+9Kf40pe+hCiKsGPHDjzjGc8A\nADzucY/Dueeeiy996Uu46qqrcO655+LnP/85rr76amzbtq3tOD/72c+Wfk179+7F5s2b0+83bdqE\nn/zkJ2332bp1K7Zv346rr7667fYwDHHDDTfg3HPPxXOf+1xs2LABmzdvXhfMADfKO+mkk3Dcccfh\nvPPOw1VXXYXTTjst3X7WWWd1Pc777rsPn/rUp/DJT34S1113Xcf7PPKRjwQA3HXXXfjoRz+KT33q\nU3jwwQdx0UUX4R/+4R+wYcMGvP3tb8fOnTvxrGc9K33cHXfcga985Sv4xCc+gU996lPr9vvZz362\n79Ee9caARjRFxx13HKSUOOSQQ7Blyxbcd999uO+++/CWt7wFgDtp//Zv/zae+9zn4vOf/zxuuOEG\nbN68GVEUpfv41V/9VQDAH/zBH+CSSy7B6aefjuXlZZx11ln44Q9/iGOPPRZCCDQaDRx99NH44Q9/\nCAA48sgjAQCHHnpoOpLZtm3bumAG9B6hfeELX8BXv/pVAMBHPvIR7Nu3L922b98+bNmypfR78qIX\nvQgvfOELcfbZZ+Mf//Ef8fu///sd7xeGIY477jgAwG/8xm/gX//1X9u29xqhXX/99dizZw/OOOMM\n7Nq1CwcPHsThhx+OV76yfVWsm2++GR/4wAdw3nnn4fDDD8d//Md/4IEHHsAZZ5yRvr67774b1157\nLe6++25s27YNj3/843Hvvffi1FNPxT333INGo4HDDjsMz3nOc3DnnXdiy5Yt+OVf/uXS7wmVw4BG\nNEXf//73AQC7d+/G3r17ceihh+LQQw/Fpz/9aSwvL+NrX/saNm7ciMsuuwxPf/rTsWPHDtx88834\nxje+ke7DjyS/9rWv4ZhjjsGb3/xmfOUrX8HnPvc5vOhFL8LVV1+N17/+9Wg2m/j2t7+NV7ziFW2P\ny5Ky8/WaXiO01772tXjta1+bft9oNHD33XfjCU94Am688cbCopCsvXv34o1vfCMuu+wyLCwsYMOG\nDYXHAwBRFOH222/HEUccgVtvvRVPfvKT27b3GqG97nWvw+te9zoALv171113dQxmH/rQh/C5z30O\nhx12GADg8Y9/PB772MfisssuQ6PRwNVXX40jjzwSr371qzs+z0UXXYRDDjkEz3nOcwAAN910U/o1\njRYDGtEU7d69G6eeeipWVlbwvve9D0EQ4F3vehfOOOMMWGuxadMmnHfeeRBC4IMf/CCuvfZaLC8v\nIwgCrK2tte3rqU99Kt7xjnfgM5/5DIwxeOc734mjjjoKt9xyC171qleh2WziJS95CY466qixv64P\nfOADeNvb3oY4jrF9+3YcffTRePDBB/Hud78bn/zkJzs+ZvPmzTjppJPwmte8BmEYQimF3/u93yu8\nhgYAl1xyCX72s5/hcY97XM8AVlb2OD/84Q+j2Wzi7LPPBuBGw+eeey5e//rX45RTTkEcxzjssMNw\nwgknlN7/j370o7b0JI0OmxPXACdeziY/KuhUUEAtURThL//yL9Og4j3/+c/HddddlxZq1BybEyfY\nnLjmmiV7QRLNImst3vCGN0z7MGgGcIRWA8ZaTtQmqjeO0BLdRmi8hlYDkoGMiIgpR6JJsdYiNkwP\nE40LA9oE+L6AnUSxKbV0DM0+IQQEwJ830ZgwoE1AvsFt/oQ26LWvbidGnjSrSUrJa51EY8KANgWx\naQWbcIjGo92qG8uugk1EVBcMaFMQyHIrVBcxxqUwu+0nDORQz9EtTUpEVEWscpyCUaWcgi5tgYZ9\nDiGGC7pERJPGEdoMknIy63RV8VoPgywRFWFAG0JsOqflYl6/GhuWvRNREQa0MTC2NZLw16LGeU3K\njGH/nfZXhdGRtdU4DiKqHga0IQQFqb9G2F6abbG+dH+UotiMfP+xWd/weBzH329waoRBJVOhRDR9\nDGgTZK2FMaMfXTSGKP0vEsjJBA1OLyCiUWFAGzMhRFuvRYvRpx57jVgGSUdOahTEakoiGhUGtAkS\nQiCYQqcIU+H10oaZWE5ElMWzyZDGlUYcpap342fakYhGgQFtBPJpxKIUWr7ycVKqOjrz2LCXiEaB\nnUKGJIRAULIa0N9e9QAzaWEYTPsQiKgGOEIjIqJaGHiEppSSAD4N4GgAqwBO11rfmWx7OoCPZ+7+\nDAAvB3ALgDsAfC+5/Rqt9YWDHsM0+NTYpEdZ2ZQcR3hEROsNk3J8OYAlrfUzlVLPAHA+gJcBgNb6\nNgDPAwCl1MkA7tFaX6+UeiGAL2qt/8dwhz09ZYKJHUNVobG2azNiIqJ5N8wZcjuA6wFAa30zgGPz\nd1BKbQLwAQB/ltx0DIBjlFLfUEr9nVLqsUM8f2XFY6h6rHqlIhHRtA0zQtsC4KHM97FSKtRaR5nb\n3gDg77TWu5Pvbwdwq9b6n5RSrwFwEYA/GOIYKslPFs7+P4p9UnfjGBkTzZpt2zaOrNBqefPSSPYz\nKcMEtIcBLGe+l7lgBgCvQXvA+mcA+5OvrwFw7hDPX1nZtlE8wU4O32uqo34/qO3Zs7/3nUpa2Xtw\nZPuahGFSjjsBnAgAyTW072Y3KqW2AljUWv8kc/PnAPx+8vULANw6xPMTEdVeM2LjgbKGGaFdA+B4\npdRNcHNjT1NKvRXAnVrrLwP4NQA/zj3mbACXKaX+GMA+AKcP8fyV1OnTVP62fj5xGWshwNEH0byS\nE2oUXgei4h0aKn1wZQ1zbSeKDfsdElHpE8iuXSsjO29+/bZ7RrWrkTn5+CMK3wueKccg39/R9yq0\n1sL0+QFiUsu4EBHNOga0EUtXp870d/TVjoOsXM1UI9F8q3gWrVLYy3HE8itHW2vTlOEogxNL1Inm\nA//Oy+MIbUSKlpHptTTKoEuncMkVIqJ2DGgjZK1Zlx4IpOyeMhggDVlqv0REc4YpxxERQiAI1s/O\n71VyO+iMfiGYiiAiyuIIbUYx5UhE1I4BraRO6b3YrE8xDrLfon102z9TjkRE7RjQSuqU3jN2+LRf\nvioyKzbFlYxSFj+OiGgeMaANIRzzpOcGO4QQEZXGM+aA3OTp9lSk/9qY/qsWO+EIjIh4vbw8BrQB\nWYt1TYP917ExlQhGvMZGNPs6zW+lzhjQBtTtGlZVmgnzkx3R7GuE1TifzAK+U2OQD3RxPHw15CBk\n0kOSiGZXFbI9s4IBbQLMlPouBoHkHwMRzQ0GtAmoSgqSiKjOeKYtqWj5F/914eToEtexhkkLGtP/\nGmtlMV1JRLOEvRxLKkrd+duLttsu23rtuwwLi0CM53MJ05VENEs4Qhuzca84LRl0iIgAMKANpUz1\n4iCjnH6Wk+EoiojIYUAbQr6X46iuOXXr7zguvF5GRLOOAW0IYdAedPKtsMooWul60qxlUCOi2caA\nNoR8z0aBwQKDhdtPt+ViBlnVGgCiOC71OCEY1IhotrHKsU82M0naWCDI9XLsN1MohEj3YY2FKCgi\nGTQFaUsucdPvsdspTRYnIirCEVqfsnO+8inHYfVTERmbcn0axzWpe1xz34iIBsWA1ieXVnQn8/wI\nxRjTlobsN32X31+3x4se24v2OSrsE0lEVcOUY5+kLP4MIIRom0g9itWsBzmOSWC6kYiqhiO0ERJC\ngKd5IqLpYEArqVd6rSgNOci+ytw/mtKSNDQ8Y13/Tf78iEaLAa0kH6iKyuf7ScH1m67r1UeSZk9+\ntXMiGh4DWp+iuBrl6lySZnbJKXSCIZoHPCsW8Cmh/GgskMXVfc0oRhS1JjJ3m9TsO4QMm3YqO3Ga\niKjuGNBKyK6D5j9YFwaqtvtP4tjaj5EGw/eOqoq/m+UNXLavlJIAPg3gaACrAE7XWt+Z2X4hgO0A\nVpKbXgagAeBKABsA/AzAaVrr/YMewzjll2XxAUpKgdgYBB3K5hth0HZf/30ng3QV6aTbc1B5TAFS\nVfF3s7xhRmgvB7CktX4mgLMBnJ/bfgyAF2utn5f8ewjAewFcqbV+NoBvAzhziOefqNhY+Jr8XsX5\nQghMon6flXJERC3DBLTtAK4HAK31zQCO9RuS0dtTAFyslNqplPrv+ccAuA7AC4d4/onINx8G3Cit\n1/0ntfAmGwpXH38+RJMxTKeQLQAeynwfK6VCrXUEYBOAiwB8DEAA4F+UUv+ee8wKgK1DPP9E+OF+\n2arCSaYH5IRGgjQcpoxokrZt24hwRJciljcvjWQ/kzJMQHsYwHLme5kEMwDYD+BCf31MKfXPcNfa\n/GMOJP8/OMTzExFRzp49oytLWNl7cGT7moRhUo47AZwIAEqpZwD4bmbbrwHYqZQKlFINuFTjt7KP\nAXACgG8O8fwjV6YbyDjTR9lqyrqp6+siouoYZoR2DYDjlVI3wSW+TlNKvRXAnVrrLyulrgBwM4Am\ngL/WWn9fKfVBAJ9XSv0RgN0Adgx5/CPVKzWU7RYyrjSSxeSuv02SsbZjZSgR0aiIin9qruTBNaMY\njTBAFJvS19aKSv2z+ukHOWu4ICjRUEr/8ezatTKy8+bXb7tnVLsamZOPP6LwveBH5px82i8f8K21\n6VpkFuVThAKi533FlFsijfPDDYNZu4p/kCSaSVwPLSd/4l23iKe1CAIJIQQaQflKom6l/lUx6qDD\nUVkxvi9Eo8cRWg82WerDk0Igis0Uj2h2xIajkH75Hp9E1D8GtA7yTYP999lrXJNMGc1qesqnZqk/\nrAglGgxTjh3ExqARBmnKLJ86C4P1fR7HmUKa1fRUMIUlbmY9zSmEQBDM7vETTRNHaB34ykWfMut1\ngmEKsjqa/FkQzS2O0LrwKTOZSzH6a2p+ocZOo7i8QUYObX0kZ3jUMUmyxM+CiOqJAa0DfzKUsr2M\n3lpAiOSaGoAgdCO5MnPRBjnBGusWFKXyuJI30fziX38X2Sq9KDbp+mUCQKPDiXPUy7kwlhERlTfX\nAS1fzeh1qnD0XT6sReGcfZHcPzamY1/GTtVr3Z5/VGkzkxxPkTpW1PV6zUSzgr/H5c13QCu41pK9\nzacdhXC3x8YiDILCxwWBTFKTYt3+O3UC6fX8o2B77LOO15tiw+toVA/8PS5vrgNar+tT2e1RbJIG\nu+X3W5Umw6M8jnhGqgh5LY1o/sz1X32nTz7562D+60DKwv6OnfZbpUq70R5Hf9cJp5Uuqcp7T0ST\nwyrHHGssZPLpPp967HTxrChw1fWEGvTRvxKo7/tARNUz1yO0TvptIpydVD3qKkciIiqPIzS4Vlf5\nSdJAUjSS3McvvJlPJ2Yn8mZ7F+YXA/VNjmWHwhDqT5XSuURUHRyhATAGHasRXYl+6+tOJ1G/lIwP\nZFLKdfvK4ol4eHwPiagTBjS0Nxu21s0jA1y1oq8QzFc85sXGYi1qzT/LLwEihKhM1SMRUR0x5Yj1\nn/jj2EIKF5SkbG2PYwMpRVrx6IKWhZQSUrbSii71mEzCRitFNuzIgqk2IqJicx/QjDFtwSabXrSw\nbdfCjLUIhExbYBlYwAJBcv1MhusrAG3SWmQUgYjBjIio2NynHJuxRWza04QLDfe25NOM+cm6oRQ9\nJ/D6LiNF+ll6hqsZExEVm/uA5i6ftfou+uIOH2ji2CBKUo15ZdOIXdtOoXjycVHvx1FODYjZ85CI\namLuU45hZmVqz6cXQyFhrAtsYZcJxcNc2+q2qnOnCslRr2ZsjE2XwSEimmVzHdB8GtFYC4mkiS/c\nqCWUomOasRNj/Uhv9rDnIRHVxXyfzax1RSFIlolZd33Kfe+vsfl/cdyeppOi93Il+cf0PrTJpAHr\nXmhik58x06o0q/i7W95cj9CCQMJYF5B82b0QIk0v+mhvrEEo/HporWpHL3strSj9aJJqyLLqHmgm\ni91ZaHbxd7e8uR6hxcZCCjfvDGifN5b9VJRdnTqKbY+qxc6fpsJAsNfjFPSqMiWi+pjbEVoraAnI\nQKQrU8cmmRiNVrRva2WVXGlzIzV3zS1bASlE51GacBvS63X9fuoa9SrWVTfKSeTz8p4Rzbu5DWg+\nTeibCkP4no7rGwtnhZnJ09aYdVWK2SKL/OOFEH2lHfPHO0/YVYWI+jXXKcf8itV+pOV7OcY9JjH3\nqhAsSj9Omn8986SfCetEVA9zFdCiOM5MnI7T27PXzFzq0VUtAhbNZoy1Zrzu+ld2X34f69n0caO6\ndjbofubt2l12hXEimg9zFdCyS8Dkl4NJvxZ+5OWaELuwhnXrmBU9vq2cX8q2ddZajx38RJtdqqas\nILekzTyQkpWNRPNmrgJaNkUY5ioXvUC62/0JUQBodJg1XZRubN9X5xNqr1RmL1VJZRIRVclARSFK\nKQng0wCOBrAK4HSt9Z2Z7WcB+MPk22u11h9QSgkAPwXwg+T2f9Nav3PgIx9Ap0/sURSvq0zMfh0G\nre76nkshAsD6wgNZUOWYFUgxVNFCmefoxviKSQxWfFGngos6vRaieTdolePLASxprZ+plHoGgPMB\nvAwAlFKHA3gNgN8CYADcqJS6BsB+AN/SWp80/GEPLr82mQXQyPVpzJ7gOjUl7nQ/r1tvxm6P63as\ngzxH9x23V3P2q04BoE6vhWjeDXpm3A7gegDQWt8M4NjMtp8AeInWOtZaWwANAAcBHAPgMKXUvyil\nrlVKqSGOe2D5dF/ZXobZpVsmNVl3XCvF8PoSEdXRoCO0LQAeynwfK6VCrXWktW4C2J2kGP8XgG9r\nre9QSh0K4C+01n+nlNoO4AsAjhvq6Afg031RbGCMxUIjgDGt7h+9TvTdVp/220aRxrLWpqnF/HFF\ncTyXhR5E1Nu2bRvb5ssOY3nz0kj2MymDBrSHASxnvpda68h/o5RaAnAZgBUAf5zc/O8AIgDQWt+o\nlHqcUkoko7iJMxaIrW951QpSxhhI2erbCGQnYXffZ/uq1+WDW2FnkcL7M1VGRJ3t2bN/ZPta2Xtw\nZPuahEFTjjsBnAgAyTW07/oNycjsfwP4jtb6TK21n/D1PgBvSe5zNICfTCOYxcYm180ElhoBYpO0\nsEoCRDNTQRgbO/AEXWtbjYx76fc5uOQLEdF6YpA5UZkqx6fBFcudBhfg7gQQAPgigJszD3kngNvh\n0oyb4UZqf6K1vr3HU4084LmJ0wYQ0o3GhEBsLUxm7bMgkOnoyli7bg5aN1EUtxVtZB9fNFqLk+Oo\nwqjLV3D6opFePSRntUpwVo+b5lbpX9Zdu1ZGdt78+m33jGpXI3Py8UcUvhcDpRy11gbAG3M3Z4NT\nUeL1dwd5vlGSUsCYJDWIZAmZKIZFUvGYrGANuJN4r0bCPmB5/jfJP6ZM70Y/960qLCxksjxOr5M+\ngwIRVUW1zqQTIqWbW+aDTxhIbFhspAUjJnNtrdcANp8uDIPiYo1ZOPkLIdoC9KCq3nZqFn4WRNSf\nuQxoAJKFPCWaUZym1mJjEUUmXR9NCNFzoJ+/nlWHE+UoXkMcGzSjuPcdiYhGpPYBzRizrjlw/ra2\nbWitaWaTdGK2wXB+5CFQbjRS9Pgy8k2Qqz76AZCsGlf9kRpR1fFvqLxaBrTsL0Az7jBvTPhlYiwa\nYZBuDwOJxUbQdhsANJsGQoh16cV0kc8SI5rYFM9f6yXfBHkWRoGNMECYvI9ENLi1iEshlVXLgJYN\nPGHQ3p3+4FoMYwyiTFWjMRZxbArL58OwVf2YXVusn44ho7guRUTzpxHW8jQ9FrV9p3wQy3bUsG5y\nGLIXxmJjYNEq/sinIrMdO1wKLbdETIlA5UrEi7d1SyP2m2IcNKXJtAZRNfHDcHmDdgqptEZB2xdj\ngaVF95J9EUgcGyw0Aoiw0/wwm47ifMVj0b576dX5o6gJcvYYhn2eIlFsBn5dRERVUdsRWkfWohnF\niI1BHCeFIXBBY7UZp82HPQGkKcbY2D6mNmaf0lVOFulVSTmJT2fsPEJEdVDLEVohASDJOvrEowsY\nSYoR7fPOpBSuNVYS1LJVe51WqPZafRz9Xos7U/hKyiKdRm69unf0a1YLN4reB3YBIZpPc/PR3FqL\nQMp04nMYSFgAC40AYRCgEYi2CsJs5WNsWhOm81WGQoi00tH/8xWNsbGQUqIRjnayteEJGwCSVRLW\nvw98b4jm09wENF/B6DphuIm/YSDTOWaxsYgjl4bMl8n6eWnZCses7DIvADI9IUXbc49K3S8SF73P\ned0WXyWi+VPLgJYNLnEyidp3A4miGCaZP2athTVuXTQBAJnAlK0+FAJJ4MtNwjYmTUdm+RGCzDT3\nzU+OHsakRiDTqny0ptxzj/J9mHSlJytLqSz+npRXy2to2RNdbCyCUCKQ7vbYAiL2HeVFuip0dkG8\nBdEKgMYWNw/2QbHTPJHsGmv5CsJZSYlN6zjDKcy7mfRrnZXfAZo+/q6UV8sRWlYjkIgik65QHSRN\niZtx7NJdnVInAAAgAElEQVSMxrqJ1ZmR1lqzVdnYLavllljpvG3Uacas2PATGxFRXu0DmuNGWq6H\nIwBrISFgfcASgDWtFKOUfpjfniaM4tiN2kyrzyMgcmlI25biBIA4edyoUgcCSK/9VYl/7f2q2usg\notlU24CWltoL4XoKwoUnXyG4YSlEEAjXSQQi7TvoU4RCiLYuIwDgB10WrXRifrkYX+GYvT0yo+3B\nKKWozIKgWbExQ/eqJKJ2/MBX3kwEND8qKsOn+pqx6wLiudJ5IEqWholig9Wmm2AdBCItFslWM2ZT\ne9mTbrcqwzBYv62R6yc5btNKSXKCNtHoNdmcuLSZKQoxsBClOtu30l7GWogkOPmJ1EIIl0hMejT6\nRh0GgEi6gcSxhYBNJ1K3qhaRFJMkz+Sfx1hI2ZqHlk05Zkdmg0z4HeQxQvg5Wp0ngI9rRFQ0cXzc\nz0tUZ5yeUt5MBDQhBMKSJ8MwCDLXt1wYi41JqhWBhYZMApVA2Gj1aQyEQBDI9NqZEG5la78dWN/H\n0Z+gjTUIROu+2cnZ2f+7KQpcgwQB2aGdVrd+kePkPwB072XJieJERZj5KK+W75RbGibpBpLMHwuk\nuwbm21n5+WnGWESxTcs/TIcyfGO7Vy1mf+EGrW70qdBx8ZPDJ61MnGLRJhGNwkyM0HrJf8JPR04+\n3WgtjBGu2XBkWsHLGMQmSdFZ1z0ESVm/zKbqkv2bTN/FfHDI9hWMjWkr2uiVdvOjQne8bmSZT1UW\nPbboPcgb9whomBFmpxTpLKrDayCaZbUYoeVPIL7CMDIAhMBaZCCEKwwxcIUbgZSQUsIkq1ZLAHES\nsLJFHxZuVBcGsu32bDox28sxkGJdAYvNbC86fl9ZiSS49rtK9ShOosOM4IZ5filEeg1ylrHHJtF0\n1SKgZWUrIkMJrK4ZNEKJZuTSio1Aotk0MNaVmPsmIEEgESbByHUIcfvoVtHonyd7acpYF1DXojgz\nsirfykkACKZ0EXjcac+6m9bPjYicWqQcs3zJurBIg5Lr1Siw1owBCwi462YCMZBUI/oGxYCbZO2r\nIdOglbTO8mX9gZTJaKo9DSl8yhK++rG/0cs0P+H7wMtRxmD4vhFNV61GaNbatIs+ADQjpHPPZCCw\n1jTYvxoB0o3YImMRZiZP+zU8s5Oq42S0lk0xrjVtep98GtKnLBuNEEFQvGyMP96qsNaumyRORDRL\nZiaglWn1FMUm7YwfG4sgAPYeWIMQyaqeAJYWAkRRjE1LIcJApJOvm5FFKFtdOPz+GoFcVza7tDCa\nt22a1X3ZESkw3t6Tk1an10JE5c1MQPOTnIuCmr9dSpFUL/pyfVdsEMUG1rbaYfnLRRauutFfS/Pn\neF/d6O9vjEEcxzBJe6f8MjLZY+sVeNNjFe2BOtsLsds+/JSDoVmDbAVllUaMQ6lgn0uiXrik0PBm\nJ6AJAZnrrdgWRIBk3pmbEB3HBlFksLQQQgoJwE2cBlwBSDMySWUhkknXrjdI9tfJ93f0zw+0uoFk\nA0C2irHMNah8Gy3/fbYXYrd9GDPc9Rp/jEHQen11Sjdmf25Es2KU/V7n1cwEtE6i2KCZpJd8mtAk\nTfKlFMk1LACwiIyBMa5kf3UtxoYFF9TCQCIMRFIk4jQjk0y4bqWuRFJanuULRqLMfcumu4y16+7b\nqSNAp/116hfZD05kJqI6mumAFkg3InNrnbkRGZBUN1qLtchVhRhjXNWjMWngik2rCjJOl44BkCwp\nY+HXSmtPy7VNdk5ShkHS5DHbwzGOO6cF033BjezK9DrM76fofmWXb5ECba+LaFzcNBr+rtFkzHRA\nc5NxfXARMHCNhaUA1iKLKLJJSk+i0ZAQScqyEUpX+ZgGn2QFa+kmNgeBRBgESWAr7vjhqxzDQKZp\nLp+6MwV/wNmU4kKjd2qsn1Rg2Ym9ndK3ROPDVBpNxswGNL/gpu+AL9NJycCDe9cAAPsONPHQ3lWs\nRQZ7D0RoBAKrzRjGAosNgWZk0IwtGqHr9iGTEn+f5nPdQVrP2U/1XBjIwqA2LpzYS1XjshrTPgqa\nFzM7sdpVHiJdXXp1LU6WfnFdQGLjmhAfXI0gBXBwNcJCKBDKIFl52n9qdIEtCEQywmmv+GtvQYW2\ntGKen3DtU5NucrVJO92P+1Nqt5TlLH1CdlWn/FRfF/w5Dset2TizY4+JGjigKaUkgE8DOBrAKoDT\ntdZ3Zrb/EYAzAUQAPqi1/opS6hAAVwLYAOBnAE7TWu8f9BgaoYQFEMVx0hjWwsBVAboVzoC1yGBL\nIHHgYIzlja6wI4oAE1ksNGQy0rNYbLg/ukCKtNQ/LwyCtGy/03YTtxds+Ps1oxgyv55LxrABZ9qN\niUfNWJsux0M07/ycWuptmLPGywEsaa2fCeBsAOf7DUqpQwH8KYBnAXgxgL9QSi0CeC+AK7XWzwbw\nbbiANxRfXBEGwIHVGHseXsVDK6u4/8GDeHBlFfsORLjtjl2QgcBD+1bRjGJsWAiw2HApwUYgsXEx\ncClC4wo8Dq7FhRexm7l+h9mpA41G57czDGTXVaSHnQhct4nEXP+JqCW/nBUVGybluB3A9QCgtb5Z\nKXVsZttvAtiptV4FsKqUuhPA05LHfDi5z3XJ1xeUeTJrbbrqtC8CgW9EnFQ6RrFBM4pxcC3GAw8f\ngAXQbJqkVD/C0sIiDqxGsNYv9Gldh30IwJp0GZMgbVJs0m77Aq1rAX6Fai/bs7HTaMkViayfxOyW\nmrFD91B01Z6zlVbspi6vg2gU+v172LZtI8JwNEO65c1LI9nPpAwT0LYAeCjzfayUCrXWUYdtKwC2\n5m73t5Xig5mvIBTJCVxKASlj7D9osNZ0qcf9q038+Ocr2La8CGssHrFlyXUNSSZUB4HBQkO6vLR1\nJfqA75JvsNhwvwzNyBWQBGjNQZOifeVnN0E525y4YImYXKVXtnIyHDKfMAtLtNcp4BJV2Z49A1/F\nWWdl78GR7WsShgloDwNYznwvk2DWadsygAcztx/I3FaKL7EHXHBYiwwAg4UwQDM2uP/hg7j3gX34\n1u27YYzBd36wG0f88iPw8IEmnvqrj8LBtRiHbNuAzRsbiI3FvgNNbNqwABH4YGPRjE0yR80Vd/gV\nr6UUySrY6/s6ZlkgXQw0r2gy9LxUJkax68xCRDQuwwS0nQBOAvAlpdQzAHw3s+0WAB9SSi0BWARw\nJIDvJY85EcDlAE4A8M1uT2CTbhp+LpabRB0jkAKhBOIYOLgWYXUtgjEWD66s4oEH9+HHP/oB7v7J\nT7C270mIEWDb5iVs2bSA++7fj62bFrC4GKARhm5NNCMhA3fhNV0GxgCRjV0QRes6WbbPovtapFWR\nyQYYuAuT/rYoNh2LTPyIpdPtwOBpt2Efn9/XqEZVQSCTn13x/Leqj+KqfnzzgD8D6maYgHYNgOOV\nUjfBZQNPU0q9FcCdWusvK6U+ARewJIB3aa0PKqU+CODzSQXkbgA7ej2JRXt6Dmil+YQwWDtocHDN\nXTu7/+FV3LN7L+78wR2496c/QISN2LBpMx54eBUblkIcXIuxuGDQWAgB2FbvR+FaX4UNkYzQWo2N\njWucuC74ZFOg/thk7lqWD3wiqdjLbitMTfbxx5qdQlCmB2S/RrkvKVxD6Fmuxqz68c0D/gyom4ED\nmtbaAHhj7ubbM9svAXBJ7jH3AnhJ2ecQQiDMpuQEEAiBZmwghcCB1Rhh4EZuv7h/P6yx2HX/Q/jx\nf96Eh3b9CPf/9D/xyjM/grt/fj/2PHwIFhsBFhckGoHAYiPAWtMAsFhtxlgMA0SRTeajuWtlPojF\nSaGI12kUFBuLMJnLFqSjM9uWouyWkhxEM26lXBdmIJ3H6kUiGqfKT6yWsnUSFPAjtlY1YpwEl23L\ni/jprr14zKO24DG/+huImqvY/IhDETcPYMPCJuw90ISUwMr+tbQHZBD4biACQdganfn/TbO9E0kS\nktKKy+zo0VdfyqRoxc+LA1qjNT+HDUmVZGxMmtZsXSPMpTFRnLYMkseEFahy7HeVASIqZ9p/27Nk\nZj4y+x+qFAKNwC37IqWAsO4HvdgIEAiBbVs3YeujH48thzwRhzzxSARhA0uLDQRSYmkxxFrTYC2K\nERsDY/0cNolG0pnfpRFbz+lzi9nOFTLp4Zj9JfMz+f0x+urF9l9E1//R389mUnDZlGbR9bY8vyJ2\nFaocpx1MieqKway8yo/QPGtbi2H6ajlrgcWFABuXQtx1zyoOPWQTpJR44qHPx4+POQaNUCIIAhxz\nxC9hy6YG9h2IsHExTFtexZHFxkUXnA6uxVjZv4Zty4tpgPD9GE1m3rLv5B8bNynbddt3QSpbyZdP\nr7lmxu5rH/x8sYvM3AdYf3Iuk6ozFhhyVZmZNSspVyIar0oHtPaRiU27bTSbcTJwclWQQlgcsnUR\nzdhg3/41PPZR2xAbi40LAkuLi1gIJZY3NLAWuX6P+w+sQQpg04YFRMYtM7MQSoQSiJI10vzSMG6l\nawCRbVtzLb2mZn060aURs9WLJpk07Rlr2yogASCKYgSBbHvc+tfem1/9Oluo0vs9rYcqpFyJxoW/\n2+VVOqBlf4hSSiCKXVcNv10KxDEghcSWzYuIIoMNSyEetXUDHrG8hEdvXcJCI8BCKLBhqQGsiqSj\nfpJqlALWuG4iSwthuryMhTtJAskaaQkLV8mI2CCQbkTgJ1X7NlpZ/toY4CsekyVqsq+vQ+l+/rWX\n/WWWJe43rj+Maf7RVSHlSjQuDGblVTqg5S00/Hw0N1qLDdAIASDAIVuXsO9ghGOPPBQ/+cUKXvGc\nw3HPrr3YtNTAgbUIYdIl5PDDtuCBh1axvKkBIVyRyIalEEIAWzYuIDatuW/uWpmvXkxO2mgVpWRP\npJ0mTgdJ4Yefe9Upcziqyr9ppxxHXcFJRNSvSge0/Jwuzy0RYwHrSvgBkVxbE1hrWjz20RvTFlYb\nlgKEoRvWNbYuwQLYuBQmqUqJ5Y0LEMJi3/4mNiyF8G0i49igGdlWqy3hlquJYwMId92mIWSa4mub\no5adF4biooWyo5puk6X9NleNObpJ1b1k06lCiLRJNMCgRkTTUekqx/z1pHxw8wtoSgkYK9I04MbF\nRjL5WmKhEWDDYgNhGGDjhgakcCtF+5Pv4kKAQLpu+HFsXMcQ2bpW5v8PkhSkgftaoDggrUuVYn3Q\ny7++bpV6nQJmflv23ySq/tK0b6Yyk2uYEdE0VTqgefnlUYSUaIQBlhYCLDYCF6RCiUZDYuvmBchA\nYMNigEMesQEmKesPQ4mNiyGakU0aGkts3bQAC2D/aozFxQD7V2MAbqQRWz9XzKZl+Mb6WWXu2pkx\ntuuyMF6zx/IubqWA8kGo10rYk1gpu2jNOCKiaal0ytFz179iNMIA1rZ37fCjKQvrmgwjmWgMV0G4\ntCAhkvN7EAawcGX4C6Fb/yxKuoUIC2zeECKUMmnR5B7TjGLIZDkZf/3MXUtz18SMNTBGrpsMnR29\ndarC899HfnXmJG2ajnyApEuJgTG2rbGvD7BFAaXX9m6KJnETEVXdTAS0bqk6l+ry13RE+r3rxg8X\nCJIAJYRwq04LA+Ha7ANAMknazQ8LpEDUNLDWXRdq6/Iv/LporbJ81+nDBbg8n0rMdjtZv719tJNN\nF/rtvd6Pfrf30q158Cj2T0Q0DjMR0ACkI5SicnYLkfZfbEYxFhsBFsJkpBYbLCRrnLnVX12AWWvG\nWFwMsWHJBURj3YrUQdIfMjbucWkDKwFExmIxmTe22nTbOy0B40dXUWSx0Oi86GdszLrVaLOl935U\nOkndqi6j2HL1XCKqrJk9O7mO+JmRUyZeWItkxWm3PZBi3cgnStY+A4CDazEEXOm9TDp3+LL8bKxy\ny9a4DvxrUZw8t9vWjNZfJ5NCIAzFumuA2e3dCjiCgpHdtMzL2m1ENJuqdcYcQCtoZZdoSa6pJeXk\nadWiMZmKwtb1KpvU6gdJhxDbVjWI9B/a9pXcnjzemtaaaf55fF9H/xzGmLR9F1Bcht/anjyuRxXk\npHACMxFV2cwGtLTVUy4FKYRAIwzSycxt5exIqhalhLWufH8xKesPApG0ubJYXYvS51iLWtexfCWi\nlBKNULruIsnzy0AkRR6u8jFbPu97NzYjgzg2XbuANDtszz+GiOZHFT7MzoqZC2g+fZctzCj7A89O\nPg6kC2DGWkgJxLFNikcENiyESYcPF0x8ZWUYCKw2YxxcixBFblHR1WaMtWYMAYvYmPRxxlpEyUjN\nGJsud9OtPZW1rbXUgGQSNzpf1/L7JaJ6K7pkQevNXEDzzYCBpIBCuGtm+aCWTr7OpBldBaRM05Ju\nUbP1QSEIWjWLQibX1GyrOTGSVWVaKUvAdSvxqUl3UK1du/SmkP54bdu/Npmga9H905lF++Pz++vn\nkx0/BRLRrJuZKkcv7FQV2GHQ00rR5dYty/ZfDN3XzcikC4cGyQWzxYUgXSLGVSRaSOGXfAFgkXbJ\nX4tM25Iw/nkXki8lWtfCgiSg+uCXTy9mR2jdKhzz9wX8qtmDfUZhSpOomiZd6TzLZm+E1ich2kcf\nnYbvvnrRr14tsrcHbp5ZmIyu3JIy7jrZgYNRur+9B5odn983UnZfI00TCtFKKY5KPp1Z9VSFe2+q\nfYxENDvmIKC1T1rOViGmqUvpKhyzFZEuOCR9Cn0qMem27/kwKZNt/nqb32/2+/Q5k3XdfMoyew0w\ne9/sMRZdJ8zflq9C7NXXsWyascxzD6xDupiIaBAzl3IchrFu+O57HRZ1IHGNjZN0ZNOkFYxxbNNV\npo2xsGitUJ2vz7DWuknYjQASvqWU23dkDKxxxxLFJm2NBSRBzrqR4ELoV8JeP8G6TGurXunHsmnG\nXg2Y+zmm/D6CeV1mm4hGbuZGaMNU9/kqR38KLbMvv0inK/dHWtrvKhJdsDHJ1xbuelozMmg247Y1\n0lxVpZvQ7dpl+WNy94mS0nyR3NcvFpoWsOT4dGLUYUL3tFQ9xUlE9TZzAQ3ovdxKkfy8tOy+OlVJ\nZoOJbxzsJ1K7/bkJ1jZdG0ykTYVNZj8muU7kM4LZCdnIBNn2ziciE3BFmoJMX0v6+HLvxaTSevOe\nPpz31080TTMX0Pw6Z6Ooysvuqyj9KJMJ2mHg1kwLw8CtZC3dKtZCJqX9yRppC40AjdCnJd2+omSi\ndRgGacoyyKQu/bbs8/qvfeVifvAThkHabLnMezGJKsZGWO5Y6mzeXz/RNM1cQJsk17qq9XUoW6O6\nZuxK9QPhJmjHxkIky8wAQCNwtf1RbNAIJJrNGLExWItM2xpqftJ1bNx9jbGIIpOW+ftmwEEgSq29\nRlR1rG6lcZnrgNarAnB9FaHM9FZEOilbwK2LZo1xVYxx7K6RWZtOwvbfivz+hV+Q02+06YRpm5b7\nJ2uxdTiutBJyRP0eu1VV+u1Ew+rUDIE64/tU3lxVOeZ1Sw8VLdYp3MQ2LDaCtEDELzwax8b1f4yt\nW/wTotXBP1m+xsrM6CwJVL4a0dcxZpvsZ6/dyQ4Lbwoh0v10W8fMX5MrlRITxfuadkqt7Gvot+KS\nJselyvmzKYu/x+XN9QitrHymz6f+ZDIZG0jSk9K1vwqkRBjINJhlRbFBFFs0I5OMuLo/91rUKgZp\nRqatKtOPpLr1h/TP6e/fi6+0rKqyWdcmKy6J5g4DWhft1YyZ9dWEW5wzOypyS8P4Xo6ZXpNo7ydp\n0/sgCX5i3QRqf40hm2p0vSSRW36mXOpGZkZnfg5et8fkPxFWZfkaYP3PohMf5Iv6e1L99dO0nOpj\nrlOOvaSVjrl+kUEg0YxiBJm+kkIImNggbATIr8tpbXbStksxWtlKiaWdRYxJ05d+n36lbXcgnY6x\ne0rCWpv2mczerZ80hhmgR+S4Un5FvTuzilJaTN3MD2MtwootkEvjx5/4gPIn+OxJND9hO9tP0j/O\np8Ti2KRpyLb0Zebk22mE5Cste6URo9gO3TNykJWqWZBJ08TFaOcTA9qAOn3al5lVs+NM+lAknUGy\ngaWVEvOdS9orF33KJDYGsDYtQImzE6yTapF8GjE7WVwIwGSWmenVGzJfQdlJmVSOEMOnKquU6qwa\nvi/d9bquTPXEgDYGLrC1pxStsemK1wAyE6wDhGHQNik5rVwUrshESpmOePxEbJ+ODKRM/3jT63m2\n1W0kXUGgbcJ2cX/GTqtpF0067/oeJKPMYdJ8/rX2Y15O9EyfEq030DU0pdQGAF8A8BgAKwBO1Vrv\nyt3nfwHYnjzHxVrrS5RSjwRwB4DvJXe7Rmt94aAHX2VpajEykNJN0F5oyLaiEMBVIHa6PpWW8iep\nk0YgCu+b57Mtvpxf5oLUrJz0B0l1RrHh+lFEc2rQopA3Afiu1vr9Sqk/BPBuAH/mNyqlfgfAk7XW\nz1RKLQL4vlLq7wH8BoAvaq3/x7AHPk3GtDcM9kHCpxezvRj90jJW+D6PaJ835uevydZoKIridPHQ\nbAsun5bMFo3k56BlU4tI5rC5UV7xiKuqBjnOvubbEVGtDBrQtgM4L/n6OgDvyW3/NwC3JV9buDnD\nTQDHADhGKfUNAPcB+FOt9c8HPIap8dWIeRZi3WjI92hsO8lmvg4C6ZaWEa2RV2zdG5Y/KXe60G2N\nhQzaqy3zXzejuG3/6/YxQACoatAYdMVuorrYtm1jet4Z1vLmpZHsZ1J6BjSl1BsAnJW7+V4ADyVf\nrwDYmt2otT4I4KBSqgHg83Apx71KqdsB3Kq1/iel1GsAXATgD4Z8DRPX6aQphIBEcSrPGJuu/eUa\nDruvO6URfXqxTOqsTDVXr5P8IGm6KLZohNULaETzbs+e/SPb18regyPb1yT0DGha60sBXJq9TSl1\nNYDl5NtlAA/mH6eU2gbg7wF8XWv9F8nN/wzAv9vXADh3sMOerkHaQlm46kJ3Pa2VFguS/pDpxOfk\nPkLYoUdB2RRoN/4Y+lucE+myOGWeg4gGExuDgHPqShn0XdoJ4MTk6xMAfDO7MSka+RqAy7TW/09m\n0+cA/H7y9QsA3Drg888cAZGOprI9GaUUQOa6m69uHHRZmLY100oGmezx9OrA4YXpEj69g9msFKEQ\n9TKN3+U45t9PWYNeQ/sMgM8rpW4EsAZgBwAopc6DG5U9C8DhAP5IKfVHyWNOA3A2gMuUUn8MYB+A\n04c49pnSLTWYbdM07DUgnz4sWxHpH5OtygxD2XEeTz7N6AJZ7z82t6I3R3A0+7KXCyalEXJ0Vpao\n+KfnSh/cqPgqx04jnXz1ZP77bIUkgDRl2Upd9v7jyz5/HBtAoOMcsig2CEruM6vXagBEs2KKv8ul\nn3DXrpWRnTe/fts9o9rVyJx8/BGF7wV7OVaAG8F0/hTmlo9pVU9atF+zMkDb6McXngR9fIoMMiO5\noMuobtDRY1HXhqpWShIVYQeSauNYdoQGbdXULVAY25ooDaz/g8p+FxX0bKzq6sBcgZuIRokBbYTc\nHOr+g1p+MdEo068x/4EwiuJ1S8ak90Xni9b9LqUxyhWwu5Gyc9eSiqfBeyo6/jg2M//aiKqMKccR\nGkX5etKvGCIZluXLdWMLBJlejGGPdGG2q0inbZ1v770szSgUpW9mPQ1ZdPzGgsUxRGPEEVrFSCm6\n9jBc6FLxlF22xqcfs8vS5O/bjDqnIssWk1B/Jl0dRzRvGNAmKJ8mzC4zk9Wt2tGlrVrpq+ySMq6A\nxKYrXbv/u6xMLculSF2gHD5dNu8pN35IIBovphwnqFOfRWsMRMkuAEKINOXol4gxxqQpStGh2jHf\n0y1b8t8Iyre7shi+WrFbNScNj1WjNO94dpmyskuk+EU8fcrRP87Y/lbndd33+xslxcZ2LVcuW61Y\ntuy/qlWZVVdU5Uo0LxjQpqzsJ2oBpNfHssUnAu3px3ywyt7WSkX2F9Raqc7OjwkKqhX9Y/1q2/2M\nHuY5NTmobMcZonnElOOMkAVpySCQaEZx12CRXwet36yU7zEZDlCV6LqbGIg+Uo1sxDqYbpPiieYB\n/wJqoPvE7PZClEEmMwdSDNWEjGuUEdEk8Ewzw7J9HTvdDrg0lJ+o7ZsJd0pLxpkqRpObWO26/8uB\n01mT7saffz1Es4y/x+UxoM2obmudtV1jE250la6QLWVhgGmrwoRPFyaBcQRz0zp1N8k/7yix4o/q\ngL/H5TGgzTDT5ZNbdpJ1r0pKIURbFWO20/4oK+eamX2NsyIv/3qIaD4woM2yDj0dO6UTfXDyk7g7\n3S+7NE3WKCvnwszq3H6V7HHhp1qi+cMqxxnl0orrb+u2HbBdqw07BYFRVs5l58sx3lAvnChO/eII\nbY6wHJ5mSZMTxalPPMPNGX9tbRKVU4M+hz/G7GTu/P9VEcXxwMcUzXlvy17CMaelqX4Y0ObMJE8Q\nw6SLjDVtecn85PCqGObtZEqtO676QP1iQJszUkoIUe3VooUQEHDL6FT9hBYGxdMgemmE5ZtDE1Fv\nDGhzxFc5CiG69l/spBnFfT9fP51J1h2LwERWzR5W1QMu0TxhQJtTg6yuXWbdtA43lg5K2WkD6fI6\nMxDUiMaJv//lsWx/jpRdqqaTMumxfIAUQqTrsvX7WD8xuhkbNLqs0k1Ud8wClMczBVXaLDQ2znY9\nGSQ1S0SjUf2zBY1Up04inb7vtbZar+fodr9+UijZDib9pl4mmarJpkqZIiKaDqYc50yntGCn74ua\nHvfiAk/3VbT7TaEYO1i6dFKpmuwochZGlER1xb8+GikhhGvVP4B8VaNfBkYKXhgnot4Y0KgvnZaA\n6dTQ2N/eKRAVNkiGm6jc/hzJti6pPAY7IgKYcqQh9OreYYzt2NzYorXeWn5/2ZvcwqLru4UUHQcR\nzTeO0Kgv/XQYKQxApZ+LzWmJqDwGtDk1TJquW6VkNp1YVBjSKdB16goiMFiasddrm4UOJETUPwa0\nOTVomq5T78L899Z2um39gqJZcWzWT67u0sux2/EXbfPHYAybAhPV0UDX0JRSGwB8AcBjAKwAOFVr\nvT9pQrUAAAx8SURBVCt3n/8N4BAATQAHtNYnKKWeDOByuMso3wPwJ1pr5pVqxAWK9aOfKDZdu41M\notzdH0O3KQVENLsGPYu8CcB3tdbPBvDXAN7d4T5PAbBda/08rfUJyW0fA/Du5HECwMsGfH7qYdQp\ntewaatkKxU4Vi0Vz2LodU3YCdf45RsU/h+TkZ6JaGjSgbQdwffL1dQBemN2olPolAI8A8H+UUjcq\npV6abDoGwDeKHkejM+qUWmxMW1Vjq3lwuUbHZZZZye5nkObJvWSPgSlHovrpmXJUSr0BwFm5m+8F\n8FDy9QqArbntCwDOB3AhgEcC2KmUugWA0FrbLo+jiipKCQpRz4UqY2MQyP4/71lrYeFGtP2mUWNj\nh2ogTQQA27ZtRDiitfaWNy+NZD+T0jOgaa0vBXBp9jal1NUAlpNvlwE8mHvYLwD8v1rrCMB9Sqlv\nA1AAstfLOj2OKqpbcUaV03euAKT/EZlPeQ4SqN370f/jhRj8eIm8PXv2j2xfK3sPjmxfkzBoynEn\ngBOTr08A8M3c9hcC+DsAUEptBvBUAP8F4NtKqed1eRzNoCqffAcNSmEQDPQ4t3iqHOjxUoiulZ1E\n1N2gAe0zAI5SSt0I4AwAHwAApdR5Sqnf1FpfB+AOpdTNAG4AcI7WejeAPwfwAaXUv8GlJf9+6FdA\ntTGO+WFVrGg0fUxOn0XZ5XSIJklUOV2ETvXf1DffAX9aqaz8KKlo1DTt45yUur/OKIoRlCgCor6U\nfjN37VoZ2Xnz67fdM6pdjczJxx9R+F6wl+O8GPHJs59UXq+J2Nnb5+EcWPfXOaqCBKJ+sVPIHBBC\nDLqiSyFT7ZE9Ec0hBrQ5UXY0VTYFLYQY+ppX0dIyNH2DrhJONE0MaDNqXCeasoFPCgE55OTnQVfF\nnoZJntirEESy69ARzQoGtBnFSrLR6/aeTvL9rsLPlnGMZhED2owKpKzEJ/leuqWtOt0eGzO11yVQ\nfKyTnEBehcnq42g9RjRurHKcUVWcX9VJv8u8GAME4XReWxBMdzWATs9Vx7ZiROPCERpVShjw5J01\nA4NwospgQKOpy6YZu41Gsgt0TjslNymuv+P00rB1Y63l+1ljDGg0MUUnkbIrSPv7ZJeyqTshBKRk\n143R4vXBumJAo4kp+lDc7/WpSV7Ponqpe5eWecczA03MqNJn/X66jmOmmKiFo7P6YkCjiSlKn437\nBGMGqBRkACSaPQxoNBHW2qn1fxwkRVmFyc1E1B8GNJoYO6XqxEFGgFWcuD7NSedEs4ABjSZCCDFT\na2RVceXouGQ1KDkM/vOHAY1oRjRY3dkXpo3nD/9CaC5ENah05OisP1VMG9N4MaDRXLC2FRB4kpsP\nVUwb03gxoNFcyPaIjA0DGlEdMaDRXMh+UhfgKI2ojhjQaO7MUrUlET98lceARnPHWsu0I82MtYjV\nmmUxoFHljPsTqRudzc8SNDTbOF2jPK5YTZUziXRgIHmSoNkwK6vTVwH/qmkmuIUZOaIiomIMaDQT\nsnPI6pIqrMvrIKoKphxpZtQt9cJKS6LR4giNiIhqgQGNZgKXTpkt/FnRNDCgEdHUTPKaaJ2uv1Jn\nDGg0EwLJ7h6zpOzPapJrvBnL9eTqjgGNiKZGTjDASCE4Qqu5gaoclVIbAHwBwGMArAA4VWu9K7P9\nJQDOTr4VALYDeCqAJQBfAfCDZNtntNZXDXboVAX+BFGnT751fE1VNcnKVf4862/Qsv03Afiu1vr9\nSqk/BPBuAH/mN2qtrwdwPQAopd4OYKfW+r+UUqcD+JjW+vwhj5sqoo4nichYthsimkGDBrTtAM5L\nvr4OwHs63Ukp9XgApwA4LrnpGHezehncKO0tWuuVAY+BaCyCGgZponnQM6Appd4A4KzczfcCeCj5\negXA1oKHvxXABVrr1eT7WwB8Tmt9q1LqXQDeB+BtfR810RjVbQL3KNgeBRVM01bHtm0bEYbBSPa1\nvHlpJPuZlJ4BTWt9KYBLs7cppa4GsJx8uwzgwfzjlFISwEsBvCtz8zVaa3/fawBcNMAxE41crxP2\nvOv13sTGImSathL27Nk/sn2t7D04sn1NwqC/gTsBnJh8fQKAb3a4z1MB3K61PpC57atKqd9Mvn4B\ngFsHfH6ikYpirjk1jICj2kLGcP7bpAx6De0zAD6vlLoRwBqAHQCglDoPwN9rrW8BoADclXvcmwBc\npJRqAvgFgDMGfH6qkSqMjsSUj6MK78EwZvnYR6Xbz9C6O/B9GjNR8U8OlT44IqIJKR0Jd+1aGdl5\n8+u33TOqXY3MyccfUfheMOlNRES1wIBGRES1wIBGRES1wIBGRES1wIBGVFMVL/giGjkGNKKaYok4\nzRsGNCIiqgUGNJobTME5dX0fuCI1MaDR3JhUCq7qJ9W6piKFELV9bVQOAxrRiFU8nhHVFgMa0aiJ\n6jSkrcIxEE3KoM2JiaiAFKKPznvjxRQczROO0IiIqBYY0IiIKoxp4/IY0IiIKoxp4/IY0IiIqBYY\n0IiIqBYY0IgqgNdJiIbHgEZUAVFspn0IRDOPAY2oAqQQHKURDYkTq4kqIAj42ZJoWPwrIiKiWmBA\nI5ogphVHz1oLY8xMvrdxPJvHXVUMaEQTxEmy4zKbS8cYa2fyuKuK19CIaKa5gDCbo5yQ105Hiu8m\nEc28/ChnEqm8Ueyfo7PRYkCjucDrFPPFYvzBgsGoehjQaC5EhgFtHKy1MBX8sBBIBpt5xIBGc0GA\no7RxsbYaq3NncfQ0n1gUQnNh2IvvltVoHQkhEPB9oYrgCI2oBGYsiaqPAY2oBCncnKGqpdaIqIUp\nR6IShBBgYo2o2oYKaEqpVwA4WWu9o8O2PwJwJoAIwAe11l9RSh0C4EoAGwD8DMBpWuv9wxwDERER\nMETKUSl1IYC/6LQPpdShAP4UwLMAvBjAXyilFgG8F8CVWutnA/g2XMAjosSoUppMjdI8GuYa2k0A\n3lSw7TcB7NRar2qtHwJwJ4CnAdgO4PrkPtcBeOEQz09UO6OqpGRFJs2jnilHpdQbAJyVu/k0rfVV\nSqnnFTxsC4CHMt+vANiau93f1g3/KomI+vDoRy+P7Lx58vFHjGpXE9EzoGmtLwVwaZ/7fRjAcub7\nZQAPZm4/kLmNiIhoaOMq278FwLOVUktKqa0AjgTwPQA7AZyY3OcEAN8c0/MTEdGcGWlAU0q9VSn1\ne1rrXwD4BFzA+mcA79JaHwTwQQB/qJTaCeCZAD45yucnIqL5JVgNRUREdcBOIUREVAsMaEREVAsM\naEREVAvs5diDUkoC+DSAowGsAjhda31nZvu6Fl9TOdApKPHeXAg3mX4luellyUT7uaCU+i0AH9Va\nPy93+0lwXXMiAJdprS+ZwuFNVZf35iwApwPYldx0ptZaT/jwpkYp1QBwGYBfAbAId075cmb73P/u\ndMOA1tvLASxprZ+plHoGgPMBvAxoa/F1LIAlADcqpf4/rfXq1I52sgrfm8QxAF6std49laObIqXU\n/wRwCoB9udsbAC4AcFyybadS6sta63snf5TTUfTeJI4B8Dqt9a2TParKeC2A+7XWpyilHgngNgBf\nBvi7UwZTjr2l7bq01jfDBS+vqMXXvCh8b5LR21MAXKyU2qmU+u/TOcSp+SGAV3a4/UgAd2qt92it\n1wDcCOA5Ez2y6St6bwAX0N6plLpRKfXOCR5TVfwdgPckXwu4kZjH350eGNB6y7fxipVSYcG2Mu28\n6qTbe7MJwEVwnzhfAuCPlVJzE+y11v8AoNlh07z/znR7bwDgbwG8EcDzAWxXSr10YgdWAVrrvVrr\nFaXUMoC/B/DuzOa5/93phQGtt3wbL6m1jgq2zVs7r27vzX4AF2qt92utV+Am2B896QOsoHn/nSmk\nlBIAPq613p2MQP4vgP825cOaOKXUEwD8C4ArtNZXZjbxd6cHXkPrbSeAkwB8KblO9N3MtlsAfEgp\ntQR3Ade3+JoX3d6bXwNwlVLqv8F9cNoO4POTP8TK+S8AT0muj+yFSxn95XQPqTK2APieUupIuGtE\nz4crkJgbSqlfAnADgDdrrb+W28zfnR4Y0Hq7BsDxSqmb4HLapyml3gqXy/6yUsq3+JJotfiaF73e\nmysA3AyXXvprrfX3p3isU6WU2gFgs9b64uQ9+irc78xlWut7pnt005V7b86BG52sAvia1vra6R7d\nxJ0DYBuA9yil/LW0SwBs4u9Ob2x9RUREtcBraEREVAsMaEREVAsMaEREVAsMaEREVAsMaEREVAsM\naEREVAsMaEREVAv/P2MDqmGfGqOMAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x119ade0b8>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"RGZ & compact\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAbQAAAGoCAYAAAAuIBCmAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvXu0LFdd7/udc1b3WnvtvfbOTiAJ+DiHgFa4YQiXoAYM\nV+SQ8JBzfPAII5LBIxHwccSgaAREjCAQbwhcHSAPg8jLgCcZ5/gAHIBkSBAjMbmSDClM4HAlkmSH\n7Mdae+3V3VVz3j9mzerZtaq6q7ur39/PIOzVXdVVs6u7569+8/f7fX/CGANCCCFk0ZGzHgAhhBBS\nBzRohBBClgIaNEIIIUsBDRohhJClgAaNEELIUhDMegD9OHJka+5TMA8f3sDRozuzHsZcwmtTDK9L\nObw2xTz84Zti1mNYBOihjUkQqFkPYW7htSmG16UcXhsyDjRohBBCloK5XnKcB75wx72Fzz/tCd8z\n5ZEQQgjpBz00QgghSwE9NJR7YYQQQhYHemiEEEKWAho0QgghSwENGiGEkKWABo0QQshSQINGCCFk\nKaBBI4QQshTQoBFCCFkKaNAIIYQsBTRohBBClgIaNEIIIUsBDRohhJClgAaNEELIUkCDRgghZCmg\nQSOEELIU0KARQghZCmjQCCGELAU0aIQQQpYCGjRCCCFLAQ0aIYSQpYAGjRBCyFJAg0YIIWQpoEEj\nhBCyFNCgEUIIWQpo0AghhCwFNGiEEEKWAho0QgghSwENGiGEkKWABo0QQshSQINGCCFkKaBBI4QQ\nshTQoBFCCFkKaNAIIYQsBcGsB7CofOGOewEAmwfWsbW927PtaU/4nlkMiRBCVhp6aIQQQpYCGjRC\nCCFLAQ0aIYSQpYAGjRBCyFJAg0YIIWQpoEEjhBCyFNCgEUIIWQpo0AghhCwFNGiEEEKWAho0Qggh\nS8FKSV85uSpCCCHLx0oZtGlRZjip8UgIIZODS46EEEKWAho0QgghSwENGiGEkKWAMbQp0i8phfE1\nQggZDxq0OYGJJIQQMh5LZ9CWLTV/1u+HBpWQ6VH2e3/BRedOeSSLiTDGzHoMhBBCyNgwKYQQQshS\nQINGCCFkKaBBI4QQshTQoBFCCFkKaNAIIYQsBTRohBBClgIaNEIIIUvBWIXVYRj+KIC3R1H0tNzz\n/xXAGwHEAK6Pouj9YRjuA/ARAGcC2ALwkiiKjoxzfkIIIcQxsocWhuFvAPgAgPXc8w0A1wG4GMCP\nA3hFGIZnAfgFAF+NouipAP4MwBtGPTchhBCSZ5wlx3sA/GzB848FcHcURUejKGoD+CKA/wvAhQA+\nne7zKQDPGOPchBBCSA8jLzlGUfQ/wjD8zwWbDgI47j3eAnAo97x7bhALr8uVJBpK9b9viBONYMA+\ns8JJowkhZjwSQlaayj/AOE5MEKhaTvrpf/jftRynTp715P9cei0mIU58AsCm93gTwLHc8+65pWOP\ncarwNZTCGg5tACVHNxzGGBoeQlaco0d3ajvW1vZubceaBpMwaP8K4AfCMDwdwDbscuP/DeA/AXgO\ngFsBPBvA30/g3HOBb1iUHOx5SSlTT8jAmPnyhuZpLNNCawMhVvO9E7LI1GbQwjC8FMCBKIreF4bh\nawB8BjZGd30URfeGYfgeAB8Kw/CLANoALq3r3PPEqEuHQgioMSdQTsD1oLVBEMznEjAhpJx5bx8z\n14PrB5f/LIt4HRZxzGTpqfyFPHJkq7Z5c9b9GIt4wUXnll4L3oZOiCTRsx7CXBAv4HWgMSNkMaFB\nqwmtDXq8XSEw597vxDHGQGXxQUIImSyTSAohGD2WtkwIIUBnhxAyLWjQakKOkW5PCCFkfOhGEEII\nWQpo0BYcYwxjVGSu+aM/+iM8//nPx4te9CL8y7/8y57tn//85/G85z0Pl1xyCT7xiU8AALa2tvCq\nV70KL37xi3HJJZfg9ttvBwB86Utfws/+7M/ihS98Ia677rqpvYc//uM/xpVXXll5f6013vjGN+KS\nSy7BZZddhm9961sAZjf+VYEGbUgSrSsZEGMMdMV9868bxkhZhREaNTKf3HXXXbj11lvxyU9+Eu94\nxzvwu7/7uz3bO50O3vrWt+L666/Hhz/8Ydxwww148MEH8cEPfhAXXHABPvKRj+Ctb30rrr76agDA\nNddcg2uuuQY33HADbr31VkRRNPH3cPPNN+MLX/jCUK/57Gc/i3a7jRtuuAG/9mu/hre97W0AZjP+\nVYIxtGExgKgYLzMA5IhZEVVTx2UFJRKyWNx444347Gc/i5MnT+Lo0aP4pV/6JTzzmc/Erbfeiuuu\nuw5KKXzf930frr76arRaLbz+9a/H1tYWHnjgAVx66aW49NJLcdlll+H000/H8ePH8cY3vhGve93r\nEAQBtNa49tpr8YhHPAJve9vbcNtttwEAnvvc5+IlL3kJrrrqKjSbTdx777144IEH8La3vQ3nnXce\nfuInfgLnnHMOHv3oR+N1r3tdNtZXvvKV2NnpSi09+tGPxpve9Kbs8W233YYLL7wQQgg88pGPRJIk\neOihh3D66acDAO655x58//d/Pw4dstKu559/Pv7pn/4JL33pS9FsNgEASZJgbW0NAPDYxz4Wx44d\nQ6fTQavVglJWs/Cyyy7Dhz/84Z7reNlll+FRj3oUvvnNb8IYg+uuuw4Pf/jDs+0f+chH8JnPfKbn\nNW9/+9vxyEc+Mnv8rW99CzfccAN+5Vd+BZ/85Cez56+99lp85StfgdYaL33pS/HsZz+75zi33XYb\nnvrUpwIAnvCEJ+DOO+/sO35SDzRoQ1I1+UMIMZL7K5juTwCcOnUKH/zgB/HQQw/hBS94AZ7+9Kfj\nt3/7t/Gxj30MZ5xxBt75znfipptuwnnnnYef/MmfxMUXX4z7778fl112GS691IrwPPe5z8VFF12E\nj370o/ihH/ohvPa1r8VXvvIVbG1t4Wtf+xq+/e1v4xOf+ATiOMall16KCy64AADwyEc+EldffTU+\n8YlP4IYbbsDVV1+N73znO7jxxhtx+PDhnnG+973v7fs+tre3cdppp2WP9+/fj62trcygbW9vY3Nz\ns2f79vY2Dh48CAA4cuQIXvva12ZGNAxDvOpVr8Jpp52GMAxxzjnnAMAeY+Z44hOfiKuvvhof/ehH\n8d73vhdveEO3a9WLX/xivPjFLy4d+8mTJ3H11Vfj7W9/O+65557s+Ztvvhnf/va38fGPfxytVgsv\nfOEL8WM/9mPZmN37OnDgQPZYKYU4jkvHT+qBBm1Ihim6HbVAd5zC3irq/mT++eEf/mFIKfGwhz0M\nBw8exAMPPIAHHngAv/qrvwoA2N3dxVOe8hT8+I//OD70oQ/hb//2b3HgwAHEcZwd41GPehQA4PnP\nfz7e//7344orrsDm5iauvPJK3HPPPXjSk54EIQQajQYe//jHZ5P2Yx/7WADA2WefjX/+538GABw+\nfHiPMQMGe2gHDhzAyZMns8cnT57sMWD9tkdRhNe85jX4jd/4DfzIj/wITpw4gfe+973467/+a5x1\n1lm45pprcP311+OKK64ovY7OSD/xiU/E5z//+Z5tgzy0W265BUeOHMGVV16JEydO4IEHHsD73vc+\nCCFw11134bLLLgMAxHGMr3/963jXu94FAHjKU56y531prbGzszP0+Mlw0KAtG4LSTcvAXXfdBQB4\n8MEHsb29jbPPPhtnn3023v3ud2NzcxOf+9znsLGxgeuvvx5PeMITcOmll+LLX/4ybr755uwY7jvw\nuc99Dueffz5++Zd/GX/1V3+FD3zgA7j44otx44034qUvfSk6nQ5uv/12/MzP/EzP63zKlrYHeWhP\nfOIT8Qd/8Ae4/PLLcd9990FrnXlngDWA3/rWt3Ds2DFsbGzgK1/5Ci6//HLcfffdePWrX413vvOd\nOPfccwEA6+vr2NjYwMbGBgDgzDPPxEMPPdT3/HfeeWdmmB/zmMf0bBvkoV188cW4+OKLAQD/+I//\niD//8z/HK17xCnzuc5/Dj/7oj+L3fu/3oLXGu9/9bpx77rk9XuJnPvMZ/N3f/R2e85zn4I477sAP\n/uAPjjR+Mhw0aDPAX1IsmjwGGaR+r6+i7k/mnwcffBAveclLsLW1hd/5nd+BUgqvf/3r8YpXvALG\nGOzfvx/XXHMNhBB485vfjL/5m7/B5uYmlFJot9s9x3rc4x6H3/zN38R73vMeaK3xW7/1WzjvvPNw\n66234pJLLkGn08GznvUsnHfeebW/j8c97nF40pOehEsuuSTL/AOAv/zLv8TOzg4uueQSXHXVVbj8\n8sthjMHznvc8nHXWWXjTm96EdruNt7zlLQCsJ/ee97wHV111FV7+8pdjbW0Nm5ubWbJFUQwNAG66\n6Sb86Z/+Kfbt24drrrmmlvf09Kc/HbfeeisuvfRS7Ozs4BnPeEbP8iIAXHTRRbjlllvwohe9CMYY\n/P7v/z6azWbp+Ek9UJx4BtgsxtGLscd9PZlvbrzxRnzjG9/Ar//6r896KAvDW97yFrz+9a/vee6y\nyy7Dm970Jjz60Y+e0ahqheLEKf3EiemhzQDrVY3+nRv39YQsGy9/+ctnPQQyB9BDI4SQ+YceWgrb\nxyw5c35TQgghU4EGbQlgRiMhhNCgEUIIWRJo0AghhCwFNGiEEEKWAqbt14zWOv3LdmsetUA6vx/j\nZNXgtSJkdaGHVjOJTifUAcYMAJw9G7QfJ+jqzPpaMeOUkNlBg1YzTr2jyrQqpZj5BEzqh0aNkNlA\ng1Yzrv8ZDRUhhEwXGrQxyd+N05CtNkLQ6yZkVtCgTRgrJMwlqKpoXi9CyIjQoI1J0d24/xzv2IdD\na2YpEkJGgwaNzBWKLXEIISNCgzYhjDFeTdpwr1vlJTd6Z4SQUaFBqxljTBYHMihP4XYGr2h7XUZt\nlQ0jIWT1oFLIBBAAhBx8r2DQTfPPXltjzI3eDiFklaCHVjN5I1LmJQkh9hgzQggho0ODNgF8oxYn\nvXG0xHvs72eXILlESAghozLykmMYhhLAuwE8HkALwBVRFN2dbnsCgHd6u18A4KcB3Arg6wDuTJ+/\nKYqid406hkVAqdw9g3AxMvSIFwshstjZMEuFFOMlhBDLODG0nwawHkXRk8MwvADAtQB+CgCiKLoD\nwNMAIAzDFwC4N4qiT4dh+AwAH4+i6L+PN+zFIb+sqNLYWtFSpGTKOiEkh9YaskJMnoy35HghgE8D\nQBRFXwbwpPwOYRjuB/C7AF6dPnU+gPPDMLw5DMNPhmH4iDHOP1OcQRo1k7AuYWJ6Z4QsNzFDEZUZ\nx0M7COC49zgJwzCIoij2nrscwCejKHowffw1ALdFUfTZMAx/DsAfAnj+GGOYGXFi0AgEDABMYdnP\nlgP0Lzzm8iMhy0cw5MrN4cMbCAJVy7k3D6zXcpxpMY5BOwFg03ssc8YMAH4OvQbr8wB20r9vAnD1\nGOefKUpVaxPjPLhxDY0QAhL979SSRNf2RSaEzAexNmgOsZZ29OjO4J0qsrW9W9uxpsE4S463AHgO\nAKQxtK/6G8MwPARgLYqif/ee/gCA56V//xcAt41x/qmRX1Y0xvS0iSkzVv6yZB3F0lUagbKYmpDl\nQnHVpTLjeGg3AbgoDMMvwToqLwvD8DUA7o6i6H8B+EEA/zv3mqsAXB+G4S8COAngijHOPzWqele+\nMREFBm/SxmZPRiUhZOHh77o6Ys7v6Od6cEDvkqLWhpmKhJBJUHliOXJkq7Z58wt33FvXoWrjBRed\nW3otaPrHxABItDNqsx0LIYSsMjRoYyIAOKeMGYaEEDI7aNBqQPYplq5CUdLJoH1GZc6XmAkhZGRo\n0MYk350aGN5o5D27QV2w+zHo3PQiCSHLCg3ahNA1pOmPQl4MmZB5hqLcpE5o0CaAEAICszEuAVN8\nyQJhy1pmPQqyLHD2G5M4Ke467fqd1emlVTkWlxTJosHvLKkLGrQJ4FRBigSImZRBCCGTgQZtTFSJ\nar7tdzZ6ckcRlLYihJByaNDGxGCv1zXJuACTPgghpBgatDEps1tVPbFEVzNQTo1kUNJHHSLIhBCy\niNCgDUFZ8oe/FGj7lg1hVCruK0T1fmdVjFqie5NZqhR3rzK8HoTMPzRofShaSiyjp8B6wL4+SqlK\n+8o+bWry45BSDtxXa1NYFF72eFymZRAmdR5m4hEy/9Cg9WGUubGuiW/SBmDa9WrTiv0lLNIlZGWh\nQevDqLYp0ePHsfSEDdq0PY5pGVDF9j2ErCw0aH0YddKXonqyRylmueI20zKgXBokZHWhQfOoYkCq\n7GPV98WepIthDJSgp0HmgGW6qSLLTzDrAcwTVZMuqpBfYhvWc5D0NMgcQI+XLBL00Dx4N0oIIYsL\nDZrHqPbM1Z4RQgiZHTRoHkLY+qwyT02nxchue+Ir7Q+IkdH7I6Q+hhYwICsBY2gegzQYDXqlrrQx\nkBCZWsgk8H+wjGcQQkg5NGhDoGSvQ9sIVM/jftJU/vODJKz87c6I0pgR0sU10SXEh0uONRIPKTRc\nZTuzHQkhpBo0aDWS9+DKGGSk8tuX2TtjQg0hpC5o0HK4pI+iYHPZc1mH6oIGnEXHkgOKpvttn6cg\neF6xf2QY3CeE1AANWgmjdpsuUq3PPzfO5D2Ot1a30cgr9o9C1e4AhBAyCBq0HGUTa5kxcPvHyXDG\nYhbLbHWfctqK/YQQ0g/OSAUUGbV+BksIgUBV9zBmlaFVtxNEr4oQMk/QoFVEil4vbVix4Tx1LkP6\nxEl5XIsGiBCyzNCgVUSNKTZchWGMmlM0oVoCIYRYaNCGoCjhAxhcKF312MMcI9EaQog9iRmBYoIF\nIWQ1oUGrgUGF0pPAJWSwQzMhhFhGlr4Kw1ACeDeAxwNoAbgiiqK7ve3vAnAhgK30qZ8C0ADwMQD7\nAPwHgJdFUbQz6hjmhapGxXpT9SxXumPQGyOEEMs4HtpPA1iPoujJAK4CcG1u+/kAnhlF0dPS/44D\neCOAj0VR9FQAtwN45RjnnxtEQUG1wz1vlyV7nxsVxswIIWQv4xi0CwF8GgCiKPoygCe5Dan39gMA\n3heG4S1hGL48/xoAnwLwjDHOXyvDqIMMcwzfk/L/G+X444yNELKY8HdenXHU9g8COO49TsIwDKIo\nigHsB/CHAN4BQAH4uzAMv5J7zRaAQ2Ocv1a0MYVajAYAKiR9uNdrY7L9qySL+McfJrlEazNQQmvW\n1JEsQ8iq00k0mrnOHv04fHgDwRD792PzwHotx5kW4xi0EwA2vccyNWYAsAPgXS4+Fobh52Fjbe41\np9J/j41x/lopEwwu0mfs93p/f2MGFzP7+8dao6EGfxGtkZj/uzb7tmjUCBmHxpCKPEeP1peWsLW9\nW9uxpsE4S463AHgOAIRheAGAr3rbfhDALWEYqjAMG7BLjf/svwbAswH8/Rjnr5V+k+6wGo7amCwB\npLz79d7GnUrYjyPx2tCULYUugpFYgCESMvcswm99XhjHQ7sJwEVhGH4Jtgfly8IwfA2Au6Mo+l9h\nGH4YwJcBdAD8WRRFd4Vh+GYAHwrD8OcBPAjg0jHHP1WKukcbb7kw2wYBA4O+Alci7XjtfVmlTJcd\n0Xu8Kp7OJJb33BjGOS5/jNXg8iwh4yPmPOA4s8EVTTB1pt2Pcv5ZMm/jIWTFqPzjO3Jkq7Z58wt3\n3FvXoWrjBRedW3otWFhdQpEavpTDqXmMQz8x5FnchJTVjs/5DREhZIWgQSshnyRi0rjYpMgfX/VR\n7y9SJjHG9MTe6qYsoTJOJndOQggZBhq0Eoo8Mb9Dcz9Ve5+ifRJdXK9mYFLDZPasL8RJkr3GxdqK\nxjspj6nMM1VS0ksjZILESTLrISwM4ySFrBTF7V7KW8CMsjSZ1cEVGQjvqbISg6I6ukkz77Vws4Ix\nR1IXvF+sDg3aEDS8YsVGQeGiMXsn+KJJbZD2Y9H2YQolOZnOHl5/UhdFcw0phkuONVJ1Dpv0Et0s\n1P8JIWTW0KANYJhEi6p35ZM2ONNuKTPphBlCCKkCDVoJmReVKnW4x35iiPG2DZsgMkkvrcywDnvO\n4fZfzs7Zy/ieCFlWGEMrIZOjymsrGkCkHpBLC6nimflxrWBIbbaqxx3EsHGdYY67rDGjZX1fhCwj\n9NCGxE+Zl0NM5EWF2v2o6hlwqY8QQiw0aEMihBgpBlaWau/Ix6GSPkohPcdl2jwhhACgQetB52Jh\ncZzs8ZSM6fYhq9oQNEn0QE8uXxjdT6m/6HWToOj9E0LIvEKDVoCbxLXpfezIe1t5Q9izTZtMAUTr\nveoi/mNfK1IpOfX4zZ7klhHPP0kjSANL5hV+N2cPDZqHi4k5Q+KU9fOtYhzub6vCL3qecyRaI1AK\nQoie/fLHcMzyR5FP7ghGNKqTNMRM0iDzCr+bs4cGrQ/5bETf1viGp1/dl38M1Se70deILNtGCCGk\nHBq0Puz1prp/+0kbVbtd99vPLW8WpfRT+YMQQgazMgatavFzvnDaPY4T3bMNA5I2+hVRF71OivKa\nMlHyGv94Vd7fqnl6VT9zQshywMLqHL6IvjH+Y5M+thNk3pPq1816bwZj+T57x2NqS81ftTV+Ifa2\n2SGELC8r46FVVbPwEyESo7PHSko0AlXaSTrRxQkjPnFJ+n5f76vP8fxzLbNaxzjwmhCyOqyMQRuF\nwOsvFid2+Uqp4sLqoE+H6e4+xZe7X4xsUEE2IYQQCw1aH/y7eymshyVTpRDfCNlYTe9rXdwtf7wi\n9X5ntMrq2ablZfSrpyOEkHmHBq0PvR2ou5mI9qIZaC9pxBVP55NB9iRsFBgNpw8pYJcY61TFH+pY\nxox0/lrOTabGND4Xfvb1wWtZHSaF9CEfEwuU/bfRUFlGYqINpJKFRddFnWaden9ZkfYovlhZ4Xf+\nPQxCyvHub8re0yRgV+7RmcZ142dTH7yW1aGHVhEhRE88y8XUnHeVV9PXufT/PMOq71dh1jdy0zx/\nUQE6IWS1oUEbgl5ZKJFlLSba7Ene2G0naLUTAMVJH5NI9pj1jVxVQeU6qLOnHCFkOVj4WWHUCVTr\nvbGsOOmqy+e3u/YuLh7mPLY4TlBUJtYIJKQEOp2k57WOfG1aP6q+x7JSgSTZK4pcF36xeVnpQFJw\nrceFyzCEkDyMofXQLcQ1MEj/l8W1tDFQ3kSqlOxZ+vInbRc/63QSSCFsPVmBQZsGBt0szH4F3PlC\n5GqduDEw8DfuO9VpwgyNGCGkHwvvoY0yybnYV/61gZLZup2SEoCATpcV3WSf90KUdNu8xA5ve6Oh\noJRMBYz3FkBX8dTGmcgDJREotafwe9A5qp6ziiJ/0bUehlETQJgdRshqsfAGbVTcZJevC5M9xgYQ\nsuu1FKnqZx6ak8tC+UTqS1jl93FJImWvHXdyrhpzmkcvaNR4oy9VRuYHfiZkUqysQXMUTZZdrwk9\nhdRFslfOULij5I9WVEhd9LyAzYwsax8TlxynKsMYqnkzaqOOZ87eBkkp+00QMi4rYdDyd4S9TTz7\nzXpdr0nAxnESrTNFDWd8+h6voNg6HUVPWr9btpS5OFb2t/Y6aVdMsvD3SQq6ZQ/Lot1ZU99yXqFo\n9DDwWlVnJQxav0mt35dFyrRgGgJSSjQaNtHDJSj4sR1dctep0m7V7lzu73zsSQgBKQVUwfOumDs7\nDvrHlNxY/H2KumUPC40DqYNRO6GvKrxW1VkJg9aPfjEv2w/NwBfQ0LrrVfnLlZ2kOCbm9nWvLTuX\nLtB+LEMNUPRItMnG6Vilui3e0RKymoyUth+GoQTwbgCPB9ACcEUURXd7268E8KL04d9EUfS7YRgK\nAN8G8G/p8/8QRdFvjTzymuh37xNr7WUxph6O6Xpn2hg4cauG6vWq0LPcZxAogcQYJLFBI9jrhcGY\n2oxO0XFW6S4v1qbn8yCErAaj1qH9NID1KIqeHIbhBQCuBfBTABCG4TkAfg7AjwLQAL4YhuFNAHYA\n/HMURf91/GHXR36ijxNrxBJtoITMMhPjJEGgutqMidZZs7JE6x6vyaQiv+7IzpMLpOyKGKfPJ4ne\ns8xY93uad1y3groamc57yx17M1ScNUsIGZ1RXYILAXwaAKIo+jKAJ3nb/h3As6IoSqIoMgAaAHYB\nnA/ge8Iw/LswDP8mDMNwjHGPjd8qxXlbee1FJ+VkTFpkbQykEoiTJKu4NsbApEt8Tr8xr7DvJmop\nu3qQ2T6eSr8eInGjLMljWokfdS/ruetQB4thKKbbqofLsGQVGNVDOwjguPc4CcMwiKIojqKoA+DB\ndInxDwDcHkXR18MwPBvAW6Mo+mQYhhcC+AiAHx5r9GNgi6vTlHshoLWGlDJr1CmRS+JIlT8kbLws\nCGRmnJSSqRKI3z+tOMNub2F2dwxJohEEvfcYZUXFWhuoYPDS4rBFyYMSaKplhw6HEKJHgWXZmcX7\nXTSvnXQZ9jd8+PBGNl+Ny+aB9VqOMy1GNWgnAGx6j2UURbF7EIbhOoDrAWwB+MX06a8AiAEgiqIv\nhmH4yDAMRerFTZ18YoW/TOW+QLHWaCjVo1VYlrhhtIYQvVJYrt1M4f6e6ki+j5qP1rZL9l76f8Gz\n95DowjY2o2DVUGo51Mxg2xmyaHQSjeYQv+GjR3dqO/fW9m5tx5oGoy453gLgOQCQxtC+6jakntn/\nBPD/RlH0yiiKknTT7wD41XSfxwP491kZsyL8rESnjh+kRi/RdklSa5u40QhkZk7iJLH7CwEhnNSU\nhJL9W5y4bb6xLFI5LosrFRs5//3Yf+vMbpymmv6kKOp8QMg801ihDOVxEaNMUF6W4w/BugovgzVw\ndwNQAD4O4MveS34LwNdglxkPwHpqvxRF0dcGnGpqs49vWBKtM49NCIFOJ7Geiejti6ZTBREhupqO\n2kvnd2n6Lukjn76v0i9qrzCwyLQm3fn9fUZ5P/nnF91D0ek1d+8jSXRlvch+QsfDHIeQKVP5S3nk\nyFZt8+YX7ri3rkPVxgsuOrf0Woy05BhFkQbwqtzTvnEqW3j9yVHOVweDJnJ/297EDWQTqM0P6Rom\nJQGte+Wy3FdPKYlOnPinscdA12A5UeOe5Ud0jdmwiiCDYlzDTtZlhnGSDPqs8gL/Zs8z5fTLgKTv\nRshiszLrhI2WAAAgAElEQVS+7DBqIa5pZ5wuTyllvTIlU9V8YdvBGGE7V7tsRyFEV9sxPZ8fv3IG\nKkiTSJw3mK9JU56X4FTyBxkUZxiL3s84DFLpnwSDzqdyXlTgqbGMAxUsCFlsVsag9SMf60q0htFp\nDzHR2xpmtx1DCmGVONLaKSVFj3BxPk7jP3bnymrTBqyPV05B93Zrd3R23qSi+sjY5yeEkBlDg4Zu\nAgXQ7UwtpbCSV8ZAiq5CuIt/pXkg3SJsb+J3Cv2uts1f5lJKIkl6vbJheqGVZUT6ezUC5yXa9jfd\n9zl87dMqeSz9sk0JIfPPyho0vzDZ1ZzB/ZsaK+n2A2A0EMcJZNofTcDpQKYHTJcdkyRJswF1qgWp\nAdiiaa21Vd8XvZOn289/3KOUn/QWUfvbE0/xf08ht5fAkg6xULuyuBvA4jJOZ4F+2p6EzAJ+H6uz\nMgYt/6Vw6vPGmB4leykllBLZcmOi0xozCSQGWEsV911htZOwcnVtSZbkIaGk9JYrRbcbtpcEYlX2\nJQR6W9D0KOV7S57Z/i5ehupelMvQzO+/R1dywRm1s0DZ9RkWTkCkTpbhNzktVsag5ZtzutiVuyP3\nJyFtrMCt1lZIWBugExsEaaws0QatdmJTwEXXI4q1tl5Qtkxp0AhUaqBSj0nuVQIB+hcsB31qzvyl\nzqJ5dBUn11l3FihqBEsImTwrY9DyRiHzeNLHidZZyxUpBRrKel9xYu/2m0Har0xaI6KkgEA3Xgak\n4sOmmxno90jz77KKkkR0H8PT7w4tTpcjnXEt2r5qzPqOtt8NyCwZJYZKyCIxqvTVwpEvbHYFtO55\nmabQa20NmjaAMFa8wwBINKCNVdgX6W2AmxsEXFNNAZkKfrhjds+pPe3IvXErt68/Tic1VVYcrdMC\nbFeQDdHtFuBeo5TcU9flxurGMmsDsChULUqf1+vpYqhYguJ6QopYGg8tr5ifx2946Qqj80uNxtjl\nRr+gWimZTgQ2jV+718Fk7p1bctSp+oc7pC9b5a9CqbQTNtBbO+YnJFTJuHOKFzauVhz78WNCe99v\n8fFHuYvPdxgY9ThkMKNmY9YVIyRkXlkagwYga75ZhF+g7ApxMw/LeWroLtsZoNupWtj/s9mOLuVe\n9HhVQHcCjwuSEnzjY4/vxiJTbysnWAxR2ietJ0FE5IuMy4uDu4bW9nkbdPxh8BVPxjnOLKhqHCbx\nfkYxTLrP95yQVWZpDJpLvCijKK4hpejxipz4cKwBnRgk2ipdtzuJTcdHauj8IubYxrDasbZLiQAC\n6e6irdeW6L3dqPP1ylL0yjJNop55kjqFizy/xnp2nuQoYsmsdSekmKUxaED/u9ZSbcP0XxePEkJ0\nO01LwGgnVSXQSRMsdnbjLIvRJX5Yg5kmikhbPO1EjmVBnCr/WKfKJPmlyESXJ3W4Iu8y/NdOWmV+\nkT2GUXqT6Zqu5yhKLPNyrft9NwmZBQtp0IZdpskXJvvHcEkYSdJNzJBpKr5OUmNm7DGUcHVgwlOy\ntY05k8RkKftOkNjFOopEhq0iie5RHokTnT1n29LYJJSy9+uSS0rjVt5rZcG+s8Be69ELnydBWYue\nfhRd+1GYF+M0Eqb4t0XqZVz5ulViIQ3a8Irxva/JGxmRFkgLYT01bazHZfucpZqIWmfF1ErZmFe2\nTCjs0qRIZbDixCAIVBYny58/f06gmzkp0uNZb81KV/VTzveLrPPXxo+R+YXcs0QIAY3Fz7Kbl+s5\nS1wC1Cpfg2nQr6SH9LKQBm1oCn5v2kvmEEJgraGQ6K6wbydNf+/EOm3qGaT9zzQ6HY1WJ4EUQCu2\ny4oba4G9kzI2McPKLyGNr/W2kHGGVKXGKNEGDaXQTBVLZGoEtakuLrxId8kNVU8HbTJ7gmA1ppBZ\nUlfH+VVgqb+NXcOx1ztqt4uNjJQCcaJxqpWg1dHQiV1ClMKg3dHQiT3exprCqXaC9YZEO9bYbSc2\nYUTZ1JE4sUuXcWLQDGTPOZKC2JdJk0dcIXQjkAikKFS9cALKPgnVKQghK85SGzRfuDdPo+DO0hZI\nGy8d3mYxJtqme+y2Y7TiBJ0krVFzef2pJ5bEGp1Ogt22TuNwtpdaJ7E1cnGaESmFSONlLr7llq/g\ndbHur0mYf3qUOBAhhCwTS6EUYif+AkUN5BU5usF8J03lFDech+OeE0gNj7AqHImxS4g28UMj0RJa\na5jUCEl0i6tFei4pU8OIbjakMd0ibQPrlWX1bOn5EzvIbPz5OrdeGS2dnS8fz9Ba9yyr1k1V5QxC\nyOjwd1adpfDQdMkH7mJUhUkTXqJiktjYWCOQkCJNyXYqIBDQiZWKajYVmg0JpSTi1HOzySECjUCh\nEUgopbC+pqy3lXpwzhtsNFRXVitNKMkXJGvj+rOJPWvnvlRXrzyWQOGCYwVj1tM2Z0j4IyNk8vB3\nVp2lMGhltTz+MpxfeO3sVaejEScandguEbY6CeLEZMah1bHbdjsJGkoiSY3Yzm5sZa5k1yC1OwlO\nnoqz4zvvyokHu2QTAAhScWNjkP7bNU6BsrEzZ1BdTM3F2ABkzUPdexdprVveJlWROeqKI/fdjRBC\n5p6lMGhV72DcflIKxLHODOF6U0JroJOqfbQ7GgICJl3KlAI41Y5t0kasEUhnLO3SYZxoKGX7qAGu\nFk3b/bVJ28jILGbmp+xbY+hifZ42Y7bM2B27s89Kdrf3SmkN72m5pJNlDsEVJdEQQpaPpTBoPkVF\nxq7YWWuDOE4Qp2n0tu7MCg53YlscHQQKgRJodRJoaCRxmn6vbQp9nCT2NdogtkrF2XkaSmbBLJUa\nPNfW2qnin2p1sjhbop2ayF5R4t2W9QKDVC3fX0cvqn9yBqknvjZE0eu4yxpxksx16YBOO4j3G+Mg\ngWtCZgG/j9VZOoPm05sgYSe1JEuesEXLxliLpjNPqOsVBSpAkhqjJNHONgEQ9niJRhCIbCJ0osUu\nPmZlsASElKk4sW0U6i8xWldt79i7xZR7DbSbdPNf9KKkmGGuURXKFfqHOsxUcQXohMwSGqbJs3S/\n8jL1+LWmghTW21lrBmh1dLdfmbVDmdxVq5NACNvMU2tgvRlgt2MNViOQCJTNkFRKIpAKgEDcSbDb\njlOBYrs82I4NnCay64K91lRp0bQtmFRKZskfvvrE/n3NrHmo/7y/fJZPdsn/YPop79fNNM81ClIM\nVvYo6l5ASF2M+r3i97E6S2fQ8oKpvY8N1hoKxpg0bma9r912YmNhcYITJ9vQxuDYVguJNthtxzi6\nvYtTrQ4O7m/gPx48ia2dTpqgYbDTjtHuaBgIrDWDNDZmhYwDa+sg0vR8AavE75YYE91VAolLCqN7\npBnTJBMlRaEczjS6U5eJHK9iZ2xCyHyxdAatTNXeGIPYq8uSUqIdJ4hjnVmNRBu0O0naLkbj+HYL\nWhts73TQUBLbp2KsNRQ21qxHFSgJnaQq/UAqLOwp3Ce20zVgjViS+D3ZJNIVymzJchBxojNPyG81\n47w2VaAqUjey5G5RcUmPEDJjFr6w2iVLdFu19E70ztDYmFPvspzdZmNNu61OmjgCtOMEwgBHt1to\nKoWd3TaaDYVj2y0EEtjeidFoyDTpQqMT2yQQaWy2pDQJbANQAwEBrU1We+bS+V2MDbDJGwJeUTa6\nYTWbuGKy9+L290sSXLdrWRSM865R/nFRweagIs4yRZJpK5XUXWzK4lVCFp+Fv63OCpL13km71+kR\nNgsRqSeVZhAKAUDbGrStnQ6kFGi1E8Ta4OjxXbTaHbQ6Gru7HRzfaiHWwENbu6kCPwAh0Yk1Wh2b\nDWlbydgzKimtxFVqaNaaQebJ+HExG0+TmacovO2BShNKIBAE3U7b/nuVUmZF5P2uUf5xWbxxEPMQ\n3K7b+NCYEbL4LLxBc+RFfP2GndrAel8mbdDZinFqN0acek5aAA8/bR371gLs7MYwEPiPB0/i4P4m\ndlsJlBTYPhWj2ZC477snccahddgaNI12J4bWBpv7AsRx11tsKGmzDI2BSd0zFy9TUnYzHWGNWZwY\ndJK9XoJfO+dQBd23h2UcozTpZqGjMg+GtgqLMk5CFo2lMWhu4ndJIDL32HaXtvVmMALNdMmw1Y5x\ncqeDB4/totXWNilEa+yc6uDEyTYAYHung/U1295FCoHdToJj220c3+5YVX0p0IpttuTmRhMw1uMD\ngH1rQWaM/GnMJYH4pknJYmPhlgfjWPc8HqdYuGoSR1H7mn5dlmfZRHSUxJRZjJf9rQiZDHMfQxs1\ntiGEQJwkEGldWCOQaHViNBsBgkCkGYa24Hq3naARSHQSjRMnW2gnGu1EY78Q+OZ3TiAxBid2Oji4\nv4kzT1tH3NGQsGr6idZADMDEOHigiVYnRiOQSIzJYmY6Xf40aXFvV2XET7/XqRG2sT6n+tHVbgQg\nuokhABBrjaZUSLTOljK7LWp032XITBC5ILbWc/0LXqsNIL0mnW587qXOM532Mt6oiSnTHm/RtSeE\njM/cG7RhcMkWfuGyW57T3uShpES7k6CjTRaTimON7ZNt7LZitDoaR7dbWG8oPHisBaWAVktDwGC9\nqXDogEQjSIurjc1gjLWt2O4kQCMQgLbHNEpmYscSqTBxWi7gGyI7PAED06MckiW0wCa86FRdBJmR\ntIknvar85YXOToFfZfHE4k4FDgGzZ/LN7+nXxQkv2WUUxpnoR0lMGXe8o1BFLHrQfoSQvcz9kmPV\nH3XXS+gmWzhPxnprBgf2Nbv7w8pZrTUUWu0Yp1oxHjh2Cq1Yo9VOcNc3HsK37juBk7ttBEriVCvG\n1k6MO7/xXWtwAJzcbdv2L9IWUu92NE61bEwtkAKnWkmqym+NTreA2iZ5dOKu3JWSEiZtDJpPGJGp\n0oiBydreS2kLvK0KRrcY2D1upAkkeXQuoSRO+reYUWrvcfzzAVY6TNVUWM1JfG8boHmAcb/ZwWtf\nnZE9tDAMJYB3A3g8gBaAK6Ioutvb/vMAXgm7IPfmKIr+KgzDhwH4GIB9AP4DwMuiKNoZ9txFd/Gx\nNlkWY/c5DaO77Vta7QSNQCDW1qvYbSdWTzExOH5yF41A4OvfPIFmILF/vYEv3x5hY/N0PHhsF+d8\nz0EoKRB+/2k4vt1Cs6Fw2uYadlsxDuwLgDQ9HzA4tZug2VQIAomd3Q72rQdYa0jrQSQGnRhoNgyU\nEtkSooFdilKi98urssQWayStF5oargHXJdFmT7xr7+PxU9aDZVY2njJCuMKN+cJfUl4UlmVZt5No\nNHOtpEgx43hoPw1gPYqiJwO4CsC1bkMYhmcD+BUAPwbgmQDeGobhGoA3AvhYFEVPBXA7rMEbmqLE\niaJEBSdfFSdWAFiprlcEACdPtbG908axnRa+89Ap3PfQKdz/3ZPYbcU4vrUDIQM8dPwUAIM7774P\np9ox7vvuDjqxbSuztdPGoQPNnlYvWgOQyJp6OqkrN2arKmLbyTRSbwsAkN6Vq1SM2CUOuB+kSr2x\n2MuEzP9Y8wkcRXZmz2tqEPhYhkljnpjH6+liuovEsqjX5DO4STnjxNAuBPBpAIii6MthGD7J2/Yj\nAG6JoqgFoBWG4d0Afih9ze+n+3wq/fu6YU9cFFTvtlsxmaSVhF0Oc0XNnU4CpWSqBhJjYy3A1qkO\n4tiqgdzz7aO4/8GjeOjocexsn0A70UhigZ1D+9BuJzix3cKBfQ08dKKFRzxsA0LYPmhCCCRxgvX1\nwJYL2DVFBFJ0i6mRFlALAyHsEqJd7nNjtuLJSsrUMAkI1c1odO/Z5T3kYy2uuNpPJAGQFZznJ0lX\nxF1UArAsd7aDqPI+F/la1Dn2RbwGrjxmEcfuU6bOU8bhwxsIavLoNg+s13KcaTGOQTsI4Lj3OAnD\nMIiiKC7YtgXgUO5599zQ9Av++5O7SK2JgI1R7SYJgoZAJ46RJECjIYFTVsPxoeOn8M17j+Pogw8i\ngYRpb0GqBpqBxLETp3B4s4mTp2Joo3FyVyNQ1mC2OjZDsh0nWEeAQNnzB0pBSgmdaMSpHIlOUxWt\ngbHLns2G/eIZ2H0ywwQDhb2emMg95xs2d12csUoPXKjm754vMnaLPgFUZVXe56oybfWaeeHo0aGj\nOKVsbe/WdqxpMI5BOwFg03ssU2NWtG0TwDHv+VPec7XgeyZBYL2wQEkbn5JW1DcIpK3lEhKNhsG/\n37+FY1staAPc8+3jMFrju/d9EwcO7MeJY0fRWNsPA4MDh8/GN775Lazv24DWQLOh0I4NIAwOHmig\nHWsc2GhmnqEQtk2MEEm63AjAJAgCq6yvjbHeo7eC4xJGbCfsvUuB7v2pVOk/v+wohIBytXcuLmfK\n9R2z2rgFW0aaNots9BZ57ISMwjiLs7cAeA4AhGF4AYCvettuBfDUMAzXwzA8BOCxAO70XwPg2QD+\nfozz9+BiTm7ZrRHIniC2FPa/QEkEUmK9aY3bqXaMB9I7mmbDYH3fAfx/X7sVjX2bOHr/v+Hg5mk4\n64xNXPCkxyGOE5xxcA3rDYlTux3AGPzHgyfRCCR2W3GmzyiETRCxgXRroAKVdppGumQKAZX2WfNj\ngs5jcr1Ci9T4OyXK/A6VGavB120ScQZ2iCaEzIJxDNpNAHbDMPwSbBzsyjAMXxOG4X+Loug+AP8P\nrMH6PIDXR1G0C+DNAF4UhuEtAJ4M4I/GG34Xt87sbJhLe48TjXZHQxv3OEGrE+O7x1u2hUti8NCJ\nFvatN9AImljbtw8HzzwHALB5xvdie/s4/v3b9+KBY6dw1hn78S/3fBdC2VYxXVWRGOvNAEbY5A8p\nBJpp489EWwFkKYVdekwNa6bbKAQEDFrtGEmi0YmdV6cRp01F7X7d9zrovrvrtfV6YH67mlGoKnkl\n0iVVUqy0QgiZDCMvOUZRpAG8Kvf017zt7wfw/txr7gfwrFHP6SgqBvaX3vxJ3HpKGp3YtXABhLFN\nPCEEjDAIlECgBOLYYOPAYZzcvwWtEzSa+5HEbZzajSEB7FsPsLXdwm4rQauZQGsNuaagYaBhELcT\n7F8PkCQaSijApE1Dja0vswobOuuUbWDHYrspG8TaZNmRVrGrW6dmDaXOjIWvMuInfnQLss2eejGX\nnuJ3KMgbvf7LVN1av0GMs9y1DIF8h/tMFu39LOKYCVnIfFDd58dWJOfUbCh0YuuluYQN5+d0OgYH\nNhrYWG+g3dnF2sYhSBXAJB001vYjWNvAwdPOwCMetol9zQBnnLYPjUDiyNFTkMIWMK83AiTa4NSu\nldZqx9oaJymw3lRITFpcncbWdnZjQNjkkDixCRxrTXtvIYSAEQLNhitoTpcPtelWJ/VJ5MgKsgtq\nmZSUPYXSWptMHit/zYroJ6VVRyyuVwpsOdh7U7EYLOKYB8F48fKzkNJX/eoyrGfSvTNOEgOlbCJH\nIAUSDRzfamNzI0AcN3DagSaMtnVf53zfmbjr7u8gWNuP9c2H4ayzzoLWwJlnbGJ9rYH9awH272vg\n7NP346ETdgly/77AelgGOP3QOo5tt3Bwo2GTN4ytOwtSVQ+dZjoe2NewAsZxYrMdDYDUW/Lfm5Q2\nHmaNsjUmTncQSBNIhCjUMAykHFgMG3gdAdzybCNQSLT1WofBvXYc7Nsa3jNwKjGrmtVGqjHK95os\nFgtp0PqSfl/dMl2zabP9OrGGalq1/PU1hYaSWF8LcGyrhSPHT+Ex33sI37j3BA7uX8ejv/dxOLq1\ni//zsY/A/d89iYcf3kBDSXzPmfsRKIGtky0cOrBmvSgAzSDte2aAQ/ubCJTEse0WDh9cw1ogsdMy\naCiFU23b8VoKwAhgraGy5p3aiLRuzVf6AAIlMsUPIQSM1lnSR5IYwOieTMZeL6f/Hakta+ju44zp\nKHeydRR/Cu+zG8ZAzau6Bpkv+nWJIMvBQhi0ouJgv2tzXpuwoVTaxNN9iQ2agQBSWal9zQAndtqQ\nAjjtwJptzZIYPPzwPqw3H4ZTLYNj2y1sn+qg0VA4uNFErO2xd1sGQWCNYqcTQ8nALhk2ZBqTCtDu\nJNifemHtWGddqKVMk0MSuxwpBaCE8JT4ZU9huIAVE5beRG9jXwbQ9v0bAO20Fi5JY2/WuHhK/ehN\nlvGNXlEc0nmFe1VFej+H/HHyhnBYTyt/3GHiOLNcIhsk8Ezmg0X9fBjPrM5CxNCKHIZ8Tymb/GFS\nCalU0FfYv5VKdRSNyOrE7D4CBw80cebp+7GxHuCMQ2t45MM3sb4WoNkIsLsbY70R4NCBNaQ2wiqA\nKGULp5U9npR2SVN4DUU30j5oNnZnl0GlkDYdHzYm1k3RFxAyNUipZwn0pt/3JG54/2ZJIM6rEcAe\nb8W461it91fe0LnX5g9b9COrw0/KCy4PIvvsS2DshJDVYCE8tOLlrPzynK09W2sGcD3HpFRod5K0\nmacVA1ZC4FRicNqBNbQ7Gq1NjYMbGru7MQQE2kGCx3xvE8e3W3jEw/bjrNM3cPjgmvWCGgoP21zD\nekNZLwbAGYf2YbedwECgGSgYY1vMdBJbfwbYUgGbkGHH2gxkmiQiEMcajUBCCUAbkRWEG88wtzpJ\nKlPlEjs8r8prYOpiWHGiMyHj3qxIJ5/Vu0RZRSlEGxQWaec9vFncR7rPvoxJ390ydkcmCb2z6iyE\nh1ZEPrjrHie6W6hs42i6K/YrgMQA+9YUYm1wqp3Y1wlgY1+AWNvEhtMPruFH/o+z8LhzzoAUAoGU\nOPPwPmysKaw3JDY3mtjcaODw5hoA6ymtBdbTarVtp2rnNRjYyTZObA3YTivJWrjEWqeCyVbs2C5d\nKgTKepeugLqRlhU4g+SLF3drw7rXo6iwOknsshhyS4M2H2VwrdQ8z9mzDvTTAyRkPlgID62I0rR1\nWM8m0RpGGwTKekPGAJ1Yo6kENASEAdabEg0VYGMtsMuE+wIoISCVxMMPrSMBsLm/gVO7Mb7/7NOw\nvdOBUmkDTwg0GgrtODVKCbDbjtFIvbRmQyGOE6tOEtjYWENJNBS8mJgXh5JdlZBMkBip6oaxXqpO\nk1tcHzQAqfETVgsyfy1E1wOTfqsaL+lCwBr5QXc283aX6OKMwOzHxuy54XF6o7P+7MhysbAGLU9P\nMbUng2W7PLtUflilDpM2pZQSibbyVBvrAdYChU6c2ImyqbCzm2AtkBBCQkmBRiAh06zDQAp0OgkA\ngbWGbc651lBAuq9b4pPSSV31GjJrdO14lOou1SWJUxPx1TZSb0+bHk+pm0CCLHXfeJ6b8uJQMq1v\nA7qJIVr3Lkn6RcB+8bWv9p3VsBnTk2gyafLn6y6j1lfE7R+vLBDvkpEKY4wVx+K8bHfzUtYRYRZM\nKwHBj//Ow/ueZ5gUUp2FXXL0M+H8ycF2dxYQwgoTQ1jDZmvBJPy2mIFKm3Iak6XzKyVtwbSSCAKB\nxBhsbjStQVJpnAxAsynR7ugsucQ1BVUSaDRs4bbtZJ3qNwKQSiIxyLpQu+xDJWX2WMMZPIEg7Tod\npMXQ2pjsOQBZXVpRpmJR8bnrKu2uk7OY/mSa/9eNxU8U8RNEpvZDy50vP6ZR2RMDzL3/omHktwVq\nb3H6IPzj9BMKmDbTGkf2W52T9z3P8BpVZ2ENmvPC4py4L2ANjEq1E+PELgd1Epu+3kkSnGprrAUS\nnVhjvanSFi5W1eOs0zdw2sF1BEri7NM3AGNw6EADnVjj8IE1NJTEGQfXsdYIcNqBNdtGJjWWGt0E\nASVtp+z1tQBKiSyz0RiTdYmWAj3FyALWkNoi567Bdrh9E92NoRUlzAghKnWR9g1ZmZhwUe1OUiir\nNRqD4k9u+6DzTSuOVUctkxCix+sNCgrjCSHDs7C/JDchBErumWSS1HBICATSZejZeq9A2iVC54kp\naeWomg3rYTlxYev1SZxxaB82Nxo4sC/A+nqAzf0NxIld5guUwMZ6A612gjgxaLXitDeaNaQynbhs\ncke6PAhkBsufgu35kKXxu5hMq5MUvHdrHPsp2sshJkm3hFe2LU+dBaqD1P6rdgOYpLh/da3L6hR5\n1YSQ8VjYGFq/pSF3Ny/StHedJocI2LiVFNZTs3JUNgvRdpm2x2o20iU5Y7B/X4A4MWg0AsQdnfZV\nUxBSpiLCBmvNNPEEgEkLm92oOnFiDacSMGnrbOedCWGNTpIeR6QG1n9PRenoLsljGAYV/w4zqdY5\nAZf1a6u63SHF5GINidap/idZVTpxMra0G5k8C+uhlWHSeJj2lOSdrRKiNzHDFVyvNVOtRa1tzEhK\nBIFb309jV8p6AVrb9Hp/2lTKGiKlbHG0koCbhw3sznFiMu8ryzAU3XiUNnZQLvMxiw0CWelBT3dq\nIbLAul9Y7P/d82/2vk1Xbis9bv769Xs86NqXkRScy72PfhRt7yk7mFBiQc94zWSXNJn2P/8UKeGQ\n+WNhDVrZl6sbaO+d5IwGAJtoEQQSQaDQCBTWmgHi2Ha5jtPYUBxrbKwHWG8qtDoJAinRCKzyx759\nDUhlDZNOi6gDKdFsKDRTbypTpRdAI5UG6cQJTCpH5ZIAsgzENKlESOF5l13VEXiJGf57dCTetUhK\nuln3lAToroTWoKLqujy3osSHUSeIsuW6Oo2a9q6Nn4gzCeZhyZGTdX9c4g+ZbxbWoMUVgyY2nmVr\nxfy6JZlmJ+7sxthYD4BU6WO9KdEIJJqBQmJsKr6vzKGkzBJKpLDHdDVurY5ONRVdY8/UG4KLjTmD\nJ/YkteQTBbrnc+fY+35jbZvEKNHtaF1FJNhdhzoEhatSlPhQpfllVbmuuhnm2iyDMZhE5/J5YRk+\nH1KNhTVoZYkJOreUFqQiwP5XWqcJFVpbz8x1cm4E3fRrAwDGYN9aAK0N4ljbejMDtBMbA2s2bJFy\nkBZa72tK653BQApryNrtxGY8KqvI34l1WlrQjWs5iu4A3XiKJhxp1yytsfSM7qAf8KDU9KokFRRG\n8uf0qRIfixNtuwpMmWGuTV5XdBGZ5s3NtFmCj4dUZK6/xf1EZ4u8mThJsjiUSxJwtVdGa7vsZ+wa\nnujmeJoAABw4SURBVEFXPd6mwetM4BcAkCp7xInOjIk1Lt3i5jgxaHfSwmNhDZVOlT3asQY8z8sN\nVwjfM7GVaKYnBqZ73nec6J5iZz9m5oxi/nrkvZokKY5f+VSJnVV9riqltV7e+O3yrdnznuYJlxU7\niHkdPzAfy56TQghkcWOy3My1QetNbK+wfxprsskevW/NGgSvrin9/apsGdLu79Ubo9FQqXdgFT8M\nTKqYLyDSpUYXa2kolS0/AkAc24zGILBGTqWeYqAkEq8YPFAS0utDlk/l745X9DzOjFzuGhQVrBYm\niQy8loMngH4drEc5XhFSip4u23UxynjKXjNOgTcn2snjx5DJcjPXaftFnZj70VOk7H15nRaiMAkg\nRGqEbGaj1UaUaQaksEoeWmOtYSfRRtop2klJOS1EIQSaQTfDrhGoTORXpLE1pewPqdWxTTmdAdDa\nQEOkS5VIU/jt30abnuXDroJ+khaM22vSSVX6q6QSK2VLF9wSn/P2+iVU5BXsx02JryO5pM4JaZRj\n2RuT0e8Bi87pSkpGhbJIhHSZaw+tDhKvw7NK79SspySwm6rtCwHApIFxkwoLe0kWSgo00sxGwCVy\naHS85UjAquO7VHoIq3BvgNSYdT0/lRo7X3fR4ccG/Tv3wDVS8x8X7Nf73ntT2v3zDMqpyU+yRTG8\nVfMsBpUYjMK4Rep5lZxJUiWJh9TPqv3OxmHpDZq/HNSOux6UgVNsl1kcyqArgmuMySbxJN3PeVeA\nlakCurVp7nVWjBhYSztIC7hMxe7ynEyXP51hdAkqgEuC0Nnf/vvwsx39u/KySc2ff13dW/Z4wDya\nv+sv8kzqyIxbpOy6SXhC4x6zTtWWQYgJnmuYBKNVY5F+I7Nm6Qxa/m5G5P72ky8CKWyLF9n10vxm\njTptO+MKoG32pDVS2mhbH4beNjDadIup4cXYeuJhUtjX2wFn8TlXBA7hxci895OP1RQVGLu/XQF4\n9l5MV61+0J22X3SdyYgVTGb+9RwF4908zJpJjCF/zHxxeZVknUFMc7lxEh5qhin/Ptdy+Dn4jo3K\nAg996sx1DG0UslhUrngZQNbNWggBAYG1NdezzO7XlN3XNRsKSWLVRpw35rZJ6eJwpiempkXqpaXH\nS9TecTmUlIUxmUApL2Gkf/ZcVvhboaO3fy6XPOO/p7LXG60hSuJGwZhSQAaDRYeHPuaIMaV+GZfD\nHq/ou2c39Ho52hgosXT3lCORL+Go21AvcpxxgYc+dZb211RWG2TQjXG5tP7C7ei2W3GeSqyRFk3b\n1HzXb8xtt7ExmWUrNtJi7vySoCukzosL52NqLkW/8H2k5yxCCLHnR+AXNvtJJ0XH8F8/yfqkSdzx\nTyKmNOzdfdl3L+/lVknoWWTPgtTDMtcI1s3SXqmyyVJ42+NUJsqfBN0SmJuUXF2ZFNZAuYxIJa3k\nlFUCsYkmifPU0sPZurRuTZxOC7hd3KMs8cJPPila6gO6aidl9JOw8v8ui8FM64627vPUHVMaZXyl\n370RjjXNpA8ynyyydzltltag9Uv9dv8pIbP4kItxZROIMV6hdloADT8WJQBt0+ddHE2Y3riQ/bvr\nZbm4WccrlvZRUvY8n+9CrXMixX5sbpg7eT92M+8/lmE9lHlI3OhJ2BkzTubit4vIoo6bLC5La9D6\n0VXiSJf2cnfB3fiH/U8Ip+nRjT9JKXoyTpzwsIFb87ZyVUIImHQ/KVxBdq/avZ8s4k+G/mM3Zn+O\n6Bq6vROHzZzcq9LvxroszPukOe61HqZ4nZBVZzUNWuoFxS6WZbrTjlPVdioezjtzqff+MqGSEmsN\nldaa2UKzTNUetkzAJaAAXcWCtUYAkxnL8qQI34uyKvqyR7XezeXuffjYNOjueX0CT3lj3g3CoMl8\n3if7vEGa9+tdJ/P+2ZDlYyUNml9oDXQbchbNNX7tVz5pw8W3XHKIC9+4uNzGmk0ilcLqPvrHd2r/\n/Yi92pwg7d3mx4icB9csaALq9h80qWjd+95I/fhJIqPExPolAJHlh7/N6iyFQRs2hpQVOHvtZIoy\nA902F8tyhdD5xAN3vN7EC9Mjauw0IoeJXfkp/UXnyG8b9FwRbkwsbJ0c/icxSmbnoAQgstx0WFhd\nmaUwaEB1o6a1VeLIT+BOiX9PvMkVO8O1a8kdq6ATc7acBy9eZ7rZk1XFgcvmsKKu1E6Vv2j83fhb\n8bn98ZWNZdBYdZ/j93vdKOerk3ELw8s6Qvg3Lvm46CiMs3w36D3GNRR4k8nBm5nqLGxhdZGCRpZZ\n2OfH7zpA5++UXYpIYYmxyzosrFlDlujh72tV+XsVP9z+7iT+WF1vNFefVtbU057Xqv7753MHzh/P\n7lQ+IbquBEW106UFwjlsAbbpe55hGHSMfJan/2/d5xp8gPE85GkwcCym7JtP5oFxBLFXjZEMWhiG\n+wB8BMCZALYAvCSKoiO5ff4AwIXpOd4XRdH7wzA8HcDXAdyZ7nZTFEXvGnXwxvTe8cZao6H6F6uW\nFSk2S4pcrZpD8Y/d/6LFSa86vRuXM0kqJyasjekxqr66fSfWWGuWt0wp+oLnVTsSrbPC3apTVd4o\n9HvveUbxPEad9P3OAcDsFOdd8s+iM67iC5ks83RzNO+M6qH9AoCvRlH0pjAMXwTgDQBe7TaGYfgT\nAB4TRdGTwzBcA3BXGIZ/AeCJAD4eRdF/H3fg9kPu9WCCGu9kXIq837wxnxnof9ECVeIBib2elrCB\nq96xp69PEo1mY/z3UWa440SXbrMlCd3HE9XuGwPfeIqC60sIWU1GNWgXArgm/ftTAH47t/0fANyR\n/m0AKAAdAOcDOD8Mw5sBPADgV6Io+s6IY+irhjEIJ1XV79hZbVmFCbPfufstSSWJzrwNf9lxEG5Z\nctjx9FcX6fV25vXOcJzPnZBl5/Dhjdq87s0D67UcZ1oMNGhhGF4O4Mrc0/cDOJ7+vQXgkL8xiqJd\nALthGDYAfAh2yXE7DMOvAbgtiqLPhmH4cwD+EMDzx3wPe6gSVxmUceir0+friPL7lxmifoaw6w15\nCR4wmUe39xy6J1YIYZcVpWd8qiy95Tt5+8zCMAy7XDir5UVCZsWw3/mjR3dqO/fW9m5tx5oGAw1a\nFEV/AuBP/OfCMLwRwGb6cBPAsfzrwjA8DOAvAHwhiqK3pk9/HoC72jcBuHq0YfeniocxaDnNxefy\nxrHM+BUtd/re3R5PLzWAKo35GdNVw3fGq2c8ED3GSwBweZpF73dRJv5xZKUIWXYW5Xc8L4warLkF\nwHPSv58N4O/9jWnSyOcAXB9F0e95mz4A4Hnp3/8FwG0jnn/iKC+pwxcr7rdvEf6XMdY6k8PKv8J1\nyAZs5+t+58iksvpkICYFxyCELBYxf8dDMWoM7T0APhSG4RcBtAFcCgBhGF4D65X9GIBzAPx8GIY/\nn77mZQCuAnB9GIa/COAkgCvGGPtUcHdI/Ty6qvJMQUGhtMNv6VKWYOJItCndx8Xk1IDthJD5p+x3\nTIoRc54hNvHBDXLpXbaji5EV7Z/fB7DZhConLuzickIKaK37Cs/GSZJtzx8/8drK5JcZXbKL03/M\ne3H557ikQchCUPlHeuTIVm3z5hfuuLeuQ9XGCy46t/RaLGxh9bQok8QCci3jkfvGFRSrCn/nrEtN\nSWJKbrvtumb3UZlo8t6xKumXF9iTFrWkIWSVWIR2SXmxCDI8K2/Qxvni+K/Nrwzk02atR+XXT1nv\nq6wuTCmZdcW2x6+Wqt5bGzfYePGHQ1YB7SVdzTMG81v/uQjM/yc8Z7gkkVFJUqFRF+zt1zHabZrz\nZeEeFmmsZHVYBCOxLMozs4QGrYSiBpzA+Ip3wms5A1QryF6k1iGLNFayOizKSsSijHNeWTmDNpQa\nPLoq/mXq6cOer1tLliZxeErn7jxJgXJ+/yLt4p5mRQr7k/agiqS+CCGjw99TdVYuhla9T5ioLMxb\nxCCl+m6LmW4Go0sjsY+rx8L8wmo/AcQdzz9WXXeAZdmRo7ZHIYQUQ6+tOivnoU2LfoXYPoGS6MQ2\nriaFSJXkxzCk8DK6MLkfQ35lkXeRhJBZQ4M2IYYJQvvq+lIOt6TZ77yTtDF5RyxmV11CyIyhQZsQ\nRUapzIvxEylcKn+eOEn2xMLKEjBELk43Kv1em39/8xg7m7fxkMVhnr478zSWeWflYmizJN9huUu+\n03Y3maOrsN/dW7u229gbb/OZZqHmPMppjdPJehFZhOJhQibJyhq0WXY59v8FgCDXZds9ThKNIO1i\n3fAKtbUxlYqmnQfnd9KuQj6hZZGNwjyPu+7rOs/vddGYp2s5T2OZd+bvtnpKVE3amCVlXk8/dX+g\ne6ceKFnJ8OXJL2XWUVvGZZO9jFukTwjpZWUN2qIoB1R5Pt/exhmgYWvmHHmDWUcqfqyZNJJn/r+B\nhCwWK2vQ6nTjR7nLrv3O3C/+HvP4RQkfRTgllUrHxOSTRhbN2xn1hqMKi3YtSDn8LKuzsjE0wCZX\n+C1f5oWszcyATEk/Hpe1qTFm7NT/fufvGQuqexmjLH2S0Zm37zQZHW3MWCIPq8RKzzKJ0bX88Ec5\nRr/XWENbkrk44LhJMv576nd+n3793GbBPI2FkLrYbSWzHsLCsNIGLZjTdhL9kj5cvVdZokYdntCg\npBNCVoF5WerbWF/phbShmM8ZfUrM6x39oHH5rWWGfW0d5ydkFdBz0jmCv8fqrLRBm0fy6vjuOR8h\nBKTnXQ7av8o5R3ndLFmksZJ6mP5nvve3SOYbGrQpUTkbsCDzrYrHNmj/KjJWi3QnuEhjJfUw7c9c\nKcXv2YJBgzYlXIfqSVNmuHx9yCIvkBBCFh0atCkRjNESZhjKVO/9ZJFEmz3tXwghZNGhQZsSwy5d\nVImlFaGULNyvp8knADGh+IDfgZusBvy8ybzAfNA5Za8ifzWqSHpNUhk/P+JpKv4TQlYbGrQ5Ztjk\nkHmgrA5uEcZORoOfLZkXuORI+jLuchInO0LItKBBI30pSzIZBho1Qsg0oEGbEuN4OsaYysr2Vc+T\npMdLBhxXyd4kk3lNABj0Pgghyw8N2pQY30uppqBf9TxOgNiY/q/JK/f7f9dtQMYy+hUFlQkhywsN\n2pziCxBb9ZB6julwyRvjCBHrmgu0kzGWNyeZuUkIWQw4C8wpeQHiOrwP3/bUIXclhShV/R+FcYzS\nMntnXEolpBo0aHNCkbJ33ZO0EPVOjv1U/weh9V7vbpmN0jgkevzEHEJWgZHq0MIw3AfgIwDOBLAF\n4CVRFB3J7fM/ATwMQAfAqSiKnh2G4WMA/Cls/e2dAH4piiL+WgEgNTaljT2NSeNdvUXX/YxAvqg5\nv2+/81VFVugpV3gekRZh1zCGZaB/Abqo5bMi8w0/4/EZ1UP7BQBfjaLoqQD+DMAbCvb5AQAXRlH0\ntCiKnp0+9w4Ab0hfJwD81IjnXzpkgcHJY2B6lgoH749s3yIGvr4mb67oPFKISu95VXCXuuh6BGq+\nOoOTycDPeHxGNWgXAvh0+venADzD3xiG4VkATgPwl2EYfjEMw+emm84HcHPZ60g5IjUARZQZnnEN\nRh01aLNgEWNO+WxSQsjwDFxyDMPwcgBX5p6+H8Dx9O8tAIdy25sArgXwLgCnA7glDMNbAYgoikyf\n15E+lE14iTYIlEhT8eu70yuTsZp3tDFQNA5kRTl8eANBoGo51uaB9VqOMy0GGrQoiv4EwJ/4z4Vh\neCOAzfThJoBjuZfdB+CPoyiKATwQhuHtAEIA/i1/0etICb6xSrSB9AyXgFt/d0tXJouzVVlW9PdJ\ntM48u2l6DEVjHTWmUPW9rxq8JqvB0aM7tR1ra3u3tmNNg1FvwW8B8Jz072cD+Pvc9mcA+CQAhGF4\nAMDjAPwrgNvDMHxan9eREVBpjEUIMdbSldYGJr3lmPayXZ0TLWNzpCiLliw/o6rtvwfAh8Iw/CKA\nNoBLASAMw2sA/EUURZ8Kw/CZYRh+GdYre10URQ+GYfhrAN4fhmET1sD9xfhvYTWQXn581WLoYZVF\ntNaVlyqmcbdPo1Qvq3Q9E63RqGnZjSwOYs7vYuZ6cMvGMEaqEyecMMjcsoTLq5XfzJEjW7XNm1+4\n4966DlUbL7jo3NJrsZhRfzIRhpkAVIX6M0JmxZIZM1IRzkpkJOQYGpD9GKazwDDHzEN1fkKWDxo0\nMn/UnNRRdCyq8xOyfNCgLRGL0LdsEEKI6sGCMXBCyIt6nQghe6FBWyL8uXlRVT6A6cQ/3Dnq7BZA\nCJktNGhLhFPTN8ZAegLGPlU9kjhJZuK9uPFPq45IyuLrRAhZPGjQlgjfsxlXG7CuOX5UwzQtI8Mi\nbEKWh1ELq8mcM6rCvqOsxmzY+h5tDIIhUvzdsZWikSGEDAc9tCVjGt7GMN5TVVUTMj7JAsdNCakD\nGrQlRc9JXIjLedNjUrWBhCwKNGjLiqkWuxo2VjWMCr+pOIa6Xrfq8OaBrDqMoS0hwxidOiZB3/jk\nj1fl+O71fjduGjRCyLDQQyMj01vIPZoxA1yvt9FeW2VshJDVgAaNjIxLQrAe4ejHmUTsh/XShKwe\nNGhkZKTqfn3G8agmEfuRgl4aIasGY2hkZOQcJyEMayTzcTxCyOJBg0YIaMgIWQa45EhIRRLNwmVC\n5hkatBXAGDM3hdaLzDwvsRJCaNBWhirFytNOoli0pI1lXJZctM+gKizOX00YQ1sBhBBQczgZL6OB\nIMVMO+mGxfmrCT00krHKBmZVJ79pfeZ6yC4NdbDK3+dVhQaNELAQe9Iw/kimAQ0aIbCF2GRy0Fsi\n04AGbYnRWte+lLasS3OccBeLSXy3yeJDg7bEGNQ/UVM0mMwDRWLYhNCgLTHzGLdIGKwiNcBmpqQI\nGrQlZtg7WD0FY6M4EZEaoHdGiqBBWwHipJpkk8Hk422ciAgZDi7TV4cGbSWoppogwGLUcdGaChWE\nzAoatBUgUKqSZ2RQb/HrKnpjsyggJssNv0/VoUEjGfOYRLJoFMUI6bERMh1o0EgG7wTHp+gastMB\nIdNhJHHiMAz3AfgIgDMBbAF4SRRFR7ztzwJwVfpQALgQwOMArAP4KwD/lm57TxRFN4w2dEIWA5kK\n5fKGgZDJMqra/i8A+GoURW8Kw/BFAN4A4NVuYxRFnwbwaQAIw/C1AG6JouhfwzC8AsA7oii6dsxx\nkxGZtuo54bUmZFqMatAuBHBN+venAPx20U5hGH4vgMsA/HD61Pn26fCnYL20X42iaGvEMZARSLRB\noLjSTAhZPgYatDAMLwdwZe7p+wEcT//eAnCo5OWvAXDd/9/e/YdYVtZxHH/P3V3c0lE2kvon6B/7\nuhCJaJa0hliLKZoVLMSSwaZlRgRKBLpZ/xhSFLVtFGi7YMKSZS0s/dKwAndEFpaEjPrC1n+GscZq\ns62u7tzbH+fOdpudO3Nm5t57zpzzfsHA3OfM3PPw3Gfu5z7Pc84zmXm6//gI8MPMPBoRu4GvAl9c\nca21at7YrKU4NVo/K31Ntmx5Ixs3bhjJuacv2DyS55mUZQMtM/cB+wbLIuLnwHT/4TTw0sLfi4gO\ncBOwe6D4YGbO/+xBYO8q6qw18M1KSylG8PaROpmb664ooE6cODWyc8+efHVkzzUJq517mgFu7H9/\nA/DUIj/zTuCvmfnKQNnjEXFV//sPAEdXeX6tE3Puir7u+HrVjB9CS1vtGtoPgIcj4jDwGrATICK+\nATyWmUeAAP6+4PfuBPZGxOvAC8BnVnl+1dz8NEmvB1NOc64brq/Wj69JeVM1/zRW68ppuLlujw0d\nL1eXRqT0H9Hx47Mje9/8w7PPj+qpRmbH9kuHtoXRr7GYH5QZZpImxUDTWBhkK1fz2RKp9gw0qSEM\nRLWdgSbVxFpHtY6K1XYGmiSpEQw0SVIjrPY+NGmsur3e2euUnUqTVIYjNNVT//oGw0xSWY7QVEsd\ndxeRtEKO0CRJjWCgSZIawUBTa/R6vbNf0nox1+1WXYV1w0BTa8zH2DguNDEkNS7drn2rLANNrdEZ\n4xWT5pnGxX8fU54tpcbqLjK9OK7bALy7QOPirSvlGWiaqElOzU1RjJwmcU7fdKTqeR+aGmtqasqR\nk9QijtA0UY5kJI2LgSZJagQDTZLUCAaa1BDeC6e2M9CkhnB9Um1noKlyjiwkjYKBpsqdcWsfSSNg\noKlyHRylScP4t1GeN1archvcq07SCPhOIkk15sU+5RlokqRGMNAkSY1goKmW5rrdcxbDXRxXG83N\n+R+ryzLQVEu9EV/K31vkf6NJ60HXfluaVzmqljZu3HBO2VoWx3s96HRcXNf6s2mRvwUtzhGaRmau\nW9+pES8Uk5pvTSO0iPgosCMzdy5y7NPAHcAZ4P7M/EVEvBk4ALwB+AewKzNPraUOqo86X15c57pJ\nGo1Vj9AiYg/wwGLPERFvBb4AvA+4HnggIs4DvgIcyMxrgD9SBJ4aorPK0HBtyzbQcPaN8tYy5fg0\ncOeQY1cBM5l5OjNfBo4B7wK2Ab/p/8yvgQ+u4fxqCEdPtoGGs2+Ut+yUY0TcBty1oHhXZj4aEdcO\n+bULgZcHHs8CFy0ony9biq+kJK3AxRdPj+x9c8f2S0f1VBOxbKBl5j5g3wqf99/A9MDjaeClgfJX\nBsokSVqzcV3leAS4JiI2R8RFwFbgOWAGuLH/MzcAT43p/JKklhlpoEXE3RHx4cx8AfguRWD9Dtid\nma8C9wMfj4gZ4Grge6M8vySpvaa8gkaS1ATeWC1JagQDTZLUCAaaJKkR3Jy4pIjoAN8HLgNOA7dn\n5rGB4+ds9VVJRSesRLvsobihfrZfdEv/ZvvWiIj3AF/PzGsXlN9MsXvOGWB/Zj5UQfUqs0S73AXc\nDhzvF92RmTnh6lUiIjYB+4G3A+dRvJccGjje6j6zHAOtvI8AmzPz6oh4L/At4Bb4v62+rgQ2A4cj\n4reZebqy2k7O0HbpuwK4PjNfrKR2FYuILwG3Av9ZUL4J+Dbw7v6xmYg4lJn/nHwtJ29Yu/RdAXwy\nM49Otla18AngX5l5a0S8CXgWOAT2mTKccizv7LZdmfkMRXjNG7bVVxsMbZf+6O0S4MGImImIT1VT\nxUr9DfjYIuVbgWOZeSIzXwMOA++faM2qNaxdoAi0eyLicETcM8E61cFPgfv6309RjMTmtb3PLMtA\nK2/hdl5zEbFxyLEy23o1xVLtcj6wl+JT54eAz0VEW4IegMz8GfD6Iofa3GeWaheAHwOfBa4DtkXE\nTROrWMUy82RmzkbENPAY8OWBw63uM2UYaOUt3M6rk5lnhhxr07ZeS7XLKWBPZp7KzFmKm+wvm3QF\na6rNfWaoiJgCvpOZL/ZHIb8ELq+4WhMVEW8Dfg88kpkHBg7ZZ5bhGlp5M8DNwE/6a0V/Gjh2BPha\nRGymWMid3+qrDZZql3cAj0bE5RQfnrYBD0++irX0F+CS/jrJSYqpo29WW6VauBB4LiK2UqwTXUdx\nkUQrRMRbgCeAz2fmkwsO22eWYaCVdxDYHhFPU8xt74qIuynmtA9FxPxWXx3+t9VXGyzXLo8Az1BM\nL/0oM/9cYV0rFxE7gQsy88F+Oz1O0Wf2Z+bz1dauOgva5V6KEcpp4MnM/FW1tZuoe4EtwH0RMb+W\n9hBwvn1meW59JUlqBNfQJEmNYKBJkhrBQJMkNYKBJklqBANNktQIBpokqREMNElSI/wXzp2Lc3cT\n9rsAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1195cc710>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"RGZ & resolved\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAbQAAAGoCAYAAAAuIBCmAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X+cJFV97//XqaqenYUdcAUR9avRoDkoXjGgBpLVmERU\niLkaDTEhEjGgXhPzA6MRQQ0SiD9y8Ufwx/UXkajkKyHwuMar6FWDEZQQiXy/yjeeBDSJwR8slwVn\nd9mdrqrz/aOqeqp7untqunt6qqvfz8djHztd1V1V09NdnzqnPudzjPceERGRWRds9QGIiIhMggKa\niIg0ggKaiIg0ggKaiIg0ggKaiIg0QrTVBzDM7t3LM5GCuXPnIezZs3+rD6N29L4MpvemP70v/T3o\nQUtmq49hFqiFNgFRFG71IdSS3pfB9N70p/dFxqGAJiIijVDrLsdhrr/1zr7Ln/7Eh035SEREpA7U\nQhMRkUZQQBMRkUZQQBMRkUZQQBMRkUZQQBMRkUZQQBMRkUZQQBMRkUZQQBMRkUZQQBMRkUZQQBMR\nkUZQQBMRkUZQQBMRkUZQQBMRkUZQQBMRkUZQQBMRkUZQQBMRkUZQQBMRkUZQQBMRkUZQQBMRkUZQ\nQBMRkUZQQBMRkUaItvoAJu36W+8cuO7pT3zYFI9ERESmSS00ERFpBAU0ERFpBAU0ERFpBAU0ERFp\nBAU0ERFpBAU0ERFpBAU0ERFpBAU0ERFpBAU0ERFpBAU0ERFpBAU0ERFpBAU0ERFpBAU0ERFpBAU0\nERFpBAU0ERFpBAU0ERFpBAU0ERFpBAU0ERFpBAU0ERFpBAU0ERFpBAU0ERFpBAU0ERFphGirD2Ca\nrr/1zr7Ln/7Eh035SEREZNLUQhMRkUZQQBMRkUZQQBMRkUaYq3togwy6twa6vyYiMivUQhMRkUZQ\nC20dw1pvhaUdiyzvPdB5rFadiIxi0Pnm9FOOnfKRzKZaB7QqwaSORjluBUERkfHUOqDNk7oG7zoE\nWo0fFJEqjPd+q49BRERkbEoKERGRRlBAExGRRlBAExGRRlBAExGRRlBAExGRRlBAExGRRlBAExGR\nRhhrYLW19qeAtzrnnt6z/JeANwIxcLlz7oPW2u3Ax4CjgGXgxc653ePsX0REpDByC81a+0fAh4DF\nnuUt4B3AM4GfBV5mrX0w8ArgG865pwJ/Cbx+1H2LiIj0GqfL8Q7g+X2WPxa43Tm3xzm3AtwAPA3Y\nBVyXP+czwDPG2LeIiEiXkbscnXN/Y619ZJ9VhwH3lR4vA4f3LC+WrUd1uUREwFR9YhwnPorCiez0\nuq/+20S2M0nPPvmRA9+LzShO/CNgqfR4Cbi3Z3mxTETmXJykhIHBmMrnbBliz579E9tWeVqsWbAZ\nAe2fgcdYax8I7CXrbvzvwI8BpwE3A6cCX96EfYvIjPEeBTOZiIkFNGvtGcAO59wHrLWvAj5Ldo/u\ncufcndba9wFXWGtvAFaAMya1bxGZXVGoYCaTUffpY2p9cCIiU1I56u/evTyx82Yd52k8/ZRjB74X\nGlgtIiKNoIAmIiKNoIAmIiKNoIAmIiKNoIAmIiKNsBnj0ERE1vXud7+b66+/niiKOP/883nCE57Q\ntf6LX/wi73nPe4iiiBe84AX86q/+KsvLy7zmNa9h7969tNttzjvvPH7yJ3+Sr371q7zzne8kiiKO\nOOII3vrWt7J9+/ZNO/Zbb72VSy65hDAM2bVrF6985Su71t9zzz28+tWv5sCBAxx11FG8+c1v5t/+\n7d/40z/9065tvOc97+FpT3vaph3nvFHa/pzx3pN6CAON/ZGtc9ttt/HWt76VK664gu9///v87u/+\nLn/zN3/TWd9utznttNO4+uqr2b59O7/+67/O+9//fq688koOO+wwzjrrLL797W/zh3/4h1x77bU8\n61nP4uMf/zhHHnkkl156KQ960IP4zd/8zU07/uc+97lcdtllPPzhD+dlL3sZ5557Lo973OM66y++\n+GIe97jH8fznP58PfOADLCwscNZZZ3XWf+Yzn+Hzn/88l156adVdKm0/NyxtXy20eeRTvA9UnWHG\nXHPNNXz+859n37597Nmzh9/5nd/hWc96FjfffDPveMc7CMOQhz/84Vx00UUcPHiQCy64gOXlZe66\n6y7OOOMMzjjjDM4880we+MAHct999/HGN76R888/nyiKSNOUSy+9lIc85CG85S1v4ZZbbgHgOc95\nDi9+8Ys577zzWFhY4M477+Suu+7iLW95C8cddxw/93M/x4//+I9zzDHHcP7553eO9eUvfzn796+W\nYDrmmGO48MILO49vueUWdu3ahTGGhz70oSRJwj333MMDH/hAAO644w4e8YhHcPjhWcnXE088kX/8\nx3/krLPOYmFhAYAkSdi2bRsAH/3oRznyyCMBiOO4s/zMM8/kox/9aNf7eOaZZ/KoRz2K73znO3jv\necc73sGDHvSgzvqPfexjfPazn+16zVvf+lYe+tCHArB3715WVlZ4xCMeAcCuXbv4yle+0hXQbrnl\nFl7+8pcD8LSnPY23v/3tnYC2f/9+LrvsMj72sY9V+rsnaUoY6O5QFQpoc8YYQxhOpnCpTN/999/P\nX/zFX3DPPfdw+umn8/M///O84Q1v4Morr+SII47gne98J9deey3HHXccv/iLv8gzn/lMfvjDH3Lm\nmWdyxhlZcZ7nPOc5nHLKKXz84x/nCU94Aq95zWv42te+xvLyMt/61rf4z//8T6666iriOOaMM87g\npJNOAuChD30oF110EVdddRWf+MQnuOiii/j+97/PNddcw86dO7uO8/3vf//Q32Pv3r084AEP6Dw+\n9NBDWV5e7gS0vXv3srS01LV+7969HHbYYQDs3r2b17zmNZ0getRRRwHwuc99jn/4h3/gD/7gDwDW\nBLPCCSecwEUXXcTHP/5x3v/+9/P616/OZvWiF72IF73oRUOPfceOHV3H9t3vfnfNc4rjL363wtVX\nX82zn/3szu+6njjxhIpnlSigicyQJz/5yQRBwJFHHslhhx3GXXfdxV133dU5gR84cICf/umf5md/\n9me54oor+NznPseOHTuI47izjUc96lEA/Mqv/Aof/OAHOeecc1haWuLcc8/ljjvu4ElPehLGGFqt\nFscffzx33HEHAI997GMBOProo/mnf/onAHbu3LkmmMH6LbQdO3awb9++zuN9+/Z1BbBh651zvOpV\nr+KP/uiPeMpTntJ5zkc+8hGuu+46PvShD3VaaIMUQfqEE07gi1/8Yte69Vpo/Y6tCLS9x7+4uLhm\n/d/+7d/y53/+50OPr2whUjSrSgFNZIbcdtttANx9993s3buXo48+mqOPPpr3vve9LC0t8YUvfIFD\nDjmEyy+/nCc+8YmcccYZ3HTTTXzpS1/qbKPoav7CF77AiSeeyCtf+Uo+9alP8aEPfYhnPvOZXHPN\nNZx11lm0222+/vWv88u//MtdrysLBnSFrddCO+GEE/izP/szzj77bH7wgx+QpmlXi+WYY47h3//9\n37n33ns55JBD+NrXvsbZZ5/N7bffzu///u/zzne+k2OPPbbz/Pe9733cdtttfOQjH2FxcbHfLrt8\n85vf7ATmRz/60V3r1muh7dixg1arxX/8x3/w8Ic/nBtuuGFNUsgJJ5zAl770JZ7//Ofz93//95x4\n4okALC8vs7KywkMe8pB1j7GgWwPVKaCJzJC7776bF7/4xSwvL/PHf/zHhGHIBRdcwMte9jK89xx6\n6KG87W1vwxjDxRdfzKc//WmWlpYIw5CVlZWubT3+8Y/nta99Le973/tI05TXve51HHfccdx88828\n8IUvpN1u8+xnP5vjjjtu4r/H4x//eJ70pCfxwhe+kDRNeeMb3whkrZf9+/fzwhe+kPPOO4+zzz4b\n7z0veMELePCDH8yFF17IysoKl1xyCZAFlz/5kz/hPe95D4973ON46UtfCsCpp57auWfYr9vx2muv\n5SMf+Qjbt2/nbW9724aP/01vehOvfvWrSZKEXbt2cfzxx3Pvvffy+te/nne/+9284hWv4LWvfS1X\nXXUVO3fu7CR/fOc73+FhD3vYqG+brENZjnOi+Dvram92XXPNNXz729/m1a9+9VYfysy45JJLuOCC\nC7qWnXnmmVx44YUcc8wxW3RUI1GWY05ZjqJAJnPpt37rt7b6EGSK1EITEak/tdBymj5GZkLNL65E\npOYU0KQ21C0qIuNQQBMRkUZQQJMtpW5GEZkUBTTZUh4FNRGZDAU02VIGSFOvoCYiY9M4NNlSWbFk\nJYOIDOK9V8JURWqhiYjU2EqcbvUhzAwFNBGRGtNcvNUpoImI1Fgr0vyFVSmg1Zj3fmoJE957kiRV\ncoaIzCwFtBkwtRvCRtU6RGR2KcuxxrLgMp0WkzFGVzciMtN0Dqu5abaY1DoTqR/dBqhOAU1EpMZ0\noVmdAprIBsSJxgSJ1JUC2pzarG6M1De7jJX36gKS6dLnrToFtDm1Wd0YcZI2uoukFQWN/v2kfvR5\nq27kLEdrbQC8FzgeOAic45y7PV/3ROCdpaefBDwPuBn4F+Cb+fJrnXPvGvUY5kld67l57/EeTJ7y\nH4VBbY9VZBbp+1TdOGn7zwMWnXMnW2tPAi4FngvgnLsVeDqAtfZ04E7n3HXW2mcAf+Wc+93xDnv+\n1PUDXQ5mAEFNj1NkVtX1u19H4wS0XcB1AM65m6y1T+p9grX2UOBNwNPyRScCJ1prvwTcBfyec+77\nYxyD5NK8n33aASVQobmZ5b0n9Z4w0J0HaYZxAtphwH2lx4m1NnLOxaVlZwN/7Zy7O3/8LeAW59zn\nrbW/AVwG/MoYxyA5Q56Qga7oZAPyJJ46f2Z6u7U3+to6/26bYefOQ4gmVP9xacfiRLYzLeMEtB8B\nS6XHQU8wA/gNugPWF4H9+c/XAheNsX8pMcYQztkXV8aTzUVX/8K32UXaaBdq8xbMAPbs2b/+kypa\n3ntgYtuahnH6Gm4ETgPI76F9o7zSWns4sM05993S4g8BL8h//gXgljH2LyJzYP5CkoxqnBbatcAp\n1tqvkH3mXmKtfRVwu3Puk8BPAP/W85rzgMuttb8N7APOGWP/IjIH5rGVJaMxNR+0V+uDExGZkspR\nfffu5YmdN6+/9c5JbWpiTj/l2IHvhdKbZMvU/GJKRGaMAppsGXUlicgkKaCJiEgjKKBtsY0W8+33\nXHXdiQw269+PWT/+aVJA22LJBov59nuuuu5EBpv178esH/80KaBNUb8rrSgMSNOUNB3eUmsnydD1\n3nuSdbYhAlmvQNOn+ZH5pIA2RYNaV8XyoVdi3lS6UtPVnKzLZzng+qxI04wzsFomJDuxDL9ajsLh\nJx9jDMGYw/ZS73WimwMqKC1NpRZaTRRBxA/oCppG68zAul2fIiJ1pRZazWxl6ygrVqurd5E6mccZ\nA0alFpqISI2143SrD2FmKKBNwbS78AaNVWtCV2LxO8zC79KU91y2lhpn1anLcQqm3V3Q5LFqlTJC\na2IWjlHqrzWhyTrngVpoIiLSCApoIiLSCApoMlCc6Ga01JP3njTV/UnppoAmgympQSrais+JR59P\n6aakEBko0s1oqWgrEp9CJd1ID7XQRESkERTQtsA0xlJpDJSIzBsFtC1Q3MvezG6achV/EZF5oIA2\nBb0tpcBULwKsVpaISDVKCpmC3pZS1noa7bUiItKfWmgiItIICmhTMM1uwyIZRF2VMip9dmRWKaBN\nwTS7DVOvhBAZjz479aILjOoU0LbYoA9r1Q9xv4STYa/Vl0NktqgEXXVKCtlig66Gq14l90s4GWV/\nIlJPugStTi00EZEaa4U6TVeld2pMSZJWTsTY7O4+dSeKNI96VapTQBtTmvpOEsakuvtGDUzrbV8B\nT0SaTAFtTFE0+bcw2aR5nlIFNBFpMAW0MU26O8D7rMU3apbjMAYzsGtU49fqSX8PkepGznK01gbA\ne4HjgYPAOc6520vr3wXsApbzRc8FWsCVwHbge8BLnHP7Rz2GJsrmedrY86sKgvW6JNd/jkyX7p+I\nVDdOC+15wKJz7mTgPODSnvUnAs9yzj09/3cf8EbgSufcU4GvAy8fY/+1ULXAcL/nxUlSsyvwyRRM\nVktPRLbCOAFtF3AdgHPuJuBJxYq89fYY4APW2huttb/V+xrgM8Azxth/LVS5gh6cMFKfih7GGIIg\nqPz7rLe+Lr+XiMyPcQZWHwbcV3qcWGsj51wMHApcBrwdCIG/s9Z+rec1y8DhY+x/5oXq3hORCdu5\n8xCiKJzItpZ2LE5kO9MyTkD7EbBUehzkwQxgP/Cu4v6YtfaLZPfaitfcn/9/7xj7n3nlVkzRRaeW\njYiMY8+eyaUlLO89MLFtTcM4XY43AqcBWGtPAr5RWvcTwI3W2tBa2yLravyn8muAU4Evj7H/mTPs\nvlK/bjrdhxIRqW6cgHYtcMBa+xXgHcC51tpXWWv/q3Pun4GPAjcBXwL+0jl3G3Ax8GvW2huBk4F3\nj3f49eO9J04SknRtQdGNFhlVUVIRkepMzVsBtT64frKAlhIYQxB0t7racUIUVku86H1+MT5t1GNS\nV6bITKv8Bd69e3li583rb71zUpuamNNPOXbge6Fq+xNmjKE14IasZ2P3yMrbGScgKZiJyDxQQJug\nNPVgskupfkEkCgLSNCVL1x8v0KTeg2fs7YjUVZKka3o5RIZR6asR9S0fhScYMgYrCAyYjQezvt3C\nCmbScBvt0RBRQBtRv4SNoMKXr8pzquxLwUyaTuM0ZaMU0EbgfdYSS3uq4o86y3SxzWEJOuV1aZ8M\nyrqpebKRzABdsMlG6R7aCIwxhBupIFxxm4P0JpnEqWdhE6atmSSdjERk2up9VpwB7TiZ+j6jTZiS\nXS2qydN7KjJdCmhbbJST3ij34dajFtXk6T0VmS4FtDGN21pSNRARkclQQBtRmvo1FTiKxI4kTSu3\nvMIgmOmuqY38riKycYkueitTQBtRkqZrupSKElUbmeds1geOJunmltVSsJR5F6f6DlSlgDaiQV2N\nSeqZp+EzrU1IUCmb1He5ratcmVF1z2iuE71TG1AeK9ZvLjOYXMJGsa++FUmGrBt1X/1+rmKzW5eG\n1e7d8Uzu/ZpXev+2xiz34EybxqFtwKAPVnl5OMEWi/d5uaw+yydZKaS8nbp9efr9/qNohZOZwXee\n1e2zIdJLLbQ6M/2vio3J6tzpillEZJVaaENs5TxixpiBEyANWyciMq/UQhsiTja/BeS9X1MTUkRE\nNk4BbQhT6vIb1L03iW4/7zc+lmuj492kWfR3nx/6W1engDZEOTW/SkLIKLJCx+GGt2OMIU11o35e\n6e8+P/S3rk4BbR0b6Q5MpjytS7niv7oupUm2oui3zD4FtAE6zfxO9Y/V5YPHgZk1y6uOFxulSzMw\n3fvzGmslM2Ld78WADF+RYZTlOEDRzO+dNTf1kHqPYW21kH4z7MaJp1VhpP+oXZpdY+DUNSEzYr3P\ntcYNyijUQltH71ViYMBsoFJHoCtNEZGpUEAbot84NGMMUZQlcVS5WRuGgW7qiohMgQLaEHGSTwfT\np7Btv+5FERHZOrqHNpQn6y1cO/dZ1VZXv2LGIjI/yrccdB7YXApoQ7Si8W9M91bl1wdaZL6k3hMG\n6gybBr3LuUmMIWsnSaeCRz+x5uQSmTtBz9Af2TwKaAVfLRtx6HN8Mb5mg7ue4NxmIlIvVRPIBtG5\noToFtFzxkUl6qm30triGtbKiMCAIgoEJI4O6MD2TmsRSRJpmJVbPTlUKaCVZQPFrb+KWWm9+SEuu\nuArbcF1GRp+FWq07kWaLlFFdmZJCcr1VP8rCriLFk89UKsa2jfpaEWmuSc3aPg/UQusj7VOPseiK\nLAe+8vLuZeoiEJHJUJdjdSO10Ky1AfBe4HjgIHCOc+720vpzgV/LH37aOfcma60B/hP413z5V51z\nrxv5yCeoPFYsq1jvScmifWccWupJTbB2pug8CaRoKXnv8Sl4s36K/rhj1CYxDGCcY+jdv4YlyLj0\nGVpLDbTqRu1yfB6w6Jw72Vp7EnAp8FwAa+2PA78B/BSQAjdYa68F9gP/5Jz7pfEPe7LKX6A4TVko\ndf8dbMcsLkRgsoLEvYOry1O4AARBQNUhJ5OYS21c44yR6VcWTGQc+gytNYnxsPNi1C7HXcB1AM65\nm4AnldZ9F3i2cy5xznmgBRwATgQeZq39O2vtp621dozjnrhiDFkUBp1WS5wktKLssSHLRhyWgDFs\nCpgkGT67dDtORk7uGCcppHcKGhGpF303qxu1hXYYcF/pcWKtjZxzsXOuDdyddzH+GfB159y/WGuP\nBt7snPtra+0u4GPAk8c6+gnx3oPPxooYIE1TjDF4TyfAFeuGfbiGXV36ddav9/qNvG4j3Ta6Ihap\nt41+R3fuPGTkJLNeSzsWJ7KdaRk1oP0IWCo9DpxzcfHAWrsIXA4sA7+dL/4aEAM4526w1j7UWmvy\nVtyWyrrdYKWdsNAKaSeeBeM7CSBxknaa/cXPcZIOzYwsM8aw3lOrbquKOPW0QgUqkXm0Z8/+iW1r\nee+BiW1rGkY9i94InAaQ30P7RrEib5n9T+D/cc693DlXzKX+x8Af5M85HvhuHYIZZN1uaakIMUBS\naomFQdCVPJG16Pp30w0aIL1ZrbO+26Le3RRFFmmdj1FEZo8Z5aRSynJ8Atn58yVkAe52IAT+Crip\n9JLXAd8i62bcQdZS+x3n3LfW2dXUznjlFtfBdsJCNNo8Zu042dBN3I10DzYlAyxJ0q6xfSKyrspf\n/N27lyd23rz+1jsntamJOf2UYwe+FyN1OTrnUuC/9SwuB6dBHa+/OMr+pqEYvDhuq2GjXYfl7sxJ\nPrfONFBURDbD3F4mp2naVW4qyFs+ac+A6mGZi6N0Lfa+ptOFWcF6z91IMO49/ml2AW60lVn1uEYt\nHyZSZ/o8Vze3pa+KLMbe1kKSera11m8FJakfKZGj92S+kW2s99yNBIre59a59Vf199K8U9JETbjN\nMC1z8e2PS2PAuq/gfddVfRwnhIHpWua973p9XMx5lqSsrMSdFl2xvKx4vNIefYzZJBUJK/2OJSyN\nv5tVkxhTpxaeyOyaixZa6j2RWR1PViiXqzLG4IEov8IvP9f7FJO/PvUQ5c9NPSx0njO4ckaS+s7z\nJmmjSSIeT2D6X8MEDbgKnMSVrK6GRWbXXLTQWqXxZIVy9Y6ildVdeHj19cVy71enctjWCllcCNc8\np5/y8yYp3WBLoglBS0RkkLloofUW0C3+Jelqt2CcJoRhQJp6sqdnlfSDrhZd1iorgmDQp7W33v5H\nsWZ+ttLPxfHWqWVRVFqp0zGJSPPNRQutUJxkjTGQV84PggATGJK8yzBO8rJXGMIg6DoxZxU/glIg\nmc4JOy1Kb/XsLzCGIKgeOKZ1vPEU3xuRptM93ermKqD5NOtmNMYQGIiiAGMgTjxRzzsRmLUfpDRv\nmbXjZKKlqtZTJDvMipYGTYtMTDvRfGhVzdeZJ5v/pauMVdGSCIIiaYTOOuiT9bZOXOkd27WeKs8Z\ntftu3CC4keMf1C0qIuPRt6m6uQpoURgQBmZNgCgvK4/FKpIuiv8DYzAm286gk3bX3GoVrqyqPGdU\n05hvrZiwW0FMZHNMszdo1jX+ncqSP1LiJKuRnKa+Mx6ryHL03ncqhxSvgVJXn+9OJvF+NUuyN9Ow\n3FLp11Xo8y7Lzj4CQ5IOnyttElLvBxZOHkdgstqMm7HtKmapK1ZENtd8ZDliSLwnMlnwKK54knS1\nSG5v8kfvskLqsxZd9nNKq2dcV1fLr8+Vlad7brQgr1iy2S0cXzruScoSbLauPqNahtJ0+oxX1/gW\nmsm7CZOkaEHk3Yjp6v2yKE/XhzwlPx181V+ctzcyH1r369cOvp7G53Uz481W1xouknVEZL41PqAV\nXYTG+E5K/uqA6tLgZFN0y6Wd+bqK13c/zrdZyg4pFzpe71jSdLULs1BOQFnd5nhdeGmF45mUfleQ\nk9p3paQZsgzWaXc/Vv0bqVt0tqkc2uxofEArAliaQCsKCYMg6x4zhlYY5ImP2fiyoBifZrq7HYtU\nf8i6KY0xtMKwdCJfm2jST9bVSNf2e4+1EKfpWF0N5WPu3fY0TGp/VbZjjCEckqizWZKKfyN1Gc22\nROMqZ0ZjA1r5qioMDQutgHac0M6TQ0x+N8uzWjy4HSeYvGBxOXEjKhXuLc9evZr+X7FF5D1xnHZt\nY9CxR8HgsWdVWoJRA4oN1916f0dphnDId1HqpbFJIeW5w4wxBGFeBST/XAalaUZ86TVBEGSBp9TC\nKV+dlZMfin0YYyqNFQmCgDhN1k2gWK+1t97Voq4mp0MTlc4HfZ9mR2NbaJAlbiRpShyn2Rgysg9n\nO05JSokfC1HWXVUkeQQVAxRAHG9sHJmqaIiIbI7GtdDSNM3/z5Iv0jRL6kiSNA9SxfxlKWDywdKr\nSRlF0WGfJ4yYfFtFzcQsIYROcDRB/2lcehM8gj4DusvP7bT0+hRSNj3HOOyKsVifJOnAOo/D1s2b\n8t9c74fIbGtgcyE7MSU+q9UYGNMZ9xVFIWBo5YUbDf1OYkXgoXOSS7oyHuk6+UWl5JDezMXiX3nc\nWT+e/t2M/ZZX7W4cts9knaA4j/R+iMy+xgW04rwUmqwVdv9KnAe1LNHj4Eqy5rkH2wkr7STvisxa\neF1jzHy2razrcnBSxqCxUOvdaxk0T9k485cN26e6PVdlhaoVzESaoLlnNrPaZWgM4D1pko0fKwce\nnz+nWG5Y263XCQ6l8153Kay8axDTd8xKsc3y6wq9Y97WvLbiybb3df1O0r5nX6Pod4yzngGm1plI\nMzTuHlonMxHDwZWE7dtCWlFImnruX1nhAUvbACg3UhZaw2eUHlYRZDVoDq74kaS+s412krJQKoCc\nJGmnIHI7TjvdoRtVdTxU0W06ahms8u+ykX2LiGy2xgS0olXlvSdOstZWK8qCWhgGtJOkMxYtCoNO\nlfvi5Fy8rhUFJEl3jcdyi628HyhaXwBFRZLV4/Fk866VtxF1pqkx+YzYq0kaveNdxgkU5SELZcYY\njE9Hrh8YP6xrAAAgAElEQVRZHKOCmIjUzUx0OVadM6zIWCMvYRUGAZ6s+y1Nfd4SM12JE937yf5P\ne072vWPaev/vZEBSykjM+jnzKiTlede6MxaDIOh0ZZYzIScx9cugbQTB6FU1JnFsIiKbYUYCWrXq\nGCtxiiELMD5P2T9kW9bd2ClAXCpIHAZZoMtadBAEsP9gTBCsttiK6Wf2H4jXHEPvXGbl+1aBMetO\nBloEumKYwKzfixIR2Uoz0eVoTHcXWr8Tf5GdeHAlxpMFm1YYEieAjzFhgM8HU8c+64YMjCHpdL8B\nBqLAkKZFUaysmHAKRNHq2K5Ceaxab8slTdOsJFZe729Y7UaTt+YGdRNm+xq8TkREZiagrT8Wq4hx\n9+1fIQqy1lcYelbaCZEJaIWwbVtEkqTEqSfMtxOFIYnJghres20hIk2zVlkrCrNA4j2tVtiZcmZ1\noLQfmPKdpL5r9uth+g2q7vce1J3urYlMnr5X1c1El2OhaIX1KqaIAdi+EHWmgEmSvFoIPhtjlqQc\naCf41He6C1Pv8XlyRidBhKzVlSQpSZKl40PWisvKaRX3xta+fb3JJlX0dl3OqnI5MRGZjHZDzg/T\nUPuA1j3Wq5hTLO3c20ryeo0eSPJK+pjsVlk53hjvSTqlpFa3vfqEUrWPIpOR1Slfys8vuhKLbsKu\n7ZTKVa3Zxzq/5ySft1XqfnxldTzWOh6TbC21zaqrfZdjuW5ikmb1GA/GCYdsa7H//jYmz2D80b4V\nPNk9tCMP347J0+V3bI+I06xKSJp6FheiUop+1vZqeyD1WZKIB9MzJ9oqQxRmXYP3H4xpRYY08V3j\n2KKebsYqXQVVuyarbm+rjDKD91aq43tZx2OSrbWR88O8q31AS+IsESMIAJ9ysJ11AR5sx1kCiIcD\nKzFJmrJ8f5v7lg+yvG+Fo484FGM86WKL1EMUGuI47aoE0knoYHU26ZXY0wqz1lkQmLzeI50xY95n\nCRwLrZA0zUphZa010xUE23FCGPQPjHGSdHVXbvQk1q8FOGgbcZJ2DRsQEWmq2l9Se0NnNuLUZ+nt\nJszC0P6DCXHq2bs/5mA75UfLK+z50UH2LB/gYDshTjyJJ0/JD/LAmI1Na+WFiyFLn4/CgCAI8kzG\noJNxX4wNS/MxY8XjMDC0orBT8Lg3cKV+8MzUxTi3Ucd09SbIDNpGMS5vver8IiJNMHILzVobAO8F\njgcOAuc4524vrX8p8HIgBi52zn3KWnskcCWwHfge8BLn3P5h+ykX0k2LavepZ9+BNnjPN26/m1u+\ndRd33bOPBx9xKIft2MYjj17iwErCtijo1HI8sJIQBYZWlGcp5if5+w/GRGFAkg+8PmQxwhgIO+PD\nspZbb0HfIliEeZArAkOcpERhwELU7/lZ8GyVqpMU29gM2dCF4dsuul5FRGbdOGfS5wGLzrmTgfOA\nS4sV1tqjgd8DfgZ4FvBma+024I3Alc65pwJfJwt46yqSQAKzOn9ZnKbcu3yQ7/3gbu6+63v88M7v\n8N3//CH79q/gvWff/hWCAA4cjAlX61OR5uPOkjSlHSedLsfAZMuKFk+QD7rOSlj1b8WUE0JWW0GD\nx5OV5zfrt41JKG+vWhX5ye5fNp/+XiL9jXMPbRdwHYBz7iZr7ZNK654C3OicOwgctNbeDjwhf82f\n5s/5TP7zO4btxBiTF/QN2F4aR3bv8kG+/i+7+R8f/V/c+4N/Zc/3/j8ec9KvcsLjH8nithb7D8Ys\nbotoxylBGBCZrCUUJ54oCmjHWcsrigJafYoTZ+Wr8m7GAccVhWtf12/Z6vPX1lUc9PxRlYNlWCFJ\nQzecZ4/uh8owO3cesiY5bVRLOxYnsp1pGSegHQbcV3qcWGsj51zcZ90ycHjP8mLZQJ0Bx6UL0jj1\ntNsJ+/atsGN7i4Xth9Ju30+0bYn7l+/hzt0/4gE7tvGIo5fYfyDmAUsLtNtZZZAwzKrwt+M8kEUB\nRQslyVtjWZHgLBAcXEnZvq27dmMxuLpQLI/jpNKHqBh+sN4caeNoJwnRGPUaRWR27dkz9C7Ohizv\nPTCxbU3DOF2OPwKWytvKg1m/dUvAvT3Li2UD9RYRzrods3tp7WR1cLNJU7YdejgGiNvZIMTt20JS\n77MWkDGE4WpgygoWZ/ezwvzEvzpP2GqXTupXBzT2m6esKwlk2C9SsrYg8iZ0H41YSV9EZJaN00K7\nEfgl4Cpr7UnAN0rrbgYusdYuAtuAxwLfzF9zGvAR4FTgy1V2VMzdVczFtbyvTasVcNTORU4+6af4\nsR97JGl4KA88bBuPf/RRHPGARbYttFhciEgST6uVdTX62LN9MWJbK8jmSPNZxZBifrIgv3dWzFl2\n6GILICt6bGAhCge2rNZLvii3zMr35OLSfGjrvT5NfaVuxI2OB9vs5BQRkWkYJ6BdC5xirf0KWV7F\nS6y1rwJud8590lr752QBKwAucM4dsNZeDFyRZ0DeDZxRZUdBYGjHKWEA7ThmcVvIEYctEoUBJ/+X\no7n9sIj7V1JMGLJ0SEQrCgjzWVnacUKUZ/G1oiAbOwa020k+ti1LBgmCbJB0EBhCY7KxZcZ0xqgV\nGY+9CR3GGOI4yVL0g2B1EHheyLj7+Sned3cFhqX50aqo8tyNts6MMZCuTVgREZklpuYZU52Da8cJ\nrShkpR3TTjxJkpW72n8g5v/917tphYZ7961w7CN2crCdcPQRh7LjkBZ797c54vBF4iRl+7YoSzKJ\nE7wnH3tmOqn2xT6Arkk+7z/QZttCNLB1drCdDQkot57a7aRvskmlX3pA4Oy3TkTqZZO+o5U3uHv3\n8sRO6tffeuekNjUxp59y7MD3ovaVQgpFN1orCgmClCQw/J/7DrB0SIsTjz2Kffe32Xd/m20LIYuL\nYT7RJzxgxwIHVuKuYFSMOet9V6Iw6HQNxqknCLIP5uK24W9TK1z7/kbR2u67qgkhWddq9yDt4mHV\nLkoR2Rr6jm6dWge03tZjceUTGENi6MxAvdAKieOEJA1JUs+2IAtWSZoS5mnxUVBkKaadAsR0uhGz\nFllxUZX6LGmkfAz9xpQVOhmQpcLGg15bBLVBc54VySblq7xiypqi8ohaaSL1Uz4/6Tu6NWod0AYl\nKgRBQAvP4TsW8i5Dz0JrkWh/mz17D5Kknu3bQtqJJzApKatzk5XLThWtpdAYDq4kpGnK9sUWcZx0\nEkUG6fdhTZIsWGb36lYDUPk1YZ/WXO82w54WXGBMaaZtfUlE6qjz/Z2xIt1NUuuAVi4kDL0ttnxO\n6XwOrlZoOGQxZKG1nThJO/OjZbEhC1hRFHSWx3GWaN+Os+7HKDLgswk9w2D1Cqv8PwxPuMiuzui0\n+nx20LpSExGZgloHtKCnddbb2gl8lkmYxFnX4vYgS+xoJ0EnYJkwIMjT0rMB1HRqFxpM3tWYtdIK\nYc9+yv8PC2xZy6r02nF+eRER2ZCZbhtHYVYxPwrI76F5Dqxk9RkXt2VFhqPQcOBAzOJCiDHZpJ9R\nGBCFAWFoNjxmK80TRkREpF5q3ULrp9/N1iDIWmTeZwOvjc8idRQE4GFhISQpqn+k2QDlYlZrY7q7\nMtPUd1L5w6CoKlIaT+ZTfAoxSafKCORj2fpM5dIveWSadHNaRObFzLXQ+p2cjTG0WiFRFLC4LSJq\nBVm5qyibFuaQxVaeXFLMQQaQBason2ut+JfkAaCdZIWJ12QkmgATGJKUrntraTpo7rPVzEWYfqV0\nBTMRmRczF9DiZHDVxCCv7FGUrwoDOq2tlTgB70nStJOWnySrrbYi0BQlrMIgH1y9JuMw+1dkGxbH\nMyh7MSgFPYB20l0fMkmrVoEUEZFhZi6glYsH91+fJ20U/3qSOgylQsT5a1KfVR0pbzco+iRZnWOs\nvO0iUBXH05kNrWd+s97WmenZT7rO7zNMeV+Dfu733PKyzTTpud5ERIaZuXtorT4VOLplqfNRFJDm\n1fnbiWdxIZ+JOszS8st5HUnaZ3yXyboRw9Jszp37aqVqH0VFkPL0MoPGoRhjuioIGGP6Vhmpqjfr\ns3OcfWbYzmamHpw1uhnU3Ski0zRzAW2YOEnzcWAG41eTO5LEZ1193ueD20xW1QPTCXpxslrfEfLq\nHN53KogUU84UA6aL4NaOkyzbku7U/mEn8zjpTihZrR6y8SDQbxhB7/g98mNvaoJIU38vEdmYmety\nHCaboDMrOBxFYTYjdBR2BmAnPu8qBLIEkezk34pCDKtdk8VM0iZPHMlOloYgCAjDoDM+Lquq313N\npEqVgKJaSZcBwWy9LrveedlgNdGlLOyzrCma+nuJyMY0KqD1jilbaWep9Du2R4SBYVuUdTUmqc+n\nmMmyGYuZqntfH4WGMJ8CpreecJEssj0vXFxOVhmWuJKmvlNXsmCMGTgIuz1kWyIisqpRAW3tlCur\nXYmYvGWE72Q1Fl1z7TjtmhW73I1XTipJ0nS1uHFpn+VkjDRN145t69omaxJQeo+9rDdLskwJF+PR\n+yfSLI0KaGXGZLNPF92BgclaYB5DK8r+D4KAKAjye2+rY9EGBZck9XjWPqdI9igKHkdh2LU+u++2\nGhjL98/W06/7sLxfGZ3eP5FmaWxAg1KFD0MnkcPjOwkS2RW6ZyEKOHAwzltrSdc2vPedLsSs1Nbw\nK/uuQJbvo3cs26jUohARGazZAS0opmPJEjmMMQSszjfm89TCIAzyrMfMoMAR9GnBlbsby/vsrGfy\nLQEFNhGRtRod0KC4r5UFgCgMWGiFWSakMazEaZ62b1anmwmCrkSMrItwcEAq7oelfYJMYLLJ/ial\nCIxKFBERWavxAQ26Ez3S1Hcm4jR5GatiTFmR8BEYWGknnWDYr0GUJGl2byz/Gc+ahJF+xzHsOVVb\nXmFPIoqIiDRsYHU/vbNEe7IU/dTDgsm6IdtxNvlnMYbMe8/BdsxCKyRJ0zXp/EWLrKjGkXVnVuxa\nHJJ0UrVrsjzWTYkNIiKZuWihlRX3wQJj2H8g7kw5U7TUijT+7dsi2nHamb06SbvT8MMgmxwUoGpM\nGTbeTERExjM3Ac33JH0U2YflMWKevAgxRV3iUrdeV3FikxclXi27NKilVGW8mboNm0N/S5Gt0/gu\nx0Jv1f12krKYV/loxymtKOhE91YeyIpCwmsnFC1q+Vff77jPkdmgv6XI1pmbFlpZnKREwWpiRTG2\nLE1TkiTNux5XW3LtOKEdJ11X30X35Eb3W7wmq2Ay3tV81elZ6thq0NQyIjJpc9NC65XNRp2dUMvJ\nIACYtePJYO3Vd+/j9aq+Z+uLfY1/NV/19XVsNdTxmKpSdX+ReprLFlpgsjJWcdw9nitJswzI3rnE\nojBYk+nYb2xaOXGkn/I2ercns0PjAEXqaS7Pqqn34FNMsFqeqshY7K2U3y/pI0n7n9DW60brVxZL\n+qvzexOVWvfSDHXuAq/rcdXRnHY5GsIw6Oo6Sn2aDZL2qxX0B2Uvpp5OOn95fXk26vX0zoYt3erc\npdevO1pmW50/b3U+trqZyxZacUIqdx2FYUAQBrTC9ctLFd2Nw+Y9K/QWO17dX/eHVC02EZHxzGUL\nraivWMyHVizz3mOK2ahL68qttc6YNLrnQoPBV1L9kgh6azwasqAWDNnOZlKig4jMurlsoRWKOcx6\nx6iV1yVpViVktWtyNUOxmKusnaQDg0GxnfVsdJ60SVMwE5FZN9cBrVAkhfTr8jOs3i+DLEMS6Kqu\nXyQJFDNh925nUl2Jo4x9ExGZFyN1OVprtwMfA44CloEXO+d29zznz4Bd+T4+4Jz7oLX2gcC/AN/M\nn3atc+5dox78pBiTlcAK+7RSwp70+t5ix7B6Ty5JU6Jg7TXCpFo/xTg2dQ+KiKw16j20VwDfcM5d\naK39NeD1wO8XK621Pwc82jl3srV2G3CbtfZq4ATgr5xzvzvugU9alAepopZj7z2u1GdTxQwNJJvc\neirGrsVxSqtVPaNSRGQejBrQdgFvy3/+DPCGnvVfBW7Nf/ZACLSBE4ETrbVfAu4Cfs859/0Rj2Gi\nikBVBLSU7mqNWUq/Z1AYyRJKTDZHmune5qDnr/ecQcdo+gwZEBEB2LnzEKINDCEaZmnH4kS2My3r\nBjRr7dnAuT2Lfwjcl/+8DBxeXumcOwAcsNa2gCvIuhz3Wmu/BdzinPu8tfY3gMuAXxnzd5iooNRl\nmKQpYelxNCCApKnvel0V4wQjVRkRkUH27Nk/sW0t7z0wsW1Nw7oBzTn3YeDD5WXW2muApfzhEnBv\n7+ustTuBq4HrnXNvzhd/ESje7WuBi0Y77OnopPKvE3yMUdq71EOcrJ2QVmRejPrJvxE4Lf/5VODL\n5ZV50sgXgMudc39SWvUh4AX5z78A3DLi/jdVv+7AQdmF/SqKjFtGR5mMIiIbN+o9tPcBV1hrbwBW\ngDMArLVvI2uV/Qzw48BLrbUvzV/zEuA84HJr7W8D+4Bzxjj2TZPFk+5A5fMVayrsD1he3G8bpdWm\nlp6MSq0zmWem5q2BqR9cnKT5/Gh5Nkupbl+a+q5lRaWQNK/SX04sSfLB1uXlIiIjqnwS2b17eWLn\nzetvvXNSm5qY0085duB7MZelr4ZJvScKswyhdtxdASQMDe046cxpBv3HpRljJpZlJCIi1ah/okeU\np97D6ti0rvUb7NIZVJx4UqoUSBYRmQcKaD2KbsRBWYudmo5p9TJU5ecV5bEmp9lV+pv8u4nIZCmg\n9ci6ENcvElwuWDxMb3HiOB1cyHgUUVit+PGsavLvJiKTpYA2QDn1vlwUOI4T4iTpKli8EVE+sei4\naf2Tb+k1j94fkfmipJABelsGnYxGwHgI1rmXNqjLsrdG5CgDsovT9Ky2XqY1CH1W3x8RGY1aaBWE\npRmuW2HQaWUl6eCEjGwe0PVbCKMkdQTGMMvn6iLpRkRkkhTQKiiu9APozFQN2Ym5SA4p/5y9plrF\nkDCfS23UY5pFWRFnZWdKdeo+lirU5bgB5bFlxYzVxezV7ThhodW9vkrQCYLZDUwbVXQ1BsYw001M\nmbpZvoCT6VELbQymq+tPV5DriWO1ykRk8yigjaHoNitaHut1i6y3vuiynJXulQ1nWprmdR3N0t9L\npOkU0MZQjEUzxqwZb9bPeuvbydrK/XWWbHBMXZX3aNakmjZIpDYU0EaUJGmlsWhZski1q/goMKR9\nrvjr2gIYNaGlSYIKLXMRmQ4lhYzIU6TPD786763YP0w4YGxbXVsA85TQMkhd/zYi80gttBGFgak0\nhqxqMBMRkfEooI2oSD+v0t3U2+WoRILJycYAVi8ULSLNpS7HMQzqIuyVek8UdM+hJpM0O4k0IrJ5\n1ELbZGnqUa9jf+uVD6uieyygiMwzBbQJ6tft5ak2Rm1uVax5OYxaZyIC6nKcqEEnVp1w+8vmntN7\nIyKToRbaJim3OpIkIUnGT1xQK09EZDAFtE2y2iozBEHQVaV//G2KiEgvdTlussDkXWu6dBAR2VQ6\nzW6yolVVpXU1qS7FJo1za8rvorFyIptPAa1GJtWlmKbNKZg7S8Wah4kb9DcRqSsFtBkQx8mGru6D\nAUWT20lSqVyXTF6kPudGKar/qNVdL/qWzYCUjbXeBrZq9N3bMoFaZ41SfJXU6q4XJYXUkPee1K8W\nNm5N6OperQSRyVDR8XrSGW4KqnZLJKUZq71fTSKY1FVgU+5HyfxQl55shFpoU1A1iKSpJ4yCrJL/\nJh+TyCzQBZhshM6bNaIuQRGR0ekMWiNFEePebpYq3S7qmhGReTdSl6O1djvwMeAoYBl4sXNud89z\n/idwJNAG7nfOnWqtfTTwEbIkoW8Cv+OcUx55Sb8ulirdLuqaEZF5N2oL7RXAN5xzTwX+Enh9n+c8\nBtjlnHu6c+7UfNnbgdfnrzPAc0fcf21577sKEff+3/vc4l+SjjamxXtPPIHCx8DEtiMishVGDWi7\ngOvynz8DPKO80lr7YOABwN9aa2+w1j4nX3Ui8KVBr2uS3pJXg1penfUDnrOR/U2imr9aeiIyq9bt\ncrTWng2c27P4h8B9+c/LwOE96xeAS4F3AQ8EbrTW3gwY55wf8rqZZ4wh6HOZkLXEsioe/V4z6qjn\ncuHjLJ6NHpSUlCIy+3buPIQoCieyraUdixPZzrSsG9Cccx8GPlxeZq29BljKHy4B9/a87AfA/3DO\nxcBd1tqvA5as6AVDXtcI/QJKkma/uvHB0PtkqffrttZ6W1KrrUA2PHYtSVOCvKW4kX2KbCV9Hgfb\ns2f/xLa1vPfAxLY1DaNekt8InJb/fCrw5Z71zwD+GsBauwN4PPDPwNettU8f8rpGKr58YdA/mHU9\nt0IR22EzYwcV9lGWpko6kdmjz6P0M2pAex9wnLX2BuBlwJsArLVvs9Y+xTn3GeBfrLU3AZ8DznfO\n3Q38IfAma+1Xybolrx77N5gBxhgMplJh4H5dkpspDHViEJFmMDXPaqv1wW1UnKSdCT+h+yqz7l0o\ndT8+kYar/OXbvXt5YufN62+9c1KbmpjTTzl24HuhLIApypIu+mc91j1Y1P34REQU0KYsS9yYTGWP\nmreuRUSmSsWJpyzLJpzctkREJKMWmoiINIICmoiINIICmoiINIIC2pSl3pOmg5M52klSabyaiIh0\nU0CrG9+wwXcyl5SBK1tBAW3KAmM6dR37icKAaMrVQkQmLRnSCyGyWRTQtkDvVC/ln4d1R4rMCoNa\naTJ9CmhbIAoHFxBOWR1fphOCzKpwyGdcNkbngeoU0GqgXUoCKXc3tpUcIgNks5zr8zEPVmL9natS\nQKuBIO+C7C0AHJjxZ6GW6mbtvfbp7B2zbJxuqVen0lc1MGimaM0gPV2z1EVmjCGKZud4ZXStCc0+\nPQ90xqyRNPWkeUtNmkl/2+mI40Tv9RxSQKsZg5JCmmyWWoGzrJxcJfNDXY410jtbtQfQxJoiG9ZS\nd/1c0l+9ZnxeGst7j4GxuyCz7aVq7clcmeRFYKLvz8xQQKsZk1cSyeZNM4TBeON5PHS2JSIb5726\nL2eFAloN9ctujEcci6Kvoch4em8FSH0poNVQv6tBz2hdj2qdiYwn0PdnZigpZEZoLIqIyHBqoYmI\nSCMooImISCMooImISCMooM0wX3GMmsbQiMg8UFLIDKuavagsRxGZB2qhiYhIIyig1VRvN2HV7kUR\nkXmlgFZTvbNVJ6mKFIuIDKOAVlNREHS1yMLAkKZqoYmIDKKAVlNB0F2yyhjTVVOuqd2PTf29RGTz\nKaDNqN4uyaaIG/p7icjmGylt31q7HfgYcBSwDLzYObe7tP7ZwHn5QwPsAh4PLAKfAv41X/c+59wn\nRjv0+WbIWjNNu68WGNPI36sJvPfZdERoKIjU06jj0F4BfMM5d6G19teA1wO/X6x0zl0HXAdgrX0N\ncKNz7p+ttecAb3fOXTrmcc+9phYrDjXTcL15MJpORWpq1IC2C3hb/vNngDf0e5K19v8CzgSenC86\nMVtsn0vWSvsD59zyiMcgPbLUfjBGV9AyeSZvPasFPV16v6tbN6BZa88Gzu1Z/EPgvvznZeDwAS9/\nFfAO59zB/PHNwIecc7dYay8A/hh49YaPWvryAApmUzOPJxpNdjl9G/2M7dx5CNGEenCWdixOZDvT\nsm5Ac859GPhweZm19hpgKX+4BNzb+zprbQA8B7igtPha51zx3GuBy0Y4ZhmguP8k05F6CHV+l5rZ\ns2f/xLa1vPfAxLY1DaPesLgROC3/+VTgy32e83jgW865+0vLPmutfUr+8y8At4y4fxlg1lsM3nuS\nNJ2JwBwYSGfkWEXmwaj30N4HXGGtvQFYAc4AsNa+DbjaOXczYIFv97zuFcBl1to28APgZSPuXxrN\nzERgNmY2jlNkXpiaX13W+uDmRZFsMq37J/N4b0pkHZW/ELt3L0/svHn9rXdOalMTc/opxw58L5Qj\n3QDpJhQu7i2G7Bm8j0nvW8FsrZpfeIrUggJaAyRJOvEgkJaKIRtjCINg4D4UgDaf3mOR9SmgNUAY\nBhO/gg8CZUyKyGzRjNUNEGzC1btaBCIya9RCExGRRlBAmzNpOloCife+NmOuZmWcmohMlwLanEnS\n0RJIshqR9Rh3lWr2bhHpQwGtAYrqGlVEI1azr1P8UEV+EelHSSFNUbEHbtSWTZ1aRJuRBCMis08B\nrQGMMYSqkisic059NyIi0ggKaCIiNaaM3uoU0EREamwlrpbwJQpoc0NXeSKzKdQs4ZUpoM2JOmUp\nikh1ow61mUd6pxpMrTIRmScKaA3Wr1WmICciTaWANmfiRDeYRaSZFNDmzGbMnSYiUgeqFDJnVDZK\nRJpKLTQREWkEBTRZQ12SIltH37/RKaDJGhqzJrJ19P0bnQLaHPN+tNmrR9mPiMhmU1LIHJvWlaCu\nOEVkGtRCExGRRlBAky7qHhSRWaWAJl3UPShSL7rIrE4BTUSkxtqaD60yBTQRkTpTp0llCmgiIjW2\nEIVbfQgzQwFNakX3CyZjWmMMRepE49CkVpSUMhl6H2UejRXQrLW/DJzunDujz7qXAi8HYuBi59yn\nrLVHAlcC24HvAS9xzu0f5xhERERgjC5Ha+27gDf324a19mjg94CfAZ4FvNlauw14I3Clc+6pwNfJ\nAp5Ih7rJRGRU49xD+wrwigHrngLc6Jw76Jy7D7gdeAKwC7guf85ngGeMsX9pIHWVicio1u1ytNae\nDZzbs/glzrlPWGufPuBlhwH3lR4vA4f3LC+WDaOzm4jIBjzoQUsTO2+efsqxk9rUVKwb0JxzHwY+\nvMHt/ghYKj1eAu4tLb+/tExERGRsm5W2fzPwVGvtorX2cOCxwDeBG4HT8uecCnx5k/YvIiJzZqIB\nzVr7Kmvtf3XO/QD4c7KA9UXgAufcAeBi4NestTcCJwPvnuT+RURkfhlllYmISBOoUoiIiDSCApqI\niDSCApqIiDSCajlWZK0NgPcCxwMHgXOcc7eX1q8p9bUlB7oFKrw37yIbVL+cL3puPuB+Llhrfwp4\nq9hq3n8AAAKySURBVHPu6T3Lf4msek4MXO6c++AWHN6WGfK+nAucA+zOF73cOeemfHhbwlrbAi4H\nHglsIzuXfLK0fq4/M+tRQKvuecCic+5ka+1JwKXAc6Gr1NeTgEXgBmvt/3bOHdyyo52uge9N7kTg\nWc65u7fk6LaQtfaPgDOBfT3LW8A7gCfn62601n7SOffD6R/l9A16X3InAr/pnLtlukdVCy8C/o9z\n7kxr7QOBW4FPgj4zVajLsbpO2S7n3E1kwaswqNTXvBj43uStt8cAH7DW3mit/a2tOcQtcwfw/D7L\nHwvc7pzb45xbAW4AnjbVI9tag94XyALa66y1N1hrXzfFY6qDvwbekP9syFpihXn/zKxLAa263nJe\nibU2GrCuSlmvJhn23hwKXEZ25fls4LettXMT7J1zfwO0+6ya68/MkPcF4P8G/hvw88Aua+1zpnZg\nW8w5t9c5t2ytXQKuBl5fWj3Xn5kqFNCq6y3nFTjn4gHr5q2s17D3Zj/wLufcfufcMtlA++OnfYA1\nNO+fmb6stQZ4p3Pu7rwV8r+An9ziw5oqa+3Dgb8DPuqcu7K0Sp+ZdegeWnU3Ar8EXJXfJ/pGad3N\nwCXW2kWyG7lFqa95Mey9+QngE9banyS7gNoFXDH9Q6ydfwYek98n2UvWdfTft/aQauEw4JvW2seS\n3Sf6ebIkiblgrX0w8Dnglc65L/Ss1mdmHQpo1V0LnGKt/QpZ3/ZLrLWvIuvT/qS1tij1FbBa6mte\nrPfefBS4iayL6S+dc7dt4bFuKWvtGcAO59wH8vfos2Sfmcudc3du7dFtnZ735XyyFspB4AvOuU9v\n7dFN1fnATuAN1triXtoHgUP1mVmfSl+JiEgj6B6aiIg0ggKaiIg0ggKaiIg0ggKaiIg0ggKaiIg0\nggKaiIg0ggKaiIg0wv8P3pdLInNGTSQAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x11a6f12e8>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"RGZ\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAbQAAAGoCAYAAAAuIBCmAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztvXvUJVV57vvMWuvrC90f2HgJIcckYnSCOMBNI4K2SFQE\nlMQrA2z1cBFla9QAh2xQboJuRdygbhl4IoqHqM0BFMbmeBSNGBWaEIYoiZI4syFjKyEqzemm+fry\nXdaqOn9UzapZtapqVdWqVbf1/MaAXqsuc86qb9V86n3nO98pHMcBIYQQ0nasuhtACCGElAEFjRBC\nSCegoBFCCOkEFDRCCCGdgIJGCCGkE/TrbkAa27YttC4Ec8OGfbBjx566m9EoeE/i4X2Jh/dllGc/\ne17U3YY2QAutZPr9Xt1NaBy8J/HwvsTD+0KKQkEjhBDSCRrtcqyKHz70eOK+417yBxW2hBBCSFFo\noRFCCOkEFDRCCCGdgIJGCCGkE1DQCCGEdAIKGiGEkE5AQSOEENIJKGiEEEI6AQWNEEJIJ6CgEUII\n6QQUNEIIIZ2AgkYIIaQTUNAIIYR0AgoaIYSQTkBBI4QQ0gkoaIQQQjoBBY0QQkgnoKARQgjpBBQ0\nQgghnYCCRgghpBNQ0AghhHQCChohhJBOQEEjhBDSCShohBBCOgEFjRBCSCegoBFCCOkEFDRCCCGd\ngIJGCCGkE/TrbkDT+eFDj8duP+4lf1BxSwghhKRBC40QQkgnoKARQgjpBBQ0QgghnYCCRgghpBNQ\n0AghhHQCChohhJBOQEEjhBDSCShohBBCOgEFjRBCSCegoBFCCOkEFDRCCCGdgIJGCCGkE8xUcuKk\nRMOEEELaDy00QgghnYCCRgghpBNQ0AghhHQCChohhJBOQEEjhBDSCWYqyrFMkiIm59evwcY/eWbF\nrSGEEEILjRBCSCegoBFCCOkEFDRCCCGdgGNoUyBpfO24l/xBxS0hhJDZgYJWIWmptyh2hBAyGZ0T\ntLbma2xjuynChJRLUj9wyvEHV9ySdiIcx6m7DYQQQsjEMCiEEEJIJ6CgEUII6QQUNEIIIZ2AgkYI\nIaQTUNAIIYR0AgoaIYSQTkBBI4QQ0gkmmlgtpXwZgE8ppY6LbP8zAJcBGAC4USl1g5RyLYCvAXgO\ngAUApyultk1SPyGEEKIpbKFJKf8LgC8BWBPZPgfgMwBeB+BVAN4rpfw9AO8D8HOl1CsB/A2AS4rW\nTQghhESZxOX4KIC3xGw/BMAjSqkdSqllAPcCOBbAJgB3ecd8B8BrJ6ibEEIICVHY5aiU+qaU8o9j\ndu0LYKfxfQHAfpHtets4mJerAej0aEKIzMdnPTZveUlll11n2diOA6vB7SPNxfttZ/7xDAZDp9/v\nlVL3XX//v0opp0xOPOaPE+/FNJITPw1g3vg+D+CpyHa9bSo0vXObFpNcd5Zzo8dkEZqyGFf+NK+7\nDESFdZFuYTtAL8fPZseOPaXVvbBrsbSyqmAagvYvAF4gpdwfwC647sb/BuCPALwewAMATgJwzxTq\nBlC8c2s7k153UoebJGJJx5R9/ycpb9oin6UMYHZ/k2RyLP50MlOaoEkpNwNYr5T6opTyfADfhTtG\nd6NS6nEp5RcA3CSlvBfAMoDNZdVNJkcIgbwrL9TRSeepU19PnZZRkftKiAlfhrLT9OVjGt24WWSc\nOOj9tu1AiPSHsQo3paZIPXQRkgaR+Ye4bdtCaf1mE9dpPOX4gysdQyMdJtrBx4lGU16SJhUjihkh\n7YKZQsjEmPKlRcCyBAWhZpryYkFIVdBCmzEmdcNFEUKM+EJ0uUPb8Qe0xwWSdAW6KQmpD1poM0hV\n7+1N6dZpqZA2w99vdmihzRhxFlXZ6IAQy2rWmNqsQUuRzBq00MjUsB0n1gXXZYFroog43t+hCh56\n6CGccsopOO2003DdddeN7N++fTvOOussbN68Geeeey727t0b2nfCCSdgaWkpdM6jjz6KjRs3jmwv\nm8XFRXzwgx/E5s2b8Z73vAfbt28fOea6667D2972Npx22mn4p3/6JwDAr371K7z97W/H5s2bcfnl\nl8O2bQDApz71KZx66ql461vfiltvvRUA8Nhjj+Ed73gHNm/ejAsuuCB0/WRyKGgkE7pTzNIx+gEh\nDdGtJopMV7n88stxzTXX4Oabb8Y//uM/4p//+Z9D+6+//nqcfPLJ2LJlC170ohfhlltuAQDcc889\nOOuss7BtW3gBjl27duFTn/oUVq1aNfW233zzzXjhC1+ILVu24E1vehOuv/760P6HH34YDzzwAG67\n7TZce+21uOKKKwAAn/zkJ3Huuediy5YtcBwHd999N+6//378+te/xi233IKbb74ZN9xwA3bu3IlP\nf/rTOO2007Blyxa87GUvw1e+8pWx7eLvNzt0Oc4QVQcsWExxEMvtt9+O73//+9i9ezd27NiBv/iL\nv8AJJ5yABx54AJ/5zGfQ6/Xw3Oc+F1deeSWWlpZw8cUXY2FhAU888QQ2b96MzZs3413vehf2339/\n7Ny5E5dddhk+8pGPoN/vw7ZtXHPNNfj93/99XHXVVXjwwQcBACeffDJOP/10XHTRRVi1ahUef/xx\nPPHEE7jqqqtw6KGH4k//9E9x0EEH4fnPfz4+8pGP+G0955xzsGdPkErp+c9/Pj760Y/GXteuXbuw\nvLyMP/zDPwQAbNq0Cffddx9e9KIX+cc8+OCDOOeccwAAxx57LK699lqcccYZsCwLX/nKV/DWt77V\nP9ZxHFx66aU4//zz8f73v9/f/sUvfhEHH3wwjj322LH3VPOrX/0Kl1wSXuDj5JNPxqmnnhpq29ln\nn+23LSpoDz74IDZt2gQhBA488EAMh0Ns374dDz/8MI466ij/vK1bt+Kiiy7CIYcc4p87HA7R7/fx\nyCOP4GMf+xgA4IgjjsAnPvGJ2HtJikFBmyFc46qYqJUphHzjBPbu3YuvfOUr2L59O0455RS8+tWv\nxqWXXootW7bgmc98Jj772c/ijjvuwKGHHoo3vOENeN3rXoff/e53eNe73oXNm90kOyeffDKOP/54\nfP3rX8dhhx2Gv/qrv8JPfvITLCws4Je//CX+/d//HbfeeisGgwE2b96Mo48+GgBw4IEH4sorr8St\nt96KW265BVdeeSV+85vf4Pbbb8eGDRtC7fzrv/7rzNe0a9curF+/3v++bt06PPbYYyPHzM/P+/sX\nFhYAAK94xStGyrvuuuvwqle9CgcffHBo+3vf+95M9/Q1r3kN+n23i/ujP/ojfPWrXx3b/ri2mfuf\n8YxnhK5vYWEh9KKot61evRqrV6/GysoKLrroIpx66qlYt24dDjnkEPzgBz/Am9/8Ztx99910OZYM\nBW2GcFBd5CHD19N56UtfCsuy8KxnPQv77rsvnnjiCTzxxBM499xzAbjjOS9/+cvxqle9CjfddBO+\n973vYf369RgMBn4Zz3ve8wAAb3vb23DDDTfg7LPPxvz8PM477zw8+uijOPLIIyGEwNzcHA4//HA8\n+uijAOBbDgcccAB++tOfAgA2bNgwImbAeAvta1/7Gr773e8CAK666irs3r3b37d7927su+++ofLW\nr1+P3bt3Y82aNbH7Te68804ccMAB+OY3v4lt27bhrLPOwte//vXM93T79u14znOeAyCbhabbNq7t\n5vXNz8/DsqzQNn3ezp078aEPfQhHHXWUb5VeeOGF+NjHPobbb78dxx57bOw9J8WhoM0QPboAG8PD\nDz8MAHjyySexa9cuHHDAATjggANw/fXXY35+HnfffTf22Wcf3HjjjXjJS16CzZs34/7778ePfvQj\nvwz9wnD33Xdj48aN+MAHPoBvfetb+NKXvoTXve51uP3223HGGWdgZWUFP/vZz/DmN785dJ6J2Smb\njLPQ3vnOd+Kd73yn/31ubg6//vWv8dznPhf33nsvPvCBD4SOP+KII/CjH/0Ib3nLW/DjH/8YGzdu\nTCz7b//2b/3Pr371q3HjjTemtiV6T5/5zGf6+7JYaLpthx12WGzbjjjiCHz605/Gu9/9bvz2t7+F\nbdvYf//98aIXvQj/8A//gJe97GX48Y9/jKOPPhqLi4s444wzcOaZZ+LP//zP/TLuu+8+nHfeeTjo\noINw44034uUvf3lqm0g+KGgdh5ZSM3nyySdx+umnY2FhAZdffjl6vR4uvvhivPe974XjOFi3bh2u\nvvpqCCHw8Y9/HN/+9rcxPz+PXq+H5eXlUFkvfvGLceGFF+ILX/gCbNvGhz/8YRx66KF44IEHcOqp\np2JlZQUnnngiDj300Klf1xVXXIELLrgAw+EQmzZtwuGHH46nnnoKl1xyCa677jq8733vw4UXXohb\nb70VGzZswDXXXJO7jrgxNCD+nubh7W9/Oy688EK8/e1vx9zcnN+2q6++GieeeCIOO+wwHHnkkTj1\n1FNh2zYuu+wyAK7Vdemll+Laa6/FQQcdhBNOOAFf/epX8dhjj+G2227DbbfdBgD4xCc+gec973m4\n4IILsGrVKrzgBS/wyyDlwOTEHUcLWtYMIZMsd8KlUrJx++2349/+7d9wwQUX1N2UVqKt12OOOcbf\nNgP3lMmJPZicmFSC7cz22k20hqvhkEMOwYEHHlh3M0gDoYU24yRly2fHnP8+8L6RKUILzSPNQuPE\nalIZ0cnZVWawIKSt8BnJDl2OM06dWfAdB2iyQZP3PtA6I6ReKGikMqIdfp5MIk1y5zH4hZBmQpcj\nGcG26QpMg0JGqoS/t+xQ0MgIZUlZljGyqoSz7HqSOhmOCxJSH3Q5zgB5XWRlZRQpM9UW31IJIeOg\nhTYD1CUGosa6yyar1SWE6Mw1E9I2KGgdJM7tNS47yDTcZFk69qo6/7pEhu5HQqqjNYKWp2MouxOp\ns1Mqct15m2s7wfnR//LWXRZ52lDn35t1s+6q6ibjaY2g5XnDLvttvE4XUpHrzttcS7jnamHT/9Z9\nz52M5Vbx906qY1zd05zLVufvnHVXXzcZT2sEjWQn7ziOPlYLW1PyMVo5H3a+7RIy21DQWsy0QtHb\nGthAPSNktqGgtRibHXgisz7WwflwZBahoLWYprgG46hjoF2IoKxpiH2bBKKNFjYhk0JBazFN7rTy\ndP1lyYR5P8oW+ybf6yTa2GZCJoGCRqZCnq60zG7XHAcsGwoEIc2GgkamQp2h0ISQ2YSCRmqnTWNT\nhJDmUjg5sZTSAnA9gMMBLAE4Wyn1iLfvJQA+axx+NIA3AXgAwL8C+IW3/Q6l1OeKtoFMRtY1xqa9\nFlnTF/okpE6atBZg05kk2/6bAKxRSh0jpTwawDUA3ggASqmHABwHAFLKUwA8rpS6S0r5WgA3K6U+\nOFmzSRHiHowmiFrXn1V2SGQSbAfo8eeTiUlcjpsA3AUASqn7ARwZPUBKuQ7AFQD+0tu0EcBGKeWP\npJS3SSl/f4L6SU6ijr2mdLJNace0oEOVTEKTp+c0jUkstH0B7DS+D6WUfaXUwNj2bgC3KaWe9L7/\nEsCDSqnvSynfAeDzAN42QRtIDuKeiyZlxO8sDuCAVhopRt7fzYYN+6Df75VS9/z6NaWUUxWTCNrT\nAOaN71ZEzADgHQgL1g8A7PE+3wHgygnqJznJ82DQTVYeliUY+EIqY8eOPeMPysjCrsXSyqqCSVyO\nWwG8HgC8MbSfmzullPsBWK2UeszY/CUAb/U+vwbAgxPUT0okrsOtuxOuu/4y4csBIdNnEgvtDgDH\nSynvg+vNOlNKeT6AR5RSdwJ4IYD/FTnnIgA3SinfD2A3gLMnqJ+USDTSUIj6rQpGPxJC8iDq7rTG\n0OjGdYlpuhiLlp3lPLpGyYyQ+Ue+bdtCaf3mDx96vKyiSuOU4w9OvBecWD1DpL28THWeWcHzsk0n\nKFg4IaRzUNBmDC1qVS4vMk37icYZIURDQZtRbKc6f+40rT+6GwkhmkmCQkjLKGt5FY5bEUKaCC20\nGaaoKDlOt0LqCSHdgILWIsoWkaLl0TgjpDzGjWfz5TE7FLQW0ZSfdRPcjXzISd1U9Ru0+VPPDAWt\nRUxjZee6zp8UPuOkbsrSMyFE6vPE5MTZoaC1iKzLvGQl7cimW0B8xkndVPVOV/fLY5ugoHWMPDqk\nH5M4H36z5YwPeR00/SWnavgbbB4UtIaTtxPJ84ylPZB8VEmUWdIzinc7oaC1gDwPV5G3xjgfPt8+\nSRT+JEjToaA1nDixySpwSeHAZae9mlYaLb4lNwu+5JCm0ypBq3MeVpPqnjSMN8+l1HvdpVbd2r83\n666+7knFu87rnmValfqq7DfEPOU1qe6sYbxJdVg54oCztHNa97HoLU9KzdXWvzfrZt0kG62y0GYd\n/SZX1gPQ9DfDwqm5Sm4HIaQdUNA6TtNFaxoIzOZ1EzLrUNA6RFIn3uTOfRptG5d5gRDSTShoLSDN\n1ThOEFLnmuXMPFK2+NhMUgeg2S8chLQJClrDMVeYHn9s/HFlpMzK046s0IgihJRJq6IciUsb3ujN\nNiYJKt2CzcK2HQjBvwtpLxS0BmK6GHXn4rrnRsPR9XfHcWBZYiKxixMhIcTEK1Rzhet0mnJvGtIM\nQgpDQWsYuvOPCpjZ2SR1gPoNO1reuPP0Psdx3JB373+TdLTmuUnZSsa1qam0ue1pdO16yOzBMbSW\nYFprOtWU7ljjgivM/Y6xbVwdlhCJb+p5oyjb4BotAjt+QpoJLbSGkpbNw3EAiNGM+PocbWkJeELo\nn5cvybG2Fqfhbmy7KLS9/aS7lvYsQwutYSSF5o/kmjOOtSzhC5DGKkGIJoUdBekCXfU0dBEKWgvR\nApaXrOfkjUqcdK4bGcW2p7OCAQloywR8ztfMDgWtBYx76EzXSdTFFx1vy1NnGx72OpnWsjl520AI\nceEYWkcJJkLDH28rOmbAsPvqybMiApkudf/2+VvIDgWtBUzyFp7nWeQgeT54nwhpFnQ5tgQhBOwE\nF5fZsZoTokdWus5ZZxNcanlJukddpW5RnaV7TZoPBa0hZOoYnODYrB2JFrYs4fv6uFYHJLS02YQk\n0dpnsQbociyRSV124+ZsaV96XEaQaVD3238RON4wCl3JZFYoLGhSSgvA9QAOB7AE4Gyl1CPG/s8B\n2ARgwdv0RgBzALYAWAvgPwCcqZTaU7QNXSBrwEWWt7RxyWXNTCNp7ahTFNj5tgv+nUiTmMTl+CYA\na5RSxwC4CMA1kf0bAZyglDrO+28ngMsAbFFKvRLAzwCcM0H9jaNoqHvZUYR510ijS6PbcApGu+Hf\nLjuTCNomAHcBgFLqfgBH6h2e9fYCAF+UUm6VUp4VPQfAdwC8doL6O010nMwcC0uaWG1ub2NABzC+\n823rdRFSFP7eszPJGNq+AHYa34dSyr5SagBgHYDPA7gWQA/A30kpfxI5ZwHAfhPU32jSXGdxrsHo\nj9ZxprOcR9vnlOkclYSQeDZs2Af9fq+UsubXrymlnKqYRNCeBjBvfLc8MQOAPQA+p8fHpJQ/gDvW\nps/Z6/371AT1N5pJBWmyc/Od3CaBs1rU1ibT5LHKtr901c2OHeWFJSzsWiytrCqYxOW4FcDrAUBK\neTSAnxv7Xghgq5SyJ6Wcg+tq/Kl5DoCTANwzQf2NJs4tqN1l5r5QWH1kPllaEEdVBBlH6PboEvxr\ntgeKe3YmsdDuAHC8lPI+uF6gM6WU5wN4RCl1p5TyqwDuB7AC4G+UUg9LKT8O4CYp5XsAPAlg84Tt\nbxXjrDbzzXRab9BceZoAtHTrosmWcRcQDX/zbnTjyiBOxEziEg7HnVtG/Wn7+SDmh/eMRLEdJ7T0\nUw4yn7Bt20Jp/eYPH3q8rKJK45TjD068F8wU0hBG1jsTYbdk1hcP00VY5ppmWTL+N/zliJDamXSd\nQpIOM4U0nKqyggBhUc27yvS0ojLDdbTL4mlLOwnpCrTQKmKcBePnUYw5RJ8WZ8WZ5SftS6OsTjcp\nQ0mZlhvXOQygNUzIKK0RtCZE+k1WRrayogmEi+iNWUfeRMbmv3muO0kYi965uLrzZuQqKqZt/62R\nbNBN3j1aI2h1um/KqFuIQNTSytZfzWCQPLkVnZgy87VzdCmaSSgyZhANRDHbk6esovei7b81kg1K\nWfdojaC1nTwuwPj5axlzMBqWYNaAjiaS9uaclFw5SpdD08vO/TmLlkrBaEPSYChoFZI02TqJsLUU\nf0zUvehago4/3tTGB3acEMeNpbXxOpvELN6/WbzmrkNBq4io8CTtiyPJ1Za0UjWQf7ypaaR1Nm2/\nNqBZY2Xs2ElXoKBVhJPweZK10JIiG6e1XEhTOuEudMCM2CSkfChoFSESPgMZJi0nlVnhGmruMaVV\nN/N0wcokpGlQ0CoiKXowi5Ck9X2J4fI51SfL0R0wjBpDF6xMQpoGBa0GQuNpCdtNimbdzzWPLMsx\nNXTCTXFzEkKaDwWtAlIjGZEeMJKnrFC5U1wTrWqRoagRQrJAQasAB+nWV1yIfVLm/bT9SceXmS3D\ncRxOSCWpzOq8NlI/FLQpEUr0i3BARdQaMgMEfBFKKDcQqexCVWb6KQc51rEoAY41tQ/+zUhdUNBK\nIu6t1MwOnzYxOnaOWcKxRSjSvSRZd3VkV+DLfvugqJE6oKCVxKQrQefNlp8nT+G442w73kXk5lPM\nV9Y0YN9ICMkCBW1K6MnN4wI+TBdiHqqYx6RTadUN3/YJIVmgoJXMqNtxfDLdqEsyS/h+WoBIXtdk\n3FpmbVtMkxBCKGglEp9v0U1zlJRFP+7ccXJkR0Qy7vhS1jLj2FUqjOQjpFlQ0EpmdH0zEXIPZrF8\noot8Rom6G6dlQzXVOGuSkDSpLaQY/Bt2BwralMhifcUtYjlyfML+tIU4k5IT57XamupuZGJfUib8\nOXUHCloO8ghC1C2oiUpE9IhpvS3qRUK78DbalMS+TRZ9kh3+BbsDBS0nWQXBEvFvftoq80P1jYOi\nWTjiIiWL0paON08GlLLKI7NNW54NMh4K2oSkRSRG8zSa+4DRxMRJWTjG9cmZRTZmxWxCCOkKFLQc\n5HUxCSFSU1i5WTfc71rM4iyyuCrNYzimNDnMP0hI+6GgTRHTpRidYK3nkvmrTCN9kvXIXDPjc94x\npSZ33mVbkHVZpE2+x4R0FQpaDGXM4XLLcf91U0vFn2OKW7A/Q70Z20CywQCPdsOXBwIA/bob0GWE\n8DKFYHRsLC3YIy4MH4gmOy7e+bLjnj68x9ViO0CPt3zmoYU2JQKXousStKxRAUvKIEJc+NZNstKU\nqRykXihoMZQhMLorTkt5ZYnuTHbOSp6xJeoZyUrbnwtSDhS0Eohd/iX2uPBcs+rXFWtXoAL7KEJI\nHihoGRknBFl0woEbHDKSLaRFIjMJ0cjOcfCtmxCSh0JBIVJKC8D1AA4HsATgbKXUI8b+8wCc5n39\ntlLqCimlAPDvAP6nt/3vlVIfLtzyinGcZIshLsAj6fjoUi1CCNi24wWQxK9eHS63+LIudQtE0sTx\nTOdmuDezCJf5ISSgaJTjmwCsUUodI6U8GsA1AN4IAFLKgwC8A8DLANgA7pVS3gFgD4CfKqX+bPJm\nV4+D9E5V7wcA23FgxR4XP57mT642RDCpLh01GY3oakuHX7SdaS8UhBACFHc5bgJwFwAope4HcKSx\n7zEAJyqlhkopB8AcgEUAGwH8gZTy76SU35ZSygnaXTnjoqiCJV/Ck6Thb3cS/o238MzkxuHM/fFt\niYb2x1G3a3NGPKuV0oVAIULKoqiFti+Ancb3oZSyr5QaKKVWADzpuRg/DeBnSql/lVIeAOCTSqnb\npJSbAHwNwEsnav2UiHPjJAmG3q7D8h3At86i6anihCiU8cM4IElAxyUrTlo2JnkRz+pcVpOEVluM\nyyYkExs27IN+v1dKWfPr15RSTlUUFbSnAcwb3y2l1EB/kVKuAXAjgAUA7/c2/wTAAACUUvdKKQ+U\nUgrPihtLHldVWe43XY7Z6eu8iZZwM4BYlnn8qFssklDfs1ICy0uPnUXbbQpoNLOIblOcFWjmhMx2\njcmuvKT7aDvOSB1Z7nneLPnj1nRLukfmcemZXJLryPtbK/s3V/TYSdpRxzM2ad1ltKMt152VHTv2\nlFbWwq7F0sqqgqIux60AXg8A3hjaz/UOzzL7HwD+USl1jlJq6O26HMC53jGHA3gsq5gB+TrDSX8g\n2o0TFRfAE4u0c2EuERNst0R8smJ9/DgLMK6Nse02vmcpa1SAExYmNUL+Y0cHx1iOeZn0752ngyq7\n7rwk3fMq6i5aHuuuru66hwraRFEL7Q4Ax0sp74Pbv50ppTwfwCMAegBeBWC1lPIk7/gPA7gKwNek\nlG+Aa6mdMUnDi1LG25iOVOz1gk7cTHEVHfMyExQLBO7HQPiCcPYsP95JLYt0Kw8ARrebLtNYqy1H\npOYklNn5lCnCHMcipH4KCZpSygbwnyObf2l8TnK8vqFIfWWhXWV5SJo7FYiCl7PR3x5YPXHprizL\nDdMPlwXoEibphJPEyEQLT/Q6xjHuCFfMUImolUkT2llmG5pwPVUya9dL0pmpidV5f/pJIfZ6u227\nY1bm/CpTarRwjQqIcYxj7hufzSOPWJgu06HtjNSdB3Nx0CQ3HfuW6ULXEyHpzJagZQxxTgo8AIJw\nel8s9H8pEYxp/ZA+N2/ARBxpK1LrraHxOqM8P79kQhlZ0mZFxx7ZAadjZ7inUXhPZw9aodnphKCV\n+ZDbqe48fUxkQrS3Pymy3BQ2faz73QkJiFl3nIDEXadth4/T58W5OqMPhhUR+FTLMHFPOk3qgKP3\nqm4m9RiQbCQ9E6R7dGY9tLLClceVoEXLFyUAQofmOzooBCNpnhwYVpwI79fjWkIgNC0giWlF1iWP\nzTnGxPHsnULZkY95afpYXpEpBU2+HkLqphMWWpkdfJJbUls4IYsm5t9gtxOyaswShRlFEjomXVTj\nhCfqrjTbmNellckdq/+NWIWTlDlSx5REMM0lG9cGvtV3g6grnHSXzlho05zsaEYGBoEWCMLxER5H\nEwJwbOO7UbZtO/6GYFxLlxuesBya+5UQZZk6qdcMuYww7n4lCXyapRZYmvn+FtEJ7HnO022cBlEr\nmxDSbDoexMAZAAAgAElEQVRhoWnyvlGnWWXmeEtc5KKOSBQicA+GovGF8CMgHbMMQ/SijFiAcVZc\nQuc9Mt4WU17RMaSqxp7qnDAbd250jHFSyraWuwyt4wDeh+x0wkIrY6zEtMKiY2CWMAM6HFjeHhsA\n/EnSwTEaYZQRlBWOAhzaTmjl6rD7MJjQnDq+FWfdTGheZJkPF/1cRr7FMiZOF828UZRpW4qT0vT2\nxVH3+CtpJ52y0Ir6yeOsG0vAn7ultwFe0If3uR/TgTuBR9GPaIw2aZIOJu4Zj4vMjI1qjLQ3a4eR\nZ+ypCG3qaONgvzsd2v67INXTKUHLQnRcSudcNJ+dnhHKqN2I2trSomD2YQ50FhLDMgjVCb++KOOe\n2V4kGEWPUYXKqqhDbYobKOt8uCzH5q03rrysgl9XB82AiHbDv112OuFyzBrgkHoMRsPoLcsKLDMd\nUm8UZc49c7wCzEAPXbAuO9YyMyoeNycsNB7mBAEkZf3emxbmPqmrrGy3Fd1ghDSbmbPQNCNv20bE\notll6fGz8GHB/x3Hm2gNMzoRoX8FwuNruu5oXsVw++LbnLY/C3FjXyY6ACQ5vVWyuJRhwZVxjSZF\nIi7LLK8MmmIZE9J0OiVoeVIzxcVQuJGL3lpnsUEVDuDYoUwfjvshJFCRYMdwJQlfR8LyE65Bzy3r\nxbi5ssydalPHaFnCD8QxmaaoxNVHCGkHnRK0JNLGrkI5GYUhZgDgWV/6WNt2MLTdc2zbxnBou9s9\nV53tOCGxEwistzh6lggdH90XjPEFUwXgiW6aJZUHUwSFELETyLOSdN5EbaxYW5qoZRwDIyQbnRhD\nixI3FhT3fZzbLyjPPBGwHTsUIGIZy1Y7MWGNOjIy6r6M662j7THD9n1hNSMpnXA5ZjBElZ2guTRP\nUTdfXMddxlSAPPQqro8QUh6dstDydKQ6utEcBwPMsPtguRXXtej4k21tz0qLdrbaStPBGhDhbCGm\ntaYTY5mZNcZZMnq3JYKOPmlKQJIVFyfsWSyAuATI4QMQu3/seZiuEcbxJ0Jmh05aaHFjS0D8XOO4\noA8dxAHHgeMNppmLcvZ7FoZD2xO4YLtlCVg9KxQUol2Z2qryg04cwBHh6EddhknPj6JMjnoMVose\nPw0gT+SgaeVpS1AIEX8frUCUzdWtzbp0+6LWozXNMbEM96RNpFneTYtSJaRqOidoadZI0KHGb7O9\n2HsdsejAFYteT8Cx3aVeHGOytV6R2nEc13IbcQWGRdSsWwgREoUkETbbGOd+SxJDHZwS7dDjOvi8\nHWGaAAkhfBEeOc8Qvaqo2mVJyqeNmU5IPXTG5ZjFtRQSlpjzh0PffgIcx7PCjAAPY4XqXi9w+QnP\ntxhYYEGmfWH861tsSHMVOpHt8ddiR4TVDCDxrcmYc4tm/SgqDGXnQixLDOmGbA/8U5GsdMZC05ZQ\n0uRk1+rS28NWSTB+5gCw4Ni2d46D4RDo9dxz+j3hC58jXFEL3H0OhLD8cnqWgKkrvttRAI6dbhGZ\nb6S248SujWZafkmdc5bxubR2ZG1jXiYVuVl2rRX9e7UZWtkkK6220Mw3djPpbyhTvnbxId6tFwRn\nCPT7PQgAA9vB0AEc27No4Imb7bgLvBiDZD1vzMyx3WMsoSMovXoNEXU/aFdlIAp2RGvMUP5o6iuN\nL2bmNXrHZQm9N/Uta0doiqPZ5izz38ogbVpAmVMYCCHtpNWCFoc/2Tm0LbDKzM7fceBaW44N2x66\nQSDeOcOhDQfAysDG8sBBTwA9CwAc2HCFZGA7sIc2el6KLN3V2kY5juHFNF80jc2+COp2mSQt3eK7\nDp2wJRa6D5HzzIjGqOsxGo2YVpYbDJNdCJPcqXViumij45VNaichJDudErTAWgvEyw+OMGTO/+QF\nWgwG2uJwx83gdWqWF+AwHNpYGToY2IHb0LZdkbMdNyt/v2dhaAfWolmX6e40qk4MrjBdLNoCG+14\ntWUZsZw8ATTdqFk76Gi4fZIF6dYbCIIpxlnqmtSiSppjWIrLjd4tQlpLawUt6vbS+J07AjHwAzqc\n0TiJoe2W07csrAwcDIYOhrYNwB2/suFg4FlrrjXnltCzYFhhbiU9yxtTgwiHrUNHURrCFhMUEheh\nGR0+iLO6gvPDdfrnjN6mWEJuRGN7kIA5IqoxZRS1cCa1irLMo0u6dyZZphDQgiNVwt9bdlopaKYl\nFsX2Ai50ULy2joLIRsf3AzqO7ZezMrBhOw6GwyGWV2wMvMCQ3XuHWFweeq5F9/SeJeAgCProub7I\nYGJ1ZGqAJjruFZdTMnR8ypiR+S9gjqPpsk1RzBYur++nnkAetXyip8cdk3QdZttLtagyklSXiLmG\nrgZXkHYS9+JO4mltlGOmCDz/u/tNIJhrZg8dDIaAEJ7bDMDy8hC2t97LyoqNlRUblgVg6JbnWnMO\ner1eKETf9sSvZ1mwRLAqmhYXBxi12IBYi2zkGkR4IrObR9ITdG8eXNARB/Vq958ZyWlaWtH9ceNp\n5jHu/vHRhWm7o9cRPm/6IkKhIm2EQZ7ZaaWFZo7VREXB7LP8CEMAQ9v2RMQVBMsSsCx3UU4hgMWV\nAfYuDzAcOhjYtueqdLBr7wrWrOq5QSBDd1xtMAzqtIfaUvE6bC/1iAM3PN8SQTtsx4hENMTHjGr0\n55I5o27HuIARf1tMYIlpUcU9FEkdvK47i4sursxEayhjGU2n7Ll1RfY1mba2u6l04ZmpilYJmh2x\nvaPjRu62UWEDgqSzliW8cTIHyys2du0dYGl5iJWBKz57lgbYs3eA5YGNxRUbtu1gz9LAjXr0gy7g\np6+CiIw92UaEI8wIyyBYRbdT7w9do3YdRq499KMWo5aQFREz93P4/Lz9TNmujjiRrLJDz1NeVXXH\n3WP/NzLluic9NrGMGusuWl6X6p5l2uVyjHWZBbujIftaNGzb9o4LsuuvrAzhegodLOxeweKKm0F/\naWWIfk9g154V7Du/CvrxXBk6WBWpSwg3FZbtON6bgSuUcIB+X4xOroYWMDeIRLseA1ehgNDlIogg\njJuDpkU7zyTjrMfH5WEsixHXKpIDC6ddd1nHTlJequWcdnNKqHvSYxPLqLHuouV1qe5Zpl2CZjzg\ncR2zOy/LjVD0hs1c958D2DZgCRsD2z13xf2APUsDDIY2lpZXsLhkBxUJoLfXQr8vMOcAjmNjaAvY\njsD6tRZWBjbm5npBfkfP1tWWoCuuQTqsoI1BFY5/Le6GwIIJzjOvMEng0kQqOk5mLvOShOnqnHZW\njll/lFPvbUtvDjtoUhetEjTTwojOyQrmRQU5FwFPyLxw+oGnV0srQ1gWsGNhGcOhg527lrC4NMDQ\ncbB3aQghgLm+hXVr5rC07GDOsuE4Amvm+nAEsLg8RM8bNHPLhydekWwlkUAQ9xoCwdOKZU4tCCUY\njl4fRvu4IEgkm/AU6WqmKWrs/JLhnSEkH60aQwuPDwWftVtvZNkSuGIjhOv+swSwsjIAILC0PIDj\nOFjYs4Jde5bxu+178NTCIn7z5C4MhjYef2I3du5exmA4xNB2sLg0hCPctdBsG7C8idS9nleP59LU\n1bvCFO8b165SLVBxmUKc6DV6rsy4Mag8ue7yCAjDheslbyYWQmadVllowGg4OpC89hbgOu90Kip3\ncrOABdeS27mwhKd3r+CJp/ZicXmI4R4btgPs3LWCVX0LS8sDCCEw1xviGfOrsHvvMlbP9bF6dQ+W\ncMP4BSzfynInVdsj89Og81MF39zIyJEoQuNzzDXr6wqPGwZh+iZxlmxe9FpxTA7bbGwHiUv2kPYz\nbbd/lygsaFJKC8D1AA4HsATgbKXUI8b+9wA4B8AAwMeVUt+SUj4LwBYAawH8B4AzlVJ78tYddb35\n1o3xXThuxo+eZYgB3M5/79IAi8tD7FkeYM/SAE/vWcHuPSuAY2P34hDP3G8N9ls35yUmdjAYDD13\npkC/5wmZZ/WZrr5+3/ItJj23DQJe8IknZJEUXJYQrqUnEHJHJgVPRH/XSb/zJKHLg557RpoN3ze6\nDV9YsjOJy/FNANYopY4BcBGAa/QOKeUBAD4E4BUATgDwSSnlagCXAdiilHolgJ/BFbzcmGNLZii/\nZQWTmrVFtjL0xtUcNyzfEoADB4vLQzi2g92LK3hqYQnbn17Czt0D7F5awW+378HyANi+cxFLyzbm\n+j3s3ruC9Wv7WBnqWBMtkgJAMA/NsswsG46OLzHcksH55r+a+KkIwXy2pKwb5jYgWejywjfD5sO/\nUbfhC0t2JnE5bgJwFwAope6XUh5p7DsKwFal1BKAJSnlIwAO8875hHfMd7zPn8lSWVxWiyAQJFAA\n/be3bTfLh21r60a4k6sdwBI9rOrbbkLhoY3BYIhVcwL9noWVgfBciW59q1db2Ls8wLOescY9F65Y\nLK0MYYk++n147kdACAcQlj/+ZUZfW4alqAM5zP36+qLjgMH+cNThuPlbeTu5JHGMc/ESQprLhg37\noN/vlVLW/Po1pZRTFZMI2r4Adhrfh1LKvlJqELNvAcB+ke16WyaSzG4tFDpo0JxA7f7rRQ8KYHFg\nY2lgY/WcwJ5FN4WV4wD7rluFvUtDNxR/VQ8b1q/C9oUlzK9bBUsA+66bQ08IDB03+nFoO1jVt/y5\nZMsDG6vmrBHvnNac4dBBz4pGJJrzjQwrU4THzIRn+kW3R8fS3G3JYpdFlKLHmK5dilp9hH4LZObI\n63LcsSP3KE4iC7sWSyurCiZxOT4NYN4syxOzuH3zAJ6KbNfbMpFmdmtrSLvw9FwuQPj7hraDuTn3\ncm0HWFoeot8D9lnTx4HPWo/1a+eweq6HwcDGnGVhzeoeIAR27lqBJSxYlpuZ2BLAXL/nipO3rIwf\nNCHc+WP+XDR4bkJrdF2zUMRm5Fr0v35gS0wUZNr4WNx2OyZCMo44a5fUC4VstuFfPzuTCNpWAK8H\nACnl0QB+bux7AMArpZRrpJT7ATgEwC/McwCcBOCerJWNe6jN6MakBAtCCKyeswAIrF+7CpZl4dnP\nWIt91vSxZrWFfdbO4Q+fsx6rVvVxwP77YH5tD/uum8PS8tCzstwJ1Y5j++7Bnrei9cBLjeVnJjHq\ntbyJ3qMRiq54JEYR+jo5uj9vBOM4P7w5YTtqEaTlZzRh+Pj0oKjNLnyqsjOJy/EOAMdLKe+D2/We\nKaU8H8AjSqk7pZT/Ha5gWQAuVkotSik/DuAmLwLySQCbJ2x/CN/9CDfwQ4fsa1efZQH9nmu5rZqz\nsJ8nVnP9Hp71jLXYu+iG6c/vswpr5ixYPQsb5lfDsiz0PJvfEgIrQxtzPYF+z80L2e95ESGelLqh\n7vCi9YXr9nSCqEbd8ZuuhNhJ096/Se4+2wlHTcYFjORxV5WSx89oa1PclE1pR17a2m5SLgwKyY5o\n+Ft1ocYNPfeezqXoODZs292+vDxEvy8wdBxs37mI3XtW8NTuZTi2g527l7B6rgdhWZjrCeyzuo99\n16/CqrkeepaF9fvMoWcJrKzYWLOm703W1laMF9bftwJLzJjDFaxmHQnXt8Z3/tEMIv7NMcQqer4+\nR48vZplL5kaCTvb0NFXQgOlaOdO41jL+HqQzZP4hbNu2UFqn/sOHHi+rqNI45fiDE+9F6yZWj8MM\ng7cdHe1oodcDHNiYm7MwsB0Mh8D6tXNYs6qPXk9gaWWI9WvckMW5voXde1fwzP3WoN/vYTC0YVkC\ny8tDzK9b7SW5cmAJC0F+RK8Ox4Ftu5bg0HEgjJ+WGbZvtnccSX1aUuaU6DlZ+8Qyus4mCNg4piW0\nZZfb/DtJSLNovaBFQ8t1iLyezOxbJo7rGrRtgb4F9C0Le4Y2Vs9Z2G/9ajy9ewn9Xg/LgyFW9Xu+\nj9B2HKxb0/MjIpdWBpjrWd53x3dtuv2YwGBoo98T3hpsTmjBT3MMbWT+GZI7sCKh89Egkrh7lnRO\nHtKsn6S6i9ZVlKRJ6k2nDS8HhDSJVghamhtLd05BXGOAXvvMjQh0J0HP9QWWVwBLuKH3tgOsnutj\nv/VuqqrFpQFs28HatXOwBTBnCTgQWL2q5wWGCFiWQE8IOMKb4WZEHPYtz35zXCtNCCMqXwSiprf5\n7sAxllqZ2QLiQv6DffmFs+Fu6xGmIRMUH0Lqpx2CBoTciGbHLqL/auEDQpOX/QnLQmBV383p2OsB\nwnHQ7wFz/TmsDG2sW9vHcOhg7/IQcz0v4/7KEI7tWmtzljthceiNTel4EOGJm2WsgWYJEU7w612I\nL2bI3rnqKQlldJxpRaSJXXJ5+S3HOmlCG0yaMtZISNtphaCFrK7Ic5/kWguELmzNDYcOej0LwvEy\n5dsCcISeuezNT7OwbrVrmdkOsHpVDw6AvpdsWAjXzegGXbh1acE0jRV/HplXtwNA+NGOERck0sVt\nkv4u2mGmdZ5t7lfbKgxFXiIIIaO0YvmYrJ2xiRnVp1NRudu9LY4Dy7JckfIOneu54fyr5izMzfUx\n17dc92LPArwJ2w4cDG2dzio419aDdkatvqdRjIqyECIszileOzO5ctoxSa6/PB7BMgWhaldkXG11\nukOz1k0xI6QcWiFoaSR15Ho+GhBYSPqbuyine+muWLnyM7DdydNCWJjrWej3hJuyCgJzcz3M9SzX\nMnP9fwC8ZWDgTp4OI/z/C0/R/LG+SJCH45l54wSpaL9XV4dZtZTEXWYb1nRro1VJSBPpgKAl7/OG\nzPwOPWoZ9XyrzU1M3BNmQmHHmxRtwXFs9L1VqXuWK4JWTwBexhDTBNOWmmUImL86NQKXaZDWSvjf\ng0CR8EXpoJN0V2Hy/rRow2lSdTcdd52TTkpNs3wJIc2i9YKmIwZHRUD4y8lExUNEerlez13brN+3\n3KTD0ONlboh/kObKrVAAcGw3wz68RMMhiw/BmBngWQki+O5nMzE6Sy2+pmVpXgvMc0voZKvooptg\nedTZhiZcPyGzRAcETaRmwTDdjaZ4BEuxuFv8oAwB9HvBsa7LyhU04amnFh+NmQUEel/UTaiDRiLt\ncxxDaIXRjkibzeMBhNaBKwK72lHiXhKy5rEkhNRP6wVNk+ZuM/VOux19VyHcfyzvuyUs1woT8NyM\nbiBJz9LTANyISD+60XZ81yXgCaATRC26C34GISLCaIeJOd4XnWcXvp7R682bRT96fhl0wS3XhvE2\nQkgyrRG0STvMkJAFpXrWWiT0X4fW9yxPEEXIhalL0FabPk1bamYovrl+mQ4IMf/T+Rb9aQYJ0w9g\n7I9apVk64ml31l3QAiaBJaTdtEbQgPyiFow3JQUMBJev9zrw1jPz5gaFsuEbLsWejoAUAoCAY9t+\nIUEzg/bqMnXi5HA7g/Gz6LVmsaSydMTT7qy7oAV0LRLSblojaJOMZcSd5jhuNnodUg/Az8YB4UY9\nDoYOhGX5qa6EcINHXFEChBUOAHEiZpC7VIzZfvezPsxNZBwIVxleu6SAkWl31hQD0jTaMAeRlEtr\nBK0Ipmsvil7BWbv79M9PzzETQvhroOkoRy06Wty8gHv3PMt1Tzq2jaFtexOxw9GOAPx8k+HVq4N/\nfavSOCcIUIl/SMzVqMt+jiaOpuSDTWqCEa6zR6cFLQ39cxsMgwwfZsQj4AqXFREb7YvUImjbTijQ\nw+pZ3jmm+9CoV+ixteB7XPquuKkISQNVoaAXq5glO4nwJAmtW27hYgkhJBczJWhxVpGeP6ZzK/pj\naAAGw6G/zxcJ322oLbPAlTjQ4iYEhLBCKa/Mus3wfdNLaWYPMUXKj4BM0KlJ3wb1OGPRsvkuSghp\nAp0UtLhxJD1WFc2LmNYZC2FFrCuBnhdIElhlwo9udNdPA0KhkGYbzLJi2qutsrhIx8ClGP5Xf86y\njEtc0El0f9L2NNLqzrJSdhpFpiRUQdzfoa42sO7ZqJuMp5OClseqMA81LSoh3GwhI+NfftSjHtcK\nzulZIrDQEBmXS0BbfyPeRSNwJIrZmWbtWNPmoelpAE30+2f6W1bcbtPFOqvjNKy7Oiii2emkoMVZ\nObrDjo5XmbkUg/Pdf83xMSBFoDwB05k+/M3GeVr4or/NIFHxqLg6xjH63ywPVJbUWEn7i46/xY75\n5Ti/TTRP9gkhQEcFLSuxa6kZQqK/R3EjHi0vfCTOgrK9f8Mi5WA0T2Oc5eRvS7DSzOjNUcsuWahC\n2f1Tjo07d1q0TcwApsMipKnMtKCZCMOcMi0p3wXp/Wc7XkZ9vyMORCIcBBJEM+o0WbpsGMeE22BO\nE8gqNuHvk+qDnWLdpYnltF2WzHpPCBlHK1aszkvejjXIJmKMkXmCpDOG2I7jZ/twAx1c9bKgs+kL\nwyVphN9H2iXEqHszOXpxfNtHr3V8p5+6DM2Yc8teFTqtLDd3ZnQ6QztXpSaETJ+ZttDiJzd7YfOW\nOW3a/WT74iN8i00nPzbHy0xZCI4bjfhLymBiO46fPzI4Vowcl5Yd3nRd5rFs8q6rViV1109IHfB3\nn52ZFjRNUqCIJbzIRSHQ7/Viz/WnA/j/M8sN/6utCy1upnUWFqDRtiW12aSKEPesD1ea6zIrphsz\ndryzJOjKJKQbdNLlCASdVJEO0HacWNdbzxLxkY9GDIdphPmRjcYxYZsvPPE6Om4X53IzyRrxGLct\ny7nj6k+vGAwHJIRUSmcttCzv3FGXnu/GSzk5uktEtgWJh0cP0DGR/gRqs1xzDK8kIYizapLEqayV\nsIN6zCkRtIAIIdOns4JmjkGN66jDY2ki5AaMHqctMDNgP27itI541ONnfgSkIW7ReWd+nY5Rxhjr\nyDaWo4k7Nuu2OJo62bpsZuEaSXvhC2F2OitoJnlcc7adnNfQMYQGCMTKxBQ8LUgjqay02E3YkUaz\n8kf35RnHSluZoAgUiexwSgIh5dBpQSvSUcRPlR5Fz1XT/41EOvrz0MxFRkcF0PZF0nQLjm4LtTEm\nOjPuWuuQlDrWYiuDMgSlaBltuD+EtIFOC1rWjsJMf2UJw8qKdFDhqDvvGMQIoBP5V3/N0N/ZMe7D\ntMAOK+YaTRdknZ1llYmF46zRsscFszBNUaMVN5vwhSc7nRY0IF+4dyiEPrJvaNshofAtLm+/jiUJ\nLQdj7EucPG181gEjJtFExGlzz7pCoY7bD8bpdqff9esjZBI6L2hZiU5IHuk3EuaYAYFFZwaHCG8O\nm58CK3KOTm8VjgZMdhOGlp4Ro3kZo9eStG/a1CWscQEsecYFy2h3U14sKHpkVik0D01KuRbA1wA8\nB8ACgNOVUtsix3wawCavji8qpW6QUu4P4F8B/MI77A6l1OeKNn5S0qIDo5GLvV5Y+0NJhCPnxXUn\no4c6I3O1kpaZEUJAGAUktTvspoy3CvUcuyrSSRUVEncM0okV5iYIRl3M8rUTkoWiE6vfB+DnSqmP\nSilPA3AJgL/UO6WUfwrgT5RSx0gpVwN4WEr5DQBHALhZKfXBSRteBraTFHKffewtfnzLFROdsNjy\nrLGo0rnZQhwjg8hoeSOpuDK+fccd708JMC6viW/zaS7acbDTJ2R2KSpomwBc7X3+DoBLI/v/HsBD\n3mcHQA/ACoCNADZKKX8E4AkAH1JK/aZgGyamV8JqyoHL0BWlaCaR4FhXPO0Ut6IWNlPkokzaYSfN\nbctiBU2SfSUP0b8LRSofvF+zzYYN+6Dfj0/Vl5f59WtKKacqxgqalPLdAM6LbP4dgJ3e5wUA+5k7\nlVKLABallHMAboLrctwlpfwlgAeVUt+XUr4DwOcBvG3Ca6gN0xJzv+sOP3pcIHKu9Omw/1E3YtaF\nOc1xNy2mcWR1+2WpdxLLiRBSDNt2RhKbp7Fjx57S6l7YtVhaWVUwVtCUUl8G8GVzm5TydgDz3td5\nAE9Fz5NSbgDwDQA/VEp90tv8AwD6bt8B4MpizW4GvssQwbw0V+DCHX9Y+ETIQrMNy82KPXdUwMy5\nZ0mMs/Ci+7NGgfLtnxDSVIpGOW4F8Hrv80kA7jF3ekEjdwO4USn1MWPXlwC81fv8GgAPFqy/EehM\n+771lTAep7fbRsRjVIv0C1hUzEaOi0bzpehLGeNj41JrxU0lYOYLQsojj3U26xQdQ/sCgJuklPcC\nWAawGQCklFfDtcpeAeAgAO+RUr7HO+dMABcBuFFK+X4AuwGcPUHbayfav2vXnbZkfDciglRXoXln\njjmJOyjTnDqgLT4dUTKSUDltUC4DSWX7+5FefJwbMinYhhBCpolo+Jt0oxsHhAM5/KCQyHyzoR1O\naoyQ29D9rHXJdOvpskzRSHIZjmubeW70mChxSZmT9o2re5IyCCE+mR+abdsWSus3f/jQ42UVVRqn\nHH9w4r3o9MTqabq+omWb4fXRGnXUnmEM+ceExS+p7GDSrpkbMuu1pR0WmlCeqbTp0fCXK0JIw+ns\nAp9VkBT1F3UV6mAQ3V3r4A8Y7sVeznlm41yBJll98HF5IYFiFlXapG9CCJkGnbbQpp2KKC7qzwzR\n19I0tMeLVNzcs6Sz3KTEWdo3nWsfF11Zt6XVhDYQQqqnk4JWRWeWJpZ6sxYdc6Kwn/cxlLl/dKwp\nTQPNzCLmOdO47uxuTd2G4nWlCXCaSNUpXqybdZPm0ElBq9O9FZ7wbAifGD3GPS4+YMNcXy2aozGu\nzrggjCofPnNZnWnc/3HjgNHvVf0GmvBbY92zUTcZTycFrQlEIx2tSMi+nsOm+2nT6hoJzY8JEDFJ\nEq6k4yYVurRys0Re5iWcYqxd8I2ekOqgoE2REUssLsNHSn9nmdGRMWVq4tyT4/IxZiVPmP60cHK0\no2lQzgipjpkWtGl1wubYVnRydXBM/DlxZSRFH2qsjNbLpKIwzhKcluiUVWot68PVWLeGdc9W3bPM\nTAtamR1w0rIvep+fKUSI8HhQnNVmlpuh7jzXMcn4Up5xrEmPm/ScaZZTpM5ZHfepou6sLvcqaatH\noe3MtKCVSdwjZYpHeFzMOEafnzBRukmPRdZnlG+npEq6/nPj85QdClpJpPX10bc1PeYVTpuV7dw6\nyeTw0QIAABETSURBVDyeNuV2EGLSoEdkKmSYxko8KGglkSd4ws8UgvD8rbzi1dQ3t3FX0dR2k3bS\npJe+acBE39mhoFVIkEFfhN2Oke+ZyyuvaaUyroOJvnFOM98mIW2n64JdJhS0ComG3yeNsY2clzTo\nbeyvuvOepM64N87pZDkpvchCUFgJqQYKWpWMySg8LkdiEnVG75Vx7tTC/RvyYltkDIQiSEh+KGgV\nEsmABWC040pan2xc/xbN61gFZQrRNEStKa6aImMgDAQgJD8UtCmRd27MOCFyl6MJUkwVteZI9RQR\nVgYCEJIfCtoUMYUlLs9haD/Ci3imkdZBlpVLkaJYL02xLkn98FnMDgWtQkbci8bnca5IIDo5u5io\nZXVl1fkM8QEmJIDu5+xQ0KZElhRTOh2WPj6tIy/rR53VlVWngcDnl5AAup+zQ0GbMtH1zsJLwYz+\nUtPWR4syzbyItebBq61mQpoH3c/ZoaBVQJJIJR8/um2WftSzdK2EkPKgoFWAmXg4LTAkmGwdv58Q\nQkgyFLQpI4TwF+rMc45JlrlqdWQLyUIT20QI6SYUtIpIcqNlca9FJaFNEtGmthJC2g0FreEIIUJB\nEnqx0LgFRZs49tS8FhFCugoFrWayuArjIiSzevJ0+WaWkWkxbu4cmS5075JZh4JWIUkdjmPsT01p\nZXymTpAo1DMy61DQKiRpcrTpQjSPGUmdhfBE7KxU5Y6kNVYvvP1k1qGgVUjS5GghhJ/L0RKGm9A4\nzg39z15X0jSBaYhOma4uus2KwxcKMutQ0CrEHAsbCeowjnEQLJ1meyZb3m6+bF1Iz+5fYj3lFUUI\nmTEoaDUQ9yYdSjys/9Pi5jiudSeSzx8tL/w9ae5aVtKOLNMwoI1BCClKv8hJUsq1AL4G4DkAFgCc\nrpTaFjnmfwB4FoAVAHuVUidJKf8EwP8Ft3/8BYC/UErZxZvfXuImT8eNj4UsN9uBA/c423bcBUO9\npMZZXIsjeSWRXUDSjmv6Qp+EkNmgqIX2PgA/V0q9EsDfALgk5pgXANiklDpOKXWSt+1aAJd45wkA\nbyxY/8xgWcIQusC9FxpfQ7GxpzzSQaEhhDSdooK2CcBd3ufvAHituVNK+XsAngHg/5FS3iulPNnb\ntRHAj5LOq5o6AxAKCZCR59ESRsQjxo89BXkiRWLASBW07Z6zbtbdtrpnmbEuRynluwGcF9n8OwA7\nvc8LAPaL7F8F4BoAnwOwP4CtUsoHAAillJNyXqXUukTKGBdhnBtRHxfdJ0zTrUDdVcK6WTfrni4b\nNuyDfr9XSlnz69eUUk5VjBU0pdSXAXzZ3CalvB3AvPd1HsBTkdN+C+D/VEoNADwhpfwZAAnAHC+L\nO48YJIlaHGYEZdI50cz+ecpvGm1uOyHTZMeOPaWVtbBrsbSyqqCoy3ErgNd7n08CcE9k/2sB3AYA\nUsr1AF4M4F8A/ExKeVzKecQjbTJ02piZnpgdTXmVRptcM3W6SwkhzaaooH0BwKFSynsBvBfAFQAg\npbxaSnmUUuo7AP5VSnk/gO8B+IhS6kkA/weAK6SUfw/XLfmNia8ghq76r/V1WUZnHpenMen6zXE0\n/b2sHI9FzzfbULSOSc+fhDa9DLDudtdNxiMa/gdqdOOqJOoujO4zQ/njjilS7rTR7c7qPpzEOqvz\nOgkpgcw/2m3bFkrrN3/40ONlFVUapxx/cOK9KDQPjVRHls4+auXkzfNYdnuylwUA+ccJi5DHEiSE\ntBNmCmkBSZOuo9RheLRJJJq6ZhwhpBxooTWcrJbFtDrqaQZhWHHZmqdcJyGku9BCaxhp0YlFx44m\nsaKiZ3IZGkJIU6GF1kDiciyOs1ri5pgllWVi5oSMw1yDLXb/lMSHokYIyQsFrWEIIWIFKMn1GITd\nx4+hWRSGyqHLlJB6oKA1mDyuwqiVFRfar7eb5SaNYyWVUwVtF4SklwtCyHThGFqDiUY2jltHLSqA\nth0/fjZOJ+uOXGyrkGnMFRJIu5l0DJpUCwWt4WSeIJ2xnEmzbVQFBYEQkhe6HFtI1CUXHXfT89aS\n3IlpQSCEkAA+J+2CFlrHyGKBZck8UgY23TWEkAqhhdZC8giO7TgjUZNxofpRl2QpojZuzgAhhJQI\nBa2DhMTIExW9zXackM5MM2nvuAhKQggpE7ocW0xcFGNUlEYi7hzASptILQQcJ1x2UrQkIYQ0CVpo\nLSE2/B75PXpRq6m8zPnOyBQCDqgTQqqEgtZC9MTdNEtrEqKiZ1lceoUQ0nwoaC0hLFzFxCUp32MW\nUYybwJ2WmaQK2p5RhBBSLhS0FqHdeHV34FlSO1XRxrJSTHE1a0K6AQWt5Uwyv6xo590UF2SWKEqK\nFWk7tu0wYjgjFLQWY9va5Ta6b9pBGVWJQ1luRbeY+HtStGyKJamC+l8d2wPD9lvESAZ9BGms6u5Q\np5XEddIi674vZPo0wVswTfgLzg4ttJZhPry9GXBDlOFqcQW/hMbElEvItOHPLDsUtI4QdTFW3dmy\ncycaumJJXdDl2DLS1kYrC64B1Tz4N0mGokk0FLQWUuYDHO0k3Y6ztOLJDFLFSxchcXRS0GbxTdac\nKD0O823fcUa/F+mH6rQg6vx7V1V3XOBPk6972h6EupjFvqVNdFLQZvXNMMt1OzrbfsKctLSoyTTR\nqvOet7HuMjrGNl43686PTQ3NTCcFjSQTXd06bn8SrvWWvH9WXySKwHtFsjIDwcylQUEjmTvXon3w\ndOanOaF/CclLW347fPnJzkwL2iz44susp7B7zfxcYnvyZkOZhb83685e9zRb1hax7BozLWiz4otP\nWgTUFYTp129WUdZ1FylnmtGhVdadF9adsL/Gusl0mGlBmwUmGROrog1NLJfMBvz9dA8K2gyQ9ODy\neS4OO0NCmkeh1FdSyrUAvgbgOQAWAJyulNpm7D8RwEXeVwFgE4AXA1gD4FsA/qe37wtKqVuKNZ1M\nSpFOedpZ/AkhpChFczm+D8DPlVIflVKeBuASAH+pdyql7gJwFwBIKf8KwFal1L9IKc8GcK1S6poJ\n200ykEV8KFDFKHrfeL8JmR5FBW0TgKu9z98BcGncQVLK/w3AuwC81Nu00d0s3wjXSjtXKbVQsA0k\nA+M6UNsBehn7V50Wi/1xvvsWhaJGyHQYK2hSyncDOC+y+XcAdnqfFwDsl3D6+QA+o5Ra8r4/AOBL\nSqkHpZQXA7gcwAW5W00ykSUdVp5JmzbFzKfoZNc8KcoIKcKGDfug3++VUtb8+jWllFMVYwVNKfVl\nAF82t0kpbwcw732dB/BU9DwppQXgZAAXG5vvUErpY+8A8PkCbSY5MC2BOMsgj6XAjAUBk1hYtM7I\nNNmxY09pZS3sWiytrCooGuW4FcDrvc8nAbgn5pgXA/ilUmqvse27UsqjvM+vAfBgwfpJASa1C5qw\nMjYhhCRRdAztCwBuklLeC2AZwGYAkFJeDeAbSqkHAEgA/xY5730APi+lXAHwWwDvLVg/KQCliBDS\nZUTD/fmNbhwhhFRE5vfRbdsWSus3f/jQ42UVVRqnHH9w4r3gxGpCCCGdgIJGQpgWe8Otd9Ih+Fsj\nZUBBIyHMfoULC5Kq4E+NlAEFjYQwgxjbEkTShbf7LlzDJLTlt0aaDQWNhAjNW6uxHXnogiXZhWuY\nBE4HIWVAQSOJtGUidVvamUYXroGQuqGgkUTa8tbclnam0YVrIKRuKGgklbLGdtzExjPuVyMzD5+B\n6UJBIyGiDxwfP0LKY9bHSqdN0dRXpKO4euY+dUKI0qLPZt2lpl8UZv0+zDocK50utNBICAfhTrfo\nIpZlQjcN6Qp8oZkuFDQSQr9BTvLglS0/XdAzrlRAyPShoJEQWTvdNKup7G6bOkAIyQIFjRTClLOo\nuJVtidCyIYRkgYJGYhk3bmVKTAc8goSQDtAqQasz2GDW6tZHJB0bChwpue4ix3ap7rJpS92z+vdm\n0FN5tErQ6nRlzVrdeWos+1qmFeLe9Hs+LdpS96z+velSL49WCRqpDv2QRR+2uIwffMMkhDQBChrx\nKdtNUlTomjD3jRDSPjopaLPauU163Zlckd58qjjLrUh5ZaDrruPv3pbxKdbd/rrJeDopaLPqk67r\nuuueNDxp/ZN0UnVfN+uenbrJeDopaKTd1OGq5Js3aSr8bWaHgkZKg0vEEELqhNn2SWk4KCftlc74\nX4V7hy4kQroDBY2UhlWSOJQljIR0Ab50ZYcuR1IIe4ruRT6+hATYXBU0M7TQSDGmaEZZXAWREFIA\nChopBEWHkGqgxzE7dDmSzDCKsTxsm/eSkLKhoJHMlDV5mR05IWQa0OVIclF2xJUpbrMUzUWXLcnK\nLD0Xk0ILjVQOH1BCyDSghUYqIUnEKG6EkLKYSNCklG8GcIpSanPMvvcAOAfAAMDHlVLfklI+C8AW\nAGsB/AeAM5VSeyZpA2k+tu1ACIoXIUVwnGqy5nSBwi5HKeXnAHwyrgwp5QEAPgTgFQBOAPBJKeVq\nAJcB2KKUeiWAn8EVPEIaCSMRCWkXk4yh3QfgfQn7jgKwVSm1pJTaCeARAIcB2ATgLu+Y7wB47QT1\nk5ZgWfUuL0MImQ3GuhyllO8GcF5k85lKqVuklMclnLYvgJ3G9wUA+0W2621psBcktcFIRNIE8r4M\nPvvZ86X9cE85/uCyiqqEsYKmlPoygC/nLPdpAPPG93kATxnb9xrbCCGEkImZVtj+AwBeKaVcI6Xc\nD8AhAH4BYCuA13vHnATgninVTwghZMYoVdCklOdLKf9cKfVbAP8drmD9AMDFSqlFAB8HcJqUciuA\nYwBcV2b9hBBCZhfBKC5CCCFdgJlCCCGEdAIKGiGEkE5AQSOEENIJmMuxAFJKC8D1AA4HsATgbKXU\nI8b+kbRftTS0YjLcl8/BnVy/4G16ozfxvvNIKV8G4FNKqeMi2/8MbgadAYAblVI31NC82ki5L+cB\nOBvANm/TOUopVXHzKkdKOQfgRgB/DGA13P7jTmP/TP9exkFBK8abAKxRSh0jpTwawDUA3giE0n4d\nCWANgHullH+rlFqqrbXVkXhfPDYCOEEp9WQtrasJKeV/AfAuALsj2+cAfAbAS719W6WUdyqlfld9\nK6sn6b54bATwvyulHqy2VbXzTgD/n1LqXVLK/QE8BOBOgL+XLNDlWAw/hZdS6n644qVJSvs1CyTe\nF896ewGAL0opt0opz6qnibXwKIC3xGw/BMAjSqkdSqllAPcCOLbSltVL0n0BXEH7sJTyXinlhyts\nU93cBuBS77OAa4lpZv33MhYKWjGiqb2GUsp+wr4sKb66Qtp9WQfg83DfQE8E8H4p5UwIvVLqmwBW\nYnbN8m8l7b4AwP8N4D8DeDWATVLKkytrWI0opXYppRaklPMAvgHgEmP3TP9eskBBK0Y0tZellBok\n7JulFF9p92UPgM8ppfYopRbgTrg/vOoGNoxZ/q0kIqUUAD6rlHrSs0T+XwD/qeZmVYaU8rkA/g7A\nV5VSW4xd/L2MgWNoxdgK4M8A3OqNFf3c2PcAgP8qpVwDd1BXp/2aBdLuywsB3CKl/E9wX6Q2Abip\n+iY2in8B8AJvrGQXXPfRf6u3SY1gXwC/kFIeAnes6NVwAyU6j5Ty9wB8D8AHlFJ3R3bz9zIGClox\n7gBwvJTyPrh+7jOllOfD9W/fKaXUab8sBGm/ZoFx9+WrAO6H62b6G6XUwzW2tTaklJsBrFdKfdG7\nP9+F+1u5USn1eL2tq4/IffkIXCtlCcDdSqlv19u6yvgIgA0ALpVS6rG0GwCs4+9lPEx9RQghpBNw\nDI0QQkgnoKARQgjpBBQ0QgghnYCCRgghpBNQ0AghhHQCChohhJBOQEEjhBDSCf5/HcXzP59kHb4A\nAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x118c234a8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"import sklearn.decomposition\n",
"for j, (subset_str, subset) in enumerate(swire_sets.items()):\n",
" print(subset_str)\n",
" swire_indices = sorted(set(numpy.concatenate(numpy.array(subset).ravel())))\n",
" features = swire_features[swire_indices]\n",
" im_features = features[:, 5:]\n",
" pca = sklearn.decomposition.PCA(n_components=2, whiten=True)\n",
" im_features = pca.fit_transform(im_features)\n",
" im_features = numpy.clip(im_features, -2, 2)\n",
" seaborn.jointplot(im_features[:, 0], im_features[:, 1], bins=100, kind='hex', )\n",
" plt.xlim((-0.5, 1.0))\n",
" plt.ylim((-1.0, 1.0))\n",
" plt.show()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.1"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
danielfrg/danielfrg.github.io-source | content/blog/notebooks/2013/01/copper-machine-learning-bootstrap-bagging-python.ipynb | 1 | 109903 | {
"metadata": {
"name": "Post_3"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This week on my Advance Business Intelligence class we took a look at Boosting and Bagging, two concepts well known by everybody in the machine learning world. The example on the class was take a simple Decision Tree and compare it to some bagged Decision Tree; FYI the example on class failed: SAS told that a simple DT was \"better\" than the bagged one, some error on SAS Enterprise Miner that we could not found. Time to see if python is capable of doing it.\n",
"\n",
"This first part is just a recap of [Post #1](http://danielfrg.github.com/blog/2013/01/26/copper-easy-data-analysis-on-python/) I am using the same [donors.csv](https://raw.github.com/danielfrg/copper/master/examples/donors/data/data.csv) that I am using for my class. We import the data and set some roles for the variables"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import copper\n",
"copper.project.path = '../'\n",
"ds = copper.Dataset()\n",
"ds.load('data.csv')\n",
"ds.role['TARGET_D'] = ds.REJECTED\n",
"ds.role['TARGET_B'] = ds.TARGET\n",
"ds.type['ID'] = ds.CATEGORY"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 1
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Since scikit-learn cant handle NANs we need to fill the values so I create simple method con the Dataset class to fill values of numerical columns with the mean."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"ds.fillna('DemAge', 'mean')\n",
"ds.fillna('GiftAvgCard36', 'mean')"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 2
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's see if we are good"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"ds.inputs"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "pyout",
"prompt_number": 3,
"text": [
"<class 'pandas.core.frame.DataFrame'>\n",
"Int64Index: 9686 entries, 0 to 9685\n",
"Data columns:\n",
"GiftCnt36 9686 non-null values\n",
"GiftCntAll 9686 non-null values\n",
"GiftCntCard36 9686 non-null values\n",
"GiftCntCardAll 9686 non-null values\n",
"GiftAvgLast 9686 non-null values\n",
"GiftAvg36 9686 non-null values\n",
"GiftAvgAll 9686 non-null values\n",
"GiftAvgCard36 9686 non-null values\n",
"GiftTimeLast 9686 non-null values\n",
"GiftTimeFirst 9686 non-null values\n",
"PromCnt12 9686 non-null values\n",
"PromCnt36 9686 non-null values\n",
"PromCntAll 9686 non-null values\n",
"PromCntCard12 9686 non-null values\n",
"PromCntCard36 9686 non-null values\n",
"PromCntCardAll 9686 non-null values\n",
"StatusCat96NK [A] 9686 non-null values\n",
"StatusCat96NK [E] 9686 non-null values\n",
"StatusCat96NK [F] 9686 non-null values\n",
"StatusCat96NK [L] 9686 non-null values\n",
"StatusCat96NK [N] 9686 non-null values\n",
"StatusCat96NK [S] 9686 non-null values\n",
"StatusCatStarAll 9686 non-null values\n",
"DemCluster 9686 non-null values\n",
"DemAge 9686 non-null values\n",
"DemGender [F] 9686 non-null values\n",
"DemGender [M] 9686 non-null values\n",
"DemGender [U] 9686 non-null values\n",
"DemHomeOwner [H] 9686 non-null values\n",
"DemHomeOwner [U] 9686 non-null values\n",
"DemMedHomeValue 9686 non-null values\n",
"DemPctVeterans 9686 non-null values\n",
"DemMedIncome 9686 non-null values\n",
"dtypes: float64(7), int64(26)"
]
}
],
"prompt_number": 3
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"OK, no missing values so we are good to go."
]
},
{
"cell_type": "heading",
"level": 2,
"metadata": {},
"source": [
"Machine Learning"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Time to see if boosting and bagging are that good as they promise to be. We create a new machine learning instance and set the dataset and we tell them to sample half for training and half for testing."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"ml = copper.MachineLearning()\n",
"ml.dataset = ds\n",
"ml.sample(trainSize=0.5)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 4
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Create a new Decision Tree, add it to the models to compare and fit the models"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from sklearn import tree\n",
"tree_clf = tree.DecisionTreeClassifier(max_depth=10)\n",
"ml.add_clf(tree_clf, 'Decision Tree')\n",
"ml.fit()"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 5
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Since I start coding this library I wanted to maintain all compatibility with pandas and scikit-learn and its respective API. For that reason is possible to just add already fitted classifiers to the ML class and then just compare them with the utilities; this is useful in the case of using bootstraping.\n",
"\n",
"In the next lines I create 20 different Decision Tree classifiers using 20 different samples (using Bootstrap), fit each classifier and add them to the ML class. \n",
"\n",
"Have to carefull here, on the Bootstraping need to use only the training part, so I only use the training part of `ds.inputs` (above I did `ml.sample(0.5)` to divide half of the inputs in training and half on testing), then I use only the training part `(ml.train)` to re-sample 20 times and fit 20 classifiers.\n",
"\n",
"The first time I use all the inputs and the results were amazing, but obviously I was using some records on training **and** testing, which is wrong.\n",
"\n",
"So in this case each new Decision Tree is only going to be using a quarter of the inputs to be trained."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from sklearn import cross_validation\n",
"bs = cross_validation.Bootstrap(len(ml.X_train), n_iter=20)\n",
"i = 0\n",
"for train_index, test_index in bs:\n",
" X_train = ml.X_train[train_index]\n",
" y_train = ml.y_train[train_index]\n",
" clf = tree.DecisionTreeClassifier(max_depth=10)\n",
" clf.fit(X_train, y_train)\n",
" ml.add_clf(clf, \"DT\" + str(i + 1))\n",
" i += 1"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 6
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Lets see some results"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"ml.accuracy().head()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "pyout",
"prompt_number": 7,
"text": [
"Decision Tree 0.550279\n",
"DT17 0.539955\n",
"DT14 0.536031\n",
"DT11 0.535205\n",
"DT19 0.534999\n",
"Name: Accuracy"
]
}
],
"prompt_number": 7
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"ml.roc(legend=False, retList=True)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "pyout",
"prompt_number": 9,
"text": [
"Decision Tree 0.541008\n",
"DT15 0.521935\n",
"DT19 0.520583\n",
"DT11 0.516007\n",
"DT16 0.515312\n",
"DT14 0.514619\n",
"DT8 0.513731\n",
"DT17 0.509060\n",
"DT9 0.506149\n",
"DT3 0.504594\n",
"DT13 0.504411\n",
"DT5 0.501457\n",
"DT2 0.499923\n",
"DT6 0.497339\n",
"DT10 0.494504\n",
"DT12 0.494483\n",
"DT7 0.493177\n",
"DT18 0.492243\n",
"DT4 0.491786\n",
"DT1 0.488879\n",
"DT20 0.483900"
]
},
{
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAagAAAEYCAYAAAAJeGK1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xd0VNX68PHvTCbJZNJ7JSGNNCCE0GsoUaQXUURArCjW\nq9eOF/Aqdn9iuVhQBCwgFqp0ghBCMI1AEiCF9N57m8x+/3CR1wgkAQ0JsD9rsVbOmVOe85zDPHP2\n3nNGIYQQSJIkSVIPo+zuACRJkiTpUmSBkiRJknokWaAkSZKkHkkWKEmSJKlHkgVKkiRJ6pFkgZIk\nSZJ6JFmgpB5JqVTy3XffdXcY152MjAyUSiURERHdHQpff/01+vr63R3GNbVixQq8vb3/1jZ60jns\nbrJAXSOLFy9GqVSiVCpRqVQ4OTkxd+5cUlJSLlq2sLCQxx9/HHd3dwwNDbGzs2Pu3LnEx8dftKxW\nq+Wjjz5iyJAhmJmZYW5uzsCBA1m1ahUVFRVXFOOF+JRKJRqNBh8fH1asWIFOp7vq475aBQUFzJkz\n55rv93ri5eXFypUr28xzdXWloKCAIUOGdFNU1xeVSsWGDRv+se09++yznDhxotPLy3PYPlmgrqEx\nY8ZQUFBAdnY2mzdv5ty5c0ydOrXNMtnZ2QwaNIjIyEg+/fRT0tLS2LVrF/r6+gwbNoy9e/e2Ltvc\n3MyUKVNYtmwZ8+bNIywsjNOnT/P6668TGRnJ+vXrrzjGTz75hIKCAs6cOcMzzzzDqlWrePPNN//2\nsV8pOzs7DA0Nu3Qfzc3NXbr9q6HT6Tr9gUChUFw0T6lUYmdnh0ql+qdD6zGuJEcdUSgU/BPPKrgQ\nk7GxMVZWVle0/7+6Gc5hpwnpmrjnnntEaGhom3kffvihUCgUorS0tHXetGnThKOjo6iurr5oG5Mn\nTxYODg6ivr5eCCHEu+++K5RKpYiMjLzkPsvLy68oRoVCIb799ts28wYOHCimTZt2Udw+Pj5CrVYL\nb29v8frrrwutVtv6enNzs1ixYoXw8PAQhoaGwtnZWTz++OOtr1dXV4snnnhCODs7C41GI4KCgsTP\nP/982Vjmz59/Ue6EEGLSpEli3rx5rdP79u0TI0aMEEZGRsLZ2Vnce++9bXJ7zz33iIkTJ4oPP/xQ\nuLm5CaVSKWpray+Zi7Nnz4rJkycLExMTYWJiIqZNmyZSU1NbX1+3bp1QqVTiwIEDwt/fX6jVajFk\nyBARGxvbZjvR0dEiNDRUmJiYCFtbWzF79myRmZnZ+vry5cuFl5eX2Lx5s/Dx8REqlUokJiaKmJgY\nMWnSJGFnZydMTEzE4MGDxZ49e1rXGzt2rFAoFG3+ZWZmivT0dKFQKMSxY8eEEKJ1+ocffhBTpkwR\nGo1GeHh4iI0bN7aJ8/z58yI0NFSo1Wrh5uYmPv30UzF27FjxwAMPXDI/F6Smpoo5c+YIKysrodFo\nRP/+/cXOnTvb5OjYsWMiKChIaDQaMXjwYBETE9NmGw888IDw9PQURkZGwsPDQ7z00kuisbHxb+dI\niPavRTc3tzb5UyqVf+u8JSQktM6/IDs7W8yePVvY2NgItVotPDw8xDvvvHNF51AIIQoLC8XixYuF\nvb29UKvVwsfHR3z11VftnpsbgSxQ18iFN8cLcnNzxZgxY9pczGVlZUJPT0+8/vrrl9zG0aNHhUKh\nEDt27BBCCBEYGHjJN+6/unDBf/311+0up1AoxDfffCOEEEKn04kDBw4IjUYjVq5c2brM8uXLhZub\nm9i6davIyMgQv/76q3B1dRWvvPJK6zKLFi0SdnZ24ptvvhHnz58XUVFRYvXq1a3bDQkJEePGjRPH\njh0T6enp4vPPPxcGBgbi4MGDbWK5UKD27dsn9PT0RG5ubuvr+fn5QqVSid27dwshhDh48KDQaDTi\n448/FqmpqSIqKkqMGzdOjB07tnWde+65R5iZmYnZs2eL+Ph4kZCQ0KawXlBXVydcXV3FxIkTRWxs\nrIiJiRHjxo0TXl5eoqmpSQjxx5uvUqkUwcHB4siRI+LUqVNi6tSpwtHRUdTV1QkhhEhMTBQmJiZi\nxYoV4ty5cyIhIUHMnTtX9OnTRzQ0NLTmU6PRiJCQEHHixAmRkpIiqqurxeHDh8WGDRvEmTNnREpK\nili2bJkwMDAQycnJQog/rhV3d3fx7LPPisLCQlFYWChaWlouW6A8PDzEli1bRFpamnjhhReESqUS\nKSkpreckMDBQDBs2TERFRYmTJ0+KyZMnC3Nzc/Hggw9e9nrJz88XdnZ2IjQ0tPVc7ty5s/WcXMjR\n2LFjRXh4uDh79qy45ZZbhKenZ2vedTqdWLZsmfj9999FZmam2L59u3B0dBTLly9vc81dTY46uhaL\ni4uFSqUSH374YWsO/+55+2uBmjZtmggNDRXx8fEiMzNThIWFie+///6KzmFdXZ3w9fUVwcHB4uDB\ngyIjI0McPHhQbN68+bLn5kYhC9Q1cs899wiVSiVMTEyERqMRCoVCDB06tM2nshMnTgiFQiG2bt16\nyW2UlpYKhUIh3n33XSGEEEZGRuLJJ5/scN85OTnCz8/vstu9QKFQCLVaLUxMTIS+vr5QKBTi5Zdf\nFjqdTgghRG1trdBoNGLv3r1t1lu/fr2wsLAQQgiRkpIiFAqF+Omnny65j7CwMKFWq0VlZWWb+ffe\ne6+YOXNmm1guFKiWlhbh7Ows3nrrrdbX33vvPeHk5NQa29ixY8WLL77YZpuZmZlCoVCI+Ph4IcQf\n58DS0vKyd00XrF27Vmg0mjZ3X4WFhcLIyEhs2LBBCPHHm69CoRCHDh1qXaa8vFyYmJiIL7/8snV/\nf77DE0KIhoYGodFoWs/F8uXLhVKpFNnZ2e3GJMQfH0j+/OHFy8urzYcHIcRlC9T//d//tS6j1WqF\niYmJ+Pzzz4UQf3wAUCgUIi0trXWZsrIyodFo2i1Qy5Yta1OQ/+pCjuLi4lrnRUZGCoVC0aaI/NX7\n778vvL29W6evNkcdXYtCCKFSqcT69evbzPs75+2vBSowMFCsWLHisvvvzDlcu3atUKvVbT6g3Sxk\nI+c1NGzYMNavX099fT2bN2/mzTffJC0tDVdX1y7dr7OzM0lJSZ1adtWqVcyYMYP8/Hyef/55tm3b\nxrJly1Cr1SQmJlJfX8/s2bPbtJ23tLTQ2NhIaWkpsbGxANxyyy2X3H5UVBRNTU04Ozu3md/U1ESf\nPn0uuY5SqWTBggVs3LiR5557DoCNGzcyf/781jiioqI4ceIEH330UZt1FQoFKSkp9O/fHwA/Pz80\nGk27OUhMTCQgIKBNX4KdnR0+Pj4X5XH48OGtf1tYWODn59e6TFRUFGlpaZiamrZZp7GxkdTU1NZp\ne3t7XFxc2ixTXFzM8uXLCQsLo6CgAK1WS0NDA1lZWe3GfjkDBgxo/VtPTw97e3sKCwsBSEpKwsbG\nBg8Pj9ZlLC0t8fHxaXebMTExjBgxAiMjo8suo1AoCAwMbJ12cnIC/hgIdGG02xdffMHatWvJzMyk\ntrYWrVZ7Ub/Q1eSoo2vxcv7Oefurp556iiVLlrB7925CQkKYMmUKo0ePvqJ4YmJiCAgIaM3dzUQW\nqGtIrVa3vgm8+uqrpKSk8PDDD3PmzBmUSiVeXl4oFApOnz7NjBkzLlo/MTERoPWNw8fHp3XeP8Xe\n3h4PDw88PDzYunUrnp6evPPOO7zyyiutHdM//vjjJYuJpaVlh9vX6XSYm5sTHR190WsGBgaXXW/R\nokW8/fbbxMbGYmBgQHx8PBs3bmx9XQjBCy+8wMKFCy95TBd0VJz+vL3OzGtvGSEEixYt4oUXXrho\nuT8XP2Nj44teX7x4MTk5Obzzzju4u7ujVquZN28eTU1NnYr/r/6aW4VC0WagwaU66zs63s4MMFAq\nlW22feHvC/vesmULjz32GG+99RZjx47FzMyMH374gZdffrnNdq5Fji74O+ftUjFOmjSJPXv2EBYW\nxm233casWbPaXLudjelmJEfxXUN/fRNYsWIFqampbNq0Cfjj4p88eTIff/wx1dXVF63/xhtv4ODg\nQGhoKAALFizg0KFDREZGXnJ/VzrM/K9sbGx47LHH+OCDD6irqyMgIAC1Wk1aWlprEfvzP6VSycCB\nAwHajDb8s8GDB1NRUUF9ff1F67f3adTf35/g4GA2bNjAhg0bGDBgAH379m19fdCgQSQkJFwyrs68\nkfxZ3759SUpKorS0tHVeYWEhycnJbfYJcPz48da/KyoqOHv2LH5+fq0xxcfHXzImCwuLdmM4evQo\nS5cuZerUqQQEBODg4EBaWlqbZQwMDGhpabmiY7sUf39/iouLOX/+fOu88vJykpOT210vODiYiIgI\n6urqrnrfR44cISgoiKeeeoqgoCA8PT1JT0/v1Lod5aijaxEuncO/c94uxcHBgcWLF7N+/XrWrl3L\nt99+S01NzWX3/1eDBg0iKSmJ3NzcK9739e66LlD/9N1DV/vrpyAfHx+mTZvGW2+91Trvk08+QaVS\nMX78ePbu3Ut2djZRUVHMnz+fw4cP8/XXX7cOv37yySeZMGECt956K++99x7R0dFkZmayZ88eZs6c\n2brd3NxcfH192bp16xXH/MQTT1BXV8enn36KiYkJL730Ei+99BKffPIJ586dIzExkU2bNrV+2vTy\n8uLuu+9m6dKlfPvtt6SlpREVFcWHH34IwPjx45k4cSKzZ89m69atnD9/npiYGD766CPWrl3bbiyL\nFi3iu+++47vvvuOee+5p89qrr77Ktm3bePrpp4mLiyMtLY09e/bwwAMP0NjYeNltXuoamj9/Pra2\nttx5553ExcURExPDvHnzcHFx4c4772xdTqFQ8Pzzz3P06FFOnz7NokWLMDExYf78+QC89NJLnDlz\nhgULFhAVFUV6ejphYWE89dRTHb4J+/j48M0335CQkMDJkye566670Ol0ba4hd3d3wsPDyc7OpqSk\n5Io+Zf952dDQUAIDA1m4cCHR0dHEx8ezcOFC9PX1USgUl/1/tnTpUnQ6HTNmzCAiIoL09HR27tzJ\nnj17Oh2Hr68vp0+fZvv27aSlpbF69Wp++eWXTq3bUY46uhbhjxweOnSI/Px8SkpKgCs/b+29Dz32\n2GPs3r2btLQ0EhMT+fnnn3F1dcXExKR1/x2dw7vuugs3NzemT5/OwYMHSU9P5+DBg/zwww+dylNP\ncLXv1dd1gepsv0pPoFAoLtmM8txzz5GQkMDu3buBP76kFx0dzdChQ1myZAleXl5MnjyZ5uZmjh8/\n3qY9XaVSsXv3bv773/+yadMmQkJC6N+/Py+99BL9+vVrbYZrbm4mOTmZqqqqK47b3t6ehQsX8sEH\nH6DValm2bBnvv/8+a9euZcCAAYwePZrVq1fj7u7eus66detYsmQJy5Ytw9/fn9mzZ5ORkdH6+vbt\n25k9ezZPP/00fn5+TJ06ld27d+Pl5dVuLPPnz6eyspLi4uLWInBBSEgIhw4d4vTp04wdO5bAwECe\nfvppzMzMWr9PcqlzcKlrSK1Ws2/fPgwNDRkzZgwhISGYmpqyZ8+eNt9NUSqVrFq1iiVLljB48GAK\nCwvZtWtXa5+Mr68vERER1NTUcOuttxIQEMBDDz1EQ0NDa3Po5a6LdevWodPpGDJkCLNnz2by5MkM\nHjy4zbIrV66ksrISHx8f7O3tyc7Obt3mn11q+3+d98svv2BsbMzo0aOZPn06U6ZMwcfHB7Vafdn/\nZw4ODoSHh2NqasrkyZPp27cvr7zyyhXte8mSJSxcuJB7772XgQMHEhUVxYoVKy5qFrzaHHV0Lb73\n3nvExMTg7u7e2hR8peftz/m5VKxPPfUU/fr1Y+zYsdTX17f+X4fOnUMjIyN+++03+vbty7x58/D3\n9+fxxx+noaHhopz0VFf9Xn3tx2X8c3744YfuDqFHk/np2NXm6MJ3fG5UVVVVwszMTHz88cfyOuqA\nzE/HrjZHXTZIYs2aNcTGxmJmZsZ77713yWXWrVtHXFwchoaGLF26tM2ncEmSrp0dO3agp6eHn58f\nRUVFrFy5Ej09Pe644w4OHz7c3eFJN6kua+ILCQnhpZdeuuzrsbGxFBQU8OGHH/LQQw912P8gST3N\npZqdrld1dXU8++yz9O3bl2nTpgEQHh6Ora1tN0cm3cwUQnTd+MWioiLeeuutS95BffHFFwQEBDBi\nxAjgj3baFStWXHaUTGJi4kXtmFfyzCtJkiSp+5SVlbWZ9vf3JyAgoN11uu17UGVlZVhbW7dOW1tb\nU1ZWdtkCFRAQcNHBHDx4sHUoqXSx8PBwRo0a1d1h9GgyRx2TOWqfzM/lffqf/3Jo31Ze+N8XzJ07\n94rX79Yv6nbhzZsE8j9NJ8gcdUzmqH0yPxcL2/MbZ3ZuoTrxdxTaq//VgG4bZm5lZdXmi5ClpaWy\nyU6SJOk6FnPyDG8//CR1O79iUm0Wdn0D+O5E3FVvr9sKVHBwMEeOHAEgOTkZY2Pjq/qWtnR54eHh\n3R1Cjydz1DGZo/bd7PkRQhB3JpP3lj5BxIY1zG9IRV9bR+69j3PvR+vQ09O76m13WRPf6tWrSUpK\noqqqikceeYS5c+e2PtIjNDSUgQMHEhcXx+OPP45areaRRx7pqlAkSZKkf5gQgujkPGL+9zb70tIZ\nLKqYam/GDudePPjqJ6j+RmG6oEtH8XU1OUhCkiTp2tIJwYlz+Zxf9wkHc7OIiorEVtvI9KHeDHr+\nDUYFXvxT9bGxsUyYMOGK9yWfZi5JkiR1qEUnOJZcSNZ3X3GuIJV9ScmUpaXyQF9XuGUED//rHdQq\n/X90n9f1s/ik9t3sbeOdIXPUMZmj9t3o+dHqBAfOFLDh9Q/IWf08h7SNHIqIYGhdKY/N6Ufwe6t5\n/tkP/vHiBPIOSpIkSbqEphYdB84Wkbn9ZwLTwjhm7YGlrROvZ0STNLwXv/UP5IGHXsPYUN1lMcg+\nKEmSJKlVo1bHnjNFZPy6k0nndvGRtSu5lo48n3ES54ZKNvTS0W/OMqYP7PwvA8s+KEmSJOmq1Te3\nsDOpiMx9+5h1bgcxZjbcXW3IncYNrEw6zGGrJrYEDmDZvf/FUnNlPwJ6tWQf1A3sRm8b/yfIHHVM\n5qh913t+apta+DY2n/9bvYkB/3sam6zDLFWYsX5XGJYnTzC4KJU3vVtoXvAS7z36/jUrTiDvoCRJ\nkm5KVQ1afj5dSGb4Meal7sRJ28BLxtbExJxBmZrMqz7O1AVr2Ny7LyvueRV7E/NrHqPsg5IkSbqJ\nlNU181NCERkRJ1iY/iva2jLec+hNsr4lGZ+t4W4nSyb1c2WLZzODx/2Le0dM/ts/LSP7oCRJkqTL\nKq5tYsupIjKjYrknew8Ty/N528GDLDtXDDDky+Romkf6s6OPlm+cPFhx96u4Wlh3vOEuJPugbmDX\ne9v4tSBz1DGZo/b19PwUVDfyQXgWb67bT8j2d3n81Fd8aWDE067exFj15uHsHL5MCiPdTMv7A3WY\n3fIEXy79uNuLE8g7KEmSpBtSdkUDm+ILyUk8y5KCg1jlJfM/ew/OOLpxtqKF2w0N+OTsAZoM4F2v\nBrJt3fjPnWvwtnXo7tBbyT4oSZKkG0h6WT3fnywkPyWNpUVh2GQmsM62N/F6Ss6W11O49wCBKiVf\nB7tzwM6MXfZF9A1+iGcnzENP2TWNarIPSpIk6SaWXFLHd3EFFGdk8VjJEezSYvnepjcn7PqQTSMZ\nh37HICuTt31d6OfWi9fdSiiwNOHFOe8S6OTa3eFfkuyDuoH19LbxnkDmqGMyR+3r7vwkFtbw8p40\nPtgWy53xm3nt9w+IrCjlUYcA9pkpialqIGXdFuY11XFgbAA1Az15o08h5sEL2LD0ix5bnEDeQUmS\nJF2XssobWBOZQ1VhMY9XHsch8Qj7rNx40XkghooyMsxsCCiq4fn8BIyG+9Js58qqXtmUmih5ZtZX\nDHP17O5D6JDsg5IkSbqO1DRq+f5kIccSs/l33QlcTx0m3MaVT0wccagpINnaBuMGNU8lp+OnzcdA\nX8cmJyt+t0ilV595rJjyIBr9f/7J4+2RfVCSJEk3sAatjm2JxeyKzeS+8kjuPBtGnF1vnvMaSe/8\nHBpMionTt+bec5VMqUjEXF3JKcvefOucQrmRhkenfsp4L//uPowrIvugbmDd3TZ+PZA56pjMUfu6\nOj81jVo2nSzgoW9jMT/4Ix9FvoVxRQYLvEewuUKBSptNWHMLqZ/9zNgdu5jZkILKpIXP3Fz53PU0\nRl6TWffIuuuuOIG8g5IkSeqRyuqa+SWhiP1JBSyujuGjpP1k27tyv+cwzLJKMFPmEGltQu2P+9Av\nKuJVvz5MdTLguIUXPzsmUGEI9976IdP8g7r7UK6a7IOSJEnqQZq0On5KKGJrfB4PNpxiyKndFNm5\nsFLjQHNBFXYGNcTamlERcYbKo0dZ1MudJX5WNBtastHZinMmsZg4T+GNGU9gY6zp7sMBZB+UJEnS\nda1Bq+PHU4X8mljInOpTfHF2D5XW9rzoPojsSi0DcvKJcFGQqu/O7KQcXErq6DV2KP2MdYRZDWSv\nfQylqjruGP8O8wKH/u0HvPYEsg/qBib7Djomc9QxmaP2/RP5ya1s5F/bzqCOPsyamPcZVRTLG+6D\nuE+/F05nc1Fq8tnp6YZPgTGfhicypaaIyb0F9ha2fODuw88OB2lyGMzHD6zjrgHDbojiBPIOSpIk\nqVsl5lWxb9MOlmfuR9/MhM88g9nRrOTWmHM499HnF19rnGv0eDX2LF66JpRWNVi2NLHLZixHbI5R\npirmtpH/5YEhY1HeIIXpAtkHJUmS1A3yKhsI37aPfsd/wszEgB3eA1hfB+OjztDU25gIayVVZ0qp\n3bWb//oE4elui4+ugHS1J5sdjckwOoKn9yyenfQolkZG3X047ZJ9UJIkSdeBgupGftqyn1ExvzBM\npSN80Ag+qNMxIiKZ222M2TNAj/xqQ/S++AX96ipe7DuIMW4K9HVVfO8wiUiLA6gtDHlt5ga8HXr+\n0yD+DtkHdQOTfQcdkznqmMxR+64kP7/HnOPcihe5PeY7coYO507voRyOTueRMzlk+7TwjZM5Vb8m\nUf3p58wyteaDKeOZ5dREur437/XqQ4TtFqaPncWnD31/wxcnkHdQkiRJXa6+ppaYz77AK+EwZweO\n4i49H5xO5fBYaR2HPFr41MwYi1ozng1PIa6iliGh0xhhUEBTcx3fOM3kvH0YJhZ6vDV1Pc7W7t19\nONeM7IOSJEnqItWNWuK378Jt70bS7XrzPyd3mkpqmHk2h4S+NkRqaqhXOHP7qUyml1RRbqwGqzq8\nG0qJNx3CMUcFWUYHmTZ0IdOGLERPeX3eU8g+KEmSpB7ifFk9O04X4LTvGwaXJvJ/ASNIalIy6Vga\npcFefBsMBQYWjMhqYcGZk1gaGZLc25wxtclUaa35znkuuY5hKDQNLJ/yGa623t19SN1C9kHdwGTf\nQcdkjjomc9S+C/nR6gRHzpfzzM5kVu04zS2736d37XmWeo9Elw4eRi78NkDLTv1aKuMqaHn3/3g0\nNYcSJ3s0jlWENGdx3GoC33j15bTN1wwJHMrrC9fftMUJ5B2UJEnS39Ksg+/iCth5pgRHM0NCTcrx\n3Pk+3zsEk2Tqhb6RNSXOe0gVFeiK1Wi3fYW6oYF/+Q+nwMeYcaVnKGy25yv7iRQ7HaJJv4yXp3yM\nu4Nfdx9at5N9UJIkSVdICEFZvZb4vGq2nC7CydSQ23zNif95PcY5JfzgGopZkxZNQzRJ6kIqmh0w\n3bqLnLRkHvToh8vQwUxuSkalULHfbCRnbarIMghjfOAMbh+5BH2VQXcf4j9K9kFJkiRdAxX1zTy7\nK5Xy+mb87IyZ7mFEw95viT9QzxHHUeCoxKcmlQS9OOJNfOhVbs+kQ5EkV9Vy/63z6e9ch3f5GU4a\nWPCTgwHl6i309xjC88M+wMuxb3cfXo8iC9QNLDw8nFGjRnV3GD2azFHHZI7+UFHfzI+ni9h9rpSZ\n/jbcblxG5MbPKWnS41enkTQ4auirrCan9iCHNB4I4cfUmBTml1ZR4eCC62g/phQmUlwDL7k2Uqtf\ny8SBs7lt2GtYmth29+H1SF1aoE6ePMnXX3+NTqdj/PjxzJw5s83rVVVVfPTRR1RUVKDT6Zg2bRoh\nISFdGZIkSdIVKa9vZsupIvYmlzLJQY/XVEn8tr2AJyy8yHOdhXVVJcEmBlTm7GOvuT1lZr6EnErj\nvtQ8jK3MCPPxZpIylT5luXxtV8EpMyNGui5g4dx56KvkPUJ7uiw7Op2OL7/8kldeeQUrKytefPFF\nBg0ahIuLS+sye/fuxd3dnfnz51NVVcVTTz3F6NGj0dPT66qwbiryU2/HZI46drPmqLS2mS2nC9mf\nUsZtVloWVCdypFDDDuNeqM1V9Cqr4Z6KHA415fGDypZyaxccdx9geGoGTw0Yyu8+/pg41zI/I5II\n01p+cWvEvmUyj469i4HDbp4v2/4dXVagUlNTcXBwwM7ODoCRI0cSHR3dpkBZWFiQlZUFQH19Paam\nprI4SZLUrSobtHwTW8ChtDJmmFUTXFnEzlp77KvUlFHOhPMZYKrHCbWWR800IOxxij1N0749NBvq\nM3LAGL4f6M9DpTHU5BXzWq9SPHqFEpA/iqm3B+PhI5vzOqvLClRZWRk2Njat01ZWVqSmprZZZsKE\nCbz66qssWbKE+vp6/vWvf112e4mJiSQlJbWZZ2Vl1aZ9/ML3EeT0H9Nr1qyhX79+PSaenjh9+vRp\nHnnkkR4TT0+cvjCvp8TTVdNHjoZzvEyfyEoj7jSr5K2kzay2mYhxWTHD6uIZXlFFnJUZm9zsMKsr\no1JPH+vsPAx/2kZqfTkPeQfSPGYqHua5TE/azVbrKqpcbLml/wekJTbiE6Qgr/hca4Hq7uO91tNb\ntmzhz/z9/QkICKA9XTbMPDIykvj4eJYsWQLAkSNHSE1N5b777mtd5qeffqK6uprFixdTUFDAa6+9\nxjvvvINRJx8dL4eZt092bndM5qhjN0OOMsrree9IFvYN5dx/fg+qjCT+4/8Advlp3JZ3jiR3ZzZa\nGtPUWI0kp1hnAAAgAElEQVRAh0JnwPTTmWQVptBcVsHgEbdhbVNLSE4Cieo6kqxVeAc+QUqqKXaO\npkycEYCpubq7D7Pb9Lhh5lZWVpSUlLROl5aWYmVl1WaZ5ORkZs2aBdDaHJiXl4en543/lN5r4UZ/\nU/knyBx17EbOUYtO8GNcPsePJHN33m94FUaT7DiEHV53Muf0EcpUzSzv50GZooVmRQs+uRWMa9Lh\n09catZmORqN+xExwY0buYbLKKlnvUIuf5wJU5QGUVKiZdlcfnFwtuvswr1tdVqA8PT0pKCigqKgI\nKysrIiIiePLJJ9ss4+TkxOnTp/H19aWiooK8vDzs7e27KiRJkiQAdDpB3Kl8Du87xcCsCF6pPUWF\nZ182+c7FPjad0MII3vF2Istcg4G2gZATZxhtbYyeTSPWWfVYnqjnV68hjLcrY3HMr2yyqUDfJhAL\n5VxKGtRMnNEHNy/r7j7M616XPkkiLi6uzTDzWbNmsX//fgBCQ0OpqqpizZo1lJSUoNPpmDVr1hV9\nWpNNfO27GZpm/i6Zo47dKDkSOkFuTiVHIjKpOXWGgMpo/OqSKQwYyEZjBzySchhQUsn/9XbgpLMV\n6pZ6+lXHsHhnDYcMqhlgbIXDgED22gbiZJbDxPg9VDbXEG5piMJ8LuYmvoyc6IWHjy2KG+yn1/+u\nHtfEBxAUFERQUFCbeaGhoa1/m5mZ8fzzz3dlCJIk3cQaG7RkppZw6lQBmcnFWNdnEVQXh3NDHol9\nB/N88QhujSrgPm0+RaVV/Dt0MGXmhgyrSuSuwiYqE+p4Nj8eA2tzim+/D31FMnPSPsa7WkFKbw9S\na4Ix0DgwcfpgPP3sZGH6h8ln8UmSdEMpL6kl7WwxqWeLyMuuoFkNzjVnCKmMQV9fwXbnQJJPl3JL\nSipudmZUCwPOmLuwdpgZqrpmXj99htraGtbExnFSW8uoxXehb5zLrUW5hFSoKe8/gt/L+tDQJBg5\nLZA+w3xQKGVhak+PvIOSJEnqai1aHTkZ5Zw/V8z5s0XUN2hptNJQUlfCLap4AtOiiHbtz9sWQ+kV\nl0LQgUMM93RC18uJOJcAYgIa+L2iGYfyOp5MTqO5WsvjEWG4DnRnZpAd0yoT6JcLDW5DOGzkR0We\nAUPM8wh4/gGUGpPuPvwbmixQN7Abpe+gK8kcdayn5igno4zY41lkppRgbq2h2dqYeFtTepWfY1pW\nBJYlWWzoNZRdqtH02/Y7k5ri6OXugLGfKxEuA4jqZ05R3nlaClTYoeCRI6dIMq8gcYge93p6c1u1\nJbblBmjNXdir50NNkw1D+6jwCx2EytG5NY6emp8bgSxQkiRdN4QQZKWVcvxQGtVVDXgFu1BlbsyJ\n/FJuzzvCcylHKVaq+MJtOMYV7gRu3Iu/uQneLuYYqK0549+PL01NMWjMZ9rviXzX2w3byio8q6P4\nYWw1I8qteC6lBYV9AE3WJhxo8qXWyJ4RM3zxG+KBUjblXVOyD0qSpOtCVlopR/el0FjfzNBxHuQY\nGbLjQDizi47hn5XECVsXTgdNoSUqF//duzA1NsTT1Rp9IwMi+weyQW2ASlvOw+fOccbEnO9c7FFF\n72G8dwPjqpwIrqpB22cgJVUKTrW4UWPiwLBb/QgIdkWpJ398/O+QfVCSJN2QivKqOLI3mfLSWkaF\nemPuasSBLVvwOvkbzzTWcK7/MA6GvkHqL5H4vv4l5iqBZ99eGBgZcL5fEO/pK6kyaGBOXjT98gRv\n93EhL/88DZ98i4eRmsUGAVT1CuIntQe6CnBw0NB3ZF/8B7qgJwtTt5IF6gYm28Y7JnPUse7KUWV5\nPcf2p5CRWsLwcZ709e9Dwqa1aFYfxtPICt2EWaTY+HLs53D8v1rJoIZaPAb5oNFXcc7LlzUaNVlG\nDUypSGVaVBG/9LJjk6s+hls2oSsq5eVhwVh53kaiuS3e+RHMHeWMxYzZKNSde9TaBfIa6jqdLlDx\n8fFERERQWVnJCy+8QFpaGvX19fTtK38BUpKkf05dbRMnDqeRGJtH0HBXHnhmDDXJp8l/7mmyze35\nYdC99NLTkJhQw5Bf32RoWTEet45EbaiioK6RNzw8STJpoq/yNM/HpGIgnPhPoCejzyZQtPsQdwQH\n43vLM1jYWNI/fQcO/gPQf/Q/KM0tu/vQpb/oVIHavXs3v/76K+PHjycyMhIAfX191q1bx2uvvdal\nAUpXT36q65jMUceuVY6am1qIicggJjwDn/6O3PvUKDTGKmLX/g/b4/v40n00FjiT22iKZcRvTDlx\nFPsZoagcJ6BNjOfT/v04at6IhyKS4Tnx3J7lxV67PqgNW/g6JQb14BF4B86mvMKIUcW7cHbphcEr\nK1A6uHQcXDvkNdR1OlWgdu3axX/+8x/s7OzYvn07AC4uLuTm5nZpcJIk3fh0LToSYnOJOJiKk5sl\n8x8ehrGlEcfiUjBa/waNWi0He00h1cIP59Sz3Ln5ezQOdjTf/yB6afEcsjFm25je2GmPYlNVjHOR\nE/2bAhHGlTxdfAqV3wBqB93P1thGTOsKmddfhcmjK1DaOnT3oUsd6FSBamhowNq67YMPtVot+vr6\nXRKU9M+QbeMdkznqWFflSAhBalIRR/cmY2xqyIy7g2gxU7PrxFkUv21leP5JvnUdR4J1ENaF+dy9\nbzP6qemIEaPRGKk4WZPGq8OdaNFW4FrezPByEyaUVGHRkE2kiS1O0+8gs1RF/Nk6WiLrGOSrJvCO\ne1BqjP/R45DXUNfpVIHy8/Nj69atzJkzp3Xe7t27O/yxKUmSpEvJySjnyJ5zNDVpGXWbD7n6Kj45\ncpLguK0MrMzna/eJbBp8C70KcnmgNAn9fQfQOTpjPSSQJHsl/3U2xqeihkeTIxlVUo6eVolWz4Kj\nmPPOqVTcrA3IDwc3VTHjx3jgGjoCpZ4cE3a96dT3oMrKynjrrbeorq6mvLwcOzs71Go1L7zwApaW\n3dexKL8HJUnXl5KiGo7uTaY4vwr/kb2JQxAeH8esjMO419TyvdetpBm5EpyXyrQgZ0yTk8lYvw3d\n4JE4KYsIc9fgXprL0IoCyoRAV2WCnpkTRULJO+mJnMvLY9rwO5gzwJ1+U4dh6u/X3YcscfXfg+r0\nF3V1Oh1paWkUFxdjY2ODl5cXSmX3fkdAFihJuj7UVDVw7EAqqUmFWPd15IC2hrz8s8zNjsRZq2ar\n63gKFKaMK0jmFnMdjtMncPKJ19HqWujlpkahKMWkpY5TJsbUN9XhUmKDudoMZdAANiQmsXb/j9wa\nMJxn5k7B5/bJ6FnZdPchS3/SpV/Uffvtt3nuuefw9vbG29u7df67777Lv//97yveqXRtyLbxjskc\ndezv5KixoZnfj6QTF5kFLhYcctYgCmOZlhmLGRbs7nM3orqBcemnGFWVi9n4EeRHnCD3sR/p46hG\nX6klzNyBw5Ye1LUk8ViSKSpzV5RTQogsUFBb3oSvkSF7334N/zvuRGFg+A8ffcfkNdR1OlWgEhIS\nLjk/MTHxHw1GkqQbg1arIzYyk4hDaVSZqYlxMsBY7zwh50/RYNCbvR534mOjYer2nwmqLcAkyIs6\nbR16O9ZgrTAgz92GX6178Y1LLxzqT7D4VDpBLW5U+gRwTNEbp7PZDLKqwfOuEFT9ZsvfYbpBtVug\nNm/eDPwxYu/C3xcUFhZia2vbdZFJf5v8VNcxmaOOXUmOhE4Q+Xs2xw+kUKJUkNVbj1pdBtMyTmGk\nteBnt2nM8LVijkEztcvfwt5Gi75xPS0x5ykvVxLn40SuuQdfOVhj1pjO6PM7uKPEE426N79Z9MGp\n9Bx3BYPVlGkonVy78Kg7T15DXafdAlVSUgL8MRy0tLS0db5CocDGxoY77rija6OTJOm6IITgSHQu\nJw6kUK5tptATUhoLmdxUw9Qzp/nSZw4KG3tec9VHtXY9LSWlmDs0U1dTR1Z8JS3D/SnwsONzG3Ma\n9erxrNhDnzIzFpQGUGxkw/HiOD49somnnn4amweXdvfhStdIuwXq0UcfBcDHx4eJEydek4Ckf45s\nG++YzFHH2stRi06wNyaXmENpVDXVkOvWQlpTKbda92JKpoLwOide7TuEUF05/p++S7JBE3ouA/E3\nOENLfiW5dr7ETh/CfiM1BaZ62DfF4l9WxlytG64FesQYqtiUtp/C+kb+99U6Ro8efY2PvmPyGuo6\nneqDulCc6uvrqa6u5s8D/+zt7bsmMkmSeqzy+mZ2nyzg9NHz1DRXkOHYQJWyiUm9Awiq7MXxjHoa\nmywYVJDJ2K8/oSbEg9S+A6ESJpXsolhtzv9GhHJWz4ByExVWzckMqDzPnGZ9vHLdoUHJJ7oKdh4L\n5+mnn+bBBx+UDwa4CXVqmHlOTg4ffvghmZmZF732176pa0kOM5eka6e5Rcfv2VXsO1dK0dkiqC3g\njE0NVuZG3NW3HxFpgqKicsZnhuMRd5JskzrqfSwwqAqmocGY3jnh9LMo4Ff73my28KTMWB+7+hRs\nOMOsKhhbZE6R0gdtCzg8/wi/nYpgzJgxODjIRxJd77p0mPkXX3xBQEAAy5cv57HHHuPjjz/m+++/\np0+fPle8Q0mSri/ny+rZl1zKodRyXE318S2uxlxRx/e25Xw46Rb8TS14eXM0HnmJLD21jUN9rYge\nWMfQIm9Ss3tTV5tKvouaSTZF/GTlzXonT3pVpGKjOsltFXBbtT3Npn2paCynwteX4KduR21qxB2+\nso/7Ztepb9pmZmZy9913Y2xsjE6nw9jYmAULFnTr3ZPUsfDw8O4OoceTObq0qgYt2xKLefSXszy3\nPQm1SsljQZbUZ53lZ10KmzVZzLB15sTGMO77Lg6nwiSM9PawY4AxI4rt8UzxZVuDko2+LST6WfBI\nyWnWOPtzTE+BT9MWQpqjea3ElcnGU6iscSSpwYqq+x9mxLIFqE2v7PeYupu8hrpOp+6gDAwM0Gq1\nqFQqzMzMKC4uxsTEhJqamq6OT5Kka6hFJ9iWVMy3cQUMcjFj8WBHIk8eY1tSGllVVQy1tGF2jR6Z\nmYLoZhOCxXn6l67Gw6oX/eK9iahr4TV7C9J87RhQWcPYiiLuz4tno5EThYbReOrVMK3WB0+TATSe\nz2NjUS4f/7aLb775geAxPt19+FIP06kC5evrS2RkJCEhIQwbNoxVq1ahr68vf6ywh5Mjizomc/QH\nIQQJhbV8GpmDRl+P96d6kVCSx3+P7KW2soERuU3cVV7CcVsDdtu7M9wgktCaT+lrH4j5fgd+NoIP\n/Xph1qIgsE5HY10L5s3lLMmK51snfdIt4lmsHkpAsw+NqVmk+Gl4Ju53GpobWL/ha0aOuX77kuU1\n1HU6/Sy+C3Q6HeHh4TQ0NDBmzBjUanVXxdYhOUhCkv6esrpmwtLKOZBaRn2zjjv721KrK+HT32Mx\nrNMyOCoTx+oKYoePpsbQjEFZe3FvKcc+35CGmGROO1jyy9QR2CmNsa034JyymgqDFiYlJPGESOej\n3pUEGngxQjkE7flclBNH8ObhMLbu2MrCu5awctWz6OvLp4zf6Lp0kMSfKZVKxowZQ2NjIwcPHmTy\n5MlXvFPp2pDfz+jYzZqjsrpm1kXnEZ5RyQg3cx4a4kx5fSlvHtmLqqSaW8OTaLY1ITF4HHmNdYyO\n3o792QKUtVqMrcwodbPnl6cXkKkwx7JOQVF9DhmGtQxLSsHavYBJJhUkCLi/IRS9gmaMpwVg/K8l\nHAk7R3rqj2z7aS8Dh94YTXo36zV0LXRYoGJjY8nJycHLywt/f3/q6urYtWsXe/bswcLCQhYoSbqO\nNGl1/JxYzI+nCrm1jzXfzAsgo6KU/27dRk5FGROOx9MY6Mvx227HoyaP2eXhGO9NwsLUAvtxIzip\np+MrH38KdVYYaY1wyowg2VqPMWlpqMwTMPFT0zu/Ad8KA6qM+mMWMh6TCSNpalGwfctp6moa+W7L\n55hZXF8DIaTu0W4T348//si2bdvo1asX2dnZ3HHHHfz666/Y2toyc+bMbm9ek018ktQ5QgjCMyr5\n4vdcPKyMeHCIE3VlRby9ax+nGuoYkJmB2s2TDJMBBFecY6JxJRa5WvK3HsBmeH+O25mxzT2AFqUd\n5g1N3Bp5iJrcZL6dPoLphYcJULdgU1xL/2p9hNII1ejbMLnnPhQG+hTmVrL9+5N4+toxdpIPeqru\n/Zke6drrkia+sLAwVq5ciYeHB8nJybzyyissXLiQqVOnXnWgkiRdW2mldayJzKWqQcu/Rrli1VLJ\nqo/XcMJIiXd1KUEmrhT6z2F07VkeNcmi/nQWJQePoxvox7FZ4whz64uB0ha3mlKGRW3BIjqGVC8L\nwqeP4f/yo3EtqcG4RUWLyhm9OXPRTL6V77ds4ac772D5C6s5tj+FidP98env2N2pkK4z7Rao6upq\nPDw8AOjTpw/6+vqySe86ItvGO3Yj56i8vpmvo/M5nlnJomBHBruoeX/zj+yrqcJO04iLgTst6gEM\n12UwzracovAkck8n0zImiL1zxxLh6IWZniuBFZn0ifsW++hMynwcKbtrGCOLc1gcf5A6hRpUXhgs\nuBuTkOHEJyTw3LRp6HSCWZMeIi4yi7uWDMPK1ri709FlbuRrqLt12Ael0+la/77wLKw/z+vuX9WV\nJKmtphYdWxOL+SG+kDHuZjwywpQfT+xi2YFKrIQOZ0M/jPVNuTv7NwKVaeSdSCe9vJLKiYPZ7utA\norkFrvTCVaug35HX8Y+uwKSvA2aTvRlVWUROUSY06VFm4I3DXXdgPnYk5VWVPPPcc/z666888dgz\nqLU+ODhbEDrDH30DOUpPujrt9kHdeeedHW5APotPknqOc8W1vBGWgZOZCn39bHampqJqqsCq2RiV\nZgAmQp9Frkq817xKXq4ChYMdGSFB/IKWCpWS/loN6RoPBp3YwqhTZ3H0scTKuIE0tSkFFvbYVbWg\nqWtEMyOUPtNvR6GnB8BPP/3EgX2/MbTfTBpqFIyc6E3fYGf5Q4IS0EV9UB999NFVByRJ0rVVWtvM\nK3uSsDI6w570Kky0pQRUmlFhPRYboWOcRp+hKb+R89Y28vr1IX7REH4SzVg3NtK3oYRUKz96nzzD\nfZmbcHTWpzHYlK12ztTYujCuoAbXwnzyBtsTdN8LaNSmAOhadCQnFlKX78gQvzsYNNwdv0BHORBC\n+ke0W6Ds7Oz+1sZPnjzJ119/jU6nY/z48cycOfOiZRITE1m/fj0tLS2YmpqyYsWKv7VP6f+TbeMd\nuxFyJIQgOi2GFft3kaszxa5RzVBDT3JaBuJgWs/A/BJG1Jyjescespw0/PbILPaq1fhXlTG66RzG\nvYIYeSSfxxKiURkoOe9vw/NuARhb2nN7WjaaxGQiPWoYteQxpnn/8XtMzU0tJMTkEB2egam5mhET\nvfDoY4tCefPdMd0I11BP1WWNwzqdji+//JJXXnkFKysrXnzxRQYNGoSLi0vrMrW1tXz55Ze8/PLL\nWFtbU1VV1VXhSNINp7ahmp3Rv/Bd3DGyFN6YGXowyrY/+aVa7I8dJtjcFqf8FAxifyd/wgB2LRjD\nSQtrBlTks0CvAr+xt9KwtpAR53ZR3GhEpIsLH/sF00ttzJ3JGVinRRHr3YzRqKE8Nv1hdDoda9Z8\nRl5mJY5mg3B2tWTKnf1xcrXs7lRIN6guK1Cpqak4ODi03oWNHDmS6OjoNgUqPDycoUOHYm1tDYCZ\nmVlXhXNTkp/qOnY95ii7OI2vDv6PqPwc8g1GY2p0G4FmHgihx+CaUqzfe4daFy/Mju4lfe4QDg6Y\nSKGBmsHlmbxsrI//Lffy+zvf4B32ISpTQ+Ktnfmg3xCMDI1ZmpyOc1k80d5N2Dx4Hw96jUGhUHDo\nwBH+/e9nES36LH3wWebcNfSGHpl3Ja7Ha+h60WUFqqysDBsbm9ZpKysrUlNT2yxTUFCAVqtl5cqV\n1NfXM3nyZMaMGXPJ7SUmJpKUlNRmnpWVVZvb6wuPvZfTcvpGnN52YC8H0vdRWHWOIpMH0DOxwV5p\nxBBXS8Z5WlK7dh3imx1UOutzNljF8VsmoxQthJSmMsezP2edJ5CxPQrD9x5m4gB9svt48bmNPRnW\nztyTmYd7UQzH3apwuX8pD3uHcPRoOJsit/P995s4lRDF7OkLmTIjhAmhY3tEPuT09TW9ZcsW/szf\n35+AgADac0UPiy0pKaGsrKxTP1QYGRlJfHw8S5YsAeDIkSOkpqZy3333tS7z5Zdfkp6ezn/+8x8a\nGxtZtmwZL7zwAo6OnftCnxzF1z7ZNt6xnp6j5hYdkZnlbDm+mfNFx6k1vh09hRPmmkaeH9OXICcz\nlC0t/PrA82TWJJHqP4DfbVzo1VDDnLwz3KKxoGDmgxz6dAeOR8JoCfBignMx4U4erLLoxeyiCoaX\nZBHnWc+wGfcyyHsc2uYW4n/PJupoBpt3vYe9vQ3/++wDrG0sujsdPVJPv4Z6gi59WGxJSQmrV68m\nIyMDgI0bN3L8+HHi4+N5+OGHL7mOlZUVJSUlrdOlpaVYWVm1Wcba2hozMzMMDAwwMDDAz8+PzMzM\nThcoSbpRXfgV24MJR9Gv3UG98SQaTZ9ggIMhS4f3xtvajJq6Sra8/jRZhblkuAcQYz2NYXXVfJRw\nBAczW87f9jDfbD6M8/x/YeLXD/ePnsNhx6esselNYYsZy88lkty7CoOF9/Fon3Fom3REHU0nOjwD\nFzdL5twTzJLntxMRESGLk9QtOlWgPvvsM4KCgli5ciX3338/AIGBgWzYsOGy63h6elJQUEBRURFW\nVlZERETw5JNPtllm8ODBfPXVV+h0Opqbm0lJSZGPUfoHyU91HetJOapq0BKWVs6+5FLKq3Mwb96F\nQudBpenT1Ilynh1tyy2ezsSdOcx7qz+jvt6UZDNfkvt4MaO5mWdOhpHkGMQ3/vdiGRND/6X/wSKg\nHzbr3iKt7DymP33EIVNnvMtrMOqdi+X8B3iszziaG3VE/ZZO9LFMXD2tuOO+wdg4mLbG1ZNy1BPJ\n/HSdThWo1NRUXnzxxTZPjdBoNNTV1V12HT09Pe677z5ef/311mHmLi4u7N+/H4DQ0FCcnZ0JDAzk\n3//+NwqFggkTJrQZRCFJN7oWnSAmt5r9yaVE51Yz0EEPZ8U+Cmoh23A+JqZNoM3g+YG2ZJ1ay6p1\nURg2+BBuP4IaMxXzjQxZEXeEY/aBfG4zhX5HwxmX8xt6/QPRfP0GYXWlbIv7jdVxBylUGpFvncuI\nOx5jjs8EmhpaOBF2nqijaaTkHuXhxxcT0M+ru1MiSa06VaAsLCwoKCjAycmpdV5OTg62trbtrhcU\nFERQUFCbeaGhoW2mp0+fzvTp0zsbr3QFZNt4x7orRzmVDexNLuNAShk2xvpM9DKnjyaOzfFZ1KuG\n42KVQ2b5duwNtTgWxZH7uSHWNa584z8Fi/oWbjeyICg1mv0WfqzTBRG07SjD9QxQjZ+AwQf/5sfs\nVMrij/PUuXj6VWUTbqHFctKt/GvyozQ1tBB56DxxxzNpIIfNu9bg6uqCmYXhJWOV11H7ZH66TqcK\n1LRp03jzzTeZOXMmLS0thIeH88svvzBjxoyujk+Sbhi1TS0cOV/O3pQy8qsameBlxRuTPCkuS2L1\nb4cpFf2xszChqeBDqquLGF/vSPBRLb2b3EizteaVAEdmFQkGtlQQXmtMSbYJPru2UtfLC+64G3Fb\nAN+ln8XxwDaeTjmFc2MZp8wFZxzV3DLrKXSBI4nYn8rJE9lYOkLkuY2cOhXHqlWrmDx5snwskdTj\ndHoUX1RUFPv376e4uBgbGxtCQ0MZMmRIV8fXLjmKT7oenMyr5qeEIhIKagl0NOHWPtYM7mVGSWUu\nb+7Zzdkaf0yMGimpjsK1bj8TCpwYkqREbaJBPWwgZ4L789KJE4RU6qGrUeAfcwLbgnyq/YNRjguh\nYagdO1ITGHX+DLenJ2CipyShtxV7rcq4P1mBecg8ThkFcioqB+8Ae/yDbbllUgiLFi3iySefRKPR\ndHeKpBvc1Y7i61SB0ul0PfKp5bJAST1Zg1bHV1F5hKdXsCjYkWGuZlgY6VPfVMuGI9+zPc0G9K2o\naMliTF0UfdIyGZFng4GpBRZzbsNw3Ahe/PEgSWVNBJ86z9DfD6PWaCgPGIpuyGCqAoyIOBPNnMwz\njM1JQWlmS/PQYbxXug37Wh13FNiRPPhBErNa8OnnwJCxHphb/vFLtpWVlZibm3dzhqSbRZcOM3/w\nwQcZPnw4o0aNwtfX94p3InUP2Tbesa7IkRB/DHz4JCIHH1sNn872xUytQid0hJ3ewcfHzlGtGk2D\nspCFilR6Hd+Pe50per2CcH59IQbevflydzwHVu8kMCqWidHHMernS8Etc6no40mJJ+TFH+Gun5O5\nq6wQ7LwwnLWY5KS9rMldz3jLodjYzOUX0YivpR2LZrhf9BPrV1Kc5HXUPpmfrtOpArVs2TLCw8NZ\nvXo1SqWSkSNHMmrUKFxdXbs6Pkm6bmh1gt/Ol7PlVBE6IXhgiBMje/+/9u4zMIpqbeD4f3eTTW9L\nOgkJEBJ6Cwgh9Kb0JuAFBEMVBQWUjkiuUpRiQZoSmoogVYr0HiChhFASWhIgpPded3feD7zmikAS\nkGUDnN8nZ3ey88zjss/MOWfOefD80M3Yyyw+uIm76s7IZY0YrY2k7sXz5OVmkO5sS7VZ8yg2NuX3\ns/c4vHU3TY78yZDImxhIkNl9AHH16pLmnIdh6G4GhNzGpEiDgWtdlG26QfB+jl3ZzE7LVHwdJ5Ic\naYediy3vvOnM2eCTWFrX1nNmBOHZPNVMEpIkcf36dQIDAwkODsba2prFixfrMr5SiSY+oSLIK9Lw\n580UdlxLxtnSiP71HWjqYoFMJiMlK4HvD64iMMUDa3VlxkWfo3p8LLHKHE5ZRtOxzXAc2/Vl59VE\nDl+Jpdn+3/G6EopkaoTCyoGY7r3Ic83H5VognZKiKcQcYy9vTOrWQDq5G7WFORvcITztLtWyB9PU\nu5bXK7wAACAASURBVAFNW1XlbPAppk2bhpeXF2vXrkWpVOo7TcJrTKdNfH+RyWQ4Ozvj4uJCZGQk\nCQkJT31AQXiV3EjKZe7Ru9S0M+XzTtXwtH0w4KCwOJ8fT2zg95vZKJUdaKHNYtTlfRR42PON4QVs\nZba0eWc1O2PVhG29hmtiBL6HduGYnoFCYcjdTt0xqKam4e1tVI/KoUhrBQ17oKrhhPb4H3ApjqTu\ng/jm8mo0sUb0rf9ffNvUIjk1gTFjR3Djxg3mz5//yGMdgvAyKVeBysnJITg4mNOnT3Pr1i0aNGhA\nr169aNKkia7jE/4F0TZetmfNkSRJbL+WzKbLiUxo6VrSlCdJEhvP7WLVxctIBo2wNqvMDONUXA4d\nI8Q+h22FgdSuMZ4I8/pEXUyhduRllMY5WJ2/hkdUDHHNvZHXNqZn9CE00bYYYouiTmscOzZH/dsy\npCxTCvqN5c/IWA4FzaOhYydGD5+Iubkxx48fZ8SIEXzwwQesXr0aY2NjvebodSHyozvlKlDvv/8+\nnp6etGzZkkmTJmFubq7ruAShwsoqULPo5D3S89Us7eWJo8WDB1z3hp1l8emT5GgdqGzehYaONoxO\nuELRkbOsqhRDlP0bFKhGk66E9uePc1GZze8O1gzceQF7cjHu5UHfrJukmXpj2WUoufuCsB7UGyOj\nfIpWfIG270hOZThy5uge4oyP8H73WbSo879mE29vb44fP46rq6u+UiMIz1W5+qDS0tIemei1IhB9\nUMKLFp6Yy/xjd2npbs3wpk4YKuQcj7zO/BMHSc6XU0dVF41ky7gmDrj/sYPjSTlsruKM1tiN1pVM\nqRt4nHBFNlvcHagTm0Hn6xfxVBVjKdOS0+otanV/m+yt+ym4EYnt+PeQju1AfT2U1Lc/YfPZQKJk\n+7CvZMuYrp9RuVJVfadDEMrlufdBhYeHU7v2g9E/cXFxxMXFPXa/unXrPvVBBeFlo5Uktl1NYsuV\nJCa2qoKPmxVXE+KZfnA3sdnZeFdywUpZi+ZuNrSopODk1qN8ZV0XyT2OjtbGNDgXxDV5FnM9KlMz\nR87MoOM0kmdyt5IZeTWa0ODTKWhS0kn5+kcMnOxxmDCUnB8XcduiDqec2nDz5ByUZhKj35yMl1Nj\n4uPjoZK+syIIuvXEAhUQEFAyQm/FihVP/IBly5Y9/6iE50K0jZetPDnKKlCz8MQ9sgrVLO3lhYOF\nkl/O7WPhhds0sijGw6UzRVpDZrR2ZktwNIsupmKnScYj9yxd41yQspOZ28CDBjka5l86TvXidC7Y\nVeH0pTx8urejyidjybt4ldSVP2PVtwu5hjIOfb+DyxaNSDQ5SYEiicFtP8S39lvs+3Mffv1a0K9f\nP2bPnl1hcvQ6E/nRnScWqL8PHxdFSHhdhSXmMP/YXdpUtcGvqTMGchnfHtnA2puZdHFrQkSaOT2q\nOfCGqyWzd1yl+t0b1MvdiLWiGq1vGvJ7I0vkmal8H3qAYpnEOQsXzJu+he28AFRvdcR14hjSf/uD\n3JPB5Pfqx6mL8cTnpZJZ7SaJ0h36thhBhwZ9uXvnHgMHDCQ2NpalS5c+ceVpQXiVlKsP6uuvv2bK\nlCmPvL5o0SI+/fRTnQRWHqIPStAVrSSx9UoSW68mMal1FZpXeTDzwlcHfmJrlCEeVg2oYWvJuBau\nxGbk8+We63SOOEuy/CAdUtxIda9NQt4duiTc5qa5iuOySnRr1IKGrkaEzVoKHnWo/4M/id8EkJNd\nSKBlPVDfJ9XiJLdME+jSZBDdmgzGWGnK8uXLWbJkCZMmTWLUqFEYGhrqOTuC8HR0+hzUtWvXHvt6\nWFjYUx9QECq6zAI1Xx+/R26xhh96e2FvrkSSJP67ZzmH4qrgZu7KuBbuNHc1Z83BYP68I9H/+j5y\nFdfpbtyKNJs4vCP3c9XRk49qtqL+/WwmTxiF0fUgIr5eRYGFE06D3+HOx19w18KVPFc7CnOXEVIp\nh7aN3ub9ZkOxNLUpiadp06YEBgbi6Oiox6wIwotXaoHavHkzAGq1uuS//5KYmFjmelCCfom28bL9\nM0fXEh406bWrbsN7TR406WklLTN2fkdgkgc1bKrwQ++6xCXdZvAPR5DLvBgevgsjMzlOyprYxp/m\ntLMXXzbuglVCBiON7XhryQTUv/3IvT/PEBMvR9a+KepfN5PlXZe41M2cVGTTskU3FrYag435o/+m\nmjZt+iJT8gjxPSqdyI/ulFqgUlJSgAcPH6amppa8LpPJsLW1ZcCAAbqNThBeEK0k8fvlRHaEJfNJ\n6yq84fqgSU+r1fDp9sUEp9agmpUbC9/yZMNvP3Iwy4Yq+ZUZePswV90q0+HuGS5bVmJ+24HUC49l\n2h/BNPtmFpaertxfvJhr0TK4mIpL55ZYSMlc9oxnT9EZmtT3ZcFbk7GzciI7O5uioiIxLZEg/L9y\n9UEdPnyYjh07voh4norogxKeh4z8Yr4+cY/8Yi0z2rtjZ/agQKg1xUzYspCQzBq4mXvyrq2Cg6eW\ncsf5bXziY7CQp1E75RKVivPZ/0Zn+rrXJWbKQhy6tqHa1DHcvnSPS/tCKMrX4HFiG26Na5BqXcBq\nm/N42dVgQN//4mxX7cGsFNu38/nnn7N48WLefPNNPWdEEJ6v594HlZSUhL29PfDgWafExMTH7ufg\n4PDUBxWEiuJKfA5fHb9LBw8Vw7ydUMgfrCpbpC5k3KYFXMutiYPCHpeItfwSm0lO5RE0ux9CkTyB\nXveusLVqPZoPGkH3tbuIWb6QKnOncR9rjn4TiG12NE1s1XDtHPKaDuy2uUa+syFTu32Hu1dzAK5f\nv86UKVPIyspizZo1el8EVBAqkicWqE8//ZQNGzYA8PHHHz/xA/7ZNyVUHKJt/Mm0ksSWK0lsColh\nRscaNHW1BB4UpmNXdrI86DjJNMGpKAjTgiDyDLuRYd4Hh5Rz1MoPp0ZuOvv6jeI/TtW56fcZsY2b\nk/7+NMIu5lLbOYdeMZuQSVZk3c3kWLV4MmuY0b+LPx7Vmz04TlER/v7+bNmyhalTp/Lee++hUCj0\nmZInEt+j0on86M4TC9RfxQlEERJeLdmFar4+cY/sAg0j3Qto6mpJflEuRy/vZHfwBlLlTcgudsG1\n6FdqpdsTbzmDMGsJx6wzTIs+z01bZ6SPFuOz5RiH114is+MwrB2tadDElSqXtlNwLJDsYisOON4i\n0i4bv9GLqeP+8EAHQ0NDnJ2dOXPmDLa2tnrKhCBUbE+1HtRfEhMTkclkJU2A+iL6oISndSs5jy+O\n3MHX3YoRTZ3JzE3iQMhmjl7eib2yJvdzGpJlcA5TdTR1UjtxtnJDEhWxvJtwg7ejr3GlfW/c3VsQ\n/NsZMi0d8arvRONW7thEnaPgt9XE5BmTrzBmn0cKVc9L9F/3C0obsbS68HrT6XNQ3377LV26dMHL\ny4tjx46xevVqZDIZfn5+z3RQQXjRCtVadoQls+1qEuN9XXA1SWDln59xKeo0VU1aUCvrA+JccinK\n2YhtgQtWRe+z260YC9l9vrp1FuesdCLenEjMzSKizoVSy9Men36NUJzeR/G8+USjJTvfmnhLNWmp\n6bQ5aE6j1fNQ2lih0WgqbPOdIFRk8vLsdPXqVapXrw7Anj17+Oyzz5g/fz47d+7UaXDCvxMYGKjv\nECqE3CINM/ZHcC0+i1H1EzkeNI2vt02kINGS2mkf07rKUBKdwkhICsA1ry05Rp04bJdBO0Ueq87v\nwTzPmGOOw4k+e58q144zrKsVLTTn0c77GG1yPDGSEUWZtkQXZKKKM6fzyE9pefwXTD2q8Msvv9C0\naVOysrL0nYZnJr5HpRP50Z1y3UFpNBoMDAxIS0sjJyeHmjVrApCZmanT4ATh38oqUDN9320qyULI\nTtjGoVgj3GRtsUnvh7dPNdIcrrMx1J9CKRuZbDSnHSS0wKTo+3SLDSHIqjXGKme89q6hdrtqWFVJ\nRHZ6L7I6jShOSef2yRtgbES0SkubEV9g3bgOAKGhoSXTgwUEBGBpaanHLAjCy6lcBcrNzY0dO3aQ\nnJxc0ueTmpqKqampToMT/p3XfWRRel4Rk7fvhKwtFBopqSV7m+JEB5r4VqXhoCoEHv+DzWFLUWhq\nE2XZiyyDPLyzzPjo9lEsNNkkNuqP243bmF88gX19GQbuKhTVW5B14CBxP+5CZlOJRFuwGdSNXu3e\nfnDM9HS+/PJL9u7dy6xZsxg0aBByebkaKiqs1/17VBaRH90pV4EaO3YsmzdvxsDAgMGDBwNw69Yt\nWrVqpdPgBOFZhdy5zOI9izDSptPQpBcGSdVp3KoqDd51RatRs+SHTwhXXyZD6kystQMOhRoGR2vo\nlvwbVPFCVqRC2v8LNo6mGDVyR9mlH6k//8L9dcdQa02w9XTlpGsKLcfPxMulYclxU1JSMDAwICgo\nCGtraz1mQBBefs80iq+iEKP4Svc6Pp8RmRDO1tNruXwnhKryN3Ep9qZ5aw/qNnHB0FBBeOAJvjnx\nNVnyqiQb1SdPIadxViVaZl7kzfSrqI1sUaZGU2Rmi1mHjhhaW5GweScptzIxNLfCwklFjrGGwzUz\nGDJyIXZWzvo+ZZ17Hb9HT0Pkp2w6HcUnSRLHjh3j1KlTJcu/t2rVivbt2z/1AQVBF5Iz49lz/mdO\nXduHWUFrGmsm06lTHeo0royBgRxJq2X1ojns0WaTbNYLSabALd+Iqhoto+5vxKJYjTwvD0lehHLK\nAkwLs4n9djV5qRpMrS1R1XfmrocBG7UheLfszdg3hmKsFE3cgqBL5SpQO3bs4MSJE/To0QNbW1tS\nUlLYvXs36enp9OvXT9cxCs/odbiqu58cwa5zG7gUeYrKSl+qpn2Ia4OavNurNgqDB30/CRcu898/\n9xFs44xtoQHV8iHbxJShSed5I/Um8sJCiq2dMXl/OrLwGyTOXQoYopWZYtXNm9CaxeyK3EGLWm8y\nzedXLIytWbduHVeuXOG7777TbwJegNfhe/RviPzoTrkK1JEjR5gzZ85Dy2s0aNCA2bNniwIl6MWN\nmEvsCl5PVMJ1WtXtR42iaaTnGePTvyZv1XswP2TB9Qj2bNzDHmMVV21UOBSA1lqOT1wafW7sRK5R\nozW3xXTSRIr3Hid5YQD5OXlgZYHt+PcIMb3LjrMB1NE04csh63CwceX8+fNMnjwZc3Nzvv76az1n\nQRBebeUqUIWFhVhYWDz0moWFBcXFxToJSng+XrW2ca2kJTTyNH8EryM9N4Ueb7zLG/WncWDrDRzM\nlUz/sClWJoYUhN0iauM+9qutOGprTaxxPjYGcobbm1Pr9F4UkhZMrLH6YCLX/zyA4qPPMVM5UGSv\nwnXJbK7kXmPlqbk4WLswtd+3VHWsRVJSEh9++CEnTpzA39+fvn37IpPJ9J2SF+JV+x49byI/ulOu\nAtWwYUOWLl3KoEGDsLOzIykpiU2bNtGgQQNdxycIqDXFnLl+gF3nNmCgMKTnG8No6tmOjZeSuf7H\nbWraGDNk5Bso5JCwditnQuIJtarCXpcUkIoZYW5BhxP7sJTlEW7tQYuh75BzLpTLflPITi2gehtv\nrHp2IrqRDV8em4JcJmfUmzOp6/a/mcV//vlnKlWqxNmzZx+5WBMEQTfKNYovLy+PNWvWcObMmZJp\nW3x8fBg+fDhmZmYvIs7HEqP4Xm0FRfkcu7KTvRd+wcHalV7NhlHPvTkaCb46dpfCG4lU02oYNLoZ\nRZevEbLmACGWHpyzzuSyVRGOWbmsCj2LtTKPM/b1MfDtRP2Iq9xdtwuNFtz9eqNoVofcjbtY0egO\nhkYm9GsxkmZeHV+buyNBeBGedRRfmQUqLy+PhIQEHB0dMTY2JisrC0tLywrx8KEoUK+uc7eOsvrg\nPGq5NKZns2FUd3owQ4NaKzH/6F24l4pTRh7vDG9M9NJfOZVhSlAlNRetilBoNEw4H0QvbTwZxpas\nrDmAPskR5O84iNLCmCrvDySyhR0nr+6m86FiUnyqULvnO7g71BSFSRB0QCfDzENCQvjmm28oKirC\n2NiYyZMnU7du3XJ/eGhoKOvWrUOr1dK+fXt69+792P0iIiKYNWsWEydOpFmzZk93BsITvYxt45Ik\n8UfwOg5d2sLUft+VFCZ4UJzmHb0D8ZnYJ2fzprc52/1/YY+jKTer5aCVoH9YOB+k3cDAUE6wqSc3\ncm3ouOwH5JWt8Jr7IVc9ZXwVvB77sMr0UvhgZBHFG6PmIJPJKC4u5qeffqJmzZriEYq/eRm/Ry+S\nyI/ulFqgNm3axODBg2nbti1Hjx5l06ZNfPnll+X6YK1WS0BAAJ999hkqlYrp06fTpEkTXFxcHtnv\n119/pWHDhrzEzwwLz0GxuojVB+cSnRzBF0PWobL433IuhWot84/dhZQcHKKSqEIMvxyzZo+7Fovc\nGFon5fDp7RDMjQwpNjLm6rUi0o3TaFe5EKe1n3POIoE159fgHuXF+B7z8LCrSdzHc4hr3xSZTEZg\nYCBTpkzB2dmZzp076y8JgiCUKLVAJSYm8uabbyKTyXjzzTfZtm1buT84IiICR0fHkjWjfH19uXDh\nwiMFat++fTRv3pzIyMhSPy8sLIzw8PCHXlOpVA9dvfw1q7DY/t/V3MuSn6y8dOZsGIOJgTmfD12N\nsdKEwMBAJAnkrnVZGRSLQ24K9pHnKNQ4c1MyYJdTDI3uxTA2OxLjIg0mRoZESDYkBsWjHT0U20b2\nHE0+TXj4Amq5etO52nvYmbtQ1cCJtFW/km1jQbxSzsiRIzl37hxDhgzBx8cHDw8PvedDbIvtV217\ny5Yt/F3t2rWpU6cOpSm1D2ro0KEPrazr5+fH2rVrS/3AvwQFBXH58mXGjBkDwMmTJ4mIiGD48OEl\n+6SlpbF06VJmz57NihUr8Pb2fqomPtEH9Wq4k3Cdb3dNw6dmJwa0+gC57EH/ZnRGAcvO3Cc57QbV\n1CEURppiW1SVSlnXWVnNnP6JkbTMSiILU6rmZ5KUInHnvoTj0ukkGl7i0KWtNKzmS+/mfjgq7cgL\nukRu4HmKY+Iwb+uDRc9OdO7Tmw4dOjBx4kQx+bEg6IhO+qAKCwv5/PPPS5reCgoKmD17dsn7MpkM\nf3//pz7oX9atW8egQYOQyWRIkiSa+J6zit42nleYw++BKzh74xBD203Ct/ZbwIP1m369lMDB8GtU\nyvsJl4zamGV7Uz/9DrLs/SxoWo934yJIVJtwP1JLA6NY8ozN+KNRX7xnm/Dz+Rk09WzHF/1/xCIi\njdzV+4gNv41JwzpYdu+AScPayAwNAfjss89o166dPtNQ4VX075G+ifzoTqkFauzYsQ9tP03HsUql\nIiUlpWQ7NTUVlUr10D5RUVF8++23AGRnZxMaGoqBgQFNmjQp93GEl48kSQTfPMyGo0toUK0Fi4b/\njoWJNZIkcSQinYDzcdS2Scc1bTvV0gZhk5VBnbvbue6i4Ps3GtHqxj2UIfdpmZ+NV31TIpwacbD1\nf3CQbSfo2g1m15+O6ZX75G1aRo5nNcxaNsX2o+HITYwficXw/wuVIAgVj85mM9doNEyYMOGhQRIf\nf/zxI31Qf1m+fLlo4nsNFBbns3T3LBIy7jOy83RqujQC4HZKHsvOxqDWSHR1yuLin+dQ5drhnXAO\np4xQVrnU4YSbG//5IxBDa3MsXFW009zl93pvo67jDpeX0TTLCfc4OUpnB8x8m2Lq443CyoLCwkLW\nrVvHsGHDMDZ+tEgJgqBbOp3N/FkoFAqGDx/O3LlzS4aZu7i4cOjQIQA6deqkq0MLFZRGq+arrROw\ntXRkwbBfMVAYklWgZu2FOM7cy2RofXtyL10lPDibN1IzqZO0h7spGiY28yXP0hIHCS598A5DLpzC\niWx+rPIub8WGYH3uJDLbKji0b4fZ+CYY2NuWHPPIkSNMmzYNT09P+vbtKwqUILxExHpQr7CK1jZ+\n9PIOAsP3MeudlUiSjD9vpLAhJIE2Va3xysjh6uko7PLu0DrlJPL0VI6kWvBT3/ZUMzTnjqUC76wC\nJl47SFy1RtzJtMQ7/ganq2fSadg0qlSt99CxoqOjmTFjBtevX2fBggVPvCCqaDmqiESOSifyU7YK\ndwclCH9XVFzAtjM/MaHXV4Ql5rH8bAymhgo+rVuJc3tDuJWRQe+kfVgWJZGUIGebSRV2/qcZ3T08\nORB3h2FRUfSKv0x0pUaowpNIcrxNYC9XhvRc9Mi6TJGRkbz55puMHTuW1atXi7smQXhJiTso4YXY\nfe5nQu6EUGQ1juiMAvq6yrh9dh8Wic44FSTQIv0Q6blq4uKN+LlRPSLqVmdA4/r8cf4i86+fw7Yg\nj6LiStzxcuZP0xP07vQhbev1fOzURJIkkZSUhIODgx7OVBCEf9LpHVRRURHbtm3j9OnTZGdns379\nei5fvkx8fDxvvfXWUx9UeL2cvHGeTYFr0Kgm08bhBgb5+wndl41tcU8aZJ3F/Oo5slQm7JS5sbtv\nPTyrVKGdvT2Z+06x6c4RCrAhr31fTtmEE5YSwie9llHFrsYTjyeTyURxEoRXQLlmfF2/fj3R0dF8\n9NFHJVesrq6uHDhwQKfBCf/OX09y68vVmEjGrh7Hsr0zaFRrDDWVO7keEkCtMFccirvjG30YeWAQ\n6TUbM6Vmcw6292Z2z+5I+SYM+GU1H0YdpsinJ9L8WayStlJgoGHe0J9LilNeXh6nTp36VzHqO0cv\nA5Gj0on86E65CtS5c+f4+OOP8fT0LClQKpWKtLQ0nQYnvJzupSYz6ZfP+fK34djZeLJy7E4stXch\nKh/f2Lco0NjjE74fYu5zq1FLPqvuQvX69ZjRox9b/rzCgqMrMFcWY/n9z9xu44L/jg/p1mQQH3T7\nL8ZKUyRJYu/evfj4+LBp0ybxgLcgvKLK1cRnaGiIRqN56LW/lt0QKq4XPbKoSF3IikNrORO2CRfH\n1iwasQVXlT1bD/6G4tgFXOiDIiueFsnhaDq0YdfRILZ6V6anVyOS0hUULF3IwtQrZFf3xn7GDH46\ntoSbMaHMGrgSN/sHd00RERFMnz6dmJgYvv/+e9q0afOvYhajr8omclQ6kR/dKVeB8vHxYfny5Qwd\nOhSA9PR01q1bR4sWLXQanPBy0EpaTofvZ82R78mXVWFin1U0r+6FWq1l+9Y9yE8eJs/4P3jFnMdT\nm0WCbwd+DwribMcGNDB25Y2D22mWEkaGgTXyUdOR163C7F+HU8XOg7lDN2CifLAo5pYtW5g+fToT\nJ05k9OjRYhYIQXjFlWsUX3FxMRs3buTw4cMUFRWhVCrp0KEDgwcP1uuPhBjFV7oX8XxGWPR5fj76\nLYm5GpSq/zCvV1cqmRpyLyKVwI27MUuJIMaoPr6JZ7HWarmlMWGdvSFKZ2uGxt2lcVoEGZIVV1u/\nRY9Rwzh9fT/rjyzindbjaF+/90Oj9GJjY5HL5Tg5OT23+MUzLGUTOSqdyE/ZdDqKz9DQkGHDhjF0\n6FCysrKwsLCoECvqCvoTm3qHX49/R2RCBAVm/fCs2ZZP27ihzi9m78aLmAbvQCZ3JN7AjU7qW+Tc\nieNCdi6hb9VlTHY0tcMuUaC1ZoVrCxoNHcBbHm78dHAu16NDmDVwBW72no8cs3Llyno4U0EQ9KVc\nd1CJiYlPfE+fw3nFHdSLp9Vq2H42gP0XN2Nu24tUeWvG+rjTzMWSK8HRxG3fhepeMFfcuyHPu02t\n6zdQFSZgWMUSS2URd01scciWE1ilPuvdrJnXowuVTYr49o+puNp6MPLNGagLteTm5uLo6Kjv0xUE\n4TnQ6R3URx999MT3Nm/e/NQHFV5OadlJLN0zi7Q8DZlWc2jpWZ3+de2JjUxh/1f7cAvaRl6xNfdq\nd6Pl3d9xkeWiVUGwcy12ODjhnSGnWi7s69mYk4Wp/Ni9KwkJwXy+fRHvtPqQdvV7s3PnTmbPns34\n8eNL1hITBOH1VK4C9c8ilJGRwZYtW6hZs6ZOghKej+fVNi5JEmdvHGLN4YVoTDugcujD57XsSL2V\nzO65x6kdcQiL0LtENG6Ml5RCx9g1pOUaEKeszIR2rclQSHxxORKpuhenOrtxNTWZdT27cCB4BWHR\nF5g5YDkF6RJ9+vQhPT2dgICAp5rV/t8Q/QdlEzkqnciP7jzTXHzW1tYMGzaMCRMm0KpVq+cdk1CB\n3Eu6zZrDXxOTnkaO2fsMcG9EcWQyFy5ep01OIGbHLiFZGlG1oQU1i66SlKTmsm8XCpKS+LJeTewL\n8vj6ZjSOQ/uxsDCL9NxsFrVtyLKd43BWuTNv6M8sWfgtGzZsYMqUKbz33nsYGIgpIgVB+BeTxcbF\nxVFYWPg8YxGes39zVZeTn8nmUys5df0gBcY9aGrXDlVCDkWXbuGbf4GiUyeQKbR41DQkOVNO9F01\nGk8HtnbpSk5RDNfqV6NvTBxvN26M7fvDGH/0KHZmZgyvYcDXW95nQKuxdGzQD5lMRpMmTRgzZgx2\ndnbP8ezLR1z5lk3kqHQiP7pTrgL192Xe4cFS8DExMfTr108nQQn6o9Vq2HRmM3uCV1No2Jgq1v54\npWixKUihjUEY6hP7KcwsQOVgTKhhHQqDrqKwMyC+tSNb7BqSYphG9/RCultWoctnw8hAy7t7/qSF\niwN2eafZfuYcMwYso6rD/5qHxXyOgiA8TrkK1D+XejcyMsLNzQ1nZ2edBCU8H0/bNn4+8jwr9n1F\nrlpJlze+wDbegqSIOLqoIrEIPUq+wgpDeRH5CkN2F/tgG3gEdTNb1jdpQoyxJT1jkrExdaHee/1o\nXcuRmympjP1zH/2qOxB9eyUKEyfmvvszZsYWOjzrpyP6D8omclQ6kR/dKbNAaTQarl27xujRo1Eq\nlS8iJuEFS85KYuGur7mXcJlaNYbT1d6H0CM3qG5wntaRx8iLMCM9KQtjo0yiLepwK0NNTlw4mz58\ni3SlBb1jUuiMlpp9B9LapwZymYzg2Fg+OXiYQe4yLl1cgF1ufdZu2EfXOsOpW7euvk9ZEISXzh1D\nTQAAHXdJREFUQJkFSqFQcOXKFfFg7kuorKu6InUxq4+t4+TlX7Cq1JGJnVYTceIeRQfWMCDrAhlp\nau4p7XGzySTVxJpwu/qkBF0nz1zL6oGtaJWhYOTlG2xr0A6fvi1p41EJgD9vRzDv1Am62tzhzPGz\n3D9ZxF2Da2zcuLHCFSdx5Vs2kaPSifzoTrma+Lp168bvv//OgAEDxAirV4AkSWwMOsbuoG8wMLRl\nYKslGB24TdKv82htFIWJpZKcpt2watkKzemL3Nh/kBiHmhgeOkN6dSMCunfBWWPH8NtnuObTFtO6\nDUqK07rQK/wacpKG+cc4tjeB6GspzJo1i8GDB4uLHEEQnkqp1eavttV9+/aRmZnJnj17sLS0fGh+\ntBUrVug8SOHZPK5t/E5yLF9sm09B3m36Nh+PY2Au6SPm4uSgpXoVDfKWvUiVORC39SD5a/Zi1smX\nm9Z1MQk+waEe9blUtSZKuTXjwq5zu1JlYus14sPmldFKEgvPnOXsjcO45Z3gzabDccq4ywerP8DG\nxkZPGSib6D8om8hR6UR+dKfUAvXjjz/SsmVLxo8f/6LiEXTo0JWDBBycSzXX7nzYeAQhI78kR2mI\nT58amGkySXV+g6gVu7GoWR330f0Iu3SH22dvEeSk5sy4PhgrbHDSmPNe2FXc5EW4zpmAhZUZRRoN\nnxzYT+K9P3Ahjkn9f6CaYy16NNf3GQuC8DIrV3tdnTp1dB2HoAN/v6o7dPUkAQfn09FnPu961uRY\n66EYdu9Jh35eFG1ZQ4xFY1L/OInn4s+4FR7L9pPp2Jw5zpY2tUh1cqWqwoNWbrb03PkzxkaGOC+a\nhdzYiIyCAsb98Rsk7aCxiycfdP0VU6OKM0qvLOLKt2wiR6UT+dGdUguUVqvl2rVrpX5ARev0Fh61\n72ow6w7MplfL//JO46ac7PY+mTUb0vvjrhTNm0hy9Y5E7z2HZogf2w7EYJERgUnwCX4Y0AEDEztG\nYEwP6wzyd+wBjQan7z9HbmxEVn4+XT8aSvyZM/ywdiFdm/7noeZfQRCEf6PUAlVcXFxmH9OyZcue\na0DC8xMYGIjMwYp1B6bRv81M3m7amsuTviI1R8J3xXg0P31JpmtT7vz6J9e7jaLobgKxOem02v8n\nV9v48J+sInpHhyGTJDRO9khqNfaffYzCxIS9R4/wwUejMDRQs2LZct56o5e+T/eZiP6DsokclU7k\nR3dKLVBGRkaiAL3EYrNT2RE8h85Nx9OtThuOzfiJ7H2ncV48D7sLu8jMgcRDR0nq2JV4pTEFycG0\n2nscWUtfhkl5KOLzMG5YB3ViClJRMY5fTiFFoWVE/zcJDb5Ek97ebFywCQtTK32fqiAIryAxZvwV\nFZ+eyB83VtLAcxA9qrVlh99CVBdP0mTz99gbZpP5zT6KUnMxr+tApNKL7Oy9dN11AZe6XlhamyBP\nz0dubUPhzUis+ryFsnUTDl/5g2UblhCTV4j/+lWMbtdH36f5r4kr37KJHJVO5Ed3Si1Q5VjLUKiA\nUrLTmLJhDM4OHegZbU7wpMFUru1B4z3LMVWZkTP1Uygs4JS7krOOrbHMSqbnlkuY1q6LRSMv5Hfv\nYGBvi1X/bqR5VmFZ0Eau/DCbHJkK8zeGsXZaX5o4P79l1wVBEB6n1AL1888/v6g4hOckMSuLT9Z9\ngL1BddovPMUtuTkec6dRb0Ab1GGXSJ32MdGyfH7xKERr3ZfKiQ40/GM5klddKle2QB4ZgXnX9lxq\nXpd1gT+TH3gCc3NXOreYQs8GbVGZmOj7FJ8r0X9QNpGj0on86I5o4nuFxGTkMGXDR7gUmtBx9TVi\nvDvQ3t8PNzdLEr6ZRfHVC2y2zcEkowZVCzuTl2pJtdNbUFR2pbo1KEyVnB02iI3XdpI44zMsjFT8\nsGA5XpXr6fvUBEF4DYkC9YqISMnjs323aZpoRN298UR3eZeuk7qhlidw7dNRJGuyuFBsTI20PkRX\nqoGpnZyic0FUVko42hkS1L4p67SRsOUTIg7FUaOqF99/+QOelT31fWo6Ja58yyZyVDqRH90RBeoV\nEBKbxeK94Qzf+ysGBRK3eo6mz9jWJOVmof76I/LzZSTfr4rhG90IN9PyVg0Drq3cSmdTLUVV7ZhU\n3xLDlE0kH7pLfqKWbxYspUePHuKZJkEQ9ErM3vkSkySJ41HprNp4hvd+WoTS3p7b7QbS/6N2XEvJ\nxOjzj5Aynbht/x/ifbpQ3MSCXvcvkLfqFxpWNuaip5LlDW7hpAxGdt2Yvh0Gc+F8CD179nxtilNg\nYKC+Q6jwRI5KJ/KjO+IO6iVUqNZyPCqdP8KSsQ0Opu+O3yju1Y9oBy/eGdEUC0UxTX6bR5BnO6Ly\nnaifch5rYwXG29OJNS4mul4xkXbJOPn6MMVrLJ6V6yF/X/HaFCVBEF4OMuklHkt+5MgRGjdurO8w\nXqjbKXl8tj8C77hI6v65C21SKold3qFOj2bUf8MVo+Jc0hZ8xgmZN5XjI3HMSyHB2YQ9ple5Ym2D\nyqwOU3sPo5ZzVX2fiiAIr4mQkBA6dOjw1H+n0zuo0NBQ1q1bh1arpX379vTu3fuh90+dOsWuXbuQ\nJAkTExNGjhyJm5ubLkN6qd1OyWP+5hCG/LwCbXYu+e07U2dkL7rUdUKukJOTnsalLxZwv6AGdTIu\nYW6STYq7iiWVgpEZ9mO4Rxuibh/HIFet71MRBEEok876oLRaLQEBAcyYMYMlS5Zw+vRpYmJiHtrH\nwcEBf39/Fi1aRL9+/fjxxx91Fc5L73ZKHvO2hdF17UoMPTxofmg9fZd+gFeDysgVcm7HJ/LHl+s5\nZdICl/qOOFZREGJixGzHZAzltfDVVGLuf8dw4cIFjI2N9X06FYboPyibyFHpRH50R2d3UBERETg6\nOmJvbw+Ar68vFy5cwMXFpWQfT8//DWH28PAgNTVVV+G81CJS8ph1IJLRt09h7mZD03WfIf/bysbJ\nCVkErjyLhZktw4c0ImTNQsZb5ZBjm4wiJZPca/asj/mO+fPn07lzZz2eiSAIQvnprEClpaVha2tb\nsq1SqYiIiHji/kePHqVRo0ZPfD8sLIzw8PCHXlOpVA89xf3XlcyrtK2VICDOhjEF9yjef5iirz4q\nKU6BgYFIkkTsmQwctKe5ZZHK+G0B5KrUGONFc8NOBGxZzujRvRk3biMXLlx45fP1LNt/qSjxiG2x\n/Spub9myhb+rXbt2mWsN6myQRFBQEJcvX2bMmDEAnDx5koiICIYPH/7IvteuXSMgIIAvvvgCc3Pz\nch/jdRgkcTwqncOHQmn3/UKa/LoYq4a1St7LKchi1865nI46DiiJUXqA1pPBVvXpPrgjpuZG5OXl\nYWpqqrf4BUEQnnWQhM76oFQqFSkpKSXbqampqFSqR/a7d+8eq1atYurUqU9VnF51+cUa1pyPY+Xh\nW7RZswKvzz4oKU7F6iL2nv+FiSt6kHH5DG/FN6dm1kQGFHVg/Tt+DBjTDVNzIwIDA0VxKoPoPyib\nyFHpRH50R2dNfNWrVychIYGkpCRUKhVnzpzh448/fmiflJQUFi1axPjx43F0dNRVKC+dawk5LDp5\nj5qVTPj41DYs2zbF5Z3uSJLE2RsH+e3Y9zjkGfHJdSV3LTqRbmSBofktBk2fKp5lEgThlaGzAqVQ\nKBg+fDhz584tGWbu4uLCoUOHAOjUqRNbt24lNzeX1atXl/zN/PnzdRVShZZdqObMvUxORKUTlZrP\neF9XfJxMuXOlNlU/HMz1qHOs37cAdVYWfeOr0sjdE4XxBS4X3eSrYxdo7O3N0Pz8h+6YxBxhZRM5\nKpvIUelEfnRHPKirZ1pJ4oczMRyNSKNxZQtaV7OhmaslJoYKJEmi8FYUucfOcPr6AQwqO9C67RCM\n5Pnc/G4uc2JyiMkv5KuvvqJNmzb6PhVBEITHqpAP6gplW3M+jjtp+fz6n7qYKRUASMXF5Bw/R9ae\nI0jFaszbt6DrwGUoLM0p2rKWUzu3Mjr4JhM++YTRo0ejVCof+9linZqyiRyVTeSodCI/uiMKlB4l\nZBey72Yqa/vXxkypQJOTS87hQLL3HcPQ1Rmbd/tiXL9WSb+SlJuDlJOF7w8bOFmkxtnZWc9nIAiC\noDuiiU9P4rIKWX0uFldrY/yaOCNptcRN+i9GHu5Ydu+I0t2l7A8RBEF4CYgmvpdAkUbL/pup7ApP\nIbtQTfMqVrxd78FMGzK5HKevZyD/W3NddnY2d+7coX79+voKWRAEQW/EelAvyMWYLIZvCefc/Swm\ntHTlt0F1mdiqChZG/7tG+Ks4SZLE9u3b8fHxYdu2bc98TPF8RtlEjsomclQ6kR/dEXdQOpZdqObH\n4FhCYrP5pHUVGle2LHX/GzduMHXqVNLT01m9ejXNmzd/QZEKgiBULOIOSockSWLm/kiMDeT81K9W\nmcVp+fLl9OjRg+7du3P06NF/XZzEyKKyiRyVTeSodCI/uiPuoHRIJpOxoIsHpv8/fLwsbdq0oX//\n/tjZ2ek4MkEQhIpP3EHpWHmLE0CdOnWea3ESbeNlEzkqm8hR6UR+dEcUKD3IzMwkJydH32EIgiBU\naKJAvUBarZaNGzfSvHlzjh49qvPjibbxsokclU3kqHQiP7oj+qBekMuXLzNlypSSIlXa4oyCIAiC\nuIPSOY1Gw6effsrAgQMZMmQIBw4ceGHFSbSNl03kqGwiR6UT+dEdcQelYwqFgoYNGzJz5kxsbGz0\nHY4gCMJLQ8zFJwiCIOhUhVvy/XVUWFio7xAEQRBeGaJAPQcajYa1a9fi7e1NSkqKvsMpIdrGyyZy\nVDaRo9KJ/OiO6IP6l86fP8+UKVMwNTVl8+bN2Nra6jskQRCEV4Log3pGqampzJkzhyNHjuDv78/b\nb79dsrCgIAiC8D9iPagXrKioCJVKRVBQEJaWpU8CKwiCIDw90Qf1jJycnPD396/QxUm0jZdN5Khs\nIkelE/nRHVGgyuElbgUVBEF4aYkCVYri4mJWrFiBn5+fvkN5JmKOsLKJHJVN5Kh0Ij+6IwrUE5w+\nfZq2bdty6NAhZsyYoe9wBEEQXjuiQP1DfHw8o0aNYuzYsUydOpVt27bh6emp77CeiWgbL5vIUdlE\njkon8qM7YhTfP/z555+4ubnx7bffYmZmpu9wBEEQXlviOShBEARBp8RcfIIgCMIr5bUsUIWFhXzz\nzTfs2LFD36HolGgbL5vIUdlEjkon8qM7r12BOnLkCC1btuT8+fM0bNhQ3+EIgiAIT/Da9EHdv3+f\nmTNnEhYWxvz58+ncubOOoxMEQRBAzMVXpnHjxtGyZUt+/PFHjI2N9R2OIAiCUIbXpolvx44dTJ48\n+bUqTqJtvGwiR2UTOSqdyI/uvDYFSi5/bU5VEAThlaDTPqjQ0FDWrVuHVqulffv29O7d+5F91q5d\ny6VLlzAyMuKDDz6gatWq5f78f/ZB5efns3LlSoYPH46VldVzOQdBEATh36lwz0FptVoCAgKYMWMG\nS5Ys4fTp08TExDy0T0hICAkJCXz//feMHj2a1atXP9OxJEli3759tGjRgitXrlBYWPg8TkEQBEHQ\nI50VqIiICBwdHbG3t8fAwABfX18uXLjw0D4XL16kTZs2ANSoUYPc3FwyMjKe6jhRUVEMHDgQf39/\nvvnmG9auXYu9vf1zO4+XmWgbL5vIUdlEjkon8qM7OhvFl5aWhq2tbcm2SqUiIiLikX0qVapUsl2p\nUiXS0tKwtrZ+5PPCwsIIDw9/6DWVSkVGRgbTpk0reS0kJOR5ncJLz9TUVOSjDCJHZRM5Kp3IT/ls\n2bLloe3atWtTp06dUv9G78PMy9sFVqdOnUdOZsuWLfTv318XYb0SRH7KJnJUNpGj0on8lO1Zc6Sz\nJj6VSkVKSkrJdmpqKiqV6pF9UlNTS91HEARBeD3prEBVr16dhIQEkpKSUKvVnDlzhiZNmjy0j7e3\nNydPngTg1q1bmJmZPbZ5TxAEQXj96KyJT6FQMHz4cObOnVsyzNzFxYVDhw4B0KlTJxo3bsylS5cY\nP348xsbGjB07VlfhCIIgCC+Zl3ouvrCwsDI72V5nIj9lEzkqm8hR6UR+yvasOXqpC5QgCILw6hLz\n/wiCIAgVkihQgiAIQoUkCpQgCIJQIYkCJQiCIFRIokAJgiAIFZLepzoqD10v2/EqKCtHp06dYteu\nXUiShImJCSNHjsTNzU1P0b545fkOwYNJjmfNmsXEiRNp1qzZC45Sv8qTo7CwMNavX49Go8HCwoI5\nc+a8+ED1pKz8ZGVlsXTpUjIyMtBqtfTo0YO2bdvqJ1g9WLFiBSEhIVhaWrJ48eLH7vPUv9NSBafR\naKRx48ZJiYmJUnFxsfTpp59K9+/ff2ifixcvSvPmzZMkSZJu3bolzZgxQx+h6k15cnTz5k0pNzdX\nkiRJunTp0muVo/Lk56/95syZI82fP186e/asHiLVn/LkKCcnR5o4caKUkpIiSZIkZWZm6iNUvShP\nfn7//Xfp119/lSTpQW78/PwktVqtj3D1Ijw8XIqKipImTZr02Pef5Xe6wjfxvahlO15m5cmRp6cn\npqamAHh4eDw0B+Krrjz5Adi3bx/NmzfH0tJSD1HqV3lyFBgYSLNmzUpWIHid8lSe/FhbW5Ofnw88\nWDzVwsIChUKhj3D1olatWpiZmT3x/Wf5na7wBepxy3akpaU9ss/jlu14XZQnR3939OhRGjVq9CJC\nqxDK+x26cOECnTt3BkAmk73QGPWtPDlKSEggJycHf39/pk2bVjKP5uugPPnp0KED9+/fZ8yYMUye\nPJn33nvvBUdZsT3L73SFL1DlJYkJMcrl2rVrHDt2jMGDB+s7lApl3bp1DBo0CJlMhiRJ4vv0GGq1\nmjt37jB9+nRmzpzJtm3biI+P13dYFcaOHTtwd3dn1apVfP311wQEBJTcUQkPPO2/qwo/SEIs21G2\n8uQI4N69e6xatYqZM2dibm7+IkPUq/LkJyoqim+//RaA7OxsQkNDMTAweGQG/ldVeXJUqVIlLC0t\nUSqVKJVKatWqxb1793BycnrR4b5w5cnPrVu36NOnD0BJc2BcXBzVq1d/obFWVM/yO13h76DEsh1l\nK0+OUlJSWLRoEePHj8fR0VFPkepHefLzww8/sGzZMpYtW0bz5s0ZOXLka1OcoHw5atq0KTdu3ECr\n1VJYWMjt27dxcXHRU8QvVnny4+zszNWrVwHIyMggLi4OBwcHfYRbIT3L7/RLMVnspUuXHhre2adP\nn4eW7QAICAggNDS0ZNmOatWq6TPkF66sHK1cuZJz586VtKMrFArmz5+vz5BfqPJ8h/6yfPlyvL29\nX7th5uXJ0a5duzh+/DgymYwOHTrQtWtXfYb8QpWVn6ysLFasWEFKSgparZY+ffrQsmVLPUf94nz3\n3XeEh4eTlZWFtbU1/fv3R6PRAM/+O/1SFChBEATh9VPhm/gEQRCE15MoUIIgCEKFJAqUIAiCUCGJ\nAiUIgiBUSKJACa+NOXPmcPToUX2HUapTp04xd+7cJ75//fp1JkyY8AIjEgT9EaP4hJfShx9+SGZm\nJnL5g2ssmUzGd999V+pzFf7+/rRq1Yr27ds/tzjmzJnD7du3USgUGBoaUrt2bUaMGPHcnsMbOHAg\n33//vc6fp9myZQvbt2/H0NAQuVxO5cqVGTJkCLVq1apQcQqvlwo/k4QgPMm0adOoW7euXmOQyWSM\nGDGC9u3bk5OTw5IlS1i/fj0ff/zxczvGi7qG9PX1Zdy4cWi1Wn7//XeWLFnCTz/9VO6/F9e6wvMm\nCpTwysjNzWXp0qVERESg0WioWbMmo0aNeux0KgkJCaxYsYJ79+6hUCioV69eSdNZbGwsa9as4c6d\nO1haWjJw4EB8fHzKPL65uTlvvPFGycObN2/eZN26dcTHx+Pk5ISfnx+enp4AHD9+nG3btpGVlYWF\nhQXvvPMOLVu25Pjx4xw9epT//ve/fP755wBMnjwZmUzG2LFjsbS05IcffmDFihXs3LmTqKgoJk2a\nVBLD2rVrAfDz8yMvL4/169cTGhqKTCajXbt29O/fv+Su85/+KjByuZyWLVuyY8cOsrKysLS0JCIi\ngrVr1xIXF4dSqaRZs2YMHToUAwODx8bp4+PDxYsX2bRpEykpKbi4uDBq1CiqVKlSrv+XggCiQAkv\nsX9esUuSRPv27Zk0aRJarZYVK1YQEBDA5MmTH/nbzZs307BhQ/z9/VGr1URGRgJQUFDAl19+ycCB\nA5k5cybR0dF88cUXuLq6ljmtT1ZWFsHBwVSrVo2cnBwWLFjA8OHD8fX15ezZs8yfP5+lS5diYGDA\n2rVrWbBgAU5OTmRkZJCTk/PI5/n7+zNw4EAWLVpU0nQWFhZW8r6vry/btm2joKAAY2NjtFotQUFB\nJee7bNkyrK2tWbp0KQUFBSxYsIBKlSrRsWPHUs9DrVZz4sQJHBwcSpbUkMvl+Pn5Ua1aNVJTU5k3\nbx4HDx6ka9euj43zzp07rFy5kqlTp1K9enVOnjzJV199xXfffYeBgfjZEcpHDJIQXloLFy7Ez88P\nPz8/Fi1aVHIHo1QqMTY2pk+fPoSHhz/2bw0MDEhOTiYtLQ0DAwO8vLwACAkJwd7enrZt2yKXy3F3\nd6dZs2YEBQU99nMkSWLt2rX4+fkxZcoUVCoVQ4cOJSQkBGdnZ1q1aoVcLsfX15fKlStz4cIFZDIZ\ncrmc6OhoioqKsLa2fqY57ezs7KhatSrnzp0DHsxUr1Qq8fDwICMjg9DQUIYNG4ZSqcTS0pKuXbty\n+vTpJ37e2bNn8fPzY8iQIRw9epTp06eXvFetWjU8PDyQy+XY2dnRsWPHJ+YW4PDhw3Ts2BEPDw9k\nMhlt2rTB0NCQW7duPfV5Cq8vcSkjvLSmTJnyUB9UYWEh69ev5/LlyyV3JAUFBUiS9Mj6ToMHD2bz\n5s1Mnz4dc3NzunfvTrt27UhOTub27dv4+fmV7KvRaEoWWvsnmUyGn5/fIwMv/rl+EDwoKOnp6RgZ\nGTFhwgR2797NypUr8fLyYujQoTg7Oz91Dlq2bMnp06dp3bo1gYGBtGrVCngwObBarWbMmDEl+2q1\n2kdi+rsWLVowbtw4srOzWbx4Mfv37y/JQ1xcHBs2bCAqKorCwkK0Wm2p86ilpKRw8uRJ9u/fX/Ka\nWq1+rRYSFf49UaCEV8bu3buJj49n3rx5WFlZcffuXaZOnfrYAmVtbV3y433jxg2++OILatWqha2t\nLbVr12bWrFn/KhaVSlVyZ/OX5ORkGjZsCECDBg1o0KABxcXFbNq0iVWrVuHv7//Ux2nevDkbNmwg\nLS2N8+fPlwxRr1SpEoaGhgQEBDyxz+mf/moytbCwYPTo0UyePJlu3bphb2/P6tWrqVatGhMmTMDY\n2Ji9e/cSHBz8xM+ytbWlT58+9O3b96nPSRD+Ipr4hFdGYWEhSqUSU1NTcnJy2LJlyxP3PXv2bMna\nNGZmZiXNbt7e3sTHx3Py5EnUajVqtZqIiAhiY2OfKpbGjRsTHx9PYGAgGo2GM2fOEBsbi7e3N5mZ\nmZw/f56CggIUCgVGRkZPLCJWVlYkJiY+8TiWlpbUqVOHZcuWYW9vX3IXZmNjQ4MGDdiwYQP5+flo\ntVoSEhJKbZb7O2dnZ7y9vfnjjz8ASvq5jIyMiI2N5eDBg6XG2aFDBw4dOkRERASSJFFQUEBISAgF\nBQXlOr4ggLiDEl4hXbt25fvvv2fEiBGoVCq6d+/OhQsXHrtvVFQU69evJy8vDysrK/z8/LC3twdg\n5syZbNiwgQ0bNiBJEu7u7gwdOvSpYjE3N2fq1KmsW7eO1atX4+TkxLRp0zA3NycjI4O9e/eybNky\nZDIZ7u7ujBw5suRv/363179/f5YtW0ZRURFjxowpGbTwd76+vixbtowhQ4Y89PqHH37Ixo0bmTRp\nEvn5+Tg4ONCrV68nxvzPu8yePXvi7+/PgAEDePfdd/nxxx/ZtWsXVatWxdfX96EBG/+Ms3nz5owZ\nM4aAgAASEhJQKpXUrFmT2rVrP1UehdebeFBXEARBqJBEE58gCIJQIYkCJQiCIFRIokAJgiAIFZIo\nUIIgCEKFJAqUIAiCUCGJAiUIgiBUSP8HFGYXA6ZNB7sAAAAASUVORK5CYII=\n"
}
],
"prompt_number": 9
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"As expected that didnt do much, most of the other models are even worst than the original but now we have a few models ready to be bagged."
]
},
{
"cell_type": "heading",
"level": 3,
"metadata": {},
"source": [
"Bagging"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Since scikit-learn does not have a implementation of bagging. I made a really simple (and un-efficient) implementation of bagging by using the mode to predict the class and using the mean to predict the probabilities. Finally I created some methods to make that possible and easy on the ML class.\n",
"\n",
"To create a bag of all models is as simple as call the method and pass a name as parameter. On future releases will be possible to pass a list of target models to use on the bag and that way will be easy to create more bags."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"ml.bagging(\"Bag 1\")"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 10
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"ml.clfs # Checking the classifiers"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "pyout",
"prompt_number": 11,
"text": [
"DT14 DecisionTreeClassifier(compute_importances=Fal...\n",
"Decision Tree DecisionTreeClassifier(compute_importances=Fal...\n",
"DT13 DecisionTreeClassifier(compute_importances=Fal...\n",
"DT15 DecisionTreeClassifier(compute_importances=Fal...\n",
"DT18 DecisionTreeClassifier(compute_importances=Fal...\n",
"DT12 DecisionTreeClassifier(compute_importances=Fal...\n",
"DT17 DecisionTreeClassifier(compute_importances=Fal...\n",
"DT9 DecisionTreeClassifier(compute_importances=Fal...\n",
"DT8 DecisionTreeClassifier(compute_importances=Fal...\n",
"DT20 DecisionTreeClassifier(compute_importances=Fal...\n",
"DT11 DecisionTreeClassifier(compute_importances=Fal...\n",
"DT19 DecisionTreeClassifier(compute_importances=Fal...\n",
"DT16 DecisionTreeClassifier(compute_importances=Fal...\n",
"DT3 DecisionTreeClassifier(compute_importances=Fal...\n",
"DT2 DecisionTreeClassifier(compute_importances=Fal...\n",
"DT1 DecisionTreeClassifier(compute_importances=Fal...\n",
"DT10 DecisionTreeClassifier(compute_importances=Fal...\n",
"DT7 DecisionTreeClassifier(compute_importances=Fal...\n",
"DT6 DecisionTreeClassifier(compute_importances=Fal...\n",
"DT5 DecisionTreeClassifier(compute_importances=Fal...\n",
"DT4 DecisionTreeClassifier(compute_importances=Fal...\n",
"Bag 1 <copper.core.ensemble.Bagging object at 0x7937..."
]
}
],
"prompt_number": 11
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's see the results"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"ml.accuracy().head()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "pyout",
"prompt_number": 12,
"text": [
"Bag 1 0.558951\n",
"Decision Tree 0.550279\n",
"DT17 0.539955\n",
"DT14 0.536031\n",
"DT11 0.535205\n",
"Name: Accuracy"
]
}
],
"prompt_number": 12
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"ml.roc(legend=False, retList=True)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "pyout",
"prompt_number": 13,
"text": [
"Bag 1 0.578210\n",
"Decision Tree 0.541008\n",
"DT15 0.521935\n",
"DT19 0.520583\n",
"DT11 0.516007\n",
"DT16 0.515312\n",
"DT14 0.514619\n",
"DT8 0.513731\n",
"DT17 0.509060\n",
"DT9 0.506149\n",
"DT3 0.504594\n",
"DT13 0.504411\n",
"DT5 0.501457\n",
"DT2 0.499923\n",
"DT6 0.497339\n",
"DT10 0.494504\n",
"DT12 0.494483\n",
"DT7 0.493177\n",
"DT18 0.492243\n",
"DT4 0.491786\n",
"DT1 0.488879\n",
"DT20 0.483900"
]
},
{
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAagAAAEYCAYAAAAJeGK1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xd4VFX6wPHvTCbJZDLpnYSEdFIooYOUgKAYihRRZAXR\nVVldXdtaFkHRXQuLrivq6ipIsaKCFJGi9ACBkEYapFfS66TMJJM5vz9c8jNSEtBAgPN5Hp4nc+eW\nc997ue+dc849VyGEEEiSJElSD6O82gWQJEmSpPORCUqSJEnqkWSCkiRJknokmaAkSZKkHkkmKEmS\nJKlHkglKkiRJ6pFkgpJ6JKVSyRdffHG1i3HNycvLQ6lUcuTIkatdFNauXYu5ufnVLsYVtWzZMgID\nA3/TOnrSMbzaZIK6QhYuXIhSqUSpVKJSqejVqxdz5swhMzPznHnLysp47LHH8PX1xdLSEldXV+bM\nmUNSUtI58xqNRt59912GDRuGra0tdnZ2DBo0iNdee43a2tpLKuPZ8imVSjQaDcHBwSxbtgyTyXTZ\n+325SktLmT179hXf7rUkICCAl19+ucM0b29vSktLGTZs2FUq1bVFpVKxfv363219zzzzDMeOHevy\n/PIYXpxMUFfQ2LFjKS0tpbCwkA0bNnD69GmmTp3aYZ7CwkKGDBlCTEwMH374IdnZ2Wzfvh1zc3NG\njBjBrl272udtbW1lypQpLFmyhLlz57Jv3z6Sk5N59dVXiYmJYd26dZdcxvfff5/S0lLS09N5+umn\nee2113jjjTd+875fKldXVywtLbt1G62trd26/sthMpm6fEOgUCjOmaZUKnF1dUWlUv3eResxLiVG\nnVEoFPweYxWcLZO1tTWOjo6XtP1fuxGOYZcJ6Yq49957xaRJkzpMW7lypVAoFKKqqqp92rRp04SH\nh4fQ6XTnrCMqKkq4u7uL5uZmIYQQb775plAqlSImJua826ypqbmkMioUCvH55593mDZo0CAxbdq0\nc8odHBws1Gq1CAwMFK+++qowGo3t37e2toply5YJPz8/YWlpKTw9PcVjjz3W/r1OpxN/+ctfhKen\np9BoNCIiIkJs2rTpgmWZN2/eObETQojJkyeLuXPntn/evXu3GDVqlLCyshKenp7ivvvu6xDbe++9\nV0ycOFGsXLlS+Pj4CKVSKRobG88bi1OnTomoqCih1WqFVqsV06ZNE1lZWe3fr1mzRqhUKvHTTz+J\n0NBQoVarxbBhw0R8fHyH9Zw4cUJMmjRJaLVa4eLiImbNmiXy8/Pbv3/ppZdEQECA2LBhgwgODhYq\nlUqkpqaKuLg4MXnyZOHq6iq0Wq0YOnSo2LlzZ/ty48aNEwqFosO//Px8kZubKxQKhTh8+LAQQrR/\n/vrrr8WUKVOERqMRfn5+4tNPP+1QzpycHDFp0iShVquFj4+P+PDDD8W4cePEAw88cN74nJWVlSVm\nz54tHB0dhUajEf379xfff/99hxgdPnxYRERECI1GI4YOHSri4uI6rOOBBx4Q/v7+wsrKSvj5+YnF\nixcLg8Hwm2MkxMXPRR8fnw7xUyqVv+m4paSktE8/q7CwUMyaNUs4OzsLtVot/Pz8xIoVKy7pGAoh\nRFlZmVi4cKFwc3MTarVaBAcHi08++eSix+Z6IBPUFXL24nhWcXGxGDt2bIeTubq6WpiZmYlXX331\nvOs4dOiQUCgUYtu2bUIIIQYMGHDeC/evnT3h165de9H5FAqF+Oyzz4QQQphMJvHTTz8JjUYjXn75\n5fZ5XnrpJeHj4yM2b94s8vLyxA8//CC8vb3F0qVL2+dZsGCBcHV1FZ999pnIyckRsbGx4p133mlf\nb2RkpBg/frw4fPiwyM3NFR999JGwsLAQe/bs6VCWswlq9+7dwszMTBQXF7d/X1JSIlQqldixY4cQ\nQog9e/YIjUYj3nvvPZGVlSViY2PF+PHjxbhx49qXuffee4Wtra2YNWuWSEpKEikpKR0S61lNTU3C\n29tbTJw4UcTHx4u4uDgxfvx4ERAQIFpaWoQQP198lUqlGDx4sDh48KA4efKkmDp1qvDw8BBNTU1C\nCCFSU1OFVqsVy5YtE6dPnxYpKSlizpw5IigoSOj1+vZ4ajQaERkZKY4dOyYyMzOFTqcT+/fvF+vX\nrxfp6ekiMzNTLFmyRFhYWIiMjAwhxM/niq+vr3jmmWdEWVmZKCsrE21tbRdMUH5+fuKbb74R2dnZ\n4vnnnxcqlUpkZma2H5MBAwaIESNGiNjYWJGYmCiioqKEnZ2dePDBBy94vpSUlAhXV1cxadKk9mP5\n/ffftx+TszEaN26ciI6OFqdOnRK33HKL8Pf3b4+7yWQSS5YsEcePHxf5+fli69atwsPDQ7z00ksd\nzrnLiVFn52JFRYVQqVRi5cqV7TH8rcft1wlq2rRpYtKkSSIpKUnk5+eLffv2iS+//PKSjmFTU5Po\n27evGDx4sNizZ4/Iy8sTe/bsERs2bLjgsbleyAR1hdx7771CpVIJrVYrNBqNUCgUYvjw4R3uyo4d\nOyYUCoXYvHnzeddRVVUlFAqFePPNN4UQQlhZWYnHH3+8020XFRWJkJCQC673LIVCIdRqtdBqtcLc\n3FwoFArxwgsvCJPJJIQQorGxUWg0GrFr164Oy61bt07Y29sLIYTIzMwUCoVCbNy48bzb2Ldvn1Cr\n1aKurq7D9Pvuu0/MmDGjQ1nOJqi2tjbh6ekpli9f3v79W2+9JXr16tVetnHjxom//e1vHdaZn58v\nFAqFSEpKEkL8fAwcHBwu+KvprFWrVgmNRtPh11dZWZmwsrIS69evF0L8fPFVKBRi79697fPU1NQI\nrVYrVq9e3b69X/7CE0IIvV4vNBpN+7F46aWXhFKpFIWFhRctkxA/35D88uYlICCgw82DEOKCCert\nt99un8doNAqtVis++ugjIcTPNwAKhUJkZ2e3z1NdXS00Gs1FE9SSJUs6JORfOxujhISE9mkxMTFC\noVB0SCK/9q9//UsEBga2f77cGHV2LgohhEqlEuvWresw7bcct18nqAEDBohly5ZdcPtdOYarVq0S\narW6ww3ajUJWcl5BI0aMYN26dTQ3N7NhwwbeeOMNsrOz8fb27tbtenp6kpaW1qV5X3vtNW6//XZK\nSkp47rnn2LJlC0uWLEGtVpOamkpzczOzZs3qUHfe1taGwWCgqqqK+Ph4AG655Zbzrj82NpaWlhY8\nPT07TG9paSEoKOi8yyiVSu655x4+/fRTnn32WQA+/fRT5s2b116O2NhYjh07xrvvvtthWYVCQWZm\nJv379wcgJCQEjUZz0RikpqYSFhbWoS3B1dWV4ODgc+I4cuTI9r/t7e0JCQlpnyc2Npbs7GxsbGw6\nLGMwGMjKymr/7ObmhpeXV4d5KioqeOmll9i3bx+lpaUYjUb0ej0FBQUXLfuFDBw4sP1vMzMz3Nzc\nKCsrAyAtLQ1nZ2f8/Pza53FwcCA4OPii64yLi2PUqFFYWVldcB6FQsGAAQPaP/fq1Qv4uSPQ2d5u\nH3/8MatWrSI/P5/GxkaMRuM57UKXE6POzsUL+S3H7deeeOIJFi1axI4dO4iMjGTKlCmMGTPmksoT\nFxdHWFhYe+xuJDJBXUFqtbr9IvDKK6+QmZnJn/70J9LT01EqlQQEBKBQKEhOTub2228/Z/nU1FSA\n9gtHcHBw+7Tfi5ubG35+fvj5+bF582b8/f1ZsWIFS5cubW+Y/vbbb8+bTBwcHDpdv8lkws7OjhMn\nTpzznYWFxQWXW7BgAf/85z+Jj4/HwsKCpKQkPv300/bvhRA8//zzzJ8//7z7dFZnyemX6+vKtIvN\nI4RgwYIFPP/88+fM98vkZ21tfc73CxcupKioiBUrVuDr64tarWbu3Lm0tLR0qfy/9uvYKhSKDh0N\nztdY39n+dqWDgVKp7LDus3+f3fY333zDo48+yvLlyxk3bhy2trZ8/fXXvPDCCx3WcyVidNZvOW7n\nK+PkyZPZuXMn+/bt47bbbmPmzJkdzt2ululGJHvxXUG/vggsW7aMrKwsvvrqK+Dnkz8qKor33nsP\nnU53zvKvv/467u7uTJo0CYB77rmHvXv3EhMTc97tXWo3819zdnbm0Ucf5d///jdNTU2EhYWhVqvJ\nzs5uT2K//KdUKhk0aBBAh96GvzR06FBqa2tpbm4+Z/mL3Y2GhoYyePBg1q9fz/r16xk4cCDh4eHt\n3w8ZMoSUlJTzlqsrF5JfCg8PJy0tjaqqqvZpZWVlZGRkdNgmwNGjR9v/rq2t5dSpU4SEhLSXKSkp\n6bxlsre3v2gZDh06xCOPPMLUqVMJCwvD3d2d7OzsDvNYWFjQ1tZ2Sft2PqGhoVRUVJCTk9M+raam\nhoyMjIsuN3jwYI4cOUJTU9Nlb/vgwYNERETwxBNPEBERgb+/P7m5uV1atrMYdXYuwvlj+FuO2/m4\nu7uzcOFC1q1bx6pVq/j8889paGi44PZ/bciQIaSlpVFcXHzJ277WXdMJ6vf+9dDdfn0XFBwczLRp\n01i+fHn7tPfffx+VSsWECRPYtWsXhYWFxMbGMm/ePPbv38/atWvbu18//vjj3Hzzzdx666289dZb\nnDhxgvz8fHbu3MmMGTPa11tcXEzfvn3ZvHnzJZf5L3/5C01NTXz44YdotVoWL17M4sWLef/99zl9\n+jSpqal89dVX7XebAQEB/OEPf+CRRx7h888/Jzs7m9jYWFauXAnAhAkTmDhxIrNmzWLz5s3k5OQQ\nFxfHu+++y6pVqy5algULFvDFF1/wxRdfcO+993b47pVXXmHLli089dRTJCQkkJ2dzc6dO3nggQcw\nGAwXXOf5zqF58+bh4uLCXXfdRUJCAnFxccydOxcvLy/uuuuu9vkUCgXPPfcchw4dIjk5mQULFqDV\napk3bx4AixcvJj09nXvuuYfY2Fhyc3PZt28fTzzxRKcX4eDgYD777DNSUlJITEzk7rvvxmQydTiH\nfH19iY6OprCwkMrKyku6y/7lvJMmTWLAgAHMnz+fEydOkJSUxPz58zE3N0ehUFzw/9kjjzyCyWTi\n9ttv58iRI+Tm5vL999+zc+fOLpejb9++JCcns3XrVrKzs3nnnXf47rvvurRsZzHq7FyEn2O4d+9e\nSkpKqKysBC79uF3sOvToo4+yY8cOsrOzSU1NZdOmTXh7e6PVatu339kxvPvuu/Hx8WH69Ons2bOH\n3Nxc9uzZw9dff92lOPUEl3utvqYTVFfbVXoChUJx3mqUZ599lpSUFHbs2AH8/JDeiRMnGD58OIsW\nLSIgIICoqChaW1s5evRoh/p0lUrFjh07+Pvf/85XX31FZGQk/fv3Z/HixfTr16+9Gq61tZWMjAzq\n6+svudxubm7Mnz+ff//73xiNRpYsWcK//vUvVq1axcCBAxkzZgzvvPMOvr6+7cusWbOGRYsWsWTJ\nEkJDQ5k1axZ5eXnt32/dupVZs2bx1FNPERISwtSpU9mxYwcBAQEXLcu8efOoq6ujoqKiPQmcFRkZ\nyd69e0lOTmbcuHEMGDCAp556Cltb2/bnSc53DM53DqnVanbv3o2lpSVjx44lMjISGxsbdu7c2eHZ\nFKVSyWuvvcaiRYsYOnQoZWVlbN++vb1Npm/fvhw5coSGhgZuvfVWwsLCeOihh9Dr9e3VoRc6L9as\nWYPJZGLYsGHMmjWLqKgohg4d2mHel19+mbq6OoKDg3Fzc6OwsLB9nb90vvX/etp3332HtbU1Y8aM\nYfr06UyZMoXg4GDUavUF/5+5u7sTHR2NjY0NUVFRhIeHs3Tp0kva9qJFi5g/fz733XcfgwYNIjY2\nlmXLlp1TLXi5MersXHzrrbeIi4vD19e3vSr4Uo/bL+NzvrI+8cQT9OvXj3HjxtHc3Nz+fx26dgyt\nrKw4cOAA4eHhzJ07l9DQUB577DH0ev05MempLvtafeX7Zfx+vv7666tdhB5Nxqdzlxujs8/4XK/q\n6+uFra2teO+99+R51AkZn85dboy6rZPEBx98QHx8PLa2trz11lvnnWfNmjUkJCRgaWnJI4880uEu\nXJKkK2fbtm2YmZkREhJCeXk5L7/8MmZmZtx5553s37//ahdPukF1WxVfZGQkixcvvuD38fHxlJaW\nsnLlSh566KFO2x8kqac5X7XTtaqpqYlnnnmG8PBwpk2bBkB0dDQuLi5XuWTSjUwhRPf1XywvL2f5\n8uXn/QX18ccfExYWxqhRo4Cf62mXLVt2wV4yqamp59RjXsqYV5IkSdLVU11d3eFzaGgoYWFhF13m\nqj0HVV1djZOTU/tnJycnqqurL5igwsLCztmZPXv2tHcllc4VHR3N6NGjr3YxejQZo87JGF2cjM/5\nfZVURvy6/xCTFMe/V7zCnDlzLnkdV/VB3W788SaB/E/TBTJGnZMxujgZn5+1GE2crmwit7qZjANH\naSuM40iVnhbT5VeFX7UE5ejo2OFByKqqKlllJ0mSdA0xCcF3KRXsz6nhdEUTrg219C/YQo1LBDme\nkUQZj/LcJ5vP+y67rrhqz0ENHjyYgwcPApCRkYG1tfVlPaUtXVh0dPTVLkKPJ2PUORmji7tR4iOE\noKa5lVKdgd0ZVUxZk8jk1Yn8N6aIIIWRSSlfMrQimpjAOzC0mfi7Pyz+52LMzMwue5vd9gvqnXfe\nIS0tjfr6eh5++GHmzJnTPqTHpEmTGDRoEAkJCTz22GOo1Woefvjh7iqKJEmS9BuU1Bt4aNMpDEYT\nrlpz2kxwa6AjY2zM2fb1lyRv/ZFSlwFo/YYxPfMAC1Y8h9Lst6eXbu3F191kJwlJkqTuUdXUyuG8\nWjYml1OiayHQyYo3pwaiNlOSnFLK19v3Y5H8Dd/Gn6ZObceUYRN4Zd5knCPPbZOLj4/n5ptvvuQy\nyNHMJUmSpA7ePVzItvRKfOzV9HGw4h+3+uNpa0lKUgkbDsTjlLKV1JREYs5UEhJ5B/+yt2bCm8+j\ntLD8XcshE9R1THZ/7ZyMUedkjC7ueopPXk0zT3+fic7QxhOjexPV15m2NhPJCWf476F0LIpPMsqQ\nyJK4DFp7hfDMQH/+eMcY7CaO75byyAQlSZIkUVSn56GNpxjgoeWJ0d64WZsTf6yATYezqGquYErh\nZozWXvw3dBGjXfK4r+IUA//5V5RWXXvH2uWQbVCSJEk3sG9OlnEkv47UskaCXTT8KyqAxOOFbDmW\nT7aqhbsTP6WXhZGPgmZRYeHEwsT9TJg1Apuo27q8DdkGJUmSJHWJwWjiaH4dH8QUUdNsZFKgI48M\n7UV1RjkvrzxMtgaiUjeiyjvOqUGT+SDgVsbmpfB07TEC/7UUpa3tFSnnNf0+KOnibpTnM34LGaPO\nyRhd3LUUn8aWNj5PKGXa2iRe25dHiKs1n87uy01traz7NJ6VacXYFccwfvcr/HvfNtbXqIix8mNx\n9CYeHe5C8AcrrlhyAvkLSpIk6bpWUKtnzYkzHM6rA8BRo2LeQDdm93Ui8Ug+738cS769GQ76Quae\n2MDXpzLYW2vAM2oRL5ibM74kjj7/XorSyfmKl122QUmSJF2HcqqbOZRby+cJpQQ5a7hrgBuj+9jR\n1NDCieg89p0spcDJEtFYzf3H1mOpqGH2vmRshkYxNnw0D+UkEDhjBNo75/7mV8vINihJkqQbnNEk\n+DqpjN2Z1ZypN9DfQ8sfIty5q78rrU2t7Nt+iuiUcopcrWi0Fdy//0NcLOow2FryetjDhIbDIznJ\nDCyNxfPtF1C597qq+yMT1HXseno+o7vIGHVOxujiekJ8Es/oiCmoY1NKBQALBrkz3t8BTzs1ddVN\nHPw+neOnKjnjYUO1oxl/OLqO3oZSXMwaeSNwChmOQxiVmcyc/ER6Tx2KdsGSHvFCTpmgJEmSrlEn\nSxr46/ZMAG7qY8f8Qe7MDndFY2FGdUUjO75NJiGzijIvO0qcLZmdsIE+pZkU6so41m8om/pMxa7R\nxPNHthKgqMHjzWdR+fhd5b36fzJBXceu9l3dtUDGqHMyRhd3NeJT29zKgxtPUac3MtLbjsUT+mCp\n+rlTdkWpjr37c0jJrabCx5ECVw1T07bRNyuBnKZKHkrNpcHNjwCfO5mSdJTbKjNxmzQAmwf/gUJ5\n+SOPdweZoCRJkq4RLW0mntyWQWZlMwDf3tMPW/XPl/HS4jpi9mWTWVRPlZ8TmW42TM7Yxey0aIyi\nlbfSMznS0IbH9MeJdPDloUMb8TTX4fbaU5gHhVzN3bogmaCuYz2hbrynkzHqnIzRxV2J+MQX1/N1\nUjnxZ3QArJgSQJibFpVSQXF+DTH7sikob6Daz4U0NxsmZO5lVtputMKSFF05TyblYTfyNsLHzOfu\nuAOMPrMb59F9sX30MRQq824t+28hE5QkSVIP1WAw8ufNpynRtTCmjz3/mhpIuLsWgKryBvZtT+dM\nVTO1AS4kYcbY3MMsTdsKDRa4agRxdub8J/wPBI7xIqK6loVHNuFs0Yzri49i3j/iKu9d5+RzUJIk\nST1Qvd7IHZ8lY26m4PO5Ydhb/fxLR9/cyrH92cTHn6Ep1IP4egMja1O4LWUjdbXgZdVGjSUs9x9B\npd0QrFssuefQNgYp6nEY4oPd40+hUFtd0X2Rz0FJkiRd4w7m1HCqookz9QaO5P888sPXf+iHtYUZ\nrS1tJBzN50h0HtU+jqR4OTK8LI1XE76iuKEJszYVlgodq7xD2e8xGmuVHyMSYphbkYadugXnxx/A\nctioq7yHl0YmqOuYbDvonIxR52SMLu63xCenuplNyeWU6AwklzYCMDPMhWAXDZH+DozytsPU2sax\n/XkcO5pPpYcDqV5ODDIU848Tn1JgqETRaEN1XRV/Si+CiGEEed5JL52eew+uIcTKhF1/N+z/+iwK\na+3vudtXhExQkiRJV0FjSxt/2nSKIGcNs8Jd+ONQTwKcrbAw+7m7eKPOQMxPmSTEFqHr40SSpxP9\nFFW8dGwd5a1FGCrscVKYeOx0MinNJnrPXIRzyGTGHdrF7U0FaG2NOC+6G8txk67ynl4+2QYlSZJ0\nhRXW6vnjt+kA7H6gY2cFY2sbJw7ncexQHi1BrsS1CoLNdMw4tpamlmxMFfb4WbbxcUEBH2aVYjf6\nZvzHLcKlqpp7o7fgZ2+Orb89ds89h5m949XYvXPINihJkqQeTAjB3uwaPk8opajOQC9bC1ZOD27/\nvrWljdjoXOJjCtD1ciDZz5U+Cj1PJX+Kuj6dwkZr+rXYYWnVxKeeHmxw9GXArUOxdApg8s6NTDSr\nw9oJnBZMwXLytB4xVNFvJRPUdUy2HXROxqhzMkYX15X41Da3smjTKWqajUwOduLVW/3xsLVs/76m\nqpHNnydS6aDhZB9XPMyNPJr6JW4lcZwwN2dQuS3DNY3sdbfjfZ/hWKi88VcH4ZmTyfyf3sXLRYut\ntxV2z72CmYtbd+/yFSMTlCRJUjcwGE2sjy8hq7KZhDM67NQq1swJxdPOssN8hXnVfPxdOjlOWpyt\nFDyY+z0BGQfY4yDQlNowQtPAGSclL/qGk60NwNssDBMqbv96FSNtTWjcLXC8YxxWM+9Coby+3kEr\n26AkSZJ+RwW1ep7dnkl1sxH4eWTxkT72+Dt1fPaoprKRL3Znsb++FTutinvqjhAav40fXVrwPu1I\ngNrAD1VlvHy6GPXMOwjzjaTVujcByfHcFfcjvTzssRnsj/2f/4TSxu5q7GqXyTYoSZKkq6jNJPgq\nqYx1cSV42Fjw1bxwHDXnDiNUV93EJ5tSOdoKllZmPGRxioh9X3DQ0cDxNlfG5hoooYzpKSUUtoD3\nzHvoHToLM30zc1f/iwhXC6zDvXF59s9Y+PlehT29cmSCuo7JtoPOyRh1TsbowkxC8MEPxyhVuXCs\nsB6AR0Z6cnuoy3k7KRyJK+K/R4vRay35o3Ueg/esJs62mV0ObgzL0qNVV/NccRk7c8uwHTeeCUP+\nQIPWlb4x+5mafpRefTywv+M2bGdGXXfVeecjE5QkSdIlKm9oIaagjg1JZVQ0WjKlrzl/uak3twU7\nYaY8NzHVN7bw5uZ04huNzLCrZ+qRD8m20PGdnzPDoi0Z5FBHqZOC5d4+HNBrGDbpIVRuEShqa/jj\nf14nLMwLzdihuPzlPsw93a/CHl8dsg1KkiSpC4QQvH+0iG1plQjA3caCMX3smdPftX2cvF/TN7fy\nxd4cthQ3ENRWx0NZX6BvKeaArw2DD1jgZ9WAyULPOi8XvnYPx67Nmj6KQOqs7BlyYCc3l2bi0dsF\nuxm3Yjt9EgqznvW+pq6SbVCSJEm/M6NJMO+LFPRGE3qjCYAnR/fm1mAnlBd5zqiiREfc0Tw2F+io\ntVbxbOF3eFQls723Bv+8CG6PycBKW85+Zzs+9g6i0qIXEQZvKhx8EOWl/PGT1+g7JAirwSE4P7YQ\nC2/PK7THPYtMUNcx2XbQORmjzt2oMRJC8MC36dTqjay6IwQHKxXWFmbnJKaz8WlrM5GVVk7C0XzK\na5o57abBWlXN44lf8JOTG3aaKCaeOIyLZTyr62v5MKcU6z89RpDJAVercOq1KiZs+5qR9SV4DPLH\n9rZx2M28DYXq2vzV9HuQCUqSJOl/9EYTKaUNbEmtILaoHpOA/8wIxttefcFl2toEMfuySTxWgL2j\nBk8/NT9k6RmYl4qqpYEfNTO4KWknPtY7iEfHvMQCShSWeE2bzUhVfwpsXLDKy+YP364maFR/LPv4\n4fzofVj6eV/BPe+ZZBuUJEk3NH1rGylljWxJq+BYQT3WFmb42Ku5e6AbEZ427YO3/pIQgkadgcKc\namIP5WLvqGH4UCfiftrG1sYQ/GvrsDDVMejEPgKddDRSx1NFVRzNK8duws2MC4lC5x6MUpiYuPFT\nBph0uLo7YDNpDPZzpqAw77lvub0csg1KkiTpEuzKqOLrpDIK6wwADPDQ8lykDzcHXHyA1aYGAxtW\nxdLUYMCjtz0DhriQcvIQb210RtvsT4C+hEGxP+Hn0ojWvZ4cKwv+aa4lvkrBsAfm4+8xgiIrLSEn\nT3BHwl7sXR3QDBqG3czJWAb0uQJ7fu2QCeo6dqO2HVwKGaPOXW8xqmxsYfn+fJJKGpga4swbUQG4\nWFt0ulzkrWy2AAAgAElEQVRTYwuxh3JJji0iYqQ3jqGOfLvtADsPO+BT74aLvokBeYexU1fS27sc\ngYlv3NSs7j0MqzYr7u4TSKaLF4aGWpb89DE2JiO2c6fgeMcUVA49eySIq6VbE1RiYiJr167FZDIx\nYcIEZsyY0eH7+vp63n33XWprazGZTEybNo3IyMjuLJIkSTeYNpOgsrGV1LIG3tifD0CgsxUrpwfR\n19W60+UbdQZiD+WSEldM737uWI3qzXcJ+dgcykHTakl4XTq9zfQYRB7+1nk4tTazy0XF+z5h6FTe\nDK13QOkZSrGAu+N/YmDBaejjje/y5zCz7Dwx3si6LUGZTCZWr17N0qVLcXR05G9/+xtDhgzBy8ur\nfZ5du3bh6+vLvHnzqK+v54knnmDMmDGYXaN9/Xua6+mut7vIGHXuWo1Ra5uJP28+TV6NHgBXrTkD\nPLQsm+SHtUXn15iGej2xh3JJjT+Da4grDT52xJ4swdZgILQlH+ucOJKH9ae3PpNBNXnYtuh5o7aa\nHQpzlCPn49dowc0qfxI9HBlSkMHM08dozC/G8v478blvdnfv/nWh2xJUVlYW7u7uuLq6AnDTTTdx\n4sSJDgnK3t6egoICAJqbm7GxsZHJSZKky1bV2EpiiY7Ywnr2ZtcA8PbUQPq6Wp93hIfzaWps4eje\nLNITS3AIcaXOxpyGxDO0KWsZXBtHobEeo4sDLm7NPJmyHQWwrbWBv6cU02xmh9etU5la7U6Rrz9F\ndfU8fXgjWjcnyhIzCH/nBVxuHtmNEbi+dFuCqq6uxtnZuf2zo6MjWVlZHea5+eabeeWVV1i0aBHN\nzc08+eSTF1xfamoqaWlpHaY5Ojp2qB+Pjo4GkJ//9/mDDz6gX79+PaY8PfFzcnIyDz/8cI8pT0/8\nfHZaTynP+T4X1elZviOZ0w0qXKzNGdjLhnt6N+OrMRHmru3S+g4dPMSZ3FbK8004hLuT0scGl9RS\nTKII29aTHHN0A5OJhcVF1BaUYN+mJwMDzxScITvfgO2EW5neZzx+Xt4cNqmJSjpKL7MWHH29KN+4\nE+VzCzht2YbL/2Lak+J3JT5/8803/FJoaChhYWFcTLd1M4+JiSEpKYlFixYBcPDgQbKysrj//vvb\n59m4cSM6nY6FCxdSWlrKP/7xD1asWIGVldWFVtuB7GZ+cddb43Z3kDHqXE+NkRCCAzm1bEmrILWs\nkXA3ayL9HZge6tL5wr9SWaZj58YUWswgz9aCUzojw7MLKFMXk2DbxuTWRu7IikPR0oxSAW3KNvb2\nUfPFaXOyaoz0HzGdfna+pNk4ElRWwKC6M/i5aGn4cjM2YYGEvfFX1L1cuyEK14Ye183c0dGRysrK\n9s9VVVU4OnbsvpmRkcHMmTMB2qsDz5w5g7+/f3cV64bSEy8qPY2MUed6WoyEEHwYU8yh3Foqm1qZ\n08+V5yJ9cLex7HzhXzGZBCd+SufkZzspcLUn0TuI4cePM0Rrxi5XE/76Kt5NS8KutQkLAak2Ror8\nvVB7jWdbSSvGwWbc3epBvnsv9FWlzDu5Hwc3B8wPHcTUy5WBH/0d+8Hh3RCFG0O3JSh/f39KS0sp\nLy/H0dGRI0eO8Pjjj3eYp1evXiQnJ9O3b19qa2s5c+YMbm7Xz+uKJUn6fTW2tPHE1gzya/U8OsqL\nYb1tLysxibY28rdHE7Pqe1LtnUkZMZZBagPPNB3jfTcV9cpW3kzbh4/BgBElu11baQiKoKnJl/2t\ngjMVbUQYnBntH8jh2lZmJh3ETWHEMikRcys1QcufwWnMkG6IwI2lW0eSSEhI6NDNfObMmfz4448A\nTJo0ifr6ej744AMqKysxmUzMnDnzku7WZBXfxfXUqpmeRMaocz0hRqfKG8muauadw4UAfDS7L30c\nutYUcJYwmaiJT+P0+u1kH0vhxMjx5IT0Y5ydgdHZu/i2rY1jWmdezDzIMF0DLagosXLjlb5GChNN\nNPTyZbh/GC51NoRr1BxSWmHe2MDozETcMtKxVCkJePZBXCaOOu+7oG5kPa6KDyAiIoKIiIgO0yZN\nmtT+t62tLc8991x3FkGSpGtUqc5AVmUznyWUklPdzAAPLbcFOzF3gBsetl371WTUNVJ54DhF2w5Q\nsS+GXN++JIy7haoHJzLVoowpKe/xqaM76+w8cWvO4JPE4ziblCRpfdkUGMqOsiIaVm3H3dqOB/xv\nxTdbzwkHa75XahmrK8b+m01oFa2EvvIXXG8dIxPT70yOxSdJUo+iMxh5YWc2pyqa8HO0wttezQR/\nB0b4dG20hcacQip+PEzZj4epjUujwcefxCFjyeobgsZSwYSaBCpKD7DHUUWhZRjOtVXcdCqLP1sa\nqVQIngwZS2NzE+V7NtFaWMWjUQvo16oh2bUXh3uHMMGyGdc1axF1Ogb87SGCZ998Q7zd9rfokb+g\nJEmSuqLNJKjVG0ko1vHPAz+P9tDVkR5MLa3UHEui4qcjlP94mBZdE8bgUE67DKBg8XxyzFQMbK1m\nfP52Tltks8FKR4n7SKx0bcw7lMqMMFeUlgbS1da8HTiIYOtcvv/vt0zw60fU+OnE9B5MtJMHYWZ6\nbt+wDsszJZy5YzYPPDMHrfr6GtS1p5EJ6jrWE9oOejoZo851d4xSyxpYcaCAM/UG7NQqIv0ceHx0\n705He6iOSaRg9bdUHjiOlZ83bX1DyRs3izxXT8odLClrNTG27CSOLVnkWqWSbAsFljfRrLRlwZ4T\nzPG0JN+zhbKafBRqKz4N1XBrbQJDcnsz8LanORA4lG+0NngY6pi89j8462oxv/9uBs+PwtNBc8Xi\ncyOTCUqSpKsip7qZ/xwt4mRJA6N87HhrSiBO1hf/RSKEoOrQCbLfXoP+TAWu82fTPPQWkspaafWw\nJBkz7JrqGJMdS7a6iuPm0TRZupJjNQ6j0oZ5VTXMObqV4j7OrHDpzf1nKqhVC5osHXg43okfvQbw\nWnggbnZWuFWUELLqE1ybdfR99o/4zbn1mn3l+rVKtkFJknRFCCHYlFJBYZ2eHzOraW0TTPB34O6B\nbvh0oUdeVfQJMl//iNa6evweX0i1Tyh7diVQ52xBotKeobVZDNOaEdOYT4bpJ+rNXMjTDAelhocr\nK5gcf5haZy1v+g4itKGc+YWpbChuJCxwIjv9R5Lj6MoAOzNU6en4/PQjbroaQp65H+87J6NUyXv5\n30K2QUmS1ONUNrZQUKunoNbAjxlVZFY1M6efK4+O9GJob1ucu/Cai/qUDDJe/YDGnCICn38Ip1Hh\nbN9ymJ8KT1LjZM9tFjVM8YCtdeWs1+2m3kxLuX0ULUo7FuiamHXwOzS25mwMHcSPtjb8PSOGjOJq\nJmWUYnL2JiT4JkadyWP0ug+gzYj1gFDC/jQTrzmTUZrLS+TVJKN/HZN1452TMerc5cRICMHr+/LZ\nn1NDb3tLHK3MCXPX8vgYb4KcNZ2vAGguLCFz+UdUHojF/8mFBM2Zwne7Y/lhYyYOBi1Tg+xQWNtw\n8EgsP5V/TLNZK7jfTFmLMzPLq5h17Ftc7BTsD+7Hu64e3F2SyXPZiTyUoyO3qoLBUQ9yW2EZLgd3\ncDQ4Aq+VbzBrbBBq80urxpPnUPfpcoJKSkriyJEj1NXV8fzzz5OdnU1zczPh4XIYD0mSOnr4u1Pk\nVOsv64Halqpast9Zx5lvduB9/x2MPfpXTpfX88KXcYTUFzHaZE29gxWH4zIptdiK3qKaYP9bSK92\nR1lYygcnNtPHtg2dTyDLHJyptVSyMv0on1iH8bfoHQwaPYXXrRpxqChn2003M3B0OC9GuGNvJXvk\n9TRdSlA7duzghx9+YMKECcTExABgbm7OmjVr+Mc//tGtBZQun7yr65yMUecuJUYmIXhxdw451Xo+\nmBl8ScmprUlP3scbyPvvV3hMv5nRBz5H5ezIus0x7Cg1ElmSSJqtG80NUNOyixrNEUZ5R1JV7M1P\nWXpezDzIUGMV+l4+nGyGf3v2ZkpVLupWD5aOfJbhPva8Z1SgOZLI9jkL8RrZn2WDPfC0U19OWNrJ\nc6j7dClBbd++nRdffBFXV1e2bt0KgJeXF8XFxd1aOEmSrh3VTa3c+3UaBqOJ1yb74+/Utao8k9FI\n8VfbyXpzNQ5D+zPi+4+w9PbkxPE81n8Zi7K1GW9DLRWKPlg1ZXDGfidu5rb0zxrNN3oH5jZls6Wi\nAINwor7ZnqM2RtI9gvEx92JLUCQDetlwv6ke/dKXKLNxQPXWcl4adnmDy0pXVpcSlF6vx8nJqcM0\no9GIubn8SdyTybrxzskYda6zGH2XUs7e7BpOVzThYKVi7Z2hOGk6vzYIISjfcZCM1z7A0tWJiDVv\nYOrtw54j+RzctIs8Ky39aypRmmzQK1sw9N5MTUMOvfICKLbyRmPfxIa8GBQtgjyNI3Euvhx2CafC\nzBqPmgzmDgmg5VgKjR9updFoxGr+Hdz7l7uwtvx9m97lOdR9unSkQkJC2Lx5M7Nn//9rinfs2NHp\ny6YkSbr+NLW0sfJwIZmVTRTWGQCYGuLM4vF9ujxGXs2xJE7//X2Mjc0EvvgXalz78H10CiebM8m3\nciSivg636laa1U24DqgiufRHNOV2FBlvpbdbK6/nJJCh6cXq3pOJcQ2iRWGikWYszyRzZtOnmJnZ\n0PjJBmr69cNvyWOMun00KjM5HNG1pkvPQVVXV7N8+XJ0Oh01NTW4urqiVqt5/vnncXBwuBLlPC/5\nHJQkXTl6o4mNyeWsiysBYPGEPgQ4WeFpa9nlQVIbTueS8dqH1Kdm0OuReylz6E35sRhO2dlySuPD\ngPpKjHoLyrVVRI33oKolk59iv8b2lD8nwwazoK6RTHN3khyD0OorqVaW0KCygMYaxHebqMzO4U6t\nL74z7mLEQzMJCfbszpBIXXS5z0F1+UFdk8lEdnY2FRUVODs7ExAQgPIqD5AoE5QkdT+TEPxzfz57\ns2sAmDvAjXsi3LFQdf3/v760gqwVqynbcRDt7OnUau2xLk7kuJMPKXbhBOlqEYZWsu0asQ+24bER\nYXyweQkNxSpK1JMxs3GlRWVL35o8hKGSWLsmai3tmeDkQuPnm9h+eBcje4Uz5c9PE3XPJJy1sn2p\nJ+nWBPXPf/6TZ5999pzpb775Jn/9618veaO/F5mgLk7WjXdOxujihBA8/20sCXXmPDLSk2khLpgp\nu/5Kidb6BnLf/5yCtZtg1Ggq3LwJaUnhoGMg6dahBDQZMJpqyLEpJ9lazR9CA6nNPEJcPRgZRIul\nlpEVqYyoSMOurp5nBwRho9YyQ2WH6xe7MZbXcKJfGKFzo7hz6k1YXkLS/L3Ic6hz3TqSREpKynmn\np6amXvIGJUnq+YQQVDS2suzHHLLqzHnjNn8Gedp2eXmToYX8td+R+fZa9H5BtEZNJ9S6hAzzZj63\nj8JNb2S0rRmHzY8RY2ZPZK9ghpypZluKCbUhDKe6Kvo1H+Sewjga2mxZEejDsYAIbq7RM/b9zRT2\nCSAzagaRc8czy8tOvofpOnXRBLVhwwbg5x57Z/8+q6ysDBcXl+4rmfSbybu6zskYddRmEuzLrml/\n5YWdWsVLE327nJyEyUT25z+Q/c+PabK2x2VaJGGKAnbaK3hPfSu+dc1M6u+BnY/g9ehV1JmNwU/h\nTEaRDpuGdEbVp6GxaGFBdjwtJktOWLnwH9++mOkVPPjZPgp8w8j/1wqmjg3G2/63Pb/0e5HnUPe5\naIKqrKwE/jeCcFVV+3SFQoGzszN33nln95ZOkqQroryhhb/vyeV0RRMA/dyt+fst/mg6eeXFWUII\nMjbuJ/uNDxFtRvwm98OrKZN0NzNetLuXvjXNDFOrGBzVi3eTdpG4w0ifttG4oENl+oxA8xDMhCXz\nSo+jbWmlSjgT62DHKu9AAnLKqKtpZUVdOk+Nn8wj0wd0ZyikHuSiCerPf/4zAMHBwUycOPGKFEj6\n/ci68c7JGEFeTTMPbTyFSqngo9l96W2n7tDOdLEYmdpMpGw9Rt6bH2HTWE74WF8c9cUYAl34RD2d\n6oIG+jXV4xzYQKr+G1K+UmKXqsV30ASarcvorSgksNKPsXkpeDc10tTmwGnr3uz16c92qxb6JeaQ\nU56Job6KNR9/yJgxY65UWLpMnkPdp0ttUGeTU3NzMzqdjl/2q3Bzc+uekkmS1O2OF9axZFcOQc4a\n3p4WiHkXnxVq1Bk4ufskxe+twUuXxfDBblirtNQOH80Okz/ZGTW02eiw8Uwlq3wrmrR+9DquRNFc\nxc65c7EzVXNfznEC6stxNxjQC1vyzAOICR3Dj606SlSNBB2O5dDJ4zz11FM8+OCDcmCAG1CXevEV\nFRWxcuVK8vPzz/nu121TV5LsxSdJl6fNJPjP0SK2pVcyzteexRP6dNrRoM1oIiejgpQTRei27SQk\nbz9+4VrU7q6IW+5g62ktJRWN5FqZY7Dcw6DGPOx1vlTGZGJbXcTJaQFke9zDuNJEJpbsw12vpw4b\nWkxu7AkYye5ePlCVRJuhmXenTyEuK42xY8fi7u5+haIidZdu7cX38ccfExYWxksvvcSjjz7Ke++9\nx5dffklQUNAlb1CSpKvviW0ZnK5o4oFhvbiz/8VrQSpKdKTEF5GeVIKjrYpeh7fjWVtISH8r1E8u\npdEnkE8+OEKB0FHkUMl9daepOwO7taEMOrqH1iFqIIwit7u4peQwd+Tvp0RlTa3Rj729B7E3OBwz\n8zIqKk4yo66Rx557BGsHO/wHyTcl3Oi6lKDy8/NZunQpKpUKk8mEtbU199xzD08//TRjx47t7jJK\nl0nWjXfuRoxReUMLpyuaLvoqjOamFk4llZASV0xNtY5BI3yZNVJN3VsrcHJSou7TRvmw8Xy1PxtK\ny6jTKBjbmE5LVT0f+XoQUneUWyuLGOyrJrPFm1XBdzM/ezOuugxqWgNItw8gesRAmlxayS1KZtyJ\n0ywZMYyQ1x+95rqM34jn0JXSpQRlYWGB0WhEpVJha2tLRUUFWq2WhoaG7i6fJEm/k3q9kf05NXxz\nshwzBedNTiaTIOFoPkf3ZtMnyJkxtwRQd2wrPtu+QJSfwS4kkKR+Qewvtsc6z40GjRmDG9Mxc7Hi\nMzdzBp7J5OmTBwhsVHHcwYtYBw82ek7hlvyN+JS1UquO4JtRERR6W5JSUYjvlhiqt2/h7v+uJnRm\n1FWIitSTdSlB9e3bl5iYGCIjIxkxYgSvvfYa5ubm8mWFPZy8q+vcjRCjxpY2Pok9w7b0SpSKnwd2\nHdbbrsM8QgiK82vYt/0UFpYq5j00FJvsExg+egfrkgoSjHAscjSN5YFoMhxpU0NfizOY/K341q2G\nm7P38HZpEw1CxV6XQZibnUGonNjgNYXZ2UcZUKbkxOjxxHtpOVlexoQ6M9JefYOMNiNrP/uUQbdc\nu72Eb4Rz6Grp8lh8Z5lMJqKjo9Hr9YwdOxa1+uo9LCc7SUjShQkhOFnawDPbswB4YGgvpoQ4Y/2L\nZ5sadQbSk0pISyimpaWNEeP6EKRLxbBxPY2NevbqqzgeNhyn1rEoTJa0qsrwccqn0K6S9MpUQmv0\n3FuqpczCneNKX4a0pOOtr2S7myvb/R7jz/G7KfDzJD7Ug+TKSuYGBXDq40/Y+v02Fk2cwjPrP0Rl\nYXG1QiRdId3aSeKXlEolY8eOxWAwsGfPHqKi5M/ynkrWjXfueo3RwZwaXt2bhwAietnw/HgfHH7x\nSvNGnYFDuzPITC0jIMSVcbf1xb36FM2rnqGooY5tDnoqvSPRmIZh16qk2eoAdVYJNAk9GQpPnCsc\nWFwTRq3Olh9tXBjYcJgZhkMcdVLSZtefU84TCKzMY+3YMIpam7jf24sVt04i6921HN1zlF0fryd4\n5q1XL0C/o+v1HOoJOk1Q8fHxFBUVERAQQGhoKE1NTWzfvp2dO3dib28vE5Qk9TBVja38Y28e3vZq\n/jMjuMOo48bWNuKO5HPiUC7hgz156NlxmJ3Jpfzfj1NeU8IWdzPanGdgEL4IM3M07lWUGr9CbWeH\nUTMHx/wq7ihvoMDgwU5LD3xN3zG59gix7pbU6PxwJ4AjSmuS7d0wqGp4sF84d4T2xayxmeQHl2Co\nqOajo3uw8pJdx6XOXbSK79tvv2XLli307t2bwsJC7rzzTn744QdcXFyYMWPGVa9ek1V8kvT/SnUG\nvjlZzrb0Svq6aHh7WlD7iBBCCDJTyziw4zQu7jaMuy0YM10eFZ+8iVVBIbHWjhQ6zqRROFBrbUGf\nIBNmtvEcObUDa8dInHNNjKkRZJn3pVplTpkqGhfDCe4v0RDvGkKx3XDSFeakuPbBpGhhYpAdT44K\nwVKlou7kaRIfXILrpFEEv/goSgv5wO2Npluq+Pbt28fLL7+Mn58fGRkZLF26lPnz5zN16tTLLqgk\nSb8vIX5+6HZLWiVedpY8MtKLGWH/P5Bz+Zl69m0/RXNTC7fMDMfesorslQ/imV9OnrkfSZ4P06LU\nondQEzZMRWndTo7nRONUH8GAssEEZpuToQklxqaJBuNBKtWJ9GuwZmKdL/+JmEO6ygGduTmtqjru\nHmjNPf0j+HbDBua+/SLvzLyXzOUfEfr603hMv/QLlHRju2iC0ul0+Pn5ARAUFIS5ubms0ruGyLrx\nzl3LMcquamLtiRKOFdYDsGCQO3+IcG9/jqhRZyD6x0yyT5Uz6uYAwgI1FHzyKq0nk2kz78v3jlGU\na11QeNkxcFgridnf8NPJ0/hZD2FcYTCBDYKj9qNJsK/FvHkTeaoM/IU7gaq7SXD15kdfD0zGKvTq\nMhaNDOP2vsNIS05m+pQpiDYTD7kFU7D6W0Zs+QDrAJ+rGapudS2fQz1dp21QJpOp/e+zY2H9ctrV\nfquuJN1IWowmTpY28Fl8KWnljXjYWPC38T7c1Mcei/+No2c0mog/kk/swRz6hzuwcLINTTvfRfde\nMuXq/vzkdB9GK2tO93KlT0AJ1RVfsDO2ljDVIAZkehCoy2S72xSinTSom74lVZODg9NN2Ghmc8Tc\nFQ99FVXGKvRU83DkSKaGBKOrq+P5Z57hhx9+4OmFDxC8IwF7JzdCV72JSnP+h4ElqTMXbYO66667\nOl2BHItPkrpfm0mwIamMtXElaC3M8LZXc+9gDyI8bTrMV1JUx/avknB1VDGmLQHVkZ00tZmTqA3n\ntM0ALOvr8YkMYG3dSWyNu3HR2DCgJYg+CWnYturZ4zaGJpMPbeJHUuxqMdNOpM6yH166UnqbakhW\n6amgjYcG9uf2caNR/e8GdePGjRz4bhszmqxQ5J4h8NkH8Zw75ZobFULqHt3SBvXuu+9edoEkSfp9\nmIRgxvqTGIwm7h7oxsLBHue98DfU6/lhzRFuUyRgc+AwdQoH9jiPpsqyL9ryQsLJI/N2DWtSluFv\n78/I1oGEHEqiwjyNZDt/jCKAHMs88mzSaNHciVpYcHPxcTwt97DFxYX9jQYWWtkwa/6dmFtrfi6b\n0UjZ9v14/Pd77tS34vvnOXjMvEV2hJB+FxdNUK6urr9p5YmJiaxduxaTycSECROYMWPGOfOkpqay\nbt062trasLGxYdmyZb9pm9L/k3XjnevpMSquM7B8fx4Go4lv7+mHrfrc/7JCCOoT0yj9cDV3NJ6i\nxq4PO0Lmk6dT46CooM+RL6lZ2If11cdQpQSzoCGCiJR0krV6Tmj9UfeKYI+lOTVqexTKQHybK7g7\n7Tu09mo+cvdli8GCBfmVTJ89DevB/QBoa9JTtGE7eR98ibqXCwHPPIDLzSNR3IBV/j39HLqWXfKD\nul1lMplYvXo1S5cuxdHRkb/97W8MGTIELy+v9nkaGxtZvXo1L7zwAk5OTtTX13dXcSTpmpNV2cQj\nm0/Tx0HN65P9z0lOpsYmKn84iGHHZqxbimi1C2DP8KcpqG6lzHiYsLRTlIXBsdsrCGvsw9wcf/rX\nFZBg406s7030jxjMilMZ5Nj3xtaQybC6Wv6Yux+Dswvv+wWQbTJnQWUzC309Gfrko5hMJv678j3q\nYpIYcvIMDsP60/8/L+EwpN9VipB0veu2BJWVlYW7u3v7r7CbbrqJEydOdEhQ0dHRDB8+HCcnJwBs\nbW27qzg3JHlX17meGqOtaRW8d6SIUFdr3pwaiOoXb7htKTxD6dpNKE4lIFRNnLEPJLP3bPRY4ODR\nQGrjCnpntLFvlILxYhhjTpnjok8lzsaLY2PmMnj4UFZvXcfHRZUobILo35DPI7nRKK0seC9oEBkK\nK+bXNPPqlPFohvRHoVBwcOt2nnn6r5jXN/FM1B0M37zkuu6Zdyl66jl0Pei2BFVdXY2zs3P7Z0dH\nR7KysjrMU1paitFo5OWXX6a5uZmoqKgLvr4jNTWVtLS0DtMcHR07/LyOjo4GkJ/l52v2c0q9GeUW\nbkTn1THeuYUxjo2olD+/d23/9h+xOnAS6zMl5Dt6UN4rkjpLJ/r0dWdYfw/2HXmfLaf+j737jquy\n7h8//jqHveGwN8oUUHEvHLm3pqWZpmnDtllmVma337uyYaZ5Z8OZprlXzlwouBVBkCFDQPaGwwEO\nh3Ou3x/eeefPBCyPon2ef3mdc43PeXM9fF/XZx7ASa3A39GPJ5Lz0HGNU4og6ob1xb26gui4Q2wu\n3U6l/Uz8pEpGJ+0loL6I5d4hxMisGF9QwUdjB2DeqS1Rx09Q+vUyNv68nvNZ6TzTuRd9XppC75HD\nmk28xPbDs71lyxb+KDg4mJCQEBpyV5PFFhcXU1pa2qSFCs+cOUNsbCzTp08H4MSJE6SmpjJt2rSb\n+6xcuZJr164xb9481Go1c+fOZc6cObi6ujapPKIXX8NE3XjjmkuMcivVLD15nYs5SkYGOxDmakV4\nC9sbq9gmFZC//TAOyee45uBDmpkvfqZlBE8YgoevE5JOw/cLp6MsU+NXZ0mXyjxyzOzY79KV7Fad\neLGFBQcPLCfF8CL2utbkuz1HL+VVHo/+he1eQZy0cmdCpZp+wwZg3jkMbU0t19fuJOO7X/hKmYaD\npwkXqkgAACAASURBVDuLN67D1rXhhQ3/qZrLPdSc6XWy2OLiYpYsWUJGRgYA69at4/Tp08TGxvLS\nSy/96TEKhYLi4uKb2yUlJSgUilv2sbe3x9raGmNjY4yNjWnVqhWZmZlNTlCC8LDLq1Tz5q9XKaup\nJ8DBnM+G+NLe3ZqiPCXH9iZSGBlDYFEi5XYexHj2I9DbhCkj2mPt4YymqoqDSz/iWlYpHlo5XSoq\niHO0Z16b59E4OvOUixGys+v5T9p5PLRevNT1XyzLtGTk1X0Y1WbzUVAvRim1TA3veTMxXVu2nozv\nN2LXpQ0d1i9kd7Afp06dEslJeCCalKB++OEH2rVrx/z583nuuecAaNu2LWvXrr3jMb6+vuTn51NY\nWIhCoeDUqVPMmDHjln06derEqlWr0Ol0aDQaUlJSxDRK95B4qmvcg4zR7+1M/vZmLBruj8JITlJs\nHut2xENJCa2VKVTprIl064pfdSKTRrfFtmNHKi5Gs++7RWRXa/CpK2S0qowL/p14PeApFJIpITX5\nFKRvY/P103jUezG/02y4lsXcZDkBpWc4ayZnsKwFi3v3w7xzW7SqGtL/8zOZP2xCEd6BTluWYBXk\n2yxi9DAQ8dGfJiWo1NRU3nvvvVtmjTA3N6e6uvqOxxgYGDBt2jQ++eSTm93MPTw8OHToEAADBgzA\n3d2dtm3bMmvWLGQyGf369bulE4UgPIoi0sv46kQW6nodr3Z1p7WRjOh9SWSkFOPbwppOmmuklFYR\nad2KAJNCnqzYg/WIcRRFX+bQz1vJNq+jd3kOAZparrTpx2tm7XBUSQRXxFMqj+RKfRaBahfe6PQW\n9snxXPt1Fx+ETMVYnUWbyioGPz4Y867tqFeqSFv8E2krNhHpasKzP8zDL7zLgw6PINzUpARla2tL\nfn4+bm5uNz/Lzs7G0dGxgaOgXbt2tGvX7pbPBgwYcMv2yJEjGTlyZFPLK9wFUTfeuPsVI0mSOHi1\nlEWRWQB0czClq4FE5p4rKK1NCW3nSnuzMqIjYvjN3J22TjrGZmzD2MmdPJUVaw8c4aolvFediL8K\nMlv24DPHHriUq/CrOkap8SmKVTV0U7Vk+MD3Mb58kuz9e5jl049rrQfTJTeBkWG+tH/zKeorq0hb\ntJrMVVvJDvXkO7NiPOx8MPF2+9Oyi/uoYSI++tOkBDVixAg+++wzRo8ejVarJSoqih07djBq1Ch9\nl08QHnr5SjXLz+ZyKr2U0bbG2JaqKE8owyzMjSee7YhBXjYnN0ZwwsCBVg5mPJ68EzAmzsuF9dYy\nLrt50ksq5d8XTnJC68T+jlNwUBbjUrKFCqNorIqMGFXrT++BA5DHRXIxMorlHr0ocXSmbUkm3VVF\n9J40ktYKQ1K+WM71n3ZAeBjr2thxKfEsn376KUOHDhXTEgnNTpN78Z0/f55Dhw5RVFSEg4MDAwYM\noHPnzvouX4NELz6hOavT6jiQXML6I+m0rKzGsa6elv72hHbwoEWAA7riEk4vP0RslSV+xsWE5URQ\nU2/NAT971tkZojFUMMLPm0lIyNYvY5PrUMpMZJSZnEYjz6JVojGdNf60H9wVTfwZDlj4scWxE1oT\nM/rX5DMgPYGlQb3o5+9Am6gjZP+8C+ehfXCc9jh9nhjN5MmTmTFjBubm5g86VMIj7q/24mtSgtLp\ndM1y1nKRoITm6sS1Mj49dA3/UiVeag19BwfQKsQZc0sTdDW1ZG06yPF4FXJjGb1Lf6NY4cRenRm7\n3G1xsDJhWvvOjPTxJ+mTL0hVm3DWto4C8wtYy2WEXtDRpt6HkEFtKLoaz3bnzhyzboWZucQgd0u6\nbd9Otok1W33aMTnjIto9B3EZ1Z+Wrz2DmeeNlWwrKiqwsbF5wFES/in02s38hRdeoFu3boSHhxMU\nFHTXFxEeDFE33jh9xCixoIrvfk2mT7mK0EAH+o1ohZm5MZJOR+XRU5zbeY5EixZ00CRS5+/ARxb+\nxFnb0N7RnNV9BhHi6MKp77ez+ucIrlqUUqCIxsfEl6HHjGkhOeE/IJD4nCI+qvUgKaADCmst4/0c\nKb6USffVWyhqE4Z1Xj5P/+dTnB4fSIsjazFzv7Wb+N0kJ3EfNUzER3+alKDmzp1LVFQUS5YsQS6X\n06NHD8LDw/Hy8tJ3+QThoaHV6vh4fSza9BLCjOSMGRuKf8iNxFCbnEbGis2ckXkhN7HEKrCMT+q8\nqFFW08fGjEXTpmJhYMzpnef5IuZXcs2PUarIBJnEwGgnQpTGuPXtyvFKOUuMOlPeElwdZDzl48TJ\ntBrUhy/weOJZNApbpBU/Y//kENwOruLE5WiC3cUYJuHhdFczSUiSRGJiIlFRUZw9exZbW1u++uor\nfZavQaKKT2gO6tT1xJ67TmREOkUSjB4eROd2bshkMuqLSyn5cQ3xubVctA4gwVNJvIEWv6pKBmdk\nEzamF96tB3Ah6hoxZ1MoMt5JoUkSpjpjrCpkDL7qikPXdhzS2XPCoQ31UgUt3U3o5uHN0ZRq7Izg\nuSsRmCQkkx2XitOYQbR4ZSKRly8xZ84cAgMDWb16NcbGxg86TMI/mF6r+H4nk8lwc3PDw8ODtLQ0\n8vPz7/qCgvAoSU8vZc/GGPLlBiQrrHhjiD9dWtqhU9dRsW4DhadOE2XfkzIfU/YoVPS1teD5vUfR\nOpngOPU1kuIqOXosEpUmA5n8FzQyLQZqiX5XFViG9GFP7xZkWTijkopp7VNLB5cgDiVXceF6Ha84\nqLFb+RM1RaVounWiy5KPyFcpee6tGSQlJbFgwYLbhnUIwsOkSQmqqqqKs2fPcvLkSa5evUrbtm0Z\nNWoUHTt21Hf5hL9B1I037q/G6HRmOdv2JGGXV8E1V1v8gp1Z3sUdOzNDqrbvoGb3JmKtW5PsMQpZ\nN1u256UwqSqHHkezyOzxGEW1blzel06G+hoj8yO5anOdk3bVtMt0xcJnGNvDW2FvJidXXo6XcxUT\nQrqw6lwJZ9W1vORlgMXa9Rjn5CJ5ueP39TxMHBVERETw3HPP8corr7BixQpMTU0faIz+KUR89KdJ\nCeqll14iICCA8PBw3nrrLSwtLfVdLkFodnSSxKITWZxLL8MnpwwXIxkjXuxCoJctADURR6lYv5wC\nrIj0mYiDrysq7zoOpCXzclwSRjIvjvuPwbwGzlfEEl4Ww4TyHFa5VFJq4YmnwTAi2vsRbqtlgI8N\nK69EM7NTZ2yNnFh4PJfnAixx+/ln1NFxmHs5o3jzOaz7dL1Zvg4dOhAREYGnp+eDCpEg3FNNaoMq\nLS29baLX5kC0QQn6llNRy66EYuLyq0grqcGmto5eymoCQpzpPzQIA0M5dedPU7PmO9RVVZzzH0e2\noTPhQwP48XocyuR8uucYUGNmh7OrMYdzLxOgyWZqQQpJRrDXK4Ai6z7UGFsz0tOYvr3bsfTieaLz\n8vmyf38OXlURm6PkbTsl6kU/oLC3wtTbHYdXJmPkISZVFh4O97wNKiEhgeDgYAByc3PJzc390/1C\nQ0Pv+qKC0NxpdRLLz+Ww60oRrtYmjGhlj7m5nLQLZQwcE4pfKyfqU5NQfvsF2qICUgOGc94tgIA2\nrnTzteHHg+dwKzbEodYINw85u/MuUZpTwcd5V8k2sObLgF6kKrrjqsqmq6OaZ5/qTV5VFS8d2I+P\nrQ2LBw1jyW8phF6+wEvnozC2NMbK3QHHVyYjBbUkMy8PvwcdJEHQszsmqJUrV97soffdd9/d8QTf\nfvvtvS+VcE+IuvHG/f8x2p9UzIrzuSjVWgCe7eDKoBY2HN+VQHG1homvdMPGzgzVzu1oty2n2KML\n57tPQ62TM2xoIMcOJxN5Pg1nTTGda3M5oNVwqNqML0oukWbmxacBY8my9aWT6io+pT/QttdwJvcc\nR0RGJh8eO870Du3xLNSw+4VPeDwlDs/QFpj4OKGY/ATmPTqyb/9+Ppg2ibFjxzJv3rwHEiPhViI+\n+nPHBPXH7uMiCQn/BO/sTSE2r4q+vnbM7OmFiaGcnMwytv14lsDWLoQPDMDAQE7lypVoI3YQ1+NV\n4orN6NLGg5aBDqxbeYqE+lI6l8cgVav5MMibuQUZKCvkfBj6IoZyiY6qiwxq6cbaxEOEh3RkYo9x\nLD5zjt3JV5lnoUA1czHKggKGdA3BsksrbJ4YhlX/cNIyMpgzfjw5OTksXbr0jitPC8KjpEltUF98\n8QWzZ8++7fOFCxcya9YsvRSsKUQblHAvSJLEmot5/BJTwFfD/WntYomkkzgfdY0LURkMGhOKb5AT\nABXLlpEffZGTLcdh5+FAv5HBlBZXsXntOWJNixmeGctmL3e6o8Oy1ojDLh3wrb5OWMlx3Ad1ocJp\nOL8c+zchzsZMH/p/zNp7kLr8IsatPUidpS1OrXzwVVdiPbQv1sP7Ijc1ZdmyZSxatIi33nqLF154\nASMjowccMUG4O3odBxUfH/+nn1+5cuWuLygIzUVZjYbx6/93b38+xI/WLpZUq+rYv+Uy6tp6Jr3S\nDWtbMyRJonzxYs6l1XDNezz9RrXFN8iBiG2RnI1VEm+eS+uSHE4FtKJtrSmnFC3pXJnOh1e+J9O1\nlk7vfEVkthm7o5bjYVFGZ/PJPL58DZ0updBNZoOme3c6VeRi2z0Um1EDMbD+X0/ZTp06ERUVhYuL\ny4MIkyA8MA0mqE2bNgFQX19/89+/KygoaHQ9KOHBEnXjt6vRaPntail5SjXb44swN5DYOKktJoZy\nZDIZ2Rll7N0US1BbV8IH+GNgIEfS6Sj74ksuZmso9OnK1Nd6o8m4zsa3d5Bq6cIVi+t41avB2odc\nswDalp/huehdFBqXU9K/P0NGvs0PZ/OJubINi8rDGKa048OgZCbqLLF2C6JdTjJWrYNweOIFDO1u\nnyOvU6dODyBS/yPuo4aJ+OhPgwmquLgYuFEFUlJScvNzmUyGg4MD48aN02/pBOEeUdfriM+v4r0D\naZgbyQn3sWVuPx/kOVcwNTJA0kmcPZ7GxVOZDB7bmpaBNx6+JJ2O8k8+Ji6/nmzvXjwxpROJH3/N\nmRo3UmwdSbTMYGJBFXu9umNVmcHCot3EuVSwzF3HC6OXEqQIYOGKY5ie20qdTyxa4zHkdXHmuSII\nvxKDcfvW+Lw1F0NHe5RKJSZ1dWJaIkH4rya1QR0+fJj+/fvfj/LcFdEGJTTF1rgCfjybi1wGbV2t\n+HzorR20q1V17Nt8GU1dPcOfCsPK5sYMDFK9lrL5/yK5REO8Rz+6GWWTGXOBZI9+XLFS0708jgTH\ntpSbWvOiJgHzwW35PnIRnQIeY3zn6WTsPEH0so3IpFJ2PWFMod0I/OsMmX76Mvj6Evz8GMzcXZAk\nie3bt/PRRx/x1VdfMWjQoAcRJkHQm3veBlVYWIiT042G4dDQUAoKCv50P2dnMVOy0Hyti85jXXQ+\nT7R24sUu7rd9f/1aKfs2XyY4zI0e/f2QG9xY90yq01A6by4ZFfXEW3cj4NQGipy9uOI1mHLDJAaU\nlLPVfyhjC08zfHBvthZpuRC5iOdDX8HsWAaRrz9FlqM7pZOHsFvKoF5nxzPx2YQZW+H63mu4tWoB\nQGJiIrNnz6ayspJVq1Y98EVABaE5uWOCmjVrFmvXrgVgxowZdzzB/982JTQf//S68RPXylgXnU9P\nH9vbkpOkkzgfeY3Tx1IY+XR7WgT8t0qvToPy6ElqNq2jQG5Kpc6VnuXHOOrXDgwVBCn3EOvahUOO\nbfjUKh2DYf3514F/E1LowDNxvpT+ZxnSoL6sfPFVCm2V1FTmMz6zht7Gpni/MAn7YF8A6urqmD9/\nPlu2bOHdd9/l2WefxcDA4L7HqCn+6fdRY0R89OeOCer35AQiCQkPj3qdxJKoLA5eLQWgv58db/fy\nvmWf2hoN+7ZcprZaQ2gPM1oEOKKrqaXqyEkqdh3EsK6Qcq0hxlojsmyruWTsR3tlNmYmsXwbPIFQ\ndT5fD3TjUGoimbPfZGCCGTbe4DllKDte8mNrWjoV6kymxGfRuaqEsNdmYB5660KfRkZGuLm5cerU\nKRwcHO5bfAThYXJX60H9rqCgAJlMdrMK8EERbVDCH1XXadkaV8jPl/J5q6cXgwIUyGSyW/bJz65g\n9y8x+Ac70WtQIFJ5OcoDESgPR6GRGVB//QoGLp7Uac04V1WFnYMHnaU4Dnh3ZY9LN16wKcHXWs6Z\nb5Zil1KD66h+eE+dwHkTe5afzUJZFoeBTsk7OXnEOqbywowfsTITS6sL/2x6HQe1ePFihgwZQmBg\nIMeOHWPFihXIZDKmTp36ly4qCPeKVidx7nolP1/KI6W4BoW5IW/19GJwoP0t+2k0WqJPZXIhKoP+\no4LxMa+jbNkaqi/GoTY0JvdiMj49W4C9J6UVMooKs+jSWoGFcTrf+o0ny8CaN5RJ1KzeyaXqMhyf\n7E3o6rfYn6NmweUSzJWXqKxNJqimhkCDK+xvpWLm419gZWaDVqttttV3gtCcNSlBxcXF8dprrwGw\nZ88ePvzwQywsLPjiiy9EgmrGHvW68XqdxPxD6Zy9XklHDytWPdkKD5vb10BS12rYsTYaY2MDnuxm\niW7bLxRm51Gtk5N55go+kx/H3UpCe72cvMxCZKEOdFbUc6VFMMut2qK4nsa43avI9TUga4g5bcct\n4mS2ASuO5tLWzQoTZSpXNXl0qU3DzqeKHl2f49WWPUCCn3/+mUWLFhEREYG1tfUDiNLf96jfR3+X\niI/+NClBabVaDA0NKS0tpaqqiqCgG/XpFRUVei2cIPyZtJIaNsbkcyqrAq1O4rMhvrR3//P//Guq\n69i26jx+uiI8E2Koi4HKyhryzsbjPXUsRv06oNm8H0ONjqtGZrRtb0YVMjZa9+GwVUe6HdqBnbch\n+6caYh/8Apk1fmRe1RHmZkF5dTFn4n6jRmvE00Z5DHl2Gv5urQGIiYm5OT3YypUrH9rkJAgPUpMS\nlLe3Nzt27KCoqOhmm09JSQnm5uZ6LZzw9zxqT3V1Wh3TtiRQWKWhg7sVH/VvSQd3Kwzksj/dX1Wl\n5uii3XTOjcPc1IDSchVFFxLwmf4UvZfMI2n7fjw3H6C6VoWyhTOdqzO4VOLKjpbdqbBT0FeeQe1U\nS46VuFJt9DSeVnaMbmnOseREDl38ibw6GwKq5LwbHkJgnxs9XcvKyvj444/Zu3cvc+fO5emnn0Yu\nl9/PMN1zj9p9dK+J+OhPkxLUyy+/zKZNmzA0NGTixIkAXL16lZ49e+q1cILwu21xhfxwNgeADRNC\ncLBoeLaF8sspXFu6nlYaFTWaenJOp+Hz8gRaLfs/tMCZ1z/EpaQcjTwfZ0cZZdev8WulA3vHPkUL\nezkutsVEZFdhoByAq5MTY0Kd2HzxNJev7EalrSbfsBtPFZXx0jNPYBb0v4G/xcXFGBoacubMGWxt\nbfUZEkF45P2lXnzNhejF17CHvW48X6lm2elszmRVAvBMexcmtXO5rWfeH6nTMinddgBldALlVbVU\n5xbQ4rVJeEwYgYGZCZcjTsDXazDVVGJirsRM0nE535rI7oOJCwrDybKEjEoLXMyUPBbQEkszGw7E\nHKWgPAqV3Jpqo5bY1cGMvDL6zXgBQyf7O5blUfGw30f6JuLTOL324pMkiWPHjhEZGXlz+feePXvS\nt2/fu76gIDRFanE1r+xMppOHNZ8P8aONq+Udq/IA6otKqPz1MMrjZ8jJU6LKLybonam4jxuC3MQY\nrU7H3nfmEZwYh6lJFXIDiQyVBYdbjSNuYAt0JlpUmlrqtVo+H+xFmdqUpcd3UlididLAFRerjgyv\nM6RzTBIhfbpj/fwU5Ka3d8gQBOHeaVKC2rFjB8ePH2fEiBE4ODhQXFzMr7/+SllZGWPHjtV3GYW/\n6GF9qovJVTJ7XyrBThZ8Mti3wX3rsnKp3P0bNRfjqMKArNOJWIwdRb/5zyM3vrFu0sXYeDQzP6Cr\ng4oKIKfelOse3djl35tiSyM0Uj1eJipm9WnFqZwiXt+7mzKthJVBPcMCOzO6TIb1b5FY9OiEzafv\ngZUFq9es4fLlyyxZsuQ+ROTBeljvo/tFxEd/mpSgjhw5wr/+9a9bltdo27Yt8+bNEwlKuKfKajT8\n61A6Q4PseaWbxx33q01KpXLXb9SlZWLcuzuJ18qokIwJXL6YNr1v9DK9mJvHmQ+/okdSNN6eBhRr\njLBo4chWz4lctrEHNLhZVPJ6z1DWxMbx3L59mGoLCbAy5KvwoQSlVlCxdT8mIYHYfvIuRi6OnD9/\nnnfeeQdLS0u++OKL+xQVQfhnalKCUqvVWFlZ3fKZlZUVGo1GL4US7o2HsW78vf2pyGQynu/khrHB\nrb3fJJ2OmktXqNx5EG15BdYjBlDefxhn3vg31naWDN/4BWaWppzLyWX1zv30XrWDQY41KLwMqLW1\nIbnXRNaUuqKTyXAyVzKzbwiHz57g37u/5qrkxhjXWl597AUsEnIpX7KDahcHHOe8iklLLwoLC5n/\n6qscP36c+fPnM2bMmAbbwh4lD+N9dD+J+OhPkxJUWFgYS5cu5emnn8bR0ZHCwkI2btxI27Zt9V0+\n4R/idGYFx9PLSC+tZdWTrbA0+d+tKdVrUZ08T+Xu35AZGmI9aiBmncI4FZFO3pxFuNob033LQjA2\n4qtDR6n4dgNjE67SLswYnYkRGb368rmuLVWV9jjpVLw6MpCk3AS+2D4HrfoaVfbjeaN1eyYaWlD+\n2Roq5XIULz6NWev/zZ+3bt067O3tOX369G0Pa4Ig6EeTevFVV1ezatUqTp06dXPalm7dujFt2jQs\nLCzuRzn/lOjF93CTJImI9DJ+OJtDaXU9fX3t6O+voKPHjUGtulo1VUdPUrnnCEYujliPGohpm1bo\ndBL7Nl+mfsd2HEuz6LrzWyIKCtm06EcGHjxHoJccH1coMjdifpfxFOpCcFGpGRRgRZVFGsdi1iND\nTf+wp/G2acVn5y7wY1wmxibG2DwxFPOu7f8xb0eCcD/81V58jSao6upq8vPzcXFxwdTUlMrKSqyt\nrZvF4EORoB5e35y8zp7EGys2T+voyuBAe2zNjG5+X332EiXLN2Dayh/rUQMx8fMBQKvVsXdjLEQc\nxfbKOdpt/w/zt+0m8KfddDCtpqWbhNZQxndBrYl0Hoex1oA2pWXYBqQTnbUTIyMFI9pPZJBGgTLi\nNNMtDZlma8ewvr0xbuEpEpMg6IFeuplHR0fz9ddfU1dXh6mpKe+88w6hoaFNPnlMTAxr1qxBp9PR\nt29fRo8e/af7paamMnfuXGbOnEmXLl3u7hcId9Qc68bLazRM3pRAbb2OV7p5MCzIHqM/tDVJkkTl\nzoMofzuB05xXbyYmuJGc9myMhfNnsb4QSc3CWfzwwttMVeXg7mcASOz0aMlm3wno5FY4VeXgUHeW\nNONTmBUFMan3XHoWa6nc8BvVTg6c7NwaWUEejz87CZlMhkajYfny5QQFBYkhFH/QHO+j5kTER38a\nTFAbN25k4sSJ9OnTh6NHj7Jx40Y+/vjjJp1Yp9OxcuVKPvzwQxQKBe+99x4dO3bEw8Pjtv3Wr19P\nWFgYD/GYYaERWWW1RGWUs+ZiHsYGMrZMao2N6a23n6TRUPLjBjRZubh8MhtDxf9mYtBotDfenBKu\nYHJsL3HdW9PilXk8HWaMyt6E07a+LPcfis7UDplWhk3l9xjWqzFw9+XNDksJTiug8sc91LbwxHHG\nc0gtvfhhwyYmu90Y+BsVFcXs2bNxc3Nj4MCB9zs8giD8iQYTVEFBAYMGDUImkzFo0CC2bdvW5BOn\npqbi4uJyc82oHj16cOHChdsS1P79++natStpaWkNnu/KlSskJCTc8plCobjl6SUqKgpAbP/haa45\nxMfWL4y39qTgbqrlMQcts0Z0wshAfsv+2soqUud9ic7MhMD5byM3NSEqKgpJknBRBHBsbxLmRSlY\nnP4NlUaDXWw87buYEG1ny7aWz1AL1Bk5YqYqxLxmCT1bTCXEzhGb+BQUX61FHRxAzqDuaJwUeDs7\n8J+IE7gZyLGtreH555/n3LlzTJo0iW7duuHn59cs/n5iW2w/Sttbtmzhj4KDgwkJCaEhDbZBTZ48\n+ZaVdadOncrq1asbPOHvzpw5Q2xsLNOnTwfgxIkTpKamMm3atJv7lJaWsnTpUubNm8d3331Hhw4d\n7qqKT7RBNW9nsipYeT6XzLJaOrhbsWCI35/up07PovjrFZh3b4/t+JHI/tu+WVJUxdHdCchzcwku\nT6TwUBQl1bVc7BvIi5pr7HfvySW7UEwrislw88VYfQnzmv281vMj/LNLUP52HLN2odiMHoTKwY6D\naensTUkltbSM0UEBPBfWlieHD6dfv37MnDlTTH4sCHqilzYotVrNRx99dLPqrba2lnnz5t38XiaT\nMX/+/Lu+6O/WrFnD008/jUwmQ5IkUcV3jz2ounFJkpi6JZHcSjU9fWz5sF8LPG1MbttPV11D+aZf\nUZ26iGLKE1iEdwJAXVvP6aOpZJxKokfBeYrSM0lOy+Z0Bz/K2rkxLy2WXe79sFWlozPPJc2lMyba\nbMLqDJjWajb1K7ej7dwWm/lvE1mjYm9sDBfy8gn38mRK2zb09PLE+L8LCH744Yc89thj9zU+DxvR\nxtIwER/9aTBBvfzyy7ds303DsUKhoLi4+OZ2SUkJCoXiln3S09NZvHgxAEqlkpiYGAwNDenYsWOT\nryM0H5W19UReK2fJyesAbJ4YekvPvN9JkkT1mWjKftqKWVgwbos+xMDKEkmSSIjJJfLgVQIcZXSK\n20dCShap9lYcf+4xOmHJm6kRRFoac91wN1Hu7igtX8JNktHfyJDe9XWoj58k5ZWJHCwr5fiBA4S5\nODPM348vB/TDwvj2GdCNjG4vnyAIzYPeZjPXarW8+eabt3SSmDFjxm1tUL9btmyZqOJ7SEmSxNdR\n1zmQXIK7tQlt3Sx5qYs7pka3L3OuU9dR/M0q6vMLUbzwNKb/XaqiIKeCI78motPq6O6iJuP/0K2W\nIAAAIABJREFUvqKgTs2vQ3pQ7uvPpIx99CjKZ5WHClNTBTnGT5Bp24Z2NWr6KnTUJEQS6eHEcTND\nfGxtGebvxyBfX+zNzVCr1axZs4YpU6ZgKiZ4FYT7Tq+zmf8VBgYGTJs2jU8++eRmN3MPDw8OHToE\nwIABA/R1aeE+Kqm+MXdeclE1C4b40uEOK9sCSFothZ99i6GDAtfPP0BmaEBNdR1Rv6WQklBA956e\nSOvXkPh5FId7tudKtx44q6OYF7cCa5WcKktLxhv1ZIHlALAwIqSshAzrfGaVq/Dwd2do2za84u+L\nxx9Wrz1y5Ahz5swhICCAMWPGiAQlCA8RsR7UI0yfdeOSJLE1rpDl53KxMjFgycgAPGwa/s9feeQk\nqsizOM97EwkZl89f5+ThVAJbO+N68ShZq7eQ4uvFoaFjqbdQ0bpoNa+nyqiWK3Az1/GbfThrPboT\naAbXi9PINKlkalEFo54Zh9MfxksBZGVl8f7775OYmMhnn312xwci0X7QOBGjhon4NK7ZvUEJj66S\nag0TNsQD8HJXd0aFOCJvZAYGXV0dFVv34vjWC+RklXP010SMTQwZ0saYjHnvEaepZ9PLM6ixc8Kq\nPpJe1/YxIccUeZteWKbF8KXHBGIcfLCUFXFEmc2g2ir+ZWKH/3tv3LYuU1paGoMGDeLll19mxYoV\n4q1JEB5S4g1KaLKrRdW8vecqaq2Ejakha8YFY2F8ezvTn6nYfYjK2GTOeXalpEhFN0+Jqg0/k56W\nS45nSyKGP4GplIld5SHGXb9Oh2orzIeOIf34Kf4d/CyVRhJF2nQGGBgy4VIcLcePxOKxbn86NZEk\nSRQWFuLs7HyvQyAIwl+g1zeouro6tm3bxsmTJ1Eqlfz000/ExsaSl5fH4MGD7/qiwsPlenktM3+9\nSqVaSxtXS957zAd786b3fis8E0/l5n2catmL9saVWOVEknw8n6qETGL6DiIptAIT6Sp9s39hVK4c\nC49QNJ3D+DLJgJPtXqRGV8jwltY8mSrDJDkVxw9ex9jL/Y7Xk8lkIjkJwiOgSTO+/vTTT2RlZfHG\nG2/cfGL19PTk4MGDei2c8Pf8PpL7rypW1fHZsQye25qIoVzGD2OCWDjMv8nJqTT5OnFvfUnp0lWo\nevejP+kY7t3NweRiKpOvseXJ/qQGx9FZq2NO/AZGF5ihmP4hUWZtmFztRaRbIOE+ErsHteGZgxFY\na7W4Lnj3ZnKqrq4mMjLyb/3GvxujfwIRo4aJ+OhPk96gzp07x9KlSzE1Nb2ZoBQKBaWlpXotnPDg\nfH8mm+3xRSjMDJnTx5ueLWxvmdS1IZU5xaR/vxXz1ESk9p3x+dcrVK7ZTGJSDskFSgxVFSyb2hkX\n60IG5qkYlHMaQ58wakbNZO2Oixx1D8ZGruP7CWGYRcdS9vFS7CaOxuKx7jcHde/bt4/333+f8PBw\nwsPDxSzkgvAIalKCMjIyQqvV3vLZ78tuCM3XX+1ZtOJcDtvji3i+kxvj2ja9qkyq05C2eje6iBPI\n/VvhtugjLF0V5Hy7lv2XczBLvEaphxVbx3TjdUcnqs79yJgyUyrDJxKh9Obw0USKPD0Isqlh8Ygu\nVPy0hYqkNJznzcDY+8b4udTUVN577z2ys7P55ptv6N2791/6jb8Tva8aJ2LUMBEf/WlSgurWrRvL\nli1j8uTJAJSVlbFmzRq6d++u18IJ91eVup6Zv6aQWV7LJ4N86eTZtAcQSadDFXWegjXbKDG0xuvd\nNwgI80WnriP+w685mFNDi4gIjvcOIqpLG+ZQQv3ZH3hSacNB34kcUjmTb2mFobaEt7o70N/WnMK5\nX2Ls7Y7rgjnIzW70wtuyZQvvvfceM2fO5MUXXxSzQAjCI65Jvfg0Gg0bNmzg8OHD1NXVYWxsTL9+\n/Zg4ceID/U9C9OJr2N2Mz5AkiUErYwD4eJAvnZuYnGrjkyldu42KCjUp3u3o+9pgLK1NKYm8wLHP\nVpJpaovP5QtsHj+AXB8rhpecptu1LAxMQ/nRZwx55pZImjwmW1cxadLTqKLOU7ZmC7YTRmHZr8ct\nVXc5OTnI5XJcXV3vPhh3IMawNE7EqGEiPo3Tay8+IyMjpkyZwuTJk6msrMTKyqpZrKgr3DufHssA\nYO34YFysbp/Y9f+nyc6jbP0OqtOzueIQjNQnlCFPtEZXVs7FOZ+zX2OKo7IOt9wEDr/7BJU1MbTN\nTaZFRTs2+Y8lzdKFKl0+4zP3M3XoEMw7DaH0xw3UJqTg/OEMjH1unxLL3f3OPfcEQXj0NOkNqqCg\n4I7fPcjuvOIN6q+rq9dxKquC8hoNR1LLSC6q5tPBvnT0aPjNSdLpqNi2n8r9x8hp0YYrxh70GRFC\nywB7sn7aye69Z0kOsqXXzrMo3SyJ7G1FqY07ZroQak3dUNSWkWxcQ/vqYt67dgzX195DZ+NM0aIV\nGHm6Yf/i06jqNahUKlxcXO5TNARB0Ce9vkG98cYbd/xu06ZNd31R4cGJyVWy80oRpzIrAOjpY0uY\nmxUvdXUnxNmywWPrS8sp/mYVSmUdxz37ENQlgGe6e1F2/AybPv6N/WF2+Ciu0nOHhn1Pj6TAKQgJ\nDWHl+QzIjeKgvTOXrd1YqKshLOs4pu99Rm1GIaULv8J2wkgs+vZg586dzJs3j9dff/3mWmKCIPwz\nNSlB/f9JqLy8nC1bthAUFKSXQgn3xh/rxuvqdRy4WsJ/TmXT3t2KRcP9CXa2aHSKIvjv8hinL1K8\nchPX7P0oCOzO4DAbVAcOse2zGCL7hVDWPomQS3ZkeA3m7Mw2mKvj0dad5fOEZOxqq5gZ3A1PBz82\n1qVjci0e4/cXUr77GLVXruL84Ruk16p49/HHKSsrY+XKlXc1q/3fIdoPGidi1DARH/35S3Px2dra\nMmXKFN5880169ux5r8sk3EMlKg37kotZF50PwKR2Lkxs54KBvGnjhuoysylZuQllQTkXnTvi72WG\n2f51XFhdxukJE7g2KgEDqRSN9llO9zDFrO48fS1iOV+mZFFqPCVGhrzdoR9v9e5J/2PbQFmBwQvv\nU/jVaozcnXFdMIdPF33F2rVrmT17Ns8++yyGhmKKSEEQ/sZksbm5uajV6ntZFuEeK7QN4P9+icfe\n3IhnO7gyIcy5yQNatVUqyjfuRhl1gQRFIAaO9nie3kfxJVMuPTWGc6pktLIC6uWTMK+Mx6x2L/4m\nftiU2hOUfo6JlUWsdw/CfOBY9oYFwjf/RmaroL7nExR/ugzb8SOwHNATmUxGx44dmT59Oo6OjnqO\nyO3Ek2/jRIwaJuKjP01KUH9c5h1uLAWfnZ3N2LFj9VIo4e+p0Wj56WIe2+OLeLKNE893cmtyYpJ0\nOnK3HaZm136uW7hSYh+K/enf0DkqiH7xFY4rs9CoUpGM2tH61D7yPH7GtN6TYMsutL1yiRY1BWx2\nDeR8u9HMHjcAy1oltZ++gzykPapaW2q37sN57hsYt/C8eU0xn6MgCH+mSQnq/1/q3cTEBG9vb9zc\n3PRSKOGvyyyr4YVtSdiYGjLCRX1Xyan8UiIF329AVQeGI0ajiDqB+uQBEt98k6MaCxwoRKWzx6I+\nnx6/fkRM9yqc5cOYcD0N57wD/OIawC++/ZneN5yw9p5os9KpWTgXWffBlF68Tp2DDs8FczCwMNdz\nFJpOtB80TsSoYSI++tNogtJqtcTHx/Piiy9ibGx8P8ok/EVHUkv5PCITOzND1o0P4dyZU01KTnXF\npVxbsh4p/RoVXXrhZA3Jny0meeIkIjoMxbY+lzpVGpnVjnSSTiGLjkDZupYPMr0xq7/ABrdA4qwe\n49ne3Xm7awAyuYz6hBjU//kEbefhlB26zGFnCxau+ZYtw/oQGhp6H6IhCMLDrtEEZWBgwOXLl8XA\n3GZMJ0lEXSvn84hMhgbZ82a4F9B43biurp7Mn/dQfziCUq9AXCc9QdE3y1kf3IKzr76DQX0iXrLd\nZNYPR2FaQJuMw2SVRGLhYM6MPGt+cQthtbsrfapdmDukE63a3nij1pw+hnrtMmpb9uLSodN8kZ0E\nWUZs2LCh2SUn8eTbOBGjhon46E+TqviGDRvG5s2bGTdunOhh1cxIksRL25PIKKuln58dM3p4NumY\nlN2n0WzbRZ2pBWbjn6Qg8hd27d1LwshxyI1dGOtfQDffDlzJhMOXfsLneClXAlLxMXRjWpmMww6d\nWOvhzBALD7q7uN5MTnX7tlK7ZycFBv4sPrifI9fT+GDuXCZOnCgecgRBuCsNZpvf61b3799PRUUF\ne/bswdra+pZqo++++07vhRT+nCRJTPzlCsXVGtaMC8bN+tYpiv6sblx5vZCUL1djUVaExdhhpF87\nxv5Tb6Hy6Eu5zTyGBFjRwjSOqIS9nLqcS1BVH/wjEknuWsWYfE+CNIakmnqzwssdN40hPaxceWx4\nKySdjrpffqT69EWqal2wHd0HN1cLTr+yHjs7u/sZlrsi2g8aJ2LUMBEf/WkwQf3444+Eh4fz+uuv\n36/yCE0kSRIj18Si1kosGOx7W3L6M8VHz1K24hcMQ8OQv9KXL3+egaGRMXadv0CSOTLM9QonYtdQ\n6ehHv1bPkvLdSfKrDxAaIOeZdDsyzVyItA9ik7M1MmtDVo17HIWVOZKmjtqln1CZWEC9gRNOc1/E\npKU3H4wceB8iIQjCo6pJ9XUhISH6LodwF7Q6iZd2JKHWSqx+shXuNqZ/ut8fn+oKIi5SseIXqp+Y\ngM8gP2Z/M4reUms8nvmM1RdyeczhENFXz/FSt3e59tMFij74mNTBGp40MMG0xoU1HqPwaO3DKlUC\npqZG7Bz/JOZGRkjKSpSfz0OZo8MoOBTXV6cgNze7X6H428STb+NEjBom4qM/DSYonU5HfHx8gydo\nbo3e/wTfnckms6yWTRNDsTNrfLmT68djqPlxHdKEpwgd2p553z2N/1UTei/4nJmHrzPaO47400cY\nmtWR9Pn/Jr1DSzKe0vJalhX5Jn7sajcQRag9S5MS0KJj37gnMDcyor5KyffjnmBTUjq7//M9tkP7\niZVtBUG4ZxpMUBqNptE2pm+//faeFki4s31JxSyOug7AE62dGk1OUVFR+Jk6UvPDGkwmjsN7WFd+\n3PUvtMk5TJ7+LZ+cLaCXawaRFzcwdJWOeP8a8sb1JsP2AMHZIWzy9iCiRUskWTnexRIanY5VI4Zh\naWzMmYP7mfXya5jKjViybBl2Q/rfjxDcc6L9oHEiRg0T8dGfBhOUiYmJSEDNRL5SzeKo6wzwV/Ba\ndw/MjAwaPUZXWEnFtu3IRw7HtVsIv3w+k+iKk7zu+zy/yp0w1iZwOukIbaLDqba5ijrEgFyrvXim\nBbG7QycwMqSnmwvXKypR12vZMGY01rU1TB82guPRF5nVtSfPrl2JoVXDs6ALgiD8FaLPeDMnSRJp\nJTW8sjOZ3i1tmdXLq0nVaDUFJTjtPIa6eziebTz5/pUxxITV8MFTSylTtOK3I5dQ1xZjIY0k9MQC\navr4ctH2CFkG/Snq6kedth4XMzOi8/J5sX07xvr5oToSyb5vf8Qiv4CIRV/gMmHSfYiAfokn38aJ\nGDVMxEd/GkxQTVjLUNCTAmUdC09kEptXBYC3nSmze3s3KTmpSyvIeO8rqvyDKfQp5JuNn+EV7s/8\n8fMxMvXkra2xaDSGhOeqCDuxkdIWjuwOTkBb2ZYA/1ZEq2vwtLbilU4deczchOqtO8ld8C0GumqG\nhDjy5FcfYBDURt8hEAThH67BBLVu3br7VQ7hD/Iq1UzZnICHjQnLRgfi59D0uetUpUrSZ3+F0tmO\ntaYbMDtSxfPdX6XrE1OIyVUyf+dlXMuzmZh4Gll5JcVZqex+wQCbPFfSAjuSWqNiSpvWvGqkpeo/\nSyjIrcHQzgLFmN6Y9x+IzNpWj7/8/hPtB40TMWqYiI/+iCq+ZmZddB7rovNpYWfKD2Nb3dWx5YWV\npH/wNWo7WOmwh/aHJcbNWYJ1j458uvsKl7IrGJ90glJ5Otfj8zBQyTj6rC1mpUac830MDwtz9toZ\nY/jTCr66nE69lTmzly7BNNBXT79WEAThzkSCaiaul9ey5OR1LudV8W4fb/r5Ke7q+ILcSnb8dBYX\n7xoOmV9g0A4TBnz9FXJ7BW9/dxzLylIeK/yNuPwaOpzPQtWnGxdaqshBTbZnW+aaael3fB/Hc2tZ\nkByLm78/X3yzCNOARzs5iSffxokYNUzER39EgmoGJEniua2JGMplfPd4IL72d7ccRWZqMTs2naHY\ndRfZyjKGrTchfPVi8gytWLQ9BpmuEFnmT3gc1+LnYIHpD8+z5+J+kkxaoJDbszn+NFVKU15PSuFy\nTSWffP0VI0aMEGOaBEF4oMTsnc3A5E0JAGyf3OaukpMkSSRdzmPz5oOk2P6Ai1JO35/r6f3Ld1xV\nmTL7yGWkumR67N1L10hjQseFs//17nwae5JEsy70LZXxbVwm5nIPftQoaTVmBGcuXGDkyJH/mOQU\nFRX1oIvQ7IkYNUzER3/EG9QDtvxcDgVVdXw/JghTw6Y9L2g0WpIv5xF9OovrNedJN91Ov6wAPCLL\n6bTjezQODqyMuUr/pDgcjkdwYEA4FYEOXKvT0OJaFW2UHnRVFdCnTQjmEztjEtCC7+Tyf0xSEgTh\n4SAS1AO09OR1fk0sZnZvb1oqmjZ/XUFOBdvWXkSyzSSjdhfK6kKGnLCj3aieeO4dTbWpGR9ujKbt\nr+s4GOBI2gsj6CSDyRcSaV9RiNzYEOf338UkKFDPv+7hINoPGidi1DARH/3Ra4KKiYlhzZo16HQ6\n+vbty+jRo2/5PjIykt27dyNJEmZmZjz//PN4e3vrs0jNgiRJLDyRxaGUUj4d7EtHD+smHVeQU8Hm\n7/aRZrYG9fVyuhb50H/k/+H6QR/khoZUVFTx5ccbsEw6xarwUBwsfOglq2XW4cPo1IXUtO/FfkuJ\nEQZy/PX8GwVBEP4uvbVB6XQ6Vq5cyfvvv8+iRYs4efIk2dnZt+zj7OzM/PnzWbhwIWPHjuXHH3/U\nV3Gajchr5QxaGcOhlFLe7uV1V8lp95e7uFa5GJ96ez6b9DNTlm/CfUR/5IaGVKel8MvE9+m2ZT2e\nw3sS7NmJ4JIc5hzfg7ZWxUkXPyb/uoELFy5gavrns5//E4n2g8aJGDVMxEd/9PYGlZqaiouLC05O\nTgD06NGDCxcu4OHhcXOfgICAm//28/OjpKREX8VpFrQ6iYUnMhnRyoHXuns0uc2nILeSbT9dRBee\njZ26Da9P+A4D+f/+dJWJaRydMhdLRyf8Dizn5J4IZh5fjaK6jowqDd/Ul5F2PpEFCxYwcKBYo0kQ\nhIeD3hJUaWkpDg4ON7cVCgWpqal33P/o0aO0a9fujt9fuXKFhISEWz5TKBS3jOL+/UmmuW7P2Xae\nGo0Rr/43OTXleEknkXROh2vHUvYlHmVcm1k3k1NUVBSSJFHx6XryunbHxbYW7Yef85JGg6ZaRaqj\nCy9d2sML019k7WuvceHChYcqXvdr+3fNpTxiW2w/ittbtmzhj4KDgxtda1Am6WnCvTNnzhAbG8v0\n6dMBOHHiBKmpqUybNu22fePj41m5ciX//ve/sbRs+szYR44coX379veszPp0PL2MT45m8HSYM892\ndGvycUmX8zgRdYbz2v8w58ml+LoE3/xOW6Xiyro9aM9cRCurx6G2CK2ynGzv9nT9vxmYOCiorq7G\n3PzuxlUJgiDcS9HR0fTr1++uj9NbG5RCoaC4uPjmdklJCQrF7bMjZGZm8sMPP/Duu+/eVXJ6mBSr\n6vjkaAaP+doxpYNrk46pU9cTefAqB3Zd5DJrmNhnxs3kJGk0VO45TObrH3E5JZ9dptZcj4wnGics\nFi+j97L5mDjceLsUyalhov2gcSJGDRPx0R+9VfH5+vqSn59PYWEhCoWCU6dOMWPGjFv2KS4uZuHC\nhbz++uu4uLjoqygPTI1Gy4ZL+Wy6XEhLhSmvN7HdKTujjANb43DxtKI28DBhtl3p03okkiRRfeoi\nReu3k2VuzvI2AwiNisC5spTkyQN4d94sMZZJEIRHht4SlIGBAdOmTeOTTz652c3cw8ODQ4cOATBg\nwAC2bt2KSqVixYoVN49ZsGCBvop032h1Et+fyWZXwo03yFm9vBgYYN/gMbU1GlITCki6nE9RvpL+\no4LxCbCj7lwoI7tMoTw+mdyVv1BeXcNP/h7YtO5KXZEJKaGenN+1nw6ZGmpqam55YxLjMxonYtQ4\nEaOGifjoj97aoO6H5toGtSQqi71JJczu7U0fXzsM5Xd+q5F0Eod3J5AYm4e3nz2BrV1oGeiIsYkh\nkiQRk1/A9qRkqk+ep6WNDUFD+2NqYMuC7WdQHvoedVkBn3/+Ob17976Pv1AQBKHp/moblJhJ4h4q\nVtUxa28KuZV1/GtAC7p7N7520onfrlJcoGT6u30wMb3x56jTatmRlMxPsZep02oZ2yqIkTNfRmFm\nzpoLuWw9sI+kNfN4+62ZvPjiixgbG//pucU6NY0TMWqciFHDRHz0RySoe0SSJBYcy6RYpWHTxFDs\nzIwaPaaitJq489k893ZPTEwNqahVszkhgfVx8fjZKXine1e6e/yv3apKXU+FWstPM0ZT//xjuLk1\nvTegIAjCw0ZU8d0DSnU9T22IR6OVWDwigGBni0aPKS+p5viBZBSOFvQcGIBOkhjxy2ZaOznybFhb\nghwabrMSBEF4WIgqvgdkzr5UonOVmBnJWTsuBHuLO7851dfriLuQTczpTGpqNPgGOdGpZwsA5DIZ\n28aNxdTwf38SpVLJtWvXaNOmjd5/hyAIQnMj1oP6C2rrdey8UsgzG68QnatkwWBfdk1p22Byykgp\nZtWiE6QnFzHg8VBenvMYg8aEYvqHqsDfk5MkSWzfvp1u3bqxbdu2v1xOMT6jcSJGjRMxapiIj/6I\nN6i7dDmvill7U5ABT7R2YlSII06Wf95JAW50H4/Yl0RmagmDx4bi7edwx30BkpKSePfddykrK2PF\nihV07dr1Hv8CQRCEh4Nog2qC6jotcw+mEV+gAqCzpzX/GtCywe7jcONNaMP3Z3DxsKHnwACMTRp+\nHli2bBlff/01s2fPZurUqRgaiucHQRAefqINSk8kSeKdfSmkFNfw9XB/gpwsMGgkMf1OJpPx5LRO\njSam3/Xu3Zsnn3wSR0fHv1NkQRCER4Jog2rEvN/SSSmuYdnoQEJcLJucnH7X1OQEEBISck+Tk6gb\nb5yIUeNEjBom4qM/IkE1QKuTOHu9ksUjAvBzuHeTrlZUVFBVVXXPzicIgvAoEgmqAVvjCgGaNK6p\nKXQ6HRs2bKBr164cPXr0npyzIWJ0e+NEjBonYtQwER/9EW1QDdhyueCeJafY2Fhmz559M0k1tDij\nIAiCIN6g7uhEehmVai3v9PL6W+fRarXMmjWL8ePHM2nSJA4ePHjfkpOoG2+ciFHjRIwaJuKjP+IN\n6k/U1utYcvI6QY7muNuY/q1zGRgYEBYWxgcffICdnd09KqEgCMKj7/+1d+9hUdZ9HsffM8BACCOB\ngpA9IpIG1KVJpQZmHnJ3zQ50ZbRp1KTGZdlmXIEa7QYdgMo8IaEmcdjtYD5G6dPhslIzFfMA9BRo\nSKgpBxMIEQVkZu79w3U2BWYGE2Zgvq//Zuaeme98xPs7v9/c9++W86Au09xmICrvnxgV2PzESFyd\nZZAphBB/hd1d8r03qjzdyswPS1AU+O/osC43p9bW1m6qTAghHI80qP/T0mYg9pODnDcYSX9gBH6e\nnS9fdDmDwUB2djbh4eHU1tZ2Y5VdI3PjlklGlklG5kk+3Ud+g+LCahH35f4TgLzoUAZ5ulr93H37\n9pGQkIC7uzvr169nwADza+0JIYSwjjQoYFPphVFPV5pTXV0dSUlJfPvttyQnJ/PQQw+ZLixoL+T8\nDMskI8skI/Mkn+7j0A3KqCj842AtGQUnmDjs2i6NnM6fP4+3tzd79uxBq9V2Y5VCCOGYHPo3qDl/\nP8iq3SeIGT2I+AlDuvRcf39/kpOT7bo5ydy4ZZKRZZKReZJP93HIEdTB38+SWXCCE6dbWXX/CIYP\nNL/OnqIodjd9J4QQfZ3DjaBa9Eae21RGP42TxebU1tZGZmYmOp2uByu8emRu3DLJyDLJyDzJp/s4\n1AiquOoM6/ZWoXV1IvXfgs1uu2vXLhISEvDz8yMtLa2HKhRCCHGRw4yg2gxGEr4ox6AorHkwpNPt\nqqurmTt3LvPmzWPhwoVs3LiR4cOH92ClV4/MjVsmGVkmGZkn+XQfhxlBpW0/xjUuat55YITZ35O+\n+OILhgwZwvLly+nX7+qsZC6EEKLr+vxafIqi8F1FAynbjpL6r8MIH2y/R90JIURfJGvxdaKo6gwp\n244SFTZQmpMQQvQifbpBHfr9LIu+/JXxgV7MGzfYdH9rayvLli0jPz/fhtV1P5kbt0wyskwyMk/y\n6T59tkEdrW/mPzaVMTrAk/+cMtR0/7fffktkZCT79u1j1KhRNqxQCCGEOX3yN6jzeiPTc37Ex92F\nD/49DJVKxfHjx0lMTKSkpITU1FSmTp1qg4qFEMLxXOlvUH3uKL7tv/5ByrajAPzPI2GmI/bmz59P\nZGQka9euxc3tr10lVwghRPfrU1N89efaSNl2lNsGa/n7rJtxUv//4eT5+fnEx8c7VHOSuXHLJCPL\nJCPzJJ/u02dGUEZFYeaHP+PqrOa1fwlqd66TWt2nerEQQvR53dqgiouLycnJwWg0MmnSJB544IF2\n22RnZ1NUVISrqytPP/00Q4cO7eCVOmcwKsT9o4yDv5/D2NZKRONOGhsD6d+//9X6GL2WrBFmmWRk\nmWRknuTTfbptWGE0GsnKyuLFF19k6dKl7Nq1ixMnTlyyTWFhITU1NaxcuZKnnnqKdevWdfl9Piyu\nofTkWaI9j1G3dh6/HiqhtbX1an0MIYQQNtJtDaq8vJxBgwbh6+uLs7MzERER7N+//5K3OLEdAAAM\n7klEQVRtDhw4wIQJEwC44YYbOHv2LA0NDV16n7VbDnA+/xXeXZbGsmXLyM7OxtfX96p9jt5M5sYt\nk4wsk4zMk3y6T7dN8dXX1zNgwADTbW9vb8rLy9tt4+PjY7rt4+NDfX09Xl5e7V6vpKSE0tLSS+7z\n9vZm+dQAmPpfpvsKCwuv1kfo9dzd3SUPCyQjyyQj8yQf62zYsOGS26GhoYSFhZl9js0PkrD2NKyw\nsLB2H2bDhg3MmDGjO8rqEyQfyyQjyyQj8yQfy640o26b4vP29qa2ttZ0u66uDm9v73bb1NXVmd1G\nCCGEY+q2BjVs2DBqamr4/fff0ev17N69m1tvvfWSbcLDw9mxYwcAZWVl9OvXr8PpPSGEEI6n26b4\nnJycePLJJ3n99ddNh5kPHjyYr7/+GoC7776b0aNHU1RUxLPPPoubmxvz5s3rrnKEEEL0Mr16Lb6S\nkhKLP7I5MsnHMsnIMsnIPMnHsivNqFc3KCGEEH2XrP8jhBDCLkmDEkIIYZekQQkhhLBL0qCEEELY\nJWlQQggh7JLNlzqyRk9ctqO3s5TR999/z6ZNm1AUhWuuuYY5c+YwZMgQG1Xb86z5G4ILixy/9NJL\nPP/884wZM6aHq7QtazIqKSkhNzcXg8GAp6cnSUlJPV+ojVjKp7GxkfT0dBoaGjAajdx7773cdddd\ntinWBjIzMyksLESr1fL22293uE2X99OKnTMYDMr8+fOVkydPKm1tbcoLL7ygHD9+/JJtDhw4oKSk\npCiKoihlZWXKiy++aItSbcaajH755Rfl7NmziqIoSlFRkUNlZE0+F7dLSkpSUlNTlYKCAhtUajvW\nZNTU1KQ8//zzSm1traIoinL69GlblGoT1uTz8ccfK++//76iKBey0el0il6vt0W5NlFaWqpUVFQo\ncXFxHT5+Jftpu5/i66nLdvRm1mQ0fPhw3N3dAQgODr5kDcS+zpp8AL788kvGjh2LVqu1QZW2ZU1G\nO3fuZMyYMaYrEDhSTtbk4+XlRXNzMwDNzc14enri5ORki3JtIiQkhH79+nX6+JXsp+2+QXV02Y76\n+vp223R02Q5HYU1Gf7Z161ZuueWWnijNLlj7N7R//36mTp0KgEql6tEabc2ajGpqamhqaiI5OZlF\nixaZ1tF0BNbkM3nyZI4fP05sbCzx8fE88cQTPVylfbuS/bTdNyhrKbIghlV+/vlntm3bxsyZM21d\nil3Jycnh0UcfRaVSoSiK/D11QK/Xc+TIERYvXkxiYiIbN26kurra1mXZjfz8fAIDA1mzZg1vvvkm\nWVlZphGVuKCr/6/s/iAJuWyHZdZkBHDs2DHWrFlDYmIiHh4ePVmiTVmTT0VFBcuXLwfgzJkzFBcX\n4+zs3G4F/r7Kmox8fHzQarVoNBo0Gg0hISEcO3YMf3//ni63x1mTT1lZGVFRUQCm6cCqqiqGDRvW\no7XaqyvZT9v9CEou22GZNRnV1tayZMkSnn32WQYNGmSjSm3DmnxWrVpFRkYGGRkZjB07ljlz5jhM\ncwLrMrrttts4dOgQRqOR1tZWDh8+zODBg21Ucc+yJp+AgAB++uknABoaGqiqqsLPz88W5dqlK9lP\n94rFYouKii45vDMqKuqSy3YAZGVlUVxcbLpsR1BQkC1L7nGWMlq9ejV79+41zaM7OTmRmppqy5J7\nlDV/Qxe98847hIeHO9xh5tZktGnTJrZv345KpWLy5MlMmzbNliX3KEv5NDY2kpmZSW1tLUajkaio\nKCIjI21cdc9ZsWIFpaWlNDY24uXlxYwZMzAYDMCV76d7RYMSQgjheOx+ik8IIYRjkgYlhBDCLkmD\nEkIIYZekQQkhhLBL0qCEw0hKSmLr1q22LsOs77//ntdff73Txw8ePMiCBQt6sCIhbEeO4hO90jPP\nPMPp06dRqy98x1KpVKxYscLseRXJycmMHz+eSZMmXbU6kpKSOHz4ME5OTri4uBAaGsrs2bOv2nl4\n0dHRrFy5stvPp9mwYQOffPIJLi4uqNVqrrvuOmbNmkVISIhd1Skci92vJCFEZxYtWsRNN91k0xpU\nKhWzZ89m0qRJNDU1sXTpUnJzc3nuueeu2nv01HfIiIgI5s+fj9Fo5OOPP2bp0qW8++67Vj9fvuuK\nq00alOgzzp49S3p6OuXl5RgMBm688Ubmzp3b4XIqNTU1ZGZmcuzYMZycnLj55ptNU2eVlZW89957\nHDlyBK1WS3R0NOPGjbP4/h4eHtx+++2mkzd/+eUXcnJyqK6uxt/fH51Ox/DhwwHYvn07GzdupLGx\nEU9PTx555BEiIyPZvn07W7du5ZVXXuHll18GID4+HpVKxbx589BqtaxatYrMzEw+/fRTKioqiIuL\nM9WQnZ0NgE6n49y5c+Tm5lJcXIxKpWLixInMmDHDNOq83MUGo1ariYyMJD8/n8bGRrRaLeXl5WRn\nZ1NVVYVGo2HMmDHExMTg7OzcYZ3jxo3jwIEDfPTRR9TW1jJ48GDmzp3L3/72N6v+LYUAaVCiF7v8\nG7uiKEyaNIm4uDiMRiOZmZlkZWURHx/f7rnr169n1KhRJCcno9fr+fXXXwFoaWnhtddeIzo6msTE\nRH777TdeffVVrr/+eovL+jQ2NvLDDz8QFBREU1MTaWlpPPnkk0RERFBQUEBqairp6ek4OzuTnZ1N\nWloa/v7+NDQ00NTU1O71kpOTiY6OZsmSJaaps5KSEtPjERERbNy4kZaWFtzc3DAajezZs8f0eTMy\nMvDy8iI9PZ2WlhbS0tLw8fFhypQpZj+HXq/nu+++w8/Pz3RJDbVajU6nIygoiLq6OlJSUtiyZQvT\npk3rsM4jR46wevVqFi5cyLBhw9ixYwdvvPEGK1aswNlZdjvCOnKQhOi13nrrLXQ6HTqdjiVLlphG\nMBqNBjc3N6KioigtLe3wuc7Ozpw6dYr6+nqcnZ0ZMWIEAIWFhfj6+nLXXXehVqsJDAxkzJgx7Nmz\np8PXURSF7OxsdDodCQkJeHt7ExMTQ2FhIQEBAYwfPx61Wk1ERATXXXcd+/fvR6VSoVar+e233zh/\n/jxeXl5XtKbdwIEDGTp0KHv37gUurFSv0WgIDg6moaGB4uJiHn/8cTQaDVqtlmnTprFr165OX6+g\noACdTsesWbPYunUrixcvNj0WFBREcHAwarWagQMHMmXKlE6zBfjmm2+YMmUKwcHBqFQqJkyYgIuL\nC2VlZV3+nMJxyVcZ0WslJCRc8htUa2srubm5/Pjjj6YRSUtLC4qitLu+08yZM1m/fj2LFy/Gw8OD\n6dOnM3HiRE6dOsXhw4fR6XSmbQ0Gg+lCa5dTqVTodLp2B15cfv0guNBQ/vjjD1xdXVmwYAGbN29m\n9erVjBgxgpiYGAICArqcQWRkJLt27eLOO+9k586djB8/HriwOLBeryc2Nta0rdFobFfTn91xxx3M\nnz+fM2fO8Pbbb/PVV1+ZcqiqqiIvL4+KigpaW1sxGo1m11Grra1lx44dfPXVV6b79Hq9Q11IVPx1\n0qBEn7F582aqq6tJSUmhf//+HD16lIULF3bYoLy8vEw770OHDvHqq68SEhLCgAEDCA0N5aWXXvpL\ntXh7e5tGNhedOnWKUaNGATBy5EhGjhxJW1sbH330EWvWrCE5ObnL7zN27Fjy8vKor69n3759pkPU\nfXx8cHFxISsrq9PfnC53ccrU09OTp556ivj4eO655x58fX1Zt24dQUFBLFiwADc3Nz7//HN++OGH\nTl9rwIABREVF8eCDD3b5MwlxkUzxiT6jtbUVjUaDu7s7TU1NbNiwodNtCwoKTNem6devn2naLTw8\nnOrqanbs2IFer0ev11NeXk5lZWWXahk9ejTV1dXs3LkTg8HA7t27qaysJDw8nNOnT7Nv3z5aWlpw\ncnLC1dW10ybSv39/Tp482en7aLVawsLCyMjIwNfX1zQKu/baaxk5ciR5eXk0NzdjNBqpqakxOy33\nZwEBAYSHh/PZZ58BmH7ncnV1pbKyki1btpitc/LkyXz99deUl5ejKAotLS0UFhbS0tJi1fsLATKC\nEn3ItGnTWLlyJbNnz8bb25vp06ezf//+DretqKggNzeXc+fO0b9/f3Q6Hb6+vgAkJiaSl5dHXl4e\niqIQGBhITExMl2rx8PBg4cKF5OTksG7dOvz9/Vm0aBEeHh40NDTw+eefk5GRgUqlIjAwkDlz5pie\n++fR3owZM8jIyOD8+fPExsaaDlr4s4iICDIyMpg1a9Yl9z/zzDN88MEHxMXF0dzcjJ+fH/fff3+n\nNV8+yrzvvvtITk7m4Ycf5rHHHmPt2rVs2rSJoUOHEhERcckBG5fXOXbsWGJjY8nKyqKmpgaNRsON\nN95IaGhol3IUjk1O1BVCCGGXZIpPCCGEXZIGJYQQwi5JgxJCCGGXpEEJIYSwS9KghBBC2CVpUEII\nIezS/wLBosSDUGolewAAAABJRU5ErkJggg==\n"
}
],
"prompt_number": 13
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Well it an improvement, not a huge one but to be only taking the mean of each model it is not bad at all. At least the bag score a better accuracy than the other 20 clfs and also a better Area Under the Curve"
]
},
{
"cell_type": "heading",
"level": 2,
"metadata": {},
"source": [
"Conclusion"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Bagging is **good**. Just a **very** simple implementation gave better results.\n",
"\n",
"I did not select any parameter for the Decision Trees, only the max-depth=10, playing with more models and more parameters I am sure bagging is going to be even better. To solve this problem next I want to take a look at [Grid Search](http://scikit-learn.org/dev/modules/grid_search.html#grid-search) and see how it can help me to improve this results.\n",
"\n",
"I really believe that the potential of bagging is to do some conditional scoring, for example only ask models that are good with high Income when the entry income is higher than $10000 for example. Also probably is a good idea to use different classifiers, instead o 20 decision trees 5 DT, 5 SVM, and so on. But is just something that cross my mind.\n",
"\n",
"As usual the code is on github: [copper](https://github.com/danielfrg/copper)"
]
}
],
"metadata": {}
}
]
}
| apache-2.0 |
google-research/football | gfootball/colabs/gfootball_example_from_scratch.ipynb | 1 | 41251 | {
"nbformat": 4,
"nbformat_minor": 0,
"metadata": {
"colab": {
"name": "gfootball_example_from_scratch.ipynb",
"provenance": [],
"collapsed_sections": []
},
"kernelspec": {
"name": "python3",
"display_name": "Python 3"
}
},
"cells": [
{
"cell_type": "markdown",
"metadata": {
"id": "VLUqsUmXvf2_",
"colab_type": "text"
},
"source": [
"# Compiling GRF from scratch.\n",
"\n",
"Can be used to create pre-build shared libraries.\n",
"\n"
]
},
{
"cell_type": "code",
"metadata": {
"id": "AakcNSxB-D3P",
"colab_type": "code",
"outputId": "ac3b6f49-2aa5-4569-8738-2b696a9ed7e7",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 1000
}
},
"source": [
"! sudo apt-get update\n",
"! sudo apt-get install git cmake build-essential libgl1-mesa-dev libsdl2-dev \\\n",
"libsdl2-image-dev libsdl2-ttf-dev libsdl2-gfx-dev libboost-all-dev \\\n",
"libdirectfb-dev libst-dev mesa-utils xvfb x11vnc libsdl-sge-dev python3-pip "
],
"execution_count": 1,
"outputs": [
{
"output_type": "stream",
"text": [
"Reading package lists... Done\n",
"Building dependency tree \n",
"Reading state information... Done\n",
"build-essential is already the newest version (12.4ubuntu1).\n",
"libboost-all-dev is already the newest version (1.65.1.0ubuntu1).\n",
"cmake is already the newest version (3.10.2-1ubuntu2.18.04.1).\n",
"git is already the newest version (1:2.17.1-1ubuntu0.5).\n",
"libgl1-mesa-dev is already the newest version (19.0.8-0ubuntu0~18.04.3).\n",
"libgl1-mesa-dev set to manually installed.\n",
"The following package was automatically installed and is no longer required:\n",
" libnvidia-common-430\n",
"Use 'sudo apt autoremove' to remove it.\n",
"The following additional packages will be installed:\n",
" gir1.2-ibus-1.0 lib++dfb-1.7-7 liba52-0.7.4 libcaca-dev libcapnp-0.6.1\n",
" libdbus-1-dev libdirectfb-1.7-7 libibus-1.0-5 libibus-1.0-dev\n",
" libmirclient-dev libmirclient9 libmircommon-dev libmircommon7\n",
" libmircookie-dev libmircookie2 libmircore-dev libmircore1 libmirprotobuf3\n",
" libmpeg3-2 libmpeg3-dev libprotobuf-dev libprotobuf-lite10 libpulse-dev\n",
" libpulse-mainloop-glib0 libsdl-image1.2 libsdl-sge libsdl1.2-dev\n",
" libsdl1.2debian libsdl2-gfx-1.0-0 libsdl2-image-2.0-0 libsdl2-ttf-2.0-0\n",
" libslang2-dev libsndio-dev libst1 libudev-dev libvncclient1 libvncserver1\n",
" libxcursor-dev libxinerama-dev libxkbcommon-dev libxrandr-dev libxv-dev\n",
" python-pip-whl python3-asn1crypto python3-cffi-backend python3-crypto\n",
" python3-cryptography python3-idna python3-keyring python3-keyrings.alt\n",
" python3-pkg-resources python3-secretstorage python3-setuptools python3-six\n",
" python3-wheel python3-xdg x11proto-randr-dev x11proto-xinerama-dev\n",
" x11vnc-data\n",
"Suggested packages:\n",
" libdirectfb-extra ttf-dejavu-core libsdl2-gfx-doc python-crypto-doc\n",
" python-cryptography-doc python3-cryptography-vectors gnome-keyring\n",
" libkf5wallet-bin gir1.2-gnomekeyring-1.0 python-secretstorage-doc\n",
" python-setuptools-doc\n",
"The following NEW packages will be installed:\n",
" gir1.2-ibus-1.0 lib++dfb-1.7-7 liba52-0.7.4 libcaca-dev libcapnp-0.6.1\n",
" libdbus-1-dev libdirectfb-1.7-7 libdirectfb-dev libibus-1.0-5\n",
" libibus-1.0-dev libmirclient-dev libmirclient9 libmircommon-dev\n",
" libmircommon7 libmircookie-dev libmircookie2 libmircore-dev libmircore1\n",
" libmirprotobuf3 libmpeg3-2 libmpeg3-dev libprotobuf-dev libprotobuf-lite10\n",
" libpulse-dev libpulse-mainloop-glib0 libsdl-image1.2 libsdl-sge\n",
" libsdl-sge-dev libsdl1.2-dev libsdl1.2debian libsdl2-dev libsdl2-gfx-1.0-0\n",
" libsdl2-gfx-dev libsdl2-image-2.0-0 libsdl2-image-dev libsdl2-ttf-2.0-0\n",
" libsdl2-ttf-dev libslang2-dev libsndio-dev libst-dev libst1 libudev-dev\n",
" libvncclient1 libvncserver1 libxcursor-dev libxinerama-dev libxkbcommon-dev\n",
" libxrandr-dev libxv-dev mesa-utils python-pip-whl python3-asn1crypto\n",
" python3-cffi-backend python3-crypto python3-cryptography python3-idna\n",
" python3-keyring python3-keyrings.alt python3-pip python3-pkg-resources\n",
" python3-secretstorage python3-setuptools python3-six python3-wheel\n",
" python3-xdg x11proto-randr-dev x11proto-xinerama-dev x11vnc x11vnc-data xvfb\n",
"0 upgraded, 70 newly installed, 0 to remove and 7 not upgraded.\n",
"Need to get 12.9 MB of archives.\n",
"After this operation, 56.3 MB of additional disk space will be used.\n",
"Get:1 http://archive.ubuntu.com/ubuntu bionic-updates/main amd64 libibus-1.0-5 amd64 1.5.17-3ubuntu5.2 [134 kB]\n",
"Get:2 http://archive.ubuntu.com/ubuntu bionic-updates/main amd64 gir1.2-ibus-1.0 amd64 1.5.17-3ubuntu5.2 [66.5 kB]\n",
"Get:3 http://archive.ubuntu.com/ubuntu bionic/universe amd64 libdirectfb-1.7-7 amd64 1.7.7-8 [953 kB]\n",
"Get:4 http://archive.ubuntu.com/ubuntu bionic/universe amd64 lib++dfb-1.7-7 amd64 1.7.7-8 [29.4 kB]\n",
"Get:5 http://archive.ubuntu.com/ubuntu bionic/universe amd64 liba52-0.7.4 amd64 0.7.4-19 [35.2 kB]\n",
"Get:6 http://archive.ubuntu.com/ubuntu bionic/main amd64 libslang2-dev amd64 2.3.1a-3ubuntu1 [393 kB]\n",
"Get:7 http://archive.ubuntu.com/ubuntu bionic-updates/main amd64 libcaca-dev amd64 0.99.beta19-2ubuntu0.18.04.1 [747 kB]\n",
"Get:8 http://archive.ubuntu.com/ubuntu bionic/main amd64 libcapnp-0.6.1 amd64 0.6.1-1ubuntu1 [658 kB]\n",
"Get:9 http://archive.ubuntu.com/ubuntu bionic-updates/main amd64 libdbus-1-dev amd64 1.12.2-1ubuntu1.1 [165 kB]\n",
"Get:10 http://archive.ubuntu.com/ubuntu bionic/universe amd64 libmpeg3-2 amd64 1.8.dfsg-2.1 [87.6 kB]\n",
"Get:11 http://archive.ubuntu.com/ubuntu bionic/universe amd64 libmpeg3-dev amd64 1.8.dfsg-2.1 [112 kB]\n",
"Get:12 http://archive.ubuntu.com/ubuntu bionic/universe amd64 libdirectfb-dev amd64 1.7.7-8 [199 kB]\n",
"Get:13 http://archive.ubuntu.com/ubuntu bionic-updates/main amd64 libibus-1.0-dev amd64 1.5.17-3ubuntu5.2 [145 kB]\n",
"Get:14 http://archive.ubuntu.com/ubuntu bionic/main amd64 libmircore1 amd64 0.31.1-0ubuntu1 [26.5 kB]\n",
"Get:15 http://archive.ubuntu.com/ubuntu bionic/main amd64 libmircommon7 amd64 0.31.1-0ubuntu1 [73.9 kB]\n",
"Get:16 http://archive.ubuntu.com/ubuntu bionic/main amd64 libprotobuf-lite10 amd64 3.0.0-9.1ubuntu1 [97.7 kB]\n",
"Get:17 http://archive.ubuntu.com/ubuntu bionic/main amd64 libmirprotobuf3 amd64 0.31.1-0ubuntu1 [127 kB]\n",
"Get:18 http://archive.ubuntu.com/ubuntu bionic/main amd64 libmirclient9 amd64 0.31.1-0ubuntu1 [199 kB]\n",
"Get:19 http://archive.ubuntu.com/ubuntu bionic/main amd64 libmircore-dev amd64 0.31.1-0ubuntu1 [21.7 kB]\n",
"Get:20 http://archive.ubuntu.com/ubuntu bionic/main amd64 libprotobuf-dev amd64 3.0.0-9.1ubuntu1 [959 kB]\n",
"Get:21 http://archive.ubuntu.com/ubuntu bionic-updates/main amd64 libxkbcommon-dev amd64 0.8.2-1~ubuntu18.04.1 [150 kB]\n",
"Get:22 http://archive.ubuntu.com/ubuntu bionic/main amd64 libmircommon-dev amd64 0.31.1-0ubuntu1 [13.9 kB]\n",
"Get:23 http://archive.ubuntu.com/ubuntu bionic/main amd64 libmircookie2 amd64 0.31.1-0ubuntu1 [19.7 kB]\n",
"Get:24 http://archive.ubuntu.com/ubuntu bionic/main amd64 libmircookie-dev amd64 0.31.1-0ubuntu1 [4,392 B]\n",
"Get:25 http://archive.ubuntu.com/ubuntu bionic/main amd64 libmirclient-dev amd64 0.31.1-0ubuntu1 [47.8 kB]\n",
"Get:26 http://archive.ubuntu.com/ubuntu bionic-updates/main amd64 libpulse-mainloop-glib0 amd64 1:11.1-1ubuntu7.4 [22.1 kB]\n",
"Get:27 http://archive.ubuntu.com/ubuntu bionic-updates/main amd64 libpulse-dev amd64 1:11.1-1ubuntu7.4 [81.5 kB]\n",
"Get:28 http://archive.ubuntu.com/ubuntu bionic-updates/main amd64 libsdl1.2debian amd64 1.2.15+dfsg2-0.1ubuntu0.1 [175 kB]\n",
"Get:29 http://archive.ubuntu.com/ubuntu bionic/universe amd64 libsdl-image1.2 amd64 1.2.12-8 [29.5 kB]\n",
"Get:30 http://archive.ubuntu.com/ubuntu bionic/universe amd64 libsdl-sge amd64 030809dfsg-7 [70.0 kB]\n",
"Get:31 http://archive.ubuntu.com/ubuntu bionic-updates/main amd64 libsdl1.2-dev amd64 1.2.15+dfsg2-0.1ubuntu0.1 [706 kB]\n",
"Get:32 http://archive.ubuntu.com/ubuntu bionic/universe amd64 libsdl-sge-dev amd64 030809dfsg-7 [135 kB]\n",
"Get:33 http://archive.ubuntu.com/ubuntu bionic/universe amd64 libsndio-dev amd64 1.1.0-3 [13.3 kB]\n",
"Get:34 http://archive.ubuntu.com/ubuntu bionic-updates/main amd64 libudev-dev amd64 237-3ubuntu10.33 [19.1 kB]\n",
"Get:35 http://archive.ubuntu.com/ubuntu bionic/main amd64 libxcursor-dev amd64 1:1.1.15-1 [26.5 kB]\n",
"Get:36 http://archive.ubuntu.com/ubuntu bionic/main amd64 x11proto-xinerama-dev all 2018.4-4 [2,628 B]\n",
"Get:37 http://archive.ubuntu.com/ubuntu bionic/main amd64 libxinerama-dev amd64 2:1.1.3-1 [8,404 B]\n",
"Get:38 http://archive.ubuntu.com/ubuntu bionic/main amd64 x11proto-randr-dev all 2018.4-4 [2,620 B]\n",
"Get:39 http://archive.ubuntu.com/ubuntu bionic/main amd64 libxrandr-dev amd64 2:1.5.1-1 [24.0 kB]\n",
"Get:40 http://archive.ubuntu.com/ubuntu bionic/main amd64 libxv-dev amd64 2:1.0.11-1 [32.5 kB]\n",
"Get:41 http://archive.ubuntu.com/ubuntu bionic-updates/universe amd64 libsdl2-dev amd64 2.0.8+dfsg1-1ubuntu1.18.04.4 [683 kB]\n",
"Get:42 http://archive.ubuntu.com/ubuntu bionic/universe amd64 libsdl2-gfx-1.0-0 amd64 1.0.4+dfsg-1 [29.9 kB]\n",
"Get:43 http://archive.ubuntu.com/ubuntu bionic/universe amd64 libsdl2-gfx-dev amd64 1.0.4+dfsg-1 [29.8 kB]\n",
"Get:44 http://archive.ubuntu.com/ubuntu bionic/universe amd64 libsdl2-image-2.0-0 amd64 2.0.3+dfsg1-1 [63.0 kB]\n",
"Get:45 http://archive.ubuntu.com/ubuntu bionic/universe amd64 libsdl2-image-dev amd64 2.0.3+dfsg1-1 [68.6 kB]\n",
"Get:46 http://archive.ubuntu.com/ubuntu bionic/universe amd64 libsdl2-ttf-2.0-0 amd64 2.0.14+dfsg1-2 [14.8 kB]\n",
"Get:47 http://archive.ubuntu.com/ubuntu bionic/universe amd64 libsdl2-ttf-dev amd64 2.0.14+dfsg1-2 [19.7 kB]\n",
"Get:48 http://archive.ubuntu.com/ubuntu bionic/universe amd64 libst1 amd64 1.9-3.1ubuntu1 [20.9 kB]\n",
"Get:49 http://archive.ubuntu.com/ubuntu bionic/universe amd64 libst-dev amd64 1.9-3.1ubuntu1 [63.4 kB]\n",
"Get:50 http://archive.ubuntu.com/ubuntu bionic-updates/main amd64 libvncclient1 amd64 0.9.11+dfsg-1ubuntu1.1 [54.8 kB]\n",
"Get:51 http://archive.ubuntu.com/ubuntu bionic-updates/main amd64 libvncserver1 amd64 0.9.11+dfsg-1ubuntu1.1 [122 kB]\n",
"Get:52 http://archive.ubuntu.com/ubuntu bionic-updates/universe amd64 python-pip-whl all 9.0.1-2.3~ubuntu1.18.04.1 [1,653 kB]\n",
"Get:53 http://archive.ubuntu.com/ubuntu bionic/main amd64 python3-asn1crypto all 0.24.0-1 [72.8 kB]\n",
"Get:54 http://archive.ubuntu.com/ubuntu bionic/main amd64 python3-cffi-backend amd64 1.11.5-1 [64.6 kB]\n",
"Get:55 http://archive.ubuntu.com/ubuntu bionic/main amd64 python3-crypto amd64 2.6.1-8ubuntu2 [244 kB]\n",
"Get:56 http://archive.ubuntu.com/ubuntu bionic/main amd64 python3-idna all 2.6-1 [32.5 kB]\n",
"Get:57 http://archive.ubuntu.com/ubuntu bionic/main amd64 python3-six all 1.11.0-2 [11.4 kB]\n",
"Get:58 http://archive.ubuntu.com/ubuntu bionic-updates/main amd64 python3-cryptography amd64 2.1.4-1ubuntu1.3 [221 kB]\n",
"Get:59 http://archive.ubuntu.com/ubuntu bionic/main amd64 python3-secretstorage all 2.3.1-2 [12.1 kB]\n",
"Get:60 http://archive.ubuntu.com/ubuntu bionic/main amd64 python3-keyring all 10.6.0-1 [26.7 kB]\n",
"Get:61 http://archive.ubuntu.com/ubuntu bionic/main amd64 python3-keyrings.alt all 3.0-1 [16.6 kB]\n",
"Get:62 http://archive.ubuntu.com/ubuntu bionic-updates/universe amd64 python3-pip all 9.0.1-2.3~ubuntu1.18.04.1 [114 kB]\n",
"Get:63 http://archive.ubuntu.com/ubuntu bionic/main amd64 python3-pkg-resources all 39.0.1-2 [98.8 kB]\n",
"Get:64 http://archive.ubuntu.com/ubuntu bionic/main amd64 python3-setuptools all 39.0.1-2 [248 kB]\n",
"Get:65 http://archive.ubuntu.com/ubuntu bionic/universe amd64 python3-wheel all 0.30.0-0.2 [36.5 kB]\n",
"Get:66 http://archive.ubuntu.com/ubuntu bionic/main amd64 python3-xdg all 0.25-4ubuntu1 [31.4 kB]\n",
"Get:67 http://archive.ubuntu.com/ubuntu bionic/universe amd64 x11vnc-data all 0.9.13-3 [214 kB]\n",
"Get:68 http://archive.ubuntu.com/ubuntu bionic/universe amd64 x11vnc amd64 0.9.13-3 [967 kB]\n",
"Get:69 http://archive.ubuntu.com/ubuntu bionic-updates/universe amd64 xvfb amd64 2:1.19.6-1ubuntu4.3 [783 kB]\n",
"Get:70 http://archive.ubuntu.com/ubuntu bionic/universe amd64 mesa-utils amd64 8.4.0-1 [34.3 kB]\n",
"Fetched 12.9 MB in 4s (2,874 kB/s)\n",
"debconf: unable to initialize frontend: Dialog\n",
"debconf: (No usable dialog-like program is installed, so the dialog based frontend cannot be used. at /usr/share/perl5/Debconf/FrontEnd/Dialog.pm line 76, <> line 70.)\n",
"debconf: falling back to frontend: Readline\n",
"debconf: unable to initialize frontend: Readline\n",
"debconf: (This frontend requires a controlling tty.)\n",
"debconf: falling back to frontend: Teletype\n",
"dpkg-preconfigure: unable to re-open stdin: \n",
"Selecting previously unselected package libibus-1.0-5:amd64.\n",
"(Reading database ... 135004 files and directories currently installed.)\n",
"Preparing to unpack .../00-libibus-1.0-5_1.5.17-3ubuntu5.2_amd64.deb ...\n",
"Unpacking libibus-1.0-5:amd64 (1.5.17-3ubuntu5.2) ...\n",
"Selecting previously unselected package gir1.2-ibus-1.0:amd64.\n",
"Preparing to unpack .../01-gir1.2-ibus-1.0_1.5.17-3ubuntu5.2_amd64.deb ...\n",
"Unpacking gir1.2-ibus-1.0:amd64 (1.5.17-3ubuntu5.2) ...\n",
"Selecting previously unselected package libdirectfb-1.7-7:amd64.\n",
"Preparing to unpack .../02-libdirectfb-1.7-7_1.7.7-8_amd64.deb ...\n",
"Unpacking libdirectfb-1.7-7:amd64 (1.7.7-8) ...\n",
"Selecting previously unselected package lib++dfb-1.7-7:amd64.\n",
"Preparing to unpack .../03-lib++dfb-1.7-7_1.7.7-8_amd64.deb ...\n",
"Unpacking lib++dfb-1.7-7:amd64 (1.7.7-8) ...\n",
"Selecting previously unselected package liba52-0.7.4:amd64.\n",
"Preparing to unpack .../04-liba52-0.7.4_0.7.4-19_amd64.deb ...\n",
"Unpacking liba52-0.7.4:amd64 (0.7.4-19) ...\n",
"Selecting previously unselected package libslang2-dev:amd64.\n",
"Preparing to unpack .../05-libslang2-dev_2.3.1a-3ubuntu1_amd64.deb ...\n",
"Unpacking libslang2-dev:amd64 (2.3.1a-3ubuntu1) ...\n",
"Selecting previously unselected package libcaca-dev.\n",
"Preparing to unpack .../06-libcaca-dev_0.99.beta19-2ubuntu0.18.04.1_amd64.deb ...\n",
"Unpacking libcaca-dev (0.99.beta19-2ubuntu0.18.04.1) ...\n",
"Selecting previously unselected package libcapnp-0.6.1:amd64.\n",
"Preparing to unpack .../07-libcapnp-0.6.1_0.6.1-1ubuntu1_amd64.deb ...\n",
"Unpacking libcapnp-0.6.1:amd64 (0.6.1-1ubuntu1) ...\n",
"Selecting previously unselected package libdbus-1-dev:amd64.\n",
"Preparing to unpack .../08-libdbus-1-dev_1.12.2-1ubuntu1.1_amd64.deb ...\n",
"Unpacking libdbus-1-dev:amd64 (1.12.2-1ubuntu1.1) ...\n",
"Selecting previously unselected package libmpeg3-2.\n",
"Preparing to unpack .../09-libmpeg3-2_1.8.dfsg-2.1_amd64.deb ...\n",
"Unpacking libmpeg3-2 (1.8.dfsg-2.1) ...\n",
"Selecting previously unselected package libmpeg3-dev.\n",
"Preparing to unpack .../10-libmpeg3-dev_1.8.dfsg-2.1_amd64.deb ...\n",
"Unpacking libmpeg3-dev (1.8.dfsg-2.1) ...\n",
"Selecting previously unselected package libdirectfb-dev:amd64.\n",
"Preparing to unpack .../11-libdirectfb-dev_1.7.7-8_amd64.deb ...\n",
"Unpacking libdirectfb-dev:amd64 (1.7.7-8) ...\n",
"Selecting previously unselected package libibus-1.0-dev:amd64.\n",
"Preparing to unpack .../12-libibus-1.0-dev_1.5.17-3ubuntu5.2_amd64.deb ...\n",
"Unpacking libibus-1.0-dev:amd64 (1.5.17-3ubuntu5.2) ...\n",
"Selecting previously unselected package libmircore1:amd64.\n",
"Preparing to unpack .../13-libmircore1_0.31.1-0ubuntu1_amd64.deb ...\n",
"Unpacking libmircore1:amd64 (0.31.1-0ubuntu1) ...\n",
"Selecting previously unselected package libmircommon7:amd64.\n",
"Preparing to unpack .../14-libmircommon7_0.31.1-0ubuntu1_amd64.deb ...\n",
"Unpacking libmircommon7:amd64 (0.31.1-0ubuntu1) ...\n",
"Selecting previously unselected package libprotobuf-lite10:amd64.\n",
"Preparing to unpack .../15-libprotobuf-lite10_3.0.0-9.1ubuntu1_amd64.deb ...\n",
"Unpacking libprotobuf-lite10:amd64 (3.0.0-9.1ubuntu1) ...\n",
"Selecting previously unselected package libmirprotobuf3:amd64.\n",
"Preparing to unpack .../16-libmirprotobuf3_0.31.1-0ubuntu1_amd64.deb ...\n",
"Unpacking libmirprotobuf3:amd64 (0.31.1-0ubuntu1) ...\n",
"Selecting previously unselected package libmirclient9:amd64.\n",
"Preparing to unpack .../17-libmirclient9_0.31.1-0ubuntu1_amd64.deb ...\n",
"Unpacking libmirclient9:amd64 (0.31.1-0ubuntu1) ...\n",
"Selecting previously unselected package libmircore-dev:amd64.\n",
"Preparing to unpack .../18-libmircore-dev_0.31.1-0ubuntu1_amd64.deb ...\n",
"Unpacking libmircore-dev:amd64 (0.31.1-0ubuntu1) ...\n",
"Selecting previously unselected package libprotobuf-dev:amd64.\n",
"Preparing to unpack .../19-libprotobuf-dev_3.0.0-9.1ubuntu1_amd64.deb ...\n",
"Unpacking libprotobuf-dev:amd64 (3.0.0-9.1ubuntu1) ...\n",
"Selecting previously unselected package libxkbcommon-dev:amd64.\n",
"Preparing to unpack .../20-libxkbcommon-dev_0.8.2-1~ubuntu18.04.1_amd64.deb ...\n",
"Unpacking libxkbcommon-dev:amd64 (0.8.2-1~ubuntu18.04.1) ...\n",
"Selecting previously unselected package libmircommon-dev:amd64.\n",
"Preparing to unpack .../21-libmircommon-dev_0.31.1-0ubuntu1_amd64.deb ...\n",
"Unpacking libmircommon-dev:amd64 (0.31.1-0ubuntu1) ...\n",
"Selecting previously unselected package libmircookie2:amd64.\n",
"Preparing to unpack .../22-libmircookie2_0.31.1-0ubuntu1_amd64.deb ...\n",
"Unpacking libmircookie2:amd64 (0.31.1-0ubuntu1) ...\n",
"Selecting previously unselected package libmircookie-dev:amd64.\n",
"Preparing to unpack .../23-libmircookie-dev_0.31.1-0ubuntu1_amd64.deb ...\n",
"Unpacking libmircookie-dev:amd64 (0.31.1-0ubuntu1) ...\n",
"Selecting previously unselected package libmirclient-dev:amd64.\n",
"Preparing to unpack .../24-libmirclient-dev_0.31.1-0ubuntu1_amd64.deb ...\n",
"Unpacking libmirclient-dev:amd64 (0.31.1-0ubuntu1) ...\n",
"Selecting previously unselected package libpulse-mainloop-glib0:amd64.\n",
"Preparing to unpack .../25-libpulse-mainloop-glib0_1%3a11.1-1ubuntu7.4_amd64.deb ...\n",
"Unpacking libpulse-mainloop-glib0:amd64 (1:11.1-1ubuntu7.4) ...\n",
"Selecting previously unselected package libpulse-dev:amd64.\n",
"Preparing to unpack .../26-libpulse-dev_1%3a11.1-1ubuntu7.4_amd64.deb ...\n",
"Unpacking libpulse-dev:amd64 (1:11.1-1ubuntu7.4) ...\n",
"Selecting previously unselected package libsdl1.2debian:amd64.\n",
"Preparing to unpack .../27-libsdl1.2debian_1.2.15+dfsg2-0.1ubuntu0.1_amd64.deb ...\n",
"Unpacking libsdl1.2debian:amd64 (1.2.15+dfsg2-0.1ubuntu0.1) ...\n",
"Selecting previously unselected package libsdl-image1.2:amd64.\n",
"Preparing to unpack .../28-libsdl-image1.2_1.2.12-8_amd64.deb ...\n",
"Unpacking libsdl-image1.2:amd64 (1.2.12-8) ...\n",
"Selecting previously unselected package libsdl-sge:amd64.\n",
"Preparing to unpack .../29-libsdl-sge_030809dfsg-7_amd64.deb ...\n",
"Unpacking libsdl-sge:amd64 (030809dfsg-7) ...\n",
"Selecting previously unselected package libsdl1.2-dev.\n",
"Preparing to unpack .../30-libsdl1.2-dev_1.2.15+dfsg2-0.1ubuntu0.1_amd64.deb ...\n",
"Unpacking libsdl1.2-dev (1.2.15+dfsg2-0.1ubuntu0.1) ...\n",
"Selecting previously unselected package libsdl-sge-dev:amd64.\n",
"Preparing to unpack .../31-libsdl-sge-dev_030809dfsg-7_amd64.deb ...\n",
"Unpacking libsdl-sge-dev:amd64 (030809dfsg-7) ...\n",
"Selecting previously unselected package libsndio-dev:amd64.\n",
"Preparing to unpack .../32-libsndio-dev_1.1.0-3_amd64.deb ...\n",
"Unpacking libsndio-dev:amd64 (1.1.0-3) ...\n",
"Selecting previously unselected package libudev-dev:amd64.\n",
"Preparing to unpack .../33-libudev-dev_237-3ubuntu10.33_amd64.deb ...\n",
"Unpacking libudev-dev:amd64 (237-3ubuntu10.33) ...\n",
"Selecting previously unselected package libxcursor-dev:amd64.\n",
"Preparing to unpack .../34-libxcursor-dev_1%3a1.1.15-1_amd64.deb ...\n",
"Unpacking libxcursor-dev:amd64 (1:1.1.15-1) ...\n",
"Selecting previously unselected package x11proto-xinerama-dev.\n",
"Preparing to unpack .../35-x11proto-xinerama-dev_2018.4-4_all.deb ...\n",
"Unpacking x11proto-xinerama-dev (2018.4-4) ...\n",
"Selecting previously unselected package libxinerama-dev:amd64.\n",
"Preparing to unpack .../36-libxinerama-dev_2%3a1.1.3-1_amd64.deb ...\n",
"Unpacking libxinerama-dev:amd64 (2:1.1.3-1) ...\n",
"Selecting previously unselected package x11proto-randr-dev.\n",
"Preparing to unpack .../37-x11proto-randr-dev_2018.4-4_all.deb ...\n",
"Unpacking x11proto-randr-dev (2018.4-4) ...\n",
"Selecting previously unselected package libxrandr-dev:amd64.\n",
"Preparing to unpack .../38-libxrandr-dev_2%3a1.5.1-1_amd64.deb ...\n",
"Unpacking libxrandr-dev:amd64 (2:1.5.1-1) ...\n",
"Selecting previously unselected package libxv-dev:amd64.\n",
"Preparing to unpack .../39-libxv-dev_2%3a1.0.11-1_amd64.deb ...\n",
"Unpacking libxv-dev:amd64 (2:1.0.11-1) ...\n",
"Selecting previously unselected package libsdl2-dev:amd64.\n",
"Preparing to unpack .../40-libsdl2-dev_2.0.8+dfsg1-1ubuntu1.18.04.4_amd64.deb ...\n",
"Unpacking libsdl2-dev:amd64 (2.0.8+dfsg1-1ubuntu1.18.04.4) ...\n",
"Selecting previously unselected package libsdl2-gfx-1.0-0:amd64.\n",
"Preparing to unpack .../41-libsdl2-gfx-1.0-0_1.0.4+dfsg-1_amd64.deb ...\n",
"Unpacking libsdl2-gfx-1.0-0:amd64 (1.0.4+dfsg-1) ...\n",
"Selecting previously unselected package libsdl2-gfx-dev:amd64.\n",
"Preparing to unpack .../42-libsdl2-gfx-dev_1.0.4+dfsg-1_amd64.deb ...\n",
"Unpacking libsdl2-gfx-dev:amd64 (1.0.4+dfsg-1) ...\n",
"Selecting previously unselected package libsdl2-image-2.0-0:amd64.\n",
"Preparing to unpack .../43-libsdl2-image-2.0-0_2.0.3+dfsg1-1_amd64.deb ...\n",
"Unpacking libsdl2-image-2.0-0:amd64 (2.0.3+dfsg1-1) ...\n",
"Selecting previously unselected package libsdl2-image-dev:amd64.\n",
"Preparing to unpack .../44-libsdl2-image-dev_2.0.3+dfsg1-1_amd64.deb ...\n",
"Unpacking libsdl2-image-dev:amd64 (2.0.3+dfsg1-1) ...\n",
"Selecting previously unselected package libsdl2-ttf-2.0-0:amd64.\n",
"Preparing to unpack .../45-libsdl2-ttf-2.0-0_2.0.14+dfsg1-2_amd64.deb ...\n",
"Unpacking libsdl2-ttf-2.0-0:amd64 (2.0.14+dfsg1-2) ...\n",
"Selecting previously unselected package libsdl2-ttf-dev:amd64.\n",
"Preparing to unpack .../46-libsdl2-ttf-dev_2.0.14+dfsg1-2_amd64.deb ...\n",
"Unpacking libsdl2-ttf-dev:amd64 (2.0.14+dfsg1-2) ...\n",
"Selecting previously unselected package libst1.\n",
"Preparing to unpack .../47-libst1_1.9-3.1ubuntu1_amd64.deb ...\n",
"Unpacking libst1 (1.9-3.1ubuntu1) ...\n",
"Selecting previously unselected package libst-dev.\n",
"Preparing to unpack .../48-libst-dev_1.9-3.1ubuntu1_amd64.deb ...\n",
"Unpacking libst-dev (1.9-3.1ubuntu1) ...\n",
"Selecting previously unselected package libvncclient1:amd64.\n",
"Preparing to unpack .../49-libvncclient1_0.9.11+dfsg-1ubuntu1.1_amd64.deb ...\n",
"Unpacking libvncclient1:amd64 (0.9.11+dfsg-1ubuntu1.1) ...\n",
"Selecting previously unselected package libvncserver1:amd64.\n",
"Preparing to unpack .../50-libvncserver1_0.9.11+dfsg-1ubuntu1.1_amd64.deb ...\n",
"Unpacking libvncserver1:amd64 (0.9.11+dfsg-1ubuntu1.1) ...\n",
"Selecting previously unselected package python-pip-whl.\n",
"Preparing to unpack .../51-python-pip-whl_9.0.1-2.3~ubuntu1.18.04.1_all.deb ...\n",
"Unpacking python-pip-whl (9.0.1-2.3~ubuntu1.18.04.1) ...\n",
"Selecting previously unselected package python3-asn1crypto.\n",
"Preparing to unpack .../52-python3-asn1crypto_0.24.0-1_all.deb ...\n",
"Unpacking python3-asn1crypto (0.24.0-1) ...\n",
"Selecting previously unselected package python3-cffi-backend.\n",
"Preparing to unpack .../53-python3-cffi-backend_1.11.5-1_amd64.deb ...\n",
"Unpacking python3-cffi-backend (1.11.5-1) ...\n",
"Selecting previously unselected package python3-crypto.\n",
"Preparing to unpack .../54-python3-crypto_2.6.1-8ubuntu2_amd64.deb ...\n",
"Unpacking python3-crypto (2.6.1-8ubuntu2) ...\n",
"Selecting previously unselected package python3-idna.\n",
"Preparing to unpack .../55-python3-idna_2.6-1_all.deb ...\n",
"Unpacking python3-idna (2.6-1) ...\n",
"Selecting previously unselected package python3-six.\n",
"Preparing to unpack .../56-python3-six_1.11.0-2_all.deb ...\n",
"Unpacking python3-six (1.11.0-2) ...\n",
"Selecting previously unselected package python3-cryptography.\n",
"Preparing to unpack .../57-python3-cryptography_2.1.4-1ubuntu1.3_amd64.deb ...\n",
"Unpacking python3-cryptography (2.1.4-1ubuntu1.3) ...\n",
"Selecting previously unselected package python3-secretstorage.\n",
"Preparing to unpack .../58-python3-secretstorage_2.3.1-2_all.deb ...\n",
"Unpacking python3-secretstorage (2.3.1-2) ...\n",
"Selecting previously unselected package python3-keyring.\n",
"Preparing to unpack .../59-python3-keyring_10.6.0-1_all.deb ...\n",
"Unpacking python3-keyring (10.6.0-1) ...\n",
"Selecting previously unselected package python3-keyrings.alt.\n",
"Preparing to unpack .../60-python3-keyrings.alt_3.0-1_all.deb ...\n",
"Unpacking python3-keyrings.alt (3.0-1) ...\n",
"Selecting previously unselected package python3-pip.\n",
"Preparing to unpack .../61-python3-pip_9.0.1-2.3~ubuntu1.18.04.1_all.deb ...\n",
"Unpacking python3-pip (9.0.1-2.3~ubuntu1.18.04.1) ...\n",
"Selecting previously unselected package python3-pkg-resources.\n",
"Preparing to unpack .../62-python3-pkg-resources_39.0.1-2_all.deb ...\n",
"Unpacking python3-pkg-resources (39.0.1-2) ...\n",
"Selecting previously unselected package python3-setuptools.\n",
"Preparing to unpack .../63-python3-setuptools_39.0.1-2_all.deb ...\n",
"Unpacking python3-setuptools (39.0.1-2) ...\n",
"Selecting previously unselected package python3-wheel.\n",
"Preparing to unpack .../64-python3-wheel_0.30.0-0.2_all.deb ...\n",
"Unpacking python3-wheel (0.30.0-0.2) ...\n",
"Selecting previously unselected package python3-xdg.\n",
"Preparing to unpack .../65-python3-xdg_0.25-4ubuntu1_all.deb ...\n",
"Unpacking python3-xdg (0.25-4ubuntu1) ...\n",
"Selecting previously unselected package x11vnc-data.\n",
"Preparing to unpack .../66-x11vnc-data_0.9.13-3_all.deb ...\n",
"Unpacking x11vnc-data (0.9.13-3) ...\n",
"Selecting previously unselected package x11vnc.\n",
"Preparing to unpack .../67-x11vnc_0.9.13-3_amd64.deb ...\n",
"Unpacking x11vnc (0.9.13-3) ...\n",
"Selecting previously unselected package xvfb.\n",
"Preparing to unpack .../68-xvfb_2%3a1.19.6-1ubuntu4.3_amd64.deb ...\n",
"Unpacking xvfb (2:1.19.6-1ubuntu4.3) ...\n",
"Selecting previously unselected package mesa-utils.\n",
"Preparing to unpack .../69-mesa-utils_8.4.0-1_amd64.deb ...\n",
"Unpacking mesa-utils (8.4.0-1) ...\n",
"Setting up x11vnc-data (0.9.13-3) ...\n",
"Setting up python-pip-whl (9.0.1-2.3~ubuntu1.18.04.1) ...\n",
"Setting up libdbus-1-dev:amd64 (1.12.2-1ubuntu1.1) ...\n",
"Setting up libxcursor-dev:amd64 (1:1.1.15-1) ...\n",
"Setting up libxkbcommon-dev:amd64 (0.8.2-1~ubuntu18.04.1) ...\n",
"Setting up libsdl2-gfx-1.0-0:amd64 (1.0.4+dfsg-1) ...\n",
"Setting up libpulse-mainloop-glib0:amd64 (1:11.1-1ubuntu7.4) ...\n",
"Setting up libpulse-dev:amd64 (1:11.1-1ubuntu7.4) ...\n",
"Setting up libvncserver1:amd64 (0.9.11+dfsg-1ubuntu1.1) ...\n",
"Setting up libmircore-dev:amd64 (0.31.1-0ubuntu1) ...\n",
"Setting up python3-cffi-backend (1.11.5-1) ...\n",
"Setting up python3-crypto (2.6.1-8ubuntu2) ...\n",
"Setting up xvfb (2:1.19.6-1ubuntu4.3) ...\n",
"Setting up libsndio-dev:amd64 (1.1.0-3) ...\n",
"Setting up python3-idna (2.6-1) ...\n",
"Setting up python3-xdg (0.25-4ubuntu1) ...\n",
"Setting up python3-six (1.11.0-2) ...\n",
"Setting up libvncclient1:amd64 (0.9.11+dfsg-1ubuntu1.1) ...\n",
"Setting up libsdl1.2debian:amd64 (1.2.15+dfsg2-0.1ubuntu0.1) ...\n",
"Setting up python3-wheel (0.30.0-0.2) ...\n",
"Setting up python3-pkg-resources (39.0.1-2) ...\n",
"Setting up python3-asn1crypto (0.24.0-1) ...\n",
"Setting up liba52-0.7.4:amd64 (0.7.4-19) ...\n",
"Setting up libmircookie2:amd64 (0.31.1-0ubuntu1) ...\n",
"Setting up libst1 (1.9-3.1ubuntu1) ...\n",
"Setting up libmpeg3-2 (1.8.dfsg-2.1) ...\n",
"Setting up x11proto-xinerama-dev (2018.4-4) ...\n",
"Setting up x11proto-randr-dev (2018.4-4) ...\n",
"Setting up libxinerama-dev:amd64 (2:1.1.3-1) ...\n",
"Setting up libxv-dev:amd64 (2:1.0.11-1) ...\n",
"Setting up libdirectfb-1.7-7:amd64 (1.7.7-8) ...\n",
"Setting up python3-pip (9.0.1-2.3~ubuntu1.18.04.1) ...\n",
"Setting up libcapnp-0.6.1:amd64 (0.6.1-1ubuntu1) ...\n",
"Setting up libsdl2-image-2.0-0:amd64 (2.0.3+dfsg1-1) ...\n",
"Setting up libibus-1.0-5:amd64 (1.5.17-3ubuntu5.2) ...\n",
"Setting up libsdl-image1.2:amd64 (1.2.12-8) ...\n",
"Setting up libsdl2-ttf-2.0-0:amd64 (2.0.14+dfsg1-2) ...\n",
"Setting up libmpeg3-dev (1.8.dfsg-2.1) ...\n",
"Setting up python3-setuptools (39.0.1-2) ...\n",
"Setting up libmircore1:amd64 (0.31.1-0ubuntu1) ...\n",
"Setting up libprotobuf-lite10:amd64 (3.0.0-9.1ubuntu1) ...\n",
"Setting up libslang2-dev:amd64 (2.3.1a-3ubuntu1) ...\n",
"Setting up libudev-dev:amd64 (237-3ubuntu10.33) ...\n",
"Setting up mesa-utils (8.4.0-1) ...\n",
"Setting up python3-cryptography (2.1.4-1ubuntu1.3) ...\n",
"Setting up gir1.2-ibus-1.0:amd64 (1.5.17-3ubuntu5.2) ...\n",
"Setting up libxrandr-dev:amd64 (2:1.5.1-1) ...\n",
"Setting up x11vnc (0.9.13-3) ...\n",
"Setting up libmirprotobuf3:amd64 (0.31.1-0ubuntu1) ...\n",
"Setting up libprotobuf-dev:amd64 (3.0.0-9.1ubuntu1) ...\n",
"Setting up python3-keyrings.alt (3.0-1) ...\n",
"Setting up lib++dfb-1.7-7:amd64 (1.7.7-8) ...\n",
"Setting up libmircookie-dev:amd64 (0.31.1-0ubuntu1) ...\n",
"Setting up libst-dev (1.9-3.1ubuntu1) ...\n",
"Setting up libcaca-dev (0.99.beta19-2ubuntu0.18.04.1) ...\n",
"Setting up libibus-1.0-dev:amd64 (1.5.17-3ubuntu5.2) ...\n",
"Setting up libsdl-sge:amd64 (030809dfsg-7) ...\n",
"Setting up libsdl1.2-dev (1.2.15+dfsg2-0.1ubuntu0.1) ...\n",
"Setting up libmircommon7:amd64 (0.31.1-0ubuntu1) ...\n",
"Setting up python3-secretstorage (2.3.1-2) ...\n",
"Setting up python3-keyring (10.6.0-1) ...\n",
"Setting up libdirectfb-dev:amd64 (1.7.7-8) ...\n",
"Setting up libmirclient9:amd64 (0.31.1-0ubuntu1) ...\n",
"Setting up libsdl-sge-dev:amd64 (030809dfsg-7) ...\n",
"Setting up libmircommon-dev:amd64 (0.31.1-0ubuntu1) ...\n",
"Setting up libmirclient-dev:amd64 (0.31.1-0ubuntu1) ...\n",
"Setting up libsdl2-dev:amd64 (2.0.8+dfsg1-1ubuntu1.18.04.4) ...\n",
"Setting up libsdl2-ttf-dev:amd64 (2.0.14+dfsg1-2) ...\n",
"Setting up libsdl2-image-dev:amd64 (2.0.3+dfsg1-1) ...\n",
"Setting up libsdl2-gfx-dev:amd64 (1.0.4+dfsg-1) ...\n",
"Processing triggers for man-db (2.8.3-2ubuntu0.1) ...\n",
"Processing triggers for mime-support (3.60ubuntu1) ...\n",
"Processing triggers for libc-bin (2.27-3ubuntu1) ...\n"
],
"name": "stdout"
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "3GjAo6Y6-LJm",
"colab_type": "code",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 462
},
"outputId": "37b447b1-f88a-4db5-f94d-5de10dc6f837"
},
"source": [
"## Make sure to set the correct BRANCH (-b XXX)\n",
"! git clone -b v2.9 https://github.com/google-research/football.git\n",
"! cd football && python3 -m pip install ."
],
"execution_count": 3,
"outputs": [
{
"output_type": "stream",
"text": [
"Cloning into 'football'...\n",
"remote: Enumerating objects: 2105, done.\u001b[K\n",
"remote: Total 2105 (delta 0), reused 0 (delta 0), pack-reused 2105\u001b[K\n",
"Receiving objects: 100% (2105/2105), 26.74 MiB | 23.03 MiB/s, done.\n",
"Resolving deltas: 100% (1094/1094), done.\n",
"Processing /content/football\n",
"Collecting pygame==1.9.6\n",
"\u001b[?25l Downloading https://files.pythonhosted.org/packages/8e/24/ede6428359f913ed9cd1643dd5533aefeb5a2699cc95bea089de50ead586/pygame-1.9.6-cp36-cp36m-manylinux1_x86_64.whl (11.4MB)\n",
"\u001b[K |████████████████████████████████| 11.4MB 3.4MB/s \n",
"\u001b[?25hRequirement already satisfied: opencv-python in /usr/local/lib/python3.6/dist-packages (from gfootball==2.0.3) (4.1.2.30)\n",
"Requirement already satisfied: scipy in /usr/local/lib/python3.6/dist-packages (from gfootball==2.0.3) (1.3.3)\n",
"Requirement already satisfied: gym>=0.11.0 in /usr/local/lib/python3.6/dist-packages (from gfootball==2.0.3) (0.15.4)\n",
"Requirement already satisfied: absl-py in /usr/local/lib/python3.6/dist-packages (from gfootball==2.0.3) (0.8.1)\n",
"Requirement already satisfied: numpy>=1.11.3 in /usr/local/lib/python3.6/dist-packages (from opencv-python->gfootball==2.0.3) (1.17.4)\n",
"Requirement already satisfied: six in /usr/local/lib/python3.6/dist-packages (from gym>=0.11.0->gfootball==2.0.3) (1.12.0)\n",
"Requirement already satisfied: pyglet<=1.3.2,>=1.2.0 in /usr/local/lib/python3.6/dist-packages (from gym>=0.11.0->gfootball==2.0.3) (1.3.2)\n",
"Requirement already satisfied: cloudpickle~=1.2.0 in /usr/local/lib/python3.6/dist-packages (from gym>=0.11.0->gfootball==2.0.3) (1.2.2)\n",
"Requirement already satisfied: future in /usr/local/lib/python3.6/dist-packages (from pyglet<=1.3.2,>=1.2.0->gym>=0.11.0->gfootball==2.0.3) (0.16.0)\n",
"Building wheels for collected packages: gfootball\n",
" Building wheel for gfootball (setup.py) ... \u001b[?25l\u001b[?25hdone\n",
" Created wheel for gfootball: filename=gfootball-2.0.3-cp36-cp36m-linux_x86_64.whl size=23940216 sha256=e2de394e25f2b6f019ba5331aad5fb9f408f2e0f8e681ef01752213103e06657\n",
" Stored in directory: /tmp/pip-ephem-wheel-cache-me8n9jh6/wheels/41/ad/ae/8cf1d92b8694b10187e5daf33e8d5c248ffa5437e234ccbbee\n",
"Successfully built gfootball\n",
"Installing collected packages: pygame, gfootball\n",
"Successfully installed gfootball-2.0.3 pygame-1.9.6\n"
],
"name": "stdout"
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "V2MEON2i-Q4s",
"colab_type": "code",
"outputId": "cce73a10-d6fe-485e-8a87-791f5019194b",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 68
}
},
"source": [
"## Small code example to make sure that everything works.\n",
"import gfootball.env as football_env\n",
"env = football_env.create_environment(env_name=\"academy_empty_goal_close\", stacked=False, logdir='/tmp/football', write_goal_dumps=False, write_full_episode_dumps=False, render=False)\n",
"env.reset()\n",
"steps = 0\n",
"while True:\n",
" obs, rew, done, info = env.step(env.action_space.sample())\n",
" steps += 1\n",
" if steps % 100 == 0:\n",
" print(\"Step %d Reward: %f\" % (steps, rew))\n",
" if done:\n",
" break\n",
"\n",
"print(\"Steps: %d Reward: %.2f\" % (steps, rew))"
],
"execution_count": 4,
"outputs": [
{
"output_type": "stream",
"text": [
"Step 100 Reward: 0.000000\n",
"Step 200 Reward: 0.000000\n",
"Steps: 278 Reward: 0.00\n"
],
"name": "stdout"
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "OVc80iJfGlWE",
"colab_type": "code",
"colab": {}
},
"source": [
"! cp /usr/local/lib/python3.6/dist-packages/gfootball_engine/_gameplayfootball.so /root/prebuilt_gameplayfootball"
],
"execution_count": 0,
"outputs": []
},
{
"cell_type": "code",
"metadata": {
"id": "rl6KRPLesF70",
"colab_type": "code",
"colab": {}
},
"source": [
"# Now download the file from:\n",
"# /root/prebuilt_gameplay_football (using the menu on the left side)"
],
"execution_count": 0,
"outputs": []
}
]
}
| apache-2.0 |
phoebe-project/phoebe2-docs | 2.1/tutorials/spots.ipynb | 1 | 175826 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Binary with Spots\n",
"============================\n",
"\n",
"Setup\n",
"-----------------------------"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**IMPORTANT NOTE:** if using spots on contact systems or single stars, make sure to use 2.1.15 or later as the 2.1.15 release fixed a bug affecting spots in these systems.\n",
"\n",
"Let's first make sure we have the latest version of PHOEBE 2.1 installed. (You can comment out this line if you don't use pip for your installation or don't want to update to the latest release)."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"!pip install -I \"phoebe>=2.1,<2.2\""
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"As always, let's do imports and initialize a logger and a new bundle. See [Building a System](building_a_system.ipynb) for more details."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"%matplotlib inline"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"import phoebe\n",
"from phoebe import u # units\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"\n",
"logger = phoebe.logger()\n",
"\n",
"b = phoebe.default_binary()"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"Adding Spots\n",
"---------------------"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's add one spot to each of our stars in the binary.\n",
"\n",
"A spot is a feature, and needs to be attached directly to a component upon creation. Providing a tag for 'feature' is entirely optional - if one is not provided it will be created automatically."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<ParameterSet: 4 parameters | qualifiers: colat, radius, long, relteff>"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"b.add_feature('spot', component='primary', feature='spot01')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"As a shortcut, we can also call add_spot directly."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<ParameterSet: 4 parameters | qualifiers: colat, radius, long, relteff>"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"b.add_spot(component='secondary', feature='spot02')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Relevant Parameters\n",
"-----------------"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"A spot is defined by the colatitude (where 0 is defined as the North (spin) Pole) and longitude (where 0 is defined as pointing towards the other star for a binary, or to the observer for a single star) of its center, its angular radius, and the ratio of temperature of the spot to the local intrinsic value."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"ParameterSet: 4 parameters\n",
" colat@spot01@feature: 0.0 deg\n",
" long@spot01@feature: 0.0 deg\n",
" radius@spot01@feature: 1.0 deg\n",
" relteff@spot01@feature: 1.0\n"
]
}
],
"source": [
"print b['spot01']"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [],
"source": [
"b.set_value(qualifier='relteff', feature='spot01', value=0.9)"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [],
"source": [
"b.set_value(qualifier='radius', feature='spot01', value=30)"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [],
"source": [
"b.set_value(qualifier='colat', feature='spot01', value=45)"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [],
"source": [
"b.set_value(qualifier='long', feature='spot01', value=90)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To see the spot, add a mesh dataset and plot it."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<ParameterSet: 4 parameters | contexts: compute, dataset>"
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"b.add_dataset('mesh', times=[0,0.25,0.5,0.75,1.0], columns=['teffs'])"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<ParameterSet: 32 parameters | components: primary, secondary>"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"b.run_compute()"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZEAAAEOCAYAAABIESrBAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzsnXd4FNX6xz9nZvtuekISAiQhlNB7r9IsIGBBQaWIXVGv3WvBhtgrKtgviGAXEVEUlaIIKGIBFRCEEHqHkLJl3t8fW7LZJIB4r4C/+TzPecjOnik77J7vvO0cJSKYmJiYmJgcDdqxvgATExMTkxMXU0RMTExMTI4aU0RMTExMTI4aU0RMTExMTI4aU0RMTExMTI4aU0RMTExMTI4aU0RMTExMTI4aU0RMTExMTI4aU0RMTExMTI4aU0RMTExMTI4ay7G+gP81qampkpOTc6wvw8TExOSEYtmyZTtFJO1w/f7xIpKTk8N33313rC/DxMTE5IRCKbXhSPqZ7iwTExMTk6PGFBETExMTk6PGFBETExMTk6PGFBETExMTk6PGFBETExMTk6PGFBETExMTk6PGFBETExMTk6PGFBETExMTk6PGFBETExMTk6PGFBETExMTk6PGFBETExMTk6PmuBIRpdQrSqntSqkV1byvlFJPK6V+V0r9pJRq/Xdfo4mJiYlJOceViAD/AU45xPunAvVD7VJg4t9wTSYmJiYm1XBciYiILAB2H6LLIGCKBFkMJCqlMv+eqzMxMTExieW4EpEjIAvYGPW6MLTNxMTExOQYcKKJiKpim1TqpNSlSqnvlFLf7dix42+4LBMTKC4u5vXXX6dXr15YrVaUUiil0DQNq9WK0+kkLi6OhIQEEhLiUUrhcjlJSEhA13U0TYvso5RC13UsFgtKKerVq8eECRMoKio61h/TxKQCJ5qIFAK1o17XAjbHdhKRF0SkrYi0TUs77MJcJiZ/isLCQpo3b46u65HBPj4+jsTEBC644ALmz5+P3+8nLs4DgIhgGH6UeFFSijKKIVBCgseCVfejKx9WHcLPQzabDV3XMQyDQCAAwNq1a7n++uvJyEjH4/FEhCYjI4Orr76awsLCY3Q3TP6/c6KJyExgRChLqyOwT0S2HOuLMvnnYhgGL7zwAg6HIzJw161bl3Xr1hEX5yEuLg6bzUZxcTFOG1gU6GKgA/6DRTg0UApqpzsZ0CODR65rSouGCdSt5eKOS/I5qW0aSXEKMQwcCpwaBLxe7BLAEfp1xrstWCw6DocjZK2UX19RURHPPvssubm5EatH13Wuu+46DMM4JvfM5P8XSqSSN+iYoZSaDvQEUoFtwF2AFUBEJimlFPAMwQyuYuBCETnk2rdt27YVc3lckz/Da6+9xsiRIwn/NsJP/oFAgGHDziU+Po558+bzx7rVlJV6SYy3MrBnJn06pHL+Td/yeH1IsMCmMthcBj8cgKUHoLSKMV0B9ZzQNg5qOiDTBuk2cOowaycsxMGT/27J9E828eH84POS1we5desSHx/Phg0F7Ny5C5vNCigMw8Dv90csGIBatWqxbNkyatSo8TfcPZN/CkqpZSLS9rD9jicR+V9giojJkTB58mQuueQSlFJ4vV5sNhsANWtm0qpVCwBmz56D3RLA6zcoLTPIquHglC7pdGmZTH5uHK/O2MAHszbQMR5WFcNmn0aRz0AIioVO0GEVIPhkJIDSNfyBYB+nrki3Cg1c0MoDNWxwxx9Q9N0gNE0jEBC++XEXr8/eyLTZhfgDUDu7Dm53PL/9tpo2bVrSo0dXXnttOjt27MTn82Ox6Hg8HkpKSigtLaNevXosXbqUuLi4Y3GbTU4gTBEJYYqISXWMHDmSKVOmVNhmsVhwuVyICMXFxSQlJZKQkMCmwvXEua3cd1VjfH6D9ZuLmfP1Nlb+vh8NsCoojfkpWQj6ixXlGSE+guJhi7kWAYxQC8S8Z1Fg0yAg4BcwJHg+uxZse/1gtWkExEJqagpZWTVJTU1mz559rF69Bp/Ph65b2Lt3L3a7HU3T8Pl81K9fnyVLlpiCYlIlRyoilr/jYkxMjhf27dtHVlYWIkJpaSkALpcLn8+H0+nAZrPj83m5996xXHzxhdx447/5zysv0zgvnkZ143h22u9s2nyQ/aUGHh1axoFLwdf7waoUSgRRigDgDz2gaQStEB1A09BCsYqwYEhUCxMWHoOgeBQHQFPQ2AXnpkJDd3nfd3fAZ8WKTq2TmLtkG7t2bqNmVm1EYP/+AzgcDgKBQCimAz6fD4DNmzdRs2ZNiouLadWqFUuXLkXTTrQwqcmxxrRETP5f8PHHH3Paaaeh6zoigsvlwuv1UrduLgUFG2nYsD4zZ75DamoqY8b8i5dfnoyugk9ZPoFkm6KeW9HAblDXCblOcOvw3X54aANYlEKP+S2FrQtRKiIosahqWhgvwWtQlAtNALDripYuYUgapFnh8jXw5uMdaNs4kYlv/8Ezb/6B1Wrn7HOHMmrUBaxbt54ff/yZpUuXsWLFL6E4ig3DCACKsrIyHA4HpaWlTJw4kcsvv/y/eftNTkBMd1YIU0T+f3P//fdz1113EQgEcDqdBAJ+unXrxsiRF1BYWMi4cQ9y2mmnkJmZzpeff87GjespOujFItDIA9u9sNMLqTZoFwenp0FiyH5fsAcmFAYHeZ1yd1Qkfq4UxhH8vnRNQ0LWSdgO0AgKho9yt1iYsJiEz+XQIF4HW5yNjZ+fCoDPZ/DBvK089J81/LLuAK3btuXxxx/C43Fz4YVXsGrVGkaPHs7rr7/FgQNFGIaBzWYhJyebNWvWUlJSyuTJkxkxYsRR33uTExtTREKYIvL/j0AgQJ8+fZg3bx52ux2LRScuLo5atWrx888ryMoKunD27NqBzabh9wvtmyVxeo9MWuQnMPRfi2npNLiypoFSsMMLS/fBgr3wR0lwwLZrsMVb+dyKoNtJSUWrwku5W8sf2mYhxo2lKQKGRI5D1Huxrw+FHroGXQvtF7WToUCzObnuuisZMWIYderU4oEHHufRRyfg8/mw2axkZmawcWMhum6hpKSEBx54gFtvvfUIzmzyT8IUkRCmiPz/YfXq1bRs2RIglGFlRSmNwYMHMnHiBN5//wPuvfd+tm7eiNcXwOnQef7OVgw5uRYWi8aefV4anPIxDS1+rqsTHIgB1hbDwj3w00HYVKbwGRV/M2FLBCpPqRAgaE3olAfZhaCQKKoOSgaoHFxXlFsj0eeItko0yq0gBeQ54MxUyLQHA/JlBjy4EQ4GwGbTKPMaxMfHUaNGGrVqZbFy5S8UFR3E7XZTUlKCpmmUlJTi9wdl78ILL+SVV16p/j/A5B/FkYqIGUUz+UfQsmVLWrZsGRr8gkWBVquNe+8dS1FRETk5DbjssqvYuqWAU7tlsGPhQC4cnMPFd3/PTY/9TFGxn8YD5lBH89PCA4+sh4t+UZz1I9y0Bj7Zo7OplIilYCOYpqsphWgaBpUFxE/IHaUUetT74XTf6EwsI9TfG9qmhY5vpaJ4hMUovC1AMOYS3q6HKhEVsK4UHi6EO9fDkv2QY4drs4KZXmf1ysRp10lNSeC8886mdu0s4uLi8fsDeL1eDMNARPD7/aHpV3ReffVVlFI8+eSTf/0/zOQfg2mJmJzQzJs3j5NOOgldD1Z0e71erFYLXq+PtLRU9uzZy+mnD6BOnVpMeu4ZbhzVgLuubIwKDbbzlm7n1MsXUOaVCq4jq6aBYVRI0Q0P8NEDuwCGUvhE0CiPX/hCfWPjGWEqxU9CRFssYcKWRoDyLC8jdF5DpIJACYCmISJoIpUyvxq6wKZgt93G4te7c9fza5j2cSHtO7Rn2vRXiY+PY9myH7jwwispLNyMruvUqZNF+/ZteffdmYgYlJaWAbB582YyM81JtP+pmJaIyT8awzDIzs6mb9++eDwesrJqkpmZiaZpiEB+fkPuvfcutm3bSN26OUx8bgKvjGvL3Vc14Ze1+7nkru/I7TWLvqPnU+otf5CyA07AYhgRARCglMoCAiHrQAQ75UIT7qsod2f5lSKgafiUwkvQ6qhqUpIAEAj1CWgaAU2L9A0fL7w/MQISvh4MA0Mkcg3hWIxGsAjyp4NQuNtLhxELObVzKt/8pws1bAXUy2vCsGGjadGiKXl5ufTp0wOHw87ateuZNetj2rVrjd1uj8ztVa9ePbPGxCQ4Odw/ubVp00ZM/lk8/fTTommauN1uiY+PE4fDIS6XS+Li4qRmzUz59ttFIlImgUCJnHpqH0mKt8q/L86XHm1SJcmpi01D2ibpMjoLcehKdBAniCX00G4DcYWaA0QDUSD20Otws4X20UB0TRNNqegHf7Fomlg0TXQQPdTXAmINNRVqltC/mlKRPpbQPtGNQ7TwsbSoRsxrVcV+NhXcnhRvlfRkuyiF2K2aJCUlyvnnD5HCwpXSokVTiYvzSMOG9cTtdolSSjwejwwadJo4nU7RNE0mTJhwrL8WJv9lgO/kCMZY051lcsKwZ88eUlJSsFgsWCwWBgzoz8KFC9mzZy+NGzfipptu4PHHn+SXX36lUaN8CtavY+/uvSjAY4FOSYr28UJjN5QYcNlK8BrB+Eb4aT4cl7ASfHr3Ehxtw9OUGABKISo4T5VSCoumIYFApHDQQtDVpJRChVxisYStCyvlwfYA5QHy2IB7uH84HThsmVTK2lKKqn7TKrSvYRiRfQJAM3fQOunUMolLz8zm1/VFfLtyL9+v2k9xqUGbdu25997bmDr1Ld588z1uvvlali5dxmefzcMwjMhcXU6ng5KSUvbt20d8fPwR/G+aHO+Y7iyTfxSnn346ycnJWCwWRISkpCRmzfqIffv2k5OTw5dfzmXYsKGMHXsH6enp/LryJ/bt30+eE55qBK80hUuyhBZxUOSHS1eCL0ZAIDh42wi6oEoJFQsSciGFhAERdMPADthF0AOByKN92N2lh57Sqop7hLeFiwihPFMrnPbri+oXFjINIqIUdrNBubtKD523qulWtJCARG8PuuLgvmzY8Ns+xoz/mdYNE/hkQgfWvn8SHqfOunXr6d//HD75ZC5NmzZi3LhHqVUri19+WcyIEUOxWHSsViv5+fVxuZwkJSUxffr0o/tPNjkhMS0Rk+Oa/fv3k5CQgMvlIhAIUFZWhtPppH//Uyks3MSWLVuYO/dTnnjiSd57bwalpSX4vKXk57oZf00Thlz/DS1sfm7ICR5vpxfG/KbwByRiBYSD1tGZUtGEhaGqFdEAfEoRkPLjhQlbFxKqZg+n4PoJBu5VFVO1G1H7hQnHNWLPL6HzRmdrhY9hRO0HoDQNv2GghUQwfC0WBf9pEJyP64t9imk7hJb5Ccx6uj0r1x7g1Gu/ZdHiL/jxxxU88cQkVq36Ha/XS8OGebz77lR69hyAruvs3bsPTVOUlpbh9/tp0qQJK1asqOaOmZwImJaIyQnPBRdcQEZGRmQadovFQvv27fjqq3loms63336H2+2hefOW/PDDDzzzzJN06dyBtEQLn73QjX5dMlj2dl/W253c8oeFTaVw1a8KbyD44ORTijJNC1ocmoZFC6XiKoVFU5FJEsOz8MZiAGWAUYWAQHlKrkWpYCYV5QF3Qi6pcODdC1UG3MOuLiM0H1cFy0YkaFGEUozLd1IVhCd8Pj10rdGpxV6BjaXBmpg+icLjueAv2EftU+by1Q97uGhQbQadPoQLLjiH5cvnsXTpZ1x66QjWrl1Py5bdqFs3mw0bfuDyy0cFLR0tuKbJqlWrsFgsrF+//jD/yyYnOqaImByXWCwWZs6cCRBJ3e3UqSOtW7fi5JP789FHs3G7XZx8ch9++mkZX389n3nz5rF40TwWTO5JUkJQAurV8fD1a73Y6jO46lcoM4KDqNJ1FILFMHACdsNAMwQ/oImgG8GndRvlA300BuUz8ka7pWJREJzSRILHFgCl8BMUDNGCKyNWcElRHhMJC5ESCcY0KLecwtaGiBBeqSpAUCiqslzCLjMtdA1hsfloT3mfRAtcnwVXpwuPvLiKGXO3sHvXLq666sbg/ayXy7p167FYLDRv3pjly3+mefNujB59Prfeei0Wi4WcnNrYbFZ0XaN+/XrmPFz/cEx3lslxRXDqDRsejweXy8m+ffvJy8vD43GzefMWduzYgd/vJzExkYKC33G5XAA89tgT3D32DhZN7UWzBgn4/QYT31zLpDfWsWb9fnxRX3MHlZ+eDIIxkHCRX6xbqoyKAe+wIEQLiBH1r0TtWx2xbqhowi6t2D7Rx61u3cLYY1Z1DbHbsm0QZ4FEHZIskGKFZAssKQoWKqLDuPvH8uijz1C/fh7Tp79IamoyzZt3Z9eu3Xi9Xnr27Eq3bh25//7HueWWa3jjjffYsGETpaWl6LpOWVlZtffC5PjjSN1ZxzwF93/dzBTfE4eNGzcG01WVkoSEeHE6nXLjjTfIpk0bpH37dqKUEpfLJQsXfiktW7aQfv36iEiZvPnm6+JyWuTzl7vLG490lLaNEsWpK8l0KBleE6llD6bIuqPSbh0xabzh9NjYNN5ws4dScHWlKqTPKhCLrpen2iolFl0Xi1KRtF49qj/hfTQtuE3TIueOTe8lZlt0O1TabvgcmlKihc6j67pYdD2ShqyiWnifkxKQrgm6NPXokmVDEnTEGkoBtinEriEdOrQRv3+7iOwSkV2yevVS8Xjccs89t0ifPj0kLs4t7dq1EqfTIdOnPy9jxlwkVqs18lkDgcAx/paZHCkcYYrvMR/k/9fNFJETg1mzZkUGYafTKa1atZTExEQZNWqkuFwuadiwoTidTvn441ki4pONG/+QhIQEueKKS8Vh1yUrzSFxNk3iLciZGUomNEJmtkZOTwsOgi4QT0hIdKXEqmkRASE0aB+yDiQ0KEcP1LpSFcTCGtonukULiCXmb53yGhNi3tOoWDcSFgwV0z+6NiR8/8LXqR2mRQuIppTYNCUP1UGm1qvY/pOHDE0JiojDpkliYryMGXOxlJRsEpFd8t57k8Xtdstvv30jn376tuTm1hG32yVWq0Uuvni4JCcnSlpailgsFgGkrKzsWH/dTI6AIxURMyZicsy54oorGDBgAFarlfj4eN555y3++OMP/H4/33zzDQ8//ACFhRt5/vnnOOWUkwGIj4+nRYvmvPLii4g3QFPl5fYcg9eawaiaQrYTFuyGWTsquq8UwbRcv2FQQtCFFb3qYBngCwXbw9OchDFEylNmCabTaiJVTlUC5Rlf0S6p6NTcSPA7FPQOvxcIBeENEUTTIq+VpgXn6gr1D7dIAD2UeRX8/XNIlxfh/uHziuAzhH8XwK/FFftZFOzyQ7c2KdSv48btsvP110tIT89nxIgr6N27O5dcMpxevQbTo0dnVq9ewsMP34XD4eD1199mz559LF48h8aNG+B0OrDb7RQVFR3iykxOJEwRMTmmtGnThkmTJuF0OomPj6d161YMGXIuXq+PBx8cz/vvv8vtt9/J3XffxfDhF/Dtt9/StWsP0tOz+G7pImrVdBPn0rmspkFjTyS+TEEJPL4+OI2JHnPO8MAaHRfQdL18gsNwDUioWSgPYlsIxkzCqbrVEQ5+x8Y0ItlWMf1VVN+wCAAEQhMhaqHrUiIVs66iPoumqQo1IEJQKKoSEoEKa51E73P/Zlh0oGL/Ai+0a5zA5xPaIb4DNGpUj1mzXqegoJCaNZuwZs1akpKS6NPnLCwWC1deOZpff/2alJRkXC4nbdr04pZbruHUU3vjcjmJi4tj06ZNh7iDJicKpoiYHDOSk5P5/vvvcblcwcHOMFi06Bs0TSMnJ5shQ86iW7eejB59IRaLTk5OPXr27E2zZk3JzEilXbNUVs48hVq147h/ffmQWuyHG36rmOUUDpwfDP0bLt6DUHV6IICV8mndw4NqtFhYoraHhSV2ynai9glbCdEcal2Q8CqIxOyn61rkmOGsrKoQo7IoEBKKSkWPocLJqq5PAc9tg1lRWVvbfNC5WRJpSXbmP9eej2Z+yNy585k37wMWLvwQTdNYu3Y9ixZ9y/DhV9Cr1xk0bNiJjIwaXHHFKHw+PxdccAXz5i3C6XTicNipVasW33//fTWfxuSE4Uh8XidyM2MixyfZ2dkCiMfjkbFj75Rly76VevXypHXrVrJ48TficDgkPT1dHA6HJCUlSZ06tWXChKdk//7dcu45Z0lOllv2LjlD5JdzZcPcARLntsjVdYJxkCynJrZQzMMa5fvXKZ8LS1NKnCA2TRNd08RG5WC6LSoOUVW8IxzjsFSxLTZQHhsUp4ptSilRqnyerXA/qoiH6DEBeRV13kPFPoh5fbh4Sd+EYExEAznwRV+RxaeKLD5Vvnmpo7gcukye/IyI7BCRHfLbb99Ihw5txG63SVpaivz005cisk0MY6t06tRWNE2TtLQU6dWrq9jtdnG5nALIu+++e2y/jCZVghlYN0XkeKVJkyailBKr1Sp16tSRbdu2SGZmpvTp01sOHjwg8+Z9IXa7XRwOh5x8cl+ZO3eOGIZXRHwyfvw4SfBYZe2c/iK/nBtp7z3dRTxOXVrHlU9+GB4k7QQD6p4oUQlnZzlDgqJVISBhsalKQCKioQUH/rAYHE5AYrO1osUiHMCP7Rc72MdmVVWXofVnW3VCUt+BuHQiAhJu7z/UWtxOi8yf/4GI7JCDBzdIUlKCtGjRRJxOhzRokCcbNy4XkW2yatUicTodkpWVKXXqZMnKlQtk/PjbIkJy3333HeNvpUksRyoipjvL5G+lY8eOrFq1CqfTic1m4/zzz6Nx4yZ0796NM888k6ZNm9O7d190Xeff/76FTz6ZTe/evVBKMXv2bMbddzcfPteNurU9FY7rdugI8FMoXqsMAxfgorzuwxdqdioG2m1SsYrbIFjBTmi6kuoKCYPnETTKiwfh8D7iaJdW2D1VVXA+HKMJX1P09ugpTapyjYUD7eEG5YH06ohe40RCxYgAa0qhJAD9r/+W8f/5neWr9mEYBoN7pDP+igYM7H8Oa9asZdCgETRp0oivvpqF2+3m4MFiGjXqyosvvkaDBnlcf/3laJqifftWdOs2iEGDTmH8+Ntxu13ceeednHzyyYe5cybHJUeiNCdyMy2R44devXqF3Bgu6du3T2RK8Ro1akhqaopkZGRIu3btJDExUW677VapXbt2xAJZvfoXifPY5eVx7SPWR8EXp8vwgdmSnuoUu1WJXSE9ksprGsJpvR7Ka0Gip3mPbmELxUowdTfWAolNtdVAdF2r9qk+XKeha5pYdF1UTH1GdN/DWi5VpOxW2D8m9Ti2b3WuLaX+nKViU0irBvHicenisGuSkWKTVg0TpEaSTeJcdnE47FJQ8IOI7JAZM6ZIQkKcTJkyQeLiPHLSSV1l3741kpWVIXfeeZ3cfPMY8XjcMnv265KTU1v0UK3N0KFDj/XX1CQEpjvLFJHjif79+4vT6RSHwyEDBgyQpk2bis1mE5fLJS1atJD33ntH5sz5WFwulyxY8KUEAmWSkJAgCxZ8KQcO7JH0tES5flS++H4aIg/d0Fzy6njEYdPk1G415YMJXaRRtlu6JCIzWiEvN0G6pmhi14KDcNhlZQ/FSaJbtPsqVgQsul6pJsOiaWLV9QrrfIQFIyIuUa3KwbyqQT8Um4mu+6jOrRUWDhV1zuhrPJSQKIgI2pE2pZS0diGNnEiNOIts/+gk2fJhT/n0yTby2NUNZWjfmpKWaBW73S5Tp06UcIykT5/u0qdPdyks/EE6dmwjqanJ8tBDd4jH45YdO36RSZMeEZfLKRdddL64XE6x220CyBdffHGsv64mYoqIKSLHEQMHDhSXyyUWi0U8Ho9kZ2eL0+mUbt26yZIl34hIQDZt2igJCfHyzDNPi4hPRHwycODpMnjwIGmUnyd5dTzStU2aeFwWqVfHI0/c0kK2LxgosmKIjL+2qcRbkKnNgiISbg83QJKtUcWBoUG6Ossh9kk+uoiwusC6plRk4amwkBzKqggH0GPFKbpFi4yu61VaD5G+VYjIoYREj6quP9KmaUrOSkJeyUU6xWuS4NBkzVtdRRadHGn/uaOppCQ5JS7OI926dZR9+9bK+vXfi8vllC++eFf8/s1y3323isvlFJfLKZ06tRWRbfLxx9PF7XaJzWaTtLRkcbmcYrVa5eDBg8f2S2tixkRMjg/uuOMO5syZQ3FxMQ6Hg5KSErZu3YqmaaSmptK+fXv8fj+dO3fhzDPP4Kqrrojse+GFI5gx4wMKNqxn+65SWjZM5KspJ7Fm9qn8a3gD0pLtrC8s4t5nVnBDdnDhqTCf7oRH1sO+qJkTlWFgJTipYnQdiINg3ATKYxAaMYV8MZ8rHDcJF/9F0mkPEXeInqJdohaHkqhzhI8TSTEOrVUSRkIvqromorbFzucVJhCoKin50Igh1LUHiw4vSzHo5ISW5y9iycryHODOzRIpK/OxatUi3G4Xdeq04vPPF3L77dcxYsQYlFLcccd1zJ8/g6SkRJYvX8HkyW9yyim9WLhwJh6Pi717D3DmmadhtVrweDyHuCKT44ojUZoTuZmWyLFjx44d4nQGnyxdLpeMHz9OXC6XOJ1OWbhwvjidTlm16lc56aSe0rp1azl4cJ+89NIk6dq1i6SkJAsgDodDnE6nXDm0rsiKIZVavSy39E0NWh7vtUCGZiAJlmC7OAtpHx+VMqtUtam8mqaJNZTqa9GCc05Fp+5WZYHomqoym6qqGEfYOoi2HqItiOpiGISuLWzlQLk7qsrpS6K2xW7/K1lcL+QgU+qWt3NTlDg0ZObDrUQWnSzG1/3E49Rl8eLZYhhb5Y03npeEhDhp06a5ZGamy/XXXy4i20Rkm7z22rPi8bjF5XKKzWaTxMQESU1NFo/HLQ6HQ4YOHSwul1Py8/OP9Vf4/zWYlojJsSYjI4OSkhJsNhsXX3wxDzzwEJqmMXTouXTt2pVOnTrSq1dvvvxyHrt27SQ1NYP77htP27ZtaNWqFZqmkZiYwLx5nzFrkY/cUz5j1R/7I8e/5bGf2LOjmPMzYGIBjFypmL9XMToruJLhgBrw44GgRWEFNKUIxK69QXCaEYVAaJEoZQT/PlQhoYiAIZWyqcIFihWOT0Vrg5hh4pBKAAAgAElEQVR9wseNPU/EAgn9WJWmIq+r2ie2Mv5Qx/8zKAWOmJGif4IwPAWG3LqcF2ZsRClFhyZJTJ/+Pkopzj13MGvWLKZmzUz27dvPs8++wpIl39OmTR+uvPJm7rzzX/j9fpKTE5k//z3efPN5Jk58EBGD9977CKUUGzas57bbbvsLV27yt3AkSnMiN9MSOTYkJCQEZ7S1WCQvr67Ex8fLeecNE6fTKZs3F4pIQK6+eozY7Xbp2rWLPPPMU/LHH2tExCf//vctEh8fL+3bt5ORI4eLSJkUF++VMWOuELfbJbddki8rZvQTm0LqOhGHhjTwaDI2D3m/ZXlM5PGGwadoJ1E1ISAWpSJWSLi2IzbmYY16go+2QPSQVRBtgVRXAxIOokcHwKuzNqqKb1S3vVKW1SGsmaO1PlTougGxq4pWSHS7ISOYCXfX6Dx58Ir60rpVYwlbHOH2yCN3BS07i0VGjjxHduxYISJbpGPHNqJpSrp37yQiW0Rki/Tu3U10XQtNxOkQm80mixcvPlZf4//XYAbWTRE5VowcOVLsdrtYrVbRdV08Ho/ccMP10rhxI7nhhutFJCAXXjhKlFLSvn07CQfSRXzywAP3i8fjkW+//UZq164lb701TUTKIm3hwi8kMzND9FCBX6u4YAA9OqAebp0SEJuuVcrGihYHQgN/dW4rKK9ID2c2VScgkRYKmodn1D2UgFQrCFXsFysWKnafaoTorzYd5Kwk5Lp0ZEKdykIytibi1JAeLZMkLdklItskENgiTzxxn+Tm1hGn0yGnndZH3G6XNG2aLz7fRhHZIhMnPii1a9eU9PQ0ufLKkSKyRd5883mJj/eIx+OWSy45X5xOh+i6bgbajwGmiJgickz44otgtXm4HsTlcsmll14qn3wyW9xut+zcuV169+4t6ek1JCMjXZ5//jkJC8iECU9F1gs5eHCf2O022bFjk0SLyNNPPy5xcXFit2mS4LFKoscibRORxxpWFhGHRauyLsQRPUCGpluvtiI9tCaHFjWgVpk2W8WgDkHLRdd10XUtYsUcyjpQqnLc5FDxk4qZW6pS+m74dVU1LUqFm6p0DE0rX4tEgSR4LJKZYhOLrsRh0yTJY5GaCVbJi7dICyfS1lV+D047rbckJsZLdnYtefLJ+2TPntViGFslKSlRkpOTIkKyZcuPYrfbZdGimeLxuOX55x+RgwfXitPpkF69OktOTi35+efPxWoNTiFv8vdypCISlc9iYvLXKC4uplevXjidTpKSkti7dy9nnDGYiROfpUGDfK6//jp69epDSUkJc+d+Rtu27TnjjMEATJ48mVtu+TczZrxL165dee65ieTk5JCamgpAYeEmTj/9DDZsKGDKlJc5/7zz+OWDvqzeUMQLb6/jzi+3EO+w0FwrY1gm7PZDqT+49G3skrKapkXiHwGRSp8jMgNu6LUY5RGFQEy/cEW4hNYXl9Dyu5H+UVlYseeIRqLeEQTh8JXvsXEOqeKzhLcFApWjIuXdpVL/4D/Bv7t6YGmxn9suqMdN5+ewc6+Pgm2lFGwrZeP2UtZuLmHtplIabS5mVUERX365iI8/nkb37p0qVMn369eD4uIStm7dTvPmvfjhh7nk5+fx6acLeOONSZxzzqU0adKA/v37UFpaisPhYOzYR8nKymTr1u3Y7TbKyryHuSsmfztHojQncjMtkb+P8MqDQ4YMEZfLJYMHDxK/3yvTp78uTqdTsrKypEuXzrJv3x658cbrpUOH9iLik7fffkNcLqfMnPm+hK2Snj27y/XXXysiZXLPPWPF4/HI8OHny+7dW0WkTNwui2z87FSRn88S+fksKf52sLz5SAfp3SFdbFYlFlVuCUD503049hEuBgyvWhjdYheUCjcVtd/hJleMniyRaiyLSAvNvxWxaEKWQOx+0W4rIv2qr5qPbYeqsD9Ue6oOcntmMPZ01+hcka/6VtvSEm2SlpYqbdq0kEBgi0THRqZPnyS1a2dJUdFa6dSpjeTlZcv48bdJfn59EdkiDz10hyQkxMuUKRMkNTVZ1q5dJHFxbsnLy4lcy/vvv3/Mvt//38B0Z5ki8nfSoEEDcTgckpWVJQ6HQ7p37y5eb6mIBCQjI0NcLpecccZgKSsrEZGA5ObmygsvTJRPPvlIXC6XTJs2VaJjIxkZ6fLCC89Jw4YNJCMjXT77bLZEu7Xi3Fb545NTIiIiP58lvuVnyM2jG0iCxyJ2LRgQtlIeWI9umqaJlaqXwrVRPtVIWEjClemHKibUKE/HrS7NtjoXVbQLq4JrLCqd96+k6FZVpR4Ur0NXr2tKVYh9ODTk5vNyqhURq0XJr78ukCZNGkqLFk3E59skYRHZufNXsdttcuDAGjl4cK107dpeMjPTxeGwS0nJH2IYm2XEiCGSlZUhbrdL5s59Qz744FVxuZySnJwoTqdDAHOJ3b+JIxURM8XX5C+zY8cOVq9eTXZ2Nrt378Zi0VmyZAm5uXk0adKMffv2cdlll/LOO29js9nYuXMnmzdvJj09nbPOOoennnqCYcPOjRyvoGAjW7du41//upE+fXrz+++/0qdP7wrn1DSFzx900fj9Bjc9+hPpPT9i5pdb6dQihRSbomuKhhYaqaMxAMMwqvzy+wFfyEUVLkDUlIpMeChUvYYIoffCPyyImUyxisWhwq9jU39jCw9DHzjoYjv0HIrVommVdzQMOeykjAnW8rtUzwG3ZcKEN9Yz5vFfK/U9WBJABBo0yOPrr2eiFDRvfhJeb9AFlZKSTN262bz00jRcLhefffYmjRrVRymNCRNeRinFiy8+Sq1aNfH7/dx//9MMHNiPUaPO4eDBYvr3743NZqVFixZHdxNM/iccVyKilDpFKbVKKfW7UurWKt4fpZTaoZT6IdQuPhbXaVKRrKwsnE4nbdq0Qdd1Xn31FbZv38qoUSPZsGEDAAcPlq+5+sADD5KZmcEFF4xk3Lh7ufji0WzdupXbb7+TZs1akpfXAKUUNpuVL774glGjLubFF19m165dkWNomkZpmcENj/xIWvdZzFq4lcn3t+WXD/qwdPkOzqkhXJJpkGoFI2YA9QFWXaswcBsEl8b1E1z2VoViGdGxEUWw5qQqIYnUdUjVtSNhYTGi+ke/H0v4eBL6rEYoLiOxilgFmqZVEpuqYiJA5LjVUUuv+Elz7HBnTXh1RiEXjV9R4b0de7047TqappGQEM/ChR8QF+emSZNulJaWAjBo0Km89dZMABwOB7NnTyU3tza33/4Qdet2YNCgUfTr1wOHw8Hixcu55po7mDz5bZRSzJ+/GIvFwsqVK1m+fPnhb4TJ38JxIyJKKR14FjgVaAwMU0o1rqLrmyLSMtRe+lsv0qQS06ZNwzAMcnJyePvtt3G73Zxxxhls3FjIU089hWEYfPTRh8yfP5+srFp88MEHvPfe+2zbtp2ePXvwxRdfULt2LtnZecyd+zn9+vXFYrHgdrv47LOPufbaq3G5XDz66BNkZmaTkpJJfn4ziku9dBs5nzmLdjD1wXb8MqMvA3pkMvmDDfi9Bp0TwabBnXVBR4ia/SQ4zXnUoOojuJ46hIoSqVikJ1Ejd7SQRA+/0aIQS7RQhC0SpVTEOjCqaGGiBaQqqrIkgv2P0mSJOXYjR+XttWwwtia89ckWzrvrp8j27Xu8OJ22yGuPx82XX75DZmYGjRt3p7i4mNNO683q1esifX79dQ3r12/EbrfSrVt7cnPrMHPmHEpLS1EKXn55Op988jrPPfcAJSXBbU6ng3bt2v3lz2fy3+G4ERGgPfC7iKwTES/wBjDoGF+TySEwDIMRI0agaRobN27EarVyyy03U1BQQNeu3RCBc84ZwkknncTKlT9z2223cc45Q9m2bRuapli06BtSUlKYMOFJdu7cypIli5g/fwGDBw+krMxLvXp5XHbZJUye/DKrVq3gwIFdfPrpR9jtdqy6xnUj6vHze73p3z0zMpiOfepnzkwLzvMEUMMG12UH3UCRQTrkxzUIikeA8rXTY60TqDwch11b0VlfVfWL3SfaPSUiGIag6Yf+CcYKSFWiEd6maeXHkiMxWQ6DiNDGXfV7NW1wVxZ8NG8bg28JWgVBEXFW6Odyufj00+nk5dWhceNuNGnSgOLiElauXIXX62XIkEsZOnQQDz10O3PmzOOZZ8bxww+fcfDg71itVgxD2LFjF+edNxiLRaeszIfX6yMQCNCtW7e//BlN/jrHk4hkARujXheGtsVyllLqJ6XUO0qp2n/PpZlURadOndA0DU3TyMwMDuQDB55O+/YdOffcc9A0jSuvDE6oqOs6bdu2iaTEPvDA/ezYsYVXX32ZwYMHERcXx6xZH/Hbb6t46qnHSExMYNWq1RXOZ7fbmTbtTQoKCmjRqh1rNpRUGFTnLd3O9t1e+qZUvM628TAgXUOzaPgAXQUXkfISHNjD1kcsAcCi61WKg0a5kISH67B1YgBoGkrXKy70ROX4THVupuqIFYfoGEy04EQLyp8l+p6mH6IIIN0Kd9eE+Yt30u/a79ix14vL5arUz+Fw8NFHU2nSpCEtWvSiVatmPPvsq9x992OUlpby4ouPcOmlF+ByObn99gcBKCvzUlR0EIDzzx/Dzz//xg03XEZWVjo1aqRgt9tYunQJCxcuPOrPafJf4kii739HA4YAL0W9Hg5MiOmTAthDf18OfFHNsS4FvgO+q1Onzl/KUDCpmt9++010XRdN0yQrK0saN24kl156iWRmZsgFF5wvjz76sOTm5oph+EUkIDNmvCcejzsynUlWVk0pLS2ScDZWIFAmmZkZ8uijD4lImeTl1ZXJk1+W6Iysu+++Q+Li4mT58sXy+ecfS4LHKoEfz4xkZzXLi5eBacGJGGPb282RRh6tQtbToYoMbYSmODlEJlZsoV94/ZHo4sPYFu77Z9Nzj6ZFH98C4lCI26LEY9HEY9HEpStxakrsGmJVURM+hppNQ3QNiXfpkpZgk1pJNqkbb5FGDqSzBxmYiFySFqxkT9SQtASLtGndVMJTmMQ2r7dABg8+Rdxul2RmpovL5ZRlyz4RkU0isknmzJkm8fFxcuDAKvn5588lMTFerrxypLhcTklIiJcff5wrTqdDZsx4SVJSkiL30OR/AydgsWEhEG1Z1AI2R3cQkV1RL18EHqrqQCLyAvACQNu2bf+6XW9SiaZNm6LrOhaLhUmTJnHmmWeya9cuOnXqzH/+8yoNG+ZzzTXBKcAnTZrEDTfcxJNPPs411/yLd999i86duzN+/IPcc89dANxxx1isVhvXXHMVAHXq1GblyvIMoMcff5JHHnmcuXNn07JlKDtHaSz7ZQ/tmiazZsMBVq3bz7WNqr7eX4ugRCksKjRJ4mFSEw2ChYJ6Ne8F074k4p5SSuEPBCotcVtpP2JiLEod1vV0uLhIdUTvI0BzJ3SJE2yaYFNEmlUDe/hvBZqCV3drrLZY2XfQz5Q7m5KaYGPr7jK27Cpj804vBdu8FO4oYeW2Enbt97Ff/FhLDH786VdSUhqFLFSFpunouoZSGlarJfJ59u7dR716OeTn50WusV+/HrRt25xhw8YwevS5xMfHcdNNV/DKK2/Qu3cX+vUbyrnnDuTBB5/j7bcnMWjQRRw4UMTixYvp2LHjn74/Jv8djicR+Raor5TKBTYBQ4HzojsopTJFZEvo5UCgcp6hyf+cq666Cr/fj8vl4tlnn+Xpp59G13WaNm3GW2+9QUFBAZs2bWL48OGMHXsXjz/+OO+++xYrVqwkJyebWrVqMX36VPr1O5VRo0aQlJTEM888x7vvvoHVGkysbdasGT/99DMAL7zwEnfeeQ8fffQ+HTt2iFxHfqMmfPDlVto1Tebye5fTPgGSrRWv9dOd8GGRjb3eAL071GDbgi30T9X4cIcRCppX7coKptMqVNQAbwAqNKBrIQGJVLVLKF32TwhCcJ/D3++jEZBYcWrthh+LoYYVzkk5xI4hVhYLD96QR+EOLyPuW8Gi59vTpXlitf0DAaHDpUv5+Y8ScnPr8MILj+D1+vB6vZSVefF6fZSVleH1+ti5czc33HAPq1atIzW1GXl5OVx22QVcfvlwnnnmftq0OYXs7CxSU5PJyalNv349KCvz0rx5Yz79dD67du1h+/adaJrCZrPRtWtX/H5/tddm8j/mSMyVv6sBpwGrgbXA7aFt9wIDQ38/AKwEfgS+BPIPd0yz2PC/j8PhELvdLtnZ2TJz5kxxuVzSoUMHKS4uEpGAnH32WTJw4OkyevSFEh8fL4sXfyUiPmnevJnce+/dEnZhnXxyP+nbt4/069dX+vXrK9GuqzfemCrZ2dkybdoUcblcMnv2DBEpqdCefPJRyc+Nlz1fny52DXmqYdB19UYzZGAqkhJnlfRkuzxxU3M58M3pcuW5udI6QZe3GiMvNUBOTVGh9dgru7Y0ghMpxrquopewJeye4siLCv+OVpWr7Iwk5O4sxK0hHdzVz8o7pS4yMRuxKOTg3JNEvuor/x6eKwkei/z+ZpdDVqvHuy0yY8arkpmZLmefPUCqc2utXDlPEhLiJTU1Wa66apSMG3ez5OTUEo/HLe3atZTWrZuJ3W6ToUMHicgmWbr0I/F43LJr10/SrFm+WK0Wyc2tLWlpKeJyOQWQuXPn/t0/g388HKE7S8l/IYvjeKZt27by3XffHevL+MdwySWX8NJLL2G1WmnVqhXLly/H7/fz+OOPcu211yIipKSkkZ6ezp49e5g//3Py8/MxDIP4+GSWLl1E48bBzO39+/eTmVmLsjIv119/Lc2bNyM9vQaZmRnY7XYaNWqB3W5n8uSXOPvsMypdS3FxMclJafTtVIP132/julrCS1tghddCbi03d17akDN61UTXg4/7zc/4nFYH9zMg6kl8pw/e3KXxzR4Dg6AloVEedIfgKKyHLIjY7K3oebiiA+ex1k2479FYFdURDJ4Hs7wOx4CEoAWyzQcPbIEUHW7PDHrlYll+EKYVW9n6cU8g+KB53YQ1TPl4E8tf6UB2ZuXg+bbdZWSf/RXFJRspKNhE+/anMmBAX1555YlKfefOXcDIkdcwbdqznHbacBYv/pBmzRqxYsVvTJnyDlOmvM2BAwdJT09h8eKPqFEjlXbtTqNTp1aMHXsdLVuezM6du6lXLwdd1/jtt3X4fL7/6r01AaXUMhFpe7h+x1N2lskJwNSpU7HZbJxyyik8/fTTWCwWBg4cyLhx42nXrgPjxo2juLgYn8/H998vJT8/H4Bp06aTkBBPo0bBoIXf7+eKK66itLSMtLQ0Pv/8S+69935GjLiIzp17kp/fHIfDjlKKq666lgYNmtG+fVfOOmsot9xyO1OmvM66deuoVTODzxZsZacPxqzTSG6eyZxJnfnx7V6c3TcrIiAAGwqLyI8Z/1KtcFWGwcN1oVW8QtcorykJmRcKKixnG/V2BfdVbC1ImEiB4Z8c5A6XYWUYRkRADld5Xha6zHQr3JsFpShuLYTSKi7pN6+iUV758rRKKZ64uj5DemXQ5qKlbN5ZWmmfn9cWkZLkQdM0cnJqs3DhDGbM+Jirr769Ut/Nm7cSHx9Hjx6duPrq0fTrdx5+v5+mTfN5+OE72LLlB5xOB1u27CA7uz09e57NiBFnM336TJKTE/noo8kEAgE2bdrK7bdfjc1mRdM0Pv3000PeA5P/DaaImBwxb731FqWlpdjtdkaNGsVZZ52FruvcddedbN5cSHZ2NvfeOw6LxcLnn88hK6s8Q/v5519kyJAhKKV49933yMysxS+//Eq9enlcc81VLFu2mNWrV7JlywaWLfsGj8eDzWZj4sSnefvtadx1122ceeYgkpKSWLLkW+677wE6derJ2vWb0RwO9AQ7P7zVi1kTOtKpRWWn/x+bDlLsM8ipongOoKYdLqphUM8BNqvCqoJrsUO5dRFLeJqTaFQV246Ww4nOn6kL8Ue9Ha/D2Ewh1aZx00bYExNOWFmiGNA1rcI2pRSTbsynf+dUWo5awvbdFWfT/fH3A2Rklv9/N2xYj/nz32fKlLe5/fYHKvTdvHkb8fFxAIwbdzMZGWmccUb55BOGYbB3735q1kynf//e1KqVwc03j2P//iI6dRpE586DSU1NxufzU79+DjabFaXg5JNPPuQ9MPnfYIqIyREzdOhQnE4ngUCABQsWsHv3bgBatGiBzWZD0xROp5PU1FRatmzLc89NigQ8V678hb59e9OlSw9GjbqIe+65m2XLlmIYBrVr14qcY+fOnXTp0pOLL76Q9PR0ALp378r55w/j1ltv4qWXJjJv3qesWbOCyy+/BItFx2q1EZ+cTceRS7li3HJKSysHWad8WEC2o7wIMYxhwJzdcMMGjX9t0MhokkrNVDtd42F4DWjuCmYt2bXypW9jq8qjia5OP1S/IyGY1VR+wUpVFI4/Y9l4YzTGrsEN6QbN3Rr/LoSCsuD2MgM2lRqMPCWz0jGUUrx6WxN6tUmi+chv2L2/XEiW/lZE0+ZNK/Rv1qwRc+e+xdNPv8yDD06IbN+woZCaNWsAYLFYeP/9l5k3bxFTp74LwLZtO7DbbUyZ8iSffDKPhx++nbVrv6J//178/POvvPPO86xevQC/30///hdy7bWjsVgsOJ0Ovv/++yO+Jyb/HUwRMTkiCgoKEBFKSkro3LkzL730Em3btqVHjx5omsYjjzzKnDmf4vV6+e67pUya9Bz33HMf9evnc99949izZw/Dhp1PRkY6a9b8ypVXXo6maRw4UBQRkdLSUtq06UivXifxyCMPkpycxIYNBVVez2OPPcmkSS8yderLGEaAlSuX8eZbU1m2PoX0Pl9y/r+/ZX9R+SD38YKtNI9yZf1RAuMLFJcWWPhUnIy5KJ8/PuzN3Emd8JUJzd3QKxFurQ0v14dbasGgVEUdp4YllA4LVCgwDLfY+bCOtvAvEDAqWBgilYVD18uTkDVNVevW8lVhqOgKLk4x6JuouG8z/HQQ1pZBglMnNdFWeYfQOV4f24yOTRNoNmIx+4uCgv3dr3vp1atLpf7t2rVk9uypjBv3JM888woABQWbyMkpz+bPyanNCy88zJVX3sbWrdspKNiEx+OmS5d2DBjQmzPPvISaNTO4+OJhWK027r77MeLiPHTr1p4tW7bzww8rQ/crQNu2h3Xhm/yXMUXE5Iho0qQJTqeT+Ph4li9fzpAhQ9iyZQunn96fefPmcffd9zB+/DjsdjtpaWkMHTqULVs2cd5553H33fcB8Nxzz/Duu2+RkZEROe7BgwepU6c2hmHQrl1ncnNzee21V9E0jdq1a7FmzZpK1zJlyuvcddd9zJr1LkOGnEVpaRnFxcX07dubpUsXMPvjGRQeyKZmvy8Z/K8lbN9Vyu/rDlDPCa9vg2sKrdy9WaN5z9p88mwHNnzUm5tH5pGRGvR17dpXRh17+fl0BQ2ccHaKcEdNgxyHiriHLLpeaeA2oMJ0u9FCEJwzq+qfXXDixIrHOlysQ6RcVKID7LH7+avxdikFZyUK56XA09thxm7Iq1PNXCchdF3x9n3NaZ7nofmoJewrCi5S1b9/nyr7d+vWkffff4VbbhnH5MlvUVi4hfr1cyv0GTZsMIMG9aNXr3MoKNhEfHwwJvPUU/ewYsUqZs78lIYN62IYAX7/fQMPP/wco0efS0pKEnPmLKBx4/qkpaXgcjkxE2n+Xo6nOhGT4xS/309JSQn16tVj1apVJCUl8dhjj1G7dm2aNm1K//6n88AD4ykqOki9evUq7Pv5558jIqSnp3PNNf8iOTmZ0047FQCv10tJSQlZWVn07n0KIsKsWe9HakUaNGjAF198WeF4s2d/wpVXXsPrr79Kjx7BuZPcbjcbNxaSn98QgC5dOjF/wacsX/4DY8eOo/YpcwkEAkzYrmhcN54Hh+Zydp9M3M7KX/8Nm4vxGcEAdCwzd8EHu6GxRzE6Xnhlu8IIBCpYHpEpUCpYEBX/rip+ER70Y987XKwjNjMr3D92v6oskb1++K0E1pXBRi94HDobRfCvL6XusGV4HIo4p0GyRyc92UZmsp2sNDt1MhzkZDp5895mnHHbTzS+4Bs8LiupqdUXoPTt24Pp0ycybNgViAiNGtWv1GfSpIdo1KgHd9zxMAkJ8QCkp6dx//03c8klt1BYuJTSUi+vvvooo0bdyIIF71BUdJAxY0bxwguv4/f7ady4AR06dCAQqG7CfpP/NqaImByW/Px8rFYrbrcbt9vNpEmT+Oqrr3A6nQwbdj6DBg3i6qvHcOaZZ9GqVUsg6Hbp3r0He/fuJS8vjxtvvI7S0jLOOWcYQ4eew9NPP8kvv/yKx+Nh5MjRrF69muXLl+LxlGcFNW3ahClTpkZeL1mylHPPvYAnn3yUQYMGRLZ7PG42bCiIiEiYVq1a8sADd7NgwVcUFQUwsKBbbDSo465SQAA+XLiNDJsiuLBgkI2l8NjmYIbTmExo5THYWFp11Xs4bgJHVo0epjpxCR7nsDWMh2V9CTyyBQ5YrZQoRVFZgDKfQVaag4aNPJxc10N+HSc3PbMar1c4e+hQcnOz2bVrN9u27WT79h2sLdjJzu93sWvXFg7sP0BxSQlWqxWr1UpZaSmpqeWTbgdrMY3IPQiLpMViwe/3c+aZF+N0OrBYLNhsVtxuF3a7DbfbxZo168jPLxeZq64aybPPTuaGG+4lM7MGhiFceOE5DB58Md26dWD37j00bdqQpUt/pKioGJfLWenzm/zvMEXE5LBs3LiR4cOH88Ybb9C+fXuGDBnCkCFDKCoqIju7Di+++DxKKVatWs2YMcFpS3r2PImtW7eyePHXtGvXkZSUFM4++ywGDx5Inz4n06hRU4YMOZvi4mLmzPmM/2Pvq8Ojurru1/jMHY+7ExcgaHB3LW7BrRRrKVKgxUpxSmlxikuRAi20FIcixWmQICGEEJIQIFiIzqzfH5NJY/Sl9n2/723W88b6MfMAACAASURBVOynueeee0bKvWv2Xmfvfe7cKTg4OBR53cqVI5Ga+ggAcPPmLTRu3BIffTQW/ftHF5mn1Wpx//6DEu/70KEjaNeuC4YNG4w1a9Zj+vRJ+PXXa2g4bA1c7JWYOdQHHRq6FLnm+MUn8BMsnUTyzMDyVODsS4s+0skOUOazhn2+ZGDdAmxFQe5Ifv7G2+SGlEY2hcf+CoEoRRbyey0CFF46DG3phnLuAsq5CXBzUBZpVkUS7867gXHjR2LRopWIiTkOd3eXN65tNptx//4DhITUho2tEY6O9li/fnEBYRT+rzW6dunSVQwZMg5GowErV87Bq1ev8fLlK7x8+QqvXr3GixcvMWfOEsTG3oaXV3XMnj0BnTq1wtdfz0OTJt0RHOyPM2cuYe7cCdi//xgSE5Nw48ZtnDmzC8HBDXD/fhIkEglGjhyJhQsX/vkvrgxvj7fJSPy/bGUZ638NU6dOpUqloiAIlMlkbNCgAWfOnEmDwUA7OzumpDwkaSJpooODA48ePcwGDerT29uLqalJtLS6deLhwwdYuP3tkCGDLYUBpVK2bt2SJ04cosmUycJZ6yZTJmUyGWNjL9PGxsj33x9OMqOE1a1bi+PHf1BkbM2a5VSrBX755XySL1mzZhTHjh1F8jnT0xM4ffpEGgx6ursYOW9UME3nWpAXWjHIQ83eDuBoF1AvE9FDKeJMT3BTQEkDira1RX7Rw//UcvZt7G2LM5b2WmqpmDIRWEEj5ghHsKsNaK+VUlBKOLqLJ3mqSan29Mf6lMvEJFPZt283urg4MSvrPgv3SS9uQ4b0ZlBQOaak/EonJwf269eNb8pUJ5M5c+YEhoQEUKfTcOvWJbQWX7Ta7ds/U6VSUq1Wcdas8TQY9PTycuemTV+wU6eWVCoVrF8/imQCr18/SEFQUSQS8c6d49y4cREFQUVBUFEikfxj98S/BSjrsV5GIn8HRCIRg4ODaWNjw7CwMPbr14/+/v5UqVQMCQnmgQP7aTbn0WTKpVwuZ506tenh4cHk5ERaCcNoNPLy5fMFx7m5mWzUqCFFIhE9PNzZqFFDGgwGqlQqenl5sm7d2pw69WPevBlDg0FPW1sbRkd3p9n8iqWRSL9+vdi+feuC46lTJ1IQBO7atZnkS5IvOXPmFJYvH07yeYFlZqZy+fJFdHdzpa1Rx5HdfGhQiOkst/QS7+Mo4gb/0glkU8Bv5U4KypuISu9ZLhL95wd/SRJ58xxLFeCiY4JUTKkIDFGLOdgeXOb1WxmTwQ6gj6OKF7+uTju9jPUr2dL0c6MSJPLr+iga9QqSqczJecCoqMqsVCmCbyKQixctD/GbN38mmcwbN45Tp9Nw5swJfBOJ1K5djR9+OIRffvkp7e1taTIlsjCJTJs2hmFhgfT0dOOyZTP5+vUtzp//MY1GPZ2c7PP/zbiQTCCZwC+/nE61WsWePd8hmcCGDWtSqVRQrVaV9WL/i3hbEinbnVWG34VYLEbVqlXx6tUrdOnSBStXroTRaERWVlZ+aKszgoJCMHPmZzCZTLhzJw6nT58osgMrJycbtrYW0TUh4T58fMohLS0NI0YMg6urC376aS/S01Nx+/Y1zJ8/B5GRFbFnz/cID6+UX7wvB3l5efjxxwOlhoaCggIRH29pwztw4LuYO3cRDhzYXUQ36du3B65fv4HMzMyCMaVSiQEDonEv4SpWrl6CLYczkE3gqVmEpgaglo4opTV5ASSFd2DBopFY7r2iKDz0ttt9f6+UieXm/a0Do49ShM4GMxZ5AGMdzYjSAqpCLyOIgawsEyoE6PDr+hpIS8+Gf5dTRfI8ACApLQsatWUftEwmw/ffb0BKShp69Hi3lPdnRp8+I9ChQ0v4+1sq8QYGlsP336/H9OkLsH37dyWuyc3NxS+/XEL//t0waFAPGAw6jBr1cZE569fvQO/eHdGrVwcsXboRKpUKo0b1R1LSOYwb9y4MBh0eP05HQEBdVKnSCnv3HoJYLMaOHXtRsWJznDx5HiKRCBkZmWjWrNlbfddl+GsoI5EyvBGrV6+GWq3GmTNnoFQqERISgps3b+LixYvQarVYvXoV0tJS0aHDO5g6dRpMJhM6deoItfq3LaJmsxlZWRYS+fbbXQgLi0CzZk3xyy8/IygoEM+fPy+Y6+rqinbt2mDu3FlYtuxLCIIKMpkUzZs3RU5ODqKjB0CrdYC3dzDat++KjRu3ICcnB+XLRyAxMQmNG7fG7t17cebMIURFFS0N7uDgAKPRiDNnzpX6WTdt2oZXr15BEBSIirBBrE6LoQlifJgiw8oU4GF2yWvk+XdP4cZU/wlms7lUoimOwvkfxaGSiGAjFcEgtYjuGWIRnGSA5g2XCGIgO8dCvs52CpxdWQ0Vymnh3/kkLsb+9v0/eJQNnU5fcGw0GnD48A7s2fMj5s9fUmTNVas24eHDFKxaNb/IeK1a1bBy5Xz07j0S584V7YN+4cKvUKtVKFfOBxKJBKtWzcPq1Vvx6NFjAEBc3D08eJCMYcN6o3v3trh5Mw45ORaiU6lUGDq0F9zcnJGXlwe9XosOHVrAz88LUVGVQAI+Pp5ITj6H7OwcyOUyHDlSdGdfGf4hvI278n/ZysJZfx4ymYwSiYQajYZqtZq3b99m1apVGRQURG9vb1q1kAsXzlEmk9HZ2ZnlypWjIKg4YEB/3r59g8nJiZTJZBw2bCgFQeCaNb81mtqzZyddXV1ZWAchs7lx41qq1WpOm/YxK1SI4Lx5M2kNVSUkxHLDhlXs3bsnPTzcqVAo6OrqQqlUSjs7WyYmxtIawipu1atX4aRJH7JwSCsx8Tq9vDzo7+/L27cvMDq6K5tUtyfPteDDHxpw1aRwNqpiR6VcTFuNlGFqcLgzuKEcaJT+c5V4JRJJkWOV1FJRuLJGxAnO4FpvsJ2NiBX9dfykvx8FpZj+GgkXeJSsyvupG6iViYuErswnG3PqgHLUqCRcOymUPNWEH/fzZa2aVVg8bHXo0HYKgoo//fQNyVQ+fnyDOp2WmzZ9xTeFrWbMGE+jUc+EhPMFY59+Op7ly4ewcPiqXbtmrFWrKskkzpgxlhERwSQTSSayXDlvLljwccHxxInD6eLiSLFYRJVKwYSEUyQTePr0t9TrtSxfPphkAvV6HRUKOWUyKV+8ePEP3R3//UCZJlJGIn8V1geYl5cXZTIZY2JiqFKp+N5777FataokTTSZcunq6srQ0FBWqhRJMpdnz55iVFR1CoKK4eHhlMvldHJy4uXL51iYLC5cOEO9XldkbPz4DykIAr/5ZiPJTDZoUI8ffjiapWkhZAbPnDlKg0FPpVJJrVZDvV7HqKhq3LBhJU2m5yxMIp98MoEVK5anlUC2bv2aWq2GvXp1ZWZmMsl03r17mQq5mM+ONCbPtSiwrJNN+dPiKhz8jicdbeRUKyWUiX97yCulYmpkEmplkoKugQqxRStRyEQUw9JZUJM/TyX9z8K5CKBSLKKtTMRutuCXnkXJ4UMn0E6Qkqea8OGeuuzayImCQsLqGnBlIU1koYdF4ylNTN85szzVSgmHd/Rgr2Zu7Nq1HUvTP7788jNqtRrGx59jr16dWL78mzsYksk0mx+yf//udHJyYEZGHMlkRkVV4tix77Iwidy/f5aCoOKxYzsYEODLuXMn0UoaM2Z8yNDQAJKJPHVqV34nxL00GvWsXj2SkZFhJBO4ffsSOjs7UKlU8NatowwI8KFCIaNCIWdwcPA/dn/8t+NtSaSsFHwZSsWCBQswZswYqFQqtGnTBqdPn4atrS0iIiLyC+SlY8eO7ejWrTuuXPkVPXv2wLZt23DhwtmCNR4/fgwfH3/k5eXCxcUFM2dOR/v2bQtCNY8ePYKbmw9ycl7BbDajTZsOOHnyJPbv/w6VK1vKV3TrFg2JRIL161eWeI+7d3+Hnj0HoE+fHti8eRv27t0Okti8eTu2bNmOjIwM+Pv7YcCA3ujXLxopKanw9Q3H8+eJGDRoBHbs2IMlS+ajZ8/ORdb19gjAJ32dEd3SrcRrApaQVJP3zuLwuSfQiYFGeosGIUgAtdgSPhLyjxc9EsHOW4+YOy/RXWeCoxx4YQKe5wHPzUC6WYKnecCTbBNemYEMk4U9VAoxkGPGUAcgVFUkAb4AmWZg6D0g/UADaNWW3fqXbr7AoNnXcPNeBpooTWhltFTqHXIPyDtVeoHCy7deoNHI88jIzEPT5k0RHd0ZEomkoHOlTCaFVCrBtGkLcO7cZbx+/Rq3bp2Ch4drqetZkZeXh2bNuuHBg2RcvnwQen0Arl07DF9fryLzpkyZj6VL1+HFi1d4+jQGCoWlXEB8/H2EhDTAvXunUL58U/To0Q6zZ09AcHAD9O3bCdOmLcKSJTPw+HE6Vq7cgrCwACQnp0EsFuHQoZMIDPTBvXtJyMwsWXW4DP8Zb1sKvoxEylAqFAoFZDIZFAoFWrdujWvXriEmJga3b99G//79ERgYgNatW6NVq9Y4f/4s9u3bh40bN+Pixd9IpEePaBw+fASpqakYO/YDrFixCnK5HJMnf4To6J6Qy+WQydR48iQZtWrVR3Z2Ng4d2gd399/qKo0e/SGuXbuO/fv3FHl/48dPxqJFS/DVVwsQHd0DHh7+WLx4Hlq3bgHA4mHHxFzDN9/sxMaN3yAtLQ1+fr6Ij78HjUYDpVKBvXu3IjDQv8RnHzFiHC6d2IHjy6uWOPfsRQ5qDPgFmVl5WPx+ENp+cAFLvH/LHymMm5nAvMdi3NpWB9uPpGLy0pv4zNEE3e9kZ61JAy6YZXidbYKrnQKP0nPgLzEh2gYwlnLdhw9EmDY6CP1b//adkcTu448wdO4N5GXmoYfWhIWpwKvDDSAopXj1Og/fn0zD/rOPcfHWa6Q+A54+y0Bubi5kMgkcHR3zf2VaSs1bSs5btJynT58VtL7VaNQQBAEajQC9XgcHBzt4ebnB19cLAQF+iIgIhl6vQ9WqzUESjx49RlpaDHJycnD16k1cuXINN27cwY0bt/HDD0cglUrQuXMrhIT4IzIyDFWrVkC1am3yEwiVuH79EACgSZMeCA0NQFBQOYwfPws9erTF9et3sGDBJFSu3AqtWjXCt9/+CHd3F6SlPUF6+vM/Xb/s34yyfiJl+EuQSCQwm80YOXIkrl+/jpiYGPTq1Qtubm5IS0uDk5MTOnfugqlTpyAoKAgSiQSF6zjNn78Qe/Z8h2PHDkEmk+H990ciNfUBxo//EDNmzIKzswc++2w2ZDIZAgJC4ezshIsXTxchEABwc3PD48dPCo7z8vJQr15TrFjxNY4e/RHR0T0AAAaDAQ8fphTME4lECA8PxfTpkxEffxUXLpyAg4M9MjJe4+nTdGi1Wly5crXU3V6TJo3B2WtP8ehpUTX950tP4NvuKMq5C/h1Qw00r+EAo1qKyxmlf4crn0nwQQ9fuDooMbyTBxpVc8CMR2K8Kfdw42PgnEmKn5dWQaPK9qgeasDhLyrDtbwDxqaIMeORGPeK/agOUAJ7TjwqMiYSidC2jiPid9TGmD5+WJIuglgEhPQ8C/uWZ2BsegxjVz7BM2k4ogePwuatq/DllzNhNBqgUgm4ffs0Hjy4jKSkX5GcHIPU1GtIS7uBu3fPQS6Xwd3dBfXr18TJk3uwdu3nmDhxJDp0aAkvL3fExydi7dpv0LfvKHh7V4XRGIgHDx7iwYNkPHv2HDqdP1QqX9Sr1wEzZy7GxYsxcHFxglqtgkQiRl6eCdu370O3bu/BYAjFvXuJSE19jIMHNxV8Pg8PV9y9m4i+fTvB1dURy5ZtgqenK4KD/VGtWkUcOHACjo52ePIkHVlZ2Rg0aFDpX3gZ/h68Tczr/7KVaSJ/HFOmTLHE+ZVKpqWl0dnZmUqlkklJSSRJPz8/urm5skqVyjSZckmauHDhAoaHh5HM5YEDP1AQBB469BMteSIGXrlynoW1j+3bt9DDw61Ay9i0aQ2fP09l8Ra427dvooeHG8kMJiXdoaenBytUiGBychyLJxxOmPABSxPUc3PT2aJFU2o0GlasGMHataP44YcjaG9vRxsbA5s3b8Rz5w6TTC8wfz93fjEmpEAT+XRoAAWlmHOGB9F8uil5phl5phn7tXJjhEbMDX4oYtF2oJ1ezoyjjQvmvjrSiD4uKkZpUWJ+WyOoFaS8tKY6eaoJd3xans52ygLtIm5bLQ5q60GVQkw3tZgjHfNzQOxBNxt5EZ3D9HMj7vg0gg0q29HezkCpVEqZTMqwsCCeObOPGRnxLK55VKlSkcOH92dkZDgHDuxZ4jyZym++WUE3N2cmJJyjjY2B48YN4+/pImQyX7y4nZ8/oqVcLueVKweYlXWXhXWRx49jKJfLqFIpeebMHlo1kdzceH700XuUyaScOPE9WnNDZs4cy0qVwkkm8PLlH6hSKdm4cW2aTPE8fnwb1WoVfX09qNGoC/SlMvxxoCxPpAx/FtOnT4dYLEZgYCAePXqEFy9eoFevXnBxsZTAePbsGZ4+TceWLZsLwgRisaVMR0JCAjp06II5c2ahfv16AABBUCMpKanIa9ja2iA9/RmUSgV8fLwxZswEODi4o3bthliyZDkePLCUMfH29sKzZy9w9OhxBAdXRJ06NXH69JEieSgA4O7uhri4eyU+y7lzF+HhEYSUlBRcvXoa/fr1xNOn6Zg16xOkpNzEt99ugJ2dLerUaQE3txAMGjQKKSmp6Nq9K1btSUJenhmNh53F7HVx2De/Ej7o5lWkQu6kvr64nmHG60LeRZ4Z2J0pxcJRgRCUv+27Vauk+HFhZfyaJ8HR33bWYs9T4GCWBIcWVUJ5f0vhwebV7fDsZQ7O52/B9XEVsPTDICTuqoP+XXzw9SspPkyTITEHeJSeg+xsE77cfh+V+p2DsflpDF7wAP6VWuKbbWswbtxwODra4969RISFBUEQirZ3vH79Jq5evYEZM8Zj9uzJ2LJlF7KySuoI27btQc2aVeHh4Yb9+zfjiy9WY/36bSXmFYZWq0FSUgqkUgmqVCmPGTMWFWgeVuzffwyOjvbo3r0dxo79tGBcKpUiOfkRQkMDMH/+SsTFWXKBXF2dkJ5u+V7c3JxhNptx8ODPMBrDMHPmV9DptHjy5BmaNasDAEVKu5Th70cZiZShBGQyGZRKJR4/fowqVarAZDJh48aN0Ov1MBgMyMjIQECAP+7etfS2BixJdLm5uYiKqo0uXTph6NDBBevpdFokJT0sON637we0bNkOM2dOR926dVC+fAQePIjD3buxqFw5EvPmLYKfXyiCgiKwdet2vHjxAs2bt8e0aZOxZs3yEg8hAPDx8UZiYmKRsbFjJ6Fu3aYYOLA3fvnlMDw9PdCgQV3cvXvP8gtKLEbt2jWwdu0SPH4ch/nzp+POnbvw8orAhg3bcO3OM3i2PoxHT7NxdVMt1KlYskqtp7MAW60UF1/9NrY2DfBwFtC1ccm6U+U81NgwJQKbX0qQlAP8+AzY+1qCH+ZHonLwbzkaSoUErWrYY9rquCLX2+rl+LifL1K+r4tPhpTDZbkCkIqhbXwMC3Znomn7aBw7tgepqTfw1VdzULt2dSxfvg6ffTYJISEBGD68ZLvazz9fgcjIcGg0GtSrVxMBAb4YNmxCkTl5eXnYt+8QRo8eCACoVKk8NmxYjCFDxuH06d/XHBcuXIFGjWph4cIp2Lv3EB4/flrk/Pbte1GrVhUMG9Yb58//WoTAYmPvoG3bJujevS1atOgNAHBzc0JGxmsAwLp1O6BUKuDl5Yb9+9fBaNQiPf05TCYTWrVqCK1W81Y96MvwF/A27sr/ZSsLZ/1xKJVK6vV6Hj9+nF26dKFMJuODBw8YHx/PqVOnUqvVsmLFirS3t6dGo2Hnzp3Yt28fyuVy1q5di7m5mSxcJ6tmzRqcPPkjktnctm0z1WqBq1evIJnNNWtW0svLk8XDWBkZTzhv3izqdDoqFAoKgsDAwAAOGTKAMTG/sPhW3y1b1tDb24vkS6akxDEkJIguLk48c+YQC+eFkM+pVCqZknKThcNXhS0l5SZDQ4MplUqoUikZ4mvkotFBzD7epCA0VdiGvuPBIEHEDX7gl16gWinhqRXVSp1rtdFdPSnIQKUcPLioUqnbb/cviKSdXvbGWlfZRxvR38uGOp2W/v6+JNNK2P7939DOzoZkKo8e/ZY6nZaZmQm0hqhevIijIKh47tz+grEjR3aWmHf06Le0t7dl8XDV7NmTaTTqmZh4scQ5MpnJyVeoVCqYmHieZBKbN2/AVq0a0RrKysu7T41GzVOndpFMZGhoACdNGkFrSMvR0Z4//riOr17doIuLI8ePf5c3bx6hXq+l2XyPnp6unDDhXSqVCubm3iYZz717V1On09LX14MymZQAuGvXrr/1Hvk3AGXhrDL8Gbx69QpZWVkwmUywt7fH4cOHIRKJ4OrqCi8vL2zebAlhzZw5A48epeCnn35ETk4ONm3ajNzcXIhEwJYtW5Genl6wpiXUdBdff70W0dF9sWrVcvTp0wsA0LHjO3j48CGePXtW5H3IZDJs3boNOp0WTk6OGDiwL4YPH4K4uHhUqVIX9vYeqF69LmbPno9nz54hNDQEaWlpWLduE/z9yyMiIhSxsedRtWrJzSU6nRaxsSWbXQHAvn0/oUKFOsjMfI2aNaujfPkwdI4ehEV7smDT7Dgq9TmHJTvuIy/vt/jVR719cTuTeGUCvnoiRuOq9qgeZiyyrtlsxp4Tqeg68RLKdT6LpbsfATIBMrkaP519XKrAXz/SBjm5Zhw6/7jEubw8MyL6nIediy9u3DiFhw9T8MMPh0rMW7hwGRo0qA0AqFMnCgEBfhgxYmLB+fXrt8HJyQGVKpUvGKtbtwaCgsph6NCxBWM7dnyPsLCgEut/8MFgtG/fHFWqNC01BLZy5Ub4+HjAzc3Sbnf27I9w6NDPBZsgzp69BJlMiurVIwEAo0cPwJo12/I/Yx4eP36K6tUrQq0WsGXLYnz++WpkZmYhI+M1Tp06j2fPXmDatA9gZ2eDzZstO/guX7aUt0lMTIbZTMjlckyaNKnEeyvD34S3YZr/y1bmifwxTJ8+nTKZjAqFgkeOHKFMJqNcLidJJiUlUalU0N3djVu3bqY1Y/3583RqtRpKJBL269eH3t5eVCgUrFKlMhcunM9BgwbQwcGBgiBwz54dLJ6h7uTkyB9+2E2rF/Lo0X16eXmwSpVKfPIkiePHj2GVKpVo9Tpyc5/z5MlDnDx5PCMiwiiXy+ns7ESxWEy5XM5Nm1axuPdR2IKCArh06XwW9j6Sk2MZFVWFGo2a8+fPYG5uGrdvX0sXFyeST0g+4Y0bp/nxx2Po6elOtVpgZJANV4wPoelUE7oaZWxqAFUKMe99W5c5J5pwy7QItqvjSC83I5VKBR0c7NixYxuuXr2IcXEXqNfr+PnnM+jn5017Oz0Xjgwo4W30b+XGhpVti4zlHm/EYF8bVq1aka9e3SOZxqlTx9Hb25OFvZDU1OtUKhVMSLjIwtnnOp2GWVn3aTan0Nvbg3PnfsziIvqxY7uo0aiZkRFPszmFzs6O3LJlCUvzNnJzE1m7djVGRATTZEoqGM/Le0AHBzuuX7+IhYX09u2bs379GiSTOG7cMFavXpFWz+PVq5sUBBXPnNnDuLifqdVqaBXUyQQOGdKD5cp5UaVSskGDmmzWrF7BeKNGNUnGs0mT2hQEFZs0qU2DweLJisXiv/Eu+XcAZRnrZSTyZxAWFkaNRkOxWMw2bdqwUaNGBSTSs2dPNm7ciKGhoVy69CtaSaRZs6Zs3LgRVSoVHz68TzKXaWnJHD9+LIODgymRSCiRSNi0aWNeuXKeZnMWC5NIVFR1jhv3AclMXrlylra2NuzcuQOzsp6RzOSTJ0lUKBR8/Pg+S8tav3jxJI1GAzUaNeVyOdVqgUFB/hw6dACvXv2FxUmkRYsmfPfd/iTTaTI94ahRQ6lWC3znndZMTo6llVgyM5Mpl8uYnn6XViKx2tWrJ/nRR6Pp5uZCjUagnVFFmQS0N8jp5W6XX47FmdHRXbhhw1Lev/9riTWUSgXT0mJpMqVy/fqv6OhoTzdnA7dOCy8gjJ+XVqFRJyuoupt7vBGDfQysWDGcL1/G00oYr17do9Go54YNSwrGZs2azKCgcixMDmZzCitUCOOQIdE8evRbGo16mkzJLG03VtWqFdmrVydeu3acGo26CEEUt+fPb9HPz5tt2zYtGNu7d0N+KK30cu9xcSfp7+/DRYum0koiZCIHDuzOunWr8cCBTXRycmBhEsnIiKWbmzNFIhHFYjGvXj1AMoH79q2hi4sDyXja2dmwZ892DA4uxx9+WEOtVk1BUP31m+NfhjISKSORPwVrmXKtVks7OzuuXbuWCoWCJGlra8u9e79j1apV+dlnM0maGBNzhSqVirduxdLZ2blE35C0tGTqdDpKJBIGBwdRo9HQ2dmJI0a8x59/PkKTKZOffDKRlStX4s6dW6jRqDl58gSaza9ZWCPx8fHi2rXLWZxA1q5dQY1GzeHDB7Nz5/Zs3rwx79y5xK++mseGDetRpVLS1taG1apV4rx5M/jixQNOmvQha9Soyr17t9LJyZG+vt48dux7lqaPODra88CBHSxOAFYzmx9z1qyPC/paCILAhQs/ZXLy9TdeQz5hZmYSxWIR8/JSaH3oZ2U94MKF06nXaxngZcMTS6rQ9HNj2hvk3DY9gqafGzEiwJbly4fyxYt4Ftc/Fi/+jG5uziTTaDY/oru7C7/6ahaLk8OBA99Qr9exRYuG7NChVYnzVjtxYg81GjU/+mgUw8OD+Z+28yYknKPRqC/Y+luvXg1GR3dkcRIhk9irV0eWLx9CpVLBzMzbLEwiV678RLVa4KJFUxgS4s/CJEIm8MSJbVQo5LSx0bMwucjlcl6+vI8KhZzHjm2hnZ2RZ8/uok6nJQAmJib+6fvi34gyEikjkT8FjyZfrQAAIABJREFUALS1taVCoaBWq+W9e/eoUCi4ZcsW2traMi8vh40bN+b7748maWJwcBBHjBhO0sTQ0BAuWbKYhUkkPDyMbdq0pouLC7/99huaTJnctGkda9euRaPRSJ1Ox5Ytm1MiEVMQBK5bt4rFRXYykwMG9GWTJg1pJQ+T6SW7du1ItVrNbdvWk3zJxMRYKpUKJiffotXryMl5zBMnfuT48e8zMNCfcrmcdnY2lEqlVCoVBaGrN4nslSpV4PTpH7E0Irh8+RhDQgKp1Wr42WeTKRKBffp0o1otcMqUcaVeY7Xr109To1GzNDH8xYt4fvTRKAqCipHBduzUwIlRYQZGBtkxLCyIz5/fLfW67OwkOjk5cMGC6Tx+fM8bvQyTKZnlyvlQJBJx9uzJ3LlzNY8c2ckrV44wIeFikTyS6tUrUSKR8NNPx/M/kQiZzHPnfqBaLXDOnElUKpVMTb3C4gSSk3OPhw59Q5lMSjc3JxYmEKuFhQXSw8OFjRrVopUoDh7cyDp1qhWQgkgEtmnTmBkZN0gmsFq1imzatA6dnR348uVVymRS7t69nHq9JUelSZMmf+HO+PfhbyMRADZvYYa3ebH/DSsjkT8GhULBypUrUywWs3fv3kxMTKRCoWBYWBgnTZpI0sQuXTqzV6+e3LRpA/V6PdPTn5A0sWXLlhw8eBCtBDJlyse0t7fj06eP2LRpEw4c2I/F9ZCDB/fRz8+3oHNixYoVOGXKJJ46dYS5uS9pJZE7d65SqVQwIyONaWkJLFfOl97eXrx58yILJxYGBwdyxozJfJMeMmOG5eGmVCookYhpb2/Lhg3rcteuDTSZnrA4ibz33kA2alSXhQkgNTWW9evXzi9GOZDp6XeZlfWQIpGI5BMeOvQtHRzsGRhYjnfvXmRpJPLdd5vo7u7C0sjAaikp1zhoULTlvYrFVCoVXLp0Lq9ePcHc3ORSr9mwYQnt7Gz5zjut2Lp1E5KpzM5O5NatK9ixY2v6+npSrRYokUgoCEra29vSw8ONDg521Om0VCoVFItFBfqSSqWiRqOmXq+jvb0tnZwc6ObmTE9PN/r6etLHx5OBgX4MDQ1gZGQ4q1WrSHd3l/ydbSqGhwfR09ONLi6OtLExUKVS5ntsqt8aagkqeni4MioqksOH9+W+fWu5fPksqtUCO3duyfbtm9LOzkidTsPBg3vwzBlLMUYbGwNr1apCnU7DTz4ZyVmzxlGlUrJKlQiS8XR1deKAAV2o1WrKkg7/BN6WRN6mx/rDfPu9jB0JAI8/oOeX4f9DvHr1CnK5HE5OTlCr1ejTpw8Ayy6Z27dvY8CA/gAAe3t73L59GyNHjsbMmZ/CYDAAACIjK+Cnnw4AAGJjYzF79lx8990uGI1GdO3aGZMmfVziNbOzc/DwYTL8/f1gZ2eHGjWqYc+e7/H554vx+nUmqlWrglatmqNhw/owGAz45JMZWL58NRo1qo81a5YW6V0CAB98MBwffTQV48aNKlIvKSUlFU2bvoP79xOxZctqLFq0FC4uzujXrwe++WYX+vcfgdzcoQgODkDfvj3Qu3c3SKVStG3bAh07WnYL5eTkYPDg0fjmm91o3Lgerl07CW9vz4LvyHLfAfXr10Zc3HmMHj0RYWG1MGrUYEybVjTv4t69+7C1tfnd/x/Hjp3C6dPnYDYzv1+JCLNnf4H33/8YWVlZEAQVVCol1GoBNjZGODs7wsvLHZmZmdi583tERobD3b0C0tIe5ydUVsfEiaNRs2ZVbN78LebNWwKz2YxLlw7CxqbobrLc3Fy8fp2JjRt3YNy46bC3t8XWrUuRnZ2DrKxsZGVlISsru8RxVlY2bty4jU2bdkKplGHo0GjY2dkUmL29LWxsDDhw4Dg6dhwEV1cn/PTTRly+fA2XLl3DmTMXsWXLbqSnP4dMJsO2bXvRpk0TrF+/EA0b1oRUKsWdO/cgFovx6lUGdu1agdOnL2DQoAkFu8Nq1IjM//cYiqNHz8BkMuXnFpXli/wj+E8sA+DS3zHnf8vKPJG3R4sWLSiXy1m3bl0ajUaaTCYmJiYSAOvUqU2rkD5t2hQqFAr6+vowLy+nYPzgwQO0s7OjyZRNLy9Pjho1glavJDs7gwqFgikp92n1QmJiLlCr1XDlyiWMjb1CpVLJ9PRkWr2P69cvceTIYQwJCaJeryNg6cleqVJFnj59iFlZj1m8xInJ9Jy2tkYePLibVu9j7txp1GjU7NLlHT55Ek/yOa9cOUmVSsmnT+NJptNsfsrz549w7NiR9PBwo1otMCIiNN9zUXDs2OE0GvWsWDGcZ87sZ3HPwmRKy/+lW3T8yJHddHa26C537pwvGP/ww/fYuHFdFvck0tNvc/DgaNrb29LGxsiPPx7DLVuW087OhlqthitWzCeZxszMRMbFneOxY7u5adMyzpnzCYcN68eWLRvTxsZIuVzOzp3b8Ntvv+ajR9dYPKTVr183dujQkm3bNqe/v+8bxfXo6E5s0qQejUYDFyyYyv8UzjKZkli5cnnWqVO9SH5IYTOZEhkQ4Mv27ZvRaNSztHDWsGG9KQgqOjnZs7gmsmnTIvr6ejIiIogzZ44lmcDs7NucPXsCxWIx69WrSjKes2aNpUIhp7OzPfV6bZm4/geBvzGcpfw75vxvWRmJvD0UCgU1Govrr9Fo2LVrV3722WdUq9Xs27cPZ82ayfHjx7FmzZoUBIHLly+l2ZxHK4lkZb2mVCpl165d6O9fjllZr1hYH/H29uLmzetJZjM1NZE2NjacOHEcraTh7e3Fr75axNI0kTFjLBqBVCqhr683bW1tKJPJGB4eyhEjhnD79g1MSrpF8iU7dmzHNm1aMDHxOsPCQmhnZ8u9e7exeGirXDkfzps3naVpIbGxZzljxiQ6OjpQoVBQqVRw+/avaTY/5pt0DgClnn/16j4HD+5NtVrguHEjSD5hz56d2LNnJ1rJ49ChnaxWLZIqlZJRUZX57bdrC0JW8+dPY3h4MHfuXEONRs179y7yTSGw7Owk2trasEaNKnRzc2ZubhJLI4f69Wvyww+HMSMjnoGBfmzTpmmp85ycHLhz52ru2bOWWq2Gqakx/D0SmT9/Cu3sbJidHc8WLRqyfftmLE4i27Yto42NgRkZNymVSpmefpWFCWTfvnVUqwVqtRrK5TLOnfsRC5PIu+9Gs2nTOpw8eQQrV44oGD96dCu1WjVFIrB164Y8eHADdTotq1WrkN93XfjzN8e/EH8biZR6ESAFEAHA5s9c/z9pZSTy9pBIJIyMjKTBYGDNmjXZuXNnurq6UiQSMTAwkFWqVGH9+vXp6GjJ+dBqtRQEgVFRURw3bix37dpJrVZDQVDx6tXLLEwgZC7bt2/LHj26MTv7JV1dXdi1a+ciu7CmTJnEkJBgFieQwYP7U6/X8+LFk6xXrw67dOlA8iUfPrzNuXM/ZcOG9eju7kalUkF7ezvWqlUjvyOjmr16deWzZ/dZmj6ybNnndHZ2KlULSU29xZo1q1GlUlKhUNBg0LFDh9bMyEjk75GIyZT2xvMnTuylq6szvb09WbVqRY4YMZATJoyii4sTNRo1hw3rz1u3zrA4MbRv34L9+nUnmcYBA3rSx8eTJlNqiXlkGr/+ehFdXJyYk/OAlSuXZ/36NVkaOfj5eXP16oUkU3nv3nnq9Tp++ulHRebcu3eegqAq2NrboUNLRkaG800Ecvv2KQqCij/+uJFkEk+csGTI5+Ym0EogubkJdHd34fTpY0gm0svLjevWLaSVQO7f/4U6nZZffDGVjo52HDNmEA0GHTMzb9JKFmFhAZw79yOeOrWTNjaGgvF+/TpTqVSwcuUIurs7s1KlMMpkUnbo0IwajUCNpoxE/gj+MRIB4AxgA4B2AOYBaPdH1/iftDISeXsAYGRkJAVBYLt27UiS/fr1o1qtZlzcbVo9jpCQYKpUKsbF3WZMzBVOmjSRtWrVoqurK+VyORUKBevWrcNJkz7i7t07mZgYT7M5hzt2fEMHBweGhYUyKqoas7OfszBZZGc/p1qtZkzM+YKx7t270MbGhteunae1Pa5KpeKNG+dZWihr797ttLOzpVwupyAItLW1YXR0V+7evZkvXyaxMImYTOm0s7Phvn3f0Eoe1rwRjUbNDh1ac/XqxbS3t2Na2i36+fmwXDnfN4rlIpGIubmppZ6zWkZGIrt370SxWEyZTMbQ0ECuXbuYr1/f55u8C1dXZ+7cuYbWMFa5cj7s3r1DiXkmUyo9Pd05a9ZEkql8+PBXGo0GTps2lsVJRKfTFil1cvTotxQEFQ8e3FYwtmrVAvr7+9BKEo8fX6PRqOfixTP4pjBW27ZNaCUMs/kB/f19+PHHowvGVq+eTycne5pMCSQT2b59M/bq9Q7JRGZnxzEsLJDNmtUlmUh7exsePbqV1atXZMeOLUgmMDc3jnK5jAkJp5ibG0eVSslff/2ReXl3qdNpOWxYL/r5efLRo/MMDi5HhULOTp1asEKFEKrVZeGsP4J/kkTmAPAEUDn/eMcfXeN/0spI5O0BgGFhYRSJRKxZsyZJ0t/fn3q9nnv3fkdrO1yNRkNHR0du2rSBVmIhTVy2bCkBMCIinGPGvM8aNaLo6upKlUpFrVbLGjWqUy6XU6NR8+LF0zSZMljc64iKqs5hwwaTzGTr1i3p4GDPO3diWDg3pFGj+mzbtiWLk0hy8h16eLgzLCyEa9Yso0aj5pYtq9miRWO6urpQLpczKqoK582bwRs3ztFsfsY+fXqwXr1aJNO5e/cmOjs70c/PpyBvpHPnduzWrQOtukfbti2o1Wq4f/92lkYiOTkpJcatduvWWdatW4MqlZJ6vY4ymZTvvNPyjV4FmcZnz+Iok8mYmZlYMHb9+kkKgsBdu9YVmbt793ra2hqL6BvHj++mIKh44sTugrGcnAcUi8VFamORqfzii0+p1+uYlHSFZCrbt2/BXr06sjBZ7Ny5ijqdlmlpV4uML1gwhQ4OdszOjmfh0NWaNQvys/6TmJV1lw4Odvzyy+m0eh7z50/O77ueyPfe60N3dxfm5saTTKSNjYEnT+5gTMxPVKmUvHXrKC9f/oEGg45W76Np0zocPLgHDx/eTFtbIy9e/D5fZ4nn8+e/0tbWSI1GYJ8+HalUKv7K7fGvwz9JIl8CsAMwgGUk8l8FsVhMvV5PAAwKCqLJZKJGo6GPjw/nzZtL0sSdO7fTwcGBTZs2yd/O+xuJuLm5cezYMVQqlczMfElrGMtkyubZs6fZtm0bymQy2tgYqdFoqFQqWaFCeQ4dOpBff72cly//wn37dlGj0bBevdp0d3fj/fs3WTzBMCnpDgVBlV+I0UIgBw/uocGgZ8+eXQoEd29vT86b9ymtnkdSUizHjRvFsLBgajRqOjras3Pn9lQoFAwPD6FGo+Hnn39WJG/E19eb69cvYWEyWLjwUwqCilOmjCuigYjFYmZnJ7M4eVy5coyVK1vi8j17duLt279QEAQePbqLPj6eLF8+tAhJFLbDh7+ls7NjifEVK+bTYNAzLS22YCw8PIQjRw5kca9jzpyPaWtrZHr6TZKpvH//Yn6OStF5ZnMK+/TpQk9Pd+bkPKDBoOORIztY3Oto164ZK1WKYPEw1v79ljBWYcvKsngIe/as4aJF0/K3Nf+mfxw+vDVfd1lOjUbNO3dOFJwzGHQ8e3YPyQT279+FYWGBXLHiM/r7e9NKIkuWzKC/vzf79OnEpk3rMDMzllKphC9fxjAzM5ZyuYwiEWgw6KjRCExLS/vrN8q/BP8kifgDWJ2viYwGMOSPrvE/aWUk8vZA/l56d3d3Ojs788iRI9Tr9ezcuTN79OhO0sSmTZuyf/9+XLBgXr5+YSGQtWvX0MbGhllZr+js7My9e/ewsB5iMmXTwcGBrVu3pI2NDXNzXzI29gpnzZrOFi2aMiDAn0ajkTKZjFKppfLq6NHv8fvvd/Du3Ws0mV6yMJG0aNGUrVo1I/mS06ZNpCAIXLx4Hs3mF7QSy9q1y2hra8Ps7DQW10NMpnRu376eAQHlKJfL6OnpztTUWyysi+TmplGpVPLBgxgWJ4azZ3+inZ0tW7RozBcv7pF8QolEwqyshwVzTp36keHhIVSplBw8uDfv379MMo1XrhylWi3QbH7EZ8/iWLduDTo7OzIhwXK+sM2aNZkVKoSXGDebH/Gdd1oyLCyYZBpPnPiOOp2W2dmJLI0c2rRpytDQQJKpPH16Lx0d7UvMs+aUVKwYzoiIEOp0GpamfaSlXaVer+OyZbNpMiUxMjKcrVs3ZmmZ6WQSJ0x4j4GBfjQYdNy06QsWJpGnTy0NqdRqgatWzSlyTq/X8uLFfSQT+OTJFep0GoaHB7JDh2a0kkhc3AkKgoparZpHj26hJT/Ekdu3f8mjRzdTp9OwQoVghoSUo1ot8MyZM3/xLvn34J8W1m3zNZHQP3P9/6SVkcjbAwBFIhF79OhBtVrN6Ohotm7dmvPmzWNERDhJEx0dHfn993uYnJxEmUzG7OxMkia6u7tz4cJ5JHPZsmUL9uzZnYVJZODAAQwMDGBubgYdHOy5Y8dmlrYLa/jwofm/HkWsUKE8PTzcqVZbamIFBPizQ4e2nDlzCtetW0GVSsnq1avQaDTwxIn9LK2roZOTI1ev/pKlCesDB/ahIAicP9/iWZw/f4SFSWTTphV0c3Phm8JTz5/HMywsmJ6e7oyNPUOpVMLXrx/wp5+2Mzg4gIKg4qhRg5mSco2FCWDKlLGsVi2y4Dg3N5n9+/ekXq/jkSPfFpnbqlUTDhoUzdK8lOfP79LFxYmjRg1mgwa12a1be76phMmLF3H09HRjnz5duH37Kvr4eJY6Lzs7kdu2raRIJKJSqWDr1o05atRArlgxl+fO/cjs7ASSydy2bQV1Oi0/+eR92tnZMCfnHgtrIY8e/cozZ77jli1fcdy4YZRIxFSrVWzcuDarVi3PsLBAenlZkhAFQcXgYD8W3+ar1aoZE7OfVsJYvHgq1WoV27VrwjVr5vHHH9cxJmY/7eyMNBp1JONpLcA4dGgPTpw4jHq9ln5+njxxYit1Og2XL1/+l+6RfxP+URL5pwxAUwA3AdwBMK6U8woAW/PP/wLA6z+tWUYibw/r1t41a9ZQJBLR19eXy5cv56VLl6jVapmQcI9yuZwZGS9Jmmhra8OzZ89w27atNBj0fP36BclcHjz4I/V6PU2mbJK5vHv3FgVB4C+//Ewym8OGDWXVqpVZnEAOHtxHQRB46tQRurq6cNGiubR6HgkJsVyx4ktGR3dn5cqRdHd3o0QiIQA2alSf33+/jZmZaSxOInPnzqC7uytNpnRayePlyySWLx9GV1dn/vrrzyTT2bNnZ1asGE6z+SmtJNKyZRP279+TvyeUk0/Yq1cXajRqisVi+vp6UaNRc+LE0Xzy5BZLe/g3bFiHo0YNKjH++eczKAgCv/pqdsGYk5MDv/9+U6nrkGk8d+5A/g4yOU+c2M3Xr+/xTURy/foJqtUCW7ZslF8LK5V5eQ957tx+zpz5EaOiKlOhsJSFcXJyoKurEwcN6skGDWoxIMCXer2WYrGYGo26IMNdKpXS0dGerq5O+fqDmlKphFKplEajnt7eHvTx8aBEIqZSqeT77w/krFkTuGLFbG7fvoyHD1se7nK5nD/+uIGFSUStFhgbe5hWElm7dgEFwdL61t/fm05ODvlbekWUSqVMS7tAMp4ffzyc1apVYKVKYWzfvgmdnOy5du0c6nQatmnT5m+7X/7b8Y+TCCxZ6t3/7PVvWC8OgA8AOYArAIKLzRkKYGn+310AbP1P65aRyNsD+YUXL126RIVCQbVazVu3btFkMlEul3PgwAGsUaMGrSGs0NBQfvHFInp5eXHWrJks7HkYDAaePn2CZC4jIsLZr19vWpMMX758QkEQeO3aRVoJJC0tkXq9nosWzaOlt/pm6nRapqcnsbgmYjK9ZEREGAMDAyiRiNmoUT06OjpQpVKydevm3LJlDZ8/T6J1x5adnS137FhP8jkvXDhGe3s7NmpUj+np92gljOzsVBqNBm7evLJgzNPTndu2fc3fI5CkpKuMju5Co9FAhULO0NBAPnsWx98rZ+Ll5c6NG5eWeu6HHyxFKIcM6cMnT25RLpcxJ+dhwfm8vBReunSYixd/xrZtm9POzpYKhZwSiZg6naX6skIhp16vo6OjPT093RgYWI7VqkWyVavGrFQpggqFnC4uTmzcuC5VKiWNRj0jIkI4btx7vHv3LMlUjho1iM2a1WfxUFZ2dgLj489y+fI5lEjEVKlU3Lp1CQ8e3MJLl/bz/v2zzMi4w8JeSY0alQtCTsXDWaSlrM7UqR/kex4HC8YtlX5PkEzg2bN7qFar6OzswBkzxtBKLJmZltLxSqWStrZGXrmyjzt3LqWrqyPlchmPHNlMvV7LMWMGUC6X0dXV9W+6W/778XcmG+oAjAewGEBjWMqfvAcgAcDut3mRt3ojQHUA+wsdjwcwvtic/QCq5/8tBfAYgOj31i0jkbdDbGxsQUb469evqdFoaDQaaTabSZIODg60t7fn558voJVEevXqycDAAGq1Wr58mc7CJBIVVZ3vvz+Kq1evoMGg59OnKSxcM6tu3docMKAvyUyaTBn09y/H9u3bFMkbCQ0N5ogR77I4gURGVmBwcCCfPXtAX19vLl36OcmXjIn5hT17dqG7uysVCjnr1q3FFSu+4ODBfRkcHMjFi+dQrRb4ySfjSs0NWbx4Nm1tbZiRkcSMjCQqFHKmpd1iadnpixZ9xqAgfyqVCjZsWId9+nSjq6sz7e1t2bJl44I+H6WZTqfl9esn33g+JuY4HR3tGRDgRwcHOx44sJ2TJr3PqlUjqVQqqNfrGBhYjr17d+G+fVs4fvxI1qtnyQcxmZL5+PEN3rjxM0+c2MOdO7/msmVzOH36OA4b1o+urs4Ui8WUSCR8552WvHLlCEvzWt59tw/btGnC0jSRGzeO02jUs0GDWvndDkvXQsgkLlnyGdVqgdWrR3LFijn5iYhxtBJFXt69/K3R8Zww4T3a2hqZmnqJZGJ+L5RTTEo6SxsbA8ePf5f9+3dlu3ZNaSWR7duXUK/X0cXFgRMmvEu1WuDnn0+mWi3Q3t6GL17EUCqVsl696lQq5ZTJZH/H7fKvwN9JIrsBrAEwCMA3AA4AOAag/Nu8wNsagA4AVhY67glgcbE5VwG4FTqOA2D3e+uWkcjbYcGCBQRAGxsbvnjxghqNpiBXhLRs9VWpVLx9+yZ/E9O/pkql4pgxH9BszmFhElm9egVdXV1oNBq4bt1qFi+8eOHCGQqCis+fp7Jr18709vbiq1ePWTi8deXK2fxfo1dpJZDq1avQ39+PT5/eJ/mSkyaNZXh4KIuHsRITY/nee4Pp4+NFuVxGmUxKsVjMESMGMy3tDt9Utdfb25Pjxo3ismUL6OfnzaJi+gE2blyPer2Onp7unDNnClNSbpB8wlatmrB//x589uwuAwPL0c/Pp9TM8oSEy5TL5UVKwJeW77FmzRcEQIlEQnt7O1arFskJE0YxNvZ0ifkffDCMTZrU45vCWFatY8iQ3tRqNXRycmT58qHUajU8dGhHqfP79+/BDh1asnQCMbB//26MiTmSn+xXOoHcv382v9ijmGvWLKDJlMiKFcPYuXMrFhbWFQo5yUSazffZrVtburu7MDPzNuVyGe/e/ZmhoQFs2LAmyQQuWvQJw8ICaCWRxo1rs3XrRvk5IPFct25+QXHHyMgwkvEFnpm1+GMZ3g5/J4nEFPpbAiAdgPZtFv8jBqBjKSTyRbE510ohEdtS1hoI4DyA8x4eHn/3d/tfiaFDhxZoIjKZjCqVit7e3uzWrRsnTpxIZ2dnSqVSVqxYkR4eHtTpdBSJRFSrBSqVSkqlUjo42DM8PIwtWzbnwIEDKJPJaG9vx337dvPChTNMTIxjVtYLWonE19eHLVs2p0aj4c2bv7I0ob1hw/ps3boFyQzWrl2Dvr7eTEuLp5UsMjJSKQhCiWq+hW3EiKGUSCxxeldXZ8rlcjo42LNFi8acM2cqjx37ni9fJpJM5+nTP1GlUrFSpQp8770BfP48nqNHD6WrqzMFQcX/x957R0dVvuvfd9pkZk9P7xACpJIQQi8xNKUGkN6bSBEQEKkqVRFEaQJKVVREQKQLSAdBem8CISGEFkIPAcLk8/6RzJjq4aue95zzM9daz1rZz7PLzE72vnK36+7evQMHDmwpIG8SFFTSlgpssaQSH98Ak8nA7t1ryf3Cnz59IuHhwRRGHunpScyZM4WAAF9cXc2Eh4fY3E35A+65x4ABb9gUewsbiYmHKVcuW003IeEgwcGl+eqrGXz++SS0WoVly74scEzXrm3o0KEFhRNIR+AGCQkHcjK4ChJIVtY1YmOrEhkZilarYLEkAymcOrUNjUbNiRObgWQSEn7N6V6YTSrPnydQq1ZlwsPL4uDgQMOGcZQuXQKL5QqQxJYt3+Ltnd2o6s6d4zg7q0hM/BUnJydSUn4DrrB79w/Y29tTpkwJ4Ap+ft6ICFqtBgcHh7/9rPxb8LIk8jI91jOtPwAWEbkCPHqJ4/5TXBMR/1zbfpKtHlzoPnZ2do4iYhSRu/lPBMwDKgIV3d3d/xs+6v97aNq0qYiIWCwWuX//vtjZ2Ymbm5vY2dnJnj175O7du6JSqaR9+3by+ecz5fDhg/LVV4slM/OFDBo0UG7dSpHvv/9OevV6QwIDAyU5OVlERF68sMgbb/SV115rIiEhkaIoJlEUk/j6lpS0tLvyyy/bxN/fT778coFMnjxVFixYLKtWrZZdu/bIqVOn5bPPJsu2bTslJqamJCZelX37tombm5vtcyuKIuHhobJ48XeFfq+FC5fIggVfyf79v4ibm4uMHj1U0tNTZNGiWeLj4y1Ll66UNm26i4tLKSlVqrx8/vkCcXNzkXPnLshPP20UL69KMlIhAAAgAElEQVRQ2bv3N/n44w8kNfV3WbRollSuHCN2dn+IWgNy8+ZtqVatkoiI2Nvby5o138nQoQOkQYO28sUXX9n23bHjV9t+VqSk3JBhw8aKp2eYTJkySwYP7iO3b5+X9u1bSHR0pIwdO1waN+4gkybNKPQ7Pnv2XFQqVaFr69dvkXLl4qRECX9JSDgkgYElJC3trgQGBshbb/WQxYtnSI8eg2TGjHn5zpmZ55wXLlySGjXipWXLxjJ//lQREdFqFcnMfFHodRcv/kFOnjwrjRrVkTJlAm2KyhERIfLWW12lVas+IiJy//5DUamcbMc5OTnJ+vVfyfPnmWJnZycHDhyT/ftX244PCQmSBw+yXz8rVmwQPz9vKVHCT/z8vGT79n0iInLu3CXRaNRy8WKStGnzlnh7e4ha7SwiduLh4VHo5y3G38B/xTIiYhGRhznjkYi8yPXzw5dhqpcZkh3jSBCRQPkjsB6eb5+3JG9gffl/dd5id9bLISMjAxFBrVZz/fp1dDodue9deHg4zs7OXL9+Das7q1evngQGBuLi4sKLF0/J7c4aOnQIQUFBaDRqkpMvY7U+LJYMEhLOs3HjGkqWLJGjBhxIgwb1qVy5IqGhwQQFBeLj442rqwtarWKrXxk7dhTPnqWR39JYvnwJbm6uWCwP8sxv27YeRVFYt+4H4AHLli3CYDDYlHtzj0ePkvn667m0a/d6TiFkduzhyJHt/FfZWfv3b8Zg0Bcqvrhp0woMBj29e3fl+fPrhIaWtSnxHjr0Cy1bNkGtVhMVFc7WrSvJbWFMnDiSGjUqA6ns2rUGk8lI06avFqhw79q1LR07tiS3JZGZmcKQIX3Q6bQFuhuqVE7cuHHKtr1t20p0Oi0jRgywzbVs2ZjevTsBNzh/fg8uLiZ69mxPbsskPf0yjo4O5LdCUlKO5KgFzKF06ZJMnz4uz/rjxxfx8HDj449HsmPHcnx98zamSkk5RN26NVGrnfH19eTixV1Y3VdZWYk51sdeypcP5733BgBJNGpUm379OnPnzlH0eh0eHq707t0BT083dDoFvV6LTqcQHR39Vx+Rfx3k/2iKbyMR+V2y3VSjc+bGi0h8zs9qEVkh2Sm+B0Wk1H91zmISeXmICAaDgW3btqHRaHB2dub58+cAeHl54eLiwpw5n2MlkUqVKvHhhxPx8PAoUFzo5eXFd98toWrVyjkB9LwxkVOnjqDRaPj++69RFA3nz5+gMHfWnj1bcXJyQq/Pbqvr4eHO3LnTC5CJi4uZrVvX2bbPnz+CwaBnzpzPyF0bEhkZTp8+PSgsHmKxpBEbW93muipbNghXVxe2bl3Fn5HIwIFvUrfuK0WuJyYex9fXm+rVK+HiYuKDD4YSFRWBTqeladPXilTlnTBhBNWrV7JtX716nLCwYMqUKZWnUr1duxb06NEeKwFcu3acihXL4+vrzdmze8hNIOnpV3BwcCgg/X748BZMJiNdu7YFbtGkSX0GDOhhI5Du3duRPz6SlXUdOzvJI3WSlXWNevVqUbNmZRIS9qPRqAtIoUAK69Z9hV6v4+uvp1GqVACQTGbmFT799H20WoXq1SshIvTp0xGtVsPIkW9hJZIyZQIZN24wGo2ax4/PAkmMHt2fWrUq0a1bK6KiQqhfvybvvvsmycn78Pb2wMnJEZ1OoWXLln/l0fhX4h8jERE5+k/s8z81iknk5WG1RGbMmIG9vT0uLi4cOHAAAI1GQ69eb1C5cmVyy5ysXbuazp070qDBa1gJ5Oef12Mw6Hn69DGnT59Ao1Fz9eolcpNIttxJbyCD5s3jiYmpUEBL6/nzh3h6etCzZ1cMBgOQzpdfzsLPzxcPD3fmzJlmI5NmzRrTsmUz4BFpaUm4u7sxdOhA8hcYnj2bHaw/c2Y/+S2R4ODSlCsXxu3bFzEaDVy4cICJE0ejKAp9+nTjyZNrFEYSMTHlmTTp/ULXrOPatVO4ublgb2+P2Wxk8OA+RUqdFEUikMqTJ1dp165FToHlOiCVFi0a069fN+AWW7Ysx2QyUL/+K4XKwCclHSlU8gRu8fvv+/Hy8uC11+KoVy+WDh1aFEkg1qFSqUhJOYKVHJYsmYnRqOfRowtMnfo+oaFlKCrw/tprcXh4uBEeXpb9+9cQHFwKLy93Nmz4mhcvEnP6sySxa9dyfHw8KV26JJcu7aZZs1fx9HSnfPkwrMTy7bfT8fR0Q1E0JCbuoUmTOvTv3wW4QqlSATg6OqDTKXzwwQd/8en49+GfJJEMETn5J+OUiFx9mYv9T4xiEnl5WN1G8fHxaDQaoqKi+OSTTzh79iwajYbbt2/i7OzMnTu3gWxdrYSES1y7dhW1Ws3Nm9eATGJiKuT0YM8mlSpVKtOjR1esBLJt2ya0Wi23b1/Fqt7r5ubG7NkzyE0iTZo0omLFCqSnp2Jvb8+LFw+xpvrOm/c5/v6+uLu7MWfONI4d+xW1Wk1aWhIBAf60aNEkT4Fh7tGsWWNq1apuKyxMTj6Np6cH9erFkZ6eAtzD1dWF48d3AWlcunSYwMASlCjhz6FDW8lPEJ6e7uzata7AfFbWHXbvXs/rrzdBrXambNmgnOQFLc2aNeD69VP8VyRidWfllzz59NMJKIqGKVPG0KhRPQYN6sWoUYNQFA1Tp46hqCD74cNbcHU1F7meknKC0qVLotGoERG6dWvDn/UPMRh0nDjxC5DCjRvHcqyL6UAK5cuHM378u/xZ9paiaNBqFbRahb59O9vUfZ89u4y9vT1Wknj8+BxvvtkBrVZDuXLBODg4MG/eJJ49u8ilS7v5/PPxGAw63nijLXCF119vQM+ebTh2bIMtW0tR1GzYsOGvPyD/MvyTJFLiJYbfy1zsf2IUk8jLw87ODjs7O9zc3PD09GTAgAHUrVuXmTNnEh4eDlgoVSqQxYsXcuXKZVQqFRZLJmAhLCyMjz/+kNTUG6jVaq5cuYiVRM6ePYVa/Yc1UqZMacaMGU1uwli9ejk6nZbk5ItkFxsuRavVcuXKWSAdjUbDzZsJ5C88nD9/Nj4+3ri5uWIyGfHx8aJq1Uo8fXqbovqsp6ffwGDQs27d9xw5shOTycgbb3TOI7zo6enBvn2byE0K/fu/gaJo+OCDd21qvXfvXsLJyTFPn5H7968wc+YkSpb0x2DQ07x5YxISjnLjxllUKidSU89TvXoldDot06d/WGS6b1EkYh3bt2f369DpdBgMetzdXTl2bBt/luq7adOyHFXdwtctlhtMmjQae3s7HBwc6NOnCxkZVyiKRDw93dm69Qeysq7RoEEc1avHAClcv34UtdqZhw/PUxiBPHlyiY8+GoGiaLC3t2fv3p/IHRd58uT3nEyqvF0Nd+78ATc3FzQaNS4uRhwc7NHrtXh5uaPVKkydOgq4QseOzejQoRl9+3bCwcEBNzczarUzN27c+MvPx78N/ydjIv8do5hEXh52dnZ4eXnZVHwPHjyITqejXbt2dOjQHrDQt28fateOY/bsWYSEhGB1bX3xxRz8/Hzp3r0rsbG1yN+QqkqVynTv3oWlS5dgMpl49CiV/PGPOnXiqFevDvfv38RsNrFw4VysZOHiYubEid/ITyLWsWDBbJtwo06npUQJf6KjI6lXL4727VsxcGAfJk58jzlzPmXZskW0bt0cNzdXdDotEye+l0fuBO7h6+vNtm0/kd+6OHRoK76+3kREhHL+/G/Mnv0JISFlgDSOHNlOly7t0GjUBAUF8tlnE/I0qbKSiJUE1q37Dk9PD0JDy3Dw4Bbyk8T48SOoXr1oEklKOkbr1vHY2dnh5OTIqFEDi2xzax3ffDOboKCSha6dObObChXK4epqxtfXizZtmhITE4ler6V9+xbcu3ee/CRSsqQ/y5d/wQ8/zMVo1HPv3lmyiwwnERwcRH7yePHiKgsXfoqrqxl/fx/KlCmJn58XHh6uPHhwBiuJPHp0HicnR/KTyObN36AoGpycnJg1axzp6eeAJPbuXYnZbESv15KaeoRevdrTrFl9DAYdRqOeHj1aYzDosFgsf+sZ+TfhZUnkZVJ8i/EvASDe3t7i4OAgbm5uUqlSJbGzs5PffvtNYmJiRERk+PBhsm/fftm6dbtER5e3HdurVy95/DhdVq1aLcOGDS1w7sWLF8r33y+XQYOGyvjxH4hOpyuwz5o1K+Tw4aMSGVlJqlWrIt27d7atqdVquXnzVqGfOysrSxYv/lZevHgharVaatasLp999pF069ZRKlaMFmdnZ7l8+Yps2LBFZs9eIKNGjZe9e/dLenq6eHt7Sf/+b+RJ2RXJTjV98iSjwLUqVoyWq1dPSnh4iFSoUFumTp0lTk5OEhZWTV55pancvHlTfvtts1y6dFgGD+5nS021fs5swYdsNGnyqly/fkpiY6tJXFxz6dHjbbl//0Ge69nb5/1cIiIHDhyR+PhOEhJSTRITkyU0tKy88koN+eGHteLuHibvvjtWXrwoPPU2NfWO6PV57/3Tp0/lvfcmScWKr0lQUEm5fv2k+Pp6S3R0OTl8eLP8/PNSuXHjlvj6Rkvjxp3k+vWbtmMVRSMJCVelV69hMnXq+2IyGUVE5JtvfpSmTevb9gNk48ZtEhwcKyNHTpKJE4fL1auHJCPjmXz22RipXDlaoqMb2j63xWIp8DtZv36btGjxpgQFBYiDg7189dUKURRFRERu3kwVs9ko9erVkAYNuoqiqOXkyXOiVjuLXq8TJyfHnPtZ/Mr7x/EyTPN/eRRbIi8Pe3t7YmJi0Gq1tGrVCoDg4GCMRiMbN67HanX4+/tjNpuZNu0z21xCwiW8vbOLumrVqskrr8Tyyiux1KpVi5o1a1C1ahVUKhUiQnBwWYKCSuHv74e7uzsmkxFFUXByckJEsLe3Z9euzeS2NEqXDmLJkvnkt0CyZVDKExoaTPny5XjrrTfR63WsXLmEotxZ8ID33x9G6dKlKF++HCVLBnDp0lFyWyKlS5di+fJFFBUof/z4Km3bNsfZWYVWq6Vnz06F9hLJPZKTT+ZUZxe0KhISDhMREYrJZGDJktlkZd1m/PgR1KxZBchW+l2xYqGt0rxZs4YkJ58AUmnYsC4DBryBxXKLNWu+ISwsGLPZSN++XQs0nhoxYkCelrk7dqzC39+HgABfDh78o9NhxYpRfPLJB+S2Oo4d+4X4+FfRaNTExlbl999/pWLFKNzdXahcORqrtZGWdhpnZxW3bp0AUjh4cANVqkRjNBoYMaK/rfDw+fNEHB0duHfvNBkZF6lUKYoKFSKwWJJIS7Peq2wLZMWKuSiKhkWLPqFevZp0794GtdqZxMS9QBKzZo2jXLlgUlOPYDTqiYkph4jQuXMLDAYdcXFVcs5XjJeF/NOWiJ2d3WA7Ozu//yYuK8b/Ajg4OMiDBw/E3t5e1Gq1pKenS8WKFSUzM1PCwsJs+9WuHSdZWVliNpvk008/k/DwchIeXk4yMp6ISuUk3t5eUqtWTYmLe0Xq1q0tr732qsTHNxWj0SjOzs4SHV1exo9/Xz7/fLosX/6tbN26UU6cOCApKZclNDREgoPLyuuvd5ArVxJt1zQaDXLr1u08n/fFixdSvnxVefHCIvv2bZVHj9KlSpWKMmvWVOnWrZ8kJFwp8rsuWLBExo4dLseO7ZbKlStITEyc7N79q23dyclRnjx5UuC4J0+eyJQpM8XXN0IOHToubm4u4ufnLd9//6NMnjxTMjMzCxzzMggMLCGnTu2WqVPHy6BBo6V69UZy8WKCPHv2XKZNmyt+fpHSv/8IqVcvVm7fPierVy8RPz8fERHRaNSSkfFU7O3tJT6+gZw+vUeWLZsvBw8eF0/PCOnefaA8fvxYRERSUm6Kp6e73L17Tzp3fkuaNOkkHTu2lKSko1Kp0h+WpcWSJQ4OeV8P5ctHyJo1X8uJE9ukRAl/iYysI+fPX5IHDx7Jxo1LbPutW/eL+Pp6ycOHj6RJk65Su3ZrKVu2lNy8eUwmTRppswauXLkqiqKIyWQUtVotmzd/K/fuPZBmzXqKxZJls0SWLl0tXbsOkQULJkv37m3k/PlLEh9fT5o0qSt9+ryX871uiZubi7i5uci8eR/JuXOXxM7OTiZMeEfS05/ImTMXxWKx/KXfTTH+C7wM02STkoyRbNmRPZJd9Of5ssf+T45iS+Tl4e7ujk6XrQRrMBhwdHS0WQdRUVHExFSgYsWKBAcH4+zsjLOzM2FhYXz00UQyMtLp3LkjOp2OiIgImwy8dWRmZqDVapk4cSw6nY7Ll8+SPyZy+vQR1Go1qanJtGr1Ol5enly/fglIp1Gj1xgwoC9WCyQjI43g4DJUrhzDw4fXgUd4enqwa9fPwCOaN29CWFhIoQ2pli5dgIuLmefPb2O1PCZNyhbtW7BgJnCPqKhw5s6ditWKePLkGlOnjsdkypY3t6r7hoUFM2/eNPbs2YCfnw+lSwdy4MAWCrNEkpJO4OzszJ9lZEF2H/VXXqmOSpV974OCSrJgwfQi9+/QoSWdOrUudG3XrjXUrFkFvV5H69bx1KxZhVq1qmA0GoiKCic5+RiFxUeiosKZOXMCRQXULZYU3nqrOyqVCnt7O/R6HZGRYUyY8C41a1bG29sTjUZN3bq1bBZJ/rF27eICnQ6Tkw/i7u5C+/bNUBQ1CxdOQatVWLXqSyCJ588v5VgvJzl+/GcURcOjR2fo1KkFnTu3AK6QlZVAWFhpnJwcefjwFE5Ojjg7q3JShovxspB/2hIBxgHhOQTiIyK77Ozstv6zlFaM/0l899138vz5c4mLixMRkcePH8tXX30lGo1GYmJipEOHDtKuXRvp3LmjiIi8++5QOXPmlIwcOVLUarWkpd2Vbt26yM2bN+Xrr7/Jc+5vvvlWXFxcZPTokfLqq/UkPr6lPH/+PM8+/fsPljZtWoqbm5usWPGdREVFSs2a9SUtLU18fX0kJSVFRLKtgZCQaHF3d5MdOzaKXq8XEZH09HQJCMhWzvnxx+/k0aPHMmTIqALfc8yYSfLuuwPEyekPuY0RIwbL8uWLZciQ0TJ48ChxdHSUJ08yJCMjQ6ZNmyO+vuEye/YC+fLLzyQh4Zi0ahUvItk+9szMTKlZs6okJZ2Q+vVrS+3azaRv36G2//6tAMSuYIgjz/rOnb9K8+Zd5ODBo6LRaMTR0VF0Oq3ExVUv8jitVpGnT58WuhYbW1327Fkvv/yyUi5cuCQHDx6TAweOyuTJ78nx49tt1kx+ZGVliYODQ6FrN2/elldeaSErVqwTT083mTRptOzdu0batImXpUtXy6FDx+XBgwfy0UcjZevWZeLh4Vboec6fvyzu7q555vz8vGXHjuWyfv02sViyZODAsbJixRxp0aKBiIhcuZJss16iosIkKipUBg+eIMnJN6RkSV8BZNiwjyUxMUUAuXkzVVQqpzzSKsX4Z/FXoky3ReSmiKSJSLEQzf9DqF+/vjg7O0tmZqYAsn//fomJiZGMjAy5deumDBkyWN555x1p2rSpWCwWmTFjpjx8+NB2/P3798XLy0umTp0sQ4a8Iw8e/BEkXrBgkbRr11pERFas+F4ePHgogwcPy3PswYOHZfjwd2xzGzeuFjc3V4mLayCenh5y7dp1uX//voSGRkuZMkHyyy9rbYHVJ0+eSEZGhvj6Zr8U7e3tZceODfL119/L6tXrbec8fPiYXLt2XXr37l7g+zdq9KocObJTli37UU6ePCurVq0XX98ImTlzvsydO1USEo5JmzbN8xzj6Oggz59n2q45Z84ncvz4LtmxY48EBcXIxo2//Jf3/enTp7J48VIpW7aKtGjRVcxmkyQmHpXY2GrSq1dnCQoqKVFRcbJw4XdWr0AeaDQaefr0WZHnv3//gSxZ8oNcvJggIiJ6vV5Gj54kixd/X+QxRZHIli07JTQ0VhwcHCQp6ZCoVCrx8fGUyMgwGT36bWnW7DURsZNSpUrI+PGfiadnlAwePKZQ1+CJE2ckNLR0gXtx9OhpMZuNYm9vL598MloaNqxtW79wIUGMxj8SA8aOHSwrV26UlJQbEhRUUvr2fU8WLfpB7OzsRFHUMnnyF+Lg4CCPHqWLj0/hhFmMv4mXMVdy/nD7ishOyXZpjZN8DaP+t45id9Z/BhGhVKlS2Nvb06tXLy5duoSjo2NOMeF1wMLq1avw8/MjODiY999/D2twPSoqitmzZwKZRESE079/P3I3qbJ2NoRnXLp0Fp1Oy9q1K4EMevToSmxsTfK7uCyWdCIiwvDw8MDLywsfH2+aNm1UQPZk166fcXV1Ib+u1vz5s9DrdVy5chJ4QLVqlejduxv5JU+ysu5y8uRepkwZR4UKUTg4OKDVKowfP4I/C5bHxJRnypSxha5NnvwBer2OFi0ac+vWea5cOYZGo8bqarp+/RTDhw/EYNDj6+vNhAkjyMy8YVuPiYni00/HA6msXLkIs9lIw4Z1uXPnArldVsOHD6R+/VfI78p68eImc+d+gtGoJyIilNOn9+Dj48W6dd+wePEMTCYjoaFlOX16F/ndWaGhZViw4FOs7qvnz68yePCbObUYY2zz7u6ubN26HLjB/fsX0GoVunZtQ2hoGZ4/T2T58i+IiYlEq9XwyitVOXJkE1Z3VmRkKDNnjgOSuXhxN4MG9USv1+Lv70316hXR6RRKlvQjd4rv1Kmj81SqZ2UlUqpUACJCXFxVXFxMHDmyDpXKic8+G43ZbMRo1CMiDBky5O89HP8yyD9dJyIiH8s/3EPk/49RTCL/GbJrDpxy5DnMJCQkoFarCQ8PZ8KE8YCFGTOmUa5cOX75ZTNarZa7d+8AFsqWLcN33y3BWmCoKAqnTx9n06YNmEwmLJYMckufzJkzE71eT2LieUwmE5s2rSU3gWRlPeHmzUS2bFmPXq9DURRatmxGZuY98pPFtGmTKVcuvMA8PKJJkwZERoZz9eqZnP4kx4B7pKZeYunS+bRv3wqz2YTBoKdcuTBGjBiEv78vlStXQFE0fPnlZ4WKK0Ia1atX4sMPRxe6Bmmkpv5OlSox6PU6Jk4chUaj5tChX2jVKh612pmoqPAi29/6+nrnWbt37yIxMVG4uJjZsmWFbX7MmHepVasq+WMhZcsG4enpznffzbXNu7iY2LdvPXCL+/cv8tZbPdBo1LRo0ShPJlfZskEsXjwdq+R7ZGQYfn7enDmzk9yxEa1Ww/nze4AbTJw4guDgIBISDqDRqMnMTMJKGKdObaNHj+wampIl/ZkxY3xOxf1oqlWLQaNRU61aDNu2LQOSadq0Pl26tMLb25MxY97GShodO7agbdsm5CaWr7/+LKdlryspKb+xfv1CfH29SEs7hrOzCr1eh52dHZcuXfpnHpJ/Cf5xEvm/OopJ5D+Dm5sbTk5OqFQqTCYTP/74I87OznzzzTd4eHjw4sVz3n13KHXq1MZaqT5ixHCsqb+5hRhbtXqdatWq0bBhA7p160x+EUZ4xquv1sPNzRUXFzOrVy9n8uSJdOjQloiIMBRFQa12xtvbC1dXVzQaDQEBfhw/vo/8RNGrVzeaNWtSYB4ekZl5Dx8fb9zd3ShbtjTDhr1NcHBpVCoV/v6+tG7dnF9++SlPwaGLi5mDB7exdu33mExGWrduxqNHSeQnidjYaowZM6zAfP7x7bdfoNNpbcWQjRvXJyHhMH8WYM9OYS0ozjh58gfodFr69+9JRkYyH300mqpVY4BUEhOP0qxZQ3Q6LQMH9iqg+Jvdt/xX8hcZVq1aEZPJwPTpE4BblC4dyDffzGLFivnodFri418lMzOZ/AKM9vZ2pKdfJj39MkajntWrFwM3KFHCj/nzp5CZmURi4gF27fqRJUtmMHRoH9t9cHR0wNXVTL9+XfIUGmZlXcVg0LF37yq2bv0enU7hxo1DQBIVKkQwZcpIrASSkLCHsLAyaLUa9u//EbjCqFH9qFGjInCFxo3roFI5odMp/8DT8e9CMYkUk8hfQrt27dDpdDg6OlK1alU6d+6MSpWdX5/dYGo9nTt3pF27toCFXbt2oCgKd+7cxsPDg19/3YWVRDIyHmEymXLI6AdOnjzCTz8tZ+rUj+nZszs1alTD3d0dR0dHtFotAQH+VKhQno4d2zFz5qecPXvMJsoYExPNmDGj6N27J4qiMHv2Z2RlPcRKFLVrxzJ8+GAKI5ELF47Spk1LNBo1BoOeihXLM336JFsjqsLUfJ2cnGw92FNTLxEeHkJAgB8nTuwmNznUrRvLiBGDKIo80tOTmTXrY3x8vDCbjahUTgQE+JKUdIw/I5D09KQctd1bha7//vtvBAYGULp0ID16dCAyMoyRI99Go9FQu3bNPCq/uYejoyOpqWfJ777KyrrJihULcHNzITAwADc3F1u1+ldfZVsk+cfDhxdzqspvMH36eEqW9MdKLg0a1MbR0QEHB3t0OgVvbw+Cg4OoXr0i7dtndy/UaJypVq0C+Xuunz69NafZVfZ2y5aNcroUJmE06jl4cC2QxE8/zUOn0xIQ4INa7cy7774JXKFGjRhGjerH48dn8PJyzyHuYhL5T1FMIsUk8pdw+PDhnC5wWqZPn47RaMTR0RGArl27UrduHV577TUGDx6ENRZSrlwE77wzBJPJxJkzJ7CSyJ07N6levRp2dtk6TCaTiYAAf2JiKtCyZQvGjn2PjRvXYDAYcHNzpVWrFmRmPqKwuIher+PUqYNAOps2rcFsNhEf35j7968Bj4iICLP1WodHPH9+l5Urv6Vatcooiobq1avaYg9eXp5s3bqaolrkHjmyE4NBX2C+d+9uKIrC3LlTbe6thg3rMnhwX/KTx82b5xg1ajB6vY4SJfyZPfsT1qz5lhIl/ImPb4CrqwsnT+6iKBJJSDic0/GvaKKxWG7Ro0dHVConnJ1VlCwZwL59G/90fxEpVN3XOh4/TqBBgzo4ODigVjtz/Pg2ikrzTU4+glar8OxZEq6uZr7+egaZmcl07twq5+XuS+5cKgoAACAASURBVHr6RfKn9h44sB6tVuH48S3odFp++GEOuUlk1qwJOZIp2du3bx/HYNDxxRcf4eTkyJMn53nrra45KdlTaNSoNv7+3kRFhWKxXEZR1Jw69TNvvNEOtdoZs9mIvX1xW9z/FMUkUkwifxmS01fk119/Ra/X21qK3rp1C7VaTUhIMJMnf4yVRPbt24uiKCiKwvXrV7lxI5lBgwaiKBrKlCmNg4MDUVGReVrjWkdKyhWcnJy4dSsJPz9fGjVqwLNnD8hNIt98sxBfXx+ysh5jrRO5dy+FyMgIPD09OHhwJ/7+fvz88yquXj3HiBHvYDab8Pb2pH//3jx4kAI8wtXVhSNHdjF27Ei0WoVOndoU2qBq2rSPKF++XIF5uMf69cswGg20ahXPw4eJNGvWkLfe6omVPM6d20/nzm1Qq9VERITw88/LbWszZnxEdHQ5rGKOer2OnTtXU9gL/9dfN+Dh4VboWm6iqV27JhpNdnviwMASNnn4wsbjx4k5/xAUTiCpqWdp3/51tFoFR0cHKlaMQqfT0rt3pwKuLLjBqVM7MJuNzJs3FW9vDx4/vkydOjXx8/Nm2bIvcppNFWybGx0dQdeurYEU5s//BBcXExkZF7GSRsOGtenTpxO5iWXhwk8wGHSYTAYiI0Px8/Pi0qXdWCxX0Om0fPHFh5jNRs6d24per2X79qVoNGp0uuwe702aNPl7D8W/EMUkUkwifxl6vR6j0chPP/1ElSpV8vSljoyMRKvVsmDBPKwkAhbKly+Po6MjHTt2QKPRUKFCNL/9tpfHj+8jIvj7+9OxY3uysp6Sm0Rmz55BSEgwkMGDB7fw8/OlTp04MjLuYSWRGjWq8847AylMeHHo0LdRFAW9Xk90dGROl8ByrF79PfndWu7ubhw6tAN4QErKeSIjIzCbTfz44xJyE0XHjq3p2LE1RVkqqamXiIgIwd/fl+rVK9OzZyd27lxLvXqvoCga4uJqcPbsfvJbJ3379iA+voFte+rUcSiKwg8/LCD/C//HHxdTqlTJAvOQyrNnKUyYkK2A++qrcbzxRicaN67P4MF90GoV2rVrwe3b5wocd/v2OdRqNYW5shYunI7BoCcmJork5OwssoSEg+zdu45y5UJxdTUzY8Z4cpPI3r1r8PBwxdvbk7FjhxIREUJYWBnS0y9z7txuTCYD+Ulk5cp5mEwGW6OqrKxrVK1agfj4+kAyFksSOp3CwYPryU0iz58nEBDgg6OjI/Hx9Ww910+e3IzBoCMz8zJqtTPjxg2mRAlfPD3dCAz0s7nUbt++/Vcfh38tikmkmET+MhwdHVEUhTp16hAXF4ednR1ffvkla9asYfz48RgMBsaPH8fChfMZNOhtYmNrodPpcHZ2JiIinFOnjpG7Wt3e3p7k5CuYzWamTPmI3CTSsmULunbthJUw0tPTCAoqRY0a1UhPTwMyMJmM7N+/g9zkkZaWzDffLKBp00aoVCo0GnVOhftFCouLZFe0u/Pbb9vIXb0+e/ZUjEYDTZq8xo0b54F7VK4cw6RJYyiKRLKy7pKYeIJq1Srj4OCAo6MjRqOBDh1akpZ2kaLiI7Vr12LEiLfzzC1btgCtVmH69InkfuHPnj2ZqKhw8hPBnj3rCAwsgZ+fj82KiY9vQO/eXYBUrl07SaVK0ej1OubO/SRPTCUx8WiBhlRnzuymYsUoXF3NfPvtHKxy8HZ2djx7lmzbXrp0Lu7urpQs6W9L6V2//htMJgNGowEvLw9iY6tisaRgjZc4OjradLIghadPE/DycmfKlNHkJpZLl35FUTRs3/4Dx49vziGfbPLIzLzCwoVT8fb2RKfLbpV85MgGrIH1GTPGEh5eFkiiRo2KuLqaUKmcKFOmJKVKBeDk5JgTXynGf4piEikmkb+MEiVK5AQjddStWxe1Wo2vry+BgYF4eHig1Woxm82ULVuWhg0b8N57o/jxxxXY2dkRHFyWp08fk5tEnJ1V3L9/h3379qDVKmzYsBoriYSEBPPll5+T23319Ol9ypQJomLFGFauXIrZbMJiecTFiyf55JOPiI6OQqVSERhYkm7dOrFo0RcYDHq8vb1o1OhVMjJSKYxEvLw82bfvF/LLoNy7l0StWtXQ6XQsWDCTwMASNuvk9u2LbN++lhkzPqZz57aEhQWjVjvnJAL4odGocXJyomfPTmRm3uLPMrQCAvxYufKrAvN79mzAYNAzaFBvsrJuA6mMHj2EuLgaWAngzp0LdO7cBq1WYfDgPnnIoXLlaCZNeo/cZLN8eXaQvFy5UI4e3Qakcvbsrzkv6Ow2ue+80xdF0dC6dbyNMKypv9mS9XktlidPEvnww2xXYKVK5Zk8+T1bplWHDq+T392lVjuTkLAPK1l8/PFoAgJ8KUwC5eOPR+Ht7cmnn75PWFgZMjOvsGjRp3h5eeDl5UH37tnf3WQyEBjoj5VEXnstlr59OwFJTJo0HJXKCbVaxd69K3B2VmEw6PJY0sV4eRSTSDGJ/GVcu3bN1io3MTERg8FAZGQkWVlZAPj6+qLT6WzFh2AhOTnJ9mJ/660/igwhE61WISUlCcjkyy/noNPpOH36GPAMFxcXDh7cQ/5gembmI8LCQnBycsLHx5uAAH8URSE0NIT33x9BWloyVqtk0qRxVKxYgQcPUggKCqRSpQq2gHvu4e3tyZ49myhK2XfZskW4uJjQ6bQEB5fBYNDj7KzC29uTiIhQ2rZtwcyZH+dR/PX0dGfx4s/x8fGiZs2q3L17mcIIJCvrDk5OTty4cbbQ9QsXDuDm5kK7di14/vw6Xbq0oUOHlmRl3Wbx4lkYjXoqVCjH1avHyW+dBAT4smLFwgLzmZk36NKlLRqNhjff7My2batwdXVhw4bv8PR0p3TpwEKbWCUmWoP6hcdObt06TbdubVGrnXF2VjFy5EAKC7z7+/uwatUCIIXU1FPodAobN35DYSSSmZlEaGh2qm7FipF4e3vg7e3B9OljgWRq1qyEnZ0dw4b1wd3dlSlTRmKxXEGrVWyWydq1CzEYdLz3Xn/mzp2IVqug0yn06tXrbz0P/1YUk0gxifwtqNVq1Go1w4cPJzg4GK1Wy44dOwAoV64cRqOR5s2bk1sKXqNRc+nSeXQ6XZ56EaPRwMWL52zbvXv3wtvbi8uXz+Ho6Jgn/nHt2iUWLvyCJk0aodFoUKlUODg40Lt3TzIzH1BYXKRt25Z06tQOa01I+fLlKFMmqIBry8fHm507N1AYgTx/fodp0yblBJUdUaud2bBhORZLGkW5tR49SsbJyYkHD66QkZFCpUrR+Pn5cO5cwXjI9etnUBRNgfn8hYn+/r688kp1qlSJoXPnNlSuXAGz2cTXX39OUQFznU7LqVO7i1y/cGE/4eEhODurMBoN6PU6PvxwJEWRxPHj23Oq/wtfv337DE2avGrrSlipUnkuXdpPfhKpWjWGiROHAyn06tUhp9K88Fa5ycmH6Nq1NU5OTri5mW3kAcn89ttadDotfn5eLFv2OT/9NA+DQc/evSsxmQw8f36Jjz4ahkajRq12Bq7wyitV8PLKTh9/9uzZf/z3X4xiEikmkb+JqlWroigKZrOZevXqodfrqVKlCgCxsbEMGDAAvV5v6zNy/vxZtFotkMnMmdMwGo1cv34VyMTFxYUTJ46Q2zqpWrUKnp6e+Pv7sW3bz7z9dn8CA0uiVqspU6Y0PXt24+jR/ZQsWZLmzZvm9OzoSnp6KvlJJCYmmilTJmAlC4vlAXXrvoKnpwe//36M3CSyffs68hPIL7+spkQJf3x8vBg16h3c3d2Ii6uJv78v166doSgSWbTo85wugX8QQbdu7dHptHmysqwuKy8vD/6MRCCNjIwUAgNL2IrxmjdvREZGMkURxPPn17G3t+fZs5Qi98nKus38+Z/h7KzCycmJiIgQDh/eQlEksXPnT0W20F25ciFGo4HKlSvQoEFtevRoT9Om2YTy2WdjbTERuEGrVk3p2rU1587tQqNRc/78bnITx9OnCfzww1xq1KiEWu1MWFhZnJwcOXduB7mD6vXq1aJ16yZoNGouXtxFVlYicXFV8fR0w9fXizJlSuLr62XrpX7nzhFUKhXVq8cU9xD5G3hZEilu81WMQrF27Vp58uSJvHjxQiwWi4SFhcmZM2dk//794unpKY8ePZRRo0ZK9+49JT09XZ49e2brEzFgQH8pXz5K2rbtkCPkZ19AgG/NmlVy795dSU6+Jm3bdpITJ07IqFHvyoMHt+T330/JggVzJTq6vFgsL6RXrx5y6tQh2bVrj4SERMuBA4fynCst7a6ULfuHkJ+9vb1s3bpe6tWLk8qV4+TIkWO2tdw9JS5fTpBXX20ur7/eSTp0aC3JyedERCQkpIzs2LFOypULk8qV60pS0tUi7tHPEhdXM8/c4sWfy+TJY6Rly24yders7P/URCQhIVEMBn2h5wHk8OFjMnz4WClduqLcvp0qDg4O4uDgKDVrVsmjNpwfqalpolY7i0qlKnQ9MfGq1KzZRIYPHy/NmzeUoKBAqVAhUmJjm0mHDn3l5s3bBY65f/+BODvnPV9a2l1p3ryr9Ojxtkye/L4cOPCz3LhxWyIjQ2Xt2q/lp58Wyccffy6VKjWU33+/LCIiQUElJCkpRd56a7TUrVtLgoODRETk2LHT8uab74qra4QMGjRGIiNDJTn5sJw5s0PMZpNcv/5HB8sTJ87K/v1HZOrU9yQz84WUKhUgdnZ2snDhJ/LgwSO5efO21K1bUxYvnioqlZMoilq+/XaNuLgYJC3tnjg6Fqv3/rfjZZjm//IotkT+OhwcHBARPDw88PT0pF27dsTFxTFo0CBefbU+YCE4uCwDBw7g0KGDGI1Gcleru7m5MmnSh3h7e7F162YgkxcvnjJnzucYDNlpxGq1mqpVK3P//k3yx0UgAx8fb7ZsWW/bHjJkIIqiMGzYEJ4/vw+k5xQ5HqKwYPqwYYPQarVs3boOf38/Nm36kYcPr/Huu2+jKBpee60u9+4lYbVKGjasz8CBvbFaGy1bxuPh4c7Fi0fIb4kEBpZgyZI5FGZR7N27EbPZRIcOrXj69Drvvz80p0th9rrFksqePRsYMKAX7u6uGAx6qlatyFdffc7Ro9n1F1u2rMTT052wsGBOnNhJYVbG0aPbcHNzLTBvsdxi+vQPURQNDRrUISMjmbFjh9k6JV69epyqVWPQahU+/HAUT59exWptfP31LEJDy9q2f/ppMSaTgZiYyDzV7i4uZvbuXYPV8sjMTKZVqyYoioZJk0Yxa9aHeHm5o9drSUjYz7RpYyldOhC9XktcXHV27fqR/G6t0qVLsnTpLKxWSOPGdWnSpB5nz27PSQrIDqivXJnd6XDmzLFAEnXr1qBTpxZ4eblToUIEr75aC41GzejRo/+hp+HfByl2ZxWTyN9FbGysTUfLwcGBmzdvotVq6devH1FRkYCFs2dPoygK8+Z9gYuLC7ldVnv27ERRFNzd3Vm79if27t1JcHAwnp4eLFv2LXPmzCQ0NISoqHIEBZXi6tXfyU8iXl6e7Ny5Jc/csWO/4ePjTUhIMEeO7MXBwaHIjCx4xPTpk1EUBVdXF3r27ILZbCI4uAyHD+8iv2srPDyEefOmk5ssOnRojaurmXPnDtjmLJY0tFqFS5cOU5Rr6saNs/j7+1KhQiR16tSiW7f2/PLLj7zxRmeMRgNms4natWuycuVXWCyptuPmzp1K2bKlgTQyM2/RuXMbNBo1777bv4Bra+PG73Mynv6YO39+P9HR5XBzc2HDhj8EHHv27ETr1s3y7Ltly3ICAvzw9vZkzZqvycq6yYwZE6lQoRxpaedp1aoJer2O2bM/Jrdb69mz5Jz7foX8sZAdO37Ey8sDo9GAwaDHZDKgVjsTHBzE1Knv5xFmzD+ioyNs8ZBz53ag0ai5ceMImzd/i5+fN5DE1av70euzs8KSkvbx++870WjU3LlznJCQIESEsmUD0Wo1vHjx4p94FP6VKCaRYhL527h//z56vR6z2Yxer+fUqVM0b94cf39/fHx8sAbVe/TojqurK+7ubuQmEcikf/9+6PV6QkND0Gq19O/f16bmu3PnL7i7u2GxZBAf3xhXV1dOnDhIbsJwd3fn11+3k59cLJZ0OnZsh0qlQqVSMXz4EPr160WnTu1o1ao5DRrUp1at6kRHRxEcXAadTouiKGi1Wj766AOKytDy8HBn9+4N5Lc6evbshNls5OTJvcA99u3bjMGgL1Ld15qRdebMr/j6Zveed3Cwx8PDjYYN67Jly8oij2vbtkVOseMfc0eObKdECX8CAnzZvXstVhJYvHgmYWFlsWZjffjhKDQaDS1aNOb58+vkJozXXqvN0KH9KMyimThxJCaTgRo1KtOxY0tKlPDDbDYSHR1RqNbWpUsHcuovCpdESUk5htFosAW716xZRFHEkXvExlZl1KgBQDJt28ZTp04NIJkFCz4hPLwsL14kUKlSFLGxlXFycsRiuULv3h1zNLiSqFatAmq1MxqNOqeLZDH+Kl6WRBz/Bz1pxfhfDqPRKI8ePZJKlSrJhQsX5Pz58/Lll19KiRIl8jQsmj9/nqxdu04yM1/IggUL5ezZc3Lq1Gm5cOGC3LhxUxwcHOTatRQ5e/aErfOgiEhkZDm5e/ee2NnZyZo1q+Ttt9+RGjXqyE8//SD16tURERHIKtTff+zYcblzJ02ysixiZ2cn8+YtktjYGqLVasXV1SwlSwaITqcTo9GQM4zSpUsvKVHCXyZMmCK3bqXK6NFDxd39j657WVlZ8vDhQwkJKVvgegsWzBKtVpGaNRvJjh1r5fvvf5Rq1Sra+oCLZPd8P3HitOzZ85ts2bJdfv31oADi6Zndu02lUsnPPy+XChWi/vS+79mzX2bO/DjPXIUKUZKYeFyGDRsjDRq0lbZtW8j06RPl5s3botfr5eTJM9KuXS+5e/e+bN78g9SqVa3Aea9fvynNmjUs9JqjRw+RwYP7SKtWPWXFinWSlWWRSZPek6FD+xW6f1JSsuj1ukLXNm3aLu3b95PIyDA5fvy0hIQESYcO/aV8+XAZO3aI1K1bK899yw1XV7PcvXtPrly5KmvXbpFz57bnXC9FXF1NMmnSHElMvCZbtnwrtWu3k0ePHsuSJT/Krl3LRUTEaNTLixcvxMHBQTZt2lz4DS7GP4uXYZr/y6PYEvl78Pf3x9vbG41Gw8CBA7l27Rp16tTBzs6Offv2MnHiBCpXroS9vT1arYK/vz+vvlqfd999h1WrVpCWdovKlSuh0+lo0qQRmZnp5K5Yz+6pnmLbnjnzMxRF4auv5gMZuLq6cPz4AawWyO7dvxAbWxOtVkt8fGPWrFmOoigYjUaGDOmfR9k393jwIAVHRweePUvl0KGdREWVQ1E0jBgxxBYTOX36AFqtkkcSPv8YNuxt9HodJUsGMGbMMHbsWMOYMcOoVq0Szs7OmM0mIiJC6devB/v2bQLS2LbtJzw9PRg+fCA6nY49ezbwZ2m+KpWKZ89uFLlPYuJxwsNDcHU1U61aRTw93dFo1HTp0qZI1V9IxcPDnW3bVhW5vn79d7i4ZFd8m0wGfH292LNnLYVlaS1cOI2yZYPIbX08fZpI//7d0em0TJuWLZHy+uuN6NKlFY8eXaBHj3YYjXrKli3FDz/M5cWLq+S3RHr2bE/btk3p1q0N1atXxBobads2nlq1KqEoGn77bS2bN3+Lt7cHU6e+R6lSAUASy5Z9jkajtml/FePvQYrdWcUk8k8gNTUVRcmundDpdGi1Wuzt7XF2dsZoNFKhQjRjxrzP1auJODg44OXlxd27t8nt0mrYsAFvvvkGPj7edOjQLk9zKhcXF06ePEJuYlmz5kd0Oi3jxr2H2WzizJmjbNq0lgoVyqPX6+jQoS0PHtwA0rl8+VRO+ugxzGYT/fv3LpRIVq1aio+PN7ldV7t3byQsLASdTsuECaOZPHkckZHhWAkjMzOVpKST7N37M8uWLeSTT8bTr98beHi4oygam3uqSpUYRo8ewu+/H6Swl/7w4W9To0Z2UP2jj95Dq1XYvLlwd9a6dUvx9fUudC33ePLkGnXrxqLRqFGpVHz33Rf8mVhjVtZtHB0duXnzTIG1+/cv065dC3Q6LR98MBRnZxXp6VcYNuwtFEXDW2/1ID39CrlJ5L33BhMbWxUrgZw7t5syZUoREODLxYu/2uYXL55OYGAAuYsKR44cgIeHG97ensye/REZGZdt60OH9qVq1Qo5v9OdWEmkatUK2NkJQ4b0ApJZtGgqwcFBeHm5M3/+xyxdOivHdabGycmR6Ojof+Cv/9+NYhIpJpF/DCJCaGgoWq2WadOmYbFYcHNzw93dnTt3bmONjXh4uOPr60vdunWwWJ5hJZFu3brQunUrbt1KwcPDnT593rQJMfr4+LBp0zryq/seO3YQFxczOp0OPz9fTCYTffv2IiMjjdw1Ik+f3sXOzg6L5REJCadxc3OlV6/uWCwPyE0igwf3p3792hQWB9m4cSVBQYHY2dlhNpsIDw/JkQ+3z+mY506pUiWpVCma+PiGDB7cDwcHBxRF86exDeuIiAjhk0/G2bZnz56ComhYterrAvsOH/42sbHVijxXWtolxo0bjtFooEQJf/R6HeXKhaMoGtq2bV5oRbuVKJycnArMb968HDc3FyIjw0hJOcWyZfMICPDDSha//76P0qUD8fX1YvfuNbb5Nm2a0b17O7KyrvPFF1PQahU6dHg9T50I3ODataOo1c48f55IbovDYklm1qyJ+Pp6YTTqmTBhGPfuneXDD4fj5OREpUpRQDLPnl3mt9/W4uZmzmmVm00q48YNwcPDFTc3F775ZrqtRkSjUaMoGu7cufNP/On/q1FMIsUk8o9h69atKIqCwWBAq9Vy/fp1WrdujUqlonbt2lgsmYCF0NBQZs6cgYeHO2PGvI+VREaNGkFsbC0gk6SkBFxcXBg+fCjwjODgsixaNI/8JLJ9+2ZCQoJtlfO7dm2msGp1SM+pGs+2TK5evYCrqyudO7fLQyRxcbUYNuxtCqtUnz9/Jp6e2dXNTk6ORESEsGfPz2Rk3KAwl9azZ7ewt7dn5szsrK+1a7+jqJf+gwfZUvf5hRm//faLHLfd53nmK1euwLhxBfu6JyWdoH//N9BoNISGlmXNmm/JyrqDs7OKhISjJCWdoHr1ymg0GoYM6cvduxfJn7GVnSKbvf3w4RW6dWuHTqflo4/+0N3q0qUNzZs3JL/7auTIgWi1Cn37duPx4wSioyMYM2YITZrUx2g0sGbNVxQVZPfz82HJkhkUFUxfuXIewcFBKIqGqKgw1GpnWrZsRFRUGCqVE2az0eam2rTpWyCZrl1bIyJERYWhKBqaNatvIxJ7e/u/+RdfDCgmkWIS+YchIogITk5ONG/enPXr12MymXB3d2fcuLGAhcaNG9OnT2+OHTuCVqtl06YNQCZz535OaGgoVlI5d+4UBoOBCRPGUq1aVSZOHIeVPA4f3k+tWjUxGAwMGNCPgAB/4uJi0WoV3nyzh40scg+tVsvVqxds29evX8bDw502bV639WMvXboU33wzDyt5ZGamsXDhbJvA35w5n9G7d3diY6vj4+NNpUoVuH37IoWRyIkTe2xNq776ajaKouGHHxZSGImsX/99ke6pdeuWotUqzJr1MdZ0XmdnZxISjtr2OXlyDy1bxqNWq6lSJYaDB7fY1gqTUjl0aCvh4dkuusmTP/j/2Dvv8KiqtW/vlCl775nJlPRCSE8gBUjoJcFQQxUEpcOJAkoVUQRFQECkS68iSBEB6UUxKE0pUgXpPYQAIYQQAoQwub8/ppiEcM5531c8er75Xde6yKysGSMu952n21OCd+5cj5eXJ5DFjh1r8fT0IDIyjKtXf7dciopu4+FhYsOGLykrDnLhwn6rC8kTjUZGrVZRpUoMOTlneB5AIJNevbrSqFE9/lVm1qZNi61ZVUqSkmoybtz7pKcfpEeP9tSrV405cz5BkkSGDetH3brVrc0WVXz11Uzc3LQIgoAkSTRu3PgPuPEOOSDigMgfqhEjRlhnnquRJInvv/8eWZZYvXoVsizxww9pjBo1kmrVqgJmZsyYjk6n4/Ll82zbthkfH2+Kx0kOHTqAVqvF39+Pf/yjG2fPnqB58xQkSeK119qTn58DFBAfH8/EiZ9w6dIpoqMrYDKZ2LhxNcUhYjDo7VMPbSsr6yq+vj68/HILnjy5i8lk4tChnRQWZvPll/Pw8fHGx8eL6dPHYwPLsGHvkJRUh4KCLGrVqo6npwdHj+6mNERWrvzcOuvD8vrrrxchSRJLljxbeNiv3xs0aJD4zL5t7dq1CY1GZsyYDzh6dCcGg56iojvs3LmR+vXrIkkSDRsmceXKsWfeu3PnRnx8vMr83E2bVlC+fAAeHiYWL57B8uVzCQwMoGfPrsiyxKhR71HatXX+vCWxwGzO5HktUYqKblKnTnXUahUeHiaOHUvjnwEEMtm06csyB1QVX+fO7cHX14uoqFDrMK7fpxqq1SpOnEgD0tm3bwMmkwGVylK7tGHDQsaNG4KbmxadToMgCI7akD9IDog4IPKHSxAElEolgYGBBAQEEBwczIIF8xg37hMMBgMbNqyzVq1bYiStW7ciKiqSEyeOIkkSpWtIdu3agVKpRKfTIYoijRs35NatdIq7tdq1a0vXrp2wZWdNmvQpWq2Gli2bcfPmJSAfT08P9u5No7SFkpOTgb+/H02bNsLV1ZV58z7Dz88XLy8PJk8eS2nX1tSp46hcOdb+un//3kiSxMqViygOkdGjh1G9ekKJvQ0bLFbF3LmTKf4wDw4uz7x5U3geRGzWg06nJS6uIt7ensTEVMDNTUenTu3IySm7KzBkM3/+VCpWjPynnz1r1gRMJiNqtSUAHxkZxqVLhygrbjJ79gRrxlXZAHny5Do9enRAkkQUCgVhZJJW6gAAIABJREFUYcFIkkhKSjInTvzI8yBy/76ltXxW1gnKAsjPP2/AzU1Lly5tycy0DMSyQeTDD/sTFRVK8fkiqamWsbfDhw/g/v3f0Ok0VKsWh0KhoFq1av+bq+1QGXJAxAGRP1x169ZFrVZbGycG4O7ubh07auall+qTkBCPUqkkOzsLMGM2F1K+fHlee609Tk5OFBY+Agp5+PA+S5cupmrVBFxcXFAoFDRrlsKDB3cpHRsZM2Yk1aolULzQMDs7g1q1aqLVali4cDZ+fr5s2fINNniYzXlcvXqG7ds38umnH6NWq+wjf8eO/QizOYeyAuxffWWzMH7fW7FiIRqNzODB/ewdfVNTO9O+fWtKWyhpaeuRZZnJk0cD2dy+fRalUsmjRxmU9YAvLLzFoUM7+OyzT6hWrQqiKKJSqYiKCi/h0nreevvtN2nc+KXnfv/UqZ/p168nOp0WUVTj4uJCdvY5npfB1ahREr17d6MsgNy9e5Zatari7e2Ji4sLL71Uh6ZNX+LWrZM0a2aJR7z8clNOn95NWSCpUiWG0aPfpTRAVq+ejySJjBr1DrZJh0qlgoyMQzx6dB6dTsuGDZ9js0pq1Yq3dw/Ozj7OmDGDCQ4uh7e3By4ujljIHykHRBwQ+cP15MkT+7CqqVOn4urqik6no6joKQUFj/D29kan07F7905s1khmZoa9R9b333/LG2+kIssS/v7+DBo0kMuXL+Dk5ERISDCBgeU4evQgxSGSlrbVWgn/bF+tr75agslkRKvV0qpVc1q2bEZISBAKhQJZlvHz8yUuLoakpLoIgoCHhzsajYaePbuzb18aRUX3KA6MH3/cbHWllITLyZMH8PR0Jzk5kdzcqzRpksygQX0oK16yd+82a8rwUFatWkRAgB+2h/qDB9dIS1vLRx+9a68rMRr1xMZWpEmTZOuERkvgXK1WUblyLHPmTCIr6xxlQaJBg0Tefbdvib3796+wYMFnREdHIUkiNWsm2LPB4uIq8vLLzSgLIE+f3kSSxDLni5w7t4+AAF8qV47h00+HExwcyPLlswkNDbKfycw8QaNGSYiimvbtW3L+/M8Uh8jIkYOtGVe/A2TSpOFIksiyZTNK7Fvmo8xl/vzxBAT4AukcOLARDw8ToaHlEUUVzs7O5OaeRKuVmTnzYyRJJDEx8Y+87v/fywERB0ReiAwGAyqVih49etCoUSNkWebkyV8xmwtZufIrJEmiatUEmjZtSv369alWrRqenp5IkoQkSSQm1mPv3l0Ud2u5ublx6tQxevd+A0mSmDJloj0FOD8/BxcXFwoKcikNkd9+O0K9enVwdnbG2dmZxMTaLFkyj/T0MxRP7y0quo9arebmzYv8+ONWkpOTcHPT4evrzYcfvsuFC0eBXM6dO2J1uz1rpTx4cIOYmAoEBgYQFhbC5MljeF5B4r5929FqNfj6ehMdHUWfPqlERoahUCjw9vaiZs0Ehg8fXKLvVmJibV55pSWyLPPrr3vIzb3MsGFvExwciEqlpHbt6ixZMovc3Mv29/j5+bB27ZcUFd1h9+7NvPrqy4iimoAAP4YPf8duAfXo0ZG6dWuQnW35zX7ZsjmUhsiBA99hMOgpDZAff1yLVquhQ4c2FBZm4unpzvz5kzh79mdrckHJ8+npR0lOtjQ/7NDhZS5dOgBksm/fZuvnW9J733yzKzqdlj171lHaOklMrMH7779FYKAf48cPY86ccdbC0D5UrRpH8+bJSJLI8OH9CQ0tz3vv9bbOjnfoj5QDIg6IvBCdO3cOQRCQZZlRo0YhyzJVqlTGzc0NvV6PRmMZR2obmzthwnjmzZuLu7s7arWasWNHU1T0hOIQCQ4OYtWqFUABO3Z8i7u7iaSkRHt8RKfTcvbsr9jgcfv2NVJTuyOKIi1bNiMlpTHh4aHIssSECWPKLDb08vJk165t9tdmcy6LFs2mUqVYRFFNbGw0U6Z8grOzE3fuXObcuSPs25fG5s2r+PLLeUydOo5hw97BYNAjSSIhIUFUrhxLeHgofn4+GI0GRNHiZnFyckKpVCCKajQamUaN6jNz5nju3r1AWRbFnj1b0Go15OWlU7duTfr0SS3x/Zs3T9O37+sEBPihUqlISWnAqlWLcHV14f33B+Dn54Ne70bz5o04cWJPiffm5FxCFNUcPvwDkM3SpXPQaORn6klGjRpCfHwsxYEwb94kJElkwoQRQBarV3+Op6cHtrnrarWKM2d+oiz316VLB6lbtzqiqKZbt3ZcunQAUVRz4MBmUlKS8fAwlRidW3z16tWF8PBg9HodHTq0QqfT8u23y9m0aTFubloOHdqKXq9DliWaNk1CkkQqVqz4Yi78/8f6W0FEEASjIAjfC4Jw3vqn4TnnzIIgHLOujf/OZzsg8sdLoVDYK9b1ej1OTk7MmTMLMHPrViYuLi7odDpOnTqJza3Vo0d3YmNjMBgMtG/fjkeP8rBBpE6d2nzwwfvYXFj5+TnUqlUDg8HA9u1b8PPzZevW9Tx6lMO4cR8jyzKVK8dx7twJ4BHDhw+lbt1a7N2bhtFooF27l8nPv0VxiEREhDF//nTKaomSn3+L4cPfQ693Q6lUWv/ddHh5eRIYGEBkZDjx8ZVITKxDzZrVrPEVDVOnfsKSJXPYvHkl+/d/z8WLR7l//xpFRXdZsGA6Hh7ueHq60759a548uUlZACkqukN8fBz/+EdnIIcdOzag1Wqe2/bk4sXDdOv2Gh4e7oiimvDwEObNm1KiC3DxNWnSx4SFBZfYa9Qoidq1q5VokVKlSiwjR74L3OLp0xv07/86Op2WrVtX2s/ExlawNnC0gCI+Po4xY54/IdFWrFizZoK9CFCS1Hh7e3Ly5A5yck6V2frks89GoVIpEQSBkJBAMjOPUlh4lcBAf4YPH8Du3Wtwc9OiVqvsQX6H/nj93SAyQRCE961fvy8IwvjnnHvwP/1sB0T+eGVnZ9tz8jdv3owsy3h6etpnrkdERBAUFISHhwfp6VcBM7t378TNTcft2zcICQkmNjbWPvmwf/++NGyYTOmg+oQJnyDLMjqdjjZtWuHl5Un58uX49tuNFHdrbd68Fm9vLyCf7Ox0QkNDCA8P5fLlk9hA0bhxMgMHvkVZEDlw4EfCwkLx8fHG09ODb75ZSlkuradP7xIdHUXXrq9hNBpYufJzynJnPX16h4AAPyZNGk1W1gUCAvxo0CCR/Px0Sj/kv/12NTqdtkRho4+PN6tXf/HMWdvKz0/Hz88Hb29PEhNrPxcgZnMW3t5ez2SHPXqUgYeHiUmTRgFZPHhwBaVSSWbmCe7fv0iDBvXw9vbkwoWD2ADy009b0Om0FBSkYwPEwIE9SU6uyz+DiG19/fV8lEoFLi4u6PU6NBoZpVKJk5MTCoUrOp0Wb29PwsKCKFfOD41GpnnzBpjN6UAGc+d+ipeXB2bzVTZs+Bw3Ny2yLKFWq+jatev//VI79Iz+bhA5KwiCj/VrH0EQzj7nnAMifxF16dIFpVKJm5sbr776Kq6urkRHR5Ofn8fYsWOIioqiadOmBAcHc/fuHcCMVqvlt9+OYzYX0KBBMu7u7hw6tJ9169ZY+1qVhMi9e7cZNGgArq6uyLJMp06vUVaA/d69m7i6uthnsJvNebRq1Rw3Nx07dmwG8nj//bepV682xeFx7951evbsgSRJ9OzZHbM5h+bNm/D6610pCyKzZ0/B09ODwsJsJk8ei6enR5lV7d9886W1xb0lmys/P4Pw8FASEiqRk3OJ4lZIZGQYAwe+WeL9vXp1JzGxNs+DSJ8+qQQHlyc/Px0PD3fGjRte5rnNm7/CaDSUCZm0tLVIkshvv+1l69av8PHx4sqVQ4SGBhEdHUl+/lWKu7tSUhrQtm0zSoMhMDCAfwWQRYumIUkiTk4CK1bMpnjA/enT62RmHufo0e/ZuHEJVarEoFQqEASBK1f2Axk8eHAeg8GNxYsnc/nyz4SHB6NWqwgKCsDSQ9ahF6G/G0TulXqd85xzTwVBOCQIwn5BEFr/O5/tgMiLk6VNiIL4+HgkScLd3Z2UlBQePnyAJEmcOXOKhIQE4uPjefjwARER4cycOQ2bG2vw4EFIksSiRQtxcXHh4cN72KrWO3fuiCiKhIaG8Npr7XB1tbjIkpPrc+bMcUqDRKPRcOnSbxSvE5k8eRySJDF+/Mds2rTKaq1YAu1ff70Eg0FPVFS4PbAOuaxcuchaYV4SILduXUCr1bBmzZf2vcDAAMaO/ZDiACgqukvFipHWFiu/7xcWZpGQUImwsGAyM08B2axduwSj0UBhYVaJs1lZF1CrVaSn/0rph//evVuRZYmzZw/YX1s62373zNm6dWvw+uudn9m3rS5d2hMVFUbv3t2JiAhFr9fRunXKM52AL1w4aB0OdYLicLh48QAajczz4FFQkM7rr3dCp9MyZcooayFjyd5atnXx4n6ioyPRaCSMRj2NGyfRtWs7IIOPPnqb0NDybN++HJ1Og0qlol69asiyyHvvvfdHXGWHytBfDiKCIKQJgnCyjNXqfwARX+ufwYIgXBEEIeQ553paYXOoXLlyf/hfrkMW/frrrygUCntfrfr16+Ph4cHAgQOoXLkyQ4e+T2FhAaGhoTRp0pjXX0+lceNGFA+qr1y5DI1Gg06nZdiwIURFRaLRaGjYMJlffz0EFFBYmI9arebUqWM0b56CKIq89VZPsrMzsEHEx8eb7ds3Urrg0BYnSUlpjIuLC6dPHyIpqS56vZ5ZsyZTGhaFhdmIopr09FMl9l99tQ3VqsWX2Nu+fT2yLHHr1jmK14q4uemeAYNtGmJyciI+Pl6cO3eQoKBAPvro3WfOQQ7R0VGMHDmE4g/9hw+v4+/vy3vv9Sux/957/fD29ixh5Zw+vQ9JEv9psaLZnEVAgB9OTk64uroyYsRgykr/7d27OzVrxlNW9bokiRw79sMz38vIOE5sbAXKlfPj6tUjfPLJMOLiKlAWQFasmI1GI9O4cRJarcyyZTNYu3YhXl7u3Lx5DEkSadeuGaKoRhAEa9cE0dHu/QXrLweRf/pD/JvurFLvWSwIwiv/6pzDEnmxiomJsY/QVavVfPfdNnQ6Ha1atcTb25uioqfk5eXi4+NDnTqWOSDFO/yeOHGU5s2b2acODhzYj4KCPEq7tsqXD2TJkoXAI06dOkpcXCw6nZZp0ybx5Ml9KlSIZM6caZTVoPHMmaN4eLgjyzIqlYomTRrw4MENnjfdMDQ0mMWL59hf79pl+e3/xo2zz5ytUiWO7t07Ynv416pVjR49OlEWGGyrWbOGqNWWGpGyYAM5fPHFTLy9PUu4ogYM6EVISBBlASE2tiLNmze2T1pMTe1ibz9feuXlXWXt2iV07twOjUZGpVJSqVI0GRknKA2Qu3fPI4pqDh3aTlnWRq1aVfnoo3dK7O3evQGDQU+DBvUoLMwAbhETE8WYMUMoDo/8/It06fIKWq2GZctmkpragUqVKgIZPH58CVmWSEysgVKpwGjUU6NGZVQqJc7OziiVCl5//fX/2+V16J/q7waRiaUC6xPKOGMQBEFl/drdmslV4V99tgMiL1ZmsxlnZ2dcXV1xcXGhS5cupKVtRxRFNBoN+/b9BJjJyEjHYLC0dt+/fy9LliwiLi4WWZZJSqpHp04dUCqV6PV6tm3bSGmIdOz4Gm3atKa4C+ubb77C19eHwMByREZGMGBAH27fvsK2besYNepDGjVKxmQyolKp8PX1sRYhSpQr58/UqeO4e/cKZUGkY8d2tG//MpBLQUEWQUGBDB7cr8yzFy4cRRRFTpz4iV9++QFZlsjLS6c4EO7du8KGDcvp2bM7AQF+qNUq1GoVWq0GT093RowYwrVrJyhttRiNen78cQOQzU8/bUOSRM6c2U9ZYMjJuYjBoGfu3Cnk5l5GksQSzRovXz7K9OnjqFWrGkqlEl9fb15+uTlxcdEkJdWmdu3qyLLExIkjKSzMpPjY3IiI57dCeffdPtbW9RbLZOpUS+Hf6NFD7Gdu3TqJSqUkN/csNoCcPLmToKAAQkICycg4ysGD25BlqUTab+fObVEoXAkPD2blytnIsoSLiwsqlRKtVvvHX2aHSujvBhGTIAg7rGDYIQiC0bqfIAjCQuvXtQRBOCEIwnHrn6n/zmc7IPLitWjRIkRRxMPDA7VaTWZmBrNmzcDV1ZXU1H+Ql5fLnj27GDCgP5JkeRD4+voydOgQe6pvfn4uoigyePDbyLJMv35v8fjxfYpXrluaEz6k9Kz14cOHolQqrcOylPj4eFO9elX693+LHTu2YjbnAfm0bduKrl07MHPmJMLDQ1GrVbz6ahv2799Rono9LW2D9Z91j3HjRuDv7/fcVimQS9u2LalXrxbNmzemdetmFBTcYteuzQwdOojo6CiUSgV+fj40aZLMl1/OpaDgFnq9ZV77ihULiI2NRq1WU69ebb755kuePLkN5NCqVQpt2jTn4cPrBAT4MXhwH57nmoJstmyxFHv26tWdkJDy7N27lcGD+xAY6I8oqomICGXw4D72WMvZs5bajevXfwWy2LJlBV5eHgQHB7JnzyYKCjIwGPSsXDmf50Fk7dovCAz0Jz//Mu3atbCCb22JM4sWfUb58gFApn3+iCSJdO/+GmZzBk+fXqdixQhef70DNoCsWDELWRaRJJG7d3/DaNTTunUTtFpHk8U/S38riLzI5YDInyMXFxf74KquXbswa9ZMPDzc7VaKu7s7sbGxxMTEoFaradSoIffu3aF4fCQ+vgpDh77HuXMnCQwMJCIinNOnjwMFmM2W4PmpU0cpDpHc3Fu0aGHp/uvs7IwkScya9ZkdHMXXihVfWNuQWLKzTp36hZSUxuh0OsLCQpgzZyr371/HbM5Bq9Xw7bffIEkSO3Zs5HkAefLkDidP7i/WGj0OlcrS4bZGjQTGjx9FdvZFSgfOXV1d7bCw7fXq1R1PTw90Oi0DBvRmy5avUatVpKZ2JiSkPKXjGbdvn+XEib2kpa1l+fJ5TJ48mqCgcgiCgJOTE0ajgdq1q7NgwVQKC29RGjodO7blpZfqUtx9ZTbfYsCAnsiyRHx8HEajnrS01ezdu4lDh7Zz8uQuLl48QEbGcbKzz3DmzE9IkkhoaBChoUFkZZ2iNGgaNkykV6/O5Oaeo3Xrpri56di0aQk2q2TWrHF4errz9Ok1Hj++RM+enZAkEZVKyfjxw2jfvgVxcRWoX78WSqWSvXv3vriL7JBdDog4IPKnKisrC43GkjkjyzI+Pj506dIJNzc3tFqt3a0FZnx8fDAY9Pj5+XLs2CFsEFm2bDGenh6YzY8wmx/RocOryLLEvHmzKSp6TGRkBDNmTMEGkMOHf8bX14eYmGju3r2Bu7uJDz8cgtFopGrVeM6f/5XiECkoyEGpVJKVdZniqb6FhTmMGzeK4ODy1t+QOxEQ4IdOpyUxsQ5nzx5m+/Z1LFgwnaFD3+GVV1pRqVIsJpMRFxdnNBoNkiSiVCrQaGS+/rpk19/Sa/HiWdbYRtnf37p1NVWrWhoy2moh6tWrSZ061QkJCcLNTYezszNqtQq93g0/Px/Cw0OIj48jOjoKV1cXDAY3Tp/ex/OslsuXLd1yy+roe/78AZKT66FSKdHpNPj7++Lt7YmHhwmDQY9O93uNhs2NqVAoGD36fY4f/4GiopvYAPLw4RVUKhWrVs3D19eLmJgosrNPYQPI7dsn0Go1rF49j8uX9xMdHYFWq7E3jFy6dDparcyuXd+gUilJSEh4cZfYoRJyQMQBkT9dI0aMsLu1JEli+/ZvOXBgn3WUrMSGDesAM599NhUfHx969bL8xrto0UKgELO5AL3ejd27d1B83rrBYKBFi2b06NGVl15KoqjoIdOmTUKSJAYM6IMNKomJdRg4sA8FBTm0bNnMmt47hqdP72MDia+vD+vWraCsokPI4/DhPVSsGIVC4WovhtPptPj6+lCxYiRJSXVJTe3C1KmfsGvXFvLzM4FcIiPDmTJlHO3atUajkalduzq7dm2mLEh069bBGnN59ntmcza7dm2mW7ffW64LgkDTpg0YOfJ9li6dy8GDO56Ju9hWx46v0LRpA3r06IRWq2Hnzo2UBZHU1M7WwPvv8MjIOEFqaidEUU1yciKVKsVYq9ifzdh68OAKXbq0R5YltFoNo0cPoXLlGHQ6LSaTge7dX2Xjxi9ZtWoBbm5aJElk0KBelM7M6tSpDfHxsWzc+AVarYakpJpotTKvvtoKLy8P9HodnTu3QaORcHJyegG31qHnyQERB0T+I4qIiEClUtmHV23f/i1JSYl4e3sjSRKzZ1vao3h5ebJ06WLWr1+DTqejR49uPHqUR5MmjenUqQPFg+o5ObeIj6+MKIqIokizZk0xGo2kpW2luGtr0aK51vngFmCkpW3Gy8uL2NhoTp78BcgnOTmJfv16UxoeBQXZLF/+ObGx0dZ+YHH2dNJBg/r+02wuyMXd3cS+fWlALnl5GXTt2gGdTkt8fCW2b19LUdFdbA/6KlXimDRpNMUf/qdPH2DIkIF4eLij17vRtGkD0tLWo1aradasMYGBAdy/f43nWS+Qw8OHN5AkkcOHdwI5jB8/CkkSWbx4FsUBcv36CURRzalTP2HLwHr77d5Ikkj16vH2GpQKFSKYP38KpQFy+HAaAQF+hIUF07Nn1xLpv2ZzJps2LaVZswZ4e3vY04dnzvyE0gD56aeNyLJI585t0WgkZs0aR3x8LA0a1KVbN8v4AFmWEEXLLJScnJw/+ro69E/kgIgDIv8x2ZoQ2mIUK1euQJZlJkz4FK1Wy9Ch7/PJJ2MJCAjAbC4gPf0ywcFBREZGsHbtKiRJshce2tb5879RsWKUtf+SyJIlC57p7FtYmIcoily+fAobSAoLc+nYsT2SJPLRR0OZNOkTIiPDscEjPf0MQ4e+g5ubDh8fb959dwCPHmUBeeh0WlavXkJISBCenu5s2PAVZQGksDAbhcKV3Nz0EvuPHt3izTdT0evdiI6OYuPGFRQV3cXb25Pvv1/HzZtnmTrV8vPIskT16vF8/fUie6X7okUzKV++HJBDTEwFmjVrVAJGpdeKFQusMZ/iw7KWo9Fo+PDDd+zpv337vk7VqpXJz7/K6NHvo9HIREdHceDA79lckI2vrzdbt35F8XjJhAkjkCTR2iQyi9DQYGbM+ISyuv+aTAZcXV2Jja2ARiMRF1eBNWsW8PTpdQoL0wkNDcLJyQkfH0/OnNnD0KH98fJyp6DgKp6e7qjVKkRRjVqtYuzYsS/svjpUthwQcUDkP6b8/HycnJxwcXFBrVYjyxK1a9eiQoUoTpw4jslkolOnjhiNRlat+gqbK6tVq5bodFr0ej0rVy7j4cN7LFu2mISEeERRJCGhCrVq1UCSRLy8PNFqNbz1Vi+OHt2PDSQREeHMmjWV0kH1/ft34ufnS0CAPwqFgi1b1pCS0gi1Wk2VKnFs2rSK0tZJeHgoc+ZMAXKZMOFjtFotDRvW5+rVkxSHxY4dGzGZDDzPSikszGbw4H4YDHqCg8ujUqmIi4u2D6D69NMRFBTcojQUqlePZ/DgvkAOublXcXc3MXr0B8+cs606dWrQt+/rz+yfOPETJpORtm1bcO3ar4iimv7930CvdyMoKJCtW7+mLJeXRiNz8uQeIIvMzJPUrVsDDw8Tu3dvBLK4fv1X1GoVjx5dxQaPwsIMhgzphySJDB7cB5VKSUFBOo8eXWXQoN64uxvx9HSnbdtmyLJEUlItCgvT+fHHb5AkkUOHvmXTpi+tKeISCoUrHh4eL+SeOvTP5YCIAyL/UaWlpdl7XqWkNLUGiWUWL/6CzEzL2FpRFAkODi5RfDht2lT73A1ZlggI8GfQoAHcv38HKCA3NwtZljh6dD87dmyjXr06aLUawsJCmTp1Aj16dCUxsQ7FZ63v3r2d+fNn0rdvbzvUNBqZFi2akpFxjufFR7p370TLlk2xwSA3N53k5CQkSWLcuJE8eXIHyOWDDwZTq1Z1ygJIVtYl1qz5kl69/kFgYAAuLpaAuELhytKl855rWVy7dgK1Wk1u7lX73i+//IAkiWzbtvqZ8xkZp1CrVWRlXSjz87KyLlCunB9arSX5wd3dyJdfPjsTvnhfL2dnJ/Lzr7J583Lc3HQkJdXm0aN0bJbJ/PlTCAkJxAaQa9eOUKVKLD4+Xhw/vpPVqz+nXDk/ilsoT5/eIDGxFiqVCmdnJypXjmbixOEYjXrc3Y1IkmhtbaLEYNA7emP9B+WAiAMi/3F17NgRlUqFRqNhxIiPcHV1xWg08uDBffLz8wgLC0Oj0bBgwVwWLpxHkyaNEUURg8GAUml5iGzevI7ShYcpKU1p2bIZxd1YEyZ8QkREmL2fV0xMRXs1tqenBxUrRtG0aSM+/HAINWtWsxb7aZkxYxKFhTmUBZG0tI0YjYZnJiCmpa3Hz8+HkJAg9u79jsaNk+nXrxeQS3b2ZdauXcabb75utTqUBAYGkJLSkMWLZzN69HCioyvw7rv90evdqFw5lj17tlL6oT927HBiYio8sz9z5gS0Wg0XLx4tsT9u3EfWeevPAiQvL53Jk8diMhlRKpXIsowsS6hUSipUiKBjx1eYOHEUW7d+zdWrxykqukNu7mUUCgU9e3ZFliVmzBhH6dhI/fp1ePPNbsAt1q9fjFaroWnTZHuxYu/e3Wna9CWKTz+sUSMeWZasbVrO8s47byKKFrB37dqO8PBgVCoVSqUCV1dXjhw58uIuqEP/VA6IOCDyl5BWq0WtVpOYmMisWTOshYR9WbFiGd26dbMWCKrw9PSgV683OHnyOFBIv359cHZ2trqQGnDx4mlsEMnIuIwoipw/f5LiMZGiooc0b97UnnKakFCFc+eOU9q1lZFxAbVazezZU/Hx8aJ8+UC++249pSFiNuciSRKXLh2ntIVhNucwYEBvZFnCYNBTtWoVQkKCUCqV+Pv70aTOgolIAAAgAElEQVRJAxYunMnDhzdLvK9q1Sp88MFgIJfHj2/zj390RqORSUqqw7FjuwFLE8fAwABmzpxAWVBo164VYWEhPHhwvcT5GTPGlzh38+ZZhgwZiCzLlC9fjkWLZhIcXJ7ly+cB2Vy6dITZsyfSqVM74uPj8Pf3tcJFRWhoEKIoYjTq+fXX3ZQGyKNH6ahUKk6c2EXPnl3QaGTmzZtc4kxQUDkWLpwC3GLHjjUYDG7UrVsDX18vJk8eSW7uBeLiKqJSqfjll2/p1KkNer3OGgdR07p16xd2Lx3613JAxAGRv4SePn1qb9KoVFoGDdmsjZYtW7B06ZfW8bki3bt34/79u9hiJF5eXowf/wlNmjRCkiTef/9de8C9bt06dOvWmeIQGTx4ICaTiRUrFqNUKqhduyaiKNKjRxcyMy9SHCQxMdGMGjUMszmXoUPfQavV0KBBEmfOHKY4SMLCQkr00Sq+Dh3aSVxctD0VuGPHdvaU37LWvXvXUCqV3Lp1ocR+bm46L7/cAkkSad26GatWWdJdnz69w/PSgCMjw2jTpgVFRXf55Zcf0Om09oD82bO/0L17R9RqNXFx0aSlrbe/19/fl40bl/M8N9bNm6dJTk5EqVTi6uqKj48XSqWSatWqMGnSKM6c2UdR0W22bVuJ0agnLCyY4OBArlw5QnGAZGefQ6lUkJd3kWHDBiLLEuPHf8jmzcswGPTk5l6gUqVo65TI8rz3Xh8MBje6dn0FtVpF27ZtX9SVdOjflAMiDoj8ZWQbqStJEu3bt6dDh9eQJIkWLVqQm5vDmTOnEEURd3cTXl6epKV9BxSyZs1KNBoNd+7cYP/+3QQHB+Hl5cm6das4deo4oqjmxo1LwCOmTZuETqe1t4mPiAhnyJB3OHPmKAkJVZAkkffee5t7925gq153dzfx9Ok9II/c3AyaN7fEbvr27cXdu9eAPNq1e5nOnV+l+EP/8uVfadOmJZIk0qFDO/z8fOnRozNubjpatWr2DCRsa/XqJdYU5LIhc+3abwQFBaJUKtFoZDp3bs+ECaNYv345p07t5/Hjm9hgkJ19EaPRwPjxI+nZszv169fl55+/o2nThoiimsTE2pw8uY/SAPLwcGfXrk2UhseTJzeZONHSrr1q1cpUqRLLm2/2ALLJzDzFsGFvW7OsZLy9PYmMDMPFxYXq1ePJyPiVoqLbFIfIhg1L8fR0p0aNeLy8PDh6dAdwi6pVK9Gjx2tUrVqJyMhQ3Nx0vPJKM+sQKsvPHhoa+oJvpEP/jhwQcUDkL6Xr169b8/5lateuRXS0JTvJz8+PY8eOMGrUSDw83Bky5F1kWSY1tQf379+lUqU4q8Xx+7RDvd6NpKR6BAcHMXBgX1atWo4sS+za9T02q2Tv3h1IksStW5extYSPiopAp9MyceInPHqUjbu7ic2bV1Pc8jh58iAVKkSi1WqZPn0iK1cutg7MssQ7+vbtaX1I1yEz8wKQR0CAH999t5bs7MvUrFkNnU7HsmULnomldOjQjrZtW1IaHlevnmTo0EEYDAY8PNwxGo3UqlWdjh1fIT6+EoGBAej1bri6uuDl5UndujV5881UevbsZk+B9fHxQqvV8MorLUu0pi+93Nx0HD26k+IA2b59DYGBAfj6erNly1fcv38FlUrJlSvHKA2bGzd+IzQ0CIVCgdFowNvbE1G0VOsHBZXjpZfq0r//GyQn18PJyYn69WvbpyEeOZKGLEtUqRJDREQIixZ9Zq9Ot1irIkFBQS/+Mjr0b8kBEQdE/nK6deuWvYCvXLly6PV6e3X7nDmziYmJpk2bl7ly5QIVKkTh5eXFkiWLkCSJw4f3U3wGe/PmzVAoFIiiiCRJrFixmNKDqqpUqUSfPr0o7sZau/YrypULwMPDnejoCtSvX4+ygupff70ELy9PypXzR6VSMWzYO2g0MhUrRnHs2M8lzvr7+/Htt99gg8LixbPR691o0KA+GRlnsMVQ3Nx0/PDDJmxpvxs3riQpqQ5qtZpKlWJZs8Yylrdbt4507NiO0rDJz8/k22/XMnz4e7Ro0RQvL08kSbJODXSia9dXWb16MXfulOzVVXxZ6miOYouJNG3aAK1Ww7Bhb9vbzn/1la3epCRAVq/+Ap1OS0REKFqtpsTwqvT046xYMZdXX22Ns7Mzoiji7OzMu+/2ISfnHHCLNm2a4ezsTFhYEAUF6YSElLfGr1xxdXXB29v7hd09h/7nckDEAZG/pGzz2V1cXHBxcUEURd55ZxB6vZ7GjRuh0Wj46qvlQCEjR36ELMu4ublRqVIcRUWPKSp6zJEjBxg8+G17FpdSqbQOxUpk7NiR7Nixjfv3b3P8+EFEUeTatbPYIFJU9IArV07TufNr9gyl5OQkqldPICamAmFhIfj7+2IyWdJNBUFAo5HRajVs2LCSsoDj5+fLtm2/Q8QW56hXrxYajcyCBdM5ePAH3Nx0XLv2Gx98MBiTyYinpwc9enQmK+tiifeOGfMhtWpV43lur4MHf6B69QR0Oi0vv9wck8nIypWf06JFEwIC/FCplISFBdubOBZvkeLq6sr16yf54INBSJJIgwaJzwyuSklpSNeur9lfZ2df4OWXm6HVali4cBrDhr1NQkIliruvbt06ZW+Z4uzsTJMmyezf/y2RkWFoNDIffDAQtVqFp6c733+/iunTx1rnrCusPbp0f8b1c+h/IAdEHBD5y+ru3bs4OzvbYaLRaPj5571UqFABQRDQarVcv34FKOTy5fNERkYgyzJt2rTGx8cbnU5LzZrVWbLkc65fv2x9SA3h7bf7ER9fBR8fbxQKBUFB5XFz01G3bi1effUVIiMj7A0i/fx8qVw5zl60OGbMcGbNmsyyZQvZsmUNP/30PadPH6Jz59fw9fXBx8eb2rVrkJOTTmmIlCsXwNatayjrgf/1119gMOgxGg1IkoharaJSpRi+/vqLMs9DLmvXLiMg4NnYyenTv9CsWWPrvPn2PHx4k4MHf8Dd3URxayM/P4O5c6eQnJyIn58PSqWCmJgKDBs2CEEQMJmMBAeXZ//+khXqtumJarWKU6cszRu3bFmJ0WggIaESWVnngGzKly/HnDkTgSwePrzGmDFDkWWJypVjSE3tjI+PV4mZJB99NNj+767Xu9mbOP5eM6N44XfOof+5HBBxQOQvrdzcXFxdXREEAYVCQfnygeTl5ZKa2gOlUkmtWjXZsWM7PXu+gbu7CVdXV1QqFUajkW3bNlJU9Bibe2vx4oVoNBquXDmDzZWVn5/N0qWfExBgcUcJgkBkZAQ7dmyluHursDAXb28vxo79iNJwWLt2ORqNzKVLv/LoURbx8ZUJDCzH+fPHSpwLDAxgy5bVlAWEU6cOUrduTVxcXFAqFSgUrkRHV2Dw4H5s3brmmVYpkMuVK5ZKcNvr9PRTdOnyGqIokpLSqITlcvjwLkwmI/+sp9bt2+dp0aKJvRGmUqlk4MDenDixl9IQWbfuS3x9vbl//wpdu76GVqth8uTR9u9fuHAISRJ5/Pg6y5bNwcPDRFBQObZvX8W+fZbBWb/88j2QxY0bJ2jdOsXe1v3atWPMmzcZURTtg7lcXBwjbv+qckDEAZG/vHJyclCpVHh5eSFJEg0bNmTEiI/w9/e3z12Pi4tjw4a1mM0FvPVWb6uloiE6uiJbtqy3wyQlpQlVqlSisDAPG0guXPgNURT54IMhuLi4EBoajCiK1K1bm82bv7HPHPn5Z0sl+JEje7GB4dKlE2g0GhYtmk1xYHTo0A6dTsfOndvsewEB/s9AJCvrEm+80R1RFGnZMoXLl39Fo5HZuHElkyaNpl69Wnh7e6FUKoiICKNfv16sW7ecrKxLmM05KBQKrlw5wcCBbyGKIrVq1SizXuXo0T3PWCLFU4HXrLH0/jIY9Hh6utO48UusW7eUmjWrotHIhIeHMHnyaDIzTwHZtG3bksqVY/Dy8iA6OtI+wMq2Jk4cha+vNxUqRGA0GuxFiPfvX8bHx4v33uvLkyc3mDhxpH0miU6n4eOPhzBgQE97IN3SNl/z51w0h/5XckDEAZG/hW7fvo0kSWg0GmRZxtXVlY4dO7B+/Tf2rr3du3fl5s3rQCEvvVSfyMgI3nqrNwaDnsjICDZsWMOTJw/w8fHmgw+GYCs8TEqqR0pKE+ARb77ZE29vL86fP0FqajdMJiNeXp58+ulosrPT6dkzlfLly/HoURYFBdlUqBBJq1bNKCsG8umnlu64CxfOwhZY37x5FbYCwvHjR6HRWDoBnz17GNsD/803U6lYMarElMTc3HTmzJlCo0YvWYP4SsqVC7DPZomICOPw4V2UZeVALseP/4S7e0lLxGzOZtWqLwgOLo/RaGD48MFcvforarWaK1eO288VFNxiwoRRREWFo1arqFOnBqIoolKpiImpwKhR7zNo0Fu88UZXOnZsS0pKQ4xGAyqVir59U0u4rNq3b0VkZBi7dm0gOLi8tXnjSlJTOxESUp7k5HoYjQYaNaqPLEvUqFHjT7phDv1v5YCIAyJ/GxUUFNgD7UqlElFUM2jQQPbs2YksW4LakiQxcuRH5OXlEBISQtOmTXjy5AHvvmtJjQ0PD2PMmFFIksSePWmsXr0cvd6N/PxsbJZJ1arx1KxZjcLCXIqKHvD553MIDw9DrVbTsWN7PDzc6dOnF2+99YZ1JG4uz+urtWXLGjQaDQMGvIW/vx+bNn3NN98sxcfHu0zLxJaR5eHhzpIlc5/53tOnd9m27RuSkurh6uqKs7MzRqMlcSAsLIS33+7Dd9+tfaaY8eTJ/XZ31tOnd1i58nOCggJxdzcxYsQQewFiv369qFw5lrIslnPnDvHqqy/j5OSEQqEgKiqc+PhK1K1bgyZNkmnbtiUtWzbF2dkZg0GPKKp5440u5OVdBrJYsWIesizRsGESGo3MoEFvYjbfYufO9UiSiIeHCZVKhUpl+W/brVu3P+VeOfR/kwMiDoj87ZSQkGD1l6sRRREfHx8++WQMsizTp8+bBAcHYTQamT79M9zdTQwaNADb6Nxhw97DZDLi7OyMp6eH9dxkiqf8FhTk4uvrQ9++vSkeFzl16jANGryEJInWlGGR1NRufPzxh4wbN5JJk8YybdoEZs+eyoIFM1i8eC7Ll3/OxIlj0Wq1uLnp8PLyRKfTMnz4e8/UhxRfCxZMx2g02OeTZGScYdSooXh6uuPubqJjx3akp5/CxcWFnJyrPHhwg1mzJlO/fl1r9biCqlWrMGrUMH7++Xt+/fVnDAY9X321kMBAS+ryqFFD7fCAHO7du4IkSezdu82+V1R0l127NtOgQRKiqKZ27RrMmjURLy9PSkPm0KEfMRoNNGvWCLM5i0uXjhAWFoK3tycrVsxDo5FxdnamZs2qZGaeBLLIz7+Kj48XgiBYU37VKBSubNq06U+8UQ79X/TvQsTJcva/VwkJCRw6dOg//WM49G9q2rRpwpAhQwRBEISCggJBkiShfPlA4fLlK8LixYuE3Nx7wgcffCQUFRUJjx49FKZNmyK8/vo/BEEQhMuXLwstW7YVLl68JACCyWQUAgL8hdDQECE8PEwIDCwnCIIg9OkzQJg8+VMhLCxE2Llzj/D99z8IR44cEyRJFPLyHtj/54iNjRbUapVQWPhUKCwsFKBIAEEwm82C2VwkFBWZhadPzUJm5k1BEARBoXAVnjx5IhQVIbi5aQWTySR4e3sKPj4+go+Pl+Dn5yN4enoIQ4Z8JNSvX0+4ezdH2LVrrxAaGiIMGTJA6Nz5NUEQBOH69QwhMjJBePAg85m/n5s3bwnz5y8WNm/+Vjh//qKQn/9QUChcBVdXV6Fv3zeE0aM/EJydnUu8Z8KEacLChUuFc+cOCYWFhcKaNRuE0aMnCTduZApNmzYQZsyYILi7m4TVq9cL7703Qrh8+bj9vRs2bBU6dnxD6NPnH8KECaPs+1evpgstWnQUzp+/KBQVIXh4mIRGjeoLkZGhQnBwoLB583Zh9eqN1r8ry9/TlStXhMDAwD/wtjj0IuXk5HQYSPiXB/8d0vydl8MS+fvpwoULCIKASqXCZDIRERFu77m1ZctGzOYCBg8ehCzLiKLIqFEfUblyJURRTVxcLLNnTyc0NAR3dxNDhrxDhw7tqVmzOqGhIXh7W4L4arUag8FA1arxDBv2nr1RY3x8ZYYPH0qtWtXRajXMnz+DoqL7PM+t9eDBTRQKBZ07W+bBz58/gzt3rvDTT9+zZMk8Ro4cRmpqV5o2bUhCQhWiosKtM8otHYZXr/7yGctlz55v8fb2oixL5t69ayxaNIvq1RPsLiI3N8ucdUvNSyJLl87l3r0r2OIeJpORuXOn8OmnIzCZjHh7e/Hhh+9QWJhFcYtj1qyJREdbOgcXFd1l/PiRSJLE4sUzgWzy8q7yxRczqFatCmq1GpVKSfnyAWzYsIyRI4fQrl0rfH190Go1aDQyrq4u9rqRgoKCP/UOOfR/l+BwZzkg8ndWYWEhSqXSOvvCnVGjRqLRaJAkkTVrvmbGjM+oVCkOJycnNBoNSqWS6dOnkJeXDRRQWJhPxYoViI2NJicnk+JurXbt2hIZGYEkSUyfPonirq1KlWKZOnU8kM/KlYsxmUxUr16Vc+eOUhZEduzYbHUB5bFx4yr0ejfat29DXl7mM2cLCrJp3bo5Hh7unDr1C127dkSn01K5cixbt66xw2Tp0vlERIRiA8fjx7dZt245zZo1QqVSWWes9GH69Ano9W7k5WVga5/Sq1cPAgMDUKmU1K9fl7feSrVmRImEhgaxdOlcnpcKPGLEEOrUqcmTJ7fp3r0jbm469u7dSlraWtq2bWHtNOBP//49qVIllvDwEAoLbwHZ7N69mapVKyNJlkFSFuirHSm8f2M5IOKAyH+FKlWqZC9I9Pf3RxAEZFlGkiQ6dnyN27dvMG/ebJRKhTUAL9KtWxcOHvwJs/kR8fFViIyMICsrHXiE2ZyPyWTk+++38OOP36HVannnnf4UFT0A8omNjWHatInYoPL48V1atWpmtXiGUVCQTXEwDB8+hGrVEuyvb9++REREOOXK+XPixAH7fl5eJnXq1MTf34/s7Kv2/ceP79C3by+MRgMREaGsXr2EkSOHUqNGVXbt2kr37p3QaGR8fLzo1Kk9Fy4cBXK5desCWq22zCD9jRuWFvAuLs5Wi8AVtVpN3bo1GTJkIGvWLOHixaPPDMTq2bMbKSmNqFOnBgaDntTUTphMRkwmI61apXDy5D4eP75JvXq1CA4OpKAgkz17tlCjRgKSJOHk5GQvIHV2diYxMfHPvCoO/cFyQMQBkf8ade3a1f6brb+/P716vWEPviclJbJz5w5++OF7tFotzZunkJxcH61WS0hIMNOmTaFq1XiCg4PIzLzMokVz8fb2wmzOBx5x+vQxjEYj7dq14cmTe8TEVGDmzCmUnkGyZ8/3+Pn5Wiu9f8AGgapVqzB8+BBKWx2vv94NSZJYsGAmWVmXqVgxigoVIuzz2x89yuLatdMcObKX775bz5Il8+yDtGwz6vV6Nxo3Tmbv3u8oDYrWrZtTo0aC/fXdu1dYuHAG1arFo1KpCAsLISioPCEhQZjNOezfn8awYe+QlFSHoKBANBqLKzA+vhL9+/di2bJ51KpVDRcXZ3sWVXx8HKtXf4ENMk+e3KZBgyTKlfMnLW0dtWtXt7utZFkiMjIMWbbAJCcn50+9Iw798XJAxAGR/yqZzWYCAwNRKBTIskxkZCRubm7W3lYaoqKimDjxU9zd3WnePIW8vGzGj/+E4OBg1Gq1fVhUSEgwY8aMpLh7KysrnYAAf+rVq0NkZARz5kyjNEQgH7M5j759eyNJIj179iA7+yoqlZKLF3/FBo+nT+9x7dppdu3axj/+0QVJkqzxD0vNh6enh3U0rDOyLGE0GvDz8yE8PJSYmIooFApcXFzw8vJApVJSo0ZVPv98Jjk5V7EBY8OGr9DptFy7doqvv/6Chg3ro1KpCAwMYNCgvmRnX2bPnm+RZcluuZReZnMO69evoF69Wjg7O1vrdCRcXV0JCSnP4cM/UtxKKSzMonnzxri56UhIqIRGI5OcnIivrzeiqEalUiGKIr169fpT74VDL07/LkQc2VkO/a107NgxoXLlyoJCoRBcXFyEwsJCQZIkoV69usLBg78IT58+FR4/fixERIQLaWnbBJPJJJw9e07o3buPsG/fAcFsNguBgeUEb28vQa/XCyaTUXB3NwkajVaYNm2mUFj4ROjY8VWhfv16AiAUFRXZl+U1wrVr14Rp02YLRUUIzs7OQps2LYUzZ84KV65cE+7cuSOoVGpBp9MKOp1WMJvNwpUrVwVBcBK8vDyFDz98V2jWrIng5+dbIovqwYMHQosW7YWzZ88Jhw7tEXx9fYQ7d+4In3wyWVi/frNw40amkJRUR+jatYPQr9+7giiKQnb2XcFo1AtNmzYUPvpoiFCuXIAgCILw8OFDISIiXujUqb3w6aeWjKr79+8LBw4cEvbu3S/88MNu4ciRY4Krq6vg4eEuuLnphGPHTghvvpkq1KpVTZgyZZZw+vQ5wcfHS+jZs5vw2mtthLff/kD49ts0wcnJSWjdurlQpUqsMHz4WOHhw0eCJImCQqEQsrPvCi4uLv+Ja+HQC5AjO8thifxXKzU1FbVaXaIb8JgxHzNv3mzKlQtAqVTi5+fH8uVLSE5+CbVaTXR0RerVq4NSqSQ0NIRevV7ntdfa0bhxA2rUqEZ0dAWUSiVarRa93o3Q0GDCwkIJDw8jMjKcqKgIKlSIJCamIhUrRqFQKHB1tYzi7dOnJ1u2rLEPs7Kt0aOHk5BQhfT0MzRp0gBJEklOTirhEsvMvGD//Pz8W0Ae9+/f4MCBH1m8eC7vvNOPypVj7S1fNBoZQRAICPCja9cOTJw4mg0bvuL06V8oKMiif//e+Pp6s2jRLLp160j58uVQKBR4eXlSrVo877//NidO7ANy2bhxJZIkMm7cCIpbKgUFWQwY8Ka1064SWZZo3741GRmnaNmyKZIkIYpqBEFg3bp1/6Fb4NCLlOBwZzkg8t+u3Nxcu6vK5uZq1Kgh69d/Q+XKlXB1dUWn0+Hk5ET//n04evQgRUWPOXr0IL6+vkRHV+TcuRMUb9qoVCpZtGg+7u4m4uMrc/r0Ecpya6WkNCYkJJh7926QnJyEJIl8/PEHzwTeGzSoT79+/6+9ew+Pqr7zOP7+zmSumcn9QkJCI3LHEMWWIiIXwTuKPLBP7boq7eKtaxW34FbE1VbFay2CUBDqVquArjdQIxYMtc8+AtZatCjUoqASIpCAAUlIMjPf/WMmEWiAccDMRL+v55mHc2bOnHz4nWS+c87vnPO7pm2+ru5jnTDhYg0EAjpkyPf1ySd/qwUF+VpQkK8/+cmVevrpgzUnJ0ddrjTNy8vVHj1O1FGjRuhNN03WM88cobm5Obpr1ye6du0qvf/+O/WSS6IDVxUWFmggEFCn06kej0f9fp+Wlpbo+PFj9bHH5rU7bO+jj85Vv9+njz46R1sPca1evVJ/9rOfaklJ19htZ7zau3dPdbtd+tBD92hRUWHbLfIrKio6fqObDmNFxIrIt8bDDz+sfr+/bcCrjIwMdbvdevfdd+jTTy/SjIxg7Nt0uubk5OjEiZfr0qXP6IUXXqDp6ek6f/4cjUQadP782dq9+wnaenX7hAnj1O/36a23/lybmnZraxH5+c9/prm5Obp7d3Xbc6+//qqWlpZot26l+tprL2lr0cjLy9WVK5e1zUcie/Tdd9fo9On/pWlpaRoMBtXni54k0K1biU6dOllff/0VbWnZrQcWowULHtZgMNA2BvzOnZt1yZLf6aWX/kDz8nI1Pd2vpaXRs9dGjRquvXv3VK/Xo+PGjdGqqhf/6VqUe+6JDoX73HNPaGXlMzpx4qWamZmhWVmZWlJSrIAWFxfpa6+9qC+99LSWlXVTt9utDodDXa40Xbt2bcdvaNOhrIhYEflWCYVCOnLkyLZi4nK5NBgMakZGhl555Y916NAh6vN5dcSI4XrWWaO1sLBAPR6PdunSRf1+v55zzlk6ZMjg2EiIX3a6r179Ry0p6ardu5fp6tWrdNGi/9FAID12+u7BeyiRyBc6bVp0eN/x48fqO++sVo/Ho/v2bdfKymd10qQrNC8vV4PBgFZUlOudd94Wu2nkVB037iLt2rVY3W63DhxYoXfddZuuW/eGRiJ7tKrqZfX7fTp9+k06Zcr12rNnj7YTBS6+eIwuXfqUNjbu1IqKch09eqR+eSfid3X8+LGak5OtxcVddMaM/9bPPvuH3nDDter3+/Wkk/qqz+fVLl0K9YILztEnn1ygY8dGxzu/7LIf6PXXX6OZmRkaDAbV6XSqCHr66acnbRubjhVvEbGOdfONM3nyZObMmUMoFMLn89Hc3IzX6yUSiQCQlZXF44//lu7dT+DXv55FZeVytm2rweFw0KVLIV26dMHhEBwOByICwJtv/hkQVJWSkmL69u2Dw+HA6XS2/et0OnA4nDQ0NFBZ+SrhcBifz0dTUxNZWZkMHFjBNddMYsyY89s61QsLy1i06FFGjRoBQG1tLXPmLGDp0pfZtOkj0tKcNDc309DQQEZGBl27FnPllROZNOkKAoFA2/950qTrWLmyik2b3iUtLY1wOEx19TY+/HAzmzZ9yG9+s5CNGz8gHA6TluYiKyuDs88+kylTbqB37x7Mnj2fW2+9ExEhNzeHHTtqaWlpwel0Eg6Huf/++5k8eXKHbkeTXPF2rKd1RBhjOtLMmTOZOXMm8+bN49prr0VECIfD5OXl4vX6+OSTTxg7djwXXHA+w4YNZdmyl3G73eTn57Fr1y4++mgzgwcPYsSIMxBxEIlEGDTouzz33AtUV9fw8cef8tFHWxg06FT69+/XdvZWOBwmEgnjcqXRr18f3n57HR6PBxEhOzub4cOHMWBA+UFnZbW0tJCZmQOQkkoAAA3tSURBVNk2HwqFyc3NQQSamvbj92ezd+8XVFQMoK5uF9XV25g69RYeeGAWffv2pqLiJEQcLF78v5xzzmhGjDifzZu3sGPHTjweN4FAgHA4EjtrzEN5+Ul88ME/GDfuQmbPvp+1a9+iX79BbNtWw/79+/H5fHz88af4/X4cDmHFihWcccYZydiMprOIZ3elMz/scJZ5/vnnFdC0tDT1+Xw6fPgZbffmCgYD6nA4dNSokTpjxi+1qmq53nvvXVpcXKSFhQX6yCNztbl5j6o26vDhZ+i0aVO1vr5Gr7zyR5qXl6vFxUX64IP3an19jbYe1lqx4kVNT/fr3Xf/QlX3aWNjnd57751aXt5fvV6v9uvXRx94YIZ+8snfY3fX/YPOnv2ADhxYoR6PW3v06K7Tpk3V3burdcuWDbHBm77sH6mvr9Z58x7SsrJubWPAd+1arBdfPEanT79Jly59Snfu3KyVlc/qKadUaDAY1Msv/9e2W7H85S9/0oyMoPbv36et87xv395aVFSo6enpsVEityRvg5mUgPWJWBExB1u+fLkCKiLq9/vV4/Fo//79NBgMqMvlUpfLpZmZGepyubRbt1ItKuqi6enpWlhYqAsX/kb79eujjzzysB54ltbcuTO1rOw76vf79Oqr/10XLoye8fTTn16rq1a9okuXPq2///1CnTt3pt5zzy918uTrtKioKHYDQ89B/TcTJozT6up/6IH9LLt3V6vb7VbVvdrSsltfeGGxDh8+VL1ej5aX99cnnliovXr10EWLHlXVvRoO1+uzzz6hvXv30uzsLL366h/r668v14ceuk/Hjh2jhYUF6na7DxrjPDMzQzMygurz+bS2tjaJW8ikkniLiPWJmG+dSCTCXXfdxW233Yaq4vf7CYdDNDU1Ewikk5uby5AhgwmFQrzzznq2bdsGKKpQUJCPx+OhoaGBxsZG9u/fz/79TbS0tOB2u3G73YTDYVwuFw6HEAwG8Hp9eL0efD4vwWCQzMxM3G4XzzzzApmZGQwa9F0+/HAzdXV11NfvoaAgn/Ly/gwZMpgBA05i3LhLmDLlBhYufAyPx82YMecyY8ZtFBQUAHDyyadxxRWXkp+fx/Tpd1BXV4fH4yEvL5ePPtpCMBjA4XBQWxt9vrm5GVUlIyPIF1/sY9q0adxxxx3J3Sgm5cTbJ2JFxHyrhUIhbrnlFu677z4ARASv14vT6SQtzclVV01i5coqNm7cSF5eLk6nk5qaz4hElPPOO4fLL/8hQ4eeRk5ODtu37+CEE/qxcOFcHn/8Sd5/fyN1dbsYOPBkLr74Qs49dzQDBpSzb98+hg4djYjw1lv/x/btO9iy5WM2b97Chg1/5/nnl/H++xtxOp2kp6fT0tJCOBymubkZn89HerqfjIwgwWCQ7Ows3n13PfX1e/D5vLS0hMjJyeaUUwZw9tmjcLnSmDlzLjU1n9HYuB+v18P+/U3MnDmT6667Lsmtb1KZFZEYKyImXo2NjVx66aW8/PLLNDc3A+DxeNo6wpubm8nJyaa4uIgdO3ZSW1uHy+UiOzuLyy77If369eH666eya9dW9u7dS21tHX/723vMnbuA1avXoKo4nU6ysrL47LPtZGVlUle3C7fbTTAYIDMzg+zsbE488QT69OnFH/5Qxbp177BkyWP06tWTNWveZPnyFaxa9Sdqaj7D7XbjdDpoaQmRmZmB0+mkqamJpqbonobb7QaUxsb9hMNhHnzwQTvDysStUxUREfkX4HagLzBIVdv91BeRc4GHACewUFXvOdq6rYiYRHz++efcfvvtLF68mF27dqGqhMNh0tPTaWxsJBKJ4HQ6yc7OJhQK0dTUROsHduupvh6PG5fLTSDgx+v1xQ5teXjjjbV0715GQ0Mj+/Y10NjYQF5eHj179qCiopzy8v4sXvw0b775Fvn5eWzfvhOnM3oasc/no2/fPqSnp1NVtYqmpmays7NieyI+APbt20ckEqG0tJSqqip69OiR3MY0nVJnKyJ9gQgwH5jSXhERESfwAXAWsBX4M/BDVX3/SOu2ImKOl08//ZSbb76Zp556ilAohMvlwuv1sm/fFwQCAfbs2UtaWhqhUAiHw0EgkE4oFB0etmfPE/ne907l1FNP4YYbpvK7381ny5ZP2Ljx77z33gbWr3+fUChEWloaPp+PcDiESLRwRCIRHA5pyyEiNDe30NjYCND2M8877zzmzp1LWVlZklrIfJN0qiLSSkT+yOGLyGnA7ap6Tmz+ZgBVvftI67QiYr4ukUiEWbNmsWDBAqqrq9mzZw/t/T1FL0R0IiK4XNFLsxwOZ2w89kjsPUooFAa+LAoAgUA64XCEhoYGHA4HmZmZ9OrVi0GDBnHRRRcxcuRIu3Ou+Vp8Ey827Ap8esD8VuD7ScpiDA6Hg8mTJx+xn6GmpoYlS5bw6quvsmbNGgKBAPn5+W1naWVlZZGdnU1+fj6FhdHb04sIn3/+Ob1792bYsGEd+D8y5qvrsCIiIiuBLu28dIuqLo1nFe081+5ulIhcBVwF0K1bt7gzGnO8FRUVceONN3LjjTcmO4oxX4sOKyKqOvoYV7EVKD1gvgTYdpif9QjwCEQPZx3jzzXGGHMYjqMvkjL+DPQUkRNExA1cAixLciZjjPlWS4kiIiLjRGQrcBrwsoi8Gnu+WEQqAVQ1BFwHvApsAJ5W1feSldkYY0yKdKyr6vPA8+08vw04/4D5SqCyA6MZY4w5gpTYEzHGGNM5WRExxhiTMCsixhhjEmZFxBhjTMKsiBhjjEmYFRFjjDEJsyJijDEmYVZEjDHGJMyKiDHGmIRZETHGGJMwKyLGGGMSZkXEGGNMwlJqeNyvg4jsBD4+xtXkAbXHIU5H64y5O2NmsNwdqTNmhs6X+zuqmn+0hb7xReR4EJG34hlrONV0xtydMTNY7o7UGTND5819NHY4yxhjTMKsiBhjjEmYFZH4PJLsAAnqjLk7Y2aw3B2pM2aGzpv7iKxPxBhjTMJsT8QYY0zCrIjEiMijIrJDRNYf5nURkVkisklE3hWRgR2dsT1x5B4hIvUisi72+O+OzthOplIRWSUiG0TkPRG5oZ1lUq6948ydiu3tFZE3ReSdWO5ftLOMR0SeirX3WhEp6/ikB+WJJ/NEEdl5QFtPSkbW9oiIU0T+KiIvtfNaSrX1MVNVe0QP6Q0DBgLrD/P6+cArgACDgbXJzhxn7hHAS8nOeUimImBgbDoIfAD0S/X2jjN3Kra3AIHYtAtYCww+ZJmfAPNi05cAT3WCzBOBh5PdvofJ/5/AovZ+F1KtrY/1YXsiMar6J2DXERYZCzyuUWuALBEp6ph0hxdH7pSjqjWq+nZsei+wAeh6yGIp195x5k45sTb8Ijbrij0O7QwdCzwWm34GGCUi0kER/0mcmVOSiJQAFwALD7NISrX1sbIiEr+uwKcHzG+lE3yAxJwWOyzwioj0T3aYA8V25U8h+k3zQCnd3kfIDSnY3rHDK+uAHcAKVT1se6tqCKgHcjs25cHiyAwwPna48xkRKe3giIczE7gJiBzm9ZRr62NhRSR+7X1T6AzfjN4mevuCCmA28EKS87QRkQDwLDBZVfcc+nI7b0mJ9j5K7pRsb1UNq+rJQAkwSEROOmSRlGvvODK/CJSp6gBgJV9+u08aERkD7FDVvxxpsXaeS4nf7URYEYnfVuDAbzolwLYkZYmbqu5pPSygqpWAS0TykhwLEXER/SB+UlWfa2eRlGzvo+VO1fZupaqfA38Ezj3kpbb2FpE0IJMUOUx6uMyqWqeqTbHZBcCpHRytPacDF4nIFmAJcKaIPHHIMinb1omwIhK/ZcDlsbOGBgP1qlqT7FBHIyJdWo+3isggotu8LsmZBPgtsEFVHzzMYinX3vHkTtH2zheRrNi0DxgNbDxksWXAFbHpCUCVxnp+kyGezIf0kV1EtI8qqVT1ZlUtUdUyop3mVar6b4csllJtfazSkh0gVYjIYqJn1uSJyFbgNqKdeajqPKCS6BlDm4AG4EfJSXqwOHJPAK4VkRDQCFySAr+wpwOXAX+LHfMGmAZ0g5Ru73hyp2J7FwGPiYiTaFF7WlVfEpFfAm+p6jKixfH3IrKJ6LfiS5IXF4gv8/UichEQIpp5YtLSHkWKt/UxsSvWjTHGJMwOZxljjEmYFRFjjDEJsyJijDEmYVZEjDHGJMyKiDHGmIRZETHGGJMwKyLGGGMSZkXEmA4gImUi0njARYqISDg2DsZ6EXmx9QrtI6zDF1u+OZVupWK+3ayIGNNxPozdULBVo6qerKonEb1y+T+O9GZVbYy9P+n3EDOmlRURY45RbC9j/QHzU0Tk9q+4mtWk0K3ujYmXFRFjkix2f6hRRG/MZ0ynYkXEmOTxxfpI6oAcYEXrCyLSW0TmisivRKQ4aQmNOQorIsYcuxAH/y1543xfax/HdwA3sT6RWKf5zcDtRAe2ekBE3MctrTHHkRURY47ddqBARHJFxAOM+SpvVtV64HpgSmzQq2HAQ8A4oJDoIFgpMcyuMYey8USMOUaq2hIbL2ItsJl/HvApnnX8VUTeITq2xDrgbFX9FYCI/AB4/ThGNua4sSJizHGgqrOAWV/xPYFD5i9snRaRM0TkOaLjcT+hqrXHJagxx5kNSmVMBxCRUuANoO6Qa0W+yjp8RE8FzgfKVbXTjsttvjmsiBhjjEmYdawbY4xJmBURY4wxCbMiYowxJmFWRIwxxiTMiogxxpiEWRExxhiTMCsixhhjEmZFxBhjTML+HyxWkZhQcAo4AAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f52232fcf90>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"afig, mplfig = b.filter(component='primary', time=0.75).plot(fc='teffs', show=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Spot Corotation\n",
"--------------------\n",
"\n",
"The positions (colat, long) of a spot are defined at t0 (note: t0@system, not necessarily t0_perpass or t0_supconj). If the stars are not synchronous, then the spots will corotate with the star. To illustrate this, let's set the syncpar > 1 and plot the mesh at three different phases from above."
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [],
"source": [
"b.set_value('syncpar@primary', 1.5)"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"Tue, 09 Apr 2019 08:49 BUNDLE WARNING overwriting model: latest\n"
]
},
{
"data": {
"text/plain": [
"<ParameterSet: 32 parameters | components: primary, secondary>"
]
},
"execution_count": 14,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"b.run_compute(irrad_method='none')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"At time=t0=0, we can see that the spot is where defined: 45 degrees south of the north pole and 90 degree longitude (where longitude of 0 is defined as pointing towards the companion star at t0)."
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"t0 = 0.0\n"
]
}
],
"source": [
"print \"t0 = {}\".format(b.get_value('t0', context='system'))"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYgAAAEOCAYAAACTqoDjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzt3Xt0HHd99/H3VxdLsuW75LsdOSEkJE5iEiV14iRACGmgEAqHtvAcKA884AOHWx+gQMhpS8vTpz0Nl9JCOfUTKH2ANvBwKRRCk5hLLuRqk3ucqxPHdhxbtmJbtmTJkr7PH7ODfhrNSitptTPSfl7n7NndmdnZ3zjRfPZ3md+YuyMiIpJUk3UBREQknxQQIiKSSgEhIiKpFBAiIpJKASEiIqkUECIikkoBISIiqRQQIiKSSgEhIiKpFBAiIpKqLusCTEZLS4u3tbVlXQwRkWll27ZtB9y9daztpnVAtLW1sXXr1qyLISIyrZjZzlK2UxOTiIikUkCIiEgqBYSIiKTKXUCYWa2Z3WdmP8m6LCIi1Sx3AQF8BNiedSFERKpdrgLCzFYBvwdcl3VZRESqXa4CAvh74BPAYNYFERGpdrkJCDN7PbDf3beNsd0mM9tqZls7OjoqVDoRkeqTm4AANgJXmdmzwPXAZWb2reRG7r7Z3dvdvb21dcwLAUVEZIJyExDufrW7r3L3NuCtwC/c/e0ZF0tEpGrlJiBERCRfcjkXk7v/CvhVxsUQEalqqkGIiEgqBYSIiKRSQIiISKpc9kGITD8DQDfghdcngFlALdGfWQP6PSbTjQJCZEKOA8cKz4NEwUDh2YJtkmYBzYWHSL4pIERK5kAn0Yl/oLAsDoMahsLBGV5bcIYCpK+wj06gEVhAFBoi+aOAEBnTIEPBEIdAWnNRGBIknj3YLt6mD9hH9Ge4iKgZSiQ/FBAiozoKHGFo/shi4QAjaw4hS2wXLxskqo10ENUkWkbZh0hlKSBEUjlwkKF+hORJ24Ltks1K8ft4XfI9KZ+BoRrFYtTsJHmggBAZIf5F3090Iq8l+qWf9sveGB4Cca0gXhaLm5/C1+G2HizfDywE5pTxmETGTwEhMkzciRwHQhwKxfoc4hM8wXMd6bc0CWsdNcFzGBTx9x4ubKuQkOwoIER+a4AoHMKmIRhZGwibisJmJVKWhwESr09rfkrWUpwoJPqB+ZM4JpGJU0CIANHJ+UDhdfIkHy5LBsVYHdPJfYTBkAyPMFTi2kk3UA/MLvE4RMpHASECDNUcIL3/ICk5pJWU9/G+kvtNBkvY9ETK8sNEIVFfwnGIlI/G04nQTdSUE/Y5hJ3P8fualG0IXtem7DsZNmn7SrtugmB9LdFQW5HKUkBIlRsAuhj+p1DL0Ek8fE4Tr0vWOMKTf3ySDyXDJfldye/tJ7omQ6RyctPEZGaNwK1El5PWAd9z97/ItlQy8x0hvX9htH6FZFiEzU3xn1Q4vcZY+wyboOL3aWXqIeqL0O86qYzcBATQC1zm7kfNrB643cx+5u53ZV0wmalOFB6jBUMYCOEIo3D9aJ8Lh7TGksFBsG28r8Ei6w4TXSMhMvVyExDu7gzVoeMeubS/JJEyCZtskn0OMHIEUlpfwljCoEj7XDyaKVwero/XxWXpL+E7RcojV3VVM6s1s/uJLiW92d3vzrpMMlPF920I2/yTITHaSb1YoIzW8ZzcPtkZPdq6sPaivgipjFwFhLsPuPt6YBVwgZmtS25jZpvMbKuZbe3o6Kh8IWWGOEb6sNawgzjsrCZYH25nKdsQfD5tVFRNyvbJcpB4He+zhuhqb5Gpl6uAiLn7IeBXwJUp6za7e7u7t7e2tla8bDJTnCB9WGssbShrsVFNcRCkhUFa01Ryf2mhMNrnBkmfykOkvHITEGbWamYLCq+bgMuBx7ItlcxcAxQ/GRf75Z6mlH6J0cIirVYRBlDyu+PXaXerEymv3HRSA8uBfzWz+OfYd939JxmXSWakZBNNsr+g2DDT5PbFrpxOkwygtGGwMHwCQE9ZHr/uRdNvyFTLTUC4+4PAy7Muh1SD+KppGDoRjzWKKW1ZKaOYxhLOv5S2LgyS5FBYkaml/8ukCoU1iLCDOfmLfbxG6zdI6+xO+974u2tStgtfDyAy1XJTgxCpnGKX15Taz5BcnjY9eFrz03gu60lum2xyEpl6qkFIFUq7CdBoTUvJAAg/kzaqKbm/saTtY7TaiEhlKCCkCiWbZ5K//pPKdaIe7RqINMUu1BOpDAWEVLHkJHlJYw1NnWiTT7FrGErdn8JCKkMBIVUonno7PtGOdsIeKzwmotj04WkT/oVlEaksBYRUobSTbbETcNpVy8WuYSgHhYLkhwJCqlDy1p3FJugL1ydNJiRGmyaj2D7VrCSVp4CQKjSr8ByfqJMn5VLnOppISHjiOfm9ye3i18l1abc3FSkvBYRUoWQNAiY++V0YEskTebHt05alNWMl9x8un4XIVNOFclLlwo7oYp3SY412StYKkjcASm5XbFna9yQ/o4CQylFASJWqI5qTabSTfxwYyQBIG8E0no7v0bZLa7aKyxEGj5qYZOqpiUmqVBMj+yDSmnOKTZkR91OMJxg8eCQ/n/bdxfok0prIRMpPNQipUvUMnzNpkKHZU2F4s9NYNYfRAqFUxZqSkq8H0TTfUimqQUgVa2bkyTd8JBWrOUxmJFPyu4rVSuLtxzNVh8jk6P80qWINhefk3ExhZ/NozUjFgiT8XPjaC9/ljGxeStvvYKJsDswd45hEyic3AWFmq83sl2a23cweMbOPZF0mqQZzSa8ZhCf4UvockjWPYn0KyW3D4Bgc5XODRB3T6n+QyslTH0Q/8DF3/42ZzQW2mdnN7v5o1gWTmayBoRFN4R3cwr6GsJaQ7KdI9lUUmyq8WF9F2BkdhlNaX8f8MY9GpJxyU4Nw973u/pvC6y5gO7Ay21JJdVhYeE6rNRCsI7Es/OUfrg9HKo1V+0jWOML9hK+bydGfq1SJPNUgfsvM2ojuT313tiWR6mBETU2HGaoVFOtbiJ/jmkTadRLxPpM1h+R+w9pK2nDXeF0D0bBckcrK3U8SM2sGvg/8ibsfSVm/ycy2mtnWjo6OyhdQZqgmYA7Df/mnNf/Ez3HncbI/gWC7gcT6uIM62Umdto94mzrUtCRZyVVAmFk9UTh8291/kLaNu29293Z3b29tba1sAWWGm0vUlFOsAznZZBSHRHK7fobCINn5nAyDZHNWvN8Bog7pRVN0rCJjy00Tk5kZ8DVgu7t/IevySLVqJmrWOVR4HzYVxbcMjSVrF5ZYFjYXhdNkhDcq8iKPOqClHAckMmF5qkFsBN4BXGZm9xcer8u6UFKN5gCLGQqGZA0grhWQsi6sAaQNWw3Xh9sQvJ8NLJ2SIxMZj9zUINz9dnRXFMmNRqAVOAj0MfyXfzgcNhkA8W+u5PDW+LNpU3h48Nl56GI4yYvcBIRI/tQDy4AjhUdYI4ibk5LzM41205/wWolksDQTdUZrllbJDwWEyJjmFR6HifomwukvahgKjuR9HMIgSNY64qGyTUQd0fpTlPzR/5UiJZtfeBwtPLoZeZ1D2LQ0yMh+jPi6hmai0FGrquSXAkJk3JoLD4hqE4eI+ikGiIa4WuF1DUN/Yk1Ed4FT/4JMHwoIkUmpJRrxJDLz5GmYq4iI5IgCQkREUikgREQklQJCRERSKSBERCSVAkJERFIpIEREJJUCQkREUikgREQklQJCRERSKSBERCRVrgLCzL5uZvvN7OGsyyIiUu1yFRDAN4Arsy6EiIjkLCDc/VagM+tyiIhIzgKiFGa2ycy2mtnWjo6OrIsjIjJjTbuAcPfN7t7u7u2tra1ZF0dEZMaadgEhIiKVoYAQEZFUuQoIM/t34E7gNDPbbWb/I+syiYhUq1zdk9rd35Z1GUREJJKrGoSIiOSHAkJERFIpIEREJJUCQkREUo3ZSW1mi0rYz6C7HypDeUREJCdKGcX0fOFho2xTC6wpS4lERCQXSgmI7e7+8tE2MLP7ylQeERHJiVL6IC4s0zYiIjKNjBkQ7n48uczM6szsnLh/Im0bERGZ3sY9isnMlhPd2Odk4Boze1O5CyUiItmbyDDXjwLXALvd/WPA28tbJBERyYOJBMRs4BiwvsxlERGRHJlIQHwJ+DvgHjP7KLClvEUSEZE8GPdsru7+hJn9KXApcKO7P1L+YomISNYmNNWGux8EfoyamUREZqwxA8LM5pnZ1Wb2ZTO7wiIfAnYAf1jOwpjZlWb2uJk9ZWafKue+RURkfEppYvom8CLRnd7eA/wpMAt4o7vfX66CmFkt8BXgNcBu4F4z+7G7P1qu7xARkdKVEhAnu/tZAGZ2HXAAWOPuXWUuywXAU+6+o/Bd1wNvBBQQIiIZKKUP4kT8wt0HgGemIBwAVgK7gve7C8tERCQDpdQgzjGzI4XXBjQV3hvg7j6vTGVJmy3WR2xktgnYBLBmjSaQFRGZKmMGhLvXVqIgRDWG1cH7VUTTjCfLsxnYDNDe3j4iQEREpDzydEe5e4FTzWytmc0C3ko0lFZERDJQyjDX35Rjm7G4ez/wQeBGYDvwXV2EJyKSnVL6IF5mZg+Ost6A+eUojLvfANxQjn2JiMjklBIQp5ewzcBkCyIiIvlSSif1zkoURERE8iVPndQiIpIjCggREUlVckCY2TfN7L1mVkqfhIiITHPjqUH8C7Ac+Ecze9rMvm9mH5micomISMZKvmGQu//CzG4BzgdeBbwPOJPoDnMiIjLDlBwQZvZzYA7RtN+3Aee7+/6pKpiIiGRrPE1MDwJ9wDrgbGCdmTVNSalERCRz42li+p8AZtYMvIuoT2IZ0DA1RRMRkSyNp4npg8AlwHnATuDrRE1NIiIyA5UcEEAT8AVgW2FiPRERmcHG08R07VQWRERE8kVXUouISCoFhIiIpFJAiIhIqlwEhJn9gZk9YmaDZtaedXlERCQnAQE8DLwZuDXrgoiISGQ8w1ynjLtvBzCzrIsiIiIFealBiIhIzlSsBmFmW4im5ki6xt1/NI79bAI2AaxZs6ZMpRMRkaSKBYS7X16m/WwGNgO0t7d7OfYpIiIjqYlJRERS5SIgzOxNZrYbuBD4qZndmHWZRESqXV5GMf0Q+GHW5RARkSG5qEGIiEj+KCBERCSVAkJERFIpIEREJJUCQkREUikgREQklQJCRERSKSBERCSVAkJERFIpIEREJFUuptoQmf5OAL3AccALDwNmAQ1AY3ZFE5kgBYTIhPQCBxkKBogq5IOjfKaGKCjmA3OntHQi5aCAECnZINAJHCm8jmsJNQy11qa12sa3LRkkqmEcB/YBc4CFqHYheaWAEBmTAx3AUaKTfBgIVnjE21FYZwzVJuLltQwPix7gGFFALAXqp6b4IhOkgBAZ1TFgP0O1hTqG1xbi/gaC5XGIWGFd2PQUB4cFn+kDdhE1O7VO0XGIjJ8CQqSofUS/8uNggKETe6w2WBbWJDxYFgfFQPCZWBwmg0Rh1ItqE5IXuRjmambXmtljZvagmf3QzBZkXSapZgPAHqK+glqGag1xGMSva4NltQyvWcTvw/CoL+yrLvhcvO/4MQA8D3RP4fGJlCYXAQHcDKxz97OBJ4CrMy6PVK0TwAtEJ+o4AGoSz8nACIOjjigI4u3CRxwClth3DcPDowY4QNQZLpKdXASEu9/k7v2Ft3cBq7Isj1Srfob6G8KTd9wklAyHsDYQ1gJgeBhY8PlahgIk/lw9I7+vDjgMdE3FgYqUJI99EO8GvpN1IaTaONGv9rgmEHYihyd5GAqMsM+hltH7ICDqZwg7qGuD5fF2g8EzRLWIejQUVrJQsYAwsy3AspRV17j7jwrbXEP0M+7bo+xnE7AJYM2aNVNQUqlOnQx1GMNQMxDBsjAIkiOX4s+EywYYHixhDcMZupaiBgZ6oLYxWEfhuwYKZVsalEekMioWEO5++WjrzeydwOuBV7u7F9vO3TcDmwHa29uLbidSuiNEo4eKXfBmiUe83hLbhK+d6Jf/YGK9B8tqo9f9x+CZr8L8s6HllVATDpGtIwqJA0QhIVI5uWhiMrMrgU8Cr3B3Dd+QChogGjGU7EOA4n8eaU1OYZOSB+uLPQM4PuDYzs1w7DE4+jRHH/slfTUns+ik+TBnDSxYBzWzCuU8CjRP4BhFJiYXAQF8mWhGs5vNDOAud39ftkWS6hCPFErrd4jFARA28cT9BMm+h2RfQvKah/jCOWCwH3b9H+78whbmn7SE5e3LuPcrv6BuzgOse8NqlqwdZO+z81l25fux5lUoIKTSchEQ7v6SrMsg1aiX6CrmsGM67IMIO6iT7f/xdQ3h+zAo6hk+q2sQDICf6GFgx5eo632ANZeeyh1/9a/8+20X8XzfIt7S6NzyNz+l9Y/fwp6vfI3fbaih5cpPQf1sopFN88v1DyAyqlwEhEg2jjG86Sd8JC9yS3tOWxYGQTgVRzCSaaAX2/1F7vvnLdQ2NLP8vAXsOGUDn/vPOzhr/Vns7Z1LffM6nr3ubk5ecQFr79vHnJXfoOnM/wYNhgJCKiUX10GIVJ4TDZhLXugWM0bWKJK1irTgSBsWGywb6Ied10L3dta+5mx2/uwmvnP9E9zUCRdfspHFixfx5LO76aKWhQsX0nHC+fy9x/nOe/+J/rs/CV1PEzU1iUw9BYRUqWPB67RaRLg8bcRS2CSVnN017SK5wnNNA/hRmH0a805axONrN3LN939NXW0dd9z2a2bV1dPWtoaDHQfZvWsPDQ0N7N53gP/X1EbH3vlw6CE0DYdUigJCqlQvI0/0ac1LpGwDI2sJyXAh/TNm+PxLOX7oGPd/5QZ++kQHl1x6CT3d3Vz8iovZcuMWHnnwEXbv2sU556xj+6OPM39eM//1623c8Gg/fujRsv4riIxGASFVaqDI8mRzUU2R5aPVNIoFRQ30ddD5+NPc/mc/YN9d97Os0fj1rbcxp7kZ3Glubua001/Kueedy769++jt6WH+vHmcfvpL+Y87n+fGv/wV/UdfRLUIqQQFhFSh+BahxfoRwmcYeSOgZGc2wWfSLqorvO7ZATs/TT3Pc+LQfhafezGnr1jM71y0gdt/dSv33nkPjQ0NLFmyhIMHD7J7127OOnsdW7fex5LWFrp6+3jkxBw67/o+0UyzIlNLASFV6EThORxtlDyhhxe+jXXVdDIownWFzzrQcR00rqV2ljHY20Nndy+HGxfy7NPPANDU1MSKVSvo7OykrraOAx0HmDt3Lq0tLezfv5/FixbxcM089m+9B44fmNw/gUgJFBBSheLRS+HEeaH4pO9F1ie3G9uJjm28+GQH+7Y9w1MP93Jd30t4x7/dyyPP7ed4dzcbLrqQdevPZvujj9Hf38/Bjg7Wn7ueAwcO8sB9D7DmpDV0dR3loZ17+e4zDsd3je+QRSZA10FIFYr7H0b7fVTs5D/aNRDFefd2HvzyT+jeu5+7WjZwfN5S4Cm6uroY9EHqamsZBJqbm6kx4/DhI5x7/nk89fQOLrn0YnY8/QxLli5h6bJWHt9zlJ6OvTTptloyxRQQUoXCmkM432Oy36HYiKW0bUY3q6mbi699G3f/75v5xvX3caSnlw0Xb8Rqanmx80XuuO12auvrmTd/PotaFtG6pJUDBw6y48mnWdN2EqtWrWB28xzMjOd272LHzQ9y5qnjO2qR8VITk1QhD57D/oW0+0gnJwxOhkiJEwrXtlDbuJBVb34tLStWMn/BArqOHGHQB3jJaaeyuKWFZcuX8ZJTX0LXoSOsXrOa4z09nL/hfDr27Wfv3n0MDgzS2fkia1etYPnLdU8tmXoKCKlC4f/28QR6kF6riN8Xqy2UGBD1i+nr6uKhz36RN75sKYcPHaLvxAnMarjj1tt52bozWLlqFXffeRcO/PrW21m6tJW+Eyeoq6ujqamRffs7WLhwAbObZ7GobVHJRysyUWpikipVbHruWDxTazjZXnjnt9KalmL9LOfOP/8ODA6ywfew4aIN3HHHXaw6dozzLjife+66h+PHj3PxKy5hYHCQjZdezMHOQ/T29dHd00Pz3Gaa5sympsY43vEiRw42MG/5JA5fpAQKCKlCNUQd1fFkesWETVGldFoXV9vcxsV/89/p69xJX3cDv/vNfRzoPJ3muXOob2zgxIlo6G1PTw+LWlvYctPPOX/D+XS++CIrVq6gf2CAgYEBOjoOcuaKuTS2pN2cUaS81MQkVSiuGYS3BA2bmmLJgEiui9cPBg9PbBPdPc5q66k9+VM0Laih64V+Tt/3EE89/hgNTbO549bb+Z2LLuTCSzdy7z1b2bN7D6e+9FSamppYvmIZ1Bg7nn6Gvr4+du1+no2XtDKrRbfblamnGoRUoTqiK5HDC+Jg+AkfhndghyOfrMjycB/h68JzTSMnWj7Msze8m4HOfXz4DZew5bkjnHt+O/teeIGuo0c5qe0kjvf20rqkFbMadu/aw8DgIGtPaaO2ro7+/gFaemugbs7k/glESpCLGoSZfdbMHjSz+83sJjNbkXWZZCZrYmQNgGDZYLBt4iQ/bLtwtFO4fCCxj6HaRf3CdVz8l6/ltZvfwFW/fwZNs5u4b+s2li5fxgt7X2Dp8mUsW7KUHTue4eGHHmblqpVgxtx58+k6eowN68+grrcW/baTSshFQADXuvvZ7r4e+Anw51kXSGaycBK+ZDNR8mTvwfK05qOBxGeTn080O1kNLH8P/b6cfdf/mLvvuIuT1rYxf+EClixfxqHDh3l+3wucfMrJtLS2MLt5Djuf280TTz5J85w5vPKMRZz77suAxvL9c4gUkYufIe5+JHg7h5LHDopMVA1DJ++0KTfCgIibmgYZ+ZsqHBqbNhIqZb8NK9nx8w76XzzAaW0rqZ83l6eefBozY3HLYrq6jtI8t5lbbrmd1YcOc9HGDcw60cO7XjaHi9fPxhafiwJCKiEXAQFgZn8N/DHRTXdfNcp2m4BNAGvWqKNOJqoZOMTQyT8czhqHQhgIYTNUKNnUNPze00PbhLUIOP3tf0jbRcYzXz3AZ797G93d3by8/Vxq6+u4/74H6Dp2lEsu3Uj/4CCvWj6X9R17eNXvr6dp5SnQtLo8/wQiYzD3yvxYN7MtQNrYvGvc/UfBdlcDje7+F2Pts7293bdu3VrGUkp12cfQCb62sCw+uYe/nWoSz2GghPeCSF5wFwr7LRx697H/5r/mtmuuY2/76/jhky/y3HO76O45zslr27DaGnqOH8f7evnEnE7WvWUjp//B66hZ81qwFqBhcocuVc3Mtrl7+1jbVawG4e6Xl7jpvwE/BcYMCJHJaQB6Cq/j5qC41hBeFOfBOhheQ0jWPEhZF66P9uG1zQz2z+L1X30zB/fMZfvzhzm8YD5Huo5y+bJGjnX38IvuAd7Zaiw77UxOfvvHqFl2SuG7FQ5SGbloYjKzU939ycLbq4DHsiyPVIv5RMNdkyf3cARS2j0j4vXJ4a7xsuRV2snOb7C6Rpa94TP4ox/lkW/9nCu6jnH+lZfDlj2smNXNgccf4I3v+SPaz+6kYd3bYNkphf3Mn/xhi5QoFwEB/K2ZnUb0F7ATeF/G5ZGqYESdvccY6jtI65MI7x1RE2ybHO6a7MROXmiXmLajtoGBVR/jnHecoGV1FzUNs9nRdhnPP9TFFf/rKlpOaYLG82DZZcH3N03Rv4XISBXrg5gK6oOQ8tjH0FXV8SPuk0jeMS4+wddSfJqNsElprNlfB6F7Fzz7z9DfC8uuYLBmLjU7/y80nQSnvhvq44F96nuQ8shdH4RIfi0E9jO89hAHRnK+pnBUU9o04fFzMiTSmrAK62avhLb3QtMKMKjBYW4bzJoPFu+jEYWDVJoCQoRZRJffHC28T/YrECwPO7Mh/bqIYldjh/tMXH8xeyVDF9wBDfOCbeqAxeM4HpHyUECIAFEtYpCoP6KOoV/+/QxvXgqHtcJQB3RyeXhNRBwQca0k3D4OgbRAiaccb53UkYlMlAJC5LcWEwVCHyM7o5M1hrQO6Zpgu3j9AOlNTQPBduE+BoLXAIsY6g8RqSwFhMgwS4G9wAnSL4iLhWEQB0U/w0NgMLFdSgf1b5cPBMsHiEJhGfoTlSzp/z6REZYDnUR9EuHwVhh5IR0Mv69EHBA1wToYGQ79hedkrcOBeqKgUs1BsqWAEEm1iGjk0AFGXjiXdiHdACObnNKurE52WIdXWBtRZ3nLJMsuUh4KCJGiZgMriUKiu7AsOX1G2Mw0wMghrrFwWbhd3CzVRBQMqjVIfiggREZVS9TccwLoIOrADudpCofEpk0HHit2P4lGYAkKBskjBYRISeqBFUQn9YNEk/zF/Qhh/0PYH5EU1zbqCvtbiO7rIHmmgBAZlxqGrksYALqIJvzrZfhw1nDyvvgWoY1EfQy6IlqmBwWEyITVAguyLoTIlMnLPalFRCRnFBAiIpJKASEiIqlyFRBm9nEzczPTlUIiIhnLTUCY2WrgNcBzWZdFRERyFBDAF4FPMHJ+AhERyUAuAsLMrgL2uPsDWZdFREQiFbsOwsy2EM1fnHQN8GngihL3swnYBLBmzZqylU9ERIYz92xbdMzsLODnDM2Gtgp4HrjA3V8Y7bPt7e2+devWKS6hiMjMYmbb3L19rO0yv5La3R8imq0MADN7Fmh39wOZFUpERPLRByEiIvmTeQ0iyd3bsi6DiIioBiEiIkUoIEREJJUCQkREUikgREQklQJCRERSZX6h3GSYWQews0y7awGm+7UXM+EYYGYcx0w4BpgZxzETjgHKexwnuXvrWBtN64AoJzPbWsqVhXk2E44BZsZxzIRjgJlxHDPhGCCb41ATk4iIpFJAiIhIKgXEkM1ZF6AMZsIxwMw4jplwDDAzjmMmHANkcBzqgxARkVSqQYiISCoFRMDMPmRmj5vZI2b2d1mXZzLM7ONm5mbWknVZxsvMrjWzx8zsQTP7oZktyLpM42FmVxb+P3rKzD6VdXnGy8xWm9kvzWx74W/hI1mXaaLMrNbM7jOzn2RdlokyswVm9r3C38R2M7uwUt+tgCgws1cBbwTOdvczgc9lXKQJM7PVwGuA57IuywTdDKxz97OBJ4CrMy5PycysFvgK8FpmEqkOAAAES0lEQVTgDOBtZnZGtqUat37gY+7+MmAD8IFpeAyxjwDbsy7EJH0J+C93Px04hwoejwJiyPuBv3X3XgB3359xeSbji8AngGnZweTuN7l7f+HtXUR3GZwuLgCecvcd7t4HXE/0w2PacPe97v6bwusuohPSymxLNX5mtgr4PeC6rMsyUWY2D7gU+BqAu/e5+6FKfb8CYshLgUvM7G4zu8XMzs+6QBNhZlcBe9z9gazLUibvBn6WdSHGYSWwK3i/m2l4co2ZWRvwcuDubEsyIX9P9ENpMOuCTMLJQAfwL4WmsuvMbE6lvjx3NwyaSma2BViWsuoaon+LhURV6vOB75rZyZ7DYV5jHMengSsqW6LxG+0Y3P1HhW2uIWru+HYlyzZJlrIsd/8PlcLMmoHvA3/i7keyLs94mNnrgf3uvs3MXpl1eSahDjgX+JC7321mXwI+BfxZpb68arj75cXWmdn7gR8UAuEeMxskmvuko1LlK1Wx4zCzs4C1wANmBlHTzG/M7AJ3f6GCRRzTaP8tAMzsncDrgVfnMaRHsRtYHbxfBTyfUVkmzMzqicLh2+7+g6zLMwEbgavM7HVAIzDPzL7l7m/PuFzjtRvY7e5xDe57RAFREWpiGvIfwGUAZvZSYBbTbIIvd3/I3Ze4e1vh1q27gXPzFg5jMbMrgU8CV7l7d9blGad7gVPNbK2ZzQLeCvw44zKNi0W/Lr4GbHf3L2Rdnolw96vdfVXh7+CtwC+mYThQ+NvdZWanFRa9Gni0Ut9fVTWIMXwd+LqZPQz0Ae+cZr9cZ5IvAw3AzYWa0F3u/r5si1Qad+83sw8CNwK1wNfd/ZGMizVeG4F3AA+Z2f2FZZ929xsyLFM1+xDw7cIPjh3Auyr1xbqSWkREUqmJSUREUikgREQklQJCRERSKSBERCSVAkJERFIpIEREJJUCQkREUikgRCbBzNrMrCe4oAwzGzCz+83sYTP7z7HuZ2FmTYXt+6bj/Ttk5lJAiEze0+6+Pnjf4+7r3X0d0Al8YLQPu3tP4fPTbs4mmdkUECJFFGoHDwfvP25mnxnnbu5kGk/3LdVNASEyRQp3l3s102yyPpGYAkKk/JoKfRIHgUVEt1AFwMxOM7N/MrPPm9mKzEooUgIFhEhx/Qz/G2ks8XNxn8JJRNPGfwCg0AF9NfAZ4B+BzxVm6BTJJQWESHH7gCVmttjMGohuYFQydz8MfBj4eOEGPJcS3YD+TcBSohvynFneIouUj+4HIVKEu58ws78iuh/zM8BjE9jHfWb2ANFNa+4HrnD3zwOY2R8Bt5SxyCJlpYAQGYW7/wPwD+P8THPi/Rvi12Z2iZn9gOje1d9y92l110KpLrphkMgkmNlq4A7gYOJaiPHso4loOGwrcJa7d5axiCITpoAQEZFU6qQWEZFUCggREUmlgBARkVQKCBERSaWAEBGRVAoIERFJpYAQEZFUCggREUn1/wFiCJkpeuoe7gAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f5223366f10>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"afig, mplfig = b.plot(time=0, y='ws', fc='teffs', ec='None', show=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"At a later time, the spot is still technically at the same coordinates, but longitude of 0 no longer corresponds to pointing to the companion star. The coordinate system has rotated along with the asyncronous rotation of the star."
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYgAAAEOCAYAAACTqoDjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzt3Xl0Xdd53/3vg5EASIACwQEcwEHiPEqcxFG2rCSynXjIShPnbYY27VLbVTdO5bSNq9U2TVa63jZN7CTOpJVmeBO3zpvYThwPsaRIFsVBlDjPokZS4AyS4ICJGHb/OPcIB5v73HsBArgXxO+z1l2490x3A9jnPHs6+5hzDhEREV9JoRMgIiLFSQFCRESCFCBERCRIAUJERIIUIEREJEgBQkREghQgREQkSAFCRESCFCBERCRIAUJERILKCp2Ae9HQ0ODmzZtX6GSIiIwp+/fvb3HOTc213ZgOEPPmzWPfvn2FToaIyJhiZmfy2U5NTCIiEqQAISIiQQoQIiISpAAhIiJBChAiIhKkACEiIkEKECIiEqQAISIiQQoQIiISpAAhIiJBChAiIhKkACEiIkEKECIiEqQAISIiQQoQIiISpAAhIiJBChAiIhKkACEiIkEKECIiEqQAISIiQQoQIiISpAAhIiJBChAiIhKkACEiIkEKECIiEqQAISIiQUUTIMxsjpm9ZGYnzey4mX2u0GkSERnPygqdgIQe4PPOuQNmNgnYb2bPO+dOFDphIiLjUdHUIJxzF5xzBzLvbwEngVmFTZWIyPhVNAEiyczmAQ8DewubEhGR8avoAoSZTQS+BvyCc+5mYP1TZrbPzPZduXJl9BMoIjJOFFWAMLNyouDwFefc10PbOOeedc6tc86tmzp16ugmUERkHCmaAGFmBvwv4KRz7jcLnR4RkfGuaAIEsAX4aeBxMzuUeX2s0IkSERmvimaYq3NuJ2CFToeIiESKqQYhIiJFRAFCRESCFCBERCRIAUJERIIUIEREJEgBQkREghQgREQkSAFCRESCFCBERCRIAUJERIIUIEREJEgBQkREghQgREQkSAFCRESCFCBERCRIAUJERIIUIEREJEgBQkREghQgREQkSAFCRESCFCBERCRIAUJERIIUIEREJEgBQkREghQgREQkSAFCRESCFCBERCRIAUJERIIUIEREJKioAoSZ/bGZXTazY4VOi4jIeFdUAQL4U+DJQidCRESKLEA453YA1wqdDhERKbIAISIixaOs0AkYLDN7CngKoKmpqcCpGQ19wB2gK/O+N/MTwDI/Xea9Zd4DlBL9e8uJygGVo5RekUKJz5UeoJuB50d8XiSXQXSOlNF/jsTrBcZggHDOPQs8C7Bu3TqXY/Mx6g5wmygY9NJ/8U9KLjNvOUQnSydRYHFEJ0AJUAVMCBxPZKzpATroLzj50i4PyeU9mZcD2jLLyonOkYrhSeYYNuYCxP2rG7hBlNHjDFxCdCEv8Zal8UtHJd7yXqLAczuzrpooYIiMFb1EQeFOlm1CBSror2nH7/194mV3Esc3oJYoaIw/RdUHYWb/B9gDLDazZjP7Z4VO08jrAi4BV4lKMtBf2jeipiLzlvkvvHXJf2sJA2sa8YnQC9zKfPct+putRIpRN9CaeXV565LnRzK/+/wm2dB6//xxRAW3q0TnyfhSVDUI59xPFjoNo6edqCTfQ3+G9OO1n5GT65MX+7TM7rxt+wKfLZOWNqIaxaSU44kUwh2ivBk3tUL6OZEvv2ad7KNIEzfZdgATic6V+19RBYjxoZtoJG/cZupn1uTPUOb3q8/5lJZipQw80eKmqzhYtBOVziaipicprB6iEnsPd9eWY9kKSP422SQLW37zbLwseZzbRIHi/m+iVYAYVTeIMn2yOQjSaxDkWO6vS2ZkP8PHyuivSfQl9iOzTy9RNf42UIc66mT03SYqrcPdwSGtf4Es6wdTU/ADil/QitfHAewOUR/F/VnrVoAYFZ1EtYZ4NFFoBJIfBPzO6aRkyd/fJ+1n6OSIvzM5AiROYy9Ru2stUBNIg8hwc/TXrpM163xqzKFt81nf561PpsVfHjoXO4mCxGTux45sBYgR1wZcz7yPO9EgPTPHgSHtIu83SeWSVvJKnhh+IErWLG4QnQRT8vw+kaG4Q1RzdURNoWn6yK/p9V6EAoJfqHP09+HFhalqogLV/UMBYkTdAG4ycLhqrJS72zbjEUtJfp+Evz6tDdZ5P5OS7avJzmvnrSvJrOsCLgINKMvI8IsHbEC4Jp187+f1ex2ImVZryKcpqpT+IAHR79FHVJu4PxTVMNf7y1X6gwMMLKXHJaRk81IZd7d/hoa1+rJ1UsdBJVQi82spoRFSyeV9wBXCNySJDNUtovMkdEHOViNI1sazSRassg1tDQWebMHKT2/chNvB/TSdnALEiGglKk34VdK0DJ+8gMcZOt9/Ta421xLvZ5Lf3JVWW4l/9hDdN+GPQxcZijb6717Op3nIH33nr0vmdf+eiGyFrGxC5wHcfdzk+07g8iC/pzgpQAy7W0TVZb/kn9bRlq2UktymlIEZ37+ZLrmslHBA8GsKye9Pzufki5fFVeqr6MY6uTdtRE2wyWZNSL8I+yP9ksEi7SIeki1I5NsvmJQcFptMYy/3Q01CAWJY3SDqkA6VbqC/KSm53A8W/smSvICHhEr//nHTbrgz77OfJj/Tx/qA8ynpEcmlg6hZKVRgiaUNrghtM1hptYlks2q2QJEUSn98rsajF8cuBYhh00UUINJqCqHOtmRG9Psb8mlmCgWYtBqIX/X2p/BI1kL87/A72eMRHPdHNVpGUxf9Q76TfW5+YSRXf9tQmov8Yw02GCSXZ7tnKfl7dRLVuMcmBYhh4ei/WPp3YiarwMkgkByxFCqV+Bd1P3Ck1Tb8Zq3QCKp4+zi9fu0kGSyyNVMlR5+I5OM6ufvN4p+hAtRQ5NPsNJRLYbZ9kuu6yD65YPFSgBgW5+gvESVHDSUzXj79EWn9ALmqxHg/k8HB3z60vz9XfvK9H4jiDsL4hG2hf5JBkWzivJK8lyFZUEl+zmUw2+Vb20irMcRChal8m8CuMRb77RQg7lk8X0xS8vkLsfhC7PcHJC/safdBpGXCXB3L2QJK8nOo2SmZXri7FpNM+8XA94skdWZecf7JdaFNex/6nGYozVD51DZy8fvt4qk5xl5/hALEPemj/5+evPAbdwcCCAeN+GfaxTtb+6hfys+n3dbfzv+etBpFtlljuxnL7awy0uJ7aJL8piS4e76j5HahfdOkFY7y3Xcwx42XJ8/r5E2qyYJVPC3H2KEAcU+u0p8J/JvR/FJ2tgybb2bOdYHP1TyV1r7rBwd/mvC0tuBk5r/NWKxCy2hoJT1P+5cgv1acrWaRXOYP/Q6dC6HBGv42aTWbtBq8v222NMLdgbK4KUAMWTfhm3z8UQzQ33TjZ7RQBi0JbBc3P/lNUNkCgt+ZHcq8/okYWg/pzWLJ972Mtcwvo6GP/sJDsmAB4bzrNz/lO1X3UISaaHMVsrJ9tz8Lgr8s/jx2BnYoQAzZZfo720JNMblqCGkloz4GluBDNYbQvQn+8bN9zrYuFKBC1f3QyKsO1GEtAyXb3bPly2y1YH+btGMMVraaetpxc41cShaqQseG6B6QsUEBYkj6iNoSSzLvQ6WjbH0QuUotuU6U+FhpTUUhyXWhznD/e9NOWL8PJXlChNqaZfzqIRoKDf3nymBGL+W6+N9LcMh1rGzNSrkCXeh4Sb30/12KW86pOc2sPo/j9DnnWochPWNE8leNL/p+zaEssT75M5aWydKCQ7a5nPwaS7aZXP3v8W9YCjVthZ6q5X933P/QkSOtMn7cYGDhKSnfi2pa02ba9kMVytuhbUL9bKEmsWz9cY6oFlH8jy3NZ+7m85lXtv9GKdA0LCkaE+LZJ5OloGSp3Lz1oZ/ZAkLoTx3q20jjf19yWm+/5BYSl/aSx0v+Tslg101/IOnN7HeT6Gl0Mr51MDBvx/kqVPiJ85Y/ceW98s/JbPk+1/nlF6LSRl2l9aHE60qIWiC6KfaHDOUTIE465x7OtoGZHRym9IwB8Zzv/s1jMPBhJ/7FOS0gpAWHtACTb5BICpXQ4oDhB7q0TF9CfwBIE6+7jgLEeNfJwMKDL60JNs1gtk3uE2q6zRYoShLr00YphZb7y5I3lPakbHcdmJb1Nyi0fP7Km4Zpm/uE37yU1j7vuLt/IG3qitDntACStuxehUpF2U7K0B3i8YWgB3VWj3fJecnSLrTJ97mm0hhKfh/s8fJpworP49AgDQg/wjRtRFN3lvQVh5wBwjnX6S8zszIzWx33T4S2uX91k7s/wZfsEwhVOdM66vyMmKt6nAxC+ZxQaf0dfvqSn5NNXX2J5cmfDt04N97Fd02n1XiTpfS0C3HaeRH67A/pHkxtJJkmfxRhaNtQ7SLt3EzrszCiGnlxB4lBj2Iys0bgT4EFwDNm9unhTlTxukP/E9XSmm1i2e6YhrszIgzMZP7UFrlKQ6GqdD4lKCP/7ZPNZaHht8nfZxyVGcTTSX9zZOg8IbEsdD746/IpgPn7DlZas5Of10PnbfJ96JLqb5/cr7jviRjKMNengWeAZufc54GfGt4kFbO42pwsoeQq/WSbAiOtCh66uzR5rFzNUiHZRjTF7/07wkOd0hZYZ95nhx5NOp4lH5gVi0vnyVF9yaaXUB4bjFwd0LlkK4ilBZ+0dPoDSrI1ZxV3QWooAaKa6BbiNcOcljGgi3CzC97n5EU0NOzNLx1ly3R+p/FgmpJCtYrkfqFqcrIvIZSOtGF8flNYN+qHGK/ii15aHglN1ge57zEY7LI0uZpqQze/hmr3+TT5JveBu9N5nzUxAb8F/A/gNTN7GnhheJNUzJL/zLQSeeiinNwn7aLul8Zdju1Dx/f5J5xf08iWFj9IpNVSstVmxs4dozKc4tpjciRPkj/UNXSOhNaFPieXDVeQiIUu6qFad7bjJzuv09JXvHOYDTpAOOdOA/+OqA/ie8653x/2VBUt/x+Zb+k9l1AfQNrFezDV6LQ0+B3jodJSthPVvyPcH/cdr2tDxpseogDh1zhDlxp/kENy+3xvtgydO/nuk2ubtD5Bv78k9Lulnbuh5cXbzDSkqTacc1eBbzKumpl6GdjMAwMzkd+fELqg5pq3KbkszVDugfAv5qFOs1CzWJz2fL7f//3VDzE+9ZB+n0A+BZ74AhyvyzZENm2bfOQTJNI6l/MJCGm1Aj9wGsU8BXjOAGFmtWb2BTP7spn9oEX+DfAO8OPDmRgze9LM3jCzt8zsl4bz2PeunbtL1jkyfOcl6M32z49PnNDYae9YwfWDka1ZKdtQW3+ftFpFX2I7SyyT8SXZ7xQXTrKNEMpVC8/W3BQbiSCRbWiuv8yvUWQ7TqiA2ZUzpYWSTw3iz4HFwFHgnwPPAT8GfNI598nhSoiZlQK/C3wUWAb8pJktG67j37u4BgH9Fz5/GJ836ufcX8HxfwstL4HLchey64Obr8Ody+H1H8g13DWXfGoM2folktv703GEOtNVgxh/4rm4INx/kK2g4q/L1hQ60kIXdv88yTa81r+R1N/Pb8IqTvlMtbHAObcSwMz+iOjBsk3OuVvDnJYNwFvOuXcy3/VV4JPAiWH+niFKXgz9zivLjOBLdDJ3NMONfVDzIDT/CTT/OTftU9Qu/wiU1oIZuB64sReufgf6OqFqDsz6xWjdB5Jt+vcqlJnzqaX4TQR+rSfZlhwHyGRAlfEj2XGbVgpP/syV17PV1vOpXeSSdh7kcwH3A5nfF0eW5aHzp/jkEyA+GLrjnOs1s3dHIDgAzALeT3xuBjaOwPcMA28upo5LcOE5mP2jUDE5Wnbx29FPq8A5x7Fvd9H88ud48otPYGWTuNm5mYkTj1PSfS7armYptB+FO+ehclbiuwbbaZdNtmAQytBxLSFXW3DyZErO76QaxPiTbGLKpz8t10W+j/Cw62yBY7CyFZZIWRcqbPm16tB+yQkLQ8GiuOTTxLTazG5mXreAVfF7MxvOcYz59GBhZk+Z2T4z23flymg+eyA0ptvAOXjn/4P2Ztj/WWj+G/puvYNrPYArmcCd9lsc+Gobb/31t+i8co073dNw3dc58sXf5tAf7sHZhMzhMyN+LvxBdMwPDOeJ4AtV33ON7Q5tkyw1xp+Lv/osIyF0R3SatCYmX1rb/1D7HvJJT77nhJ+e5P75nEtQzAWpnDUI51wofI+EZmBO4vNsomnG/fQ8CzwLsG7dulG+CjnuutP4yqvQegxqFwLQd+av2fe3X+fMt78LwGvzt/HG++f56WWPUn56H5eOXadiQhXXjx3mOlBSWsLqn1uF3cnUJO6cgY43oXoRA6uwcG9Bwv9T5VtqSWZ8v2kp2/FBz6Maj8rIr78grQM612in0ACL4apF5NvMlFabSG6fHKEY6rNLfsdoXWIHL58mptHyOrDQzOYD54DPAP9PYZMUEv/j+6C3m863X2ICQHf0hKjjL5Xy/suvANA6dS5/9PxeqiZU8tKRt1kyexpP771GXV833Us2cduV8d7bjhNfucUPbJxEzYwaKid2U3LxD7F5/wNKyr3vhaGfDPlk/rRM7Dc7hQJF6CSR8SfOG/60Lfk8MCtxbt11Z35aQWm4atZptZQ4Pf7ybPv524SOkdyueAtS+TxR7oBz7pF73SYX51yPmX0W+B5Rzvpj59zxeznm8KrgrlLP1f3s+r29zHpkJos2d3DpnYmc+N9fA6Bqxkz+rKWKO3fuMHPmDG7dvAV1U/jSy2doqK9n9449AMyaM5vr397Hnz05k+7z7wBglRWs/IVJzNy6GCufBuUNUDoZSh+A8nwe8OdLK7lk63dI2w/Sg4Xf91C8JSMZKRWJ96HO2TT+8M+kkQgISWn5PJ8RR6F1g+1TGMMBAlhqZkeyrDeG6ekwzrnvAN8ZjmMNvwkMHOIJXHyFqYum8fqX/47D32nizLSHeGDFJur6utlfMZVTe78PQH19PXOa5rBn5x4eWvggu3fuZtGSxZw+9Qb1DzzAhfebOWKNLCUKEHWL1nHkv/8adbOeZmL9pei7qhZD92WY+0WwwVb80jJ4XLIJtRmH5o7qJVx6GhsdbjIaKhk4EinZ1JIUahrKp7kon47twcjVMe2nP9ejROP+OP9mP78GlPzesR0gluSxTfH2sgybZA3CQUcLtB5n6rxaAF4unckb5zrZ+fIeSszYvn0LHe0dzJzVyIxZjfz930V9ErV1dfT19dHZ1cXWD21j9/ej5qjfe+4Av7ehlr47nbRnahJ7vvD7PP4H/4LS6inQdTpKRstfQMPPekNhh4s/BDG0PlQqjP8ugxnBIvenMvqbiNJqqPGyUCdwvsEkn3X5yDevh7ZNG9mXDAhpzU/JQFK8Ne18OqnPjEZCxpQ7N2nd+1WqSmcypfES3dWT+MtXT1BfHw1xfWTtana8vJP585o4895ZJk+ezPpNGzjw2n4mTKgEYPacWZSXV7Bp+1auXmnh9MlTXJ25lgUTjWsHX6GsfjptDQ/xp7/1Fk9ua2VS01Sq6kspu/0aTNqGTXhwiIlPu8jDwCp1/D5tFtpcD2+HqNYl40sFA2sQoala/Nlc/WAxkgHBF6pdZxs1lW3fUHNUsjbhN+v2ZV5VQ0n4qCimTuoxoAK6WuDArzCxu5W//OyrbH364xxftp7WYy/SeuMmy5csxDKl+5mzZ3LmvbPcunWLE8dP8sjaNVRUVvDI2ofZvWMX0xtncO3yFXp7e5k5ayY7b1Zzu9T4bvuD7Nr7NnAJA+a9NYWem9ET2qy0lFkfa2X50/8dKuekJ3WAbKUkn393tF8SSgYRf3uIToj41plJeaZP7i/lDJyTye9fcNydj+DuGkU+QWI0aqppNYGY38Ee7xM6TnIfiGoPlfeawBFTvI1fRakMKibCxPmUlfcxffUyXvzVv+atm31s3PgIm7dsYHbTLA7uPwzA668doH5KPa3XbwBQUlpKaWkp1RNraJzZyKULF3l4/VoAZjXN4Vsv7eZP9r5HW1U9S1euAKIs1TF9EQAVD0yjZt4yem68B+eegZv/wMB7JvKRrRkp15wycabu9d4n1yenH6kZZNrk/lDG4Dqoob926tck4O4AEGqCyleui33oeGlNSaG0+MtCfQ3JgDJcsySMjLxrEGb258AO4BXn3KmRS1IxmwDWDhOboKeNmaubOdS8iFf2HqKzvYOuri42b1rP8lXLqZ1Uw6mTb7Js+VKOHTnGxkfX8/qrr7N2/VoOvr4fgJVrVjKpro5Ht23h1Vd2AdAwfTp7Xt4BwKKlS6itq+P4zRK2LVxN5+Vmbr99lIZVH42S0/Jn0HYIZvw8WHkwxdmbk7KVdrIth7urzfErOcSxeDO+jKRq+p9J7YvzR6g5E9IvrtnkqnGEth/sPqHvS1se6nuBgedbXJAq7jL6YFL3J0Aj8Dtm9raZfc3MPjdC6SpSEwGDxi1w4zSzVk7lWGU916+3sm79agDKy0upqq7ilVde5erVa1BawqrVK9j/WhQUzrzX36Vz5043zefO0fx+M6vXPgzA5YsXP1h/+uQpzr53htO9tdxyFXTfiJqZKutr+5PUcRgufBF6k5OkwcCLdkioYzCtXTiZsf1JB5P7Jkt/xdvxJiOthuyl7nzzZZq05pt8agdD+b5c0prGcgUHR3RNKV55Bwjn3IvArwH/CfgjYB3wr0YoXUWqDCiFCVOgfgW1Vc1czrSwnD8fDUft7umltTVqUqqorOTsu+9x6dIVps2YzubtW+js7KRx1ky2PLaVt954kyuXrnD2vTMc3H+QNevX0tbWzrQZ05k5exYbt27hWksLl6/f4Gf+/HUOT99MafUkKuoyTTcV86B0OrQfob95KDl3UlpVOdsJFos70NJGLaUti38+kPI3lPtfGf33Q4RqqX5TUuh98vkp+V74k7XYNCM1LDZtZuPQaK7kk/bukwBhZv8A7AJ+AngDWO+cy2cI7H0mM+KgcTtGN6umVrNt26Ocv3CJhx9ZxY3Wm5w48QaLFj/E2nWree/ds0yd1sD58xfYuWMXDVOn8fDaNVw8f5He3l7KSvv/BW+cPMXM2bNY++hGWi5fYe/OXfT09GCZTP0bf7ObX32zmhtuEpQ2Quc70H0h2tkln0qVrYPMH2kRCiZ+x1/ypPNrFsl948+lqIN6vEv2PyUDgD/Ta2gUUa5hrrmCRSjvZutf878r2+dQ2kLNrfHn5HNSfGUpy4vHYJqYjhA9+mgFsApYYWbFOz5rxEwGHExZA+W1rOts4eDBI0yd2kDD1AdoabnK0mWLWLR4Ec1nmwG4numkfviR1bRev8b16628/eZbLFy8iKUrV7DlsW2sXLOKzo5OThw/wQt//xxNCxYwZ948AFqvXwfgkY0b6K5+gN1/c5DTf3WMXtfQn6ze9kBaQ22h/gmZbdhqqKqcXOffcR1vV7yjMmS0JO+dzVbjTC5Lfh5Kc5EvVPDJdaNbtgAR2j9bZ3yoyTe5vPiHgQ+mienfOue2A58GrhL1SbSOVMKKVzkwAUpKYcYWqlwvn9i4grNnm7lx4xbLli/m5InT7Nt3gDNnz7Fk2WJqJ9fy4Y9s5/CBw7Reb/1gGGxXZydvvnGalitXcM7R29vLyjWr6Ors5PSpU1y8cIGN27YyeUo9cxbMZ9/e13jz1Cm6+xzvfv07vPBPf4f39xrOaqEv2wzs2dp749JVSKhfIpYcrZTsnAYYynQgcn8pof/m0lAzUzL/QPYLbz6fffnWGJLHG8x3+LXq0D5ptY+46amWYjeYJqbPmtlfAoeATwF/TPT0t3FoClFn9WOUVpaz8eZ5tmxex969B2lpucbW7Rs5f/4ic+bM4sSJN3B9fbTeuMmW7VuY0jAF5/pYtmIZN27coPns+0yoquLY4aNs3LKJ6uoqNm/fytqNG5g2Yzq9vT1YSQnTGxspL49GKnV/UHDv48Tv/gW7f/klbpw+ysCSl9/sk3xlq3L7+yaF7pGI3yebl8ZhxVICark7P4ZK0qR8HsqIpsFum7ZProARSluoU9p/H5tAsY9ggsHdKFcF/Caw3znXk2vj+1slUAXV06lfuoym24dptEmUlZUx+YHJ7Nixh40b1zKhopy5c5vYvXMPW7dt5pUdu6isrGRy/RSutVzjRqYzu2Zi1F5rZly5dIWTR4/R29tLSUmUgR6or+fYwUM0TJvGwiWLcVZCzbyllE9uoOPiOW6+eYqSW89D3w9DSbJ5Jy2T5zoxQxk6WeLzM39yJJNqDxKbCNyg/14ZfyAD3N2/kJQ2q2uu/YbDUM6RUId6Wu18bAziGEwT06875/YqOMQaAGPxR1dy6913qLnTzpIlD1JaWkJlZSUOx6TaWm7ciFrhnIsyyrqN63j+ey/w7ntnWLDwoWhkU1cXm7dv4dWduzly6DDrNkUP0lu3aSPvnznLkYOHWLhkMS2XL7NnxyvsvdRNZ1c31w68Qsf5d5jyyEYmTWuHS3/GwBvnBtMp5zc3hUp8cHcHd3KbUoZp3ka5b2SesHjXRTMtf/myrRtsM9Jg5Hsz3mDOt3h9KWNlGHjx13GKVilQQ93cWWx46gkedJ0cPXqK3j7H0iUL2bf3AK/t3cfRoydZ/cgqysrL2bJ9C7t27KKzs5OVq1fy1ptvsXPHLsorKujo7GTDlkfZvH0rbW3tbHv8QzSfOfvBt9XURqOCHt22lee+v5tfeOkyZXOXAzDvhzKDyW7thK74qa35Zmi/ucnvzPZPwuR9EH478pQ8/m4yvtQQ9dtBuIM6Fg9pHUwncLwsWz9aPtKOO5jtk0KjllxiecNdexQrBYh7MgVqF7BoYxmPzJtIdXUVp0+/RfXEajZtWU9LyzXmzW/i0MGjdHXfweFYtWbFgCPEQaNywgRe3fUqO3fs5MyZM1xvbWVi7STWb97Exi2buXThIus2beTga68DcLn1Fk+/eIGKDU8wdUni5Dj/G+CS8+Ak5XOyJd/nOukc/c0H5RT7mG4plGQtIlng8G8eC9UmCjHPUr41AUjvJwmNoHJEfQ9psx4UHwWIe1ICNUuxWY/zkZ9Zysef2MSFC5e5fPkKu3a9zpatG5g9exaPbtrA7p17ATgctdqhAAASM0lEQVR06BiLliyipKyUrY9FwQHgwL6D1E2uY8nypVRWVHDkwCHqG6awd/ce9uzaze22NiqrJlBaUUFJWRm9ztFy8zbnr7WBK4E+A6qjn+1vBdIaaiqKf/rZIO1muz76A0KyXbkPmD6UP6CMC1VEF8a4BJ02zYQ/sGKwcg1hjX8mB2vk00eX7bhpI7QgPIfU2OqjU4C4Z/XQ9CNMqC3jU8sn8dhjm7hw8TIPP7KKffuPUDWxira2NgCOHj1BZWUlp06dprunBwfMaZrDmkdWs2btGrZ9+DFutd7g8sXoruyWyy0AVNfUMHXaNF5+8WUeWryQnp6oG+jzH32Y+jf2cO29anC90HsbalZAzUPkN0op+TPZpJTk3xQX2n4yA58kJuKL+uwi8WUndPdxtj6xtFdSqJaczywDpCzP5/ih9MffmwwStYx8jWh4abrv4WB1sPQp1s/+b7xUCYdKSpg+vYHOzk6++90XWb1qGQ+vXc2tm7eYPq2B27fbObj/MGbGrMbpHDpwmMaZjRw/epypDVNY+fBqqqurOHroCA8ufIjqmmqOHooe6nfxwkUqJ0zgH39kPUvPRQ8bOvSlr/L4lz6FldXA9M8kEpa8kPt9C6Gnw0H//PXJfbJ1XFcy1kpFUgglRPnkmrfcMbCcGiqzJkvk/kU3VAsZ7ECN0H5px8oVFELHhagGNfZmF1CAGBaToXIm0z7042z57Z/h6PwFXGm5xpw5M2m73U5Pbx9HjxzGgPkLmnDOqKisoO12G7WT6+DM+8xonMHB/QeZObORI4eO4JyjcWYji5Yu4trV62zevoX4xPjYtnX8SMV53MTl9Ny+SfeNq1w+Xc70J56CEv/uzLSLe7aTIVSy8z/HwWfqUP5gMi5VZV6d9OcfCJe6/em/Y7mm2h6qwfQ7ZAsUoXOohLE6gENNTMNmGnXLtvBj33iW//rEXOrrJrH/wFG67nRRV1fL2nWrmTmzkUMHj1FWVkpHewdLli1hUl0tH//kx7h16xZTGqZw6uQbbNq2hbUb1tLV1cW3v/kdOjs62L1jF7t37OTa1at87bsv0X7pPDffPE77hffpbm/n9sXbUDnbS1Ncre4he5NTLwOr4fFy/8T1q/b1jKUONykGcZ7J1pwTuvjmChZD6bOI9wuNnAqN7MtnYEdoWR1jrWkpphrEsDFgGhOXfpgferqE8r/6Ov/TlmNl5TQ3n2PevCZKMPbvO0TL5RZWrlrOsSPHefCh+bzz9rt0tnfQer2VEjNKyksp66tgwUMP0t7eTnPzOeom11FdU8PFi5e4duMWO2wpmzgPwPxPfZwFmzrh7Jdg3i8RPa/aryn4TUwQHjnib99L+Fj1aNSSDE0DcIn+PJXt4pntxrjQhT3fMm/a92brn/DXp22b1MBYnptMNYhhVQZMg8bHeOzTn+IzpS2cO3OWxhnT2b/vMJVVE1i4eCFbH9uEc9A0dw4d7Z2cP3eBJcuiexk2b9vM9//hZZyD1/a+jsNomj+PjVs3MX1mI9evRRP3/e7fv0bZghU0bt/O8k9OiOZ3ajsOV/+e6Ga5tGdG93F3519ynX8CJE/Q+FXLWGxPlWIR3wsQGhgRX+RDeTif0U2Dnbk1W9MROT6nTbcRv69nLAcHUA1iBFQAUymd8yEef/omtb//h3yty2hv76APx4SqCbz88h6WLV/M0hVL6em+w/yH5oODj//Ix3j3nXdpnNlIW3sbTXObmDN3NldbrvH63tdpappDaWkps2bPor6hnpNT5vGD/3I5VnYH+u5AXwfc2Av1HwHzp1UOZf60Oez9AJIMHJPoH9cuMlRlREHiGv35yx8G63dKJ2vGucq2+ZTu89k+NIovuY//Pk5jLWNhttZcFCBGRCUwndk/8Elmr53Lh/f8CYsWfJgXj1xmeuM0npj6GC88/zLnz12ku6uLdesf5tDBIyxevJATx08C0DSviUlzo1J6e1s0lffc+XNpPvs+D0yq4iemdLK6901Ku0qgfCF0t0QBYvqPQUlaCSwW6l8IvYeBz5yeiIKDDJ8yos7bq4F1fu11JBs7ctUk0prAQgHDiM6R6mFLXSGpiWnEVACNUL+Wuu2f4+c/WsPjEzrY+cqr3G7vYNv2zXR1dbFy9Qpe2bGH6poayspLWfDQAjZu3sDe3Xvp6urklR27eO/MWeY9tIDJE6v4lX/yQ3zOTjHj4kl62ruAPrj9RuZ2hK1Qt47sVezQU+L8V+g5D/UoOMjwKyWqScRl1VC/WchgawjZ5DpOaL1fqIqDQz33S3AA1SBGWCnQCJMqqHv882z/5r9nSnsr36uu4lvPvUxj4zQa6iezdNliHqifTElJCQ8uXJAZ4bSYA/sOMf/B+ZS4Pn58SQOLzr7Ak//uX2A/9eOcP9rDrearULMU6tZC7cNQkTaULq1t1RhYQwiNWiolmnlSN8LJSInvkbgNtDPwqXPJJh7/UaWxoc7wmhYYQk+5y7VfPJT1/rqkmnPDFYVH37p169y+ffsKnYw8tULvdfre+yZXjr3EiRMVXPzGP9B3/Rpu3TZevNrDt/Yeo72jkwcm19FypYUlixbwLz+8lHUNPVzZf4K2c+8zeWETj//n9VhpFcz9VzBpeeb4fodZPhk8WWMILavgg2dfiIyKO0RThMPdd16T8jneNtmPkU2uYav5LE/WsmsYa4M2zGy/c25dzu0UIEZTL3AN2t6FM1+n6/LbvLGjnfdeOUnXtSt03OnhzabVNFfUMrW7jTXvvUZpXw9PfvkpauvOc/t6FRdP9TFj41omrf4JqPDvYM635BMauRR/jt/XoQf/SGH0AbeA7sQyPyiEni2RJtd5kfzeXMuT7+P+hrF3L5ACRFFrA9cKLXug9RRdnaWc2X+T0t4WGmZcp3ZKFz0l02g9e5Pr53u5fbmT1T+zntIHVsLkR6B8MneXlEIPV8nVdprcLn7VZF7qnpJC6wFu0p9nQ3lyOPJpvoM5ku8rGQuPDE2Tb4C4vxrMxowasBqY+iRM3UolsGhl5mJ/5zq0HqX89rtMnXSJqVvXw5QNUB5nxtADe/A+h5bnChZxhldgkGJRRtQ3cYeof8Lvh4gNtu8hH2n3EVUTFaDGR7NrUQQIM/tHwC8DS4ENzrmxWC0YgomZ122i+Wl6oGIyTHssen0g2b7qB4HkBb3X+5zt0aHx/pWZNIyNJ1zJeFRBFCi6gTbCTT759j/EBlOYykylPw6bXIsiQADHgB8F/rDQCSmMOFD0EJ0AXQy8ISiZmUPPbsj2ObSsjP45+kXGinKiNv8+onMkM8z7A7ludvMLWT5//zKi87JYLpOjryh+c+fcSSCaLmJcK6P/mc49RDWLeC4k/96EuLTkZ3p/WCBEtYMyoqpxUfzLRe5BCf0zw8IHtW+6SR+BFHrvb1OWOLbOExiDfwUzewp4CqCpqanAqRlJZdx9Y1o3/bULf3bVuIkornFUElXNx3vQlftfqCbcTVS48h+/GxemShOvMXcZHDWj9pcxsxeAGYFVzzjn/jbf4zjnngWehWgU0zAlb4woZywOqRMZfTpXhsOoBQjn3BOj9V0iInLvNKZRRESCiiJAmNmnzawZ2AR828y+V+g0iYiMd0XRO+Oc+wbwjUKnQ0RE+hVFDUJERIqPAoSIiAQpQIiISJAChIiIBClAiIhIkAKEiIgEKUCIiEiQAoSIiAQpQIiISJAChIiIBClAiIhIkAKEiIgEKUCIiEiQAoSIiAQpQIiISJAChIiIBClAiIhIkAKEiIgEKUCIiEiQAoSIiAQpQIiISJAChIiIBClAiIhIkAKEiIgEKUCIiEiQAoSIiAQpQIiISJAChIiIBClAiIhIUFEECDP7dTM7ZWZHzOwbZja50GkSERnviiJAAM8DK5xzq4DTwBcKnB4RkXGvKAKEc+4551xP5uOrwOxCpkdERIokQHh+DvhuoRMhIjLelY3WF5nZC8CMwKpnnHN/m9nmGaAH+EqW4zwFPAXQ1NQ0AikVEREYxQDhnHsi23oz+1ngh4GPOOdcluM8CzwLsG7dutTtRETk3oxagMjGzJ4E/gPwmHOuvdDpERGR4umD+DIwCXjezA6Z2R8UOkEiIuNdUdQgnHMPFToNIiIyULHUIEREpMgoQIiISJAChIiIBClAiIhIkAKEiIgEKUCIiEiQAoSIiAQpQIiISJAChIiIBClAiIhIkAKEiIgEKUCIiEiQAoSIiAQpQIiISJAChIiIBClAiIhIkAKEiIgEKUCIiEiQAoSIiAQpQIiISJAChIiIBClAiIhIkAKEiIgEKUCIiEiQAoSIiAQpQIiISJAChIiIBJlzrtBpGDIzuwKcGeLuDUDLMCZnuChdg6N0DY7SNXjFmrZ7Sddc59zUXBuN6QBxL8xsn3NuXaHT4VO6BkfpGhyla/CKNW2jkS41MYmISJAChIiIBI3nAPFsoROQQukaHKVrcJSuwSvWtI14usZtH4SIiGQ3nmsQIiKShQIEYGa/aGbOzBoKnRYAM/tVMztiZofM7Dkzm1noNAGY2a+b2alM2r5hZpMLnSYAM/tHZnbczPrMrOCjTczsSTN7w8zeMrNfKnR6AMzsj83sspkdK3Raksxsjpm9ZGYnM//DzxU6TQBmNsHMXjOzw5l0/ddCpynJzErN7KCZfWskv2fcBwgzmwP8AHC20GlJ+HXn3Crn3BrgW8B/LnSCMp4HVjjnVgGngS8UOD2xY8CPAjsKnRAzKwV+F/gosAz4STNbVthUAfCnwJOFTkRAD/B559xS4FHgXxfJ36sLeNw5txpYAzxpZo8WOE1JnwNOjvSXjPsAAXwR+PdA0XTGOOduJj7WUCRpc84955zryXx8FZhdyPTEnHMnnXNvFDodGRuAt5xz7zjn7gBfBT5Z4DThnNsBXCt0OnzOuQvOuQOZ97eILnqzCpsqcJHbmY/lmVdRnIdmNhv4OPBHI/1d4zpAmNkngHPOucOFTovPzH7NzN4H/jHFU4NI+jngu4VORBGaBbyf+NxMEVzwxgIzmwc8DOwtbEoimWacQ8Bl4HnnXFGkC/gSUaG2b6S/qGykv6DQzOwFYEZg1TPAfwR+cHRTFMmWLufc3zrnngGeMbMvAJ8F/ksxpCuzzTNETQNfGY005ZuuImGBZUVR8ixmZjYR+BrwC14NumCcc73Amkxf2zfMbIVzrqB9OGb2w8Bl59x+M/vQSH/ffR8gnHNPhJab2UpgPnDYzCBqLjlgZhuccxcLla6A/w18m1EKELnSZWY/C/ww8BE3imOkB/H3KrRmYE7i82zgfIHSMiaYWTlRcPiKc+7rhU6PzznXambfJ+rDKXQn/xbgE2b2MWACUGtmf+Gc+6mR+LJx28TknDvqnJvmnJvnnJtHdGI/MhrBIRczW5j4+AngVKHSkmRmTwL/AfiEc6690OkpUq8DC81svplVAJ8BvlngNBUti0pn/ws46Zz7zUKnJ2ZmU+NRemZWBTxBEZyHzrkvOOdmZ65ZnwFeHKngAOM4QBS5/9fMjpnZEaImsKIY+gd8GZgEPJ8ZgvsHhU4QgJl92syagU3At83se4VKS6YT/7PA94g6XP9/59zxQqUnZmb/B9gDLDazZjP7Z4VOU8YW4KeBxzN56lCmdFxojcBLmXPwdaI+iBEdUlqMdCe1iIgEqQYhIiJBChAiIhKkACEiIkEKECIiEqQAISIiQQoQIiISpAAhIiJBChAi98DM5plZR2ZSt3hZb+aGr2Nm9ne5npthZlWZ7e8UyzNJREABQmQ4vJ15dkeswzm3xjm3gmiK7X+dbWfnXEdmf83ZJEVFAUIkRaZ2cCzx+RfN7JcHeZg9aLpvGaMUIERGSObpch9Bk/XJGKUAITL8qjJ9EleBeqJHtQJgZovN7PfM7DeK5VnjImkUIETS9TDwHJmQ535xn8JcoIJMH0SmA/oLwC8DvwP8z8yU4CJFSQFCJN0lYJqZTTGzSqIHJeXNOXcD+HngFzMPxdkO/BbwaWA60UNylg9vkkWGz33/RDmRoXLOdZvZrxA9I/ldhvDAGOfcQTM7TPRwl0PADzrnfgPAzH4CeHkYkywyrBQgRLJwzv028NuD3Gei9/lH4vdmts3Mvk707Oq/cM61DEtCRUaAHhgkcg/MbA6wG7jq3QsxmGNUEQ2HnQqsdM5dG8YkigyZAoSIiASpk1pERIIUIEREJEgBQkREghQgREQkSAFCRESCFCBERCRIAUJERIIUIEREJOj/AgscuBVijlHAAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f522337ef10>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"afig, mplfig = b.plot(time=0.25, y='ws', fc='teffs', facecmap='YlOrRd', ec='None', show=True)"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYgAAAEOCAYAAACTqoDjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzt3XlwHOd55/Hvg4MASAI8wZsQKesmRV3QZVmSdXllWZbKsR07u/Laydosp3zIG8uHrMom2a1sZWPHt1MulY9NYm0cryWtj9jWYVmHbUk0SPEUdZASJVEURfAAQBIkrnn2j54WGo0eYAAOphuY36dqarp73ul5hsT00+/Rb5u7IyIiEleVdgAiIpJNShAiIpJICUJERBIpQYiISCIlCBERSaQEISIiiZQgREQkkRKEiIgkUoIQEZFEShAiIpKoJu0ATsT8+fN9xYoVaYchIjKprF+/fr+7N49WblIniBUrVtDW1pZ2GCIik4qZvVRMOTUxiYhIIiUIERFJpAQhIiKJMpcgzKzazJ4ys5+nHYuISCXLXIIAbgW2px2EiEily1SCMLNlwDuA76Qdi4hIpctUggC+CnwWyKUdiIhIpctMgjCzG4F97r5+lHJrzazNzNra29vLFJ2ISOXJTIIALgNuMrNdwA+Bq83sB/FC7n6nu7e6e2tz86gXAoqIyDhlJkG4++3uvszdVwDvBx5y91tSDktEpGJlJkGIiEi2ZHIuJnd/GHg45TBERCqaahAiIpJICUJERBIpQYiISKJM9kGITD49+Ucv+AB4DqrqAAPq8w9LM0CRMVOCEBmXY0AH0IP3HqH/xQfoefkpDhzJ0dddhR3pY8abzmPRmpPo6Z9J7ZwlVDXMJfjJzQQaUQVesk4JQqRoDhwCOsEdDu9k35OPseG7v+LVto1sOuUC7t26i6VLF7FwziwWNB1gzjSjad8+rr1xJXNqZpCbtpAz33MdzDoFrB6YCzSk+7VEClCCEClKF9AJfR3w+hOw9xF2tB3hJ/e+yHPMYPeKizh6bIDOji66j3bTe1ILPbl5vOxOZ5dx1z9upqvrMNdcsIr3HHiFt1/dTO0Z74bGlUA10EzQDCWSHUoQIiPqBvZD31H2PvCvPP1v97G3rpG2vnq2vHiQAx0DzJtbzdHuburqannrlZdyrLubhx9+nAsvPI+DBw6y/8AhAC6+5Hxe7TrODx99narfbuWky9s55QMfo2HxScBegppEM2p6kqxQghBJ1A/sC54PbYdd91DV28u3d/Xz6LYNgHHyycupq6llz+49zGuexyu7XqWzs5P58+dxww1Xc/xYLx2HOlhx0jJmNjVy/30Pc0HrObzY3c236xr4o+//lGkNxukf+hg0rgCOA7uBBag2IVmgUxWRYXqAPUA/DOSg+zV69r/E4994iP80D658y8UsWbyQ9X/YBDh9fX3U1dSy5uwzaJ43l107d3Hs6HGOdR/jxR0vMnP6dObNnsWFF6yh73gPSxYvoL9hOr9ceQnHp1fD01+Fg1sImpqqCBLTkRS/v0hACUJkiGNAO8GQ1CqongZLruXV106l5+B+7j9Wx97X29n53E7e+tbLWLRwAS3LlrBxwyYO7j/EgfYDXHPtlfT19NJQV8dNN7+dTRs2s2f3Hva8sgfc2b7teZ7Z8izPvLCb392zlReeAn/hn2FgYPBzOQh0pvjvIKImJpGI48B+Bg/S+efd97JoyStsW7aGja8do2X5Ul6e8wq/f/RxZs1u4uiRbi659EIam2ay87kddHV0cbjrMHPmzqbzUCcLFsxn+vQGZs6cydzZs5mxbAZ79+5j3vy5dDdN48Xf7+Vox1LOPj/8TAhqE10EI6dmp/GPIaIEIRLoZzA5VBMeqI/uaOOF//MLnt91mHVHqtm4fiOdBw/RNHMGZ646He93nt72NL975Hc01Nczr3kec+fMwQdy1NXVMbupkd3V1XQd6mTxwgVsfmoLs+fM5k2nrqSqqoq7ntrFkTfN5ZbGAXj5/8KKW/KxkI/hCIPXToiUl5qYRAA4kH+u4Y2z+NwADYfv5vBrnfzwheNs2bSNd7zz7bS0LKO+ro7qnLNt02bI5bj6uqtYtfosDrUfoL+3l+qqKp7d+gwPP/gwy5YtZf78+ax7fB2nnnYK55x/Dpue2sKhA4fY+dxO9nst9XOb4OgLcKAtH0MVg7WYDqC3/P8kUvFUgxChA+hj8OdgwaP9IapqjDPfew61/3Mjhw91cKC9HcM43HWY57c/y0Vvvpje3l4e+/UjnHrGqVTX1LBl42bq6uu55M0X09nRSV3dNHLuLFmymGe2bKPn2DFmzphO7/HjfP1T7+bSZcd55sePMn/JOdTP3T/4+VQTNDENEFygtzCFfxupZEoQUuF6Ca51qM6vh2fuQF8X9O3nxQeOcVPXRo685SI2bn2WhYsXsubcszn55BXkcjnmzZ1H68Wt1NTUcPoZp7P75d1s27SFXTt20r6vnZaVK9jzym5q6+o46+xVbNm4mQsuauVdLXXMfexeFv/tezjt6nMZWP4pmLeKICmEwuV+gk7rWeX4RxEBMtTEZGb1ZrbOzDaZ2TYz+5u0Y5JK0MGQDmngjTP4pe+jZ/q1TJ9fzw1f+RCfuWYxs2ZM55Wdu9j76mus+90TVFkVTz25js6OTnq6j7H/9XbaX9vLFVdfSdehDpYsXcr06TNof30fjY0zWbZ8Gee3ns+mtg00Ht7LnFXn8/xDnfiCd1Iz72wGO6mjMYW1iW6C2oRIeWSpBtEDXO3uR8ysFvitmf3S3Z9IOzCZqvoYPOCGB2MfXDaoO+0Wzpg7n9zuuzny6GPcdtYs7um7mMcefow3X/kW+nv7WHX2asyMrq4ueo4fp7a2lueffoaBvn5e3fUSS9+ylLpp03h+23YWNDfT39tL68UX0j6zlisuX8KSCxfDgpsZOoIpl1/P5dfDjusuYE6Z/n2k0mUmQbi7M3h1UG3+4YXfIXKiOhh6lg6DTU35WkRVFTS/kyOvHue8T85hVstMLll3kJcanmPakgF+vKOHB7buoPPQIXK5HNe98wbMnc0bNnLplZfT19vLr3/xK1affx4D/f088ehvaV60iPruDq54x4WsuOpUsGqoqWUwKThDK/dhksgRDMX1SLwiEyczCQLAzKqB9cApwLfc/cmUQ5Ipq5+g9hAeaC3yqBq63apoOvePaVpwFPraWXTGIXb+0z6mzWjkpoYuDl1wDl3dPbTv3UtH+wG2btjIsuXLWdzUwGkLGzm1/lyODhgz5i1iaU0PZ605nYtfX0fHbx4id2MNVUv/Y+Rzo0mC2Lbw0YX6IqQcMpUg3H0AONfMZgP3mtlqd98aLWNma4G1AC0tLSlEKVNDN8lJoTpSJrLdqmDJh6HnNRrrH2Ppf+igqaWBhecvZen6Lv7tnk3c+dudLF66hIVzmvjMVSs5rbmHNWvP4rFbH2OgZ4DL/urDrPubTcxacJjVn30/2/75D+zf1ciC1W+JxeKRBwxPEhryKuVhQctO9pjZXwFH3f1Lhcq0trZ6W1tbGaOSqWNfZDmcA8kSHmFTz9Bahe+/F+v4GdQup3Pn66z7y+9TvfJsjp51LjMe+RkDRzo457MfYsGqPnp6FrHzp89y1ntn0Z9bwPN3P8+Z727Cm66gt+oC6hasZmhCyEXWw+WB2GvzGZrMRIpnZuvdvXW0cpmpQZhZM9Dn7h1m1gBcC/yvlMOSKSk88FYRvWp6aDIAhjU/DS7bnLdB5/1QVUPTsh5mn3kW59x2PbUzjN6bP8KOuzcx/6JLoPFc6upWcsana6C6jhrv47RPdsH0hZhVU8cAg30KSTUGGFp7CNe7Ce5KJzJxMpMggMXAP+X7IaqAH7n7z1OOSaaknvxztFZQKClEt/vgcnUjzH0f+DFswUe44Cv7qWr/KuRmUTfvTay646+gevBOccFeHKinuiacNiPa2Rx2TOci7+iPfGZ15DVjcFSTyMTJTIJw983AeWnHIZWgh8EhrTB0eGt4oI6esUNSLYI517yxrapuOVR/DgY6YealkbfGm3AjSeaNzzSGDreNx5Vj6H6i5UUmTmYShEj59DO0dgDDE0J0e3w9emCPmL6qwOdFy8cP9NHX401N8c+Pd2KLTKzMXEktUj7Rs/jwOf6Ib/fYtqTlJPFhs/EYouWSlpPiTHq/SOkpQUgFih70o81L0dfjB/VCCQSK/xnFawbxRBB+ZjyBxZdFykMJQipQtL1/JEkH6KSJ9IpVFXmE+4wnnWgfSDwW1RqkvJQgpALFp7GIH3zjbfwWey26PNYz+/i+k5aTEoGm15DyU4KQCjfSTyA+eggmttkn3ucxUqe5koVMPCUIqUBJHcaFhrSWesTQSLWRpHJJCSE6RFdk4ihBSAWqjSznIssjDTON1iZO5OAcTTiFmpI8YTn+un66MvF0HYRUoPBWnvErmaPP4RTbSWf88feM1txTqBYSv6ZhtHhyCeVEJo5OQ6QC1UWWozWE+OihpAN7eKCOHsBzsUexNYykzvD4JH2FrsSuQ2SiqQYhFaiGoQficFbUcERTeN4UrWXEz6VG6rweqXYy0mipeC0h6bPCmJUgZOKpBiEVKjw3SjpoR/sl4gf+eO3BE95TqHxctPYSTQ6j7aeKof0oIhNDCUIq1AyGnq17bD0Hb0zFDUObfKLNSkn9EvGy8WajpOaopCQVb2aK13hEJpaamKRChU000Sm0wym147O7xm/5GU0K0QN49H25yDKxcjD0oB9/JL0eTV7hdOEiE0s1CKlgYS0i6cw+qcaQ1MQUfU7qPyBhW3xkUtLnFNqm5iUpHyUIqWAzIsvx9v/4rT4hubkpnhTCpqlcZHmAofuLN1/FE8JAZHt8edbYvqLICchMgjCz5Wb2GzPbbmbbzOzWtGOSStDI4EE+vINbvC8i6Uw/miAGYmWj+8jFlgu9P6m/YSC2j2n5h0h5ZKkPoh/4tLtvMLNGYL2ZPeDuT6cdmExlM4CjDPY9RPsbPLYt+toAQ6fBiPZlxGsGSTf5SRr5FL4e7xwPy6n2IOWVmRqEu7/m7hvyy4eB7cDSdKOSyjCPws0+8RpB0vaB2HpSbaKPoc1L8VrFAME5UrQmEa2ZNKLRS1JuWapBvMHMVhDcn/rJdCORylANNAFdBAfp6D0bovduiNYAwppF0kV1YfmkqTTifRrxmkc80TjBiKtof4lIeWQuQZjZTOBu4FPu3pXw+lpgLUBLS0uZo5OpayZBcgibm6LiTU9hk1IVQ2sWhe4rHW0uKjT5X1LNJUfwE513Qt9MZLwy08QEYGa1BMnhLne/J6mMu9/p7q3u3trc3FzeAGWKmw1MJ0gU0eagsOknut5P0GyUY3jTUX9kH/EO6OjIpnhNIRd5f3hB3IIJ/cYiI8lMDcLMDPgusN3dv5x2PFKp5hCcN4WV1/g8TNEZXp3BkU9huXjNIaxtxDu/YWjyIFLWCX6aC8nYOZxUmCz99V0GfAC42sw25h83pB2UVKJZBJ3CMPSMHoKDeh9Dh8TGawbRR3+sTLx2ER3yGpatBxaTrZ+nVKLM1CDc/bdoknvJjNkEncP7GTzTD2sI4Wii6GikUDhleLS/IT7lRvjepNpGU/6zRdKXmQQhkj0NwHKCJHGY4Aw/FO2ojp7X9FN4xFOh6yJyBH0f89FPUrJEf40io5oPzAXagSMMTRQw9MAfn8wPBofOwmDNIiwzDWhG93eQLFKCEClKFUGn8QKgg6ATuzf/WryTOXptRPT6hlANwbDauejiN8kyJQiRMTGCkU5zCA78R/KP4wy/yjoc2WQEzVXTCPoXlBRkclCCEBk3Ixjt1DhaQZFJSePoREQkkRKEiIgkUoIQEZFEShAiIpJICUJERBIpQYiISCIlCBERSaQEISIiiZQgREQkkRKEiIgkUoIQEZFEmUoQZvY9M9tnZlvTjkVEpNJlKkEA/xu4Pu0gREQkYwnC3R8FDqYdh4iIZCxBiIhIdky6BGFma82szcza2tvb0w5HRGTKmnQJwt3vdPdWd29tbm5OOxwRkSlr0iUIEREpj0wlCDP7V+Bx4HQz221m/yXtmEREKlWm7knt7n+SdgwiIhLIVA1CRESyQwlCREQSKUGIiEgiJQgREUk0aie1mc0tYj85d+8oQTwiIpIRxYxi2pN/2AhlqoGWkkQkIiKZUEyC2O7u541UwMyeKlE8IiKSEcX0QVxaojIiIjKJjJog3P14fJuZ1ZjZOWH/RFIZERGZ3MY8isnMFhPc2Odk4A4ze1epgxIRkfSNZ5jrXwB3ALvd/dPALaUNSUREsmA8CWI6cBQ4t8SxiIhIhownQXwN+HtgnZn9BfBgaUMSEZEsGPNsru7+nJl9BrgCuM/dt5U+LBERSdu4ptpw9wPAT1Ezk4jIlDVqgjCzJjO73cy+aWZvs8AngBeAPy5lMGZ2vZk9a2Y7zOzzpdy3iIiMTTFNTP8CHCK409uHgc8A04Cb3X1jqQIxs2rgW8B1wG7gD2b2U3d/ulSfISIixSsmQZzs7mcDmNl3gP1Ai7sfLnEsFwE73P2F/Gf9ELgZUIIQEUlBMX0QfeGCuw8AL05AcgBYCrwSWd+d3yYiIikopgZxjpl15ZcNaMivG+Du3lSiWJJmi/VhhczWAmsBWlo0gayIyEQZNUG4e3U5AiGoMSyPrC8jmGY8Hs+dwJ0Ara2twxKIiIiURpbuKPcH4FQzW2lm04D3EwylFRGRFBQzzHVDKcqMxt37gY8D9wHbgR/pIjwRkfQU0wdxppltHuF1A2aVIhh3/wXwi1LsS0RETkwxCeKMIsoMnGggIiKSLcV0Ur9UjkBERCRbstRJLSIiGaIEISIiiYpOEGb2L2b2ETMrpk9CREQmubHUIL4PLAa+YWY7zexuM7t1guISEZGUFX3DIHd/yMweAS4ErgI+CqwiuMOciIhMMUUnCDP7NTCDYNrvx4AL3X3fRAUmIiLpGksT02agF1gNrAFWm1nDhEQlIiKpG0sT038FMLOZwJ8S9EksAuomJjQREUnTWJqYPg5cDlwAvAR8j6CpSUREpqCiEwTQAHwZWJ+fWE9ERKawsTQxfXEiAxERkWzRldQiIpJICUJERBIpQYiISKJMJAgze6+ZbTOznJm1ph2PiIhkJEEAW4E/Ah5NOxAREQmMZZjrhHH37QBmlnYoIiKSl5UahIiIZEzZahBm9iDB1Bxxd7j7T8awn7XAWoCWlpYSRSciInFlSxDufm2J9nMncCdAa2url2KfIiIynJqYREQkUSYShJm9y8x2A5cC/25m96Udk4hIpcvKKKZ7gXvTjkNERAZlogYhIiLZowQhIiKJlCBERCSREoSIiCRSghARkURKECIikkgJQkREEilBiIhIIiUIERFJpAQhIiKJMjHVhsjUkAP68o8cMI3gJ6afmUxO+ssVGZd+oAvoBY4DA4ARJIawYu75bU7wU6sG6oBZBMlDJNuUIETG5DBBYugnOPCHahhMBuF2YzBpOIO1i6P57U1AI/oZSlbpL1OkKB3AEYKaAgwe/KOMoUkhfD2pqy9HkGgOAw3AvALlRNKjBCEyoh5gP4MH/OrIa2GNIVTFYA2iJrJcnX8/sbKhY8AeYDYws4Sxi5wYJQiRgjoImoPCg3ySaK1hJFUMTxJhTaOGoGbSAXQT1CYKfZ5I+WSiTmtmXzSzZ8xss5nda2az045JKpkD7QQHa2PwZ1IVWY8uR7clCZNHdey9FtkWPvcBrxN0foukKxMJAngAWO3ua4DngNtTjkcq1gBBcuhj6ME8enAvtC080NdElqtjZQsli2iiADhAkKBE0pOJBOHu97t7f371CWBZmvFIpcoRHJhzDB7YqxKW40kh+jOKdkzHax5hwqghuRYRf28XQR+ISDoykSBi/gz4ZdpBSCU6kH+OHryTRiLFk4ZRuOkpTArxZBHdD7Gy0X13EAypFSm/snVSm9mDwKKEl+5w95/ky9xB8Gu4a4T9rAXWArS0tExApFKZDjN0aGq07yFcDy98iy5HRy7Fk0mOoUkm6T1h+WgHdnT/AAeB5si6SHmULUG4+7UjvW5mHwRuBK5xdy9Uzt3vBO4EaG1tLVhOpHhHCYaahmfz0URAbDkU1gSiB3ki5cNtudjr8WGxSTzyWjjS6SDB6CaR8snEMFczux74HHClu6tnTsrICZJDtKkoNNKopELJI35thCU850hOOGE80XLha04wpUd94a8iUmJZ6YP4JsGcAw+Y2UYz+3baAUmlOJJ/jvcxJP00on0MSZKuiUjqyI6PhoonmHh/Rfj6EUTKKRM1CHc/Je0YpBL1EVxvUKg2MNL5U7QvIrotaT/x/cXnawqf49ud4TWPbmD6CHGJlE5WahAiKQgvhIv2GURHJMXFyxErP9K2kMdeS6o9FHp/FUEzk0h5ZKIGIZKOfoaPPEqagC/pOa7Q60k1jfh7QvFaRbxsLv/oIZg2XGRiKUFIhTpG4eRQKEkkrRc79DS+70LNTPEO7KThs8dQgpByUIKQCtVH4T6E6HJ821gTQlLNIT6MNnoNRFXk9XC4a3ySv/i6yMRQH4RUqPDq5NGahgqtx8vGr6AebV9R8Z/hSEkoLKu+CJl4qkFIBQpnSo1fkBZ9LlbSBXKjNUlFm5fCOArVZlSLkPSoBiEVKLwr3GjTc4fLha59KCaZFNNfMdb9gOZnknJQgpAKFB29BEN/BvE+g0KJYaQL5iZCPF4lCJl4ShBSgQpN4ZV0/UOhTuYTUSjpTMToKZHxU4KQCjTA8D6A8LnYg/+JJoliOrNH+kzNUykTTwlCKlAxzUiFyk6ksSQokYmnBCEVKH72nsaZedJIpvhnR9c1aknKTwlCKlS5k8Jon5E07UahYa9KFlIeug5CKlx0KotC24opU8znjCURqb9B0qcahFSg8LwoeiYeXS72YJ5j8Iw+F1mP7qfYs/1C5Zyh8STdwU5kYuivTCpQDcMPuHHRg3s8CcTLxdcLHdQLlR9tn0mxqVYhEy8TCcLM/oeZbc7fTe5+M1uSdkwylU3jxJpw4jWFuKQO6Oj2cL1QjcNjy0n712yuMvEykSCAL7r7Gnc/F/g58N/SDkimsqRRTIUOyNEDNrH3xJuWRhqFFFcoMYTi/RvxJiwlCJl4meikdveuyOoMVH+WCRdOgDfS6KEqhh/IC51TJXVsh48qhtccQoVuJhRt3kqqjVQXiEOkdDKRIADM7G+B/wx0AlelHI5MeTOALoYewGHoQT4pgSTduyF8X6G+gaQO6Hj/RHRG10LNX+F+MvOzlSmubE1MZvagmW1NeNwM4O53uPty4C7g4yPsZ62ZtZlZW3t7e7nClylnWmQ5frYeH9GUNEKJAtuikvoeRupgTuqTSFpuGuEzRUrH3LPVmmNmJwH/7u6rRyvb2trqbW1tZYhKpqbDBDfeKTSza9L5U6H5kqIXsoVlcrHluEK1BhieTML3VwHzEvYlUjwzW+/uraOVy0QntZmdGlm9CXgmrVikkjQy/OAdPTBHz+jjQ16TDuADsTLxZSLvDZ/DiQOjnxnuK/45Dswc/9cVGaOsNGb+nZmdTvCLeAn4aMrxSMWYRlCLiHYoRzuOo53POYZ3XBNbH+36inA/MHLtImn/tWj0kpRTJhKEu7877RikUjUxmCBgaFPOSB3X0cQRXy4kWuOINi1Ft8VrM9HnxpG/ikiJZaKJSSRdcxneDxBvXkq65iGpaSjenJRL2B8Ubl6Kd4qHyzPIyPmcVBD9xYlQAzQA3QztZPbYeih+HUOhobDxBBOWjyeK8DPiTU3hei1BghApLyUIESBoauoHehne7AOFr5cIm5zCC++SjDR0Nd7UFB/VVAPMGfO3ESkFNTGJvGEuwRXKhWZ2jc+TFG0+KjSMdaT5lOKjneLlPR+TfqaSDtUgRIZoBg4SdFzD0A7p6LUNYY0hPHgnzcgarX0UShIkvJYjaFZScpB0KUGIDDMX6GCwTwKSm5aiz6HovEvxEUtx8RFRYZlqYD7D+zZEyksJQiTRbKAe2J9fj3dch+Jn+P2xbSPVMmBoMnFgFhrOKlmhBCFSUD2wlKA2cZTBxBDtrE466Ic1g3gtI9oRHa6HwlpDbSkCFykJJQiRERnBKKKZwCGCUU4DDJ/aeyRJI6LC52kEI6gaShGsSEkpQYgUpRZYQJAcOoEeoC/yeqEpOKJ9C+FyFUHtZDb6CUqW6a9TZEyqCTqxIWg6OkJQq+hm+LUQYY2hJv++eoKaQnSqcZHsUoIQGbcqdG8Gmco0yFpERBIpQYiISCIlCBERSZSpBGFmt5mZm9n8tGMREal0mUkQZrYcuA54Oe1YREQkQwkC+ArwWUa/6khERMogEwnCzG4CXnX3TWnHIiIigbJdB2FmDwKLEl66A/gC8LYi97MWWAvQ0tJSsvhERGQoc0+3RcfMzgZ+TXApKsAyYA9wkbvvHem9ra2t3tbWNsERiohMLWa23t1bRyuX+pXU7r6FYJIbAMxsF9Dq7vsLvklERCZcJvogREQke1KvQcS5+4q0YxAREdUgRESkACUIERFJpAQhIiKJlCBERCSREoSIiCRK/UK5E2Fm7cBLJdrdfGCyX3sxFb4DTI3vMRW+A0yN7zEVvgOU9nuc5O7NoxWa1AmilMysrZgrC7NsKnwHmBrfYyp8B5ga32MqfAdI53uoiUlERBIpQYiISCIliEF3ph1ACUyF7wBT43tMhe8AU+N7TIXvACl8D/VBiIhIItUgREQkkRJEhJl9wsyeNbNtZvb3acdzIszsNjNzM5ufdixjZWZfNLNnzGyzmd1rZrPTjmkszOz6/N/RDjP7fNrxjJWZLTez35jZ9vxv4da0YxovM6s2s6fM7OdpxzJeZjbbzH6c/01sN7NLy/XZShB5ZnYVcDOwxt1XAV9KOaRxM7PlwHXAy2nHMk4PAKvdfQ3wHHB7yvEUzcyqgW8BbwfOAv7EzM5KN6ox6wc+7e5nApcAH5uE3yF0K7A97SBO0NeAX7n7GcA5lPH7KEEM+nPg79y9B8Dd96Ucz4n4CvBZYFJ2MLn7/e7en199guAug5PFRcAOd3/B3XuBHxKceEwa7v6au2/ILx8mOCAtTTeqsTOzZcA7gO+kHct4mVkTcAXwXQB373VPDqgpAAADwUlEQVT3jnJ9vhLEoNOAy83sSTN7xMwuTDug8TCzm4BX3X1T2rGUyJ8Bv0w7iDFYCrwSWd/NJDy4hsxsBXAe8GS6kYzLVwlOlHJpB3ICTgbage/nm8q+Y2YzyvXhmbth0EQysweBRQkv3UHwbzGHoEp9IfAjMzvZMzjMa5Tv8QXgbeWNaOxG+g7u/pN8mTsImjvuKmdsJ8gStmXub6gYZjYTuBv4lLt3pR3PWJjZjcA+d19vZm9NO54TUAOcD3zC3Z80s68Bnwf+slwfXjHc/dpCr5nZnwP35BPCOjPLEcx90l6u+IpV6HuY2dnASmCTmUHQNLPBzC5y971lDHFUI/1fAJjZB4EbgWuymKRHsBtYHllfBuxJKZZxM7NaguRwl7vfk3Y843AZcJOZ3QDUA01m9gN3vyXluMZqN7Db3cMa3I8JEkRZqIlp0P8DrgYws9OAaUyyCb7cfYu7L3D3Fflbt+4Gzs9achiNmV0PfA64yd27045njP4AnGpmK81sGvB+4KcpxzQmFpxdfBfY7u5fTjue8XD32919Wf538H7goUmYHMj/dl8xs9Pzm64Bni7X51dUDWIU3wO+Z2ZbgV7gg5PszHUq+SZQBzyQrwk94e4fTTek4rh7v5l9HLgPqAa+5+7bUg5rrC4DPgBsMbON+W1fcPdfpBhTJfsEcFf+hOMF4E/L9cG6klpERBKpiUlERBIpQYiISCIlCBERSaQEISIiiZQgREQkkRKEiIgkUoIQEZFEShAiJ8DMVpjZscgFZZjZgJltNLOtZvaz0e5nYWYN+fK9k/H+HTJ1KUGInLid7n5uZP2Yu5/r7quBg8DHRnqzux/Lv3/SzdkkU5sShEgB+drB1sj6bWb212PczeNM4um+pbIpQYhMkPzd5a5hkk3WJxJSghApvYZ8n8QBYC7BLVQBMLPTzewfzewfzGxJahGKFEEJQqSwfob+RuqLfF/Yp3ASwbTxHwPId0DfDvw18A3gS/kZOkUySQlCpLDXgQVmNs/M6ghuYFQ0d+8EPgnclr8BzxUEN6B/F7CQ4IY8q0obskjp6H4QIgW4e5+Z/XeC+zG/CDwzjn08ZWabCG5asxF4m7v/A4CZvQ94pIQhi5SUEoTICNz968DXx/iembH1d4bLZna5md1DcO/qH7j7pLproVQW3TBI5ASY2XLg98CB2LUQY9lHA8Fw2GbgbHc/WMIQRcZNCUJERBKpk1pERBIpQYiISCIlCBERSaQEISIiiZQgREQkkRKEiIgkUoIQEZFEShAiIpLo/wPmMkEwXbaUFQAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f521978c810>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"afig, mplfig = b.plot(time=0.5, y='ws', fc='teffs', facecmap='YlOrRd', ec='None', show=True)"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYgAAAEOCAYAAACTqoDjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzt3XmYXddZ5/vvW/NcskqzJVm2RsuyNViWNdhyyNQmCUmHDp0ATUPTtJ+nITc0hKGDL1waHvr2bTrcS5o04AfCkM6FpoFc0gGSOLFjyxqt0dZoS1Zky7KtWapSqap0qtb9Y5/tWrW09jmnJp1Tqt/neeqps8ezStprv2vaa5tzDhERkVBVuRMgIiKVSQFCRESiFCBERCRKAUJERKIUIEREJEoBQkREohQgREQkSgFCRESiFCBERCRKAUJERKJqyp2A0Zg2bZpbsGBBuZMhIjKh7Nmz57xzbnqx/SZ0gFiwYAG7d+8udzJERCYUMztVyn5qYhIRkSgFCBERiVKAEBGRKAUIERGJUoAQEZEoBQgREYlSgBARkSgFCBERiVKAEBGRKAUIERGJUoAQEZEoBQgREYlSgBARkSgFCBERiVKAEBGRKAUIERGJUoAQEZEoBQgREYlSgBARkSgFCBERiVKAEBGRKAUIERGJUoAQEZEoBQgREYlSgBARkSgFCBERiaqYAGFm88zsWTM7YmaHzOxny50mEZHJrKbcCfDkgM865/aaWSuwx8yeds4dLnfCREQmo4qpQTjn3nLO7c1/7gSOAHeWN1UiIpNXxQQIn5ktAFYDO8ubEhGRyaviAoSZtQB/A/w759zVyPYnzGy3me0+d+7crU+giMgkUVEBwsxqSYLDV5xzfxvbxzn3lHNurXNu7fTp029tAkVEJpGKCRBmZsAfA0ecc79T7vSIiEx2FRMggE3AjwHvNbP9+Z8PlTtRIiKTVcUMc3XOvQBYudMhIiKJSqpBiIhIBVGAEBGRKAUIERGJUoAQEZEoBQgREYlSgBARkSgFCBERiVKAEBGRKAUIERGJUoAQEZEoBQgREYlSgBARkSgFCBERiVKAEBGRKAUIERGJUoAQEZEoBQgREYlSgBARkSgFCBERiVKAEBGRKAUIERGJUoAQEZEoBQgREYlSgBARkSgFCBERiVKAEBGRKAUIERGJUoAQEZEoBQgREYmqqABhZl8ys7NmdrDcaRERmewqKkAAfwo8Xu5EiIhIhQUI59zzwMVyp0NERCosQIiISOWoKXcChsvMngCeAJg/f36ZU3Or5IC+/O8BwOV/LP/bV5VfVwNU55cbbllKRcqjH+ghyR838suQ5JEB73PKkeQNy/+uBerzvyU14QKEc+4p4CmAtWvXhnfH20QO6Ca50GHwYg7F/vw0M9zwju/O/64jCRYT7r9dJKKXJCjcYGgQSH9SWQ0l6TH9+XN05ZdrSPJKS4FjJwfdKSpGb/7nBvFaQcq83y7jc8ox9Fx9+R9ISkqN6BKQiaUXuEZSiPKFN/Kwdp0GjTCQpPv4hbABkkJVN0n+qCcJFn7emhwqKjya2V8A24GlZnbazP51udM0/vqAS0Bn/rN/UVcRDw7+skU++9urIvtBEoguk4wJ6Bl58kVuiW7gLHCFweCQ5o/wuvebjsLrPxXmmyqG5rf0cz9JQHon/90DTCYVVXx0zv1wudNw6/SSVGn7iZd+YkZagsk6Lv3ervxPM0mtQqRSXCcpPKV9bhDPL6XkISO55YV9eLEau1/TSLdfy/80Aq1U2O1zXNz+f2HF6SepMaQXYOzCzrq4RyvWqZ2mYYDk4u8hCRR1Y/B9IiPVS1LDHSAZbJHVtxD2z2X111nw2W+STbe5YD8/jw54571Okk+agPZS/6AJSQHilkpL6n411pfV4pe1PiuYpGKlozBDhH0X/cBVkkujlSRzitwqjiQw9OaXw+vPv35LCQRhP0OqOlgfBocwn/i1Cr9A1QtM5Xa9ld6ef1XFyZFc9H5zUinBIS0hxdaXolAGSben6y3YJ+0baUO1Cbk1+oALDN6Q0+s/rD0Uuv6L9TeEBaIwMMSOSz8PeOfw+/LeBu4gqXnfXhQgxl0vyY0WhjcmIOxUDtcPV1awKNbsdIVkFEfbCL9XpBRdJDVXv8MYbzkrPxDZlh7r1wxix6XPFMXOGxaYILld9gfb03NfYrA2cftQgBhX1xi86EfbhzCac4QlIbh5tJRffU4zVro+HWveMcLvFykkHEnnF6RqMtaHNYpizUQxfiDxf/vbHTcHEr9zOx3pBEl+7wemFfneiaOihrneXtKhq7GST6x5ya9Gx4bujUbsXGHHXpZ0vxyDNSGRsXKOpNM35dccCvV/hflqpPnGz3thTcVvTgqHwYYBKj22F3iLm5/TmJgUIMZFJ0Mv+lKEVeHYxeoL22Ut8pM1Ttw/B2RnDhg67rsHzaUoY+c8yQ01bBqKjVgqVMAi2JaVD8LnImJ5p5qk1hLLh+H3+/nGDx79JIFv4j8zoQAx5tKx0qWWZGLD6mBoySVWbY7VOMIf/1xZ313oQbxYlbuHpCNRZDTOkTz8Fl6v1cRvyLEgUk38+s0qHMXySuxhunD0XxicwtpEmFbHYOf1xJ4NSAFiTF0j6dQN20LDEocvq5ZQqNQ/kuanWOAI05d+jo0R90df9aKahIzcZZIadqwzGm/Z/+2vzyoMlbIt65xZ3x1e/4X2SX+n/SY5kiewJy4FiDGTDguF0m70kF2lLtYkNFxZNYvhCINeD0kHvMhwdJIUolJhGz/cXDMm/znrgblYzcDfVmrhyxcGrljzVNgx7g/NTY+f2IUpBYgxMUDSnlrlLcdk1SpiF3Ts2JHe3AtJR2n4y7Gmq3QbDHYedjH4QJNIMTdIClHhzb9QE2qsCSjcr1CTD8H29FzV3HzDL9bvF2vK9beFQ2bT/dMhvBOPAsSYCNvkYzWDsBknS1YT0HCCQyxDpcLg5e+T9eS1/zktOaW/z0eOEYk5S7xfK1Z7Dkvo/k+sJpFVQy60Ljwm7HCO5Ts/XVnBK9Zncinyt1c+BYhRSx+3L/REZuzGC/FONILlYv9Fsap2+jkr2IQlrvRzmvHSdGWNLYehQWLiVqHlVrnE4PtJYjfnrCbWWOk+ax8oLQ9knSO2rlBhi2B72I8R1kgmXj5RgBiVdN4YfznrootdgIVK67Fl/1x+6aXQcNbh/heH6QyPd8FnRzIa5dowv0cmD382Ab8Gmi6n11g4csi/psP3OBSTVbr3lVKi99ORFQzC74Sbg5Qx+CDdxKEAMSqXyX5Uv9ioiFDWKIlwXakZpNi5SuFf7IVKd46hHY8ivvPc3AQD8Rut34QUik3RnZUfwlpKVj9G2hfhB4EssT6GWAEqDGx+mifWEHEFiBG7weA4brj54ol1VGdVi2P7l9KWWqpCF36hwBQ2J2WdGwYnJBTxpQMZwndAQ7xQ5Xf2+vsUyjuhUoJG1jLcHDSy8jje/v6x6X6xvNXNRHrKWgFixNJZJ8MSQyr2T1vKlBal7DtSw+3sTtMRZoxYBkyr0CK+tNAQCwrhwI1YDTlWCyDYHip2jce+o9D2dF04FDfc328q84NE2Cx7rkj6KocCxIgMkLQlhiWLmFhTU/g5VtIYaW2hFMVKX6lCgSGswjsGX4YkAkmBoY/4tZ4Olc6qnVZ5+xSrvRZb52/zb/TDDRJ+2sKahT9cPOxTCb+rh4nymt+is7maWSnz1w445yZR+8JVCj9t7ItlgJHE5ULNPMNRSlDz963m5ipxrHM9XddNMje+yEWy+wpin2MdvET28/ePnSdWyIl9b0xW/jDiTV/+ttjfmvX9F4A7i6Sl/EqZ7vtM/qfQv2w1MH9MUjQhdDH0FYRQ/EL114WjOAj2G23/Q7p/qZOFxS7+rOW0BJZ2vvmlpn6SvplekndIyOQ1QFJ7gKHNQ2G+8T87smdwLdR34O8z3IDgpyO9lv3OcAs+h+9RSf8mi2yHeD50DL6TvqXE9JVHKQHiiHNudaEdzGzfGKVnAuhj6EUe9kGEpYdYbaFY1TZcLlTFjj14VAo/Q4SlnULLWUHHnzP/EjCrxHTI7ekig82wtcG2rKYh/2Ybe6Yg61h//XALUunvsIbuX89++mBobSEcfmvesX5hyv+e9HMnlR4gSrmbbBijfW4T4SPzsc6q2LZStoeygoN/MRYbm52lWBNTWCIKjwkzrN+BdwOZ7NJ3r/udtGGJHIZey6Hw+i7URDXcwFBswEZWXkqPLfUBVv+J6/TfIv2p/H6IoncU59xNf4WZ1ZjZyrR/IrbP7cufvx4GL/a01JA1sqlYTSK2HJOVWYaTQUr97vA7wuaAsFMulSO5Qcjk1Mtg53SaP/wn9aH4UFYi24ezXKxw5Ys1SxULIln7ZNUWsr6/skf+Dbu31MxmA38K3AM8aWYfH+tEVa5ekmpz1rQZkN0pXcpNvNQAUapCT1gPV6FpN8L9oNIvfBlPaS3bb4r1A4Uva3qKWHt/TKHgEN7AY3kwVlMOtxWbpSD8zkL8SQIdlT7qbyTDaX4eeBI47Zz7LPAvxjZJlawzWPabVwg+Z7XnF1JKs89IjKSGAUObBGJpiP1t6d8/cR4GkrHWy83NMOEon7RGEcsnFjluOLXr2PrYdB7hPllKSUMsKIX3hbBfAyr9rXMjCRBNJMXDVWOclgkg7EDLunnGqpcjCRBjUfL3zzXcGkwsza7ANn+9pgGfvPrIfsAy/R0bDVTKkPBSCixZ/GNLyWtpmrKeoM6qdcTSGW5PA+jtFyB+F/jPwC4z+3ng22ObpEp2g5tHMMQunkIXVNaNtZSOr7F+urrYBe/3rWQdE1bP/eU+ZLIJ+6b8oat+vkn7I9JCly+8yY5lQWk4/JFIKT8tsTxbKKiEASr9+ys3nww7QDjnXgF+kaQP4pvOud8f81RVrHQmxljTkn9RZLX9x6rPRPYLzz1WhpvRSimpFUp72CQnt78ukuZFv23fzxcweM2Ew6zx9i+1SWek/GagYp3R/v6l5F9/5Fb62R/EUhUcW7ljfEZ0F3LOXQC+xqRqZip0M4/tW6j6Ga7LKkHFjGWVtJS/JdZ2G0tvuJ9Dw10nox7i10zWw6Gxpp7wuLCPq9RBH8X4ASw28jCswcTSD9mBw98Og/8u6fMh6X4TOECYWZuZfc7Mfs/MPmiJ/w14DfjnY5kYM3vczI6Z2XEz+/djee7R66FwExEMrT46Spv7PTxnoQt/tJlipE1UpWSA2LrKbl+V8eBf82nBwa8RhM01YS3D3+bvA/HrbCwUKvzE9gvzeaFm2Kwah79/5TYxlfIk9ZdJxmJtB36KpHmpDviYc27/WCXEzKqBLwIfAE4DL5rZ15xzh8fqO0YnVuX12xGLzWFPxvZ0n1gJxjeWJaZShPuFT4TGSnrptvQmoZFMk086DHyAobeXsDk2VuiINUFZ8OMfP076++DyN6B2GtTPhbrZYPkRV87BQDfkLtOfg+rm6cHBfjD0A0caKP1adbhP5SklQNzjnLsfwMz+iOTtH/Odc2PdwLwOOO6cey3/XX8JfAyokAARNpfEqp6+WOWs0PxNqWKdW6OR1exVbH1YGwhLfGFbsj9Xk0wuafNJbJprGHpdxPrksgpJ4X6xdv+R8NOS17UVrr8MF47lV1TTdXUpNfY2DY0XweUYqGrj1X+4xLIfXAnTH4fmpflTxUb5+YUrf2jvQPC78pQSIN69Mzrn+s3s5DgEB0imNnzDWz4NPDwO3zNCWTOahhd7VukmvMkX6neIbRuLUlNslFIs/amssdv+tjCd/d76yi0ZyXjJmqfMLzz4BYxqbq45hOcLb1PD6bMrhZcHBvrg3JeTNFVPgf7LQD+n/uFZzh34Hut/8WEaWuH0zm5OP7uLpe8fwDr3Q+MCeps+SH3dNXA5+geaqJ52P9Q0MTRohMEBxmdAytgoJUCsNLP00UgDGvPLBjjnXNsYpaVQcXpwJ7MngCcA5s8vxwSy4Y3c/8/1SwmprFJR1nLWsNmxKI2HmTNs5y3WJJTVXpwK11duyUjGS9q8lF5r4XUdNrmGT1uHwpps1n5j5NL/yqdpAOpnQPdlnDVz6h+fw+X62fFfjIc++wEOfPEPYcBx9e3NtM++zlsvXeLNbf8Xa3+0FYBj3zGWv68J5n0Spq0H85ua/NeQQiU3xZYyF1O1c64t/9PqnKvxPo9VcICkxjDPW55LMs14mJ6nnHNrnXNrp08P2//Gkx9Lw+YWX6zJpljndjGjPd6X1VyVFYSympNK6axXE9PkE/bF+aOEQrFasx8MsoaRFzrPSBnu2lFOf/Pr3MjlZyLuOQG1M7l2qRWX66eqrp6zDbP4pf90nL+bsoFTc1bx+oFuTu6qYcdv/innXj6Kc46+gdkc+co3cL1X4LWn6D/yuwxcPR35+9LPpZTTy6OSUvYisNjM7gbeBD4F/Eh5k+SLzbWUln5iIy58Yemp1AfiskZAjESsbTTcXkontj+uO+scMrmlN/M6b13WFDTpZ78ZtVBhZaybl0g6nru2Ye/8Pp2vn+PQ7/050x5cyeJPvYfmOa2cefEoF5c8yheeOcxr27Zy/+pVHNi3n2c6prJ1YBqzuM7DDa1w9m2uXW7gxHOvMnCjj2tXG6hpncrzv/rXfODn98GdH4J5H4HqWkrPb+VVyhvl9jrn1ox2n2Kcczkz+zTwTZJiyJecc4dGc86xVWjSsXBURnghF+pfyFoXM9IbcLEaSDhEL+xQHM5F7I/MyHr5i9y+ahl8FqJYoSQVFrT8Y2J5xx/dNErOwaWvwcX/CcD0VYt4/Wvf4vyeA5zfc4Cq+zbyZ2/Us2f/K5x95wIAb505w9Ll93L5wkWOHXuNr594jb9qb+OTmzZy10s17H/mGBfvWsWWbXD5r/6YaSvuwxiAN78O3a/D8s8wdOBH5QaJUmoQ95rZSwW2G9A+Folxzv0D8A9jca6xl770pFApJ1a78NfHAkjWhZ518Y8kSERGatx0znA51pmWVXOIBRWorAqq3BqxglPs2Qd/OdzfX846brQ1amAgR+7M/6Cm5x/fXdU6t+ndz92LN/GZP99FT98N6urq2Lj5Ed48/SYz58xm945d5HI57sglb2S+euUqBy7d4NjX3+SZrWdY8cAUuo/t4XP11bTeOS05YfMCuNHJzbWlyn37Yik5eFkJ+5TyRNgE51eXSxm5VGwYXqzUlLWvb6QZIytIxEYihcvFSoJp5vUvg8oe3y3jpYbsoazp80L++ljfQxhAYqPt8JbDc5XAOTj3Rxz63S9RVVvL3f90Pc0dl6lrvALAmbsf5Zf+fAtTpt5Bz8VL9PX18fLefax6aC0XL13i4U0buHrlMsePHWfh4oU0NjWxY/uLrN+0nqqqKrq7ezj+2uvs/v6NrJnTBi13QtcJ6FjLzfmicgtSRVPmnDt1KxIy8RWqFcSCSLourC6XcpGPJkgUu2n7mS2sMRSafTLsfDOgdZjpk4mvDbjAYCEnLOzEClVZ/XpZtQkytodNvxnywYFr2+hYuYwjv/9l3n5uG7XtrSz+8U/w2qqP8mu//zUAWtvauHzxEvcsXkRvXx9bnn2O2vp6enuT2Yof2rCO2oZGTp9+E4BcLsf6TQ/zwpbtAPyPnYf5iU98FDpfTb67cWbk75nYNQh5Vw2Fh6QVKsmEY7+zSkFkHB8abnAodSRUsVFZYRrzQwKHbE8flmpCJptabu57Ch8QTZdj758O+Td9f6joCJuW3ACc+xJ0bQGg9e5pg5tqWvmVz2/nwJlOli2/l5b2drq7unj40U3s2fkifX3JlBhz5s7h5ImTrH7oQXbv2sOadWt57dXjPPjgatrbW7nadY1HN2/g4sVLNDU388xXXuTygikse+9MZi6ank+5n48qN59U7hMaFamO4qXw2DZ/XfgsQsxACfsMR1ZzT7Hmpqzv95sQwrl3/Eyvy2tySp8WDkfv+Qr1NaTrCo1mCl/xGztXeNgAV1/6M25cegWXvzabpiVlZLfwQT67/RrfePEo17u7eeXwEfbt2Mmd8+aBGYuWLn73NFM7Oli1dg0H9h2gv7+fmpokIO7bs4+uzi6Ov3KCLc9vp6vrGocOHaWu9zpvfHc725/ay+XT6at40wdKKzuflFyDMLMvA88DW5xzR8cvSZWsBejOf84qwWQ1J6X8h4jS0lGs1hHLNCOVFdQK1RZi+6fb/UxpxG8GtTcdLZNFPUNr2ukNPQ0csRpA7GZZSnNoqoRBHZ3P0XX0OXZ+4c9omj2TBf/snzBlmfHG3Zv5lS8//+7ZOq9epaamhgfWruHUyZMcPZLc7qbPnMHCJYuYMvUOnv7Gt8nlkr/x0oWLAGzavJEtz29j46Mb6N73EpjR1XWNmt5WGjqmUVVfy5TaQ8DjDNa0K7sRZzih60+A2cB/NbMTZvY3Zvaz45SuCtXgfS40Iih28ceEpaVSbuLDkdXxl3XerKDgb4/NXBnObz+AAsRk1szNL9OyYF1YyICbCyfpPuE1FyvYZG3L6zkB5/+EjmXJvt1vvcPhL36ZL/7GC3zl0BXWPbKJ2tpa6hsaqKmt5d6V97N7x653+xqqqqq46+4FXDh/kStXrtLS2sKGRzbwwOoHOPW9U6xcs5KtW7bT3t7G1atXWffwg5w8+ToADVVQ29ZG25wO7OphyKXva6/8frqSA4Rz7hngt4BfBf4IWAv823FKVwVLRzNlXaSx0nrs5hwb9x07biTVT79zOSvwFKqVxI6JDXENm87S81YBd5SUUrkdtTJ4faf9Uf7EdC74SfnrYsGk1KlbgibaGxfhzG8CUN/aT+ui+wB4aeZGPv//baOhsZGdL2zljo4OHtq0kXWPbOJa1zXuWbyItvZ21j+6iZlzZrNrxy4w2PLdLdxxxx1sf2E7L+17iSVLl9AxfRot7W1cunKVlrZWDr50iGXLFvPIow9TNW8Bl19/nRnLZtDVO4eeM2kDTOUHiOE0MX2HpGiwHdgCPOScOzteCatc9cTnb/cnFQtL2LFaRdZIpFLbJbPaZ/1zF+vniB2TdT5/9Ik/iZ+fydP+h1oqveos48mARuB6sN5xcx7xry2/Dyvr+YhCw8PD78q78JdQdw+Ygxvv0LF6GTu6p/Cf/3orADU1SZo6r17l/NmzXDh/gXfeeguADY89igPezI9Sap8yBYDps2Zw/NXjrHpwNefPn+eV46/R1NpMW3sbu1/cTy6X49y5C8ydt5l/9TfPM2fOLD7z7Oss33GKD39hA4P3i8p+mHQ4xdOXSO6MK4AHgBVm1jguqapobQy9gfs31rDUXqjqW6xUVOw5gqyaQSmlrKy0ZH1HoXTEAt8kvCwkEJaMC9WqY4WVrPwzkv64HPS8AtdfxfX3crq+g++eq2b+3XcDcOHceerq67l78WIOv3yQuxctBJI+h30v7mHbc1vY9NgjtLW3s3f3XgAOvXSQTZsfYf/e/UyfOYPOzk5mTJ9Gc2sL1dVV5HI5Htm8gcuXr1JfX09LWwv09nH/RxZAz7l8ulpG8LfcWiUX85xzPwdgZi3AvyLpk5hFJQ/iHRfVJP9sfdw8YyXE37Mb8o8pNrojLbFnncc/12j6K8LzpmkpdP6wUztNp5qXpA24yOAw6LDzOXxoLhYQwmuvKli2YL+MgSFVzQDkBmaw9/Pf5MC5NrY/twOABYsWMXPObDpmzmDbc88DcK0rGWl018J72LUt2e/owcM8+t7HOHfuPJcvXuT69ev03ehjwDnqG+rp6JhKc2sLNX03mNpxB0uWLeKFLTvY+Oh61jz4AFu3vcgdK9Yxb0UrtC/K/+2Vn0+G08T0aeBR4EHgFPAlkqamSWgq8PYwj4llgKzO41LWhduHm5bhHB8b0pqu9wPEAEl5YbSjruT20AB0Mdh0VM3Q+b38G356bYWTX/pindpZBZjB9a6qicunO9j9619koK+P3KyN7+41bcZ0Dh88xMXz51mxciWNTY0cfvllVq5ZzbEjR3n4kY10X7vG8VeP8+orr3L00BEANmzexNbnt/LIY5uw6iqq62rp7e3jxRf38r4PbKb7ei/Lli+hta2Zb34rCTwr3rMQ6++CaWuYKPlkOA3FjcDvAHucc5U7gfktUUfSzp6j8H9yWHLyhRd2qTWOsVZKsPBrMllNX2nn9K2cgl0q2zSSfgjzfrIKSulnMrb529PfsRmWw+Ohp2sq5/adpnneQjpPHKEf46577qGppYVd27bT0trCwMAABw8cAGDFqpVMnzObcxcvsv2FbQBs3PwILzz/AivXrOSVo6/w8v6XqaqqYsANkOvL8fZb77BoyUJmz5lJX98Ntr6wk2XLFnH4yHH6+vrYuP5BWvo6YdpqqK5jItQeYHhNTL89ngmZeNpIXtUdNi/5rxSE4oEgti4WWMYqSBTqoyilJlLFYGnP75yGpFSkzmlJ1ZC0s3cyWLjwf0N205Kv1EIWxPJIY0czSz5cz5IPr+L6lbVc+bqj6bVODh1I5iBtaW2jq7OLtvZ27n1gBQf27uPwwUPkcjkefOhBBnAcOphMLF1bW8uqNau4dOUK16/3cOVKJwcPHmHV6vsBR11dPf39jqamRnp6+zj1xhkWLlzAzMZaDnzpOZb+6KeppYaJ0jJfuY/wVbxmkgww3OaaUjuIhzPKqBSFOqJTsSG64XH93FySS0uHU0eZRrn9TOPmkTpZw77Tz6lizz+E50h/p82d+XU1g9NpdJ1r5uyBoxw68BLzF9zFhs2PMmP2TNZt2ohVV7N9y1YWL1tKLpejqqqK+oZ6Wlpa6bnew4oHVtDc0kJ9YxMHXz7MieOv0dbeTn9/PxcvXqamppZT33ud6mpj1eoHcEBHxx10dV3jvpo+1jzxT6mdvpSk63ZiUIAYlbSamF6MharDFNkndgMPl7NGexTi7zOc4JWVJr+pwE9TPXo4Tm5mJLXtNI/4w6P9UX8Dwbr02LDQEj4fEf4Or3cHtR0AnD3Wyu7f+ANab3QCcOb0m+RyORqbmsn155h3V/IK46amJtasW8vcu+azbcs2evt6uX79OlZVxcnXvseLO3ax+sFVAJw/f4GHHn6QWbNn8sx3nmfTIw/T3NLKC1t3MmPmdFpbm7l48TIfXDuTez/xQbAmJlI+UYAYlXoGh3SGF3J6xTn2AAASlElEQVRsZFP4z53VFlvIgPcTu4m7EvYJ05UlFqDCeaLSv7ujhLTL5HQHQ2+K4XTgBJ/9ARyFrvHw+BgH1a2cPT6dw3/yNE1zFzKtvYkNj22mvaODndu2c+H8eXbv2MVL+/Zz74rltN8xhXfeeYfvnfweAKffOM2GzRs5sP8lmlqa6Ozs5MCe/Xzf+x5jyh1TeHHnHpzLp8Oq2LN3P3PmzKK1pYnm5mY++5Mf4pHvr4YZ65lotWw1GI9aO8kbtMIbfCn9CFmzXPr7Q/HAMRb9E1lBJM2kfi0pbRJIJxybTqU/8CPlNpPkFfPhA3Ew9JpK+SOUqoLPqaw30UWGjt+4TM/5s/Rfv0btzHmcfbub5pZmzr0DAwNJsJl313wuXbpM++UrvHHqDRYtXcz8BfPJDQxw+o03mTVnFh0dU3l44zp6e/vovHYNN+CYOXM6x44d56GHH+RG/w0aGhuorqpi+859/MtHVvCL77+BLfgoVM9got1yVYMYtRqS0rN/4ccUK82nhtun4e9XSpNTum+xPo5IW+6Q/dLjm9GDcVJcHTCF+BQahfrBYs1GPr9pKpzOIz3kBjOW9LL+V/8ZdVM6GGi+g1ePHePN199gw+ZHAFiyfBlXrnZy5s0z9PT0AHC9u5sLFy7yzNPP8srRV6iqqqK6ppbt23bR0NTIrh27ee3ESVauWUlTSzM7d+6hoaGBC+cvMWfOTD67fjE/vLCeqffeB3M/RtLUNrEoQIyJhvyPf4HCyDqWs4frFVZqcIh9R7G+jrTkFjYLVDPRqsxSTlMYOnon9jrbYnmn0EALx+AgCq9wk7uUfPvcXjb82ofIzZhNx/RpLF62hP7+HIuWLaZj+jQ6pndQVVXFyROvMWvOLHL9A1w4n8zUOnvObPoHHNeuXWPpsiXs2rmH1WtWsmz5Unbu2E1jQwM/8LEP0tvbx7p1q/nE1GoWvnGYVZ9cCff+NNjMm5M9AShAjJmpDLazpjWJrFJ5oRt5rAYSK8mPRqyE5n9P1vqwFKfgIMM1g8KT96Xr/P4uvznKPwZuCgbvrvP27X0LBgZgwNE0rYH+hmrOnTvPwZcP8fZb77Dl2S1cuHCRV185Tl1DAw+sXsmyFfdx5coV+vtzzJozC4fx1pm3yPXnmDN3DrNmz2Tf3gMMuAFmzpqOVVVx6ntvcvnKVWbX9DOv7yr3fupjNK//aaiaw+ibgMtjYjWIVbzpwHmSB+iKPcTjd1zH+iaynrL29x3JRVcoQMWGucaaooykWa0OkeGpJnlrwNsMXkv+O1JgaJ5wwXpfmMcy8kv9DAD6bSpb/8M3sFe+x9IlC7lw+SrXr1+n8+pV2qe009DQwKq1q9ny3S3kBgZobm5m2fJl9A3003mlE5fPC6dOvc6dc+fQ2taKM+PIkVdZeu8SGpsbOXX4VT7TfJUZ3/cQKz7zOaiZz0TOJwoQYyp9FuAcQy/62IgNf3bKrCdM/U7qrIn/hhMkYsEhLImlafLP7683konYJu5FL+VWQ1KTOMvQQAA3lf6HTIwZFpwKFaT6B9fXTqOvfx7P/dKf0XPuAlW1tXz8gTv57lvTudZ9nQX33E1TYxOr1q5m2/NbmTFzBm+/c5YFCxewc+du7px3J4dePsz6TevYtnUXLa0tzJozi9b2Fjo7u9j8ng20trdx4fwlfvkn3sOPfqydxo2/CHV3M9H75xQgxlw1ycX/jrfOv5AL9TEMt0aQdVyp/RFZzUmx70j/hnYm+kUvlaCOZGRTmk/SUUx+jQJuDgLO2zddhptrG942A+pm8n2/9V6qavqx2nam/fEx/ue+d3j1xEkAVq1dw77de9n46EaudXVxz5JFbNu6g4GBAZYtX8bceXdy8uTrPPLYRvbve5kd23dTXVtDx7Sp3Mjl2LlrPz++eRU//eE2Gjf8PNTNIxnAMbGpD2JcVJFc/LH4m9WE43fSFeqgi93AB7i53baQcBRTKftDMp5dwUHGSi1D5+6Kja6D0qa+9zu4b1Y3/4PU1A8wUD2TZ/73b/PWd7bxU4vqMTPWPryWvbv30tjcRK6/n2mzZnCtu5uHNz7EI49tpL6+jgfWrKS6tobnn9vG1audrHhgOQ+sWsHZcxeoqq7mpx5dycc6Bmh+5Oeg/m6SgtTEZ+8+4DEBrV271u3evbvcySjAkfRJ+DNV+r/JWA7XhU1UI43rsQBT6Olsv/PQ74QXGUs5kmZZvy8hHDnnX/OFZnxN14V9dY7eI3/Izv/45/RcukJ/by/9fX18Z8pKjl6+QW9fHwf2v0xPTw+bHt3I1i3b6OiYyrL7lrH7xX3U1tdx+fIVpkxpZ/m9i9k8bwq9nZ1U1dexZv0cHrt/OlMf+zdUNy8Cmsb0X2c8mNke59zaovspQNwKV4Hu/Gf/1Zzp71jTU1YQyGqmKiarZFZo3QBJUGgvkB6RseCAyySzv1Yz9BpP+/L8hzH9h+ZKzA+dR+DE/zm43LSQnq4cf/Fzf82Ztrmc6K3h8JvnmT7nTnr6etm9a++7z0S0tLVy9WonP/DYOj5Rf4X+k69w1/sf5cEfWU7jnYthwQ+BzWKiFKJKDRDqg7gl2kiek7hCUpvwR2z4ba++rNFP4eiOYgGjUH9EOrOmv6//uYGJ+HCPTETG4JQcnQwtOKXXaJp3wv6GcDBHRt5pvRfaVkPvO2BV0H2CmuoZtF06Q9ulM6yZM5clP/MwfbV1fP1vj3DX5tXsPvk2x149yYzpU/nsw3cz7+QuZr/vfSz5seXMXt4KC34Apq7Pp31iDmUtRAHilqkjmdnyEkNnRI0NLSVYF5sO3N8vNuVxVqezf0x4nnTfapJpmidGaUhuJy0k/VwXGOx7SINCOHqpn8Hp9cPm1/C6z+eJeT8Bl/fC9RPgBrC+PtoWLmbpR1czd3kXVdU9XDg7hfmn9jMf+OTK+5j6mR+ho+M6LY3NVM3+adoWraCmsQ5q26B2ARNl6u6RUBNTWdwgKSX5710K21gpsDwaWQ/ipdeBps6QStFLUuv2RzUV669Ll7Nq4ODXwgd6O7G+M1jfeeg9C71n6Xz7Gq8/9zLzV1XROvUG1M+GO1bBnMehJs0bDUyUl/7EqImpotWSdPr2kQSKrI7jqmAZilajh8WvcdQzEV6iLpNJPcmQ8W6SV5f6E0YWmuQyNlts+LxRsr6qvgXqFwGL3j269e4B7nvoGlx5GXovwrQNUNeeP0cTST6ZHJNTVkSAMLMfAn4duBdY55ybiNWCEagjeSL5BnCNpEZRrF8hfICumEJNTUZSEqr8URcymTXlf3pJClTpkFY/n4R9ewTbs571CZto89tqGqFjnXeeNDDcfv0MhVREgAAOAj8I/GG5E1IetQzOdNlNEjD8fopSmpjSWkbsqW1fFcl/ewOV898vUor6/E+OZLRTH4NDyGN9ecUeGHWRffzPtSRB4fbtYyimIu4QzrkjAGaTKzrfrIqhzTw5kndN9GXsn9Wf4KthMCjUM9lKQHI7qiGZ7gWSANFDUqhKa+DFRgCmn0PV+XNPrLe+jaeKCBDDYWZPAE8AzJ8/v8ypGW/pS999OZLM4GeENFBUkwSDdGSHLnK53VVz85QW/STNUf0M1jDCoFGd/6lF+STbLQsQZvZt4m/rftI593elnsc59xTwFCSjmMYoeRNIDRMwrovcQtWoX21s3LI7jXPu/bfqu0REZPQ0f4KIiERVRIAws4+b2WlgA/D3ZvbNcqdJRGSyq4jGbOfcV4GvljsdIiIyqCJqECIiUnkUIEREJEoBQkREohQgREQkSgFCRESiFCBERCRKAUJERKIUIEREJEoBQkREohQgREQkSgFCRESiFCBERCRKAUJERKIUIEREJEoBQkREohQgREQkSgFCRESiFCBERCRKAUJERKIUIEREJEoBQkREohQgREQkSgFCRESiFCBERCRKAUJERKIUIEREJEoBQkREohQgREQkSgFCRESiKiJAmNlvm9lRM3vJzL5qZlPKnSYRkcmuIgIE8DSwwjn3APAK8Lkyp0dEZNKriADhnPuWcy6XX9wBzC1nekREpEICROAngX/M2mhmT5jZbjPbfe7cuVuYLBGRyaXmVn2RmX0bmBXZ9KRz7u/y+zwJ5ICvZJ3HOfcU8BTA2rVr3TgkVUREuIUBwjn3/kLbzezHgY8A73PO6cYvIlJmtyxAFGJmjwO/DDzmnOsud3pERKRy+iB+D2gFnjaz/Wb2B+VOkIjIZFcRNQjn3KJyp0FERIaqlBqEiIhUGAUIERGJUoAQEZEoBQgREYlSgBARkSgFCBERiVKAEBGRKAUIERGJUoAQEZEoBQgREYlSgBARkSgFCBERiVKAEBGRKAUIERGJUoAQEZEoBQgREYlSgBARkSgFCBERiVKAEBGRKAUIERGJUoAQEZEoBQgREYlSgBARkSgFCBERiVKAEBGRKAUIERGJUoAQEZEoc86VOw0jZmbngFMjPHwacH4MkzNWlK7hUbqGR+kankpNF4wubXc556YX22lCB4jRMLPdzrm15U5HSOkaHqVreJSu4anUdMGtSZuamEREJEoBQkREoiZzgHiq3AnIoHQNj9I1PErX8FRquuAWpG3S9kGIiEhhk7kGISIiBUz6AGFmv2BmzsymlTstKTP7TTN7ycz2m9m3zGxOudMEYGa/bWZH82n7qplNKXeaAMzsh8zskJkNmFnZR5yY2eNmdszMjpvZvy93egDM7EtmdtbMDpY7LT4zm2dmz5rZkfz/4c+WO00AZtZgZrvM7EA+Xf+h3GnymVm1me0zs6+P5/dM6gBhZvOADwCvlzstgd92zj3gnFsFfB34tXInKO9pYIVz7gHgFeBzZU5P6iDwg8Dz5U6ImVUDXwS+H1gO/LCZLS9vqgD4U+DxciciIgd81jl3L7Ae+JkK+ffqBd7rnFsJrAIeN7P1ZU6T72eBI+P9JZM6QAD/N/BLQEV1xDjnrnqLzVRI+pxz33LO5fKLO4C55UxPyjl3xDl3rNzpyFsHHHfOveac6wP+EvhYmdOEc+554GK50xFyzr3lnNub/9xJctO7s7ypApfoyi/W5n8qIh+a2Vzgw8Afjfd3TdoAYWYfBd50zh0od1pizOy3zOwN4EepnBqE7yeBfyx3IirQncAb3vJpKuCGNxGY2QJgNbCzvClJ5Jtx9gNngaedcxWRLuD/ISnYDoz3F9WM9xeUk5l9G5gV2fQk8CvAB29tigYVSptz7u+cc08CT5rZ54BPA/9HJaQrv8+TJE0DX7kVaSo1XRXCIusqouRZycysBfgb4N8FNeiycc71A6vyfW1fNbMVzrmy9uGY2UeAs865PWb2nvH+vts6QDjn3h9bb2b3A3cDB8wMkqaSvWa2zjn3djnTFvH/An/PLQoQxdJlZj8OfAR4n7uFY6SH8e9VbqeBed7yXOBMmdIyIZhZLUlw+Ipz7m/LnZ6Qc+6ymX2XpA+n3J38m4CPmtmHgAagzcz+u3PuX4zHl03KJibn3MvOuRnOuQXOuQUkmXrNrQoOxZjZYm/xo8DRcqXFZ2aPA78MfNQ5113u9FSoF4HFZna3mdUBnwK+VuY0VSxLSmh/DBxxzv1OudOTMrPp6Sg9M2sE3k8F5EPn3Oecc3Pz961PAc+MV3CASRogJoD/ZGYHzewlkmawihj6B/we0Ao8nR+C+wflThCAmX3czE4DG4C/N7Nvlist+U78TwPfJOlw/Svn3KFypSdlZn8BbAeWmtlpM/vX5U5T3ibgx4D35q+p/fnScbnNBp7N58EXSfogxnVIaSXSk9QiIhKlGoSIiEQpQIiISJQChIiIRClAiIhIlAKEiIhEKUCIiEiUAoSIiEQpQIiMgpktMLPr+Und0nX9+Qe+DprZ/yr23gwza8zv31dJ7yURUYAQGb0T+Xd3pK4751Y551aQTLH9M4UOds5dzx+vOZukoihAiGTI1w4Oesu/YGa/PszTbEfTfcsEpQAhMk7yb5d7H5qsTyYoBQiRsdeY75O4AEwleVUrAGa21Mz+m5l9vlLeNS6SRQFCJFuOoXmkocTj0j6Fu4A68n0Q+Q7ozwG/DvxX4L/kpwQXqUgKECLZ3gFmmFmHmdWTvCipZM65K8BngF/IvxRnM/C7wMeBmSQvyblvbJMsMnZu6zfKiYyGc+6Gmf0GyTuSTzKCF8Y45/aZ2QGSl7vsBz7onPs8gJl9EnhuDJMsMqYUIEQKcM59AfjCMI9pCZZ/IP1sZo+a2d+SvLv6vzvnzo9JQkXGgV4YJDIKZjYP2AZcCJ6FGM45GkmGw04H7nfOXRzDJIqMmAKEiIhEqZNaRESiFCBERCRKAUJERKIUIEREJEoBQkREohQgREQkSgFCRESiFCBERCTq/wfHvoYWCZTybwAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f521b80c110>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"ax, artists = b.plot(time=0.75, y='ws', fc='teffs', facecmap='YlOrRd', ec='None', show=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Since the syncpar was set to 1.5, one full orbit later the star (and the spot) has made an extra half-rotation."
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYgAAAEOCAYAAACTqoDjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzt3XmQHGed5vHvr/pSt1r3YcuWWoctn7JkTPvAxjbGx3o5zMLuMEwMBDPsroIJYMwCAxjHMsROzAYxMFyGmVgtMEyAlyPADAynbYzvQ5ZsnZZPybJk2VZLQkfr7K7+7R9ZSb+dyuqu7q6uzO56PhEVVZWVmfWmrc6n3iPfNHdHREQkqZB1AUREJJ8UECIikkoBISIiqRQQIiKSSgEhIiKpFBAiIpJKASEiIqkUECIikkoBISIiqRQQIiKSqjHrAozG7NmzfdGiRVkXQ0RkXFm7du0ed58z1HrjOiAWLVrEmjVrsi6GiMi4YmbbK1lPTUwiIpJKASEiIqkUECIikip3AWFmDWb2pJn9IuuyiIjUs9wFBHAzsCXrQoiI1LtcBYSZzQfeCnwz67KIiNS7XAUE8BXgk0Bf1gUREal3uQkIM3sbsNvd1w6x3kozW2Nma7q6umpUOhGR+pObgACuAG4ysxeBHwBvNrPvJVdy91Xu3ununXPmDHkhoIiIjFBuAsLdb3H3+e6+CHgPcI+7vzfjYomI1K3cBISIiORLLudicvd7gXszLoaISF1TDUJERFIpIEREJJUCQkREUuWyD0Jk/CkCRwAvve4BmoEGoj+zFvR7TMYbBYTIiBwDDpee+4iCgdKzBeskNQPtpYdIvikgRCrmwD6iE3+xtCwOgwL94RCGRPw+DpATpX3sAyYB04lCQyR/FBAiQ+qjPxjik39ac1EyJOJ14vexMCxeI/oznEnUDCWSHwoIkUF1Awfpnz+yXDjAwFBIssR68bI+otpIF1FNYvYg+xCpLQWESCoH9tLfj5A8aVuwXrkaQ/xZ8j0p20B/jWIWanaSPFBAiJwk/kXfS3+NoVztwBgYAnGtIF4Wi/cBA0Oij4Fh4cBuYAYwuVoHJDIiCgiRAU4Q1RziE3bYCZ1UoP8ET/DcSPotTZId1vE+wqDoKy07UPpcISHZUUCI/FGR/nAIawDJ2kDYVBQ2K5GyPAyQeHkYEvFzA/3hEC8/QFSLmTaioxEZLQWECBCdnLsY2JQU1hqSAQD9J/rBOqaT+wjDJw6EOCTCUIlrJ0eAJqBtWEcjUg0KCBEgGsYK/U0+yV/9SeGQ1ljyPQwc4prssE7WPpJBES8/QBQSTRUch0j1aDydCEeImnJg4Mk52cxUCB4wMAyMqJkoKRk2aftK1k7CZqpCab8HKz4akWpRQEidKxKdfMPmoIbgfficJi0skif/+CQfSoZL8ruS39tLdE2GSO3kponJzCYB9xNdTtoI/Njd/zbbUsnEF4dDJc1KpKwXrmv0/0klRysNts/k8Nfk9RKxo0R9EfpdJ7WRm4AAjgNvdvduM2sCHjSzX7v7o1kXTCaqntIjPOGmXRCXHJmUPPGnncyT10aEktsTrBt/T1+Zzw4QXSMhMvZyExDu7vTXoeMeubS/JJEqCZtshqpFlOtLGEraOskg6UssDz+PP4vL0otIreSqrmpmDWa2juhS0rvc/bGsyyQTVXzfhrDNPxkS4e+TtNpBWqAkO57Ttk2+HmybZMd4+DtKZGzlKiDcvejuFwLzgUvMbFlyHTNbaWZrzGxNV1dX7QspE8RhTh5+Gr6OO5bTrmUI17OUdQi2D/dRSLxOSgZOWl9Hgehqb5Gxl6uAiLn7fuBe4MaUz1a5e6e7d86ZM6fmZZOJIu57SA5rjZUbnZQ2qqmhzL7SahmhtM/LXb0d6iN9Kg+R6spNQJjZHDObXnrdClwHPJ1tqWTiKlL+ZFzul3uaSvolyoVFsgYSXsGdbGIKywLpd6sTqa7cdFID84B/NbP459iP3P0XGZdJJqRkE02yc7jcMNPk+uWunE6TDIa0YbAwcALA5KR+YYf1cTT9hoy13ASEu28AXpd1OaQe9HLyvRsqvRYirT9iNML5l9I+C4MkORRWZGzpX5nUobAGEXYwJ3+xD9dQ/Q3JcCl3XUWyPyPtdRGRsZabGoRI7ZS7vKbSfobk8rTpwSu9QK6ctIvxdFmQ1JZqEFKHBpvOO7kcTg6AcJu0UU3J/Q0lbR+D1UZEakMBIXUo2TyT/PWfVO5EPdxf9INdAzHU/tMu3hMZW2pikjpWrmYQKxcao/1lX+4ahkpO/goKqR3VIKQOxVNvxyfbwU7YQ13kNhLltkubKDAsi0htKSCkDqWdbMudgNOuWi53DUM1KBQkPxQQUoeSt+4sN0Ff+HnSaEJisO3KfaYOa6k9BYTUoebSc1wzSJ6UK53raCQhMdj64Xd64nXys7Tbm4pUlwJC6lCyBgEjn/wuDInkibzc+mnL0pqxkvsPlzcjMtY0iknqXNgRXa5TOnlL0HKfx8/JGwAl1yu3LO17ktsoIKR2FBBSpxqJ5mQa7OQfB0YyANJGMA2n43uw9dKareJyhMGjJiYZe2pikjrVysl9EGnNOeWmzIj7KYYTDB48ktunfXe5Pom0JjKR6lMNQupUEwPnTOqjf/ZUGNjsNFTNYbBAqFQYFMl5l8LXfWiab6kV1SCkjrVz8sk3fCSVqzmMdCRTcn/ho9x2w5mqQ2R09C9N6lhL6Tk5N1PY2TxYM1K5IAm3SwZAMVie7NtINj/1JcrmwJShD0ukSnITEGa2wMx+b2ZbzGyzmd2cdZmkHkwhvWYQnuAr6XNI1jzK9Skk1w1DYbDt+og6ptX/ILWTpz6IXuDj7v6EmU0B1prZXe7+VNYFk4mshf4RTeEd3MK+hrCWkOynSPZVlJsqvFzTUTIc4u9LG+o6bcijEamm3NQg3P0Vd3+i9PoQsAU4PdtSSX2YUXpOqzUQfEZiWdxk1Jf4PKwVDFX7SNYcwv2E+2onR3+uUifyVIP4IzNbRHR/6seyLYnUByNqajpAf62gXN9C/BzXJNKuk4j3maw5JPcb1lbShrvGn7UQDcsVqa3c/SQxs3bgJ8BH3f1gyucrzWyNma3p6uqqfQFlgmoFJjPwl39a80/8HHceJ/sTCNYrJj6PO6iTndRp+4jXaURNS5KVXAWEmTURhcPt7n5H2jruvsrdO929c86cObUtoExwU4iactJGHqWNTIpDIrleL/1hUOTkwEnuK9m0VCw9moCZY3SsIkPLTROTmRnwLWCLu38p6/JIvWonatbZX3ofNhXFtwyNJWsXllgWNheF02SENypKXv8QPxqB2dU4IJERy1MN4grgfcCbzWxd6fGWrAsl9WgyMIv+YEjWAOJaASmfhTWAtIvuws/D2gXB+zbglDE5MpHhyE0Nwt0fRHdFkdyYBMwB9gInGPjLPxwOmxy+Gv/mSg5vTd7fOtkZHW87FV0MJ3mRm4AQyZ8m4FTgYOkR1hbi5qTk/EyD3fQnvFYiGSztRJ3RmqVV8kMBITKkqaXHAaK+iXD6iwL9wZG8uC0MgmStIx4q20rUEa0/Rckf/asUqdi00qO79DjCydc5hE1LfZzcjxFf19BOFDpqVZX8UkCIDFt76QFRbWI/UT9FkWiIq5VeF4iajIyoptCM+hdkPFFAiIxKA9GIJ5GJJ0/DXEVEJEcUECIikkoBISIiqRQQIiKSSgEhIiKpFBAiIpJKASEiIqkUECIikkoBISIiqRQQIiKSSgEhIiKpchUQZvZtM9ttZpuyLouISL3LVUAA3wFuzLoQIiKSs4Bw9/uBfVmXQ0REchYQlTCzlWa2xszWdHV1ZV0cEZEJa9wFhLuvcvdOd++cM2dO1sUREZmwxl1AiIhIbSggREQkVa4Cwsy+DzwCnG1mO83sv2ZdJhGRepWre1K7+59lXQYREYnkqgYhIiL5oYAQEZFUCggREUmlgBARkVRDdlKb2cwK9tPn7vurUB4REcmJSkYx7So9bJB1GoCOqpRIRERyoZKA2OLurxtsBTN7skrlERGRnKikD+INVVpHRETGkSEDwt2PJZeZWaOZrYj7J9LWERGR8W3Yo5jMbB7RjX2WALea2TurXSgREcneSIa5fgy4Fdjp7h8H3lvdIomISB6MJCDagMPAhVUui4iI5MhIAuKrwD8Aq83sY8Dd1S2SiIjkwbBnc3X3Z83sb4CrgN+6++bqF0tERLI2oqk23H0v8HPUzCQiMmENGRBmNtXMbjGzr5vZDRb5CLAVeHc1C2NmN5rZM2b2vJl9upr7FhGR4amkiem7wB+I7vT234C/AZqBd7j7umoVxMwagG8A1wM7gcfN7Ofu/lS1vkNERCpXSUAscfcLAMzsm8AeoMPdD1W5LJcAz7v71tJ3/QB4B6CAEBHJQCV9ED3xC3cvAtvGIBwATgd2BO93lpaJiEgGKqlBrDCzg6XXBrSW3hvg7j61SmVJmy3WT1rJbCWwEqCjQxPIioiMlSEDwt0balEQohrDguD9fKJpxpPlWQWsAujs7DwpQEREpDrydEe5x4GlZrbYzJqB9xANpRURkQxUMsz1iWqsMxR37wU+DPwW2AL8SBfhiYhkp5I+iHPNbMMgnxswrRqFcfdfAb+qxr5ERGR0KgmIcypYpzjagoiISL5U0km9vRYFERGRfMlTJ7WIiOSIAkJERFJVHBBm9l0z++9mVkmfhIiIjHPDqUH8CzAPuM3MXjCzn5jZzWNULhERyVjFNwxy93vM7D7gYuAa4IPA+UR3mBMRkQmm4oAws98Bk4mm/X4AuNjdd49VwUREJFvDaWLaAJwAlgHLgWVm1jompRIRkcwNp4npfwCYWTvwl0R9EqcCLWNTNBERydJwmpg+DFwJvB7YDnybqKlJREQmoIoDAmgFvgSsLU2sJyIiE9hwmpi+MJYFERGRfNGV1CIikkoBISIiqRQQIiKSKhcBYWZ/YmabzazPzDqzLo+IiOQkIIBNwLuA+7MuiIiIRIYzzHXMuPsWADPLuigiIlKSlxqEiIjkTM1qEGZ2N9HUHEm3uvvPhrGflcBKgI6OjiqVTkREkmoWEO5+XZX2swpYBdDZ2enV2KeIiJxMTUwiIpIqFwFhZu80s53AG4Bfmtlvsy6TiEi9y8sopp8CP826HCIi0i8XNQgREckfBYSIiKRSQIiISCoFhIiIpFJAiIhIKgWEiIikUkCIiEgqBYSIiKRSQIiISCoFhIiIpMrFVBsi418PcBw4BnjpYUAz0AJMyq5oIiOkgBAZkePAXvqDIQ6ENPFnBaKgmAZMqUEZRUZHASFSsT5gH3Cw9Do+8ccn/3IttvFtS/qIahjHgNeAycAMVLuQvFJAiAzJgS6gm+gkH4ZBHBDxepQ+s9K64fIGBobFUeAwURPUqUDT2BRfZIQUECKDOgzspr+2EP/JxCHRF6wbh0YcIlbaLlwvDg4LtukBdhA1O80Zi4MQGREFhEhZrxH9yjeiX/9xbSHsb4iDIlmTiGsK4TbF0rKG4DviMOkjCqPjwCmoNiF5kIthrmb2BTN72sw2mNlPzWx61mWSelYEXibqK2gg+h3VQH9IxK8LRCfyQvCexPs4NKy0bmOwv7hGUggeRWAXcGQMj0+kMrkICOAuYJm7LweeBW7JuDxSt3qAV4lO1GEQhM/xSb2RgbWLeFlTsF74CGsb4b7joAnX20PUGS6SnVwEhLvf6e69pbePAvOzLI/Uq176+xvCk3fcJBSGQxgA4bphLSLZ9BSHQhMn10KS39cI7AcOjcWBilQkj30QHwB+mHUhpN7EI5XimkDYxxCe5KE/MMI+hwYG74OAqJ8h7KBuCJbH6/UFz43AAaIA0VBYqb2aBYSZ3U00li/pVnf/WWmdW4l+xt0+yH5WAisBOjo6xqCkUp/2EZ2Uw5N//DquFYRB4InP4m3CZUUGBktYw3D6r6WIO6nDzwi+fx9Rx3XYuS0y9moWEO5+3WCfm9n7gbcB17q7l1vP3VcBqwA6OzvLridSuYP8sUO6pxv2rIZTrweKcGAzTF0GhWYG1gbCWgYpr53ol39f4nMPljUErwv0j47qC/bRGJWDPUQhIVI7uWhiMrMbgU8BV7u7hm9IDRWJRgw14F1rsJe+T1/PcXatfprTF72ENc+AIy/BvP8UZEBak1PYpBQOgy33DP21h2QwwMCL7BpK5ewG2kd1tCLDkYuAAL5OdDnpXWYG8Ki7fzDbIkl9OAg9h+h+4nu8dN9aOi7t4OHbHqLQsotnW4+x9K2XcnzXL5l7dQtTz38rWNgEFTdJhbWDZF9C8pqHOBQItgmn7Yj3HV5cF2+jgJDaykVAuPuZWZdB6tFx8OPwwr/y9L+t4ddrd7Pl/qPY0TY65s7kOz97hH/u6mHa9OnMPu9B2LoBOv4amqbRf11DLHmhXBMDZ3VNBkNyLqewX4PgdfxcLL0+QDTZn8jYy8UwV5FsHIbuF+ne8wq3rTvMb7obeeXQMXb1Fvj1xq2cd955+Kx5bN36Iq9uO8b6727g4Oqvw9GXGPhrP23kU/ycnLPJE+tbyjrh+7DGUiDqKxGpDQWE1CkHeuneci9f/r+7uHPdsxw4cJC2tjYeeegxDh08RMHgcw9v50uvNLHqh5vY9eAjTJmxA9/2v+k9uIP0/oW0YbHlwqAQPCevuk4Ll7i/oruq/yVEylFASJ06TF/3a9z3d7fzqw07WLF8Ga0tLRw5fJiLXn8h55yzlAfve5Cp06bSUCjwf+5czdx3vYOnf3WY33/2UWz398HDE3nyxJ8MisGuq4iXh9NzJEMlXr8RTcMhtZKLPgiRmvNj7LnvOxxon0nL1CI9x0/Q1bWHEyd6aG5sZPPGpzhv2XnMnz+fhkKB48dPcPPX7udTK6bzunddTkPPU/CHe2DmtaUdpo1SCpuV0m4oFHdEe8qycB/hsFeR2lENQurTvtW8vPZZfne8jUcfWc22bS+ycGEHbZMmsWH9RuadNo+mxiY2b9xEU2MTSxYtptgymX96tY3Vaw+x+hsv88Tnv0hx/7rgvB3+6k8GRbJWET7CqcFJbEewXjgiSrUIGXsKCKlDx/GDz/DPm47ybNd+rr76chYu7KC5qYmXd77MwkUdzJgxg+0vbueF556nr69IW9sknn/6GbZseoqPr/oN+7a9xOR5bTTs/hJ0/QiKPaSf/El5nbzILrkOnFyrSG6vzmoZewoIqUM9PHfXs2zdc4ITJ47T1NTM88+9QLGvj7POOYuFHR08cN8DXHzpxVz2hktZ/fCj7NjxMh2LF3H+8uUUG5v50bHTWHDdCmg9G7rvhULa/RsG60tIq2kktwtrDMlmqmJyI5GqU0BIHepl04NbeGHbdo4ePsaRw0eYd9o8jnYfBoempkbOv+B8GhsKFItFLrvick49bR6z58yhubmJBjNWr9/Chtvu4MShbmheCDaSP6XBQgIGXjsxWA1DZGyok1rqjxfxs+Yye8tBij09uEPb5FYaCw28uG07p582j/VPrmdf114KBoVCgRkzZvD0ps2cNn8+i888g/MmF9n75JM88RVjxWdvo7XiLy/X1xB2Zg8obGK7PkRqRTUIqT/Fwxxx48CBg7z2WhdTp03hoQceYe3jT3DmmUtY/ehq/sONN/CHP/yBhYsXM2XKFF547nnedP11TJ02FTCuvno5N3z341z2yRW0zj1rGF+edrV0LO2K6rRhsiK1oX9tUneKxw6xa/WLLOyYT1NTE3v27OXyKy5jyRmLaW5u5sylZ/LKK69y5PBh2tvbaGxq4vDhw3QfOkRTUzNrH3+c9mc2sPeZQzgGTXOG8e3lmobCqTWGmuivXJOUSHUpIKTuNLTN4szLFmGFAnPmzGLGjOkcO3aMadOm8dJLO+jr66O1dRKXX3kFLzz/Atu3buOMpWdy/Ngxtr3wAgsXzIeXtrD+y99l344zqbylNu1aiHD+pmR4hM1Jg9U8RMaG+iCk/hQamV1o5Pjx4/QWixT7+nj+ua0c6e7mTddcxcZ1Gzn3/HM4tP8QCxYtYu7cU5jUOokGK9A2eTJXLJnJNTefQUtbFzb3SrBKftGHNwSCgZP4hf0M8brx+74y64qMPdUgpA4VaO8xWhoKTJ8+lYcfepQLL1pOS0sLWIEFHfNZt3YdD97/AHt2d7F3zx6OHj3KgQMHeei++1l6fA9bf/MUuMPki4bxvX1lHpWc9NVBLbWngJA61MBF77uMsztm0No2mdddtIKWSZM459yzufeee9n81NPMX7iAN179RjasW8/U6dPY/4f9PP7YY1zU+Xqm7HqKF//9fnatnwUNUyh/sk87qSdrAZ5YN+2zvpT11A8hY09NTFKHGrHp57DgxE95bM9+ir299PT00tvXxxVXXs7Ro0cpNDQyaVIri89YgjvMnDmDC1Ys541LT+GyD7yeaafup7DoL1LO04Pd06FcOJTbRzIYwqYoBYSMvVzUIMzs78xsg5mtM7M7zey0rMskE1kr3r6ERa+9yJT2NgCaGhtpnzKZ3V17aG1t5bVXXuXuO+9mxszpNLc0s3//ATau38BF7GXz7Q9ASwdMPp+Bw1Ljk3iRgTWHck1JTnpohDWP5N3q4tf6bSdjLxcBAXzB3Ze7+4XAL4DPZl0gmcgKWFM7b//7d3LVmbM4Z8ZkTpk+BSsUmDt3Dlu3vcgZS5dw/vJltE2ZQmtrK47zluuvZurxfUxfupQjvReBhWEQB0AyLAYLBhg4dUbausmRTPF3TRr9fwaRIeQiINz9YPB2MhqqIWOuQOuCC/iLN7Tz9r2bWX68i/XrNnLs2DF2vLSTQ93d7N23j+5D3ezbt4+NGzdz1dLJXPOFd7PsHW20z2lj6OaitE7lZHAk+ynSmpdixWCZAkLGXi4CAsDM/t7MdgB/ziA1CDNbaWZrzGxNV1dX7QooE0w7zO5k/rnGrPOXseC5J7h0xXk88ujj3HjjDRzYf5AFCzuYP3sGa9c8wYUrltOx5Un8yD5onAqFSZxcQyg30ij85Z8Mh2LK9snaSNhkFd/vWmTsmXttfqyb2d3AqSkf3eruPwvWuwWY5O5/O9Q+Ozs7fc2aNVUspdSX16B4lG0/XsW+DU/yLFP56p3PsWfvPhbMP50HH3iYO953FYee3cSUa9/E5Bee5fz3XMYpy6bAok9FQTFgCoxks1EonI01rCWEz8llyVpG/H4m0DL6w5e6ZWZr3b1zqPVq1tPl7tdVuOr/A34JDBkQIqPTAg19LH7XB1i8+BYuajmF3ud38tWjk1j9+FreeOXl9G5/lnlnn8cFl89i1p+cw8GeFbD4T6Fhcmkfg13EFn8Wfh7WBMKgKCTeF4P1CLZrQOEgtZKLoRBmttTdnyu9vQl4OsvySL2YBhyDpsmw5P3Yrt9w5bXzYNMTtH76nbx2z2Nc+pEbObb3CJPPexu24BKmNbaXto2vRUi7+jltBtbkkNekOBTibeKrqONHvM600R60SMVyERDA583sbKK/gO3ABzMuj9QFI+rsPQyzL4Keg3Rc8hBv/Nh/YfEl09i5qJOGhgJL/vyT0H4GA2sCBQY2GxEsJ3gPA2sZyWm7k30S4bJkOBgMY2JxkdHKRUC4+3/OugxSr6YDx4EizLuGwrw3s+isV2H7D5m//CA9p74bJi8urRuezMPaQ9pVzmnhMdiEfPE2xcQ64XazRnuwIsOSi4AQydYMYDfxLUGt7VQ496Nwopum5mkM7ESOawjhdBfJJqVkv0PyHg9h7SFsSiLYJvl+Eup7kFpTQIjQTHT5TXfpfenE39zGwHCIT+YWLE+OFA9rAsn+CDi5aSmUbFKKnxtR7UGyoIAQAaJaRB9wmOjPIv5130v6faHDmkTYlJQU9lUkO6FjYTDAwJFLDcBwbkgkUj0KCJE/mkUUCCfoP7HHz8kaQ9r9HcL38edxn0KyqakYrBfuIzm8dSZRSIjUngJCZIBTgFeAHk7uUwgVODk0ehkYAn2J9cp1UIfBQOl1A9F1pfoTlezoX5/ISeYB+4j6JOI+h2TNIeykLgav44AoBJ/ByeHQW3oOAyRurmoiCirVHCRbCgiRVDOJRg7t4eRRTGmjmorB68HmZEqOZgpHLRlRZ/nsUZZdpDoUECJltQGnE4XEkdKy5DDWsJkpri0kh7WGy8LO6rgTPL4AbjaqNUieKCBEBtVA1NzTA3QRdWCH02yEw1eTcyqFkrWHOFwmAXNRMEgeKSBEKtIEnEZ0Ut8LHKW/HyHsfwj7I5Li2kZjaX8z0H0dJM8UECLDUqD/uoQicAg4RjRdR3I+pbizuoHoT20SUR+DroiW8UEBITJiDURzOYlMTLm5o5yIiOSLAkJERFIpIEREJFWuAsLMPmFmbma6UkhEJGO5CQgzWwBcD7yUdVlERCRHAQF8Gfgk5W/aKyIiNZSLgDCzm4CX3X191mUREZFIza6DMLO7ieYvTroV+AxwQ4X7WQmsBOjo6Kha+UREZCBzz7ZFx8wuAH5H/2xo84FdwCXu/upg23Z2dvqaNWvGuIQiIhOLma11986h1sv8Smp330g0WxkAZvYi0OnuezIrlIiI5KMPQkRE8ifzGkSSuy/KugwiIqIahIiIlKGAEBGRVAoIERFJpYAQEZFUCggREUmV+YVyo2FmXcD2Ku1uNjDer72YCMcAE+M4JsIxwMQ4jolwDFDd41jo7nOGWmlcB0Q1mdmaSq4szLOJcAwwMY5jIhwDTIzjmAjHANkch5qYREQklQJCRERSKSD6rcq6AFUwEY4BJsZxTIRjgIlxHBPhGCCD41AfhIiIpFINQkREUikgAmb2ETN7xsw2m9k/ZF2e0TCzT5iZm9nsrMsyXGb2BTN72sw2mNlPzWx61mUaDjO7sfTv6Hkz+3TW5RkuM1tgZr83sy2lv4Wbsy7TSJlZg5k9aWa/yLosI2Vm083sx6W/iS1m9oZafbcCosTMrgHeASx39/OBL2ZcpBEzswXA9cBLWZdlhO4Clrn7cuBZ4JaMy1MxM2sAvgH8R+A84M/M7LxsSzVsvcDH3f1c4DLgQ+PwGGI3A1uyLsQofRX4jbufA6yghsejgOj3V8Dn3f04gLvvzrg8o/Fl4JPAuOxgcvc73b239PZRorsMjheXAM+7+1Z3PwH8gOhvfmyJAAAD7ElEQVSHx7jh7q+4+xOl14eITkinZ1uq4TOz+cBbgW9mXZaRMrOpwFXAtwDc/YS776/V9ysg+p0FXGlmj5nZfWZ2cdYFGgkzuwl42d3XZ12WKvkA8OusCzEMpwM7gvc7GYcn15iZLQJeBzyWbUlG5CtEP5T6si7IKCwBuoB/KTWVfdPMJtfqy3N3w6CxZGZ3A6emfHQr0X+LGURV6ouBH5nZEs/hMK8hjuMzwA21LdHwDXYM7v6z0jq3EjV33F7Lso2SpSzL3b+hSphZO/AT4KPufjDr8gyHmb0N2O3ua83sTVmXZxQagYuAj7j7Y2b2VeDTwP+s1ZfXDXe/rtxnZvZXwB2lQFhtZn1Ec5901ap8lSp3HGZ2AbAYWG9mEDXNPGFml7j7qzUs4pAG+38BYGbvB94GXJvHkB7ETmBB8H4+sCujsoyYmTURhcPt7n5H1uUZgSuAm8zsLcAkYKqZfc/d35txuYZrJ7DT3eMa3I+JAqIm1MTU79+ANwOY2VlAM+Nsgi933+juc919UenWrTuBi/IWDkMxsxuBTwE3ufuRrMszTI8DS81ssZk1A+8Bfp5xmYbFol8X3wK2uPuXsi7PSLj7Le4+v/R38B7gnnEYDpT+dneY2dmlRdcCT9Xq++uqBjGEbwPfNrNNwAng/ePsl+tE8nWgBbirVBN61N0/mG2RKuPuvWb2YeC3QAPwbXffnHGxhusK4H3ARjNbV1r2GXf/VYZlqmcfAW4v/eDYCvxlrb5YV1KLiEgqNTGJiEgqBYSIiKRSQIiISCoFhIiIpFJAiIhIKgWEiIikUkCIiEgqBYTIKJjZIjM7GlxQhpkVzWydmW0ys38f6n4WZtZaWv/EeLx/h0xcCgiR0XvB3S8M3h919wvdfRmwD/jQYBu7+9HS9uNuziaZ2BQQImWUagebgvefMLPPDXM3jzCOp/uW+qaAEBkjpbvLXcs4m6xPJKaAEKm+1lKfxF5gJtEtVAEws7PN7J/M7B/N7LTMSihSAQWESHm9DPwbmVThdnGfwkKiaeM/BFDqgL4F+BxwG/DF0gydIrmkgBAp7zVgrpnNMrMWohsYVczdDwB/DXyidAOeq4huQP9O4BSiG/KcX90ii1SP7gchUoa795jZ/yK6H/M24OkR7ONJM1tPdNOadcAN7v6PAGb2p8B9VSyySFUpIEQG4e5fA742zG3aE+/fHr82syvN7A6ie1d/z93H1V0Lpb7ohkEio2BmC4CHgb2JayGGs49WouGwc4AL3H1fFYsoMmIKCBERSaVOahERSaWAEBGRVAoIERFJpYAQEZFUCggREUmlgBARkVQKCBERSaWAEBGRVP8fTW7GhVt9HYQAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f5219414a10>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"ax, artists = b.plot(time=1.0, y='ws', fc='teffs', facecmap='YlOrRd', ec='None', show=True)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.15+"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| gpl-3.0 |
arne-cl/alt-mulig | time-series/Session 1 - Introduction to time series in Python.ipynb | 1 | 37515 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# show all plots inside Jupyter\n",
"%matplotlib inline"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import pandas as pd"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# background on the dataset: https://en.wikipedia.org/wiki/North_Atlantic_oscillation\n",
"NAO = pd.read_table('data/NAO.txt')"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"pandas.core.frame.DataFrame"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"type(NAO)"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>year</th>\n",
" <th>NAO</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1864</td>\n",
" <td>-1.02</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>1865</td>\n",
" <td>-1.24</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>1866</td>\n",
" <td>0.54</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>1867</td>\n",
" <td>-1.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>1868</td>\n",
" <td>2.81</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" year NAO\n",
"0 1864 -1.02\n",
"1 1865 -1.24\n",
"2 1866 0.54\n",
"3 1867 -1.38\n",
"4 1868 2.81"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"NAO.head()"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>year</th>\n",
" <th>NAO</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>count</th>\n",
" <td>146.000000</td>\n",
" <td>146.000000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>mean</th>\n",
" <td>1936.500000</td>\n",
" <td>0.193356</td>\n",
" </tr>\n",
" <tr>\n",
" <th>std</th>\n",
" <td>42.290661</td>\n",
" <td>1.907480</td>\n",
" </tr>\n",
" <tr>\n",
" <th>min</th>\n",
" <td>1864.000000</td>\n",
" <td>-4.890000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>25%</th>\n",
" <td>1900.250000</td>\n",
" <td>-1.027500</td>\n",
" </tr>\n",
" <tr>\n",
" <th>50%</th>\n",
" <td>1936.500000</td>\n",
" <td>0.245000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>75%</th>\n",
" <td>1972.750000</td>\n",
" <td>1.580000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>max</th>\n",
" <td>2009.000000</td>\n",
" <td>5.080000</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" year NAO\n",
"count 146.000000 146.000000\n",
"mean 1936.500000 0.193356\n",
"std 42.290661 1.907480\n",
"min 1864.000000 -4.890000\n",
"25% 1900.250000 -1.027500\n",
"50% 1936.500000 0.245000\n",
"75% 1972.750000 1.580000\n",
"max 2009.000000 5.080000"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"NAO.describe()"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0 -1.02\n",
"1 -1.24\n",
"2 0.54\n",
"3 -1.38\n",
"4 2.81\n",
"Name: NAO, dtype: float64"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# get the first 5 values from column NAO\n",
"NAO.NAO[:5]"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1864 2009\n"
]
}
],
"source": [
"# get min / max value from a column\n",
"print min(NAO.year), max(NAO.year)"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0 1864-01-01 00:00:00\n",
"1 1865-01-01 00:00:00\n",
"2 1866-01-01 00:00:00\n",
"3 1867-01-01 00:00:00\n",
"4 1868-01-01 00:00:00\n",
"Name: year, dtype: datetime64[ns]"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Coerce data to a time series\n",
"\n",
"dates = pd.to_datetime(NAO.year, format=\"%Y\")\n",
"dates.head()"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# NAO.NAO.index = dates"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# pd.Series(NAO.NAO, index=dates)"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.axes._subplots.AxesSubplot at 0x7f9058432650>"
]
},
"execution_count": 26,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAW4AAAEPCAYAAABiCi5wAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztnXmYZFV5/7+np/eenRmd6Z4GBobFDBgWBYIirUGDGEVj\n0GiiSYho4oJrjEafH0OeGGPigv6MO5pEf9H4GOKKGIx0BEGQyYAwgA6zr9093dMzvXdP9/n98dZL\nnbp1l3PuUnVv9ft5nnmmu7rq1r23zv3W937Pe85RWmsIgiAIxaGp3jsgCIIguCHCLQiCUDBEuAVB\nEAqGCLcgCELBEOEWBEEoGCLcgiAIBSOxcCulViqlvqWUelwp9ZhS6rI0dkwQBEHwpzmFbXwSwO1a\n699XSjUD6Ephm4IgCEIAKskAHKXUCgDbtNZnpLdLgiAIQhhJo5KNAIaUUl9RSv2vUuqLSqnONHZM\nEARB8CepcDcDuAjAZ7TWFwGYAPC+xHslCIIgBJI04z4A4IDW+hel378Fj3ArpWQyFEEQhBhorZXf\n44kct9b6CID9SqmzSw9dBWC7z/OgtcZNN9301M9R/6688krr57pu2+W5WW/b5TjztN9ynMmOMU/7\nneVnuViOM4v9DiONqpK3Afh/SqlWADsB/GnQE/v6+qw3evrppzvthMu2XZ6b9bZdjjNP+y3HWY20\n2drvS16OM+vrpwqXb4k4/+gt3Lnppptiva5oyHE2DovhGLWW46wVJe301dXcjpxM/I1UEOQ4G4fF\ncIyAHGceSFTHbfUGSums30MQBKHRUEpBZ9E5KQiCINQeEW5BEISCIcItCIJQMES4BUEQCoYItyAI\nQsEQ4RYEQSgYItyCIAgFQ4RbEAShYIhwC4IgFAwRbkEQhIIhwi0IQsPyyU8CW7fWey/SJ41pXQVB\nEHLJT34CNDUBF19c7z1JF3HcgiA0LDMzwIED9d6L9BHhFgShYRHhFgRBKBjT08D+/fXei/SRjFsQ\nhIZlZgYYGKj3XqSPOG5BEBoWjkoWFuq9J+kiwi0IQsMyMwPMzQFDQ/Xek3QR4RYEoWGZngZOOaXx\nOihFuAVBaFhmZoBNmxqvg1KEWxCEhoWFWxy3IAhCQZieBs48Uxy3IAhCIVhYoI7JM88Uxy0IglAI\nZmeB1lbg1FNFuAVBEArBzAzQ1gZs2CBRiSAIQiGYnibh7ukBDh5srEE4qQi3UmqJUmqbUup7aWxP\nEAQhKTMzQHs70NEBLFvWWINw0nLcbwfwGACd0vYEQRASwVEJAPT2NlbOnVi4lVIbAFwD4EsAVOI9\nEgRBSAGOSgDKuUW4K/kEgL8E0EAJkiAIRYejEqDxOigTCbdS6ncBDGqtt0HctiAIOaKRo5Kk83Ff\nDuBlSqlrALQDWK6U+let9evNJ23ZsuWpn/v6+tDX15fwbQVBEMIxhbu7G3j8cfvXvvzlwC23AKef\nnsmu+dLf34/+/n6r5yqt0+lPVEpdCeA9WuuXeh7Xab1HVuzbB6xfD7S01HtP4jE4CHz728Ab31jv\nPRGE/HD77cCnPgXccQdw223Av/4rXSdRaA2sWAH8938Dz3529vsZhFIKWmvfJCPtOu58K3QAb3wj\nrQZdVB57DPjSl+q9F4KQL8yMu6sLmJiwe93wMDA2Bpw8md2+JSW1pcu01v8D4H/S2l4tmZkBJifr\nvRfxmZ2lHnRBEMqYUUlXl/01vmsX/Z9n4ZaRk6APaGam3nsRn9lZYGqq3nshCPnCLAd0cdwi3AXh\n5MliO1YRbkGoxoxKOjtFuBuORhDuIu+/IGSBNyqxFe6dO+l/Ee6c0wjCLY5bECqJK9y7dtH8JiLc\nOWdurjEy7pxXXQpCTZmerq4qsblGdu0Czj5bhDv3NILj1pq+gARBIEzH3doKKBV9jczOAkeOABs3\ninDnnkYQbkDiEqFx+eIXga9+1e01pnADdnHJ3r00r0l7e76FO7U67iLTSMK9YkV990UQsmD7dveR\nzWY5IFAW7lWrgl+zcydwxhlAc3O+72DFcaMx6riBYn/5CEIY4+PAyIjba8xyQKC6JHDHjmpx3rWL\nFhdubs634xbhRmM5bkFoRMbHgWPH3F4TFZXccAPwn/9Z+Zpdu8qOW4Q754hwZ8sdd0jFi5CMOI47\nKCphjh8HHnyw8jUi3AVibq4xhDuPx6A18OIX06Q9ghCXsbF4jtuMSkS4G4xGybjz6Lh5344ere9+\nCMUmbsbtddzmRFMnTgBbt5ZXf9e6snNShDvnSFSSHXxeG2mFbaH2pJ1xa03C3dUFPPkkPTY4SJUr\nK1fS/yLcOUeEOzv4vIrjFpIwPk6iy23dBm/GbVaVzMwATU3A5ZeX45LbbweuvJJ+FsedcxYW6F/R\nhbupKZ/HII5bSIPxcRJhF9cdlnGfOAEsX04r3LBwf+MbwGteQz+LcOec+Xn6v+gZ94oV4riFxkRr\nEu7eXnfhDopKWLif9SwS7sFB4P77gZe8hP4uwh3BwgLwhS/U7/35w8mjW7VldpYaYZ6FWxy3EJfp\naZprZM0atw7KsHLAEyfI7Fx0EbBtG/DNbwLXXEPPAdxGTk5NAQ89ZL9fXrQG7rvP7TV1F+7jx4E3\nval+jpc/nKIL94oV+TwGcdxCUsbGgKVLgdWrk0clXFVy/DiZnVWrgHXrgI98pByTAG6O+0c/At71\nLvv98nLgAPCCF5Tv/m2ou3DzhX3oUH3evx6Oe3w83e1lGZVoDTzySPzXi+MWkjI+TsK9apWb47aJ\nSgCKS8bHgRe9qPxcF+Hevz+Z8ZyaouuEq1tsqLtw8wHv31+f9z95kr6Va+X45+aA005Ld5tZRiVP\nPEEDaOIyPU0XjDhuIS4s3HEct41wP+95wGtfW/ncWgo3m5tf/tL+NXWfHZB3+sCB+rz/yZPUKEZH\na/N+k5PkGhYWqBIkDbKMSo4fp/mJ5+eBJUvcXz89TZ1K4riFuMR13GHlgKZw/8VfVE/JUC/hvu46\nu9eI4y457oWF2vQi84eU5ntlGZWMjZFoxxXe6Wma31gcd+MzPp7NVKhxHLfWdF3YOG6AFlkwybvj\nrrtw807XU7hbWugDrkVcwuKaZgPPMirhOUYOHoz3+ulp6vzJ6qIW8sN73gP8y7+kv93xcWDZMjfH\nPTtL17V5Vxsm3F5cRk7u3+82MMjL1BRw+ukFFe56RSVzc/TtWqucm483beHOKiph4Y7beTw9Tbeo\nq1cDw8Pp7ZeQP4aGgH370t9uHMftjUmAyqqSKOG2ddzz82RqkjruzZvp/B0/bveaugv3zAzNDVBP\nx83CXYvKkqwcd1ZRCVfAJBHu9nZg7Vq7uOWuu4B///d47yXUF+4PSRsuB1y1yl64vaWAQKXj5nLA\nIGyF+8gRem5S4e7qIvF+9FG719RduKengU2b3B33zAzwk58kf/9aC3cRM24guXCvWWMn3PffD/z3\nf8d7L6G+nDgBHD6c/nbjdE56K0oA/wE4QdgK9/79NJtgUuFubwee+Uz7uKTuwj0zA5x6KlV1uBz8\ntm3AO96R/P3NjLuWwp1Fxp1VVNLbmyzjZsdt00E5NUUXlVA8jh/PVrhdohI/4Q6qKvHDduTk/v1k\nPJNk3IUUbs5Au7vdXPfERDoO03TcRe6czNJxn3tu7Ry3CHdxySoq8Tpum9WUuN2ZdHZS+1pYSC/j\nPnAA2LiRsm6e19sVU7gfftjuNYmFWynVq5S6Sym1XSn1qFLqRpfXcyfChg1uwj0+no7DrFdUUiTh\nPuecdDJucdyNzYkTwMBAfAELgoW7rY3ujs3FEILwc9xLltBj3MbSEO79++mOtLU1vvGbmqJr5Pzz\naZSyzflLw3HPAXin1nozgMsAvEUp9QzbF3MnQm+vWwdlFo67lp2TaWXcWtO2li2Lv/9aVy/hxKQl\n3OK4G5u5Ofq3fHn6NftcDgjY59x+wg2UK0vSFu4k5cTT00BHB0VBK1cCe/ZEvyaxcGutj2itHyr9\nPA7gcQDdtq9nx93bW5+ohMsBi5pxz82RC+no8D8fP/4x8Gd/Blx/PfDud/vfZg4MAM9/vv/2x8ao\n88W1D4IRx704YCFcvz55XDI/X1l4wI4bsM+5/coBgXIHZd6Em2Od3l47k5Rqxq2UOh3AhQDut30N\nO+4NG9wcN0clSVcPL3rGPTtLt2le4R4ZAf70T4E3vAG48ELguc8FvvY1WgzVy+gonU+/DpaxMYph\nnv70eBekOO7FAZfXrV+fvIPysccqZ+rjckDAzXF7M26AhJunnPATdsZ2AI4p3HE7KE3hXrbMbmHt\n1OYqUUotBfAtAG8vOe+n2LJly1M/9/X1oa+v76nfead7e8kd2jIxQSd/bo6EKy5Fz7hZuL37/773\nUeN99NFyo//Od2hx1DPPrNwGF/0fO0YCbTI2Ro2pp4ecgOsEWXEdt9bVw5CF/MLldevWJXfcQ0P0\nj+8m4zjusKjk8GH6kglrXzaOe26O9nP9+mQZN18j/f392L+/H1/+MpXFhpGKcCulWgD8B4Cvaa2/\n7f27KdxepqdJGFwdN5f1TE0lF+6WluIOwGHhbmujbfJkUIcO0Tzn3OABmr5y61bgVa+q3IaNcHd3\nx8u54zju+Xn6v7PT/f3yDhuFRuP4cRLuNBz34CB9cQ8MkC6Ywp004+7spP0Lq+EG7IT70CHgaU8r\nR61Jhbuvrw+XXNKH5z2Pos2bb7458DVpVJUoALcCeExrfYvr65N0TgLJxZYvpFpn3Gl1TrJwK1X5\n5TMyQu7E5OKLSbi9sHD7XRCmcMep5TaF++hRuiB/9jPg7/7OP+biL7ZGjEuOHSNh47bbSKQZlfAX\nPG/HK9y2GXdQVMKOOwwb4eaYBEgm3FxVAthHJWlk3M8B8EcAnq+U2lb6d7Xti7kTYe1a2mFb8eSh\n2Ek7KNPMuCcngQceCH9OVo4bsBdur2CajttLWo67vZ0+55ER4I1vBL74ReAtb6kufaqXcD/ySPYj\nNu+7j7687r472/dhHnkEuMXZSsUj7agEKLc3s6pk9erkVSVZCXeSjLujg35etsxuoZU0qkru0Vo3\naa0v0FpfWPp3h+3r2XE3NbkNwjGjkiSkmXH/9KfAO98Z/pwsMu6WFvrZ7KD0E+6nP50arreDkuci\n914Q/EXW1lbOuF0xnc/atcDf/z3tx8MP0yixN7+58vlTU+SuTOHesSN5J3QUt92Wzcx2JvfcQ+JW\nqyH927cDd95Zm/dK03EPDlLcd/hweaFgXgvS1nGHCfeRI3bCHXWNHjhQFu40Mm6A2n6tHHcizJ3u\n6bG/HU8rKjFnB0y6rZGR6G/LLB03C7fW1LhXrap+PufcJkFRCbttILnjBigu+eQngY99jC6c730P\n+Od/rnz+1BQJuync114L/OIX7u/twr59JBhZcs899MXu0gmfhMnJ2q3sxI47rajknHNoOzMzdH2y\nOUmjHDBvUUmcqpK6C7f5zdjVZe+g03bcaWTcNsKdVcYNlL98xsboZ79OW7+c+/hxKvz3XhBpC/fa\ntcAf/RGVJwL0nrOzlYuk+gn34GA204Wa7N9PnWFx+fWvgf/zf4L/PjMD/O//AjfeSHc8tVhYgtcy\nrAXsuM2oZGEB+PjH3dv60BDwm79J7c0sBQTSKQdMS7h376Z5tIF0hbsmUUlSzJ12OXi+fcpTxj0y\nEv1tydUSWTru4WHglFP8n3/xxdWjJI8fpwYY5biTdE4CwCc+UZm5KlU58Q9QFm4+j/PztF9ZT/ub\n1HHffz+VWwaxdSu5yFWraI3DNGa2jGJysrbCvWIFCeL8PF2fW7fSoC/XaXoHB0m4Dx+u7JgEkkcl\nXFWShnDv2UPzlADp1XEXKirhE+wi3BMTdOudRlVJWuWAx47ZOe5ly7IVbr98m7n4YnJ+ZmZ8/Dg1\nwDDHze7YdYV6s1GefXb1BWNOtak1Pd903KOj9HiWjpu3PzQUP0vfty/csd9zDw2CAoDf/u3kccnP\nfhY9k9zUVO2jEqXKccl3vgNceinw4Q+7zV9iOm6vcK9YYddxHZZx82yaYUQNwNGahJvHNaQxVwlQ\nsKiEd9rl4CcmyFVGOe7bbw+/GIM6J83bd1tGRsp1yEFMTWUr3NPT4cLt10Fp47iVItftml8GlWUx\npnDPzNAFY16cHClk6bhHRmgfOzvtpw19wxsqz9fevSQ4QZ+9KdxXXZW8g/Ib3wC+//3w59TacbMY\nclzy7W/TXVZ7O/Dd79pt5+RJ2tbmzf6Oe/lyO+EOKwfk7YQR5biHh+k5K1fS72nMVQIUOCqxvd0Y\nHyfHHSbcJ08Cv/u74d9gfhn3wAA1HFf4Qg6r083Scbe3RztuALjgAioVY2wcN2A/+pHROtj5MKZw\nT01RAzYvzqNHScyzFO59+6iT6WlPs49Lbrut8hzu3Uuu0m95toUFcsjPeQ79vnkzHfPu3fH3eXLS\nLparteMGyHHfcw+di0svBT7wgeC6fS9Hj1LbXb+eXj86WtkGV6ywW94rzHHzdsKIEm4zJgHSy7gL\nE5WYJ9g1Klm7NtxR8ICPKHH3ZtyHDsVbA5OFO+wbc2qKhCmLzkmbqAQg52ze1o+OUiMMc9wA3eG4\nrBvpt2Crl6VLo4X7vPOyF+5TT6W7EZsOSq1JPJ58svzY3r30Ofi9/oknyJl1l6ZeU4oiK9tlqvyY\nnIx2ZvV03F/4AvDSl9Jnf+211JbuvTd6O0NDdF03N1Mb3rWr0nF3dFC7ijI+UcKd1HGbHZNA7ecq\nqbtwx+mcnJ+nD27lynBRZvcU1nj9ygGHh0lMXOMSdqxhJ77eGTdQ7SzZcfsJt3nRuAp3VEwCVDvu\nzk5/4T56NNkqI2GwcNs67vFxctE7dtDvnJFfcIH/4JNHH6W/mSxf7t5fYGLruOMI9/y8u7HwOu49\ne4CXv5x+b2qizNqmn4KFG6Avuh07KtugUnTuoo49rBwQSC7cXsedVh13oaISPsG2Bz8xQRc4Z7pB\nsPuxddymcAPuF9bICDVaG8ed5chJG+Hmc6M1XXSnn05fPObtbFLHHUe4vY57eJic8Lp18ZdPi4Lr\ncZ/+dDvh5gFL7LiHhmi/zzzT33HzoCKTpUuTC7eN444jJv/0T8Df/I3ba0zHvX49fa4veEH570HT\nDnsZHKT2ydv59a+rz51Nzh1WDsjbCCOO445zrvlLkuvUCxWVuGbc3GER1RhsHLdfxs3i5DLsWmsS\nzN7e8AuqFo47rBwQqHSWk5PUaLq66ByY+14r4TanL/CLStasIUecVVxiOm6bqGR0lEb2sePeu5eq\nC9at83+9n/szjzsOU1PRF/jkJLUP1xVphobcatr5y5/F8KKLaD1Y87O3FW7TcQcJt03OHVYOCEQL\nd1MTnbegc7dnTzrCzdcIz1TY1lbuGwrdP/e3Spc4UcnEBDX8qMZg67i5HJDfm8XJ5pvP3KeWFhK3\nKOFeurTy23x+3u29TJJGJVx/C1TXyHqFe/Xq2jtuFm7XSchccI1Kjh8HfuM3gJ076SJj4Q7KyP3O\nQy0cN7d714iJFxpw2RdeVgygWOhv/7byOXEcd3c3CWRcx50kKlEq3HWn1TlpVpTw+9rEJXUX7jid\nkyzcUbXXfBHGjUpcGu+xYyRsURekX1Ty1a+SeF54IfDe97q5nbhRiZ9weyfwyUNUcvQovW+Wwh0n\nKuntLY/C27evLNx+GXdWwm3juPn9Xbft0vbNmCSIuI57fj6ecCctBwSChZtruE3H3doarw8mqG1E\nfbZ1FW4+KTw/sUvG7eK4baKSpMLNYhnWK8zH29FRKdwnTtCMeZ/9LD2+eTNNxmTTOVpLx12vjDtL\nxz03R+2ku9stKlm5EjjrLMq59+4Nr0qpt+N2Fe6JCbc7QLNjMog4ws1VOGYbBJI77iVLKl1uEEGD\ncAYHaTvmF0rSqMQk947bm/1lkXHzqs5BBGXcbW1ujXdkhIQv7ILkEVItLZXCPTtLr7vsMhqw8POf\nA7feajf9ZxzhPuUUEh8e7JB3x83CnXT05MhIde30oUMkuC0t9o6bz9mmTZRzR0Ulfh1lSYXbNuPm\n93fBNSpJ03F7OyeBdDPuVavo2rJZXSnIcXs7JoH0hTvXjtvboNOOSgYGyAmFNRizHNDMuE87LZ7j\nDrsgOc/yThlpii9AgnD55XYDNIIG4PjNDMgsWUIifPRo2T0C9RFuvzpuviOZnY3OuG1Hcu7cSYNB\n3v/+ysfNGd5sM27TcdsIdz0d97Jl2Uclto6bv0jC8EYlQLpRSVMT8Md/HL0fQLBwe2MSIF3hzn1U\n4ue404xKBgfpgjIb7s9/TnMnMEFRycaNbo7bJuM2HbfZILzCDVDDcBXujo7ySMMowWSRylNUMjlJ\nx8C1uqOjtH+rVgVXlTz72dHnaetWGm6+eXO1iHHHJEDnYXo6WuhYuDdtKkclp51G5/To0eqIy6+q\nxPzCcoUHlc3OhpesTU7SuYvjuF3aflYZ97p19H+anZMuhDlus2MSiJ9xm/OUMLmPSryO2zbj5pkB\nwxqD1mXhNp/z+OOVq9SECXfcjDvKcXujkpmZauHeuJG+2aPwCvfBg+GlgIyfcEc57s5OOq82zgmI\nH5UAdHHu20f7tmQJue7Jycr31pou9Kjz9L73ATffDNxwQ/XFZQq3Unaum8/ZWWfRhF0zM7R/PM+K\n98vNxnFPTgLvelf4+5rba22NvsCnpki442TcrlFJGhn33Bxti2O+lhYS8bwJd9qO25u35z4q8TZo\n24x7YoI+zLCo5MQJatyrV1c2GO+gBC4HbG4mpzQ7Syett9dduDnjDjrpYRm3t5Gdfrq7cLe3k3CH\n5dtMHMetlJvrTircu3aRIPJ7exeUZtcZ1mmpNU1j+7KX+V9cPE8JY9NBaTru3btJ+Dkz9YtLbIT7\n4EHq37CZh2Nykr5Ew9rayZNUgxwnKpmYoPNqK0Q2UUlnZ7RwDw9T212ypPzYq15VnoGPscm4g0ZO\nuhAm3F7H7W1bW7faxW4SlXgYGKCL0CvuPCiBYcfNi+3yCtCrVrl3Ttpm3H7C7ReVxHHcg4Pxhdt0\n3LxklLdHPwvh9g7AAaqFG6jOuXkEY1inJc91sW6dvzEwM27AroOShXv5cjqPprDEFW4WooceCn9v\noHyewhw3PyfOPPN8V2Pb/tOKSsyYhPn0p+mcmtTbcdt0Tn74w9WrO/lRyKqSpJ2TYY1hcJA+cO9z\n/Bw3lyOyYz3lFDp5addxs+P2Ngg/4d6wgQQg6g7EK9xAOo57cpK2y+eGqbXjNmMfb2UJ72uYcD/4\nIC3XBvhHcSdOlDtnAbeoBCDXzVEL4C/cNlUlLsJt47j5OXHmmZ+YsJ8+FUivHNCsKAkjat/4i8em\n5C8Mv3Un5+epvUVl3OPj1J8WRSGrSryO2zXjDmuU7Li985nYCrdLwwWSOW6/jLu5mXrVo2YpTCLc\nAwPBjtsbkzCnnGK3dBSQXLh376503Bs2VJ4PG8dtCref4/aee5sZAs1KnLPOqnTcfqucuzjubdvC\n3xsoi3LYBc7nMk72OjFBx2Hb/rN03H5EXZu8HZuSvzD8HPf+/bRt7+fpPc/j48B990VPZVuYqOTJ\nJ8sN1s9xu2TcNo6bS+TM15onmMsB+f0PHiSxsJ1ekeGMO+r21TbjBuziEm/GDbg7br9yQL+YBKid\n4162rDoqWbu28r1HR6tzby8PPkiVJ4C/MfDeUts4blO4b76ZBk8xtlEJZ748F8bx4zQLootwh5mE\nuI775En6t3atW1SShuO2Fe6ojHtoyM65R+E3AOfJJ+kuy4ufcB85QhVHYRSmquQ97ymvhuHXOZl2\nxu0Xlfhl3ADty6FDyR13UIN3ybgBd+GOE5WMjvpHJUGO22W+kqSOe+/eSuH2fmkcOwY885nkuP2c\nzcICVX1cfDH9HuS4XYXbFKrTTqsUmyDh9n4xNzVV1jaPjtJCC7/+dfQ1wNPf2jpuF+FmwbddIgyo\nnGAqCBvhtolcgOpr8847K+c2t41covBz3C7Cfd555LrDKExVyfBw2dV5L5o0B+CYjjtuVOJ38o4d\no95/v8ddMu4shTtuOeDy5XRuT54Mj0rSFG6/ATi8L/PzlcfCg4aY0VE6R0qVYxOTHTvoNbwNP8ft\nvduJikqmp+lLIui4bB03UNlWjh+n127aFL3AAte72zpul6iEp0x26eNJy3FzBBqFV7i/9KXKZdwG\nB+2cexRBwn3mmdXP9RPuF74wOucuTFQyMlK+yLw77ZJxczlg0LSVAwP2nZM8qxlHJWGdk9u3A5//\nfOVjc3PlUWpRGbffABy/jBugDpCowSVpRCV80TU10c+jo7UT7o4OOv75+WrhBqIdd9jgHDPfBtJx\n3ByTBOWnSYSbJxqLiktcMm7XqGRyksSzHp2THIFGwSNr2fwcOEB3ykxaUYmfcO/c6e+4/Tonr7rK\nznEXIioZGSnfjsedq4Qdt1LBt4J8u+RtMN6M27Vz8ujR6gEoLCBK0QXFQuSFL6asMm6XqGTpUnKO\no6OVt7mcc9dKuPmcTU66CzeLaNA8Jl7htsm416wJX1czyl36zRBoK9wrV7oJt43jdu2c5GvLZpUZ\nJq3OSX7vKHhkLV+fBw5UTn1Q76hkYYHO/5VXktELO+5CVJXwYgPsuJOWAwLBjoIdt20dN2+Lhdv7\nrc74Cbc5N4hSlbmtiem4s4hKliyhbdsIN48S5C8SZs0a4GtfIwdbC+EGyucrjnCz4/YT7l/8wt1x\nd3WFjww1Oyb94GHv5l1g0GoseXTcrlGJ1uUZHMPgNha2gIitcANl4Z6fp2vW67iziEq0JscdFZXw\nue/qonnbt24Nfo9CRCUsmqbjTirc5jf52Fj5wgxy3FEZ99QUCQRPaO49gUND/o7bFMugEx/muP2E\nu6eHjiPsLsT72o4OO+EG6Px43eNnPkPZ8Ac+4C9QWQn3+Li/cJsZ94oVdO753B07RvvoF5UsLFBN\n9EUXlR9jx212ZHqFO2qEn1mF40drK23DrHqwcdzcSXzBBcAvfxk+pS+fJ1vH7SrcLlHJyEh59aQo\noly3bcYNlPdvYIA+61o47sOHSRP8DI2pXRzlAjTjZ1jOXbeqEqXU1UqpJ5RSO5RSfxX2XO6UNB23\nt457djYkTPuTAAAgAElEQVS69tE8MWZj+Ou/Bl7xCvp9aoousKCqEn4PbzkgUBYLv8Z79GhlGRcf\nl1e4/U48X8DeBhGUcTc305zEYeVuXuH+9rfL8xhH8bSnVYvQhRcCX/86OZgPfrD6NbV03EpVznLY\n1ES/m+0oKCrZs4c+E/P4liyhbfC517o6pmptpTYRJJxRjpuPx/xyd8m4V66kO8XPfjbY+bs6bpeo\nxMy4baKSw4fLk0FFYV6LWgM/+EHl320zbqB8bR44AJx7LrVXvqaz6pwMikkAaltaU7sx9emKK4A7\n7gh+D7+qkswdt1JqCYBPA7gawG8AeI1S6hlBzz92jC7GIMfd1EQnIGqF6aCo5NAh4J57gBtvLBfg\ne28VOcJgF+t13EClcHtPIOef5ja9wh30jRlWDhjkWKLiEq9wP//59gMP/Bw3s2aNv0CtWkUiY7PI\nQ1Lh9s5bAVR+cZidk17hfuwxuk31YnYizc2VxZxRKtwZmuWTUccDUPvSunoEKuAv3AANlf7hD+kL\n6Xvfq35dlnXcfG3ZRiVHjpSnX43CPK+Dg8B11/m/tw1cy33gAHDOOXT9sCFMs3PSvE7DhJv722Zm\nKoX72mtpYruHHy4/93vfK5uPoBr/qL6+pI77EgBPaq33aK3nAHwDwLVBTx4ZoQETZlWJV7Ci4hI+\nIO/iAQCJ6uc+RyeG5zfwc9xA+T3ChNuv8bJwm27IO/910AUVNgDHz3ED7sLtQphwB9HcTOfFr/zO\nSxLh3riRZvXzYgo3u1+/qOSxx2gaVy9m+wq60+HOUj+iohJ+PQt32Dnw65wEyKX94Ae0jN1dd1W/\nLsuRk5xx20YlcR33iRP0s2nS4kQlBw6QpqxfT/vCs4Km4bi91V9B+TbjJ9xtbcDb3w589KP0+0MP\nUSrw4x/T737tQ6noO4+kwt0DwLxkDpQe82VkBDjjjLLj9uu0iWpo3g/XHBk5NEQDMv7jP4DXvIYe\n8xvyvnRppePmjpP29rJLAfwd99BQeTuMX8bt6riDxPe00/Il3IB9XJJEuDs7abBW2Htz52RPD91t\nmXcB27f7O26zgzJsJfAg4XaNSmyEW2v/apVVq4INQFaO2zUqieu4+UvBfI84Ucn+/STc3d3UBiYm\n6A7K9gsgDJeoBPAXbgB405uA228n4b/+etpf7kwNi9FC983+MHyJSKOJLVu2AKBRbO3tfRgf78P8\nvP9OR9Vyez9cU5h5tZTNm2kUGlAp7HNz5aku/Rx3W1tlZ1iQ425pqRZuc9KZsM5JvwE4Qc4PoP35\n1a/8/wYkE+6+Pvs83LtPaQr30qXlzjyzwiXovblqg0fs8Yo+hw/TRQGQ4/7zP69+vdm+giKqKOGO\nEiozKgmqKAHKwjs9Xb7V9vu7Fx6AE+a4JyfpCy1u56RtVHL4sH0bChJuvluNU1Vy4AB16LLjTqtj\nEnAXbo7hvMK9YgUJ9gteADzjGTRV7cGD9DfzGunv70d/fz+A6LukpMJ9EIAxKSZ6Qa67Ahbuf/gH\ncqz3308n3c/xRNVyez9cbgwLC/5rLXLnDK8a4q1t9UYlpnAHdU729lZe2N55PWwct3d2wKCMO2pe\nhiTCfdFFlVUXtmThuI8etZvNjd/7xAk6z5yBc1yyYQO1hccfT+a4gzLuNKMSPu6g2vAw4Y5y3NzW\n446ctI1KjhwpTykQhbcCzPyf3ztOxm067qyEW+vgUZNMkOMGKC75zndo8N5Pfwo88gg9blaV9PX1\noa+vDwBFZcPDNwe+V9Ko5EEAZymlTldKtQJ4NYDvBj2ZhXXlSnKpfo06KirxfrjsqI8do8bmdWxK\nlV0WN0oX4TYb1swM7fO6ddXCbe5TUOdknIw7S+GOi+18JVkI95o19N7cMcmYHZT79lEb8xND03EH\nCXfY+ohZRCVxhTvKcddi5GSSjBso7z8vYmI7FWtQxp1WDTdQKdzDwxTBhJXahgn3hg00D81pp5W/\nZAD/qhIg44xba30SwFsB/AjAYwD+XWv9eNDzWbhXraILIE7npFckOSrhmMQPbjBmbatZWRAk3N7b\nRX4Pb7mXN75JM+MOu4Dm58ldeisvssY7Z0gQLsI9NOTmuL0Cev75wL330s9BFSVAOhm3S1VJ2Eos\npnD7fRlECTe/j1/5rN/dpQ1mVML5exhHjqQj3GyqbCuieE3SQ4coEsracfMSd2H7FybcJl7h9rtG\n/GrFTRLXcWutf6i1PkdrvUlr/eGw53odt1/+F7Xopl/GPTVFF76tcJuuy3Tcvb2VF7xXNFm4vRe2\n94OyrSrRutwwgsQ3zHHPzdGxJJ132JXNm+0m/M8yKvEK92tfC3zjG3ROtm/3rygB7Bx3ratKXB03\ni3JzM+2/377GddwsoM3NdK6i1hdNq3PSJSYB6NrcuZP+b2+vdNxZCDcXNYQRlHF76emhjFvrOgq3\nC3x7azrutKKSo0eDb5G48fJtYFBUct11wE03lV/njUpM4fbOf2LuU1DnJDvupiYS24WF8Hwb8Bdu\n/r0eMQlAteJ33RXuxrS2Xz4qjnB7o5JNmyh//NGPsnfcaUclQS4+qnMy7Dlmxh2ncxKIjkvYDJmf\nQxjmefVm3FFi52XFCvqC5mXnTMedRVRiVjwFYeu4WZTHxuJXldRUuP0ct2tU4tc5aRuVBGXcQZUM\nQVFJlOOOyriBsuuOEl+/i+eyy6jSpF7CvWlTed6GIGZn6RibLFpYGo4bAF7/euCrXw2u4QaSO27X\nqMSmqiRuxg1U5tw/+Un5y5TF3TUqYXMDRJcEDgxQTGJ7x+d13EqV23Ycx33iRLmKKOuqEr+h6V5M\n4Q47FqXKXzSFcNx+GXfSOm4zKgn6pvXLuGdmysPWg8TF23D5PfyE2+u4w4a8A/bCzY7bdLeHD9Pq\nMPUSbqXKrjsI25gESMdxA1RmdccdNJ/1MwLG73odt8sAnJMnqR1FuSGXqGRiIplw83MmJ2n+Zx6I\nlIbjjioJdOmYBKqF+2lPSxaVAGXhXrqUhHbHjvSE2+yLcnHcNvXo3d3UsRpkHnIp3GGO2zXjNqOS\nIMdtRiWccc/OVsYkftg6btvOSfPD50YRVsMNlBfs5QY/P08X+v799RNuIH3hHhmxE26edpYnmPL+\n7aqrSASDbt9tHbdfOSDXjUfdRcSpKvGLX/iz9V4Pfo77kUfIiHB9cFzHzXelQHRU4pJvA9XC3dOT\nnnADtC+PPJJNVBJU/WHCbcsm9unpobn2W1v929Nb3xr++poJ9+wsHfyyZeUlsuI47t27Kys/OCpx\n6Zzk94gS7rQ7J+M4bqByGSkeap4X4Q7KuV2Em+cGtxFunn1v715/sbvhBuC5zw1+vU3GHVQOaBOT\nANVVJXEzbvM5DI9H8GbcPBUsC3dcx+0SlSRx3GNjJLpJMm6gUri7u2n7WUUlNo7bpnOS93XXruC2\nEbWKVc2E21xsYOXKeOWAAwPAN79JWSbDjcGmc5K/1fk9zFJAP4I6J80Lm2caNAXUr3Nyfp4aAT+P\nG0VU5yTvB3dI8uQ0+/bVV7g3bqT3DhrV6eq4Afsa3lNOocEQfq766qupjQSRZOSkTcckv96mHJCn\nsw1bnMEr3LOzVIHE7ZYd97Zt5fnkgWRVJbZRiUspIJCu4+YRyF7HDeS/cxKIFu4oaibc5qhGdtyu\nc5V87GNU9mXentlEJXEdt7fh+mXcfnmWX+ckCxl35Lg6bhZunuel3o6bc+7SCN0qshbunTvtRNSL\nd5IpF+H2zkkThG1UwrfJg4P2wm3GJObft22jmMjruJubK8tOo3CJSg4fThaVdHfHF25eBafHmBlp\n/Xp6zKaSyYYknZM2wr1zZ0GEmx1SWOdkUMY9PEyLgr73vZWPx4lKbDNum6jErwfZLyrxfmPHFe6R\nEZoxsN6OGwjPubMW7qGh+MIdtxzQb0oFP2yrSgBqKwcPxhfuZcvoC2X7duCaa2hb3KFmTp5mm3O7\nRCVpOm7XqASgyeTOOqv8e3d3ejEJ4O64XTPuQjhu063EKQe85Rbgla+k0UsmLlGJn+MOm9SorY2+\n2Xl//ITbz3H7CbdXyGw7J4HKL5CREZoBkXuk6yncmzdTZOFH1sIN2NcPmyQpB7QVbtuqEqAs3EFf\nQt62xE7a/PvWrSQE55xD7cIrMrYdlCdP0j8+JzZVJUk7J+OWAwI0SZrZsbd+fXoxCeDeOemacR87\nFl+4k04yZY03KhkcpBPj7VH1a2Sjo7QiyAMPVG+3vZ3+PjsbXEJjOu4NG+yjEqDceHkRWT/H7f2Q\nzJXLeUSk92Jyybi9UUlPD+3XwYP1FW6/9Rkffhi4+27giSeyF+4sHbdfVcnwcLyoJOw1S5fS3ZOL\n4zbP07JlNGnRc55THpHndeW2Obd32Pny5ZVLgnmJ67jn5+n/9esro5KoDrkonvtcu8XGbcky4+Yv\nPNs276UuGTc7br+Lxk+4P/1p4CUvobm8vXR0UN67Zk3wQICgATg2ws23i2NjJJI8Z3dYVMLrVYat\nO5gkKlm9mkaMPflkfYXbz5necgstnwbQVJY2cOO1bcQciWXluIOqSuJEJTaOG0iWcR88SEvOmcJt\nnksX4TbbcljGvbBA5osXLLGBr0O+ZswoJk5U4uXUU4E/+ZNk2zCJI9x8PFHXZUcHtd9COe729vI/\nL975EcbGgE99ilyFHx0d5ArOOy/4vf2ikhMn7IR7xQpyFkBZMKKiEqA8kouPOWnGbUYlGzaQcO/c\nmT/hnpigkrxXv9p+O01NtC0Xx93cXClgtvBnD5Bw+4l/WFQSNLDH+/paCTffZV54IT23tZVG5JnP\nsY1KzHybtx2UcQ8P099dOgJZuLke3tx+nKgka1w7J1tb6bzYfgH19BQg4/a6lZUr/Xfa28g+9zma\ngPzcc/23295O3/5BHZNA8CRTUeWAAK2k8/GPV1atRDluoLwqC5M04zajktWryV3k0XHHvQCXLnUT\n7pUr402u5XXcLiMnR0bsbue9UUmYuPFxB/W12DhugIQboC/1HTuyd9yuMQngL9w8A2EehTvOyMmR\nEXvh7u4uoHCvWhUdlUxPk2h+4APB2+WTGdYpEbccEADe9jZa+OH733dz3N3d5dIsPpYgx+2ScZtR\nSb0dt7mIBeMVFlu6utyEO05MAtSmqsQc8WhTVRKW1ft1TnozbrOaoqeHvtC9jtsl42bChHvfvsoa\nahu4vYyN0X63tNA/jjGTRiVpE6dz0sVx5164jx+3d9ymI9qzhz7g888P3jafzDDHHTQAx0a4OzqA\nm28GPvKR8peD2XkVlM15Hbf3VsvsnHTNuHll84GB+gp3U1O1m4vrnFyE+5xzqGY5DrWoKuFtTEzY\nRSVhozGjHPf55wPvf3/5954ef8eddlSya1f4ajB+eB23+R4uCwXXijgZt4vjzn1U8qEPVa+EHua4\n2RHxYrBh8IG7RCW25YDM619PM+K5RCVexz08XHksLhm36Xw4KuHpLOsp3EC1yNXCcZ96KvCZz7i/\nB1DZvsJGTvpVlbgIN8clWQt3d3flvBYs3HGrSvwmcPNj1y7/YoEwgoT7xIl8RiVx6rhdHPf557uf\nw6f2Ld7L3Lj1VsqxvI6b590wMaMSmyHGNlFJ3EmmmOZm4OtfL2eqNlFJTw9Ns8l4G7pLxu0XlfDF\nnjfhjnsB/sEfBM+hnSZxq0q0rjYfYXBlSdbC7YWjErMT1bZz0huVhAn+rl3AFVdEb9MkzHHnPSqx\nHTnpItwuHfheauK43/nO6uHCQaUwrsLd0kK10nEdt41wAzTohSOb1lYS3fl5e8e9e3flSvBxMm5T\nPNavp6giD8LNFRRA9e22Le94R/Xgqiywybj5OfPz5cempuh8294VZBWVeAfgeOnpoefHcdzez45H\nJfsRx3G3tVGbHx0tV8M0WlQyN1eb46iJ4373u6kX2iYqMR2R7aQ+7e12nZNx6rj9UKp8Ox3muM2M\n29vQXTPuEyeqxaO7u/7C7bf+ZpyopFbYOG7z8+XP1iUmAeyjkjVrwmuh/Rx3mDDw3B1pVJUEvU7r\neMKtFG1zcNDfcTeCcAO1uXOoiePu6KBBNOa6imHlgGbGbSPcHR12nZPepctsygGD4IggqHNy3Tpq\noOzawhy3bTmgVzxOPbX+wm1GJVrHz7hrhY3jBqojoDjCPTERvXzb614HfPSjwX93jUq40iNOHbf3\nS9e8szQZGKDnsfi60NlJry+acNvOxw00kHD7sXp1OlEJAPze79HES0F0dFDjmJ+nk8sXb1zHzdtk\n4fZrcC0tdIyDg/S848cr53Vwybi7uuh5g4OV4tHbmy/hnp6m/an1qvMu2DhuILlw20YlvOBvEK7C\nvXYtta00HLdS/qIfx20zHR2Vjnv5csqFlap/W/aSZ8dds5GTXl7xCppfwYtXuE87LXpbn/98+N87\nOqhx8DwMfPEmEW6+sMM6VTjnHhmh4zDnZXHJuHkKyz17KuOmyy9Pdza0OJgZdx5dkxebpcuAdBy3\nTVQShatwNzWRQYg7ctI7wIhzbnN7SYV7YKAy4z58OJ/tpqWFNIIXr7DpnAQaXLhXrgxerokbWdCS\nTq60t5Nw87ZcywH9MKOSoEbHOXdTU2VMArhFJUBZuE3xuPHGePueJqbA5T0mAezm4waqS+HiRiVp\nC7eN8+vpScdxB702DeE2o5IDB/Ip3M3N5WvUXLwiiIbLuF3wZtw2S0VF0dFB2+TGkbRzEojOuIGy\n4/Zr6C6dkwCdB69w5wGzc7IIjjtvUUkUro4boJw7yeyAJrxQicnOne6Dbxg/4T58OH+lgED5GrX5\nsgQWScYdRJyMOwo+6dwo08i4baISdtzejknALeMGSLh3744/1DsrvI4778Kdt87JKMwpggE74f7I\nR4Df//3y73EnmQKycdxzc5XCfeRIPtsNC7dNxyQgjjt14WbHww0+zYw7LCphx717d3VDd8m4gfw6\nbu9gpLxHJTZrTgLpCPfoqP+c8y4oVTlNrI1wb9xYeaeaJCrxq+VOKtxAZcadd+G2ddyLWrjj1HFH\n0dJSnjoUSLcc0MZx79qVTsa9e3c+hbvInZNZRiXDw8liEsaMS+L0I9g6bj8T4hV9Xm3KXOvRBRZA\n03EPDOQ/KrH5HBe1cMep446CC/+9wp3UcR8/Xi4x9CPMccfJuCcm8h+VFMlxZx2VjIykL9yjo+71\n07aO+8iR6sFA3ox7zx6qkIpb8ukn3AsL+fzCb9iMWyn1j0qpx5VSDyulblNKJe5KZFGdniZRjLu0\nj5eOjvQ7J4eG6EMKmhe6pwf41a/IXXs7WeNk3ED+HHfROifZGGidfVVJ2o57bIyE23U6VRvh1pru\nDr1O2vvaJDEJUJ57nM87C3ge200jRyX/BWCz1vo3AfwawPsjnh8JTwDFbjvOZPl+dHSU3SDXZ87O\nJisHZOEO4pRTaP/9Grprxs0NPG/CXbTOSbN/o6kp2DnmMSr51a+As892z8xtopKRkcprhPFm3Ekq\nSnh7y5aVr2vOuvMcldh2TnJ/Ru6FW2t9p9aap9G/H4CjF/DZodLFNDSUTkzCmFEJD8KZnEzmuAcH\nw4VKKYpLvPk24J5xs+POY1RiZtx5j0r4856cDP/CzGNU8sQTwStBhWHjuA8epLYa9dr9+8tTCseh\no6My6mHhzuMXPhs8W8cN0PTPcaYCcCXNjPt6ALensaG2NhLFNGq4Ga+baGsjoUkjKgmjuzvacRc5\nKima4wbofPPiz0GYxzUzUzkOwIY8CbeN4z540L/D0ZtxT0yUxTYORRJu16gEoLuitOLdMCJlSyl1\nJwC/1eX+Wmv9vdJzPgBgVmv9b37b2LJly1M/9/X1oa+vL/Q9WbjTdNxBwh1XCNlxh01uBZA78bu1\n5EbhknErle6XWRp4ywHztn9+8ILBto6b15p0ie06O+nzTVLDzXR1lYX7uuvcX2/juP3ybb/XJr2r\n8gp3ZyfdZedVuOfm7KtKktLf34/+/n6r50YKt9b6hWF/V0r9CYBrAPx20HNM4bahrY1KhNKOSszG\nwcIdd64PFu6wya0A4BOf8BezOOWAK1cmqwnOAm/npN/tdt5gx+0i3K5f8NzW0nTcjz+ebVTiJ9ze\njDvpXRVn3IxSdHx5zrhdHHcSvKb25ptvDnxu0qqSqwH8JYBrtdYWBUd2tLamL9xex93amjwqsVlf\nzjvhD+PaOblqld0K47XGzLiLEpW0tRVPuEdHqaLj7LPdX28bldhk3Ekrh7yOGyAhz2O7WbKEKttq\nJdwuJJ1k6v8CaAVwp6L7yPu01m9OulMclaSZ55qdk/weExPxq0o6OqiEKm6Dc3Xc550HfOc78d4r\nS4o2chKwE26zHDCOcPN5SEu4H3qITEAcAbGNSq65xv+13hWOknzGV18NbN5c+VhehVspEu/x8QYT\nbq31WWntiAlHJUnqRb2ccUZl/WsanZNA/Fs81wE4StVmTUZXito56Zpx19txP/hg5TqSLiTtnBwe\nLv+e1HH39lZXpSxfns+oBKDrdGwsf+26btO6hpFFxv3xj1e/RxrCndRx23ZO5pVGddxJhbu1ldpW\nWsK9Zw/NYR+HNDPuLD7j970PeNaz0t1mWrBw5y2mzFlXF5FFxu2lrS15HTcQ3ym4Ztx5hddm5GXL\n8uZM/HB13Lt2xatd7uxMT7iB+I47Srjn5mgxb7+Oem85YBaf8Stekb/xCQwLd96iklwKdxZ13F7S\n6JwE0hHuIjvupib6vHjh5CIIt2s54L33Ar/1W+7vw+ubJoXbWJyKEqC8+rh37Ujm8GESbb9RpGl3\nThaNlhYRbms4k8vacdc7KuELIs9rNNpgzpRYhKjEZQDO2BiwYwdw4YXu79PVla7jjivcTU20FuXg\noP/fg2ISoFq4izCRWJo0N+ezczK3wg1kL9zj4/XtnJyYKLbbZljkihKV2Dhurip54AES7TifU5pR\nyerV0YO9wujupsoRPw4dCq6/NzPuhQU6J4tNuMVxW8IXSdbCPT2dbJIpIJnjnpgodr7N8CCcojlu\nm6jkvvvixSRAeo773HOpcz3JhGs8xbAfUY6bM+6pKTpneRsEliUs3LUYOelCLj+CWjhu/nKI67hb\nWui1STLuRnLcExON5bh5+te77wYuvzze+6Ql3F1dwB//cbJthDlu26ikKJ9vmjQ3U1sRx21BWxvl\nvlk2Er5o4wo3QIIlwk3n4dgxu5Ww84CN41aKjuuee+I77rSikjSIikpshHuxdUwCEpU40daW7lzc\nQe8BJBfupFFJowj30aPFiEkAuzpugI5n/frqVWFsWbs2P2VuUY7bJuNebB2TQH47J3Ppj1pbs41J\ngHSE++qr40+q1NxMnT2NkHHzFLdFcWM2jhug44rrtgHgs5/NT8VQkqiEM+7F6ri1FuG2oq0t++lB\nk2bcAPCVr8R/LXeKNoLj7uoi4S6KG7PJuAG6WOPm20D8ju8s8Ar3wgI56KVL3aKSonzGacH6kJfI\ni8l1VJL1ewD1y2QbSbiL5ri5FDRKuC+7DLjqqtrsU9Z4hfvWW2lypw0bKJIMWrVlsXdO8nUqjtuC\nWgp3vVxRown3wYPFcWN8zqPOfZI7qryxdi1NDcsjdbdtoxLDV7yivIK8H2bGvVijEiB/wp1Lx12U\njDsJ/L6NknEfPVqci5rPeSOce1uamqiT9cgR+n37duD882khkPPOC35da2t5uPxi7ZwERLituOIK\n4Nprs32Pegt3oznuIkUlfM4Xk3AD5bhEaxJu77zYfihVnoJisTpu/pcncrY7xKWXZv8eaXROJqGR\nhJs7Jy+4oN57YsdidNxAWbiHhqhzcp3fSrI+cM69WB133jomgZw67lpQb8fN79sIwt3ZSZPtF8WN\nLXbHzW7bdpwE59yL1XHnLSYBcuq4a0G9hVspeu9GEI/OTnJwRXFji91xA3YxCcO13BMT+VtQIGvy\nKtziuOv41dXc3DiOGyiOG1vMjvvgQXLcLsvgLfaoRIQ7R/DFW89BEi0tItz1YLE7btuOSYaFW6KS\n/CBRSR3PQKMIN1/MRXFji91xDwy4CTdn3IvRcbe0SOdkrsiLcDeCeIjjLgbd3bSaD+A2cZaZcRfl\nM06LvDpuEW7JuBPDwl0UN2Y7crLRWL2aBuK4VJQAEpWIcOeIPAh3o0Ql4riLgVLkul1iEkA6J0W4\nc0S9B+AAItz1YrEKNxBPuKWOu957UY10TopwJ0Y6J4vDG98IPPe5bq/hjHuxOu48dk6KcEvnZGLY\nkRTFjS1mxx1n7UrJuOu9F9Us2qiEV6uu54rVjdI5uWQJnc+iuLHF7LjjYJYDinDng8SypZR6t1Jq\nQSm1Oo0dqhVtbfWf8atRohKALuiiXNSL2XHHYTFHJevX02ITeSORdCmlegG8EMDedHandnR1AT/9\naX33oZGE+wc/iL/+Zq1pbaU7rXp/cReF9naaRKylJT9raNaKt7613nvgT1LH/XEA701jR+pBLaaP\nDaNRMm6AlvlyqQ2uJ52dtICAYAcL92Jz23kmtnArpa4FcEBr/csU92dR0SgZd9Fobwd27qz3XhSH\njo5iTdu7GAi9WVRK3QnAb7r1DwB4P4AXmU9Pcb8WBe94B3DRRfXeC0EIp70dGBkR4c4TocKttX6h\n3+NKqfMAbATwsKL74w0AtiqlLtFaD3qfv2XLlqd+7uvrQ19fX/w9biBe/OJ674EgRMNRiQh3tvT3\n96O/v9/quUprnfgNlVK7AVystR7x+ZtO4z0EQagPt90G3HADzeF999313pvFg1IKWmvfJCOtKmZR\nZkFoUDo6gGPHpHMyT6RSEKW1PiON7QiCkD/a22lleIlK8sOiHTkpCIIdPFeHOO78IMItCEIoLNzi\nuPODCLcgCKEUbRKxxYAItyAIoUhUkj9EuAVBCEWikvwhwi0IQijiuPOHCLcgCKFIxp0/RLgFQQiF\nJ0IT4c4PItyCIISiFMUlEpXkBxFuQRAiaW8Xx50nRLgFQYiko0Mcd54Q4RYEIRJx3PlChFsQhEhu\nvB08zOkAAAdFSURBVBE4Q6aSyw2pzMcd+gYyH7cgCIIztZiPWxAEQagRItyCIAgFQ4RbEAShYIhw\nC4IgFAwRbkEQhIIhwi0IglAwRLgFQRAKhgi3IAhCwRDhFgRBKBgi3IIgCAVDhFsQBKFgiHALgiAU\nDBFuQRCEgiHCLQiCUDASCbdS6m1KqceVUo8qpT6S1k4JgiAIwcQWbqXU8wG8DMAztdbnAfhoansF\noL+/P83N5RY5zsZhMRwjIMeZB5I47r8A8GGt9RwAaK2H0tklIs8nLU3kOBuHxXCMgBxnHkgi3GcB\neJ5S6udKqX6l1LOiXuByIvbs2eO0My7bdv1Asty2y3Hmab/lOKuRNlv7fcnLcWZ9/XgJFW6l1J1K\nqUd8/r0MQDOAVVrrywD8JYBvprmz0jiSbzsv5wRYHMcpbbb2+5KX46y1cMdec1Ip9UMAf6+1/p/S\n708CuFRrPex5niw4KQiCEIOgNSebE2zz2wBeAOB/lFJnA2j1inbYGwuCIAjxSCLcXwbwZaXUIwBm\nAbw+nV0SBEEQwogdlQiCIAj1oWYjJ5VSX1ZKDZQcOj92iVLqAaXUNqXUL5RSzy49/oelx/jfvFLq\nmaW/XVzqIN2hlPpkrfbfFsfjbFVKfUUp9Uul1ENKqSuN1/QrpZ4wzsGaehxPEAHH+ZtKqftKx/Nd\npdSy0uMvVEo9WHr8wdIYAH5Nbj9Pl2M0/n6qUmpcKfVu47FG+iwb7doMOs58X5ta65r8A3AFgAsB\nPGI81g/gd0o/vxjAXT6vOw/Ak8bvDwC4pPTz7QCurtUxpH2cAN4C4NbSz2sBPGi85i4AF9X7eByP\n8xcArij9/KcA/qb08wUA1pV+3gzgQBE+T5djNP7+LQD/DuDdjfhZel7XCNdmUJvN9bVZM8ettb4b\nwDHPw4cBrCj9vBLAQZ+XvhbA1wFAKbUewDKt9QOlv/0rgJenv7fxcTzOZ4AaATQNYBr11MPntmM3\n4DjPKj0OAD8G8MrScx/SWh8pPf4YgA6lVEveP0+XYwQApdTLAewCHaOXhvgsPTTCtRl0nLm+Nus9\nydT7AHxMKbUPwD8CeL/Pc16FUuMA0APggPG3g6XH8k7QcT4M4GVKqSVKqY0ALgbQa7zuX0q3Yh+s\n7e7GZrtS6trSz9eh8liYVwLYqmnEbRE/T99jVEotBfBeAFsCXteIn2UjXJtBx5nra7Pewn0rgBu1\n1qcCeCeoUuUplFKXApjUWvs5mCIRdJxfBjX2BwF8AsC9AOZLf/tDTXPAXAHgCqXU62q7y7G4HsCb\nlVIPAlgKqjZ6CqXUZgB/D+BNddi3tAg6xi0APqG1nkS1G2vEz7JRrs2g48z1tZmkHDANLtFaX1X6\n+VsAvuT5+x8A+Dfj94MANhi/b4B/vJI3fI9Taz0P4F38JKXUzwD8uvS3Q6X/x5VS/wbgEgBfreVO\nu6K1/hWA3wEARbX9L+G/KaU2ALgNwOu01rtLDxfu8/Q5xmtKf7oEwCuVUv8AisMWlFJTWuvPNNpn\nWaIhrs2g48z7tVlvx/2k0Vv7ApRODAAopZpAty7f4Me01ocBnFBKXaqUUgBeBxoIlHd8j1Mp1aGU\n6ir9/EIAc1rrJ0q3Z2tKj7cAeCmAR3y2myuUUmtL/zcB+CCAz5Z+XwngBwD+Smt9Hz+/iJ+nzzF+\nDgC01s/TWm/UWm8EcAuAD2mtP9Non6XxWENcmyFtNt/XZg17dL8O4BDoVmQ/qAf3WQDuB/AQgPsA\nXGg8vw/AvT7buRh0op4E8Kl69uwmPU4ApwN4AtSZ9V8AekuPd4Fu0R4G8CjoVk3V+9gijvN6ADcC\n+FXp398Zz/0ggHEA24x/a/L+eboco+d1NwF4VyN+lqXnN8q1GdZmc31tygAcQRCEglHvqEQQBEFw\nRIRbEAShYIhwC4IgFAwRbkEQhIIhwi0IglAwRLgFQRAKhgi3IAhCwRDhFgQLSiPrBCEXSGMUGg6l\n1M1Kqbcbv39IKXWjUuovFS1o8bBSaovx9/9UtMDDo0qpG4zHx5VSH1VKPQTgstoehSAEI8ItNCJf\nRmkN1JJTfjWAIwA2aa0vAU2mf7FS6orS86/XWj8LwLMB3KiUWlV6vBPAz7XWF2it763pEQhCCPWe\nHVAQUkdrvVcpNayUugDAOtDcKM8G8CKl1LbS07oAbAJwN4C3lxZBAGjO5bNAq7nMA/iPmu68IFgg\nwi00Kl8CTfD1dJAD/20AH9Zaf8F8klKqr/S3y7TW00qpuwC0l/48rWUyHyGHSFQiNCr/CeBq0MyM\ndwD4EYDrjak6e0pTei4HcKwk2udCsmyhAIjjFhoSrfWcUuonIFHWAO5USj0DwH00XTTGAPwRSNT/\nXCn1GGhqz/vMzdR4twXBCpnWVWhISp2SWwH8vtZ6Z733RxDSRKISoeFQSv0GgB0AfiyiLTQi4rgF\nQRAKhjhuQRCEgiHCLQiCUDBEuAVBEAqGCLcgCELBEOEWBEEoGCLcgiAIBeP/A9f2hFQTZSZSAAAA\nAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f90585a4a10>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"pd.Series(NAO.NAO.values, index=dates).plot()"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"year\n",
"1864-01-01 00:00:00 NaN\n",
"1865-01-01 00:00:00 NaN\n",
"1866-01-01 00:00:00 NaN\n",
"1867-01-01 00:00:00 NaN\n",
"1868-01-01 00:00:00 NaN\n",
"1869-01-01 00:00:00 NaN\n",
"1870-01-01 00:00:00 NaN\n",
"1871-01-01 00:00:00 NaN\n",
"1872-01-01 00:00:00 NaN\n",
"1873-01-01 00:00:00 NaN\n",
"1874-01-01 00:00:00 NaN\n",
"1875-01-01 00:00:00 NaN\n",
"1876-01-01 00:00:00 NaN\n",
"1877-01-01 00:00:00 NaN\n",
"1878-01-01 00:00:00 NaN\n",
"1879-01-01 00:00:00 NaN\n",
"1880-01-01 00:00:00 NaN\n",
"1881-01-01 00:00:00 NaN\n",
"1882-01-01 00:00:00 NaN\n",
"1883-01-01 00:00:00 NaN\n",
"1884-01-01 00:00:00 NaN\n",
"1885-01-01 00:00:00 NaN\n",
"1886-01-01 00:00:00 NaN\n",
"1887-01-01 00:00:00 NaN\n",
"1888-01-01 00:00:00 NaN\n",
"1889-01-01 00:00:00 NaN\n",
"1890-01-01 00:00:00 NaN\n",
"1891-01-01 00:00:00 NaN\n",
"1892-01-01 00:00:00 NaN\n",
"1893-01-01 00:00:00 NaN\n",
" ..\n",
"1980-01-01 NaN\n",
"1981-01-01 NaN\n",
"1982-01-01 NaN\n",
"1983-01-01 NaN\n",
"1984-01-01 NaN\n",
"1985-01-01 NaN\n",
"1986-01-01 NaN\n",
"1987-01-01 NaN\n",
"1988-01-01 NaN\n",
"1989-01-01 NaN\n",
"1990-01-01 NaN\n",
"1991-01-01 NaN\n",
"1992-01-01 NaN\n",
"1993-01-01 NaN\n",
"1994-01-01 NaN\n",
"1995-01-01 NaN\n",
"1996-01-01 NaN\n",
"1997-01-01 NaN\n",
"1998-01-01 NaN\n",
"1999-01-01 NaN\n",
"2000-01-01 NaN\n",
"2001-01-01 NaN\n",
"2002-01-01 NaN\n",
"2003-01-01 NaN\n",
"2004-01-01 NaN\n",
"2005-01-01 NaN\n",
"2006-01-01 NaN\n",
"2007-01-01 NaN\n",
"2008-01-01 NaN\n",
"2009-01-01 NaN\n",
"Name: NAO, dtype: float64"
]
},
"execution_count": 30,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"NAO.NAO.reindex(dates)"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"0 -1.02\n",
"1 -1.24\n",
"2 0.54\n",
"3 -1.38\n",
"4 2.81\n",
"5 1.70\n",
"6 -3.01\n",
"7 -1.01\n",
"8 -0.76\n",
"9 -0.50\n",
"10 2.32\n",
"11 -1.35\n",
"12 0.21\n",
"13 0.05\n",
"14 1.46\n",
"15 -2.22\n",
"16 0.89\n",
"17 -3.80\n",
"18 3.87\n",
"19 -0.23\n",
"20 1.44\n",
"21 -0.89\n",
"22 -1.12\n",
"23 0.45\n",
"24 -2.75\n",
"25 -0.01\n",
"26 1.78\n",
"27 -0.82\n",
"28 -2.02\n",
"29 -1.07\n",
" ... \n",
"116 0.56\n",
"117 2.05\n",
"118 0.80\n",
"119 3.42\n",
"120 1.60\n",
"121 -0.63\n",
"122 0.50\n",
"123 -0.75\n",
"124 0.72\n",
"125 5.08\n",
"126 3.96\n",
"127 1.03\n",
"128 3.28\n",
"129 2.67\n",
"130 3.03\n",
"131 3.96\n",
"132 -3.78\n",
"133 -0.17\n",
"134 0.72\n",
"135 1.70\n",
"136 2.80\n",
"137 -1.90\n",
"138 0.76\n",
"139 0.20\n",
"140 -0.07\n",
"141 0.12\n",
"142 -1.09\n",
"143 2.80\n",
"144 2.11\n",
"145 -0.40\n",
"Name: NAO, dtype: float64"
]
},
"execution_count": 31,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"NAO.NAO"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.6"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| gpl-3.0 |
rohanisaac/spectra | notebooks/find_background.ipynb | 1 | 883223 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Intelligent background subtraction algorithm using wavelets.\n",
"\n",
"Also contains implementations of other wavelets and peak-finding code\n",
"\n",
"Runs 2017/1/9"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Find and Subtract background "
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"from __future__ import division\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"import os\n",
"import sys\n",
"from scipy import signal"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Find Peaks\n",
"\n",
"Use method in P. Du, W. A. Kibbe, S. M. Lin, Bioinformatics 2006, 22, 2059. Same as in scipy.signal.find_peaks_cwt() and baselineWavelet\n",
"\n",
"### Wavelet transform"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[<matplotlib.lines.Line2D at 0x7f7ac7b47990>]"
]
},
"execution_count": 2,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAjAAAAFkCAYAAAA+BgETAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzt3XmYFNXZ/vHvwzYsyqIICLgvKMYNooILLqi4ZXGLjhpN\nolEjxgQ18ecbE7e8icurxBWNmhglkhhNTNxC1LjiFkGNCqISFAUBURzWAWbm/P54qtI17SzdPUt1\n99yf6+qrpqtOV52egu57zjl1ykIIiIiIiJSSTmlXQERERCRfCjAiIiJSchRgREREpOQowIiIiEjJ\nUYARERGRkqMAIyIiIiVHAUZERERKjgKMiIiIlBwFGBERESk5CjAiIiJScvIOMGY22MzuNrMlZrbK\nzF43sxFZZS4zswXR9sfMbOus7f3M7PdmVmVmS83sdjPrlVVmJzN7xsxWm9kHZvajBupyrJnNisq8\nbmaHNlCmybqIiIhI6ckrwJhZX2AasAYYB2wPnAcsTZS5ADgbOAPYHVgJTDWzbold3RO9dixwODAG\nuDWxj/WBqcBcYATwI+ASMzstUWZ0tJ/bgF2AB4AHzGx4nnURERGREmP53MzRzK4ARocQ9m2izALg\n6hDCxOh5b2ARcEoI4V4z2x54CxgZQng1KjMOeBgYGkJYaGbfAy4HBoUQaqIyvwS+FkIYHj3/A9Az\nhPDVxLFfAF4NIZyVS11yfuMiIiJSVPLtQvoK8IqZ3Wtmi8xsRlaryBbAIOCJeF0IYRnwEjA6WjUK\nWBqHl8jjQAD2SJR5Jg4vkanAMDPrEz0fHb2OrDKjo7psmUNdREREpAR1ybP8lsD3gGuA/8UDx/Vm\nVh1CmIwHhoC3ciQtirYRLRcnN4YQas3ss6wy/2lgH/G2qmjZ1HEG5lCXesxsQ7xr7H2guqEyIiIi\n0qDuwObA1BDCp219sHwDTCfg5RDCT6Pnr5vZDniomdzE6wwPE01prozlWKYlxxkH/L6Z14uIiEjj\nTsTHqLapfAPMx8CsrHWzgKOinxfiAWEg9Vs+BgCvJsoMSO7AzDoD/aJtcZmBWccZQP0WlcbKJLc3\nV5ds7wNMnjyZ7bffvpEiUkomTJjAxIkT066GtCKd0/Ki81k+Zs2axUknnQTRd2lbyzfATAOGZa0b\nBnwAEEKYa2YL8auL/g3/HTi7B3BTVP4FoK+Z7ZoYBzMWDxsvJ8r83Mw6hxBqo3UHA7NDCFWJMmOB\n6xN1OShan2tdslUDbL/99owYMaKRIlJK+vTpo3NZZnROy4vOZ1lqlyEY+Q7inQiMMrMLzWwrMzsB\nOA24MVHmV8BFZvYVM9sRuAv4CPgrQAjhbXyw7W1mtpuZ7QXcAEwJIcQtMPcAa4HfmNlwMzsOOAcf\nexO7DjjUzM41s2FmdgkwMp+6iIiISGnKqwUmhPCKmR0JXAH8FJ+n5QchhD8kylxlZj3xeV36As8C\nh4YQ1iZ2dQIeNB4H6oD7gB8k9rEsurT6RuAVYAlwSQjhjkSZF8ysEh9M/L/Au/hl1jPzrIuIiIiU\nmHy7kAghPAI80kyZS4BLmtj+OXBSM/t4A2h0vpmozP3A/S2pi4iIiJQe3QtJylplZWXaVZBWpnNa\nXnQ+pVAKMFLW9OFYfnROy4vOpxRKAUZERERKjgKMiIiIlBwFGBERESk5CjAiIiJSchRgREREpOQo\nwIiIiEjJUYARERGRkqMAIyIiIiVHAUZERERKjgKMiIiIlBwFGBERESk5CjAiIiJSchRgREREpOQo\nwIiIiEjJUYARERGRkqMAIyIiIiVHAUZERERKjgKMiIiIlBwFGBERESk5CjAiIiJSchRgREREpOQo\nwIiIiEjJUYARERGRkqMAIyIiIiVHAUZERERKjgKMiIiIlBwFGBERESk5CjAiIiJSchRgREREpOQo\nwIiIiEjJUYARERGRkqMAIyIiIiVHAUZERERKjgKMiIiIlBwFGBERESk5CjAiIiJSchRgREREpOQo\nwIiIiEjJUYARERGRkpNXgDGzi82sLusxM7G9wsxuMrMlZrbczO4zswFZ+9jEzB42s5VmttDMrjKz\nTlll9jOz6WZWbWbvmNkpDdRlvJnNNbPVZvaime2Wtb3ZuoiIiEhpKqQF5k1gIDAoeuyd2PYr4HDg\naGAMMBi4P94YBZVHgC7AKOAU4FvAZYkymwMPAU8AOwPXAbeb2UGJMscB1wAXA7sCrwNTzax/rnUR\nERGR0lVIgKkJIXwSQlgcPT4DMLPewHeACSGEp0MIrwLfBvYys92j144DtgNODCG8EUKYCvwUGG9m\nXaIy3wP+E0L4cQhhdgjhJuA+YEKiDhOAW0MId4UQ3gbOBFZFx8+1LiIiIlKiCgkw25jZfDObY2aT\nzWyTaP1IvGXlibhgCGE2MA8YHa0aBbwRQliS2N9UoA+wQ6LM41nHnBrvw8y6RsdKHidEr4mP8+Uc\n6iIiIiIlKt8A8yLe5TMOb/XYAnjGzHrh3UlrQwjLsl6zKNpGtFzUwHZyKNPbzCqA/kDnRsrE+xiY\nQ12kiPz61/Czn6VdCxERKRVdmi+SEXX5xN40s5eBD4BvANWNvMyAkMvum9hmOZZp7jg51WXChAn0\n6dOn3rrKykoqKyube6kU6IwzfHnppWDWdFkREUnXlClTmDJlSr11VVVV7VqHvAJMthBClZm9A2yN\nd+F0M7PeWS0fA8i0liwEdsvazcDEtng5MKvMAGBZCGGtmS0BahspkzxOc3Vp1MSJExkxYkRzxaQN\nrF0LFRVp10JERJrS0B/1M2bMYOTIke1WhxbNA2Nm6wFbAQuA6UANMDaxfVtgU+D5aNULwI5ZVwsd\nDFQBsxJlxlLfwdF6QgjromMlj2PR8/g4TdXlhYLerLSLdevSroGIiJSCvFpgzOxq4EG822gIcCke\nFP4QQlhmZncA15rZUmA5cD0wLYTwr2gX/wBmAneb2QXAxsDlwI1RMAG4BTjbzK4EfoOHkGOAwxJV\nuRb4nZlNB17Gr0rqCdwJ0ExdXs7nPUv7qqlJuwYiIlIK8u1CGgrcA2wIfAI8B4wKIXwabZ+Ad+/c\nB1QAfwfGxy8OIdSZ2RHAJLy1ZCUeOi5OlHnfzA7HQ8o5wEfAqSGExxNl7o1acS7Du5JeA8aFED5J\n1LXJukhxUguMiIjkwvwKZAEwsxHA9OnTp2sMTDuLB+7Onw+DB6dbFxERyV9iDMzIEMKMtj6e7oUk\nRUUtMCIikgsFGCkqGgMjIiK5UICRoqIWGBERyYUCjBQVBRgREcmFAowUFQUYERHJhQKMFBWNgRER\nkVwowEhRUQuMiIjkQgFGiooCjIiI5EIBRoqKAoyIiORCAUaKigKMiIjkQgFGiooG8YqISC4UYKSo\nqAVGRERyoQAjRUUBRkREcqEAI6mrq8v8rAAjIiK5UICR1CVDS7mNgZk2DVatSrsWIiLlRwFGUpcM\nLcXeArNuHXz1qzB9evNlV6yAvfeGCy5o+3qJiHQ0XdKugEgytBR7gPnkE3jwQXjrLZgzp+my8+dn\nXiMiIq1LLTCSulJqgVmzxpe51POjj3w5YEDb1UdEpKNSgJHUJQNMsY+Bqa72pVnzZZcv92WPHm1X\nHxGRjkoBRlJXSl1I+QSYYn8vIiKlTAFGUldKXUhxgMnF2rVtVw8RkY5OAUZSV64tMHGACaHt6iMi\n0lEpwEjqSmkMTDyIN58AU+zvSUSkFCnASOpKsQspnwCjriQpdStXwlln+VKkWCjASOpKsQspF/F7\nUYCRUvfb38KkSfDAA2nXRCRDAUZSF7fAdOlSOgEmnxaYuNtJpFR99pkv+/ZNtx4iSQowkro4tPTo\nUfytFXEYqa1tvqy6kKRcxAFm/fXTrYdIkgKMpC5ugendO78umjTE9culVUUBRvLxi1/AjTemXYuG\nxf+Gk3eOF0mb7oUkqYs/HHv3htWr061Lc/IJMBoDI/n4yU98efbZ6dajKbm0PIq0F7XASOri0LLB\nBuUVYDQGRsqNpgSQYqIAI6mLQ8EGG8CqVenWpTlxGMmlq0tdSFIu4kHrCjBSTBRgJHVxq0u/fqXT\nAlNb23xzugKMlIt4NmkFGCkmCjDSqm6/HV5/Pb/XVFdDp06lNQYGmu8aUheSlBuNgZFiogAj/zVn\nDpxyCixZUvg+vvtd2G23/F6zerVfQt2jR3kFGA3ilXKhLiQpRgowHdhf/gI/+EGmefiee+Cuu+Dq\nq1u233wno6uu9vDSs2fxT1VeSAuMAoyUCwUYKSYKMB3YxRfD9dfD7Nn+/LXXfPncc4Xtr9APt9Wr\noXt370JatqywfbSXNWugc+fMz01RgJFyoy4kKSYKMB1Y166+fPttX86Y4cs338y0yuRj+fLC6hG3\nwPTr5y0wxXw7gepqD1qgMTDS8agFRoqJAkwHFvdrv/22TxX+/vtQWemtIPPm5b+/uPWkU57/qhYs\ngI028gADsHRp0+U/+giefjr/+rWG6upMPZsbr6MWGCkXugpJipECTAexahXstx/MnZtZt2iRL2fP\nhpde8p+/8x1fxt1J2erq/DF7NlRVZdavWwdvveU/d+7srQ7z5+dWt9mzYbvtcg8wp57q7yWuf3uq\nroYNN/SfmxuvE7ckqQVGSl3cdaQAI8VEAaaDmDHDWy1uuMGfxwGjWzd44gkfuLvZZjB2LAwcCNOm\nebnPP4d334UpU+Dooz2cdO7sgaNvX29t2Wcf/1I//HB/zbp1PqZl6FBv5TGDP/7Rv/zjm8LFQvAW\noO22g8GDfd2HHzb9XuLLtF99tXV+N/lYsyb3ABO3vKxeXViXnHQcxX6PoTjAaAyMFJMWBRgzu9DM\n6szs2sS6CjO7ycyWmNlyM7vPzAZkvW4TM3vYzFaa2UIzu8rMOmWV2c/MpptZtZm9Y2anNHD88WY2\n18xWm9mLZrZb1vZm69JRxK0B8QfQ3Ln+pfrjH3tgePJJDy9mcOSRHmjOPddbRbbdFk44Af785y/u\nNwQf9FtTA1/5Cjz1FPz617DnnrDjjplyxx/v41w23BCGDPH5YkLwlp8VK2DYMNhySy8Tj8VpSG1t\npuWnsVaibPPmwf/8T+t05SRbYFasaLrs2rWw3npe52Ie1yPpS7ZsFGPYjeunFhgpJgUHmCgsfBfI\nnrbsV8DhwNHAGGAwcH/idZ2AR/AbSY4CTgG+BVyWKLM58BDwBLAzcB1wu5kdlChzHHANcDGwa1SP\nqWbWP9e6dCT3R+86DjDvvefLE0/MlLnmGl9+73u+nDjRl+PHezCZN89bPz791D9kQ/CBux995F1U\nf/sb7LuvzwUzbRr8+9/+JT5zJhxzTOY4CxZ4mT59vNVm4429S6hzZ39+/fU+kPjYY2HSJG/9Ofts\nOOooOOIIDxH9+/tl4A2ZOdNbfMDrt9lm8Mtfwp/+1NLfYubYkFsLTJ8+/nOxz28j6UoGg2IcM6Uu\nJClKIYS8H8B6wGzgAOBJ4NpofW9gDXBkouwwoA7YPXp+KLAO6J8ocwawFOgSPb8S+HfWMacAjySe\nvwhcl3huwEfAj3OtSwPvawQQpk+fHsrJ++/HcSOEr3wlhJqaEM44I4Tu3UOorQ2hqiqEV16p/5oP\nPwzhX/8KYeHC1q3LBx+E8MILIUyaFEKnTiEceWQI8+Zltr/2Wgg9emTq29jj7rt92bNnCA895O8j\nBF/GZd5/P4TJkzPPTzut5fUfMiSEn/0shM6dQ7jllqbLbrNNCMOH+7E//rjlx5byVVWV+XdaVZV2\nbb7o+OO9bldckXZNpJhNnz49AAEYEQrIFvk+uhSYe24CHgwh/NPMfppY/2W8ZeWJRECabWbzgNHA\ny3iryxshhOR8r1OBScAOeEvKKODxrGNOBSYCmFlXYCTwi8Rxgpk9Hh0n17p0CP/8py/HjYMHH4Qu\n0Vk/9tjMFP4jR9Z/zdCh/mhtm27qj1Gj4JvfhF696m/feWf4z3+8nj16eNfWiBE+DqdrV28dqqjw\n1w0c6AN5jzjCWzrWrvVuqNgJJ8Dzz/sYnU02ycx30xJr1ni91l+/+TlrVqyAbbbxn4v9JpWSrmTL\nRjEO+lYLjBSjvAOMmR0P7IIHhGwDgbUhhOyP9kXAoOjnQdHz7O3xttebKNPbzCqADYDOjZQZlkdd\nOoS334bNN/dulVGjMvO+/O53qVbrC+ElNmiQdzEBnHRS469fuNC7ZqZMgYcf9jE6b73lwevMM+Gi\ni7zcBRd4l9Y993j30vDhhdW3rs4HNffu7eNgmrvlQlWVvxdQF5I0LTlGqhgDjMbASDHKawyMmQ3F\nx5WcFELIZ1ii4c1KzWmqjOVYprnj5FqXsvHSS96y0aePf4HPnu2tBz16pF2zluvRwy/9vv9+f0+X\nXw4vvuiDdl97zVtuDj8cTj/dy1dWwp13etl8P4wXL/bXDB3q42A++aTxsuvWeavLxhv7c7XASFPU\nAiOSv3xbYEYCGwHTzeJp0OgMjDGzs4FDgAoz653V8jGATGvJQiD7dn8DE9vi5cCsMgOAZSGEtWa2\nBKhtpEzyON2aqUuDJkyYQJ949GWksrKSysrKpl5WlNas8W6UeICumV9VVI7WXz/T6gIe2mKbb+6D\neI89Fr79bX/ErrzSr8ZqTE2Nt1rFrShDhvjEe00FmLh7adNNffn553m9Felgij3AxPXTZdQSmzJl\nClOmTKm3rio5OVg7yDfAPA7smLXuTmAWcAUwHx+gOxb4C4CZbQtsCjwflX8B+B8z658YB3MwUBXt\nJy5zaNZxDo7WE0JYZ2bTo+P8LTqORc+vj8pPB2oaqcsLTb3JiRMnMmLEiKaKlIw33vDWgHzvEF2O\njjkGnnkGxoypv/6CC+A3v4Ebb/TxMhUV9befeSbccYeP2ena1bughg71YNiYOLDEY2AWL2699yHl\np9gDjFpgJFtDf9TPmDGDkdkDKttQXgEmhLASmJlcZ2YrgU9DCLOi53cA15rZUmA5HiimhRD+Fb3k\nH9E+7jazC4CNgcuBGxPdUrcAZ5vZlcBv8BByDHBY4tDXAr+LgszLwASgJx6oCCEsa6IuHWYA7/Tp\nfnlysjWiI9tnn8w8G0uWwG23+biZ3/8eDjooU26PPXxG4PXWy8xLc/fd8PWve7fVNtv4GKK1a30y\nwGzvvuvLL33Jx/oowEhTij3AaAyMFKPWmIk3ezzJBHwOl/uAp4AF+DwsXjiEOuAIvAvoeeAuPHRc\nnCjzPj5/y4HAa9E+Tw0hPJ4ocy9wHj5/zKvATsC4EEKyYb/JunQEr7wCO+xQHuNdWlv//nDhhTB5\nsgeR007LbHvpJXjnnUx4+e1v/UqmuKvpkEO8S2nIkIYntPvHP3ym4s02gwEDFGCkaaUyD4y6kKSY\nFHoZ9X+FEA7Ier4G+H70aOw1H+Ihpqn9Po2PuWmqzM3AzU1sb7Yu5ayuzmfJHT26+bIdXdeu3hpz\n223+e3v2WfjgAx/ncuKJfjXRt76VKT98OGy9tU8IuP76vu6Pf4SDD/YWl/vu8y6nTp08wKRx3yYp\nHWqBEclfiwOMFK9nnvHBp/H9jyQ3nTr5jMLNefNNv8LpiWimoeOOy2zr3BlOPtl/Hjiw7VpgXnnF\nW4L22adt9i/to9gDjMbASDHSzRxL0HPP+WRvzfnjH/0qmLFj275OHVFFBTz+uN9L6vTT6w8OvuUW\n+HI0U9LGG8P777dNHXbbzY9bjN0OkrtiDzBqgZFipABTQmpr4ZJL/K/tnXbKDEatq/MrbKZOzZT9\n5BOf7+SUU/zSaWk7Q4fCrbf63b7r6vy8JMfT7LuvDxR+6KG2q0NFRfHf0VgaV+wBRmNgpBgpwJSI\nDz/0lpRLL/UBuStX+hVG4Jfz3n9//S/Nyy7zL9Jzzkmnvh1VQ2Hx2GPhsMP8bt0HHghz5rTOsbK/\nTHJplZPipJl4RfKnAFMCFi3yFpfnn/e7Mn/+uQ8Uje9x9Oyzvly92kNLdTXcdRecf37mzsmSni5d\n/DYHp57qd+jefnsPMmefDVdfXfh+P/20/nNd6VS6SqUFRgFGiokCTMqefNIvxW3qr/J77vGp6OfN\n8wG53bp5N9IFF3hLzPPP+8DTTz/1uUp69PCZYJu6j5C0r4oKuP12mDs3M/D3ppv8sux+/eAnP/Fz\nmY/smYCbmhlYilsyGDR0WX7aNBOvFCMFmJTdfz8sWACvv97w9tpan4PksMMyNwaEzCW948b5jQp/\n9jOfNO2UU3z9kCGw3XZtWnUpQK9e3hozaxZstZWv+/xz+MUvYPBgn1DvySdz21fc4vL22951pRaY\n0hUHhG7d/CagxUYtMFKMFGBSFg/EXbiw4e2PPea3A5gwof76Y47x5bRpPmPsXnvBpEn+pXjZZW13\n1Yu0nJmHy/fe84G3Tz3l6+NWswMO8Ba1oUPh0Ucb30/c4jJokN8dWy0wpSsOBv37F+d9szQGRoqR\n5oFJ2Wef+fLjjxvefuedPmla9jwfnTvD/Pk+cPeoozJfeu+916bVlVZm5lcp1dX5mKY//xluvtmD\n7fz53vJ2+OF+P6Ydd/SZfWOLF/tf7L17N39zSSluyQCzdGm6dWmIWmCkGCnApCwOMA21wCxbBg88\nAJdf3vDVLYMHwyOPtG39pH2Y+VVmY8f6TSVffdW7Eg44AB5+2B/gLWw//7lvv+oqHxBsptl+S10c\nDLbeGmbPTrcuDdEYGClGCjApW7bMlw0FmMce8ysSjj22fesk6TKD+GboK1b44N477vBL6OfMgeQN\nYE8/3Zebbtp6l2dL+4sDwoEHwvjx3iK78cbp1ilJLTBSjBRgUlZd7cuGupAefti7jzbfvF2rJEWk\nVy9/XHghnHsunHEGDBvmVzMNGQJnneXlhg2Dv/7VW2369Em3zpK/OBjssYd3H86bV1wBRmNgpBgp\nwKQsnvMhO8BUV3uAie+nI1JR4WOiGnLSSXDllXD00T7fzLBhmVYcKX5xMOjb15fLl6dXl4ZoJl4p\nRgowKauu9g+txYt9IGen6Lqwv/3N133nO+nWT0rDZpv5fEHf/Gbm5pK33AI77OBXPGlCw+K2bp1P\neBjf2bzYAoxaYKQY6TLqlK1Z411ENTWZAb3gl9Zuu60P0hTJxRFH+P2Whg/352ee6Vevbbpp5qaT\n++3nLTkPPJC5hF/SV1OjACOSLwWYlFVXZy6NTQ7kfeYZv7xWJB977eU3jqyr86uVwG8xcdBBHmSe\necbvXH3kkbD77goxxSIOMBUVviy2AFNb663DCjBSTBRgUlZdnRmkGweYJUv8S0gBRgpl5rcnCMHn\nBvryl339Aw/4TUAHDYJXXvF/Z5K+OMCYeStMsQWYmhro3l1jYKS4aAxMytas+WILTHxzxjFj0qmT\nlJettoJ//av+ujlz/Oqmo47yoPO1r2UGkEr7q6mBrl395969iyvA1NX5sqJCLTBSXNQCk6KaGv+L\npl8//9CKA8zTT8MWW8Amm6RbPylfPXt6F9K77/p9teJ/gy++6DcOlfa1bp3Prg3F1wIThxYFGCk2\nCjApii+h7t7dm/QXLvQm/8ceU+uLtL2//x1eegnOPtufL18Oo0d7y8wDD/gkelVVuj1Fe6iu9rvI\nQ/EFmLjbqKJCXUhSXBRgUhRPYldRkQkw774LM2f6fB4ibalfP2+FueEGD8733OOXXYMP8l1/fe9W\n2mYb/eXd1lat8lYxKL4AE5/77t3170CKiwJMiuIPg65dPcB8/LEPsATYc8/06iUdU2UlvPmmD+7t\n3t1bYoYN821du/qsv59+mm4dy9Xq1aXRAqMAI8VEASZF8YdBly7+V+4bb/hMq7vuChtumGrVpAMb\nOdK/UFesgFmzYJddfP2kSbDzznDffZmBndI6SqEFRgFGio0CTIqSAWbsWPjkE/jHP3wCMpFiYOYt\nMn/9q4eXFSv85qKdO/u2n/3M/80uWZJ2TUtbKbTAqAtJio0CTIqSASbuMqqo8HvZiBSLzp3hq1+F\n117z2XzPPTez7fLLYdw42GgjDzT9+vnzadM8kBfbRHm1tT7LdbEphRaYHj38aimRYqEAk6JkgKmo\ngHfe8YnF4sspRYrN+uvDNdf4WJj334errvK5ZGKff+4tMnvvDQMG+OytTzzh64vBT34C++/vg+WL\nSbIFpndvWLYs3fokxS0wPXv6LM4ixUIBJkXJAAM+DmarrdKrj0iuNtjAJ2D80Y/g/vv9C/iBB7zl\n5Xe/8zLxfbwOPNBbZoYOhTvuSK/OAM8958v589OtR7ZkC0y/fh74imWcUXYLTLG1qknHpQCTouwA\nI1Kqunf32Xz33BNOPtm/5GbOhNmzvcvpa1/z0HDaad4684Mf+PP2njRvxQpffvxx+x63OckWmA02\n8N9fVVW6dYolW2CgNLqR/vxnmDo17VpIW1OASZECjJS7bbf1LqcHHsh8oUybBtdf7y0yvXrBxInt\nV584uCRvnFoMki0w8RWIybvTpyn+nIrrVwrdSEcfDYccknYtpK0pwKRIAUY6koMP9paFujr44x8z\n6889F444An74Q1//+uv+5R2CTyvw2WewcmXLjz9rFixe7D+3pAXmvfe8vvG+WsOqVZkWmI028mWx\nhKxSDDDSMeirM0UKMNIRmcE3vuGXY//nP/B//wdPPgkPPwzXXdf463r1glNOge99z8PN2rU+Z5KZ\nP5ozZYrPLDxsWMvGwPz6117X55+Hr3+98P0krV6dCQhDh/qyWMbprF7tyz59fBnfAqVYFcvYIWl7\n+upMkQKMdGRmPmh90iR//vjj8MgjPtB3k03go4/qjwNZuRJuvtkfjbn+ehgyxFtIunWrv+3pp+GA\nA3yQ7Kuvtrz+8+a1fB+xZAtMnz6w3np+yXoxiMcpxQGm2Ftg4sAl5U9fnSlSgBHJOPBAf1x7rT+v\nq/PLsOPuo5df9qkGXnvNu5WqqmDwYL+c+8knvcw552T2d8ghMH48HHSQX/b9/PNw5ZW+z3vu8cGp\nDU1Z8MorHn522qnhesa3U/jgg1Z526xe7aGgd29/buatMB991Dr7b6k4EPTt68tiDzCt0d0opUFf\nnSlSgBFpXKdohF6vXr7cf39/NGT+fB8zcuedfqn0a6/53bb//vdMmQ028MGd77zjX8pvv525eWVs\n8WLYbTfBm1oYAAAgAElEQVT/+eWXMz8nxS0vrdUCs2CBL4cMyazbZBMPZoVYvtyD2/jxsMceLa7e\nFwJMsXchNRdgZs+GSy/1rsD11mufOknb0CDeFCnAiLSOIUP8Hk433ODdQyHAFVfUL3P99T53zd57\ne2vH2LF+WfXSpb79gw/g8MMz5a+7LnPJcPwlHoIPMgYfzNsa4q6iwYMz63be2VuCmppzZdUqD2QX\nXFB//ZFHwt13++8C/N5Vo0Zl3me+4i6kDTbwZXV1YftpL80FmIsv9vFQs2a1T32k7SjApEgBRqTt\nXHCBB4AQPIiceKKv79HD56NZtMhnFt5gA++22XxzDw2XXgq/+AX8/vew6abeldSzp5c57DC/RcJ+\n+/kXYGu0Rrzyitdp660z68aO9S6kmTMbf92vfuXznVx1le8DPFQ98YT//NZb/r6PPRZeeqnwSQTj\n8BYHmGLvoknWr6EAGM9rU0y3a5DCKMCkSAFGpH1k/x+76iqorIThwzPr9t0X5s71G1Sed57PT3PQ\nQTB6NJx0koeZv//dZxi+/HIPLxdf3PCX5Ftv5T5j7YsveldV166Zdfvv761EV13V8Gvq6nzwc2Wl\nB6sXXvD18fih88/3lqLkbR4eeyy3+mRbutTrEne3lFKAaShgxuelmG7XIIXRV2eK4uZpBRiR9tW5\nsw/kBf9CW7QIBg3KbO/WzeelSQoB/vIXDzrxrRSuvNK7gG6+OXOVzlNPeQC56y745jebrkcIHj6y\ny1VUeEvQhAneSnTjjfW3T5vmLTRnnulXV51zjh/zlls8VF14oQechx6CL38Zjj8eLrrIu3+6d8/v\nd/XBB/5e47FIpRRgVq784vuNL7NWC0zpUwtMitQCI5I+s/rhpalyRx3lM+Wawb/+BYce6kGob18P\nPbfckpnL5s47v7iPmhrvnorHz9xzjw/iPeywL5Y9/ngPDTfdBH/4g4ed+CaZY8Z4mb339kAFsOOO\n/j7+3//zAHTXXfD973ugOuggDy/TpuX728kEmHiemva+/UO+4ttFZP8ci8fwKMCUPgWYFCnAiJSu\njTbyeWvuv9+fr1vnk+w98IAPyP3nP2HgQDj9dJgzx1tFunb1O2Jvs42HoJNO8oG4cSBJGjTIv2TH\njPGuoq5dPYB88olv//GP/UqtW2/18Tvg41ziFoejjvKBy716ebgZOLCwbqQ4wHTt6iGt2L/4s1tg\nssVzCxX7+5DmKcCkKA4wDc1FISKl4aijfGDoDTfAqaf6YOFZs7x1ZvFiuO02H6AbXxUVDyYeM8aD\nTFOzD5vBX//qLSq1tb6fN97w1p94f+uv72N3qqr8mI3t54gjvMtr6tTMXDaxtWvhu9/1S4yTqqp8\nXXxn8QEDWvcWCm0h1wCjMTClL68AY2ZnmtnrZlYVPZ43s0MS2yvM7CYzW2Jmy83sPjMbkLWPTczs\nYTNbaWYLzewqM+uUVWY/M5tuZtVm9o6ZndJAXcab2VwzW21mL5rZblnbm61L2mpqPLzkMg26iBSv\nTp3g7LPh9tth8mQf9Prggz7nzAcfeAvKn//sQWHyZO8Oevpp356c/6Uhffv6lUCffAIzZsCXvuTj\nWrI/N+KJ8Bpz2WW+POQQ6N/fu6imTfMxIeed53UfPz5TfvlyDzzr1vndxMFbhYrtTt7Zmgswn3/u\nS7XAlL58Oy8+BC4A4hkQvgX81cx2CSHMAn4FHAocDSwDbgLuB/YBiILKI8ACYBQwGLgbWAtcFJXZ\nHHgIuBk4ATgQuN3MFoQQHovKHAdcA5wOvAxMAKaa2bYhhCVR3ZqsSzGoqVH3kUi56tzZW1ggM2C4\nUGYeOlpi8GC/nPqgg/yz549/rH9TTfBLsM84w+ehufJKn6xv770z92fadtvWuQ1DW1q50ru61q5V\nF1K5y6sFJoTwcAjh7yGE96LHRcAKYJSZ9Qa+A0wIITwdQngV+Dawl5ntHu1iHLAdcGII4Y0QwlTg\np8B4M4u/yr8H/CeE8OMQwuwQwk3AfXhIiU0Abg0h3BVCeBs4E1gVHZ8c65I6BRgRaU+77+5f4CtX\n+hgd8BagTp38xpo9evgMtePHe3g56CC/kin2ta/B9Ok+cPjFF73rqtisXOnjfeCLg3hrazPrFGBK\nX8FjYMysk5kdD/QEXgBG4i06T8RlQgizgXnA6GjVKOCNRCsJwFSgD7BDoszjWYebGu/DzLpGx0oe\nJ0SviY/z5RzqkjoFGBFJy/77e1fWRx/5F/sWW8C773rLyznn+NVPDz6YuTwc4JhjfBLAZ57x+XG2\n3NK7uO64A5YsafxY7WnlSh+rY/bFcS7x84a2SenJO8CY2ZfMbDmwBu/mOTJqBRkErA0hZP+zWBRt\nI1ouamA7OZTpbWYVQH+gcyNl4n0MzKEuqVOAEZFiMmSIX9103XVw1lk+eDipUycflPzKK5kbZ1ZV\neajZaCPYa6/0B/muWOEDm/v1++Jg5bj7aJNNFGDKQSFfn28DOwN98fEld5lZAxcB/pcBucxJ2VQZ\ny7FMc8fJqS4TJkygT/LPDqCyspLKysrmXpoXBRgRKUUjR/rjuuvgzTc97NTW+h2/Bw70yf3icTPt\nbeVKv3R8ww2/2CoUB5ihQzODeaUwU6ZMYcqUKfXWVcW/4HaS99dnCKEG+E/0dEY0puQHwL1ANzPr\nndXyMYBMa8lCIPv+rgMT2+LlwKwyA4BlIYS1ZrYEqG2kTPI4zdWlURMnTmTEiBHNFWsxBRgRKXVf\n+pJ3KYG3zpx+urdwjBvn95PacMP2rc/Kld4a1L9/0y0wrXU38Y6qoT/qZ8yYwciRI9utDq0xD0wn\noAKYDtQAY+MNZrYtsCnwfLTqBWBHM0uOpz8YqAJmJcqMpb6Do/WEENZFx0oex6Ln8XGaqssLhb3N\n1qcAIyLl5Lvf9VmDweeb2WUXH+zbWlavztwKoDHJFpimAowG8Za+fOeB+V8z29vMNovGwvwS2BeY\nHLV03AFcG83jMhL4LTAthPCvaBf/AGYCd5vZTmY2DrgcuDEKJgC3AFuZ2ZVmNszMzgKOAa5NVOVa\n4HQzO9nMtote0xO4E6CZuryc12+oDSnAiEi5Oe44WLjQJ/NbuNAH+5rBT3/asvExK1f67Qw23bT5\nco11IcXdRkOH+hiYXG+4KcUp3xaYgcBd+DiYx/GrgQ4OIUQX5DEBn8PlPuApfL6Xo+MXhxDqgCPw\nLqDno33dCVycKPM+cDg+/8tr0T5PDSE8nihzL3AecBnwKrATMC6E8Emirk3WpRgowIhIORo4ELbb\nzgf7xn7+c9hqK3j/fb8UO1+PPurL+fObvqFkHGAGDPAAlVRV5bdEGDDAw0ux35hSmpbX12cI4bRm\ntq8Bvh89GivzIR5imtrP03g4aqrMzfhVUAXXJW0KMCJSznbe2bt9Lr4YnnvOB/lusYVvGzPGJ9bb\nc0+4+mq/Aiq+/Pm993zivR49/OaLU6fCscdm9vvII/WfJy1fDuut5+NgPvjAJ7Tr1s23VVX5ZeHx\nNRrLlnlZKU26F1KKFGBEpNx17+5zy0ybBs8+66EGfODvmjXw5JN+a4SNN/bZizt18hl/11vPn/fq\n5febAvjd77xL6hvf8Jtivv12/WOtWuXdRkOH+j7q6nyCvlhVlc9bEw8szh4jI6VFASZFCjAi0pHs\nvTe89pp33yxd6oFizhz44Q9hxAif+TeWvHrpW9/y1pSTT4Zf/tLX/eIXfpPJceMyN8Z9PrqMY7vt\nYNgw/3nmzMx+4haYAdFd8RYv9on8NBamNOnrM0UKMCLSUfXt68vevWHixMz6ujrvNurZs+HX7bsv\n3Hmnv37SJO9e2ndfH2NzxBF++fTu0Q1jhgzxbqq4BefDD71rKg4wjz4KBx7ox//hD9vkbUobUgtM\nihRgRETq69Sp8fASO+UUvy/Tgw/CoYd6y8sBB3iX1KGH+jgaM2/x+dOffJI98Lt/DxuWuUrpxht9\n/b//3bbvSdqGvj5TpAAjIlK4rl19QO999/kVT2vWeEtM7NRT/Y7bV1zhrTRz5vjYGPA7hcdz1Lzz\nTvvXXVpOX58pWrdOAUZEpKWOOcYf2fbf31tmLrrIn3ft6uvAu5lefNHHxLz1lo+DMfviPqR4qQsp\nRWqBERFpO126+BiZ557zMTP33ANbb+3bxo+HE0/0cTSff15/sK+UBn19pkgBRkSkbXXp4nfJ/vRT\nH18T23ZbmDzZL73u3t0H9O6wQ3r1lPypBSZFtbUKMCIi7aFTI992PXt6N9PDD7dvfaTlFGBSVFPj\nEzWJiEh6Dj8cnnrqixPjSXFTgElRba0CjIhI2r7xDV9uvz1ceKGCTKlQgEmRAoyISPr698/MCXPF\nFR5kDj7YZ/+V4qUAkyKNgRERKQ7jx8Orr/qNJQEeeww239yDzNy5qVZNGqEAkyKNgRERKR677ALn\nn+93sI5n533sMdhyS58jZsaMzKy+kj4FmBSpC0lEpPh07Qo77gjz58P//V/mc3rkSG81v/RS3QCy\nGCjApEhdSCIixWvwYDjvPG8t/+STzCR4l1zil2Vvtpnfa2nFilSrWc+aNTBqVOY2CeVMASZF6kIS\nESkN/fv7PZPuugtOO83XzZvnVzCtv77fUHLZsnTrCF6Pl16C665LuyZtTwEmRepCEhEpHWbwzW/C\nbbdBXR384Q+wxx6+ba+9/L5KZ53lf5ymZd48X3aE1n0FmBQpwIiIlCYzOO4476o5//zM+kmTfAzN\npZd6yGlvCxb4ctWq9j92e1OASZHGwIiIlL6rr4bly+Gzz+D0033dJZf4H6gzZrRvXT791JdLl7bv\ncdOgAJMijYERESkP660H/frBrbd6y8uDD/r6kSM9zLRXa8xnn/ny88/b53hpUoBJkbqQRETKjxkc\ncQS8+64/v/RS/6yfNKnt55GJA4xaYKRNqQtJRKR8bb21B4nzzvPnZ50FJ5zQcNnWaqFRgJF2oRYY\nEZHy1revT4b34Yf+/N57oaLCb1sQmzPHvwsmT258P88+m9t8M599Br16QVVV+c8arACTIo2BERHp\nGIYO9c/8007zWxWMGOFjY779bTjgAC/zzW/CySd/8bV1dTBmTGb+maZ8+mlmwr1yHwejAJMitcCI\niHQcnTv7HDJvvunPL70U7rzT5275zW983d13wxtv1H9ddbUv58xpev+1tbB4MQwf7s/j7qRypQCT\nIo2BERHpeHbYwbt49t3XZ/L9+GNviamu9quZrrmmfvl4Thezpve7eLG31uywgz8v9wCjr88UqQtJ\nRKRj6t0bnnqq/rqKCrjsMjj3XNh2W/if//H1q1f7srkA8/HHvowDTDwnTLlSC0yK1IUkIiJJ3/8+\nbLMN/OQnPjbm3Xdzn1V34UJfqgVG2py6kEREJKlLF3jrLejWDZ580lti+vXzbZ2aaXKYN89fv/nm\n0L17+QcYtcCkSC0wIiKSrWtXDyOPPebP4zldXnwRxo+HEBp+3bRpsOWW/voNN1QXkrSREBRgRESk\nYZtsAgce6N8VEyfC4MG+/uabvSXmu9/NzPNSWwt//avPI3PSSb5ugw3UAiNtJJ51UQFGRESa8sMf\n+kR4jz6auVnk7bd7d9HOO/vy61/39ccf78sNN1SAkTYSJ2eNgRERkeZ06gSHHOI3i6ythR/9yNf/\n+9+ZMjNn+gBggI02ylyVVK4UYFISBxi1wIiISD46dYKrroKPPvKrlBYt8q6m7bfPlBk2zANNOdPf\n/ympqfGlAoyIiBRiyJDGt+26qwebBQsy42fKjVpgUqIuJBERaSu77ebLf/0r3Xq0JQWYlKgLSURE\n2srQoTBwIDz/fNo1aTsKMClRgBERkbZiBsccA5Mm+ViZcqQAkxKNgRERkbb085/D8uU+p8y6dWnX\npvUpwKREY2BERKQt9e0L55/vPx9yiN+tupzkFWDM7EIze9nMlpnZIjP7i5ltm1WmwsxuMrMlZrbc\nzO4zswFZZTYxs4fNbKWZLTSzq8ysU1aZ/cxsuplVm9k7ZnZKA/UZb2ZzzWy1mb1oZrvlW5e0qAtJ\nRETa2tVXw5//DP/8p4+JOemkzESqpS7fFph9gBuAPYADga7AP8ysR6LMr4DDgaOBMcBg4P54YxRU\nHsEv4R4FnAJ8C7gsUWZz4CHgCWBn4DrgdjM7KFHmOOAa4GJgV+B1YKqZ9c+1LmlSF5KIiLSHI4+E\nWbNg+HD4/e/9e2fWrMwf0qUqrwATQjgshHB3CGFWCOENPHhsCowEMLPewHeACSGEp0MIrwLfBvYy\ns92j3YwDtgNODCG8EUKYCvwUGG9mcYfK94D/hBB+HEKYHUK4CbgPmJCozgTg1hDCXSGEt4EzgVXR\n8XOtS2rUAiMiIu1lu+3gtdfg29/258OH+xCGZ58t3fExLR0D0xcIQHzHhZF4y8oTcYEQwmxgHjA6\nWjUKeCOEsCSxn6lAH2CHRJnHs441Nd6HmXWNjpU8ToheEx/nyznUJTUaAyMiIu2pa1f4zW/goYcy\n68aMgW7d4I030qtXoQoOMGZmeBfNcyGEeMLiQcDaEMKyrOKLom1xmUUNbCeHMr3NrALoD3RupEy8\nj4E51CU1aoEREZE0HH44rFwJFRWZdTvt5Jdev/pq6bTItOTv/5uB4cDeOZQ1vKWmOU2VsRzLNHec\nZstMmDCBPn361FtXWVlJZWVlM7vOncbAiIhIWnr2hOpq//mFF2DPPf3nESN8+fnnkPU1WM+UKVOY\nMmVKvXVVVVVtUNPGFRRgzOxG4DBgnxDCgsSmhUA3M+ud1fIxgExryUKg3tVCeGtJvC1eDswqMwBY\nFkJYa2ZLgNpGyiSP01xdGjRx4kRGxGexjagLSUREisHo0X4zyAULYOutYfVqvwR7s83gtNPgoou+\n+JqG/qifMWMGI0eObKdaF9CFFIWXrwH7hxDmZW2eDtQAYxPlt8UH+sYTGr8A7Jh1tdDBQBUwK1Fm\nLPUdHK0nhLAuOlbyOBY9j4/TVF1eyPkNtxF1IYmISDEZPBhWrYLrr/fnH3wAP/2pdy2tXp1u3RqS\n7zwwNwMnAicAK81sYPToDhC1dNwBXBvN4zIS+C0wLYQQ31LqH8BM4G4z28nMxgGXAzdGwQTgFmAr\nM7vSzIaZ2VnAMcC1iepcC5xuZieb2XbRa3oCd+ZQl5fzed9tQQFGRESK0fe/D++/D9ddl1nXs6fP\nJVNM8m2BORPoDTwFLEg8vpEoMwGfw+W+RLmj440hhDrgCLwL6HngLjx0XJwo8z4+f8uBwGvRPk8N\nITyeKHMvcB4+f8yrwE7AuBDCJ7nWJU0aAyMiIsVqs83gnHN89t69o5GuY8dmLsMuBuZXHwuAmY0A\npk+fPr3Nx8A8+SQccAC89x5stVWbHkpERKRF3nsPKivhlVf8+c9/Dj/5Sf0yiTEwI0MIM9q6TroX\nUkrUhSQiIqVi663h6ad93hjwgb3HHgtr1qRXJwWYlCjAiIhIKenZ00NMXZ2Pk7nvPujeHT75pPnX\ntgUFmJTEY2B0GbWIiJQSMx/gG/8BPmAAnHFG+0+ApwCTErXAiIhIqTLzP8QnT/bnv/41jBrVvnVQ\ngEmJAoyIiJS6E0/0SfDaO7yAAkxqdBm1iIiUi3/+E156qX2PqQCTEt1KQEREykWPHu3/faYAkxJ1\nIYmIiBROASYlCjAiIiKFU4BJiS6jFhERKZwCTEriFphOOgMiIiJ509dnSmpr1X0kIiJSKAWYlCjA\niIiIFE4BJiU1NRr/IiIiUigFmJSoBUZERKRwCjApUYAREREpnAJMStSFJCIiUjgFmJSoBUZERKRw\nCjApUYAREREpnAJMShRgRERECqcAkxKNgRERESmcAkxK1AIjIiJSOAWYlCjAiIiIFE4BJiW1tepC\nEhERKZQCTEpqatQCIyIiUigFmJSoC0lERKRwCjApUYAREREpnAJMSjQGRkREpHAKMCnRGBgREZHC\nKcCkZN066No17VqIiIiUJgWYlCjAiIiIFE4BJiUKMCIiIoVTgEmJAoyIiEjhFGBSogAjIiJSOAWY\nlCjAiIiIFE4BJiUKMCIiIoVTgEmJAoyIiEjhFGBSogAjIiJSOAWYlCjAiIiIFE4BJiUKMCIiIoXL\nO8CY2T5m9jczm29mdWb21QbKXGZmC8xslZk9ZmZbZ23vZ2a/N7MqM1tqZrebWa+sMjuZ2TNmttrM\nPjCzHzVwnGPNbFZU5nUzOzTfuqRl3TrdzFFERKRQhbTA9AJeA8YDIXujmV0AnA2cAewOrASmmlm3\nRLF7gO2BscDhwBjg1sQ+1gemAnOBEcCPgEvM7LREmdHRfm4DdgEeAB4ws+F51iUVNTVqgRERESlU\n3m0AIYS/A38HMDNroMgPgMtDCA9GZU4GFgFfB+41s+2BccDIEMKrUZnvAw+b2fkhhIXASUBX4NQQ\nQg0wy8x2Bc4Fbk8c59EQwrXR84vN7GA8sJyVS13yfe+tSV1IIiIihWvVMTBmtgUwCHgiXhdCWAa8\nBIyOVo0ClsbhJfI43pqzR6LMM1F4iU0FhplZn+j56Oh1ZJUZHdVlyxzqkhoFGBERkcK19iDeQXgQ\nWZS1flG0LS6zOLkxhFALfJZVpqF9kEOZePvAHOqSGgUYERGRwrXXVUhGA+Nl8ixjOZZp6XHahQKM\niIhI4Vr7OpiFeEAYSP2WjwHAq4kyA5IvMrPOQL9oW1xmYNa+B1C/RaWxMsntzdWlQRMmTKBPnz71\n1lVWVlJZWdnUy/KiACMiIqVqypQpTJkypd66qqqqdq1DqwaYEMJcM1uIX130bwAz642PbbkpKvYC\n0NfMdk2MgxmLh42XE2V+bmado+4lgIOB2SGEqkSZscD1iSocFK3PtS4NmjhxIiNGjMj37edFAUZE\nREpVQ3/Uz5gxg5EjR7ZbHQqZB6aXme1sZrtEq7aMnm8SPf8VcJGZfcXMdgTuAj4C/goQQngbH2x7\nm5ntZmZ7ATcAU6IrkMAvj14L/MbMhpvZccA5wDWJqlwHHGpm55rZMDO7BBgJ3Jgo02Rd0lJbCyEo\nwIiIiBSqkBaYLwNP4t05gUyo+B3wnRDCVWbWE5/XpS/wLHBoCGFtYh8n4EHjcaAOuA+/5Bnwq4XM\nbFxU5hVgCXBJCOGORJkXzKwS+N/o8S7wtRDCzESZXOrS7tat86UCjIiISGEKmQfmaZppuQkhXAJc\n0sT2z/G5XpraxxvAvs2UuR+4vyV1SYMCjIiISMvoXkgpUIARERFpGQWYFCjAiIiItIwCTAoUYERE\nRFpGASYFCjAiIiItowCTgjjAdGntaQRFREQ6CAWYFKgFRkREpGUUYFJQE91jWwFGRESkMAowKVAL\njIiISMsowKRAAUZERKRlFGBSsDa6kYECjIiISGEUYFKwerUve/RItx4iIiKlSgEmBQowIiIiLaMA\nkwIFGBERkZZRgEmBAoyIiEjLKMCkYPVqqKiATvrti4iIFERfoSlYvVqtLyIiIi2hAJMCBRgREZGW\nUYBJwapVCjAiIiItoQCTArXAiIiItIwCTAoUYERERFpGASYFCjAiIiItowCTAgUYERGRllGASYEC\njIiISMsowKRAAUZERKRlFGBSoAAjIiLSMgowKdA8MCIiIi2jAJMCtcCIiIi0jAJMCpYtgz590q6F\niIhI6VKAaWchwKefwgYbpF0TERGR0qUA085WrICaGgUYERGRllCAaWeffebLDTdMtx4iIiKlTAGm\nncUBRi0wIiIihVOAaWcKMCIiIi2nANPOFGBERERaTgGmnX32GXTurMuoRUREWkIBpp0tWQL9+oFZ\n2jUREREpXQow7WzuXNh887RrISIiUtoUYNrZe+/BVlulXQsREZHSpgDTzt57D7beOu1aiIiIlDYF\nmHa0ejXMn68WGBERkZZSgGlHb77py+23T7ceHcmUKVPSroK0Mp3T8qLzKYXqEAHGzMab2VwzW21m\nL5rZbmnU48knoaICdt01jaN3TPpwLD86p+VF51MKVfYBxsyOA64BLgZ2BV4HpppZ//asRwhw113w\n9a97iBEREZHClX2AASYAt4YQ7gohvA2cCawCvtOelfjTn+Ctt+CMM9rzqCIiIuWprAOMmXUFRgJP\nxOtCCAF4HBjdnnUZOxYmTYL992/Po4qIiJSnLmlXoI31BzoDi7LWLwKGNVC+O8CsWbPapDK77w4z\nZrTJrqURVVVVzNAvvazonJYXnc/ykfju7N4exzNvkChPZrYxMB8YHUJ4KbH+KmDvEMKeWeVPAH7f\nvrUUEREpKyeGEO5p64OUewvMEqAWGJi1fgBfbJUBmAqcCLwPVLdpzURERMpLd2Bz/Lu0zZV1CwyA\nmb0IvBRC+EH03IB5wPUhhKtTrZyIiIgUpNxbYACuBX5nZtOBl/GrknoCd6ZZKRERESlc2QeYEMK9\n0Zwvl+FdSa8B40IIn6RbMxERESlU2XchiYiISPkp63lgREREpDwpwIiIiEjJUYBJKJabPkrjzOxi\nM6vLesxMbK8ws5vMbImZLTez+8xsQNY+NjGzh81spZktNLOrzEz/F9qJme1jZn8zs/nR+ftqA2Uu\nM7MFZrbKzB4zs62ztvczs9+bWZWZLTWz282sV1aZnczsmej/8wdm9qO2fm8dUXPn08x+28D/2Uey\nyuh8Fgkzu9DMXjazZWa2yMz+YmbbZpVplc9ZM9vPzKabWbWZvWNmp+RTV31oR4rlpo+SkzfxAdmD\nosfeiW2/Ag4HjgbGAIOB++ON0X+gR/AB7KOAU4Bv4YO8pX30wgfTjwe+MAjPzC4AzgbOAHYHVuL/\nF7slit0DbA+Mxc/3GODWxD7Wx+eimAuMAH4EXGJmp7XB++nomjyfkUep/3+2Mmu7zmfx2Ae4AdgD\nOBDoCvzDzHokyrT4c9bMNgcewm/1szNwHXC7mR2Uc01DCHr4QOYXgesSzw34CPhx2nXTo955uhiY\n0ci23sAa4MjEumFAHbB79PxQYB3QP1HmDGAp0CXt99fRHtG5+WrWugXAhKzzuhr4RvR8++h1uybK\njOh1Ma4AAAQiSURBVANqgEHR8+/hE1l2SZT5JTAz7fdczo9GzudvgT838ZrtdD6L94HfkqcOn72+\n1T5ngSuBf2cdawrwSK51UwsMxXXTR8nJNlFz9Rwzm2xmm0TrR+KJP3keZ+MTF8bncRTwRghhSWJ/\nU4E+wA5tX3Vpipltgf+FnjyHy4CXqH8Ol4YQXk289HH8r/89EmWeCSHUJMpMBYaZWZ82qr40br+o\nO+JtM7vZzDZIbBuNzmcx64ufi8+i5631OTsKP89klcn5O1cBxjV108dB7V8dacKLeFPkOOBMYAvg\nmai/fBCwNvrCS0qex0E0fJ5B57oYDMI/LJv6vzgIWJzcGEKoxT9gdZ6Lz6PAycABwI+BfYFHolnR\nQeezaEXn6FfAcyGEeKxha33ONlamt5lV5FK/sp/IroWMxvt0JQUhhOQ9Nt40s5eBD4Bv0Pj9q3I9\njzrXxSuXc9hcmfgLU+e5HYUQ7k08fcvM3gDmAPsBTzbxUp3P9N0MDKf+OMPGtMbnbF7nVC0wLt+b\nPkqRCCFUAe8AWwMLgW5m1jurWPI8LuSL5zl+rnOdvoX4h1hT/xcXRs//y8w6A/2ibXGZhvYBOs+p\nCiHMxT9z4yvLdD6LkJndCBwG7BdCWJDY1NLP2ebO6bIQwtpc6qgAA4QQ1gHT8RHwwH+bzsYCz6dV\nL2mema0HbIUP/JyOD/xLnsdtgU3JnMcXgB2zri47GKgCZiKpir7cFlL/HPbGx0Ikz2FfM9s18dKx\nePB5OVFmTPRFGDsYmB2FXkmJmQ0FNgQ+jlbpfBaZKLx8Ddg/hDAva3NLP2dnJcqMpb6Do/W5SXuE\nc7E88C6I1Xhf7Xb4JXyfAhulXTc96p2nq/HL9jYD9gQew1P/htH2m/FLLffDB5tNA55NvL4Tfon8\no8BO+FiaRcDlab+3jvLAL7vdGdgFv3Lhh9HzTaLtP47+730F2BF4AHgX6JbYxyPAK8BuwF7AbODu\nxPbeeKj9Hd4EfhywAjg17fdfbo+mzme07So8gG6Gf2G9gn+JddX5LL5H9Bm6FL+cemDi0T2rTIs+\nZ4HNo3N4JX4V01nAWuDAnOua9i+rmB7RL/B9PMi8AHw57Trp8YVzNAW/vH01Pur9HmCLxPYKfA6D\nJcBy4E/AgKx9bILPP7Ai+k91JdAp7ffWUR74IM46vNs2+fhNoswl0RfWKvzKhK2z9tEXmIz/RbcU\nuA3omVVmR+DpaB/zgPPTfu/l+GjqfALdgb/jrWrVwH+ASWT9YajzWTyPRs5lLXByokyrfM5G/3am\nR5/n7wLfzKeuupmjiIiIlByNgREREZGSowAjIiIiJUcBRkREREqOAoyIiIiUHAUYERERKTkKMCIi\nIlJyFGBERESk5CjAiIiISMlRgBEREZGSowAjIiIiJUcBRkRERErO/wfc/4UCZ3JC1wAAAABJRU5E\nrkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f7aca021890>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"data1 = np.genfromtxt(os.path.join('..', 'tests', 'data', 'raman-785nm.txt'))\n",
"x = data1[:, 0]\n",
"y = data1[:, 1]\n",
"plt.plot(x, y)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Find ridge lines "
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.image.AxesImage at 0x7f7ac7a7df90>"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAfwAAAFiCAYAAAATPmogAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzsvXvMdc1VH/Zb+3lff8Y2xm5Tm9I0gYi6pWqVRgYbN0AV\njGICFQGMLw0UxShtiAyitKgpKi0JtGlEg2UBtpRIKEAhjbApBZTWNOBCEwqYUi5KAKdAjLmED4yN\n75+/733O9I+9Z2bNmjW3vWefM+d59u99z3P22Xsua65r1mVmkzEGBw4cOHDgwIG7jenSBBw4cODA\ngQMH9sfB8A8cOHDgwIF7gIPhHzhw4MCBA/cAB8M/cODAgQMH7gEOhn/gwIEDBw7cAxwM/8CBAwcO\nHLgHOBj+gQMHDhw4cA9wMPwDBw4cOHDgHuBg+AcOHDhw4MA9wMHwDxw4cODAgXuA3Rg+Eb2WiP45\nEX2YiH6KiD5lr7wOHDhw4MCBA3nswvCJ6FUAvhnA1wP4UwB+AcAPE9Ef2SO/AwcOHDhw4EAetMfL\nc4jopwD8tDHmq5bfBOA3AXyLMeabRNh/GcDLALwDwBPdiTlw4MCBAwfuLp4O4OMB/LAx5g9yAR/0\nzpmIHgJ4IYC/Ye8ZYwwR/QiAlyhRXgbge3rTceDAgQMHDtwjfDGAv5cL0J3hA/gjAG4APC7uPw7g\n31TCvwMA/uu//I34+D/6J8A1DrNiADid5nvTREHE08mACDAmfGaMCeJOEwXfNi1Nu2HMHP/mZgry\n5vnYeDy6zMPSI8Pa+EQ+HA9j4xPN5dfqQ5bL3ubhZfllnUiajTGORpv36WRcejcPbnC6Pbl0eF3a\nezcPJjx66tblz+nibSPrkYPTyON/63f/LXzll3xNkI6l0ZaF3+f1VPN8psvg4dMe4PbRydULLyfv\nA/YeT5vfs3XIyyzpkPe0tuF1wGm9uZnw6NEJH/WMh/jwh550bcLpk+nyOtfqTvYFOV543cu2SsXj\nZeGQfW9OV6/PVD+VdH3bd38zvuJL/osoTKpN5HiR45CH4ffkWJZ1wfOS40+rF61P2Oe3tydMEwVx\ntbSNCfsnT0+Wex7XwIOn3eDRk7dL+rZtfV3ZcE97+gM8+cSjIB2NBl53FrwPa/On1rZynMkxYJ+7\nuelmcnOVpU+bj2X/kGW25fLX8di3afO21sDrh6fL09D4l5yfeDvy8k43E578yCMABr/5L34Df+Pv\n/DfAwktz2IPhp0AAtBp6AgD++L/2CXjBx3+SyuDsZDxNocvB6XRyA5I/C5nbCdM0Bd8zM0oxfLNM\nqDcAAafbk6PF5mPDcMg8LD2+cxsXzg/+k/ttw+RoDBlVWB5OIw/L8+D3JM2yTPaZvffwaQ/w6Klb\nxvAnl4699/BpD/DkE08BBEe/pJu3ZZ7hh+V61jM+Gi/4+E+K2piXhd/n9VTz3BiDR49OeNZHPx1P\nPfUIT33kEW4e3KhMgZedp83v8fLzuuV0yHta22h52v756NEtnvUxT8f73vMh3EzzJMDDynR5O/P0\nOP2lMLINS/F4WThKfU+ri1xYAHjmM57l5hA5bmy7awxf9kf+W2t/OZbtM0sz77dy/Gn1ovUJIgJN\nhNtHt5imycVNpc3bRqYny21peNrTH+KJDz2Jm5speM7TOp0MnvGsx/ChD3zELTxSbSjz5/XB60zr\n17xt5TNZZt4O5mTwtKc/xO2jE25vb13e2nws+4dWZl4+3l6yDLZs80NEnM3WOY/P89LqwT7XGb7v\nGw8fe4ibBxM+9L4Pz4sGuPBFk/geDP9dAG4BPF/cfx5iqd/hDd/zOjzzGc8K7r30JZ+Nz3rJZ3cn\nsARj4JhWDlqH0dPr7yexBanFTjbOlK8LG0YbSJLhc8jJtFTnPJ4WVrtflaYBzOmE6WbCdDtLDDeN\naeQWkTKN2vovhZumCeZkYKZ+/cylU9cUcTwJRVulBssscFPha59t6Ve5fqm17Vr0TMsiJS1O07yg\ngNImQTsYP/YN0xbk+nkNLamwrWU3xmC6IZxOBPOUqXJDb577Sv0QBFA9H1gzD8xhgbf+9A/jx37m\nH2IiwlNPPYIxwIee+GB1Gt0ZvjHmKSL6WQAvBfCDgHPaeymAb0nF+4r/+Gvwgj/+bzUN+F5ISZpU\nCNMz/1JZU2GkxNKfNqkSDNVe9p5VCy5rpauDwayiu3kw4fYRwSjqurbBuU97zGnP30QA3XCpM5RO\nUnRtz3+sBazEnnV/NjAVcKk8zc+XQRyq11NpbK/LWuYe0UD+vhYeWEwG0wSaYq1rCVLj0ha5LfiW\nMcPjvvRTX4b/8LM+Dw8e3uDdj78Pt49O+I3Hfw1/5a9/aVVae6n0XwfgOxfG/zYAXw3gGQC+IxVh\nbZ9aI63WJ75PslVZDzZhzeSkrDI2DOUeq+FzbSfVg3vjdDphuiFMi01wfCyT9sk01fsBz1z2mj+2\njl/KTD7bGfCc/qxGrwgb+CPtPy81Laytrw3FfiJrsEZ7UavpLcWvxTRNuFnMd6fTqWns78LwjTHf\nS/Oe+2/ArNr/eQAvM8b8fiqOdZLToDWCXA3y37WqwFS68zNdetY0ENJmqNGn5c/Ty62Ce0xIaycJ\ny3TnyTF2IAnthDZOuIDrIXF95ov/bJBeitaa/LS+YwfOdDN5B6KTAd2U6a4t35Y6kPU9t8uilqWw\nHVJ9upS2vNbGV6nu5T3HVJGmiZtzajR8mvnHGIOXvuSzk9JgzRgqmZVydaDNPy3ayqjvRlq0sFwp\nraRWrzJ9Y4zrN7lyOU3SYrs3JxOkm6IhhdKYrIWj1Wo/lnFQ0oa8dKV5WKtHje5aHpQzeabgx/yE\nmwfzBwa4fXTr/MxqsJvTnjHmjQDeWBt+uplKAuQqbJlkzy1kX1KqL03knKFrIIKvsBWSQGnArx2s\n1fmfDGCMk/CNMTgZkzQJ7qpZysBOasYANw9myQaYtRM3jedonbMMvfPSxspnMYav4ZpU/bu2jfFM\nHNDNdPN9s/hfzOHnXTqJJC8xFhZmMZH3R0iVBcB+/mA78C0Ntv8+eDhhejDBALh96tRklhjmLP2b\nB5NjEWs6T68O51a1RK7n8KRTK9vUyq9FutoSpgVVK1HXGIzZLyr7UMLHYri3YZCcFM6FkoSrtt9p\nnj6macJ0M0szhm1LLDESFS28pRDW5WGs+t5gupnmyRgLvUaELdHHnmvlbOGN+phIp5PTaK3B3gxH\njvuUBmGtQ5aPE/sPaWmtnSPt2J34Aj4zdxFImD50bVA1Es1bO1+GcbyEPzmpv06rUqtxKYezCUre\ngarxz+MXwy2LGS/hm1nCv06GT00zzO4ryjZy7iwMm7WzEv7EFkgZ9e2oOBmr0vcS/oh0ewl/YfiL\navaSPgdVTPqOjqV9HGXNrvXlVPrudyIcU+FPFC4qt6BbnVmJ3qn05cyzEwT553QuJyLcPLhxJvBH\nj25xuq0v9TAMn6y00lB5rXZTbRUpr93KjsWtlepbn/eArINWCaPGz2D+vUiSxkQf/9w77p2j7Gvy\n0PvDMrnRvNtgWuz2XMKX8XvY7FtsvDY8r/ObKZS+wvaI00uVJUf/msksl0+pzWppavGD2YJWTcQW\nB67QfEZqWqk+k9LSyPRdHrzvQPdBcir9JbxGg0SprbfM77x8VlvhTA4ULoZT5pvWOTFVntS8mxp/\ncnym8kzRzNvtwcPQhn/bYMMfhuHfTLNkZXFx6WrhYHuu3nql3buu1M5cUFFZE8g1CnLGLA56i6Qw\nkZWa2zxgdwfXqBJ5lT55J8Ne6N3vR7Odpyb1EbDrwsUq7OAZZa6Pk5sHu5NUhayj38k7hZLdFnwG\nTddFqmIp1nQzM/vpZm6XVqe9YRg+3VBwJGMx/AbJI70Chh8QnNmHpqHm/CxaJL4REJIjT44LbflW\nEoCTNs9B37pMtNX36WQw0eQcgIjCo4Vb6Sn6RqC9Txmbx6LxnTURTJ1ZqPct/atFis7buvU4PZhu\nToI699hqzS8Kv1SHlVxzaNmRwMer5fhav/E241DyPJepKyedS18EfrInf9Y/f/cwGc9VL8X3iyRl\nhoDT6t0QHjiV/nwS4+2j20LCHsMw/ImmeQvUAIttsoMBqGoEH69e3XsdCJn5PPmYUCJgjirhImms\nxUsO1kHPSvhu8uhhs+zYFYLJlkn4E6W3SY2COzMkdoRhY2n+3iEPcLOB1w6liLGq/JqTNs8KM++i\nsQ6O4VkB9Vg7V5+zP/MFzHQz4ebhLOETYT5S+NEVSvjTDZ31kJUSaPlzCSX1KAuGYOzwRZACu0iq\n5vdjFBEAc4KzKv1FPcjfJTAEGClWwrfqTFg/hE7o2gcHautrwK59brF7B++7UCRiKcy67jDIcDAA\nDHvniFu8FMZAj7rdMjS2Zj9N80vKrNPerNK/QgmfaFZX1K4kezPF0KmC2e8pfK7Fq0XOwW5NerX5\n1DoXcmcXTS1Loi58eL8wcqq/hCNQCUnnoY6InJ1OjOHDajrjF5rU0J1zmuP3axysAhplnTNfg8Bp\n7xQ6B/V0nGpxYKtSK1fStMUBLoUaG36r4+NaNb7sY9xhT+svso/VtqeVFGepWGgRTDoPRw/p40H2\nVe26FS1ObICVR0KzQy7/GudQnl8rUk6XtXkGebMxf/PwBtODCbBCye0Jt09dI8NfnPYmVlFnh2J/\nuWbhpHXSVQIBEPXBJAKuXnYVNZgkAJSYCWPS0+Q0GVOlXfys4LRSaH4A0OxzkMUVdfw9JeKLanh6\nz4MBE4e7nh9JI374fLhxbemzJwZS6MsyClbxMmn/X76nifDgwWz6pgmz/8Xtlar0iSiQ8M/N9GfT\ntFjZzhdLgPOYpbesBrfmGWTNTfVCr2fsQ+fYA3UCSRWlxUN6zwFsV8+WUU43s+RjbfktavLeNMZS\nlO2f8BK+s68uYRYTxF79VC1jovlyNLTSN9IE3tMZLKmFUdyHeJCUhqSsyQOcI57NY/Jj2kYPFsFs\nXPstfDLdyjrpNGVZ+owJfQvmOkD3RUleU5COt8qdSQpOjojZz+3GMnyyEr65Tqc9IsL0YLqsc4hc\n1VpckbTTFULj4cz4TMI3i1HQOc9k6io1sV0SfHKbFgmfSH9vfW16e4HT4t5NTr6/dpXwO2EUf5Rz\noGfd02Jn7wnOxKUJTjLJQHsHT8so/cuNAzbvSMe9UWjdDKbNePDwZhZM7PsNbk+4fepRdVJjMfxp\nchPZ3hOFtHOmVs2cjFq70Dkmud57+DWb8ZwRs0fNKo/IRuZIYcxHhqm1/64dpLn0c3ZAa/cG4CVm\nonDyEKr03SBVeVEfFZM2Gyv2UKQa6aamDLXlbLVznwtbJvutDKOnFqBXutJHgG/7s8+DMasu9hVz\nXgN6zI9WKxeo9EX6nP4WX45kfkiPf+4/I7WckqYSv7Hhw/kW/p0Byx784MVHJ4Pbp65QpQ+anfbc\nG8AugKBRHRO7oE/BBRAL4bq2I3Ie0qrozAvsNZOQH6xhv4tO27ugsOAYPV+ETdYz2dsxa5yVDtwv\nuL7AFosgNqrl2GUq8WCxbMdHx6lw9YJKxl1onNzq5Tqk+xoSuRlmuvFacL51+HSNDJ8I7mxwjb/u\n5ZU/XyNU53thNqJltf2KY4f1w9r60eiPmLnPhAWCYIK0LI6kJJDOpyda0+cSszEm0E5AqvRP287o\n3ibR2AsvuRARU+l79Z70tL4UgqyD7nM3Fs61UmELFP5VlVd1+uw6SB9yvBonUcrTNV08E8+D5wSX\nqANpmmnlDAsrsaZODecPLJ1Y4k8lgKLWwS3gA77j2+JGSPi23a7Uhu/PMb/0xECsxkeZonJ1srea\nOVDrIVZRuYN5BC1Xsco+hUzUYrIvpRlAao5NKHzvMTAtlS/VsQfWYZe2vvBEEqrp2fxGTItnteWi\nnwHx2D4nonydIBEKh5r6/CyQwk9FNbX5BZlFwvcMn2+TvEoJH5gl/GnSHff26mzSduW8833GipS/\nj43u3GmmypGW8CFUx/Y25/gx09dsujk/jZ6DtWi/V1T6gQ2fqfRLE0lKmlhjD5eSOq9vwKrx+Tni\ndrILy1iLZJs3otaXgquat6S918SeSzdbPyvI0bLqZu+23wah5O4zis10gUo/XgB4zVg571oa28oD\nAIqEzyVjodaPfBgaUNuntd82fo25jc+Lvq6Xup/mXWxTJOEbnK5xHz7gC5W0CZ+NEJ89Wd0+cDbb\n0CWkSTVLKjEsOxHwOPtL+DXpVuWdkGYA5gWPC0gMEkIVGDu2MlpPpu8LRBJN30/VPK46YpVqflV5\nODNaER1lWjldXKQhobYPyBH3iXPT4Luejs1YpGljEPMJxiR70aEvMrskXZ83+RP2phur0mMLitO1\nSvjL4Ts0DWDv02xXueCXpncnyGLZ34arsfiq1v0ZH/zchdlZdL5PQLgXfxCVfvzeAqtq9VVujMHJ\nnKJFwiVwR4fE7khrvjYkGozXIDOh0vc2/BHnNOljICX8PTrdpeuBMO9gu3lws+zB9+MewHW+LQ/A\nctqeP8v8bJCSO1/2qirhDXmR+K6JsqM5Q78vnFSU7LljTLQocIEQCQE1ZenBpGpU77ND3mIjm6ak\nes4ubkpk5Z63qvVdGxi/MAm0EdxjmukyveNVez2mgrf0v2SWsRl2+R5Twl9L13aHPXGAToehH5Ak\nheIgnFhYQmGoYCaCDSp9qbKuhXF//MI3TFMfr1vMVUkaG5KqEhqYWTS4vYz3+aU5zORtzSu39XU4\nFMOfpsVTv8Hu2RW8o4Ndc1rGnJ/2g2gHVxczR1HCx3EGndODhV6wHZQg7OIDqPSZDdZty7EHHjFJ\nZ17EVKxOZBY7Fa/nOB7Rd2ZkpGzYIZeE4PqIwxkfuEsdFpKo9ZHgzoc2XedUfMGJOtrKzLGGLKbS\nJ2bytvV0lS/PAeYCTPbI0I5jMy/tKRO6W0BJxsUkQ5FmqwTXMnBKC6Ct24RS5ZLMRMYxLNx8s5y3\nllabBLltIHPHH1deCqUFgig3C5tzdMwhVcZc2SNnH0Wlz397WrFKwtdoaqFbOhrqbb2KpCRanSjP\nDTnec3OKFjcVvoTsmE7kIft4qOjUDyGrdaSU5agW6oLFrCiP5PeBbWvdPJ1cJEmycvQXipWbR7R0\nibyH/sRfIW+npwafnaEYvt3/7NQWlZPDrit3RcVynxB3PvZDE/DFxDCHu/zEG4FPbFg83QNnJr9N\nr+SRXI2V/SjIn9ik4JgIxMmAx+E714rdFklCrQ/lp2WoSSTMe5eClKS5NtbAqPPTpvz2ZDOZtN0r\ncYNT9uy7Xq5VpW/gXgji3vPdqYabJj+2ouQSX8oGeZdBvm/xuwAQMEslprvimoAe6Od9i0Cl76QD\nLkUHZ3PnJ5AsWWsXjZY+Zj4hgG3LQbAA8JOdjbsizx6otOPvjXMterrMU1JVnQpWWaSg7NwcpM2r\nTD1k5JhwYex8wBeWOj271TvTKhDr91zid+NiKXMPUopj215W8izD6k1rChLzxbx7TTD8QPC6RoYP\nzI11M3sknn0x6fpMrE5xQe4ol6/t0PK3ysop7sQjInKCE4OVS83Se/ncCCV8ZTEcqD0vd1DQHR0e\nuyLHMPcaR6Ea3P++uK9KARFlEbOkaEGyKb/aukitnzphIsL0wNvwESze5jfmVafVl7T1MMarUe3b\ngPZW6asdXMtWTKg8firdNbRsTWNNPtr9iBGycBRyfL2N2ArUSwJ5e9gW2lsR2E3tQk/sDCEiTMs+\nPScpJGz5tR7JLbZxab+XtlUu4UTpV/gcaPWRo782bovdM2e/7gW5sNsD1f41kZZwKbeQ7jUbroYm\nez6XKBPpSxu5Sgcf/g19rKbv5+LJecSbteDrj2m8Qvqqs6uiJXWvJOFrY5nHS34KEn7L+BmG4Vu4\nrXlMpXq+zNk3u17jaHdnoEwQ5SihPXzEw1ViJzihmuCqtUWlfjHpZ1lsACGjtwi0EYh9DkaW2g7s\nOz7iptcs3woSC/lLzIA5B7eae3bwnHUcdKqo0GFvfn23KwXNf66a4c9e+uF5wTXIboUoIHDeqknm\nrs6fjLEA2+o0udUnF+4McMyQSwvLoTuBJmNZAFzaLm59INieCMf0Oa18rNxVx70tC+5NffmC6C1j\nSPvwfDMV+AwENYA74rmdKtzRVrRybf9f26/2rgoCnF+bO3RnApxKf1mBXe1Je056WXP4zorKN4LB\naWnIRUCoym3PM0tL8PvcnEW5tu3RmFQwgKzWslDPNehWJ1atZsmxDDSybcZqcu44xJJbhVL/5mrM\nUJ0vFsJWxQ9Jax1tm6pVxpUWskwZnUb7HCr9Afl9stiVtFbVm6I+lnlJM91cXZXS85kWwdpcrZWF\nL9ItfWdFru3YuOQLFxfVLsYC7fL8qm5nvyeKh9z1S/jkjjY9hxq9NCCuwgttMIzs7OjIYRw/Wtgo\n9rjeOw5qICcIaaecb4U+Lz3tlgfOhz2mGUWjH2eU0uqrKnOW9kUcQ7k2NhYKg99XMAZKi9HZhu9V\n+lzC9+O9Pr/BGP6ssnBMf4VzRy1SzhPqtbjH4/V0PNrTcS/lYJP7naxTxb8hiKsJAgkV8zn9Ilwd\naEfVMhu+McbNi5GzpgnraEsTqQsKS1cgpWs7CnhCodTvjABKP+XX55qwq/pUBbT6Whv3IlhR3Rrd\nsi1bnIdzC/EWJ7wtcUpI0RjkoZob5j8yfom0Uh2nwjqzQsJxT0ujxHPk72macHMzO+3RDXmzBtMQ\nXK+Ev8yy0zR5Kf/c41SsgMn9uYcghPXv+DkF3/zZEm1sCDWk9Ndz96fYnBMPrn2ZZmy3VLy4ES5O\n5CLhUtL+RVWr14SSWXHLJKikLVNT5ziVjsssnNSFi+JBKJUXaxYhF9NGKpoKu2vt5sGE6cHMD084\nsSjtbTEMw3f1TPZc82n21G9w3GvOj9tUXPZxNaodKdMvenWaPST8+L4evjS49VWxjxw9H2DCD1f7\n3LZLC832ib0ljx1F82EeqcVEDa12YWI1EgCWMSHq39ou+c4IKwUY9punjYb+1Xmib01q67a0q0BD\nnci2TEv4MouEfbvR/JYd+7WoLa8Jr3NaRCehJJh+q+aiCc7UVko4k3agtVsciW+8l76V8M2Sjsvv\nmiV8IjjPRJpwGXHRroTJXRSjrJ18QvXTqiR2RVZFFcwd24g/v2qf522bmGt2yDvRsHjnWLhEzJlL\n+Krmi4KFRWASOHB12G0skPhmP2vyJDkgzgw5x6gOiAqzv8ZxQE7bPavz7XHzBicInX5Tus0Mn4g+\nnYh+kIh+m4hORPR5SphvIKLfIaIPEdE/JKJPLKVr7aZAfLzulgFQsqNIe0qkLl2cuWrsPL1tWXuD\n14FGe0495hdDNgB/iJhRXgCardPfkzbxmWlyCULb7iY/JZT6b7CYEsk5xo1SH7UqzlBSk3SulXY4\nnRpq7J2ldHL0tNhYrwWyTXg/TI41JX4ufbWfatVfmF7DOfJ8Ghc5P8kDilT6FBt+DW1VfgOZeBGv\ncpo1fewl+Q4hmI8Clf6Nbq/f24b/TAA/D+C1UOQdIvqrAL4CwF8G8CIAHwTww0T0tJrEue3CvbJ0\np0XlOSeNIZyGKpCT4uW9VJlScsAwc7SRNvxEH+uoym5Kxk3UyiLS0qox/YjhYwhTyhA0HFiElw39\nORX1Uu2rTTTqxHMGWnbALPhOTsIHscX/OgEfD1qJMMa8BcBb5szU7L4KwDcaY35oCfOlAB4H8PkA\nvreYAVlP/VmFYe34hvqpU7OMJzfxK8+MEarUK4IQdvP0y0duQZrocYMtcFzZNIl58itqDtvma/e3\ntxHo6XTNYuTgJgTdkKtomW3fSUNmtviRUfrumboqHx/5cKbZZ+ROoNaNgtr6nF3saYu+1b45gKq9\n81qqzsPeJK4ZKfZv0rTvxlU9bS2+LdDSXe4nk1HMbYFLjtMazHvwp8V+T5NiOt1bpZ8DEX0CgI8F\n8KP2njHmfQB+GsBLKlLwEr5V6U/7nZFVVHUVE+hGyrBQ1bLwHTIRyQYcEwszBEL1GRAeauGkZhJx\nOyDLwNyEkDt3m6XFxk1ofpCqRJ7FPei8BxDqwbFpTK7VEPRerHEVeJTyRhNwb7SYEvy95TMxh71F\n023H7drR29tp72Mx0/K4uP/48iwNvkSzhbXOSWdsv5E6yyWxpR4ijXNF7zx3vTuSEmp76zRzyf4Q\nzRUEfdLmdj/uqc+29J0buWo7xlgeu9QP11SllHI1E20n0nqU0S5wTbCA35xsIi/9umfacvwS+Zfm\nTCNK+BksSo6akMS89Lm6tU8tRysuqa5KkqU7g6hpJuKvom9n5JxakjQzBlPrnHdJj1mfd+wAZBcn\nWtsuQj9TWepOezUOfEl/B83RDtZsIKR7hGMhSFOR8HkaqfqvabMarG3X2ngjLRJa6jAdpz5sqy9J\nzqk0NYfxfAj5/AJHU6B5LLRA7bfKojfUzMXzUomuNf0r5bAXpcXNdQm+IZ32rOO6/bgteZGZr43m\nZht+Ab+Luaqfj1DKfx6An8tF/IbX/XU897nPmVdsJ4PTrcHLPv1z8Gde/DK3DWlNN0o2csompA2u\ngSabsyBVXMckY5WayUQbGov+LGm/J+u9P9+3i4b9DE2I/Aw8UV59zwm2E/Rs/golfM37P4W13fyS\ni7i7iC7SL0iRBpWAzD+EEbArba2I1yXk5uoIbl5Syt8h773hBJDlJXJOur+ZcMIJ/8ubvh8/8OYf\nxOkjJ3zgD5/Ae3//fXjPu/6gOv2uDN8Y88+J6HcBvBTALwIAET0bwIsBvCEX97/9z78eL/rUT8H0\ngHD71AlPfvApfOC9T+BDH3jST3AdHPfyDnv6NM47l3WKKjkZbaHvrGMqUR+q8457yKRiHk4ZmM7m\nFBqQz7I6sG1kGLfmq+xwRc6YviXVqthoVlBZuzrfBtuy4uELB55/SDNLj+UTaFSi1YlbtygSPtKO\ne3uhIZ+z9/cdULUtsWHemtPLV0qu3mybR/RADNfUwtIGTiASYI3vX84y26lNk5rBlMbM/RH0VXRK\nbUuknkHmdwrMnyanOfUCyCzZ3yz772kiGHOLL3jF5+MvvOqL8ZHffRJv/5nfws+/9Z/iJ/63t+J/\n/q1vryIdTIN6AAAgAElEQVSjmeET0TMBfCJ8Uf8EEf1JAO82xvwmgNcD+Doi+lUA7wDwjQB+C8AP\n1GWAQK3hbamtlG7A2ka9a5Dl1lRQ/JnCiLS95ZdSz2pD2TnIKCRpGh9uFpB7brvRmWQgXuMQU6oX\nokXCP1CHvfpw7zRrmeT8LAyWYpD97ddtZ8HPkYIv/ZlMd8QxkNAyewnfHrozM/+nlkN3yEZeITit\nkfA/GcD/CS9/fPNy/zsBfJkx5puI6BkA/jaA5wD4RwD+nDHmybrkmXc+c9yzasstqjxpZ4q9n9OD\njkuDwarTWJrX0VQq036ahLRdV/OZ0OxNnPkYJR0tz3OvnmRbpSR8aZckx0PDtnU2drQzU97WunTv\n05N91GpTuDo/bJO43VzZmWrf0qA7Kqb7fqQtEXnUpFNCbV+/y+p8IK6/VJ1o9ZVqHy0cMTupNRVp\nNVszP/H+JWnb0h9S+afGgZaftJuX+nnqWek6LkDitpg3gnpiwu50M2Fa3pKHKZx7WOx0/grW7MP/\ncRSc/Ywxfw3AX2tNG4AXVsRe/FtSxMVzQKx896JAqntHQK4rSceYeLV5HWqRqBz8GeKFDwC3cNhl\nIZbxrJ81DhT5LNnFsFaW2FEoVuseGAt2Ydy7bWq7a40pYqvwtQVJhp38sW++KTT5EDDNhJXwb5jD\nHgjBi3PWVv0wZ+lL26Zb5bCzw0nOdGvzMPEqa8lZjeelPH3y3xN7DapA26XlwVbQACsmXwCJ+jAs\nYE5bck54KcEzU62vpZw3onYP0lmpLi9UC399r2ubpDofgUZf9cIWtOa6lDRfaM+zvgfVTKUunIY7\nJ+GLuqgdN1o1BD4g9tsll083OQ6sLlejzejXXZsoIQ0HpARh9MW6Nce1IjnmViKpRUCozrfn59PN\nfPCcYQx/LYZh+A6WqU9gKv3990MnJ9MgTPj7zk08qJtsuOrpqpAw4lMijN9uE0s9u7a9KTBbO0bk\nJCdpNfvTuscWrPuOnmaSMA2eSS6csmgs0LJH21U5Q6ZwZVOTg51zJr4lbwLIqvMrVu0ZDMPwY3u6\nlfCnwJ56EQhp976gWORANZy3o42CmE64QSZxaS1F5DeR1XDZMuxH76hteu3wJ1deQdsFJs5L9Aef\n515Os8mc9yovm2fsEA7eksdU+lKB04phGL4FL7g7dGfykk1LpWsrxNwhDDlHJko8L6VZi3MOnkjV\nWxseoXSvOokp6jeZ1ta60tKrCZNq87Jmx6s6eVpry5KrF2sySNKqxOdl4Dw/R+vaNtAcHLWylfrz\nVkeuS6Om7aslYUWlX1tO6ZDGaSvRlHTWFevG0ly5tU9J5B2KkeQDsu/xBcFq8xvCvNY4ItbWSSTo\nLup8mmhm9rwM127DDwpgpa4Ji/PeedT6Lu97jiID1G66NYToiZVqxDnf81Z+XoL3h3vMjPY8tDmn\nPaa9C8nyC9D4WYLWVFoH7g9KwhJbMGq9fZSFFoCQOjndZBjy6O+PcIt2p873TP9kbplKf/1cNA7D\nZ+DSI3+Tmf3UllftpGvbnPwn67R0BSg67EGs4OOHuoOPDHgGHmkS9m4ZRrNnh9oKJaIbgVqeJkqv\nBi6fKM3wZTdycnLjwaXBdavzTW2SnrfyhBoEX4YWwuNba5lAoL5sxCiMp5umimtmMs9TYcKxbC8U\nE6m2eT3BLPMEKfNfwnFvLUIJX2YuvhX0FByyayTSP23pc1X+PA9NJI7WtRI+U+lfvYQf0G8rj5+n\nP51Hwsrlci4pbwScY3fAuaFpH+aT9NJxsl78eyCnfkxMKG4NnFyIjcEkD1wGxphi/w0k4ww/HwKU\nnotTDHeUhaKE34XjHW7tW/LslrxZwj+FTnsrW2UYhs8LQMtSiQh+ax6Fn+bUM3Yhm6fPN28fytmt\ne9mw9kKqDuzv9LYr3j6obosWj9pWu5i0XxZ9NlISPsubp0MKXTn7fU27aSrHmvSsdJ/qn1zy4ZOh\nlPC32O7XIsgvECLz/awnRp3wSzbh1LzDUTO3aXlEfcEpAdrHdOs4yKUl6dPHQTr/2rraSp/kSVq+\nqXlWozW04S92fLYlL07LJlJdnJEYPpPArOo8YPRw+/Evhvsj4BfQoR0GmX/tIi/9nIXblFF9UKMs\nTKzKL5e8XYgVTS0HhoVt4kusT9ze9YzanwW+HC7KBDpCWOVmnge/HX2x4xvnn88lS/enSfM8DMNn\n9ANgNpHgNblwkn9rh4sGkHQSLKCmjzXbRS+JlXR6P4pEOyRU0UGQLlqQhP1SCaceCEJgK+uQxiAt\nNgGGXr+KHX/l5BjEZwMhlL7Y4VNqHgmNC7PZb/VW3gMRuXdcwt+DjmAspGzeWjwezI4BEveUsKky\nFMdBI5L2exQW4EpZetKVzGvNOkSUiZhkH6jznUof/h1ypn3tMwzDt/Adb57dYpX+Xhmrlzp9rUlf\n4Yq0rMpargdSe+Tm0rRzIoJGlcGIrOTTTk9LnNzixWm4UkZ8FxDBQsanJ1Y9B8bERYdS2XSQxRm7\n19bpdLNJa+W4LmQwm7Ad0/eC7gm3i4wvVPr++MNqerq+HncTXFmkV3542hn/nWu4lE1Js+HU2KFL\nA8EYf7Y6t4ePhsATnH8b5Duy61uiLpwKMpR2pW1Kp6X+PPo1+5Ltb82+GdCXoZHfJ/KvRtak/FIa\npTLk9x/HzF71q4AeJtJIsPa08WV5S7Rq16XwVmU88hi5JHr4SkR+Kkq6Uhp35iCFFtm3c34+ch5c\nWx5NW5CbRyQsjXtrdko2e3nfmHCsOdnWpseYvXXam/fgi2N1VxZrOAnfwU5gE7G9+NhtFXxWT+wC\nBtE+rsQglSiRqNOqdlcmwy0oJhWJ+D5eKa42cV8a192fL4/uzVlqj4p+dmmspe/SfTGiexnUznxN\nfkseTbPDnvXQjyT8FWUZmOETMAmVPtuTvwqFChLa3bokL92DhkOb9uRcUA/dKDQ41yztgkSysemS\ngl9RKDZpWHFB2wVw4J4jZw1iC19abZDeB5rGYv5xZkICe3tF+MohR0uCktnTDcEsLntSpb92OA/L\n8L1KHzGzp7K0H6oc9ftBfjbTKuK0DHkedclEyZ65A+ecbLK0MPNKmGArAQ1BTfhZE06qwO13aRFJ\n7K9LR1HpF1FoX24ukE6lzpRSSFouUHgbRyr91vaqHR5KuGO9sRENDKbGZKk1R2iGq6RFTgFb7eMu\nnfr42Tmh85xKWtlJXLemx3nd5Jn9LOHbA3eiyWxVXQ/L8J3UYu0Z0ku/e34s38Sje4FehW1J5xzM\nQBXwCw5Klnnu1edawSYWA925z8lnGtM/cG/R1H9l2Jw57MxoyXMU7WIJch//NMUSfsj015drSIYv\nJftQpR9WkAbNoShQa2bmv2xVJiTb3KEXPbAmXS1Oql5q05IHRNR49Oace2ry36KOzm1Bk7b7/K6E\nNF0th9lIByruBJhNy/Y7KHOxDcskBa0Tp/LodQhJTxS3fV0p1tIfOszFaZbaU45bjZ5gTLM4cv5M\nOfZJzOHbyyfzTIVPzcPyfoujX6595JxX48SYSkf7tufOOHX+8jE44WROOMl54U6o9GPjpZ/sLNMH\nqRPaORBoc65k9ViNSuZ3l+AGalF9WRFuR/gDUSie8aPADYendMKV8+GLY7jhVrGI70LzjuUerk4V\nOBoXHmfP0LfSPQjOfh/ajNcP6XEYvnF/ZiyTlvfUZ3Z79wz1nSYn1df0DrsQS0isMo+ek2AvycYl\nw5Or2PYS25ORlCiNaEKbblXaCZpXFz9h07Q0eSelPFISfmDHr0Uqs8Wmrqvp4etai8fCJpM37OU8\nrTTvgNyYuzRte6EkQZaghjHsU8hDjRukj6p+VpXehiZU5ynEWrkUaFmk+xtaHp00WxRfl9fknNPb\nBT2i/feYwA7dkZ766yp4HIYPhJMXlophW/K8lH8ZYesuSb53dVKtQbgQQc0ItWPzLNCcrpyEn8NS\nFqcJS6QXZraB0AP3C2sWFTsgqaYHqpnupRFoSZhg616Jaxl+4KEvHffa8x2G4QedKJAguYTvD+Rx\nE1tjy6bsoyUkbS8i3ZwNrT6PquBZaAfQaPd53jW2eS2ctPel4rSXoTkKixvaHpNMNBPXhfM/onDc\ns77Fjs/ja3SqfhOwWv1M27gfcZnW+B2swWppdSNG3n5Yax/OIWeDD34rfTHV7/izKt8cgyCs9ry2\nDbLlVZKoHbMy/WB+MuW5sJbOlC1fC5/yK+DjOlDnT7OEYcyt3q9XqvWHYfgeBk7VwVT3E2P6KNiQ\n1m4NGX1VeE7sPXHWpX+eyTvV7KE6/YKdg8R3JkhW/ZUT9Mfkk/cSW8eeeuZEJ5TS1p6vcjoueVZT\nPu20FmCcjh4vtDC/PIdm5z0v3Yt9+K4I7WUZhuFbh2rffpzpU1gpUg2bZf78uk9jHwuDGbwaklWr\n2s/2oKYRxKTlHJNkqvy92r1UH9IkqQeypi6Kths6iWagyW4NRpXe7wSC6bSsabgkSvTtl2/qx7bE\n7Bvy/AfeQ98y+059fxiGzxE4j9iJmVcIKAzTgkS9VXdi3lCaem1ju+zOVLbQR3HbpBz2XIRLgdsb\nCyrOWP8t0mJquqjNtywotbhR3nCdoka7xdskKKMZz3GvNzY5eO6MtCS6JdFMHvyZlofy3Pu0JOLU\nkrVDIwTmzlraEpq51eRJnkPBV2NSXnsNa7/n5usbwsncumN1T0Y7fKc933EYvuKTEDgzEM1mDafm\nPyMzOUT6VRi92lxfSj6/nDSRQpZWZsNPenSfCZeWAg+EONpjI3pXH5tb7JY8Wuz2/i15J+XQnW0Y\nhuHLAjlPY7uq4hK+4mSipikcojSknCmCMOJii6NgrfNcT7Q68Fk6UvernHsK6ZTyn59nHyfTbHbY\nYwtI3akzEU/kq8avpDlFr9uyo0j2al523EDXQJ3TeS9J44p45b4Sj7FLY22fKDl9aflsdRrOjWvZ\nR/bc9VGqq6SmTYRJzk9M89fa91N8Z/V8zcZ1qNJnL80xp+VbahNjumowDMNXwSfaSVTO4WS3K0aZ\nNPdG7WDJT7ht9/WwKVtTfRpBnAuNjWNMbsfmsSeYgebhncJeuyfaI3UnYyhECyyxB5/b76O35W2o\nm+EZPlfhR457LgzyE1ypgjLm3FSwzRPqBTv0Vn8Dzc43zETPTEO6tBObhQLStTrZu3COXpmt7+TS\nbsjjhXHKeTk7fiadS6OVSZiE9HNJlLV5/fNai2BMy74mzK17mgeyxUhlK83BDeSVNBdFDWZDlk4r\n4ARZBAKsZfi4sfvvb9nRuqck3S0YnOGHNg1eOfPjfDV3H/jDcLX9cM4iXlKL4NXeKBaa3J8dYdyf\naHL1zL5eG1E7KV+LJuda6LwEei7empj54NPhyNN16KwHTBNA7NAdx+hxwu3pVpfwDUurEg96FqIn\niAAYpsaXKyHucLWE0SaFLXb84mEOFK8QrQqNf6doOhecQL/CzsnLwMski6WqDhvTb4lTE0bavYCQ\nGW6RVHgbew/4dpttGC+k0/9Y6EY8x8Y+B2E8mY+vk7QvwpZ66Sn9BXVcCDcq1vjJtGWQz0uzxwNh\nnXqNV56+1n5ttUncP2ZtmXuM25L/TS5OKm85N9bkzzWLXKXvTNUTOWZvpfvoTXnx1FaFq5DwQZ7R\nT5PvnERKL12dV59k7grWDqqRJ98ATGquKerFvJzJayNK6ny/AK5M+0qa6q4jxURqsNfZCiNLx1UI\nzI2DFcYu4LkgyzTYIMye+Sa233Mry5oBPBTDDzrvIs74SuGVJBh9hwlO234V8K6KDpSyjUcqt0tN\ntB2dyIjCTxa9x5vJfGyQnDaDMcYW0rn9LUvbBgS0Lsy+decG9+yXtO2zR3ptvJJJrk5jMvIac439\nfnUbbVbnh9+jIKWBrYusxzNirsja72WWmqqtkg7uj2Ynz3AP/hyGO+zJPfhmKcCabjIUw09JLU7K\nj87UF9LZlo5aGXe0wbAahc7iOvvAk2kRWQcg0q8rgvO0z+L8xictOXHJYMQv9qNFfXRXxsaFcRaJ\ndIXgscrZnsfpND4u0c+0xZBKRo22kB26w9X49tu+Jc8evOO25dkM3PUVS/iaFObUmQtjnzLMfsTJ\nZmTJo4SrUc1vQOAHkgujXOfQth2vEIA8nUUQP3hH11rNmdbTd+D8uA9jb2+MdmBWACblW742LYze\nqvYDD32c9HT2lvCJ6GuJ6G1E9D4iepyIvp+IXiDCPEZEbyCidxHR+4nozUT0vHbSyKtduc2D78Hn\n6pEMqh1nstLLBrXSmZE76Kd2MkmVUd8mma+PkuNi7SEYLWFKB5E0NSGTmFNOnWsd9iTdEZ3uW6ok\nE2Xk7SE1+iKO9rsWpfFQM0Zqwqx12Ms58I6A2vmkxbm2F03NDnKpIAWSatvO0xJel2gqzVFrDvmx\nv9U+n0lH1m3Ez8QrcY0xjtkbs9jwAzNElvQkWiX8TwfwrQBeDOCzADwE8H8Q0UexMK8H8LkAXg7g\nMwB8HIDvq85B6igXdT4IAFd7ODtIQ3oJ1E7+g/P5ITFundVPaLYLhgZ9dt3Tbh9lTtqlFlBovOqZ\nyEiM8ECbQNGt7Wqz3MkP5CqwYi6TY5Ivxoms7R4B03ce+kzCd0x/I5q25RljPicsDP1FAL8H4IUA\n/jERPRvAlwF4tTHmx5cwrwHwy0T0ImPM2ypyWdL2Wzq8hC88G2Hvr9y2s4EZEc2U1mzHODdCydFe\nxM+aIBkcsetUFF43Ke1yk/67IkiBmYXSAr+fSVRZ4fdo89I2yUBSd7p6Fl8hUZaD02qMARlarpff\niuZgjQYrGYX3lRUYbWztBt6uvA1qi7+hmuxcG2zNqxaC9LGwdXtnnFG/pKqyq5YCl++U/xlLzzDe\nRsuF42XMS5876zn7fdA/1o+LrTb852Au6ruX3y/EvIj4UU+ceTuAdwJ4yaocmIQfq/QrJPw9Maz0\n2oi7Uo5K1JpxZJy81LyRqGS+YEy5QCxXd2aCBpJCBzXhgb4Y3WTYDan+1s25b5B6dItxodpfbPYT\nu7aH7lj7/a3xh+74cbu+glYzfJopfz2Af2yM+aXl9scCeNIY8z4R/PHlWRmBOVI66bHtC5HkX5qQ\nU7bcenuVFlbGSW3N24qeks6aw0BkPZfqW6unLarKFvt+yX4/X4RlTdnm52fxdY3fiEaHRmN661ZI\nn7a+9QfpeKlhvtbbyB+IkrfZt/a31vbthRSZ6zzKL7fiyfU/DSXtUGv6LXOhZo+upTfnW1Gal2rm\nkhp6fH7pMCm7fTwmE3Um5wm2Zo94l+ahr0n5QSHWsZgtJ+29EcC/DeDTKsISCvT9zW/77/Av/b3n\nYnowgW7mme0VL38FvugLv8hL8k7C96uhIIeBYBCrSw94zOaaC2XOpGa7RaYXettUq/xUZNQ1FbtR\n9X4N6K5mPjAsgmYucp9cQk23M8nMb8CbFdMU+KO5M/SnmdDTcujOrbl1tnsr3f+vb/oB/NCb/gGe\n+uAjfPD9T+AD7/kg3v1776qmYxXDJ6JvA/A5AD7dGPM77NHvAngaET1bSPnPwyzlJ/Ffvfbr8Kc/\n7cV42rMe4sFHPcD0cAIIMLfGqe9nRo9F0merObseoO6CtY5rnzNSlVRbLm63ytmweqLF4zcXlqvI\nU6pv6ThqLxs1FC6fVmZK8U9vWxUPTRxWSyMm0Es4ByO8HEapd27H5/e6Y+vCUun+ueRcuVqyiKR7\n9s3njJZFBWH2n3HmaS/ZTzdepW9g35MXeulbfMErPh9f8vlfinf/+nvxq7/4O3j7z/wafvItP4bv\nfsffqSpbs0p/YfZ/HsCfMca8Uzz+WQCPALyUhX8BgD8G4CeLicsKcxUceuZLB74lI05jY6kaMMb4\nvPPoISjnnDWdGq4ina79qblcFPbtmhgUb+Nrxpm026MwPODyDoJNVWES12fApetpM9aQ36ObWn7P\neNcs4duX5gCGTGDDt2/J63XAV5OET0RvBPAfAfg8AB8koucvj95rjHnCGPM+Ivp2AK8jovcAeD+A\nbwHwE0UPfRNvOvDqTOMqa5qY/WPiNp2SCFgsWz5AIs7Vd36G2jqQ5ba/16ymL4mSvVKz2WnxN0Gp\nL16/tT4DcSI4FqdXAK1dL7EI8mOY971+dOS0SATvwV6isQV+/Lb7o5R+a/dSO4LctUHgWxO9AVa+\nJW85aS902GNYMde2qvS/fMnmx8T91wD4ruX6qwHcAngzgMcAvAXAa1sJCysrVKcETJ/ZONc07rq9\nlelIsmPzQXSOgVxyENOwxuEqVSY5YfTevla6X3LYm6Vf6Gq5XHzWx2S5rPqef9sIchLNlUfS6q9j\nWpNbczKMntPCnffs97X5nJxzsS0XuHvn1eII155+qE2oWsiawvNsfvGcGCZdX44WocQSnZuHSnWd\nW/DXInDcm7yUP9Ei3Vumz/fgnzyjD/rexjHaug+/aAIwxnwEwFcun4bE4aT8oGmEWt+tjCamFnFq\nT1O2pZwL1+wEJW1Tdw2M6dcOoFUDLdcPa1SyJCeZelrdwkZme4WM/cDlcY4pNbl+ueLuKhceXrpH\n5LBn9+Dbt+Rxpz2f4La2GOcs/dSDZWamhen7bQ1WumfblVq1npoUtQJ5id9+n38V4rLcSgOpl9X1\nvZdAZCVVzb5VLGuCIVaNpowEXYOaYJFkQUq2CXMA+xFpBWy8QJMxwgJ5Bc45pIzxn/0z65tcMP6y\nW9HCz25ECamuTuPFfzSELcTJZt1p3grrlW8rtwwf7mNd9m7VF+fUEJ3HMAwfUCR7fr18wgpDsBA4\ncEex5wRY229a+lcwmTXE07JcS+sxHg7shKvxWxpsDITO5uRfmsN42skYJ+Hr9vtthRqG4WtdiFcQ\n4O31blUUPBeSfyVSYWsOQ9HvDdbLFtTY8UvX6rOMLbB0v8U2L59rB/O0lDFHVxzRF7NUlnopP//C\nIKu9aqYVlt/7iSVFK6dDpanTvJ7zX9jTHt6LMeX62p5ozaNlzkqFWzOH5uho9V1J0cW/S3nm0tDj\nluNoNOR4Af/m9cmZPbHPvM8cwRn61n4fqfUXmtfU5jAMPwsnyTP1pvteJridHWksHe4ymd9lV79X\ns/q+IPgisSHStkwj55TabBsmX78qCdQDSZu98XmoDpDXqus/EKD3nHCJXQRbUCb3PP3cm6Dn+cef\nGgtvv4c4ZQ+nYByGRTGzA2aDkDkew0/ZJSNmz44jZOr96r5YxbwTUccX6HcBse+o2Il6WLOyLs1P\nqoTFGGrpiE7/I59PHNnH2WvS4ztPpDm+PS17kQ8XSmH1DKK6DoruFPvU5V5r3162/MB7+1Ig8dkB\nm/yYNtK0abyDC5pwdcRNbSrPIRk3NEFbBk8TvKRPy6E7xp+yZ+33oac+zcPJmFV9cDyGr2EW4Vnl\nedUIV/mfnawNi4YD58XW7TVOk9Sxn9U671WrZF2csglCpeEQ6FXcK6XZ2u7N411xn9p1Hqd59uCq\nfLpZ1PnMYS9S6yuV6O40bvcemuH7fdPk1faM0SNg/D5OS9rJOBkP6GJcmVSjfbcHknlucSLLlL/V\nfs/plDZk+bz0OxU/tRdflqEEL4mJ/hcQopdLo6lk09bsqDI/NX2hEtDaJkfXWVDaWVCbzOo96Ov8\nRnrSYJEbQzVtUzNeamhotdu3+KmU7tXa3ktjIRW3da7OpaHVlVZvXiiVceDG5bwHnx28sxyry0/Y\n4176EdM3mKX8xvKMxfBT1AsJH1YVElTkGFL2CDQcSEBpGtu1hkaL5nf0shw4O65uTroycqtgFwBT\n4kOIGb2Q7p12caXDHjAawwdi/RmzQ3J7Cj94xxtYDqSwhwR3lTVO4jqQqgpRqUKlX1nNtaftEbEc\nua4+Facu+zpcmTr2zqGx/ntqL0ZFau0SlXDrQOg4kLgWmpujJ+Glzx323KE7mnS/AeMxfAnG5AHM\nFNuV0sLo3TxI7LMXORvSvsjA65Rlttiph6GGWQWvEtUZSlGVR8+N/nyX6qa6PiDLFVyX6JLpJxi9\nWl+1HZQ5512jF/dakvuq9NfRMAxy4zYzj55tRxS3pGXybGqGjvxBI4nED8fslwgho58CLfUs1ec8\n9FnqKzvfMAzfLDaJ0jGjwUqJnal/neLmflg7GfUazNeiRWyhc1XdbGUKFYumQxK/g0gsGEdFT2fW\nXtg6B3Wbw7hmmqn1p8VZD8sxu1y6t7b74KS9DmxuGIaf2vXrHfSIVVx4PKGtiFbnkzl9nk8bxZoj\nScrxJnWvp3S1lwYhVad25VpT36Xtea11lXM605yZIocb0ttMyzdVlpb4Jec9mU4g1WRozeVZMxZS\nB+/USP8t46znYTVb02mJXwq7tlyj2tVLTnzJ8pYsXcpYbXa2K0j6Mn7rM57XqjmNwmfqx56hL+z5\n89Y7f45+zVvy1oyCgRi+AvLfVmXPGfw0wav2VzDsLrRV4BpW6F1xoblsT5PJOT3JZb5qzpmko8Vr\njSawa9WNyczuKzYtLtZEzcTZU+DZHSvqItRGk2P2fP89cfs9ez2u7qE/E7G22sZi+Fajr4r6fKVn\nGbw8cCezPS8xAfZEzcDas4N3PdhijX3PtUMianYi0G7KMIr9Xnmm2rYRMsKSxqGIinRkmiX/hCjd\nRNJNzVwyCcg6NOxao1H61JYS5bcGmdv7atW6JdUXwSKvgsjcuO6Ai9UTIV4AC2Rps3OaVzKodRQt\nsF08L4wSsdP1bmg+TZe/JQ95L32f9frBNBTDTxaBdcbYhi+25yHPWKJ0N2BUtdwo2LL/tTbtdZG3\nxalRk/dCoNqvjuT+tEQ4sBKjzgN70dUr3auS7lfCC6QL45+k496s5jfGqDZ8FRlXtxIerC7JHnBS\nhXdSMDCLWtPbXgFmI1leOiAPRNEOQ7AVqNnetTg5EFG8+pLxDdS5dO+OLm1kOZtZjT0rdc8YE9cr\nWxFrNuq1h3bk7PX+R8oTxOe/dbIK+leibQm02DpDqVmlOZG+vE4hbQdFVgth6TLLtgFLd1SWpc1y\nNvMwnkAAACAASURBVNGcL0It2vpGfbop2mXf3QJtXimhtY5q6Vxrg075Hq2pI5uW7D9b6nzN2HVC\nIK0vR+qTzQuItCX8KF37IabWj1T59phdhD41WxfnQ0n4WTA1iWXyvDG1CfhsC+8xF/j3DrX7VUsq\nvjhCpzAtWToC06r9tnTqcQ8ErwMdMaqGYzV6F4er84kCZz2asAi2s0rfSvec2ftkFIGyEcMw/OpJ\nxjJ2xuideh/+fhglL6k2N3Cg3m2MKzCSWiuokhZpxf0ZE0nptCquns72dk/nx/0MON9vRa22oGcX\nvGuT/0DDU0eNeX6VSSiTZbLztmVzzShWqZDwwRi9k/Bpvm/IRNJ96sAdwjZXmGEYvkNUmlBdvPxY\nmLxg+hoTDyodQ3RKufWpf/r2wufHf9elUbH1Zs+6zKnBhc9K1WE7G9Z3QTK1k6cR1+xT7UTVmo+W\nTCIdaWrI0jQ601sBuRVxW1obFgZnmI+K5dNo6EmXsNTO17XauLp7a9Pakt4cOf5N8jeT7AMPfXvK\nHmF22pMOe6qHPvn6XDEwx2H4lStVZ5u0ThBCpZ/zbtbSa8cAK4YD2yBHZG00ax8NXHbzaGEm4XqV\n9ecd0Wvr4IH7g6O9G8FV+tE5+nAq/ZPipR8kw6t9paP+OAw/Qb3bmsBNmo7RgzF6dg22CACCb82p\npc3ZJk7v0tvxeqVfKkvKVNIar4Q1DntVjnBCPa/Z8pMH9rgbSJqNUjTU0snzm/txup/lDschllaU\nboY+7eAdLb8S/WtQG6/vlrq+Y3JPrd2e0PpyzkkzdW/LPJg7hEd/UMyqPq0V4XJlVh39GJO3Er49\nYc9vx/OqfTcOl3+9FlkDMfxFNZY9UYRJ8LwiuVq/tBm8ho5NsQ8E2FkYqFLn98CKPtWFnlVKKIqY\nPXt0r3CF/FfHwCaDvbHJ36onHa3hmfZ5WviTP3AHjn/ZPfhcpT9L+3KHzyKgmPWv0xmK4adhAmbv\nJC4r2TMHCC/5n1n1VMhq74mnt2RRXXeKDcunoaVbkWbJfq/cry1+qVylQziC78q4LRI+kJDy1YSL\nSdWB+XzktjyWT/fbf7z17Ob9Jfw6+nSpcHv+LVJ5XYL67aDeMuN/KwKyzzCVRwtj8t+hhlnQRCyO\nDbNczEw+ZP4ktuQZy+D56XrGLJ77xqYUzgQrmf6YDF9O+PbGwtTtNV85udVP5859H6BNCJsnw2up\nz9p1zaXKs2LSIz5BrcSdkYwP7DaWe46JvfvbJfwOIiZPi4e+YPxWhX9ijH/eh2+irXkANi30x2L4\n1paovTTAVV4ovXuVvpf8pf1Eon67Ur1N7pKOLJpUVnPoTg55m3winCrRx/bBFFK249y1qfR6L/UJ\njZZcGvZ3rhzSzl7yDNd8TuQzPS+WhvvWy1uiWbtfQku9bsG57eNr86vx05DXJf8Ke60d5KSly+9l\n2yX3qMGWXYrTquXS0gzm/Y59LTXech8tnh5Wl+yxOOth0h32siftbcBYDB9QO3N0i6n2vdqFXZ8B\nF+Tv+0Co4q/H+WglnYO3XziJKAF2ap4cQzkwBlqVuXuY+3oy3D3mmnObA2IC7IcJqfKEveUteScT\nH6vLVftxokIj0tAW4zF8CyN/GKHS9wyer6Tsfe9Nbb+FFFJTRxVbH5ITcmfkBsU5mXNQ/QnhXquP\n6gliR/t9T7h2Z+pzvlCyjNPSFkr4iMoZ9E9pEzwDavwPLo1zk7I2v4GqrAmiO++Cs9SNEF6CR70K\nJ9Nh/CaQ6h3Tj5k9f0ueYQfvWIe9k7DT27bRtN+1GJfhM8zz4+K4B87EuZRP7lktc1nV+JdeOTZi\n7YQdqLd6EVPCjpNBT0/fc5hvQnoz+VUsSGsxEnM/MMMkFrktqFLNN6R3PgfhrQP1THESycz8KPTI\nn5a990QE3NBio5+ZPH9pjtuHr9W1MGNSA9FXwfADWOln8tI8uZUAAgnpXmPjmIwG9T2r001zWqf5\n0G81XZtA4vrA1WJNvxxiIRcsXMSjJH0D0L0WgZaZnEo/lvBNdMpeoNJXEy7fSmGot+VpzeuOGBTq\n+aAyp1AdKh2WnOqVYavzxxzPuDxqBpUx/Q5Q4GluhebYlaJT3rf5Ww2LNKXw561miZwzYu5ao3O+\nl3+eo0WmEfStTJrSqS6VT+TIVcGsc45/NfBmh/BNedwcYdvtkk6pjqYNcc9N/wh1VjPHpRw6tfGU\n6q85pOqh9RCnGmfZOK7xY5Q8Lb3mTPW35DPKgTvkpHzgdtmDH52yJ5x+1TKvKMZYEr5BcQnrmbpU\n7Ycq/l1QSncAKar7YnmAMuVQNXa7SrrnqRCXS+VkGd1qKHOLSvDA9eFiZ3RsymP3LNrzaQgb2fI5\no3ee+sxpLzh0x2/JU0lwt9vbdRyGn5KC5A0CYNX50dYjefAOghXepbGHZm0IdV2PhZBmqio47EVF\nF85wxcHc2Ceko2JVHsCyddB//H2l0DY926+zCZfzDpJOEBtMLCau3yH62AZcgvxUnj19Sa4B6aN0\n9TEhsXZLYS4tzh/0cCxtK1TyZ+w6Ssup8r0G0Er2E80frua3r8V1HvqLet/Y43XZwTs2gy3deRyG\nj/zCxd7i6vzQM5J5RN6HkbQXFMnw0qpJjiTzqRwFZy/JitFZYgo1/Xvtroji/QvhytccF0WsflYD\nVae39wJwlOkmSUcFfdz8zJk+34dPE7xCP7LhJw7d2Ygmhk9EX05Ev0BE710+/zcRfTZ7/hgRvYGI\n3kVE7yeiNxPR82rS5h6JisIyGPEzX5eHGiCwI4c2fFIn0ZT9KlP+pt9APDh6NmAp7WJeVR23bDcr\n1V3puUb3Fvu9zDvc8pa2BTalU4EU3aV85LX8lqq+VHrZMaDQmjv46Nql/FbsVd6WOeecdS8pCdb9\niXmuVRBoKcce8w5PU44J7ZkWVkszG54doTux69lhD7M0z7bkGbsdT50nWN4FzUgKrRL+bwL4qwBe\nuHzeCuAHiOiTluevB/C5AF4O4DMAfByA72snK4ZbCixSPOC/3TYHJu0HKpkDF8NFVuutdv01Qfcs\nV0bdeODAgUERaZ69UBo57PE9+GA2fH6ePjtS3gqzNNsBVqPJS98Y8w/Era8jor8C4FOJ6LcBfBmA\nVxtjfhwzca8B8MtE9CJjzNvqMsk/YiYSxV5iJTi2AICt+NnT30LaYlqQrXMqlMH0m8xjaaxPuilo\ndBPpDmNEmOs7sKlbj28Rp9J+nzxs50LCZ7I8C5yHsu247kEqQftFwe/oujOMMSCTz2AEr/MD+yDb\nqoX5zAWjCu93OQ7UdBI0DAZ9Lgy1N473sDfkgRAcusP34If78L1DUmzC0x36arDahk9EExG9GsAz\nAPwkZon/AYAfdWQZ83YA7wTwkqpEs5P4UgFiBcW99P12MGLP16uEWpBM6n5pQoccnAACulY1u2C+\nq/1EtP6Q06duRUNa90xrn8VRF5dHyEC3JrYxfk0WJD/ecS+S8omcRG/Edjz9WF1WCOGc3ILmffhE\n9O9gZvBPB/B+AF9gjPkVIvpTAJ40xrxPRHkcwMfWpF0qg4FhmnqvtueMnVfw/Duif5NNjIhWr66u\nDa0LokphYCisXvSxvjeCvVePH6Z1X/rtncMVNNtZxsGowoQAp1dX6ftDd+zBO/xNeadTToLfVglr\nDt75FQB/EsBzMNvqv4uIPiMTfjMfcIVfVEKRvR7z9TQxyR5+wuMrLf7bUtfM2IgAMsHv2gNmgPXq\n0doBVeu8t6rcyj310BsCAKPWTa6OapzG1joz1TDQ0mE20kEnVR5+P/W8hr7AHyWRvkxvq+bKSRcG\nAPy4uZRavwcjaaG9F+O6mBmk2USZHtc9GDmvh5o62VpnkuaUya2UZ4oOzXlPhreqfCnV2/FsKOWd\n7730CZ7uxUDgm/ZcEr4x5hGAX19+/r9E9CIAXwXgewE8jYieLaT852GW8rP4H//2/4Dnfu9zcPPw\nBtMNgW4Ir3r1q/CFr/xCnzdzYvA6fDimPdtN/F58uIbZcYk8sFjbeprVJnSshz29kjcV9wwS8x4M\nIpL02SLhsMuPi+Qw6NHtrrTZd+2uhbRzeYdjLFTpT2Qd9bBsx1uYvhF78M0Jp5NX7UveRQDe/L1v\nxpu+5834yIeewofe/wQ++N4P4w/f9e7qIvY4WncC8BiAnwXwCMBLAXz/XHB6AYA/htkEkMXX/Kdf\ni5d86ovwjOc8hofPfIiHz3iAm8du8AiPXBjDjRcBow9tJ5bRu0Zw4fpO0MmV406LgGpG2Jo3N43Y\nW7nOb5/ZpkjUA4HCRdqaOhnQYU9joFF9LdqowHGPP5YVppiecm1gnT+T/U8lHMX6sg58zpFvAMbQ\nY/3X01l2KLSOK0pcd0g6hWBhWXTc69xIohBJjaS7Dr+d5Zj9VklVNMjyWF3Pl/wZ+vylOTPjtyfv\nGUwUH7Lzile+An/+M78Av/dr78E7fuVx/NrPvwP/z1t/At/5q2+sqo4mhk9E/z2A/x3z9ryPBvDF\nAP4DAH/WGPM+Ivp2AK8jovdgtu9/C4CfqPbQh6nrYQFzR1CR1jtyoXeICUvizk4+6MTkazGoZqUn\npORw4MBdRtTHW/t8zzknkbc2DlP3tBfmYAJABmY5WU867Nk35RmIsnQY/60S/vMBfBeAfxXAewH8\nImZm/9bl+VcDuAXwZsxS/1sAvLYm4dlu6H7Ez91OfAOybx4gbuv0DD64Br8f1ljKFlMDu0rjabfY\n8Xsja9fOkJKyT+fA7XHBPVraaUPRc7b62sN2OE3cFs4/rbTYNEJHUTAtBwXxWmygWhtI2mvoS/kF\naH4HalomHHr8Hi/PaKj1XxiVfg21fjgaWsbwudBqxwfS46IFnCekxqOcI7R7Wt7hb0XCJ3uc7nLP\nqvRp2YNvDKK35DGVPqKteUxLshKt+/D/UuH5RwB85fLZhJr+bT31rRqfb8Wbf9rr8fyTR5t8BiLl\nAMfahgn0kHmM1hcPXBn21uSdGyuGAjcFOMne8iEr2TNV/63yhjz3+2RfnmPJIUcWJ22NUDnU63EB\n5pinPAFmmwZX5wcMnsIFAAWLAWVS620uIrZQOfP82VuhkGQA0oaV1R7AtRewQuuhKStM+lmajgsx\nM2bHr0HQf+0990xJPlf3iThrMLwJqnLM1Zbj3u7Bt3Wzd/mLdvydxuwyX6lprzEdQOtPjB8Fb8YL\nr0/Gvxb31tziFreLDV85aQ+WZsny2zHUy3PqYOJZ0KpM7LdVr7D7JQw9oe2B4uTYd9RvSe/aznHv\nSm9Lv9QcJ1s69nVV853GlXX586KyS19iTncS/qLOJ1q25vFFgFPpn3BiDnvBi3PcttgYfpt6eycZ\niuGH9DN7LbPfu32JFDL1gLkzxh9s2VM+W5Cz6dTk0XO/75a0y/apdLxkWArD1dihA1u94p2fiqOf\nShXTmUOtnV3zC9iSrswjlWZrP4rSobp6cOkldhWU6vrcCGgx5fouP+9B1dhI9QPZZ2r7y5rx1TLe\neiFnl9fKnRqHOd8g92EvyfGSvSLhS5X+iTnxpQpigq8mDMXwAVSUgnmAwzN7uR8/cN7LIHh836T8\nFAaoh/G8Ls4MRa2/J6IJecus0hHnX1zc8353YBu4uXniZmW4RYDbf4/w8J3b063z0AfCOXDRW7vf\na4fFOAx/TQG4ZA/B6O1zHjQ1cw7A4LphhPlq5EVUL3qEBqM3SORRROVOjGIy0kv/wGr0rL4ebVHd\nDVZ25+0a07b7vVHMp+h3YAXQ0GEPTuLHLN3bd+S5vfeL/f4k7Pds15cn4a7a8NX+bR0ZTOi/wFZQ\nk6xwZ8NnK4Htvg8RWjt738mgX1oqckUTzL25WlMMRlHpaw57NSp9oKzJKdZhisGXClzZNl5F6CeN\n3kiqKjX1fXSPPRsJkpwCeSXyRyteM7jmc4d0o9trszlzPRPnFdFD5ZrYFxuOxHhHMA24cesl+ckd\nrYtAvc/fkqfZ760Nn1fRLNQuqDBdpTAMwzfsb01ncB2aRKNIOz5rnHOtFEfA2g6x9yr7LB7zd6Sd\na4tx9UzqwD6o0LQ1D5WdNVtDobJ4AS8ir8a3jB9E3kufyJ2wZ2Bm6d56659mL33nL6MyQsKW1dIw\nDN8K7gArDrtwkhwMDFlVB5OGgsr26n3wa/hnOQeOZlyw37ceRmORK2vLs5SjYmud1jjnpe7l0og0\nEJ3UjimHH42WOg0E78N20brd8VNrh5Y24bSPJN3n6rTGcS/12ROldtToaDm0qXS/pxOeFrbVgTV3\nxG3ufu381OKIF36H91Jzms5HQmne2/EX6Z5MuOfe2e+ZOl/0AW+/X2jf0E3HYfitoPAjVfjhxBk2\nzigYaP5MYqwa64e7Wq4iOhT8nIz/GsbIfUHJLDYUdqZPqvO5kziR35LnVPz2hTn2H9uSx1+cY0x4\n6A4vCC8SHxctRR2K4bOTBHOh2FntIVOHXVkRYfKn7wqVS/iJaquxo8g1xGBrirOhqtzVOurlq8J+\nn6cpn2FrW0WDPJNX5I+wwqmuS19KmmgaFsCjMt0UXRV2+tTnUvA+EoKOGpoKzVjVzg19bW2/jMZr\ng9/MJgbutHLsN/9gfZm4Jg6ROh/LcbregS8l4Z/MrXtxDnfYm/PQiIv9bGowFMOPoBTIzZ0Bw/aH\n7RBhqWDO2XdixAMw9+bJoQVMfX0NGEnlvAnXJEkduFps9fi+V8hUlSbhWwYPdj3Po/N78vgpe5zx\nz+p8tgdfyTea5RqacTCGb5Qr+5utfAziSVFWNpEV+pN2GE3KaWVuml2nBXucQLfWrq+htlw15a6R\nKrUX5uTu1eSp5Z2jJZV2yZ5XSidlK9bSqLHdl9o5TE+3OabS1WlPl20rRk+Pp7vW7r914Zzrl7V5\nBM9ryWEL/1L/KaGmvlJ29pbscvb73PitncvzPMUz+IDZT5hZfeSZvxype/Ke+no9LfTETm7VGIzh\n18Gq9EMGj+Xe0lBsxTU/6EvDlQi9WVxScr+q+rs0rRfM/85oTe4p9hhn16Lx641ssZmJwHvnA8ur\n8pZX4sJJ90ZI97PTnmD0xg996qSPGY/hK7Za7bGrDS/Geykflun7ewA3ASy4n/02XQel+tixvnoz\nFrq2dt6TxrVpj8zrR6ZtJTYPgWvo52dG09pEC1syB1smDyn1Mynfnp+v2e+jt+bZk2acWJsk0ADN\nnWY8hl+E94Bya56lwoMFALgaky0AeLgFvRaswcKiEnsIUNoBNjmo9BbKkGSoxH4KzUsVOjnsSbRI\nJdWH8DBtkpaH6qRUSPvi0pNzYCtvbRsae5FnxOeMyFb5zt2mKF+OvtjIzEMkeQFj4lo6ck5zzH65\nx73y+aE7APz5+ZCn7N0uzJ6/Kc+wvJb0eb+7K057NZOJYRI+l9zjrXhLBKni74C76fTSa/XTP8le\nWNNu52zrffIarBHuCgZf9wCWWeTbP5oXxU++Uexci71Wu/2eyNYf1yQL/gPyzN9K+Japxyr9WcLP\n5gNCKPm0lWMohh8LRAmnNL5L0dVuKM17xq8fPLLF0c7FkWNkZe/sMYDWOA9pTjjhapfUeLnr0rPS\n/RRaDn/R2jsMkM9DS49L9TLdFue6+WaKZpZXsIBd30952iW0OoHuPfGvPVinNVxtWlvpWZNnbfo5\nBzRjTLLPr3G2LTmzbUXVnFGZTW5ukvdyjnihU3jqmRcqrZOel/RpUdOHkr3+8X1tngrsgs3TvrbL\nDcXwAcbMswUybmselm8+UVq1CoJGGGvFeGA9hlcnj4Cjnx8YEHdm7HJeAyFcTv4ZHC/yzN4snvqW\n6T9a1PknY3A6xefo8yzNyv33FsMxfADWGyGxD9+/PNBXOMIV2ESLc+SiiGFagHgRsCTcMkFqYTdM\nsGvHwK578DOQNix53/3uwHU0+/0IqJVkNh0O1NssUujrWQnW+VaUw++O2mx7k5dKb09/gQPtKIyV\n1PyfHIqceZO7FarwQcx2T+yZ1wIYw16Ky16JK0/aM+YUDLRAw2KHolnH+Idi+HUn7QGRst+1HoTq\nBQGDt0EP7IeAye9Q12NICPt2ohWayzuJIZp6AIzR568Qew4ep8qHFzwTH0zzxywvzDlhtt9zhz1v\nw/ee+rkCGfa3BcMwfMO5fWL1wtX91i7lpHjYa2bH5y8uyNln0GZ7KoVdY8dqHdQ97YnSRmfv5cL7\neOI+hWFS6WvQDtjRvu116eCT2nxzNOhpQu03JVt+Kr3UdU3aqTrgtsUaOmsOCfJ1o5IyJM7tHzMC\nWsZybRq14VvGubxuoWMtffZam/9zeUUfeClft+tbO75P16n0xda8iNmLcdfTiXcYht+CaP0TqWaI\nafC91yQPr+I+i1MMRNc3ydWgNEdcS5Ev3zb98798mQoYnLwD+yCn5odbLLCPtd8HZ+gzZs8O3OFS\n/ulkPfRlR1vy4MxpCbamSw7P8Hl9h4ze+AC28q16ZRL2FXUFhvCTyHM13Y2JtM53q+fHSrqapYKG\n4KW0I0nShPd9QDT3+k1Mv6KMKek5y9CUxWieTqbaU2zrrfSlwG33V4se9F9jHXQSXi4mA6UEtBUE\ncWEwiq8Jg1ZRKfkCG5tOyqeZGYf2e7hve+/kFPrh0bq3i4R/y234osNZZs+ZvnF/2jA8wy9iaRkn\nxTsVvm0g8msBrgnYlN/1IznxL7d3k7hy9deQ5abtP2smjSDv9Vkn029Ks2ULZjMpcw7XyOQOHDgX\n3EKBGM9hzH6y3+QlfHbojt+WxyV8uyRImOg46h3eAgzP8FP2C8PEu8CO7JZnnPETolXcgXuIhoav\nGEs0Sp86mPOBK0LzSaBscG2zZ6+JS8FX9FQKmEzjbPfgg2iR3E+BhD+r9Gdm787SL5HSVnURhmf4\nEnwFZMCYOVPVS4c9gK/Ayo577Q4hcdy9HPdSbzKrTa+GrhZntz2cHoE6hz0ZtpQnb6c1qK27telq\nfTKH2n4g0y6lqaWTUu+f2/a+Jr8tNF7ikJ8e6W3SgDWms4/GK5Di9OtC3Pg7Lk8gmUPjEz5b3TmP\nM332cbZ8ykj3TJ2/vBpXvkDHmQw6SRRjMXyhpSh3esPU+PZbTp4IPhZ7dNIRMJzz0z2o816T617o\nTd9oXezAgd2hLEBCRo+AF3mhk+z5egvT9w57TqUfvBb3NLNBN8h6aTdmjMPwhQCRPuPCRFfBFqRE\npXuub6vQh+WOG6kqTVb1Beb6aMLtNAEnzfoFph09t783qLyzB+5I81Wq/Odomz3y0OqPIcVwS4y4\n2gTRIMmffYG5JrstJNbGHWQRdO7FZ+/80lvjMnFQnp+jvk/KM8s7lmsvRIZ0eMl/cdyzr8B1PGj+\nzNvyZvu9WbbjyaN1vYTvX5wD5rjntwEuRBg25lZ47o3D8Dkq/BGcUt81HGfmCLwmgYDfu9+jYTTJ\naUsVBeNrwLrehj25/IED6LKA2H3c3aMumxR0mBbZLRim5feyW+wUSPjhq3FvT+GLc6Qdf4PMpGIY\nhm9XNkC+rzsbvg8OftiOXVmF6nzlQATF7gLkVpjp+/zZ1hVvTmJK2lYr4kpEjoyIy5KMV5N24Zqj\npQx7vha3Lj0/+Lfa3ON0SdxLp1vrt8C/g2cV00f+8J11/a4Wpb6+Jr2W+K3hLwG1XS8g4V/apJWj\nQRsD2pxf6+MV8w49vjtwh7BI97O6Xu6/t/Z7f6yuHHOJMbxI961ddBiGb+ELWmG/l3vxo2vrQOFt\nLO77Pi1Pa9BsyzgvRp9890TX+TSV1v2t3juNvZjx8Fq7HelzdeqETHjpnn37N+TZM/TFHvzTLU7u\nWF370pzCQSBMm79myD5YEWc3mOgiH9ZtzeMqff4B/80l/Dku9Z7kKKSdqF1Nb0x6MKlp5dUhMX3y\n1mCMvsjYV7TZLpPTTvVTS+vW9U/y1dPG6NIEhde5fjokYh+ouvBXhCRzJx6mR0bQ6yd1/0xIZr88\nyJadC4r8tmPg4YmtUsJ3zH/yfmMznzn5F+Yg9NK/5RJ+oNLXK9GRx2Xiq5bwjcb041YwjN3PIfgq\ny3N7WhYC4baMfhPVVU14GZxDJXdptd8Imgq5mDl/nQxQCQcugnPOeWv6tRalKq/mnBrSS62fAoHS\nb93zEj45+72B9byf/1l1/q25dS/NuT3dum15qe2vi3ug35K+csW/ieET0dcS0YmIXsfuPUZEbyCi\ndxHR+4nozUT0vOpE5z0JPo9iYDDmDqZa8dI8TaEdhtFaTdaWOOfCFrV3sVw1xaZy/Wr3rlVdP3Jf\niEAAYJp8Dmpxre1311Bt09/Y9O6o14H7vzYPrZmbsnEW3qLynIXp2+N2ToqH/klI9/xfDUKxtw6r\nGT4RfQqA/wTAL4hHrwfwuQBeDuAzAHwcgO9blYmQ8nnh3EqH6eUDFQvAztT3an3ucOHj9JkENaer\nNZDOG9nDUDbS19tJT7vX6tBW87a8Fmx1qONp5BzhNoP3zUANW09/Touwhmae7tZ2KOVxDpTG0wjO\neiUnSYuSCn83hkzlMd89y5XzkBYmcsKTcSn4CqT4iF+IMUuE4A15ltEbLCfqMWb/6LRI+cbb9uPx\ni8UpfSGg1sUtgVUMn4ieBeC7AfwlAH/I7j8bwJcB+GpjzI8bY34OwGsA/GkielEp3bKPvg1nwiun\nyrc/4BtiWtajbDHQW7V/bRh5ZT407lm1DSe4j0bPtWFr/71H/d+p5v0dJjiGn1jC99K9SZyw5/bg\nn9g5+suWvJDpE2NplumvHwhrJfw3APghY8xbxf1PxuwI+KP2hjHm7QDeCeAluQRzDnupfsb34lt7\nSrzdLpT8fTgmSVEmk0oEC8SNDNXuUJSfbQRujK+lt/cEYD1Sg4Mm9s2rCkFb6/dbEUri69Npy7Qt\n+F6Sry5t75KVd3RKOcCudX/uCZZ/jeapt4mmhEtrQHL9llI/UnFK878UDBcOH/AQMN4zkbffk39D\nnrHb8U63oZe+dNhT9uHzHWWuiyZs/SU0e+kT0asB/HuYmbvE8wE8aYx5n7j/OICPLSYuCptzbK+f\npAAAIABJREFU3FODRCuucBEgwxnCxsG9OYFhsVUVfN9ARG4i5NfbE+6TzIH7i2sdv9K0lQjVO1eW\nP4Jrrh0Ot+BR9JuIIu98vgf/1shDd066Q55dUKjlbJ9jmiR8IvqjmG30X2KMeaolKgrUqe86z4Sb\nD99ZPrzinepF3zbhPpCagPaOkzShXWCA1dqg5bX226ZXitPLZyGHLXbjmgmj+bCiht91ierxa9OK\nDsZJxC05MWnpatetYUZGyUdmj/xyv1P3ctDmr1T79/BR6uX3syqu8kgGT9VDKl1ZJs/YKXhu8494\nCeM3VuK3jnxWnc8P3HES/ckeqxt66Ec2fAhmv1ED1SrhvxDAvwLgZ8nX4A2AzyCirwDw2QAeI6Jn\nCyn/eZil/CRe/3e/Cc/9/ufgwcMJ04MJdEN45StfiVf9hVcm4/Cy07Km4Aze2vZD5r9I9kTb9IZ3\nV7hPMskrFRRWo7p7jN4X7lm7HajAKH1iFDo0CBHf/rInu0J8uPQfqPMxM3Juv390slvzTrg9GafS\nJ/I+arT8Y0TgTd/3Jvz97/n7+MiHnsKHP/AEPvz+J/Ded7+nukitDP9HAPy74t53APhlAH8TwG8D\neArASwF8PwAQ0QsA/DEAP5lL+D97zX+JF3/KJ+Ojn/tReOxZD/HgGQ/x8KM08gwAux+RfXjlA2LF\ntnwmAm4JBDPP0eTb1BjonW/jRL51XZFFg61vNyzMTivnWj5otHI1JnRNasxNpBbqJZZyKitSjgf+\ne7nmh++oB/aMjksv0rQ5p5clqEdT8O4y+qKWISBVliEVwX5x1Tx8Pc7PuN+X5qVPi4c+ALf/Plbp\nu2+uzmce+qFKH06TQABe8fIvwp/79z8H/+LX3413/rPfxTv/6W/h5/7RT+E7/r83VtVNE8M3xnwQ\nwC8FdUX0QQB/YIz55eX3twN4HRG9B8D7AXwLgJ8wxrytnAH/ru9d3lMfC2f3v4kI0xRK+YYIoHVO\nD3cG55Tir4wP3CtUTORXyczvKy7UTLsKNueCrLtQuGbCY2jLR3R/dtizUn0g3eMkDt3hr8aVW/Ji\nCV+eU9OKHkfryty/GsAtgDcDeAzAWwC8tiWhMr+XZ+0ZEE2e37NVkVshTXw1Zlzj2PpMTWopyVk6\nZrnfYgLt6sAV0NUQuHESSNnpAsdHds/WnVyZbllQ5eqMO8dpcGadijxmuu2EtfSBKqnZ0+DUeLVO\ne0wLVbLBynJo/TSVFbF8WhDkIaRQ3tY1tHXDNTCTlJawECd3zPFa1NqsLw3Vn4Ti58mwFemX54sl\nXcTjMRqjAXPn9yk498VuybPn6Esb/qzSD0/ZO5kTJpqYSh+hWr9Dk21m+MaYzxS/PwLgK5fPigT5\npVG9EwNVYshdmR7GOAYfqPltcmx1VjuZJINeRN11DTPgtSCcqVtPr7rLSI1B9/xM0v81tMmaurqG\ncpWwl1BzTmitRspDchyfPXPSvtcuz++2959g/72x++9vZ9v9ib0WNyNgcqzclTfYWfrQClGaTIwI\nJlX6fDXGrn2QOVYqm5Vz2Sgr6EsgKHptNXSYL85Z52uyqqJPF3TKqF203t9uedXYlZ/u0CfOMRa7\n5CAFQPvTCY5MhiT/LPzNJH/noR++Nkfa7m8XCZ+fsCf34MekztpH1xdW9InBGL4Je3ayQItzA3Pd\nC2ws8A0Ay9zttaKSiRqyM3bp+ysngFBFpmg9tiJg9qRd1iFTvuw2qoZ8oiQ2DKSIjME561r6rl2S\nGw7C9/hAH5D8EUh34W+rOgdCRu6iW5X9EjjejufDzIn5V93yk/a8hM/s9yd7zn769bjEiHJPV57G\nNhjDb/bXQzRShNhu68rZWm0g2eiDT9BXiSthDldC5owOC728/nJfOlbjGtpoMBqPOW0bXPVxlT3g\nGL/TItswk69zp9KXNny3/z522Mudnhe05AZ/83EYvi2s8ZI7AJCJOy1fDRnL74mthBiDJ36N5Wx9\nIeFLBw2OnANVLkxNvDXQpNs1h+6knMVqaC2FkXVbm26qXKkDXnIvipH3atugKMEKNV4LSrQ4jcuS\nT4nmtYe0lGjhWyHdJet3PaX8HofP2DijvPzmklgz12ydn4LxXSFA1cwftfkW6UE816lzUwVPIEAN\nC/bNHfa8VH8bqPT9+fnxoTtG4eaBATqllazEOAxfIih3rgOw5QGT5p0e30n5QvUiwQWge7gw3rvM\nbgfDXccdKmONQ5l6ZsKBLuhSn3egP15iPo7NnZ6XeP4CJ9m7/fcLw/evu/Un6822fGu/Xxi/MfOz\nE1tkeypCmtyVWBQ0dJNxGT4Q++NpD2EnJiPs8WzbnZPq+Yer++EzcvFZVpKAxOLgbB1TNHDWnn0O\nmjrlkSxHgqnswmAqkgzbvJMmZ03UXsWvzXtgfn5I+NDnLuX3uqQTiQy8oFCnP1Ke83qz/ECo790t\nZhoOJXzPU+zrcJ1Knx+4c7rFI2vDZw57Jy7h2215NNe7O9kPABattnM3auzrQzH83LYEPXyk+wg9\nKiO1vlXpkzIoBu65l8KKKsltSwLup/YEOPrXgY64RFfSlKJ3uEt7IdCbKogvBki5N83fXKVvmP3e\nM/1F4l8+0fswOFsjf2G99GWgFpY/FMPXKJdM3b1RiHvq25URX5mR87t0DJ7bYFyYhF0zJ7mlnu0+\nqWv1k1kgtdjkt9Du6w3JyajFjl/zspYaevZAsr0pvLfVlpqLv1WK1frzGnpLPhbnQKou7qO0X5rH\nVqdbkaf2u8bnqSr/lWWo8ckqfoJ0OC8J7ffcYY+/6lYeuONO2Qvuz3vx5/4qymAZvQaDZo/jsRh+\nK0x0ETB96YVPU2IgcLX+wLjEIR2XrJfuk/UVtPGBK9s1cQW4Fu3SkHQKM28g4SPUJoOr85l0z5n+\nI3ek7m2wMPDMXt+fqdXMGn4wHMPPlFkJa//54L5RwOwx9jr0JuWrOG6bqbLj5yCkvSitLegxGV56\nXJ05/+xE0mXPfTrflJR1Vs1QAsV8z+A7cZ8k8F2R6+JnquOe3TiZ1iozo/7h6ZHjEeE9XfIPmT/3\nBzs5Zj//jaV7dujOidnvgaSEbx0JnKS/oTkHY/jtrofBW/N4S5L9Q4y5g31INJqNlu9RlPpxaSZa\ngSrGQsFX/OOKJP4hJQaOtZNa5YK4Od1WuC177Nah0r8aDD46zgY5TUTaXxuG4E7S4z5inL9YD/2T\nCSV8x/SXs/NPzEOfb8mLTtujkCclbf2VGIzhL6guCLPjL3fCrRRwFUYTApV+ytP+2kbBnhMa72ij\n885Lwe/RDSeJtekcOLALdule96TPcrOwUOFbZm+vLaO3Ur5z1pNvyXOLAKnS3xdDMXx3iI7dZ+hq\nIN2xDBczgobhEjyck4V6cAJC1avmeNUyIW+Nr0E7hWkts6+mhdaVe0s4WaTWw15y6vO9mCrvU/J+\nSq3PHR230FV76FLJrFCbR0079F6EbnXivOSWvdZDsmrCtbblfv0+n88W57ySw19LyimHPD5mY5V9\nSpXvt8lZpz2bjhH/whfm3LrT9Wamf8ukfF0jxR32dM3zHbDhW2j+eOXwbC++W4Xx36E63/9Op3sv\nBa+NTOhe4Iqq52jKA0DnfnCH+hTX+M51xOyanEcQv08BP8FkNc3h2fmBDX+x3T9amP2tOcGc2AmW\nCz2O6bvsuMrahllX1nEYvgm+AqT6VmjtYL+EI0W0imNhWBTRuJmML4HeDutK2fi9YU75umsm2EKd\ntE7Kq5upIR8TDrOK8J0bLXUe0woJ/9LoIeEDCIQYzTy554K9mHRAzzapX0sz+Vz75MIh5uHWLu+l\n+eUp5ydgjH5h9pGEb5iED8bwT7eB054/WheAUOs7Rs+/jBdu12Achm9hVdcNjkmBr37AsClg3nbx\npi0GcrjrEpLO/HX1WsmpMZfmVeMOlefOtU0DRmD6Z8PGdlbHeiLNVYx8lH7IpPegGIxXzEE45/US\nvuUvVo3vztGH3JJnX5zj35ZnTrOTHxB7pHH/IEvWbPFev0H7wcp43WGMlySCwhhEHcNVCMjb7g1g\nyHjlB1udWcnekFf52wZ098Aab7k2Zn4W2FXYb3tt1UD2uuec0nOCKtnIctvIfKDtNIw46dq25r9T\n8PY8feDlyijbIGX3r6GR39ck2Dmscd/BM1DVPl6ep3Ytv0u0yrRr7tXGrUWP/ndpk1fRxt3Qr9KZ\nYJahlDnQzo8pGuQcWaK7FbWaA31MxL+dxI54HgxV/qE9H5P3B7Ce9qeUDf/EXotrvA3f+yl5Fza9\n0LJw6fpJYTAJ3yR/pSTLWa6PX6Bjr4ldgzcUa8RVTGyU1ekGBJ1/p/L0SnbERYKGSzOCEkan7+px\nHd30bqGDEDJ/s8ScBth+h9pi6RNmD9O1Z+jLA3f8/nvP+IMz9HMCBs/QGfrXdbVhJPw2aN77cmue\nCRvFhpY2mkUTYLBI50zChxFSUCwopaGsjldJ/5nww9jZbTpGuV6DC0yaxnRWdWt1wKSES2PrqY1O\ngl80cGvq71KLuK355trPwFSbva4Vvc/DkGr0rlDSS+an2e+ZRO8FSGJvx1uk+9A/H3IP/u3pdlHp\nc/u9P1IX0HmDP3jHTylFTUAGY0n4ctXivfCykYw2fRFfGcE1jG/Msqf+JY6yvU8YgO9tx56TVStW\ndNcRFh8cV6LIuV6M1dx5nIlWL/yFeVum79X9TBPA4tBEnsnbK1Wd71X6t8srce1BO7lu77fnMSli\n5UAZiuFvlDn8ZaDGR6C+D7btBeHjm5G9p6IHXtvqvhe9wSE9su6uq0oA7MV4dqqIGlrdpLUhm4Mb\nA7g79TDOYm8/OvT5jeqe8zHD1PvufqBpt9754aE7numz/ffaa3ETav2IPiviux9tGIrhA1DLkOqX\nfAsEsAxEMkGDUPAh90x+AulfrPZC70xxT1xLtW3JUU4tV4VdZ/WkI8vAypyNVqI9IemWnItSuNZJ\nNeU0Nd9D8tn8oC2vNXVU5ZjJ0zbidybftYfMVNFxpdDIL5Wpl8lhL4YepVtYTKb6XGg770iPQlvo\nhMfmPJUveOkeath43pTH48YH7sTSvcrstW15Alt6x3gM36GtWFYxMpsUWYd30j3Z/6CJ22rm+E4p\nIOu4pTOOsmBW0GXwD1y+cyBV/FV1m1gg5XBNvG9vRn3tC4FzYRghfnCoGslgASCFSMtM5p1e3HZv\nlmN0T86OH780x9rv7cer9vmOhoBCdQHQOgyGYfheS8H3JBZjBd/uL1O/cMeKwFYTGPD5ak2ocBYk\nNdR7DCjDPqkgF57wUn4PYT2lKq2MS5evFerEWmDqqf7VFXv1T+32dTXZPqiog70k/BGYu6PhXLSU\nFI+RlpfF43wiCM/33iOIaIVIInjHPcfuEx76Vso3J5wWpm9P2LPb0edP7HofaUEkX7hWhg8A7kAB\nVqiqs7vZlQFE6yFo2MDZQnYAVEzcB6pxX50ex7GNrsehjr/DuP7u2R+pxbnkFe7jBcVw972yB/+0\nMHop4ZtTpNIvbUWXWoBWDMPwTcy2kVu+8Mp1v9npPd4OzyR3aaOJPnxFpRy+sKDmeg1qj/9ca7vl\n32sgyxp5tmbyTNnv9kSJPgv5gp6aQ3N8+hT1FS182n6p97EtaOkfW/KsebFR6nCdSx+csxVbadj6\nQiANNX5DW/uY7psS59ejL/Pxu9YXKDVG9fk/zxNC/uHV+txhL3odLm6Dk/VuT/4teU6V7yR9Kd5b\nRT7TPHMEDnx1GIbhA8rewqpteWGk4AAehBI8iaQi9ZNUn+yAOyD8rcIIk/SBsaH2kaPbHDgnON8I\nmD3/ELv2jnpcug9fmjO/MMc67p1Oxqn0Twlmry9klnulfXwZDMXwHSoK5IMwCZ/pBog1SqCOmR86\n2wxfqbF1qvsiuUBIqX4yaFrtdrABllBFzrUvTFbQ7xxlezIZ0Wd6ajY4nTU0b5PmtXuxZ3EyTOX9\nOlouvwoYTcKPmnbFPNUl3+qIqdtbNRDhJ8pT4QlMgGff/lA2rhEGEWjyv62KnR2oy5z15JG6t/OR\nutaLnzF+oKxZJAAwVS5eSYzF8I2uzveCuN4ZvF2DfciGZ63IGHuo8vfSv9pRKhAtDAZHzdawdeW4\ngsIfOHBHca3+I4EkXQqbTKM5U50OpraH8uHe+rOEf/IqfZjAWe+0vA73kTtp7xR45ruteVEZSflN\nYM5tjYWdMRTDN/wis4SJ7f3id7SSE7Yg1nBewpf2Hb+KS9mii4OL4nA97Pyt6G/Hy6W9Keku0Ozp\nEkE9msT9DfmnaEk9a22T3sebrs23Zu994JQ0gHTeCz2k/F71cgkfmWI+uUeZeMlHNYsBxV6feibn\neK7pTdv94XnFwkdsO55SdnznsKcfq6uep5+ohK2jZyiGn0NR1WO4A5+L5KR6aY8J1CTg6py6gXIJ\nvtZ9skxI87bDd81qhJWAguY6vXAxRmGYa+gYhfZzo3Yb3l71M+rYA8YQEBy4cMg/4IJi+Ny/IS88\nP59L9/Mrca10v7wh7zTb7k98ZxrCPuDOk5GTzoZuMjTDr91+YJycbyKJ39cVBQ3oVTJsX35Qrxfo\niReYD1MDznW8TtUw1GS/JykjTWAlXIjWofrCPUC3+i4pNM/NvTdmx6MH9ntnuw8lec7oaZrvWybv\nTthTXppze1peheu+T5Cn7M3xY/q8YKoUdkW7jsPwU7QbIOTUWjTO5P1e/EBdyhqMggadA5MIR0F4\nkf0FJ/VNg7ekKks8H2oVrqEjfVXVW1FP2e1LJXrPUN8lWlMoS6t6nLrjoqvJGAK1YzEVTNbLNR+4\nw1GkZwd61TxVSZ0zbuUIdcEbuNrf2+89n+An7Flmb8/LvwXbjufU+fZ0Pcn0lX5SMPft7rRHRF9P\nRCfx+SX2/DEiegMRvYuI3k9Ebyai51VnIAvOnfgqOgnfk+/iCKZNXNKXKpwD9wa9ecu5pJseOwm6\n0HplzPk+ImRme2SwQ5pnRywUhswd7CPCAMw3Pz5wx6v0OeMXb8oLFnqhTjtdvesH3xoJ/58AeD6A\nj10+n8aevR7A5wJ4OYDPAPBxAL6vJtFwdSv2JCbCB+oQ+8+uGNyKLjx4J7rPVnDBag78fux4FUya\nrANEmoVK1Nj51ksAMT0ph0Ttk0ovfrCKvIthswOkUt5c26910JOoeZFNDWrpqTmYqBdNqTR7p70n\nzk1jySm4l0NfKV5tPhq9OcfWVNjsnIx4TovvxQyegEAQDPlEKOG7/fdmdtYLjtVFeH6+O3DnFJ6u\nF36immJ2/AVWIOaG/wY8aI4BPDLG/H5EGtGzAXwZgFcbY358ufcaAL9MRC8yxrxtRV6r4NT8QsLn\njWmCt+qZRconF5uIrmJyuRbMA2fLoZD7wJgO0o/vNt2w29qpM63GmLNpNw4c6Auptgdmlb7w61JU\n+Y7hL6p8uf8+OEt/8dA/nU7BC3OsSh9EbIfawn9CKt1fF0x812KNhP9vENFvE9GvEdF3E9G/vtx/\nIeYFxI86oox5O4B3AnhJdeqSyVaUSJEDYMDXR3AqGbma8+oZv7rTJTf4xg4elOk7MKhktkktHn6H\nD+0zRVPC4qmMkhLXDBll2OUQbG3cMZsR+9EFEartwz42BOR8uoa2Qhx1Tqbwuf0EAqCXAF1AzwMo\nSne+7Zk+1yyfjP3M0r132Dt5Sd867J18eCetFw7d8RCsvnE4tDL8nwLwFwG8DMCXA/gEAP8XET0T\ns3r/SWPM+0Scx5dnZXSYNAJP/aCBKfjN7TJOuBedxP9YR0sKawSikSe6pvJ0rMs7JVmeuShNdXep\nrjdulz8gcaVDkS8E+CKeBN+giJeQs9k7K75RTtljR+ueTifcnvxefbcHH3mJ3Yut5FT6nh20DZIm\nlb4x5ofZz39CRG8D8BsAXgngiUS0aiWiutDJxvR7GA1Z9Qics98EL2UZ8qp6WhrLqplDOz5X47A9\nkU7lI/ZKWnuO8elrzLloIsg96sjsVaGyE+PMldHV606zeA+7uEyjVBa7yudaI5tOSdWdksakrbEn\neP9et48+7D+yrLzMrar+Hn2896FJtXnWxNnD9CG1RCUbd2/UzHW8P6ylY6vvQKqOih/4cQ0S/AFM\nwud78a2Ub7gN/9Z57tsDd/hpezn/LK7I91dMum/s8mts+D5bY95LRP8MwCcC+BEATyOiZwsp/3mY\npfwsvvV/+lv4mB/8GDx4cIObhxOmG8IrvugVeNWrXwVAX0BqZeUn6hshzVtGD/hrp6ZRdwMsdudD\n0jhwBlxSYXH4rHTEbE8cAzvRQXThbZS9y8WEaO0jJXwv3Z+8dB+9NIefoT9L94HtHnkB18sE/397\n3x50W1LV91vn3nmPMxAIThnREImEWKgg8sgDKacCZSVSIlUQE4ukKqQIgZShophUxYLAH0mwEo2p\nYKg8LAokgINoNINTYCViUKQGBTWQScABFLhjBoZ53nvnfmd3/tj9WL36sbv345x9zunfV/s7e3f3\n7t3de3WvXo/u7dj+e3/xvXj3u9+DS49cwaVHLuHig5fxwH1fLa7mJIZPRDcC+CYAbwPwMQBnAG4F\n8D4d/80AvgHAbw7l9Zof/GE88xnPwI03X4sbbr4GV113Fc5fz4sXzG88SMWIClqOAFKRl9kzdWvn\ngZ4ojADvBHvvECeFtYyu47A0o/cmtDOgOeodKNb+ygrMqHNUIeU641hC6Ovl2fXJl+4t249tpyv2\n0FcdU+UL6V4593unYRA1f8mLXoJbn/lCfPGz9+ELn7mAL3zyi/jdj96Jt336LUV1r2L4RPTjAH4J\nvRr/TwH4Z+iZ/LuUUg8Q0X8C8K+J6D4ADwL4KQAfLvbQ95YmlAxQJo1WG3kW/P5/33AqOkNzMzc3\nvTPplYmLWCSI+kkBKRaTGlNnGGvnWHrl+yeM7zbrHOedSDW6fDNJZXaiF3vvq2y7CZBtxq5rVz/M\nMjmeI4/Kd1Su0p/Wd6QAsc5+yM1a4p3GmCy5e8Y/L/2MWByRiGc8wZSF2/Ado/eX6XWWzbtV+NZ+\nj369vflozlbssBdT5csx3rIe0T5uRd44zXOthP/1AN4J4HEA/h+A/wngOUqpL+v41wLYArgNwDUA\nfgXAq+seoUZ1XH/THZGBeXHo1SOW2aO37dsXaR393GhNxO4xeZ2i5F7bJ1c6IM2NMarw2EA3+K2I\npTDThLRJ/KcNb4xcOZKrY5hU7zFb8uM9Cd/+Oem+l+C5h37n77LH1t33h2P6XIAsGhOWtOErpX5g\nIP4ygH+gjzqoHLnkK66gQEo75jEHvp6Zu413jPMeV927NZdgL1uxl66CQTHnwCed9+SvTDfcLNM6\nUcyRp3ZwLnGa2Yf9N+acFLs2UFb0XrZM8n3nyiXVh6l0Oaaaa3s+eJWUeyrGOO6VbrCT35Z3HvpL\nOaHNlffYvOT7KaX5pRz3AnrRY2SK/lO0H/vNlTXXR0qd9cxv6KTn+gsfJ53Tnot3znqRDXfU1lPp\n2zX4xmlPKXQdMhvumAb1L+0EwNOC19H9evbS57CmeKnmKCHYiB2fq2fsNXlh9mUjaGr3/CbErBtz\nv5/DEFgaGqoxZ1c5tHGRWXCd+h7unEv15P0yZm+d9eJb6hqVvpPy3R76ynwWt2OSfUKxTfZPI5Ko\nZrK7SoY/YsGQsNwzxb73MsXHcnS8U+kzxk/wCSJH1DJuxg6wmORM4lecz9GJi/I4sMEih0DqIHHk\n0g7hACcfU0g3Nrkfu6y1CipyDN2yI+0W8fGoIG3sfJ6CFCbLpEvFJcs99ExxH2fqkrHDaHVZYsfQ\nnUZMSvhOC8e3dHefxfU99N1Hc9xX8oxKX26vqzlXjI68sSPRCBXkty6GL2c59RoLcAk/vtQO0QE4\n0AB4EccNr5N5EbsuyXHg0CQeg1lUvmP8b2JSyyHOcNaAA6W9XYL70DheTj6/9yYETincS/jChq+E\nhA/x0Rxjv1cKWy3hG8c9QE8YByR8WyA1iilarIrhO02+YmG9fR5IzPqZ6l5uhGAkfGmDsVJ+zI4j\nDgDRMA4Z7u6b2B4LSg41drNU+jnKMFd+RXklmjPmKVvd9hS2TYpu5qo3X8s7VN60RFVWDtlGqd/Y\n+dK296Ul7KE6pO4Jw6aVY2gMyl0n048gwzH+AzVxY8qS6l/ZsZ0QPXeH1PgSnP2+04cKd9frfAnf\n89JnTnve0jyU07GSJwer0meGDFmHFLPnV+G5cCrx1DUI1dlR1Wth2Q8QSZXZEde5weGYabuhIQsS\nQx4z43rS/Uan3TgzgFuO55i9p873nPY6a7vvOmUnCaHDXoWzaEL7X4J1MfwJ4IoOqXLxnS/49oju\nJYfemjozLq1T5FeUI/qOhE1oVwhn4jt9/Mmgpl2r7JKnjJoBbWnt/xgt6g4tErseV/yHh+e+tB25\nhZsQgwTldfHs9LEwEmGAxwecXd6VhVgYaUZg79mQtwzPrr+Pfh2v0/vob63T3patw++Zf8JT35t7\nRCo5Aetj+Mmpy1CFI975JtybtfkH5+s2GdMG7LMv7XOr070OIvvCmOZOqsonlaQMeyCPFEl6S7BY\nowyR8B5JfDasdkvimKAxA10uW1/B+WKYqW85qwaz30sJn7chATBLvmE+fNOFHvrcft+xJXmdsvb7\nTi/Cl9wqKKAtI0Ov/x/V/VfD8IOlCRGtfFE+3v/ALuCNxP7LdYddm38sGFGXOTv12psyWtWC6h8V\njVQia5dvDnerwmonJBzRvrRguQUj5xK/jmDhcOeAUeR7Er6V7tWWLccz9nu3JC+02/f//Amz+U0N\nMON72GoYfgwxJz7TCLLKxlnPY/amIY3KHobnu814YNX4wpmDpStx7LPlE84jsd+5MPilpQHnGunY\nws8PVcKvLbdsuzEOWimnzaHyOQfSMpSUq6bstY5eY5/NVZc8bTp9zOGtPO1SqHY+jAUtUN4h2luy\nL+fGu5LylIyfQ/mkylDkuAfXD70x3+SlVfmc2VvHcMU+j8s89S2jV2YP/c6p81W4tW4lFGtUAAAg\nAElEQVSKJIxK33Iu499mEowgpXUyfGX/VdaJr8MXUj5T04fOGe7XTfKEJuDE4HYFnJjRibVdntmn\nImZ48C7s2Pt47gHjWDUdhyoMBPDU+Hxtvjs8yZ/kKjCxJA/cZs+YvXJqfNWZ9MYkYDX0omgUHzA8\nfxJV3f/WyfDh8fwAaUWH38ncuXJqesvoCV6bGkZPZF++S29mgpkC8wlErpAmeq5BvvKFH0tnXawe\nYxy0DESRuF3QM6NGpZWRz6xBqgyR8EntG5Vs/UFNXg9mmXQeqCvaJMzwrLkF/Nh7XIKWpmSZ6gdF\nD4uTafI5PCF/nj+ec9nPjfdWjQ9f+2buUwT7mZzYB3M8lb5yjnvWQ9/bS9+p86Nr661G2pUJYapq\nklwlw88xe5EqGRaV8GFOWSMKu02MKCl5sRIsMOgdy8SgIYL2ak8PM77zmPbvIIcLw+CJMXhPE6zD\nNgTaEGCZvYoye6U31nHL8UL7vZHyPTs+YhI+rPlaqvQtjkKlH6u9B5+yPFsIIr/Wtm9eqnnJjrPz\njRb868gGDYkS1dhxS+KHbH1jbbU1jHwOW/7cduLafGLpZnVITNRvyGbI049pk6SdO6UVy5oaQvrI\npc9tupMrnwlf8kM3S2OujYLmKnutz9Ac/bH2npzPUyzPofOhPEps99xO3wt+5twIfZzpu+f1G+34\n/MXfQ5857FnpvnN2e+9reTk6MEJpZPziZ4et0k9PYSaxCRo4eFLL9RNZDcQ37BhT38MhmVl3VNax\nk7LZGPAhvRONg/CEP3VIsmYSPZF/bZgtbVy4vwZf2O85s1d8SZ5T4/vqfOewFzJ+MSmLDXIjyW01\nDD9m0/NV+6lBSLHDhHDXvcgsSkrt/EXrR3E7jvSmlrYdiTmE2MEBZMr4MrJ8pfUaSleSz1KagdmQ\nKU6RNL2niYqVfmbV8RaGod52X/3cpVHzzEwbHC2YlnQwqegLNV08Zq9P5WXGaTeec2nejO2GycM3\n9bJ7PEc9uSTP2PCtw55z3nOb7chd9pxaH3B0Ee2bpkLWU38cEa2G4Rt4jM753FUMT475O8bfw6rn\nYV6qf7D37mZ9ArXD5Nr4lMHqyrVEeZaq49raTqNqCNjFpLShYW2w6n4gbr93h7X6piR8+Ovv+3Nz\n3X9Ap2M77AX75xvJXi7Ni2idTZBZbn4EEn5iPWJkDX42H8TaQrGX6GZuPF+ynB4hsyeXyubB7vSQ\nKuKOmcR+JeLdreOfVVKtfC5/NtG+27wOjVnvF7tu/tloc0h7N6I/juvDcU2V1yfl+EyJfuppagnW\nbm8kfB3psXsV2u9jEr7dYU8xOz4QHOC+ZguOaath+BaVS3W8P2X1Hc5xz6pMmJrAU9Vzlb6vvved\nO+ARO58V7lr9PHWwjqqVR6jZ0+nq8pnkXFTZ1NzRLPWFtyIIevCiClT60foV1GVquYecp2Jlq8Gk\nNk3cU+MUKNOUHlPLOKacs/VjYC9ap6hznRg7i+4ncV30bHOSycsb00V5ks58XPp3Y7zjJ066l8z+\nrNt6n8W1X8djX8njS/SMt35s9tc/Nj6pmUI1q2P4g076BTkoNm9yYRqcUKQKx+r7Q+KYC4tMBoqY\n9fyP3WX+/rMOR5LmKCr3AVStKQcOBwfaVSIa1sj5yIy5EBf4YQV8gRzDN5Z7zfT5F/LcDnudZfp2\nhz2t1lcdX5bn+lGsOzkFAytczMetEudH3LMbjBpVlDhz0n8v4RuVPKBANhVR/xWkmH2fzyTlueK/\nqv/13oK8ngs1eQ5K2wVJR3eykQ2QuG0ORq+YokeBnasJgyMvrz7PltVKISOeJTv9ypivUsrVnTdw\ncQbxPEvSpcpTgiraGlOvWDZTaC4BKfnOmnGqLTPjHhFF38Esk3bZjyL9itvgiR2c45vx3qn7pcRP\n6OC5gXvq/C22wSdx3WdxtVS/9e33pi3TS2kpIA4VnNRjdRJ+4MbLB9KS25mnX0zGd1L8wGEg7fnH\niDln0DyrNbfbyhjlvrDqd3RgOBS/iDGv/BjJRDrlIcMbwiV5/idxuUrf7rTnba3rvPVDCT/0X3MW\nCa5tnk5f62P4kMr4mvuUZ7+3r8k4BLIXa9QlfBYHLyzcSCd38DTyHnPOf8eidLY8ZAMfKnst5ro3\nKxgX2J+nYKytOPWec3RifymezxJYgvZim++UfiSnJv+hMBk/xi5fY9Mvzn8g2ZRNeGI29LnHm9wz\nc2EmPBdX+pyh81Tf4+dlB6yAR0b61/l4PmHcYY/Z8rdKOOwJ+70KPpqTe/dS8tQIktfRzsoYPh8o\nYKdAynLryjy8M6NjMkco1gZBdgZ4jPPbNPZZ3QMRko4Pp0Xip4k53/GEvJad1MbP/USI81M+3jPp\nvxck3Za63GHPbL7j1txrib8zdn0FZe33neZrcMwppdGPFlpgxFi5GoZvGkIBcfttaT76v2/Dh/1v\nHDa4TSf2oo0GwGgDOIFQjFhkeUsIbwwmMMSqjsbLvyNuEC1fwaOrB5CKNqyZgNhi5IrDaUjeNxf2\nMWniVriYSa4yj2hepdmM8L6v9tqfqY3HTnDH9uX6B1UkTaRNaU15/tG+Q9HTeN8ZYO52nA/K4+Kd\nVO9rCxQ5Rm8c9oLleGrrM35+KGUPMCnf53dxQrDliCQZQzqrYfhlKKE+abl30ynjmBdQT1Sy95do\nREuTI7KVYA5mrXbIQaqY3wra+cSUPw1rRKNBAOWTaCL4YzsT9mxb2gkAwuXffEketJRv1t9b1b7C\n1jrt+d75UsIHxMQvUfZe08BvrseKGL5zXLCeixFHhsSd9tfaWkwot+lr7+neEYIxdfBztjbfhqft\nsa5s6eu9LiPzOkG8HCm/g6H75kbM7riLZ49Zy54Lz5U5Z28ciynOYlW23irNiMpey7iqOiSSTrGH\nx/KaI03Zs+ajwZJ7au6tscGn8s+NnTmfg7F2/Gr7vefTxfIggDbk8RTo805I+ltPumdqfW7LT+4B\n4b97X/7MvKsR9Lcihq9RVQdupY/dqFg4W6LHZ3SAmBq6oKWZTbUmeo4BpkkDR4N9eoVXOdOpgfiV\nYsmNgxpWBE+yZ8KeZvaISPWeGt9bkqcd9rZssx1t61dd3GCv2P9okeyURKdXjNdXktb6GD5DxrRR\ncGfKjo+4nchMAkSEp/6RSWReDQeNUxuX55jQNmbWEMW+x8WIrwBX43vqfJM+ot6XyvyUd/6ZYPhb\nxdT5/Ct5nXIcmzvuBdpsijAbMH44rt+tkOEnp0AA4iqOmFlEBYzexXrOGuDnPkG49uZb8MZUWe7+\nmOdn9HxBhCo1GV+fx2TsewBYGnJCSIlDpkF4fpRNlRufppklXTYzq/TnkvBL6lbnHJpSs5sT/zrZ\nl2cgtNQzy24eyFOmKTkHE9L5WK4T+up+F2/y4b5bfVq95t447TGVvi/dG6avJwJb/0t5fCtdT52f\nfO+S0/VXkt/XUujqGL5H+KNF/CATbwJgwdX6QPScE4a5ZSr2atMvRL9j2r5LUYEpE6tDF1L3UP4m\n2B8OTlILEwhenMFTdJLgSX2BhM889MU++uZLeVu7l77bac849HWcwQsJNfZ2bHki1XECLao74uoY\nfgBbH/J+XLRk6PqabZBgNwfR/61Dhs3azPy4E0fcec+du7Ahh74UllpONuRAuOsJR8nzpjgUTalP\nzrksusmRuEg5HeXoora8Sw3Yc9FB7cdkSpfA1djDl2qjuT6uM6cTYKp/D/0ugWxZBh5b6kRceh7r\nZ7FrGWfU525Md+WXm+1w6T694U5i050upHu+za5oBSFwka/CHomVMfx0TWpINtLdmIelyc/N5rj6\nhx9Oix8ntHrsWGRes4S+QNkOSiMxA1YnuLHynIRUeQJV3CkW7L++2h5unJdhOrEZ5610r/9b6R58\n7b1W66t+4x3O9Lddx9T3vu3eF0S90tpf6bA3Feth+NyHYQZHPRPmq/G1HkWq6DXH99Q6JtLMCOGI\nJiCeGKJxKxohDok5VpR1+hK3+Hn+meZEXOfS7hv7KIdUZw7Y7mvs4WuS8OMZlTxrRL77eI81z4yl\nJT882icoeuqljZlafcbNh3CxBJvlYTW+RrrfmDwiLnvCYY9/Jc8eW70OX7kP6KiO8XvL9OM2/KQP\nwwxYD8MHBiSE+po75s8d+Fh2JM6NZG+CmZQvizHkGOeSL9wj58g+ksfcasDcut2GlWDm13ESUn7D\n7lFIp8RmAeQN6oiM/8R+ia2/Zw57bKMd+9EccIYf2UOfr7+3Hvqc6af7SV9EJ3AGHnsjUM3wiejr\niOjtRHQvET1CRJ8gomeING8koi/q+A8Q0ZOH8o3bTp19PnuvJ8NLW76OV/2FgoIiZcppp4TGhm/V\n/MIWFbPBxuzhjq6kDwCC+5dG7jk1dvX+fFpZJFHPbdef0zchJ9WlbIepNEP3uzEpzNeVJ17G3PVS\niPXTnN/D2HKtwX4/97PnKGcNre0SqQl9SXisH5We53xmbLgXH6a10r+Nhx23DdM3NnzPfq/V+mdd\nZ7+OZ+z5nOkb+z0i9vu4n9By77SK4RPRYwB8GMBlAC8E8FQA/wjAfSzNjwJ4DYBXAngWgIcB3EFE\nV1eXbrKTgpPppXLfzf58lay17etrndjdF3vMQlL20vDUY7t/fIPETl9Ce+NL4dg1G2uZZBgktaty\nHEfkWoz/XKVrl+Fp2723Dt+q8zu7re5Zt2X753feGnzD7KOmrIhm3y8i+WmNn98IMjtfmf4fA/i8\nUuoVLOxzIs0PAXiTUuqXAICIXg7gHgDfB+A9ucy1EJ6x7YVvNuPjG7B7L5QEYw+YvPu1TzUEARUw\nS+WdrA/JTkqJ8wNH6aCkMLLaU9/1itqaaIUOgA2rw4qHtwDcpm/V4kaKB5ha31flG20uCODfx5PM\n3px7O+wp7qyn7Dp8pW34RpXfm+9VXy5mzvfLr00LgtlPRa1K/3sB3ElE7yGie4jot4nIMn8iehKA\nWwD8qi2jUg8A+C0Azx3MPTZtKZrJ+NMlhZDd+zHOcc84dEg7vq0TXBiJQOJEw7HHwTzL6FbEZKqR\nmKUvIW0kV8qUgA80kePgMeTUKLvvjCr9XTvsFT2j5tELFlNKsynpdlYSTDwroPPE2Dp4b0YYifUl\n/17NMC0Td4zcjf2O+Xt9lACrE7afxdU++nKXPavG75m+8cx3S/Kcl779Qh6X9AGE3J79BPW0hv+w\nAQpQy/D/DIBXAbgLwAsA/HsAP0VEP6jjb9Elukfcd4+OG4T1YgT07Iep4a0DQz3ZunxEflEi1ETi\n6XugCaj60Q1YnxpwCRTXcYammMLjiOKy2uIOpg37Q5RBjnvfh2Cy4ApcFxhLyG7Q125JXudL+Ups\nusMc9uSGO847P+2sxyH91GKvRkkuNuI91Kr0NwA+qpT6MX39CSL6FvSTgHdk7hvUBv30u34CN7//\nZpw7fw7nz29w7vwGL/m+l+ClL3tpUcE8IiQty6veQU8ppcOUdeJzM7nwC0lcAwC4OIJi126LXn5u\n5hAxJ7VcRxmKz92Xu86FpxxdSp+7tMMSf4Z83pBDX+1g1u8sOL3+JnworyFHpV3C1mWwl6bB6yzr\nX9O2tc5xc21oU1K+VD1i4TVpa+K9OEqEY7h/jAGn7ZLfVNly5cz1Z6emD53+uE+Wi4iPcXEHPj8f\nw+Dtb8xpj0v33tfx2GHs93bTHYhffwLg2I5cg9//vu+Xfx7vvu3ncPniFVx6+DIuP3QZD9z/1dxr\n81DL8L8E4FMi7FMAvl+fX9Al+1r4Uv4TAPxOLuNX/fXX4unf9nTccNO1uOFrrsH1N12D89eFxauX\nQhT735/ZeZIW4GPDAQFQEVVPSjrKgt8yYVDdC/Yl9B1aOx0Y+ulra+CGI4LUxsaiPI0uV/FTL87q\na2G5t+p8vtOe9czXn8Ttz8OleJbZM0m/xk+N48V/7fvxvG//K/jS576CL/3BPbhw1wX87p134u13\nv7WoiWpV+h8G8BQR9hRoxz2l1N3omf6tJpKIbgLwbAC/kcu4TgIc4kKBix7cK3RpuErfZ+rwVDzW\nHiQJBD4hRSeZiaLOMvMuyOKoNOnEjrkxg81ehuXSe/fs6B0Vl3EEvP470Y6/hObIbXoSPyY9K6ai\nncPmL3BIZjGi/Njjxct0cSVGGMDHXAr5uAm04zlLQ2wscbZ8l6FT5ie8881yPP5JXCP1M+/8zqr0\nOb05DbR12ou1EZPus6++gqZqJfyfAPBhIvon6D3unw3gFQD+LkvzkwD+KRF9GsBnAbwJwB8B+MWh\nzIM+UuSwl8kPsGr4/po57XGkBkLB87OEOBJE0+yxc+OAxpSGI8QSjPKQoFTrg6NhNbDwmDsgBbNQ\nWOOCnyfhK8f0gz30tSr/TDmVPmf8XaegtkzStxwfetA3BRA6/VTlLNKT6yFUMXyl1J1E9GIA/wLA\njwG4G8APKaXexdK8mYiuB/BWAI8B8OsAvkcp9Wg+77IyxFT6xr7iAgCQni0o9HZ8cd7b8ZltPjh3\nH9kBsbT6MPcDxvYDm5ar70nPzqQteqzN3muL7BQ6TMPtYLXPmCpdmDarSh/xgyi5r9Qe27/qsnqV\n2OxT/gYyvTwf428QO8+htHy1SNnuY3Z88+xUPrlnzHVPSfpRNnY+fg+krfUXSZUr5ZeTu3dUPybU\nWzEZHeTiY2Xyx1U5foXXsfBYvE1nmT7/cA7Pw7fbm3PurBcsyeu2bimecdhTktkbXq+g+llF1IZv\nfm09suJlRIDNoFbCh1LqdgC3D6R5A4A31ObtZ+J+cn03V1kl4pNpuV3enruwqN3+mGfhC9TtEDx7\nG44TuyA9ZUyEp44RkwN76xzNZyR1GZZI59T/sBMBhX7RPFfpy/3zvWV5XYfoV/KYOj9g7hlVflBg\nrggwJqiRbbyuvfQBNwsaezNv0YwlX3riJ89NEFkzkGc3suklImGTCTplepiSz54x1CYHYbeU9GDC\nYgdE2kTfrkVxfxl6QGUBksx0hB1/CVt/uX1+/onBria5e+0iMdrn0RQ/5P2pfGNpjDY19kwrGTP7\nPbFzd5//GVwwLa3nrKdV+lK6d8xe7qOvbfharR9dgw/D/ONER3DaBumlb1An1zusi+ErybAlKlWf\n9r/y2D2X9Y3KXTJ8y9hThBWooaqKtnfsq7wlz60u2+JccgeoqIM3RqyoDkMMbjQDHHvbiPuG7lmN\npurAxpupKB4TKNSz2KGdjfF8zHdMvz9iO+wp1X8wx34Sl3npy0/imp32Om/9PZPwhUQrKYpsYf06\nKJ74WCR8Y+MINehTFWYpdX4iee5hY+1gC2PIfndsmFSvOcbtI2jWY6WNhhNGTKXP6ZxEAqva7wOV\nx/LjDnv9pjtMwt9yG76W7tmSPJ2x8L9JV4DY2ZymotUx/PhAnDV4RFIzhwvrdMHCjYrFzvZijh2Z\nDRsANzOEP2imHElkulxYCjlHl9J8k5tUxOJnRKruJDpfSZtNhZTSPDXbCJTQQc6xKJZXqsyLOnoW\nxA+VYcihkPc/edQ8a6gMU5opV56hZ09JOxZLaxtzNCHpOEbPJf2g9Fzm2V/zcK7CDx31zPidcuYD\nQhq1qnxPne/W4PfSvm+77/j6ewXfcY/Rlyf1m/rZfwITpXtgjQyfQVUx+lxCJQ6TO7PjS7U+/HNf\nBZQYqJuwlASfYDU0HB1qBuERA/bsE9+p2a28L5s9U6xZtg80kcHh7Pehw15sDb77YI7ZQ5857Em7\nvWD2jgXFOHidwFM7n1wXw5f8PfS/K89I/zqrPT+cTT/U/cA3+liicDNDq3Lh9iCwc877yY/njxkF\nOSk5EBRJlokkg/fO1SCFNDZk7ckV14uvKLbVCq7BhFxahki6Guk+96y8BF5Yvsz92SKt4iVEkBpn\nCulsiHZL7rfPK8lHjpsyLJKeUnmLcdoxeV96J2IPs7Z7pwGIWO+9JXnGY/+M7Z8vvfNVbh99OKZv\nqSjB71Pj2hTqWxXD750S5u1M0lkvqhcJJHzH+C0dekwfPgGZtM0emsSSg2S/J8KU+2dAe/UAVswM\nG2bBTsh8yqTDu2D777PB3E4I5NhN3GGPn8WW4zHvfL7pjpbwu65j6nt4y/MkCyqWZ6Magbr+tiqG\nH0WNvSwyMzPhiNr1nUo/bu+BpQpu9/ZtSOnNIKSPAE8zFjkbe034FFv93Pdx+1/Mx6DkvjnLWYqx\n7TrWl2MJL/g52ijlE2HOx04Cxtj155xw1PoWlIblwlOo8Qca6he5+0vpYej5JfkM+bTExtC43V7G\nSVs9vHHbSv0gL75X6Uvtk94/nznv8c/h+vvpG+98thzPs+UXarX6kuk6DKhpDlqlvwgyqj8dl1YJ\nkyUEQKiDwMLQpPshtPapxI6ba87X0971umAZ4Z7LsRPEzAQ8nDF3x+j7cd6sjed/HZRdiue+krd1\nznqBSr8T6nzhmJdkR2k7fpAs8AEoxzoZftKGFnuDmUzA2sY7d1Z8a8dnROBU9npCwGw+VuPPiQU2\nerBYvr2fgrBZIM0NLCyVNgieuUxze5evnakQxQ+XIHGewVq15bJc3rueUuZK+/2Q7b368bV2/IUd\n9yxSTC31qGptwvjyFIfH6kB+kpLycOncKgTsGB4R2ED2l2tyQ/t9zmFPbq3re+d3qoPq0E8eVCjh\nG5s+gOhEgCk2bGu4a49zVWN1DD9XCa2EGZkjZ/LuWrmMWSszChzoXERhnHdeU97IZGBOpLLcBetc\nO4MejWrGvWA7DI4AR/oOFsRaJ1k1KFOvj8l4xD1jUfwsIYCJYKfehzMZcHW+x+w7KLH2vgNj+sZx\nb2vW5LtNd/xP4sLNRhPLa0MyI3FGiXR1WA3DH1q/24M3wjhq49K9klMr8wwh4ccGdfIIK10WNfkV\n1SPWNvve5/uYnLnG2eBNvGuH3U+CjucdNBgM01B935uHLucbc/KaUO85gdDG45kAxzW0Osz6egWy\nfmT/fP2FPG6/75iK30n2QytKQnnd7P462H5HodLn9gnFTxVjtrHb4n9QzBGDZWjjlFPbO/WOoQXf\ngcw4UciNHEyCmHNeThVd4lwzCnY2m9CRxcozsQiDTigTHdmGVPrD61XjzjJD12MRbuzh00OUDsT9\nQ5jq+JWMK6CFqnYbGPRiec+5Ec9ULOW4NxY+7ZiT4fTlDnllz86WJ1OmlBNzzOnPOtVF7ufO0TFH\nvTC+L6AfziR95tDdGWe96MdynId+8MEc5qjn7PcRh70EScSbTIROMF2ti+FbdYe0wEuUcyff4mEY\nv7TjR7JmMz9uJ+KTjpQav7KIDREUDzoj2vmIlA1lSLVRo9GGIwKxQTk2ZlsBX4dxlb5bvSWW44Gp\n85XbN/+s29p1+FvhtGfW3jsvffi2eit3DnN9M4npb+CJxumOV8XwFZAejUcN0jHHvdB9D1D+TJLi\nY6HVAAl1UGqW7ROXiJ9bqE9wyBrtwRRFw2JMVBL/VG3IUDkL65EsRUnxFqSDnSFw1OPnEx3aMulz\nDntLITkkFdZzL+asuemqYo4dSPkx5ivTxsbQxCDs+U3x8RXExmfyeb0ZjIWkZjW2wnrPl+dxad9b\nkse/kKf8T+Jy+318SV6cJpa28q2K4UM5pm/bZKa+whm9b8cXoJ4IfEJCQKzGznJYqGH+B1e5vaO1\nWcMSmH3SHk0zkXZH3F7TXUr8AQLFH3fKM4FCyucSvuMMzmkv+GhO1+GM2fG7bss89J20rzrjo8e8\n8tmR4fmsxn6dmZfb6Enkqhh+6L5Qxu+5csPOosRMTUcyOz57ydbGwzfMkZszOPt9bEMIdy7yQnht\nwiSG4nMo9sSNJIuVb99ItU9JO6ZQusyqpDOl7KJl7yFe/rHtX+I/UeNoOEc5UrbslH2+ZEOSKfb7\n1Ja+pZv1LGHHn1Pyn7pstYr5ZnwCYuUIbO6ZvEIfKHMRzys11srx2aXppTh5n2HOvWd+XLoP9tHX\nnvlWyve20mUq/Up6s8M0ObbPW20K1ayK4UvM1x1i8r0KYizkrFDEWZXSGvWxKyzSrjCKUR2yPf+Q\ny57DsdZrHzil8cCz3wsNLNfYRkwMVqq3wqL/dbx+OZ7zyucHl/CN017HHPeg4G+tC9gJQWHF3OlE\nrfd6GH6JVDUuY6a8l+dMre8RgPPo9B5shX+yan8uNdt7uClgB4jPtHPpa/OvLNBghjPnNwMm8ZjI\npDB7RO5bYZNMQtK+nRuwBgazSfZ76TRVaTJcxAw/Mc+5+mUsHxmWFG5SwQNlC5gx+yUeps+ZcO7f\nx+NMvsRKa+8hbyLANQKx1V0Kyl9/rx32zuyWuk7Fb3+t/R6B/d6cAyhSYYdj+jwvez0MP4biTulZ\nN4T07p9Jmd7z1pdERfAZP+BmjhR/BSWvxc9uT0N96rEJhrRLFLfJsXFJg2Ot1xHiUPaXmEpS0my6\nSniCFzsgrpm6vz/X6nu+4Y5h+MEa/K2/va74YI7dO99+Epcxe8b099WEq2H4aSJy7JkijgypPGwD\ny8kA8wa0L6TPHPaEnJ0HbCZIYnboh0fW59NuGPrQmlZPktyzrb72+UulnROpNs7ZGu19kfNaeALD\nDkeSoWeV2ORLbJpj61R735I+BFOQWoZaakOfO01uvDHnQ/Qs7e7yN+b/FOs/OX8pIuF35flgsfGZ\nMX0m3wfr8KVKv1P8gzl6h72U/d7GmdILqT9on4xWZQJWw/AtmI3DvxzfqTzHPZhJF7PqG2c+Id3b\n35TKa4+M89CRbLrWpCeBoD8PdO+co9/QfYNjR2bgHYWVCsBrwRzDZtwMEQuM32O0AD1vYIvxlHPa\nM4zeSPvGWe/Mc9rrhHe+YhvvKGe/Z8htvJNiOEQ0C12ti+ErLY8v0mF8Wd+xfCfxe8vxAGZTcuFu\nIuDPv4qJeCjdGtT9e0KyvmtphrWUY6VYq6Z3aZT009WqwefEHvsHyZOcOt+M8Vq67yDW3web7fBd\n9nrGf8bW3RuHPcVU+jD8XizJi61k4WG9HMm0GDM36roYPuBGjQLHhmw23DYvfkw7E0EAAA5ESURB\nVJlS38/eIxBi5/CJ2WgCvIOrmrykjMDS5T0x3t6DEucmKNcmiZn7LP2jkN6CR9U8O66l3RlmMScU\nSOVJRlfhOJdeyjcwyahxzCsqR0E++8BCBDTVb8xqzsURzZP8S/v8pCaQ4I3DLsgLt5pYHWGuPVU+\nV+NbSV/50r3aiv3zt+CfwzWHp86PbLwTY/yyPSjVIMcm4Vter1Rh3cop0LB/fxLAQ50tn88WPfts\n5B3YpKfIsHeJY2rfldal0fA4nIT0vksU0GFysp0gYk/w0ue9hz48Ju8typNfybPq+21kH32n0u+4\nLZ8vx5NkklXrw/qsOc+16XS2KoYPlFUppuaw0rpwBLL2eZa7Y/PiqZbBi6UbYOc2PrPpgylnheNW\nyvllDiSdcgayzz1/6iDn19OF5Zx55P25+BLUOmgNOTKNdTAscaIqxojXMslhULTT3BvMjHGUK91M\nJ35z3sZamu9Sm++UONiV3leLEke8UudVmWeN8595Ttw5L/5csF94+RrmzPbQD5bj8Y/mMCl/q9jm\nO9r+3ynASPaJTXdy79xTSMTgy6vVWB3D5yiV88vulwp8PrcTHS+lSkqpjikygJf0r4UlqlPzAWhY\nB45B4p069hw7KHmxHyTNeuQf5IUJNT6T8sOv5bmP5hjpPvxojplswvfKH5LuvThmn4jUR/KqWipd\nDcOPjhHG3lGahyfBKxEmU0QkfOjZYX/mbE7EZl3s3P7ae8V7Sk0cIAg0g6JZtb1I553KZt99tWpS\nwjvvHJhhTI+qFnMTRgqD8gErh2jD6H47i0j4QzeOfmT23uL6zdwOJbBdqaZLLUFvpcKOKK/Hp1m8\nZ4+HGWfFfihc6vcyE5kzLYBC77AnTbvcdm+kfP+zuFq1v3VL8zwPfb7ZjrgOmH/alK+LKwcNX0td\ni9Uw/CyCmmVUzclmUJEU4cTAZh8dsCU3N6dCohcSf5hPOmpRpJ57aEzmELGmNl6B9mlRnIBwXsSo\nD/kdVsKb7IiJQj8pYNKZJ+H7f5zp+/vnsy/lqcRncfkyPLn2Xjjq5Zz2zEmUhyg96fSt1MVYDcNP\nMuoRs2LPXoLwFzLOOAlS/ywCmz16diJEzw1S9qkYSm2+NRL+kI25pAxjbYRjUdMOMRvg2PxiGCOB\nxdovZ3scopHSsi8hLc7ZbjHbfqltfSjtmM1xxqDm+XP7LozBGJ+Wob5UEjfGlyXnq1PiC5UK99M4\nqV+O5QaBfT1lw/dU+s5Jb8s89DmD986lT1mG8XNtcX/te6x5qUfQ12oYfg+mv/cqU6HXjyGgv7j9\nQJm0rLGDfGJqM0p3gFHY88x8jab//3HnB3b7wBOQEo8NO6eRhv2hUMNBbjDHbe+7zd1LzrDr/4U7\n7HGVvjnv2FfyjFrfSvWC2Uel8cj44sbdlD1wOlbF8BVrmNR4W7sRgfS4ddqQmBXfV+vLCQC3B/US\nvjsPysm1/4lwF7ZCDrtnyDb5tTs/mEi3i9I0HAJSNDIKu5rwtYnlKFDkwjN3CxU/EeG9v3CbJ5yF\nCn29J77ccEdJZr/FVilvDX64hz7ckjyNgBcFErrRXCQqPQOtrIrhA3BcPzobYlL0UDZZtwa+UI/b\nboQ9njN6SzgmiF0wBxITFcCbOMSRdKxLRKQnConZxqGAF7+w/DubNMUmbLm0mfceBO/wXS3ZXinH\ntvlU+rmbCwtZggorY6njXi1iTrl+gtoMa5+fvj/GdL3r3AH/3BtqZf/3h1onbVnBy0lgwfDMVPpg\nplpuv5esP3Da41vpqs5T6RtvfeucJ+z3nsMe4Ev+QWObn3DQIMxD2uti+NqWHt14R8WaoCDLgPH7\nDJ6HxvUs6UcZb88kCtVOc6NJvbvHcJPP/FIWlgyrNGlNSm1YAQKHdmcIDx34ELB5zXecZG+Y/lZ1\nOONOe56znvTQR3pJ3oCHfqhIJhEr/GJGtNGqGH5RBdhLnP6MiFpfM3HP8UM/11znJO6UA0rO6Szl\nvCLjY8+rQWn6XUnLJc5rpU6L+yhzLsyEu2M4r1WZdlZUlIYQJXQ/hwNuqSNwznk1N/7lHPaG7o+O\nt/DHbfYkF5IQ4rz1W2zDNiel+9dK3pWS3CuxZNc7v2DepbgWAP7wwudw/Y3X4robrsF111+Fa2+8\nBldfdx7nrtng3NXncP7q88BVwJm6givqUWxxhrPuDFtsodRWb36oYL92BIUN9fOZDW2wwQaEDYg2\nOIcNNnQOG9rgHM7hHJ3HBuewoXM4h3P9DG2r0J0pqG2HbqtsmNLn3Zl23DjTKp2t9tY86+1ASu/C\npLp+xtcZoukUOr1Bg3H0ANCfs1+pN+y6Lmi4zUbM1zTRbzb+L4iw2fCdqADo643nwQrQRof1Defn\nYx6DcHJmy23qofwZb67+fB/qfnmLbgJd565TeOTiQ/j05++KtIHuxrotiNhAoOsdawfbdBs2aEAM\nYpt415NfvwISWqkBbEi0a+J5Q2Xo2EBk25+3cR/p2lk7yaTamtepFOGAn5kISboN6hbSOkcXaX8A\nPY38YUgjU5Cqg+wTQLxe8vagz0YS8byDdhR9nMdxmg7iDI3LvlxAcpIMYrTXp6tndqaMvHxWpjNj\nke7DZOJNHz5P2KC/3pzbYHOub1+bZgPQOQKd22BzjnD/A/fj45/4ODbnCdgAZ+oMW5xhq85wRT2K\nK92jOMMZLp1dxMWzS7i0vYiLZxfx0KMP4/5LD+HBSw/j/osP4YFHHsLDFy/joUcu4eLFy7h88TKu\nXLyCs0tXsL10hu7KGdSjWyjNP8D71IagrtqgO7/B9mKHs4tn2DyyxaVHtnjoYYWrHzjDtfdtcO4x\nCmc3XsYD1z2IC1f9MW4691h0Dytc+uplfOWeh/DlCw/g3gtfwX1f/Qq+fPlek/21g+29712xiOhv\nAPjZvRaioaGhoaHhsPE3lVLvzCVYA8N/HIAXAvgsgEt7LUxDQ0NDQ8Nh4VoAfxrAHUqpL+cS7p3h\nNzQ0NDQ0NCyPVTntNTQ0NDQ0NCyDxvAbGhoaGhpOAI3hNzQ0NDQ0nAAaw29oaGhoaDgB7J3hE9Gr\niehuIrpIRB8hou/cd5kalgcRvZ6IOnF8ksVfQ0T/jojuJaIHieg2InqCyOOJRPTfiOhhIrpARG8m\nor3TdMM4ENFfJqL/SkRf0PTwokiaNxLRF4noESL6ABE9WcQ/loh+lojuJ6L7iOg/EtENIs23EtGH\n9JjzOSL6kaXr1jAdQ/RBRD8TGVNuF2lOmj72OjgS0csA/CsArwfwdACfAHAHET1+n+Vq2Bl+H8DX\nArhFH3+Jxf0kgL8K4CUAngfg6wC810Rqxn47+s2jngPgbwH42wDeuINyNyyDGwB8HMCrEdl4k4h+\nFMBrALwSwLMAPIx+vLiaJXsngKcCuBU9/TwPwFtZHl8D4A4AdwN4BoAfAfAGInrFAvVpmBdZ+tB4\nP/wx5QdE/GnTR/A94B0eAD4C4N+wawLwRwBet89ytWMn7/71AH47EXcTgMsAXszCngKgA/Asff09\nAK4AeDxL80oA9wE4v+/6tWMyfXQAXiTCvgjgtYJOLgJ4qb5+qr7v6SzNCwGcAbhFX78KwL2cRgD8\ncwCf3Hed2zGZPn4GwM9n7vlzp04fe5PwiegqAN8B4FdNmOpb94MAnruvcjXsFH9Wq+c+Q0TvIKIn\n6vDvQC+5c9q4C8Dn4WjjOQB+Tyl1L8vvDgA3A/iW5YvesEsQ0ZPQS2ycJh4A8FvwaeI+pdTvsFs/\niF4afDZL8yGl1BlLcweApxDRzQsVv2F3eD4R3UNE/5uI3kJEf4LFPRcnTh/7VOk/HsA5APeI8HvQ\nd+yG48ZH0KvgXwjg7wF4EoAPaXvaLQAe1QM6B6eNWxCnHaDRzzHiFvQDc268uAXAH/NIpdQWwFfQ\n6OYU8H4ALwfw3QBeB+C7ANxO7qMCJ08fa/h4jsRcn/5tWDGUUnewy98noo8C+ByAlyK9xXIpbTT6\nOR2U0MRQGsMQGt0cMJRS72GX/4uIfg/AZwA8H8B/z9x6MvSxTwn/XgBb9A4WHE9AOMNqOHIope4H\n8H8APBnABQBXE9FNIhmnjQsIacdcN/o5PlxAP/DmxosL+tqCiM4BeKyOM2lieQCNbo4KSqm70fMZ\ns5Lj5OljbwxfKXUFwMfQe0sCALTq5VYAv7GvcjXsB0R0I4BvQu+Y9TH0jjScNr4ZwDfA0cZvAnia\nWNHxAgD3A/gkGo4KevC+AJ8mbkJve+U08Rgiejq79Vb0E4WPsjTP0wO9wQsA3KUnnQ1HAiL6egCP\nA/AlHdToY8+eli9F72X7cvQelG8F8GUAf3Lf3oztWPzd/zj6JTHfCOAvAPgA+hn043T8W9AvjXk+\neie+DwP4dXb/Bv0yzvcD+Fb0vgD3AHjTvuvWjtE0cQOAbwPw7ei9qf+hvn6ijn+dHh++F8DTAPwC\ngP8L4GqWx+0A7gTwnQD+IoC7ALydxd+EflL5NgB/HsDLADwE4O/su/7tGE8fOu7N6CeA34iekd8J\n4FMArmr0oeu39wIAfx/9p3Evop9dPXPfZWrHTt77f0G/BPMieu/7dwJ4Eou/BsC/Ra+SexDAzwF4\ngsjjiQB+WXfIewD8SwCbfdetHaNp4rv0QL4Vx39mad6gB+RH0HtPP1nk8RgA70Cv6bkPwH8AcL1I\n8zQAv6bz+DyAH9533dsxjT7QfyL2V9BrgS4B+AMAPw0hPJ46fbTP4zY0NDQ0NJwA2jakDQ0NDQ0N\nJ4DG8BsaGhoaGk4AjeE3NDQ0NDScABrDb2hoaGhoOAE0ht/Q0NDQ0HACaAy/oaGhoaHhBNAYfkND\nQ0NDwwmgMfyGhoaGhoYTQGP4DQ0NDQ0NJ4DG8BsaGhoaGk4AjeE3NDQ0NDScABrDb2hoaGhoOAH8\nf6p+t9YLVYJIAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f7aca021290>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"widths = np.arange(1,71)\n",
"cwtmat = signal.cwt(y, signal.ricker, widths)\n",
"plt.imshow(cwtmat, aspect='auto', cmap='PRGn')"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.image.AxesImage at 0x7f7ad344ad90>"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABLUAAAFiCAYAAAAAxuoIAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzsnXmYHFW5/7/V+zLTs/fseyaZzJ6ePSEii8KDCCoqREAx\nqOQKsvwU8OJVXBFRlotBwMuVRRRkEQW8oCh7lkkms2WZSSbJTCaZfd+6Z+mZ/v0xnqKquqq7urt6\nmcn5PI+PpKdPn1Onqt73nO95z3sYl8sFCoVCoVAoFAqFQqFQKBQKZTWhCncDKBQKhUKhUCgUCoVC\noVAoFF+hohaFQqFQKBQKhUKhUCgUCmXVQUUtCoVCoVAoFAqFQqFQKBTKqoOKWhQKhUKhUCgUCoVC\noVAolFUHFbUoFAqFQqFQKBQKhUKhUCirDipqUSgUCoVCoVAoFAqFQqFQVh1U1KJQKBQKhUKhUCgU\nCoVCoaw6qKhFoVAoFAqFQqFQKBQKhUJZdVBRi0KhUCgUCoVCoVAoFAqFsuqgohaFQqFQKBQKhUKh\nUCgUCmXVETRRi2GYGxmG6WIYxsEwzF6GYaqDVReFQqFQKBQKhUKhUCgUCuXsIiiiFsMwVwK4H8Dd\nADYBaAXwd4ZhEoNRH4VCoVAoFAqFQqFQKBQK5eyCcblcyv8ow+wF0OByuW75978ZAKcBPOxyue4T\nfDcBwEUAugHMKd4YCoVCoVAoFAqFQqFQKBTKasIAIAfA310u16jUlzRK18owjBZAJYB7yGcul8vF\nMMw/AdSLFLkIwB+UbgeFQqFQKBQKhUKhUCgUCmVVczWAP0r9UXFRC0AiADWAQcHngwA2iHy/GwBy\nc3Px0ksvsR8++uijuOaaaxAdHY1Pf/rTeO211wAAd9xxB+655x5oNBrcdddd+MlPfoJ7770X3/ve\n9/DYY4/hhhtuwMMPP4xbbrkF9957L7773e8CAG666Sbcd999MJlMuPrqq/GHP/wBExMT+Mtf/oLr\nrrsOTz/9NC677DLExcUBAN5//31ER0dDo9FgfHwcubm5aG1txaWXXoqHH34YN910E1QqFWZmZvDr\nX/8a//mf/4nvfve7uPfee3HdddfhqaeeAgDcd999uPbaa/Gvf/0L11xzDR555BHceOONuPvuu9HV\n1YVnnnkGAPCNb3wD8fHxuPfeewEAU1NTeOmll7B9+3b86U9/wubNm5GZmQkA+OCDD2A2m2Gz2fBf\n//Vf+OlPfwoAmJ6exnPPPYft27fj+eefx8UXX4zExJUdn3feeSd+8YtfuHX+xz72Mbz//vu8z958\n802sX78eeXl5uPnmm/HAAw/g+9//Pn7+85+z9bzwwgu4/vrr8cILL+D8889HYmIi77qvvfZa/P73\nv0dfXx/279+Pyy+/HE888QSuuOIKvPXWWzjvvPOQlJQEANi1axd0Oh2qq6vxgx/8ADfccAN2796N\nL3zhC2yb5ubm8KUvfQl//vOfAQC7d++GRqNBTU0N7r77bvzoRz8CAFx00UV49dVXodfr8eKLL+Lj\nH/84kpKScOWVV+JPf/oT7zr7+vrw4Ycf4tJLL8ULL7yA6667Ds899xwuuOACWK1Wt3p++MMf4oc/\n/CHm5uZw+eWX4+9//zsA4Fe/+hV2797Ntu3999+HyWRCVVUVWwYAtmzZgl27dgEAXn75ZZxzzjl4\n6KGH8POf/xz79+8HwzAwm83o6enBE088gRdffBEOhwPPPPMMbrjhBvz5z3/Gli1b8Nhjj+Huu+/G\nf/zHf+DRRx9FZ2cnTp06hdLSUnz44Yf4+Mc/jr/+9a/Yvn07/vznP2Pz5s04cOAACgoKsH79enz7\n29/Gj3/8Y9x///34wQ9+wPbvU089hR07duDBBx/Enj178MILL8But+N73/seHnzwQWzfvh2PPPII\nrrnmGrz88ssAgKeeegpf/OIX8frrr2Pr1q1ITU3F1772NTzxxBO48cYb8cgjj7D9/fDDD+Pmm29m\n//3zn/8c//mf/+n2THL55S9/idtvv53991/+8hfU1taio6MDKSkp2LhxIwCgs7MTnZ2duOSSSwAA\ni4uLePrpp/G1r31N9Hdvuukm7Ny50+3zp59+GldccQWioqJw5ZVX4qtf/Sqys7PhcDgwOTmJ8847\nDz/72c/wve99DwBw/vnn44033oBOp8P999+P73znO+w7efPNN8NgMOC++1aCU3t6erB371588Ytf\nBABccskl+L//+z9cddVVeP755/HlL38Zt912GxwOBzZv3ox77rkH1157LXbv3o0rr7wSv//973Hh\nhRfi2Wefxe233473338fCQkJKC4uxi233IL//u//BgCMjY3htddeQ3NzMzZu3IgbbrgBr732Gioq\nKvDQQw/h/vvvBwDWXgHA5Zdfjr/+9a9YXl7Gzp072ftEPgeA1tZWjIyMID8/H0eOHEF9fT3efPNN\nXHnllfif//kf3HDDDQDA2lcA2LFjB3bu3InrrrsOzz77LMbHx/Hmm2/iqquuwq9//WvWjgKA0+kE\nANx6663YuXMnurq60NbWhssvvxyPPvooduzYgaeffhqf+cxnEBsbCwB49913ERsbC7VajYmJCWzd\nulX0fp9//vl4++23eZ8dPHgQ4+Pj+NjHPgYAOO+88/DOO+8AAJ577jls3boVGRkZuOKKK/D//t//\nQ3R0NMrKytjyP/7xj9n3BwCeeeYZXHrppYiPj8e1116LHTt2ICoqCmq1GmNjY8jNzUVDQwOefPJJ\n/O1vfwMA1h/cc889uOuuu9h7smPHDjz22GPo6elBY2Mj/vd//5ct86c//Qmf+MQnEB8fD+Aj237w\n4EEMDw/j/PPP5z1fALBz507885//xIsvvoivfvWrePbZZ3HzzTfj4YcfBgBcddVVeOqpp/C5z32O\nLfPCCy/gggsuQEJCAs+2A8Dtt9+OX/7ylwBW/MErr7yCp556Cm+++Sa+8IUvsM+Mw+HAnXfeiYcf\nfhjf//738ZOf/ET0/lx00UWsPQUAu92OW2+9Fb/97W9Fv//CCy/wfEhDQwOcTicSEhLQ19eH888/\nn+1TwsMPP4zt27fjwQcfRFdXF373u9/h1ltvxUMPPYS7774bt99+O6Kioti2XHjhhdixYwfOPfdc\n7N+/H+vWrcP69esBgLVx/f39+OCDD9h3uq6uDnv37mXrJO82twyXxx57DNdddx0MBgMA4Ec/+hHu\nvvtu9u9f+tKX8Mc//hH9/f14//33cdlll7E+HgBmZmawd+9eZGdno6CgAABw/fXXY+fOnbj22mt5\nYypgZTzyne98B0tLS/jGN76BJ598Et/+9rdx//3346677sItt9yCDz/8EFdccQWefPJJXHXVVXjj\njTdQX1+P1NRUtq+Xl5dRX1/PewcuvPBC/POf/wQAvPLKK6irq0N7ezvi4uLw9NNP46GHHgIA/OQn\nP8Ftt92G3/3ud7j55pvx1FNP4VOf+hR7L4k/v+GGG/D444/j+PHjOHnyJDZv3oyoqChccMEF+Ne/\n/oWLL74Yb775JmZmZnDffffhxz/+MZqamjA1NYWMjAycPHkSn/zkJwEA4+PjePnll1l/cOmll+L1\n118HANZ2fvGLX8QLL7wAAKxtWlhYwGc+8xm88cYbAFaee6fTiauvvhpzc3M455xzeGMwp9OJJ598\nEl//+tdZP/Hee+/BbDajqqoKd9xxB+677z7eu3Deeedh+/bt+MxnPoN33nkHlZWVePTRR/HTn/4U\nTqcTd955J2uzx8bG8NZbb+GKK67AY489hptuugkAsG3bNnz9619HUlISSktL3fzBW2+9hc9//vN4\n9NFHceONN8LpdEKlUuEHP/gBfvazn/H6AQAuu+wyvPTSS/jEJz6B9957j3127rjjDvzjH/9AWloa\nSkpKeD5kfHwcr776Kr7yla8AAD71qU9h+/btqKmpQWZmJr75zW/iN7/5DQCgvb0dXV1drL+urKzE\ngQMHAAB/+9vfUFpaipMnTyI2NhYVFRUAgFOnTuHw4cMoLy/He++9x74b5557LtLT0wEAd911F+65\n5x527PHZz34Wr7zyCiYnJ/H666/jgQcewIEDB3hzCmIDWltbMTY2hvPOOw+/+MUvcOedd7JzipXN\nJsCrr76K0tJS5ObmAoCbXZyamsJrr72G3/72t3jvvfd484Ndu3YhKioK5eXl7DsHrNjpV155BXq9\nHs8//zwuuugifPDBBygpKUFeXh6+9a1vYceOHRgdHUVOTg4aGxvxuc99DgDw8Y9/HO+++y4A4LXX\nXkNRUREGBwdhMpnYfiM+/JJLLsEll1yCHTt2QKNZmfrdc889uOWWW9Da2gqj0YhNmzbxnmcuzz77\nLG9OsWfPHuj1ejz++ON4/PHH0dvbi127drG2sKamBvv27QMA/OxnP8Ott94Ks9nM+h0pf/CHP/wB\nn/zkJ1l7IHw2e3t72fnBE088ga985St45ZVXcN5552H//v0oKCjA448/jl/96lf4+te/jocffhjX\nXXcdampq8O1vf5v9zT/+8Y+48MIL2bH+rbfeCqfTiZ07d7I2iDtGvfDCC/H666/j6quvxg033IDc\n3FyMj49DrVajsrISP/zhD/Gd73yH50OAlbHE+eefj+TkZLbfVCoVamtrAYC1O5/85Cfx2muvQa/X\n4+WXX4bNZmOfMzLWJz7kC1/4Al588UVs3rwZu3fvZq/p85//PF566SXMzs7i+9//Ph544AFcf/31\nsFqt7Pxtbm4Of/zjH7F9+3b2OQfE/ROhvr4ee/bs4X329ttvIz09HY888ggeeOABdHV1obu7G2Vl\nZXj77bexbds29ru/+MUvcPvtt+Pdd99Feno6NmxYkQLIvOyKK66A0+nEX//6V/z2t7/FNddcA5PJ\nBOAjf7Bv3z44nU5s3rwZAPDZz36WndP9/ve/x/XXX8/2ybFjx9j5AXesPzw8jH/84x+4+uqr8fTT\nT+Piiy9m78s777wjWgZY8Qff+ta33Prln//8J1JSUlBSUoI77rgDO3bsQGdnJy666CLe94TzbDIu\nvvPOO3HjjTfi2LFjuPjii7Fz50585StfQXR0tNv8AAD77iwtLeGnP/0pO1Y477zz8Oabb0Kv17u1\nkXtfyZiIjDufffZZXH755YiOjuaN9VtaWmC329m+Hhsbw+uvv44vf/nLAD6yO8QGc+1gd3c3jhw5\ngksuuQS/+c1v8M1vfhN/+MMf8OlPfxoWi4XXtubmZkxNTeHcc891a7eQ9vZ2XHPNNcC/NSMpgiFq\nScEAENvrOAcAarUaNpuN/bCurg6zs7M499xzcc4557B/27BhAwoKChAXF4f6+nps3LgRubm5sNls\nqKurg81mQ3JyMmw2G+rr69lymzdvZuvYsmULbDYbRkdHsX//fthsNrzxxhuoqqpCTEwMgBXDGRcX\nh/j4eExOTiIzMxN6vR42mw0pKSmw2WxQqVT417/+xdazefNm2Gw2VnACVozB4uIiamtreW1KSEhA\nWloa+73S0lJeufHxcezZswc2mw3d3d1wOp3s3/r7+xEdHc2rEwDeeust1NXVobKyEh9++CHKysqQ\nkpLCXj+3fwnCfid15+fnIycnB1u2bMH69euxfv169nuTk5P48MMPYbPZcOrUKVRVVSE+Pp7tVwDs\ntaSmpoJhGPb+OBwO1NXVoaqqCgkJCQCAwcFBGAwG9npKSkpw5swZXrva29t5z8HQ0BB0Op3ofU5K\nSsK6devQ09ODyspKJCYmwmQyuV1nfHw8+52enh7YbDZ8+OGHKC0tZQdJw8PD0Gg0vHoOHz7Ma0tW\nVhYWFxfZf+/fvx/V1dXYtGkTr99VKhX732fOnGH7jXzGMAxcLhfUajX7+3a7HW+99RZsNht6e3tR\nVVXF/qbFYoHNZkNMTAySk5NRXFyMxcVFzM3Nse8CKdPZ2YmqqiqsW7cOmzdvBsMwvH5zOBz4+9//\nzt4n0tZdu3ax93XLli0wm828a+/o6EBlZSXa2tpQUlKC7Oxs9u+kfdx3mvvvpKQk0WeSi9Vq5X2n\nv78flZWVsFgsSE5OZieZGo2Gdw8WFxdx9OhRyd+PiYkR/dvRo0dRVVUFk8mEc845B9HR0aiqqsL8\n/Dx27drFszMAsHXrVlitVmRlZbnZgS1btrA2AwC6urpQU1PDK2uz2dj+MpvNqKmpgcPhYJ83p9PJ\n2o7Ozk4sLi6y9TgcDiQkJKCwsJB3PePj49i3bx9iYmLYtg4NDaG0tBSxsbE820T+m7RheXmZtW8A\n2PcSAHQ6Hd5//31UVVUhKioKVVVVGB8fd+sTrh0oLS3lPROTk5NsmYyMDJSVlUGn0wFYsQM6nY7t\nP5PJhMnJSd7vv/HGG6isrGTt9OnTp5GYmIjY2FhMTU1J3m/yDnMxGAzs7wu/c/LkSdbmGgwG1NTU\nICoqCsXFxWz5xMRE3m++/fbbKCsrg9VqxZYtW1BTUwOz2Qy1Wo3x8XFkZ2ejs7OT9/4Inxnyb9KH\n0dHRGB4e5pXp7u5GZWUluwBDyi4sLLB+gft8ASvv3tzcHDIyMmCz2dx8xznnnAOLxSJaj9C2A0Bc\nXBz779nZWfT39+PEiRNITk5mn1cAaGxsZMtK+SAA0Gq1vL81NDS41cmlp6eH50OWl5fR3NyMqqoq\nDAwMwGazudmXuro6OJ1O1NfXs76X2+/Ly8uw2Wxsv23duhW1tbWorKzEyMgINm7ciPLycra/iP/r\n7u4WtfEAeH5H7HpSU1OxadMmGI1G3r0Ulu/p6UFXVxcqKyvR1dXFfuedd95hRYP8/Hy2HqGdJmRn\nZ6O4uBgTExOoqKjg9UF8fDyqqqpYO9re3o7KykqMjY2hqqqKHfyPjY2xfcW1Idznra+vD1VVVYiO\njkZXVxfv2oldI+90R0cH5ufn3d4J8izHxcUhKSmJfR+FdvPdd99lr0GtVmPPnj2orq7mvZ+vv/46\nz0Zx7TJpm9Fo5LVh06ZNOH78OK8f4+LisLCwgPXr18Nut8NmWxnLkb87nU60t7fDZrOx9dvtdnR2\ndvL6mltm69at7LjNbrejoqKC/d7Y2BgKCwt5tp3YOa6dPuecc5CXl8c+10J/QMqkp6ejrKwMAwMD\niI+P5z1v3DK1tbVITk7Gxz72Mbf7snv3blRXV2Pjxo288sPDw2hqauJdV1xcHCorK5GRkcF7Bjo6\nOni+EADvd4qLi8EwDO8eJiUlwWw2Y2Zmhr2XJ0+e5Pl9oT0l/mtqagojIyNsPdx7Snzi3NwchoaG\neM81qYeIWq2trSgqKmIX06KionjXMD09jaGhIXR0dMBms/HmB4uLizCbzSgpKeH54bq6OlitVuTn\n57Pv+OnTp1FUVISioiJs3rwZ1dXVGB0dhdVqxfDwsOg7d/DgQRQVFSE7OxtGoxGlpaW8Z33r1q3s\nM0NErfr6lc0zNTU1bBkpO/3uu+/y5hRLS0vQ6/U4dOgQbLaVsT65bgDsuJ9cI/m3N3/w/vvvo7S0\nFGlpaexn3GcnLi6OnR+Q+9Pf34+qqioMDw/znsstW7awY7nKykpefR988AFvrF9UVISlpSXe/ef6\nkK1btyI2NhZbtmxBbW0tsrOzWVGroqKC50O4zxeZU2RkZAAARkZGeH6C2x+JiYkoKCjAmTNnMDc3\nx36HjKXJd8nvC/0N+XzXrl28PhgdHWW/Nz8/j5MnT7pdnyd/K6wHWFlQSU1NRVFREfLy8pCQkACr\n1YqCggLW3hFycnJQXFwMu92O1NRUdgGG+LctW7agra0NNpsNaWlpqKioQFRUFICP3umJiQksLCyw\nv1tTU4OUlBSkp6fj2LFjsNlsaGhoYN8vMj/gzkP6+vpY+3z06FHe783OzrJlhPMDrp/jcvLkSWRl\nZbH3r6qqijc2Igjn2Zs3b0Z+fj4KCwt5Zcgc+dxzz3Xzc6SczWbD9PQ08vPzefY/Pj6eFQu5cG2U\n0K6R+xQdHc0b62u1Wta/ASvz7ZaWFvbfZKzMnbuQvyUmJrJ1kvqOHz+OyspKREdH89pmt9sxNjYm\n+dxJ4DFNVTASxY8AWAKQLPjcCvfoLZbe3l5cdtll7P+eeOIJVl2srv7o4ESr1Yrp6WkAQGFhIebm\n5tiHPysri/ebZJAHAMXFxTh06BAAYNOmTW71Ly4usoaeS3R0NOLi4mA0GllFn0tjYyPWrVvHtkdI\nfn4+mpqaWMOZnZ3N/o2spAArLz13ZYJLamoqWltbRf9GJvXAipiSlZXFOmAuYm2TgohAwIqhn5mZ\nYVdnxNqm1WoBgB3wczEYDKwTzMzMxL59+5CamspOZD1dDxcywfJWprKyEmfOnGHbJlUPF7VazToc\nT5B6iDhBMBgM7AACWDGcZNJNjLeQlJQUXttiY2PZMgBEX3JSRvibZrMZiYmJ0Ol0SElJwf79+9mo\nvpSUFOj1eoyNjcFsNgMANm7ciLa2Nsm2EZEYWBkokQFceXk5a5wIGRkZUKvVvPLcvuCSk5Mj+rkv\nJCcnQ6/XIyEhgX3vxVCpVGwf+AL3emw2G0ZGRhAVFQWLxYKBgQEA/HtaW1uLM2fOYGlpCXl5eQDA\nOpaioiLee9fa2sobqBG7xrVHFouFFSvWrVuH1tZWNkIiPT0dTU1NbD3x8fGifaDVarGwsADgI5to\ntVrZaBACt21VVVVe+8ZisWBwcJC1hRqNBmlpaWAYhmd7udeTlZWF8fFx1taRMuS/SXQWsDL5mp6e\n5glHBGI3nU4na2+EbSORS3Ihtl2MtLQ0tLS0sP+Oi4tzc8ieqKioQFxcHCwWC6KjoxEfHw+DwYCZ\nmRmePyPXRXwVuSclJSW83+OW4dpcbhkh3DI5OTmoqqrC0NAQ+/xy+3nTpk04efIkr0xaWhpro8Rs\nO0GtViM9PR21tbXo7+/nRbO1t7ejqKgIgLRtF+PIkSOSdgRwt+2xsbE4c+YMoqKiWKFLSE5ODpqa\nmlBQUMC2kdu2pqYmAGBte21traQP8dQ2Kbj9IoWUTSao1WqeXWtqakJiYiJr20k9wkkFwWg0Yn5+\nHiMjI6wdIfYdAOtDgBVbqFKpWB/irb0k8gD4yO8kJCTg5MmTbD+TMk1NTaw/yMjIQGNjI/t34XNi\nMpmQmJjI3h9SD7lPzc3NbBmLxYL+/n62DGHfvn2S/oDbNkJ2djZcLhdOnz7N8/XeYBjGrZ6EhAR0\nd3cDEH9X6+rqkJ6eDo1GA6vVCr1ez/qQqakp9n4AK7ad+AMuYmNaYRmGYaBWq+F0OjE4OIi5uTnR\nSRCw8r739fWhrq6O/YzYqOHhYdYWehpXVldXY2ZmhhVsufbm6NGjvPE0d8wq5quAlWc3KSkJLS0t\nrA8R2mkp+8n1VaRtniDXKpxTeEOj0SA9PZ3tN+78gPgDITbbyuIjuR6hfysuLkZUVJSof+PeH4JU\nPWLXTMYY3DJSz4SQ2NhYWCwWtq/1ej1mZ2dFv1tQUMDOYfzxB2LvKLAyp1CpVG52mti00tJSdHZ2\nYtOmTWzUkxSpqansPECsbbW1tew8hMyRuON2MR8iB2Knq6qq2LlLSkoKO1/lQnyIlAhAPm9ra2P7\nTOh3pMbGcvwTFzIGT09Px8TEBDsPEYP4Halxe2VlJTvnFCL1nJSWlqK/v1/S5nqaHwArfodEh3or\nw523S1FYWAiTySQ5jxe2ndh2rq/KyclhI73F5gfEhjocDt58sba2FqdPn/ZaL7FF5HqI3xHCnYd4\ngqthELhaCbGfUvVI8dxzz/H0oMsuuwy33XabrLKKi1oul2sRwAEAF5DP/p0o/gIAu6XKxcbG4tVX\nX2X/98wzz7DilVDUmpqaArDyEDkcDtYYCx88cgOBlYfIm6glNlniTkjISiWX/fv3u01IuOTl5ckS\ntXJzcyUNQlpamqSoxXVA+/btk3TC3IGrN6xWK2tgSkpKPIpa3ImP2APO7besrCw0NDT4JWp1dXVJ\nTry5fcB1DHJFLZVK5bOoxR1MiIlaZHuU1PWkpqbyJgoxMTFsGQCiAh6ZKEiJWnq9HqmpqbwBvJio\nVVRUhNbWVsm25eXlsfW3tbWxhrSsrAzHjh1zE7XI9jGClHP0NqiQQ0pKCgwGAxISEngTOSFCoUUu\nUqJWTEwMK2px7Up9fT16e3tFRa2SkhLee8cVqICPBj7cAYqYqEUG8ETUIvYmISFBVGghohbDMKy9\nSU5OZicXBG7bvA3ygRVbSLY2WK1WaLVaUbvGta/Z2dkYGxtjbQO3jFDUGhsbw9TUlKhgQH7f0+KD\nP6KWVJn09HQ3UUtsoiDFpk2bWCGMTEiMRiOmp6d5A15yXeSZIvdE+A5xywgnPlK2nVuGiFrDw8Ps\n88mdZJKoB64w4W3BgqDRaJCRkYH6+npRUYtMeuROlgDg8OHDHgfZnkQtKV+Vm5uLxsZGFBQUsNdD\n+mDDhg1uokldXZ3b4gPB1wmA3DLeRC3hhKSxsdFN1CovL3ez0wSj0YiFhQV2GzHAnzASHwKsTBjV\narVHUYvrQ7g+kbv4cOLECTdRq7GxkfUHQlFL+JyQQT/5DokuIffpwIEDbDtiYmJYUYs7uWhoaJD0\nB2Iiem5uLlwuF3p6enwWtYT1JCQkoKurC4D4u1pfX4/09HS2rw0GA9sHk5OTbqIWd2GE4E3UIoIO\nEbWGhobgcDi8ilqkrwGw/m14eJid/HkStWpqajA9Pc0KVFy73tHRwRO1uAdWWa1WN18FrDy7ycnJ\nfota6enpbD1yRS05k1mxeki/cecHUgsj3kStkpISREdHi4r1ZHsQFylfJfYcr1u3Di0tLX6JWnFx\ncYiJiWHtGlm0EYPUQ67Hl3oA8XcUALuIL/QHxN6Ul5ezEfvcIAcx0tLS2HmAWNvq6urYeQixuUJR\ni4gkYmKjFMROV1dX8+YunkQtqQV+8jmJKATcfbeSopbZbOaJWlKCjslkYkUtsXE72R0hhtRzQkQt\nlUolanM9zQ8AcVFLqoycucvGjRv9FrWILczJyWG3eYrND8h7YLfbee94XV0dTp065bVeMs4kC0qB\nilpi4qrwejzVI8W2bdt4etCrr76KBx98UFbZYERqAcADAL7BMMyXGYYpBPAYABOAp6QKkMgCQnZ2\nNrtX2FPXnJp/AAAgAElEQVSklsPhYB2F0AFxjVhJSQkOHjwIwD9RizhUIdyVGLEBC4nUIsaSG60i\nN1LLk6jFHVQQUSvQSK2kpCTWwBQXF2NmZkZy9ZvrTMQmPnq9nu23zMxMVtQS62tA2oB1d3dLilrc\ngbU/opZw9VsKUo9w8scN9Qb4kVpSwpG3SC0pUUun07n9prdILZ1Oh7GxMXYgSkQtqQkUV9QSOkey\njZFAJj5cpCbASohaciO1xFZv5CAUtUZHR9lIrf7+fgD8iWd9fT3OnDkDp9PJ2huuaCAUtbgTEl9F\nLeKEST1SkVo6nc4tUis5OVnxSC3uBMtbpBb5jFuGbBkljI2NYXp62m1CAniP1PIUdSWFJ1FLOFmK\nj4/3OVIrPj5eNFJLKDYBcIv2FQp7QlGLazukbLuUqEXsB7efbTYbTpw4IVmP2IIFgUS61tfXo6+v\nj/f+HzlyhCccyUWOqMV9DsiWFLPZLOmrPIla3AkJV9SS8iGeRD4p5EwavEUvCCckBw4ckIzUEnun\nuZFa5JnjCk7cSC0SBSE3Uos7kSNlEhMTceLECd6kVChqZWZmYv/+/ZJ9QCZLRNQi9ZD71NTUxD5b\nRNQSTrAaGhok/YHYhDknJ4cVtbi+3htiolZ8fLxXUSsjIwMajYa101KRWjqdTlTU8rR9g1tGGKkl\nZTsqKirQ29vLE03EIrU8LZZWV1djenqaFag8iVrcMavYAgzwUQRAc3MzuzCSnp6O5uZm9jtS9pMs\npvgaqeWvqEX6jTs/IP5AiBxRSypSiys6EkIpalksFp6oJSdSyx9/ICVqZWZmsqKW2EIPdyGWiLJS\neIvU4opaZCuslKjli80gY+2qqio22iYlJYWdr3LxJmoRm88dtwcrUotsM5MTqUVELVJGrN2+RmqV\nlZUFHKnFXUzxVEbOLhNfRK2ysjJMTk4iNTWVV8abqEXGbHa7nTdfrKurQ09Pj9d6haIW8TtC5O58\nENNSuJFa3iLCgkFQRC2Xy/UCgG8D+DGAZgBlAC5yuVzDUmXWr1+Pjo4O9t/cbVbch50ITMCKYKLT\n6dgXSafToa2tjV1p5A7EDAYDmx+LlFer1Wznp6SkiIpBarUaGo0GKpWKvSncaAu73c7WIzbw0+v1\nyM/PZw2uTqfD4cOHkZmZyXPcsbGxrFgnbJtWq+UZ5JGREXYQy60zLy8POp0ODMMgKSmJ9xCJhXNL\nQa6XlCORMQSVSoXl5WW4XC5otVq237jXQwydSqXiXfu6deug1Wrdonu4/aXT6dwmJgsLC7zfJ1Ej\nwj4wm82Ij49HW1sbW8/4+LjHqB2GYdg2JiYm8pwjd1WS1JOUlIQTJ06w30lKSuJNeLlCD7dtxcXF\nbLQPaRt56dVqNdRqNYxGI/uMnjlzBgzDsKIgKSN8zsizSfrabrez16DVatHR0cGLqDIYDLBarbDb\n7bw+AFbyJOh0Oravs7Ky2GeHTIi494Hc/7m5ObZO8n3hIII7OTx48KCs6DghpA80Go2bmMaFYRhZ\ngqbY73OfZyJyqdVq9hni9j/pE5VKxdZH/k7eHQK3j4CP7Bq3P0ld5Hfy8vJ499LhcLD1cPsgNzeX\ntZ9kkLdt2zbed1UqFeLi4tiBJ7dtpC3CaDLupIdMiEj/k/dG2Nfc6xkdHYXZbGY/45ZJTk7m3cPh\n4WEYjUa2XXq9nnWsxK65XC6enbZYLGzeKl+dprAMV+QhNrenpweFhYW8+yIF1+YajUa2DNeHLC8v\n8/yZ2DPD/X+dTge73c4rw31Gud81mUwYHx9nPxfWYzKZEB0dzQ6GuPefRPBI1SM2ySSQe2oymRAX\nF8fay6NHjyI9PZ13P6UQbi+Zm5vz6LOEPoS8n9x7mpGRwZsY6HQ65ObmQq/Xs9fDbZvD4QDwUb+Z\nTCZJX0XKabVaSRFN6Hc89SFB2EdkQH/8+HEkJibyfBWw8t5z/TWpR2inCVarFZ2dnZLPAddfk/vv\nzV8ThM8OsRMLCwu8OvR6PTIyMjA5Ocl+lxv9KuXfxO4PsLIVg5QhC1Tc8RqwMpgn7xo3Sk14/QTy\nXafTyWtPTk4Otm3bBrPZzOZo4t5jri0k90Gj0bB+Xqwu8pwxDMPeS71ej87OThiNRt7kgtwP7jiX\n1BUTEwOTyYTjx4/zFpCENre9vR0WiwVarVbynSSLBNx7Sr7rdDpFxzfEP3CvKz09nTfuIJB+IZSV\nlaGvrw/AR76K2HYCuafc8TTxicI2krqI/yJ9QCK1uNeVm5uL48ePw2QyscIO+R3idwjx8fHQ6/WY\nnJzE7Oys28Ig1xYC/PkB8QWzs7O8BZioqCj230LbTq6F2DXiD7h9TIiLi8OpU6ckfZXJZHLbujo7\nOwur1eo27pADKUP6WqVSiQqu3HrI9fhSD7cMsHJP5ubm2P/m2qi4uDjeuMtgMLC2UDgeFI71tVot\n+2/SNu4YlYgPRqORfUaF/Sa0UWL1CCF2mitckvEHib4hY2nyXSlfIjVu50L66+DBg6w47Ok3peCO\nKc1ms5vN5bKwsACNRuPmq8iip9FoxNVXXw1gRdTmfseTjYqNjeXZ3ISEBOh0OnZsPD09zROZNBoN\nqxcIbQcpI7YzSc5cwmAweOwD4XeNRiPi4uJ4ZcgcmUQbA/z7Qu4pyb1MEG63l4Jr1wBxewPAzYYI\nd1WQsTJpG9cOCq/HUz3BIFiRWnC5XL9xuVw5LpfL6HK56l0uV6On75977rm8FRdAPLRWuGIuzHW1\ne/duydUVshWGQFZVAN/y/fi6eiNcISEnKXEhCYHF2gbwV5YGBga8rsSIrfj4izBPiUajwfLyMpaX\nlyXL5OXlYXR01O1zsZUlIXq9nrc6KQbZbiKERA1wT6AaHh52628phCvz3KgrQl5eHu/3pUKfhXDD\niwliWwnJM9rV1SU7iswT3O0ZhHXr1rGDcmDFEDEM43ZP5a7ecAdvBKl+AFZWzpWI3Ao23H4TW5Um\n70GwViHkbAsEVtrGjSwiky8h3EhXMchJagQfEzi6cerUKY9b/Lj9NjQ05NG2i+FrBJUnhH1dXV2N\nEydOeIxS4qKkzSUYjUbJLR1ChD5EDKmtPUrBtYUtLS2yt73LiRT0hnA1Py8vDw0NDYrXw4W7XU8I\nNxrKX4j9PXTokKhPlFqxl4LkahFGd4UasspO8CWywRtS0VCEwcFBycgPLiqVCiqVCktLS+xn69ev\nx7Zt23jb0aUinqOiotjJtz852Nra2mCxWHhpCQh79+4VjQiLjo7GoUOHJN87soVdKhqKILXN0RNa\nrZYXeQvA65YvQn19vVukgZRtl+sTAc/bMgmFhYU4ePCgrC3sxH6S5PtiUcXemJ6e5vk14VjfE578\ngdVqxdGjRz2WF+7k4G5HVwKp+z0yMuJ1a7VcPOXu4uYD9oacnRzCMao/Y1Zf0qBwx/qVlZU4duwY\nAOlINSnkRBLv3bvXa/SaHIS7TMQQmx8AK/MQMmYh41WxlCZi6HQ6N98rjCqemprifUcq0pULiaAK\nNjExMaK7C+RGXXHxN92KXLh5egF3TcMf/xYsgiZq+Up2djZvUgaI70sWOjoSdUIQTsq45OTk8EQt\nruP2RaiS2uInhdAJc0OSCVFRUTyRgSTfJXAHr4ODg15FLbmGVA5CUUutVrORWlLk5uby+pogZ/DK\n3bIoRWxsLBuyzYWIWtzJjC+TC+G2wP7+fjeDnZubyx5VLFZGakDJDS8meBO1/E14zoUkR+aSn5/v\nJmoBUFTU8jSh3bdvnyIONdhwB3xiWzVcLheWl5e9RvH4i9xJa2FhIW+LspQ9S0xM9CiSCCdLcgUd\nKXp6ejwmY+eKQJEoah0/ftwnUUtpcdNTnhIhQh8iBndreTDgbgNpa2uTLWr5Ks6IIRTRhXZaqXq4\nePJVwoggf/AmavkqOhNRS07OkWBSWlrKikKAb4mVvSH2zHHHHYODgx4XXAgMw7iJWsQfcA8OkRpb\nmM3mgEStQ4cOSeY2EdtOSbbPHD58WHJbIdmuJ7YdnQv3QA+5iIlacn18fX29W04YKdvuizAttN1i\n4/YNGzbg8OHDskQtYj/JoSb+iFrCSBDhWN8TnvxBUlISOjs7PZYn2/UI3O3oSiB1v4eHhxUVtbjR\nalzItkA5yJkjCa/Hn8OOpPIyChEeWEVOpwN8y4kMyBu3NzQ0KHJ4kzAfsBieRC3hmEXs8CkxxEQt\nkp6EIBSoxMoIEQphwUJqwaK2ttYvUSvQeaInhKlChDbYHzsYLCJG1MrNzXUTtaSSIAonPtxBpb+R\nWr6KWr7gb6QW18BFUqSWWq3G0tKSV1FLLFJLTgJF7omJUniL1CL7kgHfVonkRmpxRTNh0ndfIrXE\n8ocoLWpJRWpxnzcSqcUdwAM0UstbpJbL5cLS0lLQRC25q9KFhYW8SFepwYq3SK09e/bw7FukR2r5\neiqhJ5QQtZSO1PJF1JITqUW2TwQLbh6uSIzUCoaoJTUA9iVCWAqy4i4lavnab5ESqVVaWspuNwOU\njdQS8zvcccfAwICsyAcxUUuYkB6QjtQym82Yn58H4H+kltRqvtjiLTdSS0rUysjIQFNTk+QJgwSl\nIrXkPv9iopaUbQ8kUktszLpx40YcOnTIr0gtf+6rWKSW3FQM3kQtb5Fa2dnZPFFraGho1YlaBoPB\no6gViZFacrZaCsf6VVVVrKglR4TnIidSq6GhQZGF5UBErYKCAjdRSyxPrxhSkVpcu+aPqCU8nCNY\nKB2p5esOMl+gkVp+kJSUhImJCd4eVzGHGBUVxRuU63Q6WCwWLC8vY3Z2FlNTU5J7S1NTU3lCi1qt\nZh8qYRmHwyE5QSG5Lch/k9MYCcIHlWs47HY7pqam3FZ3DQaDW04t7u8QYzo6OgqGYUQnJtx6YmNj\nFYsaMBgMvAR6arUaJpMJQ0NDkmVSU1NFowbkDHK0Wq3XcFaz2Sw6QFGpVIiPj2f7cmRkBIuLi6Ir\nYSqVyq0fhf1G9oJzSUpKwtTUFGZmZuByudzKSK265eXlYWxsjNduofE0GAzQaDQYGRnB3Nwcez1i\nmEwmtwMWSPu44dkzMzNu9aSnp/P2SEtFHgoFNYvFwruvs7OzWF5ehl6vd3tfPA2KT5w44VWw8AWS\nu0VpuA5Q6nqE+9v9Rew+cwdRs7OzHk8hJfYPcLdnhOjoaDZ6QAySu4cQiKMcHx/H8vKy5OQ5Li6O\n7Tcxu0ZsO2FoaMgtkafQHwSCcICXm5uLoaEhyT4QikhxcXGKR2px84d4Q+hDxLBYLB5zVHgTxbxB\nbOHc3BwmJydlT4yVELiFdtdqteLkyZOy6pmcnJSVk0KI0FdxRWOn0yk7AkMKYn9nZ2dFJ2C+rrTH\nxsZibm4O0dHRvMH/4uKiTzlufEHMrgkXGMUi2nw9+IEg9sxxxx1TU1Oi9yUmJob3rjEMg6ioKJ6/\nJv5ArVaz/kYqUk+v17MiD9ePOp1Or5Np8v4YjUZR+3nixAm3XG5RUVGw2+2w2+2S711cXBy6u7sR\nExPj1gbuxFSj0Yj2/+joqOTYjCx2cpHy8cK2WywWVgDkXo+3ce7s7KxkTjvA3X+JjXOMRiNmZ2dh\nNBq9Jpe2WCzQ6XQYGRnB0tKSVzFKzKYsLS3xxkrCsb4nhCKrsG1CUXFycpLXPwkJCWAYBna7HUtL\nS5JjY3/h3m+St5XU408OVTG0Wi10Oh075+MSHR0t244Jx+06nc7t94TPr5wk4N7qkYI71rfb7cjM\nzGTFO1/vkbdxOwC3fFP+YjKZeEIid17laX4ArFyXMPghPj5e1vZDjUbjJqbFxMTw6nE4HG52jfvv\npKQkOBwO3jvldDoVnZtIIWXb8/PzRQNCuHBz2QErdk3MDo6Njcm2LQkJCWyeSyEajYbXR8Kxsr/v\n9szMjGI7yggRI2oBK2HAnoQSTzidTrcjiIVER0fL/v3BwUFZEQBVVVW8pOGA51A84elQvtLa2urT\nSYbBIisry21rB5eoqCivL2ageFq94B73LbXPXk7urtTUVNEXvba2FmfOnPGYV0yISqVit6t5oqCg\nAE1NTV4nemlpaZiYmHD7vLq6mrfNUerYVe6Ai2wn9eZMCgoKeMfgkj4Id9SVyWQS7YvVhLcQ3t7e\nXo85QsrLy3H8+PGA2qBkMsdDhw7JDktuaWnxateEUWThJj8/n3dq22onLy/Po033BSWilELJsWPH\nZOXf8UZtbS26u7sB+JbfxRslJSW87XqBIOYP7Ha73yKSN8RWceWItb5GJwSKMHoZWJl0iS1YCE8l\n9AXhyVVijI2N+bU16NChQz7n3yHIGVc2NzcrkoNJGP3qr23v6+vzaYu82ELo0aNHfd4+48v8QEhU\nVJTfiwdzc3MehTfh3OLo0aOidq2vrw+Li4tB3Y5eV1eH/v5+LC4uKmoLgRVftby8LLpbw1+kUpqE\ng4GBASwsLCgW3UbmFFyU3PLNhRsN5W1+IDzcJtTU1NSwJ8ES5ESehRu5pyz64g82bdrkNdJTaXp6\nemSdsugLESVqFRYW+i1qLS4uore316uoJdeZSOWtEkK2qHDxFIoXqKjly5aOYJKVlcVLli4kOjra\na36XQPH0spLtBo2NjZJbLQwGg9fcXWlpaZKiVk9Pj8+iFuCet0oIORrYm1CUnp4u2jahqCW25UZ4\n/C5pkzdRi3tsMQCcPn0aS0tLYc+PFW7nqATeQnjPnDnjcftURUVFwKKWkhw8eFD2ZKG5uVmWqKVE\nDgilWGuiVn5+vqKilpLbWoINOfY9UMix7wAU3eKnpKgldp3CE9mURGy8o9Pp3CJzhPgrzvjL+vXr\n3caHUvldAkkmLEfUGh0d9WuhyBebKyTcopY/UcF9fX0Bi9EdHR1+iVpy5wdCAomI9SZqCfv16NGj\noiI2EZusVmtQRa2+vj4sLCwoLp7l5eVhaWlJcVFLyd8LhP7+fszPzyvmQ9evX4/GRv5ZbXJSwfgD\nd0u+t/mB2WwOu6g1MDDA80VSeQwjCZPJJCuazBd/sGnTJvYE9VBx6tQpxfs6okStDRs2+G3slY7U\nEuZ3kUIsUiuYolakRGplZmZ6nABxj7wOFnIitZqamiQdaiCRWjU1NTh9+rRPohYZHIciUovrnMUG\nNVKilrdtdOvWrXOL1FpaWoqISC2p0NnVgjdRq7e312OOKyVELU958nzFl1WilpYWr5MlGqkVXPLy\n8hS7HiVzqIQCJSO1giFqFRcXBzVSK5ii1mqJ1CooKJAtaoUiUssfn7paI7XETnOUQ29vr0/jabFI\n5I6ODp/7zJf5gZBgilpikVpikWxcsSlYORa5kVpKi1q5ublYWlpSNLIqJiYmYkSt1R6pRWyjt/lB\nuHdYkEgtrqi1GiK1jEYjjdSSIKJErcLCQgwODvpV1ul0ore3VzS5PCFUkVreth8GcqLYaorUCvb2\nQ08vKxE3PUVqyRG1pCK16urqcPr0aZ9EALnbDwON1CKCG0FupJac7YfCSC0SXhzuSK1wr/goQSSI\nWkqidKSWp0NAwoGSkU2RgFhidX9ZjaJWJEdqCU8LDIRQR2qJHTYSiZFaoRS1vE2aRkdH/YpKbWtr\n87vf5Iwr5dhpOQgFZH9tu6+RWmLjtdUUqeVwOBSN1Arm9sP6+nr09/fTSC0/INFDSkZqccftQPAi\ntcS2H0ZqpFZtba3b9kOpUwkjCbnbD33xB+EQtdZ8pJbZbHZLuu4Ly8vLHhPyMQyD/Px8tLW1yfot\nOfllNBoNTCYTL8G9pzZ4aqO3ScDIyAhycnKCdtKaL6jVao+DCYZhZEcxectPsH//ftFVPE/9QPrY\n6XSyJ/uJtdGbiCN1Ao9Go0Fqaqqbo/CE3HxFarUaTqfT632OjY3lnSBF0Gq1vK0RYs+b8NqbmpqQ\nnp7utY1qtRolJSXsSUUpKSlQqVQ+PZPeckP5A8MwsgVGsYMa/KWxsVGxBKie7IbL5fKazFmj0QQs\n+ii5ere0tCQ7cbqc591ms4Xc9nkSa8l7Kpe5ubmgnzhXUFCA1tZWv8r6ej2eiI+P95p0WYqJiQlF\nkxfLITc3V5Ek/83NzWySXim/4w9Go1HyxC8x8vPz3U6TJnCvc3JyEpOTk245Fj1hsVjYk//kIOV/\nsrKyPEYGCt91qWi1QCLfhfUJfYjUPYyKivI6GLdardDr9ewJZgQ5q+zeJtjCFAOEDRs2eH2OKysr\nWeGVixzbKsdOy4G0cXFxEf39/X7b9oWFBY+nOAoh/o0btZKfn+/zu+/L/ECIL/MQIXq93uO2I259\nMzMzkoeXWK1WaLVaRW2UWFu4aS2UrEetVkOlUil6Sp1KpfJp54W/yLGfcndOyEXMtyt9qA2BO7cg\n8wMxW0W+q+TuACEWi8XjYhD3GSWoVCpZieqDibexmJy5K+DbGFyj0SAvLw9HjhyR3c5AWV5eVryv\nI0rUMhqNXk9vCpQNGzagublZ0d+0WCw8UctfvKnySh+/GyhKKf39/f0ew/EbGhrClksnJiZGsm2Z\nmZlh3X4kJWqpVCqfhZb9+/e7nZgiBXdQLLWS7YkzZ874fBS9kgSSD0VIQ0OD7H4LBBLhJ2d7aCAE\na/VOCTxtLQ8WYqey+Yu3rSNKsH79esX9mz8EsjI/MTGhmFAsF6X8arB8lV6v92mMITzQQ4rJyUlM\nTEz4JGrFxMT4JGpJkZOT41NkoFS0mqfo1WAhJ++K1WqFwWDAsWPHeJ/L6euEhAT2wAExamtrRSeK\nco5Wr66udjsVNFwsLi56TRvirbwvk3NuBD9Bie2UvuLvPMRoNMpekJuenvZ4ErzU6e6rBbVaHXI/\noQSRlJA+2JD5gZiIHgp8XYCJBIhgJXXKaTDZsGEDDh06FPJ6lSTiRK1AIrXkUFhYGLGilrew7khL\nvqvUJLO/v99jKPeePXvClrMpNjZWUtTydgJksImJiRF1jiqVymehZd++fT6JWmTAnZmZ6bPSHm5R\na2pqSlFRKxR5nlwul6xVl0BFLU/bt8NNOEQtJU/wczgcsvKwBEIw/Js/nK2i1t69e4Piq3Q6nU9j\nDLHtJmIQUUu4Hd0TMTExoospvpKTk+MxhYGQ0tJS0QlKOEQtOXlXUlJSYDAY3LZ0yEnyGx8f73Ei\nWFdXx0ZLc5EjatXU1LjlgQ0XcnLheivvizhD6uGO28KRo3bDhg1uOY7kYDAYZCWIBlYitaQiAtPS\n0qioFSbOJlGLzA/CJaIrtQATShiGUTRq3hc2bNiAgwcPhrxeJYk4USvYkVrBErV82RoghbcVo0gT\ntZSK6hgYGPAYqbV3796wRWp5ErW8JcsPNp4itYIpalVVVQUUqXX69OmwR2opFbbub4JbXwmVqBUO\n4Ugu4RDclBS1QhGp5e9kSWkCEbXGx8dDEv3IJdJFLV8jteSKWhMTE5icnPRJ1FJqUpabm+uTqFVW\nVibq7yI1Uis5OVlS1PK2/TAhIcGrqNXT0+P2+WoTtcip5f7adl8jtUg93Aj7cIha/s5D5JzYTfAU\nqZWWlgadTudz/ZEEFbUiHzI/oKKWfMIpahUWFlJRS0m0Wi1MJpNfq4AqlUrWKnhiYqLXPbwDAwOy\nB3jASt4luQnul5aWJCNbvNU5Njam6B7yQPE28UhISJBlUKanpz3mRXC5XGE7YtVoNHptmy9YLBZZ\nz7ecSCKDwSAa2ahSqbyeriSkt7dXdhnuPviYmBifIrVInpBgDEbknqIxPz+vWMSMy+WSnSsiOTk5\n6KJ9QkKCx7/b7XaPg1klxQSr1Sr7tFk5hFroAOQ/U3IYGBgIuh1LTEwMySDO23NmNpv9njTNzc3J\nSsIsh7S0NFnR3774e08Ey1dpNBqYzWbZk6GEhATZ4yiXywWdTic735vBYFDEjsXFxWF5eVn2qbXJ\nycmYmZlx+zwtLc2nes1mM9RqtdtBNmT8KQeDweD11LioqChoNBrY7XYsLCzw6vHW1yaTyWMkTUZG\nhmi/yRE80tPTMTY25vV7Yngaf3oa20qxvLyM6enpkNn2zMxMTE9P87b2yEm4LMRsNns96MATcuYh\nYmi1WtkLI0NDQ5J2LTo6OiJy8waCSqWS5Se8+SqCkn7HE1Ljdi5RUVGK3x+ldif4ApkfSD3rvuTE\nm5qa8il/HrDS13q9HgsLC5idnRX9DvEHkQLDMEHPNSYF1y6NjIzw/ubrnNIbQ0NDsqNOfSGiRC1g\nZWXcnzxFGo1GdnJZb0mqW1pafFq9sVqt6OjokPXdxcVFv8N+SULX1YJSUQORmufn9OnTPifWlhvd\npcRJXMGisbHR72iEvXv3+hXdJYdwnLYmtWIuRnl5ud/bdpRavZF7FLkSlJaWrvr9+UrS3t6u2AEF\n4SYceWj8obKyMqQnWgXTV+Xl5fkU2SSH2NjYsJ70JDypNxR42hboj8DhjcTERL9EQLFTI8ONp6i4\nQMa2/qLVan32iUocVJOcnBxwqpRgRxh2d3cruiizWpEbhRuObe9SpKSkKB5JF845hdSBO3a7XfYi\n0JkzZ/zyVUVFRbDb7W4iDYH4A8oKJNq3vb2d97nSu6V8OR3dFyJO1MrPz/db1JK7YhcMUUuYDFSK\ns0nUUippcSSLWmJHNntCbnL5cGypkEtTU5PfBq6hoQEZGRlBOV1Eya1icqmpqZEtapWVlfkdRUNE\nrUCTR46MjAR9CxyhuLiYiloc2tvbg7IyFQ4iaRu8J0ItatXW1gbtt3NychTf7i4nN1QwCYeolZyc\nDL1eL5rAPViilliEmTeCMeAPlIqKCsm/+ZrfSgk0Gg0WFxd9KtPX1+fxOuSgRNR1oG3wBhW1VvBF\n1Ar1qbtSpKamejzp2h8iUdSanZ2V7X96e3v98lUbN26E3W7H8PCw6N+JP6CsQPyOMFAn0JPVhRw6\ndAjFxcWK/iYQgaJWJERqNTc3+yxqCVf9pFhYWAhI1PIW8h5J0Egtd2ik1l5kZmbSSC0fISei0Eit\n1QuN1Ao9VVVVNFLLA+EWtaRO8QsmoRa1kpKS/BJA5OTHCjVrJVIrEkStYC9cdnV1yd56t5ahkVor\nhHIhqOUAACAASURBVHNOITVfCEWkFhG1pCK1qKjFh/gdoaildKTWoUOHguLjIk7UysvLQ0tLC5aX\nl30qp9VqZUdqlZeXS/5teXkZhw4d8mnQnpSUhBMnTsDlconug3W5XOz1LC0t+ez4l5eX4XK5MDMz\ns6oitQoKChRJOuercBQq+vr6fA5jz8jIkJXAV+7vhvLoV1JPW1ubXwZueXkZBw4cQHp6elBErXBE\nalVXV8sWqqSOpJcDwzDQaDS83Cz+MDIyEpCo5cvzVlxcLFvsPxs4fvx40CO1lpaWQpIfIhwCsj/Y\nbDb09fWFzEYG01fl5OQofghATEyM4rkyfKGqqoq1n76O+fyFJHA/ceIE77kwmUyK5Vbj4u/2Q0+R\nWv7kr1KirKexsz+RWktLS7JzUoqh0Wh8ErWWlpYwMDDg8TrkYLVaAxa1Am2DJ5aWlnDmzBkaqQX5\nvmp8fDxkopa39y8lJUVxoSXQLbeBoISo5W+kVmFhIex2O0ZHR0XHAcQfBAMy9w9Xzi5/dneQ6KnO\nzk6edqHkgVgulwvt7e0oKipS7DcJESdqASthuUocGe0Pw8PDfq1CV1RUYHx8XHSf/dLSEpvg1Z8Q\nvv7+fiwuLoZl0h4o4TSkwSYjI8OvqEIlKSoqQltbW0jqIvX4u+LT3d0dsVF3/sIwTMiS3Kanp4f9\nZLvCwkK0tLTI/n4wwotXK8HebgIAx44dW9M211fICVlKRziFi2BubwwHDMOwE8lQn5C1fv36kJz0\nFB8fj+7ubkV/s6GhwW+/s3//fsntQKGmtbXV50T/gbBnzx6kp6f7dGLiauTw4cMRuX01kunv7w9J\nongAQZnMr0Z8OXU3EMiChZyAAiVxuVzo6ekJW2BGSUkJDh8+7FfZwsJCOBwOyW2bgTA2Nqb4dkZC\nRIpamzZtCtuRp0NDQ36LWmNjY6KrN06nMyBRq6+vb9WKWpGcGypQsrKy0NDQENY2FBUVobW1NSR1\nkXr8FbW6urrWpKil5AqGJzIyMladqEUH1h8RClt49OhRKmpxoKJWZKNSqVj72dXVFdK6N2zYEJIF\noYSEBMWvbe/evX5PCvbt24f8/HxF2+Mvzc3NIc1jtHv3bqSlpYV8m2SoCdbWnrVMX19fyKJW6WLf\nCsHa8i3EbDYjKSkJjY2NQa+LS7hFrUBSgJBtm0qeYE4YGxtTfDsjISJFrXBGavkram3atEkyUosr\navlzI6moFZnIzY8VTEIZqUVEraqqKr/KU1ErMORuXQ0mGzdu9OnwBypqfUQoxKaOjo41bXN9RaVS\nITMzc82IWmvRfpKIo3BEaq1mUctfvxNJolZLSwuN1AoChw8fpqKWj/T394dM1KKRWiuEMlLrbBW1\naKRWBLAatx+Wl5fLErVopNbaQe5JhsEkHNsP/b2n3d3day7SIJSiViRsP9ywYYNPkYFU1PqIUIha\ndPshH7VajfT09LBH1CrFWrOfRHQEQh+pFcrth0pfW0NDg99+Z//+/REjaoVj++HZEKlFRS3fCWWk\nFhW1VghWHkOpesKx/dCfA8WUIlBRK5iRWmeVqGW1WjE1NSWadD3YjI2N+RUOmZiYCLVaDbVa7Xba\nEsMwrBP1J0mzTqcDwzBhTejqL94M1unTp5Gamhqi1ihLVFQUoqKiJE/VkCIvL08x9TsuLg6jo6OK\n/JY3yCEF/oYL6/X6NXP6G4FhGERFRcn67unTpwN6h81mM6KjozE1NeXzMeYA0NPTg5SUFL/rB1ae\nN18Oq5CTqHZqamrV2oCsrCyMj4/L+q6/g7ekpCRZk+K5uTksLS0FNEjMzs6WfT2rAZVKhaioKJjN\nZgDwO7eR3W5X/DQqfwj2QQOhhms/vSVGPnPmjKJjoNjYWIyNjSn2e1IYDAbExMTA4XBgdnY24N8b\nGRlhxx7+YDabQ5Y7yBvcdzOU9fmbKD9UREdH+32oTH9/P4xGY0QkiY+JiQlbkmxfIGOzQG18eno6\nJicnvX5PbnL0tY5Wq4XRaAxZPUpHHZnNZq/zP51O55PfJsnZlbBR8fHxfvdvXFwclpaWMDc3F3A7\nhMzPzwftFPaItOz+HNOrFNPT0wE9BBaLxW0Pq0ajCShvQGpq6ppdWWptbcXGjRvD3Qy/qa2t9XkV\ntra2VvHEsaGgrKwsoPLB2kO9Wmhrawt4Vbq6uhqDg4N+OZrm5ma/olCFKH1qk79bviOBTZs2BT2q\nOD8/X1ZE6PT0dMCrnjabzW1RZi1Atu35G+k4Pj4e0sn32YjUCVmEgwcPrlrxu6SkBFNTU5iYmAj4\nt06dOhXQNtTq6uqA26AUoW5LfX19SOvzl6SkJBw7dsyvsh0dHRGTsyk1NTUiFgO80dbWpsg8pLi4\n2G8xkrL68La13J+dHEqfmBgptiBURKSopdFo/IpEUIKpqSmfIhG4xMfHIzo62i2kXaPRBHRU7FoO\nl25paVnVolZdXZ3PopY/ZSKBQMUMb5OWtU5ra2vAk7La2loMDg7C4XD4XFYpUUvp7W1DQ0MoLCxU\n9DdDRShEoPz8fFm5+2ZmZgJOulpZWRm2Q1qCCREB/M2pMTEx4fe4gCIPbyfyrWZRq6ysDJOTk4pE\nQXZ3dwckzoRrK4wYVNQSx2q14ujRo36VbW9vj5iJ7GqZu7S2tiqyJbCkpISKWmcRCQkJHnNB+itq\nLS0tKZb3L1JsQaiISFErnJFaU1NTAUdqCUUtktfDX1aLY/CH1R6p5Y9A5U90VyQQqKh1tkdqKZE/\npKamxu9IraamJkXEo4qKioB/g8vg4OCqFbVCcVKvXFFrenpaEVFrLUdq+Stq0Uit4ONt0aOtrW3V\nilqlpaWKRWp1d3cHFKl1NotamzdvDml9/hKoqBUpuSxXS6RWS0uLIqIWjdQ6u/AWqcU93VcuSota\nkWILQkVEiloajQYMw/gVjRAIDocDCwsLMBgMfpWPiYlBVFQUuru7sbS0xH6u0WgCyiVktVrXrKjV\n0dERtKSlTqfTa56OQCkvL/c5kV55eTl6e3uxvLwccP3z8/N+P6++EmiUj6/Rii6XCwzDBFSnGCqV\nKiyi+dGjRwPOiVNaWoqJiQm/Ilnb29sViZZTUoR2OByYnJyMmMTFvlJUVISxsbGg+qrMzEwcP34c\ni4uLHvNMzs3NBbz9sLi4GIODgwH9RiRCBPkTJ074VT6Qxa5wEMg4JlyQhPFClpeX4XQ60dPTE5Lj\n34PB+vXrYbfbMTMzE/Bv9fX1BbSwEEkJxEM94VJ6QSZYxMfHY2BgAPPz8z6X7e3tRUFBQRBa5Tur\nZe5y9OhRRcYgBQUFPufYpXhnbm4u6HM5f4iNjcXw8DCWlpZ4c34CwzB+LcQouf0wUmwBF6fTGbS8\nhhEpagErCWt3794d0jr379+vyAmDOTk5IUveTZGmv78/4DxQcvBHKDAajVhYWAi47iNHjoTkGsNB\nsAS7mJgY9Pf3K/67oSIlJWXVTVil2L9/P5KTk1eVYMCF5EsMtq+qqanBqVOnPH4nKioqIpIDRzJV\nVVXhbkJIOHbs2Jq5VrvdjpGRkVV/PRaLhSaIpsimoqICHR0dPpdbrVHPFIoUbW1tEbuNrqysDFNT\nU2vqgJ1gMzw8fHYligdWRK09e/aEtE6ljjrOyckJyak6FM9EuqjlzyqckCNHjiieuDtSCFa0gcVi\nWdWiVnJy8poRtfbt2wer1brqRa1g+6qamhr09PR4jNSKjo5GQkJCUNux2lntwohcjh07hsrKynA3\nQxFmZ2cxPDy86u9dTEwMFbUosqmoqEB7e7vP5VZzOg8KRYxIF7UmJycV2Vp+tjA0NHR2ilp79+4N\naZ2NjY2KRWpRUSv89Pf3hyS83Z9cUQaDgUZqeWFhYSEoIccxMTGrOu+B1WpdM6JWY2Pjqr4eImoF\n21dVV1d7FbVopJZ31orQ443Ozk7YbLZwN0MRSKTWar93FosFsbGx4W4GZZVAI7UolBUOHjyoSM6z\nYEBOtqWRWvI5ayO1VvP2QypqhR8aqbW6oZFa4tBIrcghkrYfRkdHU1HLC6tdGJFLZ2fnmrnWtSJq\n0Ugtii/QSC0KZYVIj9SiopZvnJWRWkajEampqT4n4faX0dFRJCYmKnJst9Fo9CuR89nG5ORkQKdC\nemN+fj5oLw4Xf54ZlUrlMepCDj09PYiPjw/4GgcGBiJyde/kyZMBJ74WQ6vVKiIohgu9Xu9zEsnx\n8XHJRMzhgAzWk5OT/bqeSEGlUsFgMCA1NRWjo6NBO4AgJiYGFosFACQTuWs0mlVx0lQ4iYmJCXcT\nQsLs7OyauVaNRoOxsTHFr2dqagopKSmK/qYnNBpNwEmznU6nYqdiUSIbi8UCnU4Hu93uU7moqKgg\ntYjijdU+toxUpqenA3qu5+bmMDk5GZSk6dHR0dDpdBgeHg74t8jYLlIORPHH/njjxIkTsFqtQfNj\nEStqASvH73Z3d4ekrt7e3lVzMspaYXh4OCJPZlgtHD58WJGQ3K6uroCOCA8WBw8eXLVHuEcaQ0ND\nEbWCSyKbIul4+UCor69HX19fUBczsrKywDBMyHwihRIJmEymoKyCj46OIi8vT/HfDSaLi4tUuD6L\nSE5OxtTUVLibQZGJXq8P6knIFP+w2+1Bzcuo1O6P7u5uMAyD7OxsBVoVOCaTCZOTk4r+ZnNzc1CD\nKCJa1Kqvr/e65UIpAj0mmeI7w8PDWL9+fbibsWo5cuSIYqJWbW2tAi1Slra2NipqKcTg4GBE5SQg\nidWrq6vD3BJl2Lx5c9BFLTLQoaIW5WzCbDYHJQnvahS1FhYWqKh1FpGSkkJFrVWEXq9XPLKFEjjB\nPmxEqTy9RNTKyspSoFWBYzQaFbc/TU1NZ7eo1dPTE5K6qKgVemikVmC0t7evaVHr4MGDId0espYZ\nHByMqC2ma03UqqurC7qolZmZCYZhQrbQQ6FEAsGM1PInH2Y4oZFaZxc0Umt1odPpaKRWBBLsvIwW\ni2VNilomk0lx+9PS0oINGzYo+ptcfBa1GIbZyjDMqwzD9DIMs8wwzGUi3/kxwzB9DMPYGYZ5i2EY\nv7KvFxUVYWhoCMvLy/4U94mZmRlFksQDgMPhCDh3wtlAsHNqrXVGR0f9DlNdWlpiT1+cnJyMqK1p\nhK6uLiQkJIS7GYoRHR2Nubm5sNQ9Ojrq1ymdSrO8vIy5uTn09fUBQFCdWygpKirCzMwMlpeXg7ZS\nm5ycDIZhMDw8HDSfODk5GfZDCObn5yMqb9Dk5KQiuTZDhdPpXFPjD4PBgOXlZUW3QUxNTcHhcCAj\nI0Ox3wwFS0tLEfVucGEYJuA8ob7icrnAMExI6wwlVqsVCwsLmJ6eDndTQoZerw/59UZHR2NxcTHg\nRSmdTheynFp2u52epioTp9MJh8MRtJ1BZrMZCwsLAQlAy8vLGB4eBsMwsFqtCrbOf/R6vaI2fX5+\nHgMDA0HN7+tPpJYZQAuAGwG4XS3DMHcCuAnADQBqAMwC+DvDMH4tL2m12qAl3+WSlpam2ECwu7ub\nnkJFCTqBCFGzs7MYGRkB4N/pjRTfKSsrC9upizMzM2EXK4CVwUVfXx/q6+vD3RTFIT7k+PHjQa1H\nq9UGLSKsqakp7AsNAwMDbFL8SODAgQOrKqLYbrevuVP2CgoKcODAAcV+r6mpCQkJCTSptoIE0y5J\nsbi4GLEinxLExsYiOjoahw4dCndTQkZqaioOHjwY0jrLy8sxMTGxqqLiurq61kxO0mBjMpmCcugU\nl8LCQrS2tvpdPlKjcJUK9gFWcvsGeyHbZ1HL5XK96XK5fuByuf4CQGyJ5BYAP3G5XK+5XK5DAL4M\nIA3AZ/xpoEajCYmjTE9PV8w5UlGLEgoCOeKWilqhp7y8nI1QCjXT09MwGo1hqZvL4uIiFbUCRKfT\nBc0nHjhwIOzRK/39/RF1ct9qE7VmZ2fX3PiDilqRT6jG6lzWWlSikPj4eFgslpCLPOEkNTUVbW1t\nIa2TiFpKJ8UOJpF6wFMkYjKZgn6i4MaNG9HS0uJ3+UjNl6i0qBXsXUGK5tRiGCYXQAqAf5HPXC7X\nFIAGAH7NYmikFoUiTiD5tEjiRICKWqGivLz8rI/UWlxcRG9vLzZv3hzupigO8SEnTpwIaj3BFrXC\nHakVaaJWY2PjqhK1ZmZm1tz4o6CgAI2NjYr9HhW1lIdGailPXFwcLBZLyEWecEJFLXlEai7cSMRs\nNodE1Ao0Ukuv1yvYImVQUtQaHBxcXaIWVgQtF4BBweeD//6bz4Rq9UdJUevUqVNrblBJiTwCMQ4k\ncSJARa1QEc5IrUgStfr7+2mkVgAEU9RqamoKe6QW3X4YGHT7oXeIqGU2mxX7zbOdcIhaaz1Si4ha\nZ9v2w1CLWmVlZZicnKSi1hqFbj/0n/z8fMV+a2hoKOgHVoXq9EMGIvm35JCcnIz29naFm+OOVqsN\nOOHkyZMnAawcvb6WV4+UIi4ujp7kFQCBiBR6vZ6dOEaiIT116lRA2ysjkaioqLCdjLO8vAyVKnyH\n3c7NzWF0dBQajQZxcXGrKvG2XIgPISd2En+gNFarVXGfOD8/j5GREaxbty7sk8TFxUWo1eqwtoGL\nw+EI2gpqSkqK4luLuru719QBG8CKv8rMzGSjiwMlNzcXGo0mop6z1Q5NFK88arUaarUaCQkJmJiY\nCGtbQhUVp9VqQ36gjtFohMlkWjXjkoWFBahUqlXT3nCjUqmC/uwaDAZkZ2f7PKd1OBwYGxuDWq2O\nmATxXJQc+0xOTgZ9wVLpuzyAFQErGfxoLSuAZk8Fb7vtNrctB9u2bUN6ejqam5uxdetWhZuqPB0d\nHcjLy0NpaWm4m7IqSEpKwq5du8LdjLOSUKxcBMKxY8dQVVUV7mYoilarDdnJOJGGw+HA8PAw0tPT\nkZaWFu7mBBUSrk38gdKkpaWhtbUV5557rmK/OTc3h8HBQbryG2IyMzOxb98+RRP+njhxAh/72McU\n+71IgRy0ocQ2EpvNpkCLKJTQkJubi7GxsbCedjc/Px/2BY9gEhsbu2pE7vn5+YjIkUrhU1FRgc7O\nTp9OpSe7ZlJSUtb82FjujpHnnnsOzz33HO8zuVGUiopaLperi2GYAQAXAGgDAIZhLABqATziqeyD\nDz4oOtA4fPgwnn/+eSWbGTQ6OjpwySWXoKSkJNxNWRUkJSWhs7Mz3M04KzGbzREtah0/fhyVlZXh\nboai6HQ6LCwshLsZYcHhcGBoaAg5OTlr3nGTcG3iD5QmLS3NzeEHChG1qqurFf1dimcyMzPx0ksv\nKfqbx48fx2c/+1lFfzMSKC0tRX9/P8rKygL+LSpqUVYTOTk5GBsbC8oiiVwiNZG1UsTGxoY1mt0X\n5ufnIyKdBIVPeXk5jh8/jgsvvFB2GbLgm5WVhdTU1CC2LvzIPbBq27Zt2LZtG++zpqYmWXNCn99g\nhmHMDMOUMwxT8e+P8v7978x///shAP/FMMynGYYpBfAMgDMA/uprXcDKAL652WOQV8TQ0dEBADRS\nSyZU1AofkS5qdXZ2rjlRS6vVnvWillarDXsi8mDDjdQKBiRSS0lopFZ4IJFaSnLixImItu3+QkQt\nJaCiFmU1kZOTg9HR0bC2YWFhYc1HakXSASWeWFhYoJFaEQiJ1PIFu92O4eFhaLXaNb/gG4rcvv7I\n0lVY2Up4ACt5su4H0ATgRwDgcrnu+//s3VlsXNt+JvZv1UiyilOxSBZncRRFcZ4lt+91PKSdvnDi\n4KIbLSCw20YH8EOM4OQlaCBA8hIkQAAfIx07yIPhpN3waQTXMOI4QBLYhm3EhxQlUaRIURwlkRTn\nuTizhp0HqXiouYqs2v89fD+AgA5J1f6OKNXw1X+tBeBfA/hf8PbUw2wA/4Gmadd6NVdYWIjT01OE\nw+Hr/HZdJfbLkd5oNxXBYBDHx8ci187NzUUkEhHfK0BCdnY29vb2xK7v9XqRm5srdv2v2djYwK1b\ntzJ2+wUFBbo/SXS5XMjKysLm5qau193a2hL9We/v7yMej1/ulSS5hEIPiX0RMrV/WkFBAZaXl9N6\nm5qmIRKJ8NCITwgGgxnbQDgQCODVq1dpua2LiwtcXFwgGo1m/N97QUEBdnd3M3qND1VXV+Pi4iIt\n95+pLA8hY9rc3LTN6ZWSz9MTotGopfcKzsnJMUVRdHBwgHg8bpoCLh0CgQAuLi4Mv31HVVXVe/vB\nJfNYFYvFLvers/Jz40Rxl+lpz5RLLU3T/k7TNIemac4PPn77yvf8N5qmlWualqNp2j/WNO1Gx0H1\n9fVl/Jj0dMj0rv6Z0NPTgzdv3ohdv7OzU5eDAIymrKws7RsEU/Juevzudd26dQtDQ0O6XnNkZCSt\nJ5ikanp6GtnZ2YbcBDOTzPR4kJWVhdLSUukYhtTb22uKieL9/X3s7++jo6Mj49dqaWnR/f7T4/Gg\nrKwMw8PDul6XjOn7779nOUm2Mzs7C6/Xa/mlalclTqc0wwDE1ZOSk3mun5OTk5Z9Io1uZGTkchVD\nJpliAXFfX1/Gj0lPBzO9iEkwQqk1NTUldn0pmTj1ipLX0tKCsbEx3a/LUss+zPR44PV6WWp9Rk9P\nj6lKrXTsOfU1UqVWeXk5Sy0C8PYFI0stsptEqZU4ZdkOzFpqJfNYZZdS69GjR7q8DjFFqdXb28tJ\nrQzp7u7GysqK2PXb29sztveMkZWVlWFyclI6hm01NzeLTWrp/aJMrweTz0mUWnZ44L7KTI8HnNT6\nPLOUWgcHBzg4ONCl1Lpz5w6ePXuW8etc5fF4EAqF8PDhQ12vS8bEUovsaG5u7vK+0C7a2tpMU2pd\nnUZiqfWDR48e6XLQhSlKrf7+fpZaGcJJLRmhUIilliAuP9QPJ7WMj6XW55ll+WGi1LL68kO97z/J\nmLj8kOzIrpNa4XDYFKUWlx9+GpcfXuF0OuHz+TK28W66OJ1O6Qgpczqd0DRN9PqJO4GjoyPxE170\n4nA4EIvFpGMY0snJScY3THQ6nSJ//g6HAz09PWnf6PtzVldX0dbWJnJU9fPnzwG8fedKKWWa47LT\nJZOPB93d3Wl9o8eOP59kOZ3Oyw30jTxVnJeXh7y8PF2eh0jcfyb+jvb09GBlZYWPnza2tLSE3t5e\n3mdZVLof36xiYmICdXV1tnu8djqdyM3NTdvpt5l09eeSOMH98ePHn/1+O/ws9XwdYpo/Sb/f/96p\nAmQdd+7cAWCvUos+7/j42NKngAwMDGBpaUmXa62srKCrq0uXa30oMYlopokls+jt7TXFPpNWkXjj\nxciHmuTn59viRKyBgQG8efOGpZaNLS4uYnBwUDoGZYhZlnzrbWJi4r1JIDvJz883Ral1VeI+amRk\nRDiJrJWVFXR2dupyLdOUWrm5uYaf1KLrYalFV52cnKCwsFA6RsYMDg7qVmq9efMG3d3dulzrQyy1\nMscsh6dYReKFhJGXytul1BocHGSpZXOLi4u4f/++dAzKEL5p82nj4+NoamqSjiEiLy/PdKXWvXv3\nALDUWllZ0e11CEstEpcotY6Pj1lqkeVLLT0ntVZXV8VLrdu3b4tc38p6enr4pF9HZpjUKigosPSE\nawIntWhpaYmTWhbGx7dPm5iYsG2pZcZJrYGBAQBvN0m3s9XVVd1WjJim1AoEAlhfX5eOQRlgh03y\nPqW8vBzHx8e4uLiQjmIokUgEWVlZ0jEyprKyEuFwGPF4PKPXSezbVV5entHrfOjDJx52/fedSRUV\nFdjd3ZWOYRtFRUUZu+3Kykrs7e3d+HaysrIsfb+ZUFVVdflru/0bWF9fR25urnQMUbFYDOFw+L2/\nB1a2ubkJj8eD7Oxs6Si6KS8v5xvc73z4ujeTj0VGlnh8u7i4wPHxsXScpNj5sSpB0zTs7++joqJC\nl+uZptQqKSkx9LukdHN+vx/BYFA6hm56enqwvb1tmjtoSg+lFJxOJ6LRaEavMzQ0hIqKCrhcroxe\n50NPnz4FALS2tup6XaJMa2lpSfttDg4O4tWrV2m/XSurrKyE0+nEy5cvpaPoamxsTPc3KYwmGo3C\n7XZLx9DN5OQkcnNzbVtm2N3VU2bb29sFk8hraWnByckJtre3paOkpL+/33aPVVfFYjHdXoeYqtSa\nmZmRjkEZ5PP5EAgEpGPopqenBzs7Oyy1bCZRamV6+czw8DBLLaI0SiyVT6eBgQGWWilKlFp2+3N7\n9uwZysrKpGOIikQiuj+mSXr+/Dn8fr+tnhvTDyYmJi5/bfdSq7m52ZSlVl9fn21LLU3TEI1GWWp9\nqLS01NDHadPNcVKL7CBxhK/VJ7Xa2tp0vS5RpnFSyxjsOqk1Pj7OSS2bTmqx1LInTmr9oKWlBcfH\nx9ja2pKOkpKBgQEsLCxIxxDDUusTiouL8fLlS24OamF2ezeqs7MTu7u7ODw8lI5iO3qOw35IKQW3\n243z8/OMXmd0dBTl5eW6/n/GYrHLE+IyUQDQD5RS0DRNOoatZOLQg97eXiwtLfFnmYKKigo4nU4s\nLS1l/M0BI5mYmLD9pNbZ2Rk8Hg+UUtJRMi4Wi2F2dlb8uXE0GoXDYZqXi5ZydZjD7tPvt2/fxunp\nqekmtTo6OnQ7HMpootEoNE1jqfUpnZ2dnNYiSwkGg7Zu8KW8ePFC9F2viooKjI6OZvQaieOE9bSw\nsIDOzk7dr2tH+fn5ODk5kY5BaZDYAJdSU1dXdzkZSvZgp33FpqencffuXekYGB4exq1bt6Rj2BIn\n3t/n8/nScrCKnkZGRlBXVycdQ8Tw8DCqq6t1u56pSq2uri7uq0WWwlJLxosXL0TLFyuXWnod3Wt3\n+fn5OD09lY5BaZCdnZ3xyU0rqqurw5MnT6RjkI7GxsZ0O0lL2osXLwwxnTM0NMRSS0hHR4d0BEPJ\nycnB/v6+dIyUjIyMoL6+XjqGiKGhIdTU1Oh2PVOVWpzUIqsJBoOYn5+XjmE7L168EH2yUFlZmfFS\na3BwMKO3/ykvX75kqaWTvLw8TmpZBCe1rqe2tpaTWjbDSS39DQ8P6/rClH5g9320PpSTk8NJmdrn\nJAAAIABJREFULRPhpNYXdHV1sdQiS+GklgzpUsuqk1rz8/MstXTC5YfWwUmt66mvr+ekls08ffrU\nVqUWJ7XsjZNa7+PyQ3PhpNYXFBUVQdM0Lrkgy8jKykJ+fj5WVlakoxiGx+PJ+ImQ+/v7KCoqyug1\nvsTn8yEvLw8HBweIRCIZuUZJSUlGbvdDVycNs7OzRf9c7aSoqIj3GxYRCARMt5FsaWmp+CEnubm5\nyM3Nxfr6umgOeivTk+cbGxvIy8uDz+fL2DWMJDs7G4WFhdIxsLm5idzcXOkYplBcXJzWN6rtdHhW\nMlwuFwoLCxGNRk2zDHFrawt5eXnSMXS3vb2NvLw8+P1+3a5pqlILePtCTfqJFFE6tbe348WLF9Ix\nDMOMa+avo6+vD5ubmzg7O5OOciPDw8OXv7brvgESiouLMTs7Kx2D0iAUCmFyclI6Rkrq6+sNcQpV\nV1cX/x0YRHV19XuPB+m2sLCAvr6+jN2+0TQ3N0tHoBTV1tZiZGREOoalNTY24uLiAmtra9JR6AsW\nFxd13waFpRaRsI6ODkxNTUnHMAwzjhdfR39/PzY2Nkxfan3//feXv2appZ+SkhK+mLeIsrIyTExM\nSMdISUNDgyFKre7ubh4gZBC3bt167/Eg3exWat25c0c6AqWorq4ODx8+lI5haSy1zGFxcRH379/X\n9ZostYiEtbe3s9S6wi6TWlYpta6+M2/XfQMkcFLLOsw4qWWkUov/DoyhpqYm45Navb29Gbt9o+Gk\nlvnU1tay1MqwRKnFZefGxkmtJBQXF9tiioNuTtM0KKWkY3zV7du3sbS0hFgsJh3FELKzsxEOhzN2\n+7FYDG63O2O3n6y2tjYcHBxk9P81U65uan31BaWep5zYXSAQsEQpSm+f18zNzUnHSEl1dbUhnou1\ntLRgbW2N/w4MoLy8/PLxIN2HWMTjcbx58wZtbW1pvV0j45tE5lNZWYlnz55Jx7C0mpoaRKNRbG5u\nSkf5qkgkguzsbOkYujs5OcHW1hY6Ozt1va7pSq1AIIDFxUXpGGQCZ2dn8Hg80jGSUl5ejoODA+kY\ntnBwcIBQKCQdA8DbzZbNOKV3dTNgvceL6QednZ08EZhsr6mpiS8kDSLxePDo0aO03u7p6aktN1sm\noo95PB5TvJHx5s0b9PT0SMfQ3aNHj0ROTDVdqVVYWGi6U4JIhplKrYqKClssuTOCcDiMsrIy6RgA\n3pZaZjwk4OrpPnqPF9MPOjo6TPn3hyidmpqaTLcnmVUlHg8yUWrxBD4iAsxTaq2srKC7u1s6hu4e\nP36Mmpoa3a9rulIrEAjg9evX0jHIBM7Pz01TanFSSz8HBweGKrXMPql17949wST2xkktordL+Dmp\nZQyJx4N0nwDHSS0iSvB4PO9tg2FUdp7UYqmVBC4/pGSZbVKLpZY+wuEwlx/eEJcfGkNnZycntcj2\nWGoZR+LxIBOlFie1iAgwz6QWSy19ma7UcrvdCIVCePXqlXQUMrh4PA6Hwxx/xQOBAE/yuKKioiLt\nJ1qFw2Gcnp7C4/GgqKgorbd9XR6PB+Xl5VheXpaOkpLCwsLLX+fn5wsmsbfc3FwcHx9Lx6A0aGpq\nwps3b6RjmFJOTg6Ojo6kYxB+eDxI5zT00tISXC4XgsFg2m6TktfS0sLnpym4ffs2tra2pGNYmsPh\nQElJCeLxuKE3jD8/P7fdhOnq6irKyspENsg3xyv+D7S1tZnu+GuiLykoKMDKyop0DMNobGzE48eP\n03qb29vbODo6Qn5+PgoKCtJ62zfR1dWFmZkZ6RgpaWhokI5AZCk9PT2mOwGR6HP6+/vTdlvT09PI\nzs5GSUlJ2m6Tknfv3j1u+5KCvr4+071RaUa3bt2Cpmn8szaY+fl59PX1iVzblKVWa2srSy2ylPz8\nfJZaVzQ2NmJ0dDStt7m7u4ujoyPk5eUZrtRK91RaptXX10tHILKU7u5u090PEH1OOl/UzMzMsNQS\nNDAwwG1fUtDT08Pn8zqora1FPB7n4XEGMz8/j97eXpFrs9QiMgCWWu/L9KTW1eVz0rq7uzmpRWRz\nnNQiK+GklnVwUis1nNTSBye1jImTWim6desWNjY2cHFxIR3F9JRS0DQNmqZJR0k7h8OBeDwuHSMp\nfr8fFxcXCIfD0lEMoaKiAltbWzg5OUnbbZ6dnSESicDn88Hv96ftdm+qoaEBm5ubiEaj0lGSVl5e\nLh0haWdnZ9z3iwyvsbHRVPcDTqcTkUhEOgYZVFNTU1puJxqNYnNzE16v11AT1nZy584dbGxs6Ha9\n/f19+Hw+3a6Xbk1NTdje3rbk6yojCYVC0DQNR0dH2Nvbk47zkcRra6WUdBTdxGIxbG1tpe3+P1Wm\nLLUAoKamxpB/ic3G6XQiHo9b8s43KyvLVMXnnTt3eILTFd3d3Wl9d7CoqMhQZdZVwWCQGx1nyOrq\nKjo7O6VjEH1VIBAwzcb/Pp+Pz8Eo48LhMCe0bObJkyemngZ3Op3QNM00b6qbmcPhQFVVFR49eiQd\n5SOJvwNOp1M6im5OT09FN8Y3dam1u7srHcP0WGoZx927d1lqXdHb25vWU06NXmodHh5Kx7CklZUV\nllpkCoWFhaYptXJyclhqUcYdHh6itLRUOgbp6PHjx2hsbJSOcW0Oh4Ollk6UUqiqqsLDhw+lo3zE\njqXWyckJS63rYKmVHi6Xy7J3vF6v11SlVktLC8bHx6VjGEa6S61gMGjYUqu4uJiTWhmysrKCrq4u\n6RhEX8VJLaL3cVLLfsxeaiUmtaw4LGA0DocD1dXVhi61XC6XdBTdcFLrmrj8MD2cTidisZgl73zN\nNqnV0tKCiYkJ6RiGweWHlA5cfkhmYaZJLZZapIfDw0OWWjZj9uWHnNTST2JSa2RkRDrKRzRNQywW\ns9WklqlKLaXUv1JKjSilwkqpDaXUnyulmj74Hq9S6g+UUttKqUOl1M+UUml/RCooKMDm5ma6b9Z2\nrLyBXWITfLPwer0oKSnhC4V3srOzUVpaing8jrW1tRvfntPphMNhzB6/qKiIxxJnSDQaRVZWlnQM\noq9KvMNvBg6HA7FYTDoGWdjs7Cyys7NRVFQkHcX23G63LgdDbG5uoqamBh6PJ+PXyhQrv64yGqUU\n3G632MbkybDT34eFhQUEg0Gx66f6Cu/nAfxrAAMAfhmAG8D/q5TKvvI9vw/gJwB+CuBHAMoB/NnN\no74vNzeXpRZZTn19Pba3t6VjGEbiyF6rFz6BQIBHZhMREb0zOTmJ3NxcFBYWSkexPa/Xq0uptba2\nhvb29oxfh6ylv79fOgLh7RsRkpO1KZVamqb9E03T/kTTtBeapk0A+BcAqgH0AIBSKg/AbwP4RtO0\nv9M07SmA3wLwc0qptP6NY6lFVsRS6321tbWIx+NYXl6WjpJRRUVFad0/jIiIyMwmJyeRl5eHQCAg\nHcX2PB6PLtt5sNSi6xgYGJCOQABmZmbMU2p9QgEADUBix/YeAC4Af534Bk3TZgAsAbh3w2u9Jy8v\nj6UWWQ5LrffdunUL8Xjc8pNaLLWIiIh+MDExgby8PE5qGYDH4+GkFhkWJ7WMYXp62pyllnq7SPT3\nAfx/mqZNvft0CMCFpmnhD759493X0iYrKwtOp5MFAFlKWVkZT/W8IrE2OxKJWLrE9vl8iMfj/NkT\n2VhWVhbC4Q+fPhlXfn4+tra2pGOQBZ2dneHw8BBZWVnw+XzScWwvLy8Pmqbh4OAgY9fY2NhAJBJB\nVVVVxq6hF7/fb+nnrEZTW1srHeEjm5ubhj2cKhP29vYQi8WQm5srluEm50z+IYAWAP8oie9VeDvR\n9VnffPMN8vPz3/vcgwcP8ODBg8/+nubmZjx9+hS/8iu/kkQEIuPz+XwsNj7gcDhQVVWFhw8f4td+\n7dek42RMe3s7nj9/jp//+Z+XjkJEAoLBIGZnZ/HjH/9YOkpSGhsb8eTJE/zqr/6qdBSymL29PdTU\n1EjHoHfKy8vhdrsxNzeH3t7ejFxjeHgYZWVlpt4kPiFxIl91dbV0FBIyPDxsq5//9PR0Wk4a/+67\n7/Ddd9+997lky/RrTWoppf4nAP8EwC9omrZ65UvrADzv9ta6qgRvp7U+69tvv8Vf/MVfvPfxpUIL\n+KHUIrIKv9/PUusDSilUV1fj4cOH0lEyqq2tDZOTk9IxiEhIMBjE/Py8dIykNTU14fHjx9IxyIJ2\nd3dZahlIeXk5PB5PRu+fhoaGLq9jdolSi+zLjqVWV1fXjW/nwYMHH/VB3377bVK/N+VS612h9R8B\n+Pc0Tftwo5snAKIAfunK9zfh7WbyQ6le62tu376NsbGxdN8skRhOan0sMall9ScIbW1teP78uXQM\nIhISDAaxsLAgHSNpjY2NGB0dlY5BFsRSy1jKysrgdrszWmo9fPgQoVAIbrc7Y9fQix2es9KXjYyM\nWGIpbbKmp6fR0dEhmiGl5YdKqT8E8ADAfwjgWClV+u5LB5qmnWmaFlZK/RGA31NK7QE4BPA/AvgH\nTdPS/q+bk1pkNSy1PmanSS2WWkT2ZcZSi5NalAkstYylvLwcADA3N5exayQmtayApRZxUkt/qU5q\n/Q6APAB/C2D1ysc/u/I93wD4SwA/u/J9P71hzk9yOBxoa2vDy5cvM3HzZHKhUMh0y7mUUtC0L24/\nZztKKSil0N3dDQCWnc50OByIx+PSMYhIiFLKVPcBRrnPmpubQ2trq3QMSqOtrS3RDYe/ZHNz07DZ\nMiXxPKyurg7Pnj1L620nivHe3t7L65idw+FAb28vXr9+LR2FBCwuLqK3txcOx7XP4zOVcDiMYDAo\n/v+b0tU1TXNomub8xMe/ufI955qm/a6maUFN03I1TfunmqZl7AiIrq4uU+1BQfopKyvDxMSEdAxK\nk4GBAQDAkydPhJMQEZFRzMzMoL29XToGpdHm5iby8j7cntcYNjY2bFdqJTQ0NKT9jcXEFP7g4GBa\nb1fa4OAgXr16JR2DBLx+/Rr37t2TjqGbw8NDlJaWfv0bM8z0FWJXV5epxvVJP2VlZWl/R4nkJEot\n7uFCREQJs7OzaGtrk45BaWTkaaiNjQ3DFm6Z1tjYmPZSK7FMz2olwMDAAEstm3r16pXlStovCYfD\nLLXSobOzk6UWfVIoFOKkloX09/cDAPfRIyKiSyy1rMfopZZRs2VaQ0MDxsfH03qbiVIr8calVQwM\nDHD5oU0tLi6y1BJg+lIrFApBKYU3b95IRyGDyc3Nhdvtxvb2tnQUSoOKigoAb/d24M+UiKwoFAph\nczNjOzakXSgUwuHhoWgGpZQhnlBnWllZGcLhsHQMXRwfH8Pr9UrH+CQjZ8u0QCBwuW/OxsZGWm4z\ncXuVlZVpuT2jqKysxP7+vnQMErC/v2+5v89fsrm5iWAwKB3D/KUWANTX1+PRo0fSMciAenp6uOea\nxXR3d2N2dlY6BhFR2rW3t2Nqako6RtJaW1uxtrYmmqGpqUn0+nrp6OgQ/7Mm6ujoAIC03U/19fWl\n5XaISMbS0hIKCwulY1ij1GpoaGCpRZ/U29vLAsRiuru7MTMzIx2DiCjtOjo6TFVqtbW1iRctt2/f\nFr2+Xjo6OrC6uiodg2yus7MTANJ2urjVlh0S2Q1LrTSqr6+/XJNNdFVPTw/m5uakY1Aa9fT0sNQi\nIksyY6m1vr4umsFOk1ostUhaotR6/vx5Wm6PpRaRuS0tLSEQCEjHsEapVVtbi4mJCcTjcekoZDCd\nnZ149eoVNE2TjpIUTdOglJKOYWjt7e2m+pkSESXr7t27mJ+fRywWk46SlJaWlrTtrXNdDQ0NotfX\nS2trq3iBqBen04loNCod4yPRaBROp1M6hqjW1lYAeO8NY03Trv0arLu7Oy25jEgpxeeqNmO313HR\naBRra2soKCiQjmKNUgsAurq6sLKyIh2DDKiwsBDHx8fSMZJydHRkiLbb6IqKinB0dCQdg4go7Vpa\nWtI2BUFkRs3NzWlb3pZOY2NjaG5ulo5hCIlyCwDOzs7Ey20jysrKwsXFhXQM0tHFxQU8Ho90DN1M\nTk6+d18giaUWWV5hYSFOTk6kYyTl+PgYRUVF0jEMj6UWEVnV3bt3TbUEkSjdjFpqPX36FHfu3JGO\nYQh37969/PXZ2ZltpghTkZWVhfPzc+kYpKNIJGKr01EnJiZYaqVbV1cX9xqgTyooKDDNpNbx8bEh\nNtszOpZaRGRVd+7cYalFtnb79m1DllpjY2O2OZjga1paWi5/fXZ2hs3NTcE0xsRJLfu5uLhgqSXE\nUqUWJ7XoU8w2qcXlh18XDAZZahGRJbW0tLDUIltrbm7GxMSEdIyPjI2NcVLrnasvZM/Pzzmp9Qks\ntewnEolw+aEQy5RawWAQh4eH3JDvGoqKirCwsCAdI2OKiorgcDhMMcm3urrK5YdJKCoqEj9GPp2O\njo5wdnaGiooK6SiWE4vF4HBY5qGObKCgoAA+nw/Ly8vSUYhE5Ofnw+/3S8f4yO7uLvLz86VjGMLV\njaEdDsflC/mdnR2+FnvH6XTyEDObicfjtjlM4ujoCE6n0xCbxAMWKrXcbrchT0oxg+rqagwPD0vH\nyJhgMAifz2eKd74XFhYQDAalYxheUVERXr58KR0jbXZ2dnB4eGiYdzusJBqNwu12S8cgSklLSwvG\nx8elYxCJ4eOheXi9XoRCIQDA0tISSy0iG9jd3cWtW7ekY1yyTKnlcrlYal2T1Uut4uJi5OTkmKLU\nmp+fZ6mVBCuWWkdHR+9tvErpEYlE4HK5pGMQpaSlpQXPnj2TjkEkpq2tTToCJSkrKwulpaUAWGoR\n2QVLrQxhqXV9VVVVePjwoXSMjElMar148UI6yle9fPmSyw+TUFRUhFevXknHSJvd3V2WWhnCSS0y\nI5ZaZHd8PDSPD0stLrkjsj6WWhnicrngdDpNc8qdkZSVlVn6yXNhYSGys7OxurqK09NT6TifdXp6\niu3tbZ5+mISCggLs7OwY+ueZisSeWg0NDdJRLCcajXJSi0ynvr4ey8vLODs7k47yRUopvoCljGhs\nbJSO8J5IJIKsrCzpGIbk9Xov35Dd3d3la7F33G63ZZ6nEn1oZ2cHlZWV0jEuWabUAoCamhp8//33\n0jHIoIx+otTU1BQ6OjqkY5hGe3u7oX+eqSgqKjLkprhEJKejowOzs7PSMb7I4/EYvngjSofNzU3c\nvn1bOobhWX1Lk1SEQiFDnuJJlA5bW1vIzc2VjnHJUqUW70jpS+7cuYPnz59Lx/isqakp7iGRgra2\nNkP/PFNRVFRkqAcGIpLX1taGubk56RhfxFKL7GJra4ulVhKqqqowMjIiHcMQysrKMDk5KR2DKCNY\namVQTU0NhoaGpGOQQbW0tBi6BOGkVmra29sN/fNMRSAQ4KQWEb3HDJNaXq+XpRbZAie1ksMBgx9Y\nfXsXsjeWWhnEUou+5M6dO4ZerjY1NYX29nbpGKbR1tZm6J9nKrj8kIg+1N7ezkktIoPgpFZyqqur\nOan1TigU4qQWWdbW1pahXrtYqtTKyspCZWUl1tfXpaOQAfl8PhQXF+P09BQHBwfScd5zdHSE7Oxs\nQ905GJ3f77fMZqRut5ubmRPRe/x+PwKBACKRCHZ2dqTjfJLD4eBG8TpxOp085VvQ/v4+D/JJQlZW\nluGeY0vxer2oqKjAmzdvpKMQpdXc3BxKS0sN9drFUqUWANy/fx+Li4vSMcig7t69i6OjI8O9QNjf\n30dFRYV0DCIiMpCmpiacn5/zzTqCx+PBxcWFdAzbCofDyM7Olo5BJtPT02P4ZeREqRodHUVzc7N0\njPdYrtQaHBzE0tKSdAwyqJaWFhwfHxuu1Do4OGCpRURE72lsbGSpRQDeTvSy1JLDUouuo6enx/DL\nyIlSNTY2Zrjl2JYrtTipRV+SmNTa3t6WjvIellpERPQhTmpRAkstWSy16DpYapEVjY6OstTKtObm\nZmxtbXGPB/qk6upqRCIRnJ+fIxaLGWaD252dHYRCIekYppOdnc0n+URkWRUVFYjH4zg5OYGmaTg9\nPZWOREJcLhf31BKyt7cHpRS8Xq90FFMIBAI4OTmRjmEIDQ0NCIfD3GeMLOPs7AxbW1uorKyUjvIe\ny5VawNt3s/jAT5/j9/tRVFSE8/NzbGxsSMcBAKysrCA/P186hulUVFRgf39fOgYRUcZ4PB6EQiHE\n43EsLy9LxyGyncePH6OhoUE6hmkMDg7i9evX0jEMo7GxEc+ePZOOQZQWm5ubhttPC7BoqeVyuRCJ\nRKRjkEFdLbWMsqRjdXWVpdY1VFZWstQiIkvzer0oKytDLBZjqUUk4NGjR6ivr5eOYRqDg4N49eqV\ndAzDaGxsxPj4uHQMorTY2NhAS0uLdIyPWLLU4qQWfYnP52OpZREstYjI6rxe7+WkFo+GJ9IfJ7VS\nMzg4yP2Nr+CkFlkJJ7V0xEkt+hK/349gMGioUovLD6+HpRYRWd3VUouTWkT6e/ToEUutFNy7d4/L\nD6/gpBZZycbGBu7cuSMd4yOWLLVCoRCmpqakY5BBORwOOJ1OuN1uBAKBy88/ffpU9yy7u7s4OTlB\nbW0tnE6n7tc3O5fLxUMhyNaKi4txeHgoHSMtpqam+MLxE5RScLlcUEqhuLgYAFhuEelkY2MDdXV1\ncLvd0lFMIysri8MFV3g8HtTV1SEcDiMcDkvHoQxyuVwoKSkReU2pl3A4jNzcXOkYH7FkqVVeXo6x\nsTHpGGRwXq8XpaWll//98OFD3TNsb2/j+PjYkI03ERlfaWmpZUqtZ8+eGXKk3SicTuflaUPcr4ZI\nH6urq+js7JSOQSbX3t6O/f19noJocR6PB2VlZRgeHpaOkjFHR0fIysqSjvERS5ZaFRUVlm5IKT0S\nSzoSJO6AEqWWETfcIyLjC4VClnnnd2xsjPeFX+BwOFBVVQUAePnypXAaIntYWVlhqUU31tHRgYOD\nA5ZaFpcotYaGhqSjZAxLLR1xUouSYYRJrZ2dHZZaRHRtViq1xsfHOan1BVdLLe5XQ6SP1dVVdHR0\nSMcgk+Oklj243W6Ul5eLvKbUy9HREbKzs6VjfCSlUksp9TtKqXGl1MG7j++VUr965etepdQfKKW2\nlVKHSqmfKaVK0h/7ywoKCnB+fs47Dvoit9v93ubsp6enul5/c3MT0WgU8XgcZWVlul7bKjweD46P\nj6VjEInJy8vD2dmZdIy0ePPmDe8Lv8DhcKCwsBAAcHFxAeDt45bk3jWxWIz7QZKl7e3toaamRjoG\nmVxlZSVisRhisZh0FMogl8uF/Px8nJycSEfJiI2NDWRlZRlyj8FUJ7WWAfyXAHreffwNgP9DKZXY\nEOj3AfwEwE8B/AhAOYA/S0/U1PT392N+fl7i0mRSg4ODul7vyZMnCAaD8Pl8ul7XSvLz87G2tiYd\ng4hIV7W1tQB+WMIu5eLiwpDv2BKlSyQSgcvlko5BFlBQUMCTzm3i3r170hEy4tGjR6ivr5eO8Ukp\nlVqapv1fmqb935qmzb/7+K8AHAEYVErlAfhtAN9omvZ3mqY9BfBbAH5OKdWf/uhf1tvbi4WFBb0v\nSyY2MDCg6/VGR0dZat1QXl4eSy0ish2jlFrn5+eG3FuDKF0ikYghpxLIfAoKClBQUCAdg3Sg92tK\nvTx69Ah1dXXSMT7p2ntqKaUcSql/DiAHwBDeTm65APx14ns0TZsBsARA97qyr6+Pk1qUEr0ntR4/\nfsxS64Y4qUVEdpR4Uildal1cXLDUIktjqUXpkp+fz0ktm7DqpNbIyIg1JrUAQCnVqpQ6BHAO4A8B\n/Meapk0DCAG40DTtwx1rN959TVf9/f2c1KKUcPmh+bDUIiI7MsqkFkstsjouP6R04fJD+2Cppb/r\nTGpNA+gAMADgfwbwb5RSXzquSAHQrnGdG1FKwe/36775t1kNDAxgcXFROoYopZQu1xkZGQEAdHV1\nQSml23WtSCkFTdP97oVMYnh4GNXV1dIxMqqgoADLy8vSMUhniceNoqIi5OTkvPe1ubk53XJMTk4i\nFNL9fUvbqqmpsfSpWkaTeAzh8zRKBz7ntw8r/pxXVlbQ0dFh2P+3lN960DQtCuDlu/8cfbdf1n8O\n4H8H4FFK5X0wrVWCt9NaX/TNN9981F4/ePAADx48SDXipby8PJyennIT0yTcu3cPr1+/5gkvOhge\nHkZ/fz96enqkoxBZ2vfff4/GxkbpGBlVWFiIv//7v5eOQUI+Ne07Ozur29/7iYkJ3aec7ezWrVsY\nGhqy7H4tRmOHxxAiomSsrKygu7s7o9f47rvv8N133733uYODg6R+bzrmaR0AvACeAIgC+CUAfw4A\nSqkmANV4u+fWF3377bdp/4PKzc3lpFaSBgcH8fr1a/z4xz+WjmJ5iXdZM33HQGR3w8PD+OVf/mXp\nGBlVWFjISS0b+1Sppfek1q//+q/rdj27q6mpwZ/+6Z9Kx7ANOzyGEBElY3V1FV1dXRm9xqcGmkZH\nR5MaBElp+aFS6r9VSv0jpVTNu721/jsAPwbwb99NZ/0RgN9TSv2CUqoHwB8D+AdN00ZSuU66JCa1\n6OsSk1qUecPDwwDentBJRJnz/fffW376tLCwEEtLS9IxSIh0qfXs2TOUlZXpdj27S0xqkT7s8BhC\nRJSMlZWVjJdaN5HqnlqlAP4N3u6r9Vd4e+Lhv69p2t+8+/o3AP4SwM8A/C2AVQA/TUvSawgEAlhd\nXZW6vKlUVFQkPd5H1xOPx7G/v3+54Sj3ISHKrJWVFctvypqVlYWcnBwemGBTOTk58Hg8733O4bj2\nwdYp2d7ehtfrhd/v1+V69PZwlJWVFekYtrC3tweXy2X5xxAioq/RNA0HBwcoLy+XjvJZKS0/1DTt\nX37l6+cAfvfdh7ji4mLMzMzgRz/6kXQUIsTjcbx584Z7YRBRWt29exeTk5OcmCEA0G0PoLm5OS6j\nJ8taWlrifnFERO9Eo1FDnwSrz9t5QkpLSzEzMyMdgwgAEIvFsLy8zCdJRDox6gkt6XaR5kWtAAAg\nAElEQVT37l1MTExIxyCDaGpq0uU6s7OzXEZPlrW4uIj79+9LxyAiEqdpGmKxGEstKSUlJZienpaO\nQQTgh0ktllpE+tA0TTqCLlpbW1lq0SW9Sq25uTme4kuWtbi4iHv37knHICIyBE5qCQoGg1hcXEQ0\nGpWOQjaWaLfj8TjW19e5XCPNXC4XIpGIdAwiMc3NzZebg5v130I8Hjf0kyUzqaury/g1IpEIFhcX\n0dHRkfFrEelN0zS8efOGk4hERPjhuaWRn6dZutQCgM7OTk5rkajz83Osr6/D4XCgqqpKOo7l3Llz\nB+Pj49IxiES1tbUBAJ4+fSqc5Hq2trZ02wuKbu7Zs2e6TYQR6c3oEwlERHoaGhpCdXW1dIwvYqlF\nlGHn5+fY2NiA0+lEZWWldBzLYalFxFKL9DU+Ps6fF1kWSy0ioh8MDw+jpqZGOsYXWb7U6urqYqlF\nos7Pz7G2tsZJrQxpaWlhqUWfZJeN4oEfSq3R0VHhJNfDUstcWGqRlUUiEbjdbukYRESGwEktA2Cp\nRdISyw+dTidLrQzgpBZ9jl02igesUWpxOZt5jI+P8+dFlsVJLSKiHwwNDXFSS1phYSGUUjg9PZWO\nQjZzdnaGw8NDOBwOeL1eKKWQk5MjHcty8vPzsbe3Jx2DSFRBQQGAt/8ezOj8/By5ubnSMegrTk5O\ncHx8jLy8PP68hDQ0NGB7e1s6hqW9evUKgUDAVtO+RESfsrW1hcLCQvh8PukoX2T5UgsASkpKEA6H\npWOQzRwfH2N7exterxehUEg6DhHZAE9XpUza39/HwcEBTz0UNDg4iKWlJekYlvb06VNUVFRIxyAi\nEre4uIh79+5Jx/gqW5RapaWlODw8lI5BNnO11CorK5OOQ0Q20NXVJR2BLOzg4AD7+/sstQSx1Mo8\nllpERG+9fv0a9+/fl47xVbYotTipRRKOj4+xs7MDr9eL0tJS6ThEtmPHpSMstSiTEqVWe3u7dBTb\nGhgYYKmVYU+fPkV5ebl0DCIicYuLixgcHJSO8VW2KLUCgQBOTk6kY5CNnJ6e4vz8HEdHR/B4PAgG\ng9KRiGzHThvFJzQ3N0tHIIs6OTnB6ekpTk9PuUm8oLa2Nqyvr0vHsKyzszO8efMGJSUl0lGIiETF\n43Gsr6+b4o0sHu1BlAFTU1PIy8tDUVGRdBQiIqIbe/bsGfLz821ZFpN9LCwsoK+vTzoGEZG4aDQK\nt9stHSMptpjUItLb1NQUfD4fJ7SIiMgSEqWWWU/YJErGwsIC+vv7pWMQEYmLRCLweDzSMZLCUoso\nA54/fw6/389Si4iILOHZs2coKChAQUGBdBSijJmfn+ekFhER3pZanNQisjFOahHJs+NG8USZkpjU\nYqlFVvby5UuWWkRE4KSW4eTm5nJTza+YnJxEKBSSjmEJr1+/RklJCZxOp2nabbOrrKzE/v6+dAwy\nGO79Yx5HR0fwer3SMegzDg4OUFBQAJfLBZeL27GSNZ2fn0MphdzcXOkopud2uxGJRKRjENENzM7O\nori4WDpGUmxRahUWFvL4468YHh7GrVu3pGNYwtTUFFpaWqRj2EpjYyO2trakYxDRNe3v7yMnJ0c6\nBn3G9vY26urqpGMQZdTZ2RkLrTTxer0stYhMbnx8HOXl5dIxkmKLUisQCLDU+gqWWukzNTWFu3fv\nSsewlcbGRmxvb0vHIKJrOjg4gM/nk45Bn7Gzs4P6+nrpGEQZdXp6ylIrTbxeLy4uLqRjENENjI2N\nsdQykkAggMXFRekYhjY0NMRSK004qaU/TmoRmRsntYyNk1pkByy10sfj8bDUIjI5TmoZjN/vx/n5\nOcLhsHQUw5qZmUFJSYl0DNM7ODjAwcEBqqqqpKPYSllZGf9900e4Ubx5HB8fc08tAzs8POS+m2R5\nu7u7PAghTdxuN2KxmHQMIrqmo6Mj7O/vIxAISEdJii1KLQBobW3FxMSEdAyyuPHxcU5pERkEN4on\nIqJkvXjxgm/wEhEBmJ+fN9VJsCy1iNKIpRaRcXBSi4iIkjU9PY3S0lLpGERE4ubn59Hb2ysdI2m2\nKrUmJyelY5DFPXv2DHfu3JGOQUTgpBYRESVvenraNMfXExFl0sLCAkstI2KpRXrgpBYRERGR+bx4\n8YKTWkREAObm5rj80Ig8Hg9KSkqwv78vHcVwVldX0dXVJR3D9F69eoX6+np4PB7pKEQELj80i4mJ\nCZ6+S5QCh8OBaDQqHcNSFhYW0NTUBKfTKR2FiEjU6ekpsrOzTXWAj21KLQCoqanB7u6udAzDWVpa\nwuDgoHQM05ubm0NHR4d0DCJ6h8sPzeHx48dobGyUjkFkCkopOJ1OniyXZjMzM3yDl4gIb0utvLw8\n6RgpsVWpdevWLZZan8BSKz1mZ2dZahEZCCe1zOHx48doaGiQjkFkColSi5Na6TU9Pc1Si4gIwMnJ\nCUstI+Ok1qctLS1hYGBAOobpzc3Nob29XToGEb3DSS1zePLkCSe1iJKklILD4eCkVppxUouI6K3T\n01Pk5+dLx0iJrUqt0tJSbG9vS8cwlPX1dUSjUe5nckMbGxuIRCKoqKiQjmJLLpcL5+fn0jHIYMrK\nyhAOh6Vj0FcsLS3xxDGiJCVKrXg8Lh3FMi4uLnB4eIjKykrpKESGEgqFcHh4KB2DdLa5uYnCwkLp\nGCmxVamVm5uLra0t6RiGMjIygurqai7TuaEnT56gqalJOoZt+Xw+HgJBH7l//z4WFxelYxARkYEd\nHh6yWCf6hL6+PiwvL0vHIJ3NzMygpKREOkZKWGrZ3MjICKqqqlhq3RCXz8jKyclhqUUfGRwcZKlF\nRERfxFKL6NNYatnT7Oys6e4TbVdqbW5uSscwlJGREdTU1LDUuiGWWrJycnKwt7cnHYMMhpNaRET0\nNYeHh6abSiDSQ39/P0stG7LdpJZS6l8ppeJKqd+78jmvUuoPlFLbSqlDpdTPlFKG+FPhpNbHEpNa\ndDMstWRxUos+5d69e1haWpKOQUREBsZJLaJP6+vrw5s3b6RjkM5sNamllOoD8J8CGP/gS78P4CcA\nfgrgRwDKAfzZda+TTkopNDU14enTp9JRxBweHmJnZ+fyv/v6+qCU4qTWDaytraG1tZV/hoL4Z0+f\nopTiCYgGt7a2xlNjTaCoqAgvX76UjkGUEYuLiygqKpKOQWQ4fB5lL+FwGHt7e+jo6DDda6trlVpK\nKT+AfwvgXwLYv/L5PAC/DeAbTdP+TtO0pwB+C8DPKaX605D3xpqbm21dah0dHb1XavX3G+LHYmpr\na2toa2uTjkFEZDqrq6sstUwgGAxiYWFBOgZRRrx+/RqBQEA6BhGRqHA4jN3dXXR2dkpHSdl1J7X+\nAMD/qWna33zw+V4ALgB/nfiEpmkzAJYA3LvmtdLq9u3bGBsbk44h5ujoCLu7u5f/zVLr5tbX19Ha\n2iodg4jIdNbX1/mmgAlwUousbHFx0XTH1xMRpVs4HMb+/r4pSy1Xqr9BKfXPAXTibYH1oVIAF5qm\nhT/4/AaAUOrx0q+5uRmjo6PSMcR8uPyQpdbNra2tobu7WzoGEZHprK6u8nHIBDipRVbGSS0iorel\n1uHhoSlLrZQmtZRSlXi7Z9Z/omlaJJXfCsAQC3IDgQCUUjg8PJSOIsLhcMDh+OHHXlZWJpjG/BYX\nF+F0OhEKGaKzJSIylePjY9NtRmpH2dnZyMnJwfr6unQUApCfn8/Nm9MoHA4jOztbOgaR4ST2VYrH\n48JJSA8bGxtwOBymO/kQSH1SqwdAMYAn6ofdw5wAfqSU+s8A/CoAr1Iq74NprRK8ndb6rG+++Qb5\n+fnvfe7Bgwd48OBBihG/rrm5GZubm8jNzU37bRud3+/nZphp9PDhQ4RCIXg8HukoREREGdPW1oap\nqSm+iWMAFRUVGB0d5dYHRJRRDocDSinE4/H3hiLImpaXl3H//n2x63/33Xf47rvv3vvcwcFBUr83\n1VLrrwB8uPnF/wrgBYD/HsAKgAiAXwLw5wCglGoCUA1g6Es3/O233+q2hCtRatXX1+tyPSPx+/3S\nESxleHgYv/mbvwmv1ysdhYiIKGM6OjowNTWFX/zFX5SOYnuVlZX4kz/5E/zGb/yGdBQisrBEkRWL\nxeBypbxrEZnM0tISfvKTn4hd/1MDTaOjo+jp6fnq702pctU07VjTtKmrHwCOAexomvbi3XTWHwH4\nPaXULyilegD8MYB/0DRtJJVrZVKi1LIjTmqlFye1iIjIDhKTWiSvoqLC1id5E5E+rk5qkfUtLy+b\n9tCMdMwRfrhX1jcA/hLAzwD8LYBVAD9Nw3XSpqmpCVtbW9IxRPj9ftP+ZTWaaDSKiYkJlJaWstQi\nIiJLa2lpwcLCAl/cGEBZWRmePXsmHcMSIpEI3G63dAwiQ3I4HHA6nTg7O5OOQhkWiUSwubmJgoIC\n6SjXcuNSS9O0X9Q07b+48t/nmqb9rqZpQU3TcjVN+6eaphlqLCorKwvh8IcHNBKlZnl5mad2ERGR\nbVRUVGB/f186BlHaTE5Ooq3tw51ViCihqqoKjx49ko5BGTYxMWHqfRptueNbdnY2jo6OpGOQyS0v\nL6Ovr086BhERkS4qKiqS3rSVyAwmJydN/UKOKNMqKyvx+PFj6RiUYZOTk7h79650jGuzZanFSS1K\nh+XlZQwMDEjHICIi0gUntchqWGoRfRlLLXuYmJhgqWU2nNSidOCkFhER2Ul5eTlLLbKU58+fs9Qi\n+oKqqiqWWjbASS0TcjqdCAQCmJ+fl45CJrSxsQHgbTkaDAaF01BCKBTCwsKCdAwiSkEkEoHT6ZSO\nQUkKBoO2PT3aaBoaGi6fj9D1HB0dweVymXZjZCI95OTkIBAIYH9/H5FIRDoOZcDR0RHcbrep7wtt\nWWoBb58McNM7uo5Xr14BAKqrq+Fw2PafkOE0NjbiyZMn0jGIKAXn5+c8PdZE8vPzsbKyIh2DAPT3\n9/ONnBva3d1FTU2NdAwiwxsYGMD6+jrOz8+lo1AG7Ozs4NatW9IxbsS2r8jr6+tZatG1JEqtyspK\nKKWE01ACSy0i82GpZS75+flYW1uTjkEA+vr68PLlS+kYpra3t4fq6mrpGESG19/fz1LLwnZ3d1lq\nmRVLLbquxJNITmoZS2NjI9f8E5kMSy1zKSgowOrqqnQMAie10oGTWkTJGRwcZKllYSy1TKyyshJL\nS0s4Pz+HpmnSccjgYrHY5Try3d1dAEBpaSlLLQOpqqrCixcvpGMQUQouLi7gdrulY1CS/H4/jo+P\ncXx8LB3F9u7evYv19XXE43HpKKZ1eHiIUCgkHYPI8O7evYtwOIyDgwPpKJQBOzs7qKyslI5xI7Z+\nRd7X14fFxUXpGGQCx8fH2NnZAQDU1tYKpyEiIpJx584dPHv2TDoGAfD5fDg7O5OOQUQ2EAqF8Pz5\nc+kYlAFbW1vw+/3SMW6EpRZLLUrC0dERtre3AbDUIiIi+2ppacH4+Lh0DMLbyTmWWkSkh1AohMnJ\nSekYlAFbW1vIzc2VjnEjti+1lpaWpGOQCXBSi4iIiJNaRsJSi4j0wkkt62KpZXL9/f2c1KKkXJ3U\nqqurE05DREQkg5NaxuHz+XB6eiodg4hsgJNa1sVSy+T8fj8KCwsxMTEhHYUMzuv1wufzAQCysrKE\n0xBRslwuF6LRqHQM+oTJyUmUlZVJx6AU5eTkoLCwEPv7+9JRbK+4uPjyRGZK3e7uLnJycqRjEJmC\nx+NBdXU1AGB+fl44DaXD7u4uzs/PUV5eDqfTKR3nRmxdagFAdXU1hoeHpWOQwfl8PhQVFUnHIKIU\nsdQyruHhYdMfIW1XDQ0Nl9PLJKekpATT09PSMUxrc3MTeXl50jGITKO7uxsAuATdIjY2NnB2dobb\nt29LR7kx25daNTU1+P7776VjkMH5fD4Eg0HpGESUIpfLhUgkIh2DPmF4eJh7FJpUQ0MDtra2pGPY\nXmlpKaampqRjmNbm5qbpl9wQ6YmllrVsbm7i9PSUpZYV1NTUYGhoSDoGGZzf72epRWRCbrebk1oG\nNTQ0xEktk+KkljGUlpbixYsX0jFMa2Njg5NaRCno6ekBwFLLKhKTWs3NzdJRbsz2pVZxcTF2dnZw\nfHwsHYUMLCsri+/mEZmQ0+lELBaTjkGfMDc3h5KSEukYdA0VFRWXJwKTnIKCAhwfH+Pw8FA6iikd\nHBwgOztbOgaRaSQOy7q6p2I0GsX5+blUJLqBnZ0dxGIxlJeXS0e5MduXWgBw//59noJIRERElASf\nz4e9vT3pGASgq6uL+2oRka46Ojouf318fMzJXZM6OjqyTLHPUgvA4OAgSy0iIiKiJLDUMo6uri7M\nzs5KxyAiG2lra7v8NUst8zo6OkJWVpZ0jLRgqQVOahEREREli6WWcXR3d2NmZkY6BhHZSHt7++Wv\nT05OeHCISbHUspj79+/j9evX0jGIiIiIDC8nJ4ellkFw+SER6Y3LD63h8PCQyw+txOPxQCnFY9+J\niIiIvsLhcKCmpoYnYBmAx+NBTU0NAHBii4h04Xa7L3+dlZWFgoICwTR0HWNjY6iuroZSSjpKWrDU\neofHvhMRERElp6mpCU+ePJGOQQBu374NAJicnBROQkR24/P5EAwGpWNQikZGRlBfXy8dI21Yar3j\ndrs5qUVERESUhMbGRjx+/Fg6BoGlFhHJYallTiy1LIqlFhEREVFyGhsbMTo6Kh2D8EOp9fz5c+Ek\nRGQ3LLXM6dGjR6irq5OOkTYstd7Jz8/H+vq6dAwiIiLLC4fDKCsrk45BN1BcXIyzszMcHR1JR7G9\nkpISAOA2GkSkO4/HA7/fLx2DUnB4eIjz83NLlZEstd4pLy/H2NiYdAwiIiLLW15eRn9/v3QMuqHW\n1la+IWggd+/elY5AREQGt7Kygq6uLukYacVS6x2WWkRERPpYWlrCwMCAdAy6oba2NqytrUnHoHda\nW1ulIxARkcGtrKygu7tbOkZasdR6p6KigqUWERGRDlhqWQNLLWPhpBYREX0NSy0LKy8vx/j4ODRN\nk45CRERpxPt141leXmapZQFtbW1cfmggnNQiIqIv0TSNpZbV9fb2YmFhQToGERGlCadwiTLH4/Hg\n7OxMOgYRERElYWhoCBUVFXA6ndJR0oql1hV9fX2Yn5+XjkFERGnC/RKJMoelFhERkXkMDw+joqIC\nLpdLOkpasdS6gqUWEZG1lJeX4+nTp9IxiCyJpRYREZF5JCa1bF1qKaX+a6VU/IOPqStf9yql/kAp\nta2UOlRK/UwpVZL+2JnR19fH5YdERBZSUVHBUosoQ7xeL0stIiIikxgaGkJlZaW9S613JgGUAgi9\n+/hHV772+wB+AuCnAH4EoBzAn90wo25KS0vhcrmwsrIiHYWIiNLA7/dja2tLOgaRJTmdTuTl5WFx\ncVE6ChEREX3B7u4uvF4v/H4/HA5rLdi7zv9NVNO0LU3TNt997AKAUioPwG8D+EbTtL/TNO0pgN8C\n8HNKqf40Zs6ohoYGvqtPRERElITa2loMDw9LxyAiIqIveP36Ne7duycdIyOuU2o1KqVWlFILSql/\nq5Sqevf5HgAuAH+d+EZN02YALAEwzZ9eQ0MDNxUmIiIiSgJLLSIiIuNjqfWDYQD/AsA/BvA7AGoB\n/L1Syoe3SxEvNE0Lf/B7Nt59zRTq6+tZahEREREloba2Fg8fPpSOQURERF+wuLiIwcFB6RgZkdIO\nYZqm/T9X/nNSKTUCYBHAPwPwuZ1CFQDtevH0d+vWLczNzSESicDtdkvHISIishRNM81TAkpCVVUV\nnj9/jmg0armNZ8nanE4n4vG45faWISL6kKZpWFlZQU9Pj3SUjLjRsw9N0w6UUrMAGgD8FQCPUirv\ng2mtEryd1vqib775Bvn5+e997sGDB3jw4MFNIl5LZ2cnpqen0dbWpvu1iYiIrCwWi8HhcEApJR2F\n0qSvrw/Ly8uora2VjkKUtJKSEhweHn70+oOIyGoikQg8Ho90jC/67rvv8N133733uYODg6R+741K\nLaWUH0A9gP8NwBMAUQC/BODP3329CUA1gKGv3da3336L7u7um8RJG5ZaREREmcFSy3r6+/tZapHp\nlJaWIhwOs9QiIsszwyq0Tw00jY6OJjVdltK8rVLqf1BK/UgpVaOUuo+35VUUwL97N531RwB+Tyn1\nC0qpHgB/DOAfNE0bSeU60rq6uvDixQvpGERERJaTKLW45Mc6BgYGsLS0JB2DKCUlJSUIhz/cCpiI\nyHouLi4MP6l1E6k+o6wE8KcApgH8OwBbAAY1Tdt59/VvAPwlgJ8B+FsAqwB+mpakOkpMahEREVF6\nxWIxKKU4qWUhfX19ePPmjXQMopQklh8SEVmdGZYf3kSqG8V/cYMrTdPOAfzuuw/TKigogNPpxMnJ\nCXJycqTjEBHRDTQ0NGB9fR2hkGkO4rU0TdNYallMUVERTk9Puek2mUowGMTa2pp0DCKijHv16hWK\nioqkY2QMn3l8RmlpKd+9ISKygL6+PszPz0vHILKsxB5psVhMOgpR0goLC7G4uCgdg4go48bGxlBe\nXi4dI2NYan0GR5KJiKyhr68PCwsL0jGILCsxdcdSi8wkEAhwLzgisoVnz56x1LKjxIkoRERkbpzU\nIsqsxKRWPB6XjkKUtMLCQpZaRGQLnNSyqZKSEuzt7UnHIKIknZ6ewu/3S8cgA7pz5w5WVlakYxBZ\nlsPhgNfr5ZuBZCp5eXkIh8M4OTmRjkJElDGnp6dYX19HMBiUjpIxLLU+g+vsicxlbm4Ovb290jGI\niGypqqoKjx49ko5BlJLW1lZMTExIxyAiypj5+Xn09fVJx8gollqfwVKLyFxYahERyamsrMTjx4+l\nYxClpK2tjaUWEVna/Py85V8jsdT6DG4eSWQu8/Pz6OnpkY5BRGRLlZWVePLkiXQMopTcvXsXk5OT\n0jGIiDKGpZaNcfNIInPhpBYRkRwuPyQzam1tZalFRJbG5Yc25nK5UFlZiePjYxwcHEjHIaKvODs7\ng8/nk45BBuXz+XB2diYdgwC8ePECJSUl0jEozTweD2pra3koA5lKTk7O5Ylg09PTwmmIiNJrZmYG\nxcXFln+NxFLrC1pbW3F4eIjd3V3pKEREdAO5ubk4PT2VjkEAnjx5gsrKSukYlAH9/f14+fKldAyi\nlLS2tgJ4e+Q9EZGVjI+Po6GhQTpGxrHU+gKWWkRE1pCXl8dSyyBYalnXwMAAXr16JR2DKCWJUuvp\n06fCSYiI0uvp06cstewuUWrt7e1JRyEiohvIzc3l8kODePLkCSoqKqRjUAZwUovMiJNaRGRVnNQi\nVFVVIRqNYnt7WzoKERHdQHZ2Ni4uLqRjEICXL1+iqKhIOgZlQGNjI05OTjjhTqZSXV0NANjf3wcA\nxONxnJycSEYyvXg8DoeDLzOJJB0cHODg4AChUEg6Ssbx3uYrcnNzsbW1JR2DiIiIyPDq6urw5MkT\n6RhEKevu7gYARKNRHnhwQ+fn53C73dIxiGxtenoanZ2d0jF0wVLrK3Jzc7G5uSkdg4iIiMjwamtr\nMTo6Kh2DKGWJF3/RaBSrq6vCaczt/PwcHo9HOgaRrbHUokuc1CIiIiJKTl1dHUstMqWuri4AQCQS\n4aTWDXFSi0jeixcvWGrRW5zUIiIiIkoOJ7XIrDiplT4XFxec1CISxkktuuRwOFBXV4eJiQnpKERE\ndE3BYBDz8/PSMWxvcXHxchqCrMnlcqG5uRkLCwvSUYhSkihhnE4niouLhdOYm6ZpUEpJxyCyrcPD\nQxQWFtpmYpKlVhKam5vx9OlT6RhERHRNJSUlmJ6elo5hewsLCxgYGJCOQRnW09OD2dlZ6RhE1+J2\nu1FRUSEdg4jo2sLhsC1OPUxgqZWE27dvY2xsTDoGERFdU0lJCWZmZqRj2N6rV6/Q398vHYMyrLu7\nG3Nzc9IxiK7F5XKhvLxcOgYR0bWFw2GUlpZKx9ANS60k3L59m5NaREQmxlLLGBYWFlhq2UB3dzcn\ntci0XC4XJ7WIyNRYatFHSkpKcHZ2huPjY+koRER0DX6/n4d+GMDu7i6qq6ulY1CGVVZW4ujoCBcX\nF9JRiFLmdDqRn58vHYOI6Nq2trZstTcgS60kNTc38wURERERURICgQDfDCQiIhKwvLyMwsJC6Ri6\nYamVpDt37mBjY0M6BhEREZHhBQIBHB0dSccgIiKynaWlJZZa9DFOahERERElp6ioiJNaREREAjip\nRZ+UKLU0TZOOQkQf4L9LSoZSin9XBPHP3l44qUVERKQ/TdNYatGnZWVlobS0FCMjI9JRiOgDJycn\ntrrjpuvp6urC9PS0dAzbOj8/h8/nk45BOgkGg1hYWJCOQUREZCsTExNobW2VjqErllpJys7ORklJ\nCR49eiQdhYg+cHJygoKCAukYZHCdnZ0stQSdnZ2x1LKRoqIivHz5UjoGERGRrUxMTODu3bvSMXTF\nUitJnNQiMq7j42OWWvRVnNSSxVLLXjipRUREpD9OatFncVKLyLg4qUXJ4KSWrPPzc+Tk5EjHIJ1w\nUouIiEh/nNSiz3K5XMjJyYHH48H+/r50HCK6IhqNwuv1SscggysuLsbe3p50DNuKxWJwu93SMUgn\n2dnZ8Pv9WFtbk45CRERkC4lTh4uKioST6IulVoq6urqwsrIiHYOIiIjI0Nrb2zE1NSUdg4iIyBZ2\ndnZw69Yt6Ri6Y6mVIpZaRERERF/X1tbGUouIiEgnu7u7LLXo67q7u1lqEREREX1FR0cHnj9/Lh2D\niIjIFnZ3d1FbWysdQ3cpl1pKqXKl1J8opbaVUidKqXGl/v/27j22rfM+4/jz082yrLtkSVFsXSwp\nvkTxJYp72da0WIAGxdCt64B13oZ2GLJ2vWxBMXRd0W4tmj82pJcUbbe12Nbu0sZF0KFrhqbx2mJA\ntzSx44scR5blKJXkybIkS5YoSpZsSXz3B8mElmXVtCi+POT3AxgIeY7oh4b9y3ajkM0AABJlSURB\nVOHD95xj96/Y57NmNhLb/iMza09dZL/uvfdejY6OyjnnOwoAIEn5+fmKRCK+Y+Sk69evKz8/33cM\npNGuXbs0MDCg5eVl31EAAMhq165d08zMjLZv3+47StolVWqZWaWk5yRdk/SwpN2S/kzSVMI+H5f0\nEUkfkPQGSXOSjphZUYoye1VQUMDBGQAEVH19vWZmZnzHyElnz55VfX297xhIs7vvvluhUMh3DAAA\nstqpU6dUU1OjsrIy31HSLtmVWn8h6YJz7hHn3Ann3JBz7sfOuYGEfR6V9Jhz7j+dcy9Leq+kRknv\nSlFmrwoKCrS0tOQ7BgDgDtTV1SkcDvuOkZPOnj2rhoYG3zGQZtu2beOu0QAAbLCTJ0+qurqaUus2\nvFPScTN7yszGzOykmT0S32hmrZIaJP0k/pxzbkbSUUlvTkVg3+IrtTj9EACCh5Va/vT09LBSKwfd\nfffdmpqa+sU7AgCAOxZfqVVaWuo7StolW2rtkPRBSX2S3i7pa5K+bGa/H9veIMlJGlvxc2OxbYHH\nSi0ACC5WavnT29tLqZWDOP0QAICNd+rUqZxdqVWQ5P55ko455/4y9vi0md2raNH1rTV+zhQtu27p\nox/9qCoqKm547tChQzp06FCSETdWXl6eamtrJUnj4+Oqq6vznAjAyMiIysvLfcdAANTU1OjSpUu+\nY+SkmZkZFRcX+46BNKupqdHg4KDvGAAAZK3p6WmVlZWpqCi4lzE/fPiwDh8+fMNzt/ulWLKl1iVJ\nvSue65X07th/jypaYNXrxtVadZJOrfXCTzzxhO6///61dskYTU1NkqShoSFKLSAD9Pf3q6ury3cM\nBEBVVZVeeukl3zGAnFFRUUGRDADABhobG9Pu3bt9x1iX1RY0nTx58rY+4yV7+uFzknaueG6npCFJ\nil0wflTSQ/GNZlYu6Y2Sfpbk75WxmpubZWZ88whkiFdeeeW1FZTAWqqrq3XhwgXfMYCcUVFRoZGR\nEd8xAADIWtlQaq1Hsiu1npD0nJl9QtJTipZVj0j6o4R9viTpU2bWL2lQ0mOShiV9f91pM0Rzc7Mk\nUWoBGeKVV17R1q1bfcdAAFRVVWloaMh3DCBnUGoBALCxxsbGtGfPHt8xvElqpZZz7rik35R0SNIZ\nSZ+U9Khz7jsJ+zwu6SuSvq7oXQ83S3qHc+56qkL7Vl9fLzPT+Pi4IpGI7zhAzhseHlZlZaXvGAiA\n8vJyzc7Oam5uzneUnHL16tWcvBsPpNLSUs3Pz2t2dtZ3FAAAstLExIRaW1t9x/Am2dMP5Zx7xjm3\n1zlX4py71zn3jVX2+YxzrjG2z8POuf7UxM0sRUVFWlxc9B0DAJCEzs5OnTlzxneMnNLX18d173LY\nnj17dPr0ad8xAADISrOzszl9M56kSy28rrCwkFILAAKms7NTL7/8su8YOeX8+fM6cOCA7xjwZPfu\n3dygAQCADTI3N0ephTtTVFSkpaUl3zEAAElgpVb69fX1BeYOx0i9PXv2qLu723cMAACyEiu1cMdY\nqQUAwcNKrfQ7f/48pVYO4/RDAAA2DqUW7lhdXZ36+vp8xwAAJGHz5s2qrKxUKBTyHSUnXL16VcXF\nxSopKfEdBZ4UFxertrZWU1NTvqMAAJBVenp61NjYqLy83K12cvedp0BjYyPL6QEggFpaWnTlyhXf\nMXLC7OysamtrfceAZx0dHZqYmPAdAwCArHL06FHt2LHDdwyvKLXWgVILAIKJUit9wuEwpRbU3t6u\ny5cv+44BAEBWOXbsmNra2nzH8IpSax0aGxu5RgQABFBzczOlVprMzc2ppqbGdwx41t7ezkotAABS\n7MUXX2Sllu8AQVZVVaW5uTmFw2HfUYCcNT09rerqat8xEDANDQ2anJz0HSMnTExMsFIL2rZtG//m\nAABIoatXr2p6elr19fW+o3hFqbVOXV1d6u/v9x0DyFnnzp3T3r17fcdAwJSVlXEqVJoMDAxQPEMl\nJSVcKB4AgBQaHh7WgQMHfMfwjlJrnQ4ePEipBXh09uxZ7du3z3cMBExZWZnGx8d9x8gJP//5zzn9\nENqyZYump6d9xwAAIGtcvHhRXV1dvmN4R6m1TgcPHtSrr77qOwaQs3p7e7V//37fMRAw5eXllFpp\nMjAwQKkFVmoBAJBiw8PDlFqi1Fq3Bx54gJVagEe9vb2cfoiklZaWcvphmlBqQWKlFgAAqXbx4kVO\nPxSl1roVFhaqqalJZ86c8R0FyElLS0sqLCz0HQMBk5eXpx07dmhhYYFyawOdO3dOO3fuVF4ehxu5\nzszU0tKi7u5u31EAAAg855yWlpZUXFzsO4p3HGWmQHt7OwdpABAwu3bt0vz8PKchbqCenh5WUuI1\nHR0dOnHihO8YAAAEnnNOy8vLys/P9x3FO0qtFGhra6PUAoCA2blzpxYWFii1NlBPT486Ozt9x0CG\noNQCACA14qVWQUGB7yjeUWqlQHt7u06dOuU7BgAgCfGVWmNjY76jZC1WaiFRR0eHjh8/7jsGAACB\nR6n1OkqtFKipqVEkEtHk5KTvKEBOuXbtmkpLS33HQEBt3bpVkrgj2wZZWFjQ/Py8GhoafEdBhqit\nrdXi4qJmZ2d9RwEAILBCoZAkqaysjOuWilIrZfbv36/e3l7fMYCcEgqFdNddd/mOgQArLi5WOBz2\nHSMrTU1Nafv27b5jIMPcd999unTpku8YAAAE1uDgoMxMTU1NvqNkBEqtFDlw4IDOnTvnOwaQU0Kh\nkBobG33HQIBt3ryZUmuDTE9Pa9u2bb5jIMPs3buXUgsAgHWIl1rNzc2+o2QESq0U2b9/P6UWkGah\nUIhTm7AurNTaONPT06zUwk1YqQUAwPoMDQ3JzDjOiqHUSpF9+/bp/Pnzcs75jgLkjJmZGU4/xLps\n3rxZs7Ozcs4xv1MoEomwUgur6uzs1OjoqO8YAAAEknPutVKL0w+jKLVSqL6+XjMzM75jAACS0N7e\nrqWlJV28eNF3lKzR3d2tqqoqVVRU+I4CAACQNRYXF1VUVOQ7Rkah1Eqh+vp6TmMBgIBpa2uj1Eqx\n06dPq7KyUuXl5b6jAAAAZA1KrZtRaqUQK7UAIHgotVKPUgsAACD1KLVuVuA7QDapq6uj1AKAgGlr\na9Pi4qJGRkZ8R8kap0+fVlVVlczMdxQAAICsQal1M1ZqpVBtba3GxsZ8xwAAJKGiokJmpnA4zMXi\nUyAcDisvL0+bNm3ioAs3yc/P1+Liou8YAAAE0oULF1RVVeU7Rkah1EqhqqoqXbhwwXcMAECSCgoK\ntLS05DtGVrh8+bLuuece3zGQoYqKinTt2jXfMQAACKTu7m41Njb6jpFRKLVSiFILAIKpsLCQUitF\nJiYm1NHR4TsGMlRRUZEWFhZ8xwAAIJBeeuklSq0VKLVSqLq6mlILAAKooKCAU6JS5PLly5RauCVW\nagEAcOdYqXUzSq0Uqqio0MTEhCKRiJaXl33HAbLe0tKS8vIYY1i/goKC1y5qTrl15xYWFhQKhdTa\n2uo7CjJUUVGRIpEIq7UAAEjS9evXNTg4qLq6Ot9RMkrGfBp89tlnfUdIic7OToXDYV25csV3FCDr\nDQ8Pq7Ky0neMjHT48GHfEQKnublZkjQ0NOQ5SXAdP35cW7duVUlJie8oyGAtLS164YUXfMdIGnMV\nAFKLuZqc/v5+PfDAA75jZJyMKbWOHDniO0JKxEutyclJ31GArDc8PMzdP26Bg4TkxUutwcFBv0EC\njFILt6O1tVXPP/+87xhJY64CQGoxV5PT39+vgwcP+o6RcTKm1MoWrNQC0md4eFgVFRW+YyBLxEst\nro14506cOKHa2lpKLayppaVFR48e9R0DAIBAYaXW6ii1UoxSC0gfVmohlZqamiSxUms94iu1tmzZ\n4jsKMlhra2sgTz8EAMAnSq3VFfgOkG3Kysq0vLzMhYaBNFhYWFBhYaHvGMgS8dVF8/PznpME1/T0\ntDZt2uQ7BjJcSUmJpqamfMcAACBQ5ubmuJ7wKjKh1CqWpHA4rJMnT/rOkhJ9fX2amJjImvcDZKps\nmhupFgqF+LO5Q2NjY/zZ3aHFxUX+7HBbIpFI4P6uMFeB2zM+Ps6/FdwW5mpyJicnc+rPq7e3N/6f\nxWvtZ865jU+zVgCz35X0ba8hAAAAAAAAkGl+zzn35K02ZkKpVSPpYUmDkha8hgEAAAAAAIBvxZJa\nJB1xzk3eaifvpRYAAAAAAACQLO5+CAAAAAAAgMCh1AIAAAAAAEDgUGoBAAAAAAAgcCi1AAAAAAAA\nEDjeSy0z+7CZDZjZvJm9YGYHfWcCgExjZp82s8iKX2cTtm8ys781swkzC5vZd82sbsVrbDezH5jZ\nnJmNmtnjZub9/wMAkA5m9hYze9rMLsZm6K+vss9nzWzEzK6a2Y/MrH3F9ioz+7aZhcxsysz+0cy2\nrNhnr5n9NHZsO2RmH9vo9wYAPvyiuWpm31zl+PWZFfswV7EuXj/MmNl7JH1B0qclHZB0WtIRM6v1\nmQsAMtTLkuolNcR+/UrCti9J+jVJvyXpQUmNkv49vjFWXj0jqUDSmyS9T9IfSPpsGnIDQCbYIqlb\n0ocl3XT7bzP7uKSPSPqApDdImlP0uLQoYbcnJe2W9JCiM/dBSV9PeI0ySUckDUi6X9LHJH3GzB7Z\ngPcDAL6tOVdjfqgbj18PrdjOXMW6mHO3+ruXht/c7AVJR51zj8Yem6T/k/Rl59zj3oIBQIYxs09L\n+g3n3P2rbCuXdFnS7zjnvhd7bqekXklvcs4dM7N3SHpa0l3OuYnYPh+Q9DeStjrnltL0VgDAOzOL\nSHqXc+7phOdGJH3OOfdE7HG5pDFJ73POPWVmuyX1SOpyzp2K7fOwpB9I2uacGzWzD0p6TFJDfK6a\n2V8rOr/3pPEtAkBa3WKuflNShXPu3bf4mV2Szoq5inXwtlLLzAoldUn6Sfw5F23Yfizpzb5yAUAG\n64gt737VzL5lZttjz3cpugIrcZ72Sbqg1+fpmySdiRdaMUckVUi6d+OjA0DmMrNWRVcQJM7RGUlH\ndeMcnYp/8Ir5saKrE96YsM9PV3xRcETSTjOr2KD4AJDJ3mZmY2Z2zsz+zsyqE7a9WcxVrJPP0w9r\nJeUr+g1YojFFDyoAAK97QdHTBR+W9MeSWiX9NHbNgQZJ12MfwBIlztMGrT5vJWYuADQo+iFqrePS\nBknjiRudc8uSrohZCwCr+aGk90r6VUl/Lumtkp6JnaElMVeRAgW+A6zCdOvzcQEgJznnjiQ8fNnM\njkkakvTbkhZu8WO3O0+ZuQCwutuZo79on/iHN2YtgJzinHsq4WGPmZ2R9Kqkt0n67zV+lLmK2+Zz\npdaEpGVFLxqXqE43N7EAgATOuZCk85LaJY1KKopd/yVR4jwd1c3zNv6YmQsg140q+iFprePS0djj\n15hZvqSq2Lb4Pqu9hsSsBZDjnHMDivYA8TvLMlexbt5KLefcoqQTit7lQNJrF4p/SNLPfOUCgCAw\ns1JJbZJGFJ2lS7pxnt4jqUmvz9PnJd234u6yb5cUUvQCnQCQs2IftEZ14xwtV/SaLolztNLMDiT8\n6EOKlmHHEvZ5MPahLO7tkvpiX0YAQM4ys22SaiRdij3FXMW6+VypJUlflPR+M3tv7M4HX5NUIumf\nvaYCgAxjZp8zswfNrNnMfknS9xQtsr4Tu5bWP0n6opm9zcy6JH1T0nPOuRdjL/FfipZX/2Zme2N3\nlnlM0ldjXzIAQFYzsy1mts/M9see2hF7HL/pxpckfcrM3mlm90n6V0nDkr4vSc65c4penPgfzOyg\nmf2ypK9IOuyci68oeFLSdUnfMLM9ZvYeSX8q6QtpeZMAkEZrzdXYtsfN7I2x49eHJP2HomcaHJGY\nq0gNi95w0GMAsw8petG4ekndkv7EOXfcaygAyDBmdljSWxT9duuypP+V9MnY6gKZ2SZJn5d0SNIm\nSc9K+rBzbjzhNbZL+ntFr2Mwp+gXCJ9wzkXS9kYAwBMze6ui13BZefD7L865P4zt8xlJ75dUKel/\nFJ2j/QmvUSnpq5LeKSki6buSHnXOXU3Y577YPgcVPc3my865z2/Q2wIAb9aaq5I+pGiJtV/RmTqi\naIH1V865ywmvwVzFungvtQAAAAAAAIBk+T79EAAAAAAAAEgapRYAAAAAAAACh1ILAAAAAAAAgUOp\nBQAAAAAAgMCh1AIAAAAAAEDgUGoBAAAAAAAgcCi1AAAAAAAAEDiUWgAAAAAAAAgcSi0AAAAAAAAE\nDqUWAAAAAAAAAodSCwAAAAAAAIFDqQUAAAAAAIDA+X9qIp/mTn3r6QAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f7ac79f5cd0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Find local maxima\n",
"# make a binary array containing local maximum of transform, with same shape\n",
"lmax = np.zeros(cwtmat.shape)\n",
"for i in range(cwtmat.shape[0]):\n",
" lmax[i, signal.argrelextrema(cwtmat[i, :], np.greater)] = 1\n",
"fig, ax = plt.subplots(figsize=(15, 4))\n",
"ax.imshow(lmax, aspect='auto', cmap='gray_r')"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# allocate memory\n",
"\n",
"# intial location assigned to peak from the first row\n",
"peak_pos_start = np.where(lmax[0,:]==1)[0]\n",
"\n",
"# current position of the ridge\n",
"peak_ridge = np.copy(peak_pos_start) # full copy\n",
"\n",
"n_peaks = peak_pos_start.size\n",
"\n",
"# length of the ridge\n",
"peak_len = np.ones(n_peaks)\n",
"\n",
"# use the max of the ridge line to find the width of the peaks\n",
"peak_pos = np.zeros(n_peaks, dtype='int')\n",
"peak_width = np.ones(n_peaks)\n",
"peak_width_max = np.zeros(n_peaks)"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Link local maxima (find ridges)\n",
"\n",
"w = 3\n",
"\n",
"# for each row starting at the second\n",
"for i in range(1, lmax.shape[0]):\n",
" # for each peak\n",
" for j in range(n_peaks):\n",
" # assume it doesn't extend, and then check\n",
" extends = False\n",
" p = peak_ridge[j]\n",
" if lmax[i, p] == 1:\n",
" # if there is one below, it is part of the same ridge\n",
" extends = True\n",
" else:\n",
" # if not search around peak \n",
" for k in range(1, w):\n",
" if lmax[i, p-k] == 1:\n",
" extends = True\n",
" peak_ridge[j] -= k\n",
" break\n",
" elif lmax[i, p+k] == 1:\n",
" extends = True\n",
" peak_ridge[j] += k\n",
" break\n",
" # if it extends\n",
" if extends:\n",
" # it it longer\n",
" peak_len[j] += 1\n",
" # find width by comparing max vs. previous\n",
" if cwtmat[i, p] > peak_width_max[j]:\n",
" peak_width_max[j] = cwtmat[i, p]\n",
" peak_width[j] = i\n",
" peak_pos[j] = p"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75]\n",
"[ 69. 69. 69. 69. 69. 69. 69. 69. 69. 69. 69. 69. 69. 69. 69.\n",
" 69. 69. 69. 69. 69.]\n"
]
}
],
"source": [
"print peak_pos[:20]\n",
"print peak_width[:20]"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[<matplotlib.lines.Line2D at 0x7f7ac789e790>]"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABNgAAAFkCAYAAADyhobVAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzt3X+8bXVdJ/7XW1EqiauNApo2zmSlmb8gDGcUTRJT+zGT\nld50xp8zWWp1bYxH853S0WnGLAV/a4O/lTsVZpmCKOYvNEUBFQPRRFREEATvRRAucD/fP9benX3O\nPefe83uvdfbz+Xicxz5n7c/e57PX3uuzPp/X/qy1qrUWAAAAAGB1bjXtCgAAAADAkAnYAAAAAGAN\nBGwAAAAAsAYCNgAAAABYAwEbAAAAAKyBgA0AAAAA1kDABgAAAABrIGADAAAAgDUQsAEAAADAGgjY\nAAAAAGANVhSwVdXzqmrvgp8LJu4/uKpeVVVXVdW1VXVqVR224DnuVlXvqarrquryqnpxVd1qQZmH\nVdU5VXVDVX2xqp60tpcJAAAAABtjNTPYPp/k8CRHjH4ePHHfSUkek+SxSY5Ncpck7xjfOQrSTkty\nUJJjkjwpyZOTvGCizN2TvDvJB5LcL8nLkpxcVY9YRV0BAAAAYENVa235hauel+SXW2tHLnLfoUmu\nTPL41to7R8t+IsmFSY5prZ1dVY9K8q4kd26tXTUq85tJXpTkTq21m6vqT5M8qrV234nn3plkW2vt\n0at9oQAAAACwEVYzg+3HquobVfXlqnpbVd1ttPyodDPTPjAu2Fq7KMnXkjxotOiYJOePw7WRM5Js\nS3LviTJnLvifZ0w8BwAAAAD0xkErLP+JdId0XpTkzkmen+QjVfVT6Q4X3dNa273gMVeM7svo9opF\n7h/f99n9lDm0qg5urd24WMWq6l8leWSSS5LcsJIXBQAAAMCW8n1J7p7kjNbatzf6n60oYGutnTHx\n5+er6uwkX03y61k61KokyzkOdX9lahllHpnk7cv4PwAAAADMhickOWWj/8lKZ7DN01rbVVVfTHKP\ndId13raqDl0wi+2wzM1IuzzJ0Que5vCJ+8a3hy8oc1iS3a21PfupziVJ8ra3vS33ute9VvQ6ANbL\njh07cuKJJ067GsCM0xYBfaAtAqbpwgsvzBOf+MRklBdttDUFbFV1SJIfTfLmJOckuTnJcUnGFzn4\n8SQ/kuTjo4f8Y5L/XlV3nDgP2/FJdqW7GMK4zKMW/KvjR8v354Ykude97pUjj9znGgwAm2Lbtm3a\nIGDqtEVAH2iLgJ7YlNOIregiB1X1Z1V1bFX966r6d+mCtJuT/L/RrLXXJ3lpVT2sqo5K8sYkH2ut\nfWr0FO9LckGSt1bVfavqkUlemOSVrbWbRmVem+RHq+pPq+onquq3k/xqkpeu9cUCAAAAwHpb6Qy2\nu6Y7bvVfJbkyyVlJjpk4WdyOJLckOTXJwUnem+SZ4we31vZW1S8keU26WW3XJXlTkudNlLmkqh6T\nLlD7nSSXJnlaa23hlUUBAAAAYOpWepGD7Qe4/8Ykzx79LFXm60l+4QDP8+EkR62kbgAAAAAwDSs6\nRBSA/du+fb/fQwBsCm0R0AfaImCWCNgA1pGOJNAH2iKgD7RFwCwRsAEAAADAGgjYAAAAAGANBGwM\n1gUXJC984bRrAQAAAMw6ARuD9f73Jy960bRrAQAAAMw6ARuD1Vr3AwAAADBNAjYAAAAAWAMBG4Nl\nBhsAAADQBwI2BkvABgAAAPSBgA0AAAAA1kDAxmCZwQYAAAD0gYCNwRKwAQAAAH0gYAMAAACANRCw\nMVhmsAEAAAB9IGBjsARsAAAAQB8I2AAAAABgDQRsDJYZbAAAAEAfCNgYLAEbAAAA0AcCNgAAAABY\nAwEbg2UGGwAAANAHAjYGS7gGAAAA9IGADQAAAADWQMDGYI1nsJnJBgAAAEyTgI3BEqwBAAAAfSBg\nY/AEbQAAAMA0CdgYLIeIAgAAAH0gYGOwBGsAAABAHwjYGDxBGwAAADBNAjYGyyGiAAAAQB8I2AAA\nAABgDQRsDJYZbAAAAEAfCNgYLAEbAAAA0AcCNgAAAABYAwEbg2UGGwAAANAHAjYGS8AGAAAA9IGA\nDQAAAADWQMDGYJnBBgAAAPSBgI3BErABAAAAfSBgAwAAAIA1ELAxWGawAQAAAH0gYGOwBGwAAABA\nHwjYAAAAAGANBGwMlhlsAAAAQB8I2BgswRoAAADQBwI2Bk/QBgAAAEyTgI3BcogoAAAA0AcCNgZL\nsAYAAAD0gYCNwRO0AQAAANMkYGOwHCIKAAAA9IGAjcESrAEAAAB9sKaArar+sKr2VtVLJ5YdXFWv\nqqqrquraqjq1qg5b8Li7VdV7quq6qrq8ql5cVbdaUOZhVXVOVd1QVV+sqietpa5sXYI2AAAAYJpW\nHbBV1dFJ/kuSzy6466Qkj0ny2CTHJrlLkndMPO5WSU5LclCSY5I8KcmTk7xgoszdk7w7yQeS3C/J\ny5KcXFWPWG192XocIgoAAAD0waoCtqo6JMnbkjw9yXcmlh+a5KlJdrTWPtxaOy/JU5L8+6p64KjY\nI5PcM8kTWmvnt9bOSPJHSZ5ZVQeNyvxWkotba3/QWruotfaqJKcm2bGa+gIAAADARlntDLZXJfn7\n1to/LFj+0+lmpn1gvKC1dlGSryV50GjRMUnOb61dNfG4M5JsS3LviTJnLnjuMyaeA8xgAwAAAHrh\noAMXma+qHp/k/unCtIUOT7KntbZ7wfIrkhwx+v2I0d8L7x/f99n9lDm0qg5urd240nqz9QjYAAAA\ngD5YUcBWVXdNd461R7TWblrJQ5MsJwbZX5laRpns2LEj27Ztm7ds+/bt2b59+zL+PQAAAABDsnPn\nzuzcuXPesl27dm1qHVY6g+2oJHdKck5VjQOvWyc5tqqeleTnkxxcVYcumMV2WOZmpF2e5OgFz3v4\nxH3j28MXlDksye7W2p79VfDEE0/MkUceudzXw4CZwQYAAAAsNrHq3HPPzVFHHbVpdVjpOdjOTHKf\ndIeI3m/08+l0FzwY/35TkuPGD6iqH0/yI0k+Plr0j0nuU1V3nHje45PsSnLhRJnjMt/xo+WQRMAG\nAAAA9MOKZrC11q5LcsHksqq6Lsm3W2sXjv5+fZKXVtU1Sa5N8vIkH2utfWr0kPeNnuOtVXVCkjsn\neWGSV04cdvraJM+qqj9N8oZ0YduvJnn0yl8iAAAAAGycFV/kYBEL5w/tSHJLklOTHJzkvUme+S+F\nW9tbVb+Q5DXpZrVdl+RNSZ43UeaSqnpMkpcm+Z0klyZ5Wmtt4ZVFmWFmsAEAAAB9sOaArbX28AV/\n35jk2aOfpR7z9SS/cIDn/XC6c77BogRsAAAAQB+s9BxsAAAAAMAEARuDZQYbAAAA0AcCNgZLsAYA\nAAD0gYCNwRO0AQAAANMkYGOwHCIKAAAA9IGAjcESrAEAAAB9IGBj8ARtAAAAwDQJ2Bgsh4gCAAAA\nfSBgY7AEawAAAEAfCNgYPEEbAAAAME0CNgbLIaIAAABAHwjYGCzBGgAAANAHAjYGT9AGAAAATJOA\njcFyiCgAAADQBwI2BkuwBgAAAPSBgI3BE7QBAAAA0yRgY7AcIgoAAAD0gYANAAAAANZAwMZgmcEG\nAAAA9IGAjcESsAEAAAB9IGADAAAAgDUQsDFYZrABAAAAfSBgY7AEawAAAEAfCNgYPEEb9E9rybvf\nbfsEAABmg4CNwXKIKPTXeeclv/iLyRe+MO2aAAAAbDwBG4MlWIP+2rNn/i0AAMBWJmBj8ARt0D9m\nmAIAALNEwMZgGcBDf9k+AQCAWSJgY7AM3AEAAIA+ELAxeII26B8z2AAAgFkiYGOwDOChv2yfAADA\nLBGwMVgG7tBfAjYAAGCWCNgYPAN46B8BGwAAMEsEbAyWATz0l+0TAACYJQI2BsvAHQAAAOgDARuD\nJ2iD/jGDDQAAmCUCNgbLAB76y/YJAADMEgEbg2XgDv0lYAMAAGaJgI3BM4CH/hGwAQAAs0TAxmAZ\nuEN/CdgAAIBZImBj8AzgAQAAgGkSsDFYZshAf9k+AQCAWSJgY7AM3KG/BGwAAMAsEbAxeAbw0D8C\nNgAAYJYI2BgsA3joL9snAAAwSwRsDJaBO/SXgA0AAJglAjYGzwAeAAAAmCYBG4Nlhgz0l+0TAACY\nJQI2BsvAHfpLwAYAAMwSARuDZwAP/SNgAwAAZomAjcEygIf+sn0CAACzZEUBW1U9o6o+W1W7Rj8f\nr6qfn7j/4Kp6VVVdVVXXVtWpVXXYgue4W1W9p6quq6rLq+rFVXWrBWUeVlXnVNUNVfXFqnrS2l4m\nW5GBO/SXgA0AAJglK53B9vUkJyQ5avTzD0n+rqruNbr/pCSPSfLYJMcmuUuSd4wfPArSTktyUJJj\nkjwpyZOTvGCizN2TvDvJB5LcL8nLkpxcVY9YYV2ZEQbwAAAAwDQdtJLCrbX3LFj0P6rqt5IcU1Xf\nSPLUJI9vrX04SarqKUkurKoHttbOTvLIJPdM8rOttauSnF9Vf5TkRVX1/NbazUl+K8nFrbU/GP2P\ni6rqwUl2JHn/Kl8nW5AZMtBftk8AAGCWrPocbFV1q6p6fJIfSPKP6Wa0HZRu5lmSpLV2UZKvJXnQ\naNExSc4fhWtjZyTZluTeE2XOXPDvzph4Dkhi4A59JmADAABmyYoDtqr6qaq6NsmNSV6d5D+21r6Q\n5Igke1pruxc85IrRfRndXrHI/VlGmUOr6uCV1petzwAe+kfABgAAzJIVHSI68oV050a7fbpzrb2l\nqo7dT/lKspwh1v7K1DLKJEl27NiRbdu2zVu2ffv2bN++fRlVYEgM4KG/bJ8AAMBm2blzZ3bu3Dlv\n2a5duza1DisO2EbnSbt49Oe5VfXAJL+b5K+S3LaqDl0wi+2wzM1IuzzJ0Que8vCJ+8a3hy8oc1iS\n3a21PQeq34knnpgjjzxyWa+FYTNwh/4SsAEAAJtlsYlV5557bo466qhNq8Oqz8G24DkOTnJOkpuT\nHDe+o6p+PMmPJPn4aNE/JrlPVd1x4vHHJ9mV5MKJMsdlvuNHy2EfBvAAAADANK1oBltV/UmS05N8\nPckPJnlCkocmOb61truqXp/kpVV1TZJrk7w8ycdaa58aPcX7klyQ5K1VdUKSOyd5YZJXttZuGpV5\nbZJnVdWfJnlDurDtV5M8evUvk61IsAb9ZQYbAAAwS1Z6iOjhSd6SLhjbleRz6cK1fxjdvyPJLUlO\nTTer7b1Jnjl+cGttb1X9QpLXpJvVdl2SNyV53kSZS6rqMUlemuR3klya5GmttYVXFmXGGcBDf9k+\nAQCAWbKigK219vQD3H9jkmePfpYq8/Ukv3CA5/lwks07UJZBM4CH/hGwAQAAs2Q9zsEGU2HgDv0l\nYAMAAGaJgI3BM4CH/hGwAQAAs0TAxmAZwAMAAAB9IGBjsARr0F8CcAAAYJYI2Bg8A3joHwEbAAAw\nSwRsDJYBPPSX7RMAAJglAjYGy8Ad+kvABgAAzBIBG4NnAA/9I2ADAABmiYCNwTKABwAAAPpAwMZg\nCdagvwTgAADALBGwMXgG8NA/AjYAYNZddlly2mnTrgWwWQ6adgVgtQzgob9snwDArHv4w5OLLtIf\ngllhBhuDZUcF/SVgAwBm3Te/Oe0aAJtJwMbgGcBD/wjYAACAWSJgY7AM4AEAAIA+ELAxWII16C8B\nOAAAMEsEbAyeATz0j4ANAACYJQI2BsvAHfpLwAYAAMwSARuDZQAP/WX7BAAAZomAjcEzgIf+EbAB\nAACzRMDGYBm4AwAAAH0gYGOwzJCB/rJ9AgAAs0TAxuAZwEP/CNgAAIBZImBjsAzcob8EbAAAwCwR\nsDF4BvDQPwI2AABglgjYGCwDeOgv2ycAADBLBGwMloE7AAAA0AcCNgZP0Ab9YwYbAAAwSwRsDJYB\nPPSX7RMAAJglAjYGy8Ad+kvABgAAzBIBG4NnAA/9I2ADAABmiYCNwTKAh/6yfQIAALNEwMZgGbgD\nAAAAfSBgY/AEbdA/ZrABAACzRMDGYBnAQ3/ZPgEAgFkiYGOwDNyhvwRsAAAd/SGYDQI2Bs8OC/pH\nwAYAAMwSARuDZeAO/SVgAwDo6A/BbBCwMVgG8AAAQN8Zr8BsELAxeHZY0D8CcACAjv4QzAYBG4Nl\nRwX9JWADAOjoD8FsELAxWAbw0F+2TwCAjv4QzAYBG4NnhwX9I2ADAOjoD8FsELAxWHZU0F8CNgCA\njv4QzAYBG4NlAA8AAPSd8QrMBgEbg2eHBf0jAAcAAGaJgI3BMnCH/hKwAQB09IdgNgjYGCwDeOgv\n2ycAQEd/CGaDgI3Bs8OC/hGwAQB09IdgNgjYGCw7KugvARsAQEd/CGaDgI3Bs8MCAAD6yngFZsOK\nAraq+sOqOruqdlfVFVX1zqr68QVlDq6qV1XVVVV1bVWdWlWHLShzt6p6T1VdV1WXV9WLq+pWC8o8\nrKrOqaobquqLVfWk1b9MtiIzZKC/bJ8AAB39IZgNK53B9pAkr0jyM0l+Lsltkryvqr5/osxJSR6T\n5LFJjk1ylyTvGN85CtJOS3JQkmOSPCnJk5O8YKLM3ZO8O8kHktwvycuSnFxVj1hhfdnC7KigvwRs\nAAAd/SGYDQetpHBr7dGTf1fVk5N8K8lRSc6qqkOTPDXJ41trHx6VeUqSC6vqga21s5M8Msk9k/xs\na+2qJOdX1R8leVFVPb+1dnOS30pycWvtD0b/6qKqenCSHUnev8rXyhZlhwX9I2ADAOjoD8FsWOs5\n2G6fpCW5evT3UelCuw+MC7TWLkrytSQPGi06Jsn5o3Bt7Iwk25Lce6LMmQv+1xkTzwF2VNBjAjYA\nAGCWrDpgq6pKdzjoWa21C0aLj0iyp7W2e0HxK0b3jctcscj9WUaZQ6vq4NXWma3FAB76y/YJANDR\nH4LZsKJDRBd4dZKfTPLgZZStdDPdDmR/ZWoZZbJjx45s27Zt3rLt27dn+/bty/j3DJEdFgAA0FfG\nK7Dxdu7cmZ07d85btmvXrk2tw6oCtqp6ZZJHJ3lIa+2yibsuT3Lbqjp0wSy2wzI3I+3yJEcveMrD\nJ+4b3x6+oMxhSXa31vbsr24nnnhijjzyyOW9EAbNjgr6yww2AICO/hBsvMUmVp177rk56qijNq0O\nKz5EdBSu/XK6ixR8bcHd5yS5OclxE+V/PMmPJPn4aNE/JrlPVd1x4nHHJ9mV5MKJMsdlvuNHyyGJ\nATz0me0TAKCjPwSzYUUz2Krq1Um2J/mlJNdV1XiW2a7W2g2ttd1V9fokL62qa5Jcm+TlST7WWvvU\nqOz7klyQ5K1VdUKSOyd5YZJXttZuGpV5bZJnVdWfJnlDurDtV9PNmoN57LCgfwRsAAAd/SGYDSud\nwfaMJIcm+VCSyyZ+fn2izI4k705y6kS5x47vbK3tTfILSW5JN6vtLUnelOR5E2UuSfKYJD+X5DOj\n53xaa23hlUWZYXZU0F8CNgCAjv4QzIYVzWBrrR0wkGut3Zjk2aOfpcp8PV3Itr/n+XCSzTtYlsEx\ngIf+sn0CAHT0h2A2rPgcbNA3dlgAAEBfGa/AbBCwMVh2VNBfZrABAACzRMDGYBnAQ3/ZPgEAOvpD\nMBsEbAyeHRb0j4ANAKCjPwSzQcDGYNlRQX8J2AAAOvpDMBsEbAyWATwAANB3xiswGwRsDJ4dFvSP\nABwAoKM/BLNBwMZg2VFBfwnYAAA6+kMwGwRsDJYBPPSX7RMAoKM/BLNBwMbg2WFB/wjYAAA6+kMw\nGwRsDJYdFfSXgA0AmHX6QzBbBGwMnh0WAAAAME0CNgZLsAb95RtbAGDWVXW3+kMwGwRsDJYBPPSX\n7RMAoKM/BLNBwMbg2WFB/wjYAAA6+kMwGwRsDJYdFfSXgA0AoKM/BLNBwMZgGcBDf9k+AQA6+kMw\nGwRsDJ4dFgAA0FfGKzAbBGwMlh0V9JcZbAAAHf0hmA0CNgbLAB76y/YJAMw6/SGYLQI2Bs8OC/pH\nhxIAAJglAjYGy8Ad+kvABgDMuqruVn8IZoOAjcEygIf+sn0CAHT0h2A2CNgYPDssAACgr4xXYDYI\n2BgsOyroLzPYAAA6+kMwGwRsDJYBPPSX7RMAoKM/BLNBwMbg2WFB/wjYAAA6+kMwGwRsDJYdFfSX\ngA0AoKM/BLNBwMZgGcBDf9k+AYBZpz8Es0XAxuDZYQEAAADTJGBjsARr0F++sQUAZl1Vd6s/BLNB\nwMZgGcBDf9k+AQA6+kMwGwRsAKw7ARsAQEd/CGaDgI3BMoCH/rJ9AgB09IdgNgjYGDw7LOgfARsA\nQEd/CGaDgI3BsqMCAAD6zrgFZoOAjcEyQwb6y/YJANDRH4LZIGBj8OywoH8EbADArNMfgtkiYGOw\n7Kigv3QoAYblrndNHvOYadcCAIbroGlXAFbLAB76y/YJMCzf+Eb3A6yfqu5WfwhmgxlsDJ4dFvSP\ngA0AoKM/BLNBwAYAAAAbRMAGs0HAxiBN7qTssKB/zGADAOjoD8FsELAxeHZY0D8CNgCAjv4QzAYB\nG4NkJwX9JmADAOjoD8FsELAxSA4RhX4TsAEAdPSHYDYI2Bg8OyzoHwEbADDr9IdgtgjYGCQ7KQAA\nAKAvBGwMkkNEod98YwsAzLqq7lZ/CGaDgI3Bs8OC/hGwAWOnnJKcfvq0awEwPfpDMBsOmnYFYDXs\npKDfBGzA2BOe0N1qD4BZpf2D2bDiGWxV9ZCqeldVfaOq9lbVLy1S5gVVdVlVXV9V76+qeyy4/w5V\n9faq2lVV11TVyVV1uwVl7ltVH6mq71XVV6vquSt/eWxVDhGFfhOwAQB09IdgNqzmENHbJflMkmcm\n2aepqKoTkjwryW8meWCS65KcUVW3nSh2SpJ7JTkuyWOSHJvkdRPP8YNJzkjylSRHJnlukudX1dNX\nUV8ANpmADQCgoz8Es2HFh4i21t6b5L1JUjU+beM8v5vkha21vx+V+c9JrkjyH5L8VVXdK8kjkxzV\nWjtvVObZSd5TVf+ttXZ5kicmuU2Sp7XWbk5yYVU9IMlzkpy80jqz9ZjBBgAADIHxCsyGdb3IQVX9\nmyRHJPnAeFlrbXeSTyZ50GjRMUmuGYdrI2emmw33MxNlPjIK18bOSPITVbVtPevMMAnYoN/MYAMA\n6OgPwWxY76uIHpEuKLtiwfIrRveNy3xr8s7W2i1Jrl5QZrHnyEQZAHpKwAYAzDr9IZgtm3UV0coi\n52tbYZnx4aj7fZ4dO3Zk27b5k9y2b9+e7du3H6iODIgZbNBvOpQAAMBm2blzZ3bu3Dlv2a5duza1\nDusdsF2eLgg7PPNnoB2W5LyJModNPqiqbp3kDqP7xmUOX/Dc48csnNk2z4knnpgjjzxyxRVnWARs\n0G8CNgBg1o3PWK4/BBtvsYlV5557bo466qhNq8O6HiLaWvtKunDsuPGyqjo03bnVPj5a9I9Jbj+6\naMHYcemCubMnyhw7Ct7Gjk9yUWttcyNIAFZMwAYA0NEfgtmw4oCtqm5XVferqvuPFv3b0d93G/19\nUpL/UVW/WFX3SfKWJJcm+bskaa19Id0FC/5vVR1dVf8+ySuS7BxdQTRJTkmyJ8kbquonq+pxSX4n\nyUtW+TrZYsxgAwAAhsB4BWbDag4R/ekkH0x3LrSWudDrzUme2lp7cVX9QJLXJbl9ko8meVRrbc/E\nc/xGklemu3ro3iSnJvnd8Z2ttd1V9chRmU8nuSrJ81trr19Ffdni7LCgf8xgAwDo6A/BbFhxwNZa\n+3AOMPOttfb8JM/fz/3fSfLEAzzH+UkeutL6MRvspKDfBGwAAB39IZgN63oONtgsDhGFfhOwAQB0\n9IdgNgjYGDw7LOgfARsAQEd/CGaDgI1BspOCfhOwAQCzTn8IZouAjUFyiCgAAADQFwI2Bk/ABv3j\nG1sAYNZVdbf6QzAbBGwMkp0U9JuADQCgoz8Es0HAxiA5RBT6TcAGMBzaathYtjGYDQI2ANadgA1g\nOPbunXYNYGvTH4LZIGBjkMxgg34TsAEMh4ANNpb+EFvRxRcn3/3utGvRLwI2BknABsyC3/u95JOf\nnHYtZsdDH5q89a3TrgVsvv0FbC95ydyJ2oHVMV5hK/rRH00e9ahp16JfBGwArDsz2NbHy16W/Mqv\nJJddllx//bRrs/V95CPJ058+7VrA5ttfwPaiF21ePWCr0h9iqzrrrGnXoF8EbAySGWzQbwK29fXD\nP5wcf/y0azEbfGY31nXXTbsGLGZ/AZttAlZPfwhmi4CNQRKwQb/pUK6/j31s2jWAtfnyl5NDDklO\nP33aNWEh52ADgLUTsAGw7gRsa2fdTYdzTW2ciy/ubj/xienWg33dcsvS99kmYPXG2499OswGARuD\nZAYb9JuAbe0ONKPkQx9Kbne7ZM+eTakOrIo2YBjMYIONpS2E2SBgY5AEbMBWd/PN+7//ZS/rLnxw\nzTWbUx9Yjf3NjKI/lhOwCeFg9YxXYDYI2ABYd2awrd2BAjbWl8/qxpgMZazj/vnnf+6C+uWEZ8JS\nWD3tH8wGARuDZAYb9JuAbe2WO5i1jteH2TkbQyjTbz/2Y8njHre8z7/QH1bPvhpmg4CNQZpGwPbB\nDyb3u58dJCyHgG3tljuYFWCsj/H69pldX5PBjZPl99MnPrH/gG28TWhr1u5Tn+q2gy98Ydo1YbPZ\nt8BsELDBMl10UfK5z+lgwnII2NbuQAHbeN3edNPG12UWmJ2zMcwMHAYz2DbHWWd1t5/97HTrwebT\nH2KrsX9fnICNQZrGDLbxINZgFg5MwLZ248HsgTowBr3rY/zliVlW68uXUv3XmnOwwUbRH2Krsk9Y\nnICNwROwAVvRODhbKkAbB0ECtvXhENGN4SIH/TX5fpjBtrlsC8DQCdgWJ2BjkKbRMdmzZ/4tsDTf\n2K7dgQK2heVYG+txY0x2wHXG+2UyVDODDTbG+Msw/SG2GvuExQnYGCSHiEK/CdjWbtxxWSr4cQ62\n9eUQ0Y0xGdwIMftl8v0QsMHG0B9iq7JPWJyAjcETsEH/6FCunRlsm8shohtjsgPus9ov4/ejanmH\n8nr/1o8gf3boD7FVCdgWJ2BjkKaxkxKwwfLpUK6dc7BtLutxY0wGNzrj/bLUDLal2u3J9++qq7Tv\nsBz6Q2w3TNv4AAAduUlEQVRV9umLE7AxSA4RhX7ToVw7M9g2l0NEN8ZkcGP/2S+TszaXcz62cfnd\nu5M73Sl5xSs2tn5bmX3j7NAfYqsSsC1OwAbLJGADNtOBgjPnYFtfDhHdGJMd8Btv7G6FmP2w1Ay2\npQK28Xu5e3d3+9GPbky9tpqbbkr+5m+mXQumRcDGViVgW5yAjUEygw36TYdy7ZY7M80MtvVhPW6M\nybBmfBVu7UI/rDRgs42szotfnDz2scnnPidcnkX6Q6yna69N3vzmadeiI2BbnICNQRKwQb/pUK7d\ncjsuBr3rw3rcGIvNYGstufDC6dSHOaudwbacK44y51vf6m6/9725Zdbh7NAfYj2dcELy5Ccnl146\n7ZoI2JYiYINlGn/zPr4FlqZDuXYHCnxc5GB96ShujMVmsP3DPyQ/+ZPJ6adPp050Jr8wXMkMNv2g\n1RvvE7U3wGpcc01324c2pA916CMBG4M07qBUmcEGfSRgWzvnYNtcgsqNMdkBHwczF1/c3V5yyaZX\nhwmrncGmzVmdyf2h9mZ26A+xVQnYFidgY5AEbNBvOpTLd+ONyY4dyXXXzV/uHGyby3rcGIvNYNMp\n74fVXkVUP2j1xuvWOpwd+kNshD7sR/tQhz4SsDFom3myWAEbsBHe+c7kpJOSN7xh/nIB2+bSUdwY\ni52DzRVb+2G1M9gcIro6e/fOrUPt9uwQsLER+jAe1W9anICNQRrvpG51KzPYoI90KJdvPJhduK4O\n1HFxDrb1ZT1ujMVmsFnX/bAVDhG96KLu6pxDcNNNc+vcNjA79Ie61/7pTye7dk27JltHH9phAdvi\nBGwMkkNEod90KNfOOdg2lwHvxhCw9df4faga7kUO7nnP5H73m3YtlkfANpv0h5I3vjE5+ujkFa+Y\ndk22jj70/QRsixOwMWgOEYV+0qFcvnE7trA9O9AAzEBtfY07ipu5X5kFi13kwGe2H7bCDLYh2bNH\nuz2L9IeSyy7rbnfvnm49tpI+tMMCtsUJ2Bgkh4hCv+lQLt9S60jAtrmcF2xjmMHWXysN2Po4g21I\nBGyzSX9o7vyb41vWrg/tsIBtcQI2Bmkah4iOG7I+NGjQdzqUaydg21zW48ZY7CIHS513kM01/sJw\nuVcRNYNtbSYPEZ1ch9dck/zZn9ketrpZfn8FbOuvD+2wgG1xAjYGzSGi9NX73peceea0a8EQLBXs\nHCjw0SatLwHbxlhsBtuYz+50rXYGm/dtdfbsmVt3k+v+hBOSP/iD5CtfmU69tpqrr07OP3/atWCS\ngG399aEdFrAtTsDGIDlElL57yUuSE0+cdi2mxwy25bvhhu52YUflQB0XM9jWl47ixlhsBtuYGeHT\ntdpzsHnfVmepixx873vdrf3l+nj4w5P73nfatehMvqez/P6O+zl9C9ge+9jhXnihD+NR/abFCdgY\nJFcRpW9e85ruW9Ox667rfmaVgG35lvpm1yGim8t63Bj7m8HWt8HWpHe9q+tjjMOPrWjyMz85UFoY\nsI3bcTPYVme8Pg90DjbrdX189rPTrsEcAVtn3Nb3LZz/m79Jfud3pl2L1elDeyFgW5yAjUFziCh9\n8J3vJL/928l73jO37Lvf7X5mlYBt+cbf7I5vxxYbgE2uTwHb+rIeN8b+Ara+DbYmvelN3e0110y1\nGhtqrTPYtO/LM+43Hihg28ph7qwSsHUcIrr++rD/FLAtTsDGIDlElD4ZX3b82mvnlpnBNv+WpS11\n6MRiA7DJga82aX3NekexteQFL0iuuGJ9n3dyvQ5pBtvYwuB7K5m8cu5qLnJw/vndF51nn71xddwK\nJttqAdv6+Mxnko99bP9llvocbyYBW0fAtv760Peb9X7TUgRsDJpDROmDcbAmYJsjYFu+cYdzOTPY\nJpetxwy2vXvn3qOrrkpOOWX1zzV04/W41TuM552XfPSj+y6/7LLkec9LduxY3/831BlsY1u5HV/u\nDLbx3+Py4/fti1/sbj/+8Y2p30r0IUxZyuRV6Pd3mK2Abfke8IDkwQ/uts+bb07e8IZ9jxroQzgu\nYOsI2NZfH8ajW72/tFoCNgZp8hxsm0XAxlKWCthm+RBRlm+pGWyLdVzWO2C79a27k/wmyVOekjzh\nCbPbxo3X42TouBUdeWRy7LH7Lt+oc+QM/SIHAra593DhDLY+6fPA3Qy2jXPIIclP/3TytKcl/+N/\nzL+vD+tTwNbpY8A21Pdj3D73oR3u8xcb0yRgY5CmcYjo5DeQQ3XLLb5t2AgLA7bWunBtKw/MDsQM\ntuWb5gy2JHnnO7vbb32ru921a23PN1STbeMstJO33DL/szP5BcF6GspFDq69dvH9+1Zux5d7iOjC\ntqaP/aA+fZYWWmwGm4Bt/YwvavCd78xffv31m1+XhQRsnT4GbH2Y4bgak+d0nLZZ6CuthoCNQTOD\nbWWe8YzkqU/dnP914onJN76x9P1veENywQWbU5eNtjBgu/HGboCyZ8+wPy9rIWBbvpWcg21y2Ua1\nSQsHKbNisfByK7v//ZMf/uG5v8fnklxvQ5nBduihyX/8j/su38oB27jtuPnmYc5gm9xO+zxYnhwQ\nT67zhQRs66sP61PA1uljwNaHAHY1+jQeFbAtTsDGIE0eIuocbMt34YXdz0a79trkOc+ZmxmzmN/7\nveStb934umyGhQHb5IBsKw/O9kfAtnwruYroes5gW+pxArbZCNg+//m5WYvJxgVsQ5nBliSnnbbv\nsq18qP9kG7KSGWwL+0HTCkonPz99+yxNGq+fpQ4RHf/eh0BoKxlqgLIV9TFgG+r21qfxqIBtcQI2\nBmmzDxHdu7dfx7wfyF/9VfLqV++7/Moru5+NNh60TQ7eJn3ve10YtdT9QyNg25eAbfmW6nhudMC2\nVKAyq4eIzlrAttA0DhGd5gy2xz8++S//pft9sfPIjJdt5TZ8MjBbKmCbPHx0PJha+L5NK4Sc/FJi\nKDPYFgspxwP9oQ74+2Jhf2Mj1+cNNyS3uU3ywQ8uv05L9Yeqkqc/ff3q1kcCtvUjYOs/ARuDtlmH\niE42Yn1o0A7kTW9KXvvafZd/61sbG2p97WvJT/1UNzMiSa64Innd65Izzti3HuP7N8u73rVxA6XJ\ngG3nzp3zBhtbeXC2P6sJ2P72b5Of//mNqU+fTWsG2zXXLL58VmewbbVzsO3cuXNF5ceB63q/9snn\n24wZbEuddPmjH00mV8lf/mVy8snd74uFyuPZL9ddl5xzztwVM7eSySvnTr5Pk+twcvlSM9g2Kpw9\nkK0yg22rB2wrbYvWy0bOYLvssu49fNWr9l9uuYeIvv7161OvvupjwDbUGY6T7cm0bYW+0kbodcBW\nVc+sqq9U1feq6hNVdfS060Q/bPYhotMK2G65JXnxi5Orr15e+Q99KLn00uTrX+9+Ju3Z0w2cr79+\n43YqZ5+d/NM/Je97X/f3t76V/J//k/zf/zu/3GYHbFdckfzyL3cDqo2wMGCbDNWGfnjRddfNnUB4\nLU499cCHBH/oQ10Y2+eZCBthqYscHOgqomv9FnNhkDZuS81g2xoz2BYb1C72WRl31sft2Hq3WZs5\ng+073+mujPuOd+x737HHJr/xG4s/7tvf3nfZuB2/7rruKoU/8RPrV8++WKw9SZYO2MxgW53FZrBt\nRsC2e3c/rvK33gHbUoP6hZ/LjQwsl3s0yIECtj6dh3Ij3Xhjd57LPgVsQw20XeSg/3obsFXV45K8\nJMnzkjwgyWeTnFFVd5xqxeiFlR4i+qQnJS95yer/37QCtg9/ODnhhP2fy2ysteRXfqUL5L7+9W6g\nMfmt8lVXzf2+UYeJfuUr3e0nPtHdjsO+iy+eX24crG3WIaL//M9ztxdcsPhgai228iGir3lN8qAH\nrXxHvnAG28tfPn8bXOz5Lrmku/3a11ZczUFb7UUO1jqDbTJgu+WWuc/vRs5g+8xn+vv+brWAbTGL\nHRY8/gJnfN96n4ttfxc5WO/B1pe/3N0uFrCN7d2776BgsS+xJgO2jbJ373Qv9jP5OZ9skzdjBtuV\nV3Zfkp5zzsofOza0GWybGbDdfHOybVvyv//3+j1nXyy1TS78HG7kDKVxP/ZAR9IcKGCb7JtvZeOA\nbS2h0M03J6efvvxJBwcy9ICtbzPY+hDm90VvA7YkO5K8rrX2ltbaF5I8I8n1STbpGogMwXIOEb35\n5m72zHJCqqVMK2D7f/+vux0fcrk/l17aHfJ11llzM1AmZ7FNhmobFWyNg7Rzz+1uP/3prsH98pfn\ndywmZ7BtxgzEccD2pS8lxx2X/PEfJ+ed1824Ww8LA7b1PET0v//37uqv0/KZz3SdkC99aWWPa21+\nAH7hhclFF3U740svTW5/++SBD0z+23+be8w4YBvfzoppHSI6GaTt3j3390YGbA94QHcYeR8N6RDR\nK65IHv7w5PLLV/a4xWYnjr9wWNiO7c/11y//f+/v5Pnr/Q38wi9zFnPllfO/ZLn++vl/j9uscTv+\nzW+uX/3Grrkm+f3fT/7kT5J733tj/sdyLCdgmyyz1Ay21QRsn/50d/v2t6/8sa9+dfI3fzO9GWyt\nJUcckbz5zcsrPzkg3qyAbfyF51//9fo952rc5z5df2s9LfV5u/ba+X3KjQxQxgHbgfYViwVs55yT\nPPrR3WdgM86LfCAf+tDK+3hjt9zSnYLlQH35yRlsq+33/93fdevtaU9b3eMXmgxg+xBWLVdfA7a+\n95s2Uy8Dtqq6TZKjknxgvKy11pKcmeRB06oX/bGSQ0S/8IWuET3vvPkdms9/PvmLv1je/xt3Jr//\n+zdmSm5r3eGLk4OfPXvmvoVfTsB2/vnd7WRHZhyw3XRT8rKXzS1fzg59NSHcuEO30O7d8wcw447J\njTdu3JXrJo0DttNP7waFH/1od0LZJz5x9Tv6yc78/mawreXQmdaSt7ylG4BMa0c6/lyNb5drMmC7\n6qru54Ybkq9+NfnAB7qO76c+lbztbXPvwThY++pX16366+LGGzf2cObVXOSgtbnOzHoEbN/5zlz7\ns1GHiI7bnY06X9N737v/jv6NN+4/8F5qBttS56pbyoc/nDz3uSt7zEqdckp3cu23vW1lj9tfwHag\nGWxXXdUdan/ppd1s6Tvfed/w7IILunOVTbZX++t0r/eso3HAtvA9m/w/X/3q/EDr8svn758Wzlyb\nnGG2XjNiXvnK5KUv7b7sSbq2cKVaS974xrXNgFnpDLbx7wv3R6vZz40H9CsNQfbuTZ75zOSxj53e\nDLYvfanbJ5xwwvLKT2MG2xe+MPf73/99F+ZecUVy//t3p/IYe9vb5pddyvXXr3zm0E03df3XSy9d\n2eOSbl0tPNXJ2FKft927538O9re9Xnnl6kOlZK6PfKAjIhYL2H7v97r+6Oc+N7+vvdS+65ZbNq4P\nuHdv8rM/mxx55Ooe/4Y3dPuFJz5x//35ccCWrP61jL+8X6/AdnJ7W+u2t3fv5l3Ua7MDtta6bXiy\nrz7+gk3AtriDpl2BJdwxya2TLBzSXJFkqbNgfF+SXHjhhRtYrem66ab1ORfSVjA+xGjPnu73/QVl\nn/xkd3v99d35wA4/vPv7z/+827ledllyl7vs//+Nd6C3vW3XOV9uMLeYPXu6Hepd7tIFEEkXXrzy\nlckjHpH86q92yy66qOvMPPSh3Te9B/qf73//vstOOaWr71lnzT//1amnznV49uzp1s22bXMzAj/x\nia7j/vjHJw972PyZgq11dfuhH0oOO6xb9r3vdQOahRczmHTSScmP/Ej3++RVl175yuROd1r6ca11\n6+uQQ5Lb3W5u+d69XSfxX//ruZ32UsbrZjxgmgyLnv3s7nWMPxdf+lI3u+qww7r/8Z3vdH/fauLr\niH/4h67D+vznd+tt3Dndsye55JJdOf30c/+l7Hves/xOaWvd/zvkkO7qVN/+dvKNb3T3/c//Obf+\nvve9rnP+gz84//FXX92957/2a3Ov50D/7+KLu4HyD/zA4vePB5dvf/vKwtBxZ+Xaa+cfGvqyl3Wz\n4sauuKLr+G/bNjf4/7u/W7qjctNN3WPucpcusNu9u3utC2ezXnJJ9z4/5jHdfeed1z3mppu6z9EP\n/dC+z33ppd16WHjfm97UPdef/Enyfd+37+OuuaZbP8td7wuNw7urrpq/nS926Nhf/3XXpk0OgL/y\nlbnHffOb3fZy3/seeIbvmWfO/X7yyXPv2ac+Nfd8rSUf+Ujyb/9tcre7zZW/7LJuVuLP/mz3f775\nzeSOd+zayKVM7p5POmn+Z27v3u7+u93twNvzlVd2X3YccsjcsptuSp71rO73pz2tmx05+dznn9+9\npptvTp761OToo+dv08n8Tvvb3969lxde2NX1Oc9Z+hxc49l/t7lNt+7HV3C+3e26tuO005Kf+7nu\n94XGM3zvfvfu8WNXXdVt/zfcMP+9/Od/7raV00/v/v6jP+r+31Of2rVZu3d3n9FuX7Urf/EXXVv0\nne909VnsS5C//MuuDRv3L7797W5dXX11ctBBc+/H+9/fBZg33DB3ns0//uO5dunMM+dmyzzkId2A\nK+m+0FjKt7514H3bWWd17/X977//csncevnMZ+Y/7+Qg+I1vnL8d/8VfzA/1X/Wq5A53mAugJ/cX\nL33p3H5vrLXu83+nO3Xv4Z493efmXvfq/t61q6v/QRM97tNOm/8cJ588f0bg1Vd363mybzK++vad\n7tR9Hr785e6UEEcdlfzX/3rgdbOY8SyypFvPY3/7t3Ptz2SYce653fq66KL5z3PJJfuu76uvTu5x\nj6XbofFRBR/+8Mr6VJOBxHiWf9Ltky+7bPnPs9B3v9vtqx73uOSe99x/2fHs9+uvX17dx32AL395\nLvy99NK5x47vH7dTy3HxxV1/5fjju3V87bXJwQfPtcEfGE1R+OY3k1/6pe73T36y286f8YzkP/2n\nrr147nO7bfzP/mz//+9//a+uzq9+9fy2s7Xu/T/88H37EXPvx6685jXn5ta3nr9ObnObrh/zzW92\ndR/ve/fu7U5PccEFXb/9B35gbnbaHe6wdPD2jW/Mv8DXBz+Yef9z0u//fveev+Y1++4LlmPcj/3i\nF/f/nk0GN+O+/Hi9nHRS97rHXvWqxfehr3td1399znP2X6dbbunei0MO6W6PPrrrX7z2tV1faHK/\nODbuf3z3u3Ov4+yzu/bnwQ/ed91cfHHX937kI7u6js9tfMop3bb5a7+27/9obX6g/LrXzX/dyzVu\nN7/61eQVr5h7jvFn8M53XryPdvXVXR9hYf9sPD5Mute+sO8x7mOO2/zzzuvavsc9rvv7mmvmxgev\neU3XB5p8/ddf322bn/98N0vwt3+7e46jj9739V97bbev+OEfPnDfbfylyuc+t/Lx6NVXdzMoH/rQ\nbp/0pS91+5lb37r7GY9zb7ghuetdu8/Su9/dta9PeUryMz8zd1TN6143f/9+8sn77wNO05e+9C8d\n0EU+Ieuv2mbFrStQVXdO8o0kD2qtfXJi+YuTPLi19u8WecxvJFnFRHMAAAAAtqgntNZO2eh/0tcZ\nbFcluSXJwrkAh2XfWW1jZyR5QpJLkvT4WkIAAAAAbLDvS3L3dHnRhuvlDLYkqapPJPlka+13R39X\nkq8leXlr7QATmQEAAABgc/R1BluSvDTJm6vqnCRnp7uq6A8kedM0KwUAAAAAk3obsLXW/qqq7pjk\nBekOFf1Mkke21npwQWMAAAAA6PT2EFEAAAAAGIJVXJgYAAAAABgTsAEAAADAGmyJgK2qnllVX6mq\n71XVJ6rq6GnXCdgaqup5VbV3wc8FE/cfXFWvqqqrquraqjq1qg5b8Bx3q6r3VNV1VXV5Vb24qrZE\n+wtsjKp6SFW9q6q+MWp3fmmRMi+oqsuq6vqqen9V3WPB/XeoqrdX1a6quqaqTq6q2y0oc9+q+sio\nD/XVqnruRr82YDgO1BZV1RsX6SedtqCMtghYtar6w6o6u6p2V9UVVfXOqvrxBWXWZUxWVQ+rqnOq\n6oaq+mJVPWkldR38AK+qHpfkJUmel+QBST6b5IzRBRIA1sPn011s5YjRz4Mn7jspyWOSPDbJsUnu\nkuQd4ztHjfZp6S4qc0ySJyV5croLuAAs5XbpLvD0zCT7nDC3qk5I8qwkv5nkgUmuS9f/ue1EsVOS\n3CvJcenaqWOTvG7iOX4wyRlJvpLkyCTPTfL8qnr6BrweYJj22xaNnJ75/aTtC+7XFgFr8ZAkr0jy\nM0l+Lsltkryvqr5/osyax2RVdfck707ygST3S/KyJCdX1SOWW9HBX+Sgqj6R5JOttd8d/V1Jvp7k\n5a21F0+1csDgVdXzkvxya+3IRe47NMmVSR7fWnvnaNlPJLkwyTGttbOr6lFJ3pXkzq21q0ZlfjPJ\ni5LcqbV28ya9FGCgqmpvkv/QWnvXxLLLkvxZa+3E0d+HJrkiyZNGV2K/V5J/SnJUa+28UZlHJnlP\nkru21i6vqt9K8sIkR4zboqr6P+navJ/cxJcIDMASbdEbk2xrrf3KEo+5Z5ILoi0C1sloMtW3khzb\nWjtrvcZkVfWnSR7VWrvvxP/ama6Ne/Ry6jboGWxVdZskR6VLGJMkrUsMz0zyoGnVC9hyfmx0aMSX\nq+ptVXW30fKj0n0LMtkGXZTka5lrg45Jcv64IR85I8m2JPfe+KoDW01V/Zt0s0Qm257dST6Z+W3P\nNeMB7ciZ6Wag/MxEmY8sCPrPSPITVbVtg6oPbD0PGx229YWqenVV/dDEfQ+KtghYX7dP14ZcPfp7\nvcZkx6Rrn7KgzLKzpUEHbEnumOTW6b6xnXRFuo4nwFp9It304UcmeUaSf5PkI6NzhxyRZM9oYDtp\nsg06Iou3UYl2ClidI9J1LPfX/zki3be7/6K1dku6zqj2CVgvpyf5z0kenuQPkjw0yWmjo4oSbRGw\njkZty0lJzmqtjc+LvV5jsqXKHFpVBy+nfgctp9AAVZY+RwDAsrXWzpj48/NVdXaSryb59SQ3LPGw\n5bZB2ilgPS2n7TlQmfGgWPsEHFBr7a8m/vynqjo/yZeTPCzJB/fzUG0RsBqvTvKTmX9O7KWsx5hs\nRW3R0GewXZXklnQn1Zx0WPZNHgHWrLW2K8kXk9wjyeVJbjs67n/SZBt0efZto8Z/a6eA1bg8XYdv\nf/2fy0d//4uqunWSO4zuG5dZ7DkS7ROwCq21r6Qbo42vaqwtAtZFVb0yyaOTPKy1dtnEXWsdkx2o\nLdrdWtuznDoOOmBrrd2U5Jx0V6RJ8i9TBo9L8vFp1QvYuqrqkCQ/muSydO3PzZnfBv14kh/JXBv0\nj0nus+DKxscn2ZXupL8AKzIawF6e+W3PoenOZzTZ9ty+qh4w8dDj0gVzZ0+UOXY02B07PslFoy8T\nAFakqu6a5F8l+eZokbYIWLNRuPbLSX62tfa1BXevdUx24USZ4zLf8aPly6vnFriK6K8neXO6y9Sf\nnWRHkl9Ncs/W2pXTrBswfFX1Z0n+Pt1hoT+c5H8muW+Sn2ytfbuqXp3kUUmekuTaJC9Psre19pDR\n42+V5Lx0gdwJSe6c5C1J/qK19keb/HKAgRid5/Ee6Qah5yZ5TrrDra5urX29qv4gXZvy5CSXpLsC\n372T3Hv8LWtVnZbum9ffSnLbJG9IcnZr7T+N7j80yReSvD/Jnya5T5LXJ/nd1trrN+WFAr22v7Zo\n9PO8JO9IF/rfI11bcrsk9x1NhtAWAWsyGm9tT/JL6Y4kGtvVWrthosyaxmRVdfckn0/yqnTt1HHp\nzvf26NbawosfLF7XoQdsSVJVv53upJqHJ/lMkme31j493VoBW8Ho0swPSfdt7JVJzkry/41mkGR0\nwss/T9foH5zkvUme2Vr71sRz3C3Ja9Kdj+S6JG9K8oettb2b9kKAQamqh6YbxC7sqL25tfbUUZnn\nJ/mv6a6m9dF0bc8/TzzH7ZO8MskvJtmb5NR0A9brJ8rcZ1Tm6HSHdb28tfbnG/SygIHZX1uU5LeT\n/G2S+6drhy5Ld8W9P56c6KAtAtaiqvZm8XOgPaW19pZRmXUZk43avJemO8/bpUle0Fp767LruhUC\nNgAAAACYlkGfgw0AAAAApk3ABgAAAABrIGADAAAAgDUQsAEAAADAGgjYAAAAAGANBGwAAAAAsAYC\nNgAAAABYAwEbAAAAAKyBgA0AAAAA1kDABgAAAABrIGADAAAAgDX4/wEXLW79n+Oe9QAAAABJRU5E\nrkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f7ac789e6d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# generate a simulated spectrum of sorts, with peak positions and the length of the ridge lines\n",
"ypeaks = np.zeros(y.shape)\n",
"ypeaks[peak_pos] = peak_len*peak_width\n",
"fig, ax = plt.subplots(figsize=(15, 4))\n",
"ax.plot(x, ypeaks)"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# find peaks using the first ridge position, last ridge position as well using find_peaks\n",
"peaks = signal.find_peaks_cwt(y, wavelet=signal.ricker, widths=widths)\n",
"peaks_2 = peak_pos[np.all(((peak_width > 0), (peak_len > 5)), axis=0)]\n"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[4, 139, 221, 274, 385, 417, 459, 598, 667, 756, 841, 907, 1048, 1145, 1188, 1278, 1316, 1384, 1463, 1512, 1577, 1682] [ 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75\n",
" 75 75 75 75 75 89 89 112 139 171 188 220 220 220 255\n",
" 256 256 0 285 285 285 285 286 286 286 301 303 330 330 344\n",
" 345 371 385 398 398 416 444 444 459 465 468 471 471 484 485\n",
" 508 508 531 531 548 548 563 598 606 611 630 648 648 678 678\n",
" 678 678 683 706 706 733 740 750 755 782 806 809 841 845 852\n",
" 858 874 874 908 911 915 0 923 925 933 933 949 949 956 959\n",
" 978 981 1014 1019 1045 1045 1069 1070 1104 1124 1132 1140 1140 1145 1162\n",
" 1162 1169 1169 1177 1180 1189 1189 1224 0 0 1251 1278 1296 1316 1361\n",
" 1361 1386 1386 1392 1398 1425 1463 1495 1510 1512 1518 1536 1537 1575 1575\n",
" 1575 1575 1598 1598 1612 1612 1612 1612 1612 1612 1612 1612 1612 1612 1612\n",
" 1612 1612 1612 1612]\n"
]
}
],
"source": [
"print peaks, peaks_2"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For now use `scipy.signal.find_peaks_cwt()`, compare with my own implementation"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA2YAAAM1CAYAAAAbz+KnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzsXXl4FEX6fjsJ4UrCKCiHB6dAwpUEhUQh0OKKFypegOIB\niwcIIq6owA+R9QAhypCNuiggKDIaL9T1QFEbRwSVgIiIKEvjogjIGa4Qknl/f3zdTE+nJweCQaj3\neeZJuqq66qvqq976jtJIQkFBQUFBQUFBQUFBQaHqEFPVAigoKCgoKCgoKCgoKJzoUMRMQUFBQUFB\nQUFBQUGhiqGImYKCgoKCgoKCgoKCQhVDETMFBQUFBQUFBQUFBYUqhiJmCgoKCgoKCgoKCgoKVQxF\nzBQUFBQUFBQUFBQUFKoYipgpKCgoKCgoKCgoKChUMRQxU1BQUFBQUFBQUFBQqGIoYqagoKCgoKCg\noKCgoFDFUMRMQUFBQUFBQUFBQUGhilFpYqZpWiNN017UNG2rpmn7NE1boWlauqvMPzVN22jlf6Rp\nWgtX/kmapr2kadouTdN2aJo2XdO02q4y7TVN+0zTtP2apv2sadpID1mu1TRttVVmhaZpF3uUKVMW\nBQUFBQUFBQUFBQWFqkaliJmmaT4AiwAcANATQDKAfwDY4ShzP4ChAG4H0AnAXgDzNU2Ld1Q11zq3\nB4BLAWQBmOaoIxHAfAAmgHQAIwE8pGnaIEeZTKue5wCkApgHYJ6maSmVlEVBQUFBQUFBQUFBQaFK\noZGseGFNmwggk2S3MspsBDCZ5BTrOAnAZgA3k8zTNC0ZwCoAHUkut8r0BPAugNNJbtI0bTCAhwE0\nIFlslZkA4AqSKdbxywBqkbzc0fZiAMtJDqmILBXuuIKCgoKCgoKCgoKCwlFEZU0ZewFYqmlanqZp\nmzVNW+bSYjUF0ADAx3YayQIAXwLItJIyAOywSZmFBQAIoLOjzGc2KbMwH0ArTdPqWMeZ1nlwlcm0\nZGlWAVkUFBQUFBQUFBQUFBSqHHGVLN8MwGAATwB4FEKkcjRNKyQ5B0KECNFKObHZyoP1d4szk2SJ\npmnbXWXWedRh5+2y/pbVTv0KyBIBTdPqQkw01wMo9CqjoKCgoKCgoKCgoHBCoAaAJgDmk9x2tBur\nLDGrBiAWwBjrB4h/2WAAc6x8DcD3lh/XfABDrDTbZrIOgNM1TdsLYDeAFwA84CpzEoBrNE0bAOB/\nEBL4tatMDIB/aZo2C8AKAMNc+RWRxY2eAF6q5JgoKCgoKCgoKCgoKBy/uAES2+KoorLEbDeAEIDW\nEIIDAP0BjLD+v81KvxfANwCeAvA6gBIAyzVNi7HKVwfQEUAjAC8COAghY5s0TWsCIA0S+KMLgAsA\nTIeQNwLYrGlaH0v2+RDSNsL6fzrCGrIyZYnSv/UAMGfOHCQnJ1dyaBQUKoF33gE6dgQaNSqdt3Ej\nkJ8P9Or158tlYcSIEZgyZUqVta+gcCxAPQcKJzrUM6BwomP16tXo378/YHGEo43KErMNAJqS/N1O\n0DTtDAA/W4E1roVo0Hwkl1sar9UAiiDEqCfExDAGQBzJ+ZqmjQWQDSFRX0FI1mYAJwNYS3KNpmld\nIFq5NSR3aZo2AsCPAJJI/qBp2h2Q6I7XAXivgrJ4oRAAkpOTkZ6eHqWIgsIRwMknAwMHAjNnAk2a\nhNPXrwfuvbd0+p+MOnXqqGdA4YSHeg4UTnSoZ0BB4RD+FBenygb/WAwgwdp/7GdN0z4HcCuAXIgG\nLA7AFAD/p2laLwDxkI7sBvAWJKjHSoh26zlN084BsBVAAoAPSG6yysyDEKiZVvj7HQCaA3hC07Rq\nVlvTAVysado9AFpa9ZxhyXJ2BWRRUKg6NGki5GvgQCFjgPz1ImsnGmbPDo+JG+vXS/6fWY+CgoKC\ngoKCwp+AyhKzNwA8BmATRPPVCUBtAOdCAmoUAZgE4L8QcvUthCC9S7II4YAdIwE0hGjIXrXqfs76\n2wCimRsD4CpIaP3bIGaMcwDUg/i5fQZgNoCJAH4A0AbAzyS/t2QrTxYFhaqFRc52XT0Qo89biL19\nFSkDAHTrFklYbdjEtVvU3TqOTj0KCgpHB2rxRI2BgoJCBCpFzEjOJzmGZCsAXQH8CvHZauUo5gdw\nKoDzIZtDH7D+d+JlAN8BaA/gCivtOkf+SQD+BeAZiD/bsxBTR2c9FwC4EcAgyGbVqwCcoWlavUrK\nUgojRozA5ZdfHvELBALlnaZQHm69Ffj8c++8zz+XfCdatQKeimJ1+tRTku+E8wPn/tj17QuMseLV\nuD92n38uk/Ts7Mjz7eP164Enngifs3490LlzuD53+3Z9zro+/zzyfEf7n+zrjMe+6I4nao8LkzK3\n/M6xc8s/erTIY6c7+5GdLXLa9dn9cMrkbOvWW4FXXwU2bCjdltc1Oho4UtpEpZVUUDi2oRZP1Bgo\nKBxDCAQCpeb/I0aMKP/EIwmSlf5BTA/XQEiOvTeYDiFpBwD0dpT9BRIwpBOA8QDWQoJ91LPym1j5\nBRCN1kJIBMZvHXXcAtGAvQeJtnjQan+qo8wsAPsB3FcRWaL0Kx0A8/PzqXCYAMhGjbzz6taV/GAw\nMj0YJH2+0um5uaSmyd+KpJsmqevy1/1/ejqZmEjm5YXTnW3n5ZGZmWRGRviczEwyNVXOdae3aSP1\nOWU2TSmflBTZjrN/LrmKO2dysZbBi2sZ/DRG5+6VZum+uOV0pyclkSkpImMwGO5HMBjZb2f/osmU\nl0fGxXHuXXdFpke7RoMGlU6zcdll8vNCMCjnzpoV7otHmYLTW/OOZIM7O+qly9nnetXhTM/O5q6O\nOm9rZXB7mk5Onhz9vMmTyezs8N9odc6a5S3z4aCsMbTHSaFKMHfu3KoW4fiH+13nPj4R4Ojz/v1k\naJ15zIyBegYUTnTk5+cTYrWXzsPgTJX9HS4xmw0J2JFgkaSPASRZ5KkEEpQDEN+vEICNAIYDuMjK\nX+Go6zbIvmQhAB0gpol7ADzpKDMXEhJ/h3X8pVXP5daxBjF//BrAmxWRJUq/FDH7o2jUyJuc2el1\n60ZO8KNN+Enu20duGZfLkJOE5crxlodyuWgRuWmT6yQ3IcvIEELiIB3My/Nu2yZdTvKSkMBQQgJX\nPhPkwZ888t19SUoScuZuPxiMlMVqa8tZGWwMkx99RDaGyV9aljFBKUt+p+zBIJmWRiYkyN+8PJEr\nLS2StAaD3mOVlydkLj29bFJW1vWzxo61a5dNxKNNwkyToe46hzcIkAAHnWUwFIpyrZ39iJI+PNUg\nAQ5OMcKTHq/z3GTcJnF2naNGRV7DWbPCZM1J2LzSnHI709xjOGuWtJuXF063yZtpkp06kaNHR55v\nk7dgkMzKknJehM9uWxE+hWMJkydzfaNMfjnJKP0+ONILIccqTJM70nVmweDG5GODlCkoKBzjxAzA\nZAAPAfgeYsr4kUWAnrbyP7TIT3dIgI5FAIIWkZoAMZ3cBuB3iBljT4jP2QTrvJ4ODZoBMZEcYrUx\nyiJa1RH2OXsIYuo4zao3B8DiisgSpX+KmB0JuMmZ47i4mFz9XJD7a/o473w/C+J8nDkwyOnTyWef\nJZ95RjjY0KFkw4Zy2r21c1kCjV+d0Zsl0PhAUi4BHvq1b09eey15003krbeS911nclV9nePPN/jD\nyZn8/qQMjuxkcPnJOieenceCOB+fbiVtD2kfpK6TF15IXnQROegCk9+flMmfklL5U2Ia1ySk8bvq\nacxHKlfGp/HbxAxe18lk9+7k+eeTwzsGWRDnY25Lqe8fnYMcdIHJb0/R+VhPg/+tn8m19TM49SqD\n6xpkcl2DDOZeK+lr6mawXaLJCy6QYbr5ZrJlvMmVp+gc0dvkgAHkA31N/tBIp7+3wR9P1zn7sjzu\nq+7j2xf4ua+6j09fH+R995EjR5L39zH5Ta1M/lA7lb+elMLC+ARuOTWZmxqlcfNpadzULIPv3W/w\n19Y6X3/C5Guvka9ONrm+mc5Xhxrc3DyTW5pn8N37DG46LZ374xP5yrl+7on3ce6QIF95hfziC3LV\nKvKHH8j//Y/cuJHc9laQJXV8LHgvyN27ycIFQYZsQuFFXt1EzmPFvKSbzjl3BPkxdL4yxODH0Dlj\nrMmSEte95iZh7r+myZXvmPwYOh+9UOoxZplln+ckuDZRs8m1My/aAoAtlzvNq6823GQ1JYWMjY0k\n4YmJoql1amud57m1qk5iRwrZs4m3zyck00nUnJNfO92tOXRqGd0TZndZJzG0yw4aJKQyLy+SGA4a\nJA9+nz5CLJ33h1O7ap/n1pY6ZTlams0jjbK0xce67EcYy980mY9UEuCBD41wxgmmPXvyCllAeiDT\nKL/wiQT1rChUIY51YvaNJRwt0vM7JAT9k1b+ACs9ZJX5BUAKJMjHY1aZNyAmhrSI1peQACIhABda\nZTZbZIzW32kALrHKx0MCh4QAFFtldgO4CRLs44uKyuLRv3QAzMrKYq9evSJ+fxV1/jffkGvXVu6c\nUEgm2J99Rr7xBjljBpmTQ06cSD74IHn//eQjj5Dz5pH5+eT69eSGDfKbP598/HHy6afJhQvJZcvI\nxYvJPXUbMQTwIDSGAG6p3og9esh8ECBHxPpJgA/W8bNOnTDJio0l4+PJpk3JIUNkHjZuHLnktN4k\nwEX1e3PkSPLtt8mVK8kXX5R52gUXkF26kOecI/Phoe3kA3fvOYZ85ACO6WrwkkvImanS9sxUP/v3\nJ/v1I6++mrzqKvLSS3moPAE+pBt8/JLw8aMXGuzfn7z+erJvX/K668gZHaS+Gal+Xnml1PGPs+Wc\nv7cwOLC5/H9LU4M3NZb/Z5z6AK/rZHLkyLDWb/9+mSv3zTD5aMtZPPdcUY4MOkvOuamxwZYtyfEn\nS3vjT/azeXOyRQvyrLPIDh3IiReHZb033n/o/x5xBrMgeVkwIojtpQnhdLvMRTUNjjtJzp/Q0M/a\ntRlxjvt3HoLcDh+Hwc/t8PE8BBkXJ/yhZ23Juzfezx2aj5f5gjz9dPLMM8kGDeSeSKllcmGszssS\nDX5WTWcXCCkbd7NJkhx3s5Crdokmk5PJs88mu3Yle/Yk+2WaXH6yzofbBlgQ5+PEtAC/qavzpiyT\nF7U2+Ql0nt/M5IEDUtaI0XnPVSbHDzD538Y63+wb4P6aPhqDA9zcRuf7z5g0Zpnc2kHn0pEBHqyd\nxL3Nkrm7fSbXzDe56TUhotvfDnL7dnL3SjFJLemcIdo4srT21U6LMsk8eJB8fUSQe+J9XHiVn/ur\nJ/FAq5RIE9o2bcJkLRgUbWRCgjcBttuySZhtypqcLNpTp7bSTeCcpDVaH6JpG51lvcxvg0GyVq1I\n0kkKKQPkRnbK4+yXU2PslMOtiU5OjmzTJph2/qBB4fRRo4QoepG67OzIsna/bMJpE1Fnnbb5rp02\neXKY9NraTDtt9GiydevIMczOll/DhpHj44SXibAtnzPPSVoHDZL6bG2qczJbnvmu3V+7j+663QTe\nXY8XaXbh0VtNLkIm85HKjU2sa2kvJNjXzk307WO3Btjuq9dk3W1C3bKlt0n8rFmS3rJl6TqOFkyT\ni2uKxsyI1XlgjfnntX2sowzLCs90ReQUDhNz584tNf/Pyso6ponZPy1yVAQxYSxxEKwiAG9bxxdD\nNon+wtJSrYeYMsZYpKsAQDtLQ7YFEugjZGnRmlj1fW1pzO602pqMsCnj9VY7Uxwas+0AAgDetMq8\nVZYsUfr3l9aYPfaYXNGYGPn2bNwYmR8Kkb/+KuTrn/8kb7hBJriJiaUn2jVqkCedRJ52Gtmsmfwf\nbVKekCDzJXd6ETQSYBE0dupEXnMNOX48+U2upVHx+0mfj6HPgqU1IU7YPmW9e3v7lrlhv6wNIzxZ\nNIzISajVtqepl60lSUsL/+xj58STDE8cnfVFa98tS0VWgZ11lSe/U/aUFLkwycmH+hDKyODBBQZD\nus5935vcupXcvzpcf0lGJos7S5lDvmmOa7RjB/ntt+SiRULiP/iA/M9/yLfekntq2S1C5L66wc+Z\nM8mnniKfeIKcNIn85ErJ+6iXn488Qo4dS44ZI/fhpElSLnCHkMI3+wb4ayudK94yD5kvhkLkl6+Y\nNJvqHD/A5MCBZP/+cktcfTX5f13l3OntpJ0HMg3e3tPk6kY6Z483+fvvUk9BATnhdpNfJ+n821km\nrz1Vzrs7xl+KtNokdRgkLx+pzIJo3c6ziKN93BgmG0PIY3fN4CeaztY1TLZNMPlZnM4rfAaD8TrP\nO81khw5yeVq3Fq7VpIlwpZgYckyitHVPnJ/JNU2uqpPJdb5U/lwvjf9tkMEZF+VxXw0f37/Yz8L4\nBBZWq82Pr/Bzf03Rak6aJAslEyaQT42U8frkqhyWxMTxmyvGsqhWEvclp3LdJybXreMhkrn133ks\nztK578MgS7p7mLl6+Tu6iZxXWS/z24QEIWe2aa1tAnzWWZGaQC/i6SRctlbSNju1ZfYimm7Np10u\nISHchhch9dDARmgvnXWmporMNWuKTLZJcVKSvLNs+Z1mxm5Nrf2OcffB+b7xMhE2zXD7dp5Ta5ub\nK9chN9fTpLqUL63zujrJvZeW2EvL7FxQiHZvWAitM/lFTZ339zF57zUmFyGDaxLSeKBtmvd1dWuE\n7bG1x8N9zznHzv2OHj8+8psSLd2JsnxCR40Sra8X3IsCLk16YXoG70E2Jw0xeQ+yxR/WvRjgxqxZ\n5ODB0qZ78SAvTwiyU3tsa6ad2mo738u8+Y+QmIr6AFe0fvf9U5Y2tbJETkGhDBzrGrPaltbJ+TsI\n4HPI3mEHrOPeVvlWDq3VORZJKkZk8I/bAeyF7FVWDcDjFllz+qEFIBEg37OOlwD4DVbwD4iP2S8A\ndkJC8SeVI8txF/xj0yayenXyzjtlLn3yyfJ97tVLzPSSkxmh9ahXjzzvPHLgQJnIzZsnJmpbt5LF\nxaXrt0ndkiXkhx+S779PvvsuuWYNWVJCHjhAfvcd+fXXMnkvPNXSmGlCzg6ZNVbEtM0Jd6CPaIE/\nbLgnAkfAxyxi4nYkfczK+0BUZJJb1T5mNrwIakXy3H01DLlZo7Xl9SG3zw0EpP5AQI7tlfZo9WRn\nR5xX9GKAB7vq3L7M5K+LTO7L1Lnt6QCLk3z872MB7mmVJsRzssF33yWDjwhx+2ScwZdeErH+M1LS\n3hhu0O+XJl66TdJmDTB4//2iCb77bnLECPKuu2QuN2ECuWaGLFgUZftZUsfHGQOCHGMRTgK8uYnB\nNm3IB+sIeRud4OcDNeX/e+P9TEqS7p90krhy1qtHXl5Hzp+KoYdIpk0g3STzOgS4HT5ehwA/0XS2\njDdZq5bFQWqb/DRG5wXxBhfV0NnntCCX1NI5sLnBrxJ19k4zmZVF9uhB3pRlckVdnf/X1eDKU3X6\nu+RxT7yPgUw/91b38cmrgpxydZD74pO4xdeChdUS+GuDNP7rHyZfvF3MnI2r/DxQPYGF8bW5pJ+f\nhbV8XPBQkK+/Tn70nGgzv842uDMlk7vaZPDHhwM8mOjj2kcCLDhb50/PB7m7k861C0z+9BP56ytB\nliQksbBNKrd8ZXLHO0GWJCbxYHIbFndIY3GHVBZ3zmThgiCLO2fyYKcM7l1lct8+8sAa8XcMfeYg\nUenp8kJt0yZMpJKS5N61TU1tLWWLFmENoWnKuQkJh94TBe8FWVQriZvrpXBPew+No9e7sqx3TzQt\naV5eBJHd8U6QB7uWQ0TL+usku+73hPvdW8ZEeWe6LGy88w5ZWEjOGyH37Krqafz1FVe7ToLpPLbf\niW4yWRETapuEjR9fPimLVpf7GkQjBF5E3xqrzc0zeR6CPNBFZ/rJJife4RizaG3m5cm9Zb8znUGc\nYmPlXnSme30/bVJva9LJMLFzap3tv7Y5sdPv1c63zZBHjRLNrbOv9nnBoKxKXXZZ+BvjNcZePrCm\nycJzda6f7VjcjEZa7X7ZRNk0y/62TJ4sZaMRPZvkKpxwOKaJWcSJov3qa2m3nkc4EuJzAEyEfbsK\nAfzXOmc8gGWQQB7vWxqym6wOT7PKLIRsHr3HImmtALxglbkA4aiMj0OiMN5kac3WWGTsFEi0yDJl\nidKnvywxy8khq1UTYkWS27fL9+Wii8REb/hw0Uq88Qb5yy9HWZhoPmbuwB82on10ToCojBVe8fPS\nGNjpRyEqY4S5WHnkrLITyAr4mFVaoxhtAlkWMauIj5l7EprmWsV3aj+d5LKsNC9Em2inpES269SY\n2pqTsrS/us5QTg5DcXE8MHosi5N8XP6vIJdNkcnvkscNvv02+cUEOf76JiF6r99lMCeHnDJF3hvZ\n2eRrw6TMszcYvPdeMudqOZ58mcFbbhEN/HXXiRbTNge+O81g167kk42l3kfr+5mcTLZrRz5yatjU\n9up6BuvXlwWlkZYJ7vAY/yFt5TD4I7TxTrNct2bT1np6EVDbXC4faVyKNC5CBq9DgDuRxJVIZr6V\n1hhmRHt2XX0s8npDXIDLtHTuRCInxI9lEeJ4f+0cflUtk1/FZXBkzRwWIY5TksayICaJP8ancHXN\nVH5fM43La2bwhsZBLquRyRVxIstKpBySvWVL8uKLZTwnXS7mrXMzxNfzkYuC7N9fzKgf6BLkrlgf\nH2vg565YH0dmBjn0MpPfnarz+Y45PKjF8fW2Y7m3WhLNk1I58WKDP52aybWnZPCRdlY/qgW48hSd\nj91mcspwk+ub63z/lgALa/kYHBbglnY6508z+fbb5ILpJn9L1vnW9ZK/7L6AEOOUDH73lMFdZ+tc\nNS3Inek6V+QIad7eOoNLHje4tYP4ds6fL1r2V14hp00jX7xgFjvUMdmxo7UgaN2zG+YYXBqfwfti\ns9m/i8nv6uuc/rcA91X38bMLxrEkJo7fXT2WRQk+rhibx9+SdS4Ya3BzW/GfnTCBnHJ1kLur+fhc\nOxm7vLuCnDuXfOEFafvhh8kHb5K6X2k0nCGA3ze+kCFofKtnLgcPlnv52muFZ0yfLguSK1aQv79p\naZrnBbl1K7n7fVlUOfhpkMVrTR7M0rn5S5MbNpB7vjMZcr3fQrrOok+CLM7SWXDXKBa0zeTfWwX5\nVaKUGzyYPPVUctMSM0wGor1Lne92ewEwPV2+UbVrl15gc2sYvQilexHQfo85ibCtOba1wzb5srW2\nqamlCfX48WGZ7W9TRecDJNetI3vEyfP+wzSj7PJWv3Y0S+Ww9ga3ti/ju2B/1+33bJ8+3gu2ffpI\nX2yTZGc9TjPmPn0iSZ6TaMbHi6mSF8kbMEDMlWxkZUU3abZNk48lHKcmpMc0MYME4FhpCUiI+eJq\nAE8C6GcRpUTIZs62b9cBAM9a50+zCFkniEmjbQZJABdbZdYAuB9i+rjXyjto1VcdYf+yzpD90A46\n2vnJqqNcWaL07y9LzC68UPxtqhwVicroBa8VMi/7fxte9v/Ol4L7BdGnTziSnfsFEQyWftG6/VKc\nq2WmWToynrNNuz5nXcGgt59FtJeVW36vQAo2Ro0Seex0Zz8mTw770Dj74ZTJywTGSz6va1TWR/EP\nRmWssEbR/bGNll6R86KRcafm0z2hcH643XVVxMcsGll1BgAxzT/uY2Yf25Mwmyza4+DWODrldBNM\nL2IarayX+a09GWzRIqzZdU4eLeIZql2bB5/0M+Tzcc8HQW7bRm75SlbNNwYM7kvN5N4OGVz/uGjM\n1k0IcNfZOpe9YXLRInJFjkU4sw1+8AG5eKJxiG19+pDBjx+MJKQEOH+0wZdfJufOFR/WWbPImTPJ\nd+6Vsp9dI2VfHWrwkyvk/68zRSM5a4DBWQOk3JedJO2N7v5DQR0IcOpVBkeMIJ/uE07bl5zKoo8M\nbkoRU90rrhAfyo4dyclnSBtPnOnnuefykGbykkvIF8+WvDmd/OzVywpIZEUgfa2RtO9v6ufgFEm7\nI9ngba3k/496yblD2xls0ULM1m1/UzfJjWbe6yTGdlkv0uyuB5C1tRYtxMpj06bSz8fulSZ/bq7z\n1r+ZvKuD1POQ5V/r1AC72wREa9ymDZnbUspPPsPPatUi2z/lFFkgsP2Rv6nTlQQ4L643Tz9dfHZ7\n9pSxtj9fzp+XX62byNuLAs1jTSYkyJw7Njac79RSB6vp/CpP+v7zz+HdZRITxeXwjDPIaxsGuTPG\nx0fr+7krxseBLYPs3Jm8uqPJlUmZ/DExlT8npnBPXCJn9gzw53rp3BefyHf+5uf+GkJO//1v8sMH\ngyys5ePXN/l5oLaPwQlBGrNMbk/TuTJXSPa6SXk8mOjjqmlBLltGbpiSx1BsHDePy+W+DJ2/vBxk\nYZt0FteqzcI26TQ/Nbl+TpDFtRJYXKs2N0zJ457OOjeMymVJbBx/vGw4S2Li+HnfHG5L1fnjh6Zo\nsuv4uOvdIPftI0sWen9PSkpkQbl3mslgNZ39Golp+IfPmiwq8niHWscLHw3y/Fi5vj3iDL71lsd7\n2L1Y6lx4dS9o2ovC48d7W9fUrCnn2i4QbrNk05QbDxDfDicGDJD0AQPCaW6CbH+rneleAZBsQudM\ns8sNHizzBSec/rLO8k4fWRv23MFLg2hrQw/ne34M41gnZu8BuBnA3yAbQv9kEasODjL0DMSPqxvE\nt2s3gP8xkpitBDAf4mfWy+rwSwwTMztk/iRLY/a0Td4cxGyMpQGzNWbfWCStXkVkidK/v2Twj6Ii\nmaNNnFjVktCblNmwv24Kxw+O5j5m5a2wHa4PQ1nnuQMhuD/a2dnysR09OrrJrN1+RaMyusfQSeqc\n5j9/NCqjXa8zAIj7nGimVn8lHzP3XyeZdPuPZmQIEbXNEL38SJ19dJJXm6CPHSt9zMkJX7ecHEkb\nO9Zb82nLYvuCus2M3WNdURNh+3x3+zYRt+XzIuGOPoZ8Pu57PsAD5+n8/WuTmzYJIT6YpTMUCIi2\n6KkA96dlcl9qBtc9b7DgHJ0/zhQT0vWzDe5Py2RhegY35xncf67OXxeZhyK57tolAW/KfC7cz4It\n87hxDMXFcd99ogHemCP+kXvfM1jURfxnvcYn9JkVNbaQ4a037HaHD5dv04UXRjVjPHBACNPixeQ7\n74jmb+XkqSOUAAAgAElEQVQgIX75N/n54otC4KdPJ19+OayF/misccjfNidHAmU99xz53v2Sv2Kg\n1FH0kRHR3qZN5Esvyato/Hi5lA88QL6pS/m8Ln7efjv5979LROLxPRzkv7mUGdDM4KP15f/7avpZ\ns6b4sgL01Ea7Ca6bfF6NvFKEcilEc+wkqPZ54yDa5CkYRgIch7GliLq7Db1akElJQkwbNBAeY5NZ\nI1bn0tfkfuzTWchtiziT9euT158pGuRnkiVC8o1Ng2wMk9/W07nvfYPf1hOT2c6dyStTJdjUVXUN\nrqqv87kxJufOJV9/nfx4hskdKZnce/pZLImJ5b5mbbh2gcmNeUIid0/KZaiOj8UBD1Nh5+KZ1+Ka\nfS9fc00kCfMiZTbcVizJyZHBk7y+NU5TVuc3yT43Odl7QdL9DbN9ZN3vHadrhPsZjrZQ6iwb7Rvs\nDFI0eHA4AJP9DbD/t30qvRaL/yD+csE/Sp0sJIiQvcPUBtNVhMWL5UouWVLVkigoHGdwfzi8wsX/\n0X3MvNp0m8kciX3M7A94dnb44xaNwLnNOsvTRnppCL3IVDB49KMyRvMxcppr2cf26rbXlgjR+mxr\nTf+oj5mX+XF5fTiCPmYR/akqHzPnPe+VZ9djL4QcCz5mNsoizW6tcUWIfkU0CtHadE6uU1Lk/nMu\nHjjKl5SQe+eL6WXh4/5DJpm/LjK5L0NIdcE5Or+ZZ3LpUnLDvULgfhrm56ef8pAZ9Johkv7lJIM/\nDAmX+ewzcsECcu0wSdt88U0kwD3/GCs+tC8GuDdD59evmvz4Y/FV/2aAlP2ir59Tp8rr77HH5FI8\n/DD54sMmN7fVuS0/PD6hEPndf0xuOEun/26Td98d1iA/29bP+64zuaWtzuK1ck7Jf8UUd/gVJvv3\nJ+feLv24I9lgzZqHOG0EQSXAAiSU0oraZHI8xvIgYvkjmnNltTR+HZ/BofXzuCvGxwkN/CyISeLa\nGilck5DKHxPTuKpOBodcYvLaa8kFTQcwBHBzYlOGAC5uM4BjxkifJ04UEj99umjul9ybx5LYOP56\n9VCGYmJZ2DyZv3xucuNGsuBbk6EMeX5D62RLmaIfTR5s3YahmFjump7HvXvp7Y/o8Q4IrTNl0cS+\np5yLVV5pzvvZOt6Wb/L7BjoHp4gZc9T73/0dsd/xd98dltU2j01ICF8g53vOfgbsKHZHCoD4B/EY\n15iVOhloYQn7BtQG01WGiRPlvi0qqmpJFBQUjllEI5nH2z5mtjmN3Sf3irA9GajqqIxnnhndHDYv\nTwisWxttaxyPo6iMUeGevB0rURnddUWrO5rGwIvoV8QvNlqbR8PHzH3tbWJnj72X5thtquzzkcOG\nyTgOH+6tmXfKVVZwqIpYVjjrqWgQFos4l/zX5O7d4qO/aYkpmuDkVO5tlcb9DZqQAFcP9vOdd8hX\nXyXnzCEX9xUSuKzL0EOEYfqNBu+7j3ytq+S9cp6fExxb2IzparBbN9nep1s3ckN8UxLg+rimPOss\nsnFjMVs96SQxe3WSRdt8dyqGljKVbQyTLeJKp12NPBYhjlMxlEWI4+1183hJisllPp3Z5wS4u5qP\nT2UFuLqhzrE3mpxwu8mvEsRUdF0TnU+NNPncGJMbm2by9zNSua1xGn9vmcEP/m1y/jSTW9rp/PxR\ng78l63wt2+S0aeQ994iWs1eS9LsbDI4eTW7b5nHdvO5/pz9iUhLZvLncx9WrhwejenVvUpaY6H2P\nHA5s2+dq1Y5tYgbgUQBdADQG0NbSfhHA+Va+2mC6CnDxxWKBoaCgoHDCw4uAHov7mLl9NOw2bQLr\nNUElj8t9zDzhJt/Hyj5mXto3O/1wojJ65bvPj9bm0YrKaNftJLj2sa2tdGqOneTPXjiwCeD48aXP\nc57v9NeN1s/y4D5v1KjS/XGWde8f6PYxcy6QxMbKniZeco4dK/nNm3sHaPIyY7bbtc0Xmwo58zJj\nLC4md+8mdzwr/n1brx/Kktg4fjcuj19OEuLz8YMGp0+X7Wne/oekvXe/wVdflS1t1l4shG5Z16Ec\nM4a8/XbyIV3K/auFEMjbWxvs0EG6YWsLr6prsG5d6bYdcMVthurlQ9q0KTn6evEDLvnEoNlMZ7MY\nk4CQzvbtyc6dye7dyZu7mfz2FJ055wW4J97HmT0D/OlMna9ck8f9NXxc1nUYQwALfKfxYHxNliCG\nRbHVGAJYGF+Ta9aQhbUT5Tgxsextlw4HFjnLj4s7ponZdEvjVIJwQI3HHfk3QsLh70N4A2jD0nbZ\nG0zPsYiZHdCjEBLV0bnB9P8swma3sxXADJTeYHqH9bcEwI8AXkV4g+lyZfHo31+OmB08KO/Bxx6r\nakkUFBQUFBSOcxyNfczs/Gh+sX/2PmZObZydX9mojLZG2NZ0uzVmo0fL+e4gWpUlZ2UR5fIiADvT\n3SZ6bo2kbaLs1H7/2T5m9rFNxsuLAGyfO3RoaTPwsvxM3fVmZjKUmsriDmksOjuD2/JNbl1q8sB5\nOre9YbA4S+f+1WJG6aUhLjxX5zy/ybFjJdjPwIFkv34S9XRkJyF32WcKSbz+NIOnncZDW8G8ht6H\nSKGtNSxAvGzHBDAEcAsSDxFDO8COrVRr2FDIYnKy3Kpdusg2UldeSV5/vfhoDhsmt+HEieILOnWq\n+IK++CJZGFONS4Fjl5hRyMtFAL6C7DV2yJzQytMtErQdEtSjLYB5Fgm7xyozHmK6uAyy99m5ANZZ\nnW5vlfkcYs44G0AyJNDIAQB7rfxqFtEqBnCPpVkbb8mzoKKyePTtLxf8Y8kSuYqLF1e1JAoKCgoK\nCgp/ebiJ4OHsY+YmqE6ta3laYSdJrKysZdVTlkmkcx8zN6mztdn9+1dtVEZbFmcAELeWzy7jJIl2\nXRXwMYuoo7I+ZtE0vmURYi+SaI/ZMNGYFTc6jaEaNRnSYrh16FgeTPTxoMXEDgJ8803xxZs+PUyq\ncnLISZPkUo0aJfuG3nGHXMLLLhNLs+7dxWW7XTtZRzj5ZLJmzbmMielFIPzr+hcgZrkQf65mFvFx\nErMkS/iZjrQ0K22UdXyrdaw7yvittNOt4/kW6YpzlFkFYLfjeCuAdY5jzSJvX1RUFo++/eU0Zsq/\nTEFBQUFBQUHhCCEa2bM1jlW1j5mT4DhNk4+VqIxlbeDt1gQfjo+ZvT+e09/sSPuWObBvH1kYd4xr\nzCBh63cA6AqgvkXMbgRQw8pvagn/CyJ9u3YCmGKVGWiRLnuDadvPrATAFVaZ16wy9gbTQyxNVwmA\nOlaZ3yG+Z3a4/GkQs8WVVn6z8mTx6N9fjpj16CGbSCsoKCgoKCgoKByn8NL4HUv7mFXUhzSahq28\nqIx29F5nABA7pObRIGdV5GOmUQhJhaBpmu1XZiPGImcDSL6gaVomxAzxeQBXQgJ1fAAxPdxPsp+m\naaMscrbGIkx7IaHubwHwIMlpmqbNh4S+PwNAikWupgN4DEAKyTWaph0A8CKACyAk8RuID9ktJBu6\nZOkLoJYl+04AS0n29OhfOoD8/Px8pKenV3hcqgrbtgH16wO5ucAdd1S1NArHEwKBAPr161fVYigo\nVCnUc6BwokM9AwpHHLNnA926AQsXyt8mTST91luBCy+USW2bNkDz5sAPPwA33yz5558PHDwIxMYC\nM2ZI/uzZwCuvALt3A4mJQEHBkZExPl7aqlYNy5YsQceOHQGgI8llR6aB6IirTGGSMc5ji6j1Jvm2\nq+gYkoMc5fIQSeiKSV7mqmuAq8xvJK905KdAojc6y3zkameIKx8Qf7j+EOL3FYB3AXTXNK0eya1e\n/RwxYgTq1KkTkdavX79j7uX0wgtATAzQu3dVS6JwvEF9jBUU1HOgoKCeAYUjDpto2YTMxnPPyd9r\nr/U+7+DB0uSrSxc5LylJyNkfRCAQQCAQkLY0DbjoIuwaMeIP11sZVIqYVQCbIL5e9SHmiTZOBbDc\nUeZU50mapsUCOMnKs8vUd9V9KoR0bS6njDNfAzAUwDSSL1htbbDKDQQwyasTU6ZMOeY1ZgUFwOTJ\nQJ8+ojVTUFBQUFBQUFBQOC5RloXfEdKUeSlhli1bZmvM/hTElF+k4iBpQghRDztN07QkAJ0BfGEl\nLQbg0zQtzXFqDwiJ+spRJssibDYuBLCG5C5HmR6IxN+sdKcsbQB87JJlKYDMw+5oFWPrVuDqq4E9\ne4BHHqlqaRQUFBQUFBQUFBQU/igqrTHTNK02gBYQIgUAzTRN6wBgO8kNkAiL/6dp2loA6wE8DPER\newsASP5g+ZA9p2naYMi+ZP8CECBpa8zmAngQwExN0x4H0A7AXQCGO0SZCmChpmn3QMwT+0ECfNzq\nKDMDwP8BOEvTtHYOWZZCNsr+y2DuXGDdOmDFCuD994GaNYF584DGjataMgUFBQUFBQUFBQWFP4rD\nMWU8G8CnCIePfMJKnw1gIMlJmqbVgkRJ9AEIAriYZJGjjushYfcXQIKHvAYH6SJZoGlaT6vMUkho\n/IdIznCUWaxpWj8Aj1q/nyBRHb93tPM0hJg9ACFlQQAXA7gNpX3RAKAGAKxevbqSQ3L08Y9/APv3\nA82aAf37A1ddBfh8wLKj7oaocCJi165dWKZuLoUTHOo5UDjRoZ4BhRMdDk5Q489o73CI2U8AXoIQ\nnFrW8QBXpJKYKP/b0BDWuHkdO9M0CIly59t12wSLHm1thRC/GEd5INIXzYkmANC/f3+PrGMDy5fL\nb9q0qpZE4XjHn2lTraBwrEI9BwonOtQzoKAAQDjCF+UV+qOoFDHTNM0H2QvsY8j+Y1sBnAXZ28wu\ncz8k4MbNAEwAjwCYr2laskNrNhcSuKMHxJRxFkTD1t+qIxGyyfSHAG6HmDI+r2naDpLTrTKZVj33\nQ0wZrwcwT9O0NIfW7B4IYVsEYLQti9VmjkcX5wO4AWKCWViZsVFQUFBQUFBQUFBQOK5QA0LK5v8Z\njVV2H7OJADJJdiujzEYAk0lOsY6TINqpm0nmaZqWDGAVZD+A5VaZnhBydTrJTZbv2cMAGpAstspM\ngJgqpljHLwOoRfJyR9uLASwnOcQhy0cAroMQvFUAvoTskdaM5O8V7ryCgoKCgoKCgoKCgsJRQmWj\nMvYCsFTTtDxN0zZrmrZM0zTnPmJNATSAFQUREH8xCBmyoyBmANhhkzILCyCarc6OMp/ZpMzCfACt\nNE2zNxjLtM6Dq0ymJUszS5YnAPwDwD8hG07vBfC2ImUKCgoKCgoKCgoKCscKKutj1hJAivU/AZwC\n4FlN0wpJzgFwhpX3qaZp8RCiNASiMWtg5bUCEK9p2l4AuwG8AAnOsd1RJhlAU03TCgH8DxLcww6l\n3wDALgCNINEfHwewAsAwVzun27JATBdtWf6FKIRU07S6EBPN9VCmjAoKCgoKCgoKCgonMg6ZMpLc\ndrQbqywx0wDsgwhoB+P4J4DBAOYAuNtK/zuAnwE8BeB1AL8BoKZpMQBuscpkQMjViwCKrDRqmtYE\nQDqAlQD6ArgAwHQAdzjK9LFkfxVCtEZAiNcEhIOBlClLlP71hAQ2UVBQUFBQUFBQUFBQACQGxdyj\n3UhlidluACVOM0BN074BcKnlS3YphPSsI/mtpmkDAKwGsBzAZxDiUw9AAcmVAFZqmjYWwEQACZAN\noQcDKABgklwDYI2maV0g+5MRohUbYcmyxtoX7Q6r7QsBbK6gLF5YDwBz5sxBcnJyJYdGQaES2LgR\nGD8eGDcOaNSo/PQ/GSNGjMCUKVOqrH0FhWMB6jlQONGhngGFEx2rV6+2o7Wv/zPaqywx2wAgRdO0\nXyGmfoshgTR+hmzuHAchTj0AfEtyjaZpGyBRFSdCtGRrALS2oicuh2i6noGEtf8K4g+2DECWpmmx\nJEscZdZANHYdrbZ7AMghSU3TFkB84F6B7LVWnixeuBwAkpOTkZ6eXsmhUVCoBNLTgbZtgYEDgZkz\ngSZNgPXrgXvvBV59VY6rEHXq1Km6Z2D2bKBbN+8xWL8eWLgQuPnmP1sqhRMQVfocKCgcA1DPgILC\nIRRqmnYGgH8D6A6HOxbJkF1I07TukPgWbWC5Y5GcXdFGKhv841mIFupVAOMBnAMxFXwO4ttVBGAK\nxPerl6Zp7QAkAtgD4C2rzP8gROs5TdPOAdAUYnJokNxklfnMqmumpmkpEL+0GgCmQjRusZANrS/W\nNO0eTdNaAWgB4CTIptT1KyBLBCzzyBGVHA8FhcNHkybAzJkIDRiIdc8vBJ0k7URGt25CWNevj0xf\nv17Su0UNChuJ2bNL1+Gsa3aF35MKCgoKRwfqPaWg8FeBBuA9iOInA7It2C0Qly4pIO5Y/4EEQewA\n4S3TNU37W0UbqRQxI5kL4AoA50MY40mWoNc7ik0F8F8A8wB8CyFDbzn2MAOAkQAaQjRkdgRH575i\nBwCMAXAVJMT9SAghfN5R5jsIOZsI4AdIRMf1jj3MKiqLjREQHzSMGDECl19+ecQvEAiUPTgKxzYq\n8vFzlpk9G8jODh87P5Dr1wN9+wJPPFF2fRVBkyaY22Icmg3sjjfajjs8Una8fdgtwhpBzmxSVhni\neqQInoKCwtHB8fbuOhyo95SCwjGDQCBQav4/YsQhnU0mgNYAbiC5kuR8AGMB3Klpmm2BOBjiQnUf\nyTUknwLwGiqj+CF5WD+ItmwdJPz8lwB0ACWQQB3rAXQDkAYxefyvdc54iJniSojWrB2AmyCk61mr\nzEKrjj0AJkG0ZS9YZf4GoBqAg1ZeoXV+a4iZYxFEo1auLK6+2HXeDYD5+flUOAoYNIgMBr3zgkHJ\nd6JlSzI317t8bq7kR8OsWaRpho8nTyYzMyXNNCWflP8zM8k+fUQGXQ+XycwkMzLIvDyydevI9DPP\nJFNTI9uYNUvqyMggs7Mj5XG26Ur/srbOLBhcUluPrM+JssYuL4+sU6d0vmmSycmS727blnXWrMix\nGjSIzMtjr9TU0nJ7XaOy5LrsMvl5wa7LfZ1cZYpbtubX2QZD3csYm7JgmqSus3ityQ8/JPevNsPX\nWEGhHPTq1auqRTi+YT2fpZ7HaOnHK9z9PYb6r54BhRMd+fn5tDjINADLGMkfmkBcsTowzGGedJW5\nBbJNWMX4VUULuhpJsIjQJRah+RhAEkTTdRBAb6tcS0vgEIBOAC4CUGyVqWeVuc0idzsg6sGJALZA\n/MLs9uYC2AjgPet4CSS64lTrWIP4v+0EcF9FZHH1p6GVfpMiZn8QANmokXde3bqS757IB4Okz1c6\nPTeX1LTS5CxauhNeH7qMDDItLZKg2eTLJmVucpaSQsbGCrlxl7f/t9sIBsnERDI9PfKDWsbkY29n\nnY1hcuBAsjFM7j4nysc42hjZ6bm5kfl2m3l5ZZ8XDEbKl5dHxsVx7l13RaaX175XekICWbt2xdt2\njQ11ndPOD5AAp11vlB6Tskidi3yvayLkd+2Z5Ux23HU6j01TyKTz2ElsnW16pXnJRlZ+wULhT8Pc\nuXOrWoTjH9YC0tZ5QRYV0fvd7bWodbzBNFmcpXP2QIP7Mo8NUkaqZ0BBwUHMXgfwPiP5Q02LP/S0\njtcAuN9V5mJLWVSdFeFYFSnkqHwygCyIWm4ugI8sLdXTVv5blvCXQAJ0LAIQtLRWwyGmk5sg+5C1\nh0Rp3AwxYwxB7DGbWB34GqItG2K1MclmnAD6We1MgWjLpgHYBiAA4M2KyOLqlyJmRwqNGnmTMzu9\nbt1Dk/LiYnLNjCBDHhP7bdvIp54iX+icyxA0/jg8l7/8Qv7vATl+MSOXl1xC3nUX+fbb5Jo15P/+\nR27eTP72G/nzz+R6w+SezjpXv28yP59c/VyQxQlJ3N0yjav/bbCgbSZ3pWQw/3WTX39Nfvu2yd2d\ndK6dFWTBOTrXPhLgwdpJ3HlGCn9KSuXWxmnclZLBr/JMLlpELnvDZEHbTBa0zeCqpw0WtM3g3tbp\n3NMhg2sXmPzlF3LnNyYPdtVZ8K3J3bvJPXvIvXvJHctN7svQOfwKk4mJ5K5dZMOG5A3nmdybofPX\nRSY3biS3bJGx2LWL3P+RjFWxEWQoRPnr87HokyAPHCC3vRXkgdo+fjc2wKIuujfZJMMTHzcJzcgQ\nspmXRyYmMpSWzh3LTe56Nwr5suEmZ87jsvJsRFkt/u3VID/RhFB9GqPzt8VmZLsVXG3ft4/slWSQ\nAC+uZXDnzmg3b3RZSo1ltLFzLwQ406LJ7B6TWbNEw+sk1TZ5M02yUydy9OjI823yFgySWVlhEukc\nZ6eW1FnOlss5+XWTTmcd5Z2joFBJ7PkgyO3w8Z9tAses5ujPwCtD5D2Ve63HQpSCgkKVoILE7EJG\nJ2aXWLwmnhXhWhUp5Kj8a0vjRUuQ3yEh6J+08gc4tFIE8AtkQ+ovAUywyrxhabNoCfolgNouxrnZ\nImO0/k5zMk4HkbJl2W2RqscBLK6oLI5+KVPGMlBcTJaUVOIEFzkradSIIYB76zXi1KnkqK5B7tB8\nHAY/t8PHHtWDbNpUrANPO41s0ICMiZEqzjqLvAO5LIHG19CbJdB4B3LZrh15+eVk48ZSLtqvMUx+\nDJncfwyd5yHIfKSSAPORysYwPcsPg58EeB0CzIJxqEAWjFLl85Fm1ZfGxjBLteluAyBvwiw2hsnY\nWPK552TYPvyQrFVL6rwJszz7cx5kAmOP3XkIRuRfB9EwDYOfC+N0tks06fORZ9czuai6zn6NDC6q\noVNvajItjezexKQRo/PyOgbzq2dyWY0M9m1ocHlsOnci8VA7PWsH2a4decklZL9+ZP/+5G23kUOG\nkMOGkVOvDXJvdR/f7uHnvuo+zhgQ5OOPkzk55Gt3B7m/po+f9vZzf00f3xoZ5OzZ5IsvkjNmCAGf\n+aDJDS11vnm3wV9a6ZwxIMgltXSeXU8I7tn1xOTz+XEm33iDnD+f/OwzIdM7O+r89m2TX35JrnxH\ntI7fv2dy6VLynXfIe66S67EiRwje0MtMbtggJDkU8rh/3ZPB8silU5PqnFB6pUWbZAaFZO96V8hX\nyKmptdtMTCTbtJFfYmJp4mv/n5fnrS11a1ftctGIu006yyP10frmpQkcNEhIZV5epCZw0CCRq08f\nIYzO85xmr/Z5NkH00kxOniymxNG0lbbW0ybAbuJs15mdHVnWae5rk2Q73S7nNN+163eTYTutT59I\nk2e7TWffvPBHNKwV1TL/yZgxI/zu2pAdCMtztEjZsTgOpslvTq6AWfuJiMper2Px+ir8ZVFBU8b2\n1vGfa8pokZ/tFvtrAeARS6BZVv5H1rHt0/WFpaX6CsBjEI3ZNovQtYNozLZAzBdDkH3I7E4aEI3Z\nnRZpGmMzTgC3W4P0EMIas+2Qzaa/qIgsHn1bAtECMisri7169Yr4/RXU+evWkddcI9/l9evLLltS\nIu+nDz4gp06VCfaFF4oVXtOm5KmnytwvNlbukpo1yXPOIXv3lvpvv11+XbtKudNOk/OvvlrmJRur\nCRkrgsYQwP+iEQEyPp7s1o18529CfBb18XPSJPKBB8gxY8gHHyTHjyenTyc3bBBZ9+8nd/boTQLc\n2q03t28P9yMUkn4YhvRl3jyZjH/wAfnxxzJ5X/W0EKsfphnMf93kvtZCpPa1TuPaBSa/+45cvpzM\nzye/+IL88WFrgnCvn3s6ZLIwJY0lHVJZmJLGfamiDVu1ily5kvz+PZN7WwnR29sqld++bXLxYnJF\njrRpjDf46qvkK6+QgQA5dy45Zw752mtCxH7/PfK6bNlCLlgg8r/7LvnWW+Trr8v5L71Ezp5NLu4r\nY7e4r58zZ5LPPy/fmf/kihZu4wOS/2bfAB9/nJw4kfznP8npN4pMz95gcMQI8o47yHvuIV8eLOn/\n7mfwqevk/7m3G1zUR+pZdrOfEybIPdKrF9m9u8wvzz5b3OzatROLz4dPkfLjTvKzUSPypJPkvomP\nJ/9RTfLujvGXIpvx8VLugmrSdh8E+Fk1nTd2NfnNNzIu33xDXnuOyU+00kS3LCLcGCYXxul8boxJ\nknxrqhBRu4ymicVlw4ayCNC+vTwD15xtcmkdnYNTDC4/SecDXYL89hSd4883uLqRzuwrg1xzus7c\naw3+dKbOSUNMPnmXSbOpzjm3Gvy5uc4ZY03OesjkLy11vnOvwV9b63zjSZPvvEO+8YZc1zfflOs6\nZQrZ+xQh3WMS/dyJJG6sm8KCdhlcb5jcsdxkcXIbhmJiGXolTybgtWuL8F6aSbcpq03CcnPJuLhI\nwud1Xllavoqc41XOTqtVK5J0kiKXvRLjJJTOOiwz20NmxTZBdGombUKcmhpdW+nUejrJszO/LBNn\np8myMz81Va6Jbb5rmmI6nZQUSYbT0uS6tWkT2bazzYYNI8fHidxceWi8TITj48Mm3s7JqU1q+/QJ\ny+v0s83OFn9UL8Jnk0qnGa+bEHsRYy9EmRQPusDk14k676wXYEGsj9+PC4Tl8ZpkOzXC7vosP1nP\nybezH7ouHzunSbzzXo7mx1wWMR41SsY4Wt+9iL6VV9I5gw9Uy+albUzeg2zuP9fxTEVr07lY4dXe\n8UJAKmgdcdjpCgoW5s6dW2r+n5WVZRMzm4/UY5g73AZxxapmHU8EsMLOt9LmwnLFqsivssTsCosc\nFVnCHURYe1Zk/UIAkqzyrazjjRBTRlvrtcJR5+0Q08YQxLzxcUjgjycdZQIAViBsyvilVc/l1rEG\n0YgtBfAmxMesyCrjKYtH366DBAf5S2rMSkpkotygAVm/Plm9Onn//eSKFeRXX8kkcMoUmVx37CgT\nYXvyWr062batkK7bb5fzHn6YfOIJ8plnyJkz5f8BA8gePYSgpafLPOSaa8jHHpNF8CuvJHv2FE3W\nNdeQB6GRAA9C41tvCfnZu5fhyZbfX7aJnA3bp6x37/J9y9ywX8SGIROftDSZ/BiGt6mZLVsgIHkp\nKTKxsida7omcXYddv3MyZxhH/iMQbezck85AwDvfLZN7fOyxSU+XyWdFr1FZ19SVF/pMTC/373do\nYhJbC6UAACAASURBVJ1yRJsgkiz8wWTBv2Zx3Tpy9Wpy6VK5r9Y8K6RuzbMGv/ySXLJEtGf7z9UZ\nWmdG1LFpicnf2+l8a6rJadPk3n7oIfLee8k77xTCetNN5D97SJ0PdjN48cXkvefI8W2tDKamkjc3\nkePrTzPYpAl5+ulk75Ml7ZIEgwkJZI0apB5reGpbnb/YWCG9C68SAvtGdz9b1zC5CJnMRyrzkcZF\nyODVyON2+Hh3jJ8FSOAu1OZ9Nf3coYlWs04duWwJCWTrGiY/jdH5QEIODyKO/6o7lrtiffR3yeOq\nBjofv0RI5hO9g/yhkc5p14sP3pThJidNknGZMkW0ns+PM/lzC50vDzb4W4rOj8cHuaWtzi8mGNzW\nQecXc00GgzLu+fnkt9/K9dkQCLI4ycff3wxyyxZy7/wgSxISWFKzFotT01j0o8nQZ0F5xs46K1IT\n6EU8bYLpfP7S00uTqPK0lW4SZhO5ss511p+eLvLZ/qRBqw+pqZFkODOTbNEi0k81PV36lZoaJpbp\n6Qw5+1Ceb6jbp9Qr3dlnJ6l1+3i631vRCLbX2Ntj5hU0qYKT4r2r5D799wMm588n/54gC2PG1Tll\na2ejjZGzr179cL4TW7aUBzA3tzQpi/at8VpwsNPteyBa38swhd7VJpPnIchtHXQ2gclXHnfIE63N\naH3t06e0rzMZ1kw7iZxNEp3aVrdW2FnWJoJusmiaYW33qFFicu0koU5SnJ0tZcsj0F5j6L4P7MBd\nbpimXAubKJtmmd+W44rIKhxRODRmHS0u8j4i3bEeZqQGbY/FZZzuWBeQR4eY1YaYA6ZANk77h0V2\n3oTE8y+BmCn2dpzzi1XmHEhUxrWIDP7RxMovgJgULrS0Wk7ydovVsfcQNjtcAyv4h1VmFmTz6ZGQ\ncP5lydIpSv8m/FWJ2cKFcjUXLCB37xbNk5N8ATJJTE4mb7lF5sjvvy9atuLioyCQbc6oCTk75HNW\nnlmYG+4PZEUCf9hwvsidq9fOD7OTnLknLHZ594TEJnjuVXl70mVPLt0y/FFEG7toJmleEyqnTB6T\nA6ePWcSkswp8zCo8ZtFI5x8xZ3HX6SbbXuTbSw4rLfSpwZCuc/dK8R3culV8B7dskcWKUMgxNhaB\nLXgvyB+mGYce4I/GGpw7l/z8WiFvxlV+fnKF/P/hZaJ5njxZCNWTT0o1rw2T8z9PH0oCnJXuZ1YW\neWdbSR90lsH27cm/t7C0lQ0MNmwoQT6TkoR71Kwp746LakYSTNvEtyzCGc389jwEuRNJXIMWLEAC\n85HGlvEmL6ghZs6jE/zcrSWwALU5vq6fO2N8vKlZkGlp5BUdRJt5VweD39XJ5Ko6GZyYFuDuOB8n\nnx3gt6fovPNSk8N6mVxVX+djPQ1+31DnqH4mBw8mhw4lhw8nH/67yZ/O1PnS5QHuj0/ib/WS+Wv9\nNP58WgYn3mFy1KiwFt9/t0mzqc43+wa4v4aPb98Q4KbT0llYPZELr/azsKaP8+4N8uWJJn9trXPh\ntTksiYnjiivHsqhmEnedkcKdzVO5s1kat7bKoPFIkL+3zOTvZ6byt7opLIhJ5A1xAX53qs7/5Jpc\ntozcmBdkSR0ft78d5ObN5NZ5QZYk+bgxL8i1a8m1s4IsSvBxxUA/ixJ8/HGmpP/yspDhjXlB/vK5\nycI2qSxJTOK2aXk80DGDB87O5KppQZqNMvhrA7ECKPoxyrMXjVC4Ca3z/nf/X8YzvWuFyR8a6WwR\nZ0qWaTKk63zh0gC3w8fnLszjro46N+YFWdRVZ7HhIYdHO6FX8lhSx8f1c4JctYrc/HppX+ZQiCz4\n1uSBpi0ZAljYuCUPrDHJ3FyGNI27J+Xy++/JH38kCwtd74ey3mvl9d09pqNGkZmZnHZjkAvjJIJs\nRoaYjUe8p8p7/5f1HbLh9f20CYzz2+jUCjuvWVkE3ybLttY4JSVM+O367cWKjIzS2vtoY+tAaJ3J\ntY11Tr7MYIkdqbccolySmsoVOVb5aIsPbtLmRTpnzQoTW9sk2VmPbcZsmkIG+/SJ/BbbRNMmpscj\nCTxOTUgdxCwdwBmQfcr2WKTscQAxjOQS3QDkA9gP4CcAN9KDc0T7VYqYWQ22hfh0HYSYD64A8CQk\nIMd+AE8DMCG7Yne0ym6wzp1mMU0n4+xldfglq8waiCrQyThzrTIXI+xfNtpqzw6X/40l0ykVkSVK\n39L/qsRsyBDx0XL6gu3aJe+D/HyZAIZCf5Iw7gAgHoE/IhDtxXokozJmZ3uvCtuEZPToyBez0z/E\ny/Tn0kvJ5s0jX0LOFfzJk6PLcjgo6+NTq5aMhVcbeXmSX9aYR1tZd6aX1f5RjMpY7pj9UVJXkTrL\nI5deWoJoaWX4mJVqIylJJjepqWFNr60l8PvD4xtNq2m3l5Mj13Ts2MiJXFkkM8qYhD41WJyls+C9\nIA900bn1dYP7M3WuN0yuXi2asvx80ZwFg+Qnn4g/4He3CYH8+kY/58whX36Z/Lq//xB7e/Nugzk5\nQio/ukzS3+3pP2Ty/EZ3P4cNE23m3/9OPtbT0mZ2Nzimi/w/LUXK3nuOwQsukK4May95dyQbPPts\nGcb27WVYW7Uirz9N8h86OSzLdfUNtmhBNmsmPqynny6vsCtPkrL315SyPWsavCdO/h8e4z+0BmUT\n1qkQMjwMfk8/VWfajPZST9+GkSS3PJ9S2xd2GPxRz9uJJC5FKrNgcBEyuQgZzILB5TFpEfLExckt\nd3Y9k4tq6Ly5icGvE3Ve3t5kp07klakmF9fUeUvNAHfG+DimRYDfJWVyVVIG7+tscEU9nYMuMHnp\npeRFF5H9MoVA39nW4NI6Oq8522TXrnIbt2tHnnGG+No21Uzm5EQ+H6EQ+fLQIFdrrXkegvwYOq+D\nkLWbawS4qLrOi1qbzMoi+3Q2ubiWzluaGvwqQfxna9cuPXaX+YJs00au+5lnymKD8zqUAIf8mAcj\nN2I8q1UTq8fzziOvu06+t9lXBrk33sc3uvu5t7qP024M8qGHxGx84h0mfzhNZ3Yv0UI/fZ/JqVPl\nMzRxIplzj0SKnXtFgHur+zghNcCPoXPsjfLsvfCCtDt4sLgazJghaR8+KAGeVgz080BtHxdPDnLB\nAnJxwOSOdJ2r/21wTyedG4Imd78vxH7fh0GZF5SlbXVr+rzInRcRdBM453vfJmHJyZKWnFxaux3N\nDzbKIuAzz4Svl7+3EZ7TRHlHFy4I8p6OUn5kJ0MIdnlE2WuR1q1JHT8+8v1u97tmTTFRTksr/c62\n69I0sl497/fsgAFyY9qwtYo2nMQnL0/yvfxs7fO8yJB93tHAH/2eH6NwEjNWkjMdzq+ypGyUpc3a\nDfEVW2ORoecdZCgRspmzHXSjCMA0RhKzThbTpKXZIoCLGCZm90NMH/daeQet+uIdxKwzgJcRNqcs\nAvCTVUe5skTp31+WmLVqJZOWKkdFojJ6wct04UjuY1ZeNDmn/4QbXi83r5WhyoRIryzKc/h3Rthz\ny+QklV7pHvuYRZDQqtrHrKJarSP5EaiMxsBL2+gm/IcTldEu596qoU2b8HEweOz7mLn75ySQ9mSw\nRQvpQ1pa5ISoLOJpt+c0v7VNdwOByOtSFuG08wMBkSU5OTyZKqus3Y6HuW9onWh8mJPDUFwc/5+9\nK4+zqfz/72eMdRa3KEuLsURGmBnRTMtw26QQaZuS8KNSytIifFVKIcoQFSIiU0NpVSp1uUoJiSQV\nZywtJPsyzPL+/fE5Z+65d86duZdhRp7363Ve957n+Zzn+TzPvWd5n8/yHBk8jHkxscxuGM/sJgk8\nclEij7RI5p6PvMxpmcK8hAT5nWNiCnTfucLg8uUSZ/ruu+SP/yfka22vdC5YILGpX35JrnlZLGP7\nnklnbqyLP73q5aJF4jXx+efk+j5y3Lp70/nNSHk4/fo5D70j5Htu8wQe/MTDnc3dnDvG4CuvCDF+\n5hlyyp0iM6a9h717y6nasyf50s1SPu8KaXv4lR4+0VrKHrvEw/btyRtvJG+6SZIEWQT62Ws9vOsu\n8q675Nmzb18xFM2YYcYSB/kPZf9icO/Fbv44RNwbrbjXqV097NtXkhDdfrtPrxdvlPjZsWNlOn/t\nK/I/9kznk0+KpfThh8USmp5OfjDB4M7mbm563cMjVauTADdc1JmvvOI7zb76ShIUDRok+l91Fdm8\nuWwja5rzUC2d558voYE1asg7u571PQVk24q3jY0lzzxTZLpUl/rnzDbe6uPh4cMy7vx8ibuuW1fC\nBkMh404WbCdyet555J11vNwT4eKzNdK5t5yLvRt7efPFBled4eajrYRk92lncEiql/vLu/ha03Qe\nKO/iiOu87N6dfLiLwZ9riuUqq1oSD5aP4ayWIjP8Gi+fu16Om9dkGHNVOW6pVJ+/V4rnXhXDvtUz\nuNLl5kMdZZmYsZ3MxFFXp/NQJRczHvDypZfIV18VQjplCjlypDzfNKwgFtb5/SWeuFOCweeek5h0\nzwixIG99JJ05MS4uec7LW1qabrJpHn6l3Ly1lcHPPyeXzja45QI3Px4kL5byNxmFr2VOpDMweZJF\nPC1roP0a7XQNT0kRUgbIiWBHjx6FywNdVS397Ndxp3tNZqb026RJYYtnRETh56pgS77YkxfZZb1e\nZ6ufYUh5Sb8sLWWUdWK2AMBdABpDknd8ZBKgKTiFF5i2jS8JOPWSf/z1l/ySGRmlrQmdSZkFi5xp\naJQEToTbRFlYx8xubbPiOayHhFMpK6O9T7sO0dFixbWTMR1j5mzRdyK1webVaT893aeXPc42mAui\nfbzB4lHt5NQelxqM0IcSa1vMQvO88EJn8l1UP8HmLlA/w/Aln7EemkNxlS+q/XBeCjiNyYb8fAk3\nyM6mWL+qurhvRDrzqrq4/R0vDYPc9KXBA63c/HWqh3uS3PTOMpiRIUmjvu8mRG7RjekcMYL83/+E\noM5vI+VvX5bOXr2EdD7lFnI3KNnDa64Ry+erpiU6vW46L72UBVufeJHt3dDDF+v4ZFJT5S8xvp6U\nvXNO3wL2+MFVUvaU28PWrUUuIYEccbaUD41OZ3S0xL1bmZkBIbNX1hPX4+xfZI6WvGFwdTXJPOxE\nWuvA4LdV3FyWIfLLM8USbCV+spJNpUKIc3y8nBqdEw2udLn5SEsPf6+axAORMXzj4nQeqODiC529\nfPhh8tWuXh6q5OKSK4cxL6Ic/61enzvrJHJ7/WQu7ZfJI1EurumVzqNVYrmvTjz3XZDAAw0Tub9p\nMjcuMrirSw/mA9x/ew/u3Elmd5X9/ECyRhYmZ4EeQ/b7hf2csJNEeztO3jXBXi4Ghn9Y//vYWN/1\nO/A/bV5TDqe4uWqch/ltHP7XgVl1LVgvhlNTxVxsTyLk9cqPXLmyuIkG3ldjYkrk+bKY5B9lj5gV\nOlhIEE2CdsouMG3r55S0mL39tvySf/5Z2ppoaGgcN5zSuJ+K65g5WQIt11udlbHorIyhEOtAouFU\nbxj+8T32By0nAh6McDtZjEsgxqxYFNV/UfoW5yIXSMqsB13D8E8IEgxFEePixl7cmIoiqKHGmAW6\n5AUj9vZyJzIZ7Hi7rFOiKOu4YcPkXK9fv5BlOBQCnZdnhmcE+/+Y5Tm/GdzzkViQswamMycqltnx\nCYUSP+VtlLVNs2Z7md/Gzd3vefhPMzcnDDTYr59Y5Xr08CV+GpTs4cSGQvbGnp/O5s3FOykujhwa\nI+UvR/qIp2WttBPEYMvtvAohY7+iLvMBvooeBMRCGhMjVtW6deUyMaheJnNUJN87vy9zVCRfbzWR\n62u5Oa6TZAUeP8DgK4MMGnXdnNHDw41xbj7zfwZfvjKTuSqSX7foy9yISHoeyOSCBbIG64FL3Ny8\nWJaO+ed7Qyz4lyTzmzkGP/iAvmuS3YvAqSzgP7d/P/nssyxIetU/0cO//w74Lwe73ljX+P795X/T\nuLH//9AyHyvl/1+wSFlMjPO5cyxQSlKIs+xbzJ4FcDmAOpBYs1dNZXuY9e+Z+6fUAtO28Z2SxOz+\n++V5RkNDQ6PMQK9jduzrmBUVG2pPiR8Ieyp9+8Os9cDTp4//w1DgQ/yFFxZ++C3KWlkCWRmDojiy\neDxZGa3fLVgyjK5dT15WxqLGWlyfwcZqGMFjxE7FGLPivCOGDPE/bvDgwpYe+1za/+fBiHNR2Ykd\niGde80TmXpLMAzMk8cy+Z9LFjblBPA9dmMCDF4rFzDvLoMcj7sb7a9QlAe49qy5nzBC3zUmTxKV4\nxAgZRr9+ZO/e5KcNhQDOP68vL7+cvKeREJ87zvGwRg1R50aXlHWp7mGjRpKBe9YZfQsIpN311WmZ\nGXvZl8rNxpUNNq9qcHn5FK4tn8B1FRO5ukoy219ksENTWeLi3gs9XFZFYjvPP19Om3oRYt38ZqSH\n3vJutqhmcMAAcU394AMZ+/dzDe672E1jlpeHUtzc+Z6XOVe4eXS86aY5fLj8hvXr+15uxcb6EspZ\nJOxEkDJSSBlAtm5d5onZa6blKg++2DDDVn+XaRE7BN8C0B5IYg5rgenZkHXMrLixbEiMmn2B6S0m\nYcszy3eafQcuML3b/MwD8CuATPgWmC5WF4fxnZLELD6+6DVFNTQ0NDROIRzrItL245zWMbNnhguM\nIw328HsS1jFzRDB3J6ud41nHzMKxxDGfiHXMrPpgi4uHu46ZRZjslnVrTKdwVkZHFEWUi8sAHFge\nzDJut9ocb4yZ9dLCiimrK+SsUMyZHda89+3r745YXFbggOOyZ2dy61ZJ0uT1kitfFCK39FkPMzNl\naaSFQ6Rsfn8Px40jR48mZ/TwFDC6Fzp6eO+95D33kGPaS/lLN3s4cKD83d4ebfBQim+Odyw3uL6W\nm5edYxRwqkByaCX2uRWSBOcWc1mYVys9yDyAf5Q7hwciorm+SgLTUgzuUTHMB5gDMB/gvsgYDh4s\niXesBDtjxsg0TZsma4W++y65YIFkMP/xR3LdOslK/vffkijPMTu5Sc5WJiWVXWJGIS/XAXgaksSD\nALrb6tLgy9bYwbSqvWeSr1GmzGSTmK0CcDGASyHpJAngWlPmV0j6/JmQeDZrjbHABCC5AAaalrXh\n5v4PoeriMLZTLsZs+3b5Fd98s7Q10dDQ0NDQ0Ch1BCNyp/I6ZuGO1amdUGIZ7SQs0PJcElkZnRKA\nOCX+sFDSMWaBiURCWfLFclsOdGsMdnwQ4nt4vcG//hJCtG6drEP64wQhd2t6ifvngkEevvwyC5aC\nWduwcwGTG3mdh7fdJmvl5phlOQDj44Xf1qghXPqMM4QrBybOKWpTSo6NiprDChU6sGLFDoyO7sDL\ny1XjFcJPyi4xoxCYiQA2m+Soo63cbSr/uK0s1pR73dyfZMok2mSsBCBu+ojZYQCRNpmPAOSZ38ub\nbX4XoNcOAJtC1cVhXKecxcyKL/vjj9LWRENDQ0NDQ0PjFISTu7IFi2CWxDpmN98sD22XX+7f/8nK\nyuiUACQYuQs3xixwTuxwsgRbxwUmwbHI7IMPypycc44vYZJh+NwXra0IN8bcXPLAAVk7dOtWcv16\nWc7l668lg+0HH8hz9JQp4kI6erS4kT7xBDlggLiRLi1XpWwTM5OUbQVQz4GYNTWV728ra2iWzTH3\nXzD3q9tk7jXLbjL31wLYE9DvF6ZMVXP/CACPrV5BYtf+MPebFaeLw9hOOWJ2331FZ43X0NDQ0NDQ\n0NAoA6hUKbjb4slYx2ziRLJq1cKxtSWZlTEUBIu7nFhGYswstG7NlSfZYhaJMKCUehniItgRkkkR\nAKoqpSqRzAYQbSo/QCm1GrLe2QRIjJgy5f81SdUspdQgiFvi02Z7Z5kyuwBcqJQaDWA6gKsApJpE\nsKZJwCIAXKqU6gZZW20AgHJAwZiiQtDllEZ+PvDRR0CnTqWticZ/DRkZGUhLSyttNTQ0ShX6PNA4\n3aHPgRLG4cPB66ZPl83C4sX+9Xff7ft+yy2y2REXV/g4q8xCdDSwerV/+eLFQEaG73tcnHzecQeQ\nnAxs3AhcfrnUb9wIfPwx8N13Plmrn+nT/cuCISsL6NkTePpp4Ikn5Li4OKBPH+mzb1+pa9gQWLAA\n2LYN6NAByM4WG5lSwJo10ta+fUBsLLB/v3zu21d03+GgTRsZT1ISsGpVybVbDMIiZgDug5Adj7mv\nAMwwP98wywjgcwDzIIk6PoWQIdrqt0ISdnwDIWQzAPSwyWQD+BjA1QAeArANwDAAI20y+QBmQUhd\nDUhSj4kQt0gLli4fAahi7u8FcEaY4y6TWLZM/q9dupS2Jhr/NeibsYaGPg80NPQ58B+Dndw5lVmk\nyl5mkTJ7ub3MfmxxpAwQsmOROIuUAcBnnwFz5gATJwL33APUr+9r88MPgSuuACpXBjp29CeAdnJW\nUrBIWevWwIsvAi1alFzbxSAsYkYywr6vlMqHrBP2gVn0N4SkTSDZyybnAbDJJnMmyfa2+nKQJB5/\n22RiSLawybSBEKvtNpk1Af08FVCvIAtPRwLoDrGsfQmgjVKqOsmdTuMcMGAAqlat6leWlpZW5i5O\n48fL/zY1tbQ10dDQ0NDQ0NDQ0CgGFrkLJHFTp8pnoCUQECJIFi63UEKWsoyMDGRkZAgpq1YNiI3F\n3gEDSqTtUBGuxaxIkDSUUn9DXA/XAIBSKhbAJZCkHwCwDIBLKZVI8gez7CoIiVpukxmhlCpHMs8s\nuxbABpJ7bTJXQdwTLVxjltt1eQDAZJJvmLqcAbHS9YSsjVYI48aNQ1JS0rFOw0nBggXA3LnAtGlA\nRETx8hoaGhoaGhoaGhoaznAywqxatQotTqLFLOxHeqVUlFKquVIqwSyqZ+6fZ+6nA/ifUqqDUqop\nxMVxG2TBZ5D8BcBCAFOVUi2VUpcBeAlABknLYjYHsqj0dKVUvFLqNohL4ws2VcYDaKeUGqiUamRa\ny1pA3BktTIAshr0vQJePAaSEO/bSRn4+8OuvwLBhwI03Au3bA927l7ZWGhoaGhoaGhoaGhrHi2Ox\nmF0M4Cv4spRYZGkmgJ4kn1dKVYGsV+YC4AXQjuRRWxt3QAjUF5BYsXkA+lmVJPcppdqaMisgMWpP\nkZxmk1mmlEoD8Ky5/QbgRpI/2/qZCYlLuw/Aw5YuAHoDuMBhbJUAYP369WFOyYlHt24Sc5mdDVSs\nCHTtKnGSq1eXtmYa/0Xs3bsXq05isKuGRlmEPg80Tnfoc0DjdIeNE1Q6Gf0dCzH7DcCbEIJTxdzv\nQdJ+5kYE+W5BwT8zYuC+vUxBCKBTJsUI+CcVKc4CaNVbbQYiDgC6du1aTDOliyNHgBkzZNPQOFE4\nmaZ7DY2yCn0eaJzu0OeAhgYA4QjfnOhOwk2X7wLwNYBFANpCLFkXANhtkxkEoC+AuwEYAEYAWKiU\namyzms2BZFK8CkAFSFbGyQC6mm3EQNwdP4OscdYUwOtKqd0kXzNlUsx2BkFcE+8A8J4Zu2ZZzbqb\nn68CeNvSxRyDlSTEjoUA7gSQBckMqaGhoaGhoaGhoaFxeqIShJQtPBmdKRaV5SRQWKlRAFJIti5C\n5k8AY0iOM/djISTobpKZSqnGANYBaGEl/zDdFj8GcC7Jv5VSfQA8A6AmyVxTZiTEVTHe3H8LQBWS\nHW19LwPwA8n7bbocBfA+yX42XQ4CGE1yTMiD19DQ0NDQ0NDQ0NDQOEEIN/lHBwArlFKZSqntSqlV\nSil7uvq6kAWgF1llJPcB+A6+ZBvJAHbbMjICEmtGSPZGS2aJRcpMLATQSCll5bFPMY9DgEyKqUs9\nU5eJAO4xF6KuDbHuRUGsdBoaGhoaGhoaGhoaGqWOcGPM6gHoA0n48SyESE1QSmWTnA0hQva1xixs\nN+tgfu6wV5LMU0rtCpDZBH9st9XtNT+L6qeGqcssAIfgW4j6IIT0/RM4OKVUNYiLZha0K6OGhoaG\nhoaGhobG6YwCV0aS/57ozsIlZuUBlAMw1NwAsUD1ATDbrFcAflZKVYBYsO6Hf7KNqgDOVUodBLAf\nksL+8QCZMwDcrJTqAWALhAR+HyATAeAlpdQMAD8CeDCgvkAXSBybpctEAHZLnB1tIYlNNDQ0NDQ0\nNDQ0NDQ0AMlBMedEdxIuMdsPSW9/IXxZErsCsJbFvscsfwTAasii0u8AyAPwg1IqwpSvCFlzrDbE\nopUDIWN/K6XiACRCEodcDuBqAK9ByBsBbDfXNYuEkK1nzf4XmnKWFa1IXYKMLwsAZs+ejcaNG4c5\nNRoaYeDDD4EWLYDatQvX/fknsHIl0KHDydfLxIABAzBu3LhS619DoyxAnwcapzv0OaBxumP9+vVW\ntvask9FfuMRsK4C6djdAc2HpzWZijVsgFjQXyR9Mi9d6SAKOSRCLVA2ItSuS5EKl1DAAYyEkajmE\nZG0HcCaA30luUEpdDrHKbSC5Vyk1AMCvAGJJ/qKUug/ADQBuBbAgRF2c0BEAGjdujKSkpDCnRkMj\nDJx5JtCzJzB9OhAX5yvPygIeeaRw+UlG1apV9TmgcdpDnwcapzv0OaChUYBsk/O8CqANbF5/JPMt\nIaVUG0jIVxOYXn8kZ4baSbjJP5YBiFZK7VVKbVZKLYUs1jwRYgGLBDAOwP+UUh0gLoTZpvLvQ5J6\nrIVYt6YqpVpCUu5HA/iU5N+mzHsQAjVdKRUPIVj1AbyglCpv9vUagHZKqYEAGprtnGfqcnEIuvjB\ntMINCCzX0DghiIsT8tWzp5AxQD6dyNrphpkzfXMSiKwsqT+Z7WhoaGhoaGic7lAAFkD4RTJkWbDu\nkBwWIiBefx9BkiA2BzAewGtKqWtC7SRcYvYugOcA/A2xfLWCZDi8FJJ04yiA5wFshJCrNeYAPjbX\nMLMSdjwKoBbEQjbXbHuq+VkTYpkbCuAmSGr9eyBujLMBVIfEuS0BMBPAKAC/QJjpZnMNsxoh6BKI\nARBXRw2NkwOTnO27uSeeci/GoTRNygAArVv7E1YLFnFtHXS1jhPTjoaGxomBfnmi50BD49RB7/1Z\n/QAAIABJREFUCiSU606Sa0kuBDAMwANKKcsDsQ+ATSQfI7mB5CQA8xCG4ScsYkZyIcmhJBsBuALA\nH5CYrUY2sXQAZwO4EkASgCPmdzveAvATgGYAbjTLbrXVnwHgJQCvQCZhCoSp2tu5GsBdAHoBsNZG\nO08pVT1MXWCzwi0HxKe6Y8eOfltGRkbRk6NRPHr3BpYuda5bulTq7WjUCJgUxOt00iSpD4bAm529\n78CbndW3/ZiZM4GxY/2tWdYxWVnAJZcAQ4fCD9bxTmMJdoONi0O660k85WmDF6OfDE7Kipq7IUNE\nH6eb+9ixomdg3zNnSnszZ/qPu3dvYO5cYOvWwno7jetEoKSsidoqqaFRtqFfnug50NAoQ8jIyCj0\n/D9gQAGnagpgLcmdtkMWQpIaNjH3k1HEUl4hgWTYG8T1cAOE5FjrlLkhJO0IgM422W2QhCGtAAwH\n8Dsk2Ud1sz7OrN8HsWgthmRgXGNrozvEArYAkm0xx+x/vE1mBoDDAB4LRZeA8dQyy7sB4MqVK6lx\njADI2rWd66pVk3qv17/c6yVdrsLlEyeSSslnKOV2GAbpdsunvY/MTOdyr9f/GMMgU1LI5GSpCyxv\n0oSMifHX2TDIhAQyNrZwub1PG7J/Megp5+bVFTz0RLh5cF1hmSLnyOuV/uLjRVd7H4ZBJiUV1rOo\ncWdmkpGRnPPQQ/7lwfrv1atwmYX27WULNp5evZzrbPrvbO5mvwQP913sMH8zZjjOqXUsZ8wo+L6v\npZsPNvNwd5Lz7xB2myWJouYwlHnSOGGYM2dOaavw30fg9bGI6+V/FrYx5+aS+ZuMMjMH+hzQON2x\ncuVKQrz23gHwCf35Q2WTP7Q19zcAGBQg087kJBUZCscKRajQQeJCONYkaDkQX8pYkzzlQZJyABL7\nlQ/gTwD9AFxn1v9oa+seyLpk+RB/zFEADgB40SYzB5ISf7e5/53ZTkdzX0HcH78HMD8UXQLGo4lZ\nSaF2bWdyZpVXq+b/gB/sgZ/k0aPk7mcDSJhJyvY8O5GrVpG7dhWhS+AN3iQdzMwM3ncgOUtMZH5s\nLH+d7mXu74aPrDmRFYskJSSE9pBhGNx+kZt1YHDBArIODP7RqIibsVN/dnJl1y0YsbTrFEg4k5Pl\nmMxMIXNJSUWTsmBzaJVHR5NRUaET8QDk5ZHd6nhIgPde6GF+fuH5c5xbh/KBLaSdB5t5iuwznDYL\n4ETmrDInMhdYFjgfM2aQY8bI72CVW+TNMMhWrcghQ/yPt8ib10umpoqcE+Gz+taET6MsYcwYbjk3\nhavGeQqfZyfqhUhZg2FwTws3U+HhX/Flg5RpaGiETMyuZXBidr3JRyowFI4VipCt8TEAnoKsDXYF\ngM9NAvSyWf+ZqWAbiGvg1wC8JpEaCXGd/BfAPxA3xraQmLORFuOEz4LmgbhI3m/2MdhinPDFnD0F\ncXWcbLY7AcCyUHQJGJdlheuviVkJIJCc2fbz88lNb3iZXcXFj9umc395F9/s4+Wbb5KzZsn9d9o0\n8tFHyfPPl8OGuCYyD4qr4jozD4pPVJ9IQOoiIshLLiG7dSPvvZd86CGyb1/ynnvIHj3I/p0Mrj3b\nzf9d4eGa6m6+mJLJfZEuTm2azn2RLg5o6eX115M33kh27kzedhv5wA0G15zl5pDLPPzZlcJ1lRO5\nEglcVzGR62KT2S3VYLt25A03kI9d6uX+SBcnx6dzf6SLQ1K97Nve4Loabr7Q0cNfz3Pz2d4GH3uM\nHDSIHDxYnqmf+T+DP9d0M8FlsHVrmaa0NPLCSgbX1XRzcJrB+++X8QwYIPMxeDA59W4vD1Vy8ZN2\n6TxUycVpPbx88knyiSfIJ+82uCY6hb9GJ3DrWYn8s24y33ja4KRJ5FujDP7V2M1FT8hN/+NJBj/+\nmPzwJYNbLnDzg4c9/OeCFP7TMJmfD/Nw+3lJPFwhhu+2SefBii6+M8DLDz4gf/iB3LSJ3LyZ3LFD\niPH+T7zMr+pi9hdeedu7xEY0iiKTRSA3l5zxlMFFcHNWLw8Xwc3ZI4ziyZkDgfp5gbTzZBtp55s5\nBotEuG/wnertRDew3KmtQJIdH0+WK+f/EiEmRiy1dmut12GuLauwndiRQvYs4u1yyR/KPkb7w6+1\nH0g67fvBjrHgRAx79ZITIDPTnxj26iUvXW67Tb7b+7STyMA+SsPCWVI4lXUvYaz90OBKJJAAc76w\nvTw5zaxn6Z3lBdLgS4t5gXS6QZ8rGqUIGzGbDGAV/fmDxVmamfuL7YYl+rz+djNUrhWqoNn4alM5\nmor8A0lB/6JZ38MszzdltgGIh8RuPWfKvAtxMaRJtL6DJBCxM87tJhmj+TnZzjjhs3DlmjL7Idau\n5wF8E6ouAWP7FmKZO6WJ2S+/kFu3hn/c7t3k99+Tn3xCzplDTp1Kjh9PjhxJPvUU+cIL5MKF5M8/\nk9u3k//8I9vixeSECeTrr5PLl5Pr15OrV5MHq9dmPsAcKOYD3FG5Ntu3J2vUkH9dP6TLDSgqnZUq\nsYBoWVvNmkKsZs4kH3uM/LpmZxLg4uqd2bcv+fbb0t+UKeSdd5KXXUa2aEFedBHZvDl58cXyDJqa\n6rOWPNrKQ7ebnBwvfU+OT2eXLmSnTuT115Pt2pFXXkledRX5SEvfDfLpqzwFij3RxsMuXYTE3Xgj\n2aED+aqtvbZtpY2+TeWYrud52LAh2aABWb8+WbcuGRdHDqo1gx2bGezbl9y2TX6DAwfI/v3JTgkG\nn4ybwcREsmlTsnFj8oIL5NjzziOHxkh/Q2PSWbs2ec455Lnnkg0bksNturojPCxfXoyEAJkKqUuF\nx2+ur67gK7dk3OU8HBIt/TxdPb2gjWDbZfByF1x8EOncBRdTI7yMiSHPPpvscIaXu5WLg6PSuVu5\neNPZXl5wAdmokYypVi3yrLPkNz/nHBljwwpCph6/3SBJPn677F9c3WBSEnnFFeS118pv18NtcE11\nNx9PEfJ9//UGb7lF6jolGPxKuXnFeQYPHyZvvlhcR4fcYfDxx8kRI+R/Pm2acIUPPyQXLCC/fcvg\n7kQ3V7zg4d4Wbv76mcH168mNG22EdD95+DCZk+PgehRowbTKgjxk5uaSHz3u5cGKLn5zezqzK8by\n6IXx/hbQJk18ZM3rFWtkdLQzAbb6skhYZqbo07ixz9XWyXIaqGcwklrUMRacSLjXS1ap4k86SSFl\ngPzR7W0Hc7m1WySdSPHYscVbOC3LpJN1xmrDIon2B0O79dIqt+Ts7rtW+16vz0qZmuorGzKEvPBC\n/zkcO7Zo3e39O2HwYCG39nFa3y2CG2jJtc/F2LHO82U/1g77HFjtHcND9Kj7DH6NFK5EAv+qa77M\nsF4kBP5GVjvWPAS216uX/LecHtatcVg6NmxY2CXe0nHiRKk/WTAMLqsiFjNPOTeP/mqcvL7LOsL1\nZNBETqMEYSNmD8AWikWf199uAOXN/VGweQXS5/W3wF5W1BYuMXvaJEdHTeXybATrKIAPzP12kEWi\nvzGtVFkQV8YIk3TtgwTRtQWwA5LoIx9iRYsz2/seYjGzJmIMfK6Md5j9jIPPYrYLQAaA+abM+0Xp\n4jC2WyHp9JmamsoOHTr4baeCn/WLL8ovGhlJPvigEKdA/PuvkK8xY+T+dMUV8lDs9LBdqRJ55pny\n4FylSvCH8goVnMuPQpEAj0KxaVOxMD3+OPndC17mVXWR6emky8Vcj5cHDshD7tGj4sLmZxmxYso6\ndy4+tiwQ1oXb4/F/UDX7dnzAsR+TkkImJop7YmJi4Tgu68HR3l5gnyX5ttepP7veKSmOuuZtNJjb\n2s0DH3uYm+rmrlUGt20j96w2mO92M+9LD3NapfBoy2QeXOBhfqIZm2b2k7fYyz//JL/7jvziCyHp\n8+eTc+eSb71Fvvkm+d2dQuS+vjWdkybJM96IEeTw4eTCG6Tuk3bpHDqUfOQRcuBAeY4cPlzknn7a\nfAnwoFjxvnvbZyHLzycXzzS4sY5YE9PSyC5dyOuuE1L9aCsf+b7mGvLqq8m7W4v1cfJgg3/9Je3s\n3i2Wxe+ihKyddRZZubLz/zcYkQ221YsQEti2koeLy4k19OLqBpdWcPPWGh5+XcnNK+sZTE6WlwiJ\nifICoXFj3zk4qLLMU/+IdDaNMbj+jBRmnSkW0KzayZzVMZOHKrn4eYd0HqkQzewKUVxyczqzK4tV\n86WX5EVJejo5bZjBzQ3cXHr7BOZFRHLdzcOYUyWW2fEJ/PMbmZPdH8q5uPdjsXbmbZT/Q5FWvmAk\n0Ol/7mQxjY6WC0pioo98xcYKKbMsgYbhH69ZlBUz8HsgIQ6EnVwGuv8GllskMZAsWq6+9vqEBCHL\nlvuuYcgYY2PlmmUR5MREmYPERP/jrWtNUbo7zam93O5KbZ8XuzXVbskNNhdO/QXG54ZD0ospX1bF\nzUduNti/k8FvkMzfYhJ5pGli0a7YgRZhC4Eu607zZrUxfLj/PSVYuR2hEuNA2Al8IHEwDGYnJXMg\nxvK5ewwOxFjuTgzh3hGMgAQjp5Zl2smN+US5N5cUSSrqGlCcbHHlGhom5syZU+j5PzU11SJmLSBh\nVZ/A3+vvGfq4RBwkHGs0/L3+rrZkitvCJWZRptXJvuUAWApZO+yIud/ZlG9ks1q1NElSLvyTf9wL\n4KDFOM3B7IB/HFoGJAPkAnP/WwB/wUz+AYkx2wZgDyQVf2wxurQKMr6ROEUtZv/8Iw+YvXuLlSs2\nlqxalbz1VrHsJCWR1av7HiKjoqQsLU0ehjMyyBUrxNq2f7+QIztyc8nffye/+op8/33y3XfJefPE\nOpaTI8d8/z25ZIk8vB+yLGZKyFmBW2O4rm2BiT5CSfxhIfAifIwxZn4PhyUZYxYuymKMWaBuToSx\nqDonhHsjD0aEw2gnJ4fcs4f86y85BzYuMniglZvb3vRwX0s3v59r0OsVQvree/Lfz8ggZ8+WZl57\njXzlFfKdh4TMZdzn4ciR5DPPkNPvlrIpd3r40ENiCb73XvK+++R87d9fXFHXvuJlvsvFw6PTmVfV\nxZfv8BYQTgK8vZaH9eqRg6OEvD1aIZ0DI+V7P5XO8uXJihXlhUqVKnKOt60sx49HXxLgg0hnHYj1\nMRXi2nkZvH779csZjI0lzzhDQkLPPptsUc3g4kg3b4j2cFkVN7vV83J5jJt94j1cWdXNtBSDbduK\nsahzZ7nu3Hkn2b07Oaq9lwcquDjvinQequjipDQvX77Dy8MVYrnzzAbMrhDNv2oncupQg5kPeZld\n2cWvb0vnkUqx3FkngYue8HD7RW5+PlViMT//XH7q7+ca3NvCzbUfGlz3scEDzZJ56MJEHkxI5qYv\nDW7cKC6327bJ77pjh7yY2rOHPLhOXlQc/dLLvOQU5ickMD8lhfR6mZ+SwrxLkoWk5rPw+eL1yrlh\nXUTt5DIhobCVskEDn4XQMOSY6OiC60T2F14erRLLHWfH81BCMaTMQnHXAqfz2uuV70lJZHIy93/i\nZW6qw3WgqGtFsM/iHoCLeFDe20LibN97jzx0iHz7fvnP/lwpkTveLabfUElbUdd6i4QNH148KQvW\nllUeeP0P7MtJb/M32t4ghZfByyOXyUud5+8PMmdFzbOFYOQ02P0zcEyhJCQK5qrs9QpBbdXK/z9l\nuS8bhry1a9XKd/4E68NhvEcuc/OPObZrfTBdrZc7FlE2DHkLFmxc4ZBEjdMKNotZEmS95I9M8rXd\n5CwR9OcSrQGshCQk/A3AXXTgHMG2sIhZQMcRAG43rVuvw5cJcSoAA77YrmwAG81jhgNYFcA4u5kD\nnmzKLIYsHm1nnG+YMlfDFw822hx0N4jVbINJxs6CZIssUpcgY0o6VYnZyy/LdXjHDtnfsUOsU61b\ni4vePfeIVeLNN8nffmPhWJ2SRLAYs8DEHxaC3ehOg6yMIaO4h4ESzspY8BBZXFZGJ93s++ES8XAR\nzlvUE92mE0EMRhoDEYzkx8f7W0DtFl8ruUowwmv2nTNuAvPLRfLQo8OYG+Pit2O9/Ha0PPwuftrD\nt98mv3pK9j9+zMNJk8SiPnq0vOQZMUII5pv3iMxLN3v4wAPkmPayP+IaD2+7jbzpJnHtve46cQdO\nTZVT5eKLydHnCIF86sx0xsUJV3nqzPQC0tk+xsPYWHm51C8ivYBEFme1tJPMlUgMy8JpHXsrMrgH\nsVyLxlyJRH6NZNaBUSAXEUE2iDT4VYSbd1XI4C642L1KBleXS+JexHBojLjodj7Ly8vOMfh1JTeH\nxE5gDiL5UrVh3BcRy98rxfOXqAT+UiWRP0Yls8cFXq6uksK1FRK4Eolci3gSYBvlYfPmMpe9eglp\n79dPPCAeeMBH5nv0IJ+40st9kS6OOU/iZf/Xxsvu3cmePcnHbjW4vpabY9p7+HuNFP5eI5njOnm4\nsWYKN9ZM5vMtZBzdKmZwXQ03X3zI4KhRYm19a5TBv+LdXPKMh/82d3PxTIOff04unW1wexM3P+me\nwSNRLv40LIN7ktxc/Z7BH34gf/qJXLNG4lBXrCBXvmNwV6Kbq8Z5uCvRzW/fMrhkCbloEfnBB+Qb\nb5BvXT+DLaoZbNZMXo5Y/1ljhoffl0/m4+XHstfVMpY3bsiQ+NruGfyrsZtfvCYvS1bMkyRK3hEe\n7mwm8bPp6eTLd3h5oLyLM5LSeaCCi+8/6i2w8r/xhnCD5+6Rtued34/5ADfUu5b5UFzQfiIHDiTv\nuEPil59+Wu6dHg/566/kvgViad7/iZcHD5JHv5SXKtb1NK+Nm3t/NLhzJ5nzW5DridfLfLeb2Q8P\n5oFmKezd2Mvl0SLXu7d4quxaZRRPFoJdr4KRU8t6W9Q1uaj7TbBru1VvWY3t9yTrvjJxos8y7HQP\nLapvklu2+F42/T7NU7yusbHcWz+Bj7T0cFdCGC8SgpG9UC2OTm7SFipUkIui0+/ao4e8WbP3VxxB\nLkv4j7qQ2okZj5EzhbOFS8YGA1hrKkiIeW49gBcBpJlEKQaymLMV23UEwBTz+MkmIWtlMk3LDZIA\n2pkyGwAMgrg+HjTrcsz2KsIXX3YJZD20HFs/v5ltFKtLkPGdssTsuuvEfavUEUpWRic4XWSc/P8t\nFOf/H3iBsF/gAi8QVt+BMRn2C6v9GMMonBnP3qfTWI73olSc+4z1djIQY8aInoF9W3EjgQkeAl1g\n7Ho7jauom+JxZmUsFifCXeVY23R6OAo1xizY23x7AhDDOP4YM2vfeqtvkUXrYaUo8hhIMEM5JnB8\ndgJpEc8GDXxufbYXAPnj0pkfG8vchAQeXODh0cvd/Od7cb81DHm59PPP5I8/kr9Mlge1/Q0TuHai\nh7sT3VyWYRS43C5YILGDlqXz7bcljnbWLPKTx+XYZbf7SOIHD3v4+usSdzhlilhCJ00i5z0osotu\nFNnZvT389Hr5/nHbdP7vf3IqTrlT5L5uIVbKty9L58jrPAXtP3+Dh/fdR47r5Cs72CiB2Qs9/ONC\ncdW99lp5douPl5+9aVOyWTOZppYtyUsvlWmfliD9v56Qzquv9v3lLrmEvPdCab93Qw//r4F871HP\nw+515fuC69IL6s85R9zWrXjfYITYKn/QjBEujgQXR6zPOUeI5LZthc+PvT8a3FTXzW6pRsFYhkY7\n9xvYT8WKZL165Li6Iv9czfRCfUdHy9+vd0M5dlXMFSTAd1VnVqsmt5fUVJnrM84orHtgXO1l8DIy\nUp67A63STaLEbfqMM6TfhhUMfmm+FNgFF29FBhdH+hITbdokpwogFut69USfJk0khrpFC/mNL7+c\nbNOGvPMygz+c6ebQyz38qYabj90qCadeus3LQxVd/PT6dB6uLOR05kxy8bNeHoly8cee6TwS5eLy\nF71cvJj89lty1Soh2Zvf9DI31sXfZ3j588/kn5le5sW6uONdL//4g/zzT3LXB0JQ/5nvFcv0XC/z\noqKZFxXF7RMzeTgphdn1GzMnKpY/9ZnII5VjufuceO5tkswtSwzufE+Oz/7CKy+Li7g3/Psvedsl\nYrm/qZqHSyu6ueQNWV4g2AvAZWO8vLq8/L7XVPBw4cIg1+pQ4mPJ0C2OTtd/q9zyW7/5Zv82evSQ\n8h49fGWDBxd+0Wv1Fxsr9U5ITS1sLbXQp488L9gRLIuw/TkhEE7PNCfinlwGUNaJ2QIAdwO4BhKT\n9ZtJrJrbyNArkDiu1pDYrv0AttCfmK2FLLjWFEAHc8Bv0kfMrJT5z5sWs5ct8mYjZkNNC5hlMVtt\nkrTqoegSZHxJwKkXY5aTIxf7554rbU3oTMosWORM47+DE7mOWXE4EW/njqVNp5uO6Z4UUlbGwDm0\n39Qt9x+v9/izMlrt2hOABCN0RekcyjEWnB6YSiLGLHCuEhIKx02FauHMyJB+GjcOHuNll3W55DPJ\nPw7TT88JE8RCMGyYs+XT6xV94+P9iWk4DzBOhDdQXytONjnZ/7t9HAH95W00JA51voeHU9zc6jVo\nGOSWJQaPXu5m3pwM5lV18c9xGdzfys11Hxv8/nvym2/IZcskKdPKleSGhQYPJru5dbaHB5Pd3LjI\n4IYNkkDn778l2VEhfYP9vgE657Z2c8dyScjzy6ei1675HmZfKvGzfg/55vwc/dLLHTskzvTw4YB+\n+/WTe9O11wb1xti3T5JrffmlnFpz55Kr7hbi921aOqdMEQL/0kuSDMtuhbbibUePlkRaEyaQ8/tL\n/ffdpI3Dn3r8+tuyRV4OPP20eL888ohYUPv2FVfo//s/8u67xWX41lvJoVdIe/0SPGzVSpJNXXCB\nzzI9sJw/ObXI9YMoTFqLIp+hyFhlT2IYc1COv6C+n2XYTqwDj78u2ssaNSShVd26kp05KkrI7lcR\n8tJl2zZJ7LQIbsZXMRgXR/a4QCzI05pJtudeF3pZBwZXV3Nz/0cerq7mZl1lsE0b8vZkg97ybqbV\n9nB9LTdnPWNw/nx5ibNoEfn11+T6qV7mxLi4ZY6XmzfTRyLHTfRZR+3noZPHQrDwgptv9idhTqTM\naiPQC8e6Xjq5zFoI5sqamSkv9xo3Du1+VdTYQo3vc5K1JwxyOudTU4VAOiUj8nrFPfUEWd+KiTEr\ne8Ss0MFCgghZO+yUXWDaVn9KWsyWL5df8uuvS1sTDY3TEMe7jplTe4FuMCWxjpl18x071ndzKy55\nQ7CbbFHH2PU6UVkZrT6dkneEQnDs47ATO2vfydJp6eX1lkyMmeXqFdhnKOSsKBfhwHkIEmPmN57S\nijGzEOyFiKX/kCFlJ8Ys8DcojhgXNT9FEOSwEKw/Bx2zs32Wrv3PSjzrn5lebthArl0rpHrZMsm4\n7PWSm/oLgfv53nQuWMCC7aOPJN58/nxybS+RWX9fOj/7TCzU6/tI2dZOfQtYXG6zBB78xMP9Ld30\nzjL40Udixf6+q8guvimdo0YJGR02TAjpkCHk1KGy3Mv273zzk5cnbqxZ9d0cdZ/Be+/1WZAnNUrn\nQx3FJdfKbpn7u8Ftjdy8t63BLl3I17sLke1RzxM063AwYmqVP1JB3Jjbu7xs2FCsmk2byiW6VSsh\njz/FpvC3mAT+HpvI9Wcmc+BNBrt1Iz31ezAf4PaqdZkPcHnzHhwxgnz+eckUPHWquM8unGxwb/0E\n5kTFcusj6cyNjmV2kwTuXGFw925JmOaE7FmZzC8XycNvZIpVMViYgvX/Ma9B+ZsMyTEQzrU+AHt/\nNPjLOW72TxQ35qD//2BtT5zoTCCtH8aJlMbElOyL/xo15FrAMm4xK3Qw0MBU9l2cwgtM2/o5JYnZ\n88/Ls86RI6WtiYaGRpnFsaxJVlbXMbNu4E7p7u0koygLZzBCZC93IgCW9fJ4szKef35w16eiyHtR\n7sOnYlbGYCiu/dLKyhjYVrC2g81HcWQ3XHIWrP3jiTELHGdRiZuCuSq7XMKuypUj69QJbhkOpY9Q\nPBns7YSahMUkskc2GNyxQxI//f47uW6duHR+8w356wNC9tb0SmdmpsQnTp1KLu4i5QtvSOczz8h6\now8/LPGgVm6UHj3I4Vd6CgjFo63EmnnZZULcsirUJQEa5ery3HPFbdXlYqElhOrA4AY0IAFuQAO/\nGFhA3GdjY+W4ChVkygGyCzJ5FJEcj748ikg+WCuTl14qGbL73Wjw51qy3uqGc2W91XH9DK6o6ma3\nOh5m1XNz2jCDL79Mvj1aSO7iZySO0zPD4Kefkp99Jtu8eSyYm6FDxTnq+igZtzvCw2eekQRxRf4W\ngZ92t3vrf2INOCrKvy2LlMXEOP9HjgXDh0ubw4eXbWIG4FkAlwOoA+Ai0/pFAFea9afkAtO28Z2S\nxOyGG8pIfJmGhobGycDxuLGWlXXMxo4tTGwDy5zwH1zHzBHFuTuV1jpmoRLjwDZDsfSFS86Ckd3j\nzcroVBaqjBVbHGgxthJ/2F8+BCanKookFoXA44LFZlmygesHFueKHUgaQyGTVttBlrApcF+sK+Qs\n0I0xL488eFASuf2Z6WVulWgSYE7laC4bI4ls3n5b3GZfeklO3QkTZJpfeUVI0vz55PprxWL5fUpf\nDhwoyWw6dpTEcH3ihTx1ryvrrdau7YvXvCHaU+DcEEq8qLXVrEkOvMng4RQ3cxZ5uLGOm3EwGBEh\nsZKXXCJxke3akfe2NfhTDTdfdWfwYEUXZ7fP4KY4N19+zOD48eT7j3p5pHIs99VswJxK0dxbP4HZ\nlaKYDzA7KoZbtpDZ0THMB5hXkqTMgknOVt57b5kmZq+ZFqc8+BJqjLbV3wVJh38IvgWgPaa1y1pg\nerZJzKyEHtmQrI72Baa3mITN6mcngGkovMD0bvMzD8CvAObCt8B0sbo4jO+UI2Y5OXL9GTGitDXR\n0NDQ0ND4j+NErGNm1QeS3OJwotYxK4p8hpuVccyYwu69VvxsTEzhJFrhkrNQdLUQjjU3GDEN1eLo\nZAUPN8bMat+esMkp83MwWAS9b9/CRN0acwhZhHN/l+VF9rzv4eFL3fzja4ObN5NZWSI2L0MeAAAg\nAElEQVSyc6ckZzl40GEuDYOHkt18a5TBRx6RZD9paWSnTpK07qHmQvhG1hQLZJfqHp55pm99USsW\n0k4Kd0DIWA7AfIA7EFNgObQS7Lhcktm0Xj35KyYliaXymmskJjMtTeI0+/YlH3tMMg+PHy8ZzqdM\nEcI7bx65oetwrgDKLjGjkJfrACyHrDVW4E5o1rlNErQLktTjIgDvmSRsoCkzHOK6uAqy9tmlADaZ\ng25myiyFuDPOBNAYkmjkCICDZn15k2jlAhhoWtaGm/p8EaouDmM75ZJ/6PgyDQ0NDQ0NjRJDSa5j\nFnicZRlOTS2+j5LS1UKo1txgZOtkZ2V0ssIaRmjkLNBqGmKM2TG7KhdVV1x5kFjL/CVe5sfGMqdu\nA+ZFRTO7cQJ/+dTg8uVkjknWcgDOmSOJcl56iRw1ShLsjB4tBq/HH5ekOffdJ8lyunSR5VzatBHr\nXdOmYtQ96ywhg+XKzSHQwW9rhtgyT8wmQuK56pnEx07MYk3lp9vKEs2yweZ+b3PfbZNJN8vONfcX\nmqQr0iazDsB+2/5OAJts+8okb9+EqovD2E45i5mOL9PQ0NDQ0NDQKCGUlXXMbrstuGusffHsQJRW\nVsZw3JiPJcbM2o+KKrCilXhsGWWd36NHxQq4a0AZt5hB0tbvBnAFgBomMbsLQCWzvq6p/Db4x3bt\nATDOlOlpki5rgWkrziwPwI2mzDxTxlpg+n7T0pUHoKop8w8k9sxKlz8Z4ra41qyvV5wuDuM75YjZ\nNdfIpqGhoaGhoaGh8R/BscZrltY6ZqGiOGtcsKyMTglATkTiDwulFGOmKIQkJCilrLgyCxEmOetB\n8g2lVArEDfF1AJ0giTo+hbgeHiaZppQabJKzDSZhOghJdd8dwBMkJyulFkJS358HIN4kV68BeA5A\nPMkNSqkjAGYBuBpCEldDYsi6k6wVoMvtAKqYuu8BsIJkW4fxJQFYuXLlSiQlJYU8L6WF3buBs88G\n0tOBBx4obW00/kvIyMhAWlpaaauhoVGq0OeBxukOfQ5olDhmzgRatwYWL5bPuDhfXVYWcPfdQJMm\nQP36wMMP++piY4H9+4Fy5YBp00TOXh4TA+zbVzI6Pv008OSTwPDhWNW+PVq0aAEALUiuKpkOgiMy\nHGGSEfZ9k6h1JvlBgOhQkr1scpnwJ3S5JNsHtNUjQOYvkp1s9fGQ7I12mc8D+rk/oB6QeLiuEOK3\nHMDHANoopaqT3Ok0zgEDBqBq1ap+ZWlpaWXu4jRrlnzedFPp6qHx34O+GWto6PNAQ0OfAxolDotQ\n2QmZhbg4IWxOCEa+9u3zkbPjREZGBjIyMoCFC4FGjYAVK7B30aLjbjcchEXMQsDfkFivGhD3RAtn\nA/jBJnO2/SClVDkAZ5h1lkyNgLbPhpCu7cXI2OsVgL4AJpN8w+xrqynXE8DzToMYN25cmbeYHTwI\njBkD3HwzUKtWaWujoaGhoaGhoaGhcYJQlIdfCVnKnIwwq1atsixmJwURxYuEDpIGhBBdZZUppWIB\nXALgG7NoGQCXUirRduhVEBK13CaTahI2C9cC2EByr03mKvjjGrPcrksTAIsCdFkBIOWYB1rK2LMH\nuPVWYNcuYMSI0tZGQ0NDQ0NDQ0NDQ+N4EbbFTCkVBaABhEgBQD2lVHMAu0huhWRY/J9S6ncAWQCe\ngcSIvQ8AJH8xY8imKqX6QNYlewlABknLYjYHwBMApiulRgNoCuAhAP1sqowHsFgpNRDinpgGSfDR\n2yYzDcD/AFyglGpq02UFZKHsUwbz5wObNgE//gh8+KGUvfOOuOBqaGhoaGhoaGhoaJzaOBZXxosB\nfAVf+sgXzPKZAHqSfF4pVQWSJdEFwAugHcmjtjbugKTd/wKSPGQebKSL5D6lVFtTZgUkNf5TJKfZ\nZJYppdIAPGtuv0GyOv5s6+dlCDF7HELKvADaAbgHhWPRAKASAKxfvz7MKTnx6NMH2LsXqFsX6NQJ\nuOUWSfyx6oSHIWqcjti7dy9W6T+XxmkOfR5onO7Q54DG6Q4bJ6h0Mvo7FmL2G4A3IQSnirnfIyBT\nSUSQ7xYUfBY3p317mYKQqMB6q22LYNGhr50Q4hdhkwf8Y9HsiAOArl27OlSVDaxfL9uMGaWticZ/\nHSfTp1pDo6xCnwcapzv0OaChAUA4wjfFCR0vwiJmSikXZC2wRZD1x3YCuACytpklMwiScONuAAaA\nEQAWKqUa26xmcyCJO66CuDLOgFjYupptxEAWmf4MwL0QV8bXlVK7Sb5myqSY7QyCuDLeAeA9pVSi\nzWo2EELYvgYwxNLF7HOCwxAXArgT4oKZHc7caGhoaGhoaGhoaGj8p1AJQsoWnozOwl3HbBSAFJKt\ni5D5E8AYkuPM/ViIdepukplKqcYA1kHWA/jBlGkLIVfnkvzbjD17BkBNkrmmzEiIq2K8uf8WgCok\nO9r6XgbgB5L323T5HMCtEIK3DsB3kDXS6pH8J+TBa2hoaGhoaGhoaGhonCCEm5WxA4AVSqlMpdR2\npdQqpZR9HbG6AGrCzIIISLwYhAxZWRCTAey2SJmJLyCWrUtsMkssUmZiIYBGSilrgbEU8zgEyKSY\nutQzdXkBwMMAnoYsOH0QwAealGloaGhoaGhoaGholBWEG2PWEEC8+Z0AzgIwRSmVTXI2gPPMuq+U\nUhUgROl+iMWsplnXCEAFpdRBAPsBvAFJzrHLJtMYQF2lVDaALZDkHlYq/ZoA9gKoDcn+OBrAjwAe\nDOjnXEsXiOuipctLCEJIlVLVIC6aWdCujBoaGhoaGhoaGhqnMwpcGUn+e6I7C5eYKQCHIApayTie\nBtAHwGwA/c3y/wOwGcAkAO8A+AsAlVIRALqbMskQcjULwFGzjEqpOABJANYCuB3A1QBeA3CfTeY2\nU/e5EKI1AEK8RsKXDKRIXYKMry0ksYmGhoaGhoaGhoaGhgYgOSjmnOhOwiVm+wHk2d0AlVKrAdxg\nxpLdACE9m0iuUUr1ALAewA8AlkCIT3UA+0iuBbBWKTUMwCgA0ZAFofsA2AfAILkBwAal1OWQ9ckI\nsYoNMHXZYK6Ldp/Z97UAtoeoixOyAGD27Nlo3LhxmFOjoREG/vwTGD4cePJJoHbt4stPMgYMGIBx\n48aVWv8aGmUB+jzQON2hzwGN0x3r16+3srVnnYz+wiVmWwHEK6X+gLj6LYMk0tgMWdw5EkKcrgKw\nhuQGpdRWSFbFURAr2QYAF5rZE3+AWLpegaS1Xw6JB1sFIFUpVY5knk1mA8Ri18Ls+yoAE0hSKfUF\nJAbubchaa8Xp4oSOANC4cWMkJSWFOTUaGmEgKQm46CKgZ09g+nQgLg7IygIeeQSYO1f2SxFVq1Yt\nvXNg5kygdWvnOcjKAhYvBu6++2RrpXEaolTPAw2NMgB9DmhoFCBbKXUegFcBtIEtHItkviWklGoD\nyW/RBGY4FsmZoXYSbvKPKRAr1FwAwwG0hLgKToXEdh0FMA4S+9VBKdUUQAyAAwDeN2W2QIjWVKVU\nSwB1IS6HHpJ/mzJLzLamK6XiIXFplQCMh1jcykEWtG6nlBqolGoEoAGAMyCLUtcIQRc/mO6RA8Kc\nDw2NY0dcHDB9OvJ79MS2Nxf7k7TTGa1by1xkZfmXZ2VJeeugSWH9MXNm4Tbsbc0M+TqpoaGhcWKg\nr1MaGqcKFIAFEMNPMmRZsO6QkC4RkHCsjyBJEJtDeMtrSqlrQu0kLGJGciKAGwFcCWGMZ5iK3mET\nGw9gI4D3AKyBkKH3bWuYAcCjAGpBLGRWBkf7umJHAAwFcBMkxf2jEEL4uk3mJwg5GwXgF0hGxyzb\nGmah6mJhACQGTeO/iHBvfjNnAmPHOh+TlQW88ELJ3DDj4vB2oydxbtc2eD/hyWMjZf+1G7tJWP3I\nmUXKwiGuJUXwNDQ0Tgz+a9euY4G+TmlonCpIAXAhgDtJriW5EMAwAA8opSwPxD6QEKrHSG4gOQnA\nPIRh+AnXYgaSC0g2A9AaYn06BMAFiQ+rAEmycTaEvCUByAOQah7+N8Sa9RaEWDWDsE0AaG+TuQCS\n1OMVyCTMgRDA1pBFrfMAdAFwF4BekCyOmwCcq5SqHqIuBVBKlYe4Ry4HxKe6Y8eOfltGRka4U6UR\niN69gaVLneuWLpV6Oxo1AiZNcpafNEnqQ8U//wB33OF887vjDqm3PyS0bg28+y6QliZl1kOCJf/K\nK0D9+s59hfNAkZWF+m8OR2t4UGvq8OAPKUXhWG7s9rHav/fuLa6UW7f62rDG4vQbhfubhgqTnOXd\n3RNrJy4Gj8WaaCN4+ZuysHQpcGRDlrZMamiUFWhSUnIvojQ0NI4bGRkZhZ7/Bwwo4FRNAawludN2\nyEIAVSFui4BY0oIu5RUSSIa9QRJ1bABwPYAciNUrFmLpygHQ2ZRrCIkdywfQCsB1AHJNmeqmzD2Q\ntcV2Q8yDowDsgMSFWf3NAfAngAXm/reQ7IrjzX0FiX/bA+CxUHQJGE8ts7wbAK5cuZIaxwiAPP98\n57qzz5Z6r9e/3OslXa7C5RMnkkrJZyjlRcEwyORkMiVFvltlKSlSbhiyud2F6xMS5NPr9cl7vf6y\n9n6cyoPodDDZzTow2LUrWQcG97cK8Vin8QXqXpQe9nr798xMMjKScx56yL882G8UbnmYGNfJQwKc\n1s1TuHLGjKLHN2NGwXejrpup8HBjnWLmN9Q2j/cYO3r1Cj5PXq/Ua5QK5syZU9oq/PdhGGTjxtzz\nkZe5uXS+lhV3Dv0XYBjMbe3mW308PHzpMd4HTgD0OaBxumPlypWEeO29A+AT+vOHyiZ/aGvubwAw\nKECmHcQwVJGhcKxQhGyNj4FYnOaZZOlzSCzXy2b9+6by10MsUF8D8EIymfSDWOj+hqxD1gySpXE7\nxI0xH+KPGWcO4HtIbNn9Zh/PQxamBoA0s59xEIvaZAD/AsgAMD8UXQLGpYlZSeH8853JmVV+9tkF\nD+x5eWTWbC/zHR7g9+8np08nM66YyHwoGo9O5L//kn8Nk/2MKyaySxdy0CDy88/JLVvIf/4h9+0j\n9+whd+wg//iDzMoif/uN/Pln8tfPDB5OSOaBZinc9LqHB5qlcF/TZK772OBPP5Hr1pFZHiFLv38h\nZb9O9/JolVhujmnMXXGJ3HdRMtd8YHDVKnLdxwb3t3Rz/ScGf/yRXP+JwQOXuJnlMbh5M/nvv+Th\nw+SRI+TRo2RuLpmXR+bnk4fXG8y+1M1HbjYYFUXu2iVT072NwcOXuvnvSoO7d8s8HDokx+fnFz31\n+9ca3JXg5rqXPcxNDeHGHkjOLOKamUnGxJBJSTy83uDhz4shWYEkrIRI2V/LDH6phFB5ItzcsTxg\nPMHIZ0B5djZ5o0sI3vXRHu7bV0SnIbZ53MfYEThfM2aQY8bI72CVW+TNMMhWrcghQ/yPt8ib10um\npopcIOGbMUP2rU9LztLV/vBr7R8v6dTQCAGHPvNyF1wclZgR3gum/xjmPSjXqUm3OryI0tDQKBWE\nSMyuZXBidr3JayowFK4VipCt8e9NixdNRf6BpKB/0azvYbNKEcA2yILU3wEYacq8a1qzaCr6HYCo\nAMa53SRjND8n2xmnjUhZuuw3SdVoAMtC1cU2rvIQ61p/TcxKAIHk7PzzmQ/wYM3zOWUK+dTVXu5R\nLvaPSOcuuNguxsv4eLJRI7JBA7JuXbJ8eWni3HPJ+zCReVCch87Mg+J9mMgGDchrriFr1BC5ULc6\nMLgSCSTAlUhgHRiOMosghGAR3LwVGQWVqfAUKevUntPWDTNYB4af4e+jj8iKFaXNbpjheFxEhMxN\nxYryGRlJlisn5QCZCrmxt4aHtWqxYIuLk/m96CKycWOyeXPy0kvJ6y40uKS8m7ec7eEPlVO4ukoy\n747z8MfIJO5BDB+E/EYdz/SyVSuySxeyZ0+yd2+yXz/y4YfJxx4jX+3q5aFKLn7SLp2HKrk4+z4v\nJ0wgp04lp00jX32VnDxZvs+aRb79Njl3Lvnmm0LAp0yRutdfJ2fOJF8ZZPC7aDcTzzCYlUUmnmFw\nebSbGSMNfvIJuWQJuXy5kO19Ld389TODa9aQv30uxHrTlwbXrSO/+IIcnCa/0coXPfxKuTnwJoM7\ndwpRdkS41sdjPcYOr7ygOPSZSb7i4+WHzcwsqGdMDNmkiWwxMVJmJ3XW98xM6dtO7Kw2XC75w9nl\nAq2/waypRY3XCeFYAsO1GlqE0Yk42suLIo4WAQ5GtseOlX4D+7GT5MB+2reXzal9iwyPGSPfb7tN\n+gjsszjdj8fCWkaJ9owZLLjO/vFihk+f04iU0TC4uprcS76LOo3GHQrC/d+W0f+5xqkJGzGbDGAV\n/flDnMkzmpn7iy1OZJPpbhmWQtmUeVBIUEp1A5AOoCuAX83OhgB4g2R3pdTnkPT0bshaZJNsZOoL\nAP8zyVw+JO7LWmB6OsQF8Tqz3U2QzIz3QhaYTgfwFCTzSWWTdL0KyQz5FiSo7hbI4tAtSF5anC4k\nhwSM7Vuz37TU1FRUrVrVb+xpaWlIS0sLea5KA1u3AkOHAi4XMHgwUKtWcFkS2LED2LDBt/3+O7Bz\nJ7B7N3DwIHD4MHDoEHDkCBAdDTRtCpx7LlCtGlCunLTz88/A6tVAbCzQpInIHT0KjHu/Dmof3YIc\nRKA88vEbzkcjbEZEBHDxxcDjVcajs6c/vuqUDm9iP+zaJW1a2znnAO3aSRjX3r1AbqebUM0zHzsu\n74z8ue+iZk3pPz9fdN+8GcjOlq1cOaB8ed9WoYJ8kkDEliw0H34Ton79AQcbJmLzuHdxuEYcjh6V\nto4cAZQCqv20GM0eaoPfnsnAOfMmoAIPI+eoQn6Fitg8MgPZNeOQny/HRK1YjCYPtMHPL3uwq2lr\n5OQAOTnA/v0yhyQKZK3vlSrJnF18sf9yZX/8AfzwA5CbC+Tlyae12ffz80VP+3bWwSy0zeyJP/7v\nScSOG463rp2OfWfGgZTfxNoiI0Wvw4eBKlWA5COL0W16G0y4yYO8PGDA+20wo7sHdfetRut3++O7\nO9KxoEE/bN0q/7H9+6X/Q4d8euXlAXftGo/he/tjaHQ6XinfD4cPy+8BiH6hXmrqIAszy/XEpKTp\neHRSHFq2BFasAJ7umYX+a3uiJ6ZjM+L85KejJ4bjSTyJ4X71dZCFmRE9sXbAdPQdG4d5Y7NQ/bGe\n6E6RqVxZ/rMxMfJZubLMT12VhYfX9cSMOk+i57bheC1lOnbFxqFCBfndIiMLb9X2Z+GGd3riu+ue\nRMpnw7H47uk4XCOuoD4iAqhYUc7PnBzz/xgh87hjB/DVM0vxyh8dMOHMpzBg1xM4fNa5iK4diwOT\nM1C1KlChS3uoDb9AZWTIyX3ddTKxn3wiE9GhA/Dhh8Dll/tiVPr0Ae65B5gyReIiu3QB+vcH5swB\nbrlF4gCdjrPHtgSW/T971x5fc/3/n+9t7jaHhBBTbhvVTOQWTm5RFN3oQqQkpCkJSUo3lKWppERf\nnJouSgpFh6P8KnRRacRn0oXIZSOz2Z6/P16fj/PZ2TnbOdvY8H4+Huexfd7v1+f9fr3fn+vz87q8\ng41/8W07v/JQZO06PfEE8NhjeXXzLfcHK16UBFyu3OO1yqdPl3bs7f3xB9CrF9CoEfDii7nLe/aU\n/VaskJul1c6YMd7j8MwzwPbtQP36cuJZ8cu+fQbSPb+56tEDmD9fjq192YkFC+Rm+vXXwPLlMp4d\nO2TZidRU4L33pNxfn1Y7a9fmXcbCWr7Cqh80qFDLXQzrkYqhXw3BvDL3YFr6cPzz+Cu4eNETMl87\ndgTXr4W775Zt+9zY52jBAqnr1Enm6/77gREj8rZ95Agwa5Y8YOzIr/0JE4CdO4G33/Y/9qeekoe0\n71ympiKn/wA8+t2N+O6iGxD763t4ut1ylFukY8wABL7nFFe5hoYJl8uVJ6fE4cOHsW7dOgAYCeEj\nF9CMM1NK3QMxCtUgmaWUehZAT5KXWfsrpRYDcJDsFZQSwTI4k8BdByE3mRALUxa81rNM85cDIMqU\nb2Ju/wVxZbSsXj/Y2hwGcW3Mgbg3PgdJKvKCTcYF4Ad4XRm/NtvpY24riEVsI4APIDFmmaaMX138\njO1myNpsZ6TFLCdHvNCqVyerVSMrViQff5zcto3csoX85BOxWjz4INmhg3wwt1thLr6YvPpqcuBA\nsYRMnEhOnUq+8AI5e7b837+/WFksq0uTJvJxeNIkMiGB7NFDPgh360Zecw2ZCTHjZCGMb79NfvWV\nuBme/HKfmBicy5sVU9a3b+ixZXbYY8rc7rwxZ3Y5p5N0ucioKIkxs6wH9pg0u6zbXbJfdwtrsbHr\nb5+b+HixygR7jAIc05wccd+0cOKEuGYeOiTum0ePei1XOTlkVhaZOXc+c3b61/vITwb3Pz+fP/9M\nbt4s3Xz1FbklSSyFP77kpttNfvEF+e0Sg0evcDJre+62dnsM7mnm5DvPGUxMlHN73DhyxAixBg4a\nRN50EznxSmlzXBs3O3eWc7tVKzFYNWlCXnQRWb8+WaeOWG7PO4/sVUn26VrGzfDw0Ky5XbuSn/VO\nJAG+0y6Rjcsa/BJtuQlx3IQW/BJteAOSeQAOji2XyDRUZhoqcWJkIg8qsWrWqiUuseefT8Y5DK6L\ncHJS1VnMQgRfqTmJaREOvnxVMn+t7WRiXze31XUyqb+H2y50cv5gN3c2cPLlhw3OmiXX/auvijXT\n9YzBPxo7+cEDbv7T3MnPXze4YgW5erVYLzdsIDduJH/4QdyGt28XN+J/3vcwu4qDaZ94mJ5OnnCL\nZTBzjSeva26oLrHWuWtZ/Hz/BhnnmSfONNA1bm8/Pp6sVEn++sZg2v/3tX4ahuxTubLcVzwe6Ss+\nPv/YVV8EmivLCupr7cxPP9/xFjTPgealoHtPgPJjWw26w+S8W7aMHFhOLGfr+88Krd9Ac+Ov3Gpj\nypTcz5RA5cG2b39e5DeHdt1NN/LDzduyPTzcd6mT0TC4ZHqAebQjkGVo6FA5F3wtQ0OHypj8WVXt\n1tZgrLL+ZKyy8ePF5dpuVbb2syzDHTv619FXFwuhPuP8ycfE5H8/0ZY0DT+wWcxamlzkU+QOx3qS\nuS1oR0wuYw/H6koGybWCFTQ7rARxB4yFZCB50CQ7H0Dy+WdD3BT72vb5w5RpBbFw/YbcyT+izfo0\niEvhWkh2RDt5u9Mc2Cfwuh2mwEz+YcrMh2SIHAuxxuWnS+sA43vmTCVm69fL0Vyxgjx4kBw7lixb\nNq8bXHS0eNA88wz5/vsSV5WRcQoUstwZLR87y60x1Jcv30QfhUn8QQZ+4fKXEMR6cNoTf9jrAyUA\nKSnXm8K6m/m6rPmJMcvzUucPpyjGLGgEIsdFcWcpDOH2s49FNo8dI48cIffuJXfsIHfvJv/4g9y1\ni9y/X+IQfcntgY88/PEl98kLePk4N994g1xzvZC3z65N5Ipe8v/y7omcMoV84gkhmk89Jdf4ontk\nf/clI0mAcy9JZKtW5NBGUn5HPTcbNSJvv1C2+1Zz0+GQe0eZMt7LFyCd4SLj685b0K89JH7Icott\nD8/JuvBwccutXJmsWpW8poqHB5WDk6sm8lCYgwMu9LB5c7JFC3nPa9eO7NRJSOzVV5N3dTH4Y3Un\nX7jCxfQyDia2c/Hnmk4+eINx0uX23nuFdI8eTY4ZI/fGRx6Rj0+PPUbOHG3w97pt+VetOP59QQvu\nrtuGM0cbJ+fymWfIVx8xuKuhk8sHunisgoMrB7v4z4XxzCgfyQ39E5lR0cFPJ3q4aBG5cCH58SMe\nZlR08PvBicysGMW0+rFMaxjHtIYteDCmDTdM9/Dfpm25v34c954fy/TwSN5ZwcVfagnp3bqV3LNH\nzpn0dG/s7L//yjn055/kbpeHWZEO/jIskVmVHdy1yMM//iD3fm0wo73EZO771uDxy9swq1Vbpn3i\nYVarNsxq3Za/zfdwV502/PuCFsyIbxPwQ0iecztYEhzkS/R/vxhMqevkxeEGd+wQuezOTr7RzcUD\ncHDBtclMb+Xk/qUenugUAvk2XYP/XuLhzp3koY/93JPMvtLGTmEOFP99YApzbKQsY2YSDUOu1ays\nvO0HvOcVNHbfuRw/nmzblm8M9nBtuJMnfjPYqhXZpw+Dv0/5zoOZxOmkK7SFQM/PYO/hgQi+vb5S\nJfnFxnqfk3FxQlqTk73Pz6Qk/zrm8/zI2WlwZwMnZ93glmNlGPmTyORkZl9wAX+d42Z25xDO10Bt\nBktsg3GTPhtJ4FnqQmojZvEALoSsU3bEJGXPAQhjbi7RCcAmAMcAbAdwh72+oF9IxMzssDkkpisL\nwAGTPb4ASchxDMDLAAzIqtgtTdnd5r5zTKZpZ5y9zQEvMmVSIJkZ7YwzyZTpCW982QSzv4GQBCDf\nmzqdH4wuAcYWf6YSs1GjJB7Lbp3Yt49ctUpI265dfh4upwp+Yszok/gjFwLdiIszK+OMGf6/CluE\nZMaM3Ddn+43V34N1wgSyadPQydCpQGFuhr6kzCcr48mv+yWclbFAhPoV9VS1WVQ9/L0YRUXJy01c\nnDCTNm28cWOJicJmKlUKbNW0dJg1S47ppEm5rSoWgbReVvIhoTk7pa2s1W5mdpCX/t9/F5L5669i\nld+8mfz6a7nffPGF3HuWLyeXLiW/GywE8qv+iZw7V2IJ584lX3lF1Hv+efK554QILe8hskuvSuSY\nMXJvu/deeecZNIi89Vby5pvFgH7tteRDrYQwJjWS/UZd6mb79jJdrVrJ1F16qVg6mzYlGzWSONZ6\n9cTaWbs22bealwBf53CzTh2JzaxRQyyhVauSPSuKzJgI6ccZ5uYomH0iMQ8htddZsZ92YmsveyVG\nZPudFxrpDdS/Pfb1S7Tll2iT5//NqsVJfcLD5VtMzZoyN7Gx5OWXi1GjY0chw7dcIXGf91Rx8XC4\ng1NiXfz+PCeHdjV4ww3iUXHLLeSNN8qxubOzwc1VnUyId3NzVSdv72Cwe3c5xRIhrG8AACAASURB\nVFq3Jhs3Ju9UEms7bVruayY7m1xwt4e/qKZsD8/JWN8DcPDuKBc3VHTy+jiDPXqQPXvKMW7VSoj7\nZZeJ54jvB4F+NTxs2VLqmzSRY2rN0/MYzRyAn6I7s6E4KiIp13xaPKNrVzkHH3yQfOkWD4+Wc/Cj\nrhJXO3+oh889J4+NmaMNbr/QyZdudHNntJPzHjP42mtihX7xRfK1CQZTL3Ly3ZtcPFrOwedbu7hG\nOTl+gFx78+ZJv2PGiMV68WKJyf3gA3LZMvkA+/nncslufNfg4ZZOblkmCat+X2fweHsnjy9KZo7D\nwRPuADGmoZCwQHL+ZKz7kkXCYmKkLCYmr2U4UBxsgOfGG294r5uXb3GL1T0f/XMcDr4cM4sEOLGD\nm5mZDO5eHeo7ia+8vw/BVrlScoL6ezYMHkyWL+/dtqyK/pCcLPX+UNj9iorCfiQu5bATM4bImQrz\nC5WUjTetWemQLIgpJhl600aGIiGLOVtJNzIBzGFuYtbaZJo0LVsEcDW9xGwcxPXxqFmXZbZX1kbM\nroDEl2XZ+tlutlGgLgHGd8YSs9hY8p57SloLBpeV0R/8uS40bhyYfCUlSX2wCIa8hEJwzvQvQ3b9\nfRMb2N1L7GPxd4xKMtX7qXgIFKbNourh7yXAMPK6wDVr5t22vkxXruz/67XVt/XiY5Ex36/Ugfbz\nfZkoDtIZjFtsKLJ2XVwukXe5Qj/21kuUnQAHOpb2fkx33+yZicxxOJjxuYdHj5ruuabL5pGnE5kd\nGcWMhrE8FhPHjNgWPNaiDfe+5+Hxlm2ZdWmcHOfISNLlYo7TyT+/NLh2rbyEL1okXb3zjhyy994j\nP/xQCO+3M8Vitv+xRGZFOrh5locffywv7h99RK5/Sl5g1z7p5hePy/9rJrv5+ST5P+vSOKYtE9fU\nhVMNvvCCEOMJE8gHHhBr4+23y++228gBA8gZvWVfV1shhBPau3nNNTxJuLp0kf979iSvv56c3Fnk\nH+vs5o03Cmnr35+86y7p45VXyN9+Y8Bz6shPBg+2cHLjWHFvdPeTfpNucvOuuyQZ0XXXkcOGib53\n3ikk/sknhdz8PEzkvx2YyIcflmfkffcJ4XnmGflAsO5J0XF/7JUkwF+a9uULL0gSolWrJAxgxgzy\n/vtF/3bt5NHTuDH5RHVp/9GoRJ5/vpwaUVFC9m+rK+32reZm+fLy+CtThqxQQWSujZT6KdWkjQVD\n3Dx6VMadnS0W3lq15D2+IIIeKAmVRU7HRIi7c78aHjZqRA5p7OHhcAen103k4XAHR8Z52K2bfOjo\n10+O0R13kFO6eZhexsEFLRN5pKyD06/zcPhwcvhwmcf77ycTb/TwSFkH32knMs9e6+GM66Vsadwk\nnlDh3F3pYu6oGMvDKpIJtV38rpqTY28yOGKEENz/yjm4omcij5V38P0xHr7+usz/4sWSLCoxUcIl\nmpQz+MsFTiaPkHHecoXBmTPJlZM8zKzs4E+vevjrr5LtObOyg1OaJ/MLJW7ba5R8HFi/Xsjsn02c\n/HySm8fbB7hfBCKmwRJbX3JmbVevLgdt8ODc8oMH5y0PZPkMVF7Y/QK9z9gz+foimI++/rbPQJR2\nYvYJZFHnGMhCax+bBOg1SJKNbACvQ1LSdwLQAhK3tcPcfwqAzQC2QBZcu8S0eBHAa6bMWrONI5AU\n+U0AvGXKdIPXlXGa2bZlMUsxiVf1YHQJML54AOzYsSN79+6d61ea1/LYu1eO5KJFJa0J/ZMyCxY5\n09AoDpwKclwa1jGzP9CTk731Z1pWRnufwXwRD9Ul1tIhWPe6QG2cTTFmvgTbN3a0bVshn3YX7WCP\nZagk2K5DYWOlrLE1bRo6+Q6G5Fs6jh4tz6bu3YP3xsivfT9jz8nx028QY8rKEnfWgwfFC+bvv2V5\nmJ07JYb8l18ktvPXOUL0Nj7v5kcfCTGdP5/c0F+I34qeiZw4Uax999xDvtNeyhe2TuRttwnp7NNH\nXISvukpi0Tt1Il9qKHLTL0xkfLycPi1aiOWxeXM5vZ+t7ZVp1Urqpl9oxsvWHHmSQb7bUcrGt3Oz\ndWuv9XJyVSkfWy7Rb2xuhQpk+zoGU+o4efRnmaPP5hrc7HCyYURuEmpZSG9AMr8s7+TaBSK/fqFB\nT1kvae1kWt46ws3atcmWLYV0X3WV98PCY1cJwXS1TeTRcg4m9ffw0UfJN+/y8Fh5B939xI35w7Ee\nLlkil/hHHwmhX7VK+kxr3pZHm8Txv6YteDSuDf/80mDaLYOZA/DYbYPlQ44/UmbBl0wVRMoKs1+g\ne0B+pLOAaz+jvZM/zba5nNpR0DOzY0f/16t1Mvj74BsZWSzvl4sXL87z/t+xY8fSS8zy7CwkiCZB\nO2MXmLb1c0ZazJYskSP5xx8lrYmGhkaR4S8+4UxcxywUN9dQXWJ9yVIgEpXfy7s/EuZb7o/sWSQ5\nPj5vueXGZR0rO8G2yHCLFiLXrJl/QliQ7gXNlW8CECt21OORvqOivPoVRMADzXdBJLi4vpoXlnwH\nQ/Kttq1EH1OmFJz4I5j2Cxp7cXxQCDRPviQ4EHkM1jIdjJw/Gats0iT5KHHxxbkswwXpmJ0tcbdH\njkiyqJydRsDzLMcpZG33bvKPh4XgpQ6axCOtnXliJ7O2G0y73MmUNzzM7uzk3mQ39zZzctp9Bu+5\nR9xU+/cXV9xevYSkzWwgbT5TK5GNG8v35Zo1yYcrSPloP27M9p8/N2aAfBVCzrahAXMAzsFgli9P\nVqkijkXR0V6X4kkxycxSEfy4wUieUBF8tWsy77+ffOghcvJkeVzMmiWW3WnTxBo8cSL5xtXJPKEi\n+H+tRzI7LIJfJSRzzRry++9lKv/6S2Kc09LI4ykyl5vfN7hqFfOep0FeyxkZkjSuaxkZ99jWbu7f\nH+B8DXTf8P2oaKFCBS85s8MiZZGRfnUqFGweW6XdYvYUgA4A6kNizV41lR1s1i81t8+oBaZt4zsj\nidnIkXLf09DQ0Cg10OuYnf51zJKTJTjOl2xZL7/jx+d+0fIlZ/m5JgVLgotqZS1svxaCIfm+pKwk\nszIGM6Zg5sm3rYIs5gVZpoMht/5kTkWMWTAfiOwEr2LFwBYlywIbDNEIktjmrPPw338l0/CePdJU\naiq5a63Bo5e15ZEmcUxv3IKHm7XhZ3NlLc6PPiLTajQgAR6q3oCvvCLxhzNmiEvxxIni7nvPPeJO\n/HEDsTwuqTWSLVvKd51GjSRONipKkihFRgqxq1ZNCGRsLPlmpOw3CyMLdIm9ONzrEusOl3VE69Qh\nO9Q1uKGik0MbubmxipM3Xm7wyivFotqpk9eC2qSJuOtGQ5L6fPG4m+sinGxdw+CECeKa+tlnEoe8\nZZnBI1c4JUvyHjLtR0nGk4ew+865Rc4sEnYqSBmZK56wtBOz103LVTa8sWGGrf4O0yL2H7wLQLsh\niTmsBaYXQtYys+LGMiAxavYFpn83CVu2Wb7f7Nt3gemD5t9syPpnyfAuMF2gLn7Gd0YSs+bNJc23\nhoaGhsY5jECxo76xInYSFgyBDYUEF5eLcWHJdzAk39rXXxyz1WagOOb82h8/Xgi3P1hW7KJ+UPDd\nxx+pOEuzMgZEsPqH8tEgUJtFjTGzti33xQZCzvy6MVqwjufIkcG5MfrZLycigmnzkrltmyRpWrWK\n/Phjyc799tsS0zd7NvnhGDcJ8J373Hz6aVl2afx4MukmKX+6h5sDB0oMohV/OmyYxB0mJJALpgjh\nsuby7w0Gf6rp5OXVjaBiI8PDhceffz7Zr4aHh8IcfK6OxEKOauHhNdeQh8IimQMwC2AOwLQykXzi\nCfnmZSXYSUqSZDGLF8sYP/1UklJ98424AO/cKW7Bhw9TksL4g3m9bBo3rvQSMwp5uRqy0POnpqJ3\n2uoGwJutsbdpVVtqkq9nTZk5JjHbDOByAO0g6SQJoLspsw2SPn8BJJ7NWmPMNwHICQBjTMvaFHP7\nu2B18TO2My7G7J9/5Cj+738lrYmGhoaGhobGacO5tI5ZIARr8SOD/2gQqM3iyMroLwFISceY2fXz\n5xIbqDzQ/gGI7+EfDO7cKcs0bdwo0/XtDCF8qx9z8803yZdfliy9ltXw/c7eWMhbbpE4yG7dyCyT\n3WUBbNBAEuVERckQy5cXy11BFkL7r1w5K3H4Ylao0JsVK/ZmVFRvxlZsziuFn5ReYkYhMEkAdpnk\nqI+t3Gkq/4itLMqUe9Pcnm3KtLDJWAlAnPQSs2MAImwyHwPINv8vY7b5tY9e/wDYGawufsZ1xlnM\n3n1XjuLu3SWtiYaGhoaGhobGacSpyAx8Ktcxu/FGeWnr0CF3eUlmZSQLjoUMxvUzVGt5QYQvkCup\n5b5o/QK4MZ44IXGK+/bJO/K2bbKsyxdfyHITy5ZJxtv588XKNnWqWAgnTpT1Lu+9V6yCC2o4Szcx\nM0nZbgAX+SFml5jKP2Ara2yWLTa3nze3q9tkhpll/cztLQAO+fT7uSlTxdw+DsBtq1eQ2LU/ze1L\nC9LFz9jOOGI2YgTZsGFJa6GhoaGhoaGhoZEvypcP7LZYUuuYBSJbobqEhoJARLC0xJhZSEriptNs\nMQtDCFBKvQzgNgC3QjIpAkAVpVR58//KpvIJSqnOSqmWkPix/SZxAiRJx3EA/1NKXaqU6gFxjTwK\nWRwaEPfDSkqp55RSTZRS9wHoaBLBWqZMGIB2SqmBSqmmkEQk4ZDMjgBQKQhdzmiQwMcfA926lbQm\nGmcbXC5XSaugoVHi0NeBxrkOfQ0UM44dA+bN8183b57UW1i7FrjpJv+yN90k9f4Q6n5r10rf0dG5\ny3fsAJYtk792REeLfKD+C0JqKjBkSO4+rTaHDAGWLAF695a+O3SQ+g4dgOPHZX4qVADS0qQ8LQ2I\njATS04GoqMLpEwizZwOjRgHjxhVvuwUgJGIG4F6IO6AbkgREAZgPiQGzQACfAXjXJveVWW7V74Yk\n7PgKskbZfEiSDksmA8ByAF0hyToSAEwy+7Nkcsx9nwDwHcRClmS266vLx5Asj20g5K1qiOMulfj6\na2DXLuCGG0paE42zDfphrKGhrwMNDX0NnAMYNCgvKbPKO3SQv76IjvZfHgwCEUGLnCUl5SZlFixS\ndtttucvt5Ky4YJGyl14Cbr65YPliRETBIl6QzEXklFI5kHXCPjKL9kDI0yySQ21ybgA7bTLVSF5r\nqw+HJPHYY5OJJNnSJtMZQrT22mR+9OnncZ96BVl4OgLAnQC+AbAGQGelVHWS+/2NMyEhAVWqVMlV\nNmDAAAwYMMCfeIlh1iw5jzt3LmlNNDQ0NDQ0NDQ0NApAfoQuOjqwJY70Xw54LWhFhMvlko8Ra9YA\nzZoBK1ficHJysbQdLEIiZgWBpKGU2gOgC4AfAUApFQXgCkjSDwDYAMChlGpB8juzrAuERH1jk5mq\nlAonaVnAugNIIXnYJtMFsgaahW5muV2XEQDmkHzL1KUqxG1yCGRttDyYOXMm4uPjCzsNpwWrVwMu\nF/Dqq0B4eElro6GhoaGhoaGhoXHmwp8RZvPmzWjZsmWAPYofoboyQilVSSl1mVIqziy6yNy+0NxO\nBPCoUqq3UuoSiLvhH5AFn0HyVwArAcxVSrVSSrUH8BIAF0nLYrYYsqj0PKVUrFLqFgD3QxKHWHgR\nQE+l1BgzDu1xyELSSTaZWZDFsNN8dFkOoG2oYy9pkMDu3cDTTwPXXCOxZUOHFryfhoaGhoaGhoaG\nhkbpRmEsZpcD+ALeLCUWWVoAYAjJaUqpipD1yhwAPAB6ksy0tXErhEB9DokVexfAaKuSZJqZFCQJ\nwEZIwo7HSb5hk9mglBoA4Cnztx3AdSR/sfWzAMAzkNi4By1dANwNoJGfsZUHgK1bt4Y4JaceQ4cC\nv/0mLrQRERK/OWoU8MMPJa2ZxtmIw4cPY/PmzSWthoZGiUJfBxrnOvQ1oHGuw8YJyucnV1woDDHb\nDmARhOBUNLcHk7RfuWEB/regkDszou+2vcxK+OEvk2IYcicVKcgCaNXbk4jYEQ0At99+ewHNlCxO\nnBA3Rh2Tq3EqcTpN9xoapRX6OtA416GvAQ0NAMIRvjrVnYREzJRSDgBfAlgNoAfEktUIwEGbzDgA\nIwEMAmAAmApgpVIqxmY1WwygJiRGrCwkK+McALebbURC3B1XQdY4uwTAm0qpgyRfN2Xamu2Mg7gm\n3gpgqRm7ZlnN7jT/vgrgHUsXcwxWkhA7VkKWA0iFZIbU0NDQ0NDQ0NDQ0Dg3UR5Cylaejs4U88ty\n4ius1LMA2pLslI/MXwCmk5xpbkdBSNAgkslKqRgAPwNoaSX/MN0WlwOoS3KPUmo4gCcB1CJ5wpR5\nBuKqGGtuvw2gIsk+tr43APiO5H02XTIBfEhytE2XowCeIzk96MFraGhoaGhoaGhoaGicIoSa/KM3\ngI1KqWSl1F6l1GallD1dfQPIAtCrrTKSaQC+hjfZRhsAB20ZGQGJNSMke6Mls84iZSZWAmiilLLy\n2Lc194OPTFtTl4tMXZIA3KOUGgigNsS6VwlipdPQ0NDQ0NDQ0NDQ0ChxhBpjdhGA4ZCEH09BiNQs\npVQGyYUQImRfa8zCXrMO5t9/7JUks5VSB3xkdiI39trqDpt/8+unpqnL/yCLVz9hlh2FkL59wQ1Z\nQ0NDQ0NDQ0NDQ0Pj1CJUYlYGQDiAieYPEAvUcAALzXoF4BelVFmIBes+5E62UQVAXaXUUQDpkBT2\nj/jIVAVwo1JqMIDfISTwWx+ZMAAvKaXmA/gBwCif+pO6QOLYLF2SANgtcSehlDoPEjuXCh1jpqGh\noaGhoaGhoXEu42SMGcl/T3VnoRKzdEh6+6bwZkm8HUCC+f89ZvlDAL6HLCr9HoBsAN8ppcJM+XKQ\nNcdqQyxaWRAytkcpFQ2gBSRxSAcAXQG8DiFvBLDXXNcsAkK2njL7X2nKWVa0fHUJML4ekIyTGhoa\nGhoaGhoaGhoagCQHXHyqOwmVmO0G0MDuBmguLL3LTKxxE8SC5iD5nWnx2gpJwDEbQnxqQqxdESRX\nKqUmAZgBIVHfQEjWXgDVAPxGMkUp1QFilUsheVgplQBgG4Aokr8qpe4FcA2AmwF8EqQu/hAPAAsX\nLkRMTEyIU6OhEQL++guYMgWYPBmoXbvg8tOMhIQEzJw5s8T619AoDdDXgca5Dn0NaJzr2Lp1q7WM\nVqrJeV4F0Bk2rz+SOZa8UqozJOSrGUyvP5ILgu0vVGK2AcAlSqnDAA5BiFocgKEQC1gEgJkAHlVK\n/QavS+BRAB9C3B+3ANgDYK6ZfXE/gMoAlpsZGdsAWAqgH4B5SqnnIATrYgBDlVJlzL4mAHhKKTUG\nktFxPyStfhJkEeyCdMkF0wo3CgBiYmIQHx8f4tRoaISA+HigeXNgyBBg3jwgOhpITQUeeghYskS2\nSxBVqlQpuWtgwQKgUyf/c5CaCqxdCwwadPra0ThnUaLXgYZGKYC+BjQ0TuI4gE8A/AVJUmh5/WUC\neBQATK+/jwG8DFnGqyuA15VSf5H8LJhOQs3K+D6ApyHEqiaA1pAMh+0gSTcyAUwDsANCrn6EEKTl\n5hpmVsKOsQAugFjIlphtzzX/1oIQvokQcvYzxC2RkDi26pA4t3UAFgB4FsCvEGa6y1zDrGYQuvgi\nAeLqqKFxehAdDcybh/Sbh+CZq9fi2K02knYuo1MnIaypqbnLU1OlvFPA1TpOTTsaGhoapwoLFuS9\nR1lITZV6DQ2N0oC2kFCu20huIbkSwCQAI5RSlqFrOICdJB8mmUJyNoB34Q35KhAhETOSK0lOJNkE\nwJUA/oTEbDWxiSUCqAHgKohr4HHzfzveBvATgEsBXGeW3WyrrwrgJQCvQCbhNYiro72drgDugFjr\nrLXRLlRKVQ9RF9iscN8AYrrv06dPrp/L5cp/cjQKxt13A+vX+69bv17q7WjSBJgdwOt09mypDxbB\nPPzsMgsWADNmeLftD8jUVOD554vngRkdjVmOyRi/sjNmRk4uHCkrzIPdd6zW/3ffLRa73bvz7u/v\nGJ0KmIQ1F6myyFQoxLW42tHQ0Dg10KREf0DS0ChFcLlced7/ExJOcqpLAGwhud+2y0pIUsNm5nYb\n5LOUV1AgGfIP4nqYAiE51jplTghJOw6gr032D0jCkNYApgD4DZLso7pZH23Wp0EsWmshGRh/tLVx\nJ8QC9gkk22KW2f+LNpn5AI4BeDgYXXzGc4FZPhAAN23aRI1CAiDr1fNfV6OG1Hs8ucs9HtLhyFue\nlEQqJX+DKc8PhkE6nfI3ULnv/23bkm3aiF7+yn3bKgQyfjW4NtzJzspNd7iT//1SiDaDGVt++9j/\nT04mIyLYu2XL3OWBjtHQoXnLLHg8Ul9YGAYPxDk5trWb6a38jGP+/MDHwDCk3vw/vbWTD7Vy81DL\nAPMRapvFiVM5hxpFQu/evUtahbMbhbl3nY2wjTcnh6Vq/Poa0DjXsWnTJkK89t4D8Clz84cKJn/o\nYW6nABjnI9PT5CTlGAzHCkYoz07iQjjDJGhZkAWlo0zylA1JygEAjU2F/wIwGsDVZv0PtrbugaxL\nlgPgMohr4hEAL9hkFkNS4h80t7822+ljbiuI++O3AD4IRhef8WhiVlyoV88/ObPKa9TI/YIf6IWf\n5IkT5JHpPiTMJGXp05K4dSt55EgIuvk+7Pw9/HwJS4sWZFQUUxd6mL3DKFZSRsPgP5c4WR8Gly4l\n68PgX00L+TAOZmz57WMYMq62bcnkZC4uX56Mj8+flJGB6/LbJ0hkZ5ODL3KTAEc0d8sLSyD9Cygf\n21raeaCFO/9OC/OiWFQy5ztX8+eT06cLSbbKLfJmGOSMGbnb9CVvlj7+CJ+ljyZ8QWHx4sUlrcLZ\nD8MgY2L4v2EeOV393ctOxQeR0gbD4OHLnexa1s09zUoHKSP1NaChESQx687AxKyXyUfKMgiOFVLy\nD6XUdEjyjFYAhpkkiJBsiWlKKTfExTBeKZUOYBaALyHriNWCuCceAlBbKXWpSYiehATJjTNlXoVY\nveKVUk0AdAFwI4DJAKYqpcoBeANigYtXSm2D+G5WhCQnaRWkLnbsNyetWijzoeEHu3YB9esDv/8u\nf+3b9eqBqbvw95L1OK9Hb3iuehxtVj6OlSOWIWxfB+S8B2Rny+/XXwGXC9i+fQQmnw88NnIUtiSu\nxqW/LcVTF7yEx8aNAB8GypYF2rUTr8YKFYBy5YCcHCAzE8jKyv0jo3FBtXm4s/UQvH/pZPT7cQpm\nxc3DgYeiUaYMEBYGlC0bjfOqzcOQNkPwbrPJuOX38kD2xTh6+yj8V14BFcph5uUu/PtgNMLCZB87\nypTx/ipXBipWxEk5pbx/y+9JRe+lQ3D78Xmo0y4affoAC2+MRrdP5+Hd9kOQ3GMe0qpFIyICCA8H\nIiK8v/BwaUeYrvWLBhrPQ48WQ5AcMxl3/zUFG++bh6NfRAOQeSlXTvTKzpZ5q1gxGtm3zkPM1UPw\n0w2T0eqgAhTxc0oNdKsRi+M/bcequz9EV8/jWJOwDOUyOuDCFKBKFdGhQgUg4vIOCH9/GSJ694Za\ntgzo0EFcHnv3BqztQoAEkqel4vadU/D67W70WzgF778wDzc8GO0Vsrsq2hOo+Lgqbv8sFVd/MwXj\n27rRe8MUfLtkHlrdFJ2nz1DazAXLFcm33r5ffujQQebKmrNOnYBrrgFSUuQisOawVy+gXj0gMlLK\ngdxz7avP8OG5j8OMGcD77wMJCVI+fLjoaI3RngzF2rbaK0wClbvvljp/58D69eKmNndu6LKnEQMG\nDDh1jevkNILoaGwf+xquGdIb9855Be06v4awN/1ce2c7oqMxv95kfLaxMx6t5sbUUuJqfUqvgWCh\nrxWN0oH9EP5jR03z7x7b35o+MjUApNF/fou8CIa92Vjf9xAiRghD3AdJQf+CWT/YLM8xZf4AEAuJ\n3XralHkf4mJICBn6GpJAxM4490IsXjT/zoGNccJr4TphyqRDrF3TAHwVrC4+Y/s/iGXujLaYpaaS\ne/eGvt9//5E//US63eQHH5ALF5KvvUYmJpLPPUe+/DK5bp18xEtLE0vVkSPkN9+Qc+eSb79Nbtki\n/aekkP9dUI85ALNUGHMA7q1cjzfe6DWcjUIiCfChsokMC8tNMQCyalWyf3/y1VfJUaPIdef3JQGu\nqdaXd90lH1DXriVffJHs10+MO7Gx5MUXk40bk82akXFxZKtWZPv2ZOfOZKdOYhQa01KsJ2Nautmr\nF9mjh3yg7dxZDEbt2pGjLvXKTLzSfVKxR9rKPldfTXbvTnbtSl51lfy6dJE+2rWTfps0kfFeeCFZ\npw5ZuzZZqxZZsyY55rz57N7Y4F13yZyRMq/DhpE9YwyOrzOfTZuSDRuS0dFk3bqyb/XqYkSpUkX+\nVq1KVqtGnnee9DOxg+ja7zx3njkN9OsI2acj3Ln+H1tWjtFjVRILbKM9PDwABx8IS+QBONitgoc1\napD165MNGohu9eqRF10k83LppXJ8YmOlrF49kWvYUI5f88oGV8PJhL7i2pPQV7bb1zHYvr3M/XXX\nkQMGkMN7GvypppOTO7v5U00nx/QzOHCg1N1yhUF3uJPtahs8epS8Ps7g2ggnpww2OGUK+fzzcp4v\nXkwuW0Z+/jn5xRfk90sNHm7p5JYkN9NbO/n7OoOpqeRff5Hp6eSxY2LRPWnFK4zF0oacHPKzyR7+\nV97Bb+9IZEb5KGY1jfVaZw1DTurwcLGkkflbJa3+LatbcrKc3DExZFSU1/rmdOZ21fXVvSiuZqFY\nUwtreS2qtbKg/YcO9bZjydmtl1a51c+118rPanv6dO9+Hg/ZsaOUeTzkhAlk06a5533GDPnlN7f5\nub6OH0/ecov/cVpWUn/H0nccvvv6zkF++xbimEyYQN4Ml9zjh7mkcPp0OWftcxiMzsG4Blv7Nm6c\n1yXeajMpSepPFwyD/1fJyY5wc224k1nbjdPXd2lHqPehknBJ1zhrYbOYJbH4MgAAIABJREFUjYAt\nFIter7+DAMqY28/C5hVIr9ffJ/ay/H6hErMnTHKUaSqXbSNYmQA+Mrd7QhaJ/gqAB5KqfjQk2che\nSDzZJZB1zf6BWNJyIMlAos32voUkFbEmYjq8roy3mv3MhCQHmQPgAAAXgA9MmQ/z08XP2G6GpNNn\nx44d2bt371y/M8GcP3u2HNFy5ciHHyYPHcork54u5CspSQhP9+5esuTvV6GCvBdFRASWUcp/+XEI\n4zqOMDZsKORl9Ghy3dMeZldxCOtzOJjxuYf79pEHDpCHDwvhy862KW3FlPXtG3psmS+sG7nbXXD8\nldstLwYtWgiLaNGi+NwYTwV8xpa5zeCJE2RWFnn0KHnwoJD2/fvJ3bvJ7dvJPf9nMMfpZMYqN49f\n3pYZ8W144AM3s+PiycjIXMdoxw5petkyculSITNvvUW++Sb5+uvk+puEyLn7JXLGDPLJJ8mJE8lH\nHiEnTZLfI4+QY8aQI0eS991HPvCAlE2cKO+U48aRT91tMPUiJ9cuME6eB9nZ5Mo5BrddKGTt+uvJ\nXr2ECDud5Og4IZSj49zs0EHI+C1XGNxyvpMvJhj8/XdpZ98+ctwtBr+q4GSr8w1WrhwcYc2PlEZE\nkOXLk7EVhfT1qeKmp6yTbWoZjI4Wstm0qXCiuDjRt0MHIfBXXikfFS68UNp6sIzM4f1IZIuqBlPO\na8td1eP4Z80W/L1OG75zYzKPVXBwbb9EZlRw8MOxHs6bJ+8Z8+bJcZg7l5wzh1w41eAfjZ38+o5Z\nzA6LYMqAScyqFMXjzeN4YLPBQ4fI/1Z5mGMe34CxLUUhnb7EKhS32GDcYYsao1TQ/hZptZNXj0eu\njfj4vOWVK5OVKnmJm+X6bCfILVqIXIsWudu37jUF3WPyI7FRUXKS+e5v7ZOc7P9Y+pLz/OaioH0L\ncUy6NTL4cy0nZ7Zx8QAcnN7KxcxWfmJ8g9E5GJJvtTFlSu5nSqDyYFEYom/WZbRswzGYwSmDDY7B\nDB6MD+L8DdTf0KFyrP2R1qQk/27Mp8q9ubhIUij3oaLeFzTOWSxevDjP+3/Hjh0tYtYSElb1qclX\nepic5kl6uUQ0JBzrOZPD3Gfyo66WTEG/UIlZJdPqZP9lAVgPWTvsuLnd15RvYrNatTJJ0gnkTv4x\nDOIeeRCS2OM5k6zZ49BckAyQn5jb/wfgb5jJPyAxZn9A3CTHQmLM8tOldYDxPYMz1GL277/yPjBw\nIPnYY2TFimJdGTRILE/t28vLn2WdKlNGXhSvv15ehufNk/vytm3kP/+IBe2kNYDk8eNiEfvkE7GO\nLVpE/u9/5IYNIrt/v1jUVq6Ul/cjNU2LWZhYzE7GnIX68uWb6KMwiT8sBHNj97UWmDFmeV60StuN\nvTAvz75jtcWYnXzxtF44C3pBtmRMIleU2LKQH+SByHaQ7WRnyweLv/8md+6Ua+Dn5RLvsWOem4fi\nnVy/0OCqVUJIXS459+fNExL0yivkSy+RL7xALh4mZG7+YDcfe0wsAQ8/LGT0gQfIu++W63HgQLk2\n77iDvPdecuxYctOLQpLSpibyRJSDM2/w8P7L3CcZYN9qbl5wAfmQackcHRbYkqmUXOvOMNn/RYwk\nAY5CIutDrI8d4RYrJDxcDSevCndzjXKyWSWDNWuKhbduXbF6tq9jcH1ZJ/ud5+Y3lZ28Ps5ghw4y\n3d27k9dcI/eSm24ib71VxjZ0KDl8ODnzBg+PlnPwwy6J/K+8g6/f6eFjj5FPPEE+84wYiBIT5cPS\nh2M9zKjo4De3JfJ4JQe/eNLDDz+U+86qVWLNXL+e/L//IzdtIn/8kdz+mcGjVzi5c43BHTvI3R6D\nx9o5ufdrg//8I/fGQ4fkGP/3n9zLcn34Keja8UfS4uPlhuvvGvElALGxXkunYcg+lSufJFBZX3iY\nVSmK+2vF8liLIO8t+d1Hg9Hf6WTG5x5mdy6AlPnOkS9RDbRvCPejn5fL+fjpKwbT08n3bxHL2SMN\nXNz3bYj9BjM/vjpaJGzKlKKRsvzGmR/RN++9/zRsy/bwMKOdk5dVMThjZOA5K7A/M4nTSeu6hUDP\nT9/5Ccbq6E/GKhs/nmzd2js+y3pvEdNgLMMBxpt5pZP/LLHd6wPpahhyjVkWZMOQl55A4wqFJGqc\nU7BZzOIBXAhZp+yIScqeAxDG3FyiE4BNkISE2wHcQT+cI9AvJGLm03EYgP6mdetNeDMhzgVgQFbF\nbmlaoXaY+0wBsNmHcQ40BzzHlFkL4HUfxvmWKdMV3qyMz5mDHgixmqWYZOx8SLbIfHUJMKb4M5WY\nzZkjz/49e2T7jz/EOtW6tbjo3XGHWCVef11eZrKyTqEyvglAAiX+sHAOZ2UsFhTm62Cgcdsf6Pby\n4rZ0FBcKQ0hPVZuBCGIw8DeHUVHyUm+31lqWFxsBzs4mMzN9XCtt+mTMmMWc8AgefmASsyIdXPuU\nh2ufEMK2aqKb8+eTKybI9vuj3ZwxQ0jT44/LR56JE4VgzhskMjN6uzlkiNxT+vcnb7iB7NOH7NlT\nXHvt7rxxceKBOfV8IZMTIxNZs6a49tasKS64UVFimS9TRm4TlpvzKBTsQmv9fMlmfRhB7RceLqd7\nozIGv1CSeOGLMCcvDjdYtqxYQitVEtfatRFO3lXZxYPKwXuquPhjmXgeRiQfr5bIQ2EO9q/rYUyM\nvPvdXNvDQ2EOPlcnkenhUdxRMZbbKsdxW+UW3BLZhvc29/DHym35c7k4blYtuAWxJEBnuJtt2pC3\n3SYeDePHi0X54YfJhx4iExLI++8Xa/NTPT1Mi3AwsUEi0yIcfLKHh8OHkyNGkI8NNJhS18kX+7m5\nra6TU4cafOgh8ul7DG6v52RiW7FM3VnRxa21nXz5YYMvvigfGhYtIt9/n1yxQj62rVsnZHjjuwb3\nXerk6ntczKzsYMoTLqa1cvLXFQa3biV/+02s8L/+Sv78sxCuQy2d/PllNw+3dPL7pQa//Zb86ivy\ns8/IJUvIF+4Xwt+1ocHMTO85azwr89yjkocjr5WxvN3XxWPlHVx9j4t7m8vHko0byc2byeXL5aPg\nF1+QH38sz8M3Bnt4pKyDi69I5NFyDq541MMVK6R+yRL5EPDC/dL2Bw1GMwfgbw27MweKn/VL4sSJ\n5F13iXv59OkyJ19/Ld4GGRnyy8yk36REOU4nM34V9+mcnQHuJ+ZzJfPh8fwvri3vu9TDryuJ3ODB\n8lEk7UejYLIQ6H5lTx5kv8ckJRV8vw7G6hhov0qV5Bdrc8W2nitJScFbhv3gr7/I3lFyH0pd4C5Y\n16gopjWM48QObrFABvshIRCCzaDr68ZsR9my5OWX+z+ugwfLTSfU/koLzlIXUjsxYyE5Uyi/UMnY\neABbTAUJMc9tBfACgAEmUYqELOZsxXYdB/Cauf8ck5C1Npmm5QZJAD1NmRRIIpDREEsaTSKWA6Ac\nvPFlV0DWQ8uy9bPdbKNAXQKM74wlZr16iatgiSOYrIz+4O8m48//30Ko/v/B3DDsMr43VvtNxfri\nV1puMoW5GfqO1frf1wXGvr+/Y1TY2KDiQGEI6alqsygEMdDXfF9LS1FjzKxty93NIpDWy0qw7r2F\nJZ1BWFNz1onV8PiMRGZXcfDwcg/37pUPTamp8uL/yy/ycWnTJrGceTyi1uaZ8sL2zXQ3P/nE63L7\n3nsybMvSOX8++cYbElv4yisSP5uURL53v+z/7ij3ybIXXxRL6IwZXmvoip5CHN8Y6OaybvL/0qsS\n+eCDYhV94AHxQni/s9QtbJ3Ix53uk2zwya5uDhpEPtvTW5beKI5Hlru5u7G46l55pRzuBg0kBrNh\nQ7JRI3GJbd7c+147J1b6eK1ZItu3l8N62WUSw3lnA2l/YH03mzSR22WjRuSA2lL+YZfEk/XVqgk5\nLojIWu69FnkuyM23IHfg+yrN56jeEr/pe80c+MjDvec15c2tjZNjGVsuuH7DwsgLLiCn1RH5KdXy\nkvyICPlAMLC+tP1tpSvl+KMvK1YUD5NWrWSuC5qb8HB5n46MlPjfi8O9HwrWKCdbnmewXj2xQp9/\nPnlplMS+3hYhBPlmuOgOd9I9X8a+bZu0FREhFutmzeS4Xn65HPcOHeSDa7du8kHkri4Gf6zu5JQu\nbv5ygZOPDTQ4eTL52kCJW11zXSIzKgo5TU4mN0z38HglB38ZlsjMyg7+MNvDb74hv/9erq/ffiP/\nXuLhiSgHd7s8NAzy3w89J6/JAwfENf7ICilL+8TDf/+VY5ZdqTKzK1XiwdeSebxlW2Y0iuGJylFM\nGZ3EzApRPFw3lumXtOE/34g7dUaGH3LrB+np5G3tDbrDxF38y/JOfpNsLi8Q4OPg5lkedi8nx7dH\neTfd7rznWZHv1f7KA33ANQw5AQDyxhtztzF4sJQPHuwtGz/e67Hj219UlNT7Q8eOea2lFpKTpd6O\nU+VuWlD5GYLSTsw+ATAIQDdITNZ2k1hdZiNDr0DiuDpBYrvSAfzO3MRsC2TBtUsA9DYHvIheYmal\nzJ9mWsxetsibjZhNNC1glsXse5OkVQ9GlwDjiwfOvBizEyfkGp06taQ1oX9SZsEiZxpnD0ryi96p\n+DpXmDaL+jDynUP7Q91y/7Himpo1y/2wz89Fy/eLudWuPQGIvxeKMynGzFfHwhDHYPa36l0u0cnl\nEpdEWxymX4tDYqJ/y6fHI8ciNtYbb+ZrvS4I+RHeQOPxNw5bfXa2xKPu2ydEeOtW+f3yC7ltlbiI\nZv7PxRNRDu6a5uLhy53c/L7BdevI1avJNWskKdP69eQPHxpMb+Xkb2/IOoQ/Lzf4/feSZMowxP39\n5At5fteQdS2YOp9Y5GLmlZKQZ/NmSUC1e7eXuO/ebXqE+MzPkRUe7tolVpcDB0x3Vqvf0aPl2dS9\nO3P8eGNkZ0t87nffiXVuwQKJr50/X6yML78sJH7GDHLaNNm2rNAfPODm1Knko4+Kl+RTT4nMO/dJ\n/YYBQh6PLHfn6vO330SN8eNFvREjxHp3113iCn3rreTNN0vyq969vUuC3Bvj5iWXeF2RJ0b6t0AH\nY5m2kjqNgiR1ag9PUDJW2WRMYhbC+Ssu5iZ4LcP+iHX58nK4ateWhFeNGsnl0aSJhGU0UAbXKCc9\n/xMi3ytWyG+cw2BMDHlvc7Egv9UykellHBxxmYfRMLi5qpMHl7q5uaqTF4UZ7NmTvLOzwS/LO3ln\nAzdT6jq5ZLrBFSvE4vrVV2KF/flnOQa7d0t4x+HD4gadsy7I+5QvObNv33hjbhLmj5RZbcTF5SZn\nFinzF0tqIZAra6Dy4iRUwTwvSrFlrYAYs9JHzPLsLCSIkLT5Z+wC07b6M9JitnGjHMnT4TmmoaHh\ng+J+yPhzgymOdcwMQ14KZsyQ8ltuKTh5Q1Ee2KFYU4tieS0KcQxmf2vbHh9UHDFmlquXRdLsL3Ch\nzq1vn0HEmPmNdypojoLdN9RjEugass7ZCRPOjBgz37ZDIfpFsSgE6s9GTq0kPwcPijUsu4qDBx6X\neNbUhR5+/72Q3PXrhWCvWCFxnSn3CYH7YUgi33uPJ39Llki8+eLF5OY7TZm7Evnhh3Kq/zhUynZe\nO/Ik+8q8JI4Hl4pr62dzDS5ZIlbsuXMlTnfaNHLyZCGjDz0khDQhgXzpQYN/NnFyt8c7P1lZ5PqF\nBnc2kCy7Awd6LciJDRJ5T3eDfzYVl1KSzNxm8PdGTg7qZLBXL/LVAUJkb6vrDpjALNDPWcbDg3Bw\nfKVEHlQO3lDTw8suE6tm69bizt2pE9m/jcFfHG25o0ocdzpaMKV6G44fYHDYMNITM5g5APdVacAc\ngJtbDubzz8s8vPaaZMZ+/33SPd9gWsM4ZlWK4t/jE5ldOYqZl8TxyE9GvtbGE65k5oRHMPvtZJEJ\nRMp8zyGj6Iucp28xuP1CJ8e1kRjtoJ8fBfUJyMcwf4iMLN4P/zaPrVJtMcuzM9DQVPZ9nMELTNv6\nOSOJ2fPPy9emjIyS1kRDQ6PUwvfl177tSyCt7aKQzlCsqYW1vBb1S29B+/sjApb1sqhZGevVC+z6\nlN/cFhBTcyZmZfSLUPv1HWt+JN+XlBVXVkZ/4wyVKIf6Ihyo/aLEmFkIxg3Zn4xVNmmSfJSoX7/w\nlmEyuPuQr5Xa33XgO/cmkT3yk8Fdu8SFdMsW+dj95ZdiBf7kE1lC6O23xVI6Zw45axb5eR8hgcu7\nJ3LCBEnidN99cqu67Tb59e9PTmjvPsno7r9MrJnx8eQll5CpEQ2EvIY14HnnyW2lXLm8RLA+DKag\nIQkwBQ1zxdCGh4v7bM2asnxOlSoy1UqRNyCZmYhgUthIZiKCD9ZLZpcuYrAbOlSssAkJ4no9aRL5\n8sMGv6vq5NBGbv7eyMmFUw2++aaQ7/feIz/9VKyKbrdYxq1DvXy5uI4vWSLZmOvXJ3tUkHFfFS5x\ny3neTwvzQc0iX77kLFB5UWDLZVCqiRmApwB0AFAfQHPT+kUAV5n1q0zy0xmSbONLSIr6ryEZD8MA\n/AtZ/8yeavIZc78eNguaG7lTTY43iVY5k8wRwOPwpsv/F7KI9IZgdAkwvjOSmPXuLeezhoaGxjmF\nM3kdM1/Lpz9rqD+cheuY+UWo/VooyXXMCkP0/dWHSl595YualdFfWbAy1scJa+3Ehg2FPViJP0Kx\nDAcLXz0CxWZZsr7rB56quFnrg4u/5XYs98UGQs7sbow5Od5s17t2kakLPTxRUdZ2ySpfmWuf8nDx\nYjlNX35ZLI1PPilrzk6fLnGx1vqcP10lFssNl4/k8OGSObdbN7HsWWuJNmwoMZVVq3rjQruWDd2S\nCMh03NfL4NE2TmZ+5ub2CyUZU9my4onfubPERfbrR46+zuDWCyRJ0fZ6Ts4cbfDZZ8Ut+LXXxJr6\n7rtC/NaskSzgGRUjmQMwo1Ik9+0jMyJlu1hJmQXzetk0blypJmavmxanbHgTajxnq78Dkg7/P3gX\ngHab1i5rgemFJjGzEnpkQLI62heY/t0kbFY/+wG8gbwLTB80/2YD2AZgCbwLTBeoi5/xnXHE7MQJ\n+ULyxBMlrYmGhoaGhsY5jMKuY2bV50eQQ+mvqOuYBWN1DETUfLMyTp+ed6H7YCzDwSIUN+jisOYG\nQ1itNosaY2a1b0/Y5Btzlh8sgj5yZP5ujHadbZbEnJ0Gs7Jkbdl//5V4u23byJQUyb5qxZ/u3i0J\nmvbv95+F9EhrJ+c/bnDECHLAAFlapUcPcfcc1lSI4K113KxTh0ElIvoHQsayAOYA/AeRLFtW3oWt\nBDu1agnnjY0VC2X79mSXLpJBeNAgcsgQmZaxY8V9dsYMIYNvvimE8O23hRCmjE7iRqD0EjMKebka\nwDeQtcZOuhOadU6TBB2AJPVoDmCpScLGmDJTIK6LmyFrn7UDsNMc9KWmzHqIO+MCADGQRCPHARw1\n68uYROsEgDGmZW2Kqc/nweriZ2xnXPKPTZvkKK5bV9KaaGhoaGhoaJzxKM51zHz3C9YyXJy6Wiiq\nNTdYEuhLyux9hJKV0Z97smEER858raYhxJj53Q4GoRJfHyJor8/JIY8dk0Q9f/4piVi2bJE4yLVr\nySyTpWUBfOMN+d4wbZos8zJ1qvx95BGJUxw2TMjYzTdLBvP27ckrrpDstQ0bSnbWypUt4reYQO9c\nvxicV+qJWRIknusik/jYiVmUqfw8W1kLs2y8uX23ue20ySSaZXXN7ZUm6YqwyfwMIN22vR/ATtu2\nMsnbV8Hq4mdsZ5zFbMYM+bqg48s0NDQ0NDQ0NE4RTvc6ZrfcEjhWzr54ti9KKitjKMS3KETQiimz\nfsXkxpiTI15ox45JFs4//iD/mlTKLWaQtPUHAVwJoKZJzO4AUN6sb2Aq/wdyx3YdAjDTlBliki5r\ngWkrziwbwHWmzLumjLXA9H2mpSsbQBVTZh8k9sxKlz8H4ra4xay/qCBd/IzvjCNmV18t5lkNDQ0N\nDQ0NDY2zBIW18JXUOmbBoihE0DfRx6lI/GGhhGLMwhAa7jUtUW5IrJmCpKm/2ayvZZK1FSa5suTc\nZh1MQmeYJOsrAG+Zbey3yUQC+BhAV8j6ZAkAHrX1AVOPtwA8AeA7CMl7EZLC3+rH0uVjSMbGNma/\nsSGOu1Ti8GFg9WqgT5+S1kTjbIPL5SppFTQ0Shz6OtA416GvgRLEoEFAdLT/uuhoqfeHtWuBm27y\nX3fTTVJfHP0UFmvXAvPm5e0zOlrKffWzEBUFpKcDkZFAWpqUpaXJdnq61BcXZs8GRo0CXnoJuPnm\nguWLERGhCJPMReSUUjmQdcI+8hGdSHKoTS4ZwjYtnCB5rU9bg31k/iZ5va0+FpK90S7zmU8/9/nU\nAxIPdztkLbRvACwH0FkpVZ3kfn/jTEhIQJUqVXKVDRgwAAMGDPAnXmJYtAjIzgZuuKGkNdE42+By\nuUrd+a6hcbqhrwONcx36GtAoduRH9KKjA5NEX1JmIS3NS9qKCJfLJR8j1qwBmjUDVq7E4eTkIrcb\nCkIiZkFgD8SKVhPinmihBsSqZcnUsO+klAoHUNWss2Rq+rRdA0K69hYgY69XAEYCmEPyLbOv3abc\nEADT/A1i5syZiI+Pz2eYJY9jx4Dp04G+fYE6dUpaGw0NDQ0NDQ0NDY1TBPraXWzwJWuFhD8jzObN\nm9GyZctiaT8YhOrKmC9IGhBC1MUqU0pFAbgC4rYIABsAOJRSLWy7doGQqG9sMh1NwmahO4AUkodt\nMl2QG93McrsuzQCs9tFlI4C2hR5oCSM9Hbj1VmDPHuDpp0taGw0NDQ0NDQ0NDQ2NoiJki5lSqhKA\nhhAiBQAXKaUuA3CA5G5IhsVHlVK/AUgF8CQkAceHAEDyV6XUSgBzlVLDIeuSvQTARdKymC0G8BiA\neUqp5wBcAuB+AKNtqrwIYK1SagzEPXEAJMHH3TaZNyCxaY2UUpfYdNkIWSj7jMGnnwKGAfzwA7B0\nKfDff8DbbwONG5e0ZhoaGhoaGhoaGhoaRUVhXBkvB/AFvOkjnzfLFwAYQnKaUqoiJEuiA4AHQE+S\nmbY2boWk3f8ckqDjXdhIF8k0pVQPU2YjJDHI4yTfsMlsUEoNAPCU+dsOyer4i62flyHE7BEIKfMA\n6AngHuSNRQOA8gCwdevWEKfk1OPOO4F//wXq1we6dAH69wfq1gU2by5pzTTORhw+fBib9cmlcY5D\nXwca5zr0NaBxrsPGCcqfjv4KQ8y2A1gEITgVze3BJO1XbliA/y0oeC1u/rbtZQpConzrrbYtgkU/\nfe2HEL8wmzyQOxbNjmgAuP322/1UlQ7s3Ck/nShJ41TjdPpUa2iUVujrQONch74GNDQACEf4qiCh\noiIkYqaUckDWAlsNWX9sP4BGkLXNLJlxkIQbgyBp8acCWKmUirFZzRZDEnd0gbgyzodY2G4324iE\nLDK9CsAwiCvjm0qpgyRfN2Xamu2Mg7gy3gpgqVKqhc1qNgZC2L4EMMHSxexzlp8hrgRwG8QFMyOU\nudHQ0NDQ0NDQ0NDQOKtQHkLKVp6OzhTzy3LiK6zUswDakuyUj8xfAKaTnGluR0GsU4NIJiulYgD8\nDKAlye9MmR4QclWX5B4z9uxJALVInjBlnoG4Ksaa228DqEiyj63vDQC+I3mfTZfPIOusDTP7/RrA\nMQAXkdwX9OA1NDQ0NDQ0NDQ0NDROEULNytgbwEalVLJSaq9SarNSyr6OWAPIAtCrrTKSaRAyZGVB\nbAPgoEXKTHwOsWxdYZNZZ5EyEysBNFFKWQuMtTX3g49MW1OXi0xdngfwIGQh6vUAjgL4SJMyDQ0N\nDQ0NDQ0NDY3SglBjzBoDiDX/J4DzAbymlMoguRDAhWbdF0qpshCidB/EYlbLrGsCoKxS6iiAdABv\nQZJzHLDJxABooJTKAPA7JLmHlUq/FoDDAGpDsj8+B+AHAKN8+qlr6QJxXbR0eQkBCKlS6jyIi2Yq\ntCujhoaGhoaGhoaGxrmMk66MJP891Z2FSswUgP8gClrJOJ4AMBzAQgAPmOV3AdgFYDaA9wD8DYBK\nqTAAd5oybSDk6n8AMs0yKqWiAcQD2AKgP4CuAF4HcK9N5hZT9yUQopUAIV7PwJsMJF9dAoyvBySx\niYaGhoaGhoaGhoaGBiA5KBaf6k5CJWbpALLtboBKqe8BXGPGkl0DIT07Sf6olBoMYCuA7wCsgxCf\n6gDSSG4BsEUpNQnAswAqQxaEHg4gDYBBMgVAilKqA2R9MkKsYgmmLinmumj3mn13B7A3SF38IRUA\nFi5ciJiYmBCnRkMjBCxbBrRsCdSunbfur7+ATZuA3r1Pv14mEhISMHPmzBLrX0OjNEBfBxrnOvQ1\noHGuY+vWrVa29tTT0V+oxGw3gFil1J8QV78NkEQauyCLO0dAiFMXAD+STFFK7YZkVXwWYiVLAdDU\nzJ74HcTS9Qokrf03kHiwzQA6KqXCSWbbZFIgFruWZt9dAMwiSaXU55AYuHcga60VpIs/9AGAmJgY\nxMfHhzg1GhohoFo1YMgQYN48IDraW56aCjz0UN7y04wqVaqU3DWwYAHQqZP/8aemAmvXAoMGnW6t\nNM5BlOh1oKFRCqCvAQ2Nk8hQSl0I4FUAnWELxyKZYwkppTpD8ls0gxmORXJBsJ2EmvzjNYgVagmA\nKQBaQVwF50JiuzIBzITEfvVWSl0CIBLAEQAfmjK/Q4jWXKVUKwANIC6HbpJ7TJl1ZlvzlFKxkLi0\n8gBehFjcwiELWvdUSo1RSjUB0BBAVcii1DWD0CUXTPfIhBDnQ0OjcIiOFvI1ZAiyd6Tizz8hpMMf\nWTvX0KmTzENqau5ya346BUwKmxsLFuRtw97WgqDvkxoaGhqnBvo+paFxpkAB+ARi+GkDWRbsTkhI\nlwhIONbHkCSIl0F4y+tKqW7BdhISMSOZBOA6AFdBGGNVU9FbbWIvAtgBYCmAHyFk6EPbGmYAMBbA\nBRALmZXB0b6u2HEAEwH0g6S4HwshhG/aZH6CkLNnAfwKyeiYalvFDq34AAAgAElEQVTDLFhdLCRA\nYtA0NE7Pw9IkZ39ePQS31l2Lv3oWkpSdbQ92G2k9Oa7CkNbiIngaGhqnBmfbvasw0PcpDY0zBW0B\nNAVwG8ktJFcCmARghFLK8kAcDgmhephkCsnZAN5FCIafUC1mIPkJyUsBdIJYn/4D4IDEh5WFJNmo\nASFv8QCyAXQ0d98DsWa9DSFWl0LYJgBca5NpBEnq8QpkEhZDCGAnyKLW2QBuAHAHgKGQLI47AdRV\nSlUPUpeTUEqVgbhHfgOIT3WfPn1y/VwuV6hTpeGLu+8G1q/3X7d+vdTb0aQJMHu2f/nZs6U+WIT6\nAtCpE9CrV159rYflxRcXGzmbGjYZa9EZk7MnF85SVtQHu31ufI+RfW78HaNQj2mwMMlZ9p1DsG3u\nWrAwlkQbwaORik2bgKztqdoqqaFRWqBJSfF9iNLQ0CgyXC5Xnvf/hISTnOoSAFtI7rftshJAFYjb\nIiCWtIBLeQUFkiH/IIk6UgD0ApAFsXpFQSxdWQD6mnKNIbFjOQBaA7gawAlTpropcw9kbbGDEPPg\nswD+gcSFWf0tBvAXgE/M7f+DZFd80dxWkPi3QwAeDkYXn/FcYJYPBMBNmzZRo5AAyHr1/NfVqCH1\nHk/uco+HdDjyliclkUrJ32DK84NhkE6n/A2m3J9elqzHE3ifEPH7OoOr4eRjnd1cDSd/+7yQbfqO\nI79x5bevOebFkyf7LQ/62AUqDxGzbnCTAN+6y523cv78wOMzDKk3/0+92MmOcHNndAFzEmybRd3H\njqFDA8+TxyP1GiWCxYsXl7QKZz8Mg4yJYfqnHmZn0/+9rKBr6GyAYTC7s5MfPOBmxv+zd+VxNpV/\n+Hlnxm4WJbQxlrJEGFlGGm6SVKNU+FHZKkspS4uEkJQlGUxJaqyZmtCqkpY7XUsKFdkiZ0qh7MYy\nY8x9fn98z5l75rozc+8shrzP53M+9553/b7vWZ/zXd4bC+f5UhjQ14DGxY7169cTYrW3BMDnzM4f\nypj8ob25vx3AMK8yHSCKoVL0h2P5U8jW+GSIxmmxSZZWQHy5XjfzPzKFvx2igVoFwAWJZDIIoqHb\nB1mH7HpIlMZ/IGaMbog9ZqQ5gB8hvmWPmn1MgixMDQDdzH6mQjRqswAcBJAI4AN/ZPEalyZmhYWq\nVX2TMyu9UqWsF3a3m9yT5KLbxwv8qVNkYiK5+OZ4uqH413PxPHmSPDBO9hffHM8HHiDHjCFXriT3\n7yePHyczMsj0dDI1lTx0iPznH/Kvv+QZ9+d3BtNaCvn5/Xdy1zcGU5vZ9neRf/8t5f/4g/z9d/KP\nd1w8XT6CM1olcv/1Du6c6+Jxs8727eRvv5E7dnh+U1KkjX//JU+ezHmaMjPJIz8b3HqFg7VLGdy/\nn2wUYXBjRQcPrjeYmipzkJFBut3+TX3aNoNHohzc+baTmW0CfLB7k7DQUDIqimd2Gjz9TR4ky5uE\nFRIp+2etwW+DhFA5g2VecpQ5l/T0dLLTJULw7gx18vjxXDrND4HPTx07vOdr7lxy8mQyKcmTbpE3\nwyBfeSX7i6o3ebOIoi/CZ73k+kv4Cko6NTT8wKkVLh5CBKe2SMz/B6b/AJYOkvvUzP/5+BCloaFR\nLPCTmN3KnInZ7SavKUl/uJY/hWyN/2hqvGgKsh8Sgv5VM7+3TStFAH9BFqReC+Bls8xSU5tFU9C1\nAMp5Mc5/TDJG83eWnXHaiJQlS6pJqiYCWOOvLLZxlYBo1wZrYlYI8CZnVavSDfDUFVW5YAH58h0u\nHgmK4NMl43gIEbzrUhebNCEbNSIbNCDr1SPLlpUmKlYk+yOemVBcjE7MhGJ/xPPKK8lWreS9FfB/\nqwbRUMVANFTVYORZpwsSSYCPI87vOvYtKIgMDiZLlCBLliRLlfLIUQ0Gp0yRaVq6lKwVYvjsIzhY\n6pUrR4aFybjDwoQ/lS8v6cHBZAzkwX5zsJM1ajBrq1tX5rdpUzIqimzRgmzblmzenLz6arJ2bbLj\n9QbXhTnYt7aTm0pG8ShC+QTkGHW+3MXWrckHHiAfe4x84gny2WfJkSPJ0aPJOQ+5eLJ0BFfExvFU\nmQi+P8jF2bPJhQvJRYvIefPI+fPl/+LF5Mcfk59+KmNOTCQXLJC8d98VPjJntMEfQx28Pszgjh3k\n9WEi2wdTDTqd5A8/kJs2Cdk+0dzBP7+TcrtdBk+1dHDPaoO7dpGrVpGje8qcfj/RyW+Ug8/+z+CJ\nE7mcv/nRPhZEY0nKh4qICCHBhiEXQXCwTIaZz9BQ8rrr5OBZ7foiwVbfdmKXW3puKCjp9Bf51RoW\nlDjmVf/hhz3tWOXsJNlKt/q5807ZrLYnT85+rGJiJM3lIrt2FZJt788i3bnJXhAN63lKtBcs8Nxn\n98YleuS5iEgZDYO/XCrPprXlL6Jx+4Pz9LzVuDhgI2azAGxgdv4QafKM6839ZIsT2cr0shRL/mzK\nrOQXlFI9AMQBeADAb2ZnzwGYT7KXUmoFJDy9A7IW2Ws2MvUVgJEmmXND/L6sBaYTICaIt5nt7oJE\nZuwHWWA6DsAYSOSTMibpegMSGfJdiFNdZ8ji0E1ItsxLFpLPeY3te7PfbjExMQgPD8829m7duqFb\nt25+z1VxYO9eYMwYICICePppoGLF3MsfOwZs3+7Zdu4EDhwADh8GTpwATp0CTp4E0tOB8uWBBg2A\nq64CLr0UCA6WNrZsAX7+GQgLA667TsqlpwMTkqrh8vQ/cQZBCIEbO1AVtfEHAGlnZNg0dFk1GF/e\nEYdvGwzC4cPSZlCQ/F55JdChg7T5779AUOd7cJnrA+yN7oT0RUtRrRqgFHDmDLBxI/DHH0BammzB\nwUCJEp6tZEn5JYHTp4Erdyaj0eA2+DnOiVPNWiMzU9LdbpFdKSAkRLay/6ag3pQ+COp0F8qPGIwd\n4xJxoO3/4HYja8vMlDpKARkZni01VeaQ9JS1/jfYMA+pUa1R/85IVK/uOSa7dgFbP0/Bpb8mY+eN\nPXHmDLK2zEzPf7fb06e1VTqZgtgP+yClx2hcEj8WC9ok4GiFyKxxW1tIiMh16hRQtqwspZaeLudD\njb+S8eznbTCrmxM1j/+MWz4ZjJWd4/Bx5CDs3g3s3i3jcrvl3LDkyswEeqdOw0snBuOZknGYETQI\naWn5O4+rIQVzVB9MrZ+AZ9+IRMuWwOrVwJheKXh2Rx/0QQL+QGS28gnog7EYjdEYmy3famvDYwl4\nckYk3hmfgitG9UFvJmBvyUiULy/nbGio/JYpI/MTiRQ8/nMfvFNzNB40xmJ+6wQcDo9EyZJyrlvn\nh32rcDQFt77XBxvuHI0bPhuL1Q8lIP3yyKz8oCCgVCm5PjMy5FwICpJ5/Pdf4KsxKzHNiMXMymMw\n8N/nkV7pKoReHob0uYkIDQVUxzuBbdugEhOBzp3Fhy82VtbEa9Uq+yRaPioDBgB9+wJvvgnMnOnZ\n91UnJ3j7uxSF/0tOY8ltjL5kyys90PovvAA8/7znNyEB+Osv8T+95hpg2rTs6R06yIH94gu5WXbv\nLvtDh3qOw8svAzt2ANWqyYln+S9bZSdP9rTpS/b8zJW1BAVw9nhTUoAlS4Bly3z3eQ6WrxjQIQW9\nXH2QENIXr5wYgMMvzUTVOS/IfOV03HPq95FHJN1XvZUrZTytWsmY2rcHnngCeOyxs9s+fhyYPl0e\njv7C37nyLpeSAnfvPmi4LgGVKgGNdi3ByzcuQ8mF2scMQODXuV5yRSOfSExMPCumxNGjR/Hdd98B\nwEAIH7mcpp+ZUqovRClUiWSGUmoCgA4kG1r1lVKLAESQvN0vIfxlcCaBuwtCbk5DNEwZ8GjPTpub\nG0CYWb62ub8HYspoab1+sbXZD2La6IaYN06EBBV51VYmEcAv8JgyrjXb6WjuK4hGbB2ADyA+ZqfN\nMj5l8TG2LpC12S5IjZnbLR9jIyLkw3pYGDlxIrl7N7lzJ/ntt6K1GDmSbNeOvPzy7FqdK66Q+p07\nk337kkOHkiNGkOPHy0fcESPIu+4iGzcma9YkIyNFIda2LfnUU2T//lK/aVPRZN18M3kaQSTADARx\nzhzy66/FtDDrK39cnH9f7i2fsk6dAvct84b1Fdbp9F8LYvmUJSYWiolekaCgGht7HadT1Gqhof4f\nIx/H1O0Wc8zjx8m0NNlSU8mDB8m9e8Xk88AByT91ijxxgjx2jDz++lxm7PAt96ENBvdOmMt160Qb\n9uWXcl6tmyKawnVTnPziC/Lzz8mVCw0ea+pg2rbsbf3+tcE9dR2cN9bghAlyTQwaRD70ENm9O9ml\niyg9nm4mbQ5u7GTz5nJu168v53+1anLNVK5MXnopGR4uWt62IVInBs6AtKoAeeON5Ocd4kiAC5rG\nsUaQwVWI5no04no05mq0YNegJB5WERxRPo6HVQTvqeRijRpkrVqiGY2MFNmuvppsUcXgypIOjr1s\nOjMQwreuHMVjIRGceq+LQ4aQTz9NDh9Ojhol1/ekSbJNm0bOnk0mJMg9Y8EC8oOpBvfUcXDZMCcP\nNHRw5UKDycnk6tXkjz+SP/9Mbt5Mbt8uJsG7d5P79smxPnZMju+ZMzL/OZrm5tcktqDnfl71ve8D\nLpdcH+XKya+3D6b9v7f20zCkTvnyosJ2uUQDaqmx/fVfDXSu7GPy/h8dnV0Lm9f85JUeINK2GXQG\nOzjjSYNLlpD3lxDN2fcPTM9fv/74vVptjB2b/ZmSU7q/8HeufByPDUsNVoPBfxuIxcSSKXmMkwxc\nk+SvttWfcr7KWGnDh5PNmmXXKlv1/NUM+xqPv9f5udL0a1wUsGnMmphc5HNkd8cax+watOMml7G7\nY91C+sm1/C1odlgOYg5YDxKB5EmT7HwAieefCTFT7GSr85dZpilEw7UT2YN/RJr5xyAmhcmQ6Ih2\n8tbLHNhn8JgdbocZ/MMsMxcSIfJpiDYuN1ma5TC+ly9UYrZmjRzNTz8Vf6uBA+VdwPvlr3JlsmNH\n8vnnyXfeIdetkxenQodlzhgk5CzLrDHQFwrvQB/5CfxhIT83du8XpULynypUFMZDyF7W5mN21kun\nLxSRj5nfyIlsF8T8JRAC76OO2+Hg6d8Mnjwp19ehQ3JdpqSQv/7q8Unctk1IzNGjpPu77OT236Uu\n/viKM+vi/WCwk/Hx5PI7hLwtax/HESPEpPTpp+V3+HAhWSNHyjWe0FPqf1VvIAlwZp041q8vpq3X\nXCNE7qqr5PIMD5etVCnfxNEyk80P6bS2EiXkvmSZ5pYvL0O+7DIhuvdUEjPnFyvF8UhQBHvVcrFp\nU7JlS7J1a/kQdNttZGysfKfp0kXI9NB7DG6u4uCEDk5uvdzB57obWSa3Q4bIx6Nnn5W5ef55ee9+\n8UXy5ZflA9Ybzxr8o6aD7z3q5B+1HJw5zODkyeSUKXI45o4x+Ne1Dn75UCLTykbwm/6J3F8timml\nQ/ljjziml4vgNy+4uHQpuWQJuWK0i+nlIri5XxwzyobxePV6PH5tI6Ze25hHr2vBDdNdPFwvmoer\nN+K/leoxNTiUfcMTue1KIb0pKXJOZGYKobV8Z+3n079LXcwIjeCOx+OYERrBfYtdPHiQPHyYPHJE\n6h875vnwkbZNgktk7DCY4jS4++oW/OfKxky/IRdS5n1uF+TDjw+kbze4s6qD1ZXB336Tds+0dnBm\nm0QeQgQT703iiRYOHtto+A4MkhNM0+BDH7u4dy95Yrlvk1+3w8FTw8fSDcWjT42l20bKzkyP5759\n8vEox48JvuDvXFnpprnrtCEGk4Pl+ERFyfnt933K33u/v8Ga/Cnnq4zLJR8sypWTDxLWx4ZGjeRr\ncVKS50NAPoJouXfJdTqru9xjs8yNfT1rDINs1IiZXbpy82Yy8/cc5iQQBGJGfDGaX/5Hx2wjZlEA\nroasU3bcJGUTAQQxO5doDWA9gFMAdgB40J6f1xYQMTM7rA/x6coAcMhkj69CAnKcAvA6AAOyKnYT\ns+xus+4sk2naGWesOeB3zDLbIZEZ7Ywz3izTAR7/sufM/npAAoD8bMp0mT+y5DC2qAuVmA0eLFow\n66s0KRqJjz4iV6yQF8Bc/WoKEz58zOgV+CMbzseojFaAhJwebnXqnD9f3Qp6M/QmZd5flXMjZ0Uc\nlTFPFMULY37aLKgcvl6MwsLk5aZRI1FVt2jh8Q/zR5NpyTB9OhkSIqoxP4+JRQjS0+Wl/tRWealP\n+9LJUy3Fp2/7diGZP/0kPn+rVgmPXbGC/OwzufcsXuzxIUxIIGfMEHFef11+X31ViNGLL0ognxEj\nyA9vFuK5+KY4Dhgg7zo9e5L33y9ErFMnIWa33SZELSZGtPSP1Rfi2Le2k1FRZMOGouGsU0dIaI0a\nok286iqyShUhg5dcQlaoINPSoazUv62Mk5dc4rE+KFuWLF2avDlY8h9HXBZBtf4/jrizSKg9zyK1\ndmJrT5teS8rGhgVGenPr39dm97HdgMZZ8pQvL7fnyEg55Zo0IW+6iWzfXrbbbiN7tjb4Y5iDXas4\nuS7cwd4Og/feK65yDzxA9u5N9upFPvigkOV77/W43MXGygfBu+4ib79dSHbDhuRDJeayGgy+8EL2\na+bMGfLNHi5uQR3eCBe/hoOt4WRyiIM3XmmwUSOyTRvy7rvJe+4R4h4TI+dDixaiMY4JkoAij5t+\nst2udrFVK8lv1Eg+BNQIkvmYgkF0A1wedCszofhkmfisb4qAnCNNmsg4+veXDx/Wx49x48gJE4TE\nT58uj6WZwwz+Hungm/c7mVLTwUUvGVnXwJtvkq+9JprpN58zuCvSwRfbOfmtcvDpznK/mDVLHnEj\nRpga6w/ITz4hv/iC/Ooruc5WriTXriU3fWIwtamDv30pQaz+/cFgxk0OZv5u+CaU+SFhOZXzVcZy\nerZIWN26kla3buCaYS8sWOC5bt560Cnjy0V+d1gYd4Y3Ygyc3FTJkaMlht8I5HmX0zOgZEm5Afka\ne+/ecrOxEBPj8TP2RlKS5PtCfusVFP9RTaWdmDFAzpSfLVBSNtzUZqVCoiBuN8nQHBsZCoUs5mwF\n3TgNYBazE7NmJtOkqdkigNvoIWbDIKaPJ8y8DLO9kjZi1hziX5Zh62eH2UaesuQwvguWmNWvL6ZY\nxQ5/ojL6gi+n9WuvzZl8xcdLvr8ojjDoFwp8BTawYB+nr2NUnKHei+IhkJ82CypHTg91bxO46647\nOyBITkTL6tsicklJgQf+yGkcRfmQDdTM2VvGQDScgdS38hMT6Y6IYOaiRGY2iqI7NJRpE+OYGR7B\nY5+5eOCAaFhOLHcxMzyCh8fE8Uz5MJ6sWY8najfiyTqNeaJRC/65yMVTjaN5un4juuvVEwaYmEh3\nGwd//9rg8uUSDOett+Rlfu5cMStduFAC5CxZQq6aKBqzvcNFY7Zmsovvvy+H+L33pFxiolhGzJ8v\n9efOJZcNkxfbjAaNeOgDJ/fVc/CtkQbHjxciMGQI2a+fkK1775XtnnuEBI2/Veq+2M7J2Fjy1lvF\nbP2mm+R9u2VL+d+mjRC62FjZ7ryTvOMO2e66S4hbv35CzDdvZo7n1JGfDR5s6ODqQWLeuKifk8OH\nkwMGSBu33y4y9Ogh8nbtKiT+ueeE/PzcR4jrmm5xfOIJIY29e0v955+XDwQrRsmY/qlzEwlw07Wd\nOH48+cYb8nFhyRIhX488IvI3bizE7+qrheRXriwEPzRU3qlLlhQid99l0u7t5Z1UKjtBLlGCLFNG\nvr1YEWPfvN+ZZb1y5oy4FISH+0fQfQW1CgkRcmfJU62aBHm6/npyQAMXjwZHMK56HI+FRHBoMxc7\ndhRXhvvvlznq25eccKeLx0tGcFGLOJ4oFcHpXVwcOlRcHZ58khw2jHy9u4snSkVwaRspM/VeF2d0\nlbRlN4ziGRXMv8rVpFGuHo8FhXJYZCI3VnRw1IMGn3pKCO6LL4p1Y3w8OWeOnLNJSUJIFy8Wovrc\nc2S9sgY3V3Zw4SMyzh4xBmfOJJ0vSvTkHXNc/OMPifZ8unwEn2rhyvqg4ghy8s47yfXryQ0b5Fr6\n8EPRLAeEQCxEfN07q1SRg9a7d/ayvXufnZ6UJB/VvElWTun5rVeY7zrn8nlxjnC+E7PPIIs614Us\ntPapSYDehATZyATwFiQkfWsAjSF+W7+b9ccC2ABgE2TBtQamxosA3jTLJJttHIeEyK8NYL5Zph08\npoyTzLYtjdl2k3hV9EeWHMYXBYAxMTGMjY3Ntp3Pa3ns3y9Hcv784paEvkmZBYucaWgUBoqCOJ8P\n65gZhsfcJynJk/9fjspIah+zovQxs481Olr6jo6WfX/nq6DkNzfkdg1ZFgqB9usPybfGNGiQPJtu\nvbXgfsz2dk2Zz+w0svwss2mx/JjT48dl+ZU9e8g//xQfzu3bhdD+8osQje+/J3+ZLgRk1UtOvvee\nENOZM2UoEycKsRk6lHz0USGoC5sJaZ3bOI733COks1070WZGR4uGsFkz8tVqUu6lKnGsW1cORZ06\n8l20Zk2yenVy3GWeMvXrS97LVSRtUcWBWQwyMVrShjZxskEDKVe1qnyvDQ8XEumLeAYFkU0uNbjl\ncgdTN8kcfTJDNLhWBOMbkV1DeiNcbFbJ4P4GMr/7r3ewUYThs/2aNUXr3ratzMM995DduokGuH9/\nOT2eeUaMDsaPJxc96uKpMhFc1SWOaWUj+MVIFz/9VLSaK1Z4bgOrVpGblxk83tzB3QudPBUty76c\n6N6bboBpPXuLia4vUmbBm0zlRcryU6+w7/OGwfRWDv4222ZyWhgA5DnoC6GhhfJ+uWjRorPe/2Ni\nYs5fYnZWZSFBNAnaBbvAtK2fC1JjtmSJHMk//ihuSTQ0NAoM7zDr5H9/HbP8msQW9IUir/p2MubL\nB9M73TLjso6VnWBbmsvGjaWcnWTby+ZFzgoyV/ZAH/ax5zVfxfUVPL/9+kNcrbasQB9jxxYs8Eeg\nMhfmnAZKmv3VTPtTzlcZK23UKPkoUbOmfKAwNcO5yXj6tLhdHDkiH50PHszFP8wQE+uD68VH0Rgs\nxG9r/zhu/Nigu032+c1s7eCP7xtcvVr8L3fsEE3ykCFCVrt0EY3ubbdJd9HRcplfd50EWLr6ajGB\nDgsjhwb7b0bsyz/3DQg5+w3V6Qb4dlBvVqggCrVq1cTy0zIpHtcwiRkqhF9cO5BnVAjf7pDEYcNk\neidMkFN19mwh4zNmyKEYN46cH5vEM0EhXNdyIDODQrhuWBLXrBFiv2+f+KOeOGGul7pL5njTJxLY\nKb/nY0aGfBC4tZSMecRNTh45ElATOcMiX97kLKf0gsBmDnq+a8zGA2gFoBrE1+wNU9jeZv6H5v4F\ntcC0bXwXJDF74gn5aqWhoaFxQUKvY5addOcme37mynrJ8ib83uTMV5/nUmtaGP36Q1y9SVlxRmUM\nZGz+9Bno/FwIPmb+XOd2ghgWJlrhojpnzb7cU+Pojohg2lcu/vWXaDUNg9yyhdy6VXxwf/nI4OEo\nBzdMdfJgIwc/mWFw6VIxNz5yWXUS4OFLq3PqVNFsjhsnJsVDh4q574MPijnxh1VF85h42UDWqyc+\ns1ddJWa0JUrI23xIiGgdy5QRAlmjBjm7jNSbhoG5kkelxFTUMol1lXAw+nKDtWoJp27cWCIHt20r\nmtVbb/X4oLZs6fHdLFdOTGu3Xu7gF885mRwsfqHjxolp6sqVouXdskXmat8+MSc9fdrPufcmYUVB\nyshsGsbznZi9ZWquMuHxDTNs+Q+aGrGT8CwA7YQE5rAWmF4IWcvM8htLg/io2ReY/tMkbJlm+gGz\nb+8Fpg+bv5mQ9c+S4FlgOk9ZfIzvgiRmDRuKyl1DQ0NDQ+MsFITAFpevbX779Ye4Wm378mO22g7U\njzkQmQtrTgMleAUhYd7pORG1IozKmCO8ZRk+XPrLyXy1IOdsQX3MrH3LfLG6kDOfZowWLJIwcGCO\n5ojZTGR91HOHhPDAG0n85RdRrH70Efn+++LPN2eO+FS+8gr53qOi6Zr/kJOjRokf4eDB4pfZs6do\nFTt3Ju+7z+N/2qOHx+xz1nBZpsYa826XwY2XOVi/vJGnZjE4WDj8ZZeJiWvt2h6r65tvFjPT++4j\njwaH0g0wA6AbYGqJUE6aJNpCK8DO22+Ln+4HH8jyOU6nmPxu2iSRkPfuFa1sroTQnL/1Eyacv8SM\nQl5ugyz0/LkpaC9bXjd4ojXGmlq1D03yNcEsM8skZhsA3ACgJSScJAHcapb5DRI+fx7En81aY8w7\nAMgZAENNzdpYc/8nf2XxMbYLzsfswAE5ivPmFbckGhoaGhoaGucMF9M6Zjkhv6a9Rd1XbqTZOwBI\ncfuYectc0CBKPsbsdjj4z1qDmzfLMk0ul6xD+tFHEqhozhwJxjNligSDsbSGAwYI6evaVSK7tmsn\n/oAZJpvLAFilivgoWprDQLfgYDl81aqRlSotYvnysQwNjWWFCrGsHdqENwk/OX+JGYXAxAP4wyRH\nHW3pDlP4Z21pYWa5Oeb+a2aZxrYyVgAQBz3E7BSAEFuZTwFkmv9LmG2u9ZLrXwC7/JXFx7guOI3Z\n0qXU/mUaGhoaGhoaFx/OZWTgwljHzCJhrVr5Ti+OqIxk4fg8nivtumW+aG02M8aMDNEenjkjgXP2\n75egOb/9JsFyVq2S5Vw++USmYe5c8YmbMEHI4LBhQggHDhQN4b33ktOu7HJOiVkIAoRSKh7AXZBI\nhzu9sg+Yv2m2tCqQ4BylvPJ228qUMX8rmL/pANJJnrGVKQ0gSCkVTvKoUioDQt4suaw+Msykg37I\ncsHj22+BGjWAqlWLWxINDQ0NDQ0NjXOI2bNzzmvVSrbi6KtnT9/lEhOB3r2BhITs6dZ+YqLnf3w8\nsGgR0Llz9rLWfnz82Xn5qZeSAvTpI/1GRkpaZKTse6fnhpzGbLXnTxt5ISwMSE0FQkOBY8c8+2Fh\nwLFjCDFZTXAwUK6cbAXC++9jw4dLCix2IAgKpLBS6nUA94VkV8kAACAASURBVAPoDomkCADhSqnS\n5v/yEFY5RCnVRinVBOI/dgBCiAAhTOkAFiilrldKtYeYRp6ALA4NiPlhOaXURKVUbaXUowBiINqu\nKjbZWyqleiil6kACkQQDWWSznB+yXNAggU8/BW65pbgl0fivITExsbhF0NAodujrQONih74GChmn\nTp1NyiwkJEi+heRk38QLkPTkZN95gdZLTvZNvixyllM/5xrepAyQ39BQDzkrTLz/PtC9OzB+fOG2\nmwcCImYA+kPMAZ2QICAKwFyID5gFAlgBYLGt3Goz3crfDQnYsRqyRtlcSJAOq0wagGUAboEE6xgC\nYJTZn1XGbdZ9AcBPkCiP8Wa73rJ8Cony2AJC3irgP4B16wDDAO69t7gl0fivQT+MNTT0daChoa+B\niwA9e+aszYqMzF0Tdi7hTcos2MlZYcEiZYsWAe3aFV67fiAgU0aS2YicUsoNWSfsYzNpH4Q8TSf5\nsK2cE8AuW5lLSN5pyw+GBPHYZysTSrKJrUwbCNH6x1Zmo1c/Y7zyFWTh6RAAvQD8AOAbAG2UUhVJ\nWqaX2TBkyBCEh4dnS+vWrRu6devmq3ixIT4euPpq4Oabi1sSDQ0NDQ0NDQ0NjSICmXOeN1nLJxIT\nE+VjxKpVQMOGwIIFOHr0aKG07S8C9jHLDSQNpdQ+AG0BbAQApVQYgOaQoB8AsAZAhFKqMcmfzLS2\nEBL1g63Mi0qpYJKWBuxWANtJHrWVaQtZA81COzPdLstjAGaRnG/KUgFiNtkHsjbaWZg6dSqioqLy\nOw3nBC4XsGABMH06smxqNTQ0NDQ0NDQ0NDQChy8lzIYNG9CkSZMcahQ+AjVlhFKqnFKqoVKqkZlU\nw9y/2tyPAzBSKRWrlGoAMTf8C7LgM0huA7AcwGylVFOl1I0AZgBIJGlpzBZBFpVOUErVU0p1BfAE\ngCk2UaYB6KCUGmr6oY2BLCQdbyszHbIY9jEvWZYBiA507OcDDhwApk4F2rcHYmKA/v2LWyINDQ0N\nDQ0NDQ0NjYIiP7qWGwB8C09cf4sszQPQh+QkpVRZyHplEQBcADqQPG1rozuEQH0F8RVbDGCQlUny\nmBkUJB7AOkjAjjEk37aVWaOU6gZgvLntAHAXyS22fuYBeBniG/ekJQuARwBc42NspQFg69atAU5J\n0eOxx4CdO4WYBQUBd98NDB0KbNxY3JJp/Bdx9OhRbNiwobjF0NAoVujrQONih74GNC522DhB6dzK\nFRbyQ8x2AHgHQnDKmvu9Sdqv3KAc/ltQyB4Z0XvfnmYF/PAVSTEI2YOK5KUBtPLtQUTsiASABx54\nII9mihduN7B0qWwaGkWFc6m619A4X6GvA42LHfoa0NAAIBxhdVF3EhAxU0pFAFgF4GsA7SGarGsA\nHLaVGQZgIICeAAwALwJYrpSqa9OaLQJQGeIjVhISlXEWgAfMNkIh5o5fAugHoAGAOUqpwyTfMstE\nm+0Mg5gmdgfwoem7ZmnNepm/bwB4z5LFHIMVJMSO5ZDlAFKQff0zDQ0NDQ0NDQ0NDY2LC6UhpGz5\nuehMMbcoJ96FlZoAIJpk61zK7AEwmeRUcz8MQoJ6kkxSStUFsBlAEyv4h2m2uAzAVST3KaUGABgH\noIq1yLRS6mWIqWI9c/9dAGVJdrT1vQbATyQftclyGsBHJAfZZDkBYCLJyX4PXkNDQ0NDQ0NDQ0ND\no4gQaPCPWADrlFJJSql/lFIblFL2cPXVIQtAf22lkTwGYC08wTZaADhsi8gIiK8ZIdEbrTLfWaTM\nxHIAtZVSVhz7aLMevMpEm7LUMGWJB9BXKdUDwBUQ7V45iJZOQ0NDQ0NDQ0NDQ0Oj2BGoj1kNAAMg\nAT/GQ4jUdKVUGsmFECJkX2vMwj9mHszff+2ZJDOVUoe8yuxCdvxjyztq/ubWT2VTlgWQxatfMNNO\nQEjffv+GrKGhoaGhoaGhoaGhUbQIlJiVABAMYIS5AaKBGgBgoZmvAGxRSpWEaLAeRfZgG+EArlJK\nnQCQCglh/6xXmQoA7lNK9QbwJ4QE/uhVJgjADKXUXAC/AHjcKz9LFogfmyVLPAC7Ji4LSqlLIb5z\nKdA+ZhoaGhoaGhoaGhoXM7J8zEgeLOrOAiVmqZDw9nXgiZL4AIAh5v++ZvpTAH6GLCq9BEAmgJ+U\nUkFm+VKQNceugGi0MiBkbJ9SKhJAY0jgkFYAbgHwFoS8EcA/5rpmIRCyNd7sf7lZztKi5SpLDuNr\nD4k4qaGhoaGhoaGhoaGhAUhwwEVF3UmgxGw3gOp2M0BzYek/zMAanSEatAiSP5kar62QAByvQYhP\nZYi2K4TkcqXUKACvQEjUDxCS9Q+ASwDsJLldKdUKopXbTvKoUmoIgN8AhJHcppTqD+AOAF0AfOan\nLL4QBQALFy5E3bp1A5waDY0AsGcPMHYsMHo0cMUVeaefYwwZMgRTp04ttv41NM4H6OtA42KHvgY0\nLnZs3brVWkYrxeQ8bwBoA5vVH0m3VV4p1Qbi8nUdTKs/kvP87S9QYrYGQAOl1FEARyBErRGAhyEa\nsBAAUwGMVErthMck8ASAjyDmj5sA7AMw24y+eABAeQDLzIiMLQB8COAeAAlKqYkQglUTwMNKqRJm\nX88BGK+UGgqJ6HgAElY/HrIIdl6yZIOphXscAOrWrYuoqKgAp0ZDIwBERQH16wN9+gAJCUBkJJCS\nAjz1FPD++7JfjAgPDy++a2DePKB1a99zkJICJCcDPXueu3Y0LloU63WgoXEeQF8DGhpZSAfwGYA9\nkCCFltXfaQAjAcC0+vsUwOuQZbxuAfCWUmoPyRX+dBJoVMalAF6CEKvKAJpBIhy2hATdOA1gEoDf\nIeRqI4QgLTPXMLMCdjwN4HKIhux9s+3Z5m8VCOEbASFnmyFmiYT4sVWE+Ll9B2AegAkAtkGY6R/m\nGmaV/ZDFG0Mgpo4aGucGkZFAQgKOd+2DV+9KRtr9NpJ2MaN1ayGsKSnZ01NSJL11jqt1FE07Ghoa\nGkWFefPOvkdZSEmRfA0NjfMB0RBXrvtJbiK5HMAoAI8ppSxF1wAAu0g+Q3I7ydcALIbH5StPBETM\nSC4nOYJkbQA3Afgb4rNV21YsDkAlADdDTAPTzf92vAvgVwDXA7jLTOtiy68AYAaAmZBJeBNi6mhv\n5xYAD0K0ddbaaFcrpSoGKAtsWrgfAFHdd+zYMduWmJiY++Ro5I1HHgFWrvSdt3Kl5NtRuzbwWg5W\np6+9Jvn+ItCH37x5wCuv+K6TkgJMmVI4D8zISMyoMBpDP26DuPDR+SNlBX2w2+t7HyN7fV/HqChg\nEtZspMoiU4EQ18JqR0NDo2igSYn+gKShcR4hMTHxrPf/IUOyOFUDAJtIHrBVWQ4Janidud8CuSzl\n5RdIBrxBTA+3Q0iOtU6ZA0LS0gF0spX9CxIwpBmAsQB2QoJ9VDTzI838YxCNVjIkAuNGWxu9IBqw\nzyDRFjPM/qfZyswFcArAM/7I4jWey830HgC4fv16ahQBXC4yIkJ+/UmPjyeVkl9/0nODYZAOh/z6\nmx4dTbZokT0vp/R8In27weQQB2PgZHKwg2nb8tFmoGPLrb55LGJvvNFn+lnH6OGHz06z4HJJfn5h\nGDwc5eDIm5w83tzHOObOzXlshiH55v/jzR0c0crJYzf4MR/nGkU5hxoFQmxsbHGL8N9GQe9d/xV4\nj/c8Gr++BjQudqxfv54Qq70lAD5ndv5QxuQP7c397QCGeZXpYHKSUvSHY/lT6KxKYkL4iknQMiAL\nSoeZ5CkTEpQDAK41Bd4DYBCA28z8X2xt9YWsS+YG0BBimngcwKu2MosgIfEPm/trzXY6mvsKYv74\nI4AP/JHFazyamBUWALJqVd95VatKvv0FP6cXfpJuN5k21YuEmaQsbUo8U1LItLQAZAv04WcjYX+t\nNOjeZRQqKaNhcP/1DlaDwaQkshoM7q2Xz4dxQR/sXiRsUenSZFRU7qSMDJxsBwC3m3z4GicJ8ImG\nTrrducicR/qz0dLOkzc48y1PjvCXIOYE77maO5ecPJlMSvKkW+TNMMhXXsnepjd5s+TxRfgseTTh\n8wuLFi0qbhH++zAMsm5dvve4i99/T9/3sryuof8CDIPHmjrYMdzJf+ufH6SM1NeAhoafxOxW5kzM\nbjf5SEn6wbGUWckvKKUmQ4JndAHQD8DzAFoDeIvko0qpLyEmhjdDopVMNwUuCeAbiN/YfjOtrUmI\n5gNIADAMwiq3QxaX/s7soy3EJHE0gBcBlAXQE8AsiAbuXYjt5n2QUPdNSUbnJQvJ4bZxlYAsQv00\ngKnr16/Xzq75RbVqwJ9/AlWrAn/84TP94PR3EHp/LNa0H4MbPh2Db4d8gpA2reB2A5mZsm3bBrzz\nDvDrr8CLV7yG4Xsex5Zr78Z1v32ISVVnYOSex3DmDFC2LBATA9SpA5QpA5QqBbjdwOnTQEZG9o0E\nqqSloPtXffBJ1GjE/jQWM29IwJGISJQoAQQFASVLSrnMTODMGaDC0RQ89HV3pB09hXJlFVCmFF5r\nmYhDYZEICpI6dpQo4dnKlxf5rHJKeX5L7U3BbUl98MDpBLirRmLtWuDuuwHj2xQsCe+DpXcm4HjF\nSISEAMHBQEiIZwsOlnaE5do2IwWOhX3wQYPR6PXHWGwcnICTlSIByLyUKiVyZWbKOMuWBY4fB/bu\nlbmrdDIFDab2wY7uo1Hr9aEot3cHnDePQ8y3Y7Bq2Cco064VrroKCA8XOcqUMcezaiUQGwt88gnQ\nqpWYPNr384kP41IQNqQPtnYejbrvj8WJ6QmIfTwyeyFv00Qfpoq7vklBSts+WNZkNO5YPxYVliag\ncSevdgqCnMwjAzGbtM/ZVVcBd9wBbN8OJCYCnTtL/u23y3UVGirpkZG+59rqd8AAoG9fT15O6bnh\nXAVQeeQRaceXPCtXihyzZ5+ddyFDB6fJwu/zVuKSXrHoj5l4t82bUHNyvp7/y4jvnIyBi9vg+Rgn\nXkjWJoxZ0NeKRjFiw4YNaNKkCSBuVU1JZhEEM9jHLgCNSG5USiUDWE9yqK1MLwBTSVbwq0N/2JuN\n9f0MYY2EkJz9kBD0r5r5vc10t1nmLwD1IL5bL5lllkJMDAlhkGshAUTsjPMfiMaL5u8s2BgnPBqu\nM2aZVIi2axKA1f7K4jW27yGauQtaY7Z3L3n4cOD1Tp8md+4k164lv/iCXLKEXLCAnDWLnD6dnDOH\n/PFHct8+MiODzMwkz5whN20iFy4kP/pI6v/zD5l2RVW6AZ6oUpVffEEeqiD7e8pUZe3aQiMeRxwJ\ncBDivOkFAbJcOfKuu8ipU+XD/reXdCIBrgjvxO7dyZkzRc4JE8gOHci6dcnq1ckrriCvvpqsUYOs\nXZusX18UP82bk82akQ0bkgMbiPbksfpOOhxkTIwowZo3Jxs1Ihs3Jps2FeVYq1bk082cWYINiZI6\nrVuTN91E3nijlIuOJlu2lD4aN5Z+q1YlL7uMrFiRvOQSskIFMjycDAsjB4bOZUxVg927y7yR5KFD\nZI8epKO6wacum8tq1cgrryQrVyYvvVTqlitHlipFliwpv6VLk2XKkGXLSj9PNRVZby/v9DmveW0x\nkPoxcHJQkByjZ8v6PkbWFhxMOkq4eAgRfLpUHA+rCN4Z4WK1amSdOmS9euS118rxuO46mePmzWXO\nmjSRtNq1pVyDBnKMbqho8Gs4+NgdBt1u8rE7ZL9tTYO33CLnxv/+R/bpQw7pZHDL5Q6+1N7JLZc7\n+Fx3g/36SV7P1mIq2qySwdRU8o7rDH5XwsGJAwxOmkS+/jo5fz75wQfkihXkypXk99+TGzfKtmGD\nHJ+9e+XcPnxYzvs8tXcBaizdbjJ5vIsnS0fw5z5xTC8dxjN163m0s4YhExUcLJo0MnetpNW/pXVL\nSsq+768m81yZmhWh5jVX5KXtfPhhj8bGKmfXXlrplkbHrom0NJ/29q00l4t87jm5QOznzCuvyJbb\n3ObH9NUup69j6T0OX3V9oZC0WSNHkl2QSAJMfjRREidPlpuEr75z69ef+bHGdO21Z5vEW23Hx0v+\nuYJhcG0506w9xMEzO41z1/f5jkDvQ+fgnNW4eGDTmD0GmysWPVZ/hwGUMPcnwGYVSI/V32f2tNy2\nQInZCyY5Om0Kl2kjWKcBfGzud4AsEr0agAsSqn4QJNjIPxB/sgaQdc3+hQT6cEOCgUSa7f0ICSpi\nTcRkeEwZu5v9TIUEB5kF4BCARAAfmGU+yk0WH2PrAgmnz5iYGMbGxmbbLgR1/uzZZFCQvKSPHk2m\npp5dJi1NyNfbb5NPP0127CgvxSEhOb94lyol1oSBvOBvh5CxdATRDfB3VGV0NNm3L7litIuZYRF0\nT40jIyJ4/AsX//yT/PtvIX7795Pp6TahLZ+yTp0C9y3zhnUjdzr997+KjvYwtsIyYywK2Mbmdjh4\nbKOQkWPHyAMHyD17yJQUcvdu8rffhHjs3EmeOCGkcLfL4MkWDu5918kzDaPoDg0l4+QYpX7u4q+/\nkp9/Lu/2iYlyDs2aJeRmxgzym7uFyK24M47jxsl759Ch5KBB5FNPyTZoEDlgAPnQQ2Tv3mS/fpI2\ndCg5eDD5xBPkqAcN7op0cPksgxkZMrQzZ8iPpxvcdoWDAzoYbN9ehtqsmRyS/nWFUPav62STJkLG\n725k8OdLhYT9/ru0s3cvOegugytLOdgg1GBwcODk1dpCQoQYly8v3KFxBYOukg7ed5mTq0o72CbS\nYN26QjYbNxaZoqPJ228n27Uj27Ylb71VyP0110ibg00y/Dji2KySwR2XRXP3ZY245/LG3F21BT/o\nnsS0shFc/b84ppWN4BcjXUxMJN97T47JO+/Ih5L588nFrxjcU8fBDX2mMzM4hLseHMWMULneTpyQ\naywzU+blLKLp67wqav8XbxJW1KSMzPuFz+XK/muZ9oaGygH1TrfL68sf1TDkZChfXn7t7UdH+3eP\nyQ+J9R6P97H0Tg9kjgrhPLitjsHNlR2cfEMiDyGC01omMqNpDmbjefXrz/xYbYwdm/2ZklO6v/CX\nEHiXMwym3yhm7c/3MDgUr/BIEz/m9kIgIIUlYyD3oXP1QUnjP4dFixad9f4fExNjEbMmELeqz02+\n0t7kNOPo4RKREHesiSaHedTkR7dYZfLaAiVm5Uytk33LALASsnZYurnfySxf26a1amqSpDPIHvyj\nH8Q88jAksMdEk6zZ/dASIREgP6NHu7UXZvAPiI/ZX5C11Z6G+JjlJkuzHMb3Mi5Qjdnhw/Ku0LWr\nEK6SJcnLLyf795cX4FtukY9/JUvKUVeKjIwk27eXl+HXXiO//JL85Rfyjz/IgwfJkyc9L2zHj5M/\n/CCatDlzyLfeIt98k/zmG/LIEXnZX76c/PBDeXn/5hsyIyiIBOTXQqAvX96BPvIT+MNCoC+Y3i9W\nvl60zhcU9OXZXt7+4unrhdMXrDImkSvQy3SgD/KcyLYf7bjd5KlT5L//krt2kZs3yzWwZo0M4Ycf\nyK+/Jj/5RLTCiYlkQoKc+6+9JtrkV18lJ00iX3qJnNtbCOKb9zv5zDNCOJ94gnz0USGhDzwg2r7O\nnckuXcj77iN79iQHDiTXTHbRHRHBQ2PieCYsghPudLFfHWcWE7y9vJMREeQgeMibvxrQaRiYYx3z\nMmVYmGhlK1WSe0PNmkIY69Qhb65hcHVpB7td4eS6cAe7NjfYrp2QzLvuknF06yYa34cekvvO44/L\n+IcNE43ImDHkxInkyy/LNnmynC7x8ULwExLIz0e4mF42gj/1jmN6uQiunuTi8uVyP3G55LisWyfH\naPNm+cCwaxf5559yD9qzRzSbBw7IPTE1Ve5j6ek5aDrt509O144vkhYVJerrvK4RX/eQqCghZo0a\nkYZB93cuZpQL48Er6jEtys97S35IrNc4Mr510d0mD1Lm7xwVANu+EG34p/EGjxwh3+0kmrMRtRJ5\n+Kd89uvP/HiTsLFjC0bKcpMvt/kz/3883WA1GDzVUj4aTR3kx1iLioDkNyCRVc+uLbZkSUryaKD9\n0Qz7gmEwI8bBQx/Y7vU5yWoYco117erZ16RMIx+wacyiAFwNWafsuEnKJgIIYnYu0RrAekhAwh0A\nHqQPzpHTFhAx8+o4CMD/TO3WHHgiIc4GYEBWxW5iaqF+N+uMBbDBi3H2MAc8yyyTDOAtL8Y53yxz\nCzxRGSeag+4B0ZptN8nYZRC/slxlyWFMURcqMXvrLXmW7Nkj+4Yh2qkGDcRs7L775CVpxgzRmJ08\nWcQCWYE+rLe+qlV1VMaiQkEfzt6kzPurcl7krDg0Hb5k97V/LpETQfQHvuYwLEzsO+3aWtMU0T01\nju6ICKZ95eLx4+TRo0JCTpyQazstTSJ+ZrZxMPXl6XQHh/DAwFE8XT6CK0a7uHChvDvNnk2+8YYQ\nzcmTZRs3jhw+XAjV00/LfWPIEHLm/4TkvdTeye7dhVzefTd5xx2i+XM4xPS3eXPhHg0aCKmrWVMu\n/8sv95jyXnKJ/JYtS5YokZ0oPh4A8czPFhQkH6jKlBF+FBpKNggVk9c7yosZ2XXlDIaHi/lxxYpi\nWruypIMDLknkERXBgZclclPJKB5VoRxfOY5HgyLYs6aLUVEydsuEumVLslu0wS0R0dwZ1og7wxpz\nc3gLDmri4q9h0dxaphF/CmrMTahHArylpJhKP/ww+cwz5AsvCE8YPZocNUq00MOGkU8+Sb5yt4up\nJSL4Wu04ppaI4KSOLg4dKprpp5+W+sOGybEcOVLqv/qEaKNfi0nkYUTwkdBEbr/KwbdHGXzzTdG2\nLl0qH9eSk8V8/ccfyfXryV8/NXiokYMrRjp5qLGDm5cZ3LZNtO4pKWLx8Ndf8mFv1y5y2zYh0L/8\nItr5TZvIX38lf/pJTIY//ZR8/RkjS7ucnu65hna+mMjDKoK3h7n45L0Gd1R1cMHDTu6+1sEP4wwu\nW0auWiXkfOtWIe7ffSdmyF9/LRrjBf1cPFEqgu/fFMeTpSL47TgXk5Ml/9NP5UPA689I28uuGUQ3\nwF21b6Ubisld4/nii/LBZPBgedR8/rmM48AB/zTM7l2GaKTzuD9nTprMv1Ya/F8Lg9+Xk3I9epDV\nqpEnNht5a5SK4h6YX9NiKz8pKftzMilJTAzi4/3XDPvAP/+QnS6R+9Duhc68ZQ0L47FrG3FsWyeP\n+qOBzAuBENacPgyWLi0vZL6Oa+/ekn+h4kLQ4OYDdmLGfHKmQLZAydhwAJtMAQlRz20F8CqAbiZR\nCoUs5mz5dqUDeNOsP8skZM1MpmmZQRJAB7PMdkggkEEQTRpNIuYGUAoe/7LmkMAfGbZ+dpht5ClL\nDuO7YIlZbKz4PZ0XsEiZFZ3R2i9bNrCvcL7s/y0Eav8f6A3Dl3+Ivbx3ZLziREFvhr78Z3zV93WM\niss3yJLtfDFXKcjLUU5f8+vV8/iUGUbx+Jh5t5cf0ukH3G7RaKV95WJmeARPvBTHzPAI/rvUxZQU\ncscOeQHfuFFIwtq18nL/7bei6f/8c/Kzz0Sz+eGHotm3TG4XLiTnzfNoOmfOlNvHtGmi7ZwyRS71\nRf3khe+dvs6stAkTyPHjhazO6SX5H98ixHHm/5xc2kb+L74pLksr2q+faEn79xdtaNeu5PCWzixm\nOPImJ7t0Ice29aQdq9WIhz908o+aDj56u8EbbhA/2SpVhNBeeSV51VXysl6zphDehg3J+Guk//hr\n4xgVJWbp114rms5ataRs9epyC776amnjnkudWTITYNcqTpYt6x+ptfugFgZJfqTkXD7SzuCOHTzr\nmtn/gYt7K9Rhx+sNdr9S+nUE+99vRAQ5vrKMcUSob5J/ySVk1yrS9toyN8m8oBOVEkJev77Mtbep\nv1KyBQeLqX/58kLiK1WSY3ZdOdECWsug3Hilwdq1PR8prrhC/I8bhBr8Rkm5b4Mc/OotGfvWrfK4\nLFtW+r/hBuExN90kU9SunfhWd+xI3nOP+OD+WtnBlzs4ue1KB1/qa2Sdu5Yv7cKF5OLFco1YBDU5\nWbTQ69cLcd6+Xab/77/JQx+7sq7BffvI41+4sj4GnTolH38yMszrNk0+CKWmesodn5vEjKbRPF27\nLs+UD+Oup+J5umwYj1atxxONWvDoL0LGcyW5Npw8SfZqI/N1e3knV5dxcOPH4oOc08fBTTNdbF9G\njm+Hsk6uXl3AG1Ugz7ucngH33Scn0X33ZU/v3VvSe/f2pMXEeO733khKknxfCLReUZmb5pV+geB8\nJ2afQSIitoP4ZO0wiVVDGxmaCfHjag3x7UoF8CezE7NNkAXXGgCINQf8Dj3EzAqZP8nUmL1ukTcb\nMRthasAsjdnPJkmr6I8sOYwvCrjwfMzOnJEv0S+8UNyS8GxSlle6xoWN4lyD63z5OlfQh5EvMmx9\nbbbMfyzz0uuuy/6lObcXAm8SllN6oOMrqofs+aB5zYl4WvmJiSJTYqKoxGx+mDnKaR1Pu+bT8imr\nV8/jb2Y3+wqE0AdiPuxrHGZ/bre8/B44IGah27ZJ8JsNG+TFfePHBk+0cPD4MllX8KcPDH73nWir\nli8XLdSyZRKUacUK0WCtXSvb998LAVizRjRwW7ZIH5aPo1+WC6bv7MktBv/+W7Rlq1YJufjtNw9x\n37FDNMf2+XFHRPDgRy5u20b+/rsQj7Q0W7+DBpEA3e1upVspumdk/yCYni6awDVrhPTPmiXbzJli\nzjxlipD4ceNEwzllCvnxk0II3h3g5IgRouV89lnRXo4d6yFNHwyWckc+cmbrc8sW+TgweLBYv/Tp\nI6bClra6Uyf5INuhg7gqPNFQ2uldw8latYQoWkGj8utLeyMkqNPjiOMhRPBGuAKqNxqjmIFgbkNN\nrodHM2wn9kqJ9rpCBfkIUbOmBPO6/noJDtWokXxUuKaEwW/g4DcJBnfuJG+pJeS3RRWDUVHkoCai\nQU6MjuPxkhEc2szFmsEG14c7eGCJmGBfU8LgPfeQl6RatQAAIABJREFU994rfTRtKlrlxES59Nes\nEY3uli1ynvz1l1wPqakSIC03EpjrBzLve6dFziwS5ouUkR5NozfJyik9v/UKk1CdT1Ys+UAePmbn\nHzE7q7KQIELWDrtgF5i25V+QGrMNG+RIJicXtyTMnXxZ5ExD47+EwiaIvrS1xbWO2bn6Ano+aV5z\n2i9sH7N69bKTNHuZvOa2EHzMzvrNrb+iftnK6RoyDJmXV14JrN/i8jHzbjsvDXNhaaLzaMft9gR5\n2rOHWQT1t9/EvHTDBiElyclCqpctk0i1H31E/vqIaB1/7BHHhQuZtc2fL/7mb78tGumFC4XgvPuu\n7K/vIfV+6zAwi7GlXdeI+94TU9hPZhicP1+02NOnC0kdO1ZMcIcMIR97TAhp//7k5McM/nmNg8a3\nnnGlp5Nfv21wZ1UHh3cz2LmzR4M8+eo49ogxuPsaIfKkmHan1BD/WIdDtNpduwrp85eoWiSyfTkX\nD6sIPh8RxyNBEex2tYstWsip2ro1edttst1+Ozmgg2gzX2rv5NbLHRzb2+DgweSa63rTDfBARHW6\nAf7SrDdfe03cUhYskA8An39O/jo6iZnBIdz9ahJTUsgjs5PoDg5h5rs5kDLrmL+XRLedhOVF5grx\nGj+5xeDv1Rx8vrWTx24oxPsEIB/DfCE0tHDfL21ax/NaY3ZWZaCWKexSXMALTNv6uSCJ2dSpYk5x\n6lRxS6KhofGfwrnSShaX5jUv4umLvNiD43inBxKV0fK79VU2t7nND4n1Hk9OpDMnclQc5kn57def\n+fEmZYUVldGXfP6OI7/zWZSkOT9aWXu9UaNEXVetWv41w6R/9yG7rGFhWcF1zirro98DB8SMc+NG\n0eiuXEl+9ZUQ1KVLyUWLhIS+8YaYQE+cSH7eQUjgB444DhlC9uolCq/772eWVu7uu80Aa6Y2s18d\nJ6+5RrR1tWqRu4KrkwB/V9VZtmzO0bHvRRJPI4TTMJCnEcJ7kZRFFMuXF/PZyEgxka1SRcxkS5f2\n1JtZciAzEMLhtZJ4553kgw9KcKannhK/1TFjJHhVwvMGf6no4GP1nfy7toOLXzH47rtC0j/7THj/\n99+LFvyHHyQQ07p1ojX/6ivRmr/yiphStyspY76lhJOvvcasCMsFgkW+vMlZTukFgY3IntfEDMB4\nAK0AVANQ39R+EcDNZv6XJvlpAwm2sQoSon4tJOJhEICDkPXP7KEmXzbrtbdp0JzIHmpyuEm0Splk\njgDGwBMu/yBkEek1/siSw/guSGJ2993nkX+ZhoaGxoWC4lzHzFvz6Usb6gv/wXXMfCK//RbnOmYF\nJWGBEpaiJM35NS32DgBSq5aQMyvwRyCa4fzKOny4kLOcPlIU9JwNhLDmpM20zBerCzmzzBgzM8Wk\n+ODB7CbFf98jmsedtw/kokWiqZw5U8xmx471EKwXXhAz2WnTpMzPMVLP1Xgge/Ui77xTgjQ1aCA+\nqdWriw9rxYpC5grqR1qmDPlQW4PHmzmY9qX4PFaDwfLlxVeyQwchrvffL5fi44+LlnT0aDEHnjZN\ntKgLFohP5LJlQvzWrCF//plMKxdKN8C08qE8fpzMLApSZsEkZ+snTDinxExRCIlfUEq9BVnoubKp\npVIAJpEcZuY/CInQeBpAaZMYrQRQAcAyks8ppRaaBCwCQLBZNhHiu3YbyS+VUn+aBKyi2cchyLpk\nvQCUAXApJHz+UQDh5oT9DtGqXUmypT+y+BhfFID169evR1RUlHf2eQm3G6hYERg0CBg9uril0dDQ\n0NDQuEgxbx7QujUQGXl2XkoKkJwM9Ozpf7nC6i9QrFwJxMYCn3wCtGqVd7p3/ptvAlOnyrv6vfcC\n1aoBfftmT09MlDr5lbGgshZWf7n1k5IC9OkDJCTIMbL2L70UWLwY6N1b8vr0AebM8ex74/33ge7d\ngf79gTfeABYtAjp3zlvWQOtZ8o0eDY4di9MzE3D6ikikpwPp6cDJk8CpU2fTsdBQQCmgdGng8vQU\nBD+Sfcypnftg0S0J+OHfSBw6JG2cOgWkpXn+e2+54V+EoSJSkQkhEQcQimvCj6FMGaBcOSAjAwgO\nBsqUka10ac9vuXJAhQqSX7aspJctK2MICwNKlABCQuQ3NBS4as37ODqqG5q6MwGgCckNeU98AREo\nk4OYI/4AWWssy5zQzHNACNAhSFCP+gA+hPiEDTXLjIUQqg2Qtc9aAtgFIVfXm2VWQswZ5wGoCwk0\nkg7ghJlfArIe2hkAQyGatbGmPF/5K4uPsV1wwT9++kkuDaezuCXR0NDQ0NDQuOBRmOuYedfzVzNc\n1LLmB+c6KiN5tm9YXr5i+a1XGCaxhaTBdbvFNefQIQnUs3OnRA394Qfxg/ziCzLD5IUZAOPj5XQb\nO1aCuYwYIb+DBomfYo8esm5obKyIERUlwWWuuUa0hZdcYjcjXUQgNttWE1ecv6aMFPISD/HnqmES\nHzsxCzOFT7ClNTbThpv7j5j7DluZODPtKnN/uUm6QmxlNgNIte0fALDLtq9M8rbaX1l8jO2CM2XU\n/mUaGhoaGhoaGkWMc72O2YUWlfFcmT1b5ovWVghmjBYZTE0VQrhvn0R43TUpiT8GBZ9TYhaSsy7t\nbCilXoeEou8IWWMMAMKVUqVJpkFMDAHgVqVUG0h4+ukQDVklMy/T3J5RSh2EhL/vZpK8JpDIialm\n2fFKqQQAbSHBO4KUUuEkj1pETinVA6LBG2K2G2rWreiHLBc8vvoKaNlSVLQaGhoaGhoaGhpFgNmz\nc85r1Sq7KWNO5pm52eklJGQ3ZYyP921+aO3Hx/s2TQy0XnKyx/TQjshISU9O9m0u643cTFIjI/1r\nIy+EhQGpqWJneOyYZz8sTPbzCcsU047K370PPNcdh18aDzz7bAEF9x9BAZbvD9FEOSHRDRUkTH0X\nM78KhGB9AWCxrZzTzAPEP82AkKjVAOabbRywlQkF8CmAWyDrkw0BMNLWB0w55gN4AcBPkGAi0+Ah\nZJVtsnwKidjYwuy3XoDjPi9x7BiwYoWYN2toFCYSLft/DY2LGPo60LjYoa+BYkRycs4+YZ07S35h\n1OvZM2fSFBlZMB/AwoQ3KQPkNzTUQ84KC5Z/3qJFQLt2hdeuHwhIY0YyG5FTSrkh64R97FV0BMmH\nbeWSIBouC2dI3unVVm+vMntJ3m3LrweJ3mgvs8Krn0e98gHRpj0ACRzyA4BlANoopSqSPOBrnEOG\nDEF4eHi2tG7duqFbt26+ihcb3n0XOHNGfGs1NAoTiYmJ5935rqFxrqGvA42LHfoa0Dhv4E3KLNg1\nZwVEYmKifIxYtQpo2BBYsABHjx4tcLuBICBi5gf2QbRolSFh8C1Ugmi1rDLZTAmVUsGQaIn7bGUq\ne7VdCUK6/smjjD1fARgIYBbJ+WZfu81yfQBM8jWIqVOnnvdRGdPTgUmTgI4dgapVi1saDQ0NDQ0N\nDQ0NjSJCblHkC2DGaIcvJcyGDRvQpEmTQmnfHwRqypgrSBoQQtTWSlNKhQFoDjFbBIA1ACKUUo1t\nVdtCSNQPtjIxJmGzcCuA7aZ/mVWmLbKjnZlul+U6AF97ybIOQHS+B1rMOHkS6NUL2L0bGD++uKXR\n0NDQ0NDQ0NDQ0CgoAtaYKaXKAagFIVIAUEMp1RDAIZK7IREWRyqldgJIATAOEtDjIwAguU0ptRzA\nbKXUAAAlAcwAkEjS0pgtAvA8gASl1EQADQA8AWCQTZRpAJKVUkMh5ondIMFDHrGVeRvim3aNUqqB\nTZZ1kIWyLxh8+60sMfHLL8CSJcDBg8CCBUC9/4S3nIaGhoaGhoaGhsbFjfyYMt4A4FuIWSEBTDHT\n5wHoQ3KSUqosgFmQRaRdADqQPG1rozsk7P5XkAAdi2EjXSSPKaXam2XWQQKDjCH5tq3MGqVUNwDj\nzW0HgLtIbrH18zqEmD0LIWUuAB0A9MXZvmiALESNrVu3BjglRY+uXYH9+4ErrwSaNxefxOrVgQ1F\nv9SdxkWIo0ePYoM+uTQucujrQONih74GNC522DjBOYl/nh9itgPAOxCCU9bc783sq2EH5fDfgoJH\n4+Zr356mICTKO99q2yJY9NHXAQjxC7KVB7L7otkRCQAPPPCAj6zzA3//DSxdKpuGRlHiXNpUa2ic\nr9DXgcbFDn0NaGgAEI6wOq9CBUWg65hFAFgF8dlqDyE+1wA4bCszDBJwoyckLP6LAJYrperatGaL\nIIE72kJMGedCNGwPmG2EQhaZ/hJAP4gp4xyl1GGSb5llos12hkFMGbsD+FAp1dimNRsKIWyrADxn\nyWL2Od3HEJcDuB9igpkWyNxoaGhoaGhoaGhoaPynUBpCypafi84Uc4ty4l1YqQkAokm2zqXMHgCT\nSU4198Mg2qmeJJOUUnUBbAbQhORPZpn2EHJ1Fcl9pu/ZOABVSJ4xy7wMMVWsZ+6/C6AsyY62vtcA\n+InkozZZVkDWWetn9rsWwCkANUju93vwGhoaGhoaGhoaGhoaRYRAozLGAlinlEpSSv2jlNqglLKv\nI1YdsgD011YayWMQMmRFQWwB4LBFykx8BdFsNbeV+c4iZSaWA6itlLIWGIs268GrTLQpSw1TlikA\nnoQsRL0SwAkAH2tSpqGhoaGhoaGhoaFxviBQH7NrAVhxAAngMgBvKqXSSC4EcLWZ961SqiSEKD0K\n0ZhVMfNqAyiplDoBIBXAfEhwjkO2MnUBVFdKpQH4ExLcwwqlXwXAUQBXQKI/TgTwC4DHvfq5ypIF\nYrpoyTIDORBSpdSlEBPNFGhTRg0NDQ2N/7N33eFRVG/3TBJCgCQsRapKEAUCoiFYiGBglSII+IEU\nUVFAAVEsYAXFAIpUIWBQikZQJBqwC7YfuHFBKQYpSocJVXoIPW3P98c7w85udje7IaHOeZ55duf2\ne6fdc99yTZgwYcLE1Yxzqowkj5R0ZYESMwXAaUgDdWccowAMBDAXwAta+BMAdgKYBuBLAP8BoKIo\nQQB6a2maQsjVpwBytDAqihIFIBbAegAPAWgF4EMATxnS9NDaPh9CtAZDiNcYOJ2B+GyLl/61hTg2\nMWHChAkTJkyYMGHChAlAfFDMK+lKAiVmJwDkG9UAFUVZA+B+zZbsfgjp2UFynaIofQBsBPA3gN8h\nxKcygOMk1wNYryjKcABjAYRDNoQeCOA4AJXkZgCbFUVpDtmfjBCp2GCtLZu1fdGe0upuA+CAn23x\nhAwAmDt3LqKjowMcGhMmAsD33wNNmgA1ahSM27cPSE8HOna88O3SMHjwYEyePPmi1W/CxKUA8zkw\ncbXDfAZMXO3YuHGj7q0940LUFygx2w2ggaIoeyGqfn9CHGnshGzuHAIhTvcCWEdys6IouyFeFcdC\npGSbAdTXvCf+DZF0fQBxa78SYg+2GkC8oijBJPMNaTZDJHZNtLrvBTCVJBVF+R/EBu4LyF5rhbXF\nEzoBQHR0NGJjYwMcGhMmAkDFikDfvkByMhAV5QzPyABeeqlg+AVG+fLlL94zMGcO0KKF5/5nZABp\nacDjj1/oVpm4CnFRnwMTJi4BmM+ACRPncFZRlOsATAfQEgZzLJIOPZGiKC0h/i0aQjPHIjnH30oC\ndf4xEyKFmg9gJIDbIaqCsyC2XTkAJkNsvzoqitIIQASAkwC+1dLsghCtWYqi3A6gNkTl0EZyv5bm\nd62sZEVRGkDs0sIATIFI3IIhG1q3UxRliKIo9QDcCKACZFPqqn60xQWaeuTgAMfDhImiISpKyFff\nvnDsyMCRIxDS4YmsXW1o0ULGISPDNVwfnxZencK6Ys6cgmUYy5rj93vShAkTJkoG5nvKhInLBQqA\nRRDBT1PItmC9ISZdkkDMsX6AOEG8FcJbPlQUpbW/lQREzEgmAXgAwD0QxlhBa+jDhmRTAGwH8A2A\ndRAy9K1hDzMAeBlAdYiETPfgaNxXLBvA6wC6QFzcvwwhhB8b0vwDIWdjAWyCeHTMMOxh5m9bdAyG\n2KCZMHFhPpYaOdt7X190qZyG/e2LSMqutA+7gbSe61dRSGtxETwTJkyUDK60d1dRYL6nTJi4XBAH\noD6AR0iuJ/kzgOEAnlEURddAHAgxoXqF5GaS0wAsQACCn0AlZiC5iOQtAFpApE+nAVgg9mGhECcb\nVSDkLRZAPoB4Lft+iDTrcwixugXCNgGggyHNTRCnHh9ABmEehAC2gGxqnQ/gQQC9ADwJ8eK4A8C1\niqJU9rMt56AoSimIeuRKQHSqO3Xq5HKkpKQEOlQm3NGvH7B0qee4pUsl3oh69YBp0zynnzZN4v1F\noBOAFi2A9u0Ltlf/WNapU2zkbHRwAtLQEiOYUDRJ2fl+2I1j436NjGPj6RoFek39hUbOHH36Yucn\naWBRJIkGgkc1A//+C+RvzzClkiZMXCowSUnxLUSZMGHivJGSklJg/j948DlO1QjAepKHDVl+BlAe\norYIiCTN61ZefoFkwAfEUcdmAO0B5EKkXpEQSVcugM5auroQ2zEHgDsA3AcgT0tTWUvTH7K3WCZE\nPDgWwEGIXZhe3zwA+wAs0s6XQ7wrTtHOFYj92zEAr/jTFrf+VNfCHwPA9PR0migiALJOHc9xNWpI\nvN3uGm63kxZLwfCkJFJR5NefcF9QVdJqlV9/wj21S09rt3vPEyB221UuhpXDmtm4GFbuWFLEMt37\n4atfvvJqfZ6XkOAx3O9r5y08QHzwkI0EOG+ArWDk7Nne+6eqEq/933WjlfGwUb2heK5bkdrhDU8+\n6X2c7HaJN3FRMG/evIvdhCsfqkpGR/PMr3Y6HPT8LivsGboSoKrMb2nlwldtzG5eAu+pIsJ8Bkxc\n7UhPTydEa+9LAD/SlT+U0fhDW+18M4BX3dK0gwiGStMfjuVPIkPhEyASpwUaWfoVYsv1vhb/rdb4\n9hAJ1DIAdognk+chErr9kH3IboF4aTwAUWN0QPQxo7QOrILYlj2t1TEesjE1APTU6pkMkajNAHAE\nQAqAr/1pi1u/TGJWXKhTxzM508Nr1HCZsB/51k6Hhwl8bi75zTfkd/cl0QGFBxOSmJdHHh8r59/d\nl8R+/chx48j0dPLkSTIvz5k/L488c4Y8fpw8coTcv588uFJlzt1W7lmqct8+cu8ylaebOs//+488\nelTSHzxI7ttH7l9gZ26EhTPuSeHRGCt3p9h5Os7K3XaVu3aRu3eTe/bI7+7dUs+RI+SJE2R+vu+h\nOrNR5eZrrawbqnL/frJRhMr1Vaw89a/KvDzKJCUA5G5Vefx2K3fPtdERKHF0J2EREWRsLKmqdPxe\nCMlyJ2HFRMoOrVL5W5AQqrRgKzP/duuPn2Q7J4d8sLIQvE7lbTx16ryaVRBFIf1GuI/X7NnkhAlk\naqozXCdvqkpOnOg6UXUnbzpR9ET49Emuv4TvfEmnCRN+4Oz/7DwKC6fFpxR9gekKwLdD5D0142EP\nC1EmTJi4KPCTmLWhd2LWXuM1ofSHa/mTyFD4Kk3iRa0hhyAu6Cdp8X0MUikC2APZkHoFgDFamq80\naRa1hq4AUM6NcR7QyBi13xlGxmkgUnpbTmikahyAP/1ti6FfpSDStRdMYlYMcCdnderQAfDs9XW4\nYAE5qYudWcEWDgtP5FFY2K26nc2bk3Fx5B13kE2akOXLSxHh4eRTSGI+FC5AZ+ZD4VNIYqVKkq5c\nOUmnHyEhZFCQa5jxqAWRUMVDJFS1oHpNqx/dkUICfBaJfucBpB1lykgbw8PJyEjpl8VC1g1Vz5X1\nzjsyTJ9/TtZWVJc6QkLIsDDJb7GQlSuTVauS1avLb5Uq5DXXSHhYGBkP+bC3KW1jw4Y8d8TGyvjG\nx5PNmslcp0MHsmVLsm5dMiaG7H6HytUVrBzUyMZ/w2KZhQgOCZFr9GiUnffdR/brR770Evnqq+TI\nkeTo0eTYseS8p+08U8bCtC6JPFvGwu9esXPuXPLLL8mvvxaOMX++/F+4kPz1V3LxYvLHH4WAL1gg\ncd9+S37/PZkyRmV6eStvDle5YQN5c7jKdIuVP36gcsUKcv16cts28sAKlWfirDy4UuWePRr5bm7l\n0dUq//uPXL2afKe/jKn9bRuXKFa++ZjKnJxivufPR2JJniNnjt818tWgARkcLAOnx0dEyMVs2tRZ\nricSrNdtJHa+wgPpV2HhRcXFkhoWRjyffNJJQPV0RpKsh+sE1dhWnWAby9fD7HayRw8h2cb6dNLt\ni/Sez1hdokR73jzne/bA1BRne64iUkZV5brK8m1aGX4V9dsfXKL3rYmrAwZiNgPAarryhyiNZ9yi\nnafpnMiQprcuWPLnULRMfkFRlMcAJAJ4FMAWrbJhAD4h2VtRlF8h7umtkL3IphnI1P8AvKGROQfE\n7kvfYDoZooJ4n1buDohnxgGQDaYTAYyAeD4po5Gu6RDPkJ9DjOq6QTaHbkLyrsLaQnKYW9+Wa/X2\njI+PR/ny5V363rNnT/Ts2dPvsboYOHQIGD0asFiAF16QX184exbYtg3YvFmObduAw4eBzEzg1Cng\nzBng9GkgOxsIDwcaNQKuvRaoVAkIDpYyNmwA1qwBIiOBhg0lXXY2MPyzG1Hz1HbkIhilkI+NqIOG\n2AYAuPFGYETFKXhk5QtY1CYRv0Q/j8xMKTMoSH5r1gTatZOtvnbtAsIe6YJqf3yNPXd0xonZX6Fe\nPUl79qxs+bVzp/w/e1bylyrlPEJD5ZcEcnKA63ak4c5XW2LFOBtO3dYC+fkS7nDIr6IAISFSTvjh\nDNw6tS/Q6QFYRryAf4en4EDLh+Bw4NyRny95FAXIzXUeJ07IGJLOtPr/mHVzcDymBRq0j0KDBs5r\nsnEjsGFRBq7ZkIbNTR9HXh7OHfn5zv8Oh7NO/ah2NgNdFvbFtocTUOWDkfioWTKOWaLO9Vs/QkKk\nXWfOAGXLylZq2dnA8ePATfvS8OaSlpjaxYabTq9Bu59ewG8PJOKr657H7t3A7t3SL4dD7g29Xfn5\nQL8zUzAh5wW8EJSIKY7ni3wf10IGktEXY29KxrCZUWjZErDZgDcfy8CI3X3RF8nYiagC6UciAQkY\n6RKvx/35ZDJenxWF5DczEPVWX/QLSsaRiCiEh8s9GxEhv2XKyPiULStl5+VJXLlycr+Fhsq9HhJS\n8LAcy0DLT/tifecE3PrtSPw1MBk5NaLOxQcFAaVLy3OZmyv3QlCQjOPBg8Avby7F+E0d8dG1IzBg\n75vIrnotImpEAvNSULo0gA4dgE2bgJQUoFs3seHr2FH2xGve3HUQdRuVgQOB/v2BmTOBDz5wnnvK\n4w3u9i4lYf/irS+++lgc8NYXPXzUKODNN52/ycnAnj1if3rTTcCUKa7hxrZmZAAPPywXOiXFOXZd\nugBbtwK1asnNpdsv62knTHCW6Wl8izJW+hYUQMH+ZmQAX34JLFzouc4LsH3FoA4ZePS3vkgO6Y9J\nZwbixPgPUH3mKLlvPV13X/X26yfhnvItXSr9ad5c+tS2LfDcc8AzzxQs++RJYOpU+Tj6C3/Hyj1d\nRgbYpy9uTU9GxYpAk51fYkyzhQida9qYASj8OXUPN7dcMVFEpKSkFPApkZWVhd9//x0ABkH4SHVq\ndmaKovSHCIWqkMxVFGUsgHYkb9XzK4oyD4CFZHu/GuEvg9MI3AMQcpMDkTDlwik9y9EOB4BILX09\n7XwfRJVRl3qtNZQ5AKLa6ICoN46DOBWZZEiTAmAtnKqMK7RyOmnnCkQi9heAryE2ZjlaGo9t8dC3\n7pC92S5LiZnDQd57r0hWypQhK1Uip04lDx8m9+4lly+XhfK33yY7dSJvuMFVslShgkirOnQge/Ui\nBw4khwwh33iDfOst+d+mDVm/vmgjVq0qkpq77iIHDSIff5y8/Xby5ptFkhUXR2YjmASYowTz/ffJ\nH34gd+6kc5U/MdG/lXvdpqxz58Bty9yhr8LabIWvxrrblKWkFIuKXongfCU2xjw2m4jYIiL8v0Zu\n1zQ/zc7Tp0U19NAhMjNTjoMHRfVzxw6ReO3eLfFHj8q9euAAmZk4m2c3eW73f3+q3DlqNu128n//\nI7/7Tu6rZe+IpHDZOzZ+/TX51Vfk/z5UeayJlSfWu5a16SeVe+paOWOoyoQE8sUXyf79yYcfllus\nY0d5llq0kHs+Lo685Ra5t+vUkfu/ShV5ZiIjybJlydBQuTV1iWU8bH5JVY1Hkybkd/cmkgCTYxIZ\nBZXLEMd0xHC10ph/BjXlo6VTmalYOKJiIo8FWdjzOjsbNiQbNRJhWnS0PKN165Ito1T+EWblOzWm\nMlcJ4Zyo4TxRysL3H7Zz2DDyzTfJUaPId96R98J778kxcyY5d67c7qmpIs388QOV+xta+b/hNh5t\nbOVfC1SuXEn+/Tf5zz/k5s1yTXftEpXgw4fJrCzy9GlRS/ZLLbeEVGILRWHPjvt7wG6X56NcuXPq\nvl7bqqpyA+lSTlWVPOHhIqa22yUuNlZ+/bVfDXSsjH1y/29snz/jU1h4gDi7SaUt2Mopg1WmpJA9\ng0Rylt5natHq9cfuVS9j5EjXb4q3cH/h71h5uB5/f62yFlQeuFk0Jr5JLKSfJYmiSmX1fEZpsS7t\n0vP5Kxl2RyDfuAsl6TdxVcAgMWuicZEf4WqO9RZdJWgnNS5jNMdqRfrJtfxNqFVYDqIO2ADigeRF\njex8DfHnnw9RU+xsyLNHS3M7RMK1Da7OP6K0+OMQlcI0iHdEI3nrrXVsEZxqh5uhOf/Q0syGeIh8\nGSKN89WWO7z0b8zlSsxWrpSr+fXXQsSeeEK+K+6Tv/LlydatyZdfJj/8UN6VBw8Gbs9UKHR1xmAh\nZ+fUGgOdULg7+iiK4w8dRXmxu0+ULtRkMRAUx0fIh41ZoX2+WBNq97a7k+0Lrf6iqnRYrcz51ca8\neCuPr1N55IiQzb17hbRs3EiuWkWuXUuuWyfEZssWsU08Z8unkds9n9vPEU4C/HygjRMmkAvbCHn7\n5p5EDhlCPv+8LI48/zz5wguyiPLii/KM685js1yEAAAgAElEQVRTfqo7iAQ4pU4i69Qho6LIa6+V\nBZZKlWSRJTRUDm/E8XxIJ0CWKiVENjzcqZp7zTWilnv99fKK6HmdnceCLBxXM5FZwRYOaGhnfLwQ\n5fvuk4Wjzp3J7t2FSD/+uLzrBgwgn3qKfOYZ8rnnyMGDnSq3w4aRw4fLXPvtt8kxY8jx48l335Wh\nnjqVnD1C5e66Vn79go2761qZ/KbK994jp00jp08X1dp99a20DUzh2bIW2p9N4ZGoWGaXieDavonM\nLmfhsnF2/vgjuWiRqOcuWkT+9hu5+iuVJ2+J46l6MTxVvzGPN2rKf2fYmXVzHI/VieGhag14MiSC\ngyqncOt1QnoPHCCzswveYg6HEN0zZ8ishXbmRVqYMSSReZEWZn4viyFnz0renBxJe87W1fCM71+u\ncm9UUx68rjFzb/dBylgwr8fzIiJ3q8rtUVZGQeXGjVJu7t1WTm2WwqOw8MueqTx7l5XZmwOsV3sH\nnfrZzmPHyJwl3lV+c94cSQcUnho60oWUOd5L4rFjYr8c0PfR37HSwzUCk/SSENScLSpvvZXs1o0X\nT02vqE6d9PjUVCfht9tlESIysmB4ERYPd9e1cnYfgx21NxKpqmRMDB09enDHDtKxQz3/e9ZUqbwq\nYSBmsQCug+xTdlIjZeMABNGVS7QAkA7gDICtAHoZ4ws7AiJmWoU3Q2y6cgEc1djjJIhDjjMA3geg\nQnbFbqKl3a3lnaExTSPj7Kh1+DMtzWaIZ0Yj40zS0rSD075smFbfYxAHIGu0Nl3jT1u89C32ciVm\nL74okyyjAwxVJb/4QqQKf/8tTimKnYB5ggcbM3pw/HEOl6JXRt1Bgqc4u13EEpfKqtv5fizcSZn7\nqrIvclbCXhkLRQlNGC94OzyR28hIsTWLiSEbN5bJjG4f5o8kU2/D1KlirDh8uF/XJD9fJqMnTpDH\njok0M/NvlbnxVh7/wcZTTa3c8ovKNWuEZP7xB5mWJhLMH3+U982XX4rN5KefksnJIoWbNk0I0bhx\nQorGjRMbxREjRDL/6qtCKhfcLcQzJS6RvXuTjz4q5lhduoi0v107WVxq2VLsJXW71NhY8tZbRbIZ\nHS1Swzp1yFq1hIRWry6SzkqVZIFK1y4ICyNLlybvCRbiaQ22sUwZCQsJcS5w6cT0WSSeI6j6/2eR\n6JOU6nmNxNYYNqmWlHNfGVfSGxoqhNab7ay/9QPSj9qKyiWajW06GpMAWyo2XnONjFN0tIxl8+Yi\nLf6//5Ojc2dyQFuVqy1W9rrextUVrBzYTuWjj5K9e4vt6dNPi6ZF//5Clh99VMhFt25CpHv0IB96\niHzwQSHZTZuST5WZzVpQ+frrrs9Mbi75Xg87/0V9NoOdi2Fl61Ab7aFW3ltHZVyc3Ac9e5KPPCLE\nvW1bIe5Wq1z7VmHiUORZiJ3s43XsbN1a4uPi5N5oUFbsT9/F83QA/LVUG+ZD4WuRSSxTxjl21avL\nvda9uyx+jB4tx5gxIvyZMoV8/31y1izyo4/IjxNUqjcIgdh1k5VfTVK5YIFIoY3PxCejVGbcYOWE\nDjbagqwc3FneF0lJcr3fflsk1j/9JM9XWhq5bBm5YoU4vVq3jtywQRZ3duwQh1XHjrF4bGiLuuDm\nTs6io+Vhi44OXDLshi++cD43nz5p890uu52OyEhurxDDeNj4bzUr87YFVl8BBDKP8PZdDgsju3b1\n/F3u00fidcTHO+2M3ZGaKvGeUNR854srlLgaiRkD5ExFOQK1MRsKoDNk37AcyJ5iNwCYC+AXiK1Y\nFYgHxJshKoa5AD4mOUBRlBkArgeQAOB7La0D4q2xHcmfFEXZrJVzFsA7AMpCnHwEAwgDUAnAXsie\nAIMh+5mFaPXsJHmToig9C2uLl/7FAkhPT09HbGys3+NyKeDWW8UeKzn5IjfkxhuB7dtln69t2wqG\n16gB7N1bMJ+u+z9rljOsXr2C+v86pk0LTP+/KDrnV4ueurGf7vYZxn56ukb+2HMY0xcnArU7KCmc\nbzs82QZlZAD33y/3d0oKcPvtV7aNmQ69TyNGyFFStmXu0PuUkACMHFmgb1QlPu+J/gh5diCyEz9A\nyOQJCNqxFadefQvlJozA0dnf4+xt0tbSpcWe88wZIG9bBmq+/DCUnDNQFAUMLY39QyagRuIrCM49\ng1LIQdDu3cDMmXBMn4lNryRja24UjhwR+8OgIDkURexeQ0LEZrbGjqVoPr4jDjw1AlWnj8Afr32P\nXdc3L0DJdDtY/bza5jT8X2JL5Nwcg2NvJiLvzZH4ukMy9odF4fRpnDt0O2PAWc6d2WkYaWuJN+Nt\n+DO0BbKzxQ5Tt6vVbYSDg2UMQkOd+fWpRkiI2GxGRMgrvm1boEmlDI/31KFVGcATfbGhWX+0mN4T\ns3vbsNbSAseOAVlZwLFjUn+1atK+3FwgLExslGvWBFqsnYLbPn0B9q6J+LSC2DKHhEiaa66RfPUP\npKH9+JbYX/duVNtix9obO2PBQ1+hUiWgenUpf8MGsXXet0+Ow4ed/TLaFeflSXhYGNCmdBq+zWqJ\nViE2LM5r4fG2K1UKaF06DQtPtsS0bjY8MrMFLBYpp29fIDVV7H+LgvBwue6hoTLekZHSrtKl5X9e\nnoxFaKjz0K+ZbpcdtWcp+n3fET/dOQLtV47Ap93lHgOcttiK4mprTAI37l+KR77oiKWxz+Le5e/g\nYHgUclAaFU/txvg6M/HQ8Zn4tlMyzlaLQlgYXI5y5Zz1h4RImUeOyPinjs/AvDJ9sapdAmrNGYnP\nWyej2SNRqHdoKW4b1RH7pn+PsFbNEbJ8KSIf7YiExt/jz6X5WOJoCatiQ+UHW2DUKGnzhg0yRvHx\nUq/f8Pd96C28WzdgwQKga1dg/nxneN++wMcfA336OCdy8+eL7em8eZJPh7fwwuK9hRfXXOdS+SYX\nM1avXo0mTZoA4sNidYlXGAiLg6gS9oIQs0YQcd4ZADMhTjbyAXwIcUnfAkBjCMHaruUfCWA1gPWQ\nDdcaQXNRD2CmliZNK+MkxEV+PQCfaGlaw6nKOF4rW5eYbYaQxcr+tMVL/2IBMD4+nh07dnQ5LuW9\nPI4ckdXQS2Ixwigpc4cuOTNhojhwqazOFfc+Zka7n9RUZ/yV7JWRNG3MStLGzL09MTHya7Bx8lud\n0R/73EDh6xnSNRQCrdcfW2a9T88/L9+mNm3Oy47Z4dBUR93G6sxGlUePihT6zBk6t0MpZEwdDrHX\n3LVLJGKbN5P//iuq0H/9JbbjS5eKyuwvv4i9bWqqDOfEieSkSaIpOWKEqPcOHChCma5dRXrZrRv5\nwAMifbznHpGU3nGH3B4NGojt6riaIpUdWTGRUVEiWa1Vi7zuOlGCqV5d/kdFie16nTpyPrKS5Puk\n/KBz6wSf3CZhgxrZeNNNosJcpYooB/hSowbIhuVU/lPVyqy1Kh0OcsFElSvCnR6Mm8FVQtoMdjau\noPJAQxnfgzeLl1/3coODRcreurVIXLt2FSls374yXoMHk6+9RiYkiD3upEki6dxb38qfh9l4oKGV\ni95XuXixSDWXLpVr89df5D8/qDx5p2yvs2ePbAGTF2/l2S5d6QDo6NNHLnSfPtIY/dyI1FQRmesS\nMPdzbwgkX3G+57U8WWtVbtpUTCqkOgD5DnpCRESxzC/nzZtXYP4fHx9/QSVm55dZSBA1gnbZbjBt\nqOeyVGX85hu5kpeKZp0JEybOA57crF/p+5hdLJXYwiYkRjLmyQbTPdydCLs71lBVUUsND3cl2ca0\nhZGzoo6VJ5LoySGIP+N0oVSGi1qvP8RVL0t39DHS1casyE6m/G3zpaKG7QuBOupyzzd8uDCfOnWE\n6UVEiD6nl37m5cneo4cPixOhXbvEWdTZTarXMcyNt3LvMpVr15JbnhHit/aJRK5MlQ27jeObG2+l\n/VMhUQcOiCro9Olin9q1qzh+atNGHD81bSoENTpaCGfNmrItTXi4qBf7a3PrbYue6ehDB8CtqE0H\nwNml+rBGDbJ2bVmHiI11qhSPvS2VuUoIf20wiHlKCOc+kMoRI4QoJiaKv4C5c0VF9sMPyRkz5DPx\n+YOpzAsK4Zr4QcwPCuG64alcs0bGNStL7FHdbVA3/aTyzz9Z5PsxP5+cP0FlWrD0+Z8qVp78J7Ay\nvEInX+7kzFv4+cDw/bzQqoyBErHRAJoDqAVRD5yuNbaPFv+Ndn5ZbTBt6N9lScwGD5YVLBMmTJi4\nLGHuY+ZKun2R3qKMlT7Jcm+POznzVOeFlJoWR72Xm1fGQPp2IXEp2Zj5s0BkJJGRkcKqSmp8VXH0\ndPYXG3PvtjLzb5Vbt5Lbt4vNX3q67KG5ahX5++/kqolC4pa9Y+Ps2eRnn0mTMyvXJgEerVib77wj\nks1hw8TWduBA8rHHhDC2b08uqCmSx08rDmLt2iKprFSJLraQxiM8XNJ8EKo5fsIgr+QxJES8C8dW\ndJLIZaWttNZW2aiR2J3edRfZqpVIFTt1EkmrboN6771O282KFaXMt1pJn9uGiXR04kSxlUxPlzFS\nVXF6lZUVoE2kOwkrCVJGutzvlzox+1CTXOVrBwGohvhemkTsNJwbQNsgjjn0DabnQvYyy9XSnAXw\nMVw3mN6lEbZ8LfywVrf7BtOZ2m8+ZP+zVDg3mC60LR76d1kSs8aN5QE2YcKECRMmCuB8JJ8XS2W4\nqPX6Q1z1suvWLUi+9LKTkiS+JNp8qahhe8Ol6pXR3/YOHSr1eVNfPZ/xDVTS6U1dVVdfrC3kzKMa\now5dDXHQII/qiHl55KlTbl5YDfkczwyiIziE+6amcvlycdL0+efkJ5+IhO3998nJk2VrpNl9hFDN\netTGl14SL7cDBoiTn+7dRarYoQN5//1CGNu1E5XYHj3ES+6oUeKJVu/zqTutfLyFytKlvUsVdZXS\n8HDx1Hv99WS9ek6N63vukfq6dpXtnLKCI+gAmAvQAfBEqQi+9570RXewM2+eeCn/6ScZ+hUrRAV4\n2zaRyB47Jt5rHQ4f11q7r9I//PCCErOAnH8AgKIo9wG4C+L+/j6ItGy2FtcTYg92AuI+XwXwtpYu\nkeRrmgOQLhDVw/4AQgHMAXCjRsx+URRlC4BqEDf8YyG2aJ9oaY0OQBwQ1cWFAB4G8DqA9SQb+9MW\nD32LBZB+OW0wffQoULmy2FT27n2xW2PChAkTJkyYuKxRVKdOer7t24FDh8TBRVqaOJbYs0fyvf66\nbGheubKEn68TrQu5OX2gzi28OQqpVEkcgOiOPjw5/tDh7rCjMMcf55OvECdIRRoj7Tx/VjJ2KlHI\nzBSnQud7LE9XEAKRuFQuT5w5Iw6XAkVwMFCmjDgjiowETp1KwfHjKQgKEuczFsdRVM1cjmXMBy5F\n5x/6AXFfvxNCjDoZwq0QVvmaISxSS/exdj5NS9PYkEZ3AGLVzrdAnIqEGNL8ACBf+19KK3OFW7sO\nAtjhb1s89Ouyk5iZ9mUmTJgwYcKEiasSF1INOhBJpzdJWteuMmnr2tU13JMDEG8OOwpzAFKUfMVh\n83ihVHR19UX90NQYdRvF06fF0c6hQ2JPt3mzSMuWLxcHLV9+KUMwZw75wQfi0CUhQVRIn3tO1Eif\neEIkhO3bk8Nqv3hBJWYhgRI5RVGSADwA8XS4zS1acyKLs4awahDnHKXd4nYb0pTRfitov9kAsknm\nGdKEAQhSFKU8ySxFUXIh5E1vl15HrhZ0xI+2XPaw2YBatS5LD6QmTJgwYcKECRNFh6/tWJo3L97t\nNnxJ9qKiXCdiaWmeJU4//CCSxA4dXMN1SVlKivN/UpJnCZd+npTkWfoVaD5PEr+oKKc0z1/Jmbc+\n62WlpZ3/ZDUyEjhxQkRcx487zyMjEXz8OCIinEnDw8+vKgDA0qVY3W4G3imGovxFUCCJFUV5H8Aj\nELXBU1pweUVR9F0gwiGscrCiKC0VRWkCsR87DCFEgBCmbACfKopyi6IobQGM0sq7RktzFEA5RVHG\nKYpST1GUpwHEQ6Rd1Qxtv0tRlMcURakPcUQSDJwjm+X8aMtlDVKe8datL3ZLTFxpSElJudhNMGHi\nosN8Dkxc7TCfgSLi8cc9k5AzZ0St0BPJS052bh4ICJHxpnbYrZvEe0Kg+fwhVP7AW5/1ss5331d3\nUgbIb0TEOXJWrNDVYRMTi7fcQhAQMQPwFEQd0AZxAqIAmA2guyENAfwKYIEh3R9auB6/G+Kw4w+I\nHdhsiJMOPc1ZiN1YK4izjsEAhmv16WkcWt5RAP6GeHlM0sp1b8sPEC+PTSHkrQKuAKxZI3s4d+ly\nsVti4kqD+TE2YcJ8DkyYMJ+BqwAlTaiKC+6kTIeRnBUXjDaKjRsXX7l+ICBVRpIuRE5RFAdkn7Dv\ntKD9EPI0leSThnQ2ADsMaSqS7GCIDwYwRIvT00SQbGJI0xJCtA4Y0qxzq2eEW7wC2Xg6BEBvACsB\nLAHQUlGUyiR11UsXDB48+LJw/pGUBNSsCbRqdbFbYsKECRMmTJgwYcJECcGXs0J3slZEpKSkyGLE\n2rVAw4bA+PHIysoqlrL9RcA2Zr5AUlUUZT+AewGsAwBFUSIB3Alx+gEAfwKwKIrSmOTfWti9EBK1\n0pDmbUVRgknqErA2ADaTzDKkuReyB5qO1lq4sS3PAJhB8hOtLRUgapN9IXujFcDkyZMRGxtb1GG4\nIFi+HJg9G5g4EShV6mK3xoQJEyZMmDBhwoSJyxeehDCrV69GkyZNvOQofgSqyghFUcopinKroigx\nWtAN2vl12nkigDcURemoKIru5n4PZMNnkNwE4GcAsxRFuV1RlGYA3gOQQlKXmM2DbCqdrChKA0VR\negB4DsC7hqZMAdBOUZQhmh3aCMhG0kmGNFMhm2Efd2vLQgBxgfb9UsCJE8D06WJXduedwKBBF7tF\nJkyYMGHChAkTJkyYOF8URWJ2G4DfIGqFhJMszQHQl+R4RVHKApgBwALADqAdSeMOAw9DCNT/ILZi\nCwA8r0eSPK45BUkC8BfEYccIkh8Z0vyp7VU2Wju2AniA5AZDPXMAjIHYxr2otwVAPwA3eehbGABs\n3LgxwCEpeQweDOzYIVuBAED79sBrrwHr11/cdpm4MpGVlYXVq0t+uw4TJi5lmM+Biasd5jNg4mqH\ngROE+UpXXCgKMdsK4DMIwSmrnfeh66ZrQV7+61Dg6hnR/dwYpjv88ORJMQiuTkUKkwDq8UYnIkZE\nAcCjjz5aSDEXH4sWyWHCREnhQoruTZi4VGE+ByaudpjPgAkTAIQj/FHSlQREzBRFsQBYBmAxgLYQ\nSdZNADINaV4FMAjA4wBUAG8D+FlRlGiD1GwegKoQG7FQiFfGGQAe1cqIgKg7/gJgAIBGAD5WFCWT\n5IdamjitnFchqokPA/hGs13TpWa9td/pAL7Q26L1QXcSYsTPkO0AMuC6/5kJEyZMmDBhwoQJEyau\nLoRBSNnPF6Iyhb68nLgnVpSxAOJItvCRZh+ACSQna+eREBL0OMlURVGiAfwLoInu/ENTW1wI4FqS\n+xVFGQjgLQDV9E2mFUUZA1FVbKCdfw6gLMlOhrr/BPA3yacNbckB8C3J5w1tOQVgHMkJfnfehAkT\nJkyYMGHChAkTJkoIgTr/6AjgL0VRUhVFOaAoympFUYzu6mtDNoBerIeRPA5gBZzONpoCyDR4ZATE\n1owQ7416mt91UqbhZwD1FEXR/djHafngliZOa8sNWluSAPRXFOUxADUg0r1yECmdCRMmTJgwYcKE\nCRMmTFx0BGpjdgOAgRCHH6MhRGqqoihnSc6FECHjXmM6Dmhx0H4PGiNJ5iuKctQtzQ644oAhLkv7\n9VVPVa0tn0I2rx6lhZ2CkL5D/nXZhAkTJkyYMGHChAkTJkoWgRKzUgCCAbyuHYBIoAYCmKvFKwA2\nKIoSCpFgPQ1XZxvlAVyrKMopACcgLuxfc0tTAUBXRVH6ANgFIYGr3NIEAXhPUZTZANYCeNYt/lxb\nIHZseluSABglceegKEoliO1cBkwbMxMmTJgwYcKECRMmrmacszEjeaSkKwuUmJ2AuLevD6eXxEcB\nDNb+99fCXwKwBrKp9JcA8gH8rShKkJa+NGTPsRoQiVYuhIztVxQlCkBjiOOQ5gBaAfgQQt4I4IC2\nr1kIhGyN1ur/WUunS9F8tsVL/9pCPE6aMGHChAkTJkyYMGHCBCDOAeeVdCWBErPdAGob1QC1jaV3\nao41ukEkaBaSf2sSr40QBxzTIMSnKkTaFULyZ0VRhgOYCCFRKyEk6wCAigC2kdysKEpziFRuM8ks\nRVEGA9gCIJLkJkVRngJwP4DuABb52RZPiAWAuXPnIjo6OsChMWEiAOzbB4wcCSQkADVqFB5+gTF4\n8GBMnjz5otVvwsSlAPM5MHG1w3wGTFzt2Lhxo76NVobGeaYDaAmD1h9Jh55eUZSWEJOvhtC0/kjO\n8be+QInZnwAaKYqSBeAYhKjFAHgSIgELATAZwBuKomyDUyXwFIBvIeqP6wHsBzBL8754GEA4gIWa\nR8amAL4B0AVAsqIo4yAEqw6AJxVFKaXVNQzAaEVRhkA8Oh6GuNVPgmyCXVhbXKBJ4Z4FgOjoaMTG\nxgY4NCZMBIDYWODmm4G+fYHkZCAqCsjIAF56CZg/X84vIsqXL3/xnoE5c4AWLTyPQUYGkJYGPP74\nhSvHxFWLi/ocmDBxCcB8BkyYOIdsAIsA7IM4KdS1/nIAvAEAmtbfDwDeh2zj1QrAh4qi7CP5qz+V\nBOqV8SsA70CIVVUAd0A8HN4FcbqRA2A8gO0QcrUOQpAWanuY6Q47XgZQHSIhm6+VPUv7rQYhfK9D\nyNm/ELVEQuzYKkPs3H4HMAfAWACbIMx0p7aHWVU/2uKOwRBVRxMmLgyiooDkZJx6qC+mdU9D9qMG\nknY1o0ULIawZGa7hGRkS3sLrbh0lU44JEyZMlBTmzCn4jtKRkSHxJkyYuBQQBzHleoTkepI/AxgO\n4BlFUXRB10AAO0i+QnIzyWkAFsBp8lUoAiJmJH8m+TrJegDuBrAXYrNVz5AsEUAVAPdAVAOztf9G\nfA7gHwC3AHhAC+tuiK8A4D0AH0AGYSZE1dFYTisAvSDSOn1vtOsURakcYFtgkMKtBER036lTJ5cj\nJSXF9+CYKBz9+gFLl3qOW7pU4o2oVw+Y5kXrdNo0ifcG94+dsW73j93SpTJJnzjRNY9eRkYG8O67\nrnkmTpQwT3Av39eHF4Dt9J14Zn5LvFchwTsp81XGxInAQw856zWmM7bd2C5v5fXrJxK73bsLxnm6\nRiUBjbC6kCqdTAVCXIurHBMmTJQMTFJiLiCZMHEJISUlpcD8f/Dgc5yqEYD1JA8bsvwMcWrYUDtv\nCh9befkFkgEfENXDzRCSo+9TZoWQtGwAnQ1p90AchtwBYCSAbRBnH5W1+Cgt/jhEopUG8cC4zlBG\nb4gEbBHE22KuVv8UQ5rZAM4AeMWftrj1p7oW/hgApqen00QJwG4nLRb59Sc8KYlUFPn1J9wIVSWt\nVvk11pGa6j08Lo5s2tQZp6pyHhtbMNw9rbd6vYVp4flN47giuCnjYWNaiJVnN7ml8aMMxsWRjRtL\ne+x2ZzpjO43h7uXNnu0MT00lQ0LYsUkTZ7rZs71foyefLBimo0MHOTzBbpe8vqCqPNbEyrda2Xiq\nqYe+6+02tt84Lnr4xIk83dTKkffaeOJ2D+VcbPgaQ3/GyUSJoWPHjhe7CVc2fL3XPIVfqXDv7yXU\nf/MZMHG1Iz09nRCtvS8B/EhX/lBG4w9ttfPNAF51S9NO4ySl6Q/H8idRgUyiQjhRI2i5kA2lIzXy\nlA9xygEAdbUG7wPwPID7tPi1hrL6Q/YlcwC4FaKaeBLAJEOaeRCX+Jna+QqtnE7auQJRf1wF4Gt/\n2uLWH5OYFRcAskYNz3E1aki8cYLvbcKvIX+qGwnTSFl2YhIPHCDz8ny0xf3jppEOpqZ6rtudcKmq\nkLKICB751l6wzEA+pp7SxsXxaHRT1oLKuXPJWlC5v6GPj7Gv+txJmJFQupMy9/L0eP03NZXzypZ1\nktjUVO/XyBfZDg8ny5Xzn4i7weEgB9S3kQCHNLF5Hw9vpNMQ/npzKeeVOz2U4wmeyJ6x3tmziy+/\n+3jMnk1OmOA67jp5U1WyRw9y4kTX/Dp5U1X5r/+6j7GRaJuEr1DMmzfvYjfhyoeqktHR/OYlO1ev\npuf3XGHP25UAVeWJO6zsUc3GQ40uDVJGms+ACRN+ErM29E7M2mt8JJT+cCx/EhkKnwBgBGRvsLsB\n/KoRoPe1+F+0BraEqAYuA2DXiNQYiOrkEQCHIGqMbSE2Z2N0xgmnBM0GUZF8WqtjqM444bQ5GwFR\ndZyhlTsVwJ/+tMWtX7oU7gWTmJ0ndPLlTs4M4VkL7cwpZ+Gy7ok8VdrCX96002Yjlywhf/2V/Okn\nMjGRvO02MjiYHFcriQ4o3FC/Mx1QOKlOEsPCpLjy5cnOncmhQ8lRo8hx48gxY8iRI8k33iDHPqVy\ny3VWTuli4+aaVn58fypPhlqY2jyRJ0MtHN3Ozn79yKefJgcNIt96QuWO6nHcdU0Md1ZuzG1VmvLV\nZnYuhpXPx9i4oZqVL3dT+eSTZP/+5LCHVW6qYeW7nWzcVMPKhMdVDhlCvvoq+dZb5LvvkpMnk1Om\nkB8nqNxd18qvX7Bxb6047qzZlM1qqmzcWEjIffeRMRaV22pZmfiCytGjpT8TJ8p4JCWRc99Wubee\nlQtfsXFvfStTxqicOZOcMYN8/xWVmyrGUa0Yw0NVGzC7TARXvpjCg42stM1WuWSJzMdtNvKPP8g1\na8hV81UeaGhl+ispzAm38J/pdqalkctfSmV+UAiXtR7OM2EWpo22Mz2dPHCAPHuWzM01XFt3YmE8\n9xVXCBZOU7kYVk56wMbFsPLnGWrBRN7IpYGU7UyTcgY1knLWfeehHG/lFnUlP9D8xnFRVbJBA7n5\njYsIERFkw4ZO6aiqFsznRrALLDwURmb+XisAACAASURBVLTdcT4E1RMx1MtzJ4ZPPintmj27YD5j\n2iuJUJ4v+b+CoH5q51FY2B0pdFyikqMLgWndZQEpoaWfC0gmTJgocRiI2QwAq+nKH3TOcot2nmYU\nLNGp9ZdJf7mWvwm1wtdojaPWkEMQF/STtPg+WrhDS7MHQAOI7dY7WpqvICqG1IjWCogDESPjPKCR\nMWq/M4yME04JV56W5gRE2jUewB/+tsWtb8shkrnLmpgdPUqePBl4vvx8cu9ect06Mi2NXLSIXLCA\n/OQTctYs8vPPyX/+IY8dc+ZxOMht28gvvyR/+UXyHz9Onq1Wgw6AZ6vUYFoamWWR84NhNRgTIwKw\nZ5FIAnwWiQRY4AgNJdu0Id95h3zkEfJ/5TuTAH8K78zOnclJk8ivvyYTEsiWLcmoKLJaNbJCBbJy\nZbJ6dfL668k6dche18vHrndtG+vVIydcK3VPuDaRTZuSt99O3norecstZL16zvQE2K+ujS1akD2q\nSdjTDW1s2pS84w4hjrGx5BM3StwTN9rYqBFZv77Ue801TqFRmTJkWBh5b4iknRj6Gu+sqrJzZ3LT\nJhnPQ4fI7t3JuOoqnys/m1WqkBUrkpGRZNmyMiZBQWQ8pIx42M6Nl6JIPc/e4my7PsbGdJ4Ovbzu\nSOFiWBkPITAJGE4CfLGU52tUqpT0KzycbFvOzkzFwtfDE5mpWPhgVTvr1xcO0beunVnBFo6rmcis\nYAv7N7CzZUvynnvI5s1lHGNiyCZN5FrceSfZrKaQqX6tVTocZL/Wcn5/Q5UdO5IPPUT26UM+8ww5\ntKfKzTWtnHlvCk+FWji7XQq3XGvl8F4qB7RVaS9lZZNKKo8dI9vWU7k01Mopg1W+9x758cfk/Pmy\nGLB0KZmeTq5dS27dSqq/qTx5p5X7l0veE+tV5rUIYJIYoHrS8ol2nilj4b8DEpldJpL50Q1cpbcN\nGzrJmqrKoEVGupIy97p0EuaP9NOfPhQWboQnEu7ebh1GabY3Ym/8Hyip8ZReD/OUXg/zpC5rlF7q\n4bqU0pP6rlFKGR8v0lBvEveJE+WIjvZ+jXr0IIcN89wXY/3G/unENz6+YJ+N/fBEBv1VGT4PIpmQ\nQHZHCglw6bMpEjhhgmgB6OPlb73+qAbreevWLagSr5eZlCTxFwqqyhXh8v79PcTKvG3qhav7Ukdx\nPO++0psw4QMGYvYMDKZYdGr9ZQIopZ2PhUErkE6tv0XGMF9HoMRslEaOcrTG5RsIVg6A77TzdpBN\nov/QpFQZEFXGII10HYcY0bUFcBDi6MMBkaJFaeWtgkjM9IGYAKcq48NaPZPhlJgdBZAC4Gstzbe+\n2uKhb90h7vQZHx/Pjh07uhyXgzj/k09kbhMZSY4dS545UzBNXp6Qr3nzyDfflG98TIxM/H1N3o1H\nSIiQhNKlvafZDiFjOVDoAJgBIWWPPUYuHGpnXqSFORMT6bBYmPm9nZs3C8lTVXLXLvLUKUOjdZuy\nzp0Lty1zhz75sdlcJ6aJiZ4nqLpKYExMQbstvQzjC9+9fF8T1UDS+ijDYbUyf4nNdWXZre2OBg2Y\nHxHBrBkpzG5m5b4/VG7fTm7cSG7ZIuRjxQpy008qc5pbefhLG0/eaeXO8TI5yho9lQ5tnBwWCw9/\nY+eqVeRXX5Fz5pDJyXIZEhNFKjh+PPnz/UIEF7ZN5LBh5ODB5MCBIllMbS5xKXGJ7N2bfPhhIVeP\nPSbxAweSAwaQ/fqRL3dTufV6K7+bqjI7W7qWk0Omjle5oZqVfawq4+Pl0jRqJKS6zw1CLsdUl3p6\nXW/jffVVrq5g5cg+6jnyu3s3OaCtyt9DrKwbqhZ6r9eC6kJWa0E9R0gjImQh4JprZCHguuvIG26Q\nuVyDBkL072+oclWElU83tPGv8lb2jFP54INkp04yf37gAbJVK0kLuC5YNKupcnvVOO6tGsP9NRpz\nb1RTLuyTyrNlLVzVS8jbkdoxtL8tqk8/z1D51VeyUDJ/PvlDkqjG/jNgKvODQ7irz3DmRVqY+5ud\nDkdg91yR7V88SUwjI+X58kYidRJWrpywfk+S10AJo6dwVZWbKC7O8zNtJE9GdVldehkb6yqhjYmR\nNhvVdz0RZHd1aT2/N1tR935o6tUeCa+xfmP/kpLkxZ2U5NpnT/1zh7c03sKLMCluF63ynypWjm2c\nwqOw8IOWKcy7w80+tkcPz5JhdwmsP7bMehkjR7p+U7yFG+GL+A0dKu301nedwLuPkaoy+7amHIKJ\nHNpT5RBMZFYTw5h6q3P2bHl59uhRcPEgNVVIvjuBvdBS5+IgScXxvPsKN2FCw7x58wrM/+Pj43Vi\n1gRiVvUjXLX+3qKTS0RBzLHGwVXrr5WeprAjUGJWTpM6GY9cAEshe4dla+edtfT1DFKr2zWSlAdX\n5x8DIHuLZUJUCsdpZM1oh5YC8QC5iE7p1n/QnH9AbMz2QPZWexliY+arLXd46d8YXKYSs6wsp1rf\noEHyDa5VSybHTz9NduwoE9hy5ZyTzqpVZQG1Xz95f3/7Lbl8uUhw9uwhjxwRcpefTx4+LJK0uXPJ\n998n33tP1PMWLiT/+08kDN9+S6akyOR94UIyFwoJMFdRnA0NVLXN3dGHP44/dLi/hM/DxszjhDCQ\nCev5TG79KcPY9kBtzPRwfTwSEnyPkyfoaTwRXl9xnhDoh1zvR0qKlJ+SIueeVtrdysnJESnzzp3k\nv/+Sf/0lz8CSJSIFTksj/xgjpG/xmzYmJ5PTpsm9P3GiqJqOHi3zuOHDZV728svy3D37rMyZJnSQ\n/KPb2PjggyIJ7tBBnsn77xcp6RNPkLa37cwvb+GBYYnMjbBwZGs7e9e2nXtgW5WyMTTUlbx5kp56\nkoZOwaBzefS4oCBZYNElulWrylGrlghsbr5ZCGPjxmT7BiqXl7Oyd20bV1ew8vEWKjt1Ih98UAh2\nr15k375CrgcNkv6/8gr5+uvkR33sPB1m4a8dE3mmjIVfPGvnR8NFrfe7F0Ul98t3VaakkEtG2Zld\nzsJ/+icyNyycOWHluO1ZGY+Ns+xcs0au05Yt5K7fVZ65y8qDK1UeOkQeXa0y524rT6xXeeqUqNzm\n5dFJQj09P54c/nhbfDGSsNhYGbjYWCcx0AlnYVJKt3odv9uZFx7JzJoNmH2bj7YYz30RXncSGB0t\ncampLu8Fx+92WdzxRcp8jYG3vAFOirf+Kosf301VeeQI+cn9sjg0IjqFx9epnsfcnZR5e+f4+s64\nk7CRIwsnZd7Kcr8G3vruadw0An3opjg2g51n4qy8OVzllMGq7z6Sck2Dg50SVj29Ht6woWt4hw7O\nxQ5P/dIJWyBSRyP0fBMmCFk0fidTU53EdOJEUTvRnx9fbXEbw7ObVGZmGsZUJ+zu0BcrdKKsqr4l\n0f6SRBNXHQwSs1gA10H2KTupkbJxAILoyiVaAEiHOCTcCqAXPXAOb0dAxMyt4iAAD2nSrY/h9IQ4\nC4AKp23XWQDbtTwjAax2Y5yPaR2eoaVJA/ChG+P8REvTCk57sHFapx+DSM02a2TsGoi3SJ9t8dKn\n2MuVmH38sXxLdu+W882bZbJ0443ayv39MkkcP14ENpmZJdwg3aZMEXLGGjX8W8k04irwyug3OfNV\nxvl6ZTSeG1fWPY2Ttw96CdiY+YVAJoznU35RpZz+5vc20W7QwEV66/gilQ6LhdkTEpkfEcmcW2KY\n+Y2N2c2sPJKu8vBhIZqZmeTxdSpz4608OmoqHcEh3P/UcOaEW/jDa3bOmkVOny4LLLoN5KhRcgwb\nRr7wAvncc0KyBg4kn3qKnNJFSF5CSxs7d5Y5Xtu2opJ6991ymzVpIu+b6Gh599SqJY/+sHAhk4OD\nE89JHO8J9kwqjcSzMJVnTxJNT+mCgkT1tm6oSluQle3LibpYbEWVTSqptIda2bmijUtDrbyjisoq\nVUQ1ukYNkYQ2q6nyjzArn6+WwmNBFr5YM4X/hsXyeFAEJ1wrKrr9ou18sInKv8pbOf76qcxFCOdE\nDefxEAtfb2Fn9+5k167k//0f+cS9KjdY4ripXAzXBjfmejQgAbYNs7F9eyH1CQnkjKEqM+pY+Vl/\nG9UbrJw6ROWIEWI/+14PO0+GWjjz5kSeLGVhYlc7JzyjcnuUlT/cN5V5QSH8LX44z5SO5L7qMfz0\nSRv3XB/H3dc15axWKcxULBxYMYXbrrfys9EqP/1UpK0//ii368qVor7+zz9Chrf+qvJYrJUrhqQw\nN8LCvZNSeCZOVH0PHJD77sgR8uBB8uBKlWfirNyxROWWLaT6m8rTTa3cmSbS6/R0cvFi8qPhKv8o\nY2Xza1XR8NCel40jRHLWqaKdrz+ickeUlT/0SmF26XDmhJbl8Zti+c8PKvd+IdoX/0wXif7atWI/\nO38+mfqcnadLW/jNPYk8HWbhH+PtXLlS4hcvlvWbj4ZL2T9FP08HwJ3RbeiAwj8eSeK778oiy9Ch\n5EcfyZhs3appc/h6rxW2COf2znIMHcqc2+I4+HY7/ywr6R5+WKTvZzeprpIuT3Uav13GRbmGDQsu\nHvjrkCkQqaPxnaZLk91tYfVF0aQk5/eqYcOCkl9fdVMWX5aFWdmpvI2n4wohrdo79GS9GI5tZ+Px\n2318F/S+6It53tR24+NdCaYRurRUVSXeuDBoJH2hoaK/74kE9ukjNg+XK65QFVIjMWMROVMgR6Bk\nbCiA9VoDCRHPbQQwCUBPjShFQDZz1m27sgHM1PLP0AjZHRrT1NUgCaCdlmYzgFchqo+ntLhcrbzS\ncNqX3QnZDy3XUM9WrYxC2+Klf5ctMXvgAbHXuSTg7gBEPw8LK3wVzghP+v86CtP/d39BGFcA3V8Q\ndrur7Yd7GfoKnzHPhAmunvGMcC+/OF5Wvsowrk56UJHxqM5iTGf8wBqdMHgit+7XyNdH8Ty9MhYK\nd1LmZeJTZHJW2ASruPJ7W803OgBR1YtjY+bel6IQVE8SU0N5jpayCn7iBJm1UKSGmSMTmV8unHll\ny/G/oSIx2/yRnStWiC2gzSaOghYtIpeOFoKXNsrG1FSZcM+d61S51UmoLun84mlJ/1l/G0ePJt9+\nm5zdR8KSH7cxIUHCRo0ScvTGG0JWp/eUNF+1FLKY2NnGL5rJ/3lNE9mnj6jmjm4j6X6uJ1LKmQ0T\n2bo1ee+9Ii1t106kpbqnUALMvCGGB1JtVGtb2fcelQ0binps+fJk+3BJ1zHSxipVyJo1hfDWrUtO\nitLaUjuR0dFiV9v1Gkn/UTmp//WIRHYq7yzjfq28lDjJ27mi7dz6WWGHLoH1x37VH9LcN3g2H4tX\nuWFDwefjv/l27rXUZ5u6Kh+s7FrvcYTzWSTyKCxsBrvH+kuXJkdUlPSvlvFM7MPCyM4VpezloXeT\nABegMwF5ddWpI2PtPj5ly5L3hIrDklfKiF3tA5XsrFWLrF2bbFJJFgBalbLRXsrKe25QGRMjUuh6\n9cj461UuK21l//Ip55yeLFGs/PED6fv69dK2ChWEw9x9twzN4NvtPB5i4cyGiTxRysI377HzkUfI\nFx9UubVKHHdWjuF/lRrwTGgEFz2ewv01Y3m2dASX90xkdjkhp6sm25kbYeH6D4SobkkWcrs7xc5d\nu8j9+4Vkn/pZnsWshXZmZZG5v/mQOqpiC5y3TWV+41g6IiKYMy+V+XfGMS86mvkRkdw9NIm5ZSN5\nolYDnmnclNmbRVrs78JddrYsarTQ7sFe19v4zz/0nE873zDTzvblJH2HCBvT0wveZy7nhX1TfC1c\nRkbKilRcnJx7WhRVVdF9B2SVxog+fSS8Tx9nmE4EPUG3GfUEX/kGDhRppSd4myP4SucefgWqkF7q\nxGwRgMcBtIbYZG3ViNWtBjL0AcSOqwXEtusEgF10JWbrIRuuNQLQUevwZ3QSM91l/nhNYva+Tt4M\nxOx1TQKmS8zWaCStsj9t8dK/WODyszHLz5cX+IgRF7sl9Msro4lLDMXteU/H+e5jVhhK0inB+X5g\nAsnvPoZGSae+OuttJdrTCrY+ESgOr4ye2hzIR9aXyp03EqlLWn3ZmLm3zV/C6Cm9P2XoaYzqsrqa\nsyfCOXWqTOCGD/dty9qggfSxcWPXtriPjae2+SK8xvr18bbZnPeVm9qvY4dIrI4cEa2LLVvIv/8m\nly2TY+lScmWqyhO3W5k5XSRm/w5P4ZFbrVySrPKbb0RKtWCBOGX67jvy55/JvxNlUrx6so1LloiK\n8O+/i8RsyxaesyH1+bwY2uywWJg1M4XZtW4iAW56OpE//SSSstWrxW523Trpx7lJv2Ynuy/Vzr//\nFgngtm2i/u/YodX7/PMkwNzWIjE7O9l1QfDECVHxX7JESH9iohxLHhDi91P7RCYkCIF/7TUh9vMH\nSd/n9LVxyBAxKXj+efLFFyXNh70kfrFWxuEvbS51rlkjiwMDBoj2S8+eZLdu5KxGkv6D+ols1Uqc\nXzVr5txahACHl5c0bUrbODi4oNS5GYRUFkZufaVTFLnFbgwpSMD1fAkYzlwEcxPqMB1OybBO6IOC\nhOBmKha+EZnIY0EW9qptZ2ysOIFq3lwuf9268qhFQeXBm63c+YmNf5SRum66Sfr/yl0iQV5wt3h7\nfq25nXVDVa6KtHL/FzauihC74kceIV/4P5Urw6189hYbd0SJfe6KFTLm2/6n8nSclYe+tjOnuZVn\nfrXT0dLDe9V9scuT/Wjjxq6LZ3p8166uJMwTKSMLml8UFu5PPl31tbBvU1G/gee7oHmRUYiN2aVH\nzApkFhJEyN5hl+0G04b4y1JitmaNXMnffrvYLaFv8qWTMxMmLnVcyH3MPOV1l95erH3MzoegepME\nFodXRk9tKMqE4WLamBnVj705BClBG7OA1H49jUFheQMhzd6eF1WVtg4bVnDsb7rJsyqcPh4lZWPm\nXocn29nC+u6J6PszefVWp35PxcQI2Y+IoMOweJD7biLzy1t48Cs7t28X0r3vVSFsGUMSuWyZkM6f\nfhJSvWCBOAj7/HNydW9J9+dDiZw1i+eOGTPE3jwpifx2iJDCha/a+PHHIqFe3lPybWw16BzTOxMd\nw52f2Hj4VivnT1A5Y4ZIsX/tKGm/uzeRzz4rqtN9+wohffxxcsgQ2Q7mxB3OMTqzUbZ6GdlHZa9e\nsgaoS5DfqZbIHneKGvCJ9c70O6Ks/L8YlU2bOm1/O0YWlPrq0t7uMEg0YWX9MJUVK5KdKtp5LMjC\n9yoOZy5COKbmVK62WPlQU5WPxatcV9nK1++2cVPFOO6o0JgZFWX7ne3VmnLsUyqHDiVX3tqHDoBH\nKtamA+A/cX2YnEx+9pmM/6JFcvtsGZ1KR3AIDySl8sAB8vScVDp8kTIdqW7pjO/YopIwP0nW2U0q\n1RusfLuNzeWa+Q3jN9D4HdNF2boWkPE7FhFRYvPLS1piViAzcKPW2K9wGW8wbajnsiRmU6aI2vLp\n0xe7JSZMmLiicKnuYxYoYfRGuC6mV0Z3GxQjObPbZd8NT/241L0yehrvoqya+zP2nsYiEPuoonhl\n9FSHL9srb+eBkFxfdQZiY+a+yFGYQyZ/0nkioXq+4cNFQlOrlnfJcCB1+HqujeX464TFJt6N//tT\n5Zo1InH9/XdRk172jhC3Vb2E7H39go2TJ4vH6xEjyO9aSfiSRkI8R1htfOghsksX8uU7JO9Lt9tc\ntrDpXdvGa6+V7X1q1iS3B9UmAW5FbZ/qxA8ilTkI4RQMYg5C+CBSWaqUqNRec42oz9avL3aJtWuL\nSnOFCmQ3Ld+sMoOYixAmNEhlt27iCXnMALFHndPXxow6Vn40XPZE7dFDPAV/+qncWr/MVHn4VitX\nT7bxWBMrNyxSuW6dqNv++68cf/4pkvXFi0VlvGFD59ZAbUqL06z8fM+3mEcY34fGhS3de11QkGu4\nTsoiIgKoxH9c0sQMwGgAzQHUAnCzJv0igHu0+Mtyg2lD/y5LYtali+igmzBhwsRVgSthHzNP7dZX\ngn3171LfxyxQ0uwN7vW6kx89fNgw1wl9Se9j5ov4FcUro6d49/ze6gzUK6PdXtD21x8i6y2dJ9Kp\nk2WdMN54o7RFd/zhy+uxt7YU9ry73wNDhxaUyhv7ZVz08LZo40uiaSSeISGiOuxJNVqXjBu339HL\n0NUXaws5c/Tpw9xccS5z5Ih4xjaqFGc8IARwU5tB/OgjGc5Jk0Rt9rXXxBPuq69K1994QwhkUhL5\n112S77dGg9ijh9i6Nmkil6VbFSFPHSJsLFeuoC2lfhTm/dd4hISQjzRTefx2K0//aOOGaqJyWqmS\nzFO7dJG9aZ98UpwcvfKK2PKOHStChpkzhRQuel/l0fpxPBbdlJvfTmVuuQievakh85UgOgA6AOan\nlTwpIy99YvahJnHKh9OhxjhDfC+IO/zTcG4AbdOkXfoG03M1YqY79DgL8epo3GB6l0bY9HoOA/gI\nBTeYztR+8wFsATAfzg2mC22Lh/5ddsQsP5+sVEneDyZMmDBhwsRFRUl5ZvOHcF0IlMQ+Znp8oJtm\nB7qPmS51cF888IeEuYd7IjS69MJoCzthgmeJcWqqpHVfZPBWtzf4SyxJ/xYNCpNoXkgbMx26GqK+\nF1Jhaoz+5PMg6czLkzllXp5oYGVmkodWybYku+faeOJ2K1d/pfLPP8W7qW5/unat2HZu2aJ5EnUj\n68dirUx8QWXPnuR995EtWoj/kUaNhCDWrElWrCjeet1VSpchjumI4SbcxBwEMwHDma8Rs1zt9xAi\nWK2acFzdwU6DBkJAmzcXCWDHjmKj2bu3kNiXXpK9fMeMEUL4/+xdeZyN1f9/n5kh24ybZEuZtAjR\nGJEpDbdUVPTLN1lSlm9IkdCmkiUqW4aGEonC1KTSQmm944r4RpbQEM8Ihez7rO/fH5/zmGfu3Dtz\nr20s5/16Pa97n3M+Z33W9/NZztSpYkL6+eey3NO334omcPVq8qOPzmJiRiEvzQEshaw1dtycUOe5\nNQnaAwnqcT2AOZqE9dMyQyCmi8sha5/dDGCTHnRdLbMQYs44HUBNSKCRdACHdX4xTbSyAPTTmrUh\nuj/fB9sXP2M754J/rFwpR/HHH4u6JwYGBgYGBgZnLYIlt6dyHTPfcrZmOD7+1BDtUAh7YR8NRo8u\nWKN5pqMykvkDeRQW+COYcsGaGgcrF0i+sHQ/yMmR9XP37CG3bSO3zvQcZ2pbWov2b2XXBGbqtEyA\no0ZJoJznn5dlXvr1k9/u3cVPsU0bIWbNmskhqVlTXFSrVvVHCGcRaOmzneXBPwAkQvy5qmvi4yRm\nUbrzUx1p9XTaAL3fTe+7HTIJOq2q3p+vSVeEQ2YNgIOO/V0ANjn2lSZvi4Lti5+xnXMaM+NfZmBg\nYGBgYGBwkijMbPdMr2N2rkVlPNXaclvLGBMjTCo8XMzDfO0nT4EZY3q6kMGdO4UQWpZoARctIt97\n7yzWmEHC1u8FcCuAipqYPQyghM6/Und+K/L6du0DMFbLdNWky15g2vYzywZwn5aZrWXsBaYf15qu\nbABltcy/EN8zO1z+JIjZ4mqdX72wvvgZ3zlHzFq1CryUhYGBgYGBgYGBwTmIc20ds1MJp+mnbfZa\nu7YE/rAJ2RkI/EGeeR+zMISGx7QmygPxNVOQMPUP6vxKmqx9o8mVLefRedCEztIkaxGA93Uduxwy\nkQC+AtAMsj5ZXwAvOdqA7sf7AIYC+A1C8sZBQvjb7dh9+QoSsbGRbrdWiOM+K3HoEPDtt0DLlkXd\nE4PzDUlJSUXdBQODIoe5DgwudJhroAiRkgK0aeM/r00byQ+13MSJwJIl/vOio4FOneR/p06yX5jc\n6UBaGtChg9Cvfv2A7t2BefMkPScHCAsDkpPl5XfePCAyEjh4EIiKOn19OoOICEWYZB4ip5TKgawT\n9oWP6IskH3XIJUPYpo0skvf61NXFR+Yfkv/nyK8Fid7olPnOp53HffIB8YfrCFkLbSmAuQCaKqXK\nk9zlb5x9+/ZF2bJl86S1b98e7du39ydeZEhOBtLTgQceKOqeGJxvSEpKOuvOdwODMw1zHRhc6DDX\ngMEZR0oK0Lq1vNwOHw58+SXQuDFw+DBQujQwZAhw5IikT58OHDggpOzgwZNuOikpKd/HiP379590\nvaEgJGIWBLZDtGgVIeaJNipAtFq2TAVnIaVUOICLdZ4tU9Gn7goQ0rWjEBlnvgLQC8Akku/rtrZo\nua4ARvobxNixYxEbG1vAMIseGRnAyJHA3XcH/qhhYGBgYGBgYGBgcM7AqY2bPDn3P331LhDCBgg5\nOwXwp4RZvnw56tevf0rqDwahmjIWCJIWhBDdbqcppaIA3AQxWwSAxQBcSql6jqK3Q0jUUodMvCZs\nNu4EkEpyv0PmduTFHTrd2ZfaAH7w6cuvAOJOeKBFjPR00exu3Ai8+mpR98bAwMDAwMDAwMDA4GQR\nssZMKVUawNUQIgUA1ZVSNwDYQ3ILJMLiS0qpPwGkAXgFEoDjcwAg+YdSaj6AyUqpnpB1yd4EkETS\n1pjNAvAygKlKqREA6gB4EkAfR1fGAUhRSvWDmCe2hwT46OaQeRfim3aNUqqOoy+/QhbKPmfwyy9i\nXrtypZgwbt0KTJ0K1K1b1D0zMDAwMDAwMDAwMDhZnIgp440AfoKYFRLAGJ0+HUBXkiOVUqUgURJd\nALwAWpDMcNTRARJ2/3tIgI7ZcJAukgeUUndpmV8hgUEGk3zXIbNYKdUewHC9bYBEdVzraGcihJg9\nDyFlXgAtAHRHfl80ACgBAOvWrQtxSk4/WrUC/v0XKF8eaNhQNGXXXAMsX17UPTM4H7F//34sNyeX\nwQUOcx0YXOgw14DBhQ4HJyhxJto7EWK2AcBMCMEppfe7kHReuWEB/ttQyNW4+dt3pikIifLNt+u2\nCRb9tLULQvzCHPJAXl80J6IBoGPHjn6yzg7s2iVBaObNK+qeGJzvOJM21QYGZyvMdWBwocNcAwYG\nAIQjLCpM6GQREjFTSrkga4H9ciSOuQAAIABJREFUAFl/bBeAayBrm9kyz0ECbnSChMUfBmC+Uqqm\nQ2s2CxK443aIKeM0iIato64jErLI9LcAekBMGd9TSu0lOUXLxOl6noOYMnYAMEcpVc+hNesHIWw/\nA3jB7otuc7yfIc4H8BDEBPNYKHNjYGBgYGBgYGBgYHBeoQSElM0/E40p+otyEkhYqdcBxJFsUoDM\n3wBGkRyr96Mg2qlOJJOVUjUBrAFQn+RvWuYuCLmqSnK79j17BUAlklla5jWIqWItvf8hgFIkWzna\nXgzgN5KPO/ryHWSdtR663SUAjgKoTvLfoAdvYGBgYGBgYGBgYGBwmhBqVMaWAH5VSiUrpXYopZYr\npZzriF0JWQD6BzuN5AEIGbKjIDYCsNcmZRrfQzRbNzlkFtikTGM+gBpKKXuBsThdDj4ycbov1XVf\nxgDoD1mIeiGAwwC+MKTMwMDAwMDAwMDAwOBsQag+ZtcCqKX/E8ClAN5RSh0jOQPA5TrvJ6VUcQhR\nehyiMauk82oAKK6UOgzgIID3IcE59jhkagK4Uil1DMBfkOAedij9SgD2A6gCif44AsBKAL192qlq\n9wViumj35U0EIKRKqUsgJpppMKaMBgYGBgYGBgYGBhcyjpsyktx9uhsLlZgpAEcgHbSDcQwF0BPA\nDABP6fT/AtgMYAKATwD8A4BKqTAAnbVMIwi5+gBAhk6jUioaQCyA1QDaAWgGYAqAxxwybXXfP4YQ\nrb4Q4vUacoOBFNiXAOO7CxLYxMDAwMDAwMDAwMDAAJAYFLNOdyOhErODALKdZoBKqRUA7tG+ZPdA\nSM8mkquUUl0ArAPwG4AFEOJTHsABkqsBrFZKDQTwOoAykAWhewI4AMAimQogVSnVGLI+GSFasb66\nL6l6XbTHdNt3AtgRZF/8IQ0AZsyYgZo1a4Y4NQYGIeDLL4H69YEqVfLn/f03sGwZ0LLlme+XRt++\nfTF27Ngia9/A4GyAuQ4MLnSYa8DgQse6devsaO1pZ6K9UInZFgC1lFLbIKZ+iyGBNDZDFneOgBCn\n2wGsIpmqlNoCiar4OkRLlgrgOh098TeIpustSFj7pRB/sOUA4pVS4SSzHTKpEI1dfd327QDGk6RS\n6nuID9xHkLXWCuuLP7QCgJo1ayI2NjbEqTEwCAHlygFdu8oq4dHRuelpacDTT+dPP8MoW7asuQYM\nLniY68DgQoe5BgwMjuOYUupyAG8DaAqHOxbJHFtIKdUUEt+iNrQ7FsnpwTYSavCPdyBaqI8BDAHQ\nAGIqOBni25UBYCzE96ulUqoOgEgAhwB8rmX+ghCtyUqpBgCuhJgcekhu1zILdF1TlVK1IH5pJQCM\ng2jcwiELWrdQSvVTStUAcDWAiyGLUlcMoi95oM0j+4Y4HwYGJ4boaCFfXbuCVhoOH4aQMn9k7ULD\n9OkyF/6Qlib5Z7IeAwMDg9MFc58yMDhXoADMgyh+GkGWBesMcekSAXHH+goSBPEGCG+ZopS6I9hG\nQiJmJBMB3AfgNghjvFh3tINDbByAjQDmAFgFIUOfO9YwA4BnAFSGaMjsCI7OdcXSAbwIoDUkxP0z\nEEL4nkPmdwg5ex3AH5CIjmmONcyC7YuNvhAfNAODMwNNzv5u3hV3l0nBjntOkJSdbw/2Jk2EoPqO\nySauTQKu1nF66jEwMDg9ON/uXScCc58yMDhXEAfgOgAPkVxNcj6AgQCeUErZFog9IS5Uz5JMJTkB\nwGyEoPgJVWMGkvNI1gXQBKJ9OgLABfEPKw4JslEBQt5iAWQDiNfFt0O0WR9CiFVdCNsEgHsdMtdA\ngnq8BZmEWRAC2ASyqHU2gP8AeBjAo5AojpsAVFVKlQ+yL8ehlCoGMY9cCohNdatWrfJsSUlJoU6V\ngS+6dQMWLvSft3Ch5DtRowYwYYJ/+QkTJD8QfB/4zrZ9H/gLF8rDb/TovGXsOtLSgDFj8pYZPVrS\n/CGUF4roaAyPGIQUNMUQDApMygp6gbnqKuDmm/PPrf1gv+qq/P1x1uf8360b8PHHwJYt+cfi7xgV\ndExbtgzsJ+evLhsObWLWn2nStRPRJjrqQVoaNm0CcjadQD0GBganB4aU5LtPATDWEwYGRYSkpKR8\n7/99+x7nVHUArCa5y1FkPoCyELNFQDRpAZfyCgokQ94ggTpSAdwNIBOi9YqCaLoyAdyv5a6F+I7l\nAGgIoDmALC1TXst0h6wttheiHnwdwE6IX5jd3iwAfwOYp/d/gURXHKf3FcT/bR+AZ4Ppi894Kuv0\nRwBw2bJlNDhBAGSVKv7zLrlE8r3evOleL+ly5U9PTCSVkt9g0p2wLNLtll9nG8nJgdPj4shGjXLz\nLEv2Y2Pzp/vKBmq3EPy9yOIPcPOZhh7+ADc3pwQoF6heOz05Oe8c2uleb8HlLCvv/+RkMiKCs558\nMm96oGNUUHqZMmTp0sGX8TPmP6u5GQ8P/7rGzximTQs8z5Yl+fr/1mulnrSrgj82J4Vg+0aSjz4a\neC68Xsk3KBLMmjWrqLtw/kPfZ479YTEnhyHfQ88bWBZzmrr5/UAPMxqfPeM314DBhY5ly5YRYrX3\nCYCvmZc/lNT84S69nwrgOR+ZFhDF0EUMhmMFI+SofBRE4zRbk6XvIL5cE3X+57rzd0M0UD8D8EIi\nmfSBaOi2Q9YhqwuJ0rgDYsaYA7HHjNYD+B/Et+xx3cZIyMLUANBetzMWolGbBGA3gCQAnwXTF59x\nGWJ2qlClin9yZqdfckmel/JD3/h/Sc/OJufPJ79umcgcKO4dnsicHPLoaNn/umUin3ySHD+eXLuW\nzMrK35WcTRazm7p5dJ3F/fvJg+8lMycigvsmJ3PvXnLvl15ml3Vxzxde7t1L7l9pMfumOGbd1IiH\nfre4f6XFjLqxzCwdybH/8XLxYnL7LxaP3eLmv/+zuHuZxYzGbu79zeKuXeSe5RYzb5X2/PXHF5kb\nLG643M1rilncto28vozFNRXdzNxg+S/g+8Lis5+d4mVWlIu7JiQxpyBS5q8+m4TGxQk5i4wUQloQ\nKbPhm+/cLyivEPz7L3lXCQ8J8N5ID/ftK2Q+AqRnZpJtKkg9/3exh0ePFtr0ySPIvpHMPyfTppGj\nRuUl2zZ5syyybVty9Oi85W3yZlny3/71nWebFAZL+EIhmAYGJ4iM10bxl/A4vnGfJ//1cQGdZ18+\nLfepyR09Rd0VAwMDjSCJ2Z0MTMzu1rymOIPhWsEIOSr/n9Z4UXfkX0gI+jd0fheHVooAtkIWpF4C\n4DUt86nWZlF3dAmA0j6Mc4cmY9S/k5yM00Gk7L4c1KRqBIDFwfbFMa5iEO3aU4aYnQL4krMqVZgD\n8FilKpw7l0xs5+X+cBcHXZzAPXCxY7SXd9xB3nYb2aQJ2bgxWaGCVFG8OPkYEpkNxU/D7mc2FB9D\nIsuUIWvVknwgVzYyUpQ0xYpJWjWIRioeopH6D5K5By72hrR9C7zHy9vyPyOOyxDDZajHn9GIt8Cb\np45qsPLIB8orUYIsV44sX5689FKyYkWyUiWycmWybpTFH5XIv/yyTNP06WS0ru/qCIslS8p4Lr5Y\nyleuTMZVtvhzCTfbVfbw5xJu3nKZxSuuIC+/nIyKIh9EEgnw+ZIJXBrpZss6Fm+8kbzlFpnfu+4i\nmzUj776bbNOG7NTE4pIybvas5eGasnFc42rE/jd6uK5ULPerSD5bMoF7lYv/reHl/feTTz5JDhxI\nDh5MjhxJvvEGOW4c+UlfL4+VcnFRuwQeK+Xi/IFefvIJOW8euXiUl+mlXfy9WwIzyri4bJyXCxeS\nixaRHg/5zTfkV1+RX39Nfvst+f335IwZZIebLXrC3fzzXQ89YW52bGxx3jxy1Sryzz/JbduETKc3\ndnP/Sou7d5MHVlnMinfzyFqL+/aR69aRY3rLnP44yMMf4eawR4MjzieNQoh0HjjJmWXJyR0eLuTM\nzo+MJGvXJuvVy9XW+pZzEvJAWlTf9FDGUFi6E/6IoU30fInho49Kv6ZNy1/OKWv/PxWEMZg6bBmn\nrJMk2+k2Gb73Xtn81eXbd3/tO9NPBxk5S4n2l29aXIYYEuCOZAcpuZC0Z5bFVZfKs+R/kRfImIPF\nWXreGlwYcBCzSQCWMy9/iNY8o67eT7E5kUOms61YCmZTulBQUEo9AiABQEcA63VjLwB4n2RnpdR3\nkPD0bshaZBMcZOp7AC9pMpcD8fuyF5ieCjFBbK7r3QSJzNgDssB0AoDBkMgnJTXpehsSGfJDiFNd\nG8ji0PVJ3lxYX0i+4DO2X3S77ePj41G2bNk8Y2/fvj3at28f9FwVBfbuBUaOBFwu4IkngDJlCpbP\nzhZT9tRU2f78E9i1S+o5fBg4ehQ4cgRIT5e66tQBqlYFLrkECA+XOtauBVasAKKigNq1RS49HXhx\n0mUof+xvZEMhHMRmVMGV2AYAuOwyYNil49B5xVOY407A19f0wd69UmdYmPxedhnQooW4Tm3YAER1\naY3LlnyGzfXvx+53PkXdukBEBHDoEPDLL8DmzcCxY7KFhwPFiuVuVTem4I7hTfHTIA+2XtUEdT3j\ncMPUp7CyawK2tu6D7GwgIwPIyZHfin+IPAB4X/Hg2E1NUHNnCqp2bIolIzzYVbsJcnJwfCu3OgVN\nBjXFgqEe/HNtE2RmApmZwMGDModkrqz9/8Y107G3bhPUbBGN2FhA6eXaV6wA1sxNQ8U/UrC2QSdk\nZeH4lp0tv1U3pqDbzKaY/JAHadWaQCkpXyUjDW3nd8W2BvehzpSn8HbTJCy/ph1IGZe9RURIv44e\nBUqVApogBf2+aIqX4z3IzgaG/9wUo+/14NqjK9Dqh6fw7T0J+LhyH2zZIq5nBw7IGI4cye1XdjbQ\nM2McEvAUnkQC3kSfPOdab4zD+AB5/lANaUgq0RUZb09Fk07RSJmehojuXfFQxlRsRnQ+2anoiiEY\nhEEYgq7IlbHzPA9PxdD3o/H282m4dkRXPFFiKva5olGmjJyzkZHyW7KkzE+pUlJ3VpbklS4t52bx\n4nKuR0QEt0XuTkPdhK7Y3HkQot8fgrSBU1GyZjQyM+VcCAuTa23nTuCblxZi+OqWmB49GF03v4yM\nSlURdVkUwj9MQlgYgHvvBf74A0hKAho0AO6/H9i0CZg7Vy5Mp0+K7aPSsyfQvTvwzjvAW2/l7n/5\nJdC4caHHAUB+f5dg/V8WLhQfQ2dbaWl5+22nf/wx0KEDMGsWULlybjnA/3/f8Qbqayjj8pcOyP+h\nQ4GXX5a0rVuBu+8GrrkGGDdO0ocOBXr3lpsVAHzzjYzN9zj07Cll7TJ2ndHRuX6XkyfnHjN/x6hd\nO/EbHT48f57t0/nll+Ib2qSJ1D19upzUn3wiJ9vQocDGjUCnTtLHTz6R4+Fv3ux6UlJy63POlZ2e\nkiL1Odv1N+e2nANPtkpD5287ICLrKC4qWxKRX85ClUWzgU8/BVq3Bh54oPB2bXTrJvv+5m7hQulf\n48ZS9q67gCeflAemb92HDgHjx8vD0YmC6n/hBTm3P/zQ/9iHDwdefDH/XKalge3aY+DKB+C55D+4\nadsneK3xXBT/QB+PYMY0eXL+vPMFwVyrzvQTOAcNDADxMfONKbF//34sWLAAAHpB+Ehlaj8zpVR3\niFKoAslMpdTrAFqQvMEur5SaBcBF8u6gOhEsg9ME7j4IucmAaJgykas9y9BbDoAoLV9D7/8NMWW0\ntV4rHXX2gJg25kDMG0dAgoq84ZBJArASuaaMS3Q9rfS+gmjEfgXwGcTHLEPL+O2Ln7E9CFmb7ZzV\nmDVvLlqa4sVFOzN5MnnoELlnD7lyJfnll+SYMeSDD+bXNpUsSdapQ95+O/nAA2TnzmTPnmT//uQL\nL8j/W28lq1UTDU5UlLgQ1atH/ve/Uuf115NXXSV1x8SQmVAkwEwojhlDfvwxmZpK5izQX/kTEoL7\ncm/7lN1/f+G+Zb6wv7h6PHm1BYHatv3HYmJyNRO2BsKuw9fMJlDe6UCg9ny1JUlJQftxHa/P9pvz\neMSMMTIy+GOkNTc5YxOY43Lx2Pde7t4tWq3ts8VkdN/QBGZFubglycs1a8jVq8n168m//hK5LVvI\ntDRyc4qYhPrOZc4mi0caubn8U4vffivn80cfyXn142AxAfpxsIezZpEzZ5JfJVrcE+Pm7mV561n5\nucW/rnZzfD+Lzz5LPv44+fDDcno1by4axZtvJhs2lHM+Joa85ho5t6tUkfM/MlKuNVszW9AWD+lb\nPDwFytWuTc6OTyABTqqVkEd7uyK8HpdGNGLXyGTuC3NxWIUEHgiL4poSMexeQ76wt6xjMTZWTtsb\nbiCbX2fxl9Jujqo2npkqgjOvHshDxVx8t4uXr7xCvvqqaD3HjpX7wpQpsn3wAfnJJ+ScOTLHc+eS\nP71ncWcdN73DPNxf383fv7K4ejX5xx/kxo1yDP/5R8xP9+0jDx8mMzIc17rTlDUqSibV99x1avK8\nXlF9lynj3yTWWS4YjWRh539BdfheW16vXB+lS+c197XHZY/D9md1jstfXU4Zu0xBvqH2tVmYX6cf\n31EmJ+fXsgbylw00/kD3nMKOQ4D0jPUWU8LdHNvH4uzRFn9GIy5HPe6t7nP/Laxd5zwU5g9r1zFk\nSN5nSqD0YOv3PbcDzaGz79qM/GCdON4CL7fXFkuKL8Y75itQmwMGSJu+6U4NtG96YqJ/M2anZjoY\nv1d/Wiy73KhRYnLt1ADb5SxLTLHj4/330bcvvnMYzPUeKG/UKDnfA5UxmjcDP3BozOprLvI18rpj\nvcK8GrRDmss43bGakUFyrWAFdYOlIeaAtSARSPprsvMZJJ5/NsRM8X5Hma1apgFEw/Un8gb/iNb5\nByAmhSmQ6IhO8tZZD2wecs0OU6GDf2iZaZAIkc9AtHEF9aVhgPG9dq4Ss+XL5Wh+/LG83Hbo4P/l\nr0QJMRXs1Yt8800xHdu8WXy6Tilsc0al8po1hupz5BvoI5jAHzZ8b87OlxN/bfu+pPh7CfL1yzrZ\nF8NQEKg9fw97f+MrqD79cnBW+JiFarYSiKyeQfOX7Gzy2DH5ELJvH7lrF7l9O/nPYotH49zcOtPD\nwzcJoVmwgPzlF3LJEjHnXLlSupPlyfvBwvrAyx8HeY5fvNO7evjKK+Sc24S8zb41QXxyAI6428Pu\n3ckePeQjyuOPyzU+rrXkz63eiwQ4+ooEVqkiH24uuUTe6UqVkvf5U0Uw85UL83IPXHzmIjGLvTvK\ny9hyFr3F3WxTwcNFJdy8rbrF668nO10lZs5vRCfwUHgZHgorzYk1EnggwsUBt3rZpo3c2zp1kg9C\nL3SwmHqZm28+4OH6y90c3s3ic8/JxyTb5NZJQseMkel9801y4kRy0iQy6TWL265zc+5zHv59nZvJ\nIy2+846Q1KlTxcT4s7EWt9dyc1GfJKaXdnFJvyTurR7L9JKRXNtDTHR/TfBycZLFPfXcXNNzPLPD\nI/hXl4HMjHRx80wvN2yQD1Prv7V4sIGbqe96uaeem962QpxfqTieG6vJOXLgAJm90Qp4f8lZ4GWO\ny8Xts71cvZr852Mvc8q6hAj7EpCYGDnQycnHr/H9c738p3oj7qpWj1kNCyBlzuvF370mmOBC/vbt\n62ajRau6EJHff5e0vXPkPFuu6vGj3l5mNHbLuIJp14aeg4wfvUxP9/OBwNGn7EFDmAPFYwOH5CNl\n6en+/ZcLvK8VNnbfuRwwgIyL4wc9vPSEuZmearFOHbJdO+a9T/lrMxAR9H3W2Qj0/Az2Pl3QOO18\nX5NrrzfvOWg/YxMT/fexoGeEJdfqrB4e8aO2zYgDyDImhjlt2/Kff+TDXtBBuwI9O2zCaxNM337b\n6YbgnVdwELNYAJdD1ik7pEnZCABhzMslmgBYBuAogA0AHnbmF7aFRMx0g9dDfLoyAezR7PENSECO\nowAmArAgq2LX17JbdNlJmmk6GWdLPeCZWiYVEpnRyTgTtUwL5PqXvaDbewQSAGSF7tOlwfQlwNhi\nz1Vi9swz4oeUmZmbtm6d3B8++kheALduDfCQOdXw42NGP4E/jiPQjfgCiMoYNAr6Cl2zZv5x2fB6\nyeuuK7ifgb6sO9ODeVD7pp9sVMZgcKbJcSgIpW+BXrps9bP9kuPU+NovZYG0tXZ748fLMR04sMB5\nz8oSgnn4sGi+du4ULdi2bUIw029xc9cnHh5s4OaqLywuXkwuWED+8IP4CX75Jfnpp3K/mTGDfO89\n8p13yAkTSE9rIZNft0jg4MHksGHke53lBfzt9h727y/+iz17kklxIvt+/QS+FyP/36mdwBYtyDvu\nIJs2lY9LN90kl2bnK6Weh6/w8NprRbMZHS1+l1WqiL+qfeuJjBQiWry4uPCFQjptmd5IOC5r/++N\nhHxy49ArX56vb6pdfmKFgSTAO4rntl+sGFknUrRJzUuKn+W1xS1GREj+LfD69ZdVimys8/qEJXAf\norgcMbzzIg8Xh8VxcVgjxsPDZahHArw9wsMrrpDbRGyszO0dd5D33Ue2by9bhw5kn/ssrrjEzeei\nk3gwwsU3b03iuspuvviQxSefFOuKfv3IPn3ko8Dz7SyuqeTm8Ds9XFPJzf7/sdilC9mxo2in3W6y\nV+Q0VoPF/v3znrOZ33v4Z8VG7IfRrAaLP8LNrqWTuC/Mxeeik7jc5WaPuyx27SrvwvfeS/7f/4nf\n7N13i8b4nrJ556d7LS9btZJ8t1ssPGLLia/vGPRhDsAfL7qT2VB8uXwiy5XLPV7Vq4smvVMn4VFv\nvEF+2MvLoyVdXPCA+NXOHeDljBnkrFlC9v+62s2kxzzcVsPNeRMtzp0rWujZs8kvxlv8p6abP/ZI\n4tGSLk69K4mecDd73SvXcEKCnJ9jxojGOiWF/Plncs0kLzMjXdz2XK71wRavxaM3u7lzqcW9e8n0\nVEtIi68vqX2PSUwMnYQFkvN3j7M/ZtrP1Jo15VlQs2bus9RXUxzkh7vPPsu9vj563FNo/3OiomiV\ni2E8PFxXxS0fO4K5Lwe6V9vPx8TE/O8RpUrlpo8aJZuzDZusFS9O3nijf/LWpYt8PbdhaxX9ITlZ\n8v3hRMudLM5TX0AnMWOInOlEtlBJ2QCtzToIiYKYqsnQew4yFAlZzNkOupEBYBLzErOGmmlSa7YI\noDlzidlzENPHwzovU9dX3EHMboL4l2U62tmg6yi0LwHGd84Ss5gYeWgUOYKJyugP/kwXrr02MPlK\nTJT8QPC9QTi/qvneILxeuVE5b6TOOmzTC2eZUaPyRsZz4nTcgAq74fn7gldQf5z1+QY2cJqX+H6x\n9T1GBZm8+AuEYMNfXaGiILJa1OQslL4FeuFxBgCxLPkK7dy3v0IX9JW+ILO6Ex1LqPNrj89pFhtI\ny+mUtYl9Qea0geoJBZa8yGb94GF209yoqDk58qHr2DHy6DqLmfFuHno3idllXdw/KYkZdWKZXSaS\newbLS/LWD73c9KPFw43c3DV4PHPCI7j9MdGYLR/v5U8/5b5g//IL+edwCdST8YImzElJzIoXU92k\nJLnFjRxJfthTXkSTn/Bw/HjR9E2eTL7/PrmmhxC7tT0SOHOmEOFJk8i33ya9bSQvpXUCP+6V+zJr\n13esVgy3zvRwy7Vuju4l5KhnT3mO2ATH7ZataVO5RT4fJ2Xfqil1d6/hYb16QnJq1BByV7s2Wbcu\n2aAB+cT1Iv94bQ/j4uQ9/dZbxWS4TRvypZfksObk+D/Pjsa5+cV4i3P6Sj2f3y7tDnZ72Ly5vOPf\neCPZsqX094475P9jj4mmdFE7kf/hvgR27Ejec48QzrZthTwOG0Z+2kfq3nb1raKpi76f/fuLlvW9\n92Su+/Yl//Mf6X+1anJali5N9i+Wn5jbmx1RNhDZtwlGv3CpY0wrD3ftkqFnZMj82AYnzs3fxwDf\nIFTVwyxeeinZItLLvcrFIZckcH+4kNOmTcnnbvHyQISL79RO4MFiLg5u5mXnzqJx791bSPbzz5MT\nO3h5+CIX59yWwCMlXJz2qJfDhsm8DR9OjhhBvv28aD2nd/VwU7SYpE7v5uWREi7+eOtAZqlw/hN5\nFf+KqsWD4ZEcWjuJayu7Oaa3xVdfFYJ7rKSLi9snML2Uiwte9fLrryUIlMcjH36Sk+VxWzfK4qry\nbr7VTsbZu6XFjz4il48Xwrp9tpcHDki056xIF4fc4WUTx0eXjh3l9Nritbirrpsrx8s17/e+Eeo9\n1Ul4nR9vfc1WL71UDtoDD+Rtr0sXSe/SJTctkOYzUHow5cLCAr9XOZ/3J0KyzuZn8kngbCdm8yCL\nOteELLT2lSZA70CCbGQDmAIJSd8EQD2I39ZGXX4IgOUAVkMWXKujNV4E8I6WSdF1HIKEyK8B4H0t\ncwdyTRlH6rptjVmqJl7lg+lLgPHFAmB8fDxbtmyZZzub1/LYs0du4FOnFnVP6J+U2bDJmYHBqcDZ\n/HXuZNYxcz7UbbMZfyZCvppM++EX6Gu074tFMOTsZB+0wZhf+euX13t++pj5zsv48QX7lhVEPP0R\nXn95Ts1qXJycPzExub42wc6bLWf7ryYlFVwuFNJc0HlmXwvBtutvDgoj9n36yLPpzjuDN5V31J/j\ncjHzJy+PHBFz5uNmqB4Pc5rKkirbtokWes8e8tDvFrOauJk1M4k5BYwpI0N8b1NTyTVryPVThYBY\nT4n57PLxXn73nUS/XThcCMg3Azx86y0hpsOHk1+3ECL30c0J7NxZTCTvuYd853pJn1AjgU2bil/t\njTcKqb7uOtESXn01OexSkXsxMoEVK4oGukIFiTZ88cUyBa3KStv3l/OwShXJeylKyr1bptdxVvnu\nDZLW7VoPq1YVjhIZST4VFpjg2ttV4RK1cu9vst7djGEWF5XMjYTsT4N8fRnRTNLj4fZabl5XwspH\njJsV97BBA7JVKyHDDz8st9wnniBf+a+spTmti4dp1d18d6DFt94iv3peohCveWAgs8Mi+HuP8dwX\n6+aqiV7uv9HN9d9aXP/X3UulAAAgAElEQVStxaM16zG7TBR3zfFy728WMxvGMfumRsx54IG8JMwf\nKbPhS7IKI2WFlfPV9vleC4XdTwu7X+j8I2stbt4chLw/2EvG+JYB5L7r+6GclBPpFLxfzpo1K9/7\nf3x8/NlLzPIVFhJETdDO2QWmHe2ckxqzL76QI7lxY1H3xMDA4KTh76F0Lq5jFohMOTV9NgIFpwj0\n/1R8mQ2mDl9SZpMw2wfTSdZiYnJVKQWRYV+z6kB+W4FImi8h951r33ly+vfUq+dfyxrky1ahfQw0\nt4XVH+g8sywhZS+8cEI+ZkGZ4dk+ZUOG5PMxC4iC6i9s7KHOZShtFqSB9le2sOBOoZBbZ9t2uYED\nRctvRwWLjMxPQrVs1hsJzCnr4u7Pvdyyhdy0SQjphg3kvhVWrk+ZAzmbZLmUjT9Y/OWXXA3yr48k\ncMH7Qn6d855xq5vfT7H4w7uijV37lod/XS1mtvfcI+aqt94qgZ9uuEG0wG0rCYG7N9LD0qVzTaBt\nzaVtsmxrRp3ay58Rx19RL8/yOzaRfAddmAPwT3UlcwDOKNnl+DTVqydL3NgmxWNvTmaWiqCnTi9m\nqQgmt0nmiBESuGnSJAl29cknMrUzZ4o2fcIE8tMOycwKi+Dvt/VidlgE/xiWzNRUcvcyWeM1Z1P+\nczQ1VWIWFHjuFnB/zcmR5S8WRMgcrK0sa7uGBOcHGWdbpUvL5IeF5U23SVlkZGjtBImzXWM2HEBj\nANUgvmZv68520flz9P45tcC0Y3znJDHr35+sWlWbgxgYGBicDTDrmOWty+sVUl2zpvx31ul8Wbdl\nA/mGnkxUxp4985tWOf8XZJ4UiCgWRCD91RPsl/NQ23XOw7kUlfFkxxSMBtpZx7noYxbMtepPS1yQ\nBjYYshGA8GZ5JNjO4WcGMic8gnuGjpeAPvMtLltGrnpTyNzK8R4uHeU5rvb7cZBoM6dMId96i9xT\n7koS4C7XlRw4kHzuOTGb7dlTImO3aSPaTbeb/KiCEMBpkb1YqZIMtVQp/9pFQC53l4tMDOt1nEA6\n820C2ayYh55wN2NcsiaqnX/ddUJO77vB4q9l3ewb6+HKS9x8/G6LbduK5tX2Qb33XjElvu22XMOo\nl271HNdI1q4tRDElhVy7VqZx+3Zy/37RCgc8rr7B2OLihJQ5SdhpJmXk2U/MpmjNVTZyfcMsR/7D\nWiN2BLkLQHsggTnsBaZnQNYys/3GjkF81JwLTP+lCVu2Tt+l2/ZdYHqv/s2GrH+WjNwFpgvti5/x\nnZPErH598qGHiroXBgYGBgYFIlhCWZBc27aiQfIHJzH09SO1zWJ92yqMyIa6IPapMjE+0YW4Qwn1\n7s+P2a4zkB9zQfUPGCDHxx+cBP5UjcnWiPq2eb5GZQwE3zKBlhGwNbC+/uH+xhJIWxTIVNlXA+5r\nOuw0QSdzzRevFHLm14zRhn08e/XKN2fZ2eTBg+Tu3RT/ukPk0aP6Q70ul/l4L+aERzBtVDJ/+kmC\nNL33HvlFfyFPHz3u4auvym3FJof9+ok5Z7du5PA7Re75OA+bNZNllW67Ldf/9N57xRT0wQdl6hcn\nWcfn4GBDN9veZB3nU/628HDh7pdeSl5xhWgqY2LI++tZ/D0qjhuiYrjRVY/ryzfigPYWD0REMgdg\nJsAcgIeKR3LKFNEW2gF2PvtMglKlpEgE5FWrZHmebdskwFV6evDKjLOamFHIS3PIQs9f6452duS1\nR260xpZaqzZHk6/XtcwkTcyWA7gRwM2QcJIEcKeWWQ8Jnz8d4s9mrzHmGwAkC0A/rVkbovd/C7Yv\nfsZ2zvmY7d0rHxCmTCnqnhgYGBgYGBicMRQW1v18WscsEILV+JHBfzQIpEUrKCqjvwAgvqbDNikt\nSh8zez+Q+au/eQnWV9Qp70Noj/0hS2J4vbJM0+efkx9+KARx4kSJQDpsGPnii0IKba3hYLfnOIPr\nVcfD+vXF3DNTp2UCedbkDWULC8slhNWrCxmsXn0WL764JcuVa8mKFVuySpWWvPTSc8DHDBK+frMm\nR60c6W7d+ecdaVFa7j29P0HL1HPI2AFA3MwlZkcBRDhkvgKQrf8X03Uu8enXTgCbgu2Ln3Gdcxoz\n419mYGBgYGBgcEEiGBIZKk5kHbPkZLJyZWlz9OizNyqjP2IZrPlxYebIp8qM2VkuLi6/xtE2X7S3\nyEhmZYnmcMcO0R7u3En+9Zf4Ka5YIZFwf/pJlnWZMUPWp3z7bVn6Yvhw8tlnhQx26yaEsEMHifDq\ndpMNGpz9GrNESKCN6n6IWR3d+accadfqtFl6f4zeL++Q6aHTWuv91QD2+bT7vZYpq/fTAXgc+Qri\nu7ZN79ctrC9+xnbOEbN+/WS9nmBVsgYGBgYGBgYGBqcQvqbDZ+s6ZomJZNmyJ07CCiJZpzJS8gXs\nYxaBEKCUmggxEWwFiaQIAGWVUiVIHgNQRne+r1JqBWS9s/EQHzGl5XdrUvWBUuo5iFniUF3fpVpm\nD4DrlFIjAEwFcDuAeE0EK2kCFgbgZqXUI5C11foCCAeOj6l0EH05p0ECc+cCzZoB6rwYkcHZgqSk\nJLRv376ou2FgUKQw14HBhQ5zDQSJTp38/weA6GjZACA9PXAdU6fKZiMlJbBsmzay+UNB5cqUAVas\nyO2Ps49Tp0rZ6Gj5nTq1cDknfMftW85XPhDS0oAOHeQlNykpt9yqVUBODhAWJv8B4MABICoKOHhQ\nfg8cCK6NsxhhIco/BjEH9ECCgCgA0yA+YDYI4DsAsx1yi3S6nb8FErBjEWSNsmmQIB22zDEAcwE0\ngwTr6AtgoG7PlsnRZYcC+A2iIUvU9fr25StIlMdGEPJ2cYjjPiuxejWQmgq0bl3UPTE435CUlFTU\nXTAwKHKY68DgQoe5Bs4zdOoUmCBFR+eSq2DlTgdSUuTF1knKAODwYaB0aWDkyLzk88ABIDJSyNl5\ngJA0ZiTzEDmlVA5knbAvdNJ2CHkaT/JRh5wHwCaHTDmS9zrywyFBPLY7ZCJJ1nfINIUQrR0OmVU+\n7Qz2yVeQhacjAHSGaNZ+BNBUKVWe5C5/4+zbty/Kli2bJ619+/Zn3VejiROBSpWAO+8s6p4YGBgY\nGBgYGBgYnCQCkT7SfzpwyjRlSUlJ+T5G7N+//5TUHSxCImaFgaSllNoOMT1cBQBKqSgAN0GCfgDA\nYgAupVQ9kr/ptNshJGqpQ2aYUiqcpK0BuxNAKsn9DpnbIeaJNu7Q6c6+PAFgEsn3dV8uhphNdoWs\njZYPY8eORWxs7IlOwxnB8uXAlCnAq68CxYsXdW8MDAwMDAwMDAwMzl34U8IsX74c9evXD1Di1CNU\nU0YopUorpW5QSsXopOp6/3K9nwDgJaVUS6VUHYi54VbIgs8g+QeA+QAmK6UaKKVuAfAmgCSStsZs\nFmRR6alKqVpKqbYAnoQEDrExDkALpVQ/pVQNrS2rDzFntDEeshj2AZ++zAUQF+rYzwYcOwZMnw7c\nfjtQrx7Qp09R98jAwMDAwMDAwMDA4GRxIhqzGwH8BDErJHLJ0nQAXUmOVEqVgqxX5gLgBdCCZIaj\njg4QAvU9xFdsNoDjFIPkAaXUXVrmV0jAjsEk33XILFZKtQcwXG8bANxHcq2jnekAXoP4xvW3+wKg\nG4Br/IytBACsW7cuxCk5/Xj+eWDTJmDzZiArS4jZSy8Ba9YUdc8Mzkfs378fy5cvL+puGBgUKcx1\nYHChw1wDBhc6HJygxJlo70SI2QYAMyEEp5Te70LSeeWGBfhvQyFvZETffWeaHfDDX9zBMOQNKlKY\nBtDOdwYRcSIaADp27FhINUWPH36QzcDgdOFMqu4NDM5WmOvA4EKHuQYMDAAIR1h0uhsJNVy+C8DP\nAH4AcBdEk3UNgL0OmecA9ALQCYAFYBiA+Uqpmg6t2SwAFSE+YsUhURknAeio64iEmDt+C1njrA6A\n95RSe0lO0TJxup7nIKaJHQDM0b5rttass/59G8BHdl/0GOwgIU7MB/AQgDRIZEgDAwMDAwMDAwMD\ngwsTJSCkbP6ZaEyxoCgnvsJKvQ4gjmSTAmT+BjCK5Fi9HwUhQZ1IJiulagJYA6C+HfxDmy3OBVCV\n5HalVE8ArwCoRDJLy7wGMVWspfc/BFCKZCtH24sB/EbycUdfMgB8TrKPoy+HAYwgOSrowRsYGBgY\nGBgYGBgYGJwmhBr8oyWAX5VSyUqpHUqp5UopZ7j6KyELQB83siN5AMAS5AbbaARgryMiIyC+ZoRE\nb7RlFtikTGM+gBpKKTuOfZwuBx+ZON2X6roviQC664Woq0C0e6UhWjoDAwMDAwMDAwMDA4MiR6g+\nZtUB9IQE/BgOIVLjlVLHSM6AECHnWmM2dug86N+dzkyS2UqpPT4ym5AXOxx5+/VvQe1U1H35ALJ4\n9VCddhhC+v4NbsgGBgYGBgYGBgYGBganF6ESs2IAwgG8qDdANFA9AczQ+QrAWqVUcYgG63HkDbZR\nFkBVpdRhAAchIeyf95G5GMADSqkuAP6CkMD/+ciEAXhTKTUNwEoAvX3yj/cF4sdm9yURgFMTdxxK\nqUsgvnNpMD5mBgYGBgYGBgYGBhcyjvuYkdx9uhsLlZgdhIS3vw65URI7Auir/3fX6U8DWAFZVPoT\nANkAflNKhWn5iyBrjlWBaLQyIWRsu1IqGkA9SOCQxgCaAZgCIW8EsEOvaxYBIVvDdfvztZytRSuw\nLwHGdxck4qSBgYGBgYGBgYGBgQEgwQFnne5GQiVmWwBc6TQD1AtLb9aBNdpANGgukr9pjdc6SACO\nCRDiUxGi7YogOV8pNRDAaAiJWgohWTsAlAPwJ8lUpVRjiFYuleR+pVRfAOsBRJH8Qyn1GIB7ADwI\nYF6QffGHWACYMWMGatasGeLUGBiEgL//BoYMAQYNAqpUKTz9DKNv374YO3ZskbVvYHA2wFwHBhc6\nzDVgcKFj3bp19jJaaZrzvA2gKRxWfyRzbHmlVFOIy1dtaKs/ktODbS9UYrYYQB2l1H4A+yBELQbA\noxANWASAsQBeUkr9iVyTwMMAPoeYP64GsB3AZB19cReAMgDm6oiMjQDMAdAawFSl1AgIwboKwKNK\nqWK6rRcADFdK9YNEdNwFCaufCFkEu7C+5IHWwvUGgJo1ayI2NjbEqTEwCAGxscD11wNduwJTpwLR\n0UBaGvD008DHH8t+EaJs2bJFdw1Mnw40aeJ/DtLSgJQUoFOnM1ePwQWLIr0ODAzOAphrwMDgONIB\nzAPwNyRIoW31lwHgJQDQVn9fAZgIWcarGYApSqm/SX4XTCOhRmX8FMCrEGJVEUBDSITDmyFBNzIA\njASwEUKuVkEI0ly9hpkdsOMZAJUhGrKPdd2T9W8lCOF7EULO1kDMEgnxYysP8XNbAGA6gNcB/AFh\nppv1GmYVg+iLL/pCTB0NDM4MoqOBqVNxpH1XTO6YgoyHHSTtQkaTJkJY09LypqelSXqTgKt1nJ56\nDAwMDE4Xpk/Pf4+ykZYm+QYGBmcD4iCuXA+RXE1yPoCBAJ5QStmKrp4ANpF8lmQqyQkAZiPX5atQ\nhETMSM4n+SLJGgBuBbAN4rNVwyGWAKACgNsgpoHp+r8THwL4HUBdAPfptAcd+RcDeBPAW5BJeAdi\n6uispxmAhyHaOntttMuVUuVD7AscWrilgKjuW7VqlWdLSkoqeHIMCke3bsDChf7zFi6UfCdq1AAm\nBLA6nTBB8gPB92HnbNv3YWe37VvGue9bZvRoYMwY/22H8jCNjsbE8oPQbWZTJJYbFJiUFfTwHj0a\naNfOf35amvTTtz+B6uvWTTR2W7bkz/N3jE4HNGHNQ6psMhUKcT1V9RgYGJweGFJiPiAZGJxFSEpK\nyvf+37fvcU5VB8BqkrscReZDghrW1vuNUMBSXkGBZMgbxPQwFUJy7HXK3BCSlg7gfofsVkjAkIYA\nhgD4ExLso7zOj9b5ByAarRRIBMZVjjo6QzRg8yDRFjN1++McMtMAHAXwbDB98RlPZZ3+CAAuW7aM\nBqcBXi/pcslvMOmJiaRS8htMuhOWRbrd8utsIznZf7rXm7+Mve/15k+PiyMbNcpNC9RuIcjcYHFB\nMTfj4eGCCDfTUwOUC1Sv3Zd69fL3J9h+TpuWm5+cTEZEsGX9+rly06YFPkaPPpo/zca998rmD16v\nlC0IlsX9N7o58h4Pj8T5Gbuz337Kctq04/+Pxrn5egsPDzUM/ticMRQ0h8HMk8FpQ8uWLYu6C+c3\nCrqvhXAfPecR6NlzFozfXAMGFzqWLVtGiNXeJwC+Zl7+UFLzh7v0fiqA53xkWmhOchGD4VjBCOUr\nJCaEozVBy4QsKB2lyVM2JCgHAFyrO/w3gD4Amuv8lY66ukPWJcsBcAPENPEQgDccMrMgIfH36v0l\nup5Wel9BzB//B+CzYPriMx5DzE4VALJKFf95VapIvvMFP9ALvw1fEqb3s8Yn8sABMiengL74Ptw0\n6WBycuC2AxC6A/O8+fNP9mFqWdwd42Y1WJw6lawGizuuL6B8Qe35krCCSJlvfTbxtH+TkzmrVKlc\nEpucHPgYFUS2y5QhS5cOnoj7ICeH7FnLQwJ8pqGn8PkoIP3lJlLPgJv91HM6ECxpJPPPx7Rp5KhR\neefdJm+WRbZtS44enbe8Td4sS/7bv75z7CTahvAVilmzZhV1F85/WBZZsybnveDl6tX0f59zXi/n\nKyyLh25y85FqHu664ewgZaS5BgwMgiRmdzIwMbtb85HiDIZjBSPkqHwUgMGQtcFuBfCdJkATdf63\nuoNNIaaBPwPwaiL1GsR0cjeAfyFmjHdBfM5esxkncjVoHoiJ5OO6jQE240Suz9lgiKnjJF3veACL\ng+mLz7hsLdxThpidJGzy5UvOHOlHvvUyo4yLSx9K4OGLXEwZ7uWSJeTixeTChWRKCjlpEnnrrWSp\nUuTYqxOZA8XU6+9nDhTH10xkVJRUV6EC2aEDOXSovMuOH08mJJAjR5LDh5Nj+1j8s5qbb7XzcMPl\nbs68P5mHL3Lxs6bS9uj/8/LJJ8n+/clnniFffJEc+bjFP69wc8KDHq6v6ubLt3n5A9x8pqGHf1Rx\nc+DDFnv3Jvv0IYd2tbj+cjcT23i4/nI3X+th8cUXycGD5d154kTy7bfJd94hJ08m332XnDqV/OAV\ni1Z1N5tUs1injpCQ228n619icdOVbr79vMU33pDxTJgg8/Huu+Ts0Rb/qeXmdwM9/KeWm5+NtfjB\nB+T775NTX7a4vnwcN18Sw51V63FPzUZMmW5x/nzS45H5/fVXcskS8rffyNRUcvWXFv+t6+bql5KY\nGeni+qleLl1KLn8hmdlhEVzSYiCPlnRx8Sgv16whDxzwc8x9iYVzv6C8QvDtOxZ/gJuvNffwB7j5\n03tWfqEgyPEWr8Uf4Wb3GlLPmrl+6jnVCFUT4Ku5rVWLDA/P+xEhMpKsXTuvdtSfxtdBsPPMtZ1f\nENH2RSgE0xf+iKFdny8xfPRR6de0afnb9CWeF8JL+gWGzTO93AMXH0QSc85SzdGZwFvt5APSkNvO\n0AckAwODQuEgZpMALGde/mBzlrp6P8WpWGKu1d9eBsu1ghXUla/QnaPuyL+QEPRv6PwuOj1Hy2wF\nUAviu/WqlvkUYmJITbSWQAKIOBnnDk3GqH8nORkncjVcWVrmIETbNRLAomD74jO2XyCauXOamB06\nRB47dmJl9+whN2wgly4lf/qJnDuX/PhjcsYM8vPPyY0bySNH8pbZto2cN0/enfbsITMzyWOVqzAH\n4LEKVbh0KXngYtn/t2QVxsXJ+2ZvJJAAeyOBAPNt4eFCzAYOJFu3JudH3k8CnFvyfjZvLqRr1izy\n2WfJm24iK1WSd80SJURJ43KRl14qfLBtJXnYdbjMwyuuIIdXlLaHV0zgDTeQ119PXnstec015BVX\nkNWqke2rSJlHqnnYsCHZMkr2/3u1hzfcQNapI+/INWuSHS+XvIev8PDqq6V8lSqiMAoPJ8PC8o+v\nS9g03lDWYvPmlK/EJLdvJ1u2JOtdbPGxUtMYGUmWLEkWK5a3bDykvXh48qQXK0Z2r+E5nuCbH2iz\n63sQSfwBYlb5A9wchIEkwD5heY+RUtJWVBRZrpzMc6tyXu5VLg4ul8B9YS62v9zLevXIm28me9bx\ncn+4i29US+CBcBd71/OyRQvynnvIO+6Q4xwXRzZuTMbHk02bkrdVF1L2SLzF7GzykXghV61jLT74\nINmlC/n44+TTT5NDuljcoMnxhivcHNHT4oABktfnPosLL3IzxmVx927y9qss/nyRm5MGWJwyhfzw\nQ/Krr+RjwLJl5Nq15Pr15NatsqWlkbt3k+npZEaGnN9BI0SN6m9venmslIvreyUwo1QUs2vWyqsB\nrV07l6xZFhkTIwehIDNcm4QFo/0MZgyFpTsRSCPt7LcNpzbbWXcgU+OTIYw2gqnDlnHKOrWXdrqt\npfRnvuvUUsbHyxckf2OwLPma42zTHwoyfR0wQDSqvuNzaknt88lh6ltgm6dirgvB0KHkg0giAS5+\nKkkSR42SG4O/tk90fuw5sMd07bX5TeLtuhMTJf9MwbK4tIw2ay/mZvZG68y1fbYj1HPwDJyzBhcO\nHMTsCThcsZhr9bcXQDG9/zocVoHMtfqb50wraAuVmA3V5ChDdy7bQbAyAHyh91tAFolepLVUaRBT\nxjBNug5AnOjuArATEugjB6JFi9b1/Q+iMbMnYhRyTRk76HbGIldjtgdAEoDPtMznBfXFz9gehITT\nZ3x8PFu2bJlnOxfU+R9+SF50EXnJJeS4cfIy6YucHCFfn31GvvYa2bmzPPvKlSv8BR4QkhEZSZYt\nK1sguY0QMpYBxRyAFqqwRg2yTRvys/5eZka6ePi1BOa4XNw+28sVK4SgrF0rmpx9+xydts0Z77+/\ncN8yX9gvcx5P3hfThITAL6i+ZWwNhL3v+zIVKM/P3Gdnk1lZhZhgBkB2NpmeajEr3s0jX3uYFe/m\n0XUWjx4VMp71pyUHMyaG2TH1eLReI25daDEtTcjG77+Ty5eTq1aJ1szjIVfMsXjsZje3zfLwwI1u\n/jlMXo52DR7P7LIu5oyVY/R3spcLFpAzZ4oGcMIEeW967TVy2DByyBBy7p1CeOfclsC+fcnHHpPz\n6+GHyZkNJe/9GxPYtq0cyvvuk/Ph4YdF7pFHyI4dyd4tLaZWdTN5pIyNlPG9P9Ti6gputo+z2KAB\necMN5NVXy7tTh8tyyfeVV5LR0WTTaIu/Rrn5QgfrOPndtIns1MSiJ0xMSIM5551bREQuIa1QQQj4\nFVeQ1atLP2rXln7Vry8fDP5T3+Iyl5t9Yz1cfrGbXdwWO3aUd+c2bch27YSM33ST1O/8YHFbdYtW\n5Tj+XVk0oNurN+J3PZKZXtrFFV2FvO2tHsOlozzcHeNmynSLX38tH0q++or8forFnXXcTO09ntnh\nEfy7+0BmRbmYsyBIUuZ7jp+IFsOfxjQqSshZIBJpk55giOeJEMbCZH1NhH39TG3tZWxsXjPgmBj5\nKuQ03/VHkG0TY2edluU/PZg5daY759YfwU1OljZswuNvfIHmySaUgebJftk9gZfie6+Xa3tYnSTu\nVS6+e2cSs27S8xFsu8HMjy/JHzIk7zMlULoTwRJjf2O3ibEfUp5xYyP2w2g+08ZiP4zm/huDOI8D\nzbVTA+2LM23GfCpIUqjX+6m4PxhckJg1a1a+9//4+HibmNWHuFV9jbxWf68wl0tEQ9yxRiCv1V8z\nW6awLVRiVlprnZxbJoCFkLXD0vX+/Vq+hkNr1UCTpCzkDf7RA7K22F6ISeEITdacfmhJkAiQ8/T+\nLwD+gQ7+AfEx2wpZW+0ZiI9ZQX1pGGB8r+Ec1ZgdOCAvi/fcQ/73v0KgrrmGfOEFMdN78EF5xjkJ\nWFQU2aCBvAy/8ooQu59+EjO3DRtEY7BnD3n4sPz/5hsxxxszRkwFX3+dnD1bXnZXrZLyU6fKy/vs\n2WQmFAkwU6lcIhKqaVsAH7OgyJnvTfgkfMzyvWj5vvj4K3uqUVB7zhc7f/vB1GePddCgwufJF7aM\nP8JbUJ4/hPogD0SOC6kne+o07t8vWt8//hAzT683V1v8+edyzn/8MTl9Ovnee0JIR4+Wc/+VV8Rk\n9aWXyOefFw3dU0+RvXoJKX30USGcw+4Q0vhyUw/vvls0hLffTjZrRt52mxCzhx4i5w/0Mrusi1ue\nSWBmpIsvxHuPE05bA6pUXvIWSHvqqw0dh17Hy0REyAec0qXl40r58nJfiI6W7brrhHM0aCCE8eab\nydaxFv8XKeagKy9xs8ddFtu2lXtHly5k9+7kE0/I+J95Ru47gwYJaZ/xmJdHS7roaZ3AY6VcnPO0\nlzOHW9x2nZvfvODh9lpuzp1gcc4c8ucRYua8/okEZpaO4oFrY7jubQ8PNHBz/bcWU1PlfrNlC7lz\nqcWMxm7uX2nx0CHyyFqL2U3czNxgBf/hI5hr2Je8eL0yQaVLy69NfGxSVJiW0peENWrEY7Vjueva\nRuLLGsw9pKD7qO99wSZiui3GxuYlgIURQd8++977TpI0b/pRtOOfjbW4Ywc55Q75ODSsThIPrwmh\n3WDnx7c/NgkbMqRwUhaoLjvd96ODb1v+5lwfo3+vjeMt8PJIIzdrlbKY+HQB4ytkTvM962zce6+Y\ncgTyF7YJWyhaRyfscqNGCUF1Hqfk5FxiOno02bBh7vVTUF98xpqx3uLBg46xt20b+ANrTEwuUbYs\nMXEJNK5gSaLBBQeHxiwWwOWQdcoOaVI2AkAY83KJJgCWQQISbgDwMP1wjkBbSMTMp+EwAO20dus9\n5EZCnAzAQq5v1zEAG3WZIQCW+zDOR/SAJ2mZFABTfBjn+1qmGXL9wUboQT8C0ZqlajJ2KSRaZIF9\nCTCm2HOVmL3/vhzNtDTZX7WKfOAB8rLLhKDddpu8JA4ZQn79NfnPPyemtQkatk+ZEnLGKlWC+5Lp\nxAUQlTFoFPSyc8cxn9MAACAASURBVLJRGZ37iYnyQE9MLJigOnGafMyCwpkmx6EiEGn0RSDNUq1a\nZEwMc+rVY85NjZiZlMzssi4eejWB2ZFRPFY7hjuSJWrltp8tbtkiRPPvv4W4pN/i5o6BojHb8t+B\nTC/t4id9vRw/nhw7Vj6wvPqqEM0BA2Tr25fs0YPs1k0+8nTuTHbqRI68R0je83EeNm8u5DI+Xk6x\nG28UTWGtWnK/iY6We0+FCuTFF5PPFM9vuhyIVIZCPKvBymN+69SC2ia3tnlzVJT0pXx5MX2+7DLR\ndt5ymcWfS7jZrrKHi0q4GX+FxWrVyCuvJK+6SjSht19l8ZfSbj5zRRL3h7s4oHoS15WK5YGwSCZc\nmcADES72ivHyoVssLr/YzbFXjWemiuDMqwfyYDEXh97pZadOoh1u35584h6Lf5SL4/oyMfwjohb3\nIZIPIokpEUJ6n31WjkliIvnmm2IBMXasvM+OGCGm3O884uWh4i5Oq5fAQ8VdnNjBy2HDJG/CMxbT\nqrs5q4eHW6vFcWu1Rkx+wsNt0XHcFt2I0+8WzVSfSkncdKWbn4yxOHu2aFs9HtGor14t5usbN2oy\n7LV4sG4c910Vw0M3xHHbzxZ3/Wox41Y3D64W7faRI+TBg+T+lRbTG7v59yI5J/9ZLJr5HUssbt4s\nlhGLFpEzh1v8pZSbcZUtHj6ce738PjCJe+Bi6wpeDu1qcesVcdxZNYb/XhNHzzSLyz+VQBk7lwqZ\nW7FCLALWr5cPi199RX7+jJdHSrg4984EHi3h4rJxElzkt9+k7TlzpP206m5+X6cPcwBuuf5O5kDx\nf10SOXEi+fLLYmY5a5bMydat2pw5WGLsvAcEeq4MGMDMBnF8upGXi0uKXNu2ch2lp1qFk4VA9ft+\nEPB6gw/IFIrW0XlPC+QLaxPFxMTc51Xt2iIb7PsA5bxaVNLN+8t5ePRmP+bOvvVERfFwzRiO/T8P\nDzYs4COE71hOVhNpB3DyV0fx4nLD9FdHly5ywzpXcZ6akDqJGU+QM4WyhUrGBgBYrTtIiHpuHYA3\nALTXRCkSspiz7duVDuAdXX6SJmQNNdO0zSAJoIWWSQXwHMT08bDOy9T1XYRc/7KbIOuhZTra2aDr\nKLQvAcZ3zhKz1q3ly/ZZAd8AIPZ+iRKFf4Vzwp/9v43C7P99bxDOL4C+N4hAXwCd+75lRo3KGxnP\nidNxAyrohuf8OumvL7bfSqD6nA8l54PHH7n1PUYFPRRPMipjoQjxy/wZR7CkMdDXfGcAEMsqGh8z\n37EEYbKbDw6NaY7LxcyfvMzZZDGnqZvp33qYGe/mvhUWd+4kd37qZVaUiztfSmBWGXmpWj/Zw/31\n3fx1tkWPh/zuO/m49MUX5CefkD+8LOTt2xc9nD5dtPaTJ+ea3Nok1NZ0Dh8uL9uDBom288UXyXce\nkjreaufhs89K2oAB4sPav7+Q1XGtReajm4U4jrjbwxnaRHd6/QS2ayfmqS83Fbn/Z+/a42yq+vez\nZsbdjJFLihiRa8qli4mGg9wyipSXyi0qRdJNlET1dtH7GhoKNSEZv1HpRilyxlGi3N9CLntcEhHG\ndczlPL8/vnvP2XPmnJlzxjCD9Xw++3POXuu71vqufTlnP/t7WYvqipUyvl4cW7eW3+fbb5cYyg4d\nyGdudmYzzHUDpJ8Z9zvZvr24xkZGyjNcqVISa1q2rDzHWm6011xDvlld2k2sEceoKIn3rFxZ3Nm7\nhUv/Xcs52amMfO9YyskOJeX7nBZx2fWBuvJaRHktmvokw4GSZmvrj1m87xaDGzfmvj/2Jrq4r0ID\nxtQ0sucSyLjWFhJCvhAuc3ympO9Y5pAQsms56fvHsNtJgJ+gBwG51a6+Wo61d5tKlcgu4RJX+0J4\nHI+pSN53tYsNGsht26q6wRVhDnYt7+SPpR3s2shgdLRYoZs2JTvWM7iqrIPDqghBtuJ7v5gsc1+/\nXl4qVKsm103HjmTXruL+fc898nN///3y0mTwYHJMX4PbqkvCqp1RDk57zuCMGRI2kFY2kmv7xfFs\nOSGnm6a5shM9bd4siVcyIyL592cuHjpEpqaSZ86QmU4X3ZGRTFvqYnp6Hr9T3r87zZvLhWq67bob\nNmRWeAQPjotnRrkInqrdiGdbtKR7lxHUi7uMDPH8sa7Bgdc6uWMHfbcz97d/6MqOD+9ewclNm/zo\n7M9KHqgl0pdnja+XooYhNykgb87tGDhQygcO9JTFxOQey65LTIzvurzaDR0q1kpfONdnl+L+n1xA\nFHdithhAfwB3QGKytpvE6kYbGXoXEsfVBhLbdQLAHuYkZpshC641ARBrTvhjeoiZlTL/LdNiNs0i\nbzZi9oJpAbMsZhtMklY5EF38zK85cPHFmGVlyR/F2LFFrQkDysqoUcxQ2Jn3LJzrOmb5oTi/nQvm\nD8r7GNr/1C33H39von29wbbeChdGVkZfOgfzJ+vPEniuMWbeuhWEMAbThyWTmCg6JiZ6HkDtLrqW\n3JQp8gA3dqzvY22d46ZN5Uk+PFz6DGYOebkI2+dkXUv277Z5uB0Opm01eOSIWIT++IPcuFGsSkuX\nyvb99+SKOQaPtXBwf6KTJ+o1IwG6XnXyk0+kuzlzyI8+EuvS//2fWKR+flMein9+08lFi8RFeMkS\nyb67caMkq8qhrz+PgJYt6V7uZOaNMu7OBCddLvKrryRe+uefyR9/9Fj79u0jM5bnfCGQMtfFVavI\nX34Ra+CBA2ZcrsMhKXYBprcXi9nJifHMyvKocfiwkKVFi4T0v/66bEvuFOL31R1xfO45IfAjRgix\nnzvEmU22hw71uPw+9pjITL1P6r/tIn38Nd+ZY+qrV8vLgX795Bn+7rvl59SyVrdpQ7ZqJe7GzZuT\nA2pLf72qOHnFFWIxDgnxnWirFSQL5nDE8Qgi2Qoun8TVW85RwsXSpXO+KLi+vMTsdijp5A/KwTqh\nBtuVlHYvYywzEMqtqMO1aMbNaETLAh4SIu/tLII7vpIkjhrcwMVWreQFxh13iLfPjTfKM04tGDzQ\n2MGdCU7+WErI+Q03yIuOsQ6xIH/RXjIuj2vvYoPSklBl71wnV5d3sGEZg4MHk8//S+KPn7nZyZQ6\nEp+7aZPEt+/eLddG6kaDmW1sSVjyskTmdY/7Ci/o1SsnCfNFykj/RNBfeSDtQkPFpfN8kafi7sWS\nD/KJMSt+xCxXYyFBhKwddtEuMG2rvygtZps2yZlctqyoNWHe5MsiZxoalzrOhTT6coMpqnXMzuUN\nqL837IWRldGXDgV5AAjm7bk9PqiQY8xyxX3lN4dAXekMo/BizLz79OU+7atNIKTZ3/1ijfX224GP\nm9/x8dYv2Bgz7zHyI8Z53T92on8uD68+xsvMJLOSxep15s04ZkZEcm+ii//7n5DulKeEsO0YHsel\nS4V0LlwopPqjj2R5lg8/JFffL3LJ98RxyhRmb3FxEm8+cSKZ9LiQwoVPOjltmlioV/SSdpvbDstm\neqfqiwX87+sdnPuqwbg4sWIv7iyyn8TEcfBgcZ3u00cs0L17i5Fn0ggjR0KUE5sN/tXQwdF9DPbq\nJWT1LdOCPL5SHO+6UZaeSd0o8if/Z3B7TQc7NzB4442e2N9OZfxbjC2rb7tQJ52hkt23enXy3qtc\nPBYSyTerxzE1NJKPNHaxa1exavboIUv49O1LPnm3wR1Vo7mnSlPurdKMxtUtGfekwQkTyHUtBtIN\n8MgVtekGuK31QCYmkp99Judi+XIh5ykTk+gODeOR6Uk8fpzMTMyHlFnwJmf+fmPt108hkaf0Pwzu\nruvgxG5Onrq1AP36cwUF5HfXlxdQePh5e74s1hazXI2Buqayn+EiXmDaNs5FSczeeUfcHk6dKmpN\nNDQ0LikU13XMCsNlJpA+vEmZpfvlmJXRu09vi0Bex/ZcSXOg4+Z3fAojK6OvMc4lxiwYgpzfcbLv\n52XZyYtU+ppnMFmM7dfb2LFioalVS1zbmzXzf20GMkZe15m9n0CTsDiddDscNJYbXLVKprBkibhJ\nJyUJQf36WSFw//eYk//+t7hAjxpFftpGSODHt8Sxf3+ye3dxNe3SRax9Dod4FNqXsOlb3clKlcRF\ntVIlcgdqkwD/QO083XLvQRLTEcbJGMZ0hPFfYUmMiJA+atYUo7sVtteoEVm/vrwHv7+ktJsVPowZ\nCONrTZPYr59YbCeNMGhc6+D8oU7uuU6I8kcfiXtsbKwkcPvqK/K77zzroG7cKBb17dvJHTsk9nTX\nLonxXLdOCH9Cgvw0OkJl3p3LOJmYGGROA3/3eLlyzPYntpdbpCw8PIhBAkexJmYAXgPQGkAtANeb\n1i8CaGfWX5QLTNvmd1ESs169xKVBQ0ND47KAXsfMd935XMfM18OxpXMgJCxYchbsuBbO9zpmgRJj\n7z7zImGBEGRf8HdM84qF8o79DYTI+pPzRQq9YsxYt66QMyvxh921z5LNT5f87tUxY3K2Gz06t1Xe\nPq8GDQJ7aeCLdNr1zI/YWgSjadPcll7LfbG2WMzS+g/k8ePiNrtvn5Afu0vxzjvF8vi/9sMYHy8/\nI6+9Jm6zI0ZIJuAnnpDMuE8/LQRy4kTy51uk3fcNh7F7d4lZbNRIkh91ryDk6Y6STp/rrRZkU0qW\niTnWwsGTi5z8X1VxOb36anFN7dtXkkoNGyYZfF96SdyC4+LI6dPFJXrBAnLZBwaPNYpmauOW/G2R\nwR1LDaY1j2ZWSAjdADMtEnaeSRlZ/InZ+6bFKQuehBpv2uofhKTDPw3PAtBO09plLTA91yRmVkKP\nNEhWR/sC03tMwmaNcxjAB8i9wPRR8zMLwB8AFsCzwHS+uviY30VHzNxuCfZ+4YWi1kRDQ0ND45JF\noGS4sGM/i1ss6flYx8yqz4+UeyPY7IEul5Ay75cHgSbhyMsyaNV7x8JOnOjbYpyUJLJjxuStS34I\nlFiSwb00KIgl0rvPc40xs2AR7WHDAnNjDKSdD9J5+rSsf3vmDPnPP5LdNyVFYu82bZJYTqdT3CyX\nLfPEoP78M7lmjcic2JzzuLl3GfynqYNvPGrw7rslNvKWW8gmTYSzV68uCY3KlMlN8mrB4I+I5lo0\n5Vo0449oyVow+DfC6QaYAdAN8DDCWbu2EM6bbhIe3KIF2bq1kMHYWEkc06+fuMWOGSPGXIsQzpgh\n3sSLFomF8Icf5HRu2CCWwc8/L8bEjEJeOgNYA1lrLNud0KxzmCToCCSpx/UAPjdJ2FOmzHiI6+I6\nyNpntwHYZU76BlNmJcSdcTaAhpBEI2cBnDLrS5hEKxPAU6Zlbbypz9JAdfExt4su+cf//idn8fvv\ni1oTDQ0NDQ0NjWKLQKyJgcoFuo6ZdzvL2hkTE5guhTUnMnCSXxBL5PnIyuhrzPwSfwTSzh/pDNaN\n1hvnaC13u4UUHjkiy77s2EHuTHBmM7XVbzm5cKEkGMowyzIATpgg70RGjJBlXoYOlc8HH5TD3K2b\nJIhp1UoSyURFkTVqiCtobkI4j0Cs11bMk38AiIfEc11rEh87MYswlU+wlTUzy0ab+0PMfYdNJs4s\nq2HuLzFJV5hN5jcAJ2z7hwHssu0rk7z9FKguPuZ20VnMdHyZhoaGhoaGhkYhobisY3axZWUsbOu2\nP1dQy33R2s7RjdHtlmUi/vxTsnLu2CFrLa5eLZbBd9+9sBazMAQBpdQ0SCr67pA1xgCgglKqNMk0\nAJXMso5KqbaQ9PRTIBayqmZdlrk9p5T6B+KW2MckeS0gmRNPmLKvKaUSALSHJO8IUUpVIJlqETml\nVD+IBW+k2W+42bZyALpc9Fi2DLj1VqBs2aLWRENDQ0NDQ0PjIkf//r7LZ87036Z1a9nyag8AZ8/6\nr0tIkM1CfDwwbx5w77055az9+Pjcdfm1W74cWLsWiIrKWRcVJWMnJ+euCxR5zTsqKrh+U1KAvn2F\nei1cKGV9+wJ16gBuNxAeDhw/DkREACdOyOfx4wVSWylpHhHhuz4yskDdFhghQco/CrFEOSGxZgqS\npv4+s74ahGB9C+ATm5zTrAOAKwEYEBL1E4A5Zh+HbTLhAL4G0AGyPtlIAC/axoCpxxwAEwCshyQT\nmQwPIbvSpsvXkIyNLc1xGwU572KJU6eAJUuAbt2KWhONSw2JiYlFrYKGRpFD3wcalzv0PVCESE72\nTbwAKU9ODr7dtGnA6tW+66Ki8iZXFwp2UpaY6CF1mzYJKQsJke+AkLHwcA85uwQQlMWMZA4ip5Ry\nQ9YJ+9JL9AWSg21ySRALl4VMkjnohFJqoJfMXyTvttU3gmRvtMt87zXOY171gFjTHoCshbYGwCIA\nbZVSlUke9jXPkSNHokKFCjnK+vTpgz59+vgSLzJ8+ilw5gzQq1dRa6JxqSExMbHYXe8aGhca+j7Q\nuNyh7wGNC47kZKBnT3m4tVvZTp0CypUDxo/PadmzW87OEYmJibleRqSmpp5zv8EgKGIWAA5ArGhX\nQrIqWqgKsWpZMjlcCZVSoQAqmnWWzJVefVeFkK6D+cjY6xWAYQCmk5xjjrXXlBsE4C1fk5g0aRKa\nN2+exzSLHpmZwFtvAZ06iWVXQ0NDQ0NDQ0ND46KGP6sdve0uNhTQjdEbvoww69atQ4sWLQql/0AQ\nrCtjniBpQAhRe6tMKRUB4FaI2yIArAIQqZRqZmvaHkKi1thkYkzCZqEjgG1mfJkl0x45cYdZbtel\nMYBlXrr8CiC6wBMtYmRkAMOGAVu3Av/+d1Fro6GhoaGhoaGhoaFxrgjaYqaUKgegLoRIAcC1Sqkb\nARwhuReSYfFFpdQOACkAXoEk9PgCAEhuVUotATBTKTUUsi7ZOwASSVoWs3kAXgKQoJR6E0ATAE8A\nGGFTZTKAZKXUUxD3xD6Q5CFDbDIfQGLTrlNKNbHp8itkoeyLBhs2ALt3Axs3AvPnA9u3A++9BxRz\nw56GhoaGhoaGhoaGRgAoiCvjTQCWQ9wKCeA/ZvlsAINIvqWUKgtgOoBIAC4AXUim2/roC0m7vxSS\noOMT2EgXyeNKqU6mzK+QxCAvk/zAJrNKKdUHwGvmth3AXSR/t40zDULMnoeQMheALgAeRu5YNAAo\nDQBbtmwJ8pCcf3TqBBw+DJQvL1kYR48GGjcG1q0ras00LkWkpqZinb64NC5z6PtA43KHvgc0LnfY\nOEHpCzFeQYjZdgAfQwhOWXN/IEn7nRvi57sFBY/Fzde+vUxBSJR3vdW3RbDoY6zDEOIXYpMHcsai\n2REFAA888ICPquKBkyclRf6yZUWticaljgvpU62hUVyh7wONyx36HtDQACAc4af8hM4Vwa5jFgng\nR0jMVicI8bkOwFGbzChIwo3+kLT4rwJYopRqaLOazYMk7mgPcWWcBbGwPWD2EQ5ZZPo7AI9AXBk/\nVEodJfm+KRNt9jMK4srYF8DnSqlmNqvZUxDC9iOAMZYu5phTfExxCYD7IS6YacEcGw0NDQ0NDQ0N\nDQ2NSwqlIaRsyYUYTDGvLCfewkq9ASCaZJs8ZPYDmEhykrkfAbFO9SeZpJRqCOA3AC1IrjdlOkHI\nVQ2SB8zYs1cAVCOZacq8DnFVbGTuzwdQlmR329irAKwn+ZhNl+8h66w9Yo67GsAZANeSPBTw5DU0\nNDQ0NDQ0NDQ0NM4Tgs3KGAvgV6VUklLqoFJqnVLKvo5YbcgC0NmOdiSPQ8iQlQWxJYCjFikzsRRi\n2brVJrPCImUmlgCor5SyFhiLNtvBSyba1OVaU5f/AHgashD1SgCnAHypSZmGhoaGhoaGhoaGRnFB\nsDFm9QA0Mr8TQBUAM5RSaSTnArjGrFuulCoJIUqPQSxm1cy6+gBKKqVOATgBYA4kOccRm0xDALWV\nUmkA9kCSe1ip9KsBSAVwNST745sANgIY7jVODUsXiOuipcs78ENIlVKVIC6aKdCujBoaGhoaGhoa\nGhqXM7JdGUn+c74HC5aYKQCnIQpayTgmABgKYC6AJ83yhwDsBjAVwKcA/gJApVQIgAGmTEsIufoI\nQLpZRqVUFIDmADYD+BeADgDeB/CoTaa3qfsCCNEaCSFer8OTDCRPXfzMrxMksYmGhoaGhoaGhoaG\nhgYgOSjmne9BgiVmJwBk2d0AlVIbANxpxpLdCSE9u0huUkoNBLAFwHoAKyDEpzKA4yQ3A9islBoL\n4A0A5SELQg8FcByAQXIbgG1KqdaQ9ckIsYqNNHXZZq6L9qg5dkcABwPUxRdSAGDu3Llo2LBhkIdG\nQyMIfPUV0KIFcPXVuev27wfWrgViYy+8XiZGjhyJSZMmFdn4GhrFAfo+0Ljcoe8BjcsdW7ZssbK1\np1yI8YIlZnsBNFJK/Qlx9VsFSaSxG7K4cxiEOLUHsInkNqXUXkhWxTcgVrJtABqY2RPXQyxd70LS\n2q+BxIOtAxCjlAolmWWT2Qax2LUwx24PYApJKqWWQmLg/g+y1lp+uvhCdwBo2LAhmuuVmzXOJ664\nAhg0CEhIAKKiPOUpKcAzz+Quv8CoUKGCvgc0Lnvo+0Djcoe+BzQ0spGmlLoGwHsA2sIWjkXSbQkp\npdpC8ls0hhmORXJ2oIMEm/xjBsQKtQDAeAA3Q1wFZ0Jiu9IBTILEfsUqpZoACAdwEsAXpsweCNGa\nqZS6GUBtiMuhk+QBU2aF2VeCUqoRJC6tNIDJEItbKGRB6y5KqaeUUvUB1AVQEbIo9ZUB6JIDpnvk\nyCCPh4ZGwRAVJeRr0CAgJQWZmRBS5ousXW6YPVuOhS+kpEj9hexHQ0NDQ0ND43KHArAYYvhpCVkW\nbAAkpEsEJBzra0gSxBshvOV9pdQdgQ4SFDEjGQ/gLgDtIIyxoqloX5vYZAA7AXwOYBOEDH1hW8MM\nAJ4FcBXEQmZlcLSvK3YWwAsAekJS3D8LIYQf2mT+ByFnbwDYCsnomGJbwyxQXSyMhMSgaWhcGJjk\nbH/nQWhfIhl/x2pSBgBo0yabsOaARVzb+F2t4/z0o6GhcX6gX57oY6ChcfEgGkADAPeT3ExyCYCx\nAB5XSlkeiEMhIVTPkdxGciqATxCE4SdYixlILiZ5A4A2EOvTaQCRkPiwkpAkG1Uh5K05gCwAMWbz\nAxBr1nwIsboBwjYBoJtN5jpIUo93IQdhHoQAtoEsap0F4B4ADwIYDMniuAtADaVU5QB1yYZSqgTE\nPXINID7V3bt3z7ElJiYGe6g0vDFkCLBype+6lSul3o769YGpU33LT50q9YU5tvcfpH3f+w+ysP4w\no6LweslxSEZbvKLGFYyUFeSP3d7G/n3IEGDBAmDv3tztfZ2jYM9pILBZE7N2puDAARTMmuhlldy/\nH6BRgH40NDTOD/TLE30MNDSKERITE3M9/48cmc2pmgDYTPKwrckSABUgbouAWNL8LuUVEEgGvUES\ndWwD0BVABsTqFQGxdGUA6GHK1YPEjrkB3AKgM4BMU6ayKfMwZG2xoxDz4BsA/obEhVnjzQOwH8Bi\nc/9nSHbFyea+gsS/HQPwXCC6eM3nKrO8HwCuXbuWGgUEQNas6buualWpd7lylrtcZGRk7vL4eFIp\n+QykPC/4G8NebhikwyGfpGff5fJdbu2fAw78bHAZHHyqhZPL4OBeVwH69KdPXnra6+zfk5LIsDDO\ne+KJnOWBHL9AyoOc164oB2Pg5L56PuYxa5b/c2AYUm9+/7OB9LPnusI5b4WKwYP9HyeXS+o1igTz\n5s0rahUufZi/MxnbjRz7xe4+PZ8w55y10+Dnn5OpG41icwz0PaBxuWPt2rWEeO19CuAb5uQPZUz+\n0Mnc3wZglJdMF4hhqBQD4ViBCNk6nwixOH1ikqXvIbFc08z6L0zlu0IsUD8CcEEymYyAWOgOQNYh\nuwGSpfEgxI3RDfHHjDIn8Asktuwxc4y3IAtTA0Afc5xJEIvadAD/AEgEsDAQXbzmpYlZYaFmTd/k\nzCqvWjXHA/vZZb4f4N1ucsUKcuk98XRD8eREIWFn42R/6T3xHDWKnDlT/rvcbv8qud1kerqM5Y6M\n5KklLqalkae/czGrgmf/7FnSvcug2+Fg5g4jWyYzIpLT+rq4aRN5bIPBjNsdPLHZ4MmT5KlT5OnT\n8nnqlIyTly52ZO00uLOWg3VCDe7ZQzYqa/D3q+TPOWgYove+lQYPH2ZgDzfe5KxlSzI6WshZeDjZ\nvHnepMyCd31hkDKSR46QXco6SYDdKzh5/Hge+udRnplJ9q4m/fSs5GRa2jmpVfjwPl6zZpETJ8p5\nsMot8mYYZO/e5Ntv52xvkTfDkO/Wp/c5sAhroIQvUPKroXEOyHhjIn8pEc13/+XMfU9fLteZYXC/\n+QJpZ1TxIGUaGhoBE7OO9E/Mupq8piQD4VqBCNk6/8W0eNFU5BAkBf1/zfqBNqsUAeyDLEi9GsDr\npsxnpjWLpqKrAZTzYpwHTTJG83O6nXHaiJSlywmTVL0JYFWgutjmVQJiXXtSE7NCgDc5M/fTrqnJ\nH34gZ/Z38XhYJF+tGscjiORD9V3s3p28806yc2fyjjvIa66RLpQiH0U8s6D4RVgPZkHxUcSzVCmy\ndm0yNFTkSpYkK1QQ3le5MhkRQZYpQ4aFSb21tYKLRxDJ4ZCxW8GVox4ga0GsWDEQK1YruHLs14KR\nq433VqIEWbEiWb26zKVmTTIqSnS+9lrylqoGnSHS16hRcphmzpSxlysHry9v8IorZD5XXy3tr72W\nrFePbNiQbNxYPhs0IOvXl/IWlTx6ryzp4L03G7z9dvL228kOHeT43n03GRtL3nMP2a8f+Ugng79E\nOPhkMye3VIzm1itacvRtTm4t15ypKpwvhMfxqIrkYze42LcvOWoU+e9/k2++Sb7zDvnuu+SMGeTX\nz7uYVjaSvzwYx7PlIul81cXFi8nly8nkZHLpUnLZMvm+ahW5di25fj25erWULVtGOp3CF378kfz0\nU3JAW4PLQxzc8p6Ty0McHNTO4PLl5Pbt5J9/CnFL22owI8bBs9sMnj5Npv8hBNW9y+DZs2RKCjn1\nWTku346RUhzSEAAAIABJREFU8zfxcYNZWUVza/iFt+W2USO5uJOSPPXh4XLimzUTEu1Nmr0tvHZi\nR3rqvcvzQkGssRaCsQQGazUsDMIYSB+WjF3WTpLt9STZrZtsec3DV5/e454vMlJMifbiaQbXoikJ\n8PCnzpw6FRPL0YXAS23kBdKjDZ35C19OKKbXrcblARsxmw5gHXPyhyiTZ9xg7idbnMgmM8AyLAWy\nKbNRQFBK9QMQB+ABAH+Yg40BMIfkAKXU95D09A7IWmRTbWRqKYAXTTLnhsR9WQtMJ0BcEDub/e6C\nZGZ8BLLAdByAlyGZT8qYpOs9SGbI+ZCgunshi0O3IHlbfrqQHOM1t5/NcfvExMSgQoUKOebep08f\n9OnTJ+BjVRQ4fhyIiwMiIyW0p0yZvOVJ4K+/gG3bZNuxAzh8GDh6FDh1CjhzBjh9Gjh7FihfHmjS\nBKhRA6hUCQgNlT5+/x3YsAEIDwcaN5bPs2eBke/UQpVTe5CJEITBjV2oibrYDUDav15tMob89iQW\ntI7DV7VH4OhR6dParr4a6NJF3Ot//x2o/EhP1Px1IXY17YG/4j9DixZA6dLAkSPAjz8Cu3cDaWmy\nhYYCJUp4tpIl5RMQ3ZqvnIybPnoSvz4Yh5TuI5CVBaSnA263fCoFVN+RjC5vtsXSsU6cubkNGh9O\nxrWD2mLFBCf+btgGbjdybIC0y8jwbCdOyDEkPXLW91u3zsY/17dBg85RaNVK2gLAzz8Dvy9OwVV/\nJGNz8/7IzITPze2WNvatXDmgY6lktHqhLWbe70Qy2iAkxDMvawsLE73OnAHKlgUcIckYvaQtRt3q\nRFYW8PavbfHaHU40SNuAe1xPYlHHOCRWGYG9eyX07Phx6fP0adElK0t0H47JmIIn8QTi8A5GnNO1\nXAspmFtyEM7EJ+COIVFY+n4KSg0dhAczE7AbUblkEzAI4zEO4zAeg+CRseq+vTcBbyVFYfLIFDSJ\nG4QnwxNwolIUypeXa9b6LFNGjk/ZstJ3ZqaUlysHhITItRQRITLBbiEhQKlScn9mZMi1EBIi99rf\nfwOLx6zES7/G4uPrXkb/nS8ho1oNVKgRgZD5Znxrt27A1q1AYiJw881Ajx7Arl3AokVyY9pj56z4\nlKFDgYcfBmbMAN5917P/1VdA69aBnQzv+L5A4/1WrpS1+LzH8lUejKwvnfIrD2RevsoB+T5hAvDS\nS1K2bx/QtStw3XXA5Mk5y7t0kRP77be+5zF0qLR96aWcfUZFeWIyZ87MWe6NIUOA/v19n78xY+Sa\nmD9fYkPbtJE+Zs8G6tQBVq+W62XCBGDnTuknJQX49FMp9zWm1U9ysqc/+7GyypOTpT/7uL6OuSVn\nw8geKXhgcV+EZZ1BmcgyqPjNPFRJ/gT47DOgZ0+gV6/8xw3k+KxcKfq1bi1tO3UCnngCePzx3H2f\nPAlMmSJ/jgU5/r7m/tprwAsv+DyW7hUrsd0xBJMixuGJY+Nx9fpvENnUxzG8HBHs/V6Aa1BDA5AY\nM++cEqmpqVixYgUADIPwkatoxpkppR6GGIWqksxQSr0BoAvJG632Sql5ACJJdg1IiUAZnEng7oKQ\nm3SIhSkDHutZurm5AUSY8vXN/f0QV0bL6rXR1ucjENdGN8S98U1IUpH/2mQSAWyEx5VxtdlPd3Nf\nQSxivwJYCIkxSzdlfOriY273QdZmu2gtZt27i6UmNFSsNHPninve6dPkH3+I1WLaNLJ/f7JFC7J8\neY+FJzSUrFuXvO02saz07k0OGEA+9hg5cqR8v+kmseCULu0Zp0EDsm9fscLUqSPWndq1xYqTjhAS\nYAZC+Oqr5Jw55IYNZFay+ZY/Li6wN/dWTFmPHsHHlnnDFcDY1ltapzOnBcLaL65vb731DkRPe5vo\naLHEOJ3ixhgeHvA5ykoWN9GzE+OYVSGSqYtc3LeP3LGD3LaN3LlTtq1byU2byF9/JdesITdulPod\nO+Qa3bKF3LbE4NlWYvWyI3OHwRO3OPjTPINffEEuWCAvSufMIb8dLW+avx3t5AcfkO+/T37ytsFD\nNzi4/6ec/axJMmhc6+BbjxkcPpwcOJDs1UustW3akK1aiVGqSRO55uvXJ2vUkGu7YkW5/r0tsYWx\nXXcdmRgdRwKMrxfHWjD4I6K5TjXlprBm/LVkSz5aOYmpIZF8q3ocT4RGcEvZphzWxMm1kWIhbdVK\n7uGWLcm7mxr8JdzByXWnMEOF8f8ajuXJkpH86BEX336bnDRJrJ7vvSe/Cx9/LNsnn5CLF5NLlshv\nxg8/kKsSDf5zo4NrJjp54mYHdyw1uGMHuXs3uX8/eegQeewYefKk6RJsufMG4+YarEusv5jQYO7P\nQPrwtkS6XHJ/lCvn2903r3n46stuxUxKyn8OecV1RkSQTZvmjh31p59heO77vCwSecXaBhqD66c8\nY7vB5DAH3x5mMPF1gz+iJdepZjxWx7QMBzpuIMfH+zyMH5/zP8VfeaD9249/XsfQW3eXixnhkbwH\nSfyroXhpHGgcwLXsz5I0eLBcS96WpMGDZU6+3JjtlulALNi+xrbaTZwoDxF2C7DVzjDEFTsmxreO\n3rpYCOZ+91c3caJc7/7aaMubhg/YLGYtTC7yDXKGY73CnBa0kyaXsYdjdSAD5FqBCpoDloO4AzaC\nZCB52iQ7CyH5/LMgboo9bG32mTI3QyxcO5Az+UeUWX8c4lKYDMmOaCdvA8yJLYbH7XAbzOQfpsws\nSIbIZyHWuLx0ucXP/F6/WInZxo1yNufNkwfcHj08hMv+8BcaKqTsoYfIt94iv/hCHpbT0wtZIcud\nMUTIWbZbY7APX96JPgqS+MNCIGN7/6B7yxRX15qCPKQW1xizYN1W/BHS8+z+4nZL/FpamhCSo0eF\noPz1F7l3rwyxfbuQzc2b5R796SchPMuXi7rLlpE//0z+/juZ/kPOlwbbPnDxm+ed2TfvjPudHDOG\nXHC7kLfE6Di+3kXqJ7R38sEHxT11wAAhmw89RL51p9R/XnMYCfD1anGsWFGeH8uWlRcsSuX+nfC1\nxUD6ioEzIKIZGiok9o4yLh5VkXyhfByPhUSyRxVXtmtu/frindm0KXnzzeTDjVw8HhrJ+OvieDws\nks9Gu3j33eS998oLoH79ZF6PPkoOG0ZOGGRwe00HZ9zv5I5aDv5nuMGXXyZfecXjcmsnodOmkdOn\nC3H/8EMh9QsnGfyrkYNLxzp5oLGDX04x+NFHQlITE+V2+OZdg383cfDXZxN5tlwk1z+fyNS6zZle\nNpzbh8cxvXwkN7/r4urVcj7XvyMP2nufjWNmRCQPfCIvKvbsIfesMHiqpYMpc11MbeHgzw9MYaYK\n4xs1ptCoLaQ3399jl7wIOfqVizt2kEe+lP1cSYzs97XLlf391BIXD9ZpySNRzZh1ax6kzH6/+CIW\n/shRgL9H7l0Gd9cVl+4NG6Ts7wVyna1TzbjwaRczY4IY13Z8GBlJ94oAfuvHj6cbihnjxuciZdkv\nGPz0nyf59jd3Py7Hn9+fxOUhDqZtNdioETniLt/HLM/jbMFM4pTtCm3B3/9noL/hec3Tqvd2uXa5\n5AaPiBB9rBcB8fG+dczr/8OQe/WT4bbfen8k0jBk3N69efQo834J4T2XYAmvpbdO1HRJwkbMmgO4\nBrJO2UmTlL0JIIQ5uUQbAGsBnAGwHcCD9vr8tqCImTng9ZCYrgwAR0z2+F9IQo4zAKYBMCCrYrcw\nZfeabaebTNPOOGPNCX9symyDZGa0M854U6YLPPFlY8zx+kESgGwwdaoSiC5+5tb8YiVmzz9PVqqU\nk2CtXy8xQLNmyQPg9u3kmTMXQBk/MWbeiT+y4e+H+DLIylgoCPINda46+3f7H7q/N+52BFte2CgM\nq0lxgK8Ho4gIiTVr2tTzkGNZVuLiPG/n/VlIrWMxZYqc07Fj/Z4Tt1vI5cmT5OHDQiB27yZ37RJr\nprHc4JloB/+c5+SxFg6uSTL4ww9CMr/+mly4UFT7+GP5vZk5U0jQ5MlCjL7vJmTyyw5xHDWKfOEF\niVd8+mnyiSfEMj9kiJDKOS1E9oMb4ti9O9m1q8Sdtm1Ltm5N3nqrvFy64QaJs+xbXR7ke1dz8ppr\nxLJ55ZUSa1qxojwnli1Llirl39IZCOm0ZIYjLlvW+j4ccbnk86qz4lgtmSlXjCUBtgv1jF++PFmt\nmszFip2NjJT5lClDtvYRL1u6tMy1YRmDzlAHO5dxcnVoNFeHtmRshJNrwqK5Oqwl2yon16IZCbBT\naSfr1ZNL6bbbJB61e3fyX/8Sgj9okJDhUb0Nbqri4Nh6iTxRIpLT2yVyWw0HX3lI4mRffFHO6/PP\nk88+S748wOCWqx18O9bJrVc7+ML9RvZ57ttXzuvIK2axFgw+/njOa/bsd05ur9yST+Ft1oLM5dGK\niTwWEsmx9RK5oZKDI+6SdsOHC3Hv00eI+z33yK3Ss6ocnxGI41FEcngzF3v3lvquXcUaHn2V9P0f\njKAboLNMR2ZB8ZWr4lm9urxXLFlSeEZsrLwQmDBB/lcXPi1xtav6xDGtbCS/H+fip5/KvbBwksF9\n9R38bISTfzVy8IcEg8uWee6XJdMNHmzs4MrhiUwvWZafd5jC5DAHh3aRe3jiRHlp8tErBn8fNYtr\n1pDr1skLni1b5L/cMMh9+8i/1xhMb+1g6kZJWOXeZfiOJbV+Y+Ljgydh/uR8/f5a3hYWCWvYUC7m\nhg2lzm4F9aejn/+NRYs89+FnI5z56u+OiODuyk0ZAyf/qGF6YQTynxEs4fXWwUrg5Ot/qGRJufh8\nkbuBA+VtlgXLqugLSUlS7wsFbXeuuERjAe3EjEFypoJswZKy0aY16wQkC+I2kwx9aCND4ZDFnK2k\nG+kApjMnMbvFZJo0LVsE0JkeYjYK4vp4yqzLMPsraSNmt0LiyzJs42w3+8hXFz/zu2iJWfPm5AMP\nFLUWDCwroy/4ettUr55/8hUfL/WBoiCuGfZ97x+V4vQjU5AfQ3sb78QG9jeC9va+zlFRpnovCCEt\njvD3wGNPAGIY8nRo37feQuf1UsHbRS6YxB92Xc6F/FrzC8QtNhhZuy5BuhlnZclLrDNnyDNbDGbG\nOHjqGyczYiTj6pkzkmX1+HGxhB5db/BsawePvpfIrIhIHopPZFrj5swsH86DY8QqtnO2ixs3imU0\nZa5YzFJGijVt1URXDvdQp5Pc8nIiCfDMKJMwJyYy/XZx1U1IkOe68ePF+vfaax4L4H/+I1x7+nRy\nw0AhdhsHxfH994UIx8WJhfD/HpMH2HmPODl3iHz/aLCTswfJ9zMNm9KY5eTuOg6+OlhI04AB5H33\nSf4Sh0OeoVu2FDJ8883kyObSdkpdGbd/lJMNGogbe82aZK1aYgm97jry+uvJwdeJ/EN1nWzaVC7Z\nm24Sl+Fu3YSYf/ed6frq4zo7dauDCyYa2XP5JEbGHdPKyTZtyBtvlNuiQwdp2rq1fO/fnxwzhkzu\nKfLfdonjPfeQ7dqRHTsK8XzoISGSiY9K33tr304CXHNNDz72mLzHmDZNjvWjjwqZa9pU/sJCQmTL\ni3y3VXmTfYtgjDD7+HcnJw8elKmnpcnxCdQN2jthVaOyBmvWJO+u7OKxkEi+Xi2OqaFCTrt0IV9q\n5+KJEpH8sGkcT5aI5Ot3ujh0KPnkk+RzzwnJHj+e/GCgi6dLRXJRpzieKR3JxMdd/M9/5Br873/l\n2Mx62eCeug7OH+pkSh0Hpz1ncP4wF8+UjuSKdmOZqUJ5sEId7q3QiCfDwvlGs0Ruq+7g1GcNTprk\nIbi/9pPEUT+/7aLTKUmgVq8WL4OvviKnTiWbVTS4oZKDU+6ReT57r8EvvyR/my7Zk49+5WJGhngf\nZEbIvOwvXQYPJg8cIA/9YvBIM0ks5Q7UHdL7NzU/wurLOmcYZJUqctJ69co53sCBUj5woKfMHxH0\nV36u7c4Vl8p/sheKOzFbDFnUuSFkobWvTQI0A5JkIwvA+5CU9G0ANIPEbe00248HsA7AZsiCa01M\nixcBzDBlks0+TkJS5NcHMMeUuQMeV8a3zL4ti9k2k3hVDkQXP/NrDoAxMTGMjY3NsRXntTyOHZM/\nifffL2pN6JuUWbDImYZGYeBSeTvnTW7tf+pJSZ76iy0rIxmcm2uwLrGFYS0N5u253Y2uoDFm3nOd\nMiUncc7PRc+OvEisnbDaY0ejo+X6adrUE2sT6HGz5BITs4lknu2CIc15XWeW/oGOayEQkm+NO2KE\n/Dd17Bi4N4bZf+Z/4+iOjOTJb1385x9xZz6zxcwOu9zJzBgH/1rlicn880/y8K8G02938PSHieKC\n6mdOJ09KaMKGDRKXu2qVDLt8uRDaxYvJL7+ULLbLXhIC8sVTTv73v0JMX3yR/LKDEL+Pbo5j797k\nXXcJQZ1aX8rjasfx1lvlsmjcWEh1rVrkVVdJVuGXIkXuuTJxjIiQn6HwcLn8S5cWS3Sn0jJ21/JO\nVqwodaPKSLsZZYZlM8jpjaSsXy0nK1USQ1pYWN4E104+N1zh4OFfJavuB2MNrizlyZLsK+Ny/VIG\n/6wv1+D+Bg7WK2nkIsZdyjoZEyMhcf36kQ8/LFbYZ54hJz5u0Kjt4LxHZA3Mua8anDWL/H6ci2fL\nRfJ/D8uLl7WTXVy/Xqyav/0mngZ7Vhg80zyaZ29qyeObDJ7ZYjCrZTTdLVsKKbOTMF+kzII3mQqU\nXBW03bnCvKfSthryoqEgv8v+/tsBubh8/beHhxfK8+W8efNyPf/HxMQUX2KWq7GQIJoE7aJdYNo2\nzkVpMfv6azmT27cXtSYaGhrnDF9uMBfjOmbBuLkG6xJbGG9mA+nDm5RZJMyKwfQuL19eHhzymof1\n3ZuMBRo/5eu4+HPJNoycMWbNmvm2suZ33HyR00KIMcuGv+vM0n/MmALFmAXkhmfFlI3PHWPmF4Ee\n/7yORUHOuz/4I8H+yGmglulgyK19bKvd2LFi5a9TRzwAwsNzk1CXxEemvSmJo/YnufjHH0JwNmyQ\nZFEHfjaY1Tb3sXHvMnjmNgd/WyRLqVgW5FV94vjdDFlKxX7cz7Zy8Ot4g4umGjx5q4Pr45w0rnXw\n8TsNtmsniZ9uukkSP9WrJ++S764oBO6Okk4q5SGKgZLJHxHNtWjKtWjGH9GS15UwWLIk+UHIQLoB\n7gypTTfA+eUH8vrrxU3b26V4atskZqowupoNY2ZIGD+/P4lTpkjipjlzyM8+E5L++efyfcECMiGB\n/Kp/ErNCwril4zBmhYZx11tJ3LOHPHHC/3qru3aJy2xB4XaT38806CopFtyt1YWkBQV/vxflynnI\nmR0WKQsPL7jieaC4W8xeA9AaQC1IrNl7prIDzfrPzf2LaoFp2/wuSmL27LMSV+HvRtPQ0NC44NDr\nmOWeR+/eEmvjcuV2lbYezvNbxywvEptfVsbRo3MSAG9y5mtMX+Q0kPJzdWcKdtxAjk9xzcqY35wC\nOU7efV1KMWaB3Kt2EpnXefB2MczruvQine5dkpjn1BIXsypE8uh4cWPemyiJf375hVy5kvz+e3FZ\nXrKEdL3qzGZq3zwv1sx33hFX0MMVa5MAD1WozWeekXjbRx8Vl+LevSWusV07UXfuFWJ5fL/sMEZG\niqXSThR9baVKkZMh7SZjWI660FCJR42MFPfcGjUkGZNVbzlmtGkjMb7duombc79+4io8YIDEnw4a\nJDGePXuKu2+dOtL+2Vtk3u1CnWzeXIjimjVySA8cIFNT80k65++6tsiZRcLOMykjiz8xe9+0XGXB\nExtm2OofNC1ip+FZANoJScxhLTA9F7KWmRU3lgaJUbMvML3HJGxZZvlhc2zvBaaPmp9ZkPXPkuBZ\nYDpfXXzM76IkZjffLIHPGhoaGhrFGIVBKPMisaNHyxOd91jWg6uv2NH8xg12QezCcjEu6ELcwcQT\n+4pjtvr0F8cc6PH3hmF4rNmFtbi4P1JxqWZl9AfvNqNHeyzDdlgWWLvHgVWeXwKQ/AivP2tidHTO\nBE5Wf5b7Ym0hZz7dGC1Y53PYsBzHzO2WONlDhyQRzMGD8v3IEVm2hElJdIeFMe2RYXSHhvGP15K4\neLFk7373XeGwb71FvvqqGDdHjiQff1wS9AwdKqTrgQeEeHXvLlY8a0kW6zTeeivZvr2Qt9hYiVNc\n/qG48tLp5PGbHLy7qeGXPIaGCm+vUkUslPXrezyt+0RLTOFLbZz87UoHR/cxOGIEeTwsnG6AGQDd\nAE+WDOfHH4u1cMkSSRLz7bdkcrKQwU2bxKNs7145NsEaMYo1MaOQl86QhZ6/MRUdYKvrA0+2xljT\nqva5Sb7eMGWmm8RsHYCbANwGSSdJAB1NmT8g6fNnQ+LZrDXGvBOAZAJ4yrSsjTf31weqi4+5XXQx\nZqmpEl82Y0ZRa6KhoaGhoaFxwXA5rWPmD8G4QQf60iBYwuvPmmi3ztn3L4MYM29Ce3yTwV9+kdjI\nL74g58+XJUumTZNkMq++Ksl4nnpKSKFlNRx9m1jehjVxskUL8YitXZvMMJldBpCn1dDfFhIixjeL\nEDZuLKenQYN5rFw5llWqxPKqq2J5zTWxvPLKCxtjpiiEJCgopeJNsnMNgLtJfmmWOwD8AGA0yTfM\nsghI7NdskgOVUlMh7onNSa43ZfqZJKwdyeVKqT/MvsNJZpoyX0NW0w5VSpWAxJD9QvJWm15/AzhJ\n8tpAdPExr+YA1q5duxbNmzcP+rgUBRYtArp1A7ZvB+rWLWptNDQ0NDQ0NDQuEIYMAfr3B1q3zl23\nciUwezYwc2Zwfc6eDbRpA0RF5R6rY0fg9GkZ099YKSlA377CARITPf2kpAC33AIcOgT06gUsWOBp\nP2gQ8OGHwMCBQEKClC1YIP3Mmwfce69H1l95fvX5tTtXpKTIPBISch47f+WB9jduHDB+vKd9RARw\n4kS2WFZ4ONL+Oo7Tp+XUlCgBZGYCaWnAmTOyWd9PngRSU4GsLNk/fVo+U1Oly8xMICMDSE+X/ZMn\ngVOn1mHz5hYA0ILkukI4UnkiLNgGJim7C5LpcIdX9WHzM81WVg2SnKOUV91em0wZ87Oi+XkWwFmL\nlJkoDSBEKVWBZKpSKgOSEdLSyxojwyz6JwBdLno4nUD16kCdOkWtiYaGhoaGhobGBURepKt1a9+E\nLT94k65gx0pOBnr2FPJlJyJRUcIAbrpJ3qjbYZGxxETP9/h43yTK2o+P902wCtruXJGc7Jt8RUVJ\neXJy4MTMm8wlJMj+mjXAqVNAeDhw/DgQEYHQEydQ7qoIlDt+vFCnY2HdOqBFi/PStU8ERcyUUtMg\nLoLdIZkUAaCCUqo0yTQA5SHmvpFKqQ2Q9c6mQAibMuX/gRCvj5RSoyBuiRPM/qqYMkcANFBKvQkg\nAUB7ADEQ98VqkOQhIQBuM61tawCMBBBqm1O5AHS56LF4MdC+PaAumRlpFAckJiaiT58+Ra2GhkaR\nQt8HGpc79D1QAPgjdgBw9qz/uoQEDykDhMj4w733+idXBW13rshr3lFRBSdlVnuLlJUrJ6QMyCZn\nOHFCPs8TObuQCAlS/lFIKnonJAmIAjALEgNmgQC+B/CJTe4ns9yq3wtJ2PETZI2yWZAkHZZMGoBF\nADpAknWMBDDWHM+ScZttJwBYD8nyGG/2663L15Asjy0h5K0iLgH8/rtsPXsWtSYalxoSExOLWgUN\njSKHvg80Lnfoe0DjgsOf5c0iZVOn5iw/flwsaDb3xosZQVnMSOYgckopN2SdsC/NogMQ8jSF5GCb\nnBPALpvMFSS72epDIUk8Dthkwkm2sMm0hRCtgzaZTV7jvOxVryALT4cBGACxrP0AoK1SqjJJy/Uy\nB0aOHIkKFSrkKOvTp0+xe2s0bRpQpQrQuXNRa6KhoaGhoaGhoaFxjvBnecsrJ0YhWcoSExNzvYxI\nTU0tlL4DRdAxZnmBpKGUOgBxPdwEZCfcuBWARXFXAYhUSjWzkn+Y8gpCnCyZV5VSoSQtC1hHANtI\nptpk2kPcEy3cYZbbdXkcwHSSc0xdKkLcJgdB1kbLhUmTJhX75B+bNwMzZkhMZKlLJmJOQ0NDQ0ND\nQ0ND48LDlxFm3bp1aHEBg8yCdWWEUqqcUupGpVRTs+hac/8acz8OwItKqVilVBOIu+E+yILPILkV\nwBIAM5VSNyulWgF4B0AiSctiNg+yqHSCUqqRUqo3gCcA/MemymQAXZRSTyml6pvWshYQd0YLUyCL\nYR/30mURgOhg514ckJEBJCUB7doBjRoBTz1V1BppaGhoaGhoaGhoaJwrCmIxuwnAcohbIeEhS7MB\nDCL5llKqLGS9skgALkia+3RbH30hBGopJFbsEwAjrEqSx5VSnUyZXyEJO14m+YFNZpVSqg+A18xt\nO4C7SP5uG2c2gNchsXFPW7oAGALgOh9zKw0AW7ZsCfKQnH+89BJgGMCuXZL2s3Vr4OWXgWKoqsYl\ngNTUVKxbd96zwmpoFGvo+0Djcoe+BzQud9g4QekLMV5BiNl2AB9DCE5Zc3+gV27/ED/fLSjkzIzo\nvW8vsxJ++Mo7GIKcSUXyswBa9fYkInZEAcADDzyQTzdFj5UrgQ4diloLjUsZF9J0r6FRXKHvA43L\nHfoe0NAAIBzhp/M9SLDp8iMB/AhgGYBOEEvWdQCO2mRGARgGoD8AA8CrAJYopRrarGbzAFwJiREr\nCcnKOB3AA2Yf4RB3x+8APAKgCYAPlVJHSb5vykSb/YyCuCb2BfC5GbtmWc0GmJ/vAfg/SxdzDlaS\nEDuWALgfQApyrn+moaGhoaGhoaGhoXF5oTSElC25EIMp5pXlxFtYqTcARJNsk4fMfgATSU4y9yMg\nJKg/ySSlVEMAv0FW0F5vynSCkKsaJA8opYYCeAVANWuRaaXU6xBXxUbm/nwAZUl2t429CsB6ko/Z\ndEkH8AXJETZdTgF4k+TEgCevoaGhoaGhoaGhoaFxnhBs8o9YAL8qpZKUUgeVUuuUUvZ09bUhC0Av\ns8ohrqemAAAgAElEQVRIHgewGp5kGy0BHLVlZAQk1oyQ7I2WzAqLlJlYAqC+UsrKYx9ttoOXTLSp\ny7WmLvEAHjYXor4aYt0rB7HSaWhoaGhoaGhoaGhoFDmCjTG7FsBQSMKP1yBEaopSKo3kXAgRsq81\nZuGgWQfz8297JckspdQRL5ldyImDtrpU8zOvca40dfkIsnj1BLPsFIT0HQpsyhoaGhoaGhoaGhoa\nGucXwRKzEgBCAbxgboBYoIYCmGvWKwC/K6VKQixYjyFnso0KAGoopU4BOAFJYf+8l0xFAL2UUgMB\n7IGQwF+8ZEIAvKOUmgVgI4DhXvXZukDi2Cxd4gHYLXHZUEpVgsTOpUDHmGloaGhoaGhoaGhczsiO\nMSP5z/keLFhidgKS3r4BPFkSHwAw0vz+sFn+DIANkEWlPwWQBWC9UirElC8FWXPsaohFKwNCxg4o\npaIANIMkDmkNoAOA9yHkjQAOmuuahUHI1mvm+EtMOcuKlqcufubXCZJxUkNDQ0NDQ0NDQ0NDA5Dk\ngPPO9yDBErO9AGrb3QDNhaV3m4k17oVY0CJJrjctXlsgCTimQojPlRBrVxjJJUqpsQDehpCoNRCS\ndRDAFQB2kNymlGoNscptI5mqlBoJ4A8AESS3KqUeBXAngPsALA5QF19oDgBz585Fw4YNgzw0GhpB\nYP9+YPx4YNw44Oqr8y+/wBg5ciQmTZpUZONraBQH6PtA43KHvgc0Lnds2bLFWkYrxeQ87wFoC5vX\nH0m3Ja+UagsJ+WoM0+uP5OxAxwuWmK0C0EQplQrgGISoNQUwGGIBCwMwCcCLSqkd8LgEngLwBcT9\ncTOAAwBmmtkXDwMoD2CRmZGxJYDPAfQEkKCUehNCsOoAGKyUKmGONQbAa0qppyAZHQ9D0urHQxbB\nzk+XHDCtcMMBoGHDhmjevHmQh0ZDIwg0bw5cfz0waBCQkABERQEpKcAzzwALFsh+EaJChQpFdw/M\nng20aeP7GKSkAMnJQP/+F64fjcsWRXofaGgUA+h7QEMjG2cBLAawH5Kk0PL6SwfwIgCYXn9fA5gG\nWcarA4D3lVL7SX4fyCDBZmX8DMC/IcTqSgC3QDIc3gZJupEO4C0AOyHkahOEIC0y1zCzEnY8C+Aq\niIVsgdn3TPOzGoTwvQAhZ79B3BIJiWOrDIlzWwFgNoA3AGyFMNPd5hpmVwagizdGQlwdNTQuDKKi\ngIQEnOk7CHMeSkbGgzaSdjmjTRshrCkpOctTUqS8jd/VOs5PPxoaGhrnC7Nn5/6NspCSIvUaGhrF\nAdGQUK77SW4muQTAWACPK6UsQ9dQALtIPkdyG8mpAD6BJ+QrXwRFzEguIfkCyfoAbgfwJyRmq75N\nLA5AVQDtIK6BZ83vdswH8D8ANwC4yyy7z1ZfEcA7AN6FHIQZEFdHez8dADwIsdZZa6Ndo5SqHKQu\nsFnh1gBiuu/evXuOLTExMe+Do5E/hgwBVq70XbdypdTbUb8+MNWP1+nUqVIfKAL58/OWse97/0EW\n1h9mVBTerTIO/RLaYmrlcQUjZQX5Y/fXZsgQsdjt3Zu7ztc5Oh8wCWsOUmWRqWCIa2H1o6GhcX6g\nSYl+gaShUYyQmJiY6/l/5MhsTtUEwGaSh21NlkCSGjY291sij6W8AgLJoDeI6+E2CMmx1ilzQEja\nWQA9bLL7IAlDbgEwHsAOSLKPymZ9lFl/HGLRSoZkYNxk62MAxAK2GJJtMcMcf7JNZhaAMwCeC0QX\nr/lcZZb3A8C1a9dS4zzA5SIjI+UzkPL4eFIp+QykPC8YBulwyKe/cm8Za9/l8l3u3VcBkLnDoKuE\ngzFwckUJB9P/KECfgcwtrzazZnlkkpLIsDDGtmjhkZs1y/85Gjw4d5kFl0vqCwrD4ImbHYzr4eSZ\n23zMw663j7acNSv7e9ptDk6628lTtxbOeStUnM9jqHFOiI2NLWoVLm0U5LfrUoS//55iMH99D2hc\n7li7di0hXnufAviGOflDGZM/dDL3twEY5SXTxeQkpRgIxwpEKFcjcSF82yRoGZAFpSNM8pQFScoB\nAPVMhfcDGAGgs1m/0dbXw5B1ydwAboS4Jp4E8F+bzDxISvyj5v5qs5/u5r6CuD/+AmBhILp4zUcT\ns8ICQNas6buuZk2ptz/g+3vgt+BNwsx99zvxTE8PUrdA/vy8y0z90pa6/LcpKAyDR5o5WAsG33uP\nrAWDfzcpYN8F+WP3Jp7WZ1IS55UtKyTN3Pd7joIl20HiiRudJMDRtzn96x/AQ934dtLP2Bgf/RQ1\nvI/VrFnkxIk5j7tF3gyDfPttD+m02tvJW6CEVSNfzJs3r6hVuPRhGGTDhlz6sotbt9L3b9nlcM0a\nBk+1dPDh+k7+07R4kDJS3wMaGgESs470T8y6mnykJAPgWMpsFBCUUhMhyTPuA/AIgJcAtAHwPsnH\nlFLfQVwM20GylUwxFS4J4AdI3Nghs6y9SYjmAEgAMArCKrdBFpdeYY7RHuKSOA7AqwDKAugPYDrE\nAjcf4rvZC5Lq/maS0fnpQnK0bV4lIItQPwtg0tq1a3Wwa0FRqxawZw9Qsyawe7fP8rMJHyO0Ryz+\n1+tl1E98GRtf+QrlOrWG2w1kZcm2dSswdy6wdi0wvupUPLZlOHbdeDeu3fg5pt/wDl7663EcOiTd\ndugANGgAlC4NlCoFuN1AejqQkZFzI4Gqp1PQZcEgONuMQ9sV4zH/jgScqBSFEiWAkBCgZEkg4kgK\nun02CD/cPg5tk8djfqMJuG3JS/ih9Tj0SxmPBZ0TkFoxCiEh0saOEiU8W/nyQNmyyJZTyvMZti8F\nt0wfhEFMwJ8lovDbb4DDAaRtTcGC8EFY/mACzlwZhbAwIDQUCAvzbKGh0o+wXM+WsT0Fzd4ZhGWt\nx6Hn5vHY83IC0q+OAiDHpVQp0SsrS+ZZtixwdlsKrnh2EA73fBjXThyK/e99heM3tEbIpwvQYEJf\nbLxzNBotewe/v/EVIru1RvXq0jYHVq4EYmOBr74CWrfOvV9AJM9OQdaAQXA5xuH25eNRam4CWt0f\nlVPI2zXRh6viX6tSsLXVIMyJGocHjfG45rsEXHeHVz9FDfsxq1EDuPNOYNs2IDERuPdeqe/aVe6r\n8HApj4ryfaytY1C1KjBsWO7yhARg3z5xE5s5049CJs4lgcqQIVLn6xpYuTLn+MHIalxy2Dd/Jcr1\nicWw0HcxN2YGVB7386WM6X2T8UhiW7zawYkXv9cujBoaxQHr1q1DixYtAAmruplkNkEwk33sAtCU\n5CalVDKAtSSfsskMADCJZMWABgyEvdlY3wYIaySE5ByCpKD/r1k/0Cx3mzL7ADSCxG7925T5DOJi\nSAiDXA1JIGJnnAchFi+an9NhY5zwWLgyTZkTEGvXWwB+ClQXr7n9DLHMXdQWs7NnyczMgrU9fZrc\nt4/cvJn8+Wfyhx/Ir78mP/2U/O47cv9+MiMjZ5t//iGXLyd//ZU8dUrKsmrWpBtgWvWa3LyZPF5F\n9v8uX5Pt2pGlS5PDEUcCHI445qYYst10E/nMM2SXLuQ3ZXqQAL8q2YNt25Ivvkh+8AE5fDh5ww1k\nhQpkqVLSTin5Xr48WbEieeWVZI0aZPXqZJUqZO9qYj3pXc3JevXIOnXIa64RmSpVyKpVyZ6VPDJN\nmpAdS8n+gzWlTd265LXXklFRYgisWZOsVUvGqFpVxg0L8z0vgOyHWaxfymCbNuS6dXLc9u0jO3Qg\nG5Yx+FDYrDzb+9qUIgfUFj3bwBlwuxhIm/uQyGUQt8plcHAcxuY6R0qRZcuSERFyXKtXl7nfe5WL\nx0Ii+WrVOB4LieSAui7edhvZvj15xx3yArxdO7JjR/LOO8mePclevcju3aWsXTuR69RJznfXRgZ/\nUA72iTaYmUn2iZb9vrcZ7N+ffOwx8umnybFjyTceNbgzysEZ9zu5M8rBySMNTpggdaN6G/yptINN\nwg3+/TfZNkr2Z483+PHH5BdfkMuWkWvWkL//Li+p9+6V6/qff8iDB+W+cLs92/nCb9NdTCsbyZSR\ncUwvG8Gsho3Ili09braNG5OhoWJJI/O2ShoG2bw5GR7usbRZVohgrJnn4moWjDX1PFteCwzL+mi3\nQtqtl/Z6kuzWTTZfcLnImBixhnr3Sea0huZlJcrL9XX0aLJ3b9/zsCyrvs5lXmNeAAvsq6+S9yGR\nBLjm6UQpnDiRjI7274pdkONjHQNrTvXq5XaJt/qOj5f6CwXD4Jpw+f11lXAwa6dx4cYu7gj2GtRe\nAxqFCJvF7HHYQrHo8fo7CqCEuf8GbF6B9Hj9LbaX5bUFS8wmmOQo3VQuy0aw0gF8ae53gSwS/RMA\nFyRV/QhIspGDkHiyJpB1zf6GJPpwQ5KBRJn9/QJJKmIdiInwuDL2NceZBEkOMh3AEQCJABaaMl/k\npYuPud0HSafPmJgYxsbG5tguBnP+woXy0FytGjljRm4SZWHfPvLbb8m4OHLoUHkorl49sIf4UqWE\neFSrJps3MbDIxDYIGTuLELoB/oGarFlTnlnmD3MxIzySxybE0R0Zyd0fu7hqlTwcr11LbtggD8TZ\nMN0Xs+7ukW9sWb4PztYDpdOZf/yVJWO5+OXVxo8u6elCls+ckQf8kyfJEycYsBum2y1EOy1N2h47\nRh4+TB46JJ///EMeOUIePUqmbfXonRHj4PbvDW7dSm7ZQm7cSP7yC/njj+Tq1TKVb74hf54v7jO7\nPnTyWHMHf3tJHo7+emEKsypEMuM/co6Mj1xcsoR8/31y0iR5fpwwgXzpJfKFF8jnnycXOoRsf3J7\nHB99lOzfX54Re/Ui+/SRzSJjnTsLIYuNJe+9l/zXv8j77iPvuYcccofBLVc5OGeCwZMn5TicOkXO\nGGNwY2UHezQz2KSJPDNZxLBXFSGXvao4Wa2akMaW1QyuKe/gUz0NWu9atm0je99qcBnEhTRQ8hoS\nItd22bIeQlqrlpD6+vWFM914o7xMaNmSbN2abNtWiHbnznLdx8bK/IcMIQcMIPv1IwcOlHm3bSvj\n2F9YdG5gcHf1aB6o3pSHajbj33VbMnl4Es+Wi+Rvj8QxvXwk1052MTlZLtHkZDmvP/wgZNP1kcHU\nus2ZUaY8Tzdszv9n79zjZKr/P/767K67XUuiUiy55JJYuQsT0Y1+fZFIiUoXJLoqQqVIZdNSonXN\n1pJ0oXQdRumGULHI2UJRLq07uzuv3x/vzzFnZ2d2Z3axi8/z8TiPmfM5n3M+n8+ZOTPndd6Xz+9f\nWtz7YT6ETkHiX/yFVW5CK5y6p4tAcaYejwje+Pic5WXLkmXKBBeYKSkiNlq0yL6vZQUuD0RuIjYm\nhmzUKOe+zvZDiaMNdA5sQelfbvffvtnNx03xTVdYXHe+i2PqJXOfiuXcG5OZ1Vyfj1DbDeX82OX2\nMcaMyf6fEqw8VPIauy2MA4jy401bcBhe4kP/Z3EYXuL+K0O4xoK1d/fd8lkHEiCnO271ZIikcB8Q\nFeSBkuGcZt68eTnu/9u2bWsLsyaQsKpPtF7prDXNs/RpiThIONZ4rWEe0Pqoo10nryVcYVZGW52c\nSwaAFZC5w47p9Zt1/ToOq1VTLZIykT35x70Q98h9kMQe47VYc8ahJUMyQC7R698B+Bs6+Qckxmw7\nZG61RyExZrn1pVmQ8b2AM9RidvCgWHuuuYbs3Vs+2QYNyGefFetS377ye+QUYCVKSJ1u3cgnnyRn\nzCCXLCG//ZZct47cskWsZHv2yPv33ycnTZKnm2PGkKNGkXPmkL/+Kjf7M2aQkyfLzfucOWSGiiAB\nZkRE+ERiuDdfQWLMwv7DJAsUY3aif0X1h70gMWb+Yx01SlRIKJYZG7tOQkLBb6bD/SMPJrZzOY53\nq8WjU2dy5075bq9ZI13+7DMRrAsWkO+8I9/52bPJN94gp0whX35ZrqlRo+SaefxxsdwNGUIOHEje\ney95111yvd12mwjTbt3Im24SceZyiXhr1Yps3VruxTt2FAvih495mBUTy60Pieh6uLmH3Sq6T1yw\nbbUVNBRrs781dD/KcjASuBexvKaUh7GxZMWK8nDlkkvkd6FuXVkaN5a+tW0rgrFDB7J3K4uryrk4\nuKGb6yu5OOQmi3feKSLzgQdk/I88Igabp5+WczRunJyv+UM8PFoqlt/0TODR0rH85CkPZ88m580j\n58+Xc/zxx+TSpeRPCR4eLyvnICM6lpuSPPzlFxHUW7eSf/5J/v23PJT47z8R7MeOkVlZp9Ca6S9e\nPB4RZWXKyKu/FTKv3zh/EdaiBY81iOfeui14aGkeoswmtzaC/Rb4x5L6v+b1W2H32RZEeSVNCvGm\n+I9l8qBkwUsWd+wgp7STh0PjGifLw6ZQ2w31/Pj3xxZhY8YUTJSFMvZA59yyyBYtuLtOS7aGh4da\nuFi3lMUpj+Uyvrza00mcTvyG29x4ozw8CPZgxBZs4Vgdndj7TZggP37OzyklxSdMX3pJlnD+S/Vx\nMrdYPHrUMfaePYN7DTRq5LMgW5b8wAUbl7GkGYLgsJjFA7gEMk/ZQS3KxgOIYHYt0Q7AKkhCws0A\nbmcAzRFsCUuY+TUcAeBWbd2aAV8mxGkALMis2E20Fep3vc8YAKv9FOcdesBTdZ1lAKb7Kc7Zuk5H\n+LIyjteDvgNiNUvVYux8SFxZrn0JMqb4M1WYvf22fJq//y7rP/wgLmMVKoiLXsuW8vv0xBPkwoVy\nk5Nfl8eQsBN9RIg4Y9WqJivjqSI/TweDjTUxUf7QExNzF6hOCtPSkR9BWhQJdA5jYsh69chGjZjV\nqDEzm7Xg0TkpzCoXy32jE5gZE8ttyR6mpoobZmoquWmTCM3ffye3eSweaeni70luHr64Fglwdd8E\nvvwy+eKL5PPPyz3oyJEiNB96SJb77hNrXp8+8pCnZ0+x6j3bUUTesCZutmsn4rJpU7n3qV9fLJjV\nq8vvTeXK8tsTHS2uy0MiQheT4QjPQO68UVHy0Ml2uS1fXkRo5crkRReJEK1eXdyR69QhL7tMTnP9\n+vKgqkEDX1mDBmIJvaG+xR+jXXyqZjLTI2P5dJ1kppaN54HIaCbWTuD+KBHSXbqIZXRYMw8PRMXy\nrUYJPFgsluO7eHjffeSAAWT//uTD3SxuqtiSW8o14qbi9fgfonkLkrm8mIjeUaPIV18Vd+3p08UD\n4o035MHXq6+K4J15t4eHSsRybrMEHioRy7f6efjyy+Qrr5BvjbT4Zy0XFwx2c1ttF+c+JwmG3h5r\ncUcdF5P/L5n/RcTy0arJTLvUxcWTLS5eLG7p33+f/cHcX3+JGP7nB4uHG7Xk/pqNeLhxS+5ZZfHg\nLxYz27mYsdk64eqbmUkeS7WY0dbFvast7t5N7ltj8fhVLqavFZdiy5KHIe+9bPH7si42q6St4/r6\nXfNEMvcilj2rePjiAxZ3xLXk7qqNuKdOS65MtvjrYvlup6+1uH+/fPd//13ckDduFIvxJ095eKRk\nLD+7MYFHSsXylzc83LJFtq9ZIw8C3ntZzpO78RB6Af51RSd6ofjzvYmcMYN84QXRGO+/L+dkz54w\nvDKC/Sb5/68MH86s5i35RBsPvy0p9bp1Ew2RsdnKWywEO75/0qZQLLp5/Ybn9gDA3h4dLRdT48Y+\nQW0LxcREuRlxbguD/essflfGxR6V3DzaOg/XbP0berhuI07pqTPyBnsIEer/RqgZdO0EToGOV7y4\nPJ0L9Ln26yc/mGcqZ6kLqVOYMZ+aKZwlXDE2HMB63UFCzHMbALwCoJcWStGQyZzt2K5jAN7U+0/V\ngqyZVpq2GyQBXKfrpEISgQyBWNKohZgXQAn44suaQxJ/ZDja2ayPkWdfgozvjBVm3buTzZsXdi80\ntiizszPa66VLh/ajZhPI/98mXP//UH4w/Os41/1/VIrSj0x+fgz9x2b/KTldYAJZ1Pw/o8KMDcqP\nIC2KBHuaX6+eL6bMssKPMfN3vatVyxdzFi7BrJJhjM87MYHecrE8tNTDI0fEpXffPvKff8gdO8g/\n/iC3JXuYGRPLHY+LxezXqR5+8400+8UXYs388EN5uPTuu+TcuWKpnz6dnDbNJ14mTfK53I4fLyLU\ntnSOGCGWvcceE2vnsGEiSIcMkZjVBx+U8qFD5f3AgSJWJ9wownRuMxGOz3Rwc0YjeT/98oQTVtEb\nbxQr6dR6si2hegKbNJF70SuvlN/p1q3JwQ3dJxTl97dJ3cQebrZqRV54oS9m1l90liolH2PFiuRz\nlWS/sZUTWLmy7767dGnymuJy/A5RbkZGyjMypXxW1Lcayr7XFA8/HnUVGp2IRQ3mElwNVraY1UD1\n7sBM3nSFxZ9+Yo7rdutsD7dFX8ZmlawTYwmlXefyWEkZ40MRwUV+hyg5tifiKhLgAtx8Ylv58nKu\nnfVLlpSHDxdfLCK/Rg0R+A0ayGfcpAl5dQ2LK0q4eHMFN1eWdvF/8Ravvlqs0C1bkl0biiAdViWZ\n/6lY3qokvnf+BBn7jz/KZ12tmlisb7pJvlO33ioPTO68U36K779fvrPP9Le4uaqL029306rh4lsj\nLc6ZQy4eLnGra+8SK/wvb3iY+pZcY2lzRajuXOBhVrlYpi/28OBBcbP3egP8vuRmdXT+l9ixrbbb\nbt269MbEcO9zicwsG8MjNeoxo2n4oiwri7z9dt938J7abm7blv03xr+v1hwP/6+81L+5gjt41s/8\numYHK/e3MDvP1/nnyxepe/fsx+jXT8r79fOVtW2b0+ppk5Ii2wOR3/0Kytnyn+xHURdmSyAZEa+B\nxGRt1sLqCocYeh0Sx9UOEtt1AMCfzC7M1kMmXLscQBc94LfpE2Z2yvwXtcVsii3eHMLsKW0Bsy1m\nP2uRVjGUvgQZXzxw5sWYeb1yrT/1VGH3hDlFWV7lhsKnIE+5CnMOrrPl6Zz/OXT+qdvuP84n0c4/\n+7xulvyfcDsTgoTKybyRKaqW17ywx5ycLH1KTvady0Duu3m59tqfcaNGIsCjo+WYjvPq9ebhoplb\nG8GEdIBxZLUXy9OOHeTmzRKP+t13YnX66CNZPvyQ/OxNmd4jbZab+2s2JgF+MdLNOXPIpCRy6lSx\n7L31llx677xDLntWboqXPePmggXiIrxoEfn559LG3r1+/Q10Q6evheOfu3n8cml3wxtufvaZXB7z\n5omlzxbubreM48jnvvPjjY1l6lsefvUVuXy5eJRYliMud4hYzI66xGK2b2yiuMvpz2H7dnHxX7BA\nRP/TT8syYoS4Mw8bJgLJtooOG0a+dYf7hNi+804RVbffLvfdAwaQr9wk2z/sKOLxzznubENftkwe\nGPToId4vnTuLSLOt1c2ayVewYUOxrvWuIsfrEuNmqVI+IRnIAt0aHu5F7An35tbw5BCsxYqRVymp\nN0RJvWvLeli+vAjWChUk3vzKihaXR7l4Q1k3l0W6WL+MxeuiZb/nokYyA5HciEu5Co25HvVIiFt2\nmTLycOHii8V63aCBPLho21bcu6+7TuKRb7hBfvKqVBGx/3ddFzdNc3NFcRdrRFhs3lys1M9dKxbk\nJdcm8HDJWD5/vYcNyoqF7fckEcgNylocNIgc1dfi6vIuPtnazT9rufj9uxY3bxZX6X/+IdPTJa47\n4LUX6u+Uvzhzrnfvnl2EBRJlZHCX1GDlBd3vZHCGe7HkEWNW9IRZjp1FBBEyd9gZO8G0Y/sZaTH7\n9Vf5JD/7rLB7wtzFly3ODAZDcAK5weRnHrNgou3JJ01WxnDwdz07BTFmjI8PLfGHTWHEmPnFROXp\njhaOlTXYQxa7rZdeCr1d//MRaN3Zv5MZY+Z/7GBjDyT0C3LzGqC9Q4fIo1946C0Xy/3Piuvzlpke\n/vijiO4tg0WwbbgvgR99JKJz3jz5KN58U4b/+uvkN7dIvS+6JnD8eJ5YXnhB4s2feYacc7eIwnfu\nd/Pll8VC/dVNst+aqwadUHsHajfiL5Pd3FnPxekjLL7wglixH39cLNYDBkhs7i23kP/3f2J97tpV\nLIQv3GtxX7zvHKWvtbi9jotDb7Z4ww0iVm0L8oiYBHauY3FLVRf3rPLVT73YxfZxFmvXpsxpqS3K\nuVldS5QQl+jzz/eJyD5xHqZHxvKVauLG/GC8h926iVWzd2+JM77rLvKJWy1uvaAlt1VqxB2VG/PP\nKi34xhMWJ0wg1zbrRy/A/ypWpxfglnb9uGiRPFz46it5cLFuHfnXpBR6I6N4cGaKxOqHKq78650O\nUabJ3GJxe20XJ3Vz83DLkyjKAHmIFQjbtH0KKNIWsxw7AzV1ZxfiDJ5g2tHOGSnMpkyR683OYGcw\nGAwnxZp5uqyphWl5zQ1/UeN0DT3XsjLa/QzU57yEe36emuenXedYQ4mPOtlZGf37ndt6fgRyOO0F\nijHzf3iQV7KmUOoFEqH2fiNHivt1tWpybTRunPPzzM8YA5U7+xrsOvA/9243s9q7uOETi199JaJo\n0SJxk541SwTqa6/Jc7LnnpPhPPaYuDi/01JE4Mz4BN5yiyRe69RJEiY1by5fz6ZNfVPYEGC3im6W\nLi3T+5QuTW5CdRLgJlTPVRx2QwqPI4qvYhCPI4p3lEo5MQ1QnTriPtuqlVgcmzSRoV96KdkvOoUZ\niOKcCoOYoaI4oXkK771Xcg2MGyfu3pMnixv4rFkizu+/X4Tx4sVihfZ4JO70558lhnnbNrEg79gh\nsad//y0xnhs2SOxmcrJcnu2VjPuGsm4uWhTax5wntvjyF2fByk8SRVqYARgLoA2AagAaaOsXAVyt\nt3+mxU97SLKNbyAp6r+HZDyMALAHMv+ZM9XkC3q/zg4LmhvZU00O10KrhBZzBDAavnT5eyCTSK8M\npS9BxndGCrNbbpEfAYPBYDCcRMw8Zr5tgW6O7T4XICtjUMJt16Yw5zHLa+zBRFgoAjmc9oJZRwI9\nPAjVWp3fGLOaNUWc2Yk/AmXYzIu8HhD5ewEMHy7iLJjL9GWXFeyhQajC1n6I0KhRTkuvdl/MrCqu\nFfIAACAASURBVC4WsyO39eOuXSJ6tmzJOZ/spmvF8ri23SBOmCAxsyNHSjzsgAGSCfieeyQz8AMP\niIB85hnymyay3ye1BrFTJ/l4qlcXV9SyZSUXSSjxpeEsN9S3uK+xi/s/cnNtRYkHvfRSsX7edRc5\naBD56KPiDvzCC3Iap06VDMjz58t4v/xS3IfXrJGEPX/8IW6mR6Oj6XWKsFMsysiiL8yma4tTFnwJ\nNcY7tt8OSYd/GL4JoN3a2mVPMD1XCzM7ocdRSFZH5wTTf2rBZrezG8BbyDnB9D79mgVgE4D58E0w\nnWdfAozvjBNmXq9kGxs+vLB7YjAYDIazllCtpyc79vNMiiXN7zxm9va8RHmo7QWbx8zjEVHm//Ag\n1Lip3Fxm7e3+WRknTPBZ75wWY1ucFfTzC8cN+mQ8NDidMWY2ttAeNCg8d8QQ9/N6ZdqRPXskKdN/\n/4lA/P13sYT9/LNYzb7+WqyKS5aIRe3jjyUG9euvJSby++8prqPOWNmtFv9t6OKYfhY7d5bYyMsv\nF71epYoIRGdMZCjLPxBxlgHQC3A3olmvnlgLr7pKTnObNmLF7NpVjBd9+4poHTZMRO3zz/sE4Zw5\nYin96iv5GFeuJH/6SSyBO3aQn35ahIUZRbxcC+AHyFxjJ9wJ9TaXFkF7IUk9GgBYpEXYMF1nDMR1\ncTVk7rNWALbqQTfUdVZA3BlnAagLSTRyDMAhvb2YFlqZAIZpy9oY3Z8vQu1LgLGdcck/fvtNPsWl\nSwu7JwaDwWAwGIosoboMn8x5zPz3c1qGTwbhuEEXVOSHKgKDudtaVnhZGcn8x4oVRoxZAYSv10se\nOSIJgXbs8FkNf/hBRN+nn8q0FfPmSYKhDK3SMgAOHy6JcgYM8GUt7dNHTvENN0jSnNatxVpYu7YY\nM847T9xJcwq/eQS6+C1FPPkHgERIPFcNLXycwixGdz7JUdZYlw3X6/fodZejToIuu1ivL9WiK8pR\n51cABxzruwFsdawrLd6+DbUvAcZ2xlnMJk828WUGg8FgMBgMp5TTPY/ZmZaV8XRZt/3nsCiAG6Mt\nCHfu5Il5DtevJ1etkrDJjz8mExJOr8UsCmGglJoCSUXfFTLHGACUU0qVJHkUwHm6rJNSqj0kPf0k\niIWskt6WpZfHlFJ7IG6JvbTIawLJnHhA1x2rlEoC0AGSvCNCKVWOZLot5JRSd0AseEP1caP1vhVD\n6MsZz1dfAU2bAmXKFHZPDAaDwWAwGM5Spk0Lvq1NG1kAoG/f4PWOHQu+LSlJFpvERGDePKBHj+z1\n7PXExJzbCrJfQclt3HFxshSUmBjgwAEgOhrYv9+3HhMj62GiFFCypCyVKweus3p1AfscJhFh1r8P\nYolyQ2LNFCRN/S16+wUQgfUpgAWOem69DQAqA7AgIupbALP1MXY76kQD+BhAR8j8ZEMBjHC0Ad2P\n2QCeAbAGkkzkVfgEWWVHXz6GZGxsodutF+a4iyRHjgCffgrceGNh98RwtpGcnFzYXTAYCh1zHRjO\ndcw1UIgsWxZcQPXoIdtP5n5FHX9RBshrdLRPnJ0FhGUxI5lNyCmlvJB5wj70q/oUybsd9VIgFi6b\nTJLZ5IRSqp9fnb9J/p9jez1I9kZnnc/92nnAbzsg1rQ+kLnQfgCwGEB7pVRFkrsDjXPo0KEoV65c\ntrJevXqhV69egaoXGgsXAocOAd27F3ZPDGcbycnJRe77bjCcbsx1YDjXMdeAocjgL8psnJazApKc\nnJzjYUR6enqBjxsOYQmzENgJsaJVhmRVtKkEsWrZdbK5EiqlIgGU19vsOv5GxUoQ0bUrjzrO7QrA\nIABTSc7WbW3T9foDeDHQICZOnIj4+Phchln4ZGUBL74IdOgA1K5d2L0xGAwGg8FgMBhOEfS3uzjI\nhxtjIAIZYVavXo0mTZqclOOHQriujLlC0oIIog52mVIqBkBziNsiAKwEEKuUauzYtQNERP3gqNNW\nCzabTgBSdXyZXacDsnONLnf2pT6AL/368hOAlvkeaCGTlQUMGwasXw88/3xh98ZgMBgMBoPBYDAU\nlLAtZkqpMgBqQoQUANRQSl0BYC/JbZAMiyOUUlsApAF4FpLQ4wMAILlRKbUUwDSl1P2QecleA5BM\n0raYzQPwNIAkpdR4AJcDeBDAEEdXXgWwTCk1DOKe2AuSPOQeR523ILFptZRSlzv68hNkouwzhtRU\n4I8/gLVrJaZz3Tpg0iSgWbPC7pnBYDAYDAaDwWAoKPlxZbwSwNcQt0ICeFmXzwLQn+SLSqnSAKYC\niAXgAXAdyeOOY/SGpN3/ApKgYwEcoovkfqVUZ13nJ0hikNEk33LUWamU6gVgrF42A7iJ5G+OdqZA\nhNkTEFHmAXAdgAHIGYsGACUBYMOGDWGeklNP587A7t1AiRKShfHNN4HGjU9/thjDuUF6ejpWmy+X\n4RzHXAeGcx1zDRjOdRyaoOTpaC8/wmwzgLchAqe0Xu9H0nnlRgR5b6Pgs7gFWneWKYiI8t9uH9sW\nWAzQ1m6I8Itw1Aeyx6I5iQOAPn36BNhUNDh2DFixQhaD4VRyOn2qDYaiirkODOc65howGACIRvg2\nr0oFJdx5zGIBfAOJ2eoMET61AOxz1HkcknCjLyQt/nMAliql6jqsZvMgiTs6QFwZZ0IsbH30MaIh\nk0x/BuBeiCvjDKXUPpLTdZ2W+jiPQ1wZewNYpJRq7LCaDYMItm8APGn3Rbc5KcAQlwK4DeKCeTSc\nc2MwGAwGg8FgMBjOKkpCRNnS09GYYm5ZTvwrKzUOQEuS7XKp8xeACSQn6vUYiHWqL8kUpVRdAL8C\naEJyja7TGSKuLia5U8eePQvgApKZus4LEFfFenr9HQClSXZ1tL0SwBqSDzj68jlknrV7dbvfAzgC\noAbJf0MevMFgMBgMBoPBYDCcIsLNytgFwE9KqRSl1C6l1GqllHMeseqQCaC/tMtI7oeIITsLYgsA\n+2xRpvkCYtlq7qiz3BZlmqUA6iil7AnGWur94Fenpe5LDd2XlwE8DJmIegWAQwA+NKLMYDAYDAaD\nwWAwFBXCjTGrDaCefk8A5wN4Uyl1lORcAJfobV8rpYpDhNIDEIvZBXpbHQDFlVKHABwAMBuSnGOv\no05dANWVUkcB/AlJ7mGn0r8AQDqAiyDZH8cDWAtgsF87F9t9gbgu2n15DUEEqVLqPIiLZhqMK6PB\nYDAYDAaDwXAuc8KVkeSeU91YuMJMATgM6aCdjOMZAPcDmAvgIV1+F4A/AEwG8B6AvwFQKRUB4E5d\npwVEXM0BcFyXUSkVByAewHoAtwLoCGA6gPscdXrqvs+HCK2hEOH1AnzJQHLtS5DxdYYkNjEYDAaD\nwWAwGAwGQHJQzDvVjYQrzA4AyHK6ASqlfgZwg44luwEieraSXKeU6gdgA4A1AJZDhE9FAPtJrgew\nXik1EsA4AGUhE0LfD2A/AItkKoBUpVQbyPxkhFjFhuq+pOp50e7TbXcCsCvEvgQiDQDmzp2LunXr\nhnlqDIYw+OgjoEkT4KKLcm776y9g1SqgS5fT3y/N0KFDMXHixEJr32AoCpjrwHCuY64Bw7nOhg0b\n7GztaaejvXCF2TYA9ZRSOyCufishiTT+gEzuHAURTh0ArCOZqpTaBsmqOA5iJUsFcJnOnrgGYul6\nHZLW/gdIPNhqAG2VUpEksxx1UiEWuya67Q4AJpGkUuoLSAzcu5C51vLqSyC6AkDdunURHx8f5qkx\nGMKgQgWgf38gKQmIi/OVp6UBjzySs/w0U65cOXMNGM55zHVgONcx14DBcIKjSqlLALwBoD0c4Vgk\nvXYlpVR7SH6L+tDhWCRnhdpIuMk/3oRYoeYDGAOgKcRVcBoktus4gImQ2K8uSqnLAUQDOAjgA13n\nT4jQmqaUagqgOsTl0E1yp66zXB8rSSlVDxKXVhLAqxCLWyRkQuvrlFLDlFJ1ANQEUB4yKXXlEPqS\nDe0eOTTM82Ew5I+4OBFf/fsDaWkgIaIskFg715g1S85FINLSZPvpPI7BYDAYDIZzHQVgCcTw0wIy\nLdidkJAuqSDhWB9DkiBeAdEt05VS14TaSFjCjGQigJsAXA1RjOV1R3s7qr0K4HcAiwCsg4ihDxxz\nmAHAowAuhFjI7AyOznnFjgF4CsD/ICnuH4UIwhmOOr9AxNk4ABshGR3THHOYhdoXm6GQGDSD4fSg\nxdnf1/fHNcWX4d+uRpQBANq1OyFYs2EL13ZBZ+s4NccxGAynBvPwxJwDg+HMoSWAywDcRnI9yaUA\nRgIYqJSyPRDvh4RQPUYyleRkAAsQhuEnXIsZSC4h2RBAO4j16TCAWEh8WHFIko1KEPEWDyALQFu9\n+06INesdiLBqCFGbAHCjo04tSFKP1yEnYR5EALaDTGqdBaAbgNsB3A3J4rgVwMVKqYoh9uUESqli\nEPfIHwDxqe7atWu2JTk5OdxTZfDnnnuAFSsCb1uxQrY7qVMHmDw5cP3Jk2V7qOTnz+90/GHGxWFc\n8VH4IrM9nosYlT9RVtB+Ovf3/4yc+wf6jML9TEPBYU2klYb//kP+rIl+Vsm9ewFa+TiOwWA4NZiH\nJ+YcGAxFiOTk5Bz3/0OHntBUlwNYT3K3Y5elAMpB3BYBsaQFncorJEiGvUASdaQCuB5ABsTqFQOx\ndGUAuFnXqw2JHfMCaAbgWgCZuk5FXWcAZG6xfRDz4DgA/0Diwuz25gH4C8ASvf4dJLviq3pdQeLf\n/gPwWCh98RvPhbr8DgBctWoVDfkEIKtWDbytUiXZ7vFkL/d4yNjYnOWJiaRS8hpKeW5YFulyyWso\n5fndJ0z++cHil3BxcEM3v4SLO77JxzEL2k9nPf1ZzBs1KmB5yJ9dsPJwsCxaNVxsCzd3XBZgHDNn\nBh+bZcl2/f6vunKcbbVPzud2Urn77uDnyeOR7YZCYd68eYXdhbMf/TuT9buVbb3IXaenEj1m71aL\nS5eSB3+xisw5MNeA4Vxn1apVhHjtvQfgE2bXD6W0fuis11MBPO5X5zqIYagEQ9FYoVRyHHwCxOK0\nQIulzyGxXFP09g9056+HWKC+AeCBZDIZArHQ7YTMQ9YQkqVxF8SN0Qvxx4zTA/gRElv2gG7jRcjE\n1ADQS7czEWJRmwpgD4BkAO+H0he/cRlhdrKoWjWwOLPLK1XKfsOeyw38Dz+Qy3om0gvFoxNFhGVN\nkvVlPRM5ejQ5Zw65c2eIfdN/fplbLDnW7xaz2vnWA5H1u8WjrVycOMTi77+TRzdazGrvYsZmi1lZ\npNdLZmWRmZnyPhy8Wy1ure5ijQiLlkVeVtLixovkzzls9Nh2/2TxwAGGf3PjL8Kio8n4+NxFmY3/\n9pMhykj+9x95fVk3CfD/yrt58GAufc6lPCuL7F1FjtP9fDePHStQt04+/udr5kxywgQyJcVXbos3\nyyJfesknOu39neLNFqyBBJ8tWEMVfKGKX4OhAGSOn8DVJVtyxp3unNf0ufI9syz+rR8gba1eNESZ\nwWAIWZh1YnBhdr3WNcUZitYKpZLj4D9qixd1R/6FpKB/RW/v57BKEcB2yITU3wN4QddZqK1Z1B39\nHkAZP8W5S4sx6tepTsXpEFJ2Xw5oUTUewMpQ++IYVzGIde0hI8xOAv7iTK8fr1qVK1eSswd4uD8q\nluOrJHAvYvlAQw979iS7dydvvpns2pWsXVsOAZD3IZFZUPy4xM3MguJ9SGRkJHnBBb465crJerVq\n5CWXkJUrkxUqiL4oWZKMjCQjIsg6JcRC1Q5ioaoGi4AY4CIiyFKlpH6xYlIGkNUg+7T128de7HqA\ntFOypLR70UVkzZoyljp1yLp1yXr1yPr1ybZVLS6PkmMNHSqnKTFR2loW6eKVFS1WqSLjufRS2b9+\nffKKK0QvXXmlvDZuTDZqJOWtLvL189uSLt5+lcVOnchOncguXeT89upF3nIL2acPee+95G23yX3Q\n9deTg260+GtlF0e73NwUHc/9EdEcUyGB/0XEcmhTD++6ixw9mpw4kZw0iZw+Xe6X5swhPx/l4bEy\nsfy5fwKPlYnlygkefvUVuXIl+f335DffkN9+K2L755/J334jN24k162Tsm+/lXo//USuXk0uWULe\nc43Fr5WL6xPd/Fq5eN+1Fr/7jty+ndy7lzxyRMRtVnu5ifF6mU2Ueb3krl3k9BFyXj56RD6/ScOs\nsEX0KccpzixLviiRkSLO7O3R0fIlaNHCd9MWSATb58Ap7HIrz43TYDUmWXSthrYwdQpUp0h2bg+1\nr4GOaRPomCeTIiq0l061uAqNSIB733dn71MRsRydDka75AHSA/XdeVc+lyii31vDuYFDmE0FsJrZ\n9UOc1hkN9foyWxM56txpG5ZCWZTeKSSUUncASADQB8Am3diTAGaTvFMp9TkkPb0LMhfZZIeY+gLA\nCC3mvJC4L3uC6SSIC+K1+rhbIZkZ74VMMJ0AYDQk80kpLbregGSGfAcSVNcDMjl0E5Kt8uoLySf9\nxvadbrdX27ZtUa5cuWxj79WrF3r16hXyuSoMDh0CpkwBYmOBvn2B4sXz3mffPiA1VZYtW4Ddu6Xs\n0CHg8GFZjh0DoqOByy8HLr4YOO88IDJS9v/tN+Dnn2V7/fryeuwYcP9L1VDxwJ/IRASi4IWFqqgV\n8Qe8XqBsWWDcRa9i4KaHMK9ZAt6vOgT79skx7eWii4DrrgOuvhr45RfgwsH/Q/XV72Pz5Tfjj1cW\nonlzaWvnTsDjEXf8o0dliYwEihXzLcWLyysgfau5YxlumNAeix91Y+/l7ZCVBRw/Dni98qoUEBUl\nS2Sk9Lf+7mWoP7A9Pn/KjZ112sHrRbYFkP0yMnzLgQPAkSMi2ex69vtWW2bh37rtUKdzHDp0ACJ0\ntKfbDWz4JA1VtizDmoZ9kZmJgIvXK+05lzJlgGtLLcPVz7TH5B5ufJXVDhERvnHZS1SU9OvIEaB0\naTnXx44B+/fLOF9b3x5Pt3WjXsbPuHXlQ1jkSsCc8kOwbRuwbZuMKytLzrWTwXgVk/AQHkQCXsOQ\nAn2XqyENc6L648CrSbj+gTgsmZKGMg/2R9+sJPyBuBP1IiKAqt40vIX+GINRGI0xuK94Ev5QccjI\nAC7xpiEJ/bGoSxJe/SAOEwam4crX++OJ85NwsGIcypaV75H9WqqUfOZlysjxMzOlvEwZaat4cSAm\nxvf9CGeJiABKlJDrMyNDPpfISLnW/vkH+PiJFXji2y5IqTsavTY+De9FFyO6SgyUHd96443Axo1A\ncjLQo4fE8HXpInPitWmT/QTa8Sn33w8MGAC8+Sbw+uu+9UD7BMM/vu9UZA8NNpbcxng6sMf6zDPA\n00/LmLdvB66/HqhVC3j11ezlHToAr7wCDByY81grVgBPPQWMHSv7OI8ZF+eLyZw2LXu5P/fcIz/w\ngc7HihUSEzptWvbyWbN8sUr+n11aGvDee8DixYHbtPcN1Je0NGDZMulPAXi4Wxp6fdQbxbKOoMx5\npXD+5/NQ7vMFwMKFwLx5OdvOrd1Qzk+bNjKmzp2BBx/M/nnZxz54EJg0Sf4cQyXUcxWgnndrGr65\nrD9mlxyAYQfGoMraTxDTMMBxzkWC/eYEKz8N31nD2UlycnKOnBLp6elYvnw5AAyC6JELqePMlFID\nIEahSiQzlFLjAFxH8gp7f6XUPACxJK8PqROhKjgt4G6CiJvjEAtTBnzWs+N68QKI0fXr6PW/IK6M\nttVrreOY90JcG70Q98bxkKQirzjqJANYC58r4/f6OF31uoJYxH4C8D4kxuy4rhOwLwHGdgtkbrYz\n1mLWrZtYfZQSK8t774mLXWYmuW2bWC1mzCDvu49s04Y8/3yfpQcgq1QRK8zVV4vVqmdPsl8/qd+z\npzysj4nJvk+1amLl6thRLETly4vlqmpV8hgixFKGCI4YQb75plhQMr7WT/kTEkJ7cm/HlN18c/ix\nZf7YT2DdAVxmTuY+hUFB++ncPz5eLDS5fEZZWeTx42K5OvyZh1nlYnnw+QRmlYvlPws93LyZXL9e\nLGS//CLLzz+LhczjIZctI7/7TsrWryfXrhVr2doPLB5p6Yg50RzdaDG9iYtfJVl85x1y9mzy9dfJ\nqVPJD4bJk+YPhrmZmEi+9ho59zmLuxq4uPWr7BYyzxyLv8e5+Ex/i3ffTd56K3nDDWS7dmSzZjL0\nyy4Ta2f9+vJdPu88+W6XLJn9+38yl2rVyNlXJpAAX4lLYDVY/AYtuTayEX8p3pirS7bg4AtTmB4Z\ny4nVE7g/KpaDG3vYqRN57bViGe3YkezQQT7Gns0trirn4pR6k5ihorjw8pE8VCKWKQ96OHky+cYb\nYvWcNUt+FxYulGXxYvLrr8nly8kVK+SaXb3Q4r7GLq6d5OahFi5u81jcsYP85x9y3z7y4EHy2DH5\nTuSbU+QSW2Ds68Lj8b3Gx5NlyuR0901MzD3mMiUl57GcVkx7e27Xbn7iOp2WJ//3LVtmt8Lmtm8o\n5WGSsVm8B8bfb3HWGIvfoAXXqMZMr9k4cL/yajeU82MfY8yY7P8pwcpDJdRzFWD9QFMXW8PDvy6T\n110NQji34VqSQrVMh1IvUNv2fhMmyE2D0wJs7+d0xw7H2pXXOcytbl7lBkMuOCxmTbQW+QTZw7Ge\nZXYL2kGtZZzhWB3tOnkt4QqzMhB3wHqQDCQPa7HzPiSffxbETfFmxz7bdZ2mEAvXFmRP/hGnt++H\nuBQug2RHdIq3O/XAlsDndpgKnfxD15kJyRD5KMQal1tfmgUZ3wtnqjD75Rf5NGfNkpvca6+V9VKl\nxCPKeQNYrx7Zu7f897zzDrlmDXPG7+RBVhaZkZFLBdudMULE2Qm3xnBvvvwTfeQn8YdNOD/sBdmn\nMChoP4tSjFm4NxvBBOkpcn/xeuW7f/gweeCACJN//yX/+ov8809y61Zy0yZx11y3TsTmDz+ICP3y\nS3LRInHV/OQT8uOPRQStWkUe/cL3wMIbG8t1UzxcNNR94sJN7OHm0KHkvOYi3mY3SeCtt/pcgLt3\nJ3v0kPuhW2+Va/zZjrL/giqDSIDPVEzI4aob6tIWcqy2cOdaLyKCLFGCLFtWxGylSjzhlnvZZT7X\n3vr1xQ33yitFG7RtSw5uLG7OU+sl8ECxWI5o72GvXuQdd5B33SXut4MGkUOHko8+Sj75JPn00+Qz\nz5DPPks+/zw5frzc99kut04ROmOGCPq335bfvvnz5QHWwoXyuXzwgbwuWOAr++gj8usZFvdc4eK6\np5J5vGwsf306mQdqxzOjTDTThiUwIzqWm5I8XLeO3DzDw4zoWG6e4WFqKrlzgTy0SF/s4b//SsKf\no61c/CvFwwNNXVzdbxIzVRRfqTGJf9QU0Zunq62+xg5/5uGOHeShpR5687rmHNf40Y0W/63Vgv/V\naExv81xEWYB9A67nF8vi9tri0m3/7W5/W75na1RjLnnSQ9tVOax2Q/lNcogwr1L0jh5TMFHmf9y8\n+uwn+JMHevh1hItHN1qsU4d8uFsIYw1XgIQq6sMRt842nC7XjbWw9njkQo+JkQcP9oMA+6FEON8h\nSx62ffSI47c+mIi0LGm3Z08ePpzLOQmHoupybTilOIRZPIBLIPOUHdSibDyACGbXEu0ArAJwBMBm\nALc7t+e1hCXMdIMNIDFdGQD2avX4CiQhxxEAUwBYkFmxm+i62/S+U7XSdCrOLnrAb+s6qZDMjE7F\nmajrXAdffNmTur07IAlAftZ9Oj+UvgQZW/yZKsyeekpugpyJDb79lnzlFbEqLF4sgm3//tPQmSAx\nZjkSf9icw1kZTwoF7ae/KAv0x1sYWRlD4UwRznkR6MYoJkaeojRq5LvJsS0roVib7XMxaRIZFUWO\nHJljn8xM8uhRsXz++68s27aRqakSA/jrr/K7seETiwebu7h1hpt7G7u4fLbFxYtFuMyfT86bJw+F\npk+X35tJk8iXXybHjRPBNGqUiKiHHiKHDCEfflheBw4kBwwQy/ztt4ugfKuhCM/X6yawUycZQps2\nMvwmTciGDeW01KpFxsWJ6LvgAokrrVhRfgdjYsSgVaKEDD1cEZqbMB2MhBMC1X4/GAnZ6raGh3sR\ny8GQONrW8GS3juq4VXv/V6JHkgDbKxG9UVHi0VC9uozRjp298EL5Ga1Qgby6ePY22kd5WL68WHcr\nVpT9K1WSc1OlCnnxxWTLCy1+U8LFDlFurkJjEuANZd284gq5X+7QQeJRbW+JBx6QZdAgclRfiUEd\n1sTNXy9wcUw/i48/Lv89o0eTY8eSzz0nuubpp8nHH5fP+6GHREgPGyaf+4MPisju1o18rPJMVoPl\nu5/V39kjn7qZel4LDsNLvDTS4vJiLvau4uYP0S7e1tpi9+5yD/zII+Rjj4lw799fhHufPvKd6XWJ\nh/sQy0eKJ3CfiuUjLTy8807Z3q0bedVVpKu6RU8xF1/GEHoBeqI7MQuK46omsmZN+Q6VKyffu1tu\nkXFMmCDPdGbOFJGfnCxC/oMP5IHLp5+Sn7wumWAXP+bmrgYufjvP4rffihX6yy/JpUvloczSqRb3\nXViXKd2SubyYi/dcY5EkX3iBLF6cnD/B4uYRM+Ua3EBu2UKmpUmc7c6d5J495P51FjPbungsNWec\nbci/NfkVa4F+f21vC1uE1a0rT2nq1pVt+RVlJD/7zHcdfvyoO8/+e2NiuK1SI7aDm1uq5TOxlt8x\nQ/6/C/ZgsGRJeYoW6MFgv36y3aZtW1+csT8pKbI9EPndr6CcpbGATmHGMDVTfpZwRdlwbc06AMmC\nmKrF0AyHGIqGTOZsJ904DmAqswuzZlppUlu2COBa+oTZ4xDXx0N6W4Y+XnGHMGsOiS/LcLSzWR8j\nz74EGd8ZK8yuvFKekBc6oWRlDESgp021awcXX4mJsj1U8vODcab8yBS0n4ESGwTaP9BnVJhPEM8U\n4ZwXwW54nAlALEueQvsnBMnLdc3fRS6cxB/+xzod4tceU6huzmFgWzqPHhUPgfR0SSKzLJtFjwAA\nIABJREFUZw+5e7e4Ze7aJcvevVK2a5dYQv9eKe61uyYlMzMmljteSebhumIx2/aoWMx+e9PD774T\ny+iaNWTaUBFdv92bwPffF8ucbYH75BNy7ZPJJMD9w7RgTk7msdbiqjt5slgBn3hCBO2IEaKrR48W\n8TN+vJyiH/tIGz/ekcDXXhMh/MILYjkcO1ZEsS2URo6U47x5m9zYHqrTiBunSgbAEX0s9usngqxL\nFxFoLVpIUqErrhAxfPnllKQUAO+v52bdumSNGiIaL7rIJwQvvFBE4KWXyr143bpiKa1Tx2cpbdZM\n2njgARE0WVkM6t4351mLc+6Wdifc6OYtt4jbbrNm8hdQowbZurVPuLdu7RNRn3eR8/NhxwRef73P\nMtupkyQ+evhhcmY/OXZatatIgCur3Mz+/UX0vfyynOu+faVrdeqI5jiZFma73miXm3/9JUM/fFjO\nT8hu0PAltXJHuBhfQaxuNWvKz0jTpnK8G24g//c/8rlrPTxYLJZzmyXwYPFYvvI/D4cNI4cPl4co\nY8eSL75IzrnXw8MlY/n5jQk8UiqWC4d5OGUKOWWKPICZNo18Z5zF7XVcfP8hN/+s5WLS0xbff9jD\nI6ViubLTSGapSP5T/lLuKF+PB6Oi+UrzZG6u6uJbIy2+8Yb8vbzzjlwbn34q4vX778XTYN06uZa+\n+IJMSiKvrGhxdXkXX+oiiZxG3m7x88/JLTM9zIwRC7LXS3qXi5X65Zs92T6HwYPluk9Pl+v0l1/C\nz6YcsrAN9jvZvbt8aN27Zy/v10/K+/XzlaWkyFMaf5EVrLyg+xWUs+U/2Y+iLsyWQCZ1rguZaO1j\nLYDehCTZyAIwHZKSvh2AxpC4rd/1/mMArAawHjLh2uXa4kUAb+o6y/QxDkJS5NcBMFvXuQY+V8YX\n9bFti1mqFl4VQ+lLkPHFA2Dbtm3ZpUuXbEtRnssjPV3ch958s7B7wsCizMYWZwbDyeBMEc55EUgM\n2+4+KSm+7WdzVkby7Igx8+97MIFpb580KXDsWSjnNT8i1v5uNWokr5YVvmX9VMTa5vY9s6+FcNsN\n5fzY7Q4ZIv9NnTqF5I1x9Kh4pxw9Ku7Me/eKiN++XdyZ963R06p86ebxNi5aX1tcv16s0Fu2kH/8\nQe7YQe7+Saxdgcbm9YoFe+1aifP0eMivvhKr0ZIlImjfe498911y7lxyyeMiQFIGujl2rM9C+dBD\n5D33iFjt2lWG2LIlmVBdROuESxLYsKGI5xo1RFTbzi0VKpDDy0i9YZEJLFZM7uujonxRCgDZXknb\nHYu5WbKkbBsWpS3fUYNOVEysJWU9L3CzdOnsxwhFfK6KdXHX9xYzM8nJj4q1086SbFuph0T4rNS1\nilncVkvO7/baLl4aaeU4bqVKZOfO5J13isV1yBCxwo4cKQ9BXnpJYpbffFO8At59l1w21sPjZWO5\naWACM8rG8pc3PNy4UayaW7eSf/8ty78/Wsxo6+LxTX7WTFuc2SIskCiz8RdToYqr/O5XUPQYMzZb\n/O8/ntz/CkD+BwNhPzEpIPPmzctx/9+2bduiK8xy7CwiiFqgnbETTDvaOSMtZkuWyCeZmlrYPTEY\nDAXGnsfM+Ud2ts9jVtguscHwF2W2CLNjMP3LAyUACSbagiUCCUWc5UfEOkWOvyDL6+bpVFtNg33P\nLEv6+9JL4bUbZowZlZLXwogxOxnnNFzRHKqoz6Oe1ytTluRo295v5Eix8l96qZjuoqPF99PRx4wM\nEbf//iuidsMGEaM//eSbbiXNbTHjqpzjytxi8VBzF1cvtLhkic+CvLx7Aj+cZPF4m+zn90grFxe8\nZHH2bLHIffKJdLFLF7k04uPl2VfNmuI6fP754hZdokROoRjMjTmYNbMt3PwKLl4ebbFcOXJmsX70\nArQiq9MLcH5sPzZtKm7b/i7F0zqlMFNFcWXTQcyMiOKSfimcNk2E4vz5Mo6vvxYXWTt2OTmZXHpP\nCrMiorjlukHMiozitokp/Pff3PMDbNsmMdIFwTNHXKbbwc3Nl4gwPSnY4stfnAUrP0kUdYvZWABt\nAFSDxJq9oTvbT29fpNfPqAmmHeM7I4XZ449LHEHYJnmDwWAoChTVoPpw5zFLTJTgoGACMyVFfPs8\nnuzHdArAvLLV5UfE2sf3F/z+4ixQm4XlnpTfdsNJXFFUsjKGOrZQ2gz3/JwJMWahPCByisiYGLEK\nn8TvrNcrVtL0dHLvh+I6+c+IBGZGx3LLTA/dbnHD/Pxz8sMPxWV50SIRSJ884SYBLhrqPuEmOnYs\nubtcdRLgrnLVOXCgWDb79hVB1rWrZNlt2VLciWeWE8vjG8UHBRSKwZZXIfu9ikHZysuWlXjUCy8U\nd+RateSU2dtbtZJTde210pcePaRv994rmbrvv19ihAcOlBjP226T2M0GDWT/IY1kzK4IN1u2lPOw\nfr3ERqanS1xzvvAXYadYlJFFX5hN15arLPhiwyzH9tu1RewwfBNAuyGJOewJpudC5jKz48aOQmLU\nnBNM/6kFW5Yu363b9p9gep9+zYLMf5YC3wTTefYlwPjOSGHWvLlcyAaDwWAoRPISmG3bFtwCmR8R\nWxDLZ2G5DOe33XBSvQeKY7aPHW4cczh9PlnnNFyBVxAR5l8eqA2ny/WpyMoYDP/+Dh8u7QV7SFGQ\n72y41upg1kzbfbG6iLOAbow2thvioEEn3BG9XnGl3btXLI2bN0timD//FDfZ9HQyMzmF3sgoHrpr\nEL2RUfxlVArfe4986y1JDDdunMSyjhghWW7vv1/E1623imtnr14itm68kbzmGonfjI+Xj7ZRI1/8\naatWYunr2FGE2yevW/TqMf8X7+K1l1kBRWNkpAjE88+XSJc6dXxe1ldfLTGR3btLYqgBA8TN9Ikn\nyAPFoukFmAHQC/BQiWguXCjWwuXLxeV32TLJhrx+vZyb7dslbvjIkfA/8tMtzBRFkISMUupaAK0g\n6e+vhVjLZuptvSDxYAcg6fMtAM/pegkkn1BKTQXwP4jr4QBIQo9ZAGpqYfaZUmoTgAsgafjHQWLR\nZuu6JQGcB2CHFlyPAVgMoDeApwCsJ9k4lL4EGFs8gFVn0gTTBw4A5csDkycD995b2L0xGAwGg8Fw\nWgh3IuVQJycPZ5JuZ9v2ft99B/z0EzBunPShXTuZgH3WLJlk/b33gIoVpbygkz2fzsnpw23LfwJs\ne/2884AFC4B+/WRb//7AjBm+dSfz5wO9e8tE6z165FwPRn73KyhBxrxnQhJ+OxyHffuAI0dkOXrU\n9z7c5c+/FaIgFpdiCE/HlCgBREUBpUoBpUvLa3Q0EBMD7N6djJ07kxERIXWiooBjx9Lx99/LAaAJ\nydUn+5T5E7YwAwClVCIkzf0lAP6P5Ie63AXgKwDDSY7TZTGQ2K9ZJPsppSZD3BPjSa7Rde6AiLOr\nSX6thdklAKJJZuo6H0Nm045UShWDxJD9SLK5o1//ADhIskYofQkwrngAq1atWoX4+Piwz0th8Omn\nwHXXARs3AnXqFHZvDAaDwWAwGE4ToYrN092Wv0Cx6dFDRFn37iKWbAKJs2BiKi+Rld/9CkqwMQcr\nzy8xMWKVgJixjkdH46C1H4cPA4cOAcWKAZmZ2YWf/f7gQSA9HcjKkvXDh+U1PV0OmZkJZGQAx4/L\n+sGDwJEjq7FpUxPgNAmzqHB30KLsJkimwy1+m3fr16OOsgsgyTlK+G3b5qhTSr+W16/HAByzRZmm\nJIAIpVQ5kulKqQxIRki7X3YbGbpoTwh9OeP5+mvgwguB2rULuycGg8FgMBgMp5HcRFebNifPWhZu\nW8uWBRYiH38souzGG7OX22IsOdn3PjExsIiy1xMTAwus/O5XUIKNOS5OypctK7gws0VZdDSwfz9U\nTAxKHDiAEtVjcN7+/QU7dhBWrwaaNDklhw5IRDiVlVJTANwGcRs8pIvLKaVK6vdlIQJ2qFKqvVKq\nCSR+bDdEEAEimI4BmKOUaqiU6gzgGX2883WdvQDKKKXGK6XqKKUeANAW4rp4gaPvrZRSdyilLoMk\nIomET2yWCaEvZzyffAJcfTWgzpoRGYoCycnJhd0Fg6HQMdeB4VzHXAP5pG/fwCLkyBGxXAVy30xK\nku02y5YFF1A9esj2QOR3v4ISbMyAlBfEZRXIIcoAyGt0tJTHxBTs+EWEsIQZgPsgqejdkCQgCsBM\nALc46hDA5wAWOOp9q8vt7dsgCTu+hcSBzYQk6bDrHIXEjXWEJOsYCmCkbs+u49X7PgNgDSTLY6I+\nrn9fPoZkeWwBEW/lcRaQmgqsXw/873+F3RPD2Yb5MzYYzHVgMJhrwFBk8BdlNk5xdhYQlisjyWxC\nTinlhcwT9qEu2gkRT5NI3u2o5waw1VGnAskbHdsjAQzT2+w60SSbOOq0hwitXY466/zaGe23XUEm\nno4CcCeAHyBxZ+2VUhVJ2q6X2Rg6dOgZkfzj9dclhvT66wu7JwaDwWAwGAwGwykit5wYJ8mNMTk5\nOcfDiPT09JNy7FAJO8YsN0haSqmdADoAWAecSLjRHMBkXW0lgFilVGM7+YeuryDCya7znFIqkqRt\nAesEIJVkuqNOB8gcaDbX6HJnXwYCmEpytu5LeYjbZH/I3Gg5mDhxYpFP/rFhgwiz4cOBkiXzrm8w\nGAwGg8FgMBgCE8gIs3r1ajQ5jUFm4boyQilVRil1hVKqkS6qodcv0esJAEYopboopew099shEz6D\n5EYASwFMU0o1VUq1BvAagGSStsVsHmRS6SSlVD2lVE8ADwJ42dGVVwFcp5QapuPQRkMmkk501JkE\nmQx7v19fFgNoGe7YiwJZWZKRtUMHoGZN4LHHCrtHBoPBYDAYDAaDoaDkx2J2JYCvIW6FhE8szQLQ\nn+SLSqnSAKYCiAXggaS5P+44Rm+IgPoCEiu2AMAQeyPJ/TopSCKAnyAJO0aTfMtRZ6Weq2ysXjYD\nuInkb452ZgF4ARIb97DdFwD3AKgVYGwlAWDDhg1hnpJTz9ixgGUBW7aIG23TpsBzz0mafIPhZJOe\nno7Vq095VliDoUhjrgPDuY65BgznOg5NcFr80/IjzDYDeBsicErr9X5+uf0jgry3UcieGdF/3Vlm\nJ/wIlHcwAtmTiuRlAbS3O5OIOIkDgD59+uRxmMLnxx+Bzp0LuxeGs5nTabo3GIoq5jownOuYa8Bg\nACAa4dtT3UhYwkwpFQvgGwBfAugMsWTVArDPUedxAIMA9AVgAXgOwFKlVF2H1WwegMqQGLHikKyM\nUwH00ceIhrg7fgbgXgCXA5ihlNpHcrqu01If53GIa2JvAIt07JptNbtTv74B4F27L3oMdpIQJ0sh\n0wGkIfv8ZwaDwWAwGAwGg+HcoiRElC09HY0p5pblxL+yUuMAtCTZLpc6fwGYQHKiXo+BiKC+JFOU\nUnUB/AqZQXuNrtMZIq4uJrlTKXU/gGcBXGBPMq2UegHiqlhPr78DoDTJro62VwJYQ/IBR1+OA/iA\n5BBHXw4BGE9yQsiDNxgMBoPBYDAYDIZTRLjJP7oA+EkplaKU2qWUWq2Ucqarrw6ZAPpLu4zkfgDf\nw5dsowWAfY6MjIDEmhGSvdGus9wWZZqlAOoopew89i31fvCr01L3pYbuSyKAAUqpOwBcBLHulYFY\n6QwGg8FgMBgMBoOh0Ak3xqwGgPshCT/GQoTUJKXUUZJzIULIOdeYzS69Dfr1H+dGkllKqb1+dbYi\nO7sc29L1a27tVNZ9mQOZvPoZXXYIIvr+DW3IBoPBYDAYDAaDwXBqCVeYFQMQCeApvQBigbofwFy9\nXQH4TSlVHGLBegDZk22UA3CxUuoQgAOQFPZP+NUpD6C7UqofgD8hIvBHvzoRAF5TSs0EsBbAYL/t\nJ/oCiWOz+5IIwGmJO4FS6jxI7FwaTIyZwWAwGAwGg8FwLnMixozknlPdWLjC7AAkvf1l8GVJ7ANg\nqH4/QJc/AuBnyKTS7wHIArBGKRWh65eAzDl2EcSilQERYzuVUnEAGkMSh7QB0BHAdIh4I4Bdel6z\nKIjYGqvbX6rr2Va0XPsSZHydIRknDQaDwWAwGAwGgwGQ5IDzTnUj4QqzbQCqO90A9cTSf+jEGj0g\nFrRYkmu0xWsDJAHHZIjwqQyxdkWRXKqUGgngJYiI+gEisnYBqABgC8lUpVQbiFUulWS6UmoogE0A\nYkhuVErdB+AGALcAWBJiXwIRDwBz585F3bp1wzw1BkMY/PUXMGYMMGoUcNFFeZefZoYOHYqJEycW\nWvsGQ1HAXAeGcx1zDRjOdTZs2GBPo5WmNc8bANrD4fVH0mvXV0q1h4R81Yf2+iM5K9T2whVmKwFc\nrpRKB/AfRKg1AnA3xAIWBWAigBFKqS3wuQQeAvABxP1xPYCdAKbp7Iu7AZQFsFhnZGwBYBGA/wFI\nUkqNhwisSwHcrZQqptt6EsBYpdQwSEbH3ZC0+omQSbDz6ks2tBVuMADUrVsX8fHxYZ4agyEM4uOB\nBg2A/v2BpCQgLg5ISwMeeQSYP1/WC5Fy5coV3jUwaxbQrl3gc5CWBixbBvTte/qOYzhnKdTrwGAo\nAphrwGA4wTEASwD8BUlSaHv9HQcwAgC019/HAKZApvHqCGC6Uuovkp+H0ki4WRkXAngeIqwqA2gG\nyXDYCpJ04ziAFwH8DhFX6yACabGew8xO2PEogAshFrL5+tjT9OsFEMH3FESc/QpxSyQkjq0iJM5t\nOYBZAMYB2AhRpn/oOcwqh9AXf4ZCXB0NhtNDXByQlISjt/XHuw8sQ+YdDpF2LtOunQjWtLTs5Wlp\nUt4u6Gwdp+Y4BoPBcKqYNSvnb5RNWppsNxgMRYGWkFCu20iuJ7kUwEgAA5VStqHrfgBbST5GMpXk\nZAAL4Av5ypOwhBnJpSSfIlkHwFUAdkBituo4qiUAqATgaohr4DH93sk7AH4B0BDATbrsFsf28gBe\nA/A65CS8CXF1dB6nI4DbIdY6e260S5RSFcPsCxxWuB8AMd137do125KcnJz7yTHkzT33ACtWBN62\nYoVsd1KnDjA5iNfp5MmyPVTy8+d3Ov4w4+LwRqVR6Pl6e0w5f1T+RNnJ7Ge4n9GpQAvWbKLKFlPh\nCNeTdRyDwXBqMKLEPEAyGIoQycnJOe7/hw49oakuB7Ce5G7HLkshSQ3r6/UWyGUqr5AgGfYCcT1M\nhYgce54yF0SkHQNws6PudkjCkGYAxgDYAkn2UVFvj9Pb90MsWssgGRjXOY5xJ8QCtgSSbTFDt/+q\no85MAEcAPBZKX/zGc6EuvwMAV61aRcMpwOMhY2PlNZTyxERSKXkNpTw3LIt0ueQ1lPL87hMmmVss\neoq72BZueoq5mLE5H8csaD9nzvTV0Z9Fl9atfceYOTP4Z3T33TnLbDwe2Z5fLIsHm7n4+q1uHm0V\nYBzOfgfYlzNnnnh/rLWLU3q6ebjFyfncDOcGXbp0KewunN2cht/YMwL/8Rah8ZtrwHCus2rVKkK8\n9t4D8Amz64dSWj901uupAB73q3Od1iQlGIrGCqVSjp3EhfAlLdAyIBNKx2jxlAVJygEAtXWH/wIw\nBMC1evtax7EGQOYl8wK4AuKaeBDAK4468yAp8ffp9e/1cbrqdQVxf/wRwPuh9MVvPEaYnSwAsmrV\nwNuqVpXtzhv8YDf8Nv4izLHu9YbZt/z8+ek6xzeFsU8Y/dnX2MVqsDhpElkNFv9tmM9jF+SP3b+u\nx8N5pUuTKSlSnpIS/DMKV2yHydB4NwlwxFXuvPudS/lz18hxRrsCHKew8Re3M2eSEyZI/21xa9ex\nLPKll3yik8wpgEMVrIY8mTdvXmF34ezHssi6dbn8eQ+3bGHg37Jz4TtrWTzc0sXBDd3c27hoiDLS\nXAMGQ4jCrBODC7PrtR4pzhA0ltI7hYRSagIkecYtAO4F8DSAdgCmk3xAKfUZxMXwaki2kkm6w8UB\nfAWJG/tXl3XQgmg2gCQAj0NUZSpkcunluo0OEJfEUQCeA1AaQF8AUyEWuHcgvpvdIanum5JsmVdf\nSA53jKsYZBLqRwFMXLVqlQl2zS/VqgF//glUrQr88UfA8qzZb4NduiC112hcOns0Nrz4EaKvawOv\nF8jKkmXjRmDuXGDVKmBkxcm45+fBSIv/P8StXoQZTV7D6H8G4u+/gZo1gY4dxauxVCmgRAnA6wWO\nHwcyMrIvJHD+oTR0eLs/vuk4Cq2/HIOFNyThYMU4FCsGKCX7k9KHzExZjqWm4Zp3+mPF1aPQe/MY\nLOqahP0V4hARIfso5RtmsWK+pWxZoHRpICICJ+qeeP0zDfGJ/XF3RBJ+z4rDxo1AmzaA+iMN75bt\nj2/6J+HoBXGIigIiI4GoKN8SGSnHEZXrW45vSkP9V/pjWbtR6PrzGOwcm4SMKnEAZFwlSki/srLk\ntUwZ4OBBSQQZ+18aqj/bH/teTsKRynFgynzUGNkbv940HHU+fQ1bJn6ECl3boFIlaTsbK1YAXboA\nH30kg/Bfzycrk9NwpHd/fN5yFK5ZOQZl301Cs1vislfyd00M4Kr4zw9p+LVFf7xVZRT6bx+Dal8k\n4dIOfscpTPzPV1oa0Ls38N9/wI4dwOLFUu/66+W6io4GkpNlfIHOtX0OKlUCBg3KWZ6UBGzfLm5i\n06bl7I+T05VA5Z575DiBvi8rVoTWV8MZy9/zV6DkLV3wUInXMbPVm1C5XM9nM9P6LMM9b7fH2E5u\nPLXUuDAaDEWB1atXo0mTJoCEVTUleUIg6GQfWwE0IrlOKbUMwCqSwxx17gQwkWT5kBoMRb05VN/P\nENVIiMj5F5KC/hW9vZ8u9+o62wHUg8RuPa/rLIS4GBKiIL+HJBBxKs5dEIsX9etUOBQnfBauTF3n\nAMTa9SKAb0Pti9/YvoNY5s5oi1lWFsO3JGkyM8k9e8gtW8i1a8mVK8kvvySXLJGH8vv25Tz2wYPk\nd9+Rv/5KHj+uC6tWpRfg0UuqcssW8kAlWf83uipvuIGMjiYHI4EEOBgJzCkxZKlfnxw4kGzfnvy4\nxM0kwEWRN7N5c/Lhh8V4dvfdZK1aZPHiOfePjCRLliRjYsjzziMrVCDLliVvriDWk5v/n70rj7Op\n/MPPOzN2M4aILBlbGkoMFVnGRCRbSopEprIUMaVFJaO0WMoQWRuUTI02FaWiO0YUWeJXGtsdRJRt\nZiyz3uf3x/cc98x1Z+beWcn7fD7nc+551+/7nuWe53yXt4qNdeqQNWuSVatKmYoVRb7Klclq1cga\nNciGDclQSJ1+1aVOrVrkNdeQ1atLuWrVyKuvlj78/aXfnMYFkIOwmEGw85ZbyF9+kWlLTCTbtiXr\nKTsHYXGu9XPaBtQSOTvA5nXdurBzDcSscg3COAHjLzpHpUvLPFWvTgYFydw0bkwODIpnkk8gp9SK\nYpJvIIc1jWenTmSPHmSvXmS3buRdd8nvvn3JBx8kH3qIvP9+sndvsnt3ybv7bvKee8h7Quz8UYWx\nbys709PJvq3s/NEnjOG32zl8uJz/l14iX3+djBpjp71+GJeE25hYP4zzxtk5darkTRhs58byYWxa\nwc6//ybb1Zbjjyfb+dln5HffkRs2kDt3ygfqo0fJ48fJc+dkS06We6rIER/PDP9ArpkYzx07yN8n\nxtLh60sGB4tgdrvcEL6+osE06uSolbTbyZAQuRhNTZuphfBGm1lcpmZFrHnNN0zto1ULadVeWvNN\neXMz37VqQ101m1ZtaG5aovyYD7sbh7Xf3PosBg3sG2+Q/RBDAtz6XIwkTp1KtmmTs5l5QebHHNN1\n111sEm+2PWuW5BcX7HZu9jfM2kuH0bHfXnx9X+rw9hrUVgMahQiLxuwJWFyx6LT6OwWglHH8JixW\ngXRa/a2ypuW2eUvMXjHIUbohXJaFYKUD+NI47gZZJHoDgHhIqPrRkGAjxyD+ZDdC1jX7BxLowwEJ\nBhJktLcZElTEnIipcJoyDjD6mQ4JDjIPwEkAMQA+N8qsyE0WN2PrBwmnzw4dOrBnz57ZtstBnb9y\nJVmpElm3LvnBBzm/UB4/TsbFkfPmkU89JS/FDRvKO19eL+8VK0r79erJ5uPjzCtVSt4DS5cmEyBk\nLA0+dABMwLWsVo3s1Ilc8lg80ysG8t/xUcyqFMjd0fFcu1ZkWr9eCOHBgxaBDfPFjN596MjFtywr\nS16m09JyeZk2XyhtNu9N/bypQ5EjKYk8fZo8eVJI77//kv/8k/cLv8NBZmSQ58+TKSlCiv/9l/z7\nb/LQIZmfQ4fIv/4iDx8mjxwhk35zypneLow7v7Jz2zZy61Yhz+vWkT/8IMP45hvys8/Ib78ld+wg\nN2+WvF+mCLE79NxMZgYE8vxkOUd/LoznF1+Q77wjhOfVV8lx48hnn5VraPRocnl7IdsxbaL48MNC\nunr1kuvr7rtl696dvOMOMjSUbN+e7NxZyFvv3mTPnkLeBnWw83/Vwzj/BTuTkmQ+kpPJmU/Zua1y\nGLsF29mwIVmnjhDhatXIngEid88AGytVEjLePFBI2ON32blhg7Tzv/+RdzcXAloXdo9Ja4UKcm1X\nqeIkpNdfT95wA9m8OdmqFdm6tYwpLEzG2K2bjKlPH/K++8h+/YSMPvkkOWIEOWyY7AcPlrJtEc+T\nCOQoRPEkAvlc/VgeqtOG/9RuzhNBLfjvda258elYplcM5O4nopheMZD/mxvPTZvIX38lN20Skr9x\no5DNzcvtTL4uhBnlKjK1aQgP/2TnmW/zQXSKy//FlYSVNCkjnWONj89ObP39hfi6puclr90uZKN1\n6+x1c0p3h/yQWHfjyC3dXd0iJOd3N7dzR9Uwvtw4hqdUID++J4ZZtxrz4W2/nsyP2cbEidlN5XNK\n9xSeEgI3pDy9fRjrKTtH9rDzKUxjys1e+gfn1t/lDm+vQe27qJFPLFu27KL3/w4dOpjErCXEreob\ng690NTjNq3RyiSCIO9Zkg8M8bvCjzmTRELMKhtbJumUAWA9ZOyzNOO5jlG9s0VpwuI6GAAAgAElE\nQVTdbJCkTGQP/jEMYh55ChLYY7JB1qx+aDGQCJCrjOOfAfwNI/gHxMfsL8jaas9AfMxyk+WWHMb3\nBi5TjdnZs6LdCQ2VF0GAbNlSPjq+9ho5fLi89DZs6HzZ9PEhGzSQ9IgI8t13yU8/FS3ZL7+IFmHf\nPnn537mTXLaMnDyZfPFF8vnn5aV8/nx5KbTZpP60afLyPn8+maGEtWX4+PDcOUNQb1++cvEx8xoF\n8DG7FJ2ys6Ew5DTrzJxJ+vl5ppkxYZaJiir4y7S3Lxs5Eedc2kn9086UWYtpt8u1vWGDaM9WrBDC\n+sEH5KJFcs3Pm0dOn06+9RY5aRL5wgty7UdECMl6/HFy6FAyPJwcNIgcMEBI2D33CDG96y6ySxf5\nKNG6tSi+WrSQ9/rmzUVL2q2bTPu/44Xc/j4simFhZA9/24Ub1tSCeqJtNrcOhqY3GRUvEL4egfG8\n5hohtvXqiVKgYUORJySEvO02Icxdu4pcPXqQ4bfbua1KGMfebOPvNcL43P12jhgh43/6aXkejB9P\nvvKKaD+mTSNnzJBnwoIFciqWLpXny/Llsn3+Ofn11/JxYM0a+XCwc45oDg89E8UM/0Ae+DCe+/bJ\nh4i//5aPE6dPy/MuLS3/1gFewZW8xMfLRFWoIPv8aCGtJKx1a2Y0C2FSk9ZM/SEPUmYiPyTW3Tjy\nImWudYvgOXgoXj6ULJ9q54EDZFQb0Zy9dUuM+Pbmp19P5seVhE2cWDBSlpt8uc2f8Xv1PDvrws4z\nt4axcRk75z7vwViLioDkN6iTWc+dZtis56lm2BXGmBz77czIcB7z/vtz/hjRvLnkW+pfcv/dGpc8\nLBqzEAB1IOuUnTFI2WQAPszOJUIBbIEEJNwD4CG64Rw5bV4RM5eOfQA8YGi3FsEZCXEBADtkVeyW\nhhZqn1FnIoCtLoxzkDHgeUaZOAALXRjn+0aZznBGZZxsDHoQRGuWYJCxahC/slxlyWFMIZcrMfvo\nIzmbu3fL8bp15O23k+XKielZ8+bykjh6NPnhh2J6mJpahAKZgT5Mldq11+qojEWFwpDTLGsG+jAD\nf5h1c3vxK0lNx+VCnD2BK7mNjSXbtKGjeXNmNmvB9FatmfReLDMDAnnsxShmBgRy7+J4bt9ObtlC\nbt8uJsg7d4pmcM/38pL3xxwbz9ZqRAL8eUAUJ02Sd8/x44VQjR0rRHPYMNkGDxYN3733ykeeXr1E\n8/dSeyF5T9xg4y23CLm84QYxZa1fX4hejRryvAkIkGePn59nGknr5g3xNB8xpUuTZcqQ5cuLMisw\n0GlyW7OmyBYUJB+irruObNKEvPFGeS62aCEfsVq1Im++WTYz7eabhT/d29LOLZXCGBkcw2S/QE66\nMYa7/UOY4uvP+U2jmFIqkC90iGe/fkLK775b9oMGCWkfPVqI/OjRYp79wgA7917dhvsCm3NPmSY8\nDX/2QwzXlxbS++ab8nFr2TJ5Xn/wAblkCRkdLenvvkvGPBHPc2UC+XHbKJ4rE8ilw+P57rvknDnk\n3LnyQWHBAvK99+Qjw+LF5Kdv2fl3cBg/7RfDJN9AvtgwhocahXHNe3auXSua9R07yD17RBN/6pRs\np0+TyTvsPN9GrqfU28J49nc7MzNzJseZmUKgz54VS4bz5+U/JyVFTIb//JNcOVvM91pVtTM5mRfu\n381jY3gSgRwYFM+ZT9n5V+Mwrp1g44mbwrjtczsTEshjx6S9tDQh7keOiDXIgQPyoWXtK/E8Xy6Q\nP/aJYmp5scw4fFjy//xT/iNXzrbzcOMw/nTLaDoAHmvRhQ4o/j5yFj/6SG7FWbPk48GePTKWPOHp\nM8lMnzqV6bvtfPwuO38qK+Xuvlvurcy99ryJS1E8A/NrWmzmG8+uCx8fmjeXh4Jrupdynv3dzk3+\nYexf08a0tnloquPjyYAApgY353uDbDzXphD+F7whrDl9GCxbVuz53Z3XIUMk/3LFf1SDayVmzCdn\n8mbzloyNA7DTEJAQ9dwuAG8D6G8QJX/IYs6mb1cagPlG/XkGIbvFYJqmGSQBdDPKJEACgYyGaNJo\nEDEHgDJw+pfdCgn8kWHpZ4/RRp6y5DC+y5aY9esnLxauKJYvyq4wSZkZndE8Ll/eu69w7uz/TXhr\n/5+fB8bl8pApqJzWP3LrH4/rH7y7c1SSvkGXC3H2BK7zFRsrtsUF8TFzNb1r1Mjpc+YtctJKegCH\nQ8xyz51zmvKePCn7I0fkRXnvXnlZ3rtYNGaJT0Uxo2Igt86M5w8/iOntV1+JNvPjj4WsLF4sxOPd\nd0VLP3OmaDanTRPNvmlyGxkpJNTUdD79NDlmDDlqlGg7TbPSoUPl8n7sMUkfPlx+h4cLWTUjey5q\nLsTxxfY2zm8qv+dcH3VBK9q5s9Nkt107IXhNmojpa9OmZLNmomgb2th2gV3+1E/aeauXjS1ayGm1\nmom7bn5+orCbUFnqRVaJYkCAXB4+PvLdKi8t6pxgqXu7r+f+qGZdVx9WPz8h4mXLikl7brJbt0FY\nzK6NDVNjl/s24b14HqhwPZsF2C/4+HrrOxvhK2N8MheSb7Ydp9qTAD9Bnwt55nis5QMD5VZq1Ej+\ngpo2Fd5x882ibW7XjryriZ0byoXxgWts3FQxjP3b2Nm9u2jOb79dTJ7btCF73ijm1p1Li1/vstdl\n7Bs3yhw2biwa6wceIAcOlPf2xx6Ta3bUKDEjf/ZZcsrjdu4LCuMHj9p4sGEYP3zNzk8+kXvls8/I\n1aulze3byV27eIGgHj4s92RSkhDnbOb1+f3g5krOgoPpqFiR6Y2Deb5JCM8190Iz7PIceeQR5zU4\noomNR4/mLuuhmHjeW1XK961m4759HneX+9g8+b/L6X+ob1+5kPr2zZ4+ZIikDxniTOvQwfm8d0Vs\nrOS7Q37rFRT/pf9kC4qbmHkblXEVgI8hIecrA3gNQH2D0DSBRFdcDDFZHAzxJVsH8Q27Vik1D8C1\nAGobbYyF2GN+CWAZyQeVUgmQkPcjAbwL4D2DpI2ABADZDjFrHG9sQyEBPT6CLPB2DYA78pIlh/GF\nANjSoUMHVKpUKVte//790b9/f4/nqjhBAjVqAI88Arz+egkL40FUxmzpGiWPgkTeK8loesUVMbCo\nUVRRGc3oi2Z+7drAvfcCe/YAq1Z5HjHTg8iXRTIPhRTds1BgjnnoUGDECGDOHGDqVJnLV18FIiO9\nk9M8x+fPSwjZQ4eA+fNlM+Y1MxNIS8sezdXXVzal4JyfyMhc+zej3ZIA7YnwGxYONWwofB6XcWTN\nnY8TUyQ67blzuLCdPSt7QOqWO5aI2xaG48TICagyayJ+Co/GyQCR04x8a5WxbFmgdGlnffNVw89P\nIsL6+0s03Ro1JBqt22vKmCeSODf+TfhOmgj7+Gj8WyEISUlyi2RmShtZWSJDuXJArVpA3UPr4f9g\nT6jISDgmROL3N77Cobrt4OcnslWrBtRMT4T/mHD43NQMnDEDqR26oOy673F8wjsoHfEEAgJE7v37\n5e/ryBHZjh93zq1r9F+HQyLyNjsVh+EfdcTbvWzYVC4UqakSDdfPL/u+2ak4PLG8I/ZH21B/SOiF\noX//PfDpp/IIOHfOGSXYnG/X45Zn4vDJ8Y7oWsaG79ND4cWrXTb4+sp5K1UKuCV9PWJTe+L10pF4\nMSMSD1f5CpvLyDWmlIxBKZHBep3d5liPRSd6Yn7ZUXjq/OvYhyBkoAzq4BCGYj6GYT7GVpbzWLYs\nsm0VKjj7N6MInzgh85+5LxEbrg9H0ugJOP7kRDyCaNRqG4SrrwZapa7HyNU98VOXSLT7PhLvdvsK\n76+tjbkZ4ag8fQJOjpmIEaWj0WVoEJQC/vhDztPttwMtWgDXXCORi8uWlb05tovgzXMqp2fnVVcB\nn3wCDBkieeHhwKJFzmMTy5fLc2LZMuC++/JOL2i9wkBx/V8UEWJiYhATE5MtLSkpCevWrQOAliS3\nFrkQBWF1AKpCWOTnuIwXmLbkX5Yas1275G/v229LWhIym6bMFabmTENDw4miWscsp6+4L7ygozJ6\ng2LwMWNIiHfmXf8hHzOSOWv97XaZl2nTvOu3pHzMXNvOS8NcAE10bu049tt54oQzaFRiopg5b9ok\nJpxffy1atFWryC++ECXKBx+I2eucOeIfOnUq+fbbpO0e0Tp+0y2KkZG8sL38svibjxsnGunISNFQ\nT5okx9/eJfU2txl5Qd24+wlJW/msja+9Jm08+6z4qg4dKsGR7rlHTKe7dhUN9B13iJvYhMF2nmju\nnKMTW+w82EiCO3XqJLdQZBVp/7lyUQyta2dC7TD+s0nKn9xq565rwti6hp116ojvb8uWOWt3lRKN\naWCgmERfe61oSW+8kXykcTyTfAP5TsMoJvsF8pk28Rw4ULSajzxCjhwp25NPkm8OF22mGTV4caSd\ns2aR/2szhA6Ap6vVowOgvfMQrl4tp3DjRjlfe/aQx+fG0uHrx7QPY8UCKjY2uw94TnAt52m9QkDW\nPjuPXB/GeQNsPH9bIT4nALH6cAd//yJ7v7ykTRkvqgw0NIT9DJfxAtOWfi5LYjZ3rpiwJCeXtCQa\nGhqXDPLrwG9FcZnzFoasRQFXMmM1DdVRGYvWPCm//ZZkVEZ38nk6jvzOZ1GS5vwGdTLrjR8vLycN\nGog9r78/GROT/8BUuc2hVdaAALEv9eDaOXtWgp2tXClmnzEx8libO1cI6pQpEtToxRfFH3fUKDEn\n/aCVkMAFN0axZ08xYW3fnrz1VjFXvukm8RNs0IAXzCl7+Nsu+MQC5G7UE8KKerma5N6LWKbDjzMx\nkunw4yMBsaxbV4hi8+bSd6dO0n+7dvIoueEGcthVscyAH2OqjWSG8mNUu1iOGSOX94wZMsboaAnM\nFBsrcxARIabba9eSP/0kwd127CATEiQS9PHjEmH65EnxPT19Wnw8ExPFHP2LL2SKTZPTXpVshac0\nMMmXKznLKb2QcEkTM4jpYjsAdQHcYGi/COB2I/87g/x0hATb+AkSov4XSMRDHwAnIOufWUNNvmHU\n62rRoNmQPdTkOINolTHIHAFEwhku/wRkEemNnsiSw/guS2LWvz95yy0lLYWGhobGfwx6HbOS87XN\nb78luY5ZQUmYt6SqKElzIfqYsWJF2XurGTaR17XgagUwbpyQs5w+UhT0mvWGsLpoM7P2yTgcQ0Rj\nllFXNGYpDwxhYqJoyXbuFO3mjz8KWVq+nPyjs2get7QdyVdekSGPHSv+sA89JHEGBg6UgENDhgiB\nHDeOjLtJ6n1VbyTbt5fTUKOG+IR6skRSfrZODew8cVMYT31h47YqsjTNDTeI5nPkSPKZZ0Rb+sYb\nMoXz5pHvvy/j/PpridK7YQO5bZuQvQMHxCc5JYXMdCVhRUzKyEvfx2whxM+ruqGlUgCmkHzOyH8I\nEqExHUBZgxith/ijrST5glJqqUHAAgH4GmVjIH5gd5L8Til10CBgVY0+TkLWJXsYQDkAV0H8zJIA\nVDImbB9Eq1aL5G2eyOJmfCEAtmzZsgUhISGu2ZckSKBmTXGlefPNkpZGQ0NDQ0PjCoWnfq+F5R9b\nVH62OflN5eX3aebPnw9Mny4vKFOnAqNGiaPewoXZ019+ueC+R/mVtbD6K0ofMxOmb9jw4cDcuZ77\niHlQz/TNTEsDzpwRHzuHA0hKkrT0dNmnpYmvY2rqxVSsYkXxgy1bFmhUKhHXvBQOZYzZsT8Rx3uF\nI6pZNH46HIRTp8S11nXzBv8gAFWRgiwIiTgFf3RpmYxy5YDy5cXn0ddX/E3LlRO5zH2FCkDlypJf\nvjwu1PH3BwICsvt/+vvL2H77bSvCwloCxeRj5udNYZKPKqXuhCw0HQQhSD9ZivwF0YqlArgfEqp+\nEoC2AJYYZfYBKA2J7jjU+L0UQsCOGmUOAmhupL8JWYz6AwCpJNOVUschRMsfEkBkJWTR6ZcA/OiF\nLG4RERFx2QT/2L0bOHoU6NixpCXR0NDQ0NC4gpEbCQoKchIQT8sVVn/eYskS90SjXTtJX7LEPdkx\n6+3bB9xzD9C3r5DDzz+XQERLlgg5+PRTKRMdLfkFIWb5lTU/cEfCzH5yC8Jkji8oyEnK+vZ1kjBz\nv2hR9mPg4oAdHTrIMZA7OfOwnjVYj/W1t1o1byfH/Zh96gfh6q+j8Xp4OLDEPQknhfi5I2zuttjz\nyRg2UsEPsjDyq2OS0eq8M3CRn5+Qs9RU4N9/ZZ+aKnXPnBHSmZkpxxfrpmKMzYqkfExGAeCtig3A\nLIg/V30IOeplyQuAaK+iLWktjLRxxvFjxnGYpUyUkVbbOF4NmW8/S5nfAaRYjo8D2G85VpBgHxs8\nlcXN2C47U0btX6ahoaGhoaGhUcQo7nXMcgrYkVcgj/zWKyiKy+zZNF80t3yaMTocskzEyZMi3s6d\nYj65aRO5fr0s07J8OTl5cvGaMnqlMVNKvQtZI6wXZI0xAKiklCpLMhWiQQOALkqpjgBSIH5fSQCu\nNvKyjO1ZpdQJSHj7/gbJawnRdKUYZV9TSkUD6AQJ3uGjlKpEMskkckqpQZBw+RFGu/5G3aoeyHLZ\nY80aoFUrUblqaGhoaGhoaGgUAXJb+qVdu+yauZy0mbnZ7UVHZ9eWzZrl3mzRPJ41y73WLL/1Coqi\n0uBaERAApKTIS29ysvM4IECOvYBSzmUaKlfOudzWog+Qnw0+XpYfDtFE2SDRDRUkTH0/I78GhGB9\nC+ATSzmbkQeIf5odQqI2AHjfaOO4pYw/gK8BdIasWxYBMVOEpUyAUfcVANsgwURmwEnIqltk+RoS\nsbG10W8TL8d9SSI1FfjmG6B795KWROO/Btd1PDQ0rkTo+0DjSoe+B0oQcXE5E6j77pP8wqx3qcOV\nlAGy9/d3krP/ALz1MctG5JRSDsg6YV+6FH2R5KOWcrEQDZeJTJI9XNoa4lLmb5J3W/KbQKI3Wst8\n79LP4y75gGjTBkICh2yC+KN1VEpVJXnc3TgvFx+zFSvEXrZv35KWROO/hpiYmEvuetfQKG7o+0Dj\nSoe+BzQuGbiSMhNWzVkBkdMC08UJr4iZBzgK0aJVh4TBN3E1RKtllslmSqiU8oVESzxqKVPdpe2r\nIaTrWB5lrPkKwEgA80i+b/R1yCgXDmCKu0FMnz79ko/K6HAAU6ZIQKbg4JKWRkNDQ0NDQ0NDQ6OI\nkFsUeS/NGHOCOyXM1q1b0bJly0Jp3xN4a8qYK0jaIYSok5mmlAoAcCvEbBEANgIIVEq1sFTtBCFR\nmyxlOhiEzUQXAAmGf5lZphOy4w4j3SpLUwBrXGT5FUCbfA+0hOFwAOPGid3ra6+VtDQaGhoaGhoa\nGhoaGgWF1xozpVQFAA0hRAoA6iulbgJwkuQhSITFl5RSewEkAngVEtBjBQCQ/FMptRrAAqXUCEi4\n/HcAxJA0NWbLALwMIFopNRkSLv9JAKMtoswAEKeUegpintgfEjzkMUuZ9yC+aY2UUjdaZPkVslD2\nZYMDB4CDB4HffgM+/BD4+WdZBqRt25KWTENDQ0NDQ0NDQ0OjoMiPKWMryFphZvjIt4z0JQDCSU5R\nSpUHMA+yiHQ8gG4k0y1tDICE3f8BEqDjE1hIF8lkpVRXo8yvkMAgkSTfs5TZqJTqD+A1Y9sDoDfJ\nPyz9vAshZs9DSFk8gG6Q9dPc6UTLAsCuXbu8nJKiR5cuwIkTst5ESAgwZw5wyy3FHy1G48pAUlIS\ntuqLS+MKh74PNK506HtA40qHhROULY7+8kPM9gD4EEJwyhvHQ5h9NWyfHH6bUHBq3NwdW9MUhES5\n5pttmwSLbvoyF6L2sZQHsvuiWREEAAMHDnSTdWkgKwvYvFk2DY2iRHHaVGtoXKrQ94HGlQ59D2ho\nABCOsCGvQgWFt+uYBQL4CeKz1RVCfBoBOGUp8xwk4MZgSFj8SQBWK6WCLVqzZZDAHZ0gpoyLIRq2\ngUYb/pBFpr8DMAxiyrhIKXWK5EKjTBujnecgpowDAHyhlGph0Zo9BSFsPwF4wZTF6HOmmyGuBvAg\nxAQz1Zu50dDQ0NDQ0NDQ0ND4T6EshJStLo7OFHOLcuJaWKk3AbQhGZpLmSMAppKcbhwHQLRTg0nG\nKqWCAfwOoCXJbUaZrhByVZvkUcP37FUANUhmGmXegJgqNjGOPwJQnmQvS98bAWwj+bhFlu8h66wN\nM/r9BcB5APVJ/uvx4DU0NDQ0NDQ0NDQ0NIoI3kZl7AngV6VUrFLqmFJqq1LKuo5YPcgC0GvMNJLJ\nEDJkRkFsDeCUScoM/ADRbN1qKbPOJGUGVgNorJQyFxhrY9SDS5k2hiz1DVneAvA0ZCHq9QDOAvhS\nkzINDQ0NDQ0NDQ0NjUsF3vqYXQegifGbAKoBmK+USiW5FEAdI+9HpVRpCFF6HKIxq2HkNQZQWil1\nFkAKgPchwTlOWsoEA6inlEoFcBAS3MMMpV8DQBKAmpDoj5MB/AZglEs/tU1ZIKaLpizvIAdCqpS6\nCmKimQhtyqihoaGhoaGhoaFxJeOCKSPJE0XdmbfETAE4BxHQDMbxCoARAJYCGGOkPwLgAIDZAD4F\n8DcAKqV8ADxslGkNIVcfAEg30qiUCgIQAmAngAcAdAawEMBwS5n7DdmXQ4hWBIR4vQFnMJBcZclh\nfF0hgU00NDQ0NDQ0NDQ0NDQAiUGxrKg78ZaYpQDIspoBKqW2A+hu+JJ1h5Ce/SR3KKWGANgFYBuA\ndRDiUxVAMsmdAHYqpcYDeBNARciC0CMAJAOwk0wAkKCUagdZn4wQrViEIUuCsS7acKPvLgCOeSiL\nOyQCwNKlSxEcHOzl1GhoeIGvvgJatgRq1rw478gRYMsWoGfP4pfLQEREBKZPn15i/WtoXArQ94HG\nlQ59D2hc6di1a5cZrT2xOPrzlpgdAtBEKXUYYuq3ERJI4wBkcWc/CHHqBGAHyQSl1CFIVMU3IVqy\nBADXG9ETt0E0XXMgYe03QfzBtgLooJTyJZllKZMA0di1NPruBGAmSSqlfoD4wH0MWWstL1ncoRcA\nBAcHIyQkxMup0dDwAlWqAOHhQHQ0EBTkTE9MBMaOvTi9mFGpUiV9D2hc8dD3gcaVDn0PaGhcQKpS\nqg6AuQA6wuKORdJhFlJKdYTEt2gKwx2L5BJPO/E2+Md8iBZqOYCJAG6GmAougPh2pQOYDvH96qmU\nuhGAP4AzAFYYZQ5CiNYCpdTNAOpBTA5tJI8aZdYZbUUrpZpA/NLKApgB0bj5Qha07qaUekop1RhA\nQwCVIYtSV/dAlmwwzCMjvJwPDY38IShIyFd4uJAxQPbuyNqVhiVLnHPiisREyS/OdjQ0NDQ0NDSu\ndCgAqyCKn9aQZcEehrh0SQFxx/oaEgTxJghvWaiUusPTTrwiZiRnAegN4HYIY6xsCDrAUmwGgH0A\nvgCwA0KGVljWMAOAZwBcA9GQmREcreuKpQF4EcA9kBD3z0AI4SJLmf9ByNmbAP6ERHRMtKxh5qks\nJiIgPmgaGsUDg5wd7R6O7v5xONFbkzIAQGhodsJqwiSuoTmu1lE07WhoaBQN9McTPQcaGpcP2gC4\nHsCDJHeSXA1gPIAnlFKmBeIIiAvVsyQTSM4G8Am8UPx4qzEDyVUkmwEIhWifzgEIhPiHlYYE2bga\nQt5CAGQB6GBUPwrRZn0EIVbNIGwTAHpYyjSCBPWYA5mEZRACGApZ1DoLwL0AHgLwKCSK434AtZVS\nVT2U5QKUUqUg5pGbALGp7tWrV7YtJibG26nScMVjjwHr17vPW79e8q1o3BiYPdt9+dmzJd9T5OfP\nrzj+MIOCMLnMBKw80xGTfCfkj5QVVE5rfddzZK3v7hx5e049gUWbSHsiUlORP22ii1by7FmA9ny0\no6GhUTTQH0/0HGhoXEKIiYm56P0/IuICp7oRwE6Sxy1VVgOoBDFbBESTluNSXh6BpNcbJFBHAoC7\nAGRAtF4BEE1XBoA+RrnrIL5jDgC3ALgTQKZRpqpRZihkbbFTEPXgmwD+gfiFmf0tA3AEwCrj+GdI\ndMUZxrGC+L+dBvCsJ7K4jOcaI30QAG7ZsoUa+QRANmjgPq9mTcmPj8+eHh9PBgZenD5rFqmU7D1J\nzw12OxkWJntP0vNbx0sc/9XONQjj8GAb1yCMf2/MR5sFldNazjgXyyZMcJvu8bnLKd0b2O1MbBDG\nUNj4d7CbcSxenPPY7HbJN34fbRLGDrDxcOPCOW+FikcfzXme4uMlX6NEsGzZspIW4b8P4znj2G/P\ndnzJ3adFCcscrFtHnt9lv2TmQN8DGlc6tmzZQojV3qcAvmF2/lDO4A9djeMEAM+5lOkGUQyVoScc\ny5NClsanQjROnxhk6XuIL9e7Rv4KQ/i7IBqonwDEQyKZjIZo6I5C1iFrBonSeAxixuiA2GMGGQPY\nDPEte9zoYwpkYWoA6G/0Mx2iUZsH4ASAGACfeyKLy7g0MSssNGjgnpyZ6TVrZn9hz+UFfscOcuPA\nWXRAMWOmkDDHO3K8ceAsTp5MfvIJeeqUh7K5/uF78gJgtzO9fRjnPGfn0aMe1vEUBvGop+zcvZu8\nrrSdu2vns21DruQddqam5kNOVxLm70+GhOROyky45hcGKSOZnEz28LeRAO+5ysZz53KROZf0rCxy\nYB1p5/4aNmZkFEiswofrfC1eTE6dSsbGOtNN8ma3k9OmOUmnWd9K3kzC6o7wmYRVEz6NSwhZU6Zy\nR8U2XDbMdvE9bf3I8l+G5QOSvd6lQco0NDQ8JmZdmDMxu8vgNaXpCdfypJCl8c2GxouGIP9CQtC/\nbeQPsWilCOAvyILUvwB4wyjzmaHNoiHoLwAquDDOYwYZo7GfZ2WcFiJlypJikKrJADZ6KotlXKUg\n2rUxmpgVAlzJmXGc1aABt28nPx4Vz5RSgXw7KIonEciIm+P58MPkQw+RAwaQ999P3nSTNAGQwzGL\nWVD8pnwfZkFxOGYRICtVcpapUYOsV4+8/nryuuvIoCCyVi3y6qvJypXJimp9f4gAACAASURBVBXJ\nChXImyrZuVaFsUsZG9eqMAbBzlKlyPLlJb9KFSkfECBppUuTdSFarQ4QrVY9Zaefn+SVKUOWLSv7\nMmWkn8qVpd8GDcgbb5SxNG8uPKdlS7JVK7LLdXauLx3GurDz8cdlmqZNk77iS4exbS07GzaU8dxw\ng9Rv1Yps3Zps25Zs3172t91Gtmkj6bfXFznDfG38uUIYH7vDzt69yd69yX79ZH7Dw8nBg8nHHiPH\njJF387vuIu+9lxzb185dNcP4xp027q0UwhQff75eI4qnfQL5fLt4jhxJTp5Mzp1LLlhAfvgh+fHH\nQo7jXotnWoVA/j4siukVA7llRjw3biS3bxeCvXUruW0buXMnmZAg7xwHDpB79kjatm1S7vffyV27\nyB9/JEf2kHO1dbqcqyd72fnbb+SJE+T580K4aLfTkQvZTk4mP3hV5uWz0XL+5o2z0+EozhvCA1jJ\nmd1ONmlC+voKOTPz/f3Jpk3lZJvjdUeCzTmwErvc0nODp1rJguJS1Rqa47fOg5UkW/M9ldVdmybc\ntVmYKK7z6SW+X2DnFjQnAZ76wpZdpktEc1QcmNhJPiCNvNGWd+ErCZfodatxZcBCzOYB2Mrs/CHI\n4BnNjOM4kxNZyjxsKpY82ZRRySMopQYBiAIwEMBuo7MXALxP8mGl1PeQ8PRhkLXIZlvI1A8AXjLI\nnAPi92UuMB0NMUG802h3PyQy4zDIAtNRACIhkU/KGaRrLiQy5EcQp7r7IItDtyR5W16ykHzBZWw/\nG/3279ChAypVqpRt7P3790f//v09nquSQGoqsHAhEBgIPPAA4OfBYgjnzgF79gAJCcDevcDx48Cp\nU8DZs5J37hyQlgb4+wM33gjUrg1cdRXg6yv1//gD2L5d8ps2lX1aGjD49YaodnofMuCLUsjCXp8G\naFZ6L1JTgTJlgMk1Z2C0fQyWhEThk5qjcfKktGluNWsC3boBnTsDO3YAQU/fgwa/fY4/m/TBnjc/\nw223iRyJicC6dbJPTZXN1xcoVcq5lS4te0Bku+7vONwzsyM+e9KG401DkZUFpKcDDofslZK58/OT\ntipWBG44EYeWT3fE12NtONIoFA4Hsm2A1MvIcG4pKcD580IdzXLm7w72JTjaOBTXdQlC9+7O+fzm\nG+DPbxNRZ38cfm06GJmZcLs5HNKfdatQAbirQhy6Te6It3vZ8ENGKHx8nOMyNz8/kev8eaB8eZnr\ntDQgORlodioO8xI64rlbbbghczse2jIGy9tFYZH/aBw6BBw6JOMyx2zFKMzATIzBk4jCOxhdoGu5\nLhKxxDccJ6dGo09EEL6ISkTg0+F42BGNAwi6MN/lygE10xOx0BGOSX4T8FLWRIwqH41DvkHIyACq\nnk1ENMLxcZdozP02CJMeTUTb6HBMqB2Nc1cHoWJFuWbNfblyci4qVBA5MjMlvUIFwMdHrqWAAOf1\n4c3m4yPXfmCgXB8Oh/R19izwzz/AimfW42lbT3zaLBL9dr6MrFq14V8zAMr0b+3RA/jzTyAmBrjv\nPvHh69lT1sRr1y77BJr+KSNGAEOHAvPnA3PmOI/d1XGHnHz7CjuCaE5jyW2MxQFznK+8Arz8soz3\nr7+Au+4CGjUCZszInp6XrEuWAA0aSB1rm0FBTp/MBQuyp7visceAwYPd97F+vfSxYMHF/Zq+Sq7n\nLTER+PRTYOVK932add3JkpgIxMWJPAXAM/clot8XA1DKcR7+VcuhxtplqPDNJ8BnnwHLll3cd279\nejI/7drJmLp2BZ58EnjiiYvbPnMGmDlT/hw9hadz5aYc7Yn4qXE43is1FM+em4hav32DgGZu2rkS\n4e1zqBiuWY3/JmJiYi6KKZGUlIR169YBwEgIH7mGhp+ZUmooRCl0NckMpdSbALqRvMmsr5RaBiCQ\n5F0eCeEpgzMIXG8IuUmHaJgy4NSepRubA0CAUb6xcXwEYspoar1+s7Q5DGLa6ICYN06GBBV521Im\nBsBvcJoy/mK004tOH7O/APwK4HOIj1m6UcatLG7G1g+yNttlqzHr39+pQWrShFy1inQ4ZDt+XLQW\nH31ERkSQd9xBXnutszwg2qLgYNHA3HEH2asX+cADomHp1YusX1+0QtY6V19N3nmnaG8qVxbtUaVK\nkp4KXxJgGnz59NPkjBnk2rVk6g/GV/6oKM++3Js+ZX36eO9b5grzC6zNjclMYdYpCRRUTmv9kBDR\n0ORwjrKyyLNnyaQk8uRJ8tRX8cyqFMhTkVHMDAjkoZh47thBbtpEbtxIbt4s28aNZFwc+d135Lff\nimZs40Yp9/PP5E8/kb98bOeZW8OYlpBd/rO/23mqRRhXvWvnokXkvHnk22+LiLFPyJfm2CdsnDqV\nnDKFfG+8nX8Hh/GPVU4NmcMhX+f31AnjCwPsfPBB0Sjefjt5yy2i4QwOJuvWFY1r/fpktWqiPS1X\nTpRY1uu/MLeaNcn3booiAU6pFcW6sHOjTxvu8GvOP8q24Pbyrfl03Vgm+wVy1nVRTPYL5NjW8ezd\nW26N3r3Jnj3JHj1ECzo41M5tVcK44KaZzFR+/LLFeJ4rE8gVz8QzOppcskS0nrGx8lz45hvZ1q6V\nc7F5M7llC/n7SjuTbw7jbyvs3LyZ/HujnWltw3h6u50pKWRqqqG9LCiKyCS2wDDvi/h45z4kRFTs\nnpr75taWVYsZG5v3vZsfv06r5sn1t6lyz00jUYS+tpl77VxXKoxvDrdzwYt2/oTW3O7TgsmNWriX\nK69+PZkfs42JE7P/p+SU7ik8nSs3xym3hLEt4nm4sez/uaEE/2vyq8E265nm2FYNsFnPao7tjbbL\nG1eEYvAP17hyYNGYtTS4yDfI7o71KrNr0M4YXMbqjtXZLJPX5i0xqwAxB2wCiUDytEF2PofE88+C\nmCn2sdT5yyhzM0TDtRfZg38EGfnJEJPCOEh0RCt5e9gY2Co4zQ4TYAT/MMoshkSIfAaijctNllty\nGN8blysx27VLzubCheSvv5KhoXIcGCgvlNYXwHr15EXu+efJRYvIDRvEPMwTZGaKGdmZM2ImlqNJ\nmGnOaL7JmmaN3r58uQb6yE/gDxP59DHzuk5JoKByXko+Zt6areRESIvA/CUjgzx3Tq79EyfIf/4h\njxwhDx4k9+0TM83ffyd/+01IzS+/CNmMixMS+vXXZEwM+emn5GefkcuXyweU9evJs6udHywcgYHc\nPD2eHz9uu3DjvtXLxuHDycUhQt7eaxbF3r2FiHXrRnbvLsSsVy/y7rvlHn+pvdT/uPpIEuD4SlH5\nIo2u5rx1Yb+ojI+PmPdWqCDDqFZNyGbdurxgltuihdO0t1Ur4QTt2wsx7tqVHNtazJzfax7FlFKB\nfLVrPMPDyWHDyJEjxfz2mWfIF14gX36ZfPVV8o035B1w2jQh6jNmyONhzhwxuTVJ6NKlMvexsTL3\nK1bI+Vi1Sgjp6tXywWD1anLlSmfaDz+QG2Pko8CuyBhm+Ady76QYnmkcwowK/jz8XBQz/QOZuDSe\nu3eTu3eT//uf7A8eJP/9V56X587JPuk3O9PbhfHEiniebR3GncOEOM+8bib/ui6M/27O4Zq1wrjH\nMn6M58mTZMaPHtxzlns8c6+dJ65vzaSGLejIjZS5qev2OL+w23nkermeNm2SpP2L5Jrd5tOCaybG\n09ExH/168kyykDCHUkLGCkLKXNvNS2YXkv7xqHj+qMJ4fpedjRqRz9zn4ViLAvkN6mTmx8Y6CX98\nvNzwAQEXp3s7Prud/zYL43cvWp71OZFIu136vf9+8SsujGtWm1RekbAQsxAAdSDrlJ0xSNlkAD7M\nziVCAWwBcB7AHgAPWfPz2rwyZQQApdQNADZCFnxOgURDXAPxP4uGrDXWDWJumALABuA0yTpKqXkA\nroWYMB4B8ByAugC+BLCM5INKqQSD6I2EmB9GAxgF4AmIA912AIchZpHjIRq3TRCTxqZG253zkiWH\nsYUA2LJly5bLbqX7CRPEqubYMTGXIgGbDdi4UczV6tQBrr0WqFcPqFq1iIVp2BDYt09MdvbudR7X\nrCm2kZ6aK82eDYwaBbzzTnZTk5zSc0N+TLKKy4yroCionNZyVnOs2rXdp3ty7orLBM11jJfaufEU\nrvO1fj3Qvbucg9KlxW6zTBngqafEFDEyUrbc5teciz59pN64ccA774BffgXHbe2QmSkmlZmZYmaZ\nlCTdpKaKeSUJZGU5TXAr74hDo8c64pfJNhy7PjSb2W5em9nXuXPSlp+f0yzXtcydu2dg+K4xeKdh\nFJZfM/qifNffGRkipymvdXNncptfdEAc4tARTyIKMzEGobDhJmzPl/luXYiJ7RfojZkYgynlxuPZ\n868iFDasQygqVgSqVBETW5P6Ohwy7qws2TdLXo8PU3piAiIxEZHoX+Er7KzUDj4+2U2cfXzEZFYp\noHZmIl4/Fo5IxwS8nhqBEGzDPVVs+Pu6UJQvj4u2cuVEXh8foEpyIu7+MhxLgibg4QMT8UWvaKTW\nCIKfn9Ns3HoO0tJkA7LLk5Eh19fp00C9dUvw/sFQdHgoCO+/77xmzz07AQcGPI+Fp/piVdl78R7D\nsaDmBIw6ORHvtopGes0gBAaKWbCPD3D0KC7IcfYscPgwUC1hPaL298SU8pF47nwkprb/CiebyHV/\n/ryYD/seSsRL+8PxS1ozjMEM/BzQBbcmf48ZDd7BovJP4O+/pd2GDeXvrFYt+RurVs05L1az+VKl\nJM2xPxFNpoVjxz0T0GLFRByMjIaqF5TtnsvIkP5bvHgXfuzwMq76ZD4WtY/Ge2uCMGkS8NprQOyU\nRNx0Og4ZAwZfGJ/VPNp6rFThXesA3D+TPHmmm+XmzwemT5cTfeiQvISUKyfPs6lTczfXzQFxccDL\nHeU+/O4FG7q8FprrfxC7d8eRcvUx6HgUFl47EfXWFvB/wZv/2pzMKcuVE7P0Hj0uNqcMDxdT9fPn\n5Tg0FBg5UkzXXbF8OTBrlkyKK/Jbr6D4j5qQbt26FS1btgTEVWprUffnrY/ZOAB9IOuGpUPWFKsP\nYCmA7yBk6GpIBMQbICaGGQAWkRxmIWYTAHxllHVAojV2I/mtQcyiIWaFrwMoDwny4Qshg1dBiFkb\niG/ZvZAw+xkADpBspJTqn5csOYzvsiVmrVsL6Srx5dZcSZlres2a8q/pCne+EY0bX2z/b2L2bO/s\n//PzwLhcHjIFldNa39U/w1rf3TnKj79LYeFyIc55wd2LRWKiELOEBLmpb765ZHzMXNubMAGYOLHo\n5tYckyfE0wO4I2smsTF/W4mP+XdYqpQcm2V8Diai2vPhOHXfUNSYOAJ/vTgH1RZPRZlDe3DosVdR\nZ2Ek/vfGVzh9g8hapoz4c54/L0T3/HmnT6Gvr7xI1/npI7R6qz9OjRqPwA/egZozB6nvzMePA6Px\nx7kgnDghRNbHBxfIllm3VCnpo8P2Gbjt4zH4+YEoxIeMvkCorWMyx2Gm1TsYhyeWd8TZ65pj38go\nVHhrIubeHI2//IIu+BWfOycEx3w/NOuGIg4L93bEIw1sWJsVirQ0adskyKaMvr4iX+nS2esDIn+F\nCuK72bixuHndey/g91ditvuW9kQk3xeO5XdGQx08gEc+6IjXutjwS5lQnD6NC1tmJnDNNU45ypYV\nAlWrFtD7wAzc+c0YfN4xCu+o0Th1SuaubFkhVzVqAM2T4vDYhx2ReG17BB2Mx4bqfTDr9s9QpYq0\nm5kpvtQHDwJHjsiWmZn3tWcSeZNs51XuhdtsGPFRKOrUkbnv0gXYsMHza93HR8ZlEuqrrpI5KVVK\nCH5AgOSXKSO/MzPlXJQu7dzMc2b6ZVffsx49F/TEL90i0frbSKwZ/RX+uU6ucdMXW6mL76da9vXo\nNKMndoaNQsg3r+NkpSBk+JRBpeRDWNR6Prodmo+Nj0Yjq04QypZFtq18eZHDJJ1ZWcCJEzL/UWMS\n8W5aOFbfOgGtv5uIjY9GI3RwEOoeWo+aw3uCK76Cb6iQSEePnpjT7SvEfpR14Ty0fjYUkZEi8+7d\nch02aOD5HAPw/GNgTun33Qd88gnQt6+QJBPh4cCiRcCQIVIHkPwBA8TP0kqyckrPKz+vegXFf+U/\n2QXFTcy8NWVcBVnUORiy0NrXEFXdfEiQjSwACyEh6UMBtIAQrH1G/YkAtgLYCVlw7UYYIeoBzDfK\nxBltnIGEyG8M4H2jzB1wmjJOMdoeBAmZnwAhi1U9kSWH8YUAYIcOHdizZ89s26W8lkdKilgMzplT\n0pIwu9miK0zzRg2NwsB/xazE1RTH6vcTG+vML4mojNZ6RW3OeyX4mJkwy8+cmd23zBvzLrMNT311\nzbG0aSMmXm3aXOxzllfdovK1zc3cz7wXvO3Xk/kx+x09Wv6bunTJ04wxK4s8fVq2U6fEnPnwYTIx\nUaLMJiSIH2ZG+zCeXWXj+dvCuOsbMdU0I9P++Se5dy/513oxa3X8ePHYHA4xhf35Z/H7/O47MbFd\nsUJMoT/6SMxzFy8Wk91335Whvv46+dJL5IgR5BNPiBnwwIFi5nzHHWI6bJoSt2ghj5RGjcTk+Jpr\nyKuukkdNmTLiBjG2tJhOj4J3ZtCjIPVmqpEXEt8OkrQ+VWxUyntz6s0BYTyywc70dPKtUXbG+TnN\nqtsinicRyGdKS7TntohnfR9ZkoY2Gw80lIjKvr7ZfYXr1hXT7xEjxFT6+efJCRNkHt96i5w9W1xE\nPvhAbtMvvyTjlth5skUY/zfbxuRWYfx9pZ0HDsg18PffzusjZafdvSlu377S+ZAhkj5kSPZjK2Jj\nST8/Z4Re1+OckN96BYUxRsd+O8+fZ+H+XwBycbqDv3+hvF8uW7bsovf/Dh06XDBlpBecKb9bwSoL\nCaJB0C7bBaYt/YTgMvQx+/ZbOZO7dpW0JBoaGgWG1XHeREmtY1ZcTvRFuVB5QeBKylx9MF3TPZHV\n6ofjLhCIJ+QsPyTWNdCH9RzmdT6Lmpzn9JHFbhd5p03zrl8vfcxYkj5ml7L/soXcOgIDmWmLZ2am\n+Jqnp4u/+dmzZFqapDkcsqWtiacjMJAcP15YUIMGEpHM318cPY0X9/R08df95x8hoQkJEqTs55+l\n67VrhY//+a0EHHLst2cTLy1BAhNtWGbnp5+SP90vxG9N7ygun2pnatvs83u2dRiXTrJz3jzx/f3s\nM3LsWLJzZyGrwcES8KlWLbJqVVn+plQp90SxA2wkwA6w5Uko1yKMnUvZaPMNY6uqdtaoQS4tN4QO\ngIl+9egA+NlVQ9ihg5DnHj1kiZuHHyYff5xc0iOWmT5+3NxmJDN9/PjD8FguXSrL1Xz9tczRzz+T\n69bJ7zVryC++IG1PxDLLx4+JPUcyy9eP/8yO5ZkzucQGIHn0aMEvwU2xdm4oJ0v37AsKY+beAjZo\nwiRfruQsp/RCgtXHjJcaMQPwGoB2EL+wGyAh6wlgiJH/hXF8WS0wbRnfZUnMxo0jq1fP/WbT0NDQ\n8Bp6HTPnOM15KMg6Zna7vP2ZketcX8qt6TnNbUGiMroSfldy5q7P4iLnhdXv5RiV0dOxFSfyq8F2\nDQASHCwMJzhYPmbkJ/CHJ88hq4Y0IECYViHNb1aWkNDTp4W4/LVeSN6+aBuTWoVx2+f2C8GCvvxS\nCFNsrHDQ6GjyiwghcR8/buNLL8nl9dJL5D+V6pEAj/nXY3i4aDb79ZMATnfcIdGumzeXtVnfqyCa\nx1m+I73SNM6A1JsBZ71SpSQ4U+3aQkSvv55s1kxOl1mmUyeJ7tunj6wtO2gQOXy4aBUjIsinnhJS\nO3asaGUffVTkv/lmqf94UxlzKGzs2FGI4t69Esk5Pd2r6c8OVxJWxKSMLH5i5q2P2UKD6FQ3knwA\nJJKsZ+Q/BAm4kQ7xB3MAWA8gELJa9jil1FKDkAVC/MbSDUI1GOJntlopdRCy3lhViDbspEH6hkB8\nzqpA/MySAFQyJmwfJDBIHZJtPJHFzfguSx+ztm3Fnj42tqQl0dDQ0NDIEYXht1qQdczy029J+drm\nt9/LdB0zj8ZWXMhvUCfXwB+kBPoYNQrYv18WWrWm5yMAiEfyvvCC+KGvXOne/7Yg8+ttwKmc/HNN\nn7J69QC7PbtvmStM37Dhw4G5c5H1wTKk9boP6eniD3rmjATaMYPPmOuvBn6/HKUfHoCUgcNRcelc\n/PbsMvzR9D6cPi3Bnqzrm6alSTspKeIXW7GipJl5aWnSl7k2q3WrWNHp49igAdCnRSJ6rwiHipyA\nUxETcc+paNgSs8+Nr6/4QuZne2pSACpkpCALQiJSy/oj7vNklCsnfoOZmdnbL1vWuS9bVmT1Bpd0\n8A8AUErdCeA2SPj7OyHassVGXn+IP1gKhGjZAUwyykWRfN4IAHIPxPRwKIDSAJYAaAigK8nvlFK7\nAdSARGd8E+KL9r5R1hoAxAExXVwJYACAFwHsJNnCE1ncjC0EwJbLaYHpM2eAypXl/2PEiJKWRkND\nQ0NDQ+OyRn6DOpn19u0D/v1XAlzExQkJ/esvqffii7KgedWqkl5QElqckYG9DW6RE4m76ioJAGKS\nMXeBP0y4BuzwNIBHfusVFG7GzPBwHHk1Gr+fDcKpU9mDIuV3+/e0gh/EN6oUvFEwAZUqSWCZcuWc\nwXL8/SUozrFjMTh8OAY+PlLG1xdIS0vC4cPrgEuVmAGAUmoWgJ6QeP53k/zSSA8DsBbAOJJvGmkB\nEN+vJSSHKKVmQ8wTQ0huM8oMgpCz20n+aBCzOgD8SWYaZb6GaNR8lVKlID5km0neapHrHwBnSNb3\nRBY347rsNGbffScf/f74AwgOLmlpNDQ0NDQ0NDSKCcUZGdgbTaeOyph3en4REACkpMABMalLr+iP\nf3clX4gmW6qUaM1M8pea6vx95oxEc83KkmNTC5iUJNpCcymL9HQ5Fm3kVhw4UHwaMz9vKxikrDck\n0uFel+zjxj7VklYDMndlXPIOWcoYq6WgsrFPA5BmkjIDZQH4KKUqkUxSSmVAIkKacpl9ZBhJJzyQ\n5bKHzQZUrw5cf31JS6KhoaGhoaGhUYzIjXS1a1e462jmptkLCspOOuLi3BORr78WUtajR/Z0k4zF\nxDh/z5rlnkSZx7NmuSdY+a1XUOQ05qAgSY+LKzgxM0gZ/P3hk5wMBASgTEoKajcJAJKTC9Z2Dti6\nFRBLxuKBV5aWSql3ATwIMRs8ayRXUkqVNX5XhPh7RSilOiqlWkL8vI5DCBEghCkNwAdKqWZKqa4A\nXjHaM5ZtxEkAFZRSk5VSjZVSjwPoADFdrGGR/Tal1CCl1PWQQCS+cJLNCh7Ictnjm2+A228vgsUl\nNa5oxJT4gngaGiUPfR9oXOnQ90A+MXiwexJy/rxortyRvOho5+KBgBCZnAjUffflvEh0fusVFDmN\nGZD0gvpNWkjZBRKWnCzHKSmS/x+Aly5wGA4JRW+DhK9XABYD6GcpQwDfA/jEUm6DkW7mH4JEXtwA\n8QNbDOCcpUwqxG+sMySgRwSA8UZ/ZhmHUfcVANsgUR5nGe26yvI1JMpjawh5q4z/APbuBbZvB/r0\nKWlJNP5r0H/GGhr6PtDQ0PeAxiUDV1JmwkrO/gPwypSRZDYip5RyQNYJ+9JIOgohTzNJPmopZwOw\n31KmCskelnxfAE8ZeWYZf5ItLWU6QojWMUuZHS79RLrkK8jC034AHgawCeJ31lEpVZWkaXqZDRER\nEZdF8I+5cyXwR/fuJS2JhoaGhoaGhoaGRhEht5gYhWTGGBMTc9HHiKSkpEJp21N47WOWG0jalVJH\nAXQCsAO4EHDjVgCzjWIbAQQqpVqYwT+M8gpCnMwyk5RSviRNDVgXAAkkkyxlOkHWQDNxh5FuleUJ\nAPNIvm/IUhliNhkOWRvtIkyfPv2SD/6xZ49Eg336aYkqo6GhoaGhoaGhoaGRP7hTwljC5RcLvDVl\nhFKqglLqJqVUcyOpvnFcxziOAvCSUqqnUsoMc/8XZMFnkPwTwGoAC5RSNyul2gJ4B0AMSVNjtgyy\n/li0UqqJUup+AE8CeMsiygwA3ZRSTxl+aJGQhaRnWcrMhCyGnewiy0oAbbwd+6UAEvj+e6BTJ6BO\nHeD5i4L+a2hoaGhoaGhoaGhcbsiPxqwVgB8hZoWEkywtARBOcopSqjyAeZDFnOMhYe7TLW0MgBCo\nHyC+Yp8AGG1mkkw2goLMAvArJGBHJMn3LGU2GmuVvWZsewD0JvmHpZ8lAN6A+MY9bcoC4DEAjdyM\nrSwA7Nq1y8spKXpMnSoRR/fsAU6cAG66CXj9dWD37pKWTOO/iKSkJGzdWuRRYTU0Lmno+0DjSoe+\nBzSudFg4QdncyhUW8kPM9gD4EEJwyhvHQ1xi+/vk8NuEQvbIiK7H1jQz4Ie7uIM+yB5UJC8NoJlv\nDSJiRRAADBw4MI9mSh6//aZ9yzSKFsWputfQuFSh7wONKx36HtDQACAcYUNRd+IVMVNKBQL4CcAa\nAF0hmqxGAE5ZyjwHYCSAwQDsACYBWK2UCrZozZYBqA7xESsNico4D8BAow1/iLnjdwCGAbgRwCKl\n1CmSC40ybYx2noOYJg4A8IXhu2ZqzR429nMBfGzKYozBDBJixWrIcgCJyL7+mYaGhoaGhoaGhobG\nlYWyEFK2ujg6U8wtyolrYaXeBNCGZGguZY4AmEpyunEcACFBg0nGKqWCAfwOWUF7m1GmK4Rc1SZ5\nVCk1AsCrAGqYi0wrpd6AmCo2MY4/AlCeZC9L3xsBbCP5uEWWdAArSI62yHIWwGSSUz0evIaGhoaG\nhoaGhoaGRhHB2+AfPQH8qpSKVUodU0ptVUpZw9XXgywAvcZMI5kM4Bc4g220BnDKEpEREF8zQqI3\nmmXWmaTMwGoAjZVSZhz7NkY9uJRpY8hS35BlFoChSqlBAGpCtHsVIFo6DQ0NDQ0NDQ0NDQ2NEoe3\nPmb1AYyABPx4DUKkZiqlUkkuhRAh61pjJo4ZeTD2/1gzSWYppU6603R3zwAAIABJREFUlNmP7Dhm\nyUsy9rn1U92Q5QPI4tWvGGlnIaTvX8+GrKGhoaGhoaGhoaGhUbTwlpiVAuAL4EVjA0QDNQLAUiNf\nAfhDKVUaosF6HNmDbVQCUFspdRZACiSE/fMuZSoD6KuUGgLgIIQEbnYp4wPgHaXUYgC/ARjlkn9B\nFogfmynLLABWTdwFKKWugvjOJUL7mGloaGhoaGhoaGhcybjgY0byRFF35i0xS4GEt78eziiJAwFE\nGL+HGuljAWyHLCr9KYAsANuUUj5G+TKQNcdqQjRaGRAydlQpFQSgBSRwSDsAnQEshJA3AjhmrGvm\nByFbrxn9rzbKmVq0XGXJYXxdIREnNTQ0NDQ0NDQ0NDQ0AAkOuKyoO/GWmB0CUM9qBmgsLH3ACKxx\nH0SDFkhym6Hx2gUJwDEbQnyqQ7RdfiRXK6XGA5gGIVGbICTrGIAqAPaSTFBKtYNo5RJIJimlIgDs\nBhBA8k+l1HAA3QH0A7DKQ1ncIQQAli5diuDgYC+nRkPDCxw5AkycCEyYANSsmXd6MSMiIgLTp08v\nsf41NC4F6PtA40qHvgc0rnTs2rXLXEYr0eA8cwF0hMXqj6TDLK+U6ghx+WoKw+qP5BJP+/OWmG0E\ncKNSKgnAaQhRaw7gUYgGzA/AdAAvKaX2wmkSeBbACoj5404ARwEsMKIvHgdQEcBKIyJjawBfALgH\nQLRSajKEYDUA8KhSqpTR1wsAXlNKPQWJ6HgcElZ/FmQR7LxkyQZDCzcKAIKDgxESEuLl1GhoeIGQ\nEOCGG4DwcCA6GggKkhXEx44Fli+X4xJEpUqVSu4eWLIECA11PweJiUBcHDB4cPG1o3HFokTvAw2N\nSwD6HtDQuIA0AKsAHIEEKTSt/tIBvAQAhtXf1wDehSzj1RnAQqXUEZLfe9KJt1EZPwPwOoRYVQdw\nCyTC4W2QoBvpAKYA2AchVzsgBGmlsYaZGbDjGQDXQDRky422Fxj7GhDC9yKEnP0OMUskxI+tKsTP\nbR2AJQDeBPAnhJkeMNYwq+6BLK6IgJg6amgUD4KCgOhopA0MxxcRccgabCFpVzJCQ4WwJiZmT09M\nlPTQHFfrKJp2NDQ0NIoKS5Zc/IwykZgo+RoaGpcC2kBcuR4kuZPkagDjATyhlDIVXSMA7Cf5LMkE\nkrMBfAKny1ee8IqYkVxN8kWSjQG0B3AY4rPV2FIsCsDVAG6HmAamGb+t+AjA/wA0A9DbSOtnya8M\n4B0AcyCTMB9i6mhtpzOAhyDaOnNttDpKqapeygKLFm4TIKr7Xr16ZdtiYmJynxyNvPHYY8D69e7z\n1q+XfCsaNwZm52B1Onu25OcE1z87a9+uf3br18tL+rRp2euYbSQmAm+9lb3OtGmS5g6u7ef2xwsg\nLvVW3B3VEXOrT8gfKVuy5GLZrbK4yp4bvD1HRQGDsGYjVSaZ8oa4FlY7GhoaRQNNSvQHJA2NSwgx\nMTEXvf9HRFzgVDcC2EnyuKXKakhQw6bGcWvkspSXRyDp9QYxPUyAkBxznbIwCElLA9DHUvYvSMCQ\nWwBMBLAXEuyjqpEfZOQnQzRacZAIjDssbTwM0YCtgkRbzDD6n2EpsxjAeQDPeiKLy3iuMdIHAeCW\nLVuoUQSIjycDA2XvSfqsWaRSsvck3Qq7nQwLk721j9jYnNPbtCH/z96Vx9lU9vHvY4ZsM3MrLaSM\n3RDGWJqJhkuRMopQWmxvWkSW8gopS6IoQ1KIiExNpUUpb+FyLZEtlKxnlLXsS4yZud/3j9857pk7\n587cO4YZnO/ncz73nud5zvP8nueec+7zfX7LExvrzdM0OY+JyZruW9Zfu/7S9HRPbBx/KRzLeLjo\nLuJk+g6fMoHALM+YMf7l1DRyxoys18+YkWU8Eho29NYxY4b/3+jJJ7OmGXC7JT+30DSejnVyWicX\nUxtajJ8ht1l+07Xn08eOZWojqedMnEU9Nmz4QUJCQn6LcGUjm3ejZfqVCt/+FqD+28+Ajasda9eu\nJcRq7wsA3zMzfyim84cW+vlWAAN8yrTUOck1DIRjBVIoy0ViQjhWJ2hpkA2lw3XylAEJygEAVXSB\n9wHoDeBePf9XU11PQfYl8wCoDTFNPAXgbVOZOZCQ+Ef181V6Pa31cwUxf/wFwJeByOLTH5uY5RUA\nskwZ67wyZSTfPMH3N+E34EvCAiFlBnz/3JKTydBQ+bRq24rIxMSQYWHMWOLOWmcwf6ZWZePieLxG\nLMtB45gxZDloPFw7l3/Ghux16oj8bnfWvgQqm9vNOcWLe0lscrL/3yhYsh0kXqzvIgEOdbr8y+12\nW/8OpvTXW0g9I+62qCe/4UtuZ8zwEmyD3BpldKKZiWD7EmAromrAHzm3YYk5c+bktwhXPjSNjIri\nz2Pd3L2b1u/Kq+Ge1TSeudPJF+q5eDSmYJAy0n4GbNgIkJg1p39idp/OR4owEI4VSCFT5WMADIXs\nDXYXgB91AjRJz/+fLmATiGngcgBunUiNgphOHgbwD8SMsQXE52yUwTjh1aC5ICaSPfQ2BhqME16f\ns6EQU8fJer0TAKwMRBaffhlauD42MbtAGOTLl5yZ0j1L3UwPd3Dbc4k8U8zB3ya7uWcP+eef8l+0\nYwf57bfkI4+QlSuT0+tPpAeKu+u1oQeKs2InskoVMixMeEj//uQHH5Aff0x+/rnwiNmzyQ8/JOe8\nrvGvKk5+1tPFPys5+cN/knmmqIOLHkjkmaIOzuzu5htvkG+/TY4bR84aoXF/+TgevCWaB26pw79u\ni+X49m4uCXHyzftd1Mo7+W5/jaNHk2++SU4eqHF3RSc/edbF3RWdnP6KxkmTyKlTyaQk8uuvyXnz\npD+LP9R4qLaTq9508XDVOB6sEMtWt2ssX55MTyfr1SPvulXj3mpOfpWo8dNPyS++IL/6Sq7/4Qfy\np5/IxYvJJUtIl0u+L1pELlxIzp+kMaVMHA/eUJ3nipbk6ag63LpA49YFonnas0zj/v3kX3+RBw+S\np06RBw6Q69aRO37SeLahk4fXaty7l9w9NpkZIaH8vcMQppZwcMcMN48d8/Ob+5KwPCJlq5M1LoST\n/eq6uBBOrpurZS3kS8J8PzWN//yicZFyst0NLi6Ckykui3ryE/4WCKKiyPBwSXe75YavUSOzptZq\nrI0xefhh63Qz4csJF0LyrK410nyvffJJeXCt6rtQzauNAo8Dn7t5BA52K5FETwHVHF0KfPCELCCN\nurcALiDZsHGVwkTMJgNYx8z8weAstfTzJWbFEr1Wf0cZKNcKtKBe+QZdOOqC/AMJQf+2nt9VT/fo\nZfYAqA7x3XpdLzMXYmJInWitggQQMTPOgzoZo/452cw44dVwpetlTkK0XW8CWBGoLD59+xmimbuq\nidm//5J795LbtpEbNpArVsjkf80ayfPF2bNSbtcuMiNDT9RJWGqZMty7lzxdqgw9AI+ULMN27chS\npcheSCQB9kIiAVoeFSqQ3bqRd9xBfhXahgQ4V7VhrVpkjx6iVHjsMbJsWevrjaNpiPzZ3VPExZAQ\n8r9Fpe3/Fk1kqVLktdeSJUqQxYuTISGkUy9PgPeVcPGWW8h4SNoDDhdLlSKvu07mw+HhZItikndv\nMReLFROlnD9ZjHpG4iWWg8aaNclly2TYduwQBV05aOyEGdn2yd/R9nqv7GsRzXgIqSkHLcdry0GI\nkHHNqxiS5TcKC5PxjowU3lCzJhkdTf6nqpvHQxwcVz6RJ0IcfD7GzVatyPbthR+0bUs+9JB8f+IJ\nmWc/9RTZpYsQ8HbtJK9jR/lNH71To6uQkw/U1piaSj5QW6MrxMke92ns25d8+WVy5Egh0++/pPHP\nSk5+81gSzxRz8IeuSfyripPThmgc9bTGVSWcrFZU419/kXGl5fzr8Rq//17m/OvXy9gfOEAeP06e\nPi33clqaHJcEblmsWDbaze3byR2jkukJCZFBNohMjRpyg/rT+Jph0vae17SZSVmgxPlCTM38mfXG\nxgrxNKebtdlmDaIV6X/yybzRCgZSh5W5rFl7aaQ/+aR8tmolh1VdbjcZH+/Vhvq2b9aGZtcHK/Nh\n4xpz+2YSbBDf+PisxNgsS06mzv7G6QLx5ptkBySRADcMTJLEMWOy3ieBtBuIebXRpypVslpfGHVP\nnCj5lwqaxjXh8v5dVsRJzy7t0rVd0BHsPWhbDdjIQ5iI2XMwuWKR563+jgIorJ+PhskqUE+bA2C+\nOS27I1hiNlwnR+d04TJMBOscgG/085aQTaJX6FqqFIgpYyGddJ2AONG1APA3JNCHB6JFi9Tr+wWi\nMTMGYgy8poyP6u2Mg1djdgRAEoAv9TJfZyeLRd86QMLpMz4+ngkJCZmOy0Gd/+OP5E03kVWriubI\n47Eud/IkuXo1+dFH5ODBMimuWZMsViz7ibtS5A03kNWqkdWry1GkiDe/RAnyxhvJiAhyF4SMnYOi\nB+BOlGHJkuSdd5JTOrl5rqSD+wYkMiPCwc3vu/ndd6IR+vFH0QBt3WqSf+JEepTi2VZt6PFjxpie\nLhPqw4fJY8fk+7lzlD83p1PUS2azvMRE68mpoa2Ijs5sFmiuw3cyZZHn8cgk/8ABcv9+Ibv7V4qp\nyoFPxWfqzBaNVkhNFflPnCCPHCH//pvct080irt2CWneulU+t28XUrFzJ/n3apHdEx3N1Bp1eCqy\nOglw00QXFy8mFywQ7d3335Nz54qG8csvyVWryKVLJW/pCCF2O/tOYHq4gydek9/o13fdTEqSCdSQ\nIeSgQWSfPmSvXuSzzwrJmnOHEN6P6iby4YfJ1q3Je+4hmzYlW7SQo2lTslEjskED0RA2bEg2a0Y2\nb07efbcMYYcGGjfe4OSEfhqPHJExOXqUfLOHxjURTjatoPGWW4TgFytGlixJNr9G5H6hsMjQNMTF\nakU1Lr/GyW5NNbpcUs/69WTLKC0gshoSIp9Fi0pbN95I3nKLl5DWqUPWry+3y113iezNm5P33Sd9\nb9uW7NCBfPRRslMnsnNnGacBA8h+/WT8+vUjn3lGyt6lRGvQC4k8AgdfrpbMveXieOi2aB4tX4dH\nqsVy7UvJPFfSQa1PItPCHNw23c1Nm8jffiM3bSI3bpSFkvXryU3zNJ6qGsP04iV5rmYMD6/VePan\nXGgzL8T/xY8JbxafTfOzOXFi5k8rkpYXvkmB1GFlLmtoL2NiMmtoo6PlJViiRGbtp7lvZl9Wc53m\ncfE1zfWFPy2pb/tmEjxxohDfiRMzE2N/5sBW42H2X7UaJ2Oym4tJ8UN1Nf56vZODKyXxqHLwy0eS\nmBHr4zdrJsS+7Zq1qoGYVxt1DBuW2TTeX3qgyKnvBoG3IOVp9WP5ohrLZ+7V2A9jebJBAPex2ezZ\nd/EgOdma6F+OGuhgn/e8eD/YuCoxZ86cLPP/+Ph4g5jVhbhVfY/MVn8j6OUSkRB3rDeQ2ervbvLi\nELMSutbJfKQBWAbZOyxVP2+jl69q0lrV10lSOjIH/3gasrfYUYhJ4Rs6WTP7oSVBIkDO189/BrAf\nevAPiI/ZHsjeav0hPmbZydLAT/9G4TLVmJ05I5PGuDjy3nvll23YUP5X3n6b7NtXNBY1a5KFCnkn\nn2XKyHvqmWfIt94SE8BvvxWesXo1uXmzTP5XryanTSOHDpXJZO/eMikfP17e899/L9ePGCGT9/Hj\nyTQoEmCaUjxyRCdawZq9FRAfsywTLfOkJpAJ64VMbgOBr+xut6jzqle3DlLirw6nk5wwIftxsoJR\nxh/hDQbBTuwMuZOSpO2kJOuJpA6Phzz+q8bDb8/g77/Lvb1woZidfvKJENapU8n33iOnT5d7+fXX\nyddek4WMvn3l3n/mGbJ7d7JrV9ECduwoGsI2bciEBLJlSyGmTqcQtzvvJGvXJitWlMWNqChZRImJ\nIZs0Id94g9w7QIjlhm6JjI0l7yniOv+wxsNFIDBts6+G9gRKnid8D93kZoUKogyoXl1kqllT3hcG\nUU5IIB98UAhj+/Zkj/s0bizl5OBGLv5RxslXO2vs109I5ssvyzz29ddlyBMTyXffJadMEXPiL8dp\nPFDDySXDXTxUy8mF0zQunCZmvWvfdvFoHSfXfqHxl1/IbdPdTAtz8PATveiB4qERE7lvH3l0npsZ\nEQ7++z83U1P1d0lePFOB1OFLXtxu+dFKlJBP8/MWHZ2ZhFn5aPqSsNhYpteO4YnbY5m6MAdSZsDq\nPWrVvtkkNjk5czAjC7PfbMfJn89qoL+Dn/T9K2Wh5JPRGnfuJN+sK5qzCQ2TJBiS0W5yspcQm9u1\n8oEN5H/Gl4QNG3ZhpCyQvluNuU6gD1eNY0O4ebKBk1WKaJwyyE9dvvVaEfrkZFlZqlEj66JCIO/n\n3AZ1Mq6zIozGdZomhDE+PjjzZdPYZnr+fU22zeWjoyXf53obNoKBSWMWA+BWyD5lp3RS9gaAQszM\nJRoDWAsJSLgdwBO04Bz+jqCImU/DhQA8omu3PoQ3EuJUABq8vl1nAezUrxkGYJ0P4+ykd3iyXmYJ\ngA98GOdHepm74fUHe0PvdCeI1myrTsZugESLzFYWP32KuVyJ2Wefya+5ZYuc/+9/8r4ODRUTvapV\nZZL41FPij7VmjWhkLhoMnzKlvAzQjsqYc9ncwN+kyQgAYmj+cvqD913ZtxqnQAKA5JGPWUDwN+EJ\nZLJZ0OBLbvV7MiM6mudur8OzMbH8571kpoc5uHeAaMx+m+zmypViDrtyJfnzz0I0f/lFNGYn6jm5\nPtHFk6UrkwDd7RM5eDD50kvkiy/KAstzzwnR7NRJjg4dxBruvvtkkeeee0Sb2b+BkLwnK7tYs6aQ\ny4oVydtuI0uXFq1iRIS8bwoXtiaIBrn0l2YmnuPQK5MGsSHcmcoVKkRWKSImr/eVcHFJqJPRDo03\n3ijyGCa3FSsKCY2KIm+/XYho3bqitY2LI9vGiCa2Z00X10Y42aGBxjvvFM1ufLzcRo811Lj+Oidf\nr53EE6EOvlk3iTsiYngqNIwfRifyZGEHh93j5gsPafztZienx0xgugrlN3WG8PQ1Dk561M1Bg7zj\nPrybxl03x1G7Lpo7i1XnMYSxA5K4vKiQ3vHjxaJh7lzxMzV8Z5OSyFmzhPDO7efmv0UdnNskkf8W\ndfCz3m5+Nkbjvignf35sAjMKhfLXB4cwtVg4D0VGc9GrLv5TJY7/VInlvMeTeDzEwWFRSdxbzcnl\nH2tcuZL89VdZiNuzR7T1Z8/KkZpKntumMbVeHE9Xjea5+nFCmnJ4t3l2aVlIdFqaWDXs3k0unCZj\nX+daTXxY9XIreifxCBzsWtnNKYM0HqwUx6Plo3kqsgbTSoTx70nJTIt30vNpMj0OB4/Oc/PoUbE0\n+Ptv0Rgvf8PNs8UdXN4hkanFHdz9sfu8BcLu3fKMLJymcX+Ukz/H9aYH4D/1mtMDxe19J/Lrr8nJ\nk2VBcskSGZOATJtzIqq+76yBA+mJjePQu91cfo2MWUKCcIqMnVrOZncWRJ8xMULKfBcPAn0v5zao\nk9X/qaFNNhYHjHRDi2ssAAbQxpktcr88cZuL5xrlQDb1xYqzNaI560kXz9yZB/8HgRLW7BYXixSR\nl4sVunYVE43LFVeoCamZmDGXnCmYI1gyNhDAJl1AQtRzWwC8DaCjTpTCIJs5G75dqQCm6NdP1glZ\nA51pGmaQBNBSL7MVwACI6eNpPS9Nr+8aeP3L7oDsh5Zmame7XkeOsvjp32VLzDp2lPm3L9LS/Js0\nXjT4BgAxzosWDW4Vzsr+30BO9v++LwjzC9X3BeHr++Fbh7HCZ75mzBhJs4Jv/Rf7ZWVenbSaBIwd\nK0cg2jzfcfIlZ76/UW7/wPMCvhMcfxOfy4Gc+Y6XseJ9IT5mvqZ3lStn1v4GA6M+K3NeP/B45P1z\nZovGtHgnj38jk6M9yzQe+FnjmTgn985x8dQdTv7xg8b168nfJruZVtLB7b0SxWSzda/zGsTkZNFm\nzpghi0vvvSfK3U97CMGb87SLo0aJZnPYMPKVV0TDOWCAkKG+fcnnnxci+vTTcit37Sp+jiObSx0j\n7nbx8cclvXNn8vHH5d3aoQM5JF7KTKkhxLF/AxcnVpHvEyolnteKPne7lPvs5p4kwJE3JbJ8ebJc\nOfGbrVxZftYu5b3a0MVtpJ7XW7hYrRp5zTXZa0INYjqopFw3OCzxPBk2CO94SPu9kJiJBBvf36kk\n1zb2IcaBaGAN/9VFSrQ7YWHid3vttTL/LlGCrBSa2We1HLTz63TG0Qkz2CRSNzX2ed9sft/NlOLV\nWKWIlqnd5zCB5xDKVzGER+Bg4xC3X3mfD0C7bNTtwl0kwM/R5nyer7yFCgnpr1VLjtq1xSQ7Lk7+\nQpo1k4WMtjHiy9o50sU1EU52dWps14584AHy/vvJJ+7SuM7h5CtVhSB3KZbEhXByxlDp+9Kl0nat\nWuJq0KWLaOeffVYWUfr1I//7XzEpf/VVckI/jXtui+OBW6J5uHR1ni0axnX/TeLRCjE8VzyMO3rJ\nQs7uj91MSRGT/4MH5fPkSXq10GbkdsHNl5xFRZElSzI9Koqpt8fwbEws011ua21nNm14POJbbvxe\nvWq5ePhw9rLuS3azw01S/pHSLv75Z46vrcD6ltP/XXYLFjffLDdT166Z87p2zZpuaBWtYPiMWiG3\n110oLvYidD6hoBOz+QA6A7gH4pO1XSdWtU1k6D2IH1djiG/XSQB/MjMx2wTZcK0mgAS9wx/TS8yM\nkPlv6hqzSQZ5MxGzwboGzNCYbdBJWqlAZPHTvxjg8vMx83jkWR8wIL8lYUBRGW1cROSGBF4IcbyY\n+5jlhED3MSvoq3T+TGovNCqj72qypmU1zQ0EOWkAgr02Jx8zQzZDM96rV84ENAjCmKs6jDJmc1lj\nLM3mu0Y5wxx4yJCcfVmrV5d6DBNcvf3Tp8l//iEPHRLt1dGjYuVw5oy+4LY0s4bVs9TNc9s0ZjRx\nMvWtCfSEhjJ14BB6wsKZViuaJ791Ma1+HM/Vi2XabG8/0uKd3L1E4+bNom11ucj588UK46OP5Jg5\nk/xsjMaDtzu58R0Xj0TWIQF+2cfF8eNl3WfUKHL0aFkjevttctIk8tv+Mime96KLU6aIeev06eSn\nn0obO3f6MUv1Gaf0O2J5eK6LZ6Kk3ZQEIZ3LOyTy3XdFq2gQ97lzxW/277luehwOesaJn+wv49z8\n/HOJcvvDD+TateSBnzWmxzvJ3qIxO9lINGZ7Bk3k/v3iu3zunPhufvutyD90KNmzpxw9eghh6tJF\nghZ16OAlUoltXOfJduvW4n96//1Cztq1I4c1lfxP7xTy+Pt7rkxd/+Yb0WA3aya3Sv36svhqaKsr\nVRKNcNmy4lveKsxL9A2tczxcQZk+FykiPrvXXSd13h/h5lHl4MASiTymHOxQxs2KFUULXamS1yS7\ncmVJi4yUBYiHb3HzmHLw7bAhTEMIt6IiN8GrGV6knIwrrbFyZbJTBQkclVg+kSdCHXypkZsdOsh4\ndukiZuL33SevvnKQKMu/ThANebWiGlu2lEWU8e1Fg+xqK9GeJz7iZr1SGlcUlfLLr3GyXimNr7wi\nZLZ9e+FAs2aJy8bhwxKpOD09h/dFoIQ1u/emLwmzImVkVveLnNIv9DozcjsvuJD/iwKAHHzMCh4x\ny3KxkCBC9g67bDeYNuVflhqzrVvll5w/P78lYfbkyyBnNmzY8OJi7WPmj7QNGlSwozIafcouEIhV\n/bmZAARSh68G9iL4mGXx+8qpD/nhY+bjE5WjiXQwpNnfJNBoa+xY7/fKlUVz7I/0+hufS+Fj5lu3\nv75bEf0LmbyaiL6nenV6wsJ46N0kpt4ew/SSYdw/UDRm6ya4uWCBkO6vvhJCm5QkxHvKFK9P+ujR\n5PDhEvn2x1ZC7L65O5EDBvD80b+/N4jRiy9K2qBBoqXu35+cd49ct7J+z/PMb/NTkja3t4svvyzl\nevUik+IkfVrtRLZsKabT8fE8b1LcujU54GGN/9T0Rqs8uEpjSgUJ7nTnnXKbD9Y1yP1CE3nHTRq3\nlHFy3wop//dqjZtvEnPnUqVkuKtXtyaoISFikn3ttaIhjYwUd5BatcQEukctN0+EOvh+dTFjfrmJ\nm927C0nv2VPG48UXydHPaNwV6eTs7t7tdD74QMxjt97VlR6AJ24sTw/Av+7tyqVLZVFhwwYJ7rVn\nD3liejI9oaH0fKq/GwMlV77lgiFlxj2Vy3e/Z5f4Fc/o6uLZhrm8r80Rb43nFpBFLIMYmv/7wsIu\n2vyyQGvMslwMVNKFnYvLeINpUzuXJTGbMkVMLI4fz29JbNiwUWCQF9rM/NjHzGpSbfTFjsron2Rc\n7KiM5vK+Muf0O1woaTaPo1lzHEjgD6t0X1KWV1EZA+m7FdG/ENNrf0T/QnzMDPj6vQZ6rXHdkCHC\ncipW9KsZDqiNQJ5Vcz3GIkUA74ejR4U/f/65aFynTxcz6XHjhKAOG0YOHCgk9Lnn5FX0+OPktGgh\ngZOqJvLuu8VvtV49IW+VK4unRcWK3i1s7i3mYvHimQngNpQnAW5D+Ww1mQ8hmecQykmhPXkOoXy2\nVDKrVZO24uLEfLZVK9HKGpGQ69cne5VOZhpC+dnNPZmmQjmpaTIHDpQAbVOmCCFPShKCPm+eRMQe\nNEhMZleuJDd/q/FUAye1xRr//JM8sk40zGe2aDxzRkxgU1NFs3/woPhuLlggga8Mk9M217nOR0UO\nCr7vTuO9azBnq/SwsFw0lDMKNDEDMBJAIwDlANyua78IoKmef1luMG3q32VJzB57TF4INmzYsHHZ\nI5h9qKyQE2E0YO9jllk+f22a67HSJvr6r+YFabZq1zwRM7frS87ycx+znPruj4QFQpD9tXcxojKS\nee5jxqiorNraQH3McnpWfa0ABg70moFblb9Q8/ZACauF5vTMGdkn82xn0Zidu000ZsfadeWWLWI2\nu3q1BJyZP18I40cfkRubiOZxVYOeHDhQfGafe06sH9u1k0iqrt21AAAgAElEQVS6Dz0kJpqPPCK3\neZ8+5MLqct1Xt/VkvXqi/YuI8E8CfQ/f/U0D2RO1UVnRbh76wsW1DicjobF+fTFN7d9f/H9HjZLh\nmzxZ+vfZZ2IuvHCh7J+7fj254yfxRT42NZkZEQ6mJyV797EBLgkpIws+MftA1zhlwBtQ4w1T/hOQ\ncPj/wrsBtEvXdhkbTM/WiZkR0OMsJKqjeYPpP3XCZrRzCMA0ZN1g+qj+mQFgG4DP4N1gOkdZLPp3\n2REzj0fC5L/4Yn5LYsOGDRs2rlgESobzOtiRlUmTb30X2581UOR2HzMjP1i/2Iu1j1mgQS78XXeR\nojLmqay5xaX0MTNgmCH27BmcOWI213k84j956pT4sO7f743I+tdfsi/mmjXk8uXkunEuEuCS4S5+\n/LFsqzRrltf/9IsvZE/U778ndy7U6DH1O32HRIrt20bIWaVKMme97rqc9841E0Mj6M8wNYQZAD0A\n0/TPIwhjo0aiLTQC7LRuLTsldOkiW9v07St8/bXXZDuX99/3EsLvvpOAOxs2yJ6gW7fKnrH//CM+\nvStWFGBiRiEv9wJYDdlr7Lw5oZ7n1EnQEUhQj9sBfKWTsH56mWEQ08V1kL3P7gSwS+90Lb3MMog5\n40wAUZBAI6kATuv5hXWilQ6gn65ZG6bL81Ogslj07bIL/rFtm/yK332X35LYsGHDhg0bNi57FMR9\nzPJa1twgUBKYneY0mKiMZO59xS7Ux8wsc6C+ornQlns8Qn6OHCH37iV37BBSaGgNf/iBXDpCiOHm\npqL9+6l1ItN05pYG8OmnJVBOu3YSKKZ1ayFnzZqJn2KdOqKwjYyUbV0KF84acdV7zCGQ4HMU8OAf\nACZC/Lkq6MTHTMzCdeGnm9Lq6GkD9fPu+rnTVCZRTyurny/QSVeoqcxvAE6azg8B2GU6Vzp5WxGo\nLBZ9u+w0ZrZ/mQ0bNmzYsGHDxkXGpd7HLD+jMpLB+4pejK2BjDbNkW592VQuzBg9Htmj8ehRIYRb\ntggZXLFCCOGPP0qE148+IocPL8AaM0jY+qMA7gJwk07MngBQVM8vrwu/B5l9u44BGKeX6aaTLmOD\nacPPLAPAA3qZz/UyxgbTPXRNVwaACL3MPxDfMyNc/mSI2eImPb9CTrJY9O+yI2aPPCJOnjZs2LBh\nw4YNGzauEOTnPmZ55St6IfD1LzV8J69wH7NCCA7P6JooF8TXTEHC1HfQ82/WydoPOrkyyrn0POiE\nTtNJ1goAH+l1HDKVCQPwLYC7IfuT9QXwsqkN6HJ8BGA4gPUQkjceEsLfaMeQ5VtIxMZYvd3qQfa7\nQCI1FZg/H7jvvvyWxMaVhqSkpPwWwYaNfIf9HNi42mE/A/mIJUuA9u2t89q3l/y8vM63junTgcjI\nzOmRkZIeSB0XgpQUoFs34NlngaeeAubNA/7zHyAjAwgJAZKTgYQEmQSHhQEnTwLh4RdXpkuE0GAK\nk8xE5JRSHsg+Yd/4FB1M8klTuWQI2zSQTrKVT11dfcrsJ/mgKb86JHqjucyPPu308MkHxB/ucche\naKsBfAegiVKqFMlDVv3s27cvIiIiMqV17NgRHTt2tCqeb5g3DzhxAmjXLr8lsXGlISkpqcDd7zZs\nXGrYz4GNqx32M3CVonNn/3mRkVkJW17DIIYjR8pkt1EjIV9hYcDGjZI/bx4wc6ZMhMPDJf8CkZSU\nlGUx4vjx4xdcbzAIipgFgAMQLdpNEPNEAzdCtFpGmRvNFymlQgBcq+cZZW7yqftGCOk6mEMZc74C\n0BPAZJIf6W39pZfrBuBNq06MGzcOMTEx2XQz/+HxAGPGAA0bArffnt/S2LBhw4YNGzZs2LCRBzCI\n4dSp3jSa9C4GMWzUSD5PnMiTZq2UMOvWrUPdunXzpP5AEKwpY7YgqUEIUTMjTSkVDuAOiNkiAKwE\n4FBK1TFd2gxColabysTrhM1AcwBbSR43lWmGzLhHTzfLUgPAQh9Z1gCIy3VH8xkkMHw4sHq1LCbY\nsGHDhg0bNmzYsGHj8kbQxEwpVUIpVVspFa0nVdDPb9XPEwG8rJRKUErVhPiB7QHwNQCQ/AMSdXGq\nUqq+UqohgHcAJJE0NGZzIIE9piulqiulHgbwPIC3TKKMB9BSKdVPKVVVKTUUEuBjoqnMNL2PlX1k\nWQOvr9plgYMHgTVrgGnTgKZNgWHDgBEjgMaN81syGzZs2LBhw4YNGzZsXChyY8pYD8BiiFkh4SVL\nMwF0I/mmUqo4JEqiA4AbQEuS50x1PAohUD9BAnR8DqC3kUnyhFKqhV5mDSQwyFCS00xlViqlOgIY\nqR/bIVEdfze1MwkSNOQlACMMWQA8hay+aABQFAC2bNkS5JBcfDRvDhw+LN9r1gQSE4G77gLWrctf\nuWxcmTh+/DjW2TeXjasc9nNg42qH/QzYuNph4gRFL0V7uSFm2wF8DCE4xfXzriTNT24hP98NKP3w\nd25OUxAS5Ztv1G0QLFq0dQhC/AqZygOZfdHMiASAxx9/3CKr4GDTJqBPn/yWwsaVjktpU23DRkGF\n/RzYuNphPwM2bAAQjrAip0IXiqCImVLKAdkLbCFk/7FDACpD9jYzygyABNzoDAmL/xqABUqpKJPW\nbA4kcEczAEUg4fInQ6InQikVBjF3/B+ApwHUBPChUuooyQ/0MnF6PQMgkRYfBfCVUqqOSWvWD0LY\nlgMYZMiitznBoosLADwGIAXA2WDGxoYNGzZs2LBhw4YNG1cUikJI2YJL0ZgirSz6/BRWajSAOJJ+\nPZuUUvsAjCE5Tj8Ph2inOpNMVkpFAfgNQF2S6/UyLSDkqizJA0qpZyGmhzeTTNfLjIKYKlbXzz8B\nUJxka1PbKwGsJ9nDJMuPkH3WntbbXQXgDIAKJP8JuPM2bNiwYcOGDRs2bNiwcZEQbPCPBABrlFLJ\nSqmDSql1SinzPmLlIUE1FhppJE9AyJARBTEWwFGDlOn4CaLZusNUZqlBynQsAFBVKWVsMBanXwef\nMnG6LBV0Wd4C8AJkI+plAE4D+MYmZTZs2LBhw4YNGzZs2CgoCNbHrAqA6vp3ArgBwBSl1FmSswEY\nkRkXK6WKQIhSD4jGzIiCWBVAEaXUaQAnIZESXwJwxFQmCkB5pdRZAH9CgnsYofRvBnAcQBlI9Mc3\nAPwKoJdPO2UNWSCmi4Ys78APIVVKXQ8x0UyBbcpow4YNGzZs2LBhw8bVjPOmjCQPX+zGgiVmCsC/\nEAGNYBzDATwLYDaAPnr6fwDsBvAugC8A7AdApVQhAF30MrEQcjULEhpf6WUiAcQA2ATgEQB3A/gA\nwDOmMg/rsn8GIVp9IcRrFLzBQLKVxU//WkACm9iwYcOGDRs2bNiwYcMGIDEo5lzsRoIlZicBZJjN\nAJVSGwDcr/uS3Q8hPbtIblRKdQWwBcB6AEshxKcUgBMkNwHYpJQaAmA0gJKQDaGfBXACgEZyK4Ct\nSqlGALrrdR+EELGTkA2n/1BKPaO33RzAwQBlsUIKAMyePRtRUVFBDo0NG0Fg3jygbl2gTJmsefv2\nAWvXAgkJl14uHX379sW4cePyrX0bNgoC7OfAxtUO+xmwcbVjy5YtRrT2lEvRXrDE7C8A1ZVSeyGm\nfishgTR2QzZ3DoUQp2YANpLcqpT6CxJVcTRES7YVQDU9euJ6iKbrPUhY+9UQf7B1AOKVUiEkM0xl\ntkI0dnX1tpsBmECSSqmfID5wn0L2WstJFiu0BoCoqCjExMQEOTQ2bASB664DunUDpk8HIiO96Skp\nwIsvZk2/xIiIiLCfARtXPeznwMbVDvsZsGHjPM4qpW4F8D6AJjC5Y5H0GIWUUk0g8S1qQHfHIjkz\n0EaCDf4xBaKF+gzAMAD1IaaCUyG+XecAjIP4fiUopWoCCANwCsDXepk/IURrqlKqPoDyEJNDF8kD\nepmlel3TlVLVIX5pRQGMh2jcQiAbWrdUSvVTSlUFUAnAtZBNqW8KQJZM0M0j+wY5HjZs5A6RkUK+\nunUTMgbIpxVZu9owc6Z3THyRkiL5l7IeGzZs2LBhw8bVDgVgPkTxEwvZFqwLxKVLCog71reQIIi1\nIbzlA6XUPYE2EhQxIzkRwAMAmkIY47W6oI+aio0HsBPAVwA2QsjQ16Y9zACgP4DSEA2ZEcHRvK9Y\nKoDBANpCQtz3hxDCD01lNkPI2WgAf0AiOqaY9jALVBYDfSE+aDZsXBro5OzvVt3Q9volONLGJmUA\ngMaNMxNWAwZxbex3t46LU48NGzYuDuzFE3sMbNi4fBAHoBqAx0huIrkAwBAAzymlDAvEZyEuVP8l\nuZXkuwA+RxCKn2A1ZiA5n2QtAI0h2qd/ATgg/mFFIEE2boSQtxgAGQDi9csPQLRZn0CIVS0I2wSA\nVqYylSFBPd6DDMIcCAFsDNnUOgPAQwCeAPAkJIrjLgBllVKlApTlPJRShSHmkasBsalu3bp1piMp\nKSnYobLhi+7dgWXLrPOWLZN8M6pWBd5917r8u+9Kvj/4/tmZ2/b9s1u2TCbpY8dmvsaoIyUFeOut\nzNeMHStpVgjmzzQyEm8UfRVzjzTByJBXc0fKZs7MKrtZFl/Zra43rvX9jcx9sfqNgv1NA4GPNtHj\nQe60iT71pKXlsh4bNmxcHNiLJ/YY2LBRgJCUlJRl/t+373lOVRPAJpKHTJcsABABMVsERJPmdyuv\ngEAy6AMSqGMrgPsApEG0XuEQTVcagDZ6uSoQ3zEPgAYA7gWQrpcppZd5CrK32FGIenA0gL8hfmFG\ne3MA7AMwXz//GRJdcbx+riD+b8cA/DcQWXz6U1pP7wSAa9eupY1cAiDLlLHOu/56yXe7M6e73aTD\nkTV94kRSKfkMJN0MTSOdTvk0t5Gc7D89Lo6MjfXmaZqcx8RkTfct66/dHHBkncZFcPI/lVxcCCf/\nXh3YdVnatJInOzn9yayPx5xXX7VMD/i385ceZL/+rOykM8TFAzUsxnTGDP/90jTJ178fvN1JZyEX\n90UF/ttcMjz5pP9xcrsl30a+YM6cOfktwpUP33dmkO/QKwJ6nz27NP7yC3n2D63AjIH9DNi42rF2\n7VpCrPa+APA9M/OHYjp/aKGfbwUwwKdMS4hi6BoGwrECKWSqfAxE4/S5TpZ+hPhyTdLzv9aFvw+i\ngVoOwA2JZNIboqE7ANmHrBYkSuNBiBmjB2KPGal34BeIb1kPvY03IRtTA0BHvZ1xEI3aZACHASQB\n+DIQWXz6ZROzvEKZMtbkzEi//vrME/ZsJvDbtpFruk6kB4qed3QSNlHO13SdyAkTyO++I0+f9iOL\n7x98cjIZGiqfVm37EhlNI2Ni6AkL42e93Tx0yKfOC51QaBr/rORkJDT+/jtZubDG7bfl8s9Ylz39\njlim79ACJ2Xm680kLCxMCGl2pMyAb35ekDKSp06RrSNcJMB2N7h45kw2MmeT7vGQncpJPR3LuJie\nfkFi5T18x2vGDHLMGLlPjXSDvGkaOXasl3Qa15vJm0FYrQifQVhtwmejACHjzTHcHB7Hub1dWZ9p\n8yLLlQxN48EaTsbDxZQKBYOU2bBhI2Bi1pz+idl9Oq8pwkC4ViCFTJX/omu8qAvyDyQE/dt6fleT\nVooA9kA2pF4FYJReZq6uzaIu6CoAJXwY50GdjFH/nGxmnCYiZchyUidVbwBYGagspn4VhmjX+tjE\nLA/gS870c0+ZMty6lfzyBTdPFXFwYuVEHlUODmjo5jPPkE89Rf7nP2SXLsInlJJqnsFEZkBxQVgb\nZkDxGUwkQBYpIvkhIWT58mT16mSdOmTt2mRUFFmpEtnwFo3LijjZOsLFpYWd7H5tMo/CwZeKJ/Io\nHGxaxM2wMPK668hSpcg7btL4S+E4/hoSzV9D6vDnQrFsCDcXQv4wFxdyslpRjSVLkhERZM0wjUtC\nnbyvpItLQp2MuU5jmTJkuXLk7beTDRpIX+LiyIYNyUaNyLvuIlvX0riimJPloJ2fH48cSZaDxuVF\nnWxWUWPNmtKf+vXl+rvukjnL3XeTzZvLZ7NmZNOmkt4ySuMKxHGdiuaW4nW49fpY9myl8ZFHyM6d\nZXyfe4585hny+efJl14ie/YkH3qIfPxx8uXHNW4t6+TbD7i40xHDkyFhHHNrIo+HOPhKUzf79ycn\nTCBnziRnzybnziW/+UbI8coxbp4r6eC25xJ5rqSDm993c8MGcutWcvt2cssW8o8/yB07yD//JA8c\nIP/+m9yzR9L++EPK7dpFpqSQP/9M9murcZFycvUYFxfByf7tNW7bRv77L73kKgdyfPYsmfymxoVw\n8pNnRSv54avaJXoQgoCZnGma3MwhIZkXEcLCyBo1MpNtKxJsjIGZ2GWXnh0C1UoGeq2R5nvtk0+K\nXDNmZCWUZhJpfL8QubKTz7eOvGjHX7tWdZvTLwYZuRj9yQMs/lDjWkSTAI9/48osUwHRHF0KvHaP\nLCA9X9uVc+GrCQX0vrVxdcBEzCYDWMfM/CFS5xm19PMlBicyleliKJYCOZR+UUBQSnUCkAjgcQDb\n9MYGAfiIZBel1I+Q8PROyF5k75rI1E8AXtbJnAfi92VsMD0dYoJ4r17vLkhkxqchG0wnAhgKiXxS\nTCdd70MiQ34CcaprD9kcui7JO3OSheQgn779rLfbMT4+HhEREZn63rFjR3Ts2DHgscoPnDsHzJoF\nREQAbdsChQLwIExLAzQN2LoV2LEDOHQIOHoUOH0a+PdfOVJTgbAwoGZNoGxZ4PrrgZAQuf7334EN\nGyS/Rg35TE0FHht0Cxwn9yEDCiEg9hYqg5rhe3HsmFw7uvR4vLinDz6omYhPbuyNI0ck3TjKlAFa\ntgSaNQM2bQKqDGyLKpu/xO/V2mDzsLlo1AgoXVrkXrJEzPHPnpUjJAQoXBgoUkQ+K+1dgi4zmmD2\nky5sL9MYd60fj7vn9cFPCYn4rVlvZGTI2JEie+RuKQ8AnzzjwrHajVHzyBI0HNwEX/RyYU/FxvB4\ncP64ZccSPDqlCZKedmHXrY2RlibjevIkcOaM1GuUNb47/5yJfZUbo/I9kWjbVuQkgS+/BLYuSEG5\nlCVYVa0z0tNheXg8gFKZjxIlgFZhS/BgosjeJ9qFTdeJrOfOeY/QUJHrzBmgeHEZ69RU4MQJIPr4\nEsxIaYI+0S7U8mxAt419MKdBIqYW742//gL27JGyVuiF8ZiAPngeiXgHvS/oXi6HFMwo1A0HX5+O\nhwdEIvnNFNzwUjd05XTsRiQKFQKuuUbkL52agkmp3TD6mlfxUuowvOCYjj2hkUhLA0oeSsE0dMOs\nJtMxfVEkhjyRgqYfd8OoStNx5qZIlCwp96zxWayY3D8lSnifj/BwOS9USO6p8HAZw2APQ2aHQ+r1\neKSt06eBv/8GvnxhGXr+LwHfxAxFm/WvwFO2LMJuDgcM/9ZWrYA//pDz9u3Fhy8hQfbEa9Qo8wAa\n/inPPgs89RQwZQrw3nvec6trrODPJy8QXz2rMikpQMeOcsPOmeNN/+wz4NFHJa10aW+/AOvvZcvm\nXq5g+gbI9/vuA9q1k3LduwPNm8t4GmVGjgQGDwZ69ZJzQ16jviVLgIoVpczIkcArrwDDh8un0b7h\nkzl1auZ0X3TvDnTubP37GXsfzpsnvqGNG0sdM2fKw/LFF3KzDR8O7Nwp9aSkSPp331m3adSzZIm3\nPt++GfmdO2du12rMjXImvPRICtp+/iiKeM4g4qZiKOOag2vmfQ7MnSt/ZsbYZ9duIOOzbJnI16iR\nXNuiBfD888Bzz2Wt+9QpYMIE+ZMJFDn13bhPLMaS7mXY7uyOkSGv4qVzw3Drpu9R8naLeq5GBPse\nysU9aMMGID5mvjEljh8/jqVLlwJATwgfKU3dz0wp9RREKXQjyTSl1GgALUnWNq5XSs0B4CB5X0BC\nBMrgdAL3AITcnINomNLg1Z6d0w8PgHC9fFX9fB/ElNHQev1qqvNpiGmjB2Le+AYkqMjbpjJJAH6F\n15RxlV5Pa3p9zPYAWAPgS4iP2Tm9jKUsFn3rANmb7bLVmHXuLBokQDQtixZ5806dEq3F11+TgwaR\nrVuTVauKZZ9xTfHiZGQkGR0tmp177iEfeIDs0EG+ly4ti/hGeYAMDycbNxart2LFeF6TFRZGnoOo\nvNKg2KMHOXq0aFdO/aCv8icmBrZyb/iUtWmTs2+ZL4wVV5crs7bAX9uGCWB0tAxibKyUMdfha2bj\nL+9Sw0r2YOQx9yUmRn5En3HyeMjUVNFaHTokmq+9e8kDn7uZHu7gwcGJTA93cMcMN1etIpcskfvQ\n7ZZj0SLyhx/kPvzyS3L+fElbsoRcvJhcuJBc+pHGE/Wc/Pf3zLIf26DxUG0n576tcdIkEW3kSHLU\nKHLWk7LSPOtJF4cPJ4cNI9/tr3FvVSfXzdXOa9g8HnLeOxr/uMXJFx7S2LataB/j4siaNUXLGhlJ\n3nijaFFLlyZLlpTbztDgXqyjVCny/eqJJMCRNyWyHDSuConj5iKiAd1YMpaDKifzRKiDk6sn8mRh\nBwc3dvORR8hHHyUfeUSe1fbtRQv6dAuNG0s5OaPeBKarUM5vMIT/FnXwh5fdTEqSR2HuXHLePPk9\nXC45Vq4kf/2V3LyZ/P13cudCjafvcHLrAo2bN5NH12tMi3fy7B9azmahVhpNK19OX02e202WKCGD\nb5z70wxeiG9SIHX4ymw2iTbKu93y3JUoIYc/LaXh42q8U4xP3/zs+pCdX2fJkt72zX0xy+yrnc3J\n5NncR6ux8pceoP9txk6N7sJOjuyu8d3+GpcjlhtC6vBkVZ/3b07tBjI+5n47nfKiMP+n+EsPFDn1\n3fd3N2m+08McfAjJ/KuKkw3h5t81A7iX/WmSzBpoXwRixpxbv1fjOsMc26wBNq4zzLHj44OTMZjn\nPch70IaN7GDSmNXVucj3yOyONYKZNWindC5jdse62yiT0xEsMSsBMQesDolA8oJOdr6ExPPPgJgp\ntjFds0cvUx+i4dqBzME/IvX8ExCTwiWQ6Ihm8tZF79h8eM0Ot0IP/qGXmQGJENkfoo3LTpYGfvo3\n6nIlZtu2ya/53nvksmXkHXfIeenSMsE0TwBvvpm8916yd29y0iSZDO/ZI5PWnHDmDHnkCPnPP+TB\ng2RGhjfP4zHVYZgzGrNZw6wxWH8k30AfgQT+MOD7Es6ljxnDwrJOtIz8guK0biX75epjFqzZij9y\nnIfmLx6P3OunT5OHD8u9v2cPuXs3uXOnmGxu3kxu2ECuWSOmmMuWiUg//SRkdP588rPPyOnTxRT0\n44/Jjz4iv/iC/PFH8sR874KFx+HgstHu84STAF9v4WLnzuTUmkLe3otKZPPmYs7apImYtN59tyyi\ntGghz3j/BnL9x9f3JAG+VCwxV6SxHLTz5rwLISa4Rp5SshhTooSY95YqJe+d224jK1Ykm1bQuKqE\nBLhZE+7kg9Ea29TRuDbCyT51XFx/rZNdnRoffJAc3NjNk4UdnFUvkf+GluS/oSWY3CiRp69x8N2O\nbg4cSL7yCjlihBDyKYMkQMzc3i7+VcXJ2a9pnDKFnDZNft7Zs3mehH7xBfnVV0JEv/+e/N//5N23\nMknjkTpO/jrBxaMxTq76VOOiRfLbLV1KLl9Orpur8WTNOJ6uGs1TteKYMiaZ6SXCeKZ6DLXFGvd+\n6mZ6yXCerRHNf95LZnq4g/+8l8zURk6e+SiZHv15yMggU7dqTG/s5Kkf3Dx7p5N/9JzA9EKhfK/G\nBO6r5uSJjX7uWTP0Z8yz1M0zZ0jPUndmUmsmINHRsoKWnHzertqz1M2jUbE8WaUOPYG8I/wRC3/k\nKNB3o6Zxf3W5n1askKQt78s9uyGkDpeNdtMTTLs+45PtO8mXhA0bdmGkLNC++46lTsq/65rMRcrJ\n079prFCBfOkRP2OWXVsGfP/rDAT6bs5tUCerYFrGooVxDxrpEycGL6Om8Ui0k65hpne9PxJp3PsP\nP+w9v9D/ZztQ01UJEzGLAXArZJ+yUzopewNAIWbmEo0BrAVwBsB2AE+Y83M6giJmeoO3Q3y60gAc\n0dnj25CAHGcATAKgQXbFrquX/Uu/drLONM2MM0Hv8Md6ma2QyIxmxjlRL9MSXv+yQXp7nSABQDbo\nMt0QiCx++hZzuRKzYcNkLv3vv3Lu8Yh26uWXyddfJ2fNEq3En38GRsAuCH58zLIE/jBwFUdlzBP4\nkydQcuZLynxXlbMjZxczKmMgKEjk+EJgNZEMDxdfM7MGNCeNrxnGWEyYIBOgIUPocTh49ic3T54k\njx4VP799+0TzuXWrLPBs3ChasxUrpPolS4SkbJooE+Ylw1385BN5p0yfTk6eLI/iuHHkm2+KFnPo\nUHLwYPK//yX79iXHt5VrRzZ38YknyK5dydeaS9orjV184AHy/vtFezmhkhDPt8slcsytXg1ilSri\nS1q2rCwuXX+9DNE9RaSepiEuFiqUO21lPKSOeLhyLLMW0YyHi2sQw2MIYy8k8ggcbAj3eQL7HCbw\nHEL5Koacz7Miur0g/RtVZEim9m+4QSwa6taV14/hO1ujBlmtmmh2Hyzl5hE4zrefcK2bFSuSlSuT\nj5R181ghB1+7MZEnCoXzt2ui2bWCixuKx3F98Vi2CnNxLeqQAB++2UWnU8a/fXuxvHj2WfKFF+T/\n4+WXhQyP6y0+qONik3j6Ggc/a5fElIpOTh2sccIEWRScNIl85x25Pd8boHFXeSdndHVRK+/kOy9o\n5++N/v3J7t3J4RVnsBw0duiQ+Z49+a2Lv0XEsh/GsnaExpXFnRxUMYknQh0cd0cSt5RxctTTGl9/\nXSwxevcWeQcOFP/Zhx4in6ouY/BKRCKPFXJweHM3+/WT/O7dxRrkwWipe3xIb3oA/nxtc2ZA8Z2o\niWzQgLz1Vrnn7rlHfHNHjBDS/803cnz7rSy6LFwoJH7lSnLVKnLFHI3/1HRy6QgXj9Rx8rfvNP7x\nhyzerF9P/vq1xmMxTv72ShLTrinOxQ9N4LIiTnaK14z44zIAACAASURBVEiSr74qFiz/m6Jx/+gZ\n3LtXFoOOHCFPnJD/+XPn9P9yf+9AX1/SYN/JuV1w8/1PjYoSTW5UlPe/1FdTHGAby5d7n8NFQ13Z\nX6O/Q/eVjmaLoi7urpgH/wuB/t9ltyhYpIiYJFmha1eyaFHvuaFVtEJysuRbIbfXXSiuUF9AMzFj\nkJwpN0ewpGygrs06CYmCuFUnQx+ayFAYZDNnI+jGOQCTmZmYNdCZJnXNFgHcSy8xGwAxfTyt56Xp\n9RUxEbM7IP5laaZ2tut15CiLn/5dtsQsLk7+VPMdgURltILValOVKv7J18SJku8Pvi8I80qX7wvC\n7ZYXlWF64VuHYXphvmbMGEmzwqV+AZnNRqxk8ZXd6nrjWt8VQXNfrH6j/FxBvFLMVfyt5psDgGia\nzMp9A4Jks7JsaSIXTOAPq/pyY7Jrda2/+ow+JSZ6zfKyI6EW9Xg8EhwmNVU0nCdOCAk9dEgmt/v2\nyQKVpkngGW2xxtOxTu7+yMVTdzi54yeNO3YISd2yRSbTW77XeKK+k39MdvFUFSE0G99xcXsvIVZ/\n9EjkggWiFf35DZk4agmipfylUyKnTSOnThUiO3OmaEuX90oiAf7dQwgzk5J4OlZMdUeMIPv0kYA9\nzzxD9ughgXuef57s148cMEDIkquttL/koUQOGyZEuH9/8sUXyS+bSN4XjRPPE+NxD7r49gPy/USl\naP4y1sVtZZ3s2UrjAw8IAWnYUIhglSpCTG69VcjwLbeQT9wm1464Qeq+r6SLYWEylwwJEf5/zTVC\nKq69lnzwWin/gMPFG24Qwlm6tBDLOnXE/PbDD+W38n1uPbtEk/nOCxrf7SD1TKst7T5V1cVKlUQ7\n63DInN8g7lFRojnu3Jn8ppmU//TORMbGCtm9/XayXj2yZUuZB7/TTureectdMpY3tOGDD0ogqsGD\nZawTEoQY33BD3pF9I98g5/3qurhrl9zWJ04IKQ+knZAQskoRja5CTiaEu7jsGied5TXGxZHdo9w8\nHuLgpKpi+jy8uZtPPsnzBLVfPwkC9cor5Guvyd/I+PFCsj/4gPy6v5tnizm4vEMizxZ38MdX3fzk\nE/KTT8hPPxUt9Ny58lpJShIN9axZ5E9D3Txb3MENDwxhRqEQHipVkQdKVefpwmGc0iyJKRWc/Hys\nJpa1oyRw1I5eiUwLc3DnTDe3b5cgUIZVwrp1ou1ueIvGNeFOvtrExUXKybd6aVy7lvx7rpueCNEg\nG++RjAgHp3RyZ/odXn1V7rW0NHm+9+wJ4h1oIBhtrNV/0803yw/XtWvmvK5ds6b703z6S7/Q68zI\nDcm6Uv6TfVDQidl8yKbOUZCN1r7VCdAUSJCNDAAfQELSNwZQB+K3tVO/fhiAdQA2QTZcq6lrvAhg\nil5miV7HKUiI/KoAPtLL3AOvKeObet2GxmyrTrxKBSKLn/7FAGB8fDwTEhIyHQV5L49Tp+RZe/fd\n/JaE1qTMgEHObNjIC1wpq3NWZNjQdCYne/PzIyqj+brcaCWtrr0cfczMhDI2VlhFjRpZ/TAttJTZ\nrrBPmGDtexZIH8wk1rcNc154uGhdXS4Z+zp15DwuLjNJzqlNo1xSktSdlJT9dcGQ+ewmdMb9Emi7\nVmOQE7Hv3Vv+m5o3z9EaIzWV3L9ftMz79glx2LFDSPzGjWLOnOLSmNrQyaNfuXg61sn1X2pcskS0\n0KtXk799p/FkAyf3vJXE9HAH0z/O2qf0dNFiL14s1i9ff01+/rmQotmzhdBOnSokasIE8tMeOnnt\n5OILL0h0427dyFn1hPhNrJLIRo2ElFat6tW+VqggxPvGG2WYihfP7HveWyWeJ5DBaKENwjkePc8n\nvnGLTuhLuCzLZtdGOWhcVdLJv9waz54lR3YXMmqYVTeEaJAHlZRoz/GFRIO9q7yTnsWitY2ExmLF\nZCHBqLdaNbJjRyGpAweKRnf0aLEAmDRJNKSzZ4sZ+rx5YgK9boKbaWEO/vWi+FTv/tjNv/+WhZ9j\nx+QeSd2qMaOJn3eLLwmzImUGfMlUoOQqt9cZyC3JMuWnpwdQ3h+s/t8Beeda/b+HheXJ/HLOnDlZ\n5v/x8fEFl5hluVhIEHWCdtluMG1q57LUmP34o/ySmzfntyQ2bNi4YFhpQPNrH7MLWQH1R3KM/SPM\n6f6CU/j7nhcrs4HU4e97crKoKmrUkHPD9DQ6Omctpa9ZdbD+U+Y6rFbts/Mxq1NHvvuOYaCTrbz2\nMTPgb5HFuF8GDbpyfcyC+d1zajM7DXSQmvKMDK/vomdcIj0RDp5eIGbQJ0+Sx4+LaeWhQ0JGTp4U\nDfW//4q/rMfh4LlBQ+gJCRFn0+rVZfKsE+uzf2g8fpw8/LUeOGqQaMw2TnJz8WIhQN99J/6gG77S\neCbOyYydmcfmzBaNx+o6uWi6xtmzvRrkH1omcvZrco153E82cHLaEI2JiWJ+OmeOaKIbNhSyGhnp\n9csvUSJrsLPckMlFyskWxbzb6ZQvL5rdT0p2pQfg7iLl6QH4zY1d2aKFaGfbtSM7dRJteb9+5Jy2\nyUwvFMr1d/VkRqFQLn0+mV98Iea0CxeK+eyvv5K//KKb0q4gFywgV/RNZkZIKP9q25OekFAem5qc\nY8Cmw4cloFem+yrIxa9fvxa/4rsLu6hVyPq7BQSrtgzyFRJinR4WFnw7AaCga8xGAmgEoBzE1+x9\nXdiuev5X+vlltcG0qX+XJTEbPFhMOjye/JbEhg0bVxTsfcyyEhczsRo71jupDjQqY1SU5JvbN0/W\nc9rHLDs/l5yiMj77bGYC4EvOsjNP8iUOOaVfCGnOTbuBjE9BjcqYU5+CadP3nrsSfMwCeVattMQX\neg9SNJenTwsJ3b9fLk2ZLRqzlH6yb+e6CW7OnSvmlp9+KuLMnCmmy1/2cZEA5zzt4siR4gv50kvy\neTCsPAlwf8ny7NhRfCMTEsSkuFEjGa6qVcWcePI1onkcj55BaS4NjaX5uvBwCc5UubKsLdWpIwHj\nmjb1Xnf//WTbtmSvBI2/3+zk2AQXt93q5BvPahw0SOadQ4bI0acP2auX+G7Gx8uj072K9DseLt57\nrxDFvXvFNzJgWN3bBls2SNhFJmVkwSdmH+iaqwx4fcM0U/4TukbsX3g3gHZBAnMYG0zPhuxlZviN\nnYX4qJk3mP5TJ2wZevohvW3fDaaP6p8ZkP3PkuHdYDpHWSz6d1kSs0aN5IG2YcOGDRsXATn5YRph\nwFu1ksMM88QxPv7CCWV2fp3m9s0yz5jhNYv1bStQgh3ohth5ZWKc2424A/F7Na618mM26szJjzk7\nma1gvk/yanNxf0TjSo3KGKi8Awd6NcO+CGZ8A2krEF9fK3New3yxvJAzSzNGA8bv2bMnPaGhPDsr\nmYcOiSntjh1iPrtqlfjibdhAbtokTR2flkxPSCgPP9aTGSGh/PnFZE6dKgYZL78sPql9+ogP63/+\nIwEsW7SQ11Tr1vLd6SR71BCS9cRtLkZGkuXKCbEz/E+rVROFaEyMxDpIGqWbcbpcPFTbybjSWiay\nGBIiXP2GG6SeqlW91tVNmwopbNeOfOIJcmBHCTo0+VEXd5V38v2XNJ4qEkYPwDSAHoBnioXR5ZIx\nMKIjb9okY7N3r2gBT5/OHEU8GBRoYkYhL/dCNnr+Xhe0iymvI7zRGhN0rdpXOvkarZeZrBOzdQDq\nAbgTEk6SAJrrZbZBwufPhPizGXuM+QYASQfQT9esDdPP1wcqi0XfLjsfs9OnycKFJRKWDRs2bNiw\nYeMqwdW0j5k/5JZE5gbBtJWdGeDl4GPm249AAz9Z9NvjdHLnQo1ffy2+kZMmkW+9JRF8X35ZtIc9\nekj3H3lEIqY2b07edZf4RHaOFGLY5joXHQ4JMJSms7w0ICgNYtGiYq56662y7mIQwubNhQzGxc1h\n2bIJvPXWBFaokMDKlRN4222XgY8ZJHz9bp0ctTalO3XhXzKlhevlPtTP39XL1DGVMQKAOOklZmcA\nhJrKfAsgQ/9eWK9zlY9cfwPYFagsFv267DRmtn+ZDRs2bNiwYeOqxKWMDBxoW9mZtF4uURmt+pGT\nKWhemTFbXWsmhmGZNWZnS4Zx2zbRlC1fLgF2VqwgFy0SP8UvvpBIuB98IJauQ4eKCeaLL3oJYdu2\nQs6aNhVCeMcdYn17663kzTcXfI3ZREigjQoWxKymLnwfU1oVPW2Ofv6Wfl7KVOZpPa2tfr4JwDGf\ndn/Sy0To56kAXKZ8BfFd26uf18pJFou+XXbEzPYvs2HDhg0bNmzYKCC4EvYxyw3JyutIyVepj1kh\nBAGl1CQAjwF4FBJJEQAilFJF9e8ldeH7KqWaKKXqQvzHDunECZAgHakAZimlaimlWkBMI09DNocG\nxPywhFLqDaVUVaVUDwDxOhG8WS9TCMCdSqlOSqlqkEAkIZDIjgBQIgBZLnv88APQtCmgrpge2SgI\nSEpKym8RbNjId9jPgY2rHfYzkAt07gxERlrnpaYCbrd13vTpwJkz3vMlS4D27a3Ltm8v+VbI7XW+\ndUyfnrUfkZGSblVHdv2OjJT8QJGSAnTrllmGWrWAjAwgJATYuFHSTpwAwsKAkyeB8PDA6y/ACIqY\nAXgGYg7oggQBUQBmQHzADBDAjwA+N5Vboacb+X9BAnasgOxRNgMSpMMocxbAdwDuhgTr6AtgiN6e\nUcajXzscwHqIhmyiXq+vLN9CojzGQsjbtUH2u0BC04C1a4E2bfJbEhtXGuw/Yxs27OfAhg37GbhK\nkZckKzewIoYnTwoJ27EjMzE0k7MrAKE5F/GCZCYip5TyQPYJ+0ZPOgAhTxNIPmkq5wKwy1TmOpKt\nTPkhkCAeB0xlwkjWNZVpAiFaB01lNvq0M9QnX0E2ng4F0AXAagCLADRRSpUieciqn3379kVERESm\ntI4dO6Jjx45WxfMNkycDERFAq1Y5l7Vhw4YNGzZs2LBho8DDiviR3u++pPHEiTxpNikpKctixPHj\nx/Ok7kARFDHLCSQ1pdQBAM0AbAQApVQ4gDsgQT8AYCUAh1KqDsn1elozCIlabSrzmlIqhKShAWsO\nYCvJ46YyzSB7oBm4R083y/IcgMkkP9JluRZiNtkNsjdaFowbNw4xMTG5HYZLAk0D3nkH6NkTKFky\nv6WxYcOGDRs2bNiwYePyhZUSZt26dahbt66fK/IewZoyQilVQilVWykVrSdV0M9v1c8TAbyslEpQ\nStWEmBvugWz4DJJ/AFgAYKpSqr5SqiGAdwAkkTQ0ZnMgm0pPV0pVV0o9DOB5SOAQA+MBtFRK9dP9\n0IZCNpKeaCozAbIZ9gkfWb4DEBds3wsCSGDZMuDuu4GbbgIGDcpviWzYsGHDhg0bNmzYsHGhyI3G\nrB6AxRCzQsJLlmYC6EbyTaVUcch+ZQ4AbgAtSZ4z1fEohED9BPEV+xxAbyOT5Ak9KMhEAGsgATuG\nkpxmKrNSKdURwEj92A7gAZK/m9qZCWAUxDfuBUMWAN0BVLboW1EA2LJlS5BDcvExfjywezewbRuw\nfz8QFQWMHg3s3Jnfktm4EnH8+HGsW7cuv8WwYSNfYT8HNq522M+AjasdJk5QNLtyeYXcELPtAD6G\nEJzi+nlXkuYnt5Cf7wYUMkdG9D03pxkBP6ziDhZC5qAiOWkAjXxzEBEzIgHg8ccfz6Ga/MeWLcAD\nD+S3FDauZFxK1b0NGwUV9nNg42qH/QzYsAFAOMKKi91IUMRMKeUAsBzAQgAtIJqsygCOmsoMANAT\nQGcAGoDXACxQSkWZtGZzANwE8RErAonKOBnA43odYRBzx/9B9jirCeBDpdRRkh/oZeL0egZATBMf\nBfCV7rtmaM266J/vA/jUkEXvgxEkxIwFkO0AUiCRIW3YsGHDhg0bNmzYsHF1oiiElC24FI0p0kpx\n5KewUqMBxJFsnE2ZfQDGkBynn4dDSFBnkslKqSgAvwGoawT/0M0WvwNQluQBpdSzAEYA/2fvyuNs\nKv//+5kZu+GmQloMFcbWGIWxDFeWKNoXiRppUUqUCiFKCBkalZQ94zdJJUsK3XGpLyJbWcIZ+xpm\nbGOW+/798TnHPXPn3pl7ZzCD8369zuvec57t8zxnfT+f5UFFkhl6nuEQU8Wa+v5sACVJdjS1/QeA\nv0i+YpIlDcCPJHuZZDkDYCTJUX533oIFCxYsWLBgwYIFCxYuEQIN/tEBwJ9KqQSl1GGl1DqllDlc\nfRXIAtBLjWMkUwCsgjvYRiMAJ0wRGQHxNSMkeqORZ7lBynQsBlBdKWXEsY/Sy8EjT5QuS1VdljgA\nLyqlugKoBNHulYJo6SxYsGDBggULFixYsGChwBGoj1lVAD0gAT+GQYjUeKVUKsmZECJkXmvMwGE9\nDfrvEXMiyUyl1HGPPLuQFYdNacn6b07tVNBlmQFZvHqofuwMhPQd9a/LFixYsGDBggULFixYsHBp\nESgxKwIgGMAAfQNEA9UDwEw9XQH4RylVFKLBegVZg22UBXCLUuoMgFOQEPbveuS5DsBjSqkYAHsg\nJHCNR54gAJ8qpaYC2ADgNY/0C7JA/NgMWeIAmDVxF6CUuh7iO5cEy8fMggULFixYsGDBgoVrGRd8\nzEj+d6kbC5SYnYKEt68Bd5TEZwD01v+/qB9/C8B6yKLS3wHIBPCXUipIz18MsuZYJYhGKx1Cxg4p\npcIA1IMEDmkKoBWAryDkjQAO6+uahUDI1jC9/cV6PkOLlqMsPvrXFhJx0oIFCxYsWLBgwYIFCxYA\nCQ4461I3Eigx2wugitkMUF9YerceWONxiAbNRvIvXeO1BRKAYwKE+FSAaLtCSC5WSg0EMBpColZD\nSNZhAOUA7CC5TSnVFKKV20YyWSnVG8B2AGVIblVKvQzgfgBPAFjopyzeEAkAM2fORHh4eIBDY8FC\nADhwABgyBBg8GKhUKffjlxm9e/fG2LFjC6x9CxYKA6z7wMK1DusesHCtY8uWLcYyWkk65/kCQAuY\nrP5Iuoz8SqkWEJevWtCt/khO87e9QInZHwDqKKWSAZyEELUIAN0hGrAQAGMBvKeU2gG3SeAZAD9C\nzB83ATgEYJIeffEYgNIAFugRGRsB+AHAIwAmK6VGQgjW7QC6K6WK6G31BzBMKdUHEtHxGCSsfhxk\nEezcZMkCXQv3GgCEh4cjMjIywKGxYCEAREYCtWsD3boBkycDYWFAUhLw1lvAt9/KfgGibNmyBXcP\nTJsGNG/ufQySkoDERODZZy9fPRauWRTofWDBQiGAdQ9YsHAB5wEsBHAAEqTQsPpLA/AeAOhWf/MB\nfAZZxqsVgK+UUgdI/upPI4FGZZwL4CMIsaoAoAEkwmFjSNCNNAAfA9gJIVcbIQRpgb6GmRGwoy+A\nmyAasm/1uifpvxUhhG8AhJz9DTFLJMSP7QaIn9tyANMAjACwFcJMd+trmFXwQxZP9IaYOlqwcHkQ\nFgZMnoy0Lt2w8N1EZD5nImnXMpo3F8KalJT1eFKSHG/uc7WOS1OPBQsWLFwqTJuW/RllIClJ0i1Y\nsFAYEAVx5epMchPJxQAGAnhVKWUounoA2EXybZLbSE4AMAdul69cERAxI7mY5ACS1QE0A7Af4rNV\n3ZQtFkB5AC0hpoHn9f9mzAawGUBdAA/qx54wpV8H4FMAn0MG4UuIqaO5nlYAukC0dcbaaLcqpW4I\nUBaYtHCrAVHdd+zYMcsWHx+f8+BYyB0vvACsWOE9bcUKSTejenVggg+r0wkTJN0XPF925rY9X3ZG\n255lzPueZUaPBsaM8d52IC/TsDBMumkw2o9sgUk3Dc4bKZs2TeTx9nJPShI5/ZUn0HN0KaAT1iyk\nyiBTgRDXi1WPBQsWLg0sUmJNIFmwUIgQHx+f7fu/d+8LnKoOgE0kj5mKLIYENayl7zdCDkt5+QWS\nAW8Q08NtEJJjrFNmh5C08wAeNuXdBwkY0gDAEAA7IME+btDTw/T0FIhGKxESgXGjqY7nIBqwhZBo\ni+l6++NMeaYCOAfgbX9k8ejPTfrxrgC4du1aWrgEcDpJm01+/TkeF0cqJb/+HDdD00i7XX7NbSQk\neD/udGYvY+w7ndmPR0WRjRq5j/lqNxdk7tS4opid0XBwRTE7M3f6Vy5bm97kyUlOM6ZOzTYeHZo0\ncdcxdarvc9S9e/ZjBpxOSc8rNI1no+yc+YKDaU29jKlZbi9lOXXqhf9pzeyc0d3B1Mb+nxsLFjp0\n6FDQIlzd8PW8DPA5esXD17unEPTfugcsXOtYu3YtIVZ73wFYxKz8oYTOH9rq+9sAvOORp53OSYrR\nH47lT6ZshcSEcLRO0NIhC0qX0clTJiQoBwBU0wU+AKAXgPv09A2mul6ErEvmAnAXxDTxNIBPTHlm\nQULin9D3V+n1dNT3FcT8cQ2A7/2RxaM/FjG7WADISpW8p1WqJOnmD3xfH/wGPEmYP6TMgOfLLSGB\nDAmRX19t+yB0ruXO7On5fZlqGk/Wt7MyNA4bRlaGxuMReXwZe5Iwf0mZN7mdTs4qWdJNYhMSfJ+j\nQMl2gHg3ykEC/LC1I3e5czg+sr3U81FbL/UUNDzJ7dSp5KhRIr9Bbo08mkaOHu0mnWT+CbAFn5g1\na1ZBi3D1Q9PI8HCuG+/k/v30/lw1X+9XKzSNqY3t7N/EweT6hYOUkdY9YMGCn8SsDX0Ts/Y6HylK\nfziWP5lMlY8C8D5kbbBmAH7VCdBnevovuoAtIKaBKwE4dSI1HGI6+R+AoxAzxrYQn7PhBuOEW4Pm\ngJhIvqK30c9gnHD7nL0PMXWcqNc7HsAf/sji0S9DC/eGRczyCYN8eZIz83GnkxllbNz1RixTS9q4\nY6qT//1HHj1KHjpE7t9PLl1KxsSQdeuSMxvH0QXFfQ0fpguKs6PjeNddZPnyZOPG5KBB5DffkHPn\nkgsWkD/9RH73HTl7Njn3E40Hatg5700H91W3c1mPBJ4rYaPz8VieK2Hj7J5Ojh9Pfv45+cUX5JQp\nZMLHGvdXt/OH3g7uvdPOL55x0lnEznGPOLj7Dju/Hqhx3Djy00/JaUM07q1m59xeDu6tZuesjzRO\nmULOnEn+8AP5yy/kkiXSn99+Ix0OMjGRTJym8VAtOx+K0HjrrWR6OhkRQbasqvFQTTt//kLjvHnk\nwoXk4sVSPjGRXLmS/N//yNWr5fePP8jff5fjyyZr3HNLFA9VimDy7fV4LqIRdydq3LmT3LePPHKE\nPHmSPHaMTEkhMzPJ5GRyyxZy3wrRKp35W+Px4+TB8QnMDA7hjqcHMq20jXvjnUxN9XHOPUnYRSJl\nf32vcSnsfLW2g0th56aftOyZ/CDH/63V+FuQnR3LOrhM2bnX6aWegoTneBmkOjycLFNGjjudZGgo\nWatWVrLtbawNTaI3baZZA+oPmfNXK+lvWeOYt7LXyge4hWw4MtfJ47DxxbLxhVZzdDnwdVeZQBrR\nrhBOIFmwcI3CRMwmAljHrPzB4Cx19f1Es2KJbqu/E/SXa/mbUa98vS4cdUGOQkLQf6Knx+jHXXqe\nfQBqQny3PtLzzIWYGFInWqsgAUTMjPOwTsao/040M064NVwZep5TEG3XxwB+91cWj779D6KZu6aJ\nWUYGefw4uXcvuW0b+ddfQgD+/ptMS/Oef9s28uBB0uXSD+okzFWpEo8fJ8/dWIkugCdCK7FLF/LW\nW8nXEEsCfA2xBOh1q1SJ7NRJyNncoIdJgHPwMO+8U0jb0KHkI4+QN9zgvbyxRUNeds3hIED2Dpa2\newfHslQpsnhxMihIFHGeZe4NcbBcOfd+u5IOli5NlihBFitGFilC2oMlrWWwI0c5zFtXTGVlaLzj\nDnLZMhm2rVvlW7wyNHbFVL/rMm8PhDou7ETDf3kAaXcpxKxyKewcjIHZzlH58uSdd5I1apCRkWSD\nBsIhXqnrZEqIjXHVYpkSYmPfKCcff5zs2pV87jmyc2fymWfk/4svkq+9RvbqRfboIeeySxdJ69ZN\n+EK3lhoTg+1sX1Pj2bNk+5oaE0Ps7POIxv79yWHDyE8+ETI99X2N+6rb+f0bQr7/b6TGr7+WtLG9\nNK4JtbNaUY2aRjYor3F1qJ2LJ2p0OMg//5Rx379fSGpamhBWUq7nC9f0pYY+WbH6Eyf37SP3jEmg\nKzhYLgiDyNSqRQYH56zxJd0fs56aTl/Hc0J+TM285dE0IZZRUVmPP/mkXFAGOTOnmUmkkZ4fwmjA\nnzqMPOa8Zu2lmQRrGvnAA7J5q8vpJKOj3dpQz/bN2tCc+pCT+XC/fjKWnv0zk3FPYmyWpYCI8Zgx\n5BOIJwFuei9eDo4alf06MZDX8THGwOhvtWrZrS+MuuPiJP1yQdP4Z1m3Wbtrl3b52i7sCPR+vxjP\nBwsWdJiI2aswuWKRF6z+TgAoou+PgMkqUD82C8BC87GctkCJ2VCdHKXpwmWaCFYagHn6fjvIItG/\n61qqJIgpY5BOulIgTnRtARyBBPpwQbRoYXp9ayAaM2MgRsFtyvi03s5YuDVmxwHEA/hez/NjTrJ4\n6dsTkHD6jI6OZocOHbJsV4I63+Egw8JE87Jgge+PytRUctMm8ttvyQ8/lI/iBg3IcuWykhPPrUgR\n8rbbyHr1yPr1ZStd2p1erhxZuTJZsSKZBCFjaVB0AdyJSgwJkbKfPunk+VI2JvWJZUYZG9eOc3LO\nHPL778l580T29etN8sfF0aUUz7R7mC4vZowuF3n6tGiC9u0TknjsmHxon9ui0dXCTjocdNntTJul\nf5TGxnr9OE1LI9P/1eiyS5ksPmbGvsfHlMtuZ+YySXPt0pieTp49K9o/TSN37SJ37CD//VdI7Nat\nZFKSEGDPc+RyubVahw8LYdi9m9y5U8r+/Te5YYOMz4YN5MaNci43byb3OjW6oqLoiojguZr1eCK8\nEVd+o3HJEtG8/fCDfJPPnSsaxq++ImfNkm4tXizXw5KBQuy29hzP9FAb/xsce4EwTJ5MDhlCvvUW\n2bs3+dJL8o3z3HNyDU2NFML7dd1YduxItm5NsF6XoAAAIABJREFUNmsmWs3oaNmiouS6qVNHeEZk\npKQ3a0Y2aSLf7B3ralxfzs6PX9F45IiMy9Gj5NBuQqqa3KyxXDmyVCm57oKDyeY6cTaT0TBodBax\n8+nGGhcvlnpWrxat5FKICamva714cSHfISHkddeRt9wi1/4dd7gJqdGvli3JNm3I9u3JBx8kH31U\nvo07dyaffZZ8/nkZq5dfFjI6eDDZv798Qw8YIGPZuTPZPFi0Bq8hlsdh49C6CTxYJYr/hYkG9GTN\nRtw0KIHpoTbuezuWGaE2Js10cseO7NfYjiUaTze0c8+YBGaUsfHUlARmRNuZER8AKTNd43nWYngr\n62liq2kyqKGh2X09ffmA5ocw5pbXWztmP1NDexkZ6T7udMqDt1Qp2XyR4YQEd//NdZrHxdOn1RM5\nmQ+XKSNyeI6R2cfWTIy99c8T3sipeaw8SV0ePoqfaKBx/fV2vlslnieDbFzQNZ6uRvp4GETWXId5\n3Dzr88e82qhjyJCspvG+jvuL3PpuEGMvpDy9QSO+pUbzhdYa+2A0Tzf04zr21V737nKuvRGQK9H0\nOdD7/WI8Hyxck5g1a1a27//o6GiDmNWHuFUtQlarvw/o5hJhEHeskchq9deKXniVty1QYlZK1zqZ\nt3QAKyBrh53X9x/W81c3aa3u0UlSBrIG/3gJsrbYCYhJ4UidrJn90OIhESAX6vv/A3AQevAPiI/Z\nPsjaan0hPmY5ydLAR/+G4wrVmKWmyofj3XeTzZvLmb33XvLrr8VMr39/0Vg0aCAEy0ymoqLk43rY\nMHLSJPlAX7RITOfWrJGP/8REeUe9845oOV58UZ7tI0aIud7cuULyBgwQTdaIEWQ6hOWlQ3H/ftGu\nBWz2Vkh8zLJ9aHn7OCzIh77nB6+3D2B/6rDbyfHjcx8nTxh5fBDegBDAh53LRbp2ZSXSmTs1udZ8\n1JORQR5epfHgiKlcu1au7fnzxfR1yhQhrOPHi0ZuwgS5lgcOlGu7Tx8hWN27C+l65hnyqafIxx4j\nH3pIlCX33Ue2akW2aEE2bSqn4O67ZVKiWjXRBIeFkVWqyD0bHk42bEi+/z656w0ht2u6xPKuu9yE\n00w6/dE2mzWgr2I80xDCwRjI47Cx061O1qpF3nWXkORGjeS50KqVbA88QD7xhGirO3cWrWefRzRu\nLm/nkHsd3H6rncNf0jhggMg8bBj58cfk2LFyW06cSE6eTM6YIWO66HONR+vY+b+RDh6vZ+fKbzSu\n/EbjiXp2bp4g/jR/L9C4c5poDffNdnL/So2ptSOYGVqGKQudPPO3xswWHsFxLsb9508dnuTF6RRS\nVqqUW8tnJkVmEuZLc2kmYY0aMTMikqfvasT033IhZQZyeo56PqMMIqa3xcjIrAQwNyLoi7zldtzP\nj+LDq+Q6nfWRxq1byQ/riObs8xbxcr49n2u5kfPcxsdTHoOEDRmSP1LmT9+9jbl+jo7XiGITOJly\nj2j4vx6YQ/9ya8/zXWfAXzPzvAZ1MsqZ/WSN57BZYzt6tMxqBUIefd2rTz7pXVZNk/vR0CBbpMxC\nHmHSmEUCuBWyTtlpnZSNBBDErFyiOYC1kICE/wLoQi+cw9cWEDHzaDgIwFO6dmsK3JEQJwHQ4Pbt\nSgWwUy8zBMA6D8bZVe/wRD1PIoCvPBjndD1PK7j9wUbqne4K0Zpt08nYjZBokTnK4qNPkVcqMZs7\nV87mpk3ysTpvnjyTDI3CbbfJR2KXLvK+WbFCtBCXDIZPmaGC033LrKiMlwC+5AmEnHmb2c+JoJpx\niXzM/EJhIsf5hSe5TUigq1EU0+tEMLVWPZ6NaMT940RjltQ7lumlbVw33slly8hffxWT2N9+E6K5\nfLnc45vihNhtv68nCXDZg7Hs00c0d6++KhMshvno44/L1qGDTOq0bCmTPM2aybOjV4TU1eU2B++4\nQ7TjlSqRN94o4pYqRRYt6l3rHu1Fo+ntWBO4tYYnUYZ/IuKCaa2h4QwKEjPiUqXIOqEalxex8+Fy\nDjqL2tmoosbKlcmqVcXkNjycrF1bSGhkJHnPPXI7NG0qfWvZkny6sca/rrPzzbsd/KucnV2jNd57\nr2h827YVTejz92rceIOdo++J56kiNsZGxXPXdZE8ExLKmQ1iebqojSMecLL/0xq3VrJzRsPxzFAh\nXNRwIM8Ws/HrGCc/+EC++QcOJD9+RWNSpSjuvj6Cu0rW5EmE8gnE84+SQnq//NI9QbZwodt39ocf\nyDlzhPAu6OfkueI2/tQ6lueK2zjvbSdnzyb/7//I+XEaD9eyM3Gog/9Vj+Kx6o248iMHj9eI4n81\nGnFxt3imhNg4PCKeB2vaufY7jevXk9u3i9XBf/+R586ZNPr6fXVqkZNnGtmZuiQXUpfLfXn+vFgE\nrPxG4zqbnXXLaPzvP3e+xFfixeesppPTh2o8Wi2KybdHMKVOFHct03jsTyHq1LQLFhOpqSLvqVNi\nlfBnrJOpJW1c1TmW50vZeGiOk+fOSfqRI2JlsPIbjYdr2/lndC+6AB5v2IYuKCa9HcdffiGnTxer\ngtWrZUwujEdOyO2Z5Ple6dePrqgofnif84IJY7t2Mmni2qXlbnbnq37PCYFAnst5Depkfs+aJx8i\nImTiwnw8Li5g8pi6Ve7V7nc6mN7Mi1bds54yZZhaO4IJrzqY2uQivBf8Jaw5TS4WLSoPIG+IiRFz\njSsVV6kJqZmYMY+cKZAtUDLWD8AmXUBC1HNbAHwCoJNOlEIhizkbvl3nAXypl5+oE7IGOtM0zCAJ\noJ2eZxuAdyCmj2f0tHS9vmJw+5c1hKyHlm5q51+9jlxl8dG/K5aYde4sHx+eOHNG11RdTngGADH2\nixcPbBbOm/2/gdzs/z0fEOYHqucDwtPvwFsdnmVGjZJZP2+43A8g8+ykN1k8o/h5y2O82D3HyZOc\neZ6jvL7ALwYCnJkv1PAcr4QEmVHJi4+ZAU8N6MCBeT8nRl3ezHm9ICNDPuxTUsgTf2k838TOI986\neKahnTuWaExyiKnlrikOptxj5/ofNP7+u5DKra+IRnBT91gu/0DI26/vOThtmmgzP/9cAu988gk5\nciQ5/XnJM+U5BwcNEs3mu++SffuKhvP114WEvvwy+cILQkS7dpVn5lNPyYT6oBZSx3vNHHz0UTn+\nxBNilvrQQ0JW324oeeKqiXyv3+VgbBX5P+a22Ata0e53Sr74G4UMv18ulhUrin/mTTeJWWxYGNmp\nklsb+ssDUs/gFg5WruxbC+q59S0q5d4unl17aia+3v5/Ujk2GzH23JSSLSiIrBokmq0nIKTp6eB4\nJgYLqSpfnrz5ZnnUV6ggfr+1S2v8TdnZqoiDvwWJFsgwDzbq74qpjLpJ4y+/MNt9u268k7uK12AY\ntAsyr/Ug6iVLZjWn99z80S4bdTvQjIT4Medk4ly1qmiYGzQQftGsmRD8tm1F29yxo5D9NWXsfLG6\ng+uus7NHO41duri16y+0FtPND+vEMznYxhfKxHMp7Pyyv/R92TJpr0EDmUzt0UOu4z59yLfflmt8\n8GDygw9Eo/9lf4177pSAVQfC7VwwQePSpeSqMU6mlXa7DRya4+Thw2Jqn5Iivz6/D/I64eZJzsLD\nydKl6QoPZ3rdSKbd3UiiHOeBPPbu7T5ffeo7mJycs6xH5jr59M2Sv/MtDh44kLPoucLf911O76aK\nFeXkxsRkTYuJyX7c0Cp6Q0KCpHtDXsvlF1fTO9mEwk7MFgJ4FkBriE/WvzqxustEhj6H+HE1h/h2\nnQKwh1mJ2SbIgmt1AHTQO/wN3cTMCJn/sa4x+8wgbyZiNkDXgBkas/U6SbvBH1l89C8SuPJ8zFwu\neSn27VvQktC/qIwWChfyM8t1Kdcxyw1Xy+yct5d6fqIyGnV404AGEvjDs668aCW9lfXmY+bpCxUb\n6zYNzIkMBkgYc5TRn3bi40W++Hi3X5zZfNdfMmyMQ0QEWbOm1BPvjkiYmSl+pnv2SCCm/fvJAwdE\ny3T8uHxUpy7JqmFN/83J5GTxUU3eIFFWk+c5mHZ3FM/Xb8Rj3zl4vn4UUyMbMXWaux/nm9q5bbHG\nNWuEGC9aJFFtp08Xs9SJEyWQzmefkb8MkI/cVZ2F8Mzu4eCIEUIQBg0SsjB0qJi3jhlDfve65J/z\nmoPjxpHjxol58NSp0sbmzToxyOGDztUoimn3NOKBeAfPVK9HAlz+gYNTp0rXR4+WKLjTp4vp/jff\nyKncG++kq6yNaaOFlKwY4eSMGTLM338vGuUkh8bzTe10vS4as+Qo0ZhpfeO4a5ebwKxaJRrMcePE\nnP/552WLiRFz5ieflEBUHTqQ998v+8YSHYNbOC742xr+qPffT/ZvIukz7pGx/CvWkUUjl5AgGuzG\njeUyqV1bgi4Z2uqbbxYSfP31cqu0Luom34GS06AgIZ1ly4oG/OabZfLgkfJOnlA2DrLF8mSQjV2q\nOFm7tshSp45MRERGSoCu2rXlkVWjBtm1qpMng2wcX24g0xHM7ep2boJbM+wIttNeRWPduuQL4U6m\nBNs4oXosTxWxcfC9Tj77rLw6DLeJRx8Vc/DK0Lj7DjvXfuKgI9jOOqEaH3lEJl2+eEY0yCuflGjP\nk551slFFWSd0zWgHVxS1s2EFjcOHC5nt2pV85RXRQO/cKefaCPyUI/wlrDk9Nz1JmDdSZlwE3rSK\nvo7nt9zFwBVuxZKLj1nhI2bZCgsJImTtsCt2gWlT+hWpMfv3XzmT8+cXtCTMmXwZ5MyCBQtuXOx1\nzHyZMvk6nhPyMwPqLY+meY/KqGnZA4AY5k/ezIy91Z+XDwB/6vA0PbsEPmbZ/L5y68Pl9DHzHAcz\nOfXHN80f0uxrksWQf/Ro9/969XI3zy4oHzPPun31PdCx9LM9128OZja38+R6jf/+S+6bLX6be9+K\nZVppG/8Y5eQPP/ACQZ05U/xBv/hCSOeoUUKqBw+W4ETvvUcuaCvE7rvmsXz9dV7YevYU4vTSS6KR\nfv110Wj16SNpc1tIOWe9nhcY4F8xciz+ZQfffFPyde9OTq8vx7+oGcsWLSQQ1D33uAONtW5N9npQ\nlphx7ZIx2rdC484wCe5Ur54Qyb7F3CT0rrIa/67gXh7l4B8aN95oZ43iGkuXlkuoSpXsJLVIEdHC\nXn+9fLJUrSqEMyJCfIGbNyd73+PkqRAbv75LyOQHbZ0XxqVvX5mPGThQogIn3W7ntz3dy+l8842Y\nx+5oEUMXwFMVqtAF8MD9MRd8+rdtkwmZ//4jU2cm0GUmU/6SK898l4OU6XDt0nikjp2zXnLwfNM8\nXtfengmAvCO8TbyGhl6y78tCrTHLVhi4Qxd2Lq7gBaZN7VyRxOyrr2TG6+TJgpbEggULBY4rcR0z\nQyPYv793DZo3wpFfkxl/6vAkZYZM11JURnM/PMlcHn3M/IKv8+1N6+rv+FzqqIyecue07+9Y5rW9\n/PiYGfD0e/W3rFFu4EAxv779dq+aYb/b8Ode1evJHBtLl/k+8JLftct9/OBB0RLPmCHfUhMmiJn0\nRx8JQX33XfKNN4SEdusmJtCPPkpOrCkkcFzVWDZpIt2rVUt8W2+5RZYFqlSJvL+0gwRo97KcznYI\nM9yOKj61mQD5KBKYhhB+Wbwn0xHCXjcnsF49IYotW4r57OOPS1Tgjh1FIxsdTb55WwLTEcK5t/Rk\nugrh1/clcOhQMQWfMUMukR9+ED/WJUtkXdQPPhByvX69rHG6a5f4nR49Kq4xZq0u6Y6KnZIivpvL\nl5MPP+w2OX28vIO//+7fZZPrOTfIV3Cw9+OhoXloKHcUamIGYBiApgAqA6ita78IoKWefkUuMG3q\n3xVJzLp0kW8ECxYsWLgiYSaR1jpmOffhcq9j5ou85XY8P6TZLL8vLebo0d7rK8h1zHLruy8S5i9B\n9re9/EZl9JY3nz5mDA/Prq31lzzmdq/275+1XL9+bm27t/z5NXP3l7B60ZyeOCFE5lxn0Zidv000\nZsceiuG6dWI2m5hI/vyzmPvOmCHmxOuaiuZxZf2efOMNMd/s1k38Fu+/XyLqtm8vj58HHxQC+dJL\n5OLqUm5OpZ6sVUvMX4sW9U0CA9mCgmTzPN6wggQfOpzg4JoydlYN0hgdLeR20CBy+HAZuokTxQT5\n22/F4mvpUvL332X93K1bRSt6vqmdpzdrbpPn4OCsJOwSkzKy8BOzr3SNUybcATVGmtK7QMLhn4V7\nAWiHru0yFpieqRMzI6BHKiSqo3mB6T06YTPaOQbga2RfYPqE/psJYDuAb+FeYDpXWbz074ojZi6X\nzMz06VPQkliwYMGChasOl2EdM7/av1j1XUrkdR0zIz3Qhb4v1Tpm/ga58FXuEkVlvKiy5hWX08fM\ngEG0e/YMzBzRRzmXS4IzJSeLJmz/ftGMbdzoXg9z9Wrp0pIlEhV27lwxff3qK1lW6csv3f6nM2eK\neebcueTfC9wRU0kybbvGfdUlAE7t2uK/WK6crBPqD/kzln2JhoPLlJ21S2s8hlC6AKYDEk0VoWzd\nWrSFRoCdJ5+UZaB69BAT2/79xf91zBgx3502TYbDIISrV4sJ6a5d4tt78KAQaJerkBMzCnm5D8Bq\nyFpjF8wJ9TS7ToKOQ4J61Abwg07C+uh5hkBMF9dB1j5rDGCX3um6ep4VEHPGaQDCIYFGzgM4o6cX\n0YlWBoA+umZtiC7PEn9l8dK3Ky74x86dchbnzStoSSxYsGDBggULVzwK4zpmF1vWvMBfEpiT5jSQ\nqIxk3n3FCsLHLEBtuUEQjx8Xcrhjhyz5tHq1W2v4/ffkrwMdJMC5vRwcNUoIVrrO3NIBdu0qppz3\n3y/NtG4tJp6NG4ufYo0a4oNYoYJYmudMBmcR6OCxFfLgHwDiIP5cVXXiYyZmZXThJ5uO1dOP9dP3\nX9D37aY8sfqxW/T9xTrpCjHl+RvAKdP+MQC7TPtKJ2+/+yuLl75dcRozw7/sxImClsSCBQsWLFiw\nYOEqxeVex+xKi8p4KbTbXsxBL5gvGluAZozp6bLu4YkTEu12xw5y3Tohg0uXCiGcN08ivE6cSA4Y\ncHk1ZiEIAEqpzyCh6DtC1hgDgLJKqeIkUwFcrx9ro5RqAQlPPx6iISuvp2Xq29tKqf8gZomddJJX\nHxI58ZSed5hSajKAeyHBO4KUUmVJJhtETinVFaLB663XG6qXvcEPWa54LFsG1KsH2GwFLYkFCxYs\nWLBgwcJVikmTfKc1bSobADz7rO9858/7Tps8WTYDcXHArFnA449nzWfsx8VlT8tPufwip36HhckW\nCJKSgG7dZEzCwuT3jjuAzEwgNBRISQHKlAFOnZLflBS/qg0Jka1YMf++ndetA4YNC0z0/CAowPwv\nQzRRDoivmYKEqX9CT68IIVg/A5hjyufQ0wCgAgANQqJ+BzBdr+OYKU8ogPkAWkHWJ+sN4D1TG9Dl\nmA5gKIC/IMFExsFNyCqYZJkPidjYSG+3ZoD9LpRISwMWLgTatStoSSxcbYiPjy9oESxYKHBY94GF\nax3WPVCASEz0TaAef1zSL2a5wgRPUgYAdesKKQsOBjZulGMpKULSDHJ2FSAgjRnJLEROKeWCrBM2\nzyPrAJLdTfkSIBouAxkkH/CoK8Yjz0GSD5nSa0KiN5rz/OrRzise6YBo056BrIW2GsACAC2UUjeQ\nPOatn71790bZsmWzHOvUqRM6derkLXuBYeFC4ORJ4LHHCloSC1cb4uPjC931bsHC5YZ1H1i41mHd\nAxYKBImJWUkZIOQrNFRIWWKiO82sOcsn4uPjs01GJCcn57veQBAQMfMDhyBatAqQqIoGykO0Wkae\nLKaESqlgANfpaUaeCh51l4eQrsO55DGnKwA9AUwkOV1va6+erxuAj711YuzYsYiMjMyhmwUPEhg9\nGmjYELjrroKWxoIFCxYsWLBgwYKFiwBvZpE06V08zSL9NGPMDd6UMOvWrUP9+vUvSv3+IFBTxhxB\nUoMQonuNY0qpMgAaQswWAeAPADalVD1T0XshJGq1KU+0TtgMtAGwTfcvM/Lci6xorR83y1ILwFIP\nWf4EEJXnjhYwSGDkSGDlSuDDDwtaGgsWLFiwYMGCBQsWLOQXARMzpVQppdRdSqkI/VBVff9WfT8W\nwHtKqQ5KqToQP7B9AH4EAJJbIVEXJyml7lFKNQHwKYB4kobGbBZkUenJSqmaSqknAbwOYIxJlHEA\n2iml+iilqiul3ocED4kz5fla7+OdHrL8Cbev2hWBlBTg77/Fn7N9e6BfP6B/f6BVq4KWzIIFCxYs\nWLBgwYIFC/lFXkwZ7wbwG8SskHCTpWkAupH8WClVEsBEADYATgDtSKaZ6ngaQqCWQAJ0zAHQy0gk\nmaKUaqvn+RMSGOR9kl+b8vyhlOoEYJi+/QvgQZL/mNr5DBI05F0AHxiyAHgR2X3RAKA4AGzZsiXA\nIbn0aN0aOH5c/lerJhqzVq0kWowFCxcbycnJWGddXBaucVj3gYVrHdY9YOFah4kTFL8c7eWFmP0L\n4BsIwSmp78eQNN+5QT7+G1D65mvffExBSJRnulG3QbDopa1jEOIXZMoPZPVFMyMMAJ555hkvSYUH\n27cD77xT0FJYuNpxOW2qLVgorLDuAwvXOqx7wIIFAMIRfs8tU34R6DpmNgArIT5bbSHE504AJ0x5\n3oEE3HgWEhb/QwCLlVLhJq3ZLEjgjnsBFIWEy58IiZ4IpVQoxNzxFwAvAagDYIpS6gTJr/Q8UXo9\n70AiLT4N4AelVD2T1qwPhLCtBNDfkEVvc7yXLi4G0BlAEoDUQMbGggULFixYsGDBggULVxWKQ0jZ\n4svRmCK9WfT5yKzUCABRJJvnkOcAgFEkx+r7ZSDaqWdJJiilwgH8DaA+yb/0PG0h5OoWkoeUUj0g\npocVSWboeYZDTBVr6vuzAZQk2dHU9h8A/iL5ikmWXyHrrL2kt7sKwDkAVUke9bvzFixYsGDBggUL\nFixYsHCJEGjwjw4A/lRKJSilDiul1imlzOuIVYEE1VhqHCOZAiFDRhTERgBOGKRMxxKIZquhKc9y\ng5TpWAygulLKWGAsSi8HjzxRuixVdVnGAHgTshD1CgBnAMyzSJkFCxYsWLBgwYIFCxYKCwL1MasG\noKb+nwBuBPClUiqV5EwARmTG35RSRSFE6RWIxsyIglgdQFGl1BkApyCREt8FcNyUJxxAFaVUKoA9\nkOAeRij9igCSAVSCRH8cCWADgNc82rnFkAViumjI8il8EFKl1PUQE80kWKaMFixYsGDBggULFixc\ny7hgykjyv0vdWKDETAE4CxHQCMYxFEAPADMBvKEffx7AbgATAHwH4CAAKqWCADyn52kEIVczIKHx\nlZ4nDEAkgE0AngLQCsBXAF425XlSl/1bCNHqDSFew+EOBpKjLD761xYS2MSCBQsWLFiwYMGCBQsW\nAIlBMetSNxIoMTsFINNsBqiUWg/gft2X7H4I6dlFcqNSKgbAFgB/AVgOIT43AEghuQnAJqXUQAAj\nAJSGLAjdA0AKAI3kNgDblFJNAbyg130YQsROQRac3qqUellvuw2Aw37K4g1JADBz5kyEh4cHODQW\nLASAn34C6tcHKlXKnnbgALB2LdChw+WXS0fv3r0xduzYAmvfgoXCAOs+sHCtw7oHLFzr2LJlixGt\nPelytBcoMdsLoKZSaj/E1O8PSCCN3ZDFnUMgxOleABtJblNK7YVEVRwB0ZJtA1BDj574F0TT9Tkk\nrP1qiD/YOgDRSqlgkpmmPNsgGrv6etv3AhhPkkqpJRAfuP+DrLWWmyze0BEAwsPDERkZGeDQWLAQ\nAMqVA7p1AyZPBsLC3MeTkoC33sp+/DKjbNmy1j1g4ZqHdR9YuNZh3QMWLFxAqlLqVgBfAGgBkzsW\nSZeRSSnVAhLfohZ0dyyS0/xtJNDgH19CtFDfAhgC4B6IqeAkiG9XGoCxEN+vDkqpOgBCAZwG8KOe\nZw+EaE1SSt0DoArE5NBB8pCeZ7le12SlVE2IX1pxAOMgGrdgyILW7ZRSfZRS1QHcAeA6yKLUFfyQ\nJQt088jeAY6HBQt5Q1iYkK9u3YSMAfLrjaxda5g2zT0mnkhKkvTLWY8FCxYsWLBg4VqHArAQovhp\nBFkW7DmIS5dkEHes+ZAgiHdBeMtXSqnW/jYSEDEjGQfgQQAtIYzxOl3Qp03ZxgHYCeAHABshZOhH\n0xpmANAXwE0QDZkRwdG8rth5AAMAPAIJcd8XQginmPJshpCzEQC2QiI6JpnWMPNXFgO9IT5oFixc\nHujk7GiHbnj65kSceMQiZQCA5s2zElYDBnFt7nO1jktTjwULFi4NrMkTawwsWLhyEAWgBoDOJDeR\nXAxgIIBXlVKGBWIPiAvV2yS3kZwAYA4CUPwEqjEDyYUk6wJoDtE+nQVgg/iHFYUE2SgPIW+RADIB\nROvFD0G0WbMhxKouhG0CwAOmPHdCgnp8DhmEWRAC2ByyqHUmgEcBdAHQHRLFcReAW5RSN/gpywUo\npYpAzCNXA2JT3bFjxyxbfHx8oENlwRMvvACsWOE9bcUKSTejenVgwgTv+SdMkPSL2bbnC9K87/mC\nvFgvzLAwjCo5GLMOtMDwIoPzRsry+2I3l/ccJ3N5b+co0HPqDy6WNtGjHjKP9ViwYOHSwJo8scbA\ngoVChPj4+Gzf/717X+BUdQBsInnMVGQxgLIQs0VANGk+l/LyCyQD3iCBOrYBaA8gHaL1KgPRdKUD\neFjPVw3iO+YC0ADAfQAy9Dw36HlehKwtdgKiHhwB4AjEL8xobxaAAwAW6vv/g0RXHKfvK4j/20kA\nb/sji0d/btKPdwXAtWvX0kIeAZC33eY9rXx5SXc6sx53OkmbLfvxuDhSKfn153hO8NWG+bimkXa7\n/JLufafT+3FjPx84uV7jMmXns2EOLoOdR9fkoU5f8vgrpzmfPh6zBg/2etzvc+freCDQNO6rZmfb\nEg4eqe2lH1On+u6bpkm6/v9oHTtbF3ULU+elAAAgAElEQVTwUM2Lc94uKrp39z1OTqekWygQzJo1\nq6BFuPrh67lb2O7TSwlTnzdvJs9v0wrNGFj3gIVrHWvXriXEau87AIuYlT+U0PlDW31/G4B3PPK0\ngyiGitEfjuVPJlPloyAapzk6WfoV4sv1mZ7+oy58e4gGaiUAJySSSS+Ihu4QZB2yupAojYchZowu\niD1mmN6BNRDfslf0Nj6GLEwNAJ30dsZCNGoTAfwHIB7A9/7I4tEvi5hdLNx2m3dyZhwvXz7rB3sO\nH/BJSeSGl+LogomExcn+hpfi+OWX5LJl5Pnzfsrm2Za3tj0/CpxOumw2znvbyZMnvaTnB5rGvdXs\nDIPGjRvJO0I07qycx7p1uTJ2aHS58iCnJwkLDSUjI3MmZQb8Gdc84OxZ8qHrHCTAJys6sp9nPwmp\ny0XGVJV6nrnVwYyMfIl18eE5XlOnkqNGkQkJ7uMGedM0cvRoN+k0ypvJm0FYvRE+g7BahM9CIULm\nx6P4jy2K8950ZL+nzZMsVzM0jUfq2BkNB3ffXjhImQULFvwmZm3om5i113lNUfrDtfzJZKp8ja7x\noi7IUUgI+k/09BiTVooA9kEWpF4FYLieZ66uzaIu6CoApTwY52GdjFH/nWhmnCYiZchySidVIwH8\n4a8spn4VgWjX3rCI2UWAJzkz7e/ZQy7s7+TpojZOrBnLk8rGQS2d7N2b7NWL7NmT7NFD3s0hIVLs\nZcQxE4pLyj7MTCi+jDgCvLAVL07WrEnWr082bkw2aiScok4dskYN8vbbRYRbbyWfvNnJE8rGQWVj\neULZ2C7UyfLlyZtvlvQ77iCjb9O4sridj93ooLOonc2DnVwKeWEmhtgZYdN4441khQrkTTeRlSrJ\n7003STu33y7t3nMP2by59KVlS7JVK7J1a7JNG/KJBhpXlRJS1qWLDNOgQWRlaPxfSTvvr6WxQQPp\nT7NmUkfr1mS7duQDD5AdO5IdOsj/++8n27cnH66n8bcgO9uXdnBtWTvfekxjTAwZE0O+/LKM71tv\nkb17k++8Qw4ZQvbtSz7zDPnCC+SH3TXuuM3OuMcd1MpF8nRIKGOrxDIl2MZh7ZwcNIicNEn4wnff\nkYsWkb/+KuR43Xgn00rbqL0Ry/RQG7dPdnLbNnLPHnLfPiHZu3eT+/eTR4+SycnkqVPkf//Jsd27\nJd/Bg+Thw+SGDWS/ThqXwc6VHzm4FHYO6Kxx714hWi6Xfq3lMtuekUHOG69xKeyc/rzUM+sj7TLd\nCAHAU3NbsyYZHCyDbaSHhpK1askFbpo48Dm5YCZ2OR3PCf5qJfNbNlCtYX7kuph15AVGu97aNx+/\nFO0XVJ9zQeI0jWsRQQI8Nd+RVaZCojm6HBjWRiaQekU4cs98LaGQXrcWrg2YiNlEAOuYlT+E6Tyj\nrr6faHAiU57nDMWSP5vSC/kFpVRXALEAngGwXW+sP4DpJJ9TSv0KCU9vh6xFNsFEppYAeE8ncy6I\n35exwPRkiAnifXq9uyCRGV+CLDAdC+B9SOSTEjrp+gISGXI2xKnuccji0PVJNs5NFpL9Pfr2P73d\nTtHR0ShbtmyWvnfq1AmdOnXye6wKAhkZQEICULYs0L49oFTuZVwuYP9+YNs2YMcO4Ngx4MQJ4MwZ\n4OxZ2c6fB0JDgdq1gVtvBa6/HggOlvL//AOsXy/ptWrJ7/nzwCNvVYbt5B5kIgjBcGFvyG1oeMNu\nHDok5YZVGIf+h9/AFzViMaNcLxw/LnUa2803A/fdB7RsCWzeDNQe9AjCt36PTXc+jHUD5qJZM6By\nZWDjRiAxUczxU1Ol7eBgoEgR91a0qPySkt5y8zjct+gN/NwuFuujeyEzE0hLc6crBdyxPxHdZ7bA\ntBgHjtdpjjrHE9HqwxaIf8mB3WHN4XIhywZIufR093bqFHDunNRr5DP+tz4wDXurNsedrcPw1FNA\nsWKSNmsWsP2XJFTdm4iVdzyLjAx43Uhpz7yVLAk8aEvEE5+1wBC7A4vONkdQkLSXlubeQkJErnPn\npEylStLvlBQg8lQi4g+2wCs1HajL9Xh5yxuYFhmLz4v0wt69wMGD0rY3vIZxGI838Dpi8Sl65eta\nrowkTFHdsPf9yeg6KAwzPkjCLYO6IQaTsRthKFECKFFC5K+YmoTYU90wptRgvHlmCPqVn4z9RcKQ\nng4UP5SEL9K74evGkzFzRRjefiIJ7eZ0w9jak5FaMQylS8s1a/yWKCHXT6lSIkd6OlCmjOwHBcm1\nVKaMjGGgW1CQXIehoe5pBaXkPBw5AnzXewVenN8Bixq8jwfWDAJvuQWlKpQBDP/WBx4Atm6V/ccf\nFx++Dh1kTbymTbMOoOGf0qMH8OKLwJdfAp9/7t73VsYbfPnk+eOrF0hZX33xdTw/cgVSR2Ki+PgY\nv2Fh4jf57LPALbdkTX/2Wffagz/9lL29FSuAAQOAYcOAQYOAoUPl12jf8MmcNCnrcU8Y7Xs7f/37\nA7t2AbNni2+oIfO0acDttwOrVgELFkjbO3dKPUlJwHffyXFvbRr1mMfAPFaeY2Bu19uYG/lMGNA5\nCR1mP41iPIfrKpbArc5ZCP5+DjB3LvDII8Bjj+Xerj/js2KFyNe0qZRt2xZ4/XXg1Vez1336NDB+\nvLwc/UVufR82TK4BL2NJ5wr8a38BQ9VgDMgYgts2L0KpWl7quRYR6P2eh2vQggVAfMw8Y0okJydj\n+fLlANATwkduou5nppR6EaIUKk8yXSk1AkA7kncZ5ZVSswDYSLb3Swh/GZxO4B6EkJs0iIYpHW7t\nWZq+uQCU0fNX1/cPQEwZDa3XBlOdL0FMG10Q88aRkKAin5jyxAPYALcp4yq9no76voJoxP4E8D3E\nxyxNz+NVFi99ewKyNtsVqzF78UW3FikqivzjD3daWppoLX75hfzgA/LJJ8mICLJkSXeZkBDRAlWv\nLtqnpk1Fu9Ohg/y32dx5zdqqBg3I8HCZ4DfXdR5BJMA0BDEmhhw8mJwzhzw5X5/lj431b+be8Cl7\n+OHAfcs84fSjbWOW1uHI6mNm7BfW2VtPuQOV01w+MlI0NB7jlJZGnjwpmq69e6XIjh3k7m+czAi1\ncf87ojH7e6KTDgf588/kggVy3f3yi/z//nty9mxy1izRvC1YIPkWLiTnzyd/+VLjyUg7kzdklf/I\nao1HaovGa8wYcvhw8r33RNP4dVeZaf66q4P9+pHvvkuOeU3jnjvt/CNeY1qa1JGZSc4ZrfGfm+x8\n9X6N7dqJRjIiQrSlN98s90BoKFmihHTdfF1fjM3QBHtuNhv56R2xJMAh18eyMjSuKRLFf4pHcFup\netxcphHfr5XAU0VsnBwRy1NFbBzaxsmYGPL550Uz+uyzZNeuogXt9aDGzeXtnBU1nhkqhL82Hshz\nxW387QMnv/+e/Okn0XouWSLnZtUq2davJ7dvJ3fulPO7f6XGc43t3J2ocedO8uw/GjNb2Ona5cf1\nFYj/UKAmsRfDNym3Orz5mZpNfT2Ply5Nlirl2+cyISFrfcavocU00nPqQ05+nWXKyMWsab59RD21\ns1FRWbWwvsbIl6+tvz64Po5n7tToLGrn0G4ax/bSuBKNuDGkHs/UqCdy+duuP+Pj6U88ZEjWd4qv\n4/4it757nneT5jujjI2PIoF77rSzCZw8WtePa9mXJql7d7mWvGmS/DFjzqvfq1HOMMc2a4CNcoY5\ndnR0YDIGcr8HeA1asJATTBqz+joXWYSs7lgfMKsG7bTOZczuWK2MPLltgRKzUhBzwJqQCCRv6mTn\ne0g8/0yImeLDpjL79Dz3QDRcO5A1+EeYnp4CMSlMhERHNJO35/SOLYTb7HAb9OAfep6pkAiRfSHa\nuJxkaeCjf8OvVGK2c6e8R8aNE/Oyu+6Ss1u1qnxsBgVl/QBs3lyI3Jgx8jH8779kenru7SQni+nZ\nnj1C9IwPXlL+nz0rH78XzBeNhg2zxkA/vjwDfeQl8IeBPPqYeTUHK2wP9vx+pBYmH7NAzVZ8EdKL\nZP7icpGpqeS5c0JIDdPMf/8lt24lN28WMrNmjUyGOJ3kb7/JfbhokRCg778XEjp9OjlhgpiEfvUV\nOXEiOXMmOW8eeXyee9LAZbNx6RAnv+riuHDjDm7h4BNPkJ/XEPI2/o5YNmsm5q4NG8r3dZMmMokS\nHS33eK8IKT+tbE8S4FtFY/NEJitDu2DOuxR2VoZ2gWSWKCF84PrryYoVxSS4alWZ4Kldm2xfU+Oa\nUDtfqeXguuvsfKqRxpYtZdLn/vvJBx8kH3uM7NSJHNpGzJxnR8XydFEbYx9z8q23yH79hIAPHSqE\nfPRomTOYPlTjvup2LnjbwQM17Px2lMYZM4T0/9//yZj/8IOcg4ULycWLhYg6HHKefv+dXDdXY3J9\nO7d84WDy3XZu+FHjH38ISV2zhtw8X+Ope+zcOc3J0w3t3P2Nk+dqRjKjZCmm1orkwT80HvvBycyy\nNp6c7+TJ+e7/p0+TmYnZnyEuu53pvzmZ1tTOnb3HMyMohF9HjOehWnambvVxzZphusdcrqz7We5l\nTRNyExUlaab/ybUa8Uz1ejmTMvP94o1Y+CJH/j6PNI2Ha8v15HTKvbZhvFyzG4Lrcc1YJ12BtOtl\nfLzum2UySNiQIfkjZf723XMsdVK+qFsClyk7T2/WGBZG9n/ax5jl1JaBhAS5OQ1TaAP+PpvzGtTJ\nPAFhEH6nUyYLypTJejwuLnAZNY0nIu38fbjpWe+LRGqatPvkk+79wvjutlDoYSJmkQBuhaxTdlon\nZSMBBDErl2gOYC2AcwD+BdCFXjiHry0gYqY3WBvi05UO4LjOHj+BBOQ4B+AzABpkVez6et69etmJ\nOtM0M84Oeoe/0fNsg0RmNDPOOD1PO7j9y/rr7XWFBABZr8t0oz+y+Ohb5JVKzD78UCZqz5yR/YwM\n0U69+SY5cCD55Zeildi2TSdOlxK+fMw8A38Y8PUgvgaiMl4U5Hd20NfMuq/jZuT1BX6xcDG0JoUB\n3j4ky5QRX7OICLKe/gFtaFb80TYbYzF+vHwADRxIl83G5AVOHjlCHjggvn2GZmzDBtlWrRK/waVL\nRZP2889CMP8cIx/MvwxwcMoUeaZMmCCijBpFfvSRfNO+9574MPbpQ772mvg3fny/lB3UwsHHHiOf\nekrI2EMPCTlr00b8MJs1Iz+pLMRzRKVY1qpFVqtGVqkihK9iRSGAZcuKtr9IETIaUnc0HHnWYuZW\nh0FMn0A8j8PGJxDPPxHJkwjla4jlcdjYBM4L+ZvAyeOwXUhrEeJk8eJk0aIyV2XU9xqkrx+GDLzQ\nflCQPDIjIoRkN2ki37ING5J33y2XQp06ur8sbHwdsTwBGx+r6GTt2mTdumS7cI2rStv5/B0Ori8V\nxQ2lGvHlcAc3lo7ixtKN+Mj1Dq5FPRJgl9scbN9ezkfXrnK+evcmBwwghw2Tbfhw8rO3xQd1QnQ8\nzxaz8cen47nnTjtnfKBx0iSZ55g8WSYdvviCnDJY4+7b7Yx/WYJZTBqg8ZNPyJEjhWS//jo5Inwq\nqyiNDz7ILEGLkuc5uCm0EftgNBuUl768Hx7PU0VsnBAdz2232Dm2l8axY2Uy8t135bobOlSuvWee\nIV+r5+TJIBs/uDGWycE2juzg5IABkv7663INPtVI4+rSdk4o1osugGtuaEMXFL+4K47Nm8u1V7Om\n+PT27i0TArNmyaTLr7/KPZKYKAR/zRqZoNm4Ucj+fxF2rvrYwZP17dy5VLtwr23dSm5brDHlHjv/\n/TCeGcVKcsVT47mymJ2dm2gkZexLlSKXT9d4bMxUHj9OpqTI5FB6usnH1nyfez4DPX1JA30m53XC\nzZOchYeLJjk8XCb7zFrQAGVcvdp9rzo/dORcRn+GHro5gh3KOLjnzovwXvBXk5jTpGDRonJje0NM\njJghGTC0it6QkCDp3pDXcvnFVeoLaCZmDJAz5WULlJT107VZpyBRELfpZGiKiQyFQhZzNoJupAGY\nyKzErIHONKlrtgjgPrqJ2TsQ08czelq6Xl9REzFrCPEvSze1869eR66y+OjfFUvMmjQhH320oKWg\nf1EZvcGb6UK1ar7JV1ycpPsLfx6ong8V877nQ6UwPWTy+zA0l/ccJ3N5b+eoIEO9Xy3mKr5m880B\nQDRNAn94BgTJzRzX00QukMAf3urLi5lsIGWNPvlr5qzXnbnMQVcLO89v03j2rASWMUxuDx8WErp3\nr2g6d+6UCap//iE3bSK3LBKN2PZJDqbcbefm+Ro3bRKSum6dfHCvWkVuniAfhNt7CplaM9rBf16S\n/5u6x/KHH0RD9913YoWwvpuk/fFULOPihB9PmCCk5auvyN9ejicBHnhBCDPj43nqHjHV7d+ffOkl\nsksXMU+NiSG7dZMgPT16CLHo25f8tYO0saRjLN99V4hwz57kq6+Snzwo8o7u4LhAjEe0c3D4ffL/\nRNUIrhjm4JZKdr7QWmObNvK9GBkpwYtuvZW84QbZrr+eLFeOfLKiTrBt0m6rIg6vprlKyfdlu5KS\n/74SDpYuLd/nNptYcdSoIdrSzz4TwuF532bu1Hisrp2jXtUu9OWLmtLus2EO3nyzkJdixciwMDdx\nDwuT9+ETT5BzoiX/jHtieddd7uBMtWqRLVoIORvdQT+vNzUjAS4r9zDbtiWfflomF15/XQIvVasm\n7V0ssm+kG+S8Zx0Ht2+Xy/rECdE251R/cLCMcenSZJ1QjcuLSMCqP0rY2S5ctNI9I5xMCbFxUh3R\nQI/s4ORrr/ECQR0wQCZThg8X65m4OJlwmTqV/OYb8uf3nEwtaePqzrE8X8rG5R85+eOP5I8/ipZ/\n4UK3VYBx/c+ZQzqHO3m+lI2bHxvIzKBgHr/hdh4uX5Nni4Zyajsh9PPjNP70E7n6EwkcldRHzOD3\nzXZy717y0CG5f48cIbdsEW139G0aV4fa2a+xg78F2Tmhr8Z//iGTF0j0ZDPBc9lsnPaCM8t5GDFC\nJq0zM+V5cPSo/4+xLM+n3CYic3o3VawoJzAmJmtaTEz24740n76O57dcfnG1vJM9UNiJ2ULIos7h\nkIXW5usE6EtIkI1MAF9BQtI3B1AP4re1Uy8/BMA6AJsgC67V0TVeBPClnidRr+M0JER+dQDT9Tyt\n4TZl/Fiv29CYbdOJ1w3+yOKjf5EAGB0dzQ4dOmTZCvNaHmfOyMzxp58WtCT0TsoMGOTMgoWLgatl\nds4bGTbMfRIS3OkFEZXRXC4vWslAygY6Q38xtKUBmNzRbifj40Wm+HiffphZZPdFMI308eO9+575\n04ec2jCTYeNaMv7XqyfquKgot7ljIJp18xjo5VwuMWXPos0JhJDnNO6G/F7azfP4eLbbq5e8m9q0\nydUaIyWF3LVLihoasE2bhMSvWiXmzFt/1ng2ys5D/+fgqXvEz/Xnn90atrXfifmsNiKeGWVsTJ2e\nvU9paaKBW7hQyM7s2eSMGeSUKaKV/OwzuXwMLeT054WAfPakg6+8IhZ8nTqRX0cI8RtbJZZ33y2E\n77bbxNy4cmWJJnz99XIpFyuWnQAaxPE1BGYGbZQbh54XDn5Y3k3oA22jMjT+UdJO7TeZfBnYRdYA\nNcyqm0A0yIOvk2jPLYs6WRkad1S20/WbgzsrS96yZcUYARDtdb16MukxYIBoXEeOFC3sF1/IWBu+\n0PPnixn0+jgn00Nt/HeKk1u3kgcSxD/w9M9OpqTI8j1m7a/XZ4snCfNGygx4kil/yVVey+UXl9KK\nBZAL1RtCQy/K9+WsWbOyff9HR0cXXmKWrbCQIOoE7YpdYNrUzhWpMVu6VM7kxo0FLYkFCxbyDbPj\nvIGCWscsPzOggZQN1CT2YszM+luHsW/2b4qMFPWJNz/M3Aim2dQrL/5TOdWZm49ZvXryVeotX05t\nehuDi+FjZsDXJIshf//+V6+PWSDnPbc2PUlwoBpoCqlIT5cJ39Qlonk6PyqWmWVtPD5PzKCPHBGN\n1v79onk6eFCOHTsmWi7D5/Ls2wPpCg6m6/bbxQIgNJSMj6fLLsGdDh1yE5u9fUVjtmaskwsXilZu\nzhxy7lzyf7M1nm4o63SakbJR4/EIOxd+Jua0hgZ5XqtYfvWelDGPe/LdomUbPlyI1tdfCymLjBSy\nWqGCDFOJEnIJ+CKJnqbKZjNmg/AFBZG3B2tMDLazY1lZeqdxJY01a8pQfGuLoQvg3qJV6AK4oFIM\nH3pINL1duojG3DApnvNUAjOCQripRU9mBoXwf28lcOFCMaf9/Xf59tu+XfydN24k//qLXL6c/POd\nBGYGh/Dg4z3pCg7h2WkJWc1gvSA5Wc5lfrBlkfgVtyvp4J47/AwU5Q8M8uVJznwdv0go7BqzYQCa\nAqgM8TX7Qhc2Rk//Qd+/ohaYNvXviiRmgwaJmckl9x2zYMHCtYVrfR0zz49og4TlJypjeLjse5pK\nG+3kto5ZLj41OUZl7Ncvq8ye5Mxbm97GwJ/j+SHNeWnXn/EprFEZc+tTIG0a+1eTj5k/96qZhJrv\nA8+8fo6voQU+dUoI5/79oin95x8hPtobQgK39IjlokVi+hkfL6J8/rlo3CZMIGf3cJAApzzn4Hvv\nka+8IgraV14hD5auQgI8UKoKH3pI1iNt1UpMiuvXlyG77TYxJ54QLJrHcegZkObS0Fga5YoWdUff\nrltX/FYbNxbT3vvvd5d77DGyc2chrj16kG+8IfMjQ4dKZO8PPxS/4o8+ksfK22+L2W/btmJm+1wV\n6Xc0HHzoISGKx4/nOuy5w5OEXWJSRhZ+YvaVrrnKhNs3TDOld9E1YmfhXgDaAQnMYSwwPROylpnh\nN5YK8VEzLzC9RydsmfrxY3rbngtMn9B/MyHrnyXAvcB0rrJ46d8VScyio8WJ3oIFCxYsXER4Wwza\nrL30JFEPPCCbNzid8rDOL6HMicT26+eOQmeW2fhwNeo3t+UvwfZ3QeyLZWKc14W4A/En9ubHbNQZ\nqB+zWWZvMLTYeemTL/giGldrVEZ/5e3Xz60Z9kQg45tbe7lpIn1pMkm3+WIVIWdezRgN6OfT9WpP\nukJCmPx1AvfuFVPaTZvEfNbhIFeulP+rVwuBPPp5Al3BITz8ZE9mBodw+esJHD9eyNWbb4pP6ksv\nSdNPPy1Bbho3ltPVurU8rho1EkV7zZriv1mhgoQKuPFGt/9p5crSjfBwefxNGawxo7n0+0htO+tf\nr10gfMHBwtNvvFFIZ/Xqbsvqli2FHD72mGgNX3xRSOy778pcyccfi8vO6aKhdAFMB+gCmFoilKtW\nibbQ8CHesUPI9PHjpmjhecTlJmaKQkj8hlLqPgCNIeHv74Noy6bqaZ0g/mCnIOHzNQAf6vliSb6r\nlJoI4BGI6eGLkIAe0wDcoROzX5RS2wFUhIThHwHxRZuu5y0O4HoA+3XC9TaABQCeBjAAwCaS9fyR\nxUvfIgGsvZIWmD53DrDZgFGjZJ1MCxYsWLBgwcI1AF8LKb/wAtCmDXD2bPaFlI1FtidN8l2vP4t0\neytvlNu5Ezh6VBYGNxbT3rdPyg0YIAuaz5sH9OyZdxnNeQNZnD6/8KzXVzuei1+b94cOBaZMAWJi\nZL9bt6z7Znz7LfD008CsWcDjj2ff94W8lssvvPTbFdMNW/tOxqZTYTh+XL5bz50DUlPd/wPZzp8H\n0qEQAtG4FIF/PKZYMaBkSeC664DgYPlfooT8hoYCZcoAe/bEQ9PiERQEhITIlpqajKSk5QBQn+S6\nSzZ2OgImZgCglIqDhLm/FcBDJOfpx+0AlgHoR3KEfqwMxPdrGskYpdQEiHliJMm/9DxdIeSsJcnf\ndGJ2K4BQkhl6nvmQ1bSDlVJFID5ka0g2NMl1BMBpklX9kcVLvyIBrF27di0iIyMDHpeCwLJlwL33\nAhs2AHXrFrQ0FixYsGDBggULlwl5JZF5gb8k0JOcGEhKAqKigEOHspMwb+TMF5nKjWTltVx+kVO/\nvR3PI1xlykCdOoVMAMEA0kqFYtvvKTh7FjhzBihSBMjIcBO/1FT3/9OngZMngcxM2T97Vn6TkyUt\nIwNITwfS0oBTp+RYevo6nDxZH7hMxCwk0AI6KXsQEunw/9k77/AoqraN3ycJnRSKoNSACgZEIaAS\nxYRVBAXBXkAFiSIgIIK9IKDwCaISmghoKGKiUVBUUF5ENiygoBRBBQTZIEjvoabs/f3xzLCTzW6y\nm0ICnN91zbU7M2fmnDOzszP3POVs9Vh9wPg8bVl2KSQ5RzmPdTssZSoYn1WMzzMAzpiizKA8gCCl\nVDjJo0qpTEhGSLNdZh2ZxqKDfrTlvMduB6pVA66+uqRbotFoNBqNRnMOyUt0tWlTtNaymTO9W+Da\ntJHlM2fK99RU7yIkMhI4dEjKeFrGzPnkZPf3iRO9iyhzfuJE7wKroNsVlrz6nZgo6wsrzMLCEJSe\nDoSGIuTYMSAsDOXS03FNmzDg2LHC7dsHa9YALVsWy669EhRIYaXUBwAegbgNnjAWhyulyhvfK0P8\nMAcppdoqpVpC4scOQAQRIILpDIBPlFLXKKU6AHjT2N8lRplDACoppUYrpRorpZ4GEAtxXbzU0vYb\nlVLdlVJXQRKRBMMtNiv50ZbznoULAZsNCAroTGo0eZOcnFzSTdBoShx9HWgudvQ1YGHaNN9Cr00b\nt0js0cO3ADlzBnA4vK9LTBTzjUlqqm8B9cADst4bBd2usOTV78jI3C6rgRIWJmas0FC3CDt2TObT\n02X9BUCgj/N9IKno7ZAkIArADAAPWsoQwCIAX1rKrTCWm+t3QBJ2rIDEgc2AJOkwy5yGxI21gyTr\nGARgiFGfWcZlbPsmgLWQLI8Tjf16tuU7SJbH1hDxVgUXAP/+C6xaBdx9d0m3RHOhoW/GGo2+DjQa\nfQ1oSg2eoszEKs4uAAJyZSSZQ8gppVyQccK+MRbtgYin8SSftJSzA9hmKVOV5J2W9cEABhvrzDKh\nJFtayrSFCK29ljLrPeoZ5rFeQcro0PoAACAASURBVAaeDgHwOIBVkLiztkqp6iRN18scDBo06LxI\n/jF1KlC5MtClS0m3RKPRaDQajUajKSbyyolRRG6MycnJuV5GHD16tEj27S8Bx5jlBUmnUmoPgFsB\nrAfOJty4AcAko9jPACKUUi3M5B9GeQURTmaZEUqpYJKmBaw9gM0kj1rK3AoZA83kNmO5tS39AEwh\nOctoSxWI22Q8ZGy0XIwdO7bUJ//YsQMYNw546il5UaDRaDQajUaj0WgKhjcjzJo1a9DyHAaZBRyZ\npJSqpJS6VinV3FjU0Jiva8wnAHhdKdVZKWWmud8JGfAZJDcBWAhgmlLqOqXUTQAmAEgmaVrMkiCD\nSicqpZoopR4C8AyA9yxNGQfgDqXUYCMObRhkIOmJljLjIYNhH/Noy3wAMYH2vbSwerVkwq1SBXj9\n9ZJujUaj0Wg0Go1GoyksBbGYtQKwBOJWSLjF0kwA8STfUUpVBDAFQAQAByTNfYZlH90gAupHSKzY\nlwAGmitJHjOSgkwE8BskYccwkh9byvxsjFU20pi2ALiL5F+WemYCeBsSG/ec2RYAvQBc6aVv5QFg\n48aNAR6S4ufDD4Ht24G//5bMo1dcASQkAE6nTBpNUXL06FGsWVPsWWE1mlKNvg40Fzv6GtBc7Fg0\nQfm8yhUVBRFmWwB8ChE4FY35nh65/YN8fDdRyJkZ0XPeusxM+OEtk2IQciYVyc8CaK63JhGxEgkA\njz76aD67KXm2bgXuu6+kW6G5kDmXpnuNprSirwPNxY6+BjQaAKIRVhR3JQEJM6VUBIDlABYD6ACx\nZF0J4LClzEsA+gPoAcAJYASAhUqpKIvVLAlATUiMWFlIVsYpAB419hEKcXf8H4DeAJoBmK6UOkzy\nI6NMjLGflyCuid0AfG3ErplWs8eNzw8BfG62xeiDmSTEykLIcABpyDn+mUaj0Wg0Go1Go7m4KA8R\nZQvPRWWKeWU58Sys1CgAMSTj8iizC8AYkmON+TCICOpBMkUpFQXgT8gI2muNMh0g4qoOyT1Kqb4A\n3gJwqTnItFLqbYirYhNj/jMAFUl2sdT9M4C1JJ+2tCUDwDySAy1tOQFgNMkxfndeo9FoNBqNRqPR\naIqJQJN/dAbwm1IqRSm1Vym1RillTVffADIA9GJzGcljAFbCnWyjNYDDloyMgMSaEZK90Syz1BRl\nBgsBNFZKmXnsY4zt4FEmxmhLQ6MtEwE8pZTqDqAWxLpXCWKl02g0Go1Go9FoNJoSJ9AYs4YA+kIS\nfoyECKnxSqnTJGdDhJB1rDGTvcY6GJ/7rCtJZiulDnmU2Yac7LWsO2p85lVPTaMtn0AGr37TWHYC\nIvr2+9dljUaj0Wg0Go1GoyleAhVmZQAEA3jNmACxQPUFMNtYrwD8pZQqC7FgPY2cyTbCAdRRSp0A\nkA5JYf+yR5kqAO5XSvUE8C9EBP7qUSYIwASl1AwAvwMY4LH+bFsgcWxmWyYCsFrizqKUqgaJnUuD\njjHTaDQajUaj0WguZs7GmJE8WNyVBSrM0iHp7a+CO0viowAGGd+fMpY/D2AdZFDpOQCyAaxVSgUZ\n5ctBxhyrBbFoZULE2B6lVCSAFpDEIW0AtAPwEUS8EcBeY1yzEIjYGmnUv9AoZ1rR8myLj/51gGSc\n1Gg0Go1Go9FoNBpAkgMmFXclgQqzHQAaWN0AjYGltxuJNR6AWNAiSK41LF4bIQk4JkGET02ItSuE\n5EKl1BAA70JE1CqIyNoLoCqArSQ3K6XaQKxym0keVUoNAvA3gDCSm5RSfQB0AvAggAV+tsUb0QAw\ne/ZsREVFBXhoNJoA2LULGD4cGDoUqFUr/+XnmEGDBmHs2LElVr9GUxrQ14HmYkdfA5qLnY0bN5rD\naKUZmudDAG1h8foj6TLLK6XaQkK+msLw+iM509/6AhVmPwNoppQ6CuAIRKg1B/AkxAIWAmAsgNeV\nUlvhdgk8AWAexP1xA4A9AKYZ2RcPAKgMYL6RkbE1gK8B3AsgUSk1GiKwLgfwpFKqjFHXqwBGKqUG\nQzI6HoCk1Z8IGQQ7v7bkwLDCDQCAqKgoREdHB3hoNJoAiI4Grr4aiI8HEhOByEgZOfz554EvvpD5\nEiQ8PLzkroGZM4G4OO/HIC0NSE0FevQ4d/vRXLSU6HWg0ZQC9DWg0ZzlDIAFAHZBkhSaXn8ZAF4H\nAMPr7zsAH0CG8WoH4COl1C6Si/ypJNCsjHMB/B9EWNUEcD0kw+GNkKQbGQDeAfAPRFythwik+cYY\nZmbCjhcAXAaxkH1h7Hua8XkpRPC9BhFnf0LcEgmJY6sOiXNbCmAmgFEANkGU6XZjDLOafrTFk0EQ\nV0eN5twQGQkkJiLzsXgsfiMVrp4WkXYxExcngjUtLefytDRZHudztI7i2Y9Go9EUFzNn5v6PMklL\nk/UajaY0EAMJ5XqE5AaSCwEMAdBPKWUauvoC2EbyRZKbSU4C8CXcIV/5EpAwI7mQ5GskGwO4GcB/\nkJitxpZiCQBqALgF4hp4xvhu5TMAfwC4BsBdxrIHLeurAJgAYDLkIEyFuDpa99MOwGMQa505Nlpd\npVT1ANsCixVuFSCm+y5duuSYkpOT8z44mqKncWNgkg+v00mTZL2/+HPz8yxjnfe8QRbVDTMyEh/V\nHopb32qLj2sPLZgoK8obe69ewLJl3tctWybrixtDsOYQVaaYCkS4FtV+NBpN8aBFiX6BpNGUIpKT\nk3M9/w8adFZTNQOwgeQByyYLIUkNmxrzrZHHUF5+QTLgCeJ6uBkicsxxymwQkXYGwD2WsjshCUOu\nBzAcwFZIso/qxvpIY/0xiEUrFZKBcb1lH49DLGALINkWM436x1nKzABwCsCL/rTFoz+XGcu7A+Dq\n1aupKQaefJJ0OLyvczhkvZWJE0ml5NOf5XnhdJI2m3z6Wu5Zxpx3OLwv99xXAXBtc3J5ORtjYefy\ncjZm/1OAffrTt7yYMcNdxuEgIyLY+aab3PuYMePs8lznL9BzGghOJ0/daOMX/e3MvNlLP6zt9rIt\nZ8w4+z0z1saUfnaevqlozpvm4qBz584l3YQLm8L+d10o+Lr3lIL+62tAc7GzevVqQrz25gD4njn1\nQwVDP3Qw5jcDeMmjzB2GJilHfzSWP4VybSQuhO8aAi0TMqB0mCGesiFJOQCgkdHgXQAGArjdWP+7\nZV9PQcYlcwG4FuKaeBzA+5YySZCU+IeN+ZXGfroY8wri/vgrgK/8aYtHf7QwKyoAsl497+tq1JD1\nng/yvh76ydwirCCizMSfm5/nMs+2FeUN0+nk0VY21oeTQ4eS9eHkoRYF3Hdhbuxe+pxUsSKZkiLL\nU1J8nx9f5y6vcxoAr7WxkwDfvt2ef7vzWP5eF9nP6I5e9lPSeIrbGTPIMWOk/Z7i1ukk333XLTo1\nxUpSUlJJN+HCx+kko6L4x4cO7ttH7/9lF8Pv3enkmZtsHH6LncdalQ5RRuprQKPxU5i1p29h1tHQ\nI2Xpj8byp5Bl52MADIOMDXYzgEWGAPrAWP8/o4FtIa6BywE4DCH1NsR18iCA/RA3xg6QmLO3TcUJ\ntwXNDnGRfNqo4xVTccIdczYM4uo4xdjveAA/+9MWj36ZVrhntTArJPXqeRdn5vIaNciICB7+1sF1\n68gfXncwKyyCp390MD2dPHKEPHiQXL6cfPpp8oYbyM/jJtIFxd033kMXFOfcOpGtW5P165O33kq+\n/TY5dy75/ffkTz+RP/5ILlhAzptHfvklmZxMzppFzpxJfjPeyf8a2/j9y3b+d5WNs0c4OW2a3Pdn\nziQ/+0zK7G7iLjP9CQeXl7Nx8sN27mwk20ydSn70Efnxx2Riovvzk09kH3PmkAsXynP18uXkihXk\nL7+QK1eSq1aRKz93cl8zGx+83slatciMDLJpU/K2K53cd7WN9hlOLlpELllCLl0q269aRa5ZQ/7+\nO7lhg3yuW0euXSvLVyQ5mXa5jXMH2nm4hY17fnHyv//I//4jDxwg09PJ06fJEyekPpI8c4ZMSyMP\n/OZkdpxY7E6dIg9OSWF2cAjTegxhRuUI7pvrYHa2j3PuKcKKSJRt+NbJxbDxySvtXAwb/1rgzF3I\nD0F6ZJ2TS4Js7FDBzp+UjbtWeNlPSeJN/MfEkFFRZFiYW5ylpMjy1q1zPrR5ijfTkujNmmm1gPpj\nzfTXKlnU22ouKg587eAhRLBf9eRSazk6F8zoKS+QxtxZCl8gaTQXKRZhNgXAGubUD6ZmucaYT7Ua\nluj2+jtMf7WWvwWNna8zGkejIfshKejfN9b3NJa7jDI7ATSBxG79n1FmLsTFkIbQWglJIGJVnHsN\nMUbjc4pVccJt4coyyqRDrF3vAFjhb1s8+vYLxDJ3UQszl4s8eZLcv5/8919y0yYRAP/8Q68P5i6X\nlDtyxLLQIs5OnSJP1apHF8BDVerxqafIh+vITXgAEngIEbwJDgLMNVWrRt59N3nlleSXuIcE+CXu\nYZ065MMPk6+8Qt5xB1m5cu5t85piITe/WNgZFJR/mQoV3PO3BNsZHBxYfd6m7pjB+nCyTh0RcKSI\nrYYNxXLWHTMKtN8O5d3tzq9s2bI55+tDhFAsRAgNxRAS4AAkECBDQkQMX3MN2aIFedNNZFwcecst\n5KDrHDwWEsEpTRKYXiaCr7d1sHt3sndvsm9f0QC9esn3gQPJF18kX36ZHDxYBPhTT8m6fv3IAQPI\npzs6uTTExvaNnDx+nGzfyMmlZWx8tZuTb71Fvv8+OXmyIaZHObkrysb5L9m5O8rGeeOcTEqSdR+8\n6ORv4TZeWcbJLVvIltWc/C1MhO/KleSff5Lbt5OHDrnFaongcDA7PIK/T3LwwAFyz4QUMjhYxJnT\nKaIsOFjUu6co8xTB5sOsp6XT1/K8KIyrWSDbFqdLbGEwxaVVZJpttS43Readd8rkDYeDjI11W0M9\nhavVGpqXcM3rWL3yCvnQQ977YR5Hb+cjvzqLmbFjyQeRTAL8a2iyu10FEWX+/JbM/jZqlNv7wjwO\nEyfK+nOF08nV4W63dtc257mru7QT6Ese/VJIU4RYhFk/WEKxyLNef4cBlDHmR8HiFWgsSwKwwLos\nrylQYfamIY4yjMZlWwRWBoBvjPk7IINErzCsVGkQV8YgQ3QdgwTRdQCwD5LowwWxokUa+/sVYjEz\nD8QYuF0Zuxn1jIXbYnYIQDKAr4wy8/Jqi5e+PQhJp8/Y2Fh27tw5x3Q+mPNXrJDnuJgYsRz5IiuL\n3LqV/O478r335KE4Lo6sXZssV873g3ylSnKfiokh27SRqVo19/ratcmrriIbNCD/gYixMwiiC+Bm\n1CMg659+mvy1ewIJcPcrCZw/XyxNSUnk55+Llevnn6WdJMmJE+lSiuntxWLmeSPNzhYhuWMHuWUL\nuW2bfN+zR6xvpqXo1Cny2HonXW1tzFhkp8u46btc8lB++jR59CiZvsHJrDgbM380ypgxZnZ7jgcF\nl0vamJEhU1aWUccxqTctjdy4kfzrL/KPP8j160Xkrl0ry//7L7fYzc4md++W9qelyXnatEm2X7eO\n/O03sbz9/HNOC9yvv5JbFrn7ln6djYumOfndd+S334oFLzlZxMqnn4q1b8IEsfR9/z359ddiVZz/\nkgi7Db3HM7NyBPe8msDM0Ag63nZw0iQRU/36iYjq0YN85BERyQ88QE5rJud0clQCb7tNfh+tWomI\nu+46mZo3J5s0Ia+4QkRoVJSsb9WKjI4mr71WRNjqCBvfjHdy1y45Lrt3k692c/KXija2rOZkhQrM\nIaqtQtoqNO3BNt4b7eQ338h+li0j29QRAVofzly/8eBguQaqVJEpNJSsVUteDjRuTDZr5hakt95K\nduhAdupE3nUXed99ciwefZR8/HF5/uvTh+zfn3z2WXLQIDl+o0aRb71FvvkmOWIE+eqrUtZWJucL\ni1GtUrj38hgebtCc6Ve24PGGTZlZKZTOTxz8+2/yv8/F2rxvroO7d8vvaedOeVGyc5mTJ2Ns3DMh\nhdnhETzzaYr8lgMRZSZF6Sbra9tidoktMN7iTB0O+WFER+deXrmy/FH66ofV6mnd1rSSei73Rl7H\nKixMLjJfx9d0T/Y8H3nV6U2cWo+Pp6grwEPxw62dXFvVxhfqJfNIUAQXPZlM11VR0i5/6/Xsa16/\nJbPfw4fndI33tdxf8uu7KYy9iPKs61vzhaB32SPOycF4l8dvCDA+2IppYfcmQEryRUdBCfQFUWFe\nKGkuapKSknI9/8fGxprCrCUkrOp75PT6e4tuLREJCccajZxef+3oRVd5mwIVZpUMq5N1ygSwDDJ2\n2Blj/h6jfGOL1eo6QyRlIWfyj96QscUOQ1wKRxtizRqHlgzJALnAmP8FwG4YyT8gMWY7IWOrvQCJ\nMcurLdf76N/bOE8tZmfOyIPutdeK+x8gL26Tksjp0+Uh8Mkn5YGyYkX3g2jFinIff+gh8vXXyfHj\n5QF97lzyhx/EjW7lSvk+Zgz5zDPy0PnYY/JQPnSouAx++in52mtiAXnlFVmeCXlyzlRB3LpVhA9J\n9w0yISH/h64LOcasKCnMw7PnPsaPF/NYSoos9+fhOJBzmh9+Pti5XCKEz2wWN8zMxXZmx9l44k8n\n09PJjGkzvL51zsggt6c6+e9bM7hsmfy2v/hCrpMPPhDBOno0OXKkGDCGDiWff15+21ZB+uCDIsbu\nukvEWYcOItbi4kS83XAD2bKlXJNNm8pLibp1RfDVrEleeil5ySVkZKRYIV9+mfy7n4jbFQ8nsFEj\nt+A0RedN8M/abLWA9sN4ZiCEQzGEhxHBx69wsFUr0QBt2pBt24ohp3NnmR54QPoYHy//Gb17iyj+\n6zIbR91h59b6No4d6OSIEXKc3n9fjtmHH4rQnzVLXgJ8+aX8NyyZ7uTB5jauGWvnkZY2rp7jPOua\nu3atWIo3bSJ3fiZCc/9XDu7fTx5b4KArXNycfbrRngs8xYvDIaKsUiX5NEWZ+bvPz7XXU4S1bs3s\nFtE81bw1s1PzEWUmedXh67/A2n5vn3ldc3klQfI3OZKP5ft/dfIniIv4hg3kG43FcvZZm/E5X4wF\nIib9ca/2FGHDhxdOlPnTd2/H3OkkW7fmoagY3gQHj7YSC3/iGz725U99KSk5/8NN/H3RUVALtrmd\nNU7W/D+3Wmz9sQx74ut3/dBD3tvqdLofbrxtr9H4icViFg2gLmScsuOGKBsNIIg5tUQcgNWQhIRb\nADxGL5rD1xSQMPOoOAjAw4Z1azrcmRCnAXDCHdt1GsA/xjbDAazxUJzdjQ5PMcqkAvjIQ3HOMsq0\ngzsebLTR6e4Qq9lmQ4xdAskWmWdbfPQp+nwVZt98I2dz7Vp5YP38c3nDbz6kXXKJPCTef7/8Xy5a\nJG/Wi+2Bx3RnNM0aZsxZIPFIF0FWxiKhKN4OmmVNi4rnm/W8zlMxxZj5RVEI0tKCh7h1fZ7C7Bti\nmHF1c56KasHj17TmXwuc3DpAxNumpxP4ww/k/Ply/c+fL7GVP/wg7rGLFpG/vSfC7q92/UmACzsl\nsG9fsZLHx8sLlq5dRWiaXnjt2pE33ija4frrxZrZsiXZt4ns66FL7axdW8JFq1QRI1G5cvTpFuzL\noultykt4BgWJ+22lSnKYqlcnL7tMxG6DBvJi6sorRQA3bSpiNzpaLLWtW4tYjo2Vn8dtt5G33y6C\n+s47yS5dRGDffbdM5rK77xbx3a+Tk3/UsHH8Tck8XjaCH8QlM61aNE+UCeXnNyXwRNkIjr3PwUGD\nxDL63j0OnigXwW/aJfBk+QjO7uPgu++S77xD/t//keMHO/lvnRjuuKQ50yo34VGE8kEkc2VlEb2f\nfCIeDXa7xJmasbMLF8p5njePXDTUwVMVIvhDxwSeqhDBhUMcnDdPfgs/fuTk/mts/GW0nQeutXHp\nLIlZXf6pk4ea27ikTzKPhUTwveuTue9qG/+c7+TmzWKpP3hQ3NldLstv07iuTv/o4Kkbbcyy5yPq\n8rkuXS7xLFg9RyxlV1d2cv9+d7kfeyXzECL4RlQKd11l4/LRDh6OtnHrDKn/xELHWY8HUrwVzPaa\ncbMbJjt4plIE1zyewIzKEtfscknZ9HRxz189R47TOttAugAeiWlPFxR3vT6RDoe8sPnqK3l5cPKk\nn9dxfv9JnveVV16hKyaGo+50cFlZcWFs315e7Li2OfMXLr7272kdD+R/uaAWbF+W4ebNxZrry2Ls\nJ2c2O/l7dRv7XW1nZqzFUp2HBflMs+acN9jOM22K4L7gr2DN6+Vi2bLyRswbPXuS5csXro0lyQXq\nQmoVZiygZgpkClSMvQJgg9FAQsxzGwG8D6CrIZRCIYM5m7FdZwBMNbafYgiy6w2labpBEsAdRpnN\nAF6CuD6eMNZlGvsrB3d82Q2Q8dAyLfVsMfaRb1t89O+8FWbdu8vDiCfmTfac4pkAxCPxh99/9t78\n/00C9f/35w/Ds4x13vNPpTT9yRT2z9B6Y7feeLxZDz3flJakC9qF5K7iebxSPGLMTCtL06biRueP\nZdLTAjpkSMHPibkvD3deT7KzxTKeni5xe3v3krt/dvJUjI07Ztt57DoRARs2yEukX38VF+zUVHLx\nYhGVG54U4bnm8YSzsYIffSQWuQkTxEL3zjti0Rw2TCz1L79MvvQS+cILYtkcOFBcSPv2ldjG+Hix\nAj76qAjRBx4g771XxFiXLiLEOnWSmNWOHWV5587yvUMHEXLPthBxmdBA2tcnys4xdeX7qFoJvPpq\nOV1RUfIcOrKmrHstNIHh4XLaIiLE/btmTfLeam5r6Pz2UvblGPvZ5LX+TM8GyXaDghP8FsPm8tG1\nE/IUy0qJR0XFiiKGm1QUC+yDENHUo3wyHWVsvL6Gk/Xri3vy5ZeLBbhuXbJVdSdTQ2zsWNnO1BAb\nrwlzsmpVOQ6miO+OGWxV3clvv2Wu6/bnMQ7+U+4q3gRHjnofRDIXw8aGQU5WqyYvHc32esbNDoD0\n0YyTzeulgR03k5A4Zl9lIyLkEoyLk8lmI9u3l9/O3XfL7+qhh8j4W8Qdu38zO9dVs3HQPU4+9ZQ8\ndz/2GNn/Tic3XGLjmJYikPtVlz5NekH6/r//GW2LlZcogwfL7/u118SCP2KEuES/+y45bhw5600n\ndxpJrfY2tXHxx2KVXjfRwczQCO56KYFZYSJOjx0TEZuZ6SG+PSnoCzdPcRYVJW9voqKY3TyaWdcX\nTJSRcp2b5+ul1nYeP553Ww987eBj9aT84w3skvWzMPh7v8vr3nTppXJye/bMua5nz9zLY2NzWz1N\nUlJkvTcKul1huZDuyRZKuzBbAKAHgNsgMVlbDGF1rUUMTYbEccVBYrvSAfzLnMJsA2TAtWYAOhsd\n/pRuYWamzH/HsJh9YIo3izB7zbCAmRazdYZIq+5PW3z0Lxo4/2LMXC65EQ4eXNItoX9ZGb1xPvq9\nXygURtiVZNKGC+XtnC9XN2tWRjJ3ApC8HpR8WUBLa4yZSVG6xBYlZruTk6VdyclijvMlkvPrh3mO\nzaDL0FDZp3FsTpwQ69XmzRI3+88/Eju7fbvEEu7da7h6GnW4IiJ4YqGDe/ZIPObelU6evtHGfV/Y\neepGG3c4nLJ9qpMnWtt4/GN3P07daOPv85xculSE8dy55OzZ5JQp0vyEBEnO8d575LfPy0Pu8gdF\n8MyMt3PoUImTfOEFEQ+vvirvAEaMIJN6S/mk3naOGuUWE5MnSx2//mok3cnjgS4r1sZDk8W9cduz\nUu+iIXZOniwZed96i5w2Tdo7caKI+O+/J7fOkIQ6J94WUbJ4uINTp0r23KQksShv+kHGSswcIBaz\nQzeIxezvgRP555/ycmHfPnkfMWuWtP+ZZ8hu3WR6+GGxqHbpIqK+XTtJhtSlC/nmrfazYtuMt42J\nIW++Wco810rWJzaXPv0y2p5DKM2aJS8MWrQQ75fLL5fkS6a1umpV+XuoWJEsU8a3EM9PnJYpI8K7\nShXRDPXqiciOiiK71nXwSFAER1ySwKPBEXzyKsfZeOHrrxfLuum2bcYTN29O9opy8GhwBCfXGMJM\nBHNr0OX8QzXhEcMyvLSMjXdEOXnDDSJwO3SQlyEPPSQvUfr0kSRQ5kuWRx+V41YfTqY1FEuwPcjG\n6KpOPvKIWKmnPyEW5F8fTeDpihGc9ZSDbeo46Shr47KRdjrK2HhTbScTEkTM9u5NPvecWKB37cpH\npFrxV7Dm9d/nKcK8iTLSt0uqr+WF3a4oOM+9WPKJMSt9wizXxiKCCBk77LwdYNqy/ry0mG3bJmdy\n3rySbgm9izITU5xpNBo3/oxjZn0LbR3HLK/YmfMpK6O3vpxLl9i88HQ9K4YYM0ZHB+bedS5jzDyP\ng1Wc+hOblo+VlWTeL1kcDvFP9bdec5uSiDHz3Levvgd6LP2sL/NHOzNvtnHvSifXryf/mSkWs23P\nijtn6kgHk5N5VqBOm0ZOmiTCe9QoiUV//XXJmvvssyJcvr5FhN1nMQns1YtnpyeekHjz7t1FTPXq\nJYKqb19Z9/lNsp29Wf+zKnDVI7JsRk87n35ayj3yiIjbTp1EsN5wg1wOzZrJaW/SRDz/eneQ7Luu\nbXKMnEuc3FJPkjtddZVYoU0L8gAksHE5sUpu+0nK73A4ua6qWFrLlpXY38suyylSy5YVsXvJJWSd\nOiKGmzaV9sTESDzu7beTL7dxML1MBGe1SuDxshF8p4uDL70kLybeeEPclf/v/8jJLzn575U2fvOc\nnbuusnHu+07OnSvusWntetIF8MSlDegCuK9LT/7xh7yI+fdfGeLm5EnS9bmHmPJXXHmWOxeizMQp\nccVznrEz4+YiFGWAvMTyRmhosT1flmqLWa6NgSuMxs7FeTzAtKWe81KYJSbKfeTQoZJuiUajKRYC\nsUyej+OYlaRLbF54ihpThF1MWRm9lctP1BXVW/NA67X2Na/fkqcoK6qsjNZ9+Op7QfpUkPoKE2Nm\nUlALtrndkCFi5b/8cq+WhEsfCwAAIABJREFU4QL30dtyh1iQz4xJoCssjC5v14FTMhdnbpHlLpe8\n2J47V8TqhAny3mvkSBFYL74oFrs+fcSY1a2buEB36kRObCQi8N16CWzZ0h3nWqeOuCtXry5WyHZl\nvVsyAfJvNCAB/o0Gebosdy2TwgyE8OPK/ZmJEL7QIIU33ihCsVMnsTR27y4WXDMpVYcO5CtXpDBT\nhfCbyP7MUiH8pEsKx4wRq/IXX0g86g8/SAzr8uWS+fndd+W0bd4ssZq7d0tIzPHjvnMSZGWJa2x6\nuljBu3VzW3C71bazyB6pTfHlKc58LS8iSrUwAzASQBsA9QFcbVi/COAWY/15OcC0pX/npTDr0UPu\nxRqNRnNeoscxk++lcRwzX+Itv+UFsbIWpl6TkhzHLL+++xJh/gpkf+srbFZGb2WLIMYsYMuwSX4v\neV59NWfbXnklpxu4Z/nCurn7K1iN8+NaYmd2WxtPb5IhYPbvJ9MfFovZ6TpiMdvbuSeXLxcj6w8/\niFVt9mwRjAkJ5KrWYnlMbd6fvXvLc1/XruICesst4lJqs0lm4PbtRUB2707Ov0K2+6xGfzZsKIcl\nv9jVvKZy5SQ/SYUK8g6qUqXcZaKrinXzvyQ7V1W28YoQSWgzeLC4HyckiOvxrFkiEL/7TmKMV6yQ\n2ONNm8Rte98+EXtnh04ic4uwYhZl5LkXZooiSPxCKfURZKDnmoaVSgF4h+RLxvrHIBkaMwCUN4TR\nMgBVAMwn+apSarYhwCIABBtlkyGxa7eT/J9S6l9DgFU36jgEGZfscQAVAFSDpM8/CiDcOGD/QKxq\ntUne6E9bvPQvGsDq1atXIzo62u/jUtJERgL33AOMHVvSLdFoNBrNBcXMmUBcHJCaKp+Rke51aWnu\n5ampQI8e7vLWcp7le/Qo+npLA/n1feRI4LXXiq5Pvurr1Qto3x44eTL3fpYtk+2mTfO932XLgM6d\ngW+/Bdq0yX+55/qpU+WBhATGjAEGDAC2bQM++ijn8jfeABITvR8vfyloW4uqPl/1pKUB8fHu/lnn\n33wTmD4d6NlT5uPjc8578sUXQLduQJ8+wIcfAklJwAMP5N9WH9tlZQHp6UBGhns6cwY4fhyoWFFO\nz+HDssw6nTwJnD6dW65VrgwEBQHlywNRFdJwzbh4BM+Qfp/ZnIZ9d8ZjaN1ELP03EocPA6dOyRQI\nZcoAFSrI9OfeMFRFOrIhIuKoCkWPzsdQoYK0PysLCA52ly9f3v1ZqRIQEQGEhOBs+QoVgNBQIDxc\n6gkJkc/KlWU/a9asQcuWLQGgJck1gbU8cAISZgCglLodMtB0JEQg3UPyG2OdDcBiyHhiPSCp6kcA\n6ATgJZLvK6WGA3gWIqSeAlAWwGwADQBcS3K9UmoZgOYA5kBcG5sB+ARAFslKSqkykHgyQGLK5kMG\nnX4dwBKS7fxpi5e+RQNYHRsbi/Dw8Bzrunbtiq5duwZ0rM4FaWlAgwbA118Dd91V0q3RaDQajUZz\nXtOrlwg6X+LLl7Azt/vnH2D/fuD++91ic+dO2e6114A5c4Dq1YtGWBe0rQXBXxHoKcpM0tKAmBhg\nz57cIsyXODPFlSnGPOd9UdDtCkNe/fZYTorYM0VaoNObbyuEQAZG7vYAceqUCMeTJ0VYZWeLiDTL\nm99PnJB1vkk2JiEoCACOwuVaCpRiYTYRwF2QTIdbAdxtEWZhECvWdJLxxrIWkLHLXiX5tlKqF4Cp\nEPfHJUaZBEgMWl2SO5VSCwHcCqA8ySyjzJ8A6pEMNeYPADhGsqExryBZGlcbFrN82+Klb+edxWz6\ndOCJJ4CDB4EqVUq6NRqNRqPRaDQXIP6KwLwsp+XKAddfDzgcudfFxwPJyW5zki8xlZ/IKuh2haWo\nrOX5ERYmJj+T0FDg2DG/NiXd4swUc6dOAUePyi6zsoDMTLEipqeLFXHHjjV4771zZzELCaSwUuoD\nSCr6LpAxxgAgXClVnuRpiAUNANorpdpC0tOPhwikGsa6bGN6USl1EJL+vivE1bAlJHOiecRHKqUS\nISKtEYAgpVQ4yaMQ98U6SqnuAFYBGGTsN9TYtrofbTnvWbIEaN5cizKNRqPRaDSaYiMvy1ubNm7B\nlpf4OHPG97rExJzWsokTvYsoc37iRO8Cq6DbFZa8+h0ZWTiXVRNTlJlizJwPC/NLnCklLoqAuC76\nw5o1wHvvFaLNARIUYPk+kIyHdkh2QwVJU/+gsf5SiMD6AcCXlnJ2Yx0g8WlOiIhaAWCWsY8DljKh\nAL4D0A4yPtkgiJsiLGXCjG3fBLAWkkxkHNyCrKalLd9BMja2NuptEmC/SyWZmcD8+cDtt5d0SzQX\nGsnJyfkX0mgucPR1oLnY0ddACZKa6ltAPfCArC/K7Uo7nqIMkM/QULc4uwAIyGJGMoeQU0q5YIkx\ns/AaySct5VIgFi6TLJJ3euyrp0eZ3STvtqxvAsneaC2zyKOepz3WA2JNexSSOGQVJB6trVKqOskD\n3vo5aNCg8yLGbOFC4NAhcePWaIqS5OTkUvd712jONfo60Fzs6GtAU2rwFGUmVstZIUlOTs71MuLo\n0aOF3m8gBCTM/GAPxIpWE5IG36QGxKpllsnhSqiUCoZkS9xjKVPTY981IKJrbz5lrOsVgP4AppCc\nZdS1wygXD+Adb50YO3ZsqY8xI4F33wVatgRatCjp1mg0Go1Go9FoNMVEXjkx/Iwxyw9vRhhLVsZz\nQqCujHlC0gkRRLeay4wkHDdA3BYB4GcAEUYiDpNbISJqlaVMrCHYTNoD2GzEl5llbkVObjOWW9vS\nFJKd0dqW3wDEFLijpYDx48Ua/eab4jOr0Wg0Go1Go9Fozl8CFmZKqUpKqWuVUs2NRQ2N+brGfAKA\n15VSnZVSzSBxYDsh45CB5CYACwFMU0pdp5S6CcAEAMkkTYtZEmT8sUSlVBOl1EMAngFgDb8bB+AO\npdRgpVRjpdQwSPKQiZYyHxt9vNKjLb/BHat2XpCRIcOAfPUVcO+9wLPPAoMHAx07lnTLNBqNRqPR\naDQaTWEpiCtjKwBLIG6FhFsszQQQT/IdpVRFAFMgg0g7ANxBMsOyj24QAfUjJEHHl5B0+QAAkseU\nUh2MMr9BEoMMI/mxpczPSqmuAEYa0xYAd5H8y1LPB5CkIS8DeMtsC2T8NG820fIAsHHjxgAPSfFz\n220STwZIYpu33hJRtqbYE3dqLkaOHj2KNfrHpbnI0deB5mJHXwOaix2LJih/LuoriDDbAuBTiMCp\naMz39MjtH+Tju4kyJl/z1mUKIqK8OewFwS2w6KWuAxDhF2QpD+SMRbMSCQCPPvqol1Wlh7Q0YMgQ\nmTSa4uJc+lRrNKUVfR1oLnb0NaDRABCNsCK/QoUl0HHMIgAsh8RsdYAInysBHLaUeQmScKMHJC3+\nCAALlVJRFqtZEiRxx60AykLS5U+BZE+EUioU4u74PwC9ATQDMF0pdZjkR0aZGGM/L0EyLXYD8LVS\nqoXFajYYItiWA3jVbItR53gvXVwI4BEAaZDBqjUajUaj0Wg0Gs3FSXmIKFt4LipTzCvLiWdhpUYB\niCEZl0eZXQDGkBxrzIdBrFM9SKYopaIA/AkZQXutUaYDRFzVIblHKdUX4np4Kckso8zbEFfFJsb8\nZwAqkuxiqftnAGtJPm1pyyLIOGu9jXpXAjgFoCHJ/X53XqPRaDQajUaj0WiKiUCTf3QG8JtSKkUp\ntVcptUYpZR1HrAEkqcZicxnJYxAxZGZBbA3gsCnKDH6EWLZusJRZaooyg4UAGiulzAHGYozt4FEm\nxmhLQ6Mt7wF4DjIQ9TIAJwB8o0WZRqPRaDQajUajKS0EGmPWCEAT4zsBXAJgqlLqNMnZAMzMjEuU\nUmUhQulpiMXMzILYGEBZpdQJAOmQTIkvAzhkKRMFoIFS6jSAfyHJPcxU+pcCOAqgFiT742gAvwMY\n4FFPHbMtENdFsy0T4EOQKqWqQVw006BdGTUajUaj0Wg0mouZs66MJA8Wd2WBCjMF4CSkgWYyjjcB\n9AUwG8CzxvInAGwHMAnAHAC7AVApFQTgcaNMa4i4+gSSGl8ZZSIBRAPYAOBhAO0AfASgj6XMQ0bb\nv4AIrUEQ4fU23MlA8myLj/51gCQ20Wg0Go1Go9FoNBpAclAkFXclgQqzdADZVjdApdQ6AJ2MWLJO\nENGzjeR6pVRPABsBrAWwFCJ8qgM4RnIDgA1KqSEARgGoDBkQui+AYwCcJDcD2KyUagOgl7HvvRAh\nlg4ZcHqTUqqPUXd7AHv9bIs30gBg9uzZiIqKCvDQaDQB8O23QMuWQK1audft2gWsXg107nzu22Uw\naNAgjB07tsTq12hKA/o60Fzs6GtAc7GzceNGM1t72rmoL1BhtgNAE6XUfxBXv58hiTS2QwZ3DoEI\np1sBrCe5WSm1A5JVcRTESrYZwFVG9sS1EEvXZEha+1WQeLA1AGKVUsEksy1lNkMsdi2Num8FMJ4k\nlVI/QmLgPoeMtZZfW7zRBQCioqIQHR0d4KHRaAKgalUgPh5ITJSB6UzS0oDnn8+9/BwTHh6urwHN\nRY++DjQXO/oa0GjOclopVRfAhwDawhKORdJlFlJKtYXkt2gKIxyL5Ex/Kwk0+cdUiBXqCwDDAVwH\ncRWcBontygAwFhL71Vkp1QxAKIDjAOYZZf6FCK1pSqnrADSAuBzaSe4xyiw19pWolGoCiUsrD2Ac\nxOIWDBnQ+g6l1GClVGMAVwCoAhmUuqYfbcmB4R45KMDjodEUjMhIEV/x8SLGAPn0JtYuNmbOdB8T\nT9LSZP253I9Go9FoNJqLHQVgAcTw0xoyLNjjkJAuKSDhWN9BkiBeC9EtHymlbvO3koCEGcmJAO4C\ncAtEMVYxGtrNUmwcgH8AfA1gPUQMzbOMYQYALwC4DGIhMzM4WscVOwPgNQD3QlLcvwARhNMtZf6A\niLNRADZBMjqmWcYw87ctJoMgMWgazbnBEGcH7orH4w1ScfQ+LcoAAHFxOQWriSlc43yO1lE8+9Fo\nNMWDfnmij4FGc/4QA+AqAI+Q3EByIYAhAPoppUwPxL6QEKoXSW4mOQnAlwjA8BOoxQwkF5C8BkAc\nxPp0EkAEJD6sLCTJRg2IeIsGkA0g1th8D8Sa9RlEWF0DUZsAcKelzJWQpB6TIQchCSIA4yCDWmcD\nuA/AYwCehGRx3AagjlKqup9tOYtSqgzEPXIVID7VXbp0yTElJycHeqg0nvTqBSxb5n3dsmWy3krj\nxsCkSd7LT5ok6/2lIDe/c3HDjIzEuxWHYkZaW4wqN7Rgoqyw7bRu73mOrNt7O0eBnlN/KCprorZK\najSlG/3yRB8DjaYUkZycnOv5f9Cgs5qqGYANJA9YNlkIIBzitgiIJc3nUF5+QTLgCZKoYzOAjgAy\nIVavMIilKxPAPUa5RpDYMReA6wHcDiDLKFPdKPMUZGyxwxDz4CgA+yBxYWZ9SQB2AVhgzP8Cya44\nzphXkPi3IwBe9KctHv25zFjeHQBXr15NTQEByHr1vK+rUUPWOxw5lzscZERE7uUTJ5JKyac/y/PC\n6SRtNvn0Z3lBtwmQo787+ZOysVttO39SNh5cXYB9Frad1nLGuUgaOtTrcr/Pna/lgeB08r+rbOwS\nbuf+a7z0Y8YM331zOmW98f3AtTZ2DrNzb9OiOW9FypNP+j5ODoes15QISUlJJd2ECx/P/6ki/H89\nb7D0eetWMnOLs9QcA30NaC52Vq9eTYjX3hwA3zOnfqhg6IcOxvxmAC95lLkDYhgqR380lj+FLDsf\nA7E4fWmIpUWQWK4PjPXzjMZ3hFiglgNwQDKZDIRY6PZAxiG7BpKlcS/EjdEF8ceMNDrwKyS27Gmj\njncgA1MDQFejnrEQi9oUAAcBJAP4yp+2ePRLC7Oiol497+LMXF6jRs4H9jwe4P/7j/yz/0S6YBFh\nE2X+rwET+ckn5M8/k1lZfratIA8ATiez29r41Vgnjx3zcxt/cTq5s7GN9eHkmjVkwyAntzUo4L4L\n+3DjKcJCQ8no6LxFmYnn+qIQZSRPnSLvrWYnAXarbWdGRh5tzmO5y0U+cYXsp3t9O7OzC9Wsosfz\neM2YQY4ZQ6akuJeb4s3pJN991y06ze2t4s0UrN4EnylYteDTlCJcY8ZwU9UY/vCKPfc1bX3JciHj\ndHL/NTbGws5/rywdokyj0fgtzNrTtzDraOiasvRDawWalbEtxE8y2GjkQUgMlzkY89eQzIjfQaxY\n/0FS2E8HcClJl1JqBSSV/e9GZ34D8AqA/kaZ35VSBwyRtgli9ZoOGSj6OaVUOQB2o/4BkPHKjgPo\nBzElmq6KebbFo1+me2TVAI+HxpPt24H69YF//5VP63y9etj363b88eEytG7XGZ9dNQz3bRiGie2/\nxcnv28A1H8jOlmnTJmDxYuDMmX7oA2BS/wFY+sZixB76Gs9gAiZN6He2yrAw4MorgQoVgHLlAJcL\nyMgAMjNzTmQkIpGIoVHxmFRtKPodHI7B4YnY0zYSZcoAQUFA2bIAKW3IygKysyNRYW8iJtjjcc8L\nQzE8aDier5qIXXGRCAqSbayUKeOeKlcGKlbE2XJKuT/DD6dhwNp4PHQiETEPR6JFC+CBFyJhG52I\nL66Jx+hGiThQORIhIUBwMBAS4p6Cg2U/onTNKRJlTyei9xXxGBc+FG9gOOZ0TMShMZEA5LiUKyft\nys6WflasCBw/DuzeDVSoEIl6TRNx7y3xWHzTULQvdyWqrd+CmbfPw2P/DMPUO79F5rI2qLsdCA+X\nNlSsaLQnpA3CRn+LRh07Y2/fYag5eRh2ffgtVP02qHBA2pqVJf0OCZG6y5aV5RkZwOnTsj442N23\nPXuAT0emod/B4bAPs+OJYcMxqk8i+o6ORPXqxsG2uiqarokerooksGhaGrptHY6PH7OjxyfD8dXY\nRNz3XGSxXwp+06aNDJ/QubN8xsUBnToBmzcDycmyHgA6dgTq1QNCQ2U5IO6i5nYmpmtU377udW3a\nuI+NdXl+zJwp+/Pm9pmWBqSmAj16FPIAQFxee/Rw99XKsmXSjmnTCl9PacA8pqmpuY+teUzN9UVx\nbL3VXdznM0BWXHY/Khz6FB3ebouTC+yoaLbPej1f6ERG4qNaQ5G6vi0Gh9rxvna1dlNKf7eai44D\nkKSHVmoan3ssnzU9ytSADBPmLb9FLpSh5vxCKdUdQAKARwH8DYkPexXALJKPK6UWQdLT2yBjkU2C\nYb6D+Fy+DmA/RJDdAvcA04kQF8Tbjf1ug2Rm7A0ZYDoBwDBI5pMKAHpCko8Mh8SrDQLwAGRw6JYk\nb8yvLSRf9ejbL0a9XWNjYxEeHp6j7127dkXXrl39PlYlgcsFzJsnD842mzwI+8OBA/IMuHWrfD98\nGDhxAjh5UqYzZ+RZ8Oqrgbp1gWrV5AEaAP76C1i3TtY3bSqfZ84AHfvXR/jhf5GNIATDhZ1l6iGu\nznY4nbLd8Krj8MahZzH+8gTMCBuIQ4fcD+bBwUDt2sAddwBt2wJ//glEj7wXV//9FdY1uAe/vDgX\nN98MNGggdaemyn/z6dNSd3BwToFUtqx8krK+2aFUPJXUFlO72fHfFXHIzhaBYK43BYQpgipXBq4+\nmIou77fFjMftcNaLg8uFHBMg21mFYHo6cOqU7NflyvnZYe9MbK8fhyvaRaJ7dxE5Lpc8f2xZlIYr\n/kvF0gY9kJUFrxMp9VmnihWBe6qm4rGP2+LVG+2YfzwOQUFuoWpOISHSrtOnRczWqiX9PnYMaHUi\nFXMPtcUTl9vRXK3DgK3P4qNmCZigBmLHDvlt+GIAxmE8nsUzSMAEDCzozxgAUB9pmI54bH01Eb1G\nRuKj19PQcGQ84pGIPeUiUamStL1iRaDGyTS8eyge4yKGYuCR4RhSOxG7ykYiMxMouysN40/EY3Kr\nRHy+MhKD7knDXd/I/JnLIlG5svxmzc8KFeScV6ok7cjMFOFfqZJbuIeF5RTK/k5BQbLvsmVz9jU7\nW667LwYuQ485nfFjm2HosPwNqLp1UKFGmFuE3XmnvLFITgYeeCCnKPMUNFYR9tRTwNSpwOTJ7nlv\n23jDV0xeUcfq+epLXn08F3gTUaaIrFMnt4gyxx70JnqXLQNeew0YORJ44w3gzTfl0zyGZkzmtGk5\nl3tSEBFr9gPIfd7S0oA5c4D5873XeQ4eioc8loaOs7uhPE6hWu0KqOtIgprzJTB3LpCUlLvuvOr1\n5/i0aSN96tABeOYZoJ/7Rd/ZfR8/DowfLzdHf/H3WHkpR2caVkTFY8KZpzAUwxH51/eoEOVlPxcj\ngf4PaSGnKSDJycm5ckocPXoUS5cuBcSAlADgMhpxZkqppwCMBlCDZKZSahSAO0hea26vlEoCEEGy\no1+N8MesZjHH3QURNxkQS1YmxHLlMpZlGN/DjPKNjfldEFdG08/yd8s+e0NcG10Q98bREAvY+5Yy\nyRALm+nKuNLYTxe6Y8x2QqxvX0FizDKMMl7b4qVvD0Isf+etK2P//m77yS23kGvWuNe5XOTeveLB\n9O675OOPkzExZNWqOe0uYWHiddikCdmyJXnzzWS7dvK9XLmcZQEyJIRs1oyMjMy97gyCSIAZCOLD\nD5Mvvkh+8gm5b67hupWQ4J/LmxlTds89gceWeWK6udm9uMwU5TYlQWHbad0+OlrcGT3OUXo6uXs3\nuXMn+fff5F9/kRs2kH8nOpgZGsG0QQnMrBzBNeMd/P578quvyC+/JOfNk+nLL8mkJHL6dPLjj8nZ\ns2XZV1+Rc+aQX3xBfjPeyYPNbdz/a87271zm5J4mNia+4eSIEeQbb5DPPUe+8AL5wUPiqvjBQ3Y+\n+yw5cCA5speTaZfbuGS6k6dPyz6yssjZI5z8o4aNT9zqZNu2ZKtWZOPGZO3acj2EhZHBwTJ5+80X\nZgoKksNavjxZtixZoYJ7XeXK5Pv1E0iAb4QnsD6cXF0uhhsrNOeW0Bb8M6I1/69FCtPLRPCT6xJ4\nvGwER3d28Omn5dp/+mmyTx+yd2+yVy/ypYec/OsyG7+IG8+soBDa44bwVIUIrnjHwR9+IH/8UU71\n8uVyetevl2nzZnLHDnLXLnLPHvLgaifPtLFx70ond+0iXducxXMdFJNLbKEwrwmHw7urr+fyypXJ\nSpV8x1ympOTcn/lpuq2a6/M6tgWJ67S693p+j4khW7fOO16zGGNtXducXFbOxmGPOzm6r5PL0Zob\nyrTgyagW3tuVX73+HB9zH8OH57yn+FruL/4eKy/zJ1rbeBMc3H65fB7wFlfrib9xtoFS0LhXczvT\nHdtsg3l9PPlkTnfsQNoYiLv+OYgP11w8WFwZWxpa5HvkDMd6i24tEWlomNHIGY7VziyT3xSoMKsE\noIkxNYUMBu0yxFAPQwidgZFww9hmp1HmOoiFaytyJv+INNYfA1AGQCokO6JVvD1udGyBUSYT4sc5\nzlJmBiRD5AsQa1xebbneR//ePl+FWVqaPPSNGUN+8w151VVyX2nalLziipwPmBUqkNdfTz72GDli\nhDwMr19PnjyZdx0uF7lvH7l1qzy8bdxInjjhXn/8OHnwoHxmmjFlQSLOzsacBfrw5ZnooyCJP0wK\nGGN2XgSmX0gxZoE+bPgSpIV4aHG53LGLGRnk4cPkoUMiSLdskd/++vXk2rXkr79KrOPSpeRPP5H/\n+x+5YIFch3PnyrN2UpKI0ClT5Jlk/HhywgTRvdOmkZ9/nvOFhSsiggtedXDSg/azF+7LMXZ27kyO\nu1zE2/v1E9iqFdmiBXnNNWTz5nLKWrYkr7tOrvE+UbL9x5Xkrc2g4IQCCcr6cHIxJP5lMWxsGORk\n+fLyM6lalaxZk6xTh2zQgGzUSP53mjeXdtx4IxkXR956K3nnnWTHjmSnTuRdd5H3308+/LD8F8XH\nk6M7O3i8bATnxCXwRLkITn7EwSFDyDffJN9+W/7fEhLISZPkWCYmkrNmyfFNTpbjaAr9b76R87Bw\noYjQJUvkHC1fTq5cSf72m5y/devkXG7YQP7xh0zmsj/+ILf+KA/NOz9z8GSMjXu+dPDM1dHMrlSJ\nGc2ieXitk8cWOJgdHsFTixw8tcj9PTubua8Hi9jLirVxx4sinD+5fjz3NbNJ4of8KMg15yHI0pu1\n5ilf4ievbb3NFxSnk/ubSZztkiVy3a0aI7/Z9SEtuP4DR8Hq9ef4eIqw4cMLJ8o895tfmz1E/1fP\nOfiTsjF9g5N165JvdPejr8UlQAqa1Mn6AsIU/A6H/BmEheVeHmgbnU4ebWXjb+9Z/ut9iUinU+p9\n6CH3fGm8d2tKPRZhFg2gLiRE6rghykYDCGJOLREHYDWAUwC2AHiMXjSHrykgV0YAUEpdDeBnyIDP\n6ZBsiIshyToSITFcd0DcDdMh8WBHSNZVSk0BUA/iwrgLwEsA6gP4BkASyUeUUpsNodcf4n6YCIkl\n6wcJoFsHiRd7HTJ+QG9DyH0GEYu1IO6PebbFR9+iAaxevXr1eTfS/ahR4hmzb5+4ZWVmAp9/Dvz8\ns7h71a0r4SkNGojLYUig0YWBYIkpyxFjVqOG+NL56640aRIwYAAwYUJOVxNfy/OiIC5Z58qNq7AU\ntp3Wcjt3us9FnTrel/tz7s6VC5pnH0vbufEXz+O1bJnEmdWpI76PSkmQ4ODB4oo4bJhMeR1f81jc\nc49s98or4IQJOJD4LU61bIOsLPmfyMoSN8tjx2Sz06fFlZkUN0vT/bbmplTc+GpbfPe8HTsaxuWK\n4cxrMus6eVL2FRLidsv1LHP/rnF4adezGHFJAqaHDsy13vo9wNtXgamPNCQiHlPwFD5EX/TBZLyI\nMbgCWzAEb2E4hqEzvsVyyLm4CcvwLTpjKIZhOIaha6VvsapsG7hc0vbamWn4MDMeX/EujMezeCto\nCIa43kIc7FhZLg6RkUDVqvJfTrpdps0Y3Kws4KoDyzDO2RlvBQ/DkOxh6F/vW/xdo83ZOFZzMl1o\nlQIuPZ2GFzfFY0wxJAH/AAAgAElEQVTFoXh+1yBEYy16XWnH4WviULEizk6mm3DFitL/oCAg7FAa\n2s6Kx1fXDMW9G4YjtUciMmtLHKzpNm5tY0aGuEgDOduTmSm/ryNHgBo/zMQHf8ShUftIzJ8PqO3y\nmz38zFDseOxlzDx+P36rdx/ePxKPz68aih5pw5HULhGuepGIiAAiIqRtu3e741dPnAD++w8I37AM\nQ37tjMk1h6Hv3mGYfs+3ON5cfvenTsm9ks409F8Tj9VZ16DXyXFYV6M9mu9bhOktJyClej/s2SP7\nveIK4PLLxcW+Vi3gkkvcx8XafzNWOePvNNQaEo/tPYbi8tnDcSwhEWWujMxxzWVmyjVat3dHrL7z\nDYR8PBXjrk3EZ79E4uWXgQ8+ABZ/nIar9qaizJM9zrrW5wpRKK7/QG//Sf78p5vlpk4Fxo6VE71j\nhzyEVKggJ2nMmLzddX2wbh0wsEUqUtEWK0fbccOLcXnfgzp1wv7whnj6dALGVR2OWj8U8pgURSxs\nhQpA167e4ybj48VV/dQpmY+LA/r3F9d1T774Apg4UdwySwsXqAvpmjVr0LJlS0BCpdYUe4WBqDhI\nko5VEJFzEGK1MpNzdIWow1DIYM4uiMLMADDF2H4KxAR4PURpEmLZIoDbjTKbIYJtICSNPo06XJCx\nycwMijdAxFimpZ4txj7ybYuP/kXjPLWY3XwzeffdJd0K+peV0Rve3CMaNfL91nLiRFnvLwWxnhSX\nm0hRU9h2Wrf3fPto3d7bOSrJVO8XiruKr7f5TZqIP2VKisw3beqe97WddXtvLnLWTI+BcK7cec0+\n+enmnJUl2TuPHxc32yNHxGq/b5/b5TYtjfznH3G93bjRbRFbvZpctUqsZ7/8Qq5YIda05ctl+S+/\nyPelS6Xbq98XS86fvcViufz/7Pw9Xr6veTyBycliFZ09W7wQfn1M1qXel8AxY8jRo8VaOnasWEsX\nxieTALf3HMLs8Ai6kpN5pKW46g4aRPboQT7wAPngg2JV7NqVfPRRcUPv1UvcVxfcLnV8f0cCBw6U\ny+2JJ8T62LOn7KN7d/KRR8hu3WQfw2zSj0ORzbn4DTv/vNTGx2528uabxdoaFUXWr09Wry5emZUq\nkRUriqfF3VVk2y7hdpYtm7+ltUwZ9xQSIlP58mS1alJH+/bke+/J+fO8brO2Orn3ahvfesLJt++Q\nep9tYWd0NNmwoVhqg4LEuFWzprQ3PFy+R0eTnTuTyTFyfBKbJ7BRI/KSS8hatWT7G24Qq+3I9rLv\nTTVvJgEuCr+HsbHiOd+3rxzrNm3IunWl/f5amWMh+42F3a9yvRrZ+ddf8rs+cEBub97Km8ewcmWy\nShXp03WXiDtot9p2rqxs493NnezUibz9djkOXbuKi/PAgRJSMGIEOWyYfL7zjlxuH3wg7uWffCKW\n57lzySVvOXimUgTX9kxgRqUIrnzPwf/9T7wCFi0SK7TdLt8XLhQL9fz55Kr3ZbvNDw9hdlAwj9S4\nnPtrNuGpsqFMuiuZOxvb+ONHTv74I7lsmViv//hDvHF27ZL+Hz0qXjzp6XINL11K3tLQyZWVbBzc\n0k57kI0fD3HS6SRP/5jbQuqKiOBn/R05zsO4cWKVdbmkjmPHCvj/VJjhYXr2lBPZs2f+y1NS5ISb\n//n5LTeJjfW9LiVF1hcHF8o92QOrxYwBaKaCToEKswWQQZ2jIAOtfWcIoKmQJBvZAD6CpKSPA9AC\nErf1j7H9cABrAGyADLjWDEaKegBTjTKpxj6OQ1LkNwYwyyhzG9yujO8Y++4OSZm/2RBe1f1pi4/+\nRQNgbGwsO3funGMqzWN5nDwp8SrjxpV0S+hdlJmY4kyjKQrOF+GcH97EsOnuk5LiXh8aKuLM6nqW\nl4uWpwjztTw/zpU7b2mMMTMx+5ycLG1KTvYZh0kyf4Fprh8/3nvsmT/HNkARe7YfMTHi4hUTkzvm\nzJ9jYBHnLheZmSn3oKNH5UH3xAny9GkGNixFXg905rXg5aWAWb9X/Dk+Zr0DB8q9qX37PN0Ys7Ml\nVvvPPyW+9o8/xB121SoR8Xa7uDOv+9rJ4zfYuH2WnUda2mif4eRXX5HffUf+8AO5eDGZmkqunuNk\n+nU2Hvsud99OnRIX6TlzRCxNn05OnSoCavx4EbSjR5MjR4rImvaoCJCxd9vZsyfZpYu8rL3zTtl1\ndLT8fVx+uYi5yy5zj15TsaJv0TkAIm4HIDA3aHO7cXAHvw+tIsvaqrzFqi936uXlbdz6o5PHj5Mv\nPODkTxA3WIC0lXHwsIrgiBoJPBIUwQ6VHKwPJ/+uY2P2T3b+XVfK1qjhHlK1TBlxte7XT0TqmDFy\nbKdOJWfOJD/7TNyiFyyQc7Z8OblxmsRT/5vk4Pbt5IGvxXU54ycHMzPlN5kvniLMl1gjc4uw/ERZ\nXmX82bawFOf9ApD/XG+EhhbJ82VSUlKu5//Y2NjSK8xybSwiiIZAO28HmLbUc15azJYskTO5bl1J\nt0Sj0RSa/2fvvOOjKPM//n6S0AlERUVECFgQbAg2TgSintiwHRZsSH4eisIh6tkVsCsqAcGCGsFT\nolhP9E6sgWC7E1A5FQTdoFhQpCMl5fP74zvDbpZN2IQkgDzv12teuzPzzDxldnb3M9/yxAbOh2yp\necxq6wloTU5UvrnExQKpoMD+5TZqlDgOc1MCc1OJQJIRZ1WNMYtN9BEXc1ZhnTUtzst7yBKJWHvv\nu69y9W5LMWbVMabVZNEuKTFRvWJFYLV63UTHqjtzVNwkQz89b2JkwQKrYv58s0R/+61t+/57s1L/\n8FyBSppkaMWQm1WamqqSPfc0D4D0dCkvTyU9LJlQJGJW7FmzTIS++640ebKJ0WefNUH6zDNS/viI\nVhySpXVzy/brtxk299tLD0Q0enTUgvxSjxyNuTqiFYeWHd+lnbJ0/6CIbrnFrNpjxpg1sX17E6tN\nmiSX8OlICrSEDA0iR0vI0JEUbNiXkhK1NKenmwW3VSuz0rZrZ1bpzp2ll3bqp1LQwvptVAqa0qqf\n+vQxK3f//tIVV0g33GCC8dULJ6kkJU1fHTtQJSlpmnn9JL33nlkbZ82yuOfvvzfPgHnzpDlzpHl3\nTlJJapq+vmOSZs+Wljw6SaVJiLLVqy2menOY/3ZEMzKydNoO+VrYLssSRlUHofiKF2flba8mtnaL\n2R1AVywubH8sZb2AfsH+V4L1bWqC6Zj+bZPCbNgwc2nY6ibO9Xg82za1ZZXcki6xFREvykIRtjlZ\nGdu3j2aui/9THru9vLHdnKyM8YI/XpwlqnNLuSdVtd5tMStjsn1Lps7qui5VtWDHJwBp397ui/bt\n7Z6pSuKPZL6HYi2kTZqYVbiK41taKq1bZ1bgX34x0TN/vllKZ8wwt+evLzcR+PnFOXrpJenxxy0Z\n0SOPmLvyyJH2POG226SbbpKuvdayCPfrZ8KrXz/pp0ZtJNAPDdqoZ09r2pFHmnDr0MGyXe+8s32l\nhJbHUQxM2sr4FyZpPWkaxUCtJ01/YZKaNrXzduxo7rxHHWWJmU44wZIxhZmCL7jAvnYvv1y68krp\n+uutLyNGWL/uvz/az+HDpaFDrY+nnWYeXOe1zFfoQnrOOZYka1MJ5pIiXoTVsCiTtn5h9nhguSoh\nGhsWidl/QWAR+z0QWsVYwo1PgbuCMk9jc5mFcWNrsRi1UqBnUOa7QLCVBNsXB3WH85CFcWZLg9cS\nbP6zScCHybYlQf+2SWHWo4e5LXg8Ho+nGokVSeGfuVjrZbyIOvlkWxJRUGCxHZsrdKsiYjdHYG8p\nl+Gq1pvM+ITnThTHHJ67snHMlWlzdY1pTYnmrTUrY7Ltvf56q6+8hxSb+5mtihtxPKH7YhsTZwnd\nGEMmmbVr/YCBKk1N068PT9LXX5sr7X/+Y5bGf//bss+++27gJjvDrJm/nGOC7puTBuqJJ8z99frr\nbXqViy+2GNRzzrGYyj//2TL87rmnxVUeeqh00EGW5btNG7P+NWliGih8BtWwobmGNm9ugu+YY6SH\nr42ouJtZcH/ukKUD0iMbxGLjxiY2W7UyC2LoVX300Zatt3dvE4X9+5uH8XXXmfC7916LzX38cWl1\nvXSVgopApaC1DdP1+edmLfzxR7Pe/vCDZVJesyZJ99IKqG1hVpWsjMcDf8LS3x+PWcvGB/v6YPFg\nK7H0+RHg9qBcjqTrgsyMZ2Cuh/2xhB4TgL0CYfamc+5roDmWnfFuLBbtqaBsfWAnLDNjKea6+Dpw\nLnAjMFvSwcm0JUHfOgEztqUJpteutcxUd98NV1yxpVvj8Xg8Ho+nVqipLHhVzT4YHvfNN/Drr9C7\nd3QS9oUL7bgbb7QJzZs1Kzs5e1Wp7czAVc1WGUt2Njz5JPTrZ9kZ49djef55OPdcm2j9zDM3Xq+I\nsOyll8IjjyR3zOaSIEto6UXZfDY4l8+WZ7JkiSWdXLvWXiu7hJlei3CkYRaXOmxax9SrF802u8MO\nluE0NgNtejo0aQKRSB7z5+dtyLialgZr1izn22+nQS1lZay0MANwzo0BemH5/E+T9GqwPQt4F7he\n0t3BtiZY7NcESf2cc2Mx98ROkmYFZS7ExNnRkt4LhNkeQLqk4qDMa9hs2qnOuTpYDNl/JR0e065f\ngFWS2ibTlgT92ubS5U+dCj16wKxZ0LHjlm6Nx+PxeDweTy1RHSnsk6U6RGB5IizR9vJEWDLibHME\nXVWphSmGSkuhKKMJdVeupARIBdY3SufTd1bw++82XUadOjYlRSj+1q6Nvl+1ymZwKCmx9d9/t9fl\ny21fOJXF+vWwcqVtKymZyZo1tZcuv9KzWQWi7FQs0+H8uN2Lg9e1MduaY8k56sXt+z6mTIPgdYfg\ndR2wLhRlAfWBFOdcU0nLnXNFWEbIsF1hHUXBpt+SaMs2z3vvmfo/8MAt3RKPx+PxeDyeWqQi0dW1\na/VayyZMSCy+una17RMmbLq+vLzElrFwPS8v+n7MmMRCKlwfM6b8Oc7iRVj4eu65Zderk6lTE4uv\nzEzbPnXqZguzlIwm1Fu5EtLTSVuxAprY+uF/bhKdjLOamTkTbBqz2iGlMoWdcw8B52Fug6uDzU2d\nc/WD940xP8whzrkezrnOWPzYYkwQgQmmdcA/nHMHOud6ArcG5wumbWQJ0Mg5d49zrp1z7jKgG+a6\n2Dym7X9yzl3onNsXS0SSSlRsNkqiLds8U6aYxSylUlfS46mYvLy8Ld0Ej2eL4+8Dz/aOvwdieOyx\n8oVX167JWebWrEk8uTTY9jVroutTp5YvoM48s/zJpSsSdBMn2v6aoG/f8oVXZubmTy7dpImZsdLT\noyJsxQpbX7nS9v8BqOzf+UuxVPT5WBIQB4wHzoopI+At4IWYch8E28P932MJOz7A4sDGY0k6wjJr\nsbixY7FkHUOAm4P6wjKlwbG3ArOwLI9jgvPGt+U1LMvjEZh424E/AAsXwkcfwemnb+mWeP5o+B9j\nj8ffBx6Pvwe2Qaoq6LZ24kVZSKw4+wNQKVdGSWWEnHOuFJsn7NVg08+YeBot6eKYcvnAtzFldpR0\ncsz+VODKYF9YJl1S55gyPTChtSimzOdx9QyL2++wiafTgIuA/2BxZz2cc80kha6XZRgyZMg2kfzj\n8cehUSM45ZQt3RKPx+PxeDwej6eGqCgnRjW5Mebl5W30MGL58uXVcu5kqXSMWUVIijjnfgaOAT6H\nDQk3DgfGBsU+BDKccweHyT+C8g4TTmGZ251zqZJCC9hxwFxJy2PKHIPNgRby52B7bFsuBx6V9FTQ\nlh0wt8lsbG60jRg5cuRWn/zjp58gJ8fiKeM0pMfj8Xg8Ho/H46kEiYwwM2fOpHMtBplVOjLJOdfI\nOXeQcy7MAdg2WN8jWM8BbnLO9XLOhWnuF2ITPiNpDjAFeMw5d6hz7kjgQSBPUmgxm4hNKp3rnOvg\nnDsb+Btwf0xTRgEnOOeuDOLQhmETScc6z47GJsNeEdeW14Eule371sIXX0DPnpbi85ZbtnRrPB6P\nx+PxeDwez+ZSFYvZIcB7mFuhiIqlCUC2pHudcw2BR4EMoABLc78+5hznYgLqbSxW7AVgcLhT0oog\nKcgY4BMsYccwSU/ElPkwmKvsjmCZB5wq6cuYeiYAd2GxcVeFbQH+CuydoG/1Ab766qtKDknNk5sL\n330H8+bBnDnQurVZzL77zhaPpzpZvnw5M2fWeFZYj2erxt8Hnu0dfw94tndiNEH9ispVF1URZvOA\nZzCB0zBY7xeX2z+lnPchjrKZEePXY7eFCT8SZVJMoWxSkU1ZAMP9sUlEYskEOP/88zdxmi3PggVw\n9tlbuhWePzK1abr3eLZW/H3g2d7x94DHA5hG+KCmK6mUMHPOZQDvA+8APTFL1t7A0pgy1wIDgb5A\nBLgdmOKcax9jNZsI7IrFiNXFsjI+CpwfnCMdc3d8E7gEOAB40jm3VNLjQZkuwXmuxVwTzwVeCWLX\nQqvZRcHrI8BzYVuCPoRJQmKZgk0HUEjZ+c88Ho/H4/F4PB7P9kV9TJRNqY3KnCrKchJf2Lm7gS6S\nuldQ5kdghKSRwXoTTAT1lTTJOdce+AKbQXtWUKYnJq5aSvrZOTcAuA1oHk4y7Zy7C3NV7BCsPws0\nlHRKTN0fArMkXRbTlvXAPyUNjmnLauAeSSOS7rzH4/F4PB6Px+Px1BCVTf7RC/jEOTfJObfIOTfT\nORebrr4NNgH0O+E2SSuAj4km2zgCWBqTkREs1kxY9sawzLRQlAVMAdo558IchF2C44gr0yVoS9ug\nLWOA/s65C4EWmHWvEWal83g8Ho/H4/F4PJ4tTmVjzNoCA7CEH3dgQmq0c26tpKcxIRQ711jIomAf\nwesvsTsllTjnlsSV+ZayLIrZtzx4raieXYO2/AObvPrWYNtqTPT9mlyXPR6Px+PxeDwej6dmqaww\nqwOkAjcGC5gFagDwdLDfAV865+piFqzLKJtsoynQ0jm3GliJpbC/Lq7MDkBv51w/4DtMBP43rkwK\n8KBzbjzwGTAobv+GtmBxbGFbxgCxlrgNOOd2wmLnCvExZh6Px+PxeDwez/bMhhgzSb/VdGWVFWYr\nsfT2+xLNkng+MCR43z/YfjXwKTap9ItACTDLOZcSlK+HzTnWArNoFWFi7GfnXCZwMJY4pCtwLPA4\nJt4ELArmNUvDxNYdQf1TgnKhFa3CtpTTv55YxkmPx+PxeDwej8fjAUsOOLGmK6msMPseaBPrBhhM\nLL0gSKxxJmZBy5A0K7B4fYUl4BiLCZ9dMWtXmqQpzrmbgfswEfUfTGQtAnYE5kua65zrilnl5kpa\n7pwbAnwNNJE0xzl3KXAScBbwryTbkohCgKeffpr27dtXcmg8nkrw448wfDgMHQotWmx6ey0zZMgQ\nRo4cucXq93i2Bvx94Nne8feAZ3vnq6++CqfRKqyN+iorzD4EDnDOLQeWYUKtI3AxZgFLA0YCNznn\n5hN1CVwN/BNzf5wN/Aw8FmRfXAw0Bl4PMjIeAbwCnAHkOufuwQTWnsDFzrk6QV03AHc4567EMjou\nxtLqj8Emwd5UWxJxCkD79u3p1KlTJYfG46kEnTrB/vtDdrbNHp6ZCYWFcPXV8Pzztr4Fadq06Za7\nByZMgO7dE49BYSFMnQp9+9beeTzbLVv0PvB4tgL8PeDxbGBtYIx6BOhBTDiWpNKwkHOuB5aLYz+C\ncCxJE5KtpLJZGV8C7sSE1a7AYViGwz9hSTfWA/cC32Di6nNMIL0ezGEWJuz4O7AbZiF7Pjj3Y8Fr\nc0zw3YiJsy8wt0RhcWzNsDi3acAE4G5gDjYAC4I5zHZNoi1lCNwjh8Rv93hqjMxMyM2l+MJspt8x\nldJ+MSJte6Z7dxOshYVltxcW2vbu5c7WUTPn8Xg8nppiwoSNv6NCCgttv8fj2RpwwL8wLXEENl/z\nRVhyQStg4VivYdnpDwJGAY875/6cbCWVEmaSpki6UVI74CjgByxmq11MsRxgF+BooBOwLngfy7PA\n/4ADgVODbWfF7N8BeBB4GItnG4cNSOx5jgUuwKx14dxoezjnmlWyLSFDsBg0hgwZwimnnFJmycvL\nK29YPDVFu3Ywthyv07FjbX+yVOXHrzZ+MDMzeaLlULre1IPxrYZWTZT90X7YA8FaRlSFYqoywrW6\nzuPxeGqGP9p3V1XwD5A8nq2GvLy8jf7/DxmywWbTBdMk50maLWkKcDNwuXMu9EAcAHwr6RpJcyWN\nBV6gMoYfSZVeMNfDuZjICecpy8JE2jrg9JiyC7GEIYcBw4H5WLKPZsH+zGD/CkyFTsUyMH4ec46L\nMAvYv7Bsi0VB/aNiyowH1gDXJNOWuP6E57wC0IwZM+SpAS6+WCooSLyvoMD2xzJmjOScvSazvSIi\nESkry16T2V7VYypJ6bcRfVA/S93I1/v1s1T6bRXOubntHD8+Wia4Rr169YqeY/x4e5/oGlX2mlaG\nSERrj8zSq1flq6hbgn7EtjvBsRvaHYmouFuW/nllvtZ1rZ7r5tk+2HAfeGqGWviO3SaI7+9W1H9/\nD3i2d2bMmCHMa+9RYKbK6odQwxwUrE8FHogrcxE2f3NyGivZgnGVTMASdjQOBM07QJNAPJVgSTkA\n9gka/CMwGDg+2P9ZzLn6Y/OSlWJmv7uBVbEdw7KgfBZ2LBCCJcApwbrD3B//C7ycTFvi+rNbsO9C\nL8w2E5BatUq8b5ddbH/8H/mCAikjI/Ef/HgRVhVRFlKVH7+a/MGMRLTikCy1JqLrr5daE9HSTlU8\n9+a0M7ZscC0mDh2acHvS166ia1oJbumRL4FGnJxfcbs3sT3ndDvP/ackOM+WJl7cjh8vjRgRHfdY\ncRuJSPfdFxWdnhpl4sSJW7oJf3wiEal9e32dW6AlS5T4u2x7+LxHIlrXNUt3nZCvlYduHaJM8veA\nxxMjzF4E/q2y+qFBoB96ButzgWvjypwQ6JF6SkJjueCgpHDOjcCSZ5wFXALcAnQHHpd0mXPuTczF\n8GgsKG500OC6wLtY3NivwbZjAkH0FJALXBs0fi42ufS0oI5jMJfEocDtQEPMr/NRzAL3LGYi7I2l\nuj9UUpdNtUXS9TH92g1zy7wImDBjxgwf7FpVWreG776DVq1gwYKNt++yC6xfz+pnJ/NDm678OGk6\n3Ub0wr02mdI/daWkBEpKYM4ceOYZmDED/pY2ltPeHsTio06jWcErvHb8g4xcdzk//QR77QXHHmte\njQ0aQL16UFoK69dDUVHZRYKMZYUckJPNV2cOpcPzwynol8u63TKpUwecs+Mla0NxsS2rv4gec/zH\nw/ng4lzW7JpJSood45wd4xzUqRNdGjeGhg3ZUC62fOm3hbS8JZu/Nc7l7fmZLFgABx0EbVMK+Ufd\nbOZdl0vJHpmkpUFqKqSlRZfUVDtXaanVGy5rviqk2bXZzD59KF3fHY4ez6W0VSZg/apXz44tLY1p\nRyksXgyNfi2k4aBsXG4upd8thJNPpKjV3sy980XqLFpIu7/3wk2ejDuq68bXfPp06NULJk+Grl03\nXq8ic94o5McTspnQeigXLRjOHm/lstexmWULxbsmJnBVXPF5IbMOzma4G8otpcPp8FEuuxwWd54t\nSfx4FRbCuefCsmXwww/w+uvm0nXccTBypF3svLyoK+b06bb/sSBMN0x6cscdltwk9hqESU/23LPs\nMeXhE6h4aoGlk6fDKb0Y3vxhctqPq/B+/iPz1P9N5cLcHtzfK5+rXvUujB7P1sDMmTPp3LkzWJ6N\nhpJOCPc55xpguuh4SW865+YCuZLuiSlzIjAZaKAEOS42Ihn1FqP6PsVUozCR8yuWgv6BYH+/YHtp\nUGYh0AFL8nFnUOYlzMVQmIL8GEsgUgocF5RZhFm8FLw+CpwYlK9L1MJVHJRZiVm77gU+SLYtMf3y\nrowxlJRIq1ZJv/4qLVggff219OOPUmlp4vKLF0u//x6zoVWrDZaz4mJp7e6tVApatlMrDR4s9d2z\nQEvI0CBytIQMHUmBykoMW9LTpZ49pZYtpRc4XQK9wOnaaSfp1FOlK66QevSQ6tbd+NiKlm6Y9aQb\n+UmVT02t/DGbWi5kvFoT0c47S5Mn27DNnCntvrtZzi5kfJXOe0xaxe10zl7r1JGaNrXXcF8bF9G7\nLks9XL4+oZOWkV7mGjVqJO27r3T44dKf/iQde6x0/PHSSSdJ13Ut0Mo6GcrtmKOVdTJ0W88CXXKJ\nXaMrr5QGDZL+9jd7f9110tCh0vDh0o03SlddJQ0ebPuuvlq65hrpyjMiKqiTpaPbRrR8uXR024gK\n6mZpeL+I7rtPevhhe4g+aZL0Sk5Ei/bL0ts352vRflma8mhEL79s+3JviWjmDlnaKy2iL7+UOmZE\nNCMjSx89G9Hnn0vffiv98ou0Zk35n+9aoaBAJU0zNOfxAq1aJS15dJJ98Nq3tyfnk4L1/fYr+yQ9\nkWUytDhMmlR2X3nbK6K2XM1q0iV2cwjdZRO4+5bZXpG7b/z5QmtovCturDW0IitRVcYqUT9i691U\nnTXM6NHSWeRJoLm35kXbVZXPWDLjk6wbdG0Sse+mzXJr/6NS2eu1NV5fzzZLkq6MBwbrm+3KWFmL\n2a2Y1asEcx9MCZbSYNsbQK9ARP2MzRdWAuyBpa5/EPgJM/0dSXSC6eeAy7HU+yuwTIozscmoj8Us\nZjnAxZJ2cM6di1nHcoKBGoLNWzYFqC/pdOfcP7H09wnbImlUXN8+wix1fbp160bTpk3L9L1Pnz70\n6dMn6bHaEnzyCVxyCWRkwO23Q5cuictJ8NNPZpWaOze6zJ9v1pNlyxIft9NO0LKlvaam2rYvv7SH\n+ikp0LYtpKfDunXw2letydR3FJFCHUqZRyvasYDWreHoo6H/mlEc8ewVfHdVDv/tMpglS+yc4bL7\n7nDkkVC3LjB2LBo4iBXHnEaTd16BBx/EDbx8Q7vWr4dFi2DtWltSU8tarurWtVcJiucXsuPV2ay5\nZigN7h1Oyaf3AdoAACAASURBVGNmmSoqMuvRunVmSYq1TtX/uZDUv2ajW4bC8OEUj7NjSkvZsIQW\nqFgL3cqVsGaN1RuWC9/Xrw9NmpghMS1m0oriYvj+e3uNtdrFr8fWGS4ZywrZ7/5s1l03lKKbhjPt\nolzWNs9EsjEKl7Q0a9eaNWbRa9HC+r1iBezy1VROy+lB/rB8WvzyKfs8dAULrszh48MH8/331raV\nK63+33+PtqukBE6aP4pL51zBg3vlMKn5YNassetRUhLtY1FRtB2lpWbFq18/askrKYHmawu5f1k2\nL5+cy6V3Z7LHHrBwIeRcUcgZr2fTPzWXL3+3foV0YypT6UF38pmGPWluTSFPumzu75BL36GZnHkm\nvPceXN+nkDsXZZNNLgvI3HCO1FSzuqal2biE1yM9HRo1ss943bp23WItmLFLnTrl7wstshkZUQtu\nSoqN4y+/wJfjpvP8ul4MZRjDGcb4LuO4YPFI6pauITXNkVK0njqLvuPXJ/9FSZeuNJgxnR369mLV\nxMnoyK5lPl9uQSHpg7NZfeEAMq7pj3tsHDz8MAwYAP37V86amYRVcrMpz8paTdbXKhP29dZb4ZZb\nrM8LF8KJJ8Lee8OoUWW3b6qtoTVUghEjosdC4u2JxrcqY5WoH7HXMn57LLVgNT3vyEKu/iqbZxr1\n5+YfB/DppQ/T7d1b7XObaCwrqjeZ8WnZMppw46qr4PLLo+cNP9uvvw6jR9uPY7IkO1bx5QoLKemb\nTfsPczn8cNhl+ovcdsTrNMzbxD22vVi0y/vOqa7tHk9AXl7eRsn+li9fzrRp0wAGYrpjN0mLAZxz\n/YF7gF0kFTnn7gZOkHRQeLxzbiI2p/KJSTUiWQUXCLhGmNUpdikCpmNzh60L1k8PyrcjarU6FHNV\nLKZs8o9LMDPgUsxydQ/wC2Xj0PIwV8N/BesfYQJvVLDuMIvYMiwVf5NNtOWwBH07C5vnbJu0mK1f\nL+29t9Shg9Sxo1lAzjxTevll6dln7SHtoEFm4dhhh6iVJC1NatdOOuUUs1zcc4/06KPSM8/YsVOm\nSPn59v6226S//lU6+2ypd2/pjDPMuvHss9Ljj5vFY8AAs5Jcc41URIoEKnIpmj1bWrYsaGz4lD8n\nZ9NP7v/IMWbVSXW0MzwmP1/q1MlMlslcI6ly13RTJPG0s6REWrdOWrJEWjk7oqKjsrT63/laf1SW\nfpsR0S+/SKseGq/i+RufZ80aae6UiObfPF5vvWWf7aeekh56SLr/funee6Vhw6SbbrLP/DXXSJdf\nbp/tiy6SzjrLPvu9ekknnigdd5x09NFSt25mSTzsMBu+Aw+0+3GffaS2baXWraVmzaT69aUmTcxi\n2bixtOuudu8OHiz9r3+OBJp6Ro5at45aakMr6JEkZ20Gs7y+Q5YuZ7TWk6ZbU27WUpehS/Yr0FFH\n2aX+85+lE04wy/RZZ9ly4YXSpZdanwcNsvt5eL+I5uyepQdOzVekTZYeuiai++83S8fDD9v9P2GC\nNHGi9Pzz0iuvSK+/Lr35pvTee9L06dJHH0mffSbNmmXL7NnSnDnS/Plmmf/1ZbMarviXWQ3Xvl2g\n0mqIU9xswvuioCD62qmT1KiRvVYUg1ne+bp0kY44wsofcYRKD+6ktZ2OUOm0guTu2/j6kqk/UT9i\nXyu652rQarpkplnqJwyPaOZM6fq2Zjl7ocdolVa13mTGJxKxmxPs9yT2vFX9nUl2rGLXg/dTJ0TU\nmoiWdTYL/4ThSfSzpq5NVS3Y4XGJLMPhcclahuMpbwzPPjtxWyMR+zN09tmJj/d4kiTGYtYZy3fx\nbyyrfE/Mw+82lbWgrQq0TDvgMszz71gl0FWJlkoJszIHmqXsHMwK9STRTIiPARFs8rXOgdj5Jjhm\nOGYJi+3YhUGHH1XUDPh4XMeeCsocS9Tt8B4sC+OFWPrKuYEY2xmLK6uwLeX06a5tVZi9/rpdzf/+\n11wRx4+PehSC/QHs0MHczm69VXr1VWnuXBN0NUJYeYqJsw0JQSrzh2I7yMpYLVRHO+MTfaSnJ/+n\nsyp/EquLbUU4J0OcuC15dpKKDu2itR06anW7g7V8/yM086WIvhpg4m32xTl6+WXphRek556z1xdf\nNKH5yit2j79/pwm72T0GSqDXjsvRRRdJF1wg9eljD1hOO82E5jHH2HLkkdLBB9t/mgMOMO/JDh2k\n7D3tXKftkK8dd7SPSP365mFZHe69oITC0zlzV27UyMRss2bSbrtJe+xhgneffax9++1nYvjgg6VD\nDom63B51lLk8H3usCdATTzRRfdpp0l/+Yg+wzjpLOuccG5M+fWzb2Wfb+/PPl676S0Rf7palR7Ly\ntKpuhh7/c54W7NxJv9dN10s9crS6XoYeOrdAN9wg3XCDueTecIN91957r/Tgg9LYsfY6cqQ07oaI\nFrbqooW7dtSC9A5aTrrOIk//bWKi94UXpHfekT7+2ATthx9K778vTZsmvfuuCd5pdxZobcMMvXtq\njtY2zFD+7QV6803prbekt9+24997T5o61T5a06dLM160P/7vD8rTyjoZerBrnhYflKX5b0f03XdR\nt/SN3HqD+6p4fkSLF1s22c29z9atk754PaLPmmWpQ8OIFi2K1vNGvzwtIUO3d5yknztk6f1nIvrk\nE6kwP6L1XbNUNK/8ektKpEWLpK9zC7S+UYZmX5yj9Y0ztHpK9PuouNjc8794PaJVLfdRKWhli330\nzTsRrbh7jEpxKrxmjF57TXrjDXt4UFSUZMeS/U4KtwcC5qbzzV279NvIhvuw9NvIpoVLTXwHVjWp\nU7h/0qSyDx86drSnUfHbK9nOonkRzd4lS1d2zldxt6yKf58KCqQmTbT+wI5643p7aLfZvwvV4XJd\nv77Ur1/iff362f5tlT+oC2mMMOuEed29FmiURYEWSVFZLdEdmBFolHnABbH7N7VUVoxdD8wOGqhA\nBX4FPAD0CRqRjk3mHMZ2rQPGBcc/Ggiyw4IOKRBQwkx/BALrWiyL4+pgX1FwvnpE48sOxxJ/FMXU\nMy84xybbUk7/Om2rwqxfPwtHif1BLS2VfvhBWrq0luNnYmLMyqzvskvlvuz32ad88TVmjO1Plqp8\nYWwrXzKb2854URZei/K2x1LDWRmTbncy27dm4sdrUlyMWWhl2W+/5C2Z4TiMHm2m8Ztvrvo1ibWm\nJhjb0IK5apV93/zyi333FBZK8+ZJX30lff65CYwPPpD+8x97nTbNBMQbb0ivvWaicuZFJjw/Pi9H\nTzwhPfJIVNDce690xx0Wn3jTTdK115qlfvBgi2EcONAsm/37S//3f2bhPP98E1hnnWVC7LTTpJNP\nNkvhcceZ1fCYY8zq2aOHde+440zIZWWZJbRrV2lABxOmI1pa+/q1zdedze39bTvnaM89pcxMW9q1\nk9q0kZo3NzFZt65dgnr1pIYN7T/qSY2j1tBXjrbzXNk5X+npyQvZQdhxg8hJ+pjQCnv7znZsefGo\nDRpIO+1kS7NmUqcdzbLVjXy9l5KlQ5pF1Lq1tOeeFnt6wAHS/vvbR3affWwcdtvNlhYtbNl9d/sZ\naNTI6riQ8TqwiQnR+Pt26h0Fmld3Xx1Jgd7B6n0Hy2IbPmxs2dJ+XurWtXGNj5uNH58GDcrujx2P\nEiyGuQSnSxmz0XikpFhfDjnEPE+OP95E/qmn2gOOPn3M2nzRRdJlJ0b06Y4mIGbvnKXr+0Q0eLB0\n2WX22ezXzx6ODDw5ok93ytIFraxvIwdb38MHrT172mf7xhvNin/77dLdd5tlf9QoE/vjxkmT7o3o\np/ZZendovn490ITsrFnSJ5/YfffNNxYzvmpVJQRmVR+4xYuz9u3tYrVvr9KDO6nk8KqJMkm65Zbo\n9brxqHytWVNxW5dOLlC/tlb+//bKt6yfm0N1/N7162cXN16cJdrerZuNYyImTbL9iajqcZvLH+k3\nOYZYYaZKaKaqLpWNMfsXFg/2IzYJ9B1A20DQdMCyK47HXBb7YvFi07Cgt1bOuUeBVkDL4BxXY2a/\nV4GJks4LMpq8jPlyPgQ8EYi0AVi82KeYW+PNwdIfS+jxLLBfINz+vKm2lNO/TsCMbTHGLDMTTj/d\nkrZtUZLJyrho0cbHxWeW89QesXEKf/1r2Ux+sXEKia5RfPlYavqa/lHiK5LJyti1Kzz/PPTpA/vu\nC6+9VnFMUxhLEcaUjdvKY8xCwrEYNsyWLRVbFk/Y5/79bQwffthiwebNg9tuq3xbw2u8Zo0FXH7/\nvV2jcePQE7ksaZLJkiUWf5iSEs3oGpuhtfGn09nxol64YcPQsGEse2oyyw/oupHECmM3JUhbWEiL\nm7Ip/r/+ZFw3AD38MGtyxvG/K3NZlpHJ77+zYVm92poH0fPsu2gqf3mwBy8MzOfLnbuzbp3FYYZx\ntSkp0TjhevWCGGGibQFre6NGFrvZrh0ceqjF8ZYXE1R0QTZLzuzProP7MPOBfApbd2fZMli+3G6R\n4mJo3tzaV1RkMau77w7tfp1Ou7/3YtXVw2g0YhhvDZrMvF27kpZmZXbeGVqVFrL33dmkDh9KWp/e\npC5ZzMLDTufL215ip51gt93s/F9+aT9fP/5oy+LF1rywztiltNQy8h62diq3F/Tgqs75TKU7a9dG\nY1BjXw9bM5W7PuzBtNvyOerG7jhn537sMXjuOfsKCON5w6WoqOx7SBxnWx7169uxaWl2jcIlvGZh\nXPYBy6czOtKLR3YbxqU/D+OG/Sczu6l9xsNYbOfKxhpL0HnNdO6Y3YtJzQdx0Q938l1aJutK69Gi\n9HsuYRyD6o3jvvb2matfnzJLo0bR+uvUsXP+9pv9nfj6zULebZPNjxdbHPV1u+RyQK9MdtkF9l82\nnTPG92LO2cNoP2kYr2RP5pHXWjJ8ocVd17trOEP3yOWc6zJxzq5p48YW896xI+ywQ3K3brVkIc7O\nhiefhH797DMfvx7y/PP2PTFxIpx55qa3b+5x1UFt/l7UAJuIMessaWaNN2JzVB3QDFORL7MNTzAd\ns3+btJgVFtrP3ssvb+mWqKylLJ7QcubxeKIkM49Z7FPo2HnM/ihZGaUt6xJbEYlis6o5xkydOlXO\nvas2Y8zijy/HarpZVGT1Lygwk1xl6k02xiw2pgzMNBjGnG0OyY5VNY1p8fyIirtnadXr+Vp7ZJYW\nTI3o448ttOGjj8wq/dJLFgOamxu1to0ebV8nd95pmXKvv95izQcNki65xCx8LxxlVsd/HJKj88/X\nhuXcc83d98wz7f0FF0h9+5rF8NxzpacPs+Pe6jBww3OC98+ybePOy1e/flbujDPM8nj00XZbHHig\nGdn22svictu0MSvlRT0iWrhPlkq+sTH6+s2I5u6epRM7mOW2SZOyFtK2KWaN/PpNK//tu5b1sjUR\npaSYVXfHHaOPMOrXN4vrrrvaX5W99zYL8CGHmFvp0Ueblf3006Vbji7QqroZyutibsw5vQs0bJiN\n4V13mXV/5Egb58cesxjmvDxzN//3v81D4Pvj+6kUtHr3NioF/faXfvrmG2nhQrNurl5tngiaNMnM\n7aEFLH69PKp6XHUQsTlZX/t7voq6VeN3BZjHSCJCV4MaoLYtZpsrzPYKGvsS2/AE0zH1bJPCbMIE\nu5KLF2/plng8nhqhMrEN4Z/cRMeErq3JxkPUljvvlnSJrYh4MRMfgxm/PRlxlCjGprztiajKWCXq\nR0Xbyzu+tmM5q1JvMuMTL8rCmOVIpGxCkJpsc3WNaU1em7i416Tvw/C4m282l+w997RA0PR0UyhV\nTUxV0RgWWLKgVXfmqCS9iUo6dkxYvrh7ltZ8ZduLi6UvvrBkZ6NGmav0bbeZm/Tf/24CtX9/E5zn\nnGOi7IQTTKSNbGMi8K7mOerQwdyWd9vNXH8bNrTnNvXrx9uvyy5f00YCfU2bcss0aCD1bTRJ60nT\nU00Hqog03dhuko45xtrSu7eJ4UsuMS/Ivn1NOJ92mjS0wyQVuTT9a6+BKnZpeq73JI0ZY/197TWL\nR5061VzMZ860vAMPPWTi8rvvLFZz2TKLOy0p2fRlKiqS/vc/cyMPXU4vaJWv//0v+UtdIaH4ihdn\n5W2vJrZqYYa5LnYFWgP7B9YvAUcH+98MxE8PLNnG+0BBIKTuwhKG/IbNfxab0eSu4LieMRa0fMpm\nNLk+EFr1AjEnYBiW+OPR4LyjgQ+TaUs5/dsmhVm/fubf7/F4PNskfh4ze781zmO2peJGqlpvZeYx\nS5RIKhKxf7a1lZUxmeM3t76qUAMxZpW2DIds6gHRDTeUbdv115sJrbyHFJv7QKkSgrWkxDIBr1hh\n8bfffGOiZ1lvs5itCSxmP5zQT2+/bRa1l1826+Zjj5lgvOsu6cNDzPL47n4DdeGFFjN72mkWD9ul\nS3Row4RHJ5xg1sxXW9txT+84ULvttnGMZWWWevWsuzvsYNbGZs1sCWNow3IHpEe0sF2WCifk66NG\nWdqnbkSnnmqxkjk5lvn7qacsg+9rr5lF94MPLFvvnDmWpfeXX6SVK008lyFehNWwKJO2/hizx7E4\nr10DK5UD7pV0bbD/AixD43qgfiCMpmPxaK9LusE593QgwDKA1KBsHhYHFs6c/V0gwJoFdSwB/om5\nNDYAdsLizJYDTYMB+wazqu0u6U/JtCVB/zoBM2bMmEGnTp2SHpctTdu25uI8atSmy3o8Ho/HkzRb\nKpazNupt1w7+9rfoPGaxjB1be/OYlVeuuuqrLFWdVzDcP26cBbxLFos5aBB8+y08/njZ7RXN11fT\nba2u+moyxiwkjA279FJ45JHkY8QSHKfeZ/L77xajGTu/6bp1sGqVzeEpwdKlti3ct26dxTqGc7PG\nLo0bW3xp/fqwX6NCDnk4m7QJdl3Xzink55OyuWHXXKYuyGTp0mjsarLUqWNzjIbLjMIm7MBKSjAR\nscKlc8lZK2jQwNpfXBydl7RBA2tX+Nqokc0lmpbGhvINGljMa9OmZWNA69a1GMqZM2fSuXNnqKUY\ns0oJMwDn3PHArZhlaycshuvVYF8W8A42n1hfLFX97cBJwLWSHnDODQeuwIRUf6Au8DTQBjhI0ufO\nuenYZNMvYq6NB2ATURdLauScq4PFk4HFlL0OnAvcBLwn6dhk2pKgb9tc8o8FC+w77aWXLPmHx+Px\neDweT5WpalKn8LhvvoFff4XevU0cdu9uyYomTIAbb4QXX4RmzWz75grs2kxAVR0isDwRlmwCkGQT\neFT1uM0hyYm9JRN6a9ZUfRmR40jDJkY+/WSxZk00cVFamiWNWbs2Wj58HybLKZ+8YIkmuJGWU1xc\ne8k/qiLMxgCnYnn65wOnxQizJpgV60lJ2cG2g7G5y26QdJdz7q/AOMz98b2gTA4Wg7aHpIXOuSnA\nMUB9ScVBmS+AVpLSg/XFwApJbYN1h81TNiOwmG2yLQn6ts1ZzJ56Ci66yL4Dd9ppS7fG4/F4PB6P\n5w9IdYjABg0su24iy1h2NuTlRU1K21pWxtqyrjdpAitXRtfT02HFiqQOXb/erIUlJWwQc2vW2LaV\nK6OZTtevt/VVq+CHH2YyZkztWczSKlPYOfcQNkfYKdgcYwBNnXP1Ja3FLGgAxznnegArsbiv5cAu\nwb6SYLnGOfcblt6+D+Zq2BnLnBiO+B3OuVxMpO0DpDjnmkpajrkvtnTOXYilyx8SnDc9OLZZEm3Z\n5nnvPTjwQC/KPB6Px+PxeGqMikRX167JuTJW5MeXm1tWsI0Zk1hEhetjxiQWWFU9bnOpSHRlZlZP\nuvxQlIViLFxv0iQpcVa3rk2VURlmzrQhqy1SKln+UizjYT6W3dBhaerPCvY3xwTWG8ALMeXyg31g\n8WkRTER9ADwVnGNxTJl0bGbtY7F5y4ZgborElGkSHHsrMAtLJjKKqCDbNaYtr2EZG48I6u1QyX5v\nlRQX23RGxx+/pVvi+aMRP4+Hx7M94u8Dz/aOvwe2IFOnli+gzjzT9lfncVs78aIM7DU9PSrO/gBU\nymImqYyQc86VEhNjFsONki6OKTcJs3CFFEs6Oe5c/eLK/CTptJj9HbDsjbFl3oqr57K4/WDWtPOx\nxCH/weLRejjnmklanKifQ4YM2SZizN56yya67N17S7fE80cjLy9vq/u8ezy1jb8PPNs7/h7wbDXE\ni7KQWMvZZlLeBNO1SaWEWRL8jFnRdsXS4Ifsglm1wjJlXAmdc6lYtsSfY8rsGnfuXTDRtWgTZWL3\nO2Ag8Kikp4K6vg/KZQP3JurEyJEjt/oYMwkeeMBmrLdkMR6Px+PxeDwezx+QinJiJBljtikSGWFi\nsjLWCpV1ZawQSRFMEB0TbguScByOuS0CfAhkBIk4Qo7BRNR/Ysp0CwRbyHHA3CC+LCxzDGX5c7A9\nti37YdkZY9vyCdClyh3dChg3Dt5+G4YNs8wxHo/H4/F4PB6PZ9ul0sLMOdfIOXeQc65jsKltsL5H\nsJ4D3OSc6+WcOwCLA1uIzUOGpDnAFOAx59yhzrkjgQeBPEmhxWwiNv9YrnOug3PubOBvwP0xTRkF\nnOCcu9I51845NwxLHhIbovdE0Me949ryCdFYtW2C0lL46Sd44w047zyblmLAADjllC3dMo/H4/F4\nPB6Px7O5VMWV8RDgPcytUETF0gQgW9K9zrmGwKPYJNIFwAmS1sec41xMQL2NJeh4AUuXD4CkFc65\nnkGZT7DEIMMkPRFT5kPnXB/gjmCZB5wq6cuYeh7CkoZcB9wWtgWbPy2RTbQ+wFdffVXJIal5eva0\neDKA3XazqUBOPx1mzar4OI+nKixfvpyZM2s8K6zHs1Xj7wPP9o6/BzzbOzGaoH5t1FcVYTYPeAYT\nOA2D9X5xuf1Tynkf4oKlvPXYbQ4TUYkc9lKICiwlqGsxJvxSYspD2Vi0WDIBzj///AS7th5++gnu\nuMMWj6emqE2fao9na8XfB57tHX8PeDyAaYQPNlVoc6nsPGYZwPtYzFZPTPjsDSyNKXMtlnCjL5YW\n/3ZginOufYzVbCKWuOMYoC6WLv9RLHsizrl0zN3xTeAS4ADgSefcUkmPB2W6BOe5Fsu0eC7winPu\n4Bir2ZWYYHsfuCFsS1Dn6ARdnAKcBxRik1V7PB6Px+PxeDye7ZP6mCibUhuVOVWU5SS+sHN3A10k\nda+gzI/ACEkjg/UmmHWqr6RJzrn2wBfYDNqzgjI9MXHVUtLPzrkBmOthc0nFQZm7MFfFDsH6s0BD\nSafE1P0hMEvSZTFteQubZ+2SoN6PgTVAW0m/Jt15j8fj8Xg8Ho/H46khKpv8oxfwiXNuknNukXNu\npnMudh6xNlhSjXfCbZJWYGIozIJ4BLA0FGUBb2OWrcNjykwLRVnAFKCdcy6cYKxLcBxxZboEbWkb\ntOV+4CpsIurpwGrgVS/KPB6Px+PxeDwez9ZCZWPM9gE6BO8F7AyMc86tlfQ0EGZmfM85VxcTSpdh\nFrMwC2I7oK5zbjWwEsuUeB2wJKZMe6CNc24t8B2W3CNMpd8cWA60wLI/3gN8BgyKq6dl2BbMdTFs\ny4OUI0idczthLpqFeFdGj8fj8Xg8Ho9ne2aDK6Ok32q6ssoKMwf8jjUwTMZxKzAAeBq4Itj+f8AC\nYCzwIvATIOdcCnBRUOYITFz9A0uN74IymUAnYDZwDnAs8DhwaUyZs4O2P48JrSGY8LqLaDKQCttS\nTv96YolNPB6Px+PxeDwejwcsB8XEmq6kssJsJVAS6wbonPsUOCmIJTsJEz3fSvrcOdcP+AqYBUzD\nhE8zYIWk2cBs59zNwN1AY2xC6AHACiAiaS4w1znXFfhrcO5FmBBbiU04Pcc5d2lQ93HAoiTbkohC\ngKeffpr27dtXcmg8nkoweTJ07gwtWmy878cfYcYM6NWr9tsVMGTIEEaOHLnF6vd4tgb8feDZ3vH3\ngGd756uvvgqztRfWRn2VFWbfAx2ccz9grn4fYok0FmCTO6dhwukY4HNJc51z32NZFe/GrGRzgX2D\n7ImzMEvXw1ha+/9g8WAzgW7OuVRJJTFl5mIWu85B3ccAoyXJOfc2FgP3HDbX2qbakohTANq3b0+n\nTp0qOTQeTyXYcUfIzobcXMjMjG4vLISrr954ey3TtGlTfw94tnv8feDZ3vH3gMezgbXOuT2AR4Ae\nxIRjSSoNCznnemD5LfYjCMeSNCHZSiqb/GMcZoV6HhgOHIq5Cj6GxXatB0ZisV+9nHMHAOnAKuCf\nQZnvMKH1mHPuUKAN5nKYL+nnoMy04Fy5zrkOWFxafWAUZnFLxSa0PsE5d6Vzrh2wF7ADNin1rkm0\npQyBe+SQSo6Hx1M1MjNNfGVnmxgDe00k1rY3JkyIjkk8hYW2vzbP4/F4PB6PZ3vHAf/CDD9HYNOC\nXYSFdFkBC8d6DUuCeBCmWx53zv052UoqJcwkjQFOBY7GFOMOQUPPjSk2CvgGeAX4HBND/4yZwwzg\n78BumIUszOAYO6/YOuBG4Awsxf3fMUH4ZEyZ/2Hi7G5gDpbRsTBmDrNk2xIyBItB83hqh0CcLTkt\nm0v2ncqK3l6UAdC9e1nBGhIK1+7lztZRM+fxeDw1g3944sfA49l26ALsC5wnabakKcDNwOXOudAD\ncQAWQnWNpLmSxgIvUAnDT2UtZkj6l6QDge6Y9el3IAOLD6uLJdnYBRNvnYASoFtw+M+YNetZTFgd\niKlNgJNjyuyNJfV4GBuEiZgA7I5Nal0C/AW4ALgYy+L4LdDSOdcsybZswDlXB3OP/A+YT/Upp5xS\nZsnLy6vsUHni+etfYfr0xPumT7f9sbRrB2PHJi4/dqztT5aq/PjVxg9mZib3NRrKo3N7cE/9oVUT\nZZvbztjj469R7PGJrlFlr2kyVJc10VslPZ6tG//wxI+Bx7MVkZeXt9H//yFDNmiqA4DZkhbHHDIF\naIq5LYJZ0sqdyispJFV6wRJ1zAVOBIowq1cTzNJVBJwelNsHix0rBQ4DjgeKgzLNgjL9sbnFlmLm\nwbuBAg6J2QAAIABJREFUX7C4sLC+icCPwL+C9Y+w7IqjgnWHxb8tA65Jpi1x/dkt2H4hoBkzZshT\nRUDac8/E+1q0sP0FBWW3FxRIGRkbbx8zRnLOXpPZXhGRiJSVZa/JbK/qMZVkxecRveeydNau+XrX\nZWnprCqcc3PbGVsuuBYThw5NuD3pa1fe9soQiein9lk6c5d8/XZQgn6MH19+3yIR2x+8/61jlnrv\nnK9fDqie61atXHxx+eNUUGD7PVuEiRMnbukm/PGJ/56qxu/XbYaYPi9cKBXPj2w1Y+DvAc/2zowZ\nM4R57b0I/Ftl9UODQD/0DNbnAtfGlTkBMwzVUzIaK5lCMScfgVmcXgjE0ltYLNdDwf5/Bo0/EbNA\nvQ8UYJlMBmMWup+xecgOxLI0LsLcGEsxf8zMoAP/xWLLLgvquBebmBqgT1DPSMyi9ijwG5AHvJxM\nW+L65YVZdbHnnonFWbi9RYuyf9gr+AP/66/SvCFjVBorwsbY+vwrx+iFF6RPP5VKS5NsW1X+AEQi\nKu2RpX8/HNHq1UkekyyRiH7YN0utiejjj6U2LqLCtlU89+b+uYkXYenpUqdOFYuykPj91SHKJK1b\nJ/XeOV8Cnb9HvoqKKmjzJrZfsq+dp1/b/OQ/L7VF/HiNHy+NGCFNmhTdHoq3SES6776o6AyPjxVv\noWBNJPhCweoFn2cronTECH3drIvevjl/43s69iHLH5lIRIsPylI38vX9PluHKPN4PEkLs+NUvjA7\nMdA1dZWE1qpsVsYemJ9katDI37AYrnAy5lewzIivYVasH7AU9k8CzSWVOuc+wFLZfxZ05hPgemBg\nUOYz59ziQKTNwaxeT2ITRV/lnKsH5Af1D8LmK1sFXI6ZEkNXxQrbEtev0D1yx0qOhyee+fNhr73g\nm2/sNXZ9zz1ZPmM+/3tkOp2O7cULBwzj1FnDGHfyZNbmd6X0XSgpsWXOHHjjDVi9+nKbFXzgIN4f\n/g5H/voKg1MfZMwDl8MDVuXOO5tXY4MGUK8elJbC+vVQVFR2kTJprVyu3y+bcc2HcsnPw7l251wW\nnZBJnTqQkgJ164JkbSguhpKSTOr9lMt9+dmcceVQhmo4NzTP5afjM0lJsWNiqVMnujRuDA0bsqGc\nc9HX9N8KufS/2ZyzOpfOZ2Ry2GFw2hWZ9BiZywsdsxm5fy6/pWeSlgapqZCWFl1SU+08pnTDJZM6\n5JK9TzZjmw3lhqLhvHpaLkvHZAI2LvXqWbtKSqyfDRvCqlXw00/QoEEme3TO5eRjs5nWYyhZDfZm\nx9nzeKbXP+kzdxjjz5hMyYyu7PELNG1qbWjQIGhP466k50wm86Re/DZoGDs9OIzFuZNJ3bcrDVZb\nW4uLrd9padaG1FQbLwnWrbP9qanRvv38M/zjtkIG/DqcN2/Ip9+dw7l/UC6X3ZtJenow2LGuiqFr\nYgJXxakTCjlrznAePjuf858bzmtjcuk1KLMm74LK0bWrTZ/Qq5e9du8OJ50Ec+dCXp7tBzjxRGjV\nCtLTbTuYu2h4XEjoGjVgQHRf167RsYndvikmTLDzJXL7LCyEqVOhb9/NHADM5bVv32hfY5k+3drx\n2GObX8/WRG2N7ZauMwk+btmbuouf4ZjberDm3/k0CNsXez//0cnM5IndhzL1sx5clZ7P/d7VOspW\n+rn1bHcsxpIexrJr8PpzzOuucWV2waYJS5TfYiNcoOaSwjl3IZADnA98jcWH3QA8Jeki59xbWHr6\nLGwusrEE5jvM5/Im4FdMkB1NdILpXMwF8fjgvN9imRkvwSaYzgGGYZlPGgD9sOQjw7F4tSHAmdjk\n0J0l/WlTbZF0Q1zfPgrq7dOtWzeaNm1apu99+vShT58+SY/VlkAyMZORAV2S92Zl1Sr4+mvTUIsX\nw9KlsHo1/P67LevW2X/B/feHPfaAnXaKCpIvv4TPPrP9++1nr+vWQY9L9yLjl28odqmkqYTv6u3J\niXvOZ84cE043po/i9pVXcH+rHB5vOJglS6J/zFNTYffd4YQToEcP+OILOOK+Mzho/svMaH060wa/\nxFFHQZs28Omn9p1cWAhr11rdqallBVLduvYaioCDlk1l0Is9ePAv+XzftjslJSbkwv2hgAhFUOPG\nsN/iqZzzSA8e7ZPPNy27U1pKmQXsuFghuHIlrFlj5y0tLft60uIJRFp1p+3RmVx8sY1bSQk89BDM\nf7uQfX6eynt79KW4mISLZPXFLg0bwl+aTeXip3twVed8Jq/ovkHArV8fXVJTrV1r15q4atHC+r1i\nBRy2diqvr+rB+S3z6Zz6KUMWXMHD7XIYWTqY77+3Y8pjEKMYzRX8jRweZHCFn7lQgBUVJd7fmkJy\nyebLq3IZeF8mY/9eSPv7svk/clmWkUmjRtb2hg1h59WF3Lkom4eaDeWyxcO5LTOXn+plUlQEaQsL\nGbEkm9EH5fLijEwGnlzImW9k82TXXNa3yKRxYxv78LVBA2tbo0bWjqIiaNLE1kPhnp4eFZixgnlT\ni3PRz0k8K1bAc4Om0yevF+91H8axU28hpVVL6u3cJCrCTj7Znljk5cGZZ5YVZfGCJlaE9e8P48bB\nww9H1xMdk4jyYvKqO1avvL5U1MfaIPxDOHVq9I9hKCJbtoxuD/8YbkpETpgAv/4KvXvbevxDhReD\n/FOvv17+2FZFxIb9iK8TovWWV2ct/Cke2reQnk+dSwPW0GyPBuwxbSK88AK89BJMnLhx3RXVm8z4\ndO1qferZE/72N7j88o3PvWoVjB5tD0iSJdmxSlBOkUI+bJ/NqHX9GeaG0+bLf1N/3wTn2R6p7PeQ\nF3KeKpKXl7dRTonly5czbdo0MANSDrCbgjgz51x/4B5gF0lFzrm7gRMkHRQe75ybCGRIOjGpRiRj\nVosxx52KiZv1mCWrCLNclQbb1gfvmwTl2wXrP2KujKGf5Wcx57wEc20sxdwb78EsYA/ElMnDLGyh\nK+PHwXlOUTTGbCFmfXsZizFbH5RJ2JYEfTsLs/xts66MV10VtZ+cdJL0xRdl969YIX3yiTR2rDRg\ngHT00dLuu5e1u6SlSTvvLLVpI3XoIB1yiHTkkfY+NbVsWbBQr732kpo333jfWuyAtaTq1FOlQYOk\nceOk7/MKVJqRIeXkJOfyFsaUnX565WPL4gnd3PITuMxU5zFbgs1tZ+zxnTqZO2PMNSotNffSb7+V\n5s2TPvtMmjFD+s9/pP89UqD1jTP09cAcrW+coQ9HFOill6SJE6V//EN69llb/vEP6YknpIcessv4\n2GO2beJE6emnpaeekp4fEdGvB2bph/fLtv+bd8z186FrIrrxRunvf5cuu0waOFAaeZq5Ko48LV+X\nXCL17y/dfEFE32bGuKFKWr9eeuLmiD5vlqXzjozo8MOl/faTWrWSdtxRatBAqlNn489ydS1160q7\n7CLtsIPUtKnVWa+e7WvQQLpn9xwJdGPjHLVxEc1q2EVzG3fU/KYHa86OR+i+wydpVd0MPfenHK2u\nm6Gc3gW66iobi6uukoYMka64Qvrb36ShfSOas3uWXj5mtIpT0lRwzM1a2zBDM0YVaOpU6f33pY8/\nlmbOtO+Fr7+26/rdd9LixdLSpdLy5dLqLyIq7pal5Z9FtHSpqtedN5YacondLMK+FhQkdvWN376p\n9kYiUpcu0hFH2PvY83fpIh18cHRfeVQlrjP2msW/j21PRWNQQ7G2pd9G9H69LN1yYUS3/V9E73OE\n/lfvYK1pX85YbKreZMYnPMfw4WV/U8rbnizJjlWC9d+PyNKRFKiwrb0uThRXW1tUNe41PC50xw7d\nUMP74+KLy7pjV8ZNtTLu+rUQH+7ZfohxZewcaJF/UzYc6zZFtURmoGHuoWw41rFhmU0tlRVmjYAO\nwbIfNhl0aSCG+gZCaB1Bwo3gmIVBmUMxC9d8yib/yAz2rwDqAFOx7Iix4u2ioGP/CsoUYX6co2LK\njMcyRP4ds8ZV1JbDyunfXduqMPvuOxNOt94qPfecCavUVBNWBxxgv0fhn8M6dWxb797SjTfan+GP\nP5aWLKk4Xmv9emnBAmn2bIvtmjlTWrYsuv+336SFC+3P+9q2e6oUomoujDmr7J+v+EQfVUn8EVLF\nGLNtIjD9jxRjlmxSj/i2xwvSyp4nhvXrpd9/l0pKTJz8+KP0ww8mXD7/3D77H38sffCBNG2a9O67\n0pQp0uuvS//8p/Tii3YfPvOMNGGCidHHHjOde9tt0j33SPfeK911lzR6tDXlx0nBuOXkqDQjQ69c\nXaAHTs3fcONe2Tlfxx4r3dfKxNvdLXK0337SvvtKe+8ttWsntW9vD1H239/u8X5t7fhx9QdKoMHk\nVElQtiaid7D4l/dcljo0jGiHHUxk7r67lJlpbejQQTroIPve6dJF6tZNOuYY6fjjpZNPls48U/rL\nX+y755xzpAsukPr1MyF9+eVSTu8Cra6XoVePzdHv9TOUm12gO++0/3g5OXbbP/qolJtr31t5edLz\nz0svvSS9/LL06qt2Dd54Q3rrLem99+z6vP++9NFH0n//a9fu88/twdWcOdLcuXZd58+XvvnGlnDb\nN99I3xdEtOZPWfr15QKtOzJLSycXqOjATipp1EjFB3XSmq8iWveOPWwqnVagkhJp7Vr77JT72QvE\nUNG8iAqfLtDa+k20cIcOWtr+CJV+W85nNpaq3HNxgmx1xyO0tkMSQjD+2ETrVSWIq2pNRG+/bWNW\ncLt9ZmfXOVhzHi+oWr3JjE+8CBs+fPNEWfx5N9XmONH/ytUFehd7ALL77tKwi5Lsa01Q1aRO4f5J\nk6KCv6BA6thRatJk4+2V7V8kopWHZumz0THf9eWJyEjE6j377Oj61vjb7dnqiRFmnYA9sBCpVYEo\nuwdIUVkt0R2YAawB5gEXKIHmKG+plCsjgHNuf+BDbMLnlVg2xHewZB25WAzXCZi74UosHmyZpD2c\nc48CrTAXxh+Ba4HWwKvAREnnOefmBkJvIOZ+mIvFkl2OBdB9isWL3YTNH3BJIOSexcRiC8z9scK2\nlNO3TsCMGTNmbHMz3Y8YAbfcAr/8EnUnfOop+PBDc/faYw8LT2nTBg46yFy2aoyYmLIyMWYtWphv\nZLLuSmPHwqBB8OCDZV1NytteEVVxyaotN67NZXPbGVtu4cLotWjZMvH2ZK5dbbmgxfdxa7s2yRI/\nXtOnW5xZy5bmP+mcBQleeaW5Ig4bZktF4xuOxemn23HXX49GP8gPj0xm9cFdKS42V83iYnPTXLHC\nDlu71m7T0E23pMTk2W7zppI1rAcvDspnQWb3jWI4K1rCun7/3c6VlhZ1y40vc84vo7jp1ysY2jSH\nxxoO3mi/xYvW0nUJCF1rH6U/jzCAS3mYaxjBXszjZm5jOMPoxWTep+y1qFvXvmsbNLAxDmNXW6wv\n5LHV51KndA3gqMc69uNLupPPrPTu7Lkn7LijudhKZa9FeI59fpnOiLm9uLveMK5bN4wr95rM/OZd\nN8SxhktKirnnOge7rinkitnZ5DQZyqDIEDoxi4H757O8Y3caNmTDEroJN2xo/UhJsbjYPz2RzWud\nhtJr5nA+/GsuxS0zN7j11qlTto3/396Zx2dRnXv8+xCWsCSgIkatEqjVYusGbngxhKJSbXGpVSt+\n1JLa1lYoYm2tei1LqxWtAhW5SjWoBdIbtb0qLri0iXAp5RasShEXTFhUoKCELYGEPPePZ4ZMXt6E\nN+ubNz7fz+d8YOacmTkzmfPO/OY8y5499hyC2v2prDRT+a1b4ZD5j/PAW0M56uxsXnkFZE0p5OWx\nZcwE1l39C/6w69usOPZS7t6Ux9MnTOCq9yfx1AX5aN9sevUys/0OHcxPtmNHu947d8JHH0HGm4v4\n+aKRPPqFiVz30UTmXP4c5YPsvi8vt2dl9Yel/GBJHm/oiYwum86bh5/HSZ+8wtwzH+DprBvYsMH2\ne8wx9jg78kh7jB16aM11iZ5/6Ku8+91SDr0lj4+um8DRj02i4sF8Oh+bXWvMVVaa+eJhoy/gzYt/\niT48i/u/kk/h0mxuvhkefRRef6KUYz8ppvP3r41rAt2ixPtNSuQ3PWw3axZMnWp/6HXr7CWka1f7\nI4UvLA38nV6xAm44oZhicll+fxEDxw+t/xn0jW+wuVd/xu2dxn2Zk8h6oYnPheYwkezaFa68Mr7f\nZF6emaqXl9vy0KEwZoyZrsfy5JMwY4Yds63QTk1Ily9fzqBBg8BcpZa39PEa6mN2K3AJljdsD+YI\n1x+YA7yMiaE+WATEr2ImhpXAbFX9YUSYTQCeC9pWY9Eaz1fVlwJhlo+ZFd4FdMNC7KdhYvAQTJgN\nxnzLLsXC7FcCa1T1SyJy5YH6Usf5pawwGzbMfGGeeSbJHYkVZbHrjzjCnpqxxPONOO64/e3/Qx58\nsGH2/435wUiVH5mm9jO6fax/RnT7eH+jZAZtSBXhfCDivViUltYOAHLaacnxMYvd34QJMGlSy13b\n8JwOIDyrq2sLv1A8hqKgrmIBfWqXUPiE/8L+IqO6Gnr+s5jBt+byZt40Tsq/kb9OKCKj5J+c+sSN\nLL1qGv8aPo69e237Ll1MmIS+nOXlto/Qh7ZjR+hbWszlM3MBqDrhZNJ+N42tN03ij+fm89a2bD79\n1IRsNGhQuG2nTnaMC0unc+FrN/LcOdOY338cO3fWnusMzys8T1UYsKmYuxbnsuXok1l65TSOyp/E\n5Ox8SjR7n1/xrl0mcML3w3Db87sV88KuXL7etYgF5UMb/Wfu1s0+IB57bI2bV8aW0lrjtvL9UrZc\nnMeMU/Lp/MkafvmXXH58fBFFOpStW+19P+xfZqadY2UlpKebgDrySLhm63Su/seNzDp+Gr/ePo7P\nPrNrl55u4iorC87cU8ykolzeOfRsBvx7IQt6XMIdA/7EIYdYfVUVvPMOrFljPtiJkoMJiKEU8Tp1\nX6uw3bV9i/jps0M58URzQzz99NqpzeL5tcYup6fXCOtDDrFrEgaiysy0+i5d7P9VVTViNixdutT8\nv1Mn6Pn2IgZNGsn7oyZybMFE/vWb59h+0pB9IjsU/FVVtT/iHPLOIgbcMpJ1l4wle+5d7Dg0m0rp\nQvdP1zH/wlkM+dcsVt+ej/TLJj2dWqVbt5rjd+xo+92yBdauhduvKmXS+jzmfnECl62cxLpJ+Zxz\nXTa9Vy0i7eLaIlJHjuSZ7z3HtPv2UkQuuRRx1ayhXHed9XnnTut/enoDbtzmeObk5cHs2TB6dG1x\nFm/9k0/CqFHmZxkVZ3WtD0mWoGsvz+QYWluYNdSU8QUsqfMALNHafGyqbhYWZGMv8AgWkn4ocAom\nsFYH208ClgNvYwnXTiAIUQ/MCtoUB/vYgYXIPw54ImhzLjWmjPcE+74GC5n/LiYWeyfSlzrObyCg\nOTk5OnLkyFqlLefyKC83P5WpU5PdE61tthhLGDLfcZqDJpgqtiliTXGifj+FhTX1GRnmEBc1PavP\nRCsabr++9Qeitcx526KPWUh4zgUF1qeCgrh+mA3a3+DBZvvZo4f5lsX6fx2I8Po05PjhcU8+2f5t\nyDFjTIarPijRXbvMd3nLFtUNG1Q3bqzxT9y1S7WqqqZUVlqJa+JZn7lfOBbi+M5WVKju2NGE6xMe\nd9w4ezadd169ZowVFaqlpeaTuWyZmcYuXqxaXKz66quqL75oprRL/lii204dpu/9vkg/PWWYvvRQ\nic6bZ2a3f/6z6vz5Zm77v3NLdOugYbr56SKtjjm3HTvMFHfOHPPNnjnTzJ7vv99Moe+806wu77hD\n9Re/MB/TsWNV8/LMTPjcc1VHjDBT4jPPNDPn/v0tY02PHubnmpmpmp5up1yXGfNYzHR6bAPNoMPt\npjNm38rbeti6HIoaZU69qPMwXfVSiZaVqY4daebVfSlREdUR3Rfq1g69dMqR07QsrZd+o+dC7UuJ\nrjpimFa9VqSrjrS2ffuq9u1r+0xPt+tz882q991X2++5sNDM0l96yf4OixebGfR7L5s/4MeLS3TT\nJstFWpUzLDET5JDRo60Do0fHX45SWGjO/4WF8ZfjUVebRLZtKi35vAD7zY1HRkazvF/Omzdvv/f/\nnJycfaaM2gDN1NjStI1NBGkg0FI2wXTkOANJQR+z4mL7Sy5fnuyeOI7TZKKO8yHJymPWWk70LZmo\nvKnE+ALpwoUmyrp3T9wPM3Z/0UAfYeCP2IAg9V3bxvqY1XWcAx2zpcV5XR9ZSkqsv7/9bcOOm0o+\nZm3Ef7myUnXnThPVGzeqrlunuulPC3Vvz1762cRpWpXZS0vnLNRVq8w3c+VK8zd/880af83QV/PD\nJxZqVWYv3TL2Dq1OS9PK/l/U6uOPt5fnggKtzBmma4pLdOVKe29ZvNj8dJ9/3jTDnDmqs2ebIH3k\nEdUFD5fo1oHDtGJV7WuzYUmJbvzqMJ13V4lOmaL6zHATfv991jT97RgTvdUfBtuUlOiWk4fpnd8v\n0Z/9zHxU771X9eKLzUe2R4/EAz9FfW5Dcdipk2me7t1Ve/e20qeP7fu44+yb2sknqw4ZYuXZPqO1\nGvSjrv20GvTV/qM1L0/1+uvtO8Gtt5o/8n33qS64rlD3duio750/Rvd26KgrJhTqkiX2cWDVKvPt\n37zZfKHXr7dYAGt+W6h70zpq6b2F+sEHqttnF2p1AqKsokJ1+/am3UtrXy/RNw4epldkFenHA5rx\nng7FV6w4q2t9MxH1MdO2JsyAO4EhmF/YV7GQ9QqMDur/J1hOqQTTkfNLSWE2ebJFeKuqSnZPHMdp\nV7TWrGRjo8C1NLGiLDY4TlOiMkbFdzzRVNe1bUpUxljBHyvO4h2ztcR5cx03FaMyJnpurUljZ7Bj\nA4AMGGCqZ8AAGzONCfyRyO9QdIY0M9NUUCOu7969ZoW0davNAq9ZYxFr337bZkoXLVJ97TXVJVOK\nVEFf+2WRzp2r+sADFvF66lTVu+6y8qtfqd52m81m/uQnFkU4DHr0ne+ofty1nyrouvR+mpNjl2bg\nQJtI79dP9bDD7NJ16KD7Zh6nMybhWcZLKdQ9dNTpjNE9dNQrOhRqVpb9KQYPVs3NtUnib35T9Vvf\nsn4dfLAJzB/8wGZgb77ZgsRNnmzfR2bMsPOcOVP1oYes3HOP6t13q06caOeVnq56RZZdnxyKdPRo\n1RUrTPw3mVgR1sKiTLX1hVlDfcweCYROmDytA1Cqqv2C+quxgBt7MH+wamAR0AvLln2riMwJBFkv\nzG9sTyCorsX8zBaIyFos31hvbDbs00D0jcZ8zg7G/MzKgJ7BBVuNBQY5SlUHJ9KXOOeXkj5m55xj\nNuWJ5It1HMdxEqQl85jFCzb09NPQu3f9PqFNyWPWGD/UZPnaNva4KZrHLKFzay0aG9QpNvCHqgX6\nGDsWPvwQHnmk9vpGBABJqL+33WZ+6M8/H9//tqnXtzl8bkOfsn79oKRkf5+zCFr4JFw1it3fvZ4u\nsx/ik/vnsTn3MvbsMX/QHTss0E7nzjXBfnr0sHLor8Zy+FMzeH/EGF4e+QCbN5t/ZllZ7fymu3fb\nfj76yP49+mhbF9bt3m3HCnOzRktGhvntpadbeIHLTitlzPI80iZPYMOPJnHO2nxW7sqmUycL2BMG\nRGpsueR7maRXbGcvgYjonsG6f26ja1fLOVpZadega1frU1MD57Tp4B8AIvJ14Cws/P3Xsdmyx4K6\nKzF/sO2Y0CoBfh20m6aqvwgCgHwLMz38AdAZeBw4Bhihqi+LyHtAFhad8W7MF+2JoG00AEg1Zrr4\nPDAKuB14W1VPSaQvcc5tILAslRJM795tN/qdd1rgNcdxHMdxnEbT2KBO4XarV9d8gAg/Xqxfb9vd\nfnvNB4joR43G0tqRgZsjEnBsoI+6AoLA/oE+DhT4I962118PDz2U2DZNJc712XttHkuvz+efWy2o\nUXl57cBIiZYwyitAJUJHzDeqE/XrmC5dakRa9+5w0EEm3KIRaDMyLCjOBx8U8O67BYjUBNUpLy/j\ngw9eh7YqzABEZAYwEovnf7GqPhusHwb8BbhVVe8O1mVivl+Pq+poEXkQM08cqKpvBG2uwcTZ11T1\nr4EwOwrIUNWqoM18bEYtTUQ6YT5k/6eqZ0T6tQnYoar9E+lLnPNKuRmzhQshJweWLYMU6bLjOI7j\nOE7Tac3IwKkSlTFem4YIusbSwlEZq6tNzKUdlknnHZEZs24Z/O35bfsiyobpWELhV1FR8/8dO2y2\nMEybEc4ClpVZXZjKYs8e2L7d1qkup7q69WbMOjZ0g0CUXYRFOvwgpjoMJlsRWZeFmSN2ialbF2kT\nZtU6KPh3N7A7FGUB6UAHEempqmUiUolFhAz7FR6jMli1JYG+pDxFRTZjdtJJye6J4ziO4zhOK1Kf\n6BoypHlny4qL44uL7GxbX1x8YOFRUBB/ZixcLiio+f+MGfGFVLg8Y0bdIfFjRVj476hRtZebk+a4\nPvXQoQN0y8qEHdshI4OO27ZBZiZdtm8n98LMmmSczczy5WCWjK1Dh4Y0FpGZwFWY2eDOYHVPEQkz\nQfTA/L3Gi0iuiAzC/Lw2Y4IITDDtBv4gIieKyAhgcrC/IG0jnwLdRWSKiBwnIj8GcjDTxaxI388S\nkWtE5MtYIJI0asRm9wT6kvIsWGDWAGlpye6J054oKChIdhccJ+n4OHA+7/gYiHDttXULi+zsxEwy\ny8vr9CUjP78mOR+YkKlLQF12Wd25yOoTdPPmWX1L0BzXpz4yM20aKyOjRoRt22bL27dbfTugQcIM\nuB4LRV+Eha8X4DHg8kgbBV4Bnoq0WxysD+vXYZEXF2N+YI8BuyJtKjC/sXOwgB7jgTuC44VtqoNt\nJwNvYFEeZwT7je3LfCzK45mYeDuIdsDHH8PixXDxxcnuidPe8Iex4/g4cBwfAylIYwVdWydWlIVE\nxVk7oEGmjKpaS8iJSDWWJ+zZYNUGTDz9TlWvi7QrAj6MtDlYVb8ZqU8DbgrqwjYZqjoo0iYXE1rU\nhLeIAAAJK0lEQVQbI23eijnOxJh6wRJPdwS+CyzF/M5yRaS3qoaml7UYP358SgT/yM83Z8aLLkp2\nTxzHcRzHcRynhagvJkYzmTEWFBTs9zGirKysWfadKA32MasPVS0RkQ3AcOAt2Bdw4wzgwaDZ34Be\nInJKGPwjaC+YcArb/FpE0lQ1nAE7D3hXVcsibYZjOdBCzg3WR/tyA/Cwqj4R9OUgzGwyD8uNth9T\np05t88E/Nm2C+++3meGD2sX8n+M4juM4juMkh3iTMJFw+a1CQ00ZEZHuInKSiJwcrOofLB8VLE8D\n/lNERopIGOZ+PZbwGVVdBSwAfi8ip4nIfwAPAAWqGs6YzcPyj+WLyPEicgXwE+C+SFemA+eLyE2B\nH9pELJF01Hj2d1gy7G0xfXkeGNzQc28rrF4NF1wAnTpZCg3HcRzHcRzHcVKbxsyYnQr8FTMrVGrE\n0uNAnqreIyLdgIexZM4LsTD3eyL7GIUJqFcxX7GngHFhpapuC4KCzAD+gQXsmKiqj0ba/C3IVXZn\nUN4HLlLVlZHjPA78BvON+2nYF+D7wJfinFs6wDvvvNPAS9LyzJ0L69bBe+/BW2/B4Ydbnsb16604\nTnNSVlbG8uUtHhXWcdo0Pg6czzs+BpzPOxFNkF5fu+aiUXnMUgURORxLRD1YVf8eWX8PMERVz4pp\nPwqY27q9dBzHcRzHcRynDXOVqs5r6YM0q49ZG2QzFqXxsJj1fagJEhJlAZYOoJTa+c8cx3Ecx3Ec\nx/l8kQ5kYxqhxWnXM2YAIrIE+LuqjguWBViLRY68N6mdcxzHcRzHcRzHof3PmAHcDzwuIsuwqI/j\ngW5Y7jTHcRzHcRzHcZyk0+6FmaoWikhvLBH1YVjC6hGq+u/k9sxxHMdxHMdxHMdo96aMjuM4juM4\njuM4bZ0G5zFzHMdxHMdxHMdxmhcXZo7jOI7jOI7jOEnGhVkEEblBREpEpFxElojIacnuk+M0ByIy\nQUSqY8rKSH0XEXlQRDaLyHYReUpE+sTs4ygReV5EdorIBhG5R0T8N8Rps4jI2SLyrIh8FNzzF8Zp\nM1lEPhaRXSLyiogcE1N/kIjMFZEyEflMRB4Rke4xbU4UkdeDZ8caEflZS5+b4yTCgcaAiMyO82x4\nIaaNjwEnpRGRW0VkqYhsE5GNIvJnETk2pk2zvAeJSK6ILBORChF5T0SubUhf/aUqQESuAO4DJgCn\nAG8CC4LAIY7THliBBcDJCsqQSN004BvApUAOcATwdFgZ/PC8gAUMOhO4FvguFlTHcdoq3bGATzcA\n+zlUi8gtwBjgh8DpwE7sd79zpNk8YAAwHBsjOcDDkX1kYPltSoCBwM+AiSJyXQucj+M0lHrHQMCL\n1H42XBlT72PASXXOBh4AzgDOAToBL4tI10ibJr8HiUg2MB94DTgJmA48IiLnJtxTVfViAVCWANMj\nywKsB36e7L558dLUgn1wWF5HXSawG7gksu44oBo4PVg+H6gEekfa/BD4DOiY7PPz4uVAJbifL4xZ\n9zEwPrKcCZQDlwfLA4LtTom0GQFUAVnB8o+AzdFxAPwGWJnsc/biJVrqGAOzgT/Vs82XfQx4aW8F\n6B3c10OC5WZ5DwKmAG/FHKsAeCHRvvmMGSAinYBBmMIFQO1qvgoMTla/HKeZ+VJgzrJaROaIyFHB\n+kHYF6Do/f8ulog9vP/PBN5W1c2R/S0AegJfafmuO07zIiL9sNmB6H2/Dfg7te/7z1T1jcimr2Iz\nD2dE2ryuqlWRNguA40SkZwt133Gak9zAvGuViMwUkYMjdYPxMeC0P3ph9/CnwXJzvQediY0PYtok\nrCVcmBm9gTRgY8z6jdiD23FSnSXYlPsI4HqgH/B64CeQBewJXkqjRO//LOKPD/Ax4qQmWdiDub7f\n/SxgU7RSVfdiD3MfG0574EXgGuBrwM+BocALIiJBvY8Bp10R3NvTgEWqGvraN9d7UF1tMkWkSyL9\na/cJppuIULdNtuOkDKq6ILK4QkSWAmuAy4GKOjZL9P73MeK0JxK57w/UJnyp9bHhtGlUtTCy+C8R\neRtYDeQCf61nUx8DTqoyEzie2n72ddEc70ENGgs+Y2ZsBvZizq9R+rC/8nWclEdVy4D3gGOADUBn\nEcmMaRa9/zew//gIl32MOKnIBuyBWd/v/oZgeR8ikgYcFNSFbeLtA3xsOCmGqpZg70RhdFIfA067\nQURmABcAuar6caSqqe9BBxoL21R1TyJ9dGEGqGolsAyLOATsm+ocDixOVr8cp6UQkR7AF7HgB8sw\nR+7o/X8scDQ19//fgBNiopSeB5QBK3GcFCN4Ad1A7fs+E/Obid73vUTklMimwzFBtzTSJid4WQ05\nD3g3+ADiOCmDiHwBOAT4JFjlY8BpFwSi7CJgmKqujalu6nvQO5E2w6nNecH6xPoZRAz53CMilwOP\nYxFWlgLjgW8DX1bVfyezb47TVETkXuA5zHzxSGAScCJwvKpuEZGZWMSh0cB24HdAtaqeHWzfAXgD\nE3K3AIcDTwCzVPWOVj4dx0mIwIfyGOwlcjlwE2ae9amqrhORn2P383eBUuBXmBP3V8Kvm0FOpz5Y\n5LnOQD6wVFWvDuozgVXAK1hErhOAR4Fxqvpoq5yo49RBfWMgKBOwkOAbgnZTsBD7JwYfrX0MOClP\n8I5zJXAhZi0UUqaqFZE2TXoPCsLlrwAexMbJcMyf7QJVjQ0KEp9kh6xsSwX4MfZwLsfU7anJ7pMX\nL81RsHCt64N7ey2Wl6ZfpL4LluNjc/CD9CTQJ2YfR2H5OXZgU/tTgA7JPjcvXuoqWCCDasxUPVry\nI20mBg/aXVj0rGNi9tELmIN9Ff0M+D3QLabNCUBxsI+1wM3JPncvXlTrHwNAOvASJsoqgA+B/wIO\njdmHjwEvKV3qGAN7gWsibZrlPSgYc8uC9633gasb0lefMXMcx3Ecx3Ecx0ky7mPmOI7jOI7jOI6T\nZFyYOY7jOI7jOI7jJBkXZo7jOI7jOI7jOEnGhZnjOI7jOI7jOE6ScWHmOI7jOI7jOI6TZFyYOY7j\nOI7jOI7jJBkXZo7jOI7jOI7jOEnGhZnjOI7jOI7jOE6ScWHmOI7jOI7jOI6TZFyYOY7jOI7jOI7j\nJBkXZo7jOI7jOI7jOEnm/wHqgUEtpMoFAwAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f7ac9b67d50>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fig, ax = plt.subplots(24, figsize=(10,10))\n",
"for w in range(3):\n",
" for l in range(2, 10):\n",
" a = ax[w*8 + (l-2)]\n",
" peaks = peak_pos[np.all(((peak_width > w), (peak_len > l)), axis=0)]\n",
" a.plot(x,y)\n",
" a.plot(x[peaks], y[peaks], 'rx', label='w%i, l%i' % (w,l))\n",
" #a.legend()"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.legend.Legend at 0x7f7ac6a0ef90>"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABLQAAAGrCAYAAADZ485KAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3Xl4lOX59vHvM5ONYUkgCZss4o64YAJCpLhgKKKiVVNX\nCiqLoFIEQWJVILgRQClCFVDkJ6LoaxdrS8GCpYIVlUWgLKIVWZQlJBCCDNlmnvePO0MWAoQwk8lM\nzs9x5JjM9jx3EhwnZ67rui3bthEREREREREREQkVjmAvQERERERERERE5HQo0BIRERERERERkZCi\nQEtEREREREREREKKAi0REREREREREQkpCrRERERERERERCSkKNASEREREREREZGQokBLRERERERE\nRERCigItEREREREREREJKRHVeZJlWfFAL2A7kO/PBYmIiIiIiIiISMiJAc4GPrZtOyfQJ6tWoIUJ\ns97x50JERERERERERCTk3Qe8G+iTVDfQ2g4wf/582rdv77/ViIicphEjRjB16tRgL0NE6ji9FolI\nsOl1SESCbcuWLfTt2xdKMqNAq26glQ/Qvn17kpKS/LgcEZHTExsbq9chEQk6vRaJSLDpdUhEapEa\nGU2lofAiIiIiIiIiIhJSFGiJiIiIiIiIiEhIUaAlIiIiIiIiIiIhRYGWiIS0e+65J9hLEBHRa5GI\nBJ1eh0SkrqnuUHgRkVpBb95EpDbQa5GIBJteh+qGnTt3kp2dHexlSB2WkJBAmzZtgr0MQIGWiIiI\niIiISK23c+dO2rdvj9vtDvZSpA5zuVxs2bKlVoRaCrREREREREREarns7Gzcbjfz58+nffv2wV6O\n1EFbtmyhb9++ZGdnK9ASERERERERkapr3749SUlJwV6GSNBpKLyIiIiIiIiIiIQUBVoiIiIiIiIi\nIhJSFGiJiIiIiIiIiEhIUaAlIiIiIiIiIiIhRYGWiIiIiIiIiATd6tWr6datGw0aNMDpdLJhwwbG\njx+Pw1E+ujj77LN58MEHg7TKUtdeey09evQIyLE//fRTHA4Hy5cv9+s6rr32Wi677LIzXV6toEBL\nRERERERERIKquLiYtLQ0Dh48yO9//3vefvtt2rZti2VZxwValmWVu75lyxYyMjLYuXNnTS75uHUE\n6/gVH7dnzx4yMjLYsGFDtY8ZChRoiYiIiIiIiIQZt9vN+OHDcbvdIXHs77//np07dzJ69GgGDhzI\nvffeS2xsLM8888wpz7N582YyMjLYvn2739YTbNdccw1Hjx7l6quvPu3n7t69m4yMDNatWxeAldUe\nCrREREREREREwsz0sWNpuXAhM8aNC4lj79u3D4DY2NhytzscDqKiok76XNu2A1J5FIgw8HSc6us+\nEdu2/byS2kmBloiIiIiIiEgYWbVyJdbSpQyOi8NesoRVK1fW6mM/8MADXHvttViWRVpaGg6H49hM\nqMpmaJX11ltvceeddwJmPpTD4cDpdJabPbVo0SKuvvpqGjRoQKNGjbj55pvZvHlzuePcf//9NGzY\nkG3btnHjjTfSqFEj+vbte+z+2bNnc9555+FyuejatSufffZZlb62O+64g+Tk5HK39enTB4fDwd//\n/vdjt3311Vc4HA7++c9/AieeoXWqdXz66adceeWVWJbF/ffff+z7MW/evHKP27JlC9dddx3169en\nVatWTJ48uUpfT22iQEtEREREREQkTLjdbuakp/NoSQg0zOFgTnq6X6qNAnXsIUOG8NRTT2HbNsOH\nD2f+/Pk89dRTgJn5dLLqq6uvvprf/va3ADz99NPMnz+ft99+m/bt2wPw9ttvc/PNN9OwYUMmTZrE\n2LFj2bJlC927dy83c8uyLIqLi+nVqxfNmzfnpZde4o477gBgzpw5DBkyhJYtWzJ58mS6devGLbfc\nwq5du075tXXv3p0NGzZw+PDhY7d9/vnnOJ1OVqxYcey25cuX43Q6ueqqq8qtqayqrKN9+/ZMmDAB\n27Z56KGHjn0/yrYuHjhwgN69e3PFFVfw8ssv0759e9LT0/n4449P+fXUJhHBXoCIiIiIiIiI+Mf0\nsWMZmJODKyYGAJfDwYCcHGaMG8cTZ1iFE6hjd+nShfz8fJ5//nm6d+/O7bffXuXntmvXju7duzN9\n+nRSU1PLBTdHjhxh+PDhDB48mNdee+3Y7f379+eCCy7ghRdeYObMmcduLyws5K677uK55547dltx\ncTFPPfUUSUlJ/Otf/yIiwsQoF198MYMGDaJNmzYnXV/37t3xeDx8/vnn9OrVi40bN3Lw4EHuvPPO\ncoHWZ599xuWXX06DBg0qPU5V19G0aVN69+7N2LFjSUlJ4d577z3uWHv27OHtt98+dt+DDz5ImzZt\nmDNnDr169Trp11ObqEJLREREREREJAz42gE7lQROPp1jYs64PTCQxw6UJUuWcOjQIe6++25ycnKO\nfViWRZcuXVi2bNlxzxkyZEi566tXryYrK4shQ4YcC5HAhGJxcXGnXMMVV1xBgwYNjrUOrlixgtat\nW9OvXz/WrFlDfn4+AP/5z3/o3r37CY9zpusoq379+uWCrsjISLp06cK2bdtO6zjBpkBLRERERERE\nJAzMy8zkwRPcN6Dk/tp47ED57rvvsG2b6667jsTExGMfTZs2ZcmSJWRlZZV7fEREBK1atSp3244d\nO7Asi/POO++4x7Zr1+6Ua3A4HHTt2vVYNdaKFSvo3r073bp1w+Px8MUXX7B582ZycnJOGmid6TrK\nat269XG3NW7cmIMHD57WcYJNLYciIiIiIiIiYaDfmDG8OXQoT1Ry3xygf3p6rTx2oHi9XizLYv78\n+TRr1uy4+8tWOgFER0cf9xjfjoGVzfGq6m6C3bt354UXXqCgoIAVK1bwzDPPEBsbyyWXXMKKFSto\n2rQplmWdNNDyxzp8nE7nSc8RKlShJSIiIiIiIhIGOqekYKemsqqkjc1nVX4+Vs+edOratVYe+0yd\naGj8ueeei23bJCYm0qNHj+M+ys7bOpGzzz4b27b59ttvy91eXFzM9u3bq7S+7t27U1hYyIIFC9i9\ne/ex4Orqq69m+fLlrFixggsuuIDExES/rONkQ/TDiQItERERERERkTAxbMIE5sTH4/Z6AXB7vcyJ\nj+fRjIxafewzUb9+fWzbJjc3t9ztvXr1olGjRrzwwgsUFxcf97zs7OxTHrtTp04kJiYyc+bMcseY\nO3fucec7ka5duxIREUFmZiaNGzc+tgNj9+7d+eKLL1i+fPlJq7NOdx3169cHqPL6QpVaDkVERERE\nRETChMvlYsDEicwYOpQnHA6me70MzMzE5XLV6mOfiY4dO+J0OsnMzCQ3N5fo6Giuv/56EhISeO21\n1+jXrx9JSUncfffdJCYmsnPnThYuXMgvfvELXnnllZMeOyIigueee44hQ4Zw3XXXcdddd/HDDz8w\nd+5czj333CqtLyYmhuTkZL744gtuueWWY7dfffXVHDlyBLfbXWmgVbYF8HTWce655xIXF8fMmTNp\n0KAB9evXp2vXrrRt27ZK6w0VqtASERERERERCSO+9sBZubl+bwcM5LFP1CpX8XbLssrd1qxZM2bN\nmkVWVhYDBw7k3nvvZfPmzQDcc889fPLJJ7Rq1YopU6bw2GOP8f7773PFFVfwwAMPVOn8gwYN4tVX\nX2XPnj088cQTfPbZZ/ztb3+jdevWVW7v6969+3Fzspo1a8Z55513wvlZFY9d1XVEREQwb948nE4n\nQ4cO5d577+XTTz895dcZaq2KVnWGflmWlQSsWbNmDUlJSf5flYiIiIiIiIgcs3btWpKTk6nq7+Fu\nt5tJTz7JEy++6PcKqkAeW2qvU/0b9N0PJNu2vTbQ61HLoYiIiIiIiEiYcblcjJ82LeSOLVJVajkU\nEREREREREZGQokBLRERERERERERCigItEREREREREREJKQq0REREREREREQkpCjQEhERERERERGR\nkKJAS0REREREREREQooCLRERERERERERCSkKtEREREREREREJKREBHsBIiIiIiIiIlI1W7ZsCfYS\npI6qbf/2FGiJiIiIiIiI1HIJCQm4XC769u0b7KVIHeZyuUhISAj2MgAFWiIiIiIiIiK1Xps2bdiy\nZQvZ2dnBXorUYQkJCbRp0ybYywAUaImIiIiIiIiEhDZt2tSaMEEk2DQUXkREREREREREQooCLRER\nERERERERCSkKtEREREREREREJKQo0BIRERERERERkZCiQEtEREREREREREKKAi0REREREREREQkp\nCrRERERERERERCSkKNASEREREREREZGQokBLRERERERERERCigItEREREREREREJKQq0RERERERE\nREQkpCjQEhERERERERGRkKJAS0REREREREREQooCLRERERERERERCSkKtEREREREREREJKQo0BKp\nA9xuN+OHD8ftdgd7KSIiIiIiIiJnTIGWSB0wfexYWi5cyIxx44K9FBEREREREZEzFhHsBYhIYIwa\nNYq1a9dyJC+Py7du5XHLYsrMmXRZtoz6jRqRlJTElClTgr1MERERERERkdOmCi2RMJWcnMzevXux\nt27lIY8Hj8fDEI8He+tW9u7dS3JycrCXKCIiIiIiIlItCrREwlRaWhrReXmMLCqinmUBUM+yGFFU\nRHReHmlpaUFeoYiIiIiIiEj1KNASCVPrVq+mV0QEl1oW2FBQALYNl1kWvZxO1q1eHewlioiIiIiI\niFTLGQVaI0aM4JZbbmHBggX+Wo+I+Mm8zExGxsbijIjA6wWPx4RazogIRsbFMS8zM9hLFBERERER\nkRC3YMECbrnlFkaMGFGj57Vs2z79J1lWErBmzZo1JCUl+X9VInLGVq1cybKhQxmQl8dPP+2hsNAB\neGnXrgVvNGrE9TNn0qlr12AvU0RERERERMLA2rVrfbOak23bXhvo86nlUCRMdU5JwU5N5X/16uF0\nRAA2EMH/6tXD6tlTYZaIiIiIiIiELAVaImFs2IQJzE1IILJhPOAhn3jejE/g0YyMYC9NRERERERE\npNoUaImEMZfLxYCJE3mzXizQhD8QywMvZOJyuYK9NBEREREREZFqU6AlEuY6p6Tw08U9eZ/6LOGX\ndLhcrYYiIiIiIiIS2hRoidQBV944gTe4iRwyyM8P9mpEREREREREzkxEsBcgIoHn9brIZRoAR48G\neTEiIiIiIiIiZ0gVWiJ1QEFB6eeq0BIREREREZFQp0BLpA4oG2Ip0BIREREREZFQp0BLpA5QhZaI\niIiIiIiEEwVaInVAfj44HKWfi4iIiIiIiIQyBVoidUBBAcTFmc8VaImIiIiIiEioU6AlUgfk50Ns\nrPlcuxyKiIiIiIhIqFOgJVIH5OerQktERERERETChwItkTqgoKC0QkuBloiIiIiIiIQ6BVoidUB+\nPjRoYAbDK9ASERERERGRUKdAS6QOKCiAmBioV0+BloiIiIiIiIQ+BVoidUB+vgm0YmI0FF5ERERE\nRERCnwItkTqgoACio02gpQotERERERERCXUKtETqgLIVWgq0REREREREJNQp0BKpA1ShJSIiIiIi\nIuFEgZZIHeCr0NJQeBEREREREQkHCrRE6gBVaImIiIiIiEg4UaAlUgdol0MREREREREJJwq0ROoA\nVWiFDrfbzfjhw3G73cFeioiIiIiISK2lQEskzNm2djkMJdPHjqXlwoXMGDcu2EsRERERERGptSKC\nvQARCaziYhNq+Sq0srKCvSKpaNSoUaxdu5YjeXlcvnUrj1sWU2bOpMuyZdRv1IikpCSmTJkS7GWK\niIiIiIjUGqrQEglzvoos7XJYeyUnJ7N3717srVt5yOPB4/EwxOPB3rqVvXv3kpycHJDzqr1RRERE\nRERClQItkTBXUGAufRVaGgpf+6SlpRGdl8fIoiLqWRYA9SyLEUVFROflkZaWFpDzTh87lsS/LmT6\nWLU3ioiIiIhIaFHLoUiYK1uhpRlatdO61avpFRHBpZaF1wsWYDngMsuil9PJutWr6ZyS4pdzlW1v\nvOybrTx0xGLGjJl0+bfaG0VEREREJHSoQkskzPkqtBRo1V7zMjMZGRuLMyKC/Hw4mg+2F5wREYyM\ni2NeZqbfzlW2vXFQkQeomfZGERERERERf1KgJRLmfAGWr+VQgVbt02/MGP7PskhMTMSyvAAUe7wk\nJiYy17Lon57ut3OVbW+Mtk17o8sR+PZGERERERERf1KgJRLmylZoaSh87dQ5JQU7NZX/1auHZUUA\nNg5HhLnesyedunb127kqtjcCYJdvbxQREREREantFGiJhDlVaIWGYRMmMDchgQIrHvBg1YtnbkIC\nj2Zk+PU8ZdsbbdvcZhOY9kYREREREZFAUaAlEuYqztAqKgKPJ7hrkuO5XC4GTJzIq8QCTXgjKpaB\nmZm4XC6/nqdse6NtmxIt2w5Me6OIiIiIiEigKNASCXMVK7TK3ia1S+eUFD6xevI+9fmm9S/92mpY\n9hy+9kaz0a2NZQWmvVFERERERCRQFGiJhDlfeOWr0Cp7m9Qutg17iifwBjfR8jL/thqWVbG90Y4O\nTHujiIiIiIhIoCjQEglzvpZDVWjVfubn4iKXaRQU+LfVsCxfe+NrJe2NsyIC094oIiIiIiISKAq0\nRMJc2QqtevXK3ya1y5EjlX8eCJ1TUlha0t64PiEw7Y0iIiIiIiKBEhHsBYhIYBUUgGVBRIQqtGo7\nt9tcNm4MP/8c2HPZNuz1TOANiuh0tloNRUREREQktCjQEglz+fkmyLKs0kDr6NHgrkkq56vKato0\n8BVaphXVxSFr2rG2VBERERERkVChlkORMFdQYOZngSq0aruaDLR8oWZ8fGllmIiISLhzu92MHTYc\nt/7nJyIS8hRoiYQ5X4UWKNCq7XzvrRMTA99y6Au0EhIUaImISN3x+6fGkj9jIYN+NS7YSxERkTOk\nlkORMFe2QktD4Wu3YFVo/fhjYM8lIiISTKNGjWLt2rUcycvj0i1bGYLFtGUz6dJpGfUbNSIpKYkp\nU6YEe5kiInKaVKElEuZUoRU6fJVSzZqp5VBERMRfkpOT2bt3L/bWrQwu9gAeHrE92Fu3snfvXpKT\nk4O9RBERqQZVaImEucpmaGkofO3kC7ESE83nXi84AvRnh7KBVqDDMxGRuspXGeSo5MXc6/WqMqiG\npKWlMWn0aEYWFRGDk0LA5bAYUVTEpLw80tLSgr1EERGpBlVoiYS5shVaUVFmt0NV5NRObjc4ndC4\nsbkeyODR92/AV6Fl24E7l4hIXZWcnExWVha5ubnHfWRlZakyqIasW72aXhERXGpZ2F5zmw1cZln0\ncjpZt3p1UNcnIiLVo0BLJMyVrdCyLGjUCA4fDu6apHJHjkD9+tCgQen1QClboQVqQxURCYS0tDTi\n4+OxK/zVwLZt4uPjVRlUQ+ZlZjIyNhZnRATeMj8KZ0QEI+PimJeZGbzFiYhItSnQEglzZSu0wARa\neXnBW4+c2JEj4HKZUMt3PVAqBlqq2hMR8b/IyEiGDBlCQUEB69fDTz+Z2wsKChgyZAiRkZHBXWAd\n0W/MGP7PskhMTMRXomXbXhITE5lrWfRPTw/yCkVEpDoUaImEObe7dHdDMIHWoUPBW4+cmNttwixf\noPXzz4E7lwItEZGa4avSKi622btX1VnB0DklBTs1lf/Vq4dlRQA2DivCXO/Zk05duwZ7iSIiUg0K\ntETC3OHDJsTyiY1VhVZt5avQCkbLoQItEZHA8FVpQQGg6qxgGTZhAnMTEvBExQMeqBfP3IQEHs3I\nCPbSRESkmhRoiYS5vDxo2LD0uiq0aq+KFVqBDrSiokrDMwVaIiKBY6qx4gGvqrOCxOVyMWDiRGY7\nY4EmvB4Vy8DMTFwuV7CXJiIi1aRASyTMHT58fKClCq3ayTcUvqZaDuvVMxVhoEBLRCSQHI5IYAiQ\no+qsIOqcksLqJj15n/p80+qXajUUEQlxCrREwpxaDkOH212zQ+EVaImI1AzT5n0jcSRy4403Bns5\ndVpMqwm8wU20vkKthiIioU6BlkiYq6xCSy2HtZOvQqtePbAsBVoiIuHC7YZ4nmUQucx67rlgL6dO\n83pd5DIN21aroYhIqFOgJRLGioshP18th6HCNxTe4TCXNdFy6KsGU6AlIhI4Kz9bSU+Wcidx2EuW\nsGrlymAvqc4qKjKXhYXBXYeIiJw5BVoiATJtGrz5ZnDXcPiwuVTLYWjwDYUHc1kTFVoxMaXnFhER\n/3O73fzphXQeKXnb/YjlYE56Om698AaFL9DyXYqISOhSoCUh6csvYefOYK/i5N59F/785+CuwRdc\nVazQcrv1Rq428lVogdl9sCYCLYfDXOr3KhGRwJg+diwDc3OIKXnbHW07GJCTw4xx44K8srrJV5ml\n90EiIqFPgZaEHLcbunaFtm3hP/8J9mpObP9+OHAguGvwVWhVDLTK3ie1RzAqtMCEaAq0RET8b9XK\nlVhLl3JFRMyx2zzF0DkmRq2HQaKWQxGR8KFAS2qN5cvh7rth9+6TP+7f/zaX8fHQt6+ZE1Ub7d8P\nOTnBXUNlgVZcnLk8eDBw53W73YwfPlztFKfJNxQezGVNzNACE2gFMjwTEamr5mVm8iDg9Zbe5rXN\n5YCS+6VmqeVQRCR8KNCSWuP9983HI4+c/HH/+Ae0awcffwzbt8Mnn9TI8k5Lfr4JI2pLhVbZGVrN\nm5vLvXsDd97pY8fScuFCtVOcBts2VVK+lsOaqNDynUsVWiIigdFvzBjepEKgVfL5HKB/enowllWn\nqeVQRCR8KNCSWsNXmfXpp+Xf+FX06adw/fWQlAQXXAALFtTM+k7H/v3mMifHzbjfBq9SqbIKrZYt\nzeWpKuGqy9deMThOOzmdjsJC8HhKK7RqaoYWKNASEQmUzikp2KmprM7PP3ab7YVV+flYPXvSqWvX\nIK6ublLLoYhI+FCgJbXGDz+YgOrgQdiypfLH5ObCpk3QrRtYFvTpA8uW+W8N2dnZ3NCxI9nZ2af1\nPLfbzfVJSVxzzTWkpqaSlpYKpNLEbg+vv073iy5i1KhR/ltoFVU2FD4uDqKjYc8e/5/P7XYzJz2d\nRx3mpWWYQzs5VZUvvCpboVWTLYf6EYmIBMawCROY4YonH/PXup89XubEx/NoRkaQV1Y3qeVQRCR8\nKNCSWmHUqFFs3NiDoiITBKWlpZKaaj569OhxLAz64gvTmtWtm3leSorZ7dBf1UaDb7iB6zdt4qHe\nvU/redPHjuXGn35i36ZN5ObmcvBgLg5+pCf7uROLy/bvp3HZvr8asmcPxMZCRETpbZZlqrQCUaE1\nfexYBubk4CoJtFwO7eRUVb5AqWyFlgItEZHQ53K5OP+mifyhJNCa7vEyMDMTl+8vGFKjFGiJiIQP\nBVpSK1x4YTIeTxaWlYvLlUtWVi579+7l208+YefOnSQnJwPwzjtmd8PzzjPP81Xqf/nlma/hrdmz\nabdpE6Ojomi7cSNvzZ5dpef5WuxGtGrFL/LzcR8+TGGhlwv4iUcAG/it08mOJUtqvFJpzRrTmllR\nIAIt3/ehU0wMNnCk5EvVTk5VU7FCq3HjQA/uV6AlIlJTEpql8C9HKu+Ty95L1GoYTIWFplJdLYci\nIqFPgZYE1LZtVRuMftllaUA8kZH2scqUgs2beRhwbNtGWloau3bBe+/BY4+ZKiOAs86CNm3OvO0w\nOzubeaNHM77kegYwb/ToU7Yelm2xc1gW4xIScP34I3b2jzxBMTFYeL1e2jRtyqCDB2u8UmnNGijJ\nAstp2dL/LYe+nZwAsrJM26hvlph2cjq1Q4fMpW8XykAHWmUrtAI9gF5EpK7Lzwc7fgJvcBMpt6jV\nMFhsu3RepSq0RERCnwItCQjfLKqbb86mKiMiNm6MBIbgcBTQoAHYhd/T27YZA/SybR594AGmTTNv\nQAYMKP/cPn3gr381b1Kqa/ANNzCuoIAGJa1yDR0Onskv4K6U3qxff+Ih9WVb7AoKoWnDeB73eGh7\n5ACXlxwLO4LGjRsfq1R6562VbNtW/bVW1f79sGPHiQOtXbv8ez7fTk4AeSXhjG8nxTPdycntdjN+\n+MmH61d3/llt4Qt+GzcuvczNPfkGCWeibKDVsGHpBgIiIuJ/hYXQoIGLPMc0bFuthsHiC7FcLgVa\nIiLhIOLUDxE5fb5ZVH/w9GZLq1WnfPyqVdChQxrx8TPZty+bjuTyXMl9LwCp77zDf+s9w/DhF5Yb\ncA5w223whz+Y+VopKVVf49GjpuLroz/Nps36TXSLcOJ2Q1QkWA7oUuzkgv9tJLnjbHAOpn17ePtt\nWLsWvv0Wbuy1ksKFS2lvxbDrR9i3DyzL4hKcXE0hWx0eLrAtCouasX69RXw89CyGX92fyf6YD3nk\nEXA6zZuqr74y4UK3bjBiRNW/hpP597/NpW/eWFlXXAGvvAI5ORAf75/zdU5J4V+pqXz5j8VEHo45\nVvXz+eF8rFt6n1F7xfSxY2m5cCEzoqJ4YvLkcveNGjWKtWvXsm/1avr+/DPXnnMOza+8EgCv10tS\nUhJTpkw5o6+tJvgCrSZNzGXjxiakzcsrrdryF9suH2g1alS6gYCIiPhfURFERkJMjKnWkuDwtRnW\nr68/5IiIhAMFWuJ3vllUj0dGsa14I39dOxsYfNLnfPUVXHllJD17DmHsffcxCfDlVg2AicCgo0kM\nG3Z8X9S118JFF8H48fDxx8cf+/PP4Y03oFMn+O47WL8eWrSAzZthwwa4gHG87IX8YvP4wjJ/sXsq\nAr6IHse6I4PZuNEEQT7vZGYyF9gCWJj2x/x8KMhvze1HvuUVbxFX1HdxVsvGHMqDfXvhlUi44cF0\nXA1h5kwzsL3sLKs//QlmzIBFi6BdO9MWuGyZOW5MDPTvf/LvfVmLF8PFF0Pr1sff16OHCTWWLYO0\ntKof81SGTZjA/R+v4rf2Yc47y8GGb71MdcTz9hns5OSbzTU4Lo7Mkllcncskl8nJyXzw7rv0+fln\nHrMsfvz5Zz7+7jviEhPJz88/Nn+ttjtwAKKiSmdo+YKtAwf8H2gVFZnKLwVaIiI1Q4FW7eCryqpf\nv2ojMUQ3TzuLAAAgAElEQVREpHZToCV+5ZtF9SEmMBkPrMoZzZ49t9OiRUKlz8nPh//+FwYNgk/+\n/nd62zbXVHjMtUBv3GQ80ZdZ8+eXu8/phBdegNtvNyHR7t0m+ImLgyFD4I9/hGbNYO5cEzp17Woq\nrI4cgdWrYcOqDKY+MpxMr6nO8nrNIPfISHjGC49NfZamrUz11/TpcNVVJgj78vMx/HvtUJ6IMLsI\nuur5VtSAh79twDlHjpCYmEjDhhYNG8KPjfNpf2Nv0qeYSqWpU825Pv7YzBr7/nsTmI0fD7/4hVn/\nd9+V/z643WYg/t/+Bs2bw4MPmsuybBtWrIAPP4T776/859S6NVx4IcyfD3fcUTqT7Ey5XC4iLp7I\n61uH8n8NHcyJ8bKnUfV3cvLNKHu5pH1zmMPByPR0OixadOyY1157Lc2zshhn22BZjLNtVu36kYK4\nOOLj40nzZ2IXQAcOmBDL97PwtR4GYo7W0aPmUoGWiEjNKCw0f7RQoBVcajkUEQkvmqElfuWbRdXQ\n4cD2QgMcPE8Bg3r1PuFz1q2D4mK48kr44r33ONGkpSeB/yxYUOl9t90G994LQ4fCs8/C+efDueea\nMKttW1OVtWYN/PCDuW3VKhNqXXEF9B88mB8v78BXkR6cThNkRUXCco+HHZdcQv9BA+nd2wRMzzwD\n119v2gLf+yCFhrelsjUyv0yYBavy82lx//3856yziI6NBcDt9fJ/ifH8dkJppZJlmTDuxhvh0UdN\nwNWvn2md7NPHrC0lxcwMy8oyj3/4YfjlL+GDD+DFF6FzZ7OmI0dMOLZjBzzwAFxzjQkpTja2asIE\nM3ussm/pzz+boe4nY9vHzy07eBD+9WkKP12cyuzcXJy/7MnKr7ryr3+d/FgnUnZGGYDL4WBATg5T\nf/e7YzO1HunTh0zLooFlYdtQHwfP2l7c33zLkCFDiIyMrN7Ja9jBg6VVWVDzgdbRo3pzLyISKKrQ\nqh3KVmhpl0MRkdCnCi3xG1+rYXenk8Ki0jcNv8DJom828tbs2fQffHzr4apV5q+Wl14K3e65h4nv\nvMO0So7/ItCtb98Tnn/ePBMOXXCBqfj67ju4887SNsFmzU689tmLF3PXuefyYWEhDR0ODnu9TIiO\n5v1Fi076NQ+bMIGRq1bR4fBhXA4Hbq+XOfHxvDxxIjfccw+vDh3KE8B0r5eBmVWrVGraFObMOf72\nJUtMYLV1qwmqDh2CceNgyhRTadWokakci4w04diAARw3b6ysO+80VVxDh5oKsV/+0lR/5eWZlsQf\nfoC//AU6djRvvletguXLzZD5/fvNLLE9e0zAt2+faRv93//Mz3LmHycwf3oR017I4L89zHq//PL0\nKsF8rYadYmLYnw25B80w+871Y1jw7rvUi4xkyJYttNu0iasjozhabH5DsIBf4KBnYQHu3NyqnzDI\nDhwoDbGg5gMtMPNEyoZqIiLiHwq0aoeyM7T0RxwRkdBn2dXYGs6yrCRgzZo1a0hKSvL/qiQkXdOi\nBe/l5pLoNTv++VgW7Le89Gsax6d79hz3vHvvNe12X35prl/mcjHt6FGuK/OYZcBjLhfrjxw/Q8tf\n3po9mw3Dh/OSw8FIr5eO06fTb+DAUz5v1cqVLBs6lCciIsgsLub6mTOPDUDPHDWKuA8/5NBttx03\nzNxf1q6Fu+6CVq1g2DAzBP5k4V1Zhw6Z9sx//MO8sXM4zM8rMrLyN9znnEOlOzR27mwq3g4dgjff\nNFViPosXQ+/ephIsNtYco7gYOnQ4+dqG/epXjNu+HcfhiGPnjG0ELVseYfv27cyMjubokSPcYVmk\nEklhUTEWRVgOC9trs48I7m8eX+m/udqoTx/zvf/oI3Pd6zU/h1dfhYce8u+5Nm823//PPjP/XpYu\nhZ49TYh59tn+PZeIiMB995k/Ah06BF26mNd2qXnffmtGLvTta/4Y6PX6b+yCiIjA2rVrfTOMk23b\nXhvo86lCS/zmwYwMpgwfznNFppUuKgqwweOBiUVw86PPUjLmCK8XRo82wcb775v2OZ8Pvv6a/hdd\nxBLMYPjDmHbD/7c2sP899B88mNtnz2bS+vXs6NiRl6sQZkHp7n6zPvwQ67bbyu3mN2zCBCYVFfHE\nGQxFP5WkpONnbVVVbKyp0iouNqHG9u2mjbB/f7NL4r595thff22G1Z9zjgkev/vODK5PSzMVXOec\nAwUFZgD/tdeWP4ev8uuee8rfPnKkuc/tNi2STZqYz/fsMe2i/caM4c2hQ7kly1SaxTeB7Tu8OIt+\n5CPLon/z5jQ9coQBP/1EZzuChs4IvHYx2DaWZTHJdnLjI89W7xsTBAcOmFZZH4fDtLkGokLLNy/L\nV5nlu9QcLRGRwCgsVIVWbVB2hhaY9z8hMplAREQqoUBL/Kb/4MHc8tpslq/byPVOJw4LsGC518OS\nyEv5/umB/PnvMHw4zJplAhMwg9sff7z0OBdeeCGX33cfT73zDq8AvwMu79ePCy+8MOBfw+zFi+mb\nmsr8U7QaVnSi4MrlcjF+WmUNlLVLRATccEP52268sfLHdu1qPn7zm/K3R0fDddcd/3iHw8wt277d\ntLht2GDeUD79NLz8snlM/frwyCOmYujzz00b5YgRKbx5Xiqfr1/MrWfH0LgJ7PtpN/87WoS3SRwX\n0QBPvQbcb2XzjF3Aq1ExeDwRFBYV8YXDwULPJbxwdtVCybKys7PNv4GlS0lIqHwjg0DwDYUvq1kz\n2LvX/+fat6/0+KBAS0Qk0Hwth9HRCrSCqWzLIZT+XEREJDQp0BK/umvUYn7X91yWWYU0wsyiejYm\nmll/XsQXX8Brr5VW6rRoAT/9VHmp96z587nsz3/mxaNHWe5ysf6tt2pk/QkJCSxet+60nxcqwVWw\nXH65+QBTlQWm3D8vz1SJvfACvPOOGW5/2WUwapT5gAn8t8kq7ow7zFH3UWKch3jbG8lDB1ryTcl2\n2xdyIcus//JpcRHXREaS7/HwXH0XngaL+M1voFMnuOiiqq918A03cP2mTTzUuzd/WrXKn9+GE7Jt\n2LXL/DdRVps2Zm6av/k2GYiPN9d9gdahQ/4/l4iImOBEuxwGX9mh8GWvi4hIaNIuh+JX69YlsKPR\nZDJKQqpxQP+XXuL66xN46ikzWHzaNDPgfOnSk88t+ODrr3kzOjrgrYYSHK1bmzlOrVqZWSI//miq\nlJYvN5Ved94JAwa4mPThRF61veTs2cMCCx497yzOPctBu3bQrh2cd14Eo1u2IMPjwQKei4zk/pde\n4rbbTHXVmDFVX5NvY4PRUVG03Wg2MqgJP/1kwrz27cvf3rZt4AKthATTGgyq0BIRCbTCQgVatYEv\nwPJtiqKdDkVEQpsqtMRviovN4O877h7MD2sqn0XVogX89rdVO96FF17Id3rXV6dYlqnY+te/yt6a\nworUVP7y3nt8HRXF0w0bmOFqZcyqn4CjQQMmff/9sX9z/TDzvQYPNjPa+vY1IdqJZGdnM2/0aD4s\nuZ4B/Gr0aG66/faAtx5+8425rFhJ1rYt/OlP/j9fVpbZTdOnfn3zvVegJSISGL7WNqcTQmgD3rBT\nXGwuVaElIhIezijQGjFiBLGxsdxzzz3cU3His9Q5//iHqTQZOhRatareLCqRyvhmlHUEVn3yCZ1j\nYo7dtyo/H6t3b94fM+a4f3P9+5uKr9/9zgy179oVGjc2s6MeewwSE2H/fvPLxZh7bmBcQQENS8qW\nGjocjC0oqJHWw2++MX+5r7jDYJs2kJNjqrd8b779oWKgZVlmAP2BA/47h4iIlPIFWpYFR48GezV1\nV8UKLQVaIiL+sWDBAhYsWMChGp5hckaB1tSpU0lKSvLXWiTELVxotkLu2BGgerOoRCrjm1HmdrsZ\n2bs3HQ4fxuVw4PZ6mRMfz8sZGbhcruP+zUVGwrx5pkKrZ0/4859L7/v8c7j+enjmGXAym0ciN3Gl\n10mRt6QVz4JrnE7+WtJ62H/w4IB9fevXwwUXmOH8ZbVtay537ICLL/bf+SoGWmCq13bt8t85RESk\nlC/QioxUy2Ew+Sq0fLscquVQRMQ/fEVOa9euJTk5ucbOqxla4he2Df/8Z+nAb5FAcLlcDJg4kRle\nLwDTvV4GZmbi8r0zPYGzzoJ162DzZrjvPhg0CNauhYkTzbD6cxjHY0Xg8UBhERzNN39BL/bAaODN\nceP8sv6tW+Gaa0zlmE9xMXz00fG7TIIJiAE2bvTL6Y9RoCUiUrN8M7RcLlVoBVPFQEsVWiIioU2B\nlvjF99/D9u2mCkYkkDqnpGCnpjIrNxerZ086de1apedFRZmh6/Pnw+zZsHOnGUS/bh30eTSDaZGl\nQ9IdFjgdUFAAzxZAfotnGTHCtNRWV2Eh3HabaYGcNw+++87cvmCBCZh+/evjn9O0qWk79GfHo8dj\n/ltt1ar87W3aKNASEQkUX4VWvXrgdgd7NXWXL9BSy6GISHhQoCV+sWSJaZe69tpgr0TqgmETJrDn\nppt4NCOj2seIjTVzowBemj6YnZd14MsIDy6XeaMbHQNfOj18EnMJP/w4kHfeMbsyfvABjBoFnTqZ\nDQ4++QTefrv8boRer6la9Nm1C+64A7ZsgS++gCZNYMAA+PprUy12773QuXPl6+zcuWqBltvtZvzw\n4bhP8ZvS+vXw889w1VXlb2/TxoR8IiLif75Ay+VSoBVMFQMttRyKiIQ27XIofrFkCaSkQMOGp36s\nyJnyzdTyp9mLF3PXuefyYWEhDR0OfvZ6eb5+NMu/XURCAhw6BA8/DHfeWfqcNWtg+nTzeaNG8Oij\nJtxq3NjMv2rRApYuNcPWc3MhLQ26dIEPPzSfJyWZ/2Zee80MCq5M9+4mQPv0U9OueCLTx46l5cKF\nzIiK4onJk0/4uOXLITr6+ACtdWs4eND/A+hFRKR8hZZaDoNHLYciIuFFFVpyxvLzzS/tmp8loSwh\nIYF+kyczvuT6OKD/Sy/RrFkCTqepqlqwwFRo/e1vptoqO9sMl9+40bTwTZxofmHZuNE8ZvZs2LbN\n/PKyeze89545dvfuZobX44/D66+bMOxEHn7YhGCPPw5ffQUrVhz/mFUrV2ItXcrguDjsJUtYtXJl\npcfKzoYpUyA11YRaZbVpYy7LVpqJiIh/lJ2h5XaXr+KVmqOWQxGR8KIKLTlj//wnHD5sWqpEQln/\nwYO5ffZsJq1fz46OHXl54MBy91uWqawqKyXFXC5bZiqxWreGH34wwVC7dmZW1sUXm2qtss46y4RL\npxIZCenp0KePCbYAvvzSBFKXX25aDeekp/Oyw/x9YpjDwcj0dDosWnTcsPxZs0wV1qxZx5/nnHPM\n5bZt/t1RUUREyrccgvljoC9UkZqjXQ5FRMKLKrTkjBQXw9SpcMklZuC2SKibvXgx/+rQgVmLFp3W\n85o2hYsuMu16l1wCN91kgqFbb4Xzzz+zNfXubeZ19etnrnfpAh07mo9uF4zll+tycDkceLwQYzkY\nkJPDjAo7M+bnw9y5Zvj8WWcdf44WLSAmxmzwICIi/lW25RDUdhgsvoqsmJjy10VEJDSpQkvOyIwZ\npgXqn/8M9kpE/CMhIYHF69YFexnlOJ0wbZppUSkuNgHZc8/Bf9ev5E6W0oYYDhw0uzZ6iuGi82JY\n/I8l3L9nJRNeSCE2Fu66y+zS+NhjlZ/D4TBVWgq0RET8r6iotOUQTNthkybBXVNdVFxsNjGKijLX\nFWiJiIQ2VWhJtXm9ZiD23XdDjx7BXo1I+LMseOcdGD/e7EjYJymTIZEm8Nq2zbxRd0bA1m8hZTN8\n8k4mHTqYSrEvvzRzvTp2PPHxzz03/AMttxuGDs2m56Udyc7ODvZyRKSOKCws33KonQ6DwxdoRUaa\n62o5FBEJbQq0pNr+3/8zv0QPGxbslYjUPS1bwlMzxvDlxXDZpXDhhSWXF0BCArwVAb/+bToPPADX\nX28GyqemnvyY559vBtqH87Dit9+Gv8+8gdQtm3iod+9gL0dE6gDbVsthbaEKLRGR8KJAKwzt2WNm\n7Xz2WeDOkZ1tBlXffHPpoGoRqVmdU1KwU1NZW5RPwwbmTXp0NOxvls8lj/Xk5WldeeUVmDevanO8\n+vQxlV+V7aQYLv7y/mz6sImRjijabtzIzFdmB3tJIhLmPB5zqQqt4KtYoaVAS0QktCnQCiN79sAb\nb0D37vDuu6YaY9euqj33xRfhiy9O/piJEyfSxrKYOHEiDzxg3oy98sqZr1tEqm/YhAnMiY/H7fUC\n4PZ6mRMfz7CMjNM+1jXXmEqvwYNh+3Y/L7QWyM7O5sCnoxkHeG14phheHz6adevUeigigeNra6s4\nQ0tqni/QiiiZIqyWQxGR0KZAK0y89JKpwBg0CAoKYM0a86bp5ZdP/dxFi+B3v4OHHz55q9GcJ5/k\nEeDNJ5/k738387PatfPblyAi1eByuRgwcSIzSgKt6V4vAzMzcfl+azoNlmXmbBUXw+WXw6RJ/l5t\ncPXu0IHnvYdpQCGe4nyiiwt5gcPc0fkcevTowahRo4K9RBEJQ74qILUcBp8v0LIs8/NQhZaISGhT\noBXCbNvMu3n6aRg1Cu6/3wx0/vZb88voo4/C669DTs7JjzN1KjRvDl9/Df/5T+WPiXM46A08AfQC\n6uPg17/279cjItXjaz2clZuL1bMnnbp2rfaxzj/fVGv26wdjxpjXkiuuMKF5SWYWkt6aPZurDh7k\nqpLrdsnHL7DoVfwz33/zDcnJyUFcoYiEq7KBliq0gqu4uLTdUIGWiEjoU6AVgmwbnnnGDIW+9FJ4\n/nno1s1UTJ1zTulf/4YNM7+Azpp14mP9/DN8+qn5xTUhwVRrVTRx4kQutG2eL7n+AtABm0mTJvr7\nSxORaho2YQJ7brqJR6vRalhRQoJ5PZk1Cxo2NK8ro0aZsGvMGDhwwA8LrmFvjhvHE5YTsLCs0tst\nYDQ2DbOzSUtLC9byRCSMVVahpUArOIqKStsNIyPVcigiEuoUaIWgSZPguefgzjthyRIz62bxYsr9\nkgaQmAi33QYffHDiYy1bZv5nfvPN0LMn/POfxz9mzpNPkgk0KLneAJiIaT0UkdrB5XIxftq0arUa\nnsjgwWZziT/9ybw2pKSYuXnnngszZsC998LeveaxgwbBPfeYlufa6MGMDCbbABGY2qwSFkzC4up+\n/Yn0/dleRMSPfKFJZKT5iIhQoBUsvpZDMDPNVKElIhLaFGgFyK5dpkXnf//z73Hz881xH34Ypk0z\ng9/btoUGDSp//C23wLp18Oqrld//j3/AeeeZj5tugtWrzXF9fK2G11R43nWY1sM4h/4JidQFPXvC\n/Pnwww+mOnTYMFiwAH7xC9Oy/MYb8N57MHYs/PRTsFd7vP6DB7O6RQc+w8KyLCzMHwE+s70sxMUz\nz57gRVJE5Az5QpPoaHPZpEloVrqGg7KBlloORURCn9KIABkxwrTo/OEP/j3u3LmQnQ2PPVa1x99w\nAzgc8MgjsH59+fts27QY3nijuX7PPTBkiBkQn5dnbmtp26RXOKavEOzJkvtFpO5o3hy+/BK++sq8\nplxxBezbZ+67+WZTQdqqFbRubQbML1oEt95aO+ZvJd26mGesaAqcTizL5ojt5WnLwS5eIitL1Vki\nEhi+ytWoKHPZtClkZQVvPXVZxUBLLYciIqFNgVaA7NplLr/5xn/HPHgQnn0W+vY1s2yqIjbWzMly\nueA3vzHzsnw2bIAdO6B3b3Pd4TAD5o8eNVUXt9wC27A40aSsF4E9qtASqXMaNIDOneGyy0xLc3a2\n2VDiD38wm1OcdZZ57bntNhOYf/SRGTQfbNnZCbjPn8yzTidYFuMti7y25wIP1sqqMhEJD77QxFeh\npUAreFShJSISXpRGBMju3ebSX4GWbZt5NQUFZn7W6ahXz1RR/Pe/0KNHaaXEzJnmTVWPHqWPPess\nmDABcnNNdUVEfS+LgH+X3O+rzloGfAwc9HjO5MsSkTAQHw9XXQVt2pgq0h9/NK3OgwfDhReax3Tr\nBiNHmtbmjz6C998387iefda8vtWEnTshqctgfujQgWnAxxERPP1sBg5H5LE/QoiI+JsqtGqPsrsc\naoaWiEjoU6AVAF6vGZTcqZOpgPLH4M8FC8zg9/nzzS+Np2vGDLj7brO2J5+EpCQTaD34YOkbLJ+n\nnzbh11/+AocPw4AXXyQd+Lnk/sNAOvDgiy+e2RclImErIsLM7vvmGxNgpabC1Kkm6Lr1VvN6NHy4\nmbk1axbs2WM+CgvNzq3p6f4fmrxzp2mFnL14Mcs6dODmhx/mrrvSaN3abK4hIhIIvgqtioGW2+1m\n/PDhuDUhvsao5VBEJLxEBHsB4WLUqFGsXbsWh8NBYaH5H+b+/aby4NprvVx9dRJTpkyp1rEPHYLH\nH4e0tNL2wNPVsSO8+64pd580Ca6+2gxwvv32yh8fGwu/+pX5PD09nYm/+x1P2TavAL8DvnU4SE+v\nOF1LROR4ffqYj9xcc33qVDjnHPNLxeOPw9Ch5gMgLq70cdHR8Mwzpb98nIniYlM526YNJCQk8PGG\nDcfua9cOtm0783OIiFTGV6FVseVw+tixtFy4kBlRUTwxeXLwFliHFBWp5VBEJJyoQstPkpOTycrK\nIjc3l5ycXCCXyEhzuXdvFsnJydU+9owZJtSaOvXM1mhZph0oKwv+/W+4667SsutTyfWa1sMXUauh\niFRPXJz5yMiA/v3hvvtgxQr45BO44w7zmIICM5erf3/T/nzJJbBkCSxfXr5F53TbFPfsAY+n8grX\ndu3M7o0iIoFQWYXWgf0rYelSBsfFYS9ZwqqVK4O3wDqkbIWWWg5FREKfAi0/SUtLIz4+Htu2j71x\nqVcPwCYqKp60tLRqHdfrhTfeMO05rVqd+TotCxITzeXpGvDii7yGWg1FxH/OP9/M8fvjH83r3ZEj\nphp14kR48UVTrfXLX8I110CzZvDAA6aa6+KLS6uqDhw4dcD1+efmUoGWiNS0ihVarVu7OZ90Hsw3\nb8OHORzMSU9X62ENUMuhiEh4UaDlJ5GRkQwZMoSCgoJjf+2JjITIyAIuumgIkVUthapg6VIz22XQ\nIP+ttbrS09PZadtqNRSRgLCs0rC9eXMzR+vjj83r33vvmYDrww/N/L9vvjFhWK9eZij9q6+aUGvf\nvtLjFRbCmDHw9dcmBLvpJhOEVXTOOWanxr17Nc9GRPyvYoXW2o/Hkm7lUHTYvA13ORwMyMlhxrhx\nQVph3aFdDkVEwosCLT/yVWkVFdk4nQA2Llc8Llf1qrMAZs+GDh2ga1e/LVNEJGRcfrl5HbzrLhNw\n7dwJmzfDwYMwebLZURFg1CgzK7B5czjvPLjootKZgUlJpm37D3+ovDr10kvN5fMjSubZjBunYc0i\n4jdlA61VK1cSsWwp3RvHkJ1duvN055gYtR7WAO1yKCISXhRo+ZGvSquoqACHAwoKCrj00iHs3l29\n6qwtW0w1wtCh1WsRFBEJNw0bQvv2ZhbXyJGwaRP8/veQn29+SbnjDvN6aVq+Sz30ELRtW/kxL74Y\nYiJXEr28dJ7NmIEDj4VbPtnZ2dzQsSPZ2dkB/ApFJNz4Wg4jI2FeZiYPAi1amKDrUF7p4wZg7pfA\nUcuhiEh4UaDlZ2lpaURHx2NZXuLj4+nWLY1du6p3rGefNVvMDxzo3zWKiISTBx+El182g+P/+Ef4\n7jvTZlhcbP76XlhoWhJPpLDQzWUx6fT72YENPHj0KNs++oi+jRqVq5gYfMMNXL9pEw+V2W5WlVwi\nciqFhaYayLKg35gxvAnExIBF+QqhOUB/jXUIKLUcioiEFwVafhYZGcnFFw/BtnMYMmQIbdtG8tNP\nZnet05GfDx99ZGbH+IaIiojI8Ro2hBEjwOUqf7vTaX5xOdUIw+ljx5JRP4fCPAc7dnhx797NM8XF\nzNi9+9iw5tkzZtBu0yZGR0XRduNG3po9+9hzK1ZynYwCMJG6p6Cg9L1c55QU7NRUVufnExEJxSWB\nyqr8fKyePemkGRMBpV0ORUTCiwKtAGjZMo3ExPtIS0ujdWsTZpUdVFwVn3xidvu69dbArFFERMw8\nG2vpUm44K4Y2bSA3ezeNC4rp6nRi5+Wxye2mf1YWs0aOZHzJczKAeaNHs2TRIqylpW2KVZl9UzYA\nUwujSN3gq9DyGTZhAnPi4ylyeikqBrfXy5z4eB7NyAjeIuuIoiK1HIqIhBMFWgGQnx/JRRe9QGRk\nJK1bm9tOp+3wyBEz4PiKKyrfkUtERPzDN88GoL7rCI2deTiLHBw9Cvd7YO7uvTT6bie9i4r5xrYB\naOhw8Ex+Pum//jWPOsz/Rn2VXJVVXo0aNYoePXrQpVMnvp81i2uysvhu5ky6tmnDNRs2cOMll9TU\nlysiQVBQUD7QcrlcDJg4kdkRXoqLYbrXy8DMTFwVy0zF79RyKCISXhRoBYDbXdr60qqVuTydQOuP\nf4StW+HddzUMXkQkkHzzbABy9uyhZRREl8y6ebUQrjocQwPPUYYBbxUV4fGCDVzl9dLd7eaDnBwA\nXA4HA3JyKm09TE5OZu/evdhbt/KQx4PH42FQQQFnHz3KYNsm5cCBYy2MIhJ+CguPHx/ROSWFLa1S\neetorloNa5BaDkVEwosCrQAoG2g1aWJ22/JtLV8Vf/0rdOlitp0XEZHA8c2zWZWfT3yLFuRgftnZ\nEOklP6IRHcmhBfAmcJc3kvx8KMj3gsfDGNvm9R93c/BgybFiYiptPUxLSyM6L4+RRUXUsyxs26Zh\nURHPAjOB55xO5o0erdZDkTBVseXQ5/LrJ/BOvZvUaliDiotL5yqq5VBEJPQp0AqAsoGWZZmdCqta\noXX0KHz8sWZniYjUFN88G6tePexGjdjv8fBmZARjL21J8zYtWYyN7XDSNdJJVCR4vUU4bcjEoqe3\nJd9vg8IiU7k1ANPGWNaSxavpcjiC8wss3G7wHM3nLKAL4LQsvrFtxhYUlNs9UUTCR9mh8GW1bOni\nkE9X3yoAACAASURBVGOaWg1rkFoORUTCiwKtACgbaIFpO6xqoPXJJ+b5CrRERGqGb57NDK+Xpi1b\nkhERQd+WLanvcOCKj2dygwYkRziIjDS/AEVFRbIMm63U42YrEYANG+DbrZCZA97m6ezZA1lZsH49\nPHJbJml5sTgjInA6iojFpn7JuQfYMK+oiGucznK7J4pI+DhRhVaTJpCbCyXj+aQGFBebHXBBLYci\nIuFAgVYAuN1Qv37p9dOp0PrrX+GCC9RuKCJSk3yth2/k5RF56618Xq8eYIY1j/vgAybFxHDY6wXg\nqAPGR0Ux8sLWJCXBZZdCu3bw1dF85v7Yk1dndaVlS2jWDDp2hKizx7CyvUXr1olEeotoXnJOG4s3\ngN9EmP6X0cCblczgEpHQVnEovE9srNkJ+8iRml9TXVVUVPqzUMuhiEjoU6AVABUrtNq2hR07Tv08\njwc++shUZ2kYvIhIzRo2YQJ7brqJ519/HTs1lVm5Zlhz6g030G/yZMaXPG4ccP/UqfypWTOOer1E\nRUG9OC//vjKeN/6SwYwZ5nEpKaa1Zd47KUTdmMr/6tWD6Gj2ARawBvDgpEOhE68Nk4EBzz4bhK9c\nRAKpsqHwAHFx5jI3t2bXU5eVrZZTy6GISOhToBUAFQOtdu1gzx4zH+tkvvzStKio3VBEpOa5XC7G\nTzPzbHzhlm9Yc//Bg/mhQwcmFRay45JLGPjww8faFMFUcg19OZNf/crFI4/AwYPw+eeQl2c2+Rg2\nYQJzExKIbd6cQ5ZFFvCmw+K3JdOJlxV62HHJJfQbODBYX76IBMjJKrQADh2q2fXUZYWFpUPh1XIo\nIhL6FGgFQMVA6+yzzeXOnSd/3gcfQGIiaOdmEZHgKhtu+cxevPj/s3fn4U2WafvHv0+SNmmgUGnY\nQcAVARUpCHVUlEVhUGdGUcdBYQQEHGVQpFA3oEWFiuj4g3Gkig687rsoLyjgOkx9ARWVKouKIEKp\nLUILabok+f1xN3ShhS6hLeX8HAdH2iTPkzsRaXPmuq6bD7p3Z+Hy5UBJm2Kokqt3qX+8Q5UXxZ2L\nh+Z0vdC8Oc1btuR+m40b7HaaRVj4bAHuDjoPnVdEGpfKKrQUaNU9tRyKiDQuCrTCLBAAn+/wCi2A\nbdsqP27fPli0CMaOLRlWKSIiDYfH42HFhg14PJ5D15Wv5DqSPvHxMHgwy6OjyR84kKXF/9gn2+GL\nwDyysz1kZsJ338GmTeFZs9frZeakSXi93vCcUESqrbIKLbUc1r3SFVpqORQROf4p0AqzUFth6UCr\nfXszR+VIgdZrr5mhoBMnHtv1iYhI+FRUyXUkoQDsybfeKtPCiH0sXbuaQfLdukFcHDzwANx5p9kB\nLRCAtWvNrMXqmD99Ou2WLWOBhs2L1JvKdjlUhVbdq2iGlnaZFBE5finQCrPQTjWl39s4HGanw59+\nqvy499+HPn2gbdtjujwREalHpQOwUAvj0+8vJzUVTjsNxo0z1boOB9x/P/zjH9CmDZx0kpnF9cwz\nVX+sdWlpWKtWMS4mhuDKlaxLSzt2T0xEKpWfX3HLYZMmpipfgVbdCAbLthyGLouK6m9NIiJSOwq0\nwizU1VH+w/ouXSqv0PL7YfVqGDz42K5NREQajtItjKNHw9atsHAhjB4NW7aYjUKuvda8GQ7tfHv3\n3fDmmzB8uLlfZZUFXq+XRYmJ3G4zP+Yn2mwsSkxU66FIPSg/WzXEsqBZM7Uc1pVQcFW65RDUdigi\ncjxToBVmNQm0Xn8d9u6Fq646tmsTEZHjQ+vWcP758MorZsfEjAxITYXsbLj6avjkE3j2WbjySvjn\nP0t+9oTMnz6dsdnZuG02gkCUZWNMdrZaD0XqQV5exYEWmDlaqtCqG6EB8KVbDkGBlojI8UyBVpiF\n3lSEdrYK6dy58pbDlBS47DLTcigiIlKaZYHLBWPGmCquzz6DH3+Em2+GZcvg9ttN69Irr8A118Dr\nr6RR9N4qzot0sWsXfPml2WW3j8ul1kOReuD1Hv57YUjz5gq06koouCrfcqidDkVEjl8KtMIsP99c\nulxlr+/SBbKy4MCBstdnZ8MXX8CNN9bN+kRE5Phks5k5W337QtOmMH8+vPQSTJ1qbr/+enjjDbjj\n+hT6bjRB1q7dZqD8r1kQBMYAS1JS6vNpiJxwKms5BBNoqeWwboSCK7Uciog0Hgq0wqz8pz8hXbqY\ny/Jth2vWmMuLLjq26xIRkcalSRMTYqWkmJ8tgwbBtGlw9W3TWN0JOnaA7t2ha1dz/02bINUPF/85\nsX4XLnKCUcthw6CWQxGRxkeBVpiV/2EZ0rmzufzxx7LXf/ABtG8PnTod86WJiEgj1bkzrFwJc+bA\n4wviiRk+iB3NfUS5TPDVogWkHfTx6MbBXHdDP775Bh591FR01VRWVhZDevYkKysrbM9DpLEJBk2g\npZbD+hcKrkJBlloORUSOfwq0wqx8OXNI27bQsSMsX15y3ddfwxNPwMiRJTtYiYiI1NbE5GQWxcbi\nDQSwgDadAixwxpJNEgDnnAN33QUjRtT8zfS4IUMYmJ7O+KFDw7dwkUbG5zOXajmsf6rQEhFpfBRo\nhVllFVqWBTfdZOadhH65eeQRE3Jp0ykREQknt9vNmDlzWBAIADA/EODht1PYu9fNP/5h7jNwoPl5\nFBMDf/oTvPOOqSQJBo9+/sWpqXRJTychMpJOGzeyODX1GD4bkeNXZZsFhajlsO4o0BIRaXwUaIVZ\nZTO0oOST8NWr4fnn4dVXYdw4cDrrdo0iItL49YmPJzhoEAv37cMaPJhBl/fjpJPg73+Hd9+F11+H\nFSsgIQG+/x6uuspUkVx9NXz8sdk9MTvb/MzatKnkvFlZWSxJSGBm8fdJwJKEhGq3HqplUU4EoUDr\nSBVaCrTqhloORUQaH0d9L6CxqaxCC+Css8wOVf/4B6xaZT4dv+WWul2fiIicOCYmJ/NwYSFTk5IO\nXWdZMGyY+fryy82flBR46ilYvBiWLYO33jK3b9hQsnnJJ59A69Zw+x+GMCM/n6Z2OwDRNhvT8/MZ\nP3Qor69bV+E6pkyZwhdffIHNVvI52u61a7nxwAEu6dKFIePH88gjj4T/BTjBVfS6hwQCAXr16qXX\n/RjLyzOXRwq0cnPB74fi/6XkGCn/O7oCLRGR458qtMKsshlaYN5E/PGPJswCWLrUDOoVERE5Ftxu\nNzMffxx3Ze+mi1mWqRheswZ++cWEV9dea77v2RP694cBA6DbmamctimduHw7Xq+pPsnzQXzAToev\nTOthMAhbt5Y9f1xcHJmZmezbt499+/bx09atXHrgAHdYFv0PHsSrIULHRPnXvfSfzMxM4uLi6nuJ\njV5VWg4BcnLqZj0nsvK/o7tc5jI0CkRERI4/CrTCrKAAHI7Kh7zff79p43jiico/rRMREakvLVvC\nRRfB44/D00+b3RPfeMOEWqfZZnC3veRnXBAIBEwrzx2FkPK3GUyaBGecAW++CffeC1dcAX/4w3Ba\ntIglGAxSVFREi507mVE8rCsJ2PTqq2o9PAaGDx9ObGwsfr+f3B07yM01M9WCwSCxsbEMHz68nlfY\n+FWlQgvUdlgXyo8FCY38yM+vn/WIiEjtKdAKs8LCitsNQ5o1g/nz4dZb625NIiIi1dW2LYwZAx6P\nqSZetQoS/5XEPyLAHWXeoLvdEFE8vOBhYIt/FvPnm++vvhoeesi0MDZpEkFm5gR2785n3zdbeDAQ\noIllIxgMEhMRwYzilkUJr4iICCZMmEDezz9z9d79ZG/ZxYEDkJ+fz4QJE4ioqJxcwqoqM7RAOx3W\nhfIth6EKLQVaDZ/X62XmpEl4Q/9DiYgUU6AVZgUFFbcbioiIHO/+Om4c27p352O/HwuwgIhIWBvh\n56v2PUh+cCwzZ8LevaaFcdYsmDvXHLt583AydxcwLODjAmwEgxAMWliWg/52u3ZLPEY6d+jART4f\nwwMOBpND7r5cVWfVoVCFVmUthx6PuVSB4rFXvuUwVKGllsOGb/706bRbtowF2hpeRMpRoBVmBQVH\nrtASERE5nqWuWEGy00luwLSvHQgEeCDKydINy7nnHpgxA046CRYuhPvugylTIDMT7r8/grObZJJA\nEMsCiyA2y4Ev37yhnOiDh2+bwb/+Bbt3V309+uS+cl6vl8X33cd9LTwEgwFuAzzZO7n55ptVnVVH\njlah1aqVuczMrJv1nMjKtxyqQuv4sC4tDWvVKsbFxBBcuZJ1aWn1vSQRaUAUaIWZAi0REWnMPB4P\nI+fOZWbx9zOAUfPm4QmVmlSgZUtITobb587mEcvCIohls3C5HNgs8AfgUTvkt5vF3/4GHTvC2WfD\nxImwbduRdyHTJ/eVmz99OmOzszkpKhZw4AImB2H3N9/U99JOGEcbCt+0qQm79uypuzWdqMq3HDoc\nYLOpQqsh83q9LEpM5PbinVon2mwsSkzUBxgicogCrTA72gwtERGR492o4tbDhwsK2N6jByPHjq3S\ncWNuvZWNnTvzaTBIhMOBZYErCtZF+tl1Xg+++34sX3wBkyfDxo2wYAGccooZLF9UdPj59Ml95UKv\nTW+XizyvhUVLbDY/vRytsa1e3aBfq8ZUdZeba1rbjlQQ17q1KrTqQkU7kbtcqtBqyEKhvLs40HLb\nbIzJztYHGCJyiAKtMNMMLRERORGkrljBB927s3D58mod9+KaNcyMjCSv+A3KgUCAWS4nC5cvJyIC\nzjsPHn4YduyAgQPNMStXmg+L7rwT/v53iIuDtWv1yf2RLElJ4c+BADN37GCvN0CU+yTc7hYE/Ccx\npvj2hqoxVd3t3w8xMUe+T6tWqtCqC6GWQ4ej5DqnUxVaDVXpUP7AQdi82eys28fl0gcYInKIAq0w\nU8uhiIicCDweDys2bDhiq2FF2rZty/j584/astixo9kh8ZtvTJA1Zgw8+ywsXQq7dsHv+05n8IZs\n/F4b6d9CMM/GzVnZPHjn8R+ChMPIadO4MyODdvv38++cXUS5LGJj21NYZPF0EEYlJtb3EsuYMmUK\nAwYMoG/v3vywcCH9MzPZ+uST9O3dmwEDBjBlypT6XmKN7NtXspNhZVq3VqBVF0IfOltWyXWq0Gq4\npt50Exd//z2bt2xhy5Yt5B7YwubNW9i8ZQv9v/+eqTfdVN9LFJEGQIFWmCnQEhERObKqtiw6ndCj\nBzz6KDz1lAkHfvoJ7k1M45qmqzgtz8XmzWYnue07IGaHi21PreTN18L7yX1tWuDqs32uMzDCZsNV\nlMMm2wEiI+FrfBzoN5je/frV+XqOJC4ujoyMDIKbNzPe78fv9zPB7ye4eTMZGRnExcXV9xJrpKoV\nWmo5PPYq+h1dFVoN16CRI1lY/G9BMOgH/PiLzPcL/X4GjRxZ30sUkQZAgVaYFRaq5VBERORoatqy\nCLD5wxQePBXOOgvatDGBgNcLuQdgnA3uG53CG2+UDOSurdq0wIWOfeyee8oEW1lZWQzp2ZOsrKzw\nLLKU0CDlme3akWlz8DeCvH7gF/ZbRcwlloF/Tgr7Y9bW8OHDcebkMLmwkKjiEpooy+LOwkKcOTkM\nHz68nldYM/v2HT3QatcOfvmlbtZzIqss0FKFVsM09e672RAby1d+P8GguS4IfOX3syE2lql3312v\n6xORhkGBVpipQktEROToatqyCKad7hkgMgI6tIeTO8Kpp0LXM+G9jrApN5FrrjFBwaRJkJoKzz9v\ndkx86qmSWTpHEgzCihXw309rPni+9ND67BdeoPC11w6FYuOGDGFgejrjhw496nmqG36FBilHOxzk\nWx3wWhbjgkVMyt7FFlLIznZX+TnUlQ3r13O5w0EPy8LnM1V3AOdYFpfb7WxYv75+F1hDVWk57NgR\nMjKOvJun1J7Xa3aULM3lUoVWQxUREcGkBx5gnt2OD5No5QWCzLPbmfTAA0SogkBEUKAVdgq0RERE\njq0+8fEEBw1iXal3oifFwHcOHzHDB7P6w3588w3ceiu8+KK5vPFGs2PiuHFwzTWQlGQCr9WrzaD5\nuXPhP/+BN98Evx/efReGDvUy8y8lg+f/6rVx//WJHDx49NKv0tvNHzx4kNtzc8nOySH/vfeYOW0a\nXdLTSYiMpNPGjSxOTT3iuaoTfpUepJyfDwcONiEY3YwuBOliA2dksEFWAy1JSWFy8+bYbQ4CARMo\nBgJgdziYHBPToIfYH0lVWg47djTPd9euulnTiergQWjSpOx1qtBq2EaMGEHw9DP4Z/H3C4LAGWcw\nYsSI+lyWiDQgCrTCTIGWiIjIsTcxOZlFsbF4AwEAvIEAi2JjmZiUxCWXmNlbs2fD7t3mZ/Mbb5jj\nRoyAd96BmTPNbYMGwfz5MHUqXHQRXH01xMbCVVdBLNP5y85s8vbZyM+Hnd/buO7nbK6Kn8HatfCH\nP8BHH1Vc4RGqknICWTt30smyGFNUBLt38/68eUwt7qFJApYkJFRafbU4NbVa4Vfp3Q13Zgew2aBj\nl3YUNm/OtDZt6ByZwtatNXrJDxPOtsmR06bxb8uiefOWgPlvGvAHaNmyJc9aVoMbYl9VVanQOvlk\nc7ljx7Ffz4msokBLFVoNW0REBLf9fSorcfMyRXwS6eauqVNVnSUihyjQCjPN0BIRETn23G43Y+bM\nYUFxoDU/EGBsSgrucj1Fdrv586c/mWqZ556Dr76C996D116Ds882l6+9ZnZQ/Ne/zP1OPyWNCaes\nom8TF9u2wTcbTRXNAI+Ltukrie+bxtKlcOmlcMYZpsrr/PNNODZsSBrbnl7FmUUuvv16F819RVhY\nxGEjmJ3NSL+fZwv9BILQ1LIxPT+fvw4YemhOTEhWVhZLEhIO7Qh5tPALyu5u+FT2Lpo2gQiHjXYd\nO/Jvm40uFyTy+efh+W9QncqxowlV3aXbowAHECSIg++jorAGN7wh9lVV1QotgJ9/PvbrOZGpQuv4\nNHjwcLLpytM0g5Zdaz1Prz436hCR8FOgFWaq0BIREakboRBk4b59VQo9mjUzl+ecA5ddZloPv/7a\nXF5zDVx5JYwfD6tWweDuKdwRDV27mvu3bwennw6dO8Hcs+C0qBRuuAGGDzdBxPz5sHOnCba2fJTC\ntTmwefNBmvhziCiykZcHeb4ixgSDbASCAT//yfOT54PfYafjNxu5akjZ6qtxQ4YwIz+f6OKWx2ib\nCb+OFiB1xuxu6CzI4fvIAwCs8/mwBg9m8NB+bNhQtTliR1LdyrGqmJiczHynBx+xWJafIkcsz3o8\n3J7U8IbYV1VVKrSaNoWTTjI7eMqxowqt41N+fgRwG/twc955t9W6Oqs2m3yISMOjQCvMFGiJiIjU\nnYnJyeweNixsoYdlwcCB8Ne7zeB5CzN8vm1baF4ciC1xwP+sTuT55+HVV80A8/R02LzZtI0tWj6N\nT06DJhG76eAClxOckWCjgCXASGAM8BKFEDQVIlOBze/PwLLg0Uch7pxU2nyeTl+/HX8AAkGzw1d/\nu73SAKn07oZ7LLO74ZsHfyGrqIhFsbHcnpRE797mDfy339b8NapJ5VhVuN1uWl04h6cczXG5WvBP\nmldYdXe8OHDA/F7YosXR73vmmebvz7FSm/bQxlLRogqt49OBAwDDgRG0bVuz6qwpU6YwYMAA+vbu\nzQ8LF9I/M5OtTz5J3969GTBgAFOmTAnnkkWkDinQCjMFWiIiInXH7XYz8/HHwx56VDR4Hkoqnc6P\n74dlmetcLujWDaKjTfvYxZfG475qEJkdY9lrmZZHhwM2OBwcBM632XjWgtHOCCIjTYj2eAS4zpwF\nwF13Qe43M0gAioo4tOuf12vefCcAz1RQXVB6d8NAZAe8WNxCEeN37ToUDPXsCTYb1GbTwJpWjlWJ\nI54vPINZ6mrCauuy47bVEEpmYoVmZB1J166wadOxW0tt2kMbS0WL16sKreORCbQiiI19iAMHalad\nFRcXR0ZGBsHNmxnv9+P3+5ng9xPcvJmMjAzi4uLCumYRqTsKtMJMM7REREQah8oGz1elGmxicjIv\ndujAwehoDgYCeINBFrtcXB8VxYeBAJbdTm+7HYcD1kX6+fncHny9aSwFBbBsGYxJTuL/OU11mKN4\nDlhEBBT5YY4fTh04i1Gj4Pnnza6Mod0NezldbNkK+/Y3wd+0GV2CQToBweIBXU2bwlln1TzQCrUa\nXmw3lWPePPDlw0VW5ZVjcHiVT2VVPzt3wsm9kvmi1zB2eJMoKKjZOhuC7dvNZadOR7/vWWeZQKv8\nHLVwqE17aOjv1biYGIIrV7IuLS38C6wjqtA6PplAC1q3Nv8Na2L48OE4c3KYXFhIVPEnEVGWxZ2F\nhThzcmo9l0tE6o8CrTBThZaIiEjjUNXB80c69tXWrclyOHgcGNu+PSefdhr32u2MstsByA0ESHY6\nWbh8OWBCq9//HqbdP47tPbrzX5sfp9O0LUZGwH8tP+8EevDs82NZsgRuvBH+9je4d3QKV/xqhpDn\n5EDnztDl9JLdDZekpBxaW58+8OGHUPy0quWZGTOYgml/LMg3AYzfD3k+mBKouHIMDq/yKf+91+tl\nxt8nsX69l9693Yyb9jjg5pdfqr/GhmL7dlOZ167d0e/brRvk5paEYOFSm/bQUAvrhICNXbthTL6N\nRYmJZULIUCvXoEGDDvvT0Fq5NEPr+BSOQGvD+vVc7nBwtmVRVGQqXwHOsSwut9vZUJuSVRGpVwq0\nwkyBloiISONR3cHz5Y+1LruMt5o3Z33TpvRu2pQnbTYunzKFh4urBGYAo+bNw+PxHHZ86ooVJDud\n5BYnT7mBAA82cdK273IuughuugmGDYNnn4XVm6Yxaxf88AM0cYMnFuy2kt0NRyUmHjrvuHFmXtNz\nz1X/9RidlMQjmIr0QNAEAqHfex4qgjGzZh12TPkqn8WpqYdV/cyfPp2Wby+D7Bn061fSphfugKcu\nbd8OHTqY6rqjiY83racffxzemVW1aQ+dP306N/+aTdYvNnbtgv17bIzYvZtzo6PZXDzwKy4ujszM\nTPbt23fYn8zMzAbVylVRoNWkSc1DEqkb4Qi0lqSkMLl5c2w2BwUFHKr8tDscTI6JKRP4i8jxRYFW\nmBUUqOVQRESkManN4PmJycn8ds019LzhhkOh2Iw5c9jWvTsPFxSwvUcPRo4dW+GxHo+HkXPnHqqu\nmQGMfmwea9Z4+OQTWLIE3n3XBCf/83w8OecPYlesj1NOKTlHaOZX6SAuPt7sznjvvWY2V3WMGjeO\nH87qzkeFfhwOsNsgwgGf2f28G+zBn64v+1xCVT63Fwcqf8NUCI0OvT42G/+49VYK33+fG+wxDGYl\nEbY0Tj3VhGUbNlRvfRWpr6HmP/5oKuWqIjYWzj0XVq8O38yq0u2hQaCwCPyBI28sEBIKIWN3udi7\n11yXmwstvv+eKwMBrjr3XMC0csXGxlJYGCQ/vyRwCAaDxMbGNqhWrooCraZNSwITaZgOHDCtoc2b\n1zzQGjltGv+2LJo3bwmYDwiCgQAtW7bkWcsqE/iLyPFFgVaYFRaqQktERKQxqc3g+dCxd82eXSYU\nS12xgg+6dz/UaliZUePGHTX8atsW/vIXePXDZP63eyz+iKPP/HrwQTOvyu02wVZodlNeXuXDyZ97\nDq64At7+cgV34yTfXlI59kCUk5+t5TzxBOzdWxKUhQbVu4sDrdzdGUzPz+eZjAwAnMC1W7di7dnD\nwQMwOdLGaw8lUlDg5dxzaze8PqS+hpp/9hlUp0Dp8sth2dI0CNPMqlB7KEBhcVWKz3fkjQVClqSk\ncDOwb7+pHOvSBfxF24gOBrkHaJOfz/gbbyQiIoIJEyaweXM+GzeavzuFhZCfn8+ECROIaECf8lYU\naEVHm6BOGq4DB0zwWJtqulCl7bcRUYADCGK3O/g+Kqralbci0rAo0AoztRyKiIhIeeVDMY/Hw4oN\nGypsNSyvquFXdWZ+nXGGCacAHnoIEhLMDo1utxlQ/tlnJpT6+GN4+GEYPNi0OG7fDtdf72Hw5Lkk\nFe/yOAO4+bF53H67h8REU23UpQvcf08aOW+sosN+Fz9th40bD+LLzKFfkR3frzm8teUAmbt2MTgQ\nwJGbS9r+A3iibYzJzmbBjBnExcG6dVV/jStSX0PNf/7Z7HL4u99V/ZihQ7202p/IqIPm1/OJtsNn\nVlVHqD3UHzDVWXa7CaeK/DC7kvbQkL/cNY0p6ebr00+HKJcPN3tpDywCkoGvnn+ezZs3M2TIcPLz\nYzGT1SAjo+FVZxUVmd/RK6rQ8nrNHDhpmA4cMMFjbdtDJyYn84Tbg49YwI8zJpZnPZ4aVd6KSMOh\nQCvMFGiJiIhIOFUn/KrOzK9XXoHffjMVXvPmwTnnwC23mEHm8fEm3LrkEpg2DVatgqQk+OYbeOkl\nmDPv8MqxuXNh1ixzrm7d4N+zU7h0G+zaBd6DYA/spo3dBCo3B+G13F/w7cnBFbQxIh/eKcggOhr6\nuFwEV66kc8c0tmypvGLsaMq3O9Y2IKqONWvM5QUXVP2YtKXTuS8iG+9es163rSTcq4lQdd8HPj82\nGzgjwR1lNhZY5aq81RXg2y3xLCsaRLrdR5MmsG3Tt3QAPgcsoD8wG7iuVy+6do0AJnDaafm0bQu/\n/prPTTc1vOosqLhCq/Tt0vAcPGj+LaptoOV2uzn993P4J82BFjzrbl7lTT5EpOFSoBVmmqElIiIi\n9amqM7+ioiAmBmbOhMREeOcdSE2FX3+F224z9+nWzbSp/fADTJ9e9vjylWORkXDffTB5MnzwASx5\nfxqfdYPzzjPnOfnUtuREmjenL7hguDNILODLh6cD8NfWbYiNNeceA2xbk0J0NLzwQs1eh/Ltjk7g\nio0beeyee2p2wmpYswZOO80Msq6KdWlp2FavYmBrF7/tNTtVggn3/O+9x/jrrqtREJf87xUkFreH\nWpZpD01yOtmSt5zKTldQAA88ABf9MZm038Wy9acfiQ4GsWGqs4r/anApcLHXy2+ZNzJw4HDaOSod\ncwAAIABJREFUto0lJiZAMBhLx44NpzoLYPduc9mqVdnrQ4GW2g4brrw8829VOAb4N2sRz0oG8zJN\nyDznMrUaijQCCrTCTDO0REREpD5Vd+bXuHEwezYU5z7ExMCCBfDLL7B2rRnIXHrQfMjRKscuHRxP\nxNBBrPf5AGjSpAnBZs34xO/HataMwV06csAFG+wBHC2aMahDU4q7GFkEjL43kRtugEWLzLD0X36p\n+msQajXs7XIRCJqqsMxdu+h78CDZL7xQ7dbD6g6WX7Omeu2GS1JSGI0JXJo1g+9/MLOuAK7MyGBX\nDWeAvf66h3TbXGYV77Q4AxiSMA+/31PpwP1nnjGtpbNmmRbWlN9+ow0wHxgLhP5WBYG7gdN4kfff\nj+DWWydw8GA2TucEvv66YX26G9ots1Onstc3bWouNRi+4SodaBUUmPbRmtq3D5ztknmaYfQeolZD\nkcZAgVaYqUJLREREGoN27Q5v0aquicnJLIqNxVs816tpmzYkO52MbtOGJk2akNcsmiecNiZ3anfo\nmNI7M06caFoWBw0ys5x27Kja44YCIjDHbNhwkOD+HFra7YzOzeXxadOq9TyqM1h+506zO+Oll1b9\n/COnTeMZwGbBKaeWrPvXXw/yTG4uMzp2rPYMsF9/Ne2ft91Rtj106n1jiYw0c9LKe/ttU5335z9D\njx6mhXXHWWfxMOZNQ+/i+xXvIcBs4MzLbsRmMzsejhgxgri44YdaLhuK7dtNYNu+fdnrVaHV8OXl\nmR1PQ/8W1aZKa98+6NDBjc/1OF6vWg1FGgMFWmEUCJhdghRoiYiIiBw+qP4JYOQjj/BM8e2vtG5N\n/hlnHLp/+Z0Ze/SADz80g+mjo80g+xtvhJUrj/y4oYAoGISsrAAudtKiuLLjHcvCl5tb5Wqr6g6W\nf+klU63/xz9W6fRAyeyzdT4fdpt5A78/J8D7O3bgjmhG76ZNqz0DbPZsc3n33WXbQyMjoWVLuOsu\n+N//Lbl/MGh2v+zbF55+uuT6d9av5992O2eXO/9HwEdRbt58bzEAERERPPTQQ4wcGcHbb8P771f9\n+R9r27ebMKv87+ihCi0FWg1X6QotqF2g9dtvpgK1aVPNTRNpLBRohVGoBNZur991iIiIiDQU5QfV\nj7rllkPf2y+/nGlPPHHEnRkvucTswvjssyboWbcOfv97COVK//u/h1duhR7z/QwfDnbRzioi6LdY\nFwhgb9aMaYWFVaq2qu5g+f374ZFHTIVT8+bVe51KV7N16AARrl940w5Dctuz97fKh8R/9x389JN5\nbDC/j375Jfzzn+Z183gObw9NSTH3fest2LbNfCg7c6Z5badPN3POQtxuN8vS00kCQp15B4BE4LUv\nvzjseYwbZ1pUly2r3vM/lrZvP7zdEEoqtNRy2HCFAq1Q+FjbCq3mzc259N9cpHFQoBVGoS1/HY76\nXYeIiIhIQ1J+UH3p76u6M+Pvf29meqWnw9lnw2WXmTe6w4bBiBHw889muH1oXtJtM5OZmunAZdtP\nswgbB4JB/hVwcHu7dod2UjxatVXpwfJ7fwPvb5XvPJifb6qy8vPNjpDVVbqazW47yGJymHZaR9rE\n2Pj5Z/AHOGzd+flm4H6XLtC9O2RmmoqsXr3MGIyJEyt+rBEj4G9/g6eeMuGT3Q7JyTBnDgwZcvj9\nzzzzTM4dMYJ7Mbsc3gP0HDmSM88887D7WhZcdBF8+mn1X4NjZfNmM6S/PLUcNnw+X/gqtHJzzYw6\nBVoijYcCrTAKVWgp0BIREREpUX5Qffnvq7ozI5jfs5580oQ2l19uZiOlpcHAgaby6JJLYM8e+POf\n3WQWNeNVB9gd8C87XFrQHoff/Po7BjNrqzKlB8vn+UwV1E8/QdtsF/vfWMmaT9IIBk2rnt9vKpzS\n0mDp0oqrgaoiFO49tmMHzaKj6dO0KR07mt8xv/8efs0qu+633jLHXXihGZrftq2pEAMTVMXEVP5Y\nY8eaIfQtWpjvu3aFI40WW/jcc3wUFcVs4BO3m4WLF1d63/79zRyxrKyKb8/KymJIz55kVXaHUqo7\nkL/8sTP+Pon0dC89ehx+u9ttAjiFGw1X+Qqt2oSPOTkKtEQaGwVaYaRAS0RERKT6qrsz4/nnw8cf\nm0Bnxw4TKG3dauZXZWZCmzam5c1qlcKXzaNJLSoiskUzzrY3ZdN3sG8/PJoD192RyKJF8PXXZc8f\nDMLjiSn8PgO+/c5UhTns5rwZGXDpjzByUArR0WZ4vsNhqpvuuMNUJ9XGxORkfhk2DEebNgA4I6Fz\nZ1OZsn07TN8B105KJBCA1NSSaqidO02V1sknw+uvm9ljR3LeeSYEy8yEl1+G9947+tpe/fJLnnE6\neeWLw1sNS7v8cvMaVjZHa9yQIQxMT2f80KFHfczqDOSHsgHY/OnTafX2Mtx5MyoMtCzLhH7Z2VU6\ntdSD0FD4Zs3M97UJtHJzTVWeAi2RxkOBVhgp0BIRERGpW+3bm8Dpww/h+uth4ULTXvbJJ7BtRzzn\n3XADG5o25e8d2nFWN4iIhDe+95G6bTAXX9qPsWMhPt6EYTt2mPPcdhu8+Mk0Htxj3lA7ndCtO7Rv\nZ0KQRUC/qxOZOZNDQcmECabdr7bcbjf/euUVIi67jHU+HwCxLaBnT/jW7uOV3wZz5R/7YbfDBx+Y\nxw29DmvXmva6q682wdbROBym3fC666p2/zPPPJOtPl+FrYaltWsHcXGwZMnhty1OTaVLejoJkZF0\n2riRxamplZ6nugP5oSQAu/eWW7BWreIGRwyDWUlRfsXHduhggj1pmEIVWqH20Jycmp9LgZZI46Po\nJYwUaImIiIjUvW7dzB8wuyDeeGPJbXfNns3kDRsgNxdnJLTpFOAfW2K5ZUoSRUVm7tWCBXDDDSXH\nREbCgEHxBAKDKMpYQU+nC3vxx8CFXX2cO3QoifPMrK/Jk0uqwsJpYnIyk9eto3tuLm6bDV8wwMfn\nx/LPSUmsW2eqimJiyq7b5QrvGmpj6lQTMI4cWRJsZWVlsSQhgeJOSZKAPyYkMOzqqw8NrA8JDeR/\n1Gbj4EEYVWRjZmIi3Zcvr7SSLxSAjWnWjElvv018+/ZkZ0eTEGUjdV4ilw46/NgOHUx1mzRMpXc5\ntKyaV2gFgybECgVa5TeSEJHjkyq0wki7HIqIiIg0LKWHrQOkRgR4+pMUZs92M3cu/O538MIL8Pbb\nZsD8HXeY9r6VK+HZd5J51hNLPuZYbyDAv1vG8vdZJbO+bLbwh1kVrXt+IMCtj6Zw/fVuHnnE7Pr4\n2GPmTX5DdO21cP/98D//A2PGQGEhDD9/CPfn5RNdvGtktM3G9Pz8ClsPQwP5o2w2vtsEO7+38ddf\nKx7ID2V3pMzctYsZRUU898suMvcHaO+pfJh/x44KtBqyUKBls5kgqqYVWl6v2c1TFVoijYsCrTDS\nLociIiIiDU/5nRTPjy+7k6JlwVVXwbvvmpAo9LtcRaHS2JSUKs/6Cve6K9sBsiGyLLjvPjMg/5ln\n4KQmqXTblk6fQjuFheaD4CDQ324/rPWw9ED+PRkl52yfXfnulKEALJiXh5WTQ0u7nb8WFPEau4iJ\nOXyHyJAOHcwOmdIwhQItMHO0alqhFTpOgZZI46JAK4zUcigiIiLSMFVnJ8XS6jtUqum6G4LISPjx\nR3juOWhXOIOE4usLCiG/wFTNFBbC5CJ4plT11JKUFG7wmWqcX3ZBm9YmeNqTCX/2Hr47ZekALGv3\nbloU7z7Z028jxsrh6wKTXlS0s2XHjqZl9ODBY/lKSE34/ebvR6iVNjq65hVaoeO0y6FI46JAK4wU\naImIiIg0TNXdSbG0+gyVarPuhsBmgxEjYNyDSSxwQYTDVNy4XGC3mXDrwSJYkzGLFStg40YYeOM0\npm6GLVvN7pJt20HrVuaYh/bAqMTEMo+xJCWF0cVf+/xt2ekDb55pMRvvgCUZpsxrEYcf+7vfmcvV\nq4/xCyHVVrwnwqEKrehoVWiJSFkKtMJIgZaIiIhI43O8h0oNwZR7xrGte3fS7H5slgmznC5Is/lZ\nRg/8jGXoUDj7bPjTtfGsZBBf46NtO3Nfy4KdLXy8kTOY3Lx+fPSRqfD66SeIu3Iaj+dCkR9yDzQh\nh2YUOQJEuWCxA0a1acM6n6/CCrvTT4euXeG11+rlZZEjyMszl6VbDmtaoVU+0MrNNVV8InJ8U6AV\nRgq0REREREQqlrpiBclOJ7nFM8kOBALMbupk+cblfPQRzJkD//43XHIJpL6ezJr4WJrGlgzkf71L\nLKf1S2LAALj0UrPzXZcucPPYeP714yBe/taHZcFZPdqxz+VgbdCP1awZ3dxuFsXGVlphN3o0vPQS\nbNpUs+fl9XqZOWkSXq+3ZieQCpUPtMJVodW8ecmuhyJyfFOgFUba5VBEREREpGIej4eRc+cys/j7\nGcCoefPo3t1D//4wbRqMGgUffghXX+1mwryyA/nHP5LCu++66doVLrwQevc257EsOOfSZGYXxdK8\ndQCn04a7XTtmORzc3q7dUYf5jx8Pp5xi2g8feQS2b4ePP67685o/fTrtli2rdAdGqZnQXLPQf7Zw\nVWg1b26+3r+/dusTkfqnQCuMtMuhiIiIiEjlRo0zrYcPFxSwvUcPRo4dW+l9KxrIHxsL334Ln34K\n69ZBQQHs2QMffODm2f/M4Y3WJgB7JiqKU6+6iv/JyTnqMP9mzeC//zWVYQkJ0Lmz+Xr9evj8c5gw\nAV55peR3/dJCA+nHxcRUugOj1EzpEAogJgb27av5uWw2E44p0BJpPBRohZFaDkVEREREjix1xQo+\n6N6dhcuXH/W+FQ3kt6yS2yMioGVL83X5AGzO009XeZh/ixbw+uuQmgp33gmtWkGfPqYKbOFCuP56\naNPGBGm5ufDrr6bVcFFiIrfbzFuqiTYbixIT1XoYJuUDLY/HvO41kZNjzmNZJYFWTau9RKThUKAV\nRgq0RERERESOzOPxsGLDBjwez1HvW92B/KUDsJoM87/lFnj0UUhLg1tvhRUrTIgFkJUFF19sKrrO\nOQemjp7O8B+zcfjNWyq3zcaY7Gy1HoZJ+UCrZUvIzja7V9bkXKHzNGtmLlWhJXL8U6AVRgq0RERE\nRETqT7h2pDzlFHjiCbj8cjOvq7DQtDb27g1xcZCZkUb2y6uI2eni669h209ml8U+LleFrYdZWVkM\n6dmTrKysWq3rRBIa2l460PL74bffqn+u0oGWWg5FGg8FWmGkQEtEREREpPFxOEwb4tq1ZrZWfKcU\nxgCnnmpaEbOzYcMG2Po9jCyEJSkpZY4fN2QIA9PTGT90aP08geNQaO5VaJfDUGtpTdoOSwdaTZua\n1kMFWiLHv1oFWnfeeSdXXXUVL774YrjWc1zTLociIiIiIo1XaH7XQ89O48POZlB5h/bQrRu4nCYk\nmfwt9Lgs8dAxi1NT6ZKeTkJkJJ02bmRxamr9LP44EwqhQq95uAItm820HSrQEgmfF198kauuuoo7\n77yzTh+3VoHWY489xtKlS7nhhhvCtZ7jmnY5FBERERFp/C6+NJ5m1wxivc8HgDsKevSA3E4+Pmsy\nmDvu6sdzz0FmZhZLEhKYWXxcErAkIUGth1VQOoSC8AVaYNoOFWiJhM8NN9zA0qVLeeyxx+r0cdVy\nGEZqORQREREROTFMTE5mUWws3uIp5d5AgJc7xbJoaRI+H9x0E1zebQj3HcynSfHbrmibjen5+Y2m\n9dDr9TJz0qRjsrNj+RCqRQtTXVWTQCsnp2QYPCjQEmksFGiFkQItEREREZETg9vtZsycOSwoDrTm\nBwKMTUlhwAA3q1fDjdenEp+dzvl+Oz4fFBRAIAj97fZG03o4f/p02i1bdkx2diwfaNlsEBsbvgqt\nnJzar1FE6pcCrTBSoCUiIiIicuLoEx9PcNAgFu7bhzV4ML379QNgwADY8fEMEorvZ7NDYRHk+yAY\nhATgmUpCoIa+I+KUKVMYMGAAfXv35oeFC+mfmcnWJ5+kb+/eDBgwgClTpoTlccqHUGDaDtVyKCIh\nCrTCSIGWiIiIiMiJZWJyMruHDeP2pKQy149OSuIfERARYQbGR7lMhVZeHszxw+hZsyo8X0PfETEu\nLo6MjAyCmzcz3u/H7/czwe8nuHkzGRkZxMXFheVxwhloqeVQpHFSoBVG2uVQREREROTE4na7mfn4\n47jd7jLXjxo3jp/P6U6azewcZbOZUGuN5efNwh6s+njsYW1vx8OOiMOHD8eZk8PkwkKiircgjLIs\n7iwsxJmTw/Dhw8PyOL/+Ch5P2etatoTqFq4FAvDbb2YGV4h2ORRpHBRohVFol0ObXlURERERkRNe\n6ooVJDud5BbP2TpIgDnRTs69YjnPPWcqhZ580tw3K+v42BFxw/r1XO5w0MOyyMszs8EAzrEsLrfb\n2bB+fVgeZ88eaN267HU1qdDKyTGhVulASxVaIo2DopcwKioy7YbFH1SIiIiIiMgJzOPxMHLu3EMh\n1Qxg1Lx5vPyyh/vvN9fdeiv07g392hXviGjZKCyCptXcEbEuZm95vV4SRoxgQnQ0BB0Eg+Y9UEE+\n2B0OJsfEsCQlpdaPEwyaQKtVq7LX1yTQ2rvXXMbGllynQEukcVCgFUahQEtERERERARM6+G27t15\nuKCA7T16MHLsWNxuSE6G7dtNW92Gz1O5rNDsiBiqegr4q7cjYk1nb3m9XmZOmoTX663w9lBQtmPH\nDq678EKu8Pm4a88eIiJaAqbyrMgfoGXLljxrWYxKTKzW41ckJ8e8BuUrtFq3hszMks6YqsjONpcV\nVWgFg7VeqojUIwVaYaRAS0REREREyktdsYIPundn4fLlZa4/+WTIyIBuzpIdEUPNHoWFEOTIOyKG\n1Gb21vzp02m3bBkLKnmMUFB2zXnncVF6OoFAgE5BeNkbJMLhIDIyCDjYHBFVZqfH2tizx1yWD7RO\nP928Lj/9VPVzVVahVVRkBvSLyPFLgVYYKdASEREREZHyPB4PKzZswFN+yjlmQ6m7/l8SC1zgdkOU\nG5xO8AfAlwezi+CK22exbh2ccw5s21b2+NrM3lqXloa1ahXjYmIIrlzJurS0MreHgrLJdjv99u6l\npd9PICeHC4qa83ZgL8GYkwgG/fiI5XGn57CdHkPrq24rZGWBVteu5nLTpiqfqtIKLeCwofwicnxR\noBVGRUXa4VBERERERKon1Jb4id+PBTjs4IyE/wT9vFXUg0f+31juuQe++QbGjIHdu8HnM4HMiIuH\nMCM/nybYKPJDdBVnb3m9XhYlJnJ78Y5WE202FiUmHmo9LB2UFRYU8CDwvN/PNXkB3tyXwZ3uFswi\nj9jYFjwV0ZyNBSlERbkPe5yatELu3m0u27Qpe3379tCkSfUCrb17TUBYehPKUKC1b1/VzyMiDY8C\nrTDy+1WhJSIiIiIi1Vd+R8Q8W4A5zZy8+9VygkFYtQqGDYMPP4R27aBzZ2jRPJVTv0snLt9Ong/y\n88GXD78Llsze+ukns8tfefOnT2d0VjZFB20EguC22RiTnX2o9XDcEBOURRYW4ggGiQamA1MpYBxF\nbIvMo5Nl8YTNRpM/Xsa3m/uxdm3Zx6hpK+QPP0BMDJx0UtnrbTY488zqBVpZWabdsPTGXS1bmsvy\nA+aPNk9MRBoWBVphpJZDERERERGpicp2RDznHA+ffQavvAJLl8KaNbBoEVxxBZzCDKYWBzWWZSq7\n/H7IL4C/++DB8TPo0gWuvRa++AJGjIBrroFV75lWw477XGzZYm7buRM8u118+chKepw2jZO/Tqd3\nvgV+P6EmlIuBLgT5wVZERH4Ol0VHs87pJGVREu3awSOPlAxsr00r5I8/wimnVHxb167VC7S2bzez\nykoLtTKGWhtDjjZPTEQaFgVaYaRAS0REREREaqqiHRHBhDvXXmsqlC64AEaPhqefNrO35juhiRvc\nUaa1LirKnGuuDXZFzgLgvfcgLg5eeAHeeANuHpJCr6/gl13mvjYbZOyB7L0wBvD/8DiTCgEKcWBR\nejPABGBxoIixwGNZWcx+4QWio90kJcFrr0G3bvDgg/DXgUO472A+7uK3nFVthQRToXXqqRXfVt1A\n68cfoUuXstfFxEBERNlA62jzxESk4VGgFUYKtEREREREpDYq2xGxIuMnmgDs41BZFGCzYL3TT0av\nHmTtH8uBA7BjB7z5pmm/mzsXilpOY1Hx/bt3h17nQY8eZkbVZ91h6K138Ahgs0XgL9WqZwFzgTEO\nB/ODQc684opDuxqOGQOTJ8OWLTDjvlRO/jqd8/12fD7TBhkIQH+7/aithwUFkJ4Op51W8e1du5rn\nUdUZ89u2HR5oWRa0alUSaB1tnpiINEwKtMJIgZaIiIiIiNTGkXZErEj52Vu5gQDJTicLly/H5TJD\n1Fu0gD/+0cySmjIFdmfGc8q4QeSc7CPKZc7jcsLOGB+RQwfz6BNz2B3Xnf+LCILdTtAyVVofA9st\nizPsdtbExjLnqacOrcOyIDHRfH0KM5iKqRZzRkKguA0yiKnweuYILX2LF5uw6i9/qfj2s882l19+\nefTXpqDAtFKWD7TAtB2GAq3506czNjsbd3GgVX6emIg0TAq0wki7HIqIiIiISF2qbPbW0QKxex9L\n5pXOsXiLgzBvIMCi2FhuT0oCSoKyfIeDIsviADATeCwyklkOBzOfew63u+yuhi1bQl4e3P1kEvNd\nplrM4YDISFOh5fXCnCIYM2tWpetavhwuushUjFXkjDPMLoXlB9BXZPt2CAYrnscVCrRCrYa9XS5y\ncuHgQXN7H5dLrYciDZwCrTBShZaIiIiIiNS1ymZvHYnb7WbMnDksKA605gcCjE1JORRSlQ7KHJGR\n3GdZXN20KfODQU79wx+48JJLKjyvywU3jy/bCmm3mz//wc9yWw9uGlPx+lavNq2RF11U+bptNujT\nBz777KhPkW3bzGVFFVrt2pnqrSUpKYwGCgtNu+R3m0oG24/B3C4iDZMCrTDy+xVoiYiIiIhI3avO\n7K2QPvHxBAcNYuG+fViDBx+ahxUSCsrmFRWxvlUrHK1asaVHjzKthkdaT6gV0rKgMCLAg24nWwuW\nY7PBjTeaaqhgEN55B/bvhzvvNMdeddWRz92/P3zyiSkoOJJt20yQ1rHj4bedcoq5feS0aTwD/PZb\nyW2hKq1FwKhQH6WINDgKtMJIFVoiIiIiIlIfqjt7K2RicjK7hw071GpYXigoe2ntWvZccQUvfvrp\nYa2Gla2nfCvk2Mfn8cILZn3PPw9Nm0Lv3ibAuuAC+OYbWLLEVGAdycCBkJMDH3xQ9vqsrCyG9OxJ\nVvHE+G3bTJhV0Xu0U06BvXvh9LNMqPfpfh9Nm5gA7MABWOfzVRjyiUjDYQWDwaPfq/xBltUL+Pzz\nzz+nV69e4V/Vcermm02Z6po19b0SERERERGR+nd17970++or/q9nT15ftw4An89UYz35JFx/vQmR\nXnjB3H/PHrMD4ZEUFcHFF5sZWT//bNoQQ48V/9VXfFb8WMOHm8qr1asPP8fatdC3L3zxBZx5ppcL\nY4fyUnQuwTwbhY4AC86J5tHly6sU3omI8cUXXxAXFwcQFwwGvzjWj6cKrTBShZaIiIiIiEiJiloh\nXS547DH4v/+Dl14y1Vrvvw+bNh09zALznuuBB2DXLkhPN9ctTk2lS3o6CZGRdNq4kcWpqXz5JZx7\nbsXnCA2K37IFCgvdfOWbwzNRAZxOeCy/7DwxEWmYFL+EkXY5FBERERERKRFqhSzP5YLzzy/5fvDg\n6p03Pt7snvjqq9C2bRZLEhJ4q/i2JOCqKQn8mHs1vXpV3ILp8Zh2xPXrwbIgQDzWZYN48fW3WMmf\nWKRWQ5EGTxVaYaQKLRERERERkWMvKsq0LT7wAFxx7hDuPZhPVMC8vW2Cjbtz8+nIUPr2rfwc/fqZ\nKrE33oCePeH+x5PZ0HsYP+clHRoMLyINlwKtMNIuhyIiIiIiInXjoYegf3wqvXal09dvJ7/AFBkU\nFsGFlp2rIzfy3w9TKz3+wgvh00/h5ZfhmmvA7Xbz9xmPA26+/77unoeI1IwCrTBShZaIiIiIiEjd\nsNkg8OMM7nOC2w0OO4dCLYcDptngmRkzKj3+uutKvr7mGnN57rlmjMz//d8xXryI1JoCrTBSoCUi\nIiIiIlJ3RiclMc8CC4h0llwf4YC5wJhZsyo9tk0bePFFWLYMzjrLXNe0qQm1tHO9SMOnQCuMFGiJ\niIiIiIjUnVHjxrGte3c+9vuxMLO1olzwScDP9h49GDl27BGP//Of4fe/L3vdpZeaXRf9/mO3bhGp\nPQVaYaRdDkVEREREROpW6ooVJDud5AYC2Cw4SIBkp5OFy5fX6HzXXAMZGfDf/4Z5oSISVgq0wkgV\nWiIiIiIiInXL4/Ewcu5cZhZ/PwMYNW8eHo+nRufr2xfat4fXXgvXCkXkWFCgFUZ+vyq0RERERERE\n6lqo9fDhgoIqtRoeic1mqrTeeAOCwTAuUkTCSoFWGCnQEhERERERqR+pK1bwQffuNW41LG3wYNi5\nE7ZtC8PCROSYUKAVRgq0RERERERE6ofH42HFhg01bjUs7YILzOV//lPrU4nIMaJAK4wUaImIiIiI\niBz/WrSAc8+FVavqeyUiUhkFWmGkQEtERERERKRxuOIKWLbMbP4lIg2PAq0wCgTMAEERERERERE5\nvl17LezdC2++Wd8rEZGKKH4JI1VoiYiIiIiINA7nngsDBsB118Gttx55x0Ov18vMSZPwer11t0CR\nE5wCrTBSoCUiIiIiItJ4TJliLp98El55pfL7zZ8+nXbLlrFgxoy6WZiIKNAKJwVaIiIiIiIijceQ\nIfDf/0JcHDz0EKxdC3fdBX/9K2zYYO6zLi0Na9UqxsXEEFy5knVpafW6ZpEThQKtMFKgJSIiIiIi\n0nhYFsTHw9VXw9dfQ9++8OijsHgxnHceTJ3qZVFiIrcXD1OeaLOxKDGxwtbDrKwshvQ33aE1AAAf\ndUlEQVTsSVZWVl0/DZFGSYFWGCnQEhERERERaXwmTYK33oKlS+H11yEx0Vz/zNzp/HFrNoW5Nrxe\ncNtsjMnOrrD1cNyQIQxMT2f80KF1vHqRxkmBVhhpl0MREREREZHGp0kT+MMf4MorTbXW7NmwbGka\nVzpX4dntYuv38O13kLEH+rhch7UeLk5NpUt6OgmRkXTauJHFqan1+GxEGgfFL2GkCi0REREREZET\nw/JFKTzcFVq1gk6doHUr2LkT0r+Fa3Ng8ZwUwLQaLklIYGbxcUnAkoQEtR6K1JICrTBSoCUiIiIi\nInJiGDltGs8CJ3eElh7o0AGaNoW8PLh3G3z1ayKff25aDWfk5xNd3M4TbbMxPT9frYcitaRAK4wU\naImIiIiIiJwY+sTHExw0iHU+H2AGyJ9+OnyNjw/tg/lPWj/69k6lzefpnF9op6AQAkFzbH+7Xa2H\nIrWkQCuMFGiJiIiIiIicOCYmJ7MoNhZvIABAPgHe6xFL2tYkxo6FU5hBAuAPQGEh+HwQLA61EoBn\nKhgeLyJVo0ArjBRoiYiIiIiInDjcbjdj5sxhQXGgNT8QIOGpFLp0cZOaColPJrHAZTYPszBhVp7P\nhFsPB+EPd8yq8mN5vV5mTpqE1+s9Rs9GStPr3fAp0Aoj7XIoIiIiIiJyYgm1Hi7ctw9r8GB69+sH\nmBbE0ePHsa17d9ZG+IlygzPSHPNBoZ/X83twV+JYsrOP/hher5frLrwQzzvvsEBVXXVi/vTptFu2\nTK93A6b4JYxUoSUiIiIiInLimZiczO5hw7g9Kemw21JXrCDZ6eRAIIDDAX5ngNlNnfzMcgA8Hrj0\nUnjhBdi3r+Lz3zN2LBelp+P1egmuXMm6tLRj+XROWFOmTGHAgAH07d2bHxYupH9mJluffJK+vXsz\nYMAApkyZUt9LlFIUaIWRAi0REREREZETj9vtZubjj+N2uw+7zePxMHLuXGYWfz8DGP3YPHw+D0uX\nmus++ghGjICTToLffoMDByAz09z26Ycf4l+6lCl2O8GcHC7Iy2NRYqJa4Y6BuLg4MjIyCG7ezHi/\nH7/fzwS/n+DmzWRkZBAXF1ffS5RSFGiFkQItERERERERKW/UONN6+HBBAdt79GDk2LE4nXDllSX3\nsSxz2aIFREdD69Zw771eZt90E9OLirBbFhOB53ftYsSvv6oV7hgYPnw4zpwcJhcW4sLC6wVn0OLO\nwkKcOTkMHz68vpcopSjQCpNg0PxRoCUiIiIiIiLlpa5YwQfdu7Nw+fIy12/bBnv2QFERrF0LPXtC\n9+7Fxzw0lr9lZnFS0E4gABFFFqOLikjbu7fC1sMdO3Zw9kkn0Skigs2bN9fVU2s0Nqxfz+UOB2db\nFn6/uc5fBOdYFpfb7WxYv75+FyhlKNAKk+JNLRRoiYiIiIiIyGE8Hg8rNmzA4/GUub5zZ2jVymww\n1qcPfP45fPMNPJKSxhXWMi4utJFfYHZHLCiE8wI2gjk59Dp4kCUpKWXOdX2fPozYt4+YoiKu69Wr\nDp9d47AkJYXJzZtjdzgOBVpBwO5wMDkm5rDXW+qXAq0wCf1l1y6HIiIiIiIiUlM2m2k//Om/Kdxz\ncit+s4HdBjbLXF9QAH/1wyOZmYxKTDx03Mxp0+iTmclUoD/QxOtl/I031tvzOB6NnDaNf1sWLVu2\nJFhctRIIBGjZsiXPWlaZ11vqn+KXMAkFWqrQEhERERERkdoaOW0ab8Y0IbJlM/yRAaKiIDLS3Dav\nIMgm/xXkFf7/9u49zMqy3v/4+x5mQAY5OUjggVQwLcWfGzxAJrk5qKhp7h87apOa9tuGB7Zb00D9\nJQcTHcNdGLbTMstfiJpdGmZt01+aUijspDRS1PKYIjLKoIIcZt37j3uNDMOAM8Mzs9aaeb+ua661\n1vM861n38rq8r/V8+H7vZwR/+hPce+/L3D9nDlcCAbiKVFn0+Pz5th62wOEjRxLHjuX57t2JlAMR\nYjnPd+9OGDeOw0aMKPQQ1YCBVkYMtCRJkiRJWakPV17abTdWl5dTFyNdusCTXev4RVkVL7/3fUaN\nSmtu/dvJh3N1LkcvUqDVE5gNlIOthy00ZdYsfljVj/WxCqhjPVXc0q8f58+cWeihqREDrYwYaEmS\nJEmSsjRl1ix+tPvuVO6xB28C62PkGxXlzLrtJ3TrVgnA/ntP5SRWMSr/npj/+0fgk9h62FKVlZX8\n07RruIHedOu6G/Nib740u5rKyspCD02NlBd6AB2FgZYkSZIkKUuVlZV8+ZpruOWcczitVy+mv/02\ng089lQkTj+HR38P110PlyrlMI1VmNTYNOAF4dP58xq5cudW+XC7HsGHDmDNnTjt8k9IyYM+RPMA4\nhlbewwMbj2Xu/rYaFiMrtDLiXQ4lSZIkSVmrbz28p0cPnj34YK75/vcBuOoqWLgQPnvhBVSTqrIa\nisA1QCVQ27cva9as2epv1apVDB8+vH2/TIlYswZqmMWy4SdSw0xWry70iNQUA62MeJdDSZIkSVJb\nmDJrFm+cdBILHn30g9a3XXeFz3wGZlRXs7R/fx5u9J6Hgd8Dqwh07b3vVvtijFRVVTFhwoR2GH3p\nqa0FqGTKFXOBSgOtImX8khFbDiVJkiRJbaGyspIZc+dudx2nO5Yu5fKyMtbmX78LXAZsBjbu/U1e\nfHEDK1bAc8/BW2/Bhg0bmDx5MhUVFe30DUpLCrRg8OD0aKBVnAy0MmKgJUmSJEkqhEGDBnHcxRfz\ndVKr4eWkNbWOPP10/vrXf+PAA6vYvDmydi288EKkstLqrB2prYWKChg4MHVhvflmoUekphhoZcRA\nS5IkSZJUKPWth9XAb4H3Kiu58cc/pqKigiuumMzgwRs4+GDo0mUD5eWTKS9vujpr9erVHH/ooazu\nxGVJa9dC794pzOrVK71W8THQyoiBliRJkiSpkO5YupTb+vRhTXk5dz7xxAfbJ0yYQFVVFRUVOQYP\nrmLx4gmUlcENN2x7jrOPP54xy5fzlfHj23HkxaW2NgVakNYqe+edwo5HTTPQyoh3OZQkSZIkFdKg\nQYN46u23eWnTJg444IAPtldUVDB58mRqamqYMWMyp5+eqrOqq+Hdd7esGfXjm25i3+XLubiigj2W\nLeOmphKvTqBhoNWzZ/pvpOJjoJUR73IoSZIkSSpWEyZMYNKkSUyYMIFbboEZM+CVV1Jgc+SR8MYb\nq7n1kkuYAWzatIlZdXXcetFFnbL10Aqt0mD8khFbDiVJkiRJxaqiooLZs2dTUVFBWRlceCGcdBIc\ncACsWAFH7X08U9duoHuEUFdH37IyZm7cyBePPrrQQ293tbVp7SywQquYGWhlxEBLkiRJklQqevWC\ne++FZ56Bf5lwE8duWs5RlLFpw0a6xHTM6BDYf8WKTtd6uGYN9OmTnluhVbwMtDJioCVJkiRJKkWv\nLprOpeXQpWwT5UQigVyESGBajNw4dWqhh9iuamqgX7/03Aqt4mWglREDLUmSJElSKTpr5kz+oyxH\nl1hHeQgAxJj+rguBj/Xpw9LFi1t9/pdffplD+/Xj5ZdfzmrIbaqmBqqq0nMrtIqXgVZGvMuhJEmS\nJKkUnXH22TzSvTu/i5EQIOS3P0KOZ8u6851+/bi1urrZ57v44osZPXo0Y8eOZezYsYwbMoTP19Rw\n7JAhjB49mosvvrhtvkgG6urgrbe2BFpWaBUvA62MeJdDSZIkSVKpumbBAv5vWRnv5HKEMlhHjlmh\njAvr9uc/N8IZ06Y1+1zDhw9n1apVrFixhj//4SmO27SJrwFjN21ixZNPMnz48Lb7IjtpzZpUmdaw\nQstAqzgZv2TElkNJkiRJUqkaN348e40ezRUhEIDpIXD6HnvxevlmbvzbOBb+cgQjR6bqpQ8zYcIE\neveu4tVXNzBozSquzG+/CtirpoYjjjiiDb/JzqmpSY8N19Cy5bA4GWhlxEBLkiRJklTKfvjzn/NI\nZSXX5nK81L07E/tX8dBhVfQePJMrr4THHoNTTvnwiqWKigoOPHAy+/A01UDP/PaewDXAaUcd1arx\n3XYbnHpqq97abPWBVuMKrfplhlQ8DLQyYqAlSZIkSSpllZWVXPPTn7KgWzdu3H9/vpPLcc63qlmw\noJKrroIFC2DRIrjrrh2f55VXYMEtT3ASdYwCYv4P4JiyMg5btYoZrbhz4qRJcM89LX5bizQOtPr0\nSS2Ith0WHwOtjBhoSZIkSZJK3bjx4/n8+efzs3ffJYwbx2EjRnDIIXDZZfD5z8MnPwn//u9w551w\n/fUp7AGYPx+WL4eNG+ELX4CPxu9wKVsWmAeIBIgwLUZ+PnduIb7eh2oq0IK0tpaKi4FWRrzLoSRJ\nkiSpI5gyaxavn3gi58+cuc2+G26A3XeHiRPhggvg8cfh5JPhi1+Egw+Gbt3gd7+DoyZdQHVIcdaW\nUCuQi3B1CHz2oova7fu0xOrVqc2wa9f0unfv9GigVXwMtDLiXQ4lSZIkSR1BZWUlM+bOpbKycpt9\nhx4KDz8MP/whhACf+xzce2/a96lPwRFHwHXXwQ9+Us2S3Xfnt6R2w7IQKAvwW3Is6tWf6bNnt+dX\naraami0LwoMVWsWsvNAD6ChsOZQkSZIkdQZ77glnnglLlsD3vrdl+yOPpJCr3h1LlzJxv/24v66O\nniHwbi7HNLqw19FLdurzN2+G8jZKM2pqtrQbwpZAq7a2bT5PrWc9UUYMtCRJkiRJncns2WltrVWr\n4L33tg6zAAYNGsRxX/0qXw+BAFweArsc8TWWLRv0wdpbrfH++zs17B1qHGjZcli8DLQyYqAlSZIk\nSepM+vaFq65Ka2o10Z0IwIzq1Hp4TS7Hf/fvz1cvm83f/w5PP936z23PQGuXXdK6YAZaxcdAKyMG\nWpIkSZIkbeuOpUu5vaqK25csYfRo2G8/OOEEeOml1p1vw4Zsx9dQ40ALUtuhgVbxMdDKiHc5lCRJ\nkiRpW4MGDeKPq1czaNAgevZMi8pv2JCqu1qjLSu0Vq1KFWcN9enjGlrFyEArI97lUJIkSZKkD7f3\n3nDuuTB/Pqxf3/L3t1WgVVcHb74JAwduvd0KreJk/JIRWw4lSZIkSWqef/5nWLcurb31+9+37L1t\n1XL45pup+2rAgK239+5toFWMDLQyYqAlSZIkSVLzHHBACrV23RXGj4fXX2/+e9uqQuuNN9Jj40DL\nCq3iZKCVEQMtSZIkSZKaJwS48860MPz69XDHHc1/b1tVaK1cmR6bCrRcQ6v4GGhlpK4u/Q8ZQqFH\nIkmSJElSadhtt3THw0svhWHD4JOfhAcf3PF72qpCqz7Q6t9/6+1WaBUnA62M5HJWZ0mSJEmS1FI3\n35xCqmXLYPFiGDcOfvObrY+Jccvztgq0XnkF+vWDbt223u4aWsXJQCsjdXXe4VCSJEmSpJaqqoKz\nz07PN2+Gww6D006DK69MFVu5HGzcuOX4tmo5fOEF2HffbbfXV2g1DNVUeEYwGamrs0JLkiRJkqTW\n+O53010Pu3SBhQvTcj5XXJEqtubMSWFTvbaq0HrxRdhnn2239+mTgrb169vmc9U6BloZMdCSJEmS\nJKl1unSB7t3T84ED4a674F//FXr1gqlTYcSILWtWt1WgtaMKLbDtsNgYaGXEQEuSJEmSpGyMGAE3\n3QRvvAETJ6a7DB5/PPTsmdbayuXgoYfSYxaeeirdcfHAA7fd17t3ejTQKi4GWhkx0JIkSZIkKVu7\n7AKTJ6fnZ58N06aloOvUU2H0aLjssnQ9vrNuuAH23hsmTdp2X32FVm3tzn+OsmOglZFczkXhJUmS\nJEnK2qc/naqxTjkFLrggbVu4MD1WV8M3vrHzC7Y/9hiMHQtdu267z5bD4mQEkxErtCRJkiRJyl4I\ncMwx6bFHD7j22rTO1m9/CwcfDDNmwAEHwGc+k1oUly1r2fnXrk0thyNGNL3flsPiZKCVEQMtSZIk\nSZLa3iWXwGuvwahR8PDDaeH4556DX/wCBgyAYcPSeljN8fjjcNBBqetq7Nimj+nRI13vG2gVFwOt\njBhoSZIkSZLUvqqqUnXV6tVw9dVbtjd83pS5c1PF11FHwauvwp57wj77NH1sCKnt0DW0iouBVkYM\ntCRJkiRJan+DBqVga9q0VEU1ezbceCNcfDEsWrTluN/8BhYsSOttXXll2lZXB3//OyxZsuPP6NPH\nCq1iU17oAXQUuZyBliRJkiRJhdS7N5xzTrr74XXXwfe+l7YNHQr335+OWbgQamrS82HDYI89mnde\nA63iYqCVkbo673IoSZIkSVKh9ekDf/hDCqDGjIH33ktrbtW7/XY48UQ46yw4+ujmnbNv3y0hmIqD\ngVZGrNCSJEmSJKk4DBuWHu++O7UUjhqV7oo4dmxaM2vMmLQ2VnPtu2/L756otmWglZFczgotSZIk\nSZKKyWc/u+X50KHp8cADW36eIUPgpz9N62+1JAhT2zGCyYgth5IkSZIkdUxDhqS7HNp2WDyMYDJi\ny6EkSZIkSR3TkCHp8bnnCjsObWGglRFbDiVJkiRJ6pjqA63nny/sOLSFEUxG6uqs0JIkSZIkqSPq\n0QMGDjTQKiYGWhmxQkuSJEmSpI5ryBADrWJiBJMRAy1JkiRJkjqu/feHFSsKPQrVM4LJiC2HkiRJ\nkiR1XAcdBH/5S7r+V+EZaGXECi1JkiRJkjquoUNh/Xr4298KPRKBgVZmDLQkSZIkSeq4hg5Nj089\nVdhxKDGCyYgth5IkSZIkdVwf+Qj062egVSwMtDJihZYkSZIkSR1XCKlK68knCz0SgYFWZgy0JEmS\nJEnq2A45BBYvhjVrCj0SGcFkxJZDSZIkSZI6tvPOg3ffhauvLvRIZKCVESu0JEmSJEnq2PbfH846\nC265Bd5/v9Cj6dyMYDJioCVJkiRJUsd37rmwejXMn1/okXRuRjAZseVQkiRJkqSO72Mfg1NOgTlz\nUnGLCsNAKyNWaEmSJEmS1Dmcey488wwsX17okXReRjAZMdCSJEmSJKlzOPLI9Hj11bB5c2HH0lkZ\nwWQkl7PlUJIkSZKkzqBXr/S4YAFUVxd2LJ2VgVZG6uqs0JIkSZIkqbP40Y9gjz1g+nR47LFCj6bz\nMYLJiC2HkiRJkiR1HmecAS+9BEOHwiWXuEB8ezOCyYgth5IkSZIkdS7l5eluh4sWwcknp4Xi1T4M\ntDJiy6EkSZIkSZ3PmDFw++1w333w8Y+n9sO1aws9qo7PCCYjthxKkiRJktQ5TZyYgqyKChg5Eqqq\n4IEHCj2qjs0IJiO2HEqSJEmS1HkdeSQ8+2xaT2v33dPdD11Xq+2UF3oAHYUth5IkSZIkdW777APX\nXguHHgqTJqXCl1WrUsClbBnBZMSWQ0mSJEmSBDBhQgq3APr3hxdeKOhwOiQjmIzYcihJkiRJkgC6\ndk0h1u23p9fnnQePPgqbNzd9/Lp165hxwQWsW7eu/QZZ4gy0MmLLoSRJkiRJamjiRLjnHvjVr2DU\nKPjWt5o+7jtXXMEe993HvOnT23eAJcwIJiO2HEqSJEmSpMZOOSWFWQA33wwPPQSDB0N9MdbSxYsJ\nDz7I2X36EB94gKWLFxdusCXECCYjthxKkiRJkqSm/PrXsHgxvPIKjB4Nf/sbfPGLsGbNOm6eNo3z\n8xUyU8rKuHnaNFsPm8FAKyO2HEqSJEmSpKZ06wYjRqS1tOrdfTdcdNoVfLmmhsp8oFBZVsaXa2ps\nPWwGI5iM2HIoFcaCBQsKPQRJci6SVHDOQ1JpuPDCFG4BlLGY+OCDhOW7sGJFWkQ+Rjh8l11sPWwG\nI5iM2HIoFYY/3iQVA+ciSYXmPCSVhoED4cEH4dVX4dQjqpn0ftr+zrtQ8xY8/1fIRfgycGt19Qfv\nmzJlCoNCYMqUKYUZeBEy0MqILYeSJEmSJOnDfOpTsOeeMPXbU7k5v22//dJjbS28VQM/AM6YNu2D\n9/zXvHmcB9w/b157D7doGcFkxJZDSZIkSZLUXIePHMkDjOVJ3me3vvDRj6btC196nwWrxtF39xHk\ncrBrCIwHpgLHkV7LQCszthxKkiRJkqSWuPuRWfziwCrW5XLs3g/23C/HN6niyddnMmQIjBgxhYOA\nq/LHzwYOAlsPgfJWvm8XgKeffjrDoZS2DRtg5Up44olCj0TqXGpra3nC//EkFZhzkaRCcx6SSlOP\nHnDq1DO5dPZszigv55Yumznpogs4reoZLr8cXl86j68DzwL1dVlnAVfNm8eZZ55ZuIE3oUFGtEt7\nfF6IMbb8TSH8CzA/++FIkiRJkiSphE2KMd7W1h/S2kCritS6+SLwfsZjkiRJkiRJUmnZBdgHuD/G\nWNPWH9aqQEuSJEmSJEkqFBeFlyRJkiRJUkkx0JIkSZIkSVJJMdCSJEmSJElSSTHQkiRJkiRJUklp\nVaAVQjgvhPBCCGF9COGxEMLhWQ9MUucUQpgeQsg1+vtLg/3dQgg3hBBWhxDeCSHcFULo3+gce4cQ\n7gshvBdCWBlCuDaEYIAvabtCCEeHEBaGEP6en3dObuKYWSGE10II60IID4QQhjTa3zeEMD+EUBtC\neDuE8IMQQo9GxxwSQngk/xvqpRDCJW393SSVhg+bh0IItzTxG+mXjY5xHpLUaiGES0MIS0IIa0MI\nb4QQ7g4hfKzRMZlcj4UQjgkh/CGE8H4I4dkQwhktHW+LL/BCCBOB64DpwD8AfwLuDyH0a+m5JGk7\n/gx8BBiQ//tUg33fBk4E/jcwCtgD+Fn9zvxE+UugHBgBnAF8CZjVDuOWVLp6AH8EzgO2uQV0CGEq\ncD7wFeAI4D3S75+uDQ67Dfg4MIY0T40Cbmxwjp7A/cALwDDgEmBGCOH/tMH3kVR6djgP5f2KrX8j\nfaHRfuchSTvjaOA7wJHAWKAC+HUIoXuDY3b6eiyEsA/wC+D/A/8LmAv8IIQwriWDDTFub67czhtC\neAx4PMZ4Qf51AF4Bro8xXtuik0lSIyGE6cApMcZhTezrBbwJfD7GeHd+2wHA08CIGOOSEMJ4YCEw\nMMa4On/MV4BrgN1jjJvb6atIKlEhhBzw2RjjwgbbXgO+GWP8Vv51L+AN4IwY450hhI8Dy4HhMcZl\n+WOOA+4D9ooxrgwhnANcCQyon4tCCFeT5rxPtONXlFTktjMP3QL0jjH+03becyDwF5yHJGUkX7i0\nChgVY1yU1fVYCKEaGB9jPKTBZy0gzXEnNHd8LarQCiFUAMNJKRoAMSViDwIjW3IuSdqB/fPl9n8N\nIfwkhLB3fvtwUtLfcA5aAbzMljloBPBU/eSZdz/QGzio7YcuqaMJIexLqoRoOPesBR5n67nn7fqL\nyLwHSVUWRzY45pFGwfr9wAEhhN5tNHxJHcsx+TagZ0II3w0h7NZg30ichyRlqw9pDnkr/zqr67ER\npPmJRse0KFdqacthP6AL6V8kG3qD9ENPknbWY6SS1OOAycC+wCP59R8GABvzF5INNZyDBtD0HAXO\nU5JaZwDpx9yOfv8MIP0L5gdijHWkH4DOT5Ky8CvgdGA08DXg08Av8x0z4DwkKUP5ueXbwKIYY/2a\nxlldj23vmF4hhG7NHWN5cw/8EIHt93lLUrPFGO9v8PLPIYQlwEvA54D3t/O25s5BzlOSstScuefD\njqm/EHV+krRDMcY7G7xcHkJ4CvgrcAzw0A7e6jwkqTW+C3yCrdcz3p4srsdaPBe1tEJrNVBHWoiw\nof5sm65J0k6LMdYCzwJDgJVA13zvdkMN56CVbDtH1b92npLUGitJP7J29PtnZf71B0IIXYC++X31\nxzR1DnB+ktRCMcYXSNdn9XdcdR6SlIkQwjzgBOCYGONrDXbt7PXYh81Fa2OMG5s7zhYFWjHGTcAf\nSHfNAD4oQxsD/L4l55Kk5ggh7AoMBl4jzT+b2XoO+hgwiC1z0GJgaKM7rx4L1JIWSpWkFslfNK5k\n67mnF2lNmoZzT58Qwj80eOsYUhC2pMExo/IXmPWOBVbkw3tJarYQwl5AFfB6fpPzkKSdlg+zTgH+\nMcb4cqPdO3s99nSDY8awtWPz25s/1lbc5fBzwI9Jt61eAlwITAAOjDG+2aKTSVIjIYRvAveS2gz3\nBGYChwCfiDHWhBC+C4wHzgTeAa4HcjHGo/PvLwOWkQKwqcBA4Fbgphjj19v560gqEfl1+oaQLvye\nAC4itfC8FWN8JYTwNdKc8iXgRdJdwg4CDqr/l8QQwi9J/7p4DtAV+CGwJMZ4Wn5/L+AZ4AGgGhgK\n3AxcEGO8uV2+qKSitaN5KP83HfgZKWAfQppHegCH5AsPnIck7ZT8tdYXgJNJXTL1amOM7zc4Zqeu\nx0II+wB/Bm4gzVNjSOt1nRBjbLxY/PbH29JAK//h55IWIvwI8EdgSozxv1t8IklqJH+71qNJ/+L4\nJrAIuDxfIUF+kcA5pIm2G/BfwHkxxlUNzrE38J+kNSXeA34EXBpjzLXbF5FUUkIInyZdODb+YfTj\nGONZ+WNmAGeT7vjzKGnueb7BOfoA84DPADngLtJF4roGxwzNH3M4qVXo+hjjnDb6WpJKyI7mIeBc\n4B7gUNIc9BrpjmBXNCwqcB6StDNCCDmaXsPqzBjjrfljMrkey895/0Fap+tVYFaM8f+1aLytCbQk\nSZIkSZKkQmnpovCSJEmSJElSQRloSZIkSZIkqaQYaEmSJEmSJKmkGGhJkiRJkiSppBhoSZIkSZIk\nqaQYaEmSJEmSJKmkGGhJkiRJkiSppBhoSZIkSZIkqaQYaEmSJEmSJKmkGGhJkiRJkiSppBhoSZIk\nSZIkqaQYaEmSJEmSJKmk/A8PFOeGjR2rowAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f7ac7842910>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# find peaks using the first ridge position, last ridge position as well using find_peaks\n",
"peaks = signal.find_peaks_cwt(y, wavelet=signal.ricker, widths=widths)\n",
"peaks_2 = peak_pos[np.all(((peak_width > 1), (peak_len > 5)), axis=0)]\n",
"\n",
"fig, ax = plt.subplots(figsize=(15,5))\n",
"ax.semilogy(x,y)\n",
"ax.semilogy(x[peaks], y[peaks], 'kv', alpha=0.8)\n",
"ax.semilogy(x[peaks_2], y[peaks_2], 'rd', alpha=0.8, label='filterd width')\n",
"#ax.plot(x[peaks_3], y[peaks_3], 'bx', label='filterd length')\n",
"ax.set_ylim(200000,600000)\n",
"ax.legend()"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.legend.Legend at 0x7f7ac6abfe50>"
]
},
"execution_count": 13,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABOoAAAGrCAYAAAB+PnixAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3Xd81EX+x/HXbEgIoROKVEURRFSQgIIKBwoiiuU0KoiH\nYiOKopyo+POUcqCCCBYQvRMbInqH5VROEQvYUEosKFE8iqKCGCShhNSd3x+TTTa9kG3h/Xw88tjs\n9zs739lsCJt3PjNjrLWIiIiIiIiIiIhIaHlCPQARERERERERERFRUCciIiIiIiIiIhIWFNSJiIiI\niIiIiIiEAQV1IiIiIiIiIiIiYUBBnYiIiIiIiIiISBhQUCciIiIiIiIiIhIGFNSJiIiIiIiIiIiE\nAQV1IiIiIiIiIiIiYaBOqAcQTowx8cAQYCuQGdrRiIiIiIiIiIhIiMUCRwDLrLW7An0xBXVFDQEW\nhXoQIiIiIiIiIiISVkYCLwT6IgrqitoK8Pzzz9O1a9cQD0VEDmXjx49nzpw5oR6GiBzC9HNIRMKB\nfhaJSKilpKRw+eWXQ35mFGgK6orKBOjatSs9e/YM9VhE5BDWuHFj/RwSkZDSzyERCQf6WSQiYSQo\nS6RpMwkREREREREREZEwoKBOREREREREREQkDCioExERERERERERCQMK6kREwtCIESNCPQQROcTp\n55CIhAP9LBKRQ402kxARCUN6UyoioaafQyISDoL5s+inn34iNTU1aNcTkfDQvHlzOnToEOphFFBQ\nJyIiIiIiIoe0n376ia5du5KRkRHqoYhIkMXFxZGSkhI2YZ2COhERERERETmkpaamkpGRwfPPP0/X\nrl1DPRwRCZKUlBQuv/xyUlNTFdSJiIiIiIiIhJOuXbvSs2fPUA9DRA5h2kxCREREREREREQkDCio\nExERERERERERCQMK6kRERERERERERMKAgjoREREREREREZEwoKBORERERERERCo0efJkPB7FCCKB\npH9hIiIiIiIiIlIhY4yCOpEA078wEREREREREanQ3XffTUZGRqiHIVKrVSmoM8ZMMsZ4i31s8Dtf\n1xgzzxiTaozZa4xZYoxpWayP9saYpcaY/caYHcaYmcYYT7E2A4wx64wxmcaYjcaYK0oZy1hjzBZj\nzAFjzGfGmN7Fzlc4FhERERERERGpHI/HQ0xMTKiHIVKrVaei7hugFXBY/sdpfuceAs4BLgL6A22A\nl30n8wO5/wJ1gD7AFcCVwFS/NkcAbwLvAd2Bh4EnjTGD/dpcCjwITAJOBL4Clhljmld2LCIiIiIi\nIiKVNWHCBE4//XQGDRpU4uP0009nwoQJYdm3z759+7jlllvo2LEjsbGxtGrVijPPPJMvv/yyoM3n\nn3/O2WefTbNmzWjQoAHdu3fnkUceKThf2hp1Ho+HcePG8cILL3DMMcdQr149evXqxUcffVTQ5oMP\nPsDj8fCf//ynxLheeOEFPB4Pn3/++UE/R5HaoE41HpNrrf29+EFjTCPgKmC4tXZl/rHRQIox5iRr\n7WpgCHAMMNBamwqsN8bcDdxvjJlsrc0Frgc2W2tvz+/6e2PMacB4YHn+sfHAE9ba5/Kvk4QL5a4C\nZlZyLCISgSZMmEBycnKpa2N4vV569uzJrFmzQjAyEREREanNEhISePvtt4mNjS1xLjMzk4SEhLDs\n22fMmDG88sor3HTTTXTt2pVdu3bxySefkJKSQo8ePVi+fDnnnnsubdq04ZZbbuGwww4jJSWFpUuX\nMm7cOMCtUWeMKdH3ihUreOmllxg3bhx169blscceY+jQoaxevZpjjz2WgQMH0qFDBxYtWsT5559f\n5LGLFi2iU6dOnHzyyQf9HEVqg+oEdUcbY34BMoFVwJ3W2m1AQn5/7/kaWmu/N8b8BPQFVuOq6Nbn\nh3Q+y4D5QDdcZVwf4N1i11wGzAEwxkTnX+tev+tYY8y7+dcB6FWJsYhIBArGmxgRERERkeISExN5\n/PHH2bdvX5GwylpLfHw8iYmJYdm3z3//+1+uvfZaZs6cWXDMV6nn9XoZM2YMbdu25csvv6Rhw4ZV\n6vvbb79l3bp19OjRA4BLL72ULl26cM8997BkyRIARo4cyZw5c9i7d29B/6mpqSxfvpy77777oJ+f\nSG1R1amvn+Gmqg4BkoCOwIfGmPq4abDZ1to9xR7zW/458m9/K+U8lWjTyBhTF2gORJXRxtdHq0qM\nRUQiUGJiIvHx8VhrAci/qdE3MSIiIiIixUVHR5OUlERWVlaR41lZWSQlJREdHR2Wffs0adKE1atX\ns3379hLnvvjiC7Zu3cott9xS5ZAO4JRTTikI6QDat2/P+eefzzvvvFPwvn3UqFFkZmYWBHcAL774\nInl5eYwcObIaz0ikdqpSUGetXWatfdla+421djlwNtAUuKSchxnAVqb7CvqoTJuKrlPZsYhImPJ/\nE/Pzz5Cc7I7X5JsYEREREZHSlPyjcc39sTiQfQPMnDmT9evX0759e04++WSmTJnCli1bANi0aRPG\nGLp161atvjt16lTiWOfOndm/fz+pqW5CXZcuXejduzeLFi0qaPPCCy/Qp08fjjzyyGpdV6Q2qs5m\nEgWstenARqATsAOIyV8fzl9LCqvfduCq3fy18jtXVpuWwB5rbTaQCuSV0cb/OhWNpUzjx4/nvPPO\nK/KxePHiih4mIkHiexOTnu7exGRkqJpORERERAKveOVbTf6xOJB9A1x88cVs3ryZuXPn0rZtW2bN\nmkW3bt1YtmxZQThYk0rrc9SoUaxcuZJff/2VTZs28dlnn/GXv/ylxq8tUl2LFy8ukQeNHz8+qGM4\nqKDOGNMAOAr4FVgH5AJn+J3vDHQAPs0/tAo4vtjurGcC6UCKX5szKOrM/ONYa3Pyr+V/HZN/33ed\n8sayqqLnNWfOHF5//fUiHyNGjKjoYSISJL43MfXquTcxqamqphMRERGR4PD90djr9db4H4sD2TdA\nq1atSEpK4pVXXmHLli3Ex8czffp0OnXqhLWWb775plr9/vDDDyWObdy4kbi4OJo3L/z1f8SIEXg8\nHhYvXswLL7xATEwMl1xS3gQ9keAaMWJEiTxozpw5QR1DlYI6Y8wDxpj+xpjDjTGnAK/iArEX89eD\nWwDMNsYMMMYkAE8Dn1hr1+R38Q6wAVhojDnBGDME+DswNz+AA3gcOMoYM8MY08UYcwOQCMz2G8ps\n4DpjzChjzDH5j4kDngGoYCzaSEKkFkhMTCQ2Nh7w4vGomk5EREREgsP3R+Ndu3bV+B+LA9W31+tl\nz56iS7g3b96cNm3akJWVRUJCAh07duShhx4iPT29yv2vWrWKZN+aNMC2bdt4/fXXGTJkSJHNMZo1\na8bQoUNZuHAhixYt4qyzzqJZs2bVf2IitVBVd31tB7wAxAO/Ax8Dfay1u/LPj8dNS10C1AXeBsb6\nHmyt9RpjhuF2ef0U2I8L1yb5tdlqjDkHF8aNA34GrrbWvuvX5l/5VXlTcVNgvwSGWGt/9xtruWMR\nkcgWHR3NMccksX37RI4++jZV04mIiIhI0CQmJrJ+/fqA/LE4EH3v3buXdu3akZiYSPfu3WnQoAHL\nly9n7dq1zJ7tamIee+wxzj//fHr06MHo0aNp3bo13333HRs2bOCtt94qt//jjjuOoUOHctNNNxET\nE8P8+fMxxjB58uQSbUeNGkViYiLGGKZNm1Zjz1GktqhSUGetLXf+p7U2C7gp/6OsNtuAYRX0sxJI\nqKDNY8BjBzMWEYlsHTokAutp00bVdCIiIiISPNHR0dx7770R03dcXBxjx47lnXfe4dVXX8Xr9dKp\nUyfmz5/PddddB8CQIUP44IMPmDJlCrNnz8br9XLUUUcVnPfxr5Dz+dOf/kTfvn2ZPHky27Zto1u3\nbjz33HMcd9xxJdqee+65NGvWjLy8PM4777wafZ4itUFVK+pERMJGXl40cC95eaEeiYiIiIhI+IqO\njub+++/n/vvvL7dd3759efvtt8s8P2nSJCZNmlTquREjRlRqbXePx0NUVBQXXnghMTExFbYXOdQc\n1GYSIiKhlJvrbnNyym8nIiIiIiLh4dVXXyU1NZVRo0aFeigiYUkVdSISsXwBnYI6EREREZHwtnr1\nar766iumTZtGz549Oe2000I9JJGwpIo6EYlYCupERERERELLGFPqunXFzZ8/n7Fjx3LYYYfx7LPP\nBmFkIpFJFXUiErF8U1+zs0M7DhERERGRQ1VeJReMfvrpp3n66acDPBqRyKeKOhGJWKqoExERERER\nkdpEQZ2IRCwFdSIiIiIiIlKbKKgTkYilXV9FRERERESkNlFQJyIRSxV1IiIiIiIiUpsoqBORiKWg\nTkRERERERGoTBXUiErEU1ImIiIiIiEhtoqBORCKW1qgTERERERGR2kRBnYhELFXUiYiIiIhUztq1\nazn11FNp0KABUVFRfP3110yePBmPp2gscMQRR3DVVVeFaJSFBgwYwOmnn15hu3AZb0WuvPJKGjZs\nGOphVGjlypV4PB4+/PDDgPQ/YMAABg4cWKPj8LV95ZVXamKIIaegTkQiVk4OxMQoqBMRERERKU9u\nbi6JiYns3r2bhx56iIULF3L44YdjjCkR1BljitxPSUlhypQp/PTTT8EccolxHGy7YDhw4ABTpkwp\nNVwyxoTVWMsTyHGW9j1X2XEsXryYhx9+uFJtI5mCOhGJWLm5UK+egjoRERERCa6MjAwm33wzGRkZ\nEdH3pk2b+Omnn7jtttu45ppruOyyy2jcuDF33313hdfZsGEDU6ZMYevWrTU2ntoqIyODKVOmsGLF\nilAPJWwtX76cZcuWVeuxL7zwQplBnbX2YIYVVhTUiUjEysmBuDgFdSIiIiISXI/ecw9tli5l7qRJ\nEdH3b7/9BkDjxo2LHPd4PMTExJT7WGttQKqVAhFyhlptCosCpU6dOtSpUyfUwwhrCupEJGL5grrs\n7FCPREREREQOFWtWrcK8+y7XNWmCXb6cNatWhXXfo0ePZsCAARhjSExMxOPxFKz9Vtoadf6effZZ\nLrnkEsCtLebxeIiKiioytfOtt96if//+NGjQgEaNGjFs2DA2bNhQpB/f+mybN2/m7LPPplGjRlx+\n+eUF5//xj3/QqVMn4uLi6NOnDx9//PFBPef09HRuueUWOnToQGxsLEcffTQzZ84sEqT9+OOPeDwe\nZs+ezT//+U86depEbGwsJ510EmvXri3R57///W+6detGvXr1OOGEE3jttde48sor6dixY0F/LVu2\nxBhT8HX1eDxMnTq1SD+//vorF1xwAQ0bNqRly5bcdtttlQr4Xn/9dYYNG0bbtm2JjY2lU6dOTJs2\nDa/XW6TdgAEDOOGEE0hJSWHgwIHUr1+fdu3a8cADD5To85dffuGCCy6gQYMGtGrVir/+9a9kZWVV\nOJ7169fj8Xh48803C44lJyfj8Xjo1atXkbZDhw7llFNOKTK+4msPVmYcAwcOZOnSpQWvm8fj4cgj\njyw4b4zB6/Uyffp02rdvT7169Rg0aBCbNm0q97mEI8WYIhKxfFNfrYW8PIiKCvWIRERERKQ2y8jI\nYMHEiczOD7du8nj468SJdHvrLeLi4sKy76SkJNq1a8f06dO5+eab6d27N61atQIqXjetf//+jBs3\njkcffZS//e1vHHPMMQB07doVgIULF3LllVdy1llnMXPmTDIyMpg/fz79+vXjiy++oEOHDgXXyc3N\nZciQIfTr148HH3yw4DktWLCApKQkTjvtNMaPH8/mzZs577zzaNasWcHjq+LAgQP079+fX3/9leuv\nv5727dvz6aefcuedd7Jjxw5mz55dpP2iRYvYt28fSUlJGGOYMWMGF110EZs3byYq/xeMpUuXMnz4\ncLp3787999/P7t27ufrqq2nbtm3B169FixY8/vjjJCUlceGFF3LhhRcCcMIJJxRcy/c16NOnDw8+\n+CDvvvsus2fPplOnTowZM6bc5/XMM8/QsGFDbr31Vho0aMD777/PPffcw969e5kxY0ZBO2MMf/zx\nB0OHDuXCCy9k+PDhLFmyhIkTJ3LCCScwZMgQADIzMzn99NP5+eefufnmm2ndujULFy7k/fffr7CC\n8rjjjqNJkyZ8+OGHDBs2DICPPvoIj8fDV199xb59+2jQoAHWWlatWkVSUlKR8fmr7Dj+9re/kZ6e\nzi+//MJDDz2EtZYGDRoUnLfWct999xEVFcVtt91Geno6M2bM4PLLL2dVDYbpQWGt1Uf+B9ATsOvW\nrbMiEv5iY6096SRrwdoDB0I9GhERERGJVOvWrbOV+V3w/ltvtWu6dbM2IaHgY3W3bnbGhAkHPYZA\n9r1ixQprjLEvv/xykeOTJ0+2Ho+nyLEjjjjCjh49uuD+kiVLrMfjsStXrizSbt++fbZp06Y2KSmp\nyPGdO3faJk2a2DFjxhQcu/LKK63H47F33XVXkbY5OTm2VatWNiEhwebk5BQcf/LJJ60xxg4cOLDC\n51Z8vH//+99tw4YN7aZNm4q0u/POO210dLT9+eefrbXWbt261RpjbIsWLWx6enpBu9dff916PB67\ndOnSgmPHH3+87dChg83IyCg49uGHH1pjjO3YsWPBsdTUVGuMsVOmTCkxTt/XYPr06UWO9+zZ0/bu\n3bvC55mZmVniWFJSkm3QoIHNzs4uODZgwADr8XjsokWLCo5lZ2fbww47zF588cUFxx566CHr8XiK\nfE8cOHDAHn300aW+3sUNGzbM9unTp+D+RRddZBMTE210dLRdtmyZtdba5ORka4yxb7zxRpHx+b+u\nVRnHsGHDiny9fXzf3926dbO5ubkFxx955BHr8Xjst99+W+bzqMy/fV8boKcNQjalqa8iErF8U199\nn4uIiIiIBIpvWmqv2Ngix3vHxh70NNVA9h0oy5cvJz09neHDh7Nr166CD2MMJ598Mh988EGJx/hX\nVgGsXbuWnTt3kpSUVGTdsiuuuIImTZpUa1xLliyhX79+NG7cuMi4zjjjDHJzc0vsyDp8+HAaNWpU\ncL9fv35Ya9m8eTMA27dv55tvvuGKK66gXr16Rdodf/zxVR5f8cq5fv36FVyrPHXr1i34fN++feza\ntYvTTjuNjIwMvvvuuyJt69evz2WXXVZwPzo6mpNPPrnIdd566y1at25dUPkHEBsby3XXXVep59Gv\nXz+Sk5M5cOAAAB9//DFnn3023bt356OPPgIKq+xOPfXUMvs52HH4u+qqqwqqIH1j9H8tI4WmvopI\nRPJNd/X9X6mgTkREREQC6bkZMyhre4ergSkzZtD7tdfCru9A+eGHH7DWMnDgwBLnjDFFwi9wmwi0\na9euyLEff/wRYwydOnUq0da39lt1xrV+/XpatGhR6rh27txZ5Fj79u2L3PcFhLt37y4YI8BRRx1V\nor9OnTrxxRdfVHpssbGxxMfHFznWtGnTgmuVZ8OGDdx111188MEH7Nmzp+C4MYb09PQibYs/J991\n1q9fX3D/xx9/LPF1B+jSpUuFYwE47bTTyMnJYdWqVbRr147ff/+dfv368c033xQEdR9//DHHHnss\nTZs2LbOfgx2Hv+LP23fdynx9w4mCOhGJSLm57lYVdSIiIiISDKPuuIOnrr+e20s5twC4YuLEsOw7\nULxeL8YYnn/++YI17/wV39nTvyLMx+ZvFlDammi+c9UZ1+DBg7njjjtK7aNz585F7keVsdB1da9f\nnrKuVZH09HT69+9PkyZNmDZtGkceeSSxsbGsW7eOiRMnlthQojLPyZaxm29ln3fv3r2JjY3lww8/\npH379rRs2ZJOnTrRr18/5s+fT3Z2Nh9//HGRSrmyxlRTr38wX8tAUlAnIhHJF8zVr1/0voiIiIhI\nIPTu25f3Bw1izdtv09tviuqazEzM0KH06tMnLPs+WGVtLHDUUUdhraVFixYldvGsrCOOOAJrLRs3\nbuRPf/pTwfHc3Fy2bt1Kjx49qtznUUcdxb59+0qt9KuOww8/HID//e9/Jc4VP1bRJgzVtWLFCnbv\n3s1//vOfItNID2ZH0yOOOIJvvvmmxPHvv/++Uo+Pjo7mpJNO4sMPP6RDhw7069cPcNNNs7OzWbRo\nETt27Cg4XhPjCNTXN9xojToRiUi+YE5TX0VEREQkWG6aOpUF8fFk5FcwZXi9LIiP58YpU8K674NR\nv359rLWkpaUVOT5kyBAaNWrEvffeS65vuouf1NTUCvvu1atXwW6p/n08/fTTJa5XWZdccgmrVq3i\nnXfeKXEuPT2dvLy8KvXXunVrjjvuOJ577jkyMjIKjq9cubLIVFKgYCfb6o69LFFRUVhri1TOZWdn\n89hjj1W7z7PPPpvt27fz8ssvFxzLyMjgn//8Z6X76NevH59//jkrVqwoCOTi4+Pp0qULM2bMwBhT\nYVBXlXHUr1+/xDTf2kgVdSISkTT1VURERESCLS4ujqvvv5+511/P7R4Pj3q9XDNjRkFAE659H4we\nPXoQFRXFjBkzSEtLo27dupxxxhk0b96c+fPnM2rUKHr27Mnw4cNp0aIFP/30E0uXLuW0007jkUce\nKbfvOnXqMG3aNJKSkhg4cCCXXnopW7Zs4emnny51TbjKuO2223j99dcZNmwYV155JQkJCezfv5+v\nv/6aV155ha1bt9KsWbMq9XnvvfdywQUXcMoppzB69Gj++OMP5s2bx/HHH8++ffsK2sXGxnLsscfy\n0ksv0blzZ5o2bcpxxx1Ht27dqvVcfE455RSaNm3KqFGjGDduHADPP//8QVWYXXvttcydO5e//OUv\nrF27ltatW7Nw4ULq+6YsVUK/fv2YPn0627ZtKxLI9e/fnyeeeIKOHTvSpk2bGhtHQkIC//rXv7j1\n1lvp3bs3DRo0YNiwYZV/0hFCFXUiEpF8wZyCOhEREREJpt59+2IHDeKJtDTM4ME1Oi01kH2XFeoU\nP26MKXKsVatWPPHEE+zcuZNrrrmGyy67jA0bNgAwYsQI3nvvPdq1a8esWbO45ZZbeOmllzjxxBMZ\nPXp0pa5/7bXX8thjj7F9+3Zuv/12Pv74Y9544w3at29fqSCq+Hjr1avHhx9+yO23387KlSu55ZZb\nmDFjBps2bWLq1Kk0bty4zMeWdXzYsGEsXryYnJwcJk6cyGuvvcazzz5L586diS22U++CBQto27Yt\n48eP57LLLitSKVbZ16C4Zs2asXTpUtq0acPdd9/N7NmzGTJkCDNnzqxSf8W/Tu+//z5Dhgxh7ty5\nTJ8+nf79+5fZZ2lOOeUUoqKiaNSoEd27dy843q9fP4wx9O/fv0bHccMNN3DZZZfxzDPPMHLkyILQ\nsrLPOVKYSFtUL5CMMT2BdevWraNnz56hHo6IlGPbNujQAaZPh7vugi++gGosYSEiIiIiQnJyMgkJ\nCVT2d8GMjAxm3nknt993X41XvAWyb6lZJ554Ii1btmTZsmWhHopUU2X+7fvaAAnW2uRAj0kVdSIS\nkXxTX7VGnYiIiIgEW1xcHJMffjggQVog+5bqycvLK7Gz6ooVK/jqq69qbNMKER+tUSciEan41Nfs\n7NCNRUREREREaq+ff/6ZwYMHM3LkSNq0aUNKSgpPPPEEbdq0YcyYMaEentQyCupEJCJpjToRERER\nEQmGpk2bkpCQwIIFC/j999+pX78+5557Lvfddx9NmzYN9fCkllFQJyIRSVNfRUREREQkGBo1asTi\nxYtDPQw5RGiNOhGJSKqoExERERERkdpGQZ2IRCQFdSIiIiIiIlLbKKgTkYikoE5ERERERERqGwV1\nIhKRfGvUKagTERERERGR2kJBnYhEJFXUiYiIiIiISG2jXV9FJCL5gjnt+ioiIiIiNSUlJSXUQxCR\nIArHf/MK6kQkIvmmvsbEQFSUgjoRERERqb7mzZsTFxfH5ZdfHuqhiEiQxcXF0bx581APo4CCOhGJ\nSL5grk4diI5WUCciIiIi1dehQwdSUlJITU0N9VBEJMiaN29Ohw4dQj2MAgrqRCQi+YK56GgFdSIi\nIiJy8Dp06BBWv6yLyKFJm0mISETyTX31BXXZ2aEdj4iIiIiIiMjBUlAnIhFJU19FRERERESkttHU\nVxGJSDk5bhMJYxTUhasJEyaQnJyMx1Pyb0Jer5eePXsya9asEIxMREREREQkPCmoE5GIlJPjAjpQ\nUBeuEhISePvtt4mNjS1xLjMzk4SEhBCMSkREREREJHxp6quIRKTcXDftFSAmRkFdOEpMTCQ+Ph5r\nbZHj1lri4+NJTEwMyHU/+AB694ZilxUREREREQl7CupEJCKpoi78RUdHk5SURFZWFqmphRuAZGVl\nkZSURLTvBaxhY8fC2rX6nhARERERkcijoE5EIpKCusiQmJhIo0bx/Pij5bvvAl9NB7Bjh7vNygrY\nJURERERERAJCa9SJSETyn/qqoC58RUdHc/nlSaxaNZ2srFgOHMhiwoQJNV5N579xxe7d7tiwYe57\nQxtXiIiIiIhIpFBFnYhEJFXURY7BgxOBeMBLkyaBqaZLSEhg586dpKWlAe4jLc197Ny5UxtXiIiI\niIhIRFBQJyIRSUFd5PB6o4EkYBcjRwZmbbrSNq7weoMz1VZERERERKSmHFRQZ4y50xjjNcbM9ju2\nIv+Y7yPPGPNYsce1N8YsNcbsN8bsMMbMNMZ4irUZYIxZZ4zJNMZsNMZcUcr1xxpjthhjDhhjPjPG\n9C52vq4xZp4xJtUYs9cYs8QY0/JgnrOIhIfcXAV1kcKtFZcIjOSMMwITmPk2rsjIKFyYztrAb1wh\nIiIiIiJSk6od1OWHYtcCXxU7ZYF/AK2Aw4DWwO1+j/MA/8Wtj9cHuAK4Epjq1+YI4E3gPaA78DDw\npDFmsF+bS4EHgUnAifnjWGaMae43loeAc4CLgP5AG+Dl6j5nEQkfOTlaoy5SuKAuGrg3v7ouMBIT\nE2ncOB733xB4vaqmExERERGRyFKtoM4Y0wB4HrgGtxhQcRnW2t+ttTvzP/b5nRsCHAOMtNaut9Yu\nA+4GxhpjfJtbXA9sttbebq393lo7D1gCjPfrZzzwhLX2OWvtd7h5VRnAVfljbJT/+Xhr7Upr7RfA\naOBUY8wP7+PgAAAgAElEQVRJ1XneIhI+ik99zc4O7XikbP67r2ZmBu460dHRjBiRBGTlX1fVdCIi\nIiIiElmqW1E3D3jDWvt+GedHGmN+N8asN8bca4yp53euD7DeWpvqd2wZ0Bjo5tfm3WJ9LgP6Ahhj\nooEEXMUdANYtTPSurw3QC1e159/me+AnvzYiEqE09TVy+Ad1/p8HwqBBhRtXNGyoajoREREREYks\ndSpuUpQxZjjQAxeElWYR8CPwK3ACMBPojFugCNx02N+KPeY3v3NfldOmkTGmLtAMiCqjTZf8z1sB\n2dbaPaW0OayMsYtIhNDU18gRrIo6AGt9G1dM5JxzblM1nYiIiIiIRJQqBXXGmHa4dd8GW2tL/bXY\nWvuk391vjTE7gPeMMR2ttVsquIQt55ypZJvyzle2jYiEOf+przExCurCWTAr6twU6ERgPX36qJpO\nREREREQiS1Ur6hKAFsA6Y4wvOIsC+htjbgTq5k9B9fd5/m0nYAuwA+hdrE2r/NsdfretirVpCeyx\n1mYbY1KBvDLa+KrsdgAxxphGxarq/NuUavz48TRu3LjIsREjRjBixIjyHiYiQVR8jToFdeErmBV1\n7vvAbVyRlxfYa4mIiIiISO2yePFiFi9eXORYenp6UMdQ1aDuXeD4YseeAVKA+0sJ6cDtyGqB7fn3\nVwH/Z4xp7rdO3ZlAen4/vjZDi/VzZv5xrLU5xph1wBnA6wD5weEZwCP57dcBufnHXs1v0xno4Oun\nLHPmzKFnz57lNRGREMvN1dTXSBH8irrgXEtERERERGqX0oq0kpOTSUhICNoYqhTUWWv3Axv8jxlj\n9gO7rLUpxpgjgcuA/wK7gO7AbGCltfab/Ie8k9/HQmPMHUBr4O/AXL/ptI8DNxpjZgBP4cK2ROBs\nv0vPBp7ND+xW43aBjcMFh1hr9xhjFgCzjTG7gb24EO8Ta+3qqjxvEQk/qqiLHMGsqFNQJyIiIiIi\nkazKm0mUwr+KLhsYBNwM1Ae2Af8Gphc0ttZrjBkGzAc+BfbjwrVJfm22GmPOwYVx44Cfgautte/6\ntfmXMaY5MBU3BfZLYIi19ne/8YzHTZFdAtQF3gbG1sBzFpEQy8mBBg3c5wrqwltWFsTGuttAh2f+\n3wf+oZ2IiIiIiEgkOOigzlp7ut/nPwMDKvGYbcCwCtqsxK2JV16bx4DHyjmfBdyU/yEitYimvkaO\nrCyoWxeMUUWdiIiIiIhIeWqiok5EJOg09TVy+Ad1WqNORERERESkbArqRCQiKaiLHL6gzuMJ1q6v\nUK+epr6KiIiIiEjkUVAnIhEpN1dBXaTwD+qCVVHXoIEq6kREREREJPJ4Qj0AEZHqyMkpukadqqfC\nV2amC+piY4NXUVe/voI6ERE5dOzdCwsXhnoUIiJSExTUiUhE0tTXyOGrqKtbNzgVdTExwbmWiIhI\nuLjpJhg1CnbtCvVIRETkYGnqq4hEJP+gLiZGQV048wV1deoEZ9fX6Gh3PVVZiojIoeJ//3O3Xm9o\nxyEiIgdPQZ2IRKTc3KJTX/PywFq3s6iEF19Ql5cX+Cq3nBwX3MbEqKJOREQOHX/84W5zc0M7DhER\nOXgK6kQkIhWf+uo7FhMTujFJ6bKy3Pp0eXnBrahTUCciIrXZhAkTSE5OxuPxFFTUXXyx+z/X6/XS\ns2dPZs2aFdpBiohIlWmNOhGJSGUFdRJ+QrVGnaa+iohIbZaQkMDOnTtJS0sjJycNSCM9PY20tDR2\n7txJQkJCqIcoIiLVoIo6EYlIxae+goK6cJWV5XZh9Xphz57AXstXVamKOhGRwPGv5CpOlVzBk5iY\nyOOPP86+ffsAt/aHtWCtJT4+nsTExNAOUEREqkUVdSISkfwr6mJj3W2gp1VK9QS7oi46WmvUiYgE\nkn8lV/EPVXIFT3R0NElJSWT5/YdnLWRlZZGUlES0742SiIhEFAV1IhKR/IO6uDh3e+BA6MYjZfMF\ndbGxwVmjTlNfRUQCKzExkfj4eKy1RY6rkiv4fK8FuNdCr4GISORTUCciESk3tzCoq1fP3WZkhG48\nUrZgVtRp6quISOD5V3Lt3194XJVcwed7LcD9p6fXQEQk8imoE5GIY60LZHxr1Pkq6hTUhadgV9Rp\n6quISOAlJibi8cTz3XeWtDRVcoWS+5rHA14aNdJrICIS6RTUiUjEyclxYV3duu6+grrw5h/UBXPX\nVwV1IiKBEx0dTf/+rpIrK0uVXKFUp040kATs4vzz9RqIiEQ6BXUiEnF8a9H5prxqjbrw5j/1NdAV\ndf5TX7VGnYhIYJ16qqvk8nq9qqYLIa8XIBEYmf+aiIhIJFNQJyIRxxfI+QI6rVEX3kIx9VUVdSIi\ngVevnqvkysjYpWq6EMrLA4gG7s2/FRGRSFYn1AMQEamqsirqFNSFJ19Q5/EEb+qr1qgTEQm8qCiA\nRI4/fr2q6UIoN7fw85yc0I1DRERqhoI6EYk4xYO6unXBGAV14coX1EVFBWfqa1ycpr6KiASDC4Wi\nGTjwXlRMFzr+QZ3/5yIiEpk09VVEIk7xoM4Y97nWqAs/Xq/7Rc63Rp3XG9hfIjT1VUQkeHx/EFEV\nV2ipok5EpHZRUCciEad4UAeuikoVdeHHF5b51qiDwFbV+TaT0NRXEZHA8/2cVRVXaLk16hy9FiIi\nkU9BnYhEHAV1kcM/qKtbt+ixQPCvqMvOBmsDdy0RkUOd7+e5lhoILU19FRGpXRTUiUjE8QVyxYM6\nTX0NP8GuqPOth1e3rgvp9AuLiEjguJ/xGax792Yy9NeykNHUVxGR2kVBnYhEnNIq6urVU0VdOAp2\nRZ1/UBfoa4mIHOqysyGeexj841LmTpoU6uEcslRRJyJSuyioE5Eq2bzZbQgQSpr6GjmCXVGXnV24\nRp3/9UVEpOZt/mEVg3mXy6KaYJcvZ82qVaEe0iHJf406VdSJiEQ+BXUiUmn790PXrrB0aWjHceAA\n1KnjPnwU1IUnX1AWGxuaijqtmyQiEhgZGRlsemsiY/Hg9cJNHg8LJk7UFNgQUEWdiEjtoqBOJIzs\n3BnqEZTvjz9c8LFjR2jHceBA0Wo6cPe1Rl34CeUadf7XFxGRmvXoPfdwY8YuYvGQ54U4j4erd+3S\nFNgQ0Bp1IiK1i4I6kTCxZg20agW33hrqkZQtPd3d7t0b2nEcOOAq6Pypoi48aY06EZHaZ82qVZh3\n36W7x/0FxrckRu/YWE2BDQFV1ImI1C4K6kTCxEcfudvZs+Grr0I7lrLs2eNu9+0L7ThKq6hTUBee\nQr1Gnaa+iojUvOdmzOAqwGvdfeu3du3V+eclePzXqFNQJyIS+RTUiQTYDTfAjTeCteW3W7sWTjoJ\njjwSHnwwOGOrqnCqqCse1DVoEPpxSUnBrKiz1gVzqqgTEQmsUXfcwVMUvrfx+r3HWQBcMXFiKIZ1\nyNLUVxGR2kVBnUiAzZ8P8+bBm2+W327tWujTBxIT4f33Kw72QiGcg7pmzWD37tCMR8oWzIo6X/Wc\ngjoRkcDq3bcvdtAgknPcD3Tfe5Y1mZmYwYPp1adPCEd36NHUVxGR2kVBnUiANWzobtesKbvN/v3w\nww/Qowf07w+//AKbNwdnfFURzlNfmzVzm11IeAlmRZ3/tXxTXxXUiYgExk1Tp/JwdDyZeLEWMrxe\nFsTHc+OUKaEe2iFHFXUiIrWLgjqRADpwoLD6bMOGstt9/727PfZYOPVUMKZwzbpwEi4VdRkZpQd1\nmZna+TXc+Idn0dHueztQFXW+a8XEFIaCWqNORCQw4uLi8HS9n3n5Qd2jXi/XzJhBXPHdniTgfGvU\nxcSook5EpDZQUCcSQL/95m47d4aUlLLb+c4dcww0aQIdO8K33wZ+fFUVLkFdWRV1oKq6cOMfnhnj\nArRAVblp6quISHDF1u/Lcgax2JumKa8h5AvnYmMV1ImI1AZ1Qj0AkdrMF9QNGABPPeWmI0RHl2yX\nkgJt2kDjxu5+ly6FVXahNmHCBJKTk/F4PAVjWrsWBg0Cr9dLz549mTVrVlDHtH8/tGhR9Jh/UNe2\nbVCHI+XIyioM6cD9EhHoijoFdSIiwZGdDbuYygJy2KYpryHjH9Rp6quISORTRZ1IAPmCuoED3Zuo\n//2v9HYbNkDXroX3u3SB774L/PgqIyEhgZ07d5KWlsaBA2lAGjk5aaSlpbFz504SEhKCPqaffoL2\n7YseU0VdeMrKKgzNAOLi3NTlQF0Liq5Rp6mvIiKB437uxvGHfZh69TTlNVRUUSciUruook4kgObO\nnQAkM2+ey8QvvRRatnTnfNVo9903iw8+gBtvLHxcly7w6KMuZPAFDqGSmJjI448/zr59+8jNdWVR\neXlgrSU+Pp7ExMSgjicnB7ZuhU6dih4PRlBnLXi9EBUVuGvUNsWDuoYNAzd1WptJiIgEV1aWW4ri\nwAH3/3Oo37Mcqnxr1KmiTkSkdlBFnUgANWmSQFTUTg4cSCMqKo1du1wlmn812ooVkJYGF15Y+Lhj\njnFvusqqwAum6OhokpKSyMrKwut1x/LyICsri6SkJKJLm8sbQD/+6K5fPKhr0sTdBjKoGz3abfjh\n+zpIxfbvh/r1C+83aBC4XYN91XMxMeDxuGnmCupERAInO7vwZ7wqmEPHV0VXr54q6kREagMFdSJV\nlJsL06a5AKIiTZokEhsbj7WWevUK1+byr0Z75RU44gjo0aPwcSee6Nb0Wr06IE+hyhITE4mPjycr\ny2IMeL2WZs2CX00HheFl8aAuKsqFdYEM6p59FjZuhJdeCtw1apu9e1045xPIoM6/og4KqzxERCQw\ncnMV1IUDXzhXt64q6kREagMFdSJV9O23cPfdsHJlxW03b46mWzdXjRYb69bm8nq9pG/dyujRo/F4\nonn1VVdN51tsH9ymEsceC6tW1fz4f/8dtm2r/F9cc3NdVd2wYUlkZ2flV65lMWpU0Wq6jRsLp14E\n0g8/uIqp4mvUgZv++vvvgbnu7t2Fn3/ySWCuURvt2+emu/oEM6gL5Hp4IiLi3iP4dmFXQBQ6WqNO\nRKR2UVAnUkU7d7rb7dsrbrtxIwwc6KrRGja0ZGbC/h9/4bKMDLavX89nn7kNJ/ynvfr07Qufflq9\nMebluem0eXmwdCmcfbar5svNdRtbdOjgApO77iqsDvvlF9i1q2g/U6e6sOPCC+GddxLxeOKJj/cC\n8dxySyJjxrjxP/ywW1dv1ChX0bZ3L6xbB8uXw+TJkJ5evedRmq+/dlODS1snrnNntzFHIKxb525P\nOMGFtcGQmprKWT16kJqaGpwLBkDxirpgrVEHCupERALNP6hTRV3o+K9RF4w/moqISGBpMwmRKqps\nUJeR4SrXunaNpnv3JKZNm07dqFxOStvDzYe35sn33mP+r6s47LC+9O1b8vGDBsGTT7qpnsWneZYm\nL8+FV/fe6wK2rCwX0H3zjdsl9bzz4MMP3fFbb4UHH3RtAT7/HObMcVV811/vwrDPP3e3gwbBq69C\nmzbR3HxzEi+/PJFZs25j375oHnoI/vEP18eQIfDii/DCCyXH9skn7lx8fMXPoyLr1kFZG8326AHP\nP3/w1yjrug0awAUXwOOPB+Ya/iZMmMBbTzzB5fv3M+DIIznspJMKzvk2Ipk1a1bgB3KQ9u4tWVG3\neXNgruW/Rh0oqBMRCbS8PPezFhTUhZKvii4mRhV1IiK1gYI6kSryBXW//lp+O99aap07Q69eicyb\nN4/O5kuS8qJo2rQp5/9oeeariZxz9Vt4PHElHn/eedCoETz3nAve/FkLt90GH38Mgwe7qrmvv4Ze\nvVzANn68e+yUKa59jx6uuq1JE3j6aRgxwoUnkye7Crs5c6BVK1eNdtNNrjpu61aYOBHuu8/1fdRR\nEBOTSGzsesaNSyQ6Gs45xz321luhZ0/44AMXDG7cCHPnFo733XehTx/Xz4EDbhrpnDlujKee6vqp\njKws1//VV5d+vkcPuP9+VxlYE6Ggv7VrXUB43HHueyA1FZo3r9lr+MtIS2Pg/v3cYgw/79vHsh9+\noEmLFgBkZmaSUFZaGWb27Svc6Rg09VVEpDbR1NfwkJvr/lhbp44CUxGR2kBBnUgV+dZAq6iibuNG\nd3v00W6Nt05NmnC6zaIu7dmyxbBvt+E2dvG9dxLwQInH16sHI0e66q0bbnDVeb17u+q4O+90lWt1\n6rhgLjERhg93gd0NN8Ds2W5n0tRUaN0a7rjDBXSDBkHHjq7/e+5xQZwx8N57cOaZ8NBDrk337i70\n8AUeJ5zgG1U09/rK8HDB4KJFhWMeONB9gJsOO22a6zcry1XcnXEGJCcX3YnzmGNc5d8XX7jptz16\nlL7+HLh1AXNy3HVL49uQ4+OP4fzzy3xpqmXdOvjzn8FX2LZsmXt9AiE1NZXv/v1v/pV/f7K1rN72\nM5mNmhITE1WwEUkkKG0zCU19FRGpHXJzVVEXDnJz3XvCqChV1ImI1AYK6kSqqLJTXzduhKZNXWXX\nmlWr6LptGwPim7NzZ9OCjQku7RrL3OTlrFm1it6lzH+97TY3tbR1a3f/9tvho4/cJhOdO7vwaNMm\nF6z5zvt4PEWr2q69tmjfxhQGGkOHuttbby087ztXXR6PCwN9Fi92IWKLFvDzz259vGOPdWGXx2+1\nzDp14O23Xajnb+5cmDDBVeb17l36NTt3dkHaAw+4ikT/DToOxs6dsGWLCwgPPxz+9Cd46qnABXXX\nnXUWk7OyaBIdTU5ODvWNh2nWy/UpP2CP6ciECROKbOQRzopPfW3YMLAVdca47yFQUCciEmhaoy48\n5OW5//vq1NEadSIitYE2kxCpoqoEdZ07u+DguRkzuNoYOrRvy9FHmyJraF2NO1+ajh1hwQI3LXXE\nCHjiCRfSPf44vP++q07yhXTh7s9/dl+zbdtcVeLf/w7DhhX+JT4mxm3ScOqprqpv5Ej3pn/rVnjs\nMRg3zgVkzz9fNNjzZ4wLBz/5BFasKHl+6VI3hbU8u3a5qcX+HnvM/SIyeLC7f9VV7uu/ZUtVvgKV\n8+w//kHHb7+lf1QUUXXqAAZr4TQ8DMk7QN6B7IippoPg7/oaE1MY0CqoExEJLP+KOk19DR1V1ImI\n1C6qqBOppNRUt17bG2+4IGD79sI3RqX54QcX1AGMuuMOnrr+em4HGjeCbt0gJxsMsAC4YuLEMq97\nxRVuN1Vj3HTW3393wV0k863t1qgRBdWFe/e66sO33nLTaW+4wU3r3bbNBXaXXw7PPFP6bq/+zj7b\nrZc3dqwLA887D6KjXfXhsGHu9dq6Fdq2hZQUt7Puhg0uHNyyxT3uoouga1e3zuDKle61vvnmwnFf\ndBHceKMbj28dwKrKzXVTmLdudesQ+ioSnpo0iRf92nhtHSAHjzHcbi2f/bYzYqrpoPSprzk57jX1\nBdY1JTu7aCVoXBzs2FGz1xARkUKqqAsP/mvUqaJORCTyqaJOpJKmTnVrv0F+0JYDn31WdntfRR1A\n7759sYMGsSYzE4AoD8TGwprMTMzgwfTq06fca/sqhDyeyA/piouJcR++zR/q1YNrrnGh6NatLqjc\nsQMWLqw4pAP3tXrmGVcZl5jo+h040FXqgXsz266dCwmPPdZda948F/CNHevavPwyPPoofPllYeWk\n/7Tg+vVdheArr1T/eU+fDrNmwZIlbrMNn6umTMG3l6t7s10HjzGAZSaG1n1Kr74MR7m5bvOQ4hV1\nEJh16vzXVQRV1ImIBJqCuvCgijoRkdpFQZ1IJeTmwksvwS23uIDlmWfcWmtvvll6+/XrXQVe166F\nx26aOpUF8fFkeL0AZHi9LIiP58bqlmTVcrfeCnv2uDX6qhpOHn+823Tj/fddELdzp6vQS011a9wN\nH15Y6fXxx65qzz+Iu/RS9xqmpLg+nn665AYXw4a5HWgvvBAuvtjdzptXctpsaax1z+vGG91mI6+/\nXnjuiuuuY0u3bqzIzcOb56oBo6Pr8JG1rIg7ggN5Y6r2xQih/fvdrX9FnS+0C8T018xMBXUiIsGU\nl6epr+FAa9SJiNQuBxXUGWPuNMZ4jTGz/Y7VNcbMM8akGmP2GmOWGGNaFntce2PMUmPMfmPMDmPM\nTGOMp1ibAcaYdcaYTGPMRmPMFaVcf6wxZosx5oAx5jNjTO9i5ysci0hlJCe7sOeSS+D//g8SEtyU\nysWLiwYBycnu3CWXuADm3HMLz8XFxXH1/fczNz+oe9Tr5ZoZM4jzvcOVEg7mS1O3rqukmz3brX03\ne7arrlu1yr1uycluI45TT3Wh66xZ8Ntvbmrxiy8WBnMDB8KVV5bsf8gQV5W3YYMLbF991QVvM2e6\ntQRff73wr9pbtsAffxQ+9rvv4NdfXdiXmAj/+lfhFGCAf7z9Nv9HXfbhpU4UHPB4mBwTw5nXfMIP\nP1T/axJsvqq5YFXUpadDkyaF9xXUiYgEjrXa9TVcqKJORKR2qXZQlx+KXQt8VezUQ8A5wEVAf6AN\n8LLf4zzAf3Hr4/UBrgCuBKb6tTkCeBN4D+gOPAw8aYwZ7NfmUuBBYBJwYv44lhljmld2LCKV9c03\nbkql/8YNN9/sqrbq13ebO6xcCZMmuQCoQwd44YWSa3D5psA+kZZWqSmvEjgnnggti8X2LVsWrkNX\nkUaNXNiWkgJffOECvnHjYOJEV713/vkwYAB88AF06uSqAn2bT7z2mquUO+00932Uk+N2wQXXZ0xM\nc9abB5gW5aY7TwKS5s0jIaE1v/xSWKkW7koL6nxTnHftqvnrpaUpqBMRCZb8vztq6msY0Bp1IiK1\nS7WCOmNMA+B54Bogze94I+AqYLy1dqW19gtgNHCqMeak/GZDgGOAkdba9dbaZcDdwFhjjG9Z/uuB\nzdba262131tr5wFLgPF+wxgPPGGtfc5a+x2QBGTkX7+yYxGplG+/hSOPLFrhdfzx8MADbp2zsWPh\njDNcZdWYMbBsGfTqVXpfN02dyvZzztGU11qgfn0X4B5zjAv4Hn7YTZndudMFtykpcPrp7peZ3Fz3\nPXLHHTBtGlx3nXt8q1YwZw7Mnw9nnuk2uWjcGPZnX8emY7sxMzubH487jlHXXMPRR7vr/u9/oX3e\nleWrEmzcuPCYLxz17Z5ckxTUiYgEj69yS1NfQ08VdSIitUt1K+rmAW9Ya98vdrwXrlLuPd8Ba+33\nwE9A3/xDfYD11tpUv8ctAxoD3fza+C2vXtCmL4AxJhpIKHYdm/8Y33UqMxaRSvn2W7eBRHETJsDX\nX7s1z3r2dBV3111Xfl9xcXFMfvhhTXmtpY47zlWN9e8Pv/wCa9a4wO6mm1xF3cyZ0KYN3H9/4WPG\njHE7wL73HjRr5n7pmTwZnn3/bd7v1o0n3noLKNycpEcPV3kX7rZtc7f+6/s1buyqCQMV1PmHgr6g\nrjLrBoqISNUUD+pUURc6WqNORKR2qVNxk6KMMcOBHrggrLhWQLa1dk+x478Bh+V/flj+/eLnfee+\nKqdNI2NMXaAZEFVGmy5VGItIhax1U1//8pfSz0dFwaJFrp1vd1YRcDv7+iorJ092nzdv7qbd+m+w\nAHDvvXDPPe4xhd9LzXn7yy8L2sTHu11wn33W7Th7443BeibVs22bm/bqH54Z46rqAhXUHX984X3f\nL4+ZmYVTs0REpGb4grq6dd3PdgV1oaOKOhGR2qVKQZ0xph1u3bfB1tqqFLgboDI1DeW1MZVsU9F1\nKjsWEcAt/P/LL249sfIopJPyNGsGo0aV3yY21t2W9730zDOwfTs8/zxcf717Ux6ufvrJVdMVfz6B\nDOqKT30FV1WnoE5EpGb5AqGoKLcmr6a+ho7WqBMRqV2qWlGXALQA1hlT8KtXFNDfGHMjcBZQ1xjT\nqFglW0sKq992AEV2Z8VVv/nO+W5bFWvTEthjrc02xqQCeWW08b9OTAVjKdX48eNp7F8CAowYMYIR\nI0aU9zCppd54w/2Sf/rpoR6JiDNhApx1lquw+89/3DqJ8fFu44lwsm1b0WmvPsEO6vbvL9zEQkRE\naoYvqKtTxwV1qqgLHVXUiYjUnMWLF7N48eIix9LT04M6hqoGde8Cxxc79gyQAtwP/ALkAGcArwIY\nYzoDHYBP89uvAv7PGNPcb526M4H0/H58bYYWu86Z+cex1uYYY9blX+f1/OuY/PuP5LdfB+SWMZZV\n5T3JOXPm0LNnz/KayCFk+XIX0qkiR8LF4MFuN9mkJLezLLhNKbp3h6VL3Zv1115zU2wPPzx049y2\nza3dWFyrVrBpU81eKy8P9uwpGtQ1a+Zu//jD7cQsIiI1x1e5VaeOW3s0Kyu04zmUaY06EZGaU1qR\nVnJyMgkJCUEbQ5WCOmvtfmCD/zFjzH5gl7U2Jf/+AmC2MWY3sBcXnH1irV2T/5B38vtYaIy5A2gN\n/B2Y6zed9nHgRmPMDOApXNiWCJztd+nZwLP5gd1q3C6wcbjgEGvtnnLGsroqz1sOXdbCunUwfnzF\nbUWCqX9/+O9/XWj3v//Bb7/BO+/A3//uKsgefBBOPdWFzA0auNDqqquCV3Xn9cLmzfDnP5c817Il\nfPppyeMHY09+3bR/UBfIHWZFRA51/hV1deuqoi6UVFEnIlK7VHkziVIUX+9tPG5a6hKgLvA2MLag\nsbVeY8wwYD6uym4/Llyb5NdmqzHmHFwYNw74GbjaWvuuX5t/GWOaA1NxU2C/BIZYa3+v7FhEKrJl\nC+zeDUEMz0Uq7YgjYMMGt9nJBRdAp04wdWph9ecnn7gPn2uvhb/+1YV4Nem33+Dpp90YjjnGHUtJ\ncf92Tj65ZPt27Vy1XV5eza2xl5bmbv2DuhYt3O3vv5dsLyIiB6d4UKeKutDRGnUiIrXLQQd11trT\ni93PAm7K/yjrMduAYRX0uxK3Jl55bR4DHivnfIVjESnPunXuVkGdhKvoaDfF9ccf3Zvz55+HQYPc\n8UsvdWHVv/9d2H72bFdhd+ut0KjRwV/f64Xzz4fPP3cbrzzzjDu+cqX7haFv35KP6dLF/UK3bZsL\nG+ueJ1YAACAASURBVGvC7t3utvgadfXrq6JORCQQFNSFD1XUiYjULjVRUSdSa61bB23bujW1RMJd\nVBRccUXh/Q8+cNO3u3eHP/3JhXcvvuiq7qZOdevXDR4MjzxS/TUY//MfF9L17QtvveWCO68XnnoK\nTjnFBWXFdenibr//vuaCuh9+cLcdOxY9HqiNK0REDnX+QV1sLGRmhnY8hzKtUSciUrsoqBMpx7p1\n0KtXqEchUn3GwF13Fd4/6SS45BK48ko48khYtMhNU331VbeG3WmnwVFHwbnnwsaNcHzx7YP87N0L\nDzzg/o3MnAn9+sGTT7rd/5KT4bPPSn9chw6u+uL772HIkJp5nuvXQ5s2JXd3bdFCQZ2ISCD4grqo\nKFXUhZoq6kREahcFdSJl0EYSUhsZ46rfvv/e3f/sMxg6tHDjhTffdLcxMW5h8NmzXft169xOrWPH\nwnvvuUrTq65yIZhv44rrr3cfXq/bxOKkk0ofQ1QUdO7s1s8bN65mntfXX5ceKrZsqTXqREQCQVNf\nw4fWqBMRqV0U1ImUYetWbSQhtV+fPvDKK/C3v7npsV4vdOsGq1e7DRruuMOFe77d/ObMKXxs+/bw\n7LNuLTxjYO5c98vCP/8JV19d/nVvvBHGjHFBeJ8+ZbfLyMhg5p13cvt99xEXF1dqm9xcV8FXbBd1\nwAV1335bwRdBRESqzBcIKagLvdxcty6rKupERGoHBXUiZfDtlllWVZBIbTFwYNHdYQH+8hfIyIAv\nv3RB2o8/wpo1Lrxr1crt9DpjRtFwzOOBf/wDpk+H5s3Lv+Y117h18l58EdauhXPOKbm+HMCj99xD\nm6VLmRsTw+0PPFBqX08+Cb/+6gLD4lq1chWAIiJSs4pX1GmNutDxrVHn20nd63X/J4uISGRSUCdS\nhhUr3FS6igIHkdoqLs5NKTXGTQU3xgV1TZrA5s1ujbvStGhRcd8eDwwbBg8/7O6vXu2q84wpbLNm\n1SrMu+9yXZMmzFi+nDWrVtG7lG1kn33W7Txb2nqSbdq4EM83fhERqRnFN5PYuze04zmU+daoq1On\n8H5MTGjHJCIi1ae/tYiUwuuF99+HAQNCPRKR0PKFW77bJk3cbVkhXVVcfbVb/65ZM1i4EBo3hr/+\nFb75Bh55JIN5N0/kxvySgJs8HhZMnEhGRkaRPnbtcrvOnntu6ddo0wZyclw7ERGpOVqjLnz41qjz\nVdRpnToRkcimoE6kFM88A1u2wMUXh3okIrVX797w6aduuiy4aow5c1wl69Sb72HoN7uo5/Hwxx9Q\nJ9fD1bt2MXfSpCJ9PPWUuy1r99i2bd3tr78G6EmIiByiFNSFj9Iq6kREJHIpqBMpxcyZLqTr1y/U\nIxGp/S64AF5/HbZtg3btwMMqBvMunTJj+W0HbN4C33wLPerEsnvJci4fvorsbDc9/W9/g5v/n707\nD2+qTN84/n3TlkJZpewgoqKisigFhREXlEVBnZ9aRUBFR8UygoiDgsugoCA4gCKIG4jbyMioow6K\nCyjoIArKqOCC4obsUJYWSkvbnN8fTzMNpUvapk2X+3NduU5zcnLyhmqa3Hne5x2ZG8jl1aKFbRXU\niYiEl4K6iiNvjzpV1ImIVG4K6kTy+O47WLfOmumLSNmLirKpq61aWVjX8/gpjKxtfeU2boJ69Ww6\n+ldfwXm/wrKXp5CQYPc5+2yYPLngczdrZtuqHtRt2gTvvx/pUYhIdRII6qKitJhEpKmiTkSkalFQ\nJ5LHK69A7drQq1ekRyJSPT347Bg+agvt28MJx8NxbaF1a7ttLnDZ8LFkZUHv3vDaa/YBsSAxMdCk\niQVZVVmPHtCnz07OP+UUdu7cGenhiEg1kHcxCVXURY561ImIVC0K6kSCZGfDnDkwYADUqhXp0YhU\nT127d8fr1Ys1Xjp169pCFk0ag/+kdI68rjePzOzGd99ZSFenTtHnO/lk+PTTsh93JP36K7TifM77\n5htuuuCCSA9HRKqBQBikqa+Rl7eiTkGdiEjlpqBOKo0XX4Szzirbypjnn4cNG2DYsLJ7DBEp2ogJ\nE5gbH0+a3w9Amt/PM43iuW/W+GKfq18/W8X5wIFwj7Ji8DyI4iku4hv+El2Do9auZe7jT0V6WCJS\nxalHXcWRt0edpr6KiFRuCuqkwsvKgs8+gxtugBUr4NprQ7vfgQMwY0bobxz37YPbbrPedF26lHi4\nIhIGcXFxXD95MrNygrqZfj83TJlCXFxcsc910UXWO2nixHCPsmL46quddOJ27gX8HtyZDk8Ov11T\nYEWkTOUN6tSjLnJUUSciUrUoqJMK7eOP4eijoVs3OOkkmDkTliyBjRuLvu+sWXDrrfDyy0UdN4vW\nznHjjbPYuxceeCA8YxeR0glMgX1yzx5c79506datROc54QRbcGLiRLj/fjh4MMwDjbDbrzyfB8mg\nDj48D+Lwcb8/gyE9NQVWRMqOetRVHHl71KmiTkSkclNQJxXWihVwzjkW1D3yCLzxBgwcCDVqwD/+\nUfh9Pc96zQG8+mrhx84YMYKbgc//MYK+fXOb1otI5I2YMIEt/fszfHzxp7wGu+MOGDMGxo+3AD89\nvWpMhX3uqac4+edvOAP7dBaoouhBFG2/X8tzT2kKrIiUjUAY5PNZRV1mpq3QLeVPFXUiIlWLgjqp\ncNLSLFy79FJo1856S40cCUceCfXr2zS2v/+98HP8/jv88AOcfTa8+27BFTSNatTgAuAO4Hxg1eIa\nYX42IlIacXFx3DdjRommvAZzzqrqZs6Exx+3xWKOOKLo0L+ie+bee7k1KxNIx5FOdnY6YJdRWRn8\nbfhwRo8eHeFRikhVFKjici539e2qVrFcWahHnYhI1aKgTiqMAwesD13TppCYCFu3WhVM4NvBgMGD\n4csv4bvvCj7XihW2ve02m4qxZs3hx8yaNYtjMzMJtK2aBByblcmsWbPC8XREpAIaNgxmz4ZRoyz0\nHzgQ+vaFlSsjPbKS+dP48UxzPsA77LaHgH2NGpGQkFDu4xKRqi9QxQW5QZ2mv0aGKupERKoWBXVS\nYdx2m1XK3XEHrF8Pu3bBNdccflzfvhATY5V2Bfn0UzjmGOjTx9605PchfMaIEUwB6uRcrwNMBh4d\nMaL0T0ZEKqxhw2D6dOtfOX48/PwznHEGTJtmXxB8+60dl50NkybZ7RXVkKFDWX5ER5YDONvngOX4\nWeSryVHHHUdiYmIERygiVVWgigtygzotKBEZ6lEnIlK1KKiTCiE52XrKTZgAf/0rHHusTUtz7vBj\na9WChAT4z38KPt+nn9oCFDVrQocO8NFHh94emPJ6dtA+B/QE+ubcLiJVm88H48bB2rWQlASjR0Pz\n5nDyyRbWvfoq3H03tG9fsasTmnR5h3t8NdnvWXOo/fi5Cx/bYluTlJRETExMhEcoIlVRZmZuUFe7\ntm3374/ceKozVdSJiFQtCuqkWJ54Ai65BFJSwnve11+3BsRXXx3a8T16WG+p1147/LaMDFi92oI6\ngCFD7NgFC3KPaZKZydgCzn1nzu0iUj3Exlo13eDBVlnn81lYN2CA3X7gANx+O+zcGdlxFmTPnkbU\nPG0a453DObjPOdbHtSIqqqmq6USkzGRm2gwHsC9XAXbvjtx4qjP1qBMRqVoU1EnIMjNtytjrr8MX\nX4T33C+8YAs/NGsW2vGXX27bW245/Lb//teaGQeCultugbPOgmefzT1ma3QMkws494PAjsAcDhGp\nFmrUgBdftErdTZusuhfg+OOtsvfhh6FxYzj9dNi+3VaOnTo1smMO2LYNzjhnGGvbtOERz8+SWrWI\niatLbKyq6USk7CioqzhUUSciUrUoqJOQ7dqV+/Nvv4XvvN9+C8uWwdChod/ntNOsmm7TJvj4Y/CC\n+qh/8olNee3Uya47Z1WAixbBe+9ZZczurIO8DSzNuU9ghu2HwLvADjVZEam2mjWzKfjffWe9MBcu\nhMsus9tWrrQvAWbMsNeSSPM8C+qaNoX5y5fzTFwcNY49lnr14klLUzWdiJQdBXUVh3rUiYhULQrq\nJGTB077CFdR5ni0e0bIlXHpp8e7bvbttzzoL5s3L3b9oEZx5plXIBFxyifW269s3twrmjGtmMhbY\nl3NMKjAWuGXmzJI9GRGpUtq1s9emfv3glVfsg88HH8Avv+QeM326VS789FPuPs+zqfzlYd8+m5rb\ntCk0b96c++fMYe/evfTtm8SBAzGkpZXPOESk+gkO6urXty9GFdSVP7/f/u6ook5EpOpQUCchCwR1\nDRqEL6h77z146y2YOfPQYC0UzZrl3uf112379deweDFcfPGhxx51FOzdC3/+MwwcaBUozz03nJ9i\nYrg755i7gJ9jYxk+fHhpnpKIVFFRUdCzp1XyrlxpH0r/8hd7fWnbFmbNgq5drcddeS0evW2bbZs2\ntW1iYiKDBw/m4outmm7r1vIZh4hUP8FBnc9nYZ2CuvIXCOXUo05EpOpQUCchCwR1CQnhC+oefNA+\n2P7f/5Xs/r//DpMmWeB388023bVBg/zPFxMDjz0GL70ETZrYvp0HD7II60unKa8iEooWLex1a8cO\nWxW2Sxc49VQL5z7/3I6ZPdt+zsiw187ffoM+fSzMC6e8QV1MTAyTJk2idWv79Lx5c3gfT0QkIDio\nA5v+umdP5MZTXQVCOVXUiYhUHQrqJGQ7d9o3pp06hSeoW7HCetPdeadVppREkya2wMWJJ8LcuRb8\n/fortGoV+jlGzpzJ42jKq4gUT3w8PPCAVfS+8go89ZR9efDWW3Z7167WL7NxY5ui//77FuZt3Bi+\nMeQN6gJatLCtgjoRKSv5BXWqqCt/gaAuKio3qMvMjNx4RESk9KIjPQCp2EaPHs3q1avx+Xz8+qu9\nCVi4EH7+Gc4910/nzp2ZWsKlD6dPtx5Qf/xj6cbYoAEsX27f4gY+nBbH8OHDNd1VRErlmGPsAvZF\nweuv22vStdfavp07beGbM8+EI4+00K5Xr9I/7rZt9rrcsOGh++vXt76cW7aU/jFERPJz8OChbUuO\nOAJ27EjjvpF3cseDDxIXFxe5wVUj+VXUaeqriEjlpoo6KVRCQgLbt29nz549pKbuISpqD1lZe/C8\nPWzZsp2EhIQSnTctzapO/vQnq9Irrbi4koV0IiJl4Y9/hCFDrMJ31y7rn9mjh1UQR0dD795wwgl2\nzIsvWiPwH34ofk+5bdussjjv66hz0Ly5KupEpOzkraiLj4efV46jxVtvMeveeyM3sGomuEdd4Peh\noE5EpHJTUCeFSkxMJD4+Hs/zyMoK/rbOo06deBITE0t03vfft5UKS1tNJyJSkR11lFWZHHusXZ80\nKbff5w8/wPPPw9VX5wZ3Rx8N27fbB+BPPy383NnZ8M47uZV8ebVooaBORMpO3qCuccMVnLx5MTc2\naID3/vusWrEicoOrRlRRJyJS9Siok0LFxMSQlJRERkbG/4I6e1OWQb9+ScQEv0MrhjfesL5yxx8f\n1uGKiFR49evDmjWwahX4/fDyy7aKLEB6uoV6zZtD9+7WZiCv9eth+HB47TX47DOYPDn/x2nRIrz9\n8EREggUHdWlpaez8ZCxJfh8HDsAIn4+5Y8eSlpYW2UFWA/n1qFNQJyJSuSmokyIFquqysjyioiAq\nygPiOfHEklXTZWfDv/+tajoRqb7at7fVYp2DK66A5GRISbHtlVfmrpw4ezaccYYFd2PGwDnnwHHH\n2QrW11xji/v06JH/Yxx3HPz4o32Avm/kSH1gFpGwCg7qZo4bx21ZycQ5H3v2QJzPx/XJyZoCWw6C\nK+qiog7dJyIilZOCOilSoKrO78/A54Ps7Ax8viSSk0tWTbdsmU39UlAnImJiYqBuXVsU4umn7UNW\njRowbRr88ov1rnvoIXv9DEhPt1CvIO3awaZNMHWs9Yx6+K67FNiJSNgEgrpVK1bgFi/mtFo1iW8E\nO7aDB3StWVNTYMtBcI865yysU1AnIlK5KaiTkCQmJuJcPOAnPj6eZs0S2batZOeaORNOOglOPz2s\nQxQRqVJGj4ZmzeD7721Riq1brefc3/8OK1bAggV2TEFOPBF8rCD7ncUMbdCA5JdeIvOVV1ThIiJh\nEQjqnp8yhT/l7KtTBzKzbFo/wPXY7VJ2givqAlsFdSIilZuCOglJTEwMdeokkZGRTFJSEk2bxrB9\ne/HPs3s3vPkm3HyzfesnIiL5u/9+C+bq1bNFKZo2tSmwgwZBt25w+eW5H8zyc+SRaRzPWIbs87F/\n/36Gp6aSnJJCxrvvqsJFREotENRdM2YMz+TsC0y99OdUec0FhowdG4nhVRvBPepAQZ2ISFWgoE5C\nFhWVSKdOg0lMTKRpU0pUUffxx/Yt6wUXhH98IiJVic9Xui805j00jkn1k9m1Bbb+tpGjnOP6rCx8\n27apybuIlFogqOvavTter16sSk8nKueTRXY2rEpPx/XuTZdu3SI70Couv4q6zMzIjUdEREpPQZ2E\nLCMjhosumkRMTEyJg7ply+DII6FNm7APT0REcgR6Rv1f25rUitlMg/QsfM7R1ecjOjWV7r//HrYp\nsFqsQqR6Cl5MYsSECcyNjyfD2ZzX1Cw/c+PjGT5+fARHWD0E96gLbFVRJyJSuSmok5Clp0PNmvZz\nSYK6jAx4/XVbtVDTXkVEyk6gZ1Ta/v0c4UuhpufjYIZVNF8PrNq1i4y332dlGKbAzhxni1Wo951I\n9RIc1MXFxXH95Mk87rOgbkaWnxumTCEuLi6CI6we8lbUxcQoqBMRqewU1ElIPA8OHChdUDdzJmzY\nAGPGhH98IiKSK9AzKnnLFhr7bAXZ7Gw4kA5PZcN5Wc3o/i1MvqVkTd5Hjx7Nueeey+lduvDTk09y\n9vbt/PjEE5zepQvnnnsuowtb5UJEqoTgoA5sCmxWz168zB62tdeU1/KiHnUiIlWPgjoJycGDtg0O\n6vbvt0uo3nwTLroITj45/OMTEZFcgZ5Rv8THkwzEREOtOFjt87PjYD2O3F+HuUBag7GsXg2rVxfv\n/AkJCWzduhVv3Tpuys4mOzubpOxsvHXr2Lp1KwkJCWXxtESkAjl48NCgDuDWByYwh/6c1l9TXsuL\nVn0VEal6FNRJSNLTbRsI6po0sW2oK7+mpcFnn0HPnuEfm4iIHG7EhAnMb9WK/XXrst/v54Dn8ULN\naAbVaMGG+umknt6bdxd3IyEBEhLgX/+y++3bB0OHFl41nZiYSGxKCrdlZlIrp5dBLecYlZlJbEoK\niYmJ5fAMRSSSMjOtWjfYEUfEkVZjBgcPaspreVGPOhGRqkdBnYQkb1DXtKltQ53++umn9s3rOeeE\nfWgiIpKPQM+ofzZtys7oaGYAQ49sycknw3ud4pn67HiSkuDVV6FvX7jqKhg2DOrWhaefhmnTCj73\nl59/Tt+oaE7MdmRk2N8IfzZ0dI6+UVF8+fnn5fY8RSQy8k59DahXD1JSyn881ZUq6kREqh4FdRKS\n0gZ1S5dCfLymvYqIlKeu3bvj+vTh9fr1+bxOHbrUqcNMvzV5b9cujscfh0svhddeg0sugSeeyL3v\nM8/AiBGwaVNuxUbA4+OmcNGO+mRmReP3g+eHg5kQFR3NbQ0a8PyUkvW+E5HKQ0FdxaAedSIiVY+C\nOglJIKirVcu2jRqBz1e8oO7ss+0+IiJSfkZMmMDuyy7jlIEDeXLPHlzvw5u8x8XBCy/A+vWwcqW1\nKrjoIliwALp3h8aNrSJ61ixYvhy+2jGGJw86GjduTM1YPzE1wO/343ONuX+To9c1YyPzZEWk3Cio\nqxhUUSciUvVER3oAUjnkraiLirKwLpSgLtCfburUshufiIjkLy4ujvtmzCAtLY2HgDvG59/k3Tk4\n9li7AJx2GmzcCOefbx+6ly2zi+lO10t7sfX7RdQ/EA1Z2UA0n6TW4tXo3vzwZDe6nZFbfS0iVU9B\nQV3dugrqypN61ImIVD2qb5KQ5A3qAFq0gM2bi76v+tOJiEReILCLiwu9yXurVvDll7BzJwwZYotO\nDB0KvXvDtOcnMK9RI2rHx5Ptz6Zxq3hWnNmIm+4Zz3vvwYUXluGTEZGIU0VdxZBfRV1mZuTGIyIi\npaeKOgnJgQO2DQ7qWra03kVFUX86EZHKK/Dhb9488LzgFga2WMVLSUkMzsjgxYb1ufGhKXQ4NY51\n62D+fPj9dzjyyEiNXETKUmFB3ZYt5T+e6ko96kREqh5V1ElI8quoCzWo+/BD9acTEansnDv8dbxr\n9+7Quzdv1a6Nr08funTrRmwszJ5tHxYXLozMWEWkbPn9dlFFXeTlraiLiVFQJyJS2Sk6kZCUNKjb\ntAk++cR6HImISNUzYsIEtvTvz/Cg3ncNGkCXLvDRRxEcmIiUmcDUSgV1kacedSIiVY+mvkpICupR\nt317wVMfAF58EWJj4Yoryn6MIiJS/gK97/Lq0cOmvy5dan8jPv0U+vSBDh3Kf4wiEl4K6ioOTX0V\nEal6ilVR55xLcs595Zzbm3P5xDl3ftDtS51z/qBLtnNudp5zHOmce8s5t985t9U595BzzpfnmHOc\nc18459Kdcz8454bkM5abnXO/OOcOOOc+dc51zXN7rHPuMefcTudcqnPuFedck+I8X8lVUEWd5xXe\nh2TRIujbF+rXL9vxiYhIxdKzp1VV9+xpod3o0XDZZTBoEDzxhB2TkgJr1kR2nCJSfArqKo6sLGtL\n4JxdV1AnIlL5FXfq6+/AGCAh5/IB8IZz7sSc2z3gKaAp0AxoDtwRuHNOIPc2VsnXDRgCXAtMCDqm\nDbAQWAJ0AmYAc5xzvYOOGQBMA+4FTgW+At51zjUKGusjQH/gMuAsoAXwajGfr+RIT7c//NFBNZgt\nW9q2oOmvWVmwahWccUbZj09ERCqW88+H22+Hiy6CV16B116DH3+0Krthw+z2+vWhY0dbVVZEKo+D\nB21bo8bht9WrZ+8bA8dI2crKOvT9uYI6EZHKr1hTXz3PeyvPrnucc8Ow0O27nH1pnuftKOAUfYF2\nQE/P83YCa5xzfwUmO+fu8zwvCxgG/Ox5XiDgW+ec6wGMAt7P2TcKeNLzvOfBKv2wUO5PwEPOuXo5\nP1/ped6ynGOuA75zzp3med7K4jxvsTdcwdV0UHRQ9/XXkJYG3buX7dhERKTi8fngoYcO3ffVV/Y3\n46KL4N13c/d/8AH06wfTpsGAAdCuXfmOVUSKJzDTolatw2+rV8+2qakQH19+Y6qusrMV1ImIVDUl\nXkzCOedzzl0JxAGfBN002Dm3wzm3xjk3yTkX/Ce8G7AmJ6QLeBeoD5wcdMziPA/3LtA953FjsGq+\nJYEbPc/zcu4TiIS6YCFk8DHrgA1Bx0gx5BfUNWxo/ec2b87/PosX2zetnTuX/fhERKTi69gRLrgA\n9u+HX3+FrVuhbVsL5xo2hPvug+uus9s9L9KjFZGC5NcSJSAQ1Gn6a/lQRZ2ISNVT7KDOOdfeOZcK\nZACzgUtyQjCAvwNXAecAk4CrgReC7t4M2JbnlNuCbivsmHrOuVigERBVwDGBczQFDnqel/ctQvAx\nUgwHDhz+Zsy5gld+9fvhySfh8svz/7ZVRESqr9hYOOooaNoUpk+3qbBXXglz5tiiE3XqQP/+8OGH\nFtgF+mEF+P3w6qu5YYGIlC8FdRVHVlbuQhKgoE5EpCooyaqv32O94xpg/d+ed86d5Xne957nzQk6\n7hvn3FZgiXPuaM/zfinivIV9d+5CPKao799DOUbykZ5uH6zyKiioW7UKfv4Z5s0r+7GJiEjlddFF\ndgl491345z9tMaJFi+DGG+Hll2H5cut59cMPcPfd9jfm0UdhxIjIjV2kujpwwLaFBXWpqeU3nuos\nv4q6vF9uiIhI5VLsoC6nj9zPOVdXO+dOA0ZiveXy+ixn2xb4BdgKdM1zTNOc7dagbdM8xzQBUjzP\nO+ic2wlkF3BMoMpuK1DDOVcvT1Vd8DEFGjVqFPXzLFM6cOBABg4cWNRdq6zMzPwbBrdokX9Q98UX\nthLY6aeX/dhERKTqmD8f5s61BSiSkuDpp21/hw65x5xyim0/+URBnUgkqKKu4lCPOhGR8Jo/fz7z\n588/ZN/evXvLdQwlqajLywfkU2sF2IqsHrAl5/oK4C7nXKOgPnV9gL3kLkaxArggz3n65OzH87xM\n59wXwHnAmwDOOZdz/dGc478AsnL2/SvnmOOB1oHzFObhhx+msxqrHSIz04K3vFq2hNWrD9//xRfQ\nvn3+VXgiIiIFiYqCunWtV92xx8K4cTY1tm5diIuzSp5eveCee2yxiksusTYLnmcLWIhI2VNQV3Hk\nraiLiVFQJyJSGvkVaa1evZqEhIRyG0Oxgjrn3ERgEfA7UBcYDJwN9HHOHQMMAt4GkrHpsdOBZZ7n\nrc05xXvAt8ALzrkxQHPgfmCW53mBIu0ngOHOuSnAM1jYlgj0CxrKdOC5nMBuJbYKbBzwLIDneSnO\nubnAdOfcbiAVC/GWa8XXkiksqNu0yT4gOZe7f/VqKMf/jkVEpAo66yxYujT/2wYNsv52AwbA7bdD\nly5WhbduHRxzTP5V4CISHoUFdbVr23tCBXXlQz3qRESqnuJ+99wUeB7rU7cYW321j+d5HwAHgV7Y\nCq3fAX8D/glcHLiz53l+4EJs6uonOed6Frg36Jhfgf455/oSC+Gu9zxvcdAxC4C/ABOA/wIdgb6e\n5+0IGusoYCHwCrAU2Iz11JMSKCioa9sW0tLgl6AOhF98AV99BT16lN/4RESkeunUCT74wH7esAFe\new2uvhpOPBGmTIns2ESqukBQl9+CYc5ZVZ2CuvKhVV9FRKqeYlXUeZ53QyG3bcRWey3qHL9jYV1h\nxyzDQsDCjpmNrTpb0O0ZwIici5RSQUHduefa9NY33oBRo2zfXXfZtNerrirfMYqISPVyxhkwdiz0\n62fVd3//u+0fNw7OOQfOPDOiwxOpsgJBXUEtThTUlR/1qBMRqXrUzUVCUlBQV6cO9O4Nr79ubVIa\n/wAAIABJREFU17dvh8WLrbl3dDg6IIqIiBTA54MHH7RAbvp0m4b30kt221lnQbNm9kXS559biwYR\nCY/0dHufV9B7PQV15UcVdSIiVY+COglJQUEdwAUX2Mp7W7bAjTfalIdLLinf8YmISPU2ahSkpsLA\ngRYiLFgAHTvC//0fdO1qlXczZsAtt8CuXfCPf8DOnUWfV0QOl56ef3+6AAV15Se/HnWZmQUfLyIi\nFZ9qniQkhQV1555rbxL+9CdYsgRmz4ZGjcp3fCIiIoGqkthYWwn2ssvg0Ufh7bdthdiANWtskYr2\n7WHlSti2DZo2zb/fVnHt3LmTq3r14sXFi2mkP4ZSRR04oKCuoshbUVejhoI6EZHKTkGdhCQzs+A3\nZCecAM2bwzvvwMUXw9Ch5Ts2ERGR/Ph8cOutdvnxR9i71/raLV1qId7Chbbw0erVdvyxx8Jxx8Hx\nx0OHDrbt3NnaPORn9OjRrF69Gp8vd4LClpUruWrfPs45+mjOv+kmpk6dWvZPtJrJ7989wO/307lz\nZ/27l7GiKurq1rX/36Ts5e1RV6MGZGREbjwiIlJ6CuokJJmZ9qYrP85ZFd3VV8NNN5XvuEREREJx\n3HG2ffJJWL/epsK+9JL93apTB44+2irtfvrJvngKOPJImDYN1q6Fb7+1KbVz5ljAl5CQwDvvvEPN\nnMRiz44dnL9vH7c6x8b9+0nbsycCz7Tqy/vvHiw9PZ2EhELXI5MwCGXq6++/l994qrO8FXWxsXDw\nYOTGIyIipaegTkJS2NRXsB5AKSkW2omIiFRU116b+/PQoRa4NWgATZrYdL7//hd277a/a2BhwxVX\n5N7n4outEu/EE+G++xKpU+cJDh7cx9692cRv3Mi9ngfOMR644p//ZOfkyZoCG2aJiYk88cQTpKSk\nsOunTeyv0Yo2bXx4nkd8fDyJiYmRHmKVpx51FUfeHnWqqBMRqfy0mISEpKigDhTSiYhI5XPSSdCi\nhVWk1K1rq8X+8Y/wyCO5VXhgLR6uucZCuvbt4bvvYMCAGD77LIk1azI4+PMPTPT7icMCowYxMdyb\nkcFNF1wQuSdXRcXExJCUlETaht8ZkLoXkjcDkJGRQVJSEjFFvWGRUktPL7ynY/36mvpaXvKrqPP7\nbUqsiIhUTgrqJCShBHUiIiJVxciRsG4dbN5s/e3Wr4e5c2HZMvj8c3jsscCRicRFH+Ri0vlDztsq\nz3M4XzRn+aI4au1annvqqYg9j6qqTatWnJGWzhVE05sUUnenqpquHBVVURcfD8nJ4HnlN6bqKr8e\ndaCqOhGRykxBnYREQZ2IiFQ3zlklXdu2EBdnH4bPOssqVv78Z/sgvGBBDCfEbud2PJwD5zyciyYj\n3abSjkiHh26+l/nz9cE5XNLS0njunnu4vXYjwM/NQO3NG7nuuutUTVdOQgnqMjIgLa38xlRd5VdR\nB+pTJyJSmSmok5AoqBMRETlUjRpw+eVw04MPMtU5HB7OOWJjcz81PxINm2LuZ9Agm2I7dCjMn29/\nV6VkZo4bxw3JydT2xeOIpibwFz9sWbMm0kOrNooK6gJtGXfuLJ/xVGf59agDfTEgIlKZKaiTkCio\nExERyd/1w4axtk0bPvY8YqKjifJBrThYWSObjae0Z+P2G1i4ENq1g6efhkGD7MP00qWRHnnls2rF\nCtzixXSpWZMD6Y5acY2BbLrXaYpvyRJWrVgR6SFWC/v3W5VpQeLjbZucXD7jqc5UUSciUvUoqJOQ\nKKgTEREp2Pzly7mvRg0O+Oyt1T6/n/trxvLkokXUqQP9+8NHH8Gzz+bep2dPuPtu2LMH3n7bKu2k\ncM9PmcKfcn7OSId69Y4gOqoh0dFHcH3O7VL2UlJsZdeCqKKu/OTtURcI6lRRV/F9/bWtNC4ikpeC\nOgmJgjoREZGCNW/enJtmzuS+nOv3AkOmTaNRILHApqcNGQLz5sGVV9rf1cmT4YgjLMgbNAjmzIHd\nu2HrVnj99Ug8k4rtmjFjeAZb1fJgJtSs6ahVqyVZWY65wJCxYyM9xGohJcVWSS6Igrryk7eiLjD1\nVRV1FV+nTtC5c6RHISIVUXTRh4goqBMRESnKkKFDufSpp3joq6/47ZRTmH7DDfked+21dvE8+O03\nWLIEOnaEiy6CG2+EMWMsrPM8W212yRJo1Qr69SvXp1Mhde3enXfOPpubnnuRIRxFbKyP6BhYlZGO\n630BXbp1i/QQ/2f06NGsXr0an+/w78X9fj+dO3dm6tSpERhZ6aWmFl5RFxdnlV2a+lr28vaoU0Vd\nxVXQa0KvXpX/NUFEwktBnYREQZ2IiEjRnnrnHa7q1YsXFy0q8ljnoE0buP56u/7xx7BxI9x6K+za\nZfvat7fG/Y0bw08/FV7FVF0452iVlsYCNnF67JFkRfv5W0Y8H40fH+mhHSIhIYF33nmHmvmsupCe\nnk5CQkIERhUeRU19dc6q6nbsKL8xVVcFVdQpqKt4gl8TPC93/549lf81QUTCS1NfJSQK6kRERIrW\nqFEj3vnyy0OmvIbquOOsb93KlRbazZplId3FF9sHuVNOgVde4ZAPeBVNWloa940cSVpaWpmcf9WK\nFdRYupSr67QhixT+m7GPJ6P8/BQ1hbjCVjeIgMTEROLj4/FyfmF+v/3uPM8jPj6exMTECI+wZPx+\n2Lev6NC4WTPYtq18xlSd5X2PrsUkKq7g14Tg309lf00QkfBTUCchUVAnIiJSPmJjoUcP+POf4ZNP\n4J//tJ9//hkuvxxOOgmmTYOZMy3Ue+89+PDD0M69bRssXlx2Y585bhwt3nqLWffeG/Zzp6WlMXfs\nWG7K9rF7T22S4uox8bff2NLhHPakdqtwFUQxMTEkJSWRkZFBWpo1jd+wATIyMkhKSiKmkr6x2rfP\ntoVV1AG0aAGbN5f9eKq7AwegVq3c66qoq7iCXxOCfz+V/TVBRMJPQZ2EREGdiIhI+XIOune3D94P\nPQTffWcrx3boYH3sRo2C00+Hvn3h3HPh5Zdh6FD7+dtv4c47Yc0auwQqm665Bnr3hh9+yH2cF1+E\nTz8t/XhXrViBW7yYoQ0a4L3/PqtWrCj9SYPMHDeOG5KTydhrb1/btW3JjXFx1MkppNu+PawPFxaB\nCpqUFKuqS0mp/JUzKSm2LaqiTkFd+UhLs56AAaqoq9gCrwnZ2YHSaI+GDSv3a4KIhJ+COimS59nS\n7wrqREREIqNGDWjXDs48ExYsgP37bVpsly52e0KCrST79NNWXXfyybaibMeOdjnuOLjrLqu+A7j9\ndvvb/ttvcPXVFgh+/72FenPmFH98gWq34TlN0kf4fMwdOzZsU2ADIWCXmjXZvQfq1YUaMT4uPPpo\nWn63FB8r2LAhLA8VVsEVNAAHD2Zwww2Vu3ImENQVVVHXvLmCuvKQN6hTRV3Flvc1ATIYMqRyvyaI\nSPgpqJMiZWbaVn8/REREKobYWGsgv2wZfPMNfPABTJwIb79t4Z1z8PrrMGAAzJ0LNWvCgw9a37DJ\nk+HNNy1oadPGzte0qS1c0bGjrTxbq5ZV2X31FTz7rIUBs2dbpd4PP1g13969ueMJVLvF5QR1cT4f\n1ycnh20K7NyJE0neuJH9fj/79x9azfXnmtCSKaxdG5aHCrvExESiouIBPxDPySdX7sqZ1FTbhjL1\ndds2W+xAys6BA6qoq2wSExOpVSv3NeHccyv3a4KIhJ9WfZUiKagTERGpmOLirGcdWMUcWNWdc1C7\nNvzxj7bv5JPhtddg0iSIirJjFi+GJ56wCrrzzoObb7ZQD6xar3v33Me5+WYL65o0AZ8Ptm61/nkN\nG8KuHSvo+stimsXUZM1uCwpatIB2Xk2eeuJ9/nPhCnqcHXSyEqhZrx4NU1N5ZMNm+vpbEVc797Z5\nDmKPHstXX5XqIcpMTEwMLVoksXv3WA4evJ1ffomhc+dIj6rkijP11fPsv5VWrcp+XNVVWtqhPeoC\nQZ0q6iqumJgYunVLYv36scDtHDigD1kicihV1EmRFNSJiIhUHnXqWEgX7PTTYcoUC+kA/vAHGDfO\npib262cf7mfPtj53Bw9a5dy4cTB4MLzxBgwaZFV7Rxxh7wsWLLDzZGfDjq+mkJhi1VMZByElFX74\nEX76CQbsg3tvnMLSpRbaJCfbfQ8cCP35rFqxghbffss1RxxB2t69fMO+/1UQrUpPx/XuTddu3fj6\n61L/05WZqKhE2rUbTHR0Ilu2RHo0pRNqUHfUUbb97beyHU91lplpl+CKuuicMgxV1FVsbdsmAoOB\nxP/9PyUiEqCKOimSgjoREZGqr0YNuOIK+/nEE2H8+NzbLr7Ytp99ZlMfW7WyFWgBVnw8ho9HDOP2\naMCDrGybMusHnouGpT+O5YOedp+NG+0+gwZZ6Hf22dY/75RT8h9ToPfddJ+P2BYtSNy5j6m+jVzu\njuegH+bGxzN9/HgefRQWLrQw0Lmy+NcpnZ07Y7jyykns2UOlD+q2b7cwqEGDwo875hjbrl8PZ5xR\n9uOqjgKBd3BQ55wF76qoq9jS02OIjp5EVtahbQRCNXr0aFavXo3Pd3jdjd/vp3PnzkydOjUMIxWR\nSFBFnRRJQZ2IiIgA1K9/+DTG7md2x+vVi8/T03EOYqLh2GNhV8t02g3vze1junHqqbkhHcBLL8Fj\nj1kweOqpVrmXn+Ded1mZPjz/kQxwWczavJmZfj83TJlCXFwcHTtagPjrr+F5nr//bqFfuGzfbtOG\nq8JKqBs32vMIVGcWJC4OWraEH38sn3FVR4G1WoKDOrDQXRV1Fdv+/faaEPi5uBISEti+fTt79uw5\n7LJ9+3YSEhLCO2ARKVcK6qRICupERESkMCMmTGBufDxpfj8AsfX8vHZsPKMmjmfyZFi92qp//H67\nvP22rUD7z3/aIhcvvWSVV02bQv/+NgU3eKXX1H2w9huIialNwhEN2LF7N5tOPpku3boB0KmTjSMc\n019vuglat4YhQ2xMpbVnjwUqzZrZSqiVvaJu40YL4ELRtm14/g0lf4GKuuAedaCKuspg/35o3Nh+\nLsni2ImJicTHx+Pl+UbB8zzi4+NJTNQCFSKVmaa+SpEU1ImIiEhh4uLiuH7yZGYNG8YdPt8h1W4B\nNWvmHn/BBbk/p6bCffdB164War39tl36d5zC+A2wr5lVpNWoASedCLgWDPk9m8eCGju1aAGNGsFH\nH+UuoFES//0vPPWU/fzCC3a+n34qunqsqHOCrai7fDl8/HHJz1URbNwY+uIQJ5wAK1aU7XhK6oMP\nbNXkO+44tKdjZZpSWFhFnYK6im3/foiPt6nKJQnqYmJiSEpKYuLEidSoUZPNm62dQFRUBqNHjyZG\nH9xEKjVV1EmRFNSJiIhIUbp2tymwT+7Zg+vd+3/VbkWpWxeefRbatLGQbehQ6NEDFn09hql74Pvv\nYfduC+KioiDK5+Otli25/u67/3cO5+BPf7KQLTm5ZOP3PEhKslV0d+60xTR++w3efLNk5wv44gsL\nUtq1s0AxeApwZbRpU+hB3emnw9q1JevBVZaysyExESZMsN6GwSrTlMKCgrq4uJKFP1J+0tIsIC7N\n7ypQVbd9u8e2bbBzp6rpRKoKBXVSJAV1IiIiEooREyawpX9/hgevRBGCK6+0yrPXX4cnn7Sqs8Uf\ndMffsxe/1EmneTNomtPPKbDSa94gcPRom1b78MMlG/sXX8DKlTBtmlW6jB8PHTrAq6+W7HzB5z3l\nFAsZ27WDXbtg69bSnTNS/H7r3xdqUPeHP1gA+umnZTOezExYvBiyskK/T3q6LYaxe7ddf+edDZzS\nqBEbNmwADp9S6Pfbc6iIUwoLCurq1ClZ3zMpP/v32++tNEFdoKouI6d8Misrg6SkJFXTiVQBCuqk\nSArqREREJBRxcXHcN2PGIVNeS6pnT5i3cAJLOsdzRHM/Ph+k+f3MjY/PNwhs3Nj6y02cCPfcE/qi\nDZ9+aqFcjx52jl69cm+79FKrqAuEOiXxxRcQKMIKZy+9SFi/3kKF9u1DO/6EE6xh/gcflM14LrsM\neveGLl3gu+9Cu0/g375jR1vEZPmLXRmYnMyVp50G5IYfBw5k8PXXFiD/9htkZFS8EKSgHnW1a8O+\nfeU/Hgnd/v2lr6gDC5ajo+MBPz5fxQqSRaTkFNRJkRTUiYiISCT8r/ddziIV+fW+CzZsmG0nTrSp\njf/5D9x+O5x2GowcmXuc51n49sgj0L279cg7+WR4/HGrtgpISrJqrdNPh/POsym6OUNhxw5YuhTG\njLGFJ37+GebPt552ASkptuppIKg7+mj7cF5Zg7qVK23bpUtoxztn/QgXLQr/WL74Av79b/t9ffUV\nnHlm0YHqvn02RRrsuezdPoa+WTu4w/nosn07940ZA+SGH5mZVlWXnOxRp07FC0FUUVd5hSuoi4mJ\noU2bJCCZ+PiKFSSLSMkpqJMiKagTERGRSClO77vjjoMXX7SKuhUrrDpu9mxYtQoefRQuvBCuuspW\nX23YEEaNsiBv+3Y75rLLDj1fs2Y2FXfzZpuuet11tjJtkyZ26dkT5s61VWqPPRYGDYJzzoFPPoGD\nB2HWLDtPIKjz+eznyrqgxKpVtpJrw4ah3+fCC2HNGgssw+XgQVsduEMHC+c++sh6E374YeH3e/hh\n+OYb+71u27aBnUum8QAWxk30PN6bNo0NGzbg98ewZ08SzmXQqRM4l0GLFhUvBCkoqFNFXcWXllb6\nqa8B9eolAoNxrmIFySJSclr1VYqkoE5EREQiacSECTyUmckdIfS+GzzY+sA99JBNZ33rLauCu/lm\nmDfPjmndGu66yz4k33WXVX4V5Oqr7ZwAS5bYpWZNq8Br397CwU8+gS1bLLy78EIL65o3hw0brP/e\nSSflnu/CC+Hee3M/qFcmK1dadWJx9O8P9evD00/b7yQcli+HbdusUq9OHaumO+ooC0AvvTT/+xw4\nADNnWoXfo4/CgK5dedCfTR18eB7U9fmYmJ3NlaedxrUTtvL774k0bPgEPl8qTZvG8803FS8E2bvX\nKgpjYw/dX6eOhc9ScaWn25TlcAR1+/bFAJPYtSssQxORCkAVdVIkBXUiIiISScXtfdewoVVxLVxo\nIUatWvDMM7YQwsUXw/vv2/TYu+8uPKQL8Pns0rs3TJ5sU2UvvxxOPNGCkrPOggEDrMJuxw5bwXbD\nBnjhBZsO6wt6x33JJRYalXY12fKWmQlffglduxbvfrVqwYgRtkjHO++EZyyLFlkoGuj5BxbKLl9e\n8H2ee86q7mbOhBefHsNpO3Zwjs+Hc+Bh06F7+nwkbN/O6OFjaN8+hr/9LYnk5GQuuiiJ9etj/tcT\nrqLYtAlatjz8v2FV1FV8Bw5Y4B+OoG7vXvv/bNeu3Kn5IlK5KaiTIimoExERkcrm+OPtg3CwVq3g\njTfstrISF2c96Favtmm2ebVta6uh3nGH9dQr6ZTQZctskYPy8vXXVgVU3KAOLNg8/3yrTszOLt04\nUlNtuvGAAYcGoJ07w9q1+Z9/1y4LWBMTbYryGzNmMCZnVddAxuXlXMZ6Hi0zZ3D99XD11YkMHjyY\na69NxO+Hb78t3djDraAVeNWjruJLTw9vUHfMMRbS7dkTnvGJSGQpqJMiBZa8j9ZEaREREZEi1awJ\np55a8O133WUhyxNPQN++uV+KhurAAZte26ZN6T/kh2rhQqhXr2RBXVQU3Hkn7NxpVYlF9ZIrzOzZ\nFtbdcceh+zt2tH+Xd989/D5//KNNBb3rrpzrI0cyJacMzbmcsM4Dzw8P4uhw0W3ccos16p80aRKd\nOsXgnE17rkg2boQjjzx8vyrqKjbPC+/U1717c/87SE0t/fhEJPIU1EmRFNSJiIiIhE///rZq6Qcf\nwC+/WMh0wQVWERaKxYtzf162rGzGGMzzYMEC669Xo0bJzhHobffhh/ZcS7LybVqaTaG97rrDK8kC\n02D79z909de1a2313+eeyz3mvilTWNm4MR/mzBMMTH9dip9lcU1Y8OakQ6r1ate2FYDHjbOVfCuK\njRtVUVcZZWba/1PhqKjLzrZwrnlzu67fu0jVoKBOihSYQqCgTkRERCQ8One2nnbPPAPt2tkU2Asu\nsA/taWkwZ46tbpqX59nqpe3b2wq0H31U9mN9/XWb9nnDDSU/R40a8PjjuVOPe/SwPn758TxYutR6\nsAW+MN692/rL7doFY8cefp/GjeHWW+3nDz+0c6ek2Eq8Rx9tVXXBXl61irujokj1+3EO0vBzty+K\nt75bme+YbrkFMjJsQY2KwPMKDuoCFXU5s3ulgklPt204grpA5aSCOpGqRUGdFCnwBikqKrLjEBER\nEalqrrsO/vUvW+BiyxbroVa7Ntx4I7z6qoVOTz6Z+35s1SrbN2kSnH22hV9r1pTssf1+mDIF1q0r\n+Jgff4Trr4d+/Wy6bWkkJdliHh9/bCFFQYv4Ll1qIWarVvbYnmcr9Y4da73ujj46//tNn26BxWWX\n2Sqw9etbYLdw4eGVgK1bt6bPX/7CPTlTYO92jvPH3EHr1q3zPffxx0ODBrBiRQmffJht3GiBT9u2\nh99Wu7b9bjMyyn9cUrTAoiSBoK404VpgqquCOpGqRUGdFEkVdSIiIiJl6+ij4cEHLZzq18/2zZhh\nwVRSkq1Qu3mzLaJQu7ZV302ebOFRoPdacS1YYOFXhw42FTfv4hSeB4MHW7Xaiy+GtkJuKOrXh3vu\ngWefhfvvPzwofPZZ2550Ejz/vP2bBCqHevcu+LzOwciRh+6bMMHOk5/AFNjJfj+fN2nCvZMmFXhu\nnw+6dbOQsSL4/nvbtmt3+G116thWfeoqpkBFXa1a9v9yacK1wO+4adNDr4tI5aagToqkijoRERGR\nsnf77VYx99Zb8Oij8NlnEBsLY8bAQw9By5bw669w6aX2BerRR1tV2sKFcNtttlhDaqq9d/v4Y6uq\nCuZ5dvv06TBwoIVwnTrBCSdAly62OEX//rYvMdEWj1i1CmbNgiOOCO9zvekmCyTHjYM+feDzz21/\naiq88ooFeN98Y0Hd5s22OMecOTB0aOHnHTPGpskmJ1vV4Y03Fn78y6tW8Y/4eP4RwpzWXr3s3zUQ\ntETS999blWCbNoffVq+ebffuLdchSYiCp77WrVu6BSAC923WzLaqqBOpGlQjJUXKzrZvKH2KdUVE\nRETKxfDhNkXuvPNssYn337eebf/4h/W3C7jmGgumRo2y3nVRURaq7dxp1XfPPmuBwO7dFmI9/XTu\nfc8+21ZJXbLEAjqw93wJCTBvnl0fNcoCqnCLjYV//9tCucsvt9Vk+/SB996z26++OnebkADHHGPP\nIxQNGtj2zjuLPrZ169Z8uXNnSOft3RtGj7bFPC68MLSxlJW1a206bn5fpAemQW7ebFOppWLJG9Sl\np1u4XpLZS3kr6hTUiVQNCuqkSFlZqqYTERERKU/OwR135F7/+GPbV6vW4cfdeiusXg0vvABnnGGL\nUIwZA3/9q02DDLQxCZg92xajaN/eArMLLrBFHs4/P7eX26hRVoHXsWPZPs9LL4WXXrJee36/hRej\nR1uPuYCCpq6Wtw4dbPXaESMsADvxxNKdb8cOiI8v/pfh2dnw5ptw5ZX5396ypW03by7d+KRsBPeo\nq1vXft63LzdgLo5ARV39+nY+BXUiVYOCOilSdrb604mIiIhEUlxc4bfPmWNTZzt0yN33hz9Y4LZy\npVWtjR+ff7jknC3yECz4PGXJ57NpuAMH2vW0tKKfa6Q4Z4Finz5W8fjmm9ZjLCUld7ppqHbvhiZN\nLJT829+Kd9///Ae2bi04qKtXz/4NN20q3nmlfAT3qAv0E0xNLVlQF6ioq1u39P3uRKTi0GRGKZIq\n6kREREQqtho1Dg/X/vAH63O3dSu8/HLpK8DKQ0UN6QI6d4aJE+GDD+zf++mnrZpp2bLinWfWLNtO\nnWpBX3G8/bZNdezaNf/bnbOqOlXUVUx5p75CyReBSE21sDscC1OISMWhoE6KpIo6ERERkcqradPw\nrdgqcO21tprsli25i1ucc44FJqefbtWNnmeX/Hz9td3/iiusoip4inNRPC93mnJhU2ZbtlRFXUWV\nX1BX0gUl9u2z/4acs6BOq76KVA0K6qRIqqgTERERETGxsdb/78MPISnJgjuwxTySk22lWZ/PFpz4\n/vvc++3YYdNm+/a1Hnwvvmir2z79NPzwQ+GPed99NkX2sstg3brcxyxI27YWCErFExzUBU99LYnU\n1NxzqKJOpOpQUCdFKukqRCIiIiIiVVW3btaz7umnLTAZORLWr8+tkHv7bZtu3K+fBW1DhtjqvVu3\nwr33QkwMDBsGDRvCk08W/Djr11t/wTvugOXLbfGQs88ufGx9+8K338Jvv4Xt6UqY5LeYRGkq6gLn\nUFAnUnUofpEiZWerok5EREREJD/R0blVTQAPPmiVb7fdZsHakiWwaJHddtNNkJkJgwbZ9dhYq457\n7DFbYKJtW+t5d8IJVkE3cCD89JP1IFu2DDp1yl2ZtzC9e9u558+HsWPD/pSlFNLT7b+Z6Ojw9KgL\n/LdXt27JAz8RqVgU1EmRVFEnIiIiIhIanw9OO81WZ01NtS+8t2+Hjz6Cq646vLfc+PHw8ccwb97h\n53rvPdveckvBi0fkp359e6zp0+GPf6wcC4lUF+npVk0HFqZGRYWnoq5+fdi4MTxjFJHIKtbUV+dc\nknPuK+fc3pzLJ86584Nuj3XOPeac2+mcS3XOveKca5LnHEc6595yzu13zm11zj3knPPlOeYc59wX\nzrl059wPzrkh+YzlZufcL865A865T51zXfPcXuRYJDSqqBMRERERKb66dW0l2zZt4Jpr8l8AIi4O\nFiyAUaMsmJs2Dfr3t3DukUcscLvzzuI/9gMP2EIiXbrA6NF2/d//LvVTklLav9+mqYItAlGaSrjg\nirp69WDv3vCMUUQiq7h1Ur8DY4D1OdevBd5wzp3ied53wCPABcBlQArwGPAqcCZATiCfV4pSAAAg\nAElEQVT3NrAZ6Aa0AF4ADgL35BzTBlgIzAYGAb2AOc65zZ7nvZ9zzABgGjAUWAmMAt51zh3ved7O\nnLEVOhYJnSrqRERERETKTuvWVv0GNm31tttKf85mzaxS7447LPwDq+B67jlYs8Z6602daoteHHFE\n6R9PQpOamlsFB/Zvv2tXyc61b5/9nsEq6lJSSj8+EYm8YsUvnue9lWfXPc65YUA359wm4E/AlZ7n\nLQNwzl0HfOecO83zvJVAX6Ad0DMnUFvjnPsrMNk5d5/neVnAMOBnz/MCC5Wvc871wMK493P2jQKe\n9Dzv+ZzHSQL65zz+Q865eiGMRUKUna2gTkRERESksmnQAJ56Cs47D+Lj4eKL4corLbDLyLAqv9q1\n4csv4eefoWPH3OBHykZwFRxA48awc2fBxxd1rrZt7WdV1IlUHSVe9dU553POXQnEASuABCz4WxI4\nxvO8dcAGoHvOrm7AmqCqN4B3gfrAyUHHLM7zcO8GzuGci8l5rODH8XLuE3icLiGMRUKUlaWpryIi\nIiIildWAAdCrF3z+Obz5JqSlwd//bn3v6tWD446zlWIHDLBFLB5/HL77LtKjrpqC+8oBNGoEO3aU\n/lz161tQ53mlH6OIRFax66Scc+2xYK4mkApc4nne9865U4GDnuflLbjdBgS+l2mWcz3v7YHbvirk\nmHrOuVigIRBVwDEn5PzcNISxSIhUUSciIiIiUvmddJJdwFaeHTQIvv0WkpKgfXsL6D76KPf4e+6x\n/nhxcZEZb1WUd+pr48bw448lP1dwj7qsLFusolat0o9TRCKnJBV13wOdgNOBx4HnnXPtCjneAaHk\n+oUd40I8pqjHCXUsEkQVdSIiIiIiVdNJJ1k499hjEBNj+5KTbVrsAw/Y1NihQ0te9SWHyjv1NZwV\ndaDpryJVQbHrpHL6yP2cc3W1c+40YCSwAKjhnKuXp5KtCbnVb1uBvAuLNw26LbBtmueYJkCK53kH\nnXM7gewCjgl+nKLGUqBRo0ZRP/BKl2PgwIEMHDiwqLtWSaqoExERERGp2pyDX3+FgwehYUNbdOKq\nq6BfP1t4YuFC+OYbLTxRWvv22SrAAY0alaxHnecdGvoFPr6mpKjPoEhpzJ8/n/nz5x+yb285J+Dh\niF98QCzwBZAFnAf8C8A5dzzQGvgk59gVwF3OuUZBfer6AHuB74KOuSDPY/TJ2Y/neZnOuS9yHufN\nnMdxOdcfzTm+sLGsKOoJPfzww3Tu3Dm0Z18NqKJORERERKTqa9Hi0Ou9e9uiE/PmwbBhcMYZ8OST\ncOaZkRlfVZDfYhK7d9tnruIUR6Sng9+fW1FXr55tVVEnUjr5FWmtXr2ahISEchtDsaa+OucmOud6\nOOeOcs61d849CJwNvJhTuTYXmO6cO8c5lwDMA5Z7nrcq5xTvAd8CLzjnOjrn+gL3A7M8z8vMOeYJ\n4Fjn3BTn3AnOuT8DicD0oKFMB4Y6567JmXb7BLaoxbMARYxFK74WkyrqRERERESqJ58Prr8eRo2y\nBSbOOgvmzIFZsywsqorS0tK4b+RI0tLSwn7uvD3qGjWybXJy8c8D+VfUiUjlVtwedU2B57E+dYux\n1Vf7eJ73Qc7to4CFwCvAUmAzcFngzp7n+YELsamrn+Sc61ng3qBjfgX6A72AL3POeb3neYuDjlkA\n/AWYAPwX6Aj09TwveHZ/oWOR0KmiTkRERESkehs/Ht5/HxIT4cYbYcQIOP10eOqpqrfS6Mxx42jx\n1lvMuvfeog8upryrvjZubNviTn/dt8+2qqgTqXqKVSfled4NRdyeAYzIuRR0zO9YWFfYeZZhIWBh\nx8wGZpdmLBKa4pZhi4iIiIhI1VKzJvTqZT3qXnnF9vn9cNNN1ttu0qSIDq/URo8ezerVq9mfkkKn\ndev4i3NMfeIJTv/wQ2rXq0fnzp2ZOnVqqR4jb185yK2oK+6CEnkr6hTUiVQdJVn1VaqZ7GxV1ImI\niIiICHTuDFdcAe++C2vWwMSJ8OCDtujE999HenQll5CQwNatW/HWreOm7Gyys7NJys7GW7eOrVu3\nhqU/VUaGFUGEo6IuENQFzhUTA7VqaeqrSFWgoE6KpIo6EREREREBWx325ZehTx+7fueddn3lSjjp\nJFi0KLLjK6nExERiU1K4LTOTWs4BUMs5RmVmEpuSQmJiYqkfIxDGxcfn7qtf34oiiltRt2uXbRs2\nPPRcqqgTqfwU1EmRVFEnIiIiIiL5cc4q7L791j4z9Otnq8f++GOkR1Y8X37+OX2jozkZx4E0m9YL\n0NE5+kZF8eXnn5f6MbZts23Tprn7fD6b/lrcirrA4hPBQV29eqqoE6kKFNRJkVRRJyIiIiIihWnS\nxFaFbdsWtmyB44+3nnZDh8Ly5bB2LXz2WaRHWbDnp0zhtvr1yc6OxsNWtM3OhqjoaG5r0IDnp0wp\n9WNs327bJk0O3d+oUckq6urWtSmvAaqoE6kaFNRJkVRRJyIiIiIiRWnbFr76CubMsetLlsDTT0OP\nHtChA3TrllupVtFcM2YM85zD728M2CCzsvw0btyYec4xZOzYUj9GoKIub1DXpAls3Vq8c+3adWg1\nHaiiTqSqUFAnRVJFnYiIiIiIhCIuDq6/Hlavzl0oIdjzz5f/mELRtXt3dif04kt/LWrVjCYqygMv\nmvW1auF696ZLt26lfoxt26BBA4iNPXR/27bFnyqcnHxorztQRZ1IVaGgToqUna2gTkREREREQnfq\nqTbV8/ffrYpu714YPBiuuw7+/Gf4979tFdTHHoObbgLPi+x4PQ/+9Z8JTHONqNMoHsgmzYvnmfhG\nDB8/PiyPsX374dV0ACeeCOvWFa/aML+KOgV1IlWDgjopUlaWpr6KiIiIiEjxtWplC07Uqwfz5sH/\n/R889xxcfLFV3k2YAE89ZZV2qal2n02brGIsK8sq8377rWzHuGED1KwJP/wQxxX3TOYfDetTv35D\nZnn1qdN5CnFxcWF5nC1boFmzw/e3awcHDtg4QpVfRV29egrqRKoCBXVSJFXUiYiIiIhIacXEwL/+\nBbt3wyOPwN//blVmZ5wB115rQdMZZ1i416iRHZ+QAG3awC23wC+/2Hk8L3fV0/zs2AG//lp4lV5G\nhi0YsWIFXHYZHDxo+8fe3R169+b9I2qztX0fXnujW9iq/X76CY4++vD97drZ9vvvQz9XcvLhFXWN\nGxd/UQoRqXgU1EmRVFEnIiIiIiLhUqMGjBwJCxbAhx/Ce+9ZVd2UKbkLLnTokLs9+2yYOdMCtRNP\nBJ/PgrwXXoBPPoGLLoJnnskN27p1s0CsSROYPx/OO8/6wP31rxYOHn+8nadWLfjDH+Dzz2HGDBtL\nbCyMmDCBLf37c+e08fz6K7z5Znie908/2TjyOuooq+grTlD32292v2BNm+ZWIopI5aU6KSmSFpMQ\nEREREZFwu/zy3J9vvNG2t91mFXeNG1vPNl9Oacljj8Gtt0Lv3rmB1jXX5N5/4UKbSutcbiXdzp0w\naFDuMQ88cOjjN28ODz4IrVvDOefYfQHi4uK4b8YMPA969rTpupdeCjf/f3t3HmdlWf9//PUZGEYx\nWWQQpMQtpdwBF3zkgoi7qdlkmiWllRT2MxVcMkMxKcolNZf4mZbZ18rtq79cKE3LSsMlDTc0pUgR\nEBdQEIGZ6/fHdU4cRubMDMucYeb1fDzmcZ9z39d9n+v4eHgx93s+132NyVVsL74Ie++dg7GWmj8/\nh2hbbfXBY1VVMGgQPPdcy6711lvw9tuw5ZYr7u/XL3/311/P303SusmKOjWrvt6KOkmSJElrX9eu\ny1eLrSq5W/3613NAdffd8Mor+R7l0UfhttvyM+0OPzy3K4Z0S5fmoO+mm/Lz72bNghtvzMeuvRYW\nLsz7Ro3KYVwxpCsVkafq9u6dP2e//fIiGUcfnSvjvvOdPH22JZ56Km9XFtRBnv7a0qDu5ZfzdmVB\nHSyvSpS0bjKoU7OsqJMkSZJUSRHwoQ/l1x/+cA7xdtkFPvUpGDAA7rgjh3T33APPPpvvXyLgmGPg\nC1/IFWbHHZcXrDjxRGjp+hA9e+aqu6JRo/JKtl/5ClxwQZ6SW5xyW873v5+n2w4ZsvLjO+6Yw7yW\nrPxqUCd1bAZ1apYVdZIkSZLWBQcdlAOxphTDvtb46ldzBd6SJfCzn+XFLi65BOrq4Iwz8nPtiuHZ\nyrz3Htx/P4we3XQBxLBhsGBBy55T99JL0KtXrvQrtbKgbvHivMpua1aUlVRZBnVqlhV1kiRJkjqr\niFyBV1294v5vfSsvTAHw0582ff5nPpNDvn32abrNrrvmKsGHH26+Py+//MFqOsgLUmy0Ua74K7r+\n+ryi7oknNn9dSe2DQZ2aZUWdJEmSJK1o8GCYPj1Pg504MQd6EybkKbizZ+eQ7IUX4K67coC2/fZN\nX2vDDWHo0Fx515ymgjrI+196afn7X/0qbx9+2NVgpXWFQZ2aZUWdJEmSJK3c1VfDqafm1+PH58q4\nj34UTjgBdtstV+L9+9/NFz/svz9MmZJDvlLz5s3joJ13Zt68eUD5oG6rrZYHde+/nwO6z342T939\nxz9W40tKajMGdWqWFXWSJEmStHJduuRn1tXXw8CB0K0bnHIKHH88zJ+fp7625Nl4X/lKLpA466wV\n93/1oIPY75lnOOngg1m8OD9vriVB3bRpefXb4rTXlq4qK6myrJNSs6yokyRJkqTyqqryyq1duuSp\nrCnl8G3YsJadv/nmOdz75S/zuRHw88mT2eKZZxjXrRunPf00E8+fTH39V5tcPXbrreHVV/PCFI8+\nmvuy555QWwszZqyxryppLbKiTs2yok6SJEmSmterVw7pIAdte+7ZuqKH/feH116D227LU15vGDeO\n8wrHzgd+d9E4Iuax444rP3/33fN26lS44478+euvnyvwyq1MK6n9MKhTs6yokyRJkqS1b+RIqKuD\n446DEVsfxNkL3mf9hnzbXrOsivOXvc92Gx5MTc3Kzx80KIeFd94J992Xn08HBnXSusSgTs2qrzeo\nkyRJkqS1raoKbrwR9txtMnvPf4ZPVHXh/SW5eGLpMti3ugv7L3man0+e3OT5++8PV1yRp88edVTe\nv8028MwzeZ+k9s2gTs1atsypr5IkSZLUFmpqYOmL4zmnBtZbL9+Lvb8kH+vaFcYB140f3+T5J52U\nt4cfDv365def+ATMmwfTp6/dvktafQZ1apZTXyVJkiSp7Zxw/vlcBARQ0w2qIq8mWxXwQ+DECy5o\n8tz99ssrv9566/J9e+yRA78HHljbPZe0ugzqVFZDQy6PtqJOkiRJktrGqK9+lRnbbccf6+uJyAtC\nVHeFP9bX8+/tt+f4L3+57PlbbpmnwRZtuCEMHw4337x2+y1p9RnUqaz6+ry1ok6SJEmS2s7ke+9l\nQk0N7zQ0APBOQwMTamr4yT33rNL1jj0WHnwQZs1ag52UtMYZ1KmsYlBnRZ0kSZIktZ3a2lqO/+EP\nOa/wfjww6uKLqa2tXaXrHXVULsD4zW/WVA8lrQ0GdSpr2bK8taJOkiRJktpWcQrsD5YsadGU13J6\n987Pr1vFgjxJbcSgTmVZUSdJkiRJlTP53nv5w3bbrfKU11IjRsCf/wxLl66BjklaKwzqVJYVdZIk\nSZJUObW1tdz75JOrPOW11L77wqJF8Je/rIGOSVorDOpUlhV1kiRJktQxDBkCH/4w3HZbpXsiqSkG\ndSrLijpJkiRJ6hiqquCYY+DGG2HBgkr3RtLKGNSpLCvqJEmSJKnj+OY34e23oWfPHNhJal8M6lSW\nFXWSJEmS1HF85CPw+c/n11/4AsyZU9n+SFqRQZ3KKgZ1VtRJkiRJUsdw7bXw8MP59b77wpgxMGAA\n7L47PPdcZfsmdXYGdSqrOPXVijpJkiRJ6hi6dYNhw+CQQ3Iwd9VV8NprMHUqbLst/OQnle6h1HkZ\n1KksK+okSZIkqWO6+WZ4912YPh3mz4crrsj7R4+Ggw+G4cPhuuugoaGi3ZQ6FYM6lWVFnSRJkiR1\nTN27wwYbwDbbQI8ecPLJubLuiCPg3nvhkUfgxBNh772dEiu1FYM6leViEpIkSZLUefTvD7fdBk8+\nCe+9BxdfDH/5S54SO2IEvPhipXsodWzGLyqrWFHn1FdJkiRJ6hyqqmCnnfLr006DBQvg/PPhoYdy\n9V2/fvCVr8DQofn9tttWtr9SR2JFncqyok6SJEmSOrfRo+Fzn4Mnnsjv58yB734XPvUp2G67vBiF\npDXDoE5lWVEnSZIkSZ1b//7wy1/CDjvkZ9U98QT84Q/Lj48ZAyeckKfM/uc/ecqs2qdFixZx3imn\nsGjRokp3RU0wqFNZVtRJkiRJkoo+9jEYPBj23RdeeAGWLIHjjoNbboFPfxoGDoRhw/J+tT9XfOc7\nDLjrLn48fnylu6ImGNSpLCvqJEmSJEkrs/XWUF0NN94I8+fDj36U9//jH1BTAzvvDNddl1eSVeWM\nHTuWESNGsPsuu/DST37CPnPn8uI117D7LrswYsQIxo4dW+kuqoRBncqyok6SJEmS1JwIOOWUXOxx\n2ml531NPwYknwmabwT//Cddfn7cpVbavnc3QoUOZPXs2afp0TqqvZ9nSekbX15OmT2f27NkMHTq0\n0l1UCYM6lWVFnSRJkiSppaqq4KyzcrHHRRfBFlvA0qW5+u6EE/J29Ojl7evroaGh/DVnzpzJzrW1\nzJw5c+12voOqq6ujZsECTlu6lC5LgvcWw/oRnLp0KTULFlBXV1fpLqqEQZ3KsqJOkiRJktQaffvm\ncO700+Hll2H2bPjmN2HChHx88mTYZ5+8Yuxuu8HIkbl9Uz67664c+8YbHLPbbm3zBTqYJx97jAO7\ndmWHCJYVinEaGmDHCA7s0oUnH3ussh3UCgzqVFYxqLOiTpIkSZK0Kvr1g0svhXPPzYHcvvvCn/4E\nzz6bV5B94AG47LKVV9add+aZ7Pb665xZVcUuc+dy3plntv0XWMfdMGkSp/XsSZcuyytwUgN06dqV\n03r14oZJkyrYOzVmUKeyilNfraiTJEmSJK2url3hrrvg9ddh2jR46aUc3I0bB7vvDuedl8O8p5+G\nF1+cye8uvpjvFh5qd2FK/O7ii50C20rHn3kmP4ugV6++QE5D6xsa6Nu3L9dHMOqssyrbQa3AoE5l\nWVEnSZIkSVqT1l8famth++1hyy3h6qvz1NjHHoPzz8/Hd9gBjthxVybW17NhVY4uNqyq4sL6eqfA\nttKue+xBGjmSZ7qsD3QFEkFX/rn++sT++7PLsGGV7qJKtCqoi4izI2JqRCyIiDkRcXtEbNOozYMR\n0VDyUx8RVzVqs2lE3BURCyNidkT8ICKqGrUZHhGPR8TiiHghIkatpD9jImJGRLwXEY9ExK6NjtdE\nxJURMS8i3omIWyJi49Z8587OijpJkiRJ0to0aFCeGvvLX+b39fWwad8z2W/x6+xFFQ0N0FBYKXYf\nYMicOQzabDNGjhy5ws+IESMYO3Zsxb5He/aNCRO4rFsti+lDRD3LqvtwfW0tJ59/fqW7pkZaW1G3\nF3AFsDswEqgGfhcR65e0ScBkoB/QH9gEOKN4sBDI3U2OcYcBo4AvAhNK2mwO/Ba4H9gJuAy4NiL2\nL2nzWeBiYDwwGHgKmBIRtSV9+RFwKPBpYG9gAHBrK79zp2ZFnSRJkiSpLXzuc7DRRvn1RvMv4yxy\nOpeAlPJPRHA20GXmTN5+++0VfubOncvQoUMr1v/2rHv37my85/f5v117st56G3EVPfnypEl07969\n0l1TI60K6lJKh6SUfpFSei6lNI0csA0EGv+fsCil9HpKaW7h592SYwcCHwOOSylNSylNAc4FxkRE\nsW7ra8DLKaUzUkrTU0pXArcAp5Zc51TgJymlG1JKzwOjgUXACQAR0aPw+tSU0h9TSn8HvgR8IiKs\nk22hYkWdQZ0kSZIkaW17/vm8SuyR3zyFH0RQFVAVEOSqupSC7wGzu/db4byUEn369KGurq4i/V4X\n1HTfg0d7788dNRvwYPUBTnltp1b3GXW9yOH2m432HxcRr0fEtIiY2KjibhgwLaU0r2TfFKAnsF1J\nm/saXXMKsAdARFSTw8H7iwdTSqlwzh6FXbuQq/ZK20wHZpa0UTOWLcshXUSleyJJkiRJ6uj69s2r\nxJ43aRJT+/blwdRARL4nDeBBGribnry1qJaXX4Z334VFi2Dx4vcZPXo01dXVlf4K7dabb0Lfj0/g\nbzscyqwl51NYo0PtzCoHdRER5Kmlf04pPVty6JfA54HhwETgC8AvSo73B+Y0utyckmPl2vSIiBqg\nFujSRJviNfoBS1JKC8q0UTPq662mkyRJkiS1vV8/+ijndOnCOw05rFtIA9+q6sKv/vY4W23VhwUL\nEtOnw3PPJd5802q65rz1FtTWdufYr1/G4sXdeffd5s9R21udirqrgG2BY0p3ppSuTSn9PqX0TErp\nJuB44KiI2KIF1yyX50YL2zSXCbekjQqWLXMhCUmSJElS2xs4cCAHnH463y5M8TongoPPPIPddtuK\nCy4YzaBB77PVVtC9+/vMnj2ahx+2mq6ct96C3r1z1SLAvHnl26syVimCiYgfA4cAe6WUXmum+d8K\n248CM4DZwK6N2hQnl88u2fZr1GZjYEFKaUlEzAPqm2hTrLKbDXSLiB6NqupK26zUqaeeSs+ePVfY\nd+yxx3LssceWO61DsqJOkiRJklQp502axB4/+xnfnzuXx/r1468TJwJQV1fHNddcwzvvvMOAAX1Y\ntqyOffbJ57z0Emy5ZQU73U4Vg7pi3DF/fmX70x7ddNNN3HTTTSvsm9/G/6FaHdQVQrojgH1SSjNb\ncMpgcgVbMdB7GPhWRNSWPKfuAGA+8FxJm4MbXeeAwn5SSksj4nFgP+DOQr+i8P7yQvvHgWWFfbcX\n2mxDXvzi4XIdvvTSSxkyZEgLvlrHZ0WdJEmSJKmSfv3ooxw+ZAh3Tp36333V1dWMHj2as846i3Hj\nxnHYYdUMHpxDuuuugx13hL32gk02qWDH25m33sqr6vbokd8b1H3Qyoq0nnjiiTZdTbhVEUxEXAUc\nCxwOLIyIYkXb/JTS4ojYEvgccDfwBrATcAnwx5TS04W2vwOeBX4REWcCmwAXAD9OKS0ttLkGODki\nJgHXkcO2OnIVX9ElwM8Lgd1U8iqw3YGfAaSUFkTET4FLIuIt4B1yiPeXlNJU1CJW1EmSJEmSKmng\nwIE8uZJ5mnV1dUybNo26ujqqq+HZZ+H44+HCC/PxkSPh0kvzYhO77dbGnW5nUvpgRd2Cxk/0V7vQ\n2lqp0eTquAcb7f8ScAOwBBgJnAJsAPwHuBm4sNgwpdQQEYcBVwN/BRaSw7XxJW3+FRGHksO4/wO8\nApyYUrqvpM1vIqIWmECeAvskcGBK6fWSfp1KniJ7C1AD3AuMaeV37tSsqJMkSZIktUfV1dVMLEyF\nBejWDa6+OlfTVVXB2WfDDjvkY9/7Hhx3HGy6aYU6W2HvvJMLcXr3tqKuvWtVBJNSKrv4RErpFfJq\nr81d5z/AYc20+SNQtrYwpXQVeVGLpo6/D3yj8KNVsGyZFXWSJEmSpHVD797wrW/l14MHw9FH58qx\ns8+GRx6BUaNgjz2gf//V+5yZM2fm6bhPPMHAgQNXv+Nr2dy5ebvxxrDeelBdbVDXXq3Oqq/qBOrr\nraiTJEmSJK17DjwQ3n4bXn01T4O94w446qj87Lr6+tW79md33ZVj33iDY9aRObVzCktq9usHEXn6\nq1Nf2yeDOpVlRZ0kSZIkaV0VAQMGwG9+s3zfP/8JN9/c+muNHTuWESNGMGizzdh17lzGAUPmzGHQ\nZpsxYsQIxo4du8b6vaaVBnWQp79aUdc+GdSpLCvqJEmSJEnrut69Yd48WLgwV9qddRY8/ngOsF55\npWXXGDp0KC+//Ao9Z87kgsK+C4GeM2fyyiuvtOnKoK01Z06+t+/dO7/v2dOgrr0yqFNZVtRJkiRJ\nkjqCPn2ge3e44gr40Idgl13ys+oGDYIXXmj+/Lq6Orr+ZwaTgA8V9m0IfB+IGTOoq6tbpX49+STM\nmrVKp7bY7Nn5+XRVhRTIirr2y6BOZVlRJ0mSJEnqSLbeOlfT7borbLUVLFqUn1v3/vvlz/v6id/m\n4IZl7F14nwo/w4EDli3jwm9/e5X6M3jw8tVp15Y5c5ZPewXYaCN46621+5laNQZ1KsuKOkmSJElS\nR1NTk1eB/ec/4amn8qqoRx8Nt94KDz6Y27z3HlxzDbz7bm73519cxllANLpWAs4G7rjsslXuz5tv\nrvKpLTJnzoor3fbpk6cCq/0xqFNZVtRJkiRJkjqi4jTQHXeEiRPhrrugrg4OOCCHdd27w9e+Br16\n5Sq8N3uewg8iiAiC0sAumEhw5GmnVeR7tETjirraWnjjjcr1R00zqFNZy5YZ1EmSJEmSOrazz4Zp\n02DSJFi6FPbdd/mxQw+FL30J/vCXSUzt25cHU/rvsQD+ROJuNuYLX57Y9h1voZUFdVbUtU8GdSqr\nvt6pr5IkSZKkju/jH4dx4+Cww6C6Gj75Sbj9drjjDrjuOthuO/j1o49yTpcuvEue8vou8K0uXXil\neiq33976z2xoWMNfogmNg7o+feCdd2DJkrb5fLWcQZ3KsqJOkiRJktRZRORwbvZsuPNOOPLIFY8P\nHDiQA04/nXML01+/HcFBZ5zByJED+d//bX3w9t57a6zrTVq4MP80rqgDp7+2RwZ1KsvFJCRJkiRJ\nnUnXrnlV1KacNylPgf0B8NjGGzN+4kROPBH+8hc46qg8M62lFi1a7e42a86cvG1cUQdOf22PDOpU\nlotJSJIkSZK0ol8/+ii/6tOHX02dCsCnPw233Zanyd54Y8uvs3DhWupgiVdfzdsBA5bvs6Ku/TKC\nUVlW1EmSJEmStKKBAwfyZKNytCOPzM+3++IXYfPNYZ99mr9OW1TUzZyZt5tuurIy57UAABGPSURB\nVHxfMaizoq79saJOZVlRJ0mSJElSy5x0Ut4OHw7nntt8+7YK6jbaCD70oeX7evaEqior6tojgzqV\nZUWdJEmSJEktc9hh8PTT8O1vw/e+BzNmQEpNt2+Lqa8zZ65YTQc5pOvTx4q69sigTmVZUSdJkiRJ\nUstttx2MHQs9esCWW0JNDQweDLfe+sG2bVVR1zioA4O69sqgTmVZUSdJkiRJUuv07An33ZdfL12a\nK9iOOQbuvhv++leYPj0fKw3qWrNabGu88AJsvfUH99fWOvW1PbJWSmVZUSdJkiRJUusNGQJXXAE7\n7gjDhsEnPwmHHrr8+IwZK059fe+9FZ8jtya8/z68/DJ8/OMfPFZba0Vde2QEo7KsqJMkSZIkadWc\nfPLy17/9LRx/fJ4Cu3QpbLEFfOQjy48vWrTmg7oXX4SGhpUHdX36wD/+sWY/T6vPqa8qy4o6SZIk\nSZJWX3U13HQTLFkC06bBBhvAK6/AV76Sj99wA9x7b16EYk25/HJYf33YfvsPHnPqa/tkBKOyrKiT\nJEmSJGnN2n57+P73czh35ZV52uu4ccuP//rX8NBDsOGGq/4ZCxfCz38OF1wAvXp98LhTX9snK+pU\nlhV1kiRJkiSteSefDFOn5kq7Cy7I+zbcEA45BJ56Kj/P7pBD4I478nPm5s9v3fUfeCBX7x155MqP\n9+kDCxbkabhqP4xgVNayZQZ1kiRJkiStTZtvDrNmweLF+dl111wDX/taPnbPPcvbvPhi+Xv0117L\n9/HXXAMTJ8I226x8xVfIFXWQp7/277+mvolWlxV1Ksupr5IkSZIkrX2bbJJDOoCTToLHHstVdMcd\nl/f96195mmzpSrGQK+JSyq8HDICBA2HSpPx+7FiIWPnn9emTt05/bV8M6lSWU18lSZIkSWpbETB0\nKPToATfemIO40aPhm9/MK8OOGwcnngjXXw89e8K+++aFI4q++90c4BUXqliZ0oo6tR9GMCrLijpJ\nkiRJkipv4sQcvk2fDhddlPddd13e/vGP+WfnnfNCFaNHN190Uwzq5sxZe31W6xnUqaz6eoM6SZIk\nSZIqrXdvuPZaeP99OOssOOIIePpp+PCH4d13YdNNYfjw1l2vb1949tm11mWtAoM6leXUV0mSJEmS\n2o+aGrj00vy6NcFcYxGw0055hVm1Hz6jTmU59VWSJEmSpI5p553hyScr3QuVMqhTWVbUSZIkSZLU\nMe20U15N9u23K90TFRnUqSwr6iRJkiRJ6ph23jlv//GPyvZDyxnUqSwXk5AkSZIkqWMaNCg/8+7v\nf690T1RkUKeynPoqSZIkSVLHVF0NQ4fCX/9a6Z6oyKBOZTn1VZIkSZKkjmuvveChhyClSvdEYFCn\nZlhRJ0mSJElSx7XnnvDaazBjRqV7IjCoUzOsqJMkSZIkqeP6xCfy9qGHKtsPZQZ1alJDQ94a1EmS\nJEmS1DH17g277Qbjx8Mbb1S6NzKoU5Pq6/PWqa+SJEmSJHVcN9+cQ7oLLqh0T2RQpyYtW5a3VtRJ\nkiRJktRxDRwI55wDP/4xPPVUpXvTuRnUqUlW1EmSJEmS1DmcdhoMGgTjxlW6J52bQZ2aZEWdJEmS\nJEmdQ7duMGYM/P73cMMNle5N52VQpyYVK+oM6iRJkiRJ6vgOOihvR42Cyy+vbF86K4M6Ncmpr5Ik\nSZIkdR5bbgkPPABf/jKccgrceWele9T5GNSpSU59lSRJkiSpcxk+HCZPhiOPhKOOgqOPzuGd2oZB\nnZpkRZ0kSZIkSZ1PBPzqV3D++XDzzbDffnDMMTBhAqRU6d51bAZ1apIVdZIkSZIkdU41NXDOOfDu\nu7m67k9/gvHj4aqrYOHCSveu4zKoU5NcTEKSJEmSpM5tgw3gtttg1qw8Dfbkk+EjH4G77qp0zzom\ngzo1yamvkiRJkiSp6LLLYORIePtt+OQnc1j3739XulcdixGMmuTUV0mSJEmSVNS/P/z+97BoERxy\nCBx2WN7//PPQty8sWZLbaNVZUacmWVEnVc5NN91U6S5I6uQchyS1B45FUvvUvTvcc09eIRbg4INh\n001hk01gxoyKdm2d16qgLiLOjoipEbEgIuZExO0RsU2jNjURcWVEzIuIdyLilojYuFGbTSPirohY\nGBGzI+IHEVHVqM3wiHg8IhZHxAsRMWol/RkTETMi4r2IeCQidm1tX9Q0K+qkyvGXUkmV5jgkqT1w\nLJLar/XXhwceyMHcggW5yg5gyy3zAhQzZuQVYovZQmOXXHIJAyO45JJL2q7T64DWVtTtBVwB7A6M\nBKqB30XE+iVtfgQcCnwa2BsYANxaPFgI5O4mT7sdBowCvghMKGmzOfBb4H5gJ+Ay4NqI2L+kzWeB\ni4HxwGDgKWBKRNS2tC8qz8UkJEmSJElSOZtvDldfveK+DTfMgV11NRx0ELz66gfPu/r00xkDXHP6\n6W3RzXVGq4K6lNIhKaVfpJSeSylNIwdsA4GhABHRAzgBODWl9MeU0t+BLwGfiIjdCpc5EPgYcFxK\naVpKaQpwLjAmIoqTLL8GvJxSOiOlND2ldCVwC3BqSXdOBX6SUrohpfQ8MBpYVPj8lvZFZTj1VZIk\nSZIkNeczn4HZs3MF3eTJy/fX18P99+dVYv/1r+U5w0Zdu3IwcCY5JNrI4OG/VvcZdb2ABLxZeD+U\nXCl3f7FBSmk6MBPYo7BrGDAtpTSv5DpTgJ7AdiVt7mv0WVOK14iI6sJnlX5OKpxT/JxdWtAXleHU\nV0mSJEmS1BL9+uXtqMKDy3bfPU+BPeKI/H6LLWCzzWD48EvYur6eCwvnTQS2rq93CmzBKkeWERHk\nqaV/Tik9W9jdH1iSUlrQqPmcwrFimzkrOV489lSZNj0iogbYCOjSRJtBhdf9WtCXxtYDeO6555o4\n3LkU/zM8/zy8915l+yJ1NvPnz+eJJ56odDckdWKOQ5LaA8ciad10ww0wYABMnw7f+Q4MGQI//GGe\nAhuvns65wAuFtkGeDnnh6aczvLg6RTtSkhGt1xaftzq1hVcB2wJ7tqBtkCvvmlOuTbSwTXOfU67N\n5gCf//znm7lE53LUUZXugdQ5DR06tNJdkNTJOQ5Jag8ci6SO5RXgpCaOtfP/3zcH/rq2P2SVgrqI\n+DFwCLBXSmlWyaHZQLeI6NGokm1jlle/zQZWWJ2VXP1WPFbc9mvUZmNgQUppSUTMA+qbaFP6Oc31\npbEpwHHAv4DFTbSRJEmSJElS57AeOaSb0hYf1uqgrhDSHQHsk1Ka2ejw48AyYD/g9kL7bcgLThRT\nx4eBb0VEbclz6g4A5gPPlbQ5uNG1DyjsJ6W0NCIeL3zOnYXPicL7y1vQl4dX9t1SSm8A/9OS/w6S\nJEmSJEnqFNZ6JV1R5DUYWtg44irgWOBwlk8nBpifUlpc0uZg8gqr75CDs4aU0l6F41XA34FZ5AU+\nNgFuACanlM4ttNkceBq4EriOHLb9CDgkpXRfoc3RwM/JFZNTyavA1gEfSym93pK+SJIkSZIkSe1F\na4O6Blb+fLcvpZRuKLSpAS4iB3o1wL3AmJTS3JLrbApcDQwHFgI/A85OKTWUtNkHuIT8HLxXgAkp\npV806s/XgTPIU2CfBL6RUnqs5HizfZEkSZIkSZLag1YFdZIkSZIkSZLWjqpKd0CSJEmSJEmSQd0K\nImJMRMyIiPci4pGIaLw6rSStkogYHxENjX6eLTleExFXRsS8iHgnIm6JiI0bXWPTiLgrIhZGxOyI\n+EHhuZ+S9AERsVdE3BkRrxbGnMNX0mZCRMyKiEUR8fuI+Gij470j4pcRMT8i3oqIayNig0ZtdoyI\nPxV+f/p3RIxb299N0rqjubEoIq5fye9Idzdq41gkaZVFxNkRMTUiFkTEnIi4vbDYaGmbNXI/FhHD\nI+LxiFgcES9ExKjW9tcbvIKI+CxwMTAeGAw8BUyJiNqKdkxSR/I0+Zma/Qs/e5Yc+xFwKPBpYG9g\nAHBr8WDhH4C7yat1DwNGAV8EJrRBvyWtmzYgP8N3DCt5xnBEnAmcTF6Yazfyc4OnRES3kmb/A3yc\nvLDXoeTx6Scl19gQmALMAIYA44DzIuLLa+H7SFo3lR2LCu5hxd+Rjm103LFI0urYC7gC2B0YCVQD\nv4uI9UvarPb9WGFh1N8C9wM7AZcB10bE/q3prM+oK4iIR4C/pZROKbwP4D/A5SmlH1S0c5LWeREx\nHjgipTRkJcd6AK8Dx6SUbi/sGwQ8BwxLKU2NiIOBO4FNUkrzCm1OAr4P9E0pLWujryJpHVRYEOzI\nlNKdJftmAT9MKV1aeN8DmAOMSin9JiI+DjwDDE0p/b3Q5kDgLuAjKaXZEfE14AKgf3Eciojvkce7\nbdvwK0paBzQxFl0P9EwpHdXEOR8DnsWxSNIaUijImgvsnVL685q6H4uIScDBKaUdSz7rJvIYd0hL\n+2dFHRAR1cBQcuoJQMoJ5n3AHpXql6QOZ+vCtI+XIuLGyCtgQx5/urLiGDQdmMnyMWgYMK34j0LB\nFKAnsN3a77qkjiQitiBXrZSOOwuAv7HiuPNW8ca44D5yRczuJW3+1OiPBVOAQRHRcy11X1LHM7ww\nHe35iLgqIjYqObYHjkWS1qxe5DHkzcL7NXU/Now8PtGoTatyJYO6rBboQv4rcqk55F9iJWl1PUIu\njT4QGA1sAfyp8HyV/sCSwk1yqdIxqD8rH6PAcUpS6/Un/4Ja7nef/uS/Nv9XSqme/EutY5OkNeUe\n4HhgBHAGsA9wd2GGEzgWSVqDCmPLj4A/p5SKzwxfU/djTbXpERE1Le1j15Y27KSCpp+jIEktllKa\nUvL26YiYCvwbOBpY3MRpLR2DHKckrSktGXeaa1O8uXZsktSslNJvSt4+ExHTgJeA4cADZU51LJK0\nKq4CtmXF54U3ZU3cj7V6LLKiLpsH1JMfYFpqYz6YhkrSakspzQdeAD4KzAa6FZ6NUKp0DJrNB8eo\n4nvHKUmtNZv8i2O5331mF97/V0R0AXoXjhXbrOwa4NgkaRWklGaQ78+Kq1A7FklaIyLix8AhwPCU\n0qySQ6t7P9bcWLQgpbSkpf00qANSSkuBx8mrCAH/LYfcD/hrpfolqeOKiA8BWwGzyOPPMlYcg7YB\nBrJ8DHoY2KHRStQHAPPJD1iWpBYr3AjPZsVxpwf5eU+l406viBhccup+5IBvakmbvQs3zUUHANML\nf5CQpFaJiI8AfYDXCrsciySttkJIdwSwb0ppZqPDq3s/9lxJm/1Y0QGF/S3vq6u+ZhFxNPBz4CTy\ngH8qUAd8LKX0eiX7JmndFxE/BP4febrrh4HzgR2BbVNKb0TEVcDBwJeAd4DLgYaU0l6F86uAv5OD\nvTOBTYAbgMkppXPb+OtIWgcUnoH5UfLN7BPAaeRpZG+mlP4TEWeQx5MvAv8ir5i4HbBd8a++EXE3\n+S/BXwO6AdcBU1NKXygc7wE8D/wemATsAPwUOCWl9NM2+aKS2rVyY1HhZzxwK/mPBx8ljyUbADsW\nCiociyStlsK91rHA4eRZTUXzU0qLS9qs1v1YRGwOPA1cSR6n9iM/D++QlFLjRSaa7q9B3XIR8XXy\nA0z7AU8C30gpPVbZXknqCArLcu9F/gvx68CfgXMKVS0UHi56EfkfkBrgXmBMSmluyTU2Ba4mP7Nl\nIfAz4OyUUkObfRFJ64yI2Id8M9z4l72fp5ROKLQ5D/gqefWzh8jjzj9LrtEL+DHwSaABuIV847uo\npM0OhTa7kqerXZ5SumgtfS1J65hyYxHwdeB/gZ3J49As8gqJ3yktlnAskrQ6IqKBlT8j7ksppRsK\nbdbI/VhhzLuE/By8V4AJKaVftKq/BnWSJEmSJElS5fmMOkmSJEmSJKkdMKiTJEmSJEmS2gGDOkmS\nJEmSJKkdMKiTJEmSJEmS2gGDOkmSJEmSJKkdMKiTJEmSJEmS2gGDOkmSJEmSJKkdMKiTJEmSJEmS\n2gGDOkmSJEmSJKkdMKiTJEmSJEmS2gGDOkmSJEmSJKkdMKiTJEmSJEmS2oH/D/sJaZIpddX8AAAA\nAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f7ac9bc5450>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# find peaks using the first ridge position, last ridge position as well using find_peaks\n",
"peaks = signal.find_peaks_cwt(y, wavelet=signal.ricker, widths=widths)\n",
"peaks_2 = peak_pos[np.all(((peak_width > 5), (peak_len > 20)), axis=0)]\n",
"\n",
"fig, ax = plt.subplots(figsize=(15,5))\n",
"ax.plot(x,y)\n",
"ax.plot(x[peaks], y[peaks], 'kv', alpha=0.8, label='scipy')\n",
"ax.plot(x[peaks_2], y[peaks_2], 'rd', alpha=0.8, label='filterd length and width')\n",
"#ax.plot(x[peaks_3], y[peaks_3], 'bx', label='filterd length')\n",
"ax.set_ylim(200000,520000)\n",
"ax.legend()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Estimate Peak widths\n",
"\n",
"Procedure from Zhang et al.\n",
"\n",
"1. Perform CWT with Haar wavelet w/ same scales as peak finding. Result M x N matrix\n",
"2. Take abs of all values\n",
"3. For each peak in peak-detection there are two parameter: index and scale\n",
" a. Row corresponding to scale is taken out\n",
" b. Search for local minima to three times of peak scale or next peak index\n",
"4. If local minima do not exist:\n",
" a. Peak start or end point is min(3 x peak scale, next peak index)\n",
" else\n",
" b. Peaks boundaries are minima and min(...)\n",
"5. Repeat for all peaks"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAhkAAAFkCAYAAACNTikJAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3XmcW3W9//HX9ySZTDKTmcnsnZa2lC4s3ctWQSu0CIIr\nXq9WUBQviqJXuVd8yM/rRb33KuLCvepVRK4Csl3hKiqytgwUkFK60Z22tKXtLJktM5OZZLKd7++P\nk8yaZLZkpu18nj5iZs6S803KJO98V6W1RgghhBAi24zJLoAQQgghTk0SMoQQQgiRExIyhBBCCJET\nEjKEEEIIkRMSMoQQQgiRExIyhBBCCJETEjKEEEIIkRMSMoQQQgiRExIyhBBCCJETEjKEEEIIkRM5\nDxlKqZuUUoeVUiGl1Eal1HnDHF+slPpvpVR94px9Sqkrcl1OIYQQQmSXPZcPrpT6GPBj4HPAJuBm\n4Bml1HytdUuK4x3AOqARuBqoB2YB7bkspxBCCCGyT+VygTSl1EbgNa31VxK/K+AY8FOt9R0pjr8R\n+GfgTK11PGcFE0IIIUTO5ay5JFErsQJYn9ymrUSzDliZ5rT3A68Cv1BKNSqldiqlblVKSd8RIYQQ\n4iSTy+aScsAG+AZt9wEL0pwzB7gUeAB4LzAP+EXicf491QlKqTLgcuAI0DPeQgshhBBTSD4wG3hG\na92a7QfPaZ+MNBSQro3GwAohn0vUemxTSk0HvkaakIEVMB7MeimFEEKIqeMa4KFsP2guQ0YLEAeq\nBm2vZGjtRlIDENEDO4rsBaqVUnatdSzFOUcAHnjgAc4666zxlViM2M0338ydd9452cWYUuQ1n3jy\nmk88ec0n1t69e7n22msh8VmabTkLGVrrqFJqC7Aa+DP0dvxcDfw0zWmvAGsHbVsANKQJGJBoIjnr\nrLNYvnz5uMstRqa4uFhe7wkmr/nEk9d84slrPmly0t0g1x0qfwJ8Tin1KaXUmcBdgBu4F0Apdb9S\n6nv9jv8lUKaU+i+l1Dyl1FXArcDPc1xOIYQQQmRZTvtkaK1/r5QqB76L1WyyHbhca92cOGQGEOt3\n/HGl1HuAO4E3gLrEz0OGuwohhBDixJbzjp9a619gjRBJte/SFNteA96R63IJIYQQIrdk/gkxJmvX\nDu46I3JNXvOJJ6/5xJPX/NSS0xk/J4JSajmwZcuWLdJZSAghhBiFrVu3smLFCoAVWuut2X58qckQ\nQgghRE5IyBBCCCFETkjIEEIIIUROSMgQQgghRE5IyBBCCCFETkjIEEIIIUROTMYqrEKIU9STT8KG\nDQO3ud3wta9Z90KIqUVChhAia771LTh4ECorrd+jUXj7bbjoIli9enLLJoSYeNJcIoTImu5uuOEG\nOHDAur32mrU9GJzccgkhJoeEDCFE1gSD4HL1/Z78WUKGEFOThAwhRNaEQgP7XiRDRig0OeURQkwu\nCRlCiKwJBgeGDIfDuklNhhBTk4QMIURWaD00ZID1u4QMIaYmCRlCiKzo6bHu+/fJSP4uIUOIqUlC\nhhAiK5L9LlLVZEifDCGmJgkZQoisSNZWSHOJECJJQoYQIiskZAghBpOQIYTIimSQkD4ZQogkCRlC\niKyQPhlCiMEkZAghskKaS4QQg0nIEEJkhYQMIcRgEjKEEFkhfTKEEINJyBBCZEWy38XgkCF9MoSY\nuiRkCCGyIhjsW6ukP2kuEWLqkpAhhMiKVOuWgIQMIaYyCRlCiKwIhYY2lYC1TZpLhJiaJGQIIbJi\nuJoMrSe+TEKIySUhQwiRFZlCRjwO0ejEl0kIMbkkZAghsiJTyEjuF0JMLRIyhBBZkalPRnK/EGJq\nkZAhhMgKqckQQgwmIUMIkRUSMoQQg0nIEEJkRTCYublEQoYQU4+EDCFEVoRCmWsypE+GEFOPhAwh\nRFZIc4kQYjAJGUKIrJCQIYQYTEKGECIrpE+GEGIwCRlCiKxI1ycjLw8MQ/pkCDEVScgQQoyb1umb\nS5SSlViFmKokZAghxi0atdYnSRUyQEKGEFOVhAwhxLglA0SqPhnJ7RIyhJh6JGQIIcYt2d8iU02G\n9MkQYuqRkCGEGLdkLYU0lwgh+pOQIYQYNwkZQohUJGQIIcZN+mQIIVKRkCGEGDfpkyGESEVChhBi\n3KS5RAiRioQMIcS4ScgQQqQiIUMIMW7JppBMfTKkuUSIqUdChhBi3IJBa32SvLzU+6UmQ4ipSUKG\nEGLckuuWKJV6v4QMIaYmCRlCiHFLtzhakoQMIaYm+2QXQAhx8guFrH4XtYdrefX4qwP2uewu7Plf\nIBTKn6TSCSEmi4QMIcS4JWsyPv/E56kL1FGYVwiA1prmYDNfLp9DJPJBYjGwy7uOEFOG/LkLIcYt\nGASnp5t9bQe55wP3cP2y6wErZJT/sJxGdgAfJBQCj2dyyyqEmDjSJ0MIMW7BIFC+B41mUeWi3u1K\nKRZVLqI+trPvOCHElDEhIUMpdZNS6rBSKqSU2qiUOm+E531cKWUqpf6Q6zIKIcYuFIJo6U4UinMq\nzxmwb3HVYo6Gd/YeJ4SYOnIeMpRSHwN+DNwGLAPeAJ5RSpUPc94s4IfAhlyXUQgxPsEghIp3MLd0\nLm7HwGEmiyoXURfaD/aQ1GQIMcVMRE3GzcCvtNb3a633ATcCQeD6dCcopQzgAeBfgcMTUEYhxDgE\ng9BdsJNFVYuG7FtUtQgTEyr2SsgQYorJachQSjmAFcD65DattQbWASsznHob0KS1/m0uyyeEyI7u\noKbDuYPFlYuH7FtYudD6oWqHhAwhpphcjy4pB2yAb9B2H7Ag1QlKqYuAzwBLcls0IUS2BEwfPbaW\nlDUZhXmFzPTM4WjlTumTIcQUM1lDWBWgh2xUqhD4HXCD1to/mge8+eabKS4uHrBt7dq1rF27djzl\nFEKMQEe+1bGz/8iS/s4pX8TRqp1SkyHEJHr44Yd5+OGHB2zr6OjI6TVzHTJagDhQNWh7JUNrNwDO\nAGYBf1GqdxUEA0ApFQEWaK1T9tG48847Wb58eVYKLYQYna6CHThwM8c7J+X+JdWLearqbgkZQkyi\nVF+8t27dyooVK3J2zZz2ydBaR4EtwOrktkR4WA38LcUpe4FFwFKs5pIlwJ+B5xM/H8tleYUQY9NT\ntJNq4xxshi3l/mXTF0GhD1+geYJLJoSYTBPRXPIT4D6l1BZgE9ZoEzdwL4BS6n7guNb6/2mtI8Ce\n/icrpdqx+ovunYCyCiHGIFa6kxmOpWn3L0701TjUvRO4dIJKJYSYbDkPGVrr3yfmxPguVrPJduBy\nrXXyK80MIJbrcgghcqMnEkNX7Ga261Npj5lbOhdi+RwJ7UBChhBTx4R0/NRa/wL4RZp9Gd9xtNaf\nyUmhhBBZsbvhINjDnOFJ3ekTwG7YcbSfTV3pzgksmRBissnaJUKIcdlyfAcAC0rShwwAV+ciGvSO\niSiSEOIEISFDCDEuO5t2QqCa6qKKjMcVdi+m1dhN3IxPUMmEEJNNQoYQYlz2tOyEpkW43ZmPKwkv\nIqZCHPIfmpiCCSEmnYQMIcS47PPvAN/iYUNGWdyacnyHT5pMhJgqJGQIIcYsEA5QHzoMvkW4XJmP\nLbFXkRetsJpXhBBTgoQMIcSY7W7ebf0wguYStxsKuhdJyBBiCpGQIYQYsx2+HRgY0Hz2iEJGfvti\naS4RYgqRkCGEGLOdvp1UO+ZDLH9EIcPWtoi32t6iO9I9MQUUQkwqCRlCiDHb0bSDaXZrfoz8/MzH\nulxgNC1Co/uaWYQQpzQJGUKIMdFas9O3kyq9GJcLetdNTsPthljDOSgUO33SL0OIqWBCphUXQpx6\n6gP1+Hv8lNn7dfo8cgTefHPggU4nrFqF263oCbiZWzpXOn8KMUVIyBBCjEmyA2dxOBEyIhFYtQqO\nHh168O9+h9t9LcEgvLtqkXT+FGKKkOYSIcSY7G3Zi9vhxhmabc2R8dBDVsDYsAGOHeu7XXEF3H47\nLqdJTw+cU76QPc17Jrv4QogJIDUZQogxOd55nBlFMwjVGRS4TPjBD+ADH4B3vnPggd/8Jrzzncx7\n8wngA1S7T6Opu4loPIrD5piUsgshJobUZAghxqQuUMd0z3SCQbi850+wbx984xtDD7z4YrjoIhY9\n8X1AU+qYjkbT0NUw4WUWQkwsCRlCiDGpD9QzvWg6wW7NdQ3ft/pjrFyZ+uBbb6V0/0bexQa8tum9\n5wshTm0SMoQQY1LXWUdNYQ3zjtdyZufrcOut6Q++8kq65yziG9xOsVHTe74Q4tQmIUMIMWpa696a\njA+/+X0OlyyD97wn/QlK4bv+G7yXpynedZQ8W57UZAgxBUjIEEKMWluojXA8zDlvh1jRto6nl35j\n2Nm4wh/4ew5xOuW/uYMaTw11AanJEOJUJyFDCDFqyVqIpfc+zdG8uew56yPDnuMusvNDbqG89lHO\nD5ZKTYYQU4CEDCHEqNUF6pjfAqVPv8jdJV8nv8A27DkuF/yWzxAuquCG9X6pyRBiCpCQIYQYtbrO\nOj75BuD18rDjU8OuwArW2iVh8jmw5ou88+Vj+PzHc15OIcTkkpAhhBi1+kA97znqQF16Ke0h54hC\nhstl3R9ecAXOcIzqvRIyhDjVScgQQoxaS9MRlh2LwiWXEAwyopBhs1lrpR2rWE60IJ8LDgQJhAO5\nL6wQYtJIyBBCjFrx1t04TDBXXUJPT18txXBcLghG7HResJR3H5EJuYQ41UnIEEKM2unbj9BR4qJn\n9pnAyGoykscFg2C+axUXHYX6lsM5LKUQYrLJAmlCiFFbvKeNY8vmUx2y5sZIhozfNTbyamfngGPd\nhsEtM2dSlZfXGzIKr34/rm//gMirL8OZV0x08YUQE0RChhBiVKLtbSw5FmXjtcsoDlnb3G74r+PH\n+erBgywsKCCv38Rch3p6eNbv54WlS3G7HYRC4Dr3Qjrywf3KJvjMJD0RIUTOScgQQoxK+7onqNAQ\nf9c7CQatbeud9dxx8CBfP+00bp8zB9UvZOzp7mbV9u1csWMHjpIlBIN2sNnYOq+Q6a/vnaRnIYSY\nCNInQwgxKtH1z1JfCCWLz7dCxmofP9T7uammZkjAADi7oIBnFy/mQCjEwc/upDMSB+DNRTXM3lsP\nPT2T8CyEEBNBQoYQYlTyX3mN2tOhpmg6T3c1w617+WB+NT+dN29IwEha5vHw1KJFdFUHeGH1LsKm\nSf25C8iLmvDaaxP8DIQQE0VChhBi5Do6KNn9Fi/PsbEv6uC22B7YUMGPqxdgDLNA2oXFxVz85CJa\nazq4du9ezIULaXcbUFs7QYUXQkw0CRlCiJF76SUMU7NnYTVfe+stZpuF8L2zKHRnDhhJs/xe5v1x\nAY81N9Ptmc8LszRaQoYQpywJGUKIkXvhBVrL3DSfvZpNgQAf6TgdYsao5slwb6pkcUEB683pPD9L\nw8aNEArlttxCiEkhIUMIMXK1tWxZUISv4r1c4PEwt90LjHzGT7cbQt2Kf509m50RB389dyEqEoFX\nX81hoYUQk0VChhBiZPx+2LaN3168iDZHNbfNnk1PSOF0WuuSjITbbVVafLi8nAX5eRxadh2REo/0\nyxDiFCUhQwgxMi+9hNaaP1/wIU5TXVxRWkowOPJaDEisXRIEQym+c/ocKD2XP79/DbzwQs6KLYSY\nPDIZlxBiZGpree6KKwiWns1Nha0opQaswBptj3L0e0cJ7g0OOE05FdNvmo73Em/vtOIAH62s4tqt\nz/G9q97P333y84x4OVchxElDajKEECOia2v59qeuhc59vLe0DEjkApem8b5GNs3fRP0v6613FVvf\nreetHt649A32fGIPnmiYYBC0tmozZra/wLaq09k4dy688spkPj0hRA5ITYYQYnh+P7U2G69Omw47\nb2XGRfcD4DjWxTcaDrDv0x1Urq3kjB+dgbPGOeBUbWoa72/k0NcPcfofN3G1nk04OJ38AoOFqpWm\naAvfueEGnnrxRbjsssl4dkKIHJGaDCHE8LZt4zuf+hRnxLqgbSM1nhrq76nn0kc24zGjLFm/hLMf\nOntIwABQhmLap6dx/pvnE1lVxRd5ix3v2kYsEGO6p4bSpid4etkyNtXXT8ITE0LkkoQMIcSwtr35\nJhuWLOEiRx3FzmLCL4TZf+N+3pwzjbsvOBfvpd5hH8PhdaC/Mp8vsZye/UH2rN3DdPd0uuufYn53\nN/95xhkT8EyEEBNJQoYQYlgPRaOUd3XhCe7l3K5z2f3R3ZReXsqzZ88jv3DkbyNuN+ylCO9/nUPb\n020sumcRrcEmrtUmf1q+nC6pzRDilCIhQwiRUVxrHj7tND5WX09nXRtf+tWXyJ+Vz9mPnE0wbIx6\nCCuAPreUeT+bR9FDRXxw0wdZPc1D0OXiT7t25eZJCCEmhYQMIURGLzU1Uef1slY5WX37apwxJ4ue\nWITdYx/1qNPkscEgTP/CdFw3uPjyU18mvsvgHXv38lB3d26ehBBiUkjIEEJk9OCBA8yub8D76OlU\nH63mjX9/g/yZ+cDop7boHzIA5v1kHpvmbiL6pRjXb2zkmeJimiORLD8DIcRkkZAhhEgrbJo8Fg5z\n8z1v0fScyR0fvgPPeZ7e/eMNGd4CLz/6+I8IV4Y555llqLjm0ebmLD4DIcRkkpAhhEjrqdZWeiI2\nlv5tMZ73eXj+7Oep8dT07g+FRj+tePI8AKUU3nIv2760jR5fCf981xEelM6fQpwyJGQIIdJ6qKmJ\nf7qrC2Ju+Ja1bXrR9N79463JSD7e7lm7qbrKwWV/qWZHYzeHZel3IU4JEjKEECl1xmJsfqOF1U+4\nOO0SH40ljQBM94w9ZDgcYLcPChme6dR11jHnv5fgiCpu+K3mkaambD0NIcQkkpAhhEjpjy0t3PAz\nTR6tzPxqFXWBOgxlUFVYBVjrj4RCo1/TLLnce1KNp4a6QB3OWYXMrnmO9/0Jal9pQGudxWcjhJgM\nEjKEECltevQYKzfCAvPn2C5YSn2gnqqCKuyGteRRJAKmObo+GdC33HvSdM906gP1aK2ZsboTCju4\n8o4ednR1ZfHZCCEmg4QMIcQQ9R0h3nF7N91ndlE+/TCUl1PXWTeg02cyKIylJqN/yKjx1BCMBukI\nd2Ccu4SF4R+x9A2o/c2R8T8RIcSkkpAhhBjixe8foMoHy2r+D7VsKQD1XfVDOn3C+ENG8jHrA/Ww\ndCmV4Vc4vspg5n+0Eu2Kjet5CCEml4QMIcQAsc4YJb9oY8fH8qnZ/RQsWwZAXWfdgE6fyX4V4+2T\nkXzMus46WLIEgJkf8VHUBht/enjsT0QIMekkZAghBjj4y+PYQ1D6D4Xg88HSRE1GoD5lc8l4+2RM\n80zrfXyKi2HOHC46/CovXabo/lkjZsQc1/MRQkweCRlCiF5m2KTuzuM8+x54T88xa+OyZYRjYZqD\nzUOGr8L4m0vy7fmUucqoC9T1Xs+2fTutX/SS3xjH94BvHM9ICDGZJGQIIXo13t+I0RRjx2fc1Gzb\nZtUszJ6Nr9v6oE/WOkD2QgZYnT/rA4mZPpcuhW3buOj8Kl66GA794G10XIazCnEympCQoZS6SSl1\nWCkVUkptVEqdl+HYf1BKbVBKtSVuz2U6XgiRHTquOXrHMV5dpThveTls32594CtFY5c1EVd1YXXv\n8dnqkwFQVVjVG2RYtgza27m8u5tH1kJ0fw8tj7eM9WkJISZRzkOGUupjwI+B24BlwBvAM0qp8jSn\nrAIeAt4NXAgcA55VSk1Lc7wQIgua/6+ZnoMh7vu45qqyMti2rbc/hq/LCgBVBVW9x2erT0bycZPX\nSF6zdMcOvBcWcex8B0dvPyqTcwlxEpqImoybgV9pre/XWu8DbgSCwPWpDtZaf1JrfZfWeofWej/w\nD4lyrp6AsgoxJWmtOfr9o7RelE/rOXbOVwoOHuwdWdLY1YhCUVFQ0XtONptLqgure2tLqKmBigrY\nvp0ry8r49d/HCWwO4F/vH+vTE0JMkpyGDKWUA1gBrE9u09bXkXXAyhE+TAHgANqyXkAhBAD+Z/10\nbe/ikWvgitJSbDt2WDsSIcPX7aPcXd472ydYQcFut9YjGY1UIaOqoF9ziVLWdbdt46qyMl5abqKX\nuDh6+9GxPj0hxCTJdU1GOWADBncP9wHVQw9P6QdAHVYwEULkwNvffxvnuQU8dmYPV5aVWf0x8vLg\nrLMAq7kkuWZJ0miXeU9K2VxSWEVnuJNQNNFZY+lS2L6dxQUFTHfmsfmzLtrXt9P5eudYnp4QYpLY\nhz8kJxQwbAOrUuobwN8Dq7TWkUzH3nzzzRQXFw/YtnbtWtauXTuecgpxyuvY2EHHix00/Hoahurm\n8tJSqz/GwoW91RSN3Y0DOn3C6FdgTUrV8TP52L5uH7NLZls1GXfcgWpr48qyMv5nhZ93zbNqMxb+\n38KxPE0hpryHH36Yhx9+eMC2jo6OnF4z1yGjBYgDVYO2VzK0dmMApdTXgK8Dq7XWu4e70J133sny\n5cvHWk4hpqy6n9eRf0Y+j54f4cJYEWUOB+zYAYsX9x7j6/Ixs3jmgPPGEzJSNZckrzO7ZHbvzJ/s\n2MGVCxfy64YGnF+aTcvNR+g51kP+afmjv7AQU1yqL95bt25lxYoVObtmTptLtNZRYAv9Om0qpVTi\n97+lO08pdQvwTeByrfW2XJZRiKks0hKh+dFmqj4/jec62q1RJaYJe/ZYNRkJvm7fgJElML7mklgM\notG+bcmmmN5+GXPnWrUou3ezxuvFoRQvv8fA5rbRcE/D6C8qhJgUEzG65CfA55RSn1JKnQncBbiB\newGUUvcrpb6XPFgp9XXg37BGnxxVSlUlbgUTUFYhppTGe60RHYc+7KYrHufK0lI4csSqajjnnL7j\nurLbXAIDm0wq3BUYyugbYeJwwIIFsHs3hXY7q0pKeCLsp+raKhp+3YAZlanGhTgZ5DxkaK1/D/wz\n8F1gG7AYq4aiOXHIDAZ2Av0C1miSx4D6frd/znVZhZhKtKlp+FUDFR+t4K90UJOXx5LCQtidaJ1M\n1GT0xHroDHdmteNn8vwkm2Gj3F3eN1dG8vqJslxVWsoL7e14b6gi0hCh9YnW0V9YCDHhJmTGT631\nL7TWs7XWLq31Sq315n77LtVaX9/v99O11rYUt+9ORFmFmCr8z/sJHQxRc2MNT7a2cmVZGUop64O9\nqAimW+uUpJqIC8Zfk5FxGCtYNSm7d4PWXFlWRlhrNs6MUnRhEfV31Y/+wkKICSdrlwgxRdXfVY/7\nHDcty/N4MxTiqtJSa8fu3dYHvFIAKacUB6smIlvNJcnH720uAasMbW3g8zHf7Wauy8VfW1upubEG\n/7N+Qm8NegAhxAlHQoYQU1C4PkzL4y3U3FjD021tOJRitddr7UyGjIRk7cLg5pJgcHzNJanmyhhS\nk5EsD3BlaSlPtbVR/tFy7CV26u+W2gwhTnQSMoSYghp+04DhNKj+ZDXr29tZWVSEx26HeBz27h0Y\nMrp8KBTl7oHLDeWkuaR/n4wzzgCnszdkXOb1cjQc5ggRqj9dTeNvGjHD0gFUiBOZhAwhphgd1zTc\n3UDl2krwGNT6/X21GIcOQU/PkJElFQUVA6YUh+x2/IQUzSU2G5x5JuzaBcC7SkqwAev8fqZ9fhrR\nlijNf2hGCHHikpAhxBTT+lQr4WNhpn9hOlu7uuiIx1nTv6kEhjSXDO70CbmpyQhEAn1Ti8OAESZF\ndjsXFBWxvr2dgjMLKLmkRDqACnGCk5AhxBRTf1c9nnM9eFZ4WOf3U2izcZ7HY+3cvRtKSmDatN7j\nfd1D1y2B7Hf8HDIhFwwYYQKw2uvleb8fU2tqbqyhY0MH3Xu6R18IIcSEkJAhxBTSc7yHtifbmPZ5\nK0Ss9/t5d0kJDiPxVrB7t1V7kBhZAqkn4oKxd/zMz+87v7/kNYaMMOnogHqrxmKN10tbLMb2ri7K\nP1SOo9JBw69lBlAhTlQSMoSYQny/82G4DCo/VkkoHueVjg5Wl5T0HTBoZAkkVmDNYnOJUmlWYu23\nfkmvQSNMLiwqwm0YrPf7MfIMqq6twvegT2YAFeIEJSFDiClCa03jvY1UXF2B3WPnlY4Owlr3dfqM\nxWDfvqEhI0WfjHgcIpGx1WSAdd7g5pJydzmGMgY2l5x+unVwImTkGQbvLC5mnd8PQPV11USbo7Q9\n1Ta2ggghckpChhBTROdrnYT2h6j+tNUssb69nUqHg4UFiWWBDh60kkO/kBGKhugMd6aciAvGVpOR\nPG9wTYbNsFHhrhjYXGIYcPbZvSNMwGoyeamjg7BpUri4kMJlhTTe14gQ4sQjIUOIKaLx3kacpzkp\nucRqHlmXGLqqkv0v0owsgaETcWUjZAyuyUheZ0BzSbI8ybJhdf4MmSavdnQAVm1G619aibZGEUKc\nWCRkCDEFxHviND3SRNUnq1CGwh+NsiUQ6Bu6CtYHeVkZVFb2bsq0bgmMr7lkcE1G8joDmkvAChl7\n9vSOMFlSWEiZ3c769nYAKj9RCRp8D/sGP5wQYpJJyBBiCmj9UyvxjjjV11nNHi+0t6Ohrz8GDFmz\nBNKvW5IMCNlsLkleZ0BzCVhlCgTg2DEADKW41OtlfaJfRl5FHqVXlfYuWy+EOHFIyBBiCmi8r5Gi\nlUW451upYJ3fz1yXi1nJ8aTQN3y1H1+3D0MZQ6YUTzZ1ZLPjJ2SoyUiWL2GN18umzk46YzHAajLp\n2tJF166usRVICJETEjKEOMWF68O0PdPW2+ETrPkxBgxdjUZh//6Uw1fL3eXYDNuA7bmqyUjZJ2Pm\nTCgoGNIvIw68mGgyKbuqDHuZHd990mQixIlEQoYQpzjfgz6UQ1Hx9xUAHO/p4c1QaGBTyYEDVtAY\nFDLSTcSVq5qM6sJqApEAwWi/BGIYQzp/zsnPZ5bT2TuU1cgzqPpEFb4HfJgxmTNDiBOFhAwhTmFa\naxrva6TiwxU4ShyANXRVAZf0r8lIDhEdwRwZkMOajFQTciXL1W8Yq1KKNf36ZQBUf7qaSGME/3N+\nhBAnBgkZQpzCAlsCBHcHqbquLyis9/tZWlhIeV5e34G7d1ujSsoH9r3ItG4J5GYIa/K6AyRHmJh9\ntRSrvV4oQt7bAAAgAElEQVR2B4M0hsMAFC4rpGBhgXQAFeIEIiFDiFOY7z4fedPyKL2sFLBqNtb5\n/QOHrkLK6cQh0VxSkHrdEsj+ENaU65eAVbZgEN5+u3fTpYnnkBzKqpSi6roqWv7UQtQvc2YIcSKQ\nkCHEKcqMmtbcGNdUoWzWsNQ3g0EaIhEu7d9UAmlDhq8rdU1GMAhOp9VdYizSNZeUucqsqcVTNZck\ny5lQlZfHooICnu/XZFJ1TRU6qml+rHlsBRNCZJWEDCFOUf5n/URbolR9si8kPN/ejl0pLi4u7jsw\nHLY6fg4KGcFokEAkkLJPRig09loMSN/xMzm1+JDmkhkzoKhoQMgAq1/J84maDADnNCfeNV58D8oo\nEyFOBBIyhDhF+R7wUbCwgMLFhb3batvbucDjodBu7ztw/35rxbPBc2QkahPSLfM+1v4YkL4mI3m9\nIc0lSg0ZYQJWk8mRnh4O90ssVddU0fFiBz1He8ZeQCFEVkjIEOIUFOuM0fJ4C1XX9tVCmFpT6/dz\nSar+GGAtRNZPunVLwKqFGG/ICIV6ZwofoKowxYRcMGSECcC7iotRWOEpqfzD5RguA99DUpshxGST\nkCHEKajljy2YPaa1rkfCru5uWmOxof0xdu2CadOgtHTA5nTrloBVCzHe5hLTtBZ9HayqIMWEXGCF\njL17rVqXBK/DwfLCwgEhw+6xU/6hcnwP+NCpUowQYsJIyBDiFOR70EfJu0vIP61v2vDn/X6cSrGy\nqGjgwRlGlqSaUhyy01ySfJzBUjaXgFXGnh44fHjA5ku9Xp73+wcEiqprqwjuDtK9o3vshRRCjJuE\nDCFOMeH6MP71fiqvqRywvba9nXcUF5NvGzhFeKo1S8BqLqlwVwyZUhyy0/Ez+TiDpVy/BPrKmKLz\nZ30kwoF+D+a9zIuj3IHvAWkyEWIyScgQ4hTT9EgTyq6o+LuK3m1xrXmxvX1oU0koBAcPjmr4KuS2\nJqOqsIquSBfdkUG1ENXV4PUO6ZdxcXExdqUGDGU1HAaVH6/E95APHZcmEyEmi4QMIU4xvgd9lL2/\nrHcacYBtgQAd8fjQTp/79lm9L1M1l3SnXrcEstPxM/k4gyWvOaQ2I80IE4/dznkez4B+GWA1mUTq\nI7S/OHC7EGLiSMgQ4hTSvaebrq1dA0aVgDU/RoFhcJ7HM/CE5Ad2upqMFJ0+ITsdP5OPM1ja9Usg\nZcgAuLSkhNr29gH9Mjzne3DNdUmTiRCTSEKGEKcQ34M+7CV2yt5bNmB7bXs7FxcXkzd4is5du+C0\n06yJrgY/VprF0SC3NRlp1y8Bq1/Gvn0Qiw3YfInXS3M0yu7uviYWpRSV11TS/Fgz8VB88CMJISaA\nhAwhThHa1DQ91ETF31dgOPv+tCOmyUvt7b1rfQyQZmQJpF/mHXJbk1HmKsOmbOlHmEQiVj+Sft5R\nVESeUgNm/wRrYq54IE7rE61jL6wQYswkZAhxiuj4Wwc9R3qGNJW8HgjQbZoDl3ZPSjOyJBgN0hXp\nmpSOnzbDRkVBRfrmEhjSZOKy2VhZVDSg8yeAe54bzwUefL+TJhMhJoOEDCFOEb4HfDhnOSm+qHjA\n9lq/n2KbjWWFhQNP6Oqy5pxI0x8DUk/EBbltLkleN2VzSWUlVFQMGWEC1nwZL3Z0EB80AVfVtVW0\nPdVGpCXFzF9CiJySkCHEKcAMmzT/vtlacdVQA/Y9397Ou0pKsA/uj7F3r3WfZiIuSL1uCYy/ucTh\nsFZwHdX6JUlpOn9eUlJCeyzG9q6uAdsrP1aJ1prmR2VlViEmmoQMIU4BrU+1EvPHqLpmYM1DTzzO\n3zo6hs6PAWnXLIHM65bA+GsylOpbvySVtOuXQNqQcUFRES7DoHZQk0leRR6lV5TKKBMhJoGEDCFO\nAb4HfBQuL6Tg7IIB21/t7CSs9dD5McD6oD79dCgoGLLL1+XDUAZlrrIh+6JRa3DHeGoywDo/XU1G\n2vVLwAoZ+/cPWfgkzzC4uLh4SOdPsJpMOv/WSehQmlQjhMgJCRlCnOSi7VFa/9I6pMMnWENXy+x2\nFqUIEuzalXFkSWVBZcopxZPBYDw1Gcnzx9RcsnChlXL27x+y69KSEl7q6CBqmgO2l3+gHFuhDd+D\nUpshxESSkCHESa75sWZ0TFP58coh+9b7/by7pARDqaEnphlZAsPPkQHZqcnI1PGzO9o9dGpxSDvC\nBKzOn13xOK8HAgO229w2yj8iK7MKMdEkZAhxkvM94MO7xotzmnPA9s5YjNc6O1mTqqmksxOOHUtb\nk+HrzrxuCeS2JiPjhFylpdY6JilCxgqPh2KbjfWD+mWA1WQS2h8isDkwZJ8QIjckZAhxEut5u4eO\nFztSNpVsaG8nDqlDRobpxAEaAg0Z1y2B7ISMdDUZ0wqn9ZYjpYULUw5jtSnFJV4v61KEDO8lXvJq\n8mTODCEmkIQMIU5ivod8GG6D8g+XD9m3zu9nltPJGanaNXbvtsaQnnlmysetD9Qz3TM95b5k7UMu\nO37WeGp6y5FSmhEmYIWqVzs76Y4PnEpc2RRVn6ii6ZEmzKiZ8lwhRHZJyBDiJKW1xvc7H+UfKsde\naB+yf317O2u8XlS6/hhnnJEyKZjapD5Q3/tBP9hENJeU5JeQb8+nLlCX+oBzzrGmFu/pGbJrjddL\nVGteSjPKJNocxf/c0JoOIUT2ScgQ4iTVtb2L4N5gyqaSxnCYXd3dqZtKIOPIktZgK1EzmrYmYyI6\nfiqlmO6Znr4mY+FCME1rsbRB5rtczHA6UzaZFCwuoGBhgcyZIcQEkZAhxEnK94APR4UD72VDg8T6\nxLf4lIuiQcaRJckP9smsyUheP23ISE4glqLJRCnF6pKSlCFDKUXVtVW0PN5CLBAbsl8IkV0SMoQ4\nCem4punhJirXVmLYh/4Zr/P7WVxQQGVe3tCT29qgoSFtTUayiWJ6UeaajFx2/ExeP21zSXExzJiR\nsV/GG93dNEWGrldS+YlKzJBJyx9axlJsIcQoSMgQ4iTU9lwbkYYIVZ8c2lSitWa935++qWSYkSX1\ngXoUKu08GcGgNS2405ly94hl6vgJUFOYoSYDrPKnGGECsDrx3GtT9MvIPy2fkktLaLw/zWRfQois\nkZAhxEmo8d5GChYW4FnhGbLvQCjEsXA4c8iw22HBgpS76zrrqCqswmFzpNwfClkBIVV/0tEYUU1G\nZ136ybMWLkxbkzHN6eQctztlkwlA9aeraX++nZ63h3YcFUJkj4QMIU4yUX+UlsdbqP50dcqRI+v8\nfuxK8c7i4hRnY30wz5sHqZpSIOPIEhj/CqxJw9ZkeGrojnYTiKSZPOucc6yl6rtTzAqKVZvxXFtb\nypBScXUFtkKb1GYIkWMSMoQ4yTT9b5M1jfg1Q6cRBytkrCwqotA+dFgrkHFkCVh9MtKNLAErGIy3\nPwYM3/EzWYa6zgzDWLXuW7J+kDVeL2+HwxxKMczVVmCj4qMVNN7bKNOMC5FDEjKEOMk03ttI2XvL\ncFYP7RQR15raxPwYaWUYWQLD12SMd5n3JLfbmubCTDMv1rATcmUYYQKwqqQEG6ScYhysJpOeQz10\nvNwxmmILIUZBQoYQJ5Huvd0EXgtQ/enUU35vDQRoj8XShwyfD5qbx12Tka3mEkg5nxbQFzLSjjAp\nLLSWqt+5M+XuIrudC4qK0vbLKL64mPw5+TTeK00mQuSKhAwhTiKN9zViL7VT9r6ylPvX+f0U2myc\n5xnaIRSA7dut+2XLUu6OxqM0dTdNWE1G8vFScTlcePO9mUeYLF3a95xSWO31st7vx0zRJKIMRfV1\n1TT/vpl4dzzF2UKI8ZKQIcRJQsetacSrPlGF4Uz9p7susbS7w0jzp71tG3g8Vg1ACg1d1oJk6ebI\ngOzXZGTsl5EYYZLW0qXWc0rTr2KN10tbLMb2rq6U+6s+VUW8K07zH5pHWmwhxChIyBDiJNH2XBuR\n+kjappJQPM4rHR2Z+2Ns3259MKcJIcPN9gnZ7fiZfLx0ajw11HdlqMlYtsyaXOz48ZS7Lywqwm0Y\naftluGa7KLmkRJpMhMgRCRlCnCSSc2MULi9Muf/ljg7CWmcOGdu2WSEjjWStQaY+Gcl5MsYr+RgZ\n58rwjKAmA6znlUKeYbCqpITn0oQMkDkzhMglCRlCnASGmxsD4Km2Nqbn5XF2umqGri44cCBtfwyw\najKcNielrtK0x0x4TUamPhkzZkBZWcZ+Ge/xetnQ3j5k6fekio/InBlC5IqEDCFOAsPNjQHwZGsr\nV5aVpQ0h7Nhh9V3IVJMRqKPGU5P+MZi4jp9g1WQ0dDVg6jTjXJXq65eRxlVlZYS15vk0tRkyZ4YQ\nuSMhQ4iTQMM9DWnnxgB4KxTizVCIK0vT10CwfTs4HBmHrw43RwZMbMfPGk8NMTNGc3eGjpnLlmWs\nyZjndjPX5eKvra1pj6n+jDVnRvsLQ9c6EUKM3YSEDKXUTUqpw0qpkFJqo1LqvGGO/6hSam/i+DeU\nUu+diHIKcSLq3NxJ15Yuam5M/+H/ZGsrDqWG7/R59tlppxOHxBwZGUaWwATXZCTKknauDLBqMo4c\ngRSLoSVdVVrKk2mmGAdrzgz3WW7q78rQNCOEGLWchwyl1MeAHwO3AcuAN4BnlFLlaY5fCTwE/BpY\nCjwOPK6UOjvXZRXiRFR/Vz3OmU5Kr0hfS/HX1lZWlZSkn0ocrCaFDP0xIFGTUXhi1WQky5VW8jll\nqM24sqyMY+Ewu9Ksc6KUoubGGlr+0ELEN3R5eCHE2ExETcbNwK+01vdrrfcBNwJB4Po0x38FeEpr\n/ROt9Zta69uArcCXJqCsQpxQou1Rmh5uouZzNShb6n4S3fE4L7S3c1WmppJYzJoZM0N/DLBGlwxX\nk5Gtjp92u9V6kylkVBVUYSgj8wiT+fMhPz9jyFhVUoLbMHiyrS39tT5ZhXIoGn7TMJLiCyFGIKch\nQynlAFYA65PbtFVfuQ5Ymea0lYn9/T2T4XghTlm+B3zoiKb6+tRzYwA87/cT1pory1LPAgrAvn0Q\nDmcMGYFwgEAkkLFPhtbZay6B4Zd7txk2qgurM9dk2O2waFHGzp9Ow2CN15uxX4bD66Dy45U03N2A\njksHUCGyIUPdalaUAzbAN2i7D1iQ5pzqNMenf5cF7r/uSZ4v2ItO8WVPK93v54HbUv6urN91YrtO\n/m5Y96ZhbTMNjTas301DEzc0pi3xs83EtGnidpO4zSRu08TsJjGHSdRhErPFiDpMtN3qNa8GvKdp\nlAaVaD9WWls3EvcaDNPs3W5oE8NM3MdNbGYcQ2ts8Tj2WAybGccei2OPx3HEouRFrZsjGsUZjZDf\nE8YV7iEvGkUBqd5edWK0gR6wDTSqd7+pwFQq8bN1H1eKuGEQVwrTUMQMg4jNRtRmI2IziNpshBwO\nQg47wTwHIYeDrjwHHa58ehyOTP/kw1CJ/1f9fleJ/9lQ2kBhWD9jw6ad2MjD0E5s2olDF+LUXpy6\nBKdZglOX4jarUBPUV1opMJRmzcP1dM0p51t3OikogPJyqKiwbpWVcOaZ8GRbG3NdLuZn+uRPfsvP\nEDKSH+SZ5sgIh62gkY3mEhh+ufdkeTL2yQCryWTjxoyHXFVWxhf378cfjRL1Ozh82FrGJXnz+6Eg\nUsPFRxr5/tVtNMwsS7t4Wy5EVRdBo5Gwaies2okY1n1c9RAnTFxFiKswJlE0cTQmWplo4oAm8Y7V\n72dI/dc8MoZpUtwTxtMTxh2N4orGcEeiuKJRnLE4jrh1y4vHccRNbFpjM00MrbEn3p8MrTES72VG\n4pakEu9z1s991KB+M8l9McOgx+mkx5lPj9NJxOEgarcTceQRcTiI2e3EbDZiNhtxm42YzY5pMzCV\nQdxmEDesn7VhvTdZ71MGpmG9N5hKgQJTWX/jve95qq8UvZ8XpsIRNbDHbDhiNuxRA3vMwBY3sMUU\n9riBLa4wYgaGqTDiCpuZ+NlUKBPrXvf9rrTC0Crx3m/dk/jZel0G/mzdD/y97zUc+kHY/5jLfnYB\nS86bm/HfP1tyHTLSSfdZNubjn97/v7iNggHbVrrezUWuS/oeZNALb5jJ7X37rX9Iev+Brf8QSPyh\n9P3HYfS7t5nph/sNJ2bThPNNevI1YadJyGUSLNAE3SbdBSbdBZpAkUlnkUlHsUlnsaaj2MRfAqbd\n+gDXyiBms2EaBqZhEDOSf2Q2dLrppVMwzDjunh48XV2UdHVSHAhQ3BWgJNBJZVsrFf5WKtus2/Tm\nJgp6eqzXikQQIvE6gRVyTLBpjd203mgcpvVznqlxjuCbYtCuaMu30+qy01Dg4O2iPI4U5yXunewt\nzSds7//8hvylJbb2/rUm7k20igPWvVYxtC2CNsJoI4JphMEYOqeCirlwBs/A2TUPZ/dcXJ2LKWq6\nAnskZfeiMUm+v5omzA50UNQa5H9c89jzR2uai5YWq+Uj6fQ5Gv8vW/nY9GHKsG2bNZV4cXHaQ0Yy\n22ey1mGiajKS5clYkwFWePrNb6wU5Ew9AucKbylx4Ipv+dn8w8oBAaK4GLxecNg9zHQWUlhbz4bT\ny1DKCnzQdz9emjjd3tfoKt9AuOCAdSs8QCw/9TwdKu5EmXkYpnWvtAO0DaVtYFqBubdSWveF6ZTf\nuJIf2VpzWiDKPH8PszojzO6MMDNxKw/FKO2J4e2JDxupYwoiNkXUsG5xw/piETOsLxxx1fcFRJP4\nEpIoZlwpfGVl+ErL8ZVa902lZbQVl9Dh8dBR2HfrchcQydBhOZXkFyxbPHEzTYzkTWsM08Qd1Hjb\nFMWdBkUdiuIOg6IOg4JuRUG3gTto4O42cAcV+T0Gzp7EfWTsXzZMpTENEl9O++61wvrSmviiaxqJ\nd67EpUxj8Bfjgf/Eqb9MD7z2q8FaXg2+wJ/+8dd4K4oA6OjI7SrEuQ4ZLUAcqBq0vZKhtRVJjaM8\nHoCHXr2P5cuXj6WM46a1Rsc1Opq4xTRmxERHEvdhjRk2MXtMzJBJPBTHDJmYQZN4V3zALdYRI9Ye\nI+aPEWuNET0YJdoSxewe+JVK2RV5NXk4T3OSf1o+zllOXHNduOe5cc1zkTctD6UUca2JmCZRrQmb\nJj39biHTpDsepyseJ5C474zF8MditMVitEajtEaj7IlGWRcO09r/0w2YlpfH/MQ36PkuF4sLC1nh\n8VA2khoIrSEatZbgDAahu9v6FO3uhs5OaG3F3dKCu7WVGc3NLKmrs0YQbDtsHQdWNfnChXDuudZt\n5Uqr2jwLnwahaIj2nvbeW0uwhbf8b3Gg9QAH/Qc50PoYh9t/iKEMVs5Yyfvnv5/3zX8fZ1ecnXGO\nidHYc209AbuLx/eVoJKfIRo6Oqyw8fbbcOfj3fw1L8y9N5ZhXwJf+QrMm5fiwbZvH7bTZ7K2YLgp\nxWHiazJePvZy5oOWLbPS1+7dMOh9IByGhx6Cn/40H75UwL6SVn72s0ouvtiqESor6z/gRlF/dw37\nv7Cf157oIf+0/DE/t/46w508+9az/GX/X3jywJO0BFsochYxv2w+80rnMa/0EuaVzaPGU4M334vX\n5aUkvwRPngebYRt/Afx+2LABNm/uu7W0WPsMw5rUbPYCOH8WVFVZL0p5uXUrKbFWvC0shIIC6+Zy\nQV4edptt2A+RmGmyJxhkSyDAvmCQ/aEQB4JBDoZChPvVWjiVYrrTSVVeHmUOB7PtdsocDkodDopt\nNgptNjx2O57Ezy7DID9xcxkGeYaB0zBwKIVDKev9LxgndDBE6EDIun8rRPhYmPDxMD3Heoh3DPoy\nYYCj3IGj1IHda8deabfui+3YPDZshTbrvsC6GW4Dm8uG4TKsm9O6qTxl3TsUyqEwHImf7QplZCmt\njsG1XD5k29atW1mxYkXOrpnTkKG1jiqltgCrgT8DKOsdeDXw0zSnvZpi/2WJ7Sckpaz/eLADWXrz\nHSzeHSfSHCHaFCXSGCFcF+79YwkfC9O5sdOaFjnxN2sUGBScVUDBkgIKlxRSuKSQksUFOErG/qbZ\nE49TH4lQFw5zpKeHA6EQ+xNvHg83NdGVmFFxdn4+53o8nO/xsNrrZWlhIcbgD16lrHf2vDwoKhp5\nIbS21qo4eND6dr55M7z+Ovz2txCPw8yZ8MEPwoc+BO98p9WzcAxcDhcuh4tpnmlpj2kINPDkgSf5\ny/6/8N0N3+Ub67/Bqlmr+M8r/pOl1Zk7WA4n0hKh+dFm5nxvzoA3JaWs9/ySEpg7FzbPa+P5wwY3\nrynmnl/APfdYeeLMM/s9mNbWa3XzzRmvWR+op9hZTEFeQdpjkoEgmzUZw4WMEdVkJMPltm1DQsYn\nPwmPPQZXXQULZpfx/JkN3PgOPfS/yYTKtZW89bW3aLingdO/k3ohuZEKRUP86G8/4vZXbicYDbKw\nciE3LL+B981/HxdMvyA7ASKdo0fhT3+Cxx+HF1+0/j4qK+G88+Cmm2DFCmvOlBkzMg5rHq3mSIT1\nfj+vdHayORBge1cXPaaJwnpvmOdycYnXy+dqapjrcjHD6WS600mp3T7mgK7jmuD+IN07uul6o4uu\nN7ro3tFN+Hi49xhbsQ3XGS7yZ+ZT8u4SnKc5cc5wkjctj7yqPByVVriYzBBwKpqI5pKfAPclwsYm\nrNEmbuBeAKXU/cBxrfX/Sxz/X8CLSql/Av4KrMXqPHrDBJT1hGUrsOEqcOGanT7FmGGT0CErtQf3\nB+ne1U3Xli58v7M6DwK4z3JTfFExRe8ooviiYlzzXCP+w8632ZjjcjHH5eKdg6+tNW+FQmwOBNgS\nCLA5EOA7R47w9UOHKHc4WF1SwntKS3lvaSnT0lRnj4hS1ressjK44IK+7aEQvPyy9ab6xz/Cz35m\n1X+vXWt9uM7NfvvjNM80Prv8s3x2+WfpifXw1IGn+Obz32T5r5Zzw/Ib+LdL/43KgvQzdGbSeG8j\nKKi6bnCl3kBPtrZyWamX/7jNxjdvgcWL4ctfhmef7Vehc+yY9U12uJqMEYwsmYzmkulF02kJthCO\nhXHa0/y3U1AACxYMGWHy7LPw6KPwwANwzTXwcnsp/7v9KJsDAc5PE27tHjtV11bR8OsGZv3LLAzH\n6KvGtdY8uudRbnnuFhoCDXzlgq9w0/k3Mbtk9qgfa1QiEava5uc/hy1brJB96aXW38OVV1ohPFvt\nPgkx02RDRwfPtrXxnN/P1kRN43yXi/M8Hj5WUcEKj4dlhYWZh1iP5pqdMTo3dtLxtw46X+mkc2Mn\n8S7rS07e9DwKlxRSdW0V7jOtml3XPBeOckfWahnFyOU8ZGitf5+YE+O7WM0g24HLtdbJKfxmALF+\nx7+qlFoL/EfidgD4oNZ6T67LerIznInai7MGfhM1oybBfUG6tnX1/lE2/E8DaMirzsN7uZfSK0op\nvawUR9nYvvkbSjHP7Wae283aKuuDMWKabOzs7H3zueHNN9HApSUlXFNVxdUVFRRn6U0Hlwsuu8y6\n/exnsHUr/OEP8Otfw113wdVXwy23wPnnZ+d6g+Tb8/nwWR/mffPfxy83/5LbXriNR3Y/wm2rbuOr\nF34VQ438g0qbmoZfNVD50UryytN/w2yPRnmlo4P/nj8fsD6w//M/4f3vt3LW1VcnDkyOuhhm+Gp9\n18hm+4SJbS5JlqmhqyHzh/Sg6cUjEfjHf4RVq+ATn7C2XVhURIndzpOtrWlDBkDN52uo/2U9rU+0\nUvHhipE+HQB2Ne3ii3/9Ii8dfYkPLPgA6z65jnllqdqwsqijA+6+2/oPoL7eqrZ55BG44oqM/XDG\nSmvNpkCAB30+/repiaZolCqHg8tKS/nKjBms8XqpGc+XicHXi2sCmwO0Pd1G29NtdG7qBBPspXaK\n31HMzG/OpOi8IgqWFGT8mxGTQGt9Ut+A5YDesmWLFiMX8Ud0y1Mt+uDXD+pNizbpWmp1rarVmy/Y\nrI98/4gOHgpm/ZqtkYi+p75eX7Jtm1a1tdr5wgv673bt0s+3tWnTNLN+Pa211sGg1nfdpfXcuVqD\n1qtWab11a26u1U9Ld4u+6a83afVtpT/358/puBkf8bmtT7fqWmq1/yV/xuP+1+fT1Nbqt0OhAduv\nukrrWbO07u5ObPj2t7UuL9d6mNd45T0r9XV/vC7jMc8/b72Mb701zJMYoauv1vq97818zC7fLs23\n0S+//XLmA3/wA60LC7WOW6/1D3+otc2m9RtvDDzsY7t26XM3bx62bFtWbtHbVm8b9rj+Nh3fpIu+\nX6TP+vlZ+tmDz47q3DEJhbT+1re09ni0dji0vv56rXfvztnlmsJh/d3Dh/XcjRs1tbV62iuv6H86\ncEBv7uzM+t9wLBTTTX9s0rs/sVu/VPqSrqVWbyjeoHf93S5dd3ed7trblbv3jSlky5YtyWFJy3Uu\nPqNz8aATeZOQkR09x3t0/f/U650f2alfdL2oa6nVm8/frI/++KgOHQsN/wCjdCwU0ne8/bY+57XX\nNLW1esXrr+uHGxt1ND7yD+NRicW0/r//03rRIuuT5xvfsAJIjv1222+1+rbSX3jiCyN+Q9y+Zrt+\nfcXrwx5/3Z49etGmTUO2HzigdV6e1v/6r4kNH/yg1mvWDHvdWXfO0reuuzXjMU88Yb1r1NcP+3Aj\ncs01Vu7LpC3Ypvk2+ve7fp/5wGeesQq3f7+uq7Pyxj/+49DD7m9o0NTW6sZwOOPD+R7x6VpqdefW\nzszXTdhct1mX3F6iV96zUnf2jOyccdmwQev5861/7Ftu0bquLmeX2t/drW98802d/+KL2v3ii/rT\ne/fqdW1tOpblD/l4JK5b/tqi93xqj95QtEHXUqs3LdqkD/3LId3+cruOR3P0/jCF5TpkyAJpAgDn\ndCfTrp/GwscW8o6md3DWw2eRNy2PQ7ceYuPMjey4agctT7RkbZKiGfn53DJzJjvPO4+nFy/G63Cw\ndu9e5r72Gj87fpxIticosNms9oMtW+A734Gf/MSqXn/ppexeZ5BPL/0093zgHn65+Zd8+akvJ4Nx\nWivLTA8AACAASURBVIGtAfzr/My8ZWbG9uO41jzV1pZyQbS5c62WoR/8AA4dYkQjS0xtUh+ozzhH\nBkxOx8+S/BJcdtfwc2Ukm4O2b+frX7eaYr7znaGHXVFaisLqz5JJ+UfKyZ+dz7EfHst8XWBbwzYu\n+91lLChbwNPXPo3H6Rn2nDHr7LQ6br7rXX3L3N9xB9Rkbuoai22BAFfv2sWCTZv4Q3Mz35w5k6Mr\nV/LbM89ktdeLLUt9HEJHQhz65iFePe1Vdl61k87XOplx8wzO23Me5+04j9P/7XSKLyrGsMtH1slG\n/sXEEPZCO1Ufr2LR44u4qOki5v9qPpHGCLvev4uNp2/kyL8fIdwYHv6BRkApxeWlpTy3ZAnbVqzg\n4uJivnrwIOe8/jp/amkZ9kN51BwO+OY3rTfmsjLrjforX7GG0+bI9cuu5+733c1/v/7ffPXpr2Z8\nTsd+dIz82fmUfyTzvBcvtbfTFI3yofLUx916qzWQ4Fs3tVljXYfpj9EabCVqRoftkzEZHT+VUiMb\nYVJZCTU1HP3TNh580ApZJSVDD6vIy+Oi4mIea86wsitg2A1m/NMMmn7fZI3cSuONxjdY87s1zCub\nxzPXPkORcxSjpUbr5ZetYdv33Qc//akVks86K+uXaQiHuX7fPlZs2cLu7m5+NX8+b194If8ye/bI\nhqiPgDY1LX9pYcdVO3htzmvU/byOyo9WsmLbCs7fez6nf/v0If3LxMlHQobIyF5sp+aGGs7dci7L\nX1+O9z1ejn7vKBtnbWT/F/YTOjTMJ8QoLPV4eODss3nj3HM5PT+fD+3axeo33uCN/9/eeYdFdaV/\n/HOAoYoUAemgoqgI2BCNmmbWdJNsEk2y2ZRNstkkbnrf9N3Nxt9uEk3dVJNNsaT3xGSzaSYWLCAg\nTSkiRaki0rm/Pw6DoMDM4AyIeT/PM49y59xzj4dx7ve+1VwXw55MmKC/oJ98Ep57TkdL1tXZ/zod\nXDPtGv595r95asNT3Pvfe3sc01DQwJ7Vewi/LdziE9vKPXuIcnMjuZfgRS8vbawp+TJVH7CyRoY1\nfUucnfudGXwY1gR+mtdl0ZIBtE+eQuHHW0lOhssv733cosBA1lRXU2lBXIb8IQQXHxd2PdmzNSOn\nMod5/5nHaL/RfHXpV/i42z/IspOVK2HePIiOhvR0nUbkbN8U2Ia2Nv5eWMjY9ev5uKKCZ8aOJSMp\niWtCQ3G307XaW9opfa2UDRM3kL4gneayZsa9OI5Zu2cx9umxeE/2liyQYwgRGYLVDJ8+nPEvj2dW\nySyiH4pm73t7WT9uPZmXZrI/3X5CYNKwYXyVkMCn8fGUNDUxJSWFxTk51LcdXoXziHB2hptvhi+/\nhF9+0VaNEse1+r52+rUsOWUJj619jF92HV72pfjJYlx8XAi5svfaHKBTBt+rqGBhUFCfX8bnnw/n\nj9pCo5OHbiLWB9ZU+wT79i0B6ywZYGWtDCB/+GRi6rawdKmuMdUbFwQG0m4YfGDBmuHs5UzYDWGU\nvlRKS1V3QWIYBtd8cg1+Hn6suXQNvu49mE3sgWFod8jFF8PChfDNN1po2Jk1VVWM37CBhwsKuDY0\nlNzkZK4PC8PFhqrBfdHW0EbxM8Wsj1lP9pXZeMZ6MuXnKUzfNJ3Qq0NxGTZYBagFRyIiQ7AZk6+J\nqHuimFkwk5ilMdT+WEtKfAoZF2XQsMM+lg2lFGeOGMG2pCSeGDOGV8vKmJySwjpHlMCdN0+boSsq\nYOZM/ZToIG6bdRvTQ6dz7afX0tJ28KbVUtVC6culhN0QhrNX30+M39bUUNHSwkVBfdfgUApO9N3C\nNhJoo+85d+/bjUIx0qvvuhz2avNuxlpLRuiw0L47sXaQ0jaFEMpIjuq5RLeZYDc3TvT1ZZUFkQEQ\ntjgM2qHk+e4i57Wtr/FD4Q+8cNYL+Hn4WZynX7S26viLu+7Sbr7//MeuhbNAd/FdnJPDqWlpjPXw\nICMpicdjYvCzk7mqvbWdkhdKWD96PXk35+Ez14fp26YT/1E8PrMcaPkRjgpEZAj9xtnTmfDF4STn\nJRP7ciy1P9WyYcIGcm/Opbmi2S7XMDk5cXNEBFunT8ffxYXZW7Zw386d9g8MjY/XDbb8/WH2bF2C\n2QE4OznzwlkvkLE3g6XrlnYeL3m+BNo7bmgWWLVnDzEeHkwZNszi2DHlv7CuPYlMC1VmSupKGDls\nJCbnvm8sg2XJCBseRkldicUYnU/KdR0Utc5ygeBFQUF8W13Nnua+P6uuQa6MvHwkxU8V09aorWkV\nByq44+s7uDThUk4edbLlf0B/aGrSwcovvqjrvfztb3YvpLWutpYpKSm8WlbG0zExrElMZKydfsGG\nYbD3w71snLSRnOty8JvvR3JOMhPfnMiwSZY/u8KxgYgM4YhxMjkRclUIyTnJRD8cTdmrZawfs57C\nxwppb7KPGBjn6cnaKVN4ODqaJbt2kbx5M7nWPALbQliYFhfTp+sYjbQ0+87fwdSQqdw440Ye+v4h\nCmsKaWtso/ipYoKvCMY1qO+n1Ob2dt6vqGBRYKBlv3VpKR4lO1ir5lpqUMruut0WXSXgGEtGc3P3\npm89EeodSn1LPfua9vU6pr0dPkuLoNYnUlumLPDbgAAU8J4V1oyI2yJo2dtC+X90C6U7vr6DdqOd\nx+c/bvHcftHeroNK1qyBTz6Bq6+27/SGwUP5+czesgU/Fxe2TJ/O4vDwXkut28q+DfvYMncLGedl\n4B7lzrTN05jw+gQ8Rjuo74Jw1CIiQ7Abzp7ORN0TRfKOZIKvCKbg/gI2Jm6k+ttqu8zv4uTEfdHR\nrJ86lQNtbczYvJmvqqrsMncnw4frXg9jxsDpp+v+Dw7gkZMewd/Dn8VfLKbs9TJa9rYQfmu4xfO+\nrq6mprWVRRZcJUDnjbZq4hyLIsOa9FXQIsPelgyworR4x9r6isvIzYWaGjgwfa5VqckBrq6c4ufH\nqj17LK9zrCcB5wWw6/FdfLfjO17b+hpLTlnS77LxFrnzTli9WpcIP/10u05d29rKOenpPFJYyAPR\n0aydMoVYO/1SW6pbyLkuh80zN9O2v42ErxJI/CoR78kOTOkVjmpEZAh2xzXQlbHLxjJ963Rcg1xJ\nnZdK5u8y7Zb2OtXbm/VTp3Lc8OGckZbGv4qK7Jvq6u0Nn3+ufd+nn677ftgZbzdvnjrtKT7f/jlZ\n/8gi4LwAPMda/qJftWcPEzw9meRlRWrfjz/C6NGMnhPK+vV9D7XWkuEId4l53r4wr62vDJN16zoa\nyJ05R5eVtyIraVFQED/U1lLSZPmzGXFHBA05Dbz4jxeZHTGbq6ZeZfGcfrF0KTz+uE5R7awNbx9y\nDhxg5ubN/FhTw6fx8TwYHW2XwE7DMCh7o4wN4zdQ/lY5MctimL5pOv7zD6/jIvy6EJEhOAyvOC8m\nfz+Z2OWxVK+pZsP4DZS8YNmvbg2+JhMfx8dzV2Qkd+zcye+3b6fBntknwcE666SsTHd0bey9TkJ/\nOXf8udxdejfOhc4E3mG5P0ZjWxsfVlSwyEJWSSc//QRz5zJzJmRm6vYWvWGLJcPe7hLzvH1hFhl9\nWTLWrdOZyR7z5+qOo5aUFXBuQAAuSvGOFS4Tn5k+VE+r5rSPTuP50563qR+N1axeDbfeqi0Zixfb\ndeovKyuZsWkTABumTeOMESPsMu+BvAOknpxK1mVZ+J7ky4ysGYT/ORzlLGmogogMwcEopQi5IoQZ\nWTMIvCCQnD/lkHZqGo27jvym7awUj44ezcqJE3m/ooITtm5lr4UgPpuIjdX+8A0bdL9wOwebtje0\nc9qnp/Fdwnc81/CcxfFfVFVR19bGokArGnbt2wepqZ0iwzBg48aehza3NbOnfs9RbcnwMHng5+7X\nZ4bJunU6OYgJE3QArxUuEz+TiVP9/a1ymeyt38sDMx4gsiKSEZ/b5wbdje+/15+zSy6Bf/zDrlM/\nXVzMmdu2McfHh3VTpzLODr9Eo92g+JliUhJTaCxsJOGrBOJWxuEWar/GaMLQR0SGMCCYRpgY//J4\nEr5MoD6zno2TNlL6aqldrBqLgoJYO2UKRY2NzNmyhSJ7Wh2OOw5WrID33tMlJO1I8dJi2ivbabyx\nkedTnqexte91r9qzh0QvL8Zb4yr55RctiubMYdw4Xfmyt7iMsv063dNSIS4YPEsGHMww6Yn6eh2n\nO3MmukDG7NlWBX8CXBQUxC/79ln83Lyw6QV2hO3A50IfCh4soO2AHS1nJSVwwQUwZw68+mrfRT5s\nwDAMHszP58a8PG4JD+ej+Hi7dD5uKGgg9ZRU8v6cR/AVwUxPE9eI0DMiMoQBxf9Uf5LSkwg4L4Ds\nq7LZdvY2u8RqTPH2Zu3UqbQYBrO3bGF7fb0dVtvBuefqOt33369v3naguaKZoiVFhF4XylXnXsXe\nA3tZmb6y1/H1bW18UllpXcAn6Kf4oCAYNw4nJ0hO7l1kmK0D1maXOMKSYVWtDO/QXmMyNm3Smmrm\nzI4Dc+fq35UV5eIXjBiBu5MTq/uwZjS3NfPcxue4LPEyxj82npa9LRQvK7a8aGtoa9MWDJNJV/W0\nUx2MdsPgz7m5PFJYyJLRo/lXTMwR9xoxDIOSl0tIiU+hYUcDCV8nMO7ZcVJIS+gVERnCgGPyNTHh\ntQlM+mgSdSl1pCSkUPl5382qrGGMhwc/TZmCr4sLc7dsYeO+3tMdbeahh2DGDF11sabmiKcrerQI\nDIi6L4qxI8Zy5tgzWbpuaa+Wnc8qKznQ3m6byJgzp7Ougllk9DS92TpgTUzGYLlLQK+vN0vGunUw\nbBhMnNhxYO5crVy2bLE4r7eLC2f4+/dZmOudjHco3V/Kjck34jHag9DrQil6rIiWSjv0vFmyBP73\nP3jrLbDGFWYFze3tXLp9O8+XlPDSuHHcGRl5xHO2VLWQcUEGOdfkELgwkKRtSfifItYLoW9EZAiD\nRsCCAJLSkvBO8mbbmdvIuyXviOtqhLq58cPkyYzz9OSkrVv51l6ZISaTTiesqYE//rHnu7WVNBQ0\nsPvZ3UTcGYFroH5qvXnmzaSWp/J94fc9nvNGeTnTvb0ZbY2voqlJx5HMmdN5aOZMqKyEHTsOH15Q\nU4CnyRN/D8s3jMF0l0T6RFJQU9Dje+vWQVJSl1YeU6fqyW1wmaTU1fVoATMMg6XrlzJ/zHwmBmoV\nE3VfFBhQ+PdCq+bvlZ9/hgcegHvvhZNOOrK5Omhoa+Pc9HTe27uX1XFxXG2H7qw1P9SQkphCzbc1\nxL0Xx/hXxuMyXKwXgmVEZAiDimuQK/GfxhOzNIbdz+1m88zN1GcdmavDz2Ti68REZvv4cNa2bfYT\nGtHR8PLL8M47ugJjPym4vwCTv4mIWyI6j80bNY+4wDiWrV922PgdDQ18VlnJn6y9WWzapLNh5s7t\nPDRDF8LsMeEiuzKbcSPGWZWxMpiWjHEjxlFeX05tY/c0GcPQnpFOVwlol0NyslXBnwALAgIYaTLx\nzO7D3TG/FP9CSkkKNyXfdHD6QFci7oxg97O7aSjoZyn96mptGUtO1pYyO9DQ1sY56el8X1PDZ/Hx\nnH+ElpH21nbyH8xn60lbcR/lzvTU6QT+1j7WFuHXgYgMYdBRShF+UzhT102lraGNTdM2UfZm370n\nLOHl7MxHkyYxt0NofG8HFwegg/OuvVa3h8/IsPn0uq11lL9VTvRD0d16lCiluCn5Jj7K+oid1Tu7\nnfPs7t34ubhwibWukp9+0m1Yu7R3HzFC90jrKS4juzKb2BGxVk1tb0uGu/vBeS1hXmN2ZXa347t2\n6UzjbiIDtCXnp5+ssjq5OTnxp9BQXi8ro/aQ8qNL1y1l3IhxnBZzWrfjEbdEYPI3UfBAgeXFH4ph\nwDXX6Cygt98GOwRjNra1cV56Oj/V1vJpfDyn+B+ZK6OppInUeakU/q2Q6Aejmfy/ybhHuh/xOoVf\nFyIyhKMG7yneTN80ncALA8n6fRbZ12TT1tD/CH53Z2c+nDSJ2T4+nJGWxo/2EhpPPqkrgl58sa6J\nbSVGm0Hu4lw8xnkQfFXwYe9fmnAp/h7+PL3+6c5j+1tbebW0lGtCQvCwttX2jz/CrFmH3bhmzuxZ\nZORU5lgtMuxtyXBy0kLDWksG6PV2xWydSU4+5IS5c3XTu+xsrOHa0FCaDIPlpaWdx4pqi3h/+/vc\nlHzTYXUxnL2ciX44mvI3y6n5wcbP1vLlOmPplVcgKsq2c3ugqb2d8zMy+L62lk/i4znJ78gatlV9\nXUXK5BQa8hqY/N1koh+IlroXQr8QkSEcVTh7OTPhtQnEvhpL+ZvlbJ65mQM5/e9R4tFh0Zg5fDin\np6Wx1h5dXD084M03dYUrG9Jai5cVs+/nfcS+FIuTy+H/9TxMHvxx2h95ZcsrnT063igvp66tjevD\nLAdlAjrFYu3abq4SM8nJsHVr9xv6vqZ9lO0vIzbAsshob9deGHuKDNDzWWPJ8HbzJtQ7lOyK7qJh\n3TrtyRp5aAPZWbO0irHSZRLi5sbCwECe3r2btg7rx7MbnmWY6zAuS7ys53OuCsFntg9ZV2bRVm+l\nIC4t1QW3Lr/cLhU9m9rbuSAjg/9WV/PxpEnMOwKBYbQZ5D+YT9qpaQybMozpW6fjO9dBLeyFXwUi\nMoSjkpArQ5i6YSrtTe1smraJPassF0vqDU9nZz6Ojydp+HBOS0tjvT2yTiZP1lUZ//Y32L7d4vD6\nrHry/5JP+E3hfX5pX590PQ2tDby29TUMw+Dp3bs5LyCASHcrzdSZmdrX3yXo08zMmboR2ebNB4+Z\nb9hmK0FfmMWJPd0l5vms7XU3bsS4w9wlnUW4DsXbW/+erAz+BLgxPJydjY18UVlJfXM9L25+kWum\nXsMw1567hipnRezyWJrLmtl5984exxzGn/8Mbm66dPgR0tLezkWZmXxdVcVH8fH85ghcJE1lTaTO\n1+6RUX8dRcIXCZ2ByYLQX0RkCEctw+KHMW3jNEacPYLMizLJuSGn39knXs7OfBofT6KXF6enpZFm\nRV8Li9x/vzZ1X3NNn9VA21vbyboiC7dIN0b9fVSfU4YPD+fCiRfy1PqnWFNVyfYDB/hzuOXGaZ38\n+KN2kxzmO9Dd7D08urtMzDdsW0SGIywZ1rhLQMdldBUZzc06zrVHkQHaomOlJQMgefhwkry9eXr3\nbv6T+h/2Ne1j8Yy+y3t7xngyeslodj+z23IzwA8+0G6Sp57SgTJHQLthcEVWFp9WVvLepEmcegQC\no/q7ajZN2cSBzAMk/jeRqL9EoZzEPSIcOSIyhKMaF28XJrw1gXH/Hkfpy6Vsnr2Zhvz+RfObhUa0\nuzvzU1OPvFW8h4fONlm7Fv79716HFT9eTN3GOsa/Nh5nT8txFYtnLGZH9Q4ezttGgpcXx/v4WL+m\nn37S6Zs9VAU1mXQX+24ioyKbkGEhDHcbbnFq83YNpiUjdkQsuZW5tBta1KWm6ozdXkXGnDmQnw89\nZI30xo1hYaypruaZjE84e9zZRPlajpkIuz4M3xN9yfpDFq11vfStr6mBG26As8+GhQutXk9PGIbB\nDbm5rNyzh7cnTODMfgoWo92g8NFCUuel4jnBk2lbpuF34pHFcwhCV0RkCEc9SilCrw1l6i9Taa1u\nJWVKChUfVfRrLl+Tia8SEvAzmTglNfXIS5Aff7zONrnrLp3mcAj70/eT/0A+EbdH4DPLOrEwK3wW\n4UEz+OWANt9b1QzNzI8/9hiPYSY5uXsaa3ZltlXxGHCUWDICYmlobWBXrd7r9et1tmqXRJrumPfC\nBpfJhUFBBLg4kWkax+8Tfm/VOcpJEftqLC0VLey4vYdiJKDda/v3w3PPdRZJ6w+GYXDXzp38u6SE\nl2JjudDarKNDaKlsYdtZ28i/L5+ov0SR+HUibsHSd0SwLyIyhCGD91Rvpm2aht/JfqSfm07uzbn9\ncp8EurryTWIizkpxSmoq5UfaVG3JEhg+HK6/vlu6ZHuLdpN4jPEg+uFoq6dTShE6/npU637O97fB\nilFYqIVOHyJj5kw9xPxgb2v6Kgy+JQMOunnWrYMpU3SIQ4+MHAljx9rkMnFzciKudScEn8rsUfOt\nPs9jlAdj/jWG0hdLqfqqqvub332na6ssWQK2uL964NGiIv65axdLY2L4Q0hIv+ao+aGGlMkp1G2s\nI+GLBEY9MkqyRwSHICJDGFKYfE3EvRdHzLIYSp4vYfOs/mWfhLm58U1iIvvb2vhNaipVVvS46BUf\nH/10+umnsGoVoJ82c67NoT61nvGvj8fZ3cr0U3Ta6nbnaIzST/ih4Bvr1/Htt/oJefbsXoeYQzU2\nbIB2o53cylybRcZgZZcARPtG4+rs2hmwumFDj+En3Zk7F/77X6vXYxgGu7KeRTm5sbLCttTU0GtD\n8ZvvR+YlmQeLyjU26iqxc+Zoq9cR8FRxMffl5/PX6Ghu6odYaW9tJ/+hjuJao92ZtmUa/qdKaXDB\ncYjIEIYcSinCb+wo3lXfRsrUFEpfs72j62gPD75JTKS0uZnT0tLY19qLL90azjkHzj8fbrkFamvJ\nvy+fsuVlxC6PZXiS5XiHriwtLqbBgPHNOby97W3rT1y9Wt9QAwJ6HRIWpnt87NgBu2p30dDaMKTc\nJc5OzsT4x5BdmU1rK+zcqTu798l550FWFqSnW3WNzaWb2VmewsleBv/ctYs6Gz4XSikmrpyIa4gr\naael0VTSpNu2FxRoS8YRdFd9uaSEm/LyuCMigr/0o7ZG465GUk9OpfCvHcW1vp2Me7gU1xIci4gM\nYcjiPUW7T4IWBpF9ZTbbf7edlirbLBITvbxYk5BAbkMDZ27bRn3bEbTvXroU9u+neMFyih4tYvQ/\nRxN86eFFt/qisLGRR4uKuCU8nCvGn87H2R9T11Rn+cSKCvj6a7jooj6HKQWjRulYSLPLYSi5S+Bg\nhklxsW5gOqrvhB2YP1/3ul/Ze5fbrry97W2CvIJ4YVIyVa2t/K3Qtv4kJj8TCV8kQBuknbSRln88\nreMxxo+3aZ6uvFVezh9zcrghNJQlo0fbFqcD7HlnDymJKTQWNEpxLWFAEZEhDGlchrkw/tXxTHh7\nAlVfVLExbiN7P+y9m2ZPTPH25ov4eLbu38+56ek09ldohIez57fLyPshgfDfmYi83fbOl7fl5eHr\n4sL9UVFcNOkiGlob+Cj7I8snvv++jgc5/3yLQ6Oj9YN1TmUOJieTVdkTcHRYMkCn2+ZU5lBQoH+O\njrZwgqurLnq1apXFEuNt7W2szFjJorhFjPEcxr2RkTxZXExWD43T+sI9wp2EL+Np2llHuvOjtN12\nj03nd+WDvXu5fPt2Lg8O5qmxY20SGM17msm4MIPMhZn4nuwrxbWEAUdEhnBMMPLikSRl6I6uGedl\nkHlJJs0V1gd0zvTx4dP4eH6qrWVhZiYtfdS96I3q76rZvnIMQT6bGZN1i37MtoGvq6p4r6KCf40Z\ng7eLC1G+UcyJnGOdy2TlSjj5ZLAi0yA6usOSUZFNjH8MLk7W9c04miwZRbVFZO3QJ1nlOVi0CPLy\nulci64EfCn+gpK6ES+IvAeCOiAgi3Ny4MS/PZnec17ZPiW+9k7r2WLZfk4/RZnvn3i8qK1mUmckF\ngYG8HBuLk5UCwzAMyleUs2HiBmq+q2HiqonEvROHyd9k8xoE4UgQkSEcM7iFujHpo0lMeHMCVV9p\nq0bZm2UY7dZ9uZ/g68sHcXF8WVXFwsxMmqwUGoZhUPpKKdvO2IbvCb6M/3AmatNGePFFq9fe3N7O\njXl5zPXx4eIuQuGSSZewZsca9tb3YZ0pLdXZCxZcJWZGjdKWDFvSV0ELAVfXLu3U7YQtgZ9A55q3\nFOUSEnKwyVqfnHyyjlXpCMztjbe3vc0o31Ekh+loUndnZ5bGxPB1dTUfVtiQNl1bC7fcgs95Y5n4\nTjwVH1SQdkYazXusF75fVFby24wMTvf3540JE3C2UmA05DeQfl462y/Zjt8pfiRlJhG0MMhmF4sg\n2AMRGcIxhVKKkb/TVg3fE3zJ+n0Wm5I2Wa7E2MFpI0bwwaRJfFFZyTnbtnHAgjWita6V7ZduJ/vq\nbEZeOpJJH07C6cQ5cNVVcM89UF5u1XWfKi4m58ABnjnEHH5h3IUopXgn853eT373XX3nP+88q64V\nHa3dE9v3WJ++CvZvjmbGVneJec1Ze7Mtu0rMuLjoDrp9uEyaWpt4d/u7XBJ/SbffwVkjRnCGvz+3\n5OVZ/Dx08sADUFcHy5YRsCCAhC8T2L91PymJKVT/z/Jn8b29ezknPZ35fn6smjgRkxUBoy2VLeTd\nmseG2A3Ubawj7r044lbGSWlwYVARkSEck7gFuxG3Oo7JP07GydWJ1HmppJ2Rxv50y+XEzxwxgs8T\nEviptpbT+8g6qdtSx6Zpm6j8uJIJb08g9sXYgxU9lyzRN7bbb7d4vZKmJh4uLOSGsDAShnXvkRHg\nGcD8MfP7dpmsWgWnngpWlpUeNQowHaB4f5FNIsPebd7N2OouGeE5ghEeIyjcn2056LMrF10ERUU9\nt6IFvsz7kprGmk5XiRmlFMtiYihtbmZJUZHl62zeDM88Aw89BBERAPj/xp/pW6fjOcGT1FNSKXi4\noFf3yRtlZSzMyOD8wEDejYvD3YLpqK2xjaJ/FrFuzDpKXy4l+sFoknOSCfxtoOW1CoKDEZEhHNP4\nzvFlys9TiHs3jobcBlISUkg9NZU9q/f0WcjrZD8/1iQmkrp//2F1NBp2NrDj7h1snrkZZy9npm2e\nxsiLD2kBOmIE/N//6W6tX3/d63UMw+C2HTvwcHLikV4eyy+ZdAlrd62loKbg8Dd37dJlzRct6msb\nuhEdDfjnAtjkLnG0JcOWkIfYgFj2GjZYMkDXqQgJ6dVl8nb62ySOTGRi4MTD3ovx9OSOiAiWFBX1\nXY6+tVXXwpg4EW66qdtbbiFuJH6dSPSD0RQ8UsCWE7ZQ8VEF7a0HP4f/3r2by7KyuDI4mDcn4i4l\nqgAAGmlJREFUTOjTglG/vZ4dd+xgXdQ68u/NJ/j3wSTnJRP1lyicvezs0xKEfiIiQzjmUUoReH4g\nSZlJxL4SS9v+NjIXZfJz6M/k3pRL7S+1PbbpPs7Hh28nT2ZHQwPzUraQuWI3qaemsn7MekqeLyH8\n5nCm/DIFz7G93HmvvFLHAlxzjTad98BDBQWs3LOHJ2Ni8DX1HJR3zvhz8HDxYGV6DymYq1frcpfn\nnGP1fvj6gmekbemr4FhLRlsb2FIPbaxfLAc8bLRkODvDhRfqPTvE7VHXVMfH2R8fZsXoyj1RUUS4\nu3NaWhq7m5p6HvTEE9qS8fLLulnMIShnRfQD0ST+N5H2xnbSz01nXdQ6dt6/k8fX5nFdbi43hoXx\nYmzsYTEYRrtBQ0EDJS/rInQbJ26kdHkpIy8ZSVJmEmOfHotrkLhGhKML68LKBeEYwMnkRMiVIYRc\nGUL99nrKlpdR9noZu5/aDQrcR7njFe+FV5wXylnRXNaMqbyZD0vcqM6tZ09tLu1JnkxYHkvQwiDL\nzc6U0gWY4uN1fMYzz3R7+7HCQh4pLOSx0aP53ciRvUwCw1yHsSB2AW9ve5u759zd/c1Vq+CMM3RZ\ncxsYPjqb9vYRjPC0vrGWIy0Z5vldrbxHBjnHQsC7REUZgA0BjRddpDug/vQTnHBC5+GPsj+isbWR\nRXG9W4S8nJ35JjGRuVu2cEpqKt9PnkxQ1wVnZ+tYjFtvtViG1O9EP6anTKducx0FL+wm98ldTPm7\nwSdjTYRH1JM1cjuuwa64+LnQWNBIfXo9BzIO0La/DRT4n+rPxNUTCVgQgJObPCsKRy8iMoRfJV4T\nvBjzf2MY9fdR7N+6n/qMeurT9avs9TKUUphGmnANdiUgwRv/U/1ZMqWWN0bs476oRh70sPKLffRo\nXfHxppt0583jjwdgWXEx9+Tn82BUFHdFWq6ncdGkizhv1Xls37udCYEdJS537ICNG+G222z+95uC\ns3Hbb7m9e1cOHHCsyDhwQFdot+qchnHgVsew4DLAhv4dM2dCZKRO+e0iMlamr+S4iOMs1gyJcnfn\n28REjt+6lVNSU/lu8mT8TSZtGfnDH/Tcjzxi9XLyxsIFV9Zw4HwnXt0eTOwOaC5vpqm4ibpNdbRW\ntuIW5YZXnBeB5wfiNcmLYVOGSSMzYcggIkP4VeNkcmJ40nCrSn8vNwxii4q4Pz+fn2treXvixO5P\nsr2xeLE20V91FaSm8mJNDTd3lId+0MqggtNiTmO423BWZazioRMf0gdXr9Z36LPOsmqOrjR752AU\nxtl0jiPdJeb5rcWpSrt56j1ysElkKKXjV5Yvh6efBhcXqhqqWLNjDf+a/y+rpojx9OSbxERO2LqV\nU9PS+CYxEZ/nnoOff4YffrBqkwzD4KXSUm7MzSXOy4tv5iYyar4DNlcQBhmxswmClTgpxb1RUXyT\nmMi2+nrGb9jAA/n57LXUxdXJCV55herqah554w3+lJPD4rAwm8pDu7u4c+74c1mZvlIXhTIMWLEC\nzj4bvLxs+ncYhkGtKZv6olhsqTk2EO4Sa6kvHgPtTuyszbb9gosW6TLsHU3TPtj+Aa3trVw48UKr\np5jo5cXXCQnkNTQwf8MGfnn9dS0m++iAC3rvP6us5PitW7k2J4crQ0JYO2UKoxyh3gThKEBEhiDY\nyEl+fqROn87lwcE8vmsXUevWcWNuLoWNjT2OzztwgD87ORG+ahWPjhrFHS4uLIuJsbk40qK4RWRX\nZpNWnqZjMbZt09YRGymvL6fR2EdbeSxlZdafdzRZMooL3HBvHNXZjdUmpk6FyZPhvvugrY1VGas4\nIfoEQrxta5s+2dubNfHx1JSWctzjjzPrsst4Z88eWntQbq3t7bxVXk5iSgpnbdtGq2HwaXw8z48b\nZzFFVRCGMuIuEYR+EOzmxpMxMdwXFcUzu3fzVHExz+3eTYyHB74uLp2vurY2vqiqYoTJxB3R0Vx3\n9dWMLC6G9eutrmth5pTRp+Dv4c9H614j8eYVurjUb35j89o7b8yVseTnQ2iodecdTZaM/HwYERbb\n2eTNJpSC556D2bOpe3IJ3x74lmfPeNb2eYCkF15g+9138/maNTxhMrEwM5MoNzeO9/WltrWVmo5X\nSXMzFS0tnO7vzzNjxzLXx0cqcAq/CkRkCMIRMMJk4sHoaG6PiODN8nJyDxyguuPGsrelhVbD4IVx\n47h05Eg8nJ11amNysm7YtWaN9ekUgKuzK78d/1tilryCcQDUsmX9WnN2ZTZOyon2qjEUFMDs2dad\nNxCBn9ZSUACR82PJrvykfxedNQv+9CfcHvoroX8yOH+i5cZyh/H++3D33Tjdey9nnXIKZwGb6+pY\nVlxMXkMDfi4uRLi5Ee/lhb/JxPmBgSQeUmxNEI51RGQIgh3wcnbmWmtMAmPGwIcfwrx58Mc/6gBE\nG55o/9icQNLPL1P419uJstYEcQjZFdmM8h1Fja8b+fnWn3e0uEsaGnS7lt/4x/JW9VM0tzXj6tyP\n+hCPPkrd26/w1g+BBHgG2Hbuxo1w6aU6Y6hLNslUb29enzDB9rUIwjGKxGQIwkAzZw68+iq8/rpO\nb7WWlhamP/wCWyJceHpqz6XOrcHcGM3cKM1ajhZ3ibmy95TIWNqMNnZU7ejXdUucD3DDb5qZu7Ec\nPrHBIlJUBAsWQGKiFolW9BURhF8r8r9DEAaD3/1O97b4y18sdgbt5IknUNuz+PKO37Iq+13aDdvb\n0YMWGeP8xxEdbZvIcJQlw9VVG3OstWSY1zxrnK7z0a+4DOCdjHd4P96FlvnzdGZIfb3lk/btgzPP\n1K1fP/rIMRsiCMcQIjIEYbB44AEtNi6/XBeH6iufND8fHn4YbrqJOQsWU7yvmJ93/WzzJRtaGsiv\nzu+0ZNjiLnGUJUMp2zqx5ufrCuFTx4bg7epN5t7Mfl13ZcZKTht7OqbnX4Q9e7To64uiIt3pdtcu\n+OwzCArq13UF4deEiAxBGCyUglde0WXBL74YkpLgq6+6dworLIR779XBogEB8PDDzI6cTZh3GKvS\nrbSAdOHLvC9pM9o4KfokoqP1fdOa7uWtrbq3iKMe3G3pxFpQoJubmkyKE6NP5NOcT22+XkFNAeuK\n1+ky4qNHw4MPwr/+Baefrl0nXTdlzx64+WYYO1anDb//vm6AJgiCRURkCMJg4uamb1rff69N8Ked\nBieeqOM1FizQfdmffVaLkB9+gGHDcFJOLIxbyDuZ79DWboVC6MKqjFUkjkzstGS0tsLu3ZbPM1sZ\nHGHJMM9riyXD3BhtUdwifin+haJaK1qwd2F1xmrcXdxZELtAH7jzTnjtNais1Ps+ZoyOl7n/fi1C\nli/XlqedO3XTO0EQrEJEhiAcDRx/vG7a9emnUFsLV1yhzfIvvAAlJbBsGV37mi+KW0R5fTnfFXxn\n9SXqm+v5JOeTziZg5umsicswN5G1sbio1Xh56XAHaygoOLj2BbELcHN2Y3XGapuutzJ9JWeOPRNv\nN299wMlJu602bNCvk0/WWSOPP67jNfLzdfyMpKAKgk2IyBCEowWldFDh5s36Trp5s24T38OdfUbY\nDCYETGDZeutrZXye+zkHWg6wMG4hcPBGbU1cRnGx/jMszOrL2URYmHUWFehuyfB28+aMsWfYJDJ+\nLPyRLWVbuGLyFT0PSErS2T+lpXpRjz1mc+E0QRA0IjIE4WjDyQmiovqsn6GU4q7Zd/FJziek70m3\natpVGauYFjKNMf5jAB0HMXKkdZYMc9qoFQ1j+0Vk5MFr9EV9Pezd282ow6K4RWws2cjO6p1WXeux\ntY8xKWgSZ4w9o++Bvr7g52fVnIIg9IyIDEEYolwSfwkRwyNYsnaJxbH7m/fzWe5nnVYMM9HR1lky\ndu3SBhVH3XMjI/U1LGEWRF1FxpnjzsTDxYN3Mt6xeH5qWSqf537O3bPvxknJ158gOBr5XyYIQxST\ns4nbj7udFdtWkF/dt1L4JPsTGlsbDxMZ1hbkKirSQsBR7TYiI7V3oqmp73HmtZrdJQDDXIdx1riz\nWJVhOdvmsbWPEe0bzaJJi/q/WEEQrEZEhiAMYa6eejV+Hn48/svjfY5bnbmaGWEziPaN7nbcWkuG\nWWQ4CvPcluIy8vPBZIKQQxqmLoxbyJayLeRW5vZ67o6qHazOWM0dx92Bi5N0VBCEgUBEhiAMYTxN\nntw440Ze2fIK5fvLexyzr2kfX+R+0ZlV0pVRo3RQZ0tL39cZKJFhKS6joECHqxzaHf2MsWfgZfLq\nMwD0nz//kwDPAK6cfOWRLVYQBKsRkSEIQ5zFMxbj4uTCU+uf6vH9j7M/pqmtiQsnXnjYe9HRutCo\npXgIR4uM8PCD1+mL/Pzu8RhmPE2enB17NqszexYZpXWlLN+6nJuTb8bDJKXABWGgEJEhCEMcPw8/\nrp12Lc9ufJZ9TYcXm1iVsYrjIo4jwifisPfMsQ19xWU0NOiil44UGR4eukq3NZaMrvEYXVkUt4i0\n8jSyKrIOe2/puqW4ObtxXdJ1R75YQRCsRkSGIBwD3DrrVhpaG/h3yr+7Ha9prOGrvK9YOHFhj+eZ\ngzn7issw18iIOFyj2JWIiP5bMgBOizkNb1fvw1wmNY01PJ/yPNcnXY+vu699FisIglU4LPpJKeUH\nPAOcBbQD7wE3GYbRY6vDjvEPA/OBCKAC+BC43zAMK2sBCsKvk1DvUC5LuIxHf3yUtPI0YvxjiPGP\nIa8qj9b2Vi6YeEGP57m5QWho35YMR9fIMGOpVkZtLVRX927JcHdx55zx57AifQXTQqaRV5VHXlUe\n63evp7mtmZtn3uyYhQuC0CuODLF+GxgJzANcgdeAF4BLexkfCoQAtwLbgaiO8SFAz49hgiB08reT\n/wZAVmUW/83/L2X7ywA4IeoEwob3XqrTUst3843fHDfhKCIjYc2a3t8vLNR/9mbJALh40sW8mfYm\nZ604C3cXd8b4jSHGP4ZbZ91K8LBgu65XEATLOERkKKXGA6cC0wzD2NJx7M/AZ0qp2w3DKDv0HMMw\nMoCukWn5Sqm/AG8opZwMw+ijD7YgCCOHjeSlBS91/ry/eT87qnb0KTAAiy3fd+2C4GBt9XAkZkuG\nYfRcj8O8xt4sGQCnx5zOpj9uYqTXSEK8Q6TgliAMMo76HzgLqDYLjA6+AQwg2YZ5fIF9IjAEwXaG\nuQ4jMTiRAM+APsdZY8lwtKsE9DXq67VLpCcKCnSj2pEje59DKcXUkKmEDQ8TgSEIRwGO+l8YDOzp\nesAwjDagquM9iyilAoD70C4TQRAcxOjRutFrfY/RUgMrMszX64m8PG3FcFTVUUEQ7I9N7hKl1D+A\nu/oYYgAT+pqiY4yl63gDnwHp6GBQi9xyyy34+Ph0O3bxxRdz8cUXW3O6IPxqiY/XLorMTN2A9FCK\ninRzWEdjFhm7dsHkyYe/v22bXqsgCP1jxYoVrFixotux2tpah17T1piMfwHLLYzZCZQBQV0PKqWc\nAT+g57KEB8cNA74CaoDfdlhALPLkk08ydepUa4YKgtCFiRN149e0tMNFhmEMnCUjKAhcXXu2ZBiG\nXt9ttzl+HYJwrNLTg/fmzZuZNm2aw65pk8gwDKMSqLQ0Tin1C+CrlJrSJS5jHtqSsb6P87zRAqMB\nWGAYRrMt6xMEwXY8PWHsWH0TP5TKSl2MayBEhpNT77Uydu/WsRoJCY5fhyAI9sMhMRmGYWShxcJL\nSqkkpdRs4GlghTmzRCkVqpTarpSa3vHzMOBrwBO4Gi1SRna8JIJLEBxIfHzPIsN8w3d0IS4zvYkM\n89rEXSIIQwtH3rwvAbLQWSWfAj8A13Z53wSMQ4sKgGlAEhAP5AElQGnHnw7O0BeEXzcJCfpGbhwS\nMTVQhbjM9FaQKy0NvL11czRBEIYODivGZRhGDb0X3sIwjELAucvP33f9WRCEgSMhAaqqdJZJWJey\nGkVFuj5GYODArCMyEr799vDjaWl6jZJZIghDC3FDCILQGetwqMtk166D/U0GgshILXQObT1vFhmC\nIAwtRGQIgkBUlHZHHCoyBiqzxExkpG49X1Jy8FhTE2Rni8gQhKGIiAxBEHBy6jn4czBEhvm6ZrKy\noLVVRIYgDEVEZAiCABwM/uzKQIsMcxZLV5FhXtOkSQO3DkEQ7IOIDEEQAC0ysrKguaM6TXMzlJYO\nrMgYNgz8/Q8XGaNGwfDhA7cOQRDsg4gMQRAALTJaW7XQAF0AyzAGrkaGmUNrZUjQpyAMXURkCIIA\nHHRHmN0TA10jw8yhtTJEZAjC0EVEhiAIAPj46Lbvh4qMgbZkREbq1FmAvXuhrExEhiAMVURkCILQ\nSdcMk6IiCAjQvU0Gkq6WjG3bDq5LEIShh4gMQRA66ZphYi7ENdBERkJtrX6lpYG7O8TEDPw6BEE4\nckRkCILQSUKCzijZu3fg01fNmK+5a5cWGZMmgbM0HBCEIYmIDEEQOjHHPmzbNvgio6hIgj4FYagj\nIkMQhE5iYrR7IjUVCgsHR2SEhGjLxc6dkJEhIkMQhjIiMgRB6MTFBeLi4McfYf/+wREZzs4QHq67\nsTY2isgQhKGMiAxBELqRkABff63/PtDpq2YiIg6uQTJLBGHoIiJDEIRuJCRoKwYMjiXDfN39+yE0\nVKfRCoIwNBGRIQhCN8zuCZMJgoMHZw1mcSOuEkEY2ojIEAShG2b3RHi4bgE/GIjIEIRjAxEZgiB0\nIzBQZ3gMlqsERGQIwrGCy2AvQBCEo49TT4WRIwfv+gkJEBQExx03eGsQBOHIEZEhCMJhLF8+uNeP\niIDy8sFdgyAIR464SwRBEARBcAgiMoR+sWLFisFewq8O2fOBR/Z84JE9P7YQkSH0C/kiGHhkzwce\n2fOBR/b82EJEhiAIgiAIDkFEhiAIgiAIDkFEhiAIgiAIDuFYSGF1B9i+fftgr+NXRW1tLZs3bx7s\nZfyqkD0feGTPBx7Z84Gly73T3RHzK8MwHDHvgKGUugR4a7DXIQiCIAhDmN8ZhvG2vSc9FkTGCOBU\noABoHNzVCIIgCMKQwh2IBr4yDKPS3pMPeZEhCIIgCMLRiQR+CoIgCILgEERkCIIgCILgEERkCIIg\nCILgEERkCIIgCILgEERkCIIgCILgEIa8yFBK3aCUyldKNSil1imlkgZ7TccCSql7lFIblFL7lFLl\nSqkPlFLjDhnjppR6VilVoZSqU0q9q5QKGqw1H2t0/A7alVJPdDkme25nlFKhSqk3Ovb0gFIqVSk1\n9ZAxjyilSjre/1opFTNY6x3qKKWclFJ/VUrt7NjPPKXUfT2Mkz3vJ0qpuUqpj5VSuzu+Qxb0MKbP\n/VVK+Sml3lJK1SqlqpVSLyulvGxdy5AWGUqpRcDjwIPAFCAV+EopFTCoCzs2mAs8DSQDpwAmYI1S\nyqPLmKXAmcD5wPFAKPDeAK/zmKRDLF+D/kx3RfbcjiilfIG1QBO63s4E4DagusuYu4DFwLXADKAe\n/T3jOuALPja4G72X1wPjgTuBO5VSi80DZM+PGC9gK3ADcFidCiv39230/4d56O+c44EXbF6JYRhD\n9gWsA5Z1+VkBxcCdg722Y+0FBADtwJyOn4ejv5jP6zImtmPMjMFe71B+AcOAbOBk4H/AE7LnDtvr\nx4DvLYwpAW7p8vNwoAFYONjrH4ov4BPgpUOOvQv8R/bcIfvdDiw45Fif+9shLtqBKV3GnAq0AsG2\nXH/IWjKUUiZgGvBf8zFD78Q3wKzBWtcxjC9aEVd1/DwN3fum6/5nA0XI/h8pzwKfGIbx7SHHpyN7\nbm/OBlKUUqs73IKblVJXm99USo0Cgum+5/uA9cie95efgXlKqbEASqlEYDbwecfPsucOxMr9nQlU\nG4axpcup36DvAcm2XG8oN0gLAJyB8kOOl6Of7gQ7oZRSaDP9T4ZhZHYcDgaaOz6cXSnveE/oB0qp\ni4DJaEFxKCORPbc3o4Hr0G7Xv6O/QJ9SSjUahvEmel8Nev6ekT3vH4+hn5yzlFJtaLf9XwzDWNnx\nvuy5Y7Fmf4OBPV3fNAyjTSlVhY2/g6EsMnpD0YMPSjgingMmAnOsGCv730+UUuFoMfcbwzBabDkV\n2fP+4gRsMAzj/o6fU5VScWjh8WYf58me959FwCXARUAmWlQvU0qVGIbxRh/nyZ47Fmv21+bfwZB1\nlwAVQBv66a4rQRyu0IR+opR6BjgDONEwjJIub5UBrkqp4YecIvvff6YBgcAmpVSLUqoFOAG4SSnV\njN5XN9lzu1IKbD/k2HYgsuPvZegvVvmesR//B/zDMIx3DMPIMAzjLeBJ4J6O92XPHYs1+1vW8XMn\nSilnwA8bfwdDVmR0POltQke+Ap1m/Xlon59whHQIjHOAkwzDKDrk7U3oIKCu+z8O/eX8y4At8tji\nGyAe/WSX2PFKQT9Rm//eguy5PVnL4e7VWKAQwDCMfPQXbtc9H452q8j3TP/w5PCn4XY67key547F\nyv39BfBVSk3pcuo8tDhZb8v1hrq75AngdaXUJmADcAv6A/zaYC7qWEAp9RxwMbAAqFdKmVVvrWEY\njYZh7FNKvQI8oZSqBuqAp4C1hmFsGJxVD20Mw6hHm487UUrVA5WGYWzv+Fn23L48CaxVSt0DrEZ/\n0V6NTh82sxS4TymVBxQAf0VnsX00sEs9ZvgE+ItSaheQAUxFf3e/3GWM7PkR0FHPIgYtCgBGdwTY\nVhmGsQsL+2sYRpZS6ivgJaXUdYAruqTBCsMwymxazGCn19ghPef6jk1qQKuv6YO9pmPhhX6yaOvh\ndVmXMW4dH7wK9A3vHSBosNd+LL2Ab+lIYZU9d9genwGkAQfQN70/9DDmIXTa3wHgKyBmsNc9VF/o\nGg5PAPno+gy5wMOAi+y53fb4hF6+w1+1dn/RGYVvArXoujEvAZ62rkV1TCYIgiAIgmBXhmxMhiAI\ngiAIRzciMgRBEARBcAgiMgRBEARBcAgiMgRBEARBcAgiMgRBEARBcAgiMgRBEARBcAgiMgRBEARB\ncAgiMgRBEARBcAgiMgRBEARBcAgiMgRBEARBcAgiMgRBEARBcAj/D90gJm4ZNIHaAAAAAElFTkSu\nQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f7ac6412c10>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# analyze the ricker wavelet to help build the ricker wavelet\n",
"points = 100\n",
"for a in range(2, 11, 2):\n",
" wave = signal.ricker(points, a)\n",
" plt.plot(wave)"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# note, all integrate to 0"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# make a haar mother wavelet\n",
"def haar2(points, a):\n",
" \"\"\"\n",
" Returns a haar wavelet mother wavelet\n",
" \n",
" 1 if 0 <= t < 1/2\n",
" h(t) = -1 if 1/2 <= t < 1\n",
" 0 otherwise`\n",
" \n",
" Numpy version, not accurate right now\n",
" \"\"\"\n",
" x = np.arange(0, points) - (points - 1.0) / 2\n",
" wave = np.zeros(x.shape)\n",
" amp = 2/a\n",
" wave[np.where(np.logical_and(0 <= x, x < 0.5*a))[0]] = 1\n",
" wave[np.where(np.logical_and(-0.5*a <= x, x < 1))[0]] = -1\n",
"\n",
" return wave*amp"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# make a haar mother wavelet\n",
"def haar(points, a):\n",
" \"\"\"\n",
" Returns a haar wavelet mother wavelet\n",
" \n",
" 1 if 0 <= t < 1/2\n",
" h(t) = -1 if 1/2 <= t < 1\n",
" 0 otherwise`\n",
" \"\"\"\n",
" vec = np.arange(0, points) - (points - 1.0) / 2\n",
" wave = np.zeros(vec.shape)\n",
" amp = 2/a\n",
" for i, x in enumerate(vec):\n",
" if 0 <= x < 0.5*a:\n",
" wave[i] = 1\n",
" elif -0.5*a <= x < 1:\n",
" wave[i] = -1\n",
" return wave*amp"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAhkAAAFkCAYAAACNTikJAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAHCdJREFUeJzt3XuUnHWd5/H3lw6XdGjDTUgAURxaUs4Omo7isOqMA7Ic\nmCPOsM5qTI/uuuNl1BlO3FldHXMc5TioR2G8sRqYXcVu40FFB3ZwWIFdVxFkpzvCrlZMswYQEjDc\nYpNOgFR++8dTnVSadKcT6tu3vF/n1Hn6+T2/p+pbv6SrPv1co5SCJElSux0y3QVIkqS5yZAhSZJS\nGDIkSVIKQ4YkSUphyJAkSSkMGZIkKYUhQ5IkpTBkSJKkFIYMSZKUwpAhSZJSpIaMiHh1RFwXEQ9E\nxM6IuHAS67wmIgYiYntErI+It2bWKEmScmRvyVgA/BR4D7DPm6RExAuA/wbcDLwE+CxwVUScm1ei\nJEnKEFN1g7SI2An8USnlugn6fBI4v5RyRkvbGmBhKeWCKShTkiS1yUw7JuN3gZvGtN0InDUNtUiS\npGdh3nQXMMYi4KExbQ8Bz4mIw0spT45dISKOBc4D7gG2p1coSdLccQTwAuDGUsoj7X7ymRYy9iaa\n0/H265wH9E9RLZIkzUUrgK+3+0lnWsh4EDhhTNvxwG9KKU+Ns849AH19fdRqtcTS1GrlypVcfvnl\n013GQWU2jHm9Dr29cMklcOqpVduGDbBqFfT1wWz7FZ0NYz7XOOZTq16v09vbC83v0nabaSHjNuD8\nMW3/qtk+nu0AtVqNnp6erLo0xsKFCx3vKTabxvyCC2C01MHBKmTUarvbZovZNOZzhWM+bVION8i+\nTsaCiHhJRLy02fTC5vzzmssvjYivtqzyJeC3IuKTEXF6RLwbeANwWWadkiSp/bLPLnkZsBYYoDqm\n4jPAIPDR5vJFwPNGO5dS7gH+EHgt1fU1VgL/vpQy9owTSZI0w6XuLiml/IAJgkwp5d+Ns86yzLok\nSVK+mXadDM0Sy5cvn+4SDjqO+dRzzKeeYz63GDJ0QPwgmHqO+dRzzKeeYz63GDIkSVIKQ4YkSUph\nyJAkSSkMGZIkKYUhQ5IkpTBkSJKkFIYMSZKUwpAhSZJSGDIkSVIKQ4YkSUphyJAkSSkMGZIkKYUh\nQ5IkpTBkSJKkFIYMSZKUwpAhSZJSGDIkSVIKQ4YkSUphyJAkSSkMGZIkKYUhQ5IkpTBkSJKkFIYM\nSZKUwpAhSZJSGDIkSVIKQ4YkSUphyJAkSSkMGZIkKYUhQ5IkpTBkSJKkFIYMSZKUwpAhSZJSGDIk\nSVIKQ4YkSUphyJAkSSkMGZIkKYUhQ5IkpTBkSJKkFIYMSZKUwpAhSZJSGDIkSVIKQ4YkSUphyJAk\nSSkMGZIkKYUhQ5IkpTBkSJKkFIYMSZKUwpAhSZJSGDIkSVIKQ4YkSUphyJAkSSkMGZIkKYUhQ5Ik\npTBkSJKkFIYMSZKUwpAhSZJSGDIkSVIKQ4YkSUphyJAkSSkMGZIkKYUhQ5IkpTBkSJKkFIYMSZKU\nwpAhSZJSGDIkSVKKKQkZEfGeiNgQEdsi4vaIePkEfd8aETsjotGc7oyIkamoU5IktU96yIiINwKf\nAT4CLAXuBG6MiOMmWG0LsKjl8fzsOiVJUntNxZaMlcCXSylXl1LWAe8CRoC3TbBOKaVsLqX8uvnY\nPAV1SpKkNkoNGRFxKLAMuHm0rZRSgJuAsyZY9ciIuCci7ouI70bEizPrlCRJ7Tcv+fmPAzqAh8a0\nPwScPs46v6DaynEXsBD4j8CPI+K3SykPZBUqqU2OGaL++DBsqmbrjwOLm9NmW9dhXXQf2z1dFUqa\nItkhYzwBlL0tKKXcDty+q2PEbUAdeAfVcR17tXLlShYuXLhH2/Lly1m+fHk76pU0Cfc9MQR/+SJ6\nfwj8sGXBO3lG2/r3rjdoSFNozZo1rFmzZo+2LVu2pL5mdsh4GGgAJ4xpP55nbt3Yq1LKjohYC5w2\nUb/LL7+cnp6eAypSUnts3TEMwCVL+7jg5TUA6nXo7YW+PqjVoL65Tu93ehl+ang6S5UOOnv7w3tw\ncJBly5alvWZqyCilPB0RA8A5wHUAERHN+c9N5jki4hDgXwA3ZNUpqb1OPbJGz+Jm6N9UPWpHQc/i\naS1L0hSbit0llwFfbYaNO6jONukEvgIQEVcD95dSPtScX0W1u+Ru4Cjg/VSnsF41BbVKkqQ2SQ8Z\npZRrmtfE+BjVbpOfAue1nJZ6MrCjZZWjgdVU18d4DBgAzmqe/ipJkmaJKTnws5RyBXDFOMvOHjP/\nPuB9U1GXJEnK471LJElSCkOGJElKYciQJEkpDBmSJCmFIUOSJKUwZEiSpBSGDEmSlMKQIUmSUhgy\nJElSCkOGJElKYciQJEkpDBmSJCmFIUOSJKUwZEiSpBSGDEmSlMKQIUmSUhgyJElSCkOGJElKYciQ\nJEkp5k13AZLmltMegaPX1+Goan5+HZY2pwDzN9dZuhHm31WHTS0rdnVBd/dUlyspkSFDUtt03X8f\nQ58H6N3VVgMGW5p2za/u5RnWrzdoSHOIu0sktc28ka0A3PrBS2BgAAYGqPcN0EM1ZWCA+j/10fMO\nqP9T364+9PVVTzA8PI3VS2o3t2RIarstp5wKPT0AbAPWAttqQA9s2wRrb4dtZ9Rgcc90likpmVsy\nJElSCkOGJElKYciQJEkpDBmSJCmFIUOSJKUwZEiSpBSGDEmSlMKQIUmSUhgyJElSCq/4Kamthk46\nibsPP5TB5iXC6w2guzkdhvr2BhzZXU1HLyPeaFT3LGk09ri0eFdHB92dnVP/JiS1RZRSpruGZyUi\neoCBgYEBenq8RLE0na78+2/wjt9a1NbnXH/mmQYNKcng4CDLli0DWFZKGWz387slQ1LbbDuk2gP7\nVxsfZfnrzgWgvg56V0BfP9SWQP3hdfReu4K+i/qpHbekWnHdOlixAvr7YUnVVh8ZobdeZ7jRmJb3\nIunZM2RIarvnPbmDnq6uaqYDGIJaB/R0AU90wBND1I7oaOnTAUND1XS0TdKs54GfkiQphSFDkiSl\nMGRIkqQUHpMhqa1Ouh/m3zuP4cHqVNRGHbqb02GgsblB98ZuGnc1GN7UPF117HmuQGPrCN3rodEx\nwvCCqltHVwed3Z5pIs0WnsIqqW2+9Ilvs+SDx6a+xpnrzzRoSG3iKaySZo2O7QHAfW/fwh+/62wA\n1tVhRS/098GSGqzbvI4V166g/6J+ljy3eQrr2PNcgXVbR1hRr9Nfq7FkQScj9RHqvXUaw57SKs0W\nhgxJbffkiQ26eqpTUZtnsNJRg64e6NjUwdDtQ3Sc0UHX4tHTVcee5wodwzDUgI6XdtLlaa3SrOSB\nn5IkKYUhQ5IkpTBkSJKkFIYMSZKUwpAhSZJSGDIkSVIKQ4YkSUphyJAkSSkMGZIkKYUhQ5IkpTBk\nSJKkFIYMSZKUwpAhSZJSGDIkSVIKQ4YkSUphyJAkSSkMGZIkKYUhQ5IkpTBkSJKkFIYMSZKUwpAh\nSZJSGDIkSVIKQ4YkSUoxJSEjIt4TERsiYltE3B4RL99H/z+JiHqz/50Rcf5U1ClJktonPWRExBuB\nzwAfAZYCdwI3RsRx4/Q/C/g6cCXwUuC7wHcj4sXZtUqSpPaZii0ZK4Evl1KuLqWsA94FjABvG6f/\nxcD3SimXlVJ+UUr5CDAIvHcKapUkSW2SGjIi4lBgGXDzaFsppQA3AWeNs9pZzeWtbpygvyRJmoHm\nJT//cUAH8NCY9oeA08dZZ9E4/RdN9ELXfvkWBhbfcwAlSgefxhGFp05o7Jqfv3MnJz3d2KPPjs4F\nDJ98yh5tC+Z1ccqR3bvmu7qgu5tJqdeb08er6Q3/u079yOrno9fXuQC49Vs3sOWOquPdhx8Kpx7P\nmuu/z4+e3MH8e+fRzTF850u38OSJjWe+gKRJO7f3X/KC0yb8Wm2L7JAxngBKO/tfv/prHMmRe7Sd\nzdmcwzn7X510EOj9Gjxw8u759b29dD/wwB59uv8C7j52zIqfWw+P7k4W69dPHDS6upqv19tsOKYL\n/hJWre3d1ee0R+AC4JWXrtrVNnTSSVzc18enTzwGgJMOhT7glCsXTvIdSmp1MzdzC7cA8IU1l/L8\n0xezZcuW1NfMDhkPAw3ghDHtx/PMrRWjHtzP/gC87h1/yvMXv/AZ7UM8OqlCpYPF4Rs7OOXKhXzk\n7kfZ9vQOfnX4PD594jF875LLGHryaQAW3reBV166is++uI/HXlQDYMMTdVat7aXvm8PUjqq2TPT2\nwvDwxK/X3V0Fkd39urnvifVs3bHnite97D7mjWzdo231/3uQbYfs3qu77tIOOrbHs3r/0sHqFJby\nb1kK7N6SMTg4yLJly9JeMzVklFKejogB4BzgOoCIiOb858ZZ7ba9LD+32T6ui955Nj09Pc+6Zmmu\nGx4cZuDKAd504bl09XQxODzMpwcGeNUbzqdndLPD4CBcuooLzqxB8/dqcBOsWgu1GvQs3r/XHLul\no4e9bfrw91eaa6Zid8llwFebYeMOqrNNOoGvAETE1cD9pZQPNft/FvhBRLwP+EdgOdXBo2+fglol\nSVKbpIeMUso1zWtifIxqN8hPgfNKKZubXU4GdrT0vy0ilgMfbz6GgNeXUn6eXaskSWqfKTnws5Ry\nBXDFOMvO3kvbt4FvZ9clSZLyeO8SSZKUwpAhSZJSGDIkSVIKQ4YkSUphyJAkSSkMGZIkKYUhQ5Ik\npTBkSJKkFIYMSZKUwpAhSZJSGDIkSVIKQ4YkSUphyJAkSSkMGZIkKYUhQ5IkpTBkSJKkFIYMSZKU\nwpAhSZJSGDIkSVIKQ4YkSUphyJAkSSkMGZIkKYUhQ5IkpTBkSJKkFPOmuwBJ02OkPgJAY+sI3euh\n0THC8ILmwnoD6G5Oh6t+mxt0b+ymcVeD4U3DNOrQDTTqoz3g8I0dU/wuJM1khgzpINPRVQWBem99\nV9tqYCt1BvbouRp6t0JL62pWs3X1VgaabauBrb27e5zCQgAaR5Ss8iXNIoYM6SDT2d3JmevPpDHc\nAGDd1hFW1Ov012osWdBZdaqvg94V0NcPtSVVv83rWHHtCvov6mfJc5ewrg4reqG/D5bUqtW+cd33\n+ehpx/D+pxvT8dYkzTCGDOkg1NnduevnjmEYakDHSzvp6uoabQWGoNYBPVVbx6YOhm4fouOMDroW\nd432oKMGXT3VWtvu3MEDJwMbpvDNSJqxPPBTkiSlMGRIkqQUhgxJkpTCkCFJklJ44KckAOojI7tn\nGg3o7q6mw9VVMOrbG3BkdzUdHt7bpTT41eF+pEjazU8E6SDX1VFdN6O3Xt9zwerVsHUrDLRcPWPZ\nanrv3Qr3NtvGXkrjxGMAmL9zZ27RkmYFQ4Z0kOvu7GT9mWcy3Gi5tsW6dbBiBfT3w5LqOhn1h9fR\ne+0K+i7qp3bckr1dSoMffet7nL/qfQx9+JPT8E4kzTSGDEl0d3bu2dDRAUND1XT02hlPdMATQ9SO\n6KCnq2tvl9LgwSefpvuBBxia0uolzVQe+ClJklIYMiRJUgpDhiRJSmHIkCRJKQwZkiQphSFDkiSl\nMGRIkqQUhgxJkpTCkCFJklJ4xU9J42u5n8n8zXWWboT5d9VhE8yvw1Kq6aiF922Y+holzViGDEnP\nNHop8d7eXU01YBBgde+e87u78MrmdEfngvQSJc18hgxJz9TdDevX77rNO0B9c50V1/bSf1EftefW\nqNdhRS/090GtVvW54Y46F/+8l785+ZRpKlzSTGLIkLR33d17zG7bBGtvh21n1GBxD9uAtcC2GtBT\n9Xnscbj7oakuVNJM5YGfkiQphSFDkiSlMGRIkqQUhgxJkpTCkCFJklIYMiRJUgpDhiRJSmHIkCRJ\nKQwZkiQphSFDkiSlMGRIkqQUhgxJkpTCkCFJklIYMiRJUgpDhiRJSmHIkCRJKQwZkiQphSFDkiSl\nSA0ZEXF0RPRHxJaIeCwiroqIBftY539GxM6WRyMirsisU5Iktd+85Of/OnACcA5wGPAV4MtA7wTr\nFGA1sAqIZttIXomSJClDWsiIiCXAecCyUsraZttfAP8YEX9VSnlwgtVHSimbs2qTJEn5MneXnAU8\nNhowmm6i2lLxin2suyIiNkfE/4mIv42I+WlVSpKkFJm7SxYBv25tKKU0IuLR5rLx9AP3AhuBM4BP\nAS8C3pBUp6T9UN9cr6aPA4ub003Vsg1P1KetLkkzz36HjIi4FPjABF0KUJvoKZp99r5yKVe1zP4s\nIh4EboqIU0spG8Zbb+XKlSxcuHCPtuXLl7N8+fIJSpE0WV2HdQHQ+52WQ6reCb0/BH64Z98F87qm\nrjBJk7JmzRrWrFmzR9uWLVtSXzNKGff7fu8rRBwLHLuPbr8E/hT4dCllV9+I6AC2A28opfzDJF+v\nE3gCOK+U8v29LO8BBgYGBujp6Znku5B0IIYeGWL4qWEA6nXo7YW+Pqg1/6yo16H3T7oY+H43/jpK\nM9/g4CDLli2D6vjJwXY//35vySilPAI8sq9+EXEbcFRELG05LuMcqi0ZP9mPl1xKteVj0/7WKqm9\nuo/t3j2zqXrUjoKexS1tj05DYZJmpLQDP0sp64AbgSsj4uUR8Urg88Ca0TNLIuLEiKhHxMua8y+M\niA9HRE9EPD8iLgS+CvyglPJ/s2qVJEntl32djDcDX6A6q2Qn8C3g4pblh1Id1NnZnH8KeG2zzwLg\nV8A3gY8n1ylJktosNWSUUh5nggtvlVLuBTpa5u8HXpNZkyRJmhreu0SSJKUwZEiSpBSGDEmSlMKQ\nIUmSUhgyJElSCkOGJElKYciQJEkpDBmSJCmFIUOSJKUwZEiSpBSGDEmSlMKQIUmSUhgyJElSCkOG\nJElKYciQJEkpDBmSJCmFIUOSJKUwZEiSpBSGDEmSlMKQIUmSUhgyJElSCkOGJElKYciQJEkpDBmS\nJCmFIUOSJKUwZEiSpBSGDEmSlMKQIUmSUhgyJElSCkOGJElKYciQJEkpDBmSJCmFIUOSJKUwZEiS\npBSGDEmSlMKQIUmSUhgyJElSCkOGJElKYciQJEkpDBmSJCmFIUOSJKUwZEiSpBSGDEmSlMKQIUmS\nUhgyJElSCkOGJElKYciQJEkpDBmSJCmFIUOSJKUwZEiSpBSGDEmSlMKQIUmSUhgyJElSCkOGJElK\nYciQJEkpDBmSJCmFIUOSJKUwZEiSpBSGDEmSlMKQIUmSUhgyJElSCkOGJElKYciQJEkpDBmSJCmF\nIUOSJKUwZOiArFmzZrpLOOg45lPPMZ96jvnckhYyIuJDEXFrRGyNiEf3Y72PRcTGiBiJiO9HxGlZ\nNerA+UEw9RzzqeeYTz3HfG7J3JJxKHAN8J8nu0JEfAB4L/BO4ExgK3BjRByWUqEkSUozL+uJSykf\nBYiIt+7HahcDl5RSrm+u+xbgIeCPqAKLJEmaJWbMMRkRcSqwCLh5tK2U8hvgJ8BZ01WXJEk6MGlb\nMg7AIqBQbblo9VBz2XiOAKjX60llaW+2bNnC4ODgdJdxUJlpYz76K3fDDbt/3rBhz2Wz3Uwb84OB\nYz61Wr47j8h4/iilTL5zxKXAByboUoBaKWV9yzpvBS4vpRyzj+c+C/gRcGIp5aGW9muAHaWUN4+z\n3puB/km/CUmSNNaKUsrX2/2k+7sl49PAf91Hn18eYC0PAgGcwJ5bM44H1k6w3o3ACuAeYPsBvrYk\nSQejI4AXUH2Xtt1+hYxSyiPAIxmFlFI2RMSDwDnAXQAR8RzgFcAX91FT29OXJEkHiR9nPXHmdTKe\nFxEvAZ4PdETES5qPBS191kXE61tW+zvgwxHxuoj4HeBq4H7gH7LqlCRJOTIP/PwY8JaW+dEjef4A\n+F/Nn7uBhaMdSimfiohO4MvAUcAPgfNLKU8l1ilJkhLs14GfkiRJkzVjrpMhSZLmFkOGJElKMetD\nRkS8JyI2RMS2iLg9Il4+3TXNBRHxwYi4IyJ+ExEPRcR3IuJFY/ocHhFfjIiHI2I4Ir4VEcdPV81z\nTfPfYGdEXNbS5pi3WUScGBFfa47pSETcGRE9Y/p448Y2iYhDIuKSiPhlczzvjogP76WfY/4sRMSr\nI+K6iHig+Tly4V76TDjGEXF0RPRHxJaIeCwirmo9eWMyZnXIiIg3Ap8BPgIsBe6kuqHacdNa2Nzw\nauDzVKcQv5bqhnf/PSLmt/T5O+APgX8N/B5wIvDtKa5zTmqG5bdT/Z9u5Zi3UUQcBdwKPAmcB9SA\n/wA81tLHGze213+iGst3A0uA9wPvj4j3jnZwzNtiAfBT4D1UF8rcwyTH+OtUvxPnUH3u/B7ViRmT\nV0qZtQ/gduCzLfNBdcrr+6e7trn2AI4DdgKvas4/h+qD+Y9b+pze7HPmdNc7mx/AkcAvgLOB/wFc\n5pinjfUngB/so89GYGXL/HOAbcC/me76Z+MDuB64ckzbt4CrHfO0Md8JXDimbcIxboaLncDSlj7n\nATuARZN97Vm7JSMiDgWWsecN1QpwE95QLcNRVGn40eb8MqpToFvH/xfAfTj+z9YXgetLKbeMaX8Z\njnm7vQ7454i4prlbcDAi/mx0oTduTPFj4JyI6AZoXk/plcANzXnHPNkkx/h3gcdKKa1X3L6J6nvg\nFZN9rZl0g7T9dRzQwd5vqHb61Jczd0VEUG2m/1Ep5efN5kXAU83/mK32dUM7TSAi3gS8lCpQjHUC\njnm7vRD4c6rdrh+n+vD8XERsL6X0ceA3btT4PkH1V/O6iGhQ7bb/61LKN5rLHfN8kxnjRcCvWxeW\nUhoR8Sj78e8wm0PGeIK97H/Ss3IF8GLgVZPo6/gfoIg4mSrMnVtKeXp/VsUxP1CHAHeUUlY15++M\niN+mCh59E6znmB+4NwJvBt4E/JwqVH82IjaWUr42wXqOeb7JjPF+/TvM2t0lwMNAg+qvu1bH88x0\npgMUEV8ALgBeU0rZ2LLoQeCw5v1lWjn+B24Z8FxgICKejoingd8HLo6Ip6jG9XDHvK02AWNvTF8H\nTmn+3HrjxlaO+YH7FHBpKeWbpZSflVL6gcuBDzaXO+b5JjPGDzbnd4mIDuBo9uPfYdaGjOZfegNU\nR70Cuzbrn0PizV4OJs2A8XrgD0op941ZPEB1AFDr+L+I6sP5tikrcm65Cfgdqr/sXtJ8/DPVX9Sj\nPz+NY95Ot/LM3aunA/dCdeNGqg/b1jEfvXGjnzMHppNn/iW8k+b3kWOeb5JjfBtwVEQsbVn1HKpw\n8pPJvtZs311yGfDViBgA7gBWUv0H/sp0FjUXRMQVwHLgQmBrRIwm3i2llO2llN9ExN8Dl0XEY8Aw\n8Dng1lLKHdNT9exWStlKtfl4l4jYCjxSSqk35x3z9rocuDUiPghcQ/Uh+2dUpw+PGr1x493APcAl\neOPGZ+N64K8j4lfAz4Aeqs/uq1r6OObPUvN6FqdRhQKAFzYPsn20lPIr9jHGpZR1EXEjcGVE/Dlw\nGNVlDdaUUh6cdCHTfWpNG07NeXdzgLZRJa+XTXdNc+FB9ZdFYy+Pt7T0Obz5n+5hqi+8bwLHT3ft\nc+kB3ELzFFbHPG2MLwDuAkaovvTetpc+f0N1yt8IcCNw2nTXPVsfVNdvuAzYQHVthiHgo8A8x7yt\n4/z743yO/5fJjjHVWYV9wBaqa8dcCXTuTx3eIE2SJKWYtcdkSJKkmc2QIUmSUhgyJElSCkOGJElK\nYciQJEkpDBmSJCmFIUOSJKUwZEiSpBSGDEmSlMKQIUmSUhgyJElSiv8PUZ8oKyojj+AAAAAASUVO\nRK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f7ac6384950>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"points = 100\n",
"for a in range(2, 11, 2):\n",
" wave = haar(points, a)\n",
" plt.step(np.arange(points), wave)"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.image.AxesImage at 0x7f7ac68c6ad0>"
]
},
"execution_count": 19,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAfwAAAFiCAYAAAATPmogAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzsvWusbFt2HvSNMdeqvc859/ZN3E23nzjGFiRyDMKdGPlH\nAsI/rPArEUgGIfGI4AchUoQQCkhIRA4CFGQrOIoFioTwD0CKSCQCEnEEiiJCFAejOLHBUZz4HcVt\nt7v73nvO2XtXrTkHP8Yc87Heq6r23nXurXF17q5atdZ8rTnneH+TRARXutKVrnSlK13pk0383A24\n0pWudKUrXelKj09Xhn+lK13pSle60qeArgz/Sle60pWudKVPAV0Z/pWudKUrXelKnwK6MvwrXelK\nV7rSlT4FdGX4V7rSla50pSt9CujK8K90pStd6UpX+hTQleFf6UpXutKVrvQpoCvDv9KVrnSlK13p\nU0BXhn+lK13pSle60qeAHo3hE9G/S0S/QER3RPTXieh3P1ZdV7rSla50pStdaZ4eheET0Q8A+CEA\n/wmAfxrA3wLw40T0uceo70pXutKVrnSlK80TPcbhOUT01wH8hIj8kfidAPwKgB8RkT/Ru/ezAL4f\nwC8CuD97Y650pStd6UpX+uTSLYDfBuDHReQ3525szl0zEbUAvgjgP7NrIiJE9L8D+N6RR74fwH9/\n7nZc6UpXutKVrvQpon8VwP8wd8PZGT6AzwFwAL7Uu/4lAP/EyP2/CAA//F//EL7jH/92EBgg/YFA\n6f8oPpVXkK4VlwpPRemzyM/VnwEAAogAIoJwEHRvDxAvcC8acLPG8yEACHIIIEeACKT/swDBLCpB\nAM79SXcHSbfrB0nP5kuC+qZ86+Ce3n1T1+03ESB0Ad3Bg5hARHi4O+Cjr9zh1Qe3ePGqBcV2I2ir\nu33A3ZsHvPnoHl/3hffR7hxAVBaMEHr1+ADE8gG7nVL77Lvd/0M/+l/g3/9D/+GgvURUjYd9tr6k\nbtq4BqnHtnh+/9DhZ/7yz+Ll517h27/rW+EaBhFyf+15fdXVDOobynznEXzsCwNEhOAFQQDHWiYx\npfEWAdgB7PJcs3olCCS2P3jB4dDhq1/6EHev7/Hr/9+v4Tu//zvx6v0XYEeDtpbfy7aKDyAikKNU\ndu6fQAKwfzhgd9OCGJAwKAZB9H5mSq+bqB4L7wX3b+/R7hq4xoGYUz1FpYPxG6PQn7A9+jP/45/C\nv/0Df7jua9m3WEkoJmOcAqP1i6D6oX5OBs+EiT6Jz/Uyc3F/UV7I87brOhweOogX3Ly60TVCw/4A\nAu8FzLZ31f1MnZD6We8DXv/aR/jwH3wV3/BPfvPEHNHn/EOHX/2ZX8YXvv0bsHv/FoCkNTtGwRcT\npTf2wQeETsCOdO+L85psf43zzvrW3Xdodj0WxZRfWhAE7/FLf+cX8Or2FT73bV9I4ytBdMzSHiD4\n3/72n8fv+51/IDevfB8ceYm9k/gsFe/Lrh3u9xABmpsGzAzfdSAiuJtW936vfXU7h/blDtw6OMeg\nhrWIIAghwLVNbGuAP2i9HPcFcoymcWh2Dk3boGkdXOPwcPeA11+7wxe+9XP4ln/2M/jzf/d/xU//\nzb+Dn/4z/zcQeekcPQbDn6Ji+Cu6BwD+3A7u62+h7C8zdK621ZI5ZIEg/1rsOpG4z9iLkisKOikg\nAuoEcucgXYC7LRj+WFF9ptkpw++vOftAQfLFsV0yMay6/GpzkbGLfYY/3sY5F46EuMh9gBx83MgJ\n4b5B+1LQvH+D5tUuLXjdEwQ4BLRvGM37hObzt3A7V20KUvY7ticEUWaaX2bd3t53unVovvG21985\nhh8/29Cmzb4YEKvHmrbv8PLb3kfzwQ2ab75F4xggAhcbYogMsb/p9ceVuwBfMHwmgvf6LHMsM25e\nvovXHdUMP42zpM3TewEOHW52B4Q3Drs3r9B+0ws0xvD74z66OYsyITKho2h7EIS48cpDi+ammWT4\nyvQErC8ytrmeexwCwltOG1YSYoqbaiY2TWFm7gIA3zq03/Ri+hkTmsq6+3Oo6h+qzvTb3G/PQLgw\nGT4ywf77KMsLxqCCwHUe9NBBQsDu5QzDF2VaJjjmvaNuR7n/WHv8bcBds8fuW16C3IhCE99t2Hu8\nePM+dv/oS9y8r+tvluGHCYYfmbvvvM7xOFEkSFG/ACG3u3nw4F3dNmZOgmwIAeIFrw4fYNfc4OZb\nXxXKCAYMn3/O4eZbX+Xm+ZDXm83hUE/0MYbv7nfavpsGxIzQeYBJhRM2QSTAtQ7NyxaudWDHqa4g\nuv6a1qUx811m+GCCY4ZrHJrWodkpw2dm4MHh8BnSvfDzN7j5+D3c/oP3rIWLLvHHYPhfBuABfKF3\n/fMYav2JfuQH/yvcvlcv1u/+vt+N7/6+7xnwWRoRAvKnWvUaaPLlfSWJ/hMI4AG/9zohdi5v+GsY\nfogbCGR4T8GQKqZWMfxesSMa+ehvvbbIxPU5VcqYpASBNw2QCN3B4+3hAbu3DW5CWzMiAL4L6PYe\nd90DvvL2BdyeBxp+3/ogId5SCm9pGCR9t/vfdG/xc29+ftjfclFL7qz1JW3mI9pPX7sLPuArn/kK\nQsNwD1BNBBhu0n2BpDfGApXaTePTcTRhQZk/MWLlcZMUgHytoVPqf+ocQhAEL3jbvMH+psNXv+5r\n+GX/K7jd30SLTDXsmOD3cRy0HX1h0sbO+wB34EWGWDKkyloFXQ8H6cDewYF6nSo/LjP9JSvAndzh\nl/yvVmWNCcpzc2Cuwuo5oF7jAIR6UnbiPbneKYYvxldYIBxwgIcEQdu2AEaHDRAVOsiY50i7++sO\nAMQLDr/lAR8+fIzm5ZdHGbgqPwB2AW++4S3oM19B+2JXtWWMaqGnbqsKt5nJ2lqqrFKlEGTW0oKI\nKa0/EyIevvkBd+EA95ldXpflGo1F7tsDfvODrxZtDYmh9y2Mqb5ibltZ4YVXQbeNik3QN2zfJTJ0\nbhlu14Adg5wpDpT2WFMkJQiCC6l/FAVxZoZzDEcOThgkhP/3p34KP/uTfwuudWh/jPHhw0d4+/Hb\n6RfSo7MzfBE5ENH/A+D7APwFIAXtfR+AH5l67rv+le/BP/JtXxjMpp/90s/N1NZn9kvXx+8pGh//\n6qIIIYAcz0q0o2VMbSCx7PxhWoIY34CW6i4/Tty8UEbJ9JXnamce9h04ENqDQ7mSlLnpBH/oOty8\naXVi9xaJ9CoZMqP4TOp4UYYIXvs3+LnXPYY/0rd+PYMu9xgzIY8VCfDmgzd4ezhg/3CXN6K+9WGB\njBH2u2IWEQJlYUeK60TDMel1zMreuwP8jcfrr3uD4AW7fVu5QeoeTjQy3V8PivHfEAJYeNI2l5iC\nzZPRauI6EgIFqrpUl7WCFjj+W7nDL3e/PF3u6HyY4/hz1Y+sMJr4NVmspxl+eY0c0FGAiKhVpCfE\nVbXYOqrmfm+S9z8GAVzAh/Ia4YXMbZKgIHj7DW/x8PIAt2sxO6f6DeztRwy1UCUmWsz7/jMSrVB9\nd4Mx1CzICw67Pe7uD5APppsFAIdmj6988JX0PUR3VCy5t/+kCodd9OaCUwGWRBCg1gfrVwghafUU\ntfa0Pm3/s7qjNcXqo/iXjfETgYRBAfjMFz+L7/6u3wtqHG4+5/Cl+y/hN/7+r+On/8u/Ot/5SI9l\n0v9hAD8WGf/fAPDvAXgJ4L+beuAXf/NX8eWXr+uL/c1hA989imI9zDro3s8vhjGa0oYehY6spj+c\n48Xkhe0I8EEQHgLYudHSmAhdF8BvaHnMxipc4FOVhl8+P8GMjiFmQvMZxlc/eoMP91+bbNpqmhro\nKevAmrkmgGOCOAEccP91B3zoP4Lb99/LiXTsGI/cSwR1CfiztGySVMP/lZk7jhOCN96mRBOfV5Bj\nQmca3xZlI5GM/amofeXwurnD/Yt5K7AjQngl8P515W46pknMVMc5nIluPuvw4UdvcHh5mL1voOHL\nfDzCFGUlIe6PDHRBKqE3lV0U37fSUHGhPypj7SLRfTbsBA8PHfw/DGhaQufXL6xHYfgi8mdjzv0P\nQk37PwXg+0XkNyafoQDhkCXukh6Z0Q+qI47a1qSePFPWMJgHOE8X1FUwLHfumn0ur61ZtgRO2qhz\nBCdA5/NYVYGTBDTM4GZDLzcy6i98zzejaRdafsIgE9Rv9ur2FnfdHrubZQZq4/PU5JjAxGAiuJYR\nIHB8wmb8iETQebvkfz8Hff33fAt2t/V7S29nTItfujb1+wYak+2WSnDM8EGwvECOm3tEwE3bAg7Y\n7Zpp109sCxPj4bCvAg6PqBUuMvxyDNaMxxK99+IWHQW8uL2Zve+bvve34b33cxxQkBh/spH6Sp1j\nigw/k7paVhmOJmjEGhXrggAeHvv7DizbWPijBe2JyI8C+NG19+92DW537bZNNDKNgZ9lI/Xrc8xg\nJvggkLFopbmyJjR8Kv2XRxIvcfexayMcn4ixtNRsshIBjXOAAAffpWey+VhAxNg5h33nzci/2Dgi\nLsZ2SUQhvPd7v2O246eOL4PQOIcPXr6Hh/0BN7t28Zm5udqPcyjN3qN+wpHrw0JNMCE4dmjY4X6/\nxyF0YNq2GS9ZolKbjhRqsutCn34Khv/BPzdMAjLz6Llo61jUbpaS2U2X0zqOe8+8wmHC1FZNlUB4\nsdth51q0TTP7jhvHaFyDtw/3m+dYv7GOKMbxnY/lExE+ePkKEoCb3W723q/757+z+n6sht+3VLjI\nK/plA6OOn3zPzLjbeumX0zAD0DiZg/foe0+X6Cmj9GepbRrc3rTbpK7IlYa+z23Uj9hvnEsvMUid\ninOciS3WcjLDP8/GRQsLt9TKmAit02ly6A4WRFu1hYlx07TY+wN8WCcgMXE1tqeSMpYTGD4Tdq7F\n5977AG8e7tC2KzT8Gc2I45wKccTKfJOAMHvvFFkZjjlt1nf7B9x3D5vnJYNn67M2Hc/wdR5ZBH9Y\nOS/ORSUjPH7NDmnrGrTgUwIlBk40Lzi0zhUMf0Yoi2VrpsR6ZkxEeHVzi7Zp4JyD9PbcUvRunMPO\ntfi4bZMVqe/t6T8z9t180rKB4a8xAjIRPvveB+h8h107z/D7JBIW98Ix6jP4cYav831O0J3jJyE9\nX5fTOo2h2oc9Xt/db95DL4bh37Sq4W9h+MQUUzT4JIbfXyytc3Ds4EOAl8I/skIY7Ucpl9dPkpCB\ns5ltl9pBoGjhCHDMaF0DAuGhO6QJVraFyeG2bbHvDujCOn8Sk0OQ8zl1VZs8fnwcE3Zuh89+5gN8\n7f5jTclboLkF60gFBps/TJw2ed/rd//eKbIyHDNumhvctC3u9vd4s9++jJfG39p0rNnTBIVPGsN3\nR1hSSguOYJk571wDHyO/5zZ0jlYtkbBpb2FmvH/zEm2jqV59fICSWtfgtr1Ba2lhRxKDNCJeaiFy\nVqBcwfGZCZ9//7fivnvArlm2ypV0PMPnSrHpfwf0vQlkdt7PsRNvjD4+b993rgER4W13h69+9DH2\nB1liSRVdDMMn0jQElKkS8bexmCZBTGO2nOaTGH79MDPDsfqwEXIOvkhvco42sPQBlreezvBP86Fl\ncsSzk40oWyMcs5r0QXDiQXH+lgzfMaNhB+/CrEZStSH5Kc9D2uYTNqTYz51rNAeW3eKcWmT4hXTP\nJpCMSPz9eyfbCBVsHWlbG9dEa1QvDXIFOfBsDJ0xfJZwkknf5skjx+sNyOJdmE6x+wyJeVtwJPcZ\nvkhKz5qixjUgigxDpu/j6DIJQmBa3y7HhLZp0LhGtVNi9Q2PUOsatK5BwwoecyxRjDkR1Otmag31\nt9bJvhBj17S6Hppt70ZkYwaW1ckM8pnn9L9b2SIBfmZPmnUJRmHcx/ZRAEDqdsz78/a2XwzD3x86\n3O/3vVSJeTJt+lQpvs/EO/Zw7NB5rxL2wuSsy5oOQj9FAwXOZ9Jf1PDjhMoafgcAeDgcEkMvNwjH\nDnvX4aE7wAe/ivecW8PHiQIVE+GhOeBFe4uvfvwaN7tmkdHNLVjHDJGsodmYltem7p0ic1s4Zjw0\nHdqmxduHO9zt7zcLg0suFWvTqT58FZzxvBr+GcvdPs55YzaT/tI6bk3DX2HSV4a/TcN3TNgfPL72\n5mM0zs1acdqmwU2zw9fevF5l9ZpsaxTIBXVK7pxbbI2K74jBYHz5ww9xe7PVpH+ci9Yxw/tQMfzy\nu5UtMgRnquq3OBcMezkw6QflQ2ptBT568xb3+wMkLOFP1nRZDP/hsO0lFD78U6j//ME5OCIcvM/A\nFsDJJv1T+fW5TJMaszC/kZtfionQNA4iwP5wSG0o26JCwQEPBzX5r2nnudMX1bhygg+fCLumxc61\n+MpHH+PVi5vFfsxr+KyIWnEumHk7jGzi/XunyDZ4besejXN4c3ePvd/DDdIl52lqnpZtMm3sFPqk\nMfytQrvhxBjzygxuzof/uEF7TIT7/QFf+/g12tbFuIIpDV8tSR+9eYO2PZ5dmJtQ1kbpr1TxmRki\ngi9/+CFeLkTp9+lYd5VjRhdCaqJjRud9NYYaupzxTMbI5sI4w+8F7YkxfN2LP3r9Fg8P+xiDsb7t\nl8Pwuw73+8NRQZtU/P8o6j3asJqf9l1EVEpS/XLjqLDoL1RzRDvPxfCX73DRh28M33vBoeuS9aVm\n+ATHDfaR4a/RgpYYzjF00tZOwE3TgJnw1Y9eq6ViydI0Mx0ejeEj4gVE18Prt3fwISSYzrW0huGf\nI7Le2XkBT4VN0aNzMnstcFuJnATb/rY+Z9LnqOEvNCX+b15LHm/T/X6Pr370GrtdA9D02mkaB0eM\nj9/eYXcCwweiEqFS5KKKv96kT/DB48sffohX3YuFu2s6KWjPZ8uvY0LX+RqGt2TYS0riiPJjX9Ma\njePUOocQAj56c4f7/QEvbmYYzghdDsOPGv4lkIvwhvuDmrK3mPEilPI7T6bhE2mkrvcBh64b1SRd\nhIHc7zsNSrrQnPAlumkbBAR89eOPIbROcJmiMud47trc9TEiIjjSOUlEeP3mHgJNaz0njeVMb6EU\npR8Z/pOBUV0YHWPJsrV3WsLaNDET3rb3+OpHr3Fzs5sVFprGgUB4/fYeNyfOsbFo9ilKmCMLY+eY\n8OD3+I0PP8SD329qz/Em/Trv3jHh0IVRV/Sad7gakKjYiz96/Rb7Q4dd07ybJv2Ged5HdMZI29Hi\ni8/GwGyhbtn4nxRpb1C3CYLbzXx9GjB8DhowNsHwXczVf1cYfhorIL38m7bF7W6Hm12Lm12jftEj\nh1C1eaDUUcaiefO96zdCJs3Dd8w4RCvU+Rn+MvjLGiuNi+torH8pBqf4u4UeiyGekzbvB6R7oY+H\n8wz6Z4YCsvHbPgZMhBc3N3h7/4Dbm3Z2n2gbDdjtvF+FTTFH2xm+LKr4DTNe3dzixU27yYdPMXNk\n6x6p6w+DtDzn/Oi+l+Z3bz8uLX99q/CcoNM2Dl0IaBuXzjvZQhfD8F08DnCKzplaM15+/tywi5pJ\nfCkrgwiB8c176sS+s1MR03AKwy8nNTHpJPNq3mfXO7+Q1DfXNg0MIrKMTL5USouM8oZ5u9vh5c0t\nXtzscLtroYiLx5Y/1FCci8E9PbLUqDXE0d3knALvHLoOIYTzM3zH8bS/GYa/yMzUNTTlw+/jol/6\nnElEvUCrmbZvd11RMunbiZJT5R07XkyM925v8fbhHre73azEcNO0ADQwcNc2s+98qT2OOKWXLVGZ\ntjdHDTu89+IFXr64wcsX6334jLhPbxxCTS+kQdCeujtrhl8etDV1jgL15xKQFKfyvngzdq5BFzx2\nbYND599dht80LkqT43SuCPUpKgeucZHhRwlza0DMgOFvEBhOI506hmJ3bFYAk/bZB4FjoGkaND6A\ngQGWPlMM2msbjSjVCCA8WZePJGOyZYbHi5sbvLq9xe3tDrc3u9nsjyUGNRaIM6XhbMEY5wira+lS\n+24P7x9Dw1/Wxta028UUtFHLRny+/LuFtvquz0e2SUvvytit23ysRJp65UOALwLDyt8tJoDLs+E3\nEBPj1e0LvLy9w+2unX3+tt0BIHjpsGvb2eyOpUyBTRo+lv33gDL891+8xKsXunbXku7TdobuelJl\nBnE+Zx/+vlPslpLyfogB1sEcw7cIf2Ao8OyaFp1Xhn//cEhHmK+li2H4Sxr+VsCLrVRuNqcw/DEJ\n+KkYvtW9BKaxRC6GjirDV+3de918+gdoOFL3x82u1fOp4wR3F66tJYbPGaHvxU3U8G93aSOcEjRX\nmVJ7K3lSw3eE4FcyfKfY5ruYLnV/uEfnw8kBVX1yUcuc23XZcTrrfZQo4zWM95vTmeTV2eSr6XmM\n+oR6nZtVa/ruDQwfcb0Fj86HoYZfMHwLiNy61BypVvzxww1u23Z2CF+0ykS9HNA2zWw67RIWwJRL\na4woDtvSyLWuwfsvXqqGvyFKf4vwUT8X53MPeKfpDiMMP4+TpTin34K5i0f8/jJE2DO6aXboQodd\nq0G7W9/9xTD8iyKyP+eKJH/KTYl6f08oYup7/7foCK/m5mXze6WRNlLUyE5mJbRl/qxnCmm4C7r8\ncLjjfM1ryn0+6r+zpUWyoVj7SL0LON5v368jBcnPlkXJNfUsc2zFshgZovMVvrG09NmMOlL+uLWR\ndr8MrthVtQRsK/ViGL73AV03DcQS6HHzeHN+eTbXPhwO75RJPwMRnWbSN1Ad0/CDAF3n8bA/DFDd\nHGdAmfv9HrZJLHX5OYMbgXGTPhPjbXOPt/f7BDt6dBxE/F/ZxXOY9C2gtPMBvhO8vd8rQNQRAUhL\n9Vgu+FS5W0z6/Tzl8vljTfrPR30z7PwhSlvmOZEejdsFP2/Sn7E+LZFjRkMN3t49LAZ+SQAgwNu7\nB3RteDqT/kpPyMF12LkWb+4e4Hg9Oztew897Y3lt33VJw7e2+wgzbgGCZnElqMZve8/Qh5+DXEvg\nLkCPbO+8x/3DHl3n0bTvaB5+13kcZhj+U/nwiRCDZWJanmyN0h9O1KezbpsP/7QgqHJSWx7xofO4\nfzigcVwFMTJlhv/wcABAYLd8kM1G1+bZKY8RYLIzEWHXPODt3QNu2iYGKE71Y143MsCViuE7ioFw\nvXu3MHynPnzHAV0TcBcZvmwUTNfUkxj+FDOLQCqTRDkPf4yx5LMw8t9N9ExO/DELy6RBfyvDB6Fr\nPA7ejz5XmvSP7bpjhiOHu/vI8CfGnaAMX0Tw5u4hBu5elg+/dQ4tN3jz9h7OucV9x2jLmisp7419\nH/48wy/3Y0MxtcOPxpREGTB8DZZWht/hYX9Ad/AIN2HT/LoYhr+k4T9VWh4zwZMygv1+ex7+2AJ/\nOn5PeRM8YTMsGb4VdejiJHNcjYcF+AWBAieB4NxyXsJzM/y0o/RMqK27x9v7B7y42Sl2+JEvz4Sg\n0qQ/5cPcshHq0c0Mpg6HrsPbuGmDzszwmQsNf/yeZZeF+ZlFmUWPsZyalvestNKif4xbsPUNuphu\nOSw3V3zseDnWcxff3j3g4Gvfcp9CnANv7x6OYpB1vVt8+NrPpT1CLXGE13cPaJqn0PDHffhllL4J\nE5aZwvFcFntfzNniZQiE/bG1OZPKiCnCXRfQecWsOXQe3su7yfC7ENDNBQA9ESnojmojZnFg3mKS\ne2ZGdgaqGD50Y9kfOjw8HND0Ts0iQq3hE606xOISx4lAaJoH3N3vcf/isPkwjpKmgHdGTfojEv5c\nuRyDdRw73D/sk5Z2TvyDNSb9teUEEXh/GpDRu0rHzHMFufKPlqpowGJ3D3t0IczCMoegh/i8vXs4\n2eP9GBr+oWMFErp7SGmDa+hUDb8rLFYKvJPz8G09lwy/X0aJzDc3Lv0yfBPQmfLVqdtny6q6GIbv\niGclzTXUX1wpMCVqcmumAtuGCsA7B4Fsalet4Y+okRdC/XVRtpKjPZpIwKxStEDgfYOm4R7DV399\n27iEtf2uMvybXYubRkF32tbFUwKPI4t9KKVvxwQeWdjbNHzNwSdSmM1d28Bz2LTZra5HJLm3xmjJ\nXK1CiUL0KnATDX7fOgfGcvcvOYefizHqGwSqmK6Cmsbl5+j8dg/nKIJLtWhjtPcoEemR5SHo/W0z\nbdlYsc0lDX/FvWstI22jx6rf3mh/1k6DLdaG/nMA0PTy8Jk5WbAyw5f0vS6DEp6Gfe+vf/tmh+OY\nv79tHIgiGBq9w8A77Pik4xeBoaZkA2qmsTVLhzke6UkqXQXBaoZfCRjo+276y3vq+5p7yn4cV25/\noowxfA4BznFk+IBvAxo3ZPiWurdrG4jIIsOn8r08Ah27+d/uWuzaBru2xa5p4Bp39GZrmu2aoL1j\nGD5THnPvBG3bnDXOZY2Gv8Y/3bhPOcPnnL1SjlVu75D72RqTmCd+7r41jhKiZNs2k5YXJl0TPgTc\n3LTY7doBdLh5aYLkz1NkgbLlvdO8P5r0J39XatsGtztNo1V0zLUa/nqwq/5zgMWk2DWKR6rrBeox\n/P77c0xg71NQ9SjDNyFR8hpkIrRRsG+cw567dzctzzGddPwiMDTTmMRlWsqawdEXxzF4LyAElYjX\nUJ+RXfJm1IeNrYNKYghA0InVtk1ES2vgBgxf4S3bptH7JCz60qz8x1LwCfW7WDv+N7sWu1Y3jl2r\nfT0l8PGxGH7jHIgJN61uwt4H7Br35Cb9Na6IczN8q3Ps7yUSR6RBAFWAI81wvIYZzoV0/+ZgxgVq\nHCcNf9c2k+UzEW5udH6VDHVMqVrzDpJvu7h3iqHb3FgKRdpFOGzT8J+C4RNQnZanSmKOUVHeUQh4\nvSY5JrguBz+PMvxgVqFsZWMm7BqzojJ0C19puo50QQx/iFS0uQwH+Op79EWTpOCyJTINn4gQmgDv\nZbXlgSIns/d8yelGcwzfctE5UEJAVDz0kMxXRiptqhVg1zqEsOzDf+wDVUrhbkvs4s2u1SNy2xZt\nq1j1x262jjn68OugPR4N2hu/PlVu61wCO6pM+mecZ44ZLmpjU+O3BJVKoHjeeoDnMNiYGIRtp3nn\nOsf+XiKVa6VkMHZ9LFjRMcGFaR/wqdQ4VgZ+o5asqX3RsZr0DUf/pm0HzImZYpqZJA13iiwbo7x3\nUqCMRtEpIOQpAAAgAElEQVQlQWK3i+df3OxS+9bQ8QyfABCa4GE2Y4oMv6y7L+yXpCZ9n7Iaxhh+\n2TYfdO04ZrWiQs80Ic44CWvpYhi+YPl40MUypPb7pAEXXVZrdEoRSj5/kzDXMiaSmpFpWQKRy2P4\nQrWKnawS5jsr+q5Ht6rUGUhApWkS2eyk9y6P19ZxPYXWVpH7EYr+bChgUK+dZy6Da1P3ri4XuX32\nfoIINsSWrqpn6V0KLbdbRM8EH7tPU7y3NTr1feTvJVJ5pn05BllLrluu8zC/1/jg2dsU4nsJEkAT\nYV9k7Yj3BRGQ1Ohvto3Yb3PE8dnyXk37HKkbxTis6YsE7YusFI5k/ECn5ef0fyGI7pRE4IBB3fn9\nDXtHcf8zYbc/pkD9vTbvF2tqYl3N0cUw/ODDKPzmFhKpTfrGaO0QilUavvlMgkZeqpa2bhLZs8mS\nYybRCzwvl4lGNXwzh4tIOi2NQDgcOhw6r4FcBWcpTXz7gwLALDne1IKwfbNfS8eY9In0iGYmxsPh\ngP2hQ+OOd8cEDgMpP3AYNd1PXZ8qVwTgGLCzP3ToOh8tL+cTLK1NcxqW5zAf6UxIzGIU4GWdDF5R\nRyqQjf29RFLtXDs5cDdGZtkfFgsoeywNPwSHxh3wsD8o5OuEBVMxNjTl7P7hkFPIzmnSn7Ag2R60\nZKETUahgxQhpVruFz+HDt1goZj0e1/VM+pVgVPTBMQ2i/Oc0/BBENXxiIGZMHQ4ewese805G6fsg\nJzP8IEBpYbQxTAx4xX7oolbORDHtYb32wCHCUJq2fME+/L4Z0UyLKhjpNR9MFVfhZ3/o0ARXpSmm\nuAkBDoeuiHyd7nM/uPHsVMgyC7JHIo7Mk4iw33fY7zuEeZjx2fodcWT4tUm/HxlMBHhaHzGsx81m\ngeZhHxl+PP/hXJSYzsxGvhR7QERJ8Bln+Nud+J+8oL2aCPnMBf9IDN+7gMY53O8PaHyYdMGZktRF\n0C07qKV8ZWtdZwTth4/nbczELAIoFImFBSyic/X+QbH+u5UM/9Qofe9V0CQmOCIcCpwJpizYGJXv\neyvDz8iKASDCfn9A13UInQqFS5aVki6I4Xt0YQZ4ZwVRqE36FCwwxMxGy5uCMIFZF+rB+025mnak\nbnrPpsFc4F7Ub5I1s9T8fRAI68RThq+5wRXwDhNCBJbYHzqduLScD/H40LrbWL5jRIYPPOxVwzcn\nx+aaCfA01PDdiCZPpNr6+qC9UDG6/UEBOJrWLSKdbSFnjDqEyXKXGX7GI1Ao0V45R2j4JiOM/b1E\nOgZatwkROtkbDsi5GT6jcQ4PDwf4JkwyPosMP3QB9w+HGMSKIxm+Hisbegx/6jll+Gahm+mM6L3G\n8JvmcRl+CtqLDN9Or+y8rxi+Bbwa9Rl+H5p3juHHAvSkPiBp+NKpa2FL5NvFMPwyjeF46j+/9H2M\nTEvXM4/n8pCHtVP0Da26/SLJjn8ETMNXIKLOewWLIFS+Yid2YhfFTSrEYMmFAJ7tyt2jkoiiX3FH\nCeaZjtxolYkPo/RFhgubCQi0PkpfpE7T6rqAw0HfzRaAqDX1GKOeKnesPyWpabME3rmgF/5EtAVU\nCbB14dB5nyyeZx83UajsQ+dTfM5oW6ABfofOR5eew7HaSz5Wdq1gOwSuGi+X4VynTLDrEGQd+xsT\nvtc+B2g/DB/fcaiAd4yBG9Muz+sAgNBj8P3vAFL+vZEJX4rqp+tdhad31Id/DuCdk4isHRSPII0Q\nsSQpL39JWeTIxaZuOUKhWU19ffZYwwKTRX6K9j1G4AcRNFEzKE3HjhnsWH9rXMoRnW1r4V9/LCoP\nGVlr0m9jRkLbNmgal/yBYwLffH56lvJLMuCdEheC4l/mrBHMCZiKeaDj2zYOTcMQcRGQY1vO9lwf\nbNPiMI3gx0SzzKgUfPTey4qkn1qP5zQWbNbwmdDEeIyOVMPfvC8umD8sq8bApdrGTarnBujUtg1a\ni+g/wqQytSamaG2qqqXQ5lTatQz/xMNzfIAIg2L+PRXze5ThWwGkQGXO6rbvqmWmeoLwwELArO+t\n807P+SissWvpYhi+psM9n10upaRFPACCLjwPSS90iYmmPPZnUF0tJeukw0iQF6aIIJD6E5vGwYeQ\nmGB5brmhRmn6HietYG5DWIuTfQol3651aoGYdHNrGhf76ZJvc6yMWYaPCMYxAq2bAjljmRSLLiPi\nlxi+CVZtSplEunZOhk9BEGYZPmatWTYOCTjkwhi+CSP2Luy9nDMeYKuQT6QoalT5eE9HIC3JsDUU\nXIojIx9/dhfRM3etQ9s0YD7WhUKREa6PVVlz765tY0pwxs44Z/ljzwFAxxq0x8QpPc7SgdlSWkOd\nvmxU4sUQ5b2qtgb2YgCAmuGzuki24jBeDMNXBLHn2xDMv0gUcxyhf0EhavoWbTvHyJAib5+abE8I\npJ/t71Yy05FqZRI3hMjwTcMvgIhcBCpqXISilTV5+IwtqWjH0Njxt3NEUNSuJi6qJlotgKFJDkB1\n3OUYjWkQphGHeFKWCWTGFEI8gWsu+M40fGP4jVOGb1r/FqY61wezRswx/CVmZgw/AYf0sB+emzLD\nV03pMRj+5jZFHBANkNNrWxn+UkBjEzEz2rapLHPDcoDdzhh+g13rJstcbpOa37fgTTgJs0oBkWr4\nTYSYnoUJHil/bVv6zwEAs0Xps2K8FOtW1z5XTD03Ogf16W+UDDHlfpj3g7rutm3UfRCVqq0z9WIY\nviHcPWf9RrbRW5CKgc1cdDRwZMLBC9hR+ruVCADFxRBYEiNvnIdrnP4rymVmNEnDV6bTOLfg+ogM\n/xFFIyZGMMl7zbIgJLS6ttD0AYyWEWKwzhQpeFO9YFNaEptmXzBAQX19ptwmAu+0sY2CPOZbAvfm\n+mDtD3Oa+QLHt01eOIC8bYiXs35MyysROXmlgPhYlBh+dfzqVoYftXDWrKW+AKlm/KwR9910Jd20\nDSCiSJpNcxKYmDHCc9672zVouNDwVzP89W3pPwcAXaAY5KxrmMgnxYB7wElKUbiPGn3C2S/BeioF\nQQbtM/dqE/cpUjS5Te2/GIYf5EgghHNR4Xu3dphZhVT8mgSJMFqj8TyaDz/OrSACCvnvVhIAHIEl\nRATCmkddgT1Qeb8gwEA8JB0LObdpWpmPaQoJHFJbaUXeCkkMrop9VFhlM/dCgYoKkiAIPBHdDMpj\nVmWN6FniEk39xAEUB1PiGNr1uXKDkAoIIZ/KpcAfNNmmMZrtgyDWNf2eqAd0NfY7YlaBlpNz0i+B\nKAKmIKggEiRAQOBzAmUVAt3aBwgG6x2qIlaXYDE4geKcqkvgaFrX/O6gLrziHtunLMjO/NE+6PhY\nmeV+Nra39X8HOJ6+t+aZfO9UPTpOAi/alzKte+yZ+tpIiuzKPgCZOQuFNE5M5uswH74UdUsqpNTw\ny7dbYchgqOEzIe2vEkIC3tmiOF0Mw5eYAvR89Wdhib2+npQLK9nkMsfITLI+9vdTyMpVDOf8dysp\nU8kMHFAtXs9h9nEzKTR8E4QI6DqfIt3nNABOGRmPGLQXLFhq3RkKRIo14DhGMB806pYix++XYeBM\nU2VxsCj9MhpXishaigKZmfSKoL2pcqPZUE3lOim7mC6p7aXJZ8dorg/CttFPR/8vBaSVQC3enzeL\n4BwUKCLNFUGkqy1Ca4ki01jZdU1zFXTBo+t0Pwxbx63H4QbzXwDHGtVOnoB2XFEkIhyaDodDh33X\noTm4hCuw1QiiLp3pFMA+BY6wzQsa1O7QwRNjf+jQHjo0K7X2cKoPP6hJX7/H426jed7K7medWZAd\nj2j4Sz58u2b7lO+CAu+EebdHny6G4fsgCP75NoRAPgGMcAzQ64o8/DXWB3tuahPcmqKzhRLmQNzE\n5zbzOWJGwjOw9cCdx8HrBkTkEQoISccCcdqnzgd0XQCzB80sPMcGh7m5easp+xqBNToSR4ElcGSi\nXacxJUSjZcwJf0y5/nLNu8hEq6C9yBBSznG8Pt4nBXdCEdXfpZQpE1A2MvyJ+wNnzW7KSroYtBfb\nW6flXY5Jn2gkJxw4axMtQnvtundM8KzAO13Mw/dbTfqgBKQlGHvHhg7n7evoPGAC9geH/UGFysZ1\nYHeca9PWxBa8iaV7CcC+6SIaoI9gWU+Ulhfz8F0M8D74bNK3svsaus0FLuJ7zEVQBu0CtQKQr7nE\n8IP3EXhnm+J0MQw/+PXS32ORpIMg9CVYHj6wLpBHeP5QGGEaSH1no9J0WEr4G8kV5kyD1uWIDNV5\nD+I6CyGdPYBaw6cZrcSeeUwXTt709NsSGdCSC4KDV425aXxapAOGn4yaY2Xl+sspLXGhl+2i6IZT\nQ9J8eylqB0lzDjmf+tB5ODfdpjGa64MwwYsgzOTPMwNzS9bamxk+TfbtWai/ToZW1pOJowSxdq4H\nVmHuHHn4U9sAxXYdIrgU8fgsYCZl9l3U8h3DBT5qaykP2VlDY7npY9Q2DZhChMLm1ebtteWPPQcA\nnVf8fhdcsm4aw7eyBwy/l7ZXltfHHOjn4evFbIn0XYB4tcRuMZRuZvhE9HsA/AcAvgjgGwD8fhH5\nC717fhDAvwXgtwD4vwD8OyLy9+bKDXhmHz5QHQQBKQ96mPfdV8/3tLr+74/WRxn5fJRJP1MIeliO\n+Y1CGJriCaophUDpdx8CeAbhWU2cjw1QNDYg00SIwhiH5D+1MxjKMmo/31S5+S5b2MbI603GgsT6\nG2E9vkZmHg8hRCkBabxz3MSavpa1SHUt30PpvZdUb/bDTZP6X0gR09Qfy9mX+SkhVSIkw8SOUcGZ\nyeIzfDH2ZzaM2JxRa1NA8FNBtoqMZ65NO7XtOIpK1OpFv4YhR+Q+IgQf0PkAdmuVxuMYftkPKdxB\nvsoIGmf4XLzjpPhJFISML5hrdsSdEWI/vQ8pzugpgHdeAfgpAP8tgD/X/5GI/iiAPwzgXwfwCwD+\nUwA/TkS/Q0T2U4U6mvf7PiaZfGuamUuSmG5QhiG9pD1pjipNYhtr/55/w5szVhgD0nkkMYo3RuI7\nzaRw/Tx85+CcXhdRgJ659DDN89fgwEshi4AlaBSzc5qa17fsrAFSKfEkLGBQfZj5u5FpPpOBhUXq\njUX4usbpuJNiRlik9epjnAufdf9a2S7EXPCy3NKcO9afsXLMImQa/oUmujwKJb/uBsAZjkBfEXfn\n7PgFhjPRNvPHWbuYfdOEEKP03dFtyQfLrB8H4nnt1VJTQVThZ6wrf5hFs0ikfErrFohwNOnn9qhJ\nP2e4lGRjxxHjwj4DGBywFuK5LKXVKWdJRVcj02YBbDPDF5G/COAvAgCN27n/CIA/LiL/S7znXwPw\nJQC/H8CfnSqXnjEtr97AKDEuQ9rLDB+z3NL8f1Nz1Mp/bpprQ+l/BklkKA7O+fg3vqdYhotpRCYI\niCAe5DLH8GMQ5Nl7djwZ+pgKLC71e8DAFvzWQM3wTfpL737A8KPAObERUrGmleFzwkMgipt3ZwLX\nus3Omlf2oy9rK2a4BpDV53zne3WDq02RY+Xk4MkMNPRpIRNyhIc+WaMyt92w2c2vTsiM5FxkqV1N\n4yCBRgVbIOZ9OwfvQsJ8OBYrJeWvb8jDX7q3z/Bbl1OD15W/cUzJTqwDKEZFl+NRMnwOhNArP4Pz\nEALVByNJdNuko3CZBvuM7UsNZ7Cfvs1xic7qwyeibwPw9QD+D7smIh8R0U8A+F7MMHyOGstzUJKy\noFKTi5tUBlIoAVimy6FksJxY2KDVEu5j0myuNpU+ppA0d9P0OQIkmd7pnGokSRBwiNCg83UAuCiO\n3zSqzYQgaJpCw++J0IZxMEclToHNCHZx8+51Ol2ncQmIuBbQOCLtmSZjiICNc6sF5hKzoX+trAfQ\neI1yUytzsAmA77V7rBxJbg0a9OeTTukYWEzH9lQMPzJ98gCDMuM/M8NvIzKmafhTDF81fK8wvM3p\nDH9tILExzbmVZkA0Isga/gqGT4gC7UaGb+8HiP0QiUJ2tuIlDX+W4SP9lqP0Ef9mxt+3Cln/nDOG\nv114PnfQ3tdDe/+l3vUvxd8miTEEiHgqKjdKjtjwEkJl0gfM3L2mjXP3PP9mt2SWU4YlybytpnzV\n8g0YJMF+GsPnjEznFkz6l0iNc2hdA08+oo/xqHnQOYJfkFRcxfSkd03G751g+CXimn7nyhqRXC4b\nxtzqLPvhBoya01HT5W8eUgs01DsRcKycIjqfmAZWgE8yle9k6vx1Q4W0LAsuNEF79+dcT6atN85F\ncK3xueMKKFcTEk7X8NczfL9wrwkkkGy1eEwNv0TTIw+1LDCn+b+k4QP5PfY1fKNyjvieYmHrPDH8\nIxbSU0XpL9sdVvhGH4sskI7i5wQiIznYhgBk7KvjaJvx5RFpAQDdgHvseFQ92zlnLASWZIGm6McN\nEaDDhwAXFgBWLmYgMlkfrb9dDFQaxG1QHXk/RiWDTlJ6NM0Pc3OL+0bGRNOqrAiCQMfX8CFSAJbf\nMDvjy6uBwMrKtZ6EI1B0SA0/WWP3/XYX5Rg0i40roFrrOXFtLp2k+BBkfOJI/E2HmjRDIs0/qJvw\nXOuFcoCZzXU7o36MLFjP+1AB22wmyeWtvX/xXtHsLtunVreRDKtkW3/UEhOF5Ri8rHK6ZqEkS0xs\n+/CI2/geKdddDXs5R2QY4Gjr3oL2FHhn29w4N8P/Neiu8wXUWv7nAfzNuQf//v/0M3C3dXM+98Vv\nxOe++E1nbuKQRPKpRiwBPpohbWAjXFv0px638shWLh43/3wNzQF5MGJqYUCCHe3Yp7xgB1awjrhp\nW/6CcNwcuoCO/WxAnsVqPya07lYin9MKvQ/oupgW1fdJy3KKVZnTkfJtJ6KU7d6po0BL1DcigIXj\nKWo6l7qIj9D5qK+vYKZWZtmPfj0hMLz3MT84/6amRiruq9/jsL2SBChANbxPkUU/YRjMnR2hVhJJ\n8UIcGD7ktDyLlTgHEREO7CGiRyuHYGeFDMvXEzJ9Oo6VHR+dZWR7znrgHVkE3gmsKbQhiB4Tzd0q\nK7EqKUNgnDXPmTtUUQcFwmrSP1RpeTLK8O09KrSuafj2qzHvwqTfax6zxz/8iV/Br/61X8Tbt/cI\nneDtzsH59X04K8MXkV8gol8D8H0A/jYAENFnAPwzAP703LPf/i/9Tuy+/r3B9UfLWy9IUmAVQYjA\nvoAsNRhJGl8Ua0kDcGTWl/dURDMqlhDF9MLI8D3Bcy09V24N0bEJkoUC9jQr1Ei05lwOu9d338XU\nns57UEcJWbCksEbbGmAZxOwNjKQlybggUNZXtjHhvcMn4J2u8zh0YbVDz8os+1HWo2ZlZdLKqOzH\nGsxIA/nrdvfba/PI5o6UUYixzOGuXl5b+n3umXOVc/wzLg5yH3WxvK/y4Yc6D98yM87lw2cidJ1q\noYd4pjrH2Jw+iQg6F+eX9+COE8jWVrK+r2X4a5BXbf77oEiOh8P6A9jybryNXBRc0tpIoGMqhNvp\nkNMMn+IxwfqbzQ/jCyXD7+8zHQGf/13fiJvf/lvxSz//Jezf7PHqs6/w4k7w8z/6k6vaf0we/isA\n34G8bP8xIvqnAHxFRH4FwJ8E8B8T0d8D8IsA/jiAXwXwPy+VPWXyenSyDY1Vm+fA8aVJ0ryYTdo8\nbuERScRCfn5r9pyVwsCHBLqZk1cEt85MSYBaO9IDBDI8aa8asvM8z/B5eBzkc5MyfF8AnnSa19vf\naNe4I87I8FOdiClBRAntSwRJQOk6PwmgMlUe+vzHPlJk5jEXvDwOucwJrzHBh+U40khjX4HIXNaJ\neY9NmdGtm+wupjF2XYAPqrqd03/vItNRDd/DB598wn1S/37W8B2fouFHhLrVwDth0upV3nPommiR\nCwA8XPe4DD/1w0sS4gjAwed3FSaQ9uw9lsA7mcEXFjcz7feXVhT+1PKs0LpPkYf/uwD8ZUShBMAP\nxes/BuAPisifIKKXAP4bKPDO/wng983l4Bs9HwMoN2VJklb+V5o1jzTpF2bspX4u7Mcn01z1Ff6D\naXfRUSTmMCq0cxGk72aSSgcOzTSgNF9dAkl870GkkrZHWzjX7J4FwPoYRANTh3CZ9X3zbSzbimqO\nDjXIFTSjyKa5iojmRcPnlqxVeQ5ls/8lvfOnoC3v1+4v3+uWZ1eVT3X5xmjGvHxj982u67l6o7K0\nfhwsLW1mfklGNrX1u7r8I/dxKdxh5R5RvufyHSpR+g2o97783Pjvdd1xfw2iAbXpvvXc4Zg8/L8C\nzMCo6T1/DMAf21JumfKg362s+vtjkkXHOiYEMQCekM6nPoVS9O2qSRnNnsV9T5XKxGZyFbVKuJi1\nYNkL9jlHDxM4gk+wY7AfgvMM6kjJ7Jej6lkaXhCJKYY08d6XVHyqsecL4B1Nm62fTeXPuoso3qvv\nxzmHJmpbjim13RXvZZ76ImX9kPoqCUAoIpOHBSscQ7/d+T7HSHCi+Znxsj6pNJWdMUZEcT3ZmHX6\nx76Xe+Kx2wHHnHXHDNcwyGPyeFzHFDNWXMJ+ODZKPwNMrWu44+W4BWsfEVLb1gLvHEsZQEjdzU2R\nlgfELK/Ydo98r/7l9I7tmTQ/RJDjDXOcTFV3xNpg1vRWS9ncQheDpW+gE+V3IEs6T8HwbKNjZpBo\nAI2A60V4JBmCHa0I+qLYmFIweCqMgvL0JhJK+fX1v+xTtLx8IILwuCInf6aOS4NYTQBDIacpuZH3\nvoS018dqsH6auX2Qh59y2ifKLNwnullE1MPGaUZEkapTon7NNDCz+6m1RXm+cQwyGlt/Y0Gs5X1p\nTRcGgnPnlF862Ya+Zr4TF/sPkPhIxfAJkKD3HkMMQhuZRuMcAinT7OMnAIiCu0PjQmL6rjmS4Vua\nYQirBBbNZZ938VpaHnlK67c5sn1rKeEJeEIgQdOY+zKuFxd99CTVnLe/xPoOqMfwRbLwLAB4BAUw\npeUZENwR6+hiGD73NXxjPKH+/phEyBKaiC48QUjXTiEX0bPU/rOAIIUIzlDsEbNgOWckk8TtNDsD\n1THGbsJPysPnGorYtOI5AcnxsR60xyEiJBwBH7LAwo4H426H1kyRjV8m6V2vn3UFwx8rtRQgCMgC\nlXNpvppFZQ3wTrLgIAfEjs1tY9R2wM7Y+lONrXZR9YX2JNBQfuq58DaegzJK4fJsN0TPBNYj9n4y\nJCugx/oeO4YEJKCdxjE8KeOfYvg59zuDUR1DHONPygDF2ft5HP1vrH2Aws42T6Dh531NtXjnOFpi\n436YgLQAC54nygJb2gcicy9RLH1h0RiDCEj7Emdo3a08/2IYPlBrB2nSxwCvp9JwXWL4RdR+Txg5\nhrLpFpAFwAeOph9LlO67Ox6T0oSOB2WUmr2B7pSmYxMIys9mBZiv43lPRizJ4JSdc3A+VAy0P+6q\nfU23fSjo9AE2xgN5LDVrqbwS9dBX393smI+VR4O2lfVQ8hHOaRN9F1VVPkX3htSWh3cNlOkU2mLS\nd64G3JFQM3wrK1CZzrWdGjszonEgb2iaYybkaCZPzJSPZvgZUnadS4KZR5lev30JWjeugWPbt5ZK\na0vwatIXc6gjvyMuHPvlfO/PhzGQLmDc6WVuCzbQHZMsNqhOF8Xwy40jHSYUAOCxT1bLAxwi6I6E\nHJgxe9LV2vKrvi0VFkFVzOQqcrwNbyNJ9NsmwCHKp+SFICAIPIWsKUa8AhDyyVpOFkyY4SxjejYi\nOz0spCORBTGVrLezCkLaiMfIxs8oWwMUGMcij6l4AhiPygWgmwkhlWnt5JBPMPMhphIW9821L322\nSOGeEGJ5Gj6exjVp0gcN2l2WxdEGHUIG3jHwoE8Nkb23NZM9Mnum6rhwe9IOM44w7ke2B/CdB2K0\nt0/1jM0bS8mNKbccjo4dSAw/hOo8hikSWQbGEWiWSpkF0nm3sAJOIxt3HwKC1xRVESlQ8Si5XdL7\nq0JlevOhGNByjoz13cB9KuCdIBg5SHeSLorhl4zQXBjJz/jIe0Qym4oe9arRkAbOELAQp7hcfrHJ\nLWELKC5A7SuWxx6ASGyeZkP+YqoYC6BjJaaFEOBCnsSWfzqHBSHgzShXj0qEuPlpmpIPASTjOcMk\nCz58qZljRtTKzK9k+FLcNxbGWPr/AAARF4FJ22vHZfqYQrhkBqUeiE7/mtUlomMyy/CJBu+xKp8J\nAkIXU4jsmTkciE8exbWxcP4CoBHgCv6VmbFe19+DZHcbHzmGRMokQUiCoqbRDvc3gZqcDdhp6SyR\n+XoNQz4qUUsmfRliyY/do2BZIeXF27n0j0V28qMpBkgM39Y5p37atVAE7qYo/1BJAbFMi9Ift/Z1\n7EcZ/hbp73IZvmn4FvT0yNpgsmRb2oNkrdZacgqVU3ARTIiiT7fUnJ7o0J3osc3pdSHDfOZNO7sZ\niELCvA7xniV4S0v1uhQFH0AFLmQWi7F+rAna40pqt01bN/NSa67qnwxmoiJqXr93keEr/K8kZEDz\nAc9T3rSngvY4ml4XNXwagwouBQrd4HRzLFHjPoUMf4WGH8yNKKx4EH341YitJDLu411DhjcBIAJl\nBbguTALqdBxxHnwAkT8+WDD68MPKoD2WZaWAhSscCuFxsKxzEkfBaMjwzVomEVgnM/wywDlZrhN/\ny7gnCbo8wvaW9xEB7Cmt+xBz8bfimVwWwy8WRf/cuceP6s46V6BQIe2Nm7u2lj5m5l1syvDao5Nq\nohCBFwEHyjjVcQF60oAViZs3+ww3aVr+fHs5mrYvh+WblpAsGZJdFTUt+cyoDsSxTZuOZ/hADu4R\nENgHdJSFE2s7+7AimGvMZ1g/Y3UZeMhUKp0jwA92m3yfixp+ibT3aUvLkzXASpEIMS1PzFQdx0zy\n7wBGLUFriZngokm/i4Ji48Y1fAKhI5/uU5fxcTWngMOBS2vq/mUN30VEwqzhEw7dCFjWGYkLiGBj\nzCKlYK8+9gS8UyxqLmJZrGdObF3nMzpqQSevUUoKVq3hv7MMv6R+H56cNUj+k+WtTHNTamxCj7V/\nctDdOY0AACAASURBVOJP3fzYlHhZ0fle5UkMk+jDLzyMFY3xEuuw9Ms/sc1nJOm99+FLKm6YfXk0\nNLX1+12Ohf2QxnWqvixw1G9FMNOokfYtXeuzl+E9KfGoqrYnpVYDWbf/3aaxfvSvze0Cw/fUX2X1\nL7XKc+4RnCpPkC1BY/vgsfWsKWdVXdpA/SiRAT+FQCmjH+s2yzBeRwYsH0jrpLo+sldYGYrAU/R9\nfX8vhuFbsMpzUToCN6WUhSItb5hKNB0cZS+5ZyatBOgs1a0EQ30yKvspkJiSmFPtUlqeabKUNTmN\n4qf0DFBrrCbsGgBROIMv91zCfOPqTASJoDYGBTvYuuM6G6vefOlpYSLO7/hggJnJC1O9uVAw7ie1\nIEnNgHBRKwtVqo5jBvGKXPwF0tQhggLvTB+7m4Gkxt+DHaOsiVISy/5kROiPu3Zqhl+6d/pZGFOa\nsuVYR96V3GfnMlMbUBNI53wIlnY7lqkRs0FidLg7IUo/A9asExnWAO8Y/oRA8+F1TxoHEToXldY7\nlghMhuxi4ZTZk8UjW9Ple7S5YBlPhnaoGWlSCVlWhuGDmHvkmM3vYhi+Wvqej/klPwvZAQgcfS4E\npmF61uQCFM2o7v9efs0naB1vInssqhl+TlPM/yzljnLecMxFdczwjisBKTE6xEltwX4G2Xtqe8+1\nEboi7dBFhm8pMDQUy4LIZFS8LUiRAEjOywUQg/o0KtrGIl2XfL1PtmHkPPyIGZDeSRbMThUi+2b3\nqfx+IiQgqbE2Z0RGrja4d57ie+8z/L4QUG7w/fTFSYYfU/NKxe6sDN8p4wDFlM5Q5HYP7uXqnwnF\nx9artMK1QTUa3XSZmkoroulxBETkvUfaU6l2rUkEvhLJqyXhB1DB8MmY/pDh65oFKB11W2SGlVUT\nVSl5id9v7OvFMHxaFXD0aLWnNBGmmIcf4ssI8cjKPgOfkiKjUtf/vbJsm1IXZsp5BiLUGli2bnCP\n8ee8e4Ui1g09gcBQBirSk91yhxMAEdA7kP04cmdKV7RNrdTwk0WDRpioaIrMmD6dUpBEN3oqTQGF\nXbQai/71QaEFwzcwJK/Cln7PUMCnMnyKZVgpk5t8UmTCaJuzdUQ+eQyfaJCeSVxfo+JdpDMJit/G\nSIFb1MRrd0wBHx1DzpGi5UkGrpnS8JueZr8Emb1Ur9Iyw2eiGBy4oOE3LsUfJACeR2T4CVcCUIsc\nAY5dVPBi26P1kyvrnik+VADKFQzf2VKyYOZ4ZoHUdbsIBJaycd5lDR94PoZfppvYBi9cwOGOSNhT\nmqUs/A4U/I7Op6Geg/oR5go6xAl4qPwHZNN1AioqLQF2T2FillC7RuQMfT+X+S6BC5HCjEqgZG5L\nQEgFSaC88HqU5ktQ4KbqDkICXqraPnW9oFLwKs34lbvlDNpgdgtkV830zcP3mtsbNzdGSiP7JKDs\nJYFuBESpvFYzUZr5LVPSIIUr/++5XCEVMmayEs1o+IX1aC2a41S9AFZZ9dgQ5BbuNYHE0DG1nidi\n+E5AIVvD+u9JpJjzxZq03wNyEKtjs3baHKEhoBVR6lsC3cF2nn9BDB8DE9lT1pujSDUPPwHwmJml\n98xUAKnEQIqZU0NzWMbIfc9JpFw7fc+ZChZ1qoA0LkTNTTQERccqpKwGjdIvEPti74MIEKI0LGsA\niFbQGQbQ+pDTD/Xdex+U+Udtvq522ndt+PP5BLu4IcR1bek8aSwwvN5vnzLWAAq68ZQpkCHo2fWN\nE435O3G/Y4nHHae01Pkxtvc68gssFetc6a2XQGTvt9fnIPVxpQrCZJ/r7Jxp8CF9gZbZQPHlnw+s\niNIx12Ua6thb6bxG5qc51gUwH9sOHYk12Qqawrp8bzrO2o7uFoFvwqNZTZMrEkDnRbFK4m8Zb8P6\nICkTSRLDz++xD8hlfbX1Zr+nUyaJEvBO8Dn/XsK2WKiLYvhnYQDHUqyaLP/eGJgIyM42LWgKB2cK\nKKjchFOwtsijAwptIVLOl76b0ON9iOMhCkjDIZqoQpVqpuenR0Q+OwiCsp4iIhAKMIH2HO/7HIBE\n2u2ckhdiemHnPRpyIIueKusVGb2ubaIUpBUKhk+kfDEEHTcbC2B4vd8+szR5r6WVYEhl2mQK6DmB\nDFTJhLelt2TvdUg5FXGQU/4Ok76P4SFYfR++MS79XM93GdmkVRCODL9Igy0BW04lEUITGXyX0jo9\nxhDomdVl1RUM1fkjLQ0b0hPN8rl0L0dQIEPaCyLoQjgalGiRCHDxhdp42CtNDL/Y221fTAy/eI95\nLug1UyBCdAXY7yl4jwjeFfttPCJ3DvVzjC6L4T+jupvM7NA8/HzusH5H6J+aNt5Wif/r/16ayvPL\nnC7nOcgAV4xCyIApwfJKieACx3YzmCJATbIGBHhfRprnaNuUf15pv6fRucx3xtxMmzEBgEM02fXe\nU9Lcx94fUfJv+yj8lEzCBKLSDze43qMU+UsKvpHa6muGL8Snz6nY/mStWaDpw1DUJRT8unLeLYrv\nY4YCsgk4RIjw8rc+MQEhumX0nXogulTG7j+GXGTgkAwn3fkwSGUjUqAXFTJ9ZF6au38MWflrEAeZ\ngUC0eC+zts0EF1VOPMIjwZATAZIwKnSf4B7D54LhB2P4RZBzbfMBAEKI8SAhMo8SoyTBX7OOPUdh\nsAzw2yIMXhbDf0YNP+2RIvARac9HDV+RdXttW1R7et+LOVhJrpfD77WNxTtQEB0BJGu9BEFwwcwB\n6ucPlEzSPghAARSyF9hI4neJPv9zvO9zADKZ1GztT9q+DzEGYViHGdzGlprwED2LotZvVhO1kEja\nQAzdEfF6v32GtEie4IHM6IMg+AJ9q4gDPJas/V607KUhtvc6/EFjYUqUxoua76fQMr+P90QG0QvC\nGntJQgQSQIgrxEc5x0stKvZeI8sNTrrjYfk5qjyb/gNB3XlH1guc26RPidl77+GjNZL6e/WZSDMz\nrG4z6Zsp3ixYWbmxNS0RW6N6j0kwsKwl0+7rczWyckhgDhDOGr6Z9LcoThfF8C8hnIcGH0a/Hlno\nQlkXMAClCdIUVftfUuIKq3H6W1yvnyvKHqtLRn54aqJsKdB25wZNGRCmm0yDMbFyohsvmeir8vtj\nPGhfcV/fbE9Ujf9pVLRBULzMkUbFm8ar1MZYn9PLpt49qaJz0BNPpDXVpS5OjePIAzQ1SU6n6FxK\nVie70m9cnmLx13qibqxz3XO9FszKVOXw6AUVltI6WtGuftmLMlw5Hmnj6o9frtsY+eh7rC4VG6FK\nfPF3SQJj3piL9h+hMF0Mw39u4B2TZokt6jxHHqfjCI8tuzDtAXOT+Hk5nwr62gYhAUIJtlOk4xGn\niFVNY7Q0thi1n9LyxvvD8QhpEdVcn7/flu5WZBmIgVxs02iIaveNaeZ2DraQVH1Ox0CToNixBu2z\nq/2jijPYkWVUnHjIU9F+YYHGaYzAribBcILdE1KbXLQcScS0WFvGMW2/NEpzYYXWaSmVhgNi6uT5\nMhtI0/IibgY7RhM4pnbWdVhUeD4qWtf2miOYB7VSmf0jmNoBk9BNFvMyrb1Sah9BULYvRrKvmAxL\nOAp96mfAWOpu6lfc+5TRCyioAb/kI1NlCmKsGDQ2SsunZK2w9W6xPNberQLYxTB87m2UT006KZHS\n0AQZ3YyrCXt82UZT+9tzg/AwIW3uIgHgnGpnzAVAYuy6qetiC8EYvVTCwVQ9hrtTBjY9FznOaW4p\nDz9IYqRbaLApxMVrYEWC+ijSlMbTu95vn/3mOOfiVxgJLrf/FKraHwKEeZST2nqYcssYgJXOJ9E0\nM6k3vaUyjmn7pVEJvLNEieE7Q9qLbpwzoCdaWwyvAaJAWRKZeT/djplzHr7nlN9+TFoecYFXQVK5\nDfv3AcrybLVMBaURU2qfIObfS07LW6OgLeEo9Il770EPyikYPjIYmZVDkGLfHBOcYxq4QvlUBs9Q\nzAFTSsSMZIXBZcu0vxiGT5HZPmf9VG5SJCBiEKmGc0rbqNCcAU3bGqPnxyTJErwPDEcROpKLfFHk\nzdzuHwgCKR98uh6K5l09IezxezZHo/nsSdDZ1jidK9WVVEffGAiUUJ319X777Do7LoST+C9t2tsF\nlLm6AMYUMnmCTp4IxksAJEwAGE6QrEBVGYKIMHg6XSJsb9Zrl9+LZVg41tgH8wefA1vB2tI4p4we\nKtBK/N4H1GHiQR6+MZ2txAOwrQnLX7nHkhpFwkQWjrWPmeEQAWzsL9Oq/bpfNhNP1jfoR7TCZ8Ei\nwmLHui3PPlDB8EfwPAgq0EEkWTQs6JBCXn2miKT4n6iMbp0VF8PwMcsgnqwJhW8owxf2XaZbaQjL\nO1X/82so2VxkUehD8KGxz2YKNksNLb7PrPk8d79NgDFLDvX+bSqLqVqEJWSzfR/7fQy+t2zfaFs5\nfz62vXN10cyGkl0RU5t3bo8CWRFCqOe4WdDk2LNeZ9p+abSmZabJZ7dSnjtnYfjFnDFAJZb8jkqq\n4bRLl9H2dlRCqPnzlu4DdNAm5kbZrr77NSskCxSGfZ47d7gGyooMNzKHEFNiqXBnCggIeV7294ZU\nLlEMflYxwUSVUKy/BHIWqz7W5HM5DN9Abp4pjJdgJmYZ/Asiq0xykxRqJj9pwnzmzCWiHFVuvqwQ\nJXLLr9drku+P42PR5wmsZ2qToiQca0yK5GMhn4sopsJYDn7qSwUYs5ZCZc0pATYIQ7AWi26fryeX\nae8hpxCGKp3wVCqj7cto4bE2zbc7JIZvbRwq8ktlbKXLS/1LMTEr9jVOcWA97IJzpFrGtqgbLsQo\nfZ1HhutQksAi8jPWg5DAHyGclS2fA3IqUtPTg2HC+iNiSIHlkdYxP55pSqaoqF+2zNSX2kfWj1Bo\n+HF/JIkYI4QgIWX+mJZugdAlkbn5xICbchvqdcEJF8bSxW3/3HI64OUwfOiieC60PRBlxl4wes0y\nk0kz/BrqG7Gm+vjc2xUVrQiJ4WfGnz5LAOLZzmRYBcb0g8CTmqdGLaxx0pcAFc+tl1GRdmhpeYon\nIAjNtAlylAKqzTml1YQoWMS5lX27ebwn89mLMkPgAg2yRjesEA6PpNK8PseI7bapuSyhQByMKIb6\nA1f3QM4n4p/JM3BWsn1jjUwjZMh6XK03vX4Ok76AAoHjuzBUSY+cRpvJwHYo4j1osKnnMORaS/2S\nkB6ZS7Uzc7op0kFm9koKcEVeevCau66ogfOm+dyuumzDX5m8n+p+iEiywiThLGIIiAlJsQ8GqDWE\naNd3Yml5pmQC/fUXivTnkJl92BatfzEM3wbmucB3zNJEMYpUCgbGJAgnLLhcNqrc7AE9MwiPmpZM\nw9f2elJQjiAZPIWDjpIjxX4OgRLTT+PGYdRUqwoMIcEVC56934CiemXQnUKLXgEtW1KG0dRnbIMj\nqLvDR4Eyb5qU75sYC0O+AwCOYEAucMzB13Y7Vq3idKkxtyvMoOwtaa6k0a4AsjCoIxlWl7G95c8t\nOg5J5ZuhZWeUNGoWglAJSeUhPKcQEZThB1JtuLAiDAQKy/u2tREjzjs+QvgoTOEDPIJe+7TqqHpI\nRrIbu9c7BoeYix+ZaxcCHNbJJP2yS0VkjALl4Gtl+DGoFSgwE6ycAnU0xnCNZS4Jm5Y/hNWt5wyp\ndUWysGE5+Ft05Ith+ACSlPMcZPusafmVSR84i0k/GXenynpmvkc995ryH0UZ9KWGHycmxXSrypQf\nBIhCwKhFn9RHVS3m5+43MrRuhthV0JnNAij1NPyQOylEhSaf67b7pjR8oXz8bCmMlHDAPlB6L6dQ\nrl0WgE+W6sn2z1JYrBCozv7in1twHCMVetYAzljMjEh2gwCIRyqfieH77K+3sxgAjGj4agkwDd/u\nY3eMtaFg+CvGIQcOz9/bmIZv0L9ARCd8HCLKwohZAvtIe2bASrwjKBy5pt6NOd91fpSKYIlumm9j\nkA9pr0om/SAjZU7TRTH8FBw34supvo9dm/q+5h7bfCkHKhn2QVnlYFg3lGtfBQt93FDuqnvWlksY\nMmjJfj/7q/2hNE5pzKi4nv5iQDnlhlTKWtPeRyYLWqqD9QBYIN2Gdlj/laQagzIIzsrNY6oXJses\n+L0fSGnvJ5dzGuVAQu3DyeUMyvx0ECEzaqa+JWOos/eDRevA2DNYMKgIABRRy0EYL79eE/X7S3Nx\nbbXFIloTS1eO2RylrKD0jIwGIJ6LynHgyPz7watJmKqeiWNczAebC2mvSMK+YGz95fQ9AEU5W+li\nGH4Z0TsqBA0e2Ph99p7MoJhYUysE0ZSWN6yxpq2pu3qBEnWcc/RxzT2rnxlhNhTTq8iiYg14JwJM\nGPAOEaTYTNLvJhH0qiLSACUZE05H2/u4XIKZYh67tj/hCnBhhlvZBAbymdfSzzsHIOr+SAIF5Tak\n60DV5yxYxbz7eC62fecibapKHTpmLCqBxSw+6/tflWV51QEJQvjU9r1LxKAUUkEglA6SJPQWRJxT\n8wBK6XN27eRsfMppnZqWxwgFbkaVkBnXBBGqtD0XcRnG2j9ZbZxTgnUgW+WYzfalSBV0TlPWLI3w\nUYjKTBCNp+/XZd81LijyELJnuRAIdC6k/cGASVSHt+qqtDx2HM/bgE0gu2k1XRDDNx/y0+fSVhsq\n5TxK3ZxyIMkxyEawspEn/bkOwjgnUTWZMxkYiKX02DVLYVMUQgZLsXEUjHIgpZMuZCFBWBHxOyIz\nnJ0cxTx2KnPxQ8JkmBT0xoi0PEAXdYUxT4CDncNEFXMlSLoO9LSbOGYchRHHlBAhmQmOirSpidSf\n1c0vNSQKKT/gmHeQxoEFLg4Dndi+d4lKwJngeidj0lDAVgHB1puOG4Sy4nEixgKBEnBTkBDxJ0Ka\nQ2X5NteSkJnWPmeNemVzzH8tQRDcMncqx2y+L5xy0x0TSCKAlnucGZb6IaKtpJAZtmn4KeJQz+Aw\nKB17f6UQDOQ1IgQ7YQlUrBsLyHMUBcDiqO65VN4puhyGn5jKc9UfNyPbTEM0F3ExuIWZbWvZiOVr\nXub52n0umtpQknZhzB3IjKXIzRU2YIkQmQb3JOK6MpKo5q+gx86vNi2hym+nrDWnDW5DeUAM4OnD\nKhI0/NjGxvYLoXQdGOkzWQ5+Rj3LwglHbSybYY+m4p0JIiAItvXfKGsvSPC558AKeFeoFL4GGj4N\nx5RQggcRnGTIauB0UCUC0jyHRGbZA9ZJbSeqtPr82QT5LQxf+5XFx+X79e/0vUSKGshMcBLbGiRZ\nMB6DklldVJAnKQCo4j35eyj0dPstW0kHGr5+i3/zQVO2bgwcLOf7b9FCMl0MwwfiInjGuJu+laTf\nnuP0+/r5bSEWT0dT0uIAYAdZ28uWkd5nKu6Z6uyGd/3Y/KES5tLn+Fv6fVt5ADTQc0zeGRsbqr+P\nyknU892DRsZ/W1tn20+S3tExZY778E9v37tCFYgRkDJggJ4lpaD+eiuvnUPwNcucBY6Wc7EGXSrr\nx6AtYwLLHJX7x+pn1pRX/YvCxWNNsGpMJFndgKEPv8ysKdtcnZ2Begypd83EbruWLMw9RrSFZV4U\nwy+j9K0/T8H/U12S22DpDimiXsw0s71FVr7llS6VYILBUxLFIJ4+pXx80cjQAJ2YrBDpVf59PtM9\nRpgShmlixYtdnZHxyPnVBryT8tqrrIOgVp+1B7wQEtysHXdZ/gbpR9/Gv/3x6PWZqB5rPWo3VONu\n6ZCr27rU/lj2WHs2lRPH0wKTPi0aPhWDVkZhA7qG+iiFpUJgc0/3i2TkPrE9gI9n3JfzJqeCFSmT\nRCky31JWgeziE8oMak29AkBm0jz79wPzeyARpVTBnE6rmQ18JuTGsTolCkvpOGtkTIOSLIo/PZs4\nRz8CP6Tx0dTVfH5AmckUKGcR1cA7eEfz8OPfEsWNsA6w4lQqgR4YAoSCORv4BQTC23Ie++UjgiQs\n9YloPh/0MYgI4JH9JE2+Ms+e1LctQSXVwIIgIS0CzeQLGqDW2xSyuXglwhptm9DHEBHiRsFpMWke\ntKZT2fE268rKpjYDbyp/K4E1JBQpUr182r42qF8zwE7atENAJayE08RFJoK39RCCehko5k9voME4\npLTD9Yzi3acCZKjIrwbMolaPAxGBkZEtLbeci9PTTiEi0hPcPCWBNtURIWpTy9kYap0iyL7QqLfU\nK6Ga+0v3A/PrnogiaJAknADDLngsDT/n0UvOhe8B79grDVKATcHeLcFOTivPubf++lALA+V4edI0\nySRICHIe/gYB54IYfvyveMmCp2F8SdI2zR5FHqXVbxrKCeWnjX5Fp56a4cc4lAGFos0JUY/jUY4c\ncQsKsJpSwyeaZj2rASMkrZFHo2yhKCTomDseIg7B2hevYKQ2ZrXWnvAHIghN6WrsWwMqw4Cl7Igh\n7EkUUkrLBKd+nOozMkZkICmj2RSLZeRehGCwofGAkYt0ap2fKIQ0brpHly94GLHOrJs3UYZmBZCu\nnbonMAu8JzBlUKkQBEIBLnC1zgSAi9q/IfIBGkimZ4utnxTMApIYsLzCSMGc580UUeyDCeu2Djof\n8FiHKFmWgSoroeJPJd4GgKQApfayAMUYS7FHMGdr8hTSHqW1XyhW+tC7qeEDQ5P+U2n4WeGwRVUz\nfmvbGnP8fPlKS6ZswtMzfGDcp54mXzJz68IyrdMYvjFHw8YPHIWjXpmWhDGHojVsxLE9WkcBBcKe\nFP8MeIdlfRuoBs+pzfeSLUdRwkrj0Z/o5WNQ4SAEIFDfpB8SsI0PAazHrB1NJfhS1aaNZZbolAlp\nr+c3/qRTPBkYwBSITP8aqW+YCuENKMbs1IWgPjYOtXWIECGkK8k6m/TN2gAoyiYnzWD1okj3rgUg\nWrqXCEmbDwVCpvcB3j2WD3CsH8acQ/ENSWEwYoxD65oTx5TLSYZPAk8hW1ILk/4WZrGJ4RPRfwTg\nDwD47QDuAPw1AH9URP5ucc8NgB8G8AMAbgD8OIA/JCK/Pls26o2ALDhhQ2eWTOFLG4393C+nv0md\nHhSlf8WUsZHgjqf34o/1qwxeM1Oe+WFR/euDdPTfZ78OEhqXME7vxcLvI5usnaFtbR/5XJc9LCN9\nmpwrFlSkC1zHpxjfyXdOI2Mcr3H53Y52nuv72GZT/1Y+b+d0Tz8/X04ZfBQTVIo+f/K5ftnNDJoy\ncz/R4F95/eT2pDlCo2s2vTvk4D5Qfk5kuS39FWLz3IhnrH55/6XFe7nsC/fWxUp3w9bdpw6wG/42\n7Gt+5zaGY/Pe2i49AafeR2IGzonrZquG/3sA/CkAPxmf/c8B/CUi+h0ichfv+ZMAfh+AfxHARwD+\nNIA/F5+dpJSWlya5Xt/ij6HBBjX8fYxSKiXbJCcQhd6k56Jt2wZ9GAtnBk+T4Osb1BT+9BviWDss\nJ9RS1iSOQwJ+IU4T1vLWmXLK3lQdasY6fx+XXk2/TqKYllekGJY57S72qSx7rIz6c7noe1paiHO0\n2LDyfWObgf3VMbU8fBBy/j0XbZ7BseiPTdmPWvCIbe+9o7GxVcF4bN4Ua1fPWoryXV+I+uRSfyyX\nSN9r3HOEUu57unYi6dzRnHqCpXqp28Hy6wHdixOWBulzHA8EcUUu+Rip66ne29ZmE5aM3r5Pmau5\n6Iv9BYr+rRivrbFBbq7foOo9adGc8+gjXslYCS4KU4hWPI1bQuVitXdA8QCfFCOzcVpsYvgi8i+U\n34no3wDw6wC+COCvEtFnAPxBAP+yiPyVeM+/CeBnieh7RORvTJWdJJieRrRFDmOqc13Hfh+vO7ch\nSbCltJik4flypqh/e8621E1+LOf6OfbDfjtKASwx8eJ6+U8SkwxVfv5UHYLHsWEs4Tb1T1QjRgbc\nSYJKkY/PnKRqK3usjPR5YK7J9+imIMlyWuXMF+bfsbItBajciJmz0JUFlZlNqTc2ZT/G0M2Exu+p\nyui/yMjsjWkAgKSzFTIT+FQw/N5YLpHNNYrgLlycLHhqDr6Vbzn3QCjmkgLvpLn6/7P3vqHbPst9\n0Geu5zQnTdtj29ST5LTmhdq8KFWbHBsb6B8wKK2CIoWSIkITK1RikLySgkV9IQhCCMH0XYrWP4ik\nBClilKbY0pgaTaGl9DT+xdSIIU3TnNPTnN/v/L47vtid3ZnZ2b12r/u+v9/7OfnNw/e573v/zM7O\nzu7M7rUzl8jUUWJpHFyDvnh//a4NOspdrPZbjzVPZv7hDOv8yDA+nn9XYk9kenKsAkYL+jUzfAVm\nr8IN6VN3A7jzmDiMXGdDOdVH0sdxDGMXHMdR5lENyIvEbMKU1Jgg1OTqyqnPrc/wfz3y6P2d8vuz\nBeePSQFm/mki+hkA3wZgqvBll+/TVyHHhp4teAOFXz5FqZvjq6MdH53hGbY7SKBEdYL77EdfVIvA\nT2RS/a6nHwda0J2j7VK1MtLHbaM27vCel7gPJ/KS3E7LKHZNe7HIW6jThjvCUcHNadZlqlGed0Hm\nCN4/Qg3q6TC6ABq/ZQyOXpZmvNH98CdrQF60ojIaGGzoJrTdhyy6WW8x5AUVtcxXOHhenoEoR6L8\netejWWF38sE/SrAakZ8DLXS2NS4OIhzvsmp5OXKQm5SOoSEv8O7IL4mR58+y827I05AXbQetNX6s\nuN8p4yVHCyxhiIuyn+3GKwxwj0AbEV0XDi4nE8XIJQblW8217shQOujIXjnpUPeFkjnl1aeqdWcv\nO/0NZXFZ4VOesd8P4C8x898oyV8P4ENm/rwr/nMl7wTpVWrWql9D39e6deqR+xHhe4blkPx3QtVg\nK/TNyjysfyenI/7agD7F8f2lUoBU2RGOCTm2btdAX3aEmyq9Qb3y37Tvvh6P8yTtrEy9h6KIaSdm\nrR21Fg5xfSXDSn+pDHCTSbZ596Ch4m/y5NsQg0yr30pPIH++EWL7TghTnCf1xeisRS0Punaq4mt9\ngpwMLzBs1z004lX9zbB9ZUt/NG8NLlbzTf3WZeL5t9eHW3b4fxLAbwPwuxfKKlURw1/7T38KfET4\nigAAIABJREFU+FWHej8z8LXf8hl87bd8Zpmgs5vfo9vxVcCYlHtEuzGZcmZdTndf4evHqd3kzL/S\noGx0XeqhV/miI2V1Y1T807PffbZEU3FVrD76iQGJkx+5x5Q2xDXt3kCpTQwZJqL23U8QTihuSgwg\n1T7IzXfxSJCyIxy1fTfY1a0xqFtpZev+qHe/rPpDLK/GdTxXnhKzkKf+BNO4wKaefpkDo/oeR04o\nG3lC9auSG9T15SkU4/pKA8/Lc8iyxqTcr8R9K/KZ3YYcawJobmxVllITNKa8KuUTyOb++ZIYR8ov\njRkBswo6VX5rPqTJvJe6ev4O12ySwETIr/kV7yG0d9WfcmPbFarh9B4EnErAK+Gh8kyRuvHrcRve\nlyQuuzZmAwC8EIMo4ef/l5/Fz//ln8GXf/kj8EvCR5848MFGDy4pfCL6jwD8cwB+DzP/vyrr/wPw\nVUT0KbfL/zTyLn8I//i/8i1Iv/GT+OUvfVjayOk7FkxK8/KRX6edlOLbiPocisUXGW0rs+JLqsGf\n5CSlfBh2F6XCj5tFQm6sPspdj4JFOB3AoaI+VT/RxEhUFgrKR1lawJNM1MCtRlix5Za31Q/17niW\n4zRSC1BfPpUY1YTDRq4r7j5txzrGIdAdm1fXqr6u0MqqnLiuhf2BMkKg4geIm95LQjpoeMTndzSe\nFk+/H6NoR9SNIWXD5CCCPF1LnKrLEVG2CH4lBN/xvDwDKm6a4u6a3VwrhpvpIRxIL1lhi7JPJbjO\nizZsiWqZTHuL8vbyEsuWQBdzhOy9Eh+RLqprg1HFfHuhrCDJRaADcp98FMOwve2NWzN0kuuHzEEa\nKvyxKyOVCzzNv77HTwQkIvyGb/4GfPCZr8bf/dlfwpe/+CG+6td9Ep9MhF/4zz+31IdthV+U/b8I\n4Pcx88+47J8C8BGAbwfwI6X8NwH4RgA/McPrd2Ar0ZY6HBrRKN9BFu3Wtg+8U33vmbe9T3UbGkww\nH4dP7+SNC3eQdk+IpsdR/L4Bu4NPB+djOwaOcgJiQuuW39HLcWSdf5jCZ9QBrcFsDqVQg/Li20pl\nhy8BhuqCWF95iSGOCm7zU+NKBHU7WlF2RAqJLgNWCh4l+Ifb4b+bBAnyOrajxdHfKfzBeHk8XPDU\n0yExFhPXZ5C/AvR9x8uzhYOQcOCoO7xYYVwHQkLifBW8BZrKSvJI6qKbGPPFYtOGZSKeGmtEsl62\n39qCnUXXrHiNwh+VTdVY0dEmpY0Vg3J3/dGhkn0/UgmyJDysvFUGm4SdGuGtoayZO3khYiRK9ZQV\nxYDO0fbWn/fs+uH/SQB/GMC/AOCLRPR1JeuXmPlLzPx5IvohAN9HRL8I4AsAfgDAj89u6GvwY7A1\nJmcjOMivVqm0p3ap2hDREfm2yHLWpjFi9OzQtDhh57JLfdQOHwywV1bICh0oR/AiZKws0WII6ShR\n2mDqmhF+PuhIn6GMCtldM4Y7LC606AiBzbjJu4d3Sj5GOAQ6pRoYdZ5WPdYpsXHh0v2pBpemVUXd\nenlJSJ8YO3TO+C15mn6/qK2Ml8Yj3zVP5VDzV4K+n/FyWL4afmx3uHeY+MQowXQOo8QrfSJ3DLzU\n43+0AE8pB3+ZXlqOFnBv+JzVLeWngXeS8JRrrP/Mq15Z3gvMeLp+tM1F46cPXKUfN0Z4Jdyx1Ldl\nWkCwurYqeVmF3R3+H8uk439w6d8J4E+X798L4AXADyMH3vlRAN+9gjwKmLBuu1yD7nJKTgShHEui\nLLoRLeGxkRI2dwlFtxmcC9uyjhcEVHoeASR0OTorbw59mUgFe9GfCscoQAcp3I8CwSzH5VHfdFlx\nmdGBO7Rr3panSMfD8/JaAUZ80zytrnfRWKgAJFdhNUjKFp782FgF3nnsrH70mrEKnpdnoN00RQaN\nXNxIT37HfXMf03FG6vcC7w4bdyT74adT189RuwIrm1Hvjz/CWV2Giy++3GF5WCz9WT/c4wgQWe8V\ntVYCTadIXq4L4CivRCagbYnUPMdt8r3rh396rsTMHwD4nvK3DFT+u8Ut7wocaiIZP3xuUZzyjck1\nl0EO8n2xyOU6KnuY/D7tniALgKeJlCDniR8oRFB5HWRz4xtNvNqPwOa5Z1+AZqQRjflGpNzbVB/E\nTY9O3JA8+LJnC1wOZkT1rgQCvulYCNYPX7lBOgPsKvhFbYjpZJtu8AAoLxkYRhu7Jzx4yVgGM44L\nE1fiKgDICuNoL7S5R+yC6sutAu8cKvCOdhvTv+t3plM//FG7Ar3/elSeupOBuC+5wDtG54f/CDjz\nw89l6nbDlPGbB1ZPOkx/GfmlZCrENZyhD5njsrhtrKPPE0ufrB/+a01as4ulpuSJ225P52mIBEuf\nJlUfdlfmoP7iny9LQOffnOlY7to2+KM6rTxqgB3K9FdffCrBOZQVKrgi/uiUR/WlTjml+EdrQF34\n3h11vHUQGx+D4bRtz8OF8vo5PaNvj+rCaxdcE/tA5d20w9eL/mnhNTzEBCQGH6nKyyPhWv/1nute\ndLTvx4ofvlYIIBx8mPem37r50TEbuMTTON7pmA5txCWwDQAcL6nI3NGVW21XYMXbIK8zPOVZpk+U\npw1G9aiX58z7Ia8PPtRvE5Er+9FLMCpms7bW/qaU39XFVAMDERHekWxAmhXeNqfrfXgehY/Yin20\n4tdWeF7wURWbpkfyRnUF9CsUhpH9gOFrY3252e97Q7SzrP2vwV36HX4u0IIWSd1p1LeH9GDcxqi9\ntqOnajAfR15s6/cbdvhnHa1GlLjtLe3w88Uu/1hF/74KPojQEDZ2+IKH0+N2Xxp2A2MBODnOuEiH\nQ38GOrwtl2MpuZFBuNgvh/94l9tgLsfgR1NUZof/Tu/wRcmnGpVyt12BpR0+ZffoGc+0YueDs3GS\n+Kl2+N6zQgfG4qQMedPfEl+XAHFzIRUJFGin4VfO9x91QrwPr7Sj/xg+Bg8EdMqrLryvcbtsow0x\nSuI6z3kVjgff30e4sMYu4/VwT15V/GxlOmpXl61EsNh4jx3BZd7KHFD01c8nETLGOTmj/vrrssM5\ntNnXp9rhA2yOOmoq6+O2nL/rQ6nBBDZReOQWur5V3G6mo2tTv76yXqaFfb1htNka4go2Gf6g8ZHP\nvTsX2aM8VmKUW/rO7U5/Vv9R1ffqm9M68hqKdLTBjdqkQ27UZj9k7X5IJO41i8sQoXOXXrmdrcuJ\ni12MXrlHKVe39rrcFgfhEjj6p7edT3b4Htqt5RS6Jt0Tzt9LF8Diib7Qfq74bC9Z/T8u3Xgjga70\nS2hGcrECgl/LsrxHniF+31TLissbSl7iVN7m1m6Sr7es3dnmdfNj3bLmTviViMyN9kwjAOISU2CD\nxEXQKCM/fF1KuwkCbfxENplRftv+6iBV8vY8OgBScUJKUAuIa94OPJnCl0WZT9JudU/j4Fs+5pK2\nUqfse4UhL+rJbmmVsoo0DZ5YpREu7p81+24+yg8/ojPLFJl3xGt3PFICp93D8u8WyIMKLjNhHqjw\nR8dWUZuH9C0xjsP2Iy+EXGMRnAKje8HMacCVYsy2iHzcxeo3bjuKXla/SRa9gZG5Al6HT42Vk25p\nlul3fauAbg8DuurKsjDM8gj1PJAOm8caZ+XlXo9UyTxrgXeiR4o7QCVWux5TI0OJIDMnG//NvbMa\naywytkNIiSmvcM3pLAYbz3mWKFVcSRsubNeee4I2JHs//P63TjsISEeq73qRS3u+v3pMqotmyuNH\nnCMImg0o81bUyidU+IMdftvgP3CHb/3IZQeVf/fWlLbp2tg2hT/aNCRB6HBFmyYfyPJRijLcsHHZ\nVSpl33a+bPzbWeUDqMF5gGYQvUY/pC8RhG2mdqoDUv2Q/gUKeNq2N+TO5DTHba606Yne4dQLgg6G\nwlzD7kqo4ytggvys0H6Gq5Ld4loQcw1k9Ci4EtRncYMPiaZ2enLjkJ2WL4GKhDd68QeQX616w5wh\nAnAkpOJbL7t6aeel7N5zWUYiqopaTgKANie22p4ErPFwqNvps7KJ2g5aQv/KGGb3vPvL2GngHQAy\ngVrkP5WsDTpkOfX9NSHKlSLJETeLYZOgdvh7u/ynUvijE0Su/0m5+z1JYvedCyFclDL7PFO5KLuR\nAcIchngclgVCY4cHBso9gfVzidpWvlDWIjqJQqTuMUdShhJgA8hUgwmoEv+oftS+ROlBm3nhswq+\n9hN54i54o6o2ztvUIAepUiwKWOTzRn8See8qyCK0SvsUl6oqi7Hw9Hjg2ANLG/XL9eod7NOTG3va\nc1ZeAhXVQFfKyEZJv4VrB/IJgjZe9WM4vSuWQFo6UmILIMXbhuAsYE0H3Gyl6Q6fGx36u8znKMrn\nrXAaeAeogu/DAjO3uV7TApxiONi5J/PbrgEV8Wu8Le8RoDwObHr9D3WHT5tCN21XfZrvJM9X5pd1\npGwlkG1eVz5QrpLuyx8u7VFxCcj+Z+iR98SL21o9iqq3+Kne6K+LhnIxknHV41v7IXxwbd/clyg9\n8oSgRispumtwkqP1caXdpcA79cSKjOsgmJsMaO+R8tveyOfqYdAC7xz1+xXw9N8z8E5iKHl48Jn+\nA6F5ofS8IffD88BPeT+vNf9lbOXC9q2Bd7Istxv2LOsocb2FrwPZiEcIc3aB+4heKtX6Ud15w71M\nzeAIygrbdFW9vmha6+9HHOlP5sbhZFt85uXcocUosfNa4yTKvE4sj+XY4M9lb5tDT6PwmwKJFuXe\nErjnohH52psgPBjTJnl6D8guz0MUeAdAdQ3r8Lu6jwAh0wq1UoRVqajvNZ+AEoCnxhNQk44o062H\nsXsvAeFul7lGohHxzvqvK9e3QmxbPNZoWwm8k086UC/sKFOx8MnKmswNTVtSyr4G3lF9uAK+7i2e\naub5demXDMyjIqG9BlTFGylwst+9PHcGgsr2BjOIwPm2ljFAb6H7nXJZYwmCxBJPw83dMify2ySV\nAnXzegV2AhBFZeueQGW908ZLcgr/QnCgFfC06fFned9GKcPKsBKe+ccM0XwrdyvR3pNbmjuaDBi+\nE9YHAs+k8OF3jeOCt64Xvv49FX4/qQMDZvDEcGTFG4X/oLVS0JrAK6LECaDUAu+IT74sFEV1GR5J\ncB7B7ZWHNFMffd2gqEZ98RDxrsYTkMmk+iYW+M6u2Run4aXNcranT29qMKaiKPSCRUANZEQS8Ci1\nXUMLgrQfKKijfyfwziqeVB7rKL/u9xXqDp/7x3jGSKv/ZXjH1B0De6POhl4lHJx5dmzKYATZaG++\n66lcKuQS+KnOZWonW8dx5HJHCxjjjfqVds18ODl+pqCsf6EaAHMikYTWcr/oSnCgFfC0+SN7TWNK\nB44jX7wkqLXS6x4/35hygCqQO0E4SvvFKqi49mTiaRQ+qsIIchbTLresLFZlyCqLm3vLyteXPHfh\nYLTDT8Ee/9mC77RAD20HecArybIQJRt4xweAGfVDRxJ79M4vNKaU0gTsDp/c96U2vAwH1ViO4x1/\nmLjuCqPgO4fsvIjyIic0KkV/Kx+XA+9s4OEjK7sjxX17n6DtdHs31qkhQ+hcNn15o/CJ8i4y5QA5\np/gXIMecLzhYzTlClS3p3rvjyGW5HfEDdp5eomenitsU6Pb0Dv9IrV9ENu9h4Mffy7ScACT9yM1r\n+2C+UR7z5DZ/pq7+OtFLETyNwn/eJWDjKeZi0VGxeN9/mZotiNoVelgnyFdn3UZ0Rc/eAlQV38o7\nrM9ghiGikSZ59WLiDW0Px/qkv+axkK1YbUp2Zes9nnNSQ/DU3EvWxH3o3njfEhiRDLfv0dCele/y\ndTkKr/0sA5X6IxnJcp4vgAktg7vFW/R4PpzV0eU9reYIHbYPuowTt7uBp800ESx2+l6d8N8oa/fb\n7RVtXV2Abf5OX59G4e/C1RvE0U6t3kBl/b0PvDNyedKufJ62+BWxg1fHJj7V+A+74OysaaJGj/S9\nuYyIAIsbGNfAPO3WPmrgiHCXWydDmym86e4z60cE4QJ2cA1yAjT/2fYK2nJLf4U0AgD7fuqoTxJI\nyueJnFXeK7yp+OLWYDvc3o3NiZHqTV4V8GgX3K7llvHQm5/m611Oc95jlW/65V2z1M1wCo6uz8rn\nY/2Sp+Iq4Eg5tjqdrw8joBK/WXzoObkxKXnZ37sF3knJuZgRIzHlMgs34T0fznwNdHkpK37mxsNA\nud7VOVBiByRO2Lm5vgqeNu3/XgMklTKJU52r9XSnjGOt4059JNCS9uEXN3WdVw1oscred4W/osyv\nK75gAa44SSkiCZDTAu90Jpqi1yp8m+dhFMFsFKjH1j0pcBH8HYQDVOgh4xOc3Uu4BKxp7kJJ86lM\nBpmgo+BDgObVSpTt9X5EEPKujLGOdKf92V8S493A0Iva9k1ErkXCI99fMayE9x7vUZW9jQYpvvvi\nV33Vg8XTf4sfvj8N0q5T9/SweXVQpHfP5NWARjv8s/JUr23aIEtIDCrK7aovPhXlYiJjJjUmKfu2\nyxFxU57Fz72OXQ56Q3QsBTjqd/gnCt/skO16qtvTAbF0MCox0h9xvdnTZtd5edFNM0JkfhIzUnFV\nIX1xrw137QdzqjErgGwE0CFuz8r9sOqmrwCFvwKMa9H23gUzUftQet/TtrvPrp1RkzoSGsFezokm\nqATz8dC/bqGHmxbhKcjz+tL/em3kKBG/2Ah5/V0sWF0GpR+pmsBjntfJjHPrf6cfEUS8o3L5RmgV\nX/Yc0SrvdDhx97KjUdv5mE7tRAYKP+pvnsQJ/ZUdyqcofBTDq/E6ld1+DoJEdcG4BmTaTcUwuYRJ\n7WRSkvmaFN73E0y//NiqvHfB7vesPKu3KDGnOtYvTDiO23at7468M3+RwDvqxC7/LgY6S9kDNSiU\niu/AuSPL9Hg+vJwscLp8KyuLjuKXmrMtTkiOTPiSjjutJWe06ROHsrk5RMZb8JxsrKtxVODlqdZR\neuhgObWA2t0XZSRpi/D+KvyL4xlF8lttR45bp2UXFMOoRGIODZIRPXcFucsjClg9c2rWZCvDaCcb\nYJtm6ivcs37coFvCfkQQ8S7T7fpW+6qe4a/p+67saLxGOEXGTD0zBuy+t5MV/XcJXLv3Crwj/NU8\nfl/BrwcuV+VFJ4Fn5dvjoF4OzW2aC3QLflHw1oC3edTmNuDKye81ejwfzmTKPA7ryrLJa7ySE1ad\nd38hm9GmeRfRYMcRLr1996ca+dSCmjyowGC13fc38A5hVayv3u8a+vnD3niMb+nPXQbzsRx1Sr8P\nxhL3UFzbZtAu2Wpt2m5367wdv/YoYEz1E699b6OTnzfSgF+NV6M+5QvAZyO975k/4190cTffOs43\n3xlsbrsTbD+utN2/G6H1uffTZiNjku+DsWhXwcPd1t+h94x+P0YjnG3v10oYFyrkx0AmKMl7CqtB\nZFZkISovvGFqgXd0+jmBY/zaC0Dmr+gK+Q3qy+bb+21nGr4yetKuhmMUhKTgsK53g7JkYwMkkXnv\nSXDGsh2b4Iy2ox8/cwGf4hgZXp5YjU9up81tVhnkPlfhaRS+DjhhznkBGN1Wv9LegJnGLN66SJV/\n+nsmp32fLaRSRltckW/9CMeKjFY+cfudd4WdZtkSBr9QV796+aTsj5+4Ta4adAfqt1b4FcegHyfj\nl1HtCfSsdLwIN992MKoffnVXOlo/VtuurlWj0yS25XT6oWSsjYVS9uWd6S0Ih3LN09EQryh8R7tW\nOCG9qp6XQR94h7gpvFv8yd8aNOWzfpDLPztZjCK1sVoQ1t1Cx/i17zojy7qE8m3zt7mmVhfRg4yx\nkn3C9Ro3picyVIb6PlCIob6XealiIuSYArqv5/za0vcntB31xUNK8auN3SiWgg+809w+ixld1l27\nFghR7nMBnkbhA005dsI96tCFdcOgdpOpU1jR76BRa8lFbXqrbkzb6g5fW/4J1k+zBnbZ8EXVykoU\nbVV2WskXGrwAH7CKUYR0FD2wBpqZ0bTAj1E/Ihjv8FukLu+XP/ShnbQtZVPq21RvIe1wtrelkckn\ntF2Vjg+gadU7gau++NJOpRNWVkc8EPtc76pM2fK4lwb9fp9AU37mdu/n5Kx89SmvhQiJj/rMd5Vn\no3EXJdlC6xYZqXJ+qNOisqsXnMn6tb87Drv5Ghj10q75HQQg0rSbtXRQthov0pdENUYIIP08TtXD\nzn0oTxt84KV6VFKp1z/MyZzBq/jKtV77ZLRxyy/48u3swVMpfEB2fucDcc9NwtaR/gJN5CdDp/AH\nR/pB2a5M+awBaw4CJXaWYs67suhrATwMX6i2pXcDTf7cb7VbGPXj7CLcVcU1xBekVYUphpM3ZI55\nP8J2NN9cHjurv8/r+S84ZVHWxqhR8krpXw+va2mf0VvpLh4HEp1Q46m4VN/e5yN9DWe96HiwUNYe\n6aO60a3ybGYYvDsOO75OzvXOWLf37rDrkm+jbRLOgQjDm8k93risNn6BfKRvH09Qr6Aj2HAL6oMk\nwb6W1rXFbi0nio2Q8ZG+Had64uPrbvAeeDKF/5zLgLtVsblY8YU6GxR1lzxs2yirtvqE+w5LnviI\nE6G/WCaXYtBfihm/4S3u/qpxzZ72SnScNuN0dFHOXF4yF6VafkdvxEvVtm9n1AdTjlqax9Ns4P5y\noZSrl3qkT/b5V0ivT/O2dnhlKpAhSWJu1OsLm+zqD3k5o3eUv9nHS3hUnpYvjspFvCRXPqijL8gC\naOOoxnuF3v6yWmNGHR9qxLQxUZfBiNwcsGNv8QA9s3XbPYR8Q2u7pXHfbxJZj+Rf08sKTywQQ1YF\naZ42NrT1A1vpqfUjvqHns0uvfYVbq1SlnfuJT6Xwd0EWQYH8PHve+2gH7W+nSlrzLS8+56FEWJwr\nNM1oXBk7LeyVVtjfQAnfa1bbuBGCVTLyXQd/sG48ebJklxEp08oJHqFr5Id/fmO3GAtRsSDNR66K\nqnRNMuo77+3N98LD6oPMFpH/zurINgn96vawWSxRcWs8dTKTzdevZNXjUBfpxOAjv9M8f7d+/CN6\nfZp5AVSR+Rm9+odx2wLa40uhTy1M5ij1bGwXx361j5fwqN/mScUiL2Vs0wA3MfLzZ26xK/pAVrxG\nbyf/uQCRxHjIeGoQlxpwqpzCSFAt7YJWgjzVfkswmZJEwCC2Qn9vIfuSB7QDte1aVnjm+kiHuKSW\nJM+rVIIIdUyyiDr30Bl/HW2iG7pFpbzn2PvIiwst0dGNfW5Gzze2xju3dai55an1YkVpFHgahe8V\n2FIdWF4fYllN6hxBbvMWz76qgCik3Erjsds5BTgjmvzJ0cgP+V1QNoKsbBvNzMChakresXxm1byv\ni30KwlHrtwBEImBZwehFTLuHAeVWdqErBTzrFsAhVevSbH0VwgLofd+LC1LKKrIFtSn9ED/845yX\n0k/hJivetPZaj/z4CJ/rZSnhPwjih68NEgmGlJVBAiVSgXc2VgFFv6bdj9FInkTmCS3KXzL+xdK3\nEpxkn7SnAS3Ls3VK8zKXHZdntbVvMT1SCSizx7OXwQw4wKBE1c8f3ALWCP7jSHgB5TVLnVc3o7e0\nwQmH4cP4aM2vtzM+SNu1Xb+Y1nQqkSZlrZbAO2W+1OfdMU2GmEXoaFN++CbuSjlJYbY8A+coe94P\nv86TOt+aH782EiT2ho6dgKqf1k+Qn0bhXwK1awCQj6JwcsQx3eE3hdD7PE+WUHnuNqKJvdAPJv7i\n/YWk2yh0RZuv1QAn+sVSLPPkUMocOihE+60nbwqEkQuO6MVVaRB8SANjUzkQY3ZVJ1psCHqHL2Pd\nAo1I0JGzC4aA6qfiGwNmd6Rb9+OT17cWJawabrL7Uz642uLPBkuOgMYlAtkVpapdjfQYj+j1tIss\nAv3Rt/gQAwhfHPVeANmde5owxLtt8aQ8EVr4WFl/5LRml2eT+0FMXNsRWRP8TJzvC1AL5SogRm/9\n7UP80nhx9Dv86cke2ROB4akGYIJh6UigQm86aFi3ITnJX6TNKHx5rKLkXZryoXQBe7IqJy6yZtT5\nnVq4XU5cjYPtPuA9V/hhXx+4ljBOjMaZUXBvQtzXqN1VWpjdURrix1k7Lczo2qJtsRxwfqTf7++V\nUtZKWvP3wpia8jw2bMIxU2PBYdnGWW2ICt3VYN2kOaLJr8s766f9bml6T9V9twDs6pPZbJGTQ80j\nxgWejRQk5VZqO34TI99Zyqq6ToaZ2V4gmxmCbj56XJ52XX5kF1S+OOaw+tzYvK/BhDZtwJD63c0H\nzzdVpp/HrR9+fven4e/rDn/hlropDuosWho+9D1rWlwCKyndrXudFuNAloqLgXd2aL3nsik3Qetv\nSauLUD5m1u1KvueN7morEzwGoUj9btLtBZ16Xnft+t+HvdFLKC4wctSpb8SrelFAmlHb5tm467Pm\nMRC4JoGUbLrb+d4Vr97gj6g498zvfYQ9vTGOES90WXn/es5boeY5wd+qXil3Vp7IesRI/UMtSLd6\nNuRb7coPX9okWwZoc6LRd+DQgXdo3QukK3dgqoy9X/q4L2q3DVT5n9Knt9O7QBPajqNa6gQ134O1\nMAq8kzf+5XRSTqnLcRJzWxNy1d5dfKc/T6PwtcJdV/rOuiF5bjauPwweUpmqFizH2JHykrQcXAOm\n/dgtb0zDCogCvhccTlMLHw5qN1llAWJM+OP6OuNZeZfE7XQ7OHVr9OuPcnXLv+2Y1cXPTXjzbFtP\nPt8e7OLg+1xdiyT98EqlKXHtMkhlASdCmN/Tce6+0/sIW3pHOCJeaGVCSR4TtXbeV9c86562Vm6p\n/GFlSKZkDS5zY+wCCShV22EybpS6jYOOWk7S9W9S/vwr7ZrfqZ+Do/Ijdh1k6TnYubQN6NPr9BUY\n0ZbfY4G2Xorcm7atUaJpIspXK1jW1xKrQ2wsUuuTqX1BJJ5G4QO7yr63bvLiSpeeXxKagsq/5Z9W\ncvOdSaXdte9r3Kqsd626JXwK8mLcFI0EhKGD6jPAtvMk8xuOV6PAO7g4TjO6z7hK1L+N+t6MAAAg\nAElEQVSY1QfEqDvlF3L5tr1KuzYS40btTy8boiChj/PbiiGGsNnFo+0KJQqaLOYjGV2ZW52cknVd\nGuEgtnXksxYl/9ho7yTvWaCjeNKHFVnQZQ/NLJTTgANAGhuTO9BkpSg9aVMNXmfk6rpkca3SE4Xg\nHU17y4fJDt/RxyWt2swDOa3G9RLljjbHA02b7NEPOvJl5ZphJ0/EN+lzGeb6ncAlWFWZ3zJnrJhs\nK/3nUfhlodtVhoE8bTPBLvgNL5WVVauJFTnvaPKDfOuRfv3vPjA6gZD4zURcj8lqwB9SPJLfagfY\njqHiEc3G2W18uBpNzuA4ZIdf8qkp+PZbJp5ejNqR/xkdOtf32S5C9nRK47ZH9m23Znf8ZMbAt3NF\naWhZHeGIgvPonUzmn+3b+7rD17Dbg1n5nq/tMQ5wO7/0o5/8O8u+3u1KGzpAD2B3mBrXarsackTL\neN77x1HjRyBeDvs5G9FXZfKCxo8C76jmwalE60xNzg2Nao7G/ZE1kepc8WsQBPMNsvA8Cv8Nn+mx\n3X60dPX/ryQQdvhLYOeX2exlErmdHSqJO7DV41iZB91FtEJn7e8gX1+s6vLVqcZKm1FetAgKbsGr\nXR+bRwG7vLixFX57+ntenONovGwLn76YJO3c/VLVK8AZf0blVsoLu6iWtbELtvhl8GjZ1kYXd14Y\nkp9dO226L7dKjy83vXkPdu5+Y5yWnmTSRpf2tDfWLshb62LarDdXWIZzfIxozaos4f677k9zwVU8\nnMz5CJ5I4V+7xCXvoPeTLHz3OcZHY1rYpb5fRCO/0C48qruFelAfD1or0hmuGezEgT4DHzSjeRQ5\nn9BOwXDAL630E5hj7+3OT/USuHdLLxiNfnKklHccNYgH2PgdyzvJAUIysQ7KDh+o6aP2TfCars/q\nnd4uR3BTOQdt4yCugm0MCFR8t4+x7J/ML0+/H6MRDttequd01ac/6YVeDKQrB6tvCxF/VsqtlD/K\n6Q6rsuIiCuzddyFuYWYlrkP2racaS4EZNWCNgASYyrEp2vh05RKg3553RouG/Fr3AR+YTMCf0fpA\njr6X6sImfTtMHIHWdjFAL6w7bYx62rKOSHhJh+Vbt+6nbhwFbzMYiktwwQlQxS/z3Rv2O915KoXf\n3CvWe5At2N7iHKMY7IAoCCdZFPzMcuwCubi2Y+GOLeQdg+eeO6ROCSILokTqYxRlo3zntUEk9CTF\nH0YxJBLHfvgbu4QReN/kyZ0o066GZqS0gBl2t8AlQhmZ8TH9lBv2C212Ox5RiqE8ZNz5+T5Vf1xN\ndzP4GSR+vCFfz6XL09/v5AbSrBJrZEVGVToiFzXwDui99MX3/Bm+BGZQf1a+vVOpKSUT8GZjslDF\nItH1Cv4cLrSik+A+lb6ULx3nT6vcjOHHAB1r9Pindmmw2cl0K6HBTOHbPG0AA1kfhEZvnbMXFD7D\nDKyZ06ncq+dkcHc0eOWANvbMNpYJM1R/UHfydYePlvZe3tK/Cv7YU6dHMHyOqXauFW/ZdZnAPF5h\n+GfUfpGkOPBOSN7GDv/qTdMY1yhDnRy5Se8tzaaA9EQA0hEHgdHGw3XC3c8Fjc/OxE5HXiiOYWjd\nMvFcP5wenLY/Crxj6g4Jznj1CQsndIF3pJ3kxkA3c3ZlwtPfHfkOcHhesEQPNYZyW8iOY2+Rehbw\n/PGyNCq3Uj7zpaW16HFl0d9hmFpGcpTItjHSBytaSQI5cBMVl1RyoXR1OSLGkdbWqj7K6HjsffKI\nXwk2iJHQpxV+VJebxt8GdvdrTCCi8kjBbzwNzyBGndMFhxjsMAa99IeIkdJR06ru0Gg2+rOyKWpE\nE/0xIvqrRPRL5e9/JKLfr/I/SUQ/SER/m4i+QEQ/TESf3mnj2qP821ePyxgCI+4rBaZ9WTA4ZiXu\nwSd2f5fqsJ05ZzRHbZ21P6Nxpe4orXtmOMHj6Yj+Vho/qxfT2wzmVVqe8W+FF6tyEJWfTamrdI5Q\nRpsOnlVwdF7l2VlfVspFfVlqg/doX6aNG19GwOozxMnq9xCPuk+kjxg3YHeH/7cA/FsA/vfy+48A\n+K+J6Hcw8+cAfD+APwDgDwL4PIAfBPBnAPyeM8RUzqG2b75SvGuPNsujZ2vTW/qDtFE7BOq2Qfay\nB8Pf/L8C97zkHN3SjzwN8q39THd1ATO8sfUid7aWd1v/Da7oVuwA/O1aOg7Vj3aTmco5Wndr3x3t\naxpG7bcon3G9nBPzo7o/kvXJ97+Bs8A7wTNo1WZEP4mv4CKOWsbfzEY56i+M0Lx8n6B3X10rt1K+\n3i8yN7OvBSvSMlBdNmED0jBQx6PRlz0/fPAn7wYnZVcgKjeb+SbOwaCJd8dh8Ap9fBZ450aIXAYZ\nPOyjX2uq55LzxCnZkgCJs6IDCYnLM5UylU+b3dxS+Mz837ikf5uI/nUAv4uIfhbAdwH4Dmb+C6Uz\n3wngc0T0rcz8k3Ps7arPli++fPrFalA2Vj7Nt7kNgPXPruW6+n6BZdN6dUvThZiBAR2rcE9x9vT5\nCFy5TMwL73dty4x4ttfXM5gFvunKujMtH6xGLoA2l0TrzpQvYcY0DBd6dWw3on10KasLtnNofud3\npmvaRvzWbQn4gDmxol7HIRCOt/pyL1ez14bexWyt3Er5qgicAX0lWJGezyIf1UBUrmlZSWr6rKwZ\n+rxb2qMC7xhFHpfxgYAOCSJUtDCdGL5XIQq8k1j90GUZSC5d6DocbytOAiTwDtXNBqwRRnYumc8F\nuPwMn4gOAH8IwNcA+AkAny34fkzKMPNPE9HPAPg2AFOFnwV8f+daFWqQ3qUt4LAKrO2edNoM51C5\niWXNsZvaLtxTYZJjvN5pCOTFAtW07RTlaKF4RYW/Ijy+hA28w8pIyaV9H8QQCGkYtE+Qy3l9vt5x\nRSB4ZdGNDKxqsB5jfuu2BNjnBbLt6ZrhqPUGeNpC9X4q/Ig/K+VWyh+yzjiFT6bMBr+qAdvwk9qp\nJwJ8yFxRRjryJBDvmC/v8M+q6fVjiNPu8Ln8Njv8UcCvG8D0pXyNZ3XZ4Uf1PS9df5kk8E4zePQO\nvwmIVI9m6Ri2FT4R/XZkBf/VAL4A4F9i5r9JRN8M4ENm/ryr8nMAvv4Ur/ofRP0DkUFadSlz+VVP\ne17ocuU7uWw5dqw0lbdBkco3uE/ajo5fwnE667f6bqy8Do+mLaLX1qkKXjXjy8kO4UXaF4Wjih5E\neFF1DlFEAW1R2iq9PW3UlxvVcdMzilN9lNCccmvZBpEpj2NcO0bJ+baJ8m65G1tlYJqHeH2+LLqi\nCJidstf56PF0NAJq7gQGmPBD0xyU8/nh2AoeX/d9U/hAP+936ozKC1/dfBNlXYtd4ZcyEG3gHS5B\ncFrRGs3RK3cVmEpwrtLSycupwscpf71B0h4vUq022gjeAv70MpMbq3yi/u2I2ljvoGym8py2odNl\nDWoyIRmOmAW4ssP/mwD+CQC/HvlZ/Z8mot87Kb9kgphnnNHth7O06OKGW4tGdfSQ6QsYNVfdj6jV\n21rZtV3uVSicZbGbk9v5w4/o9e0IHeGlD47TjF5lK7R1vikdpL1BpE/M+lkWOheRxNzviNl8LNPb\ngaPF83dYxwgFtX6oG+/1NbSleEpcj/O6y05VXpRC823LDfuAnuhCW5dP1MWFqBeQBC+7W/t6EdA0\nRixS7Xhe+XGK3FC7dnxa1PeAnsfD0lI0qe5lLJrEweKrJ9EAJ6NMpjwh2/qjjP1lfgU0dB40QJVz\ngerCp08hi/zrtQbMxl9+RkfkoXRSSRcOS+TAQKov6rXRudoGrzbAr381baB7ukuRZZ01tAmfjbut\nHS9m6m/oy58n7AS2FT4zfwTg/yw//woRfSuAfxPAfwXgq4joU26X/2nkXf4U/sqf+kkcX/0OH70k\npBIF5Wu/5TP4TZ/9zC6Jmlbze2SV6gWydzOzg3uG0wdQoYHQR0O0a8FrvFE7cyiXQ0L61PfymeBc\nwLj/7V3CvOCOaL8Vmg/zORieob2fWwLv+CBDlX5ubUW0z2iochSMelJlIhC8npcdfUB165nh8nTN\n6I/GboZjmDaQgdcOvZPV/XW5i/hzVma1vOZ/tOgT1vkV0SC+3s3AZLDzwxc//aRiZzD3MTeAtcBf\nEc1n9TTtQznu4gQk68JIXE/n7gpB/0frGzj2w5c1R8BsCmF98WtcBJZYHMDf++s/jy/81Z/Dy4cv\neb4fhC9vTKR7+OEfAD4J4KcAfATg2wH8CAAQ0TcB+EbkRwBT+Obv/J34qq/7NfjiL3+Av/+lD2r6\nLYqBtVkaHZd35Sv78z8j6DogS7bUouWDK80Nl25blL2hTdXd65+lo/EqOtu2adlntNDveNO+klsg\nYoXT8m2/xNI+Vwrn9PbcaWmJxxd8POhjtuPwlnS/2Irylw1Nqrrf0jYbuxosJ+hDXTgMTpuf6Wyn\nEQBq9LNKazk2F3rdQSoARtJsJSsv0o6huxs7FTWy4HHmbe5lZOCyH1NYenpy++9R/qyOS8sRJJXi\n2mzb86eOhyo3k8PkV3ouN7k1vUCNUcGs/MmPojwX6A1pYBUTg2BjNohsUwL4sHKmDcvU2kmJT8fp\nOPo0YziM6hSo/HLtGL5ABQXThu+RWpS//SUlTNOPYducRu/zL3ND84iQowzKbycvEp+gm9dcVuGy\nVn3Nb/ta4Ot/Nb74C1/ER1/6CJ/45CfwiS8zvvhn/y+swJbCJ6J/H8B/i+ye9+sA/MsAfh+Af5aZ\nP09EPwTg+4joF5Gf7/8AgB/n0xv6Yn3eF+xujofPOpjbEZZd/BGkCU4ljA5XVXoEkD/CKYhC22PT\nIrUGjVbUGjmHaYz2Ksd+gZaJ4ie+4klyv5WSbHgYo+M1m3RObw+qHcTBfSLwEcP8KU47OmvpOo52\nbOKpCHMnbfq6c7JzvtCZNJ3cArOIHEiwDk6iSSyN+djYJHXtmNQuOJL6HRIu88RmtgA+Abb50J7n\nz+r4NHIKf7PtPmqcOmIdlPHlI9xaH5E2ArnVOUbH1AG9o+BI1cBXcm2MkHI7PBsGVGkWGWtR/4Ak\n73ON6JB+BcNrgjkN6uiyUR8zfS1RglDpHf6RGGr/FuLp4CRNRxO2kf78xFHpuu2j7PAVHulvDbjD\nNviO7PBlzMyJo9FHa7C7w/86AH8awDcA+CUAfw1Z2f/5kv+9AF4A/DDyrv9HAXz3KnIChkr5Y3h7\nMKL1FTJMa49RzifVa7DDtzF8hDDJewu48cn5VzZQ+PVV2g3b6xIHVD2RkD0JGQ8HYz9sKnqBXT/8\nP3qS/wGA7yl/WyBeB/ccvO7m9KRcvXVZnmnrm57m9mcl9rxNCtLlNOEe/exvwK5jpXL6ENVtN8dR\nOyH+6ZKg3cJqn9ztXe+2J6BPVO4JKziNSExoPojyc9WgzAjv0B3u8Cca6yDy5+modDpXveOwt7GX\n2wnop+BIVsqONudCR9SPEI+Dq3wa4dOQ34eA4XvWz/HbispLdVjGlA+OgLrAOmUMmVFvZwtePR93\n6Kz43dpEB5lTKfEEMXEnUG6Ip8Bb5cQXv7vVLhv2k7W40jPywycytCQWntm5cUbfLnjaRFajmATM\ntgyRc7FV+kbjO+rl4Pa93tB3a1f7XJ80TxRLn6pSuZcyMO+xxxgvqUGoA8ES6IAqHgmMETG+Qn7o\n0rVpFR4QRZrbXqR1/xSdq7WJOKSv8kDtzUTZC90HHVZwgUAo20LT+2bfd8+3opRzOcszH1VM+nQc\nBzglIxszOOgYLsYSae4K2Oh6eqHQRpdP2w86Mg68Y+kWmZaHBBH0Y03g4MpZ5Mt9y0t1znzDiXJw\nlqsX91YMmanCn+DU6x5BjM22ja4K4yqdbm4ChIMOsPPDJzqcG15sQEbuezM68lqKHHhnsc7oEVkf\nJ+AwCl54ee84D562JqtROzJ23Iz2g6oO8cHCGj7hvd1EhT250L2nUfhVIO44RqPddlSOYAfALrDW\nyp5N6rUd/hlFa3DTDl/97+uaHb7b0dvf+U927AcRksPzfDt8R1+3eEDtsKyyPcU7KLJng/d4q2Gi\naPUR+HTZFXo9xIF3ekVNpSzTODpgrBj7tN2wq2dwusAbub4AAX/6B/2TtWGC8yCYulVJqHLLCiwo\ndwQy4ZWiPjHSa0AKlI4O4rNCR90E08lsWFizPd1cfrOeByv07UJA2+jJhnhdyGejmazx5mSSy48E\nOeGQkOZq/PRas9nF51H4aApGlMg9cC63Te07Q/NUCSiZj612fdo9RPFWnLT53dQlPWYIH3V0+bUu\n3XZ2O6Jps4woL7LEAXL6Aenn+SOY6dpCFMdYWIDDLTJtzqtdv8sf7gimJAY1CN0FMKMMBn3qMAV4\nRm1e5dMIX1+o/nc77OJa3CiIvPg5dYuRHMmED7wjishHlKtR62zy3gajKuONh/8D/P7EwQfeuULf\nNgg/5dmLz5aT3rpxcPT5OnoeS6C3yjOc2Ejr/Xwahc/Bt3vinrEk32DNjNW3WFkypFzZmWoKI7zR\nQU/GO+/lVfHU/buK119gneGTdH8Jtbvtr3AZ/Hz1UHUMJ3Oio0s+xZPA0CY39NFuSp95/fFg4pfM\ny/1NSua0S5Pxw+/6M6Flh/6IbuZu7Lsigzphm67eLXIx3CSIgSn9u3yhIuCpxzXj+4Q+dvQZXpS8\n3t1ync5uvJjtjfkCKSUkF5a2C7wj+M74SHZe6c8l2gdlfeCdlFLgaTSOR3EZHG3Ni6BvRyfl9UON\nn97QqjGXd903tMIzAtd8h3xlHBQ8j8If8+4OuOU5dDxdZNGUkwVx3WH/tI/LhRNFpMepF2B/jB2V\n0XDVIo3cCnfxWvo0L1p+73KnlSMHZZSRFEzIe8LqqZDQ6vug6Rr9zeA88M61/kqMAeGlXjjroluV\nMFcXpWOzvZFCjpRyzoOfHabeGR4gDiRzi1xE+OTYnZWyvNpGaNw7XNONRTQ3C32jwDvyWwzaM8rD\nxwxSdyTnJU2i7PmgNVHgHWIePtJptCgcCtdqndE4+cA73mU1KnMP8LTNjBjha3WjBXDkixmQ8dY4\n9XjowDsAcBCbWAN8g2X8NArfa/p7KoRqPU9wMmVLClrZ+4WKgBY5odTr2lIKZUCLn3wjXKvgFfOt\neHMfyClHhd8YRoEC0ngC4+YR1vc6NkuzV45asdYJOIlet9J+3iFd72/R6d0ikxfnJnPGANvkb2Sw\n9IF3AEAHC7pR4QfVb+FT/Oa+3C8dPc7HOF+Bkc3scS0H3pHy+ihNotslu0awRMBz1aMlbXQx3a85\nItPaVzwdqMGbNN4qV8qiYmLjTx6B4YW0odo7qzMaJz44DrwDm0YXxnkGnra6NgbtVN95OeNkzvxF\nkUe2OAUfp9YXv7Zqf/ycsb+WPo3C1zuHu+Nm4CzwDpc41k2x9bSEdoM/BYWaLOYEyMyguJ8Xz/SZ\nW92reK2iFl7o4+K2EJAYRRx/arq4yrtXAjs9XICgjQj0uDa6dX7Up8F4KbgWeOccGFwC71DZxeh+\ntB2a9KMFDto80g9W4XjBPVfJfhyio+M1THsQ4WuvMW3Bma6MBylcGjyu5cA7DjcjB9fR5VjRewTe\nBXlHHuPr2gagw98n7ufswShR6tz4pdQUjrTB548XNC/qOtIFcxrXGfGrP9LnruxDdvgD2iI67ZrB\nZXwrpjqWXiYloBbQAu/4TYhX+jvT6GkUPoDt547PCDvPkp8eQusmsHbeo077CzAzkXsGcdQkBPd8\n7khjcPEI9xlWwnVXuGvtqe8UpLnynrKIpaNrkDvsD/EO6BvtKSyO3hV3JA+9q+QAJwV0upvk8v2S\n6NHcKHJFKzDG7YX3TaN+3BH0GMXyZEcxlqkYX02jklMy7zGDnkbh11vfDxiomcuU5PcuK6g3W7vJ\nd6IlTi3fC7eoz/BF32/FUfvK4hOaUytv6mKVFx7Px8gtTyzTR96gnd3V0Pnerc2n0aBMBJHbU8N5\noROqrnHN07SD3Lj0rnq77dyD7tgt7/VAN1/5ddjvBtxKGioQxLENPK6py25wRODdgAFkYdIHkia4\nkqXJM3bUfnyznaqLpZQ56OgC1hzlta36iMO7s4b9DfIPEHii8S2NKl1p/K4vJXYAG0OeHhp4xwSl\n8u2UU9AETSMqvxGMueA7Cp/zaXI2q/J8VicqWlY2u/g0Cl8op8KQeyqEo9iHM+vX75Zs4B1LZrSg\nVMhn3nGeLnKHwDuNJBVAJ7ADV/DaCaSsy3yoLKMDCdbTKX0iHAQkwxursDzN94Qdo0fa1kFtSkaJ\n4pWP0A+KZWPU/nixvb6/be8oL4tsXRi8MZKP/6KoXCsQG73XqI52k6+5w/e+5UDWVfq7Bh/sJ/Lf\njpRrhGsme7PAO/UlOqWtFnjHtm3dNPtZNDY67fp3IMsUq/VNFJLvP8scgOXrTuCdRvN8p6rr2CsA\nbY2zgYGaK6Eex6gft4KnLUGNj4JUrDV9hyAretFvLU3LZK0HAOASaS+OBYOWtKX0n0bhG2vn7rjn\nGA/qPa1FoBPZU23CPMDHyu7dT55bQdNzVcgjHEJn6nb4NOQZOTyCSz5fmM3vR8AIt2+77pxNyNAy\n9kXpG8t8ArMyvCATZ3jNYkxASjbIjsgl0bXFLqL/Kt09HuBIjxvvvn29NRQl05RE//TZ3j47wq14\nvC517yWcdDN86l3waoXMIBzgGkhG0971rYvtG9N5uEA0NWx0OU0AxKCkrv/p4Br8pfWzL9d1LSCE\nI5oHdTS/ElJtL0fW053r190j6Met0NOWOjozOSVmHum6Za4ql0fdD8GXSJQ/ICOZ9ZALVnZxOj2P\nwpdPpfhftX0/b4wZ9Z48oH4U9GtK/nQC/T5CR7XZHd6A504wPrmwyn7+tHCvHZ12D2+K15aMaNys\nrLrMhSP9nbaulPX02ePpCY7F9vvTm/JISOEgyPrrm2gbAN3slSmv2zun2dIgv3v6Spo/0n+g4On2\nfDvqkNeWh03vxlU/xuEJf2/o2NMo/LcEudVsLDi5ZRnewCxfRlb/bLA8DgVvqTP9LX2z6KgLI8wA\n0+B2O3za69zS7yfcHLnqVnejfexeOKfBx2ew9MzrTvHWG9ukbv4qF7zU+L7jVTBqx6ddoT3GtY/n\nKqwEqNHkeNqiW9czfLMLZaM2Pd7cZFvtR7wX2pReOKUPQHk3u5JzMBKaPOly/pa+ljudNvN2OOPX\nSj1dzt+K1/t5udmuyXm4Hz603ERrW+/aCFD9FLr1OMr8ta+TbvOe2yS3i9gGPJXCf6t9tCz82gqu\ni2dQtlJaL1aofKkT5Fk80aJyP43v+3Na3nxn6JvVuT9Nwri4CLEyZYWHZlEQXIx6PKnbuBs4Xp9h\nroFMqpFiF7LQD/kEK/szPEPe9b4KXnH3tAE6VFAU+VfSd+9IRPRfdSf06naFf/cEWQ+n80+Pebhg\nOzjDtTDXQkOU1OJPrZzMnR6HrVsNQsz7m5jN3bLqvqkUkwTeCd0qnQID83kY5ICe0xMjswa7eanT\n/eYs9TTvBp86BUdbXR/9ZiYwpBLn+0/a7tJzTvAl1ReJHZFUpD1tGKgGl+GpFD7cAL9q00C/00Mv\n/GwC7/TuRnmxiaPL2XLBZL5KfIj/OsbcB7WYcBMyoyzNeI3TYHDFk+QWWD161v2R33HsANuPWwPv\n3NLXtsg1upqvvZxCubzE4GO/zc64varwuzlzzr97gtvMxmWUgvBzOPJtPwuoM8uP2vR4mdEFBop4\nVgO2kC172l9m6xevDUe5wnAAlLijU0LX+kA7M6Py8Gfsio7ZZBkF3snKsKX7csmtd8wJ6c73RkaB\nd/pxFV7ZtbC9ArfgcGMuhoL0JfLDl7kOtbfamVpPpfBfV8WrdpmDHeiYkS29X1nqTgzzHXa8i1gm\n+RT03fql8kZRUzmG7/OZUaIS9kdrYhj0v/vjyXuu/+werZwq57JDaBPp7Eh/4Wg7eGzR6p/1YEJr\n3UXYoz0xRn3gHdkJ7Or76JHEVbpXA+88CricMcx08Oz0Ijx9m9DvlelOm1YJt91e/pzRls/g9BH/\nrL9ezlvgHdueDvxi6/o5sRcmt9a7IfBOVbDM5uJfeCrxioF3Ro/DXApaJFeSlC7wjjaO25jZ0z0Y\nmZkbUB6eSuGT+v/1271QL7ocBOH/Gz6Qx30fDxSEfdLqI4MHs2IX/ejyzyVkDwd1YYps+uhi0r3u\ngsR7tCt4Xjfwzr3hjJ3L00AZ0f7y2uzSXkcL9TJ8Nt+7S2SOrvadAtqoLxfUNfgnF87qyUDRVTMc\nng+RzMtFQ1125dJexOMOT/3PlUObG1LHjO9gDKcXMFfgxmn0VAofeJuLa7EPcltQOwHIBeIpRhKw\n5bzNR8Iu+ug2eE1jNmn1TzfEXNxHPB/jvr7GrX5pw1vb4tdMdJh+Mee3WuUgHpYfpq+TtiJQnk/n\nICtHxdvc7LQbIafGW/8nxsAOxGO0hWKCa++06R7QFGLc7k7fRjIsoH38Z9DcraBuxDdl2nD0CtbQ\notpru/q5gvOBcuR98UxWzg8i4zoGAClaH2vgnkF7A2KC8PoGR+/r7uqruaDr9Ov3uetv9CqAg2y6\nXsst/1QH0BtJEWg3WmnLG1PaUNH9MqcVHb/WrYCnUvix8L9OuwfZCUaQwXcTqXw/AiEAUE75zy/M\nHdGx4R377PTGKVg//DJhyu9UHHhEuA6SQCFtwouvcLdbqAaQJSbq/1UYLi7kXjtagQGQWTyOw/q2\na9/840DXt46GCR1M57fGBeSFWsawJALRUYMCpVTag1p0y5gcJwvxkP7AgM2PSvbHyS+0Cfcd7zVo\nMQkimEV76zDRPK5Bwhq/EwiHqBPKc0qvI9V2zl74IY3NoMsyINHcjMwEcHQyIfxBvWQpcn+UNlpd\nNuWEjqMYzRGM6MmPnqn+ykHDGg5zsVDzS/IPmQuqHPWBd2TOzMDjzvUOl66C43RLfTl6L+NFlOPr\nSc/6gE6yyVBtyZjLWBNa5MNDGwJBB8h9LsBTKXzgdRW9brOzENWRabTDn+8czvgnDLEAACAASURB\nVPvwPu3wiVkJnt3h1100+tC6gPBx3t6jIE9AdGdrdQKbkKXZmBFj0xsuCPrmkE5kYr2vVO5FmPYP\nqrTqkyf72eftQGSwkI5nuoOrk4G3g3uMid9R9vlrfTwI9SKZOSUD7K46a/KwTV/P7I4nbfu5eeg0\nmdtQQZtUWWZbDlARIAeWzpAWhUYuAZrAV6qo5pdu93AnEIfjiS43g+hS33GQSTe7bF0O6iSAACTO\nQYxSYyb5S45kT090P+wJat92x9GLk+rpFD7wNkq/J0J/eX+fP74WREe2WYm8Pi2ehq3RGymIhXbu\nBZ4ECrkru6hIKdyh0dLuPZ69v9UMuts6coJntRVfjibfR/yiSb15216oYiUreZHJdp62Qoclodyf\nPS2rE0dzwTPt0jRYpqPtBMtWwYzbSp+uSuctcv2UCv8twJ/8Npen/uZyFdSA7+VS+umie3ah47WB\n1W0TfwEFsHNJ3+7VN4ulPCupr2F5u/buR/uIb1EcBU+DxCuoni6TG8nHZIou+ekvgg7OkcdB39K1\nt/GT47suswOhC5jcqtqE2C1vH88tUPk2yOf63znkoDW302SXk3z4W3e73FRo88DocaRyIK7JWTmH\n8fI7kpP6bnlyafWeXf4i7yfpXg98QofQq2kwr9115Tx9Ivfk+tIF3gm8DTo6Iv52fOfumb7U1TyR\n+Bc2rW9P024C77DHa8fH394vjdjPBXhahf+afrutLa3x24JhFn+q/03wrbR5hdLHgeaA2K0tqEeW\nPB3kwytGBrqFShbdsL1X6D8rWuN8PYnapOr98EUWJmPuLSSdt6HwtEKw9aM/mO9tkdj3e4+K77r8\njHDNxuCRIBcxI9jpW76DcDukwJCsp85yeQOxDGow9QreszsE3vhpwXR648z7yjOnTtlInIfON3+w\nA9cgbutcDEqNw/erp6/44XuDJLl4GimOe2BxBUZucmMEVNc5GtBW14bk0hR6KrRrKy+l1l9br5cB\ns96Whe3KPH9ahf+aICrLW40RQ7ma0/HN4zwe57eSQ1/fN3za6XppjnP9ToDrP1/GmpzZd7ywy3Xt\nnm5aI76dKRpZBEnKGSXqy2J60SvLxfUTAE1zYxoghleN7yByCf29XR9q/vq8tSuN6L+qpN860h5Q\nHkcwT45/NsaE7/N4QPNBhqe+IKfs9oiUT3ZAH3OZmeTWqhP6dCQ/+R2NSyqhdcmlNR/42mhWVhEL\nT2hh3z+9tvh++ZVJ5NucxvY++xKdbkpHRLyXC/dVLm/m9th8Z1WhCwSEdopTjRVW4w/NE617rCEg\n30/7MYCPFX6BpsjLb8SyrI+AowW1HuVcONJ/y9tNVoiymW6UvNuZNOVDLr3f4Wdd4pXAHYmfHOnP\noBopcqTvds4el+5rRMPcuJiSYsvW//IBb4LlbU+r7Y8sgFsGZED/1TGK+HDX8V4Bt3PyMDvuD0rf\nhf4okExvQ9oIlyEtQBcE5szpoJ+rkyN9xxv72Egb+P0dD8L5acgooA7Q9yvqhw+8E5+gnR/pRxAa\nWSWNGOAaGVGvh3aj4/M1ppzXlDxVvrZPZh1tsaXXkxdZn0RJbXTzqRT+U1zWO4EzGr9ig4wsDE3e\noVjLOtrdPwtEl5VAwaW5IO31wHsS6JwxXfegd/7g6j2HN+icb9IP0er6F8nnbp2o/REN1oNnjnul\nD9HTrxHerlxQVuanLttuuo/pWLUHKq7BQjZ5mufKrZvgMY+o/745z59K4QN7TLlbm4gXU3FPMZdK\nKC6vK84udwk88n3wV+BQM8S/w15ONXRZ/WfKuLJw7kBde28E4vJyuElUfduPPv2M5iifkXmz0l95\npilt5k9UOmVhOw5CYqq8ze8qzzv66r6HmO8jGPvh74Pvaz4KvYDogbC7ztxDXvlAtxO38leUisyp\noTHX+9Sf8dfLOgfyL/R046fSUlDOGwQLKr8/Gahrznm5o8SkEAgDA9G5O+XqxsyufaWuQptwwMer\niMauxvhwa6kpT5TnXZ3vi5baIjyNwhffY1Gmr7rbV4tplKaXBkLbBYY0lvO2c/p7YXvLE45mMfa8\nKJ7hTgk1oaxl6rhxxSn867t2v+3VFb5pOav1mfs0U25Ow5yOhf4y1XsCbTiUb/2h+O/pYjcmXp5P\nIFKAV2ORd3xwz49fA05lwp+L34pvAXJwNrvH94a0bmvE/8PJYvapP2nb1fHzt5Y7+jRdTjYzeo0w\nBsKCws8+7LZvre/zctr49Wm6rJSZB0xaG/+2GWp902NzhIZJhAd1fdW0a3x6bQXsvOlQSrkNOX4a\nhZ9hc5W6X6u9hQi1iLsdPoLyNn/Bxn1D5R5BdFxUP92CbYO89GUMLsRD+ub9DyzoZlWP0uc0xwZg\nfIchhn6HD7QQnG3xaoFGNF1mXJbbFIzBHLg4Rt19Ddy0KXkIrM7TVv72HkQY4nk3b9OHvl1SsqER\n27cR7YqjELCG3kHgnCEQQC7oTTVmz8oRdf2v4YD1bX856ZocfXjcw3IBbf5UwwfxGa150WbCf+Zx\nybNmWPaiOD6Vwif5e2tl8DH8CoFezu4uec5gvIjkLqR8DG8Lec92Hzyz368Nu+2Hhs8G3lvL7sJb\n8xfYvWQ6hqdS+M94Qciv1eLpM/L4Wd3NRDrgLe0cuWhHNAi8476PbunLp/RFyganvHeDS3wTV5rB\nzXSffnYTOvMruuFr8U5JCugQvP5GdXPNa2OBcsM7+ynTnmcA9UTe7ZZ+eIv6sbAiEzuXtu4RRyB6\nTbCJ9xDchB/h2RX5PvAOOpmquN0DaE+33BeRtFHgnBGI3Po2fP2oHAe3720sCoWPGaTwenauDmnU\nP1s3duP1IHO2C4CkyvtxsenKXe+iOD6Nwo99Tl9nlYhcroyPs3bBAHBmq69Q/doL4BkYcgj5eXJd\neCwfiqpUisYKo10c7GW0mv7W/Scy9AsM3fISn75wJcplhfMMLJ+szPmYEJyJVXIqv93CsAijBeoK\n9Iv0683lHdgyiO7U3tT1MUkam08POmDLetvWp30cZ+Q8TWI8SNoocM4IooA6Na4+zcsxUxdQJ3E/\nZzkBTFzLRgdtqzIZ9S/i0RnuJDEUzDjY+eHHxadLBXafq/A0Cv8tQZSSCbwjn5GQFOmJHj1I9mmb\ngUC85aOMSg8RwHZXI8pEl22WqTUCJF/6ImW757p3VABX+HYWxKLf4QPHhOZ8MhIYra69KU2WQEEc\nLs6a/+24r/jgJwYfd1D4gaF2BddbKPwVmVimaTC2u3Cm8NklDmMIYP+YOZ8KnCv8fDo0V/j5tMCt\nDwVW6EpZIGwbQf2wHEc7/BY/oNYFQCWIEFAuAHp2Lo5p1D9vfK8ofEnyCr+L2jdR+BXtRXG8KWIk\nEf1xIkpE9H0q7ZNE9INE9LeJ6AtE9MNE9Old3K++IxjscHqFMCxe0teFyP+9JRgajBI3SS2de9pj\npYGYt3f8uwU6fDIp2f/xKQ0z2nb7UdP0WCh6chbXcbBl5rQu0897OHZ588i/FVjGdYGf8d8JHm1I\nn5XbbXtxLFOAu0vzuJSSWqMlKBfVn5UL/szYsgoiNPpb5t1JnSA9Aj1fDW9dfaG/X3NzounvqLEB\nXN7hE9HvBPCvAfirLuv7AfwBAH8QwOcB/CCAPwPg92zif12lP7lVqek4s2BXvXuf4SKIBns71t5K\nZdhTi3o7XP1m9dnhjXirvvMg/ZFA6i/Mp/73+dj3wJO8UVmNr964D2miji65eT3r2wi6y2A33DLz\n4/ts8g5s0OS8TgQi1sxwUjBD5uWv5fWFe3kYyf9B/QqWXd4Mur6uWzOm5Axo9HneQ0rS+tMb7tdp\nsh4H3fzd0S3B+Hd9X8AXzcvK26L0K/6TW4hXT4MvKXwi+rUA/jMAfxTAn1DpnwLwXQC+g5n/Qkn7\nTgCfI6JvZeafXMR/hazLkAeBurRMix3L6q88IHGV9GfzRCA14Tq3IGYr9JH7F8eBd0b+6SbNTNTX\n4UvkIpPTIzrishFOD7IILfXLCFqWycgFstKPnr/a3WqXlx0vbtDUGlf0SOcZYJWmTgkV2H0sR4Hp\nMy0/IW/L5XIkP6H8n6cdQVrktjemJ6bR5+W4BRaiwECJS/ApvSkhgA4y/v36OHvHjvUueJ5OQg7+\nY+vEeOp6adKKXJR1Vuav5DPrS5re6t/oCK7v8H8QwJ9l5j9PRH9Cpf+TBeePSQIz/zQR/QyAbwMw\nVPidwn3FBUIWyT5NAs4EZQcL6i27mbdcE40faO2zFjMKyjhffGdR9/hGcJvCv8K30YIHRP7J5wq/\nryM1d8CedXhlbxaK0uhsId9TCoHCv6zs0dP6ynDPueTnf/0elj0xCjfK303hH2Tmr9SPZET8131b\nJk0Zo7peyTqnJygU1T8oeBuf+Neb/UI/Z2vsCoVXDILdg+MjiDNg+9AbtLHC7/lWN5AFj19/8mfb\ncNU8whqzHWwrfCL6DgC/A1m5e/g6AB8y8+dd+s8B+PpT3LUNhMfDbwHkCKmKbFR+B+8TwcyKdRv8\nInTWKtdlorJ9e+07B/x9NOidcERXlH5GW7gI1x3+OU2eD0Jf++7oD+hqC/k+L/s+X5+B/gTn2eQd\nuG4oVtjd4TP3G7Spwh/zf0fhR1HsIpmSsmdpoqJ02k7o4ahfUf2spLkrd7jAO6nKvN04+NMA+cZ0\n/urcU9rIG+f+0UOPR89ZnwZwMVzYjEtdW5epncOWwiei34L8jP6fYeYv71TFmf5WXHjt+3ofwzV4\n1mezD4Enlcl44X9SYj+Gj+EecOvC81YK5pTuMV1Tijf6s7vD/yyAfxDAT1Fbad4B+L1E9G8A+P0A\nPklEn3K7/E8j7/KH8FN/6n/Cu69+h5fESCnhJSV87bd8Br/ps5/ZJHEfInbp25ImXW1lb5O5vd3B\no8G45bm0fENUl5W/zAvrGtbjPXPL40H6Gpw9Lohhdru3fbYrd7W/Iypofsl03y0v/1dv9jpavVue\n7ReFfZvBiP6r47HipvQo2JlHK3SdPbffwbfDl1vlqZXNnylx3TFqudIQBZjyLm+mrHxX/u7n9AS4\nysviyZSL+ZVgaYzmsrjlERredrF9b27o04B26jkfx3AuBXnVzZDF5U673zkvBAa+9NN/B3//c38H\n6aOXEhuE8JK6poawq/D/HIB/zKX9xwA+B+A/APCzAL4M4NsB/AgAENE3AfhGAD8xQ/zZ7/qn8DW/\n+dfhlz/4EF/64EN86YMv4yWl11koyiLZp3EnHOKtb8MnXGoySr0B423QVBsqL7hJqOEDU1swMi9i\nX3HUPN1CRdk33pVaAOJLbBMjppcvO9kEoihpXb0oVXi2QqPmAzFQFbcYHC1fL8LWGNNGwkKbE/r5\ntM8BlPHwRtzrbqr2leEqvjPjdIYu4sNcqc9xrYLM54QcbU8HqvFoJErjGd25cNv8yItoVvy8I1yp\nCE0feCeqm6CvsWWl6ctyMV6UUcItb0cezUt5gj4wRnT2eA5QOF+h1iLuvrcx+ORv/Q3gr/8afPBL\nX8LLhy9491Xv8O5LL/jSf/+3lvqypfCZ+YsA/oZOI6IvAvgFZv5c+f1DAL6PiH4RwBcA/ACAH1+9\noZ/b2aHqdggXavmMJigRbj1Wev92+NoqzQopf1IxCOJx293hXxn8K3zTijFq3hsDZzvmx+3w4x0M\nF4b3dMblz+B+O/wY1+u62K45x8YGX4TukTv8a7h22KnnMaGFnY12utFufiRLDKUAy+ca32Nc/rnv\nKPBObJjGdEuQoIpPWtvhn/pe7wG49WtV3n3ZxAAnNnV0X2zfmnFw1s4I7hFpz7f4vQBeAPwwgE8C\n+FEA332Hdl4dogXhRj1v8DwTRBO2V0Dqp2JEJPC62sygWk0fwVXXMcaYtlrG2UBntE1xLVPW16m0\n+p1BgLvuCC60uTNOI5Dx6BblTTy3AIlRfgr7p3S3yECUf1Vmduhuei4fAZvdoy8bKNQUpGl8FRnQ\nfq/Q43D5+sMTlPZfTYsMd1GUCSjvlrgohVq5k1yx09lrcpQ3SK6uwuXnsaknadzavAI3K3xm/qfd\n7w8AfE/52wMtK09wrVduSYe78TvgBvIgPkFX2417k6aVnr3t6mlu/qQ+fX5LP5Lb1+DH6Ja+L6Pp\nofrfvLwGkZ2zPo340G7ik5OZtovtxwLDvDMgqVQWsatj4XfFfrwfOcbLJz4DmX1U+5oPZ2Vz3h5t\nI1xebvUNcFulf9c8UILDhKj72/srvB/1q3dZ8+VG93Uou/B17eQ/CcBz0BUTL6bP39L3ZsyIDZ7n\nei2NxqXDU9OvTaCniqVvfLtfq81BW3rB1ItxLX/jitVatTH83wpaf7Vib4JsuqsUZU3WWsYUpbB/\nNS14Br/Fj6sKqdLm0ileCM+MgxEp7eTkhNARHyhTqaOGVcUhRovCbfzwV9r1ZKiVhvmCbJL5yPQa\nOjjLz9PI/P3pGGG0fJiXRVB22uZkzezcLaXn5GaAKEdPY5BWMnrZW6F1UMq72/V0DOqSBP3y5Kl4\nIeX3LfadMbIN38rWfQVHsOrU8XC8rLlnY7uhi55K4Xsr9DWeaWu/5TC9s2ILf+9GX3u+/ZY7fU1D\no8MOiA4GIXypPCjP6UdBO4Z9Y+5WvV2+XuHbKPBIVQPewqntxI2N5HWZtAEf6t9Bboz0Dj9S+Htz\nqOl5bfBdA9+uxSMG5OOE/d6od/FNd9qLZc/aDderBXq0DPc7ahg5a3THO3c/zl5hr9I+6kPfxwG/\n5MRrMH/kEmIUyGcHdP+8TvAnINM+duPR8iTNrLWh4ODSBH0qhS/KdLawPqLNaT7B3drorbFL7TY9\n+aaKXkALWEtTR7C6LNYXnJEBWvsP6s6zX4MfoyP9aAK28nPC4sVo7Ugf6B8dVcVOUfATVCPM0uwX\njLN24z5wof3qWBheuCP9qQH4yvAIOoZy8sAjfZrgihSnfHp5j470x3PYll0NvjPql6/vy0W0lZIh\njVJen0aeveJ6BiaIz4XAO5I+Gw9fptIfrM9X4Ka35T0OnmQ1CCG6YvGVA695mTo3+MrtncCo/6sX\ncy63O8yYtzq7LPms8My0va9wL55uXQa880DeeiGyK+8v8m3WH7XfX3S8EfFZu3ITV77f0JOn2uG/\nurLBmHWzweW667/+UpDI5e053PLa6YW5Ca5vjfp65SggGr8zt7xIje66k10B6Vvkh5/zffkJXeV0\n4ya3vJG7EekYB5aetghYuqsbD63dTNY8lGAqbdyvXRwbuSkxAHqw8bQjE7v8uRWnzhtdCF7B09E0\n4enYiA3GKTES2S3XKPCOx70qK0NcyT7WWnUTZZ65EyqZns3hFboLfX7d6H5P2pnnNaXeu+WhTspO\n52/06akUvlevr+W7m4UhmEDFH8JOUgBMNTDKVWuromSN4e32PrVlJqvklWKufGDl2gNUZRf59Z4G\n3omMhGuU79USI8WnV2O6pzf3rV/8Ce191l07RilP6BnwIU/2FoBHcErgpyyiTYiEfrkSsLgET9pe\nQtDh8kZhLO+PgvUW1vp3H4ns+Tk3fOa0uUz9/K3DExss0fi2SHukyo1Q24BlOvLeDEb9yoFpZuVm\nm4rISG9zJ9O3pRuH9Hk87OiazZsxL1u6LlMNeDR9pBrenqNPpfDfSt2FC/Ugj7Wep+s37JOxCPP3\nd2+4wxd6jrIz1GlAb9HqegdR6AtbcTB3fUsTKd0x9K7ybLTDN8aOy6nK1cFRniHO+jTLm9FInOsm\nZlCy42F3ATmdOEdL06cDZ6B56B9d7NL9LpCd6PcjjfkdmTh7VDN7Nj6CVTl4R3RZZnwfp/2Y7Ch1\nG1TKHkxGzn25Ee7VoJcjXAesa50vJ1ECIxqiwDs1cE8xfs+jZc5B6GOey/dMCUfBhEy98tlCFavg\nWvWz00pbfXgeeCuNP4Azch64Zj0fnPT1tU5jHg7DyTjr4+v3/fzE4CtkPB4Mp3P8Vah4Gwg3OoHi\nXD4nupFZZzI7MmlOm108ZTtHw+bTp7vm9vGvtMs2bVdAn2qHX314B7dCH9jkdh5w2zN3uf3PeL2+\nzqDzq4e7pa9dRqJ6FAcx8eV1OjCeHI/mie/D2T2KmXuhv82vIQq803jap1m8zSNi5O6Y+0Lwbzy5\nl6vnLfV93ADdx2eQeeD1bumPAjDd65b+jIbVG+PGDbRLH+Pw38+9WeJ+9fEk3A5/dksfEW/b3Inw\n7UL16c9HISZH/9Zr26rHg+RJneE6Q9KeanoDnkrhRwEfHt/o2A+/ZAeLLYZ5y80iW6z6yPAtL+1F\nfp92AopSd8pm8F3Xi2IWqEPkKT2rdO+Cp1sTNhrz2fHu2Rg6M6CkUVsrgsXILsCx/25bHKLxWOPP\nVOmc1h7j6n3x9fHxwBK8A+zIxErJXRlb5eeZq+fVPJ9/ZsQKHEXI5XOFzpkheoX2+Voyws11bYrK\nR/PnCrS1r09Pbq3UdK31IR6zcA6T+9yA51L4ZD9fp82B/7jkBVuvyu8bCG2tPlukPZ2mLFet0JyB\nSZIfWaXoI0s13MBQ4T+YJ3rczSKMNtG68hTT5ewFA1zTqUutinrw8LPuKIJWjdwSVXuh0inG2a3x\nIm6or0fYyBKskfKW8Ag5i1VS3N6s9XvwfobHS1bbDVsMIoNnNLaNwhltgxLdumLLRVEApTARdXNI\n+ne3uVCNfsBE1iMGsSOeAZH8iKYQf1kLmAdGQaD8d3XQUyl8gdfc6Ypiv1r3crulcnTs8xYQ7VCJ\n1PGzSvO7FMkPDSeK+6f7H9OzTPol8Na0PXK1yknTc0ZX5C7l6/nHJMDgfQ1ldQlPHKB2MJKAfkdw\nKx9vqU9qkIWvz+CCquERZIR9e8+O9E05rB3pR23Hdc77FR3BDx8tcBx4R9LayeSNR/p6vrkjfY27\nvkDqwpF+7gt34+LpmP2ewXNd2nsj+PiCU4PTy2CvQ8YrwPhy3mv1kt1nXGicG12wml8ufFvQZD0n\nhR9DKFNPP1pn7o13on+A5p7TbRSXhBn1lv7ZpcEZPOUO/zXh7N51eJNVPvm2wDty6fIZdj01gI56\nxGAD77BKa5b2SuAdBDsE7cc/pGcBrvPfjmPfz56e+AazpeEsqAag+qx4MLwxTVSVuLRTaQnw6500\nD04OZvTP6F6BES/El1glbOG9SsMKbAW4uRGfztcnS/emyweCGZXxYwSQeYd8VG7UjpbPVdo8eBnv\n6Y3wjY1f6YteZ68C5xP3gG+9rI/7MF8jbF/yetzVYVtnB55a4b/KTqUOTn8Ua3wfTZ4+1LlGY5Kd\nJDff0+MNLekElInR7tprn9EmdDnokLCk1uM48E4C4aB+olaX8kGXV99xcZVnOVgNt7bMJO0JS4kK\nP+Y0eLp10A/VeP2oMhTgTUCOSsdsFuFkFgaU/JxHKl3L1gxmPEyb7I14Uekza5ZcWb0/7MrErI9X\n5CviuZ4X0t4Bno7PLXQZvMPAO71cUlEw+hKalq8eSU/TmcyNcOlVNQXliDnuS50HfTsHZ1mL8O0C\nFTw9P+zvujam/vh+tIbUPOi+qHkOO9+Hu4QTeGqF/xpwJsdRvrLlLl8EsRabrNZvu8OX6HMILHXZ\nnWWhaw/ydYCX0Q5fl9fpJwStEX6HHb5ua7TDB8Y7fGzu8A0RJ0TWue3GxRtXmu4amW+lDUf/Et2L\nuCL6WkL97/5wxx3+Ffla3uHesMM/o2vK+wI+HG01ThNwHDp9Ua5v3eET7Oni4u54dPrWlKXslG+X\nN0YcwOdeO3xdj6iF1VYLwU3T5nmf4T9oLbgPsPn4GL5yWPGc/YiMhden4mP4yoeBKlqre6tMPkym\n74R4sAt8xEm0PrGQzXx7jKfDnO/hfbodfn029RyXeAfQ32jfxlAugjPedGPfgXcx4/pd+ecPb+b2\n0nd2u/fOm6tlGNNFNd9vXmY3bH19AftsfW9RbDeMvQ9+PjGZ3cS2t3zX24xouAd4ft4T963wGjf1\n7bPucTld/nYPiybLcX4kJ48NvDPrVx+Hxbc1CbwzuaWPEz6swjjwTgG3nkfr5XwNbQesuq9U86vT\ncN79XzBknkbh+wXNL3KPbjcSLnG3iFyixA/tFpe+Zwq8I+2biUOkhK1MyCqMTgGhCarBOUnPs2Ms\ntCv8uMx/iuVL+yH7iTqSScMLKezL1G/rk3QUOIQAMLHhLbk6mv5zN6lx/i53h0FFAPi+P0red/HO\nSt8iXxXU4xjd3lkwmFvpOltXxvO4T5/h0BRHc72rM0nv5tKE3gYcGgPajU7PkatQ8YjfXWseoPrh\n2g90W8QjbmlZXFiNh+MFDb4vwPMo/PrpzJpXajdKJ4r10epCOm1X6jJXRfqWoCdGS0Ndo+tkGynv\nwYQaTbR6IjDd4T+OKSO6joEFPvJRjvDqyvpGdknYo3G4aMSLtdCuF4m7yOmNQLJ9eQDuW+ERdMx3\n+PG4dTjuRMNrKfwleeN1z6ZunZnREXgCtY3jAl2LENJQDQAuytryvd/MRrRkPSAnIHrjAa0TSX2/\nAE+j8AVu7M/FNi9a8be0WT6f5Uif3Gf+bo+NZmMzNJwGGWIkTF10hjm3w5jepmT9MWxnaQ/qT9s7\n6bOvQ5AIY3263/VHdNy6s7nXGCjb8e64b4VH0GF3ZNbYWdmg+d3iLTRMNzWD8iZ9IkM7awEAMFEY\nvXQFt6erpoty9I+MYNefe4xzxNM2VvF62dcP+Kn40k4R2roDNc8jw2YVnvfS3ivCq7j/Re26z7eE\niAb/jOgKm2Z13orvM2i3aKPbwCv1L95QPqFphGt843de92N4PXhGOd+B+9L/iAtu46fZr8n59Wfq\nsadB+w7zvd3Ul++2zs74PM0O/62mxMiSninjmrdxPBU33lynGOWlFW8Ezb1OWZBs+8oQ/242tFY/\n0QHeyNSd1RFYeRf7VZ6NvFuse5uiJTH4Xfxe8IgXHqTejpwnZhDnyAhJ8Txx/j18XWh1UyKAJj7U\naCcFMxp2YDQeKeDLLu5baRjBjI6r8rXat1E5ib1wC12J8z2P0fgn30Ytn5+dWQAAIABJREFUbyfH\nlBaXftDgnfWq+Gq/fDkaTlpr/JKaJ4daW2+VN+GNx5PJ6gPkpNRc61qfMn0RLdpN0rrlWaUvfTaf\ni/A0Cl8LzooP6T3bzTqM+nRlVdksUkeU1+nznhVvGcKSgHJbpPHCW5018A5bWmugjYBXIIC4P8au\nOGYnAAt0X+VZ9W0N0v3EzemTWAOaBnd82/n1b5DLlR4bWa/RiJBW8aNm5Jd6nDc5X6B3YGyE9M08\nStp3ZWJ6CnUnKrfXsYGs1ewtQYqNAz8F9M5Rr4cjudd1Vuma4fL1O9yOLo+zlZcvsu5Q26zcCBH9\nXGnljp/+6kpZYqM9vuoDlzls53/t2UVlDzyRwn8rVTdq94ynmfG37fCbfJZvb7nDRxPcer/M5LMS\naja0GmH0eDleb5Ym4MoMvbrDx4hep6BVjUi5ehq2Au+cEqkVe+P5KNCIbqsuHhR2RtEePlG8Tvdg\nPEI8jzLmN2Xi3oF3TnEulruVriozUzmJjdPY2F+gceGOymq/rgbeITNPinrduDszpi2mwShkx8/e\naEELcBb0w64zeXNVd/7cytg66/C8z/Cf4SbbEN7KPPkYHg2zkX2UfnoMvFfEfgxPAgO1/spUPCm8\nJRsmRtcOPM0O3z9LlN+vceFl37RoN6BvbbcePr2xfaN9PsN8494S141mxAzfyrHkI/gS+ezqPGlX\ni565pX9CEwW7lOhexDmdjdbetWd8uqT9j03bUdmTzqzw3x34DPF0m8H639vCI+fe2Ro2GsN7Bd6p\nt7wn+e03AFwPvKPLj2CnX9E6E9cdB96JPq9CDXuj8GTZzyu5nwd63p7R0g5j4tgv94KnUfiaA9rV\n6NG+uiNF19yzxoF3/EK83zar768TaGhMyzxgixXe2wPvAGuvTlnye98Ekauo7hEo2K69ocEzpqnp\n+/VXxjTF3QfeAY15a/x/T2T0bI6t0cq2zSEedmk9L+8BuzIxK32zUX+D/N5KV5nNcVnuZWc0j1f9\n8M/KarqGebrdIC/uiw28Y/vRG8BXoa4btvEs1tGcD/gZGfAVD7K+aUpfodVzXxG0K59Po/CjwQ23\nBQ9u16dH+ZFCvNa49b18S2gBIVSazx8s6iNfcI03TF8Y20fwhYhwDPa2dmydgpJFZWMRv0fgnSMw\nsM4WYb1Y3KLQl/i/cJeFgrm8wsvXgEfOvas7fOB2W2hNTgKFj1jeRjhW0gR2PJuWjQlSc9OXV3hu\nNt4iuuQWHqjrW2yEDALvlC1+TtZ4uk6FyavwNM/wY8EzBaJK6/mTOnSCJ8y/Q9tGoW7Qu9vOCp5w\nLjjtT2h/Oj9Kk+8d3k16RSfotnXaKZ4g3ywOHb0U5ncWuqLD49H5XdqIxsGYdH01bUdRv6KFr+eb\nxTnhFYK6QR9pgEbjmfZxoZ3VtN05Om77hvkmP1fapkm/Rn1caVtkOcIza9PXCWR+NE7w7Tjc0LgH\n+ZjhCes4nqh2NMp7yVVErx2TcDha1oQvUPzWczlANUicw9Ps8E+f1Z/d8l29BRz4TRjLbHh7stUp\nQRDbiF5su78I/qA+LuCphuoQjxw6tU/J52Gdwivq66zSy10DjZ45veN2xMWto0fd9q3Juo66PdvR\n4W41j0jzsjSrJE3JvVzSeCpN/TXg7ELY16kV1efZmNixHXyXn5Mx4UE74bSftHOWZvqzKg8D3OEJ\n1OYcHfU7lG873YL1QdG20rbafXZ4WGSo4WNVTz946m6bK3qrB06AZ+S2M8vXPI/KjeSlS+fyum+0\ntS3sA9bTKJSXaB23tBK5LM23AA8r+Z2KcpB3Bs+j8J+s3WAOqry8lN4t8A5wO64bQVx49MUTdvna\nzSc6to7n97jO0pifSPMVnlXlHVTVirlvurkmzmgYuQ71NU8JVQaIDeKx5pbXeD+CM/6tXJrVSm2E\nLxzvgJe3wlV5uBeuVdxn+bPxzTC+SKdx5DgMkcHh22hywmTpOpM1QxXd5pZHVUn3VItrWoQv6qOe\nKyt0nYGmrbbh2onat/MWcVk0Ptssbv3T4zDAcwZPo/BHi9Kjb+kzc7H++kVbM7+nQwKaXKdPyy93\nJugbATVexL642YYfGO89nwjSOWdArHZ3UuhEmZ3Vi6ompSx1PtFo4Zt7G3SLQbxmjetLHWazuOgd\nWmxg2PGa4p+1v6LwleIeGtADA+recAXjUJndRsop/rM6c8W4IPonSs7ITkVInUztKPwVeZrSNMM9\nUvgYyZdqM8C3C3WtDtdFOw90uRoLoJYZBCKrfbA7+84udkp/R1C3nuET0b9DRMn9/Q2V/0ki+kEi\n+ttE9AUi+mEi+vQK7nsMyFXYbXVsBNzQ7hsre2+BdvlOCH3d8YIwqLPIdTEMor+rPJudLoz4UNvt\naIqUbR8YR9ffotMtVlFaXM/yfsjDUxrO/3S5GZ4ubRH/zt8VuCeuHvcckZYVLze39rXJyehPyQlr\nQ7eP5LjD/1GfVvpl+eLyh3VjZT+S0Vtlayz7MZ/6tvtyUgZg15Z7zKh4nL+cy4GGK5f2/jqArwPw\n9eXvd6u87wfwzwP4gwB+L4DPAPgzq4jf8ET7Y/gYAFy6B/MxfAzvP0SXz1rma1Lyhm0+OwTafZNN\nV470P2Lmn+/aJfoUgO8C8B3M/BdK2ncC+BwRfSsz/+QMaRU3GrgtPAhGrZD69GyurmY3kmhvdr6t\ngJ+65UH5sg5ojVLr7d3u9vL8qLlDsp68gG7sl2tdmdjlxX2JcADIu6YgbYNQR0/Bw2zmiH8+qT0N\nSOG6AqtueUs8ifr+BFb+W96dGbbN8zs9KyTP5ys7uQJkVuZvrV6+1T+Z80He7C7HCr+z7Lo1Q9Eb\ntdfdJyiI7uWWp9sCUOU5xtu76BmaymcrLvcMct1HwRWF/1uJ6GcBfAnATwD448z8twB8tuD7MSnI\nzD9NRD8D4NsATBW+uCB4Rjx8MgaKrtFDAOWzJDt4QHWtuIE+IqUQbsR1K+S+5o5VMlyfa79HC8BW\nkKLVQ/3Z4nZ+cSnGN/anr4pS3WXQedKXRkHPi3q5B9pw5Jq2TieqbGojhUvDuguahuMQvjSNP+LT\nmcytvnonosPjiTDdW+SvzKFRH19jPg4VI054PzBYPW6R2SAXB6FeXNUKSdYCPaZDVvj5sKBcZ/1q\nF+Py+uiaGtkuTd47fGr+3KhIG4/sXJZWtd0rwXM0DfJDr6OqC+P+DQlynwuwq/D/MoA/AuCnAXwD\ngH8XwF8kot+OfLz/ITN/3tX5uZI3hSpuC4J8T5jI8TB/tDvcb/x5Au8cdaK2NE0REdUy0as5CXNe\n+Tqk+r5K273gUH3xIIvkcRBS917RuC8RfiC/RVB2HfrVtjt0Ct817xNzXcSEZr/DF6VPCtcVWH0N\n6wpPzl4t/FbwljQMXyeM24OkHEUAojaY7ZwmZzxrOU+T+QLE+EflXxZkBRBjt18zorqJ+jkgOPzc\nuQf4uVyNFIOecRwtQZ+kRPQk2eETun7MYFdvbCl8Zv7v1M+/TkQ/CeD/BvCHkHf8IU1Y2Nh0R5Cv\nAQvWqOSbBfVezeORhzevB1P+vf16vgWznfA91ot7uAcBbScmdIWn5e8b8z+Gu8NIBrwsT6fwExhl\nZzA6V3o2uMuc3Bg7Dze55THzLxHR/wrgHwXw5wB8FRF9yu3yP428y5/C//xDP4F3X/0JJGakxEgp\n4Td+8zfgN37LN9xC4hwWnj3esdpTgz5+lt/LZWcKrBT2dXZpi+CWIYjoybeA201ik1dvGduDwcEJ\no1Tq0i65aKHngdAa3VDWt4H144UIzni4Sq0/3lzFc2+D954y9hpT/GyezWBt7AYzj61cFdFux9Ow\nMrtKJwVps/IeRvXP8IbTinPwHeHArbI2ouGMJnt0n6mJ6JniKZkf/h9/Fx/8b7+I9FGe5C8H4eVl\nvWc3KXwi+rUA/hEA/wmAnwLwEYBvB/AjJf+bAHwj8rP+KfzOf/Xb8Gv+oU/hgw+/jA++/BE++ODL\n+ODDL+MlpVtIPIWRImL3afNuUV8KDz/PDp+dFeMnufk9uHgTz7mCly8G3intRXB151GVt6vPzEh8\nrkh1RsgHMRpO0nZoNS5+ug8Kt63jDIWLPFzyw1f4Z5e1Qkx3OO3QcItM3AvXre1K+hnv18ZuoOrY\nyRDc+Cn5P/WdD+bDankPs/pazjy+MPBOKS+G760na542b8SP/PNt22U83LGcn9MWB9dCv+of/geA\nr/vV+PDvfYj0knB84sC7DxI+/HP/z1IfthQ+Ef2HAP4s8jH+bwbw7yEr+f+SmT9PRD8E4PuI6BcB\nfAHADwD48bMb+h2YTj9OJdaBIOrkyC/6PR3ngn0G1rf9OVS/DrqjSarKLv8aKPegHwTcFngnt7ee\nuoBtMPl7v+GWR6QmpObLrJ1AjneGmcsOBdzjqgo94rlKZx/71JdboOGczoZpvEsZBUa5r9xflomR\ngnkjWFH4K/TNdrZG4ZfLyWajc0Hhr8jTFFeAE5g/CmvKctJmgHMXegUf/W7fW3o0CjatzddeJ/g5\n3vngb3Rrd4f/WwD8FwC+FsDPA/hLAH4XM/9Cyf9eAC8AfhjAJwH8KIDv3mzjLoPzSAg2hxcR3QHH\nncC7y3QGkBPO1QMO4ZWvs7G/HyvJi2Mgk8qPYZt0Qf8lD7DjFp2WDhTwdVo5lJX57pDcIjFo4ISH\nq3SbDcwGnrtP88sycT9ce+3OFOlJ5dOxawbjCH9TLhZnr/Bn7fQ0Xe4XxWWaso3wzZR9W3tulrUR\nbXojxFF6+y5rYXTvxq87oaJ3xsCuDtm9tPeHT/I/APA95e8meBWXmIe3sEDAEyn9XynwPlxCMrBJ\n7vvWvY/hbWBdTN5eoD6WaQtExdF1ky/PE0tfgfThtXzwpzQg1sn3oOyZZNi7GvpAKeb3yKVtAe8I\n/yKRe+UnaCK6dJAbHzMAcMFsJrREzyF9sI5zIhVNoLD+zC1P++03fPv86+ZglYHy34lMGDxR359k\nJX8rI/DWADVnuKf+8Co/iiXR1uE5f6K8W/s1oycn1P9qfvcYIGcM+3gV/FyUtv0dpbAPhe5uDXG4\nfPa94CkVPpQL1CMnomZ614wICjGIAzruQF8+amoD/ZaQfXYb3w8ASU8ooPqZHqMFIAq8Q4h5xRy+\nrW5Oo2vuIs8IOeiIH/QDEsEOOJQTdEqE4ygLX7nKfEzGX/vha9w+7YxGWeSIepxErBYQS4deWCrv\nnZ+1LjuDw5m7tX201x4z5vwQPFHf/ZjeCldlwvfzFlxb7Q7ayH74c+PwdOyIhvxliFxJWYvTro1j\nPLquqR8Y1NKbWb+kvi9DZX2qvxt5SPXxXDQX23p1xs8z8LSJPMtamY/qWxuyhrQ5mmk8ypqo+ZYq\n/pPnhTrrgng+ncJvgnIfv+eztoZ56jO6c3EP0rrxfUMIrVG/a+S5cRKl0sDz1OO/QuNVGO58Bjt8\nUobMiiE63Y0v9lm3Y3ZiGqfCHe/wdZlr/OvkQu0+8rFiTjvDPRrvtzZ0BZ5th49H7/DZ5kfzfwlP\nULfWiZr9/9v7/pj9kuquz3m+C8UiPyoU1qZIUSpiQxXaQqkKRJKSxrSxmtCoCTURU2ubVBNLNbGB\ngEbFNFZNMURiY0rR4I/4c+mGNo00VEqAiq0gKm6hdNk1u26XCsvu+77P+MfcuffMmTM/773Pc+/z\nzueb9/s8987MmTNzz5wzM3fOeRZa4fuT3XAM8PtrrfCJ724Z4006Uit8jR+qWOHLZ1ODucGcFoWv\n5M7LyymxFaW3CjbYtIvpbmbYlaTTsHCaajoWRo18NE0UC+/NoZdPP510lkx4h2+JPAkCCy0MN7fC\nPyWKD5tvZBW+JmRf5E7lluqA2Iy+pUslT61GTZ7S904kIzwt6+oeJvLjZ4yH+On5Ch4xPQ8To2lC\n90FXvz2l79PTOj3Xh9HTz8N//JR3itapTunPmegUHkdYFHNO6eefHXfLDFLBnT/k8+PjtvSUviyf\ny6/Bp6HzM3A/vmOM8mcMDEKX66UxevBET+8D4zkgWJ64DvHpiHsI+zJ3ncIuDL7zlVc1vvR3iKVr\n98wQQoeYUAzb7Nwn0uv0obwBjfma6hajdbU2xqyUJjSsHyYXNHvDgBfR6YwKhNVDnlLx+ZB97n3X\n7nGLpb0OKewrN0DlPUvTuNZ6feEqDZ6T0r+GyRCvO1AKahsdzBgvYHwWmPqXt8HzbeZlnMIf2xXr\n33RfcX6lDJjReTuidHifa9m4gBT1S8G9QpnX5Le0X6L3KssYzjurW1P0tTI/SHG0r2wcEPYcGc0g\n7gOnI/i1Y8LnzWsX/PtGymIEXD9M393FVNi1Q443R2TkfbZciTYax9s0Djm//tb8MC7JdZpPLNS7\nw3/88XGdwvLXzE83b/CnBiqSYWTvJ9KVe6qs+f0Z5pHGqrHuk5fJ0PEMINwg8mnyniOESswZo6CM\nMm0fDcBYUHzX7gmNEj1BLr8HdbvIXMxIs8E1+eLzZz1E63KD1R22ND7tWNVO8XhJahsx0TXO6GM8\n4KgG4An63CnsSXkQMAZX4fVpz9HrK9Hno+4zlp4/AVDe2zI6sX4J70W+F9zz2lM5dpwMaGcwiulU\nlpmUO0S7lehxUkbks1PGo74zhMl4OJknMz290TAxXrx6/M+g32S7vLpZu5R0xwOTXsujeCZkDBsT\nUPpqmkypPuuVcqWluzZOsu3XwxcKAEB8vJAw+OPky7Dyrm/T/Z+aNEls3uB3nAa5wDt+XqB0WhnL\n2hJYKSjSuPU62FK2CJBhRP17rm63YvYWUgoPS23pc3o5uyjrL93Sz/VhjGdJzy7yjD+5K6FTLwZp\ntMoE7+NGGq31xtMyhbPPLrWlPxkUK9vk0fO29DO8cHtKysQ0ll9Nc2wE409u6QPcsKbka3EZU+rg\nn/I+3GLB6JtPMRqO99Gus4vWwDubOrQn0X/t63Q4+cHBTT1aSn4b75yJ5/0cMtwNowr2zHsbhnXn\nYvK1BJ3U+Nsv8m0pae2c0/kO217hr/zMU+Qpk+eSxBGwAsTbdKBIIAvEhU27eyB92kbae80CHpeA\n9Sv2g9K44zTTyXftsCELZhNpFxD+Xja/X7yzQROvMRenke6BcDwa75rIKmBerqX/pJ+4dP+b3lOm\nDUfqeW/BS4UIOJxhVEf98E3Z78bnaMdouBUzDa+oZD4+PihBx+UtSXPjoaRd8nnE9MiYpumrYVy7\nzyXBzzQciMbfsx/TjcFBBC8Y/fhF39qXHHZ8ZN3yZjZjkwafK6tVlYE3Y5pum2FvygZ7mBSaXxb6\n/QqokdjOhNGI8X7g822vLyL8VgXese8Nq3iUj6Cxz5x8OYJk7H92u577ymoKBHaCkJBPL3iJh/Jf\nEBgD7zhlFbTdeLxyNmjsdL+c+siyfWiiV0TTtevP+AQ53vYlRb9VJuyrp8hYXxHpyXNaWopiH0Sy\nuJPiNOyhyzFN4yBxcp6qJ86PR5PVnuLZ5eA/RM35CcrABrE5KtI3jo84+42YJNqOtFBf8LzE+tjX\niYA7E6TpnET1+vcMNmnwR6w88FLUKZPn/GuSZaEGiVhghR/NO80fmnlsRRBIZLDiBBdpz67wtRY5\n5ZFSIrFDX7HgMzoNx1p+y1Uqiimwh9ALDf0XC7zj0nLBmDw6W17hA6vrG7XeqEVeN/COC5ZEkQVN\n7roprVBWgPB5JMu4dmorfDZeFwU/RDDULVf4sT4Mt+YNIyV/SpcTcBOfdrY3+w5/tQfViLX42Er7\nbguWmu2f4qnlVlbAfuRnH1yeFnt5dvtFbtk2g3I1yZk8mMj3Smx7hd9xNuRO5ZYKfCxvi8xKnlr0\n5XQKX0v0TyRr9RnvPZu++l7klL59tZp95x8LvDMFTZn6SSOV68OS09mynhifLXXUYk82lMdX0NPT\n5bPPLkMj9fxaTumXjoXSdqVO6cs69PE8vBunYTAtiqnC/Cl9gEh4+AwL9fAkPi9vfNdKk9cHOezC\n4M9tZI6uF3iHpYWuWfwhU3BvCV7OhcnnfGqX5vM9XEVohO2Y3nKJ/kOLop/fRzx6WEjdjj7Vv92W\nFq5OkX5wn7IvYhMNldHhLWZkkPP74bOa6ucRyVr6L6XEgLxM+PxGU6v5ugRoB80cUq5mxUhMKEL9\npo1bP2+8mkSakq+0XXJCkqpf5dFZ15XEyxtnga3w+4U/62GpAHc1xgARixHDlORo+Efl0sbzJg3+\nqWxfcnadyXNpKkq2R1t9TLqhPFzuGJkOYhXRMg69KbM7KFNLwrBAGQA/a2PGr5Mh5bAnaodUNlkM\n6og0LreiE0QmRZJsjzaxEJMFvmRy7R0+c9vKRvS5b+9NViY4nbi9l4oaU0XaOabEvT1tkwcR50S7\nQgPmp2efnftf6Ssrx/Hn54/bskh72njUJ6ui3YI3Zwxl5LrYlgaPGKjWo8lSpVxp6XJi77ULftvN\nEFnPncqHa884LkKd49E1fFIgZ+FB06PYpMHvOD9KJkOldEi5agq8EydcTSi26PWD8CTSUuQjiS2T\nxJIy2k6CZ+Pdd06wkJmgzyOXOXJV8pQjXHpvB0g9k2S/lNA2kUGiyLc2uecljfZM+FhIV6XfiyUO\ne908n4gL5BfR59chb3PlqnRcR/THmDzww1mK5xUTABPer0E3+B0jSu1njZ2N5tVm0wvXnSIi6Wis\nyAWFvWYnbOPkVZo1Ta7qY7E17DkghAd9q+Ap/cJ8tdjPmnxZpNo9Zz7L6UeNJMLFa47WnPT6vNOm\nd65MbhyW11kOPhZi4zq2AaM9lyLdMPOEPrA5gx//uc91asunpZT3JYHgbxFq7Rv7pNItj6YL737L\nu5vZrkoAnI87hx9AxhpQPfBOQT9EzgnUtJm78CTllDSDz34rXGy01vafnz++lNq7W945kHsFMrtf\nEm554xZ+Yjuey3na9U4vP6WH8lnAOuMgMw6IxuA3sl4MZJZ3y2N1CX3BdYnGj4sp4I0s5toXW70v\n0YJNGfzYBGY1heAZoOm2e19kH8y0bxX6bs/jb0uBd0BTcAh37SdPfUGxAZQLvANWzqA68I5kq7XP\nvHa6e+wzOjN3Soim61SwkTClIvAOMcOt1jH1teSDhk4f76dW/Nk+9NcysRZEZSJbMt7fLTj7OKpA\nur+A3JqvZJIVtfeDfLiVvvr8mBynqipxoQ4mjhm+ZT5nJNX80CcdXJctbu9l/Zk1umN/GtMiHa7d\nib6JtaGibZsy+AAG5k8zaJMrJ/HZV/j+jD9GI7gXGCL3HdWBd1J1F5eP0RkP3KRW+P6kNLfClyta\noprAO9NqIKPWA0Uh+1nlrRBa4JRsvlh6X+F7SLZ7gRV+ygiPgXeGQx6qrBfyWmLsWxY3Md2hZFTl\nq7h8A0is8FG7wo/RpXRo3dxuSw6bDLxzS8f/xeNU3hdJ7Ey49sVtHJfSjktEfzY7gKI7Ww7ubW+F\nvwWjcEvhuc0tkE/mtWEwaLzfyiPQbrezvsCqe49eX/y+TrymzY62Vob76kJxSYoF3pE8lD7rqaY8\nv/H0eOnFJoK0L+OVD6qULl/7/GJpsd2sMchUjpdhgyn6+kDxIklB2yBLHWKMxQnwyq9oV3yvHhPc\nB6axzMe0Ni4lz/bPP6k/J2bLpgx+zL1ijaA0/tZJe+Ad+wDn87eVwDvj20PFiHAjo9NQyjGa9tqM\n99uaPK+f3LOWb5S5u53+3Kd+OVngHaaQAzrM0IdKwX2Sx3uK5xh8pRsZoAV0021fRvYzb0A3h/QE\nan7gnVywnLGOiA4zIm+cWJoPuaVf2i5PJZlcEKGY7pnyLAmpHzR3Xr/OSTqNdy+k4U3mhzHnBd1x\nRLT7GWzK4J8Sxhh7MjKWLj5j6ZcCOzn1w2mqeUQ+NZ3f85b4/vc2ez9N0tqKG+8zli7v8RVzth8S\ntMvtve0rW8avQyqXWOCd8Xv0PXz+MJOnqNMZk8+kKvBOM07n4bME8iv8dHpR4J2YLGI0J8j50OcN\nvjVmMX50+Yxj2lUok734Ct+o35eANplItZOfC5oC9FCSBl+EjJ8GmYGYxsYM/qWZ0X2htPdrnlJE\nlzTr+KUkpKoNXua8ElpikijtdEAnocy8eRXi63sq8PZeSiaSCruwjjwTC7iynRBz+myJOuQqVXNV\nTS0AHGp3Vory8gmi0fnj9JILlEr+ahHfeUjnz+27jROZaeblpSUrj2BjBl+cqsyeUO5YEjldmd7I\nTpfR6mo1+nNkosUgxIrUUqpRjOPpfO2kLsITyLHAO1rZ2FUuf07pz8ES43xPxh5Itzk/FZtXhwF7\nrwy973JeOyX1NOflHi1U4AWCUD4p8j2F0n7XN+tF/RV6Q+U/d5ofplpINmXwAxci7eZidWUCmojP\nlDBdAgjw/FhVoaRYb6TLqH1V4aIW56OhbANt/97UniYXt9I2k+s7pf+YGx6RZvBZ4B1xkC3lshfl\n2SHGO0HjUmYpr6cRO7P32Vcga7rlwbgDtPF6CCiS9WQ9Wv6CvJ7up7T8OFc1NdBVRZ0AyneJeF3a\ndr1Sp3TLIz9xoLHgGy4FmzL42ju4WmGqqi2i/OyWqIv6Z7x7Wv45/MV8Nk+Nqb3TtUxPXdt7WuAd\n0vvKAE2O+ArNJcvSmEd/1z1sPM3go6zNLhqgM+hBupn8cWUe/1nK/rf3pu9L8J6PkEmZZ72I/GcM\nw9aQM6L58nn6uVWiM/hatkmOCiLtzRiTGj3tZow8OR7k/lW1wa/RxUI/RO5P9U99xMetpGHtTIGO\nGGZjteNmUwY/MPZyedKxKvIKZPhSYaej21ozZrJzFEt2gKgTmWX4qFrgJwYzn3Q4Y8sfSmoVX78r\nMX2PLvBp3jOR9dwWJJ/FsNqbX0eU/CiPcfku3w2q4bU0rzdRTeXDwGuwwq+tc1pl5yAW+IAJx3c4\n9uK8xGhE2GzG5gLvuLZM2x7rr+5rymgHWzo6NguTvOzo6NgDvBOWIqliVG9qhX9qaKclZVruxPWl\nLEycG0zuVK5zCdPmS7mTsj6dduMz5/1mts6sq5R/aLaWjeJT78asaI+JAAAgAElEQVRNJiksY7iP\nduivPZYzygnmxDtGnY+8V4LzF0q+k66opxXnfi1Wi1O45UVdRIc0Oe6D+rk+SGzx1IxJY0aKEXI0\n1T9c57w8lnLLS/WZzDd9ca99/XI1bnmub33PCa4H6toRwy4M/lqBd8A6PqhCukQETDlCy/B39p0C\nI/y9I8JruyQSFMQo7TD6jkhmzKdZZf/XF+aBc3TaqaAnxAPiUEI+UhWUZCMWhENxu+OBdwAjlALb\nGjTGewaCUp4PniWS3fYDxTMUVLWM9O9r/yJpxBIyWEYB4ZiWacNsMDae7LQRox6M8+PqKe//dNuk\n8UtWPvZVGHiHyX3xTLuwFU4HwPWNDJoTq3N6JvzJTPyzGBuME057tEtDmZqjULsw+GshN2tM5WH2\n/iLgZvBFK3xAbXhkDpCm0wBjDO6stMLPr7rYs69c4lftarD+kWWOzBhIJePuAYPRl+UZ3ZI+lD85\nqvNqlVOK3tx+L0GrTJwLub7Npefam1ut8hW+RutoDA5MH8T4IRCOmefv15tu251hAeby3Mmt8I1R\n6Xn3KuSrRhb5REOWOx6n6zt3phW+4+vA+us40vCJT9Etx1nALFS/wyeiryGinyKih4joS0T0cSJ6\nmcjzViK6f0h/PxG9cB6bHadAiSwttoba12JMRX0TKkrkJgcZRZ7J0tFRJb9L7kCWTfXlrtY2hXlN\nvridl3WdJPAOET0TwAcB/ByA1wF4CMDXA3iE5fkRAD8I4HsB3AfgbwC4l4hebIx5oo69jlOgZl1U\ne9I8nhb6zdbwsBaq+qJ2f6ei88pcqkLSJSerW09Up1jvp/TrkffDX4a2pOPtACU2qUK3ttgKv1Km\nQMjuQxN5p1dqA+/ETsjHIGW7NL97NWxQfkpfTUPYu0nPBDpN4J2/CuCzxpg3snufEXl+CMDbjDH/\nfmDsDQAeBPDHAbw3RjjmM3ku5U5KnpoHsieMwXF4vyfyxjS/LKMGjRnp5Md8DHM8N1rc8sL6i7MG\n5UqLcLe8sF8xvpafXOK4SxGx+/pzKec5NQImhmYH3rmY0VSOVIsNZso5ox/QsS/mx7Ecq8enEefY\nBYgq5o0LcCwP/5/S1LXAO4FPfpY/bqkr8rOxJ812qGtcexTdSFrgHYUHUuhWiEmtwf9OAD9DRO8F\n8GoAvwHgHcaYd1me6QUA7obdAQAAGGO+QES/BOCVSBh8jqCbVrL6NYF33H3Ooz9ja+NxiYhac8FX\nk5OvqFxBDtcGgBJgx+YxkBO3cJZLE5lzBN5B2lDTSD/O21g+o4j0suXbI47XcIBbJT09M6ZIvHt6\nQBw98EcJYrxvI/DO3nYJ1gy8449pkXFY1ruVdlngHWfQdGbXDryT6ys5KYjqryj8pXn5BMEa+Sm/\nt8/ASXp9JPvLn+CZsUwUw2xs7cA7vxvA9wP4MQB/E8ArAPwDIvqyMebdsMbewK7oOR4c0oqx+bHL\nlf4MST+3sR+YqMq6yJY+2l/jz+qy7FKzZvW7HpwSy9Xttlr9T5cWKVvBuJwIx/LMFeMtDINTY83A\nO2k58FeTcTmRRjNVXy1/5XlKtvNJKJRwkpuuK7WYS+UnRzxYnad50CbhJa845wajqzX4BwAfNsb8\n6HD9cSL6BthJwLsT5bL6/cPv+kXc9duehKM52hOaxyO++pu/Fs962e+sZHF92K0wwG2NGeSFcg+4\nhDZkkVio7BG5n/vt6OhYF4uMvKwbi/24uu8LuPr0b+J4PAJH4OZAoJtjcTW1Bv/zAD4p7n0SwJ8Y\nvj8Aq06fC3+V/xwAv5wi/PI3fhue9vxn4IknrnB9c8TjT1zhiasbXF1fV7JYDq775UzXiM9YeWCe\n/djClj6MgRFbYiXt9kmEZ2/TrjTtA2XVPiswnC4gSaVXXugiV5Cf1+fz4H/3fHSHJ+lchqQvdu3v\nN3ixE6KM9sA7tci6gNpM0fTcoT8nM9rPJxtMY3Z24B3UBd5xtOOrWhoXU2P+TFulW14qCI5KI7go\nzM/dZ71T9D4NHnhnyjut1h0VPo75n6v0rq97GvDcp+DqsSscr4+486Q7oMeucf3z9yf5dag1+B8E\n8CJx70UYDu4ZY+4jogcAvBbAfx0a+nTYrf+fSFLOjPelVzDj4TMmSIEPZMIqDa+yB2Lz+Dv36swQ\njT7lZpJeP49nYUKej0a5rxzMWSLwzhHAobGwDViTNky5oCfGDPpozcA7gxU3hoL2WrE0jM9JMRyP\nwOHA8hkK6jxinBIU8TK6E8fGAlk+k88kU1X5GiWOVpk4F1JtduPkmGhSqr18MXMMliRmGKvjV2gP\nyModRj0Y44XI4Jh7/pK2sfxrNA/k13dnZFaHHbO+7gnaXLiCBiZ5LsnveJSBd6QOORz8gkdYLwQS\nk3M7lu31kamXwCWP6ds1A+/8PQAfJKK/BnsA7xUA3gjgz7M8Pw7grxPR/wLwawDeBuBzAP5tinB7\nGJZ2MHsdTUtxtS/1Eoe6gkzlj9EoyMfzN/df7dJaFE1tyRSF1XSHnir5qN3V4INdrnDCFb6Z8hp3\nWCvSz8O98kApudn48N+MFX7xwZAULm2Fr0ysPSTay4PmxPp2kg39pD6XOzcRjjCC3PPXaCOywjej\nERy4o3zgndyKvmpRVbEaUX3j1Wtlhe8tNt34na7dpN9jZeYwqTL4xpiPENF3A/jbAH4U1s/+h4wx\n/5zleTsRfSWAdwJ4JoBfAPAdc3zwz70C7lgBO36kbs6QmTtESi7FRMnEZHc2sMPDuoNkmlCiQJBP\nOWB3rBwGlJis1GsQtovv5Q++V3ZVdWhdY8w9AO7J5HkLgLfU0vbgnTJtD9LSkcdZ3n3OOKY/65B+\nwYnfcj4ajiY3yLHKsnCt090kK+gV1B9jfQnxofE/H2vWeW6UvIOXa9vSSVzJmM6d0he5EXOtLDnV\nrtXNP7VE1/bSU/pcVnTXPr28lLGYLGpleL3ye6p+imXK8DoXm4mlH7iAQLoxLNsDWlAT/4Gl/fBd\n/rX4OyW48E1KQDwPbwIWDkT9nlKXq8e4/xp5buzvrAuZ8ty1uh2dKj5MuavVJH/T9ynNvrfjftKy\nLGuO6gIk8yV5mRoQ5TVHryT+gF4+XWe+/HaR5Ve1xqawv/PuwtyVM5Z3lLHElr2LCVHT/+RoR9KG\nyj0eYjDqGEBwHacRyli53374fLT7chy7SYWcsBM7GObbJk2ZRlhIYDMG/9SI9dFo8JR8Uiz2pV7i\nUJVnKv+Me1OdmLFz197zcyPC8Xy1BoZoeO9fUYf9DLmeqtYC60z1cTqsRDEPfv7YCq9gNZnNEAt2\n0l7n1pFqgcHw/MIDGMX9nctFLmhMauLgPgmIRsejdpnSypEQt1xbaJAdflpFi7QX5zFcydUE3jGe\nkXcLH3ftc8G/ahOe6TQ/EAzsBbBpg7+zCXvHiTBHLrJli7ZCTyOYyW1PpzCFcQ9pJBRqJR9rb+lr\ndG7rlr5ruMyyypZ+IY0UyVaZKqFZslMhFxD6Cl8vr23pl2y+jPUoW/oxHjyeE/Rz6a2o/rW8tXEJ\nW3WXjjJlcsHP7ETnSZaoph996WjFbs5NlRxgPQEbVcg5vjDvGnGKY1a1m17hr4nYGxiZnnQHydDY\nC7R21IqVll+9Z1zAjRmiu+Lp8yK3PLTx3uqWp/3Wt++GN93zJ1pDuE9R1nPZKsD4W92Z9BTNbLsN\nVNfcXJ0cNW3aAnK/d2+UPjGsXOq1UomclbjG8mefHBuVMiXpS/AtekqcZsfAl6Qjrw+Ixz1Q3ppk\n3cQnDwfjfY71iwADh0Polqe9tpnGsq1ldM1zfLUqnwHbMfgmebn8bFM5TulVMfpBpmgMn7Sj2bAG\n1hfGiHvjZdzo2Av/nv7+0d0apLaxywzSgXGSZQvK5QPvGMA0eo4UFuGBd8I0yeekdLhetCQo2La1\nvV/O+yQTkfTxM9VpmTrI6O+IM3X693Y8BgWkX/aUwNpOWoaRQEEdA73sxMNMxiZBq6X/469sxEQ2\nRcPVL/zeZZ4kAX4Zk0WljKvXN9Rhu6Zrp2sBmOEUheFxBHgwLV4+qkyr9OhmDP6pB2tcNPz0Enu/\nd+jKcy0aBs7ZaIv9V2rEW3hvXeHrwUkmI+9PAPQX4UbOBCpWY/nAO+HkOeQ3V0lRrrBOjp2t8JsD\n77AVfqzNJT2Z22GwVbEpeiK/FryrBDGaBtOE2s6v0yv8bOAd+YI9ydT4Xz5rZIUftkuu8G0dMqiQ\nOnHQMjRic+/wJ2zRHHTMRsOs9HKwYKNrbONytXacFJkJwYm4OA8uu3U+IpMeYe2X2EXezApfYnLb\n6LgoEPs88ZgukaU15Y1qVhl5Yvxjoh9mCU8Lt1SV2J1YamGtnUivLbMntATe4a8R557jLnGN5UHP\nkifq5/AQqfcUgXfUjaLxvzj4ppZ9VP4rPu7ZEh2H7j4/ryDbwRiZ+9O4wIYMfvShjopt2ZEd81Hm\n6UEAFqH0Usp2TyjxjODX3nv6Md2/F32cQ55zBt7JZSgPvFPHg3zHnmZjCryjphueRyiF8fvwh1BR\n1AZJCX9zL6S1fOCdujJ7G4NtgXeGZzG4bdW4Y8by5AL42E+DpLVpGA9IU/T4Wy/wTihjqVclYTkS\n166+cBwCcqz6Rp/TpilB4y6SlsdmDL6DFELCOovBrN5X8oVvZS4DWjvkPTmDzebP1XmOFX6JEiyl\n1Vh/S+AdnRajOWYUEwQmxB6tSsU8HcDUeV+qXwM6BX21NyPPkVvhRw2UcdHvErSL60/38RgIxl4k\n6mudgEcmLCJPbmIQrrDFBCBWV+QsSNFkbMg7eR5p9fPIiArf8M8XeIF3Rs7Dr63YnMHfNM5gpLaC\nS2h6k9E5I9K8aLsyMoe+i1XbwmFxEj9RXUkvWQ9Dibxt52nVo0gegxt2JC7R7pKVrDZ/VPM1MlQi\n4fnFgxKxrrAuTcbcIjMFub4PeRryeVv64SQkRYPTma7l7L0OmzH4eojFuvjMTfVuSMFvBbU/dbsX\nlLRhS+6VqV/TKqQAgIKd4czmbISXXC3z0eT5MHzucRQXyWNwY/DKmKf3GbmMj3uKF4EWfqLnQlAu\nV1o8AW03tka+SvPG8vkudRjezft9XaqPfPfwxGGaAmzG4J8aOUWhCnr8/MyuobVDUzQlNKLlFXKt\ncrtmfxcPwgYuWt3yYjyMvCQy2t14X3VStVueoxHPkJuYFLVbujbVlMls+24RRW55itIxTOnPCbxz\nHAQy9ehK3fIGZgpq1ekrxDzXU3/GGl7n3eKg6jC19sTrK1ku55bn3O9csDGf7TjPx6MZ+tyvdO56\nZDcGf8mVl3daOiakgxDxZx8aQUdwWyvDamh9oSjf5KAy071Y0B2/XLvFNzP6u6RYzojaTI08FBZJ\nBd7heQwX0CAdMMa9g/VXFtW8Z1b42TgaJf0+owzlOdgVooF3hnFjgGHZGml1kY+9pZfLWhJ4h9A2\nHqKviWjayTga4/mPG8A7C+MMYyrwzpix4J6cIOuMDx9mGodyVT9Sc8GvSPY1G5NM54xtYUR528YV\nf4PA78bgL40CfT5+ieW9FAVTOA6qaJT0b2v/5Q4Mz0FRaF1lC7GMdl2bU3m1wDvJemf0V5bvgh2D\nonY3TaDcCjTu0bBVlES4i2Zhh7zU5Jr6F1jhpwLjFPEg72M6LGgkfeMHkioJvOPKVTBWmC29wh+u\noL5aS5RxOsatjcb0mQvLDQfeYdjbSO7I41JmS1VYsNG3sv86bg8Sk4sTcnFWLGDgJTa1wo+9hVvL\n3BfRJbuivHQhi51qNcr3GpqyDCmJWj3Julc4ETzmKZlcttbPXyUh3kZ3ELfMP1qc/E2cpnf11MJ5\nb6X4LaIDXR44TfffGOshV4b8zz2hxC0vCLwDjAOkRF+m+q/UV9+ttH1XMX+UtnZ/yIKlObZdHNwm\npZBzTeVy77sckuB/oCR26qRc2RW5IvWG54u55RVtfI1ja3oeYldnYcHelMF3CASRlj9Nn43eNAga\nGQPDTsT6QlVOb8tIBd6RygOAEGzfb1T6nKoTCeePzvtPqUe75743Bfmgsm3fXOAdm6eeBy3wjt5u\nGhRd8ojJ2J5U0BGXTqKva3h37x+j/BZ402jlJR1HK5Wu1e3u7G0IZg86Gv0wZG3gnVj/xdzFZD4r\nRP45kGCUNuro+JSFvImv1x7l0J4+Bvw+CPkLp0O+XJmATn4KystPvERd82iaOvFJVDzwDtL3M9ik\nwXeYjM7yIzlHMWZs5IzwEpBTwvaGmEJ7SWFAmZK+OXX/LRd4p00iSwPvTEY6oYjZCr96U6JSMQ/6\nPstLcf3JuoachVuZ2sR0LxiNqQLV2LNFdSoYTS5QDc9Xkqcs8E4b0oF3pklNSn5dpL1s4B2QYDS+\ndet24/QJF6ZxHF3hT5OA/Dg2bDdBLKiiZdqwKYOfbYhmeSlzrdwbgxekdAqJ+jRFFFuuSV5m8rs6\nXQlvn0kpo/UbmxCQm9KmTv/L/kz1r8gzUmvuh3jdo2wk8zDatc8t1263s+S1UylT+26P81/Db4LO\nyK+Xzr7LdmeeNW+zifVTSd3nHEsVdKsnSkzuUu0m91+Gl5LnRnJc5+Sush9SPcCHWeoZkJuA03Q7\nJboeOwkdw9WfhIuOF0xExr4SJPmKPXgGoY9JdoXfiE0Z/PzPcBbcK8kTuyfTeZ7Uqc9RaBrqbcmz\nNF0pVJ5/SQFdWSagkei7ljyx/tbuqXnidU8uL6k8hXVp17l2u9O5moHz8lQafM4/hkfeJGcKL9zw\nxp5JgTyoCjhXhk8CtzCWKsqU/KSskRfOkHCDLekC/o5MhBfPoEXz+M9Ny+a1oKUflCycNm+PZ+/d\nPccXyxP5lei0rmPXTq6i7DPvBY2WFPfxLAZnzNhLrVd5m3jgHdVEVkz+N2XwT4mYrZPp8nsNjb1A\na0eNOZEDrrR8pcka0drfy/FU4Kc/h74b5IWESnjxFWXe0KTKh4kLBd4ZaLXk3+MZGm44onkCgzQY\niHHuG7bbGFPkJqf9CFYsjxHXPuzsQ7OnJTwkDb7bKle2u/nksMQtz8jT1yYhZ6NOS0xOWT1a/dOt\n+Pjw/e8Vnvnn8J8/AahTRJs0+GrDWzWsAu99S/JBKNGOvDyO4LL8nRpaX5Q+AxlRanqfla4v1a9Z\nNPa3faZlirDE3i4ZaMTDoJiyfcj+4vlIbXct7+ns+f2GkuqIUSpnr3KCsBPEDIm96fpJvlOyoFi5\noI4xczwTEXJGydIgzxCWIjeOZErMKJbFo9AmT/GanU7TKuQG35iw/vBambCMaT5/Ez2DUVEmlUE8\nSWJTBn+TsbI2yNJWUWVDNtqvpYbQqPuDS/GAbKCcOd23dNcv1RUx/ZqtG8vUf2oUG2U1AQhPzrOk\nivpLVvg5fqhxhY+coR4m9+qBNnav8A1QDVtFZWL55JZ+rnwsnxphz8uQ5k9iH4F3Oi4Ke94Ncdih\nfenoCLCkHK81Jm7rWJNqUp2YVXbOplb4fLa69iu5HHliX6RL0o4XFSrUE62NNIr7RunXtVHkvlbk\nqlRITCtbmCnr1y75WaLeLZSvdMvzj3DvG6S8UvPkwL3LHj5jz73KLa+w68YT80qlFWRUHrK6mOXR\n4gs4F9bcjgU5Zh2K3jPFTv9NyfZxhIF3RM0FVUW2/TmxmaK+KYPv4ActoODeQpVk03ngHQ+KVdvj\noaER6sxRG9j6tpo9VDNcCxeZaJXIb1snyzf0N2HBwDsNPPB+ytVvP5OZRkWXIkpu8uDpjIafnU70\nRxG9wtldygEjVnfJBGkP0IMOsS1dsK1zyshgQX8c3JgtGhSDMdWSZjwDaywTsuVkXLrk2sSBNT9A\nTpQN8tOKjtNo9t67cDrFp8bPMTH2M31UcX6FIt8z2KTBPwWKV/hK3r7CF3nJBZQZ/EkLZ/yn7r/l\nVsJtS5riwDsFBnTOCr/FNmbmHrPKcxwGYsfCFf44obkAHFg7bob283tHY3AgwtH49yWWDLwz5m0o\nU0SXoJ5D8POEC0BJ5ECk9pmE7M8cNFrHohU+wVmKw6FQq4wT/dhBibD9tc9jU+/w/ehhK63sOzxo\n24jtxLyPDaJoeV2UZc02rk3/snD7eiq7mXIaNraDM9qINaLABnUs2L5NGfyOfWM8sboC7Yc/dv8K\nVBUUnZxu98MvYgGbdWJQsSSvOQ8krXaX/6GPnkhGVoLmZun6g58Gl/cCOqvzqfPQOiYkvbDNZvyM\n/+XpPfyx+7N9V8LbmIbJsyyk5z/D+rrE6XxOa8YDvrUGP9dvRnznf6U09gLZNtnebF+ZUexHAjEa\nJfVofw9/7POz+7vIDaqCVr0vuylqa4lG8uSwQGF6dTR0YpLnwn4t+3P/CvObSemebFK4EnQdY0Sf\nyDsaoUI5a+RN8sDvtyCk57cvLwN+X8RoWR2i8V0ij0o5b6Lht73EeGs94eiM48qIZHeDje0a7Ood\n/lLuXD3wzgT57gnymiEXeMcJt3Eni5IV1xke7znM6O9sMWXFoPOTCMwxp35gCLeZzlsTeIdkX1P9\nDkUqPyH/PMrrm+SpKj9C5bpnaIF3nLxxuVNbGzzwdB1l/KTKOR3aZvJLA+9E8xWPWa0/s9xp1Y38\naN/1a25n0vo1NPQFDSvErgz+WXAZ+mN7OEO/GuTfb5ay5VaWq7zDW9hoaRHGlmR7SW6rJyLuvwt4\ncZ2Kwiav+eRXo7Pm2SfJk+dJ2VBt8pnT1J70xLaM3pIT3VSdsbTUswlfFyi7A3JlX9meW7ulX4pu\n7y8IS6/+VhSOLncdHbccK+xWbWGF/xQA+M1ffwRXN9e4vr7G9fGI65sbXF/f4Pr6iKvra9zcHJfb\n0j9M85w7EZeJm6OBOR5HV48U7uzYk4D3BWD74+YY2XI6HqN0bobZpzEGVOCGMjmtlOHmsWt88XOP\nWh4b+/twOGRdZG5ujri6vsEx0gcTLbJ/lbyUyNMB9lXLXXfdidMZ5PP65ojr65sEnwcQAYc703Mm\npF2X1PoyfOeeSUm75+AOEW4eu8IXf/3RVes5NVr7XY5rDanxnOLDiLHBx3vL2Ey10dGjwyHJ7/VN\nvi1chywB3g9SXxwFrwf2PGI6yNEwMLi6usHjjz+BqyeucfPEDW6ubnDz+A2OV9cwj98Aj19bfXsg\nmMfHup6S45nO/c6LiP40gJ8+KxMdHR0dHR37xp8xxrwnlWELBv9ZAF4H4NcAfPmszHR0dHR0dOwL\nTwHwdQDuNcY8nMp4doPf0dHR0dHRsT76ob2Ojo6Ojo5bgG7wOzo6Ojo6bgG6we/o6Ojo6LgF6Aa/\no6Ojo6PjFuDsBp+IfoCI7iOix4joQ0T0LefmqWN9ENGbiego/j7B0r+CiH6CiB4iot8ion9JRM8R\nNJ5HRP+RiL5IRA8Q0duJ6Owy3dEGIvojRPTviOg3Bnn4LiXPW4nofiL6EhG9n4heKNK/ioh+moge\nJaJHiOhdRPRUkecbiegDg875DBH98Npt65iPnHwQ0U8qOuUekedWy8dZlSMRfQ+AHwPwZgAvBfBx\nAPcS0bPPyVfHyfCrAJ4L4O7h7w+ztB8H8McA/EkArwLwNQD+lUscDPs9sMGjvhXA9wL4swDeegK+\nO9bBUwH8FwA/ACUuExH9CIAfBPB9AF4O4Iuw+uLJLNt7ALwYwGth5edVAN7JaDwNwL0A7gPwMgA/\nDOAtRPTGFdrTsSyS8jHgffB1yp8S6bdbPtI/ObjuH4APAfj77JoAfA7Am87JV/87ybN/M4CPRdKe\nDuBxAN/N7r0IwBHAy4fr7wBwBeDZLM/3AXgEwF3nbl//my0fRwDfJe7dD+AvCzl5DMDrh+sXD+Ve\nyvK8DsA1gLuH6+8H8BCXEQB/C8Anzt3m/jdbPn4SwL9OlPl9t10+zrbCJ6InAfgmAD/n7hnbuz8L\n4JXn4qvjpPj6YXvu00T0biJ63nD/m2BX7lw2PgXgs5hk41sB/Iox5iFG714AzwDwDeuz3nFKENEL\nYFdsXCa+AOCX4MvEI8aYX2ZFfxZ2NfgKlucDxphrludeAC8iomesxH7H6fAaInqQiP47Eb2DiH4H\nS3slbrl8nHNL/9kA7gB4UNx/EHZgd1w2PgS7Bf86AH8BwAsAfGB4n3Y3gCcGhc7BZeNu6LIDdPm5\nRNwNq5hT+uJuAP+HJxpjbgD8X3S5uQ14H4A3APijAN4E4NUA7qHp5+luvXxs4cdzJGp/V6VjhzDG\n3Msuf5WIPgzgMwBej3iI5VLZ6PJze1AiE7k80w+6d+wWxpj3ssv/RkS/AuDTAF4D4OcTRW+NfJxz\nhf8QgBvYAxYcz0E4w+q4cBhjHgXwPwC8EMADAJ5MRE8X2bhsPIBQdtx1l5/LwwOwijelLx4YrkcQ\n0R0AXzWkuTwaDaDLzUXBGHMfrJ1xnhy3Xj7OZvCNMVcAPgp7WhIAMGy9vBbAL56Lr47zgIh+O4Df\nA3sw66OwB2m4bPxeAL8Lk2z8ZwAvER4d3w7gUQCfQMdFYVDeD8CXiafDvnvlMvFMInopK/pa2InC\nh1meVw2K3uHbAXxqmHR2XAiI6GsBPAvA54dbXT7OfNLy9bCnbN8Ae4LynQAeBvDV5z7N2P9Wf/Z/\nF9Yl5vkAvg3A+2Fn0M8a0t8B6xrzGthDfB8E8Aus/AHWjfN9AL4R9izAgwDedu629b9mmXgqgD8A\n4A/Cnqb+S8P184b0Nw364TsBvATAvwHwPwE8mdG4B8BHAHwLgD8E4FMAfoqlPx12UvlPAfx+AN8D\n4P8B+HPnbn//a5ePIe3tsBPA58Ma8o8A+CSAJ3X5GNp3dgaAvwj707iPwc6uvvncPPW/kzz3fwbr\ngvkY7On79wB4AUv/CgD/EHZL7rcA/AsAzxE0ngfgPwwD8kEAfwfA4dxt63/NMvHqQZHfiL9/wvK8\nZVDIX4I9Pf1CQeOZAN4Nu9PzCIB/DOArRZ6XAPhPA43PAvgr5257/5snH7A/EfszsLtAXwbwvwH8\nI4jF422Xj/7zuB0dHR0dHbcAPQxpR0dHR0fHLUA3+B0dHcX1REAAAABySURBVB0dHbcA3eB3dHR0\ndHTcAnSD39HR0dHRcQvQDX5HR0dHR8ctQDf4HR0dHR0dtwDd4Hd0dHR0dNwCdIPf0dHR0dFxC9AN\nfkdHR0dHxy1AN/gdHR0dHR23AN3gd3R0dHR03AJ0g9/R0dHR0XEL8P8BT515AEleFf4AAAAASUVO\nRK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f7ac68bd1d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"hw = signal.cwt(y, haar, widths=widths)\n",
"plt.imshow(hw, aspect='auto', cmap='PRGn')"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.image.AxesImage at 0x7f7ac6c80cd0>"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAfwAAAFiCAYAAAATPmogAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzsvWusbUt2HvSNqjnX3ufcR3fbcbttN3HcedkWYDltHg5Y\nSPiHSX5AEEIBRQIS+MNDipCIDBJSQsIrQbEshxghESA/eCgQIQJCcYQDgeDElu3YTpyY0PEr13Y/\n7O6+t889Z6+1ZtXgR9Wo16yaj7Xm2nudvmtc3bP3nrNm1ajneI8iZsYNbnCDG9zgBjf48gb11Ajc\n4AY3uMENbnCDy8ON4N/gBje4wQ1u8AGAG8G/wQ1ucIMb3OADADeCf4Mb3OAGN7jBBwBuBP8GN7jB\nDW5wgw8A3Aj+DW5wgxvc4AYfALgR/Bvc4AY3uMENPgBwI/g3uMENbnCDG3wA4Ebwb3CDG9zgBjf4\nAMCN4N/gBje4wQ1u8AGAixF8IvrXiejniOgVEf1VIvoHLtXWDW5wgxvc4AY3mIaLEHwi+t0A/jiA\nPwjgWwH8JIAfIKJfd4n2bnCDG9zgBje4wTTQJS7PIaK/CuCHmfn3+78JwN8F8H3M/MeKsl8J4LsA\n/DyAh82RucENbnCDG9zgyxfuAfwGAD/AzL82VbDbumUi6gF8EsB/KM+YmYnofwfw7ZVPvgvAf7M1\nHje4wQ1ucIMbfIDg9wD4b6cKbE7wAfw6ABrAZ4rnnwHwWyvlfx4A/oN/64/iE1//G0EA3D8AFEER\nhYJEBFLkfw9F4ntFABGST8J3zAwKH8XnoTkF/y1B9Qr9Gx0MWeAA8GDBDMBWsA91AcyA6hV4sBFB\nSvBVBIUEB18fg0EocRPECCDRwhCAqJFh5NoZ6/9mriEKcNIB+ZYr9Rk2GPgIBTcee7vH5159Fl9x\n/xV4pp6DKFqCLFtYHvDCvMDn95/H1z3/ODrqY398vTlODAPry9Aiu9J//O/9J/i3/+AfgB2NQt43\nBvuXXBmfcf/TfrwaXuG/+/H/FV/zka/EP/6JfwS96gEAKukvM8Oyxz1ZZ6mmjMEYeMBgBgCAVhoA\nMNgBDIYmDUUq1DvYAYYNOuqglAKBQjnBzY2ha/theMAvvPsOfu39L+AnfvZn8Xt++z+BD+0+hE6N\ntzP5OSz7mq25YjyknZfDSzzvno/6l44nM0ORCnWle42ZceQjXg4vsVM77NQu4CL12cqmso31W0KJ\n05/6o/8V/uXv/r1ZX9K6yjbjWkmA6u2Hb6QOtqP2TfKdtdaXYxzNMTxTWruDIinjvuXQ9qv9A14e\nH2CsxUfeeHvc76RuwYGT9W5sPAcivtJ3A2sZ7/zq5/DOp38Nf99v+Q24033oOxFgrfvWgvHqsMdP\n/PTP4Rt/09fiQ2+8GcZG1nTWf2tG/XJturaHwWAYDLTW4by0bKGV8n0IQwMw49V+j13fZzSghMFa\n/PRf/3ncvXmH3/wNXxPqEjytBZRyP//m//DX8M3/7LcGHI216Dqd7QPLNtvvAip59P6rA5gZz+/v\noBSwPwxQSuH+bgfl+zUYg77TeOP+Ge66HXZdj051IAKMMbBscdfvAADHYcDBHKGIoEgDBNx1Pe67\nO9z3O9z393je30ORwov9S/zyu5/Ft3ztN+Ejf+fj+Iv/xf+Fv/XOT+FHH34I8LR0Ci5B8FtQO6cB\nr8bvD3fYPdxnhxOpdCrc36qg9CnBhy8f6kh+MJLzWfmn6ZmtyB2OGqBBYad6GBjgANjBL+AJgh/+\nPGrYwUamoyD44XlK8BlJefnMMy/JM4FI3MrnKRFPCZBAevilX8R6GYBmA8WdH2sCrMLdw3Pc8XPs\n6PmI0FkMuBss7vd77PDME3yEgZejJsXTsPXztIzgK6uwe/WsSfARDuTYF4Tx8CW4TfCZLdgovH38\nMN46fBh3L58nBD8ljIgEP/0+IR5MDG0HaDvATbs7HDs2YDAUFJRS0KTBzNA8uIMvYQTcQaj9+HEg\nMNbj+Xz/Fh72Bm8fPoRnD2/i3rxRJfiAX0sJzxiYFqLQj5IwWrawhnCnnzkiUCH4DAtbEHxFBMsc\nmRYeYI+End6hVz0UqcC8SFsl1JiAouHQjxSU6XD/6o1s/ad4c3g2ZgKy9isEP+6tSGzLcrZC8BmM\ng2f8rHXEjYsyKZ6WLejYgw49LFs8V2+V2z8wFsyRyKe/W5v2k0f1G2vx1uGADw0Wb+7fwk73fkgp\nzLXUpw97fHhwe+KN7nlg3GtEMRDZdMwTvIbBYDBuDBQBll3Zzh/ibm/FEe8OB+y4z/tfbH5jLT5i\nvgK74Q5vHj4ETbKeY79lTXa2x5uHt8MYWWvRGZ2fZ5aDUJlCegaowwFgxj3toBRhdxygFOEOO2jf\nL2MNetPhOd1jZ3rshoTgWwNjLe6MI/iDGdANRz8ublx3XY/7boc7s8P9cIf74R4KCuZIeL5/E88f\n3sSz45t4k9/CM35TUJs1iV+C4P8qAAPgq4vnH8VY6g/wn/33fwLPds+ywf/WT3wbfttvjM79jgYW\nxDzTAIyfhbIpxQ9VUPaMQIAClFbo7rST8I9uEeTsZ1p3zlWoTsEaG7uRvi/xT7hZVJiUTFWRdWks\nncenYzxjuRoTkB+IrpsWBgaeBcLAR7x3eBdf3L1AT7uRZGjZYG/3eHF8gZd3R2jSGbpc4MSetRD9\nSpt/j/D+F17hUz/y82Eaa+Sn7OtoFCqHf/ibgaM9wv6ixas39/iFz/5SIKCJHigQKyo4sZxwOIbG\nsJN4ZBNbNmDAa07c5nbE1cAKI0AqSMfynbQpmpKDPeLzr97Fi/0r6M8SPr37HL6oX3jpZjyacYTd\n6NX6UI4Ns8XeHnCnduGb8YhLPZFxEEIvc2TY4GD20KpDR51f/5wwZpV6Z/2KckZO4OHdPX7pxz+T\n1Vmb8/is1nq9/VIj5uajJPjjdpkZg5d8mRlKqSqzI98yGIfhiMNwdAT0DijnNDAWXODlq7NZP3OC\n79Ybg19Y3L/bYX88YFAOP/IChk2I9PF4xLNf2cEYg/3dPjynCsHnCsFP+2mNhbEMVjZI+MwMFoLP\nyZwywAPD6CE7B8u9by3jjc/do3+vhz2YpK5knvx+4pcM+ykTcGQLWG0KXPNjNzxPHx7cuNreuLoH\nC0uEoR9gRXNhLaAZDz1hUAYHfYRW7ly01jHKB30EPANwNAaKojauVx0e9B5912Gne+x0D4LCT/3M\nT+Jv/MxP4wd3fwHdYYf3Pvce3j+8P0a4AZsTfGY+EtGPAfhOAH8OCE573wng+1rf/bav/IfxVc+/\nOh/s94FP/fWfDX+mZ+yIoCYwoQEaVUTZM/cxKUB32kkaJtmYtdOhaEspBWsTCZAaZVv6jpQZabTR\nOvDK9+0yiTRarTdVhxMYFg/DK9x1X4BCSVRcWcMGe7PH5/V7Ve5/TGC53tcGvP/Fl57gR+mx1bV6\ni9nL8TtmWFjY9wxe3T3gF3bvBMm8ZF6EoGUEf9Q/Gw5e6Z9InmLKiOptUbGryOglJihhmGR2DBu8\nPL7CYRig3if8ypc+55isyriX+Kf1ZRuFy7FhDGzQ+TForaNYTRyRlCljthjYOM0FVGiSk3ka1zoH\ndbbv4d0H/NKPfTp/OupX2sP8/XT75Z7j0actRsNy1D41hjz71liDwRpnEumGMSY1nCv9rDK4fh3Z\ng8XdvsfDFw5hv1L2vStnjMGzL/Uw7xk86EN4W9uzkRlqPLfeLFVozEbCgQdrLAbFRUv5vDMDb754\nBt1rmC+Yog9xzJkBvGCY/8+GEsyAGRGLEiPfavrIMMAMoz3jYi2YCIMaknXPsGTBmqHUMTPhBe1J\nEATETBgb0qScxK80NCl0SgMgfMR+FN/21W/jo299Fe5fvol33nsHv3x8Bz/M/+cI5xpcSqX/PQD+\ntCf8PwLg3wTwHMB/3frgnU/9Et5T7y+S9gAsoOrngVI0VmMuIfheHduCS2I9f1CeVhuRgrUmk05K\nIBAsxqrureD9/Ut86od/7uTvl4wNASCl8Erv8e7xPbRnq3YoVFponWa1auvnTL11FqaDoEH4lV/8\n3GK79xrICNQEf5WhXVB8LkrNVHcWvDoc8M6PihLxEi3ksLyFFSUDI+5+ebkqcGkZqwS4/XpPHfb2\nMLnumBnPsIMliz2bcYHqhE6xTOug0uII3lT3IEU4DofJcnyMEj4Qz6y1QH5dW0qxYwxFXQbA4MvU\n2Yo4ePWjgQIznQ4zs4W5Y2j6PF6+fInBjpnCFlyE4DPzn/Ex938YTrX/EwC+i5k/1/zIm5sSMrOe\ndKSHzWrIDyRiBbInHKJEIN6G6I1ME3Plz28xaTse+M7uqgEzVtcFlwrl7NHW2ovwYl+rfj20vcRy\njcgqrXB/fw97MMEOenKtyQ4dqQk5HuyZxDex3LLviaAUQSnnAOZUpevWapB6Ks9KXFcBFz+BtjZr\nY/i4/nrssFv+wQUWarPGJWOQaBlTTdXylhcefgR0XQdYzBILIoLWCmawba3aUgwra26qLDBfnohw\n/+we5mBwoEPyPP+WCPj19Am82b+Zfo0mc9LQxkRtVq7dmjRDVV9Ncf/Jey62kpy3g3YmyJX7/mJO\ne8z8/QC+f2n5XbfDnboPf5c20iUw8sZf823ymxym1qvV1uGgUHrJn4KPw2Tld2ceYJk/RLDFErTW\nYDjCUm568QLXWjuHIGMW4S1ztRR+M755psKIzypILC+q6/D8Q8/x8MVX6Lt+XT2jeovTopybKsWf\nGI/CmVV1GrrT4MFiOAyjNbcIv1F7/gAkL1nw+XTaOZ/6uirMYn4on6f6+K34e9cid1I7k1W1qlhA\n7ULUkCJXdM3ZU+XW2kX7ux7mYGFrUntaVivoTmN4GBCjhRbiI2PKcU1tTvAV4dlbz3F47wFD2peC\nlhMBH8KH848npnyS4PuOhDJEzs+rVkmrD7X9X/2WM0FAaVd+2A8YXr1YTZ8e00t/Evp+hzt9F/52\nDnXrNqB4Y06FcUx9G35XClp3MMasPkhr9uWWbXW2rpXfKYpE+rT2KPtdmCetO4CA4TigJAFEzgGt\n67WzuQ3DIganxhidA0RUqMmWfwf4fu46vPHhN0GvAMb97LeT9SaevjXPXzkgynJL6iOtoPsOeqdh\n9gOGV8fV0hepxiFVtHUuCMGvE7D8VJY5RHLY1hj4hXRtHtJ+nkfvR87Etfdzh7OMu9IqOAovndc1\nwg4pwu75HY4vjygdD0tQnUa367B/scea4yjsR4rrf2rN1XAEpveEK6fwxle8gfftC7Batn8E2KLZ\np3LPpvtVxjr0iwjWVCI7JDyy0gdZC635Ck6HlrPvVed8qF7xC7x49aKO/ARcDcHfdTvcdQnB94Rk\nDShFsJahVh5Y4o3u/4BWGl3XwwzHajjSWjiFAQEAqsS6TrejcM7JleU8UApsLUgpdLoDKcJhH512\n0nJKKfS7DmawOB6OiwiGODduBRJ6tpZYhe+I0N33eOsjb2P4/BFKncakCQgnDqC6Jq3hcTnTXmtp\nOeo0ursO3V2H48sjDrRfLYorTeP2PP11bW2kh5cD0vKY4Jcin0pU2YlJpGEAPRvozDnO65IQ2jpi\npKZNNlIH4HN5mDaxaH27lOArTbh7+x4P+mGWcVK7Dt19hwd6gPMbWyimKxU5Mx8MX11zEzgC03sC\nAHSn8MZXvQV6SaAuzudoaelxR63h6nNgvGfT/SqMi3xPimCOlcmVfAmVPrAPSWidVymzkDITundh\nhPbVcrt9CldD8AmUeXfnBL9m7xifDIoUQOsl/DI5iZYYaWXnd2kJlcOo5rW+BNRqgk9nnYUpg6WU\nggV5bYcGKa/aLza78gRfqw7QBlbbZYeOUidrIuq4U/bzlO86rdH1PbTWGxD8ZC3DZn/Ls1q5JfUp\nraC7DrrrYLWtJkFZgt+ovUDwNySEBEARWDydZsqOdnXNGoLT13jWXtLPc7UG7uCmtoQvYzCJj/tY\na+0jPHhSas2+9RqzJUKS0oSu66H1MNtnrTt0XY+u84z8Qj6QNPkxpSA4KA3YhWMsS3quvO4U+r6H\n7jov/fr2RwR//K2l+nMAsCZ/J3go7cda2fA9kQLVcjd4Qk1Vh17nqd+aL1Y+ssNwTNYGp3EhIhfi\nd8J6vRqCfxwO2GMf/pakLGvgdAk/JRTkCL4+wpjBh1CcBydL+CsZBdpSwi9U+qScSn9shyWQUuiH\nDtZYHIdhUeuiQdgKogrxFAnf9bM3O+Bdhf3hIWQNOxmfhGGQAy8F6XtZbkl9qlPQxw7dvsPwcMTw\nsN55pzr+MhZKbSbgk89gCTsOYxvZ8GX5AmEJVwnxBST8U31/YmX1JFmxrXl1dpDwOxWlwjVG74Vc\ni1KEPe9xfHFwXuoTTaheo3vocHjhtXtL14VoawgBr0tJ+Ka3ePn++y5RmoewtjKtVQ5TEn6p0s8k\nfH82BgmfXL9GJhtJgDRh35+14Zcq/b0CiHAYDtDKJepas0+vhuAfhgP2nIagjFOCzkFwNDvJaS+X\n8JXSMMYnzDjXOzX7jSu/196fQvDPOwWbNnzl1UjGjsK/nCaG0B07l65yMIsO47VOe0vhHAfJbujB\nXwT2hz0ejg9nEbx06qpSqq2Um/LST8qR1tB7Dd1r2IOBOZqwVtfgN2rPLz+STJQOq1X1jhtKOj5j\nw4+G+6L5CxH8bRwB0qomJPwFmnBBR2ntc3mMHR0nP17stEe4H/YY9gOMHSbx0p3zFxkeXDbIxRJ+\n0OjHc+QSTntKKQww2L//gINph+XVhmVquNY67Tm+KUc2qOVrnSidVWoI+B8pwddei2EH66V8whpN\n6dUQ/ONwwN5ECT9wzFiq0D/nDMjz77tsZy72nIjOjnE+WXW9muE5fxzSpkNYnnJe+sQYhX/JQdd1\n7pBiywsZpI1EyGq964sTgO7YgzXDHge8ePkC51H84rQYUfwKh7/QS1/MKKpztl42NuTtX4Vfq70N\nCeE1w7bdpOzHOaCV5PJYzhSvoPcAEfaHB8AyDsfD5CpXSrn8/4ZXxXtP4bi0LLCQ4JsBZm/wct/O\nOLcpwfdnVxqWR5igE5VOLBTwR3/IWXyn7xzBV7QsWYGHqyH4h+GYqfSfEmIqVDubSOeDAJL/XCvd\nJCyd7tw48fLLT64Net3DWoNOdXjx6ksX0UBsAZJ+N7XdH2aSjtzgdQCv0vdnzhoCubaVu90dSBEe\n9tOaLCLnx6NI4Tgc1zXCxc8LAIEw7F1k0JdevneZRpbgUYs64uzHiVD4TElWxDc/hF73q/3Drobg\na9LoaAU624j21Uolp7GxNoT6rakhaB/WcN1XAmWefIIjLOGylZoKiRyxFGZgllBupC2erPsE2HU7\n3N09w3A4oO92qCO4RDOxBImWrjr9flyG4Lh8Rc6JchgMQJwUq+nBWji1T+StpmjrqS7pSNnOY0Fp\nkjrXnJbCpYUMIsL97t75qfSpKro0OSJc6CL3AJxDwUc+GwuUTHNHiVYK9/fPMByPuOvv47cexTVS\nfHwxPsNzvOLcRwk/JiWL37SQX67dLM9Sdxa7BGeW1ueJuR6Cr3Xztq8WpMlhNgGKi5zIqYrWKp7T\nBXJOIqD5di5zxI0IPhE65aR3ttY58JXEgQi7rsdhOC5agEs380rE0x8nwV1/j+f3z/Du4RCurqw3\nNI34Et+Lmkc1ezVuJCZ1L95OuSiCTvd4oFdB+yL4pTn6U7yJ8sNacKjhEmKNz1y/5XW450Jkouvq\n7kvti1E7uBTDQUGlX3OQBc4XIogUnt09w8PhwUXX+J7UzlOtOyfdmyN63oky+6Qzt8YkNVN1L1w3\nWnd44/kbeP/FCzy/exbrBaIPBNWxDdc4o8ImJ9+NGDui6HQrf7MdcQkt06ZT/3Myh+MzJV57nEPn\nha/jMGB4nQl+dwrB35iginpE+QNVnVJ/QvHXhMqshUsdbFnsqXVcfa97WDYYhgFclHG4KNz1d37h\n8+xhJBfiziX9WAfk/z19XJ7dPcOz++d4970vuv5U6lqWQGUBwW957pNnGITYFmUIQK87KKXRdz2M\ndVfuImEyZQJSL/zobITsfZpvIQVZ+3wmdZHIjy3yWUh96ZWnAoLhYxH8sv1TI3HGEDVq4UIVeeMm\n8ewzT5HC82fPR9c8h/M0cT7stLuP/uHw4Pp4xplbai6mNBmpWXUKOk/w968esPNMumgkxP+qDLsW\nEJPtiOBLyBzcXixxdtpfk/9t4q1+cu5PMTMuBbmcWSNyH74t902vOxhrsT9+ETDxFs2lcDUEX6sO\nnV6ODsElPLDWnh0zLSC3o0kctuPETHi+CK+EIMiCPjUOf7KdDbOhpZCOpbu/W2PX9TDWgrAHvE0v\n+4YU7nf3YLawjfuky/LAtrb+cD3rGQfh/d0zPL9/Dgaw6++qdS0h+EvyJ7jLiPTomXwvB0ZZhgD0\nXe/mpd9hf9xnayzNX2FtGqZEXoKLYyQ41HARgnYuw/pYBB+AP6Afi+CPCcEWIL4Zlu0o1FL23blz\nopXGG8/ewP6wz87c6DsQzXZ9t3MhhWCXgMs7p53S3zLZ1lTyLenrXLhp1/V4/vwNvPfFd3G/u0/q\nZR+mHU2RJQjtKHlayxyEthrORMoR+OTv45DcOugJ/hQzY7xDuCtfnikcQvnSOgiEvutgrMEXvmTB\nxKvP0Ksh+KfCprezUfornW6uosbvG8LplrR1bbhfgvxUbS8+JazKt31l4Mxx5zMO20DbdEDFb4v3\nwAr7FK02ZjXquZDnWbXHDdXtpeDpVsi5LdNkHVT546l3QwtaPTnL5AG/8huVXP5oiHtvPBeux8Gf\naiUyV0PwjR0wYF3YB1mvXlqavmkGlL/K0CoNozWOw9GpO2lF3MOXoUqf2bo7uo0BeCzBOw0I43Dc\nI73nvgXXqtLXSqN/2EGR8n2ptHIFKn1jDTQpDNa4NYqYnKOt0qe4Nheo9HWQ8M9T6Wsf4XFT6S+F\nKOGPL+GK96mf008J5zoMBwwmJtOqmUh3ZgAI2B8PIO+lfy0qfQJwGHqoVxrGGrzav3Qmx1Kln2gs\nUphX6VOoI8WLVCLhk0j8x9NV+hUJv6bSJwCDHmCsQac7FzU1DKvOvKsh+IMxGHglwd/Yhi8DZ5SF\nsiZk2luJVELwL+e0dyk2M8WV/cHK1hF8Zq9CopLguw12GA4uLG/OqU2cxjZ00y+l3lNAKUL30IOI\ncDgeqkRqicC6ZL7rl8IkRDvE+eZlhOArUujM4O8ApxAhQUEKKJyN4ssRDjVcIkE7T48kIZ3bOe1R\nhnf2zhXYpJ1ZPJBfkrWVboHIMdDTTnvn2/BBwOF4ADgyYwU/CABhXRkzONV2pcxSKEPXpi7QiszN\nlFBA0OoA3TsHa4cr+3qTtS2dKyAIY8USHzsW5jg7gm2Kv/397nACDcNORiC4NqZs+OG3pLdAFwh+\nj053UOph1cq7GoJv7HqCvz24odPKJJO4zv6YTl5tA20Hl1HqZ5wuHO7GWhgzQPk4/LJFsXMN5giA\nMtvxZCNbe+mfORwEZxN0Ev4Bpnp16Lyqe8nhX/N05nBgSPbtujd0ZwYQKXTazwcp7I+SpTJNWJX7\nkZdDJDjUcAle+jhvhSlSs+lbT4LWNDyS7vlSBB+4fFieEPzjcMBgTCReoU+xN0M3hGfH4eiH/cTI\nqHLOprbSwjNCKXd9r0j4VZf7Fqpz7xo4EyVpkikKPIFR8N/E3VMypuWNqu2BKMt1yiU4e/P5W9h1\nvfN1EGfcBXBdBH+lSv9SYK3KJIjXNZHMVmCtu+e+0x2OZpx8Q5xQjDGZB+vrBgRCt+/Q6R6H4XC1\n/TDWgEA4qhhVcjheZ+KdW+Kq9XDxOHxHtcBsHWM7sc4H41LqdrrD/ngdidFSIPJ3fRDh1f7V47RZ\nMns0k2lvQxg8wf/wWx9B3+9WOZQDV0TwFakM+VQaubRzWtYoCDqEXjg1DTFtgkAqubXfb5hX4ERI\nFzTB3axFdHRq5GLJEMjHhHc44hg44DVtXA6mLzQpYdfvsOvusD/u48UUJ09FjWufEkuXjgWh9wec\n1h2Ow8Gr+rpNTUdhfiY33xzeFMP7Jvs91j1MD/yjnQirYe7cmsU8UekjCbc8CxkgUzMqItzv7rA/\n7F3EB+smVrtuF3DZYTeH/SQqwEhYPkvAJzhm9353j/1xj7v+btXKaM1TXS6PbVLiv+H+Vtkaj98G\nvXxRSWIXTPdsoUnm4jeC2/PGDBiGI/qub2DZhush+P5KWgeiaoz2jsdwxhHPfE3aOTGJkwq2OV4k\nyUPLuHNRm/8CiHGhFOyuRAq7vs9wS+N0HcHX6LsucLhLrmt9HIIfpZklcNffY9fv8P7DC3S68+vv\n9ANuCblfa90guLA8IhVCdJg5PNsKgoZrwiY1T+69uYfrNvxTmfnrIPf13uc+BuOhmzXxkRM4ajb8\n1RgmWkrKCL7GXX+P4zD4ENB27oy7/t477B5PuoY5wSaxXY/xq+EOYHIMXAhjhztP8CUOf+mebfmw\npPNXsijO91UlNnzK/k77FVEf+2LU5qXsa5p8RxiNTnc4KoWjGXBn234CLbgegk8KOvEUjjffXc7T\nfYyDG3yRltjawHRsIXU7eyY3Cf4l4/aXQPS+95Y667zEd90OYMJgByjoTIqPBL/3Hr9+HGeHa41U\nezqsIvi7O+z6HY6ee05j2tdClGzzZ+PYcXeILPUTUUToOxdJsOt7vDo8wBrrtTDbrZugVp6gUHNp\npxWRr6ceL5x63KfNzBFF+eZKKH8G6XnVcsycIkgitV6S4GsvFb/avwz5F6o5JwDc7+4x2AG8d1k2\nz8GlVHuf66WvyGkW7/s7vMuMXX+XfTsH6V0p6TfRe59HDIrbrwrGtr301QzDtpzgRx+yVJNK5Pwp\nohZo+Tq5HoKvdJb8QwbFOYSNk71cBAc/6W5QXdgTWLi4808W7Ql+ayFoUjBsoZ+I4Icx9ionSxZK\nK/T9DsyAPVp0ciWjEHxyBH/X71woG3xq4rmTeIm7+waQhqnNwV1/h113h2EYcL+7h9b6DIKfq/nk\n2eh6YYxDf+bq3Xnb3V2/c2FvZNHrflE44FLQlISGNQn+tK1ZkfJhnVy1E6fhUxkhnKH4T8kUz4E4\nsKY/U6gmdXYnAAAgAElEQVSFQKaQ3l1hrVm8dqt1JYQlHS+tNO5291BKYdf1gGfMKsjgbncHbTSO\nwwG7fney4HMpgt93Pe58wh3BbyuCP3I2JUBB+Rv6dMCBlMJxiO1KnVN9k3dluxl+wWncenW+9omS\nGK/2r9ztpIt6GuFqCD4YY4GP4Ta//Lw0CsQi20LsZ1uqnYVjbNXJyX9PARkj4vEU71PhNgNuyQ+S\nMr6OxZLJped0pRLB9TfGx0o++1OgNtdT4WlLxyytN7UaBvX7RiBjMYXXXLhdun7A41UtbQAqq0eu\nYm7WO7GHnhrifuHqXrDMUDNjptg51FkJKTsTH1dvJCaWfThcWDKMak4Mprj3+dz94DM9JkTNAmiF\n3cnTqbA8933UHgl+S13nmG3Awdaej6Rn8kxA7IcFoFjWZHw2tXdcyB77sjF9ckulL3snXVPCTK9l\nwK6G4Fs2mRQg3KmFC4GwZy/9eVD+8hLXvirwOb9+hlfpNwm+4yoZ16PSd3evH3H0cbiy0FOVvlXu\nmUtGQSGBzExruDaV/uF4gIJC523jLv3l9an0AUm5yyE2ejADsFECKgCwZGBEZdiYzCUq/eDQVCHS\nuUqfE0ZrmUr/CjX6hQ1/vUofIJhG4p1TcXG/pxK+wYN2axzmOImTUgqDVx+fEwniqt/28hz5Xmsn\nbR+Hg187W9nw6z4aSumQeCfY8LNc+jkDXq77NP9AOi/lfEusvjAyxro02IfhiL7b+Tj81/R6XGMt\nDOUElhkgz2USX35r2zDpjh914U9+4Deg+ATja2+/56TcY0PMWOgJPjMUK9CRfIIXwGm58k2rfDTD\nYIw/xOcPqkdz2lsxb8fhCCJCr3tP8O3J016LyKj3WeLjl42FEFBxtnJ58FU1XPIcMKmneAuXmTkU\nu2PU/ozNGUK01xDva4hkacH5BB9Jpr0z90diNsud9hS0crHr1q+hJsEnCqF51p67xkomf4rpX+LO\n6oQLl8+ecDgewYnQNg+t1Zc+H7fpzDUm/F0m5ym/rSVQijH7Sd6MioQvjt5Oqh9grQuNfuP+TUfw\n6TWNw2drYGspbE915T0B0pQlBII1BqBoQ/myB5IfMSSLrFPFHQfnpWutt00lZRUZuPS7A5hc1qtZ\nE/6jEPx1syYSTNf1ODwcQpaxawJKDjnLxtkbof1NhtuNpyLjCf55mhhxfgLKQ/HLE9LQ2lZypclV\nSYVt+5wpTacuaVKRcuFd1oDZBAe0ehWO4CutcTg7Dv8yBF98Ilx2TIPlxOJEgh/mx5WLmKaDHed5\nxLg15qVsjsEh9a+YGl2CswG7N3t3k+HKS9SuhuBbNG7+4eLnI0FwpOIPduIdAmGgAcaYkGCnHI/g\nYGMtoHC1CWvmYDCDS6+rXYjh1RJ8MJT1OeqtBTSq83IOhJvTzmTMyrzmN5iHrcZ+qv7jcHTMu7WT\n2iFRX/dEmzOVWwAB0INzrh3M8VHOnqUOuVvcClrWwZpdErSuR6f1aufVqyH4EsJzaZiX+Qidtwml\nXNgHQsJHrvoT55BO92FxK6VAnEctaKWhVecOdjgv41RV1YKnzDlQg13v8lMf/YUUa65rfiwQk4Mi\nBd11sPYhXG+rNvT9iAfYVhI+oPg6PeuXQpp/AoBzZMO2a1i8zA2buhR4Rr0CSjnvdmOH0KfWbr3r\ndjiS8zPpuq6pubgUzLW163foux0OwyFcKHNpCGF3BW4tXEc2/ISRi/eKxH+BqBWQ/aNY+Tj8HsAB\nxjhzzFoG7GpONCL1OAR/pg2XzEEHVT4YPiHQsgXeVgQh8wMY2XWK908FJcHXPsELw3opXwMqL9cp\nFy4iqkGtu0X9uSaCr+Di27XSePnwCgBV444VaPZyIJWsFSkrz8pvVdjwqUIwPxDSESIi9D6HttYd\nDoc9rLVhzS7Bs4aLKta3Ui4slTDP7Do307bTl/Okdj1slXtdINsfYvbakuB7wUexym9A3KBeAa00\ndt0O++MepBgKqtnGrr8DvB2/13kCrpUIIPhDLcRXfD+mWnKhtDvsDw+rGPQph8G57yTRDrPLUyL9\nElzTumvqfBetkM+tC5YYE/yY1Y9DGKLcXuoiAdbhfzUEX2eZ9i4HboDbS0hRPOgNmcDBL/XWboWX\nzxL8ayF8identRad1uh07512bHASScs5gt9DqUPQCizJXeDilKfn47HAEfwe2nslu9S14/V4KYJf\nEl/bIPhOOtsFgg9y46iL1LpbEPyQSGQDgm8k7vgK5vpkoDFDDMbouuhzQJFT0yo7uOiXjepP05Zr\nrdH3PdSDApGrv5WTfdfvwBA1sstPYtmszuFe89KfLh9TMk9K+Ls79P586rzma039a0HONWudlO80\nChRyJkheDQlndA7fyfegMIZAnJcYouogvZyHfHimThKcCcOxluJfDcEnH1d4aXALYoLgK3cLGXNM\noqHV8gQszYVERZIFW3gsLyCQjwGpE4j1N7J1XedUjMeDT5CksnK97qF1B3V0YSOdJ0Rzd4RbUiB1\nHcYSRS6jIBHhaI7YdXfRtFOUm7PJ1ZJpRFuc49bLsulz5cMz5fdMcvfq2DTrlrEGu/4um5O0jhZ+\nZRKUrIxSgHH6qrlDdCoRjlJOUiXv5HStCXOWQnq/Aluvtdjw3IoEP15CtUX9KYHuui6sIeUZ2xYB\nv+t3YGY8HB7QdZ3P869OIPjrLphpqc3H+N0FZ+Ju50yLa+pfCyLMGDt4gu/MHIM9grymJCTe8X41\n6fxFgi9JemI6+RSflD5IPgatO/SdywQqPjuvrUp/VcKWM8CCQRODxIwwGTE5AvsY/XlgNER8UHYA\njz2WCeen2dgArAp2CcsWbN2BzTYmt7BsXbnwiYWykUO1bEFMs2Hhlq13PrsCIKfBkA3rJOca42bn\nY+Yp36zps9G38tyrh0dt0PhqWTE1Get+ip0v4yGn8KzhQuP1Le3U3uXleLJMWDML6rpmCDkn/LBd\n5MzyTJvbe3L+bDBmKSPvnfWYnW7GOdvWN6uxTn0MRig3Vb4FLpHScifEkFxqxnxgrURQUZaEZ0ED\ns5q6Fl6O4LvxI0m2Yy2IGAQV6pY5TOePvGkjEHQVPfm5IPhi2rOe6SFrfJQUB8GLPAOytCtXRfBL\nqfcSQFMpvJCHVsghxdYsJ8YtnT6oUAeOJfxrUG1bsolKyqmMXCpJZ5+31gBMsJQuYrhnnmC6a3KB\nuf4wc1bPU4LEG4MQbIE1L/25ZDNSRkDKyrOMsCfP3eE2bqPUkjjnHacNs8px+E7CMdmym8Iz4JK8\nr7UjEuZc0quQ277WFic2/IlyrwtQysWK096GCY+UitEwQa27Bb1X0XudvdbSWgsmF+GRvk/hMPQ4\nDkcAjMEMgei0yrdhZb4J0CKCfxg6aNX5/WtAC730T42AEJW9EHyj3O4QRkM0GSHLpOVs/qJJwGvw\n/Di6ozYVCKNmw3rqwyx5+w167fqtVdv/ogZXQ/ANG5hHSDjjEvi0BygIVnAZ/kBiTznPaQ/Ifdhq\noZlXQO/HC5Zdkg53MQ6Hy3/SRSbpE4y10Er5a4XnfRDDor6CflsQBh+e1HUdjDEYKvHJdsFBkRJI\nKSvPym9rz9M2SmKrrEunGQg+c4gsyNKnTuDZarNsx/iY5rnpcVJIg+DbGMI0Ve51gjIL3KZOe5ZA\niDbezcAkTKi2LtzOWijyUrEZ94HIxbYfhwMY8ITfn3CV8lNwqg1/MgkLAd3xAK1cLL6xQ10rN1n/\nOhAJPfgXWB/3Hzzmow2/zeAkVCKMY14uMDoc63CMpTMndNqH5a1Mr3s1BJ/tY0l7M1InuUUmccOS\nce9cgl9+XZa5mmOQEvsvO4lfa0fwoyTJVYStNZ7gD5P7NMByPuri4JILDQAcATXGVCX8JZJBGaqT\nPquF6JTP8zYKpz25oEMpKGWChL/nfZ4KegLPVpspSGjYksNkys6axpS7vOFXMuFXCqmte0l62VOA\n2UmHopo/Do04fCJ0+uCSbunI9J8EJ3rpz8FBa2hloYhwGOp79pz6a9/JKS8ZWN0TyqR8cV4WwekU\niJdJ5eeIsc6B0mk21KrgrtUEn4i+A8AfAPBJAF8D4Hcx858ryvxhAP8KgA8D+H8A/KvM/Kmpes8Z\nmHUwp9IHnGCfp8hcaiRplZr7+irs2EAgwmHxgkJ2vaieze3Kliws2WAGEGemRZ26ko6HDcsMpZ1f\nwTkmplYa3Tart3B9UeH4xggqwu1MYgT2kt+pB6OrxWlvhNA/feKdXK1cMlaYYFweDYThviDBN2SS\nsC7VXjde3W98+mZn9z8Dlyn15yllCbDGAmyCgHZxszAl6yZ1gansE/bm41MytUqWvfRvsE+w5U0y\nSqnVN2SeIuG/AeAnAPyXAP5s+ZKIvhvAvwHgXwTwcwD+fQA/QETfxMzN2xcUHifxjkOy/UqRDnaR\nYGchNfnN8mZPz5y1JMHDNkDu0hPvfOKSPXSBcyaiPHzSv9f+2txFXsuBc70Atfd1t0hr6xkB6H2G\nvaNxObljEo/c7BAkFZFairrTmWHOP+fwcKwKTvNrt/DVPi2q1ipkTBuMCWMuubdb/c7wLfqQllf+\nqmZiQPLl1OpptZPWQ74CYhrZeebqWTuPoz4mzwTKZ1x885QgTqPGJreonXBm1JK7CHRdh053OPiQ\nWK119TyRJE+iJtdaR7+FtSOVDPai72lBWQL6vgeRwvF48EnCLqy0JhEOoiZYXnCDsFMWjDpmOgXS\neWY4mpjtJ3L+RcLci4CyBlaPDjP/eQB/3iFQVSb8fgB/hJn/F1/mXwDwGQC/C8CfadVL6nES73ic\nmu9cnul417EQsE2SX7wOBJ8cwVdeWicf7y1OPhKWEou7REXap3lk7+Q3hd9FJBfvLHnqPEkWK8MG\nD4eHmMzG1z0yycy05Th+mascx8z2m9oEF9iEldJenaddGN7epwSWEMcV/W/2wa8Bsq4Ppy79NETJ\n9e+JQ08LtXJ5ick562criDkspi8umoO0b2Wf+m7nQuwO7rztihwOsQ4XAirpdwNTf4LvjZSXdT43\nzqnjcKusS0K1A4HwsH/wZq7L0hAxuYSQSU+znIY6no1u6N34K84ZA6K6/0d6HubaZfedUoSu61xa\nZB8B4MZoOf6bskNE9A0APgbgBxPE3yOiHwbw7Zgg+CUhuSRMMRaKtLt6lAGiaIveghlJr0U85VsB\nd5HCZRZ2mg/A+ktaXOpcd7uWu4c5SvgSD66Sw0DCRVogm3JL9Vu0m42lyKXfd10HmHg7mEtjmY+J\ngIzNHD7pgSXPooeu5/yT5wRMqum0H+9OR42KMYOT0lbmsmj1geDWG5HNLidZC04b5O9fsOzMEY+Q\na2MKH6BO8AMhe2KCr+Wec2Mym/BaSKM0dLEX+64PWfPAgNJ6VEba7boeRgi+7tx8svVawFUUH2Im\nNWyr7ZVtz5UVgg8wLBt0qkd34dS6YS78T+2FG2N9xEySVyM1YYUzwGtQJRFV2jdTeOkDiNkWFYUE\nZ0QPCRO9Dv+t9R8fgyORnymef8a/awJtRFSXwNShI1dHphyW2igpkEtacfq3Apbzv7eElLiRV/d1\nunNZ3YZDkOgDXp4hEIIviSam8Avq5w21FCmzcQoI48JAIPjSzxrBF0/5qfoCES8IvvRbNEdiPkqf\nt0D7NMYilTG7LGh934Owbp22+iA4kSXYmX5OgVLKHWhEALZLInMqjEOiov2alIvKeUr8gEjwgfMS\n7whhlt9T6Ls+k+o7T8hLCDn3jcNDK41OadAJBD9b5wsIvszNVFmlFHZd76/4tVDd5VX6YS68d31g\nMHyoUkrwUyfa9MxTRD4RVT43lBB8WZchAVdg9H22Q6/Sv9bEOzWz26jI4zjtTauSGT4hReIZuVWC\nDYvTnV7ypD15Moctgfx/YO9sYl3ayDzzU9I2xwQt6XhN4mcr9ZyLN3tzyRlVSnasoKZj6xU85MM5\n87JzbQkXLt8KUQn9tqLWx+h5C4hcNIQRouwZMBcmNI/Tkj6kh/OSfraBAeIkyQs2iSk/FUgRiNOE\nSi4/AMRJ1y53zr0YkHN4zW4/PEVKoGQ9FblH3J0Yct5KWthxG5JSVwiXy+Hu1/UZBN9drz3dJ5dI\narpsGKfAVOdE9hIQwmV95Ja05s5HDriOkgCFOSQwUXVuskx7IuGHZGbOYY+sAryZWZ1gBt+a4H8a\njrh/NXIp/6MA/trUhz9jfgqac3Q+Rl+Hj6mPb4xiVJNU3xFA1jlDpN7mWywkRXwykVOykOAWgZrZ\nMCcDkXcWiUzOYEy4WctJrUkSD3Z51FP1tcu0NzXGMWvfhogD4FD3WmC45EKDGfxFQMbnE/Akvzjb\nmKfbchnMOLPhE1PGPDLZqg1/ul7tw/FE9U7QnSf4bFf1v9kHb8N3hHoanymwnKYZdcT01Lq2AGG8\nQgZNTlT6LJnant6Gr6y7uEj0tafk9UlTx47TJvv87cwgij4gozpY4WiOGHzYnjHGReT4CIK1Grpg\n0ppIxRzK2vmyZClc8yv+Q5e+0lqupTbWeuabwpnHDKjkbEvPN5lDAsEmBL+WhttVIM9kfTLAjHeG\nX8AvDn8Hz77wHN17HfbHB7y07y/Gf1OCz8w/R0SfBvCdAH4KAIjobQD/EIA/OfXtN+q/H8/sG6Pn\nlwjlKaW1/CWFrGUSb16GoZ0KTKdrCjgh8O6gvpQk4jjQmCwFMHZwDA9FzjuUJndoSMieookwn9CC\nP3g3laYcwT/VTOBU40PINwC4RCMhmUZZfqYtOaz8EkpRzD10yb9gzp9P4alUIAYSRSH5tdf0v9kH\nAtjP41me60TQ5C/OYZ4ds4uDjLVn4kHF7+d4KG4EmhiGco3aKbuEKGZeJMqFFaVifDiRz1BHY4FG\nW41BH3E07jIpY43/LhnKpfgke94N87QAFZN/tcu63BnHcO4wHoHgi8o+MdUJMDimjismLYsMIVTn\nJiUNFJ5Fp1Jmi6/pPo6v1B/FN3z0E3jrzbfxmV/9FXzq838bf2X4i4vwPyUO/w0AvynB6RNE9C0A\nPs/MfxfA9wL4d4noUwB+HsAfAfAOgP95ru4pyXtLmCOWxroZEe6Sk8P4vIY3/PaCQ8Wk4mUuDAzK\nuNuyfNhanuDFOZqx4mD3ZjNncgjL+QLYn3ZgKy8dDN4BDgAe7B4xe92Y5E+1pUTiTspFu1bc/vlI\nZMdCFTQzjDJ+TboaOt3hcDysShA11QcCYCUOH6fPEkHWkg1S0Bnsw9lQrjqq/P605N6NFygnKFub\nOjWJRshrLxtE0ioLPWgMw+CyTxamvVWwdssvMQJTQvCVW2fDcGGCryI9IKhwPhCcqj2dq5YH/hIY\nMROWYcTxEewuK1Mq+E4thVMk/G8D8H/Aa5cB/HH//E8D+H3M/MeI6DmA/xwu8c7/DeB3TMXgC2wr\n8U02NI0DR0xCMpmntu09EsSkEl7Cp5RwOSgXdVD/+8dzSZS88v1CPThRiiT25hIOVwCnG7gm4U+3\nla4b9uOafjs+08bPx/WLligd4zQioPxmSqrOQgaz53DYMoMXHLytNljwFSma5enTwBTPzI0yjw1M\nHLVAsp+2JPjkb1/j8ToqyzktVTRDLvJlqq2X9Bk3ntf46VZ5X1bwkcQ2qVZ2Eczz16NyKT3wJ59/\n6ccoHoJ5Fa1xW8gIyXqQc/aUMFzgtDj8vwRg0gDDzH8IwB9aU++SsDwhRrVkBZuoCslxv46Li/nF\nT7FXjapewO09dUiQA0pCejiE5IljGCDhZDI23kufFAYagppQT0YRnCM3LuvDWtBKoVMaRmkYM/gL\ngNJ+tE6keltKKW+4q5WbO+Xq30kki9Yu74G1DGP2mRd1va02U1KV8MnNa8B/dl2263GJd1JJ9RrW\n+GlQG4ZE47oI5qwG8frVeI/BlsyxhJ9qpTEE6VhXcZKIEKO7wAiTnjmjaex83Tr7pnIF1MqX9Yl2\nS/IEAOzDU5dNRhrj3vqEEyZV8koII0RE7vpqX4QR51aicYReWe8vEepN+kJFP50vwDhnC5GLmjKD\n07RIHP4auJpc+jKYc2XKWNm5BbMWRE0SwvLA1bCstfC6EHx3pzNchjXEFI5KKVgTr48VXBW5Q4EQ\nnVfmxsupwoLId5E+rAVHRDtoa3A47mHskGVYLOvMVXljEKaoVq717Ug9CM7KEPnEO7pzBJ8sHg4W\ngx2S/ZMzp+66mjqOrXdC8AX/ufFs1+NC+sjfv8DEJ83NtUBtTa87f8QmPWEK8nfUB58CV/sJ2NaB\n1DgzZi3THlEk+IPuMJhjCBecqz8zzVLl7ONxWWpctxvqokTAl7MH5MMGB+yPewBw99MvvLo3tE3y\nT61QjHUnRdD+7DLe3CXfuevDKbQtER9CRygwev69HwQ5Y9IxE2fKkk4o7QQvJ+knqcxXEP2rIvhz\nm0aRu9Ql82xE3RP1NCTcgaqV87BOGYxz608XYctXYelCvSQoqHDYWMRFppXjLMMh7udKewkfQAi7\n0UpP9kX5TXMptb46keBLCuE0f3g8XPI6xZLZakuS6tTKtb5Nn8v4qIzgk5sPObDhuHyR8IXJSA9v\nO4Fj612Iw5/5fraeJPOZmIVOmZtrgVoCIg5x/PP9Yu9pPVVWKRUSsVrrozg2FAQURYLvkEJVKiaS\nRC8uydNxOITkTnP128JHShUEnytlW9cmp3VlybWALJWu9bkBtO4WX8Esdctar4GY+QTHQAesASEy\nH+IuG5KKielNkqQxu5+JBgBwmsWyn+znvUzS5vIl6GiG4TFTMAdXRPDn07E6TinfACHGeYNNIYTd\nha0knug4f9NlTEojNOnR7hKYgJAwx7PToq4Xz14gV+krzwy4b/0NazMMkgqL9jIhWqckJXLpgd1B\nKLHHaXKSUZ083VaQhmrlWt9mz0U6iOMompagaiUT4uQVKa95KfYRT4xH453yOdYF/9nxbNbjCT4D\nxjrV5qUSRj0G1BLg2LAPlhH8ueRQebKiAcDpiY9a9fdJZszAoNcIvk/0opWo9PUsLk6jk2eYKyX8\nzDSYJEGqgbzPznz/e+fTTAMuLp68cLJ0vObaFkgTNUminMC0BIZ2CCp3qdtaCwvxCcrbCQQ/KR/a\nE4YPKbOj0KkuMggi4a/UlF4NwZ+V+Dgpl9o7/IstHFsYDPI3LpXeqOfWn4YXtup6+tvEgFRlJ4lo\nLFEeJuTTpAII4yXl01jbqTZKR8BtYT1zZq11tntrHBMDJBtqXGfsX6Mtn6CkVq71bfpc2k6PIlET\nSopjl0AlZoa0/rKb9HCc8oxvvWMTzTNLPOubZTy+1ieRIdDFEkY9BrCVO86TZ34vB/UwxsdveOal\n27KeoKqGP88oTbxDy+pe8B6+/sGYcFcGyCeRSQkq4DQLALTfEwBC/vYc37wdRgzbDZb2VLvp26Wi\nbOsskHTT8DiBE00oc7jGWpGkuDWLz5XQ9oSjX5Yfw88NgBACK22FG/EkV5KNKndZ8+k8Snx9kPht\nJO+hvcyub92149Bey6rD/TNr0qxfDcEHpomqOD+kA5h+s8lBwnBHEhnYdKI38NInmy/6uTJPBUwI\nC5nZwpCJt3dRqmp05QkGJmSmi2aQueRG2GBMJ+tfCeIoZczgb0uMm7ZWp2gnWm3J9bK1cq1vs+dJ\nlETA0R+Txgwe38HZFZW7q9wdjrlXmEvG08Cx8c6pKlXAf248W2XYO3+mBH8uw9o1w9k2fE/wJ234\nzIBycxycHDc8FpgtBjVA+7wZkge+bIM8vp0ZwnpjtrNJ/1yZdM0iy3uSqfSTsi1tX0g8k+ImTqDh\ntsgheKzLtb9LQOq2ZJtD7DTnEUf2Z50QfFnOzgQc+2G9+Ubs8RH5pGIIXUM2ZsHhr+iHMWJiVtBK\nQXWqqp2Zgush+AucD0JoQkooEsl/CyCRaBOCNBdmtqjedNE3cJ1MCPRIQMQJwWcYGJ9Mx2TPYxcI\niiT1Jodb9SbD8s5IQLS0D2vBErnEO17CJygYs08uMMnrjAd9o61A8MflWt+mz9v1awxkQKScpOa9\n9gc7uLvBkRMUd0DUcZx6pxL858azVYZBIMU+kZV3tn196T3qlLeuAarDfFlWjlAMxkTasBzBWbAE\naDWAOd5saa2pagbACLkpKDBv08TUpzDJ68qY3XrZlqyTlhc/RqlPkcuOaUTCJ8IwDIszEwYhe5ah\njTiWXvoJAfIVcfhGtBiSdZSDXgShnOTPz8csnsEpDNZAex8GRQpKq9U3uV4PwccClTYXP2vvzgAC\nwSrrM4xFD8t5FfWyugWaBH9LVv5UIOeAZSHZBQnamzi00pkaTsCIp+rS8arpHreEUyV84xIMKS/h\n79MDrqxz5uwWCb9arvVtTTdbKaPUAGWVk/CJ0KkOBxxie2VbTfFlIf5z49ko4ySgaNYI9x3coAnM\nCqzc3IqD49ZmkE4IPqJ6ujYvzAxt3C2Zwsg7tfJ1gCYdCL6ETl8avzQRW5q+WKKb0nNPnG/lXF8z\nj/JtCswM+IvKlNKO4L/OKv2nhqhB2J4eLTnonvowlEtzSoJc+ldkuQ8qKKflq0zMCVqZMh3vJHN0\n4jDm+FDoR62fref+0/EiKsYTSDQ6vvzoedmXFoMA5FqXEqep8ZjB30koS9TVlUdUjNGlGb1Lwla8\n+BIGKhRNpceN2k/QWFw2k1CvB0YE8fERyP4oNRuphjiUL9U2jT1dZoMNJm0pIEfHSmfyqyH4ROtv\n/tkWAcGDfOIdizSDcxW3KQ1f6/3aco8IwfOeVMBPJ7cypd61Uj5GNQBEQ0gJKuM1mRf+UgT/BHAe\nsM7DdzDuoqAQglhpK+XcR7h6aWPcPVHyFX3wusq5vomzjoRJWmUwDENw8CJ1foKoEv+pfi6pJ903\nBLrgHRBL4RSuo52YZS2UeURKCBExmU13Xu28HCiE14lPVN1L3YXlSZKnkFDrpPvma+oteT53ELbm\niqCVhAQzDsf06u6lg9Vqu92m0Aaxs0vOjLJckByTqtN5jCY7GXvOnxd9YHA4n7IY/GUdDXA1BF9h\n20nRhf4AACAASURBVHjTtRDCr4S4+WetDRovPskhHNozfUmn6hoS7gDJGGQEX4dwnBCeIsScXJiV\nVnG8xDkrZMOa6NsaO77Us3WiJQGtNbRyca4Hu4fEs7cyQE4d3CE0rshLm/lAICGsIDDZ2b6Js472\nB7GxomZ1NvIl2SqXQMR/nkDN1RMuGynWxVNBzTa65JutKG6Iy26AEHyd+jQRNmtfwu3gw+VENV3W\nL8RT/g9M8EwIW42dyuY8IVJlVr4pp8haP7RK4/AfQEyrcsu32p5q0wk+KnFChd8nYvqjxHG58KlJ\n5rEUnqKDuK+nQEGYfaWUy5BorYuC8c6BS+FqCL5bc093GMjBJBuu9E2pxam2JD8GN98LiD3nGg5B\nAQl3CQSfXeIdxwTpUYw9KYoSCVxfDJsQu5/WWYM1lyXlGaym6z0FtNKhr5JWF96fodbWFCGUWHPi\nnLET34i0D4SYoGeub8JcaaXRqQ5GDRnBn0t4tBRCrLyPtji1TkWyDjiEKz11cqn0wpOlEJJRbQDM\ntIjgg9ntN88QbnVGSHIawDPo1lYT6qQJepTS4OG4SMKvMVRpIpzUGz2m8B6Xq5Uv61Se8QXYaxZ9\njoGFY9Vqe7pNd7GYRFS5FLgI9MIxua5fpqIRjQTffSDjGSIGRKWfOUZ7Bke7/XTEYTYSqgXXQ/Bn\nEu9cvv0o4dey/pW4TZofeD6JTpow6FoIfsr0AHAEz0uNKjmoU02AqPRTh72UiZkah1YCoinc5Jut\nzT/aZ1iUW7dkDltJhISpm8KVKZcWFLm0mGkfUml6rm8y1pLQRnCVqIgtMkLm7TMszd9dPlWPYwaT\nexieOLmUc7Ra+812yYJc2OtMpj2lwKzDgS4pk7cAlajBUy1cOS9KueiPNLHWkvVVSu1SV3ifaC7c\nfRO2Wi5AIypA8HOpZv3NpkgYpiXQanuiTaWUv5s+/y4l4EQEWAtbaDnTeRS3GDGHxjaj3b/UAod0\nyD5KgC1nGsMlcDUEf4tY93PbB1zstaJxWFmJW+0+ZKmHEW9waraXOnJcCdhEnSRe+la5TG42UU+F\nsfKJQVzYFYJaGUBRpg5rFmp6Y9dcvaeAZQtjjJ9/FdVyjYiDScnX2TcwvmUQYNisDy5kh0bP60Ag\nSyH1r0QUaKXDlbmbjIvHX8LyTq7TmzQkLA94+uRSMgdrv9mKJbewUJOb3qnW5CpaIkok/S2Ag0Yo\nzTNi2RSlGMo4bUR6Hba10/fYh9i5oq7we6KCZkS1d1kuPGsQX07GaUjC8iQ50BJotT3VphBYGYcY\no+9+Guu0g5ww4eEdx3j/2J7J2hwl6UlMAG6/k9/zCiRe+isyMV4NwQfWEYCtIajY2am50sQ7wBi3\nljNTKMeYdFBKPV+vIhwPAFkf2kI2OIYoqyAx5SHxjoSiWKf2NlZBnM6qZRqwyoZvCxv+xkmKAhH1\nOfSVUjgej65PlbaY68+BKP2XxI2Qc+Tue0mnUz6vgDcZmkD0bci0J1qWU9R8U/hP9XO+HoDhEruw\nXGG6AX7nQH6l6fJvtoJScmu9lwQyLpRxO4aDEZP6TIXRko/3JkPBxMXezDAFNQmf0nMUkeA7ad9W\ny4XyDQaRPOOQ5gmQnAJLR6vV9lSbci4GAYjdKo/+FjFpTspQjdpOGAUxraTPyyXCzDBkwKDgvEea\nsrsXlsAVEfyNpJMTQXL0W9lkfkOIx2y5ScXDtQaTIVtJmbl6HhuC30EinUpWPZE2CAkh8HZua413\nXInjZUuHlQpck9OeS6dsYCW1rlI44jipyWnjIFcMNySFRh/m+uYYSIKSPN0Jc6JIYbDHjTRGEf/z\nnPYYbCWxy/yeuG7YjuRO1eVdZ3wmt5QR3MiHAC6pjxApUj6FcsGIEVm4fFpOgydJk8xM4p2KgA9K\nTHfpOyI7+nuEb2O9EFkwdJ5alyhcJLUEWm1Ptskx8U4NZ7ZxDEppPp9H/4zi9bnpc4GQi4Gtu3US\n7hrvPA7/NST4DLRH+lHa50j0JfFOqYoqys/Vt7TdqwHxPeAooRsyLgmLtdEj1o+PaDGUVZFB8hfo\npOaBrXCb/PtMEOc3Y21i50SePGcOJw8u/KxG8AsfZpbSxTpo1Os2t4ExBKNMyKmvtYY2CsdhG6Z5\nhP+JY03kXOSCSpqeXqU/moNFX2zHXM5q9LzkasVxFM6hazN2gxWMHoIQoyB+IGNCKf5FcpGUEwCW\nE9RLA5cSPikc7fGiAhQrDmlzUygFEnnmspTGdLslEyD+TqXGN9RHiSnMutTLquuhtAq3Ub6WBJ82\nVZydjIT/sb2KfUmmvVbZx1b5S0ha9juNywBxoZdx8umzKbgKkwYh7x97SYtPwC1ZQyIVpc9HSeel\nvM9CV22P0l+piW94vwTH2hIs2pmsKxdUqu8F11Syj7kHZnAs6y36e96SeULn4Lm2CaP53VKZRcn6\nDNrjhpNCxJUmyz0VCEOS+tu4FxduF+NtnL0Mv+aFaOLdHO1Jn+d7aF1nr4bgYyMP4/NQoOgEkdz8\nJu/OIkzpZM9lLivLPuImC+F0HkfHQSooG2NPRZUv5YOXvvU2WtEULKE9j9y/Kg6IdjGJcw0H48ow\nspQRUqzirYJyaBZ+Henz1ljEOuP1uPL/cTh6By+TzcscjjX/kuxQIZpcp63+pO+zyJucdszupdY4\nZXW9BlCT/KbKxqgYHS5m2UILmHqKi/bqaI7BN0dUx6m0KF7wWkWny/KMPsXck5qJZs1YE+8lbNAo\njeNwCGfTUjoiWuXZnClJmZhLvzBZFkxoKiwER+bKPApdKb3ty/DGEIdPFLSrKPzMlsDVEPxa8oen\nwIGUOH/EQRdp5xy7cZbYYU7CL8o+ZtheCE/xmldhgCQ+HRQ5a1fe2btjHGkSWrYA7cfuXw0k5EUS\nDBm2jnkBr2ZC01CnVOpoHfyj5zWCn4ZBKp0xJ5ZtcDZcukZrjlVpO+H3qesQZghZPHgpHkycj88U\ntMbpdQOH9/jmsxpImCuIXOIdTBPDNRCTZUWCL/5DLqFOTpwAl33SrTMNYwe3HwqP8FOENMsx1DM7\nLxplW+8lO6ZWGofE52o5wRfHxWm3N+uTJREkrDOq1FqJpWr3aNTmMYbqRSYiMAucCxDarw05V9wW\nEa+PZXA1BN/ti6c/+OOmi96TqeroVEgXYesShVJNLmUfU/ORxuADCHcuK1IY2F1MkV7JKLHrsBzs\nfSKlLBmvx+5fDWLMsfKXhBgYuI23NpVolt6WYjijHJTlxUPp85B7voIfkEj4XvIS+6D8v/SqzDRr\nYq2d+ABtf4JGf9L3ckgSR7+PyChOz3lrnIA5h8nrgugEu4QR8zZZOFt7vJjl/FwdklhH1o9IpGwY\npCmJtY/jHPaEURiMWwjlflhzcUv4Jkk+FPOR1OuZet/pzu0Fq8DWXZu+63Yxtn0GnImCZ/sgvl2A\nT7VtOWhfwrciIMk4+mgvcYwE6kxL2rb0NVw/btNyTsJ3/LNnoK0n/It66+B6CH5puHoKHPykOtXo\nGJdzVPqZ9NTY/OTVNWXZxzzcSgksJd6lisn99Ac7JXHyhRZgsr1H7l8Vh0SV2pLMl0JL5dmSbLPn\nXG8vLROSHfn/rb+NzrKFxjKC35qbEW4T5pY5ST1VrRKSpEwLJfzWOLX+vlYQpqd943qEIGzAEWY2\niTnxzP5mmURJBeaydBJL16+UJa/GruFxkoSfaM4s6qaCtGzrvUjzLrlTDDNcLOGTC7NTNE17LEQL\n4FPrqpg/ICbZyv+26ZqvCHKhD5kgWGgDi/NWTHaZv8JKuBqCDyDaJp6qfR9n6cKRbOZEtTajUQmp\nd/JUOB+QawA2S6ayFDxq0qa1NoTupPam8F4IjrUZwZpLPBSae+z+1cAiSMkucUb0fl2LG1u/ZpyW\nLn4vP8r60ufcMPfENN0wZGCtu7LUcEy8k0UVLOlvrZw8ErNkJRy1infrfbIWrIR5FuPRRLExTkCM\nqHkdgHwo5RKVPlN0YjU2iePeoL/yucT4g3NNSYgDT5qRa3ODfwjGUSunoMVsIz48brcs23rvTFlD\nSHYj9nWzOJLAS8gzfXD3H/h5hCTeyfEKSZIkIU8lDr+mDeN4VMS+VvMR+L1jGVo7U4uYn9cwg1dE\n8MUm8YQYiG3E+rhUr/YSW9dZN31lUVeNeiqPH5sJksQoaWY0Zb1pA3kICeBVtdbCchJrjfqirbb3\nxEwe4Bgsw8bH4Vsv2fg0lnadZ3KQhDh3xAkZtIpxSZ+3ogJiUijHUBk2UP7iHJFwlNLNDGG1+mrz\nExjN1Ht7oo6pMinTmmY/qzG1NWiNk7x7XSR811050qdBkrg4U6IJ62GL/sbEMpHgAzmDnpeLBD/P\ntDdO0LMWHAOTr4dWPVPvXZY9A2MSYYQZPJMcqKwbM2GP7oyKop/lmDAo9MMzx1m/in1UddoLsfkJ\nc13j+SUOn4G+99pIJZcFvYaZ9phnJIpHQwTOYYtz+4vkLT4VUg591mmvKPuo0oxwrCLBK5c+V2Ls\nxS4dVN4wsFaFZ1LGWLMI72uQ1sRXwyTJbLTnnNPDcVll3kwBCumJ5TmAcV3F8yoB9WUUMcjCSfgq\nzxmglcLRmmWZ7Fr0J7geLGDaWv1J3gfph01wQFocOtUaJ3n3mtD7WrjqVFl35sT9FExpZx6L6Zwa\nFdPCBqnYE8mU4ZQUvOIQCiQ5OIp610CpOZ2qZ+q9sQbKS/gh8U6SxnktLovw9TQq9a8QIKbICCOa\nSqYy7qVlyr5mztteq2CZ3dmkKFxetmYOrobgA+erzbdq3yKqICVc5dxNt4ZZKMs+BRMUPEb9JRBp\n4p1scTJ5T/Ek176oyhbi/dRMHjGF0DZjRGrWjmivNTdw3MTZt60uLul6wjQ4da9I+FGl70IjD8vw\nncFFpKXJuubwTohy6ml9cjKfsvwTywWXAiZ2yYpSIruhyYuJE7WzE2hSFXUKxhiwcuU7JdfQ1rVD\nTwGS8ldMDkopDGZYodJfD87uPz7bFKmMEZBnKcFvzWOpNY0RFZGQi1Ovi0TQWUTZ0tsBgSsj+GXs\n4VPhUIoPT43TY0HKWQaHrcRZpFXWOTomL3lcrgZrx3UUm7qRmFd12gOf3FaI6gC1zTSVOifbSxwh\npW5x9HMhb9uNS5jbZLyXzGNZJjjoFeOw1bw9CTTW+SINRKt8+rgSERR8QjYAklSsXEinI6KR5ARI\nPclPxmVOJbS+7FaOtsuhcFqszHN4X1XU0bhr5K/NpmlG2PVTOXNFtESshqsh+K5D5x0GSxiGqfoD\n1wQCkHNnow24ASxRJz0mZITE73Fnz6ZMOht7jROYFAxMJs2lZWuwVlIoOeGtNjYRhTA3pRSOwzHY\nUFv9mDpcArEHqodj69vJvvmDIUr0zkP5aHzinWTczw/hStSXCw7RVpmUUEj0icL5+D05LDHPnEjw\nJReESpzjagz3qaDJOXhKNE1YN0WYJMGF74nkLL4sp0YMUNCUzmsrlpQlUAhPZcs42mMwpS2+Hncl\nkKxdcaBLZEMxS3LMlhS/SyNTGgQ/PJtgBLVSYNioCQ/7c/k5ejUEX6TEc+y5wrnOlmm9U8JduzuP\nydQlnM0OLL4kN7oeMgnSUtjs8iyo/SiqrZXSLlYf+VWQS8Ov1uI39fepoJR2h5tXj5V3zLfaarUv\nB47yF220YHIt1ognIajztB93O8Qoia3GvBZjv6TO0fxI/DGr4PQpRON1hZSZSx0Jy+e10LC0fCt0\nLIbN6egDQqeFv9VAaxXWEiE6pZa2YGGCARd7f7RHSFjaSQQ/MJHL19FkWULCpGvw8QBLbg9oWpc7\nYykEx0BC0KzFsDy3z8NlN4n/Tsr8x7C9lEFXmf2/qh3wZ3F6puQJeJbB1RB84X7OOQwUqVnv36mN\nE+Obo4QfvNOTFKtbbb5rSDqTgiSNEQm/VHWLNKApsSHJeKUZp5JNN5Wadu1VqcGBKcF3C9Deyz3E\n9FoLqxwhFdtl2VYq8ZSQptKsRXaEu65rdXoo30mdWiR8icP3oYSZhH/muIQ1qdq4LulPllI0nHm0\n2bw9BWTaG24/r+7rpHyb4CcSvvWaEbVd2nHJ1ChzIpEeZUId2QtOYnb+IQDCDW2r203Ohy3KBq2c\niqlumTlkB7wExKx4CNJ1K9MeODp6B0Y8nUeOdSrSsImgXka0pOWITEboX9vUusJxXrSJxcxEcRB/\nQG34soCzwywWThZ4otsCLmfDL1X6G62XVHIRs5Ckgm21JYlLajiM7HwFnGLDj9J7ZMBS2+WW4xLa\n4m1s+KP6r8iMtRbSQz3VRpbPqxqhtHxrbFIbvpckM0JyJqQS+pTWkpIkQKU58zQJPyZh2qJsdjYl\nJqhLapBqWfHKtVDbOyXOZflgShWzQKPf8RwWBno9Xboegh9MH6cT11nP8Jmqw+Hp45SDjZ1yvLby\nUn3qqIQShEt14R/xdyEsqdNJGs0AixiXmhBN8DSXvrbvpYfwVt7L4qVPRDCcxrZH9VnZVrY+Rojm\nZUqYqjNU0UrQY13iHUsxhFDs+hKSdPa4JEl15jyMp/qTjYM/jOfWxLVDejCn/Rg9r+U1SvvdGgJ/\nkLv8FkkI2EZDZsnAJIyirN80KgAAmBC83a3c04C2R/8clIl2zi5LlOUJCLZ7bqd7PhfSJDlhb5R7\nPd07Kc0o5jFNQMXk+hoioxpnhvWavNTMqpQzhS+F6yH4OJ8AWtjqYJVtTLz0tpSoIsq4x6SdLcCx\nFtdz+IndXgi9IgVLBuTvzE6lSsAvQrJO9ctJHD7iIU92QjJc67RnCwl/ou5V9QqT44moSDdKaRgz\nTLZV7YOK71pZs2p1TvWNk7sdLEuiIJvZMQOjdu64qNQ+WMd1SX/ScRAGcm5NXDuk0mPLyZK5YcpJ\nyldvKySCKJbSePJWfaeAW9vWJ4/hbL+noIjDZVnCDIPGmfaWtyt9WeC0t6AsUcxqZ7xQIgT/UmF5\nlKQjlvOunBfJZ5AKSKnwwxTnFJB9Hesr+yggoc9yxkocPikVzKlL4GoIPot3yhnrmoknv09tidX3\n/mBS/ncwnC0blNlXt9p84A3r2gI4/hQJnixBEbLDQbhVd4BbsI0crUKSnAcL5mMlftk3Gw2d3DhH\nyjM6yt0QqFW8NKRsa0rVLX4fLUk29KFRZ+udYuWZEgsidwC4za+gvARdmiJOAbmIJBvvJfNY4myj\n5M/gqOa8oiW/FoKmAsj6UT6vru1seisEn8kRO9HSeHV+GSJ6DlhrYJQ7z0RadM9tbpVLCKc1Npjw\nSsl1KZSZ9c4uywgMiTUxta5NJOWtgTg6JnOBozCz5doIApJfE+VecfuCs32ROvmF7jLDcpTww75f\ncTsgcEUEX+Cshb3k05mDK8Rg+59Z4p017SyFKzr8pL+BoCe2SJfwwXvyclRhpTn1wdFxqxbLvgV+\nU3+fCuRTB4uErEgHJ5lyY8/hBEQb7tzBM4X/6J3nh92BxiB26Yw73bkNn2oVNhiXkblhQZ2tMkFV\n2Uha8tpBC31eUGbifWrjDbcsSjjsVswtxdsVU5NU2QaBYaxbVMaaLOnWtZhkjDUg6yV9irdAXkql\nDxTJo4CMsMu5mJaV8Q1nZTmPNQVh8GHItUa2IuFfNJc+Ef07AP5pAN8I4BWAHwLw3cz8t5MydwC+\nB8DvBnAH4AcA/GvM/NnZ+p/ImSc4q4kjCOrOWK3vUphyvGqVmyv7aJA4Tso4hEUr0mNgPik4yLiy\nCoCJ/SLUQywr0tEl+lGFWpu+D5nTHueEacRxt3BPxiY42HD+bvTtwjqBONYyJ+QPH4evzWyyTUhf\nc/155pjVGLNqHcX7zDlsQnq5gQPxAk8d0YC417ZqI4QeJ8SoFgbqHERzZzXgck5xa0Bs9qLKF2JY\n68um7ZJCzZlwNEc1hm4JXqXWKPlWmIr4br0JfK2E/x0A/gSAH/Xf/kcA/gIRfRMzv/JlvhfA7wDw\nzwB4D8CfBPBn/bdNKD0uHxMCkVMRB7FnTyVDqR2uwWGt8X4Oh6eEdPwVJwcDAcqq6gKMV3rayBSg\nfUgFjcEFKX5rDVWlcYlvTa7aHIzJYttTJmgK97TdLCRt4tu1dQZcPb7GDvG2wom+1+rLmNOUwBBB\ncUWzNVNH+b5MvJO+uwai8RgQQkkXLPeU8ZQc91uNV5gTrb1GKM+bkWXT82teK8n9EPd+NWKnaGMO\nWkSq9n2trJRLk2UZY8K9F0tzBUz5YIwbRRSAeKIPwkQV5uXWuI18P5DPS1pOws4Z8NoEIPyxEFYR\nfGb+nQUS/xKAzwL4JIC/TERvA/h9AP45Zv5LvszvBfC3iOgfZOYfadWdhic8NqSbKnK2PCLeJW7N\nRcUz75Mys3U9IkhCDiBKeS7GPlFRJ30LeQuU8vQ+vxylNpdl4omL9aMCtTaFqZHDw0nNxyxSIV0f\nBGrinrYrY5Im2KjhMDce6Z5wRF5nzMlxiKaIlEC0IL9/u5EIJpm7Gl6tOsr3IR7a5uUyDcKXOZCi\ntk2/UlaRBgExux3giO6ZcfhianPrnDJ7NJCvM5dt1DmCum8MBnFebc0drSD4jfwbtfwMtbKSL0Qr\nyQSowTiEsktzUbTyXlTxSzSB4HGZoFlIbPMjbW/lTCzbtYgJqgBE3ylxSrQAxIcgmJ9nuxrgXBv+\nh+G6+Hn/9yd9nT8YOsH8/xLRLwL4dgBtgg8CnuggCAdUyl37rE1BcqrgVtuE6SRPbdLWwf+UIBsJ\ncBxqIOaesx14AIMDoRcvUVIqLOMyOU+tDcBpDC7ZjxrU2pTQllRqdhdVWLCPTMjikamNu7RLoDCW\nUrbV77nxkDalrITgCRFwV8/azOY7BVkCqaTN9DmBYuaw2pg16ijfp+OhrPL+EWpUx5czCBO9KOGM\nUsHpVRw0gbiezsYDCGuH2NUb9qt/LmWFsZS/gyZA1YnpGibO3cDZxnGurJzTYR8g97kivSxRUVp3\nxsQ22nQ/db2M9ePk9w0xBY99INGeFkNUtiv7qZTww3nrDQrBOXelovRkgk9udr8XwF9m5r/pH38M\nwIGZ3yuKf8a/m6nzVGwuDx8EiSTlPuPvbTUUFf+taeOiKv0GLk21OaJ2KWI3to/Nqt+L8auZd1q+\nG1PjESQvkRIqasClkOI45W8yhVerjiq+/udV+qw8AogUvaS/GdGk8btz8XA/XW0t05L8nplXF5gy\nyzomcWmkzK19Xysb9irl64yZQ1TVElxaiZAm8fNSellmap+P/DHKOpN2l5wD58A5Ev73A/hmAP/o\ngrKEGV7kx178UPCWFvgofR0+Rl93BorLIIt3ZcYo8Y6UK7pQjbFOVDlTDhVL6npsEBW2gAsZiV74\nI0LDMZlEebGOlKm10Xq3FTTD4RptBhu4iv0kr90QZyAghi5N1QN4ySlRs6fvym+XjEcaysOJh7VI\nzBJ/nJlUGpCOTZZbokgiM7WGW3WM3lcS+JTj8eUOIU3qkvXuk7AAiOvOn5znjhdbd5YZG/MhhPON\n8rA8SRttfL4E68Pzgpmntb8WpspujUXt++oZaxkENUoMJM6sTus1j0uWFyENu675DYC8fwBn6zl8\ngyJ6oahC/DhG537Rbhbal4Dk1/g0/xJ+5sVP4sd/4TnUr2iYw4AvvXp3tq8CJxF8IvpPAfxOAN/B\nzL+cvPo0gB0RvV1I+R+Fk/Kb8Mk3fjvoQeHh8JA9fwxCmF5aIIl3ZPCnCFjL7iqTOmWnLif+GhLw\niKNi+Du50EGkFJFYZAErdiWECGWJd2rSn0248Qv2owatjUyWMsZF7gcQJ5mUkGPKYceKFEWB6JdJ\naUZag5nxkDbld0uRkWAbY3LZ330wRxjSscmclpLnqW23OmaNOkbvxYSfjEOQhF7j5DtrIGiFlqx3\n5VTtQB4mx3x+sqLg6OYTS3FxOVTpn0OKQF74Sp1XGdy2wT+i0x5RzPgniXfSfbe1016YR4q0YQmu\n6bua82ZNiBKGLNWyiHD1Nerj+Ja3P4mv/3u+Ac8+8gzv/+r7+Bvv/AT+ty/8j7P9BU4g+J7Y/1MA\n/jFm/sXi9Y8BGAB8J4D/yZf/LQB+PYC/MlWv4zafVtKNE2nD72LHak1ytZ4FKtZrjEVO8w7I307N\nlDuPBE2Ijw0lAriIw2/FDqfS6iX70XhRLSu3uUElh5vPXsfDcUSs2tV7OyfihR7xk/q3S+sEPAPG\n8SY/0UY4L2pPqGckm2xsuP5cIYk1nprDufdpGlFOGIkJLcmXG8zlR8/AOmU7EAkEccJgn4sHIezX\nENOdJN4JzFi4R8NL0In2biqxzdKbTpsmscr3VaHB57nIJPyEOFprF+FS7q25Nt0vBFTmozRbBXNW\nQrAn65V2G9OcpuVNLzRTkm1vIayNw/9+AP88gH8SwPtE9NX+1bvM/MDM7xHRnwLwPUT0BQBfAvB9\n+P/Ze/+Yb5arPuxz9r2+Nr+MMWAbE9LQ8qOUpAm4GJsSJw1qCUKNSpEIaaQGEFFCDUL8kVKkIChp\n1CgVhCIRiTY0LQUUIVOUohCsAA00BuKGJFCE7RZiMBi4wejWtq7te9/32ekfuzN75syZmTOzu9/d\n7/N8z9Vz3+fZnT1zZnZmzu+zwFtKEfpHgzRfWjdYrU3LJj2FAKCYnHhhnaeGpyIflS+/i1kLjlwg\nCi5/fXdo6cNhOcQcN+kvgT9mIUUw94ip5Z414vT4vKvAFxiZcpEHDLOGX11HBjq0+IUemuU8hEPx\nBEv9UtCyr7nbjDPZLebM47gb7/BomJhkzqXj4CbhgzHQR4+Wr+llTfIribQ+7wWhcDYxDd/T10qL\n+SwvbgshBAgrQ84FLEGLp+Epe94CA0L4pLcVWjX8v4xpyP9YXP9KAN83//4NAO4AvAlT4Z0fB/BG\nC/IjA3miIBBKgzLW4NXA8qKPAC0TwZvquX8p+MyYKS0n5ZZABrscAdE4IgsGM+VbgQXVcXM8h2jM\nFC7m58JbyGd/vdfqOa1eaFk9j7S4JFad35l5uNh79lFDte5qY9ya3AJNUS48axR+X/1qWZ7/eebL\nvAAAIABJREFUMMRuHL4WgZDyBkxWO27+bw1grgV59rTlhbLGYXJv+Wf2CrAu0RbtF2LBe3zexH7n\nZ2lJoPCKlBf+vMV17qBpDK15+FXbgXPueQBfN/+YIYkMvTD4CfXmXKK0AEIPbS0H3NkY/jQnkwav\nzUX4vjNNdfYiUy1dz9ijwjs04PHdY7hhKmELtL13voZ9meJsWyZkFgWleS6J5d+70c2Fd+7mL6vZ\n8vDLxC801WivouL7eWTCzIX2tz8ca/1VGdDG9JZo4nUwpi9QxnO2lhbP6H2QJxD3wfFP7R4BcKHo\nlm/bmkJc84/3tPUfjCIAg3N44pYqn3ulOFtpy72nyAqBWIBK3IaZZyeX3WzxcWhyNQMnqqVPSBfd\nJWHAwPLwCc4HqWQ2RAteCbmXqrW9NMgCLN4/zIPF4BYNwOfgj1jmy0ukplxYX5jmwLEPwyM8ojk/\nOXyAY9Lwg7ZrBFnLQPOpR2OmRcL31721ZEGK4GKgEKTnpo/93I3hoxohzqJXeGLafY52M6qBgvAg\nPxB1EeHOC5xUZpS1MW5dL8CNLl8nYi6tC7jpi4Xjspdq47CAX0MDPZoCBCk+3wbmCx6GpY7GQHd4\nMj6ZkSBqZ+3Xw6YMfw6uHcc4kI67H7aEEm1uZAx8/jiRd41FVlD/rRG2DiKGPy7uCN6HH+8SYO41\n/bYxnIbhg03KMd1LDX8MQSqAcgg34FVBeVFHCTs5GvwBMc4m/Scurra1lNUFfLAR9z1axuNdJ0eO\nfSkwBAyDj663l6uVuDwQKBRP4cDHTDSb+UZxHfF74PPtNXya3Sz8wz88zqIZKP5wh0a7FXi1Pecm\nYWa1QNIAXMMvvb/aGLfWFkcaszh9kSvMPvSRmNWG1tMyFW7yBXVcdL7JQln8K2zDMAB3aBLkZb8e\nWgSsUls/jmEWVByWL3jupuEXaOPraKAhvLvoeRYXxNeBFxD89XxmwuIm8IpXK8c/XqWM4HiGdwMJ\nDyDCiuZANbhmifkSsFiEcsQRbnvnvkDmHW+wLmkWJkwmYJf8MuHYWzA3jvMaVvtusQTE9ntjF+fR\n8Gc4JF2HFqmJayM+J9JPag9t2Vx9BdfRufiEOI97wBAVeQnmXrgoqh1YxhOVijQUC/HPHTl2XprW\nOZ7b7maTeQNtI6LAHO1ZH/wYavXPEcd8TUif/ogR5Kbv3ocvg41LWh7ggjbd63sP739WMlelg81R\n3rwAUc1PuSX4ICof0Z0DbYxRENXGy5KnVxXbjWOyt7b47OtISxotP9+8pSi0GzydLrF0tdIRBbtZ\nNHxXb+vXFoiWwjssxXAPKI2DuzKjokkM+LvnvxOYhp85a3x7HqXP/7XCeRj+BQ+DtG+IggpuOQh4\nxGUPbVmBXQ3HPBQcXPhKGrAwYW4uI6IoWCQcRi4uvAPYBCRzytuOMLqlSpZPNfSuHaBN0Asfv0A+\noEamWTm+3qYLSXufGx/n4S/fNcD87YM1h10wH4uArh7w8xCECJeOe0/wfUXMW2tXSZXaWhD1CoV+\nc/lVEwBXu0JmAZTY3uVCfJSmN94Bw7K3uSumtepfrVBTT1tfLMu5NC1vryqONdo40wdEUK5QbPg6\noDEtdCVdUb79Esszx3WwmCELnIfhz3BUQQ4fNDVpA6zwDsXpT1v2d0aQYwwLdHRJKpgbHdzAtBC3\n+Lms83WGeeCflx0dy20npkkYwTNnj0uX6xRN3hXmwgFuTj2asgf8+mSFd2Zh625ytnaDP7DWMmc/\nD9zfePF3bemzentjmks0sWXGixWNGLeZvzkugAtBIbWNFd4Bpup14THGUIN1rwFqRW162pJbNHte\nO8PBhYI8W0OJNh7g7e89ojh4UAr14R24OC1P09j9sy8aXhRr+CyOygKnY/hHQSRNsxcjJbRmvA2b\n9AzMr1ZUg1s7ZI10Lt16n7i53wPH7tg4RjcuGQhKylwd2dK+tmZyTFXrT7qaeKW0ENA3DMCTlXO5\nFWPOzMPF3rMT/67FsyUYrH5B02OMZC0t3JIUuSxFn9PvI5xbzr4kYKyx363bBqUDLhJIovnaGGq0\nRUwbqdae7HcnnptB09iDxYqnu3oNv8HwcyKGf1R8/tw7i6CUZs3V6TBiZFUpV5gho03ZsevNMytS\nfzjTk24N7zPj9znd/MDKgWUsu68KWop4AOyTs8Lv3DOH3o8sQQpP8vqCKs2YCBI9Lek8PqPAfwBl\nVdEoYuvP5WmtjkfMAz+Ej93pK4HFZ5jacZDPiDbR3mNrh59Ha6bOr58Jp1tMyT7+i/XP28o0PPme\nu8AZn+VzxtpL+nicCI+7MuM3b2+9SE70jjL4knUv2xTWFHcT8n9bo4zPw/AJAGMwF++ep+Vh+V1K\nZT30tR5wsv3aA7Llebnp+WHAJVWewjj14ULwD8d1Sdq78NOcquSZE8257eRz8dtSybiQpBWvkT6+\nIi7J8H2BoJBWNWD0hXd4pb01/N6vexHMZhm/pJfPA/dbXzPDt1p9VLOsFOhEm6TwDhekFKbcCsva\nATCva36+xWl5j0JbLxhw/3JuDFbwZ4ilndYXp8+5AXdP7uLUTyNd0pJbA3kOarSVni39rVl4fDvp\nz4+fs8NpGP50qK5b0Kv75wx/ZvqhgAKW8oatIIvK1AKB5AHJcfQEESUfxCkcuFEeOQsI8b5sbw5c\nKtN5XMunKeeOprzfQuanZSx7F+TxjHTRfAaM7nGsMVTGIfGF4CGkpW75mGvrgt/n2v1AAxyNGAbC\nkzmLIJTWXSlkRcVAxkIxIIVu3oavHTkPZygw1QvelNpTsEc+I9tEvtghjjbn89oLxHLr/Wf5ZJBY\nENJEHv6TJ1MNDh8rkhuDFUoFiGQ7rS9On6NHGN3zwbIVgtqMdEjcJYgYPn+flFpiq8qPsKjKojtS\nGOM4p7gY16rgn4jhT+z+MOmfa/UECl+MkodwD32JZFcxuRJR0iaYRzvMtUn/hTEkGj67zhfgMl9x\n4R1uAq8JSJax7C0ABs05mPTnVDJaMhQGDGY6aho+H3NtXUhNimv4zk0CgPfnT+V1XXOajoQorZLG\n6BDNgVYwKNIW5+A9bVzXBl6Q6SnYI5+RbSJNbkTIHMrNayvwAlMer5szVHzhHd8/r6U/jPFHpHJn\nRAuUChDJdlpfjyIN30UWqUfDIzNdHr+1/TAsmTDJGhDLWmrimobPr4Uzh8VscEUzcqsy1C0xC6dh\n+ABWmSK3hOND504ITv55P2dpy1FtH+EdB1xBCFdb7J8czTXLUA/OqwSHpFSw3qy9TRQDU3gP/SAC\naQvxJVoe+db0tD4bmbzZWNQg1xW4i+2Eq2sNqHNcQO2tK3KvtwjQ52L4MxyRmhcdpFikRj+5SbBE\nA0grQQ2H90VpODbpP7OqIpP81DB6JjI/YflCGyBK6mLJ6y2Z7S1j2bsgD2E2XYciJ+NiNgfCVwKt\ndHCzNjfReYhynSvrIrrvAHLDVCRorvU/zrT67xk8co+CxtYLXpsD9FxwDdQ2QgMpjfuawFv/anPM\n59GDfEa2GYfFouJGcRbNE6rhtcKIEUOwXKUa+5SjT4GWYc47l2mpUXGuTnpGN5qezfXlxhGOFvqS\n+h/GJebxW8cxDqNaJCcK5qv0xZ9JUjH5fabVh/N1WL75AqL5A2ZXyPCl9HZE/4uPhPntBZPrRJ70\nVWuftAnnaAcN1kcIyUHtQX56NZjRWDWwKM7Bj6EisW5G+wpwbvky3hL0M4DA6o130KFW2StoWLl3\n7ukKjJ4H6c2mfrhJOAkfOekEzoxl3nAOtDY+Vcr/XtMsrwmkf1YDTagpCnSYmI6fJylslfCawS3M\n22FZ6/598D3uq9iF65mgsV56rEJ0rq/RjaEQDl9rgO39SPxmgV4pkjPdiP+uBdp5OpMzlZ2hMh0S\nQMiMWvLwKbwnC5yG4XM4VMNnJi0e8blGw9f66m2zVhiqmmaFVh9+nwP1PHifsePBPw5hIVrydc9g\n6p0YqVukdp/TO0wxJf4TtC34QjBRZpNnny3dGx0cjbGGP7rp4yE0AMNcJfFu3Rr168MLay1rNVlb\nXg7Y0Ax6NFgEoKhdfLHeZgbP8L2FyfJMDWgk5idm14lZFcgLHHfwn1pJGOoW9BjXVu48igRKIZAk\nAqYBf2v75Hek+y6Jwq+dBy62pEYZM57h+7gpAubKYE2utlMx/JO48CPYIsBoC3/Slr6ykkm/xdKi\n+dGiYD3rpq70sTvIFDRlE7XQUfPDWnEmPksnf0bQ8NRikTCmjFU6VXGYfZycIdI6XKcEK+mWdgUB\nIMtUV0zdiDGUzuYKTdSPIqSp7Tagp/lZYfFalLA0G6ZZ6F25JOXZqTFhixCYw7u4X4bIejDx/itl\n+P6EOCJSX0aVE6syFQVI9NLmHzvrWcfTSvw/FE5sdUFHC88xZuOwxD8wfAlsMRcrlwqB9PRDlmur\njsNFSGKcVFjHcsy1dcHeBXl//TzvIb6ApeVl+1XoDH0m2UKplq4+r9EdporieciN+x6DTNOqtZWR\n4lre+xo64lQ2F0zikSuO0cJT9BJ8pTVTgZLCYWlLiIt+ad+QsKSntgieFgWg9p5q8yZdoNw1sZy/\n848Drj4tL7ykIw4DQtwv006idKlufr8wjTNqOHzeuUkp3CdKDv+F4ROI3OLH8mOk8kFgiXY20b3m\nefKHm/97wOieRLEJ2jg47fJeKYVSjrm0LjjeiU4KtQ/cPPejm8z8jrkl8vw+HYM2f/xdl8ap0R2l\nj/mhOcqP+x5DxABqmlxwI81/sw+1bLHGAYQAz4keoaWTENKU6pOMoOyaN0FmLlQcStvFouVrZ6Qm\nfFOaXcPxk9Cm0VV7T7V5c+J8mP/mKZQ+Ocdxpt8wkNMwfACYecchh4EsPOE1fqnp9UrbvtjIGZk9\nMNM3Dy0U3KCl2I/XfD1M0aHDEpVPy3x5yXQYhjCPGmwRrb22iMt00PLDbclNBuIvhfFxlAroLMVN\n0v5yxXVy68Lf9znUXksbacq5d0+Wuvo8U6KEi9OivZ9Qc6EyTo1u3yYKWqJyUaH7CpyBWwr1RJX2\noBfeWUMHr7TnP60c+4eXks1+7wLAOK+zgI/SQlQtBXhyc2EpVuTbxdaKWCBZviDZR4eFtuTzuBAB\neEw7DzhK8zYz8fChJFZbICjDQYFYrKitcBqGzw/VM5n0AV2DacbfIO0fAYk2z/91FDEBAKEYDc15\nocQK1fhmmpky6nNNzXeF7q7nveCCRbOR6ZlcsAnPlQroKBYS7bmoTUXr8XO9fLo3Nun7AjxAfo0m\ndDpKxiXblcYZgNEuA47C74WiQvcVZBGjWtvoU6ez8lMT4lroCIwQwEiLmThSZihuJ8cxkZYqPi0F\neHJzYSlWxMex+LHjwEYQTJ+Nrb2TEm3y2STOQWHGxXmjORDRiVoMM5ogqHl/fjDpX7GGf58hRD8f\nkIHQClrgXpZs5+AoL21qZuotrRxSGOPBg5a+yc1aDk12Tf48sBy0pUIk4d2KecvRptGfm5N487sF\nLxNKvDuGZ5PU6PTjC+bCAm3atcAsRH/yfm3ctfdkfo/KM1vh6X2mFM2u0uviZ+V66qaXWSmj35G+\nO+9+0c6ApG1mrDXI0VtKXYueERlA0T4AzAHDLe+2ts7ltVKf1jXicXEXW1CImfuVGqxlp2L4friH\npuUp6XdbpeVF0tnJIKp3PtM3Rjn2aWrO6OaoX3Y4WXJPS/fXgOWQ0q4tnwKdfpdfz1PHkTkAgHje\n5P2sYFRLYfTpg/OP/51bHwYacOfuqkx/GbeLtEjWSKU3ytGvjMevJ7mvcvTkrrUKIhFtG+HpfUbW\nNCg9QyMFrR6I8/A5k+6hNzBCN4D82uQ16plQ6+CmegA05+Hz2BCOVwgkLe653HhytQs0wYfXDHDy\nGxLORk/pnchruSJZ2nmWEzS0+9m6F8BsPWV0EJY0XCIgWPqKw4zgVAzfc5qaZLZPzy6S5Pzf3MWw\nii639HNKcFg02PD9m5g5JD6q0U2+ZCyLVbYpDXeTuViJYsRcwMbXC/f16GcT2jDOTFSMxcV/xCSN\neWaYjLm2Lvx9n4fvRozjAF54h3zhnWGqGVDDFdGiNM0ykUrbpI2nXTM7nnQbbAmRNmcY74gxyg7S\ntNhV9LgRzher4Wl5Tig1mARKmt9bqfBOHx3257OCIi8MNI6LJgz9vFpLR8+zcs5K60DemwSYBbyA\nw9PyaCBgQAhetMDJGP4Eh2r4nsltrOGfltHP4ODSADJ+1ru08M6U1zvCebOhi4NbmgpgrKB7DQwY\npgI2QxykFz6XOxDcXRAHm2iwlLit0c/vD27A6BwGN0Ya/hS1jyjHuqUveb1mhrfQyz8cVK04eE8h\n8cdW2k5fQZznbN473sK0Zr74B5DGIbU+ecYUBb75fY0xKbwj2/I+LJAbi5rVorQlR1MZYix0+5gW\n/7dW1tpKh4U2+azMZFBjGhTLg4wVi+LI5t+9tWcKppyY/mQNmts2qPinZPg3uDa43sN72rjx9iVm\nWz0igDQHkxYw0+o1tLki4JZUbsGMZRDTQ4SWeQwC5Q6WQGmp4/3lVs70/oBpydXf5SZrxoiDjwMw\nWtJWwl7jK+JVpnwSAkRgbcPuPxnD16OGL9RznEqUM99ixfFKKd7TMBRi42IBIQAmzV1ofXK+osI7\nEdoYZ4A9ZATrVPq+iX9nnsLFyacfa0LV90T8VyVKPzdest1f6gVM1odxjlQeW2nN9Zd7pNZOo5vi\niGQCZdsVgb2n7P2TbJ+1wPdTMEez8ZOjVWP1MR78c9bcVRm9L5+qCgJY7E4UD2AU5uRarFo6pEsw\nN5Yhrix5N96pVoutIDsOl28TtfM0GddsYuKHT3lGEMJ64DQM30stEdO9aP+Cgfm88nniexa71of0\niZ5FC0rSzpiJzGEp/CDvyzSsqI04RDjsYdK1zqXv2+cbRwchEe7G9GM6LX37eeQ5t9nDix1apftL\nOp4XUEbQMNVG4LT6d1WjMxHMMs/U2qkmV0azpV0O+HvK3T/L/lkLIS2ZhBuAMfs1Y/VrfWHyi6sy\nzPPcf9gTABwNGMZZsGTvw6qoJOulwqgssQLy7HHk8MQ9iWtGNPi1raDRVlqjydyi/h5zgZr8Xbml\ncTPzPw3DD9o9rZNkV3QfMzxOhFUbKqKfBQhRSeksGkqU6iG098DwebTuIBZuRXNMJOQNquxJsB5C\nvm+v9QzsE5NhY4nP/tYV/HQuIv9cZrzhAK7c98ze0zrOGk5CqwNyWTpRAKqx8l2tnUa3PNi0Snul\nPiXuEm2nsZCthMDwBwLGxaLm53KtNTAIi2KjBk2SFhqGYPGaqKCBgLvpET/nvQyfdV1vn2kXLBBe\nsPSMjwRz3RASvuQVfL6ulfuRlYao/h4JIR4qCHx+DXDGHph92zhOxPCX+TqDST+S5jYw6YcNrQRp\nnAEiDVVaO4qFd+I2MnAlZxXZouhOaQzFdm6haTINMkuFN52t0PCXi2mfueeq92dTPo/SDQFdQivI\nranI4mIshFNrp9Et9xARFdvlgL+n3P37ouHz4jgjjVPQY8Za1oufa73BmuCFeIdgAfB7wrccaMAd\n7hLhoGVcHkrBr7J9qUBPpOEPcfzDHlZi+T0BT1tUmEoI/VLD9/+aNHzhMoi/wMnnr43rn4rhnwk2\nzxGfc57PClz40IqxVPPE4ZI2nFleIiq7tQ9PMz+EIteNPxQbg5a4b3QtzTLgKtDLGH0kVBXILPXV\nEjBlaRPcYYVntujzEuvqEhDmir3fXJsu/H69BAXfhViB4BqZteQk9931rW35bKCj9D55MF5u3WRS\nFi3+/17gef8W/JZaGDWQypJUSkEAZiXACidi+Hbmsk/vLrvYpG96y/zNI8ZaBW8+8vn47HDwaz4w\nH6ldCpNcNkXswHFHxWR8Co83zc2R70GLxoC7u3Ixm2w/LQJT7f5Mo3Nu+j3Kw2dWFtiqOVrHs4pu\nsX5aYe2cXRN4TXscpvXIC+9sAaHeRAiuXVK9Ag2zljyOY5Tqxcv7cqXA2i+H2nOlYkWcTjenDQII\naYMRQ95hbWj7mZ972hnYGsPAccjxRLELzArbYsw4DcN3zDJxhNSeSNVu0VQ2kxydWDRn0k5mU53/\n3dFiIuMaMJfwJcOXLopos4uh7jJ2I0puLvM+8JGNa9lIAwZyeIInbX0zoSjpM/Oc5b7PvecV9yap\nfzEHS7eKub9s9+V2Kt3zOg91HXJaXeV9SbOmev9EW2gNBA1/dMu6NL4jK/4p1mNmkhiXte5ddvN6\nnWJBUmbjz4gWZto6hqh9pq0XXjyNzsWFdzzNW0JioZX7yKXrNcwZw2Fds3I8oxvxiB5Nefg+SGcK\ns2hyX5yG4XM4q4bPzW69fSTXTqKl8AMaSA8c51zkN/OFQSJJ1yH+qhTT8M9q0p+K2SwHIR/nQAPc\nMCaCWq1vP4/bF95ZvorHK6UtH0QRftmG/jY36TPBIzcPN5N+Cr5Yz9bFimSxGi8w8q/KBaF9nAru\neBhFuekcfbl+W8aQ+2gZB18si7AIKNE+mK1fW0OJtpqGLxWjbB/MbB8VEgqWR1ZpjykmVmjKXSCi\nv0xEv0hE751/fpaI/jS7/2Ii+m4ieg8RvZ+I3kREr2jso6X5DU4CZxFcWqGaJgQ6J1PpNJNfDE5M\n2plhr7UmNcuaEMX/W9tvCy57W9byQvtgqzlZA5NAEF1oglYN/zcBfCOAX53//goAf5+I/phz7m0A\nvhPAFwH4UgDvA/DdAH4YwB+3IF9iES7M9EmJ0q9ImlvQKM3khwIxOlgqSDBPKYyPm53Ch1uUNryP\ni+yV3HTKvglplD4R7sa7WdNa/KjVdxQNU0SXN4xZXROEIMkPPtsjitJnHzmy0lsZQyvdEg93hYWA\nMDm2PdbDCbZSDyTZDyB1vXbjB7FiOpOmlwTgze+Nf2seQIhvkVZPa78ctmCWvG7G9LeLPhrlLUxb\nQ+Ladfn7oU0Oh0aeEMhygZvTZResqi3QxPCdc/9AXPqrRPQ1AF5HRO8G8FUAvtw599MAQERfCeBt\nRPRa59xbS7g5sz9Cy5epaH7x+xcrD6tNaOS+noOBB4nwuQjjJr1IR5R6JYIb5buUkf97j0eCZoZb\n0t18+yUtb5xNl9Y1yaNpAaTfJrCAsiY8c+dpeT5ox5v3gYXh9+6hJMCo811p88APyKifjZf+GfZS\nD2iFYrT12gsh4MvjpiG7p6faFCw9zo3RdzG8MGdm+hv71onVzZjGMrmxfMyQQ/8eqPbts3aEApSc\nc8ICl0TcF84nv1d4DFQcjDsz/Znxo2FOu334NIlYXwbgwwH8HIDXzPh+MgzAuXcQ0bsAvB5AkeH7\nZQTa50XVwKc0ycMK0BfpFjQGvBT3dwTkGD6/Hwq7KG2krwrQGf6lwMqgvbbAx7FsVqbhdzD8Hsj5\nAbmGD6blcw0/RHY3BvJI+tdCbh5a5nJt39cGqoZfadMCMg8fWOIs/Hvx5Wonhspy9sXeDv5lIzlR\nbn3DZ3Sz+IZYw6dhhHsSx189Gh5tL0z6PZcx6ycCs4sFAstZ6LV2TZhwEXO/gIY/d/6HMTH4lwB4\nP4Avcc69nYg+C8ALzrn3iUeeAfAqA+bDGR/vO/dC9vDpHs3sJQ2S+dXa+7bedJtts8PcaZArq5lz\nSSSCzTji0fCoKZ2MC0wcv9ZvK3gza86iIgOChrbQnIRedqFLI8u998QCVFhfvXCGvdQDCcN3ugtt\nDf5onXvmNaZ9pCbzqfBOiV5zvxsU3OIBhIBuSdtLu4/cdJn9UTvntLNiflAPHHeLhu/89VnDb41h\n6NHw3w7gjwJ4GSZf/fcR0RsK7ffw1O0C3hQE5A+6UwZwbQBy7PwwzvmSwr8OKnPkOPkze4P8fncO\n/Gbh45W5ydaDI2jWO4w30AnB3GdapWVGzntLP9HfK7NRpMCTrI+dc6WvCbS9k7RZMTa5P/1akkIX\nX2se1IwBmaZW6NfyTYkWmNxsscsBiNeblb4m8PxX7MW0WXmMOdokPi2Ox8fwgFmkW4SbZobvnHsC\n4F/Nf/5zInotgK8H8EMAniailwot/xWYtPwivPV9P4NH7hGe3N1hHO/mBz8Rr6JPbCWxGYJvmZlS\nTC9tIzhztLU/KLzfKohvM5PnxVUAwSDdZQ55K6iCSzCJD/BfyUs2UYOmGwlOGUbXQ2uIKwgMfymc\nEtxR8zfVub91DWz1ruTheOb1fhRowtamZwx8PMryd7SnsbyXhcGnpnwPI0aztm4pptMCbnRTuiz7\nW2rNWlDd6n7nva0pQlxwyvnpa2OXLl55jgw04DcfvxP/1zP/BE//f09jeGrAeOfw3Affbx7DFnn4\nA4AXA/gFAE8AfAGAHwEAIvo0AH8QkwugCK996RvwYXcfhuc++Bw+8PwHImnqEpCYF12qoU6XFzPL\nWtgS15bAzcKc4XuJkmvGvn0QClgevqZVXGSss1CSML3kz4WJDnwMLPbAb7zqOpyFAr5ewkHXMObc\nmpBzPka0Tv5UX4e9d54jkyhoFZ5kHpwyth1sf+FQRhxYpZlZa9cu+cxU+omVI85YzCS09D3M1ekI\nCF+/44zS97nUpkC4DsSxGf5+rW/+vBxH91y5EeTimiFEtNS/mGNvZD+bvFt25s2/JPMUnhUuFH6O\natq8329egNeCXf+NF38KPudj/n28/BM+Fi9+6UvwwnPP4//99bfjB37jf4AFmhg+Ef11AP8QU3re\nRwH48wD+BID/yDn3PiL6XgDfQUTPYvLvfxeAt7hKhD4Hh8trAIt/RDCnAmxpOjyDGdI5t/i+HUIZ\nV2A5HAbwz2u6sBi99gCkJu1obJcapsbsC+18mU4f8a6Zyar4OBPzl1asYzlv3hIRDlpNw6cl2Kpr\nTUVdrnhZYi6yjGuP9cDefW0/165d8plwuM+gFo5R5svat4MLJWgdlgDPKP2OmaolLVzj5G2tY9Sg\ne35HYKC4MFAkpDuKPue753rwIAUD/m+Cr/Ae+bNeGLtzk8U7Nulj2vMDoSVcoVXDfyXGjlfoAAAg\nAElEQVSA7wPwCQDeC+CXMDH7n5rvfwOmDym+CZPW/+MA3mhHf60hNw8YZi3tUgF5W0MaYHY6g0sA\nzdp02h1zUrJucINrAm7xmQSaeWN1BiW25uF/deX+8wC+bv5pgmUobUEI0g/Fr8f40zbRfZmWV/FP\n1fDVoGT+OQKkGXugReMYaIjSd7g0Guj2ZvSOcan+/wuApz+U0p0/+TuOY9AavJXClJYHitZFax5+\nbu6CtD8oZXS9mXCee/6hk1bIuq868cj0vCPec04gahnblkKV1OQ8WPLw19AS1g/idLtI4yT22Wuu\nzfuPNgmf9RbzYhFapatJKwx0N94tefiz2dyarZKjIfeuNLoAm89emvkTfOwM1T885C2r83tr3KLn\nqaXv84t7FhIZNkKhjTxYefucX8rUZwMcralp0d78IPB/Bz8TWJQopjrdk6s2NVWaabjwHEzj5Hn4\nFMUoAGy8FoYv1+4SIdVBXMw4va9++h3h93EONAQWH6w0v5q7lGPsNHVIRp9aUS7I8HPvrWFsmwoo\nzB9b6oNAKo29tIRvyLN34vuQArwUPoJgKRjvJvNi2VtsHhYBXeThj4vg4hm4OXUwtx4z7ypHl3xf\nGu/gfWn7LXI/sPEs1xEYfQe/Pw/DZ8aKLg2/Jl3VFkDQokg/pHLte+F0Gr7G8MNNgEYKwVe8TU6L\n43hrcJiGT0uVvanv6SBJAhLhsrn9Et8aZhZpUGx9efoGWiqM+b4iWtnvXRr+RvMv5+FQDX+Dvvag\n18TwN6Ql7NdZAKfZahVV0BN7WvbJ16evC7EFtOAhoqRvvw88eIvcpemT86SdhRHdCt4gWGl+fm/J\n82/smjX8SWNcFlxLwJP6QmYTc7FN4V7tJR/NoLcGKXnyd6AdPsT+A2GTghqXBq41AzGj8j6zpnWY\n0WTXxjYsghijFcs7iqwqKwIFk/dMffiSeWicxy0hK4A1jO0SJv2EySqFd9bQsjB8sX40LVTQohXe\nWUMLhx6TvmScucI7q+kLxlybSb8dvWLSV/6O27n4n8Z9dRqGH5kwGgexBDRECOttCvcsOZP3ienz\njZek0ylzEaJ5M9LsNUCI0I/GGvvAWw4OuUG3CmL0eKI4Cm++p8U21iMsa/2Ev1fiyVl9Lgm5d9BC\n0x7BqLW5ztLdSYtzDuPoMJBYP4iZPndneZAZA3utb2vbJItgXPf5ZThA2+I8L34taGdIjb5UKGTV\nNr0w0mjJOBHDF3+3bshK81IbLukmeZYr+myBszHMkqmYB4lJhs8Xn5ZLXOvz0uCZvgeelsddHD20\nyTXV9KxkAPNcjmx9StOlc0zr32Aut3of2liOhqNoyPWrCQBb0hiEWwV/bc/m2m1ClwGPJoBwZtij\nsEVt4VQLpUXp8+D3ncVkX8MXrKZMsJqKajEr+EDBD36VDB9MamtZ7H4ycuYQdqEI8lD3UmTW7LJy\nvbfSd1EgRB/KCUU6vLlv9iPxNqp/1hk39EZz2gpeWxij9z5GgUt+zDktQuKLDiLk/XG558UFRpeD\nG8dQYSzk4Qtf/0BDKDzSClutSW0e/JpZg7eXlsLN9ThaIUxBGSffW1vRQo7gWT63FoU96+Yv4wmN\n3tfbXyPMZ8EZxsT3AebCQNwqkbHwqrUMsl2ok112/ShWZA5qUJ6INVDxzUw8KrxDs4bv/yNCUPSv\nkeEnGn6jmWdNuxD00eiz3PIg2MNs2EjAYroqLGRuAuSbnhfnWVC6Xd7jZhCsFHFVMenH1HydOXzT\nAwuuNWPiDNILWPJTuFHkNdf2e/rdavqVeYhvX5TjnwNHBafZnbJCCBvdGHYnV2i4Jqkxcv9tCi7E\ntTBTA3FNbSfa08I7cbPtBBIL+HNRC1aNaIqlFxVPxNSxFN4ZhiV+IZxPjRp+32e1doItg2Oa+75H\n/vij4Mj31wtbv/c911E9kvtEZqLrWwr3GtbsTTWo+RQveAlAvK8QC4Lcf9+310+j4ftXJv2nGvRK\nbsVIfeGvtSyiNYd71fxzYdBMwyH4iij4uKLUnOx35GO8pak8ch5klL7vPym8o7krcviM47X493hE\n/kDi87hzP7lYCwu9Gv0RPZ2HipwHLXjv6PXeA7XAq5Zoc/lMqfBO4hvuYHC+aJPH4wvsSDNzWGfc\nJaMU3uE+5h565FxYI+EXc/YAwmyYHAjjXWpxqKXSWtd3T5R+zpUnz4ckAJK9D15ISFoZnf+f/zHC\naRj+4pBgB8bWXWRweqlJmkRlBKvEsSWNR0upMkjNHwZAzFyAZW7kM/6eBwdb/npExwXnYRJs4rXm\nNxYfazDzV2hLBFVi7iLZ1iJQiveRpBCSqBnuvNGwr/hOLdOlBY+cU4nr6PXeA6qQ4gr3Mm01nKr1\nxom/rf0oIAVGj5Obmf2ethbekWNoArkecjiUdrFQEn90iNNXpctqrrfSxte0mwSl5D5l5o7FdshY\nl+Xv2B3g5kstgvlpGD6BS28HaPhi41nyyu+rhj/QMEWBzkKz1/Ajv5gQkDQLQMBdGNuR8+ArdiX+\neuemQCWmQVvSXxJGpxxEPRq+fx9TtbTp4ye+Lx6DsFrD32juk3lwscC4ZV+XhKqFsGNIYf8M8cM0\nMg2bafi9/QzDoDIbGa0f9j5/1qWBoNHe3+BdWnH4CPVhOoAANwe3KXtny/VcAzVORRFWpCAiccus\nJ4YwRufYhWvU8JNJuKA7UhMwrvFAWgUk/ywHqtUWbu36WSDRrCoWniIu5SSWOPwh20ynn2+iWdLf\n7kDjfXBYY9KP/u4c89mgZNI3MYWCST+Zs9zaI52OGpTWubxusj6tdDGsMunPzJ5mNbEUjN1CQw7M\ntHUI2NKkz/dKSp9Cr8tcz8BpGL6EPSJ5szgd85M4PVK1CZ8CNeZxdJQ+OQomqBCtW6HXZzYATHNl\nm0O2scCl58FHIIf+2Ti4RG6hSxurnMf8ZlbwQbwPN8K5IVmjiekf+mFuol/pvxXkPGhr6ej13gPa\nmeDHoX0eOtfWQ3D3kDL3ct0IM28r+E/jSvDnkqd7dCMGF5v0ZZZOuEbpfStYsxK0ds45wI0A+6iX\nKozV8uiNk5l77zWFqNqvU675Zyl6YLG+BIEH08+ASQkwwmkZ/i7nQQ4nIVr0U9P4Bagvt4HG6uI6\n+PxzxIpPeL9QcB0pApCbDwdf1pKZ+j14N0BT2d0LzoODgxtH0BB/E9zHdAALE/W5yEV8lI51VXoV\nPxAEkw+xBV7rB+LDwBn7EPQ305jD4wRzSBr14T4SkvkBUj9raakn0+vCu1IFIhddiJ9pBG62D7Ee\nIgjPt9OED9kuokmblypB4s8cDqWdp3/g9CpzstWZq9FWFXIy74gLJ9G75OiEFcf3H1Xa8wpJo+vi\ntAy/NKHd2kHhMS5Rh8NVSl2y7xYy/CEcHt3mcN0Dwthd/LemvUdaKOIgPYul5Mh5WDTnWAPnG4kw\nWT7ucFelbTqEhuSa+t5V3qHPhYMLwXlRRD5EzQC30Mw/dGSFrd5FslY0q8aJ1rsVikK/RdvNvPPw\nvhhERa1ya6gByE3rwvu7+VoKa8jphXe49YIHmbVYqxLQhB9ju4keAjAuGr4ScFqtFWBl+Abaci4T\n2b52Hvhzh58j4xyYGDF3muI+pv1uh/My/B1OhBxO7XDS7lnxZRp30XYp4FYM6wHjnFvcABmTful5\nFecF58EfHvL9e01ZBiVZNAapDVhNlaU2XDCRKXi88A64xK9ojYYOtwHJBBXER6/3LiiR3DucHC8p\nuVd6+KuwDPn/eAyBJgD7Z6OgQY+nILy2E2hvN9E3idchqFac04kFY2fatBiMFE1d8JVnDzALa0Rz\n4CXb496s38DxT8Xwzx7gtQZaA8CuDXoCd44GubEktL6vPecgmOv935HZz6EUvNTSB4c1+O7zXq6B\nNciLPZA8Zwma9TitQXaLYAjd2pBJP7UEXbasfW1czUF74jmLMlejIQcl5t0CpfRc1aWj0hKQNfcP\nnIzhA3HU6h4MUg1cKfhBShuqZLZR82p5M82ScOAZyfvXzFPSNy39R95v25KWVz1EdmYak0lML7zj\nWNpLMGnW0vIUAaL03rVgwehZZmGQ8x2CCRWtvzf9bY3AIs2q0Xryh9qVp+VZoWUew3mnpHQC+Tnj\n56SpH5ESxs34vB/tLIysfxV6esE8DsXyBuhfzLNmHGxFG4fS2VabN9XCAh97MV8L/2uD8zF8QjBX\n7PGNdW2Cs2YUxIUpJA71Zc2BW8m92nho/aZZBZQflz+8+UIcwCJGsWwuPlfBx9w5rr3nY4p8JRDz\nl/mIfAcX6hDkNB8Nn8W0Z7nH7/vc4yT3mQA3uvkLfxOj5x86svQh6Y+g8UCJLRDlQ+0aLUJWyAoz\nynzyNcPz32mkpH1ufi0w0JKH7/epdr5pefieFhnT1E1PZh4sbf1e8DSAgClcRReYs+usYW3nFLsS\nlCwO6rxJF6r4OzpXnZs0/PBTHUKAUzF8H30InEfDb8WF2Y+r3mOXNA3/SK0nOngyGn604aXG2VF4\n52gNv1h4RwRxWujRqgpaNXx5j9+fCu7EtHIBS9Pwc++yhX4ZSFaCRMMXDF8eYvdZw89Vl9Tmk++7\n6DmCWuxG9tFk0lf2NV87/gxK1gHFH5fS8LVU1NTmwTpnfi+EMYAwUvp1yNxYSjTkQMMhny9mNjCa\nAP098jK6WhprULiYit9j1T/Vx3OAiSeGgIQrhS7t5YrHC1zvAX6lZAORgHj+2JD7rNGvgeq8VG8b\n51UaHHOBqGd/TQ30XeuZlIOJN/Irrpnpn0rDj2CnM0zmbHItqXWBlKLXU4t+xWLh0gjvi8IU9zX/\nGleZ09wajv0HCM1VMe33kbTvfExR+i7aRJr5Pmj9FXq09156JjHTZe5zzT1EKDsXxRZ4jUaaMZsy\nJEqR4Zbn5XjYepKocrnT9wFaMjN44SeZHqqZdmt9WGniUfoSb01bDfEFnfSoWRvGOSvRp+3ZFhqy\nbQt7c/4jgZIgps2bdJdAyPLT3h6WfT4Qpoh9NO2jUzH8OCihfsD2d6RcorzfRB6gxXQUEQQT36ow\nwQP5vTTvTeSwv52YB5HLq+eF64d9wFEb8M7zkT08SPdB1w41ny+b4ON/Fw6KZD7ccp3n4U//jnCj\ni5m9n3seb9Ewh4mZsuVQFO+Zz0U2X/v8hokuyJmLa/PJn4s+iqScNy0maWCqh5+bf7mvZf66PAc1\nAaXJ/aMJPsY583shuubEucOuWwXuEmi05eK6wt+K8ijPV46bz3EUDD1f99/R4Cl5oYsGRfVUDJ/D\nZjmUCt5ogc9BdjkNv2gyU3n2/OJkgB7p7XN0XRoiX6DX9rm/CII+wcyjDUCIff69r3JvhuAA50bw\noL2wDrgViFUgLKJTKu0Vn8lob/J+YPRzOVE3FxsZ3YhhmP36nuFDBE82zOHqSnt8PFrlRt704PW+\nJ1irxk2XROU1dj2ZNzG/4ZphGlUFRLlWK60LYDkbNHoskFO4DG1HKPQtkgsjccq2yc7Nmn0hnndQ\neIfWrxP/QrxH/xwxJSNU2VsCd4NC4vf9tTJ8b67cvR/Wh68h33P4tEiPliDEvU3YJZAmfPm3BHkg\nRcE8iLXMM5v0nXPRhg5Wivj0sNHj0sNhjYYRuVSEWd9fWzSbZfNH6VZNJ5u9aYlej4t/m6Ha/j5B\n47A04azJjGzoL4dPs0hl08K8MgMle2ntq7Q+79KxeCE9GQtTSC5CGwONn6jnaSJLMUsdFmXDByBG\nJv3pges16W+VN3mDy0DO7F3zn50Zzrr+YpPlcggExs9dMitOOU3bXIPnIULpsK+19czUoiC09G99\nH8Fsz9cB6Uy2tw/rXGjtEmEciPZADe9Wc1oU5DviweSzujAWOo9+b4FTMXwA81m272EhGVUpLU+b\n+Byu+QHdxCPatqSvXQpkQYsoBcxYeAdA4jvrTcurPb8WQiCMT7uZN1sovAN/ebFetNJa8+lLa4iG\nz+dGh49nYPk9WFlmM3+UupOhqUh/j6WLB00FxYNpKdAFwKPX+17QMofS91xaL9b5Uhn+kJ5T3BLE\n+4jOQ6cE4Wb2w1ohz/I8gfQ6AVD2Flt//Pkepl+izeoukXTlnuGCe4yHn6tsnzcM5zQMn+AnYoo8\n3FNDkOZaaUYBYCq8k+ACsoV3tM1VpOvCEOXh+7kIrrGYKZH4jz/PzZOqebyHtp3mJTBPr83MvjEp\nsPi/5YdxLLRWaa+sdS6QhqAdt9AdmDwtdEr/eBMDYgd9K8g8fKktamO7j6Ae6Jn5lFbNsO8ofcas\npVeUDY6Pn2+E2GzMn9UC4NQzzgKFuai1HUTdjEBfxhqg4l25tms4Si4sy3moxUZFCgjcrOHPqn6D\nNfU0DN/DJY4AbcH0ahsPScOXWjufN24ByEnaEg7X8BGPwWs9UrIOB+JOGn7JBbIw+6XwDv/xXwvz\nuHm2RI6mEshCIBYItDPhRRZHOeN63ws012RuPlWGj2nOSoV3SqAVipHX/Bml7VW/3jzdst9cVLy1\n+E5uLpKCPy4NuuO08bF4uiJ882ev5Rc8e5hMqSjVZhq+P3eYsqRZVubGkZJvhdMV3gHd34PgBjdo\ngivbBvdVY7+XYHxVp3una8k52XDaQLPStMHpNPyVsULGLpjUzMxa3f5L1RKVanLXHKUvaeOR46BK\nEMvKce01L35czsVlLQHd7WPRDrR5Yn+YnuHtHcXR+YFu/x1wb6UQ/0bdNmg1/nPBPXPO+4l+L5g4\n7yUowyq94+jdhJiMyloqda+k0Wn1IDR8an2NjLYqn5efms7Sl1sPpZoVnL5Mu8SaljOH967tCm0c\ntHlQo/TjBstz3lrmjWfCstcruJyG4WvxB7sdCNqGLGwI/vLUBRMTHTZs2m1qJq7RdQTUCu+EA4nE\nwZARmqwHRp6g1hEY0c6Hx7hcWFJ8cn7CCi3JIV07KFzmOru/MP0RYN8Ad1iYKo9HGGiICrfwfizQ\neihq/cjCO2de73tAL7P2bQPj7XiH0mROoKRYDbCszeR8c27B4ZZ+a+4p/3wNcm0shZ8c2grvWPHW\noIQjcaEptMwNI7rS20yAV1yDfI9P4W60/BjhNAx/gf1PgcQv5tCdSpF9eYpvrOazPjKVLUrrkmle\nCjOXB1KRqa8c1m7z4jxuJ/5W3EoEuLH9MKu+88r8cO3e0+rcVBLYORcK70SHQcn3Z4QttKDe6/cR\nehl+dH3FfOX8zEmsgRvjjBzF0rCWHrOlIsPwk36ZFsxB+2RuS/+ttHHQeElQlCrzllM4Yu2eZvc3\nmrT9VT58IvomIhqJ6DvYtRcT0XcT0XuI6P1E9CYieoUZaU3j2QF6zDM30DW33ujwI8BhYaCqRjWD\nJbJ2T5AWl4nmURzYwqTf21ejdl/C81DBKf+V2mp/r5k/rW8pOKquK7C1xveEMetDG3frXJjaybGg\nrKxZ8ZagBccWWSnJmSNM+iGTrXGvdzN8IvocAH8RwC+KW98J4IsBfCmANwB4NYAfNuJcTJQXPGBN\naRI3SCArxSq/nw0Wxhj/ZA+zg60v82/hX7/xYyFg3aF2g+2AxH+ldi3Xu+jgMR5Ce+RrJZetJNPe\nLOtLjt8yF/JZ9V7C+GaLVk1r3nI+O/lFs5VHae/dqwFf47nUZdInoo8E8P0AvhrAN7PrLwXwVQC+\n3Dn30/O1rwTwNiJ6rXPurVXcwUexX7U2ggh62CAzgKd25STOa0/LU9tyn1Pmda1Ny7PgasaT8ZV5\n0302MKjSfyktr3e8SQok+1tqYrkgq1Vafyk1zOXnhq+RM673PcHKYGoWmZ60PA2/NdCrxUKUnKPy\nXicUBSRlz4YSztKNyujbkuFHfbe4qzKuB/lMFGQYgl8VgauDPfb68L8bwI86536KiL6ZXf/3Zpw/\nGYhz7h1E9C4ArweQZfhev1r+2k/Ll5YELimGNsbCOxFODy7dDNEzjYzxEsA3ejQXbpkvbgbUtAY/\nXzm8CXQs2NIh04pHLeIB0pmmsx2GPe+9iE/OM+J3lGP4co2uWluM7uSwxfKRnGTsjOFrY7/PDJ8X\naSppdtU15eK2rWt/wBDWOe8nCqrEsq+zhW00913GIuD71Ydjtw5o+frTV+NEHj7NtEnUJNbgBuDH\nFQU1ClBpma/XzkP/rG8b9rLn8fxccq5VwW9n+ET05QD+GCbmLuGVAF5wzr1PXH8GwKvqyBfmsqeG\nP3UV+6TWLohk82gavm9D+oLYS8CxQmAmiA9wLvzItv73olSeuddset7AEhNQKUKev64JeWGzVt5R\nUcPvGa/G7Nk1X3iHp+/pqFZo+Jn3Lu/nxq4JgmtpOjvwuSDoUfK+nToPhCRgrkvDVyxEwLSnfR81\nenL9lvbDGiE/CLnyy5OAKmTIs9fDgCESkLfwdAUBwul9eqgJeaVnuMBQPzN2NOkT0R/A5KP/D51z\nj1seRYUyuUFucA5Q/UhH+Ygdur9saO/iRP5vh7xG505GKxah6AYxdL2nc73azeBsa/bS0OuWQY9w\npUCrhv8aAB8P4Bdo6eURgDcQ0dcC+NMAXkxELxVa/iswaflZ+Nln/zGewlO4G+8wjiPuxju8Aq/G\nK/GJjSTaQKZf9ablSXxBSruitDw5B9IkVUoR4qbkHGw6rg0ZXW5cRS3CkmYn8K2mUfHN83ckXTGa\nRr3VO8jFNsx/RH+HEMIHmJaX5G03jlWbt575GjECbtJ2o3fj4j0e2su0vEK/OdN16LfxGdkul0qo\n5eEDOuNL/OErwY/LklqXo8WUlictqMNkkfm1D7wD73rvv8Kj330KwyPCeOfwgQ89Z6a/leH/BIA/\nIq79zwDeBuBvAHg3gMcAvgDAj8zEfxqAPwjg50qIP+9j/iQ+3H0UPvT8B/GhF57HB5//AO7Gu30k\nQq45uSXoIz67FmYgzbJFmnIMiV8/m3bmSfFxDU6JynWx6Yybn/h/UgotjfPQOXAIpnB5XTNVevN5\nHW2eIfaONwhV4sB2E7FxQJ/3EW4pGPWsdyDMV3XP3EdIllVm/BkrzmYZFw66YMv2a3S+FYT7RMPk\nZ6fSr37ZxO2zbUc3YnDCh+90d1tJGO0GQZvGI2quv5IbIIjsLAicu2Q+9SM+A5/zss/DR77ypXjq\nJS/Ckw89xjt/61fxP73tu0zkNzF859xzAH6FXyOi5wD8vnPubfPf3wvgO4joWQDvB/BdAN5iidCP\nO2tq3Yg61Y6sGn7OH1mTxq9FwwfSAzrkuoqDIbS9oIa/GS6CSndOww8+1bNo+D44T0bvQ6F9Azos\neJJ7ih96D5quAVqZTakyXnPfBSautjX2Y9XWk2dWtM3tWUAJKB3FObYhU6nhsmZe5J6NXNwshifa\n38R+jLBFpT1J/TcAuAPwJgAvBvDjAN5oQiRNlje4CEhh5yHM/bLWCiZqBkf6pjVaOcPncCYf+kNi\n6BKse2jvuIcgkGcChXPto/Og4z2uOUOKVkGN4aOurF3C2rXletcyKJb0yljIb4HVDN8596fE388D\n+Lr5pwkm4reNqsz2JU22O2y6XB+lRXPEgS3NwXzucweSGtFf6kO5v2YTrp2nUpR+i3ZVmpvEKtIx\nXsKSKhWZDTMpUVuvLQ1faUy1COQtaLpvUFtDtbYV5MvaYW7MEi3aWmvO/igEm66B7J4d08/4Funr\nJgBFl0MJ+HlQc33m3MLTv4vQs3ta3t5ApL/U7Tuq/J2Bppec6YOQKUTCN+URQIv/KYprIKQpMqT8\nm5ma7LjWbP6V87QcgopQppjus+9do4O/Z+FHbKJxnreJuQ8RrZ7hJxpPye3QM2caKtLvqzUN4JJ2\n/P5D5/e5OQhzJ+etmd97rZC57hS/c2ivBayW3JFZfp8R/HI+fyMMNCR9hhQ5jcbN+T2pMV8SVFoc\noyc5TuNvl3A8obCQ3EsOE8dv4PqnYvjTIln8E3sy/Uir1aTaxsI7pT6SZ3Lvh6BKqXtDkDqVfN2w\nSIn5yrC04dpDLr4hO64Ve3/tPHFmKvGqfkyXPyAl3mxcSMd4/fsYNL+eX5+Kb1+zzHTNmfY6M2PS\nmFegIYfnxvDL70WGRTS+Q194B4RQsCb35bfoHFS3a3oO5ujJFd7JRe9bQV0zlI8n2Po8HTBki+7U\nhHs1KE+09+OQezt1d7cxeg+nYvhc4dqb8R1p0ufMU94/0sQZMXLEZmnJzFtM+rlxndWkrwl5NdeG\nek1YPZrHS+wQpiHqi7teEoa/ofm8xaRfDFS6mfRVkFXjAsxrZ61JXwZ1AotGnHNfaUJwFn+Gntwz\nWjGdFlDxBplSEUg2Xl9EVC26U7vnaRMXkqDpkKkhmf7M76NrRlj1tbx9oCLx3gM4czDTQwjYK8HW\nNQN2e15hBkfD2ei5BsjO2QWmMpd5c1/gmvhIMfamEKDXKtCcS8PnsPPas6bhre0jgDd5X6pATQNE\nJui55GZNa+TSaC3lsCd9pwar092YBC2vaxtsoCFbCIQDnwtpbu+iM5eWx3CrGplmUtw7Na9RCNlj\nXdwX8AVzJLS+wxFLIZ1QF4Frigr+0Y1mQSB3L1t4Z+UalLRxnHumo4b+MZpwcpebBiUcSVoec7UQ\n0VyEx/9gMYsb4LwMHxfQGPy6Jz3VIxfc0hVt7ZipOHMwlhbIruC7FGYl/y/3K/F7WjtV4nR6sM6R\nGmGUrsSvsyIe0oRuKbwDH/Mw/67NVRetws3g3PxOtCArxQXTCzUcid8yc/ao693R6iCuq4fMnMl9\nuAa/DPbiZxBf52EvOxfRxGN3UvRtFoq145G0+Wt7uA11AuIzz0NyXnhLtSZU6Rej9xHiKOY9PoTY\nBe6iwcL0jXBahr83M9Byz7f297QW3zlK4+Eavq9Vr2n4mtR/9Rq+ZOJON6HlrEG1d7ydhj9GMTr8\nnagavogf2IKWGp7W93zT8Kc50ALcSoVxmvsQGn3R9+wc3OgiZ2+tfRMtWzB8AV4QTwrvNBQRaqLB\nMIZs2qwShJd7ljB/MZAwxfAQBSZPBGCgoOhb4YQ+/MuBTGfata+HfrJdCVxLcJqH5twAACAASURB\nVFntMDsbvTc4BqSFKdLiDc/MF5rXk8v8txZaGPglmX02zXoDmiah3gs0M7MPuK9Yw5cmkb37smhw\na/tgf4RrxQCNAw9qOf85l4Z2rUb3Fm6RGs6mZwtR+rwGvIfDCu94350wvXINwhJbUKM5ByUBKOeW\nasXzoIHqa0i7vhZ/Dk3OnXX2wju57JQ911fR8uEtiMazPieYqbijW20Teh6GLxlubqFu1t1itvX9\nRAKA8g34mLw6bWpUZcavU3pmb4hqEnBTFPPt83QaLixFefiZlBvN7LyFwWPNXCVjZdeDnzAyAGXS\n8hRzenZtdIyZ08nfCy+8E3XBDpkcHU3zlqFZXcelPVvC88ChGH3t6m2ruCtCBW+r7Ysiwy+l7Gkm\n7ZUb31edjPrJzFWNvtVQGopDtpyxxm+idsz1srj0Mh27Ch0CzsPwcVkN328CdfIFdC/SSMFnEnsJ\n3ZHnHz8YPB1zUBHXfENACdL2WSk7kefqHxOy0Nv9aBBUFP+3S99TU6UxMXcLkj46MfvtIBk+9MI7\nU5NCTErLvOVopvSe9p5NeB4wFOcMUIWqVvy1dC6/ZwfMVez8j2irWhsy9OQK76wJ0gxj0c6S3Lm6\n5/oSCoG813TW8/gKx1wiuYp9vg/XFgdzKoZ/SUgY2559iGtnNunnCu9obedf4r8LuDmcwaSvaT6+\n8A6w3qSvWQlaaRzmgjuRSX/WHIIpU9Hyi3gb5q3FpH8rvNMOucI7W5n0SxYnLfNEM+mXumy1Iq0p\nvJMLhPOgrbGc4LEF1Ez6WasW4jNW4uLMPmX6aa8tetODDtq7QQr3rfhGK/SYLvPI1tOSS+GZ/rG5\nGS4FD33t9MCRwbw+na0Xasx386C9K1teq4VZb4Ummo0u8/+lhaOhm1Np+Jd8nz4tb88CPLwgBO/P\n8swlISq8w1P0vKZbKLxjBa3OwVpYM1e59BgfECch9+6OKLwj/058mo6KsSJbrLGt0sZuQoIOW80v\nL7xT7ZObk42ppRd936Q/L/cBrxtw5HmqMnyDmzBYMpg7FTyOh7k1NBdHCc7D8F0afbC79OvmRVEp\nvAOk5pcm2pzYTGcTVT05bEMl9DrdzMiLp+Q0zpyWerR2MwXnjcn1xKTJ79doZn57KSj1jDeY9TCG\np91c7csLaFE9CX8NtPpDJTWaNb9l7vA53Zo/C2TmTHMr9eIv7b9orbvJXSTPqNMU3smMxVffa6Jv\nA8jxhyQuTLj1NJr4uwj/ze5FHm+kMf0WOA/DvzAEjXue6GKQ04o+ACy+3IyEqj5zQVhVeCcTiSph\nl5zYNRq+F1IU/3c2u8JAw9aFdzwOqeHXaDtCw68GKe1EyzWDwwUL7xhoUTX8ktCXo3MnRtui4efa\n7w2ejoGGKUaCbU8LbVyIX7ImlviKiE2JAMsanMqHf6gWsGfXD/tMu8EKKB38D51Z3qAfWgvvaFzl\ntv7qsJ0SuWQohIp78/UWOJWGz40yewceadHZe/XBI7/3iNKvCUpWnFGaIuyFd2pj0nBsJdz1bijN\nz+bNZ6MbU4tGht5slLKwGvWOlxcI4u+G5+GXcvGzeI1WrRa6S7ha1/xW/Z4elEyR6XJ+3bSMNxul\nr15i64vv757CO7l+1rjwM2Pxa3ntXHmwWntza9TX8VjccfW5k66/YC2T1gHnhX3bWCSch+F7hivM\nGft1l/ZTKrwjX5qFtggflv6Kiz5zABSh8vJrwoy18A4XANTCRU5n/NHYjTRboVdQ44w0ug5WtUts\nNu0g0ArveDwRdI5XFkNx4tro0q93cdN6ViCZTf7V+Wuhu7R2C3hUGqz99uyXk0EuT97BpQF3jeMt\npbJxoSLZ00rhHe0MtJ4tHtYI+rmxBIHEpX3k0h6LYNgX8t1oVhEfQyOZucZvvCuF/+6cdPc4f3P5\naZzP8zB8CK1xbw2/wOy37kNeK5nCSnmzOajmXRvHFglBjE6uTWo4LdkHycbfyBzYzfCV955kUnDU\nGXJzh7WWAdIzZs7sl8jdReNXtfuKuZ+/z+rB1kBziQHU6Ont18J0zgw5+gmkBqm1jrfE8LW22jO5\n8ygKKKvgnB9QLQtWKDH8gD+52ScQWgThkoZPoGp8U/ZsYIJL1AdH13l+nobhTy+FLr+BT3ZWXKu2\ncm2H7kKvrqFbTfo68rXULbQsh9y8PwhwLhZWekz6e0DPGli7bq5t3Uko0a8J0q3jLbmcvIWo9kyR\nxspij+7TOkG/x/2013laU3J6Alj5s17DT7N8XDezB04UtHdL27luuC8BPJuMY6Op0HyAlujpHivR\nFtAVQb5ysq593bVGwG853lKEfW7NNfch/rsvYJkTGQvRA4mFD7S4v1kbK5xGw780BHPmbGbaMy2v\nxax76fQ1SVti1gZUjdGatmOhYQ304l1S3EQePtLcdmDxedf6DwGaLr7fe9gtgTojvJvSuXwePoBQ\neKeYMiXo2wK6tJqCaXS3Pq8Aclaa1vHKFLtan+rvOcFScSm19NEKubEUNe1eIbTyWDEItRCD1pKW\nF5j9bNmL9rr81wjnYfhzZGNyec/dzHxKMuBMSqTSvNtEV+SGqTzb4edaNUf8UVoWO6dTbrSE+TPz\nk7rIcwfXgRDGJAPzXFwAgwMP4iwg9o2jQ7v7oHNC03dsvl0cbOX7IaJJEcgEUXIht959gw+fFWFa\ng6elfanPq4DMfufvmkPreLPnjYuVnMRXzPZGUFyMe1v209S+iCovBJXiDJr7yfAigTjLH5L4IMMc\nRMF8/PwhBM0+MPzFwzc90cD0z8PwLwxJQFVh0azpA2jU8HfQWLbQ8Es4r1HD9yRr/u+shk9IN2/G\nx7pYENaNmzN3jtMLAT4KOaG3IpxsRZ+ktWftrtX6DpYd14GypoD8nGym4Rf6dBAR6Cs06C0F+0tp\n+GueA5a96Pcmr3jZrOGDQPMngZe/aeHxjSzrND58CdcejHOD+wfXFFBpskbc4MHCbW1cB8hsqOUI\n6juLTqfhT5LM8vtemqGmEW3eh4LTchC30NJkckW52AoP9uJ05sYh8Vr676HbirPpuYxASUQYxzGU\nGPaQ0y5KUdBZk2kLncyPJ/vkPtRAG3MBWPGXoHV99eCRz/XM1TUJYxxygV2lddMy1mwAp3qJwr3o\nLKilEtfo8bdXbvnSXLWsrxLkzPSldrl78t8SbTl38jTvsbtlud4O52H40QHsnRQ7plUwn0jwlfBD\ndcPCOwlzqbyrJutGw3vXgklkvm1kzmb+6FzhnQhvzmesPLOVgtGdh1/I6c3594H0vaumf6Vd93i9\nr44f3CyAp7fwTo7+BFropkJ/BTyt+8OE40ogx5CDwKh86W6rPHzObPj+jM5FLAw/J3zU6OGprmug\nuGdz5nEDfREwNMXnSn55F1+T7k/1/OUxAQ7RGaQOzfEf+7yeh+HP4DV8H5W4t4bPtaW9+pDXamNq\nWaBNhVHmSPOSdss3PY9B8H8nASmwv6eWWAYrdB/0mce81uyQFs3RrCOlueRxIr3j5dG6QQhmDN+N\nqeWhScOvzF/T+iocrtY4ktY+cziuBUoMP2IC4hkz/tw7UaaYn4nS2lfso8bwQdn91gIlhl97zgIy\nPqL0nCVuoBawy8ejZUUtmr7m93fs/3Y4jQ8/lXrqJnfNzLnHM1V6L9x3Tz9cO+zBU6VjxaYr0rsB\nbaU+rQy8pe/N1oPC7H1rCx2lftautRy91uet1/Z492eC0li2cDvWhPvSuqvhaKHhqHfWKhy1PrfH\nmR0gmO8VJIzvt1hOTsPwa1BL7bKmfvU8U6Pn0n339MPNRT14qnSsqC9QpHcD2op0CTwW7bLW92br\nIdLU+f26b7DWz9q1lqPX+rz12p7v/gxgyaSwtG3FzzM9cvfk773QYnGy4NoLonVnrV2ww5kdgJi1\nhbuHmfxP1CZ0nM6kv+cLvTQNPWl5W/av4a2ZrXJpeVHKDsR9K+PZYVxr0m60sXtTvuab92bWUv+b\np+WxlDzy3UfXFBeLtwoYur72tLwtcZwJSkyyZaxZpl4S2Chev1UBt0YPYdJEN0hR7en/kql5amwT\n9PM/GwRMy+/cErPcI9BQttjm4HQMX8Je0nxY0JQezLH/ZILopaG+CeaGar/VZxuG3DQ/FfMP/9gD\np1PSLA92Pl+atBnmSzyzCXSgCUFImu/bLQFM0VhmSTqpPV7oPwTeYMV4HRO4KP47opUF//BDYu1a\na6G7FLRZxCOFqC6pof2RM0DuHRXXTctYM3uen2GBBrfcA4ABQ2QJyO1t8xpa+Y48zYMwTPPYIvW5\nFgEpPqRs7cBcZRWGn7wPNudBUKcYX9Dq4YUApumDJjXfCE0Mn4i+BcC3iMtvd879O/P9FwP4DgB/\nFsCLAbwZwH/hnPvX1j7OIKlvpuGzDSWvWZ7bGjRzrtwoQYOXDL5AY49peSvYlDm4RfNPfPtIr2n9\n+zZrTOcafv5e+DVZeMfBhQyTFvxbQC+uLWi4VjN/j4DUMlaZbRJdz+GdmZIjpwrGzfRsJtu7hWGS\nuF57rre/RqjFy0icWh+JosFieUI8DzPpt0CPD/+XAbwSwKvmn89n974TwBcD+FIAbwDwagA/3NHH\nPQrLucHZIBuQc1t0N7hvsHJNn1KQahjTGRTINZAX3PtebI9J/4lz7veS7oleCuCrAHy5c+6n52tf\nCeBtRPRa59xba4iDqWL669DIzi0Wyt5peWtoLEXv+n+jGASlK+5vau1zy43YE0VcGv84jrEVJOMC\nsPS9Ji0vmOaZZO+teJj/krEC3Nxv7aMErWl5ufVgWfNr18Q1publ5szHi6ga4BZpeVpbYY7OpY2t\noWcNRCZyiq/30rf1c1psU60PzbWYu+cxI+DOolahh+F/KhG9G8CHAPwcgG9yzv0mgNfM+H4ykOXc\nO4joXQBeD6DK8PlbXCwX+ywm6V+JXq5DuJczzVroKuG2PLcnqD4nLKYjSWfIK0d8KET/1grv7PUu\nG/HKw0zi0mI0cjEKyd8S5woext+Hnz1HBHKLD0+NRWD/1eZm03eyYr9uQcdRCsIayAqemD6Soxbe\naRhnNiWOvavgP0bmLJgaZc3Pl5p39TxFfE5rz1xiTZbcntL9qZn9QzuHhQ2q4RsOznFG33bAtDL8\nnwfwFQDeAeATAHwrgJ8hoj+Mybz/gnPufeKZZ+Z7Jrhp+BfQ8Klw0GQ0fJWZNx7we2j4Ocbd84y/\nLoMUw1xoVo6Lafizr366AaIRPogwCYg8UMPP4btp+BnI7KGtNPzsXq+s5bDuFIFjFT0rQMtIsfR/\nTRo+38vqnnDz/2Ylf1cN3zn3ZvbnLxPRWwH8BoAvw6Txa0BoFUNusCtsJUhdo0YF9NNt0ZgPAa4V\nHAhXyXAPhtJ62kQIyuDnwm3x+ZO900sLF6cEl/ndAKvS8pxz7yWi/wfApwD4CQBPE9FLhZb/Ckxa\nfhF+9tn/A0/hRRjdHcZxxDiO+Hj3any83ThwAyNoOehdeE7AAHtosERAW6P0LweFnc20uJCqdwCt\nW62rhwSl9btnwJnVCtRiLboEcFr2XGu9a3nrKP3JJbPA29/3y/jVf/02PPqNp0ADwd2N+MDzHzDT\nt4rhE9FHAvi3APwvAH4BwBMAXwDgR+b7nwbgD2Ly9Rfh8z7mP8BH0cvwwuPn8fwLH8Lzj1/A8y98\nCE/unqwhsQs2S8sTi8aK9xIbLArIq/Sd2/Q5HLU+N4WM2dNCi/pumH88gtn0mguwCc0M89lCo8/l\nTw4KVngnYRg+/sVgjt3ynVhysvek40yMaS2U6nU05ZXnTM+az1nWIvHrr/JSLzXvER3MblxNG7xg\n4Z1oK5L/h7lDJUolVso/E1yPzLX3GR/9R/CaP/Q6fPjLPwLD049w9/wT/Prv/Br+x3/5t0zktebh\n/3cAfhSTGf8TAfzXmJj833POvY+IvhfAdxDRswDeD+C7ALzFEqE/QT7wYWsIUc3GwjtAHORioku6\nX6xFWIxDXjU3WkDIXHhH+rGj37lv26X5+pL5RM+59Pom0IiqxLgd0kp7PCq4pfCOxNsMLj54NbzR\nwcDAX0voVfoo326gu9DUsuZXr4kr5Pe5gLMtCu8QUbLvFhTxmtL2p8z40CwRa4S8VuBnSaQ1ryi8\nU1xzDetZDYLOxE64eKLD38EyxwQFr+EneINVr82W16rh/wEAPwjgYwH8HoB/AuB1zrnfn+9/A4A7\nAG/CVHjnxwG80Yr8LAL6loV3Suac0nN7Q8507Tdwchg04Kj1uTW04vWHmabh50zi2YM5s/F7aUvo\n9Acv6UxhGEThnUaT/tbvpBffFnRcYt9sDbW91XpPNMy2Vy12Ys9zpl/u5sIavu+OxPXac739NYAa\ngc+tEVJwV/rgz0WZOjy7KAQwoil+pzVo789V7j8P4Ovmn2bgApFqVr3BZeAWZnkqyLpMbvvjBgUo\nudqsAmEp5e0GB0KwALXByWrpp1rVMVRss8hz6SNbRMZuncLETVLerFRNyzPSKttv7fPbIi2P+85C\nqtsGfW+Rlif74b577ufn90s+4Bb6L1V4Zwso9X9WKOXhl9wc1jXfsjdUc3QmdiWh9QLzLt1sWgqx\n+lyGvjXncFNaHupWkuiZiuszwuXQxPVPxfD99Cb+0z36Yge87NNhqUdeMm3XaEvykq2+twvsHtXn\nxHxIScDXrPWr0euV4hxRfzuMrRVnzu8938wyS82XmcyHxNnkAk+Lcix+PFYFm8aJFi+UsXmPAq2U\n9yVhy/dxeIQ+Hack9EI2bc4zqcz6sYxTDeicwVG5iBQ/CzQ3n6TzkmfW/Ed0ppSE29I8mPsrQC6m\nS+MdJTeo5zvefRe1Eeh54Z0WUfpUDB8ZreviZDxwDX++8GA1fKt2bOl7Cw1f0uvccoiNblQDEP0Y\nqgx/Qw2/hO9SGv7hQkcrZJhlVas2jDMr1AKqIKFp+JZ4kEvNe3bP1vZghr6tNHzOLzQN39JX9Azz\n96vPMa3eNWr4PR/P2Q00Df+scG2aRBU2GM69mxMFHsIYe+Ea9u3ZoLSe1s5nDfdW7+vs7/3s9FWh\najS0c/xTafhnCQ2xaHcW7ensUfqJyYj0vi0Rw1aryB5j68FZyk/OaTVHROnn8ETuhcT7Mh/mhq63\nfB/ezXAkXFuAWW7Oaulupr1WslS5dA9YMnNy/Vziveci3KtR+p30bRWlz8/aGs7ErcJiqpbrCH8T\n+78FTsXwc+AnTDtcSwwndw1ASF+Sefg8WCbns9L8MWrfmQ1VHU/DQW2dl+SaZHh+zUhfEeLUHN6X\nhifH8HhKTRe9pXfbsC/9Oy+a2CivFYxurPatrRH5u2ynHQjen+eE3S4K1CPdZEmOgvukOL+VuUve\nd+Gd5ObD42nZoz37+toK74TzR5vG3H5rWPPFde74rylOzRydjQcwnllrISf0VvPwM/RV15VB4OL7\nye/FgC+Th5/rW+5jz+zDv/7+zP9DJluDMHN6hl+S4moSae6aJnmVnrHSmPTjhPaV2VDJtQYSrPMi\nr3lmEglAQissMWmOB4B90VU2noVRJtda56u0kf08aOPRNqvEJa0kmQ0ur6n3fUCec6DMYaeaZimO\nuyjOb+day9FbPXgbr7U+Y6kueBaQwp64mTK4xjVfWuuqQlNoW+yn8t53Ayf+zTUz0medj9wzibXN\nH40sEK80x9rzce69v84YPZEMfSvCaRn+kdJ6D9PP4Tm1SV8KJJm+S/QUD61C+y2hFWfQjjOQDVTK\nmV7Fs2tok88GC4sovOOtLgOlYThW98pa+i6B79r6b4Xcu6oyWcM4S+vAUniH/VGFS51Z2t+WvrdS\n5GqgmfRBiyBaw5ma9AdWUc9r+yxgsZG+UwXtcbj6QIsbnBZ619YRQmguwljz3d/gBrvACdbZNQfL\nrhOGlGdXTMXpNHzNh7G59FiZsK367E7LMxzmW6TladKoRmMpLY8/cxQ0p+VlmKi/d7bCO9OPl82d\nWngnsiQdVHinhO9SwtLRa7EHsgJdxpWWe0Zr01ugJzqDCnS00NMFDtk4Fd53T4rd1oV3pAuFWyDM\naXk8rY8cnEO+5LzRpcHhdAzfw57Fd/jikYwOWMzdGuNPfDbGfuaHrQTuLtGqQSY5U7anKeMfDeMs\nHVA7jqcVd/EgJBxSeEdzjfBDN+pn9t8RzR/HEfMe/LNOpzGid4e9dSQc3X8r5IrChHefWT+WcRb3\nM8rrmJ8NPrCwtLf3mncfZ6TNk9Vd2ktfi5uSx0X5Z7UYqJwLNB9T4dhP2i/UO3k4HcNPij8UFv1u\nNJxAw99a87LS9hA0fM8s9VsnK7zjDzuPZ0K2HMZu0fg93DT864Kchl8Kulur4YdUNbe0TZ71ypAh\nEHJPDT9YuQrKSA2O0PCb+prfd6Lhw22q4Z/Kh69Nr4X53WAjWDnN16JdXQudgGZqvcFDgYtY+a4E\nronW7aHA0Run5XQa/hlgz4jTlujpngj/Fjqk35dA+mdYNXOTuL8HjVZo6Tdo8IXCO7xtrZ89o/SB\nRTNYzINpf5r/tWaV2Yq+vfFdW/8tEKw0uXVVGIo1Mr24b8UHl6KlO/vOrbDXvIezpVQ8Z6csgtZn\npNtNc5n0RekPAHk/3oJf/GKC0zF8y0G8FvyhT6TXQPY+l7WHZc7sUx1LzizEbqyeD/F4mIvgdhKH\nQSlwR+JSFveuB3EH6lJBkpzPEEDKRKuvsk0YkvO+mPkW+10w2TNTfqnwTrFvI/1mMKzdXeF6+H0R\ntMI7cQMDjrB29HsJ/oo5Oqdl14STVeDP4kyBIg8lC0COvt5zWHtWFby1ODTlfM3hSArvhKp7E/MP\nRXgaeP7pGP4ZYFcN3+DL9As08ctuSJfm981Fu9b6PrrCWUv/NZ96pOGLnZSbm9CeS+AdtKn0OMnw\nBZ1KPELk86ydaRu/u2taC0dDaS3WxmE9R0qCbSLUR8ShyJx66OmGkrJhRdFB39r4FY3ht8QN8H0c\nrvsjJgTuoknJP5UP/77DmkV7TabKs0Pv4VQNcNvLrBkY/sL4g4b/oH2bN+iFJu32BEfPNQlyW8LC\n9FkQZhSM2bb/T8vwLxGod+nDck1/t4N9O7imwjtAPor7tiRu0AtN58kJ1tlDDdzWzxxuuWk7k05p\n0o8CFwxFFVZ0dHGwjketj878QGu1yS3T8nybMzHEnmekxtz1npT7a+Yll1oVFd5R3DP83xr+EjSb\nNTVBZIP12kTDSoHu0swlK9ChPP+WtZcTDBMfdCbwc25cfX97zVkoMrVynfak5WWfzcyHPDOToEgD\nWNagYvAzw2kYfhzhWC6ysEl/hcI7Pu+0lo9fo0l9acYXpKYjMp/a2vlIAkTYf5kHivm4fK6y+fo7\nSVgteIOJrFR4x0vQij9ezn2yTlcW3uE4o1xoTQAkwjiOSVCSDAwtzc/m74RSnI7cRT9qs8XeuASU\niotZaKiePzOzz7UrrePoudmfX9rXe86ZBX/tnN7SuirXsxqI7RCdH9rZKLOwZABlPmDTLU9cK8P3\nwIMTpn92KK3r+zpAxe/V8KWkfrbCO0T1ALG94EFq+F4DxPk0fKtGtBdco4avMfxa9LtVw89qtzMj\nz+GqBbi20NILFg3fsrbOpuFnMx74GnQKjdyS7/gFG5zSh8+DFALjN5h1bnCDG9zgvsAtbufhQiJQ\nCEVY3DTjPZ2G7+G+xmS25GMnpqSKybyVDmlSyllTTPUGDjybtP65BqxeN9Z7kHNUaq8d0FukE6ml\nc2e8mrnSv0eLdWFrzbtn/WwNXf0Jl8hWULJQRmsxUSLL2n1os+J+bcwt87BrKrNmMuf3ranOK/q3\n4Cq5ZeR5lHPLBheed8cQgem9vKH8xQSnYfiXXFwh2IlVlYvML0bGamKEyjMm+pUm4bktTKRSgARF\nxS1kjm6Jbj+f0d+XPvhz7q6K6S257mKztMpMRZGmMlnt9RPC+mOMPTEPutjcWYodKPa/kqlIUF0/\nFzbp93bF99eWYAl4k2uyWnhnulntt7QXpc9Ya8NpAQpC7U6v1+OuMfyqjz9zFhuJSP7OxdyEa8JN\nwwOufd+achHn2/u/p59g8WaFd1rz8E/D8B8KtERrWgq/rKEj0hr94ZArAlI8d/bb8BbQaM75H1sK\n7/D2/hl5gEq/nYW2Fshq+B4v6fEYQRioZFdsXnjn4LUAbDPnW0HJyrKm8I6ljYPLV6iTMlmBIXJr\nUi8ta2CLomNr6Ov19a8tvOP/DowdXgiAlwGWHyOc0od/g8vD1qbf++h/PCqGJGspUjSb+zjvN9ge\nmvazYg3k/x4NqsBfccXtCabsCQseYbnjxXYWC0LbOzgXw78F5R0G1YjfxoV16U12CThTnQHv47P6\nF2/wsGArpjM3jmDLWKItQLWsHUjb6tiKqHHe/TjhaRvnyU36++Z37glrtcG1aTJF3EijQKQfSjNV\nn7m8ZW6+a+mHQNlHmfhWFb9baYn2puVFufi5MWBJ3cmNx+I/zkKn7/3a0vJKLqEtwIqL7zPLurGk\n5eXalVxXyTW3+JyzOf1HpuV1pA2uqZNfjAGCfl72Ft5JwwdYnInDUoTHCKdh+Bprz73i1YU1cgFZ\n/vrs96zVACjRkct/tRYg0XJzA2xwdib4SdDM+5g1yRrtNcl/1+IcWt2CTDtz4R0BWTN6Zj2xB1Vc\nObNjHKGrH9pRYJ8S8MXHUFynlYO0551ptF608E4r81HeT02QM9NSOSOivwuBl+rzK/Lw4eL+iwyf\n0aLt7WwfW4DThV4JoxuL91vntvh8FOvI4gtKcU5KEKbc/6b4F7f8EmKrrpHhSwhH6EFm/q2Eii37\nz6WaNePOFPrI9eFTv85iwtMgy+Bz47Rq+AYNuXaod2nJ7H2ogTzz529HNxaFB2s/mZurrBMcLqrh\nb+B+2lTDN9LD955l3VjN9tn3QQjMYu15s5cw7+eitk5r0LqvS8/nnpXBjVFwr7G/JEAyt/9c8osJ\nzuXDN8Ct+M4NzgRnFoLWwn0e2w1ucB1QsR42wmk1/KNhizSQNcJJ7vktDCzUXgAAGtVJREFU/Ogl\n2nIpQmc//EvpcTyFTcstjtpafN68CfNPb/m+uNaeK7wT/JuKadhqji/S1/nKa3EPe8NWe2QLyPri\nqRwvYpmzEo0Wn3Nkml6Tp16hZS3Uzp+1c2WloQZJGl7kMU39+jUc/m+ffx+sfYTlp1EQOA3Db2Up\nvYcIzzXnhXei6xVftIWGbE57C90Z3+8WB2hyKFP+kLYUvzD1eamD38k/Z4Y8x2bkipz4Z4s+SQeM\nyPgLG99X6TqnVTINXheB+/slHf4jH73zvtn72mDt7Am70pYZu/peghXXdv5U+6X885ZzJCccrzWP\nt4DlLDYV3hHPr6FZDdzl/yoxPdqcaXhksC7Pv59vzNd8fAaaeP5pGD6Abo3ijFCKaDU9v6OGX+tX\nu3bmCH3AqOFXrgEdGj7DtYeGz5k+x+m1noEGXcM3rr893uvRa+UqNHyU1+nawju8+JJl/VsK7/TS\nshauVcPfpPAOw0NEoGG6Gmn5DWym2YdPRK8mov+ViN5DRB8gol8kos8Wbb6NiH57vv+PiOhTbNjP\nzVSa4ORDad0AZ9bQ7jW4wmHstfxcnv4NTgtrrIcXhxORosIZ6dsiw0PNTpi0+uXejiZ9InoZgLcA\n+EkAXwjgPQA+FcCzrM03AvhaAH8BwDsB/DcA3kxEn+Gce6HSAf/jquvw7BGl769vcRhk89YV/F7K\nPFpzK4Ep/Unxm16i7zXup1wePjkKMQmJBcCbCw3dlmhfs856swa2gpb3nKNvq7Wi4smg9uvFlIdf\noa8pJbB03uTK8zbSUwLNIsUj1rfIJlmT5WTZx1GEveJSMVkiOA71GZcN3LdAq0n/vwLwLufcV7Nr\nvyHafD2Av+ac+1EAIKL/HMAzAP4TAD+UQ+xf6ZI7Ol+9Zq6/BnLDZqk0/agrKS4SP2V8jmeC0jJh\nfjBrsZIcqP7MWt8d08bxqjTREieSHJYOdr95aSmseec8YOmItdNybORI2+roUV9fluOHOJLqnBW3\ncX1dBuEi01bWJSmTUumvBg7J86EeCpVx5+KllIZLX61g2cf+Pi1xOMstm9DEcUR/R/f791Irw/+P\nAfw4Ef0QgD8B4N0A/rZz7u8AABF9MoBXYbIATPQ59z4i+qcAXo8Cw59A+DxqC7oTaoVSoo2AenBe\nqY/k+okK70R/gwWcKAwfqNO+Nm94DWj+Mq3/ahEPt2jN+u1YAud9t7yvkiTP6czRG96FS32cPIq/\n5svfo/COivfS/L5FUcjQtoWyUVqLtT5r+60qvBrenQw0y/bB5kjd57Ryvlz6vF9/1j1bgkjY7xHA\ntXMRIviugleLReCCnSYUaCjjo6ltMK0M/98E8DUAvh3AXwfwuQC+i4g+5Jz7fkzM3mHS6Dk8M98r\nAlH8Yo70Qx7tA93TpF/aPDmTvqXPrdwNPWA2X1Zea/W9i+HtVXinRAsP4tEqjLX0t4WptIb3ZtK3\n42lZL2vp44F9Gi5vSjcxU1TM7hVQBVNiTL+Au5SNIOn0fbVCs0lf6afHpC8PHJ6hM/1dRRlBK8Mf\nALzVOffN89+/SESfiUkI+P7Cc1WDyFue/Sm8iJ7GOI5wbsToRnzC8El4Bb06RTYfeF1VwB6qi4DB\n2gyCEt6HBnvN5RngIb7PhwQWBnbk2ubpifd1j9UhtsD8yrO/hLf/5i/j0dOPJoF/HPHBDz1nxtbK\n8H8HwNvEtbcB+E/n3393pvCViLX8VwD4FyXEn//yP4WPfvRyvPD4BTx+8hgvPH4eLzx5jMdPynF+\ne8Haw26vwjubgOIv4/1arp0NSml5/n4wyxWtgxVtRgZTMXPi1ml54cBja4EfgtXCO/O9kml+j8I7\nEu8RgsMZUvNKxW9qha+2SMurI6jjMefrb/CKS260Go1r8G/1bOSO0dwTlkBM4gw+dmcQET7z5X8U\nn/3Jr8NLXvZhePSiR3jy/BP8+u/8Kr7nn327aRytDP8tAD5dXPt0zIF7zrl3EtHvAvgCAL80E/lS\nTKb/727sqwrdpplM4R0Nb2/6TC6QpInmTNMtDtBS4R3NFLVFtb2LHfw5n7mbxlljcqXgPh+Mo46l\n5uPL4Mv2odAa/p7/8bEuWuEdf99yaFtp6wKDj/VI2I22kt871yVzo6yiy9VN3WYTs3RjdZ6VrbQE\nQXreC9lnGwvv9NJZc/3weAjNPZEugWVfJjiwBLHz69NFgbpBL2xl+H8LwFuI6JswBeB9LoCvBvAX\nWZvvBPBXiehXAfw6gL8G4LcA/P3Gvh407KrhV/q1XDsbmDX8Gp6ahq/48vYqvFPV8FEovMO1/5J8\ns9O7PXrN3DT8CgM0FN4B6to1b7dWbsrSUOn/3mr4NDP9WaifW6ziC00M3zn3z4joSwD8DQDfjCnP\n/uudc3+PtfmbRPThAL4HwMsA/J8Avqiag38DE5xZU7rBhcG7Jx6qe/NKoIfR3Pb5AlUf/j2dKq7h\nw/++cr83l9Z1zv0YgB+rtPlWAN/aR9INgJ2j9BtXzJHR91aojUmazC7Vd+/c8chkuem5RYG7KmRf\nVu0s69/faJ2dOUq/J+W2mZZMSlftmTXvzrofam0J+xbe0TKC5L1aJgx3g1jo22s9cvN8yUVRw9Ga\nKdQC56ql3whrc4QtTLV2YFvyaaPrLXn4OdP0yoNIrd5W2VBAnXZr6t4eUDKn8eu1nF7PRANT1Uz4\nYlPGgTYK5GIKcjSAIlrV9+UWEz83p/KcXh53UTzUG+hugTV5z2vBbPYs0LbWpcbdMMn7q+G2zBmV\nz59aKpsmUKp4lJiVZA+sMTVz1HxMLE6lhlump8ozPMKx4XqM4mNcXqgItTGQCuYcV0BVjL+Q78IO\nV83w7zOUmNZq/2TrvlQCTk4HtTGR+NcIJm2ghLN37iqmO354BSFQ9uWMfef6WfvOPd4j1o71PZdo\n20g2DZaY1mcspXVzNFZoj4SByvqVcSBcqGzpU0UvhAkt+DSYsgs4JEhLVzRXe61HN/dLGeVICOXx\nrUVoaLZANDR/sAx/iypV1wpHmfT3nNOtTPrNc7NT4R2rSd9rNprmYI3Oz9JvNJXW8D50k/7WuCx4\nLf2F4M6N1m/XGMUa6zXpt9B3dpM+UNh3qhBvH0/z1/LOBK0mpFzq0g1u0Atnj21YA/d5bDc4PpPC\nSsNWUfqXgC0Eu0XYn34igUeiJ+1iHh6shl8LjjjTItoaWlP+tjoYTAEpvbgraXm8XfF+hzmNayIl\nuprQOhf2ca6egzZm6Tcm1E3DRW1iBRzJUI5Iy6utO2tba9+lVDgH+zqvFt4xzoPWruaayKW4WnDn\ncLTQtyVsmZbn+X1AQyz2ith939YIV8/wWw7oYNLxk899R4opyYI/d3/tAt1igZc7EH+WClsgDgBb\n1+0FmEChi2q+sKsHCW1ZeCdHozcLZusi8IAm/58SDR7wdMz7Vu/qzMLzprTV1p2xrW9fo61UkKbF\nfLyWjiKumk+6cD8ybxeY2qUK7+RAugtbCu9kcUgtP8LH4y/aVKirZ/i9cFhhmxMcfkdp+HvCYRo+\n63tzDb+Ao0XDrzKXe1h859o1fMsyXKXhV9YXx7Onhm/BUboO3FMN3/8drvn9jSWQsoN9ndaHb0mz\nusENbnCD+whnUAyuBu7pVPlqe9Hf4Q/xrxFOreHfR0a/VcT7KhpacvBxDpprYDVs7RFDsEeUfmIR\nVMq0co1hzfvJ0b9VZsZRa6fFzNuLYytakvYnKrxjfYc9tOTwyjz6SsensELyGKW1UfrqPefgHCY3\niPimhhVOyfBjE0Z5wfVsyCML77QUzllbvCeLV/FRW9Jerr3wjr/XUnhHAxl8uEvhHe6XZ7iDqd4t\nB4tm2vXXeAGhbH87Fd4JuA86i7cwm7coHZu2Nc5ZschUidEaC+9487GlJoCGxzQnErU3WTuEYLXi\n48b4oq3PnqQeQSlUgRXeKeGCs5jrWX+uTZw+JcMHJktGFLG40aFxL6wGK+ejterXJsV+dgbLe60F\n4+3Rd+/cld5RiENg6yDn5+/pi/ezCui4tVMT7ADb+LZaLz0pxGvoa6kzUlu/AFYJR0ValKA9v0+9\ncmQaywmOJx4flA22NeAo3vMBu17TB5rGflofPizS5xrsV1x4Z2vazjzWTcEwzDPNRU1jstB6pKB2\nprm8QQpWIfnSNDz0+K2iWV+70LDHT8zwbbDXgljlE7VIzDe4PFgjn08CvVoCh9t6u0EOzLn+F6bB\nmkFwX0FaNXzsHvkUPIoaAw17/LQm/VPYaB4I7FkQ51JQSo0LbXZaU7ul5ZH4W/xbSkX05tC1NR/W\nwKFpeYWUtSY8xjE0uQ+orjlvkQq3ReGdLWgp4cgGt7nl963o2xNqbtK2tDxpxZt+lqh98pdSAaAC\np2T4rS/Q7KtkwSd7Fd7hxX3W0FsLlFnDvJKcYOQLePBnrqLwTgG9JfjIB80cXXgnPJvRgHhQ6VKk\nQ7SbA7Oy9BrpWAuHWE3mgK9ykw3pqi4rdtYY3kdvsaRAiylWznAOGddOqfBO7X5yhs4FhRxcsbhQ\nQmspSHHNfBr6lQGQqwrveG0+4EJSYW958FZ45waNcNPw29pofecia7u1D3k4VEyfZ9Tw98Z9ib6P\n0vCty7Bbw7cW3qH1hXdqfSR4HoiGr+1PDQ8XIiIBv+PIvgof/rUzoxvc4AY3uMENWkAVIjQtvwFO\npeHrptQbs98bWorWnCmojYNlDFu1UZ/JPLam8E61eEqu8E5Xd4pL4KTv2go9BV9acPTSYsKpmIBr\neKPrxiwk655Ym+eeu1fDm3NXiUaHa/k+5qal8E6uTXauQrEdu9VFwqkYvoc49cjQvnFT1opStBTe\nyfW/Z+GdFhwmvFbmMvvUcnCGwjtF37sqUCaNqmZEWQFst8I7hVxyU+EdLP5+y/u10H1NUMv/Xo2j\no93UeDuTfi6trcYoQ+GdCi0h1qlCT3fhnRrehnoKPef0GrAU3vH8o6XwDmAUYBzQkpIHnJDh763h\nb52mdB/cDVYp/9QaviWneMN331K4pLfwjqUgUtMBUcMl4GitaS3cCu8UnmMavqWtSZjvSEe2RK1f\nQ+EdGUMUxsWsD9bCO/p4HRNs5v/V5bAETuXD9ykIPjVBalDZ56yHYyMt3ebdC8DF86vpgD4PgPsg\nwN3gBhawnJu+3Q36YFVabvR3rmEb3lMxfOfFlujv42g5MpXpdOCuX+OzwDW9v2ui9QbnA1nLodTu\nBn3QKyzFzzHBTIYLNSpipzPpp2tr28VWS1dpxncPUtossGce6xZwycI7vM6377vXZFmC6loVqL2J\nvze18L5BtS75ShwcWtwHlvNni1S44nPc/1zpyrqekvoejI41mm61ZsEJ1m4uLc/HSbQV3vFxGN4K\ns1hjJnwz18/HCmfhdAxfrr7WV5lbHFFhHeeSYg69hXdkm0sV3rHiUZ+T5iJDYQs3f7RhLdPcTWgw\not2i8I6fh1KwDu+vp/BOTfuShXcAduiwx4iMhXcaAwuvAkrvxbxgNiKlo5iYicZMk+qe9nvZEDRn\nI6OMq6XSnmhgfleHF95hAZBx4DmjSwmulfFA4fwJOFiLmdEvv/N2dTgVw9dfyJUfOvcIzswAZOT8\nWjwlkIdgMZVmxZzVrEdqxcReIfDE77YXthjTVul7mlJQecAEGn0W/GalpoHhJkVkMkpUC1gY9Rk+\nEJVo+OId+L1szSSINPzpQsjD99fnB5rgVD78s8EtWOUGN7jBg4bbEViEfQVlQ6psY/en0vBj08YS\ntX+D4+H0aXkGh5YpItmiHRV8lVqfXWl5lnQpgXvN9w7uY1oe0J8OZsGxBR35B2A+zGvaZekZa/re\nmdPyLHj2hqTwDou/sdYJkM/FN7TG7XSeiuFPwPwWZFu88dO29DxL4R2L/zOHZ+/CO6W+W/GamJwv\n1LGBX9Rq/m4aH9WZ5G6Fd0p4cz7W2pqqjCcpvMP6i8y14kM7xT7vIWwxrhYGmgURV1GFhsM8oc9w\nbnoTc3Vs/nbN16/gisbZyY8tNCYFcAq4tgTZb8QrKG5XKryjnXtJnJVv4xAHtjt5oQynY/jxXugI\nQ7zBLkCYv1p1IUG6R9DbuhZDDs6k4Ue8foWWc9Pw23FsQUepvYlG6tTwM77nHJxZwz9r4Z2kCI8l\n+LFipYvmq+M4PpUP3xfc8b9Pf9k3Sm/VKfWZjbTnewMd1pZLwmYV0c4yxpOQcc1wb/ciA3W9Godt\nnZ+HMI+XgBZ3m1kgbVPwz8XwzwRn9VUfBg3RunvAM3h38f5W2qg1ZdL6TPecWVOhNgKn/HdtINcI\nN6OuGVseSxuuPeZUG6O1m9L8RP9ZawJU5qV37raa/9oZshqI/0rJ722Wl2FpTexfiYKkVbwMN4Zf\nAFMVqis8GHug5SDZrD8Gz+C3q+0v9t1sucFKaLv5veGgtQZ1WVQ+p/xcGahrRBtX69hyOFpxOfsa\nbFqrgh7LmcR9wrUfM2Oea3Vk56Vj7hKcGn3GuaqdIWsgFMUJF5D8brKUEHNj8GI7WOIZWHp+E7MH\nTujD3wK0IIhwz0dMPtDCO2pAiKHwzpo+e3HE7SrSvEM1stmRTSiw+M8jX1upzwsW3tGAaPnaWXX+\nMn1cDyhznRlC09g2moYWJt6kvWrvbqPCO54WS5tagLM2fhNua7XDzBm+ZBe170Vrn/LMiAQAWmgq\nfW3UPxfwLZ2EHPzph+Nt4/r3juFf3yF1HWCtu30kbF02OQe5ohoqTSvWYwkv0HYQ1ui4r/vmEgKq\nNe6DC2nVto3CQSs9/pkt33uNjq6+XF14OcO5VAqcDFlfhn3oBYe4xC4LsFRM+i1w7xj+lnCGhbQ1\n1JjIDSa4pkClWirifVzHN7iBhCQqnl3faw9IrV77HbBnRZRwMGQmXBqcgeG/BACeffz7uBvv8Pju\nCZ48eYwn4x2e3D3Gk/EJHrvHuHNPTMhGRYIaFDMKuTh8YWDhDKMbZ1xjs1Sq9WWhcS88EggEKTDL\nudDAuTEYxY6AJ3iC9+O91XaleSM3RO9Zgzt3BweHoTInd7gz9dvzjjy+Er2jGzFiWqdPufw2Ht0I\n58ZuOq4JrGtka7DsVWBZC3vtbU5PbU8758L62QvkOLc6ryT4c2kItSnic2pwhBFul/WxjDF2rcl9\n63mKc+U59+/t6fFpfOjuxfjA4+fwHL0ET49P4yV4CR65p/A0XowXPX4aw1MD7h7f4feee8Y//pIa\nvXS09E9E/xmAHziUiBvc4AY3uMENrhv+vHPuB0sNzsDwPxbAFwL4dQAfOpSYG9zgBje4wQ2uC14C\n4A8BeLNz7vdLDQ9n+De4wQ1ucIMb3GB/uOXh3+AGN7jBDW7wAODG8G9wgxvc4AY3eABwY/g3uMEN\nbnCDGzwAuDH8G9zgBje4wQ0eABzO8InojUT0TiL6IBH9PBF9ztE03WB/IKJvIaJR/PwKu/9iIvpu\nInoPEb2fiN5ERK8QOD6JiP4BET1HRL9LRH+TiA5f0zfoAyL640T0vxPRu+f18GeUNt9GRL9NRB8g\non9ERJ8i7n8MEf0AEb2XiJ4lor9DRB8h2vy7RPQz85nzG0T0V/Ye2w3WQ219ENHfVc6UHxNtHvT6\nOPRwJKI/C+DbAXwLgM8C8IsA3kxEH3ckXTe4GPwygFcCeNX88/ns3ncC+GIAXwrgDQBeDeCH/c2Z\nsf8YpuJRrwPwFwB8BYBvuwDdN9gHPgLAvwTwRihV3onoGwF8LYC/BOC1AJ7DdF48zZr9IIDPAPAF\nmNbPGwB8D8PxUQDeDOCdAD4bwF8B8K1E9NU7jOcG20JxfczwDxGfKX9O3H/Y68PXSD/iB8DPA/jv\n2d8E4LcA/JdH0nX7uci7/xYA/zxz76UAngfwJezapwMYAbx2/vuLADwG8HGszV8C8CyAp44e3+1n\n9foYAfwZce23AXyDWCcfBPBl89+fMT/3WazNFwJ4AuBV899fA+A9fI0A+G8B/MrRY779rF4ffxfA\n/1Z45t9+6OvjMA2fiF4E4DUAftJfc9Ps/gSA1x9F1w0uCp86m+d+jYi+n4g+ab7+GkyaO18b7wDw\nLixr43UA/m/n3HsYvjcD+GgAn7k/6Te4JBDRJ2PS2PiaeB+Af4p4TTzrnPsX7NGfwKQNfi5r8zPO\nRbW63wzg04noo3ci/waXgz9JRM8Q0duJ6G8T0cvZvdfjga+PI036HwfgEYBnxPVnMG3sG9xv+HlM\nJvgvxP/f3t2D2FGFYQB+TsQIKkskGLYwhmCwENYfMI2CCQbS2cYujY1YWUhqwUotBUUEQSIGtLGQ\nRLEQFRVCUvlHFBVtvBF/CIoRZRmLc9aMN3ETVnT0nveBU8yeucMM99vznTv3O3e4HzvxVvs+bRm/\ntgF9bBwbyy4cOyR+FtGyOjCvN14s45tx5zAMq/he4qYHx3AQd+MQ9uBoOfeUme7j47/w8Jx5F3mq\neSyCYRheG21+UEo5ji9xwF//xPKlxkbipx+XEhMX22ctISRu/seGYXhxtPlhKeV9fIa9eGOdl3YT\nH1N+wv8Wq2qBxdg258+wYsENw3AGn2AXZthcSlma220cGzPnx87aduJn8czUgXe98WLWtv9QSrkM\n17S+tX0udAwSNwtlGIYv1DyztpKj+/iYLOEPw/AbTqrVkqDdetmHd6c6r5hGKeVq3KAWZp1UC2nG\nsXEjrncuNt7DytyKjv04g4/EQmmD98yfY2JJ/e51HBNbSim3jV66T50oHB/tc1cb6Nfsx6k26YwF\nUUq5DlvxdftT4mPiSssDapXtQbWC8ml8h2unrmZM+8ff+8fVJTE7cAdeV2fQW1v/k+rSmL1qEd87\neHv0+k3qMs5juFmtBTiNR6a+trQNx8RVuAW3qtXUD7bt7a3/UBsf7sEKXsan2Dw6xlGcwG7ciVM4\nPOpfUieVz+Em3IufcN/U15+28fhofY+pE8AdaiI/gY9xeeKjXd/kJ8AD6qNxz6qzq9unPqe0f+V9\nP6IuwTyrVt+/gJ2j/ivwhHpL7ke8hG1zx9iOV9o/5Gk8ik1TX1vahmNiTxvIV+fas6N9Hm4D8s9q\n9fSuuWNswfPqnZ4f8AyunNtnBW+2Y3yFh6a+9rS/Fx/qI2JfVe8C/YLP8ZS5D4+9x0cejxsREdGB\n/AxpREREB5LwIyIiOpCEHxER0YEk/IiIiA4k4UdERHQgCT8iIqIDSfgREREdSMKPiIjoQBJ+RERE\nB5LwIyIiOpCEHxER0YEk/IiIiA78DiFvRr5fzvunAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f7ac6acd8d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"ahw = np.abs(hw)\n",
"plt.imshow(ahw, aspect='auto', cmap='PRGn')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Search for local minima in in the row corresponding to the peak's scale, within 3x peak scale or peak index"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"75\n",
"75\n",
"75\n",
"75\n",
"75\n",
"75\n",
"75\n",
"75\n",
"75\n",
"75\n",
"75\n",
"75\n",
"75\n",
"75\n",
"75\n",
"75\n",
"75\n",
"75\n",
"75\n",
"75\n",
"82\n",
"82\n",
"88\n",
"89\n",
"89\n",
"95\n",
"97\n",
"102\n",
"106\n",
"112\n",
"0\n",
"0\n",
"0\n",
"0\n",
"139\n",
"0\n",
"0\n",
"0\n",
"159\n",
"0\n",
"0\n",
"171\n",
"175\n",
"179\n",
"0\n",
"188\n",
"0\n",
"194\n",
"200\n",
"207\n",
"0\n",
"220\n",
"220\n",
"220\n",
"232\n",
"0\n",
"0\n",
"245\n",
"0\n",
"255\n",
"256\n",
"256\n",
"0\n",
"0\n",
"285\n",
"285\n",
"285\n",
"285\n",
"286\n",
"286\n",
"286\n",
"0\n",
"0\n",
"301\n",
"303\n",
"310\n",
"311\n",
"0\n",
"0\n",
"322\n",
"323\n",
"330\n",
"330\n",
"0\n",
"0\n",
"344\n",
"345\n",
"350\n",
"353\n",
"0\n",
"0\n",
"0\n",
"371\n",
"385\n",
"391\n",
"398\n",
"398\n",
"0\n",
"416\n",
"0\n",
"0\n",
"0\n",
"0\n",
"0\n",
"444\n",
"444\n",
"0\n",
"0\n",
"0\n",
"459\n",
"465\n",
"468\n",
"471\n",
"471\n",
"477\n",
"479\n",
"484\n",
"485\n",
"0\n",
"493\n",
"498\n",
"0\n",
"508\n",
"508\n",
"0\n",
"0\n",
"520\n",
"0\n",
"531\n",
"531\n",
"0\n",
"0\n",
"0\n",
"548\n",
"548\n",
"555\n",
"559\n",
"563\n",
"571\n",
"577\n",
"577\n",
"0\n",
"0\n",
"598\n",
"606\n",
"611\n",
"0\n",
"0\n",
"0\n",
"630\n",
"0\n",
"0\n",
"0\n",
"0\n",
"648\n",
"648\n",
"0\n",
"0\n",
"0\n",
"0\n",
"678\n",
"678\n",
"678\n",
"678\n",
"683\n",
"0\n",
"0\n",
"0\n",
"0\n",
"0\n",
"706\n",
"706\n",
"0\n",
"0\n",
"721\n",
"0\n",
"730\n",
"730\n",
"733\n",
"740\n",
"750\n",
"755\n",
"0\n",
"0\n",
"0\n",
"782\n",
"0\n",
"789\n",
"0\n",
"0\n",
"797\n",
"0\n",
"0\n",
"806\n",
"809\n",
"0\n",
"818\n",
"823\n",
"829\n",
"0\n",
"841\n",
"845\n",
"852\n",
"858\n",
"858\n",
"864\n",
"874\n",
"874\n",
"0\n",
"0\n",
"0\n",
"892\n",
"892\n",
"0\n",
"0\n",
"908\n",
"911\n",
"915\n",
"0\n",
"923\n",
"925\n",
"933\n",
"933\n",
"937\n",
"0\n",
"944\n",
"949\n",
"949\n",
"956\n",
"959\n",
"964\n",
"0\n",
"973\n",
"978\n",
"981\n",
"985\n",
"992\n",
"994\n",
"0\n",
"1002\n",
"0\n",
"0\n",
"1014\n",
"1019\n",
"1022\n",
"1025\n",
"0\n",
"0\n",
"0\n",
"1038\n",
"1038\n",
"1045\n",
"1045\n",
"1058\n",
"1056\n",
"1060\n",
"0\n",
"1069\n",
"1070\n",
"1079\n",
"0\n",
"0\n",
"0\n",
"1094\n",
"0\n",
"1104\n",
"0\n",
"0\n",
"0\n",
"1119\n",
"1124\n",
"0\n",
"1132\n",
"1140\n",
"1140\n",
"1145\n",
"0\n",
"0\n",
"0\n",
"1162\n",
"1162\n",
"0\n",
"1169\n",
"1169\n",
"1177\n",
"1180\n",
"1189\n",
"1189\n",
"0\n",
"0\n",
"0\n",
"0\n",
"1212\n",
"0\n",
"0\n",
"1224\n",
"0\n",
"0\n",
"1233\n",
"0\n",
"1243\n",
"1246\n",
"1251\n",
"0\n",
"0\n",
"1261\n",
"1265\n",
"0\n",
"1278\n",
"1284\n",
"1286\n",
"1291\n",
"1296\n",
"0\n",
"0\n",
"0\n",
"1316\n",
"0\n",
"1328\n",
"0\n",
"0\n",
"0\n",
"0\n",
"1345\n",
"1345\n",
"0\n",
"1354\n",
"1361\n",
"1361\n",
"0\n",
"1367\n",
"0\n",
"0\n",
"0\n",
"0\n",
"1386\n",
"1386\n",
"1392\n",
"1398\n",
"0\n",
"1406\n",
"1411\n",
"1416\n",
"1419\n",
"1422\n",
"1425\n",
"0\n",
"0\n",
"1440\n",
"1440\n",
"0\n",
"1448\n",
"0\n",
"1463\n",
"1471\n",
"1474\n",
"1477\n",
"1480\n",
"1486\n",
"0\n",
"1495\n",
"1496\n",
"0\n",
"1503\n",
"1510\n",
"1512\n",
"1518\n",
"1521\n",
"0\n",
"0\n",
"1536\n",
"1537\n",
"1544\n",
"0\n",
"1551\n",
"0\n",
"1575\n",
"1575\n",
"1575\n",
"1575\n",
"0\n",
"0\n",
"1591\n",
"1598\n",
"1598\n",
"0\n",
"0\n",
"1612\n",
"1612\n",
"1612\n",
"1612\n",
"1612\n",
"1612\n",
"1612\n",
"1612\n",
"1612\n",
"1612\n",
"1612\n",
"1612\n",
"1612\n",
"1612\n",
"1612\n",
"1612\n"
]
}
],
"source": [
"for p in peak_pos:\n",
" print p"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.12"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| gpl-3.0 |
profxj/xastropy | xastropy/casbah/CASBAH_galaxy_database.ipynb | 4 | 14053 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Building the CASBAH Galaxy Database (v1.0)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## SDSS"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Targeting\n",
"I am unclear on how to sensibly extract targeting information from the\n",
"SDSS. But this may well be an issue for various analyses."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Extracting Galaxy data\n",
"The script build_sdss loops through the listed fields with SDSS\n",
"coverage and calls the grab_sdss_spectra script to grab photometric\n",
"and spectral data. It is currently grabbing DR12.\n",
"\n",
"Here are some defaults:\n",
"* Box of 2deg on a side\n",
"* Photometry is Petrosian ugriz\n",
"* Galaxies are cut down to 20Mpc separation (LCDM cosmology)\n",
"* z > 500km/s to cut stars\n",
"\n",
"Here is the basic procedure:\n",
"* Query photometry all objects in search box with spectra\n",
"* Query list of spectra from SDSS in search box\n",
" * This list often contain duplicates from multiple passes\n",
"* Cut on 20Mpc using redshifts, RA+DEC of obj, and RA+DEC of QSO\n",
"* Loop on sources to build table\n",
" * Take BOSS data over SDSS\n",
"* Generate a binary FITS table, including photometry, redshift and spectra"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"grab_sdss_spectra: Found 12 sources in the search box.\n",
"grab_sdss_spectra: Grabbing data for 12 sources.\n",
"Wrote SDSS table to None\n"
]
},
{
"data": {
"text/html": [
"<Table masked=False length=5>\n",
"<table id=\"table4446065744\">\n",
"<thead><tr><th>RA</th><th>DEC</th><th>Z</th><th>Z_ERR</th><th>SDSS_MAG [5]</th><th>SDSS_MAGERR [5]</th><th>TELESCOPE</th><th>INSTRUMENT</th><th>FLUX [5000]</th><th>SIG [5000]</th><th>WAVE [5000]</th></tr></thead>\n",
"<thead><tr><th>float64</th><th>float64</th><th>float64</th><th>float64</th><th>float64</th><th>float64</th><th>string640</th><th>string640</th><th>float32</th><th>float32</th><th>float64</th></tr></thead>\n",
"<tr><td>212.35102636</td><td>26.3415403908</td><td>3.21771526337</td><td>0.000997702358291</td><td>23.70004 .. 7.34031909445e+223</td><td>1.576056 .. 6.013470017e-154</td><td>SDSS 2.5-M</td><td>BOSS</td><td>3.5592 .. 1.35632e-19</td><td>2.65591 .. 1.35632e-19</td><td>3592.52587891 .. -1.22810024928e-296</td></tr>\n",
"<tr><td>212.349627859</td><td>26.3058613203</td><td>0.0</td><td>0.0</td><td>16.10909 .. -6.11925950261e-220</td><td>0.004779854 .. -2.78592920103e-305</td><td>SDSS 2.5-M</td><td>SDSS</td><td>0.0 .. 1.77053e-38</td><td>0.0 .. -1.21568e-37</td><td>3811.53564453 .. 1.57733159326e-52</td></tr>\n",
"<tr><td>212.370094746</td><td>26.3254555654</td><td>0.327256381512</td><td>5.58089996048e-05</td><td>21.36104 .. 6.013470017e-154</td><td>1.245788 .. 1.83037365249e-94</td><td>SDSS 2.5-M</td><td>BOSS</td><td>3.59836 .. -1.19132e+14</td><td>3.71348 .. -9.48227e+21</td><td>3590.87353516 .. 8.31176848954e+46</td></tr>\n",
"<tr><td>212.363198097</td><td>26.3766678271</td><td>0.673991203308</td><td>0.000221190101001</td><td>21.94763 .. 1.76807794921e+258</td><td>1.772229 .. -1.47312822905e-204</td><td>SDSS 2.5-M</td><td>BOSS</td><td>-0.0600585 .. 1.35632e-19</td><td>2.7654 .. -1.47499e+12</td><td>3592.52587891 .. 7.86200159392e-51</td></tr>\n",
"<tr><td>212.272722288</td><td>26.305233155</td><td>0.321305960417</td><td>8.39712593006e-05</td><td>21.33263 .. 3.00282156321e-142</td><td>0.844611 .. -1.19464315864e-195</td><td>SDSS 2.5-M</td><td>BOSS</td><td>-0.931015 .. 168.798</td><td>2.87149 .. 3.81592e+09</td><td>3590.87353516 .. -1.10999478584e-51</td></tr>\n",
"</table>"
],
"text/plain": [
"<Table masked=False length=5>\n",
" RA DEC ... WAVE [5000] \n",
" float64 float64 ... float64 \n",
"------------- ------------- ... ------------------------------------\n",
" 212.35102636 26.3415403908 ... 3592.52587891 .. -1.22810024928e-296\n",
"212.349627859 26.3058613203 ... 3811.53564453 .. 1.57733159326e-52\n",
"212.370094746 26.3254555654 ... 3590.87353516 .. 8.31176848954e+46\n",
"212.363198097 26.3766678271 ... 3592.52587891 .. 7.86200159392e-51\n",
"212.272722288 26.305233155 ... 3590.87353516 .. -1.10999478584e-51"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Example call\n",
"from xastropy.casbah import galaxy_data as xcgd\n",
"reload(xcgd)\n",
"radec = (212.34957*u.deg,26.30585*u.deg)\n",
"tab=xcgd.grab_sdss_spectra(radec, radius=1.*u.degree/12.) \n",
"Table(tab[0:5])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Open questions/issues\n",
"1. Should we be recording other observing meta-data?\n",
"1. How about SFR, M*, etc.?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## DEIMOS"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"### Targeting\n",
"\n",
"* Pull mask target info from Mask files :: parse_deimos_mask_file\n",
"* Pull other target info from SExtractor output\n",
" * Requires yaml file describing target criteria\n",
" * And the SExtractor output file\n",
"\n",
"#### Sample output of MULTI_OBS file\n",
"\n",
"MULTI_OBJ file:\n",
"\n",
"| INSTR | MASK_NAME | MASK_RA | MASK_DEC | MASK_EPOCH | MASK_PA | DATE_OBS | DISPERSER | TEXP | CONDITIONS |\n",
"\n",
"| DEIMOS | PG1407_may_early | 14:09:34.10 | 26:18:45.1 | 2000.0 | -96.1 | 23-Jul-2015 | G600 | 3600.0 | POOR_SEEING,CLOUDS |\n",
"\n",
"| DEIMOS | PG1407_may_early | 14:09:34.10 | 26:18:45.1 | 2000.0 | -96.1 | 24-Jul-2015 | G600 | 3600.0 | CLEAR |\n"
]
},
{
"cell_type": "code",
"execution_count": 75,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<Table masked=True length=5>\n",
"<table id=\"table4454366096\">\n",
"<thead><tr><th>TARG_RA</th><th>TARG_DEC</th><th>EPOCH</th><th>TARG_ID</th><th>TARG_MAG</th><th>TARG_IMG</th><th>INSTR</th><th>MASK_NAME</th></tr></thead>\n",
"<thead><tr><th>float64</th><th>float64</th><th>float64</th><th>int32</th><th>float32</th><th>string136</th><th>string192</th><th>string512</th></tr></thead>\n",
"<tr><td>212.39539331</td><td>26.1409489801</td><td>2000.0</td><td>556</td><td>23.7325</td><td>pg1407.V.mos.fits</td><td>DEIMOS</td><td>PG1407_may_mid2</td></tr>\n",
"<tr><td>212.386193606</td><td>26.1464415539</td><td>2000.0</td><td>703</td><td>23.8043</td><td>pg1407.V.mos.fits</td><td>DEIMOS</td><td>PG1407_may_mid2</td></tr>\n",
"<tr><td>212.365282515</td><td>26.149680065</td><td>2000.0</td><td>742</td><td>20.7288</td><td>pg1407.V.mos.fits</td><td>DEIMOS</td><td>PG1407_may_mid2</td></tr>\n",
"<tr><td>212.392594184</td><td>26.1567769971</td><td>2000.0</td><td>901</td><td>19.9971</td><td>pg1407.V.mos.fits</td><td>DEIMOS</td><td>PG1407_may_mid2</td></tr>\n",
"<tr><td>212.390583821</td><td>26.1596075882</td><td>2000.0</td><td>1037</td><td>24.3026</td><td>pg1407.V.mos.fits</td><td>DEIMOS</td><td>PG1407_may_mid2</td></tr>\n",
"</table>"
],
"text/plain": [
"<Table masked=True length=5>\n",
" TARG_RA TARG_DEC EPOCH ... INSTR MASK_NAME \n",
" float64 float64 float64 ... string192 string512 \n",
"------------- ------------- ------- ... --------- ---------------\n",
" 212.39539331 26.1409489801 2000.0 ... DEIMOS PG1407_may_mid2\n",
"212.386193606 26.1464415539 2000.0 ... DEIMOS PG1407_may_mid2\n",
"212.365282515 26.149680065 2000.0 ... DEIMOS PG1407_may_mid2\n",
"212.392594184 26.1567769971 2000.0 ... DEIMOS PG1407_may_mid2\n",
"212.390583821 26.1596075882 2000.0 ... DEIMOS PG1407_may_mid2"
]
},
"execution_count": 75,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"#### Sample of target file\n",
"fil='/Users/xavier/CASBAH/Galaxies/PG1407+265/PG1407+265_targets.fits'\n",
"targ = Table.read(fil)\n",
"#\n",
"mt = np.where(targ['MASK_NAME'] != 'N/A')[0]\n",
"targ[mt[0:5]]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Testing"
]
},
{
"cell_type": "code",
"execution_count": 77,
"metadata": {
"collapsed": false
},
"outputs": [
{
"ename": "TypeError",
"evalue": "read_table_fits() got an unexpected keyword argument 'fill_values'",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mTypeError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m<ipython-input-77-8e522a9ae1fa>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[1;32m 1\u001b[0m \u001b[0mfil\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;34m'/Users/xavier/CASBAH/Galaxies/PG1407+265/PG1407+265_targets.fits'\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m----> 2\u001b[0;31m \u001b[0mtmp\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mTable\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mread\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mfil\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0mfill_values\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m'N/A'\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m'0'\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m'MASK_NAME'\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0mformat\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;34m'fits'\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m",
"\u001b[0;32m/Users/xavier/local/Python/astropy/astropy/table/table.pyc\u001b[0m in \u001b[0;36mread\u001b[0;34m(cls, *args, **kwargs)\u001b[0m\n\u001b[1;32m 1954\u001b[0m \u001b[0mpassed\u001b[0m \u001b[0mthrough\u001b[0m \u001b[0mto\u001b[0m \u001b[0mthe\u001b[0m \u001b[0munderlying\u001b[0m \u001b[0mdata\u001b[0m \u001b[0mreader\u001b[0m \u001b[0;34m(\u001b[0m\u001b[0me\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mg\u001b[0m\u001b[0;34m.\u001b[0m \u001b[0;34m`\u001b[0m\u001b[0;34m~\u001b[0m\u001b[0mastropy\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mio\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mascii\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mread\u001b[0m\u001b[0;34m`\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1955\u001b[0m \"\"\"\n\u001b[0;32m-> 1956\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0mio_registry\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mread\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mcls\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m*\u001b[0m\u001b[0margs\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m**\u001b[0m\u001b[0mkwargs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 1957\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1958\u001b[0m \u001b[0;32mdef\u001b[0m \u001b[0mwrite\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m*\u001b[0m\u001b[0margs\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m**\u001b[0m\u001b[0mkwargs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/Users/xavier/local/Python/astropy/astropy/io/registry.pyc\u001b[0m in \u001b[0;36mread\u001b[0;34m(cls, *args, **kwargs)\u001b[0m\n\u001b[1;32m 324\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 325\u001b[0m \u001b[0mreader\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mget_reader\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mformat\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mcls\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 326\u001b[0;31m \u001b[0mdata\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mreader\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m*\u001b[0m\u001b[0margs\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m**\u001b[0m\u001b[0mkwargs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 327\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 328\u001b[0m \u001b[0;32mif\u001b[0m \u001b[0;32mnot\u001b[0m \u001b[0misinstance\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mdata\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mcls\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mTypeError\u001b[0m: read_table_fits() got an unexpected keyword argument 'fill_values'"
]
}
],
"source": [
"fil='/Users/xavier/CASBAH/Galaxies/PG1407+265/PG1407+265_targets.fits'\n",
"tmp = Table.read(fil,fill_values=[('N/A','0','MASK_NAME')],format='fits')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.10"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| bsd-3-clause |
gasabr/AtoD | experiments/abilities_clustering.ipynb | 1 | 76354 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## TODO\n",
"1. (One day) Write distance function which is going to use nmf classification of abilities texts.\n",
"2. write a method to binarize columns by given column name\n",
"3. would be nice to use some anchor abilities as centers\n",
"4. try KMeans without numeric variables"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import numpy as np\n",
"import pandas as pd\n",
"from pprint import pprint\n",
"from sklearn.cluster import KMeans, DBSCAN\n",
"from sklearn.preprocessing import MultiLabelBinarizer, LabelBinarizer\n",
"\n",
"from atod import Abilities"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>2_times</th>\n",
" <th>3_times</th>\n",
" <th>4_times</th>\n",
" <th>AbilityBehavior</th>\n",
" <th>AbilityCastPoint</th>\n",
" <th>AbilityCastRange</th>\n",
" <th>AbilityCastRangeBuffer</th>\n",
" <th>AbilityChannelTime</th>\n",
" <th>AbilityCooldown</th>\n",
" <th>AbilityDamage</th>\n",
" <th>...</th>\n",
" <th>wolf_bat</th>\n",
" <th>wolf_damage</th>\n",
" <th>wolf_duration</th>\n",
" <th>wolf_hp</th>\n",
" <th>wolf_index</th>\n",
" <th>zombie_interval</th>\n",
" <th>ID</th>\n",
" <th>damage_per_burn</th>\n",
" <th>lvl</th>\n",
" <th>per_hit</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>DOTA_ABILITY_BEHAVIOR_PASSIVE</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>...</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>5003.0</td>\n",
" <td>0.6</td>\n",
" <td>2.5</td>\n",
" <td>46.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>DOTA_ABILITY_BEHAVIOR_POINT | DOTA_ABILITY_BEH...</td>\n",
" <td>0.4</td>\n",
" <td>1037.5</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>8.25</td>\n",
" <td>NaN</td>\n",
" <td>...</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>5004.0</td>\n",
" <td>NaN</td>\n",
" <td>2.5</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>DOTA_ABILITY_BEHAVIOR_PASSIVE</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>...</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>5005.0</td>\n",
" <td>NaN</td>\n",
" <td>2.5</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>DOTA_ABILITY_BEHAVIOR_UNIT_TARGET | DOTA_ABILI...</td>\n",
" <td>0.3</td>\n",
" <td>600.0</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>70.00</td>\n",
" <td>NaN</td>\n",
" <td>...</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>5006.0</td>\n",
" <td>NaN</td>\n",
" <td>2.5</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>DOTA_ABILITY_BEHAVIOR_NO_TARGET | DOTA_ABILITY...</td>\n",
" <td>0.4</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>13.00</td>\n",
" <td>0.0</td>\n",
" <td>...</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>5007.0</td>\n",
" <td>NaN</td>\n",
" <td>2.5</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>5 rows × 837 columns</p>\n",
"</div>"
],
"text/plain": [
" 2_times 3_times 4_times \\\n",
"0 NaN NaN NaN \n",
"1 NaN NaN NaN \n",
"2 NaN NaN NaN \n",
"3 NaN NaN NaN \n",
"4 NaN NaN NaN \n",
"\n",
" AbilityBehavior AbilityCastPoint \\\n",
"0 DOTA_ABILITY_BEHAVIOR_PASSIVE NaN \n",
"1 DOTA_ABILITY_BEHAVIOR_POINT | DOTA_ABILITY_BEH... 0.4 \n",
"2 DOTA_ABILITY_BEHAVIOR_PASSIVE NaN \n",
"3 DOTA_ABILITY_BEHAVIOR_UNIT_TARGET | DOTA_ABILI... 0.3 \n",
"4 DOTA_ABILITY_BEHAVIOR_NO_TARGET | DOTA_ABILITY... 0.4 \n",
"\n",
" AbilityCastRange AbilityCastRangeBuffer AbilityChannelTime \\\n",
"0 NaN NaN NaN \n",
"1 1037.5 NaN NaN \n",
"2 NaN NaN NaN \n",
"3 600.0 NaN NaN \n",
"4 NaN NaN NaN \n",
"\n",
" AbilityCooldown AbilityDamage ... wolf_bat wolf_damage \\\n",
"0 NaN NaN ... NaN NaN \n",
"1 8.25 NaN ... NaN NaN \n",
"2 NaN NaN ... NaN NaN \n",
"3 70.00 NaN ... NaN NaN \n",
"4 13.00 0.0 ... NaN NaN \n",
"\n",
" wolf_duration wolf_hp wolf_index zombie_interval ID damage_per_burn \\\n",
"0 NaN NaN NaN NaN 5003.0 0.6 \n",
"1 NaN NaN NaN NaN 5004.0 NaN \n",
"2 NaN NaN NaN NaN 5005.0 NaN \n",
"3 NaN NaN NaN NaN 5006.0 NaN \n",
"4 NaN NaN NaN NaN 5007.0 NaN \n",
"\n",
" lvl per_hit \n",
"0 2.5 46.0 \n",
"1 2.5 NaN \n",
"2 2.5 NaN \n",
"3 2.5 NaN \n",
"4 2.5 NaN \n",
"\n",
"[5 rows x 837 columns]"
]
},
"execution_count": 2,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"specs = pd.read_csv('../atod/data/702/abilities_specs.csv')\n",
"specs.head()"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"(519, 97)"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"columns_to_drop = ['lvl', 'AbilityCastRangeBuffer', 'levelkey', \n",
" 'HotKeyOverride', 'AbilityTextureName',\n",
" 'LevelsBetweenUpgrades', '_sa_instance_state',\n",
" 'OnCastbar', 'OnLearnbar', 'LinkedSpecialBonus',\n",
" 'ID', 'pk']\n",
"specs = specs.drop(columns_to_drop, axis=1)\n",
"specs = specs.dropna(axis=1, thresh=4)\n",
"specs.shape"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# encode AbilityBehavior\n",
"# get all possible values\n",
"behavior = specs.AbilityBehavior\n",
"behavior = behavior.str.split('|').apply(lambda x: [y.strip() for y in x])\n",
"\n",
"mlb = MultiLabelBinarizer().fit(behavior)\n",
"binary_behavior = pd.DataFrame(mlb.transform(behavior),\n",
" columns=mlb.classes_).drop([''], axis=1)\n",
"\n",
"X = pd.concat([specs.drop(['AbilityBehavior'], axis=1), binary_behavior], axis=1)"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"flags = X.AbilityUnitTargetFlags\n",
"flags = flags.fillna(value='DOTA_UNIT_TARGET_FLAG_NONE')\n",
"flags = flags.str.split('|').apply(lambda x: [y.strip() for y in x])\n",
"\n",
"mlb = MultiLabelBinarizer().fit(flags)\n",
"binary_flags = pd.DataFrame(mlb.transform(flags), columns=mlb.classes_)\n",
"\n",
"X = pd.concat([X.drop(['AbilityUnitTargetFlags'], axis=1), binary_flags], axis=1)"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"target_team = X.AbilityUnitTargetTeam\n",
"target_team = target_team.fillna(value='DOTA_UNIT_TARGET_TEAM_NONE')\n",
"target_team = target_team.str.split('|').apply(lambda x: [y.strip() for y in x])\n",
"\n",
"mlb = MultiLabelBinarizer().fit(target_team)\n",
"binary_team = pd.DataFrame(mlb.transform(target_team), \n",
" columns=mlb.classes_)\n",
"\n",
"X = pd.concat([X.drop(['AbilityUnitTargetTeam'], axis=1), binary_team], axis=1)"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"target_type = X.AbilityUnitTargetType\n",
"target_type = target_type.fillna(value='DOTA_UNIT_TARGET_NONE')\n",
"target_type = target_type.str.split('|').apply(lambda x: [y.strip() for y in x])\n",
"\n",
"mlb = MultiLabelBinarizer().fit(target_type)\n",
"binary_type = pd.DataFrame(mlb.transform(target_type), \n",
" columns=mlb.classes_)\n",
"\n",
"X = pd.concat([X.drop(['AbilityUnitTargetType'], axis=1), binary_type], axis=1)"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"immunity = X.SpellImmunityType\n",
"immunity = immunity.fillna(value='SPELL_IMMUNITY_NONE')\n",
"immunity = immunity.str.split('|').apply(lambda x: [y.strip() for y in x])\n",
"\n",
"mlb = MultiLabelBinarizer().fit(immunity)\n",
"binary_immunity = pd.DataFrame(mlb.transform(immunity), \n",
" columns=mlb.classes_)\n",
"\n",
"X = pd.concat([X.drop(['SpellDispellableType'], axis=1), \n",
" binary_immunity], axis=1)"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"dispel = X.SpellImmunityType\n",
"dispel = dispel.fillna(value='DOTA_UNIT_TARGET_NONE')\n",
"dispel = dispel.str.split('|').apply(lambda x: [y.strip() for y in x])\n",
"\n",
"mlb = MultiLabelBinarizer().fit(dispel)\n",
"binary_dispel = pd.DataFrame(mlb.transform(dispel), \n",
" columns=mlb.classes_)\n",
"\n",
"X = pd.concat([X.drop(['SpellImmunityType'], axis=1), \n",
" binary_dispel], axis=1)"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"X['AbilityType'] = X['AbilityType'].apply(\n",
" lambda x: 1 if x == 'DOTA_ABILITY_TYPE_ULTIMATE' else 0)\n",
"\n",
"X['isUltimate'] = X['AbilityType']\n",
"X = X.drop(['AbilityType'], axis=1)"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"X['AbilityUnitDamageType'] = X['AbilityUnitDamageType'].apply(\n",
" lambda x: 'DAMAGE_TYPE_NONE' if x is np.NaN else x)\n",
"\n",
"lb = LabelBinarizer().fit(X['AbilityUnitDamageType'])\n",
"dmg_type = pd.DataFrame(lb.transform(X['AbilityUnitDamageType']),\n",
" columns=lb.classes_)\n",
"\n",
"X = pd.concat([X.drop(['AbilityUnitDamageType'], axis=1), dmg_type], axis=1)"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"X['MaxLevel'] = X['MaxLevel'].fillna(value=3)\n",
"X = X.fillna(value=0)"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"{'0': ['mana_break',\n",
" 'spell_shield',\n",
" 'culling_blade',\n",
" 'thirst',\n",
" 'trueshot',\n",
" 'enchant_totem',\n",
" 'aftershock',\n",
" 'blade_dance',\n",
" 'tidebringer',\n",
" 'fiery_soul',\n",
" 'invis',\n",
" 'morph',\n",
" 'morph_agi',\n",
" 'morph_str',\n",
" 'morph_replicate',\n",
" 'necromastery',\n",
" 'juxtapose',\n",
" 'phantom_edge',\n",
" 'ethereal_jaunt',\n",
" 'phase_shift',\n",
" 'dismember',\n",
" 'unstable_current',\n",
" 'mortal_strike',\n",
" 'great_cleave',\n",
" 'gods_strength',\n",
" 'electric_vortex',\n",
" 'overload',\n",
" 'craggy_exterior',\n",
" 'grow',\n",
" 'thundergods_wrath',\n",
" 'sprint',\n",
" 'bash',\n",
" 'kraken_shell',\n",
" 'brilliance_aura',\n",
" 'permanent_invisibility',\n",
" 'black_hole',\n",
" 'rearm',\n",
" 'headshot',\n",
" 'take_aim',\n",
" 'sadist',\n",
" 'golem_permanent_immolation',\n",
" 'call_of_the_wild',\n",
" 'hawk_invisibility',\n",
" 'boar_poison',\n",
" 'poison_sting',\n",
" 'time_lock',\n",
" 'coup_de_grace',\n",
" 'refraction',\n",
" 'meld',\n",
" 'psi_blades',\n",
" 'nethertoxin',\n",
" 'corrosive_skin',\n",
" 'dragon_blood',\n",
" 'elder_dragon_form',\n",
" 'frost_breath',\n",
" 'teleportation',\n",
" 'wrath_of_nature',\n",
" 'rage',\n",
" 'feast',\n",
" 'consume',\n",
" 'strafe',\n",
" 'wind_walk',\n",
" 'untouchable',\n",
" 'berserkers_blood',\n",
" 'hunter_in_the_night',\n",
" 'darkness',\n",
" 'incapacitating_bite',\n",
" 'insatiable_hunger',\n",
" 'spawn_spiderite',\n",
" 'poison_sting',\n",
" 'jinada',\n",
" 'wind_walk',\n",
" 'geminate_attack',\n",
" 'flaming_lasso',\n",
" 'hand_of_god',\n",
" 'haunt',\n",
" 'reality',\n",
" 'devour',\n",
" 'infernal_blade',\n",
" 'greater_boar_poison',\n",
" 'charge_of_darkness',\n",
" 'greater_bash',\n",
" 'overpower',\n",
" 'fury_swipes',\n",
" 'enrage',\n",
" 'goblins_greed',\n",
" 'chemical_rage',\n",
" 'quas',\n",
" 'wex',\n",
" 'exort',\n",
" 'invoke',\n",
" 'global_silence',\n",
" 'forge_spirit',\n",
" 'ice_wall',\n",
" 'summon_wolves',\n",
" 'howl',\n",
" 'summon_wolves_critical_strike',\n",
" 'drunken_brawler',\n",
" 'primal_split',\n",
" 'earth_spell_immunity',\n",
" 'earth_pulverize',\n",
" 'storm_wind_walk',\n",
" 'rabid',\n",
" 'true_form',\n",
" 'true_form_druid',\n",
" 'spirit_bear_entangle',\n",
" 'spirit_bear_demolish',\n",
" 'chaos_strike',\n",
" 'geostrike',\n",
" 'divided_we_stand',\n",
" 'living_armor',\n",
" 'multicast',\n",
" 'spiked_carapace',\n",
" 'mirror_image',\n",
" 'spirit_form',\n",
" 'recall',\n",
" 'summon_familiars',\n",
" 'summon_familiars_stone_form',\n",
" 'overcharge',\n",
" 'relocate',\n",
" 'tether_break',\n",
" 'spirits_in',\n",
" 'spirits_out',\n",
" 'essence_shift',\n",
" 'shadow_dance',\n",
" 'summon_wolves_invisibility',\n",
" 'mana_shield',\n",
" 'berserkers_rage',\n",
" 'fervor',\n",
" 'battle_trance',\n",
" 'stampede',\n",
" 'reactive_armor',\n",
" 'bristleback',\n",
" 'warpath',\n",
" 'walrus_punch',\n",
" 'call_of_the_wild_boar',\n",
" 'frostmourne',\n",
" 'borrowed_time',\n",
" 'moment_of_courage',\n",
" 'duel',\n",
" 'stasis_trap',\n",
" 'magnetize',\n",
" 'conjure_image',\n",
" 'metamorphosis',\n",
" 'icarus_dive',\n",
" 'sun_ray_toggle_move',\n",
" 'launch_snowball',\n",
" 'spin_web_destroy',\n",
" 'minefield_sign',\n",
" 'petrify',\n",
" 'arctic_burn',\n",
" 'control',\n",
" 'walrus_kick',\n",
" 'tempest_double',\n",
" 'attribute_bonus',\n",
" 'mischief',\n",
" 'untransform',\n",
" 'jingu_mastery',\n",
" 'primal_spring',\n",
" 'primal_spring_early'],\n",
" '1': ['activate_fire_remnant'],\n",
" '10': ['rolling_boulder'],\n",
" '11': ['leap', 'rocket_flare', 'ice_blast'],\n",
" '12': ['adaptive_strike',\n",
" 'shackleshot',\n",
" 'shadow_strike',\n",
" 'scream_of_pain',\n",
" 'viper_strike',\n",
" 'dragon_tail',\n",
" 'poison_touch',\n",
" 'spawn_spiderlings',\n",
" 'ignite',\n",
" 'spell_steal',\n",
" 'ensnare',\n",
" 'split_shot'],\n",
" '13': ['wild_axes', 'sun_ray'],\n",
" '14': ['spirit_bear'],\n",
" '15': ['ghostship', 'dragon_slave', 'meat_hook', 'sonic_wave'],\n",
" '16': ['arrow', 'the_swarm'],\n",
" '17': ['wave_of_terror', 'time_walk', 'penitence', 'timber_chain'],\n",
" '18': ['ball_lightning', 'whirling_axes_melee'],\n",
" '19': ['powershot', 'assassinate'],\n",
" '2': ['mana_void',\n",
" 'battle_hunger',\n",
" 'brain_sap',\n",
" 'nightmare',\n",
" 'frost_arrows',\n",
" 'echo_slam',\n",
" 'x_marks_the_spot',\n",
" 'light_strike_array',\n",
" 'voodoo',\n",
" 'doppelwalk',\n",
" 'flesh_heap',\n",
" 'ether_shock',\n",
" 'voodoo',\n",
" 'shackles',\n",
" 'mass_serpent_ward',\n",
" 'lightning_bolt',\n",
" 'amplify_damage',\n",
" 'frostbite',\n",
" 'focusfire',\n",
" 'frost_nova',\n",
" 'dark_ritual',\n",
" 'maledict',\n",
" 'death_ward',\n",
" 'malefice',\n",
" 'demonic_conversion',\n",
" 'laser',\n",
" 'reapers_scythe',\n",
" 'shadow_word',\n",
" 'primal_roar',\n",
" 'decrepify',\n",
" 'poison_attack',\n",
" 'moon_glaive',\n",
" 'shallow_grave',\n",
" 'split_earth',\n",
" 'sprout',\n",
" 'force_of_nature',\n",
" 'open_wounds',\n",
" 'surge',\n",
" 'searing_arrows',\n",
" 'death_pact',\n",
" 'repel',\n",
" 'enchant',\n",
" 'impetus',\n",
" 'burning_spear',\n",
" 'life_break',\n",
" 'void',\n",
" 'crippling_fear',\n",
" 'test_of_faith',\n",
" 'doom',\n",
" 'nether_strike',\n",
" 'unstable_concoction',\n",
" 'glaives_of_wisdom',\n",
" 'alacrity',\n",
" 'arcane_orb',\n",
" 'storm_cyclone',\n",
" 'disruption',\n",
" 'reality_rift',\n",
" 'fireblast',\n",
" 'bloodlust',\n",
" 'mana_burn',\n",
" 'unrefined_fireblast',\n",
" 'mana_leak',\n",
" 'grave_chill',\n",
" 'spirits',\n",
" 'reverse_polarity',\n",
" 'test_of_faith_teleport',\n",
" 'ancient_seal',\n",
" 'sunder',\n",
" 'fates_edict',\n",
" 'flux',\n",
" 'spirit_siphon',\n",
" 'wukongs_command'],\n",
" '20': ['berserkers_call',\n",
" 'counter_helix',\n",
" 'blade_fury',\n",
" 'shadowraze1',\n",
" 'waning_rift',\n",
" 'rot',\n",
" 'eye_of_the_storm',\n",
" 'static_remnant',\n",
" 'slithereen_crush',\n",
" 'windrun',\n",
" 'voodoo_restoration',\n",
" 'death_pulse',\n",
" 'golem_flaming_fists',\n",
" 'trap',\n",
" 'battery_assault',\n",
" 'power_cogs',\n",
" 'diabolic_edict',\n",
" 'pulse_nova',\n",
" 'guardian_angel',\n",
" 'shukuchi',\n",
" 'firefly',\n",
" 'desolate',\n",
" 'earthshock',\n",
" 'rocket_barrage',\n",
" 'ghost_walk',\n",
" 'sun_strike',\n",
" 'thunder_clap',\n",
" 'fire_permanent_immolation',\n",
" 'savage_roar',\n",
" 'poof',\n",
" 'natures_guise',\n",
" 'telekinesis_land',\n",
" 'rip_tide',\n",
" 'hoof_stomp',\n",
" 'double_edge',\n",
" 'frozen_sigil',\n",
" 'natural_order',\n",
" 'land_mines',\n",
" 'dark_rift',\n",
" 'savage_roar_bear',\n",
" 'natural_order_spirit',\n",
" 'cloud'],\n",
" '21': ['exorcism'],\n",
" '22': ['illusory_orb'],\n",
" '23': ['plasma_field', 'static_link', 'shapeshift', 'pounce', 'boulder_smash'],\n",
" '24': ['fatal_bonds', 'upheaval', 'rain_of_chaos'],\n",
" '25': ['heat_seeking_missile'],\n",
" '26': ['illuminate', 'spirit_form_illuminate'],\n",
" '27': ['healing_ward',\n",
" 'reincarnation',\n",
" 'track',\n",
" 'empowering_haste',\n",
" 'empower',\n",
" 'supernova'],\n",
" '28': ['static_field',\n",
" 'command_aura',\n",
" 'spin_web',\n",
" 'soul_rip',\n",
" 'tombstone',\n",
" 'song_of_the_siren',\n",
" 'stone_gaze',\n",
" 'atrophy_aura'],\n",
" '29': ['blink',\n",
" 'enfeeble',\n",
" 'bloodrage',\n",
" 'rupture',\n",
" 'replicate',\n",
" 'dark_lord',\n",
" 'nether_swap',\n",
" 'frost_armor',\n",
" 'blink_strike',\n",
" 'tricks_of_the_trade',\n",
" 'blink',\n",
" 'plague_ward',\n",
" 'life_drain',\n",
" 'phantom_strike',\n",
" 'lucent_beam',\n",
" 'shadow_wave',\n",
" 'wall_of_replica',\n",
" 'inner_vitality',\n",
" 'time_lapse',\n",
" 'ice_path',\n",
" 'holy_persuasion',\n",
" 'cold_snap',\n",
" 'last_word',\n",
" 'deafening_blast',\n",
" 'drunken_haze',\n",
" 'true_form_battle_cry',\n",
" 'demonic_purge',\n",
" 'phantasm',\n",
" 'glimpse',\n",
" 'chakra_magic',\n",
" 'arcane_bolt',\n",
" 'press_the_attack',\n",
" 'stone_caller',\n",
" 'reflection',\n",
" 'purifying_flames',\n",
" 'splinter_blast',\n",
" 'cold_embrace',\n",
" 'boundless_strike',\n",
" 'tree_dance'],\n",
" '3': ['flamebreak',\n",
" 'shadow_poison',\n",
" 'earthbind',\n",
" 'shockwave',\n",
" 'skewer',\n",
" 'snowball',\n",
" 'ancestral_spirit',\n",
" 'geomagnetic_grip',\n",
" 'fire_spirits',\n",
" 'launch_fire_spirit'],\n",
" '30': ['soul_assumption'],\n",
" '31': ['impale',\n",
" 'waveform',\n",
" 'spirit_lance',\n",
" 'hellfire_blast',\n",
" 'storm_bolt',\n",
" 'magic_missile',\n",
" 'paralyzing_cask',\n",
" 'venomous_gale',\n",
" 'stifling_dagger',\n",
" 'shuriken_toss',\n",
" 'earth_hurl_boulder',\n",
" 'chaos_bolt',\n",
" 'impale',\n",
" 'whirling_axes_ranged',\n",
" 'viscous_nasal_goo'],\n",
" '32': ['march_of_the_machines'],\n",
" '33': ['homing_missile'],\n",
" '34': ['spectral_dagger',\n",
" 'ice_shards',\n",
" 'concussive_shot',\n",
" 'earth_splitter',\n",
" 'spark_wraith'],\n",
" '35': ['carrion_swarm', 'breathe_fire', 'dual_breath'],\n",
" '36': ['laguna_blade',\n",
" 'finger_of_death',\n",
" 'storm_dispel_magic',\n",
" 'mystic_flare'],\n",
" '37': ['mana_drain', 'cold_feet'],\n",
" '38': ['marksmanship',\n",
" 'omni_slash',\n",
" 'shadowraze2',\n",
" 'avalanche',\n",
" 'anchor_smash',\n",
" 'smoke_screen',\n",
" 'chronosphere',\n",
" 'nether_blast',\n",
" 'vacuum',\n",
" 'ion_shell',\n",
" 'purification',\n",
" 'degen_aura',\n",
" 'liquid_fire',\n",
" 'scorched_earth',\n",
" 'astral_imprisonment',\n",
" 'soul_catcher',\n",
" 'leech_seed',\n",
" 'decay',\n",
" 'telekinesis',\n",
" 'dark_pact',\n",
" 'whirling_death',\n",
" 'aphotic_shield',\n",
" 'echo_stomp',\n",
" 'echo_stomp_spirit',\n",
" 'remote_mines',\n",
" 'searing_chains',\n",
" 'flame_guard'],\n",
" '39': ['chain_frost'],\n",
" '4': ['gush', 'quill_spray', 'death_coil'],\n",
" '5': ['starfall',\n",
" 'requiem',\n",
" 'vampiric_aura',\n",
" 'warcry',\n",
" 'ravage',\n",
" 'freezing_field',\n",
" 'inner_beast',\n",
" 'poison_nova',\n",
" 'nether_ward',\n",
" 'blur',\n",
" 'lunar_blessing',\n",
" 'eclipse',\n",
" 'infest',\n",
" 'dispersion',\n",
" 'flak_cannon',\n",
" 'essence_aura',\n",
" 'feral_impulse',\n",
" 'overgrowth',\n",
" 'tombstone_zombie_aura',\n",
" 'tombstone_zombie_deathstrike',\n",
" 'flesh_golem',\n",
" 'null_field',\n",
" 'gravekeepers_cloak',\n",
" 'focused_detonate',\n",
" 'assimilate',\n",
" 'assimilate_eject',\n",
" 'time_dilation'],\n",
" '6': ['blood_bath',\n",
" 'fissure',\n",
" 'torrent',\n",
" 'toss',\n",
" 'shrapnel',\n",
" 'psionic_trap',\n",
" 'weave',\n",
" 'macropyre',\n",
" 'ice_vortex',\n",
" 'tornado',\n",
" 'tether'],\n",
" '7': ['silence',\n",
" 'shadowraze3',\n",
" 'dream_coil',\n",
" 'silence',\n",
" 'arc_lightning',\n",
" 'crystal_nova',\n",
" 'midnight_pulse',\n",
" 'lightning_storm',\n",
" 'sticky_napalm',\n",
" 'chilling_touch',\n",
" 'call_down',\n",
" 'acid_spray',\n",
" 'curse_of_the_silent',\n",
" 'emp',\n",
" 'chaos_meteor',\n",
" 'sanity_eclipse',\n",
" 'fade_bolt',\n",
" 'thunder_strike',\n",
" 'kinetic_field',\n",
" 'static_storm',\n",
" 'blinding_light',\n",
" 'mystic_snake',\n",
" 'overwhelming_odds',\n",
" 'suicide',\n",
" 'sleight_of_fist',\n",
" 'firestorm',\n",
" 'pit_of_malice',\n",
" 'false_promise',\n",
" 'winters_curse',\n",
" 'magnetic_field',\n",
" 'mind_over_matter'],\n",
" '8': ['hookshot'],\n",
" '9': ['chakram', 'chakram_2']}\n"
]
}
],
"source": [
"km = KMeans(n_clusters=40, tol=1e-6)\n",
"km.fit(X.drop(['name'], axis=1))\n",
"\n",
"ability_by_label = dict()\n",
"for name, label in zip(X['name'], km.labels_):\n",
" ability_by_label.setdefault(str(label), [])\n",
" ability_by_label[str(label)].append(name)\n",
"\n",
"pprint(ability_by_label)"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"97\n"
]
}
],
"source": [
"print(len(list(specs.columns)))"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"{'0': ['mana_break',\n",
" 'spell_shield',\n",
" 'culling_blade',\n",
" 'thirst',\n",
" 'trueshot',\n",
" 'enchant_totem',\n",
" 'aftershock',\n",
" 'blade_dance',\n",
" 'tidebringer',\n",
" 'fiery_soul',\n",
" 'invis',\n",
" 'morph',\n",
" 'morph_agi',\n",
" 'morph_str',\n",
" 'morph_replicate',\n",
" 'necromastery',\n",
" 'juxtapose',\n",
" 'phantom_edge',\n",
" 'ethereal_jaunt',\n",
" 'phase_shift',\n",
" 'dismember',\n",
" 'unstable_current',\n",
" 'mortal_strike',\n",
" 'great_cleave',\n",
" 'gods_strength',\n",
" 'electric_vortex',\n",
" 'overload',\n",
" 'craggy_exterior',\n",
" 'grow',\n",
" 'thundergods_wrath',\n",
" 'sprint',\n",
" 'bash',\n",
" 'kraken_shell',\n",
" 'brilliance_aura',\n",
" 'permanent_invisibility',\n",
" 'black_hole',\n",
" 'rearm',\n",
" 'headshot',\n",
" 'take_aim',\n",
" 'sadist',\n",
" 'golem_permanent_immolation',\n",
" 'call_of_the_wild',\n",
" 'hawk_invisibility',\n",
" 'boar_poison',\n",
" 'poison_sting',\n",
" 'time_lock',\n",
" 'coup_de_grace',\n",
" 'refraction',\n",
" 'meld',\n",
" 'psi_blades',\n",
" 'nethertoxin',\n",
" 'corrosive_skin',\n",
" 'dragon_blood',\n",
" 'elder_dragon_form',\n",
" 'frost_breath',\n",
" 'teleportation',\n",
" 'wrath_of_nature',\n",
" 'rage',\n",
" 'feast',\n",
" 'consume',\n",
" 'strafe',\n",
" 'wind_walk',\n",
" 'untouchable',\n",
" 'berserkers_blood',\n",
" 'hunter_in_the_night',\n",
" 'darkness',\n",
" 'incapacitating_bite',\n",
" 'insatiable_hunger',\n",
" 'spawn_spiderite',\n",
" 'poison_sting',\n",
" 'jinada',\n",
" 'wind_walk',\n",
" 'geminate_attack',\n",
" 'flaming_lasso',\n",
" 'hand_of_god',\n",
" 'haunt',\n",
" 'reality',\n",
" 'devour',\n",
" 'infernal_blade',\n",
" 'greater_boar_poison',\n",
" 'charge_of_darkness',\n",
" 'greater_bash',\n",
" 'overpower',\n",
" 'fury_swipes',\n",
" 'enrage',\n",
" 'goblins_greed',\n",
" 'chemical_rage',\n",
" 'quas',\n",
" 'wex',\n",
" 'exort',\n",
" 'invoke',\n",
" 'global_silence',\n",
" 'forge_spirit',\n",
" 'ice_wall',\n",
" 'summon_wolves',\n",
" 'howl',\n",
" 'summon_wolves_critical_strike',\n",
" 'drunken_brawler',\n",
" 'primal_split',\n",
" 'earth_spell_immunity',\n",
" 'earth_pulverize',\n",
" 'storm_wind_walk',\n",
" 'rabid',\n",
" 'true_form',\n",
" 'true_form_druid',\n",
" 'spirit_bear_entangle',\n",
" 'spirit_bear_demolish',\n",
" 'chaos_strike',\n",
" 'geostrike',\n",
" 'divided_we_stand',\n",
" 'living_armor',\n",
" 'multicast',\n",
" 'spiked_carapace',\n",
" 'mirror_image',\n",
" 'spirit_form',\n",
" 'recall',\n",
" 'summon_familiars',\n",
" 'summon_familiars_stone_form',\n",
" 'overcharge',\n",
" 'relocate',\n",
" 'tether_break',\n",
" 'spirits_in',\n",
" 'spirits_out',\n",
" 'essence_shift',\n",
" 'shadow_dance',\n",
" 'summon_wolves_invisibility',\n",
" 'mana_shield',\n",
" 'berserkers_rage',\n",
" 'fervor',\n",
" 'battle_trance',\n",
" 'stampede',\n",
" 'reactive_armor',\n",
" 'bristleback',\n",
" 'warpath',\n",
" 'walrus_punch',\n",
" 'call_of_the_wild_boar',\n",
" 'frostmourne',\n",
" 'borrowed_time',\n",
" 'moment_of_courage',\n",
" 'duel',\n",
" 'stasis_trap',\n",
" 'magnetize',\n",
" 'conjure_image',\n",
" 'metamorphosis',\n",
" 'icarus_dive',\n",
" 'sun_ray_toggle_move',\n",
" 'launch_snowball',\n",
" 'spin_web_destroy',\n",
" 'minefield_sign',\n",
" 'petrify',\n",
" 'arctic_burn',\n",
" 'control',\n",
" 'walrus_kick',\n",
" 'tempest_double',\n",
" 'attribute_bonus',\n",
" 'mischief',\n",
" 'untransform',\n",
" 'jingu_mastery',\n",
" 'primal_spring',\n",
" 'primal_spring_early'],\n",
" '1': ['activate_fire_remnant'],\n",
" '10': ['rolling_boulder'],\n",
" '11': ['leap', 'rocket_flare', 'ice_blast'],\n",
" '12': ['adaptive_strike',\n",
" 'shackleshot',\n",
" 'shadow_strike',\n",
" 'scream_of_pain',\n",
" 'viper_strike',\n",
" 'dragon_tail',\n",
" 'poison_touch',\n",
" 'spawn_spiderlings',\n",
" 'ignite',\n",
" 'spell_steal',\n",
" 'ensnare',\n",
" 'split_shot'],\n",
" '13': ['wild_axes', 'sun_ray'],\n",
" '14': ['spirit_bear'],\n",
" '15': ['ghostship', 'dragon_slave', 'meat_hook', 'sonic_wave'],\n",
" '16': ['arrow', 'the_swarm'],\n",
" '17': ['wave_of_terror', 'time_walk', 'penitence', 'timber_chain'],\n",
" '18': ['ball_lightning', 'whirling_axes_melee'],\n",
" '19': ['powershot', 'assassinate'],\n",
" '2': ['mana_void',\n",
" 'battle_hunger',\n",
" 'brain_sap',\n",
" 'nightmare',\n",
" 'frost_arrows',\n",
" 'echo_slam',\n",
" 'x_marks_the_spot',\n",
" 'light_strike_array',\n",
" 'voodoo',\n",
" 'doppelwalk',\n",
" 'flesh_heap',\n",
" 'ether_shock',\n",
" 'voodoo',\n",
" 'shackles',\n",
" 'mass_serpent_ward',\n",
" 'lightning_bolt',\n",
" 'amplify_damage',\n",
" 'frostbite',\n",
" 'focusfire',\n",
" 'frost_nova',\n",
" 'dark_ritual',\n",
" 'maledict',\n",
" 'death_ward',\n",
" 'malefice',\n",
" 'demonic_conversion',\n",
" 'laser',\n",
" 'reapers_scythe',\n",
" 'shadow_word',\n",
" 'primal_roar',\n",
" 'decrepify',\n",
" 'poison_attack',\n",
" 'moon_glaive',\n",
" 'shallow_grave',\n",
" 'split_earth',\n",
" 'sprout',\n",
" 'force_of_nature',\n",
" 'open_wounds',\n",
" 'surge',\n",
" 'searing_arrows',\n",
" 'death_pact',\n",
" 'repel',\n",
" 'enchant',\n",
" 'impetus',\n",
" 'burning_spear',\n",
" 'life_break',\n",
" 'void',\n",
" 'crippling_fear',\n",
" 'test_of_faith',\n",
" 'doom',\n",
" 'nether_strike',\n",
" 'unstable_concoction',\n",
" 'glaives_of_wisdom',\n",
" 'alacrity',\n",
" 'arcane_orb',\n",
" 'storm_cyclone',\n",
" 'disruption',\n",
" 'reality_rift',\n",
" 'fireblast',\n",
" 'bloodlust',\n",
" 'mana_burn',\n",
" 'unrefined_fireblast',\n",
" 'mana_leak',\n",
" 'grave_chill',\n",
" 'spirits',\n",
" 'reverse_polarity',\n",
" 'test_of_faith_teleport',\n",
" 'ancient_seal',\n",
" 'sunder',\n",
" 'fates_edict',\n",
" 'flux',\n",
" 'spirit_siphon',\n",
" 'wukongs_command'],\n",
" '20': ['berserkers_call',\n",
" 'counter_helix',\n",
" 'blade_fury',\n",
" 'shadowraze1',\n",
" 'waning_rift',\n",
" 'rot',\n",
" 'eye_of_the_storm',\n",
" 'static_remnant',\n",
" 'slithereen_crush',\n",
" 'windrun',\n",
" 'voodoo_restoration',\n",
" 'death_pulse',\n",
" 'golem_flaming_fists',\n",
" 'trap',\n",
" 'battery_assault',\n",
" 'power_cogs',\n",
" 'diabolic_edict',\n",
" 'pulse_nova',\n",
" 'guardian_angel',\n",
" 'shukuchi',\n",
" 'firefly',\n",
" 'desolate',\n",
" 'earthshock',\n",
" 'rocket_barrage',\n",
" 'ghost_walk',\n",
" 'sun_strike',\n",
" 'thunder_clap',\n",
" 'fire_permanent_immolation',\n",
" 'savage_roar',\n",
" 'poof',\n",
" 'natures_guise',\n",
" 'telekinesis_land',\n",
" 'rip_tide',\n",
" 'hoof_stomp',\n",
" 'double_edge',\n",
" 'frozen_sigil',\n",
" 'natural_order',\n",
" 'land_mines',\n",
" 'dark_rift',\n",
" 'savage_roar_bear',\n",
" 'natural_order_spirit',\n",
" 'cloud'],\n",
" '21': ['exorcism'],\n",
" '22': ['illusory_orb'],\n",
" '23': ['plasma_field', 'static_link', 'shapeshift', 'pounce', 'boulder_smash'],\n",
" '24': ['fatal_bonds', 'upheaval', 'rain_of_chaos'],\n",
" '25': ['heat_seeking_missile'],\n",
" '26': ['illuminate', 'spirit_form_illuminate'],\n",
" '27': ['healing_ward',\n",
" 'reincarnation',\n",
" 'track',\n",
" 'empowering_haste',\n",
" 'empower',\n",
" 'supernova'],\n",
" '28': ['static_field',\n",
" 'command_aura',\n",
" 'spin_web',\n",
" 'soul_rip',\n",
" 'tombstone',\n",
" 'song_of_the_siren',\n",
" 'stone_gaze',\n",
" 'atrophy_aura'],\n",
" '29': ['blink',\n",
" 'enfeeble',\n",
" 'bloodrage',\n",
" 'rupture',\n",
" 'replicate',\n",
" 'dark_lord',\n",
" 'nether_swap',\n",
" 'frost_armor',\n",
" 'blink_strike',\n",
" 'tricks_of_the_trade',\n",
" 'blink',\n",
" 'plague_ward',\n",
" 'life_drain',\n",
" 'phantom_strike',\n",
" 'lucent_beam',\n",
" 'shadow_wave',\n",
" 'wall_of_replica',\n",
" 'inner_vitality',\n",
" 'time_lapse',\n",
" 'ice_path',\n",
" 'holy_persuasion',\n",
" 'cold_snap',\n",
" 'last_word',\n",
" 'deafening_blast',\n",
" 'drunken_haze',\n",
" 'true_form_battle_cry',\n",
" 'demonic_purge',\n",
" 'phantasm',\n",
" 'glimpse',\n",
" 'chakra_magic',\n",
" 'arcane_bolt',\n",
" 'press_the_attack',\n",
" 'stone_caller',\n",
" 'reflection',\n",
" 'purifying_flames',\n",
" 'splinter_blast',\n",
" 'cold_embrace',\n",
" 'boundless_strike',\n",
" 'tree_dance'],\n",
" '3': ['flamebreak',\n",
" 'shadow_poison',\n",
" 'earthbind',\n",
" 'shockwave',\n",
" 'skewer',\n",
" 'snowball',\n",
" 'ancestral_spirit',\n",
" 'geomagnetic_grip',\n",
" 'fire_spirits',\n",
" 'launch_fire_spirit'],\n",
" '30': ['soul_assumption'],\n",
" '31': ['impale',\n",
" 'waveform',\n",
" 'spirit_lance',\n",
" 'hellfire_blast',\n",
" 'storm_bolt',\n",
" 'magic_missile',\n",
" 'paralyzing_cask',\n",
" 'venomous_gale',\n",
" 'stifling_dagger',\n",
" 'shuriken_toss',\n",
" 'earth_hurl_boulder',\n",
" 'chaos_bolt',\n",
" 'impale',\n",
" 'whirling_axes_ranged',\n",
" 'viscous_nasal_goo'],\n",
" '32': ['march_of_the_machines'],\n",
" '33': ['homing_missile'],\n",
" '34': ['spectral_dagger',\n",
" 'ice_shards',\n",
" 'concussive_shot',\n",
" 'earth_splitter',\n",
" 'spark_wraith'],\n",
" '35': ['carrion_swarm', 'breathe_fire', 'dual_breath'],\n",
" '36': ['laguna_blade',\n",
" 'finger_of_death',\n",
" 'storm_dispel_magic',\n",
" 'mystic_flare'],\n",
" '37': ['mana_drain', 'cold_feet'],\n",
" '38': ['marksmanship',\n",
" 'omni_slash',\n",
" 'shadowraze2',\n",
" 'avalanche',\n",
" 'anchor_smash',\n",
" 'smoke_screen',\n",
" 'chronosphere',\n",
" 'nether_blast',\n",
" 'vacuum',\n",
" 'ion_shell',\n",
" 'purification',\n",
" 'degen_aura',\n",
" 'liquid_fire',\n",
" 'scorched_earth',\n",
" 'astral_imprisonment',\n",
" 'soul_catcher',\n",
" 'leech_seed',\n",
" 'decay',\n",
" 'telekinesis',\n",
" 'dark_pact',\n",
" 'whirling_death',\n",
" 'aphotic_shield',\n",
" 'echo_stomp',\n",
" 'echo_stomp_spirit',\n",
" 'remote_mines',\n",
" 'searing_chains',\n",
" 'flame_guard'],\n",
" '39': ['chain_frost'],\n",
" '4': ['gush', 'quill_spray', 'death_coil'],\n",
" '5': ['starfall',\n",
" 'requiem',\n",
" 'vampiric_aura',\n",
" 'warcry',\n",
" 'ravage',\n",
" 'freezing_field',\n",
" 'inner_beast',\n",
" 'poison_nova',\n",
" 'nether_ward',\n",
" 'blur',\n",
" 'lunar_blessing',\n",
" 'eclipse',\n",
" 'infest',\n",
" 'dispersion',\n",
" 'flak_cannon',\n",
" 'essence_aura',\n",
" 'feral_impulse',\n",
" 'overgrowth',\n",
" 'tombstone_zombie_aura',\n",
" 'tombstone_zombie_deathstrike',\n",
" 'flesh_golem',\n",
" 'null_field',\n",
" 'gravekeepers_cloak',\n",
" 'focused_detonate',\n",
" 'assimilate',\n",
" 'assimilate_eject',\n",
" 'time_dilation'],\n",
" '6': ['blood_bath',\n",
" 'fissure',\n",
" 'torrent',\n",
" 'toss',\n",
" 'shrapnel',\n",
" 'psionic_trap',\n",
" 'weave',\n",
" 'macropyre',\n",
" 'ice_vortex',\n",
" 'tornado',\n",
" 'tether'],\n",
" '7': ['silence',\n",
" 'shadowraze3',\n",
" 'dream_coil',\n",
" 'silence',\n",
" 'arc_lightning',\n",
" 'crystal_nova',\n",
" 'midnight_pulse',\n",
" 'lightning_storm',\n",
" 'sticky_napalm',\n",
" 'chilling_touch',\n",
" 'call_down',\n",
" 'acid_spray',\n",
" 'curse_of_the_silent',\n",
" 'emp',\n",
" 'chaos_meteor',\n",
" 'sanity_eclipse',\n",
" 'fade_bolt',\n",
" 'thunder_strike',\n",
" 'kinetic_field',\n",
" 'static_storm',\n",
" 'blinding_light',\n",
" 'mystic_snake',\n",
" 'overwhelming_odds',\n",
" 'suicide',\n",
" 'sleight_of_fist',\n",
" 'firestorm',\n",
" 'pit_of_malice',\n",
" 'false_promise',\n",
" 'winters_curse',\n",
" 'magnetic_field',\n",
" 'mind_over_matter'],\n",
" '8': ['hookshot'],\n",
" '9': ['chakram', 'chakram_2']}\n"
]
}
],
"source": [
"dbscan = DBSCAN(eps=.2, min_samples=3, metric='cityblock')\n",
"dbscan.fit(X.drop(['name'], axis=1))\n",
"\n",
"ability_by_label = dict()\n",
"for name, label in zip(X['name'], km.labels_):\n",
" ability_by_label.setdefault(str(label), [])\n",
" ability_by_label[str(label)].append(name)\n",
" \n",
"pprint(ability_by_label)"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>AbilityBehavior</th>\n",
" <th>AbilityCastPoint</th>\n",
" <th>AbilityCastRange</th>\n",
" <th>AbilityCooldown</th>\n",
" <th>AbilityDamage</th>\n",
" <th>AbilityDuration</th>\n",
" <th>AbilityManaCost</th>\n",
" <th>FightRecapLevel</th>\n",
" <th>SpellDispellableType</th>\n",
" <th>SpellImmunityType</th>\n",
" <th>duration</th>\n",
" <th>name</th>\n",
" <th>radius</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>16</th>\n",
" <td>DOTA_ABILITY_BEHAVIOR_AOE | DOTA_ABILITY_BEHAV...</td>\n",
" <td>0.4</td>\n",
" <td>900.0</td>\n",
" <td>14.5</td>\n",
" <td>0.0</td>\n",
" <td>4.5</td>\n",
" <td>90.0</td>\n",
" <td>1.0</td>\n",
" <td>SPELL_DISPELLABLE_YES</td>\n",
" <td>SPELL_IMMUNITY_ENEMIES_NO</td>\n",
" <td>4.5</td>\n",
" <td>silence</td>\n",
" <td>300.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>82</th>\n",
" <td>DOTA_ABILITY_BEHAVIOR_AOE | DOTA_ABILITY_BEHAV...</td>\n",
" <td>0.5</td>\n",
" <td>900.0</td>\n",
" <td>13.5</td>\n",
" <td>NaN</td>\n",
" <td>4.5</td>\n",
" <td>80.0</td>\n",
" <td>NaN</td>\n",
" <td>SPELL_DISPELLABLE_YES</td>\n",
" <td>SPELL_IMMUNITY_ENEMIES_NO</td>\n",
" <td>4.5</td>\n",
" <td>silence</td>\n",
" <td>425.0</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" AbilityBehavior AbilityCastPoint \\\n",
"16 DOTA_ABILITY_BEHAVIOR_AOE | DOTA_ABILITY_BEHAV... 0.4 \n",
"82 DOTA_ABILITY_BEHAVIOR_AOE | DOTA_ABILITY_BEHAV... 0.5 \n",
"\n",
" AbilityCastRange AbilityCooldown AbilityDamage AbilityDuration \\\n",
"16 900.0 14.5 0.0 4.5 \n",
"82 900.0 13.5 NaN 4.5 \n",
"\n",
" AbilityManaCost FightRecapLevel SpellDispellableType \\\n",
"16 90.0 1.0 SPELL_DISPELLABLE_YES \n",
"82 80.0 NaN SPELL_DISPELLABLE_YES \n",
"\n",
" SpellImmunityType duration name radius \n",
"16 SPELL_IMMUNITY_ENEMIES_NO 4.5 silence 300.0 \n",
"82 SPELL_IMMUNITY_ENEMIES_NO 4.5 silence 425.0 "
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"a = specs[specs['name'] == 'silence'].dropna(axis=1, how='all')\n",
"a.head()"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"count 228.000000\n",
"mean 17.807346\n",
"std 46.467843\n",
"min 0.500000\n",
"25% 4.000000\n",
"50% 6.500000\n",
"75% 15.000000\n",
"max 600.000000\n",
"Name: duration, dtype: float64\n",
"count 80.000000\n",
"mean 9.689812\n",
"std 9.111374\n",
"min 0.000000\n",
"25% 3.402500\n",
"50% 5.750000\n",
"75% 13.250000\n",
"max 40.000000\n",
"Name: AbilityDuration, dtype: float64\n"
]
}
],
"source": [
"print(specs['duration'].describe())\n",
"print(specs['AbilityDuration'].describe())\n"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>AbilityBehavior</th>\n",
" <th>AbilityCastPoint</th>\n",
" <th>AbilityCastRange</th>\n",
" <th>AbilityCooldown</th>\n",
" <th>AbilityDamage</th>\n",
" <th>AbilityManaCost</th>\n",
" <th>AbilityType</th>\n",
" <th>AbilityUnitDamageType</th>\n",
" <th>HasScepterUpgrade</th>\n",
" <th>SpellImmunityType</th>\n",
" <th>duration</th>\n",
" <th>name</th>\n",
" <th>radius</th>\n",
" <th>vision_duration</th>\n",
" <th>vision_radius</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>459</th>\n",
" <td>DOTA_ABILITY_BEHAVIOR_POINT | DOTA_ABILITY_BEH...</td>\n",
" <td>1.0</td>\n",
" <td>500.0</td>\n",
" <td>10.0</td>\n",
" <td>450.0</td>\n",
" <td>246.666667</td>\n",
" <td>DOTA_ABILITY_TYPE_ULTIMATE</td>\n",
" <td>DAMAGE_TYPE_MAGICAL</td>\n",
" <td>1.0</td>\n",
" <td>SPELL_IMMUNITY_ENEMIES_NO</td>\n",
" <td>600.0</td>\n",
" <td>remote_mines</td>\n",
" <td>425.0</td>\n",
" <td>3.0</td>\n",
" <td>500.0</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" AbilityBehavior AbilityCastPoint \\\n",
"459 DOTA_ABILITY_BEHAVIOR_POINT | DOTA_ABILITY_BEH... 1.0 \n",
"\n",
" AbilityCastRange AbilityCooldown AbilityDamage AbilityManaCost \\\n",
"459 500.0 10.0 450.0 246.666667 \n",
"\n",
" AbilityType AbilityUnitDamageType HasScepterUpgrade \\\n",
"459 DOTA_ABILITY_TYPE_ULTIMATE DAMAGE_TYPE_MAGICAL 1.0 \n",
"\n",
" SpellImmunityType duration name radius \\\n",
"459 SPELL_IMMUNITY_ENEMIES_NO 600.0 remote_mines 425.0 \n",
"\n",
" vision_duration vision_radius \n",
"459 3.0 500.0 "
]
},
"execution_count": 18,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"wow = specs[specs['duration'] == 600].dropna(axis=1, how='all')\n",
"wow.head()"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"0.946385036281\n"
]
},
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>AbilityCastPoint</th>\n",
" <th>AbilityCastRange</th>\n",
" <th>AbilityChannelTime</th>\n",
" <th>AbilityCooldown</th>\n",
" <th>AbilityDamage</th>\n",
" <th>AbilityDuration</th>\n",
" <th>AbilityManaCost</th>\n",
" <th>AbilityModifierSupportBonus</th>\n",
" <th>AbilityModifierSupportValue</th>\n",
" <th>CalculateSpellDamageTooltip</th>\n",
" <th>...</th>\n",
" <th>stun</th>\n",
" <th>stun_duration</th>\n",
" <th>tick_interval</th>\n",
" <th>tick_rate</th>\n",
" <th>total_damage</th>\n",
" <th>transformation_time</th>\n",
" <th>vision</th>\n",
" <th>vision_duration</th>\n",
" <th>vision_radius</th>\n",
" <th>width</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>AbilityCastPoint</th>\n",
" <td>1.000000</td>\n",
" <td>-0.057620</td>\n",
" <td>-0.035359</td>\n",
" <td>0.109001</td>\n",
" <td>0.074305</td>\n",
" <td>-0.039983</td>\n",
" <td>0.161782</td>\n",
" <td>-0.528439</td>\n",
" <td>-0.038064</td>\n",
" <td>-0.278236</td>\n",
" <td>...</td>\n",
" <td>0.966788</td>\n",
" <td>0.169499</td>\n",
" <td>-0.137262</td>\n",
" <td>0.052527</td>\n",
" <td>0.840270</td>\n",
" <td>NaN</td>\n",
" <td>0.510858</td>\n",
" <td>-0.206439</td>\n",
" <td>0.017562</td>\n",
" <td>0.266958</td>\n",
" </tr>\n",
" <tr>\n",
" <th>AbilityCastRange</th>\n",
" <td>-0.057620</td>\n",
" <td>1.000000</td>\n",
" <td>0.093588</td>\n",
" <td>-0.054303</td>\n",
" <td>0.007771</td>\n",
" <td>-0.057877</td>\n",
" <td>0.025149</td>\n",
" <td>-0.975417</td>\n",
" <td>-0.117079</td>\n",
" <td>-0.346410</td>\n",
" <td>...</td>\n",
" <td>0.693253</td>\n",
" <td>-0.255013</td>\n",
" <td>0.091893</td>\n",
" <td>0.039942</td>\n",
" <td>0.968309</td>\n",
" <td>NaN</td>\n",
" <td>0.448456</td>\n",
" <td>0.110587</td>\n",
" <td>-0.208976</td>\n",
" <td>-0.231706</td>\n",
" </tr>\n",
" <tr>\n",
" <th>AbilityChannelTime</th>\n",
" <td>-0.035359</td>\n",
" <td>0.093588</td>\n",
" <td>1.000000</td>\n",
" <td>0.338586</td>\n",
" <td>-0.490522</td>\n",
" <td>NaN</td>\n",
" <td>0.349292</td>\n",
" <td>NaN</td>\n",
" <td>-0.998033</td>\n",
" <td>NaN</td>\n",
" <td>...</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>1.000000</td>\n",
" <td>-1.000000</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>0.987829</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>AbilityCooldown</th>\n",
" <td>0.109001</td>\n",
" <td>-0.054303</td>\n",
" <td>0.338586</td>\n",
" <td>1.000000</td>\n",
" <td>0.108005</td>\n",
" <td>0.325100</td>\n",
" <td>0.435086</td>\n",
" <td>-0.215375</td>\n",
" <td>-0.157530</td>\n",
" <td>-0.049340</td>\n",
" <td>...</td>\n",
" <td>0.640529</td>\n",
" <td>-0.088940</td>\n",
" <td>-0.107227</td>\n",
" <td>-0.592137</td>\n",
" <td>0.254605</td>\n",
" <td>-0.418323</td>\n",
" <td>0.864358</td>\n",
" <td>0.151425</td>\n",
" <td>0.260934</td>\n",
" <td>0.959416</td>\n",
" </tr>\n",
" <tr>\n",
" <th>AbilityDamage</th>\n",
" <td>0.074305</td>\n",
" <td>0.007771</td>\n",
" <td>-0.490522</td>\n",
" <td>0.108005</td>\n",
" <td>1.000000</td>\n",
" <td>-0.190768</td>\n",
" <td>0.436528</td>\n",
" <td>0.812392</td>\n",
" <td>-0.293812</td>\n",
" <td>-0.917273</td>\n",
" <td>...</td>\n",
" <td>0.439186</td>\n",
" <td>-0.089634</td>\n",
" <td>-0.946729</td>\n",
" <td>-0.341644</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>0.736366</td>\n",
" <td>-0.075727</td>\n",
" <td>0.470650</td>\n",
" <td>0.561690</td>\n",
" </tr>\n",
" <tr>\n",
" <th>AbilityDuration</th>\n",
" <td>-0.039983</td>\n",
" <td>-0.057877</td>\n",
" <td>NaN</td>\n",
" <td>0.325100</td>\n",
" <td>-0.190768</td>\n",
" <td>1.000000</td>\n",
" <td>0.128627</td>\n",
" <td>-0.528604</td>\n",
" <td>-0.293121</td>\n",
" <td>NaN</td>\n",
" <td>...</td>\n",
" <td>NaN</td>\n",
" <td>-0.249354</td>\n",
" <td>-1.000000</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>0.943483</td>\n",
" </tr>\n",
" <tr>\n",
" <th>AbilityManaCost</th>\n",
" <td>0.161782</td>\n",
" <td>0.025149</td>\n",
" <td>0.349292</td>\n",
" <td>0.435086</td>\n",
" <td>0.436528</td>\n",
" <td>0.128627</td>\n",
" <td>1.000000</td>\n",
" <td>-0.196490</td>\n",
" <td>-0.338138</td>\n",
" <td>-0.247456</td>\n",
" <td>...</td>\n",
" <td>0.210674</td>\n",
" <td>0.003476</td>\n",
" <td>-0.026331</td>\n",
" <td>-0.623760</td>\n",
" <td>0.792128</td>\n",
" <td>-0.489887</td>\n",
" <td>0.546979</td>\n",
" <td>0.168106</td>\n",
" <td>0.378375</td>\n",
" <td>0.735394</td>\n",
" </tr>\n",
" <tr>\n",
" <th>AbilityModifierSupportBonus</th>\n",
" <td>-0.528439</td>\n",
" <td>-0.975417</td>\n",
" <td>NaN</td>\n",
" <td>-0.215375</td>\n",
" <td>0.812392</td>\n",
" <td>-0.528604</td>\n",
" <td>-0.196490</td>\n",
" <td>1.000000</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>...</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>AbilityModifierSupportValue</th>\n",
" <td>-0.038064</td>\n",
" <td>-0.117079</td>\n",
" <td>-0.998033</td>\n",
" <td>-0.157530</td>\n",
" <td>-0.293812</td>\n",
" <td>-0.293121</td>\n",
" <td>-0.338138</td>\n",
" <td>NaN</td>\n",
" <td>1.000000</td>\n",
" <td>-0.684186</td>\n",
" <td>...</td>\n",
" <td>NaN</td>\n",
" <td>0.216217</td>\n",
" <td>-1.000000</td>\n",
" <td>1.000000</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>-0.188982</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>CalculateSpellDamageTooltip</th>\n",
" <td>-0.278236</td>\n",
" <td>-0.346410</td>\n",
" <td>NaN</td>\n",
" <td>-0.049340</td>\n",
" <td>-0.917273</td>\n",
" <td>NaN</td>\n",
" <td>-0.247456</td>\n",
" <td>NaN</td>\n",
" <td>-0.684186</td>\n",
" <td>1.000000</td>\n",
" <td>...</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>10 rows × 88 columns</p>\n",
"</div>"
],
"text/plain": [
" AbilityCastPoint AbilityCastRange \\\n",
"AbilityCastPoint 1.000000 -0.057620 \n",
"AbilityCastRange -0.057620 1.000000 \n",
"AbilityChannelTime -0.035359 0.093588 \n",
"AbilityCooldown 0.109001 -0.054303 \n",
"AbilityDamage 0.074305 0.007771 \n",
"AbilityDuration -0.039983 -0.057877 \n",
"AbilityManaCost 0.161782 0.025149 \n",
"AbilityModifierSupportBonus -0.528439 -0.975417 \n",
"AbilityModifierSupportValue -0.038064 -0.117079 \n",
"CalculateSpellDamageTooltip -0.278236 -0.346410 \n",
"\n",
" AbilityChannelTime AbilityCooldown \\\n",
"AbilityCastPoint -0.035359 0.109001 \n",
"AbilityCastRange 0.093588 -0.054303 \n",
"AbilityChannelTime 1.000000 0.338586 \n",
"AbilityCooldown 0.338586 1.000000 \n",
"AbilityDamage -0.490522 0.108005 \n",
"AbilityDuration NaN 0.325100 \n",
"AbilityManaCost 0.349292 0.435086 \n",
"AbilityModifierSupportBonus NaN -0.215375 \n",
"AbilityModifierSupportValue -0.998033 -0.157530 \n",
"CalculateSpellDamageTooltip NaN -0.049340 \n",
"\n",
" AbilityDamage AbilityDuration AbilityManaCost \\\n",
"AbilityCastPoint 0.074305 -0.039983 0.161782 \n",
"AbilityCastRange 0.007771 -0.057877 0.025149 \n",
"AbilityChannelTime -0.490522 NaN 0.349292 \n",
"AbilityCooldown 0.108005 0.325100 0.435086 \n",
"AbilityDamage 1.000000 -0.190768 0.436528 \n",
"AbilityDuration -0.190768 1.000000 0.128627 \n",
"AbilityManaCost 0.436528 0.128627 1.000000 \n",
"AbilityModifierSupportBonus 0.812392 -0.528604 -0.196490 \n",
"AbilityModifierSupportValue -0.293812 -0.293121 -0.338138 \n",
"CalculateSpellDamageTooltip -0.917273 NaN -0.247456 \n",
"\n",
" AbilityModifierSupportBonus \\\n",
"AbilityCastPoint -0.528439 \n",
"AbilityCastRange -0.975417 \n",
"AbilityChannelTime NaN \n",
"AbilityCooldown -0.215375 \n",
"AbilityDamage 0.812392 \n",
"AbilityDuration -0.528604 \n",
"AbilityManaCost -0.196490 \n",
"AbilityModifierSupportBonus 1.000000 \n",
"AbilityModifierSupportValue NaN \n",
"CalculateSpellDamageTooltip NaN \n",
"\n",
" AbilityModifierSupportValue \\\n",
"AbilityCastPoint -0.038064 \n",
"AbilityCastRange -0.117079 \n",
"AbilityChannelTime -0.998033 \n",
"AbilityCooldown -0.157530 \n",
"AbilityDamage -0.293812 \n",
"AbilityDuration -0.293121 \n",
"AbilityManaCost -0.338138 \n",
"AbilityModifierSupportBonus NaN \n",
"AbilityModifierSupportValue 1.000000 \n",
"CalculateSpellDamageTooltip -0.684186 \n",
"\n",
" CalculateSpellDamageTooltip ... stun \\\n",
"AbilityCastPoint -0.278236 ... 0.966788 \n",
"AbilityCastRange -0.346410 ... 0.693253 \n",
"AbilityChannelTime NaN ... NaN \n",
"AbilityCooldown -0.049340 ... 0.640529 \n",
"AbilityDamage -0.917273 ... 0.439186 \n",
"AbilityDuration NaN ... NaN \n",
"AbilityManaCost -0.247456 ... 0.210674 \n",
"AbilityModifierSupportBonus NaN ... NaN \n",
"AbilityModifierSupportValue -0.684186 ... NaN \n",
"CalculateSpellDamageTooltip 1.000000 ... NaN \n",
"\n",
" stun_duration tick_interval tick_rate \\\n",
"AbilityCastPoint 0.169499 -0.137262 0.052527 \n",
"AbilityCastRange -0.255013 0.091893 0.039942 \n",
"AbilityChannelTime NaN NaN 1.000000 \n",
"AbilityCooldown -0.088940 -0.107227 -0.592137 \n",
"AbilityDamage -0.089634 -0.946729 -0.341644 \n",
"AbilityDuration -0.249354 -1.000000 NaN \n",
"AbilityManaCost 0.003476 -0.026331 -0.623760 \n",
"AbilityModifierSupportBonus NaN NaN NaN \n",
"AbilityModifierSupportValue 0.216217 -1.000000 1.000000 \n",
"CalculateSpellDamageTooltip NaN NaN NaN \n",
"\n",
" total_damage transformation_time vision \\\n",
"AbilityCastPoint 0.840270 NaN 0.510858 \n",
"AbilityCastRange 0.968309 NaN 0.448456 \n",
"AbilityChannelTime -1.000000 NaN NaN \n",
"AbilityCooldown 0.254605 -0.418323 0.864358 \n",
"AbilityDamage NaN NaN 0.736366 \n",
"AbilityDuration NaN NaN NaN \n",
"AbilityManaCost 0.792128 -0.489887 0.546979 \n",
"AbilityModifierSupportBonus NaN NaN NaN \n",
"AbilityModifierSupportValue NaN NaN NaN \n",
"CalculateSpellDamageTooltip NaN NaN NaN \n",
"\n",
" vision_duration vision_radius width \n",
"AbilityCastPoint -0.206439 0.017562 0.266958 \n",
"AbilityCastRange 0.110587 -0.208976 -0.231706 \n",
"AbilityChannelTime NaN 0.987829 NaN \n",
"AbilityCooldown 0.151425 0.260934 0.959416 \n",
"AbilityDamage -0.075727 0.470650 0.561690 \n",
"AbilityDuration NaN NaN 0.943483 \n",
"AbilityManaCost 0.168106 0.378375 0.735394 \n",
"AbilityModifierSupportBonus NaN NaN NaN \n",
"AbilityModifierSupportValue NaN -0.188982 NaN \n",
"CalculateSpellDamageTooltip NaN NaN NaN \n",
"\n",
"[10 rows x 88 columns]"
]
},
"execution_count": 19,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"corr = specs.corr()\n",
"# there are 2 very similar columns AbilityDuration and duration.\n",
"# they there left as is because some abilities have 2 durations:\n",
"# duration of stun and duration of slow for example.\n",
"print(corr['AbilityDuration']['duration'])\n",
"corr.head(10)"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.0"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
Gorgel/minkpy | analysis/notebooks/V3_analyser_dtbox.ipynb | 1 | 335012 | {
"cells": [
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from __future__ import division\n",
"import numpy as np\n",
"import scipy as sp\n",
"import matplotlib.pyplot as plt\n",
"import pylab\n",
"from scipy.signal import argrelmax, argrelmin\n",
"import pickle\n",
"%matplotlib inline"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Load all data into memory"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from IPython.html.widgets import interact #import interactive tools\n",
"filenames = np.loadtxt('../datafiles/dtboxnames.txt', dtype='str')\n",
"\n",
"def data_selector(filename):\n",
" \n",
" global plotname\n",
" plotname = filename\n",
" global data_dict\n",
" #open pickled object\n",
" with open('../datafiles/'+ str(filename), 'rb') as infile:\n",
" data_dict = pickle.load(infile)\n",
" \n",
" return data_dict\n",
" \n",
"interact(data_selector, filename=filenames.tolist())"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"with open ('../../redshift_files/all_redshifts.txt', \"r\") as myfile:\n",
" redshifts=myfile.read().splitlines()\n",
"\n",
"#set upper value and lover value of redshifts\n",
"z_upper_limit = 11.313\n",
"z_lower_limit = 5\n",
"\n",
"# selects redshift indexes between the limits\n",
"indexes = sp.where( (np.array([float(z) for z in redshifts]) <= z_upper_limit) & \\\n",
" (np.array([float(z) for z in redshifts]) >= z_lower_limit))\n",
"\n",
"#use the above indexes to select the desired redhifts\n",
"redshifts = redshifts[indexes[0][0]:indexes[0][-1] +1]\n",
"\n",
"thresholds = data_dict[str(redshifts[0])]['thresholds']"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### V3 as function of threshold $\\theta_{th}$"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<function __main__.plot_explorer>"
]
},
"execution_count": 26,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA6gAAAImCAYAAABejKc0AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl8XFX9//HXZyZp2qS0pUARCqVARaAFZIcipWUTBFF2\nsC6I4PJlEX644ULdEPnigihfURABEWWHr3zLVmhBWWSXXZYuWAotpXvTLDPz+f1xziQ305lkkiaZ\nJH0/H4/pdO6599wzd+5M7ueezdwdERERERERkUpLVboAIiIiIiIiIqAAVURERERERPoIBagiIiIi\nIiLSJyhAFRERERERkT5BAaqIiIiIiIj0CQpQRUREREREpE9QgCoiIiIiIiJ9QlWlCyAiIiIiIiID\ng5kNB4YQYs00YDFpjbsv7Gh7BagiIiIiIiLrETM7DtgXaAA2Bp5z99+Wue32wKXAj939HwVp3wcu\nKLHplcCXOspfAaqIiIiIiMh6wsw+Bmzq7ucllv3GzL7k7r9rZ7sjgWOBFcChwE+KrLYpMJUQ+OYA\nJ8Sc5wNfL6d86oMqIiIiIiKy/vgC8HjBssuBj7e3kbvf5e6fB37RzmqL3P0v7n67u9/p7v8LjAe+\n5u4ryimcAlQREREREZH1RxNwqZltkli2K/BsmdtbO2k/a7Oi2T5Arbs/VG7hFKCKiIiIiIj0AWY2\n1MxuM7PlZnZmXPY5M9uzG3fzc0JA+qqZfcHM9gcOAn6wrhm7+8r8/82sKubZqXwVoIqIiIiIiPQN\n3wT+AZwCjDazGwj9RZ/srh24+1PA4YQRdq8EbgJ+6e6Z7tpHdDrwkLs3dGYjDZIkIiIiIiLSN/zC\n3ZcCmNlbwJHu/t+FK5nZtcCoMvN8z90/m9h2Q+DLwOeAPQmDFz1pZifGPqPrzMxSwP8DTu70tu7e\nHWUQERERERGRbmBmhwIT3L29AYm6kq8BM4Fp+X6hZrYDcC2wLbCFu6/pII+xwGxgsrs/XGKdA4EZ\nQF1H+RVSE18REREREZE+wsxOJjTr7dbgNNoBGJ4ctMjdXwEOji937Kb9HArUdzY4BTXxFRERERER\n6RPM7PPAEne/M7424EJ3/3bBel1t4psDagtXcPcVsUnx210ufFu7Ays7XKsIBagiIiIiIiIVZmbH\nAZ8A5pjZ5sAKYCpwReG67v65ruzD3V81s9fM7Ax3vzyx76MJAxq9G18fDlwHnOzuMwqyybfCTbez\nqw8QprPpNAWoIiIiIiIiFWRmmwIfdPdPmtnWwB3AxsA3umvgooTjgG+b2Z+A9wk1qi8D5xasV0Ui\nXjSz/YCzCVPUOHCtmf0T+LO731Gw7RxCbW2naZAkERERERER6RM0SJKIiIiIiIj0CQpQRURERERE\npE9QgCoiIiIiIiJ9ggJUERERERER6RMUoIqIiIiIiEifoABVRERERERE+gQFqCIiIiIiItInKEAV\nERERERGRPkEBqoiIiIiIiPQJClDXU2Y21sxyZjank9tdE7f7XE+VbaAxs1nxmB1Qof3XmdmPzew1\nM2sws3fN7CYz26kS5ZHeZ2Zz4zk4ppPbTTKz75rZnWa2IOaRM7PaMrYda2Z/NLO343k3x8x+ZWYj\nu/5Oek5f+G0zs5SZHW9mF5vZg2a2PJbpyTK3P8DM7jaz981stZn9y8zOM7N0T5d9oMmf672wn1Pi\nvv7YiW0q+jdFRKSnKUAVz/+nk0Grd7yKRJ549CozGw48CnwbqAFuB94EjgOeNLMDe7tM0r06cYHb\nlfPvMuCHwMeBTcvNx8x2AZ4DPgcsBG4DmoCzgGfMbLMulKW3VPK3bRhwI/B1YDIwNC4v55ifCswE\nDgaeBe4CRgOXAHcpSO2S3jwXOruvivxNERHpDQpQJckLnqV7fBbYASirFqSbXQLsBNwNfNDdT3b3\n/YDPA4OAG8ysrgLlku7XE9/b+4DvAYcDHyhngxgI/YUQbE1z993c/VPA9sAfgTHAVT1Q1oGgCbge\nOAf4COHGQIfMbCzwW6AZONTdD3b3E4FxhBsFHwX+Xw+UVyrHKl0AEZGeogBVkvQHrwe4+3/c/TV3\nX9Ob+zWzjQmBaDNwurs3Jcp0LXAvMCquI/1ft39/3f0b7n6hu9/r7u+VudnHCcHoy+7+o0ReDpwJ\nLAUON7MJ3V3e/s7d6939s+5+mbs/CtSXuek5QDXwB3efmchvGfCV+PJrZqa/+SIi0ufpj9UAZ2a7\nmdldZrbMzFaa2WNmdlyR9b4PzI4v8019c+01+Y15/y3R3+kxMzu+nbKMMrOfJ/pCLjWzh8zsMwXr\nDTazF+O+zyySzxZxn5muNlFN9uExs33N7J54jOrN7O/t5WtmW5vZ72O/vkYzWxy3P6KjfRUsHxH7\n9/0rHot6M3vLzO4zs9NL5LWfmd0c+wM2mdk7ZnZjbFJZ6GNAGviHuy8okv7X+PyJUu+1PWb2/YLz\npNhjZpHtdjKzq2OfxIZ4/J4ysx9akf6JZvaJeEyWxPVnm9lvrUh/ymQzdTOrMrNvm9lLZrbGzJ4t\nKPc0M9vWzK6PxzFjZl/twnEo+3Ms2PdWcd8LE9+fQxPrHmdmj8bv7VIz+4sVNI01s1nA1fHl5wqO\nfbEmv2ZmH4vn+EozW2Ghz+KunX3f7TgqPt9YmBBv0vxvfNml8y7PzAaZ2ZnxGC2Ln/HL8Twa2s42\n37bW36D5ZnaFmW3Swb6GW/jtmhe3e9PMfmJmtaW+33G7lJl92kJ/0iWJbS81s1Hr8v4L5I/5XwoT\n3P2fwFvAJsC+67ITC7/hPzGz581sVTx/Xonfx/FF1t/ZzP5soR9yo4X+77eZ2cQS+ef7Sm9lZkfH\nz3aVmb1nZteZ2aZxvToz+2k8lvlj+vUSeSZ/6w+y1r69K+P/p6zLMUnsJ/nbk47n2b9j+RaUc54V\nyXPv+N4bzWxqd5RTRKQ/qKp0AaTnmNlBwP8RmnK+ALwIbA3cROhblvQscCtwLLAauDmRtrhI9vsC\nvwfmAPcAmwP7Azea2Th3v6igLNsR+kdtBvyH0BdyGHAgsL+ZfdTdPw3g7g1mdgKhSewlZvawuz8f\n80kDNwAbAj9x9wc7e1wKHEGofXgOmA6MB/YD7jGzg9z97wXvYyKhuewGwGvALfE9HQQcamY/dfdv\nF9lPm/5CFprVPgZ8CHgHmAWsIfQZ2wPYAriyYN/fBC4CssBTwMPAtsDxwCfM7Dh3vyuxST7oeLrE\ne88vLxbcluNZ4JoSaROB7YBMcqGZfR74HeG351XCeVBHOA7fAWYQ3ld+/UuA82I+DxP6M+4BfAk4\n0cwOc/cniuw/BdxBOL9mAc8TvgdJ2xGO4/K4Th3h3C9bVz7HaGzc9xLgAWAbYG9CX8GPAnsCF8b3\nfDfhnDwR2NnMdk3Uht9NuAmxH/AG8I/EPpL/h1DD+mVC/8ZHCL8NuxGaf37EzHZz99c78/5L6Oi8\ne4bQN/XDXd2BmY0gfF/3Ad4HHifUNu4FfBc42swmufvSxDZp4E7C+11FaEHQRPjNO4TwG1lsX8MI\nn8NOcV9/I9RWnkHoJ5ofSMcLtqsm/I4eBayk9fPeFTgbODaWsVMD1RUp33DC+eS0/10fQzjmj3Rx\nP7sTjvkmhO/hfYTWGdsCpxHO/5cS6x9DCJirCb+vMwnn+SeBo8zsTHe/osiunNBX+avAQ3GfE4FP\nA7ub2X6E78yWMf0NwudwsZkNTtbaFziG8Jn9i/AZjovbHWBmn3X3P3f6oBRnhL8LhwEPEn4nJwFf\nBD5qZhPd/Z0OMzE7knCTJwMc4e4zuql8IiJ9n7vrMQAfQC2wgHDx9K2CtOMIf/RywOzE8q0KlxXJ\n95q4Tg64pCDtQMLFeQb4cEHak3Gbq4GqxPLtgPkx7csF25wel78MDInLfhiX/QNIrcPxmRXzyQIn\nFKRdFtMeKFg+mBBc54AfFaTtC6yIaYeV2NekxLLPxWV3Fr4PQiD1kYJlR8T15xQ5tkcSLrSXAhsm\nlt8WtzmrxDHYMHEMarvx3Nsnngergb0Sy/eO58Ya4KQi2+0GjC54XznCRf0eieUGXBzT5gKDEmlj\nE+fnm8CYIvv5fmKd3wHpdXivnf0ck/v+74K0HyfKvQzYO5E2PH4PcsBnS5Th6nbKOTeuUw/sn1he\nlThP/lDG++3wfImfVxbYqUT60TGfJ9bhuN8U8/gTMDSxvIbQzzUHXFuwzTlx+esF59kw4O+Jz6Xw\n+OZ/D/4ObJBYPopw0y+/3aSC7f47Lr8XGFVw/uY/64c6eJ+TOzpWwM5xnffbWedXxc65ThzvDYC3\nYx6XkPgNj+lbALslXm9G+D3MEroXJNf9JCGwbSo8RxLn6cqC839Y4li/Rgj86hLph8a0FYXnJq2/\nv2v9FgJTE/vbrNi53oljNDaxn7cJff7zaYMJvxE54NaC7U6h4PtLCPgzhL/hHy6yr/x7mlRu+fTQ\nQw89+tOj4gXQo4c+2DAwTw54vkT6LawdoI4tXFZku2viOvMKL1Ji+v/E9KsSyybFZe8lLyoS6fkL\n7NeLpP01n1+8WMsSajG2XMfjk/8Df0ORtI1i2hoSwUvimL5cIs9pMf3+EvtKBqhfj8vOLrO8T8T3\nfkCJ9PwF6FmJZffFZaeW2KY6fxEGbNpN593WhNqVDHBMQVr+Au27Zeb1YFz//CJpaUKgkQOmFjmH\ncxTceEis8/2Yvoh1DMy78Dnm9/1G4feHEITmy/7DItueTZFAkiIXuEW2nRvX+UmRtN1j2ptllL+c\nALUprrNNifRDYj6vdPGYj4/bvwpUF0kfQqjNa6LtDZvZcbvjimyzUyxzmwCVcKNvdUwrFigcljgm\nye/3RoTfj8XJMiTSjVCzlqNEIB/Xm0zHAerEuM5b7axzYVznt1085udS5LetnfUviOvfWyI9fxPh\nyhLnaXvnfzOJ4C+Rnj+ehTcKZsXlj5Uoy3SK/C7lP9dOHKOxie/vl4ukbxHPyQyJG2eF319afyNe\nBcaW2Ff+PSlA1UMPPQbkQ31QB64D4vNafZKiP61j/re4e6bI8uvj8/6JZZPi8+3uXqwJ5fWEP9rb\nmNnmBWlfJNQankoIcCDckf9P14q9lrsLF7j7+4TayEHAxomk/Pu4vnCb6Or4PNHMOhqwJj+i7zfN\n7OTYTK8oC4Md7QEsdveHSqyWb4q8dwf77TGx2eX/EZoAnu/utyXS0oTpLxz4Qxl5VREuvB24tjDd\n3bPAdfHlpML0uN2dRZYnzXD3cgehKaXsz7HArMLvj7svJ9Q+OuHmQqHZ8bnwO9IZa53vhBqpdc23\nNx0Wn//X3ZsLEz30c32aUDu8B4CZbUkIIBrc/ZYi27xA8Sa+uxMC3tfd/bki291DqO0uNJlQm/ug\nJ5oZJ7ZzWpva7lNk+74mf8yvbnetVvnv5Frf3YJ8in13of3zf54Xb4r+ZnwuNYXRDSWWF/ubtS4c\nWKu5sLvPJwSWKcIIzYWqzOxKQnD/T2Ciu8/tpjKJiPQrClAHrtHxeW6J9HnrmH9H+W5RpCxzim0Q\ng4234svNC9JWEIJTCM3M/pAMfLpBqUB3ZXyuSSxr930QmnU1E5pzbdTeTt19FqE/6SjCxcz7FgaG\n+o2ZFV4obR2fN7ESgxERmjxCCA7zVsXnUtPIJAeSWVlinbLE/na3EkZvvdLdLylYZWPChf5qL6P/\nFeH4DQKavPgAT9D6OYwukrbI3Rs72Me6fgc6+zkmzS+xfFU76fm0miJp5XCKnO/unv/sC/vodlW5\n511Xz7lt4vPX2vk+fCyuk7/BlD9H2ruxNbfIsvx27Z0rb7H2CMr5Mh7XThn/q6CMXdXR8YZ1P+Zj\n4vO/y1y/o9/K9r67Tvvnf0ffnVLfj7kllhf7m7UuliW+U6X2Vex9nwR8gRCIT3H3Jd1UHhGRfkeD\nJElfUqrWMTl64a5mVl2s5qSLct2UT6e5+3fM7PeEaTkOJNxV/y/gv8zsOnc/Ja6ajs9LaB0BtZRX\nE//PXwxtWWLd/AXZkm6oSbwCmALcT+u0Fkm+jvl3VjlT+nTLtD+d+ByTOjrveuq87I3zfR5h4K0t\nKV4ruUViva7Ifx/+CbxSRlm6Q3vnb7Fjmi/jS3Q8//FLHaR3JP8eR5hZXYlWKut6zHv7+9veeVqx\n3+we9g/CzchtCN1Fzq9scUREKkcB6sD1dnweWyK91PJydZTv24ll+Tve2xbbIDbnHEO4CHq7IO0E\nwoAR8whNuA4k1Fh9rQtlXlf5shV9H4SLwGpC4FPW3W93nwf8Jj4ws0MI/W4/a2Y3uPt9tNb6rHb3\nU4vnVNQz8XmPEum7x+e1mi52hpmdT5hL9UVC/75iF5DvE45LnZltVkYt6vuE/lqDzGyL2DyuUL6W\n6u0iab2qzM9xffEMIUDdg9C/r9C6nnf51hb3ufu0MrfJnz9bmpnFJraFxhZZlj+3xhRJy9uKtQO4\nfBmf6eR3ttPcfbmZzSWUf3cSo2AndMcx354wWvUzHawL4bh9iPBb+ViR9Ep8d8d2sLy7yjLCzDYo\nUYva3r7mEsZjeJDQZWCQu5/XTWUSEelX1MR34Mr3VTypRHqxOdXyU1eUc+PiuBhYFvpUfE5eJOX/\n/0krPj/h1LjPN5OBi5mNJUxlk4n5foowsM25ZnbY2tn0uPwxnVqij+nn4/MjJYK0Drn7/YSmshAG\nbsHd3yYEf1ua2V6dyG46YfCW/cysVJMyCNOxdEm8gXAh8C5hKoSiTdtiM+4ZhFryDi/YY//MR+L6\nny2y3zSQnz+3VL/ciin2Ofagznxve0O+lv/EwgQzqyVMu1JOH+FS7onPx5TR1xto6f83l9D8/pgi\n5ZpAGA230NNAA7C9ma2VHqcE2rDIdg8QmvsfHqci6mn5Y3lyYYKZ7UMIsBcBj3Yx/3vjc7nBdv47\nudZ3N/p8wXq9Ya1jExX7m7UuLJFn68LwG5wfMLBwCigA4tgKBxD6hZ9rZr/upjKJyDoys03N7Adm\nptipF+ggD1y3EIKGnczsG8mEOD/d0UW2eY9wUbVpHPCmPVsSApNkvpMJFzBZ4PL8cg9ziT4NjAQu\nSwa2ZvbBRD4/TyyvIgzwNAz4gbs/5u6LCHeYAa41sw90UMbudjOtNQM/SCaY2d6E+Tod+EVHGVmY\nhH6/IsuH0zqAxluJpAvi81/MbK2BRcxskJl93Mw+lF8WB3u6mlCre6WZDUqs/znC1AwLCSNqdlq8\n8L2WMHXJUWUMXPUTwrnxXTM7vkh+uxcE0r+Mz1+PczDm10sRpunYllCznpyzt1d14XPsCfnawR17\neD9J7QWGfyM0vd3BzL7XskH43H4NjADudvcXu7Jjd3+GEASPB/5sZqPWKly4kDi9YHH+Yv+i5HkW\n5zn9nxL7qqd1QJ9fm9kGie1GAT/LvyzYbiHwW0L/0tvNbGsKmNkIM/tSvNmyri4l3Kj4gpkdmNjH\nhrS+t5+VqDkux1WEkZEPMrOfxj7nLcxsSzPbLbHoSkKf0IPN7LSCdY8izGnazNrzcfekfczsjIKy\nnAwcThipuawBoMzsOjN7pTCvAheY2bjENoMJfxOrgb+5e8nfhNjn/gDCtFJnmNnvyimXiPQcM9uJ\ncE19Ab37t3b9VelhhPXouQdh1NQ1xOlmCKMYPhpf/5IiU8oQan1yhEEs/ky4MLkokX5NTP8toWbh\n1ZjvTELwkQW+U6QsH6R1vtN5hOaP02MeOeD6gvUvissfLJLXJTHtfsC6eGxm0c4w/bROdzCmYPlE\nwqidOcJF+A2E2pJMfO8XlrMvwgVljvCDdzdhJMn/A5bH5Q9TMD8nYUqT/Py1LwK3E4L4hwmDn+SA\nQwu2GUaYmD5HCJRuJNRM5qfROXAdzq8HYj4vx/Oi2OObBducTrgwzW/3V0JA81qxzyPxWTcTamBv\nIAzUkiM0A96rYP2xdDxV0vfjOhd0w3esU59jR/sudd7FtMkU+U4QBjfKz3n8JOGmwVXAKeXkG9OL\nTqlBaF7/eOKRn0bjicSytaYNIjTxzX9Pnomfc/4znkvBnJNdOO7D47HNEQKhR+K5cRut82UuKNgm\nTagJzBG+L3cSbm4sJnQfuIPi86AOI/x+5gg38W6J6y4jNF/N/6buU7BdNa3TeTUS+szeGPf5dDyn\nsyTm8Y3b/U/i2Obnvl1Z8Dl8rMgx+XzML0P4bcy/t1w8N7s8b3TMf09CLWyOEKzelngvmcJzmnAT\nNP/7/jTh70n+tycDfKk7zv9E+jUlPr9Zcfll8fg8E8+VxxNl+UwnvhP5/Arf71haz+/bCb+v/xc/\n8/z3cw6wecF2p1BkmijCzY3n8mkk/tahaWb00KPXHoRB9zw+dq90edaXR8ULoEcPf8Ch79FdhGlT\nVsQ/yicS+k0VC1BHEu5+zyPckW+zDqG2LUtourV7/AO8hHCR+Dgl5p6M225CqCV9LV64LCM08fpM\nwXoHx328V/jHPKZX0Tov6Le6eFzyAXWpAHVOTC92obQ1oenxXMKF52JCs8Mjy90X4QL+p4SmXm/H\ni5m3CRfdp1Fkfse43a7xM5hNqLlcSmugdzJF5qckzOX443jc1xCCqZuACet4biVvSuSKPLIUv8Hw\nYcI0R/+J58Gi+HleQPE5Iz9BmHZiSVx/DuEGSbHPZmyx87pgnWmxbN0RoHbqc+xo3x2cdwdQ+qbN\nzoRA/z1ab5ZcXU6+Mb3Uxfi0xGdZ6lF0/tX4WfwxcVzmEAL6ket63GP+aUKLivvj+24kBAJPEG5s\n7FNkm0HAdxLfhfmE37tNSPy2FdluOOG366243Wzg4vjdeiNuN65EOT9JqPF9J56/Cwlzdl4OHNLB\n96rUY60yJs6Ru+N3ZTUhsP5/rGNwmsj/A/HYvkL4/VlGGOTp18D2Jc7LP8fPJf/ebyNModJt539M\nL/r5kQjmCHPwziTcQFpB6O95UCe/E/nPp1SAOjuem98j3ExriN+BK4BRRfL7HCXmMSY0H38q7u+6\n/OdIB3+/9NBDj+55AN+gNTgdXenyrE8Pix+AiIiIdIKZbUWofV3p7sX6okqFmdksQnA62d27q59p\nsf2MJQSnc919m/bXFpG+LHYz+ytwLOGG3F7uvqr9raQ7qQ+qiIhIO8xsrZGwYz/W6wh/R6/v9UKJ\niEi3i2NIzCYEp9cAOyk47X19ZdRHERGRvuoeM2skNGd9nzCl1G7AEEIT++9UsGwiItIN4oB2s+PL\n/3L331ayPOszBajS75nZtwhz9JXjdnfv6vQWA1ocbfMjHa4Y/N3d/9CT5akEnUu9z8x+RhgQphxX\nuvsjPVmeEi4GPk6YMmgkob/rq4TBcC7tT3fXzWwjEiOmd8CBr3kYEby/yvcfExEpycz2pXUqroPc\n/cFKlmd9pz6ovczMdMBFRESk33D3suYcFumPzOwzhC4bEAZ8+3clyyPqg1oRlR4Zqz8/pk2bVvEy\n9NeHjp2On45f/33o+OnYVeohMlBZ8EtCcLoc2NgVnPYJauIrIiIiIiLrDTMbTJhqal/CvO4fc/em\nypZK8lSDKiIiIiIi6wUz25RQY7ov8BPCnNQKTvsQ1aBKvzJ58uRKF6Hf0rFbNzp+60bHb93o+HWd\njp2I5JnZBOCF+PIEd7+5kuWR4jRIUi8zM9cxFxERkf7AzHANkiQDgJkdBtwdX+7p7k9VsjxSmpr4\nioiIiIjIgGVm59EanI5RcNq3qYmviIiIiIgMOGZWBdwAHA/8G9jD+9Hc1esr1aCKiIiIiMiAYmbD\ngDcIwemfgPEKTvsH1aCKiIiIiMiAYWZjgTnx5Vnu/pvKlUY6SwGqiIiIiIgMCGa2D/BYfHmwuz9Q\nyfJI56mJr4iIiIiI9Htm9ilag9MdFJz2TwpQRURERESk37LgZ8CfgZXAJu7+aoWLJV2kJr4iIiIi\nItIvmdlgYAawHzALOMzdGytaKFknqkEVEREREZF+x8w2AZYSgtOfAgcqOO3/VIMqIiIiIiL9ipnt\nCLwUX57k7jdWsjzSfRSgioiIiIhIv2FmhwL3xpd7ufuTlSyPdC818RURERERkX7BzM6hNTjdSsHp\nwKMaVBERERER6dPMLA1cD5wEvAHs5u4rK1sq6QmqQRURERERkT7LzDYAXiMEp38GtldwOnCpBlVE\nRERERPokMxsDzIsvv+rul1WyPNLzFKCKiIiIiEifY2Z7A4/Hl4e6+/2VLI/0DjXxFRERERGRPsXM\nTqI1ON1Rwen6QwGqiIiIiIj0CRZcDPwFqAdGufsrFS6W9CI18RURERERkYozsxrgPmAS8HfgEHdv\nrGyppLepBlVERERERCrKzDYB3icEp5cAByg4XT+pBlVERERERCrGzHYAXo4vP+Xuf6lkeaSyFKCK\niIiIiEhFmNkhhGa9APu4+z8rWR6pPDXxFRERERGRXmdmZ9ManI5VcCqgGlQREREREelFZpYGrgM+\nBcwBPuzuKypbKukrVIMqIiIiIiK9wsw2AF4hBKd/BbZTcCpJqkEVEREREZEeZ2ZbAm/Fl+e6+6WV\nLI/0TQpQRURERESkR5nZnsAT8eVh7n5vJcsjfZea+IqIiIiISI8xsxNpDU4nKDiV9ihAFRERERGR\nbmfBRYS+pg3AKHd/qcLFkj5OTXxFRERERKRbmVkNcDcwBXgEONjdGypbKukPVIMqIiIiIiLdxsw2\nBt4jBKe/APZXcCrlGhABqpnVmtlsM8uZ2a+LpH/IzO4wsyVmtsrMHjazKSXySpnZuWb2qpmtMbO3\nzOxnZlZbYv2y8xYRERERGcjMbHtCcLoBMNXdz3N3r3CxpB8ZEAEq8ENg4/j/Nl8AM9sWeBTYG7gY\n+DowFLjXzA4qktcvgZ8DLwJnAjcDZwN/MzNbx7xFRERERAakeP37Sny5r7vfUMnySP9k/f2Ghpnt\nBvyTEBz+AviNu5+dSL8JOBrY3d2fj8vqgJeABnffPrHueOAF4FZ3Pz6x/EzgMsJdoL90Je/ENrqJ\nJCIiIv2CmeHu1vGasr4zszOA38SXW7v73AoWR/qxfl2DamZp4EpCB+zbi6TXAUcBs/IBJIC7rwau\nAraLczLlnRyfCycNvhKoBz69DnmLiIiIiAwoZpY2s2sJwelbwHAFp7Iu+nWACpwLfIjQFLfY3b2d\ngUHAY0V1RHxqAAAgAElEQVTS/hmf90gs2xPI0jpPEwDu3gj8K6Z3NW8RERERkQHDzIYSWg5+FrgF\n2NbdV1S2VNLf9dsA1cy2Bn4A/MDd3yqx2ubx+e0iafllowvWX+zuzSXW39jMqhLrdiZvEREREZEB\nwcy2AFYSKou+7u7Hu3umwsWSAaA/z4N6BfAGod9pKfmRdxuLpDUUrJP/f7F1C9df0YW8RURERET6\nPTPbA3gyvjzc3e+pZHlkYOmXAaqZfRo4mDCnUradVevjc02RtMEF6+T/v3GRdfPre2L9zuYtIiIi\nItKvmdmxhOa8ADu5+4uVLI8MPP0uQDWzGkKt6f8BC81sXEzKN6cdEad/WQwsKEhLyi9LNtFdAGxv\nZtVFmvmOJjT/zSTW7UzeLb7//e+3/H/y5MlMnjy52GoiIiIivWrWrFnMmjWr0sWQPihOt/gj4DtA\nM7Cluy+sbKlkIOp308yY2QhgSRmrfg34HSFQfcTdDy7I53uEPqx7u/uTcVn+SzfJ3f+RWHcw8D5h\nxN4j4rKhhEmIy8o7kaZpZkRERKRf0DQzAmBmg4DpwEHA48AUd29ofyuRrumPAWoV8AlCc9ukUcD/\nEKac+QPwvLu/EecqPQbYLTFXaX7EsTUF86BOIIzWe7u7H5dYfhbwK+DTyQmHO5N3YhsFqCIiItIv\nKEAVM9sIeBMYTrgePlcXs9KT+l2AWoqZjQVmA79x97MTy7clTBvTDPySMNrY6cB44Ah3v78gn8sI\n09bcTgh2dwDOAv7h7gcWrNupvOM2+k6LiIhIv6AAdf1mZh8CXo0vP+vuf6pkeWT90O/6oHaWu79p\nZvsBPwW+RZi79GngMHd/sMgm5wBzgS8CRxCa8V4GXNANeYuIiIiI9HlmNgXIX8/u5+6PVrI8sv4Y\nMDWo/YVqUEVERKS/UA3q+snMvkLoOgewjbvPqWR5ZP2SqnQBRERERESk8swsbWZ/JASn84ERCk6l\ntw34Jr4iIiIiItI+M6sjjK2yI3AbcGJiekWRXqMaVBERERGR9ZiZjQZWEYLTb7r7sQpOpVJUgyoi\nIiIisp4ys92Bp+LLI9x9eiXLI6IaVBERERGR9ZCZHUNrcLqzglPpCxSgioiIiIisRyz4IXArkAU2\nc/cXKlwsEUBNfEVERERE1htmNgj4G3Ao8CRwgLuvqWypRFqpBlVEREREZD1gZiOBdwjB6a+BfRSc\nSl+jGlQRERERkQHOzD4IvBZfnuLu11ayPCKlKEAVERERERnAzGwyMDO+/Ii7P1LB4oi0S018RURk\nQGtubsbdK10MEZGKMLMv0RqcbqvgVPo6BagiIjJgZbNZ3nvvPZYuXVrpooiI9CozS5nZVcAVwAJg\nQ3efXeFiiXRITXxFRGTAymQybZ5FRNYHZlYHPA5MAO4Ejnf35sqWSqQ8qkEVEZEBK9+0N5fLVbgk\nIiK9w8w2B1YRgtPzgaMVnEp/ohpUEREZsJIBqrtjZhUukYhIzzGzXYFn4suPu/tdlSyPSFeoBlVE\nRAas5OBI2Wy2giUREelZZvZJWoPTXRScSn+lAFVERAasZICqZr4iMhBZMA24HXBgM3d/vsLFEuky\nNfEVEZEBSzWoIjKQmVk1YRCkwwm1px9x9zWVLZXIulENqoiIDFiqQRWRgcrMNiRMH3M48D/AngpO\nZSBQDaqIiAxYqkEVkYHIzMYBr8eXp7r7HytZHpHupABVREQGLAWoIjLQmNkk4KH4cpK7/72S5RHp\nbmriKyIiA5aa+IrIQGJmX6A1OB2n4FQGIgWoIiIyYKkGVUQGAjNLmdnvgKuAhcCG7v5mhYsl0iPU\nxFdERAas7qhBdXfMrLuKJCLSKWZWCzwK7ALcBRzj7s2VLZVIz1ENqoiIDFjJoDSXy7UJWMuRyWV4\nd9W7rGhc0d1FExHpkJltBqwmBKffBY5ScCoDnWpQRURkwCoMSLPZLFVV5f/py+QyOE5Ttqm7iyYi\n0i4z+zDwbHx5lLv/rZLlEektqkEVEZEBKx+gptNpoPPNfPPbZ3PqvyoivcfMjqI1ON1VwamsTxSg\niojIgFUYoHZ2oCQnbJ9zjQAsIj3Pgu8Cd8ZFm7v7c5Usk0hvU4AqIiJ9lruzqKmJFZlMl7cHWpr1\ndrYGNR+YOq5aVBHpUWZWDfwv8CPgX0Cdu79T2VKJ9D4FqCIi0mdl3Mm4s2YdRuCF1gC10zWoyVGA\nVYsqIj3EzDYE/gMcCfwO2M3d6ytbKpHK0CBJIiLSZ+XDw1wnR99t2T5OEbOuTXwBsp6lmuoulUNE\npBQz2xZ4I748zd3/UMnyiFSaAlQREemz8oGpA1l30p2YjzRf+5kMULs6SBJooCQR6X5mtj/wcHx5\ngLs/3N76IusDNfEVEZE+K1lvmu1kLWoyQE2lwp+7da1BFRHpLmb2eVqD0w8qOBUJFKCKiEif1V0B\naldrUJP9TlWDKiLdwcxSZvY/wNXAYmCku7/RwWYi6w018RURkT6ruwLU/COXy7X0S+1MHmH/ClBF\nZN2YWS3wd2A3YDrwSXdvrmypRPoW1aCKiEiflXMnuzxDriFHZ8PDZIAKdKkWNdnEV6P4isi6MLMP\nAKsIwek04EgFpyJrUw2qiIj0WbmM46tzeKOTre3cn6xiAWomkyGbzbYEq+XmAWriKyJdZ2a7AM/F\nl5909zsrWR6Rvkw1qCIi0mflcjFAzHqnm/jma0rzAWpXBkpK1po6rlpUEek0MzuS1uB0NwWnIu1T\ngCoiIn1WS4DqkMl2bYqY7mjiW5UKtbeqRRWRcllwPvC3uGi0uz9byTKJ9AcKUEVEpM9KVprmst6m\nyW3H27YNULtSg5rPoyVA1UBJIlIGM6sGbgd+ArwADHX3BZUtlUj/oABVRET6rGRA6tnOjeTbXTWo\nhpG2uK2a+IpIB8xsBDAP+ARwFfBhd19d2VKJ9B8aJElERPqsXDYGmRD6oVL+H65SAWq5Naj5YNSA\ndCpuqya+ItIOM9sGeDO+/LK7/66S5RHpjxSgiohIn5WvMK0yI9PJgZLyAWq+aW9nm/i6O2QypN9f\nRnqEQY2a+IpIaWb2EcIcpwBT3H1WBYsj0m8pQBUR6SGd6S8pxWVzod9pVcpozjiZXA5Pldc7JZfL\ntXwG7k4qlcLdyWazZX02Oc/hzc2YgzU144NSZLKZDrfN19iKyPrDzE4B/hhfbufur1ewOCL9mgJU\nEZFu9NZbbzFv3jyWL19e6aIMCEtXNpJrzDE4laLRnMHDqqktcw7T+vp6Ghsbqa2tpaamBoBly5bh\n7owYMaLDQDKTzbBy9VKqG5sYUlXLisGhqe+wmmHtbpdOp9lkk0344Ac/yPDhw8t7oyLSL5lZCrgM\nOANYAnzQ3ZdUtlQi/ZvpDn/vMjPXMRcZmGbPns1bb73FhAkTGDlyZEuTUum695Y2QGOOuqo0qz3L\n4A0HsUFVefdWV61aRWNjI0OHDm0ToGazWUaMGNHSJ7WU5mwzK1csprqhiaGDhrJkCBjGyNqR7W7X\n1NTEggULeO2115g4cSJDhw4t782K9EFmhrurWUARZjYEeAjYE7gXOMrdmypbKpH+T1dPIiLdwN15\n88032WOPPdh4440VnHaD5M28FEAnR/FtlVurP2o5I/mGOVAdIwyUlMo5TsdT3QwaNIixY8cyduxY\n5s2b14XyikhfZ2YfAFYSgtMfAocrOBXpHrqCEhHpBvX19aRSKdWWdaMcgDtmRio2x82P6luOEEjm\nyGaXk82GGR46FaC6Q84JLfggFXdd7lQzo0aNYskStfQTGWjMbCfgHSANHOPu09Q8TqT7KEAVEekG\n2WyWqjKbnkqZ3MFD7WW+v2gu13ENZuvmjnsWMNybgdYAtfxryTAPKnQ+QK2qqiKTyZS5HxHpD8zs\nCOD5+HJ3d7+9kuURGYgUoIqIdBON3lpcfXM9jZnGTm/n8R8DSBNqUXOQ69RUM/nPpe2cqGXXoCZ2\nZbnwotwAVUQGDgu+CdwVF23h7s9UskwiA5UCVBGRCrn++us56aSTGDduHHV1dWy11VZ84hOf4Ikn\nnii6/kUXXcTxxx/PNttsQyqVYuutt+7SfqdPn94yeM9GG23ECSecwNy5c9fhnZSWzWW56CcXccIJ\nJ5Rd7ptvvpmJEycyYtgwttl6U4785CHc+8C9pIwQoMb1/v3vfzN16lR22GEHRowYQV1dHdtttx1n\nnHEGc+bMiUGotwSouVyWGTNmcPzxxzNu3Dhqa2sZN24cX/ziF5kzZ85a5ciRC02MC2pQlyxbwlln\nncXo0aMZMmQIEyZM4Iorrui2YyYifYuZVQG3AD8FXgaGuvvblS2VyMClUXx7mUbxFRmYVqxYwXPP\nPcekSZPKWr+hoYHa2lp23XVXjjjiCLbeemsWLFjAFVdcwYIFC7juuuuYOnVqm21SqRQbbbQRu+22\nG0899RTDhw9n9uzZnSrnbbfdxnHHHceuu+7K6aefzrJly7j00ktJp9M89dRTbLbZZp3KryOZbIZB\n1YMYudFIdt9t9w7LffHFF3P++eez2267cdKnPsWa1c3cestfeeHF5/n95X/gqBNPYtiwamrSaR58\n8EEuvPBC9t13X7bYYguqqqp4/vnn+eMf/0hVVRUzZ85k9OhRDBtWTSqV4s9/vpNTTz2Nbbfdls98\n5jNsscUWvPjii/z+97+npqaGF154gc0337ylLPXN9TQsW0xtrorBVTU0Wo4lqQwfP+TjPP+v5zn7\n7LPZYYcdmD59OrfffjvTpk1j2rRpLduvWrWKJ598kilTpnTrMRXpTev7KL5mNhx4EdiCMM/pae5q\nRiHSo0IfHT166xEOuYgMNMuXL/eHHnqo7PUzmYw//PDDay1fuHChb7zxxr7pppt6LpdrkzZnzpyW\n/48fP9633nrrTpWxqanJN998cx87dqyvXr26Zflzzz3n6XTav/jFL3Yqv7L2mWnyZ15+xhevXuzN\nmeZ2y/3uu+/6oEGDfOedd/ZMJuMNmYwvWrjaF7+9wneasJNvuOFInz1noa/OZNrd58033+xm5t/4\nxjd80aL53tDwnjc1LfaJE/f1mpoaf/31133p0qUt61911VVuZn7ppZe2yWdV4yp/f+Fcb1i4wH3x\nYm9avMj/+5f/7Wbmv/nNb9qse+yxx/qgQYN83rx5LctWrlzpD8x4wJsWN3lmTftlFumr4nVLxa+f\nKvEAtoY4nDd8udLl0UOP9eWhJr4iIhWQTqfZf//911o+atQoJk2axKJFi3jvvffapI0dO3ad9vnQ\nQw/xzjvvcNppp1FbW9uyfJdddmHy5MnceOONZLPZddpHIccZs9UYIDaZbcejjz5Kc3MzU6dOJZ1O\nh+6fOaiurubkk09m2bKl3D39rg77oI4ZE/ZXXV1NaxNfqKurpaamhuHDh+OJPPK1xoUjMDuOJXaV\ncrj1plupq6vj9NNPb7PuOeecQ3NzMzfeeGOb5bnmHLnGHLl6VbiI9CdmNhHIN/U40N3Vjl+klyhA\nFRHpY+bPn09NTQ0jRozo1nyffPJJAPbdd9+10vbee29WrFjBa6+91q37TAaC2Vz7wW9jYxhIKR88\n5wNRM2NI7RAAnnn6ybXC3MbGRhYvXsz8+fO57777+NKXvsSYMWNamkjnx6765jfPI5PJcMYZZ/DC\nCy8wf/587r33Xs477zx23HFHTjrppILC0zLNTf69PP/c8+y0y04MGjSozap77rknZsZTTz21dh6A\nZ9S1Q6S/MLPPAI/Elx9y95mVLI/I+kYBqohIHzJ9+nSefPJJTjzxxLWCoHW1YMECAEaPHr1WWn7Z\n229377gfyQC1o9FvJ0yYAMADDzwQNw5PZjBr1qxYvvlkc22DvSuvvJJRo0YxZswYDjvsMKqrq3n4\n4YcZNWpUm/UmTZrIjBkzeOSRR5g8eTJjxozh8MMPZ9ttt+Wxxx6jrq6uzfqhxtfjKMJpli9bTkND\nAx/Y7ANt3hdATU0NG2200drHLx+gdmL+VhGpjDhS76XAdcAyYGN37967diLSIQWoIiJ9xOuvv94y\neM/Pf/7zbs+/vr4eCMFUocGDB7dZp7t4Yp6WrLdfgzphwgQOOeQQ7rzzTr75zW/y8iuv8Nprr/K9\nH3yHe+65B4A1a+rJZdsGukcffTQzZszgjjvu4IILLuDNN99k8uTJzJ07F0u00Z05cxYf/ehHGTVq\nFL/61a+4+eabOe+885gxYwYnnXRS8TlLHYwUpNPUr1kDhONXLNgePHhw6ePnClJF+jIzGww8BnwV\nmAFs6u7vV7ZUIusnzSovItJDcrkcixYtarOstraWYcOGrbXunDlzOOigg0in09x9991stNFG3V6e\nfNPZfFPapIaGhjbrdJdkgFrO/KE33ngjp512Gj/72c+45JJLABi71Vguv/xyTj/9dDbYYBge50JN\nxaa3o0ePbqkBPuqoozj22GPZc889+e53v8uf/vR7AJqamjj11K8watQoZsyYAcAGG2zAsccey7hx\n4/jKV77Ctddeyxe+8IXWsru3NvFNp6kdEpoZNzY2kvMcadJtyp4fmbmNxFv2rGPp9XYwVJE+y8w2\nBf4DVAM/Bi7wwmYSItJrVIMqItJD3nrrLTbffPM2j3POOWet9ebOncuUKVOor6/n/vvvZ/z48T1S\nnvwUKsWa8eaXFWv+21nPPvtsy/+TQWmYl7R9I0aM4JZbbuGdd97hnhkzeeD+R3nx2VdbBjLa7oPb\nhblQ27l23Gmnndhll1149NFHW2pQX3nlDRYseJePfexwhsRAM1+e4447DoCHH364TT7eMngnkE6z\n4YgRDBkymHfeeWetYDvfD7bw+CWvcdUPVaTvMbMJwLuE4PQ4d/+eglORylINqohID9lss81aauvy\nkvNsQghOJ0+ezMqVK5kxYwa77LJLj5Vnr732AsJouQceeGCbtMcff5zhw4ez3XbbrdM+1qxZw4UX\nXsjNN98cah4Tl3nJ2tSOjBo1ir333ZCm5c1Yypg+fToAhx58GJ7zDkfyXbNmDel0aw1nJhOaF2ez\nmZZBj/IBar5pb2ETX8/lQhNfS0EqRSqV4sM778y/nnuBhsYGaqpam0o/8cQTAOyxxx5tC5J8/2ri\nK9KnmNnhwPT4ck93f6q99UWkd6gGVUSkh9TU1HDggQe2eWy//fYt6fPmzWPKlCmsWLGC++67j113\n3bXb9v3uu+/y6quvsib2mwQ44IAD2GyzzbjqqqtYvXp1y/J//etfzJo1i+OPP75NUNcV77//Phtt\ntFFrEBjbuBpxJNxOBKn5Soxnn3maq666igMOOIB999o31KACCxcuLLrdzJkzeemll5g0aRL5CHGn\nnXamtraWO+64k5UrV4ayxQD1mmuuAcJIvHmZTIZ/v/oa8xcswFIhQAU44ZOfpL6+nquuvKrNPi+9\n9FKqq6s58cQTC95E4r+qQRXpM8zsa7QGp1sqOBXpO1SDKiJSAStXrmTKlCnMmzePs846i1deeYVX\nXnmlzTqHHnpom5Fo//SnPzFv3jwA3nvvPZqbm/nxj38MhDlSP/3pT7es+61vfYvrrruOmTNncsAB\nBwBQVVXFr371K0488UT2339/TjvtNFasWMEvf/lLNt10U37wgx+UVfZrrrmGU089lWnTpjFt2rQ2\nae+//z4jR45ss+ymG27i7flvk/Mci99b3G65v/e97/H666+z1157UVVTy3NPPctfb/wTW265Jddd\ncx0pDHIh7P3yl7/Mu+++y4EHHsiYMWNoaGjg6aef5sYbb2TTTTflggsuiFPMGIMH1/Gd75zHd77z\nI/bZZx+mTp3KyJEjeeaZZ7jhhhsYN24cp512Wks55s+fz8Q9JrLfPnvx9+n3QDoNZpz2malcc9ON\nnP+N83ln/jtsv/32TJ8+nTvuuIPvfe97LXOw5rVp4qsaVJGKM7Mq4K/AscCrhJrTVZUtlYi04e56\n9OIjHHIRGWiWL1/uDz30UNnrz5kzx83MU6mUm9laj1QqtVZ+kydPbpOe3HbKlClt1j3llFOK5uHu\nftddd/k+++zjtbW1vuGGG/rxxx/vs2fPLrvsl112mZuZX3XVVWulPfnkkz5t2rSW10vXLPX9Ju1X\ndrlvv/12nzhxoo8cOdIHDx7s47bdzr9+3jd8+fLlnsvmfPWiBl+0aLWvbG72m266yY888kjfcsst\nffDgwT5kyBAfP368f+1rX/P58+f74sXv+ZIl87ypaYlns03e1LTYr7/+D77ffvv50KFDvbq62rfe\nems/88wzffHixW3KMXv2bDcz33/iPu7LlsU3s9SbFy302fPf8NO/fLpvvvnmXlNT4+PHj/fLL798\nrWOxcuVKv/f2e73h7QZveLvBG99tLPsYi/QV8bql4tdP3fEAhgHzCG0brgHSlS6THnrosfbD3HVH\ntzeZmeuYiww8K1as4LnnnovNSge2Y445hpdeeomXX355rSbBTzzxBHfffXdLzerSNUvJeY666jpW\nN6+mJl3D0JqhZe3n/RWN5OqzjBg2iOra0OCn4f1GVjZnGbRRNcOrq0tu29jYyKpVK0ilGhg6dAOq\nqjYgk1kGpKiqGsGSJUtIpVJsuOGGRbfPeY6lqxZTtXI1w4duBMOGwYoV5JqbWFqdIVVdw4ZDim+b\nt2rVKh69/1EO2PuAlmWDNhvU0vxZpD8wM9y935+0ZjYWmBNfnunul1euNCLSHjXxFRGRsmUyGWbO\nnMnVV19dsr9qMgBzd8g0k64OyzqaC7WYVCI/S6WALB0NCBzuwubLYpilASM/74uZkcvlwp3aIgGj\nu4PnaJOSSpHCsKyTq+p4RGIAz4UbklZleMbDVDNV/f5aX6RfMbN9gUfjy4Pd/YFKlkdE2qcAVURE\nylZVVcXSpUtLpudyOVJxQKEQJOZIraonna2BmvLmQs1vm4vBXTJKTMd5RLPZ9vMJLVVymEEmY3GM\noxDcuocyZrNZcrlc0UA7BKhxBN98ABvfVxojA2RzWdKpMgaVskSAmnH95RXpRWY2Fbg+vtzB3V+t\nZHlEpGMaxVdEpBvkA571Xb5mEuKIve6kMFK5HCmMnOfKClK95R/aBKikYq1oDrLtdJcIAaqTyxkr\nV6ZYvZpYiwrQGkSXmps1X/b4psJzDGQtBs4dvY9Mc4aUpbCUtdaa6hQR6RUW/IIQnK4ENlFwKtI/\nKEAVEekGtbW1NDY20tjYWOmiVNSoUaN49913gRgk5lqbyaZivFcqKEzKh54pszYBqqUs/OHK0eFc\nqKEGNzTxzWZjbSjgnm1Ty1uKedx1QQ1qy/voIEBd8v4Shg8dHmpQY82vppoR6XlmNhj4B3AuMJMQ\nnC6ubKlEpFwKUEVEukEqlWKLLbbgueeeW6+D1NGjR7Nw4UIymUxsJustgWE6xmZl9UP11hrMNn1E\n05CyMGVLewFqa+CZirW64N5ag9oyT2uJYDkEn06ILosHqO0Ft0uWLOH1119ny9FbtjTxBU01I9LT\nzGwUsBSYCFwEHOTu6++Pskg/pJ4wIiLdZPz48bz00kvMnDmTmpqakoMIDXSLFi3i1ltvZeNRG7N6\n1VKqGpsZOqiO+jQ0VcHg6sEMrhrcbh6ZXI4Vy5tIZWHYiEGkqmKT3OYcq1c005x2ajeoZnCJY1xf\nX8+aNStJp1Nks0NJp4dQW9uEWT2pVBXNzVU0NDQwaNAgamtr19q+KdtE/cqlDGrOUTt0BAwZEhKW\nLQtptYMYVDWI2uq227o7TU1NVFVVMWHHCYysHomlDGIxVYMq0nPMbDzwYnx5orvfVMnyiEjXKEAV\nEekmZsaECRPYcccdqa+vL6sp60BUV1dHU1MTO+2yE8sWv83g+mZGDBlOfTUsr4Eh1UMYMXhEu3k0\n5nIseqeemixsvHlta4CaybH83QZWkWPYBwYzvKr4n7GlS5eyatX7VFVVkclsQlVVHcOGZaiqeg+z\narLZOpYtW8aQIUMYMWLtsqxuWs3KxQuoa4INNt4MhsapcRYtoqFxNUs3qGZwTV3RqWaqq6sZMmQI\n2YYsmSWZtk18VYMq0iPM7KPAPfHlXu7+ZCXLIyJdpwBVRKSbpVIphg4tb67Pgejggw9m5syZHHvS\nsWTX1FJX5QwbvAE1KSdXZ9SkaxhWO6zdPBqyWdasrGJwDoYPr2sN8NxJrR6EZbPUbTCYYSXmQs1k\nMpitoapqMNnscNLpWurqnJqaBkLP0hFks1lqamoYNmztsqSaUtBQxwbNKYYOHw51dSGhqYnBa6rI\n1MKgIXXtv48Yi9Z7jqGEINWzcaqZtKaaEekuZnYu8Iv4coy7/6eS5RGRdaM+qCIi0q2mTp3K7bff\nzqpVq2If1BCM5acOzeQyHeaRg7AttB0kyYx0OgUOmXammgkDJMU+pOSnpsnPh+qkUmX0Qc2XPZX4\nU1lVRdrSkM2SzXXQl9ahMZtlRTbDikxG/VBFupmZVZnZXwnB6evAMAWnIv2fAlQREelWm222Gfvu\nuy933H4H5HKkrHX+UMt5+dPM5OIASQWVjekY6GUz7QeokGsZxRcgkwmlADAL25aaGqhlgKfkIEkA\n6TTpVJpUtuP34TknRxh5uNld/VBFupGZDSMEpScCfybMcbqysqUSke6gAFVERLrdKaecwjV/uAbP\nZtsEeemc43iHtaghQAzTzLQZxRdIV6UwIJstPZJufh5UsJZRhDMZMAs9W8y8Zc7WYnnk50ENAXLb\nABUglc3hdBCkepwKx8KcrapBFekeZrYVsBwYC5zt7p92L2d4cBHpDxSgiohItzv66KNZuWolt9z2\nvyHIi4MZpWNw1lHz2GzLFDNrp1nawvyoWW9Zr1Br4NlagxqmZU3H/2daRlku1sy3dYqc4gFqy5Q5\n7b2PXGyqHFokk7WwkWpQRbrOzPYG5saXh7j7rytYHBHpAf0yQDWz7czsh2b2uJktMrMVZvasmX3b\nzNaaL8DMPmRmd5jZEjNbZWYPm9mUEnmnzOxcM3vVzNaY2Vtm9rNi+XY2bxGR9UV1dTWX/fYyfnTR\nL8ZgypoAACAASURBVFj43mIYNAgovx9qPu7M9xVNsiojHedCLRUe5mtQ3VOYpVpizGw2H6BmScW+\npcWa+TqOlWjiC5CO76O9OV1b+sHGzTP5Jr6qQRXpEjM7GXg8vtzR3WdUsjwi0jP6ZYAKnAqcQ+h7\n8APga8C/gR8Dj5pZywR7ZrYt8CiwN3Ax8HVgKHCvmR1UJO9fAj8nzKN1JnAzcDbwNytoZ9aFvEVE\n1hs7f3hnPnXC0Xz1uxfg+RrUXKxB7aA1Xj6IK1aDSjp258xSsgY1BIc58jWo+dlostmqmN5+DWrJ\nQZLyTXxzZdQE52Jf2vgmsjEb1aCKdI4FlwA3AKuBTdz9lQoXS0R6SH8NUG8GRrv7Z9z9cnf/vbuf\nBFwI7Ax8IbHuRcAw4KPufrG7/xbYH1gAXJ7MNE7wfBZwq7sf5+5/cPfzgP8HTAFOKihH2XmLiKxv\ncp7j3K98gUWLF/PFs88mm82WXYOayzfxLVaDWkYT38I+qPnZaPI1qNBBDWps4puyVNso2SwMlGQp\nyOXaD7SdOEhS3KMR/urmSvedFZG2zKwGeIhQGfEwsJG7L65sqUSkJ/XLANXdny4xUttN8Xk8gJnV\nAUcBs9z9+cT2q4GrgO3MbM/E9ifH50sL8r0SqAc+nV/QhbxFRNYrnssyuKaGu//yF96YPZvPfvWr\neFMITPM1j8uWLSu6ba69Jr5pI21hTtFiAWq+aW0qZeRyYfvYwjgGqFZWE9+io/gCpNMhcM1k2h0k\nyXMe3kfcvNlb5z9VLapIx8xsE2Ap4eb/xcBkd2+sbKlEpKf1ywC1HVvE54XxeWdgEPBYkXX/GZ/3\nSCzbE8gCTyRXjD+G/4rpeZ3NW0RkvZLLhmB0+LDhTJ8+naUrVnDC6V/ivXfebal5POKIIzjvvPPW\nChI9184gSSkjnTLIQqZEgAr5+VfDn7l8DWoYyTc2041/ATs1SBK0TDXT4VyoHpv4xiBbI/mKlM/M\ndgQWAUPg/7P35nF2VWXe73ettfc+59SQVEIGEgiDMiokoRFQEBPj8EoTB1oQUXEAvHK1sXkduQ6I\nt73abdui7cDr2wg0toATIvTFobkvKuKlFSFhUAEFMpGQocYz7r3XWu8fa+8zVJ0aQEIlYX0/n7Kq\nztnD2ruC5/zO73l+D+dYay+xvvTA43lOsM8IVOHecXwSSHA9CgBLs+9buuySP3ZA22NLgZ3W2mSS\n7ReIfEbBUz+2x+PxPKewmegUSlEqlfjhtddy9OGH84pTXs01V15DqlNuueUW7rvvPtauXdvhpppM\noHYxUAFQmROpuwi9vP9UCJHNQXUCVQg3mgbyUTOTz0K1zR7ULi+TSqGEQugZlPhmIUlKCJ/k6/HM\nECHEq4AHs19PstbeMJvr8Xg8zy77jEDFleW+GLjUWvtI9lievNutHKQ+bpv858lKR8Zv/1SP7fF4\nPM8ZrLVYo10pbGZVFnp7+fwnPsGN3/82P7jhB5xy8ik88MAD3HrrrRx++OG8+MUv5uGHH872d8eR\nqvvLVBBk5bnpJO5n1n/qUnzd41m+UXPUTOv3LiFJmTMqZJfzB4G7rmkcVGssFlemHGWLSPPDPYWJ\njfV63fesep4zCCHeD/ws+/Vga+1vptre4/HsewTTb7LnI4T4e+B9wDestf/Y9lQ1+17osltx3Db5\nzwsmOU0R946n2rbtUzl2k8suu6z58+rVq1m9evUkp/R4PJ69k2YKLm0puFmU7rFHHsUPf/pD/uO7\n/8GFF16I1przzz+fCy64gFNPPZVvfetbHPOilwKTpPjiRs0IwGiLsdaFJmU4MecSfMW406epS/IN\ngskd1I6ApG4CVSmEEEht0ViMNW7b8ffAOPdUAEGe5KsgZOYOaq1WY2hoiL6+PubMmTOjfTyev4Sf\n//zn/PznP3/Wz5tVwl0LvAV4FFg5Sd6Ix+PZx9nrBaoQ4jLg48BV1tr/c9zTT2Tfu5Xa5o+1l+g+\nARwlhAi7lPkegCv/Tdu2fSrHbtIuUD0ej2dPZ3BwECklAwMDM97HYhFmnMjLBGpgLFJK3vr2t/Ke\nC97DXXfdxZVXXsmNN97I0UcfzVlnncW573o3H37/pV1TfKEVlGRS19s5XqC2HMeWg5qPmklTlQlU\n12NqjMHm/aZME5AErVmo2RxWbfQEpzd3T5EghWgJ1HzUzAx7UHPxHMfxjLb3eP5Sxn9w/ulPf3q3\nn1MI0Q/cAxwGXA+ca+00s6g8Hs8+y15d4puJ00uBa6y1F3TZ5H5cCe7JXZ57cfb97rbHfoMbr3fS\nuPMUgZXjtn2qx/Z4PJ69Dq019XqdarX6lMpMjTVgTGfIUJdZqEIIXvKSl3D55ZfzzW9+kwULFiCE\n4Gtf/mf+6ze/gkYdc+pL0Jd9ouP4TqDSNck3L/F1/adigkCdbhbqlAFJ0BKotu1ax9PsPxVIIMxL\nfF2I8IwFar6uNJ16LI/Hs7cihDgIGMWJ04uttW/x4tTjeW6z1wpUIcSlOHF6rbX2vG7bWGvLwC3A\naiHE8rZ9+4ALgIettb9t2+U7uDLei8cd6t24FLlv/wXH9ng8nr2OduGWJN3y47pjrXUCtb3EVykQ\ngsAKapUq/3HLf/DBD36QE044gaVLl/KVr3yF4447ju99//s89Nh2Tn7xy+D365G/ugv51a+3GlNp\nOahkLuaEc7fNQB1n4DZnoU42aqajPLlrjLC7JsXks1CbDqrIHFQpETi3F+GWNxORmq/LGNM1zMnj\n2ZsRQpwIbMh+/W/W2i/P5no8Hs+ewV5Z4iuEeB9wGbAR+P+EEG8bt8k2a+1t2c//F/AK4GdCiMuB\nMZzgXAKc3r6TtfYBIcTXgL8VQvwA+DFwNHARbt7pdXQy42N7PB73JvupOnGe2aVer1MulwGQUtLb\n29t8TghBqVRqupDt5A7qhD7OIEDplP+89f/lO9d9n1e+/JVcfvnlnHDCCRQKrqU/NYatO2qImoWh\nne5cu4awWzYjDlzmjqPcJ6xW09VBdf/GJN0dVIEQKhOo7skOBxU70f0dTxBMPWomc1CFao5BRQlB\nai1agTKuDzWfizoZ4z8g6HavPZ69ESHE2UCezvtCa+3vZ3M9Ho9nz2GvFKi4+aIWWAb8W5fnfw7c\nBmCt/bMQ4hTgH4BLcLNLfwe8xlr7v7rsezHwOPB/4ETmDuBfcG5tB0/j2B7PcxJrLQ8++CBbtmwh\nDEP/JnsvIo5jqlWX9xZFET09rXByYwyNRoPFixezfPnyjr9rq4+zi0BNFK9fexqvO+sMlvQtafZ+\ntvZ1/yMAhgZbj6+7pylQWw6qmSBQnagzWCuQstWDKrOlGOOSfIXQXYOSmiW+kzmoAEq1knxn4KCC\nK/NNrUVL10syEwd1vEAtFotTbO3x7PkI9x/854CPAjVcUu+O2V2Vx+PZk9grBaq19l3Au57C9n8E\n3jDDbQ3wxezrGT22x/Nc5YEHHqBarbJ69eqmS+bZO6hWq9RqNQCCIGDu3Lkdz8dxzO9//3vuuece\nTjjhhObjxhpEtyTcZlCSG1qtrSYQnS9F1h0AKUAMDbUeX3cPrH094NxbpSSkmlQbF42bb9cs8XUO\n6vjTx3Ge5Bs3nxvvoApLZ3nyeDKBKtJ0SgcVKZq9NO1JvjCzJN+nW2Lt8eyJCCEKwE+A1cCvgFdZ\na+tT7uTxeJ5z7LU9qB6PZ+9Aa82WLVs47rjjvDjdC2kXSN16IKMoYvny5QwODlKvt95ndoQkdROo\nNgsNMhPDf4y1LQd1uOWgivX3dWyngkzw6W4lvm7MDHSaoOP7ULs5qM0e1KlKfJVqlfh2y3OxbtBN\nPmYG2oKSpFvvTBzUODbs3Cmp171A9ezdCCEW4KrSVgNfAF7mxanH4+mGF6gej2e3UqlUKBaLRFE0\n20vxPA3a+4WttV3TZPMRNKOjo5375T2oXRSiysRZN/fR4vKQJMCuXc3HxX0PdGwXBFnwUDpRoOYp\nvkLISQRqkK09/33yEt9aDSZoc6VQwgnUbim+NksqFlI0S3yfqoPqSqjBGEmjodBa+/5tz16JEOIo\nnDjtB95qrf2w9f+YPR7PJHiB6vF4divGGN9zuhfj0mNBZGW4kyXJKqU63NbchQQ6HdTs30KQbdrN\nQW32oArRUeLLI3/GZoFN4PpQhRATRs3kIUlCdIYkwUQHVWZu5oSQpKw8OU4EQ0MwMjJukUGAEAJp\nLMaaicKxOWam9ULbTPKV2RqncVDze6+Uwlq3cO+ievY2hBCvBP6Q/fqSLoGTHo/H04EXqB6PZ4/j\nN7/5De9///s55ZRT6OvrQ0rJv/1btzw0uOyyy5BSTvr1VJzbW2+9lZNPPpm+vj72228/3vSmN/H4\n448/Q1c1kSeffJILL7yQZcuWUSgUOPjgg7n44osZmaCGpr7OL36xe8v84OAgH/rQhzjssMMolUos\nWrSINWvW8Ktf/WrGa/zpT3/Ka15zGsuWHcDhhx/OOeecM6N7YjOBKtW4qIMsqUjC5CNaADIHsj0k\nSViLvX99a0PVChsaL1DzMTMgu1UYY0zuoGZO7ngHNStP1sap2zget8hxs1AnXIeZWOILmYsqBVq4\nbXKntRutDwcEUoYY4wWqZ+9CCPG3wH9mvx5irb1rNtfj8Xj2DvbKkCSPx7Nvc+utt/L1r3+do48+\nmpUrV/LrX/96QtJrzhvf+EaOOOKICY+vX7+ef/qnf+J1r3vdjM554403cuaZZ3LcccfxhS98geHh\nYb70pS9xyimncPfdd7NkyZK/6JrGs337dk466SS2bt3KhRdeyDHHHMP999/PFVdcwS9/+UvuvPNO\nSqXShP2+9KUvsWDBgo7Hjj/++AnbbdiwgdWrV1OtVjn//PM54ogjGB4e5v777+eJJ56Y0RpvvPFG\n3vzmN/OCFyzn0kv/kXL5Sf7n//zGjO6J0c4ZnSBQAYKAIA0gTUmDKXpQBTA0DIA9eBliwyZYfy+8\n5BQgT/KFdNyoGSdQXQ+qEJ0Oam7ma527q5M7qAKBsfkYGkgSCPMwpqy3Vlr3pDaaQLau1VqLsWBF\nQhoPocI5BEE/gRAk1qKlJTDO/RWy+79trTXGuBLqMAyJYy9QPXsHQggFXAO8DTcZYYW1dnSqfTwe\njyfHC1SPx7PH8d73vpePfvSjlEolfvCDH/DrX/960m2PPfZYjj322AmP/+IXvwDg/PPPn/Z8SZJw\n0UUXcfDBB3PHHXc0R6mcdtppHH/88Vx22WV84xvfeJpX053PfvazbNy4keuvv56zzz67+fjJJ5/M\nW97yFr74xS/y8Y9/fMJ+b3jDGzjooIOmPf7b3vY2jDHcd999LF68+CmvL78nBx64jO9+98csWrSY\nJBni1a9+FS9/+cunvSc2cyRFt/LuIEAJhUiTSXtQsU6YiUFX4mtfvgpxzb/D+paDKoKsv1Nb2rtA\nW3NQnYPaLlCFcCJVa+eiSpkghOtX1Vq7UuW2kKTUtuzXDoEKHX2o3RxU5+OmCAHG1IH+tj5U4bbR\ntiOBuOMQxmCMIAgkSiniWHiB6tnjEUL04UbuHQF8F9dzOvGTKI/H45kEX+Lr8Xj2OBYtWtR0D59O\njkalUuGGG25g2bJlvOY1r5l2+1/84hds3bqVCy64oGPO54oVK1i9ejXf+c53Ju29fLrcfvvt9PT0\ndIhTgLPPPptCocDVV1/ddT9rLaOjo13DinJyB/YjH/kIixcvJkmS5izTmZLfk3POeRuFgsDaOtYq\nXvCCF7Bq1app78l0DqoQAqUtFjtBpJrsby4EMJiV+L785e77fa0k33wWqtWWdAoHdfykmOn6UJsh\nSaLloEL3Mt9Jg5KyHlQhDBLI359PSPKdIijJCdSWg5okTPl393hmGyHEMmAMJ04/ZK0924tTj8fz\nVPEC1ePx7HN873vfY2xsjHe+852Tlga389vf/haAl7zkJROeO+mkkxgdHeXhhx9+RtfYaDQoFosT\nHhdCUCqVeOyxx9jVlmCbs3z5cgYGBiiVSpxyyin85Cc/mbDNrbfeCsCyZct47WtfS09PD319fRx5\n5JF8+9vfntH68nuycuWLEEKjdQObuYkvetGLpr0nNhOdLqhoHHmSb9Z/Od59NFl4kLQGBl2Jr1jz\nKvf9vgddvS0uIVcJAbolaqG9XDcfJdP19M0k31bZr1tHtxJf6CJQgwAlFUKbCSLbWuucYJGN2sFi\nTDIhyZcpPvfQ2glUpZQLg7LBpEnKHs9sI4Q4AdiY/foaa+0/z+Z6PB7P3osXqB6PZ5/jm9/8JlJK\nzjvvvBltn/dkHnDAAROeyx/bsmXLM7dA4JhjjmFwcJD1bSWrAOvWrWN42ImyTZs2NR+fN28e73nP\ne/jqV7/KzTffzOc+9zk2bNjA6aefPiFA6qGHHgLg3e9+N8PDw1x77bVcddVVRFHEueeeyzXXXDPt\n+vJ7smjR/k2Rn2vAvPd0qntitUYgJi3xhcmTfPPziOoYwhhsfx/iwGXY/RchyhXso39qbpvPQk3T\nth7SpuB1L3GTC9Tus1CttQiY4KCmaVMbZydXboxOlxLfXGTnPa7uuEkzyTfNk3yncFDzawpDkWVL\n+aAkz56JEOIs4DfZr8dYa386m+vxeDx7N16gejyefYqHHnqIO++8kzVr1nDwwQfPaJ+8/LVQKEx4\nLnc5n2qJ7HRcfPHFSCl505vexI9//GM2btzIj3/8Y84++2zCMMRa23HOv/u7v+OKK67g3HPPZe3a\ntXzoQx9q9pf+9//+36lUKs1tx8bGAJgzZw63334755xzDu985zu54447GBgY4GMf+9i0pdP5uYMg\nytKCXQCvMRBmjZiT3ZP2Hs4J9bXgLEshUJnY6+Y+AsjhrLx3/jz3+ArXa2zW3dPcNgjc8bWe3EGd\nvMS3cxZqvp+xxqX4tjmouc7ucFFzgZqmXa6B7Njt63I7B0IgAkE6zaiZONbNawxDCIKAJPEC1bPn\nIBz/D67XtAEsttY+OMvL8ng8ezleoHo8nmcdYwzbtm3r+BodfWYCHr/5zW8CcMEFF8x4n7zvtNFo\nTHiuXq93bPNM8dKXvpQbbriBsbExTj/9dA455BBe97rX8YpXvIK1a9cCTmBOxfz587nwwgsZHh7u\nCJLK+3fPOeccgqDVAzowMMBrX/tatm3bNm3Jcn69tVodpQRh6Pop0xRqtVrHNuPJx7RIIbsL1Cyp\nSGXu43gHVWelv2LElTjbeQPuieXL3ePr1zW3lYFwjmTamkU6Uwc1TSdxUJnYg5pXY48XqEoqRJdx\nOUZnZci0O7tOWAZCIJRAw5QCteWgtgRqmgpf4uvZIxBCRMBtwMeA/x8YsNZun91VeTyefQEvUD0e\nz7POxo0bWbp0acfXxRdf/BcfN01Trr32WhYsWMAZZ5wx4/2WLl0KdC9ZzR/rVv77l3LmmWeyefNm\n1q1bxx133MHWrVv5+te/zqZNmwjDkMMOO2zaY+QucXu/6oEHHgjA/vvvP2H7vDx3aGhoyuPm9+TJ\nJ7cSBIIgcOWqWsspS6Kh04HsKlCh2b9Jmk4Qd3nekBzKrilzUFmxwn1f15bkq/IkX5pS0JipBWpm\n4GKMwtqJDmoekiSFxGQpwLm53mFeZg6q0AZjTYcrbbIQ4fYJMtamWGubfaipdON0JhOpaVb+G4aK\nMKQZlOQdVM9sI4TYD9gBrAEuB06x1tZnd1Uej2dfwY+Z8Xg8zzpLlizhtttu63gsF0R/Cbfccgvb\nt2/n4osvbpahzoQTTzwRgF//+tesWbOm47m77rqLuXPndp21Ohm33347xx9//LQOKLiE1uWZMwiw\nbds27r33Xl7+8pd3DVEazyOPPALQMUrmpJNO4hvf+EZHD2vO5s2bAZeUPBX5Pbn33t+wdu0qlMrH\ntsDdd9895T2xOAdVCDFRHeYoRSADRFrv0oOalfiOZCW+8zKBuvKvABD3tyoI81moibZoa1FCYIzO\nhKecSh+TJAKtFUpJrNUTHFRrBCjX/xlFbr8OBzWre1YItLUYa1BCYU025kbkDqpCiCATqAmhcM6t\nlrhRM6lFqIn3KUkMQkiCQBCGLizJGIXWKcYY5GQX5/HsRoQQRwJ/zH4911r777O5Ho/Hs+/hX908\nHs+zTqFQYM2aNR1fRx111F983Ly8d6rZp9u2beOPf/xjs0wVYNWqVSxZsoQrr7yyo5dz/fr1/Pzn\nP+ess85CdQv7mYTvfe970zqU3TDG8P73vx9rbccMVK01IyMjE7bftGkTV1xxBQsWLODkk09uPv6G\nN7yB/v5+/v3f/73jerZu3cpNN93EkUceyfOe97zm45Pdk8WL9+f737+eer1GGLrrf+CB+7jzzjs5\n44wzJr0nxhqEtUgmKfEFCALnPqZ6ovuYl/gOZ/dwv/0AkEcejS0WERs2YbP7K5RwnaaZQG0dRyCE\nnFQft5f5SjlOoGYOqs1eIvP+2yBwvaXdXNSOoCSbublSIHHCXspCduyJSb7dHFStdXPEjFJkDjZA\nkK3Bu6ieZx8hxBpa4vRkL049Hs/uwDuoHo9nj2PDhg1861vfAuDBB51bdvPNN7Nxo5tg8Pa3v52D\nDjqoY58nnniCn/zkJ5x00km88IUvnPTYl1xyCddeey233347q1atAlxv35e//GXOPvtsTj31VC64\n4AJGR0e5/PLLWbx4MZ/+9KdntO5rrrmG8847j6OPPprPf/7zU25bLpc58cQT+Zu/+RsOOeQQRkZG\nuP7667nnnnv47Gc/21wbuNCjQw89lDPOOIOjjjqKefPm8dBDD3HllVdSrVa5/vrrOwKeBgYG+MIX\nvsB73vMeXvziF3PeeefRaDS44oorSNOUr3zlKzO6J5de+ln+9m/P5/TT13LBBefx5JND/I//cQUL\nFy7kYx/72KTX1j5HFClpGIMCgnax2pbkG+OSfEMVZvs7r7YpUOfPb+5jX3gU4nfrsOvvQax+BSiQ\nQmDTdoFqcZ+/imkFqtZB5kRqjHFC2VqDbAtIypcdRS7JN46hadDns1DzoCQF1liMtdist9UJZbeD\nMQlh2IvAOaiTJfkaY9C60wVuD0pK07RrqJfHs7sQQrwX+Fr266HW2sdncTkej2cfxgtUj8ezx/HY\nY49x6aWXNn8XQvDDH/6QG2+8ESEEL3vZyyYI1GuuuQZr7bThSEKI5lc7Z555JjfffDOf+cxn+PCH\nP0yhUOCVr3wl//iP/9js25yOPD23UCjQ29s75baFQoGVK1dy3XXXsXXrVnp6ejjxxBP56U9/yqte\n9aqObXt6ejjzzDP5r//6L2666SbK5TILFy7k1a9+NR/5yEd40YteNOH47373u1mwYAGf//zn+eQn\nP4mUkpNPPpkbbrhhwrzXbvdEa81pp72eK64QfPObX+WjH/04URTx0peu4uMfv5QFCxZMem15D6qU\nEiMEg0mCFILFeZ0sdJ2FGhJmAUvZNs0e1Pmt/ZYfC79bB+vugdWvyEp8BWjjQocygekk7tQlvu46\nO2elpjptBjx1E6jVqhOozT9vWx/qeAdVSJN7sE2Bam0ryVdnSb6qi4PqxLJoOqhAWx+q8A6q51lF\nCHE18E5gE3CstXZiSYfH4/E8Q3iB6vF49jhWr17dNipkZnzsYx+b0tXLufrqq7n66qu7Pnf66adz\n+umnP6XztnP77bdz2GGH8fznP3+CAB5PGIZcd911MzpuFEX867/+61NezxlnnDGjsKhu98Rai9aw\nZs0reOc71xKG86lUxiiXNUmSoLV280K7XGczJEkKUiGwgLaW1JiWi5olFQVWgLXNPlSTnVsIgRga\n56ACrFwBfAvW3wc4ca2UhFSTaoNVktxBdaK7+zXnAtWYfNSMxdosyXdcgm+7QIWJJb5KKFfia1oC\n1S3OIIUrNZYyBERHUFKs3H2ZykENgokOaqXiS3w9zw7lcjn/8Z3AD4A3W2t9jLTH49mt+B5Uj8fj\neQZI05Tbb7+dyy67rGO0y95KPrbF9T46sReG7rqMyVJoJxl3YrM5qFIFpG29pfH42atB0FkeS14e\nnL04ZSW+NutBBWDFce77ffe3DpM5jDptlehaK5iqxDd3JXMHNReBqU6dQEVg2npQs+Ui3dhTmp+f\nBFmJsHa9tNBe4tvsYgXocFFDISAQJJPMQjXGYAwoJTsEchAEaC39qBnPbmfz5s309/fnv37UWnum\nF6cej+fZwAtUj8fjeQYIgoChoaHmDNO9nVygKuV6OcFdY7vgy0OFxmN09h5WunTbnHi8K942aiZ3\nUG32PwKaDqqY3xKoYkWW5PvgH51SBFQgszW396CCCyfqfn158JG1Aca0ZqEmaTKpgwqt3tNmmm/m\noHbMQs2rlIXJXNxc6Lb6UIOspFoLXJKv6RSpcayzW9Q6uRPIAmsVxljvonp2G7/73e9YtmxZ83dr\n7dRN9R6Px/MM4gWqx+PxPMPsC+M/ksQAhjDsFFiuMteVn07qoGZCdEYOqlSItJWAawCMdUK4WeLb\nJlAHBrAHL0M0Gpg/uAAtGUgEYLTNSsNdD+pUJb7Z6RFCkqYCpURW1qxbDmoXgTph3IxSrXmuuQts\nrJuDismkfe6gup1nkuSbpu4ehmHnv6XxQUnT0UgbPDH2BLWkNu22Hg/A97///WZf+/333z/N1h6P\nx/PMs/e/i/J4PHs0SqnnVDmilJIkSTrGpuyNOAfVEAQubAhcv2cQKIJAkaa6w0FN07Q5diZ3UIVU\nHQ5qal3pa5MgyGah6q4lvmIwc1D36wxksiuyubHr73XfFSghsNqSWtdL6npjJx8zk50eaCX5Wpt2\nlvjORKBKiZQKYSymrQfVAkLaZg+qu395iW9CIOWUSb7uA4JOBxVaQUlpOrOgpIZuAFBNqtNu63lu\nY63lk5/8JGeddRZBELBt2zaOOeaY2V6Wx+N5DuIFqsfj2a309fWRJAnV6nPjDXJvby9BEDA8PDzb\nS2kymqaMPsVy0CRxpbJB0BJYAGGoMhFumkFJaZoyPDzMwMAAADYTau0OapgpxUZ7mW+mEKU2naOa\nFQAAIABJREFUWCza6FaJr7Uw5O7heIHKimPd9/Xr3PNKoASgIc0cVGunHjPTdnq0VijVmoUqTKvE\n11jL9rRBOfuQZbKgJCkkVmcuqqE5Zqa9B1XKAJBZUJJxLqpywv3pOKgzEah56XSs473+QxPP7iOO\nY1796lfzmc98hhNPPJHR0VEWL14828vyeDzPUbxA9Xg8uxUhBM973vO4++672bVr1z7/JlkIwbJl\ny9i8efNsLwVwKbGJtSRA8hSSkdPU4kp8Wz2o4Nw7l0brelR37drFb3/7Ww444IDsuU4H1eBeaEqZ\nDRmPc1ABl+SLE1MuxRdEeQyhNbavt6UKM+yKle6HLChJBPmoGZsJVIsTp5OPmWk7PVoHKKWwVk9w\nUGNrQEDF5DNNnUi0tk2k5r202pUqW2ud0B7XgwqtPtS8zFdko2Z2l4Pa6u21TTfV42ln165dLF68\nmNtuu42LLrqIu+66i1KpNNvL8ng8z2H2/qhJj8ezx3PYYYcRBAEPPvggo6Oj045g2dvZsGED3/rW\nt1i1atVsL4XEGCpZKW5BSkp5fO00bNo0SprWWLo0Igh6UcqJRGMMQ0Nj1GoNenoCFixYwGGHHcZh\nhx3W2lk7caUzdTg8JJCRhF7dGZQkhOvhREAWMmRRYCxyOJ+BOm/C2uTKLChpfSZQlUBCW4lvPgd1\n5g6q6xvWpGlKFGYOKtINrJGdY3LC0InTOM5Ck5RC4mahGmuQJnNMRS46WyLTlfk2MCYmFCVQgtQa\nGJc3lQvUMJRYa5oiNwxdsq8xEq1TTDZvthu2bXwPQD2tUwyKk98Qz3OOhx9+mCOPPBJws6Tf8Y53\nzPKKPB6PxwtUj8fzLHHIIYdwyCGHADzlGad7G3/4wx949NFHOe2002Z7KVS0ZrjmGibDSLFonBvZ\njTS13Hffk1g7zDHHzCEM90PKQvP5LVt2MDxcpqdHsWDBPObOnduxf+6gWqncSJZEkBqJKUEqbef8\nVKUIZNBM8hUqcj2oI4PuGPMGGK8xxaHPx87pRzy5A7ttK2L/JSgpITEkWgMWa6eegwp5SJKbhepE\nnitbJgCBxCJA2uYxGtYS4AzdatUJ1N5eJgYl5QJVOoHa7qB29qH2IAIxYRaqC2uySKmQMiGOd6LU\nHIKgr7lupQLSNCVJEgqF1t+m4++YiVNZq2OKBRqpd1A9LW6//XbWrFkDwK9+9StOOeWUWV6Rx+Px\nOHyJr8fjedaRUu7TX3/913/Nj370I6y1s76W1FrskMEOGTTOqJt2n9RtUyyq7LGw4/meniKFQkSS\npBPKTPM5pAJBKgTG4hxSIK07R3J8ma8UshmUZMAJ1CkcVKTEHvtCd751vwNABe4cSZI7hp0zTCdD\nKbDWCWkhsl7YNMUa4dRrm8DN3d+uSb6iVeJrTC5M8w9i2kt8W0m+oZQIJUjoHDPjZqCKTDTH2WOV\n5vMzLfNNTYqoVCmO1QkrdbTVJNqPpvHAFVdc0RSnjz76qBenHo9nj8ILVI/H43mGecELXsABBxzA\nbbfdNttLIWkYMK7P0zYs9Rm4141GPoMz77vsfKmIooggCIjjZKJAxYIxSCHRQmAMzZEqpt49KKnd\nQW2m+A5nI2bmdRGoAMvzoKT12WGyWahJ55qnqyZ3s0WDTJQ7gW3S1LmnwjmozftiTNs+oDUYAyjl\n3FpjnMjOBaqEfNxNjhAKF5Skc48WI7PRNFkwktYaY9yHBErl6cYaYzInPAtKiuOpg5JSk0IcE8iA\nQuLW5PtQn9sYYzj//PN573vfy9KlSxkeHubQQw+d7WV5PB5PB16gejwez27gHe94B9dcc81sL8MJ\nVKBPSWzdUJuBQI1jt42rHBUTBGqhECGEwI0MtR1jhIw1YFw4UCoE1oDMbEihJXFCZx9qHjCUph3u\nY17iy36tGagdrFjhvq9zSb5K5Q5qLthcr+1MBCrko2YE2qboVGMNmUhtbWtoBU11uKjjQpKMcS6y\nFBPFPbRcVGNiF5SUJfnmfajOQQUpRZsLC8a4Waa5QJ2Rg5qmKKmIkJCm1NP61DfEs89SqVRYvnw5\nV111Fa9//evZsGHDhPJ8j8fj2RPwAtXj8Xh2A+eccw4//vGPZzXNV1uLaRikEBSUQtQNqc2Tbicn\njjXWaoJAIoSkltQ6hE0UKaQMEEKhdaeLaq1FWOscVJzLGGS9oJEQNOqQWNtKc85KfJWxGGvQ2drk\nSOagzp/ffZFZUBL3PQC4JF8BGG0w1mZO5fQlvrlANSZP8k0xOsVa4XaW3cfkZIHFTqBKiZKBE6g6\nda4q7r53e5lt70MNhYBxSb5uBq0b6WNtKz1J65ZAjaIQrUVz1E83Up1AmjoHVRWQjYREJ+5DBM9z\nii1bttDX18eDDz7I5z73OX74wx8SBD6GxOPx7Jl4gerxeDy7gfnz5/OBD3yACy+8cNZG6yTGYBNL\nIAVCCQoIbGymLfONYzdCplCQaAND9SGGakMd1xFFYdcy36aDikBLibWghKCnx43gSequLzVpE6gI\ngcqWlGRurBzKHNT583FJS51rFseuwEqJeOgRqNezWagCk5jMiJxZiW8eapymyglUk2C0ASs7elCL\nmdJtZOse34eqwswVTRMXAtZlxExz7WLcqBklOmahdo6YyUuWFS7EqY4QraCkOO50sNtJGzWSGHbt\nDKnXBYXUunEzPizpOcU999zDgQceCMAtt9zCJZdcss8nqXs8nr0bL1A9Ho9nN3HJJZewceNGrrvu\nulk5f9zQYCGKJLIkKSqFmUGZrxNImkJB0tBOgY2fo1kohIThRIFqsWAtxoIVAmFEtr0TdaGVNOJx\nZb5KobIS1DzER+QO6rwBkm1PYHbu6Fij6OmBw5+P0BrzwH2ZQAWb6myW6tMp8ZUYDMZojO7sQW3O\ncTVOvEeRe7pVUeyCkkySoK3BYvKYpgnnzGeh5iW+jEvyTdNcoIqmgyplT7bPzMp8tdGQJMSxZCSM\nGK1AQQuwfh7qc4kbb7yR448/HoD169ezdu3aWV6Rx+PxTI8XqB6Px7ObiKKIq6++mg984ANs3Ljx\nWT9/UnfiJixIZFESSYloWBJr0ZOVhaaQphqlXAJxvS31tb3Mt1AoEAQBjUba1UE1UoEQCOsUopRQ\nKrlS2VptYpJv3oeaZjNbxfCwu4b+XnZVdzI8tgMancLKLj/G/bDud6CcU2tTjTMipTNAZ+CgulEz\nLqG45aB2pvgGUhIKgcW5v7mLaW0mUpXK0ogNqdUgLXJSB1U1HdFAWISCxNJ0UONYN9eGm8SKUrlA\nrWOtbSb5Jkn3oKTUpJAkVIykGgUMoxA6gkbD96E+B7DWctlll/HGN74RKSVbt25l+fLls70sj8fj\nmRFeoHo8Hs9u5Pjjj+cTn/gEq1at4s9//vOzeu48ICmIBCIEJBS0E0KTlfmmqXtzq1SKkIJEa0Sm\n0tpLQwsFhVIhxkjSNHbzQ2nNQDWZ4yjHCdSClMQx1PXEJF+hDXGaOahZiu9YyVmc2mgolzvWaldm\nQUnrnYMqAZMaUuvCiWZaxeiqjAOMkWiTopMEa50YFbL1QlnIy3y7BSVlAtWmKYlOQehJHVRolfkK\nmyACgWlzUFslvvm2KvuKAIsxdcIQlFKTOqh5QFJsAqwKqEcRcUMRJgZjjR83sw8TxzGnnXYan/70\npzn++OMpl8vsv//+s70sj8fjmTFeoHo8Hs9u5qKLLuKSSy5h9erV/OEPf+h47uGHH2ZkZOQZP6e1\nlqTh5noKtYsk2YEoCAoyS/PVuut+WrsxJ0oZEpuCkBSCAoEMOuZoulErYSbsWmW+NjuullmJbWaU\nSpmJ1KJAWUG11krEzYOSSFO0cQI3d1DN3DnuuFjnoLaJMbHiOPfDffchhEAp6a47tU9DoCqsVVhS\nrHE9qEYIt+7sQFMK1CBws1BT7RzUKXpQYVxQknQqONEGayxad/a55sdouai1Dge1Ww9qatKs3DhA\nhAGmEDFSM4QNd2zvou6bDA4OsmTJEn7605/yvve9j9/85jeUSqXZXpbH4/E8JbxA9Xg8nmeB97zn\nPXz2s59lzZo1/OAHP2gGDt10002cdNJJPPzww8/o+dLYJcHKoIEQFms1IkqIpIS6IbYW06XMN0ks\nxhiU0lmvoqAYFCkGRWB8mW9EECjq9bgpUJsOaibqhHEJvnmabk9PlzJfpZqzUBOTOr920IUkibnz\nEQhMLjYrleb5RZbkK+57EKzNejYNaWKRUk2b4JvjBKrEmBCsIU1ciq+RAilaL5SRcF5ynkLckeSr\nFEoqRKLRNgtJAiZ7mc1HzeRJviJoBSXlDmoe4JSPzJGyCAiMaQDG9RZLRRybpoOdkzZqVFOLCCOU\nEkQ9AXUpsQ13n30f6r7HI488wn777cfg4CBXXXUVX/3qV5Ez/Y/A4/F49iD8/3N5PB7Ps8S5557L\nd7/7XS699FLWrl3LY489xkc+8hE++MEPcuqpp/Kzn/3sGTtXXHNCUUU1V7erNTZsIKQgSgXW2q5h\nSfkM1CCAho6RIphGoAYkSasP1Zqs1FcqN8sT0eFkFotQVJIkhWrSclBdD6rGaEOqk6aDOmfRMoQQ\n2J4eDBZqNWfzAmLpAdgF8xHDI9gNj6ECiTEGrTtLfKdLUW4FJSmEFAibkqQGY51IzB1UIQSRlFic\ni+pc5Mx1JivxTVISq0FM3oPqjpUHJbkkX1Rr1EwrJMmS6IQnKzuoJlWEkEhZoL3M193/iX2oaaNG\nLQUVluiPJKUS1MOItBEh6zGxjmc8bqZRr0y/kWdW+cUvfsERRxwBwB133MG73vWuWV6Rx+PxPH28\nQPV4PJ5nkVNPPZV7772Xl73sZZxwwgl84hOf4DWveQ3f+973ePvb386XvvSlCYJqZ3Un2yvbn9K4\nmqRhsGmNsDYMuwZh1y6sqSNCQUEIbL37uJlGw4k/q1wYTyEoIoUkUhFSSBKTuH5QoFAIiKICSWKI\nYydczTiBGiDanEDH3B730jNSaTmoCIG0bo7p8K5NiFRje3solPqc8ItCbKHgUolyF1UI7Ipj3fnW\n3ePGshhNmgikdALVWMOTlScZrg9Peq9ygZqkEiUlCEuqLVa4MKT2F8pCPg91/LgZrVAqcA6sTqd1\nUJ2AdkFJCt10UE3iBLaUEikN9bSBRVCOXf+tlKXsPtfaBKqYMIvWxA3qRiCjiLlhQG9RYIsR9RRE\n9hnDTMbNlIeeZGjjQ4wObp12W8/s8I1vfIPVq1cD8Kc//YmXvvSls7sgj8fj+QvxAtXj8XieZaIo\n4qMf/Sh33303g4ODrFy5ks997nN86lOf4qqrruKCCy6gkSXWNtIGjbRBohNqaW1mJ9CaZMcwZngr\ngW2QGEGcpjA2gigkrpeybomN6SjztdYlyAoBRrrxMqWwt/l8QRWAlovqBFIJrRVJUsMYg9XaHVMp\nsM51HF9l2N8rUAgqNUva3oeKpFoZQQxud4/NG3DObwoWgel1PZhUq26xAMudQGX9eshGl2IF2jp3\nM3cKa0ltUscwF6hpKt1arXVlutm622dGRm3jZqAlUJMEZBCCtug0wQozpYPqjut2VmhQkFrQscYY\nF4AkpSYxCSBITUpq0o4y3yDQzVEz7X2oqUlJkwRrXJBVIRQUpaQ0N6IhwFbcuJmZ9KFWhocZHYGx\nHTuaHz549gyMMbz73e/mwgsvZP/992doaIjnP//5s70sj8fj+YvxAtXj8Xh2I41Gg6GhIQYHB4nj\nuOO5Qw45hK9//ets2rSJt7zlLdxwww088cQT/OxnP+OYY47hkT88wvDOYeItZZLtDcaqY1OfzBgY\nHcVsfpK4WsWqBvXAMtLXx1gcE4+NYEUZIQRh4gaYtLuoWucJvoaEBJDN0l5gQplvEEAQREBAmro+\nVKs1GpAyaCb41uvVjmsPQyiFAm1grJ4JzSAgNimNRgU5shMAO38e1Z0VRh4ZZHTTGCZQbqCqMU6k\nAqxYCYBYvx4rLdJa0AKdlRbnotQyuSATItfTCmtcmbCxFpElPLW/UEZSInF9qCabhwquD1UFURZy\nFKPydKgpXmbzMl9JgsySfON6itP3bgZqYtLMaYVaUssEv/s7KFUnDEPStLPENzUpcZKCUURhRBC4\nOa6lHkE9DDCNCFNrTNuHatOUsaEqjQaMDKWMDW2fcnvPs0e1WuW4447jyiuvZO3atWzcuJGBgYHZ\nXpbH4/E8I3iB6vF4PM8w1lqq1So7duxg165d1Go16vU6O3fuZGhoaEKgTalY5KQjjuCtp5zMqYce\nQnXXLjY9+ijXv3oN8/9qJYe88GiWvGIVOx/bzmC1MsH5xFoYG4Pt26FcxjQMScEwNkeQ9PYgCz3Q\nN4/ReBQ98iQEUEBg484yX9eqqkmMc2qjoOB6QzOKQRGBINZxs9w4ikLCMKDRSGg0aiRxmYauoU2Z\nsZEn2bLlj+zc+Qg7dmzouOa8zHe06s5vlKSSVBBJSm/FnV/3zaW8cQgBmMQ6sdnX5w6Ql/lmSb5i\n/f0gQWHBgMEJT93m+tWSyR1o56JKrHb9ucba5iukFJ1xwFFbmm8YuvO4WaiBm5+aOAcVRIf7Oh4p\nW32oYeCOWc16h8NQYmyKNrolUDMHPS/ztbZKsRhgraBeT5t/kySu0TAaRESkFEHg1hwqEH0RFokZ\nc+NmYt35oUk7jeoo9YahFgQkiWXn5h0z7lv17D6eeOIJent7ue+++/jMZz7DzTffTJgndnk8Hs8+\nQDDbC/B4PJ49GWNNs1evFE49rsEYQ6VSoVKpYEyexKro7e3FJgnVP/6e9PFHGd2wATZt5Lo77+KX\nGzZyx8goylpWAX8N/ANwBCA2b24eu7BxM8Uf3cjmt72L/ZYuQkg39zOo1QgqFQJrCYCgVKJBxFC8\nAxsZwqCfHrEfY4UIKk8yWtnJvDlLKcg+ynVNIzJYaxFCkKbuGrSooJSkFIy/XksgoJ5WKdd3UAwi\nhNDAGLXaLioVQZoMUamNkAwGpHEBdICUlnRcefJAr2DLiHNQrYXhtIxAEFlFYdQ5xWmxFyEsUimM\ndiNzKBScmkxTqNWQLzgGG0WIRx/HlkcRWNAKkzmo2rYEaqxjtNEdojsnCMAiwSqM1aTGNl3Q8Z/k\nFqSkbgwNYyhlAjBJIDEKgQSTYoWZsrwXWiW+1jqBWhNQbzihGQSSJHM4I1XEWENqUhKdEKoiaSqx\nNkGpNBs3o0mShCiKSOpVYgOoIkUpmz3AzTLfwQpyDFjsSsgjFXVdX31khMFYUyv2MTdUyLEGg9u3\ns2Cxn6k5W9x777381V+59Oof/ehHvO51r5vlFXk8Hs8zjxeoHo/HM45Yx9TTuuv9NK3SybF4jIHi\nwIQ39EmSUKlUqNVqbc5iRG9vL4XH/gzvfBviP2+nv805fRS4n5YgPbinB3vIIdiDDsY+/3nUn3co\nTxw4n/Kyg5jz8wc49GMXs/i663jsrHOwuxrIXoOpODc1Blc3299PImHrE5spp2X6wl5SvT87hyCg\nn4pdRG+yibHRx+nrPYYwBo0r8y0p1XRQU+oopSgGvW5sSzqcjTaxKFslTUepiphIzs3KfEPqdUmt\nVqM6XGW0nFLs66EUDdDbM58k+TPGdM7qLASSYgT12LJ9pIwmRYqIfiFJNm8DwMyZS//SOdSeiLHG\nkmoDIc5FHR52LuqCBdijj0CsfwAeXI8szAEjMLje1yRzUJVQaKupp3V6o17GEwS40CWjwFiXGDyJ\ng9otKClJXFCSQCJ03YnpaYqU3JzUAGvTrA9VECcWtCs5djNnXUCVEC4oqZbWCFWIlEWMqaJUDaVU\nsw81iiKq9TpaQyEqEYattRelpNgbMBJKehuKuJJQl3X6C/0TF2ctwyNjjDTqFPrnkyhIhits37iD\neQsXuTApz7PKTTfdxBlnnAHAunXrWLFixSyvyOPxeHYPXqB6PJ7nPKlJXRiRbkwYvyGFJBAR9Til\nalKq9Z30hD3MKcwhbsSUy+Vmf6UQgmKxRF9fH0GjgfzkJxD/8hVEPoLlgCXY5x2CPvAg9lu4hE8v\nXEqy7FDkIYdRe/5hFOeVkEXBmDXsrI8xUh8miItEZ5+C/ufP0Pfww/Te9V9EK09gXqEXNSBJCwXS\n/n7SKKKc1BkZGSQxFVRUIBJL2DEG4a5tBBiKfUsZrmwjSXcRmiGi3rlUU0tdtgRqI21gZUygSoQq\nJEl2YW2SXZ+iFPYzliQkNiQI5tHbqyiVeti+fZRdu+qEOkCF/cybv4R+uR+6ISmXFaAxRiPb3Ms5\nPZJKPWbz4ChLFgTMKw2w9ZENzNu+A4DowEWE83sQOxTCWpJEQxEolVxJcxy7r+XHwvoHYP29qJe8\nzP1NtelwUHujXkYbo9TSWleBqlSWfmtdyazWCUzioAZSooRAWxfyFEWSSsU5qBiJMBrL9A6qu6dh\nJlBTRAC1VIOxzpU1CUJIQhUSytAJ1KTGnMIclOppCtQw7KNeb/Wh1ho1jBH0lHpI0wZbtw7S19dH\nX18fAgjmRAS7LOWRGlFvgrEGOW6tulphsJGQCsW8UoGeXsvY4CCq1mDrph0cePDiaa8NoF53f6qB\nAfBVqE8Pay1///d/z6c+9SnAlfguWbJkllfl8Xg8uw8vUD0ezz6NThLSeh2RpkRBAEphhaBBSsMk\nNHDpqO2EMqQQFBC6SNqIqNdBWkiSMmPxKJurO2nUN1OSvRRVCSkDSqUSPT096FRSu+67DFz2IYIn\nXIlu+c1vZ/TD/8C8gxYiUw3G6SzbqJEkZUwEI3KUWiMmlSWMlNSSCnODgCgdQBSLNN76dnr+5YvM\n/fY1DB9xNHNUH8g5RIv7icCNIUlHmWegWAiIwznQGKBgLaUegwwt1MqkpcVURjazdfhxDjj4GGwd\n6oHru9RaUE9qBL2GnqhAmg4hZQEzJlBiPrKgCEJJKRSkpC4duFZnZKRMHGsKxTp9YZGgp4+e3l5E\n1bl3QdZfqXXaKVBLgofjMQJrKcg+ajvH0CMNwlE3EkYtXogxhsHyKGNKsijJ/k5CQE+PUz7lMqxY\nAd+6HrF+HeqlqwCFSTOBmrnWPWEP5bg8aZlvnuSLCbIU4HRSBxUgEoKatcTWUsiDkkwASGya4Lzp\n6QWqlBHG1FCkoEIaqUYZQRhCw6ROoMqQUIUEMnABSDrOXFVFEKRICWnqRs24gKQErCKKIrSuIaVl\nbGwMIQSFQoF0oEBjsA4VlzdVT+v0hD0d66qWhyknBoICCwuSJJSUFs5ldOM2xLbt7Ld4IaXi1Nen\ntTO6jYGhIVi4EKZoyfV0IUkS3vCGN3DrrbeycuVK7rzzTnp6eqbf0ePxePZivED1eDx7NNZYbGKx\nxiJCgQxab4qttc7FshYNaGvRxqAbjeYXmUBJdII0KUUbY0yalWA6AhVQiHqIwiJB0EO9EVBtuJJQ\nVIxQEhlYAmMIGhbSBkImpEGZoC9g0dz9CVWIePRhei95H4X/dZs75zHHMvYPX6N+2ItpVAw7tmgW\n7geqKFA9irmlucxlLuVymR0jI2wfGcGOjlLqKdAfWSIZYXURMTJE8W1vxn7ty8z/xS94olqjvKyH\nfhuRjqaUozLVpIpA0GsVNdNDI+1hQbHAgmKMUophYwj6UpYmBTZVImpxnQ1/eoI5RxyI7XNlvmkq\naZgqASmRqGNtCT0mkI15WAG6odFoaMBQdYhhM0x/qZ+AgJ6ePvr6IiKdUpPKhQOZXKCqLCG4Mxyq\nkYwhgwQTR4z92aDHYsJA0aOzftW5c2k0GohA0Wg0qNfbAn16e504rdfh2OUAiPsfyPotJdoYEK5v\nVQqJFC6RuJpUqSbVCWWtTqBaMAHWCLSd3EEF14day/pQe0KFUqC1wmqBMGk2Q3VmDiqAsAkqiIgT\nQ9EKgsBSMSlSlgike6kuBsWmixqpCClLWFsmilInNOsJjbhOagyCiDAIMaaV/Dw6OkrY14cqRiQR\nRDVBvWpoRI0JAnWwPEatnlIqDDAnjBEDC9huDGbnTkZ37WTL5l0873kLJ4wQamdoyIlTIVzL8Ogo\nzJ077S3xZAwNDXHUUUexfft2LrzwQr72ta8hfWm1x+N5DuAFqsfj2WMwicGmmSBNrPtZWxJjXHIt\noCXYUGBCsJFAhNK9+41jaDRcM2DWG2itITYJsdLUQ4ExBmkk/TZiQIUUREAkAkIZUKtBbQTiuDWK\nJAogCBKMKRPrlMLAAIX5IQcWlyAjSYMG2mpMdSM9X/gaxcu/jmg0sHPnYP/vS5HnXURv2dJrDDtT\n0IGiHEoWLhgnsotFQqWIRkcRjQa6PMgwKXPDhURDuyjKBnLpUsza/4b80a3M/9F32PGhT9BLiaEd\nQ6Q9KUF/wEBxgMqTOxgds7Coj95CTFLbydiuXQwViwwsWkRfpcxBC/vYsHkb8dgoOzYO01Paj7Df\nECcp2tYQjBLKAWy9gGrMQyhBMCfAppbKSIXR0VHGKmMooZgn57EgmoO2DWo7t2LMCHK/HoQRtEac\nBmjtHNQcN9u1RrEAo5sso2md/mLInCUDBGOj7t7Mn0ecJKgohEaDkeFRWJqVNkrpXNRKBXH4UQCo\n3z+EdN2nGA3GtvpPAUpBiWpSpZbWuvZdCmnASrRVKDTaagSqaxJvoS3JF1z5qtaQ6hCsweqUmTio\nTqAKrE0JAkmaWlIEViQuLEmGzfOXghLluEw9rTOXuUhZQusyQeB6huM4YaTs7l0k84Ard8/7+/sZ\nGxujMTZGo7cXOSckqBnGhhs0+jvfCph6nV2VOrGGBTUDI3Wi4hB9/Qqz/zzKj27lyQ1/Yt78/dhv\nfvdrzCuwlYJ582DXLtcyXCq1Zsd6JudPf/oThx9+OABXXnkl559//iyvyOPxeJ49vED1eDy7FWsN\n1uo298xijcEmFpNobOp+ttpgTUtYNowmMYYGBhsCSiHSXkSiILaQxIgkQSUJgTIEoSCIJEFBoANB\nXWnSQFIIeykAc4WiQYAWIQUVYaREiYBqVVKrGExoQGpEj6EUaaIgJq6NUKtUEMYgjKGsc636AAAg\nAElEQVQvjunZf3+CQiFbp6X8w+sofvASwsddOW/y1rNQn/8SurQQM+rEiyxJ9l8csHOnINHOSZoz\nB1JjGEpTEmsJlOKQhQuRacKfto5hyjVGdmwnaEj651mYtwAu+jv40a0s+u4NbL3wYh4zDfqMQJYl\nA30D6Ipl244yo3FMX2OUuKCIR0fBGEKlqEpJYe4A/aNjHLSwn63lIcaGQwZ39lIulwgbw1g7QjEI\nsUmEqs1DSEEwEJCQMNYYI1EJPQt76OvvoxSVmNc7j7giiUZLlCsGE1cp9YAdTKnvbCBDQViybrZo\nVkptrGG4PoxOLcVdmkoMiQrpPXgByeM1gpERAMRcJ1CD0L1UVSuVZuIw4FzUSgVRLGIPWILYspVg\ny0ZU73LQliQXqFk5byEooIRqS8PtbIqUgROo2BArLFiDFN1fJpUQBEKQWvcBShRJ1weqI8AJ1Hw8\nzFS0gpISAqUx2pIKg1AppBCpQnPb7mW+AUGgm0FJo5m4D1Qpu1caIQT9/f1IKRkZGaE2NkYpDLCh\nRNYM9YYhLsXN8K/h8ii1OEWVA3r6DGEYEVYFQTGlb1EPZmfC6K4hNmzYQG/PoRSLndeUJM7cFgKK\npTKjo4MUivtTr0UMD/tS3+n45S9/yapVq5o/n3rqqbO8Io/H43l28QLV4/E8bay1We9igjEJxqRo\n7Upo3e8arRN0Q2MTS0FFRDJsCtF2tDUkEmIJqQIbgAiEc++EoGBSgqRK2IhQNYU0BmxmltoAbQJq\nsWY0NZjIIkKJRFKKivQWeykE7o1+TWu2lTVDVUuSJPRKRZ8MiHokPT0BYZhSLtcZrtWhUEAUi/T0\n9tLXaCCTxKnLBQuwjz+K/bv303/LrfC/2Xv3WN3ys77v87us63t/3733OXO1x/aAh4vrBKVpSx3U\npkoRJDU1gSp/pCoFSkMDapDaSokpKhAnIkoU2ooatUAoBSKqlHulooTQFokiwq04eBh7fJmZM+fs\n23td19+1f6x99pnTsZ1IVWOM34/06t1nn73fvdZ611rv+q7n+3wfwL7wPJu//b2YP/GvkTSKaeOQ\nSqJnGlUMQmW5hKur4eLdSU+fOCKQCMFCa7SUVL5lmaWEOmXTRkJ/oDrJoaqYfNm/TPiSF0g+9GHS\nX/hJzv/c1zJZrJi5ks0rFfcuHlA3e8R8xKgIJElOURRErYlJwrau6U5OGM3ukISek9kl6XrLJ7fn\ndOMzNhf3yRJPGnO6K0kfG8RI0G4dvbVoISiShNlsRklJYxtc5hhNx4zjnMtO4qVhXGikGiprwkfo\nBKHzhLuDYNx2W3rj6F5pGPuCfiIoz+a0GCQKtb+poE5nOOfQaUKiNbZ3tG37qAdPa8hz6DriF7+A\nuHef7A8+jPyyd0OIuJvqoRKPz3KtbX2bhvtGlIpD9dVpwmAa5zPpqExKnPf0NwIVwAY92Medhc/4\n248YgpIsSnucD0PiMMOImeQNAhWGKurBHB6z+SbJASkd1goaU6EEFElJjB4pI1oP6zkajYYZvdst\n+75nJhyZh7aFbtyRqpQYI5vdFncJORk6MyRygnQLRk2HL1tmzz5JX7/I1asf4pOjCc+/4+TW6hvj\nYO2NEWx/n2p/Hxcj81GLyp7HOXm0+n4GfuiHfohv+qZvAuAjH/kI73jHOz7LS3TkyJEj/+I5CtQj\nR458SmIcBFzfD4+u6wDDYBkchOjD6ig8LjhjiMQ+EGwkGobZkChqLEprirJgNBkRM42VkV6BV+Km\nMibQCFIpyYUk73tk0xJMQ4iD/VZmJXq6QhQFrQzUxtA3PcEM1VjlFYUoKESB3EtELWiEpU80XadI\ng6QPHic8MfdQBkaJoK9rdrv2tko3Go0Yj8dD31eMt+rS/53vQ37/f4tsO+J4RPyu96O//TtI9w3N\ndouNlj7tWa1WZPkbKmAJTKeRV64c51eB5QnMMslM62HdY6S+eA3ahkkcoWYap0eIkaduGorDAfcf\n/Yfk3/6f8Zaf+vu89qe/iusQ6OWGzeuWfr8jnSlmz5xx92zBMs/BOWKa0iiFMgZjDFUyIh1PYHYg\n3jtQvPp7fPj0DpurhlHomVQJ8vRAPh3jomDbutt5rn40YicE3isq5/DU5KOSJMkQSuMkUEryVYaL\nEk0k7BUxRLw31Kbm0LRUH9+yEDNEodBvn1IdJLXRFEKhdoNAtcUgqNIyJ89zmuCp6/rxkJjxeOhD\nfec74Zd+mfSll5BfJon+0YiZNybUFkkxCNSbNNw3onSEKIlR4QkIwmc06WZCUDOMmxklQIx4kqE6\nGDz/vAJ1CEpqwPdEAUIKrBv29VQ9Xp4skhuB6tpbm+8gUD2HRtG5mmlRkmQlD+29Wj/6qB+Px5yE\nwH67Ze9rJrag3xvaWc80g6rpaC8agokkWUq+cAgUYRdJDinMExCaVfGAdrfhlY9+iCS8jWffeopI\nMs53ke2hpz68TpJtEQiU0qyrAyf5A4R48mj1/RSEEPjWb/1WfvAHf5CzszNefPFFFovFZ3uxjhw5\ncuSzwlGgHjnyecIbR0nEOPTLhXDTN+fCjQi1GOPoOou1HucsIfSE0BPfOHpFRqSEJBkuPpNEoVAo\nL1BBoYVGSo3MNLJUqFQRdaR1HV10rEXkQd+iY0peFORJQaoUmRDkUpJ5j2gaaKubEqlCpSt8EnCq\nw2rJIR4woSNEBQrkRFLqklE6QgdNNJHQB5pdoK4izkZE5lCLhDwXLEuNyiTrvmdTVZx3HQUwvRFi\nDy2RtwhB+Cf/F+IvfzvqY58YtunXvw/xd74f7jyJ3TgKW5AWKVVa4XLHzu5oQ8s8n9/M4Yw0iYM8\nQgMcNNNSDYLGObqL1/FtQ+ICMeSIImH5xBhbBNr797ncXtB++b/Cs9Mxs9/5fU4+/E9ZPz9m7+Ys\nZpGFmKEXI9R8RpEkQ29ujDTG0ElJs91yvtsxm81Y0sOogHSDulqjbY0rVxTNCEFOH6dMl3N8Glhp\nzThNiYC9CaaKIqEOgdq0iKRnHyV1hKb3FLald0MMlc4lvhs+akzfs3Nb9h9bMxUjiknK7G1LzoOn\naiKulzirUPsh2GcTAuvdDj2Z46wDnWKtxRhD+lDdpCmkKfGFFwDI/uAjSNRg8cWRwGOJvalK32ST\nfYhSERD4kCBFxDn7KRN8b1/rZv8wYUgM1gqcUPgA0nl8BMUgPj5TuM3DoKRgDShBlMO2Qr+5gqql\nJpEJNlh615PpDK0TsizyYF1jTMsynyGTFOcOSPm4QAWYT6fMrWVXVbT7Gt84Dk3KMrXsXt3T3lT/\nixNNniSoPIUgiSZS2kCTjclWX8rd7v/m5fMrPuIK6rpC5zn1paBrK/Jph4oJJ3efIkrB9eZV6u0F\nxXIM/fRo9X0DTdPw5V/+5fzO7/wOX/VVX8XP/MzPkBxn8hw5cuTzmKNAPXLkc5gQAyEGfPCPvo7+\n9nvGBtp+eHbuRpR6cNYPFS0XCH54SIakU2KAaBA4Eq0pCkWWlaRpznDKGPreBIpoBbGXhDbAjX71\nDEFGSSFJSgmFoJURJz26GKGMQbYttC3RWoL3hLYlyXMyGMSpe8PYlywbeg3zHOs6anOg6c+JwYAQ\nJHrGNL9DkRSPKmUKWgcHp3AZRBlQe0ueBMa5I1tqvPdUh4rYNCh/Y+UsChiNyNL0MUERX/kE8Tv+\nU+Q/+Nnh329/jvi934P8s+/FiwJ3aSEOluR8kVMmJZ3r2HU7etfz+ifvIXyGnE9hLDlZSLzQBCfZ\nbmFZdrDdUnd7hHOMsgWHLsGOxsSTEbv9lpd2l5TrC6bTKfv3/Tss/95P8Paf/5/5J3/lTzEdnVKM\nL1iWhr0t8fuAKiA6y267pY0RNZshQiBYS4iRkE/I0474woqnXlTc27W0neGtT59wNp2TrpZcNDkp\nkTulZJE+umD2N32XLi2pbYv3Bp3kIBNqC/u+YWMctfGMtEADxgfuX1wim4KClPlizOztJyAl2gSy\nPLI+eNzlAeEcvshYVxUuBMbjAne+I51OCDHQNM0jgQowGiG/+EsBSF98GSUVIYLzjti0nP/u6yxP\n7jB75zPAm22yD5EqEP2QgIt0eGc+YwVVCkEiBDZGTAgkCQSpCH6woIcbF8LV1RWj0YjpdPqpX0fe\nBCV5g1AgFBhjSROJkm8WKkVSYHtL61oynSFlQZ47OlPhDCS36zQcRzK+eS1OZzNM12G3DzDXezZl\nQdntafd7kAaxSkiSHTIaXMgpn5oR9oKxjFSTwG48Qdo7TOM1F8bhXt2xSjYQWiY5zLJTVqu3kcYh\nmbgVcyq3JmtehzTDuexo9QXu37/Pk08+CcB3f/d38/73v/9ThnIdOXLkyOcTR4F65MgfckIM9K6n\n9/2bxGi8bcIcqqGmj7eBts5GQoAYAqbvMcZgGZJUhRhCUB9WQmXiETqgtCNNIcsS0lShdURLjVYZ\nic7IRU7qUlwTcF3EC/BpwCsIQhATSdQStKTzgb339IdwawDOGrh7knNWlqRC4Iyh2e3ot1u6y0u6\nm0pTXhQUyyXZckmUktrW1NX5MPYF0HpFKh2ZDCQyQdAiGKyQTXPT43mjcbWG8VySP5Fgry2hsay7\nPb3ob628Z+MxxXjMIQRMjKydowiB6f3XEX/zryN+6EeRxhDLgvDX/gvUX/4rsK+wn7gmFDMoCtRI\noaaPEl9znZONMi7PX+O6uk8XPQueY97NWCw0YiW5uoLuquLAgbwwHExLEBrvMq6LAjXNiK7j5evX\nuHIdS6V5++SE8pv/EvFHf5LFz/8Sy2/fEdQa4R0xzyHPh5sPV4Z9+wDXdcjJhPlqRZ7nTNsWl+ck\nZWQUFCEdI/unKX/995HdNWb2gJMvXrAX4KuIbQQmauxysCjDEBCklOI0H5PgKGQgH6XsspJrn6Cx\n5EhaIlFEvFbc2+3Jzg1np2/l9GzJ7G2DOA0h4LqOtq15cGVZXlwC4KcTUIJZMSavKmR1IDlZEgK0\nbct0On10E6EoEG9/nphnJA+uSKstfT5jc39N8+LvIXaCw/k57yxS0mfP3mSTfYiQw/EkZU4QNd5/\n5goqDH2o9mEfqpZ4IYlBIPyNQO07YozUdc1oNEKpTx2cJITG2gYlhsqzc4GRyj+lWCl0wb7f093Y\ngJUqUHqPDTXegQjDR3sMFr8e+r8dDj199JGfCRgvZ1Sbc+RlxesfrbB3S+axR5cGwQQlGrQs8AIO\naoOJU0wb6DX0mSQ/u8MdZRCvHairEy7rNc88L1g+M2OWT9DUECHtUqbpCm86dnXFLD0n8jR1Lcnz\n4R7U5yO/+7u/y7vf/W4Afvqnf5qv+Zqv+Swv0ZEjR4784eAoUI8c+WwTwqPHje/W2I7ONJi+xXnz\n6P8fjk8JEWchBIm3ihAE0SuEkGghSZDY3hCDg2hJk2GuotQSMUlRowJRpIjEI6QFcSN6CcQoQGQg\nUhCK4AP9wdF2e3Z+R6pSpsmUNEnJxhKZSWQuEUoQYqTxniY4Eh+RHgoPOkpCI4fnnSBfRmTXopuG\n3HvCaESnNY33GKVoioLK9HT3Pk7UkazI0HqwNpZJeVstDcHg3JYYDbvdJV03JYShP1FrmEyGoujD\nzdyqlsODA5GImitGi8HK+1A0ZEDtPdXHP4b+vr+B/NEfRxhDFILwdf8u4m/9bdRbnsO3HmccmB4R\nduizHPn/GtXhvWFzuKQ+tEidobIWHa4Yiyl+5wmVI232XFSW6wiEFh8FhcroswlelCjVst1fo4Jj\nPJpw8sRzTJGkJ0/Q/xt/mvyX/yFP/8KPsf22byKsx2zakuStCaJ1XF9cE6uKfKxY3L2LLgq01hhj\nOD+ck2QTrEgoihFbqUnTFbnZE5Tl6sEnyJ+dcHoKuk7wTnB9DavVI5EKkN3YT3vfMysFmc6RMaGI\ngYVKSDJBmQRefdWy+eQ1k3nGE3dOmT53QtN1tG2LMYbWe1wIyAzyfhBdcT6lSBRj51BZho6euN6g\nnlwSlaRpGsbj8aOFmc2wzz9H+nsvUnz097jfpGzXv4E5bMiyGetdy2T+Mm/JFfps9SabLAx911JE\nlFAYBN71GNOwr1qK0ZwkebOSyqSkuhGos0SClPggkSESCBhjbl/7cDgwn88/5WlAyhTnIkp7Ygx4\n/3iC7xtRUt0uf+c6cp1DohEhIL3HkRBdIGwMIg43oey+ImaA9MToiNETnCMpFKUI2KritfMD47eU\nxL5AhRGpDgS1pJIK5TooMoRJmLWCrBDkOqVsDImO/FbY4LMZbZazWjyFlvamP/2ADzAKM0w4YesN\n/WGDmpYk7oTtFs7OPv+svj/3cz/He9/7XgB++7d/+1aoHjly5MiRo0A9cuT/d/xNhcgbQ3RuGLFy\nIzjjjeh0wWNuLjZtsPiHQpTBRqhIwBdIpyFIpNckQpEIMYxaVAKZQQg9PvR435BNhgtTIRLSLCNL\nElIlgGGuZ6ztTQpqhsgLZDFFqhIpB3ugbz2hCbjODVVc1VOLGp96tumWoiyY5TOUUnTe09hAHx5V\nS1MlKBNJoRRKCPwE1hcOe91w+aBjNXNoDUiJHI8py5JSa4w1XGwv2Bw2WGcBMK1hMV6wPFk+VoES\nIsWYU/b7Lc61wJY07ZlOZ5TlUF3zfgjWqR+OKBkLMpsx1mPyUX6bNguDlbf4wPdS/siP3QrT+mvf\nS//XvpPZu/84ArBbS2gC5CPkMqB1j6i3UJyA1sPoGbNl1+8wa4MQmpPTt3KIr2PoWIsL4mFG2NTg\nHSIqjNRU64bFTHD65JNsqwmu3TOddLSN4ywtWU3uYrzn2jjKdSR+3TeQ//I/5PQnfpzuO76ePkoI\nS3Z7T6H3jEUg84KpnKJuSlRaa6RsSGNH2ySMpnfIbUfd7tGjEcvZ07h4j53pifdf4y1vXZKdCTab\nIel1vYaTk2G2JTwulGzoESIgnIS2p7t3H79JWDd76ssL9CGSnKa0U013fk682ceFEExvkoY7EZnG\n4T13o5Kw35EuzjCTCaQJwVrSusX2HY3WjwvUssR94TtIf+9F/P/+j3n9hYzNZM1knmHnZ3SvvY78\n+BXT8YKlCBTTHBse2WSH4y0ifI9rHYfrS1y4YFTVaC/IpxueeO6dbzq+UyGG/SJGiB6hI1KkhGDw\nzmKtvV3Ptm0fuyHyRoRIsNajlMcHgbXx0wpUeIPN17bkOkckGSIGsBbbSYzph5mwmSXoDbGLhJ1A\nzx7+bUnmNcaWnNy5yyf9mh2G9aUlGS8pkjFlKvGUqGxELmrK0pDYETSG/fkWqwMum3PRv8LoiRyh\nx2g3Yb/1nJ2dEmOL9xVy5PD9jkk6x5sle3vFor+kVymZn35eWX1jjHzgAx/g/e9/PwD37t27tfge\nOXLkyJGBo0A9cuT/AzFGCBDCTU+ej7gQcW2H6wy+6wnWgb9p0BQCoSDKiI0WEw1OeZyAKAAlIcnQ\nOkWpHEKBDTmNl0Qhb8sMDwNZshQkDhk6ousRQaHFCC3GpGlKURTkeQb0eN/iXQu9h15BH1ExRfYp\n0mqoWoK0OJ/gvYabERxSSXSuKUYFC72gtjWVqWh9z3p/nygzinSMlhoBFFJSKkX2xrkTbYuqa06C\nYe0EvRVcHTKWT5ek0xyEwAVH1W1pbYvMJat8hY4a6STOOIIPXF9fc3JyghDy1srrvQAWZFlOUezI\nshYhDMZMaBpD27a3YqgoCiZnE6jB1x63diQnCbz2CeIHvhfxIz+GtHaomH79++j+6ndyeOcLBKCr\nexaVQAZAgp5qVHkyqLaug/Wafj5iYzaYaPE7j7AZqcpZtxVXXSQfSYLYMWKHLmZomzKRCn2+Q1lI\nl2coXbBv1kgVSBOJkCUqV5TzOR+7uublSvEFPpL9q3+K8Pbn0C9/nOwX/xHiX38vm77j+qrlZCJ4\n4qkJIyLRRdwB9DLi3JqikBSNojIpxpf024qGGuYLpqZkO11ghEG6jnh5H86eZLHICAH6Hq4vAydz\nhwxDU3PetNh2RycOsN6g9hZ3L7DZv8Z2XyJEjwktqYoQNJdNw2mSkGUZRVFQFAVCCHzfs+5bRD3M\nQLVpivGWejajnc2oRiXRC1SSErsKd3FBPx6T3ST6xr5nd/eMEpAv/haX7/wKzOIEd3fCsu45KM/H\n1/cQLxm+zL7A/NmCMBZ0IWIM9O2Bi8uXuXptTXs94bptyBxMdEbiPVlbs3qqJU2Lx84B4qYP1cRI\nGyJpEnBJirOOvq0JQaK1Jk1Tmqb5tFVUIW4qqMrio8T7+KaApDfy0Obb+8Gq7lWKlh7XBNp1YLx0\nyJEgWQr0dHBaSJOhZYHUCaGFojY0WUk/uuLJJwXVxX3qygMNo1VCIhQ9CTIbMdYOFR3CXBA3kVxH\n+pXiD7IpcjzlJHWcPLOi3iqurixar1mtVkhZYrkgjA360JHJKaO051DvKBdrepNCnX9eWH2ttbzv\nfe/jF37hF3jXu97Fr/3arz2eSH3kyJEjR4CjQD1y5NMSw3BxH+3wHGzA+TeIUB9wcQiMid6BsWDN\n8PyGsSsSgU4T0AqLp/MO5wMIDTIlCZApSaYzlMyADGsUPghQIJREJoIsA5lEZBJx0VB3LXXb4sOj\ndN1Ea/I8R+Q5VjgCNW2/RRPRQpCoBDmeoGYFUmZgDLHr8NsWv++Iprt9LZEp1LxETgpEng/imaHf\nTacp+25PHSqibzC+Y5mNOc1nJOrmtOLc0BDaNIO/lmFdVs8UbMyI1mquGxhri5MVrWuHn0FQJiXj\nG9ELw42Aq6srjLG88sqaPF8RwiDW03SYNJLnBTGmNM05VXVF37+OECVaTynLkvF4/CjNdAbRR/xH\nP4b/z/8m6id//DFhynd+F/JL3kUJZD5wve2pG8cOybJISBYJQt14EhcL3OUF2+oBbWvxsxnd1qLW\nCVoGunlP5zyFzDGXe3TasSqmJCceLUvCVU1b9BySMc1a8vvba9KFZDHLWOUTLveXSCmZFSWmPtC7\nnl0m+cJFhG/49+H9/xXzH/opXv5jX4lNrom+QDOlzEv0vMbuI77z2Ks1ahooihFlmdO3lua8xYtA\nKEH3AStKtNBkRU5RTth3O5KrBJWkLIXkau2xJrK+gtViSK7NQ2TXGqrO4Q8efEHlekxf4cen6Jlg\nNZuQfMjSWchUzuhkzkQrIBKjHay1sSe6Dr1/AECdpVxog0g7Xvror3F571X0+JST5G08LVLivqL+\n5CdJ7t5lu93x4T94lS0lXw0sLu4jFneRU09RN+RIxl5x1Tzgtz7pubra8tSH58TJgXiWMEoXCFHy\noN7S7B3RTalygV6myCefo99c0OzX7C6vOH3qmTedKzIpMd7TOY/WHqk1zku6pkarCWmaMplMaNv2\n01ZRpdR4H5F40BHvBVp++jksSipSlWK8GYKqXCCxirYTWNMhRoONXWuHUIJkMiG2mlBLSMDtHJmQ\nJPOUrUwYdQ2rRHNZJUxcpKouEKMTgkpIUkFmNW77gBhAJCeoLOde11ELxenslLtFixBb0uVzXF9t\n2WwsUm5YLpcoNSPma1xXMWGFszOC9vjDjjDO8O6M7Vb9kbb6brdbXnjhBR48eMA3f/M388EPfvAz\nJjsfOXLkyOczR4F65POeGCPBeqINBOeJxhNdwDuHjZ4+OEwIuOARQgEKokDYAG5InJVEtBRoCbqQ\n6CxB5zkxkfRJpAs9LjpEgMwrcq/RaFJShMvwVtPthhZUAElEyUieQZYFUg3RBow39H1PdI4SKISA\nLCPJc3SWEYSjdw3WX+NuRbJAigwpc0qRs9AJUgiCDYRW4tsMdAaLCLZHSYdUFikCYGBncJsNrVLU\n4zHhJj11kk04ySd41+B8Rww9V80lIy8ZO4k09tFGTlMoy6EhVAgWgFsbzjcVDyrDZBIZjR4J0zeO\nBXm4Dlm24vz8CmMMWbbhzp0lk8mjqkvXdVRVhTEQQooQ9iaUV5BlY6R8dLqLn/gY8gPfg/57P454\nKEz/va8dhOlNGmwMEX/w+MaTWsPG98hJSVxqhBS3+87eVOzSmr7f0R1a9LUj4xSBIFtkdKOUVZYR\n792jajqsk7hVgcbhm9cJ5ZhunBL3HawLmgtF3o+4c3eENT0AWZaxXsNEl1S6J6wECAjv/RrE3/g+\nyl/7Hfinv4/941/KE/MzZnHM5tJwqiRqJenMmmg8apyR5CeMxy31xSW7WGGnQK4w2qJERiITFmmB\nTsb4JLK7eJVlyBCzGat5weVGY9BsrWI6EsQOgvDYMrIvK/ppBqUiKVJynfHkSUqerxFnkbKKyGrD\nZtaThMH6ffsOB4+rd6jdawBURcHWH9h/8vchCHyz53znCB9/kfXdKfH1e4yqBuESLg9QeUG1PCEK\nWKzPmetA1e6ZzgN35HPk05TYGi7aa16LCZttj4o7/Eckkzvw5N0CmZXMEou3migE81ixMltamXPe\nBy4frDl58uk3BRdlUnLwns4HtA6oNMUaSdfWjMcTkiRBKUVRFJ+xiuqcAjxKO4RMCE7AZ5g2UugC\n4w2brsaee0YhpUoLXOYI2XD8DaNzQE8ybOexlxaZSYQW6Lkm0QLbJox1oAw9opzhXQJhx2Z/IF3c\nId1uUSHgoyIWCjfKeHDeYdeeZJVy921vpbz6BF1bk55ULBYLNps1Wdah1DDWKIQSNalxmx0jPSfG\nnsoZJnZLRYLyJ+x28GladD+nefnll3nHO94BwAc/+EG+5Vu+5bO8REeOHDnyh5ujQD3yRxrnLNZ2\nWNtibUdwHlxEhEh0AREj+CE5VgiBB1wEC4PA0wISgdACFS3KObS3qOBItEAJgUYidYrISkRW4JKE\nPgZq1+JiRNyMPklEQqYzMpUTXYrpJV0HQUNMIiKLJESyJJIlkOqIM46u7tisO+xDwacgmSaUy5Ky\nLFEKQmgIYUeMniGrRxFEShA5ngwP9CHQhcD9Xce4h9w/unsvUoEaaWSe3V58R+eGik/TDH101kLf\nkyyXjEYjipttRprhTc9he0572FAFTyMko3TMeHqCGI+HXtcbOtdRmQqbGLJS4LJ2o/YAACAASURB\nVCpFaEuKomSWP15RcA7qeuh/DEEynS6pqiuKoiNJdmTZjKZpqKoKdxPbq5RiOn2CPE9utonD2ku0\nniFffUD869+D+NEfR90IU/c178N9+19F/bF3kcyTx4Rpa1v2fcXOeg4KzKbluul562SBiY6r+gFN\nu8XZnjyWLESB2ETySWD8lrvok4L14YA+HFiWJa/UI7ZZZLs1PJFLvAjc05fsUEzOJuhJhu+mYAR2\n7ehcjROBymcoBYtRSUi2WG+pJhPSUtJ99b/J+Kd+kTv/y0/R/Vt/ktUiJa8F/bXjqu2ZP+URMoNW\no9wSIRRpn6KDREZLk0eqtUfqSErgNJ8gZCD3Kb3s6UVg7yqmcoE8XbE8Tbl41XPYBXwfGY8jQUk2\n8YpquscdCnQYoxrP+NRSFAeWywntOsHVhrQVRCM4KMlCJzf7myCrD7jKEasKgEM24sGrG5559pSi\nmGDLls1FzYOPtFQPtvT1Nd2Da06sZJWlrBYTll88p75zwvjBFaev/p/Yk7exKM+Y5QGlC7w4YbST\n7NKSrJTo+hkMW2SQCDMlz/Zk6RbXt3TSkdFQ+g1JnnFpLIdGcthtmM6Xj+2nqZTIm2NMaY9OU0Ir\n6duW8ZjbkTj/rCqqcwoXHGkaSchwTvCZXK9FUrCtt2yu9mQHQZklZIsRXnmsrchzjVICkEitiXao\nckcXyd+aowqF6x0xTRHWMBIOEzWzbMS42NMZT3f1gOXdMWQZev4sDVuum/tsDzMmIaWczCGXZNMV\n/eZ1QnvFeDIlxgX7/Rqta6SUjMdTYuyRpSGte7ScMs48bbuhmFUcugSaGUXxR8vq+6u/+qu85z3v\nAeBXfuVX+Iqv+IrP8hIdOXLkyB9+jgL1yOc83nucc1jb3wjRFmt7nOvxzhJNIJhINOHNvxvjIEgl\nOHnT2KkFItEopUhNIK8cqQ/kQpAmmkRrkjyDVBNTDYnGiEjvezp3wJtHMzylUGQ6J1MjCDl9pWiM\nJEZxa2XTGoqJIM8FSTKsT9d17NoWEwwUEPOIdprUpmQqI0kVsenw4pqQPVovIRKkLFCquKn2DgQT\nsE1k3Vg6H1kDuRKsxhl6pJD6kTDsQ6D1njYEYppCmiKBoqoo25akroeFLsuh97KuUX3PHM04W7CP\nHV2mOOQ5tewYB80ojh4J02Bvto3kidUYORux2wmaGohDBeXmZen7R+9VnsN4rIElV1dXXFxccH19\nTZ7nN9txCM152NMIEOMpzu0IH/0Q4W/9N8j/6acHK6+UhL/wdfD+/xL5/Bchri2+8oQ6EEWksQ2V\nrWiNoe0DOkTmSvO6gteaDS/f+xjK9iSkZDJlnJ6QljMMkLiW/hARVy2biwM+ehZKYMYFT3zhF1N9\n+LfYbnfM7j5NNW7Z2g1SFNwZvwORTnHPgqs928pz2HS0XWT1hCRZBk7uKFhnPOg6zl1PvrlE/7k/\ny/infpGT/+2XeL2u6McNTywK7j/Y0LQVshkxXY6IriR0ERccsY+MxiN6uefysGNvNXdzwaTz5DIj\nZBFz6FiYlqvxiHoqSXxAv7omjJbMNGwCrOuebVojVwHZS9oLRynnSCuJ8pIkuWS1OiVNC/LRHfr5\ngUWy4tDm+HECOiGRkrDfUx2g9QX6MFi9951CXmcUqzs8PX6GxN9nGzpcmCBqxeU+sJcWP3U8sZgw\nLRNePzRcPnOH8YMrTl5/meqL3k5W9iRiQ9RzsskZyeiMcZowGSlWZyfs6/v4bo2012y1woYFOlvC\nSNCImutuh75KyYOgtYHr+9dvEqgwiNQQwONJc4FpFH3dEVZ+OGYAlSQUUtIY86YqaozgvcLjKNOI\nMgnO/zP8rgbEVtAbTwwt8zPB+cUCaz3GbIlxjtYaIRR2a4dANQkiG266mZuQNnXTA56lGtlEjO85\nWZywXluMa9lvHdMv+AKsFmwPFfuDIykjJ3JJLgMt0I2n5Ic1bVMj5weKYk4Ic+p6AxxQSpFlM2K5\nxnYHJqzYupIkccRqjxoldCZju83/yFh9f/iHf5hv/MZvBOCll17i+eef/ywv0ZEjR458bnAUqEf+\n0BLCUEEbineRprFY626qoj3OdRjTE4IlBM/Dvs/gAtEMZVAZNVJlt3M8VSoReUDkkZiBl0NoURoj\nOgRkjKTGoLuO1BgG2SYAhUsSnMxApwiVIRAEN8wlFSoCGkSJ1pCphEQkBCvpmkBrIcYO6IADSSLI\n84SiyEjTlBAUfd+z27W3YymAYSZonpPnOVmWEkKLqWrcviOa4eVkpkjmI3Q+QspHfsBgAqENhC4Q\n/bBtliKhLyKHNBJzyZrATEjS2/Ew4TZBWDBYF0spyaVErFZDKtFmA6++eqOsi4cLCkWBLkuWSYL1\nln2/52AObNstNtjb8TBKKMbpmDIpbyqwQyrs9TVcXsL9+zCdcjurtSyHh9YPE3k7jDFUVUWMkZOT\nE87Ozm6F6i0xEn/lH6H+7t9F//z/ioiRKCX+L/x5xPu/C/lFXzL8mB9moXbnDXWzoU8PyDTQmkD0\nKfOkZFrkSN3Rb865tGs66ZklmjyZcnd2h+X4jCRm9JcGn1pUd0n1WqQZjdCjEYxnbHXGdL1hlY54\npd7woeaC1WSFFprT0ZxSSTYdjEbQa8X5tWe3FywLxUgLJsIiSZgUBQ92O17fn7PKEu48/y/h/sSf\nRP/Gr7P8yb9P/Z/8JawNzMotVxV07oSJniJUj9s5ZCoRiWD29Izr+2uudg1JdobSPVlmKFRBGwS2\nrhAxMj27w7oJbK7WrFIJokbMMkJWUx0CWMFJmJB6ge0viK6lLCb0fctoNCdNc5JkhUo2yEIQ8RRe\nUO8c10lgvKvZrQ80PhI6BVdrAPqkpIxz7p48QWgPJHTk8UArdqzuvp181FPXBV7sOV+UXDtJa+7x\nxHTBc8Dy1Qe8YgPSjpFnZ9ydTJgUEmuvCNGSTTMS9tw9fQu1y0i6A7qybKWnl5HeTslsjXAlQgbw\ngVA5tpsDxhrS5PH+0ExKYowYPONC04eI7wPK26EP+4aJ97RXV7TrNZO+HxKWkwSPIjqBUIFEebRS\nWMunxVVDNVSJDPIGGyqyrCArVvTdBdYegDFKFfg9SBMQWpA9lRHt4BKoJkPI09w5Wi2wyYg8OoKo\n8N2KyWLJbn0frOV8vyYWgs6MEE4ym2fMZEDYQbh3iWQ5XtBt79PtrpgtJnif0TRTrN2y2+04PT0d\nbqBNa/xmT6lmNN5ghad0BzZRoe0Ju53+nLb6hhD4tm/7Nn7gB36A1WrFSy+9xHL55psaR44cOXLk\nU3MUqEc+68T4SIg6B8ZE2tbS9w5rLcYMFt0Q+pv5fY9XQqUUiKhQPkGHFCUSkiJHjXOkVgQNNgWj\nwbzhrrwEMg2TDKbCMAoGZcxtdTDGSNCamOeENCUIQd3WHJoDh+YK6x9dPWqpmRQTinRBIicEk1LZ\nh+sXUcqTpo4sM6SpASzet7Ttls2mw1qLEAmQoFROUUwpioI01cTYE0KNMRsgInOQeUpsE2hTREyJ\nW/A5xMITbSS0j0QpgNACWUhUqciUYBwjG2vZOseVtUghmCqFFAItBKV8NB7mlq4DY4ZH09zOZOWJ\nJ257SwGsH0Z3uOCIMeKiwwZLYxvKpOTO+M5j75+1g4XX++FlH/bhPvPMINaEGNIvt9v6NpE3TVNO\nT0+x1pIkyeM9gX1P+In/Eb7/v0b+7oeG9yBN2X/tV7P9jm9FvPAuimROUjXIbU/YVphuT73bEWzA\ntBKKCWU+JhuNKZeay3bNbnMf4bY8HTzJbM787tPMypJIJPpr/H3DzEfKpzJUTHlQt+giMHtyhpYZ\n+09u2PYtlDntvMA6Q7JvefL0LcyyhL7fU9eSpimZzcC5HlFKJs+MmK8koQu4jcNph9vt6MUenrjD\nSJT4r/uL6N/4dc5+5Cf46Df/eZp0wUhGVssFh2zCdgvTwGDvLCP5aY7KFTvhkFGgTEqS9sTEIKwk\nWwfieEwHjELCxhrcZIQTjo779HpKkikWShO7KWabU/eBvm0Y54I0LZEyRwiP1iuiFWAFdudwtiMz\nJbtgWeuKnTGUQmELTb/ZI7fXAKSnK87urNj7S+6cSdz5iL3dI6zi6Uxx9tSY8/t3+WQ15l4X6aee\n9tzw2lPD/jW//wr9wVN1I55Nx5zMI7uyYHcuiV5R25QsbZGhIYo5ep5zN7lG3N+yVx0hTWm9xjQF\nUklS0eKMoDaeq/tXPPns46NBMiEIPtIFz2Ks8A6c90huzld5DkqhnKMcj6kPBw7rNfOb+Sq29aSb\nDb24RmmPdAtc3sE0GYbPviFQ53bUEaBnJdpssVVHVGPKcs768gF93yGlx7ceugw0JKsh3MtcGEzj\naFNQiWTlHB/XgkrmTDG0ylM1MM4Vq5M5drfmanvOOMzAnDDLHdNphwwtoh2RNhEzg348Ja82tHWF\nmR8YjebEWNI0Dq0r1us1Jycrgu4JhSFre3o5QaiAbXdMph37eoOqTygK8Tlp9W3blve85z385m/+\nJl/5lV/Jz/7sz95avI8cOXLkyD8fR4F65F8YIQasjRgbH6+MtubGomtvqqOWEMzQryQNSlmSTJAX\niiJLyNOSRKXokCF9Ck4hYoJ8GFyjwGVgErAJBKAQg56yhsHP20VEbUgOBqylipFWQZ4LsnFKNi8Q\nRY4UAuMNnevofY/TjnSaspws8dYjvMC1EtNJ9leRje+BHiEEWZYymWRMpynTaYoQmhBS2ralaSJ9\n390Msh8qpWkqyfPkpl3zGu89bQtSJgiRIYREyhwpS6TMEJkgziJu57BXFntliT4ic4kaK2QmkblE\nFhKZvOHiNgSaEIa5jYCLkRgjDXA3y5i+oV8UYwb1ODSBDt8ry0E5PhTzXYfLElrX3QrTh4zSESfl\nCQCVqYhEKlMxTse07WDjfVgw1hqeemr4U0pBVQW8bzGmeWyWZFEUjMdjkiThcDhwOBzYbDYsrUH/\n9/8d4gf/B+TFFQD+9ITDN/wHtH/xP0bNF0R7gX3wOr7dYJtA61t636MSSXInw1UjdDchT8fop0eo\nZeTV9RV12KGWGUv5FM+TcwgZwqYs0gVdtWb36hWmsfQJ9MUENT0lmkDRtsy7HUhJKw/cNz1hNOPk\nVLDZXGJ6gzeKbHzCvXtbrq93FIVE65y7d3u2W1A6p0s0mbPsrnZ0siNLPMs0oyhn7KqU5Vf8GdyT\nd8k//iqTf/x/0P6Zf5u5XpIWKS4R1PvA9SYwjyASgSoUa9MRM02OpghgI3g6RFWT50vap1a0xlD2\nDt0ZrjODT3oKB2pfMb77LKPJiNdfhwdXcLHpiHQkmWcxfxsXFw1ClLjKECsFvST6SFCeXgZcdcCk\nPXEmKeYJm13Lvr+iqPcAzO/e5cHhit4vuGjHxOUz5KMtIux5thQY23P2tlPuveTJdnviRY9Llpw/\n927gHzB/cJ9Mp5wqTZ5H6r5Fq5Q8m2LDFu3B+pKSlpSErVFMipKTMjIOni7zVI3l+nBFru+goiZN\nod5ENufXPPHME4/dGNFSDq4KAkkx2PidAfUwrCzPh2MHGM//H/beLNbSNS/v+73jN61x711VZ+iZ\npg20OwRugiMSiCGT7W7c4I4QN0EkUbCioOQuQpE6lygXkaIQIYckNrYSJXLAjc1gYwERDnYwadvp\n7sSh6fGcqlPDHtb0je+Yi29XnXMYghQbNw37kZZqq1Sl9e5vrfWt93mf5/88G/onTxhCmGdRUyK4\nnsBsty1zJIw9YXeC4vYDslqR6wZ/42eHiAS90SQZMZMk5ECbA00511R5Dzn35FAi0eilfnEfUI3i\ncONJR1iuEzYFYlnQ7x0rDUlHTs5hnaSpMq6RZDL7J4mXLxbUdaQsR3IayUNF5WEKmV4rzpsN4+EJ\nw+Gae/eXTJOiqpYMg0MIx+FwZLVaw2KHn04s8jmHVKJtgu5EWRuOwwG933zVWX2fPHnCq6++SkqJ\nj3/843z84x//bYFad7jDHe5wh98bdwT1Dv9UkfM84+ZjYHRhDtlwgX4KOPd8VnS26YYQiHG25koZ\nkdLND+2oSkVRaLTWGGOwtoFgwSvGXuKTwMiMkQmjFKIAd0tKg3pryQsYISilpEiJQjrIIwhHqm/r\nQLVkoiCakq4oOOSEu5pIYo/QDlMknh+AK6EoVIlMFSlZRj/XhVqdMWYiJYcQE1J6imImq/u95/LS\nk1JC39bAAChVUpYbqqpCa0jpRIzzI+fnVTWSnCNKgRALpKxRqpytxUOcldIwk9IcM0yAnF+H50RV\nSEHM+cVc6XNiCrDWmvvWMqWEy5k2RmIIrKcJOY5vypkwqzjP/bZCEKeR8ekjxptr/FGQthuQEiUU\nlamodIVRb1qOjTJctTveuD5ioqSQ82Zdypnv1vVMTPt+5NGjgbZ1CJHZbBJVNSegNk3ztmCZ5XJJ\n+uSvo370v8L8jZ9F3AZJTd/wDZz+nT/P+Ke/lxrYDgM8PlF1idNxz4lnuHoFmwL78pZoNri4gqXk\nsHecdOAwnvBXA67f0RB47/2XWdcvIZMgPn1Kv9/TPnvG2i6xcUvXePwrBl8aHrsTKMUrOjG2B4br\nJ8TtEv3yPYgLluIeY9OzP9zQ3kTeGDWHwxI4sV7vODvbcnnpWK8F1lqOx0z2B9I4IMRc2xLkwDRI\nBlsy6Gfwvd/F5r/4C1z89z/J4Tu+C58C1jSsqkT3KBCS5ITkvFT0g+c6dFhjeFBtcaPADZ7R75C6\nxhQLxqLGFwXd4Qnd/orxQiE3NRejZaFqRJTc5hmRUouSI27y1BeKsqwQYktsR8JxQKkFZmHQG027\niJiio/SRBYKulnzuZuB4/QYLWVC287wmtUAKx2tHeP/2nE09st1kYqk4dXtoXuLZ5UQsTth8w0Wz\nxKeXuLovGOuGsuso6TDxSD5YQpNYlIG42hKOB+rk6NMWx0SjPMcx82wMPFgsWYaGV6zmukuUlUMU\ngoPw3A8G1UN3mLjZnTg/W73t/qdSBjJJzW/snAGf5iTetxz8KKVmFbXrOMXIZrPBhYLxbAI7oM9b\n0nVJUiXJGqT3pJs94SaRdYFQAn2myVrgXaBMggAMCRoj0LokBEGMLdlvEEIjzFuIUiOZbub7Rd05\nXPQkXZKkROvA2kQGH5imTGkn6tWKoTW4ZGnbPa++ekYIFYmBXPbocYHpE2ElcMs1Zbdn6Fpa17Ld\nrrm6EhTFlnG8AgastVhbolY9cXekkmuG7BCyoQkt11LQTgXFofqqsfp+6lOf4hu/8RsB+Kmf+ik+\n+tGPfoVXdIc73OEOX724I6h3+P+FmCIhhRdkdJgCgwtMUyC4RJwiOSWS9/hxZBoHso8oLVBGUlqF\nsBHZRGyRMUZhjEbrEmsNAgvZIH0BQZEOCTKEHIg54vEM0uNMxltBAnTUaAwmaBpTsEDRpIy6TZ99\nG9mSElkVVOfzbOcUHe04cepO9GPEe0HOcyenGUqstFhlMcryW3NLjJmV17IsMaa8VT4HTqcTbdsy\njuPbFMCUEvfv36dp7K1993BL1EHKEqUawCKlunXR3irK0TN2zxCuQMbVi3RgoQSqUdj7FqEE4RRI\nQ2I8eqajw1WC1IgXJ/lKCKrb2VJ9axtcxkjfthy7jiEEHLCWktLa2b5bVaA1MUUG3zH4YQ47Whrk\nTUL6TH2cKB+8grXV265PzvPlH4aSqV3TjnuEOHDRSC42JWU5py23bc8wDKSUsDYAkWmCqyvHZuMZ\nhsDpZCiKktJYzM//Avq//m9Y/29/f34eIbj5tm9n+Pf+Q/gTf5JFyiyHnjzNtvA+elqZGZcFuSyo\nlw2r6hV8WzNmSasSrgms3ytxN4Kh7fE3HdXas9qe0aklJgkWw8BSCIaUmFyg35+wZxdsvvY9qFpz\nNZ7A7xl9z2M5wdWXafpAXRe8593n9MeKbvC0bUMIjuMJ/LBDqXucnyfOzzv6/jE5K9brBd4PPHnS\nAZF7K8NK1bg4cRIToo1EceCw1KiPfQ/rH/2L1L/49zj95m/SvvxOVv2aOHg2S7jpJEEXHDuP04HJ\njCy1ZrHYsh+PXD+5pDqLiLWEeolxcLCBLo5YBOXkWVdblqst7HZ0j48cbUE/Dmw2R9o40PSW4Cuk\nXZL6ieF0JOaJYrshKsNxl1i1B0plMEVkcJInjxyncMVWlvNhVHsCIJytGbzGmCWVGHh5lXlSL3kW\nHF2jOO5buumAyJGLRUORJVxExPEep/f9ccrP/BrLp0+5fvd7iI+/THO+ZPXOJUJndGpQZceUAuO4\not6cKKcTu5NnFyzF+QIdBEWnuLeE4azgEDXZZepK0R0D129c/TaCahBkMmMImNIgR40bHNTMpy9v\nwWKxoO/n9/xiscD7RMiBojCYsiLWFvQCv67Rx47w9BrYIV6+j7lXIqSgv71vNFnSCZiEZKUTWltC\nUMQ4kYRHKI3Qb964upQQC0XZZfL1wGQnpKrn3mULG5N46KHrJ1Z1wImGRfkyh35HWY70fUdVLUlp\nhGoijxWVExxjptOa82bLeHhMf7hicW/BZqO4uVGEsGaabjgej5ydbZHGkSpHOTqmvCCrIzJE1rXj\n+rTHtIay1PzW8fI/aPiZn/kZPvzhDwPwyU9+km/+5m/+Cq/oDne4wx2+unFHUO/we8JHj/Mjburx\n3jEODu8ifkxEFwkuI3KCGBE5E0Oc1bwYsQpWVmMrjV1plIoolWfbrtEoZRBSgjQIUUEoYSohGTJy\n3tRJCQUkNZPR0WRGGUjJo6InJ0/KARs91o0UzkEItHGuOzFSY6TBaIutV6i6wWnBFB1T7HDd7sXv\nWjbQLBRWFYSxZGgtXStphzevh1KwWMDZ2RzmI2Vmmib6fmKaphd1JwBN07BerzHGkFJiHI+EMHB9\n/QW6zrBaLW9TNvWtfbdEyjfnlZKfQ44YIsn1pHQEeqIcMdUW2yyQxUwyU86MKTE2MJpMOEbyeBsW\n1UGxMixXluL5LFtK89Bn34Nz1ECRM3ulmIqCm7KkLgoaCS5ODP0eF98S4CQkZbWieuc9ikM7e7Z3\nRzg3+KyZppmYOvfmuGqta4p1IuojQl7RjSXX1+MLEj9fu4C1sF4L+j4xDHMuU9NA5a+w/9P/gv3L\nfxX7xlMAYlOz++hHePzd30N85R2sjODe8HmED7gkQBt2JuKNQVU1q+W7MHEknQr2B83gEpFAs4RN\nAnuQaCU5tBMjI7UqqIqa1EeO/WMcsJGS5UsvcXPtadXAhc2o9oas1pxCICNYaEUKglwUZJfIak7C\n3WzgS096TrsKWxgoAtZEct6xXp+jVMK5A8NwwrlziqK6rUGybF/ZwHGH6S3pKBHhkrxY4zYLlHof\nw4f/FPVPfoL6v/vL7H7wP6LcJtQCqgvNvfuK62eJ158mlgT0RaRRhmyWdKdH2BzwaNz5CjM4fNtx\naHpUWXFuFYWZSAJiYRl8QbufmMQTxAqKYuL8XuTQ1giWXD30qFiSsiDWEweVOMZE7jt0TlRu4mld\ncH3p4HTD8kxDaTHP5iqnYC3t8iVWMeDkFQvxXrStSBi8MbzW3iCVxPeCl+s1Y55w6kRImgfvehfi\nm74RPvNrvPtqz2+qC077Rwyq4/6rAaMdqV4TU0eZJpw4Z5gGykpgdh1Ta2lfUlAvyUHDOLHOHdfl\ngkBLtYL2qaR9fU///kBdvvk1apKAnOhdpKwL+k4zdSNciN9GUJVS1HVN13W3NUmakDyN0hiliXoe\nTxiHQOkKsBVSTBjZgpgZ23RruzfeYaXFyYIoRoyBaTKkGMjCg+FFd2+6DUSTjaTpAmmITEREZckS\ngvSsskYag4sDY5eYjOW8LHj55Q0hzASzKObAo0RPsh3WrZBdJKwEfrGk7HYMXUe7blmXa5ZLgJKu\nW+L9if3+wNnZErXYE6YjC3HOkYokM9UwsmgM++4Gu7/H/fvirSO4f2CQc+ZHfuRH+OEf/mEAHj58\nyKuvvvoVXtUd7nCHO3z1446g3uFNxAgxMo4dw9QzTMP85xgYxkTvIAdQgBEaIxWl1BQJVM5ooREq\noSqNtpIsBVJnTCHQhcKWGomYnycERJKzx3aU4BXZZ8DdPiBJCBpCIXClJgk1/0VWGK1ppKEQijJr\ntPcEP+FTxidNALxWRC2ZioJOCbxIjOEJ6ZDQUt8qogYj535STQGxIHrN1M78TStYr2ci+vwSSQkx\neq6uHE+eTGjtKIr0wsEnpaQoCoqiwFqNEJ6URlJyNI2l6wJt65imxM2No2lq1ustSilyzsQxkqf8\ntvRdAKVrdFGRTQvGAS0jjuiXTFngc37T2qwF5bnFBDBtRgegB+EDuQ6IaZzZ43PmKCWUJaqqOC8K\ndm7gauq5audu1ZWSFLczdqUuqUxFqd+UNdJZyfT4BneYcM+u8MszsPb5S40QIETEGIfvRp7eXHPT\nXpFS4KzaYG8DgetaIqW4tXZrNpsSP9X4v/85Fv/zX2H10/8Dsp8toMOrr/L4z/1b3HzkoxQXK0o8\nw5PHdIODsuLi/j1oGvZ6JNhMUcGylBhpeXJj2fmRVLXU97ecVZoqQBkEuMjNzREpYdkmFq97ypsB\nsYkcTGa0lsvFgmW0yNLhi5q+6JDdjpvdIw5liVo23CvXLMIWdb7kVO6YVOa1h4/Q9btJqqc2FaXJ\nXNyPTLuIdxPen8i54dmzHcNw4vzcoNSC+/dXxFjhXKZYOWLXoWPGnxK2lIRqS0+P/7e/H37yEyz+\n6l/n+vv+Xfr7nrMLgzSSCohNJErY3TheWot5VnG3p7GGMVl6Y5l0IrprQtogKkFh11RFD2ru0b05\nOLzc4KYvIfKBYlXTNIZOaO6fLRmuC7qhx7maWBU8CwONH9GnjkUO5NDx0FvaIRHikXtSMkZL7zXj\n9WcBmBYLbLVklR/RVYYpGI5ZgrXsLveIwrNaaB7cfxfFUCADOO+xmwX3zkrih+aE5ovXP8vp4lWu\nHj+jv+wYhpHtcon3S/yhYGEcOxkZxw2ivqawgZB74ilyWmfkckvUz2hw7VGhDQAAIABJREFUND7R\nCUnVRCprcaPn6Zcuee/XvfzmPTSDEhkXItZqtBCMg+d3Y1dvVVHHsSTkgDEKLQ3aCCaXcF2kzAr5\n8hnG7+eDoMMBNpuZoMaIip7S1rRYhjBQFNC2imnIpEV4m3raxkgGKqWwdmSIDu81WUm0NmgJIkis\nCozBsT8V1BuLMXDvXsl+X9P3PbvdjouLM5wbZhV1ClSTpEuZ1hi29Ybx+IT+eM3CLlguFfPZ3ZLD\nwaHUxOk0sVxWpGVHPpwoxYqRiZQLNnli1IKbYU953P6Bs/qGEPjYxz7GJz7xCT74wQ/ya7/2azRN\n85Ve1h3ucIc7/KHAHUH9o4ZbxpBCIPg5kGhwA8M4MMSJKXoimeBhmvODIGmUKimKEtUUlIUhi0jE\nM+IRCpAlSkqUyBQmUxooraAyBi24tZdKSAa8RWDJHigAO6utOc3WXS8jQSVSDvN6U4Lg0W7Ceo8N\ngdJ7RM4z87lVWXVRoKuKarEllBanBUMY6VzHFCd89IQ0W4RhVgBjkEzB0kaBzAIj4XklqDFzYfwc\nvhmZpuktSmlmHMUt+RJMU8liYdlsChaLBEyk1BJjeMvFFyhVstls2GwsXTfQdR1DP9HvHlOpitrU\nSPHmZlZo8WbYUTHXWEzJMISe3u+IeQI6pFqiVDPP2t7WwqjbChdsIB5H4mVP7ie8zOiVRJZq/uWq\ninRrcx5Dz9TuSDlR5sxEIiAYRUFlKu7bGnm72fZ+DvadJvBeEDknTDtiOxL3N+T1iqgF4GjbE33f\n45wj34YyDU6RlGfPwEvb+whRkrNC6wKFRf/v/xD7cz/N6m/9NPq1L724Jv23/Iuc/v3/gPjhD7M0\ngs1xYHz0DLcfkfGMm/HIICv6UCFURhUldVlytthweeq5ObTMvL9ju1WcLyzr8gJ5a7++fHqJsI4q\nHKlKTzxa4iBQWXP2zhXHrWF0kWfHCUmkXU7sZOIiZdo+UPYTr9glq8353J2jLM35+9l9+XVa39Nv\nHtLUmq+7mOf62rYlRYPIjsvLh+z3inEsMMaz2SxZLDQxltzcwDB0KHWNXGWKrmbsA2Wq6ZVkKkra\n936IxYf+OdSnP8Xil34O/y98/Qty0oaAWSaqlWC8iuyeZJbrDu8t9bKmq8/o/I5n7Y4lS2qx5oHa\nMiEY1UhRWK6PkRgdNgFNonSBOh6pqleJpwk91lw0kjdioi0FsdOsxolNvOQ8Br6YWnbhDHUK5Kqj\naRwml6ijYqda0pNZFQ/LBatlZC1WjApakXG95HA60k8TdSf4Y/fXFFqChSa+DGEgyIfknBi//kMA\n1L/5G2wf1OxvCkLfEXZ75HaLkAmt1ijzjCIOeLUmujVTeoKVPcRAOnh6pUnbNVZDLTPHLEkpsn61\n5MnrE6cvX+Pf9wBj589mJlFIgQsRUZYYpQgukKXid4rKeauKut8fSDmitUSrCq0Fo3O4SYJVyELB\n8mzuYup7vNYkY9AxkokURQNBM4aBqga110yDhIUgSw/YF+opwFIppHT47JmCIfdQG9DC4tvMAseQ\nA71vKINhsZjXvF6vcc7h/WzLr6oGaIm2pXRrui7hloK0WFL2e4au47Q6sSk3bDbzgdVyueV4vEKI\nEa1risLgi4lqcjgWBHmkCrBtIs/2A9fHAq3rF2v4SmO/3/PBD36QN954gx/4gR/gx3/8x1/cF+9w\nhzvc4Q7/5LgjqH/IkXPGnXqmQ49rB5wPDNnjosPnSMqB57qbTwqXFJESq0oqW3LWLCgri1EBqz1J\nTIzRE3MmZIHPhkxA2ozWEWMVQkgC0CJoHeAtMhh00Kgs5q54ERFkkhKkEqKRZKMQ4s1eAQkU3mPH\nkWIY0N7/NpscWs8dglrhiDh3wg3XL0goSmGVotQWYxfoxYaQCvoxcuomRu9u/+2AlAPWQmUUy8qi\ngBAyh0N8MUMKMyfebDRFUSBEQYyGvp8IwbHb9ez3iaLI1HWmLJ8n7xa3tRu3NjufqGWNkYbj/sgw\nDhzzkVa2LDdLludLVKWQWuLSrFxNPuJSun21LOh76HTE5glLRykiWm2RMb29EiZGFCCbOT05ZYtP\nJbksCE1kCj2u2/MW/RUjDQtd8ECXuCy5cSOtj5y6E2VQTBOMU8b7xOQyMWYQicxIzteE04H+csBZ\nTbJzCJZSYCoorWXZVLy3uUcfJnyICJEp1ZLy732S+m/+NZpf+huYJ49erMdvz3n6L/8Zvvjdfx7x\nTf887zkXrLqEaQ/IsacxNfmlhrAoWVeKxzdPeHZ6hj5qyrhkmCo+9+UjStfUdcV2OXKxEKi8g/AI\n78CaM3aP3iDudhgi63sZIS0ivULoSqITSKdY7jOunzi4Fl8GpgxFkhyXZyyaezRtzypLePSI4RRo\nU40/W7Io7iHFFV5fkwvLdn3Oqqi5+mLL5bOB+4uAEAPH48R6vebll99D0wRSmlBqT84Luu51qspR\nLM7Rmy3d42um44T0cwVNr2vCx74P9elPsfnJv8blf/If0/seoytOt8TkPe+0/ONrz/hGSx/WCKVQ\nFwvM4UCYWk4tFIsNr1BDMEw5MEgBk6XtI17suags9qyg6gWVUaSDJx0MMmRW25qrJXStI95AfOOG\n6kHijTFwLdZoD3U4YYoBW1TkTiLzwHjpqbpx/thuV9iq4TQJlHXsuoH28SWn0SGiZ2lewpgCwYi5\n9w7OV68y3nye19+ItFcd5dd+PVkpzJe+hBxH8sUF6nRkuhpx2x1lUTHUDWG0NLLjVG5pDw1pVIgy\nI+Ue3S/IUbKTkndJRWUiOimyEFBHisIwDSOXXz7xyteuIUHOcVZNI3ilqK1iHEeGIKh/l3v0cxV1\ndzoQVaA0NVJqrBGQPW40YOfDKrSCzQZ2O6bdDrZbihhxKUJZUcYFfTwhbMIYRZgKQshkOQINXYwk\noJQSfdvvFepICA0cM9WZQ+mKTnhsDJTW0ftMnOyLoDghBNvtlqurK9q2xdotIBGVJztPNSqGRaYt\nClbVmvH0lOG0Y2EXaKk5O4OrK0lVbTidbhBiQOsSvYx4d5xTfUXJmAbWLjOu4HQ6IHeKEArW669s\nsu8XvvAFvuZrvgaAH/uxH+MHf/AHv3KLucMd7nCHP6S4I6h/iJBjJriEmwJTO+JOA74b8dExuYEp\nTUSRyFKjjUVIA9QICmSqKaWl1BYlJTkHZHIwdTDtSCkz3j6PyJGyyBSVuLXvzt16SWRCkKRsCNEQ\nnSYmQSSTgCknopyrX7yGaHnbTkN6KFKivFVIixCQOZOEwAlBqCpsWSLLkqgVEwEXHdPYEYNDhAxx\n9gWrpLFZorEQDGnUeA9d6MhlQiyWrEyNqUGZgDSOkHuO/ZF+GNgfZqUPbpN7TcGyWrJpNpRliRDp\n1rbbkrOjqmYlse8Fzlm8LzidLMNgbzOGMiLM9t23Wnclks1mw0qtaF3LlCcOomd3HLBpgS7LtyUS\nC8DephKX0qDFfeJ4JA5XZHfA+0co0aDlW6xmSoG1CGvJ9yX9aaTfd8TLI2IPcg1SCCwKLRQKQQ6R\n0O+5Gjz94Dm1gaddZIogoqaSBdIopE5kGUHOFUExTqQ8keUBI08stEEtK6qzJXVtMNbcpvAKhIgU\ng8H/4t9l+XO/wNkv/h3s9c2LZccHD+j/1J9m9+HvZvgT/wppkpjXBbyR2D/q8HIAMkVtKB80VK+s\naGpFTeJke270QD96mmLLYW8I3lGIkXOjudesqEpNCAI/PsPvPsvhOjKNGaOWbC5KqA1qeQ9tNoi9\nRx4jfdvTPevwo6c+k4xLTa1KhqQ5IahLS7NY0T4+MX75KakfSPcsWkPzoGYzFkzuQBCK1rUUeNpj\nS9d5hqrgwWZL256IMVJVDVprvL/E+2tSekRKAe9LVqt34puArSxDPxA/36K2FrlqcH/uu7D/5X+O\n+ewX0L/yKzz9l76NqtRkZtVMq8DKHukDHHea8l1bjDgxyQmrEiFo6uaM3E3YcQk5s/cSJk3MHbGc\nMPaMuo7Um/vw9ER8nEhuRFqBO69J+8hS7ylPgcvHJ3RlOMqXSfEE7oTQGkNDHgWT7uiHzMI0NIfL\n+bVfb+mZ19zuW4485Nh7/FSzlCUiVcgs0JsND156hfNzxb5a8PCxoN9P9NuE/8B7sf/4c5jPfhr7\n/vfgt1smP+KudyzvNwz6ZURusHqHzC1SG/AbnL9mUi0bGxlbw+TgRmaaylD6TJdHyjCyuFdzfNJy\n8/CK+68ukEaQScjgEUaQioJSMc+Fx9+doD5XUSfvcH6kKtYIoVAmQ/Ykl0k5v2nTrSpwDrfbIXc7\nbFEw5EhSlsYs6MY9gRFrNdFZYhJkOZJzprs9pFgoBbedwnGtCZeCPGbq7BFlRS8yhZ8oascNkRTM\n20ihMYbFYsHpdOJwOLLd1mBaou6owoahS4wLwWq5ohwODF3HdXXNWXWGUeaWpFq8X9L3R4SY2GwM\napHIp9nqO0nHGBP3bEas4HC8JhxWhLDg7Ox3dU3/vuJXf/VX+dZv/VYAfvmXf5lv//Zv/2e/iDvc\n4Q53+COAO4L6VYicMjlkkks4l3A+MY0ON3bEqYexx8cJH0ZcHsBm9LqgXFiMtahoyd7e9uOVCBQp\nQIwjWXQkGVHPv/zzrApIMc9YGsVc63JrWMsTxE6An4mgSvp2RhWyyEQNvhR4m5lKgSwl1gg0s7qr\nAB0Cxjmkc+TbDVQGBiFmn621BKvxpDk5dtphXaJ8vkNRAqVrjLTIXEC05KiZHPQ+zfOuIgAelXps\n7rFuwG4qYmUZvWfq5nCjkhItNd56kkhII1FGYYwipYkb95Allkq/tUFeoFTBYlGyWhXkrOhOiW6f\ncW1gvEzchIxWsFrMrlqh5mshCoHTGY9CpDVxmuiOR5xzcHOD1prtes2qrrFCUOSM9H7eXE4T6Xk6\ncC6IyRHzhNMDKFB2ixeCKUy4/ga3GyAnSIE0etLOobNEa4XaWIIBl2bRdRyhbeefQxCIpGmEQuAh\ndxS6ZRkSSiVSdOTsyDKjrcWUJXb1Ko0JFL7Hlha9XsHmjIwhnAL5F34Z/dd/Gvu3/zZq92ZI1fTK\nA8YP/xuM3/0Rrr/5m+h9IrtM0z5lKwq2C097TMQssWuN3DTkxZJRKfp9pr92PHPXJJVRdsu5kQx7\nxf3lGWcvaYw5MU0jp9OJbh9ZIDFZc2yvOLU9ttzSvGoJ1ZyobPWKkAKDGThOR3yYu2aVUGzskoYF\nXSV4bRx5Ojr6XlCIiiQ3KLXD2IlqmajEJWw2XD8cWFMwUvPs8hkxJJpiSVtpFpuS1eoluu7/IoTA\nMHRobUgpEOMJpU5ACbwPISR5yBht6E4d/X5kfb+mOrd0eUn90Y+g/tu/hP0Lf5H9t3wLQk9sbcVS\na/bP3qC2A9VqxY4Vx0OgyFdkkVk3S4xd4SbPIBR0ge4IY9bofESpE8IqpOlpmjXZaQgVIZzI/Z7h\nTLNJCr3bsdYjk/U8HSvCoWFTa9R0IMYerS8IJ/CypU9QrGs23rHq52Mwv17RucD+5kiMe4Z1ZL0q\nwS354t7T9wa1epUHD9ZsNh1CrNGlpDqv6AfBaXdk+sAHZoL6f3+K4hs+wFgv6LwhxBHljpipwauG\nlDsa2dKWC9JUI8IRlwKlObCtGg6HHd2DhCkKSuHYRwXRs1hX7E8d/nRk/8bE6lVLzomUAloYjLUI\nLRApMbr0/3lPr6rFHEYXR2QGISxCRSSB4DNB5BchRwB5tcK1LcI51GE/W/lVRaEKlMxk6TCFIXSa\n4BSoTOs7EoZCSqyUMI646EiVJVlNygE9ecp1zVEmrOwRwwhlojCa/R622zfPFJfLJdM04ZyjbSN1\nLRFNgL3D9grXZLqiYFVvSd01Y3viKic25YbKzPUxOTfs9w6lBk4nwWpl8ONE7R1OLnD5SDXB/U2F\n0SO7/RF/8oSw4fxcYMzvfD1/P/ATP/ETfP/3fz8Av/Ebv8EHPvCBf3ZPfoc73OEOf8RwR1C/SpBT\nxu0nurbF31a7hBzIfiS7AcaJkD1RerIMyFJgmoJmsUaoEpkrZFqQvCGJSNIenxw57xHCoSqPvf2y\nTymQ5WwRs1ZjrUUpAyjIChENTIY82rl4VEEmk0TG54QX4FUmGTH7dMkQwfSgh0whE6WMFDIgcW/O\nZglBNgZvDaMWjEYyxcCUBkJIxAwuZ3KGUQjGrKlyQU2FipbJv5n58xzKSGxjsXYO+ZC5ZLq+Ztzd\ncHrNkYFc1+SmQWp9G25kMEYiRCRnj48DUxgZ0sAUHbuho9Ml2+oepVkBBjykMRF8IrmATWANBAH9\nAEOGKAU7LzA1NGdivlZ5vjbPYYzh4uKCaRzpDydyP3I8PqZNmcZYjFbzmgWznJoTKAlSgFwyZsPU\nXxGmK3z6IikbIoZIfGF71kJjlEVfVIRTJEyZ6WlgyoasSnIqkGiUtJRLQ1NqBCNaDZzh6UNPDCPO\neZY5Y6zG6pKiKNA6YW3GmISUGnyJOHTw5T35//h59N/9OxS/8r8ibqtEANLXfA3pox/h5s98B92H\nvp7oBCGUTHuHTNCQsdPINF4hDaSXJF6smbZr3vXOJb2D/eg59oFn3Q4fA1YV3Ktfob0cmQ4Dh+HE\nO//4luXyDH88cnzyhKltOQIuOHokxeYl1i+/AyFP+NARCOynjigsUpYkmVCtYrFZsLi3mEO9hkw5\nQkqSUy+IMvOaHnhPDqxfrijqxbyj955w+ZSuO9KNE2uWTMowRY9uFO/bViAkz26O5Fwj5TP2+9cQ\nYnXbk3uPqgqMo2Yce/yxwF06yqokC0VIkSYKLIKDlLg/+z288y/9FdY//0s0bzyiet+CjVlB2zIe\nb5CFZPuO+zz5kmPfT5Qk7m9LLs7ewbGduOkTIUN9OaBiSV5GRr9naSVjEbCVJI0S0a0Qi9mZ0Pcj\n+mqcw7zGnpOPpOUCE2pM0Ay7N/BuwAqIAVzscIWkMQ2vvNPw8GHCnuZi1aMxPD1c0idH4T1nheGV\ncssuPOHRXuPNSzTNO1itTsQ4oNSKlBLNquGwNPRTh/vA1wE/h/1/Pk1pvo+jEARVkNcNPkyUfkeQ\nZwhRUagTUXQoWYDf0Lee5SsjJpYUJ4nvIqk21GpgLzRRJmIeWS1rJt9zc3mgqjZAIgZPIYuZoN4m\nbI/TWz7kvwNmxVQic2YaRkTdoLRGJUeKAS/ffmObUiJtt5SXl8T+hIjAWYEQAisVIUdUIXFxnrGX\nWnJw1yCXLMxmnut3Dpc8QTVkrdA2YmVG9pFsCkIA7QTNRqDM/N67uprTy59PWmw2Gy4vLxmGAWMs\nxiSCbqnDlqlP9I1guVyyTYljf6Tze3brRMxrFtUC7yGlNbtdQCmP1oJqpfHXRxbpnKMsOMaR+53H\nbLcotedmN/Cs8/h4xr3z3/8KmpwzP/RDP8SP/uiPst1u+dznPsfZ2dnv75Pe4Q53uMMfcdwR1K8C\nJJd48tpDHl4+mkN3UkAmjyQiRETICDpijEVVCyg3OFFhWJLbJVo0CCHw3r/o21QqURQGpeZgGEgY\ncztHahRKGXJO5BBJ40QKEYJGJHubyDoH3USbCIUlGkmw4oUNTQIyZmwG4yLGBcwUye1EHmfVLwCJ\nRKolcaHwC0XQgphvq0zinBhcS4GWBURDjoYxGfpJMITZdrwjY3BUSrI0irIQKBWRMpBzIITANEXa\n9s3fn9UK2baY4NDJYX1C1zWpymQ6YkzkPF8XcqaQUBYLnM6000QYMk+Pl5T5xEKsUFLxgjkmQAqy\nEsRCoKpMJQXHE9zsM6ED9VRQLxNKZiQCxay0aOcRISB8oAmBcfR0Q0+cHF2a00OXiyVCSrIALzIx\neXwMuHh7SBEjIfUEOSK1wRQVVXmGLReIwpCVwkVD6yxjZZimTHYCJRRCCYpzTVUJmiYSU08IR3Jy\nDCHgnSNrxaBWWGOQ1vKgtDQ2U+mAyhH6nvx/fgb5Dz6N/OSnEZ/8FPKLX3z7e/pr30/+N/91xEf+\nLOKDH0IkzcrDzZMbDiJTaM398pyzwmBiT7ZHwtoyKjC14ele8nA88vDLe7ZbjZGWUPY8KAVlLrmw\n9zgdJaN6fjBx4vOffsRLy4pllThrFviy5MY59scjPi7IEU79FcIaXAxIZSD3CDFiZKRRK2RRo5TC\nXljGLnF8GNidAonEu1aWWIMsI7E/knKGzfnsALi+5snDL3C4fkaVFLqaePd738vlyXF97NHViFIT\nlw8dNkrOzxdA4Hj01PUrWJsQInM89ky7iePhETqusec1VbWgfdozjBPpCk5uRLz7Pdz7176D6ud+\ngZd/4n+k/c/+U0J7JO6uSWTsxT3GKYHpkUFTypo8Jcoys99Du5eMxYQIUE4BddGRcsapQFVb+pNj\nyZoMnGo4ypL0+R3lsKevtxzyBSwDdlLYvGdqXyOmCpMSU5QMwwlvKs43DffuleSsadXI5lZNb61m\nP0ysm5qzymJzSS4ky0Zx8eoGsVoQgqDrCppmIqWenON8EFUWuKKje/8HOAfMZz6DVgatBTEmvF4x\nqiNLEelvWtLtQVwjOw5GIsYaF3u61HKxXc2KfRegNBiTsd4wEinCQNNsOfmW4bSn3y1JhNmeLRTW\nGIKY61FCTjPh+12+cb1P6MKioiBMnhAi1pZz0Bme30pvp5zn+frVivj4yzBFGBNIKJTCx4gpFSMG\n7wscFSlP6HRERkF2FpEzkwIfBCJK1CqihEKeJLKx+C6Sg6a0hu29ERVnQnl5OSupRQFaa9brNfv9\nntPJs90KZBPh4NC9JjXQlyWNlKwOEj22nK53HDdzj/ZmtSEESYwbDocbpIxoDbIBupaCBU469tPE\n+e7Ig+UKc9FxvfdcD1f4ZxvubcvbCpt/+hiGgW/7tm/j13/91/nO7/xOfvZnfxZr7e/9H+9whzvc\n4Q7/RLgjqH/A0d90fOG1z3M67XGDp7QGo+agCikzSVuSrXGyYMgW0RfovsQoi0sJ5/aE8IycHVon\njElYm1BKoNSsjq7XNcasyCGTfSZ7iRgNOczUaZbqAjEHJhxBBbweSWZEmFubbRZIr243pIoqSUyM\niPSmtS2rjF96QhkZ47ynCqiZzfYRhogwAlkqpC1mm1u0kAwxyhfqqAHWQKMiExMTniw8o4x0k4Mu\nYFPCAjFGUgq3NskJiBSFnDdXKzET2K5laifoZhudXCyRy9X8/EkjgkZ6RRrTHG4UNJ3vmKYex44T\nT6h0jS1qkhFEBYGMy4lIxudMfP5Q4CeBHwXxmFgWUNoIPkDO5JiQKaNSRsVELQT3GoUrMv3kCUx4\nN6AKgwuBIDJRgJcZYQyFrtC2QJtXMEIiGRE5k4LBdUvC9RY3KlKCivmhraBYJsocqJaCbHo61dKe\nerz3OO/RxtDUNbKqSEJwZgy9nDsWu8/9Q8p/9CncJ/8R5T/4NMVnPot4S6gUQDaG/PVfR/5X/yTy\nY9+L+NqvIx9HQjuRH/fklDmkSJE9RTpRNS2LOlEFM8cFW4NeX5DLkhACjRo5PRkZxpGudQh1hSJi\ndcXFakORHYNL3C88764mjvsDh1NgHwKJLSdZUWwKfHeJXTiCS/T5wPHJ62hTsj3/Y5w1DyhUxoiI\nb0eS7Am6w+U1p9ct8f9l701jrlvP+67fPa1xD89+3umc4xM7tmP7+BgnadwMFFLAQnxJhQRRmkBR\nA6paJAJEQqoUoYgPkZAagQS0oUWEAKKFoBIiBGoqIQKkDCmxIY1T+yQez/F7znmHZ9rDGu/p4sN6\nX8dJXDtjmyrPT1p69l577fWsvfa9917XfV3X/28subVMPtAoeKk0TDZzLTPdPOONQfU95X5PjJEr\nm9F1zb1Ysglh6SfOGwo1ULkjN/MFUWVMfgFj3knbCjFO7PcntltBoqKYXiD4gYmedr3H3CkgFhzr\nE2kYeMEV1H3CrleEP/fnqH/mf2b1X/63dD/4r9PLaRlj6zWDzogMKBTvPGvxdma/7zHGovUGJ55u\neEIhhkbdY6scoUgUdcnTY+Ys1cRG6JpMDj3Dac8cZ+yQiXODs3co5jeI4ZLuJqHsxKaGSTypH6nU\njjublt3OkaTgKgRev3mLr+uuAEjFmgerDbrZIMNb6DTg9H2ae+/m3ZuZzi7CZX3fEqPn7KxfJtQE\nqqpiiiPjN78CQPnpX0H2EWM0GGGOi4XR9m5NcUjM04wUYHRPVo6t2XGREkNO2JVANZN9SQ6Koiqo\nIgxec2Y9tnIUriCFkavjhMoTUiVat/g7ezTWQZKE93/vAHXyHmM0Z5tFprbvJ8ryDKtACIT8mzOo\nsASjXV1BnNA3J/J2Q2UdoyiMyqA0PgtdrtD2nBUdOY+E/gKTC0JhCF6jsqJYJ5w3+NlSZMWshUiF\nzaDszN3div0exhGur2G9Xvygm6ZhmhYv4+Mxsd0agjnRpjschkTXKtq6BudobgxmNByu9wzrQMqJ\ns7MdKTlCWLPfH9Ba2G41eRppUkVwW+Z84nKe2YbA3abBnmmu7MzhdE28WhPjmrOz31vxpCdPnvDy\nyy8TY+SHf/iH+ZEf+ZEvidzdcsstt9zy+8vvOEBVSr0IfBtLvuj/EpHrr/GUW34b5Jh5/PARbz7+\nItNxYJpguz6nsQXRaCYKgilIWIpcUmlHWThE/NJLKgPGBFariNaBlCaUWpRUrdVYZWAO9ENgeDJh\nVEXlVhRFS1lUGGvJWghaiE7hzdJPqgxICKgwYMOEnSaKOGFzwogiZ8hZ0SUISRGTJmCZlSMogziL\nKqslKHWCJGByMBpk1hANkjQgiAFVJrKNZBXIOaBUQGRGqRGtAyKRlCI+z0ySCCxluUpnrE5UWtE4\nKI3CWv1MoGcRNJpnUEoDBqGG6wnpExI6chpQtkWKGiWLRY5SS++tcoqkFcm2nKRnUDMxzDAfKKsV\n1haIViijcM8XpWhIlC7j6szYBfwpY4aAGjO71uNMxlQOCkc2hqgVIUe8THR5ovMjN/2RgGDKks2d\ncwpb4kxJa2tq26KlXEp0c4mkgmm07PeL/6MSgBFbbWmc0NZCXUSaDPX/AAAgAElEQVSsXc5tf+x5\n8vqeqZ9AgW417Z2Ge5sdVVNRVgXl9SPsJ34B/t+/DR//O9hf/BSm63/d2BWl8O9/H9OHv5n5Gz+C\n/5Y/Cn/sI5ic0ZcHdNCYzmLdFrtTpOg5ykxWgUZn7krNMN7QP/wsKVuKosWfnRFyJj/rSV47x/qF\nc8aD4np6RFlbVI5sYqY7vc4Xr4ScDGdNyeq8YLPaUJ5OTNphzrb0U+Rzn/si/dxTN4aXXn4JSZb+\ncMLkgjKUxC7SbDY4VxKHA9PYMZpEPB1R80B59wyzKrlzx1JMmXrS5KNHXz3lIEfUZo1SS791RaDc\nnXHn676e7WVPvrlm/MynmNUZ27OWsqrofc2srykrQ1XtyFnQ+pJ56Lk4ntiWG2pbMZf1YtdUHtnL\nFTei8QirKrEC7nrLHkv/xz/K6oPvR7/2acqf/En6f/6f41AIXixnnCHOcNZsqIylm08cDhljLOt1\notJHhuyJYsFFHpxvMJPj6piw9TlPYmJSB85OE9NwZOgj+3KHLRT1vsfI59F2v1g7iaGMG8Yg+O4p\nVVlwtsqsy4JTKrjcXzF21+y7nnJextKqvktlDcdCUJ2lLresX34/W/+IcB2YSdR1wNodw+AQCUCP\nCBR1je73hDt3yA/uoZ9c4L7wRdydYgnYoiBiiGVBeV/hH43IzYBtPU4Cih2WFWJmxjCgS01OA6I0\nyjpq7em1ZVYBmzo2VcsxHTkNB1z2EKEoKhBhthYpFBIDXfclu+HfxDDPAJxtNijlGceZnBerKGFR\nTX9OzJkoglEKlxKprchRo0aFXF1g70GjSnIMJCOMSZhCoK1q1m5F8FfI3NP5a1J7BxndMunTeoqi\nYOwMReeZjCZoxypCVh4Qdrul7/N4XJYQFlHh56W+McIwzJSNhdOE6R2pEcaUqK2Fu3cpD47zznBz\nuMH7wNUusT07J6UG7z2n04hSM5u1Ie0PrONd+t05fh646HuarmNrLa5xWBvZ70+8fRMIYcedO+o3\nCb3/TvjlX/5lvvEbvxGAn/qpn+K7v/u7f/c7veWWW2655bfM1wxQlVL/FvBvAh74ERH5a0qpPwv8\nRRYXS4BRKfXnReQv//4d6h8epuPI51//LNeXF3TXAe1q1quGXiUOJuPUhlKtqakwWGLwJD/TS4/W\nAaMzIgGtPUUlVM7SNDscyxsePfiwlHbNGWJKeCWc0gk/H4g2Eyyo0mKMRvUJFQTxER0Fh8aKwogh\nC4sgURYCgaQSXgWSyiirEaWJMRFDJAaF5ArDFrJDZwfZoIhLeSwKvJCnRPYBJCLZo9SELgLYhC4F\nZZe+IKWW5ZkNKlorWmvJ1pFQJBQeRcYRMDQ4bHIob1HBQDDkWUFi6eFCocWD79BxBg85CGFdk7Y1\nyYIvhPl5vy1CUiVeAmPsERJWeSqJ7FTDKoMNEZcS1nus9+icUSmxFiGIpfclgy4ZU0u9FmyVSQrE\naKKFWYHXmiwGo9ac33nAeOxR2VKMNWebO1gqZLbEcenBFcnM88g4joTw7KK4jTh3TVV56tqh9ZoY\nE3OGQ+8Z+wk/R9hqbGlY5zWb/QXtr36C8o1Poj/5S+hPfgJ9cfmbxmt86SXmb/pm8kf+KOW3fzvj\nu/8Iwa4WS5xSk2tFGgSfDXgLfoLjDfr+jsnBZABKrK7ZWEuMEf/2RG9OQKTZ1DTWokKgSonKe+qc\nycHz+pNrbB+wdcH7v+4eUcOjzpMlomqNfaC5LDXGOQZT0HcHZj/iUyYZj3UF2/U9ZKiwSvHCbo3W\nkWEYOJ1Krq+viUdFmRuqzQPUJuHSNVU10272XElingw2V1yHSDhMcHXEKrB3W5q2RZclp3CgViVN\nVRHuJ/I4M15HdOFoy8zZC+9kDi1P9ECqr4mxh6FExRV+viTlHrdp2b1g6Paa00VNlIxSAzCzsgN3\n7Y6KiPGe4snMrDP993wP6x/5d9n+1Z/i4Z/6Xt7yj1GDYlWsOC9e4u0M080yAaTUCe813jdstw1p\naEj+RFZHcmhQnXAnbDhWBZdcMl5dcxMt61CwdyvmOZCJ5HBD7jTVeUmyjos8M3ZC2wm2eUDbHnB1\n4K35gvFRZEqJ0SdWOrOaBwDU5oz1XNO/+CLohvtnNXfva/RTKIyGJCgVOT8XLi8bhuHIOE5LeajR\nVHWFRoivfpDiyQX1p38J98f/MeYwkBNoXTLPnvbeltPJEq5Gii5QXI+IvcN29wJX/i16IkpZcu7J\naiYnR6l6tFsRckLSRFU84DAdiHQMQ2JrNC4VaBFG41C1QeOJcck8FgVst/w6gZ9hWsShmqqkaQzj\nmOm6abGHkkBmUfLVSi3lvUD5rLc55YTcvYd+qyQPHUUfaTYFY/KIhkkUwQeapkEpg8trIhXBjIR4\nIk4OparF7zlrkimwYUCiIbqCVisE4Tgf2ZQbViuFtXwpmxojnJ9rttst19fX9L1Q7ATRHXW6Qzcm\n+kZRG/PcowtbFNzZG/bjDf7pE27OA+3mHjlvubyMGCNoPdLWDsYTu/6MabdmqGuGw4HJe1anxItO\nY8+E6+PE49MFIZ1z/679XYkn/czP/Azf9V3fBcDHP/5xPvKRj/zOd3bLLbfccsvviK8aoCql/gTw\n7wNPgQH4L5RSE/CXgZ8H/huWKsE/A/wlpdTfFZG/9ft7yH+wUEsK7geBfxV4F3AB/HXg3xGR4bez\nL8nC0zcf8frD1zk+6einSLFuSBreDEeKUlP5SNYTUT/GGgtZcGQkCyH4JWOhBK00WhSnm8xhziAG\nMBhtqCpoG4UuFViQIjNLYvKR2WemfsL3njxHVAKrNEZpnNG4siK1FeIsUUPUQjIarAajQClS0sSQ\niN6TnpWuAhil0GrJdCi7AlU+6wldMqFKZSgT5ixgyM+jaIgKpw1GLwrAblVSrBzWVhht0KpA62fh\nt2gUS2lw8o5pVMyDIk6KU4JBYK0NTv2aR4HSCnGQnCIVIKUi4UljR8hhca5RmlQ35LJAITgNNYJN\nkTJHKnNGnE9MwxEtHqNm6qTYiEF5v4gYWUN2Dq/AayEq8CpzM0SmaJDR4kThmonwLKOixGIoqM0Z\npdtgpEQnzeGwZ4yB/VNhuy2oqgIRIQRhnsOSRVYBayNV5SmKAMzAiXEUlDoRgmWaZlRMtG+8wf1P\nf5b1516nfO0zmE/8KuqZYM2Xkzdr0jd9mPxN34J843eQP/wd+N0DbnwgTonyRmjf1CjlaVYGU4Pq\nAK3ITiGbc3x3yWQDT33HyRT4LFRas1KKi2FA7/egLGn3IlOrmK2hMA3nWVMOA2YYyPPEdX9JnSMx\nOlbjmv5iwtQFRVpzvnI0dwODHulCxzRdkXLierxmuBjYNlvun93nPS+9h5wqLi8PdJ3idLyL9xHn\n/NI76BVhPzIysdnM3G1a2vac8frE229fcnAdFiiMXS7yN4aVX3O0NdrsODeO3kxcDEcmPIXJNEbT\nrtbMfYGzK9aVQV3uqfpE61tijBzCF6jDOzFSgm7QZcfkMm8NF1zsHSoUONOycy1JLimKEXN8izA5\n7ACta5iPmeOf+tOs/qO/hP3kr6B/+RO4D76DylZILHntzSvi1FANE2O85P47JpRqUCpTljX3dMGb\nlxMDjvkCKn1OF0bwV8hwwTgZ5mLHRY6koUeHA7P2GA951OT9RMee0/WEm++zerBj3WRmZXhrOBBO\nR3yjaYoCnQyz2lINy1emvf9e3nHvA+gXG+arHlPMKJvR2qCVYKwhZ4XWkXv3ah49Wqx6Yiyot0JT\n1xg9M7/yAYr/7W9Rffrvoj/6T5ATkAWRink+0LaR8nzDmBLh6SOKqxPuXk9cF5jQkvLEMGXWViNy\nQqlzXKEpA4yzZlN4TAFNUXETRw6xZ0uJnixFnTDWEYzm3iawPoPTaVHGvrhY3GI2m0VwaPLL570q\nNKtVyzwPzLOnymox25FEEKFU6tfKe5Ui+glRILYmn+1gPKL6nmZV4bPCOs0ggXEMuPPlO0/NM85s\niSYTvIc0onWH0ZoYBN0a8iGjU40uzaL4K0IfesY40riGVbni7l3N9TVf1pda0bYtfQ/7/YFdu8Kd\nRlRf4WvhGCOtMUtfbdOgnWN3bTl0V0wXF3Rbj2secHZ2xvX1FVo77DZQ6Ez2NdVVSVVb+u05kx85\nHo/YObLzUNaJJzNc9Jf4eMYLdyvq+rfz67vwoz/6o/zQD/0QAA8fPuTll1/+7e/klltuueWW3zVf\nK4P6bwCvAd8mIr1S6seAnwD+P+CflEVFBqXUfwr8Ckum9Q9VgAr8Byzn6aeBfw94leU8/BGl1D8t\nIvLVnvwcP3o+/5lf5dEbT9jfTExWMNoxxply7VjbisZZxHjGcM2YMjfBA4myMDR1iV5pjFjECzEb\nRApybpDakLUiaM0kQsjLRYUJQukUViLMBhc0LkbWbCgcaJ3wORMkkW0GqxAreBkosWyrAuc0RE8I\nmTwoUgCSgVwjCEopjDEYu8xqizqQGREuwFq0aUFBUoGMJ+YJpQXjFLYAbSyuKJFcIN4hk0VpjXIK\nsyvR2pKDQiYNs0JmhcyenGZIUAoUsogNj4UwG8XoNKvKUtSOaDVJK0RrfIIgEBIkUUhVoiZNMY7Y\ncaYcJ0rnqNoVRcrYlCiUQisFWEgbJJb0c0c3n7gxihutKcpzynpFKizRCGINYjQimZQSZSXMXeSw\nj4zXEUVF2yicAUtJZUpGbZgUiyiWShhTM44jMXacTpdYW2NMQc4JEcE5oa4FrWEYlsWYBj0E7Cf/\nNuWnfoXdZ9+k/czrVJ97fbGu+Q3k++fEV76B8IH3Ej/4AeRbvhn7yochaSQJkhcFYp0vaWPiuk/0\nToNznO0axCqW4WAQo5Z+WRFmXdNf3aCuDmx2O5qyoHQGHWb04QZyQDuDbFaMp45j3HNhbgjFhtKU\nSFnQWY/aPqC0BffMlv3TxE0/Eq8mtO5Y20Q4LP3KO6WWyRRjQSr8NDNlIW0bPvf4BrLCSocrKmJY\noZTg/RVFITSssbsC6hO5OPLo0VPCHFAHRVc6yhd3nNdCWyrKskBfP4EHkFzFYbri8iLj3MCqmlCu\nJSvDSENflPRqprUt5MT8+Mh0ecEDZenu10x2ZLU7IP4OORdkc8aoC8I0MZ564klx784ZjXeMvcP0\nM/RH+mGk3b1MLDbkquSwKin+5D/LvR//a2z+k/+c3V/5i2zknXSniZv9nmG44I4esKqjMJkHLzlO\nNxZ/hHhsKacto1j2jVCMHYN6xNFXTONIQOFiS5aJLnQwBVw2nLCom0uaSVGdFzSrGmMVzgrX0ZDG\nayq9o/KajQvY1Zoxeda2oRxHAO5+6F24+w5lLG8Wlhvfcy96nDZoAyoJKUGMkbp23L9fcnmZmCbP\nDNx9qaC04F99FYDyM58C5TAWtBFCUIAgkmnaxDBvOd6sKIPF7S9J5ZF79T26m7cYfKI2IHFP1A7n\nMlUUDjg8E23qaNyaSzMw+hu8eglnC/TNjDYGsY4UA1WdqWtN1y0WTuO42Dm1LQxzBKB+5hPcNCum\nKdP181LmmwI+Z0qt8c8D1JTwOS6p2GzBOfKqRuYDrj9RSkFdF1zOE9NY4p73T04TMUdyu4ZBI6nH\n2hPkSMgOXQu6y2hxmFTiipK7Zk2nI1Oc6HxH73tqV7O7s+J0sEzT877UDdbOzHNJHwZqDXWqGKZM\nV0GfEqXWtMZQOoe6f5+zouC0f0p/c0NsPbp+ifV6w/F4QGvP+Rmk8QDpDN0XtD2UrqJbO2LoOYwj\nhTc8oOPKltxM14Qna168s/4tiyfFGPne7/1efvqnf5pXXnmFj33sY6xWq9/ak2+55ZZbbvk952sF\nqB8C/mMRed5k9uPAvwb8xPPgFOBZ8PpXgT/9+3OYfzBRSn2IJTj970Xke75s/RdYSqC/D/jJr7Wf\ni7ef8Jlf+TQXbx94fDpiCkNZNJitptLmWcYlUzQZZTRVbvAyELUDFvEO7zVlXlO4OxjXkESTjCE5\nS7SarAxWNGXU5D7ju0gKkdAHtMqsK2g2HlRcekNLRSwEWxkcguRM8p7+2DP0A37MpEuPSpaqaClc\nsQSjTqPcki0tnaKwYHRCEckklFpDMqi8J6ceyXucLWiLCms0hWsw2qGxi00JFh00IhrBEAOEq0wa\n8hKIFh5baUAtmQSlSErIVpEKRa4VuYai0lirOUjG58wFQoFaFC9FyDFjRXA5U4ssWbGUKKxg24w2\nM7brIShycKT1Bu8UQwgEvyh3ighJa2IB0SZ6iUwGsu1R+UThGxwlGoehIEdDTOBjBhSmLDCxglQi\nvqFuS1ZtXoJSMkj8NeubEFBqzfFo6boREaGu4fx8xSYdWD9+SP3kIfXjN6nefkjx1kPcF9+gfPgQ\n9RXmTMK7vo751Q8SXnmV+QOvMr3vPfhNg0LIA1i/xmSHfTPiWrNMIliFtkIcIlSKphZumohfCb0K\ntNYgz210BCRppqiYjcLExPo4c2cfKdc7VN8vTW2Lyg2sV+TrSKKiiokTnqMZKdcF13piVhmFYl2W\nXKmZ8UzxpKvRpuZdDwLlViiiQs+CTgoVLXMf6Z9m2ssRU0E2PdIkgj5hasEViXbzlDNj8UOgu+k4\nXFyD2qKVQ/lMzhqlFJNNhCQ0g1C0LVoLMl0Tp2twlmpr6JxmPpYMXaKeW97xzneSTcmpjzzdD5xu\nPLEJ2PN7uCYhxRV1bSkqzZNSuLA9iYF80hR5zfm9HU5NrC5uOIwdpy+eyKfEVBTs2nOGcqb3J1Jx\nhWxrZFgRbhKP/pV/mbv/2X/N9m/+HG9+uiPtBpDEymjsasCqa+JxYhoU+dSwxnA9rhmHivF0zaF4\nwtjNVL1iPh6J7cTsNDn0WPMWKji6EMnHjqwNRaFp1/eoigO1TRzahssxMx2vSOmKsprZ1gOt+QBt\n07C+A8cUicriTkcAmnffIRjNxiuMFEzSsR97GmPQGgxLv3sIgbquKcuWszPP8aiZZ+Gw17z49RvC\nq/8IAOVnXiMpx6yFwnvWzQalKrz3VFXE6oKxOKMp1xiJlPEKyjMmW+HziWFSaDKJGSUdTg5ot8NH\naNWILc+WUtt5YCoEZQz5FLFKoYxlzpmUIs4WrNdLUHo8LkHq8ZR58iSjMJTF0kC52Zwx9Xt8TIun\ndPKcUmIfI31KrI1Bp7T8T2uXABWQpiTjMJJpu0RZa/zkiXNe7Ly8h5yZSWBLtDTEaKmqIxbDmHpE\nKVQbUF2JTTVRZ5xPnO/OCSnQ+Y4pTgxhYAwjVV1R6RXT4DgeFc7tMCYxDAOu8lQyUc4rQqMZc2Z6\nthilaLWmOTtjXRSYq8ec+iMqvMHsXqAoak4n0PqGe/c2SDqQRoXMDj1XbH3BrFYMzjHHDk3FNs9Y\nNXEKwhcvAi/4Hefn6quKJx0OBz784Q/z8OFDvv/7v5+f+Imf+JJWwS233HLLLf9g+FoB6j3g0Zfd\nf3779a+w7ReA+78Hx/QPE//Cs7//4W9Y/+PAXwD+Jb5KgBrnwGc++Rqf/dWHvHlxxcjMql1j1gZT\nZSoXONtqTAHJT8ynxeqkKu5SeY2aHSFqpiQE0USl2ZcKW5XUqxVWW2zOlCkvjULBY+eJInmsC4wp\n0InH50wKiqPWuNZQNov9S/Igk0GJgexQrCnUDlUJWkb6fCKQ8RGs9qw3FeWqpCwVxi7zF1EyUTIi\nCqXMsx5Zi1EbFCVCeJa5LLFqg2WNShZJCnq1iCbNgviEygIZssoEFcg5kWYAhT43SK2R2qDKRaDo\nOVmEEBNhjqQkSPCkGJglQ0rsFDhZpJIsgs4RLYJGyJIQSSQlBCXIsEf8jHqakdUKrEGLBoGsLFIU\naFfhmpodDp+FIU4k8RjJVFbhrGGON8wykZGldFEZGuu4uyvx84m+F3rJzBOsN4JZquxIUTFdT5jX\nH7F6+ogHT96ifush9eMvsnr6Ns3jR9juN5fmfulcWMvw7vcxv/Iq0/s/wPjeDzF/w7dCe45SmZgG\nRI6ARwbBmgbb1MQiM48ZGUE3ilwYgs+Ey4SkvLyG7VJ22V2NaC2sjeLcGBwJqzJTylQ50Qg0K1jL\ncSnhHh+SgLw25PaM1DqyDiQcWVlMPkOGG6a542Z/Te1aVrqgcWviaSm/ngdHOjmythznAmaFErD2\nmTjW7Dn1j9Cu5P6DFyDN2KnnvEmM8xOmYWZizaF4sigOO0f2J6RUKOux7j7GVBRFizHwtj6Qrnvk\nZqKrPcMA+nCipKW8s6GQFdtCeLvqGI4jrW/wnxEkj9ROUR8L5mzQtefGThw2iUFvuS/CWkWqbmSa\nj7htgXcBm1aoi4gbPa43eL1izid8njhEz800o5JC9wnMhD2PaIlU046h+Vb6D36Q1ac+hfs//3fS\nP/6drIuRsLc8aLfosuWLU+R0PfF5fcKqJ4TphutD5vp6ZmqvuTkeWI8N7ZDxF5DrjiFNRFUjhaWR\nxJwUUjXMlWIsKlw8YYYT/XHPxY3Q5IpK7ym3Cbu7w1l7n3svfx2bd9U03ev0lxdo75GyQFqDsQ6X\nNJtY8Qg4DidsDBzjgTkbJl0Q45J5VEpjrWO7nbjoJmKomIYV6hteIRcFxaO30IcDaWO4SYGYMjux\nyDhyr5ioq4ocLFOxZtvMJD/h0tucNzvejDeMkiBvUW4FOVFwhdYj8+yZ7YFCr1ApIzoieSYUBhcj\nZhZUXeIlkaLH2cWiROtFXGi1govrQIxCDiU3NwqlhM3GUpc1Ex0xnGhUhAxdTgx5CTYfDwNz9OSy\nxCXzzE86ItsWHaHM4HyHaCH4xW7LPet1nQtNzpBmjVLQthssiSyZnPeI7kjVy1SqxYQj8zRRAc44\ndvWOlBOd75YgNY5gRqQuicMKQsk8r9F65jgf2GmLCw3FUdM4zWxhMJkkwjElTilRFQXNg5c5u3zC\nYbimljfx+i4plJxOG6oqsl6X6HVGVoE8zqRRsKlgS8mQt0xxRAFOe9rpijGseUsiPi59qV8p5vzC\nF77Ae97zHgB+7Md+jB/4gR/4e3533nLLLbfc8vePrxWg7oHdl91/njWNX2HbNUuf6h8mvpUlP/QL\nX75SRGal1C89e/wrcvn4Kb/w87/IF15/xNWwp2gMzbaGJtCWhnUNJkXihaLEcOZWlLlEkiHbitCc\nk4sSXUHtMqWZ8AyE1IMcmfdvooAKRZkhhZGcI6IisyR6Y0lNgawLYrD0gyaeLPpoUWIpnaKpNMYk\nwJPzQJaA1osn6KbRlDvIeSKlAe8nlisooYqOpqmpqgKtF+VcpQ1KFClBzgYlG5AKSYbkAzFACgaR\nhpgalupRQRCiEVKjEAOySKKinis+DXHxq8kZCkHXQpaMpERKkRgCkhNKMjpnSsBJplbCKJlsFHuE\njYbC2kWQiBqUIStNRiM5wRSQ2UPZwnxCzRE1Kdico1YbTNmAsZSiqFDItGSdG8ls8oo+7jmGa/bx\nLQqraZXj7jTQTDP15CmGEd136K5D9wMcOvJhQPcDdugpxh57OlE8fkxxffNVB2WqSsI7XmR88ID+\n/gOmF15iePAi4R3vRt7/YVS9JosmppGYJ3Lu0RgQj7iAGIVxZ2i3QbReevZSWix7TgFOCUxA+wQp\nYmzGtIlyhEoJJZmTJCYtHDRUBvYpECWBeNZa6JzisUTM07eR7Bdjxfv3ULUHrkEtWXGtDEo7sHB1\nfUFMCisND/QLGF9gsqPvwZ+EF1H4lJg+NyBroWgzugBdCvvTNUlPVOeO3faMw8VTGAf66YpWCwUt\nrbakGIlxIhw8cYhIOVG8uMfUE8iGNBtuJk02mtbuaOaC4W0hZY++yTgrON+iLxSuEI7xRCwyQ+xx\n/m2iGKJYLrzDVYrNHJkuekKaEPHEe2f4GGF/wb0UqfcDQ63xWZFDx02XCafMtSoZzV1COiPEnuI4\nY6ZEfNuwrw33ncbamXx4zNHXvPmhb+KVT32K3ac/xvTRb0fPBjvB0O2JcU9668ipvWI6aQb3BAmZ\n8KQm7yv6fcac90we5HJPpmAyBR0jTgdUfUZyHjcN+By4HhpmbzjVPQ/GETt0bMyOdXnG+mzL7u7E\nvXe+xFavQO/Z76/pp4S6WTL7st0Q8x7VVuhuR0uJyzU5ZlCKIJ4xD8RJsIcD1OC0IWExRrHeHkFV\nSLaMfoP/hvdSfeo1Xvjca4Rvex/7mEkoRlGMUyI3EVNMDGPCRoN7cJeRgHMTruuprKOfBo7jzHlz\nB6VfwGlNOWvGJEQ1UKQnSD6iyhMqnzh5uFsKblbooSS0PTl4+A0KvtZCuwm0q0AcKlKCmxuN94bG\nrND6gCdQSmBrHFkJKEWjNTkEuhyZdQVBcGGiUIlSg6w2cDPSSqBKkWme6bqO6njEiDCVCu9BZY1z\ngnMKPdeIbsjyBjLO6PVAE++SRxjbQDWOi8KTWbQMttWWdbmm9z196Ml2RjUz+6OjMmv6bo1zA6fi\nxNY0qHkDMxRA8cwaazLCbIShEEarsHfuU7oCDk/YxKdcpRVDXLHfF4SweAFrHTEmY+qMIaH8ROnB\nWcvgLUyZ0rR4OeBPA09SZAo71lWFc4vAk7XwsY/9PN/5nX8MgJ/92Z/lox/96G/1d/+WW2655Zbf\nZ75WgPo54H3P74jIpVJqw1cORN8LvPV7eGz/MPAScCmLx8Fv5C3gH1VKWRH5dQH9z/2v/zcf+/jf\n4fpwRcyRelVTmxW7ZGi9ZSUF9dzQFCsKKTFWY0wBVYnyA1bdYOPl0uPX1IvKRs6sszD7kVN3zXE4\nceUjWSmUtjhTUdo1qqxJpsRkg84amyyVsjS1Iti89HBNEyFHhhgpy0jVJFaNYExajNQXydtFsMRp\njK7JqcLPkeAjeRKGITGbSF231HWzRJTZItGBr0jRkMKSGY0kYCDTgeqXbIirKcsKjKAqQGeUWXxN\ntYDEjI5CJuF9xveZuGiIQsMSrLJkRrUCqxTaOrTSKKXJ2lCjuM6KPgY6H6iGxCoKapoww4AeBuw0\no4NHxYSOER0CKgRU36GGATNPqBzQKWHnATNNGD+hxgE1j7nqGkQAACAASURBVOhpWafnGT3N2K7D\nDSNunH/Hgy5bS3jwAv7FF5flhReZX3yJ8f4LPHYlN84uwXHToLXCOUdZlGgNMj5FzY8XBWQDlp4o\nB3KcEWkRsWRakpSIaNIz6yBEk4F4I8ghowG7UtjWgFHoTnPMiSQgKAZRnLIwCGRRFNqgBWpTobSB\nLJjuhD5tYRrR65p4WaB1xqiMVhmDoHUGMkPq8XlklgFfTAzuhDEgkhhPFp0T2zZRGYOcDNwIVcpg\nLd04EPoJ4wrcdkN3fYUgDMMe7xJy5x5le485L++xSQHbT6g5kkTj3ziCfB6jd2QKBm0IucCOhied\nIqsC7TL0M3NZER5PGJ1RLtCrgLcjcWfI24BRmeEmEyOUMiP7G8orYYchY6m7nlkbugiPhz2tdDRW\nE6uMX5/oMJyM5uQt3ZMCb6ApFbtkSYfA/uGEsiOHqKmKI6s64eaCp+99F68Axcd+if/nT44cD8LV\nVQJ/QsY3SJcnVtqjvwAdjxm1gC8Y/JY5B/J+4Kx9AtPAKMLUrAkqYGKJGTWpn1n3M8VYc9+WpLZm\nvV1TnyfaceZ8rqgevMp7372lrN9gs3GYU8U8Bbq+o58n6sdPAIjrFcfTQNl2mDLhrND2FSvTch9h\nNjcMyRGiIgTPGEYGiVxPHfvxhDfCvTsaZc4piobTe16l+tRr1J95jd13fAirZ0pXoHMgYEkpkWTC\nC/S15W2rse0WYzLr5LmTA5/uM900cRYGcl7jbEGpDKHaEZNBu0QQKJSm4MSh+zxrHbHGYrJjGoRp\nHinauHwHob7kqTn5gLWZO/cUu11iGCwhaK6OgvcrsrKc+o7We3CKtTG8WJZEYEYQ5/De0AVPUWZm\nyaRkaNsztD/S+gNeNMfrE+PhikDmymvCVBCOA0UxMQ6ROJYE1aDMiqwnbGloqwNhSgwd7OyziTGl\nlt8cY9DGsDaGlV7TM9PrCbML7PfXzAZubhxnbU/z0glXFEhQZC8QFCZrVlHTiGI6JUaE2YF3G2Rl\n8Ke3qeOJ2I+c1F3G0aFURin9TLl9mTyFEWsiNiuKrDBO4edMGwwwcbp6RBh6bqxBG4fWhr/xP/0P\n/Nt/fsmW/i8/94t88IMf5OomUBaGwulFDVpzyy233HLLPyDUV9PwUUr9BeDbReSf+qo7UaoAHgL/\no4j82d/bQ/yDi1Lqc4ARka//Co/9Vywlvmey1Ew+Xy8/9upHnnlSLr2aThbVXYvDYkEEQZG1kIyQ\nFc/6KzMZcClSxIQmoVLGK5jQRKXICKglmMhKQC8qtVppNAYjBpvdYs+iMkpntE5ok5cffwC1+ATm\nbBEMiEZEodUSnFolKFHonCErtAgqg8qCyhlJGYkRnUGLYDIYpbGAXl4ZSjJKBP38NoImYdTyurRk\n1DP7FyXLfrRklvAHEFCAQr7s8V/bdtnns/8hz7cTbM7PloTJGftrrdR/3xmLgqkoGYvyS7eHoqK3\nNb2pGV3N4Cp6U3PSLWNVcli1jFsLRiFKgLyITMWATzM5J3ycIWe0MTR1jTV2UUhG0IsPDWRBE7HW\n44oZbRIpaIa+gWfFgoggz062KIWKBh0NJlqyKCYXCEUkiyKjn5VXLJlPBGa3ePWCopgClU9LqbcI\nVQzolBHs8qaRCErj3ZIlEnn2Zkoi6BkhYxWgMuiEQ+MoCL4EBcYEShueTWI4UnAYLTg9kqJggFoX\naKtR2pDRRHqyCKgapaolaysalSw6GpQI2WacmVBqJme1+PlqARb7IB2W2mudR9Lz14wlizDlpTc5\nKYuxBi2JOkeStyDgrKfKEyknvGi0KTG2QFAkowhlwJJxviBmQciYablqjhpCtgSncDbg5ozKgsTI\nrDKiHAqFMRktiSJnfvxv/nco4M/8M/8inSmI2aBVQghohFYpDIrE8nlhGSbMsmS7tBXaFDBWI2VF\n1hnjDFpXWBIuC66ogRXGGMpKgdHkmBjnADiECHis1WhKlChCmgkI73v7i/zg3/jrfPaFl/grf+L7\nwOllDARhjgGtHYVkUpyZRKFZBIuMdqASUxiIMZOUxhhN7RpCUnznL3+M7/vY/8Hr5/d47cHLS/nP\nM8sTUSBaISh8gpwFsQplDf8/e+8aI1uWluk967b3jr0jIiMy85yq6uquLsDg9gDN2MIMeCxDj0Fg\nkEYeecCNDL6M5JFGGGl+gJE9ljWjEWIsIX4geWSNLCNLZlpIYFn+g5tB3AQ9IDwYMIZRc2mqq+iq\nc/ISGZd9XTf/WDsiM0/mqe4BuruKzleKyjqZuXesWHvtnev93u97vzD+3HuwLiAkSJF+V4xrdHwa\npVptn1o8SQ0CiUQgZEo7ij7eKju4iRAjwaUWMvIQMhapR3RMLbXSA+/6eCmS63scn/fpRh1/j+tz\nAPjxGbd/bo63J/tHgSCm8+1/K8b0ayLVbu73CEKIG6e/+z7XSMcTSX+Pxjd9mzLQG0c++424P9uN\n9/mMfAc5DOLGESFGfurJG/z86oxCSv7Bl3wFU/1snF4c/ituvu0XMP7O7/4LYowPM/GABzzgc4ZP\np6D+/Rhj9xmcpyS1WfntP/uQ3lVogNPn/Kwg/V28ozZ/z+/+i8/mmB7wrwgnRDI3EjJ9lRIvBF5I\nrFTp3+PPrVIMSjNIRa8Ug4IgwGpJJw11ZuiUxkqDlRonDIPMGGQ6pjWGrdKsJ6nfqYySzBu8y3De\nEILmeqsYULpDih4hWjqnCJsdcuPJzA5EwAWP9Umgj2lXiRIy9VINgRVX5DpDaJM25OOZVe7QJqQk\n6iiTE7GAGAbaLvWQTH1hIyDJfaoHBAg4VExb8EFDlJYISJGOCUriMwV+wMi04ZUEXHTkw8AkOMS4\n7WxMqskrvUUREU5jtSZGQYxgpUXEtOFXziTiq8CFQNtnxGSXg9aRNmjG6mmc16nGLkSUGpBKoeSo\nWkdQxiGFw9pA9A1KZiiRCJmOBhB4FfBj1MOYkN6bsYbQOnQAGUhfcTjh8GO7kBDBiUBEIoLCSkUk\nMviITQkIaBcQUSO9IAhAB4TrDvth2XqQEINHBTkGd/Y/DfggiVbhvCeOzq7IkOp5cSAS6QKoEfzB\n4pgPrC74sovX+b8fv3fsHXy9ee/GqFkUqS5R7EmPCGOQR9JrkwiRHQmTDSCakfxERDsQ2dzgUzER\nIX+TVOyDQnuJKv3si56+BcAlkjeePhnTvJPTbhgPF/EuPbmftkRgC8BvZRM+DLx6ecarl2c84AsT\nHfAh4FeBvwb8dAhkv/+FtmX50+HvfL4H8IAHPOALDp+OoL4phPgIybX3uawqxngF/B9/riN7d+BT\nwAeEEOaeNN+XSem/d+p1/7PZ4hDF/spJzlcUJTEc4rVpQz5GzZPiNUaz9yfYy69jtFvFdCH3v+PF\n2DpFJNIgRETIFIkOIiTlLabjRUiqUXol2nAzTHrY/EVJiBKPJiCIQiBlaiMT97qokKPqIEc3XQgS\nrIhYPA7SsVIitQGpCJLxGEHYE0WlcEpCDsIEghAEFL1Lim4MSRkVqckRe101IFJPUwTKZsigCRKc\nDDht0fjRzCj9rpcSjySMBLTThqac4IxCxkA2WJRPm+koSARkJEBBJtUXBCIGpr3FBIGMis5MiVLd\n0QzEqEhKAQsCjbBYb3BuQqZyslGZkcqh1YDWkPKbx1hHlPT9FB8UwU9Reo0QYSSHEqMNRueHjXrf\n9zhvEUCmM7TJUNJj8gEhNUKAdwZrk6KXFx1CBeIMuq4EIZBeYnqD0AJExBpL0AERJJnNARgyS9CJ\ncNpcY3VyI5EukFuL05I+y9DesdjuMD5glaLTGdVImrUPTIeOGAVNnuOUpBct+ajW56FI1xwYxEDt\nJCHLKURGkddEUSCjPOg1Pgo2G0GIhqxwlIVChP09EdBZD1Gy20Wc90hlyIxGeIm2migjLhvSfROT\nCZg3kMcMnMa4sL/9qJrkAF0X4I0GBDFavHBp/mIKTjihEANEK1AyoHWPAELbpBNNqsNaiYAwPU4M\nBJuho0EGCV7uGTEOjcNg5EAuI9o5BIGWtPbyTIMU2Gix3vEHL7+PD6wu+CvdhjdeeAkhBVmuiH5A\niEhmFMJr0BlSybHmE4SCzlmCj+jg07MpM4QQsd7iEUgfUMEjtcGHlIqpNEQCBHDW4exINMVAEhMz\nog+JTEvNoydvAGCripOjGcgUDPAxYt1ADCm1PHiPR0CqnAaViLa3LqWjj/eYUunP21uTkn/8NV/P\n6W5LHDMxUnKJOGRyqFFO3K8xSUSPz2Axfj/GeK8bbNzLkbefmOnZsH+sv43od38W011V8vok4wnj\nzbe78SbimV+FW+//GeqPf364J6hw64efA1x5z3e99Uks8OHpEf/5fMkvvJ217xc4fqtv+e3+hjax\nvfr8DeYBD3jAFyQ+XYrvJ4D3j//8f0k9UP+3GOPl52Bs73gIIf4h8PeAfy/G+Ms3vl8AF8AvxBi/\n7Zlj4kf+p3+K8o4v/ZIXeOF9L+NLjZuAUxmBghhTXVQIgeA9wXsUqY4yk5J5UZDnOUVRkGVpE0cI\nsN0S6g0hdITYEycaqulYTCOQMkfKHBegtj2dT3+ABIIqq5hmU6S4W3gTQyQMgdhH+jpwdRFTv1NS\ns/npDKQGmUlEJtJXc11jtYf3ntVqxTAMCCGYTqeU0yl9CPQhMMTUJ/MmZLSosMPgyKVAqwqt54h7\nxnl70BF/1eDPG2LTQvDomUaVKbUPYyDP02s/h6TN4to5mlGRyghkWBrbEG6kA0shyVRGrnJynaOF\nSo0A+z6df7lM7VKeQQiptUTTQNd7Vt0KFxxlrnn55JiqlM+tfXLOsd3W/MmfNAxDRGt46aWc+XxK\nnuf3HlPXNZvNhhACk4mnqtKmXQiN1gukvPnZA9aeE6NDiAzZLvD1WG+cS/RC30pTdFuH3yaVT5xo\nrqLHjRv8I60pb9hmNpsNm4sLJHCyXKIWi7uDXa+hrolKcTGVDMGipea0PL21Lts28vE3zgl4vvjl\nOUdleedU2+2WJ0+21LXi0aNHvPji9bxae0kIHUpVQMXZWVLVHj16RLgIRB/RxxpVXI/f+YE3mrdA\nSF4u34O5Phn29z9FGEB98XvQcwPAk90TfPSclqdkKqMPgQtrqVeCKmQsl+neGYaB849/HBMjj77k\nS2D8LN43OHfFZbcjyinLYoneaUIb0Iu0jt/aOj618jwqFe87UfDmmyAEF1lG3/ccHx9TFMVhLI//\n+W+iv/nbCH/5Kzn7v34b7+HRo8DZ2VuE0HJ6XBAuc5SeoRcad+mQhcQcG66spQmB5WbDxFo4OcEb\nzR9v32TnYVn3ZO2a4vRVmu6YLIPTG7kl3sOTJ9B1NVq/QVFEltP3cP6JmiEOFK+eYH7wH3H8j34Q\n/7f/Fuof/hA8vjaFX4/tVY76Hnv2Bm92CpG/SCZrjo5yFouC11//OG9dCnR1zAvLlsdHc7LshVRz\n3geas55VfUUnzuhcxWz2Poy8wm9rdGj51Lohrw39bIo4LfnLRWBDRzufsDnLqVcdi9k5lZ5hwwwt\nL2lsYBuWXL71cZr1BS+evMTx8SlD8xZhFVi8/4O8+KWL597TjW34o0+dcfFWx/seVbz8skTKCUoc\nYZ9ahBFkjzJsCJxZixKCF7IMzs/Zbi/YzjKEeEzsK9r2CVm24/jIwDrDZguaRTJUWgwDrNf0RnJR\nBIY2o7vMEKLm0aMGU0tW9oQozhHNFVfFe3lp/phHj+4f97sJv/M7v8NXfuVXAvATP/ETfMd3fMfn\neUTvPgghHlJ8H/CAB3xO8ekU1C8mZcX8F8B/RGqn8j8IIf5P4H+JMX70szy+dzp+Avhvgb8L/PKN\n7/+XwAT48fsO+qKv+jJe+4PX+aPXO6Ra894XTtHCIAsJlSOoSBQFXk5wKHyMhBiTQZCUoBSF1mTj\nricESwgtYdITDVA76Cw0DtlF5PQYOTtFjIRBKchNhQuObb+lde2h+XppSqZ6ChZCH4hDJLpr0qhJ\nG8+mE9SDpNcCJyRHc0F+lyfcglKK45MTzjcbLrdbzlYrxHbL0dEReqwDUkKQj0Q8lxIlcmCKczu8\n3xJCcgzW+gilJrffwLlEELsOhgEVk6uvc5EwKJzN8GGCeaFCmPv73AkhmGuF7VqedBsGb8mEYGEM\nucoodEGuczKV3T345ORAssau9ew7xXddIqV9fy22ZEbxyuyYlguiHGjFOSUnwO2xWWvZ7Xa0bQvA\ncilomglZNiVGgzHPn/OyLIGGy8tPsdt5vC9ZLl9G67sd7IWQGHNC35xhVw34gMmOUDOFnt59VOiZ\nJtrItrFszyz6OK3Jpdbomzvyuqbc7RikpJ1OWZXl/Xnx8zmx77nYPWVwGr04vkNOvYf1WjDLZ4Rs\nRRs2zGJx63eGYWC321FVgul0SQiS1SpdnhB6QugAiVIzhJCUZUld11y9ecVMzRBG3CKnAE2UIDSF\n8Mg4cLBjbRpUpQgqxzcBNYsMfsBHj5b6sE4ykdre7LpImUXyPO31+r6HyYTcuRS5GAlqCClVeJof\ns7UDta2ZD/N0nbJ0rDJpIflBpLUPoDVFUdD3PV3XYTKDjx4pJOrf/QZiliF+63fwZxeIk5OxNnks\nyVQCkSlw4HcpMLEPSMgx2OT319V7VJ6nyvHoiH4YF1FaJ88Ssv2/U2BJEqMDFRnsQBQRYwxqNcY9\nF0ue7Qmy/5cXKfClRAAliUHgnEv1oDESokBKTW5KIOJ9g9bTpLIKQRQKhCSTHh8duSzwtqP3lqA9\nOjcEBUMw9KGlEpo2BMgGhFD0TnKUBXofCUKTUYOGrsuIOKYFSDNBOEHmO9owUNeHx8AdWG+xNqCF\nwZh9rac8PHP389+PAbNiP5HO4YIDU8GgCWHslywiIggQGj9OmpEyPYCA3oxZOiHH2oHJZEBLifcy\nFfxHh5cZWr79c+Xdgp/+6Z/mW7/1WwH49V//db76q7/68zyiBzzgAQ94wGeCtyWoMcmrPwf8nBDi\ne4APk8jqtwPfLoR4HfhfSWT1jz/LY33HIcb4O0KI/xH4r4QQPwX8NPBvAN9LUk//6X3H/Vtf/UEI\ngddef5NPPl0jJyUv+xPEPEf0PTK3qCogTZeULDUhiAJnDDvvsTHytN+RMzCV7mBPA4AyyMVLqGgQ\nux7RddB46M5Sd/jp9GC2oaVmOVkyHaZsthuaumFt12z8homeUGYlSiqQd9XRXAjmPvGxroOrq0TA\njo64tbGJMSaFdPzqYoSiYKIUw3qNd456teJ0Pmc5nd4mNjeg9RSlJji3JoQO51YEX6NDiehtYn7u\nRja1EJBliKLAvJATgsJdOaKPDBcOfQRqcnsT3LmO1rZ0riMSmUnYRIXREzAlR/nkEBR4Lo6OUg+D\nzQZ/taW58jTmCB/EYVhFkXhIElgl83jCRXOBDZaL9oKTyQlKKrquY7fbMQzDeKygLEum0ylSKs7P\nwVo4P09Bg5tDizHgfY33NVoHlssF63XNMJTUdeDo6P7h+zoS13OivUCYDrHI0JN71E6S4chmGtm2\ngegieR05PXmGuDdNWiTA/PSU3hiGGNk6x+wZc5IIXBaRYWPRXeBEVLeIZ4yJ94cAy1lBLHI617Hp\nNyyKNMYQAqvVihgjs9mMqso4O0vLY7eDLEt+ZUpNDyr8bDajrmuai4ZiWVCe3I60+BipvUerCTPR\nEEKDUkUaUNsijUTkFTFAaAO1qAGozHXKrhCCOMhUT6kDUqa113UdFAW5Hdew96DUgaBW2YLandP3\nPcMwkGXJ6AkgyIhWoKJkaIZUHTsS1PV6Tdd1FNNEpDOVISYl4Wu/GvlLHyP75z9L/A//Y7zfO3KP\nz4QyI2wSQZWZTKndpMARQNgTx/E4JQ3gcLYjh+cSVCEYDXdEUjRDwAVLiAEtdUonX40uscvFnRMc\n3n+ssZbCg5REL/He41y6R8Ih+JO6noXQAFOEFOkcQiKFQUtHHyyEHCy4mNpYKeXJy4wBSUvGifRk\n/YDJJFZYtMvS81YGCBmZ2GKHHcgilSiIDq0zYiyJ2ZamX9M0j59PUEPqyaqE5vp2UNcEdZz/foxq\n5WIMRoSAExGkRASNcw6tE6+PLiLQOJlygE2MpJ4ygl6n2pJoDdbWHB05NNmYFu6IwWHRmL8ABPWH\nf/iH+f7v/34APvnJT/K+973v8zyiBzzgAQ94wGeKT6egHjA60f4T4J8IIT4A/C3gu4H/Dvh7Qohf\nIBHVe1XDv8D4u8AfA38b+DbgDPhR4L9/3gFGG77i3/xLiBB4/ekFf/LkEl4RvLddYoolUgnCqiHk\nPbLqiHoANhhZsBSwczU7b2lJxg+lypmbCqUmt1I2Oa7SZmazSSxyu4WmIZQzoswJQyD0qUZsypRC\nFtTU9LKn1S297qmqilk1S0T1GSgFx8fp1Ot12gOdn4MuAvk0MMSAjfFWlZEEMik5mkx4T1lSbzY0\nTYPd7dg4x2KxSCrxPRBCYeQRvg24+ozQp9YQWs9Qqhyl4TFttyhuu14C5rHBXTlCG3Arlz77DFrX\n0toWH0fVCEGhC45NyftUzsq5Q4rmTKl7XB+vESN0sqKJmv5iDaGDLGAeLSinksnkHnVJSE7LUy7a\nCwY/8PrF62PP2zRzUkqqqqKqqltzc3oKFxfX8356CkJcE9O9GY2UBWX5iCyLXFxcUNc1UkpmN3bN\n0cc0N31ACkW+OCFMroiiwTl1R3HtQ+DKOXyMZEtNdRUpeomvPaoa10rTpMgFwNERsqpYjvO4855C\nyutUWWDVreiFR82POBkMarOF4nrC1utEyLWGxQJCPKJ3PY1tKE1JpjKurq7w3pNl2eHzLRZpntbr\nhsXCYowe03s5zG9JySZsqIeaaT699Vk3zhGBSlfo0BFCT4wB0bSJLec5qsxxK8ewHejLHoFgYp5R\n+AeZrkkWAEUIAWstQkryo6OkoLYtoTRAQAiDlJrSlGzqDa1tyaf5uM5SOnyegxoE/c6SCcAYlFIY\nY5Ly3u4AMDKxjfihD8EvfYz8Yz+P+5vXBFWMde2y0IQt+MYncjReyv1VuqmgAkiVAS3BdqBzwnjA\nfbdwMmWShCBS4KpvEVqQ6Sy52F7tCepdBfWg4AJGSJSw2JiIHXisTQR1XyKQmRIhBmJ0eN+lgIJI\n95qUEhUHXHDEvkIIgZWCaFPn5UmpaRy0MSfEmqkVNCUE6fE+x4kOLSwRTZQG5RqEEsg4wYmBQnog\np9MC6RraYaBpMu7JRMcFh7MRIw1KufFaSMZHEUKnuRpCcljPRzU0xohTAoEgBoX3A8aMBNVHpNA4\nlUpQzTBAjITMYKPFO0l0qR9olgmii3jGFi7RY0VOJbN3LUF1zvGd3/md/ORP/iRf+qVfym/8xm8w\nnU4//YEPeMADHvCAdww+Y4J6EzHGfwn810KI/wb4D4DvAb4Z+Aaek9b6FxUxxgD8yPj6jFFNKv61\nD34Z8Tc/zqfWG56cbYiP4f0FMMxR2Tyl2V51+KxHVA5IKZ6lkkxURR00PRm9NFwEmEvFnT2Q1sTF\nkrDtCWdrwq6HkNIKmaX6VKEEIhcUWcEkmxBkYNtv6VxHQ0Nbtyn1N5veS1R1FqhOIuebwFUdCFtQ\ndapNLYu0qcqFIH+GkAAsFguKouDq6oqu63j69Onhe+MEJ2Vp/3IOBcg4w0lBUA6XB/wE9OQYKZ+/\nqxJCYJYGlzm2l1uaywa7sugjjTQSIw0TM6E05S3l7sQYts6x9Z6N9wwxstT6Vo2ttYmPtSNngRx5\nekzRrqiyDsMZ5Cfc6CNxB0UoODs/o7UtSihOqhOWR0vKsrxTz5s+T0pbvbiAvg88ebJjsWjG3qGJ\nmCo1O8xJlsHx8TGXl5dst9sD8fWtx61d6lijBHqhkXlSna29xPvt2HswkbqNc+xGgpJLyTLTRBlw\nlw63cQgjkK67RU6p0rGZlFRKsfOelXM8MgYhBJftJZ3r0uc+fQV1NQZVxtzcpknzK2UKiggBSiim\n2ZTtsGXdrSkp6boOKSXL5fIwT3kOZRnZbLbUNZyczG7NZwyRgoKt3OIyR9/3h5reIQTakRwcaYN3\nBSG0KXW0SfcjVYUqFH7jqdsar3xSuZ9Rf7Eyta7IwkjQ+nF8ebof9wS1uL5+kJTYzbChc90hvdeO\nRKzMBQwwNA4q2MtwRVFgrWVbb8mr65R08aG/Bv/gB8k/9ougk+IMoPapvEoj8wA+pfjvU0wPCuYz\nBFWNa8u7HnQOnxFBVYSQPr9QhizLGFxEjutFLI/vKqjj1yDHHqIkv2YjNdBj7d49Oc2LUQopqjHj\nokapIrXbkhqFQggPwuHrgFSGqDNs7YkyoiaCvEnjbLSkihrte6SO+DZjiDsMliFOQGUoe0ZUFUIV\n+GApMk8vNSIU5MbR9lvq+uQOQfXBE2Ig+tQGbE8IhVCEGym+wxjky8b0Zqwd03sNImpCZKwbH3l9\nF/FBghZoIRA2GQb0oxqLzxiGAWMixkAcAi5qBDUEyxA1i3epgrrZbPjgBz/Ia6+9xnd/93fzYz/2\nYyh192/WAx7wgAc84J2NPxVBvYGvAf468O+M/+7/jOf7gsLxfMkrf+lV5P/3Gm9uGy7rlgi8fxkh\nOEwxR7gJ2AnxKhDzPhn9mAlCKArAhsDG+4OiVXvPXGuyKAhdwLeeaGNyeSwXQIPoagQd0jnkowWi\nuq30SCTLyRIXHLthR2tbalsflKoqmzGMKbs3jY2yCo5zaLYCYSVyKzFWsFiKZwWRWyiKgsePHx9I\n6uWTJ1RKMc9zhHM3HDJJG9c8T6m7+XsIWJxbE6PD2nOUqsbawruEbq+2daHDTxMpE06QbTNmixmT\n2eTOMXvMtMYIwZVzdKNhyUJpXC+p60RQ98iylMI7mWhEPEl5qXuZc7lMjGlECIG6rqnrmhAC82yO\nUgpVKHSpyYrs3s9yjcDR0Y7z8wZrA5eXcHJSkGWze8l6nucsFgtWq1VSG688uUjjkROJPtKIMd1T\nyhytFzi3wrl1csYNmmE0QrqlJheKOIv4rcf+yYbM1NshoAAAIABJREFUNKlLyA1yusdca4Zx7ayd\nI7odneuQQnJSnqSUz8WCfW5uf7FjPSQFZJ9Bvcc0myYFfGjZbDZMzITFYnFnU1qWO7ZbT99nxHj7\nOvutRyCYn86pZTKVejS6w2zGtPGpUknFU2Wq9+6uwKZ68L0ZlqwkzbYhNpFyeZuNDAMQBVUhkSqZ\ngt0iqEWR1ra1hMGOzrTpvEoqtNMMDAxyQKNTqjwwLQTdDlzniCWIGwR1u92ybRJBNSqtBfm1f5U4\nKcg+/i9xF29hl2kuxMEZXCInSYULbTikmO7p4s0U3xAjUig04IPFE0c38jsC6Lie9mYrKcV3GDqE\nzshMRmsD6jNUUPc1qMlV14zzmxTUvQe5VorU/Ww71h07kKCUJAZNCBGhLb736DzHqYBzyTQ7Csu0\nqKCDOhimcsC0A5NyQtsGmgEe5ZHOQkAhXIuLGYWZEuIlQ9xRSElQM4YcfLtimBzT9+LmrY8NlhBA\nRHVo+ZOgiG7sXaoFQ7gOBgGH+tNYaETc3wyOGD1KCWJIbupiJKj7h1M/Bq5S/WlPUQSMEcQGPAof\nO5QHlU8wRtzrWPxOxmuvvcarr74KwI/+6I/yvd/7vZ/fAT3gAQ94wAP+1PhXJqhCiBeB/5RUi/qv\nj9/+TZLD7xeUevrngRdOHmG/zCI+/inOdgOqDPzx9or3TyNEh5kvkULhG6Cf4AeIk4CeJeXTSMmJ\nlHTes+4dfeN40g3kPm2qtZQpta2Q6fXiAhHnSd3qe1ivwPZp5//MjkRLzVF+RKZLrvodG9twZtfE\nZsssn1PotNvaGxvlUpJnElkJmiZlFg8DPH2aSl9vlL/ehvfIvudYCJquY7te08aI1ZqjxQJTVdep\nu8+E9SU5xjzC++2Y2rojhGSiFNH0vqdzHYMfDi68AsEkn1C+XKIbTagD1GCdRS+vCdqzKJTikZQ8\nqS0XdeRTrWWmNBOVNphlmV63MoCFTLm3+yLdy0tYLHDGpLrHpjm0mcjznOl0ysv5y6zaFa1ruWgv\nOJ4c3zFlSjWmuzGVN7JcwtVVgfczNhvDycnz19xkMsF1jtUnV6zDmqPlEdXjKjkcP4NkRBXY9ivW\nwwVKL8hUzlLrO2q4nmnipiFcXWE1mFdPEM+Q0z0WWnNuLW82l2RxoNKGk8lITiHt1hcL3JMLVmc1\ncZEzOzZMnokhCCGYZ3PeevIWwQeOj46v1fcRIThi3DGZQN/P2W4TB4JExHzjQcDsxRn9ZY+1lqZp\nEHnOECNKCKZqrwzmCKGIuytCKJGz64m2mcXjMc5guL1OR38rjkqJJ9CFkOpP4Xq8kwlhtya2HUzn\nhwBDcIFc5AxqYBADJeWBoBohCCZiraMfBMW4+IwxBALOuzHlc7xWec7wb38t+S/9AvqXf5b+276N\nGOOooMrUqiob6xRdTFni6n6TpH1gqpCGgYiNniLKw+V7FtcKqhwVv0iWKbTWBGuRY62yWCzvnECO\nLbSCSPqpkpEQA3JsJWNtT4iBEDVKqPE5I1CqHO+THUJWSPZ1sBrjHC54JkVBsOCHABOJDz3TmaHt\nLEPMcAxkLjLJJTWOYdDIEnCeYRDgAkYGssLgvWbwHaXIEPkUR0cpGlrX0DTVbYLqE0FVyGRSdaN9\nWPRxbPEjsPb6Wo8fFh88mAmEa4Iagk2fHZP69+6PsTbVn46GWMLnWLtjPrdoobFBEPEIAk5kmHdh\neu+v/uqv8nVf93UA/MzP/Azf9E3f9Hke0QMe8IAHPODPgs+IoIoUpv7rJFL6zaSMqyvgH5N6pP4/\nn7UR/gWHFJKXHr+AGyzyj89YXQzo90x5bdjyioB4dYYpl5iTCaEN+MYTmsDQDqhSIXJBHCKyCyxc\n8kPauUgvwepANVXMS426teFTKTe0rhOLHO1l/dER1hhsjLgYD18B0BUTmWP7DS5YumFNHkselwvM\nPWm/exOg/em327RJPzqCPLubtns4rijIioKrtmUQgnOtmWYZs7epIRJCoPUcKSfU3RM6t6L3T/BR\no/XsYIazT+Gd6Ml1qvIRhCIc6i+Hp0Nq4/GMi6v3+/YwAlyGcI4QPa1ylNPACzP99krnYgFKYS8v\n2X3iE3R5TpxMEEIwmUyYTqeYG7vC5WSJ6ASNbbhoEknNdX6HmAKpLYWa8sIL5lCTenGRLvF9Spbb\nOLIuY1pOqfuand6RqxzF/TL3LuZsYkGgIQ8bTrLHz6ynEW2LFjusgljMcL7geftcLSXB7WhtgxWS\nl6fHB5XvMOc652KYEXxNOVwxm55ytz8kdHWHiirV62V322Y5twIi83nFxUVG2yZXVa3TXBBBVQqp\nU13uarViu90eJm+m1K1rKynwXY+XEnkjb7NxDbKQlL7E1x49T4/XGA8mqixKyUWAbd+jQkBrfa32\nTibE7VkyXppft1iJfSTXOTuVlGa4TvE1UoJyWGAImpvUXGWKlLV5w0QN6L7uG8h/6RdQv/hz+G/5\nllF5U9etmwKIXEAA33r0VF8TREjkMQTcmOY7kZo+RhyBfSeK+5ZHMkpKRHgYLHkuyMs8uQYP1ym+\nLO6m+EIiqX5vdEQgioBS1wqqix4pi1E9HedAVWPQqkXISSLaUiOCRA8OGy1kE7CSGCWpW7RH5ZKJ\nUTTWUxuDERoztKAM3mc4HEZY6gBRZJTaE4PB+wl923E0kQg/RUWBEBu65oqhuB2sccHhPUihUv9j\nCSBgb6imbqdzm3He8R5HSOtz0KOS7IGAEoaIxo3Kt/EeYsRJ8EQICtsHpIzJNdilfrpCeKK370qD\npB//8R/nu77ruwD4vd/7PT7wgQ98nkf0gAc84AEP+LPibQmqEOKrSKT0PwFOSDvinyeppf97jPEh\npffPAUYZXnrPizjrkX+yYv2kQ74847VQ84ooifUlwc7ITmZk04zhfMBdOYanAwSQpUwbbCOZVRmz\nXFDrSOM9LZHeWmZaU40bt7gnoEWB1Rq3WmH7nvD06VibOjtInYIUhddCYHTBS/kE65Nzaog9F80Z\ns2xGld1VyqSExVGkNI71hcPtHKunPYWyzKbxmjyNabv7l1aKU1I9UV3XbLdb+r5nuVzeSd30wT+j\nkkqcl3jvkMKjo6TMTqny5b09XiH1+DSPRgOlLtVSxioipoquE7TtmKI5Qil4eaYRuWAXHYGU8nv8\nbHuVETFGuq6jGQZ6a6HrEH1PledMX3rpuTVSi2KBQFDbmovmjHlmMCJwm5jOkDfqWvc1qfeR1OCS\nOVS0SZ2ZvzRHB81ut2O1WnFycnKLJPsYubQWGyNGzziKgkL0eL9CytPbvWhHK2cB6FeOsV1OaALe\n3DBNuoF1t4bQUypNkS/YBW6Rq71jry9n5L5nUaU+jjzTP7VtW5qm4ag4IpaRzqd1sFecndsSo02K\nmZlTVcnNd7uFo2kgtAEEqFka42Qyoa5rVl0Hdc1iOr3VzxVA9WlugolEmepK9+tQV5qyKfGNR80S\nse26xCuyDHIjMIOg7ntMCFQ3JbUsI0gHziOdYM/uQxdQUmFyQ4iBwQ/sOz9pIZDKsQN6f/txLk26\nPt76w/dCgP6vfiPw95G/+EujSVJyFRZifD64iCwksUtpvoyxISkEPka8lKgQ0rFCMBGGK8Di96Wp\nz1VQx/9jGBxZZsgKk0j0tkb2fWqDU5b3RlYUqc1MkDItEBEObWu8d9jgUrDqxrFCKKQsCKEj0qJE\nBkKl9WA9nfA4KVE6QwLWQy4FhJ6qymmuPLU3PFKG3G2RWuOGDEuPFo5hgKg0RQw00SHljDBsGdgx\n0ad4OWeQO2K7obOPcc4cMiwOKb5BIk1qIXarxYwWqb1YjEjGOuDxQeTUvl2MHtuPJdIZbUSMBkkA\nZgz+9aOjLz7HWjvWnwqCC/hoEFhE8FhRMFXvDgU1xsj3fd/38SM/8iNMp1M+8YlPcHp6bwOrBzzg\nAQ94wLsMn05B3Sujr5PU0h/7Qmwn87nAxEx48X2P+dTgkec7dm+1yPdO+aSyvCIFDBv8kwGTHUFM\n9YLRpwg4jM6Nc4maKoQUHAGVlFyNhja7vicChRBoKW8567Jcpn6Oux2m69DWYhYLTFHcS7iMLCl0\nwbpb07qWdb+mHWoWqkIHkiK6f3lPBjzS0EjYOeisoAs505P0et5uaD6fUxQFq9WKYRg4OztjPp+j\nMkXve3rXY4N9ZmyGWfkimdLI2IztOnq8u0Loo8Mm/FkIKTDHBrv17J462kuPJaDmGqnlgUOX5c0S\nUkURBCvnsDGmulSdUn6BQ6po27YHMxo5nVLN51TWJjVnt+O5PV+AWVbh/Zpdf8HKwjyfU+bHd4jp\n4XOIuyT1eBmh86m3ZUwbX71MxlBz5oQQaJqGi4sLTk9P0VrTec+VcwQSCVpqjRbHWHtBjAPWXpJl\n42Zwb2YUI8xmyNkM3fnbpknZ9Tra9BtqWyMQvDp7zDqIO61nLi9TZqIxcPzFCzg/S1L8ZHK4AN57\n1mNa6PHymKADm37DVXfF4+oxIVi8Ty62Wi8QQjCdpsSBtoXC+rTxr9SttO7pbMYbTQN1zXvn87tz\n3PZImRGqZJikVEltx9YykwoVFKEPhCagKkWdfnQwySmkpO86QggHMyZIG+5QKNgJZB9hMn5vSCR6\nUk2obU1nO7zID6RFYZESnDD7LjVprenkWCuCwPukknoP7qv+CmE6Rf7+HxLfeJ34eIlSGftK0+gj\nqlApPdhGggtILRNBJNWhKudwLhn15Mn6iUDE+YBAvi1BjVFgrSfGQJ5niE4gLi/Sz47miNsFmQeo\n1KcGxuwHsXfdFhoIdMOQzLyeCUQpVRFCR6BDkhFjavmDs8jCI6QgxgwiOJ9KIogdeVWh1wPOSYLW\nSOfQuYBB0drAUnr63iOEJsdSS0+Rlbi+xmaWSS7YiZxoMzLb0tqaYVig9RgkDI4YBBKJEHZsPaTS\nJJPu030Gi76R3gvXBJWgca7HGNB6TA1GEVREA2okqMOBoGYMQ0+eg9YRGnBRAw0iOqzI0EK/4wlq\n13V84zd+I7/yK7/C13/91/PRj3701r30gAc84AEPeHfj0xHUnwL+Z+Bn4r5Q7gGfNczzOfZVyxMX\nWGwt9Zst/r0Vr5vAeytB1nTY3qKKGWZZkr9n3KhvfWqdsnW0tSVMJKGSuFEpjUAz9iDdktwgl6Oi\nqkWqYzWLBXI2S7WSw5C+VhXM57cLR0fiKZ1j6QSTLrCtVzhvuUBQmYoqq65TIoVIuZRaU840xcsZ\n6zaj7QSbAM1qTPt9zt5CG83R8RFnqzNWuxVv7d5CG818PkdrjRSSXOXkOqfQxTMq6QTvG5zbEELH\nMAxoPU8taW5gbGc5KqUKbwSuceAiurbMHmvKY3VrGg7jk5JTY1g7RxMCF8OA6HvMMKQN/IgsyyjL\nksmY1kvfJxZW12Njz+Wt84YwHOppK60hzqitZRcMhnx0L70fe5J6fhbprzxPn3oWR4m4qEqh5rdT\nVheLBTFG2rbl4uKCbLEY/aJhIiWLG47Fxhxj7dlIUq8wvrhFTvcNH9UN0yS3cphTg1CCbb9lN+wQ\niEPasnym9Uy9kfT9dRsjoXRah+t1ej16BEKwWq0IITCZTChH9tfY5mDuldECEaWmh/ZLUqZlvb0M\nbK8CR8fX6ukevVKYPIdhwDYNk5skdUxJl9mMkBu8b1CqpLVpxipTIStJ6AO+9sRcMQzpfff1s7kQ\nWGuJQtzaVIfQQ54j67F/MclJlwgiS21raluztS0iy69Ji3NkGTRK0/eJCO8JUJ7nGGnouo6qqlI2\nvdbYr/068p/9Z5hf/kX83/wb47q5VlAB9FRDTL1d5UymgEqMBydf7z0Yg4wBozROSHo3UGbFvffK\nNecUh/Y2xiisArVKBJX50f3yK9d1sHFPUMfonFKGGAP94JBK3slI2BspIf2Y4quQThFCh6zSOJKK\nyJjmC4QBkQsmmWTbR3ZOYKSmlLCJlq6TqCOJDy0SRS4jOlpEbrDrjD7WTE89mdV4O6XPOmx9Rd8v\nKEsOgTURNTF6tI6p/vemgqrE7fReONSfhkwhUYQgCMGne1sBQ8SP6e76huKaDJLkof60qhzGKIIH\nj8DTjwZJBcaI512CdwTOzs545ZVX6LqOH/iBH+CHfuiHPo2R3AMe8IAHPODdhrclqDHGb/9cDeQB\nCcvJEvtFjss/POeoFdRvtfj3lLwxCN53qiglCLXD0+HiFC9z7BT6PNJvPb4PYIEtqEqiS8VMKY6N\nYQjJPVSQasECSc05qKRaJ0Of3S4Vj15dJfJRlon1POuoCxRI8uKYrWto4sBWBxozcFSdkBfVXTdO\nYDmBfcamtUnlm0xgOgt4Bqy32GCx3h56k6qJYiImuK0juki/6amOKk4Wb+MGBChVImUxtptoce6K\nEHqUWtD3KX23768/lhBQTiXFqcEMntB46B1uFdCL+w2UhBAU3rPbbjmva0KMGCE4KQqmZUlZluhn\ne6fmeWKRl5fXvWmOj/Ghx/sdMe5zipPRyzJ7gdx2rPs1V90VMcZ706ohtU3xtWfuPZcD2AHWjeT0\n/Qpd3L/zXC6XWO952raE83NOjo9ZZNkhLfz6s0q0PsHac0JzidsEtCpvkdM99EwnBa4L2EtLN+vY\n2UROl5Ml+WiydbP1zOsrR94ZlBIcH99YPlWVFFRrYbdjE+MYcNAsbqT9LooF58056+ZNlnmBVjlK\n3R7XdArrTzq6AY6K22TdhUDjPfMxWFPXNVVVXZOeUQ6V02OgJsaBut/io0+1e8okEUx7ootsLjyg\nDrcQkAyBAGEMPsYD0QyhA60RpkrroeuIfVo3spBolQIytbdkwaP1SLysJc+h0dcE1QZLJDKdTKHn\nNkEFwtd/CH72n5F/7GMM3/E3xk+/N0BKX9RUHYJfzO72Qt0HYGQMGGlwQmG9PbgPP4v9Y6bvLSBR\nKpEztEZeXQIQj55PUA+tZkajJEEYDcZUIuTeIbTA3LNmQYJ0IwkV+A6ED+hpJNjAMCTnXyEl3guk\niITQU00Nu97TWslUKHIcUWqcy2mGFk2PykqC25HhUt2oL/A+YLOewksGVeH0BaGp6fpEFK0fCWpI\nuvT+8SCEupXia0cH35sGSfe1mIkxJAW1FXgE6BR4xKXU56AVEs0wRCCQZR4ZNTZIED7VtYoM8w5P\n7/3d3/1dvvzLvxyAj3zkI3z4wx/+PI/oAQ94wAMe8NnAn7XNzAP+nJFabRzj3u+5+sNLFqFg+7TD\nvTDhjavI42WFdy02dEQ6hDBoNUWqDLPQ5D6idhE1REyb6t3UNNWoCp0MNXbeU3tPNxLWiRDMYkzp\nYNaml/epUG8YEokqy6RijWrozZfQmrmUTLzlqrvCBstF2FHawFzO7639VNozW1pWG8vVxnLWWOKl\np6pudyWRQh42/stiyftP3s9uu6Oua/qm5+mQ+qZmWXbnPfYQQmLMEucK6npN23b0/QVKHSGlQYjE\nFyeT9No7gFJqfCEOtan2zI49QtPneTaFV5J6prZaYyYTZJ6TaX2rJu4WsiwFBC4u8O0V/skZ8Wg6\nbtDl2DKnOtR67pXpq+6Kdb8mxMAsvyZfMUb8zuNrP7rZwMlLkvWgsFGy2sCJud84qQ8BP5uBtURr\nEdstk+fUc0mp0X6CW72FjwExnaOeIad76KXGnlm2zZZdvyM7ylhOlhT6NomZa826DlxtIqVyfNHp\nPUYtiwWcn9NfXLCTEmEMy+XyFsHMVEYhNTu7Yzc4Tmcv3FFX4uCZmEjjBXVQ3BTvN94TgXmWEcuS\npmnYbDapr6r3KZohBKKqxjrMml1/ASK7FTBQlcJeOeqLgFqoWz0wu64jEwKd53QhMB0J2b6kX06P\nYZPykINN59yvuVzlXDlL9D3HWZ4iK96T5cn8Z+xcw+BTgGNWzmiHlmEYEolz41x86N9P5/vYr1KP\nQZdnFVRVKkITiC6lGavx9/atZoL3KdgVPJnKaITEBvtc9e1aBHTjPZlSc9HiQFBZfHoF1YvUN1SL\nQCSORDfSDZYyF+h7TNuEUCBSXXrok+FTpiXkAtc7uj6SK4XUgsEKJIIQWky1IFsJ+kFhjSKTFpTB\nOUPr12gcSpdY36K8BWHJVIFzii4MTLOAGAwiKoQfaIYe7ycHBTW4fVuefeBPjWm6I0H1N9x4YwTn\n8DGknrNhb8JlidGNDr4aJ5Iaa8aAYi88CD22l7muP4024tGAS+m90ryjDZI++tGP8i3f8i0A/Nqv\n/Rpf8zVf83ke0QMe8IAHPOCzhQeC+g6EUYaT6RL/amD3RyuWYsb2sqc7KXjzcsdkMmFSFBjRonFk\ncU1OQWGOkLmBEsIQkvrRB/zGE+qAmirkRDALgcpadm1L23V0ztEDpVJU+36PWsMLL1w77e5zyN4m\nH9cow6PqEbthx7bf0tiG3vXMshlKKgY/3FFGMTBdjFy4l/SNQTrDo+OMqjDXbrs3cHR0xGQyYb1e\nY63l/PycqqqYz+cHMnKzDNba/f9PCCHD2jUwIOUFs9mMqqqeu6lWhUI+lrhVcvntz3sGnfpR2hvN\nT40xt1J4r5yjDYFL55jGyPxZBZWxvlD0+LknXtYwOMTKoU5fQZr7e7mWpkSQSOp22BKJzLLZHWIq\nC4maJeOs03hdk3p5mTjxzVNvxzrlCLx0coK7usI7x+XlJScnJ3fH0feodQNqiis8rvSIYO/tuyqE\noC5rNtsNwgpms9kdcjqeEnYaicXMAkEn5fEWjCEUBVdPn4JSzF599Zap02GOdKTuBX2U2BDJn7m2\nfpMCIb1OJljOpeU+hNT+RZKce+NsRtu2tG2bXJa7LpGEsgQpkZT0dk1r1xT5C0z0dQ8cWUraJ+C6\nQKECWl8Pou97cinRRZEIKhCCJcZUzyjLGWwbwq4lyglCy4PhUaELXLfD+yEpr6OKqXKNjtfrfa/Q\n5f8/e+/WY1t7V/n9ntM8rPOq2vu1DY7BIS3R0IoQrXAIhoiWQHwDkCW4yVWkKEgWEhKfAIEQiG/Q\nCLC47xZKIOruECIOUiARiBu3scHYr9+967AO8/gc/n3xzLWqau/atpTgA2YNqVR711611rPmnFX7\nGXOM/xi2JBaRYRjo+54Q8hrtv/7XpM0a94UvYv7ub2Hz3ecbIZIeKk50rYnHrKLqxUPVTBBBYsQq\nlT9ri4ghJD/Vpbx97Z5+xsZxCjOyBpGEGNC7SUGd0q6fgzkpzRNB1SpXzSilERFGH5mrdxFUizIj\nIhE95r5UW2iiEjCeGAWjHUpFQtRolS3XyinqyjJ4S/AGS492CelLmn7AGUHZkm7QmJiwLuBsQT/U\n9MPIcjVS9QVdrBj0ET80DENNOIUHpLxWaydSqvSTipkQcrPr4z7Tx/On+XtiTmJWRU7wfSMgyU/H\nXcWScRwoiny9J5+IOBQDpMBIxeKblKD++q//Op/61KeA3Hf6sY997Bu8ogsuuOCCC76WuBDUb1LU\nrmazWJK+Qzh8bscmbRiPgbh22GHAjYrZbE5dK0gNhBY/HtEUGLVAi0LbRPKBsB+RIRLeTyhycIuu\nNSulmGvN0Rg6Yzg6R+Mci6piXpY5rATyrvfu7sGPWxTZJ1k9b+WrbIWI8Kp5xdEf+YfDP1CaklW5\nOhPOkzJamAJnHN+2cgRv2O3yyx3vIdaZDz9HHoui4OXLl9zfH7m7O3A8trz//kBdL3GuftOJfEZZ\nGjabK5zbI3IEdsQ4oNTmaSrtBBHBB4+vPM2xob1rkSToUlNcFcznc+q6fosobZ2jiJH9RP7GlNg6\nh1FqqopppqqYBBrU9YcwuwETLdx1cP1moerTa0MpxW17y/5mzziOLIusYD4mpiecZ1Jf51N4d5dn\nO5MIdyGcbd8rY1hYS3rxgtevXzOOI7e3t1xdXT2Q1NPsrAhm/R4yE2JsCOEW5168FUJ1193RSYdb\nOZbdEtc5ZClPrNKny8sozYc3ljQL7EKg0PpMSs7PFyMRKOHcTfoYIexRRJblhiY6dsOOl+blef2x\nzdZbUyiWK3NO9N1uYTdt6BenmzTGMJ/POR6P7Pd7rk/+2EkO1drRhUwsS62fEHmlFL1k+2ZNtnXm\n9QVijMycQ6xlFCGJZHsvuWcVraEokKYD1aOuH5TZ0pYkgRjGTN9PN0mco5z46jDASFZQC1OQqnQm\nqDFOBLU0+B/5IYp//79S/PEfw3/73ZzVuylICzLRjseYk4QXk3Kqde5AjRGjFClmwml0SYhCkHE6\nQ0/xWEEtSzNZlLOCau5OCurmq1p8o1IYpdDI1G2cZzdDSiRJOPu8gqq0IhGg02AMZubyPLENxCSQ\nLNrCKAqSBpNIaaBeWO5bS+osTieqEsYusd9HXlQWaxUhKgo0hQyIcSS1zOfadFS2xlCT7B7fHxjH\nF3gznbdoptM3zddGdT7+PiWErJ6q5whqfJzgmyDmedto8rGy0+PHqROVWOD9kapK+fVawScL6oiS\nQKD4plNQY4z87M/+LJ/+9Kf5ru/6Lv7iL/6C5TvcGhdccMEFF3zr4EJQv4mxrtaEFEgfTey/sGc7\nbJh7TQhHhq6j/+ADBhGqqpq44kAi5e2wrrB2iVaGYgHJQTgmJEDoNUoK9LrEbCrWRcE8JfaT7XcP\nNCGwmBRVrM3BNMdjnsE7SXHWIvM5Y2EYU54bzVUvWcarXIUgHMcjgtD5jqvZFZtygzVvX3qmhPfe\ne6gBOc2HLpfZejuOj9XQ00jsAmMqmiYTtabZUZY9V1eraRPMlHCZPx44xCr3GYZ7Uurx/hXWbokx\nB9iMY1ZIQwic88EcuI1Dd5pZOaM2Nba2T8jgY8yNoVCK2xAYRfhg6FjrASM9D1Ux5RTiU0I5dasM\nQ2aT19fPJhyLCLazLPdL7tt7Wloo4Orl1TvXolQmpa9f59DdV3eJNA9EEcwUmlVMxEBrzfX1Na9f\nv2YYBu7u7ri6unpCTk8BWpY8A5fSgPcnkqoQEW67W4Y4oJXmxdUL1E7lGp/7gLvK7yulfM8jpXyO\nt1vDnU90KXHnPS8eWbePxyPDOGLWa7bW5jnpRTOpAAAgAElEQVTpqjqf1Jza2wCKVf3t+C7bzY/j\nkWW5zBbowzTTvDQsyodEXzuLePKxeDx3u1wuaduWYbdjUIpyscg3aKbz0E9GgDdV2nGEVBiMibgU\nkZQJ0jB5cKuqImlNP6m2Nk323tP85mxGer8F6dHl4w25QmtLSp6QRuyJNFtLafP7abtIrCJaaYw2\nVFXFbrej6/JrGJMPmf+RH5kI6p/C//Q/ZvXOPwT0QE4CVpMdlFFAZ4tvUApSygrqaU7SVgyRdxLU\nnNkzIqLOM9ki+QaN2d3lB63eraA+tvhaFEYLQVK2LSvJN6XSU3fAw2vn14vjiJaSWGi0sxAjorL9\nOUWFdY5RKWLQWBNJqcdWq1yxg6FQlpmDQ+gZOoVeaiqX07HRlgpPLyParUhpRz+0zIsNRTlDHzQx\nthzaEbMUjLI5lFiDnkikTJZfZR8FJL2R4OvPw7iWEALG5MouiUISnQm/UqgQslulMhhl8SPEGCiK\niDWGEIVEIqYeKxpT1BjzzvsDX3ccDge+7/u+j89+9rN88pOf5Ld+67feWcl1wQUXXHDBtxYuBPWb\nHNt6S0iBQ0jsv3xAbpdYO6O0BUk1+DDQDQN9tFSzJdVMgx5JWjHqEePmGLdCG0dhDMmTg4ZGIQaI\nt4JZBMz8IUhpPxGqXQg0MbI0JlenLBaEWYU/7Bj3d4xdR9gHROusKk1JMEYZClNQmIKXs5cYbdgP\ne1rfMsaRm+6GRbHIdtVndpOLRXYRv3qVc5o++CBvOpfLMzcAHgKCq8qy3V4xji1tu0frDqUGyjLb\nd98FEUuMC5rmA8axxfsvofUMaxePXkPhnKMoCpxzVFWFEoW/88go+Nceu7aY2fMbJ6sUVzpwN+7p\nY88NwtJY5m4xEdNHBPTEIu/uMou8ucnS3mSpfnPGtNAF282Wgzsw2pFd2LF122fXAQ+puJ//IHA4\nRJbAdqHZWnve/D881pxJat/33H/pS2zyIjI5fVSNY+0p2dcTwh3Gbrhpb/DJY5ThenadLaAbYfxg\nJPWJ2EV0Zbi5yaOdZfkQZLy2ltH7J9Uz3nsOhwMAm498BH08ZsK838N6Pc1X3pFTe5do7VhXa163\nrzmOR2ZuBl3exCunMHU+X/M5HA7CF3eR5TqryG8qocvlksPr1xxFKD/0ofO/9aFH6ZLCFBiVa1NO\nKnzbZpK32GiQRGwjdmHpp3TesiyRiaB2MbCQkawETuS3LEkekBFtH+wAQSSHS/lAH3qqkE4ngbLM\nl1DTe4oSClucz6W1lrYNaB0oivxrf/zEjzEH3B//GUGyvTRN6bonBRVypVX0EboE89wBG6eZSJMS\nMlUoOTuDQYg8Kg1+hOxIzu/TuXKqXso31Mz+Pr/vr5Liq8gudq00mjyDGiOgFSnprD4+S1An9Xeq\nFpLKonVCxRFxmfjFILiyQivFOCrKMgdX2WJNYRS9MkiyuOQJSYjRYSqDwiNi0cZihgGMo6xe0PuB\nrutZbDy2KCgkjzns+yOrWR6JSCk9Iag5NCm9M8FXRIhW57l+McQ4UFX5Z1tCTvDFqlyhOwUkYSuI\nBcMw4ly+5yVBcr2MSpAiQTnsN5F6+nd/93d8x3d8BwC/8Ru/wc///M9/g1d0wQUXXHDB1xMXgvpN\nDq00V/UV6SrROEvbOES53AWor9E2EeMRRU+jBOWhrpbMagUMQIdKA0bNMWqBshrZCKEP+IMnDQkZ\nhHSb0DONnue+QwmeQwx4SbwvgkZYGEOhVXYrbmbQa1TbUkQo+kQRPMVyg16u3tpkbqoNMzdjP+wZ\n48hu2J2VrZmbEWNWnYYhfz4JQ1PbBzFmdUjrTLJyj9+bm9EZ2+1JLerOn9frNcYYxnE8K6Pe+3M3\nKVTEGICA1gPOWer6JWVZPTvjCFC8KAi7QGxiDlEaE3b9UMeS0kCMHSnlqpO1AYuhkYJGL9CqZPVc\nVcyJpN7fZ5Zze0tarEmpIHZvz5iWrqSIBbfdLV3ooMs3NZ6DiHAgoJcJuQdpDfPa8szoKADWWq5X\nK27/9m/ph4H9bMbqIx95q7c1k/hrxvEVPjS8au9A11htua6vz7ZupRV2ZQn3gbiP3Dca7xXW5rd8\ngp4U3VP1jImR/d0dIsJiscjVLMbkOxhtC7MZUXWIhBwaZrPiWJiCmZvR+pb7/p7FId94sKuH475Y\nwJcPkaYXVgtFXb59o2FuLW2MeBEGrc/aYOMblNLMyw0gUyfqnJSyKqsULF8a0n0iNQmZ5+RhdaqX\nmQhXH1rmWjCmOl8/4oGiRKUBNfTg8tqDCKUpCb5hCENO7Iac6qoy+dgPI4ywKh9OrHOOGCMx+rN6\nGb/7e4jXW8yXXhE/85/hX33bOSDp8fivqQ1xH1GDwDxbw8P0821TYjxVxpgaaCcF9XmEMKK1wto6\nz59KtrHqM0F9t8X3dG1ErZFJQZWQSElNXaa5B/S5bz8pqDIGtFKk2iIS0DHPOyulEMCaAq0UISSU\nspM7wFOUmt45klgKNRAkIuIQA0Zn27gUGjsmrA2YqiCMM7xviKrD2RWOktG0dMOeaiyY1SeLrjzM\n7cZHCuqkTNtHAUlBcrWPURYfIaWAUoIxCgYIZMXbpQQijCpLyio8BCSd5k/TKSApBbxyOP3NkeD7\nZ3/2Z/zgD/4gkIORfvInf/IbvKILLrjgggu+3rgQ1H8CcCarQcI9LD3j6On7LLJNYZCkZAmhQaSj\n6AS9U5SlmxyQI3BDToatMWaWFYXFFKZ0zGFKDMAup3eamWFlFF0UjikyinCbIpWxbF3NqqgpZi9x\nL11mkMdjXlDTQttNvTGLJ3OUhSl4MXvBEAbu2j3HNnB7tyOFhkovqN2jkJk8hsdqBR/9aCauh0Pe\np50+Lxa8Ba012+2Wuq559eoVNzc3vP/++zjnWCwWT9Qxay3OuUkhfYExiRh3U1hNizHvTgYGMiEt\nppTfNjGMLWYdENXn+ozzmkq0rtkWNVVK7Ka51CjypGP0MWS1JnVCfH1A3r+BVfY560rnsKviYRde\nmILr+pqb7oYudEgnbKun6bZ9jOxjJIgwK2G9cQxHzd1dDk16a2MaI+z3uK5jO59zFyONcxhreU6T\nVsqAXvK6+c/EFJiVjhezD7+V4GxmhtQlbj9I9ASqK8f19duq16l65rbr+OzdHVtjqOua1amT1Nos\nfx6PpLtXxLUCFNZunjzPqlzRh57uvsMFRz2vz4m4eeECVYQGdGfhaUVuxn7PbDZjrxRt11FWFSEF\nxjiilWZebInxbupEndO2+fqsKnAzzdhki2y36xARiqJATyzKKUUnA2NKzN3DTHcaElQVOoyZ7U4X\nuxfBaktlHDEF/JhDeU622LIEv/cw5uviBOccIfRAOP9IxpTofui/Y/Hv/zfUf/w/4V/96EOCrHmk\nIhuVM4+E3IOq1JmgmhhJcaqb0QVOe5QeGOP45PVPyAoqk4KaZ7BFBLPLBJXluy2+kHlzVAohW4xR\nCRFNEgD1FSy+hjRCkog22XqRRsGhCVFA+6zwRoObWVJKhGAxBlLqKMsqjzQMBuU96JhDoUIBNWhG\nBAspUpiRnoAxS0Ru6IeG0i2xxRwZj/TdPeP4Hrp2pORRKqK1ftqBahXhscV3SuQNp0v3nOAbcoKv\n1pAMQeUbQe7Uf3pKB44F3nfMZlOCb5sIYlF0SAqMqv6mCEj69Kc/zSc/+UkA/vqv/5rv+Z7v+cYu\n6IILLrjggm8ILgT1nwhO6a1jHJm5rGSIZOLWtsIwghQLYgy0bSaqhDxzWhYLqjqhVEApj0oHjK5x\ndoFZlKhF3kBLI8ggKK9QR4WbOV4uM4HqRDiGiExKQ4MCNFYEVRRZAps6Kul7aFukaUlFRZovidoR\nY37IMJSk+BIVesLY5GRfvSPqhuvVgtWsemuj5FzmvIdDFs1On5fLc2YN3nuGYWAYBsZxPJOAk2Iq\nIrx48YLlcolz7vzvj6H147nUG4xZYO3qnedFV6CvBsabA6kf8QOYtcVWFVrXGFM/CQ6aGYNVilvv\n6VIies+Vc2eLbRqyHTT1CWQGlUBzxIQDutbo7fNrccbxYvaCm/aGPvTcdresqy1dSrQp5VAboFAq\nhzWVivt0Fml58WLiBSL5HB6P+c9KUVxfs/7Qh7i9u2O/35/tzo8xhIG74YDScyrds3YWJIB6m6T0\n1tIOI0oSm3nCmOcVsyolmrs7xhjxVcW3P5ZZAZZLpOsI/ZfBzTDLD72VJKyVZqEX3Da37Nkz//BT\ner0PgXoGodPEQeP9G2S968B76sWCvQh935NSohlzH2pta6ytSWmPiCclT9vmJzi5y83cEO4DzW0D\nVbb3nt+j1rRpYFCw1A9fT32CqkRH8zB4be2ZtMxtSej3DGHAVQ+suiwhJI+M+Zo4IRPUXElyIqgp\nJYYf/sEHgvo/84QgPYbSWZ00oogKRq3RgI1xmiPVpKRw2qHfQVBzb2rCWofWuRpGJFt83X2eQZXF\n9qsqqGiNoEEi2ghIIqERUSDqWYIKIENWWm0pjMoQASuKGAWtIyhFiFCXJfQ93quJoPYUxRy0IUZN\nKQpnEoOQCarRWO3RWEBh/EBaB4o4w/uKvu+ZlZ6irFGjZmh3DOMLDC6Tc5Om2cqHiplkIMWcXKwf\nBSQ9nj+djupUMWNRyhK05PMSQs4vcAajDMFrvPcUheCcJgQhYBE8hkhQFVbbbxhBFRF+8Rd/kV/9\n1V+lrms+//nP8/Lly2/MYi644IILLviG40JQ/wmhdvUTlTF/EdhkMWHihYyzl8QYaZqG8dARy4Qk\nmM0tVQnGBLIcklUDY+bookYtVK4eOEwEqcsbZTM3LBaWRWlpU+LgI30Qmj5AghJDrQwkR0pbIpF0\nbEhNBzKpt0WRd+zT5lxr2C4rPlRUJN3RpQMhjQzcsvMFS7XMs3aPYEwO+ZzPYbeDrot86UsDKQ1U\n1Ygx8cnji6LgIx/5CFpr2rYlhMA4jrRty/oNm+oJuZ/xihCOxHggxiMpjTi3feiJlGznzB9T8MwV\nsHcwlKhDjaZ6YiV9si6teeHcQ3hSP7IZFbrnvEFFZRuvvlpjUjW94SNoectie4LVluvZNV88vuJu\naPnSOJ6VVKfUuUbohM3modrz9hZezFrU8ZC/CJn5L5dgDBWw8J7j8cjt7S0vX748E/zOd9z397ny\nprpmYTUxHvH+lqJ4+YSgdx0cGoVbWpYqoJqAzN1bKvIwDNze3rLUGluWFOs1XYx5FvrhZBHnIENA\nNT12/ba2KyIUx5xOGqpAR8eCyS6bchiT0fDhpaVrMi/fPnZIT3Over2mGga6rqNpGjrVAZy7T7Wu\nifFI17WEsMbahzYmXWvYQ3/sUVZRPUq/LvBAYsA9XF9RMlHUoOezhySn5RI/2dKXrub+cMuYxieM\nWtuQVcVoQfS57cU5R0qKGLOCmlJWLv0nPgGA+T/+FESeVVDzA4AIOglenYKKQIWAnAY/k8YZh9YP\nPayPkW8aQVXVpOTJbyWnGJ8UVFl9ZYJqTgRVkX/p2YQkTUwRrS1a6cm98LYKK4OZfq4ElCEBNkFS\ngtIjSit80KzLktT3jGOirk22jruEUYqoHKMXCjza1YTg8IxYFVB6jqJHBY+uImWs2O1mjOMNcdZh\ninkmxGGgHz0xmGkGNU59zJo0VcwE9XxA0uOKGRFBqQgktGgSBrEKDZgQ6KJHZhaVCsbRY63gnEBS\nSDREiUQZsKLRpkLrryhef80wDAM/8RM/wR/90R/xiU98gj/8wz98chPnggsuuOCCf364ENRvETzO\nKYoR2tZQliuGYU7TNLx+3XF/H7FWMEZjbaIo0kRWd4gcJutvjdaOSCI2kdgleBURIqY2qNqANoQY\naVNiTAmIKCKV1syMwWkDixVqvsAMLbpr0AyYYcAqS/liiV08rqipWVLT+pbDcDgHKZWmZFkuz0qM\niJwV0pQGxjFwPOb3ezjAYmF58aJkNiuf2CgBFosFTdNwOBzouo5hGFitVsxmz3k6wdrFpKbeITIy\nDF/GmBl51vAhhTenqmalVL9X5pnUfSAeI+IFu7VPKlVOMEqxDZqb3cDYJ14BG2cpC4Oe6XyszyQh\n925yd5fJikhml4+QRGinc6LcOltOk6cb7vno4gXVM6nJMCX7/sNAfH/PvfaZnBVFJsFvyCmr1eo8\nx3t/f8/V1RXN2LAbdvkYFwtW5Wo6V+GsQjuXa17GMY/WAmw/bHBdzGFd+4hdP6zvRE5FhPVyyYvF\ngvvwdvVMSiPRRSgrbFhkEr99On8b7gMShOV8yX6+pxkb5m6OUord1P26MIbFUtG3D25a58h3e04l\nqbMZM2Pouo6b/Q3FKoeA2WmOWOsZMR45HHpEVsxmT4OWKLKC6Eb3RH3W+Fw9pCvGlCi0zvZeyFbk\nup6ieVvSYnEurKldxT6mnJptNKcrfYw5CEdFxzDkb8/r04gYUopAJMb8GvIv/hvSR16iv/SK+P/+\nP/DyX+baI/2MgoqgkiLoRJqcAHifU7tNVjBLW6K+CkEtyxKRwIk9Cwl9n68hWV1NxOt5GfQsICqF\nEkFN9SpjiBiT1cI8T/6UaaWQIGq0U5hCkDSRbG2IPqJ1QBtLSIrSlfRKTa6LCogkBgqj6JRhHBOO\ngCstIRQMsUGrlC2/Ai4prEt471FqicgtQ2xxdpFDkHRCUqTrmAiq5PPzqGJmfEeC72OC+iTBdwpI\nUladLcFj8uBqeDR/6pwihUSizOvwgaBcrvz6yhMNXxO8fv2a7/zO76RpGn7hF36BX/mVX3nnub/g\nggsuuOCfDy4E9VsQxmTha7kE7w1tu+J4nHM8tlMXYiRvDg0QKAqhKMh312mm6pMZel6iyocZ1XiI\ncIjYSjNbaFZzi2ihlUhQKW94TMJYzcppamuABcg8b/aPR4ge9rfQubzAR2rSzM2obSaqd+0d9909\nN/c3GDFUOqfnPsZ8rtluS0Io8b5EKcMw8ES9evr4+blyo+977u/vzyFK9tGsbEoBEY+IBwwh3JJS\nh/eZiBizwphs4dW6erKhMnODcopwF0hDwr/y2K09z4wmn0htOgcebbHsTGAo4TDLM5qz52SMqsq1\nM7e3+VimBNstowjNVA90osylsXzn8j3a/pYkkUN/RzG7fmselBBQ+z1X0nObYBDLzqxYv3i+3xZg\nu93y6tUr+r7nizdfhGlTuy7XZzURwNot3r+ekn1vUer63FCzWGQVPJUW/8oTm5jV4lLT9z13UyDS\nfD4/K93DpHbuQ2Dr3JTam9mu2X47+mZil7PZ+eTHLpK6XGMyfzmnH3rGONL6FmtrhpTQwNIYlDqP\ntHI4wNVWzuop09xrWZZYa7k93jIf5mzXD2Q4V78U9H3A2p7Z7KnTwetMMFx6SvpT6imVZlAl/Ymg\n9hNBrTQUU81TCIRhAKUyMQQK0QxATziPzvro89vviycENUYwxiIS8f7B/m6sJv7YD6J/79/B//4H\n8DP/8m31FE41rhjJKb7oHKbGVMMkSqPQWKMnopcrTh7bjE8EtSgqvG84ZZSF4wHd94hzqOUSCTlp\n+Tk8WHyn4CCVe1BHH9G6QCtDCJ43a25Sl1Aq3/xRElFJMslOuVM2xIBz2aIbQz7Xfd8Tgp4U556i\nWtD1jv6YMATKuUNEMfSSM+sk5uAhV2HjQK8GiqLKJHYcqO2IWEfyCYaOtk1ni29eZD7IX6liJhqN\nQqHEEkKHtWBMVr7DKcF3mlcd1PS8sWAcD1SV5ATfMSf4KvG5/1QV35CApL/5m785z5j+zu/8znn2\n9IILLrjgggsuBPVbHM5lMWy9NgzDkhiXeD/S9z193xGjzu68FIADRZGo65Ky7FDKYu0crWeQcsUJ\nQwLJ9RCEvIm+nhnEWZoYaWMkkriLiUOKzI1hpjVqPs8M4DRA6j3c3hK1xlcVYaoSCSEQQkAlRRwj\nbWhJktixo7Y1V8sr5vWcsiyfKFEp5caREw+eHJG8KZAaY7i6uppSfu/p+wN9f898npXXrOzIk++x\ndk1KJTHmY6KUnipinpccdKFxLx3hLhD7yPDFAV1qlFXnnkkAVSjMzPCyLjjGyCFG7kMgiLCyz/xo\nFgVcXyM3N7RtSzuO+M3mnAZbTcFC5UQ+FvOX57qX1+3rh0TdlB6GeEUwTrP5jiWvuzlNBNs8zE++\nCWMM2+2Wz37xs/Rtz9XVFe8t33vLep6Tfa/w/jXH48jxuMeYFXV95ntom5OI4z4SdoGwCOx2u3Na\n7zkQCVhZyzCOdCkxSwmTDlNqb4Et1rA0+QLY7eC99/KGfZfDe+zaooxiWSy56W44jkeU5OO7fBRS\ntVhksbLvwd83uBjzMX90E8WVjnE3YntLdf2UyA/DDJE9RdGh9dPjMaYRZRSlKUk+oV22oooEKmMZ\nVUGfEitycBnwEOY0DV/7toX5/Fw7Up4IqopngjrGkaIA8ZmgnhBCtvmK9Hj/kOSrlJD+hx+B3/t3\n8B//E/zM//LW/Ck8WH5VFixB6ycKasShUJmAmuIcInUiqDl0KGCMxrms7p7qhbl9nR+zXOUgoiDw\nDrJklMp2YqUhJZTO5ac+BLQusdpOv8ueIpN+g6410kaUKMTmnwXxWdE0RUJQhFGxnAjqOArWakTG\nfAPPWPwgKB1YvigJ90LTQW0Vzuf+1+QiahhRxUDBnMNhxjDcsZx5lHPQapT3HJu8Tnci41MCUq6Y\nmap7tH4SkCQKrDaEADFGcqD1lOAr+XeMi4GY4rmOJoX8u3W9BmsVsRGiWFADKkVG5Vh+nQOS/uAP\n/uCczvsnf/In59TeCy644IILLoALQf1nhQdVsWC9LoAV3nu6rpvUgjzX1DQdx+ORsjTUdUNZVhgz\nw23mKFWQupQ/hqwGpjb39s1mmkXt6FRW9YII995znxK1UtRKkUTwZUnY7wm7HWlSBnAus6KqOneP\nvpy9RBvNIANDGjDWEImMZqTUTxUSrR/mU/f7PFd5f58Jx2oFzoUp8TIro8Z4NpvE4dDRdd1Ebh2r\n1YqiqFHKoZSbZsNsTgFNYbL8+kcBSssn65AkpDEho+Q/N1mBBlCVwl05zCwrOdo+KJpLa7FKcT8l\n/AYRtm8k/PqUaIButUJub2EcMXd3zK6vmTl3tr6ej4nSXM+uue1uGePI6/Y1L1KFabspAXWSDZdL\nnNZsqyzQ7vdZha+eEVJFhCY1uf+xUaheUW7eNS9mOByu2O9vgZbZzLDZPGW+dmFJXaLZNxzvj5iF\nYblcslw+Pa5GKRbGsI+R+7FhoxqepPYuFudAI45HfF9A4myXBiht7izd+R6hZVXMn8zkaj2pqPvE\n8f0j2zUPbPoEl8m3jvotK2rf18CBuu6nJOipezMlhmHA1IayLEldJqjZKg6lmWEkp7aOXZ7rVk49\n2Gwnghq6Dubzc+1IpRx7pRiJyMT2Qgo4q9DuIZTMuZNT2ZISk/VUTe9ZwY//aP7zH/1xJn3PKPin\nteiUFVSlVL7eppAkUQatHgjqqfN4PmU+j1OqbFkWudJF8geAun0FgKxW2SrsJc/WPwM9nagckpQV\n1CRCTII1NVrrSUF9QAoJ8YI2FmpNaAI65lqYCKgASgRbJLxSBA/lIl/TwzCwWJSk1GFdrqYaI8yc\nwxWKOwJjJ8xKRelzsi+mRPuAnntUUMASkTu8NIhVFEqjY+LQDlQW7KnndqqYEZOPsWYi5E/svYLG\nEtLppmLAWg2dJiiFsgrb5psDVA6dSvoxoHXC2nyNx6AJaBIjmkjUJUabrxtB/c3f/M1zr+nnPve5\nc9/pBRdccMEFF5xwIaj/zHGqWVmtMlnt+56uc4Qww/uBvm+BHVVVUlUl1tZAAVUBhcYfPaENxDGS\nXieSJMQIqlQMLtHGeJ6nUkCpNbUxlNbC9TVmGHDDgFUKJ4IF7GaDqp/uUJMkjuORZmzoQ08fekpT\nsigWT8KUjAlsNoG+9+z3ga7LH2Upb7beoJRhvX7JfC7s9w0xKnY7y2JRslqt3pqF0tpSFC8JIYcn\nxXgghg6TNuB1Jqb+qfpqlgY919liaBTKqGwDfsZGWRuDmRJ++5R47T1LYxhF6FM6J7hiDOWLF8x3\nO6oYMxO/vn424UQrnStobr9A2L3mNgpX9RVmNs/k69EBqar8pf3+4Skfb1qTpDPZXS1XrMyKFBJ3\nd3dcX18/eV3v88hsCI6iWDOf31LXe0QsSj0ltGMxcj/1YK5frN8ipycsbFbpB39HaxTLYot+3CW7\nXsPr14Qv3iP1Faq0T2ZbARZuwT/0LcSGb6/fTkReLKD78pGhS/irCvdoME9EGNJAWZZUqqJtWxZT\n/UvfQ0qKsqwoioYY2/PNi7ZtERHqdY2O+VpgxZmgal1SJkUrQtcFKlS2955gLTiH73sYR6xz4D1a\naVw5Y5A8i5q7PCXPxpZZIB+GfA6zGFycCepJQTVG4OMfRz72UdTffQH5q/8b9aM/9PbBn5ajk5zJ\nk7U2V8zEPH+Z3wuUJp/fx3OowyTnVlVB5qoqhwKlhNxkBVVWa9RJQX0HTjdhZCLpSkVighiFwuZz\nFeNTBTW1WY00tSMZhRDRoojWEvseFQERdJEgZQXVWoO1ec4zxmwBx/hMdsVQlDUFAYwh9JpQJiyB\nlDTeOYrkcTowyoBzNSk5+jCgjMJJhVbQdUdspdA6v1+ZLL5h+jE+WblPUniwGohvJfhqNIgh6fwf\nuvM+ByS5GokF4zhO6b1TCFuyOWMgjpTKTKMKX/uApBgjP/dzP8fv/u7v8vGPf5y//Mu/fOKSuOCC\nCy644IITLgT1gjNOZHW5XBJCmMhqxzDkj7bdA/fnxytlc8dnWYKxeeZvSDACXRbo1rWF2jAUihHQ\nxpCcIzrHsiiYW5ttbCfrb4yZ2RyPT2ZUtdKsyhWLYkEzNhzHHZ2/pxtvcFozswWFcZzsudbmAKCc\nL6MYBov3lvncsVw6jHlITS0KmM1ecjgcOB6PNE1D3/es1+sniauQFVLlZ6je4ts70tgDX0abOdbO\nc0pooVGFyrZepzJxiIK/9YgX/Ounc7Gw1hUAACAASURBVKlPzoFSLK3li8NAG3P1xcYY3BQOVE82\nXqNUXvikpPL6dX7Db8ogXYc6HLj2mjvRjFZ4XQsvNuts930Di0VW296sn4kpctPdEFLAastVfYWe\naV69esUwDByPxzNZO81xiuQlbrcVIktiPBDCPc69dyb/TdOwb/Y5KVovqMK7518BFqplINKkgrV5\nw4dcFCRTEY9HCAfsh1++dZPBK4vRDiSQYg9vPIcmMZOGBjiw5HGxTRc6kiQ2yw20PCGoTW6dYbms\ngYaUWmB5fo8Ay80StVM50GaIJEZyyFZJhdCmRNdFKmWfdrUC1HVWUPsedzpJQFHOss039Ofz6bSj\neERQTw/XWuOcJqV4VjRPhyf9+I9h/u3vov+v/4D68R9+67ifLb6i8gyqUhhjkBghxTNBNQaMnsKK\nJBJTxGhzfr0HgqqBrEKfLL6s11kd/QoEVU929qQ1BoVWiSFFUoLCFlhrAE+McapuyfOnAGZh8jqV\noFMkKE1iGmMVIamAKzWKfIOlLEtCCHifZ/RF+XxRG4cxCodHu4LoJSvUGpIEgl2AVtnm6wZKWdA0\nJY2+x2hHUcwQAd81pGLxEFo8WXzj9PeTlftMUJ0BeZOgRowqCRiw03/oITCKB7dCuoJhOFLXQlFo\nkvdESiCgUsBjcV8He+/hcOD7v//7+cxnPsNP//RP89u//dtP5v4vuOCCCy644DEu/0Nc8CystSwW\nCxaLBTFGui5bYXOtigdGlBK0VmgdMAb0dYW1NcqXqEHBo3FOpRVUir4QBgNehFaE1nucUtRFwey9\n99BdlxnONKOarELmJVK6s0W3ILJ1ijYk2rFjiJHBg9UFi2JJXawmW65ls7Gs15bjUdFOOTqnTft8\n/rBBB1gul9R1zf39PeM4cnt7S1mULKtlVr6G9GjzrDFcoeyRZDpU2SJloJxfP6lVOUEZhXuR51JT\nn/A3HruxmNqQRBhSop8+BKi1Zki5I3JMiSvnWL65odM6y5x3d1nCu7nJJLUopj6Xw5nIKOfYbv9r\nbukY4pDtvrMXz5LUx/UzNzdCuTrQ+gZBcNpx/ShwabPZcHt7y+FwwNqCti3oszDIYvHYIbskpQGR\nkRB2OLfheDyy3+8BePHRF9jGIl4Ih4Bdvv2rKaUBKx2VNnizYR8Cm0c7a0lCSDPQDcZ5dBzBPRDe\nKMIxRuZugY57juMx9ws/vggOB+YzoU01fXRPelFP3afb+Zb9sD/XFhmT5z2VgsWiwHs7pRgPjKMQ\nY8RamwlPHYiHSGw7mAlKFSilKbVAFMYxIRVv3bxIZZkTfIchBwVN57WqFhymc+okL7QwBaXJ6xnH\nzKmmh1PXjhAifd+jtZo6aDXqx/8N/NvfRf/xfwLzS28d+5OCqqIQp78aa/ESJ7v4g4J6WkMX8rpq\nVee5cqUoy7xGkQcFVd3c5m/abjJBje8mqJBJalQKQaFJ+DjkEKjCTUFHuffYGEPsIhJz6JJ2GkaT\nfxelCLhs8Y2gVb4+SgeanDhdliVN0zAMnrI008zwOPWe1ig/YgshkRiGnA6sY8DrEtERhh41HzHR\nkNKCMXyAEJlVW9rmSBhaRj/LNmsUJJUrZrRA4pzGOyVcZf4ayQpojBgjWX2N5ARfp3ExkiQRjDrP\nn47jOIVyK+JR8rywGkA8XlfYrzFB/fu//3s+9rGPAfBrv/ZrfOpTn/ravdgFF1xwwQXfErgQ1Au+\nKowxZ7L6GCmNpNSTUj+FCyWggbJF1xVKSmSwSJdrEGiEsoFSQ7QwOBis4C2MYWDnA04n6pWm6Edo\nDtB76AHrYD6DqiarTo5l+YJlaejDSBMGEopjgn70LIqSmX2wCa/XD/OpfZ8/n+ZTH7uJjTZs51sa\n37C/ybUkrc5K2Ww2y92UjxRS7V6Q0kAI94gExvEV1q6mSpqnUCrPoIZ9YDwEmpsBP1OkuX4Sy1Qo\nRWUMHy5yeFKbEscY0Uo9mZmcnjST0ru7TEq/8IUsH5/IrLVZia5rFHAlNTfdzcNM6jtI6tUVfP6L\nLa/2B2wfudoqZm7Gulw/IXRlWbJYLHj9+sBnPrNjs7nGOc1m83aSsnNbxvEVKbXc33vaNs9CbjYb\n6romuYR/7YnHKdXXPZC0x6m9m/KKm5g7eWdT8i1MlTKi0NcrrGlyYFJZnu9CHEJAgE1REf1wTvQ9\npw9P0rE2ivpDK44Tx7+6yum4PnmMMtSuJswCh8OBpmkwUw1SXeeXypUze2JsaZqs3s2n1Clda+Ih\n4tsGOwOtq/O1Ufh8T2d0wps6sjcGjMGllFnnNJfoqhnGj+fUXKXUuYvUufzQYcgcR6lMUA+HnnEc\nKUuHMQalNOrf/ES+/v/sT1DnMptHl9k0gzpl92QYQ4pxevLnCeoYR0wyuY+2KHKgT34kSmUFVZ8I\n6maDKiwieW708Yz2Yxggao0ohULwqSclhVF2Iqi50gce2XvnZjrOFozChAi6IkTBpBwW5VNkUWSF\ndhxhsylRU90MFPl3nBrAFRjt0LGnLCGmQD+CmStIHjElokaMDyTnkSFh7YIuCqiBqiwZmo4wDgxh\n4ExO5ZkE39PdnrIkTJbwnODrn1TMnBRUF/L8qViLigXDMGKtUJYOpUK+AZQ06Kx8e21Zmq9dgu+f\n//mf8wM/8AMA/P7v/z4/9VM/9bV5oQsuuOCCC76lcCGoF/x/htbFlGS7IqXwiKyOpNQBHRQKXRWo\nWEBf5GAl7yF4ii7gxDPi6XXCOwgOeqdRBqrNmnqMlL1HRVAHUJ2g63lmAy4TA+eymbLzHYfxQEiB\n+/6ew3BgUSzOKtnJ9jsMmaB6D7c3gk2JZS1YeVBIS0quN9ccjgeGONBIQ1CB7YvtW9Y0rUuce48Q\n7kmpmz73WLtBPap28SeVtMqfwyHCEYzXzLeO2hgqrbNCNmGjNTYE9jGyC4H4roTfqsoK6n7/QFrf\ne+8p+yYToev6+kxSb7qbh3TfCUMY2A97zNzDABJKnF+xWT6/ixVZ0jSecRzpunu+7duuHmyLT17b\nYO2K29u/53jsKMuXbDZb6mmN2mnM3BCPkXAfKF4+zH/mcKqIUgWFXbAgcJiOycuiIDYxJ7VqsB9e\nwa3PLONwgNUKn1LuiCUnAnu14La75TgeHwjqyZc8n7NYGtphSvT10MSsnp7SimezGcfjka7rYSJ0\np+RjY2bEeGAcj/S9whh77tvVNtu+UzeQRo2bP1DRwkMLjM8c5iACVYU92QBOkqi1lFJyHI90vmNZ\nLs/drGWZD8F+/2C3PiVfD8NAVRm0zgFgfNt/RfrOj6M/97ekP/9T9A//yNNzpyd1L8pkzgXRGkkx\nz6CqUx/s9F4m0n4iqMDUTXx6xvwsMQbU7V3+0nqLKgwSphta7/jf6Vw1ozQSA1F8TgQWQ1Hkb/I+\nz4umIV8Tup4ScpXNPa9kZdUrA+TfAYLBOkGHrKAqpSiKgmHISriIR9tIYUuichTKUOpIIiDeoAxo\nLSixeK0oRaNiIJkB5wpuDwbjeraFoQ0VSENMDSHMkJiJMTqfa8U0gzoR1FQ4UmyzKho1MUaKYpob\nDUJIuQPVDp4hjMjCQchrzzViGhAIFo8ipQFDIuoqzzJ/DQjq7/3e7/EzP/MzAPzVX/0V3/u93/uP\n/yIXXHDBBRd8S+JCUC/4R4HWFq0XwAKRdCarKQ3ZFqyGnMxZg0qCjAm8wJBwEYpUwGAYek0vhlhY\n+rJgLDV2bpgNA3XbYmLM0mfT5N1ZXWdyVhTUrqZ2NX3oOQwHfPLshh2H8cDczZkXc1RS2JTYFkLb\nJvb3whBhIG/ol2tws9zJqQpF/dGavu/Z7Xb46Hn16hWz2eytEKWcPLwlxooQdqTUM44fgFkz4uge\nhxwBrjbMCoO5j1RBo3fgrvSzJfULazGPEn6jCNvTjvLUqxNC7tTRU7qpc5yLJt/Au0iqIOyHPX2Y\n0mWd5eMfXtHsKsY+H/LH9TOnceFxhO12wzC8pqp6mubwzqCj49HTtgGlhOVSncnpCWZpSH0OmwrH\ngF1YvL+bAoU0zuXu0YUxdCnhRTj0nmKf36vd2EympsAkmgZmM3bTsTjN7xpb4bTDJ08zNszVZItW\nCpbLc6Lv4QB3u0AsOxSKucsHwJicyHt31yPSs9nMzpt8pTRalzTNjpQsi8Ubs7BlhC6Seo1+ZGUu\n/KTeOd5KCA4iUJbYrsvrTIlTsk0lFbfdLUMcuDYPYVVlmde/3+dLo6oyQU0pTUm+p0dmW238738U\n/bm/Rf7DH8IbBBUySY1RUAmMVSRjSCkrcYmnCqozDq00IQX6IV9PxRQ4lR+jAE0Swd6fCOoGVVoI\n6asHJU1JwEgiiQc0mqygZktzeBSOZM7HUqls8VXkHuJRNIJgJIGyoGOeuY75R6osS4ZhwPtESh5l\nI3XhENGgHQUeIRK9EGMOt7IEoi5AFw9zqOWG4dZSmkhlBVRFkIiEPTEuzoOn0eSpCDfN2k5MOc+f\nRrDa4kN+f1UVcwXOoIkotFW4JnBMHtwMfME47lkspvnTkEAckUiII5W2KFWh1NPwuP+/EBF+6Zd+\niV/+5V+mqio+//nP89577/3jvcAFF1xwwQXf8rgQ1Av+0ZF7QmcYM0NEJpKa51eVUmhrse5U3+Ig\nGcQLaUgUo7AIOSm0ayL9ITKowFhqdsUSayJFP+DGkSKMmJ0H2WWyWtZIVWGsZSMbBj/QDA1DHBgZ\n2cmOiorKVTjjKB28fA86r2mDJhjFzmhmBpb1w2a7qirKsjxbOk8hSqvV6m2CZWqSKjgMt7Sxw4+v\n0KrG2iVWa6rp49RVKqXgb756eNLjhN8uJdJux1Xfo2KusHls5aWZ7K27XSYyz5DFxyS1Dz2fu/8c\npSnROncnLovlWVl0KhPRx/UzXffw9NbCdqsR2XBzc8PhcKAoCso3PL739/e0bYtzGxaLQFFAjO0T\nO7RSCrux2ep7iES7yzc30Dj3MN+rlGJlDDfes3s1cK0tbmEx1aQEn2qLjkf2Nzf/hb03i7Ulzav8\nfv9viGkPZ7yZWZVZRQFq08hgGTXN1BZdVd0tY7AsIVNviBZt3hBCQkI88IyEMBayjZAlPyBckpEQ\n4gkeWoKqot0M6kZYUA0NqBswFJmVec+0xxi+yQ9f7H3OuedmDRTV0BBLujqZ95wdO+KL2OfGivVf\nazGcnmJEWDwYkV6Ui3sVtR9/Fc7nxxM/m+WlfGe9YnGaOG1mj5Tmpml4882BGPe8972PR7pFatq2\nIyV9HO89fq8ca1CG4khE4xCRBLZQRC30MVI92FcXI4whZrTt/b6SU3NDDLiQR5APKIrMt3e7fM6q\nKhPrlLIv9mAQFxk/f9/0Qfi//y/kE78KL7GhHtQ9FRNGJI/Zhjg+CHlMUCGrqJ3v2LZbSl0eCWoW\nQBUxKkJMFDdj8NrZOWIV8JkJ6rFqRgQV46igKmQkqM7lsdwwfjZUc79TBwVVjQTVi4aUj0eASDxa\nuA8+VIBhSMQ4kPA0dUUMiZg0yfdYG1G7yDAUFKcWIx6fLGgL/R6p++yFpUaJItFhilNSSCS/Z3AC\nLyT42ocG4qLAk8m2pEzAs6XCo0Xl/dBZcRXv8SmAtvhtVqibRmMMuF0iYhEJqBRwGIq/4vHevu/5\nlm/5Fj7xiU/wjd/4jXzsYx97EjQ3YcKECRMmfDZMBHXCFxUigtYVWn+GmxQFGI59lSnkLlHbaxZD\nYhgC3ZATTgdgoAQpQRyqHyiGARsHrDisbEArqCpsVXFqT3GSVbI+9OzVnja22NLSzBrmzZxSFMuY\n1ab9Pt/Qj5WTzOf5hlpEWC6XNE3DarWi73tub2/Z7XacnJygjKEN4ajqoZakZFFhSy0dDYHGvFCL\nwhie9Ozl4UkvolCKC+e4vbvDOceNCGd1jXrRSDubZaZwd5cPKsasKL7k3FS64u3t2zlkR1leX7zO\naX16DEGCvOkQMkG9ucnc71BfW9c5VCkLVAWLxYL1es3t7S3Pnj07EqK7uzvatkVEOD+/wJiI97d4\nv0ap8lGwlCryqG+/viLddtjzCmsvUOrxnXSlNcXtQOsTuzJysXxhzRYLut2Obd8jbcvZC6p3dVBR\n2y3tLlKXsyPpg1GgLDuGTc9+p3j/2eNKDGMqQtCk5NF6AO5Hkvs+EiOU5X2NyAFJhhzaEypiH9GV\nzqOoQF1rdkD3gKCmlI7qu6mqe8X89PR4Hg8VMyk9fi+l7tXAg0qmRhYZggNKDgpq+kcfytv7td/M\n5OhBxQ7kazWQkCQoyQpqSuOIL/cpvgcUumDTbuhdz6ycHd9XKY5dqD4m1G0mqOniAjGj1/VzqZpB\nIHqixOw9xqC1EKNm2Ax467GNfeRlPiqoEiEkgmgiCZMAESLhEUFtmuzTDSHQ9zn1bT4zrPeJ5DUp\nOoyNSEy0nWJRaWwcaFkQRGNcxKmAl5aiqCHUeHqSSmgEfEfvPXEQNMcg35zge3gQUZb4OIadxcNn\nICf4GlUwxDztYZ3L/lNrkHjwn0JVlaTUj15Vi0iXA5LkrzYg6erqii/7si9js9nwAz/wA/z4j//4\nSydCJkyYMGHChM+GiaBO+BsH0YKu9ZGk2ZCoh8jpkHAhMpBwKTIkTaRiEBi8g75H+o6CQKFaCt9S\nKIttaprLM4IR2tjSupaQAtu4ZbfdUZqS2tQslxXzubBe34fg7vdZgBwthBhjuLi4oG1bblcr7rqO\nT7ctpq5ZzOdZIQYqpajtkkIWOHdLSgPOXaP1DK1fMh48hieFbcDf5jATsxw/ns5lL1rbYr3nQoSb\noqCfzbhqGi6s5QmdrUcJ+OYmM+4Y4ezs+O3e96z6FT56TqtTdm5HZSp88pnkvHBfOZ/nXXjzzSzq\nXFxkm2vTvPhzc4ZhoOs6bm9vjym/3nuUUpyfnx+VtDwC3uLcLUVx+Wg7sV6TNh3JCWo4RZVP76JD\nF5j1QifQnyh8Sll5OnwfuGsaWK1Y7vfYl3QuLsoFd8/fZusC9cWrj2OdgWDWKAVFWuK9PLqZ3+2g\nrmtS2tC2e8qyePC9HVrXzGaWGPcolR8QpBRJaUBXBtkXxHYkqN2BoBp2BLoH49ndmOZciKCaJl8P\nw/CoUkiNoUYhhSfHCI8P61i/ciA9ook+Ia+8h/iVX4H6939I/M1fQ33zhx5vRIFPoGJW67IGm4CU\nQ354qqC6IYdLFQ/IrlIHBTWn+epRQZWz88+JoB4VVBQxOGLykAw5eCl/Rvu2J0igah4/GBNRiFLk\nmpVIQBFSxKScDBxiOPLysRnnOD3RdZ7ZzFDUQKcJySAxYTX4EOmdoGqLaj0SFF4rKjQMA15tsUVB\nbGe46FEatNcY4wjRMewVdTkm+DIqqGO9DGWJD9v839GMqntAJCJRxoAkwYYxIKmwpFDQdd3oPzWk\ntCc58EkQ8RA9ThmqvyKC+gd/8Ad85Vd+JQAf/ehH+c7v/M4vfKMTJkyYMOHvLCaCOuFvPA6ElTpf\nsA+HakNKDDEypII+1viUcM7huo5d1yFxwO4dxX5NYS1VWVLbGYNOtDh639G6TFq10tSmZr5smM0s\n63W+Sb27u0/8tUWijZFWa9LpKWG7xbUtfr9HDQOvnJxw+sJIZ1Fc4v2WEDaEsMt1KeZ0DJi6h1ka\nxAh+5Qk3LelmwNT+fowXwFr0fM5FVXHjHENKXDnH+aFP9iHKMjPJm5ujb9GfLlkPm6PP1CjDslzy\nXv3ezxicdGj+OVhcD/bfl+H09JTnz5+zWq24ublhPp9jreX8/PxIjgCMOcG5Yaye2WJMVi8zoe8w\nJwVpvSRuhdSkYxcnZJXd33m0CMvzgp2BlfdcPiBCt84Rq4q675l5nyXgUXU8oPJgfcIp2BfCQ769\nHbZEPCdzSxmaY6Iv5DVoW8YR7w1t27JcLlFK0fc93nusnVNVQggtxmSCmmuaQDc1qRNiF4khe25R\nUNQGM2S/8jAmFO9HstqMSb7H3phRLfXRY7XN/sToHh1fegnPOyiZcfxZkftql/SPvxn+/R+SPvYr\n8AJBFZUVVJXyQG8MgShCEgUhPQnGekhQ7UMyfVRQIURQd7lqiPOLrG7q3BucwuNzfsDRgypCCD1I\nQEs9VteAEUMaEr7yx3CkR8dhDDCgYiAqg0+JRhKRrKBamwm994wqeMn19TXeR6w1GBtRoglJk5Rg\nUyAQcV4TUIhOFMHjVEFSFhkcQUW0qlBqSZIVQ79F2wpRAddtGaw8IKjZJ3/8wBUFfjeGYkWD9x5j\nxksh5ARfMYLxnjY6kq2JzuLcnvkcikITAhAsDvCpw5CIukGJelEo/7zxy7/8y/yzf5ZToH/jN36D\nb/iGb/jCNjhhwoQJE/7OYyKoE/6zhhah1vpIWmNKDMYwVBVDjLhhYOg6hq7LbPMgi0C+ydWKXiIt\njkGDmAFhhVGGWVWjipr9VhE6eLuDpBK2zNyvtMIrJyfY5ZJuvWYYBvarFb5tOTk5eXRTbswcpaox\njdY9UFMX92pq36OHFvEt7q4jRnBWsBcVMhvDoEZPnAIurOXGe/oYuXaOc2uPlStHFAVcXhKvnrPZ\nPGe/fYt0eorS5pHPFHhpcFLwmtXqfqT3jTfyEnqfee/FBU+glEJrzXq9JqXEcrnk8vLyybifiMKY\nU5y7JoQNSlWEsD4GIhWzC0LIVSH+zmMv7tfT3TqIoCrFcmHoRrK+D4FGa1beM4zewtPzc3j+PMvh\ns9kj5ZH1mlkx47ZMbN2OZlyPmCLbIatW7zk/4e76PtH3YAONEZpGI1LSdR1t2zKbzdjv9wAsFieI\n5FTrENrsTx6rQrSpiUXu1vV3mXwcvMeVUmxDVlEV0I9f68O5Pczqjkm+QxiOD1diigxhoNDFqFDe\ntw4dxnxfVFBBk/z4EORDH4L/4/9EPvGJJ+c1qjHAJ2WCGWMkKsmkLMaXJzePymrS90z54YhvBPRq\nJKgXz/JrzEhQ/WcgqKMHNUZPIpKSOhJU6fNroo0vHTE9jooHT9QFIUWIHqMMclRRNX1/70N1zuFc\nDnpK2mHF0mNIotHRo1Q+ns4bqkKhnWNIFtEF9Bv8WClkzBkhrBncHmstxkJo9wxR5fUVQYugDr+n\niuxT9tEjCCSN98OjipmQDBjB7B0uODAnDHdZ2Z7PC1LqiS4iqSIQCN5RaINI+QUHJP3kT/4k3/d9\n3wfAn/zJn/CBD3zgL7+xCRMmTJgwYcREUCf8rYIaO0QPg33JWlzTZJV1GIgju0rDQPKe5AMGaDC4\n3tP5HR0eZzW3ZotYSzFrwNWEriQGUK0idirfJFeClHB2dskwtKxHonp1dfUk7VcpQ1E8w/sNIWwJ\nfkPc3WJ8jXKHsBlQGopXG9xek0yF0wWmMY+8dDAGHVnL7RicdO0cZ8Y8Ctfx0bP1W9oqkNoB8YHZ\numPxni9BGft0e4fgJDfwx2/dUHOBEoUx2cZaltnTeHWVJxDv7h6LkiEEbm9vGYaB5YOR2hjjI/X0\neL5UidYzQtjRtn88qqjq6DmVZcL1jthHwj6gG43feNKQyYs5zaTiRGtuvGftPQLsQkCAM2PySOd8\nnme2Vyu4HMeJ93vwnqqaY2aCi46929PYhnW/JqZIbWoqW9A0WUXebvOk9C63ztA0INLQdR37/Z6q\nqui6DhGhaRpSUnifa5cyQe2Px01NPq7V2PtaPSWoB9R6TKIdw5JQ6viwxYX89GBRLIhEOt9R6IK+\nzwR1sciKYN9nMiIi44jtQIyR3MOZv6gP/9PcL/qbv0Xa75EHM9xBMsnU8f5coxRxHPt9kaDGGFFJ\n5feS+2M5ENT88KFHtR3JGNRpVpnFyFhvlLJF9sVr5ui5FWJwQERhiFEQSegxaSjYdxl3Hq9DlSJR\nNFFApYQojRIZR5LvCWo1npeUxgOUgNFCrw0ugvhAMXa27ntN3YDde/ZUOFFYnxj8gLWOub5kuy1w\naUAVikIpYjeww7MQC8jj8d6qOvpPjTL4Y4JvQmshDePRq0RyHUkJSWr6fsDa7D+NcUtyiUCJiEOi\nx4mhUH/5gKQQAt/93d/NRz/6Ud7//vfzyU9+8tHnfcKECRMmTPhCMBHUCX+rISIUIllZNOaxaTKl\nLIkdPH3OkVy+I+58z75t6bZborojGoMqSkrbQKghVgSn6XqhU4qVCMYWVNUlg9/h/X3a72KxOPZg\nEiNm0Ki9wu+uSXHAIWjdYOrzY22OGINNCX/jiX3MCb/vEp50Zi16rKC59Z4lYAlsh+1xlFe0pn7l\ndRbbARMSXI/y5wvyiYhQpwvevr6h945O3/D+Z+csF+roY9Q6j7peX2eOp3UmQYfgqBgjxhje//73\nj12hLbe3t1xeXvIyaL2k7z9NjDtCUFTVB45hUqIEfaLxNx6/9iAQtgEEzNlYKUMOTCpjZB8Cf973\nzLVm+XDseT7POzsMWf6sqkxYAZZL5jpx292yHbZYZdm7PYKwLJfHl+92Ryswzj0cc67QWuOc4+7u\njpQSTdOglCKlGlgRY08ILRARsYhoVJW9vn7jsYVFlXlfC5UdpT4lNt5nsns4Du+zKl4UjGyFIWSi\nOi/nx5qgZbk8VGiyWOTD7vssIIcQ0FqjVMJ7T2nHChYjyOUz4n/1X6J+598Rf/3/Qf7pf3s8T+HQ\ncTr6XWMIiMoESWLkxecPwzBgtcUqe9xHeOxBlU32n8blEqw57gd8Fh+qypVMLgyIRBSWlITURbTS\nSCGPSPHj11oQkODwPhCUQmIOLVI6V+M89KGmlHK6tVKklHtTbRFhsMRWg3eUtiIh9M6iioCIQ3kh\nWH38PWOKRJEKhqHBpx1GG2wqIHlCDLQjn37iP4157YwydAFC8Gjt0Urhg8qj4UQGP5CMgVAwDD1V\nlUYCGiFofFIIHsF/QQFJ2+2Wr/3ar+UP//AP+Y7v+A5+9md/9kk39IQJEyZMmPCFYPpXZcLfXYjc\n3+yPvlEZvV/1+Cf2HX2/p/Utw25LZHt8ucFCKEg+/4lJGHM3iTEwuC2iHL58h7YuWC6XWICUUEBR\nXOBVT7CBUBVEA8aU9+RMBHth9mxjIgAAIABJREFUsyd1l8OTYh+zV1U9Hl1cGoMC3ul3XO+3FATm\nxiAIjW2YF/PsKW1Sns3t+yyDnp8f01q9z4roMAin5Tk7e0O96On1FYlLhHuJzNqsJN7cHMKkNoSQ\nCV9VVZydnSEinJ6e4pxjGAZWqxUnL0kT9v4WpUpi7LKyyGNioStNrLOC2v1phzkx6IV+UsdzojVv\n9T0uJU61ZvaQMYlkE/GhL8f7LAUXBVQVNdlz6qLjre1bGGXu14xMquo6c9x33snH//BZR9M0bDYb\nrq6uWCwWx2qZrFbWxLjHuZvx//NDEFGSw6gCT8ZZK6W48Z4QI6fW3hPtcaz3cL2m/R4v/tjRuh22\n+JgJT9/nfT85yRPOB86THyDkMWz/oHP0+P4f+iD8zr+Dj/8KPCSoo4JqkuDJ/m+tFAmNjk89qMOQ\nR42DyhU4h0qdRyFJNzd5n5YL1Hi+PleCqkThxhRfJSaPDO8DWLALS0xx9Gu++BAmf36UBMKQiEqj\nlKBjPl8+emZlvmRyPlmHMQZjDCHkfSuKCKLoQ0QnobTQR8aHAgrRjiIGBgxdikg/YOYeGQCWJK6I\nsqMwFSl4XLdl7+ZUgA3hvr9Ja9oh/1ZRqThWzKTk0aLpk0asYL1niANUlqEVQgjUtUIplx8EhOzP\nFxUgerwu/lIBSZ/61Kd43/veB8CP/diP8YM/+IOf3wYmTJgwYcKEzwEvcQ1NmPB3GErlOdb5HM7O\nUK+9h/p9X8r5G3+PZ699OYvz91Auz5Fmhi8VvnbExQ5Ob5H5Cqla0D57AssTCDPunsM7n2r5s//w\nNu+8c8PWe/x8Dq++inn1A9jT9yOmHL2pV3i/ebRL5sRgTk2exNxHhncG/NYfv59SYu/27Psbklvj\nwsA+JoJUvDp/lZPq5D7wSCQrp3Wdb4Kvr0ldz3qdScwwHBRS4e+9cU5dFPjoudpfEdNj4liWsFhE\nbm9vePPNDcOQq3jOz8+PY80iciSru92O9lCdMcK5m5GYVlTV+xHReH/3pC7FnBjiNhLbSBwiZvH0\n2douRuzo4XtpuUVd3yuPb7+d/+5BR+y8mNO6lrvuDi2aeTF/9PL5PC/Z3V0WxV4kqG3bjj2v9pH/\n+NDz6n1WC5V6kCz7Lr+BK6VoQ6BPKYcj3S/Yo/12+w2JdPRPViZve73vjhzH2vz1kK0UQsBag1IK\n72OOO+aeGPKhD+evH//Eo30auRnFeBmkMSQpIsi7EFQRoakbEukY4HSobYoR1O0qb2u5zPVQfG4E\nVSuFIJmgpojRGkIiDmPY1KIYl8s9ea2IHrtQIyFkH60ImHRQZd3Rm+l94PnzFWVZ0jQNzsVMtG0O\n6ApRQcxBSVh1HMaQQmFxxGTZp4AJidIUoAesbRgGUOwxtSUFRRw6dmNQlb2PDyamSO97BMFKPe5/\nAAIqKXxS2X/qPS44ojG4Lq/xYpEf+qSUkFDmgKQ4BiSpOj8A+zwI6m/91m8dyekv/dIvTeR0woQJ\nEyZ80TApqBMmfDaMpFWXJTNOOMQKDWGg9z196LNCxIMb6qRIg8W6BSeDZbfZs9nvWHmDXQn1sGO2\na2mairIsKYpLYtwSwo4QNsTYYR70pupGo0qFX3tiGwnrQNgF+qanlfZYL7KwJWfVKR05ivTOB86M\nPA2LOTsDpeiud6yv7vDNEmlqZrMsNOYfz57Uq/0VLjqu9leP0n2dc+x2NxgT8F4jckpVPTUNWms5\nOTnh7u6Ou7s7tNYURXEkp9lzeolShmHwpOQIYX1MvgWIbUQKgTYTmOjiI09uGwK7EFhozQxw49/V\nL86dLpfwp3+a53UPptoRlalofZtTcZV9smbGZIIaQv7zcNNaa2KMR5Xw8eVTAJK7KJN/lN4sMqqo\nCVJMR2XciOQ+XaB8uL2HCuow4PotVCWFzVdlqUv2bs9q11Ewo6ru99176Pt8nZSlHQlreKKgyjd/\niKQU8m//X9Jmg4xkOAog5FFYIMVIFPAo6hcIahrTtEWEpmrYuR297yl0cVRQUxLk5jDiu8AYfb8f\nKifUvmw9D+utROG9I5iIFkPqEinmz4oVS9d1eO+fvFZEI1rl68wnklEkBwaFHxVUyM8y3n77lrKM\nXF42lGVJ1+0ZhoGyMFgps/8WhY4JO9cMCbpOMa8Evffsnacnci41RjRe7bD2hK6zzEqHNhUmGfzQ\n0fqBi1ShHxDUvduTSDkAKyi892idcrduIFfdGIGuzT24esbQO6yFoshBSRIKYlJEBuIhIInPLyDp\n53/+5/nIRz4CwCc/+Um+6qu+6nN74YQJEyZMmPCXwKSgTpjwl0ShCxblgsvmktfmr3FenzOzM4wy\nIBEpe2S+QZ3fMHvdc/6BBfVJgQdu14FPven4sz/f8uabN7z99tusVo6+LwmBUU19jvf3I8WiBXtm\nUWeKTdrw6c2nuf70Nd1Nh0mG8/qcV2avcF4teFZkp2A3hifFFxTJEOA2nnDjl3iXsPsVl/WOk5PH\nnZkiwmVziVX2qKT66Nnv91xdXRFC4OKi4I03nmFtyfX1MevpEZqmYT6fk1Li5uaGrnv+hJwCGHMG\nyLGOB8CvPH7lUaWieE+BKMldscealchqJCKn1nIxykLrEJ4osRjDuMBP9nEzbKhNTaELfHpKbIAX\nSNj9fzvnRl+nGoOHXsSoCj5QoVNMJJdQlcqeyfb+e+2oBhdKMTx8owPhMgaqKo91djkUCTLJFoTt\nPq/PgaAelLK+z+9RFFlx9T4R/fi+B5H99JT0D/5rxHvSv/7V+7ceyaJBkJQV1KAkv/CFFF/n8kiv\ntZbS5IcABx/q4edSEtRdJqhpeQLmfgMHsvxuKuohKMnHQIoBJZo0RFIC1aijgv0yBRVAlEGSEP0A\nKqcJS4wUypDIqbltu8rBatFwenpKWebx+773IAFrhITKncUhoMcwpd1O8vi5DPRdS9SGk+oM6QfQ\nHSGCSIWYPHJr+oKAw8lAGmSUYOVIUAEa2xACTypmAhpUIg0tKEUIOXG4LMHa8bz6Ep8SSITo8Mpi\nxI6BWS9dniNSSvzwD/8wH/nIR7DW8ulPf3oipxMmTJgw4YuOSUGdMOGvAIfxysOIZYiBPvRHhRXj\nUcZzUkPZZZVlt/esuoGr64EUI1UJs0awRlDSUxaJurqlqZZU5SUimp3b0fqWtEwooyjagrnMKXYF\nGk1aZBJhleLSWq7HupVDDY0WYbfLvtEYQS3nLE6FmV/BfgUqZJXxhWO7bC65aW/ofMd/fPM/UsSC\n0pTM5/NjeufVVb63vr7OQbkv3vwul0u89+x2b3F9Hbi8fOUROYWcdKz1ghDWuOEW2ZznjlDJY766\n0QxXQ+65XHnMieHWeyK5huUwDrsLgSElNiGwfCgTbTZ5VhfuA7KsJcTAbthR25rK5OTU1rXU9r7s\nte/vvajG5LCkw5jvbrejqipizL5H5x53f4ockmDvVdY4kkV9ohGE0Ab0LO//PkYqpdAidDHm4zrI\nt0plhlJVDMFBH7HaHs+VpmBwDmd7iiJfj4clOCioIgljLCEohnbIirF5cMI++I/h3/42fOyX4b/7\n70kpZRKnQJH9mj4GIpBUnh9WKXBgucOoAhZFQaELBGEIwxg4dBj/VujbkaCeLOGBr1qskFyumuEl\nY6hahATEFCCBDCBJkEKhjMKM/7S9TEEFEG0gCSm6/K+gKBgJah8Cm90G59oxjTmPqJdlyWazwbl8\n3mwRiEpQUdBA0Wj2XaLrEiKaPm2RBEZXaFNTBU9bJYbYolQDkkihw+hTvHji0JJ2dX7yURT0YcCP\n9TelKdmO49nG5ARf30cQg5WIi45kDMM+jSFdmpQGQKAtcDEg2iPJ46TB6s+e4DsMA9/6rd/Kr/zK\nr/D1X//1fPzjHx97fydMmDBhwoQvLiaCOmHCFwFaaRrV0NjMYFxw9KEfq0sCcRbxp5ZdW7DbR4Yh\nMQw9d9uBGIcxu8kRVzfAp7DWUtdn1PUpZVHm4KNnczSasAmEfSBsA7GN6IVGNxqjFM+s5do5XEq8\nuXPIzqDGONa6zlOuSs2gVdlcud1mIvSwO4ZMfE6KE26ubth1OzrV8b7T9z2qljg/zyTVuZxFdH7+\ndF3m80TXRbxPbDbC5eXTX0HGzPHdHnfTIemOojrFnN/X7Ngzy/B8IO4jt3rAFXkk9vQBET01hufO\nsQuBRimMUpnc7feZrb32WmaYY+3Mql+RSDS2odQlt91tVlQfENSx3pTLy3yM220mqDFG2jaTmYuL\nC9q2ZbfbcTquYYxuHO0tUaoYK2eaI0E1S0PYBtKQSCExSCKkxExrIrkHNaWEPFRPgVhYgiSU85j0\ngNyFCnCgexgLlx4qqEUBWgtKGULQuN5ha/u4c/TDH4b/+SfgE/8KyOopgDUKfBbjUgyElEDn99AS\neRlBVaKwOif5DmE4KqopCfqgoJ6cPBrlPfpQXYKXcCIFBCJJQCWIfcre41qNSzR2mo4q+pOxaz0G\nHqWcRBwSSEpYbdn1O242N9Sm5vT0BK0t3udRdRHBuTFoygZSjLgAtrREE0kq0vdCjIqdtFixKHNO\nnzxzD21KeFqMMXivkOTRhcZHjx9awmaAOVBVj9RTOIQ2e4rCY4zG7xQIFMlnglrWDOv8YCg/g0ng\nCoiC1+SApBTwWEoxn5GgXl9f8+Vf/uWsViu+//u/n5/4iZ946aj1hAkTJkyY8MXARFAnTPhPAKvt\nUeV6hDGjZ3CRzTawayPORwbX0w0tMbWE9Jzot2zXV7jdhmV1iq5PaGuhrmeohSEWiv7GE7aJsPYk\nE1AzQ9KKFCy3naMPCXDUVnj9wrCsH8xk1nVW5m5vMxOLEc7O8CEcU3jbtmVmZpn8zgyddGyH7TFM\nSKmcv/T8eU4zXa0yAYY8Kuj9LSn1nJ1dsFolhiG8NNk37AKsFxB6KHvUuUfZB75NLZgTw+a6Z3UX\nKC8t5+Vjz6gZ1dRdCKxC4EKpnN57SDc6Ocly7zDQb+7o6FCiWJZLlCg2w+aRihpCPqZDxtTVVSYM\nXQfe78dx2orlcknbtrRty8lIurzPQUDGPAM8IewzQe3G3ttKkXwi7iOhDezLTAbnWtPFyJASfYxU\nLxDUITooCqwb42MPyb6+BDZE3QInx5fkVNqAtVlB1dqSIvjBI/PHPmX5bz5Ishb57d8h3d0RRh/q\nmGOETrlmJgFxvK5V9BzkzgNBPajIpS6zZzv0lKYcu1AV6u4QknTCw2SrzxaUpEWOqcI4IQ0RVWso\n743Bxhicc3jvH6nZ+RoyxATiB2gEVPbVGjSruxU6ai6WF9R1Q9vmS6VphKIo8N4yDEMep06RFAVR\nFkNEFxB72Ow8XjssikLNcWpLGRW6dySlSZIQCpQMJAGMIg0dni1pZkiFpes3xxTulA7eZ49SHoXQ\njwFJDF1OLJYaN3isTZTjNZS6IgdFNwq3brEkus8SkPRHf/RHfMVXfAUAP/MzP8N3fdd3vfwHJ0yY\nMGHChC8SJoI6YcLfABRWcXGmuDg7dG3WdN3pWCvxpfT9hpSu6bo9tzee63hLCHeARqSkrueU5RyT\nLNIKKSS4dahaYRaGM1PQ6UCqAtUssRXHMAgLYyhHU2C0lmE2w739NsPNDe6tt4inp49mdeu65j2n\n72Hv9qz7Net+TYiBkyoTIa3vCdxuByI9dd2OftOIiKYsL7i4SFxdXbHb7TDGMJvNMoldeeI+IiiK\n01NoNoS4RqfqOCYLkEphUyTooNkkzEOyPWKpdU7CjZGu66ja9hBvev/17o719V/A+SmLcoEa32Ne\nzLnr7o4q6n6fue2Bx89mmYBvtxDCDoDZbIbWmrIs6fuetm0pS0VKAyIaYy5x7h1SGvD9ADETMWUU\n1Dmh2e8DXa7pPI4rDyHQxUh18FMe/JXBQVVRBJ/V4JGgBmcwylCUWbE8+FMPqbTeg1KSVcaQcN4d\n/acHyHxO/Idfg/r1f0P81Y/hv+1/yG99SNoNY4pvgszKciouZJUvxojWGj0eQ2UqNsPm2NF68KEe\nRnw5O/28CKoSIZLHjmljJpjV42vgMxFUZWyuX4kxj9pK7p7d3a1xzmEKw8nJCfs9DwgqY1CSpe93\n2PmASZGQ5JigZaqI6zXPV3vqpaKyBvFCOqkZtluaIWFMoo97TuuGKJ4UHSIWFXrS0NK7Ezw5dK0y\nVa7TOVppPSkFtBREDGIgdllp9bEgxkhdK0QCKQJDkdfJBKJzaGsRKkR4KUH9+Mc/zoc/nFOcf+3X\nfo1v+qZveun6T5gwYcKECV9MTAR1woS/Yaiq/CfGfHO83wsiS2BJVUWc6+j7DX2/pe97UtqP6aJv\nY4zBFhUlFVVsqG1JQcTONcXSkJJiHyMb79n2PbebDeI9RYyYQxhPUWR2GQL67o7itdewZZn9hGNn\n6qyYoZXmtr1l53aEFDirsldP657FouXmpuPuLpOWsgQRe0wmVgrOzs64ublhvV7nJNS9ziOdCsyp\nQVc58CXGDu/vsDbPDKeUuPUetdTMglB7hd/4J9UzIsLSGO76nvXtLSWZeB3jd5uG3d07ONdjuoHZ\ncnZ8bWObY6foet+y3+U505ED0jTZzrpedygVaBpDOSYCN01D3/cj+c5rqvUCpRRa14Sww+93CA2q\nzKRKlQoU7IdA8EJTGJQIlVKsx7oZXlRQwwBlie3Gws4Y6Z0iJZhXJUoNx+RcyIQke2TzEhhjIAaC\nD4/Hew/40Afh1/8NfPxjhJGgGq2AhEqQosfHBKZAeY7793C89wCrbU7dHTtalcqBUscR37Mzcv/t\n2Dtr8vhqCp9BQSURU0R6IZHQM0MI9z9jraVtW5xzT7yTSpvcw5pcDlHWlm4YULsWpRTzkzkicqgI\n5j5Yt0REMwyeKB4tkagMqAJxjrIW+rvIet8xOzXMyhIXEr0q6ERogiEMDtE9ZVniB0OKA1LVKL/G\n+z2DvEI3jvfOxnRm7/O5UyoiEpAo+GQQlcB1OZG7U0BkPo9Ags5mb3MlSAwQHU4ZjFi0fuoR/6mf\n+im+93u/F4A//uM/5ku/9EtfuvYTJkyYMGHCFxsTQZ0w4W8oDkrdbHY/TqqUQqkGrRuUehURj/d7\n2nZN12XCGsIKWNFFaPcatSmp1wvKuiFVCa890Xt8COzD6CMESq05q2sWiwX24oJiu0UdOlXq+nGv\nClkVu2wuuW6v2Q93OHfLSVkjZDK0WMBmY9lsasqyoige/7o5jMTePb/j6p0rzk7PKOoi+03NwUt4\nyjC8Q4zdcTR25T0uJQqlOD+3+BtP2AZUqXJ66gM0ztFeXeFCYFfmUKcDYopsKgU7OHFqTI26f/28\nmHO9u+PPn+84q2qahiNhEcnn5epqh1Lw7Nk9ua3rmtVqRd/fMQwFRdEcu1CVanKVULvH0DxS/XSt\n2a0cqRNmdV5roxRGBJ8SQ99TwL2CGh2IUDQL6HOab+fy+5zMS3qyYrkoF+NaQoxZQT10kRpVMKQB\nnzz2xTSiD/0T+JEfg49/4uhBNTp34qhIJrdJUNaiYjrGN7+MoObrq6T1LX3oUaoZCWoe8eXsnJRC\n7igdIVry6LOPx+vhEVKAXpGcoCvQRj0iqMZ8hqAkpYlRIPhMOGNkt9+yPD3l7PQMbbIvNPfFHghi\nJr1KKZyTHIQljiCaoEpUSpRFYhe2+NZTmwWmssje0w2afVlSbXvsvsWWETGJsC9IIphGo9eOkFo2\nHiR6tOijX/fgPz0m+PpEQmMIxOSJxtCvEyLQNBEQ6PJr+zJB61AEnJRYVfDw1MQY+Z7v+R5++qd/\nmtdff53f+73fezJ2P2HChAkTJvynxERQJ0z4zwDG3IfPvvAdimJJUSw5OYEYB4ZhS9dt6Lodg3W4\nfstms2K9UwgaURpdFzTLmvNlQ7Alg7bISEB7EQpjUHUNNzdZPrq6yqlHIzlKKeUamNhxYgI3bksf\nPddhx3n9DGsWnJxUKGXY7bK19dmzJxyXioqyL2lDy7pd88rrrzwiIyIKY07x/gbv13RRs495GvTM\nGLRSpHkibAL+1mOf2WOXKOs1bLcsleKqKNicnlJx/0tv02+I1lDNTymTzT//IByqNg2bux299yTd\ncXpaPdr3svQ416OUoiiaR9+r64rV6tN0XaBpXjv+vVIWkiEOHdEOyAOm4EvwJEzPcewaoFKKrXP0\n3mfSp7ISGVPEKINqZpmgti19yPuxnBVc9woXHSEGtNJYm1NgnYtorQCFUYaB4dj9+RDqH30zqSxR\nv/t7hOfvwMUlRisSEfGRmCIuQaUNWg2fUUGF+57ZzneINJkgr9b5mxcXjyp4II/5Jj8m+b7kX6ok\nARkEHwUzB2PkUcXRZ6qaUUoR0UhKxOjY7PfMyYpnmM3ofHdM0LU2JzgPQ55sKIqCYbB0Q4coB2ic\ntswkYmJPl3YQhIIZUjh06yh9iVvUrO5aigHKwuNwlGEGOuBkYDYEUuq4Di0XCZoH11R+ThTQOqE1\nDEMADCr1hBQYaEghe0+LQoh9QmJBtNAbYBiwybPDUqn7gKTdbsfXfd3X8fu///t8+7d/Oz/3cz93\nJPYTJkyYMGHCXxemHtQJE/4WQamCqjrn9PRLePXVv8/rr/8XvPeND3D5pc9YvNawvKg5O6m4mJUs\nYqLo98zimgt1RxOvSf6G1t3yvLvhnX7N/qQhlRZCIF1dEdZXuOGGYXgb72+IcY8S4aJ5lbI4B33G\nygtRCpQynJzcjytfX3NUuFJKuBtHWAeWJ0uqiwqWcHt7+6S7VOsKpRp8Clz1z0kpcGpMTuYFzMIg\nRfbd+pW/f7PtFkSwZ2c0l5ckEW5HEuWjZ+/2CMLy8vUsKe73PDD7cXsLpcwxBuxs82St23ZHXUNZ\n1uz3j+clyzIAkb5PiDwmargKEiTdPQom6nRClFBHRXT3TKsaJbw+xuN4rwt5P62yeYFF8PsBP0S0\nzs8RSj0qaCH3yWYFNRJCQimVfbGHOpaX9b5WFekb/2E+B7/6MYRMAgFUTDm4B0EZm4XnGI81O0qp\nJ77Ph32oOSRJMOuRoJ6fA08JKry7DzW6gAoCKKSUo/h9uMa01o+SfJ9ADAhs727x5BqZk/k8r+mD\nNX7ZmK9SlrbvkegpUGAqUJau26LLiBGL6y2qUCQG5lEhxrARg0JRpB6lPUrXtFqR/J7GG5JKrPwW\n5+SY3gv3CqpSAWM0IahcVTT6n7shH3zTjOexKxAR9kUiAXpoczWPzkq/tfAXf/EXzOdzfv/3f58f\n/dEf5Rd+4RcmcjphwoQJE/5GYCKoEyb8LYVI9jzW9SVnZ1/Ga2/8fZ594MtYvu91isUZSjfgC8Iq\n4a8cduc5JzCXAeKWzt9y1b3NW+WOtb5lcJ/G3/0Z8e0/g80KSRqtlxTFq1Tlq7wy/xIaOyemyPX+\nms53AJyd5Zt87+Gdd2C7irjnLqfYKrDnlmfvf3YMtbm9vX1yLMacsIqGmCI2rqjUY0JozywoiKuO\n8P99Okteh8Sm2Yyl1hgRXEqsvWfV5VqZWTHD2PJenl6tjl+6DmZlzeWF4JM7Hg9kgt227TiCPTsG\nHwPE6BEZKIoSmNG27aN9Vb4i94MMR9UwpUQbI6oSGlHE9p6sFUqhncOnhD8GJ40qpS4yuS5L+h7o\ne0Yr7LGT936/A0pBjCkHBElWUIGXKqgA6YMfzO/ziU9gRI7qtPhIShGfBKUNSguEwNBnMvwiOQVy\n3YyyWXmNPbgB3XYkrZHTk5cqqPDuBDX0jgRIqUikY9frQxX1M435JjT7/Za+34HWnC2X4P2TNTms\nZ9vmoKzsQ7V0fQ84rNIkU5CUoW3XFFVW39tWcrCX9khKVEEIZcMmRhoXqKyQjKZPBXR7CiXsjcMN\newglWt2PGxwIqtYeLQofBDTIkM9t7/J6z2Yx+3aHkkiir0BCoE4BjEFSPphPfvK3eeONNwD4xV/8\nRX7oh37opWs8YcKECRMm/HVgIqgTJvwdgYhGqRJbzqnOz2je+wr1xauU9WtY9Rq6v4TVCfX+hGdy\nykmxRKsKj+aumXG9WNAWMxQzir6huI2YrUfGIBsR4aw+Y2ZnJBI37Q27YXesZmkaCG3g5k8cN+8k\nohKKZwWqVMcOUaUUXdexHpW1kBJb73nuHEmdUKiCpYo4d/1IFRMtGNPB7TX+rs/VJ8+eHeUvEeHM\nGAS46nesXYsWzaIYe34O4UnDwO6qHROIs7B32uSf2fT3Kup+vyfGSNOUzOeGlHKuFEAIayAxm10g\nYtgfClRHpAFEFagSYszktY2RBNSNQYs8IqgA1Xis+1EmPBDUY3VRVdF1QNcdCVVpSgSh9/04kh1H\nD6OMKuNIUOXdCap8+J/kbf2rf02tVCaoAvgIRAKKmEDZkTh3mTC9ON57PI6RNLvUI3c3eb0WCzCa\nJwqqfXeCGkOEPnsu82uP4vKToCR4+Ziv89B2LSTP/OQMawyEcCSoLt4rqEWRt7vbZdJrjMXHROgH\nrIZUlnTO4/uOqtJUuma3cyhVIEVOcp55gaKijRGrwBIZUiBIRREHlIa9BEK/R4f7UKcYGQOdAiIB\nLRqPQSSC74miGQYNeOZzRWwTSpXsbAIRau+J0ePEoMXyL//lL/C1X/sPAPjd3/1dvu3bvu2l52rC\nhAkTJkz468JEUCdM+DsKEUE3muJZgX1m0TOLkgIZSljV1KsFr8ZnnJfvoSzfS6rfYH/2AZ6fv5fr\nsmYXI2G3y7LozU1WLYGT6oSTMoesrPoVq24FKTFXniUeJeC04jZa9t29Eqq15vz8nAS8s17zZ6sV\nbw8D6xDwKWGU4pX6GUpZUnJ4f5NJakpwe4sedqhKYLbAq5NHgUcAVinmSrHt16y9Z1bM70dsx9qZ\nvof1m1tIidPTTEwa26BF46KjdZlQ7nb31TIH8TUHH/djpY5iNnuGUophGI4EKbqscGlbI0YIIZPX\n3ciq5qXJ3suQiMM9YWtGWbBVKtfxRI8gx3HUVFYMXiFuoBo7MJUorLYkEn3oCSGMfagJ5yCF3H1q\nCpNHrl9C4uTrvpHY1BSCDW6AAAAgAElEQVR/8EfU77yd/07JyJoSKQkgR9/wMJLxdyOohzFfl3r0\n+hrIBFWs/rwUVL/3QEJbfaS1n4+CGmPkbr1DgLoqMFWJOlTFiM7pt/Ge6S6X+et2m7df5lhqXDdg\nTQRrWHmHEcVJUZAkMQyJGDWqVMQ0QJsooiJaSy+JWYhEgWgUNib2YUe0Bu0dIeQ05rzvjA9jPBDQ\naGLSpOQhevaDoNFUVUBrTeoKQkoMNUhKLPZ7XHQMUvC//i8/wr/4F/8jWmveeustvvqrv/ql52nC\nhAkTJkz468REUCdMmICyCntqKV4tMCfmGFATNgF7FTjfCadRUzpIXtHphttiyVvO8PbKs3prQ/cf\n3sb94VsMf77G3lnmqznh04HVn614/ifP8RtPWcNrX25YvMcCwmqV85ecS+xDYCNCP5uxjpHr9Ro3\nDDRKcWEtrxYFVmmsvUBEE2OP757D8+d5/lIpzAdeQU6XJJfw66eqoKQeRUQpg3vBG+psw+2uIPnA\nUmd/6QHLMjOUdb+m67px3FJTVRXWZiIbI2w2Wfk1ZoFSmqbJPsKDihr7zJ7srEFEk5Kj9z0uJRRQ\na40aO12PKmpK2BAwIgRj2Po+j7QqcyTYvVMkYylMRPr7UeSDYtn7TFCtzR2o3oPErDza+t1VxtYY\n+m/6hrx2n/iV8WIBUpb1AkJE0EXeluv7sZ7l5QS10AVKFCE55PY5MCqoAk8UVJFcfxOf1s0M2wEl\ngio1IeWamRc9qPDuCur19S0RKApNVWSlOalDx2sOlUqko7JcFPde6s3mQMBzZYyxiqhg5z1KDHMx\nmDIda6JUoZDC5xCjLUhREJRHOdCFgIqQNFs6TLCUohn8cPS85gcfOSBJqYRzAcQSQouI0LuD/zQQ\nuoCiZq8SWEW92yHBs0+Rf/7P/yf+9//tR/iar/laNv8/e28ebetWlnf+3jnn16x+7eY091y5QgC1\nUEDA2EUBo4kmAmEoEksy1CE2VRF7EylraMAmphwOLcsyBo1WxVSUknIUGLQkFfVi2YFcwEtzBYSr\nApd7mt2t9uvmnPXH/Nbaa++zT3MV5Z7L/J1xxtpnre+bX7PP2Gs/63nf551OuXjxIpFIJBKJPBqJ\nAjUSiawRJeieJj2fkuwkJ8SSOXT0J7AzE4YzSBeC913KbMwROVeWjmuTgtnlfZqPXCErLFvZOJTt\nUnBoD5EtwfQ14zFsb3sqsVxe1rzr4YqHJiEIqJPn7A4GjERIZzP6IidSbUU0xuzAosBd/jD1ci+k\nvpw7h3Q6mK1Qtmpndi0IAayzTMspI2MYZSOWzrFo1YxzwQR2/SHdjqfP7IQV10k6ZDrDesvlw+Ak\n9nrHo2X6fXBuwXxeI2LQbRjNSqAul0u89/iyLYfOBKWCAp41wY3ttv2lq3tul63Smk7BOfJOB5Ti\nqO07XM03hdAvS56H8t7ieoFaNAXOhQAlrVtXzgZxm+ZhnbME6sJaimd/fvjHb//2+v8I3iPO47wC\nBJVoqqrCNw3GHAvns8h0hlLg98N9tMNRmHl6ykGFs11UVzmaukEbMKnB2lB2fLsO6nQ6ZbksMUnG\neNhDmpoTC1h7XVASBBd1laVlTIazlqqqUZmidgvA0EuHqMaS5G1J9gJAkIHD46nnjgyNGIV3CYlr\nUFTYRlEah4gnTxKqekFZhqCu5TL0NXe7IcG3rh1gkKYtD68TnGsYDhV+KXgSytwjdc2gKLi8f41P\n/6wv4Pd/93f52q/9Zn7/99903VzYSCQSiUQeTUSBGolEzkRlimQrIT2fogcaSQWVKXRX0xkkbG/l\nXNzJ2dnN6X3CCPPkC9h7Rix3DQcDyySZ4vWEc7td8vMpbsuxV+9xebHPXlVyKBXJVoPKHd5DOVPY\nI8OuSrlna4utXg/vPfv7+7hN1eE9ajIjmWvwgusIzThdz7BRicIMW2Fy2OBdEAuTcoLH00+6nMuC\ncDxqGmrr1gnD2SBlfLG1ylYJsy2jfISzjoPpAdbbtfgEyDKPUhOshboerp83xpCmKc650LdahRk5\nKgvzbL33zOrgrnZbEa6MCv2XDty8YtUQ29neRoBpU+C9P+4/pa2uzvNQ3lsUrOpDjTJo0VhvKaqi\ndVDbiTA2HC/tnC1QrfdU3tM89+8DIPf+bnhBsy7xdWwI1LoG527onq7vlQkCde2gjkZnOqhwtkC1\nc4v1Ft3TGNF4JydCkjYdVK01Sql1km9ZlkynU5wTxttjRKv2Xnn8Kthpow91szfXmDAOOPQbtwnI\nHqw0VM0SvNBJB0hdk7YTiRaLBpEEpQXVszgHemZJ+xneK7zzaBpK12BzQ6IE7TX1csbDD/tVYQCj\nUYMxDq1b91sU3i1paov1OUpVdDIDdcbCO+goOtMp7//AB7j0tGdweHjEv/mxn+GHf/h/Jcvi234k\nEolEHt3ETPlIJHJTRAtmYGBw9usJ0CP0yZX9lMINKJZL6vk8iJ7JDI2n1pYj39DIFNEH5FmP7e6Y\ne7YTVK2YHAm2CSW/gwGMx2OstVRVxf7+Pjs7O8jK6qxrlE5Jth5PbZZYN4dGY0xoCNU9jSscrnRB\npI48y2YZxspkQ7TSlM6xcI4/v9rQcynGhMRh/DCIvMUCer317FejDNJISKGVGrXh6lo7pdt1TKcZ\ni0XOhrlKr9ejqirmB3NGarQOhRIxlD7BUaB9hVHZeh/VUdjaYq8coDIPvR46SUjrmtrWFOrYQa3r\nIMp0ojA6DfNQyjLUpBJc1Hk9Z1EtSCTBmCCybCUoWgd1eb1AXbnLyWd8Jr6TI+9/EL+3hySjIFCt\nxyqF33BQ4cb9pysynYVwo4MrADSDEanIbTmo3nlc4bBYkq5GTRXON2sDdHUvNjHGUFUVRVFw1KY0\n93oDSrKQsms9Co83Jty7psG013A6PGo4DI7mcgk4AVFM6yWJsTjpoxB8M1sL1OXSIpLjfQWdBnQC\njSO3GpSnroRUKkrlUDpHeYUSw8HVhmpUMRxm7O7CbNbgfYMxmtIqHA2KmlnhSExGtzvFLR1ecorU\noxcL7vu93+OLXvxiAF77m7/GZ3za89D6utbsSCQSiUQedcS3qkgk8lFBRMi1ZpwkXBwO2T5/nu7u\nLirPsQiJNWw1CaNFzejwiOGVD8NfPID90AfIJlc4b/bp1kcwmzG9vGDvoYphd4jRQfwcPvxw6Det\n66BGzp1D9cYYswUI1k7WoUMAeqwpfMHVw6tcuRbEUD/tr8d3jIxhORWmS8/cNezstL+8a81aYbaC\nZoWqFVo0OtfrwCTvLdbO6XSEJBlS18czMwHyPEcpRTkrqasayTZmn7Z9sDnliePojoayxB0t8G2A\nE0DeJu4Wzq9dvjabKujRVenmxmibVZnvsgrPZe3x66LtuTSCMSEoabMUdtm61p0swz89hOn4+97U\n9oWGHlQvKjjCiaZumttyULXSZCbBHB4C4IZjUAK46+aVnhaodmHDDNnEgxYMgncKDygdzted0rmr\nMt/Dw0Occ+R5TrfbR3QIiVIehAa3WeLbutOrJN8VSh1PJKqWCtBMqwU6tXRMj8ppEp1gXIUYR117\n6rpNBa7nuM4MUQ6zcJBmaATtClwvZ+nDhyDTa4aqarC+ZjAI/9WbpsH7EJDUeE1tCxKgrAzOVfT7\nCl8IhVNI5nn1q161Fqdvuv9NfNHn/2NEhDOm/0QikUgk8qgjCtRIJPI3Qq41426Xi+fPs3PxIqPx\nmLu2tnni7iU+cftu+vkARFiUU64ePsRscpWhmbJtJpjZIc3lPQ7ec41sv8RcvUr5kY9w7coVSqXC\nCJlWUGidY0xIDW6aI5bVEYfFIVeWV5hmU0pb0swacnL6aX99fouFYAqDEkhHFisbymYwWI+dWfV0\nrvpIt/vbJEkSSoa9p2nCWBmlOvT7QQHMZsdLiQi9Xg9femazGSoPP3Yb52jIUQgZFd4fW3+iBSkm\nocw37a1tL+WbkFGkDLYVc6uW0zxn7ZquVSvBaRWEog59qEGkCKv2SjFyXZhQ5RyN9+hV/+8zPx0A\nf99bwrxZ14AXQOEVNN6HIB9CWe2tyExGMtkQqOue1Zsn+bpFeF06bd+paMQHF1frMHbmtEBdXZv3\nHq014/E4jG0Rj2iNWFA47IZANcqsk3xPi+Z+PyQh2xqKSmi8JU81HZNjxSBopG7IOuHcl0swZhtr\nBSdLfHqAeDBNhqJBXIlPUxxdjqYpZWlRqqY3mK+vJQjUBvEKMLhmgQBlY3CupJcYvM+Zi+W7/7tv\n4Du/93u5cOEcD/zlAzzjKc/ANm0gVhSokUgkErkDiAI1Eon8jZOlKb3hEDMawdYW+vwFRp/4Sew8\n8dPI7v5E7O42037CZVNSDjzbj8vpbmV4k7AsU5wdgSTU3S57zrF/cHDC7fOSsmiEy/MrPDz5ALPy\nAOcdeTdnZ2uHi/lF+stjcVqWocU0UYpLO5okhYOmORYjG64lkwl4vx4tszveJdUp1luOir12lqlg\nzJBuN2jJomj7PFt6eQ/xQmWrdfDOwrkgXk0HEbD22PVkPkcnHpIEp44DbRrXkClFqlIWNvQ01nU4\n3TQliOokCSqtFakiglEG5xyNr8gyhXeKugQUrbN2UqCu3NNVXyzP+oyw1n1vRZTgrYXao5QB8cE9\nVYpU63X/603/P+gM07rTzWC83uW6UTNaQIUUX1tYfONDwnTi8d5jlCbIS4/HhfAlf3ZQkoiwvb2N\nUioIVDyiVXBQXYNbCev2G2eUOZHkuz4ngcHAIc6zrASfKIyCMLbV4FUoFTZtUNJsVqF1jlK7eA+m\nb3HuCO8VSe0wWEoc1XJMWQmiarZGDb6ZUxRhfq1zDqU8jfUgBlxJWdZ41SFJHInz7M1qvvgffBav\nfvWr+eIvei5vetebefxdjyfRCavq7ShQI5FIJHInEHtQI5HIxwyjDFu9HQadEdNyyrJZMgMWUtG7\n1GPs+xwdCbYJ7lhVL6jmM8qyYLFcojLB5IbGtyJCcowqycUy6myTmBzf8dTXanwdHhkmHBwI3gcN\nOhgYrlWOynsOm4at1W/x3W4IKKpr6sNDqqpCKUWe5xhnuLa4xrR4mCQfkiVbiChEwm6zWfg7Hoel\nfOXp9/vM6hmTyYRz586tReAg6YGtcG4B9NezTFSuwAxwRSh9FQkCt6M1TicsncPUQZDl+YYJ2ekE\n1bpcEmJ9QRPEl3U1WueIE+rm2KHcFKjee5ZtI2dnLVD/bri9b307Xgch6S1BECtC/6nWobzX2uNE\n3BuQmYxiEgRqNdpqT95zZlCSFrzz2Ek4J9VVWG8RCeXCzoXZsCuBam34uzr1LMvo9XpkWba+zpVA\nVUmCAcRZrEjYqS1fNspQu5rGNScCqQDyjgVXAprCJijxaKD0GkyC1AvMIAjU+XxVJpyg1BZaX0F3\nhHK6B42CVFPPOmg9pJGH6Q0aEjPA1RXzsqLfJj9rDU1lwWuUK5nPKkQbennDhz94lU/5rM8E4Hu+\n45v5lpd/B6PB7rq8eyVQb1F9HYlEIpHIo4LooEYikY85Rhm2Oluc654jNznOO6bVlMPmMt3xjG4P\nECFJekgy4PKk4oEP7vGnD17mzx78CNNJQS/pcXH4BC4O7mGQdXH2EOea4BDuJEgi2NJz+X01tvZ0\nu8cm6VaSoAjO4XIzZWc0CuE6Dz0EztHtdsN6OiHXgncV02qO1sfubK8X9NZyeRzYY5ch9dd0DXVd\nczCfY70nESEznXYmaoNz1XqsjHQ7qEEHPLgiCLfa1aRK0TUZjfdM2pLX7Dhf6bjMd2PcjGp/1Dtp\ngovmFM7S9n6eFKilc2FGqAhmVVr8qU/F5zny4F/A4UFwUL2sHdSqqoKDmiTXpxTdgOQopCSX/T6O\ntpT3rKCkZKPMV4D28pSAeFBe4T2I8qsg5+vKfEejEfnqvsCGgypoBFYC9VSZL1wflATgvEXUApPk\nYLepqoYksaA0zhmU82SJQxSUpcNai7Xhw4QsG5GkfTyeuZqw2HdsmR6SgB5UiHZIZamLGVeuPczD\nD++35clQNVA3DVpZikqBanjwfe9Zi9N/929/gm/79n9Ob7izLme3NlxvDEiKRCKRyJ1CfLuKRCKP\nGhKdsN3Z5lz3HJnOWqE6oTCXyUYH1NnDuOyQ/jhla2uLTA+RYsT8cpcP/lnN3hVPVY1xrgM4mmYP\n7y2iBLOdsD8TmsqjZjXD/rGK0SKMWnFy1DQsioLDw0Me3t9nvyioyhI1n69nn3rv6eow7qMhpWiO\nxaDWQSN6D7Opp7pW4SsPCoa7YQTNlXaEzXr2qQoja2xxFNKDRWA0OjGHtnENzju0aHq6Df5ZBDG4\nob2CyDpV5rtyUF3rNGsJDrL10h5fobXGOce0tds6m72kxuCf9qnh67e+Gect1glaKTyOsqoQY4LQ\nvU2BaiZTABa94Q17UOHY5QVQucK1vcIKQZRCMCccVLj1KTgXvodiDIJCORd6ejfKfG8UlATQVAWi\nKjp5Rq6HHB1ZTBIOWnkdeljrCpP5dixN3RqzDhGH0n28SpnMHSpJ2cktw36JyjtMi5JrVy+zf3CV\n2fyIphG63YzBoE9jFU29ROOobMYb3/gGvuSfvACA/+tX/0++9IueQ7p9jnE+Xp/r6nOKWN4biUQi\nkTuFWOIbiUQedSQ6Yae7Q2UrpmUIOirskiSFXielYzrkpkNdKSaTkqtXJ5Rlw0c+csD+fsZgMEAp\nT5KU5Pkevd4uk4mCQUJKw7jvqK/VJDsJKgmqRltLPZ1yuFhwzTm223rIZHubzmxGt9NB1TVojbVz\nwDHMt5lbw6SckJscaYVWvw+LiWP6wYZs26MSwWwbMpMxnc9ZFAVmueSuUQh30rqLtVPc4VW8HyFt\nSJPKg2voSoetgwBKdUpXa/aWlmXjGKcereXkDczzUNdZFJBliBcEwRHWMKKwgOV4vyRJqJuGWVWR\nZ9lxee+KZz4D3nwf/i1/DF/8BJwD5QVra6z3dFYq+XYFauugLgbDG/agwkmBqrua0rWiWwkO8ByX\n+N7IQT1NGOPqEA1KdHBRsVilgpS3FpOF6znLQZ0Wh3jv2Rr1qE2X+bykaBZoGWMxKEmQuiHJPPVS\nmM8rkiTHOYdWNVXlOZhC1hkzGvbZ1TMmRcFDM48+2mdbMkzaIUuE0eg8w2FFtSzwTmObJZWt+Plf\n/I/8/C/+LAC//Ru/xV1PGJGOt9ju7QLhWz+bHSdKx/LeSCQSidwpRIEaiUQetaQ6Zae7Q9mUISDI\nZOvSSwCdQ55nnD9/jslkzt7elKIoODwMgiDLEhaLhoODA5JkG62Fc09OcJMat3QsHl7Q5A2Vr2ia\nBuM94lwIzOl0OD8YhJCd2SyEJR0c4Le3sISY3kF+kbqYBCFdTRlmwSFVjUXPGqoaikYxussgbTmt\n7vXwRYFdLKAVqCIaVXlcWeCyLrqtPRYlqEzhCkexKMAE8a5FoBIcHlIHnErO7XRCqXBRwGiEa3sq\nRZXUtiaRHiXQuJMCtVgscHXNqNNBySnR+6xnhnN621txX/IinCi0Vzhb4RSknU4IGLodgVoUqMUC\npxRN3qVyDRlh1MxpVBJG2Yhu70UVenK1aBpRCMENRR6hg0rYB9GtoxyCktYCtU3ybVyz7gGmPdas\nmOA9DAcD6rTPlaND9o8Khh0ovcEpjdQFaQcWh8FBHQ6Dg0pjmezVlK5hdH7Aud4Osw/uQzUF11Cp\nmiTvs7NzHp8kLCuLcw1N40AMZTnlm77tO/mDN/0xT/mUp/Aff+4XkL5ikGXs7DyOohBms+O+U63D\nByabs3kjkUgkEnk0EwVqJBJ51JOZjIzsptsMhz36/Q7T6ZTFYkFdz6lrAao2PGefnZ0+YChMwWQ+\noZpWYVzJyJD2UjqdDuMsY9Ku6VaKp98Pqmc+p7n2FzDuoNIBSqWMshHXFteYV3O6SRdmYGeWXhdq\nrSlzg2yYkS5JSJOE1Dnm8zn9fh98KDt2gOsFwbRCdYJALecljIJoB5BaAw3+LIFqzGqAJlTVWqBq\nXdG4BtWe0GkHdekcqmmO03s3eVboc5S3/Ulwdb1Ce6FpKlzig0CdTm9LoPqrVxCg6Q8AYWkrBmRn\nO6haSHaTtcC33gKh1Dlchw/5Sty4B/XEsX34K+LxeLQkGC/gG6xOSeBEku/poKRls8TVFYkYsqTD\n1oUOVyfC4axilAvea0QnUE5Jx+GcF4uGXg+WS4ddWIrFlJoarQ028ejsArsWlnnFYVdCaFZZIcpQ\nNiV13VA1jmsHB/zDL/kHHBwe8mUvfDGvePn3UJUVvY6mv/V32Lum1+nRK2Ha7W5UUEcikUgkcgcQ\nBWokEnnMoJRiNBrR6/WYTCYURYH3Cu+vkWUpe3sfoaoalMpQeUZCSmpTOrpDd9BFd9tezaZhai2H\nTcO5JAnu2WiEsyVutoCDEnPxIhAczW7SZVbO2PvwHmM9BoHuBUMx1+tA3U4HyrbXcTQYoCcTZrMZ\nvV4Pmc9RLoEkxeU69M1K25+aKzyesihJegmJSkJQrlVoBd44nPfXO555HpzfosBaS6ISvEDjajo6\nzBHddFDFGGrA1DX5GbNM1ac9DZ9lyPv/HD87wtFBo7BNhTOKJM9vX6BeawXqYAQeKlsBGWc5qMC6\nDBtYzybVWuG9AhxeQsmuak/7Zqewek2UB+dRrdD13mL1SQv2LIE6q2Z4W5PpHNGGbi+l2zXM5zWL\neYV0DbU3aBTOVSiTUtdweFhz7VqBqg+p5pfJxwP6vRG9UY/t3jbqw33KwyvM0orD2QGD8ipJ5xKV\nLSkKz3vf+wE+9+99IQAv/7bv4ktf8BKWiwku7ZJwN/NF6GM25liYRiKRSCRyJxJDkiKRyGMOYwzb\n29vs7OyQJBkiY5ZLqGuPUkG7jUbCuXs0w4uC1pb6oMbOgzAZGEMqQtOOnllhBxrSBO0zZP9wbdX1\ndR+/7ymXJaUvSXYSdFfTb8N9Z6EimEUrfLbynCzLcM4xOzqC6RQRQW2dD8exi/UxRQSfh7mfshBE\nhLIMzw87Cr+x7gk67fzU5bLtfdQhCbau0UqjElknywKUgBIh9R571npJsg5KUu+5H4vgKgfi0UmC\nWqXw3E6J77VrADTDEYKibGqcd2c6qKfZdFA9gkYh4micXTuoNzuFlbsaHFRQaBIP+I1ZqO0Cp4OS\nVqXm4iFTKUonoODcuQ4intmioKmhxmDEIHVD1gn3+UMfmnB0dICtDskyS28w4PH3PImtrS06Ox1U\nv8sFvUOn2GHmhdJNcO6AejnhjW/8/9bi9Bd++if5R//wS9m/ts98KiR6TD64QJLA1hacPx/FaSQS\niUTubKJAjUQij1myLOP8+fOMx1uMRhe4ePHJ3HPPU9ndvYc8HwAe6dTQm1Lbh1nuX6E8muC9u270\njLUFzpWwtYPOtkIZ6P4+dmlp9hr6qo+kwmKwWI9G6XRCqWVdw7LwFC4MVOlqzXAY+lXnDz+MsxY6\nHXQnpK+GmajH2K4FBaY2uNqtk1nHreO7PKumNUnCwa3FFgWJTlAKmrpBRGHScI6rXsWlcyRpSkcp\n6vr65FogBCUB6t3vwnnBlTVKgV6JU62D4r1FSpHfawXqYIxRKd4H8XcjB/XEvXAW8MH1FI1RgghY\n/LoH9WaHX7+mHE48ogwawWOPk3y9P3PUzKwKnzSkYvAelE5BoNPp0e06ar9kMRccJpT5VhVJ7ttb\nYun3Pb2OYzgacfHSpdDfTOg11hcHjHLFdjGkcbvs2wpnC/7vV7+KL/uyLwfgtb/6Gzzhnk/mIx+Z\nUhcNOhtx1yc8ju1tOHfu+DOJSCQSiUTuZKJAjUQij3l6vd56FqaIRuseabpLml7EmDFJv4sZGTwF\n1dEey70PY+s9elLiveWoaaiaIwCMGSK7u2AMzX5B8/6r4KA36pGfy3Hi1kIGWLuoVyYWD+RKoURI\nkiSMclksmM3nMByiVIqIwXsbxHBL7Wt0V5OohObIrqbHMOoqtAi199RnqbJOh6PJBLdYYHQYf+Js\nEFxJdixQV6XHnSQhEbmxQH3Ws8I9eODdOBTOWpTi2D29HQsT8Ht7YbPRFlplgFDa6rYcVOcdeI9W\nOoy6EYUWT+0sImHW58008gkHVYESg0GDtyHjeOMaNgVq4xpKW6JEkYsJ5cHaICJ0OgN6PUdDga+F\nYqnwyiB1TX9kGAx6XLjQ5RM/cQjeokQzGG+fOC/dT0nGGbsmp1/mXHM9fuhf/xQ/+MM/ys7ODvf+\nzn300h0uXz2gmFYMu12e+EmXuPQJ+ckxQ5FIJBKJ3OFEgRqJRD5uEVFo3SVJdsiHl8h3ziMqxy4s\n1eGc1M9ImqtU1WUO6iULJ1TklN5TMMAugbrCuCnJOFnPn5xVs7Xr1u0G0XRUOA6PoKOO+zsHbTrs\nQilWkm49E7Ut813WS0pbonua1KQUU4ctHGka1l2Ng1mcocjm1jJfLJCqYjwekmgDjdDYhqQVNU0D\ny1ZQDrMQRHVjBzUI1OTd7wkHr8J25hEKVFoH1Q63MJLivadoasDfVKRaZ/Ec99t6HwKlFNC0+90q\nKGlToOLCPFWNxnuHdU1o4myvYTPJd1qGua0dSfE4EIVWGhSkaYYxCXm3RHzDbJ7gxSCNxVNzzz0D\ntrYyqnpBU9cYk9HrD647N3NpyFYnoTuH73/Zy3nt6/8Ln/95n82vveH/QSVbzOZ7uPmc7rDD4+85\nx/l7tq9bIxKJRCKRO50oUCORSIQgVpNuj+75CyTJRXQ1xk0ShiZBiaPxnjk99suayx9ZcmXecGXQ\n52AoHPolh/v7FF4QnVM6x0Fx1K4LvVEoJ60LYbqvgn5bLjHOkfd6uG6X6TQIIK07gDAvD7g8u8xB\ncYDzjtzkZMOMooRm3tBqyXXi7vKUKCyKgklRgNaMu11SBUYl4DS1q0nyIPKqyq9LhG8lUNVTPx2f\nJpi//BB+OgXvUEohK1V4uwJ1fz9sNtpuu0hDL21t65sKVLcSoe01OxQaQSuwLjTT3mrUzGaJL95j\nlEJUAi4ESK2vYQKXEocAACAASURBVCPJF0J6ryD0VI7zHsQgsB4/k+d9ej2PyIKmhqMiwSiDr0rK\nusY5R1UcIiJk3QHJGUFU0utw6Pd53j/7Aj705w/y5S95MT/14/8LvhlR2AKRCZmznNsaMvqEi2eu\nEYlEIpHInU4UqJFIJLKBShXpbopOOqh6iJrtciG/wHZ+gb7LSfYsSQM6VaiLOe7CFiWwmM2YTiZY\n1eHQOj64nPPgYsLlqmKhG7a3YZAo6hquXvGUV8Mwm/6lS4hSLBYLmqahtDV7yykHxSFVM8Mow1a+\nxU53B93TVI3gK0/CKmlWkYjggKJVZXVdc3BwgPee4e4unU4Hv5yRKIN3bYlvK1BntcMDmVKkxqCU\nwlobZnaeJk3x/80nhy/f+w5S0aRpetw5erslvvsH4XG8HfovSQBFaStu1ocaApKC6wngvKBFMCI0\ntPNRb9NB9eIBjzKC1hniPM5b/CmFuwpKgjDuSPtQDi3aoPTxW2ieh0GjeS8434dTE+Rz3bCsKhrb\nUE0noBTdwfjEKKEVb3/723nic0Kf7/d8y/fxpS/4cq4Vc0b9Bi97+MkBRg8Z7+wwPn+9AxuJRCKR\nyGOBKFAjkUjkFCpRmB2D6CAG/YEmL1M6E89IG3aHGZcudbm7m3Oh12NnZ4ex1gwWC/p1w3Y+RAvM\nyilN29+ZGLjngqbTAT+dcbhnmVUput+n1+tR2pIHLz/I/nIfi0YrzSBJON87TycJ6TfWCr4T0njV\n8lgEdvVxWJK1lv39fbz39Ho9+ru7APjlAqMSxAYHVSeC1jC3DmuPS4WTtlz3hmW+T3tqOOZ770eL\nkLeu6zpgKJzoTe+vHLQCdWs3zKElRUQomvKWJb5w7KB6CSW+gsf5dtTMbTqoDts6qBpRGnGC9w1u\nVeJ7ykEF6Kd9fFMHDa0MakNj5nloNjbJkk4KjdXMywyqiqppmJdzXF2Q6JSs17vuvF73utfxjGcE\ncXrvq9/ACz/z7+MXhr3phPlsQX00QZaObnfE8NIFUhPd00gkEok8NokCNRKJRM5AGUWymyBG8LXH\nTix40ANNsp2sSzu1CFm3S3c8ZqAU49mMe3TOpazDjhF6VOwmCeeSBKOEraFlqEKI0kRGPHy1ZCkF\nR9UR08UU21h2endxoXeBjjE4dzzmpixBdzR5V/CNxy6CCuuo4CkureXa3h7WWvI8ZzQaQZaFute6\nRFmHeI0Xj8Mh2lP5RyZQ/ad9GgD9970bwZOasL17BAKVlUDd2Q0OqjeIBOHsfHPD3VYOqgDeezwa\nrUKJryMI1EfkoPqQ/CuSoLwH32BPO6gqWT+mOgVb4zyIThB9rFCTpIPWhkaVDLsWMMwWCb4KDup8\nMcFWJZ2sQ9o7jtv13vODP/iDvPCFLwTgoYce4jM/7zPY3jlHVkK5v2CxKEgmc2gS9HiHixdHN7+/\nkUgkEoncwUSBGolEIjdAtASRmkoY87JtMANz9sa9HgwGIUJ2f5+RDmFHy3qOJvQ6AjCZ0Ot6uhcM\nh37CQ4d7XNlr6OQDhumQvMnpJt22F/XkyJnVeJneblBhdtqWvIqQKcX+/j7TsiRJEra2to7PrdPB\n4/DzgkRnoMNsz0a3jqRVa8F9S4H61KcBMPqz92KM0EmCg+rg9gSqtchh6M/14+0w59ULiWQhLKle\n3njXlYMqqhWoIcVXEQTyI3FQvQoC1Wgd3FAfRs24oFjXC2QmY5yP2e6EQCJbtxHK2sCGgyoi5HkX\nUaBlQZYKViXMJ1BXFbZYosSRd/sn7vHzn/98vv/7v5+nP/3pzOdz7rrrLrKtLsPzY8ZO42uPK4Ry\nukTpjK27L9Ht3+D/YCQSiUQijwGiQI1EIpGbIEpId1Oyixk6v0VZ5WAQhKr3pIdTupLi8RyVQZBR\nltSzCfvFIdNexWBckqaKXIYM5AkkDKjrmrIs12m+zgXB5j1UVdBO3bFGEsFbj50HIVVNJlRlSQVs\nb2+vBSewIVCXGJUiWqhtTaWCWkvs8XXdssT3kz8Flxh6D32IrCoQG8KJrPewKe68P3t/59YClfEO\nSiucg9yEWOHS3kSg+lWJrwSB6gWtFEoU1jk8t9+DCmEWjdEKIUE5goMK1wntbtINib2AszXeEUbM\nqJN9pHneQ0SwdkG/Bw2auspwVYOvCpQkSJqTJQkHBwc87nGP49d//df5xm/8Rt761rfS7Ybvuerm\nJB3DztYAU8Hh4R7FsiQZbnP+whaRSCQSiTyWiQI1EolEPpqMRtDpgHMMZzXKeYqmYF7NObj8F+wt\n9yg7CUobtrpDnvK4C+wO+4CirgfMZsJkMkGpBJEE7y3WFpRl0HxpGjSgGQYXzc4sk8kEWxQYpeht\nbeFPB/CkKSjwVUPqNGhYNBWifUjBdcdvBcaE2Z5N0+BPi0zn8EnC8glPQLyn/+A70e0mbrXtbShE\nOQoBUTLeCX2+XkhUcGKLurjhrV2l+CpaB9UrlNakOghW6+xNHdTVfFQRcKzmqQqiFMopwNM4e12S\n74lzsE3YT6cnHFSATicEF1m/5Hd+59epbIHCIFUNZYFWGp2n/OVf/CXb29tcvnyZn/3Zn+VVr3oV\nSp18O862uuyeO0fHg54cYJxiMNphvNu94f2JRCKRSOSxQBSokUgk8tFmPIYsQznPYFaDc0wOHqYs\nZqgkpb99kQu9C/TTPkoJW1swHEKv16UoEq5caVgslmi9clEX6/Le1XgZlSkkFRazBYcPH6KU4uLu\nLkmSnDkT1ecpWI+pPKKFSV1iTOg9Pa3DbuiiOofzjumTngRA9z3vQHxQaWs9eKsy36JAZnO81sh4\njEhwUI1K0EpjfU1tz3Zvj0OSjh1UUQqjBJyjvkUP6uo5pcDiEA9GK1AKTSv4N0fNnL4G54JAleDa\nnhaoWmcYY/iV1/0q3/jfv4R/8S+/Di8aKQqkUShlePs73sGTn/xkAN74xjfyDd/wDWdea77dJR8O\nyBJD1tdIp8N45xx55/r030gkEolEHktEgRqJRCIfbURgexuShJ6kZEdz1HRGL+mxe/HvMMgGJ0tw\ngX4/7DIY9ChL4cEHZzgXZqI6V1IUQV3l+fE+LnccTg6xC8twMGTcCX2ry1PqzHsflK1VJHWDShRz\n1+Bx9BOF9yfNwpsJVI/n6IlBoGZ/+o51ie91DuoNBKq/djVsPxyG8lolOBfEY65DH2ppy+v2c74t\n4RUNeJxzeB/EpVEKvKdxDpEgQJ27vsp4dVtEQuqv0M5NFUH5VqB6C6eSfNdYG5xXpRDUdSW+SiX8\n2q/9Jq/4wR/BOceb3/yH/MTP/GvG6YhukvCff+u3+Kdf+RIA3ve+9/HsZz/7zHsEYDJNNhwy7m2h\nPPTyPluXLqDiu3YkEolEHuPccW91InK3iPwPIvJGEXlIRGYi8k4R+VER2b7BPpdE5BdF5KqILETk\nj0XkRTc5xleLyNvabR8WkZ8Tkd2PxtqRSOTjBBHY2QFj2DEDLnTPMRjuojo3LtHMMrjnng6djqEs\nLR/8YEFV5dS1p64LtN7UTg2Hs0MkFfqdPpnLSJXCiGC9p9wQqd5bSBK8JGAdtmlwHvCWThreBja1\n6EqgVlV18gSdo6orJk8Ks1DNu9+Bbh3U252FuhKodjxCKdY9qCBkJgUcZXO9QF25p0oU3ru2/Fgh\nWpO1irRZlQDfoMx3LVCVxwHiQevQN6t9Gzzlb+KgNg1haqxCKX2dg/rLv/zLfPd3/yuKIpz/crng\n/3jNf+L1b3g1P/ozP8KP/PhPsLOzzf7+Pk9qXeibkY67bA1H9P02u/0xvd3+LfeJRCKRSORO544T\nqMDzgX8FXAV+FPg24A+AbwfeLiIXNjduRevvAS8Efhr4VmAG/IqIfO3pxUXkO4D/HThot30V8JXA\nvSLSPbXtI1o7Eol8nKFUsEVX4UGjW48H0Roe//g+nY5nOp1zcJBzeKiwdkGaBhXpnGN/fx/nHP1z\nfYaDIXZu8dbTbdXZ8oS4apVZO0/Vtc5gijvTLLyhg+o9VVkxfcKn4IxBvf/PoO0ntbfpoLJ3LZzD\naIyWkJS8clAznQGeylbX9b8eByQFBzW8HEp8dWgfpV6VAN+gzHf9bwkCVwjlwqgNB9XVx58CnL6G\n1kH1olCnHNTXvOY1vPSlL6UoTvbQLpdLvuX7/iWv+c+v5XM++7N575/efzJh+Sbk45z+7jkGvR7j\nuy+RZrG8NxKJRCKPfe7ErPrfBe7x3l/ZeO7nReRNwM8B3w38i43XXg48Hni+9/7XAUTkF4A/BH5M\nRF7jvZ+3z+8CPwS8GfhC3/6GJCJ/DPwaQQz/yF9l7Ugk8nGKMXDhQlBH+hYpwC2dTs65cwmHhzVV\n5TDG4H2D1lepqpTDw5KmEdI0ZXtnm+awwS0ddmbpDDUTa1k6x8j7doxLEK+SdfCFpaks0jEYLK0W\nvc5B3QxKWpcjO8eyLHF5RvGkJ9P90wfQ73grXHrObZf4srcXlhqP0UpQStG0LqyIItUa5x2lLdfJ\nvrDhoLa25SrwyChFqhTimrVIvqWDKsFB1d6HETVaoZwB63Fi8e1c2TMFqrOgUpQcO6ivfe1r+Zqv\n+RqWyxsnEGul+K7v/A56N3HQT5NlkG7vcN6k+E533X8ciUQikchjmTvOQfXev/uUOF3xK+3jp556\n/quAP1sJyHYNB/wUsA38441tXwh0gJ/yGx/fe+9fD3wA+Gd/jbUjkcjHKyK3LU5XDIdDul1Pmk5J\n0zFp2iNNFXt7l5nPL+PcIaNRjoiERF8Bu7AoB5lSeDZ7UR3eeTApZWYwKNKyxLrmhu2Wpn3hhIvq\nHMuiBFFUT3t6uLQ/uQ8heLTe+1sL1IOVQN1GtyW+QWw6RFTrol5f5nvsoK7etgTvQZQi1Qr8cYnv\nrRzUdYkvEjSmFgRDGI3anJyFuunkrnpQVyFJCl7/+tfzVV/1VTcVpxB6dP/5N7+Mo9n0ptudJt3u\n44cjzNYg9p9GIpFI5OOCx9Lb3Se0j5dXT4jIXcAl4I/O2P5N7eNnbDz3d9vHP7zB9p+yKvP9K6wd\niUQit02apmRZhjGOXm/BpUsDiiKnaTK0TtjeHuDchKq6jPVzVEfAQzNp6KzKfFtF5r3FNx4RTdHJ\nSHRCt6xpXIPWHpEgUDe1WJqmwEmBauuaug5jWOwzngWA/MlbUbLRh3pLB3U/bLu1hdJBYIYSXwco\ncpPhvaNoTpbKHo+YOXZQvQfRmlTrEJLUithbO6gO78MboCiFGIWIahOJHc2m272xiK8rPB7EoIA3\n/L9v4MUvfvEtxWk4X8/B4SFf+rwvu7639ybkHcF3e+S9R/YBRyQSiUQidyqPJYH6yvbxP2w8d6l9\n/PAZ26+eu/vU9v4m28vGmo907UgkEnlEDIdDABaLObPZlMVigTE9Ll78ZLJsd2NO6gSbXaNxR9hF\nTWbDD6vSOaz3IVTIeqwX6k6GAgaNxXtHs+GinhWUtClQ67LEOkeSJLhnhM/f1P33o9xGku/NYnS9\nh4MgUO14Cy2CMtJu6hFRGGXQIlhvadyxrXs8YubYQXUuCMykHTPTuNtzUH2wStG0Tmm7pHFn9KFu\nWsu2CSJcDG/8vd/hK77yK25LnK7vX11z//3387KXvey29+l04Nw5GAxue5dIJBKJRO5oPmY9qCIy\nAr7jEezyk977gxus9V3Ai4BXee/v3Xhp1exzfSQkFKe2WX/tvb+d7R/p2pFIJPKISJKETqfDcrlk\nOg2loePxeO1uat3BuQprZzgKyAvqxQJ/2CUb9SgwLK0lIwjUwgGZJidDGkNVFNSdmiRJqOugxdql\nzxSoVVniPJgsQ574THwblCTTOQx7WO9JwokFNWg3RrZAeO7wMHw52gohRSY4ok3jgKAsU51QOk/Z\nlJh0Y/wLwUH1HItNbRRG2jEzt9mD6rCAR4uAyDrsSJEADRZ7vYPqHN5bnAh/9Edv5utf+lIWy8Vt\nfy8B8jzn7rvv5lu/9Vsf0X6rPuFIJBKJRD4e+FiGJG0B309wLG8VTeiBXyQk655ARL6ekOb7euD0\nx9Kr3x7OipbIT22z/lpEsjNE6untH+nakUgk8ogZDAYURYH3nuFwSKeddbpCqRSltnGuQQ1nFMUh\nTTFH5wVWaWZ+QKosWE/pBNFCt9ejWU6RZUE9rM8MSjLGXBeUVJcl1nqSNEV3O/hP/iTUu95N8vb7\nqJ797JOjZur6BgL1KHw52kJESJKgJq0NDipAblLKqqRoCnppL7y+HjMjWMC5NlhJq9CH66H2YT6q\n1mp9uE3WDqq0DqoEB1V0WEv7sF/jajDtTVkJVGvx3vKHb7mfl37dyx6RcwqQZRlf/VUv5id/+lXk\nm8NsI5FIJBKJnOBjJlC993/OX7PEWES+DvhZ4DeBL/fen256eqh9PKvUdvXcZonuQwSxfDchFOn0\n9m5jzUe69ppXvOIV66+f+9zn8tznPveszSKRSARjDFtbWzjn6HZvXJShlEGlYxh2qScTZL5ABjVV\nvUdlEqraYb0iTxRpmoFJkOWUuinJWy22Wc0qIhhjqOuapmkwxtBUVQgjTjOMVrinfzrqXe/GvO0+\nePazbz1qxlo4CJ8z+vEOCOv+1eCghreEVCUI1XrczOqPEoVIW07cik1lwrFWvam1dyRKrQ+3yVqw\nqhABrJETJb66HTXjXAM6P3kN1vIHb7mPr/6aRyZO0zSl1+vzQ698BS/5p8+L4jTyqOfee+/l3nvv\n/VifRiQS+TjmThwzA6zF6b8H/gvwQu99fXob7/1HROTDwOecscRnt49v2XjuzcA3AJ/L9QL1s4H3\neO8Xf8W112wK1EgkErkVj0TUmEGCXw5xTZ+uK5ipKUtrqWuPaEXXaFCKpNOHxR71fEpy7jxw0kEF\n2tLfmrqug1C0FpRCtMZohX/GM+GXfgnztrcDnHRQ4WyF2DqofryDKMHo6x1UEU+iEypbUdoSLWE9\nLXo9H3XloKq2PDfxod/Cekemg+5ctcFuTMkJx6Z1UNXJEl9pBWrjG2iF70q1v/mP/oh/9JKvZbG4\nfXHa6eR83uc8h+/9H3+IXl6g01irG3n0c/qD81e+8pU33jgSiUT+BrgjQ5JE5GsJM0//K/BPvPc3\ni0T8ZeCJIvK8jf018C2EkuHf2Nj2dcASeJmsflMK2z8feALwn/4aa0cikcjfOCKC7mtEhM4yxyTn\nqfyYRrbAyDrhV7pdjDKwXOJo1rlGm2Wxm32oVVUF19EkIIIxAs8MQUnmT1qBejsO6qrEt3VQtb7e\nQfXerWeglk25TvDVSrOSwese1CQcy6wc1FWY0qmgpJVYVYqQ9ut9cFCVWrW+Ynz4wrr6xDXcd999\nfOHznsd8cXtdG8YY+v0+P/ETP8S//Z9+nHGvQ0crTJbe1v6RSCQSiXw8c8c5qCLyAuDngSPC7NOv\nWA+RD0y996/b+Pe/Ab4C+CUR+XFCae5/CzwL+Hrv/Xy1off+moh8H/BjwH8VkVcTynW/C3gA+J9P\nnc5trx2JRCJ/W+iexs4syoIpHBUpSENqBLNKEMpzjEpo6oK6LkkSQ1kGFzVrO+s3BaptXVTRBhGF\nUuCf9ky81qj3vA/mc2y/357AjR1UOZoA4Mfba4EqIusU33bDdh4qlLYk0eE8gpPqTyyttAJ//Ga2\nmoW6GZS0ymxaPV/5VQ/qSQc1lPgKzgenGKV4+/338wUvehGz+e39OO/1ejz96U/nl37pf2MwUBx8\nsGCAxqGDuI9EIpFIJHJT7jiBCjyD0Cc6IvSfnubPCU4oAN77fRH5ewQx+c1AH3gX8JXe+9ec3tl7\n/+MiskdIGP5JghB+NfDyVXnvX3XtSCQS+dtCDzTNYUO6gCoNoq6XbfzIF8H0+nC0pJ5PMKZ3U4Eq\nzuG8QycZHgkCddDDfdInoR94gOT+t+E+9/Pbg99AoBYFMp3hlUKNxqwMTKUUzrnjElzvSHWCFk3j\nGsomZNZppfE+lNyuS3y1AivBQfWe+gajZjYFqvMePCcFqgAeRDTONzhX8673vIfnvOhF6wTlmyEi\n5HnOD/zAD/Dt3/7tQM1yeRn0DGpBGYVInGUaiUQikcituOMEqvf+lRzPPL3dfR4CvvoRbP8fODlP\n9aO2diQSifxtoLvBRc1qYTpvECBPTgqkpDeEo6s0syn57l3A2UFJTdPgmwalNd4atFKIgFfgnvp0\n9AMPYN76FsrP+byw4w3mvPi9awjgRkNEKUQFoSsi6xJcgFXeXWYyFvWCogmTu5Qorivx1eFEjCjA\nn+mgbm6vFFgc4kGt5qACogRvPcprLA3veNc7ec4LXsDkNsRpt9vl7rvv5rWvfS1PecpT2mtIMcag\nM0+zdOhUc4d21UQikUgk8rdKfLeMRCKRxyh6qFEibCnDVmJQ5uREr6TbB6VoygWJCkrurKAkIJTn\nKg1K1sFEogT/1GcCkL7tbTgIIUYiwcL0/kRTq9/fC0ttjUPH6AkHtX0ibAmwLvP17b83S3xX26o2\n6Chpm2ib23BQG+fAu3VIUnihvWdO8/73fYDnPvsLOJpMbnmPO50O3/RN38Q73/nOtTiFILpFDPkg\nQ/qWdJBGBzUSiUT+//buO86uus7/+Otzzp2aNpPEAAEBKRFEqUqRFhVdAUFZAbGASBMVXFx0LQ8V\nwVVZFkQB15+7rFIU1rKy7oqrC9IE6VUQKZKgIaGkt2n3ns/vj+85t829M3cmM5k7yfv5eFxv5pTv\nKR5y8pnP9/v5ijRg0mVQRUSkMXF7TKG1QEt/WhipKkCNopiovZNk/Vqsby0woyKDCiFA7enpCQWS\n4hxEUbHyrsWG754FqI8CIb8ZQ4gQC4XwydKZy5aGbbq7w/QyVloVCjRlhZIS3BPacm0YVgpQo5gk\nHyLNQiEdNxpHUIhCwSP3UACJYTKoiZeKJGUZ1NjwAef5P/+Fvz3sWFatGjo4bWtrY8aMGfzsZz/j\n4IMPrrmNWSttbW30tPeSa43LxtiKiIhIPXpbiohswnLTSr+HtNgGr586DYD8+tXkciHpWR6kZhlU\ncyeKcrgZubJ2fLe98Cgi96dn8PXr68+F6g4rlgOQdHWFNs3CNKRRhHtloST3hMiiYoEkqMyglg4T\ngsxcOq9Mdvx6GdQ4hiSdZiZnUSmSjeC555/jiLe/k1UrVxWns6mlo6OTow4/imeeeaZucAoQRS10\ndnbQ1TWDadOmUiwXLCIiInUpQBUR2YRFbRHxtJh4eph6plpLx1SIY/K9PeQIkWl1gGpmRIDFObAo\nZC2z9qdNJdl5Z6xQoOWxR+pPNVMowMqV4Y/d3aGDbhofZmNQSxlUyMaaZt18I4vSar+lMahZgEsU\nEUcx5qGKr7sPmUFN0gGvcVQag/r8X5/nkKMOYcWKFXWD01wuZsrUKfzLN/+V66++nunTpw95783C\ntDKdnR3EcawuviIiIg1QgCoisonLTcuRm1p7REdL3IK3tTGQDNAyEAqVl49DjaKIWbNmMbO7m0Ih\nqejiCyErm7xhj9DWww9SHHFaHaAmCaxYAYB3VXbxzcaghgxq2C8LRLP5UONicOe4O+5RKUA1I7KI\nnDvuSehmXCeDijkJTuSOpV18//rXv3LQYQexfMXyusHplM4O9tlnT377u9/yniOPKQ2XHYJZmLYm\n/anmLwhERESkkgJUEZHNWEvUgne0k0/y5NJqudXjUFtbW2mJYwYKCR5ZKC6UicB33yu09fBD9bv4\nJgmsDAFqoStkUEtdfA13KBSSirlQIQTQ3e3ddLV3pcGjk05jGjK7ERBFaZbXSTx0882So9UZVEun\nmYncMTNeWLyY/fbbj1eWvpJmcCuZGZ0dHfzjP3yaX9x4HVtssWXIJkfDB5tZoaTwZ2VPRUREGqEi\nSSIim7E4iona2ilEq4jph/5+BnKtgzdMEpLEIVeVQY2MZPc3AqFQUk+x4fpdfJMZ3WE0pmWbWnoI\nJ/u9aZZBBeho6ahaZsUAtTyDGiVO3r0YJEdRqU5TcY7VNPCNMZa89BL7H3UUL7/8cs3gtLOzg1dv\nNZcb/v3fmbfjq3kl9rBnmv1tRBS1UigMoN8Hi4iINEZvTBGRzVxL1IK3t+M2QNTXQz5fKkJUlCSh\niy+VRZKIwXfbG48iWp58mkJPGqLWzKCmAWrXzNDFN30D5XLhD/n84AxquSxADRlUqxiDGllE7E7i\nXtyzvJtvMUCNwoWteGUp+x91FC++9BKFqvlaAdo72jnzzDN47K672HXnnQEniQySqDh+thHZONQs\nkyoiIiJDU4AqIrKZa4mH7+ZLklBIPFTsrcqgWueUUCgpn8ceeSisqO5jWyjAilKAmnXxhVIGNZ8v\nFUkqz6CWZBV8bVAXX4DYHceLc6FmhZLy+ayoEiSesGLZck449kMsfvFF8lUX2tbWxuw5r+KHv7iG\nCy+8gNaONHsbgUcRhhFZ4+NJ47iDXG4Gudy0hrYXERHZ3ClAFRHZzLVELdDSwoA5LVEB+voqCiUB\n4B7mD42iYkAJFN8iye67hx8feqC0rjyLmiSwclXYtmtmWJ42k2VQCwUfMoOaLQtFktImLPsfyKUn\nU6ByqpksBo0iWLp8GR955zG8+OJL5Ksyp50dnRz9zqP5/WMP8qb930jB85BLM5+RhQrFSRSOMoJ6\nR3E8RWNQRUREGqQAVURkM5fNNTrQliOXA+vtqZtBrVXFF0qFkuJHHi7tUz7XS6GApQFqYcasYhXf\nsFljGdSswq67DZpmBkpFFQaSQsXhs2B79eoVvP2QQ1my6IWKzGkul2P69Ol8//Lvc+2/XEvX9BBA\nFzwP6TywnotD2JtWD9bbU0REZHxoUIyIyGYuF+UwjIH2FuL1jq3rrcyguuOJU/CQrIyjyi6+AP6G\nfYBQKMnTCrnkctDfX8qgrkozqDPSLr7pvlkGNQSdWduDx4WWMqjhE0VWmUFNA9gsQC3PoK5evYr3\nvOcgnl/4PPmyi5syZQp77703P/7xj5mVm4UPOJGHHfPJALS1wOzZJL4a+tcQeTiWpowREREZH/od\nsIiIhCxqd9PaOgAAIABJREFUHOPtBklCfm1vaWWShHlK03lLjcFdfP11e+NmtPzxKQq96b7lGdT+\nfmz1WtwMn94VWqiq4juSMaih+WIKNlxD2mDeK8egrlixmmOOOZgFC55loL8fKE0f841vfIPbb7+d\nrbbaqhgwxx4BEYkn4TxaW3FLKwMTV1y3iIiIjC29YkVEJIxDBZKOHFEEybqeYuXbLEBNLAST5dnD\nrLurTZlGYd5O2MAAhUfTbr7Z+M2BAXzF8tBU1wzMooqpWkoZ1DTzihHmO60sJZwFrdnQ0TjrapwV\nWyJkVAtJ2DeOYd26tbz3vYfy3HNP0Z8Gp+0dHez4mu158De/4eyzzy5dTxp7xg5YTMEd93CwQpqV\nNY9K1y0iIiJjTgGqiIhUjEONc4b19TLQnwaI7uQLCW5GHA0OzLLMY37PPcLmD94fVmQpzP5+fGUa\noM7sKtY/yoK8UPDXKBQ87R5cr1DS0BnUCCMmzHWaAD096zjuuLfw7LNPloLT9nbed+pJ/O7G/2KX\nefNqXoclYVqYxB33fHomSTg3Ir05RURExpFesyIiUsygDniBlimtISjNuvkmCUmNAklF2XQue4ZC\nSdFD6VQzWQa1UICVK0JTXV2DigxFEURRFLoRu1Ovm2/2c5bZjcpPxQzzsGfiCWvXr+cd73gbf/rT\nH+jr66OtrZ0tttiSa//nBj755c/S0dpWzLxWX0eUAMQkUMygelIAN+IRTDEjIiIiI6cAVUREioWS\n8kme3LQw92d+TU9YmSQM5BM8impnULNKvnuGQknRQ2kX3/IIckUaoHZ3E1HZRTYLUEN13qRsSpba\nGdRCoSqDmjYSWUTkTk9PD4e/4x08+uij9PX10dHRyRFH/C1/+MPT7LnfvuBObDYoQM2uI0ozqAVC\nBtU9ZGTxKFQf1ptTRERk3KiKr4iIYGbkohwDyQDeEYMZ+XV9IV2ZZVAtKo37LN83q+T7+n1CN+An\n/gR9fdDWFqLPJCkFqDO7KwokQXkXX9IAtV6hpKyLb7ZfWSNpZrPQ28vpJ5zCHx56iHw+z7Rp07n0\n0qs4/PBjmDEDlvctxZKEyKLBAWraXpSOQU3cgUIIUN1DlaiqcxcREZGxpd8Di4gIUBqHSksBb20j\nP+DQ2xuq+oY5YGjJ1XhtpAnP3LTp5HfaARsYIPnDo2FhlkUtdvHtplgHKRWSmVbs4ltvDGqpi29a\nFCmujHIHBgb46AdO5aF77sOiiAMPPJB7732Kww8/Jj2Qk7iXMrhR1bWUHTa2HA4kyQBQlkFFBZJE\nRETGkwJUEREBSuNQ88kA0ZQO3KGwtgeSJFTGrdfFt6y4UP9eoVASWaGkbBzqypVAWRffsnZCrGjh\neIWhppoJqdPSGNRSGwOFAsedfiZ333EXcRxxwTe+wa233spWW21Z2j0KRZiiLAVbp4svCcRRDtIu\nz9k4VHXxFRERGX96zYqICFBWyTcZoGVaO5gxsLYP8nkKBYfIhiySZAkM7BUKJfHgg+m6LIMaAtRC\n1+AuvlCaaqZQGKqKb3WRpGz+1DzHnHQS/3fb7ew0b0d+9rub+cjHPoaZEcdluxs4jrkP2cXXk2yM\naowD7v3FLr5RjXMXERGRsaMAVUREgLJKvoUBci2Gt7WTzwP9/eTzSRiDOkSRpMhhYO9QKImsUFIW\nIa5cBUDSPbNiDtRM1l13qAxqNi9qeRffQqHA8ccfz69uuonPfuIT/Obm/2HbHV+Tjh8txcdRRDpt\nTFkX31pddSPAwRLHyFFwJ0kGSAhzoJpZRfZXRERExpaKJImICFAqlJRP8licx9s7yPeGSr4FD118\na2VQiwFbAoW0kq/94Y/Q318KUNMiSd41s2YGtRSgelmRpELVkRLAKookXXvttTz44IP8/qab2G+X\nXVhs61jlTiHdKDt8FGX5VydyMGoHqBZbyKB6yKAm5HEfICFMf1Pr3EVERGTsKIMqIiJFWRaVaADa\n28knEe6hum4UW2Xl3Ez6JvGCE3d1MbDTDlh/P8kfHqmRQZ01aAwqlALUfL6UQS3v4ptlT8FCd2NC\ngHriiSfyxBNPsP9++4UuvRhYCFDdvXj4OA4Z1MQToiSpm0EtVvLNpppxJ3QMBk+MSBlUERGRcaUA\nVUREirJxqB4NYAb5XDuFQgjRolyYa7SaZYWDPCQXS4WSHigWSbJVaYA6o3YX31pjUCu7+CbFYyVJ\nlh014jhm6tSpxWAz8lBU2HESoKUFuruhqyu0ELr4pmNQq6v4QvGtGCVeNtVMCG4treKrDKqIiMj4\nUYAqIiJFFeNQc5C0dTAwAAlOFFvoGltDMfNYgIE99wwLH3wwpC6nToWVqwFI6nTxzQLUfD6bB9XI\nqvZCeQY1KgaoFdncNNiMCFnOxJNiN9+OjlIGNRRJGrqLL0DkhlmumMN1gHQMqgJUERGR8aMAVURE\nisor+eZyQFsbfVEHSUdnmA6mRgYVKGUeywslPfxI+J4yBVu1Gjcjmd5dcy7R8jGoQQhQS1nUpLg8\n2yYuHw+btmdpEaTQnbcU4AJpRV6I3IcukkTo4gsxBbwYHEeeHkNdfEVERMaNAlQRESmKLCK2OIzV\njEORot6ObvJTpxBF9QPUYuYxgYG93hiWPfYEDAzgy5cB4F3TIYpLXYLLZMFmFnyahcGjpQA1Wx7G\nxJpZZQ/digxqyLhWl1gqpBnU4swzw45BNRKPSqGxp3sqPhURERk3ClBFRKRC+ThUCPOOujtRNDjz\nmSkP7OjqIr/j9lhfH8njj0EaoCbdXcVxqvWq+IYiSQyaCzULVN0pBqgVp5IFqA4xoYtvdQa1kLaR\nyw4+RBdfPH1BFgslWVbDV29OERGRcaTXrIiIVMhF6QxkaYAKkJAQx4118QXIFwsl3YcvywLUbnDH\nGBzolhdJKm+wOoMKRpLUCFCLXXwJGVRKY1AzxalnsuVDdPH1ghNZmGom7+kUM8XdlEIVEREZLwpQ\nRUSkQlYoKbEBoihkT0MGtX5glmUeLY0nB/baK/zhwYcqM6hpcFkrg1peobeRDGrNLr5p5jPxhPIa\nwFAWoBYzoUPP6RqblaaasagYfOvNKSIiMn70mhURkQrFQklpJV9Ps5e5eIhXRkVxIRjYO4xD5aGH\nYdlSAJKZM0NwWbZ9cfcom0Imq9hbO4PqbqHQUXWwnE0zgxGb4XhFBtWzOVDLY+Mhuvh6ko1VjRnw\nBCMqdvFVBlVERGT8KEAVEZEKuShHZBEFLxDnEpI0SIyHyqBGpS62BvTtGSr52mNPwMsvA6UxqJHZ\noCCvPEBNkmRQBjX7TtIfa8aIUQgho7SCb3mAmpDOZZqeY/1GKM3p6mBRGwmtEHWkJYDr3gIREREZ\nA3rViojIINk4VLeBhjKoxeJCSQhAvbubZIftsd5euPOusGrmTKw4/nNwG3EcsqOhm29lBjWb6iVJ\nrLjt4JMIgW/kYXqa8i6+2RyoEZSKHQ1T8Cl2wyzCWmYRWUfN6XFERERkbClAFRGRQbJxqMQDxQxq\nS274Lr5e8OKLxdNCSXb77wBIumcWx6jWClCzQkn5fP0MalZEqeZ42CgKRZzcsTSozrKoCSHINbMh\nu/hC+XjasiJLaeCtKWZERETGlwJUEREZpDjVjA0AThyDDRGdFec29VIMV9g7FEqyVauBUMXXCEFe\nrUxkFnSGqWayDGo2m2lpDGr5tlUnEQLUJClmapOKbydyD118h8qEVo2nTQ8cFuutKSIiMq5yE30C\nIiLSfLIMaoEBZnS1Yf1DTDGTsshCcaEEMCjsvU/F+sLMWTXnQM2UTzVTr4pvIY1X62VQDRuUQW1J\nW0lIiPA0mB6iu3JZF9+MF6e2UQpVRERkPOl3wSIiMkhL3IJhFJICLa0FWlsbGH+ZvlGybrz5vd5U\nsdq7Z9acAzUTh7K5FArlGdTBVXzLt61QnkHNAtR0VZJNleNpJnioa4mz6yjr4lun+rCIiIiMLb1q\nRUSkplyUw3H6C/1AAxnUuDLz6LNm4dtvW1yfdM0iMupmUOO4PINqZH2GPe2eC+VVfOtkUM3SSsKV\nXXxDC6GLb2TRkAFq+VyoxSt21xhUERGRjUABqoiI1JSNQ80C1KHGoELZVDNJKTj0vfcsrg9jUKn7\n5skq84YxqFR0863u4hvXqiicdtuN3YgMEk9KRZLc0zlY0+C3gTGoJBBbKVi1smsUERGR8aEAVURE\nasrGoWbTzAyXQa0uLlQAfJ+9i6u9a9aQXXwLhQGeeupxenr6KhoMhZIcCNPQQP1pZgAsLWiUlE01\nk6TXEWXddofKoKZte5JmTaE4f6syqCIiIuNLRZJERKSmLIOaGW4MahbYZQFq4o7t88bw564ZeBRj\nFlKR7s6zzz7Lvffey7333st9993H448/zqtfvQNXXvkjdtzxVZhFuJdX8rV0jtT6RZIgzHMameHu\nFRnUxMuKJDXSxbdQHI5azAorgyoiIjK+FKCKiEhNLVEolDTSDKqlScqCO7bfgXjXDAq77waJ871/\n/w7XXv99Xnz5RWbMmMF+++3Hvvvuy/HHH89OO+3GkiX9zJjRVtGgez60a9HQ86CmQWfkIbAccK/M\noHo2BjUesopvcU7XxIvXHGWpU8WnIiIi40oBqoiI1GRmxFFMPgkBYiPTzECo4muEoNC6uvDnFtDT\n2gr9MHvWLBY8v4DW1lamTp3KgQceyMknn8yMGTNYt26AJUuWDRqDWp5BHbKLbxp0Wtod16kcgxrm\nQR2+im9xTteyIklZZWIFqCIiIuNLY1BFRKSubBwqNFAkKS4VFMrGbibuWHc33tYGDu875v3c/7v7\nmT17NgcccAD33HMP22+/PR/72Mf405+eAEpFkmplUIfs4luWQU13BEImN0l/jmD4IkmUzYVayK69\ncrmIiIiMDwWoIiJSV/k41Ea7+HrixZdLlsF09+Jcoq/b9XXcfffdPPLII3R0dPDoo4+y5ZZbctRR\nR/DpT5/CSy+9CJRnUPNpazZ0F9+osjtulPY1zhenmnFwH34e1LJracFoMaO92H956N1ERERkwyhA\nFRGRuioyqMNlHbMqt2VdY7NcqBMCVwMw2HLLLbn99ttZunQpp556Kueccw7PPfccO+64C8ce+xau\nuuoq3K2qlVIGdbgqvuGg4XsgnTzVcEiSYedBhVI22Bxe1dpKRzZmVW9NERGRcaVXrYiI1NUSh0JJ\nscXDb8zgSr7FMaAQMqhmxW6yU6ZM4YYbbmDevHkcfPDBLF++nLPO+izf+c5/cNlll3Hkke/m5ZeX\nlto2o1AIDQ+VQS12x6Uyg0qWQR1BF1+y4a/F2WmUQhURERlPClBFRKSuyCK6O7rpau9qcIfwFacB\nXVKji295N9k4jrniiis488wzeeaZZ4hj47WvfT133nk3e+yxB+985/G88sqyYuNpMrT+GFSz4hjU\nLEAdSM/BKFUYHrKKb9l1eJqxzb711hQRERlfquIrIiJDas+1N7ytRWFaGksMIq/o4lsrQIWQlfz4\nxz8OwJNPvgJAFOW48MILieMBDj/8ffz61z9hiy2mD93FNzQWuvC6V2RQPSuQVLbdkNdRVvCpdAHK\noIqIiIw3BagiIjJmimM3k1IFXUjjvCR0rx0qyMsCz3w+ob29hfPO+wcKhQJHHPE+br31ZpIkLYRU\nr5puFIUiSEmCxSG6dCDxhMjKMqgNFknyghezv8qeioiIjD+9bkVEZOxkXXzTzGMxAZkGeVHZNrXE\ncViZTTUTRTEXXPA59tprd77whfNIEieKhghyswxqkhSLJEGo4BtR6v7baAbVE1f2VEREZCNSgCoi\nImMmKy5kVUWSnBAvFiv91pHLhZXZdDIQYWZceOGX+MUv/ofHH3+4fvdegCgqdvGNrCxAdQ8Z1OKJ\nNlgkKSkbf6r4VEREZNwpQBURkbGTFvvNMpVJOv7TKXWvHSoTmXXdzTKo2Vyo3d1dfO1rX+Mb3/gs\nSVKouz9pF+LQxdiLMWUxcTqKLr545TIREREZP3rdiojImCnPPKZTopZmMS0Gh/X3z+XCaykrhlT+\nmnrf+z7AlClTufHGn9VvoGqqmSy6TDypLJI0TBVfMwuH9jRIRV18RURENgYFqCIiMnayt0oCURrQ\nFechzTKo9QocUVkkCUoZ1HRPjj/+FH75y/+sf/z0mMWpZsqmuYnMiLIQtYFgMztPz2uKGRERkY1F\nr1sRERkz5cWF0t6+xXGo5gw7jjPLoJaPQc0kiXHggW/l8ccf5pVXXqndQJoZzQJRK/bPTaeZabSL\nb/mhsx7FSqCKiIiMOwWoIiIyZopFkJJSPFech9QYNsjLMqiFYrfa0mvKHTo6Ojn00MP4z/+sk0XN\nMqhpv+IsQHWcyNMxqQ121S0G22kGdajMr4iIiIwNBagiIjKmskAu9rIuvmnAOtw4zvoZ1Ki47Igj\n3s0NN9xQu4HiGNT0OGVdfC1b3miAWt3FV/GpiIjIuFOAKiIiYyur5JsWOiqkc6AaDPvWqVfF18yK\nhZPe8IbdefLJJ+s1EL6yYaNpn17D06lnomELJJXaCl9ZkSQFqCIiIuMvN9EnICIiQ1u4cCGLFy9m\n7dq1E30qDcmvzZMMJBQ6InqjJPT4TaBlbUJ7W0zLtJb6++bzLFq0ljiOWbRoGklSIJ9fjVnM+vVt\nrFjRw5QpMYVCgRtvvJGWlqq2+vth3Tp6LE9vW45c3EaeHP2FPlqTPqasL9Da1gHTpw97HYW+AoX1\npSlt4s6YuC0eYo+NL4oiZsyYwXbbbcecOXMm+nREREQ2mAJUEZEm9vjjj7Ny5UrmzZvH9OnTiRrN\n/k2g/No83ucUOmBdFj8OJLSsczrbcuSm13/1FAoFnn8+BKTbbTedKIJCYT2QY9WqhBUreujqauXt\nb387u+22G3Pnzq06eB5WraKHPOs7crTl2um3VgbyPeTyvUztKdDWPqWxALW/QLImKf4cTY2aLkAt\nFAosW7aMxx57jF133ZWtt956ok9JRERkgyhAFRFpUv39/SxatIjDDjuMXG7y/HUdt8cknpC0GgMt\nWZGihNZWp7UtR661/rUkSUJbWyvuRktLK3EM0ArA+vU9tLYWaG9vY+7cuaxcuZLtt9++6uAxtLbi\nRORbc7TlWpnR0klPv9PXV6AtydHa2gqtrcNeR2IJhb6yDGp7TNTSfL8g2Gabbejs7OTRRx9VgCoi\nIpNe871pRUQEgGXLljFr1qxJFZwCxTdLlJQt83Tql2HGcUZRRBSFokbZ9KmZbAyqGXR1dbFq1arB\nDVg2vUxa4Mid2IyEBEZaxXcSVe2dOXMm/f399PX1TfSpiIiIbBAFqCIiTSqfzw8eYzkZZG+W6giT\n4av4hm3CdxaQZpI04I2iiIGBgZAJrbOzpfsmlEXJ7hhRwwHqoDdkk78xW1payOfzE30aIiIiG6TJ\nX7ciIjLZZEGouZUSplkV3wZiw2wu1OoANYt3o8jo6+ujra2t1sHBrCKDmn2bZ/O0NphBtcqMrzV5\nGd9Ggn8REZFmpwBVRGQT8sMf/pATTjiBnXbaiSlTprDddtvx7ne/m/vuu6/m9kmScOmll7LLLrvQ\n0dHBtttuy6c//WnWr18/ouP+6le/4s1vfjNTp07lVVu+ivef+n4WLFxQesn4CBKXadfa0lyoaRNp\nsBlF1A1QL7nkEuYffTTbvmF3tp65NfO2n8chhxzCf1z/H+EkoOJEhr3+8rdkBL/+9a/5m7/5G7be\nems6OzvZaaedOOOMM1iwYEHFeTz99NN8+ctfZv/992fOnDlMnz6dvfbai69//esbdG9nzZrF8ccf\nz8KFC0fUhoiIyGShAFVEZBPR29vLSSedxDPPPMMHPvABrrjiCs444wweeughDjjgAH70ox8N2udT\nn/oU5557Lq9//eu54oorOO6447jssss46qijigHhcH7+85/zrne9i76+Pi6++GI+/elPc+fddzL/\nnfN5eckSIM1gQkNvnSxAHdzFNxuDWj+Dev/997PD9tvzqY99jIu/9c+cdc5Z9Pf387FTP8bnPvul\nQVnGYa+/7HyvvfZajjjiCJ5//nn+7u/+jiuuuIKjjz6a6667jje+8Y0sXry4uO33v/99vvWtb7Hz\nzjtz3nnncfHFF/Pa176WL37xi7z5zW+mt7e3gTs7+N5+5jOf4Y477uDAAw9kSXpvRURENimhEIU+\nG+sTbrmIyPD+8pe/+MMPP9zw9vl83u+4445By1966SWfPXu2b7HFFp4kSXH5448/7mbmxx57bMX2\nl19+uZuZX3fddcMes7+/3+fOnevbb7+9r1u3rrj8/tvv9ziO/SOnneZL+/v95RU9vv6VXs/35odt\n8+WXV/uzzy73FSv6K5b/9a9r/Nlnl3tvb7+fdtppvmjRotoNrFzpvnSpL139ki9dt9Tz+by//g2v\n99bWVu9/8UX39esbvv6B1QPev7Tf+5f1+4EHHuhtbW2+bNmyiu2vvPJKNzP/1re+VVz2wAMP+OrV\nqwed2he/+EU3M7/iiiuGvQ/17u0jjzzicRz7GWecUbH9Lbfc4mvXrh22XZGRSP/dMuH/ftJHH302\nn48yqCIim4g4jjn44IMHLZ8zZw6HHHIIL7/8Mq+88kpx+fXXXw/AOeecU7H96aefTmdnJz/84Q+H\nPebtt9/OkiVLOO200+js7Cwu3+MNe3DogYfy85/+lEKhEKr4NtjHt9TFN6lYnmVQkyTM/Tlnzpza\nDaTHidIxoxYZW261JXEcEUelIkmNXH+xkq/BlClTaGtro6urq2L7rbbaCoCpU6cWl+2zzz5MmzZt\n0Kkdf/zxADzxxBND3IGg7r3dYw/mz5/Pj3/843BvRURENiEKUEVENgOLFi0aFFzdf//9xHHMvvvu\nW7FtW1sbe+yxB/fff/+w7WbbHHDAAZUrYnjTPm9i9erV/Pnpp0sVjkZQJMmrehhnPy9btpTu7u76\nFY6jiOUrVrDslaU8/aenueD8C7j1t7dy7qc+SVQWoDZ0/dn5Gnz+858nn8/z4Q9/mMcee4wXXniB\n3/zmN5x77rm87nWv44QTThj22hYtWgTAFltsMey2de8tsN9++7F69WqefvrpYdsRERGZTCbZ5Hoi\nIjJSv/rVr7j//vs56aSTKqZmWbx4MbNnz64Z6G299dbcfffd5PP5IedhzcZdbr311hXLzYyttwrL\nlixezE5b74zRWKXZWhlU93Qcq0F7ezvvete7hmxj3n77sXzFCiBMv/KP//SPnHnSh7KTK577sNef\n5ImIIIL58+dz8803c9xxx1WM5z3iiCO4/vrrmTJlypDnVCgU+OpXv0pLSwsf+MAHhr0P9e5t+bIX\nXniBXXfdddi2REREJgsFqCIim7BnnnmGE088kW222YZLLrmkYt369etrT9VCCAKzbaZPn163/awi\n7aB2DNrb2iu2MWzUGdTyALW7u5tjjjmmfgNRxH9dcw3L8j0seukl/utn/8UXPvMFli9+kYu+8KVi\ngNrQ9feuZ6pNxTBuueUW3vOe9zBv3jy++tWvMnPmTO68804uv/xyTjjhBH7xi18MGcyfc8453HPP\nPXzjG99g5513HvY+1L23VP7/IyIisilRgCoiMokkScLLL79csayzs7NmELlgwQLe9ra3Eccx//u/\n/8usWbMG7bd06dKax+nt7cXMKsY+1pKt7+vrq1hukdHb11vcxpwQnDYQoNaaZiYLUN0TXnrppdBV\nt+wcqq//oP33Z22c0Nca8ZGPfIQTP3giF196GScceTR7p+N0G7n+qdOnwnoYYICTTjqJOXPmcNdd\ndxWDxne/+93stNNOfOxjH+Pqq6/m1FNPrdnel770Jb7zne/w0Y9+lM9+9rPD3wTq39vs/Mq3ERER\n2VRoDKqIyCTyl7/8hblz51Z8qov8ACxcuJC3vOUtrF+/nptuuonddttt0DZz585l6dKlDAwMDFr3\nwgsvMHv27CEzglkb2fYVInhhSVi21dy5IUAlzaIOo9Y0M1mAumTJIrbZZpuhrz8NXrMjJZ5wwgfD\n+NDf3XNPMYPayPW3tLbQ0tXC0wueZvHixRx55JGDMprHHnssAHfccUfN6/nKV77C1772NU455RS+\n+93vDnv9mbr3tmxZre6/IiIik5kyqCIik8hWW23FzTffXLEsC2QyCxcuZP78+axZs4abb76ZPfbY\no2Zb++67LzfddBP33nsvBx10UHF5b28vjzzyCPPnzx/2fLICQ7///e9561vfWlphcN8D9zFjxgx2\n32UXbE0abDbwa1EzwywEqEkS4s2su++cOXOGvf4sAM2C4sQTenp6wuHLiiSN5PqzILZW1dx8Pl/x\nXe4rX/kKF1xwASeffDJXXnnl8Bdfpu69Be655x5mzJjBvHnzRtSmiIhI05voeW429EP4587dQAL8\nT51t5gLXAK8A64H7gWOHaPMk4OF02xeBfwNmj1HbLiLSiJHOg+ruvnDhQt9+++29u7vbH3jggSG3\n/cMf/uBRFPl73/veiuWXXXaZm5n/6Ec/qli+ZMkSf/LJJ319Oo+ou/vAwIDPnTvXt9tuu4o5OB+6\n/yGPoshP/fCp7u7ev6zf+5dWzmtaT39/vz/33HJfuHC159NpU3t7E3/22eX+l78sr7vfunXrfM2a\nNe59fe5Ll/r65S/70nVLfenapX7I/EM8jmN//M47PWt0JNff09PjU6ZM8blz5/rKlSsrtr/wwgvd\nzPzSSy+tWH7++ee7mfmHP/zhYa95JPf2kUce8SiK/PTTT69oQ/OgynhA86Dqo48+G/lj7lV1/CcZ\nMzsL+DowFfilux9dtX4m8AAwG/gmsAj4IHAocIq7X1W1/aeAS4DbgOuAVwN/DzwP7Ovu60fbdrqP\nT/Z7LiIbx1//+leWLVvGnnvu2dD2a9asYY899mDhwoWcffbZvOlNbxq0zTve8Y6K+UM/+clPcsUV\nV3DMMcdw+OGH8+STT3L55Zdz0EEHccstt1Tse/LJJ3PNNddw6623cuihhxaX/+xnP+N973sfe+yx\nB6dclMy8AAAZvElEQVSddhqrV6/m0ksvJbaYe267h2132ZaBZQNg0DKz9tQwV111FaeccgrnnXce\nX/ziF1m0aDXuMVtvPZ2WFujtTXjhhVW0tRnbbNNVs41HHnmEQw89lOPe+17mvfrVTJvZxcJXXuTn\nP/05f37mz5zz8TP55vlfhZkzi1nUkVz/RRddxOc+9zm23357Tj/9dLq7u7nrrru47rrr2HHHHXno\noYeKc6F+5zvf4eyzz2bbbbflq1/96qDqxVtuuSWHHXbY6O9tHPPggw8W52AFuPXWW9l3332HrSYs\nMhJmhrs3NomxiMhYmOgIeUM+wDbAKuAcQgb1v2tsc1G67siyZRFwL7AUmFK2fDawDrgHQvCeLn9X\n2sbnR9t22XoXEWnESDOoCxYscDPzKIrczAZ9oijy22+/vWKfQqHgl1xyib/2ta/1trY232abbfzc\nc8/1devWDWr/5JNPrtmGu/svf/lL33///b2zs9O7u7v9uGOP86cefMr7l/d7Uki8f2m/9y+vn0HN\nspZXXnml5/N5X7hwmT/33ErvT3dZty7vzz673F94YWXdNpYuXepnnXWW77H77j6zu9tbWlp8zpw5\nftjfHObX/PgaX/fiIvelS0d9/e7u119/vR900EE+bdo0b2lp8de85jV+1lln+dKqdrN7Ve//i7e8\n5S2jv7fHHefPPffcoO2UQZXxgDKo+uijz0b+TOoMqpn9gpDhfCOQp3YGdRGw3t3nVS3/EKFr7vvc\n/afpstOAfwVOdPcfVW3/LNDn7ruVLWu47bJ1PpnvuYhsPCPNoDabgeUD4BB3xRRWFiCGlq7aGdS/\n/du/5YknnuCPf/wjURSxaNEKBgYitt66i7Y2WLeuwIsvrmbKlJgtt6w/7Q0AhQKsXMkACas7yqr9\nru6lo7UjZFA3QcqgynhQBlVENrZJW8XXzI4lZDbPdPekzjZbEcaI3lNj9b3p9xvLlmX94e6us/0u\nZtY5yrZFRDYvxTK6VT9Xyefz3HrrrVx44YXEcVwskhR+k5o2kVb0tUb+mZwVSao6oJk12ICIiIhM\nlElZxdfMZgCXAf/P3e8bYtOstOPgGv2lZeU1+ucCPsT2lm7z7CjaFhHZvERAAp7NZ1onNszlcqxY\nsaJiWRyXTzVjZD1PokZ+rVo1zUzaUCNTsIqIiMgEm7AANQ0yPzWCXb7t7tm/YC5Kvz8/zD7ZDOaD\nZzmH3qptin9290a2H2nbIiIjEkURSVKzg8ikYJHheDGD2sgcqMV9000LhQSIyW5DdbGhoRqw6uEU\nm3gGNUmSxu+PiIhIk5rIDGo38GVCxnK4N6oTxnSuMLODgdOAD7n76mH2yyruttVY1161TfHPZtZW\nI0it3n6kbRd95StfKf55/vz5Dc01KCKbn6lTp/LUU09N9GmMXvo3ezGDOoJBJXEc0q9ZYFrq4tt4\ngBq5hQlUQ3/hsG9DKdjJp7e3l3w+T3t7+/Abiwzhtttu47bbbpvo0xCRzdiEBajuvpDRjYG9AngU\nuM/MdqpaN8XMdgRWuvsyYHG6vFZX22xZeRfdxYR/Um0NPFdj+6SszZG2XVQeoIqI1DNjxgziOOaZ\nZ55hp512mnTZsSyD6snIC8NFUbjWLIM6oi6+UMyURg6JEQLUEZ/F5FAoFHj88ceZO3cu0SYagMvG\nU/2L8/PPP3/iTkZENkuTcQzqtsAM4Jka696SLr8C+KS7LzGzF4ADamy7f/r9QNmy+4DTgTczOEDd\nH3jK03lQR9G2iMiI7bfffjz44IMsWLCAadOmTaoApNBbIOktdVG2ViPX2dhrZ9WqdaxcmWfatE5m\nzmxh+fJe1qzpo7u7henTGxg9sWYNFAqsaknwOIKBAaYOGLm2DtiEqtwWCgVWr17NFltswW677Tb8\nDiIiIk1u0k0zY2ZHAdXzFBjwU0JAeCHwrLs/lm5/EfBp4Gh3/2W6LCZU6t0R2Nbd16XLZwPPA38A\n3pxVB06P+Qvgi+7+9bJzabjtsn00zYyIjFhPTw/r1q1jMv39UegpkF+VL/4cT4nJTWssQF2+fBWL\nFvXS3T2dV7+6g+efX8uqVevYZptOZs6c1kgD0N/P0raEfEsEPT3MHmgh1zkVurpGe0lNJ4oipk+f\nTktL7el7RDaUppkRkY1t0gWo9ZhZQu15UGcCDwKzgG8Suua+HzgEOM3df1C1/d8DFwO3Af9B6K57\nLiFwfVOWQR1N2+k+ClBFZLOQ9CUMLBso/hxPj8lNbSxAXblyFc8910NX13R22KGT555by8qVa9lh\nhyl0dTUQoK5YAT09LGt3+loMW9/DnIFW4qnTNqkAVWS8KUAVkY1tMnbxHRF3X25mBxIyq58ApgJP\nACe4+09rbP9NM1tGqDD8bWAVIVD9XHlwOpq2RUQ2K3HljyMZQxvHEWZQSAssZUWSQvGkBpSNQQVK\nRZIm2TheERGRzc0mE6C6e91/tbj7YuCkEbR1NXB1g9uOqG0Rkc2FRVXB4AhiQzMjisLUKUlSClSj\n6jbrqZ4L1T1MczOJxvCKiIhsjvSmFhGRcWGRVQalIwhQoygiisDdSZKQQQ2zxDQ+zQwogyoiIjLZ\nKEAVEZFxU55FHZRRHWo/M8xCBrVQCIFqiC9HlkGNilOwWtZww+cgIiIiG58CVBERGT/lb5kRZlDN\nHHcnnx99gGppgGrZXKwKUEVERJqaAlQRERk3FpcFhKMYg+ruo8ugVnXxtarlIiIi0pwUoIqIyPjZ\ngAxqeYAalo2ii2960CyTqiJJIiIizU1vahERGTejHYOaBajlY1DBR5xBjdMANbaoYrmIiIg0p01m\nmhkREWk+G9rFtzxAHU0GNWcxr+rsJu5dAQN5BagiIiJNTgGqiIiMn7J+Og0Hl9QegzqiADXbLklo\niVtAVXxFREQmBXXxFRGRcVPs1juKuDBOs69JkpAkyaiq+OLp4NMkSc9DAaqIiEgzU4AqIiLjJw5f\nIxl/msnlwivK3UdexRdIU7ClDyhAFRERaXIKUEVEZNxYbBCB5UYeGEZpUFtIy/jG8QjbyILR8gBV\nVXxFRESamsagiojIuDEzWrdoHVnmMxUyqIVigBqNNAsbRVAohO697sqeioiITAL6VbKIiIyr0QSn\nEAJSs2yKmVEEqNlxs4lUFaCKiIg0PQWoIiLSlLK5UEfdxTfrzqsAVUREZNJQgCoiIk0pC1CTtAKv\nMqgiIiKbPgWoIiLSlMwMM9+wMaigKWZEREQmEQWoIiLSlKozqKOu4ptlUFXBV0REpOnpbS0iIk3J\nzDasi6/GoIqIiEw6ClBFRKQpRVGE2RiMQVUXXxERkUlDAaqIiDSlLIOaUQZVRERk06cAVUREmlI2\nBhVCbDnqDGq9n0VERKTpKEAVEZGmlFXxDX8OP49IdVEkBagiIiJNTwGqiIg0peoM6gYHqKriKyIi\n0vT0thYRkaYURRFxHP4cx6MIUNXFV0REZNLJTfQJiIiI1JPLGTNmJORyIWAdEXXxFRERmXQUoIqI\nSNOKooiOjlCFVxlUERGRTZ+6+IqISNMqD0pHHKBCZRZVAaqIiEjTU4AqIiJNq7xb76gC1PJ9FKCK\niIg0PQWoIiLStMY0g6oqviIiIk1Pb2sREWlayqCKiIhsXhSgiohI09IYVBERkc2LAlQREWlaG5xB\nVYAqIiIyqShAFRGRpqUuviIiIpsXBagiItK0xqyLr5kCVBERkUlAAapMKrfddttEn8KkpXu3YXT/\nNsxo71+WQR1VcBp2rPyepPT8jZ7unYjI5KIAVSYV/UNj9HTvNozu34YZ7f3LAtNRB6jlGdRJTM/f\n6OneiYhMLgpQRUSkaSmDKiIisnlRgCoiIk0rC1DLiyWNsIHwrQBVRERkUjB3n+hz2KyYmW64iIiI\nTBrurt/wiMhGowBVREREREREmoK6+IqIiIiIiEhTUIAqIiIiIiIiTUEBqoiIiIiIiDQFBagbgZlF\nZvYpM/uTmfWY2V/M7GIz65zoc5vMzGyhmSV1PjMn+vyahZl91Mx+lD5/BTNLhtl+rpldY2avmNl6\nM7vfzI7dWOfbbEZy/8zs5CGeycs35nlPNDPb2sw+b2a3m9liM1trZo+b2UX1/vvUs1cy0vunZ6+S\nmb3KzH5gZo+Z2bL03ftnM7vWzN5QZx89f6mR3j89fyIylnITfQKbiUuBs4GfA/8MvA74JLCXmR3m\nqlQ1Wg48CXytxrq1G/lcmtnngJnAw0AnsHW9DdN/+N4JzAa+CSwCPgj8xMxOcferxv1sm0/D96/M\n1wjPZrmnxvi8mt1RwHnAL4EbgDXAfsA5wAlm9iZ3fynbWM/eICO6f2X07AXdwM7Ar4HngR5gHnAK\ncJyZzXf3e7KN9fwNMqL7V0bPn4hsOHfXZxw/wG5AAvy0avlZ6fL3T/Q5TtYPsBC4ZaLPo9k/wLZl\nf/4lUBhi24vS5/LIsmURcC+wFJgy0dfT5Pfv5PT+HTLR5z3RH8Iv4ubUWH5qeo/+uWq5nr0Nu396\n9hq7r29M79NVVcv1/G3Y/dPzp48++ozZR118x9/70+9vVS3/N2A98KGNezqbHDOz2MymT/SJNCt3\n/8sINv8A8Ky731i2fwJcTsgiHjHGp9f0Rnj/MmZm08ysdcxPaJJw9z+6+8s1Vv0k/d6tarmevTKj\nuH+Zzf7ZG0b233N/1XI9f42pd/8yev5EZIMpQB1/bwIKwH3lC929D3g0XS+jtx8h0F9pZivM7Coz\n22qiT2oySu/bXKBWt6170+83brwzmtT+G1gF9JjZI2b2wYk+oSayTfpd3r1Xz17jBt2/Knr2yphZ\nzsxmm9lWZnYwcD2wHPh22TZ6/upo5P5V0fMnIhtMY1DH31xgqbsP1Fj3AnCAmeXcPb+Rz2tT8Djw\ne8J4lxbgLcBpwNvMbF93XzKRJzcJzU2/X6ixLlvWyPjLzdk64EfALcDLwA7AJ4BrzWxHd79gIk+u\nSZyffl9dtkzPXuNq3T/Qs1fPOwlBU+ZZYL67P1G2TM9ffY3cP9DzJyJjSAHq+OsE+uqs6y3bZvXG\nOZ3mYmYzgE+NYJdvu/sKAHd/V9W6n5jZHYSX5PnAGWNzlhNvQ+7TCGRVpWs9r71V20wqG+n+4e4/\nBX5adezvAQ8AXzSzq939+ZG2O5HG8t6Z2bnAscD33P22slV69kpGc/82yWcPxuT+3Q0cBnQQukWf\nDdxqZke4+/3pNnr+SkZz/zbZ509EJoYC1PG3nlAVsJZ2QiXa9RvvdJpON/Blwn2wYbZ14BqgbuDg\n7teb2deBI8fsDJvDmN6nOrLnsK3GuvaqbSabjXH/ajfm3m9mFwNXAe8gjD+fTMbk3pnZaYRCNL8k\nFIkrp2cvGO39q93Y5H/2YAPvn7svI2T1AG40s2uBx4ArgT3S5Xr+gtHev9qNbRrPn4hMAAWo428x\nsIuZtdTo5rs1ofvvZtu9190XMvZjoRcCB4xxmxNqnO5TtcXpd62ubNmyWl3gmt5Gun9DyTIHsybw\nHEZlLO6dmZ0C/Cthyor3unuhahM9e0No4P4NZdI+ezD2/+26+xIz+y1wvJnNcPdV6PkbSXu17t9Q\nJvXzJyITQ0WSxt99QEwo5lNkZu3AnoTuLzK2dqJ+ARGpIx2z+wK1g/v90289r6Ozc/q92T2XaXB1\nJfB/wHtqjcfXs1dfI/dvGJvtszeEDkK2MAE9f6NQcf+GoedPREZMAer4+zHhL/JzqpafTvhL/kcb\n/Yw2AWbWXWf5Jwi/8f6fjXtGm4zrgR3NrDi+18xiwrijFcCvJurEJgMzG5QlSMeAfZYwvu03G/2k\nJpCZnUzo1ncz8G53rzc1BejZG2Qk90/PXiUzm1Nn+euAtwEPuvuaslV6/sqM9P7p+RORsWTuPtHn\nsMkzs8sIY4ZuAP4X2JXw0rvT3d86kec2WZnZOYQJ6/+X0IUoB8wH3k2oMnhAOnZms2dmR1EaK/Qh\nYB7wJcJ4pBXu/p2ybWcCDxK6Y32T0PXt/cAhwGnu/oONeOpNYYT3bzFwG6HC9MvA9sApwBbAue5e\nPR/yJsvMjib8nbcK+AdKxWYya9z9F2Xb69krM4r7p2evjJl9i1Dc50bCO8KA1wMnEjJ/bysv8qPn\nr9Io7p+ePxEZMwpQNwIziwgZ1DMIf2m/QsisftndJ2vhhQllZm8m/GZ2T+BVhJfnc8AvgAvdfbOs\nilyLmf0A+HD6Y/YffFYsY6G771C1/VzgQuBwYCrwBPBPaZXGzc5I7l9aEGQ+4b/z6cBKQjf/b7v7\nTRvjfJuFmZ0HnEf94ix69oYw0vunZ6+Smb0NOJMwf+kcQo+xvwK/BS5y9wU19tHzlxrp/dPzJyJj\nSQGqiIiIiIiINAWNQRUREREREZGmoABVREREREREmoICVBEREREREWkKClBFRERERESkKShAFRER\nERERkaagAFVERERERESaggJUERERERERaQoKUEVERERERKQpKEAVkU2Smc03s8TMPjzR51JtPM/N\nzG4zswUTfR6NGsn5ioiIyKYvN9EnICLSCDNLRrD59mV/9jE+lbE0Xuc20nYn+h5N9PFFRESkSShA\nFZHJ4kNVPx8CnAF8D/hd1bqlwA4b46REREREZOwoQBWRScHdryv/2cxaCQHq3dXr0vUbfEwzm+bu\naza4IRERERFpiMagisimzszsI2b2hJn1mtlCM/tMjY0WmtmtZraXmf3GzFYCj5at39nMrjWzJWbW\nZ2YLzOwiM+usaufVZvZ9M3s+Pd5LZnaXmZ002nNLN3xP2s5aM1tjZnea2dEjuAnvNrOHzazHzP5i\nZhcALQ3u+0/pWNU31Fg3I23zhrJl7zOz/y67B6+Y2Q219q9zvIVmdmuN5TXHzJpZm5l9Ib2PPWa2\nIj3+no0cT0RERJqHMqgisqk7E9gCuBJYCZwI/JOZLXL368u2c2Bb4LfAT4CfAlMBzGwf4BZgOfBd\n4AVgT+CTwIFmdqi7580sB9wEzAW+AzwNzAD2AA4CrhnNuZnZx4ErgCeB8wEDTgb+y8w+6u7/NtQN\nMLNjgP8Enkv3LwAfAd41zL3LXAV8Bjgp/S53PNCWbpP5BKGb9feAF4GdCNnuu8xsb3d/dpjjOUOP\nSy2uM7MW4NfAAYT7exnQBZyeHu8Qd39wmOOJiIhIk1CAKiKbulcDu2Zddc3sB8DzwNlAeYBqwGuA\n09z9+1VtfJ8QlL7J3dcVdzD7LfBz4IPA1cDrgHnAP7j7xWNxbmbWDVwEPAvs5+5r0+XfBR4GLjGz\nn7j7qloHMLMY+DYhYNzX3Zeny78HPNbAOeLuT5rZA8AHzOyz7l5esOqktO0by5b9jbv3VJ3HNcAj\nwKcIAexQRtI/+yzg0PSYN5Ud71+Ax4GLgbeMoD0RERGZQOriKyKbuh+UjyNNA6d7gZ1rbLsM+EH5\ngrRb6hsIAWOHmc3OPsBdwHrgHenmWZD4VjN71Rid29uBTuCyLDhNt11DyBZOBQ4b4hj7ANukx1pe\ntv9q4P81cI6Zq4Gt0vMBwMxeA7wZuN7d81XXgQXT03u1lJBR3ncEx2zEhwiZ5Yeq/r9pA24GDjKz\ntjE+poiIiIwTBagisql7rsayZcCsGsv/7O7VXUt3Tb/PB16u+rxECB7nALj788DXCAHrEjN7IB2/\n+cYNOLfXpN9P1Nj2j1Xb1JJVM/5TjXVPDrFfteuBfkLGNHMSIdtZ0XU5Hcf7S2A1oetydr9eD3SP\n4JiN2DX9vMLg/38+QnjPzR7jY4qIiMg4URdfEdnUFUaw7foay7LuphcTxjrWsiL7g7t/ycy+DxwJ\nHAycBnzGzC5y989twLlNKHdfbma/At5jZlPSrs4nAn8sH+NpZtsCdxAC0wuAp4CsW/S3gCmNHK7O\n8lrvLCN0Vf77Idpb2sAxRUREpAkoQBURGdrT6Xfi7rc0soO7LyAUNboi7V76G+AfzOxidx9psPTn\n9Pv1QHVl29el37UysdX771pj3etqLBvK1cB7gOPN7GlCdvazVdscQwhC3+Xut5evSLve9jC85dTO\ncNea2/ZpQgb71hrZbxEREZlk1MVXRDZXDQUz7v4wodjOmemYywpmlksLGZGOt2yp2r+PUvfaRru3\nlp/bTYQM5NlmNrXsuNMIxZTWpNvU8yCwCPiImRWDPjObTqgiPBI3ErKRJ6WfBPhh1TZZVrji/WJm\npxMqFjfiKWAXM5tbtn8btYsrXQNsSZ0Mqpk1ekwRERFpAsqgisjmaiSVYk8kTDPzWNp994+Esac7\nETKGnyMESm8F/tXMfkbI7K0lFCk6FbjH3Z8Z6bm5+yoz+wfCtDX3mtlVlKaZ2QH4aHmhpRr7J2b2\nKcLUOfeZ2b8RgshTCMHmqxs8J9KpdK4nVM7dB7jJ3ZdUbfYr4ELgWjO7gtDV90DgcEI2t1433XJX\nACcAN6fVhlsJxZBqdcH+NqFw0z+b2VsJWebVhCmD3kbI2L610WsUERGRiaUAVUQmq+HmymSI9bX2\nrduWuz9qZnsBnweOJmQe1wALCFV/f5tu+ghhvtH5hKlnYsK0MV8DLhntubn7d81sCWEO0vPKjnWM\nu/93A/v/p5kdC3wZ+AqhuNNVwO+A/6t33XVcTcjcTmHwvK64+3NmdjjwdeALhGD4TuAQQpC9XQPn\n+3szOznd/yJCBvi7hGzwb6u2zZvZkcDHCb9I+Eq66gXgvvR8RUREZJIwDdkRERERERGRZqAxqCIi\nIiIiItIUFKCKiIiIiIhIU1CAKiIiIiIiIk1BAaqIiIiIiIg0BQWoIiIiIiIi0hQUoIqIiIiIiEhT\nUIAqIiIiIiIiTUEBqoiIiIiIiDQFBagiIiIiIiLSFBSgioiIiIiISFP4//A1+Rq1cAAuAAAAAElF\nTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f0edcef7050>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"from IPython.html.widgets import interact #import interactive tools\n",
"\n",
"#setting plotting visual parameters\n",
"pylab.rcParams['figure.figsize'] = (10.0, 8.0)\n",
"pylab.rcParams.update({'font.size': 18})\n",
"\n",
"#define function to use in ipyton interact widget\n",
"def plot_explorer(plotnr, ylim_pos=5000, ylim_neg=-5000, local_extrema='True'):\n",
" \n",
" # plots all data\n",
" for z in redshifts:\n",
" \n",
" V3 = data_dict[z]['CV3']\n",
" thresholds = data_dict[z]['thresholds']\n",
" plt.plot(thresholds, V3, linewidth=2, alpha=0.1)\n",
" plt.xlabel('Threshold value')\n",
" plt.ylabel('V3')\n",
" plt.ylim(ylim_neg, ylim_pos)\n",
" plt.xlim(0,-35)\n",
" \n",
" #selects redshift to highligt from plotnr parameter\n",
" z = redshifts[plotnr]\n",
" V3 = data_dict[z]['CV3']\n",
" thresholds = data_dict[z]['thresholds']\n",
" #plots highlighted redshift curve and annotates it\n",
" \n",
" plt.plot(thresholds, V3, linewidth=2, alpha=1, color='red')\n",
" plt.title(str(plotname))\n",
" plt.xlabel('Threshold value')\n",
" plt.ylabel('V3')\n",
" plt.annotate('$z = ' + str(z) + '$', xy=(thresholds[20], V3[20]),\n",
" xytext=(0.5, 0.1), textcoords='axes fraction',\n",
" arrowprops=dict(facecolor='black', shrink=0.05, width=0.5, headwidth =10),\n",
" horizontalalignment='right', verticalalignment='top',\n",
" )\n",
" \n",
" if local_extrema == 'True':\n",
" \n",
" V3_maximums = argrelmax(V3)[0]\n",
" V3_minimums = argrelmin(V3)[0]\n",
"\n",
" for maximum in V3_maximums:\n",
" plt.annotate(str(thresholds[maximum]) + ' , ' + str(round(V3[maximum])), xy=(thresholds[maximum],V3[maximum]), xytext=(-20,20), \n",
" textcoords='offset points', ha='center', va='bottom',\n",
" bbox=dict(boxstyle='round,pad=0.2', fc='white', alpha=0.3),\n",
" arrowprops=dict(arrowstyle='->', connectionstyle='arc3,rad=0.5', \n",
" color='black'))\n",
"\n",
" for minimum in V3_minimums:\n",
" plt.annotate(str(thresholds[minimum]) + ' , ' + str(round(V3[minimum])), xy=(thresholds[minimum],V3[minimum]), xytext=(20,-40), \n",
" textcoords='offset points', ha='center', va='bottom',\n",
" bbox=dict(boxstyle='round,pad=0.2', fc='white', alpha=0.3),\n",
" arrowprops=dict(arrowstyle='->', connectionstyle='arc3,rad=0.5', \n",
" color='black'))\n",
" \n",
" plt.savefig('V3_threshold.png')\n",
" \n",
"interact(plot_explorer, plotnr=(0,len(redshifts) - 1,1), ylim_pos = (0,5*10**6,1000), ylim_neg = (-5*10**6,0,1000), local_extrema=['True', 'False'])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### V3 as function of global ionization fraction $x_{glob}$"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"collapsed": false,
"scrolled": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAp0AAAIOCAYAAAD6J7bTAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXmYFNXV/7+nuns2hkUYRRZRXHBXXNAkvjGoWQwmkSju\nRH0Tt18iBo1ZzSu4ZBFNNKIR40aMwahJfBN9iRqjuCsoJi6oiIDLgMgMMzDMTE8vdX5/3Kqe6urq\ndbpnYb6f5+mnZu5Wt9b+9jn3niuqCkIIIYQQQiqJ1dcdIIQQQggh2z4UnYQQQgghpOJQdBJCCCGE\nkIpD0UkIIYQQQioORSchhBBCCKk4FJ2EEEIIIaTiUHQOUkRkFxGxRWRNkfUWOvXOqlTftjVEZIlz\nzj7XR/sfIiJXi8hKEYmKyMcicr+I7N8X/SG9j4isde7BCUXWO1JEfioifxORdU4btojUFVB3FxG5\nS0QanftujYj8RkRGln4klaM/vNtExBKRk0TkGhF5QkQ2O31aVmD9z4nIP0SkWUTaReQ/IvI9EQlV\nuu/bGu693gv7OdvZ111F1OnT75SeQNFJUoFaixSiDPBaOOr59CoiMhzA8wB+AqAawIMA3gMwA8Ay\nETm6t/tEyksRX1ql3H83ArgSwFcBjC60HRE5EMC/AZwFYAOAvwKIAZgFYLmIjCmhL71FX77bhgG4\nD8D3AUwFUO+kF3LOvwngSQCfB/AqgIcBjANwLYCHKTxLojfvhWL31SffKT2FopN4Ud+WlIczAewN\noCBrRZm5FsD+AP4BYA9VPU1VjwDw3wCqACwSkSF90C9Sfirx3D4G4H8AfBnAjoVUcMTNvTACao6q\nHqyqpwPYC8BdACYAuL0Cfd0WiAG4B8BsAP8FI/bzIiK7ALgFQBzAF1X186p6CoDdYcT/lwBcUoH+\nkr5D+roDpUDRSbwMyJu4v6OqH6rqSlXt7M39ikgDjLiMAzhXVWOePv0ewKMAdnDKkIFP2Z9fVf2B\nqv5MVR9V1Y0FVvsqjMBcoapXedpSABcCaAHwZRHZr9z9HeioaoeqnqmqN6rq8wA6Cqw6G0AEwB2q\n+qSnvVYA/8/591IR4Xc+6VN4A27jiMjBIvKwiLSKSJuIvCAiMwLKzQWw2vnXdbPbudztTtsPecYP\nvSAiJ+Xoyw4i8ivP2MIWEXlKRL7hK1cjIm84+74woJ3xzj4TpbqHvWNiROTTIvKIc446ROSZXO2K\nyEQR+Z0zTq5LRJqc+sfl25cvfYQzXu4/zrnoEJEPROQxETk3S1tHiMgDzvi6mIisF5H7HHemn2kA\nQgCeVdV1Afl/crbHZzvWXIjIXN99EvR5MqDe/iJypzPGL+qcv5dF5EoJGO8nIsc752STU361iNwi\nAeMTvUNERCQsIj8RkTdFpFNEXvX1e46I7CYi9zjnMSEi3y3hPBR8HX373tnZ9wbP8/NFT9kZIvK8\n89y2iMi94nNLi8gSAHc6/57lO/dB7nYRkWnOPd4mIlvEjAE8qNjjzsHXnO19/gznh9ffnX9Luu9c\nRKRKRC50zlGrc41XOPdRfY46P5Hud9BHIrJARLbPs6/hYt5d7zv13hORn4tIXbbn26lnichMMeMz\nN3nq3iAiO/Tk+H245/xef4aqvgTgAwDbA/h0T3Yi5h3+cxF5TUS2OvfPW87zuG9A+QNE5I9ixvV2\niRlP/lcR+UyW9t2xxzuLyNeda7tVRDaKyN0iMtopN0REfumcS/ecfj9Lm953/THSPVa2zfn7qJ6c\nE89+vO+ekHOfveP0b10h91lAm4c7x94lImeUo599jqrys41+ABwDIArABvAfAH+EGd9nA7jB2a52\nyh4P4AEnrQ3mi8z9zPO0udApc4vT9ltOu08CSDh5Pw7oyyQAjU7++zAvx/8D0Omk3eMrvw+Adif/\nAE96CMDTTp2re3BuljhtzINxaS0FsMg5T7aT9tmAep8BsNkp87Zz7E/AWBNtAD/Psq8kgCM9aUOc\nc2c75+VBZ/9PAdgEYyXyt/NDp3wcwAswonGZkxYF8BVf+evdY8xyDvZz8j8p8Rwe77tPvJ+3nbb/\n6avz3865tQGscO6DvwN4x3+OnPLXeq7H4875fsdJ2wTgMF/5XTz32MMwlqLFzn7+4pSZ65T5I4zV\nba2nH+cUeQ6Kuo6efd8FYKNzLIsAvOg5zqMA/MC5zv8CcD+6n503AVT57olnnLyVvmvwTU+5tU6Z\nX8A8p085989KdD/zexRwvLZznepylHnVKTctS/4sJ/+BHjy/I9D9LtsI4BGYcaMfOWmvA9jOVycE\nM8zEBrAFwN9g3nkbYcY5/6+Td6av3jB0vxc2OnX+F+Y98DyAZ508/70b8bS52bmWDwBY5aR9CGBi\nnuOc6pRdmqPM8HzXBcBfnDLf6cE5PwRmfK4NYL1zvu8D8LJzr17uK38CgC6n/HKYYQPuNUsAuCBg\nH2ud47jOafNx5/53r+ubzrV/BcAnzvl81LOf/wloc4mT9xtnv684fXGfuSSAM7Ld60Wcn12cOmth\n3gOdMN9xfwKwzslbA2CMr97ZTt6dvvSvwHwHbgbw+SzHdGSh/esvnz7vAD8VurBAnedG/5Evbwa6\nBeJqT/rO/rSAdhc6ZWwA1/ryjnYetASAyb48VxzdCSDsSZ/keaFc4KtzLrrFSa2TdqWT9iwAqwfn\nx31okwBO9uXd6OT9y5deA/NFYQO4ypf3aZgvMhvAsVn25RWdZzlpf/MfB8xYy//ypR3neWn5z+1X\nYMRKCzxftDBfCjaAWVnOwXbI82VV4rn9lHMftMMjCgEc7twbnQBODah3MIBxvuNyxeWhnnQBcA26\nX/BeEbaL5/58D8CEgP3M9ZS5FUCoB8da7HX07nueL+9qT79bARzuyRvuPAdBosjtw505+rnWKdMB\nz48pAGHPfXJHAcdbiOjc5JTZP0v+15FHSBXQj/udNv4AoN6TXg0j6G0Av/fVme2kv+u7z4ahW7gH\nnV/3ffAMgKGe9B0AvOGp5xed85z0RwHs4Lt/3Wv9VJ7jnJrvXAE4wCnTnKPMb4LuuSLO91B0//C5\nFp53uJM/HsDBnv/HwLwPkzBDe7xlp8MIypj/HvHcp22++3+Y51yvhPmhP8ST/0V0/5io87W5xHON\nZvnyzvDszy8GSxWd7g/QPTx5NTDvCBvOj19P3tnwPb8AzoF5V66D733vOyaKTn76xwdm8ooN4LUs\n+X9GpujcxZ8WUG8hui1J4YD83zr5t3vSjkS3lWBIQB33S/PdgLw/ue05L+AkgGYAO/Xw/LgP7aKA\nvFFOXic8gsRzTjOskE7+HARb9zJeEDCzU20AFxXY36XOsX8uS777pTLLk/aYk/bNLHUi7osVwOgy\n3XcTYawhCQAn+PLcl+5PC2zrCad8kOU8BCMebHisFEh/8Z+cpd25Tv4n6KHYLuE6uvte5X9+0G2x\nsgFcGVD3IgSIQ2SxlPjKrHXKBFniD3Hy3iug/4WIzphTZtcs+V9w2nmrxHO+r1P/bQCRgPxaGEtc\nDOk/wlY79WYE1Nnf6XOa6IT58d7u5AV9+R/rOSfe53sUzPujCT6Lq5Mv6LYIB4pzp9xU5Bedn3HK\nfJCjzM+cMreUeM4vRsC7LUf5y53yj2bJd38Y3JblPs11/8cRYJX3nE+/+F/ipL+QpS+LEfBecq9r\nEedoF8/zG2TFHe/ckwl4fgz7n190vyPeBrBLln25xzTgRCfHdG67fM7ZZozxcfhDD9v/s6omAtLv\ncbaf9aQd6WwfVNX2LHUSAHYVkbG+vPNgrHvfhBEtgPnl/GFp3c7gH/4EVW2GsRpWAWjwZLnHcY+/\njsOdzvYzIpJvUoc7k/2HInKamNBGgYiZEHQogCZVfSpLsWec7eF59lsxRGQEjDtpexih+FdPXggm\nlIsCuKOAtsIwX6YK4Pf+fFVNArjb+fdIf75T728B6V4eV9VCJ2pko+Dr6GOJ//lR1c0wVkKF+cHg\nZ7Wz9T8jxZBxv8NYjnrabm9yrLP9u6rG/Zlqxo2+AmPFPRQARGQnGFEQVdU/B9R5HcYl7+cQGBH7\nrqr+O6DeIzBWaT9TYayuT6hqS0A9BfCc8++nAur3N9xzfmfOUt24z2TGs+trJ+jZBXLf/++r6rsB\n+e8522zhuBZlSQ/6zuoJCjN0Jz1R9SMYsWjBRCbwExaR22AE+0sAPqOqa8vUp34DRee2yzhnuzZL\n/vs9bD9fu+MD+rImqIIjID5w/h3ry9sCIzgB4+K5wytmykA28drmbKs9aTmPA8alEodxpYzKtVNV\nXQIzvm4HmBdUs5jJUzeJiP/lN9HZbi9ZJuzAuBsBI/hctjrbbCGRvJMt2rKUKQgRicCMG9sLxnpx\nra9IA8yXd7uqri+gyVEwoj+mwZOggO7rMC4g7xNV7cqzj54+A8VeRy8fZUnfmiPfzasOyCsERcD9\nrqruta8qsV0/hd53pd5zuzrbS3M8D9OcMu6PRvceyfVjdW1Amlsv173yATIjB7h9nJGjj9/29bFU\n8p1voOfnfIKzfafA8vnelbmeXUXu+z/fs5Pt+VibJT3oO6sntHqeqWz7CjruUwF8C0ZcH6Wqm8rU\nn35FuK87QIiHbNZB76y9g0QkEmThKBG7TO0UjapeJiK/gwkxczTMr99vA/i2iNytqmc7Rd2gzpvQ\nPfM3G297/nZfcDtlKeu+ZDeVweK3AGYCzD/RHaLFi/aw/WIpJDxVWUJYFXEdveS77yp1X/bG/f4+\ngANh7rsg6+F4T7lScJ+Hl2AmceXrSznIdf8GnVO3j28if3zeN0vqUTfuMY4QkSFZvEk9Pee9/fzm\nuk/77J1dYZ6FMTDsCjNU68d9253KQNG57dLobHfJkp8tvVDytdvoSXN/me4WVMFxpU6AebE1+vJO\nhhlU/T6M++RoGMvSpSX0uae4fQs8DpgXewRGzBT0K1VV3wdwk/OBiHwBZhzrmSKySFUfQ7d1pl1V\nvxncUiDLne2hWfIPcbYZbsNiEJEfw8xKfwNmvFzQl0IzzHkZIiJjCrB2NsOMf6oSkfGOa8qPa01q\nDMjrVQq8joOF5TCi81CY8XJ+enrfuV6Rx1R1ToF13PtnJxERx73tZ5eANPfemhCQ57IzMkWZ28fl\nRT6zRaOqm0VkLUz/D4GJ7uGnHOd8LwB7ovu9kotGp+xuMJE2/PTFs7tLnvRy9WWEiAzNYu3Mta+1\nMPMbnoAZrlOlqt8rU5/6DXSvb7u4Y/9OzZIfFPPLDR5eyI+RGY5Y9HO6s/W++Ny/p0tw/LwznH2+\n5xUjYlbZ+B3MeM/Tnc8nAC4WkWMzm6k47jk9I8uYTTfI+nNZhFdeVPWfMG5qwExugKo2wgi6nUTk\nsCKaWwwzweEIEcnmzgFMWJeScH4U/AzAxwCOy+ZWcoZQPA5jzc77JeyMd3zOKX9mwH5DANz4rtnG\nufYZQdexghTz3PYGrjX+FH+GmDXbv4bCxtxm4xFne0IBY6cBpMbTrYUZ+nJCQL/2g5kF7ucVmHBk\ne4lIRr6IfAkmCoSff8EMtfmy9M6KX+65PM2fISKfghHNn8CELCqFR51toQLafSYznl2H//aV6w0y\nzo1D0HdWTxBPm92J5h3sTqp9NqiiM1fhczDjrC8Wkfll6lP/oa9nMvFTmQ/SQyb9wJd3AoJDJkVg\n4p11ARiRpd2F6J6hd40vbyqMNSsO4CBfXraQSXugO2TS+Z70MMwvZBvAZZ70L8EIqQ0AduzB+VmC\nHLP/0B0vzjvL0Bsy6Upf+cPRHSKkkJBJXwdwRMB+vaFxTvKkT0d3OJ2MPsOMx/sqgD196bc69RYj\nPbSQGzFgPUqcwY3u0Ehb4QlplKP84c690ek9Nk/+IQgOmdQC4BBPugVj7bZhxoZFPHm7+O/rgP3M\ndcpcnq/PBRxTsdcx576D7jvf82XDTE7xprtfZC/n6GfWdp38gmbquuUQEIXCd33edMr+jy/9Dif9\n4R6edzf+5SJ4whF58kcjM1SPOwN7JTJDJrmxf9Nmrzv5NznpTyEzZNLrnnr+WdNuLOTHEBCPEybe\n5PnIEbILBcxed8rtDCOOYwCO9qRvB2OZtAFc2oPz7Q2Z9Ev4ogbADKXwhkzaEd0h5M7xlf0azHug\nC8B+Pb3/PfkLs1y/JZ5r9B1f3mnoDpk0tpBnAmYC41sBbe3i2U8jgN09eTWee/ZBX72zkRkyaTS6\nQ0TdGtAH95gG3Oz1Pu8APxW8uGa2sBt8/TWYF7QbnNcNHL7aV8cNIrwGZmLE7QB+4cl3H2w3OPzb\nTrtPOi+LJDwi0VPPKy7fh3E9LkZ38Hp/cHhXVGS8YNAdMPyfAKTEc5PzoUV36I4JvvTPwMxWtZ0X\nzyIYq0bCOfafFbIvdH8hfQwzo/gemJnfbuD5p+H7MoIJz+P+WHgDJgDxvU7ZNif9i7463sDWH8AE\nc34O3SGhji723Hna/pfTzgrnvgj6/NBX51x0B9Jf4dwHD6E7SHm24PBuoOhF6A4O34zsweF7S3QW\ndR3z7TvbfefkTUWw6KxC9w/MZTAzhm8HcHYh7Tr52b5gz4EJou1+3C/VpZ60jBBYMO519zlZjvRA\n9Gvhi4lYwnkfjm6huNW5pxfBxBx1v6zX+eqEYCx2rshwg8M3IX9w+NecvI0w4eb+1zm+F9D9Tv2U\nr14E3aHpumDGoN7n7PMV555OwvNj0Kn3W8+5dX+4tPmuQ0bgfRjrYRLmHfFPz7HZzr1Zclxjp/0p\nMNZS98fqXz3HkvDf0zA/yNz3+ysw3yfuuycBj5GhJ/e/J39hluu3xEm/0Tk/y5G+IEMCwDeKeCbc\n9vzHuwu6729vcPj7kB4c3i9uz4ZPdDrpDTDDIVxjjQT0gaKTn/71gbEePQxjLdriPGinIEsgeAAj\nAdwGIwxj/jIw8dWSMG6TQ5yHahPMi/9FZImN6NTdHsCvYL58ojAv7af8DzyMWE7CvODHBrQTRnfc\nyh+VeF5ckZxNdK5B9l/cE2Hc/mthvkyaYFx+Xyl0XzBfyr+EcbM0Oi+oRpgv0nMQEH/QqXeQcw1W\nwwT6bkG3eDsNAVZLGKv31c5574QRSPfDZ2XowTl04xv6P0kE/2iYDBOy60PnPvjEuZ6XIzim4fEw\n1qJNTvk1MD96gq7NLkH3ta/MHKdv5RCdRV3HfPvOc999Dtl/iB0AI943ovsH0J2FtOvkZ/uCneO5\nltk+gfFBnWtxl+e8rIER6SN7et6d9kMwFvt/OsfdBfPlvhTmx8qnAupUAbjM8yx8BPO+2x6ed1tA\nveEw764PnHqrYRYoqIOJuZqEx7LlqzsdZsjBeuf+3QATU/JmAF/I81xl+2T00XOP/MN5VtphxPIl\n6KHg9LS/o3Nu34J5/7TCWLXnA9gry335R+e6uMf+V5hwQGW7/538wOsHj0CDiRH7JMyPwi0w4yeP\nKfKZcK9PNtG52rk3/wfmB3LUeQYWINgqfxYCRKeTtx3Mik9uiDjL14cBJzrFOQBCCCGEFIGI7Axj\nJW1T1aCxnaSPEZElMIJzqqqWa9xm0H52gRGca1V119ylBy+cSEQIIYTkQEQyIkA4E0PuhvkezbZg\nBCHEQ3+Z7UgIIYT0Vx4RkS4YV3IznLXGYRY8WAHjsieE5IGikwx4RORHMDHkCuFBVS01VMs2jYic\ng+Dl2YJ4RlXzLmc50OC91PuIyHUofFWe21T1ufzFys41MNEh9ocZ994FM4nyQQA3qOrWHHX7FSIy\nCmZ8aiEozKz35gp2qdIoej+4PckCx3T2MiLCE04IIYSQAYOqFhQTNx+0dPYBFPoDl7lz52Lu3Ll9\n3Q1SArx2Axtev4ELr93ApsA1GAqCE4kIIYQQQkjFoegkhBBCCCEVh6KTkCKYOnVqX3eBlAiv3cCG\n12/gwmtHXDiRqJcREeU5J4QQQshAQETKNpGIlk5CCCGEEFJxKDoJIYQQQkjFoegkhBBCCCEVh6KT\nEEIIIYRUHIpOQgghhBBScSg6CSGEEEJIxaHoJIQQQgghFYeikxBCCCGEVByKTkIIIYQQUnEoOgkh\nhBBCSMWh6CSEEEIIIRWHopMQQgghhFQcik5CCCGEEFJxKDoJIYQQQkjFoegkhBBCCCEVh6KTEEII\nIYRUHIpOQgghhBBScSg6CSGEEEJIxaHoJIQQQgghFYeikxBCCCGEVByKTkIIIYQQUnEoOgkhhBBC\nSMWh6CSEEEIIIRWHopMQQgghhFQcik5CCCGEEFJxKDoJIYQQQkjFoegkhBBCCCEVh6KTEEIIIYRU\nHIpOQgghhBBScSg6CSGEEEJIxaHoJIQQQgghFYeikxBCCCGEVJxtQnSKSJ2IrBYRW0TmB+TvKSL/\nKyKbRGSriDwtIkdlacsSkYtF5G0R6RSRD0TkOhGpy1K+4LYJIYQQQgYr24ToBHAlgAbnb/VmiMhu\nAJ4HcDiAawB8H0A9gEdF5JiAtq4H8CsAbwC4EMADAC4C8JCISA/bJoQQQggZlIiq5i/VjxGRgwG8\nBCP4fg3gJlW9yJN/P4CvAzhEVV9z0oYAeBNAVFX38pTdF8DrAP6iqid50i8EcCOAM1T13lLa9tTR\ngX7OCSGEEDI4EBGoquQvmZ8BbekUkRCA2wD8A8CDAflDAHwNwBJXFAKAqrYDuB3AJBGZ4qlymrO9\nwdfUbQA6AMzsQduEEEIIIYOWAS06AVwMYE8YN3iQCj8AQBWAFwLyXnK2h3rSpgBIAljqLaiqXQD+\n4+SX2jYhhBBCyKBlwIpOEZkI4AoAV6jqB1mKjXW2jQF5bto4X/kmVY1nKd8gIuES2yaEEEIIGbQM\nWNEJYAGAVTDjOLPhzjjvCsiL+sq4fweVDSpfbNuEEEIIIYOWcP4i/Q8RmQng8wA+q6rJHEU7nG11\nQF6Nr4z7d0NAWbe8esoX23aKuXPnpv6eOnUqpk6dmmWXhBBCCCG9x5IlS7BkyZKKtD3gRKeIVMNY\nN/8PwAYR2d3Jcl3ZI5xQRk0A1vnyvLhpXvf4OgB7iUgkwMU+Dsb1nvCULabtFF7RSQghhBDSX/Ab\nw6644oqytT0Q3eu1MNbIrwB4F8BK5/Okkz/TSf8WgNdg3N+fCWjnU872ZU/aUgAhmLibKUSkBsBk\nX9nXi2ybEEIIIWTQMuDidDoTeY6HLwg8gB0A/BYmfNIdAF5T1VVOLM0TABzsiaVZDxNLs9MXp3M/\nmFnqD6rqDE/6LAC/ATBTVRd50gtu21OHcToJIYQQMiAoZ5zOASc6syEiuwBYjczg8LvBWDDjMKsN\ntQE4F8C+AI5T1X/62rkRJgTTgzACdm8AswA8q6pH+8oW1bZTh6KTEEIIIQOCcorOATems1hU9T0R\nOQLALwH8CCa25isAjlXVJwKqzAawFsB5AI4DsBFmNaLLy9A2IYQQQsigZJuxdA4UaOkkhBBCyECB\ny2ASQgghhJABBUUnIYQQQgipOBSdhBBCCCGk4lB0EkIIIYSQikPRSQghhBBCKg5FJyGEEEIIqTgU\nnYQQQgghpOJQdBJCCCGEkIpD0UkIIYQQQioORSfp16gq4sl4X3eDEEIIIT2EopP0azZ3bcbGjo2I\nJWN93RVCCCGE9ACKTtKvSdiJtC0hhBBCBiYUnaRfk7STAABb7T7uCSGEEEJ6AkUn6de4YpOikxBC\nCBnYUHSSfoutNhSa+psQQgghAxeKTtJvcV3rAEUnIYQQMtCh6CT9Fq/QpOgkhBBCBjYUnaTfklRa\nOgkhhJBtBYpO0m+he50QQgjZdqDoJP0Wv6VTVfuwN4QQQgjpCRSdpN/it27S2kkIIYQMXCg6Sb/F\nda8LBABFJyGEEDKQoegklaUHLnHXvR62wgAoOgkhhJCBDEUnqRxbtgAffwwkSls33VYbAqHoJIQQ\nQrYBKDpJ5YjHjaUzFiu6qutat8RCyAoBoOgkhBBCBjIUnaRyuK71eLzoqq5rPWSFYIm5TSk6CSGE\nkIELRSepHK7oLMG97grMkFB0EkIIIdsCFJ2kcvRAdLru9XJZOjs6gA0bSjK6EkIIIaQMUHSSyuGK\nzmSy6FnsrnvdEislOr3B4oslGjXdaGnp0YR6QgghhJQIRSepHF51V6SJMWXpLJN73Wt0bW0tuRlC\nCCGElAhFJ6kctkckFuliT43pLJN73at/OzvNhxBCCCG9B0UnqQx+H3aRotPvXhdIj0Snq3+HDjXb\nzZuNu50QQgghvQNFJ6kMPRWdHvc6AIj0bClMtzt1dUBtrRGhLS0lNUUIIYSQEqDoJJXBVXmOWCxm\nTKeqQqHGwunUd8VnT0WnZQEjRgDhsIlZv2VLSc0RQgghpEgoOkllcFVeKGSEZxEz2L2udZeejuv0\namARYLvtzHbr1pIWTCKEEEJIkVB0ksrgNS2GzdrphbrY/a51oGeiU9V8XKMrAEQiQH29+ZuTiggh\nhJDKQ9FJKoPXtBiJmL8LdLF7Z6679FR0Akb/eqmqMltOKCKEEEIqD0UnqQxe0VmspVOzWzpdK2ip\nXfHiilCKTkIIIaTyUHSSytAT0WmXd0ynGy7JLzpDjqal6CSEEEIqD0UnqQxepee61wsUnb3lXrcs\n0z3b5tKYhBBCSKWh6CSVwWvpdGewJxIFqbtc7vWeiE6/pRPotnbapcedJ4QQQkgBUHSSyuBXekW4\n2IPc667Vs5zudYDjOgkhhJDegqKTVAa/T7sIk2Kl3Ou5LJ0UnYQQQkhloegklcGv9NxtHve6rTYU\nmuZaByozphOg6CSEEEJ6C4pOUhlKFJ1BrnUXSywoFFrkrJ9c7nWO6SSEEEJ6B4pOUhmyic486i41\nicgKZeSVau2ke50QQgjpeyg6SWXwKz3Xt12Aex1Ahnsd6LnoDHKvcyIRIYQQ0jtQdJLKUKJ73XWd\nS4BZMrUqkRanEGnpJIQQQvoeik5SGfwDKQsVnXBEJ7KLzmItnX01prOtrQ3RaLT8DRNCCCEDEIpO\nUhlKHNOZa5JQJdzrgBGequUVnolEAm1tbWhpaSl64hMhhBCyLULRSSqDX+kVOKbTJci97o7zLOdE\nIm/XyuliTzqNqSo6OjrK1zAhhBAyQKHoJEURs200x+NI5hOPpY7p7GX3OlCZcZ1JT2Pt7e3la5gQ\nQggZoFD+ivyVAAAgAElEQVR0kqLoSCbRZduI5vNFlyg6c1GJkElAZcZ12p7GEokEurq6ytc4IYQQ\nMgCh6CRFkXAUnF2qpbPAMZ25Zq9XYkwnUBlLZ9hZc57WTkIIIYMdik5SFK7ozGuvVE03LRY4prMS\n7vW+GNPpWjrr6+shIohGo0gkEuXbASGEEDLAoOgkBaOqcOVeTktnkMoro3vdXSqzEFQz9a+fSlo6\nI5EI6urqAIATigghhAxqKDpJwSQ8gjGnrTFo5k4ZgsOLCARS1Prr+VzrQGVFp2VZGDJkCAAjOhk+\niRBCyGCFopMUjFd05pROPbB0ah7HfbEu9nyudaCyE4lCoRDC4TCqq6th2zY6OzvLtxNCCCFkAEHR\nSQrGGyapaPe6+7/r785D0JhOoHjRmS9ckptnWaZsOQyRtm1DVWF5zKuutZMTigghhAxWKDpJwRTs\nXs/m0y5gMlEu9zoAhKziAsQX4l735pfDxe661kOuCRVATU0NQqEQ4vE4wycRQggZlFB0koLx6rGc\nYxNzWTq9+UFV+8C9DpR3XKfXte7FO7aTEEIIGWxQdJKCKdrSWYLoTBXtRfc6UN5xnd5JRF7q6upS\n4ZOS5Zy1RAghhAwAKDpJQagqkqoQdN80Wcd15hOdOZRdPvf6QLZ0WpaF2tpaqCrHdhJCCBl0UHSS\ngnAnEYVFYDkKLqu9MpvSKzBAfC5KFZ19MabTb+kEwPBJhBBCBi0UnaQgXNd6SKTnls4CxnTmc68n\ntTB12BeWzqCJRC6RSARVVVWwbZsTigghhAwqKDpJQSQ8lk7X9Z3V1phtIGUhojOP9W8gjOnM5l53\nqa6uBgDE4/Ge74wQQggZIFB0koJwDYBlsXQWoOzKPaYzn3u9EpbOIPc6YKydAEUnIYSQwQVFJymI\nRCljOkuJ01mge73cE4ksy5Sp5EQil3A4DICikxBCyOCCopMUhHcikavfKjKms0D3eqGTcAp1rwPl\nmUzkrkaUTXACRnSKCJLJJCcTEUIIGTRQdJKCcMMlpbnXsxUuR5zOHCrREgsKLUiwFWrpBMozrjOf\na92FLnZCCCGDDYpOkpeEbUNhBCeA0kMmFRKnE5rVte5SjIu90DGdQHnGdeZzrbtQdBJCCBlsUHSS\nvHgnEQE9CA6fZ0xnoa7mYkRnb7vXaekkhBBCgqHoJHlJrRLk/J83ZFIP3eu5XOtAaZbOYtzr5RCd\n+SydnExECCFksEHRSQrG1W3uTZPVMllinM58M9ddtiX3eiKRKH1nhBBCyACCopPkxZWIKdHZU0tn\nDyOwV9rS2RsTiUQE4XAYqkrhSQghZFAwIEWniEwSkStF5EUR+UREtojIqyLyExGpCyi/p4j8r4hs\nEpGtIvK0iByVpW1LRC4WkbdFpFNEPhCR64LaLbbtgUpKdDrKreSQSQWO6cznXnctoflEp6r5FCI4\ngd61dAIc10kIIWRwMSBFJ4BvApgN4F0AVwC4FMA7AK4G8LyI1LgFRWQ3AM8DOBzANQC+D6AewKMi\nckxA29cD+BWANwBcCOABABcBeEh8aqiEtgckfonY49nredzr+SjU0lmMa91brjcmEgEc10kIIWRw\nEe7rDpTIAwB+pqptnrTfici7AC4D8C0ANzvpvwAwDMAhqvoaAIjI3QDedMrs5TYgIvsCmAXgL6p6\nkid9DYAbAZwK4F7PPgtue1vAKyEtGPe6qmZaJl3zYqkTico0prMY17pbzrKMe922CxerXkqxdNK9\nTgghZDAwIC2dqvqKT3C63O9s9wUAERkC4GsAlrii0KnfDuB2AJNEZIqn/mnO9gZfu7cB6AAw000o\noe0Bi3/2OpBjBnsupZfP0lmge71Q0VlMuCSXnozrLGQ1Ii90rxNCCBlMDEjRmYPxznaDsz0AQBWA\nFwLKvuRsD/WkTYEJS7nUW1BVuwD8x8l3KbbtAUuQRMw6gz2feVGke7BliVTK0gn0bFxnMa51s68Q\nLMtCMplMWUgJIYSQbZVtRnSKSAjA/wCIA1jkJI91to0BVdy0cZ60sQCaVDXI9NQIoEFEwp6yxbQ9\nYPHPXgdyzGDPp/RyTCYqd8ikYsd0esv2RHQWaukEaO0khBAyeNhmRCeMS/xTAC5X1XedNHfGeVdA\n+aivjPt3UNmg8sW23W9RW2HH8lvavG7vrDPYC7F0esulVS3OvZ5v4lFvWzqLGc/pwslEhBBCBgsD\ndSJRGiJyFYDvALhVVa/xZHU42+qAajW+Mu7fDVl2UwNj9OvwlC2m7RRz585N/T116lRMnTo1yy57\nh8SWBOwOG5FREVjVmb9DAi2dzjZDquYbSFngZKJciAgE0u/GdBbrXgc4mYgQQkj/YsmSJViyZElF\n2h7wolNE5sLMWL9TVf+fL3udsw1yc7tpXvf4OgB7iUgkwMU+Dsb1nvCULabtFF7R2R/QhBGAdtQO\nFp0BAjFr2KRCLZ0Bqq5Q97rZv4WkJmGrnbJ8ZutKMe713rZ09rZ7PR5vgWoSkch2MCNSCCGEkG78\nxrArrriibG0PaPe6IzgvB7BQVc8JKPI6jPv7MwF5n3K2L3vSlgIIwcTd9O6nBsBkX9li2+6/OOLM\n7spt3pOAv4t2r+ca01mgex0obFxnKe71cozpLMbSGQ6HISK9YulMJtth251QjSEeb4ZqDwKSEkII\nIUUyYEWniFwOIzjvVtVvBpVR1a0AHgIwVUQO8NStB3AOgJWqusxT5T4YCTbb19S5AGoB/LEHbfdf\nHN2mCYUmgyb4GIqaSJRNeJXBvW72n1909sS93lsTibzLYVbS2mnbCSQSW5x9hqGaoPAkhBDSqwxI\n97qIfAfAXAAfAPiXiMz0FflYVR93/v4xgGMAPCYi1wNogxGRYwAc562kqm+IyM0ALhSRvwD4B4C9\nYQLGL1HVRUin4Lb7M2p3C0C7y0aoLl00+ZfBBHoYMslbLm0/xbnXgcIsncXOXhcxgrWYJTSB0tzr\ngLF2xuNxxOPxlLu93CQSrQAUllWHcHi4IzhjiMebEIk00NVOCCGk4gxI0QkT/1IB7ATg9wH5SwA8\nDgCq+p6IHAHglwB+BBNb8xUAx6rqEwF1ZwNYC+A8GOG4EWY1osv9BUtou3/i0X92NLvo9FJyyKRc\nYzqLsH5Wyr0OAOEwEI8ba2e4iCckmUxCRIpyrwNmXGdnZ2fFXOzJZDtUYxAJIRweDhFBJDIKicQm\n2HYX4vEmhMOjYFkD9XVACCFkIDAgv2VU9b8B/HcR5d8GML3AsjaAXzufsrbdH0lZOQWAImfopEqP\n6Uy1XYBKTK2IVGb3OmBc7MWKTtfKWazgBCo7mUg1mXKrh8MjUufNuPVHpoRnItFM4UkIIaSiDNgx\nnaQ8uKJTQgKJCGBnCs+gZTBT7vWMBvufe70U0QkUN66zlPGcLpUUnV63umWlR/dyhadlVTvitBm2\nzdBNhBBCKgNF52DH1X4WjOhEdwglf5GCJhL1IE5npdzrxRofXd1YjLe7lJnrLpZlIRQKwbbtVDvl\nwMxW70q51YNwXe2WVQPVJOLxJtg2A9UTQggpPxSdgx1XI1oCsVxBmF4kSAr2eEWiHNHX+zJkElCa\npbPUSUQu5V6ZyFgu25w+Dc97TiORkbCsGgA24vFmCk9CCCFlh6JzkJM2plN8aT7SlsEUcYeBBlPB\ntdeByoVMAnrmXi/F0gmUf2Ui41a3YVl1CIVq8pY3fRgJy6oFYDv1CSGEkPJB0TnYcTVnAZZOv3ZL\nudi9AjKfi7wX43T21L3eW2M6gfKO60wmOzxu9WFF9mM7ABZU4xzfSQghpKxQdA5y0iydli/NLZNF\nIGZ1sQM9GtPZH9zrIr3rXi+X6PTOVjdu9VLGmBrLqG139qgvhBBCiBeKzsGOq9ksdKvILEbIDEtn\nUPEyrL1eCK7ozCaIVYsP7u6lWGtnT93r3uUwi5lQ5SeR2AzjVq8t2K3uJxSqBUDRSQghpLwwKN9g\nJ8i9bgcWybBAigigmjmDPRd54nSqKj5Y+wE2bdyEzs7OnAKsJdoCKDCiZkRG32wb2LzZiM4RI4rp\noKGtzcxer68HClkkqLW1FaqK4cOHlyw8t2zZgmQyiaFDh6YmFhVLLNYCAIhESrNyusTj5njC4WGw\nrP6xWlFNTQ123HFHTJw4sWSLMiGEkL6DonOQU8hEIkWmlRPIshRmT+J0qmLFGysQjoexz177YNiw\nYTld7a3RViTtJEbUjEDIJ4ySSaC11VgsSxGdW7cCXV1GdFZX5y/f3NwMEcHIkSOL31lqn1vR1dWF\n+vp6VBeyUx/Gtd4KwHLGZpaOCbcUdSymdT1qqxyoKtrb27FmzRo0NTXh8MMPL2gYBiGEkP4DRedg\nJ89EolyWxtSYzrT2Sp9I1N7RjpamFnz12K+itqo2dzsA6qQO8WQc1dXVCIfSb+VEAqipMSsK1ZTg\nZbZt09VIJH/9ZDKJmpoaWJaFmlJ25sEEbA+X1I5txxEO10AkgnC4Z/2w7ZAztMBCJNKztspFbW0t\nRo0ahWeeeQbNzc1oaGjo6y4RQggpAo7pHOSkrJqeMZ1BIZMCLZ2OgAyUmSVYOjc1b0JDQ0OGgMyG\nG1opaCxoqZOIXFzvbY5wop59qVOnZy5ft36pAeJVTT2RnrueLSsCc1Mk+9UsdhHBjjvuiKampr7u\nCiGEkCKh6BzsuKJKEGzpdLMD1Fvg7PVCJsE4Y0H9ZePxOKqrCncrF7L+eqmi0x2WWYjodGeu99Td\n21PRCbj1yjPe0V02UzVWlvbKRVVVVUWWDCWEEFJZKDoHOx73uvnDpLnWu1wSsiRLJ5B1MlExs9fN\n/rPPYO+ppbMY0enuv9QJRN37tGBZVsnLYZbT0mnaqQIA2HZXWdojhBAyuKHoHOS4rnRXdGYLEB+k\n3QIjLBWi9vIEiA9akci2bVx//fXYa6+9UFtbiwkTJuDHP/wxOjo6YAfMn/c33drait/85jf44he/\niAkTJqCurg577bUXzj//fHz00UcZ9S0LePvtN3H++Wdi4sSJqK2txfjx4/G1r30NzzzzTFrZZDKJ\nRCKB22+/HVOmTMGoUaMwbNgw7LfffrjqqqvQ1tYWeJwrVqzA6aefjjFjxqCmpgY77bQTzjrrLGzc\nuLGHojPzsXYFbbbPz3/+84A6YQAhdHRsxa677grLsjBr1qzAfT/yyCP40pe+hHHjxqGurg677747\nzjvvPKxZs6bg/m/evBmzZs3CuHHjUFtbi/322w8LFiwouD4hhJD+DScSDWJUNXNqumdcp1jSHbA9\noL4rbQKDw+cii+jMFRz+4osvxvz583HCCSfg+9//PlasWIH58+fj1eWvYvGjizPK+1cjevHFF3Hp\npZfi85//PGbNmoWGhga8/vrruPXWW3H//ffj+eefx957752q/847b+OLXzwM1dU1OP/88zFp0h5o\nbGzEbbfdhqOOOgp///vfMW3aNHP8to1LLrkE9957L4455hhceeWViEQiePLJJzFnzhwsXrwYL7zw\nQlr/Hn30UUyfPh177LEHZs+ejdGjR2PDhg147rnnsHXrViQSCVRVVRV8Ss25swFIoKXznnvuCawz\nd+5crF69Gl/72tcC27WsKlxxxS9TYyiDrs3dd9+Ns88+G5MmTcJ3v/tdNDQ04I033sDvfvc7/OUv\nf8Hrr7+OsWPH5ux/LBbDF77wBfz73//GRRddhL333huLFy/Gt7/9bWzYsAFz5szJfxIIIYT0b1SV\nn178mFPeP7CTtkYbo9r1cVcqrWtjl0Ybo5qMJVVVNZZMamM0qhu7ujLqR5285lisO/Hjj1UbG1WT\nyew73rjRlPG1ufT1pfrssmc1kUykpb/xxhsqIjpjxoy09OtvuF5FRO/8/Z0Zu+joUG1qUm1vN/+v\nXbtWV69enVHu8ccfD2z7sssuUxHRe+75u8bj3emrVq1SEdHp06en0j755BMNhUJ6yCGHZLQ/c+ZM\nFRH9z3/+k0rbsGGDjhw5UqdNm6aJRPqxdnV1aVNTk27ZsiWjrVwkkwmNxZo0FmspuM6HH36olmXp\nYYcdlrXMsmVLNRwO63XX/UxFRGfNmpVR5ogjjtDq6mptbm5OS7/99ttVRPSGG27I25ebb75ZRURv\nuummtPQTTzxRq6qq9P3330+lrVmzRl977bW8bRJCCOk5jm4piwaie30Qkxaj08EfID7nmE5nW/RE\noiLHdN57770AgNmzZ6eln3PuOairq8Of7v1TRh2/l3/nnXfGxIkTM8odc8wx2G677fDmm2+mpQ8Z\nMgQAMHr0mLRViUaPHg0RQX19fSotFAqhuroao0ePzmh/zJgxae0BwIIFC9DS0oJ58+YhFAqho6Mj\nNTHGnUyUSBQ3Y7yU8Zx33XUXVBXnnHNOYH4ymcT551+AL33p8zj++GlZ2xkyZAiqq6sxwhcQ1T12\n77nKxqJFizBkyBCce+65aemzZ89GPB7Hfffdl7cNQggh/RuKzsGMq/G8d0GWsEm5Zq8XPZEo25jO\nLHp12bJlCIVCOOyww9LSa6prsO/++2L5K8sz6vjd69nYvHkz2traMgTjOeecg512moAf/ODbeOqp\np9DY2Ihly5bhtNNOw7Bhw/C9733PcziCSy+9FI8++ijmzZuHVatWYe3atVi4cCFuueUWfOMb38Bu\nu+2WKr948WIMHz4cLS0tmDx5Murr61FbW4sjjzwSr776amoykV3ILKYUxYlOVcVdd92F+vp6nHba\naYFlrr/+erzzzjuYP/+G1NCHIH784x8jkUjgrLPOwmuvvYbGxkY8+uij+N73vod99tkHp556as6+\n2LaN5cuX46CDDsoYUjBlyhSICF5++eWCjosQQkj/haJzMONompR1E5kTiVIhkwKqu7PXiwoOD+Sf\nSOQTrOvWrUNDQwMivvUoRQRjxo5Bc1NzhmWw0GGmP/vZz1KCycv222+Pp59+CZFIBMceexR22mkn\nHH744Vi5ciVefPFFTJ48OVXWtm1897vfxS233II5c+Zg0qRJ2HXXXfGtb30Ll1xyCX7/+9+ntf3O\nO+8gHo/j2GOPxcEHH4y//OUvmDdvHt544w1MnToV7777LoDiQie5ls5CwyU98cQTWLt2LU466aRA\nS+SaNWswZ84czJkzBzvvvHvOtqZOnYrHH38cTz75JCZPnoyddtoJX/7yl7HbbrvhhRdeSLPyBtHS\n0oJoNIpx48Zl5FVXV2PUqFFobGws6LgIIYT0XziRaBAQizUBUFRVbZ+WHuRe91s6XQtXztnrQQqv\nEEunz5Lnutf9s9c7OjoCl4W0xEqld3R0YNiwYUV1489//jOuu+46fPnLX8bZZ5+dlvfhhx/iS1/6\nIlpaWvGzn12H/fefhHfeeQfXXnstpk2bhqeeegrjx49PCcP58+fjyiuvxIwZM3DiiSem2r/qqqtQ\nXV2Nn/zkJ6m229raYNs2Zs6ciTvvvDOVfsghh+Coo47CtddeiwULFiAej2cI7WyourFCC/sdefvt\ntwMAvvWtbwXmX3DBBdh9991xySWXOGuvh5z9ZArhJ554AtOnT8ekSZNw1VVXYeTIkXj22Wcxf/58\nnHrqqfjb3/6Wcy35jo4OAMi69GdNTU2qDCGEkAFMuQaH8tM/JxLZdlKj0UaNRhs1mYyn5SXaExpt\njGq8tTs93hY3aVtMWkcioY3RqG7yThbysC4a1cZotDuhsVF13brcndqyxZRra0tLfvG1F/XZZc+q\nbdtp6fvtt5/uuOOOgU0df8LxalmWxuPpx7Z5s5lIlKXb+n//939aVVWlhx12mLb5+qGqOmPGDI1E\nIvrcc29qa2t3+uuvv66RSERnzpypqqrxeFyffvpptSxLTzvttIx2Tj31VA2FQvrOO++k0urr69Wy\nLP3Xv/6VUX7ChAm64447Fj2ZKBbbpLFYk9p2jglcDs3NzVpdXa377LNPYP4f/vAHtSxLn3vuuVTa\nqlVvqYjod75zQVrZrq4uHTdunO62224a9d4HqrpgwQIVEb399ttz9qepqUlFRE899dTA/O23316P\nOOKI1P+cSEQIIb0HOJGIFIrXMuVfWSZtCUyHlGvbN5wwm8Ewp7UzG0WGTBo7diyampoCV6FZv249\nRo0aBSsUfCsHWTofeeQRnHDCCdh///3x2GOPBbqXH3/8cey9997Yc8990gyy++23H/bcc088/fTT\nAIxr/ZlnnoGq4qSTTspoZ8aMGbBtG88991wqbfz48QCAHXfcMaP8mDFj0NLSAsBMJlq3bl3e1XeM\nldMGYBVk6fzjH/+IWCwWaOXs6urCJZdcguOOOw6jR4/GqlWrsGrVKnz44ToAQGtrC1atWoXNmzcD\nAN566y2sW7cOxx13XIalcsaMGQCQOlfZGBoaitraWnz0wUew4+k3XldXF5qamgJd74QQQgYWFJ3b\nOKrdYx0zVpbxLIGZIjWxPH1FomxLPIp3XKd/yng2siz3o9DAwPCHHXYYkskkXnrppbT0aDSKN157\nAwcefGCG6M3WlUceeQTTp0/HPvvsg8cffxzDhw8P7GI8HkcymYRlmW56m08kEqkxpLZtp0Rh0Ixz\nN82bd/jhh0NV8eGHH2aU/+ijj7DDDjukJhNdd911eP/99wP72H2s7nks7HG+4447UFVVhTPPPDMj\nr7OzE01NTXj44Yexxx57YNKkSZg0aRKOPvrzAIBFi+7HpEmTcMcddwBA6tiDxp8GHbufZCwJSQoO\nOuAgvPqfV9HZ1Il4SxyJrQnYcRtLly4FABx66KEFHRshhJD+C0XnNk4uS2fGEpiAZ0H1tCJZcW8g\n1cy11LNXKmKNSQCnnHIKRAQ33HBDWvptt92Gzs5OzDhlRtr66x9//DHefvttdHZ2ppV/7LHH8PWv\nfx177703/vWvf2WE+PFy2GGH4e2338by5S+ldfWFF17AypUrMWXKFCfdxsEHHwwAGROGvGlueQD4\nxje+AQAZq+089NBDWLduHaZNm5YKndTU1ITtttsuaz+B4sIlvfzyy3jttdfw1a9+FQ0NDRn59fX1\neOCBB/DnP/857fPb3/4WAHDsscfgvvv+gK9+9asAjOW3rq4ODz74YMr66bJw4cKMY08kEnj77bdT\ngtuOmhN76imnoqOjA7ffcztgA9qlSG5J4tfzfo1IJIKTTsi0IhNCCBlglMtPz0//HNMZi7WkxnRG\no41q293ByGObYhptjGqiozst2ZXUaGNUY01mMORWZ0znZt+YSZeNXV3aGI1qVzJpAsI3NpoA8bno\n6jLlNm5MJdm2rc//53l97uXnAqvMmjVLRURPOOEEve222/SSSy7RSCSiR37uSG1qb9KuRHeg+bPO\nOktFRP/2tyXqDg9dtmyZ1tTUaE1Njd5www36hz/8IePj5ZlnntGqqiodOnSoXnjh9/Xmm2/VSy+9\nVIcMGaJ1dXW6fPlyc362btWmpiY99thjVUT0yCOP1Ouvv16vv/56/exnP6sioqecckrG8Zx++ukq\nIjpt2jS9+eab9Qc/+IHW1tbquHHjdP369dre3q4bNmzQ448/PiOAvMvOO++sIqKJRLvGYk2aSLTn\nPu+qesEFF6iI6COPPJK3rJc1a9Y4YzrP1VisOW3c7TXXXKMiohMnTtSf//znesstt+jMmTPVsizd\nY4890sbMuu1MnTpVk7GkxppiGtsU066uLj300EM1EonoJRdforfefKse/5XjVUT0sksvS5VLbE3o\ne6ve45hOQgjpJVDGMZ19LsIG26f3RWeTIzjXazTaqIlER3desxGdyWj35JNkzIjOrk+MiGuLx7Ux\nGtUtWURncyymjdGoRpNJ1USiMNHpltuwoXu/djKn6Ewmk/qrX/1K99xzT62urtbx48fr9773Pf2k\n5RNtam/SaLx7EsvZZ5+tlmXp3//+VCpt4cKFKiJqWZaKSMbHsqyMfS5dulS/8pXjddSoBg2Hw7rD\nDjvojBkz0lYXamtr06amJm1ra9Orr75a991335S4PeCAA/Taa6/VZMDqTIlEQq+55prU8YwePVrP\nOuss/eijj1RVNRqN6kcffZSxUpKXUaNG6fjx4zUeb3NEZzRrWVXVjo4OHTFihO688845ywXRLTrP\nD9zXvffeq//1X/+lQ4cO1UgkohMnTtQLL7xQm5qaAts56qijNL4lrrGmWOpHT2trq1544YU6duxY\nra6u1n333Vdvmn+TJtoTGmuNGeHZFNOVr67UV196tehjIIQQUjzlFJ1i2iO9hYhob57zWGwDVJMI\nhYYgmWyHZdUhEjFu5VhTDBpTRBoisKqMy1uTitiGGCQsqNqhCm2JBNqSSQwLhVAfEPamJR5Hp21j\nu3AYtQCwYQMQDgM77JC9U6rA+vXGze5MprHVxkuvvwSNKz5zyGcKPr6OeAc6452oi9ShNlKban7T\nJjOec+TIgpsKpLMT6OgAamuBurrM/C1btiAej2PYsGEFhzcqhGQyifXr1+OSSy7B/fffn5H/2muv\nYfLkybjrrrtw+unTASQQCg2HZVU2Cloy2QXb3gqRKoTDQ0tux07YSG5OAhYQHhHOOmY4rU7Sht1p\nY827a7Bl0xYccPABBdclZKAQi8WwceNGxGKx/IXJoMCyLAwdOhQje/qFViIiAlUty4uWcTq3ccwk\nE4Fl1SGZbIeqZzJRUOR3dyKRnT6RKBtugHjHhuu0l+feFDEfd4aOuaGdrOLua8vpsHp6Wmg3Cmo/\nz/DTUvudD3dMp9m3Dcu3tNJjjz2GyZMn46yzzkI83uL0ofAlMEvFsiKwbYFqHKp2wXFB/bhjOa1q\nq+BzZ4UsWPUWrDoLaAXsTjOJKzwyDCvM4elk4PPuu+/ivffeQ0NDA2pqavq6O6SfYNs21q5dC9u2\n8alPfQq1tbV93aWSoejchrHtBACFSBiWFYFICKpJqCaNQAmYSJQSAD61mXX2uruvYq23oRCQSBg1\nFwplXXc9H6nZ856JRNuC6DT7NoLMzKJPF1WXXnopLr30UqSHS6q8xU/EgkgEqjHYdhyhUHBA91xo\nUrfJoWsAACAASURBVKExBQSwaooXi6HqECLbRSARgcYV8Y1xhIeHEaqrvOgmpFJ88skn+PDDD3HU\nUUdlXSiBDG7ee+89LF++HEcccURfd6VkaB7Ypkmf1Sxi1rVOhU7KtsalZfJUNecymG7RVFPFqD1X\nRHlC7YjH4lkortAKqlcODeYaHLOtSOnu1y8Ky0EoFIKq5gw5VOzyl+XAvY/SrOZFYEdtQB0rp1X8\nRbJtG6FICJGGCEJDzI+nRGsC8ZZ40fcPIf2FdevWYeLEiRScJCu77ror2tvbMyKzDCQoOrdh/ILE\nsszLzBWdgctgIj1AfMqSl2UfgXE6HWwbyDosyWdCVFUMqR+Cza2bs1TIsn+47v3ufbtWyXJZOt2R\nAEHYtrv8ZPmtjMOHD4dt22hra8taptjlL8uBZVUBEKgmoFpY2CsXtRV2l12ylRMAWltbUV9fDxFB\neHgY4e3CgOW42zfGYSeK6xMh/YFsS/kS4iIiqK+vH9DLAlN0bsN0C5J0S6eqs8KNApAAweQJEF9U\nnE4Xp73WVqCpCYhGAyq6JkSPmhs5aiQ6OzvxwQcf5NmrZ/+O2LKLFD/FEGCUBVBZKycARCIRjBkz\nJs/5KDxGZ7kQEedeUth2cZMdXCunVAkkVLxQ/+STT7Bx40aMGTMmlRaqNVZPiQg0YdztyY4spmlC\n+imqyklxJC+leAT7ExzTuU3jChLL2Rphomp337RB7zhvgHjJXsxf1OteTyS6xWZ7O5AxJt6n5BTm\nhXvIYYdg9YrVePfdd1FfX59X0NlqY0vXFgDAiBozKz8eN/sMh4GAFS6LZutWM/x0yBDAO0E9mUyi\nra0NlmVVzELR0dGBxx57LHBcJwAkEluhmoBl1SEUqqpIH4JIJmOw7Q6IhAqexa6qSGw2QwVC9aGi\nJv+oKtrb25FMJjFlyhRUVaUfqxW2EGmIILkliWR7EonWBOwum7PbyYDHtm385je/wa233or3338f\n22+/PU4++WRceeWVqAsKqRFAIpHAbbfdhjvvvBOrV69GPB7HhAkTcMopp2D27NkYOjTzGV6xYgWu\nvvpqPPnkk2hpacH222+PKVOmYMGCBdjBE53k/vvvxz/+8Q8sX74cK1asQDKZxNq1azFhwoSMNpcs\nWYKjjz46sI/HHXccHnrooQLPSuH86le/wkMPPYSVK1di06ZNGDFiBCZNmoTzzjsPM2fOzCj/i1/8\nAsuXL8crr7yCtWvXYuedd8aaNWsC277nnnvw8MMP4+WXX8b69evR0NCAyZMn47LLLsNhhx1WcB83\nb96Mn/70p/jrX/+KTZs2YbfddsOFF16ICy64oOTj7q9QdG7D+JdHNF++AuM3hyctHbHEuKsVcIMk\nZPviTpu97sFr/e/qMqItLeKSz9LpiuChQ4di6tSp2Lp1K9rb2wv6Rffx1o8hEIyuHw3AiN3WViN0\ncyw6VDCbN5vQScOGpYdNisfjaG5uRjgcDlzdpxzU19dj5cqVOOOMMwLHesViTVBNIBJpqHi4JC+q\nilhsIwAbVVXbF2RpTbQnkKxKwqq2ENmuuPBSIoKampqsy5a6ZcLDw5AqQWJzwrjbk3FERkUoPMmA\n5eKLL8b8+fNxwgkn4Pvf/z5WrFiBG2+8Ea+++ioef/zxgu7t8847DwsXLsQxxxyDK6+8EpFIBE8+\n+STmzJmDxYsX44UXXkgr/+ijj2L69OnYY489MHv2bIwePRobNmzAiy++iLa2tjTRecstt2Dp0qU4\n8MADsfvuu2PlypV5+3P++efjs5/9bFra+PHjCzwjxbFs2TLsuuuu+MpXvoKGhgY0NzfjgQcewJln\nnomlS5fixhtvTCt/2WWXYdSoUTj44IOxefPmrOc3Go3izDPPxEEHHYTTTz8dEydOxLp167BgwQJ8\n+tOfxt13340zzjgjb/9isRi+8IUv4N///jcuuugi7L333li8eDG+/e1vY8OGDZgzZ05ZzkO/oVwB\nP/npf8Hh3cDwyWT3aj2pIPGxuAkCv6Ers55npaImb/D3oH0kk9oYjeonXV2qnZ2qjY1qN2/S9eu7\nFx1qbFTdvNlX0SmrmzaZfsWj2rilUZs7mos+zvVt67VxS2NqlZyODtN0S0vRTQWyZYtpb8uW9PRo\nNKqNjY0ZAdDLyUMPPaT77rtv2qo+6X1Yp9HourQVgnqLWGyTRqONGo8H982LbdsaXR81ixF0Bd9L\n5SQZT2rXhi5zj2/s6pPzQ0gxPPvss9rcnP7+e+ONN1REMhaJmD9/voqILlq0KG+7nZ2dGgqF9NBD\nD83ImzlzpopI2oIXGzZs0JEjR+q0adOyrobm5YMPPkgtgPGd73xHRUTff//9wLJPPvmkioj+/ve/\nz9tuJUkkEnrggQdqVVWVxn0Ln6xZsyb197777qsTJ07M2sbTTz+dkb5hwwZtaGjQ0aNHF/Teufnm\nm1VE9KabbkpLP/HEE7WqqirjXD7//PO60bOaX2+AMgaH55jObYBoNBoYSLh7IlH3ZU5NOHGtoAF3\nQGpGseafSBRk6YxGjQGzqqrb0tjR4ZtnFOBeN/sp3iLlH9epCtgxu3uiVA/JNoPdPTeVGtMJAEcd\ndRRaW1vx6quvZuSZ66sQCfWJJc+yTKw4284/k9LusAHbjOV0FyKoJFbYMhbOsEBjisSmREFWc0L6\nE/feey8AYPbs2Wnp5557Lurq6nDPPffkbSMSiaC6uhqjR4/OyHPHRg8ZMiSVtmDBArS0tGDevHkI\nhULo6OhAPB7P2v5OO+1U9DtQneEy0cAB/5UnFAph7NixCIVCGX3fZZddCm7Db60FgB122AFHHnlk\navx5PhYtWoQhQ4bg3HPPTUufPXs24vE47rvvvoL6M1Cg6BzgbN68GZs2bUJTUxO2bNmSluefSGRw\ngqnnmnXtCxAP5B/T6Q2Z1NFpUocMMS71qiojQtOiPGRxr5eCKzqTiSQSbQnENsQQ3xRHokwhdLKJ\nTnfmeiVFZ3V1NU488UT88Y9/zMhTNeMjRfpmlEwoVAPAgmrciQmbneRWc/JC9b044SkkRniGBHaX\n3WfCM2HbaEsksDEWw/quLrTEGdqJFMayZcsQCoUyxgdWV1fjwAMPxLJly/K2EQqFcPnll+ORRx7B\nvHnzsGrVKqxduxYLFy7ELbfcgm984xvYbbfdUuUXL16M4cOHo6WlBZMnT0Z9fT1qa2tx5JFH4uWX\nXy7LcX33u9/F0KFDUVdXhz333DPDxV0JNm3ahI0bN+Ktt97ClVdeicceeww//elPK/L+/uijj1Bd\nXY0RecZ32baN5cuX46CDDsoYpz5lyhSISNnOeX+BYzoHMLFYDO3t7an/Ozs7fRNazEwgr7AUsaAK\nqJ0EEA5UkylLZ/fQz7yWTlsVUEU8bsIkWUO6Jw8NGWLS2ts9YyKzRF0vxWIncUG8NY4O6UBtuBZ2\n0ulwwkxciYzIPn7QVk0dQzbcsajZRGclrYzhcBgnn3wypk+fjl//+tdpEwe6RWffBUW3rBrYdgds\nOwrLCp61lexMQpMKiQhCNb3bVwkJIg0RxJviKeEZHln5yUVx20anbSNq20j4BGanbVZS2i4cRqSC\nP1jIwGfdunVoaGgIXGJ33LhxeOGFF5BIJBAOWKLYyw9/+EOMHDkSF110EX70ox8BMO+tn/70p7ji\niivSyr7zzjuIx+M49thjcfLJJ2POnDlYs2YNrr76akydOhVLly7FPvvsU9LxVFVV4fjjj8e0adMw\nduxYNDY24o477sDs2bPx73//G3feeWdJ7RbCpEmTsGnTJgDG+nv99ddj1qxZZd/P4sWLsWzZMpx5\n5pkZQtJPS0sLotEoxo0bl5FXXV2NUaNGobGxsex97EsoOgcwruAcOnQoOjs7kUgkEI/HEYlEUq71\nzPiN6ZbOQDXpsXQWYo8RGHGqqsaaKYK6uu44mbW1wJYtZlZ5akKRbylMr3tdVZFMJpFMJlOB0b3u\nHxdVRXJLEtqisOM2ElUJWHUWwjUhRKoAicVhd9hIViVTq9XYquiybfNRRVIVAiAigohloUoEERGE\nPWIgFALQ0YFktBMYUmNUNHrHvQ4Ae+21Fw4//HDMnTsX8+bN8xx/31o6ASAUqnVEZyeALKKzD6yc\nXiQkCI8KI9FsZrQnWhKIjCxuIlMhdDkiM2rbSHqEZkgENZaFGstCCEBrIoGYKpricQwLhzEkxJWU\nyP9n783DZTvLMu/f+75rqmlX7emc5HAC8RMiEpBJMQZMCGkZgqFBMhgEEjE0XDJJBDHQwQjRltEg\ncuEndIMSE7C5JK02NoOhmZpGWkXxM0Bok5BzTk7O3rt2zWt6h++PVat21R5ORnLOIfve17qq9qq1\na71rVe313ut5nvt+tsdoNNrRLL5sk3lP/D3f+c53cuWVV3LBBRfwwhe+EIBPfvKTvP3tbycMQ978\n5jdPtu33+1hrefGLXzxDAp/85Cdzzjnn8La3vY2Pf/zj9+l4zjzzTD71qU/NrHv5y1/Oeeedx0c/\n+lEuv/xyzjzzzPv03neHG2+8kSRJOHjwINdffz2ve93rWFlZ4W1ve9sDto9bbrmFl7zkJezfv5/3\nvOc9d7t96bd5tM/4RPbk3A67pPMEhXOONC1M3qvVKs45BoMBSZKMSWcZQZyd0DZqOsckb5uOMJN1\nU5G9o0WGpBCYcZFwngP+Vosk3y8ihTMq9qlWmCWBS9OUw+uHt6QfPc+b+ce0qUV3NM44POWhIoWc\nk/hVn6QP0gMv8kBrdFeTSstAui1RJ0kRD86cIzOGMm4cSsmi7xfFqP0+augwBux6iswyaLUelPQ6\nFHfl11xzDc985jO5+OKLefKTnwwcH6RTynDcXrVIsW9W0JvE4HKHUAJVOYYRWU9uEM/Ekrfz+008\n3fgGpiSa0zF7b4poBpu+H0tBQE9rBsbQ1ZrUWlqed7cR91089FCtVlldXd32tSRJEELcrW3St771\nLa688kouvvhirr/++sn6iy66iEsuuYS3vvWtXHDBBZx22mkAVCoVRqMRl1122cz7nH322Zxyyil8\n8YtfvH8HtQlCCK688ko+85nP8OlPf/oHRjqf9rSnTZ5feumlvOhFL+Kaa67h+c9/Pk960pPu9/vf\neuutnHvuuSil+Ju/+RsWFxfv9m/Kz66cyzcjSZJ7bIt1omA3t3OCIk1TrLUEQYBSanLXWxZm322k\n0927SOfRpsPyNWOLaKaQgs1ZhW2z6dusLG2SPM8jiqJJWmm6kD3v5ORreZGyDQSVPRW8mocZH3PJ\nK72qQtUUqTasraTk1iKBSEqansce3+ekMOTkIGDJ95lTioqUSCAdjRgcPlx4LxmDCj1oNNBWFsWp\nq6vY8Zi2I+TWWUb5iMzcO/P07eD7Pnv27OHtb387L3vZyyaiseOBdEKRYoftBUXHOso5jZJ4IguT\n+nx9Z3HE3SG1lruyjLbWjMaE0xeChlIs+z57goA5z9tCOEvMeR4LnocEEmtZyXOyndpe7eIhi337\n9rG6urqtkOfgwYMsLS3dbWr9pptuwjnHhRdeuOW1Cy64AGstX/3qVyfrSuuik046acv2J598Muvr\n6/f2MO4Wj3jEIwB2JNg/CFx66aUAfPnLX77f73XbbbdxzjnnMBqN+NznPsfpp59+j/5ufn6eSqWy\nbQo9TVNWV1e3Tb2fyNglnScoyjujkmz6fuFFqHUplpj16CxRktCippO7r+m8G/X69B6StNinH2zd\nepsGRDMKdkcRuU2SLsZ0WFycY2FhYZJWN+OCSjMyhRJagNf0CJaCSd2M3iRmEQJsQ9KVFqcd1T6c\nFIYs+D41pSYpdCEEgZTUPY95Y1jodKDbpZ9l5J4HCwuovUtQq2Hml4pQbZ5jjxyBNJ1EOp1zjPIR\na6M17hrcRSfpsDpapZt075dwpCTez3/+8znttNO44IILiON4fGMhjmlNJ+ysYreZxWUOJMjq8XGp\nKVXtk7aZ94F4Do2hnecTojmnFHt8n+UgoHEv6jQjpVgOAoJxpmAtzxnoowuydvHQwlOe8hSMMXz9\n61+fWZ8kCd/85jf5yZ/8ybt9j5Kw6m2+W+W66dd++qd/Guccd9xxx5btDxw4MOPR+UDhlltuAZhR\n2CdJco9S1PcVZdr6/maqbrvtNp7+9KfT7/f53Oc+x+Mf//h7/LdSSp70pCfxD//wD1scaP7u7/4O\n4B59xicSjo+ZYBdHRRzDXXfBdAvu8gtaEi4hxDit7siybAflOkw+8lIEs016/V7XdI4jfWnqxmPa\n5i23i3ROMVFjEtbXv4/WfWq1AGO6OGdR423Ki2IZOfNaHqpWtvcUKKFwOIw1k0indpZ2niPnPaq+\nopoLTLJDe8Q8h7U1aLcJjKHu+7hmk06rhQvDDQW78GB5GaKoqIvtdMh6bdbjdQ4PDtNJOqRmfEPg\nRQgEw3zIymjlPkc9Pc9DSokxho997GNEUcTznvc8hsPRTJTzWCmipQzGKXaNtRskzgw3opzHkzm7\n9DcRz849J549relqjYMiqhkE1D1vpgb43kAJwVIQUFcKB/RKQrurbt8FcPHFFyOE4Nprr51Z/6EP\nfYg4jreYjx8+fJhvf/vbxFNWIaXy/U/+5E+2vH+57qd+6qcm617ykpcAhXXSNP7qr/6KQ4cOcd55\n593n41lbW9uyLk1Trr76aoQQnH/++ZP1d911F//2b/92n/cFBbEcDAZb1htj+MAHPoCUcscOSfcE\nt99+O+eccw69Xo/PfvazPPGJT9xxW6013/72t7eQ+UsuuYTRaMQf//Efz6y/9tpr8X2fiy+++D6P\n73jEbk3nCQAhinrIMsPinENrPSGaJcIwJMsy0jSlWh1HKMUOkU5ni+jldpFOISbFjs45EOLoNZ3j\nxzQrKkiDcOu2R0uv58kKA9sjyxKqlXlqtSbO5RjTx/MKcYrWGjMyOD1WQW+qD/SkVwiPrMY5hbaW\nts4Jfaj5isa8X3SpGdlZBbUxBZsvi7WlhEaDRrVKmufkztE3BqW8yeYIgWk16d51B6POKm5VI/Mm\nNBqEKqTqVwvCKQTaatbjdXKbszZaIxA1QhoYIyZCq1JTNb2E4cY5g4J4ZlmGEILrr7+eX/mVX+b8\n83+J66//CI94xDIAb3jDG2i323zwgx+cRMAfLEhZwZgB1sZIWXwn7TjyfSxrOXdCSTzztUJslpMf\n1eXAOUdHa2Jb/N+0PI/KAygAmvM8QilZz/NJun3+KOn5XTw08NjHPpZXvepV/OEf/iEvfOELec5z\nnsPNN9/M+9//fp7+9Kfzohe9aGb73/zN3+RP//RP+cIXvsDZZ58NwFlnncVznvMcPv3pT3P22Wfz\nghe8AIC/+Iu/4Ctf+QoXXXQRT3jCEybvce6553LJJZdwww038NznPpfnPve53H777bz//e9n3759\nXH311TP7/NKXvsSXvvQlgIm9z/vf/36azSZCCN7ylrdMtn32s5/Nwx72MJ70pCexb98+Dh06xHXX\nXcf3vvc9Xvva185E9VZXV3esizz11FP5/ve/P6mr3wnf/e53Ofvss7nwwgs57bTTWFhY4ODBg9xw\nww1897vf5Y1vfOOWVPjHPvYxbr/9dgBWVlbI85xrrrlmst+ydWa/3+ecc87h9ttv5zWveQ0333wz\nN99888x7PfOZz5xEhg8cOMBjHvMYzj77bL7whS9Mtnn5y1/ORz7yEa644gpuu+02Hv3oR/PpT3+a\nG2+8kauuumrbdqInNB4ol/nd5QfXkUjroiPOnXcWv6dp6g4ePLilK0HZIWdlZcVl2VrReUjHM9sY\nk7skOeiGKwcnXYe2Q9nN5cAwdoeS5KjjW88ydyBO3L99e90d/oeDzva2dqhJkuIYZpr3DAYuv/1m\nl9x1s/v2rV93f/ftr7jD7cPjMR6adFM6dOiQO3jwoEsOJzuOuRN33MHeQTdIB251zbpv3pq6760n\nrp1lzjnnrLEuOZS45FDirLYbgzp0qBjYoUNFy6GpDhKZMe5QkriDSeL6sXEHDzp3+8GRWx2uuoO9\ng+4fb/lH9/f//L/cke/+kxveeoszw8HMmKwtdtHrOXfroZ77x+8dcn//3YPun793xN12R+YOHnQ7\nLnfe6dxwOHV8nY677bbb3MrKihuNRm40WnNvecsVbmlp0b3vfe9zWms3GAzcBRdc4M444wx3Z/ll\neZBgTOaS5KBL08PF75nZsePV8QSTmkmnpGw9234ba91KmrqDSeLuTBKX7tCd6wEZj7WTLmCHksT1\nN3VL2cUPL7brSOScc8YY9573vMf92I/9mAvD0O3fv9/9+q//uhtOXyDGuOyyy5yU0n3xi1+cWZ+m\nqbvmmmvc6aef7qIoclEUuZ/4iZ9w73rXuybdhKahtXbveMc7Jvvcu3evu/TSS92BAwe2bHv11Vc7\nIYQTQjgppZNSzvw+jXe84x3uZ37mZ9zy8rLzfd+1Wi33jGc8w3384x/f8r433XSTe/e7373tuVpc\nXHT79+/f9rVprK6uule/+tXu8Y9/vFtYWHC+77u9e/e68847z914443b/s3Tn/70HY/nnHPOmWx3\n6623TrYpX59eNn8O5fbT71Gi0+m4V7/61W7fvn0uDEN3+umnuw984APbju9E70gk3G4a50GFEMLd\nl3N+111FlG3vXhiN+vT7fer1+oxVhnOOw4cPA7CwoACN7y9PIk/FNpYsO4zuWDyzjLfgbeudmK1m\n2NSy1nRIX3LyDpYOAF2taccGe2DEvIlZ+JHmxFaoRJ7DykqhYl8uAnOYYRt95DYy5XFAK1KX88j9\nj6Qe1tG6jzF9hPDpdiHpJSz4C/gVn2B5a/5+mA3ppl1qfo21XpXO0LJ3SfKwxsax5+s5NraoOYVX\nlcWAjCk8nebmNtL9U+hrTd8YrM1ZOzDCYtmz16KkpLvSJfIiHrG4XAiOhIClJfB9hsMigDp9I57b\nnJHtIFSO7wvmwwUCFeIKi1OcA2Msw2HCaFRYRkmpqdc1aTqk2+0SRRGtVgtjukDKgQMd3vSmtzIY\nDLj22mt56lOfyu/8zu/w4Q9/mBtvvPEBUWXeU2TZEco+8C5W6K5G1RRe8/hOqNjMkq/l4IpSAG9u\nY7xFxFyjncMTgoX7kUq/N+iP1e2Owkmh5Xmo46hEYRcPPL761a/y4z/+4ywsLBzroRwX+PznP8+3\nvvUtXv/618+s/+d//mee8IQn8JGPfGQiBnoo4Wtf+xqPetSjWFpaetD2KYTAOfeAXIB2czcnCMos\neq+3ISLa7O0lhMDzPJxz5Hk6XreZSJUtLo9S0zle7wBnji4iguJLlGcF6fV9Ngw6p7fZlF63Nkfb\nokg1GYKQimq1Oinq9rwGQng4l+NcjBkWnp07qaC9sVVPP0+JTaFSX/Bnyc7Eq3NkYX29IJxRBPPz\n2xJOgIbn4WzOymidkczxhE9FtNhT3UMjbBD6YeF4X6sV5vh3tVm9y9DtbrQCrddhYQFO2efz6FOW\nOHmxRqXiyNQ6UVVTrRqUGpLnqyTJYZTq4Pt98jxhNNKsrECWRXiej1KKSqWClA7nLA9/+KnccMMN\nXHrppbz0pS/lcY97LEGguPrqt/KsZz3rQW2hNi0oKlPrYhtR2fEGGcjCPkkUNcPl2DNrWc1ztHME\nQrDk+w8K4YTie7fg+yghJkr5lSxjoDV6V+W+i4cItivr+uxnP8sTnvCEhyTh/GHA8R2C2MUElUrR\n03w4tAwGOc2m2LbbQRAE5HlOmib4fn2bmk4BCJwbe2Pu2Gpo/Gjd3YpApBBkOQRskOPNmFavO2fR\neh2UJE3B5CCqYosBvOc1yfM1XDLE5j5GmB3rAz3pYZ1jXScI16TheahNhFqGsujF3R1g/QRZ8Taa\nw++AVKfYvAfCEUQRNdvCc4oNS6px7/m5Jv11Q7ye4Lw2anmJ1rxga4BY0IyaZHlGZ9Chvdam6TUn\n7yOEIIoi5uZ8TjpJEcceSaIQQrK6KlEqplYTBIHCWh9rIctGXHjhuTzveT/L1772Df78z/8bX/jC\nV/ipn3oir3rVr/LlL3+ed7/7mnFdqkQIH6UqD7jqvajr7GNtgsuKmlIZnhj3tTKUqIbC9Az5eo5Z\nUHRdEWmsjCOND7YYKpSSZd+npzWJteTOkRtDzxj8sQ9oRcoHjQjvYhcPJqy12yrL3/CGN/CGN7zh\nGIxoFw8EdknnCYJKpYgWHjqUMRoJlpaCbSfBMAwZDHpj0cn2pEIIOXZUsjuSzjLSeZRNNralSJ/7\nzhUka4fJWcqCdGo9wDlNmkMcCxCWubk5nHCIqb1JGSJlFZF10XYdF+3cdUNJRd8YcmuoIagote0w\npDKYwRBTEciTW7NqnU1IdUo7bqME7A3rZH6NwZohyxSVyoYxfJJAtwvGn0f5q9T8nLq/jgi3psmy\nLKPf75MlGUmSkNsirbuvtY8oigjDcOZzrVYhTTXr60O07rK6mqAULC4OEUISRQFRFAB1hFA87xkN\nnlGf5ztPfjIf+uu/IcxyPvCBD2M+/0Xe/8gfRay1QRtMcw5aLcTcAswvQmseMd+CZhPmW4gnPh7x\nsH07npvtIKWHED4mS0GnqDDaMZJ+PMKre7jM0R9kDFdy1JJPXSnm7sYH8QcJKQSt8Z1cai2xMTME\ntG/MxIi+IuVuW81d/NDAubsPeDwUcaKXRO6SzhMIhaK5kLBbu31IMQgCnDNkWc7O1RMSHDhhd/yn\nFqpoR+ns3X/Bs7SoR1Se3YlvFnuVYIwjz0dYm9MfCBTQqNXIwpDYJFvGI3UDRQche2SsYe3Clq43\nAIkxaCQSQ7Xsy7kZ1qLSLgaHVTVcEOxIqBOdsB6v43DUgzqNoMHhNGMdR5xaGtbhHPT7cuIqEISC\n5iMX8DsrkCZFLcS45rYkm2VphFKKhy08jIEb4PkeMpBE4Ybi3DmLtTHGjICc+XlIU8GRIx5x7DMY\nNFlcjPD9PQihuPUzn+OL/+n3+PL/+jJf0poO8LPAG4GnAU/4zi1437ll5w9nu9P12MfDM58FJsvl\nSwAAIABJREFUz3k28uynTcLYzhVWWtt10JGyQp7F4GL84MTrpDGoOQYDi8igPoK5+ePnEhlKSTgm\nldOdkLRzDIxhYAxKCCo7dEK6VzCmuHncJbEPGoIg2LEzzUMRP4wtIB8IpGl6tz3dj2ccP1fUXdwj\nKFWa+U6LHTTtuE3Vr5LohE62BnqIP1hjca5B6G2u/ZTjuyV7VF4K96ymM02KLfzy/+Cokc5kTMCG\nKNWi2mhQq1a37cbiXNFbPQqWUY0+eZ6h9RqetzhDPJ1zdI1BSY+KcLi8TH1vesNOB4FF1gJsrVaI\niqpbo8GbCedcWBDHipL4viU2lsHAsrYGniepVqHRKLVTqijgXFuDwWBiuVR2ipJSUq/XqdVqCCGo\nmzprozUG2QBPekTKH1sPJWwwZ4lSFZaW6ggxYDAArSsMeyHNL/41337nO3jON/43ZwBnA7/2I/8P\nj3n4qehmk3yuiV1YQO8/BbHvZMRyYW7vOh3c+ipm7Qius4br9qDThW4fudbB/+Y3kf/yT/Av/wTv\nfSe23iB92tkkz3wm6XOeif2RU5GAL2XRt368KFXBZQ7nEsQ21lnHK5xztLUmxeHPe9S6EMZgq/a4\nLBEoCWiTovY0sZZ43PN9moBWpaSu7oFPqjGQphvL9P9jST63e9zpNc/bsU56F9tjeXmZAwcOcPLJ\nJx/roRwX2L9/PwcOHDjWwziu0Ol00FrPCIhPNOySzhMMnrdBOl1hockwG6Ktppf2io2kI85ihmmC\niNu0ohZSSDKTUQ/qTFphcpRIpxQkKaysOxZD2EYwDhRzU5qMvSUjt32EcQwpYTRqMxqtU63Wi9rF\nIIAsKzokCWbS62ZocMbhV3wib5E8b2Ot3kI8u1pjnKMqfQIsidF4chPpHA6LolgpkfsWsD2HGZkt\npHOYDemlPRyORtCgETYmr1WVIggt7VXLqG2xFqpVwdLSVD95gCDAzs3Ru/12kiNHsEtLSM+jVqtR\nr9dnznmgAppRk/V4jdXB95kPKwTKBwRSRkhZRakyAqrxvAH17E7qH/gUjT+7DnXwdh4D3Fap4i5+\nEbz21cgnFh0xPCDr9RgOBgyBSq2GV6uROYcZL4UXhsXZBGdHODc2sE8yoq/eTOUzNxH97Wfxb/kO\nlf/x11T+x1/DFZD/6KMYXvJiRi+/jLTRKD5cKZFSovsGJQxCxFRc7YRQXfeNIbUWJQQLtRAh7KS+\nM1gOEOr4PYZgHNWcA/Ix+SwjoH1jGFlbtHidJoHOQZYVBDNJYHO3GqU2LBUKW4V7PzApi+i47xeK\nOt/fJaJHQUmyvvGNb7B///4tpTYPNVSrVW677TZWV1cnTUIeqrDW0m63ufXWW3nsYx97rIdzv7BL\nOk8UaA3DIW7UJwiqKOWRJCD8hFG+kYJQQrFQbdHORvgiwuFYTzZ65VpnqaoivY48igpWQn9QzDeD\ngSCpFELvzYhjkK7ste6wuSVNEuRYSa+UmtSg9PvrrK+3aTYF9foCrVarUJEDTmvwN0zonXUb3Yea\nHn7Xx7l5nPNwzqD1OkGwTDyeVAWwGET0s5TcaqJp0pllRaoboNVCRQF6kOIyh9UW6RUkvJt0GeZD\nAObCuTFB34AvJFks6PYd2liWWrC8LNlc8meMYW04xDiHAmpSUt+7d9sJxDlHIAwBMQMzYj3J2Fs/\nhcBvbhGBqX6fxlt+i9oN1yHTInKa7/8ReMWv4v3qy5DbWK3UGw0yITjcbpO121SShOaUeEqNuzl5\nqo4SDSQWYfpYL0Y++ykEP/8cZP4O7HdugU9/Br5wE+JrX8H/v7fQuua3mPujPyR55atIXvoi8jBE\nZw69PiJTA7RK6HktAs+j5vtUgqAgHdPLcZC+Nc4xNAYBLJRtLOuy+H6Me7QHSydGOssf13XOUURA\ne1qTOce61gyzjKbW+FlW/E9M14ZJWdTvlMtmglouhRJw58fyeZ7PRk+n91MS0JKMHgffgeMBnudx\nxhlncODAAe64445t+60/1PCd73yHm2666Yeu//i9hRCCubk5nvKUpxTz5gmMXdJ5IsA5aLfRSYLr\ndIo2kc5wpDvErxUkyZc+zaiJJz36RpP6dRp+k2rUpJt2x2/jGOZDPDeeQMXOpDNOBHkOUhYTU6fD\n1ogeRQBRCkG1AsO1ESudDibPNzr8TKHf7yEEzM3tZX5+vlg505R9Y6LTPV1k/yOJDCRqkiKcQ4g+\nzuWkeY+uLUoHmp6Hj6SfQW70xjfbju2RnCu8i8bMWVUUZlj0cRcNwXqyTqITBIJW1KLiV2bGrjW0\n2+AjkcIgo5xGA5SanTCzLKPdbmOtxZ+fZ8EYlJRMwtJTMGaIMQOcM8yFdYxTGBHQyzVLvpjeEPvB\nDyF+6yoa7dViPz/7VLL/8Ov0zn4e0lcsN6fPXlHjWka8XBBQm5/Hrq8j0hR6PfYsLqJ26jRl6uRx\nH5v0sXoFqeaRe5bgsl+Cl72k6Mj0uS8g3vF7yH/5J6rXXE3lw3+Me+3r0b9wEYlfZ+QPSU2fREsG\nCNoUBLciBDUhNvreS4VTEuH7yKiCCCOk5yOFRAr5oER6euO2ltVNQhyv5ZGv5LjMoXt6xr/zREAg\nBEvWEo9G9OKYzBhWgaoQNJRCBsEGyTxajViZRod7F6ksyWeWFY8lEU2SYimh1NaI6EOUiHqex6mn\nnsqpp556rIdyXOC0004D4KlPfeoxHskuHiicWFfRhyr6fdB6o/941mFdeAQBLIxdhqp+lUAVE4dS\nBVE0Bip+hcgriNYgG9DP+rTjDjbuslDf2fC9X3BZ6jXwK2CzgruVxu5QzCXFkAxp3CHu9QitpRJF\nEARorafalDl8XzM/P0+9PmVqO55cnDWAQiCw2mLjQjZfGot7XtmG0hCGLfJ8lXa6jvWWqKqAqlI4\nV7yXscV5EgJYaxcnIgwnoh4AWZWYoSEf5Kyrok2lEor5yvzkPJYo27JbC61IkewxdDuGNJ1VV8Zx\nTKfTwTlHFEXMz88j1tdLr6ui8BOwNkXrLs7p8SkIUWqOvYHHymiF3OZ00y6tqIW96YvwutcV9ZWA\n/ukzufPKX0X+5OPZt+90snVBkhTjW1pyDG0R+TXjKJYAIimZr9XYX6nQbrcxec6w36fZbG4cpNbF\njUIcgzH4BORGYoVGeyO86knIqDYRE6kX/yL80sWY//opxG9fjfzXbyHe/EbkH1yLfsVrSX/lXETV\nJxIBmfUY5RqtLT2jwRhC7ag6S7SdEtPzcEGAC4OChEo1IaBSSAIVUPEqKHn/U27ZOB0tYYtKXUiB\nN++Rr+WYgUGG8ris79wCa2EwKL5zzlEBIqDveQx9n2EQEIchc75P9QeZtpyOnpYo+/mWS5YV60oy\nWsL3ZyOvu3hI4hd+4Re4/vrrueiii471UHbxAGGXdJ4IaDTAOXQQMFo5hHUxBItoLaj5NWpBbWKO\n7pwbByMEZQOBkhg1wgbWWYZ5Tm4tK70uI2/fRDPg+0UkM8vAWoEXgAqg1nCYbjFH9PsT7sRwWBAt\n53roMENJSaPVojnuyjMNrftUKtDtVnFuaqIrIxp6o2bMdM2kO0xZS1eSTq01UtYZuZDcpXimSys8\neXKcSiisMxhrEL1BcTCeVxjAT0H6EiMN7X4bfAirIQuVhS1EJsuKCKe1hW3V/LwgXpOsty391HHy\nePz9ftElCpjtFNVoTEinq1YxboAxw/F4PZSam6rZhIXKAivDFZJbvot+67vwbvxk8bk+7BTc770T\neckLsQf+P0xedCyan/dYWXF0E8PqYUNr3KrYF4KqUlSk3FCZK8XCwgKrq6sMh0NC3y9I32gE06k8\n34cowgsW0XJQkGSR4nuNScWttprMZKTnn0P27J/B++Rf0vi99xDccgsLv/0mGv/lFIZveAXisl/C\ni5ZxOHJrGdpCiOVwZIB2joqzhJmGOMXEMTo22FGKtQnadnGej/ECjBdg/QAhEqTsUQlC6mGFWlDB\n88R9ytb3xjdyNaW2V+MHs/6dx3V95yayCUxIm4gi5jyPqrV0x/WrHa0ZGkPzwezxXpZVTNfqlES0\njIhOR0YHg3HB+BQBPYYWVrt4cHHhhRdyxRVXsLKywvJ0xGMXJyx2/3tPBAgBzSbD1bvok9H0QuZy\nkJUWjSCamWid00gpkdLHGLPF66wZNakScWt+hG6coBo5vvQRorjWZ2MdiZTQmIORA+EKzra6WswB\nYVjwlMOHuyRJzNKSxa9U8KTE38FDzNoRUoJS1Rlh7Gx6naIbTApIUA01tVnx3IwnzBE1BEPmZGEt\npFRhz+PJoubTjHog4+Lczc9vYSO5yemIDtZZoixiaWlpSyo3TQvC6Vzhl1mW0rQqhfq/lziklHQ6\nHUaj0aTuZsbkfkzg7KiP7tyOq0eAQKkGnjdbMwqg4pTWNe8j/IP3IZMEF1Wwr38j8i2/gazVsDal\nUomIY81wOMSv19ENwyhxmBSyvuRhC2pHv0bf95kLArqHD9NZWWF5YaE4t1IWB1mpTG4YBOC5AK3b\nWJsySu7EiDqJydB2SngigIueT//fv4Dwo/+Nyh++E/+279F63X/E/sF/gb/878jHPLo4dw6yzNFN\nLb3MkOSOvi6+Y3PSI2ooRJ7jZUUtYGgybGpwicU6ixUZsS+IKx5xnNImRYguoYqoeFUiLxx/zzaW\n8mbK82YrHGJjyJxDCUH9KBG/0r/zuK3v3I5sVipFOcmmmz9PShalJBmbzOfOsZrnVKVkzvO2Jd4/\ncGxHRLOsuFlL04J8Tqfky21LEno3Yy4svtyktrx8frRHKOrjpZCocaRdihMgyv1Dhkajwfnnn8/1\n11/P6173umM9nF08ANglnScIEp2wMljB1arMBw1sBmmiyfPZ7JNzRcTK94sLuNYaf2riSRLIhh4m\nrgAJzu+xb+/iRMxqzEZ5VfcuASMQ1uFHhSXQYFCkcuM4IU1j5udheXmB3PPoHzlSpHW31C6OcM6g\nlI+UwawQtkyvG41zDtu1SCReY7YDTBnpzPKcjtYIIWiGC/iuh9Y9pIwQQqKEB3kfM0qgHhVMcdPE\nm5mMdtzGBY5IRbS81hbCmSQbpaC1WuGZXmIukghn6cc5d62s4kmBlJL5+fktrUkBdAVMtw1GIGo1\nvGDW8mn8wWGv+zjiyjdROXgHAMPzfx757ndTOe3HpjYz1GpVOsM+d3S7zIchQgr2LAqyjoefSbIY\n/NnmTjPp85oxZEIQW0s7jll++MO3V4kx7hevFcOkg7EJiDbKm0dJn1CFhF5IoAI86aGdxlzyUtwv\nvwT7qU/A269G/t9/w/y7f8f6f/8q2b5HjD97ASiqKDxnGWLQ0jKUGqkcc5GPlD5C1JHCIfMUmaeI\nLEVajbWO3Dj6nqCvYJQlDNMRvVEbZwShivBFiCe2Xt5KEqqUo0OO9AULoaI3rs1VSqGUmojgJm1Z\nj8f6zntBNjcjUopQyom90shakiyjrhT14yGSGAQbdabWzto5GVMc83CIA7QS5L5E+wrtSbTV2HHH\nNXc0O417CYGYIaGbSakSavJ8Fw8cXv7yl3PZZZdx+eWXb+lat4sTD8fB1WUXd4fMZKzH6+R5TqXa\npHXyqfRu75AOh+gkIgynPSsL0hkE0ZhEmgnp7HaLa7VNIJB1giDFr8QkOiHyoi2lU5Nr5zhNPzdX\nXPOzzDEa9VlYsCwuNomiCGsMjG14NsOYAQC+X0T2ZiKdUzWdZmBw1iEigarNRp5KIdFamjJvLZFS\nzPl18jzH2hitu/j+PMoA3R7Gi4rJtzIrCCq7DDkctUqNar2KM7Mq9jguhFOl9mizJZqUApuN6Hb7\ntEct9rWqLCwsTIhxicLeaR0nc4hCVO7h5VWINm339W/Ar70e+b+/Wvz+2MeTvvsddM98HEoooqlo\ndWIyus6SeiG5NuRJwkmNBlGoSFQRme31xnoMzxUHMxpthLCLD4LWwx9OPhiQW0s3TWlOkc5Up8S6\n+F5YN/6wVBMFhJ4i8gS1aM8Wdb1NLc5BKgPSF1xKctbzWLjo54i++ffUn38uqzd+BXnySXjexo2N\n50l8XzI0mr4xOAxSOprjtpNaG/LcFRlXT5LHBoY9RJoiKQRktUqFuAKxjtFWYyxoC8L5+FTwXISz\nHlpvcLPYWQbO4CHIpDcOtjkqFYgiN7lvklJOiKhUEjdweKlHqEL8qn9sLG22I5tRVJRy3A3ZnIYQ\ngobnUVWKntbE1tIbE9Cm502M6I85pMRFEXmg0LUAncboeIgeDbFZskWF78YCKReFICWCQjB3d4/A\nzHPrLMaa4tFtPJq7sY8qyakUEl9t3JztktH7hrPOOoszzzyTq666ive+973Heji7uJ/YJZ0nALTV\nGGOoqArztXlEpULQyhiOYuLVIbWpMJy1Ben0vIgsy9Bak6ZFLWaWFUHIWgW8mkejUSPH0kk6LFeX\nt9QzunELQzHVlWhhAY4cGdBq5YShP7nzLL0Yi0DWxkRsbYpzGiE8/LEifIZ0jnOeLtEYrRE1gdfa\n/msZUwg/sJb5MUP2vCZZlhbEM1d43R44iwnUFrY4bfpe82s0oyZ5nONih8sceMVcXrorNRob9asl\n8jyn0+kgdFGX6fw6y8uLW8iHMUO07gEOITy8hUcg18asv1YrJsdDd+Le9GbEn/0Jwjnc4jLut9+O\nfOXlVJRiOFolMxn9rE/Vr9MzhmEW45yjVm/gBhm1PCcap4ajMc8etDO6349ZqsUbJ1vKgoBXq+D7\nCGA+DCf1nX7gY5VlmA0xbmNS9aVP5EVEXoQn95HnqziXk+er+P7ShHgmiaO/6kjTcuIGUZ+n/+ef\nQv37Z+Pf/K/sffEzEV/+n4jtrJ08D+kcd41G9POcI8ZQL214pqEUcnERkWWo4RBpDGGWURchonky\n2pMkNiE16VSUKyVQjsiLCESFPBfcmeRE2tJwHlKLwqvUWbLMkiQ5YZjj+zlCaAp/sSL1alODHVhY\nBbUoiKpVGo0WlUodIfwtRPwBRUk2R6ONz/U+kM3NUEIw7/tUxxZLuXOs5TkVKWk+iCn3MjppnEFb\nTW5ytNXF9c9tInqRB1ET4Zp42uJri58ZlHV40kNphRiNhUxRVCwPAIneQkKnfi+fT353psgUjC3t\nfOkTeiGhKrIDR7thKbVVJb8tK2CUuttqgh9KXHvttTzucY/joosu4owzzjjWw9nF/cAu6TwBUPWr\nGN8gIzmJWkZLdeThmKyXYPQcyhv7W44V0Z4XAhn9vpnM20oV5Y0qh1grRKVKrHwya1lP1lmqLs3u\nWIz/cMZZyQADpGRG/ayKnW9Jr5dRTqVqk2YlJZeYbOZ56H4OtRxvjzeJOE4jMYaYIjHbYKMFoxAS\nz2uh8zZm9fuQFSE0Mzebhtmpy5AMJTa22NTSzxSjEWNbp7LD0AZ6vR7D4RDnHI1IkooGftggd46g\n9Bd1Fq07445CxXErNVdMMNHYiHttDfNH/xn5zt9FDvo438e+8jWIt12FnPJga4ZNjgxXODTqUIsU\nSnoIDDWpaDUXWMna5HlOlmVFW7QkoZH0ibuGzECMpdIKC6IZRVtmK9/3qdQrHDpyiJXRCgtLRX2n\nJz2qfnVMNL1Nf7NInq/hXE4cr5FlS6SpIB857AhEIIhCMdmlPPkUss/8V+w55yP/9VvYZ50HN30O\n0WiMb4hS0jQlyzKstSjnSI1BU9xkLIUh1SDA93183ycINk3WcVzcJYzFKE5FuLl5rDAk+YBRPiLR\nMcYNGWrHwFkSFDIK2RuELI9TuMYUN2WjkSBNBeBjrU8YWoIgx/cNWhtMRZCRkw8NpmOIRU4cd/E8\nj3q9RrVaQ8pgTEDLMoH7qRD/AZHNzQilZDkIGBpDfxz5TLOsECDdC5X7NBmzrhCNlc9LYrnda0eD\nFBJPepPFl35BLjc7GJTeoGU9aFkLKkQR/q9U7hcBVVKhUPgc/byX5yA1aSG40ym5zcmznAEDnBUo\nAhQhHiESH603iObR2msLMUtCp2uYp9cdL4HqBwJLS0u8733v46UvfSlf+tKXOOmkk471kHZxH7FL\nOk8QCDer4haeImqGjNZT4js71Pe3xnEdCxRCosJ33TA/X8xP9XpxwdKZQyBBQCucYy0ZkJmMYTak\nFmwwrTLSidm4ApaWQNVqdab/60ykcwxrc6xNx+MphD4l6bR2Q0NkcoXLHRIzIx4qocdKW8/zCD0P\nuallplIRrDt0nmOlxdarOGEnIqo4j+kknW27DIlAFFaehx22WYyv1ZotcXTO0W63SdMUIQS1Wo29\nex3pXYI8g5ExBFKOrZA6OGeAggxPK9Op1bAfvQ7x3nehDhbt3eyzn4v4/fciH33azDE550icYOA8\nRibFpj3215cJUAgkQiiq1Sr9fp9Ru02gFOQ5AphrKtazGr1KhWhBbYmMOOeIdcwwG5KTgw82sSS9\nhIfve/iWtqkbfwdZJkmSRYbDVbTOEaKNUosoa6k2oLYsCTd5F/v7f4zsbz6B/4znI//P18me9VzW\nb/gYZhNhUkoR+T4t32cgBHZcU1nxvEk0dzNs6OMWG7h+G9vv4Lo59IBaFb9eoxlWaIYVEp2Q6JRB\nntDLM0ATupg1E1LxKkRehVrNo1aTaC0YjQSjUfFca4HvQ7UqmZsTyAXIVzRWQ+IGxGpAnid0Oj26\nnR7VaoVarToRvwkhEfgbRNQLkffU7ilNi+LiHyDZ3IyaUkRSTlLuHa0ZGUPL8yb+qjuhn/bpZ/17\nvc8yrV2mpaeJ5bbkcicoVdxkVavFOStJ53RN6ANEQI8KJ8FKPOuDAWUhzjJGacooT8lNjnMphWqS\nsRXYOAoqQwJfTYgkFIdizMa1c3MDqe1Q3uSXJLQsa9lOVHci4KKLLuI73/kOZ511Fn/7t3/LKaec\ncqyHtIv7gF3SeYIgG9fkTYuCgoU6o26OHiQwGOBqRfpaCEm/r0hTCIKCdM6UNjoQQo1LNS3NqEk7\nbjPIBlT96kYkqbzOj5nkYDAgTVOUUlt6vwohkBSUt6C901HOjfcsr+8l6XTWoROBw+GFdiLcmAx1\n3E3FAvUgQOT5xK90gm4XlQnwmuRVD0Y9jBGT1NxOhLM4esl6R6AzRzBnWVyUM/O5MYZ2u4goqrHl\nkJSS4XDIXKTIHfQSS40u1g7Hxxjiea2ZCJf99GfhN9+E/NY3i98f9Wh47+8jf/7ZbMbIGPrGYJyj\nFjZwNqUmLYHTCBwgEEJSlZJBu02c58wtLyN9HxoNKtUqw9Uictfvb1QZZCYjzmNiHU8iS0oo9u/Z\nz7AzxFlHMkwImxukU+uNOXujiY3EuUWUWiUMU2q1Dsqv4nLwq1vN8tM0JW7uRX/sA+y58FcIvvZl\n5i67nN7HPkJYrxOGIWEYznz2cxTtTYfG0NaahnPUlcK5HGsznMuwNmMShq9KiFrQGyASXRgXZBrR\nnIdqjSAQzCHwshyhU5TNCEUhOIkdxLnBN5K6Vy3EUTVHM4LhwDEcQDZ0ZG3oOEclhEgqRE/juxph\n1EBHmsFoQJom9Ndy+qJHEChq1QDfl0Ayc16E9JFehPIqKD8ECUKJwo5JjZ+Xfl3OPShkcxplyr1i\nDN2xyn8lz6kpRWObXu7GGtaTdTKTIRD4qjD4n65vnCaV2732gKN0ZKhWi3OYJEVkfDsCGkXFRfIe\nEtDp9Pd0hPLokcqASAZEYQNE4cRgSNGkIDVSxigVIxUI5eFPCfWm60HLpk/lvqYJ6XaP25WgltHS\naRJaPr8vcEcLzW7Z933/rK+66ipqtRpnnXUWn//85/nRH/3Ryf7f+973cvnll8/6D+/iuMMu6TxB\nULZEm44uehUfmk30cL24mNbC8c29Is8VUsL8vNmspRnP0+XEYYtaNxWQmYxBNsDhGOUjOknOcKjJ\nCcjDgKSf4EmPVqu1hRwCKOewFG0FhTPjFLNAqQ1roPLPSpW87mnwAkQgUNu05eyOa8x8IWiEIe3h\ncLaQv1RHCYFa3I9nNZ4YYUyf7ugIORKH27atZRlEMlLg+Y7FppuZ07XWrK2tTcRYC2N7oZL0ViuK\nIZb+sMuc0lSU2mKFZP/+H+E3fhN502cBcHtPxv3aFciXXAInnzwznnhMNvX4Ah4IQdMPmZcLdNMu\n3XSdlg8iy6G3gspzQiFIlGIUBNT37Jm8V7NZWFyt9zK0SshdPFMXF6qQWlCbNA6oLFZYXV1lMBhi\nTICUlYlQuEQ5PxdONQrPWyhS7XZIHhs8v45TjtFoNEmbbzQHUNhHnsb6DR9i8cKXUfmfnyd8/RuR\nH79u2y43zlka0oBJ6OqUtTxnKCwtNUtQhFAIEYxT2gFy7/6CBfR6BcnoDSG30GqROUcKVGTIsqqB\ndiRZwigZkWQJqU4ZMCBUIXPBXFHPCkQVSCUMR5DmMMxgiMQXHqHWhKlFoVhcXERrzXA0JEkTjHX0\nBuB7HrVqSBhJrMuxJsXZHJPlmKwPyGLsIkSKqLhZSRLoryMkiHod0ZhDOsmDnTEtVe59YxiOle7J\nJqFRqlPWk3Wsszs2WDjmEKIglZXKzgS024UgwEUVtF/BOLmFTO5E4jajjDB63qx9V/l7UfsbjRcm\nqfhUp6Qmndwwl215N5cXeNLD8zyC4OhT+DT51Lpwn9J6dtl8moQwgEbK4rGoazZore8VudwJQgiC\nICAYl80EQbDtfLITrrjiCmq1GmeeeSa/+7u/yy//8i8jpeTAgQOcccYZ/OVf/iWPetSj7vc4d/GD\nwS7pPAFgTKGYLFW0JTwPCEP0QIHOMUnC6hqARCnJ3JxETKWZSzjnECicZJwKLnqNr45WZ1JjThWW\nI1mScGh1FYXiEcuP2NYWCIroSO4cBhBmBDikrMyIK6YjnTYfdx7yPVTDQ+jxFXK8UTLVV33e8xDj\nC94k0jlFOFlYgCBAZgFhME8nvZWV4R00aw/flnD2ekWZHEC1KalhC3IyDu+macr6+jrWWsIwZGFh\nYUPVau3YAqqPMjlpYsjmFHP+ElIWrNXdcQD3G1ciPvFnhUioMYe94jeQb/w1ZFlrNhqz4BsGAAAg\nAElEQVRBvb6FbPrjNoVlStkPaoyyIdlwjWHSpS7roIrwRG3fPpI4ZgSUR5ibnNjGDGxCf2Tpa8fC\nYiGwqHgVKn5lplbTOTDGx9omR450EKLLwoI/tg3a0GJsbZPt4/vz9NcOMup1saqDcLN3OL7vTyKZ\nvr8XvWeB7MaPET73F5Gf/Dj28jriP/8RDo21Oc6VS/EZR4CQlnVtiZ3AoFgKIjwZjonmNmlXz4OF\nBWx/iFvr4IZ93MqQ1ahGKjzmhMLIyRHQFE3mgjliL6Zv+mQio+3aVFWVuWgOqSQ1KagrgXEwigWj\nBJwTZNqSdjWhtFQcBCdX8GWVXGuGoxGDwYDMWvrECCOp1utEUQvhNOgYZzLQGdgYTIyw4IY5qpMg\nnYeoLSD9GqJb3HQKKZChQIYSFRXNE8r/7MnjAxw1FEIw53lUpKSzSWgkzIjRmBhFXkQrah3/Ku1N\nBNQME7Jegh4k5FlGnmc418UFIVQquHA2BV9GCY+23NuPQElFVVap+kUZUm7yCQkthVSZychMNvN3\nAoGSaqYUoVyEEDNetdMo6qkNcVw8ls/z3GLtVmIpBPi+wPPEmDi7SYR0+1O88wmw1k5uSksUBDqY\nLJudQDbjFa94BU95ylN45StfyUc+8hE++MEP8vu///s8+tGP5mlPexrXXXcdP/dzP3fU99jFscEu\n6TwBkGXFxWYumk1pl8XiNoiwNqd3ZIiTRRRqbg4GA0WeW4wxs//EjsIPSWyQzkAFRF5EohN86dOK\nWlQtrFUG5OttjGfwQo96fauheQlVkkLnEOOuO9NRznLMML777hWdh2RNItIAkY9vxcMQ6xzdcUhh\nbqqWTAhRmN6vryPieINwjomwc2Cdz1APqRtFI6jOEE5jiuhmqeRvNKAaCfIjFAp2YDQa0e12J7Wr\nrSlxT6FwXifLVgmCgNBWiG0Fq+pI6eOGQ+x/ehfyve9CxqNCJHT5KxFXX4XaM+6o4XmQJCS9Hv0g\nIB+fN29MNivTkT9rYThkrp+wMlhn6AbUGq2i8LRaJQS8cclBZ9AhFzn52MGgUock8fFdRENGNGqz\nM0+aFsGeJCl2I0SVMCycAKxdZ8+e5W0nFWMMSZJsiIDWDSYeIesJAYpKpTkhmmpTFFOpOcxTTif5\n+AeJLng58qMfJqsp3Luv2jRTS4TwkDKg5vlEgUfHOLRzrFtoSY9ounxBW1xeuBDYvHiO80DNw2Cd\nOE1I+wmqWqc+P4/0JcITM0ukIlquRT/rM8yGZGS0RZt6UKce1DHOYaxFepag5uiNHMOhI6043LqG\njiNY1dQe5lGpF8QmiiKSOCYZDNB5zrAotEZKiR8EBEGE8muFvRUpDLsIOoimw9SquGoCbq0QyOU+\nJB4inTpPvkCEAhFKRCBmJntBcSPol4uU+ELcZzW6PyU06uQZB4dttM1pKMVJldZMPfjxjLLpUbEI\njKkAFag5UAlSJfgmQYoUlacoJ1CVAFWvoOoV5IPQkcpXPr7yJ9cu6+wk+jm9GGsmz51zWGsni0Ag\np36UUwgnJk1DSgixIfB3jnHHOA/nPJxTOOeNu6dtLauAjQju5mWn4KUxmjzPxgLCjSVNBzBWJkgp\n8H2PIPAJAh/fLy9E4/a+QvG4xz2KL3/5b/nwhz/Kueeey3nnncfll1/OJz7xCX7xF3+RN7/5zbzm\nNa85NrZmu9gRu6TzBECsY0aMiMRWA2/Pg9gLObLSx8gRYqHC/LwkCCCOFXmebyWdFgQKpJiQToD5\naJ7UpJOUa5IM6fa71FHUvTq1Vo1EJ1T8zfn6AqWYKDcxPnac9twsFike85HB1xYkyIbEDXyYIp1d\nrTHOEUpJbSa665GvrmK0xvN9WFzcMJEGhtmIUR4jhI/v+VTUxnEnSeG/ae1GZ8wiAiARSqAzTf9I\nn1QXd+CNRoPG2DPJOYcxfYwZko8tUIKgju8vMxwZ0syib7gO9R/fjBqbu9vzX4B49zuRpz1y5hwk\nnsfQ2sJjNElQUURDqVmFsNZFFHc0AucI8YiiGiNPMJirElarG9v6sNpbReWK+YV5lFBU/AoVr8KC\n79PpwGgA9WpxeuO4WKb1WKWuYs+eFu12jtY5o1FvUrubZRlJkpAkyZaa2kDU8eoR4UmasBri+4WC\nu5gE06kIZoZzplh39unEH303lZe8nuAD/y95s4X47TdPqb5nL00KWJZFfe8o06wkKdX/n703j7Y1\nres7P8/wTns+4723qhgKEKkCKXFAoEHQJiGJRlfSamInahQSNdE4pNPT6pXuOMR0r5VGaSeMaKst\ndhww6up0BjthkhksEIQSsMCa7r3nnH3OHt/hmfqP59377HPuqapbRYGBxW+t975377OHd7/T832+\nv9/v+/WSnhWx5viC5mehBSJPYLDPcnFCUi3ZTgxZMo+g/YK0vhCCQTYg1x0Oy2OmpuSoOSJwTCcb\nrK8NgKyIizWCqp9QPmgJZWD5pw6zq+mNFN0ODPt95GBAU9dUZUld19hVvrOtV65CILEWvTRo1UWO\nuqTDvN1vjpA6AiXBQTAKmoTQaDApWAkLFx11WgBKJkELbIhAvYR1XvgMEG3BqHoMA7MKBswJIlik\nUOhkSElC5v2jNhp9psP7TYAZz//zGWIpV1r0gnSvIEmKWDu9mYIPNSxqWE7iBHfVhPRpBjSr+/cm\nmPTegwfpJcGFaElrmygxFVogGi5OhScyoUgKummXLM3OGCGs1heBtBAuTs1vnMbt60I7pjiEcCjl\nUcqhlEHr1eNwBuhC0qpwRCWOuHY0TbwFQrwuIxsaQajWsbxACMErX/nX+fqvfxm/8iu/zqte9e2E\nAN/6rX+Dn/mZn+Luu9/LT/7kq8myTluKIz91NYnPx6cU4omo0fh83HwIIcJj3efGGQ6XhwQCe509\nEtWmcANcuwbXr0NvcZUiO6Z4So/+aBelCiaTCYvFgtFoRGcDpDQHDcEE/PAQqQVZdsuZ7/PeM51O\neWA2ozqx7Iuc4W1d5io2Go3yc+3J7caUDzzAcQionYSR8mi9hVJnAWpZRqZRLxqG3YAeakRHcPXg\nXpLJnL2dJ1ENh4ytRQJ7aXpmQBx/4hNU4zHb29vkt9xyBnCWpuTqyQnHxwKZzBj2Z+x09hl0bmM2\ni001EMeL0ejseHFy3wmzwxliINBdzXA4pChWuqIWa8frlG9ZeuZzz2AwIoQBh7//Fi7/8D+i+/53\nx9c/5y549auRL/+q030aAou2XMCFgFgs0NMpnW6X7qan8CrtvrL8W/lO93rULLg++wRC9djvPQXj\nDfNmjnGGg+sHaKm5/dbb6eVn2eVr12I5wXmnwSQ5zTJu4i9jDNevX6eqqrUOq99AqFJKsiwjz3PS\nJMVet9G2dLfCmAlgUapLCJ4VM3EakcG0dhK34TfeiP6Ov4fwHvc//BPUj/4v6wMTfCDYEBlM2zKY\nNrCwjql3BCBBsKU0SSIRiUAkIrKYiUC06gtza5k6R2Ite/N5HClbmQKfZWtgZkPAhOgRv/q1ta2Z\nN1OMM0iglxRs50M6OiWRscbytOwiMHvAsjjxWAtyqFGFIsui/NZmVYozBlPXNGVJU1WYyQTRzohC\nURCKAklkv7Vy5JlC6kBgpRsqQAi8CWB1BKAuQZIiVoBdCUIqsIozy/pIblwAEm5gRPWmDk+7TMyc\nhSuBmE4v0iHTtulNQHQ0ehjg8pmK5fLUPfOimkWtTw2Pbqp5JoTTlEBdn6LWFXIqipuy43y0sNbS\nNA3GmPXyWMaKaH98ugQCHo8XUTfUBINUcp19SFW6Lre52ZKITVAZgiUEhzFxsda3a4G15/SY1xHd\n25KkBfkpZJlASkHk5kWbzfIYY2ma1b6w7W4XrHRzwSMlJIlCKdEyrop3v/tufvEXX8+//tf/BmMM\n28MB7/3ln2HLeTieILSG3hDRGyKGI2RvhOj3EYP+E3IcPxdDCEEI4QnZMZ9nOj8LIlEJ3bTLvJlT\n2pJEJZRlrEmczeKNtRY5t+44UM26hnLTr/xMtPexyCY5QnAIofDeRwme5TLe7ISgP+izpbokUjJn\nvmYBLwolRBSD9yB0egPgjN8JdmERTUAMo/OQ8w5a/UXfNJy0I8VA67MMzHKJbjtObb9/A+A8qU7w\nITBIhxSdPg1/wryZgL2V+VxcqL/ZNA0nJyc0TUMIgUIVbO9vrwvbnVu2ACkgRILWI5qmQsoZjMd0\n/6fvZ/irvxhfu7eP+Kc/ivx7375GcY33LNrmi9XwoYWg2+/TqSqEtaeNDGV52qUgROy67XbXo6I0\nS/IkZ1yVfOz4Y2vwn+mMK1tX8E2bVm6B5Qq/rswBVmNkvx/HyfODrXOOsiypqorlcslsNmM+n7Oz\ns7MGmVmWnWlms0sbu8h1g/AO7+d4X+HcHK13kOvay7MMptZDjDnE/82/jDOvRX3nd6J+7IewxzPC\nj/xzgoXgLh5we6km14oT4fBaMNEwStWFWpI+BOYtKOpnGYs0xR0fY5dL7EMP4bpdwmBww0CzYgP7\nWYcreRfjKhbNDB88dXOCCh3SrH+uXlkwfFJCd2Cpjh3LpcE0DVUC1XWDxtJJLd3M0japx0PV0nAm\nTWmyLK7bkokGaIRgWTqKLKPX3UIpjycyxygDqoGsIfiAbwKhkQiTQJ0glxmJUKeqkgK8CjgJVgus\nClgJToMXgs2rWxCBqAZk8MzNlOAapJQMsiHdTIM6IReCKbAEZlJSKkU/TcnPa6p+msPamMnYNN9a\nsZgR5MTlMW/S6lrclGFaMaCrtIGUZwHoo26rXQPLFdA8DzCFECRJsrZjfbTlZqKyFaUp1/qhjWuY\n1tMIQJOCXOcIIrBcgcrN9UUpBSlXzYWwUtaI44nCe41z6syycgZbsc/z+dnjc9qsuN5Z+IeuYv7s\nPtx9D+CuXiUcH8cSq+kUOZkgpxPMyQnvPrjO206OubZcIJzjCnBbdYB+xTfw6EcFgpTQ7UGnC90u\nodON/+/14Pbb4a674Hl3Ib74uYhHKDX7fDx8fB50fpZErnPmzZzKNNjFKRHW6cR7X55nLEvoFDWr\nZpgV6DyfDg1tobhQsr2ZOLyHo6Oj9WvzPGenKLBVgEVM5Sit4ozZmTXbevqhAeEbjJ2jwhZSPkx9\nl/e4uUNq0MN4+gXCmlGZtB3P2XlB6ra7VGsNgwF2429ndTgHWNuhkwZ8yDieVhiWpEmXra2zTN90\nOmXedhMlRUJXdUmL2EkZQmhF3st2X56KvHu3IPtXv0XvR38YeXRASFKufuv3Mvlv/3ue9cwosF+1\nzUGrek0BFG2pQCrlKVtydBQR4eoGFgUhz8i3OO+obMW8PKA2JUvnCFgEgu1im0xnNEnD4eEh0+mS\nEPpn8GuSxLLXTeWdVazqM8uyXMtyAfR6PYQQ607TvQ021nvbShZVNPMl3nhURxKCROttXFvPK0RC\nktzo1hS/WCHqDk15QvOX/iLpj/8S6Q9+O/pnX42ZLgj/64+DjnWX6/rLlskUQpACRQhMrGXZaknW\n3tOTEgeYlrkcG8PUOVIhTicwwyFCa8R0ilosUMagtrfRSfKwdY+56tJLOut6z4VZUNqSftqnm3RO\nc4zGoJ0ldxVJZWN6VylqFQfb6RLmStHvQ7cvT8FLp0OytUXS769ZRS8Exjmquma5XFK2afIiz+n3\n+yTtNeBdQ/A13tcIX0PLMHvj8cYjnEb6AuFzggtIHyKzuXlZuhaIytAyogGnPQ2BqSmZlhO8t2ih\n2EkGNCT4piEhAtOhEHRC4MQ5DHBMZN46aUony9A3TSs+vlgsIpsfQvyKXi+Clyf86zZlmJw7BaDR\nWSAuK/evPIcswzl3BlxG694bwZvWet3NvTJDeKJBe65zMpXhvaU0cyq7oDQLGmOZlbFOJVMJRetC\nduP3yzZNrdo09er/ep2+frQIAZo6UF87xv7ZQ7j7ryKvXcUfXMVcv4o7uIo+uIo6uoo6uIY4PkSG\n8LCg8d8C/xvwLuALga8Evhv4VWCr1ycMBvj+gKo/JAwGyOBR5RJRLhGL1nRhsYiPGwOzaVw4bc67\n4TcIgX3q03HP+SLcc5+Lv+u5+C++C/HUJ4OIzX1CCBSRZFBCfEYnYP85x+dB52dJJDKBILh6YNjJ\nAlJG15deLwKK46OMcgyduka4WCu50vRcyS2tY50d0oRgqOuS2azGWkuapoxGI7TWHDQNTrfIxUUg\nujALalffADqdXeLtSbxIZXZGNmgz/MRGndBcIbOzN6iFEGTeo4xhaxMdWhtz8iGghkNomjV7uwk4\nB9kAYXpMiBe8r4cslxUqHbO/110DzhACx8fHVFWFEIJ+v0+v16O51hBcwDUNjpN2Zi/RerhmbcNH\nP07xyleRvuWN8fe86CsJr/1ZDgdPx7jA8cLhkqhrCJEx67RgUwpxKuezGqhW4peXLq0tKiFan1bN\nkspW645V60qEEGwXOwRaX2edYQzUdcrJSUJVGeq6Is/zM/gVYhlGHCM93pc3AE0pJXmerxnNEAIH\nBwc0TcV0ep2iSNZ1metTqfaRAS666KSIzVTBt3aZsSwhSXZio08d8E10f4qESR4pttDgvuEvYIf/\nCv2qbyZ5/c/hqZG//LqHkVM6TYcrISAExm1X9cqPPZUSGwLT9jwZJQmZlOiWwdSjEbrfR56cxDzs\nycnFNlTrE9whnGPgE7p0mZRjqnrJxF6nQjFKBmcEzHUR66ZtKcmVpjtMcb2ceZ1QG8kEWMwX9L2h\nGJ02hm2GBLIkIWtB5nw+Z7FYUFYVZVVRFAX9fh+dROmd1bd7b2PGIVni/JLgLYEpMAeZg8vByQhK\nrV+XLQTXLiaqVggfOGHOQpb4RJL0B6TpkLkULDxRTcJ7hA/I4ElDbP7w1uKNxTWOsikZLwSZEHSE\noKOjYxhJgtgAomJjeF/ped5MbDYGQjx8FxDXn55QKn5htxs3ZMV6GkNzfMxiscA4h9M6esGn6fp8\nVkqdAZc3OG09gRFNOpatRbJbX7+JgCSR9HQvMqC2onaO2lkaXzI1hkJ36aQ9ct1FSn1ToPKGaBr8\n295J+E9vQrzlzYiP3kN6/SpZ0zz6e4kAz23v4/cuwaXLiP09xPYWYjSCrRGXZ3N+wDa8+AVfwfDW\n22BrhB30cN0uM+8pm4baGGpjsKG1syUOgypNo7JGqtAqEJoFYXaCnM8QswVysUDMl4jZnOSee0k/\neA/pH3+Y5GMfRd/7MfS9H4Pf++31trrBCPOFd2CedQfNnXfQvPAr8M94GiiFlhItJaq9D+n2ObWS\nO3gkOYDPofjc/4WfI+G9YDZJsK7BUHLbXmd9fqYpICVW5xAMYjaH7W201kgpsdauJZe899RlTWMb\nnJrTNMdAB6X6pGnKzs4pMxUAlIjpFhvIdMbCLKhsda4jfIG1x0Ag0T2EHuFWgGAj7MwiXIisVfd0\ngA4h0HjPUmkyB6MQTpmmSMHGdVGg+n24fj2mgs8Bzl7aY97ex5ZL8GYLxDVUfkJRRPcKay3j8Rhr\nLUoptra2TtPFCdh6hlvUqI5ombpthFCE5RL/L16D/Gc/RFqVuMEQ+yM/RvY93wVCMDxp+NMDy58c\nOJ50RaGEoKfUaRNUVUU6ZkMmhBWr1eoSWSUo6xmVrdYd6BA1+jKVodSAVCak6RUenBxwdNKwPKnQ\nbT49y7oYc4IQC/b28rVMinOutZlsGI8dR0eGnZ048AghyPOcoijIsiyC9fUg1VAUFcvlEeOxYHd3\nu2VfojamCClBSkQiSYtTHiI4kG5EUx1gzBxjPYpzZgK6lf1J9nDyCIQj/M2X4LffgPzGb0S+/pdw\nVYl//S9jtV4zl7a1Wj2TiBSCodZM2qacpfeR2QS2tWaoNaOLRNWlhN3dCDgnE7h6NV5M/f5KR+pC\nYUYFbJNSBc/EzahpOJAT+umIbme0VtpWSkHlsMcWF0BayfauoGlg+uAcdzyN4DMZMdAdHknZUkrJ\nYDCg1+sxmU6YzqdUs4rxdIzONJ1uB6nk2gN8tYdC0ARfRsY+mPX+EiJFJB3kRio42HidY8FUhpPl\nCdbZ6FyWDChMisgqfBYb6T0CIwJWBs5UQigg0wQvCMYSWvZXWItcOgohKERkgFbHIbT7LCRxLXSy\nFo5XUqGEWv9fCokSinIpWcwVoU2UjEY3ldn+9IRS0Oth85zpeEw9nyNa6yAdAjoEEudIioKk10M+\nQXWgjxTe1zg3b13hNkNsMJNxnaaaAYqAoHb1OgVvgElTMjOxwTTXOYlMHtkhqqrwb3074Y1vQrz5\nzYh3vwNZlTe8LPT6sH+JcOlKnHRfvky4dBlx5TJu/zJm5zLN7hWa0T72HFSJEk7xcn1mErgjCXgR\nWGzcJ+zqPpFlpEASQixZaVU3TNPg6xrXNAhAK0WR5+TDJ5PvZyhhEb5B2ApcBa8wBGepnadalogP\n/ynqgx9FfvhjqI/8Ceqej6Amx6h3v5383W9fb6u9fAvVC15E+eIXMXvxC/B7u/hVpiu0talELepC\nKrI0jdelTvE6w4sEgsR7AUGSpfLTmTT4tMfnG4k+w/F4GolCgIMDmFUl0+aYvR3FbVuXzrzmoYcc\n1fIaV5Ijcr0D+/ugNcfHx5RlydbWFlJKxodjzDUDCuSOI4QTtO7Q7V6h3++fmW1fbxpsCGwdBSSC\n5HLCtcU1AC71LiGFbAHnJN5cxw3HqkOzs8NuksQ0chveeMxhHPSOTAJacuVKvHnUtuEjkwfRjeMp\nJomyTNvbp4DTmHh32d3Fe8/Vq1djl/0ov0H4fTaDBx6IeKLXg6X4ECqpuTx4JsJrTk5O8N6fEXsH\ncK6kmZ1gjw2yI8l2Bmg9IPzZfYTX/BTiF/4l4ngMQPl1f42Tf/o/s3PnHagkYe4cR03Dvdc82gqe\nuZdxeagiE9SmbtbAZZWe63ZBKdxsSnV0jVJ6mq3TvLcUMjZq6IJUpYQA8/lDNI3E+8tMywXTZkIi\nE/Z7e20naGA8vkpVVWit6XQ6N6Tyjo6itePeXsr2dkaWacC2Tj+xy/x8889stmSxMKRpwaVLtyGl\njmzjzGIODEIL9ECfgpb27T4YrDsEAjrZRhcdZCaRaVQLWIV1DbU5xvgmary+6Q8ZfdPfRs5nLF/x\ntZz8+q+eQROCtsFmY0naFNZ8Q8B84RzbScJlpaJ16sNZyKzEwqfTeM4l0XRhfVcXG36C5xavJFO3\nZNkqGmQqY5SPzgzKvvGYsYmqEakg0RViOWdZCmZqhE1yfPAkmaPX90jlz3iVr3y8XXBrJynvPfPZ\nnLIs1zq8eZ7T7XXjZPOc848QguANIZSI0LQ/SyDRKN1FyS5SKkQLOk6qE5x3SCMZMEA1Cu98ez8K\nBBGiRFMuIIMgoAmexntM8NS+ZZNaZqkJAYtH+kDqHNIYMucojKU4VycYQsARj0No2Z8VGEUInIPJ\niaBp4jnU7Qi2RpFB2gSlK7C6eu7TGc45ZrPZ+nhIKel2u3SyDLVZt72ZVl8hp1UBY/rECOo7V+Lc\nvL2WIeo2d5Ay30iL38TntGU9pS1v0AdVQpGohFSl6LIheft7EW98M7zlzYj3vhNRnwW6/gvvgJe8\nFF76UsTzvwxuufyYaiJXKgSz0jOvPLUJWB+B5WqPJgkkaVxWpLI6d59QxOekEAjvacqSermkWixw\nxqzvCaI1JMnSlKzVDvWhvU+GOqpK4KL0oFKgYlmPuzom/NGfID54D/oDHyR9+ztQJ8dnfkv9Bc9k\n/qIXMnvxC5h+xZdQZx1MEzMOvomZQOUE2kNGnHAGneAkGAQi76BVRioTijQhTQRae7QOJIlcZ6qe\nSOb8iWwk+jzo/AzH4wGdKyHzJIEmuYZQjv3u/hmB74MDw3x+xG62pE8eQc1wyGw248EHH0RrTVEU\nBBuQU0nezencUhDCEUIosuzyDd97rWlwIbB9AsJBsp9w3BxTu5rtYptEuHUXsqaHOppzLCXl1haj\njZrM4ALm0BBcQPUU40pjbZzcKgVXqwUPzq/TlylfULUD/P7+KeBcSSO1IPbe++5lUk3Yv7x/xtrS\nGLjvvtNM6S23QMODHM0fRNicnG0AiqJgNBqtWT1rJzFtbAP2QKKzAenH3w//+48jfvcNiBYw+i/+\nUvjhH+bw+V/KvK7p7e5i223yITBeOuxEc4uE/d4S2VSntZurQrOiwAVPaUtKU2Jcg7x2fZ1iz7Mu\nhS5inWZzOlY1jcXa64BG632Ugnm4jtSGrbyL9JKmaZjP52tgrXXswo+p9gStJd7H/SOlZX/fIMRF\nQtCalcuPlBlCKK49eI2mbMh1zrAYxn01sfjSowYK1TkdyDa1L70oMXJCkAKhd/BCR71LonPVJmvp\n3QzvolZf8s73c+m/+jvI6YTmq15O/du/SdLrxcFjs2liE0y2S900fLSqaJxjC3jy+Ya087Fpcr0C\nnlrHc67bvSlrxMpWTKrJ2vWpl/bIdb4GjbaxNIcNfjIlzGegBW6vRxjmLGvBYiFarVQoikCvHy78\n2pUY+ApYEWC5WFKX9ZoJ7HV6DAaDGzRSVxGCx7kl3i/XigyxqzincjAzkZUqdMEoH51255tYGuEr\nv9a0XW9XIpC5jEsSN7zxntp7Ku/Xtc3Ge0rvsatBXUpyIeg4R7ctraEd/DfBdggB5x3zWnJSaqxU\nkEB3C7Leo4OoleXmeSB6Hpw+1gghMJvNWCwWa/Df6XTo9/sXN/fEWpjzvrIxNjtysuzC0pJH2g7v\nV2AzHlMhFFJ2Uar7KQMQ590afDaTY9Rb30n6lreRve2dZO9/P+JcCZe78znw4pfCy16K/OqXIi7t\nP8wnP/rvWp1D1YaqxKoRyay8FYxAESeeK6CZaUGWiVOlAt82fm1OOjfCWkvd2vbWbWPp6t4gtSbN\nc5I8R2cZpAonPY1f0tglxm1eS20IiQiS7P33kv2nd5C9+W2k73oXsjq1xA1KUz73y5m96GXMnvfl\nHD/7TsrhAKzBVyWhWYIpka4hDR6Nw7hAHRJMkuKSFKU0qUxQQlMkKZ0CssTRy7GwLvwAACAASURB\nVFMynZGpFBDotIPMNTJ77Laz/1mATiHEFeD5xOqsPwghjJ+IDfpcj8cDOiGOhd0uzMwJS7OM4u3J\naQ3YyUl00Bn1FP2ypLGWejRiNp9zeHiI1pq9vT26WZesypCZJNlJaJprhOBIkv0btBGv1jUe2J0L\nQh3Q25qlWDKpjimkp9fOzLUeoXwCBwcstGYyHJJLyXaSRMB5ZCLYbb/zsPUF390NzIVl0pRMqzG3\nFn12Z61Wp1LxzrIBOEMIzJoZ9953L847nv6kpzMsos/ubBaB+XQaP/vJT4bBIDCZHvKxq3cTguKW\nwRcyHAzp9Xp437Spp6o9LgpFF/vzv4N+7Y+jPvAeAIJShL/61+AHvo/w4hex9J5PPvQQjbXsX76M\nkpJCSnpSMp5OOXigpFcLRhHzs6mXU9s61sTaep3+lEJSzGvyxpMOdyiTAVUVf8PZXoMGKQ9bx44+\n3tdMlhMO54coodgtdlfnF1JKlsslzpmWtOtQFJpV5+nRkaCuBb0eDIeq7SpP1h3m+MjObQqtW2M5\nODoghMDWcIuiU0T2TkB2JUPmUabIiYCBlvFq01x2QvALQKGSvRvqwtbSQEKgcOAmKCzy7g+Rfe1/\njTg6wr/wJYg3/Doiz1nrsTyMyfXUOabeMw+BgZRopdhNU+SqZuqR7GNCiKi8bNOB/f6ZzisffNRD\nXIlzt+zjSrz7pDqhsvGcSlXKMBuegpnZgvDglNCA7/chi2URMpGIVFG5hNoqBJG1G/TjoqQ8k1q+\nKJxzzOfztfKEEGJd8/lw4BNWKdgl3ldM6ynzZoEQmq3OJYbFpYd9X/ABX7UgdF2jG0MogexIVO9U\nOsmHQNWC0LqVDau8X0uIpS0AHWhNT6lYHrHh2+hrw8mhXTdQFnlgOIjA3BPwWuGkiGstcUriCety\nAx8854oyLowVENVSk6qUVKU3Nk0SwdBisWA+n68zCUVRPCLYv+BDWM8sq+pGfae2FvSRtJ2ifvAC\n7xfrWs0o5N5Dqc4Nr3+8Ee67n/BTr4X/7z8g7n5vVN1Y/U0ImjvvpH7hC2he/ALMV76AsLuNQKz3\n45oVlY+eE/Yt0Czbc2XzqK0mKpvs5aoUa1P0f00qb9TayuBIk1MnJa1BpQqV3pjBCErFMbRpWCwX\nLKoFjWvWOqiByGavmr90osnTlDxRKOHRBJQUOCtZzaOaBvyyIXvX3eRvfSv5295E+qH3xTKMjbCX\nbqG6406Wd9zJ/Nl3sviiZ1Nf2kb4itQ3yLpEBkNwBmcCRiUYlVKZDFPFSaFwim6SkmeQ5J4kU2RF\nQZb1CKJDSAtUruh2o9ua9D5mE9qJ0vn7zGcUdAohfhD4h0AD/FAI4f8SQvxd4DWwbigrgX8cQvjp\nJ2KjPptCxBH0+4DvBJ4CHAC/DvyTEMLygtc/LtC5iuiJfkKuc7aL7fXzs1nJtWtjrK0Z2WUs3h4O\nEZ0Ok8mEPM+59dZbkU5ixxaZS5LtBGOO8b68UFPzobomAPuVwi0caqAo1RGHiwfpJDlbxTZKDVEq\nj1fVwQE+SbjWCorvqwQ3tgQbU3HJTuzGHI+hLAMMLCL1WNcQzIR+2mF77uChh047AlrA2biGk+oE\n6y1HB0fkMuf2227HOc10Gr9+1acTbd+WeD/DOcfh4qME5XnKpbvo58W51JNAlgH5ut9AvubHEX/2\nCQDCcIvwHa9C/MPvoX7SrSzbmTbAtYceQgO333orXWujM1JdM7GWqQ3U05xut8vubTkyjcdsaZZr\nFkwgYuo8KchUTjk11Pcf0FiJ2ztlnFeZtyTxWHvMcnkVYxRSntZHjqsxKNjt7zLqDNDat53lDdPp\nhPm8tSjMM7a2tlGqwLmUw8MoX3TpUkwzhSasgeYNUkUispelKZmWU1Sq2L+0jzmwGBFgP7lB33Lj\nrSghCPYI6Ru0ysnS3chItH+7YdbtPa46wVZHhPd/mPRvvAp5cIB/7vMQr/8VxNbW6WtXOpLtYGGE\n4LBlKHbSlCnQhIAWgt0kuWk3njCbYSfHWGcwicIMe5hg1+nthwuBoHHN2k5WC80wH9IjRY1jo53c\n3gFVIBoB9VlpKI9gYSR1kIhUolTrmnWT+OEi8DkcDs/o9F4Ux+WYWXVICBXDtEuRFAih0XqElI+e\n9l0xoL6OTUlA1G7tqjPgcxVNez3V3rN0jnKDyUqFoJCSjlIkQmBryXImUEGQBc+waym0OatWfj5W\nHeQbzXkr8LkCopvrFat6ETCVQq4BaKYyTG2YzWbrZsZ8pSZwUd3wYwnnznrBn+9wXzWbJAlBK5yo\ncNLEWRsgRNqCzRtNRB5v+D94O7z6JxC/81troBmkJDz3efDir4SvfhniZS9BbG1FkXoXReob10SX\npHP7c9NDfsUuRyAqMQgqH0s0Nt+VCkEuJXnbiPOo0ZbL2OmSZt5EIGpErAstitPc+9rl7nQuugKj\nQnosFbVf0rhmrUBgjcUaG1UgkNF+VGkSmbRqHxJrNc4lOKcQIqa9hXCEYBDCrecQSRLw4+uE//BW\n1BvfTvLBD5Pec8+F9a9+OKS5806q5z6b6gVfRvX8u+KNobawrPHLBpzDeEEVUkqvmXtPhcQGRZ4o\nUrWk0J6OEORBkomcQEatLD6t6GSSrNMh9LrsD66cmSB8xkCnEOJrgd8FrgNj4AuAbwZ+DXg78Hqg\nAF4J3AF8VQjhzU/Ehn22hBDiJ4DvBd4A/L/Ane3jtwAvP48wP1XQ6YPn+uI6Pvi1UHzTNIzH17jv\nvhOkLLh1JMnrimQ4pLhyhZOTE6qqik0zpNhji+xIklGCtXOcm6JUD63PNns8WNcIYLcBc1JCvsR1\nGw6XxxTpkEv9208Hk6aBw0PIMsaDAcva0p1BJ8gzgBNgfBx4YGLoDAO9rqCLZVqfUHjF1tEiMk29\nHjzjGQQhmNZTFq2/cyIT3MLRVJ403cX7FdsaGwnG45Lr1xd0u4aiCLErNJlzXN1PqnMu9W5pj4NC\nXpsh/o9fQP78a9f1mv4pT8N++/fiv+PbaK70KVsmBiKAyoVgct99ZMZwZTQ6HRiEoEpTxmnKolSw\nDAjd0B1W6xuvlppu0iVTBU0tz2hNy/EhwjTovS2K7QKtLU0THYBiE9AC72dI2SPPt9d6mZaKo+VV\nBIa9YuvM4C6EpmkCk8kCSNA6KhMkJIyvexaTQKY9W2cPe/TzTluh9VSuZYpcCFw9OmK6WOCtoi+H\niEKitk5vTloIUhEFxldroO1oPyB61p8716w9axnTpupCcFg/wX/84yR/67uRDz6Ev/OLEP/23yBu\nuXJh+vGgaTAh0FOKgY61p4fGYC4AniGEM8DjvMUgdY08mazT7X5rhEwiW7Pyut5M00ohN5g9z6Sa\nUNpo/VQczxkmPWR/ECdTm9d00wK20q8BqDEwm4OVEpErsp5gZ0fcTKYfOK0xXC7jvDfPc0aj0Q0p\n3xACx9Uxla2QQrKVb6FFdN9aTcyk7KD14KY7l30TZdF81V4bElRPoboXi8a7FbPlHCfWUrXpd+fB\nzAXCxC7fLIPRAFJ1VsQ+gQiIVszo6jxaRZqeyjg8yqRjBT5XAKp20fscoKoqFvMFzjq01PSKHjuj\nHfqd/iN+5uOOVSp+s+TAmZbZrFhbRiYFKhsis94pI/qpAGBj8P/3b8JrfgL5nncCGxmfv/NtEWQO\nh4/6MSEEjDdrEGq8We9LiKUWK+bbtBOkFcvcUQldHS1wU5WgxE0YDhgTa+g37dZW+qmdDl6nNM2N\nbkqrLHsIgcpWa8WQQHROSrSkm2V0spROnlBkGq1jXbUxhro2zGaG+dywXNp18mVjjkCaCopCoXWg\naUqaZolzNdG1aSXsr8i0Qt/7SdIP/DHqA3+M+qN7UB/6CHJ8fOPP/YI7KL/khZTP+3KqL34eXNlD\nFQInGha2Yr4ssUZQO4WzAl9ZhKnoKEtPWoKoMQJE2gXZQauUtCfo5YpbbnsGujhV8vhMgs5/B9wG\nPD+EsBBC/CTwLcBHgBeGaDmCEKLbPvfOEMI3PBEb9tkQQohnA38E/FYI4Rs3nv8eIhP8t0IIv3bu\nPZ8S6ASY1TMm1YRgAolN8N7j3IzxuEKpPZ562x695UEclC9dYrFYMJlM6Ha79HQPO7GonkIPNN7X\nGHOElBlJstPWBlU4V/JgUyGCYz8I7JFHaND7OYdViVYZl3sbdaB1HWsws4x50udgUpMi2O9k6G29\nvmFUznHf2DKbw9ZQ8OSthMZWHB/dT1FZtlQP5nNCv8+ymzJLYupSIOilPTq6z/33HzMelwyH23Q6\nOb0eaF0xm804PLSUpWBnR7K31yFNPU1zyIPTjxFI2O8/ne7dn0S+5mcRv/0b61ok/6XPJ/yj/4bq\n67+O2YGhEQF9KQLapK056zQNYbnk6kMPoZTi0t4epClNqmhSRekaHqhLfAiokxTnYDQK9IuchC64\n05ve6fnQZs/MFDU7wEqo+/0z2qrRAq4mSRydzg5KZXhftV2pnsPlmMY1DLIhg3wbKfNWkF3hrceW\nlqPrR9TLGhz0Oj3yrMvhWBIC7F8SZL04Odhs8rHe07SAoFnVX4bA4fXr2HFDT3fZedIWWTdKFD2a\nr7c3Jaa82nb0dmNJxkopejPWOyW2pzplsfd+mOQV34T8xCfwz/kiwtveiOydBdkr5yEtBHtJsma1\njLNcNzW1c0g8Q0n0ankE1nKVGkyQJCcztAtonaK2d86KvT5KlKZk+uC9hLpCZDmDW25/WBvZuI82\nAKgN1FUEn86BSgVb+5Ks104I9KODwLIsmUwmeO9RSjEajcjapiwfPOMynjtKqFinvZFKjhPSGRHc\nSLQePKaUrW88buZi+h0eFXxCO/B7z3jpuT521C42LXX7MOhGsHnRe9dSWKu196jlMmYhLgAgj6Vp\np6orDsYHLMoFxhuCDHR73bVjmUCcMqE6W7NeT2R4b3B2hm/mLQi1SK9RPkVyQTp/E/Gs1pvuUhdE\nODjE//TPIV/704iHHojPjbYI3/ZKxPd9D+L2p3zKv6NylrltWFhD7Uw76Yvi84poe5zLi2sON+tv\nVxM+hURXDaqqH/dEozI187pkXlUYE2K5pxUoMhJxsV7pprjFqgQ8Vj94hDBobdDa4r2lbnV2o9f8\naUPWSvw/TTVZpkgSg5QlSRJIkpXIfooUOfKhY8T7PoR8992It74L9YfvQ9TVmW2yT34qi+e/kJMX\nfAXT/+IFmO0tZDUjqxeERYWvPMtlw7EPTBPwRUYnEQxlzqjokxYpqUvRMmXvWbdRpH8+TOf9wE+F\nEH6sfXwX8IfAd4UQfu7ca/8Z8K0hhNueiA37bAghxI8A/yPwkhDCH2w8nwFHwJtCCF9z7j2PC3QG\n56LOmLWUVcn9J/cDsFfskeiENG0AwXy+Q5YV7HM9Duh7exjg4OAArTXbxTZu5lB9heyC9yV1/SDg\nSZLdthg64EPgqnFIBFeyDHMAwmdk2z0OwgE+eK70rpzKK1UV/v4DnEsI/S2uugbRkdyyVaDbesyp\ncyycYzGHZi65daQZdSzl8XWOJ9fo6ILhzq2UwrK4eh8Oj9/ZJs27FGJEXeq2yXhCWS7Y3e0xGAjq\nulyDtNlMI0TClSuQppENCMFzcvin8HtvYvS63yF/73vjNktJ+Mt/leYHvp/yJS+iapta7LUG4aC3\nBb1gSTZSXdZaHhwf4jsZg1v2aXBnwMv12mKsolN1qKY50mdkqTw3znmktEjZIGWDtQ3eOeTBAXiP\n391FpilpqsgyRZpKrD3C2hlK9c+UQQiRYIPgaDlDhYz9fB8s0ea08Wca0WfzGbPFDJEIVKowIcfJ\nLv1Rzmj7tLlnZQfpzp2nqmUxhbWMP3KNBMWVO6+gMx3vwt6f1lqe7xZvTa+dX2L9FJAkahspk1U9\nxFlvwvPnf/CYT34E/bK/gvzkJzFf9zWYX/tpvFAEFE2QXDfggmMoBUqcBZQ+BI6tw4SoT7ilFXqj\ngWQz1bdaNr48Siq1rCG93g1s5cPGbIafTpiYOeVWD6R8eCvZc+FtBKBu6Tk+CDTRjIv+oNVelayZ\n6DUjLS9gEp3j5OSEuu0o7na7dHtdxtUY6y1aanaKnQsbaUKIzYKntc9pm3K/eb2W8+BTKIHqKWTn\nRnCxuatdCDjtSAce5KnEzIrlFEJgWpbs4e6oElB1jSpLVNOclnUkCarbRXU6DwvCrLVMp1OqtpBU\nKUWv16PoFJEFtfWawduMTRCa6/zCmtCbjRtljwRKdVCqd9qFvnmNbbCiF9U7n+6YFnwKgf/wPfDa\nf4l4w28g2tRuePozCX//HyC+/VsQg8H6tY8nQgiUrZqE2dgmtZE2z9oxYpV5WNVLW2/Xj88c5ZUb\nVJsqEkKgVILq9FDdHjrNz1zT52sUjTMsTdRBdhu6w6lK6SQdcp0jhVyDy5UAwap3oCzPuqGmaZzP\n9HoroQ2DMUuMqYjaqAHn4lop1TZ26vY1C6wtWd2sYwNYQZYVpKlGa0GiBKExuNLGGvuyhPf/Efp9\n7yF553tI3/MeZGt0sv6NT34q9Ze/gMWXfQnju57JbKuLkwGLxC0doRZ4meNWpgRGIIMlzQV33nUH\nRfeUwf9Mgs4a+M4Qwv/ZPt4HrgJ/KYTw78+99u8SAeoTo/vwWRAtE/zVQCecFgmu/vYHwBeEEPbP\nPf+YQWc1mzG7915sURBa8eqT+gQvPfujffaH+xgzxvuK8XibEHJGYkInLAi9Dr6bc/Xqgzjn2ClG\nhKVHDQKyEweBpjkAHEmyhxAaKVOCyLluAlomXM4yfO0xR7F+aNKdYLxhN9tFOx3ruSZLOB5DliP2\ndlh0odSBQgiUlCydw9PK3ZQCc2jpiiXDomFpS66VR8jRiKw7iEX/x1PE3JDpEW54G9YJvPdYa6jr\nMcvlIb1eTqdTEIJFCE+3qynLlPqhMTv3fYjsgx9Evv+PkR/4EOKj96wLtl2/z+Sbvxn3fd+Pe/rT\n8G1jirCWzHuSsSGZNeiBIGSxQcQriUkVs2A5mJyQJCn9wXZMzbgEGVKEzyi9ZBk8RQAzgcXC471D\nKUeWWQYDS6fjOethHD2E03JBamr0sIfeGbGJGJvqCO9qtNxFiS7CpYiQgZMEFzgqj6hdTS/pMUgj\nIAoh4BWEVOI1hAQqb5gtFizLEuM8h4dRxHz/SsHWdic6PrWhhCANgSwEUkC3oNLXlqOPHVKWS7qX\nU3Y2ywweKVpwaZjjlUHonKS4glin4MONUkEbjTo+ePzdd7P9F74OuVhw/I+/m9l/9yoAjp3DeOjo\nhL4ukCJFqwLdagqq1i3lxAU8glzq2Fz0WAbSTdubLIOtrUfubK8qGI/jqLSzQykck3qCD55MZWwV\nW4/J83pyFJifBELjyXVg0LtAeUDH0ojYnNSqCLS/cT6fM5vNaFzD3M3pD/oUacFOZ+dRt8O5Cucm\n7TkrWoeu/g2g8ZHC1x47s+vO9/Pgs65jZY1zcZdtavVXzrE811iiRTRe6CiFbydKj6jnuing3p6v\nQghklqE6HVSWRZUD71nO5zRVhQgBLSW9Xm/t0nXD7wp+bSlZ2/oGgKSlptDFTQHQmGmq20xGxWmH\nlmz3effmyhxCOAWiq/VqUthOCP2//4/wup9Hvu0tp7/lxS+FV74S+fKvuvHcFhvSYY+2JqbPl23Z\nxOpXqLZet5ByXXpzs+FNg13McMs5zsSaUYfHJRqXp4RHEGldmQ+sjpMLbq1okMiETtqhm3TRMmbl\nVlJj3gvqSq6bOzdDytNa0LiLA2UZLYQ3DVmUUhRFRqeTURQpUlqiaWyJUr7dXQHvRVsPKmmqBle7\n04ZO63FKYQUEbZF9kB2PkgEZQC2XpO/+AJ13vJfiHe9Dv+8PEYvFme1tLl2muuNO7J3Pxt55J8tn\nPYP5/g62NpRLS+U8XghUSHj+V3wJnc6fD9N5DfjnIYRXt493ifWdLw8h/Mdzr/1BYvPMo0/hP0dC\nCPFHwG4I4coFf/t14BuANGxoKTwu0Dkec/KJT0Qf3uGQbHcXmQgOl4cEHP20SyZijYi1fY6PE5Rv\n2OM6Qgu4tMd4fExV1eQup6d6qJFEdxOEyNqZdINSBUlyCSklxnuuVw3Kw56KXejNQYOfeyZhQlM0\nbGfb5LpNNdYVLI4JW13c5W0W1nLVGIJz7EkJzqFNQ8801HPD+Bh0aij6lmMch6EiS/rkokewCu0L\nsuMpvlpglKLJE7KOp2OOae6/n+qBB+jWJSPnyOYL1LXryA9+BPGhe9DXr96wD4NSNM96JtNv+kYe\n/Ot/hSaV4AM93aErEjICOniCD5iFpz6xuI5C7Bf4NMMJhfeBxaJkfDChSPvsjPZJZIpAYIzBOUvt\na05CQycJ7KUSKR11HVgsAt57QvAkiafT8RSZJs8VRZ6ilYTGwrVDQOB3dhEhIXgNQWHMCQFI9WUQ\ncZCNssKRxWuE5bA6AC3Y6e5DpggqnDJfIZxZe2upFgvGh0tmY0OmAnvbgVxrBnlOR2s0rH1iVpaY\nAG7paU4sR8sxdD2jwZC8k+OlIAhBkCKyyKu1VnitCETLU+cd1hzigwGRINXopruLAdLf/XfsfMsr\nESFw8suvY/71/yVzb9DBcylNUG3qLYZk5QUNkoBgbD02CBKp2Eny9rU3KSPSNNECx7k44mxtXVw/\n51wU1/U+oqdWk9B6y9HyCBfcIzKMDxdlGYFZCJDowKjrEa2L0Hlmex0iLkIKFvWC+8b3YYwhTVKe\nvP9keoNepATb1yDbteDMPolszay1OQ1R8WHVSPgY4jz4RArmTlG3zF2axt16URO4C4FlC0DP1Fq3\n4DM7B2R8Cz7Py3S5qsItl/iVNA7Re34RAssQCO35XhQFvW63VRAQSFiv1bnHq7UArDdrkfVNJm0F\nQIukWLPpq5KmU6B5ehCjskTxhMgeQWyQC6/7JcRPvgbx8Y/G54oO4Ru/Gf7BdyHv+MJTYLqi+Taz\nGI/2+StVghAwUkYvc6WirXGSkCfJKWu6WjYfn4+V1ehyeTZ9rvVpo9hKa3mDIV3933rLvJmzMIsz\nWqNKqHUz5/mOemtZ19uvvlKIKNWWZ5KikHTyU11YZx3lsqSuGqwB7xTBa5KkQ5LkKJXgvcO5Cu/L\nM9JKQiQoVSBCFr0brAcT97c1BusaFk3JxDSENCBTgeoIEiVJgiepFuhqhsKQaI8qElQnQypF8773\nkb31XXTf8Yd07v4QcnlDXzNuZ5fyOc9l/tznMHvmM1g+5WlUox3u+pJnk/85MZ1vA+4OIfz9jed6\nwHJVz7nx/E8BLwshPPuJ2LDPhhBCfBxQIYSnXvC3Xwb+NjAKIUw3nn/MoPNDv/mbHL/hN8msQ+BB\nQFASGzw1MR0upEELgfA5dZPivUA1NalwuDTDCkFTG2gkWuiYY1SrG3RACBOdh0J0PQgISimQAbLV\n9nrACGywGGlaFkkSZIDgULbBSYXVCQRPQ7x9Cu9R3qG8j9IMVuCMIHOGwpck9ZKkLikaR9FYUhP1\n6wQgg0N5S7Fckpcl6iZufE2SMt6/wsEtt3L91ls5uPVJHNy6j88MwgGuQ+WW+FDH2S4aj0RIiRcS\nhEIsWymdvkC24toKiTeOqnRkqSLvJEgZECLEGafwCGABIBQjKVA6prFEEHinaRqNC4L1cBlWraeg\nEOi6QjkHRQd00hazBzxThAKp+rQ7BqQAEdbIcOEqjK1JdU5HZUAU9W8xB6J9HPFEtIwUQnB8HChr\ni9YlqTrXwStkCyTjwCCUwpWAF9jEUfsaqTWDweB03FiDlTVkbf/dvGd5QigheITMkSJdf59sJYJW\nQLc9AqjVcZCK23/t13jWr/4CJi/4/R/7F0yedjsdoUhEZJYDhijedGP4AEtr8AGUiOxoHO/Ext5a\nbffmcvoXFnOEa49Btwfn083zE3AhIqjirLWmD4F5M8WHeAw6WS9ekzcZLkTS1bu2SbsDSQvQvA9g\nImMcVuWy7SVjfU1tYoOEqz0qxDdpLci6HQQPwzytjmn7fx8cIZTrRgshJEp318f3ZsGRd55m7ikX\nAR/i+4qhpOjeHAPWBI8hYDeGIiUEmtjEJh/WOXsjgseammq2pK4WxLNfoNKCrN9BJAleiJucDp0N\nKeIesc7Ehhofp10xTl1odLsPT886CVKjZIK4qF7zcUTn4DpP+39+j6e98fdJl5EBW27t8NFXfA2f\n+IuvwPZuthnKnwWlAQie4BzGBxrnCD4+Lzht+nrYc+t8COJnrrp9vGV91f3/7L15uGxpXd/7ed93\njTXt8QzdDYIDot4oRDAQVB7EKCIimkTDk+R6gwoSB2RyimK4FxQcUXFCxYAXW4WrCGqSviaGa4LT\nlRDRSAySeEG6+5yzxxrW/L7v/eNda1XVPlW1q/ZpGlrO93n2c7r3rqq1ao3f9fv9vt+vlLXs25se\n8Ev2sTaa0lRUuqKpjVusmwH1fJRouisu2KCqDGVpKWo3tuk10CKVvcmxylpLVZYU9WhUA6U8fN/F\nmwqEE+PZ0hnLG1xKlxW4hrCPsRKTG3RVrwj1VUgKjAQtLEbVD/zGulwmo6FwDge2OaQ85WJWhUDb\nklTnYA0ITcfzUVi2Dw/Y/9CHuPShe7l8719z+a8/SCeZr4YCZGHE8FfewuVnfcl0tzyApPO8K93v\nAk+Y/YW1dnz2RUKIAFfVe/sDsVIPISTA/pK/RbjD4ebHiw0x/O1/x+f80q/c6sf8jUCqPEaez8gP\nmHgBY99n4gWc+iEf7Pb5YHfA9aiDbW58hxkcvg/e876P7IrfxgMLa/mGS3fxpBsf4nHf/hJe9rc/\nl7H/kcpAvI3b+OjEx41P+ZK/fj9PvHEvqiZS/32ww7+98xP4472r6A8dw7/65Y/wWt7GA4X1Ho5i\nuPIouPxJXMkSPml0zKOGxzx8MuRhyYh+nvFe4GJ2/ufjPNL5cmttds5rADo4n8r33PoqPaRwL/Ap\nQgj/7EwncBdwYG+KKYCXv/zl7X8/5SlP4SlPecrKhcSf8Rh+5+rH3fLKU0IwiQAAIABJREFUfjRA\nC4kRAi0EmfJI65+s/smVIlcKM/MEa4Rg5AeM/YByzVbkA6odbZ6+m38f6IWc/Vw78/sPO5r2+xrL\nbNZzdoIee2vre9HtKQQ/+6jHcDUd8wnjU1743nfx6k9/InrDObGbrtKL1uHWzCZu4zYeXFjLp5we\n8sy//ksec3wDgEoIfm//Lv7tXR/P/+hPfW4flEvMbTxo2Gh/CsGNuMuNuMvvX67139YyKAs+L015\n2wxPeSBxXnv9GOfJ+Xpr7bs+LGvwEIYQ4hXAdwJPttb+p5nfRzj1+jseKPX6KlhrKIr7EUIRBGdS\nRG7ccIMp+/vO3ue6i3sMrgRz+ddnkRvDYVm2yUKz0EZzbXINJRRXevXyJhMnO+02UTzLUVVw/brr\nlFy65CygRsVoLkN9FbTWXLt2zdkWXZn/vtdr0X4dPX9muUO0HqNUH89b3U7SqXZ+prWJfoPhcMh4\nPGZra4tut7vwvc22C4Rg/yJ5ysfHbnhvawu63ZtsrVah0AUHycH8vlkDjc1qk0C6jLtVwwo91q3l\nFky3SRAE7O8vK/wvRxNQIISP7++v1Z411nKjLDEf+CBXPvuzkdevYb7m65A/99MbLVtby2FZUtWp\nOHv+BexuTk5quXWt1m+GEuPl1kizmBQTTnMXJ9v1u2xF53sgziLL3Co0sfG7u9N5yJPMJZgJBNvR\n9lK7piRJOD09xVqL53ns7OxsZHZuTF7Hybpn7EXentY6HVajb/B9t5nOnqc60eiRbj1LZUfi9b2V\n16uz0NYy1npOxOILgcxzqiRpjd2DIGAwGBAsO09ro/H2Z/ba7ftOshxFN831GlPU22O2FiGRMkTK\nuI6XrZ0/rG3nP7Nq6uvbqOBdiER4/uyvMei3vBXxA9+PfNcfuc+OO9h/9jWIb3kJt2p5lNcK9Fkx\nly8EXaWIl9gcLf6gWnmeZfNzomHozpkoOjd6tlGfp1XauocIBLEftzHCZxc5Gs2LgTzPLSqOl41l\nu6CFNE3b1CmlFJ1Oh06n0yZPGVPOpNu56oSbw+21Lg861eixxpZTEZ3sSlRXYYBRVZHW21UCPaXo\nKoVwdi1TdV2n40zhZ8SXk3LCuBi31oJb0dZcWuEDgQezvX4CPB94fi2aeT3wptuRly1+BWeZ9ELg\nP838/rk40/xffDBWYjpeu+BEDUNHOrMMgsDN2yx56fxnTof0z0JJhUC0mchzF5s1LjzNS1pty4al\npMbg2qyY71y0GqKeG7S2uPmPZ5cR1ssozljv1MtcmKtcI6hnucra13JjEhPHU5Vttzuzf8+v8gYq\nwJc+pSlJy3SlJ+Tc+4LpYkej5c8Nje1Ns30A+v0+aZpSFAVJkpybfnMWnrdNWZZYW1JVp/j++VrE\nYVWhrSV8xMfBr70V+/mfh3z96zCf/unIb/6GtZetaqJ5WJYUNQHdmHhu1+v7gQ+4m8Ndd61NOAG6\nQRclFcfpMZNygraanWhn7XWIIvdMeXTUBoOxs2OZmHnT97M34ll0Oh2CIOD4+JiyLDk4OKDb7dLv\nr6dQlzIkCC5TVaP6BpxQFBme10epLkXhiHFV1aPS/VZbdRNURyFjiR67G7VJDEVaOI/PBelGCz9D\nCLY8j75SJFpzMJlwMBxSVZX7WxRxdXub6DzPVSHcvoxjd8FqIiuzbGpPNBq1DMaGIVo5m6N6yyBl\nhFKOaC5ehEsoi7yoNShPq5S8ysm1+wEXjNG8bk4FXxSY1/8C4jU/iHrfXwBgd/Ywz/8G5Iu+CXlp\n8wfBWWRaM5qxOxLQugYE63YWbD2IPJnMZ577viNSUXRu1ry1lqRMmJSTOZP5xuYo9uKbjo2zZFOp\nqX3nglRRAIqiYDwek+d5ex+MIpcyF84o5M9GKdO6OkztrHRSk83qZscGC4xqG8GmkdZTip5SSK2d\n73Wz4kHgLsoz7DgtU4b5sBWqRV7EIBysFTX6kcR5a/cJwOcBzwH+AfAjwPcJId4O/Ly19p4P8/p9\nVMNa+2e1gOobhRC/iksk+lRcItE7rLV3Pzhr0th/LLgARJEzFqs9+mg7o6sv3Od1TJVUrVLQE95q\nT7gzaBZ9U8rbms2BRmBiF5C6uc7vGTRxfsacTzqFdAbcjSpYBvNEd9X2E0IQSNmmbUTrZjE3CEP3\nJFu4aLNppvJ6n9MLehxnjsCsSzrBiawboWi3e/NF2RqnkkbMk84mavHo6IjhcEgURStJ+Vk48/td\nyvIGxiRoHaw0Ic9rKxYBbHse8rP/LubHfxrx3OcgXvpCzKd9KvILnrr28s8Sz4OaeG5kp2Rr0VBj\nUZNlG5nIR17Efmefo/SIrMo4SA7WsjJq4Hmua3B87Bb9/nuPCToZ/e7Npu/LP8Pj0qVLjEYjxuNx\nW+UZDAatEfr5n9FHqU7r7VmWpxwfp+T5ACECfN9x9POKqEIIvL6H6iiqYYVJa6/PxKAGChWvdy4U\neU46GhGUJV0g933CXo8gjjkBOlXlbvLr7GshppVNmCegVYUZHVOdnDphZRShOvt4ndWdiUXfO/ad\nut1aO0c+S1NSFiWjYoQSiiDJ6fzMLxL85E8gGzP3h30c9gUvQvzzr0UtY/Vr4izZVELQrcnm2ueG\n1lNjy+aC3yjPVzG/GVSmYlJM5qqaSihiP6bjdxaSrEVks9dzhHPZqqdpyng8bu2OhBDO07bbnbOS\nc1X90UzxQs54p9Z+o5OabNbVeuEJVN8dt9ZaJloznrER7EhJ3/NcWWE4dBdha92KDwZzD7GlLjnN\nT1s1vi99tqItAvXQcKtcucfrPvDvAL8jhPgG4Nk4AvoVwFcIIT4IvBFHQP/qw7yuH614IfBXwPOA\nZ+Cy138M+O4HawVWVjprRRu1fVFbvz/vM8/5uye91pJi7qRfqyrSrHfzb2OKu/5NXilFVVVt0kq7\n3itIp7PO8bG2xJjSGZOvWs9Aoktnan2WdJ5HqkIhyIHcWjZOQm5ubk2kW9SQzvUISGNs3OQgr2tO\n3VQBGjvK3d35vy+qcrbLjCKiKCLLMobDIdvbmzmnSelyvqvqmKo6ra1iFpnEW07rIIC+Us5XEZBf\n+88w7/lT5Gt/GP7RV2L/6I8Qn/QJay9fCReR2URmHm5CPCcTt5+2t90DQ5o69rezsxHx9JXPfmef\nw/SQ0pTcmNxgr7O3duVCCLfP/r/rR2STjHKk2PL2UJ3NKh/9fp84jjk5OaEoCo6Pj0mShK2trbmb\n7/L1UPj+Lnmec3AwpCwrhDhiMAjZ2dla+zgGVxnyd3xMz1CdOpul6rhCTzTewGvPy7PI89x5ktas\nQynFHdvbdDodcmMY123icV1piqWkp9R62d4NwtD9bG1RpUfoZAwZCC3x8ghZ5DC6NrX2WWPbzX13\nIej4nbZV2pDP7EMfIPrRn6H3hjcih84YpfrkR1O++MUE/+yrUOGtZa8vIpt9pehs8vBcFI5sZjOS\nkChyT7Mr/DRnkVc5k3JCVk0/I1Qh3aA7teo7+54NyaYxhiRJmEwm7ciFUoput0un05m7zmudovV4\nZmRi3jvVWks1rjCTaZyt8GuyGbltl9TbtrH7iqRk0Bx3SeIuvMa4le31XEugsaozmmE+dNG6OOLd\nD/sPeCv9w42VM51L3yTEpwBfjYvEvILjKO/Akc8HpaX8UMWHY6ZT6wlVdYpSXTxvQV/06AiyDDvY\nphgqhBIEV1Y/FU205rSq6CrF1oKL5Wl2yqScsBVu0Q267kwfjeY8CVfhvvscQbzzzunc2Xa0vfYJ\ndHBwQFEUXLp0aW72rPncO+5YfJGpqlO0nqDUAM9bvZ4601RHFTKU+HtuGTdu3KAsSy5fvrzyBlwY\nw0HpbKwuX2Sus4kV9X3KbQ9jUjxvd21PxGZONvZiduKd899Qwxg3F2tMOwbcojwpMYnB2/JQ3Ztv\nQFprrl+/jrWW/f395XNyK9DsHyG8OqxgficOq4qx1vhCcOns52uNedozkP/+Hsyn/i+IP/g9l6ay\nAUxNOBdltS9EUbj9ZK1jfFHkbhzjsTsANySe4Ij1UXpErvO1WuOzOE6PSauUIpd4xT4SDyndabnh\n1APgZj2HwyHGGIQQK03SZ9Ekt1gLQozp90f4vnviVap37rm3DDrV6OHMvGcs8QbTec+z6UtNitCi\n+euyJp3ZzIxiJCXdBX6fy2BMRVWd1FUv11716DiylaY3RzN2u+54uIDnpn3f+7Hf/4OIN73BzfoB\nxWc9gdEL/zn5Mz6/fZr3pNe24TepfqV19a0hm54Q9DYlm2nqdvzU4NIdeItaJ4u+44IWusCR727Q\nXfoAVhTumGsaelK621C3u+w+UDGZTEiSpC16+L7vEqdmqorOQzVB60k7r+z8aXtI2Wk7bk1lsxkg\nFoGr1DcP6JnWDLWmqpcVCMHAc/HBZJlb+Wab1Q8yzfay1jIuxoyLcW3o5SKhe8H55+EDhQdzpnMh\nrLX/DfhWIcR3AE8HvgF4GvAUHqQ5xo8laOvyr726bXsW05Nhye4MQ0c60xzorFXpbLDsKGtO/na2\nZkMiLUTtkTZrCbmB9m7ZXOeqSqf7fQBM1p/rFG6us2njr1vpDKREgktHMWazCgpMW+xlia20M+xe\ns70O0PE7jIsxWZVhrFm7TdtcrIdD9zOrC7J5/fQeLt64Sin6/T7D4ZDT01MuXbq09vo28LwtjCmx\ntqCqjvH9abm1qoUMTVt9wQog3vJL2L/zROR7/yvmH/+viLe/9VxRwizkTKu9nGm1q8VlElfRtNZV\nJBpyORi4A3A0cn/f3t5oxlMIwV5nr30YO0qPGIQD93C3AifZCWmVIoXkrp09JB6np1OhUVOM3YRD\ndDodoihiNBqRJAmj0ahtuS+ah6wq95XLclqsGQx6WBtTVUOMSdF6iDEJnre1dM5xGVSskJFsb/Im\nNRRZgeoqSr9sc+ZlnSLU7S43VfelZEdKdN3uTGoCmhmDX1f3Vo3GuIf9Ic7n2KvjQWuS1+u5n7Kc\ndiyKwv1IOa1+riHWMu96N7zq+xBvfQuyvv6YL3oGfNu3ETzlc9mt50BznZNVWWuIPi7GSCEJVUjk\nRYReuPA6kNbVt+qiZNMY9x1n5zWVcoxvRczo3LY0mkk5ISmTtoXuSY+u36Xjd5buw03JZjOvmc1U\nYBfNa1qr0XqC1gnT8TUPpXrt6I+1lmrkqu7LyGZhDMOqopjZtgOliKScEvS6c4NSjmzOnFdZlTHM\nh+19NvZiBuFgo0CJjzbc6sTp3wG+FHhS/f/5itfexgWRGcNpVdGRcgnpbAazlxyIzcmUZuB1FuYz\n3/yZy4VEMCWds2kb7g3rzmW6f53H8Obt9VViolUfs9Fcp6jnOguLLSwiFGvNdDaIpCSpb2K9TUkn\nzLTYJ9CNN2pLKukSN9IqZVJM6Ifrmj+7C/Zk4i7ozWiiKV3LSCiB9JavR6/Xa2PgxuMxvQvMlfn+\nDkVxA2MyqmrcVsWSuiLVVWpphJ7Y2cG+/e3YJz4B+Vtvx3zzS5A/9sMbVZZkXeGcnfHcX0Q8m2Si\nMHSkcxZNW2w4dIwPNiKeANvRNkooRsWI0/yUXOdsR9sLiUNDUKWQ7MV77UjF7q67tw2H7sZ8/fpq\nEc8iSCnZ2tqi0+lwcnJCWZYcHR0RRRFbW1vteEtRuKaKMTeHNbmW+w7GdKiqIdaWtSNDXKvc17+J\nCiHwejPznonh6N4jkjxB9RTdnS7b29trzxWruurUV4qJ1kzqPPejqsLTmr5SxHMjPJqqOmnz0F2L\ndbD4muD7jkg0A9PNidWIahohTRzfRM7Mn/5XeMm3IH/737jleh7mK/8xfPu3Ih/z6XPbo5kDBdo4\nzqzKnKCwStuWrCc9AhUQqhCNIrFcnGxWlfsOzfxh8317vbWP9aaFnld5Kyg9r4UOm5PNLMsYj8ft\nuIUQgk6ns2Bes0DryVwylHMc6LZdJmvqyuYM2ZShRPVVO+7RxLZmjeq9GVEQ4maC7nnTbVavfGUq\nhvmwHS14qM1trsLGpFMIcRX4Ktxs56PrX/8XnLL9dpXzw4CwPhDzJdXEcyuddUCsTUug4mU/+Aqi\nQcR3fud3LrVFWUdIBBevdNbJmJu+beb9N5PO86qc7m8KITysrTCmai0tli4nkOiinusMZVvxXId0\nxkpNSef5X2nBB8SQJNg0qUnnZk+33aBLWqUkZbIR6WzUxScnjqxE0cw8Z3T+jXx7e5uDgwNGoxFx\nHM/N3K63fEdQyvIQrUdIGSCET1JfpLvnkAnxqY/G/OIvw5c/E/njP+KSf177mo2Ip1gkLvK8acW6\nueMp5djVIjTMbjicVkQ37HH3wz6+8jnJTsiqjOuT62xH23M35NPstLVFWiQaimPHixt9wnA4rXpu\n4IqE7/tcunSJyWTCaDQiyzLyPKff7yNlj9NT9xXj2H32YjFfSBBcqquEI4xJKYqsriBt1i4UUiD7\nsh0pwEDXdunpHpTAhlkBQgh6nkcPN3s3rqt/x1XFSGvXdrcZWo8AgxCqrm6usaBZFXxVTaufZems\n5poTrdvFJgn2u16OeN1PIKrK2R4952sRL30xcg3bo0AFBCqgH/bRRrcV0EK7vPJRVTDRQyoLnlTE\nXsCe32GrjYQ9B3nuSNPZec1eb34eZwkagdSkmFCaWrRTt9B7QW/lDPOmZDNJEsbjMVVdTVw9rznb\nARNI2UGpbjtbfh7ZLIwhrao5m67W/ggQ4/E8QQ8Ct/IzlU1rLaNixKSYYLFIIekH/XO7HA8lrEU6\nhRA+rqL5HFwbXeHslH4S5+H57g/bGt4GXt2qbXKDz1Zc1lI3hyGMSigKHv7wh/ONL/5GfvmXf5k3\nv/nNfMZnfMZNL29J55KbgCc9Z5tkbq3S6ZLUpr506+KipNP9PcDaCmtzzjsFZOisW0xh1m6tNwjr\n/VYs2W/nf0CIlQKK0kUuboiL2ieB40ZN5ydJwD+ntT633CCg0+m03o+7ZxVJa0DKEKX6aD1y4iK5\ni8HNQq0zqiC/5IvQd78Z+U/+EfInfhRTVcifeu2FiOdRVTnv1apyxLOq5mc2V61Pr+ded3o6DU1f\n4u+6DJEXcbl7uSWeR+kRXb/LIBy4G1Q5aQnnskqIlNMu/+mp4zoHB25VZrQKa6Hb7RLHMcPhkCRJ\n+NCHRuR5Rr/fZ28vZJ0xWnczb1ruCVo7AqrUYO255TRNXTvdGuLLMYN4gEwltrSUh6UTcfTWV7rP\nolNX/Jo5x8JojopDBDkdIen5PXx/e6PuQwvPc5XPWbuImsiZn/l5xPe/Gnl0gBUC85znIl71SuSV\ni+XDKKnoSCdGSrTmuMiwukBRIE1JLC0xJVl5SlaeooQi9MK2GjpHQpsKXTN72IwJ9HprzWwsaqEr\noegGroW+bATIWsfPzy66252eXvOvt0wmkzlxkOd57bzm1B/VoHWCMZOZbuG8OAjAVAaTGHQyQzYj\nRzaNgokxpEXVVozB+ZfGUtIxBjkazXu8LiHosxZIAkHX79IP+2uPRj1UsPKOK4R4DI5o/hNgD8dF\n/gOuqvlr1t21b+NBQCglaV016861egxupugc/7oowpoxFDnP/ern8pM/95P8+Z//OU984hN56Utf\nyste9rK5quc6ITNSSLTVaKNRF5jpdOs/ba9vgob4NReV5rPWe2+AMQnGFCi1mgCIQIAAW9p2WZtU\nY5btt3VhIx8KICtc7teG6AZdTrKTje2TwN0Tj45gOLRsG4M4Y5W0+r0DsiwjyzLSNF3bcmcWntfH\n2gJjck7yQ/B2NhI1qK/4coz3f8GzvwL5up9wxPNnfnKjGU8hBLuex3FVkRnDQVGwd3yM38xxriOW\nakjm6SltOXDDsQMpJLvxLpNiwjAfMiknHKaHzjpHBezGu2uJjcKwDmQYuZt4IzDe2lpbVOzWR0q2\ntrbJsg5FMULrEmMO0TrGmK21HsyEkPj+dt1yP619Wo8wJkKp/lJ3CWstw+GQSe0yH8cx29vb7rzs\nM7WrKWul+8iFGajO5udfrBQBJRN9zISC0goSOaCwMV1t6CqxmbXWWdQWTOZ33wkveAHyT/4zAOax\nj4NXfg/y736WI3ZabzaMO4NZxbSQHlvKp68GREpR6pJCF64lr3O01SRlQlK69GYlFEFeEWYlgZWu\nCtnMay4rL55Bqct2vrwpMAQqoOt3V16TmgfeJJm6LTUOG4vIpjGmJZtNgWCROMiYCmOaec1mtMtv\nH4SEEFhjqSbOqqsxdAdHNkVPkitIdEU58zclBB0piaXEa2T0TUm2EVT1enOCKm1068vaWCAFKmAr\n3FrbdeShhvMSiZoy0geBNwD/6mPYGukBwUXV65nWHNXGxpdnzKuNKSjLA4QICIIVJsDWUv33D6ET\ni/eoO3j3f/svPPnJTyZNUzqdDnfddRdvfvObeexjHwvASVmSGMOO583NM83ixuQGpSm53L2MN6xb\nB2smsdSCenZ3YWIOyXXOfmd/7ZmVLMvaubKmkqY1XLvmzunLKwoD1mqK4hoLE5wWoDwsMbnB9AzH\n4+ONkndSrTmuKkIp2dukl1nDZCPK6+9D+l38Ox59/hvOwFrLtck1jDVc6lza+EJ2cADZyBCXJf1d\nQbC//kxRkiScnJwghGB/f3+jhJsG1hrS4jrXigJfdbkr3t1YsWl+418jvuLvI/Ic8799DfLnf2Yj\n4tnguCzJDg9Racp2t0uw6iBbhCRhrR70OahMxQdPP8hxdoxE8rCth7HfuUgSlCu+NtWjTsc9aKyz\nabSemtFLCUEwpijGrYin3+8vTexa/pmu5d6Uk1y1uzfXvq6qqjWwb/xhl4URrDLmXucYstbWfqNJ\nuz5aDpgY5xULrn3aaQy9L6JIv+9+7Eu/DXn3L7j/v3IH9v94JfIffpkjLLP3Cs9zDzlh6P49h4Se\nFQitI46qTEVe5Y6Ijk6wo+F09rCe1/S6fTzp4UsfT3p40lvYls+qjEkxac3tBc4Evxf0Vl6HmuLv\nbPe+Ef4vurU0yUGzSvQwDOn1eq04yKnQM4xJZ8zcqY37u0gZutekxv0UZlp5kY5s5hHkyomDZv5E\nXCcyBQ1Lnk1aknJKNusTq9AFWZW1oq8GSigG4WDj4sCDgQdTvf6rwM8B//cD7vNzGxshUgq/trOY\nNRyfttbP2ZVCYL0AbAZlweMf/3ie/exnc/fdd5MkCe973/t40pOexAtf+EJe/vKXY9e4gM7GuK3d\n264x69X54LfXFUIorNVrzXWKQEA+M9e4AWGJpETgLlTG2o1vTNZXIBVUxt3hNyRujdffuBgzKSds\nq838MwcDSA8NSQr9K5sRtU6nQ1mWTCYTjo+P2d/f32jbgauGFWILOCCwCcZ0126/NpDP/GLMr74N\n/uGXId/4elfxfOPrN64c7ZQlJ3lOJiVHvR67xqyfyALu5qPUNOZUa/fUteE2yauc0AvpBT2UUBS6\n4DA5dMKjDVStTQzteOyKMk2X94wX9U0oS0c4tXY8aG8PlOqhtWu5N23vJEkYDAZzquBVaCpNTjU8\nwZgcY/K6CtWjKGjV6Z7nsbu7u9K2THVcdVNndaxmaalOKxiB6ipUVy0VVToD8JP6+irwvAFKdfGB\nqCYejd1S4/XZkM+1xmjKEvNDP4r43lcgR0Os72O/8YWIl38XsplPMMYdJ3nuhhmralr+cxtsSkCD\noK2gnfXZXIdsNvCkh1cVdEcF6JAq3KGQljwOKHzX2Woqo7OQwlVBm+Mx1zkCgZIKKaSzPPK7S4/P\nRgCfJFMx93luS41YMcuydtY+jmN6vR6+7zsrIz1LNKf9O6U6SNlFSg+dacq0xGRmrsUnY4kNBWng\nqsUWwLjuX1xXNCOYzudWUwJJELQCMYN1wq7cOQwYO71nzboLRF70oFkgfSRxIZ/O27g4bsWnc1xV\nDOuB9sY708XOjdbKEy8/cII5GOLf1UNe2eX4+JhHPvKRDGuDYXBE4Y477uBn776bRz/mMex63tKL\nVZOeshfvEY7qE6/xKjwHp6euvbe9DRPrKqabVOKqquL69et4nsfluuLURAAGwbzVz8JtUed9e972\nyvQbcJZJ5UHpnty9CZ1OZyPz86OyJDOGbc/bzPOOev+e3IvKBN7gKmsNzJ2BNprrk+sAXOld2XhG\n6PpfFGQTS//hPjuXNq8QNp6qs1XpdWGt5VpRUOqEXZngCUUQXNpYVAVg7vl3iC/7UkSWYp79T5Fv\nesP6xLOq3MFlLSe9HkkYIoBd31/b03Hus46O3L9KuXNmzYeJ2Zz2nWgHKSQn2QnaaqSQbIVbF6qU\naO2qnk03MIpcy/3s5smyqSYqDN2qn71P5nnO6elpK96I45jBYLCRoGzqjzjGmIrT0yFpWqJUl35/\nj62trc0r3rlx89l5428zQz7V9AFa6yFau9a9EEEtFlpMbhuvz7RxtYBzjebNb92DeNE3I+rISvMF\nT0f82I8gPuWTV3+BspzaLuX5TZFuuRCMPI/C98H38Xz/JuX9SiSJe/qYrWzOWoEBxpo2FKQyFaUu\nqUxFoYubstAby6N+4MRwvppWRhuxUFlOsxWa26LnTd2W1rE9miWbnudhTI7WDdGcIXht7n2ELXEp\nV+l0ThPhhKMylhSBJakLPA3CmmjGQjif1OaBoEHd+7dRRCFMS77PEnRf+oReuLGP6kcSH3Gfztv4\nyCCoJd/5XHVv/YhE69cVh8wFbO/s7PCa17yGF7zgBe18VJIkvP/97+eLn/IUvvrrv55XveIVREvK\nHk1l0rJ5pXN2pnP6uwem0rne+4P6Cbg4l3TKQIIEXWis3DxLPZKy9f/blHSCgShCZJW7yF2AdN6K\nfZLVlm5syTPIKnmh0bKdnR0ODg7IsozRaET/rL3QCmTGYIDY6xIIMCalLI/w/b2NRRzyaX8P8xu/\nBc96JvKX3+Qqnr/0f66XFDOjPt8eDBBVxURrjsqSnRUPZgvhee6p6PjY3bQODtby8kzKpCWc29F2\nSy4vdS9xmp2SVinH2TG5ztkKNyNlSrmKZaNuz7Jp1bPpko/H7m9SuRkEAAAgAElEQVTgfre1IIcC\nXGvz8uXLc1GaWZatbSwP7lqgVBdrQ46OPkSWlYCm34dOJ68DHpZ7cC6CDCUylJiiJp+Z+1dPNDKW\niE6JYdRWN92D/OrZ28brsz9DPhNjSI0havLJa7cL+773Y1/0YuRvvR0A+/GfiP3h1yC/7JnrfYGa\nTLY7pKogzymyjGGWUVQVlCUqTelLScf3p1XQMFx+nK9BNtttKGSrjofpvKY2msiL2lZ7oIJpap2t\nqKqqtW0CyFJBkfpY7eNLHyUV/a5PvycXzhbneU6e52RZ1j7MSCnpdDq1LZub08zzlFmiKURQ595H\nYCQ60ZRJ1YYLAE5w1lGISJDiPFurJnwA1z7vSom3iCFLSRV4FIGi9CSFzqiycdu9A3efbEjmTeKs\nj0HcrnQ+yLjVRKL78xwDXAkClBCU5RHGZPj+3rnWHcW1AjuaEEQpQgK7u5gg4DM/8zP5kz/5k5te\nH8cxV65c4S1veQuPf/zjb/r7XJLQsH7q29tbS5HQBBj1+5DK61Sm4kr3ykYn5H333Ye1ljvvvBOY\nhviEoVuNVTCmoiyvI4RHEJw/m1celQwPhyQyYfvy9kbEydTVOoCrQbDRjbLZv95xhTLezTFBa6LQ\nBQfJAUoorvTOn2NtoBNNdVIxKiRF4BPHyx2CVi6/KDg8PMRay+7u7kJj8UU4KAoKa9n2PGIpKcsD\nrC1xOd57F2pHmf/wu4hnPgMxGWO+7B8i33z36kpjkzDUBJzXy2zSkQSwdYEqNjAt+UPjpL7wZWmZ\ncpKdYLHTFLAzSMqEYT7EWIMnPbaj7QtVUoxxq5XWHKHZNI3h+ywRPf+zTKtyB2dZs7W1tdb+b9wP\nrLX4vs9gECNEujSGcFOYqiadSUmlT7FkiFDi92L8aPfcsZtF0NYyro3m207tZEL/e3+A7o+/BpHn\n2E4X823fifq2F2+m3jqD0hhGdYsfQGpNX2s6VYUoiimJbCDlNLozCKb+Q2uQzbPIqoxxMW6reALn\nFdr1u3PdKmttWxXNq5LTUcVorCkq3a5SHFs6XYtSjtT60kfiIoh1oTGVmRObNrZHcRxgrWuf2xm/\naBehG6OUs5nTqcYkZlrhBoQnkLGralol2nCA5hWeEHSFoFOWblvmOWiNtdbFC/uSIvQofIlh/n4u\nEPjKbx0AArXZNf+jEQ9kpfM26XyQcauk87gsSY1hy/PoKkVR3MDaEt+/fO5FMr8/BwNBL3eeYf0+\n9Pu85z3v4YlPfCJpmi58XxzHfP3Xfz2vfOUr524Ww3zIuBi7m+CoLo2sSYomE3dj6/UgldfQVm9M\nOq9du4bWmqtXryKlbElnFN2cG75we+T3A4YguHJupVhPNEd/fURqU/YevrexSOKwLMnPEWYtQrt/\nsxA5yVeXmM5BI/zaiXbWbsGWxyUmNciBx8FIYa3jXRfQBDGZTDg9PUVKyf7+/rk53pUxXC9LJO4h\ny134DGV5A2s1Usb4/gUYMGD+4zsRX/x0xHiEeeaXI3/1VxZ/qeagEsId22de04y8AAyUordhvjYw\nLzCKIsfqZ25SWZVxnB6vJJwNKlNxkp1Q6KKNy9uksj2LPHfF2IMDRzh7PXj4wzdO9QTcQ8fp6Sll\nrVoKw3Bplru1lpOTk/Z61Ol05trprn06bs3Zmxk95/O5GfHXekJVDKkmJSa1KDFAyY6rinakUytf\n5MHGWiZVhfnFX6H7nd+Bd+9fAzD5B/+I8au/B/8RH0coJYEQS4MOlqEyhuEs2aT2glRnHEy0ns6D\n1qQJmCbhwHT2cH//3CeJRRGV68xrNl74s65BnmcJ4wovLKmMa9FPsglpmlIURXucQF0pDEJ6nR6d\nKCQKBMKWSGHbUSEhvLp1HiOlt9DmqBEEqY7z1czrhLO8EQZZS1iWdKuKqKrQuRP6aKMpTUkpLFUU\nYOJwrt3TOEgEKnBjBNJ/yJPMs7hNOh/CuFXS2aihYynZ8f0Z4nTHygPdWktxXwECwh3rZspm2Nnz\nn/983vjGN87Fg80ijmMuXbrEm9/8Zp7whCcA03zvQTigN8zc1WVNRpIkboas24VMOdJ5tXd1o3nD\nsznoWea+1rrVuLaK6O2g1GoSZkrDjb+8QVqmXP6ky0sVs8vQZNk3+21dFMU1rNUEYg9xcOgudlfW\nr1TOIikTTrITAhWsrXZuH1SuBIwTwWi0XiV5GY6Pj0nTFN/32d/fX3nMNpXE2RlmaKrUB4BxWdfe\nxUi4+b0/QDz9ixDDU8wzvhT5a2+Zf2Ayxs1xau3Ke0tsjpJ631rczX9wEeI5G+fj++68VGqOcA7C\nAb1gPaulUT5qs5p96bMdbW/sXFBVjm+fnLjVa2yVziT1bYSzWe7dbpd+v98eB2VZcnx8TFVVbRLS\nMrstY8ra37O5Zom6wtU79wHcmLK2aXKVOiljlBxgJnaeqNQ2YTKqCegaaW4A5t1/At/0zch3/j8A\n6L/1GSSv+RGyJ392K/BpIHHzgs3PMiGStpZhbd1l6/d1a/HSWiRnOHQ7tDGlb8wum505q45vYni5\neERl461ZN3kQovW/JwhcFbwJGMjzHGMM2mgqU2EwKF8hPIHyFYgca1LsbJKcUCjVwZddPC9CIpG5\nRGQCUU5FTCJw7XMZu++T1mSztBbKEp0l+HlKVORgKrR162ClwPq+80sOnVBrtorZ+CB/LLTLb5PO\nhzBulXSWxnCjLPHrqL6iuA+QhOHVle+zxlLcXyCUINhXzltohsCcnp7yyEc+kpMmsm8J4jjmec97\nHq9+9auppIvq6gU9BqNiI9KZpq6K0ulA5t2PsYY7equJ81kcHh6S5zn7+/sEQTD3mevofKpqjNbD\ntYnLfe+9jyzNuProq8TdzcQaum6xz1bt1kGe3wdAGN7hMgyr6sIt9ln7pHXsqUxpKG+UCE8QXA6w\n1h02xqw9RbFwHQ4ODijLkjiO2VnydNAIiAxw2fdvEmU4q7BDwKLU4NzZu2Uwf/j/Ir7oaYiTY8zT\nvhj5tl+bfrHG12sNlp1qzUlNPM+S5LVxxocoG3Q41i6ZpB/0N65YFrrgJDuhMpUzmw6cqGOdY6+p\nchrjDrXBwHGWhkDEsSOfF0l3bXw2G4sbpVRLPE9OTtp2+u7u7lriI2OquvKZMo0ujOpEmXl27IRC\no1ooZBemCrXWOVndkp1VNAc1AY0XE1B7eIj9ju9GvP6nEcZgd/aw//srkF//vLY6ZmqBSm4MeR0c\nMQtPCAIhWhJqgVFVkdZkUzAlm+e6YSzKRW/a6J43Xwm9SZikmUhNJuuDQMpzIyqNmSZjNotruG23\nC1qXrX/vbDXTrZZPGIZEUUQQBPVDhYukrExBpUu0tRh8NB5WKIx1PpomMdjMzlU1ReTiUvEUFRKN\nxFSaMs/QWQp5SmQ0kahdRcQMyQx8VBi3oqemgvk31TvzPNwmnQ9h3CrptNZyX01eLvtq7blEUxnK\n6y6lI7gUwP33uyvEHXe0rbw3velNPP/5z29FRcsQxzF7e3v8wt2/wKMf+2i6fpetUeFulpcvryXM\naKqSUQRFcDHS2VTNmhnBpnq6Luk0Jq/znyN8//x+/P1/eT/pMOXqJ14l3tpcIdzMJ65yBJiFtYai\nuH/qJ9oMwt5Ci72pTkdexG68+jtXo9pYu6vwttw+bcYiGrudi0BrzY0bNzDGMBgMFuazNxX9QAj2\nlxBsrTOq6hiwa1Wrl8H80bsQX/SFiOMjzBc/0xHPPHdfVEp3TK/BrnJjOCpLLGxc0W5hLRwfk09O\nOSpOsf0+va1LDMLNBWQNZquenvTYCrdWGslPJo5gLrITnUzcIWiM2yT9/sYBSy2qquL09JQ8zxmN\nRpRlSb/fZ3t7m60LHN/W6tZuaWr6rerqZxdrq7q6WeFa8l2UWk3CrbWOfKZnCCjOSk3FylVAMZif\n+lnEd38X4vgQKyX2a74O8apXIM55YNGzJLQWzoHLRE/qipwHBEoxUIqd2TjWZViWi75qZrMssXlO\nMjlmkpxSVTM55V5MN97Ci2rbrzpaGc8DIRa20JsY9jC0ZFnKZDKZI5pSSsIwbH+UUlhrMCZF62Rm\ndrdRnneQMmoIECYxVJOKqnAtcG00NrCUoSb1NJmpyPMMUzjVv9AajMEHOlI4FbofIKMYFXfwoy7e\njML+b1qL/FZwm3Q+hHGrpBOmYqLLnkVXR0gZ4vurL2wmN5SHJTKU+Hu+G9QqirmqmbWWJzzhCfzx\nH//xWilBcRzzlf/0K/neV38vd1aeu9CtSTqLwq1CGEIR3IfFcmf/zrW+f4PT01Mmkwnb29t17OK0\nZb/OPWtTMdH9f3U/6VHK1Y+7Sry/OcFp5v86UrK9BiExpqQsb0yN/6vKVTulhKurK9tLP9Maro2v\nYbHO1H9VzvFBgS0s3q6HiqYkuSm4rpkDsBB5nnN4eOgSf3Z3b/JynBUQrRLoOEPxU0Dg+7vr5WAv\ngHnXuxF/7/NdxfMffxXyB17l/rBhSbeoiafBtUx3vc1vXnmVc3TjA9jxiJ7fZbBz9cIPGQ1KXXKS\nnbRZ102M5uy6Wet4dmMDWY9834SzQqMgcMT0IsVdYwz33XcfBwcH7UPI3t5ea39zEUztlhxxcXGH\nQ6w1SBnjeYO6urnZQ0FLQOufloD+3jvxvvvFqPc6MaZ50pPhtT+K/MzHXmjdR1XFsdaMq4rSOh10\nVNswKeE8Qzwh8IUgkBJ/di50WS56t7vyOK5MxaRwLfRGee1pS9d6dLRClOVCe5A0hUmmKKwPSiE8\nRdRVdAcKGcAkTUnTdC5CuNPptESzgZvTTeb8NN0DQwelOu2srsmdzZFJp9vfSihD0KGr7ld57gog\nVYU1Bms0HgbfWpQn8OIYL+rgxV0876FhWfSRxm3LpI9xeEJQ1KpAdxSsUzVrLB7qX/i+Y35l2ZJO\nIQRveMMbePzjH79UVDSLoii45zfv4SXf8hLu3KrnDG8he31TnI3C3NC1qZ77EnPKx1WwXr2AcvXr\nliFWak4AcO7yWjuseqd5nttvZeluKhcYrJNC0g26jIsxo3zETry8vW1L2860zaLfd63X4dCtwkUK\nAmEY0u/3GY1GHB8fc+nSpbaVWhlDYa2zKzmnouMqWAatR5Tlce3isHmFUT7ub2Pe9nZ42hci7/4F\nTLfriOeGMwSBlOz7PodNXntZsuv7a4cC5FXOUXqE7XXpxQMGqZmGTl+U2QG+8rnUvdTu90k5Iasy\ntqItIi9Ca7dPi2Ka077s8JJy+sBxeurec+PG5jnuZVlydHSEEIIrV64QBAF5npMkCUmSEAQB3W6X\nKNrMNLuxW1KqS1meUhT3Y9pZQFuHQqS4GdD1t6cQrrKpYuXa9P/jg/DSb8f79V8CwFy5i+pfvAqe\n/ZXI2AU6SG+9+YOqtlpqFNS+EOz5vovhFAILlNZSGENlLWX9kxgD1iLSlGAywTfGkVCl8Jqe9opj\n5mxqEEDkRXT97s3V8Nqg3hQVk6EmGTl1OdYiZUE3qO3V0pThkRMEISUoRdjp0On1iPt99zshsEWG\nNinGZli0O3CEnBuNsNa6NLisNm837tpUYimFplQlWlaQFDCqFfFAWI8nBFGEN2ugf5F5kNt4QHGb\ndD4EoYRwsZamwmc9j86mZ9POITUXotkUBeDTPu3TeN7znsfrXve6paIicPM3d9x5B7/+27/OnXfd\nCaNq6WsX4axP5yZpRA3OenVuSjrdayXWaqzV525H4Qk3K2QEVtvWUHpdqLo60aRKnW8qXhtOz65X\npzMtR11QzdELekwKRzq00QsH4ZtWogxvVu/G8TS9Zji8eBGu3+9TlmUbaXqp7tcn9f6M1xRIuIx2\njTEJVXWE7+9fyDxePvlzMD//Bviqf4L82Z/CPPLjkf/iWzb+HK8hnmVJYS2HZcneGsSzJZxYV4ns\nb0G3nLLBizC7M+gFPSIvahXuR+kRysSYdAtrJJ7nNEzrcNsocpz8IjnuaZq285tBELC7u4uUEq01\nk8mEJEkoioKiKNrqWKfTWbv6aUxVJwoVeF4fIfZrb94cawu0HqP1uPZx7LSZ22shzzHf98Oo7/se\nRDLBhiH6G16EedG3Yr0OVKBHLgVJKIEIBTJwgpazJDTVmqRuqzcIhKBTRysuWidrLZW1FFVFORpR\nTSZorSmBUilst4vtdJBC4BlDUFWOiAqBJyXGGqdCLybo+sG2UaF3/M7S7kdBwCQPXAvdA3bqFnrH\nEMicyXDI9dEIU7fQpecRBwHdZr/VCQTaZBibYmxBW9XEq8VcHRA5Js8pCzCFm2KtgBwoPUHlG1CV\ns/2r3IxrKASB5xGGIX5DMn3/wufJbXz4cLu9/iDjgWivN6rejjkhlhrP2z03GrAaV+ihRvUVXt+b\n9rcXxPeMRiMe8chHcnx0tPCzgiDgEY94BO/43XdAF6eGHml3Ubl6da2nySYnXUqL6d6HFJKrvc1a\nxmmacnx83ApSZr0/17XRLMtDjMnX8jm99957qU4rrmxdwdvxUPHmxGZUVYwWKLIXYZo2NSOUMcZt\nOHAisAs+uZ9mp0zKiZvHjW5mjdVphZ5o1EC5Yfyb1q0N6LmwhRK4G+iNGzeoqop+v0+v11spIFqF\nxo1ACK8mnhtum3rQ2PzKryJf/AIAzM/8PPK5z9nsc2qYmnCW1uLVlatlyuQmyrIhnHP7xNops7PW\nMcJ1mN05mBQTrh2POR1aBJJLgz53Xo4vdJ8+m+MeRe4cXHRcNGMxAN1ud+H8prWWNE1b8tkgDMO2\n+rkITijkCGUjFFJqa+76aExZt99njcRlbSLeWVkpN2/7TcSLX4T4H3/p/v+Ln4n4kdcgHvWJ09fk\n0xb8rAk5uPx340PqWVLPQv3g2piQd6Q830JpwQCl9X3KbpcyDCmMoayJ6SxKXZKVE0qdOQIqBB0V\nsBX1ib3FpDvP3WKybCoMmlWhG5MxmUzIZ5J5giCg0+kQxzECsGWJqRJMMcaUEzBV0+JCihBFhDDe\nVLxVuL8VtdCq8MGEAhEJR+JxleCwJplBFM3FgN7GA4/b7fWPcfj1xSEzObH0kHKNuZSzlc7mblDd\nXKHs9Xq86rWv5cXPfW5r6txACEFRFLz1rW/l8uXLXJ9cdzYaF8xeN7dAwBelEm2wCvVrPSA/t8Xe\nLEOF09mii5DOSMrW0Pm8AuFN7XVwGy6K3DBVkiy18TkPvaBHUiYkZeIyvM9UO9uc+XDxDdDz3KJH\nI0c2LioqEkKwvb3N4eEh4/EY6/uYWr27CeF067RDWR5ibTGTWrTmwdDkQALy674GU1bIb3sx4p8/\nF7O3i/z7z9r0qyFronlUVzwPypK9BSKQpuK4kHDC1JE9jqfM7vDQVb0Hgws/eJRJF7+M8OUpfpQj\nOsccZynb0fbGUamNsKwRGjVEJQwd+Wwsco6Pj8nzHCEEW1tbS63HhBBtdbMsS5IkIU3T1l5HKdX+\nvRnL0DqtZzfdeeNa7IObjgEpfaTcQqkBxmRoPamrn06E5LLeu7VoxW0H+xfvw37zC5H3/Gv3/5/0\nydjX/AjyS55+07o3yUdsOQGnLVyLOM0046Ikz6fXPF8K+pFHN/KQUrbXtIVY5EFUh5ML3ycAApyy\nHdy1tTCGYTHhtJiQVDm6ziiXKiTwOlgv5NRAUpb4UuIhMIVAF5Ismxe0e547BKNIk2UJx8dJO9rU\nRFF2u90699y0mefG5qAsxBLifr19OwgbYXOoUu0U6JElD1zVt/IsNgQRCoQA31pCIYjqtrkIgs2j\n0W7jowK3K50PMh6ISqe1lvuyMbo6YD/oEodrJOqclJjEzFforl1zN9srV+ZOYGMt9+U5X/7Up/Ku\nP/zDlnBFUcSjHvUo/vRP/xSA++6/D9MxLuVmbG9Sw5+He+8Fi0H07984KQfcTNiNGzfwfZ9Lly61\nwTFbW+sraqe2ST08b7lCuMl6l0h22GlthC6C60VBZS37vu+iTZdgadpUU6W+Bc9OgOP0mLRKneXV\njDq6dTpQguDK8u9orat2VtVKG8u1MBwOGY/HDIVgsLt7oZx6t06mTi2q1nYlAKb2SDPeteZbvgP5\ng6/GRhH2X9+D/Lwnb7w+bp0sR/WMp8TltTf7vSGcxho6foftaA3bhfHYMTtr3THQENI1YYz7ukXh\nTtXtbbDeNM1ICskgHNDxN/Oinf38ycT9NKRFiJKiOML3NUopdnd38Tcsj1tr23nPRgUthCAIJGFY\n4fui/p2P522t9zDernPVio9mYxQZ56hXvhb1kz+BKApsr4/9Fy9DvuSb17It09bFKqbGoK11lc/C\nElTQqQSeOXOtlExb8aFEKm62PKozvul2lz5w5FVOUiZkVdbOzEshibyYwOtgEO1caKGtq2imUOTu\nsGrESnEg6HUkg45AmqKNNG3uYb7vt+QfTE3im9SoqdeUSwmKEDbAZtJVgUtLWY8WFNZSBSBiiQid\nHZUvBJGUROtUf2/jw4rblc6PcQghCERFAhR4rHW7aVojs95yvu8uZGU5RzptvYwf+9mf5amf9Vmk\naUocxzzucY/jnnvu4V3vehdPfvKTuePqHfzZX/0Ze3t7FxqoFAK0tig2y11v0FQ4bm2m06vfu7rS\n2VxkvcCDCmxlLzTXCa7aOa6TMFaRzuk6nSFfTSupzl6+aJu1H/bbPPZe0GurW7auxIhw9XcTwhH8\nw0PHgeL44sWHfr/POE1J8hxvMuGOi2Rt4qrCvr9HWR5gTEZZnuD75xC5pizXKGhqyO//XszBAfIN\nPwdf9qWY//COCymSRV3xbNLEDsuSgecRYDYnnODYfVP1bAw109TtjHN2QFG4l2vNmfnNTjvrmVUZ\nJ9kJk2LCIBystFdahMZKqddzXOnGjYSTExdn2e2GPOxhO/j+5iSiMZPvdrsURcFkMmIyucFkkjCZ\ngOcF9HpX6PX2VlcMF66zh5QDPG+A1ilGp5g33o3/slci63GW6tlfif2+V6Ae9gg4h9CejagE16Hq\nhh5xPJ3VtNpiCmfHZAuLrZxCnolGJxNIJwjPteVFFCAGPUS/g/Bu9gmtTEVSJqRl2s5qCgSRFxF7\nMZE3FWRpDSIHk4HMLcpYQmtR0oBn8SNLEFmsLRmmKdfuTzBaI4VACkEURXS7XYQvSU1Gmp6Crepl\nui6UEqEjmlUAhYDMQKXR1j2AFaJpm0tE6Nr9YU0yIynXFt/dxkMLt0nnQxShsCRAZde7y7ezRbMv\n9313sy2KOVFKQ7A+8VGP4pu+6Zv4oR/6IT7ncz6H3/iN3yAMQz73cz+Xe+65h6c97Wl8+sd/Ou/9\n4Hu5KjaP2hPCKdeNYaqq3wDLhESbrYOq37taCDVr+SFD2fr2qc7mLCusSWdmDKu22sL2eoNOx6l4\nkuTCpNOTHpEXtQrWxnz8vNb6LMLQ8Z80dfqmdeJHF0EIQdDvI4oCnSRU/f7GlbDpZyk8b7cmnglV\n5S03j298guDmVrUQyJ/7aUc8f/PX4elPx77znYhP+oQLrdeO7+PVM70HeUqaH9NXzk1gbcLZQCln\n55Qk7jhozuMVxpmzaZth6BTos19XCsluvEtWZZxmp5Sm5DA9JFQhg3CwsTG2e6g8JQgm9PtgbZdu\nd6uNm+/13GG8Kay1SJnT6RREUY809chziTEh43HJZHKtNRmPomhjAip+/92ob/lW/D94JwDmMY+l\nfM0r4Ul/2/1/eQjI2jsyar0jwXWJRjPZ6wLnwNBVamG1TqipIh7AlhXmcIgdTTCFxhqLFRE27rmH\nzRzI62uVBKssmc1IbUolKkdOPUHgBcR+TMfvtA+TVTV9vipmg32EYNARRBFEkUIIV1EejickeY6x\nFmkM0vOIOh3CSCEoqMwRVTH7sC4RMgIRQh5AbrGZgdkUIYUjmZFChrJVmUd1JOhtb8y/+bhNOh+i\n8OoWULmm6tuauno1W5lr2kNnkiFmAjj4l//yX1JVFa9+9avnSMAXfuEX8ra3vY1nPetZPO5THsf9\n//ndC02+V6G5Brt2zsUuNlJKjDHO4sc27bX13z+tdK5HOoVwSlSTGkxxcdIpcRYoxtoVT/QG15pa\nQjqb4bnGqfsC6Ad9RzpLV+0UQmCK9UknuALbrODgIqJ6ay2VUnTimDjPOTk5adXsF4GUPp63Q1Ud\no/UQIbzFYrvh0JV9wnAxA1IK+ZZfwnzB05H/6R3YL/gC7O+9E3HHxXxS+54HpuJ/podU1qBkhyvB\nxY3f6XTcBm+MM5t/t7bmVDwN0QNH9gYrFhl5EVEvYlJMGBUjcp1zI7lB7MUMwsFasX/GGI6Ojmr1\nueCuu7aJ45gkcdMBVeUKtaPRlHyuc96endv0vC47O3cghGrtlprEm8Z9IwiCloAuVb9bi3nbb8L3\n/wDy9/+j+9XeJewrvhf5dV9NKGUtQMowJsPasp5ZbKyXAjLrM7Y+FonARaL2142orCoYjxFpirIW\nBh5EPWy3h0VhtauCNh2WNEtJsoTc5G2RQApJ7MV0vA6+5yOUoFKarDAkuaCytRBHCaR0h7wjmm7b\n53nOcOh8NZvP7Po+URQQhhLPs7XyvL7eSokVPkKEQIgtfJd3npl2Vt8isKGEyKn48V0FM6xb55vO\nbd/GQx+3ZzofZDwQM50ARXHAtXyE9C5xR9Rd2YqYy12/Y6YqZoxLJhLCzWI2n20MB2W5Mg2mweve\n8Dqe/5znc/XyZf7nH/wB0cd//Nrf4cYNSPIS0b1BJ1w/D3wW169fp6oqrly5wnCoSFNXbduE+LT5\n5sHVpYrnJEk4OTlxWdHd/lozj6twVJZkxiydXbRWUxTXVhvXN23VWxyoPEwOyXXu5vjoUB7MJFet\nicaYXymXD7BpwaJJIPKFwJ6ctGr2/ro2BEswbx6/P69MbmZjhXAqmBXqV3t6in3y5yHf827M33oM\n4j++A7FO7NUZlNpVD0ujyaxHN9pGAttrplStRJ67naBrz8NuF9Ptc3Qs5uY3NzH0t9YyKkZMChfH\nKRB0/A79sL9UbNT4b2q9fH4zTR35bJ53lZpGJS46ds5mpSD2+mwAACAASURBVAsR4HmDhXObTaZ3\nk+s9e731PK8loEEQQFFgfuFu+OEfRL73v7rvPNjCfu3XIb7r2xFLY1p1S0DzKudEV5T1YiLpsxN0\nCVR8vmdsVU0fHq11Xz6O3fl85ngsdena51XqiJ9xsY+BDYhFTCjClpiaCiaJ+2k6/FJC1BDNjkD6\nAiMMaZ6SFikajfSchZzvQxR5hKFgbsYV2vlMTACFcvOZxWxUEwhftHn163qV3sZHL27PdN4GoPGF\nRAtJWSv7lqIZ5j87fyjldDawLNvKSFvpXIM5fPlXfDmTyZiXfONL+VtPfSp//hd/4S7ma8DZjVou\n6A0PzLfYbT1qsHmHRgEaayuEWLzuc5VOTyKU8+q8lbnOrB6iX0Y6HVZcsDudW1axg1Oy52nOpJgQ\n4di6DDa7UXQ6bjWKwt1DV1XSFmFSiyS6SuHv7HBwcMB4PCaKogu32aExj69q8nnGw7NWqy+6wZ+F\n2NqCe/4N9rM/B/lnf4J5xrMQ//6ejZ5uKlNxmB5irKHnd3hYtM1Jnal9VFX0rGVwK7YvYegYf22v\nVB6POfpAju4OUJ2Q3d3Nra2EEAzCAf8/e28eLktV3vt/1qqh5717D4dzGGW6CMhBJWAEBTE4JGji\nAIKCgqiRiDLd4L0akkdiyINgjInADf6MEyBGI+ZGBRPn4AACAkEiYoxehHOAc/bUc9e01u+PVdXd\ne+i9u3vvCBvr+zz99Dm9q1atququ+tb3fd/vW3AK1PwaraBFI2h0CtAKTmHRdaLRaFCtVtFak8lk\nmJiYWDG8ncuZV7ttyKfv0ykELBTM32zb/A7CsIZSzXg+FpY1tmrL015fT601nud1CGgYhtTrdeqP\nPUbhhs9S/PjHsB7fCYDec2/0+Rcizns7cg3zWSEshMzTUC4NEaGlh6M9SjIkKzWoOoGq041UWGYd\nYZv3UEG9hWj75vjFDwkUi0uKOlXHZSJU3WiMIx3ymTw5J7eI/EeROYaNhkZlNNLSZCxNIavJ2Boi\nUyjYrMduAL6H1gqtfaQVkcvZ5PIOlmUj/IAwNH6b0slgOVlE5KLbwhDNUNMtFoir9mOiuVJf+hQp\nICWdmxZaK2whiJAEaxiNJ/mcK5Ij111OOnVi2Ls2pJC8/o2nw+4qf/zn7+fYY4/lhz/84UAmzsm9\nSqn1hdfNGGqkQiKzvI3W/qrFRJ0QVrw94Qp0S68rrxNYZAq9eHsrGMMvGySzIQVFGTuDa7n4kU+j\naYincIc/H+WyUa8bDUMaBiU4SzsQCcuiUChQr9fXHWYHsO3xjjJlrJSmEUmMN+lHPQDEtq3or30N\n/YIXIH9wG+rU05H/9+aB/AG11p2ioayd7XSCmnAc3CjqeO8GWjNh26MXUcT2Sr6VY/aXVbQfkGGO\nifEc0hpjpORpwJIW5WyZoluk6lVph22qXrWTC5y1siwsLHRC2sVikbEBnjyS8K7nGbLkeYYzV6sa\ny6rjunUyGY1tCyyriGUVh+5OlCibAP6vHkH91d/gfurjyJrJ5fUP+h803v4O9FlvIFMqkc1m1+zx\n1ogiamGIwlhjjbkFirE9k1Je/Gp3Gk+Yh1rMdbZWh7aXTBAKRURpHGEphG4gIotIQSNo0wq9zoXY\nElYnT3OpgXsQdM35zaVKkC8JisVuFpXv+6b6P2oQyBYq44ETkrElOSeLa+WMeqolIsggQhcpMp0U\nJHN17LleSbpq5gpNJFKkWAkp6dyEMIREY0sLX4hlJsDLlk+KiFa63yTMwPeX5bQNcglJyOI73/Jm\nWp7Pn37gA5x00kl8+9vfXjOBX0pTSGSiSusjnVEUjVRIBIMVE3WIeDzPTjHRiHmda3cnWqWIqBcb\nUFAERu2ca81Rbxh1UTjDnw/bNmJNvW5yCKcHzJZYqQNRqVSi3W4TBAG1Wm3dYXbj4TmD1gFhexdO\nPb55DtlOSRx0AOpf/gVOfBHyli+hXn0K4vpPItaooJpvz5sOYtJhIrs4ZFuwLBwhmI9tlXYHARO2\nvaqzwWoIQ5irOejJKfKqTtmqQbsJu9pGgh6leieGLW0mc5P4kU/Vq+JHPruqu6hX6uTtPHk3T7lc\n7mve3g+ZjHkZ8tSi0aji+1Hsg57DdcfI5y2y2dEaEeif/gx91V/h3HQ9IjYyV799HO0LL6T1khfj\nx32625UKlUoFx3E6L9u2cRwHKSW+UlTinuhgIhbjtr3I9N8UGGUAQ7q1jtBeC11dQLd9wELbWXQu\ngy5kQQo0IVqFRCqi5tdphcaWSAhTfZ6382QdC2ijQg8/vu56nqTRkJhdEkgpyOXM71DrkHY7pFoN\n8P2AMGyjVIDWAZmMS34iF7cYtZDSRcoMQrgIbXdyR3vzSHVoojodojlkNCRFCkhJ56ZEooLZi55A\nV0G/8Dr0PgZ3x4/fB1U60RqN5tKLL6aqFFdddRWvetWr+NKXvrQqmUzC6+tJcV3JIH4UpRNWJ529\n4XWgowRqb/TJZ6UkiK2TlpLOvnZJS7FBBUVZO4uNTTts047aQ9vkJCiVTMQ/aZqyll+q1ppmElrv\nmbsQgokNDLMLIXCcuKJ9fjdBYOGU9xrIa3Ep5HOORH3py/CKk5G3fAn97OeiPvMZ5AkvXHH5mlej\nHbY71eEr/SZcKdniOB3imdgqFYbM80w8OJUyCmJ5sghR3CS93TYpBUmh0TpC+a5lcrBnFmaYXZgl\niAKQpsOQHMEOCZIHuznyeY98HoLAJQjG8H2XKKLTcaxrUr42AVW3/xCuuBLxlf+LjC806hV/AP/r\n3cgTXkgeyGN+371h+CAIOl6gEPttAqFlmbxQx2E6m6Vg26s/MHseolZD+D4gwS11k1fj77vWiiDy\nqHkVmn4TjUDKDFnLpejksOJQdW8kptkU1OuCMDTHTakQx/GxbZ9WK6C2Qlti27YpFrPk85M4Tg4h\n3JggLz+Io6QMpUgxCFLSuSkRV25KCzQDK50rXkiS/rRh2ElkHyanUxjm2FECr7zySiqVCh/96Ed5\n05vexA033NB3nN6Pn9zweqJ0Dh5e783rVKEaKVk+09OdaGkgcqDwupnQhnQoAihQoE2bhm4wvma/\npJWReHfOzXW9O1fjwU2lUJhjsbSS1XGcDQ2zC2Fh+1kCL0BZEWFejnwBlCe8EP2je1CvfwPy3rvh\nd04keu+fYV32p4ty8rzQo+bXEAgmshOrVn4nHYySUHslDPHjYrNBfotam+MehoZLd2pgLMtU17Va\nRhX3PJMHUSwO3i92CZLuQr7nM52fNk4HLkQ6YqY5Q8bKkHfyi7whVx8vJAzn4rxqk7eZyXTzNn3f\nTL/d7tbeJAQ0m12SzqE16su3mkr07/+b+ch1UaefCf/rEuQRhy/bvpSSXC5HLq6ySkhnEAQseB4L\nvk+kFDKKyIQhru9TbTSoQkcJ7X23lTLHOnmYl9Ic7yWVUqEKOw8lGo1tF8g7+WVdwnR8ja3XFQsL\nAe22TxAEaO3juj7ZbBRfxh20trFtcBwbxzEk2XVdHCfbl2SmSPHrQko6NyESQmIJG6HXbiW5angd\nzNXa980rkxlK6UzIok4qL4G/+7u/o1qt8pnPfIZSqcTf/d3frbxuj0/nesPr683pNPsweHgdunmd\n2tcj/ZLc2Dop1JpI6yV9uQcMr8OGFRRlyGBJC2Ur2mGbrD2C9xFdEpA4+Kzm816PVc5iH0VvbGys\nozxVq9WB8gT7QilkvYVtjxOOCSJVQ0TOylZKA0AccjDiju+j3vOnyA9/EOvyy1Df+hbiszci9tuX\nSEXMt+cBY8Q/qHo8Ztu4QnSKjMI43L6Wvcz8vPkJJ6bvy34HiTxYqZjvSqKQj48Ppfh6saVVUp1e\nLpfJZDKGFPl1GkEDL/LwIq9r4+Pk+/p8KuURBPOAQggHx5lc9rDluuY1Pr6cgNbr5mXbkLv92xT+\n5CLkT+4HQJfGTCX6/7wQuc/eA++j4zgoy6Ju2zjZLFuADJDTGhWGhGFIEASE8b/DpJ1wGCJqNaTv\nY9s2Iu4XK7JZRBhCpYIQglCFNMIG7bBtihOFJO/mKTpFbG0T+AGhMGP6fsTCQkClEhAEEVprHAfy\neUUuB0JkeohlNy0gRYqnIlLSuQnRaxpuxTmdoVL9b0qrhdfBXK19v9NmbdhCoiS8nkAIwWc+8xkq\nlQrXXXcd4+PjfOADH1i2rrkpblx4ffScTolh5KqTR7UUvebwnW2v0yQejMLXUoq2UotCqQOH18Ek\nw1mWuQP7/kghYwDtm97fdadOzauNTDrBpA56niEHCddZilYUEWmNExtE90O5XGZmZoZGo0Eulxv9\nhlqpgFJYhTIUM4RhhTCcR4jp0dUf10X+9VWok05CnHM28ge3oZ/zHKLrPsbcK45HaUXOzlF0h3sY\nyFoW03GeZ6A1u4OAomVR7OP7mETPE8/4vocz8U3K57t93GdmjAI3NrbmE1vSrhRMW9xyudwtrhOC\nUqZE0S3SCls0g6YpTgsaNIKGqbh2FldcG1eBKqCRModtl9d8AF1KQNttaD/8BIU/u4TCP99oxt2y\nJ423Xkj49nOxJsvYNlhtc6mzrNV3M1SKak83IUcIxlfJsQ3DkMDzCOfnCet1oigiFAI/m0UnBqRx\ngVWgAup+HS/yOscsb5tjokLNfFQjiiCKBFGU/KRF59qWzcLYmEWx6CwimSlSbBakpHMTIlHkhLA7\npDOi/8lcU+lMcrvip/WhlE6xXOlMPv/yl7/MiSeeyJVXXsnY2Bh/8id/smjdjTCHX9oK02x7+HGE\nsGLrkBAhll/E+ymdwGKPuiGRjUmnt4x0DhheT5DkdjYaI5NOFShyTo52pk2gAlpBi5wzhKljD5KW\n4AsL5rVly/IOjWupnAl6w+zz8/Ns2bJleGU8YcBSwvg4lmX1t1IaAfIVL0ff/++oN56N/Oa/Yp1+\nCtmzz0J/8P2Up/dce4AVYEvJtONQjSJTLR338B637UUk3VjkmO/95OSArUhdt2uvlAzQbvft4x5F\nkQmn+8bip1Qq9W0GIYTx8sw7+UWtGQMVUPEqVL0qWTuLK3xsYb4DllXCtocP9btWhP3J6yi9708R\nlQW0m6F+3nuonf+e7pNOY/l6lmVeCQm1bUBqWiLE0wqNuVyW1sqr1Rq73cau1813a2IC8nl0sUio\nVOe65IUeNa+G54VIN4sb5XDJkhEFtLJotzRh2E1T0j0pS7mcpFSymZx0yWYHS7VIkeKpipR0bkok\nSqeNLQQeJkTbL3i3ak4ndO9SidIZfzxQTicmp1NptYztSSn51re+xTHHHMOll15KsVjkggsu6K7b\nU0j0ZIbXzTo2WgcxoV9OOpcWEsHG5XWCsU5KVFZzs0m6EQ24M/l81zNlhIIiFSpQIGzBWG6MhfYC\nNb82MulMppRwvfn5xdXs7dgeyBKC3AAsaWmYfXyYqnOtu56cpVLn+76ildI6buhi21bE126lfcWV\nZP78fZQ+fT2FO3+E/od/QBx5xGhjxipbTspO1fRsEJCLq6a9tqBaNd/5iYkRKrtLJUMyK5W+fdzb\n7TYLCwsopbBtm4mJiYHVNVvajGXGGMuM0Q7bNIMm7aBFvb0DrXws6VDMbqPoDF9Rr354F7zjPJNT\nC6iTXo74P9dQOuRgippYMTTP0iu9R1Ec4NGaugppJ2RTQNE23YSaQtCKvxKJnWbyb1otZN10tBKC\nRIYEYSOaABbtwGehWaMVeESRQFAgbxcoOYVF/pqua8bsJcLJv1135PrAFCmeckhJ5yZEV+m0sOOL\nYL9ioo75uliF2PVROgdBcuHUfdaybZsf/vCHHH744Vx44YUUi0Xe8pa3xPPv6b0+IjaOdK5eTLS0\nkKizXpLX6Y2W1ymFwBUCX2v8jsn/kConmDtUJmNIZ6u1dtn4EiRqrXCMSlX36x2VKj8CIUhQLpsI\nbmL+naRkDqpyLh6rG2YXQgye31mrGYbhusuOyyIrpXAOx5kaeD4rwdch8xe8GXncc5h+6/lYD/4H\n+refh/rgXyPfee5oX07i6nbXpR73bm8pRbXmE1ZtctJifHy09qOA+f0v7ePueehMhmoY0oivC7lc\njnJ57fB3P2TtLK608YRHK8zQDkHLEo0woBnuImN3i49Wg56fR//vP0V8/DqEUug990Z96MNYrz+1\nc3yFMLtl2ys7iSkFXqCp+BGNIIIInBAy2iKrLSwtiMI+ziC+bzw+k+p2x0GVTF5s2AwJVItQBQTK\nx49MIZEUkoJdoJQt4DpymdKavFKkeLojJZ2bDEYZjDAqmIUr4vBNP+a2Vj4nLFc6E4I1wHwWVa/3\nuRm5rssDDzzA/vvvz1vf+lby+Tyvf/3rO4uvJ7wuhIgNmdfBXFm7mGil8DoYc2TVUqi2wiqMntfp\nxzlkGSl7cnaHHC+fN4RhEK+iJdBxD7/Ee28sM8Zca46aVyNn50YmGokCNzNjhFjXBel2zeDzQ0g4\njuMwMTHB/Pw89Xq9E+ZdFUHQjT2voI4uslJSHkEwh21PjLS/kYqYb82j0eSPeyHy3+9FnftO5Gdv\nQJz/DtTXv4745MfW9PRcDUXbJmdZzLRCds0rlAqxxiKcrM2oxu8dJH3cq1XCWo35mRmCIEDYNuNb\nt5IvlUYmzQBR1CYMF5BCU3QnmChMEvSE39th2xTWxAp/ck1I/i0A94YvUPiz92HN7EZbFq13nEf7\nsv+NHBtHxC4BYMzsLWF13nvPp9KamopoEqFdKLqmKUEp9tvUunMp7DzIag2EIbpSBd1G5TWhUHj5\nHEHGIYyqBFGAtkzkRgKuhrwlGc8VGcsWcEbwvk2R4umGlHRuMnQJiTl1Tk8FtNJ6WScTrdbI5wQT\nu5HSPP5rPXz1utYolofXe5HNZvmv//ovtm7dyhve8Aby+Ty/+7t/YEg0o4fXzfQlYRihtcKyRrvx\nJsdzJW0jya9aaY4yK0GA8k0v5FHav2Vj66TkwWGgFpgrDpTtFhQN2aFI+bG6Gt8Ys3a226UoaAxd\nCNMLxzEKZ6US92cvRyCMKfqw5z2bzXaIZ61WA1ideC4sGMZQLPaNPQthYduTBMFsHGqfjSuohzv+\n8+15Ih2RtbOUMiXIgLjpetRLX4q44J3IL30R/ey7UZ/8FPIlLx5q7EVQAmoOYzIizEW4Rc1MEJC3\nLMZGOKaLICVN16UiBDqbxZaSyVIJO4pg1y7z1JDPE5dNDzxsGNaJohqmYCiPbY8jhMC1XFzLZTwz\n3mn3GKhgUb90NFj/8TPG/+elZG//AQDe0Uez8DdXEB0Z2x8FKyRu9u6WkAgkLS3wtDBkVFoULYdx\nx8XtsSdKVNIEURgQVOcIa1XCKCAUiiCfQRfyIHzAN6oqJp3AkY55txwyVibNwUyRogcp6dxk6A2t\nJ3CkxFMKXymyS2I0nXzOtciQZRnSGbd2M9tY+2KZVK8PgkKhwM6dOxkfH+dVr3oVt976NQ487LcH\nWnfVOUgJRHHO2aiks39Xon6hdbOeMFXs7VjtHKGK3ZGLXQjEKOH1BMWiYXf1+sCkU2vTbQTBok5E\nJbfEbGuWul9f1mN7WBQKcavDlqI6r5iaZGjj8wQDE89Gwyidtr2mH6WUDo4zHXtF+gTBDLY9iZSD\nXSIX2gv4kY8t7WUdh+Q5b0K/4NiOp6d46e+gzn0n4q8+gBjS4irx4owiGM9bTE6aB5ZG/Gorxbhl\nLbsODDa2ZmFhgVZccJXfsoXx8XFEEJjQe7vdtVarVLoN1Nf4ngXBQqd3umWNYdvL91kIQcEtUHAL\nnbloNKpeh8sux7r6bxBBgJ6YxP/Lv4S3ns24FJ3letfRcY55qEIiHRFEIZUooKm6ThlZKShakiAS\nzPjm4blXHRUIgsgnqlXR9Vrcq1egczl0aQwhLVzLWUQwHemkBDNFijWQks5Nh8VKJ4AbFxP5WrMs\nGyphkGtxMds2N+goQicG6APMpl/1ej+MjY0xOzvL1NQUJ5/8Mm783FfZfsyRI4fXwZBBrU1e56jX\nfEPwRNwrebGquVIR0aLt59ZHOgEyQtDUGk9rMqOG16Fbxe555nwOUPChA5P3K5zFhUsZO0PGyuBF\nHnW/btS7daBchpl2hB9A1LKQmdHP+ZrEM4pMfiKYsPogD1DSxnGmCYIu8XScSaRc3Q0gUegEom/H\noY6n55+9H/GhDyA/ei36X7+K+vuPI086ceD9npvrnlbjxSkYs23yUrIQhvhaMxeGZOMqd2vAH0QQ\nBMzPzxOGIVJKxsfHO0bpHY8irQ3xbDbN96vZNC/LMt+7fH5RYqLWqnMsQWLb5YE9UYUQ6C9+Ceui\nCxGPPAyAOvutiA9+gMyWwfqrKq2pRxEqiihoRVZFuBLyAgSKSEVEOuq8hyokJE7kbLWQtTpEEZaw\nsAvjWOUJHDeHYznLep+nSJFiMKQ1cZsMK+X79VZAL1teDaF0gslbij8aNLxuDOpXD6/3YnJykiee\neAKAN57+e9x/373rqxqO87DWQzrNOCsXE62mdEJPiN1T3XSGIZGNx24rNXp4Hcw5SPI5Yz/FtbA0\nn7MXYxlTrNMIGuYcrwdCkxlTSAE0rbhf9OhIiKcQglqt1iGfgCGcWhsiNESagRASx5lCyhygCIJZ\noqjVd/kgCqi0KwCUs+XVyYjrIq+8HP2DO1CHHYH4f79AvuTFqHecjx7gXM3PG66XNBjq/a7bUjLt\nupRtG4n5Hu3yfSpxW029SjSi0WgwMzNDGIY4jsOWLVu6hLMXQhhlc2oKtm416rFt0+lR+cQTMDsL\nzSaq3SCoP4r2aoggwlFFrIDYVDMudkteCXmNX/o/HkS9/BXIU16NeORh1BHPRn33+8hP/T1iAMKp\ntaYWhuzyfUM6gbxls1c2z57ZIuOZImOZMSayZaadcbZaY+ypi+zhO0zVFeX5FuWmZsIZY4/y3mzZ\n71Am9j6IscIkOSeXEs4UKdaB9NezydAN/3ZJZ9LZJlgpr3OQQiJYVEw0SnhdM5jSmWCPPfbgkUce\nZd999+FNr30lB991O88/+vkDr79oDrHSudqNdRAY26QwPsbdn0a/IqLuej0hdk9h5YZXKDNSIgBf\nKbRYh9IJhnQm9klRtGZZbCef012+f47lkLNztMIWNa/GeHa09phgKtYdB6ZKEtkUHf/O9djBrKh4\nZjJdT84ROhiZ4qIJwtAiiuqE4Txah8t8JJVWzLXm0GiKbnFgeyn5vKPhvh91Vc/rrkH/y62oj38C\n+TsvWnGdarW7S1NT/U9p3rLISkk1DGkq1Qm7C8x1IhMb8TtSLg6nY9JfBraisixDOkslE25Pwu+e\nR9SqEKoKoJHCxZZlhKiuOaT6yUPw2c8hbvo0st1GF4roi9+NPPct5sFhbm5xqXf8UlLiK1Oc5itF\n0JOXnpWSkhA4Spn5BYHJeU58k2II4pxMJNi5bkrGSuQ7RYoUIyMlnZsM/SqbXSlpxybjvb6HAxUS\nQTdzPoo2vHq9H/bZZ2++ftu/89ITns2xxxzLT37yEw477LChxoCuAmnC4kOv3kH3mC5WOtcKr0Nc\nxd5WqNZopFMIgRvn5npRgCvXQTqlNApfo2HI5xpEotcuaSWUMqWOx+LSntCDQmtNM77JbxuzqEZd\nW8ip9bkULSOeYmaGYiZj8lvXwWhtewwhbMKwQhTV0DrCccqdv8+3TOFQxsp0FOGBEaue6pRXo998\nDvLBB+AlLza5nh+8YlGuZ3IaE/N3e42rthSCsuNQiDtdeTER85TCA/NgGYY05uextSZn20xOTJAd\n1XMpDr8rFRDVd6FaLdAOUuZx7PLiZXt/Q0Kg5+bQ/3AzfO6zyPvv7fxJvfLViL+4DLl1D6NYB0HH\noiiI7cV8rQm0JkwMNBMiKiVZoKQ1ThTR15Ot11dp6SvNzUyR4r8FKencZOhHOjMx6WwvIZ0dpXOU\n8PqAF16J6CTwD3up3nvfffmnr32X17zseA4//HB+/vOfc9BBBw01xsaF11e2TVorvA5LQux9Kt3X\nQibOzW2rAFeu0wKnUOiGLEulvuRLK22KzSR9ze1taZNzcjSDJjW/RjlbXnG51dCIFfRsrLJNTMDu\n3XFxUX1dLeOBbkvGhZ07qVcqUC5T3HO0TkC9sKw8QlgEwTxKNQmCCNuepObX8CIPS1hM5FZpLr8G\n1lI9G41uamq5PFyzKSc+1iVMfqOvFJ7WzFarVKpVtNa4ros7Pk5NSvwwJCMlrhiiKQHmmhSGNZRq\nQUZAZgrbLmFZfWy7whB167/CJz+FuPVLSN94WeqxcfQpp8Hb3oI8zkQ9lNb4UYQfBPhhSBCG6IRI\nxg7vUmvcmGC6UbR8/lIaIuk4i4llaoyZIsWvHSnp3ETodqqRy+xcMvFF1l8SYl6zBWaCWD7RMekc\nhjIJBBrQYrj14hmy3/4Hcte9P+KY5/4WBx98MA8//DD77bffwCP0htc3hnSunNO52o1YSIF0JcqL\nC4pGUDuzcdcZTyfneB07Y9vGQqnVMlJZn+rtJLQundW/ICW3RCto0QpaFN3iUHltWmsasdqUVKxL\naUjU7KxJB0xqVdaDXGwZVRWCKkCj0bdV4zCQMoPjTBGGcyjlUWs9Si0EKWwmc5OLOsuMhD6qZ+uc\nd1F57xWQLzA+vr5Ib9KEoFmpkG23sW0bp1AgUyx2QtJBFFGPQ/GOEEghkMTpI5jfthSi845W6KiG\nVi0EGiEkllXEsoor2k2p+/8D/YlPIv/hJuQTjwGghSA88SVEZ52FOvXViHyeCAzJ1JoouZ5J2fmS\nOELgxJEBVwhsKbsthpJXQjRtO23nkyLFUwgp6dxE6O25vhR2bLsTxRfqTtXqoEongGWh41wnuVYM\nrwfJyAo9tDaX3A8OP+xZ3HPPPRx11FE84xnPYOfOnew5oFK1UUpnkie7VOkcJLwOcRX7OkinOYcm\nNy3U9G1rOjCKxS7pLBZXDBkmRUQr5XP2wpIWBbdA3a9T9apM5gY3OG8pRaQ1bpxPmCCTMVy4Vuu2\nyVyX+FSrkXNd2LKFBcuiWq2ilBq8c9EqSCyVWt4ustm/qgAAIABJREFU5luzaARThWfgWMP2nVxl\nG7HqGf3p+5F//QFyn7ga++u3EP1/nyD7uyvneg4K3/eZn58niiKklGydmiLTU2Dlx2H4JBTvm6e4\nFcfSWqGiOlo1SNqdCZnDskrIyEKouLNZ7O+U+ew/kr/hBjL33d0ZIzjwYJpnvJHmWWei99u3O3i4\n+LcnMalDvSRzxd9h2tInRYpNgZR0biKsRjrBWCe14tytfHwB7lSvr1VIBGDbhnQqNZRiKRFEDNc+\nswPRrZV/7nOfy+23386xxx7LXnvtxa5du9iyZcva29+gQiLjySiGrl7vrJ+E2NvrCbFrfCDQG5BT\n5jiG2SX2Nit0KVorn7MXRbdoemeHbYIoGJhwrdbyMqlD8Tyjek5PjyhMRVGn81Bu61YIQxYWFqjX\n64Rh2KlyXx8k9dACYboCuaJFFJncxY3yZwyly9wll6Nf9GomLj4H9z8fwD75xaijjoH/cQj6kGfC\noc9EHHoI8rBnDtT7slarUa/X0VqTyWSYmJhY9l12pcTtCcUnzSaS2IqOH2ajqE4Y1Q3xFCBkHqwS\nYKHiZQlDnH/5OoXrbyD31a8gfGNToEpjtF59Ku03v4noBceagi2SjkMGiYrqxMqsnaqUKVI8rZCS\nzk0ErU0ifV/SKSWt2CQ+b1ndvuuDXrctyxDHOMQ2KBLe2K//+upIjJ3N/57//Ofzne98hxNPPJE9\n9tiDubk5JiZWz5lLbvjrVzqNZY7x6ow6ebODKp2LQuyewsqOUMUuoAa0tGD4zMkVUCx2EydXIJ0q\niMPrK9glLYUUkoJToObXqHpVpvJrVwC1o4hQa2wh+hqWT04awun75n1qagTi2WuR5DjkHAfLspib\nm6PdbrN7924mJyexh1Dwl2KhvUCoQ/KZrYw7Nlq3CMMKUEXKHJaVX9PTczW026aBklLg/vbR2Pf/\nCPW+9yP++krkj+6EH925aHktBOyzH/rgQ+CQQ+CZz4RDDkEcfijiGfuigPn5eTzP67QMXbNtKN1Q\nfGc7WhNFDSJVB6HAtpCygGWNmQc1pVA//g/4zm3w3e8ivvtviF2Pd+aoTnwJnH024nWvoVAoMFyD\n1hQpUjydkJLOTYS1lM6leZ0DdyNKIKVRKoYlnQnpG4F0Jvc2rbpbfNGLXsRXv/pVfu/3fq9DPFe7\nWSZKZ+94o8LYJkVoHfb4dg6mdEJcxe7FVewjkE5X6Lg7kaAdRSN1llmETMYonkFgQu09iYEqVKBA\n2GLg70jRLdIIGniRhxd6ZOzVkwBWUzkTJFXZs7NmmnNzhngOfC59f0WLJNd12bJlC3NzcwRBwMzM\nDOVyeaQq7YbfoBW2kEIykZvAljZRlEOpJkp58XsTIWykzMcFSIMz53q9WzCUz5t8V3DhysvRl1yE\nuv8B+OlD5vWfDyF+/p/w/36BeORhY57+7a8vGk9nc4T77U/2oIOxDz+c3POOwTn6t/qmWfRDFDWI\nonpH/Zcyg6XzcPf98G/fRX33NsTt30fOzy3e/oEHo954NvKcs5D7D56fnSJFiqc3UtK5ibCW0mn3\n9GGPtEYM2o0oQaKOKrWsh/tqkDFFHUXnFD3h9V787u/+Ll/84hd57Wtfy7777svOnTvJ5/N9xhCA\n2CCl0wa8RSH2QQqJEsishMp6qtgjCtKijkV9I0gnGKIxP2+YTQ/p7ORzDhBaTyCEoOSWqHgVFtoL\nTOen+1ooJd6JlhDk1kpNiP0nZ2YMh5ybW26A3hcVY86+kkWSZVlMT09TqVRoNpvMzc1RLBaHyvMM\nooCqZxhhrwG8ZWWxrCxaR0SRIZ1ah0RRlSiqIWU2Vj/7E3OtjbrZapl9LZWWV/KLLdOIk06EpZ2L\nggD1s5+jH3wI8dBD8LOfEf30QeTP/xNrbgb3Zw/i/uxB+OqXu9srjaEPfRZs325eR25HPPdIxJJo\nQhS1YpuoEN1sIn/4APL79yC/dzvirjsQjcVm9nrPvdHHvRCOPx5edDzy2dsH7oaUIkWK3xykpHOT\noDfku1o/6EwcYveUIjNMERGAlIY4Dml91Amvj3KPEYvD6714zWtew4033sgb3/hGDjnkEP7rv/5r\nUfFDgo3K6TRYXkw0aHgdTO6scAXa1yOF2LVWZKWkhd0xu3bXm9eWyxkZLQhMDDdW+pJ8zkFC670o\nuAXaYRsv8phrzTGdn17x2NRilbMgB6vE7yWeiYfn5Fr1Ss1mt796n0p1IQTlchnHcahWq9TrdYIg\nWDG3cSmWGsBn7eUqqRBWbBxfQikvJqBtlGqhVCv+zeY79kudsZUh175v9n1iYqjmSeA4yGcdhj78\nUJrNJvV6nSg+5m6zSenRnTgP/gwe+DE88ADiP36MmN2NuOt2uOv2RUPpvfZBHX4Y6lnPRD/rEPR4\nCXH73djfvxP57/+OiG2NEux6xgHcceBB3JXPccTLXsrp578r7TueIkWKNZGSzk0CpcxFX4jVc8Z6\n8zrd0NwEhD1keH3IQqLe6vVh0blP9WGsZ555Jo1Gg3PPPZfnPOc53H///ThL+olvbE7nctukYcLr\nAFbOIvRDU8U+NOmMEEJQEA51bcLTkxtRTFEsGkWwXu+Qzk4noiGUzgSTuUl2N3cTqID59vyyavZ2\nFOEphaRrkzQILMsQz9lZw4/n5w0ZWxFad2PSAyiXhUIBx3E6eY4zMzNr5nkmBvCu5Q5kAC9lBikz\naK2WqJ+1WP3MIESGMLSZn7fR2sa2BzN9Xwqt9XKy6bqUSiUye+0FBx8MJ56weJ3HHkffez/63+9D\nP3A/4oEfIx96CLHzUaydj2J94+vLttME7jngIO7cuo070dy581HmFuY4xjqI337OkRz+4hNTM/UU\nKVIMhJR0bhJobUjnWoUKSV6npzWFWKwbhnQmhUTDhNc7vHEkpTFROvtv7+1vfzu1Wo1LLrmEF7zg\nBdx+++1YPUQmCa+v16fTjLVc6RwmvA49Ifb2KL3K4xxI26EZRLSVIlAKZ73EM5833kS+D76Pdhx0\nqEGMRjqFEEzlptjd3E07bFNpVxa1yKzGJKhk20MrYAkJm53thp3LK1VV1WpGLsxkBqrihsV5nr7v\ns3v3bsrl8oq9xmte1wB+GIsoMAVptl0EiijlxwS0hVIerZbHwoJR5zMZGBuTaG0ThjZC9L76n/NG\no7Ey2ewjlSoVorWHms6gTjoSTjqi+8coQvz8EcSPf4b48UPIBx40bP+Y5/GLQw/hkPPOpbD7CY49\n+EBOPfVULjvhBA455JCBH8JSpEiRIkFKOjcJtE4IzOqqUa9fZ+gb38yhSefQSmec0zkC4ROyf3i9\nF3/8x39MvV7nsssu42Uvexlf//rXl9z0BKDj4zT6zXClrkRJeH3Qm+zSELvMDD4fM3+BlDZ5yyid\n9ShiYr03eCFM9XqtBvU6ulgGbQjnqGFRSxoyNtucpRE0sKVNwS3Q6KlYH0bl7IXjGOI5N2ci6Mva\nqIdhxyJp2P7qUkqmp6dZWFig2WwyPz9PEASL8jy90KPm1xAIJnIT6zKAl9JFShetx6lU2lSrIUKE\nFAohY2MhEKJUuNKaywhos9mkVkvIpsBxHMbGErLpE4Y+vfnRWgdo7S+zATNjukaZdTOII/eFI49b\nNoODgavqFd7//vdTqVR473vfy9lnn815553HwQcfPPIxSZEixW8m0kfVTYJ+7S9XQmJ3EsR2OEOF\n12NT6KdKeL0X73vf+7j44ov51re+xSmnnLJIWU1uyuvN6xRCxMdYd4j+sEonxGonELWiNZbswmxP\nd/alYFkIoB2bq68bhYI54O02umG8E4fN51wK13I7bTGrXpV20KYWG3yPrbMIynVNaF0IkxVQq/X8\ncYlF0igol8uUy2WEENTrdWZnZ/F9nzAKmW/PA6bvvGuts1USRmCemRE0mzkcp8T09ARbtmwhk9kT\nx9kD256MLYjycQqNBBRa+yjVpFbbzWOP/T9mZ3fi+1Wk9Bkft5mczGDbfid8b17VzkupVk8ueB7b\nnsB1t+K6e+A4ZSwrt2aV/SWXXMIXv/hFfvnLX3LZZZeRyWQ47rjjOPnkk/na17627mOTIkWK3xyk\nSuemQUI61yYJlhBopYmUBmeIQiIh0HFLuWGoyHqq17venoPN8UMf+hDVapWPf/zjvPnNb+ZTn/pU\nJ7wOCXFbb8W3BSS2Se5QhUSdEXIWUTUayii+q0aZ+SdV302lqEcR4+vwmASMXFgqQbWK2r0AhYmR\nQutLkXNyRDqi6lV5pDmL64xTdDIbUnmfyRjiOT9vSKcQUHQ8k/CZ7M86kM/nsW27k+fpeR6zrVm0\n1BSzRcbEGJ72cBxnpHByFBl+3GqZ/9s2jI8vLhgyhYHLz20Q+DSbNZrNGmGogTy5nL1KGH35L9CQ\nzcxAD6ur4SUveQnf/OY3eeUrX8k73vEOHn74YT7/+c9z/vnns337dq699lq2bt26rm2kSJHi6Y+U\ndG4SJKrbIDcPCRDGtkmDqpzJdmLSKdTg+YgbYQ4/6OaEEHzsYx+jUqlw/fXXMzY2xtVXX91DCNav\nCBqvTj92DBiuiKgzhiWQmR7Pzvza562rZne3VbQsmkrRjCJKljVUru2KKBaN0tlugqojtg6Xq9h3\nWLeIFwU80aohowW2ZbZtyLhg0jXLZUM8q1XAq1LMYAjnBuQVJnmetVqN2fosoQ6xlEVGZagmhUoY\n+yXHcRa9rD7EWmujztbr5t9SmkOfiM39EIYhrVaLVqtF2GkJ6ZLNFiiVSiN5jG4Utm/fzu23384r\nXvEKfvnLX3Lttddy+umn8+d//ucceeSRfOhDH+LMM89Mq9hTpEjRFynp3ARIwq6DZkNYQqBDbRS2\nUUgnDEc64/dRwutSdnunD7w9Ifjc5z7HySefzDXXXMP4+Dhve9slQG/u6+joLSYaJbSeQOYN6Ywa\n0UCks6tmd5e1pSQrJW2laEQRpfWqnYAeG0c/0oJ2ExmVYA2D90Eh7SKO9LB0QLU939dKaRTkcoa8\nVXY2qFcDWhmb0mSBjaJgUkqcvENWZsmN5ZjITKAjTRAEnVcURURRRLvdXrxeTEBd18VxHHzfolo1\nKieYDICxsf78OCGa7XabIAg6n1uWRTabJZfL4brrD/FvBPbaay9uu+02TjvtNM455xxuuOEGrrji\nCk455RTe8pa3cMstt3D99dcvc5hIkSJFCkhJ56bAMPmc0CWdEUPkc8ZQI5DOpMhiWMqZVJsLhiOd\nYG72t9xyC8cffzx/+Zd/SRA4nH76uRtEOrvFRKOE1hMkIXYdaFSgkM7qDw39isWKltUhnUXLWjeR\nU0pCsYD0GsaZfI891m15EyhFSykmsuPIsNrXSmk9yGcVllOj7oCXG2NuzuR9jo+PnNbZgRd6VNrG\nZL6cLZN1DJ3trWqPomgRCU2IaBKW932o1yVhaIhooeAwNWVTKLjLlPIwDGm327RarUVEU0pJLpcj\nm832rUR/slEqlfjyl7/Mgw8+2Pns6KOP5q677uK1r30tZ555JjfddNO6Wo6mSJHi6Yn0qrApMHho\nHWI9NIJImzDvMEiUTjlKeH1I3qLpWhyNUidjWRa33XYbRx11FFdddRlCuLz73RcMP9ASLPbqHC28\nnkDmJVEtImpEyPJapHPlhwtXSlwh8LWmqdTIFeGd7QQaCgWEE3STDsfH115xFVSS4iHbIe9Od6yU\nql51IH/LNaEUzMyQcRSZvbM0s9mOA9Tu3UYJHRszPp/Dou7XqXk1NJqCUyDnLLdPAvN9S9TH7rQU\nrZbP7GxAoxESRSFCRGSzLVy3Ra1mclGT0Lxt23iet4xoJormU5VoLoVt22zfvn3RZ5lMhptvvpnX\nvOY1vOlNb+KGG25IiWeKFCkWIa1e3wToFpgMF15Xo4TXYxYohmCBAkwR0gjMMVE6h+C4i2DbNnfd\ndRd7770vV175J3z2szeMNtCiOXXD6+tROgETVhegWgqt1jo+/YvFkrB60st8PUg6EYnpuDS80TAt\ngEZEO4o67S6LltWxUhII6n69oyCODKWMaWcYGklzYoJ83gi0pZLZhVYLdu3qFrUPAq01c605ql4V\njabklhZ5ja69PjQakmo1i22XmJyc4MADt/CsZ21h770nOwU/UspOWD7phiSlJJ/PMzU1xbZt2yiX\ny5uGcK6GbDbLP/3TPzE7O8vFF1/8ZE8nRYoUTzGkj6GbAFJmsO3JgZVOIQQy0kYfHfKxohNeH5Tc\naN316RwywK61HimncykymQzf+tY9PO95h3D++e9g69YpXve61408niF9xrJmWI/OZWMlBUXtuKCo\n0P8cLq1e70VGShwhCLSmFUXk1qF2qthKS+YdwFSzryfM3jGC7wn9u5bLRG6C+dY8jaBBoAImshN9\n+7T3hdbGrDMIDOGcmurMMelVnvjeN5umcKfZNJ8XCv2HDVXIXGuOUIVIIZnITpBZI7dVa8N7Y399\nfL+bt7lYabWw7cWKaBRFxo4pDHFd92lBMPshm83y+c9/nsMPP5wzzzyT5z//+U/2lFKkSPEUQap0\nbgIIYWFZWaQcLHFNK43QAiSoYUPe8Q19qPC6ECAEash8yvWG13uRzeb5ylfuIpPJcNppp3HLLbes\na7yE4CsVxP8fPedR5mPPzsbqRH4th4JiTDTXo3aqUIGKDeylMCXVrmvYU2V4RTIxgneEIL+ECGft\nLNP5aWxp40c+u5u78cIhFFWtjcLp+8ZraGpqxWocyzLV7Vu2GCsipcyuJMpno2EcloLA/K0VtNjd\n2E2oQhzpsCW/ZUXCGYZGQa1UTD/4xx83ofxKxXweRYYHT08bW6fVngMsyyKXy63aNejphHK5zAc/\n+EH+6I/+qKcKP0WKFL/pSEnn0xA60lgCsATDRq11fOccOLzesRRKQtLDscdRC4mWjyPJ5ws88MBD\nALzyla/km9/85jrGM0GAKEp63o9OOq2shbDilAdv5TNijpvpptRvWznLworVzvaIxFMHcWjd7dlG\nuWxORLM5VJhdad01gu+Tu+dYDtP5abJ2FqUVc6056n59gInGCqfvdxuyr6E2J0Jo0sc8DI3yWamY\noXbvhp/9qsJPH55n94ymVc1jedM06haNhiGStZrhuY8/bkjr/Lwhrb7f3UahYA7ZHnsYovsUKSx/\nyuGMM85gamqKa6655smeSooUKZ4iSEnn0xA61FiYynVvCMVSa40WcbB80PUStiiGD7F37IjkRpBO\ns/1SqcjMzAxgDK2///3vjzheonQaUrXePtOyEKudzZXJ4koenSuhFD8U1EYlnXE+56JORLbdbSW5\nsDCw7FyPIhSQlZLMKsdHCslkbpKSW0KjqXpV5lvzqz+gzM8bAmxZRkocIp0gmzWEcHLS7FahAG4m\nohbN4KkGIChYZXKiTLstOsQ0MaD3PPP1t6xu2Hx6GrZtMyRzfNyE9NMamdUhhOBv//ZvufLKKzs9\n4lOkSPGbjZR0Pg2ho7gDjmXISX3A8JYGkDKufh88pxNGa0OZENROJ8x1EM8uWdNMTU3x2GOPAfDC\nF76Qu+++e4TxDKPYiPA69BQUtfsVFA1mi5Vfp9qp/DiEv7QTUaEwVJg90ppGFCEYvN1lKVNiKjeF\nFJJW2GJ304S4l2F+3sTDE4VzxPzVbNZkD2QLHlFmhlLZZ8+tNkccMM3+e+c7YfGEmOZyJhd0ctIQ\nzK1bzd+TDITU83x4HHHEEWzbto3vfve7T/ZUUqRI8RRASjo3EQYldDrU5C0LJ/aF9AZdD0DG4d0h\nlc5Ri4nMJpMWlkOv2oPeNpiwbds2HnnkEQCOOeYYfvzjHw83Wie8vjGkU0hh+rHrldXOfh6dK2FU\ntVNH2oTXxQqkE4YKs1fDEI0hwfYQKnDGzrAlvwVHOoQqZKY5QytodRdYWDBxbim7cfJ1oO7XmWvN\nEemok2PqWA6WZYhkLmdI5fi4IZilkiGrG9DoKEWM0047jc997nNP9jRSpEjxFEB6ad0EiJoR3uMe\nUX0wkqFDY18zlTXJZuGgpLMT7o6/FsMUE8XrDFNM1GkxKdZPOldSWvfZZx9+8YtfAHDkkUfy0EMP\nDTFe1zYJ1h9eBzqV66qx/BgNGl6H0dXOhOzKXJ+80d4w+/x8N5FxCbzYCF7SJcDDwJIW0/lp8k4e\npRXz7XkW2gsEczOG8EppFM51OL4HUbDMDmkyN9lpZJDi14fTTz+dm2++OS0oSpEiRUo6NwOEJUDR\ntwhlKXRoiJftSgQmFDqISpqMPhTpXEchUSe8viEV7IuVzgQHHHAAP/3pTwE49NBDOyR0zdGEBQii\nKIg7J60/tipdibAFOtJE7aVkcbiuU6Oonappjs2qLTkLBZOwmHhjLlE8ldYsxOShuI5e8EIIytky\n5WwZgaA18zizM79ipjVLreAQWcNfmoIooOpV2dXY1TGnl0IylZuilCmNNM8U68eBBx7Ili1buP/+\n+5/sqaRIkeJJRpoKvwkgXAHCVB6vRYC00kkRNEIK7FgRi7TGXoMgJJxPSmly+6Jo7fDm0pzOUcLr\nG6J0ivi4LCfKz3zmM7n//vs58sgjOeigg/jVr37FvvvuO8CYlimu0tGGKJ1g1M6wEqKaCivbJX+r\neXSuhLxlUYuijtqZXUNxjNqRyfW1xeIiopVQLpv3ZtOUfU9OGi8iYCEMibQmIyXFDaikyTt53Eab\npg+etPHHi/h41BpP4FouOTtHzsn1VSiDKKAVtmiH7UX5oZawyDk5Ck5heG/QAdBut6nVah0f1xSr\nY9999+Xee+9l7733frKn8pSH4ziUy+UNu+akSPFUQko6NwGEMERBeQrlLSYrS5FY4iR9vpMwbKj1\nmid7UXg9ioZSOkWHOA5fvb4ROZ1ag2VJIEIpteyCvX37du6++26OPvpo9ttvPx577DG2bdu26phC\n2GhtQuwboXSCCW1TNaq1jnSnTelaHp0roWRZLIQhtQFIZ0flXMWcfhGS/M5GwxDPiQkajkM7DqtP\nbETpttawsIDdajOWG4fJSTyLDon0Ix8/8ql6VUNAnRw5O0eoQtphm1bYWpFoZu0srvXf42MUhiE/\n+tGPWFhYYHx8PCUGA+KII45g586dPPzww0/2VJ7y8DyPZrPJYYcdxn777fdkTydFig1FSjo3CURG\ngAfa05Dtv1wSWk/aXybq5iB5nesJrzOC0rkovK6HSiFdcQpd8rryHH7rt36L73//+7zgBS9gzz33\nZGZmhqmpqb7jCmHHSpbaMNIppEDmJKqpiJoRdin5CQ6e05lgULVTq9gfVMSkd1CMj5uTU68TzM1R\nLRYhk6Fs2yOH1TuIom6nISlNFU8mQwZTbKS1xos8WoEhoF7k4UUeFSqLvmOWsMjaWXJO7r+NaPbi\nvvvuI5/Pc8wxx6SEcwg88cQTPProozzvec97sqeyKVCv17njjjsoFAqrXqNSpNhsSK+amwQyExfq\nrJLXGTWiTrHIUtI5SOZfJ7yekJehConMdobtSgTrD693rULjOawy7+OOO45vfOMbAExPT7OwsNB3\n2W54PdxQgpHkVCbqIyRKpxhK6YTBcjujZgQaZFZ2ztPAGBtDF4vMhyG6UqHg+2uqqmvC941Te9La\nMmkl1AMhBFk7y0Rugm3FbUxkJ8ja5mnLEhYFp8B0fpqtxa2MZ8d/LYQzCAJmZmY4/PDDU8I5JPbY\nYw+eeOKJJ3samwbFYpEDDzyQRx999MmeSooUG4r0yrlJIB0J0iiZOlrOzpSvCCtht+NMbIljDaF0\njlS9vh6fzmWh+YFXXRGJ0rlWnt1JJ53EV77yFcBYK9XrK3fIMeF1vaHhdVhcUKQ8Fedz6qFUzgSD\nVLIPVEC0Cqr5PGGhgKM1Y0mT81HRbJoCJaWMN9EAxu9CCHJOjsncJNuK236tRLMXjUaDQqGAtV7S\n/RsI13VTg/ghUS6X+16bUqTYrEhJ5yZCP7VTR7pj+p3g1x1e71SvjxpeZ/1Kp2UNTnxf8YpX8PnP\nfx7P83jGM55Bq9Vatkw3vL4x1eu96PRjb0ZDeXSuhNXUTuUpdBgXEGWG/7m3o8iYwBeLTExMGI+A\nhYXRiGel0u14lLiwD3lcN/o8DIOVcoVTDAbP834jes5vJKSUaaFaiqcd0ivoJkKHdLa7F6KoFeE/\n4RNV47C6JbBKVieMasVtLSOtUWuQsUXV6zAYC1xHIVGC9RYSLc3pHPRC/brXvY5PfepTzM3Ncdhh\nh+EtM0SXGCumjb/wW7meDkWxF+goSiesrnZ2vDnzw48d9dgjjds2dqlk8jzBkMe5OdPc3PdXP3mJ\n/VKjYUhm4sKe4jcGnufhpk3qU6T4jUdKOjcRZLardOpIowJFuLDYcNmetHuKUwySvtjtNciYGiW8\nHmMUy6SNMofvks7hQ/xnn3021157LQ8//DBHH300QRB0/qaUQggLIXotjTYGwoqVRw1RI+l6NHrY\ndiW1UyttHlDEaKH1+SBAATkpySch5UKhW9nebkO1CjMz8Pjj5r1aNR2FknmEofm8t496Ljfyfj5V\noZTiwx/+MIceeii5XI799tuPSy65hOYQivCJJ56IlHLF1z333LNo2VtuuYU/+IM/4IADDqBQKDAx\nMcFznvMcrrjiCmq12prbOv3005FSsn379mV/+853vtN3Hr//+78/8P70Yj1K5xVXXMHrXvc6Djzw\nQKSUHHDAAX2XvfHGG3n961/PwQcfTKFQ4BnPeAavetWruPPOO1dcvt9+lvo8FP3jP/4jxx13HMVi\nkbGxMU444QS++tWvDrU/lUqF888/n7333ptcLscRRxzBddddN9QYKVJsVqTV65sIncrnlsJ/YuVu\nMUlYvRdZKWkrRVupLnlYAVFM1qxhComWENWhOhKRhOZNodOvK6dzKc477zxqtRrvec97OOGEE/je\n976HZVmxJ6pEyiSvc2Nz+WReotqKsOljZWDU8DqsXMm+ngKiWhjia9PZanypPVI+b/IxPc+onEFg\nXr6/uIuRZZmTqpTpOTk5+bTtL3nxxRdz9dVzTP7kAAAgAElEQVRX89rXvpZ3v/vd/OQnP+EjH/kI\n9957L9/4xjcGTgvYsmULH/7wh5d9vpRoPfDAAziOw9ve9jb23HNPWq0Wt912G5deeik333wzd9xx\nB3YfW6uvfOUr3HzzzeRyuVXnde6553L88ccv+myfffYZaD+WYj2k89JLL2VqaoqjjjqKSqXSd87t\ndpuzzjqL5z73uZxxxhkccMAB7Ny5k+uuu45jjz2W66+/njPPPHPZeieccAJvf/vbF33mrNAN68or\nr+S9730vRx11FJdffjlaa2688UZe+cpXcsMNN3DGGWesuS++7/PSl76U++67jwsuuIDDDjuMW2+9\nlfPOO48nnniC973vfQMelRQpNil03K1ms7yAvYH3Av8G7ATqwAPAVcBkn3X2Aq4HdgNN4C7g1FW2\ncRZwb7zs48DHgOkNGluvBypU2nvC0+0d7RVfKyFSSu9ot/XOdlsrpfqO/bjn6R3ttg6jSOsdO7R+\n7LG1J1SpaL1jh24vzOod1R16pjEz8L5U2hW9o7pD75qv6x07tF5YGHjVRfA8M92HH67rHTt26Eql\nMtI4l156qQb0y172Mh1FkfZ9Xz/88IP60Ud/rMOwPtrk1kD7sbau/+px3aw9osOwua6xGmGod7Tb\nepfn6Uh1vydROxpqHC+K9M74++JFA66rlDkRtZrWs7Pmu7Njh3nNz4+wN089zM7O6u9973vLPn/g\ngQe0EEKfeuqpiz6/+uqrtRBC33TTTQON/6IXvUgfcMAB65rjO9/5Ti2E0N/5zndW/HutVtP77ruv\nvvDCC/X++++vt2/fvmyZb3/721oIoT/96U+vay69uOGGG/RnPvOZkdb95S9/2fn3s571rL7HKAxD\nfdttty37/IknntDT09N669aty65/Qgh9zjnnrDmHxx9/XLuuq4888kgdhmHn8yAI9Pbt2/Xk5KSu\nVqtrjnPttddqIYS+5pprFn1+yimnaNd19cMPP9z5bH5+fsX9SZHi142Yt2wIh9uMssPvA+/DkLyr\ngAuBHwAXAfcJIbb2LiyEmAS+B7wauBa4AENUPy+EePPSwYUQFwOfAubjZT8KvB74jhAiv56xNwLC\nErh7uLjbludHJRXrSyGFwBUCDfh95EStTdciAVhSmvDpMIVE6wmvP0k5nUtx+eWX8653vYuvfe1r\nnH766URRhBD2f0t4PYGVt9BEqLYaOaczQd6yOh2odjU82l7YDeMPCE8pY4+EaXPpDqpMCmHUzGLR\nKJrbtsEeexg7pKTD0dMUn/3sZwG46KKLFn3+h3/4h+TzeW688caBx0ouzNVqdaT86MRMfCWlDoxq\nqLXmL/7iL9YcX2tNo9Gg3W4PPY+l2LlzJ3vttddI6+6///4DLWdZ1jJlFoxd0wknnMCuXbvYvXv3\nsr9rrQmCYNVK8R/84AcEQcCZZ565yL3Atm3OOOMM5ufn+ed//uc153jTTTdRKBT4wz/8w0WfX3TR\nRQRBwOc+97k1x0iRYjNjM5LO24D9tNanaq3/Rmv9ca3124F3APsAlyxZ/j3A/sAbtNaXaa3/HjgJ\no0j+lRCikCwohJgGLgfuBE7SWv+91vp9wBuAwzEEd6SxNxqLwqUC7HEbZ3LlGw108zr9PoSsE1pP\nQlfJ+1oEbkl4fZgb5ZNZvd4PH/nIRzj77LP5whe+wB/90R+htUBK2Sn22WjInAQdoVoR6wmvJ5hy\nHDJSEjQiFsKIqhOtWUAGhmzO+D6zQdBpc1lab9ch2zY+nE9z3HXXXViWtcz4PJPJ8OxnP5u77rpr\n4LF27NhBsVikXC5TKpU45ZRTeOihh/ouX6vVmJmZ4Re/+AU33HADV111FS9/+cs57rjjli175513\ncu211/LhD3+4b85iLy688EJKpRL5fJ5nPvOZfOQjHxl4P5Zi165dI5POjcCjjz5KJpOhvMID0Be+\n8AXy+TxjY2Ns3bqVCy64gGq1umiZpMgwn88vWz8X5yj/8Ic/XHUOSinuuecenvvc5y4rqjrmmGMQ\nQnD33XcPtV8pUmw2bLqcTq31T/r86fOYMPizlnx+BvBzrfUtPWMoIcTVmLD4ycA/xn96NZADrtY9\nzEVr/RUhxC+ANwJXjDj2hsMqWUS1CHvMXrO9oRMzu35KZ6LjdfqzS2kIp1ID5eEJYYpinoze68l6\nQog4hXD0anMhBJ/85CepVCp8+tOfxnFsLr/8j//blE7pSLA1hKA8kOussbGEYNK2sYKQulB4WcHu\nIGDcslY0dfeVohrnbybrFy2L/NM09/K/Azt37mR6enpFdXHvvffm9ttvJwzDvjmWCQ488ECOP/54\njjzySCzL4o477uCaa67hm9/8Jt/73vc44ogjlq1zzjnn8MUvfrHz/7PPPpuPfvSjy5YLw5C3ve1t\nvPzlL+fUU09ddR6u6/KqV72Kk08+mb322osdO3bw8Y9/nIsuuoj77ruPT3ziE6uuvxLe9a53PWkt\nHW+99VbuuusuzjrrrGVk73nPex6nnXYaBx/8/7d373FS1uX/x1/X7Hk5n1RAAk95wFLMTFECVJRM\n/eKhTFNQv9rBNL9oefqFSXhIM0NTy6zwVB7yXKGpnFIoNEg0xcQDKiDCchbY3dmZz++P+75nZ2dn\nZue4s8u+n4/HPHa5574/85kZdufa6/oc9mTz5s389a9/5fbbb2fevHksWLCAbt28vEHw2s+aNYsL\nL7ywRRtz5swB4KOPPkrbjw0bNlBfX590//mqqir69evHypUrc36eIp1Coer0pb4B++KtbTMj7thA\n/9h9Sc7fy7/vxrhjd/nHdk9y/h/wYrPaXNqOu88VUqQxszF3wbjOj+uTj/v81B8PuDEc9g6sXeuN\nx2tsTN/w+vXOrVzpItu2upWbV7qPt2QwDjS4dNt6t3LzSrdp63a3cqVzdZkPB21h2zavq2vWNLqV\nK1e6tWvX5tZQnEgk4kaPHu0A94MffM/V16/Ku81kotGo27r+Q7f5g+WucV0br3WGmj5tcvUr6932\nugZX19joVtbXu5X19W5DY6OL+GPaGiKRFvd9XF/vtoTDacf8dnWpxnTuvvvubujQoUmvOeuss5yZ\n5TzO+MUXX3RlZWVu3LhxSe9//fXX3axZs9xDDz3kvvWtb7mKigo3btw4V5/wc3799de72traFuMj\nhw4dmnRMZzLRaNSNHz/emZmbP39+Ts+lENKN6Uzm7bffdn379nVDhgxxdRn+grn++uudmbnrrruu\nxfFjjjnGmZm77LLL3JtvvunefPNNd9lll7mqqipnZinfo8CHH37ozMxNmjQp6f1DhgxxI0aMiP1b\nYzqlo6CLj+lMZar/9d64Y0E9J9mfj8Gx+D87B+EtV5nqfItrM9u2iyJUkdlbGDKjzIwo0JQkExgr\nr8cuyHDZpKC8nsuOREUqrxdiQeVQKMRTTz3FgQceyM0338EvfvGromQ7nYt4s8stFFsKK1/B2pwV\n3croV1FBr/JyQsC2aJS14TDrwmHqwmEaolFCQM+yMnaurKR7eXlJF1/vrGpra5Os8eqpr6/HzJKW\nZTNxxBFHMGrUKObMmZP0Mfbff3+OPPJITjvtNO666y5uv/12XnjhBe68887YOe+88w7Tpk3jRz/6\nUcbjIxOZGVdeeSXgZQ4LadOmTaxevbrFrRA/w++//z5HHXUUZWVlPPPMMxnvYf7DH/6QysrKVs/z\n4Ycf5uSTT+bmm29m+PDhDB8+nEcffZQ77rgDgJ49e6ZtN/g/kO7/Sq7/T0Q6i5KV182sFzA5i0tu\ndc5tSNHWpcCpwF3OublxdwU/wcl+yusTzol975zL5Pxs2y65SjO2O0fYuVZvfBB0tiivQxZBp2FY\nScvrzROS8g/cwHtOTz75JOPGHcWVV06jd+9d+M53LihI280i3lJY1RUQ9hb7L++e+49lNBzFhZ23\nSUC19ydEt7IyqkMhNjY10RCNEvH/2uxWVkb3sjIFmnkaNGgQb731FuFwuFWJfeXKlfTv37/N0no6\nw4YNY968eWzYsIFddtkl7blnnnkmF1xwAX//+9+ZPNn79XrppZfSt29fJkyYwDvvvBM7t6mpiYaG\nBt59911qa2sZOHBg2raHDh0KQF1dXc7PJZmLL76Y++67r8Wx5cuX51WOX758OWPHjmXbtm3MmjWL\n4cMTR12lVl5ezsCBA1s9z969e/Poo4+yZs0ali1bRvfu3TnggANiwek+++yTtt0+ffpQU1OTtITe\n0NBAXV0dY8eOzbifIp1RKcd09gGuxssstvWp5/DGSLYKOs3sPLxZ7H8BLky4O1iZOdkCcdUJ58S+\nN7OqJIFn4vnZth1zzTXXxL4fM2YMY8aMSXZawVWYsR1vXGfi0MFgm8yybIPOgJk/ptJLoWcSyATB\nYeFmrxcu0+m166ioqOCll57noING8t3vfo/u3Xty5plnFqR97zG8vpbXVuI2+fukd8+9vchWfwei\nmpYZ8DIz+lVUsC3iTSzqpmCzYA455BCef/55Fi5cyBFHHBE7Xl9fz6uvvpr3z/eyZcuoqKigb9++\nbZ7b0NDQarvODz/8kFWrVqUMvPbaay+OP/54nn766Tb7AbDzzjunPS9bl19+ORMnTmxxLJ/HWL58\nOWPGjGHLli288MILHHDAAVldX19fz4oVK5JOxgJvNvxOO+0U+3cQdB533HFp2w2FQhx00EEsXryY\nxsbGFuNLg8XrDz744Kz6KlIMc+fOZe7cuUVpu2RBp3NuOXnOnjezc4HfAM8Cp7jW9c9V/tdkZe7g\nWPyfnavwAuDBwHtJzo/GtZlt2zHxQWd7qgyFIBJJOoM939nr+JlO8Mrm1ubfEYUvr5uRdeCbvl2v\n4Zqa7rz++kvsvvsXOOuss6itreXkk0/Oq+3mx/CDxKoKomWGa3JEG6OEKnPYtnJrxAtajZQTy9Jt\nDiC5Oe2007j++uuZPn16i6Dz7rvvZvv27a0WJF+9ejUbN25k6NChsZnPmzdvplu3bi2W4wFv56EF\nCxZw3HHHtQhSVq9enTTrGcwwP+qoo2LHbr75ZjZt2tTiPOccF1xwATU1Ndxyyy0tspzr1q1rVYpu\naGjgmmuuwcxy3pUolX333Zd99923IG198MEHjB07ls2bN/P8888zYsSIlOeuX78+aSA/ZcoUIpFI\nRs/zX//6F7/97W8ZM2ZMiyC1qamJd955h27dujFkyJDY8dNPP5358+fzm9/8psWEpOnTp1NRUcFp\np52W6VMVKZrEZNjUqVNTn5ylTjd7PeAHnL8FngMmOOfCiec45z42s5XAYUmaONT/Gr9GxcvA+cBI\nWgedhwL/dc5ty7HtkqswIwSEnSMcjVIRt8xRFO8vgFCO5fUg04nzdiUKZbHmZL7l9YCZl02IRCIF\nCTqDjGkoVE5tbQ3vvvsaO++8B6eccgozZ87kK1/5Sn4dBoJ1A8xChGpDRLZEiGyLZB10Nm1pIrLF\na6u8ZzlWpixme9l///353ve+x+23384pp5zCV77yFZYuXcovf/lLxowZ02qnmiuuuIL77ruPOXPm\nMHr0aABmz57NJZdcEtvasry8nJdffpkHHniAAQMGMH369FaPOWrUKEaMGMHgwYOpq6vj+eefZ/bs\n2RxxxBEt1oGMD0DjXXrppfTs2bPVH1Djx49n8ODBHHTQQQwaNIhVq1bxwAMP8M477/D9738/42zc\nsGHD+PDDD/OuPNx///188MEHAKxdu5ZwOMy1114be4yg8rBlyxbGjh3LBx98wEUXXcTSpUtZunRp\ni7aOOeaYWJZy2rRpLFy4kLFjxzJkyBA+/fRTZs6cydy5czn00EO56KKLWlw7ZcoUli1bxiGHHEKv\nXr1YvHgxM2bMYMiQIdx///0tzl2xYgX77bcfo0ePjs1uB2/t1hkzZnDJJZewfPly9tlnH2bOnMmT\nTz7JlClTSjbDX6TdFGpGUnvegLPxPq2fA6raOPcmvAzl8XHHyvACzHVAt7jj/YGtwD+BUNzxE/w2\nrsq17bj7k08PayebwuGWs9Sdc42RSGwnm5hgSvj69ekb/OQT77ymJrfm0zVu5eaVrrEps1nYwfnh\nSNitXOncqhwniPubIrlPP/V2H1m5cqULxz2/XNXV1bmVK1e67ds/dfX1K11Dwxq3YcMGhzfcw82Z\nMyfvx2hsXOfq61e6pqbtLtoU9XaW+jj9zlGJwhvD3nWr6l3Ttqa2L5CcpJq97py32sHPf/5zt/fe\ne7uqqiq36667uksvvdRt3bq11blnn322C4VCbt68ebFjS5cudV//+tfdHnvs4bp37+6qqqrcnnvu\n6S688EK3KskPxrRp09yoUaPczjvv7CoqKlzPnj3dYYcd5qZPn57x//1UOxLdeOON7rDDDnMDBgxw\nFRUVrnfv3u7II490Dz30UEbtBvr16+d23XXXrK5JZsyYMc7MnJm5UCjkQqFQ7N9jx46Nnff+++/H\nzgnuj78lvuZPPfWUO/bYY93gwYNddXW169atmxsxYoS74YYbXEP870LfE0884UaOHOn69u3rqqur\n3d577+2uuOKKpCsTBH2J719g48aN7sILL3SDBg1yVVVVbvjw4e6OO+5odZ5mr0tHQQFnr5sr0KSL\n9mJmJwJPAJuAy2ietBPY4px7Ku78vsAioB9wC15Z/HTgy8B5zrkZCe1fAtwMzAUewiuVXwp8AHzR\n+ZnOXNr2r3GlfM2bolHWhMOEgJ0rKzEz6iMR1jc1UR0K0TeYCNHQAOvWeXtspxtL9sknEInAzjuz\nrmEjDZEG+tf2p7Ks9Y5JidZsXUNTtImduu3E2k/KcQ4GDmwut2dq0ybYutXb+GbbtjoaGxsZMGBA\nyl1ZMhVkVfr374dz64AQVVW7UFdXx4ABAwBvp5LDDkuW7M5MY2MdzjVSUTGAUKiC8Low0YYoZT3L\nMppQFN4QJrrdK6mX9ymPTR6Swlu/fj1Lly7l8MMPL3VXOrzXXnuNAw88kBkzZjBp0qRSd6dT2rhx\nI6+//nrSXZZE2pM/bK0g5bPOWF4fgTfushfeeM5Ey4FY0OmcW29mhwM/Bb6HN03jDeAbzrlWC7c7\n524xs3V4M+tvxQtuHwKuiA84c2m7IygPhagKhWiIRqmPRqkpK4tNIiqPj/ZynEgE2c8eN8zfatK7\nZRt0xj9c0IdCTCYKnkdZWTlNTSEginNR+vfvH9vWb+TIkSxatIiDDjoox0cJyutesBiq9ZZOimyO\nEN0epaxbGaGaUKuhAs45mjY0Ea2PQggq+lbkNA5UpBiee+45DjzwQAWcItJCp/uUcs5Ndc6FnHNl\n/tfE2+5JrlnlnJvonBvgnKtxzh2cLih0zt3rnDvQP3cX59x5zrmk64Rk23ZHUB1siekHVcHsq7Jc\ngs4UE4kyEQR1Zpb3ZCK/C7FZu4XIJrfsX7l/zHu1Bg4cGBtn9oUvfIH//Oc/OT5GFLDYOqdlNWWU\n9/LGZLqwo2ljE42fNNK0pQkXdbF+Na2PCzj7KeCUjuUHP/gBixcvLnU3RKSD0SdVF1TpR3gNfkCZ\nV6YzcSIRmQd88cFpPkFn4ux1KEymM2jDCzrL/Mdq3oP9M5/5TGzdw8997nO8/fbbWbXvBbAuFnAG\nyrqVUblzJeV9yrFKgyhEtkRo/KSR8MYw4TqvBG9lRkX/iow3CJD8lJeXEw63mq8oUhSNjY15re8q\n0hHp06oLqgiFCOEFm+FolMZoFKM5GAWCCC7zoBNimc6oyy7gC8rrCc1lLD7oLHSm0/xgujnT2dTi\nnD322IM333wTgL333pvly5dn0X7wOiUfh1lWU0Zl/0oqBlTE1t2MbvMXfy/3A85y/Qi3lx49etDY\n2Minn35a6q5IF7B69erY2HGRHYX+jOqiKkMh6qNRNkciOLySe6slhoKBltFoc+YzXny0B7Flktq7\nvF6MMZ3xffO+Jg86wVtn8NVXX+XAAw9kt912Y8WKFQwe3PYOqEGpPjHTmShUESLUJ4SLOCJbI7io\n85ZFCmlZpPZkZuy9994sXLiQffbZhz59+rRaV1MkH845GhoaWLFiBWvXrm2x7qvIjkBBZxdVaUY9\nzSX2mmRBZSjkBZypgs5ALDDLvbweNN9RMp3xpXXva+qgE+CAAw7g5Zdf5pBDDmHXXXdl9erVGeyq\n0nISUVuszCjvqR/ZUho6dChVVVV8+OGHvPXWWwXb/UokUFFRwU477cTIkSOpqkq24Z1I56VPsC6q\nyt+dCLylAKpTBZ2QOhJMyHRmO5Eo/pqONqYzCFqDINYLOi1l0AnwxS9+kRdffJFRo0axyy67sG7d\nurRbFzZvoKVsWWeyyy67tLkHuoiItKYBYV1URSgU26iyKllpHdqeTJQYdGaR6Wxdvm7ZZDbaJ9MZ\nTCZyRKOpJ5McccQRPPfccwD069ev1faDLfsdPIaCThER2fEp6OzCqvwALWmWEzIPOn3ZTCRKzIZ2\n9Eyn136Ff1/qbCfAuHHjePrppwEYPHgwW7duTXFmZmM6RUREdgT6tOvCepaV0au8nNpUkyEyXTYp\nx4lEUPjyehAkFnoikfd9EHS2vWzOCSecwIMPPsjWrVvZfffdqa9P3DhL5XUREelaFHR2YeWhEN3S\nzb4NAi6V1wEIhTIPOgG+8Y1v8Pvf/541a9YwfPhwGhsbE/qt8rqIiHQdCjoltWzHdGYxkajQ5fVg\nWdHiltfTz2BP5pxzzuHWW2/lvffe45BDDqGpqSmu/SiQYjytiIjIDkZBp6SW6ex1Xy57r+dbXk+I\ne4ua6fQykiGci8Qt7N6273//+1x33XUsWbKEsWPHEo1GM16jU0REZEehTzxJLcdMZ0YTiQpUXk8M\nOoM2nXN5BZ7JMp3ev7MrsQeuuuoqLr/8cl566SVOOOGEWLZUpXUREekqFHRKam2N6Uw4L5bpbMfy\nerKgsxDZzmQTibx/Z19iD/z0pz/lO9/5DjNnzuSMM87yH0NBp4iIdA1aHF5Sy3Jx+Njs9RKW173v\nm8d1JmYqM5WsvO79u8K/P0wuOyDeeeedbNmyhT/84Q/06FHNr399Z079ExER6WwUdEpqWc5eBy+I\nzCjTmaK8nu38n2JnOhOD1myWTUrGzLj//vvZtGk9v/vdA/Tp05+f/ewXOfdTRESks1B5XVLLciIR\nZD6ZqJjl9ULMYE9fXk+/HWZbzIxHH72PUaMO5eabpzNt2rSc2xIREeksFHRKasE6RBmO6YTsJhPF\nn9/RxnSmLq/Hb4eZT+AJzzzzMCNGjODqq69m+vTpObclIiLSGSjolPTS1b2TldcznExU7NnrXpfz\nz3QmGxOab4ndE6G8vJx//GMBe+21F5MnT+Z3v/tdHu2JiIh0bAo6Jb10JfYkEV+mk4kSg9K2Kvkp\n22nn2evesfyDTm+dT6OqqprXXnuNgQMHct555/HHP/4x5zZFREQ6MgWdkl66tTqTjenMYlei+PM7\nWqYzuDZ5pjP3ZZO86yKAiy0MX11dzbJly+jRowff/OY3eeqpp3LrtIiISAemoFPSy7W83lams0Dl\n9aBbxch0ptqeMtcF4pvbDl7L5jWXunXrxooVKzAzJkyYwN/+9rec2hYREemoFHRKepnUvXOYSJQs\nE2pW2PJ6rpnOVJOIArluhxlo3gKz5UKfPXv2pK6uDoDx48fz97//Peu2RUREOioFnZJekSYSxc4n\n/tqWzWaiGOX1dJOImh8jKLHnku1Mve963759+eSTTwAYPXo0CxcuzKF9ERGRjkdBp6SX5USi2JjO\nLMvr8c3kG3TmW15PN4mo+TGCEnv24zqDTGeqLTB32mknVq5cCcChhx7Kq6++mvVjiIiIdDQKOiW9\nLCcSxWavt7VkUoryeopmU7fjWnbT+7645XXvvubtMLMVlOQTy+vxBg0axPLlywEYMWIEb775ZtaP\nIyIi0pEo6JT0MtmfMoeJRLHzi1BeD4LOSCSS5IpM2sykvJ77ZCLnGvw20u9CO3ToUJYtWwbA8OHD\neeedd7J+LBERkY5CQaekl2t5PcvF4eObKUTQaWZFznTmtmxSNBrGuQhmZbESfTp77rknb7zxBgB7\n7bUXH3zwQVaPJyIi0lEo6JT0irVkUoHL64nxYT4l9swyneYHntlthxmN1vttV2d8zX777cfixYsB\nGDZsGKtWrcr4WhERkY5CQaekV6RMZ+L58c0UMujMpcSeyUQi7/7sS+zRaIPfv8yDTvDGdf7jH/8A\nYPDgwaxduzar60VEREpNQaekl+2ORDkuDu99n7LZNO20vDZQVuZN0skl05lJed27P7tlk5yL4lwj\nYJhVZt2vQw89lLlz5wLeDPcNGzZk3YaIiEipKOiU9LKdSJTpmM405fVs4sRiZjrTlde9x8xu2aTm\n0npVmwFtKqNHj+bZZ58FoH///mzevDmndkRERNqbgk5JL115PckelB1h9joUZkxnW4Fhttth5jKe\nM5ljjz2WJ554gmg0yq677sq2bdvyak9ERKQ9KOiU9My8W7ryelxGsCPMXof2Kq9nvh2mcy7n8ZzJ\nTJgwgT/84Q9s2bKFPffck/r6+rzbFBERKSYFndK2ZHVv57xbQgm6o81eL2Z53XvczJZO8sZyOswq\nk25/mYszzjiD3/zmN3z88cd8/vOfJxzOZUtOERGR9qGgU9qWrMSepLQO+c1eT1fJTyaIe5MlJNsj\n0wnNJfagdJ66zebxnIV0/vnnc8stt7Bs2TIOO+wwmpqy35ZTRESkPSjolLYly3QG3+ea6SxAeT1V\nltPrVvtkOkOhWv9xtsbtqd5aocZzJjN58mSmTp3KokWLGDduXM6L4ouIiBSTgk5pW7IUZLJNzynM\n7PVCBp3FnEjkPU4FoVAN4Ghq2pL0nGx3IcrF1VdfzaWXXsrcuXM56aSTMp7IJSIi0l4UdErbkq3V\n2UamM9rGxJrY+XnMXm8r6Mx1K8xsyusA5eU9ASMa3Z50d6JCTiBK52c/+xnnn38+Tz/9NBMnTlTg\nKSIiHUp5qTsgnUC68nqSwMwwHA7nXIfKCJ0AACAASURBVMrArdjldfACz0gkQiQSiY3xzKzdzMvr\n3uOXUVZWSySylUhkC6FQnxb3F7O03rIfxl133cXmzZt54IEH6NWrF7fffntRH1NERCRTCjqlbVmU\n18ELfpxzOFyLTGa8YpfXwZtMFIlEiEajGQedzqUPllMpK+tBJLLdz3Z2j1vDM79diLJlZvzxj39k\n06ZN3HHHHfTs2ZPrr7++6I8rIiLSFpXXpW1ZTCSCuHGdGUSPhSivp0pI5jKuM9ssZ8AsRFlZNwAi\nkeZdggqxC1G2QqEQf/nLXzj88MO54YYbuOGGG9rlcUVERNJR0Clty2LJJO9Q25OJ2qu8DtnNYM92\nPGe8srLuQIhotCE2jrO9Suut+1LG3Llz+fznP89VV12lMruIiJScgk5pWxYTiSCzTGd7lde9rmae\n6QzOzTbT6fXDKC/vAUBT02Z/F6JGv732DToBysvLeeWVV9htt9246KKLmDFjRrv3QUREJKCgU9qW\nakciSDmmE9peNilxvGdHynRmM/EoXllZN8zKcC5MU9MmIFrQXYiyVVlZyRtvvMGAAQM499xzefjh\nh0vSDxEREQWd0rYsM50hP8BKlelMtQ5msYLObDKdQYCaS6YzUFbW03/cbX5bhd2FKFs1NTW89957\n1NTU8I1vfIM///nPJe2PiIh0TQo6pW1B1i+LJZMgdaYz1fGOVF7PNdPpXVuDWfMi8KUorSfq3r07\nH3/8MQAnnngiL7zwQol7JCIiXY2CTmlbkPWLL1NnUl5vI3pMtpySWWnL64XIdIK3hJLXt+LtQpSt\nXr16UVdXB8C4ceN46aWXStwjERHpShR0StvMvODSueZIL5OJRKkynWm2mUw2fDSVjjaRqOVjV1Ne\n3ofy8r55tVNo/fr1Y/Xq1QCMGjWKV155pcQ9EhGRrkJBp2QmPtsZBJ8por22Mp3pJhhlU2JvK+g0\ns9hWmJluCVmI8nqgrKymw2Q54+2888589NFHABxyyCG89tprJe6RiIh0BQo6JTPx4zrTZDmh7Uxn\n4nktjhUw6PS6mN1kokKV1zu6XXfdlffeew+AAw44gLfeeqvEPRIRkR3djv3JKoWTmOmMP5agzUxn\nBuX1QgWd2ZbYC1Ve7wx22203/vvf/wKw77778u6775a4RyIisiPb8T9ZpTAKmOksVHk9zQT6mGwm\nEwX7rodCoXbbsrLUPvvZz/L6668DsOeee8bK7iIiIoWmoFMyE5/pbCPay2f2erIdN1MpdKazq5TW\nE+2///7861//AuAzn/lMbKKRiIhIIXWtT1fJXXyms63yegFmr5diTGchJxF1Nl/4wheYP38+AAMH\nDowtrSQiIlIoCjolM8kynbmO6Wyn2eteFzMvr3fVTGdg5MiRzJo1C4ABAwawcePGEvdIRER2JF3z\n01Wyl2xMZ6ryejvPXk8XI2ZTXu9Kk4hSOfLII/nrX/8KwE477cSWLVtK3CMREdlRdN1PV8lOITOd\nJSivZ5Lp7Mrl9XjHHXccjz76KOFwmKFDh7Jt27ZSd0lERHYACjolM6GQF91lMXs96pJnF0tRXtdE\nouyccsop3HvvvWzYsIG9996bhoaGUndJREQ6OX26SuaCYKypqeW/E8Qyne1QXm9rZaNcyutdPdMZ\nmDhxInfeeScrVqxgxIgRhMPhUndJREQ6MQWdkrkgGAuCzrbGdBaxvJ5JljN4jEy3wtSYzta++93v\nctNNN7F06VJGjRqV0TAFERGRZPTpKplLXEQzx0xncDxdprOtxGSmQSdknu1UeT25H/7wh0yZMoWF\nCxdy7LHHZry7k4iISDx9ukrmEsvOba3TmUOmM9PF4bMJOjMd16nyemo/+clPuPjii5k1axZf+9rX\n2swai4iIJFLQKZlLDDLb2pEoRaYzmGCUz5jOXILOdKXhoPyuLGdqv/jFLzjnnHN4/PHHOffccxV4\niohIVspL3QHpROIzgGZpI76QhYg6L5BLzGjGyutpMp3tXV7XeM62mRm/+93v2Lx5M/fccw+9evVi\n+vTppe6WiIh0EvqElczFB2RtBGfpFogPMmQha91GKTOdoNJ6W8yMRx55hKOPPppbb72VKVOmlLpL\nIiLSSSjolMzFB2RtBZ1pFohPN5Eo00xnG5sitZBJplOTiDIXCoV49tln+dKXvsS1117LTTfdVOou\niYhIJ6BPWMlcfEDWRrSXLtMZG9PZDksmQWYTiZTpzE5ZWRkvvvgi++23H5dffjm/+tWvSt0lERHp\n4BR0SuYKlelso7webHyUTrHK68p0Zq6iooLFixczZMgQLrjgAu67775Sd0lERDowfcJKdoKgLJ8x\nnWnK65BZtrPQE4lUXs9NVVUVb731Fn369GHSpEk89thjpe6SiIh0UPqElewE2c62yusZZDqTldfj\nm06X7VR5veOora3lgw8+oLKyklNPPZWZM2eWuksiItIBKeiU7BQg05lunc74pguV6cxkK0xlOvPT\no0cPPvnkEwC++tWvMnv27BL3SEREOhp9wkp2gkxgnrPXDStIpjPTGLGtErvGdOavd+/erF27FoCj\njjqKBQsWlLhHIiLSkegTVrJTXe0FnpWVaU9Llelsq7QOhc90em2mn0yk8nph9O/fn1WrVgFw+OGH\ns2jRohL3SEREOgoFnZKd6mrYeWeoqEh7WqpMZ1ulde9a/GtTt59t0Jku06ktMAtr4MCBfPjhh9TW\n1lJXV1fq7oiISAehbTClKFJmOtNsgRnIZIH4bIPO8nLvv3o4HKa6urrFfcpyFt6QIUPYtGlT7HUX\nERHp9KkdMwuZ2T/MLGpmf05xziAzu8/M1prZNjN7xcxOTdPmRDP7t3/uajO728z6F6LtriJVpjPd\nGp3N1wbnpm4/26Czws/MNjY2trpPk4iKQwGniIjE2xE+ZS8AhvvftwpTzKwv8BIwAbgD+D7wKfCI\nmZ2d5PzJwD3ABv/cu4BvAHPNrDaftruSNjOdGZTXC5nprPTHoIbD4Vb3aRKRiIhI8XXqVISZ7Qpc\nB1wN3JLitCuAYcAJzrm/+tf9HvgHcLOZ/ck5t9U/3h+4FngZOMr5aTkzewV4GrgYuCGXtruaNsd0\nlmAiUVlZGZFIhEgk0qKUrvK6iIhI8XX21M4dwLvAbWnOOQN4JwgKAZxzUeCXQF/guLhzJwA1wC9d\nXLTknPsL8B5wZh5tdylBJjMIMgPZlNcLmemE5mxnYold5XUREZHi67Sfsv64yeOB7/iBXrJzBgKD\ngH8muXuh//XguGNf9L/+I8X5+wQl9hza7lJimc4cyuvFyHRC87jOxBK7Mp0iIiLF1ymDTjPrhZfd\n/LVz7uU0pw7yv65Mcl9wbHDC+S7N+RbXZrZtdymxMZ0pJhKlK68XK9OZajKRxnSKiIgUX8nGdPqB\n4+QsLrnVObfB//4m/+uVbVwTTPxpSHJffcI5se+dc5mcn23bXUqqTGcm63QWO9PZ1NTU4rjK6yIi\nIsVXyolEffAmADlIE4F4HHAfsMHMRgHnAWc65za3cd02/2tVkvuqE86JfW9mVUkCz8Tzs2075ppr\nrol9P2bMGMaMGZPstE4tZaaTwozpDO7LJugMhUKUl5fT1NREU1NTbEkflddFREQ8c+fOZe7cuUVp\nu2RBp3NuObmV928HlgAvm9meCfd1M7M9gI3OuXXAKv94sjJ3cCy+PL4KLwAejDdxKPH8aFyb2bYd\nEx907qiCoLIY22DmkuUMVFRU0NTURDgcbhV0KtMpIiJdXWIybOrUqQVruzN+yn4GOBBYBrwddwMY\n6x//MYBz7mO8wO+wJO0c6n/9V9yxYHzoyBTn/9c5ty3HtruUYm6DmU/QmTiDXVtgdnwNDQ3cf//9\nHHbYYfz73/8udXdERCRHnfGTdiJwasLta/59//L//du48x8E9jCz44MDZlYGXIS3APzMuHOfArYD\nF5o113/N7ARgN+APCX3Jpu0uJZ9tMM28W6ryer6ZTmiewa7SeseydOlSZs2a1eLYI488wq233srC\nhQvp3z/pxmAdyltvvcX48eN56aWX8jon0cyZM5k4cSI33HADZ555Jvfff38huisi0m463eLwzrlU\nW10CrHbOPZ5w10/xgtI/mtkteGXx04EvAOfFL97unKszsynAzcALZvYQXqn8UmApMD3XtruafLbB\n9K73gkvnWgeXQZO5JCcrKiows1jQqUlEHctll13G0KFDOeqoo2LHzjrrLDZu3MiWLVsYMmRICXuX\n3l/+8hcee+wxevbsyXPPPcdVV12V0znJLFiwgEmTJrFs2TJ69+7N1q1b2WeffejWrRsnn3xyoZ+K\niEhR7PCftM659cDhwJPA94BbgR7AN5xzM5KcfwtwDt7i7rcC3wYeAkYHpfVc2+5qDMtpnU5IP5ko\nn0ynmVFeXo5zjnA4rExnBxKNRpk/fz5HHnlkq/tmz57N0UcfXYJeZe74449nxowZXHLJJXmdk8zU\nqVM56aST6N27NwDdunXjjDPOYNq0aXn1WUSkPe0wQadzLuScOzHFfauccxOdcwOcczXOuYOdc39K\n09a9zrkD/XN3cc6d55yrK0TbXUmybGcm22BC+slE+QSd0LLErklEHceSJUvYtGkTX/7yl1scj0aj\nzJs3j3HjxpWoZ9lJzO7nek6goaGBOXPmsP/++7c4vv/++7NkyRLWrVuXdR9FREqh05XXpfOIH9eZ\nuIRSJuV1KHymE1ouEh8Emwo6S+fxxx/niSeeYMmSJQwYMIDJkyfTs2dP7rjjDgAWLVrE5s2b2b59\nO1OnTqWyspL58+dz1113MXjwjr//wvvvv09TUxM9e/ZscTz49/vvv0+/fv1K0TURkawo6JSiMTNw\nfqAZzEjPsLxezExnMIM9HA7HAlCV10vn5JNP5uSTT2bChAmMHj2aX/7yly3unzVrFpWVldTW1vLj\nH/8YgFNOOYVbbrmFn//856Xocrtav3494JXU43Xv3h1AmU4R6TQUdErRJJvBnsk6nd793tdiZDrL\ny8sxM5qammL9UKaztCKRCPPmzePuu+9udd+sWbM455xz+J//+Z/YsU2bNqX9Q2HSpEmsWbMmo8ce\nMGAA9913X/adbifBerKJzzdY9itxhy0RkY5KQacUTeKYTudci1J7OsXMdAaTicLhcGwWu4LO0lq0\naFHS8ZwNDQ0sWLCgxSzvbdu28c9//pPJk1Pvonvvvffm3Jdnn32WW2+9NaNzJ0+ezDHHHJPzY2Vi\np512ApqX9wps2bIFIDa5SESko1PQKUWTmOnMZAvM2LVpFojPN+gEr8QeDodjAbHK66U1e/Zs9t57\n71iAFViwYAGRSISRI5v3a3j66aepqqoqWrA3fvx4xo8fX5S2czFo0CBqa2v55JNPWhwPyuqf/exn\nS9EtEZGsKeiUogkyncGM9UxL69Cc6SxGeR2aJxMF/VGms7Rmz57N6NGjAa9sfOONNzJlyhRmzZrF\noYceSlVVVezce+65h0mTJlFRUcFNN93EZZdd1qq9Ham8XllZybhx43jzzTdbHF+0aBEjRoxgwIAB\nJeqZiEh2FHRK0QQZzSDozGQLzECxM53xQacCztJbvXo1J57orXg2ffp0zjrrLMAbz5mYdVywYAHT\npk1j+fLlVFdXJ20vn/J6voIyeLDxQLbnPPPMM0ycOJEHH3wwtjbpt7/97dhuRD179qSuro7HH3+c\nGTO6/HLAItKJKOiUoikzr2Qdy3RmsAVmIF2mMziWb9BpZtp3vYO48sorefDBB6mrq+Poo49m2LBh\ngBeMTpgwocW5F110Effccw+9evXiuuuuK0Fvk5s/fz633XYb//73vzEzJk2axJe+9CW++c1vxp5D\nJueANzkofoLQ+PHjuemmmzj//PM54IADWLJkCbfddluLyVUiIh2dZbNIseTPzFxXec23Nm5lU8Mm\nulV0o1d1LxqaGli3fR3V5dX0remb9tr6eli/HmpqoE+flvdt3AjbtkHv3lBbm3v/6urqaGxspKqq\nSuscioiIJOEnaPJI8zRTikeKJrG8nukanVDcJZMCWqNTRESk/SjolKIpC7Usr2e6BSYUd8mkQE1N\nDdC8WLyIiIgUj8Z0StEEmc6I8yZLZLoFJrRPprOyspKBAwdmFASLiIhIfpTplKLJp7yeSaazEPN/\nFHCKiIi0DwWdUjQhC2FYTuX19sh0ioiISPtR0ClFFSuxRyPNi8NnOJHIrLhjOkVERKT9KOiUooov\nsWezDSakXiBeQaeIiEjno6BTiip+Bns222BC6gXiFXSKiIh0Pgo6pajiZ7Bnsw0mKNMpIiKyI1HQ\nKUVViPJ6skynAk4REZHORUGnFFX8/uu5ltfjM53KcoqIiHROCjqlqJJlOrMtr8dnOhV0ioiIdE4K\nOqWo4pdMymadTlCmU0REZEeioFOKKtns9XzGdCroFBER6ZwUdEpRxc9ed7iMS+uQPNMZibS8T0RE\nRDoHfXRLUSVuhZnNXufJMp319d7XyspC9VBERETag4JOKbr4cnq+mc4g6KyuLkTPREREpL0o6JSi\niw86Mx3PCa0Xhw+HvfJ6WRlUVBSyhyIiIlJsCjql6FpkOvMoryvLKSIi0nkp6JSiC2awQ37l9SDo\nrKkpVM9ERESkvSjolKLLt7wejUJTk1deD4U0iUhERKQzUtApRZdreT0+06nSuoiISOemoFOKLth/\nHbIrr8dnOhV0ioiIdG4KOqXo8plIZOZlOhsbve+rqorRQxERESk2BZ1SdLmO6YSW211WVWn7SxER\nkc5KQacUXa6z16HldpcdYdb63LlzS90FyZHeu85N71/npfdOAgo6pehyLa975zd/7Qildf3y7Lz0\n3nVuev86L713ElDQKe0iCDxzzXRWVrbMeoqIiEjnoo9xaRfBDPZcx3Rq1rqIiEjnZi7Y7kXahZnp\nBRcREZFOwzlXkGm8CjpFREREpOhUXhcRERGRolPQKSIiIiJFp6BTRERERIpOQaeIiIiIFJ2CzjyZ\nWcjMJpvZW2a23cw+NLObzaw2izaOM7MFZvapma0zs0fMbFjxei2BfN4/M+ttZheb2XP+ddv8du4y\ns13bo/9dWSF+9hLae9jMomb2eqH7Kq0V6HdnuZl938wW+78/N5rZIjP7VjH73tXl+97579t3zewV\n/zNvs5n9x8ymmFmPYve/KzOzK83sT2b2nv/77v0c28kpbtHs9TyZ2a3ARcDjwDPAfv6/XwSOdm28\nwGZ2MvAo8G/gbqA38H9ABDjYOfdx8Xov+bx/ZjYe+DPwAjAbqAM+B3wbaARGOueWFvUJdGH5/uwl\ntHU88CTQALzrnPt84Xss8Qrwu7MSeBoYAzwA/BMoBz4LbHPO/ahone/iCvDe/R44G5iF93MXBsYC\npwELnXOHFa3zXZyZRYF1wGLgYGCTc273LNvIPW5xzumW4w0YDkSBPyUcv9A/fnob11cAK4H3gdq4\n4wcATcBdpX6OO/KtAO/fUGC3JMePStaubh3nvUu4pjvwITDd/1l8rdTPb0e/FeL9A6bhBSujS/18\nutKtAL83q/3Pt1eS3He/38bnS/08d9QbMCzu+/8A72V5fV5xi8rr+Tnd/zo94fjdwDbgzDauHw0M\nBH7rnNsWHHTOLQHmAqeZ+Vv5SDHk9f455z5wzrUqTTjnZgEb8H45S3Hk+7MX7zrAgCn+Vym+vN4/\nM+sGXAw86ZybZx6VZdtHvj97YbyKwidJ7gsyZFtz7p2k5ZxbnmcTecUtCjrz80W8dPLL8Qedcw3A\nEv/+tq4H+EeS+xYCPfFKRVIc+b5/SZlZL6AHyX+pSmEU5L0zs0OA7wGTnXNbCt1JSSnf928UXoZ6\nsV/q3QxsMrM1Znad/lgvqrzeO+dcBPgJMN7MLjOzPc1smJmdDXwXuN85925Rei6FkFfcoqAzP4OA\nOudcOMl9K4H+ZlbexvXBucmuBxicR/8kvXzfv1T+H97Ysnvz6Zyklfd759//W+BvzrlHi9BHSS3f\n929v/+v/AScBPwC+DiwArgR+V8C+Skt5/+w5527ECzCnAm8D7+G9Z7c45yYVuL9SWHnFLbl8oEqz\nWrwyQTL1cedsTnM9KdqoTzhHCi/f968VMzsV7wPwGefcPXn1TtIpxHv3Q2AP4MQC9ksyk+/7F5TS\n+wDDnXPL/H8/amazgYlm9lPn3FsF6a3Ey/tnz8wuA27Am4zymH/4VGCKmTU4564vUF+l8PKKW5Tp\nzM82oCrFfdWA889Jdz0p2qhOOEcKL9/3rwUzOw74A/AK3ixMKZ683jsz2xNvDOe1BRjjJNnL92dv\nu//1n3EBZ+A+/+vo3LsnaeT7s/c5vIDzYefcac65R/zb14GHgZ+YmYaVdVx5xS0KOvOzCq+UUJHk\nvsF4JYimNq4Pzk12PSRPYUth5Pv+xfjLJz0OvA4c45z7tHDdlCTyfe9+DqwHnvTHlO3pB6LlQJWZ\n7WFmAwvfbfHl+/595H9dneS+4FifPPonqeX73h2JN2HvT0nuexQvLjk8715KseQVtyjozM/LQBnw\npfiDZlYNHAj8K4PrAUYmue9QYBPeeBcpjnzfv+D88Xhrzb2Jt0bdpgL3U1rL9737DN7YpDfwfsaC\n2yBgL2AZcFdhuyxxCvW7M9kmDMGxNfl0UFLK970LgtVkw/vK09wnHUNecYuCzvw8jFdK+L+E4+cD\nNXilVgDMbBcz28fMauLOm4e3RMR5/hIgwbkH4C14/Cd/pp8UR77vH2Z2DPAEsBQ4yjm3sbhdFl++\n790P8MaQxd++BqzFW7PzVLwSoBRHXu+fPyRiPvAlMxsRd26Z30YYeK5ove/a8v3ZC4KWZBOGgmOv\nFKivkoeixC2lXqi0s9+A2/AWs30MOA+vbNcIzE447x7/vNEJx0/FW35iMXABcAXeUjurgIGlfn47\n+i2f9w9vN4ft/u1ivPXpWtxK/fx25Fu+P3sp2lyOFofvFO8fXlZtC97uKj/G2xHnJf/cH5f6+e3I\ntwK8d3/1j8/DC17/D/i7f+yhUj+/HfkGnAX8yL99gjfMKPj3mQnnFjxuKfkL0NlveNniS4C38GZu\nfQTcTNxK/f55M/w36ctJ2vgq3ppXW/3/AI+QZKcb3TrW+4f3V3nUPx5NcouU+vntyLdC/OwlaVM7\nEnWi9w9v29mn8DZj2A4sAiaW+rnt6Ld83zugEm9puf/Q/If7ErwKRKjUz29HvgFz4j+jEj6/Ev9o\nKHjcor3XRURERKToNKZTRERERIpOQaeIiIiIFJ2CThEREREpOgWdIiIiIlJ0CjpFREREpOgUdIqI\niIhI0SnoFBEREZGiU9ApIiIiIkWnoFNEOiUzW25mc0p1fZp2h5lZ1Mx+nMG5Y/xzk+1D3W7MrNbM\nbjOzD82syczeL2V/kukor5WI5K681B0QEcmR82+luj6T9jtCPzJxOXAh8DPgNbw9zdudmR0ITABm\nOOc+SHJKR3itRCRHCjpFpLOyEl9fCPOAGqCpxP0Yh7fn/OUl7seBwNXAbCAx6Owor5WI5EjldRGR\nEnGeRudctMRd2QXYkMmJZtajyH2BJH8QdKDXSkRypKBTRDoMfzzkY2a22cw2mdmT/rGMx1+a2QQz\nm29mn5rZFjN7ycxOTHP+QWY22z93nZndY2YDEs7pbmbXmtlCM1trZvVmtszMbjCzmjyeb9JximbW\nzW/7Xf+xPjaze83sM6muN7NzzOwN//zlZvbDDB7/bDOLAsOA0X5bUTO72r9/uZnNMbMRZvY3M9sI\nLPHv65HNa2Ke8/3zt/i318xsqn//NcDv/dPnxPVlRkd4rUQkfyqvi0iHYGb9gBeBAcCvgaXAl4E5\nQC0ZjOUzswuA2/1rp+JlzM4GnjSzbzvn7k64ZAjwAvAo8AjwBeBc4GAz+6Jzbrt/3q7A//rnPYBX\n4h0DXAaMAMbn8pzjxJ6bmVUAfwNGAn/CG2f5WeC7wDFmdrBzbmXC9d8BdgZ+C2wEzgJuNLMVzrkH\n0zzuPP/cXwBrgev846/F9eszwCy81+dPQHf/vsFk95rcD5wB/BO41u/nvsApwI+Bx/Ayrt/y+7HU\nv+7dhHZK9VqJSL6cc7rppptuJb8BNwFR4PSE4zf6x2cnHF8efwzoA3wKvA10jzveA3gH2Az0Srg+\nCnw/od3/849fHnesAihL0uef+Od+Me7YMP/Y1Rk85zH+uRPjjp3vH/tpwrnH+cfvS3L9CqBH3PEa\nYA2wIMPXvsVrmeQ1OjfJfdm8Jl/3j93bRj/O9s/7ckd9rXTTTbfcbyqvi0hHcQKwyrXONt2c4fXj\n8DKitznnPg0OOue2ALfhZeiOTrhmE3BnwrE78QLUk+LaCDvnIgBmVm5mfcysP14GEOCQDPuYiZOA\nCHBD/EHn3Ey80vb/JLlmhv88g3O3AwuBvQrQn3XAjMSDWb4m38TLUP6gAP2J19FeKxFJQ0GniHQU\nu+FlJFtwzq3FCw4zuR7gjST3vZlwTuA951yL2dDOuUbg/cRzzewCM3sNqMcLxNbglf7By7IWym54\nwXey5/wG0MMP7uK9l+TcdUC/AvTnXedc0qENWbwmewEf++9lIXW010pE0tCYThGRNpjZJXgZ178B\n04FVQCPeWM97KP0f8JEitr0t2cFO8JqkUszXSkTSUNApIh3FcmAvM7P4zJqZ7QT0yuD6YMLJ/jRn\n2wL7+V8Ts1y7m1mFcy4c93hVwO40Z0fBm2zyvnPuK/EXm1m+E4iSeQ841sx6Jcng7Qdscs7VFeFx\ns5XNa/I2cKKZ7eScW5OmzWwXfu8sr5WI0HH/EhWRrudpYCBwesLxTMcBPg9sBS4ys2CGdbCu5EV4\nu+w8n3BNL+CChGMX4E0+ejLuWJPfVux3ppmVA1dk2LdsPIH3u7lF22b2FbzF05/Ooq1i7t6TzWvy\ngP/1JjNrsQZnwr+DsbiZlro7y2slIijTKSIdx414S+rMMLNDgP8Co/CWw6mjjaDAObfJzC4D7gAW\nmtk9NC+ZtDvw7fgJJL53gR+bKmxNCQAAAbBJREFU2f7AYrwlk87BW67ntrjzHsWbrPKMmT0B9PT7\n2pjrk03jHmAScLmZDcNbRmpPvGB4NXBVFm0Vc9eljF8T59yjZvYwMBEvm/1nvMXoPwscA3zOP/Vl\nvBnm/8/M+uL9EfGec+7lFH24h87xWokICjpFpINwzq0zsyOAn+OtlemAucCReMHI9sRLkrTxKzP7\nGPgh3tqPAK8CJznnErNeDvgI+Jr/mKcDDXhZuR+45jU6wVv/0fDWpZwOfAw8jBf0xJfhc9HieTjn\nmszsWOBHwGnAyXgB2sPAj1zrdSdTBePZ7FOero1Usn1NzsALCv8XmII3tvI9vPU/vQdz7iMzOxdv\nL/g78ZZlugfv/W/VnxK9ViKSI0sxKVFEpEPwF41fC/zaOZdYChcRkU5CYzpFpMNItn0izeP1Esdj\niohIJ6JMp4h0GObtr74c+DfeH8VHAV8F5uPtUqNfWCIinZSCThHpMPy1HyfibSVZgzfm8nFgqnNu\nawm7JiIieVLQKSIiIiJFpzGdIiIiIlJ0CjpFREREpOgUdIqIiIhI0SnoFBEREZGiU9ApIiIiIkX3\n/wF/hPpr8Yzh9QAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f0f0849c550>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"from IPython.html.widgets import interact #import interactive tools\n",
"\n",
"#setting plotting visual parameters\n",
"pylab.rcParams['figure.figsize'] = (10.0, 8.0)\n",
"pylab.rcParams.update({'font.size': 18})\n",
" \n",
"#define function to use in ipyton interact widget\n",
"def plot_explorer(threshold_value, ylim_pos=5000, ylim_neg=-5000, local_extrema='True'):\n",
" \n",
" i = 0\n",
" for th in thresholds:\n",
" V3 = np.array([])\n",
" ion_frac_vol = np.array([])\n",
" for z in redshifts:\n",
"\n",
" V3 = np.append(V3,data_dict[z]['CV3'][i])\n",
" ion_frac_vol = np.append(ion_frac_vol,data_dict[z]['ion_frac_vol'])\n",
"\n",
" plt.plot(ion_frac_vol, V3, linewidth=2, alpha=0.1)\n",
" plt.xlabel('redshift')\n",
" plt.ylabel('V3')\n",
" plt.ylim(ylim_neg, ylim_pos)\n",
" i +=1\n",
" \n",
" #selects redshift to highligt from plotnr parameter\n",
" th = thresholds[threshold_value]\n",
" V3 = np.array([])\n",
" ion_frac_vol = np.array([])\n",
" for z in redshifts:\n",
"\n",
" V3 = np.append(V3,data_dict[z]['CV3'][threshold_value])\n",
" ion_frac_vol = np.append(ion_frac_vol,data_dict[z]['ion_frac_vol'])\n",
" \n",
" #plots highlighted redshift curve and annotates it\n",
" \n",
"\n",
" plt.plot(ion_frac_vol, V3, linewidth=2, alpha=1, color='red')\n",
" plt.xlabel('global ion fraction')\n",
" plt.ylabel('V3')\n",
" plt.title(str(plotname))\n",
" plt.annotate('$th = ' + str(th) + '$', xy=(ion_frac_vol[11], V3[11]),\n",
" xytext=(0.5, 0.1), textcoords='axes fraction',\n",
" arrowprops=dict(facecolor='black', shrink=0.05, width=0.5, headwidth =10),\n",
" horizontalalignment='right', verticalalignment='top',\n",
" )\n",
" \n",
" if local_extrema == 'True':\n",
" \n",
" V3_maximums = argrelmax(V3)[0]\n",
" V3_minimums = argrelmin(V3)[0]\n",
" \n",
"\n",
" for maximum in V3_maximums:\n",
" #print V3[maximum], ion_frac_vol[maximum]\n",
" #print ion_frac_vol[maximum], round(V3[maximum])\n",
" plt.annotate(str(ion_frac_vol[maximum]) + ' , ' + str(round(V3[maximum])), xy=(ion_frac_vol[maximum],V3[maximum]), xytext=(-20,20), \n",
" textcoords='offset points', ha='center', va='bottom',\n",
" bbox=dict(boxstyle='round,pad=0.2', fc='white', alpha=0.3),\n",
" arrowprops=dict(arrowstyle='->', connectionstyle='arc3,rad=0.5', \n",
" color='black'))\n",
"\n",
" for minimum in V3_minimums:\n",
" #print V3[minimum], ion_frac_vol[minimum]\n",
" #print ion_frac_vol[minimum], round(V3[minimum])\n",
" plt.annotate(str(ion_frac_vol[minimum]) + ' , ' + str(round(V3[minimum])), xy=(ion_frac_vol[minimum],V3[minimum]), xytext=(20,-40), \n",
" textcoords='offset points', ha='center', va='bottom',\n",
" bbox=dict(boxstyle='round,pad=0.2', fc='white', alpha=0.3),\n",
" arrowprops=dict(arrowstyle='->', connectionstyle='arc3,rad=0.5', \n",
" color='black'))\n",
" \n",
" plt.savefig('V3_global.png')\n",
" \n",
"interact(plot_explorer, threshold_value=(0,len(thresholds)-1,1), ylim_pos = (0,5*10**6,1000), ylim_neg = (-5*10**6,0,1000), local_extrema=['True', 'False'])"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.10"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| gpl-2.0 |
tensorflow/docs-l10n | site/zh-cn/tutorials/load_data/text.ipynb | 1 | 19130 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {
"id": "DweYe9FcbMK_"
},
"source": [
"##### Copyright 2018 The TensorFlow Authors.\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"cellView": "form",
"id": "AVV2e0XKbJeX"
},
"outputs": [],
"source": [
"#@title Licensed under the Apache License, Version 2.0 (the \"License\");\n",
"# you may not use this file except in compliance with the License.\n",
"# You may obtain a copy of the License at\n",
"#\n",
"# https://www.apache.org/licenses/LICENSE-2.0\n",
"#\n",
"# Unless required by applicable law or agreed to in writing, software\n",
"# distributed under the License is distributed on an \"AS IS\" BASIS,\n",
"# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.\n",
"# See the License for the specific language governing permissions and\n",
"# limitations under the License."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "sUtoed20cRJJ"
},
"source": [
"# 使用 tf.data 加载文本数据"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "1ap_W4aQcgNT"
},
"source": [
"<table class=\"tfo-notebook-buttons\" align=\"left\">\n",
" <td>\n",
" <a target=\"_blank\" href=\"https://tensorflow.google.cn/tutorials/load_data/text\"><img src=\"https://tensorflow.google.cn/images/tf_logo_32px.png\" />在 TensorFlow.org 上查看</a>\n",
" </td>\n",
" <td>\n",
" <a target=\"_blank\" href=\"https://colab.research.google.com/github/tensorflow/docs-l10n/blob/master/site/zh-cn/tutorials/load_data/text.ipynb\"><img src=\"https://tensorflow.google.cn/images/colab_logo_32px.png\" />在 Google Colab 上运行</a>\n",
" </td>\n",
" <td>\n",
" <a target=\"_blank\" href=\"https://github.com/tensorflow/docs-l10n/blob/master/site/zh-cn/tutorials/load_data/text.ipynb\"><img src=\"https://tensorflow.google.cn/images/GitHub-Mark-32px.png\" />查看 GitHub 上的资源</a>\n",
" </td>\n",
" <td>\n",
" <a href=\"https://storage.googleapis.com/tensorflow_docs/docs-l10n/site/zh-cn/tutorials/load_data/text.ipynb\"><img src=\"https://tensorflow.google.cn/images/download_logo_32px.png\" />下载 notebook</a>\n",
" </td>\n",
"</table>"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "GEe3i16tQPjo"
},
"source": [
"Note: 我们的 TensorFlow 社区翻译了这些文档。因为社区翻译是尽力而为, 所以无法保证它们是最准确的,并且反映了最新的\n",
"[官方英文文档](https://tensorflow.google.cn/?hl=en)。如果您有改进此翻译的建议, 请提交 pull request 到\n",
"[tensorflow/docs](https://github.com/tensorflow/docs) GitHub 仓库。要志愿地撰写或者审核译文,请加入\n",
"[[email protected] Google Group](https://groups.google.com/a/tensorflow.org/forum/#!forum/docs-zh-cn)。"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "NWeQAo0Ec_BL"
},
"source": [
"本教程为你提供了一个如何使用 `tf.data.TextLineDataset` 来加载文本文件的示例。`TextLineDataset` 通常被用来以文本文件构建数据集(原文件中的一行为一个样本) 。这适用于大多数的基于行的文本数据(例如,诗歌或错误日志) 。下面我们将使用相同作品(荷马的伊利亚特)三个不同版本的英文翻译,然后训练一个模型来通过单行文本确定译者。\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "fgZ9gjmPfSnK"
},
"source": [
"## 环境搭建"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "baYFZMW_bJHh"
},
"outputs": [],
"source": [
"import tensorflow as tf\n",
"\n",
"import tensorflow_datasets as tfds\n",
"import os"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "YWVWjyIkffau"
},
"source": [
"三个版本的翻译分别来自于:\n",
"\n",
" - [William Cowper](https://en.wikipedia.org/wiki/William_Cowper) — [text](https://storage.googleapis.com/download.tensorflow.org/data/illiad/cowper.txt)\n",
"\n",
" - [Edward, Earl of Derby](https://en.wikipedia.org/wiki/Edward_Smith-Stanley,_14th_Earl_of_Derby) — [text](https://storage.googleapis.com/download.tensorflow.org/data/illiad/derby.txt)\n",
"\n",
"- [Samuel Butler](https://en.wikipedia.org/wiki/Samuel_Butler_%28novelist%29) — [text](https://storage.googleapis.com/download.tensorflow.org/data/illiad/butler.txt)\n",
"\n",
"本教程中使用的文本文件已经进行过一些典型的预处理,主要包括删除了文档页眉和页脚,行号,章节标题。请下载这些已经被局部改动过的文件。\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "4YlKQthEYlFw"
},
"outputs": [],
"source": [
"DIRECTORY_URL = 'https://storage.googleapis.com/download.tensorflow.org/data/illiad/'\n",
"FILE_NAMES = ['cowper.txt', 'derby.txt', 'butler.txt']\n",
"\n",
"for name in FILE_NAMES:\n",
" text_dir = tf.keras.utils.get_file(name, origin=DIRECTORY_URL+name)\n",
" \n",
"parent_dir = os.path.dirname(text_dir)\n",
"\n",
"parent_dir"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "q3sDy6nuXoNp"
},
"source": [
"## 将文本加载到数据集中\n",
"\n",
"迭代整个文件,将整个文件加载到自己的数据集中。\n",
"\n",
"每个样本都需要单独标记,所以请使用 `tf.data.Dataset.map` 来为每个样本设定标签。这将迭代数据集中的每一个样本并且返回( `example, label` )对。"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "K0BjCOpOh7Ch"
},
"outputs": [],
"source": [
"def labeler(example, index):\n",
" return example, tf.cast(index, tf.int64) \n",
"\n",
"labeled_data_sets = []\n",
"\n",
"for i, file_name in enumerate(FILE_NAMES):\n",
" lines_dataset = tf.data.TextLineDataset(os.path.join(parent_dir, file_name))\n",
" labeled_dataset = lines_dataset.map(lambda ex: labeler(ex, i))\n",
" labeled_data_sets.append(labeled_dataset)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "M8PHK5J_cXE5"
},
"source": [
"将这些标记的数据集合并到一个数据集中,然后对其进行随机化操作。\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "6jAeYkTIi9-2"
},
"outputs": [],
"source": [
"BUFFER_SIZE = 50000\n",
"BATCH_SIZE = 64\n",
"TAKE_SIZE = 5000"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "Qd544E-Sh63L"
},
"outputs": [],
"source": [
"all_labeled_data = labeled_data_sets[0]\n",
"for labeled_dataset in labeled_data_sets[1:]:\n",
" all_labeled_data = all_labeled_data.concatenate(labeled_dataset)\n",
" \n",
"all_labeled_data = all_labeled_data.shuffle(\n",
" BUFFER_SIZE, reshuffle_each_iteration=False)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "r4JEHrJXeG5k"
},
"source": [
"你可以使用 `tf.data.Dataset.take` 与 `print` 来查看 `(example, label)` 对的外观。`numpy` 属性显示每个 Tensor 的值。"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "gywKlN0xh6u5"
},
"outputs": [],
"source": [
"for ex in all_labeled_data.take(5):\n",
" print(ex)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "5rrpU2_sfDh0"
},
"source": [
"## 将文本编码成数字\n",
"\n",
"机器学习基于的是数字而非文本,所以字符串需要被转化成数字列表。\n",
"为了达到此目的,我们需要构建文本与整数的一一映射。\n",
"\n",
"### 建立词汇表\n",
"\n",
"\n",
"首先,通过将文本标记为单独的单词集合来构建词汇表。在 TensorFlow 和 Python 中均有很多方法来达成这一目的。在本教程中:\n",
"\n",
"1. 迭代每个样本的 `numpy` 值。\n",
"2. 使用 `tfds.features.text.Tokenizer` 来将其分割成 `token`。\n",
"3. 将这些 `token` 放入一个 Python 集合中,借此来清除重复项。\n",
"4. 获取该词汇表的大小以便于以后使用。\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "YkHtbGnDh6mg"
},
"outputs": [],
"source": [
"tokenizer = tfds.features.text.Tokenizer()\n",
"\n",
"vocabulary_set = set()\n",
"for text_tensor, _ in all_labeled_data:\n",
" some_tokens = tokenizer.tokenize(text_tensor.numpy())\n",
" vocabulary_set.update(some_tokens)\n",
"\n",
"vocab_size = len(vocabulary_set)\n",
"vocab_size"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "0W35VJqAh9zs"
},
"source": [
"### 样本编码\n",
"\n",
"通过传递 `vocabulary_set` 到 `tfds.features.text.TokenTextEncoder` 来构建一个编码器。编码器的 `encode` 方法传入一行文本,返回一个整数列表。"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "gkxJIVAth6j0"
},
"outputs": [],
"source": [
"encoder = tfds.features.text.TokenTextEncoder(vocabulary_set)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "v6S5Qyabi-vo"
},
"source": [
"你可以尝试运行这一行代码并查看输出的样式。"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "jgxPZaxUuTbk"
},
"outputs": [],
"source": [
"example_text = next(iter(all_labeled_data))[0].numpy()\n",
"print(example_text)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "XoVpKR3qj5yb"
},
"outputs": [],
"source": [
"encoded_example = encoder.encode(example_text)\n",
"print(encoded_example)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "p9qHM0v8k_Mg"
},
"source": [
"现在,在数据集上运行编码器(通过将编码器打包到 `tf.py_function` 并且传参至数据集的 `map` 方法的方式来运行)。 "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "HcIQ7LOTh6eT"
},
"outputs": [],
"source": [
"def encode(text_tensor, label):\n",
" encoded_text = encoder.encode(text_tensor.numpy())\n",
" return encoded_text, label\n",
"\n",
"def encode_map_fn(text, label):\n",
" # py_func doesn't set the shape of the returned tensors.\n",
" encoded_text, label = tf.py_function(encode, \n",
" inp=[text, label], \n",
" Tout=(tf.int64, tf.int64))\n",
"\n",
" # `tf.data.Datasets` work best if all components have a shape set\n",
" # so set the shapes manually: \n",
" encoded_text.set_shape([None])\n",
" label.set_shape([])\n",
"\n",
" return encoded_text, label\n",
"\n",
"\n",
"all_encoded_data = all_labeled_data.map(encode_map_fn)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "_YZToSXSm0qr"
},
"source": [
"## 将数据集分割为测试集和训练集且进行分支\n",
"\n",
"使用 `tf.data.Dataset.take` 和 `tf.data.Dataset.skip` 来建立一个小一些的测试数据集和稍大一些的训练数据集。\n",
"\n",
"在数据集被传入模型之前,数据集需要被分批。最典型的是,每个分支中的样本大小与格式需要一致。但是数据集中样本并不全是相同大小的(每行文本字数并不相同)。因此,使用 `tf.data.Dataset.padded_batch`(而不是 `batch` )将样本填充到相同的大小。"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "r-rmbijQh6bf"
},
"outputs": [],
"source": [
"train_data = all_encoded_data.skip(TAKE_SIZE).shuffle(BUFFER_SIZE)\n",
"train_data = train_data.padded_batch(BATCH_SIZE)\n",
"\n",
"test_data = all_encoded_data.take(TAKE_SIZE)\n",
"test_data = test_data.padded_batch(BATCH_SIZE)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "Xdz7SVwmqi1l"
},
"source": [
"现在,test_data 和 train_data 不是( `example, label` )对的集合,而是批次的集合。每个批次都是一对(*多样本*, *多标签* ),表示为数组。\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "kMslWfuwoqpB"
},
"outputs": [],
"source": [
"sample_text, sample_labels = next(iter(test_data))\n",
"\n",
"sample_text[0], sample_labels[0]"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "UI4I6_Sa0vWu"
},
"source": [
"由于我们引入了一个新的 token 来编码(填充零),因此词汇表大小增加了一个。"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "IlD1Lli91vuc"
},
"outputs": [],
"source": [
"vocab_size += 1"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "K8SUhGFNsmRi"
},
"source": [
"## 建立模型\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "QJgI1pow2YR9"
},
"outputs": [],
"source": [
"model = tf.keras.Sequential()"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "wi0iiKLTKdoF"
},
"source": [
"第一层将整数表示转换为密集矢量嵌入。更多内容请查阅 [Word Embeddings](../../tutorials/sequences/word_embeddings) 教程。"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "DR6-ctbY638P"
},
"outputs": [],
"source": [
"model.add(tf.keras.layers.Embedding(vocab_size, 64))"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "_8OJOPohKh1q"
},
"source": [
"下一层是 [LSTM](http://colah.github.io/posts/2015-08-Understanding-LSTMs/) 层,它允许模型利用上下文中理解单词含义。 LSTM 上的双向包装器有助于模型理解当前数据点与其之前和之后的数据点的关系。\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "x6rnq6DN_WUs"
},
"outputs": [],
"source": [
"model.add(tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(64)))"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "cdffbMr5LF1g"
},
"source": [
"最后,我们将获得一个或多个紧密连接的层,其中最后一层是输出层。输出层输出样本属于各个标签的概率,最后具有最高概率的分类标签即为最终预测结果。\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "QTEaNSnLCsv5"
},
"outputs": [],
"source": [
"# 一个或多个紧密连接的层\n",
"# 编辑 `for` 行的列表去检测层的大小\n",
"for units in [64, 64]:\n",
" model.add(tf.keras.layers.Dense(units, activation='relu'))\n",
"\n",
"# 输出层。第一个参数是标签个数。\n",
"model.add(tf.keras.layers.Dense(3, activation='softmax'))"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "zLHPU8q5DLi_"
},
"source": [
"最后,编译这个模型。对于一个 softmax 分类模型来说,通常使用 `sparse_categorical_crossentropy` 作为其损失函数。你可以尝试其他的优化器,但是 `adam` 是最常用的。"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "pkTBUVO4h6Y5"
},
"outputs": [],
"source": [
"model.compile(optimizer='adam',\n",
" loss='sparse_categorical_crossentropy',\n",
" metrics=['accuracy'])"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "DM-HLo5NDhql"
},
"source": [
"## 训练模型\n",
"\n",
"利用提供的数据训练出的模型有着不错的精度(大约 83% )。"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "aLtO33tNh6V8"
},
"outputs": [],
"source": [
"model.fit(train_data, epochs=3, validation_data=test_data)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "KTPCYf_Jh6TH"
},
"outputs": [],
"source": [
"eval_loss, eval_acc = model.evaluate(test_data)\n",
"\n",
"print('\\nEval loss: {}, Eval accuracy: {}'.format(eval_loss, eval_acc))"
]
}
],
"metadata": {
"colab": {
"collapsed_sections": [],
"name": "text.ipynb",
"toc_visible": true
},
"kernelspec": {
"display_name": "Python 3",
"name": "python3"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| apache-2.0 |
fastai/course-v3 | nbs/dl1/lesson3-planet.ipynb | 1 | 532527 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Multi-label prediction with Planet Amazon dataset"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"%reload_ext autoreload\n",
"%autoreload 2\n",
"%matplotlib inline"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"from fastai.vision import *"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Getting the data"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The planet dataset isn't available on the [fastai dataset page](https://course.fast.ai/datasets) due to copyright restrictions. You can download it from Kaggle however. Let's see how to do this by using the [Kaggle API](https://github.com/Kaggle/kaggle-api) as it's going to be pretty useful to you if you want to join a competition or use other Kaggle datasets later on.\n",
"\n",
"First, install the Kaggle API by uncommenting the following line and executing it, or by executing it in your terminal (depending on your platform you may need to modify this slightly to either add `source activate fastai` or similar, or prefix `pip` with a path. Have a look at how `conda install` is called for your platform in the appropriate *Returning to work* section of https://course.fast.ai/. (Depending on your environment, you may also need to append \"--user\" to the command.)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# ! {sys.executable} -m pip install kaggle --upgrade"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Then you need to upload your credentials from Kaggle on your instance. Login to kaggle and click on your profile picture on the top left corner, then 'My account'. Scroll down until you find a button named 'Create New API Token' and click on it. This will trigger the download of a file named 'kaggle.json'.\n",
"\n",
"Upload this file to the directory this notebook is running in, by clicking \"Upload\" on your main Jupyter page, then uncomment and execute the next two commands (or run them in a terminal). For Windows, uncomment the last two commands."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# ! mkdir -p ~/.kaggle/\n",
"# ! mv kaggle.json ~/.kaggle/\n",
"\n",
"# For Windows, uncomment these two commands\n",
"# ! mkdir %userprofile%\\.kaggle\n",
"# ! move kaggle.json %userprofile%\\.kaggle"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"You're all set to download the data from [planet competition](https://www.kaggle.com/c/planet-understanding-the-amazon-from-space). You **first need to go to its main page and accept its rules**, and run the two cells below (uncomment the shell commands to download and unzip the data). If you get a `403 forbidden` error it means you haven't accepted the competition rules yet (you have to go to the competition page, click on *Rules* tab, and then scroll to the bottom to find the *accept* button)."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"PosixPath('/home/ubuntu/.fastai/data/planet')"
]
},
"execution_count": null,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"path = Config.data_path()/'planet'\n",
"path.mkdir(parents=True, exist_ok=True)\n",
"path"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# ! kaggle competitions download -c planet-understanding-the-amazon-from-space -f train-jpg.tar.7z -p {path} \n",
"# ! kaggle competitions download -c planet-understanding-the-amazon-from-space -f train_v2.csv -p {path} \n",
"# ! unzip -q -n {path}/train_v2.csv.zip -d {path}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To extract the content of this file, we'll need 7zip, so uncomment the following line if you need to install it (or run `sudo apt install p7zip-full` in your terminal)."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# ! conda install --yes --prefix {sys.prefix} -c haasad eidl7zip"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"And now we can unpack the data (uncomment to run - this might take a few minutes to complete)."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# ! 7za -bd -y -so x {path}/train-jpg.tar.7z | tar xf - -C {path.as_posix()}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Multiclassification"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Contrary to the pets dataset studied in last lesson, here each picture can have multiple labels. If we take a look at the csv file containing the labels (in 'train_v2.csv' here) we see that each 'image_name' is associated to several tags separated by spaces."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>image_name</th>\n",
" <th>tags</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>train_0</td>\n",
" <td>haze primary</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>train_1</td>\n",
" <td>agriculture clear primary water</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>train_2</td>\n",
" <td>clear primary</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>train_3</td>\n",
" <td>clear primary</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>train_4</td>\n",
" <td>agriculture clear habitation primary road</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" image_name tags\n",
"0 train_0 haze primary\n",
"1 train_1 agriculture clear primary water\n",
"2 train_2 clear primary\n",
"3 train_3 clear primary\n",
"4 train_4 agriculture clear habitation primary road"
]
},
"execution_count": null,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df = pd.read_csv(path/'train_v2.csv')\n",
"df.head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To put this in a `DataBunch` while using the [data block API](https://docs.fast.ai/data_block.html), we then need to using `ImageList` (and not `ImageDataBunch`). This will make sure the model created has the proper loss function to deal with the multiple classes."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"tfms = get_transforms(flip_vert=True, max_lighting=0.1, max_zoom=1.05, max_warp=0.)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We use parentheses around the data block pipeline below, so that we can use a multiline statement without needing to add '\\\\'."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"np.random.seed(42)\n",
"src = (ImageList.from_csv(path, 'train_v2.csv', folder='train-jpg', suffix='.jpg')\n",
" .split_by_rand_pct(0.2)\n",
" .label_from_df(label_delim=' '))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"data = (src.transform(tfms, size=128)\n",
" .databunch().normalize(imagenet_stats))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"`show_batch` still works, and show us the different labels separated by `;`."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA0IAAAKACAYAAACxCch/AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzsvXnwrltW1/dZa+/9vO/vnNsDgxRTAxFMVAYtUoqUgBCjIQMVDIlGBNNEoqghSUkR0EpiO4AZiJCEMljRWHSAGFTApC0TJrsZbIJBSBuoGAWbbhAaerz3nvN73+fZe638sfbe79uHvkNP95y+9/l2/W6fd97PtJ41fNd3ibuzY8eOHTt27NixY8eOHS8k6MNewI4dO3bs2LFjx44dO3Y819gDoR07duzYsWPHjh07drzgsAdCO3bs2LFjx44dO3bseMFhD4R27NixY8eOHTt27NjxgsMeCO3YsWPHjh07duzYseMFhz0Q2rFjx44dO3bs2LFjxwsOeyD0bkJEXEQ+4QPpu0XkFSLyLe/r732K3/p9IvLdz8Vv7dix4z2HiLxcRH7oYa/jqSAif0JE/tLDXseOHTveM+w2ZscHAvZA6GkgIq8WkS992Ov4QIK7f6u7/86HvY4dO3Z8YMPdv9bdd/u7Y8eO9wue7zbmUQ9EHxXsgdC7gAT2ffNuQkTyc/hb+zHaseMRxPvCDjzHtuQ5+60dO3a899htzHODD9R1v7t43jmSIvJ6EfnjIvJTIvI2EfkrInIUkQ8SkVeJyC/3518lIh999blXi8jXiMgPA/eB/wn4TOAbReRJEfnGB37nN4nIm65PFBH5AhH5iWdYX+rl2J8WkSdE5MdE5GXv4n0vEZFX9vX+rIj8J8Pxf5DqJiIf12l1uT/+Z0TkNf37vwf40Kv3/i0R+fIHfut1IvL5/d+vEpGvvnrNReQ/EJGfEZE3i8h/dbWOl4vID4vI14vIW4FXPJiB6J//IyLyj/p6/oyIfLyIvFZEHheRbxeRpb/33T1GXyEiP/bAtnyFiHzX0x2DHTteaBCRl4nId/Rr6y0P2rP+nl8rIt8jIm8VkX8oIr/76rV/VUR+vF+zbxSRV1y9NuzPHxCRNwDf359/nYh84QPv+YMi8k9F5BdE5CuuvuMVIvLXReRbRORx4OXXdu7q81/Sf/9tIvJl3Q6/TkTefr1N3cZ8f9/WN4vIt4rIS69ef72IfJWIvA64JyJfKSJ/44H98d+JyDe893t/x47nP3Yb897ZGBH5ahF5Vf/354jIP7h63/eKyI9ePf4hufhsXy0Xf/KnROR39ed/HfBNwKdL+LBv788fROTrROQNEj7sN4nITX/ts0Xk5/q6fxH4K8/y8H9gw92fV3/A64H/B3gZ8MHADwN/FvgQ4AuAO8CLgL8GfNfV514NvAH4RCADpT/3pQ98vwOf0P/9U8C/fPXadwJf8Qzr+0rgHwD/HCDAbwA+5F189yuBv9nX+nHA/wf8gf7aK4BvufrOj+ufzf3xa4E/DxyAzwKeGO8Hfjfwf1599jcAbwGWp1ivA3+n78uP6ev40v7ay4EKfHnfZzf9uR964PP/K/Divm/PwPcBvxp4Sd+H/05/77t7jA7AW4Ffd/WeHwe+4GGfh/vf/veo/AEJ+L+BrwfuAkfgM66v1f78G4Ev6dfWpwJvBj6xv/7ZwCcTybNPAd4EfH5/bdifV/bvuXkXaxjv+Z/7ez4Z+GXgX+yvvwLYgM/vv3FzbeeuPv9Nff2/EzgB3wV8GPBRwC8Bv62//xOA39FtxK8CfgD4hqv1vB74CeI+cQN8BHAPeGl/Pffv++cf9vHb//a/R/1vtzHvWxvTf/+WSGJn4BeBf0r4RTf9teE3/lvAR/Zt+j39Nz6ivzb3/9V3fwPhk31w/77/DfhzV8egAv9F365fsZ+fj38PfQHv8w2Kk+/Lrh7/K8BPv4v3/UbgbVePXw386Qfe82qePhD6KuBb+78/mKhSfMQzrO8fAv/6U7zm/eJKRMDw669e+0PAq/u/58XbH48LOBPBSgXuXr3+bVcX+wgefk1//HXAX3ia9TrwuVeP/wjwff3fLwfe8MD73+nC65//rVePfwz4qqvH/zVXxuM9OEb/PfA1/d+fCLwNODzs83D/2/8elT/g0wmHID/w/LxWiRvoDz7w+l8E/uRTfOc3AF/f/z3sz69+mjWM9/zaq+f+S+Av93+/AviBBz4z7dzV5z/q6vW3AL/n6vHfAP6jp/j9zwd+/Orx64F/94H3/G3g3+v//teAn3rYx27/2/8+EP52G/O+tzHADwL/BvBbgO8Gvh34XOBzgNc9zed+gu5j8iv9MSECpY9/4Nj9k/7vzwZW4Piwz6nn8u95R43reOPVv38W+EgRuSMif1GCZvY4Eb2/VETSU3zu2eBbgM8TkceISssPuvsvPMNnXgb89DO850OBpa994GeJjMQz4SOJ4OHeA58FwN3PxAX1RRIUt99L0ACfDr9ifz7Fa0+FN139+/ZdPH4M4D08Rt8MfKGICPDFwLf3bdyxY0fgZcDPunt9mvd8LPBpnf7x9k6j+H3AhwOIyKeJyN/ptJd3AF/GFeW249nYgufKlnyYiPxVEfn5bku+5Vms95uBL+r//iKe2S7u2LEjsNuY972NeQ0RmHxW//ergd/W/14z3iQiv19EfuJqn37Su1jHwK8iGDc/dvX+/70/P/DL7n56mnU97/B8DYSue24+higpfgVBR/s0d38xcXJBRMgD/sD3PPj4nV90/3mChva7CCf82dw43wh8/DO8581ECfdjr577GODn+7/vESfzwIdf/fsXgA8SkbsPfPYa30wYoN8O3Hf31z7Det7V/hx42n30buLdPkbu/iNEBuMzgS9kd1527HgQbwQ+Rp6+8fWNwGvc/aVXf4+5+x/ur38bQad4mbu/hKCPyAPf8WxswXNlS/5c/75P6bbki3jm9X4X8Cki8klEtvZb34fr2bHj+YzdxrzvbcyDgdBreCAQEpGPBf4H4N8nqHIvJVpDxjoe/P03E8HcJ14dg5e4+2NPs+bnPZ6vgdAfFZGPFpEPBv4E8L8QXMhb4O39+T/5LL7nTUQvy9PhlcB/TPBRv/NZfOdfAv6MiPwaCXyKiHzI9RvcvRFVm68RkRf1k/2PERkHiNLnZ4nIx4jIS4A/fvXZnwX+L+BPicgiIp8BfN4D3/9awAha2jsFDhKCBK94YM1fKSFk8DLgPyT25/sD78kxgjgG3whUd9+lInfseGf8KJEg+c9F5K6EeMxvfeA9rwL+WRH5YhEp/e839YZbiGvzre5+EpHfTCQdnha9WfjlDzz9n/bK7ycSvQLvT1vyJGFLPorozXxa9CzoXyccsh919ze8n9a2Y8fzDbuNeS9tjIRww6uv3v53icTwb+7v/Ul6VY1gy0D0QjlBS0REvoSoCA28Cfho6YJU7m5E4PT1IvJh/TMfJSL/0ru36c8vPF8DoW8jOJU/0//+LME3vSEi4h8hyoHPhP8G+Dcl1EP+26d4z3cSJ+d3PkBHeyr8eSLI+W7gceAv93U9iC8nKj8/A/xQ36b/EcDdv4e4uF9H9Ny86oHPfiFxsbyVCCZe+S6+/5VE8PbgoNWXEQIT1/ib/Xd+Avhbfc3vD7wnxwgimPsk9mrQjh2/Aj2x8nlE/+EbgJ8j+PrX73mCaA7+t4kM6i9yaZiF6A380yLyBPCfETbsKdFvvB9CXMfXeA3wjwnBlK9z9/fX8OU/RTRjv4OwWd/xLD/3zYRd3G3Jjh3PEruNeZ/YmHfyvbo/+feBn3T3tT/9WoKC+Ev9PT9FJLRfSwQ9n8w7+2/fD/wk8Isi8ub+3FcR++dHOqXve4mA6wUL6Q1SzxuIyOsJgYPvfQ5/86eBP/Rc/uZ7CxH5/cAfdPfPuHruo4G/5u6ffvWcE8IK//ghLPNZoUs//hLwqe7+jx72enbseKGjV6L/qLv/3v7444B/ApRn6CN4qBCRjwH+X+DD3f3xh72eHTt2vGs832yMxOiV3+7ub3loi3uB4gUxLOn9CRH5AqI0+f0Pey3PFiJyh8i+/IXr59395wgFkQ80/GHg7+1B0I4djwY6RfUDiqbaxWP+GPBX9yBox45HG883G+Puv/HhrGrHHgi9F+h8zl8PfHHnXo7n/zbRvP8gvtbdv/Y5Wt67ROeCfgdRDv22h7mW9wV6BVAI6codO3bseLfRxWXeRKhMfe5DXs6OHTueZ9htzKOL5x01bseOHTt27NixY8eOHTueCc9XsYQdO3bs2LFjx44dO3bseEo8EtS4z/n83+FiEZOJgqZMPsZr2YxmidpHZJptkBO3W8x7KpK4WQopgfXvcHNygtri8ZPnM7TGkFZPJaNimAWbrSQlL8LpNqpj1gyVhEs8FjFSWkhLfN/5VKnbxlJiTUUzaYHb84ZozP48kEEgKKHw+PmMrZU7d0MgRdUxa9TafwNBkmDW11DBHUr/TcmCuuD99fNpQ8vC8aavaT3hpuSkmMR2yeasFUqKw3ynJCqwWvQRJoUkivdwuNWGAq0XCTd3soBKl6R32MxRjTe4xn+kVxWbCBlh6/s1GYg6ImD9WBRNSIJzjTW4OIcl430/+WY40DeBzTfEMzm12G9ZqSRSi8do4pAy99atf75hOKmvOadMMwd1xOIzzWHJBe/bUdvGnUNhkBs3EwxjbLagfN93/B8PzgfY8QLFJ3/ap3rt16G7k4R5rqSsnJuQvJ9rphwOmUO/jltr1PPK6QxpfGZJnB2yd9tRANr8PU2ZJ+rGdj+eu7kppJy5ffI+AGXJaE6IWv+8slXH+vflJLjAeoprJGGoCs2Y18mhHNAivOOJJ/u6E4vqzJRZdRCh9WvGktPWlWM+zDWUlLk9haGuzTiK03J8vxpISrjm/rhiqlhaEWKd7b6z3dtgic8sh4VchNx3lDXHcNoW23naNu5kYe12veSFzZzW7Y+1SnLhTonf3MQpObOk+L2tVowGHp8XlHVtpMXpph+rQlbB+hMNwVfHi/Zj0xBxsH5vIUGDx+/HfnB1bpaMjW20DXEjpWP/vHFQZdybziKkVjH3ef/yvj06DobG+aZ1nIOJExvHpZ8/OfP3f/jv7fZqBwC/5V/4TNcS50px4cV37/ChL40xhEUP2HrGhraAG+oNa+Oe77imOAeHP0Scr06/zlxwhMEuEiw+189pRXCgjfE0blSE3K1LQ3BvnFqs4cn7G2+7v7FV60uwfu4LqbusJhtJC6L9uvMzbgnt13ouSmvGIDy5x7yQ4fMJRlJhzGrXlFAFGf6XhH3etrC5LglNoGpsbaxLsFVxCbt6XAqqinTfRFLGxDnVeLxuFREhpdhu2xSlcbPEmg9LYm1wfw3bkVEQI/UL30VpzWP/AuaOOqSiSA5nVGrFRekmjtaclATva24O5n2HAM0FzDh2u05J8Vx3htatoQjW1xD7x6+mJQkq8Zx1O5oXQZpAHTYzfEjp+8mQOJL93uOS+Lvf/wMP1V49EoFQ0oQMIy/ELWPsRI8daRIXiQnQtnkyeQ1nxN3ndzjC/VO9nPQqiAv9fETMIuDqB85bwzdl6Te3JhYO/LjzuGJmbP1Crf1EsHEgF2er8fgg44ZX8eQMh0mqkA+FMp1vAxXq8PgtNCR7zIK5483xbizEFQO8O0gpRdDh3WAlyZyrIe7IuNBao5lzOIybrOFNSDn1XW24MYMrd8eMafAWlMbFJRMRktu8CMwcF0OnwevO3bhoYuFctU/R3Di4If14ZkmYQ+r7RXOYzdqjMT8LJzOWvu+PckSdacAOuaAYh9QDRMAaJBvHVjAx3Azvx6uooFk4rSMYS0hKtG5gRBRaw0dEuLsUO64gCfKhO9P3NgzF+jmeNJEN+n2Haoa2xt0eABxL4q2nGs5sd/AdwVujTnullJzYumKqNjhIiWgi3oEB2h3flJWsymnrCquiqCm1JwcsO3eKsvUTuZmTUiRB+v0Tt8p6FrQnchLCtlbO3Rk5HDOPPZY4nboTsEGWgvRrqq5nmqwsZdyBE2vbyFnnfkiq5GE7UtxUixdMw8Kc1amLUrr9ObijpXDs9qyKc64bp20EWw5LIaXYiG1taLrYcSNxMqN2C+Y5sWTFuqNyuq3cHHJkhIAnTye8gVcl6bhJO64yJwwmVU7Z0DZsB6DX1AqjNqaDplnYVkNL3/cbKMohxzemkjivlyTdJg5uGAJysfUqEvcdwHCyZWpPaBlObTbttPega8cOuPgSEEHFaV1529viNV3OcbvvfkhR5SiJlC73dE0Jq20GPng448ZIIFyc8/g9QHUmWcydCuSR7DTHXUiMwAkc55jDRt7cXbhZNp64F4mee2sEYSlr3NyB6hmReeni3LAsMv2ndWsIFx+tedht7b5JEgG/JM/Vw59pbSRLjRtVNMl83BrYlua40dpWcllgBF+pUFLifBvrPp9uSQrajWxOiuMcuh0/Ae4NSZFMkpy4o87WM9PryZFmeLcVpIaZk/p+P2jGtWHukajqGxpJm8u+X0+V1G1qSgdKlpn0zV7ZME4jmVQjUFlKD6w0x3d3G51EwGQmz03ibmSt0jz2Q9rAsEt2cBNaMpaRBFMhq857x/ly6jw07NS4HTt27NixY8eOHTt2vODwSFSEzKD0zKHjiDu1Z+tFhKSK9wybCLgraWRPZZROE+dOmUAVUi/7AVkjytWeFam1Uu4ssyLUvNJM8F5VkEXIOc3Xz6tizsyqJMDVSDGst5dgneRpVmgQWLKy3UZWtonwopJpI5ROQQjJPTvQ+sYMahwIJeukQxiONPD+hGZn2ypp649VsbZiKSM11rCKRCayZwNcwGqb1LcsIO1Slcp9v40KyNoccZkFkabCkmRSBmmCiJBHHdaj6HnQkZGN6lprMrNDmhPN26SvpBTrGr8hqogYm40MBKjUmX3atkZRQXoWWCyyDyO7FOeCMsqDrbWg6ikso4KnQjWblTMVj+zEKCnWhvhM/Fwdkx07go5ro/JL5XDIvP2Jt8drJeF2ybipOWwzkYl5XKsqThsZVZfIkvWqAcVInqH131AwNcqxl29Q6tboxRuOx0I24bz2ioEFXU/7+Z2SUjVhRCUllcLmhkpUJCBoGOupTSqvqFO3S2X2QFDjBk0LCMrYNiiqjtNYela3pYpvsNVRXRZUbNoOt7jAHJk02CzCclSk/8amkOrG22579cVTVEs6reMmKSXnaRuyOGBITwtvtSKkae8Smc2N89a/zyqIzsq/udDMoio06HLirLVdaIcp80F3Ft5xP6jZ2xqZz85uYVmcugY1GyCXzBN1Zek2JGewJpNevCFUb8g2MvAa9y8V2qgIqVBSwga1t/UK1ThWOEuWWWFU2StCOy7ICni3HWLcPzfur1G1yPcTuRRytwPJN+5Jo3TXsCzCQYWcdF5HtTVuSLOC46JgRusVymaOO8w6qgiKT7qWiUDzSaVTCf8sj8fJeJEmitwF4KXecHGaCU92yuk71o2KkLrNSyK0JSM+DK2SVLFJY6uIBqUYgpqrUqY/ZW2lEb8BsOQjt+t50rlWM1JLlKWi0itXZaFqVJPiR1r4gYfwC7d1pbbMoRuDXEq//mM/lYNwOht169S6omzAIlEhOvEkZg3r94FFlWMpaN+R3irWggq89UpWTpmkUb2CYLiJCq2Ne0PDW7R7DKR08VtPpwrFQeJ8SRo2bEAsWgaGX1pF+z1D0G20ljiulUSv1IuRJGHdLtt25pSNNKlGPHQ8EoFQdZt8UQAXm5SMnJQkNs82NaX6FR0rB3msVmFde3CUel/KqMxVRxOUzsuwmqjnyvFOnLCchRXIo4coJZLkyZN1a7N8G2uKwGb4BCLBhnWNm298hwe9rwc+7kYTKKMPJYWzpNadHTHaVQn7oIKpMM4Sd4segkEJxDi3DenlRjSzLIlSEv26IolQ8qR74s2odqFh5FxoWabBUoJG1u0ZSkKSAZ3G1koEpJNSCCQm575a5+KOkjiGudHMZ0naPMq71o+3q5JEsb7dzRpFnNEztrqFUzIcKHdcdDAnsa1iqdHZMIg7S9JLTKNONumGOdA8Ap9DL/+29cxW6zQWQUGysdnshdMd17htG8fhhObotckSPR/nc1gK7ReduqMqrHUkRDwoJuqTCqcpUXrCB0A1+hMHTc1bXDcjsHHrnOt+Xt67f+aQy+TVliQkYQZrRxWwxmncHUUwd1IWzud+3SWoW+PcbQfeaDh3j4N74jxx7zY4bUBpCbKz5EsQsTW/JKPcuXOT8L4NqsaSha1etmk5Ki0Lt/fGvgoK2bS7ySEt1HNciAqkvMwg45gyYjL3dRWhbhs3/dgsIqzJSZ2akpKT3S5UDEmIJkq/0d8cnPu+gjmtBx2iikoia3fykvKSY+HJnqg7396immYQYtWxpFh3yNbaqSv9WC9LwS7sGmQz2nZxXHJS8HF8+74iqChig7bYe2m7b2sipBWQ0T/Bjh0TtTmljMA+R/LQhoNfOa+V0iP5JQdN/Lbf/OSU0fUeSRS18JdcjbookuNxToUkMunpYpVt23hyOCJuLA1a9+nEQV0vFHqRSGDOfKOh7ty9GW0G/bw2Y+3X0cHAznVS2Tw57Ww8drf33pVCqyt5JEzJQZHv/REtFba6Yd1f07yQRRG9+HhpSdPHs8WhKpIufZOj/2jQfbMUmrVJEjzeuQm6fX+9NUc8TfsmKmiGrVuDx29v0aJzzblkqmQOPXjLvQ9L+w+vLrgrOV3Zgta4PbVJOyslkQW82+mNSpE06XXukVgZsU5xxTLoSGi5sXnjZlDtJGEaPjp9z4r2LrDuOG5btGSM3qflRtnWM7Xb/iUdqW0j99+w0bPyEPFIBEJFbF6YiCCW8F7V0N7oOxrvcKc1mxGpZEVMWVubN5ukikoPoIjso5arpv/qbAaljQvXaSIso3dGHWvOud8xK5WMXm7Q2RAS1g/8UYN/L0nw1nn5qqxnx7tDv2RFBDYZPT29kjE6pj1F9N77AlZPmPmgiUdGRkHHlenC4VCwwbsVJWuBxsw2FpOomI1sAD0LrPPKjf8fd06PwGVkWBUQk9lb4zjZ07yJkxopRQMzRCAk7lw6jSPbLeYjdorMuPiFgyyKcwnWqkW4OaswoiSBJXVHIh8x21gGB1+Fhs1MtffjP7JNuQjJhK06dRhNN0RyLLB/R60+s8CaFRWZfR++x0E7rrE6h958vNy5y9vv384qRLVo0B/nn0vEDqPBdrPo5XCR2Sx6KT2OYF/jyXrJ4qUls3V7ZHWl3DnQuj1a799HbhQdWV2FTBpfx2mr1NamY20S1/iyFNYuEHPvtLKZUXuFRxGWknsiBLZ1wy1xfKwHa8C62RSQKUlxyaxr62t2UpEZZJxkRVRnP1DqCY7WmPx2oWeG87gtJXIzrMhcUxJIXQRi2xpN0uSz+7pyb6tI56ofDomb5LTePWMNqjC562URtrax3fa+g7WRJI7NqEpF7wCs3f0pNN7SztyMREsJAYkeo1BNyIugnS2wnjaOIhx6Nc/N2NYN68mjFx1ukJK413smS3JacpQ0+xxhCEB0myYK7nS9IPxGyQi1O3Ujs75jB8DptE2H/rAkxJnVRfMQVZHRC5gySdNsfHdfaU2p4ni9BYJBc+8svOXJOAFVnUNWbkoPjCSa89dugO4cMndvDpMF0mqlNr9iWhgiPv0zd8g06gw5pP/PeclN/EZyJTmc+zUiZtxuxtYTFDk1mrXJ+hANmzzW4HVDs1N6sKWt4aJs6xC5MQSPhDZwJ+XIa0tBhj2x8JRGEt9ao3qb9kY1cSBPO7xuEbilfi8I39Wmn1EOR8wbW69YC8IhyfRrz61RfaWbPw4sqBTW2ri/ht/42BKBz/jNukaSK81+VMLP635jKUHHmUIHZWGtK6OhvpSwwbcW35/EUVmmKEWEQNFbPmKjrp0wRbQUI2meQhenupKPhUMP+ExH9u3hYXfxduzYsWPHjh07duzY8YLDI1ER0pRHcj54mt7YOrVgcWVznxm6aiH9elF0C/qYmV2kFDWyB2XIDqZGtVlTQsW6RGCnhfQIWXvGra2VzS78UhFH8oXGli1h4pNPv24GKdQ80iDCJsHw2S+zqUelqW+XdLpDGTSy6tTqszizaGSMfZSEJBKZI9L33hczkn/xvJPESb0KVZNg1WY1RhNU14ui2qD8jd4pHBTSoNsZoRAytilq2oz4WYmK0yxSmYdM48h0m9MkVK1GP4N3SUuZUpwNsVBuG8fO6iVLckiCFCH1L9hU0I0gFhN0R21wmuJ7wjYkHgFfQ7Gmp0IYO1Pw+RuqiVYvctnqCuLz8T50eMc1mvtFThQ45MSTtV5etxoyyoQCoarP6/aK7DqptubeqVX9mmhxzY5icZPG0so8D2szSm1DZRpy4pAVyUNhsuH4rB636uSmrF1tTTmwlOipXIfUqzramLQL7T2M67DLolScm84d16Oja+Nel+Q+qpIOeVLIbjcN6l+v9GdJVIetxRpuypGtGj4JfoSSnl96EM2c6hf5WJGgmHmvIJ3NWdQuFGh3SlouB8rjnjBoIq06q/lU9AuasbB1ye9iiXwj0DKbDNlcKO7U2dsEp7ZO1dJDzpysTmnNZs6yXPp1ckohDzzsERI9ZsOmImQppP57uThZM+ttmz1jo+Vx7AeAczNkG8dXSGlh7WyEvYK94xol66Qttc2CntvPpaw3bHXlNGhs6mTb5v02awKFrflFalriOhi2w9S41xJyiqqBeNB/pZ/TL2aJfsg6GDbe2S/M78v5YgkcRSSRbVDso7XBUp5+4EvuFg750gdu28rbzxajUoB2FpoYt4MVJBL0vu6zaVKyp+nTRQM2k5ri7qHy1iXsV4G1bWiy2SM0mC6DSWKEQlyro5/Z0OKxD6FT8R0btEPVaD/o9ithJJHZRlBlA2T6eM3h4GXagahQOUWFx5aLIpvIReUSBFeZqpViuVeceo/i5izpYoPNax8HMWxmjbaSNtgE4Z/X9eI7kYI1NGxiTokikPq9otaNc2scWefj9ckzbRlU7odvsB6JQAi4cLKJ+KSkq4vALhdJTtL7dfrOa0E7EYzjYXDsM+ttRdLlSltbY/QiuwTfsnK5MBeMJKPJP+b1zKBFQ/fAJs99AAAgAElEQVR+MMpi5s+lZ6h65UCmVUOXIWYQxmPrv5FQamVSuEzjAtD5HSGfO0qOLoImYWOUbkMUddL8kyM5TQEIN8e7kMF1c7/bpI6jhMhEv045oqxNaPXCs81cGnlrq7gLgxWrOSgZbbscKxGh9SvVaohGXItKJIkLeKwopwW3bc4UcBNIPoUpaq1Rlh7eTXKq6hRDwM6IwNrnHiQvnNtl9pEhtM1Ifc3VwvAvKminPp5r426+OJbWglN7kYUgFjybitixY0IX5ckxk0e26O/ptmPzdhXsBA2zbkIpgyKbMJx1M9qc8xN9Ies2emGcZVF8NOBrJicu9mhTtm3Du428ORZ0Ebw3q97eOim1SUNrKtH/16+RgxoiCavOuTtAd1K/Ieu4AQr30sqLDsG5l5sD51qRFO8/mYZobr9hbjXox6lTBG8WuLc27navvBxC/jr1jaonQ5fMvSfucSzRHLwsOfokp7iLhqDBmKejYM2oY74Iji6JbTQ1WiMveQaIyhmSYud+E0fAhEMZCawNjCkyQXKOmnG/2IKijopz6rTEUiKRs/Zg7JAzba1Txlc1Ai4b9BaNMQ1z7lRzmip3eyB0ajWobjb2I6zqFDdaPxZLDjrTcIikC2RfTKThZaGe176fHr5jsePRQSqF1S49a4qRx3yvVMlLnuJTW91IUmj9/tpcWNKCqlGmw6+0dGmYVxGa+KTbiUunlMb7nzxvnLaL/LZKARGG9EtGUdtY+jNZMznlydwPMYUWwco454tw12SKaJ2WI8t2muNL0kHBE+/oIwRSaiE6MoIKURrK2pMgmkIIRgflHse9Tmf+fI7f3thYxoYnBXT6W5IcE5tJXzFhqxfp/JLCdzxtN33LPWzR4JQtiaOkKZOva+X2vM3E8kETSWX6TpkEYoSU1EgeFcwN1T54cxUkJ0q3se4by3JgrSMwdrbks+e1GkhrpP5+cM7nUxQr6AI85mydiicqFM8h5jJ6rpvBZpx7m8dmRlGdNMXH8oHmPoV1XC5JxIeFRyIQUuDcL8SMIKKzkuIeVYQZuEvXH59RcjQdJ2EGBWYVF5u9K6qKrNFcBqGOlhed6kNJhMJFaSynhFvtYgVRITkb5DHISgWhzDUYGyIF8zNlaKWLd0GFbhyazyZliKGdReG23zBtM3KSOQOjtqi0eN9wzxU3mUIGWTXW1/eL1pgR1MSw4Xy4RBZBL0HB2McAp+bBV+/HIalAYw5kzZow0TkHKKGoNc59Xomk3pDdXxciA5sHf94ACRGSyfbVjVYv1TlyzH8aDXNmHga0b2fLsLjNwDeXS9A89uNWfapyqURWe2RNYgCkhdM0eP454SKzZyhJr25x1RPUfM5X2gmkO65hdmk+PpYDDcfXe0DYDrs6YcQjcz+ED8pNRoWozozTyx1Roc4qU6Ko4j3wSVWBduGiLwYuSA90SDmc73ENKVAFKXNIUCSUOoffs8a1Ww16IvjJ88bxkKZCkAEZx/t23r2TOJ6FrVd47t0+ia3LlMPbFLIpx0MXJiDm+px7j5G0PqC63wxXGmwxBDWNGTveaCY0hqpbglqxwSWvysFsJqRKc7xtWI3vTJK4KWXaL1rB2kWJ0y2xZOF4lL4NcF7PFI3hkks2ikWSZdSVRIQqwlL6draKapmc+43YptEjJuKs55V86DM1ULZT5bY7ZDEcVvDuaHqreDrMe0+RTBNBbENHFhYDZw51xWOGXOv7bWsb5nk6Q+v68Dn3Ox4dhIBSd8ZLRsRwD0f53Jyj5+kDbBXWdZ1Rjiq82IWsmStBXJJeKo9biyr1GEbqKKKJ4xRIgtV0BiFmGyZ5OvwiGzkn7nVVyyyNOxx58RhyJqdodGnKcTrXDclKJ79wY4o/duSxLoClKnFtD8ZN6zPFxhyiBqAzg1oOBc2X+UlJLMRb+jaczUgIi5aZhM0SNq2HHKgp2XT6V45x285s09kJcQPKVWbVZfp41LCLNo6GKCUXtJewjRhsOlQh2xYDmk18+lywUlLBPfbD49witxXpghMpJ+6f73HT7bQeIhVfB/sJxTThvW8nmbAtB2oPfDivaCksSyTIfPRQus/ZkIbBImgPhI+WEEncykheNxYXzvXhB0ADu4u3Y8eOHTt27NixY8eOFxweiYqQew0temIiu/iVBKhFNn8MLHcjwrepsGRIDj7nSLFWi1kTg0ueF2HJyjrU0ERxhTzoWBJSjj7Khe6YXKhwm0WZc/S1uIYG+lRWUcE0+oRGZi96luDS4tO5DZ0SYc1ZDYbsPS6oKDIaelpIFOrICltUa3Q2BQU/VEevTRKsKdvW5nMu4IlZBq9b8EfnNHgXXLXP34jsJZYwGZKSKcrePRmgRagCrWe3xTeyKEsvH29soMo6wusWJ1h1ZoY16HZK7Ws4aqZZm/Q6t15iHwoym7Ac01wzxMTq2YbUGupGHUp5CC46aZFq0etQuey7UhK3521KbB8OBZrNypd7w42pVOjzt3fsALY2++iWBW6dyT236mhK89zChGbOuVdr7mghZyWpU0ePYvXgVXcj17wikvB+Tp9p1LXN8zDnoG6NguWG0apO9bWmMZco2ej9C7WiIb/dalRt16ZT1jthJNc5YsAlKuRjzpnVlYRyfx1zOhLNKtYN3J3lGDLPUynIOZSF1Cvc29ko4lxSl4K1kPAevXpiyu16ZthxNUO5zM2oVtHspKHuWArnU4VedSp9vw+KYSbmwd323oUM3DnIpV/RBZqRhm6vxvrsvM6quppi6TJLw84btm3kZdA64FDStNPn00oz6MU3FoGqwk3Pbq+tBbW6Z3WXJVFTpvb+ns0NUsKzTGqQWxzjQS2xraHOlAU/SNj9Ya/abILasSPu23fGPd9ipsuQYveaIQupn48HFFsb1cbsLqe2tStOXhQjxS8VoRhFESpuAJjioqyjsuGwmMxpFIYjfukRcpz7rc6Kd2vGVm85p1Cle9Gh8JLjDTepcv881u1gOqtQuHNTtKvBxgLvlsRL73TKH/DEvY233e+qvrWiKpPeV0pCsUm1c42eyFGNKV7BhWY6+6eSxBCXOi43PWOWeo8yMecxl6nCKy6EduelSxS3i80cc8zGqJiUOCwFOuV53SptbZcZZTlRmwCFsnQfzFZcG6XFfniMG0za9OlyyRwtI52WXUrqNODeJuINPys+eoAOiSOCaRi06Jt3tFfdR9uDKvP+omRqNVq3iTmHtlzpTn2ikETZuhLdVUPTQ8OjEQhJfqcBT6Gf3EuawXWaOz6GcV2a7RNGzomima3z3c1CdGHwtlNvehtiCg4gTN16FcG00UYZ1SEhnK9uLOqX2TcmihafNy+aI6WhXIaO4dFIN0QdooHtIvogmS6jG28vi5IkTQpNzo12JYUd5BiZAYIgZE2XIWUWfS7e0qSGtGjimQZoUCcG/z16E/zyvESJtI4LV6Izq3VHZdsqq9Xp9B3TXUwa25DcPWRoRhk19GKIGVUVs9FslygHnf1VuFLbee6HMVOgdP6oaGz32C8SuozTiFazOD/GAETVLirR95tAAWq1y6DBHHtgUOVSEhqKrSO49t7K3h2uR+BC3fHoIJeF8xj42yqn88qdLo/89vUd3D3cRXzc1BNnGmUZ/WmV5hqCLnKRRT0smSmWoApZQ3iEOP9rk3keHpaEaOZ+nwHkW3x0DDbOLrj65OhL6KNeekxEMTW2eprXwHE5okVnj+PNoLX0AO7+qbGUoKICmCWS2ExQHZOiOV+CGhGKCNJtwZPbCk059IEXrdaYASRt9rSIwiJ6uS+m6EMavS+qIXyy9CijGazWuHPofZRJuXeurH3NxyQc+ny1vmggc9sldtMiZFug00BUMtU2kggj3steEXJw/4B6ctxaT7xF8KUpzYxWTSApI6MHaGtoEW66I+FPniIA7nZ8ORayw3k0L7dKWQVNOmcwtVoxfAa2ePRujFl6h7ygts7HrHviZscF9VwZt76DRm+sa+8BOTh1s8kNUkBLJnMZB+AmbDjHHtwH2ZzpwIpHr96go9sWI06qXwKhJJFAhshbOHX6GY2YBTZ8p7ZBahu3nfd/WxtnFz7szosiaQnkUjmdbqcUNX1kxphvM/r8hv/l6jx2J8/+w7qFD3LqNH+vK5ZkBohI0MSGLdIlox7+0PCnmhhaG62LltxulXLUKed/pyTOfY4iQDZDpc4RBUkFSdcDnWEzRccokSrk6yhBEsmNdewoiaDEWqX1JP4h5z4Yuj8ugpQcgl6Ev7SUzHkMwl4jWz2FKpQ+M2Ak7KP3afpOKdN8u9h5lfC9/JKAySok96Bej53pTPuUspDUsSHqVa98/4eERyIQknRRMrNmaLJoogcQCd7mKM8Qg0xHNkJzQlxj8FM/WOu2kdzmtGRRgXxpzqsW/R9Dgz65YC6U2TzflU1m0BF9LGlkM8Wp1cj9BE6a46D6lSIRCtZIQ8VIHasVmcbBObhMjmtKMaF3zhXqQclowpZe8Jp7QaJrJs0nnK15cM5Hb1OKk9SHWsvWKKXMhsDztiF22bU5h0LJuM68D64dCkhx7WRKHkosK5DmdPrWQnmljGoMCS8Jaz4zN+OCGoHLVkP8QKdCTAQ9Sx41pMZ5bZSlX2Q5U9XpiWyqxXEeXGD3iHCH8RGNgZfObIdgwVFpc46Lt96QreMc7JngcSj2CYU7riD5klQw6fMpTnHjWcoBrqquYCwezjNAZombliiaewPz2SL5Mht5I+ExKheJyCZOVUMETzKnoHtrSJLZpwJGq1B9CDo4zaOSACCl0kTQlLjpfSY3B43v63f55ZDBewBDDIrOIhx7maKdGinpnJru7rS6kroToCJsHiI0EDdouRoGmIgp6lwpHLlH9nDTUSGqV0ONiUysXzqwRLQbwL4fznC/nck6+nUS1tJlZoo5t+fTnJ/2WE7cPzplVHPM0TUC0TxEb0w4mU27u/Vfsyvxg/BcerU5F05rm9Piqwt3S5qJvJT6se62RkxZ121+X3PQ3LjJhcZFgAP3i9OHsDXDam/0XhZSSaSb+M510BB27AC2M1g3LketnJrNIZ0pZ1Qr1m+o69nQkpimBGNrGzcpU0c/szmnWmf15ZgXjDqVENUE88ahX4cbzn3fuCNdJCC3mBvZCwKidF95NPrGc9vor66Zx+/d53Q68aKbLqyi0ft9N/cBqsmR88qpDiGn1IejjgSqkctl1lGrK7U5T57iGvvl2xNsac7gcgfdHC8295M7LCmzzIR5qPpa7xJSh21byd2p20r0s2u3Z2ojAdRtpvbf0YtolyDT9xWCOXTqCffsghx09jJvWzRhH3JGRq/mKcQVWrcB6ofoKcyXYKuJczj2Y7P1vT6S3ecWie4hsNWM1pTlcnNCpZB6RTyLUNuZZjXUdoGtru80tw5rXb1zrCFmfmpnEsmkTzw8PPwV7NixY8eOHTt27NixY8dzjEeiInTF+AIXUla20ZciSsoyM7C+WshU9xCuudCykUVntSVJKINpHspzLWbo3I8vXfKBW2NST0RAXccwXWqLvqSh4CaacWRST85to7XG4TAyj5m6Rr/M4GyZR7lxFFe3GtSUpVdPKoK4sQ2Knyspp4tyWTOkMSlhUbqxaw3V6IXqNAglxSRfvfTTKIJccXNFY6bJKEopQ/p68IcTYnVWV7L3WTqjLWlteGZ+/6V3ppeb141S8lTn06QcU1TGXC/TlpvVKScbDNVLT4VLZFVHdaaujohNah1utOaMGN49xWf6sTrdB8Q5jIqhBE2y6HWWPnqrxrGxzUORb/RbiUCS2d/VJt9xx46o3g76QvMGSdnqhRJGs0lPNRcWYfbvaImKtJmQu0TpnTuKi89KrqSQtPehRFYc7b1HAGdf8bVOW7E2Yck+s3rmlXVrkx5653jAq/F4G5PgleWcUVeGMFONGjhDL21RaFudMzIwZ13rrFIdjwlFOCyxDalk3G32QkWfkyJdLnvJMR9sVJ8PKbF6A71QlrGQsS09s1g9ZqnJYWRgFVvXyCYD+c6RZbnI4J9tQz1PtSpRYa1tzoNzN+6hs/J/I5CXzKHz5dvqSA3qYev7urFhdeNm0AmKktBJt4vJ88LW5bUVRTx6umK/FDZr5F45y8eEVKHWYfAq5+1MmnPTCinH/WjtN8G6Rk/SULBKEn1ntavDNQpFdWZYW9rt1Y4Lmq7z3rdZZpFeGQWWteBqU5JZk4QPcx72LO6Sp7NxzL1XhWBMjH7m+7YhzVmuXBXzxtCxV/GQ3h5z+xYNydl+TanQq7ajKS6qItLvu5uubBjVCuftPgDHknhxOZCHmqOHkuZwJFxbzAgalPlB9x+tCUSP4Z1+7R/OjXvnbaryeu6r6ZJwuVr4XLlx6FWlrETPt0alq5QbTnaeLRpaNSiy3QY6hpYj0itGmi493gCH5EhSbIxYsdrlqrubXj1GCvRtKtnCWguT6tg49e2Lz5wbKJdxIlsxsqdpE1tzqlfGMEhr0T8/JcHpfdg6Hmu8tY1+VI82EM9Tcl0NbvTOHO+AbmBXqoIOpso2evIfgQL2IxEItdZo64U6JekyRCp1vfpxvhgWO3w6IoLUuCnLaJjPGo1ww7FtDu0yk2cRpVyYUDQZ/TfxWFMEXuPzWRWTEA6IRTiC0Wq/GeagsxyWizy2GNGEO9bdHJErWWcPkcTE6IVpOJltzgUyXHRKXpcu6T0Zgp7JReca6xbUOO39BwOmc+JS9FfZZU1CnIwjyLzRRCoFGXx3iZv8kCH3pQsVjB4joDYPjX9CmrG2jSUd+n700JBHLnxhQohgzmTKGsd2HG+6CMXoc8LAhGPvA9ia4ebzwsxeoJ2xMRehBL1y7QYxEUNqs173awWFcQZfFg7toFvG8WYa4n2Q0I5riMV5D0SQb2NCRjj8uQjn2zFHJqNZGO2E989nyDFbYfT33dwc8K2ydee5dPGVYfOSwOo2+3VwIS+KjhuLVIzDnNOxbo3TuVFGV60oN8thJnrU4HSupOTku713ZYOz1Wl3N1/DRo2exUNmNdD+JTdp4ZAL5c5l2LKfMycfTf8he3/P4sbcWjTM+lXAWMRJorNXYJMIRMbl5h4JjiFictoqajbFWFI1RG1y9FFhuRq2fa4btl1kx0s5cINRuyNxcsNN55iELI4lp2awrhBjtZGqIMNpUyWJz3uBZuX2dGZtg6O/cFgWbvtgR1XDm04LkjWR02WI4mqNe7dtJt0OB6GUjDXH64WanVXm4EEH7hwWnuj78tQ2cpPL7KI9DtpxhawpZs4QrR8pJUq70EXNmUmXXITmxv2ePlUPyXm3ytYvvJzB88VfuqOgUmj9BnrbNrbWKP2mflwSh3SYjnGrFVef4h9iDprn/EHzhrtjw5+TGFfi6AxsTpuQqTzRg477rSLiHPt2vqjcoMlA+qiPTjsbzpD4O9OPcxJM5ZI0qSHkMvqhkyokpdKoQ/ZZlYZRa+8zwnks3cVu4vVqa4wjGYOwbUMkIb1fUFzm8FmAtfWh7sNhUyVJucz4kY1GpQ5KNJkzhm0bhzxshQKXOYxba9HuwKBmH2jepkiOmyGJmWQrqRcl8jAiMYKFae+A5px732aTxlELi+aL0ITErLyLIer7cfRvIRiXxHR+BJqwH4lAiGZTBS5lRVxJ/cBtW4vG+aEqR48ox5wZPC5MZwZCorlXh/qFVY22waG3nVRacPQHt1wjWziUyzSBo7MSMJrA6ui96YpK43xNKuQkobDWb4jNQrnpsqZwbMYgPnfHejUDYkaE+GXir6hSVeYQWPWQFxhNbWaGVZkO2Noaph48/LFdBiI2FYqaeaiWDOU6s4j85zDT6LcZMcvmMbhvTAxORBA1T1uNjO3oVWgeghNDq1+b0KoSM7jGdjeyFySP7HX0GcvMJjnS6uzPqdUQF7Z6CUaib6ob0RQRzXUXj8pF4MGaseQcSjmDJ1sBszkMUgCXC6dVPBoptWeij0thx46BCP0HBzvjDbxz7i0ZkvIcZlo0FIhkqLGZs24tBD16SvSYldV0zq1qgG+G9N84ZuWQuNxoUqG2xu06VmS41NkDt50NQWfyoJmR0Xndn+ptJBs8cRzJxqTYE8oy1e9qVLUHv12Ug4XCHUB1i4bneV326nTPCi6a+kyveFWpmMilh9KiCmx2dcNsRl3rtB+HQ0FTpvSAIFtjc59TzlNWFGWdTABFRab6Xt2M7Vw59Mz0Y8eM05C+o7ytrFWoZdhUqNvGwZ2l7ztKZkke9wzC6phYZKAB34SiBeuqcm30sPZkkEui1W1WoVJOnBx8u2SyS9IulhH3seRCdaeOqiJCSYk6Ym8Px+7QU/CmIczTbNjph998vOPRQVmWObNT3EFg6coH1eEm+5Xv7azVKRq9N60JORubCben/h1t6+fkKO9qVCT7lxxcyKTLYPfVsbJd/JBqSI6B8QB4JJ1tehYe/tBgnnTPx67UYcViNpGvo+9EqdlmwkGKcUfyZH0kjES6yqiH45G6fbuzZMzh1Aes3q6RMClDiKVEgryebc5vs9q6QmcPIkTZOLO1IQoRTJOxX0RLF2m6iHrVxFyjNsOMuR9SUUwamvrAe3WEPBX+3BpGqP7aGutebo6YXpJmR09RkJoSfUbKwpU6VQg29H6vWlsUAcZ+dCEXnX5nFrB8qTCJZkCDTTN7gCKYbT2Jj6UuKtM/4w7GFFxIj4Bs3CMRCCXPXG7jjlSf0ntFI2ioo7qDY+4z++CpZ90EvA3qQIzPHG21zSrNKsu4EDFEdN7UFaVkvSiKmHKuPql2IadtUy47JSjpUhnRpCRpmCj04X/JhfN6n8PSy6hJqbVx20/QF6fCOV0mAtOi8W5cVE0yx1SvMs+Ewz8i/W2Nys8cGGaIBL3LuoER7zPIp4S3kvWSnTQclchqQGSEs7UuyRi0NVUnjwsPi+xFd1RaUbImxh1aaiLrldaKG9IMRDikQXcxsDovLCXUs9o4vuoghndnJ0vPJA+VrpwRdDpULjaHFMY2++DDxX4yQUegNbI92quMwwCp4l4mlVJRkjt5eedy+o4dACmVy/klzk1W2hyD3uWbe9CyVSM1vUxyX5Tz6uQiDKXXU40b1zjLkqTL99DlmfNFP8jNqPdPsxq8pMK2RvYPCIpZVu50haXT2jhRWbeRsCi4OHeTcurPLYuQS7lQSKSA2gx0VBJIm8MBjzcLoj6lYosJ1TeOnWuXFDwJ3qknsPFEO3H0CBDOzfAGRX3SWpcktJKnYmhOwmndpiplToqmw1SfupWVbTO2MT1+CUpr79FmIdG2NLcJbTSBtQtbJE2UpavQEIOaTxUkG3fLpapda6MXtmibR7DbnaEsmZSEZVC1q3XHrlewTbg9bzz2WLx+ONxQ15Vt68Mjy8KL7i4h1kJUGre1srrM/aKmNI/qOoTDtWIsOhJaLQK8/vrmD9+x2PHooG3bFA9aNJzaUQFSQhZaptBU5VwF6c53a0GPT1k43onPrM1Y7CID3aqh1qYggyRBJNP6EM7bZmxAGuqyOROMqkFTG/SqwQpSJCnqY6Dwxtm78z18GTNWNUoPjO7fv4/VzKGLU933jXoMLxCgSOOQmA39IQYeARzAi26Ux5aFx7vYyzuePHNrlbVXnEoScjPU+8BZiAxuWmbi5ewrYkoZNDR1Wms9wQ05HXFsKo6KCVp0qtO6awR7/Tqufa7tcQhMAdXaTMI5DZUSw+GHCqU5tfH/s/euu5HjTN7nL4KklHZVd8/MLgbvAnv/t7b7YefwdFfZKYkRsR+CpDxzAW8XMBlAN+ByOlNSSmQc/ofVqMGNh5c18bnCKF7RsU6be64dY4nMQYQtqFypmjnozIWH8NQZs9kNey24dZ5jvypVaaVRxwb3JOksLKpJFh4rrfraxf6b4iWW8IpXvOIVr3jFK17xile84n9c/BITIZF7TBoIqQo48YM1kXN+SxAGo6UPlOqUIoTIgnQ5gRZZ0LYQ2N/2ZWxVi1NqSVlSIIrRQ5la1vk+QZnGpAWIe2RZiw4D0zGN6ZbQOmxBKKoUHtu+uiZJaAve5mSEGLjdcQwePAV2nSNIoRML4pWWZrpEBkJrEtVGJK0mx7STVKvhOfUalfleckzbV+dFErIzsejiPHvqwEPeHOmnM/CkkZMYH0TfVsD3oI/raK6U9gWmJlBL4unviXRKSk6PE+udqGWdt0QQxoL3baVA8cUJKhV61yRjjtsk3z/WvSQ3Z5KK5oi+zBE7A6/jN89M8vOmT0eQI2rOKQ38mgi94g7rtgygH1uao05T4tOF59mXIV0ArUH1OREauHCLMckkOYdxi3L0sLxXJ4eRAS2dEF2Hwx0dcKxH2fg8PtYzsbVKaV8kVEWw68k1u6PaqEVouyweSg/hOI7Fl3krj3wmRpe31cLV++IlfSuCb4WPZ37G8+y4gZfBLZAtfckGFt26se2PNHAEjudn4vSrLbnrtpU0gh0dUJHg53EuCEVrlSYwLi3NCr3BNsjEreTxHgMzWLSkOMX0MvpxoXoL0hRNyPE0S43ropWKqtDGdTCHfrD4VV5yj7IvP0NMbnlyOY9OLXPKdKXx4lgz/eqIxRJTaNV47O8Lfu1n+o6kovDcO4a+8BTWaUo/bVkvSKTozeRGvbqbr/gaaVs1chWJAdOfUwnj8kjODzkhIOS2s1ABV+pWqAPt8tg1ifx9TmySL2SDH+iW1iPzOXPSYqBPbGd0CrKQJqqFMFseQEJCtyYqCFHa8A6UMQWdE9fp31aAn8Za8w4L7LRlP+KaYgfb4gkrErFylb2mSMDvQyymifKP88k/fg4Z/M8L3QqiBZsQet0QbPEq3VOUaeZfmxZK07TnIDk93YKY50UQHWIaXmqmJtNi4OoJL5u58VYUFV10CSdSzEL85j/Xyi7QmBLdnY9Po0zOj6bH0ETGWfoqrHV+r1u+ZnLIror1Y/HOQxUUHmPNtjBEMp8uc1G0zhlOG55x6XogS1AISV7anHwty5i/MX6JQh6S3r0AACAASURBVKh7Z8owWTI2FpFYiqJiy0/Cu1D8dl1X0ZGUCPOOdEney0yGc2OVBekSFA9Z2PJmMfyLRlIgMsh18/0EXNjXxiRJdGMeU6rMaZE1ci6l0QJsuOcefqLaFrwuQijcrsLPcDpKGYmDDzW3xRuQoGr5ogBXMLe16RWpaA206HoQF55/bKAPSeGDQWfI30csrK/AgrIB2Pz3qcQSg+Q25eH7SAQmxDDya1xwv6rUWpLbsPT9ndruTX3bcgxuE5KDU+Um3qG5wc+FuY9yc179Jmk06fOgyNntPCeXhO80h2vyNIg0ChufoZH45lVIa/pEzWSo1Vdq8Yo7DFsYa6VwWl/JfBHNZGLO/UOIAj42Ir+CvSjH5WxT8KMVWtv4x5+fQPLiosmCM4RBEVsNihLKWdsq0H+60V1XBty2RiU4fubaU2sjOsvzZ5NKrckHmEqJVgJTWRBUO55YLdSxmbkZYTdu/8d1sdfHanCoQKkb5yDRbi25Bv/x14CRePB919szoz9RF4rWBc3V4Sk0ycBacr0pZRY6DcHXeRw9k7rJ1gwXwivnSMiap+/Hxyj2/DKk2Vq3H63xfX8sIZerXXwvyunXgiUa6Yc0z7MBJrqaKAIQrKZZKQXZGueVWLqK8ICVBH58XLztlfMc0BTJtX6mRme/UEluJsu3biSw4zO7j8R2noiCjCZUnuhcC1/xiuQlz+S6RzZK7u2yctl1w9QG37asRLdzPC/OftLGGtYewnV1rikIIhVtZa0d7lB3YRu8t6W6unrCkbD9mTcTQKzknHD8Wo8YocKuqabW7V4rxAwb/N3f3t7x0/gYwgWXBXHGgtxTy39puNdakGKrsaMoXTrfpq9a22nP4BxeXc+j00Mxs+Xzo5om9rOoLFIoWtIHjsEDLIFMVUo1VO91uNaGmi6VOXNPz7jZ0BjKdbrUQGV83riOo6ksUtY1dj8pRW5z26ps+53TRRiBsw21T+9J+tYldBBgtxlqcHFaLOGoqoHWL1yrUIolCWWb+1Uon2YLut1qA3H6Ne7B0+nqy9to0ib+zvglCqFadRHuz7HpLNPP85NSy+rAigobwTlBjQEgFFkDnUEAk6VaoqJcPRYvBRd678TYnKxlXjO/OPeUKPXx5WtRKJHy2ACeBq5zHqMEUgpVC+eUIQyja9xmpVKI5OeNvxkPxlQtcRnGiWMq4U6PWAuUDt5AGwT+3juYLwK0tMhuqt6Y08uyUzgVjQSlabkXIMvjmxjX6yQbj5O/ExPvu1qPRNiX6yLEJdSRqFyRD9JUgdqLJr69BDHIBWFpkDsTMBUh3JnCTxUnoi7Maq0pnz4VYePp9N6XlPm4Ke6FoHt2wMdJ1giaKAdGifv7D5dbaY5Ug5y5a9HkWEz97NmFesUrANwr15A2rkW54qJNQQ0TyulrYlBaRV3uaWRkQ+OMvjZMCeMhj1XoHBy0qLzJUHQTJdTn4JZuxnU5fUjRtS3YduUxNtiyFUq/uX5Pc07XRa5vJTHem5TVDNgq2P7g88ef+TcOGwKPoSBpgg5p6TxooT87fVwHJ1WeZBxD96DEPandW3KKZvOv7Rt2OVFZa8G5FJTG+vXZc9Nl8mcuLsupC4B6YBHYaA95L7yxrUnb83jy29u2FJUslM/r5PsQMqjaOIPVqfRQRAMz4Tn+TTGKsAwEr6Pj5uxDn1+LcPiFDI7Ps1+02jgmsXyaw869iFzv3h/5+rM7f/48UhCIXHtToErxWSAOMZ/JZ3CMordRtkSu+/M9+vniCL3iS6gsU+EhIbYaj4kguZVhVQX34K+Pn8Coxauk+uXMjy7QaKmKC1x2EldddXsUyWnynFLgdDN07rdKTgXmpMQFysrVs1GJUUYT5urGVdNu5ByKbQVhLzl9B+ilc0a5J9iWnO4YTZHey5gi5TOzb+/s246PIsTPbGbPXkKP4G1vfB88S+vB87rofk+Le3dK2Rb/U7Qkn9xuoa/rMxZ6ad+gla/CAwXdFB/ndFk2sst8v8g8cH53BUDLmqRc/RpCXXVxyU+7aKps+/0ZIrfYVMTgVPdZvCWneuWyW0H6jciRCnLe909Yohm+znDOCAyfemc0ct2/RlHau6fww7w/VKDoUg08fgFO499fir3iFa94xSte8YpXvOIVr3jF/+b4JSZCrjXhcaT6WS2FNjtw/aL3jg41kMde+Hl29vG3lyfOVfSeXKjKMOabnI/E3bdpUIhAnOwTGqXJx5l1sXhOWibcqtWKu09l2OxcBqvTmHrvOaWZmmyuOSqd3ctw4cmFTkkjc7oH+8RRqg3I3px7Jg73lpB0kEBGt7OIIF2+dBpTJ9/clhdRGsMaw38QU6WKcD2ntHTQ2t25KVu+2+wOecTC6+ch54RKlsKb5n9LBjO7kdO+5DwuojhbbFgZ3c0As0LUvJgfPSEfbTYFig7u1uyKaHaW5wQp0iQ2yq3E0krhWpBCBpZ4zdmRkp2P+d1YaHa5ZpOsREIW58BojO6nmtTELr/iFQBbLXw+J/QtKNTF+UhzOluT2r1lt9VG977uDbuc1hptyh9758f1iY6p0kbh+XxSNO/pbXuknP/oyl1nT27Pla+XVnh/U+LI15/dwIIBsMJ6x8TX1KJL8m+ksnwz6PmMlImbRXD5MiXF6Z7nDglZvo6+TPG0VQRfRqMM2Ma3t3wOv71ttE2XCt3bVuma8DydVIBa6KWsDqkjFFlzfILgeTk+9oq3WkEabRgcPq+TP69P7HN0O93xrS1z5V6Ep5XVyf7pnf3qC57cmqZPGcE5YD+lKbUJZUyYjxLYBVom/r1gV197SRwJ9Z5TcveLTrBNT7pWcZU1/Xua4h8H2/fBu9wEQtF6d7ftafS4YYwpAwwuozsumsiCiS36BXw5XvHrxGOvTCxciFCNlW8hyYdZO5yA45TpH6ZAESKE8xjTF3FQ4a0OP5KWVIOFtiuJNplT8LzVv1AX8DSAnyifkhSABY3T3JOX12AY3ZyqCesDUPdha5Ev+riCkLL4JqUZnLc9SYTQTdde3sNR3dCReHS/KC5LRtq707Twr7/9AcBeTv78OPhxdPpMqEJxTsLf7+tiN7KIUhC3pdiXxqhKDNjt5/GJbPUehZVK1MHDIbnnh8fix+8iNLl9Ik8O3Hq+fkH8CkYwEMr0Lb+L+R61CHvTNUFyZSkVAxyfT1TrLfkdglYhxjinq4PdipWG49ZptSzYYZPCXip9TPz6FcgX6kmtmhC7eR6/gGH9r1EIdV9E4K3kePEciYMlLuAmiIUQJsgkf4kMT55YsoWP2rgErumkjgyjqslDEVS3meem0an4SpSniOxKvkkZxL5GeGnEVccOG1bSQye+Gll1ipYl0NAdqpXl+l1VMWvLaPGSoIRzzWPyhNCs1WD6VjynjLQMHtR9HTwiPSymK3Dkv9cBzwjLpWlCMn2aoy5xhIGpXaZijm51wVvwSEnH8dy8FyFE1/uleakzl8TelfeWrharzomhMT/Jxmc+GEz4ip1cluTFfBMhLDjGdfvBBSV4m0WtJm524ZARTH2ZKIYEqbopi58lKjTKIiiLDpM4nwVkSobeZChe8YoVWoS23xwPLcJpsxByWlNanfyyoLvyvCbkFVoFV8WOCVfQ3ExGXhHlTBn8Kd4SCR2dxdRxpIDqtjSbYW+N59jsnh8HaUKc7aJH2+D5xAdeq5U39rcHiHMMaMl1plT+t/0xTjITmfmMXBF4Db5NnlJRjtrpx4C+SbC1ez2zaqhsbKOwuryjvX1p9ARv7wNiOCF9mvYAzym+ElkwTMEZLSlNHUswRqgFjjPd5rftwfPz5HrmQexbw7qzv2/jGC6+PeqyMvfrotcvLhYqaaPgdXnKiTnubfGWilaothIFAO1ywzui0fuxGnk7OxGs6xSRROZzSH5fPRImOP6+MkwdVW/4b00vteWSooGixEBjVslEaMr6xgvK+4ov0fvIJRjQN/ElNiA+cp8JW0LZi9w+WWR+Zr0jTFGTDYvbfFmlUqWsRk1L17CVCO+PSpUdzoEXDWeoF2UUycblbFxrejPO99sfmo0VL8kXB6JsfHpfCX5JRv56tonIvX/yc9ww6+j4/X/ygwjjn9++AfDt24OfHz+4xjpdWsEvz8YE8BtKK2+E/+DpM79J+N5sgrEFRSoT/1ulsm8b/ZzUhGxK6cq/Arl8NZJVIq0PdK77sGtdtBAIevQlQvDYd+zyzGfm4MAuosB1TJ8yaMLiYTYKImUVU9eULp9UBJW0WBrF2XUZhcI28q1tyzxywv8CR7TQit4Fn/iA+I5BQothvTKLL+dnN97L5Erxt8cvcAjk9GNtJIZ+eUgetWIFdKjuXN0QCSbdo6gg44chjZ6qKCZMkQobjkLzdqoli6epyHZ5H5vJ7III9lXprAfX1fO4SB8hiVhcGe8+HgCjyxwbDV3+IXFk3dMsdDr0arZbV0e1KKKFutzig1KUa2x+ibeHmLwVav5mEutUCZ83243glFnskIm+4sgAwpoZVpa8OyCpfjfV9hAwX4UUErw3WQozVYUTWd+dRRBlWyIVJlcWE+7oEolIhb71fVvAA2a1cYWztZtbcJoxTKDzPD0L5Smm0C2v61w0EU0j21U4BxWBMHzcJ9KU6KzNwSO4Ootb0EpgdvtxzEngK14BcP482ZZXV6R58lcFkQo2CnkT4U2Uc6oZRVA177XPa3ZlK6d3fo4E/lEr21bW5uVn+onN/bZHdti+/5GFzunCx9XX/b1tikawzzGrBlcr1OmDVrPvEDRirFeHpxdOfRvncRn9cPr02CF4L7r6MlqgUfE56VXlPC/auA61FC5SaQlIlbOb/kMPpxTY2tvCljtC70afC/dYykTuD22PLBwhlw572hJTeNsL/3gWyj6NhISOMPKQ5ClV4RxFCf3CjZVouBsqBUXSE470lIPgGBVedWHbdHkZTcLy9Rwt2O2i1MJslm9UugSfg4tQAUR59jl1N8q23clRGC6BCV/8y5xa6sLYmxlhiozuoAhoFX5+joRLl9PuK16BfzFnLlXwqvg06w3j6bHEqFoRpCl7malhNldN73xHJRvS53gmHqVSCpzPqRCZEySbuY0potfivLVQxP1WRWT42XzloSjpZUYm5SKBxMmu+WC5Kn8F2DiG3d55cq3mNZIT5JkEmjghQV2NZ+ff7JPnyM/+9fcH+96oksXaadlAlbFmbq1SSlDKO8dAA/zbz08+ze9pzBXIw5GRR3oNnnauoqPUStWyzE6J9NdZ5qQC/er35GxcI1tF6RCY+KKm55554UT1VEqax29jfWr5l3PhTeNaWw168SkL9lXh7863hEToTORAkZzcz4l3E8EGwXuKSJgnOmoWU0VKcsymON74zKVM+PcPhF4coVe84hWveMUrXvGKV7ziFf/z4teYCFm/PTUE8C8zDU+VoCmD2JuN4cGcAml2ECKhFJAjy7jiHtXVnOLoFwfxMF9yySBYYXUstlags6ApZ1wpFV0HzlJSIW7KIgqOhyNV0XFJl0DJ5NMUwGLhYsuQ856Vdq0leT8TxkZQVJfXUSstYWdfeCwpHT5PQXEZw8elRuV0Y8nL1qKECzKuS3YR5L4JquaodmF5A+KWldbxv6nw9vPqiIFus3vqtAptSqE72AVFY03tPjE0Cjo9A2qgEusz3uoGGozmEnjgpVN8djByzD+ZA+EdV9gfc1o3oJNT0ntLfleCYScERwhhdZ5nd2xxzEI4PJhjyanu9YpXAPy0zu8DdpYu3MK8Xa8zFXIeU4mxG0dc+CDCvEvixC9LTgrAcTohjT+2GzZ7aHB+5H15Oum7NTqJiqNbSUw6IKUiCtdz8OZaoSLr/o6W/hnnOTknFyKFbd+WbxBF8FIWtK2IIFWXbOpelVIrx1xLLHA/mZSgWpWPq9PHtPihDekX1+x2aq4j87qUraWfmPiSlo4AjUrRqZTpxBXEPmGFwT/vj4nc5a+PD0R1eYWYw9vWljrV8+xcfuGj3f3HtrPVnfOYTu3JBbQJPyjpk3aaL55ke2tYD7YxZCmb8Ch6u6Jj2TmuN5zFn86UudweOZEfze2cPtvt47E9Gq3E8mh5HldaFHiszrFE8P4t1ncjMiwJLP/mDEfFl9KTveSzX/EltAc+FbrMUMk1BjIn4PSlsirDv+wcil9acl/ULxLHwUFYLFXVWnbqti/J+evqY1oxoLrPE9VYPJNDKipGnaqIKFLKtDsEPKcSlsdwmlJL5du+rcm7cRIXxFgM/r/zB6XIF0iyUlxX/pWa4ECZkw+IU/irp2VBxMX/+fs/Lzjx9aOj6Jo4FU1+0bdt463cU6bjHz++yP9v0G1NQghJzs64Lv3s7E0Wh6gUpautiY9GcJwX4XOaIzSR23fIEim1pM63REGJGmV8Zo+CIUuaulSlW6cO/JlG0C9fUO4iNakM0zJlXJ01YRJBTOnznAxayFrvdOS57rFQPhJD+W9Rx5MnNZU3tybsEsvDbk7H/874JQohiVg8kwgGefWGZGAdmbiAXrDyxVNDwEW5PJbB6emdOC35RcAbQq2yNnWLwQEpE4LhCHXBtyzSJGvxWDQx/3MzU9VRyIwHwgKtTlyFfYg6nPXEPShjsein0bQuvwnRoA3+DCQfycPWeFg0ZVanUaMOeJhPY7RxhWThMjMhyx12EALtQijLB0cloW8nc1RbULkLG40UXJhy2mXwBFaVEhBFsZFQiQgavqSti0756yGLaXBiYIbb9BNRpMUai2uR9eAAaC14D9r0NxmiBWstiDSilCk3G4MvMU0RI4e+WleGlqN9fMHp3FOIYi7+TVP+fJY7naBLLINVX9XmK14B+16wIc4RJNRSl5fELXmcUTF5rmaE1yTeX09b3Lzz6sNIdJj5aYq7TM+MfkVKs36BrG6PDTun6EmHYpTlT1Hp54VNiVRV9LKVWHsUoneu8nPxb0rJxswxcP2PVtlq5RzE4GKSDQkbz1Wp1MfO54/nOuailWvg967dqQjHKMaagrS6NtS2Nwxns7a81oJsUE2jRZc+8Og3BOzgyfZIHpNcwtbq8jfxw3OdjrE2nMImwXRfKyTpd/miFcVLJhszTAP8TgTME948el60Lc27r8Un7FmkTgPwKkNUJl/vGH4q21y33THrC8LzeFTUHZnXfdu5jgu808cGpFE4DqNPjqMkRHGumZcZ13GlJwhZZL7iFTN+2LGEo1TTOmISM6I0tloXNzlIYv2Sc5f8Vw9D5nPpAZ7QfQC5TlSEvcwEX0CUY8rgdwP3+7k045OLNp7Dbx5YcdpoqG6iiBW6ZFHSmrNvhW/7zsfPH0CKI3x+fnBMAy4x3v2xEvzj6jxarIZEXIG6srfxbIRyqS8Bkj+fncP+5LdHrldv9YFYv2WkRRBPj8OzzuIo+OP9jX/8lWugmRG90/YJG2t46Td/1CwFuKa1gm6U4mudNnfMbDWnqlQetS5z1K6a5vULOie0klC22RxqYpwWXBN91yu9xOIp7aWy7w/0OsZ5Ka6Cjzy1mGcOOf0rDa5yN4mLJpXk83MMDapTkKR2TGeFiOR9ja8mzNgovK1Gc+EKeEYWoU9bXaW/LX6JQsiFpVYUFlkRT7xoGD5U2QB21VQ9WqahjkVBVLl8Fh2paa46yVk5BVgeh0M8QaYxx+hMmk8M64ZEv52OJShaqKODW0oKOBwD9y1S2aVxKoROXGzg4YsH4C5suyGjUDJJw7HpuxFuI+G58aLZKRjJjhuidwGR5Y4nUJ4sBlNnXrjGxi9FCdebbKd5sWf3QMXBfSUaXYQqd1FamnBa3H5LrmyqvNfZwU3ich3HdCpcWD5MMExnU2FGZSr2DQ5XzOIsOQ7zRrx6Fjczj+wIV8gSLDARdtFVtFZpfPZrdU1EGUpTA9srFS3Ch/eF8w8xasRSmNFaCNVc4AHrF9pZqoHXMFV7xSsgmxjXUFC6gN+2x1JT+7a/0y/DJ6GHEy3lXnsu4zOCv54n77+/AfCoynXFWivMhK7ZgAEo6uyt0SfB1SwnKlMl7uocx8Uf34dSXRU0dBUhZsHToM1nUIRTlA1d3jQEfF7nMgfcHi2nSHY3HFTLwpJ3N1opPLa38ecJLBeZynbG/lDqJDMPL7ApCnBGego98QXQfmuNM27ugHsMQ9P8+XhePIA6pmt7bchwSodc76roMpLeW07d9pLH+PFhuPxFe0z3eIFSmHIJV+9cPZOjNginxpgcr8skmN8TI/XhObcmQsFjuwuf88NxFbY5pXoGIco2ihWNNHeeKl57U7QEZwjOnXgefx23quDeUjxhFkYle+utjUJ3ymG+4hWkKtzcT/eW5vJ9KEhKOGd16uDedOu5/0+vrppNEFFBljLmhj06z5Hgf57Gxcm3ISDzXhoXQRvdg5/lpERdudFl8PCNc3iQ/ef5k33f0JifqelDMzyA3lSopfH7t/flZ/MzPnlrDZ9NV1XO+ER8cIhC6XJQyGffriO92OaV0ECkLH6K4RzRaUto5OQhX9fHziZwuS9lue9vBdWL5zPzg8NI/vMxuZ8flFp5exu+ZT0RQH1pH1iaau9DzOW6+PbY13MuCFcY8oWPI8M7LU9SUvAqZDWfkcJWM/cEML/QpgtR4+aYn0sN+IqextbjtE1KImRmc7tk83wuKSUi+T3cvCBpyW9/TPEe7xxuTCK/hGBR+Tn2K5WLUhttivno318IvThCr3jFK17xile84hWveMUr/sfFrzERcrsVJ8zxCV0DYEwc5rgwUi4ZubuGYCBwLInaoFZdo9sqOeJbmMWL9Ivwe2KkcWvIS8QYXeTrS+Tnr1EwqWa2pjHRh7rSVxxtpG59z1L78VCi3prxElBK4bqm0oqlSshUdtp2SthSL2JgVOfvlUjJ7okbj0BK0EpdMBwt6xDHcQuucWNMA3D+i+Ka7LcvkJlg17Vkw2tViirbmAgdV9BxfHoOdEt435dxchFBpKBTRQsH8dtzwAHzdZwT6/51Wmpmq3NTi6DFlnJU+jvFcinWMTw6p9LK1Smq2XGdk6oiVJGl1x+AudDnRDHSV0jnhJBXvOKOq7N4KQVJyOuAYEhL5cY//xweQC09XuYzdXTHBR5bW/dX1fT2mbAy2QQpjW0b0+PjoISjQ8o1zob2Cx0QVu2O9rImv7VVwJa6kbiw1cKjThWm4BnG1ofELPnMOImBh/QUcjVanR3WTonCNnDefx0XLVh/f1nKOy/1vIDDHR2T/lYV7XorS5nBQ2k4fWLstdEesjDJj/rGedxqeZs4/epcE9/+2Nc1AwakLtZEZNsrW93RscZ+mPGoZfkGVRWoQox94zjTub4VXdBrPGW757SYq3Fp8BzYk70UHntb6IPnxxOvdUF3P39+0nZhq9mZru9O7x2ZipXinNKXXHGJIR/sQR1Txk87h//c2K5FOJ73mtjeldZyCpjX9gXlfcUd//JP39aUtbtzHUYMONalnupdk/eiipuxWU45zJXQRJbMPby2zNPs44Zuer1VeNUTBtbHc9iagCoyoL+P7hjCYxAMw3bcDB/P1HUF3oOYktDeeTTB+idBTpG+qfL9n974PtbQzy5Uh3PAbHs4/0f9Tqk5dfi3HjytLzpDCdASN4coEpp2DJRQiBL1CWOaXGNA0FQXVWCToGyF8s+/A/DXx8mfV3AM2Nlfx8VbCG+PGzZ7RU7YIKfsErLer1XNw5kDn8gJlI5pTyOVgRelxkdOR6cO2KEW2LTxcfzMl0gQ55c3LYp34RxQXFWhlBsl5NiYGuXLqwrRYh2ziiJuY48ZcuwR2DlZstBawQw+P/O7KChSrjV5L5pc+GnDORVY/874JQohRXl+DHnRUkgI6+CpuGByQw0OTUjFlOzDBCkp4TfFEKJoSpiWyRkyig/sI1k0uExww4hg4eW7dejGNi6PbXmMs8CIcKwv9B5IPngga+ToGmxVmXtSVEXsThzMAvHbB8jHTV0m2U+cT4u1AWvtSFFkGLI6nbhY+NMqwptuQ5JQx3soWgyd4gWR+ODJU2qiHDLBLoNLCCtRsLAcsS7pa7gk4RyM1wl6G2d1oYcwlTd1aNI3/BbDIPHDy3OML6IWJLci5XLvz6iiq4gt+QKmx2kPZyu6CqHwHPdP3C21c2nhcvtSXBdMb1lKfxqdWMkMkSTSNQ7W1+D0FV9Cbkz2RuYQUwq02EYtxkdJbxsN5fM03sd61gkeAuXRbnJxhzdR/mNILsil7OIp2gJ4vOGwii3ipF8KOnzSRHjflO+T2xephuvczYGwAUMD3lohnhcfl1JHYoFobnLDALXpxmUn+yiEfhyG1UhuE9DPk/j2YD6nboaboeMhe687Zdv4HN427gm5ndAWenamZHhnQBaCZavU8XAfHlhR+vA/6tah1WWWLNeJ9VhFB6L0s691uTTheRz3Oq0JOVyFkEhCc22SvK8UUJAUkYE0p63ltmLQGoT5bVItyYGYHKLHVpAq2DQ7rcntOiYshKC0oAwYyXWlpcICL0klPDDJggxAT9h2WZCYbpEqNHP9Onfcs0jM++nvh5q84teJbgcfI1FtZUtbiOWbXHDrPD2Td9dsJNu4P2t3agmkG4zCpG7CRaUuM9JOtUZc+cz8FR88n87Q/+D9kQInc08+wvh4HrSxJm6yc17H2o+3ugFCGYINj6b8XgoFZduSH+h2cZgvKfytaib0LQsXR9OCYHA5t0elRuHnmefZo1O9rOcuMw5b7xdWkKr8/tvkXTb8eVHDblisCFKU72+5RtZW0MP49x8D4nyl1cIUdGhNoRTq2+QfXlzRlqiERnonzYzMQtlKioEB/OzPlLceOLYIp3RJoNqyGznTnd7neQXUWBLeUoYHUEzKRuFA2GYDy2ztH3kMjvbb0D40Bwh9FK061soIwVYemFDFOvhYlQLab26mpxT7NU2mfwEO9i9RCJWii69hI/mfHJIwQ1SXSIBqagDNS1eaUjbh+XT26cgrKWiw/G0GL3mqA9WRThXRQQAAIABJREFU9E6MdZBJ/jQsDA2oN652k9w8r7HRiAThwjVEA/atJl+GW9Hjac737U6uTzupUokpyGCdCFtJtgQ5dRo8pMscEed9JDfpK8HyEQrxnLzMIqLUTDK0ffHdYCQmM1lJM8dZu4snB2il+SJE3HyG8zDcWJMw3OkWt+GX6jAxn13lPsxqZ8JWUBFc4nZj1jb4O/dkq0owj6K7p0Hu3MtD0GGcOA4xH7qY3SjDJFYBGjL+dhxDmqoFcgllGOBKTT7QJJ+nC7av61BRWqvYvNb+Szwmr/hF4q3p4o/VCDos49EWB3tpa4P960hvndlB+2NLjs8uLPGO0zvbtvGt5iZ/fXa821KVs1CO/sE+xRQemqInxxQiaGgtnHO9uy7cgjbN1jSJtjGO+ceR3hZ29uVTphq0qlTGBKgE0SvHwL9fll5rc3K/lR2nLF4lIWjNjRugbZWt3MckHnSBAQvnkhSKqU34nPh1FeporgBUcdSdGPPj/QFRymqSdQkqLIXIcE+O6djFr8NSdGYKNKiS3qMjgQuQ0/jxnCISybNUKnV0q+XsXF/WyCbC9raho9AxGdd7JIG/fXvDxfn5TCJwLQ2nLMx+eiWVZQL7VnMyqFPJ0yLXWAm20Un+MOGz+1pXlcq+11XQoXCetxiGrHn7K14Bj8c772Pi8+k9ucYjRTAD18Y5pqYRgarQRzLfCWRzvAN9eqVVjLLyrU5BH8K//PFP+Z6n8/+e/8Ex9vzndSGSamMA52V8bxu/fcuiZYsdf2z84/MvIIUOPvvJ//W//hWA//uP3/mX93f+8fHk80cWR0+7OC5bBqjhlaceS9DB3JAjeBu8peu6EBHetqH2SSDi67nE8/k/h6jT4cbTdrY9f/+v2wZNOfxJ7TP/cTzO1ZCoTXmzWM3tRvr5zAn2ZZ362GhTdYsTQakzV9FpbDq56YlEmhyhUhS5+s2vbpo5X8AVQ+WvK73GQgucV0e6LN+gkOQYPVpeh+PonNfBVDpQLTQti0+qZlxy8Bx7jVzKt+3BY+xNjmLhXHZ+4a8LtSmPfXzmlciApXd2GmFwjUL3+cVP6u+KV6v7Fa94xSte8YpXvOIVr3jF/7j4JVrdpeqaYvRRkS/vGhGq3B5AKjJGazfcS0J52+vieIgH9L74NRLCVYRtisQZA8s+OoME5n3NBN5q4von3EVUON04ry8YR27cv2yOUDBnyRZ+q4pq3F41JJZyqpmpJN9lwsJC8/0mzj8wtmCdQ/J4ZOHxapP8mwmf0VQPUeFWPxvcJh3HWXUoL47z6hi1sEavyW7wNVZtoikjPToW+Tap+Q9QoudnzaGUyICI3NdNS45Cj6nktOXk7LKpOhIUSaUkSPnG7qxjTjElX/dHjo99OdxLKN0uti9YpfhijewAYVwu7BNuqXAcBzpw+rrXhLsMSE6tOdX6qkz4ilfMeNTCc05Bu/G0T9rqRCo9nJg+Dp4Tnd7nJDe7fo4sd+5LhGeX1UHlMlqta1rsGFDXWvL9fU9O4FAz1KJYGB/PXDu3SvITp3JiUWqRpW5Ed8pekb2saUqrCcud8v1HD5pWPifXTjW5cgMyo6Si2j7Wnx4X2tp6plwlIWNzrXFDLc8VQErBzDjsi3WCBCXg51iPSu+crsyFu+0bbnCO93hTRZrzMWXGe0f0lnG1COi21vXf3x44wefofjuBU9fa0qrTz8CsIJPvQE6gJzTkOjtFC++PwbeicsbJc3w3z8uh3NYLtSQEZn4X12WY2bpOh3c0rjXYd4S2VdwcXw7yznXdmHoEytuGjH+InhOrOSmb8OlXvAJgo7C95bS59pPDzqXo5W+pSnmekx8tdDOeNSdCx2X07kQ4LRGq/NXHpHXc0/umbFoxSWlraY3vb4pcA8YfwmV9cZH3vfLYHuxjjfz+Vvm2/xPlP/KZ+vn5wTd9533cxr/vG8d18P/8+7/xY/KIvHNdLIhqLx8YRhvwvbe68XgIfeYiReHqg8KQfMhShffxrHSBtFEZi4c2ROA/f+RkV7rz/v7gQcGW7UpQaEtduAa0WvjXMek6tvRxnJBWl4skcEysbqHH55LD5mrIpqlXzbBx6cE2qQgOpW7YUNtzK6g0RDplImqKEqacA/fjkXSNcam5rkQDyJjkb6WytbbyqcC57FqWAloKeKWONdhPx70vNNVxBtoqtTS03YrHEZ1+TZ/N5F/N82xb4Tov2kAfyIsjNEJmmQNIQqHmztC2ktLXc2NSgcsWRl9qpHxp+JI69CicdBZkq8Ljy+akRSiha6OxCMxtyf+1VnNTnsl0gNu5bl/RgkosUzIZ73d5R6YspeYG5WPBKZFmqPEFiqLK0u+nFarenhYWwYFS5+T2TFzbggTWgjocX8xPpRZCgj6wId2Egg4cJxBCgtDmg5UbqM8NFaGTnh8AshU2GGS7HHk2USZOza6Ly50yzrGVgoUvTL4ME9tusTwutGaRMouvkCHNOY5JKnDeeHjRhBdOThDiQ7xxjnIr3ySWZ8E2Pn+pXoZAgDZZD2J4UIsujKpIJGTm/iP8ugmDXwUnXvGKzs3xCDThmBNudZ18PFk8lq0WuiU0Lf/AKUUw1YUFLxTsMupoQOgOqCyYbalCd1kSy+7BVv32yFBLbtzi2hQ6ttYrtaDu9TYO3gPZguJ2G5yWkhygUSRoFHoDhuTt7oWnX7yVb0ASdyXOJFAC3x8NUaWPTz0HV2fKaXdzeve1oVYNdnPUWGTgcOEDWRCv9D7xBSeuWtAKA4rO2dPvjTaKrdNp2nm8TRxt5TxY0LjDnMuvVSgcZhTvxOBPXCEUzUbXEmEI2GtZa2b3hNQtHlIxSrk5i4eB2OeCQloMn7kJn1GodV/wYvHOFfLFmDboYQm1HudZd0W9rGvpMSBMq2mW5tt1XIc6tXBf8Qrgs5+Lo9taI8rN11GcuG5LRY20umjjXvqtNYTg7BfH8I7Rrabf44SAbSCiHJOv04Lv7+9cP5Owf/Zgb/VOhNsGtXCMtaI/f/Lj+OAcyc1jV87oC653nAcfxycf/eScAldXFm1lJEjvj41Nhbfh4XP04NltGaI6ELWsBzfNnMsSgjKPFFFaXjhCRCzo75/PJ7I1/vj+nX7mefXT04R55AeC8y7KmybszB7w4+gcg1Lx4wwuN3yYHz2+VUK2Sb3ieGZeO59fxRFnwf6l2IChxTrGvQmPtlHHGvdxGke/lihEAwxdMFrvaQegbeZXHaEt+eyzG+fl9CFd/nik6fT0lfLqmZvN94scOlRuE3FKNsFu37s0cZ0oatmVrcmC0v0CFKFfoxCyK1Yh5AzTr7Hbbe1BeKwHoDipGDYEAKoAnl4MMzE44krDr8kBKjIGBKM7IMHlzjVJaT2dlucNaOGZsAycpHdJYu8XDGRI0Mbr/QIf6ivLZTgKbix1M4HsFI4T7VdQLl/cGE12zeIa4E6rSptTJyqIpncQWbSkEdZENzpSCr33NZVyc/B7Q52Tl+lsbBKjeh+vD6cUZUjxpxrbFYuQJU14Wkc+5xcXaCQBL48x3dDnlEul4pad5om5RwvWbS0wpRRUdRHtPByJchuZ8d9DIXR1MIqk50YbHRCj0HZdC71b4lOLWBq75SEQlNXlVUge2uQWRGDB6lS/VONe8TXMfamKieS6MB9DK1DlS+Eewt4cn/RTr1QNPDo+OR+SeO/JQYzLaUW4vqg/Vuk8x+//+jh5e5ebNxmpgCjjQ/ulnL3j45HbtuCBsuuYYhQfxqJO1JGMIKlMaRPXbTzPuKU2m1KsIKOb9IwO4aiMNrHkZjyLFDNPRcfh+XOYIa7Lb8lbCrccLquBVbrw/PzkGrvB9tboAWU2sDzXsMVrikjPoHHe7iDS+Namt5Hi5+cXrqhzdqcMfs+35vzDL86RHL1pYW8P9l05r9kkyy7vdHvvgFzCMZmWOsxNv4jaOMIxvES0bIiwOtF73ailco0LZR7JIRqLzeGB9U5RoZ+jsadCEWUbBd5xGefT2adwjg3OQ5s+Uq8V6xV3HNf15f5MAaO5FxIMqcLZ9UsxIhuqcaGF1pRaKtLmM+FJfF+LnmPmHDFJ/EaRyhXT30t4tDe2GLwUP7mOczWF3YzeDRkKb1sBo7MPLs1/Pj/5fD45ezDZHEU65VGpmpMuLZJ8lckf7FciWyaXswxO8EIJZV43aZQSjnisny1y/ZpNk1Dhx/Hk38L5X9//AOCMH3z6sY5JJPPCmVdIBG+7cA4lus9nYGrLc0zdRoWWn7nvG91jiSsoA/Ez8kzpyYecE2z3A/RB97LMl1FhLywlXxOhcq0Pqa1ABMdYA6sqvR/0Pvn1F1Irw5WS47oQVSqzgHTCfKFl2qbpCym2eNtypYLfTN6c4NG2hSwKoFu5BxFLzebvixdH6BWveMUrXvGKV7ziFa94xf+4+CUmQiK3THTOOm5fGIuUfHO/YQAhk6+SCnDdjHBNjXeA6Kk8NjumkpOZ5RvkKb89O48qhdZkwdoMp5S68FW65XhyjmofodStEqMDckl+XtFyy8PmwSaUj/x7Eb541UAXXZV1+u1APyeetAyluwFnKTnS9Im5j07gPB7ZRXl+noj3nLSMVnDgqN7XKoohyuooiCiX+cK31/G/OY1ZevZz0nYE/brYJma/ZJdSlxpMTx36pfCXnZRS6oL8JcTnHq0WEaoKfTSWzx7UCrvO8wSExTUQBGqs7jfOgKbc3AVB7q4JgsaFqlJGl+TiwKOgkwtVhfMyPqaPiygiLJWmib1/xSsgp9Jz2mxjKjH9ddrW6P1c69nmhaigNu//E+8lndDP0ZWLtAA4x3PYilK0rufq6Adm15JtLRKYC8WnF40h4guW5mK0oimzTD4frQj1bXjbWE9HcN1SMYiEZKmxvLV6BAVBxyTX3REpC9L66RcbdUnxH3pwXL6m0SEp2TpUo/He2beKDznujUIvwfPwJcfv2mnfGt++eBft1hGmV8iJui7VJGLAC5cuvhBy+2wUDahOW5B+p32ZvDkbm1SKzulOJRDMhI8x0SkeyKPxmLBrc35ErPMunlyDcxyjD9hImapNx0l5Y/kzqSgRtmCPrsEuOnyC4HkdnJ+d798fTJyEXFAfcftKiVPMadODYBNaLWsvWQv3K15B8miPyVkTGUqy/60LL/f9G4AO3yslaCJIVdqY2Hw+f1I11yiAz/Pk1E6b/Bo3tAr//Mc/A/C97HS/uAZM7fOv4DBbuZGbJCfH5wS0sLe2jul5dbRU/tgaHzbXuApVFrLEL8O9MJX0w6GfF327qQnBraYmV/KebE6IVBEC+yKnXUsQI2coElx28WHBoD7xru9cP4717BcfnKSxHpUiuDlvWz6Pb63w82IpRF4/U5rcx6T3r+eBjAkcZL4lbgwVatySTvGY/MSuHOfBKbagcfQgwUOTn+MUtjV10ao0NbaBc2lt4/P6WP5vrZRUz5y5su25Vo31qvuA7429adsbWhkjtplfG5d0vqT0RPSVu0YAWpZv1JT9/zvjlyiEAlvwrCIJQJtJgFkaeW6TxOuGIpQxXnT3JFupsI+b2kul+7VgVVqEIgkxyBekh8zcNt6rsu1wnQN2Zh0tDZtMvGEFtYQOSknJwvn7SNy+0fk6ZJNS14anogO5N/k4yXNZEBsSjzrhd61uhHdscmGq4P0k5vjRHARk6OQ3gZDU2u8DNiiWR708eEriXmdBGCGICY+ViEjiNeeUNYSvnilY4vVlEsFrLhAz8TARSmuUicVDqMhUsh7n7UkCn7BFd/plC6vbO8R2G3wJLOnHed0aLF1886B7oHbzKULuEbhrEDKInVOv39P8sQ/JycsbEoUyrluMZGbCFO2FuX/FlzBgGsf06MM3Ie+Vx8DLf/YveK7ITRny3nJk3Fuj8SIpaPD+bRCaS8WvjltiUM8DJHakHusYrsvZxnNhKJt/8Swrxt6E5xcZ6as425abXxHj+jROc3xAJN51R0XQZUwcRPHVLFCP0VGZQipOjZt3+TwSJlen/0itxKELIlZrEmonouzjeKIVdgQdkD3H8O4wJLajB49W1vp19KATNJ1E30IIq2lWa3D0C/9Maepve6VqXRCc7s7GtviD//nxRPXGx1cRkODHcTE8o9F9Q9UWBzE02IS1XhXN1l3bZmEseHeuuU6LcPXAysTDp4DOOa7L/qio6EpUrDs4nOc1VXRRhX3blvfat7ZRd+Esk/gdvLEnrIlszL3iFTOeZkui+TwtrSHGYuH9QFqhDl5LiGFXJ7YB020FcWfbyiq8m/6eHoljf7zcuLxgA1seXdlxfGBaP+0HZrFEhzL3Eh7DE+jzOEBkQe8KnnnPKIS0bPy2VT7V8LGOHv0iDPpoinS/kLPznzY52Plvek4T6ZF52Z2dh9w/plnp3aAIkcz9xzN2lCF8Avz7n/8A4F9++43v337jxxCpSZlsX0VEFOEh0Eaa/fFonHpSBnT1fF4Eio01tmgKrcwQVY6z00cDvrTCppXHng2RzoW6pCDDWFe3rdGKLKjc8+q4ltX0lxAasgQX+nWhtVHGGqyRa/9s2LtfnN3WYZVQSinIFJ4qBTgypx7fv5lSyrYaWCKCWyz6g5kTpbBNWOP+9+dXv0Qh5Kw1f1qWroQ/QtHQ1WENyyJokk1TSy2nSJPTYc4oSWbHIfOW6YdTCKhK7zfh63JZvJO3R+Vte/AcONnrcIqUKZiUrsdVFg+leHYTurLMsZA0aJ0FXkRqP01cZFHJIm7iaiX5NesYCxzXrTLXTDCRNZ0JlIqmQh4pGmDB8DKa18o5cb4Nwy93J74UWyqCtrZ4AeaOWawC71EaZ8htflqhi6ybJsz56Eab7xeSD/nkQUVkZyYCm0TtkitSTB8Oz+nNsnXVoJojbXY4HKljLERi8Q1ZynVdYlzzu6DsbpPjjbiP95flLSSRRWmZKktSiVA2uTOPHr466i/RuFd8DYtKGQ2IEspnv80ty+MNDYPh04BeicdfPDzh47hoVXk88rm8bBBJx9phON19dVj3PQVD1PLn57PTuzCdi1tTrvCb0yZCK4pN/wrPZsA0cHV3zPPZ3EYLNbIG+CJKAhIF75Or2SDk/llLqmmONdBMkAq1DYKhBpec7GPRfNt3PHRNn4sLe6m0wjJE/euZU6cfH1kAhl/8/vaNa/l5BS1YjvX0xKzPorRuQg1ZnchnH5PdOem3jkdf6344oL6ugY8mnAhsg3T99v4gwvhzHJMrRC6E+fMW2AX7KITUlOdnLA7Gt6ZstaKzWR4pVvMYlzkcqLZ89GoNxITzeWPuf9s2ailLnUpds4/0RfzlkItZe08vlVe8AtIMdKqEuUN0X+qQpzt7VMIzMRYKW7s9qrIhrTxPX1OGVoRQv/nMqtjZ0bmHF+HwYynDeu+YOo/hg4YkP3fmT+/bztM6xzHyLRHqrmxj/Tuj8++fOVFwnbwS5+mx9vSCcMISIlDRzA3HWlGLUJss83cCitY1pTgjkIgUgyJzow/S1wsgRg7ZNPjHyI8O+Qf/+v4Nn9zy3kFu7qaTz6KPxs3vv73DB3x8jPVs3yju9HGd9q2CxCogtipZoMxcRjLfu9YExal7zd8PtWXFqDmiyfO+UlVUYoq39PSXa7OJ5rhfxDinqg1qWR53EpICMz4KJdX0XRxiCicdi456XXwss5xkTVROrQLi1NFA7+Z8nhcxpnP1nh38bfELHMIrXvGKV7ziFa94xSte8YpX/O+NX2IilEX3PbJ0fGEWiyRsao32NP6LDPVAtKaHzZwnRXY8++iobaKAro5FKgHp6hacGMXKzVuJgln/IredKkwzZHgQlaU5nyoa6jDHJyqeWNzpAySGUBa+vQ/AV5/tyxIJ6bLJIQrKlw5IDxkysgPbiVO1re6oiGD9wju0CWdRxUosmMdJcqNqm7yk1PT/HCpwZ08Z3imdWSRvkIkHvTTQaAtaZ5pTtMkLqFp4bLefUz8F9+xw9Imp70KRtvT6LXI8PLsHRYWisr7/BELeqoJ5skH0u8PVLWhjUtZRwm5YW2mkGpbE6hRfnhO42eWwAJG+vquIhNwt9btXv+AVX0Lc1wT7fdv5KX35YLn1lPIfMDSpG8cPW7CQkFQAe2+V377la34cBz8+OzY6faKdVuuCfG2aPcKvXV2c5Vjeu9EehTKNZiyfCZ2YL7cB2x3HoIX2qGj31fkraghyTz+LUCKVjyBhaqZBH+3JZpV+XVzjWf++PRKaNx6Vs6e881SLNHHOyxZMVoe3kZmhMiHJkf4SAyqhW07LbI66Cni/1ofUoZo5u7xaoQ+5cgA1G4qg+XO4Yu74XIu04BXqNiV306l+b4KMNfL0znGeq7udneyEYkP6Nbn31XHN19gth90AiSUd280gJNWbgHM0ted1rsNOwMWWrGwrSlPhHGvm0y7isrUuRXGuS7EBSbb/zv94xf/oqBiHTJXW9CqsZWJvNq6rE2Xe3zlNOac31/lBRdm2nXO+4ZbqakvgVjy90/qcWP7/7L3LkiQ5sqb3qQIw88ismjNDIRcU4fs/GrkZ4Ux3V0a4G6CqXCgAi+YDTKXIcV20dFZEuJubGwC9/JeEptW1P3UjDtkcRiLwVnjZgoMaEUKrOScVTd73PQm5MEvPG5lTJYmOuLFT2CK0R9l7ZFHhet3ea3yjJax/CrEhX7mlBoPnvGc1rUdmDunA5YL0m3NoYvw/z865IMfL/mQNyizwb2iWoyqHNn6x/NxSXfRY6BfveDi21Y0rrZT7u9H0zNxek+68Xqngt+T6I1Jie33SVgqmbE9MG5Yedm1NvsrWIQbo1rHr2u/x82z8UX8yJpT3ugaBIIuzLU4UmfDiySe9LrxfG3ZYD6GVhk6y0xFletLc9/Hvjt+iEJL4NppSQaPsAzRIiNJm9BSBcHyR5mYSPTyIb9APD93eNFomcfYb1KkivFZiPIwg+JgH8HDj1ROPDqAjkqu0CP8Y1e5l5QpaKrhlMcPiy8kNZxAB4k48Eid3/75CUSX6Ito1rtpZ9Zdq+ivdJnvgxTfXhnhREAzZfjjlhCq+oW9Cig4sXw0tmqNYvTcIt6CvhRmexqZy83lEDJmylhQBG5vPoy3o0rfcY8UxIWUpF15UD0RiL8wgx/CL6CuSi3dBH0M8BSMWtEim3O6C33VH9N5siuT3E/+G+y+M1w3AFClIGDrHwSFKOctWEB3XoExvDrghdO94B0BER2fy/Kt/ofg2LPw4T2wMnra8cQI52saNj+65lpEN2ZI4EXvSJnb8PBrdB6+F0+4JlVubdZXcc9aWKMBZ6jam+7rSh2btqY92QNzk5mvAUYPjj2MXaOO66OX2qHgUTfLyeo8aVNEtxNLdudw4z7kXHIXiY0N5E9aiuylSSlBK7OLNQjldbo16sqnVgTa5BadUSmvbV2iYcY3gsYotRiZjE6bxoz6wU/l6zuZQzD1vN9HSnHshx5SCqHPWlSQIT3H+rAWfv/TsV0Ll5nt2CzqdMr+NeKUfyYIxvmLk7y9Cc4HPa2xxheRgybYo0OEwbtNrLY63PJ/WPlvOQrcbhvgaI0Vh5tnSqjDEdiPQ38Zn7/gWZrY51fEMXvi2vDCLhFzNvUEkm8gfR0J7uyuKYBg24cAuSnHdJp6BoYXtFWhmHK3Q57qUCbP9nLwU1RtyC2yRmDKhvnqAD0sbFMCjZmNIIdb+QaHJzYUZKH+0umG04s7Pj8ZzEiUzQ5DteTg8PX22F6RqQsoWVxlB8K0QXktyqt0cW8IEV+WrBH1C+s76QKrsLU0lCBu32TYX9RD+/JlebP96vXZjBECtEOiW2g/vRHFs3gdthaPolucmCuqGR9yiWmRDZ9uPiHK0srlUdVQGY+ajUFAkbnl/SqOGb+GDbLiw9zdtihEbzhcRiFfs2zNVW+5dNs8KnXYN/RvFoJaybVxWc+3vjN+iECqArmSz5M3d0xYh0/v15ZvmtGQumiJCD89BjK0pUU5j2jzgjpZJ7vryzCdfx+4D87oC0YUvHYjU7YKunrjzZSBWJJLct3CY1CT9y+3hEFMZbRnxiafJ68Kk4pqdwFUIkUXdKpS0ONigLmWogFpvvor1QajeRrOxFrPsB+uoJ8ODa/Jx2tA5QVpFiDDc9mIvJbsksZ5YTSGKXa93aI2tvIIH3eFcTRklyc6rUzSLrmTwzM8tTuc++ImSmNhY9z5oRbZruvc0sNwGq1GSu7POeolpRDsxrG50Z9lMIa2iVZLf0Nd72sTirpCpGDM3ZBGGlv38/HiLJbzjW6SqzyxSNDlzsZL14vThu2MWAx7VqD8zsfj8HFh3/vn54nMSf02VYcafs6j4OKGMQp94d7tGvubq4hWQEbS2khel94saywBMJvl+Hn6HQIExX6/3wSGKm7Lg5iFK0SXoAngqeW6hFZlF3eJdhqG17W5oiDEY9OfcE1W4/FZ1+qgHTYJf84CVonyOwR/H1pqinY1g7Im2I8ToYPNz+qB7bJGIUZRmvqfJ5iDF9iFPOLWVXQhlU1hoa0TkwbiEr5lo1FD+aMozjLp4RJZu8yv5OUtDxPf+ddE4xNOsERjXE+ZUO69JGJ3dga1M8YYl5iKBFs39nuT/mDtR9FtClaaNf63RvcDH0XBWR10JZDdujt/iVH/H7xLPyzhj8TeMlxnnj2zcPI7C1Z+7eD7Pk1BPJTdyChOieL+276JaGgxfq/D2RpWRpuVMMSkt+ORYDwvcLtpUg4wgDZtnI/I8GxYzd5ivF/jmJsdluBQ+n9feK3p0iEhOC7nTjW77TDd33Hqat5Ic6m4X/R4zJbdJlqrcLBxm/lZnk1rnurVumfO54JOAfHnnMGERAN1eqJx8zL0g9440h4UUFviosc8GbSdfv4J/XinuomFI051DuituRimz2RRT3GB+xloqtab5/Jq028g51/oTD89iZTWK2yx6Vz7lkep98zNc1mnU7f82IlXiHvNs+lEPukGfZ5drqvEJ5Taj1dxLl/fnEPBqtLXO8e2uAAAgAElEQVT3V6Va8Jz7cpPJp/0b4435ecc73vGOd7zjHe94xzve8Z8ufove0SzOgcTQ5zDlhoAJsiFkPuFnS4VHFX640BEsVrcyoR9lv2iqNY1Y0LbAu9GW26409GRDS6RUwtmqJk2EowhjqdLhHOWGZ9mwVGEq+T4Al6U63WN2bQ3Hr1TBA5CWWH+Z0JEQRanEkmGdOuz1nB0JdySUpdlWp7LHFjqTVHGycGRLj6cSyuoGDBHOUtIVmpyEhTm+8O+aEyHrt8KbSdmTs3ZUvOqEosG4LCc1u/up2NA93SGCEMeDzVcw8hrXSLrVnJnF7MDWWhLmeC1pWCe+TU4L0Pv9/deq2dFYsLaR07clA5zKfDnBW5yfokGtujtOFr6lZ9fzI8rG+fel+fuOd5DKSmtNEA4/G8+lIe9G4NTVkbsCGYOYkxMtiqA8I3guqMD0uFgT5x4j/SvWdGak5P3m4pWC9SdteojZ1amHYlND9SiV46h8/vor39NOpNUNT7URjGE4L7otKG5KZ+9hSqQq1O7ySq7FtWjq0YjuXLOzaGNgERsGMghe45btFRSv4NdcZyMtAYbZhsV+1MJhumGFf9bGxWBsh/qEyy1jtLMoaMfXdIWEvI454ekX/HjodmqXUhGMWOp8w7nGoMmE5JSFHgi+psfTVx/80Buqq6IgZatLXWEU+Qaz9uDUknsKCXd+PNpW7KtNGVenfE3FSndKu53aVYRSSnpGLbiKpLT4kvc/j0YRtmP9mPYTW2l1kULf8Q7g4/FIRTMmN7ayFSpLVc7j3NMZs84YvqGcZrGxEgtBP2zC7RaqQ0Gq7K66atIX1nlrBohuFL97UJHdhg9JAcxNI1CnSsXXfuh/YRfocXOJD1GssPkJPsae7uSLek6Y5l7SqqC1ciw0y1SJq5takJNYm9Mal9xf6hytvLgoKBe2VRlPEpnyOffAD+DreeFThbKdSkM3/09wapGNoGl8IOeTudXwusq8z3NSUkGPso+BPHLqRhkxnGv6Fq2czqtwatkc+svT5uDObXNb2V6SCj0i7VgA+xq4Jp8pf/9IesKmhTjBzS1N5c0g1DYvW4Ghuujs/DweXHZBn/BgLVzX7bW31Aj/zvgtCqE8XOeNjSBG0Bc2kySI+ZJzrMKhNwygx8Bi+cnMlxNBmmyxg8Q7xpZaZKRk80rOJUqaEn6TjLTX4LFwlGdBi2winoQkXGFuLh4JRleRnbyE539bD3GQpNoF21CSvL/VtiXmIst/qwtVGrEe4AkJWw/0eVael23+T8hdoNSFD/V8YJdhIRJQ5H4PghDdnCEkSYvr0B+Ro9ZzJgrUlLxdD7xLyn/7XpcB+Ib76fRQQWRzdrCgBPuaQjxH5btwSTjJ2hSTSiX3pitK+KDKvaGF+SbmjQmV8VUoz2erlMLYhka5eWwT30hO2eYIkQT1zVN65xXv+Bb1qDw/5xroxo8fBy+Z8CpJ074N84iBtgOdG1r34FELRSo+T8CiKfSygB1+BeadvjD5CtK/8WlE0aK8XgmVOmql1bIhra6GVjjaWrcVRPE64adHcFk2YdZ+EnFmorOMrEcKQpyLVC3CEF9nG6cIVgqv5SUygrO2DUPTKpyum9+DO7WmsSvA0wcf5ZgiJquIDKIEsUwxygev8dqHuk/uzSIwizuujTaTm9DcCyJueN7rGrtgdB+0udYh/SyEWwzFIhOHLHTzuxnXYLQsoCCThqi3iTQjiKrEdI6VISB3IhGlUCrbY2P4yObU6mBJmjiuvcanzH8JY6WWokIfY595VSqXvZj2IpnYSvCabPYfb6DHO75FrSsjAKmVg3ET1dVhsH2ssm1aNhc5jcyTR7xFSCTl/Bc/B5u+fqtSiukHOYuIEYM+YpvdiBaucgsgPSTzt0XQdzOKFB4zP/vj/A+efRBDKLOKUCP5OnNdpn+gwM59UqBkpYDDOhrfLTOEsNj7V4ShxO6HxvRUXA2uMZJnJbAbx33ChVfBdkWA3mJSz9fgoc5j7qHigobwmLSOL3H++DiwkfvTy550d+y1OEJCaULI7Vcp1O01pKVQe3Ax+GvvszBK3Y2aokp3p05IYBFQj5QeJxvol92S3e1oODd3fbjTu00LkyxyigiP2bAflvmaW+z7Esw9cd57mc/Hkhj6fH7ycZx739X9dP598VsUQoHcPguW3jubn+75G6ti6AbSyu4EYIIxv4R551XzcFs+MOaehqTffBdUb/NAIdC4E+PeLQ215ql/zk7E4vcVl/Sz8TW1Sgy3ShJhYQo0fDOmYv5sm6AnhYjNVFG9O4ArxPcEKMQZtpuhvMbAr3ta4nURpG/lJ5Wg1bKJb1f0JBnOhRshqc0/r1Hm7db5Zdgs5o62hAwEN9tcK4Gc7CxD1uFzE5zXX/KDVtHdjQ5yIrU8TswtTblmchLmyUtYHQsRRO8a1if/a2GaE1v/rRsloNwcjVp0EsV1cypsjOQ/jPUawLfbL7Nuvmy/6TveseM1Lsbikx2VX2Nsj4Q6H34ba11X7NV5nat5kLyQpoVp3s4wp+qx+TTj2fFgTypMjJcYusjIGtR28rpe8z3hFcHH9CVqUlBsjzRf5sRz7IKiClRR+pDdtcvtR9BV6Vgm5GudmRmXGcckoPyXx8FwiHkNRUp6F82FeFTl8xq0jzzkL7toUqbHRSolqeYEaplKdwvsZVs04l+vF60WnnvYZvw4b0+5HiBm1PNWbXIvRGSBqK3SXy/qqhhabit3f0yy8FhT+uEMG1RVjtWA+uOgGthsvFy9cwY7aatlci1nUatUzvOk1angpqlGtfbQ65USPvUxn48ujLh1Kc2dGEYJo06VpVoUf3V8cqUudSJ0c4RqKFUUncnKeHdu3vEtfLxuRUkNvMfev1rP1GQ3I0IoWdnkz7VSxNIwevHm5mm+pgru/u9ee5IiTst0sx1zgrAaP2Szcg/RZ/OzrOamdTjGVgp+jXzWLYLr81ZxK9yTjj5zo+0d6UJpNzIEycbHUn+smkgSszvnQ7KBA1Aj95c1jQ4Prsibte5VrZpomy14laISiy8qorwqfBxzXyZVRVfx9ghhtODPH9PMFuWv58XnnB6P0aHUfaYUzbwzZpMmPc2EQ/VWhaueiczqfZdCG+DzNV+qiXRaW8ShHM72PqqtIX57koU7j0M3j9xIcYdbryETWVXh9hHq4D6LaPiUV6qLXvP5qYpIoS6OUPn7Gze/RSHkCP1bkeKxc/eEfgl79Fdqmq2uA3r0TqltigTMxd6EMYLuS7EtOwhrCqGAqn5bJCl8YLOr5x6c7QG6KvF0gw9LaUXRD7r1/fBApPHrcJgHvYrgXPcDiaRa2szoLWbRsaZOkuosq9EoeC66WTBcw2ntY8v07imXLAjZJDorfEyJI1MIH/gcSbrDoyl9VSpjwvpm57nWlg+4LthGdmbW5CzMGGb/dtCmCNK6D7kA9544zVIpt9RrD0dG3GN2j7lJr+ptku2+qciNSfiD7H4KsrsuUlIxcIlGuEQWwmsqhTCGY/7a0KJShRiCrvGvSk6S5jNVQ3BndzAW0u8d7wDggkNuFZ1xDR7z0FdZKpQzYuSUZJ76B5HPY5RtNnqI8qv3PR3ez3pZBPuS02pfDYeLLjdMJMThm2nx19dFuG31SLegtFuSvraSamo1IcQAH0flf3x98V/aH8D0ag3bIjZjOOqy19DXFBGos1iTYrTjJK7cI8fLOWrDF6xNkzy7EqZCCru8evBoSzjA6Y09NcLS/LnNPdW74x6MuZ+Nl1GOiswOlUnw+XLGM4uzHz9ShGfB1KoIUgSZfz/HzXwtSCGCKcgR0zEdCOXFBT7FeYr8WwOrlcrn14uimey84snLgx9Tdas5/LrGVtJsorz82nCYMEkj7Cnk4sN41DNV61ZzkOB8wPNr7nFDGBF78n+m5ChlJnlf471hveMOKbFtOEQq2nSjWyIMlcJHe8x/98yHJoRD6lR+NaHVCcV1pfevLX6ABBa3/YjGFDpZGxqFhhNLxcMHHp0o+fcWF7UdW7AgSsGj5wZFQsJEShq4zyKgBDTqVpBscjAYy+c4IfNyF3wSkyqx3sONEEPqEhhpKW6wciUZSBN8rnvE6R45GZY1oX7QSoUJnVdJZJHPyfzxKJRSt7CKpKLVN5NWo4oiZ/78v2rlPJT4RzZy/nplQbIKoeNR+aiFqVPANYRSFZVCO57zcykf5eDypbhXUA1kQmQKxuNH3c1scEYVbpSjMYbNpj48joqFo0tO3YMRcqOnSgEVIpw7NZ0T7mV+K5VxBTLPwFMOPl9ftJln/v1l0O9xDe94xzve8Y53vOMd73jHO97xvzR+i4kQsDv8qxu6rRA8K+LYUwgl3Beagcd5JrGUoK4pgAeG3BAwgvKNrCeL/7G5MZGwrvn7TYVSbL7uhNZpRSaOxM0YwzeOUoskBEvuTqGEZ0d2XXY42uqWgWbkaFnnaKRKCkIsvo6TEIo16RCyi7HMAGWkcejm3hSduvexr5vI11gdURHlOCrPLTOuDL82tldK4nfXvaV3eh/8mtLUlWyibijwnEBtZWwCc+dY3Kv5wyq64SgJZIRrj40EJbbGvJBa+atb7uG43br1KpoyudtQN03U1iWLxJSunSPvhRO24LYZS56Zbr8koMcmVRfN7tOCv/wOGNZ3/D5RpbJmPmHGxyG74989Eioy1+nzEiptNTd5vQyZ8u1ldkhLq8Q1Nsb6aIUI39CnQHNKspZ1KK9uCXslJZklkqg7/yBNDOeiOM9cg3WtSxWuEZzV97pM7nLh+pqwCxKyusRf0oSR29vo+USlpmgMc3qlzmVrmtOT9DyJw8oACR4TJsIQrBuvr87H3POa1n8TmhjkFr1EbaxMKd7VeVQHM5agrCL40/Z0xnGOo2yOnzEo7bz5W4ciF4wJG/kM5ajpYxazW9lCuKzvfbtoRVU2JEdRgkpfpq4EGpVr4fwLSI3NKRo1qF42tMQ9hRKWn1PTwqO1lNydfkqvcKoIbd26Tg7fZ/s72rR0WzDH9371jm/x9bolm4+Hp9jxmmCPNJAPXYiK5PmtxNAjnzMLuZ/x2pBSubEfkVOnWJDVwN3wCYVSVUS/mabzYEhHPferkI+0H1n7myseJS+OHOJYpKXGn5NfU6WgWrGZsz39Su7SMhsVYXCnX8qyadmZAkULC/NVUcIGYwlJDcVckMU9kMwXHeGYU3An6GLbnLaTXO7FGfLXRZeOzg3rVQsU57H4g9O2YwH76xRoWlLVX91ygr7MUsX4sv4NNTTXeig2eRw+vhiim/NziDO04Ita0hV7BX/8/NifwaNvTtgoJa0A5uHRJxJg2QPkZhqUlZ958klLYeeiTVIwY3kXfSh8/Gz0LX7RKSY7V77WF/83xm9RCJVIchswFcXkG0NdkKJbHS2IHMMtDOtZ+OoD68axMvRaGSMYk6B8Hunm7rpIaJE10IJTRSY0ZQsTpJmWL8NDcVS+WPodNpKLsyBjtSnmaWh3u9Mo4jeWcgkILKO+IZ78lrUBmVPKN4WQiIRkLV8hnHG9kI+bMxTKnumJelaP8c37gwUXnYlGVRDfnGuz9OdZGH3RoPqt9vKipHjF+qJaQTy20p0RCWVbP4/cDBdPoDZheOrcLxtqn8XTKnSbC/5tx6olr1YnHIYwArtVUWxq4+/vZmKWl29LAMiG1n11w0M5aqWsZIb0+VhKTaOnK/Ye5ZeS5ras7+zvX6jv+H1iRGDz4KjA49G2ImXvRh++k+1DK+dZt+LX1+fAwjkP2c9XhHMcwudY6oQH7n4n8G48VHmWBdV0qsTtM1PrxPDnv0splPP2/2pnS3jGXHR/PQcgHFXw2ZH4K1486rHXfkxBEWOpnaVgTLPcv/56vTC/iJ8JqUmYjG6fj2s47SONXgH+9VrwvMVjcezqKGP7kwg/4duhncqczrX26VJxv4UIzlYwKXz+lZ/0v/23k+fh22xtDCNUOGcFUWtJvvaCxs29bjm7vzwwiYS+zf3GxDhK5bl3uSQWiyzugPLzEP75a3mLBOfh+ISivLpznLrPjss61UlDNqDzpKnwWrCRQ5HqFP/WiBPBrnI36moglmcIwNBUfVq//y6E3vE9CorJ9PR5KaG6DaERYch3jm1BJx8ZEqppfTDC0AmFM+uYJxQW4PzOKSapBXyDoZnfRHqAejiFgi56Q/kL1ZPwVcRkg2F7samDC8fROKfpPSNzHbsd5yno3ndfwzhq+aZGDKayxVsWF3nsM94Yyvb/SjiaUOpqqsDVkxpgm6PjVAq1Lo7iRSkH0ZYwDrgV/udsirQR/MfjoJQFU5QUR4jVBBHOqvyXj+UjFHy9xr8JaF1eNqQs3DB/JRxv7tPiynA236qIpPjBatxEIWwk32leg0hQl4DMlRDCLfYig8t8N8TyjwZjeUgNoY9O89srLUQItw23++yDQx+bHlEi92Sd+/6Iv3+/+i0KoSG+N2+dD/Qyt4wSIHITQUenHQWdVXKfvJUe7G5A1ZwsrYIgNMl0C9upLWUNn0uOVgJXvZXMNJP3pZThI/CqW8lMyuS+LIlJN2RONmwXV2lIeHOEApXAZxfEtfBoiq4pk6Sx6UqwhgUx2JK6IiBHJk2QKYeXb//uKZsdev+NSnJffBl+CTzdd9EZMdXzVhcEQG5zrlpSTOFRFj40pbDXfRhdeSi7W5oFyX4lzpbXleoy83dEkBDK1unNe7d4ki55D8bGMMu8e3cxouguTiycWr8lYJ1UU2q7fc6cY90mYSZ40W26OsYgwjdeWFtuIEvJ6fkbdCze8fuEkYcDpJR1WLC6o0WBWvic2tj6KNmdnOd1O2BceTCvBoXjPHvfzR+p+Te6C/BschwrXWkpiHJMMYQ0eI1b7EMTNx5TJKB4HoZLIlXDMQleWlgN0pcPugWPmdxoGxQvKJM7wAWqfD4nB8gi+TJL3TEMLIhj7pk9664X930SMy5bPEyo1WlNtjjCeHY+xTf/qs5mzzI1fMjJ1/PJ0p95fDROEfgxiwwfoOzCJiTpuKuwEksD6Sr3fqatcC49WzP66Hl27O52jpQPltBKp/64JzpmRhFle0yTE7eVeIzLKF63kt3rykJqT6NFqVVvxENE7v02idiAVMEK3/6djbGyRn4WvPzmUZbfgHz8jt8pxj5vPWeWtFU/HGln4WNOi82JKkj5Ns0pB9WZ+xyY5nm6lVyn0tDCZQyM79ThlFbwvb8dctJ58jnzkEf5SYxxK06KUkSRtiYGV6JEauXzV5qP9uEcrewpdxZfZe9HEU7vsfc3Skk9vKkGkwJMMXE3Ock9SyKHAJ7hDM+CDTIfOIogHsTibmol3HiN17wNwiGdci0+u1Jq32u/d+df/uKP4z8AOI+CjM61GmCzKPl5LCGWB//8fPKPOen3rlDbLjCizJwM3/e6lPpvyKSXB6K6m8CUihRlXTIayfme9231y+YwD0WQcyXQIGUKMczxz3kUzlZwz+bafV9iX5P7hWnf+zqX8bRvraXNMf/74r1jvuMd73jHO97xjne84x3v+E8Xv8VESJRbxtCCVmSbVoUYw4M+R5qKTEnlWfE+LTXjRbbEqbikEtls+RuOxdhV8VkFinLObmV3zwnUMhdUweVbhzXBEFxLdSwg5SHnBEFmQe35bvm/Pc24/k1WEmICuVtJ2djFEXo+U2lj/bs1wwj6luNWHkWIPevN0XKfF2UaoJF+Q9Pdr3xMC5E5GisR2IhvkJxUC1nKdR4J9VgF+nGketo26uueCnxrzNpyUrM6RRpC4fYbcAtCQfrtV1pN6CLpt0FOkWrNsTCADxhm+FR+8oiUBZ8TwJTOte1JkB+t3iPwmF4gCyYpOX0KYUMdzUFtUObjfxTF5RvEryT86TaQe0+E3nFH8K37rkofvqWvtRSKFGR6P5xN6d5ZHpcuyZsxv6GYdjl1CDZhZEU1DRo2UrMwcNqUdvWSENEyJyWq8DK7OW2iydObayR6T4uB+fvHR6FGQk2M2Rq8FB8QSzVJ5yfV7EY2zclXTD7NQxvRcnoPKU2rYbTFYazKGLrvS8EZHtuk+o8fP3iI5gR78ULx9EJae/9sT7Y53XX75HEGdXZ1D8lJ2IIov66LIpU2J9iu6fezIDtJA735XPGaxsqz6/ujCUNSgXJMUx4fTrixWsvmgUfhmJvkyzpeYquetgJnDZaE0lEkVbTWlF2Fy5Vym96hteyJtsegj5yBr4242EE5dHMNhjsuQpnvcV2ennLzNdbnf8c7gPTzWftTpEfWa04h7DLqUag+JyVAlMYEriTvpqQ88uJEx4CjlG+pTVIFzj2VKIiwpaqt9zRorcvXrPAf8oM+FSaDnmr9E3JGLbgLOhXbBAFzPF4bCeLufD4dmTL1Zy0Yt1/hcT7Ax+aeH9IoItj6DCyl2ZWHJA/dRl5TDXiVG0XbEApOOevmEqOVKCfjNf/GZ76y8it3Win49FMqON2df8xxyx//ITzKT/5h/8rfj0HRts+FVpyPD+V/TsnwL3MOva1IylFxGtZtqtdB85T37lM1TmrmP4ufZf1FyEAWOqo0DhEaCQEcGB55nkBaMTQqsviHLkRVXj0fkB7JkRoe3+grqfpbJrTobA1UNpRXasXthl0vI/C/M36LQqhEjhghZQ7tmzSoRsK5ziVLTeIfdV762QQzpZvfpNrLkaZbnzw8qNWxRfxFqcQmCL4sGCM21E0kv/ANaxUlTLejr0ekFPb8eTocz6JimfnRiHHDFGqr9H5RjgUBhJfduH2Zh6XfpCIM38l4EZ0S3JPkWEryZ+RO7nOU7NtYFVGs1C1LOXrwCqMurGZlJhXzg7jAiG8uxP8/jkxNEt5KLKSk4/06gEUKRewmPUZuOBb3WJ1h0Mp+zaqCyG2CqEdC2xaB2T0otVAX5NDT+HbtqVIhJLhi78Kox5a+LqVQQujDNs41pbGhzM9RWuXQik1NW+sB9YYLvCH37/j3CM7VBCmahs+WBUUDvj6vfdAUd2qBcd18j6jJeXw+83nrkx9YF4TVjef13IX6gwceeq9LGZxStrcDGnQv2+OnRfJFlpiCl8TOr/z4x9FyTxNJE0AgSkHR7Y1ml+XRP5dAbRXson7MIoIkyS4T2KiFojds9mWdosJCgD3Og1+Xb2Ksu3OV5FuupMsi9/8xzUfLWWCUG0tuzs92cp55aPfrxedrbCPRawx+/lk3rn+8Bq1U+rQ96FfnOB/b3FYiITzLkiA9IZV/fXa+Jm76PCpnEc55885aEgq8CNMxwIM6rymdRBSd8BgnBXMW90DbQTXbHEkhaMo2S311cO9EKVt0prvhdkOxFWcM36asw5IdtBpU5u8N6x13tFbQ9bx2pp3EbAKP4HqW9J8Bhg1+lti8lwzHR1BXuS6aEsnrObt7jvPH2ahekFdKgXFDxCIyB/gxPcY+f/2Tenygk8unTYln3zQDNAsrqvCxGghHSjmvhgRT+2rB2bUU1BUZ+e9LLpyg2i10kLYpqynsXA6xC4qg2Nhw1JDMMyJ2nwaJNJj+mOt04NQRtxdbRMLm5llwItSj8euV8L7//nXyf5zw50xm/hrTjH42fmzk9/bzkcIG4xr0YbvJ2wgQ/Td+YPf8f2sPkGlAv1J9rQpy7oZWvwbdbOfTPz4qRZS6TKzdGOrbwL4dR/K1J5/LZjPdVbbVy+gDqQWJdQ1ppjrGaorNQcWse/cN/RvjtyiEwtiYbCl5aKgsUltQQnbHP1Uy7glSa0nor8O3ealFwZ6dn4/5ULfKGIUx1pc7MaTLIMYlXX9XkeJLZ38dKFlRL+Jv1xz/7EWnM+mX2KIIEoHLrXAUGLVl5Qy5sMan0ZbnTwRuYyvT9WGYw2NNSjx4mm/FktWh0e34K4SMOeVZBWBBRvC1HH99PoTzPfG5sLe3kWBmyPLVeBzI0dD50B9NGWG8ZgLX3FNfZvmgWZLy6kpcBlO9r2yPJ9c0F1yFUBa1snlGw6YjtN3XVEW3b5RIoZ6xVU1Kzc++OBsmQSlKKYuzIahLFpRLWELAvSBxF0uj3wR3d0PL/XP5DTCs7/h9ohXdPhvXMPrV+XnONRfOr6/PLByAryH8oXonwu5oU3SwD4YROTlah3rglCK0eUCGCjXuDts1csK6MNdmjrlso75asiO3CoSCU4VN8iUq0YTn68mrL5PVloaAEzweAAJS5z48srgri5t5OUVicxTxQR/H9o7wKFQLZCYJF/BxPnjNAzjMMQrXGNsUWhocj7a9iaKn/8lfaavBh1Ycx7ZHBvSX74ZVaY3HeZuTXjL3lWWYKorF4JpJwuXJvXrsg1gpRTlLbDLxx0ehRCRXiKlgaiCraJ2p0tEWGqHixOYNVE/RlaVYebRUq9uf2fJcWvmdO3y0ihW9jasjuF7s/eujTP5QrPNHaQrHY36913u/escd1zUmjzD5w8mBnVOKaDxf/VZq7M7VA5mNHY1INVkvW1ksJBjR0fn8NU2D+3FT1tKTb/FMIpvKK1HuwK/wnaz//PiTwHeOJwrjrKt+yMQ7Ah+2+c6lTS+bnfBPkaXVD9VsCvsUJmg0PAxbC2/J3a4JkUQq1y04iyhmN08zJI2NJfz2e5sGrb48LlvBexDLXJvco/YkN5KnuXLEf/3rC5Xg//rxvwHg1198Pq+NRKql8PDCf/1YC/uL//HXF2MpdapQSqXWsjk+Hg6R/kJ5X5LnvQolKZKN3lmklHogBF/zbPjnXxettpvfpZJiNlNUJ3jSjoYuDjeCtuSLLe+18PyfPfQm96hlLCvm9HFtJJLujt7fF3//FbzjHe94xzve8Y53vOMd73jH/+L4LSZC8EonYeAo5/QDmhWnCA9VdOLjZSqI+YRPuGmOentgZcGtgjBD5oxSVTHv26shpt78gie4O6pCXX4WTaeD+VJoa1nhzqt1LOEMy0o3ptv4nAIBU0te9qTLSRWR5dDLnCCtn2t1tFTWeEXptBJbJx/LrkrMbmhE3oeyVF8rE2kAACAASURBVKYdzGRq0s8p08sIu6XGS2tTinp+kI3nn53op6fC0rov5qjGHmmbBoNbacVDOUrw5TfcD9/weC5LiGNUp8yOqFXlkMJLbvWoPlWsIKeD5rJhjKqFvLx7DJ/djTkBMk0Z8DVp86AW2Z3rMhtTqmV3d9SV7vck7Bqdlxmv+UwdUnP0O29UfU+E3vE94pvSjSj1KBwThjbCQRsx12ArlrjqOTHST6d/wUfTzfEp3RndOM+laKSUehCbJ5mvtvYWLUJUtrv3GEFD+LG6pRo5xSzf4BAMzqkAd5wHEc4guOZkyw2k3RDVpXy2oCQvT1+hPqfF3Ts/jo8Na+g2sBjEuCcp4+nYhMI9NAi+OCeeWFQTzhJK1MX/JOE383P20VOe/FhYlMI/fn1uuMqP88wu7PZfqtTS6BPiml5M3GpVNVXk1n5oU3VzdWARQXGOh9Jme7vVAApjQuWiJDfLvua4DedxHujEEH5Fx4L9uZHBKXVPlD4oRG1cEw9oprjfXWM5KlI1p23zHbor/jJ0WXk0pZ7wfK3uNelNMrvdm0f6jncwlS23H2HyfeqEjwZCO86trnbICxPfXGazwdU74+q3302TlL+fe8UpjhSZktM5bCjxjRinCirUOYUyDV4vu7vw54Nhtnly0vO1X1euESmKhpAau0uCOdfMUkezMDTAZs4WZSQkbSkJS0HiViPmWw6Rb5JWJ0tRV9QJD2zxWpDk4UR8m9QqmG+IspZCHOzpr3nKkS/Yq5lD952zXeb8z1/GIb/mvR95vYsmIpGQ6Qlb/HEWfr0q18xjr8uoLfPVRckwmXDbRQvBMVUOXd9nAH2jp2opaFF05dMBr973tKYe6dd0PFZOeU0E14I5CiaalIR9Pg3MbuU6RXBzlqFD5vBHWr78JvFbFEKC7kWSuoaFWLrm4SC+tepLE66+iG5w2eAyGMKtr65OO+ouMp42D/hFU4mOeN3Qp/ySBJ0Hbq2F57hHnhGB977hEEUUKbELqYRfxMzVJ+QLQUvbiyY85bTXOLmoMGrsQ9rHemxi/7ynaU7eFlGO88ZSugUltnVqeh+VgnlsaVeNyDHzhG2cIXzFQO2Wd4xJYoYcmyrlG5ZXk7u0PoMmlG6NMhckcB3ihcBCFnwUjSQ8pzz2zX26hlGmH8llY0qkz3ttWWie02fj1JLE8gUbmuIJviE5U2p83oejHog4ZRVnBEYQI3YCFBo54p73/mWGmdzfd8mf18lLK/JbLJN3/CYh6Pb4EXUerWyYLB6cPx/4WMn8oIvwsXywUA6MboMyoW8FzQbAgiN4UPSgL5fh4hNvPddZwHjFlpfVVtAeuXgAl4rEoMdKthPfLxP/8noZw67k1a0904wmwuORuP2uQpHCVMOmR3Ii11o/UH7Uxq/F+Qmnqq1L4PmZRsi1TB8iKbyusffoUgSXhAvb3I9GH/TryXnmNZTWOB6yYYXjV/Drr2u7FTWp1FZYjZ+Poyb7c2qV95fTGknUBlprXG7o8nI7nM9rYBv62+gjeF3GakiNSymHMutBzir8eZz841fi9T6a8l/Pg9fkgH1+Dcbzbp78+LNytsY/PxNq9BrGo9bNSxrD0dLQlXAdB7jh3L+DXenxtqDY5Plgs9nzHIMxBj7hLaW896t33KFy0wZUCmbBmA2Ldh70/tr+hoFmAbDEq9wIhFrbho4XAI8tLT3M+da7TrNWVUpd8HZHpG4hg4Int3Kuy1d/8Ro3x6iWhG7JhO1qBK02VPJ38z0lbTPWwZ+yTWnsPK9PNHbTxOXCYZufOultdPsPKhKBrkaNGPVG90Gp0/C+ILoc2jSpBstCwIxSBbEptCKaEOCZ24Z4Nq99NZYV6cZ//9c/APjjPPjRDtq8j6M7IsKx1v15Yj+d//7PKVQwlE76zS3Oqnug5bYn6RPGu3ji7kZpyjlpIxGGD+dj5jpxgHfhWl5JbtgotMmBbEfLc2lB8WxgIy0BNpPEI+0fltG1Cj3G5n2XODDKhmMuLtHfGb/HjillK4qIpALcbQg1iLiwtYo8U9s5GOFp6UPzqI0+O2IaWYjYknmbhlJ1m0QpVXTzUtJUSjcJLWc5N8HVh80va3UJZXr+zC/wSmKwFqGPxQUIotjuYEQE1m0TDLUF8s2sVLVg5rfnheTiXEVIKszpNiYNM1xi81e85r2rQzb2NpZi2itv1pckVvjb3oEgjLnhHHWakq0kb/5sfcyDbNbqN56ThexCapm5LvPAmFMzcdlrZOVz2+soIjfhnVlCE6Gcd2FU538HEu8aur2O3JWquvkRhEO9hS6cyRsSIWx1anLKtfDEjmDuc/KUXY4S3zD43zyM3vGOUg96X4psOXF9zk2+1kKrcG2uoDLctyhBLemo7cGtbFgUPHhdC1Sd5s7y7WDh20GjBYqxGzlwQBiTn88ZKWJSZ2PHuhO18FwmeiM5LS3s9gGymPyYuQ9b+kCsPbBfyj8/n/uA/XmeWMSt1tiz3xezYni+vjiPRpkePdc1kPv8zE4lToRv/kJ/Kl9f1zRnnRPpEHy+xqcZRQttCcbM7vZqLRvG8xl8TXPTr8+O/Gz8fCzFB+WHwXMlBZZk8TH37FOhqfJX79vcsbvQHH7OZlKrOQ1bRoxFGhFKzLOnHZXrV2foPPRptFI45338q18wnJ9z+ufPFzGEcuS/nzatCusWPU1lwm9KhRHpV9f7UnZSjuPgNfI+1W2e8o53MAuUZeQeiPg9NfVA5VYcNBGGVPSY52kPCkJrBZlT7+M4cLl9Y65ujOHb36uEZH9l5WwBmPOa/JuqwiF18/AGTqnlW+6jaUw6OSd5Fgtf3XcyPQbIobs5rVqRUnehM3fZ24+QoLtsFIhkZvANaJJp++I0FilZNC4+oijDKypjc2GyESy85vT4+Rw8mtKWQsx88TGLiqMWKLd3m8xC6bU85qrzxym01ZBlIMEtGlGFPx4nX7Pp8q/PT16Xo5ybpy04YwTXzrgqYYO+fM1w1G40TJMDqzG/TwAlqqN9nR0vwoQxp8/SCsd5N8uJ5ITFsJ1PqQqlgfclyJF3t2yxn0C5ePWFmvj796u//wre8Y53vOMd73jHO97xjne8439x/BYTIVHhXApI0THrky+TFW5csHoWPkegY0HKXGiqOQZaI0dPNx/dLVUjTKhb/bGA3VhqrYrIrVwW3dJHZndsQVw2HEt9ThfWRMmzC+dx+2QIBa23rv0gX2O1RFUOtNh+j+5K2MBnd7JooZQbhrZmVduA3AyapIoeUAW6ZB9E1t8coCaMnnKNZ6mc2nhO9ZaUxBSOklCUyzuEUaeqXDfHn3FzGRDcgmtBdkSoyIYFVQ1GgC71Pk37DTMoSyUpIkfEc9qS0z+/+Q8uhJQlPpWSmKJ7ZP01JH2r55PrYfgY3yS/a3oSxT21AtnTq3zGstO9naxhSnjPxyVySrQgNfEdS/yO//TRpGCzg9bHxEIvXosl1OAh+5fxrxteKqrpe+ZOm/tVDSWK30o+pTG+SSwfRwEbN/RA4dBGn5PegtPKrXD0q6ffxGN2Lr/UGdY3jKSWgtlA5IZw+YSb+vKuEaOb85qveV2DYbdsfWmacs1zKlEAlUpMLN0PCkJgE4IjRWhF7m5oVawnR3DbGhyKjNjTlfpo9N4ZS4Wye/qI1bX/RConrUm+GeM1bkU3ga+r83jkhOlk4NLw6YFRG3x43V5I3QaXCZ9P42PKhD/O/L6WlHVV4fPqW8XyOTpMjkRec+Xowq9n4v4/P1/U2mhTGrj1wF7Ga0G7UR5lD58pFngPrteTY96sU0+6jb1f+eREyppYi0KVVOqC3e1/xzuAtLVYkxAFrWVORMDGIOQ7CuTikLZht1UOMKitEZMfaG549OT5AUc7Ub3oY/HmKqPL5s6IyL+d+ao1r8MXR3IlNYtG4DltnpOC4cY0AoTJLQ6B1yjIyk3CwW1zgCLhLtgCBXlM0s6N7ihath2Ja9qR+IKohjGs0/vMzwAtPT0PF68yHAv2ddbmmDmtLK7nIErhmvwbCaU4jLXPq8CUlgb4Vzfqc/B//vwJwKmdr9dr54gu8Dga/+3Pebtk0H91KEpfsEJJdMDaM/GcXS8rhdYq/k0ht+vIF17fv3dMHdXkk0YT5HVxze9+mHGcB/MjUltlfCW9YU+uRk6MbKGXJphqTfzG6IzBtnvYXI6/MX6LQsi+w5Rc6GYbggGkidU6BIYlPzfPFaqsY8z3/ZRIWMk2/hShjzvRyNxYbvk+DbqxZRElgqrf3l+FovC1ni1JLOYeJ5P/No+NkzVJLH9ZiD7LMer6oMNGGpDOzeDlaaC4pPnDjYbtazRyjLr9eLjJaMz3F4QI3X/zQ440rdrVk2DBhrIVN0RryiOSkAsC7BX7NYnYsplmDUIY8yIPjymbmP9uCuGyoXMWgE8Z2DUl98DFt9cQ7gR2f1e1cVmktC1wIMkjWM+HBG36GOSfJylybRZSQKRuA9fQ5Ez2b94aytwPlwGvxIb/5c8VVHfhrN9/+I53MG7BEHeu0fElj60pEzvmA19FKWqU5StUCl8GrcGym0ho5y01/fyaUrLLL+Is9F+deM7NRYNyFsYqYiZMbvNSJEVN1rKvKK/h+/VVBHdPuPBMJMbXwC/ntaC4RVCC/poJk89G0iJE+8xbZmJRD01S7NpbqjKuG4P/cTaK6g3votD74OqWWD3Ah9O0bo6LWBaWxzKaFaE1oU1YWZSEW9S5UD/dcfr2GXJv/PPrk39Mw8M/oxH0fQAfTQgcn3vwsMF1OedZ+fnI9/hxVL565zkbXA+tDDVqW7AguHoKIuRrOB8fsc1xv7rTPo3BJH4zxVpmgtakoKL0zbPM8/Dqvo2staQ4woIcE9PYen5udeH1Grx+LZGIvz+xeMfvE4rvhqpL8nPKY9l0CDXkbjRHIQiqLRiTzuLA0uAY6OPKfGwm02e70kOsZfIsbkjYnXbgFNEpPEJ6yMT4xiFJ+LrGFHeRQkTBrmmqThofPz4ONObaB16X3A2KEim+outzzNpnXsPwYHSjbZSsIFiKKuRVIXGbwBaps0iazSZNIRW87M9lnjD78zHFDD4+pnDTxjRzmPCxbBDMwYxL1/6jNJXdfArgc1x8Rjamf9ZC7WXD+4Tcu3/ORnV8/AC7+BrXporIkRz2xYO8xDPHWg2rVvECslL/4gi+G/B2NrC4eeE+aC245uubGb2P3Wx/1JNeDTkqY0quj2sQVraYjxQQPW8eUzXCbuEK/Q32q9+iEMqqJf+vunKUthdunEoh6Nf99JXIwgSghAKB+W0YqCU7kLaLiMwptogAubg3vjSShLcMDEUK1+u5+Te1VV7GzZxLyOqeSoWQhH67jfEQwZ3bfItADsUWxjVymnJX4oHI7V1jYTQq50cu/GFGv8bG5LvkItxLTpRHK4yIvXB6tFnk1HnrglePXWSWmpO0heWE/B5uZlVq9W8FEQk+AZmJi1A45nvmNWdXZh3qUtP/R5RdyJpnp2YrrSC8QvgvS4NeNPkJ64pU6OPmQqkEFN8KgFIEhtwTpgGob9Uu8dwMzXybyuXR4N+UCPN9V+1bi3K0utWqluDFO94BcHnQF/ZcfPJrlmGhE8O45sN0SKOU+4AV1fT5KrKfq3oeeHd0dUSLERq7EK8ijLPRf00Sbheqepoqzwi7n9NWNbuqa6pahKO0W5Upkg8UKuianpSC98GYnb9Lg/NQzknIrwQmF8tmI/dPvUVJVOgvp88TUyS9crZFjwjj6nt6LDptUiWbHQCd7BS3bx4YxevmFoQG51m/GYc63YPnM+9LcRAfbIP6qgiFPg2VPkelnXDMcXOplXpA3b5C2aj58SiZrJFnyfj03WE9W+WHVv65MPY16PjyQERUqIdy+FTl6p3Pz19bNe44DkoxHlMMppvgIcjcz56kaesjDvBMLC7rSKm8ZlFaSk6gYhbX1xUMiV2kfuuPveMdmA2KrilFqqGtEBFMbz5ijQM1GHO6o6Uw3IiR3BPIXEbLsRUknQIEPrPxKg3Vhs+fC4nC0Zk3mA/4pvR6hRFe0blhFUlkyiLJHQRnKbjKjRSSZBnG1PL9HJMzuLl7pJLZ/PdDSHjK4m5K7sPbI1AKLk6Z13i0QmsHX6/F8QbnxMeFbO9G8Nedm5ZiaCs7f7KRoktl5nCOERFbBEUkPYnWnlo06AX+7//3nwD87z9+8kerEK/5ggIIZe7ZHx+CS8H/8t2cNg/MBm2J1LSCdN08cJdUGr6mIl+NQiH4Wiq+T0ftVlRGjLM2jmN1ogPVoHl+pqaVdlYQQeaeJ6dylFvNc2CEXUlkz5eYys+zOaR//4b15gi94x3veMc73vGOd7zjHe/4Txe/xUSo6O2RUXX6SMyOW9GUFu2zYjVzgls5KNTpw5ByMzlCIVQotlR2EuYRC0qApOb8Yt5ojikXnKpGeu0sPPtZCsN8a8r3kjKTxdbECKQ7T/Hd8TyAkNgQCEJopjx/zcq8VajZFYAceUbxNYlFVdAKMsdc49UZ7pTHUlMT3GR7J4kkp8DN8amWFzUIC44tkQtUuyVsp+LSc0lplrJxnfkLZXKAZrdBlFp8qzghglfBZ0fEn440IRamtTvaFOQ77DCxw1tzvgkux54AdrPkP62JoCScT7cSHnx12xCcKoro3ZFXTUnwpUoXRk7hPIjVDVLFJG5deykUE3R2WI8j5ih8jR15xzt2hMaWcy8tpxirs3i9Bl7Kbs4/rVOU3f3EA6XSx9j+NWXCcr8mt6NochA33NMFH76lqc3Avy4+/vgBJHTK5HY8f47s0S7FI46D6LalZbUoSVeMDT/BnR8/Dl5zw3p+XZz1Y/sj9eiUuLHo3XPyZWv6fAXX0/ak9uPjJApbNl/cskO65GkBKhxFNh5Yma+5J/MJZx5TTc908GctGzIorvx6dmxyEh+14KVxTe7UcZ78PBXviwcQhLMhgr0FOmSfgqco9ITWru/iGp1ucU/GRPBycvSE27WjQndetq5BGaabT6EMqGX7MSFKiFHmRn95oFGICbUr7oQqTuc5J0CtKE38ltNWQcrdxeyWE6KPj+Wb9/dDTd7xG0Wp32TydWJaV341JZe3UpkDguiElxKIVHDf0+O6+NhTFtrDaSro/Bs86Ix9vtYiSLHNidTIifOa1lRreBivsbwhnVIKjzmVrR+N2hrdYu8FUhytgC2AsWFuORllKkAihC7V3YN21Dsv8GAMz1yDzJ9K0Q2Rf3EhUm857pEcJRNBl03B8ESWLCicCIzY+VWtLf0lbUHAcp9fiBzrHavBcN1/nv47uTd8WuFsJ2VC6dSMHn1TPCrKHw3+OgrPz5Tzj6jUWhlrsiWk59w8G7o96SGbLzpGQP3mM0SgNfjZlkFlTrZimZiZTY5+3oPPrydeHC3CMa8z70psuGVthYFuu5LRk8t1HgmlbG9oXEYtt0Tg0NRO1283zcP2YWdoChmwxrRZ0GTRM//GghKCTwiEh6Be0LrgdUEU3YT8dhSoB9c8/LoZWgrHhnWkpOlahF6F80N3MiRMApwLdeFgKQxPvgCkid8XxpjSsLr2olk4hQ4ohvYpN2uBlc7n54SU9TkZXWQZS1sqWfCX/4+9d0uSXMfVNT8ApNwjMqvatnXPf4h99jlVGeESSaAfQFJRPYG1zLbjoWpFxsXlcgnC5b+oYhOut2726+oJt9v+OI6MoMtNShRVjrqkEgN32avzWgXXW/awmhAYZTaYvQfXt2+T2EA5kC3J2yJ5QyPYzZEUeGjw78UjcpnQodkYhVD0xsxjjlG24aoR1Igtr44qZx/7JrPpEVTnee09MY2isotVK5PAuQQ3IniY7Ju9IYQPXm1BH//6G/Udf58Y/UImVj09snTjoUsR4oeEvRpUK9snpgSZl4az8SjXmPlg/g0MPDah1Y+WMLflgRFCMHbOPMwopfI14Q69BeWQLPLJe8sKG/YWUggxKsHoN+enHrYHUK8WDG6vrREDcd15t3sw2t3Y/Pn6Tvz8ytNe0Dq5mUBraXIskzh8XR0zqMaGjQ0ZXN55LH5gYmpYYF0JTR7AgrQ253xdHHMw03GQgk/p6oJTf33yv/87hQuKpQHj1xyAPbrx3Zyn3XCY56OmN91rid4oj2flaQvn3wkvm2zudvCIyveUU79eHXXdEOlejCJlk4t7DILCn34TTrX8MKNU5XU5tSijJldgtIb1sTlBEUK/7mFS60HR4HksYZ03lPcddwyFNgVC8MmlXvxYM6DvVBThSf1Zvo7GJD7q5iCajCS/z2f26J6CU/P1QpNjuxBPA5+GqIsn4BzF9iBIJXCCx7y+C4WiZfMwpVb66BOqn9f4aAlXLfOZ/XlAc+Oc0+yzOeVx+731cH7YNiaVgdiCD0jWlnWSz80D6b55UUqhn9+ECrEaH03rjq00EcyJ7/racgi8m63MYWfP4VMVRbENk3XvKVoza7yvy1FpfMzcU81Q9z0EFskG5LMq5+pTIu1dfNIARs9aR2aN90sr5xjEKn499W7q6pRcGeHbXL6UChHEyMGPj+Q1LAdLj6SnaOimJ4ik6eyC8j61YKVSVr7iRYm6hSra9eKvjr9FIxTue/p+RqdKnWQPOHubpliLFKcgtj0WGgOVQRm+cflB4uBX/VqAKLInakpwBajNRkk9OTrbfEsY3XksPDuCSzqTw6Q0xU3ol8gbLdyJiSkdZYkqzAJIgo9Stzt470kk/nFP8SEF/8zX+HOmct0a85opZQQ681mU3HItfH3yoQR+3KjDU6xh8XGI9C7aah5z8rxBrXjWWvs8DnToxssHyQ9ayYGR0+vfn8t9fqqRzGT0KLqXe9sQtQhf7nsb94zkP1FvblWM2IWlD6dI31OXasLx/KTPplWKoGGUWOTljkbsCYcArjpdnvMlDp0+UJvUGKl7Lz8mM973pMZ9n6B3vAOh7Eb8ipNoyhI+GiJIUWQ2GJV8UKz5xdkaYUq4bYXJb3dcOh9zoCqq9O9GWQbKV3qQ7dc34VFsG+0JkZPEpUZEKqn5MhDu6e+1DAxHz6necdyO86pz8zrVzR5Heh1ts2SpHFX5mlNbdcc0dt7+9fnBn68LnUbJonBY0K81gRX0qfshzzR2Hq6bYyghVLPtBRJKrj1W3laIantINtyoWve0EzS9dVaxhGBj8HsSw+tH4ev75Nk/AOjSiAt6mX48VnNTrEJZfiII//XxsYu+f51ftHZtsYSPyGLJtkeZMGRwzInqRxO+W0Onl1EJyy31vD5EEo9v8zyrzMJw+ObB6kdBUm1nft7CGLJVtq6rU9T2Mb8a73jHDqNs/nTUHPIt/EzIqjHWRign+oxVnCq45f/Poqv7mLXS3DCTg6DVZKgkx1fqPTDtV7BEUUSE46eHIiBR+Ocs1p+1Ilr47680Gm1nFvzPZ9n+bHEp5rcBauuaQ91dqzRecQ8E1Aev87WFVWKiZ1b+EwnQW1Tp8qCP2HzEIwJXp+rNX5dI89gxB0ytJ/957Nql5xZtDT1qQRWerE2+c4UDS1J3pNBBrCEu/ItGn/nvdy0cavcAZAwc4R+Pjz0Q/1/tRXjfRZ+hnKMTs8gz/UWtsFzvew+IQZvN2q+H8epsZeCqgxgNX4q7w0HH3qojs9ESoc3XiDEoCrq23t8DKW3XeCZ58j5mQXY91lbvr4s3R+gd73jHO97xjne84x3veMf/uPhbbIRs+rxAYqyFSCwrUKPidk8ekZQxXK7aJ44VYZTC1CHCCIYKzyUZ2Zyj3KJvTcB7bKjc9cptSvR7TRoB3xMQbzEoHEwIJH+8MU7b60EJcsPkwkTcp6rTD6z2EOFRhD4nqq8YiNtWVXKE14S8QCq2qctWiVMVhpeteqLktCLmFMXbxHdGoL5gY0upZCl+JJ53/VFD8R63g72lT9Dq/sMHrmzcbQR4V8a1xkvBx1Ox6dNhr1fCCufrW9FUnImbQyEiqBjPpbwyIlW31hZL8gPYn3ckhn9B4zpCjb5beCe9kPZ22gVX2YolPjdMHr4ljgPHTNOxGvDoIDfcTkU5r759o2K8N0LvuKOWuqG6xYVx3fwcrRX7Ad9SiYSRTR7e1QcmztUG1hYPTikP3StLl4SLrW3KUSzvm5nfahUex4FOvNXwkdvfLbctmAhj3Yc+cBHq3FJcr5FTQ719yOqRW/Y/c53QW0cs+JyTv6NUYLBXX5Ky+etvPmvCWfv0AHqo5IJ6Ei3NguJwzZwaEXwziC5b0pYRWAn64ix+HMiInetNYVihLwXKuDiqbRWl6+r0V9uePG6Cq6c6JnBY4btejKnGFiTiQKcvyPfD0ZlbnrY+C+O7N76m8px7pp6y/Ec8KLXyOG4Is4dvDP4lmupQ4+ZHEL5lf0OcM1LNE+BhikrwfZ5bBfD4fCasZqXEEKTI3ir9+jh4HMp53u/rHe9Y0aLviff3d6rh2swdWiq1JBQNEibefdDHUob1fPDrLUbYenKh18bSRWnm+xlcY3KBJy/OnHyO24LNOqfflhe/zahSKDNnYrmxtgkZi54bpn//q2FLcrkqZnUrPv6Lbw4zZHmCRSda8LDp31WTF3mNm4ckofs+VpnbsU13EMJ9w4m/x0U35xj9hz9SLp+XIlu4o1b3RhuVqZg2T5wrxOBrJJ/nOISBbXuAEEP0th+RyO3cyndZW+nO85ljBlqU12Pm1S/nuw3q3IIfVfmUwnkt+PA3z+PJa+aKLkGR2F5uf06hPIyjLu660l1wT5iuc4GM9Gqcx6iJ+UvuGBChyEGqIgPjO/AetLURdGHESZt89+fmoPx18bdohK4RaF0cEMXCNs/lm+R/LE8FVGYvMB8SpVBEGMq+YAyhiG199iYJc1vrv7OPJL8t+WufMrLLzyIir1m9H4ZKsK/oGPS4pbJdAhkCBn2uOYuV9NBYDd1xMERpS2ISxS22FKN0oA1iFVCTarhkoEMFom+onQRE1Q3nQwbDAxdB62oCLCVyp+xl80jPken2qIcg0WGLaQAAIABJREFUw3/ANIzRfUv91gJmNy43Ai7G7R2CEkP4/pp6/6OnHORMDN1HNo+i2zPlK3qurxdEVTM/rsJSZiGw0q5bkjvrgs5dg9fptwFhpB/UcgNYEgirEPG5sg+P++aVbJxmjkRd6a1t07kIn6TFxRFaj4B3vAPGaBvaqXKANYZkofyoR8KYZvGtqnyd14YahHt6lInyz3/kXXG2SEnaWZC/xuByR2ZxLKZ8PCoSN99QRWlTNto1JViXyStFeNqxeSjuSY5d+XChNXob2/BZJfkrrynvH3px2LEx9KJwDt98wWepPB66UbXeO//8fPJN8nGGBr3bLVBixtU75zwPyQdwOgOfA6j6OBJWM3EeGvC6XozJv1E1osbO8z16QkWWdP6Y0q5LFMIFqhGzoeyt8ev4tWV+x+mY1TRTBMa/XpQQ7GnYkclhtM7365tre6YcswKK/ZpdbyK5Fqc1tk1CAEULNqHdlwcuI/lYAEMoMXjtZu9BicFRCqI34XkIuyEsInkM8098FqE+lHOepz34esc7gKdWbD3zT+cafXP5ZCjE7WvlHtObb+Hc5rPfldViV1WwmycSoxPdKXMoog79urhWchAF+jb8LaY8auXXhKk9LOu+ZZqhlLQGmcOlqze0FupRkNmw9e6M1wnTE6zOoU9dxsaPJ2fvyVci4fHCoC6hglqRZdJKwtnSgzFfs+sLMUNf9+DmGBWnbW6xSKFfP3xVVFEZm4MtrlSv6IQ4Nx+0PnJIBGCWAi+LLz0Ej8Yxm7NHFTyUc9EjFEQLn6vm05LD7hg7v9hx0HvHxl2bPmrl8ZGvcSa7lI/HGsQYrY/Nqc7Bsm2DaALK8YGuJUFxxI5Nvwgc0bQ3WZSJ8E5cUCybp+MDKLE5ZqN3vr6DPvOV/w3qq79FIxQR90R1ttlL7WMQxHbfTJhhE93qbEhuCyImyRhy8+HJ2YE0qDtLbPJd8eCr+zadqkUYI406IZNBmO4Hqkh25tfimFCIH5h7dUGr5JO7TTw6uXlahUMbF3LexDkX5XetPOb3Tw963KpzQpL+l/JKOLiMPTVWMYraXawzNysP2+Za2VMFrdzvy0T3h94vx1vb3JgiFefHQ37+jZUTu0C/bjd6O4ze+1bEkuVLMgsZ9yBcppHWLE42zn39Tk6NFwZfQtHK3giGO5cHv+ZncRl8XRe2C5NKsbp9PJBAJfZ58RhbNfCxeEoq0H9geSPo1/wMgRaRhq3zjR/219+o7/j7xAhlrYfjclSEOkVQYvbwexsskQOTyS8sPfCe1+3zmQ+KsEG7Tsa4/SLGiG2gKQSfR9mKbN2Dr+HzIQxVjWucW/xlfCpNdQuQQPA86m2GOtKDJjQ30QBHSbWyhaEffqDoHgaNCEQrwhcAWp5IUa5red0Mqlaez1QC+j4vYujm0hyiXCHolo8sQKqrLZz/7+OD3nw/+L/PC5xb7EUF0diFxDEOxJVzvvHWB6aF52NxpfJZ4WU1hDlW8plbvq4rN8ZrxnI2vAsPu72MMIXyoEySRYTw8rH93nDDz8ZjChVUVZ4P5b//neelcICxVeQetUCpW3Up/Ul0q6aKKNeA51Op02DSAhpG5zV/ZnJPZz47eyCWPK78m++d0DvuaKNha3P78eAYB23yE5t3Iu5BJD4HDktwQwwpqSr3da1rONuWZTSutXJF22gXD0+j6cnjVVOeh3LYUqLLfLBM69VynCuxTEAV/2GSjggewfHDO0vImq9t49eD3totuhWDWuzmfrjn0GdtnaaH47pXhjvDBzY3tVJr3k+PWUP2Qe8N+SEC4eFzMz7rJ60oHZP5LJCgc200QFjhqAeLExQiE32zjsk5qLveOt1RvcWrWnOeGjeKyHuupIK9hfpVjZe1LZzz1ZSv9trqnw/7YFiwrSMZKbrwY9vceicm6ud4aNa1c5LtZ5vGnIsjJPQhRP/BYRRj9JvXKkU4hq35OTq91npb4+u/vr56c4Te8Y53vOMd73jHO97xjnf8j4u/xUaI+DFdIKf4fdxcmZ+bM4FUf5MFf8jpmFq9YWM4SGxeSp14TzbXRXjoPQl0kTkpnJuMAZjcsLOA1jt9ThseGFrTTRlyqlpMsHpPC2gjtQXna5yt86zHPoZSjbAbzhcEjm4p6q4kXm6qe5iDieLlPk/ywztEEKzkubJjQUXAr9jrYkQ5qtImRv5sjnTZzr7VglJ8TyTEcxO21qCOUC32MXoYQxSze+Lq/oOvM0ivJE11qPUzo/sWSkGDc6QfEKSPVERK9+ZrSE475rn3ayCDvTnzee50YXuneuXa9lw9lWWq2paQFPWE+S059DHQGHu6NCLyc1wO92v68Y53ADDQiTV/jeS/PKfUcYxARLcHmUfHTPnnxOR/q/P6GjxMtiePmIAYbcEZOrkNntd0cUE1sJrblvP7xIdv5cxRwNvYm3O9noQFdfEHYyDKnlx65HIoJW+nwtq0H5iiccRXEL2jE8I1cLwUHuQxfF0vLim3rYEJ17ioSzGyVrrF5tmNuMBA9Pbu+pCDU9mv+fKL7n1DQ1IozallykjTKSZ8PvI1XtdARLeCZPNAitzKvyI0uXlQX98XH9Wok3tQS2G0kzZ/v/dIqByRvEFye+RxqyiN4fm8OBYUx+ijbShcqYbJA5sbn3YGXgefSwGQIEJ23m7hHNi2RYiRuel1Nh5H2b/zrILMsayIcp1tT4pH7/TvW177sPd88x13vK62N44QVLHNMxGURI7OrzVhl6smQA0T5xDBt7JryjTf1ILBuOB7bqiPMvgoxvE57zMzfpVjb4S6N4qloi0kVD086Cy0TL5+W/SHxyO9aWJsDx6rhRGDmH5eY6QH0EdJRcjoY3Ki7+2ocKv4RgyKyt4EDFFixA+J7wBvdx6XhM5/PA+6r/z0YvjY/L9/jy8O++SjLoXjCbGfuUQl/eSK/kAPuGyOoxy5fFkKuMOdn3K3LsKIrBPzFyzhhAF13vv/9StpAPHnmu8rPTcXAgcZIBscQO8DIXlA+VmkxcBaELYGjX7LZfeAEVvuH4PAiB6MpTRoilH3hk9RtNxcdNNCrWWjCeh//Ubob9EImcgPghn04dt/QmQaDO77WNAxiCmP3Bl0hKfsWjkNTpH9cBHyxl0FunriqxcsxD03fWtNGgUqwRlzpdnyBlkeGmE6G5QbWiXh0CVxp6R06/C7UXExJgUPSGlZM/ZN0MfAR9+Y3AOhozceVQuo3yvrajgpBAB5jszg1WMni5iN2McsHB6h9B4IyxwQrN7chIrkunb1fx4gd/IYkTKJNmE+pkGJwbUfyIPegj6LIdPIhCKDi9WkJv/Jl3zn/B/9AUMcI/b7VK2UYpunM3BUdBeJEZLk5P1Zjtkc3TK+qkKpxp3jguGyIX5RC0jZzVq48yg3cXK8oSbv+BHDg9c07dTwJLkuzP0UEVgq0d6dIbKlrhmRD/AxdgE+RBP/JKspGRwP29CQkLzu1zV+us+hzRyanJ36w5RTTQlrfCzj0CbEAC83zHYMgSLIJOqO0RGDY/pPyHM1GOu+G1SJLWrjw/EWlFkpPIvx76vfSbYWTHxLvY5wsLrv8zYG9oBHD86vmV9qevmsHFhMqQ7fkQ9Mdcck6NvfLUVj1qBHNf2OYjZrIgXxc+fDNkVUwhbXQZKDuYrCwzi0ouG0RbrGGWffQzGbI6tlHiiR0Mhby0dwGs9nfv9lQevOa+ZEGR2pus+DaTDcdjP34uTzOLhkUCfE5uvqVIHP39kQtm+S2zkLLDPj1Xvq7QLl+R7cvOOOx3ET7L0HlLi5fQjuY/OdVbJQWjDbTkL2Q1IkBuDVO46gazjZg2qGZQ+CEnxq5XHkzxcTTGLDSctREPF9DB1ljM7XfNGHpIjBmpWOlqbJdlResyZTV4jAHnmvF1H+fJ3M2wh3mwapqwGYw2PWAFWA2FC6Fp3hI4cSJN2ijZacQKA+n7y+ne/z2t5Fpg9UHfcUP5DxJL3Usgm5ULwU6vItezzw8zahJnJIuxrCX/bBv89/89WWIfQzBazWwEuFCzjnMdf5HoIcxkHWuYfdAjSmippt6XNX55AP5LFqne80op12NRUoxZDlRdl7Ck2sB1oVtLB5TWifnEmhTCivUojKFkfoTYhz0OdBqRrNbzjw3yFb/S0aIS372UcfkQ+fJXwgq5HZXQwqSh17FcLThC6xOTtHkexyl9oGgbTbJwjN4iKWmSBgD8UWgSyEMQZ9XPNrS+8ZbuKwwL6ghdw+eR/bJIoQDonbUV6D0LGN9Y7DUDMWilUkzb368u0ICNFtDqg4prpJbaICfvN1EKf7gHarBklAKbonhG7w6m0fYyG4bCB9iUAITvAxpwvdE+faVsM3BQdsXtBB+qIsvGloFnS2mrciaOQUdRUOlwfj6nMCTTqkD6Eca1vnEDdXQcVA4jbrMvb2MI+hM3xhbadAg9gujoxs3iRiF6sRwuj3ebIam/w+fyA3V5vs+W6E3nFHEPlwAWpPjPxSNVSywVibkCaCX8GrzIdbKXybU8xuUnsbOUVbJpxcPGrFdpMyeJ2NJU0gMzuWtfltjrjx1TNfqRjxCfSyj2nIQBahtih1bmbrfEBePU2Il2eYWBbra7DjkQ1gXW7vNYcv21MD5flUrjPz1dd3Qy34PD7nWzxRM3QSaHt7zU1+wSUnia+rU+sTt7tQmGTMfE19pCrkdU+ze7CNkBUo0u8BhzBd3ac3Un3iI7jmjT1G5/Nx3MWTNYKRm31bvj85+Dpn41tL4ajGWMpNjBzWre1xyQntx5z6elz0l3JOYQsk8+5jfhYayuNZ6FNRq7++4Wn84/F7T7ODwCP2uW09BSWedRWvRg82Eby+N9jv+BGi5UZMVAFXfD7zQ5PsvhVwXVArXLMwpjVeLVVWH8toXSw3B0tcSISi8Jz39sMMU93qagoQfvN7JI1OVyHsMfiKjk8PsnN0Tl70sZAogBojghLTkN7WxnwOQYpjJXhd2ZRUU/oYuwEsapjdIlzncNSdNo/hsxx0CcZY9xhYlM17kpHCBvhzewuNOZAa6zjHQIpsQRg80GLbc8dfQYc9cDWDy5UxNyOv60Ip6DJDDaeP4DFrpxa5jfk9B9EDQaKDODKWkIry8fzgc+bIf7XBoN+NbhjXeGGzaakVHvLgnPyv4QMtgi0vtjGylp15/xojuaerrDXNxlCDPnPgNXKIsxrAqM4Ytmus9IlMg9u8HlbL+9fFe4f+jne84x3veMc73vGOd7zjf1z8LTZCUWLDE/prMMJvl3SbkKw5jYghdI194KoJR6ghm8uhPpA5RYNU9yjIhsKhEJ3/kI41Y2+hJODyxJ1CwtdEEtCVP0B2+0uFaR6XUBdaJbcKoltWt4hBV47HjfPGb8+M0QMJoU3eSiM4HkbomgoLVeWG53mnR/Bc31edk+GxwbdWhGpyK6m0QNz3WjMkMC8buxkCorEhm21A9Fu1TzT9npbwytUH321sVSc1S6jdnPyMkmAeQfZSpeBc3PLXVQ1Xud3hdboxr4mDRHIcZs9uJWCwZcXdnZCy5UATgSNb6a11JcJTmZC1Ncrfq3uqm4CXtqCQw4kGNnXu33K07/iP8KDO+3gglBK3LKsOruZbCtYvUvVobkDH8PR40LInoqMMHqrbE6OJg0B9TGW65nydnaX3eMwt79oIDYKrd/45p3ynn4z+gW0JXCjOVp0rmnCYz+PY3h1XD7w7YUueP7Ek+z6NzFej3ypLRsfn5taBdvVUWwQ+DqFLZ8iUsCQY7UxICwlDbq1x1Mpjvs///effXOPg1+QERXSGXhyPOwcOV9oPVcwxxuY+hQzaUJYY0Xf7wxid//o1p8YYUZUxk02Ng1e/PenGcB5FsMedrzwyHy4vtVoKhx285vbNvFOKbT8lCUkYdl9qU0GpttXzztbozVlWDL+fhf/nMPzI7/8fhIjMfxvXj3P1wOa5+34NIpyPybkYEbmd0/v59o53rDC/vQFFLeGhS4pfEnq1FHYvUaz3DeWNUhnheL/VZZ2gGPxesDFLiMxSgTNlep6tza2AKD7vu2sq5LZZn3WP9KqZxzsBq3vj6a6MEbQx6D/sR5JPfvOdfz2efLG4fJ1DdFMP1kZk1XghaZGyEDnJY/GtpuffAaZb+lqJ5GQjeL9h+giUCRm8WLy9G6LczkGb5zohZXIr9GklBJ5rU1ZScXep1+KChkwOV8Joqw/O+Zz4tLlzCe66U4Kiyq95TP/n/AIvFFu8SAUbt5WCKBK+VMhprskTmdudKsrw4FwILQuK2YYHokH3dIlZMGsfWWOqLmicE65byrxK2jnYx6RoxDJX+evi79EIXbDORRp5ySZjGcIIub0i5s20vh+WIgIRdksAatC8b2hT90jvjSU7eEEpgh03R8iHbEnTGiCFjRctaoT4LUvqQqjff28EowVW2A84JLGbOteYapLSi/MCax7YiM198hi0Nm4ek+hcZy9cZcLCtm1QGDpuwrW7TyRJrrYhpbsD52vcUJMF44O88TRic6myo2MTJbU43e8V+KGS/IOtCDFhZ/MrJZPhIhKHQLTkHK3Em/wf3Z/foxiXBmV+vpdHmp2VtW5OntKlyyMjxTL6tSQpHUbZBZh5UES3+W2xg6tduA9KXwVTpulVL5jkynnxrXoAVrIggdvo7R3vIKVf1y21SKqryZDDUFXO7wWr9YmBmMMEnIca1X4MaiToIxt+AEzpLeBxw0XbCOrHeqAehAfnhHFYFRBLHhyZy84x+FgYfQnOPjbstkjBpBBoSoEz81QftMk7ka4Ml9tYT402YuenIpOx5D/u0x+w3GHCoxjPWUhcp/Cv79fmHgRGWMKZVwH1UQ+uV9vNUj2EZ33QVxPpJ6oH1x5MBCYwJmyNUEwgNoRQKKVsudnhcH11yhxwDIsccs3P4WtAD8dEuSYkZvTBcdQ9gNIC3U5e02D1MZR6/HjfI/97G1LKAJMtHXtY5ezXHtyoGS91ZBYFD/uFmNCibXhKkJ9nuZVxQJQyny3ijXD4ns3Zr9+/eMc7VrTWJ0c5C9lq5a6VaJRSaGu6IIPRBq9lTl8L1QrBsYcaGk5FeSx4sKXc9kbp//+Q5EE2IIve8IrGCJneRIu3E7fQlGrCeWMrKoGmqMD1Z5oGR8pWL/jwwYBi/J7N2usMRnPanIr0QQ6k9D7IARv628PBhDJz5mGA3s3ZGM4YDQ9nMQme5UGtBzKHR49DaJfcdAiE49BboIGOe99c9ojg8TCqJM8JU8Z17fMkLlgtu2Esk9xxroGWOFXb/NfZhODpHbmgusB5XZsW4sNoOLpqGskhyxr2itTJP5g/r54w6fUeetZc65hq5FG59811qhUeRVF9rLeVdd+iGZlgLhsy2Pz/d8H8BfG3aIREbfNtzApCbLKXhGDOfQGb8rQfHb4oSKLfD11O65LiA7NpUoMNSCQvQCPSTIzJ5//hsn5GFjuLMNbMkQhiXoBRsklZN1F46uZbxG00ZfNmXU3F3KasbUyno3Grlojn/G8Re4tJKiatY8bz5+f3XYzB2FybI5RalLM6Nt936wLEbT5qqTqy1O/m4Hlzq2Iarm7ir6dh6bqAezjVZRvTuko2h+uYRSkWt8CD5/u94ofrtBklgiVA0yFJ3b4zM+jYJOtgUgVWfzm9pUPPdTnQRt/JoxbDim3Mc965HQf6IlXHoItsTKuZ5Hmf10OZcgs+bsGOd7xjhdbC1dfWs8K4tmkx5EBiDRf0SKEXX/nMhdYdO3yLjIQWRh9bnCVV5wyfxXJR5VctzDqXKOkutq55U51bkXzNIxKn3XU9MJMDMGtzXm3kZFCDMSnJWgUL4+z3xjlcaH1mII25fZ9feoGA5yw8WsBLbDcAg8ajVtaoUq2CtN2MBZp4dRfOuQVXr4zR+Ncrcf6/7cHH47g9fCS9i+S6t2v+Y1OvMVL9ad77T6s5gJrn6fu78ef75L/0H3leqjL8Njc9vGIk52ht8CI6KsGvf2Rz0c+L3oO6kmRN7PsxnxXqwXnu7EMtyjU617V4S87xLFssYUQSsNemzSKVMod3YglXSKHfWlF0GRxi6Dwv6U7v+yfWVPsd7wD409reDld0Dm2WcIFyvvrmBH3U9BKMNocRJvw+jPosDG61M9HYA0LR+I/mJ+uiuIcD7lzudF/CBEJidtZwKIdAq/5yT4+hNdDtLQUGRNmKjz06o/XtHVntwNuVQlbMZ7oaY9zcF5GCyWMfMxI/NtSOiSBruFCc69v3QLWFULRQFI7ZoIUP+nUPlrUanTQshRzQE2DH8pAr6NFpM0e6N1TgGmvYpJgINt/j63Xllv6HAE1XQebvnxJo0Smis7jkMqfFU8HPCs06Q1dN5v9hel/LVMmdBfefr28epfI4dgHOaNu3lsuEq99+l95HCptJ5qn5j4namYVjKYr+uEZUHCe4pnrxGiL+lfG3aIR+Krghi+A+m5AxUrZ5iQSYUNM9DkjivIhRFR7zxvlX64TccrFVFTE2SbaR9FlZzddU37jneppbqH12guhsSUE5SMPP5WAupO6hjA2JCZHZCM3fkZyIrGYKywtwrawjf3131alid6+sEWjcwgdFJSely4gPwApP1RRNIB/iHmxHZ6QSU3QB8saLuM1HY56D9T7LlBVfBdeQuRZfU+QQ0LK3O6UKiNNaVmy964QXBlYXzHA1fGtF7bSLrSpnkts7kft9a7CnwkLgErfx2VTSWxPXUgSVOw336HM1pZQ1gZrbX/lRpNUy9gqaEGII41qu02/y8Tt+hArHvL5eY3BQGMwNZQ9MjCjrAZsisHvD2UjBlACZ3X2xiunB6zU3RD4wGZzzmq+qPKriU520j059FPScW/PIwuE11j2U+aHOrca3zofSfKB+v16UXwoYx1QmGwRdA5l/IzQHRmsTMhB0sFWYXn1gJhxTq1pNOIrvjc+rXbz0YKzn6RiUAmebf68Hh+Sc4nzlcR71wf/1+8G/zj/5O56b9lVY4IPrytyc57rTA37/yuLm8zDONnbjk3DY2K9ZRHnWD655Iks3vnvsfHg8H/gYvK6+nz9VC4zAr7XBUUqATygcAQPdKqfeM68stMGhhe/etrmtGtR6K271EyrHhi+Hdp6lMFBeUxzh7DHhwPNvXBd8HNvw+9WdHoPnErF5Q3nf8SNMK7Zk7K9OIFsmOhgcLluy/kONXnVvBD4/0nKjAI8lJ2sC1w2blcihbZF1/TlDbNdHQ5yX33AsEAjB5+DHARNjTVxljKQ/2BJtcrw5epSNwnl4buUXUihlnpTeVt4dHCbolNMWv6aK7rxP3RNcN78WnXXiJO5rKC898SlRaQK1PHKrM3Oe94H72Fsnawdmthu4iCkCtu5HA/OCrtomag67bDWAadkyzsw11xh46/zzmBveEKJBe6yhifOgUiVuFV5RYnQ+Jpz4Hx8Hw4W2aRzK6OcPiobwMMHKDSFsfzrXUq4ryqFGWY1UVPxwWtt4PYgc/i3hnB7C6/WC+TerKCaFa8mIj0JnEOtvrOLtL4w3mvgd73jHO97xjne84x3veMf/uPhbbIRCbvnjEIcxuBYuPBI1NVGUSEw5wjVcGJGyjKL863vKsHr/D2nFgSLOnsIliuSmoooK7jfG1UywckMuel/kr0Wsy0njjf0MSk0p2cUdKENSjOHHOrhwG3xpGAO2zG5MadoNlpPcgiyyn0YKCrQ5mWwWhHsSb4EQ43euwbaU4p9JOlxSsMOdQ49NFhZGnvsNhM21qi48XkmTwb2NqUY4G28qEpQpBbzO4xjK1+LiRFDFMez2CVKnwN6c9eEJA1nTzqNg2IYQVhVkJJkb8lpQDRbwX1Es+uYtmSU0ZiyJXM8pSa6B5t8IT0GGdQV4elHp4jvMLdOYxMxtsvaOdzD5eUsl//uLrnXDOp5Po7nfE/7miW+fUAOpQW8dwahLBvVqhFWOdf2FoFW3qXCL9LtYuG5pAUU5z3lflkF92JSKZnJvDCbp1r8bRcv+uvf0nhGB19xk2Sh4HxvWWlH+9LEhxabOeQlz2MlwKPafxscaji1SLgMdgs/pZh8vFNt8IDHBsdxe2eJ9dqoWPue0MgB+iLu4AyJJKmZusdpJn5uxz9+fPIpxtnO+5kBVt5DFQ4SoQZ9rqphS/z5hIq8YKMHH49gbPCuF7s6Y5/YwS4L5kgbWAG6/uDEpYWuiHpoT0Q1TtNwYjuva7/EMp8g6T4PWgwTozn+LQC/fU1/3QmjdmzEfnRGdj5JPycVbe8c7AP7vZ9kiA32Qm4i5jf4sxvPDKDW3DhIOmkbrkBvMXZvt5+WEvo373wPlWpw2DRq3RUYbaUexiEmr5lmQMmPC8hcjx4Matk2Nz6sRKHKemzeH6txITYiXF64OvvLZMovetUmFMbbo1og8zruOSH/Etdm9Wqfq4+YpaXCdF1UrMdfe9aj4cNrMN8g0fZ3JodiUYlic7Nt3ZR8DCHVt50Tp49rn56NUwo3OguI5MowqC7aYyyZBbsltFDHfefr3p/LnZAs8yKGY1c3xeVhasthGHgl82IbODb+yLJytwqM+6S3St4y0qnk+hNbYNdf6HDd7PBLhtdgtoQ6u1E1X+es32H+LRkj85ud4TBWRxc8w5ai2k/taQy4RgeHB2TrD9DZdpTPKrfxD98S4z0LjabMUn/eUy0g/w7WajYSFrd+/euJA10M8eq5Yt7CBJo7fmY0cyY0RZyutLPTcQqmlkosytgnPoFbbl0RV4SnB6UvtZIo1rDcpyyxrXV0kjylugp+iU8xg8ZRuzs16nwkf2b+Auu518xiBy+ZDp+NxxD7G0DFJ0xOKMhwfU2GKTLpWjM/Pg4VJlmgYwjmTaPfkPZXliTEbn+/FMxoBw9KcFXCNvFYWLtcjFf0W+U/h6m1zihblSXTcTaglob1PLP15Nqr+aNYA944sHtrYZ+gd70DjhmZ+m9Hlomr65YzIa2cljxFB8QW/ncIGVLwHsR7SGN4bYovXXxlWAAAgAElEQVSfk/40toi8OFcb/PrIQvdZDr7Oc/t1eR/wKJuPWC1Vx9TXPZQFzfIIIgqXNz547BzYxkDCMF3XulHofM9r//dhDNloBz6qpungzMcFAy3EhJYcekxzvol3R+m9YzNXHA9FTIk2sPkQ7z047YaKiHg2V/N9HVK54obVZi5Qprk8L3vxOB7E9PA5x4tqssVfLjyhbPMhbkUp1ehzuHS1lskiLEnD+WkT7sR8n9+983mUXWh8fB58/zk37FCnqpQtKEpRTIznUvhzx89OmbnlOxrPiD2k6Z48UyFgqgA+GHynaVwe9xDEfRcriPEotp8FSw3zHe8A+OfTuDYi3yDKLvA/ijKi79pmxMii9Zh8IIAxKwhbkHvw+mOIq0GIcp5LDS15L2swM9wn6P7mronYzj2C4Br4wqaPQI/Yw9JHKaCV5i19BQG/eqrTLc6QQOt91yI2mFzmOcwGYsTtXTM9ypbiLcA52uZ+9tZQKRz7PDitN3of+BxaeB/UWvj1K5tIl87obG5n61k7Lb77o2TT4W16qXlPoa7Jzzrs4Ch1V+URkud+maV61mQ6ofo6hHBnKBtuZ5L13+IcMpKusKgJhyj840Gf3+90Xt7RcecMKbLpD5B8yWmpyau/qPXJ799rsJ18bOGGJHsU5IdZtylc7dxQyhEd3BYlO6/Jvzj+Fo2Qie3NyUnkxb6SvgZFg3OpjnmHxi4SmjeuftK95NQzfwuNe/uyJKPXQ/mzGOfo2y3XgSbJZYGcNNoP0yhGYOUWKhg90HJL5IrkhsN/NAmuqUC4bn0jhQUWPFRNMILX2iCVZCJv8YTITdnCqhPCiLELEUxTWW4TDJ1vb0n4W9yoEC6PzVNSlTzmeVDN85i2uIEEapWYsoemJQUb1iR6dFrYFjIoKCHO95wEfCapaavMPWrh0wqPUvievKE2Fknb97nPxuTeMgWdMj/vEAFjq5aYliT3zRPtEkT0TU4fU5Z8TaNcQCUVamTxlEoSsNb79sF/mPqyPvolk/k3MPx6x98nmt6NcSnpur0mrN49ifY/lAY9YjclEUJR4+wXr8mNqc+K4ZT14Dgcxfa9rd2ngtEaMARjeN4b8+9LBMeasBbNn5n3TC06j2EZGgaIMPrY5sT1eXDKLZvbepr/LX/3c6SR8uIP5qa474lrTNrmEhFoCi93jiV3a8b/+eo79/w+lNDBVz9Z9Xyf7+n3YzYRFa7rbpTKw2i93dNNgn/8+kgeIHBMR/RdgIWiLXjWlUOZ6nz55UOFS4XPua37LMoYg4ixrRMCUO6c9rqcJzKHO7Px8YH7j0JDgljKFGcOxT7mNu7rFZy98Tlx/7+qcraTY27SWocIpVsSsQGidcyd51xDuhWOWpgLQY4inKduLud3f+erd9xhCs8lvIFmbRKr2nZU693UmGQjvie2krlHdNdTPaBJv0WTIgeu1xwWHIdxjkGfPBNTS+GCpcTosS1LYNZPKptT1KPnkHLm1Ec9cBcOyjZlDVVKuQ2fewjQqbPGs0gxg7V90VACu+uGMQfLdW2oC947NiXpqcE4O2fqtvCoxuMovJrvJkOE3L4sQSwMKXfeHb1znkHM/GPk4NrmMRZ38FvSu0XHQnZj4FOI6jamrfRoe+NyjovDK0UKMmWXheRqLUEslYMPa/x75symjdF0Sk6tOtrwVTpHWrQsoTBvynDfjfGf17+okUMyyEbIypGf4drcr4H9MuWNFOza59YbFmwOLD+ep39VvDlC73jHO97xjne84x3veMc7/sfF32IjpPQtrcho9MFeWVoRzGwreEUYPm5jUWJQRAgJZHaWMQxvwdoOVpSiG72QnkDKLYfdnVFuXsrwQansLUUO4mL9B2ZpLHg8J6TDe0LGgj3FDc3ufKnhaQRXxBbISIhabKUNLbkFWjylzvxwFp52w/XmlLALobkOBjhwzgIfYtsbZEgqM62tp2gq2e3NVgzE5fYVmtC5ewKhc2tyr0qc2JsTl5wQL66UK1AKjzmFqSZIDM6vc6+Th4O58pzr3ssmzn5vcHLeIUvhzXKKsjZrqkKZkD5IE8fA9lRGJNVX1ucw5rRJRDFdngPB6X7D6+aS7PaJItdDS379rZ/9jh8hMfYW1IBf5eA11xpdHdVC99yAilRCfBtyjuaUI7cX/2fCMAqBT4lRgNAyB2pLvlERVa5zScG29IKY13xBkYgNARtjgP/INaa8mie3CEDg+Xng7d5Q+9mJSIx5vqTwecSWu26XJ9x4fn1ezjkGv+aQrxiIGaXnPfY9oRIb4qxBJ7Dlb6FGj0EpB7IUQC+fuWTmRNdU29yqQpLb2uWrUY3D4LEw9jG5S7qm340x4CyLn2NU2DKvPYSjs/lbpRb+33//4Qi2Op5r8GEVn7l/xIthgzaxIrUdMH7AgyW35GsjreKIBO3Hc8FqoW/vkQftHIxprH1eg5DG4wGPucH+04VhcJSp8Fc0J9uLI+SBVEOmvHGb/KN3vAOgI/sRnvWGbJSDUHAfaF1mmAnxbwtS1i5ED8LT3Dh/qNCGMtbzs6UU9IIDN4dHgQ9LKO91XbTRuL6nGmR5MEKQ+ZoawdX6rt+OIrTBVqQcw9MTUeOWtZfG6zLq8uGQg8MeW90syG33ayn7dpn2I/P7xRA3xsyxokKMZf5M+vAMY0w+4cs7DxPQ4PFxmyerxKa4jFBaXJSpxHk8LJWHJy7x8hM8VY4BRhvpwTRz5EVusJ6Rvy+ivLrz3F6SI33PNnTOM7+a3ZBBv/Cf6sXmnL1v76FqB+E3TcCOgkbcFA3AzbYv42BQ7N6XHMcHET/qsT6tborujVCqs8dWRW1G+rnNz6ZIen7+mlvJy+/z/lfF36IRCk93WgDzWW5PDNjzcaAq/JkPigDcfGuvSxilFFzZ5PboHVe9MfNFGcVYDqst0lPjnB++D8fMtowqkoljuUGkOINsQr648HOZ1gUOCeww/Huui4UJvVs3bjY3jx9YcId9I+vU3vf989nIbdgaSbJdTcc1Bm7Cwpq4DH7JB86gLbM+zwt2ey75QOS+8dyDcG5ujCw57XWBJudnmbY+MQ4R1m3gJXhE7JvGNR/QC+B3jiC84SMo8/PUolhxdL5G9ZGQmO0pMPuTlfB0Sm7vGi7yhptFwFifz/o4NAhN/gKkT0I60N/iB70oosJDl6GX0/1GQuKJjVsJx/RvcZu8428SOpRr+TCo8DyUa7vkVVwFHT9MjcV2YTzcKSNhHbrufTHU7YYSIBPSub6S2VRM0qxMg8758JOS/hVLpTVCKHKTjVWT3zg9iDGD89Uw19tRPBptsCEWKsZRBD9vfLpobIJhRPCQevvfTEn7mAas1X2aYS8s+kVVdmN1DUdFKUehrIcyAwl24/OohjI2l+/fvU3S3zz3GI1O+QEZ7N2RZQIrWQ6MH4bRJoPHkQVaQXB1lk/CcOcwpf4wjb7G4LuPH5BnA605/AKiDVScPqdHl2Rht4jk/z47XoKDRSQvfADUCTU5XyAxBRLyvF7SOaTsZ8M/yoPz1bbb+6HTDHLBrEteZ8jiDL19hN5xR9OyYWaqgbvg8/kbmkIC3+2GOvXet59hm8JFbVzY4vWOlgPQRcRl5NB38e1VcygyzZTrkV43ZRqHDjJvXLNhL4+CMtCV3/Tg93GwavN+nvSrU6sxUWW46ITDLXjwxRhO25xq4cOUyrLAcHrIroU8Ih1/luGq94TTzdwzutB9I+fSYDnyddfwOkbwHXFDmAHHGHon2g8rxLGGKj2N3Rf82GUKdd3NmuvAV8NAoeq4hyyeQ+eVjUqtswGKLUWOBCqyB/ARycXsr2XwnRzSxc+hBUNs00YYznW1XYfWWvE+MF0NoxND8WmMl55lJ1UPjpmf3AfN+/b+VC14CG1yyKopj4duS4EFCf8r468/AuAa/VbmkiTSrRvRVLImXsRfAUw4lhJaT++YEbEvKI+eBfm8iF998FEP2ixWWoucbC6jvpBJwF3TBGhtbEK0qfGfVjKSqmLbcFPQKjwUvpaL+ZnHvIrrUCiDXaCbpMLZwpNGZCGzOULkJOfm7+TUwrdxY6eI7c4fKbg4EUrx+338B/jRc8K5HupVlQb3ZIdUzxt+83UEeM7LxMr40arlRAK9CdQlIhOMLJJkik6pyBZcOCKokoUgwHW25Cxs0QdNTtYmcXdkKCoLAztoEfv6qMXoDt7uCaxa2e/RSuKDdcjerjmBmGzS4RCIq7OyrCN4v/Yx255Iv+MdOUBY25oxHrzk3jarprDKeogfR8VK8P2VD9zWs8j+iME/J4FeLQvb6EuKLg0G14ZHJbezdU5Qi0xfrVnwajEOlNcqdixo7rtRyq4edG3MPZWgaoF6rElww8c95ECF8xy74XuUtXWd953ldmtvJfrg/H7xnNyZVMgca/ZE00rRYEyz1H+NxtMOHkfs/KFVcCnUyZcZ4bxenTYnqi6NX/VJmXj1Uiod36pKXQYlFGlL9MSRuaGD3B6rOX1uiH6b8L/G4DEnk94ah0KtZeflf1+dcOdZbt8N97tQPD1NC1e+evVEKPz33N7VSIJ02TO2oLtwrK2WO66CLaW87xeIEuie8qpCN9ub+4ajSE6QmfwG5/a5e/ueveNH/O/vaxep0YJ6jI2o+fPdCCm7cD6vF0RsXrAzkRSdPZnx8LmZnY2RGOLHNiD3HnS1u1ESSeGhaWZagfrrzolyBWqKlPz+w4xrdLYJWSR6xVR/oHpSOXh5E4Un57fOZ/VhRkRwTF7KYcKfs21VuBCwsJ0j1SVrrFtLOJUtr+V15CCV4yhb9CH6yCH6MpWWPwifjF1/NeyHR6ZGoVrZ2xTRvLcXL7N82tzUrPrpSgvEHxvviNjKwd6dovA0vefAzHp0+SvJ4CgPnh/Lk6lzjZ4ceNJUOqpu3yAfjlXhMWvf3DwrfZ63NhS12FuiMTqtXQzGNrMVNR7PI59B5NDrsEJdIjgGzTX5/twb+r8y3hyhd7zjHe94xzve8Y53vOMd/+Pir2/FSDWMRUxZWxGf3JfeO+6OL6iTFAjdikndHUZnNKcveFXJVd9SXHP3VDhZ5h8jcsKwpBZL4OJbQQlxRh+pZsf8NYvtESTi+Bgbr2pVkQHnxZYlNAcWlpucIs/9Ur7PkRCvNeXL14eFlhSR9EiaAwpD8KXHn28SE9lbrtQmFCRkK6k4nWply2N75N879rQHqrMGEFNqWnYnf5igD9mu6r0PzG5YWnFFhFsqNmC47GlDjFR3wW7ulEBOeBavqHsq3a31nRqG81p79qnfvYacIk6p5ZY6x4jRtkKNUjgeCUdaB+HhyTmLxdMIzOBaEyuX5D0tfLG3FDLZMr684x07rtGpdm+fv5vvbY1KKkL2dU+MhlvdIycRQUfwHY3H1FWVMxKKtZUwXzzKwTVVw3qS4m4Z6UPh6nsiGwTXuOFbZkIfsvHvWucmY22XIxhRCBP6UnnrSjTbTwQV4erJa4TMBf98PFjsk0Lnf/U/LHh3aKpHLZhbeDAUfK7G5DwRrRsiO8IZ18WIQX1Ojk4pDIEh814OKC4bNlur8uuflS3FT0tI4LYgmKdwK3EKJcqeGks4j3psPkSTAA/KgkyTeerq98a5WPqGrKGlRtCvjk7+g6sTZhxzs9b6d0KSF9xvDEbYnXu6I0N4TDRCPSrXNbZn3fFRCU+49cpPcikthM95zZ0h0H1DbKoErsq5Ic/vhPWOO65rbFW4Isa4POXuAXdLronfW4a8B+aNrYbUkfXK4g9GYci1OR+HJXews7yKOu7H9rmS0FRenDXed2t81spzbmsuHwwZ6ET0tFDCSTVYkh7RR8p6L1sfKYaJb37O4/jgbNetbOdCFTY3RhabYdV4ngqV90YpVeRiQ32FWpTHlMZuNjCplCr4hNNdPnlNCzlERV03R1sk8DE4F1qFwvHx2LBaIQgNpCyoXJ8cwTzmZ33wNNl8RcFAgrHpEMHZBmfxLZ3/0Nwmr7dZwnlW4TXWVkqgPFiilt2dp3fahNaVSBXnXSoPGBSs3FBwWruRSaJYKYxxPyvKITxUN6JKhjPatbnlI2Bop06Uj94GLn9Z/C0aIScbE5j1QjjrCm9XZ6Lh8vsiDE/Z7PkvfF3BU4XPCYG4NIuDhWhSSUKy7dUuXK6bFFJK/tvXkkUEHrXui8t9UPyWjh0xkjO0IGURedPfRka5SSbQ9QAcgXCbsu6Pfms2OzF+mE4RePvBjVEQi/3ATYznrSmfviEwxHmtC9IMM91eH+4J81reRoO5So71vibsZzYh/x9777YkR46z2S4ApHtkqvrvfbPf/wnnoqdKyggnCcwFSHrWPMCUzDpg1matkjIOnu4gDt+h1IKJ8jNm+TOyaVlFnRUhRDcJu/sgutAWjE3TsFWR7aOCDNq4E1rKgrM9nnRdmw1Lmz+55D2BWu/r4j3FLsqE05RqqAXeVzNXuHrQ/LpFD0agIXvNLhLY49jrUbkql/kmby5YyzveAfB1NR7TDNWqUMqx7yUfkTBMXxw2p7XY3bSoc34WPE5eU1K+qnDIPbAoWhEpyMRl63C0KDqx1CLJ61vwvPBBjLGfie6FKsIxOSZSklbzteDF4VCdMBgbfpWmnzLhKE6aD5ZFLpaZP7/J6n4+Ks8l06rJZVrmpD5glNvCIFAIxybh/6MnFn6ge2gxJFJKdh3SPYUS5DGFcz6SKLz4VqUUuK6dvyRA7PZ/e5wH/hz7kBdVWodz8jifEkg4P1dBVxRRSyjv+l7ViQ7XNzKxIJuUbWFcr7avfS0H42p7eHJFwpUXdHe0QZliGDA5ZBGErqJhpB9bh6+vWZyUipRxQ5gjuMJJp6a0c3iOQYl9B/GOd6w4qt/2EsWIDiPSBFQj/cGWf45amZ6Js8m2Qfc0WW8985UVgVH4mIOcMZRG4+PjI/8e4fl8sXywhuVwdomacARfr8YxhyJ/nCevfu0m5ArHfNwm6ZIDidf1tZslJChnJXxxfC5C/B72CHjXLdKkVThKQZa0tabp+hoZBDm8ec1a6fNROWvgMxmVgO5P2rAUhgBMOmfVGxKG0VrnnI70MnnHXhdXptF621D7IcZo3PYmgDK2AFYTQCo2r2MQuMTmlp6qqAoN4WNBHxGij2/OPEIVoczXvAKwoJSVSyptNM7JWXxGQ16DUxOmeKjys//aHlEPKzQ1xuqkIkXKzsN2Hm7XYIhzzs9UiqDVGLGum/GQx/TUy0b4n47fImO6+8aSl9lPbPMlknxvujCLg8bY+Glxp6jgBtcSR4ig9/vgoAjP5pSlSqLKWY1YhC8Jwp2Psoi9Wezr5hQlnn4V896Vs+o23PSxlOB9P8zl1Dn9nQfq7O2WDr6ZZeOxthIxFdXWQyOCnFvfgSAQu7cTRfMG79fiHjiOUWqhzmljknZv7pNoQfAt236sa7wO7ddAw+8NSEg2LXv7kj5ESwxB0Dzk13aHfBB34yCaQgzf/JDE4dnZ6i02gmbbgzgbsfDdEFYrhLBVlZrng7WwvFIEM6XMAkslpxwbS9wiOUff2OehyeFYU48iwlHubZ5IFkXrNdam8R3vAKjHsX2BOoOqJ6+xOEPB5Q2dqohFjS5sHHn3fE5k+gnlz8Bfo221RuPAnY2hdk1PrrVN9hjgsjH5MKhR9nP69Wr8mAd/vqCm6d5UeNPp8leQneOwoKvza+aTWtIUNBar1p0Rez5BH4Gq7QnV6D0HI/N8vKLhL9+JXM4D04o/J3fm44PqwX+ua2/aDxKj3mYTeRYh1Dfn5ZOD3satPEdOPFf2FWaRtoZJ7pmDZ8F1deev54s/53e2CsdHSZQBgBW8ZmNyTYM3kxS1WYJ7w+GH6lbVWg3NclUvarjCx0de7P+8/iJeyjG+kbRrbP5hFeFRjZ9fWZiKQzkKNoSv59yE6UBMaMu0NQTR2GTjMdJ7ZGzRG97xjh3RY5LaU+XLQ+8TLQa16tIf2Qade05ZoY/0yupTKfGICihf4xawqhzJWwSaDFTL5sr4M2gxaPM5PFU59dw1wZc3FNvGooJgUhizQH71F6aDj1oIW4qPDnEbNH/1njXTuveHE4+xjUErRpC1Iyyek21uuiqIVWrNBkAL/OeXU8rMV6UChohy6GO+iecQfw2YFIrqLTRhKcigy/CLDqdusQPmwGWpF9fifH4eBFNUonv+PtZnBpCYYl3JFfw8jLOw86zOfLXe0QE1S0EpwEYqNC/lupDIrdhMZH88fjDi4uf1Kz9iE/RI0RqAV7t4jdhLgmKKRKJtNruqaApvreZMBLVA5uDGfd4Pq6n9DTZC71n3O97xjne84x3veMc73vGO/7r4PTZCna2OFmVuP+bfBZISz2vKF5HqZ0uZQ2XCMhIiAktSWe9XCbDujCUVO/0s1tpUpmzrgq2FBFfvlOXxYzW3CO2ZPx/OacFNGkqFkohb7ayaMWLQZp88ptraWhd6eE5w57+PLnRkq6lVUbw5Wr9NHv3ehMTczyzImIUDhqpS56Tl6oEMv9WnIPlR8zoU1QnZm/hPCZ4eLM217nNqskbVKQG3J67DPT0sNo9JuXxsPo+SinImynNOmscQWgTVbi6VmvKY0+yXpGR3XVv0A64u+1KPAR/HvUFSEY7T8Pm770OQHnv93FHMIqcS3yelcvOWak335qWH55JqWH1OXup4zwvecYfavRmJLvzyCzvWlC8ockvWX5IQ2b3JNfb0bN1/PSIRZ2t7bPNenpj7Kie9Ddrkwf3xUVATrl+5RTj1wA7dcqXyUxmSvBIAHUJrt/LZRpybEQuSLMlhnG9BG8LHWW5OIs6rj3ur2gctuGG30acJfW5CzAsjBsf06BFTem/ba2J05+Mw/iWFMXPYlTtm1qU0LLlEyzMsnNH7niz+df3i0LKnlUuR89rT7YFZ5TEn0S1eyRecj3MP4XMIVhevyfEuuMeGClUVcN/5RG/s8vzeAzPfSnZ4akRthSQNxnBey3dInTqx/gAhilKp6yS+RvqgFeHxmd/z4wFDlGUPZEOwevCaMMRrOKpO3UqrvOMdO8Rsb58jxkS2rPs4Yf7fuXshwbgm+gVB7aCecIylquoUi20r4RG8+nOr9krk68jMN7U61gKZZ3TzziCYVka4Cz+qUebWoiE8+2tzmUtUTApaD54LNnZ5QlQXb6kkjH4l2qYdLuM54Xxf2jntpEzYWhHodm9bQoTe297sHnEyrtemQ+BZx5jdvG+pablia2MzsmZ4zSQa0dBpRwCTb/MCPXxfp1ShXHlLwWPnM5sQ6O0JxFSaW/UXzrMJP0pwnPPaT6n/lbWDpCysH1LXVLLrG8PEiBu59OvrLz7OB2MqmArBUWtu2ud1VddU0SP5pj7VkX1vdpIPdk3ElahgRe8z0zMfHvOskN9Alfe3aIT6cIYuOFdesC0yQOLVY2PRU2DgJtcrpvka64KGSmrCL2hTgBfZByAqKTU9sZ6vSJ37tdwrQA9lzORRDeLVKavC3+vA9ZmU4YNwT9w62WR4j32IR8wCahbXMVbjNBsjhWgD8/kr8Z6wjvmRPWLa28wCfww6scl+9mFJ+g/fTaV6tpTr8O7uxEhyI+RNjN8ymGO++rphhUDsLl4miHVzowaByMDmulpRmo3tA+IOlQDv2wNFESLG5gSFpc/PSgYuWdAsGOLVg9YGbZm0qnDFYNZX+Ehd/zaX+Y5S7KZeieR3FO7ff8DfRB5Uky+0V/kR9Na3n5Itfd93vIP0d4jIoQiRUtTxWtA4wUQ5Ziffi6B9bDiEWGAhiDjXgpSOJOd+TkNMLSk3X+fEQkZMCNqExvVBFZlwubQYUL0N7Y6jYsr+88+rpQXARiBEatiGb1lUFUNLIFNaGjXssD2wuFx49r69baKkZL0s7w8WmXp+z5KcgHNCMFob9FdDFmnXjDDloxqv15KLTX+Tx7HyiyQXczYA1zVwtS2kY3ow5B6bDcncvb53a50RwseUpn4UYTR4PNYBrITqblJHgPTMF0vj9nl1igk2v7dZIZxtLHsUYYTu5uPyzF3L+Pqwghrbt0MxrJZbJAcIBjLhzF07r+YcUvmYfNByKBbGa3ZCvTtnOfbQLKInf0PWv/8tjvV3/C4RwrHMlsXgm3Rxj0DFOc6Va7JuoSw41khD06PsAek1hC7BazYyR1WORyFmI9Q7RLuImRu8ghfFll8OQTXdrzdIXl/4ykVgpfI1n3PxjnWw67kUuKklKKq3ObyXOVuYtY8IXS/qGizrgTPS1JTk9nmwBxKqgh5l11+1CMU+dt0ypqCEmuCLltEntEwX7LlnnTHrKaOkBcnMHe2VthyrtjlUs/77hhAbI/ZgyIslt321NYuHvrmCkrwmD/7w/RJ/q+GUKfwwa9k/feAIy7qnkDyxmLDG8xCsRA6AyHyopCBCfkfnENs+aO11cT07EmzBoFMP0J1CU5zHfXP2DQgzrtf0kSp3s/hPxW+RMbXGJulCQWywDMCKGmFCLFB1jJw8zD+XQ5LIFmxtfJNbDT5fcXalSwmoHjzbtU2hRKfgwTc+jhWIhfuPAd94K6nKFHsCRySu3IONR/fZli/TOzTVpLZoydwgLXNTifuhzn+fCm+r8fHuWMjNe4ospMos5qsdqTHvfuvYD8fVqPMm9+Eod2feRzo1743RJG3bXvGkmtWaBijQxjcndgSzFKIA+NWcyk0sViuYfCPWkQIOPQY7YVVFCL7WdYrVBM+k24Leg74KC0kPp2t5HS1j2pmc1jS4zwtvBN0VibETVLZFbAUZd6H12OaQYwx8jF38vMUS3vE93K+tiDQiOHWwTuiI9B9bBNpz+mrdpsOTHyTC81q8N+VxCD6bp1LTsHXMRugwQU0pk8P4qzfq0L2FGhI55FiTQ/E5aczP21pwyb3V+OMEOWqqUC6j6mKEB59/JD799Zzb3sV1GgGhOw+bGiKDckxMPY5WuTfYHkBsM9TeByM6tS5Rk6CLIy6bD2oOh9o2eB54Ot2vYoU8VBeJujlXzP0AACAASURBVONIdz4nrzI8eUvHvE7ISRuNMYubUpR6FOo81KUqMiQVRUmYfQ65c74JqYBV7Lw37yjt6juxqyVJeDWUhHC5p8IT8HGeqLC5CYfoJirn/ZLu8GP/7iplNB5yCwS9hvJQ2znuJUG7Oo/HnLhroZlsVa+1jXrHOwC+rhePpSr2OBk6GNdttuwhXHOza2YEQZ2c2wBe10V7xrb1Ge7IlYNPIJXPRO6BxHD8m+KtYliRzcmNNk//7ZMmuAa+VTDhUevmWbYRKcLi+g2dodnDyGrYAullD3LMJtdyPqctOhKG9OUHFnh02mp0EOzx2A2A9wutdddX/RV8texD6rkU9oI+fNYzUKtxYJubqaoEnbGuPZU2HF3cKovMmbNes1Ew8y3UEjFSSGZNddsgkM2Xd898+LqCX0tp7tT0TlviPKJoNHyiC4anWnFdim4aFPfNE29tINJ30dNdGP2JzesuLoQ5dW7W7Kw5RO6wh2CaNfKq6D00N+WrflahvwbHaoDknx80v0u8d7zjHe94xzve8Y53vOMd/3XxW2yEjnLwnDC1UhM9v9TQSlH6uCduGkr0ICaU7jRhdLaeGUwEl9zKczKxUMZa3Xr6bkyoW2Jag2tpzhNUtY2xR4VimpwZwNxRZWNaf7bUk6/c/hEy1dpuTk9Ogje2fKQ30loXihgSznItHjH/6f77/GSyZVuFwPaf+xhoCnazpJvElCqDmO2+RX6P9Rn7CCSEOq/bx1lQNfpYfJvkSUVZvADnG74mIYoq2xMohASof5Mh757+TranuGMq4M1rXyZPaMu8pf78ckZ2xt9UtxDh+qY6VyUn4RsOOM2il2eBYhw24X9rPRcQLvfWSE9e7YXvzZUiEfv3+1Zhesf3qFJTtQgYdLQYMQHvLsk0a1NmrIRO6NTyeFGe0TnOQtc1Zctt9trE9ui03vCZC+SslBCmijQ//eBrNP5nQqGkJNRlTWglIqVZ9Z6wXs/G+Tk3LWEUd2hOXXh3gS8k/zuJfAhu/p+E8HxefH7mxujj8eC6/kLLgoGke/zaFo+vVDXqS1HJcsq7ZO7VhPDBz9a3f5us7fPaEHWH4VuVUrQkH3TxrZzc5C5PJ09luOU/4p6T4bVNFhOslA1b8ys4D2PM393zV8NL5fGorGFl6yBVdj65WidGzHMqEQkeslIe0QQ8kLmV+vioKVu+1nM4YWPnGusFKcrra553JjQcl/M+S3qnl+A1+Q6v1omj7MP7PAqPs+7v6e/55ju+xes18PmMdF5oLff2OCR9Grlh/ijbzuQohUcRut8ICdHE3pQFy0fxbvh87qqAHo/tfzM81c+WqpyJEQFfGwoXlGLIlrEFFeWc+U2LEyqIlZ2viIShLg5PaPKCt5owczP+/VkINvolRNFg1z6iCTP79co61EejHGxOkWAUOsYFY22VAGN/Br8Gfhiua6NzIX7zlzVy+7WUg8MNurHcI7vnFkhWXhcj4t60hQiO0vu87qJp/WFgx8wVC7m0KRmOhCMLTuyOFNn1dE/yxEYJlfNBH4NxLTsbZbT4Rl1JKJ1PKWy14KiFKLdFikqS9peaJyimY9fnpklxaQv19RtwsH+LRijUN8Zaguxgthxg3qCLW3PFIOzWPu4EPZyELc4bCGDcfhP5e0nSKsBr9PTAWoVwTL7MairckUs4D73fow1sYa9DN1wTFul5NikTezskX+cu2JNg056LSAeYpNHn+szeNuTPfRHl5lvO17yVqSWxozMZPVvj0DPXzFuWPRgq6NLLZnIJWEVZGgcuf5KjpBzi1/xi1yVQ5fZfmrLiS4s/V7Y3bG24Z1O0NSQSwmFHIea1bVefTc7NUxp9b7ihJNl48+cEVJ0yi8IeymjCY62LaybzBS1RS2L6cgUSzcIiXDYOtlbFinHNhPI1Em6p0//IisNRdhG4oDnveAfksznm4VVcCNft2fP69cJO3fCtEGi/2i4iPg/lGr7x05DwlNDYzbx5Om/ZNg51hvctJ2v1wK7Bax5W1fMwem2JeecshfWMtTEoKpR5v/tDQQ0X3wbOZQzOSE4epNFnGbHFFMb8nG3yVEzgen1Rz2yMihoht8iJFxivTl1QYQoSfcvVikMbnatn/s33DELugdZ6n7pFbLJYWPnmwxSraUgKoKXweg2ir0NaqVY3TK31hkkQ8zOFR16zhQSWhLmpssnjH5+WpIflKSeOa3AseAoy4drs76nBN3l/OFyJ1xrsdKLrbv5GREryznPAR3qi5dE076mrow2e02BXJKXN7yIQ9JB9Rr4nN+/4Ho967FtCVScfMP/crj7FqBZmP4HjCz6qNZ8h7c6YjY5K/eb3CJdfRNg+L8MCTL/5OE6Y3KzpVquyJOjVx4Qarzoj0B70CSHrMujDieZb9OFRZJ7zGb0n1wlfYlSRtQp/fxZunnhC+9dnchEiFJmiJ6M5Hi90cmEsjiRGqmwfoVKyhVifSdwYHneexmdjsy8t2MEqu717ciyXuJQqjLavwwhPmOG8jmVWOb6hvMpHKfyolX+fCVG+vp4gd40XYyBi/PjxmX+vg1d0fBK8fKQty66/R2D+jSfuzlFviKGPlhSSxYNSpYrm73jVlQSM+8+CEnJ7P0ZMD7tlT9mf/NPxWzRCg7F7UnenFOUxO/HRpsrJ8qGJPNRtO7sLiEyn98WGD5zYfBxT5dX6nk5+aKF334pux1GmmencMqlRq/Fc5oEyUKvUmT3UnV+982uyeEMkk4cqPrcvXRZ3ZXbmVYCxPMYQUUqp28dDPTge5xYiCElvpZtUq0TEVnBLCpLvaYMPISwf/IW19ebIcV8WCUfLYCyn40h1u8VDGh6MPlYvx3kePKru4sjDcUtcLJAFgcfmUqWyxU3us9nErt8HJG/Jvun9x8imcJ3hOWW6tfldgkN1e2i0K31EYiawcLC4Vbm2Ge/CM0fgpBLd9jQxTQNDnYm2X6gc+zA4rEBJhZf83rzjHTtcBo+pePOLn6jfROJ//VEoevLqefP00fJZXtMwM9KXVL/NKmUqruVzVWo2N7Yao0hlMNkT1fS5esVtqGphW8Xpai0JrCtXqMEYuwiQRYEx2Q9eiocYZSwDwaB759qqSslFWY+Zi2Cl7gI+1iZsFuuj52TQr7VhKlyhPJa6kQjtq8+B0ORGSW77t3+IJOfn3GTkVK57LJGAIrQ+vnlaJNdPZ2FiapSz3ApJ/neuqIgwot/F1WfBu3O9bpdDK4V+pbhFvqbSveNzihktp92v+b3PD4FDbp8OnOK3j8c1oHdh0YSukYOj5a5uNlKN8zj5nM2YTgTDErlRKZRvkzglUkxn8UnjvrPe8Y7Pz7rP19zz+q4jisnk36/tcQpRPdvajCSyxboSC1GhidRYXBafao9LGMUQ8JvrUtF8RmWhQnKwcs7PUCn08Ps5HYMuA5kPibjlRqk1ymMdxgeG0eeWVBCk2hbVcndUbTdCguTWa22bVcDZz0yR5F/bfE6P+qD161a59Jb/sxtZ1Dx53YvLpLUQ19j+bjIbhCU0kK5D9xDYZT6z26dRcepdr6lgTXcBEjIb1lUzRmoRv6LwtYQoROdAbXWhyq9fFzM98dUGPTplnhUWg7Cbq36pUoptHmM0J+h7GF5E6SE5AJr3h0d6OG1Pucg8vASwlJGDpU2jHHl+LCXgf54i9N6hv+Md73jHO97xjne84x3v+O+L32IjpNxbCUZAvaWNx5XKGb64MSOwKFsOskVQVDjNtlpZ4JNjM1/DA3f51iQHjdibD2+BG3vLoCYQN7o0QrGiXEvto3U8AlsYVp0QCRHGxGIeRaAetIVfGJ2BbjUp1VRSkb6mfPnLWJ02DiFBWZuwki7va93Ye0943p7olr3PXN/78uBfZnuKq+I4sqElaqBV8KkY8zVS+W5NUT414WFLVekaHdnK+1DDac6G3rka7o3HkhCvye+6XtfG2BMT1Tg/VM8t+lZIElEIp69JdChSSLlycgqi+s3CKTXF98Q2ijHagIXTzRdBYa/7iwnNb97RGZUotyS72+RzLbWq90boHd9CpeATNvvgBzBuzqJWEKE9F4co+PhR95Z2KIzRGf3OBcXA+g3bCInMKXO7/HSo58mYW6brdVEP3T5now9GeEK7gGolHcCnz8zn+UA+bMNTr9bpF/xxwMdUcVNNXx2Zm/jmIFa20qKoY9V4bTJMzlJXLimaMJHFAxATVCrSb7UiFaUtnmWxnHiaUCavSCU3VEuytsxTYVkMlCpbEQ9y42Plnpi6w1GPG9YRjr9GwmRIKIuZ4d+4oD7G3pxZzSmse9n5Rc0JbfcEvUA/4DnPgnPkJs4mZt68oUfZcOOIkflz+cc5tO6bW+UIETcc5qMUjprKU4sT5FUoqnysSz9kQxDX9xj9zstryv2Od8DyMJzbGPeEYWyPREsPmXVvSd6TG2q+6gGxzc+5IlKldz5XpxqqwcW137PE7ekzCApGmxCL7vkeqzIJwMqtZ1s0t+XHlGMOlEONZo2xoGyhnBr0uWHuV6AYZXqwSch3OjMyc+qWMovMNd8tVkQGbeaG8yiYfqTEXb4jx2npJTQ/w/BE38jczL+enVJ052E8MDVU1vdoSDhMfqG6pRT3/HkZAyj7PatUpOazDeBmOHavLxR6OFdvXK+8tnVWkBuaq0opZXOfCE9Oz1LoE7JuXReq+7SCyT+aGK/eqN9kxWu1rc5LH6CalgL7awfP1ohpaSIhHOIsWebunSjKpyWs+rQFcPzn4rdohKKzJZoJmY3ILK5FqUBbp9tZMbHtn4NI3uRm8Fx4dp+H38RxR65hX/MX4e6UXBADeTOpGufEg3oksW81BKemy9B6cLsYI+LGhpqj5nl4zpv+LxoPbxuG4apJ3FtQEiJvjN3/BckGyFDysFywj2hB631X5UVn4bAkKHs2dlrSLBZIKexvWN1ShdF1Nw2l5DO1id8jm5SFF/1qF1eTDUvL/kX3mnTR+FaSNVWaKFqX8Vr68fQubGuLCcVbW3ZzCEsoIUCVTGCbKCxMUt1NIFQp6FJejIkHXgWbD7x7Qt9gwugmtGg+mFxKqnEu2I+CxJZHr5GY41h+S98JHe/4r49XH7gnrvlTjbPcz+EvdyTaluJnGMWExxQZeF4XowetdWpdB7/xar4PH3l6/t3isiAcVejzMPp6XYiw7QKQFAuR7YkBtX7wnJ4Z7o2PWvia1f1nPXhdnUHdz1GgjJGfH/L520UQcIrRhnMsWFnvPN23mWCTQimSOQqIEVgtWy77a2Rp9TVhuWcERMraH1NAwSz5gs850PIYfJSDvoYas4iLmWMzR+9HH/DkAC2I2HB03FAxVSMQrtlgqAoa+T4A2oGSUMLXczYhrshgN0ujBepszxN3S4+k9csLpbbgsRMcDLuLMpVgeKPPfPbHjw+u9kUbNzSpRXBobNEaUIrJlva9vgYhwrE4sRr01y3Rvp0q3/EOkl6w7t/zmJyNxUWONfhl/jm9tQ5bpp4TMoYgS4Y+sulYjRAM9DudYchsnmaD0BqhsaFypjV9BPfEYsLjWZ8hP8+S3jdN3yGVsgcx7p3mg856tgVvF8PW4LjkUPdbTpSIzW/uMQdO3zx5TNlwLomRsK9Vf9mJjCeYUZZohCRvaVw3H2dsaBpYKE9e6DathqpsQQfVbEDWrLwTvMI3PNnEkg+/voNo+mPaLYrDSDjxNaGMxWQP8vNDKeeh2MzLRef79iUo00ErxzFrthH5SebvqsXgtJJFGlP86uq769EkcS/AJfNi8jiVo/yxP6eoEovz5YWwWzZcfgMO9m/RCCGxSbQRbLNNmIhWv32EzqKc1TbfJ29c4RnXbhIC0Cj7hiwquCjnvOPykAadB0mVjmjepADdI6cYsxB5WBYabRlGVTibM2wd2EDPJcRSSrEwusj22FHJA3+ZZXV38NhqQ30a8a2N0KMYWpTBalIG4YOlKW+1ZLEyr5NKmmLJdH1e31tF9sPuI//9+kzdBxZ7F5ebFc1pLkB7jk3mBahquMpu14Y7okLfTYhTKPjk3tQ46JFa+kvdrlSj9W+eA5r+TWvqcXxUxhibeFlVKGL0jY9P5Ttb195liuTdU+HhQVnJSPPfeMS+Z1SW+t5Nwk4luclDGgFiW2lH9Z50veMd5SH4r8nH0Zy/69y+XCGM4WwPXgnaCGSsZ2bwfDUeR6VOH5hDC1/XkzYPVLHcmJxTJk49uXWrUrBq1EeBls1YeEmMvC5OSRbHu5ixqaDmi1cXhHRer5tPKJYO44uIKw52yDwYcy51vcYeclStfOrYyordGxK32eloUJrhydElwtNzbB6gvfXEzEcK0cAc7Ehs/kzFqFX3c3u9klR9nhO3P8eQsifPmQdXjo0YhJbtgTHiorvsSY979ppL6ODlHW1KVd3n0et1YRqcU0buGg5a9xTXdPGUFpkYsLInrCrGIen1BNBG41EE3wbQnQPbB7GE8HTn69Vpi+MVnr+P2QAuz4/FGerDudrNlVrbq3e8AzJtrDviHuCuZyDwPvaZL66pvrZM0ofThjM09gY6n2N285QJC2ySPTTSGHixIE0ql7e98VF3xoj7PS2FW9Y2+fKBihN91oRaKGZTcfJ+tn0IssURHDYHJ7/X8FutNlywb7wlBMx0o0KiC/6N19K6J2/puWopTc6R9xSRYg7AxZBZF14+cN+YnhRKGPcGx81TM3d58pyCpQpNXieE2gZHSeGDw066N7ovM3pHVbnWDsADdcGG7K13kE2kfCvqdCh9DqCu56A4W8zH5yDoXA6rPiZP7M4hXYM+N07eoVhJryFyuzfG8m3K//aolbCDJWg2xqC3FzdkKZJ7tDlj/3y++uc/wTve8Y53vOMd73jHO97xjnf8P47fYiNURG/N8RB8+FYOEmRuiW51D74pZ7Q2KFY4Tbd+uw6I+AaRmPCwud3j2S6qVup0IX6E8uXB15LWGOmqbo+p9hGKifBjTT8lJ5NruOBTTlCFreQkoqnBPtfDJYQXga3VrA90GEy/iRgp771keNUORPSWkByJjdeFly+FcV2b5/T4MC7vMHzzbZbpxlo5C4IP2TKsLqlQVWY/XE4hTGjPKZfW54ZueWpM3tU0j6dHcCCbW0Wko/HiMb26A5EKSmuVWgyNjk9uVIQzZGwuVAxPdac1kbDkRcWEsakZFjemmWC5rez7JyT2Zi4iFZXCB22u36wIUe5NmZC8jbV1DBHOGttVOqZvwDveAfBxGD9fc6vaE4JrO30NemfnnqKCVOU1N0JG4rZHb9Q+obiaKnFra9pkwkL0VgIar+A5cd4fP5IHV6dyXa9CvwZl/vxAoF388ZGTRQX8EqZZPKoJTc2Nyl6D5+R3bmeqFpSCzK1SyuaPrWQXGuhxbIWkYietNQ7NN2mPwWsMYvrjiFQ+Pj/25vevrxenGiWCiNf+N+m8Njc4ZXqcLSivAKbfYGrO6M+1nIFD+fe/jz3d+8/PTgA+c2zVQnv1na+GJmFx4eXHGGAJ8pjLF/QCs4rNTVj4SDuHb5yL4yjElujO9+wTy33ESCuFDSPKs2gpa0r3yUvKP796qnFF7xtWKDKRAks1sGr6t82X/NWc1xh8zK1V2QfAO97BwoUBSUMIvXmvhwhPYVtLIE5EQ+ehXyRhdFfErmXGEl/bthkdQXYNdxzJcfuaViGqBett0xmchKGvJ6IP56OWvyFZIOi+PBUdhqAoNjcX7kHEvUm9Wno76lRD6+G5+Z75qZOc4Fg51WeWWVx0Bq3F5lHSDTXdynVBEPVA+3V7FbX8bF3ye4oIElmbwawrou8NraJUCj5rutGCWmyVgHRvqMamBXz1Z77It23P5b7/vlp+Rlc2l9NJBV35ViBFCWzCsKPA0xtlHQal0Pugzrw8Rm6ddKFhTPC4ttR5xyi1ID7V+kSJPmgDXtfkgIXM++uuzDwcneeVCKnYN6/14hb9k/FbNEJK4Zr+FGopPboODkPTW2IWwpc7eqWEbf59UCdmdcHIiNStD1vFcN7I6wY+ygPDdnP1ImFjY+IsUUvTq2X4dSpalD7Xia9fgz7GllFUSbjC+EY6M4JD2LCNKwwd34CwYjRxjoVfp+LlbiIinBiBf03IRc8H4axr3cxUDJj8HDLXDe5DUCLwGBtaYqEU083X6RMytvgNVTQNAWcxY9VTWnNzFZwSY/sztQiKOLrINZ5cqLVubu5TCEFvHOzlM0HcfkqmgsSSS1//bX4JT4lJn+9hsxlchUR3pzpsVHxkgbZalzZ8Yli5G1dRZDgyuVTC/PllABcCl6N1vqq+F6fvuEMiNg/DdJLV17njzqOULSONpk9Xnez2/rNzFEs8+ZJ+NaN+GK817NGSELV5P55n5a/eN+RUEWQoPg9pVWWMzl/z9foYfBzK5/SWUC38GS/6JCsfcqBbCntJ4GpCrGbOexxBKZXnle95YNRSvnliZLZdzVtEY4RT5pNnNajlJOZQpfmL67UaR/DRucbARHisfFMK0tky4s7gEjbEhpICNtvWQHPgYTM/iQp9DB62WLvK1cdujGqV6Rc3uVmW10DjPjcsBHXfjY2G8iGFax0NxVLIZcI+SgzKoYz5vb6egXvf5rXFMqMvL7JyVkYPalmfQbCiWxzGr8G0YdlNplYBF57LpPcQCrcpYtXkyC7I89tG6B1/i9i1NKhwjbGPNDXjUNkD1Y4wuvNq0xrEDszS02wsOOeEQ21uh6Rwy5gv8ufXRS0HrwmTlcmVPh6Lgz3tUuaPt0guSlmfSXK4vGTwI6anTr/5MiGTkrAsT2pC6mPya2opSTSYz1BzR4ptWfvWG23EHmCJePKJ17Mzsk4psxB59s7rzydFDbUpiFULVStl1i5PLiRiC5mYGmPIHooNnO6DvmSjn87z9M1bki4pz7+47DSweufcmBDjlUuKIZbQsmUFc8oa0axcEDBicztLBJd3iq/aJ4f8u2/SIFRu2Fo4QuFxTloIBfHBApPZYWkP4XBdE2Z4PQEnlkS3OjXu62AqdPfNdaq/weDm92iEqlDjfgpqsY2XDx2pwrGKbYXe/J7yWaqgacRWJPLI2vW0b4VuH3vLBHnA3Q9/YHIrqTDJ991vIh3D6c+ZCFoakcY3jw0RobXYnXiW72V7DzVpmDhtNR2WXhKLl+IyCNEkrwEadpNXyAcyJj8mv1MWAMtbxCU5PNB2URYpPcU9Mi1878XMUrlpqQy1GDMRzANY01F9TQeIqRsvi0cQtBbYMTcrIx2EYxN/E8eb04D5Hs0xrdRpXuqSgNb1HI7RUEsuEeQEy4lvggWB1LtwuDwnUZubpcpD7nmIe2TDq/oNl5+FbJ3Fzph5YE1VjpqF6BLX2IXSO95BTh/XVsI9Nwh7oBrC8RBk5ie1NMXrX7+AfObMDCkHv6ay3MMnyXW+yFlyylfmxKLI5N/NQ3wAwtgGDEpuPNdTdKjxeRY+lhqbGv0qjP5nfsh6IC+jtRef00Dw8vx3Ohub5+uiHJ+0qSjZaTw+HtOvDZ5XJ9qdM8OzIVvCA/3qfJ4V/WM2OZfAgDIbyEcRnp4k7sU9kBH8er2IeUiPEXwcuieqrQ7ogc48HyKEHdujJzx4/my8zln8jORrxfz75whKLRwz96RwlKe/CInBP85PnIGuXF8y767CsBalojv3Jzn6VstDBSkDXWtzBYYxrjWqMXx05Lj5P73H9tQwz3NF6oP2Nd+zKqYnxfLPa/+02AgRqaa3hon2exzr7/ht4hs3hspo30w8PSjjnsqrBOjYPjN9eG5MZY0Gsh7ygA0EQbfYCiTfOXTs7U2xLKy3DZFYClxtk3QYTXZdgaUBusz7WE0hetYem09o6b12LEGsAWG74bNwqhhj5WkJ1jY2P3Qq3C4xK9NKlECWcMsYWJEt3CIhlGopUjMvlrvnQGjztisx/FacFKWWu6YbozDcacsHqCcfew2OrRYavodLhxYi9DYi7Y6V2Nu6NiJ9NRFe89p9cObvY3E/I1EKi0/4eRZ03PlqxPSbW80VmRcXR7L7BVI316oP/y6LQEFpFpjA52x0xZJjtO654YPRYy8mTJSuF3VxtMddl/9T8R51v+Md73jHO97xjne84x3v+K+L32J0ZOGYLdy2MNwZSwkUwyX2pLJo4WUDmVsHn3jD12hMaCav4YgYdU4L2nCi+1aR04lB3c63IZjU2yEnUn55YV5FDdNbEa6J0+TmqSR6NVJh6dtWKYbjayJB8qAWx6eWwKXQpyB7GwP3zrFGFlPNbX3v1PeP2zl5aMpOrhXmSHyrjPu/Oanhv4aRn0VyyzOv+2GCG/TnNwiGsKUXl5LeWoH3ETi+YR6hOc3ZythVEIFrTm1eQ/hxyHSLX3CXSBf1OS0yUslmr+4lKGZU+8j3lJYbvv27UnrkNAZSuc5UNy+qq1BE6GNBDIMe8Q0wmPDLKwyfY9hDFO/fOGbkCn47Z4/vP/2O//boIzbPxMxzs7u2Fr1hGFIXzhtqhVju4qJoCKXAx+bNTTT1loBUqsmeVo7RcR/fuDE5nRyeeK2fz+RUfs5891EPjhp4nxM3C75aY/g95U2eim7fjMMq7Xry70fC6f7880/6df1NbUoI6oLVNuijYctyQAMxvf3fmlI0+P8/f+TrlcZ/fn7xmlus46j8iMFrwHM+q/XyhEwsCGsfjE/h55ibERc0ZMvahyf8RObZ8WoXr+H8z7wOVm2fI+s6E7Gvm9aE5azkoEfhywc1YsN0HKERtImNe5QPgoLYxPkP8B4JuQNO1b8pUA4UNaHMF+zXINz5z58JGfzxkXyKBV9GhcfjoFCQY237O8S1p7aiyZNdG2xCcXfa+gz//ID1Hb9R1CklDVnrdD32+QmDKy6sL07ICaUQfnPerv5CLe04IMse17jrhBC0GOf09Dm8oFLpstTOBCgbWgee3KMNYL+46MiEl1aMw46tWClxG3VsuWsTDG57EhFG0VumHiFoextciqU6cSzob6GPCW31VAAAIABJREFU8U1FzgjvGwbfBly8Niqo1pq+Yz72ZgvSumO9RozOGFDjsa/dqL63Mx558exep3ADxnKrJXHz48fkhZfF11JByjd44IgJmxvfEAoD/2YhkN9NNqqn1oKb5VYQ8N6I0bcVQ6gmP37WQiZQ5DvSSbJWX5s0jE7kdnBZnkRuur/JCmJmaF2/C+WhDx6T07gsF/7J+C0aod7H9uhBskGRdXN58LoShw1gp1BCaPvmCvCghu1fpukgYooRkIXDiNj4z6LGdJ3K1+jwJDb20gXkuHkor9cTKboPN9HEfW9TzyFUzfXzNu8zxRGeC/fPJJbN9xyeePWVkHySlY9zEmQjEd/2zc2zx9jN3PD4mw5+RMy/k9uAkCmduep4gdbjNhqTlM9dBMEjOpcdlFkcaUkYz0qiYzV3K9ksJ1S9IYg+YuPlay1IzSbQthDBSM7QBrJnIbmKGZMjYYC2IIJCVdvfoblMMmX+h7NayqlPftdQmd5C8ytqXoDi0GeyFw9Ova+LSJ1N5HrY87otPHHEt6Tyjv/6uLrvg6GaEM23WZwieW/PZ6RSeRzAbEJePrgC3I1x3pAwBDTmgTBaFrXzGXnidOU2yvQOcWwoiqEUqTymF0Q5AqsH//uV8trtz0AtOKd4QpvcHDP9dlwGDbBlZnqeXL1PuG1KNxvg8zNqER5n3QasfTQkdEMuHvXk4zj4S+eBqwOTQOeHDhUetTIIvma+KcUox0HxdShHDjTWoS2WhtDP9e9z8DJRPAx1uJzX1xSVOE9qLVzLFNGF3m7RCAH6a9wyv6r054VWu7kCPrj62KRrZODI5vj4cIrGhhZdQ/jqwo8pluBH4buvj0oKLVyTQyZHmuz6+rMJbsoVN5zJvxQz9vCox0BGbN6lN8dVttDO+Rtg7t/x+4RaTXg/eb9qZeerUOVxHruRh7SNqEtISAXCstBeXh8MRIJlOe8Cjb4LfFFhjJ5+M2RxbuXYUN/hneZyN/al8hEF31SD4IrBY82EsWlYb7cc9qEpVNDXgHwKmGxZ6KCTZscAH6K0vwkmdY6z8jUhsL+eP6lmm4/TehohL1npgtMFDg2aLVjZrKW2k3EkbHDZi8TAr4bJUqlJuf66oHVkfbtqxqs3GPdQOEgq4pDFtZr81FXAjeROm3n6aJKDl4jCakIUQdypss6nHMT8a3J+vgy+rr6HUYck1HH1aqZGqNAnRPB5OUVl+34Ou9BIA94l4lA0aR1l8ZI0OaMLwmyaohevOeBq490IAVlYLO5LeBakS10oRMCUOi/iAalywl20igSjd6wuE01jjMavic2UOXto89C2UxHuyWOXVLWY8NB5o97VdIQngX5NI1BKsMmBfXSExP+HL7KegI2bCEcKE6xnpo6cOrxWg6BQ+IaTVQM3YhuJBmp6b0ZUUP9muDofIKv3Dfj06X68busIWvftjIznpGAltOGTHrWSzcKaLkMvY/OqmN+qxl1MBUEbKw3Ax1GmMaxvYYnwVNdbjQquuAbn/P2eNfGo61V6JOdJJyG6hsI3P4BiKZ4w5rRKw+kS+/XPBlv07Vt9oKKbEN19EGPcE6/I77KXe2+K0Du+R7+VGb0oQ7IxyP8wQMbmzflLGP32C3OHjwJfr7G9sECJopsb0yyfet/3nxLRkyxM5g2tspP35YGWu7PvEhzYdjwfvfGoto1IRwxS4ZE9tIveUVN6nx5gx4FfsYcej0fl8yxbbirJrmCzwFIphATbI9yvPDTnp/QxHe5lEYFzimsRWQCQRtVHKE1yW/LxqLjf/l+lQpjx3DyBilgqcgI87IDS9nPeYyACxiJMC1VTcQ3gasGrO6etjXcn5gZ8oQEiBv1y1rrOY2B6b9GtBOdRdiM0ulNaNq4ApY88ZcftO9TN7qlu0RwRl8VVcMYreQJjnx0l29SldtdSZeua90P3mCa60+NpGeK94x3Ar9fXrhtsDoFvfrPSn2NvclVJn7297VFGdHq/9mZCQvibsbob3jrrphdVRlwb/WKqvLwRvya3uBqjd8TyOS+1cl1Z/8BUBtbga6kkhqKapq5Lsta703rfolo/Jt95CwtI4K/Oc+abX6Sxq8znsOjB50fZObRzQBHKVFfTcJRj8/BaZO05EH7MWuQ1guZ9I4uqHYgK1+I8piQXujZf0VEZ9CnKm0oN34as1Sjl9jBTlVk3Lq5yIJTdOD1HAwIdW3yY8eFEjD3UN5SX3bVuiP6tYTzPB7Xe5rWIZ97ZnoqOXbdp7Os18Hrn/SpnbvNGbP/PSwbhsv3gVNPAPsjG52oDEUlPNn4Plct3xnzHO97xjne84x3veMc73vFfF7/FRsjjhn0sNsfiDGHKYbrlHluPW/aMhD6pkBue2aWaKIgxptfHaUapxsdck4YpGp2YmNWiQci9XUmkSmyZaBXl2X07IxtzJbpXmE5H5kRjTkmkpDfQlLRtmupHMr9Ij0j507W5KLkmWfLXqUQ19tSv1EpVvf2VPN2O24bHRCoW6Tf43QDG7XcUgFncq1kRCm17H4UaxWJD/kAQl80RCk9PosWVKqoJJ5kYz1YMUb8hZXRGDGqxPVlJ4fIbhuY4iO1lrJpx1rrfs5nxvPo3vHCkqtKC44nSubdYeL7SktQdPojooMLHgg5N6U6Ppeef27VR1r4uVW5s4vrbusjveAcpQVrnvTEkeYHrfjU1Po6Ta0pdM1IS+ZYzSmj9YY4v6fyaP98XJ+jKZ2JJbps6RWJPcRvCM5xz5RoNVBp95wKl0Xf+umgU9z01VEnIhKK0NSmWlOuvurweBNe4J4UEZ63ExI7Tgr/U9993ANUN1b1ejeezbR4UOqfIS2UuEqqiotQJP3l+DR6nca5jSQ5c24Z9BClHe6Nqc4t1Ped18UL44LHV9QJQWlv5CzglZSIhoSxjcNaP+fo91SrVkJl3X1djjMGxyFFjQjnma1RTPuuDvhQpizPMONfENQa9wVJT/zQjinHGPIuWtP+8rqcJrQnCDSXplhj8mDylmHLZa2t+9cGPw/iYOW9h8d/xDoDn1zOVd4E/Pg5KUWRuKZoPht75KyT5188l4axMqxCZhGyoVhMds6gE7jB0iVjSZQDGY9ZblzcKNxzehlMflWKTXziEj3pzuMXjbzyXr35BKFX13kQU4ai3nH+Lqca4bv0QjuOBLr8bhM/6IPYz07mi53cBToLwSC8xADNssH3TkMy7iPJzaekLaCkbmqsijAG6VeIyn4wJJ27XoJbYXkYWgMEsERGLhM4uKJykLczaejXveOt8zM3vMRWU9ai4LCqJMOzergHouD2ZendChBGrPnK8D2ShBVwJb5vPZVLxcGTyLv/nrFni6l2nnlIQ/UYhcKHF2BsfleS264TjxddAzpOy4OP6z+er36IRylte9v9PnNm8QUtKg74WDGA4jypbhOAwgZ430a0BnxCFLWlrlc7AJybxoOIm2wtC3VnGrZDwFZV7PehMku42lQrMlM/V1LjTI1fCq4vokryBa96AxbOoPzapLfGty9S1WmI7FyfIpxGo2iIQBmcIv8YN46DoXRRYCiFo2O034srLYstQDu9Y0e2f48M5DP6zuE/uU8B/kbgDIvCJ69FI+dh1wx9VcfzmTomjWrZmvYqgWjEzyix2lJQAvyan5+cXHKac8zOpCvYoG0pXRRGX3ayNadp6TUPW9J10fF5n78kdKLOIuPwiPOWOlz+JmfG8fJvIKUIIfyNIH6rYXFH/84vbd/xOIbIZjTya0jS2Z8ZZLacU86CRkrDfNvHy/bpoWD6H259qiqAs/h+AdHw2Ga0lGd8mNOURjj8bfRFgi2D2sX4SCaWNwfP1lX9uAg/ZObQewnClIZzTMPXnBeEjQewkN09D6FNtoL868sFulP6KX6jJNiGWaXu0nxXNr7Mgqt6TAbAMD7GBhaXU7j154RnO5+c5r0MavC7IBZFeb+uqyRyiyHyu/+fD+OW2m7N6VAzdhGeR5De26+ZzncdjC9A0EWoA44YKPY6Di0497b627WJ908ON61fbAjKnKM2cMeF+16PQrr4Lk8fDeNTCS5JQHQr9KrcZbhuTU3kTlA9NHuaCW1ZiCgitwR+TwC37Nd7xjhX//vGvje92cTqdNc/wDphvyP4YAx+DcxLZdQ4wFNvnZRjQb/6y1RwiryGIS1ZKseDsHgz1LTAjpNDB5jerQ+eWlRaltUFdPpCeA1PnluAeYzZK60xHaBIbJhsi9Lg2bwU6h1aqTW81qxN6OmuVkv47ffmquecbL26VL2GD23RVh2DOfg7dHdds2ADEDtrld070SG/IWcvIhPVvIZU52liQ5hg5aGuztgnPxu2Yv5u/fBA4jw8l5hA30LRi4ZzXIfNrxJIZ7zy7U2PVmYPeW3oWMeHGMnZdKTgcsXnn+3c2c1NvkvU29xJDFKTqtsSRsIQdLzGXxwmm9Dkd+rr++Xz1WzRCVHbBH3PhE7OYf72EEbJvpoZQ+s2DCQ+u6HxI2cpNEXngrV9mp2Oi28vhNQQ9bavsuA9OtX3grouysORpHxXExGxfBIcqdbn1DqV3aK1trf1DhaayNefD4/96sBz9Zu6HKb07PouV0VIpZd2AYcHLB2NPcCeWdxb8IoBEiijMz9DV0VDGtTY+wam6P2PgfHXho+ZDI5Guxb5x/0HE2MpSUpLQHH4nGx9sjKyEE9RvDtGFWgpmur/mUSo/Ph83F0Ebqs5jqk9prvd2MrlMqfYN1z+m0e24uVeFm6fkspyX54RkfnCRcjc6nuu8W6lO1gXNP3ogMvYUZf/gO94BuAxE85k5fxyo9xv3jaSf2cbYO7+ebftXiBRweEhhzIOiN8/G41grm9zI3CKWnrOJ9Vw+jPFy2nzT8ll5HA98CjIMnK+rs6xEVdIhfvmMSgRXT++h/lgHKGA5UIIcxKiCZr3ONTrPV9v+OB6dQ5VrPqc/v774/CiMOaB4eefD6iZME7m5Wg2FSeHPq/NsF4uM93FWrt74axYCtUN/tq16+cePg7MOtCw+YPCMu5hBnaiSZrRMQYoxvjmXG21ORCFRCNlsrEGO4B6M5vzxY/IhHoXwW21KNDfOY22scf68nvhsUj9KbuelrV94GihuAjXG/1cqjznoe7Uv/td4UuaGaIx0li/K/p4gjHHtRrlUI3DmYJgTxTS2r0vr/3xh8Y7fJ4qVPSwYvWVjsVQNPbCq23uqaAoGrO2zotgURuhT+CSWi98C7YjSo/GaD2poQc1Y2i9VEm2isrgyjnvjei0eSuPzuAUdBOWwsu93xef/DWzXibKFEiBzS3Iu57OMpJjUzE9jDF7XxTWvQ62VWuseGgRTHGoV7zJAx87Baspwz1y9OT/JJRwzX5kYeNBnrrjCiXDKEq/SoOh3nbj/w97ZLjmS62b6AUCmVNU9jvX9X6TXPtNdyiQJ7A+QzDo3sNMRFiKOwzVdJSlTSRIf70c2j9bPqs5w3eTQGMkVXE3kKMbVBuGvfQ2uyr/aycNzo5Ya0+Npibvk9mqzEKpFkW/7Q7FUR76NZSOn9qvwwTBje7lFxL95coYHqoUidvsGxUCILYAmkvv++kwiRiCUWbwttM8/GX9EIWQqG/rmYxUd+XN3R7BdNadz751YX95xDUyMc1XzkUfcWuztWmZOaxoD0WKT0rB00D3WjzGVn1a3gFQNaatKnpA2H2uyktVb9NxUAGqpELecY4zIh351LMKz2/JNbttM8XWAqqLhfE44V6fTnT3CllowmzKWwOiT+FuUY32uCK6hQCZMapYLcSnGCIiP7WSsUvCw7ALkb+TvzFUiqlgEYyVLQxguu+2rnp2e1ek2U2opu9sC8Hwe/Pz5RGbH4vnomMg+9GOM7FLMovN4GFYeMDvufgXndas2LUDldsqe1x1zoa73VoktXBEhmMRWuUnREt9kdSU7TFuS+y2W8I5vYaVgUx77dWUfT2Zy3UZAv2FpRMptL0NhVaP1MRs1Uwgl0hd8iZYogUZB12FWppHdfCAtUoJUF5yhD05OljhRiqMoz9XgqAEWW/GtvQZjWE5KZwF3HMo1ZE9bmjjHoXzOddp88F/+GzvXZESAQTuvfZ1FhD73o2fNqe41mzBdBmXIPtQfH5UznH7dzaLDJkxuoe8kaEU2TO0aFx9WKXPV/x6DYXe38nUNHlVZot/DnX45x9zYxZTX1XYDpFqqUX5MpU5X4devk9Hhek257J8HUnUf1oOcKC9o3NVank3zu7rO4HTd99pCE34z8vW+rtcUM1jngKCHsJWFVRHmZG5+0LMPxldH6oIFKWOeg/m8GIdMwjpwSyO/4x3wOs99hkeQ0M/VKJSGt9iqraKA+VZYTf2xbAzWOeHx0RniGznSPZUOy6zMRxd6iw3XEgu63cnmaE54y84q4J4Gn7ENNuH549jqsxIdCwd8Q3mFpADUZVBfClXh1yT1D/cU2Zr/rvpgDN/S+SMC8/uaRHOSXL4VBCHg8xpfr5NAKfVgjNe8Ls37NXO6jlPR3YAyVSxuIZ0ug5BbSIWWueTKjtzzFbZSpwUtRjbWABmJDNh5axVKGP5yepmNZas5/Zmw/5CZg+7mtgD3WVBEUzBr56UgOm4xDR8MMVYyZGaUuC1YEEcs8/ItDBYB3W/hCnXQkkIdwGiBimLfLCX+6fjnP8E73vGOd7zjHe94xzve8Y53/H+OP2IiNDqUOZKsJrzim+z0JJB5WfhopR6GL8NMhCc1JZC/iyiYbalEkMQtyt1Bw9i69RqRHj/cVTHc42P3gX1WejYCCHEQ5fwGrRJ84vhnNwAlFJosMnFDQr5Joubvrs8UOOL9JhRO4YVrG+IIhxptdRo18NAtbNDpvJrz83Fs6EdRo42WZmIkD2mE381HKRD9xqwypoHXnCjN8fLTlsBDSvcunI/39C5a07qiKW1dSfJxMU29eRU+j2xX//zxyc/Pz/2ZfnwCwpbpva4TH23DHFWU3i7kPNdtwIfvMavP72cbEgaI35Lg88LwMW4jRSrX2NPffDa+Gc2iyRlacLy3j9A7/i1M+X3ONdMG5UM39CQi+Y6PPeEWtFaiTALtCed1oaJ8fC5JZWO0sddyLYagfJ3zeQ2m588C9qfs/Zqu9N7p/TY8tAO6Dl7TI+OvWpEe+IS0+jCKwG+Tvdkd7jxE9jo6SqGqbpET8dynF8wswpGu9DnBLmKMLnvvqZrCCH2t0xjIuEVvTIW/nk/owuu6ycRiQamrM9z4PA5GXZ1heHmHZUIdQZGy4S+qikpQphnkdQWj3RPsRxGepWx4sYryeFaO6VHXi9F/vRATZPkEIWgMfHZhx7QTWE1MDeEoxxaIufykihLTM+X5yH3la/lw/PfvNIJdsDYpKUgzP6OZ5HRRlHNOpa4+8FAefU7NvYA7x0Lo0Om9Ux9zAvhmNb7jW4yrpfY8Cb+K0TYUDrE58ckflZxay+MWCkpDc9+QL8h1vLxlRAXTiteVb3XidM4FXasCTbji+5QhtqBIeR5075wTLi9X5lgrR/DFIhfBZk5XzSZ0fRq/Xi8ub4x5XWpHAuYXTK05R1XKFPj3JciwIIODmYQsmOxApCYXG7DHQbTMGWSKPFyt4d035K+a4txTqqDw6l972lstJzJlvuavHjAgVm5rAuE5bWNOuahoX7luoBq0KaYwXp0qih33xEZFMAayhMFQivQ9qR/RERtbPAPSkuRaYi+R1IBFE4kyP+Pcx5s7QfoAARgpijBibCGc9ND0fV4pggy/KRfFGN2Zj8ONnvgH448ohKzHEiShSR78m0gsKWJQdT2gCRPB70VVrNK8Ib6wbcLoynqoiylmusUTjErIjXNczsXXItV6YJYjXMjD8Bps9Q4GHM/E4kMKM7SePj8L0vXVGtVuNbwejoVso9giM9neBDNl9LLhWBqO06nbZ0gSN/5YQP+FfV0jb6Wq5aaxuAXifFTjmptFmRyiYxY2LQYolKVbTx7C8U3X3ce4PTVmoqRLsEEz+VqFgkdgVbC5IT6OyqMUTHWrLv2f//iLz88nj5KHdh+D7p0+YR0SAy+GLsC7wDWCOke9V6Rh6lbsi+DywCdUpZhSjsAnzO3qk/rjwTUW1NE59Nu9l0Ct3CavOhjdbx+h+FZUveN/fRR0Q1JP79RvBNkEaMsWJDEJ2nVSx1RQGp0iBb49U1Vz/2uvhJk9fn6iougWMEoFw/Uc+giG9w25UBPc4dVXQ2OukYnl/R/vfHzWbXbaoyFaKb2z98hSOKrxGkvxKH1DViHkCI/yTRWuOZeP/Zla70QIx3OJLSQ0wibWJC6BYtsIW7twcRFhDMnrLq6UcndFTArVhPmSnFfQW/BcIjXS+bDYEGUrxvB2cxaZBeRuaAXFYu9vMhOGq307S4pmo2V+N73/O+dQVSd2f/JHe8JbyvwuvojZcMq/T7+yO6mLHvz+6smBIGEjNwAbCEc8+auLi/nAiEfZHMaunga2vtSnDHfdgGb7A1SY3vHnhJjQRjYSwyfczVbDQxGp+ywczemMmyvouVVJ3P6D5aF8Hh/8PQ2bv64GXnbzANHkttS1LoXWlGNCOw+tvLxviP7DDtwKx1x1v+LKRH03IBM4HJ3btFWywXrOvKBIwazs/Qmy0zlW/jT/V5fv4vQRXJDX3gcxLmx2KBKqr7tQOrTSy2BE5zH5gMfD+HoNxuKrz07RFlyIr6QTzCIiOU1jQ8KqJbxvQ98098uYBeS4Ai2y/z5M8BDMF43AE56H7Mavj1Q9XhtYlYQB6uZbGQwl6toDofm5vSbHbJgtTRsZOg1y52eYxefy/hkeiAdF7lw3Bw96DxSmCu/KfY2RfKglRvUHIHn/iEIo0D0RQAYM3/LZ4sLwwVhKHWZJtluYbddUzYkbpx04xYRz8XO6c5puQQZF6GOkIzyZu2hJehfkTemDrThyiBFDeM2fTfOLXVzW64qcGpnsAu7qjqrtQ3g9rqtzrKZMFee8TlHCnWMVhB6IGKes31C0wGMWFC2C6L6Ns1QUsSTKra6uSeJvdU1wWFLaq1I3ut/JUBZj96jkA2VIqksBk1g89n0xE7TaNr9tY4DrdnN+HA+Oh1Gt8Hlk4fPXj598fHzsDab/TmO02045GHETmhXBBWLtgKEsYcH89yR0rvuuks/Q6kb4Ul8K0Pm4m64+0kzyNKUudUnkSuREaj1z5Y9YJu/4QyJEkHWYfeSaWmtOLNfQIvgv4ee2k3sjSoofrH5DDZsqk3NPOwdyyMbci6Zy0BJSCQe3ga3pi2kmBVOFR1s2PBY3+efx4O//aRzPXCPPo+ShFbcAjBXh43kwzsXHcU4PdE5RDy25rtfEugTn17n6UVytUdU4Jum/yyBCqHNNHd15mMIkXF+unC07uLoJypLS30vNsUybgXVIy8gtfnKhPnrNwmp2SM9XgyEca6JkAdfYiknX6Uj4FmxQU4hBW9xACRChiOLfRG6GB2zOjyChe/I/ZHD1sYtSKYK6b56OS/IPlmH4mCqCyy7AJZs5o2Wi2npgRVE1XlMWvNTg52fdBpZ9BBZlJ3nd8qHos9HzKO9C6B13fPx4cizz98sxUb4JMYJ2+rmaukE5js1FfnzPR2ZTo7nz++yMuJ9xH74FrFSUUnWpa6foit+6UI/jwDDafOZxR4Zu0YDPRyFMN4/JPDnhWuTfuHquio7VrI7Z0F6EfCBkK9uVj8BHKv5C5pzisfdccOS417UmZIi6eeUDkcERtyplKWktIvcr0Npr5y7HcUzrl8UZiryvspBITjOI2Yi5ek7J1icaEvffAIFxtoZtDadUDQ6XnT/Xysx1MgTAbCeaaoVBu+U8GdNiZD4PSOal90Uxgo0SIm5RmRWJbJKtvunz9baKnACj76aahmXhPd80NnLrn4t3q/sd73jHO97xjne84x3veMf/uvgjWt0it2KSh2Slv+rskIQzzIp3pKD7ngAcmvr24rFNNSMEK2DLtNMD751j4bw5aXGjU8rIjkKZE6UqSu+xJylaEp63RJxMlK+vweNjcWNgWCCFG07lc1I0r/E4LHkom/IjOXKcP/dX8m1cF2SiU6nTnAwKwcNsv8F1Xqhz4+nDZwdFbsgXIOL7S/YANLZs+JPgt3/TuVdhRHCsey0QXTeG/uw9lWLmZy5iPKpuHpSPOcSer19V+TgOfjx+bDPTZ62UEP6+cqz+6+uLv3//vWEeAFJSySQvLLvsj0e2gX+/Os3ZM/JokR9pNhVEgzZiQ3bCnNfZeBSjLn7ChACuPsTyidpD9eE0hGONk/+AjsU7/pxInP3smJoxhm9YQBuDNsbuRH4eleEFvsFTecaUpJ3TF88RZzmW18OY3cv892doctqWZHytuNyTV0HwUMzmVKEBAcccL39FRz98G0arKHijqlLmxObz8eDHUfg9eZAF42sIj9n9/PGzMjQ2vE5Rno8HbfpPiKUS1Wuqo3kEZrLNm49SpyfJnGoNxztT8vZey3349skIGclnmHJ4jlLMt5JTCNB1Y+bdgw+5Fdkemip2fZEip7FfXVKyWkgB0AULGdOAWojJQyoaOSH6xickbEMhR0mI9OJPPEwB39Ob6EJUx5dZ85Ud3wUtSdjS2B3YdUZ09w2/PKryrLKsqbi+glcEHwseXiqUQp9Tq2h3t/Yd7yAC/cb9CynQEo7667pw4DEhYWaA9JRxhskHmTy55YE4nJO/d8721ELzwWvuDc9a+Si2uX8RDjI453PZrhefj2MbRn+9+kRuTM5krVT6VoiL7gwRtAo2TTlNPH3I2lKITI54bLSKYcqW2A6CPuCjLqRJpJLmQsN4yoSX77QA2r4P2gO3nObsSWwPrPj2G7QwCpVzjmd6awlvnbnIcWgq9q2F7Hlf6nZkhRK20U9O52onCyP9kAkeXJCzEYj++1RKLeFwaxrnMXmrG2boeO8waSTDYv//6wEoJdC+PoPzUcv2Zey98XWdO9+qxRglc3DdKJyeZ6At7lQl/EZYJeLmhgDKH7DiTmbrAAAgAElEQVRd/RGFEOpcc3R72JPh45tMYib49ZtH0HA2Mcs0SXi3CCFoKNZX6gGoUhlb17xHmq0uPKkcWYwtr4/LHffYsq6QY92P5XA+JvRhYfZDsFrmC9yQrn6NbWJudUEtZiKgeWXbTVkzedja/KUS/RvxVSQldHdFmBvSlmYcnlY4Cub3a15xk9SKwCHsn1EHj12ErPH1OsRBJjn635/UfchrEnXrnnk/Eq06SdttOH9fL0wqf/38nPe2Mzp8vTJp+6///m++Xl+bvFePB5/lccuKk9wr2TwA5XgeM7kEMcfbRZvPz6OkD4Iss7fUu00T1zW6JVDZKJ/kY3z7D9F1qjKs23Bvju94R0TQZ6L8/CmUalxTPKF7cjSWAIn3wHpQJhzr0nPDW5cPWR/ZqHnMQshU6K+gzTVin49sCDy/QXdDWPiWq7fEk8895lmTn7PWuXfnWese/xeb/JnPuq/pX18vXufXNl1Flc96bANUFSNMEJZTe1DNNhzmHEq/fPvrxMgi55qHXVGhUGjz54sBLsm1rHejpYfcQjmactsLMiMzC5DFgewBRTnmMeZ07CG7idZGEJ0NvSuH4MNuzqNP48cN6XDacMRvL6JuINW2YIyGYA9NewTyLLhGu/dlmTzL+R6j9/Qlm0mijNwXn2vfZ0JI5n22aGmmPZSP2YDykn5J7WsWfM1hOGN+3zKSSP45vdj+BF+Od/w5cZ03llwjkNoTiguzGLHN37jahQzZ+ZUehcBQEZbMUmBUe9KnKbpoYHL7/uBOmO5GcpeE9J/LhsOdrwHH4usAhxlMs+bhnV/nF7Uu0+GC6kBFNoxs4Djjlp4GalWufks0d03uCiR8rJjc3mpISlHPTfGpiotsjncuX9u2B807HtlMeixhlN4YIin5T+Zb9bBdWFy901qnLBrAmV46OuHBi5O8+IUxsgl7p52R+dn0rLuk89BClPUZk0bg+LY6/LCDZ6msycHQhBNvgZi4ONT4mk2ThxTKcew9scqkeZT8LoyBmm87EgeKVfAlrqDEyEJrFzpmHFb2va0VvJfdUA46Mg50dtz7HyDu8ocUQncXy0pnINuA7pFuXPsBVTHG1ZeEfX4BEjhC3Ypr+d+Xkk9RAetbjWOMNDBcIgFifLPkTHU0ppgBZOexWOwpxZjd2ZVoyDpQh2yXYdVgyD1JCHKfWD5CFkJ8w7T66PQ+toZ8KdDTeCg/kw+49C6o0m55c5CKVjpwnY06sbznSF+OhcF0zWtbExv1AFfukiN19ZcKXBsy+TXf2Gzhu8gghNcVPHeXZdBaJnsA8hU8vfLii1+/ZrIzPqAHvybR8l9//2aMll4bZMEYHDuRWKXlMml9HhBeUjAD6Fnp7KJWBSIKMe+9FUHVQJWySIgjOxJlGageuVGuexk+C6XNzOQd79gxut9+OM8HV8Dvry8Ajmr8KMavr3xofp8Xfx22OXGfz0c2QUbszks/B4LSVz+hVl6943U1WkiluG0OGJncz+ZAHzktWRNPDeUafTd21IR/XRefS9xFH/x8fPI9X/7dOq/eiTm5/aHJgVw9gHNcOGWbB8YYKZ4yJ0a95xTrmB1bqqI6OPsSIgBqGpxC7oO9Ofb4xCcPqVQjgtugEAMr+z2uMbLRswxRI8uI1VB9mHKpIVPwoYRgVfeeqx4c1XbTpI1GEqLXYSKUgPFt4tfPTMDK3HetFvq4j25VQcc9VfIRmNxebeVRCFfaTCJFOnENYqzibWLl9z4+v8tHxdd0zZSrda5ZCAnBUWz/zTkuihSOWQiVtwH0O76FFqFMcaL2urI4X1nqCPCe6q5AOQ487nXer4Fejai2cl/Qax6aa/9J3ltdggsj+IpO67fH2PF48lx+XjRav5XqSi0pPvLNUNW00mdTphxpouwed4HmyhjBy+9JrLhs7l1o5oorj3QG1XUT8zuZuK9pRCHofnGtz6yGFaXKEk/I15OwbbCu5P73NdXuDjNE4hZdMuGnPbch/cAx7fc1mABKmT9LTc7huvdimh49uxfu2WReE3HG3qfWdVcVHuX+rq7ek7Okq9CpEL+36hsIVzs359VCUDe6TF8iUhnU51jdrFBNN6rIW8eboOUWxyiqOPckfnSf17g+d+Djyskk/JuC3T8V7x3zHe94xzve8Y53vOMd73jH/7r4IyZCY7Cd2dcUZKmhFRNGs61OFBqJkfgOnxAQynbLReB3KD++tfKH24bbEZoqGGs0uwYve7SXXcc16ksoVeCzgq2iXN5uHKYIZWFqt3S1gOkNU0v9M+KbLDhMOBwpP+ti36Y15HXO6U76gOT0af15yNS/B7DgvCLd6lfXVTxd0mfX4IjITu4qf914lLIxhIGj2JaG9TZxu+uaPLIrsyYpMeg98AUTcUEYXNNt3t1xH7gHY3VpHydG3F3ZdiEIfb7J6IGPwO2eQqWY0+w2mKJie4JXRHgcFdPFU5pTnwU9KTkWHh77GQuSYrSQteNy/JvztRabWNw/B8P6jj8nTNlr7Hw1XsHtu+A5wzzWyFqTu7gacEWEVzjjGow5cXQVnvWx18DpDW9t+wKppgRznZbkv3oHuXJaDnwcZU+lATxSG+mc6xA5sAL1mV3h51EZ3rncOaa/l5vyrzM4Jq7/w0pOTPaUNKdA2wcoCiaKTmW7xNzrVpzsqvQIrikJrkWQGtuCQKIg6nO/m//NgiKyPeI0SHntuabNBTPdXCeXRm+dx4JNPwtlKBOliIegRXldtyrTkxsO0z2n44vfUw9Bn4KfNyQ5IrukZUF31XBv3yb5yctcW2rvjhW7Oa0j0Bhb+clFeH48aEt5KrLruyba5yWM3vj5eKCzQ/51DR5xw/FOOs0Hhy14XjAI+liTtHe8447AbwsInc/0OsNL2ZAvSLl5HzBeM78qBloRH5uDJn3g7dqqluBco+9nPjxQC2pZ6oyFAfz+SqTIxyOlsdcaGK4UuSdEroEetnMdH064o/XmADUXhgcPbqRQhGxrj4ajevs6Vj0SRrYTycmdmX/fA4Yoz8fP+e8Jbx4zTxGb7Gv3zX0iEiq29t2vkSq+ZY6oixauMZB65yrihtRlV5L/VzayCOpRNrJp+ODqbU99Cou3vigeOU0uKtjKZTUIuXObQJIqsBSQrfBx1FupzUryHuf0eUgQTelznDMk88EFrTvE085hHWgTjWV6q/yNMfCIrf4ZPXC1WwXVKlL6Pu/0D0iw/ohC6KHBOVfR6wweD92LyEPxkA2FguAouhONLlOmOmQXBT0S0rUlAKcs6i0ZmA/1WrieL7ux5wq56CZWxYdzamw9d/Og986xihkP6kQ4tKlrryIcpX5/S4RvOMqR7x/zIai1EhSOlT9JQs2ek0/gAq/L9+sVBYrcePcxEsepx/bQQeFszko0fEAL3xAblxQa+JhvevYs3LzfN8JCaBtDP/83r6eIoox930VyPLr4Ez4c6Z3ena+ZlJm9psz4hHWcHdXC2lMPnOadOh/NUiohhZjjZyPl1ce8z7t+3b5ScwPfvhzJM9NvKvcxH4f1VbTLiYdSly/L3GvW+nz5P79Q3/HnRBD74Xi1FEdYiDBM6BH7+a5FsaKb8B89CBoxBu1aizk1T+0baf8anecCuKMU5VuDwrna4K//nIf8oxCjc841MIbh47zFQHrnWQr/eaTRsVTjv3794mx9Q1KLCBa6+TQRBR+CzeSnqNAkdoFgmjC2icaiaOU8BzF5AybG5c5j8ViKJjRtmTuHghgiTkwipYhSTLftAZqy3Iu39KGFMYI+myRn84RAr+LsdKSMO8kj96sSKxGZ/NG517Se7733iuFZ5JrcEBpL8+2/VyPnctSCX1P692qOjNufxDTAnJg1qCHZ1FtNGCkowjmTKX0YetStLezDkeZogE7jRpeOuDPRwTzDpidS3svHIYweE9PN9oB5xzuACW9fz4ZSv4k21eOg94t7ySkw0GM2ZG3ysV3udaUfjHFRp2nwGJYE+c2vEZSyuXqZaPuW/78kKQRjnunRlWGyuTRShKJGeebzf55fjP6i9B+bg4insEGZzYHhnsIES047Gs2VNmFstebuKttCQ7BvhVCCVAcaq8E+ecOen6GRktCyHXcyf4LYDQsQ8M5YO684Qvk3nneY7vwsBXPupn4aXvu3PDU4TIidpg9cApn7X3WljyDkNrJ20m5mS4+X9CNbMGk34efHJ+fX73zFPng8dFnOodppQ9DJwe4RhDfKMpE9G+LC8XzO3x9J8zDbcEsZjjib46i903psSwEZCSFcNBD9A/KrP6IQGpoFD4CFU002H6dfimlwzKTgNZwoulXDhPTwiOF7amQKFnO6xGxSTtNUSHK8pwA7wMSebr4q3gUL38S6NO10PncncS6fpRevJd8k2C7AHvlua7LV+kAjbrUhH1llL2U6LQixzbZSt14xz4V+tS98yDbiQ0HFb0NVhKKSBn1zLDXCMNPdIWyuFGR3QJXkyqzrGMOzWJu/LwiiICtRwTlK2ZMVl+Q2rIUtXAiayn6AqGfXFd9qU9JSYWl7ffgk061OTutc8uJjcaFU6dy69SqZNy7PlNMHvXd8FUYC7ra/a5aZWOzBVhY5KvgsdMUyYdna+B6I3gaF/a3C9I5v0SNFOwDOczBapzzuA7cLmxNUHgoafE3seTudDwmOj2M7szudr27URRbuF8/yvE3tJIgRfE3T4dDEvP89eUkf+sQ0GEs1TIWIQjmW8V5H9du6b8HVHQm20d6jKI+i20H8io6Ne4peBX7+/CD6anL0NKpe2PSj8j9fF6tb+XkUztY3D8+KJBb8m+jACOGX+/byEAX95gEWWmnntRMDK1ksndcyh0xPlDWF7+ao37I5hTRJHnMDPGqavK8ObMxux2pwDQLtU4nTlrrdfLWVIJlR9OBaZtwSlGJ7yhQMPNJ/DaC3LELX5H+bE67ciGzQLcNCFUGt0K4r0Q9AVEOH0npe9+N5IPbgnM+DSUHEN6dC7I841t/xh0TBaCs5kkhRpLKKmPRPlHl+jnOAyvZxhA8iXqjqzZl1KLXeSmSeTZwl1mJPYfTbs6dfAx23kShDOD4rca6GbeYxS6eF0cEFn90ECaXoA+c2d69Fc5rra88zisbmnTx74ffZt6CMeRY/vpAnoSmStHLECJRC6GrAQ7SOzn3+USw9GlvbucVTCxf5e5B5RLje+5cbKrp5kVULI4Qy958mjraeKp7AwBjRdu7rzSkItazJWWC1wua6d3qAuvOYX+9nLRz1QZ8m1dE1xSuWYExV6vDd5DUEGUGdJrFf7YXpsRvLXZyqz13cqULRG5EjGD06x0gDWoAwg3qLj6HKy19cZz5jjxGI5cAjf/+fJ2G/OULveMc73vGOd7zjHe94xzv+18Uf0TqKW9SCajU7eW1VnINQ3x2K6p5d/lnSmiW0aQRb/UcjcHxPLlQShraQJjni/TYBiMRY76Gnwim2lYAsAvEc+QEpjRu2JwpR0v033LdiSBvB56FblrJ5jlv3NCVyeLldhyXhbrvr0tt0X55YTQfkdmv2UNx9TYLZ+nM9pSvXa6IQs+PwdMuuxYKukfKLr9WKiRvDD6mIJHHj5U0FEd+fMT0vvvsW6eyG5t8XBr0Jtd5zpuaD1h2NpRgiqDl9Qk+apgLM6m6GXzSHc/oejHbRrpPz14SmeHZFxlKYEQMxysQ5dg3EBQnZOOg6cdKUxUWQ9BxYEBoGHfZov77bBe/4FqY3rLY3x3twLbXHhyUmf3Uai4DLhme5kZKryJ4SHGjCal854alqNB176vARlY7T5hqpZtTngSxvhzESyjG7of2C6CfHY2H0c7/715xK/W4Jb3g+jj1FFxU+H5UxO4lqyTlZamlFnBGxO8ttdJ5aeR7JOxKco5btcD66J1xmdiJVhHooS3gK4PoaIJJYd+CDQIZuBSSP3At8Qr2Ow/j77IzXmu0G6A1ty+08NkQjJNfwkrf17tPzab6/O1XZ+0JEXm/32J/hKTbhOBO63Qeut5Ckzn1l7dOJn/eE8AK/r4GpbfjLs5SEr+ja1wOuvifmI4IfdkB3vuZr/JCS+/b0H2mDSUZdsGinaNl+Sndr/R3vmBzn+Tz3DmEduab0dTjyDf0CDUOpzHWtgFT66Hu/6u1M38U54TmOgqrenJ/oXARzK6GYwlH4YHnRBOaCLy/AqtQRPMaEgmpyTLaYoyoePicbi2uXOc/rnBBTCfwwfiwkSZFUXlw8Ix8oY8tMmySfxpf1hye8VKaCJVKgGj7V0zQqxlyHi0MhM7dcNiqa6KHFbSoorsFHzXvp3flqg99zH38cywZmIWgK0b95GZUCcaNpenN6b4ytqJxejVVtK/I9joMPFf7v4gtGMAzKhLr5EM5+bRjj2D6Sa2L9yXU6zyWfXRxMNlXBewNJVFQ+PxNVpGPnpjJyT+/fJoYfVjieaw91HuhC8t5InX8w/oxCqOuWw3aCa4w7sS1KrccufK7W6cM3eSsiYMlhzwdUIlPYunCSUji/OQ0JkvCoudJEPH141sMgKau44C2doITdC51brADyMPSI/ZkBnsXoo+G+CM82depnwt/zAdTl4fMw1G6icC504fccJ7ooj+f9nsISebjxpx5jyk7PMehcZD6ztj4x8rIO4T4o3fahPeZrLr8llfyci9ekEhMKt+69013QeQAfJf0zFnEvX2YwJDgWb8mDYjdBzlQYo20p8vNqoMbwX/PhSE+Pa0EOSQ+nza+QTAw30tcHZrEg96gIpoWg3aPaklA5v9bndDzG5ke4TvK5fYNWvuMdM0R0H8gRwaAzJvHk8QBG4LE8f4zG/Qwdqtn0EKHpOsQrw5MvByBPzWR+VSmqyedbAjJVcHli6zO0C49bBv+w4FTdhqzhQVXBpwdHacmzFA1+zfcMCT4exw0XRjD33QwYbozX2Ic8UrlOp9f5mTX463nw6yv3q69X4+ydj2PBT48k1i7+oRiiyXWZXGL0SIPpBeZ9+eAwNh/UYxKql/+bJAxwWocgIlR0WxiYwPBvfMSRhqqreyRWeTzK9siIIdRik6w8C5NT0rtuMbkj8BjYMkUM4WztFrEpR/KapmKDx0joy9r+zobUwjFJkaM7ehiP2fj79friMqFWo/bJTxjOUY3HI//m1zWvY0OVnNSqWBDlN5T3HXd4DJYjsGqaP49rFf/OYQNZxLkZ50rmpaMY7vdTVcxy3U1C/TU6z8djE/JFgkeRzVn0EMwLX9vLZtDPe12aCgPnJJubhGJhN19RFYmEnC3unkg2XtbGOgagevt3xaDHDZtt3VFNnmH+faF73z5nOt/3WrL3JQVvfDeGlUEQMrbP2UWgalsIBXes3sXX67yoUSiTFzkkQDwbI8ABYEabRWm/To6qjNmo7uF8PB67Ia/WwX2Lgomkb2PygmZhI5LiXfPCTxFCCkMndcAB25TENJPnbmarCsePwtfvbMp14NPq5laJCX2MzetUyXww2ri/T7PkiW2vtECLbXL54Y2vFthsiz3qvz97/0T8EYWQe+yHqUiqBG0HcwuGsxfhkJzknG35xChEdlTXNKZqTnCuhZuc59Ai2qnk1GRhxfF0E1+skB7g5tu7RockBn9NiAhUhbLIN6LpoxHB6hWGZHG2sJo6H7XF6XFJvlA5VsbOFHyYm4coMoJii0BYeJiw8oiElssWByjVcM9CaHWje1Z7e/MIT0PW+MYRAuGSRbIOqh7oVKrz8ORfrYISRdD996LCaLHJuaGCim+dfPdclDoEedxuyt0H0pYruqNzsgQpXnKVKx2VyS7K5WM7PD9KegSdK8kLIV5tbz6Pp04NOtmfWZEkd6+VWFIR78Y4CyH3daQZ0Z30rU7sO94BED6W4CR2CMaDvz5mN9MN9bEP5OQS3sItYtlY+DUcnwfiGJ5k362GlqR5nz5BrTANAafQQC00v7HprooK36bRissgxuKQKIgzf52jGH99HpzAy3OdnW2g3KasOQKH31P17WlKrWXvLX4Nhgx+z4bEw5RhQZQ12lceYZtDRIdX9E3iTdJvXueaCJloTpyWO3zknr05jt3RFtuQdoyBFMnuLVAksGKU1fhpztcY1LJMYR1fPiFALYnrX4WTSMkJ2DdFq/PKif/+/iI5pIylhnfQRucxi5JiySddD8gjDugXOkndPqf6tgjSJpxX4zHJyMUqKulVdO/tiotv5boiPdEBSzXOLxiDssnp7/3qHXccVhmWi//rjJxs1MWPboQWii7lqMoIZylH9R5EXLg7sUn+TjkOal0CMA3BdnKNRhZPM3d5tYaf7EmHHTJN6WcOcMotegSgKQK1ciEZI9eoKWOqm71+nzyOyjGbA6ZCxF3YBIqrp3gJoBo4wau91lukeME26VFEHYuVV1y0AcJM0otApDHyWocXnhwbXcbGmoIHsXhMWaids2A8VPkotifYKkEtxzakv05neM+igcx9/v76os7ibUyBmVgeitdAFj9xblA/nx/8VY2rZSHTWs8iad7bfjlfV2d8K1IV2V4+Sg4f4pFTrNMj90Omr5DV5FuvAlKyOMoteDXJ0pB37fUhzoixJ4ifn//B8eX0uYfaH7BfvXvd73jHO97xjne84x3veMc7/tfFHzERajQeLAhZqupsLGgkj6TJgrkpI24pvio5Mh0iu6wTyY7CGikmR+Z2EW4e2IitviGR/JzVHbDQVElZ6EUDNd140iWVXZbaWuR0xQlkdT3WrbXZ1fCcfC3g68dRIMaWlBQEl7hxuCM7KHV2CkUkFdEWWsYkNd9nB7aYTIPy2N3qxG/KlHlMGI+HoIvPwPybiS0xc45Dd7dgoS/+DYaocTsBi3JU3x2QiAkBXF2VEagpojdetIkwRspuA/jExC6u1Ks78Xfb1zBc6OKUeT8vSV7TUpkjnBi+4Xgi3PreJMyvTw+h5UUULaW0l+xu9DKhhW29KYyyr2s1jd7xDpjw0TmdKSa59ubz3BG+Tt+wgNCBIBvK6eJAcH2BzL3heQgfopRjQXE7uO5nPOF3Yz/jtSpHGL+m/Gzioow9jXaH6MsaguenUYpu1R4XhVo4Ymwp1tIC7xc2seH5EQr07KB+9cFRbeO5nYQcL7XPc8L9tnqaJu9yrSGd+zgbjpwqcGqFrwnPo+W1tgWZCMv9a8IwzrOjYnz8mLK612D4DWkuU+zt91Tja93p3pJ4CLQxKFV5zG5nH53z66JMP6ZHNSIG47o5h4fBZbGVnTyAdqMDalW8JfcLkqf61Lq/2y3pO88aXWqUj7yGGsLX719cUwnvKA+GTwf5CTlW8utdXVgjVVUXIuHXZSiDM78q5PHmCL3jjs7N86V3ojj2SPlj61A00ScwebJDttmEFKVgjDGwTZYd9H4ha1aryuts3zx6gi6Nj7nO/irB7+Y8d46nOO1G2IgiYuhct2bGKYPeFtVBsJpeNTYn1s/2ILrjU1FNnoWHG9e5Jl3GEXIf3g/wJvSJNBkyqKVS53U+nxV145qcoObQzhPRm3v8sMLZGza9ErQI3T1/GYgx0uZl5VfHg0PhvHJhVj04rPLfU+2zFIVybZW4oxQuN3TuHdWm39jihpJq3j/kE4Bf7W9qwKEHdX5OkcCs0tqyFzmSgiE3NFL83P8+xOiX8/k5p3vRwbnPhelPtqSujUjax5y0vVqnYBxme6/3CEoRdKqgvvrFqzc+Zsp2inA8jNIf8759Z47+M/FHFEIfjw/qklWVxLDaPPwaMwHfU7csgnwSYMMUunDIjWFNXYHba8hVYNwQr+ET3rbVE/J9bI4XvY40rlqYVlXGYBPthjOT/YmbxJHhqN+FkKoTQuJYAe+Ja7UJiPcTKjeOf/QgLLZXSJXEuvtGziV0b0nqhgbSFg8o/Tbcg1rKljYkUjAi5mv2EM6z81HyAVRzRhsbYjMUvLLxxCKCWb/lZiONyuoi28RARXbhA5bj2yWm4B2iMbyyvG4tglqF85rJiTuiQp0399fX4Hw5z5VoHklArrpI2iO9NrYrbEIBb+5UTMDfGssmdCbkggVxc0PUt4eKa76G91VJA8VuFp/88wv1HX9OqCo2PS7qeFFNt/Fev/LpW/LvLsLrbFvqGCQ5O9Vu/2ZRpAra5mHjU/V1Po7nVyOic3ys7ToQfEO+rpG8yVXoC0atunktgfCvr7G5gPSErX7UB+bpJ6GPhHispWxLfuWb/P+v14uYG5AdhpklNI0kXYfrNvVsl099gPlzONWD01cxZxymiOheZuM1sEPRheOPxgjh9FsmuhxBrfdn+J//ftEnjKdKnYfxgiUOBrfsdEE4jopMfwt/kb5OC5qiThnTBECXt9qJRf0G3+iEjixwgOEpI77gdUgKxqzeSWhwdnhs/mkWz76kscfg58cnXzM5euG068WnFT7mM3aNRjvz/Mjryk5cX7LfMghRdF7XayZe73gHkA/dPNM/5x6yeMDDHngfm2NyjpFFz/gmFHUUaqk3QX7Cyvq3wjyzkwWvS1nr3/NQftiT6M6vkc+4toPPp7FYATIGLxu3R9DrSnPllZ5GoD2h688p8zx+GN0H1/Tj+hyGfChSlkjASEsRW/Dji2LJ/QHoQ5DwfQ3nOTBzYgkoeUXbwSDhW19fL3g8KIdxzYapZYVJW2Ir6BSQmkVlO7H65GPmqqcPFNmcofCE4C4PMrWBn/CacOTHZ+GjGueyQ7lATmiW/15QNIwWui1Tcou4OdKG0bXf+bMpH7XyeWQhfHkKJrRlEssAd+qE310eeI9bAKs4Ugp17kWHD2IMzmGsA0vVCGNTLD4Oo5gxluDVcK6vjq38O/75xs0fUQhJrPR1OttyG4WW1VSMXQlh1ahTJSNazy/fbrxnC+fDdD9wPeYSnYnCIeQD/E2u4gCuuXCf5UAIut8Pl+pAYj3AClG20SgxaDhB8FiEMdF0aV58VmmZGEyluaMEZ9wmih5B+NgO40U8vWxWzbGnIKsaC3zcUw01TefiuP+baIoLLM7OIOIi0PUAACAASURBVMDGjZs1A3x3Cy6JbD4sxZEjSXibeisTE7pNMCbPZnOtsoO0SUljJFb4270XifRhWlOj7inLtsnIUEuShfND5FRrdSC85+Rt8YRVJEUvvv08JPbzw0jcranut1iF4lifgZzEralVauXf90XknyfzveMPCoHH7I5eJReFzeT9bM5oF19TJEWG8fXVdpEC6XfxrClAAEnadx13MT+SR7TdwnGixxYuCIf+bUJkGOfV9jRGUKzW24AVp+jgXiSZKIxUGgHgQOgitDWh9pGKkHsaKvTOdDbPvUH1Fn8JgvCgLxJj6xzHsTH9/YKut28RbSBSCL1NVvXj4DVeHGtdSiH62EVJk5OP8uBjXcZRaEX4mvv0q530KtRteq5ECG12YY7nkUXUa3Krrk592N0QIWgj+9RL98aV3Lvml6OhuNg9TQ7PsnSf5U7rfU/RaxFOCR5LhMIqat94lp5Nm/Xd9+Y8H5UIuOb3fXoKV6wpZMepEfTVXEKhBHV2cfXtI/SObxEx7jNZK+IDXyqtIZx9bFXD1jOvGEsZLTybG3Kf0Wk8Hvs1JA/+7WNGBCE3FxkuVG/OtkmjjbanO+UwrN99xz48m9Ky+DoBYyA6eM2XfFrBDtkm6OfrN8/jwTGnVOcwXG7l4HEGvcdWwaQ7WDCHFkR1vk62eu1RoJaBzD36KEaVAsI39eDAVHjMJu7QnOSuwVgfztfv37R5VmgEUW0XZ80TEbQQOy6CFvZ9PV/OR31s8Zg2PaBGmebOlMxNPThmEfqf/+c/+ZTYZ4GPni2tNREyeB4HtgzuRdBiO3fufVADzsn/eqJ0bWxlu5Kv4Wuyb5ZGzxL7NQThCp9NwanKGdD4xv3EuM5ZGPPPx5/wGd7xjne84x3veMc73vGOd7zj/2v8Ea2j4c6YnUQTScD5rC6Pqv8GjTNNGBybx5L47cWhmf8RsbqV6HrvycWZcCqrwqv5ngwsX6HHll1N9OsaFrrE7oJASjQPj63FHkMS0mGx4XPFAnlydwqbggQ6Oy2uknpmsWBkTnxTaBNTNPL6AHwMhrJ/PyRV28oeq2r6GEXf6hzinhOlJZ0ZAt73a4ZHjriXtK8YLdrWVrRI6e2lNF9VKboRg6lIJ7LhgIORPkPzn3Xq6CdBavEd5nXP70bUiTCuTXcIarnvfhNFW3ybGAkSur0/iqYM7+5+h4P3raAVkR0TV+E7eDL89i5CDSJhMpAd9RD2qL/Iu1/wjjuKCX22N4sqHrfSjwyld+X1tWSlR6o1zu7m52fhcRSK6MaCDwnELfHZgNbEy+9pjAZNYkPhEMGcPbGOYZQIjrUGVFJR8haVx8zYf27wOzrauH3NkHRFnxtW70HXrTSNSQJgFp+mTPWzRVP6/Tr5+eO5oSaoYMKWxWcCVuvqjjp4H7gKMe9d/an4v+Bam0EoHoOPIzHxl3fwkRwqoITxqMqE/dO6E9WQY3pgxMDG7XtWFHrr+6wZY/IkN6w24YGG8nuqy6kLtd7eQ8Mj97gN35tTroVhnqqcPs75XT45hK22ZyOIGBu60tpA5fZkCReexXGBNuEubSpn/vWc98lq8j/nM1irchy65dHHH3Gqv+OPiZlbAHRLhIjuvCLS52dNmy2pCed8/sMTAZPH7cw1XBCJbXmiWhA7KFNhraoyGHsvUQJMKCx+oEI4fi1kxqArO294Ph5TRW5CP8OTHxdBneqzQuYSS1mzq3NdwVEXjDZ4dd8y949HRZ9x53QxkS3L58wFJbA92Q1c2Z49osoZF6PfkL2c0QcyETSZavlGv6jlxEoXjGyqyC20is+xzbJMEdKT7GMq4fWudHeOOZ1BOzLi9sf0oEejR6GkGDf/8dd/YP1rQ5q7N+Yul+8lMccf876NgVm5pfePSoyxc+OEOsv2rItwrlfb+9fjWSkmyOBW/hXoMbbtSjGjatk+d+NqhNRtX/MnOAn9EVummOwxmlSQqrM4SW+E8Bt+VRSq2DbcdAKZ2vh1mZNOKcexTeqcCLZMoWge+PN7wecDrbb4OqkSsE0RxdBymwU6KXfb2k2oNTGs3BCt3gd8BTenPxfyriF8KrN/k+Ae+MZLhipDPUGc5GZRbYvRJrwM2clRxAAVitg2ju1jvtxMXuQQjik1Pt90Gqau/5AF5yoq8CQJykxezJQWg7EwhUFKR8q670qMGxbiI2+HyI2bHe4UvSE3MmXD562ki+ZmMd/j6h0ReH6TzxYvt8dTwHHILpRHD1rMYpnc8Lp7GqruN4UYbMgglr+3aEf7ufi2wb3jHSs8nGuSTd1jNg50/1sX31DOXIDBrcweiEKqkM7DpTe8l7vWD4cCY3rLXK+Tz+fBThUCzqt/k9oXquoufALHQzbmvnhQ1ZBycx7P7lh1pq8xrTljxEbQOGkJsLgx9dMYPah2JyL+LcHyPmivi2PxA5+GhOyGBLr2lXmIF5mmq0HM6/j9yzGUtuWzByVkCw/8+PgkGLymB4q2i0sXxBekWPoGLcRyJFbePlazSGjD914z3Elu8FKgCaykMW2ZFd7BgRWlzWTl9JEiOVN2/FGeuJ1bmIISKfAz5bIFxUz2XnJ5p1RNojTZ8Bpj7K/WGbQeoLr/poRlU2YWRh+lcnbweTZQQUewPsKb0viO79E9KQYA2gKpbClsEcV724Ik0S4Q3WejiaFFMZEtINJGFvK2zlg1qt0QV4v0A/P5jHv3bBDP87VKQbhhtefMeVYqFEoe7KtBosahQWNsLktToarcIknD+TpPvq7FSzJKrbsgcIfxDa4nmlC/Bfz3nrL9ttalCG0obBGJzE1BdgEzRk9LgpXwTy/H8ri5mqXGzjtcNQ1MV15ZQcN3Y3l9B8yCslRSsGuJJ3jey93IVkuqQLTd/GjtJHrfZrUWycFchU2oEe4byk0MeruoSz67FFxtG4APwIpgO08VLo/dCDItmW+W2Hu90xPauJponv5L6mvvN1wUiyWe8c+XIf/8JyAxgwtzaNO2+9jZejCUO5EwBY3daRSZizTuL8skjbVWN1OyGbmFBlwSY1/n0hvTsXgd4pk8RyqAkDrnrffbsTxyorAfWw004KFlq591a/QrdlUcEvi4/ZKWfvt2NXfBr5usd2hQgV/7LinVvk0+hmA9uCYRWKa4gurd4RyRhYHamnzIxKfPz4TgIzZxN6dSt6+GksVDyDI07Ei7zbeG5kLesgVLhW/9B29AxfTuSAzaTHxWUWqp77f4OSONb1d3UyWwKpR5XxPTf+Cz8/xqA3zsqVUWXX7zv1yIGMSwG+cPWDXKvM5Q57rYxXcps+P07bB4xzvusD35kEkU3jzhPvhhUJ/L4yX4dY79DHko9EFUReehGy/DvbOoHb0ntvtxfABwjcFXG9j0JPsoT67WafMhr09An/SZAT+tcPk9xYglHTIPqqtHDlxL8PFM0uzZG2pCTAJ+uxqmyuMzhVWsgPd2q+HNqfia8DyPB3TfvMz6SBPGayY7qjk5Xtv6UAjNn2MmG+fV+JSyRQDowlHrNhiUYhSFrzkx8ojkPy0unykSwdmWKE4qaC6/E6Mw2rn3bdE8rGMWFFE8F75+2/sNPu3gWv4jCEph7V+/WuMoSpufWQeMyfPJz5jJV5n3Saaq57Gadhr8utid6KqOlce8rvlJzWgn+/vufuEhm48lV8eej92oW03Cd7wDoH29aJMbo6LEVb5NixsR8PExC/ePJ+PbdFpIFVkffRs4Dw+6xC4IbPQUipp8mq5l+vqtjkMqpK0zunvHuM9jofJEs5lLcomySZH7Xa0leTV6NxgiAvPAVrPn+UnzsdftRSC979xEAPmm/qhTXEt2LpScnvWZTDLn6Ksx7dm8jhBi8ZVjIOhEsIC6YhqJvCF9zS73fZ/YasirQtBEo/TV7M5/Wp9JNWDA2JMzaEN2g//TBrUKKsb5yj3x//73f/GUwCdHVRl4sBWPmSbZxxL+Bc4W+zo/ZCCUXbSaOkX13q+q8CzBeS3hg9T4VLNdPKcRrrAmPblnys1dt2lUuzrPf0B69Qd8hHe84x3veMc73vGOd7zjHe/4/xt/xERIIrb6h83u5cYbRqSi3C26hPfY3YlrDLqWxCnusi7VznbhjXLFrX7m3VHGrFxJ/GqplCWZeg3cncqq7KeAyZ5hBsNvlYxAGJYS2m3i9ocH1xhcszv5KIJ6bPlGJFXc9iREhFIUmfKQotmxWNjNy4PusjlGEfD76rdSlDimiztwQ9NcZPd+0lNHNmbeSnZWNo/Jp8/Q+lHmxGde9hkd9bInY6ZOjJu+kyPgGw6YsLnE0C/pV/F0ku/r3lpB8Y2z7aNP9bYJfVSlWqFMZSeV5O+U2T4/PAhvhH6b7o05AgSG9OxGx9heCZTJh1ij+wGjtT3iFgwruqdvva0e8jvesSAhC/oWKIHMNWcMugi6uqOmWGn8P/bePdi2La/r+/zGY86197ndTbdgwkOCiJaG+AhGBUOVXRGsRKgKSSXiowwNQrSSWEJSGqNIdSJJLCsRqiRKKiZFeEhporHUhEQtq6VQjJoSqQpIUMSWYHg0fbvvOXuvNecYv1/++I0x5rqnz7l9gXv7nOaMb9XtPnuvteeaaz7GHOP3+z6kOyiJQnRKQ22dDTOnmcXhIy1spZBbHsxbT5m7s7E1C+582Tw5vTPlamBfLrwte3dnPd3wsn7gSGaPmWxwv/V9huQilMYh91+672X7HllY7IgMkCpEXKsEuO6pGEt7gtysmfvLfkR4JaHsQmidEKuVHNOg/t7dX1hyGlQN8C7UJQm3jcp7jsppEc6l01sUyWlYlYNXG3VYayoaWkYc7khZQ0L3rnGEIjJoaKvkpi1t7++aAy3c9IEV41HZSa1zlvbi2237rFXYLjboddo69533H7Nwc7OMjnYprtE8OuSCxoOmK5Yw8+dHT5QPAXQNV2OkgRxsg3KGuEbWk3/my7MjNHGFZV2GS+tWC6JGbC2B1DQrw5EyZH8edz1PTIQaIRqam2a2GqoHuyWkiKkNtzTDHXz7VEetum6u58zgrJ/x96qcw8ZgiUgiSqIMd1d37d3toM8FmiyvTT7uL3uzx+7jk2soa6Ob5ShOyW9/75RcHc94QQh2ZCiWKizLMro9Voxg6vKFvk0VYojjPvXvbYNGq+Jav9HhkcZWGtpyo4pQWo7atlckQer3fUyEYCOjLgA5uW02eJddgxBjhpZ/9CPvez8vrZnSqNsiGTGljnHc2QnNmZ+bKq+KWLGqr26PBHfTHXp68Uy6ziq61MK2K6Hq0RkLAVPG+bY2RvcxL4hvrVMrh8PvM8RzsRCyoFwlL6B6aErEnDbW5whWdGTSAKQgLAsQnB4HPtmupR65QeZt2P5w0mItc6JRvlDWkEeWURVzXUm/OKI/fHobVvCo1jCcEXzBtpm2wETX5ygQcp+tCHkNjNWZmOfsqF+RIRk5hSEgi7iwrVNVTI1tr8SeqRETJmVYKwbx69cfsseVfMggndtrytAO1OrZH7FzToXGa+sLPGOrdogeRVApY2Hkm5GxuAsqYxAAyEvGqrKVbfBko0Q2O2wtQ3ByUafHxJiadXATI0chx3RY6O5GqGVkieTkE6lOPTpfLr69nkngIiQEG613s0BMDIqfqSBNV+a/CBgBawNeFztOTABgcGr33Vl3JHihBVzSl1fhlVeaPWkW1yS20GJR5SZHsmQ+cPew/U6wqqP4k6KQLVLbIkViQGIY4cv7vmPEERCdo40FBsDd5RGhKOsQuAqbbmgjku/7BUmR25THZCMQiJHDZTdELLglNUCSTE55sBkiwsPzxsNLv8+EkMLQPe27cloisRV2LneFvZRhHRtjpJSKxcDS7vVTTm6pO4o9EVlyd/hm341Syhg7PCcttMBsCAbV9iNAWsDiMZEwqwTjyPHIOxQZlJ1aGcHYsWsvg0JVJLSHjqg//LtOKQrFAmujQsoeqLUMCmDQQNKEjgBej3PoFB4MRAOdRmKqbGZultPGPLHd81xin2i4zW4f503hsm9X04lZuJk4EHOCVkQJEgg5jBBPJJDZ2FpwcpCM2MbeqizpZMQQyOm4z2I17redR42OJWX3pVPXE5r7M/VQzlLcRGlYyi83hCQjnxARuMRRRAkLEJS1TU93rxQ5jb8NUNmEejWBj+b6whF8nJSocRRliV4UHtOT4N+9zzMBv+e79bWpF6e6TMDXgh5k3zPhxCf7d11PGBKluoEB+GIrSBg6pRSkaQO7RmP3MbdHwUhAgo7joupzFa73McZjprxXtrMSbwqWffz5wP3ZZSHdgEF8YthzhojBC/m1Zyq6cdUxZzT/r3+mCrvVUWzqz4sj1yUS8TGoaxpdniBXgeAB00oM3dzH4wP64syeA+nBc7EQErNjpW5KqTIEYUvjlvbVZKlGkoPLifnFvQTvmgAkDeQIe99qaZ2KNqFPScBkBFVJDVTTsXIneKdG0sEn3U1HhkYIQhIhNh54iOIOSMbBe8Q5nrmrFKuHfvYKheHVzKObopjkIYjV9l17hXaNLlYs7eqRsHhKcBcWt5wcM8aCkPbXl2HzZu54VXvCfGKJkb2H+5l5ptNR7EavnKXybfZE6V6K7mGoXZMkQlUbk50UI1Urd1qHzmgJ4oNxz0AJiujRlYrtS/TFV47uWDOqwCZEEtq0VFECuqexmAtRMPWKuu9UbAvlMBZbpvZqRz68e3UY0/kSqWueRsV5YgIgGPdtUZJDYNPCW3qukET2+zJEt0hwV55WLKibBxSHZCMXJkRjIw6x6ZIDqwQPi6ZNKsQIbfFfQmXb68i9yjUQCNw3rcudbqwpI80jyUy9+KBd8xhIKXHKJz54f7gsheTGCr7fQBTK1nOCdq8sa9/nSLhcaNl/nHIirZnaqpuyCUWUtX0HywnVOgT9NBOcutcxeSF4wKq05PZlrzyqO21egVSlXHSE+61RKEGJPdhahNgyTMDv6x5aCH4/3+TMTdNelZS4f+ROUODdZMQzxKr2TpZz/rtLoAY3qijNyCLUQLpJrC2Q5BIv7Jt1nTchC+dY0TZpvMmBgHUPHKL3n5ue0ueEPurX4ViF+iSyF5zqbpjCuvSFEm4icfZ92s/jKE9MUIp3UwBOIkhOQ8dSqFTLSJuk5rhQdmkucW0RE7yCr90xMgqnsAzzhK3shCCjkJxzonBM6NeckajU5tJaraA1Hs6LgKVjLnRaV6Iod3eeM4NCaGNikT6GeUG6d4g4rZ7dOERBCuHQDAVzjXbXBafonVft8y11p83Y9dBqoIVtPxYx0lx+u9FJFmHTo6OjoqDhVTlBhasFggkxC7EF2kv1MOZlbTrN806RgpaupfJMsj43CuKa6eFimwShUuzCuc0L076REizWC8k+dvQFnYmgQante8coxHrkVSIBkzrqahKCG9YMF16h6sGuicG1rmZHh1Davlov1KBYOFRpIzet69Ds2ec0Pvul2MTExMTExMTExMTExEcYz0VHSEXGinSvvnLvzmWmXvHqfNOLKmaHrWtKgRwSxsFBTNncnamtWkWEEK6oUAgSjNw6GxKDp4qX3hkpxGhDd3KuRinufQ5OwTCMkDq/9Kqr1SuBYu652J1ZRVALg7dfzHhwezrS46XxvlsxL0W3sg1jpR5JmVEdsKIskgeNJGKI+nFMjf9ZglMMB80weOp61/gEAqpGaWv12GzKB2fTmtNKXy5XoxaGlqqUSszNhaodCXdb6dUDWpf1aLWq9HZxO9+qsDk1CJxKFFLEGm0xBt9fbZUZSQbp0E5J8awTaQcqSUZiGVS5ogYqhCRoO3i11MZTbpWXqkTscJ5rHNfh+HfExk9MkAXuu1W1BS4G6Yo+WiSOiqqa8vaTsQav+j2MO/e1UqJRuyiowksPFrZLozO0zuyl/bycMjFU9kbBuJVEjbA1C2fVDEG4dBtXcx1Mv4eCGEu4pSb/+30X11aqXnXaK2s8HCfVBKqyNl7aXitlg/WmVysreVl5eOeUGpMKUZzuC6SwYlsZdp9LzlStnLfegQqEENiqchnHLlP3inrB1K29iw2LWxN3wuvj+IZANULqtJ8E1Sua/bgG821Aq9guRuk0tOLRCoPlYQKE9v+NEgNc7iux6yqzcZsjtfNoc0DFeHi+b9tQ1uVE6C5yGJdtp5fktVlS6uB6u01urwIHIkSh1m1QbEJwzVDXeVgU9l25SZ0eDHsxukLr8DOdmIAgkdv2DL/f7pBdyW2A2qoiFsmjK2sgivW5kfr84f5yD637S06saeWll7yzum+ZrdQxzyh1h2CjIxSidyIQn5iU/cymFW336Us5UrR28zTUKms43Nk6BT9y5Jp5PqFnEgIkK2g5nOlCdLlFp5cStXWWW1e1a9B751fdW3MoGVLCpemdChaoQQ6tp28E5WC39AzH0Dq1yyLse2VvLexFwqA9A9SQG42/UQhtB4wl+3FdtLLHOPY1GEg85sJmrnk06mA73W0XFoHT6tsQSqOqtX3WSogHO8okY/E8jltUBVOsLw1MUA6K4JIipnFoqQQfV30O3KmOOB2vSy7YXC8+8kna1KtdYyO+4BniuVgIIS7QA4hWMGw8nM7FbaQb5Z6UBLXkPuX45H6vbklaug1qu1j6yZd+4MfFL4AOAStIa6H21l67ibod6blQNXHqlK81cGYfJ3IrG2Kwno7sDr2oa3LaJ6wpvUoSZvjkvfvam8K+X7G72zy909B23UBt+L9LMJIxDBtq+5+YDq2UqlMoqvYWtYc0dv1N3ZUiXAl326JpHCcjLULs1DmVtqA7KGNZfDvgfHqftLTPr0pQIZHo2Vnb5cJyWjsDEFUXHHfbcWnf+9oOG+2TFB8OzWTQWaT4INZpQtK0Cn2iEWNFgh+frhsSMSjq/FtovFw9Gu27Cz87p3lOKyaucd51XK/7bkSEtmYhWUVzGnkXWio3+S3DdSCHlbvzhfMjGSHCb7tdWCRQQr+XXd/YFz6pBESN2sY3vRGWmLC26FhzIOXI3oosu1Vk21kXX3yV4Jlqnc63LJGyVR7d7axNNZtN2LWgI+shYbITW4BhvRiXs5HWPhb4Ym/tbgmiBBGq9BDQHaLRmf8prYQUKS1odL9U0s1KKDpyhHKMbsbQqbeYB7u26pC5CmBEKUQTJKRRqLho8UDULjYeOR2duiLUzbhcfNGSkxALY5Fzf9mwGFlOcRRBtKhPdOIxHvmzpVFDRDif9VW06xxlmN6UbjneF5i7sYtbpAMEE/Kq5KWP65FSCzFltmF6IEQCuX3mHgIEHVlr5q43Y5+Hw8XEBG0+0xYEy2nFLBJye7Ztrn0eeuiWW1PbPZfIaFVUhKUZFvm1VodGupvH7G2xH2sgqgyxPLUQoh4W8TFSqdzvPqnTfEOMh7j+7nJGT+vQ8gWXtVDr7sUPIBQjJhk6yRQjMYehCaqqlBYHAk3fI8d8SaRRcttCqJqXEfoYTAqsFtBeUN0KFKXGY77kttgyFglC9p3tCgsCtzeRvWmKdFe2y9Y/smUkJpb90DgGEWLT+xiJpVa0DRamHgjd7bglud4rBhm3/Me99BKrGFt7dqy4dCSMhcziRd/qY+Dd7ouvrrVSEZ+PLb0RYUTNXtgHrO6o2VEsr4ZZaTE2naIcgHjowKV1M4Zk46DZ+fuffaH5uVgIaSnj4qlVqGZI7AfRL45ewUgxuJNcv8IVyr5Razi4lABJhyDQmj7n0Jz5hL+/HkPX+PRVsveXurHBmoW9CKF3mIgsYtAmO7VWbvJCSIeeRMz84rgKzssG0g0aqqFVhgZoWXGRbD8m6tXZ3nWKRdg3JV5l9fjS7eDDh+gv2PH8JEQZ3E1EqLsNPrBowBY5yix+sNHOh285HCNgldC6SFcXroYhihQMsYD16mdbfKYYoH1mkoxYHBOJgFeTj2qSCzqlp5o2g4ZO/o2aqUW59NTA4knL+1U1IhDHwFCCH2GrjEAvxfMB+rEXCYQYB+/VqrUKUXNrmROLiWtYGJN1K2eqQC5egbu9XbBzHQF3KcCPPHo0Or9LCuSYqXvh1F0LDc57GQWLmtoYODjXyqbKTeOWp5y47JcRgpfWTE6JvPki45xuSbpzf986RrmZjfR7TmFpbpI5H2MkloexQKkFiXqE3pkhpuxtMRZTxMrG7dorh+odmy7l051oiXTbTAfUuLvsY+Jye3vL/X4hRCO072FRfVLWhysLqJYun/EFT4TYg9ab1qm0gobeXwg3Su2VRzWQwNq1nBjn887eDB7SGsjrEVRrN+odZzEPWMT1QDnFo8rbgmu3ZiLBuZCXyE1LdifD3aPzyOWQmFhDr8SBZsM2IfXk9+K6gri2cT67C1wS5Vz680hIEsbEIpI475XldBRqjEDunzErNxNXUGy42VqvCvcVg7qZQtcruqg9Edr1WM4ViZklL+TWHba6s5UyAp9Dt49qBdNdK5tV174BiYV0ZZ4Q8ayzMT8LgRzCMEVJKRKWdIwDKLUqVWzoekvxYOquF9zP1YsJo0ClSD4YObI7s2XovNU1Sb1zS/R5TdfliYlrA/u8lELEoCYq3Y0zYRW0Hds1CEYZGYfF/N7uOm6JgSQMR1GznU0L29aZTBGqsrS8uNQWel3brBI8l2ywpSoBD5bN7XfvePAWllD5sfe/z9/DiZTqyNh8+1sfkNMNH2jizoevvEKwdYz76id0MG6qKls9Y+07pSLEkA/9YjQvkJsQ++IpNFfePiUTG3MqaOuhcPgAHJSjZ4fnYiFUrY4LrjSK2BK9mhmSkQh0PdUSA+dSxmS/e8OVUul+GiEGNDB+NgwLsA0XCyHnPB4YgouJh+00xikxLq6okJZDDGhsmMQjdM8CS/b071EFCULIcTjNETxMqy91EuJC2dad2c+FGGXsYxSjFmHtOrKYuNQykvdicIvW3hkJwa0YfTXY9rsZwPUbp5oPDJ22EyJgx02yF6XsdlQro2A1jAqjhAAljAlaTt7q3bovgbkRgo3qKGziHZlksu7jlAAAIABJREFU3Y7T3FJy0POMECN7DxVTL90YhzWg1MNBqUYlmB6Blubpxkt/bwwetNj2Md7CtvkErruYSJRmy9er20YxoV9UfYnULW17VWhiAuB2zbzSQztrQtRIvViKdwc66y2uC1Yre7/2bCFYwGoYlUUJyhb2oxtTA5e9jBmtRDdQuJx9o+eHHuJ5+8DHSILwqCq019MSsRCobXgP6lb5S3cvEiHlyH04nDRfuWzkEMltwn++vxB0EEPY1OkVl1YkudGdaj5OArx0WjlXpXZDJVGSpiGYvVjlfrvjJviCMZgRVKgEbl7q4uIdK4xusSCEq7EC686P7ec1oRWWNjbo4iLw4YqpXum+Xdf2HTZCUqRVoi1AFGXr4mSJPpkpjONyqZBXG8YTIUWyJM6tQHXeKstVYPSjzem7273v4zpE1r7L9ey07NSpSedK2ZWlhb56AaYJtzvDL7hb1l13qqsXkEpt+60x+OSlne9L6RymiQl/rIVeoM0RsnhwPZCXiO5H8SEIJFmPUPawEfPi0oBhtV99bGp/s+mOYk5NxZ/JtYK1iUQN6lKF1spNMVNCIDQOf90qG8oi3T0yu3xhME8UsybM70YoRbw40/ZIRKn1iDFYgpCijCBRU8NKHQWOQnZKWqffuXUVuX+mGaVWaqcfi8//BB3zo/vzBvUwvSkIKR620BYTqIxidTHc8Ko5UKaYeEkWtN/oppRSKOafWVWwCtt56CWgboQh0XApRMihOU/Cjz98hZ99OnGbfcy7KxU0UfY7/x4PKjcPboblt2qislNad/lmCYQUWdqcp4pAUH8eARcz0uIOfX7cfbHmcpHe6fFwXJMefN2YBr0QLT716p39vu/PEs9+DyYmJiYmJiYmJiYmJj7CeC46QmKMFmYKQlAhX2n3uOIQhhbu1Kv0Vb19V43DfpbgXSQ9ugYBGbaGVSsx2ghgLaVXTJqWJmSCCD1/MIbAui5DDLadN85lH/S8iFtxh90OQVjw7sxgqXXtTd9m9LasdkEzGa2V2ASydfdMnp6ZFFKAeCV6w1fjh5bGT2Yx6GqkjFBVhnWm5+LYsY0ApDw4rvu+Y1KG1W9OgTUdIjdFQW1wXNfg8bdXzDnXJbWlfpVOczuqvDlJPyFtn2rTBbVunBpqddhgqiS2IKR2rHNjye3t5xD8PIoeVpxRIjeNblOzEmxDS+XSqrxWKnkJLO0i2y/+manb+0f8XPW++1Vu1cTE3bZz0zonN2Flr8qp8dnv6sa+79x2Pn30LnAtRwfUpGDRRsf5do1YKZzbTbJvgf2iLEsTApO8u4rnDrFHQmLQ7YpWFgLndk8U9Wt55HuZW67W1KmhlWKBxaVygA+xlTKocIYMGhhAiAkLOgJYt+Jd1FOz9L493aLnjVOztU+nzMNL5fLKfft7OKVlhDlfysZulXgKo6u9X3ZSSkM8jAo5hEF7TRG2fR+W3jlCyifKGCTNOfZtYL80rnwsg3Dstrmn/qVht6MLH4C8etzA0lp8oRS2S+HBA//5bq9kdNBVblIECcOs5VShEgfNx+k3MsY/asBiIay+j6fbcEXChv1SQCJVI7HpsUTN9Zy9El12blKmLl0rYKwhUq5E2RMTHTUe8ynFCHp0UhKBjTIMj6pUUjVW6xewYlyIwa401wEJjAzDmPKR20d7tJuyty5D2Q0178gALCH7wNMZNsXZI33eYC3Lq4fNG5GYK0Hi0N7VaI1J1EVCiVp3rN3rMZqLIwdLNrryW484ABUw7Z2NfnzadzIQ6tBZBmgavSOGo1CQzDBsEHFt++js4x0pLcfcxirE1jaXJD6edpaiKmMSAujmnbBOIZQAIZ2OTB8tiBlbDeQ2ld+KcbEjzzGFgGkhtA7Qw7t7Xjn/KC8/OrfjoqRTHFpP14UHNzegPa+0HCZgwQ2xOnXO1PVCu6q3w4F1WYmSRsBqMZpZVY9z8G109lR+Dsar52IhFCOHUL0aJejIYdiqO1n0yfelmOtUOh9ajdJunL4AUDOq1sFrxASLhze+hODrlHZB78UnCp36hvlroT3NUs8CaRONC02k3x3fUkII1FKGYxoYZVNCyxGS6jfG+IgkmOm42Yv5oqk/MPdaMYHStVIYOUS6CUoxH5g6/9RU2GmTnp4ardLMCBrvVZ1m00W1tXrq65gm1ELQOEJgSzE2rYP7Kab+RfpfxOiD1uB6Gtbocf4dYBEf8/rkJofWTh2GCs7jj9e9eTsWRqecXJLRjStUET3O/ykmFomUq8jpJR7BtAkIVd1JbsRrJGoVd9fCJ30hGEubu55roeyV0lr1z8VNMvHc4OF54y1topxkocbK3vO91A1JdGmDfIBKQJohgBZ/MBR4FRVOLQ8NW92NJMKpjz/Jp8o3N/5Q3lZFq3L/sFG8MJY102V1QZVajlBhtUJaTpzWlwD44MN79qTcrpFz0xGVfSffLEeaezQ3OGkPvBuMSxb2dqOZcyE49zXFvpOyYe0Xl4uxRKM24e9WLjxYbuk5fpdduWjlwR45q3+PUl2v2cylPFFeZFB3ixbWJbAP2kb0xUyn4Jj5GD5Eui4U3vY++ankvJJY23H2NHtp1JQVQYs7uvWwv9slUnZGbtDezFu6c2aOsVWhutaqEkpkTcdiS6JR++RJlRSVPpCvN9G1CG2MvrvfyDG7dqrpF1JO3O30/O8Wfiss7cCICCWEQwfSHxITEzQNWXdIxWA7XOOoQozxoJ4XRVJ0VzbcZOWyF4RAvtqeP8P12D5OaQcgebDpqWv/1sDZdqz6jX1Xd3TfBoUsE7Hi0oLr7V16/leJ5AeBJUWkT/j3s9Pe2qJi14iYjV2I1rRQPRg2RVQiNvJ1KjmEsb2LFfbt0LEQmx6x09wUNmvusldudiLmk0Gcymuaxmf2eVbPJloWV01t1otJCkUJXQ6dnXp3WEoKEiOpz7eSsKsNTVIMgSUIGuMo8m/7xsuXw8V0SaHNjBut+rJxd74f4fJrNF9wpd5YMFLZ0c5bI5FjGAV7xOfRnQqco7DFSGVH2nx7K7vP37tjsiWfobcHVJTQFontuF0top8Vnos5Xq02JutVIWQZAZwSlK1uZPrPTTR6ZUpwGxYu22UsOmIKlHKEjaq1JsQQmwq2yRC0VnWe500X2plx2Su5P7wkEEsd7mn+3BO0V1iju6lVhNofyhTykkc3q5TaXEv8O4dgFD0Sfc0K1dYRHGpRWCLUnuaMuGanHzNVsDCqn2aeTB9zGtbimBBFkXAYKtC0SdA1Q3VMTmqCpabhMIIUF+e1iYqIa7W6PqtgbfLWF0quPxhua40/KqbDdSTE4K4zzdWEIKTrROigWL0KNCQitg9XpiCRcmW4GNNCSMuwvcwherW+VyNKpdTCOR7XhykQApt2PrAfy0urqJY9ciQtH5X1iQlwIa11IXvYuc2ZsrdATCI5V849ZK8KSwqkxScB51rcmrYcD92tVlIy1tXfE6KyZsbC3MS546l1X8yE/d647wnn5krJfPI/0CKoVtoahLI3l8U2DsTFXKNUldomG+74tA/daogRV+P0bnAhLcJbW6dLMddbtwHt5Q8+Yj2lYQ7z8Fx5a1jo4j2xShU73D6rwSZcSkFi1zlCjnnY5pLEK8Oxj+P+MB37pJmLKmXvWoKApEMYXouiaty3cf9mU+JJKL0ApoUQ4rjTa/DJnvP0/T0PbhYvvLUulIRIDcbSjS4QrFSWdrA1elhq7xD1SVFo2s6yK1aEXPpXdJ1UaROTAJhVdhPSqCwHlixIm/Sty0oOjCr/Xjz4sTMWjuz5iQm/prrLl7vI1qNDaUK0OsyMsoGVbYSsR8lEIjnoMLAyc6F7r+hXCa7paZtciEQJWHsoqxlyidQ2x3tLOLEtaQSsWuoLksaGKUqtlb29HgCtiT0YadjNVmqxw0DGCmldCE1zXWpl3wrSxoKkrpXunddkgijH3MaUVz3mq7iTb26LMTWKVqrJMSezQLwKYhfxkvyIODFDi47FlCRx/fqlLQhChVRH9yW3xUyPCwjBrbP7wgeV5kDZzk0M5OSWTl3fbttOYOdBOw5k8a7OqwJVK4+aZelWFQ1KoC9ShK3CMordAQmBdRRXfJnaZ6IhGguBTEa6VkrVNVvdFlUWUjKWpgmzLGjYqfdXxfBnjGffk5qYmJiYmJiYmJiYmPgI47noCG07pJY/seaIhDTsjyUYu9qwGFyztBV4X0Uqm1UkHJSsbauIGrF3AIJRVVh6q5bAXutVTox3Wxi8xwLo4Jvu4pzSfrQCQknCTTrchpyOZ6MaINEtv3vRVtXpcH21j3YaXHcMcZvrzqEPUTklYWv6nGBG1aOjhIlT/OhdLSWGQAw6Ol8mAUmMymJV1yt0O2zZlb0qqfVml5C8e9SocJgh1aitU3JavFLcLXSpBbU4LHjVvMvUw1H7PsYYRjBZCB7iqqOT5S32XlUxVbfwjN0ZZUfL8TrmIbo9A2pJHoZ70zx1Y06tc6bjD7xlHQdHdS/KTYqHnbZ4N81G4JeRog17vWV5Lm6TiecEIegIK73UShF3GAIP6HPnJX9vLa5V6d3kqpVaoGyHZfweAu8Imbc88OrmZS88fFTZ2+uLAgq6tgrbo+aG1O211eg5PgAVJcsxHtas7KUM2lsgEcG7Wn04MmmdlUZJvV08eFh7FykRk4yOkVRgV883w6klqQZyp5OGSqGOzv6yLJgo+8gEMlIwtl2RVuW9WbPr8+h6qrY7bbxKBDY7nJ3MCtvOCKmO0bU492en+92fjXUJvNRclixGyq5jLIoxUlWHTb6FQIyRFOHhpeVw7JGYhdrjG7I7YoWm+dqDcNadUFolWoVLueel1s6reNxDexSx5IBZGC6CxZSqdXS1bDdUKjELS6dFB2NNcQSsxhgJ1KHZqPjY1V26gl2XtidedAQ7Yj3cI1ePgPIIUZbBdr9ZVi7bxv3uGpJlERDYJJG6JSROPR/dY9QDUVuX/N6UKIEiPTxZSCzD+bdKZU0npHVZbRHq/e6Bx4CSKUA89bEkEmul1m3wQ09rAivuMgxwm6laRrZalsS6wp11SpggJnTpZgqZQh36Qt09i7BHZSRxHzkb7R4Xb/iUrY0XCFWcxQIQLbpD2mA3CW+7OWGjQ21c9n1op9b1BpaMdc2Qbi3Lsc3fgmty9tEZNpYYRpiziiIBYlW21tlfJfLSchoa1XNVRMroeAQSi2SSvuKvb4YsIC3LyKRyafICwM/Z7cE8igi76sE6alouCzaYRVojKa1UaU51GNu+t4cGhJoRGCyeNXTP32eH52aG1x/iSwyEJQ7yU9kVIQ26RFUjJLlqRwqxtESY3rqtzhU9EsNdpGaNnrBVF7sOgZwISu3usyRzCl5v2Sne7ust0c2qWzmGfoH65KWaDj5nELd+7YYKggvEDoMGt6CMuV9gETXI69F+3k0HHUJDajbPjTcuRpI46DW1GpI8e2R47aMkUQ73WW8N9zyKbtPasz/S6gu4/vda6NFC/rMJsdqR0VNd6zCYdEGotbKMNHpvJyvHCi4Hz3DqrdWEeNJxpykWhXDkRrmr9ZW4M3uWUdcAeVZSHBaUEp3a2BfO1vKagoTBoxULBGl244CmRCxhBOheasUwbpql7Wl59jfqxPODKMKmPThUOClYy4a4lEJKBxV0SRniYSkfiU6D0sDa6aISoVGuAEheFOn1hH0zrMowMYk5wLaz9okCiZwjoYd4xgt3Cqe2gTWu3LMRB887ud2pHSTTLRRWMW6C65DqXrkUHbbRb0mRU0pse8+P8DGsa19Q54ZLe7otqVFGhmzAqTG9+BQkELOyjFIOJEmAoF3AXAopHcUeMyHUeiTOq6EihHZfxxgpwN4Xc9EjDELXziRhq8rN2q38b9j3C9IWNVKFzSq11KE37boD63qdmNFauC9tovjgBjHxBz2u1TzFPEJdUwzclToMH2KKJAlchpC8a8faccmBGJ16XdtkI4qSCYMKhykqQ1VLEIhUaN+rj+cTE+C015du/RmmZqwhUDtVs1Tqfojh9+gULWkayEikBJ9DSCsoFK0gdRQzk0JOeUR9lL2yl4qN+AkIoRBbAbUmELsM7YxUCDmjtevsjFNeiI0/mkJkM3XqZ+6GMCApj8B5LYbIQQotpl5YboNLkMouMuijl3LvWqce47Eaq8owQrBS0XxQ5C1EAh4ibbVrGr2QNPSfCiEnGgOMfa883LYx10E8TKBT9Ku4bvncnw1WCKzUttOnZlCz9H0UY682THJyTE7hFSEk34fTSfjEj/0ESvFFiD28w4qNMVO1sCyZ063HGGzsnl/XKzUxcBKhxK4xiuyl0i8QQwm4sZbvUyTF3DT3flyCVsp2kCWlFqJklqYyizlwd9k8sgRIy2GG9qzwXCyE1ixse+uulMoaMrddKBwqF1XEunOGi/IOHYtQK0Srw/2sBtev9cMb1C/F3o2xZs3QFyUa/L1p2Km5eULPotFaEYSWV4gQSUtE+yLFWrK42NDjBMQf/N0DIIoHTY2MH2kGAm2frDr70vrKXNA2YW97iVFHtUARitrofEgQYkikIMNdyOToi9A/yeQQaYfAGhjCOcGP6wg0Nw8h2+rxGSGGI99EffG2teN+swRSjePAS4DdvCLVq9tBPZhxLGRrc7YbnTPfh37jFmuOM32Is+oDTtvA/UXIeRsONqo++PUg2t0KStMhdFlS8AVW5/EHAxUbYuRMJAQhtYll6mWkiQncda0XSeqeqaKE3k1uXZY+FlksvO300sjaOktBSiGscYQaLjkQsnB/75PrWsUX3210vr/f2LZDwS9SWdfAshwTiao2OrUmyhpjS/iGu+3CqS7EFn5aUOqlElGW5l72jnTiXAqXdpstggsKWtVjidG1UaP7EolJ2LolpYKooH3wCAG7MqwpIbpLXu3jl+sC8xq5bwsR3RVb6mES2gIqevBxDG1c7KY4La2853icUqCqcWp6nXxyke528YH7dJvZRdj7RKZ49zi0G3/bdi7BeCmnsWCzYGO89F1yX6m9U+hbR1333o1JnJY8KqZV3CyB6y69HMWmbVd3dmrHaVn9eqIF2ILnA6kdjlalPWtS13EEIec0Cjtd/jExARBEuTTNIrEJ3a+MNwIn9paXc9l2UjgmvssirCmhoRUp8c6GIe7MhjusBbUhtJBgzbCl3UMxUEMcmT5lb1qabseafQEynMpSxPLRrd7LTq3qnaH+kI6GaR1slbq7uUvPENtqE+X34GvMmTw9fxAjhTjCmlXVQ6lz7+zurs3p8zfxW1gy9NZWKWe0HsXq0Iq0DO35hRTWwSiRJAQ9NIxSFbvqrlhNILC0uYsEJRjD7TPESNx16LmMSKW6kVbPTiuFkOAm3QLwgVc+gEYZum7BO8y9KIwUaq1Ye0AttydOMbAN7zLl5Bal7WfDdsZ8TPt5VMbYr1oxUULuWqiM7EZt59tq8AVlL8LVY3x9VpgaoYmJiYmJiYmJiYmJFw7PRUcIiazdAYcKwdi12/kpO8Zt4yxGcR54GZQMQ7xFMGgYEUGv7B2D+M+xbeMUK5se3Zob9+/uIcOUlkE0HN6I3oLt3tfBgDpeN1oHwg7KXjDhDKyjEuhdom1YensFpX9mrbV9ZquKZKfCKP17W+titKpKFRaz4VwnIp72azYcRGIy57g22s5+ObOeluH2klImsnHf+KVi0bs+3fYwH7ofgFQDSKK2NxSraIHculhRDVMh9QaKGVt1J8Dc99PANIxzo81a1lpVIKiQgldv/NgaetXZKnshRiN2PvElcCL6zuIt8kTkpvnx72rs2+7V6WGVI6QYnEdH6yKFOo5bEGHJgdS6kocfzsSEuwX1an3FXKMifWwJaAyjc/IWueGt64kPtC7EXTFiXolmg89eipLK4Zp6v23kBydu2zW9pQDxntC4UaccqVsdZax9K9xdKkbLccjN+r+7ZFrgohUurZuTBY3q2Q7mPI51gV3dMQ2gpkiNcNO6SCLGdq5srXK43ghryuydUrO3rqx2vWDFglK3VjkMGyXEYZVqUohAWhZeaq3aV2rlNjq9ECDn6B3sXllWc4e9nqshHg+QxjjsdOdT0+ckIpdaCc2mda+FJLCf2xiqF9Y1Yt0tVJyqu8aIjiawa3o6Da3uFbCRo3FflRwD1nWWayTHSOlGT1rJIkjrrBVtja6u/5F26bQvcd72ZkUMa8+Jas+nTnmrZlxKGZF1+SZyE7myN57j1cSBaGnMXXTbCYsMRkUIzYmsV/g1sORIGVlchVICYkuXJPqcxWTMfyQoFfVcANxdNseMNHqV1kq97MMRl5hapGJ/xnseYqh9rlSQWtFGSS+1uCtuNe7aIJklES0OLfFZz9i1FqpRWntWW7XorKAhcgyYMrrNiKAC5zZOA8SYSH3+Zj6/M2W4WC5rIoU8qLv3uyEaxrFdl9VpY107I565M/IJqxFi5bZ19i8XoZqNLlaRQjCGHCLElSTxSoNUUalIiqNzXzAeauXtbQw8Bbg3G8+nrmXvLnI5+0yrMxb2yx0f0Myp06VSou67u3zibIOmQxnHWa33hbo2vD16OnvJ/Brp3CbU6cH3233bxKTGAaDleKgHhcWM0oV5VbjN4ViD4FaB2ici5qSxFGTQVayqT6SHtsXPXbfTli58acdfo+d8HEFZPhnuMpRExIqO7Sdzvvu4iWIgBx2BWeA89ZgOnZKqeHu2jSaXqiQLwxyhqDodqxsyRMAYD2kzz87pD+RiO/vV4s7Z9cbV5eaLDuMQPHcjhn4TLMKmYdga1qoUkUGpkWhorSxjQFK0lEEpRCLLooNSuJfaBH7NDlID2ZRdbQwoEHwB2o5DFgjlaN0qSljCWPCpaqMo9p8ZoboAWgqbHHqvaoqkhXObgO37zrZv0G3Xfce9zZwOylstm08ucR6shHhoE3j2N+rE84OVNB7Iy5LA6likaKPF9UX1o1rQR/djHAghuGXyVkbA750qFwRrRgJLdjFpp0xsdWMvOsbAO/EPur9vC58UWJfglCmA4GPd0q73uwhlU/azb//2wcpeK8HysK7+4KNCiHVMTuqu3KbEbbtHNnVjg/Ol0WSTsqxCbq+fMeoOy9qKJAF2OVYppsJ5L0MHkFPlrQ9WUk5s3TrarFljN849rjOQnmNWwOyw6M7iY96IA2i0k54xltU1SX38kmjoXkcgq4hnfPTJ0xJ9UrCjY6Ig5kzgPnbeX4pHEnQqbnHKTg9xavmqXReMBEHVhk25mm+rL6TWJSEBtFsNl0qotdGD2j5QIco4v7UaZS+DkmzRWMRpMgBmk8o7caBmOPVpwbpisYyYj70UllUGpb9uyrlCbhMRqwHdhQvnI4dRPVCzF6O3bSPnxGlt+VxVKXsdz82Aj2V9QVBVCSEOvQ4ayGIja9CCIirUc8tJCx67ochYjGFQtm1k0aQluAFEGwJzgJCUSA8K9eKUdqODsbg4siLFDgprqS3Go2mPgwbXeCehtm0GEkEy0kwh7HJHyWHojpIlrF6GjrISiBLHmGtmaGSY5iCCqrLvXbNRWVOCpndWdgiR0p4TIsGrzBIO8ykKd/f33LYB6JFWqsVjom+eraZN47NbxaIHVwNsdaUKdD+shUBcEtopiNUz7LYudZCm65eEDEGWa+h7Yc8L4XHIOgpKDYV+QUinOz5DPB8LoYNW6SF8lXFQJUR3E+mcbWur87ZyWkJL0TXoAeOuzju45dUEVIazxqbmi4HhgKQEOzJ6MEOSDIGslp0Q42HYYIWidVQGVkkYAetaIRrnVMJYVKQgiMhwTUoakKRjcr6sCznK6FIZRh41XtdAoceUXBvr9dQvpgKavQrSzQzUBDgCT1OKoJXY80iqUfZ9BMfGGNkwlpHoHCC6W1P/TkV3pFV9l7wQA+x71wwp0gYs6Asxc3Fv77ZEIadjIgCRvVzGICg9BK1XYqqfz6tCD4aNAMLdhLzpOPmSAtX00G9Vn3CewkLoXSTzxXQXsAvN1a/tkQT/oD55qeuxuJyYiCmP6maOzXGoL6Jbh6CH7j3SjXI5Agy3s2J1R2IijxvVk99Ls91ZQyKl4GnduAfMzYMbtrN/5maV2xjocnkzY0kra+tKqBQ0QGyTmVMAk43YJipBIuzK/fnIRtsuOw8e5KE72veKIkcmjxW2/SiS7HtF0JHMHr2mOxyNDKNu4Qh8Rtwkpd23YYms64KJDL3NSuBeI6kvGvCCV9eHUitrMHKrNOe4EIIOs5ZNd3cM7S5zaWGNcVSufXJTiTd9ey6eHmYwMTTXyzrcP7ubZy/uCNIe7P315iraQxLvhBRkdMBDX9p1bVUbe7oRRs6RlNo5AdQCj+4VQVja996tIlQPYgW0Ci/d3oyiW62VGBKl9GM/VUITB6RWtnbtRBViiKTcM8syYGOBkGOmRtfWAsRqaFD//24gooFSdkq7zpIESjHum+BGd2Xbd1K3BZPQsmxor/euRhs7sj/yx3goC2pnYtdA4vrtYjbGH61tjOvF6h00yDB0qOZOjD2kNUjFxIZTWVXvAHWTJjUjS2BpXfgluD65T9JlCaBu9NTnlRLcfbi7voXkna6ekKpmPtfonS81ajRiC1eLS6VqdOMsWvbRfuRfRolsVd1wh9bxLpVOuVGrnHJGTVj6sWXhR973furFx/oYTsTKOL+hzee6UcVNjtyd9zG/kgynmMc8thY4l204LktISKycRmHaSICpjjGOaIgWRJtBRyhU8pXzryKcyKdmuGDPfn41NUITExMTExMTExMTEy8cnouOULLAuVUe7xHWaKx95R8h5UgYbVh3HOoOFaV1PFLy9htA3SrhMDdrzkJHV6GokdTQ9u2VSg5x0NSiGVrMHdLwrpRZPTYorWPTW6DSOOFmowKhmJsuNVrHEgMI7D1s15r1YluKxhhIwtDOlFrY65UmqDVJRrUAIS/LoIXsUdHabL3b0nuz9jkSx2fs287a85RMG+2jvw6r6tAEeQq8ULpVYnAEyuj3AAAgAElEQVSebRw8/+YM06vAGti3irXjFIOvtE85szatgQVj2+vg0INnDQ09gwScl99OXaf3dQ1RpLnrtQ6TeVW6V5UTnmnStQi7VNYc2LtNZDt2Wo2qvcXcOk/tWKaYUBX25nKyjvLwxAQ81G1YnC7idIreoRSaTXu7Ps+7Uoph3dVHoNYAdnRmb28CMcXRVTrdZiqJ+4fuIqexulZn62IYI0jl3Bzbyq5U2TmdGiVqTYRqlFbNDOJ6k9rGs1q8m4Mqj5puSBJUEZbuYCTeMVVr1U0iKR7OimbKZdfBuZfkLkzdrVGrj497y+OpoZKWTKe9FZSiilEGl9xiRcqZbeQdBepevTONswaCMfJKlgwog3IhlkjxSs9TlVL2kQ0SY0RDJrVKc1KBvRBaOTUXcdtdZIwfYgHRcOgqR85R5zx7t/+VNm4n9fPbO2lLo4RIzyFS49FWBsNhTStLFEJjH+xFOKUFCWH8jVTYL3XoivISWNdAKf49zhdjrzqef1pmR2jigCFctpZBRSBHyN0RVQKl1oOB08aznu1VQiBLaPEe7XmZXFZgja6yWcXK3nqf7nIYEGK7Z2qbU9RjhxDCkDdYcUpbaB1NjcXdZdtwtgS326/lcET0e7uS+ngTXIcwHNi0UnelLp2m1iJUuhV1dp3UmGdgVCrWmSXm6WKZ3pUKKIW6b4erbnD9eP+ey5oRDWPeoKoUCf6MwIdvw6CxgqoEqoXhEhdjIkcb3RizihXFmg4q5Qj1yEq61B2WhBblro3jIQgPbl7i7bdvA+DR3fuBMOayPlSGQS+Woq6779RtIqqHnCKEgIVwdIzUO2ut6UUKPv/dA8PCm10QM9qjAzOPm3jQnnfVlF0fcoqdofDslyFiz0FbamJiYmJiYmJiYmJi4iOJSY2bmJiYmJiYmJiYmHjhMBdCExMTExMTExMTExMvHOZCaGJiYmJiYmJiYmLihcNcCE1MTExMTExMTExMvHCYC6GJiYmJiYmJiYmJiRcOcyE0MTExMTExMTExMfHCYS6EJiYmJiYmJiYmJiZeOMyF0MTExMTExMTExMTEC4e5EJqYmJiYmJiYmJiYeOEwF0ITExMTExMTExMTEy8c5kJoYmJiYmJiYmJiYuKFw1wITUxMTExMTExMTEy8cJgLoYmJiYmJiYmJiYmJFw5zITQxMTExMTExMTEx8cJhLoQmJiYmJiYmJiYmJl44zIXQxMTExMTExMTExMQLh7kQmpiYmJiYmJiYmJh44TAXQhMTExMTExMTExMTLxzmQmhiYmJiYmJiYmJi4oXDXAhNTExMTExMTExMTLxwmAuhiYmJiYmJiYmJiYkXDnMhNDExMTExMTExMTHxwmEuhCYmJiYmJiYmJiYmXjjMhdDExMTExMTExMTExAuHuRCamJiYmJiYmJiYmHjhMBdCExMTExMTExMTExMvHOZCaGJiYmJiYmJiYmLihcNcCE1MTExMTExMTExMvHB4JgshEfk2Efmin+Y23ikiP/RG7dMbCRH5BhH56me9H6+FD3f8ROSTReShiMQ34bN/i4j8pTd6uz8ViMjvE5E/8az340XAz/T7/icDEfm/ReSdH+Y9b9g9+GaMSc/i3nnex9Y34hr/aIWImIh82rPej492iMi7ROQ7nvV+PA0v8jNTRN4jIl/6Bm/zTRnTROTrReQPvNHbvdr+G34snvI5H/ZZ+dNFejM3/jSY2b/2Rm9TRH4Q+FIz+ytv9LZfBDx+/MzsvcBLb8B2PwX4R0A2s9K2/S3At/x0t/1GwMz+i2e9Dy8KXtT7XkS+AfghM/vK/jsz+/QP93dv1D34ZmHeOx+KN+Man3C0ydA3m9knPet9eZEx7/vnDyLyLvw5+Nn9d2b2O57dHr1xeD3Pyp8uPqIdIXE8l3Q8EXkmi8KfDD4a9vGjCR/J4/kin7sX+b5/MzqqE288frrXwUf6Gn8D9veFG49exO98jTfi+380PTOf5+fOxPOF132RiMjvFZF/KCKviMj3iMi/0X4fReS/FpEfF5F/JCL/QWuRp/b6e0TkPxeRvw7cAZ/6eEtNRL5MRL73atuf0X7/qlb701qIIvJNwCcDf6FRSX7Pkyg0IvKDIvI57d/vFpH/WUS+WUQ+CLxLRMLV93yfiPxpEXnH1d9/t4j85qufP1tE/oaIvCwi/6Styp907D5fRL6rve9viMgv+XDHtb32LhH56yLyNSLyE8C7xekyL4vIJ7/Jx+9T+nkUkd8oIn/nsb/5ChH58+3fnycif1dEPtiOw7uv3vrt7f9fbtv+LHms9S8iv1pE/raIfKD9/6++eu09IvIH23F4RUT+koh87JPOydU+/7si8sMi8k9F5D+6eu+Tzvm7ReSbH/v7L27f4/0i8jtE5Fe0z3lZRL7uans/T0T+artWflxEvkVEPubq9R8Ukf9YRL4beCQiv1tE/sxjx/GPisjXPn5Onhc87fqUF/u+/59E5P9r1+u3i8inX732DSLyx0XkfxORR8BvA34L8HvaPv6FJ+zTrxSRv9Punx8RkT/Sfj/uwatj+lr3wlP363We63eKyA+14/ij7f75AhH59SLy/4jIT4jI77t6/5PunS8Skfe26+L3X733o25svXrPH23H9O+LyK+92sZrXuOPfcbLIvID4mPdu9p3+lG5otHJa4yjV8f3t4nIe4G/KiL/q4j8zseOx3eLyBe0f/9FEfm9V6+ZiPz7IvL9wPe3373W2PvFctyfPyAiv/2xz/rd7Rr5YRH5ksde+83i4x4i8nPb9w/t5z8hIj969d5vFpEvf63PFJEHwLcBnyB+Hz0UkU94revqScfsSdfQs4SI/BwR+bMi8mNt/7/uCe/5hSLyl8Xvv+8Tkd9w9dpP6pppv/8Z88xs5/4vXr32pHvyE0Tkz7fj9w9E5Muu3v8rReQ7237+UxH5OhFZrl7/XPH7/gPte8jVa4+PF58mIn+tvffHReRPvZ5z+ITz/Vpj2odcLyLyi4CvBz6r3Rcvt/eO52a7pz7/ajup7WN/5n6mHOPt35OfJBWt3YdfKSL/WHxc+0YRedvV6/9Oe+19IvIH5NXPvxsR+R/btfO94s+fH7r628ef33+6bf8Vcdrcv3T13s8Qvx9eEX8e/il5PbRDM3td/wH/NvAJ+OLpC4FHwMcDvwP4HuCTgLcDfwUwILW/ew/wXuDTcSpebr/70qvt/r/Ar8Avsk8D/rn2mgGfdrUP3wB8dfv3O3G6SX/tB4HPufr5Va8//h7g3cAOfEH7TjfAlwN/s32XFfhvgW99yvH4ZOAV4De17/SzgF/2hP38DOBHgV8FROCL2n6sr3Vc22vvAgrwO9uxu3nKeXkzjt+n9PMI3Lbv+vOvXv/bwG+82tYvbt/hlwA/AnzB49u5+tt3Ad/R/v0O4P3Ab22f9Zvazz/r6vr5h8AvaOfoPcAfeso56Z/1rcCDtk8/9mHO+btxusX13389cAJ+HXAG/hzws4FPbOfy17T3fxrwufi18nH4ou9rHzum3wX8nPZZH9/O78e011Pb3i9/vffhR/o/5n3/pGPyJcBb2nu/Fviux/b1A8C/3LZ/ut7/p+zTdwK/tf37JeAzn3Tv8GHuhdexX1/9tO90dewK8FXtfH0Zfv/8ybbdT8fvh0+9OpaP3zv/Xdu3XwpcgF/UXv9oHFv7e76i7ccXtnP7jtd5jfe//+K2f1/d3v/ftGPw69r3fOknMY5+Iz623QC/Afg/r/b3lwLvA5anHFcD/jI+5t7w4cfezwN+Hn5//hp8YvkZ7bV/te3fv9D250/y2H372Ge/lzbOAd8H/MDVtfFe4F98HZ/5Tj703n7qdfWkY/asx9PH9j0Cfw/4mrZ/J+CzefXz8QHwT9o1lPBr/seBT/+pXDNP2If+np8Rz0yefE/+NeCPtf37Ze37/dr2/l8OfGZ776cA3wt8eXvtY4EPAv9W285X4Pfzlz7ls78V+P0c4/5nv85z+A28jjGNp1wvV2PNdzy2P9fb/SrgW65e+zzg77d/fyI+bvz6tu+f237+uA9z/b6HY6z7EuAfAJ+KP8P+LPBN7bV/HniIX9sL8F/h11S/xv5QO0dvx+/j7+Ypz3j82ju3fY3Afwn8zfbaAvxj4He18/VvAhsf5rlnZq9/IfSEg/BdwL+OVxl++9XvP4cPfXj/Z69xAP8P4Hc95TPe7AnRtz/2+vfSbpD288e3E5aesG//CfC/PGW/r/fzjwN/8LHXv482MDztuF5d3O/9MOfhzTp+n/LYefxm4Kvav38+/gC/fcrnfi3wNU/azuM3Lf4Q/luP/f13Au+6ula+8uq1fw/435/yuf2zfuHV7/4w8N+/xjl/Nx86qH/i1evvA77w6uc/Qxson/D5XwD83ceO6Zc89p5vA76s/fvzge/5qd6Dz+I/XvD7/gn7+jFtf992ta/f+Nh7xv4/ZZ++HfhPgY99yvV8fUxf773wpP16PQuheyC2n9/StvGrrt7zf3FMtN7Nh947n3T13r/FUSz5aBxb3wX8MCCPfae+aH0Pr32Nvwv4/qvXfnE7Rv/M1e/eR1vkPeHznzSOfurV6yvwE7QCFT7B+GOv8X0M+Feufn7NsfcJf//naPcs8D/w6kX4L+C1F0LfBPyHwD/bztEfxospPxd4GQiv4zPfyYfe20+9rp50zJ6n/4DP4v9n781jbduy867fmHOutfY+zW3fq/detQ4xDjZgISFiIJ0QkRxDjCUTx00KYwidg+UE2STCMjFEMg4iICFCcEho7Bj3womVRhjiuAjBcYREBHFsYSvl6l7Va29zztl7rzWbwR9jzrl33br3vvvKVb63qvaQ3rvnnL3XWnPNNedYo/nGN8woDw/8/VvYvx+/HvibD3z+Z4Hv+XTWzEO+377zefHO5IE9iTlUGTg/+Nv3Af/jI47/I1TdA3wz1ciuvwvwUR7tCP0g8N9yoAOf5BnyhDrtUevlwTVz8LfD834xBzYbVqPd7Lk/RnVaDo79X4B/9S3W78+x13V/HfhDB5/9Fvb78I9zEPTCAusL+/ffPwC+8uDzf4PHO0L/28FnXwZs68+/EwuuHurr/4MncITeDjTumw/SdXexSNBzWMTtIwdf/chDDn/Y35q8B4tyPg15cFzvA37q4B5/CdtELzzk2Ccd9/uA72jnrOd9DzZvj5vXR43x0x3Hr1d+GIsYAnwT8BdVdQMgIl8hIn+jpmvvYS+45x5xngflnZgXfygfwqIUTT5x8POGty4gP5yzD9VrPOyzR8krBz9vH/L7GYCIvENEflREPiYGG/ghPvW+H7zeDwDvrz+/HzMQnlk57vtPFjFI4J8Ug+Lcx5Q0vL09+6D8QcyQ/GUxeNLvfcx3H7oXnnBcTyJvqGquP2/rvw9d/29nfHxu6laAj2l9o1Z5u/rkwblDVR+lT55Ej/brqeoM/DjwfjHY2Tfy1vrkcLyP1b0i8lUi8rcrnOcuFoV97uDYB/Xs4+QDmCPzOzHH/+cw4+53YUZieYJrPkyeZF293f34GyXvAT6klUToEfI+4CseWON/AHMo3/aaeYx8Pr0zH1zjb6rqxcHfDtf4l4hBSD9Rx/Of8Ig1XvXA4+bij2LO0t+pkK0GF33sM3xAHqfTnmS9PFRU9VexvfHVInIC/EuYTdeu+XUPXPO3Y0GFJ5UHdcmHMCfoBT51HjeYs3x47FvZEofy4DtmJQYffyefqq+faO8/kSMkIu/DIA/fhqXNbwB/D3voH8fSWU3e85BT6EP+djjQ3/yIzzaY99jkYQvnUde4OjxWrGj5+bc45iPAV6nqjYP/Vqr6sbc57ge/970PnPNEVX/kLeb1UWN8O+P49czfg/IzwHMi8k9gL9wfPvjsh4GfBt6jqtexNHm7h7c678vYRjyU92Ke/acrh2vwvfUaTd5qPG9Hvq+e78tV9RqmpOWB7zx4vb8IfLmI/GNYdOuZYM97mBz3/UP3/TdhGbHfDVzHIqLw+D372DWnqr+iqt+IQUn+U+AnxWoi3o48ybiepnwu6laAd4nI4TGfTX3yOD36qOv9AGZU/fPARlV//i2ucXj8I3WviExYJP9PYRmsG8BfPRjPx/lUPfs4+QDwOzBn6ANYpPa3YY7QBwCe4JoPm+snWVefyWf0mZSPAO+Vx5MCfAT4wAP3d6aq31o//3TWzMPk8+md+eAavyUi5wd/O7Qv/hvgl7Gs6jXgu3jEGq964GHvObuo6idU9d9U1XcC/zbwZ8RqXd/qGR7KI3Uaj18vT/KMfgSz3b4Gy6r96sE1/8ID1zxV1T/5BOds8qAueS8GI3yFB2wFEVljcOcmT2JLPIl8nE/V1090rifNCJ1iE/0aWEEjFl0Di0j9YRF5l1jR2x97wnM2+fPAd4rIPykmX1xfYmBQhm+q0c7fgynNR8krGD6xyf+HeYr/oogMwHdjUILHyfcD39uuLyLPi8jXtA/Fira+pf76PwG/W0R+v1jh2e3qJDwofw74d2rkRkTktI7pnMfP60NF9sWJX1T/9Nmav0+SGoX4SeA/w7Dl/+vBx+dY1GUnIr8VM8qavAaUx5z7rwJfIlZcG0Tk67F0519+xPc/SR54Jk3+QxE5ESsW/9eAH/vUIz8jco5hX++KyLuAf/+tDlDVHTaPP4zBUj78WRrbZ0KO+55PWWPnWO3LG5jD9SRUso/dWyLyfhF5vkbF79Y/50d9/xHy6YzrN1I+F3UrmHP67SIyiMjXAV+K6azPhjxOjz5UquNTgP+cByLlYoXj/9FjDn+c7h2xffMakETkq7D6jyY/jhXOf5lYhPl7Hrj2t4hR27dx/gqWGXg/BrW6j+2Lf5nqCD3BNV8BbstBETZvsa6ecfk7mPH2J+vaXYnIb3vgO38Ze0b/Sl2DgxgRwZfWz9/2mvl8emeKFc//3GOO/QjwfwLfV+f3y7EMfHOmzrE6oEsR+UeAQ+fkrwD/qIh8rZjz8e0cBOUe1Bci8nUi0gz6O5j+ybz1MzyUx+m0x62XV4B3ywHRw0PkR7H99K18ciD7h7BM0VfWd+5KjDjn7dDU/wjw74kRo5xh758fO7Abv1qMmGXEYOCHzsqPA/+BiNysa+Lb3sZ1D+Xnsfn+tqrPvgb4rU9y4BM5Qqr69zFF+/PYhP/jwN+qH/85LFvw/wD/N6ZcE0/4IlfVnwC+F3swF5j339iE/jDw1Zhx8AfqZ4+S7wO+Wyy1952qeg/D0P95zPu/wvCdj5P/Eouu/IyIXGBFmF8BUB/g7fo36mb8F4DvwHDafxcrVn3w/v4vrOj4T2Ob41cxPOdbzeuj5D1Y2vFj9Ryflfl7xHd+GIs4/8QD6dk/BPyJOmd/HFvY7f43dXx/q577nz48oaq+gUV5vgMz4v4o8HtV9fXHTQJ86jM5kA9g8/zXgT+lqp+t5q3/MVbceA9Tmv/zEx73A9izfqZhccd9/9A19oPs99/f51PX3sPkvwO+rI7xYffye4BfFJHLOpZvqC//tyOfzrh+I+VzTrdW+QWsJvJ1bL3+vqqzPhvySD36FvKD2P390AN/fw+PuefH6d4KJfr2OoY7mIH90wfH/jWsHuVnsXl/kJHtYdf+AAa9/PDB74LpD57gmr+MGVz/oO6ld/KYdfWsS4WgfjVWv/FhTE99/QPfucCM12/Aou6fwLLGLbjzttbM5+E787FrvMo3Yhnyl4GfwmpzWiD3O7F1doG907oDWG2Qr8OK+d/A9MDhtR7UF/8U8AtVj/80Vtv2wSd4hl3eQqc9br38LPCLwCdE5KG2k6p+HNOH/+wD9/kRLEv0XVgQ4iOYg/p2qMf/e+zZ/O9Y38gdRkSDqv5i/flHMUfuAiOEmOuxf6Leywcx0qWfPPjsiUVVF4wg4Q9itsP7MSf0Lc8lnwyn+/VLjeJ8v6o+mHL/nBYR+e3Av1shLE9zHN8NvKaqf/ZpjuNZkAefiTykeeuzKGJ0m78MvFgjo5/zctz3R/l05VmZ4wd1qzykSeGzKCLyzcC/dTjOGs39CVX9Z57SmH4GMwR/6Wlc/ygPl8+3d6aI/F2MLOOzFZx43JiOttinITVjdBeDI37wIZ9/KxYMfBwS5Emv9QuYXfI/PPZ7v15HSAzv989h0eEXMIzv31bVP/LrOvFRjvI25XNBqYsVNf8XwDVV/dff6vvPqhz3/VE+3+VzwRGqsLSfxdjifvBpj+con1tyfGce5TdCROSrsWyjYJn6r8Bo8VVEXsKg4z+PZd3+CvCnVfVt91cUkd+Fsey9jqFJvh9jTfz44477THTdFSzdeQdLcf8SlqI9ylGOciBiBfD3MZ7+73mLrz/rctz3n4MiIt8l+4aUh//9tac9tqO8PRGRr8SgLK/wyZj/oxzl80I+z96Zn3PyiHfFpYj8jrd5qq/BYIEvY87ON+g+CzNidOIXWFDnL2F9nz4d+S1Yr6V7GOT3972VEwSfBWjcUY5ylKMc5ShHOcpRjnKUozzr8pnICB3lKEc5ylGOcpSjHOUoRznK55Q8jr/+N0y+5Vt/v3qxzJQW+9eL+WhZM6U4XIWvigxkjbg6dHEF5wOCkOp3CopTB/UcSQvbOBOjEVo5dYgHccbgF7zDOUDt+6qgB7TsDrHf6uci4Ci0ZJqKopUNMBe7Rk7KEBzeextDKYgWnPh6jYIo4O0kKxk4OfHssh2f5kzaLZ2C6zIlnDi8q2MApDgaffzF1czmauFkGplGm5ulwCBKqO7u3Zw4kUBjWReBxU4EQJxnG1elqRcFPwiu3kMhMAqcnxrZyTA5cizE0mbKRjvVeZ3CQHaKF1CVeo5CLkKdBsBBUUqunztldEJdDiQV1Ali/fZICGhhqD0fQxgQ74nZnr1iz2J0doEbZ2fcuHGdaRiIS7RxDwEfBiTYd85OBm5few6p6+WDH/sIv/bRV7i8vARg7QN/5r/6C89KP5ajPGX5f3/6v9apGBFNyAugfd8XdbYj/QBAFk8qymuv21r6ex/8EJto68wH22dFFDTgqw4pPpEXZV7sGiqenCIp1T2gmZSU27esXdIXvfMF7t+7zyt37BrbJZMp7KouTXMh54z6qu8IDIPtg1vnKwAudzvmORPrHpasDOJwdhusZOBL3/cu3v1u67G32V3wy7/2YT762pt2zagsEaTeg/MO0r65hQ+elDK52D2MXkAhizJWXeDxTFNAqq5QgVKUUvd+KUoGfNUvTjyaFS22r1ejJ/iROZku2MSZpRRKHcXkAqP3nKyMYXbyns2ysElzPd7xrts3ec9zt7i2Pq/3Adtlw70Lm9vT04mXnn83cbHfP/6Jj3Pv0hPrOV64dYZguhfgbD3hpfDGnXsAfPjVe2ySsks2ppgK22XG1XtaYuRiN7NNmVifd1EIXpC2XpIiHnzV65IK85KJS313qPLzf+NvHvXVUQD42m/4Wp3rRjwNAeccS31f7qpNVOpak+C4fe2k77GYZ3KCBdsvAKfeswNyXOwcWSkK3tf3v5+IOVOS7UtUyAq+vpOLCEtMiKv2mPO4xaHVGl2HQI6Fbd0jbrB/pcBc7aPRC4qwqrF8DeBUGIdq8zmp46v25OhYojLUfem9crkoY9VX26KEUsjVBnBOSMV1u24MZkc55zjMH3jJpNy0nHA6BZZY93ZJOBwNdZXa2ercypBxaSBnG5R3iiDkvL/fpRTee9PsredvXeeDL7/JvU2dlxBRBoqWrmedA6fKONo15igklJxszOvJE4KjtczOUnClUF8VOFUyDsXGFDworiu01WlgEI/WMd9LO+Kc8WGkmqYMwRELLHMtOSsgklkNpnfN/oKr2daHpsxf+rGfeqr66pgROspRjnKUoxzlKEc5ylGO8gUnz0RGSLunDYhFAH310RZNgKLOXNaiIKLkmjJwUr1YLZSWohHrMNeyOrn+PNXwZlaloEj3AzM5C1IzPk5qXLOmTrw3b7179kXJuu8I5ZwjqlrGprrWqgWKds/a4XDB0dNISQhOUNeincKcM0Fr1EQdS972jNDIQMmZ2LJe6tCkLbhAylBKQItQgyJEzexyYaqhlpGAuH1ENWlGKT0ioeIR9bQoijjBieyjDTgQZanfz0v9e400ow4RQWV//lznKmn7TkFUcKV+J1sUuocDFkFWU88IZQqhSM9qiUDJ4GtK6XQ1MS+RVM+3mgJhFVg5i6KcrVYE5ykp9Wyb84HJwTSsAbhxck4IA0lbpGXgNATSaBcN/hhcPcqBKGjLDltuFlf3sRQoqmjLWKKAEJq+cnbsMAhDjbDuysyAsK3RymW3EFPE1ejk4AWCQ6qOHBjIPpNrhnPeZnYpM6d6TTcyDXBas1RXQ0LjxL3Zshi5FFzxDAQoLRrpwcWufxYyOS9U9cWFWzh57VVaSHUKhZunay63ljnZ3bkgK+SavZnEgZiuBMgkis8920NxOHEMIz0bQlLgIGuO6SAp9rvzEEqhdB2rODKrlen1cfAowqZGuUWUwQta6rPSQioQtzUzfKL4oOQru/xWM6iHArFmmc5OTsEVlp3p3fOza4wrz+bSMkA3z28Rl/vE+i4Z/cCcl64DEVivT3jvynSN9xMfff1NXD1fdILqwDCYjr5+uma62nI5LyxVXy1LIVEYaqZ+8XZsrgH37TYiIj3bNpe324v3KJ/PUkJhRUN1KJaqre/4XIhF+751sVBSZnVi0XuRgTlmgmrfp7uklJyZKxTEizANDg0VWZIKLgvVTDB7KxekvsRzzgQR5lQz1IMl0JuOXHJmGoTzULMaqeD8hAj4stRzZgYCqR5TIowjDBXlgSpFpOsKJ4EQlE3dd74oTkFCg/XArN50LaYGUMXVm4iLkgcImmnbK0YIzuHG9i4oZmPUIcxRQQtTve/JF5Jz/d1BTKiUbmfucjZ7q15gFEO2nE6mOy6uZhaF07Oapi+eq5jIRZFq/6g6EhBjRci4AAi+Io9KLmxS7AiGMHiCdx2xIwheBKn3qKmYkT3Uz4sQBZAm/xsAACAASURBVJaaDUxzIVdrfZrsxsWBy5BSQwGpIQJoY4iQlFITRrs9pOipyTPhCDktaG6T6HFI35hSHJqVOqd4KWSVhnoDUZwIhdLhdAhklb3TUQoeIdZUrKjB3ZofJG5ESzHnhQaFc33jlzIDY4ciBIFUzJGxAxwxR4IDqTiP4EfE7R2hQTJJHDUjjTqhiDP8B5BIsCi7usDAcX52rX++izObWdntWm8oT/ADqW46FzzrteNs8kjdmOwKKSu5wnjUOyiOXDdiQQg+0FakxswYAr5uzBJy3YQ1fZwWRhdYV+gdXklp7yA6Ae9cN+CcFkvbmk9o9xkLqWTGoRo7RSjsz1GyUuLeSGyGUajGUELZzAlfnxXiyDnj68NZr1e8ePMWpT2a4nASwEXOfKjPzzOGifMzM+Km9RrvHKUaHms3sFqP7LIpnPbcj3IUE0e1rckCHkF0rJ9ktBRc21M4RCekwk+99zgvpJxZqm4oS2I9jkxdnXjC5DgJdf15UFlx7+ICMH/BBcf92fb1m/fush5HfH3hemDyEOs+XDFQRuW6nAJwsWzJRZl3iYu6uM9PJ9argWpncG+7Y1eE1AyPXHj53v2+b1+8fcbajZxXXXBHPDtNuBY8whyusY4hzgnxwio0+LHDO89KoEU91Fd9UPWqF6GUQqAFVhRKom5T/KiMfmB1YvC+85VH3R7OcrnJbGLuugcx+MxcPYj5KhE1c9ksm9nx8ctLxiGw2m0BuKWJk2ng+edvAHD92nVyzMxbm/vtbrEXf9X7827HLK7D+WLMsIJQYW0v3j7HifLBl63n4ZsxU1BSd5xHBj+wonTo7hgKc85obE6oJ82Fq/quKAXCGDipztRJv+GjHAUG57qTvIjitXRjPlGDwlU/iXjuXl6xi9XOcJ6YlExhbDAzIKaEq+/s9WR6al6qo5MKeHp4M2ehuMyq6poheDKCrzafC5iBUJWqJiW7PVxp9COycgSFWexaLgGYM2M/KTnDXOFYydmJtRpcmzlRckJq8CC5QonK0uxOcYyDoFX/zTHjRfqYUxaKCjHlPdzXO/y4dzIohZxcD6iWrJQcGYIFZS+T4p3ipEFehZIzJxVGrSKoh6kGPCbJ4AOno71bXr64ZJkTvgajUjF7MmfpGORBlDA4xNsxRQRyptRnsWQLTg+uwoOdQzBnuM2DiGNX10vOMDntJRlZCpohtliLN52qKDm1RISVS6R6DtFCyh5vDw0nQipC7iUaT19fPROOUCn73IzHonZ6kIdI5J4xUgclHm4i6ZHDliXIUmwRHmRnvEivATl0eIBau0PfeUqpb2Xq5x5R837BMirBKW1L+OI4cSNoIdUcjhOHamzlNyQnFKm1S4BKIcbFnCFg9J6U91mt7W5mLNoxr2HwrFCWpW1Me9371O4xs0hhFhh076CJ90iLsDqbp+aBl5QRJ4QaeRlXnjEEpDprPgycrEdWg23kOc84BF9f0KluKq33nMioKkPHAmvH57fagaIWMW8xABmUQYPhUDHny6NoNSSdVWP1eS0F8pL6M5zdjMq+piw4hx8GpqpcQnCcrFcMw9idzGWzA+/xrtUOCLjA5aWFhu/NV2zmbXfOTk9POMpRmqiHXB1zKQE049qK1oJo7kEY1UjJELe29mLKgJCLclEdGYfn2sozNlx+XAgSOJ3MwB+nwLwkOLF1eLHbkYvDO1Pfu2VhPa4Y6j6WrKh6RmkZpw3bJbOujtX5NLAkJcfC5ZUZ/IJy+/oJ7tzO6YbCkj3bZMcsKeGkkLTiuiMwKKVaVINzXAu+1yU5sbqgfamlp7h9ZtghphMUWtrJB4c43+tE1allrytmflSI+J6hHUbLfq9rf/Yb185ZhYkRcxidU7i67HUQTadrqx0tSs6Kr4N0pbC52vEKF0y+OTIL73nhOdbXbrSnz+XlPa7uW3ZtKQV1ocfcLpZIUUeoTkkqCWWswTQYQuD29TPu1vrDi+UCp0Ku68OvPOdhIIREalFXV5h8QapOSw6CT8hsv99VcFLwLZp9TGAf5UAKsKRm6BbUKallmwertm6BHY2OwtCNWvGF4IUgQ7fRYpkRVaZxquf35Bh7/U6aC2FwtADqFIT1sCbX7EvwwuhG7l/t7HyLoVKkrt/V6MAppekKVeKcyeLRupd3JeH8Puh6MgWCF+aa7S0O8J4WL81ZEZGW2KAED8H3usyUClkdse2dkihFyK0+SWAlhYjZFO2+Ne0D6OKFqIVc7asgggxD1w3DILCUbgv5iibomBtVchFiDSa5Eri2dhTfsuoFcfQgb0YJQQgDHdUjmF1a6gONSSkl9iy7OCGIEMwPIgTL8uRqqIbgcCLsqkMoClrsvsHsrKVE8M12HpG0sCSY2zyo1Wk3PT6I4D0MNRBdMhRNhBaoO6sK/CnKMdZ9lKMc5ShHOcpRjnKUoxzlC06eiYyQoKTqkWYRHErDP0SKMY3VoJ5kARGkgxgNMhGc37O4FQFJpFbz44SSoDRoHFh9kDR2jgq1a2xFKobdbBnPDKh2tjXFIppD/YP9Y+NsbBrOW0aqZWOKOrQopeVmi1h2o0WOEZJoZ1ZZnXkkd6I6KHCyHvCcAbCdE5r3fqyb7GEqyraytZSkSC5oSz2qA5E9bCMlnKcz2/kQLMvV8s1F2O7mzsY3rkbISq4wjoLgKQ0SSxQhIAw1Uu2lgJQ6txXWgWOlY88IzbtoWb0WTQAI+/orwQLCOdRrOmd44jpPwzhaWte3CJbH4xgrQ8nZ2cStazcI4YQ3G7Ro9wY5JfJSI675BHHKnYu7ALx65w12m6ueKTup+P6jHAVs/5e6/nIJiCqN9RJREN1H+QqUnLlz/z4AV/NMUo8T3yNkq2FCJRNq1ns1WqzQhb16LiXha5bidBpJKfUor2bH5bLbh7WKgDqiNnhDJpdc6/8MCZtSxnnpmfbdLvKm23Lr3KJzN87P0Lxjs+x1RdHUa1828xXTdKvDh8PoKEbrVOelEPzYI5W0CKFrtVKKc4V9fLSqW91jAVRgcJ656p9JIR/AvlYhcLaauH5iY16vRhzCONk93XLXubZe89o92/cXmwVV7RmTqJlC6rDaKYw4P7CNiU1lnitvZm6uTnj+VsM0g5NMODX9Mm8iTgKTbxDmREB6pDpnZVmuWCrEcJ4jPgTOanZvPey4e3HR4YBzUXKJVhNUH3+KwrgaeN/NazYmlNe3V9zf1gi8VzQWYhvi00eaHOUZkjlmytJYV5XV4LqdsZSCo+CrKZjFMY5Dh19p1PoedCzR7IqUhJMw9Yh+LIXUMP9ACQb7ap8H72yP1b0fCPjg94gdwPvDPSNIVqaavomaSKUQGNhV20OrnbGqxscQgtXW1EwHybGk0jdDSpa9ruRprBnNJKl2wzgJLvheMzlvPVkP6hcFg/mr39tLIsRChwOH4ClLYelToUxTIFXjdY6JoBkGy+ROzpOSclnnLjggKjLsa92D98w1I75blKyOsaaExAsuOOa5dL0oFBDdw85yRryxfoLVYjln2SobYkGCMFYdGKOiGtFWn5gM5jbU99tVLoSwL5AvWREvSKLXYoY2X61+KykxK2WqdZHJId71jB/L01dYz4QjFLOyLwlRUCW1jVkiroTuMAiKc0qpBaOaPHg1N6QukKwFEWFqD0KVpGrF/lh9jhwkw5yjki3sC57F+W7MiCpSUqdJNDrp0M/nJYNTvAi+GjeaK+1rq7fx4HLpRWlOPRoctcbaDAOkpxxBKa77DyCFlAMutE0EuhTb7DYxDG5AJaG7bkpgpVL7equcYagKZ1oNBO8Zpga/M+pf7YV3SoKeJs+7xQbUnsUBnTgY7MXwyHXenYIIHumEChFzKJtjm0JBQyHvGpGBx7mJ0vgdwSBDdWdvSiGnzDBWrDAekUKocL3z9TXc6Fmd2nO4du0m6/U5aEbqZCsZ76Svuc32inhRuHPXKG7zNhJ84F03bwPwrhffxVGO0kRU0VY/6AKZzNKCIipkkY65pxj++s0rg11uFkFlYeUH1hU7vpKBrBlX99m4WiMpUqrxHIsyBOlkL8ELwin+vhn4Z9PEtB65s7P9+MbrG+5trzp01wEnq8AwNDixY7nKSCl9DyvC5mrpZCzPZ5hGaICYs5MTvA9cLnYfl7FwnQVf4VolXZEO9J8PShDfqfXVOWIpaA1geVdwXiiqHaKckr3Em5EWcAwu9FoqL7BarQwmiMFBVDHLC9jsFtI8U2qAwznH7bMTdhWCeLns8N6xWlVnbwicD6HXIF1tE5t5i2jpEJltmoksSA3uzNGMg9FbcGRWM5CaUTd6x3ocKslP7UygM1LJW7bz64S0Zqr3+Ny1EzbbKxZaPdDIdl6YVifEbPC5afS84yzwzudv1ue94qOvv8qH1Z7FdlkoLuBqsfrSuLuPchSoEO8Kx1IhL3T7CTIqrusBXwvfG1V/jplYYAwBrU5CycomLcRGYOU93g1Mde87ybiy15GtHUmzSnZlxhfp+9z5Gqxtwe5KZVW5YNglZ/XIUjq0LRdBC8z1mvNmRyyJodJGO/FMzgKjAAOFXByu6lAvinplqcb7qXesJLBtowyK54CiHgvCrorvhC+F3LhVbJzbRFFltW4QZaHkQjPyJie17Usbo8Hl3MHcT0F7axGflWEceu3yEMyGuTvvoXfTFPCDo1Q9naMiqTCGZncGBi89qDIMgTH4DvvfLZFlLrTJ3y2JpAnfivLVWpkk2Ttnmh1DHeQ0KNttgUIvNVC1/4nfJyJEitWOYUFsB3vn2T19N+Tpj4DWd6YVzxsmsWjjIM+4vDcsvBozUKutUe8AZYb9d7BsRWzFyMVqgFrsUSorXEt8ZM3mcBz0rxBHx48GJ6RUSDUiEooyIFRbHHGBVBZSLt1gT5opoRDaC06dOQb1c3Fi2PQWBRFl8L7jwsV7vJMekRBnDkFOjfdfiZqp650wTEBl5qhRjkUFVXCtnwiJrPseO8PkGNzEUAueXWhFh9XQSErK+zqAklvUtt43yhB0T1TgxArnmvdW+/9kjKDADjLl0XC2Z96Rs5CnaiAFm/XYT6EE58itkLJky+613kd+Z86b1lqGPCNl3Z05QRARYi7M9fntYmQKgd28qc/KuL3GycJJL9y6SVjBP/ye32y/336Roxyli7Ocsv1seVipNW0lDGSdkLyrXxXuX93horP4CGPwBOf2jJGSLDJQC1iD7pkXAYZJuXl+k1VlUyjFimzPa/bGO880TUz3rabo1TfusZkT09r23M3zU567fsZYgeF3Ly5YcuZiu+2RQeeVbclsL+p9zJn15LohcYNzzlZw48SyEjdOrxFcZhxtTzkXGAu40DL1whB8LwzORQiTZ259hNwIKJoS0l5DzoImTb/kecdmWRhrZswPnuIip9p6NFlgpmPP54UYF2I1HErMvJGLRUmB58/PuXn9nOdvWL3P2bVzztYDsQLiP/aJl/nQK9GYNqu6eu7sJierk37OzeUdLu/d4bLVNxQzKm5eMydlCFaveTZZxufs9BoimbgzXaPXniPNMxf1+BMPL107407NpF0tO+asxO2WsZLePHe24steep7r1w0NMPiBu/fvEbzVd52vT7jazd3QlPZiO8pRgCmEztiV1dRXW9/iPQlHWVrmZCHHvM8waECzMobQ+wn6VMgKS9kXvzsRSv09lWgB11rHXWq5UAv0qAj358iu2hkxZ8Ige+PbwXoIvfZYy0LJyulq3ZEhaGHJkck14oBsfcfmakeGBdHQe0WKL4yDWH8zbI8qSi1zwhUl5d7pB+88gX1mPwGDeIbgu21aEMLgmWv/rqwW+G21Tt478qJ7u9JbEKp5TrucWYd9UD7naEH7xb5/62xkGDybK7ve1UZx3jOGlr1Z2Gwz107WxDpO9TXIXp+9d8Fqj7Rl46xuqBEZxGyf5fp+8iJMYWSuAatTBDcILWqcojJjfewANEcEx+A80oxRMmjp5D0WgNfOjJnVnOlG0KBxH/R+WnKsETrKUY5ylKMc5ShHOcpRjvIFJ89ERsi81QolaPDD6i16EdTvU7si5ZPqe7QURBy+QEOJqRirW4NwWe+hPRguVGaNXp9judt9V3Scccz3aAIEcQzSWFIMDtF40tUp4izz0ZgyiljfIlczGSlGowDvOH2DzlWkG76mCxu7Ry4GF+ywMwRNaU9NPQbrQ1T2NNKiNjitcBWfM3703Ntd1bm0Pj+NPc95j/Paqchb/5NPwpjL/p6WYqxsjZ3bA+Jcr49QZ/0IejRCbW698yyNjtEJXkOn8xSy4eP9Pl3sFWsaYmclC2iNLgwIbj0xVcpOTRGPMNaJHIMHFZbatXi7vc/psCIVRRp8JQSmweOCRdBdKiQtrGt46Nr5GdfPTrl9+90AnJydcpSjfLK0VV4QjJHI/uoo6pCaCY6p8Mblhm3vp2ORVKfSMzSaCt47kttnPUOKhMmOeeH2O7h+7aR35hZx5FzYLJYRiLuIG1ecnTYK+ZGLOXGt0qm9cOsaL9y+xeXGshKrJXDzZOR0ZdS47S5CWphbTVAR0jbto5tyheaB525dt3MMhtttsA2FysxZM+LFoVgvD2j9KgSpmDNniXycb8C0Fijd620kIJ5e47jEhBs8pXLcDk7w4npPjOtnp1x3Zz2q65z12NmGxuBWIBfmOg/rVSCcjqzPbX8v6Ra7nNjEhbFmmW6dnXDr9nllwYJxXHPr1sjN643pbgAnhKp/cp4Zh8B6ZbpFFOZlRlLT+5mdM/gcwMopg56hYs/y/tWWXYyEQSg1CjsOE2Fc9/fRG5f3+MTF3V47pQbS6b2r5BjePMqBuGEAbWy2aq/aZldkSBRyzeYsS0aDMlX95Z0nlmKomgZhqnXOJ4OtcT/YHmxIEtWCLw5X9VdSSHMm1ePWfiLmpWdCnFhWeA/J9yw+oVU3+WHkLAj5oPejC4YeilVXeCeMK+kImSV6djFTaq2fYOUOgYq4KQUl4KvWuUyFooFVs40oRCk9m7NEQBMiqUO+rJdk6VXSVt5w0D7Eq2X9W8JDPKXs7cYYMyUL0gvgldHT65vnYsyarS+YjIFJxEoxgHvRWp0sxcpFAKbBnulVpRE/ccqcFIn2eSwF1T2jcnCCCEyVoRSUUuCklhqoqtWYtmcrAZReU6R4xIHkPQuz1s96OWdWfKgtbbC1IM71vmhTK/R6ivJMOEJguHv714pqG0d9RoloL52JwKi6B2bWF6ogVHgosxRcCZ1QQUXx6jvtYKWg74scLbXfz762puPjqA6St40EMBRHIXdq6ETBZeOxb/zswTfnqC7y4qDsYWclZnIpTNUYctkKGXuNEYYtLQ2XiwPZ98jwAqtpomm0WAop5Wpc7J2MnKEy3qJazFGoxXg5Kg4luH3PE6PwPnguQoe+aVFzosLhZ74TF5TqYLYNUXJB1Gq3W83hIJ6ipRMuUB3ZBkFNta6q1RQVvNF0N6yuZE4mx9mZYfR3syfmglRjZxDHnPYED9Y89g7iA7HWDpQM4h0nlZ9fVoHX7t7llddetXnJmZfeeZvnrj9n933SlMRRjgIWKqkvYDIOusFvWO2Cq/DQbUy8eXnFrjY1TipkhVWR/uKPKoQCg+yhIsVl3nFuEK5b168xngihkZDgKSK9X9iGK642VwyV1OM3veM53HCP8/r72enEySogUo3zMrMehFSsOaKNSzkbrxn1N3DvasMbF5mLWo9z53LHZrcwNziMFm6enxscmNpE0dErAbIqcSm9oeo4FCiO0HqYlVJhq+xrMcHIEqouKGLQ3kZAo0XRTDdelIDuMutVJYfRNVMIOL+H0o2TMtSGqxf37hFzYbsYLE3uZZZly6pCYoMI733+BiEExlWjLh+Z3IrtpZFdBO85u3ajv4/aPUutPRCsl1J3jEtkSdphRcNgMNz1mUHnNvfuE+PCeQ3s3DgNzCi4oUO9X3v9Lhd37/EPvfg8YL1AtlcZXyncBxV8XqgIHVonuqMcBazGTFJrMlzR+c32LvZubvqr70ff9EI0B1wCpRvDGG1zg8p5R3Culys4VYqXTnOvOZF9wXdHpzCOQ69HDMlZbzRfCbJKIe8cUh0ADYVcBgtmt2BREDQWNO/rwLczfYzilYL0Nho4td42ucHWBI37emj8SEB6Py8tiUXAVcNDo7UJCevQdVpKarVIVb9AoaTCbtvsKdCwb5kyOMHjUVdLLKZAKVDj60iBMFidNcDkhZATu60FbmKM7CJE31o3FFIuRApDa7PiAl4K53WMG43kAkOdpzmZLdV6jlmdlh7AFh2xJDZ1vVxfDdbXc27P3pvTPDSIoeC9IKL7oDxiPZwaHG8oqEjjoWCaAjFptwl9I7h4ivJMOEKi0psqWX29I9eR5SJ4zQcvS7F5PjDWe0ef6tj42nmmGdcDA0lyn3hRj+bca1m0kgq09EuqZAuN8CjgmPCda32mOguusacNwIBKJNW/eRxktzcMvFAWZTvbS3jygdU47JWFs+xW0tb81IP6HuWjFGs86vYEBeWgg3gQgSAogRJbX59SHaQ9HlTEdTa0uFiRb2lZqup4tRitd9bQsBkmToSBwKpNrHfg6Aowl2yNcOs85qIMagwybXPb00rsPdmGz2yGpFLwjHWuncJlTN1nDR6SwGaukZ2a2YuVKe8T9+9wPq45Gc2QSREut1eEccS1Yr1hZLVeM4xmjKxOT7mKM0szAi8vcB9Tbo4ftfUzPgM79SjPjDhcrzsx+LvQSo8LIJrw7YWahTnGfeFwjogbmYFc6wHXg0dl3/PCOeV0NXL7tpF1hPWIV3o0VPMCPjBNpiQlTezmDZLtfLdvXefsZOrEKifTwDiOHR8/OeuhU1BC3SdBhHEI/b7u3d/xa6++ykffvAPAZme9PjTbXhi85/U793j59TcBWJKxGLXsTc5QdF9r4HMhFWGszlwpBS+BLHnfzV2xGBR74yYn7XMbBFJe8JV1aXGwLDPcsfu+uLxgXI09MIPCi8/dZL222polbLncXhD8qs6j52Mvv0YsZmi8cOs5Xnj+FufXrrGezuoYFu69/jpvvPkKALeef45r56fdCLSm2fteIM5ZjVOukWjNC5Lzvvn2aKHs0DLa6zWoQ6o+u5VO2eYd2QmXW8sSvb67Ykml9z966fZ1zk9WaG3qusmx1pO25pBPH3N/lGdH9BDdUtEvnY1Wag+++n72GhARfGt4rlYIbwX2LdPqiXnHrpgtE2JgNYbOootYfbJ0FjGHL5nsGpmCEAKdZSwmh1fpbGyhvtNbY1KyIqFQaIFNczJaiLj9QYo1Fgar4y6T7yRyqsqSCq0jzmo8RbP22j/F7K+59560G3HSkEmK4Mm59L0szpFVmSurQ46RlBxDdSIVa/xaYyQENzCu9s5V0MCy7IPlmguFQIvo31yvyaq9TvPEO8qopPoeiIOSUibFFh43MgzNQqlFYCMF5x1D2SMUipRuC6eU8cFRWipNxLiAWwPenHG6RyotMSI+kGLTdxDViLZc7/UoNfBfz1GU4pShNfx25kD1vENv3vT05JhEP8pRjnKUoxzlKEc5ylGO8gUnz0RGSFV7ijOrWnCisRmJ0Qu2NJtzDnF7GFzJYscfnE/KnlUMLAch8Enfyc64zds1PIesckMNCdQMETUz4hvLk8HoJLXpSwbncuAba64zCsgWJCmq+CEwVMajIB5BetdzFQFHr98BIR/cV3Zi3dgb5MKp1SK4xspUcM5zbTWyCY2vPZJy6RSQS84UN/ToZVHI6SBTFgzU1lOWWKf31s4kxoW4m1kNjcbXY3Hlmq2rpT65B2mEUtn3OkUuEaUwNjypiGW5pFGRG6a2UcAWlBJjx72LD8zF9SzX2jvw9KjMnDKsCuF67dESEvM2sdnsOK1MTqeDJ0xrprFGvXImSOiR46uLDXc39/m1114G4OTGGUc5ShdNyEHfq0OUrc8JKcl6WgDDGHnppZfgTavT+0i5w0BhrNTyYCw+YVBWNZp5ul5x42RgbHVzMbGZLxlqDVtcFnwQTk7O7ftnp0jQvifSElnGQK57wovgSmSscIZhOKt1Ahlf9ZGEbMD7GiF9xwu3uHHzGl+ysXG/fveCj965wwvXjTXu/PSEj736MbZL019GwRsbVC5GwPWMtyCEYIh6sDqoTMbjO3tQyM5aH9S97sRb9/SasY4sDH7oVK5lUTzCVcXc77Qw6NJZMedUuNy9yhjesHkpC0UCAcuknOnArZvnjP4WAM/fus44ODZ37nI/vw7AkiOb7Y7TypZ3Mp6xxNT1cMCjUpBWAxkzqaQeqC7sGZdsfQg5OJbKVFdE8KvAaVW6p9vE6K4Yp3NitHGeDtYk7n6y3987BM5Ob7IajV5bLy4oWrisrJgaD990R/lCF6WQ6vu29aRpYC5X8TSlMRmrNxROrRHxA2gs5Bw7rAyBwY8dCrXEQsmpH6NBGNy+X1cWoeCsBySGyiuzUtrv6g1q3JKm3huFdkPsKKTFKO2HljWfHDKo9f4BNGakuJ65YMxISjRCsoJBbpt9tdkt5GxAfgBSAlzXPcEJOgSo8L0s4Iowq3C9n7NAUZY6p5N4wrSH/DmxPo6l2q6RwqCeod7o4B3q6WNIY0GLsPQePjPLUnpPM1VrSdBoqrNX1k6IXjrKh1KIWohdP1n23neK6oK6tEf5FGHth57JLxTW3hHS/r3gi9VighGbLovVVAN45xgGZY6FuZncudiK6za8AckbXXZWj/eusxmXZyAd80w4QriDJnpqeMIONRCsuWkVEUsDNmIEqzGhIfPrOSCR+6IPWP1N7JTKimff7NRauGpPUQap6eO+EdWchm3rgeEYw4CvfRtyVhLKIJ58kLB1fg+N8zmwaNovSIFMoVQsZhhW1vhV96neRuYARq/tnexrp7I2wvF2uopbTz1FuRpXSAmEuuB2szlm/ayV1rL9LgiDdz1N6J1jCgGttQsrP6LB73kMMJxnh/0UwTtHabhaLZaSd/T6rMCEt8snZAAAIABJREFUc6VTLfoE0ZUOf8kFVmjn89/tDFscppZWHdBUOszNUQv36k3MqbBdMqdVmawqNbum3Bt85RLJObGrCiyQCEPgbGWJ9M1qYo709HCej1CTo+zF5bkbEiIWKGmYe1cKB72Y0WHgnS+9k7Nzg1/d/5UrdlERUcaGd8/FGhtW6MCN8zU3z05p1vR2e8m83XDnjvW5CoPn9Nq1DkktKRGCx9d6w/U0UVRY6rqNcUtcYi+IDsExrU5YcjIoKzAyELV0Y0byTBjg1i0jEjg7XXHj+gkntV5OknL9bOTjd5s+EpaSOg48EkGU00pIcr4acWEP59UyIgjOKb5aTPOihCwHxCmJokJp1PnqDZbYyFmkkHPC9fqrwsqvmBqpRFAoC7vqGCw5Q8kd1na3JF564TrvfdFqAderFfevNrx25x5zpZOd1gMn6xPOTk/qE01sLzZcNL0dAtN66gXSIhYJyr1WYcJJ6G0PYsxsl9wdIS2C8wUXGtzGGhSOwPPV+dqlO2yuZkZvY4gpcXI6dSiRFnDqDoJFT7/4+CjPjmwuUw+GuqRGXdyIpMSop1tQZjUCJVPLafHRyGBKoPdRHLzZBb4Z36OSdP8+LQVSLLgK0bTeP47Uapeds33YIGLBag5bIMf5gF9JL3bL2fp1Td7TLIXAwMprh7PPmtFFaQMPzpOyMNQo7molDBmWnQULFqxfT6uNAUdxdAj/4I3Maqi6hCGz3UWGg1pzQZm8sGoOn4dtyr20IISBpJnYShhSMhKv5kh52CXpPccy1oz1vAaa/ajcv5u4rMRPJSujlN4PDm/XFPY6spQKIaxfybNHSibVd4mIMPg9vXaMkU3ZcX66qvNidVZ+OHBi1Po9AkaUoA6p8yYOMoK6si9FGTzeD59Uxu9UidoGlYhJOszR+6dvXz0TjpBxuteXnXjDQkv/EBB6iYkzJ6lliFSKYazlELevJKUzy+EVymEURGwxtywUcR/SBbJUl6q06hUHOXK1bb1BHCdrOCkN82peuqraJrdh4oqjtF4h1U3LDb4uhueU/tIvxBwZXWOmU1DtGFVX1PpDyH5a9IBFxUCy1sSsFeaGEXBjnxdxkRhzJ6YoxVO8diznIJ7Ru309jhOmIKRSm5cOig5YxNMGWZ2ihh226EZvWiy1pkkKc20MNDhPCL6fQ9voWi2BFosE10HktLAO9AJoY2VRXMPhVie6BxUENrvI3YtW3OzwhMrAZ9/axsy0u2RdayyKm9gukTzvNztAqYp5V+u6jnIUsOL0tsZjfa+1miAjSVC0Kv3N1SWv7e4QVkZ88JteepFPvG6GdmhsZhlOVDk9sczjrds3ODsfeh+zvETGEBjrOhQvrFerXgujaTbyBNfYejJLyr27OMHhZUByYzob2cSF1954jfs143Oyuo4EeOfz1jPr9PQMt9uQ2zHO8cJzt/Z9NWLiXS/cYpftJX1vq6Cl125GTQzjxHMn5kjdPDvFD45d7Z8jzvqmjcNEypbpuH+x483dzI1aP3M6rrh3teXNq8t6TkfJ2jd7Kg4JwRjsMCbPwUnvSD8FT/COUrNem+3GCGXaC3h0rE/XhEqWoCJM08D5+Zqz1u8NYfS+1Y6TlsTVZuZObWabVZmmqQe8FEHKvhbhZHXK+elpJ6FYYmJJibk2eaUIwTvmOs+Xu2RNohHWdVzXprX1qqtzfbVbSDn3xrGhBEqaO6LB95flUY6CBUDqkoi5oEmp8Q7cEFizb1ivUogl9kizG+D0xJzuPFd7yZkTMdV9dB9YLlwnaRpGh2gg14bQczJyJG2sTTKyGjxS9+kgasGMyipXpJCjkDoTp6K1LjvUIv8tCecEVw2qlfPsfOy1wlIcqQitmamLNdld98boFFXpTafRgneyt21QJLte8y3eavD0AG3kvBA6XQ44lznNhdh6PYoS04xWPZ0zzI59M9OYEe+6qesx/Tae1Yela+Ky6zpVFWLJhObVIqgKJYEbGhmGw4vvRBPDaaDE1OuKRAXNrusjnDAOnouabTbmYGHVmN+SkRy46v0VsXG0us4shmigKOtqo+Edl3PqQf5x5TnxAamECzstjDikkQX1VNLTk2fDESqWoAWzQbPujWmxKjb6TlZBO2cTttClVsq1gvvKYNGSK15ssZVeMFgQ3RfCOYynOh0sOC0F3+AvCrE4VpWBJKGIZnLLOHkhJjOA9kwq9jJrjaucNkdsXxic8T0im2PGjwNLVRbeBYN4tEGJwfvavHhRy6Q1h6GIwQuVft+USMGxOm/saA6/yaRdzXSJ4kS6YaBOjCq8bgJxQqb0TsdOFJGAp9HRKqLaU78qhZKEfQJP0VBAC7mxtTg1ZrrmLCFopkdRssLilKkaN+58AnVo09xFKyxwD1t0yL6hWC5cbGZisgg8ORNOVgxuINXSydVa2EQ4LwYtCkW52lx04+b+ZoNDWWoB86aythzlKADJeTq2QAvhQCM5KWSB1GkST4h3rtiUuwC887l3M4SJj7/xej+HijIhTJUF7uxkzWq1RmjEKULyylgpl4sXvB968XzxgXm35XJjDoNzwrg63Y/JBVLMbCqN/ulaGP3I2eo6r9+1v7365qts4mLGA/BFL76LME5QCRg0JUR8hwRezZeMYeSLXzKK+VIjjY11KWfbw62wuJTMvJsJ61aEXeFykjg7Nwfw/PwW70IYml52kRfKDTb1Ja0R5lzIraFhUVbD2Nmmyk64SjvGxojkHc4503FAKSe1QNp07I1r51y/cc1oJIH79694885dfu3ll8m1mnxedoxh4MXnjbjidLVms8u8cWnniDlyPlnTSoCYMtmlDgn0EjlbpX3x8ZyYl8Jcs1Q57aAMvFmf3XZOnKxHpnHqxszJyhiY/MqCZOtpYLMsXGyMTOFiWdim2HVsg7kc5ShgMNRUC9KDg8VDs1lVCikpOTWIvRkQvu6Zs+mUs5MVMS+U6qynlIlLZtNUIFCYibuGoPCU4nvkWTQjCaSiYaYpGCtsMwJwLL50BreUDI7XnJglKVkrtLb6UmlOzBWa3w5yLjD1QHJiDMpS98TgjOKmN/1Uy/i4um/NVssd0pwxREsje0GN2dYQM80WzeSUmCsRweQBL7hKg6aqrFan+6Dvklk2ewih9/ZAVlVXBHUsWlhXOunBCcM4dtis91YiUpFy7ERYe4M9thYCWQs+aGc0XnbJiHCa4+Jq+4Zq1BVxbEruOQNXhKLK3LNzjUSj2aEKTojN7oyKozBr7nbhGARx2qFvZrN7Y44AQvJEgbERUZSnr6+OoaOjHOUoRznKUY5ylKMc5ShfcPJMZIQK+4L9ItZHSLoDKkiRfcuf6use9p4QBNXS4VOigv8k+BxGZlCvp4Y6s0JWLL03eNczGSUrwbEvckuwy6mPMXhHcY5coXMOZXO1gGTWtYlhCM6gCvWc4pz91+gZqWiw5gwXy+4MNZqQcj4ocay9fIoRGtg1QYsSe2NSh9Ymry3ZKs545VvUZAoBv/bEivdMOaJ4o94GXHAMYTAKWKweK1I6zeUym/fv6kRpbSBWGhdnsaay7XwJz6SFWKRDhXCwLKk3DXNitN65Rn/EWxy7LczgxXDANZObVS3l2jJvar2l2nrwxZq+tnm9v92xLoU5rCjJCqB3ac2N9UsdVrhJkavNzL2dwXa2u8TpMPa+UZuK0T3KUcCIS1o2J5QWLetpWHCe3Cr4Rse1a7f3Bf55y//P3psuSZIk950/VTNz94jIzKrqazgYggOCSy53hftl3/8R9g12hSAwwMz0UVdmxuFuh+4HOzzBB2C3CMJkuqezKuPycDdX1f/1h3/3He8eD3z5Uumb62qsMbHGis6c18jDw6mG1wG6TDhfSG0UmFOkFCXnfr7C68uVr5eG3kwH3jeND0CQzMPpxHJs3HMczjtEPL9viM9r/InXy8Y//aXaYZ8Oj0yhjOC84Byz+pHX5aPx6fNfByL9/rSgwZNeK0rx5bry4ekdvn2Gf/rpCx8/PXNpYabZpOZqOGU61L1gDhPLVLVE9X173j0eB4XVPPhl3jPJnMeJEdqUdzslPuiJaW5TYRN8KbtmpoB4IbQDo+qIaeXHH2t+2P/4l1/4/Lzy5bIRm7X5lgUl8Xz72I7LxJZs6CUsG+VgfPe+osvv3p2YJnhqlEA3eVxJ/Pxz/a4/ff6FS2YIrIM4nEB7Od69f89hXvj4+kwDrnjwRzb3MvY4rBrhdEbClqn0P6vnQ+Bu939f+3LisIYIBA8Sree646h2xp2GVsxAAv2Ol0VIW+Z23YaIvxRhhpp3RUUNirmR9ZdTjdAoqRsgKU4YLA8vRrzFkcejoji312f14YK2vWWSZhSFsjVIyBfI5CEDOMwTZnDrOWdTYPaOY6sbJnVccx5xJHnoxTv1SPCimDT2jBreFbRVIrecKvXfbMgZchHc5Hho70Etk52jbM3cpRTE8giGNanI1kjbKVUjndrfb1PhsMig711yIVraDWaQShvs9VcpXJMQXBiB8oaRSx721mwtrKSh5OJrXdjRGjGr+tQRgWJMXkag9M1g3TZ6Uq0rNGlKR7yVXAQ1N2z7U3YcfUAf3ujhy0ZnQ3mnLSen/rXbRee/2vpNNEJZhJ36BrxxDEGoeG4/GXa0DahNSDXF95h1UW3PqdkbHS9vHmtUjLA3Wx40l0G3ErMGjbb3V4zz83lkYITZs8XMPLeCXyeWeW4QaPtSRaqrSteBNS1Bp0hghqjgvI6fTfOgykmuznL9ZMlUHmZuWhvNiriycz0lIOaqjqi9hmOq0Y8j7DETvA2zA2ceyzLEyt4riI0LbUbZ7I2eJ9WLoHOBDfufGsxKQ+kpx5pLzb8ohdfGiV+3emxCM9cvWul8qW+qlcg7WkAvghMZCfZQIfU90FDbqdMubCccp0CRnvGkbBFCWXltELbXCbVCbo5XN4vcbiuxdIeYapzRC891vXJf9zVWMbRdd84iaoX9sjaivQ219MxHa+c1kIwcIw+H45usmsLL6ysvrz8DcFnPXOM7QmtC/LwgrlBcvYZS3MDS0IzELdX9qjcIvpq0WPt7mQPL8TiEw0huxXPidKgi2e/fPfGyXXh3qCGsL19f+JdPP/Lhqb7H//i7PzBNaaTJnw4nrpeVP32sOUNPjw+IKV9eK8Xr9Rr5299tPLaBxz/86S/89ePtzV5UCxsRuOVqAhHUMftAaO55QTNPh8DsO+W5XveHln00LxPfvzvx7bt39btwjuB83TcByLjJdSEjtiW8+hHm/Pp6IbiJzx/re/56rsf33WHm2oq2KRvqp5Hufv7yTIwFbfeCyQXMItoGOY8PE9+9f8+xhdmWkvn0yzN/+rk2mD9/feW8pZGR8jQvPC7zaKTeP33gfD3zfD5zbsGMH6YDh7A3N9fLle2a2ZoGI28r4jyuhXlvw3rmvu4LTPWNE2zVtsQ391fzNoadyoYXHaZNUgqX240rO83MFanGHO2aKFZIwjCCCq3YGm60rtcxjQ66RVJkD0l3zc2u1Q0Jw5EHPW+aQtXzFMZAVUOt70KrPpZZySbEdk9PWybeEqHpDa8psqaqqgaYQq1V+s+lNAlA109barLlpnPxNV8npz0kep4mvBNurbZREzYTYguhjjHy7jQNCvNlq7T+bnIiVggKsR2IlGCzMtz4Pr5+Jec4huElFbLKXitZpbIl0nhPwQlFBekDrKOSb4nUzF+kOFxwrO015g4CtNe4RiPGjXOrnzR0A5j23XRNdttiglZJRTBX84MAdRFMiV1nKYBzSKMw51igKGVILvjV12+iEQq4cXPKVDTIxglZTQB2Nqkg4gbv28yqjoWtjgypk8KUq3NcfUzlVg4TNrOe6lR/xFjjaMRxpZC1haICpWwsh4VbE3tJNqbDPBqKSQUflJwZJ+BljWgybOpPWnVLQ/hW6nu3IWy1qqZ7YzkokpvxN3TMox+XLW2Vs+r7Z5YW9CgU1+0Wq3tRyf2DKyp+IDaSN6LYCOLLZEqWqj+iJVDj8K0JTRgxp+FcF4JriNyOvLk3J7WYcStw9J6l80ALhMkNhz6xmhY9joP5+rna8wzwp5tMlGqUMOSCokyWWYcwSkhWRuN0CB4nVTT90jaodPvC43LgcmuFpQgimQ8t7f1ZDEcZuqOXdC8s7mtfLm+4bszSUkBLTxsHNmMUGqlNBHPu+1tme46ocxy6/fXjwul44P2H+nNOKymfhwtcLlsV6XarzBCQkpEmFJ4WCCGMvUCc4gVCc2zT4BDHcFt7uW38+NcfibdCbJrE03zkv3z7R64tJPF//PUvfL1dcG1g8Wf5mW/SE9PXimwsxwMfvvmGf24//39/faakyDX1oqDgf5n4NNVr58eXyGu2mrxKRWNwBZFCvw2lDBYTW/ud4Cva0QEdrzC5iXNDaPW8sa0FawXY+8cjohBTM2Qww0/THjmwRVJJ4zPftshWVj7fuhlKwU2OD+/ecVyaO544pjBxa0Y5r+dXzpeVtb3HXAQko23PDbPiw0Rqk+vzeeOff/zIl68V7VuTgHN8aBPabx8f8MFzbTrETOIwHfHm6UXYLUY8fmhUv6yJczJyOzAPj4+ct8twYeoC8vu6LwDMRqTFzWqjMnW0RVutJLvbGlZG0/P8sqITMNUaB2CplBzyiDypqFPQff+hmzsBMtX6K992RMnkDapKRXWlXROzGJ4whkuqMuJVfKsT/BQIpVS3GuAaEzg3aplJ4BB0vMbmahirla6NyXjRUetsphQVvOtGUIoX/ybQvjZ/poyBuVHjOs6tLlRTCm7sBVNQYtkR69kU1UDw7V6RlYygDfHWXEib8fW5NXNslVnUB/SioDIQc8tVr0UuQ7ekTgmyNxk+GKl4rDuI5kwpEdcQpORrLZW6S6A6EE9KfQIv6CxoByIyLbal/b6XOoR7UzcagmiAUu8FuYATPwbNCUeg4OVN7fsrr7tG6L7u677u677u677u677u677+za3fBCLkkGGXbFLtna3s3WUN5ujOZlT6lnWrbIVmnT2QCQooSIMRFCFma9a2FXSRN1CtN2M1Q7tdtrUcoOEHXykXrk8stKJH3UYxlki2GjDaEZ2vzxdKNN69qxSJquGRMZUVaXkY/XNIhSClfSUiWi23R9AVux04gAd1O18Vhbhd8d4N2kYWh2Udmp9KWZOR5eG12lqO8NlGUXTtuGUTnBRK44uGqSC5DFciUatUz/ZzksLS4OH6npszXzEObVptgPldtyQiFGxYelspiO6TGpOCmRGG7kgQ7we8XKRquvoMdM2Z65oGDzc4iBZJq46wW7Tw05fPbM229+H0yMP0gDQ9Q8lGShtbg5OX210jdF/78iXj2KeZBRtkpAtCqQSU9ieJImlk+FgqJANJRrFKCcMSp4cHHk6Vhna7gHfLSCZe87VSyhrlK4SF9fyVWzsvTY1lOnJsjmwp3gjTPLR8IkLJ0DKK+fT5lf/+4xfylsd1WUpmmgJfXyoy8XVNHOcHHqeqdcmW+emnL/z8XN3vvIfvv/kd//Vv/1h/ln/k56+RS6N53JLy5bpir80a+3VlezNJnLRu6WKFEnu+UUWuOpLvXKg5PX7AweCM1CaNQT3nbeOnT5We51Rwp7nay9H2Gt01kyogLgwqxlM48OOPH4fd7RwOPDwe+d3TA/OponGTd3gn5FIRopTfc7lsfG0Iz+V6Y56U9+8qmvfth/fknFmbJewvP3/i55dn3r2r3+3vlhO5JJZ2LzkuE7e48amhWDFtgEPVhoPV59uFhPHNw4f63dxWzlviqbnI/f77DyzuW/5yqfS7L6+/vh3tff12lpFJW9d0VGr513bNBTUOTobWuEC11u5UXwEzwaU9HDljjerfKF4Ks9ulCUVqXEhoiLYrGcFhrY6IEgkYLr+h2BuUhu5MTqqrbunMFGErNUrES3e3q5li2vIFrWRSrs69UJGN4vYgUJ/q/ll8s+iOVW9srtcyDkcZrr+EgGqh5D2rC62Mm9hpYjlDMY4t9ycXiLmiHwDTrBSDW7P0NoGADT3g1qy4j02zvcX67qcW9J43hxWP6whSEcAGq4jmHIzonkpqlauQU6dN18o4dyfgUsDciFTpSGF7yywK54sxH/bzZc17fS5U9K/f3QrdkltYm9U4lqqaxXr8TKEUG86FZpmooX1fkOWeIwRUu+sRZpqFRNlTaYs0q9U3Ah8zeunrUUQEx+47XzUeNgoHybU0GQS7Iqgz4rjYW2Bq+3ZDt3y1LuarTcFj45sWywQTfIMXz2vm9fnMNM8c670Jp4pJHnxPaVqdLnxzLX9HBxVOWtI642fQ8fuYUMQGTDpNjiQ2IMtUHGaObPtjitXQ2GF+QN0w0N4ITajbm8rLeUWdI8/9PVTjgtKpdK5xg1OnDJYaINtu2LO6ej0OnFEJuVBE0Aaru5J5va1Ea6np0xFxb8O1qoi655dIUpyXkdPhpNp1d/2O9+0INO5wKQVFRthbdIWTC2xrGbkH8zzjFFzbwMI8I87hpH7w4CfUjGujM9k9l+O+3iyxPOxJi0E2z7VdA5USZ8MZdvEzUaqNM0BOVeieUmJrN/709SuWEqf3tek4LCdeXz6yNvv2x8cHUoycHmsWUc6J23ojXtpNfZ4RbuMaCt5jKaKtEAn+yPVyGyGhn74+cznfSCmTmiX3h2khm7A2XVFYHJPzXJsN/W2DNaZhG72Z8vXyJ/6v//T3APwf//HvePz5Iw+fqp7ury9fuWZju3VBtUPSLlKOopAykzimqRcjBS0wtetyDr4GQPcIAqd4c0jPECut6GrP6cxIOSOt4PLTjOUN6yLtw4FlPu6BrckofBzp9GJCIBNt5dC5JeYx3KADu1KYvHB6aHtHMLw6np7m9h5qM/PaAlO/nl95PL7j+29rE5PiymsSlkaH+f6bD6QSmZoualsTz9dXovPkJgtaV8f5dmMK9dg+xxtrMawVVH/vjO++eWQ6ddOa2qze130BVafb/tuLwzkl0G3uIy/FYf1+q9Jk2e1eGYRSHFmMEhu1LRnLMYwsmZKhaCHHfXitkkGbeYspOUZ6RI9gMO0D2lKqjXMvyF5TrsPaVneEWZgRvMkwuHLOuKXMlLrQKCNFxr6bcqKk3QTAyYR6N4YLSqkZPF1P7Sv7vjP4t5xYiozGqLiWO2Q2xl5T8TivY5BciiCpHu96HAo+KCl1DZDgJoY+h1JHPlvq1DfhOAmh7W+rU3JZsdx9yAXJQhpU4Zo4ZmZs7X2fL5FDkDfhypBjohdlRVrt3L7vLmvv8tGYE4WNmNp+NhmLOtYudrfaHPXG2SN4V2UEpZk+lFSHc4epa7KFLTHs0UUEYx0RArP/9eur30QjlLfElnrAE1VM30W1KpUb2fN2MKai5N4Wa0UNasJwvXMUK+RUhhtFbrFZpTuniGDJ9hC8pknquRvSQlu7EYEizN6PQjpmJRLZGrf8FhOX1wsxFlzzsT+GmeLL6AlUFESG5qeQEdG9OcOwMtq9ioxJGZzXyku1vTHK1SSgz/6yFSRobTrGQLD6ue/PWp9noU43r2IIseYo0Zuv/k/9P3uDnFUkTYfjjCUhOxlIVbaMlD23I5gSxbeLsaFnYhU9sz693lj8ROgOWcVh2bj2398SMzoQIKc1ryTGhtKUOvXpFxkIiwsjrE2dgHhOs+K6M13w+OCZ2nMep1CnPG0Dm+eFa05vchPuGqH72lctFfp+5Fht56KndrWJ1Ebf6czDcUFbk10ybGtmjZHLVn/ndrvy8eWZ1xaY+uHdB+KW+fJcESP1wrcffhg6yrheAGF5qo3TVqwGFvbpnhmWC/OxodGasQy3c0UxJCeOoZoIHI8d6YjkCN+9qwX78XIma+Gnlq2VEpyCHynpKSZ+jJHHv1THtf/7f//P/Le/e+L/nf65/r3c+OXzDWtDF3NaB0utocg5oq6KlXd5X+XAO9eNCOoUeuQAKYgmtOmW1NXmSFrjFEWZDXze96vlcGJuBhBhdqgLaJtUbmllOQR+aKj967mGH+bMyBADRymZy7keh8t1JaY89t3TYeZ48FxaU7rqxjQvvLYQ2JyFwyGwNo3R9Xolu8LxqSJIzinr5crU9qtlXkDAhzTyRD7aC9lSdSsE5uNESMbi6zn1fEs8/+XPTK3xlbfMgfv6N7/meRp7h5VatE5T0x9uxmWLoynJqQ2Ie8aLBPysLeewFfS+mS/soYaYtXst1G7CIDUtn5OJlGsmIdQiuYpSeg3nat5XD02PN7IJWVoDEDPOgw8L3do3Z0NjJnb02CvVjKwzZGrd2OtItJBYx4BdvEPMiN09DXDeo72Yt6qXHsGiCplCXBO5aYLMh6rJbs+xbZkQwhjCWjHiZlh7joNUx7xp6k3JzGXLxNbFBC1tGNWRMCNnN4ZuhyCYZlLsaE6oSJYDL/U9bRQukWG0M2s1NOjf1aweww8UPlPwkxC078tKCAesa1o3Q7QMkxunjpSN2P5+I9d9O+kYMIlJ08D3hk9RKfh2XBTBoo4BfBn16q+3fv1W7L7u677u677u677u677u677u63/x+m0gQuyaIKcQ3nAY62DCxvCgABfLY5ovDsxVLUynUORc4b8+0VdtNLc30GzB8N3OsRSk2Ei4dd6z2e587cUQb8NFbMuZ8y0TmxPH0yHgvv9Assj51jrtnPBiPD7VaSNasR9tSEjOEdGCaOdNCl72IUtl2eY3iJFrXPcOP9djkweqZXik0QbbUkXIw0FNEFQdqXX/lmqac0+D94cJKYx8HYdi5F2f1bRTsTkiWcyUrnWiarKs8YHryxtO67Sl84sTsKjiQp1miiqatXJKaNPMQnXQA3JKRN1PUyGQcuR8rpSdZVmYpzDQveA9uLLbhYojxVRh5KVxlqV+9znX7+qSIpoduSE/YgWnOtz2btsdEbqvN8uM1JDaqBMZj7jmZFZWCn5YyTofcMHv+5nAyXsOLCyp7g2368L5cmG91XP6L3+98eHDNzzgYKMfAAAgAElEQVS9/wao9rEpxpEL5PyEBiO16/TpMBO3daDmt1vmeo3gXttr3piXD7z78FTfvhiv5xtbzKT2mD9//YT6mT++q6/p5gN4uF0qanWh8HA8kRo95nOOBODTa0Wt/vzjX/gv/9t/4g/fVUTprx8/g64cmtPZ3/7+kY/Pr7z0SWQqbDFWq7iuNaDqRXuaeVBHcG7oJBM1WyS0Y/90mng4HTi23KAQQkXd27UfbyveOQ4NKVHvaj5J40CrCt98856HhpxdLjdCWBDvht1sjoVYEq5Zdp/CEVVhCs2dKgRm54hD77CBTfiOak2B4+HI+4f6GteLb4yH+vvn9UwqeWQdbSkBkYf5wGPTET2+Ux6nE7Eh2j/ogQBDT4oVvsbdCexdo3Df130BqPjh6KZaLeQ7SmGL4Hy1hQa4bDe2bMP9NfqCi1b/rP2h883Zt03yO6XMmpbFmVHU0UBxkis4P+F9Q6UsVvaMNWdGqmV0d4olhBoU1K7zLRecC+B2eYMvtTbpEYbVTc6GTknUYWrkrv9zAS2pFphUJ0aHjH16co5ilXIHcCQQYxkMnOO0UFJCXWF+bMyjVHAig/omohWRks4cqo9dhmSj6nw6YDtNRnLK2jSNIkIgENpxPRdHLJm57Q1WrYz7RyDnXFUJtleJs3PcUsF15pETfPBI6TTElofZnuS8Ggfnya3G8Vbw3g2HZS2Vctj3uxQLTgpPhx5Vo7zcMmuJzKMGWyjCmxpemB0s7TmiCSnI7iDqfn0E+zfRCOFl3DCLZQRPGSdHpcVJE4N5K6wl0Zl0WaUGBKKDH2pWb/a9I8jU/+wnh3lFyx4K5UmsthGH4ExqMd5ziZBqQ915/gYxFS6tkF5wzHNgMcetNRmXbQOXyO1Lnsw1Qs0uYJaWiVNfUmqAav8QziHqR3PXtS+9SVHRpm3q+p9qY1jybritLauoe8yLVGqZjuwhapHRX5IaTDuyiqaMNzd0eEjVQCzWwrsmX3VD7apZSw0+tSZ+M0rVRpjgeraQgZ9rs1u/m9qWdr/HrRS0GEuD7j0OUx0wa9U5CdetN7kZ9X40Y06rTbrknb8cRLBJxs3AeYeocmvPYS83ckk7NVK0Wj42yo2NDKP7uq9KvY3ScmKmBVdqJheAi54shdAosuKtEbH7sEDJ1PyrpYndJ+9ZjqdBN3j58pF4e2Gem/21KEZi7TfcVPj8+pn3Dz8A4CfP7frKzx9r6OeXlxupGL8f5grG4SBDxCsIc5iAzF8/1uyignJQ5R9//rH+jhnfPrzjw0N9D2GLPB5mSq4W85u7IDkgTQD7y5dn/ub8yodv63v6+7+5ofIXUsv1WKaAs5l/f6iNUsmFP/30E8+XndLnBLyUlgMHFgJuEkK7tn3pIaqVtnZajnz77pG56WtQ14ZJ3WjF46YwiqecrQ5GmtlCzBuKH3qdeT7hgqOUPcsjbomc0ygCwzT/q5DqmDcwOLZmK8aFtJ1512iLx8PMcnxk8v27UFKG9VKb1Hi74HXCmu347APH999RxEhvTFou6cbtWul50+HIcZZR5MWU+cPTN4Nys1Oj7+u+ILKS017bePKgKaWSKJZGhs/xJFiGrd0b11hajIeisQ0oipBD1TtCHSwaxra25/COsDikm5xIARJbMxBJlnEqSDMJyGvGOx0GJVsUSkm49vjJNW3MGkdzJCokJ8NOexLHGhOuy2k0k4sOM4BogOrIOJymqnHqOrsYI0506AWLz4gac5s+BQd5k5rd082knCNvqWlwAJScrWYjUhsA3uijpZSq2251aUqKKwnXhiLLPPEQHM+3qgW0WPAlkFqT6kKt/qR9ZneAFDNbsnGsnQqL6LD9tlvmJtJjgBDROohuRV2QFbuVkSPFwaHyRhfd9fNtnxf1mEa2lnGW1NeaDh06xxCUoIrrOrRS3qR61uOE6j7036f/v9r6TTRCs/fDIcQ3wb/Kboaw2R5g5yxy8PMuYwm1DSqFkbEz+KvDDM1RnI0bhPbA1BHqUy/kEXVTMvomRwa0NSi7hugwOQ5Tn5AIJaeaWt4EYo9+qhkc7eekgrN90oJUR5EhbTEbgn9o7h684U+a4VWHN38pULKMZg9p3Mu3J5UIUspwThEELbs5QrEaSNsfIupr7km7MJ0GFOuhwhSBk0Gedi6wlTLC1ybgUmrBApCsXrhO6nPvn3MXm5sZqHW/BV4uG7JFDs11YpoCyWSgM07rZx/vWeqx6ht7LrU57MXPqVkEzkWJTQjunXK93Dj3XKH8ldNh4sNjLW5PhyNJFVohmtK9EbqvfSUR9hLV4UMe03k/++GGA7UoN+qAp/0JxaopgHtTsC9qI807fPc9kg1r9kJlS8Sc8C0X6Ho+k6zqSwDIIG5mPlTEp7wkvr5eSPGX+oqLkdYN5np+p2vk5bby88evY5jz/unEEg6klvURZs/r9jqyjILMBO/55nBqnyvw6eV5FBZZlJQLp6bH+a//+T/y3fsTa9MJ/PXzR7xnCKy9n5Hynn/48SvnW9cvAEud3kLNE/ndN+85znVfvL6+UorxeKoBqkvwkFcaSMVBa4ZP10RO88SyHAaiZCtktxIb8rblDdFlDJ/MEmgdlIxw2mlhkmrkADDPhzqM6S6Xm5C2yygcDSH4Gd/ME26XF1K68tJqJU2CLspjqJ/hdttY441T22sQ2LaI9x5rNpfbeqOUG+tr1RnNznN69wGLLbPpcGBSz9p0k90V9L7uC4CXG9n1oYrjWjKpIb0FEKeENq0PTjBnWGjTfTEEx+QUKXt94jFKu66iZbyB78yRBGWDIK2xKRsxp7EvmpUamN5SOb2CwxHfBNpbLuQenroIOdPycxra0gbluZ3zNgmHOVDGgNVwzvCu10uJ+W0ukCmTE649RygJLsBjL4n9btgE1V+qiGDsNVjOkZecd0dQPIKNIFg/+Yput5uFIeRSRv7S5CrSMjWzgMVrzVWTjjY7rjlzfW16nFk4eBkuvorh1cDrromWOojWZsCQspGwUU9P6qGkkekDUw2fd93BzdCyo1rWAQbrbBlPZNeDuUmZC/iYsNShLiEVhv4q50y2vdgt1GFi+xij7v41110jdF/3dV/3dV/3dV/3dV/3dV//5tZvAhFSleHmUQqEsnewKqBlGjkdTj1vaJjVVrpY9bvvKINUI4tiXetStTOMXI1Km5NOlSuCBl/FRNT8Gyu7NuTgPOJcNxVDGkLVneu2beN823gMJ7ZQ2//j7FEX9veZS+2KXe+0m42k9UmiVl7rAHSsIi7tM6kq4nRoX6B21buNb8ZZ/ezB9qcwhOEwWar9ayeAlqYx6llExQqlxJ0ilh2iO6QpNM1Wt4dUQ1UI7TSKvjCXzC+vDdrdCg+HiWUJQ2ckXup31tE750CUtU2mz9sNjQlf6lTYl1ytIHX3vZ/9xEy3pMzMx8OY2JJbJlH7uQCzN7Ia2uC1c0rEnLlt9X2WBMdZWLRmfZzmBeccr02HZPtg6L7ui+QOLSsInOVqzdrpWaWAxZ2WK1Kvp0adM0tt2lkG9daJQvBjoiYxQoqkli2TU2TNiuXn+qRSc7Q+fa2Iz3z6FmW3nS7VAJVya9dMqgiOlkqt2q6ZHz994V9er5xaDkfKBVsKy0Pzzs+FNQVOriI8/uQIIpzbNXS5XEiWCU3HUtGpQskVxVqWA3/8D39HahPb73/3Hbdr5nqp70FwfPP0SlHj50ub0qZCcDMfnuok+W9+/8Tf/7vf8/iuoieXlxfOrzfy7bm9Z0Unh1sakqYBp37YaweFuEZe2+9bKmhw47iras0lcfumqqKoBWKnz6UbMjJKIK6pWoFr1yIY03IcCHQxoDBQd18e+OlPf+UcKxXub3//7xGUreV8rFvktka2dsIkUXJKBL2NiXQs9Tt9aNShp2XmJGBN82jeoalShIGRfXJf9wWg8zIQ6zVFSokjE9GJQ0wJ7X4cTEjyBvWIwtFVd9tLszs+TPW+P4/iZkZdjT0BUFOcCNfmihkj+EmZe7VpNWdtuLiaYqLk5tSYqfWdSZNHZMfBC7lY1QADPsysaaOs9T1MQTk9LKSGkl5uETXl6XQcx8Gysrb96RI30tVzzV3bqQRRTg2YnaeFtRS0sUHUecQlTuoHur9tmceDI5f6ntIqZIns5YJhJWG5o+CKes+t5RfGUjBVZuna5Qoe+baXXDGOy8zpUI/7y7qySR71WcDxskVEPK7XU1bwwtB9FynMMiFtn58F4pZJXZNtha0ofvhtC04gdWlBLC27s/71Od3IUQjtU84+VGdjtUEXXtdEyZUlBdUhGdizQXPGxJjacTs+/Pp4zG+iEQI/fM+VXKlqg6bW7lM9IkGV8KbpKUaD/oT+bUkzVxjxL9bg1l4cF6nheq2r2DwsJezZRVTb7neN1mbiSMXYGlXFeSF4N0S95xRxcyAEX6FHquhOxQa1rQC4/QZZNUIgHRe0hDkZsKhUodNo1oQK1UoXOfaHjXu4oLlyxlJr+DR3L/7e8NUaoHNUtViFQhucbFSh3HhyqpWmf3Mck+zviVKpeN1T3nBMysgzSWpcE8Rr5jC3DYvqK69dAIhBqeYEAN8cD1hm//t2DGRYM1ZB4LenWqA95w3IwyqdUOHgXpiIGIirTeTb8yN4lhaSGImYCdvIgqmc5aKd03zvhO5rX9nYqQNSSFbQZqWPCOmNH2g/5/JWb7hpu7BuERPF9/AGKTWLo9M6LCFi47GmnlISRXvOlbDMJz6/1Eb+9eNPlBKZQtPziOOgnulUqXKHMPH6+St/6RbQlxvnmFjL/hplCkSno2BKeUO8crX6uR7LI58vZ356qc+RY6mNR5uy5LVw/vrCy6E+/vT4AefDuIG+f/eEPDliqWYM2xb57tsP/PC790NboLaRzXM81sLg8eEAbsJaJs+23uo+2dPWpsTD8WlQU0raiOtKatfxVRPZtNmNQ5iOHPU0mhizTMk1mBFq75qJbCmzbp16Uzn83Xgnl8rRDz2DbHLwJpeDUinW29ZyhK6vrOSR6bRthW27sLUiMZcaHdFF2hMtbsBsFKO325mDC/yHP3wHNHqwvIlFyIVoaeyB8qaxu6/78lMgtSGLE2NePKHpE71INU3pmWY54sLEqZkZ3YhcY0RMR4ZhSlJlAz1bS+v9u+frHOcjS3B8zW1PpNrguzHFVTDFtwYgllTrnXYJGanqXtofnMqBclCW6UBo1+phVh7miVvXEgu8d4pOdWjyKb3yEjOvbZhtBufrjdD2jpgz1xzHQKuQ+DBNfPuuZblNgWRpaI1vG3x8ydw2hrY8hIk5BFwrkPJsPN9sNITV3sohTbt3vV7JRYm9/hKj5IJvk+vjfOJyvrG9GVSbgW9DtFkzGUG7DEAnKEaOlX4GVJ2gKHPLh3Naa6zc8yxzxovRJ+pFQpUyyPhmKCKEroeQSmXsoMJmsea2NZpbipnoHcguR8ixWnx3XbcGYZ6XEXky+cBm2665/w0weX8jjVBBeiBmQynsjQhEzfbATXU1y6bd/ISCaHcT2Qtdrf49AGgpLXS1T8oyRRXXvwBzpJJG+FZFnAQX9lThYuyhiAXUxSGQPkwTycB8YqJNZaVqcbq5gUibFv5PfEhpJ0sCvM1QuvqgI2K946lJxl2/Y0Xq8Hmcr6GGIToZYr5iuTaAvfmyptXpnPnW6fcwteIKwfnxnLEYzmRwOKX//tAcGRYTr22q8uADeMd3T3UKc94ir+fE6/nKUVtxc3zARLnKzmF1OY9jO80TVvbvXyiYWQfzMBFS3oa2wYvDezfcX4TckK03E1qUxYfhzCSN9+zaBz2bseXIeasbt7t4ljBVBO/td3Bf9wX88uWF06nmwCzO1yDQN8MCfdM4iwkpZS7nikrcrlcKGQ3zELCWvKIovhXL0zwTpgNqO2qQJ8aQpOQLlm88vWuGDLbw85fP/PNP1SzhukWKZd61wuT59cI/f/7McyvOU65I9NMy8f59vVbDLASvY3vyDwdiNnIb/rzmG0WMdw+1ULAkvFwvQ5eSzom//qKcDt1dKLOt6zBaeXp4QnVm3TqaUyg546fAd9/XAv/p9MSaVm4tcydvQmLln/7pHwH48y+/ME+B7081WNZPnuv5MnKH0Mpx73OcGAUTI0xN+/f4nuNxprTbXrFECBOho3lZKHnjdr3gmuGLnwXFs6V6HMIU8MGPom29blzLK1LeaMBEiU1AHVzgb3/4A6nc2neX2HKitD0TEZSw35vEqjlGKaPgeno4Mi9HjkvLS1o3lDzed4qZS941DZ1NcV/3BaAoVur56yfP4hkB9ilCjGUMNwuKi8p03AewNxTRahgAtf7JhTG8VDVUlakZyETLBDyn5sbo1ojhRh6fiaEm3JqtnKqwuGkgB0ECDiN0R7ipcBDjDx++59Ky0K5bfc5+n39OGx+fX8eAqt73w8iCdFSk9Nb10QKxudpC1aKnJHx9aZqjxXh4OLG0Ae7xkPn8/Mot5WF49TB73MBvQOcMtzI0h6p16nxrQ5VbSmjZc4FygCWAtZpvjRvXtA7GDSpsEsdgO2bjwDQaRLOEn5Qt5VGjDVe9tide01YLtx6GC3jvCO27i9pqrV7jUQfk3XAmNz19b4zehQOGst2axswryRUmrxxbPfz8XHBh4xjqvSL7Wt/17KrZTZxvma0Z6bycf/366tfHpO7rvu7rvu7rvu7rvu7rvu7rvv4Xr98EImQwqAe9s3WDf1rRldJ6Nk+10y6Dc1Zq3o2OIV2NoWH3W08xsybjFHq+jTZLWhuPUO8G1UDbexr5Oa6SMUqzn7Xrxi3ZoIxNk+C84ZzfP0fTLemgmTVh0+C0WUVmOtJlikmsnw8amiQDsizanPMGAmRoMLQn2pfCWjIVhd3RkWo/3l9SGgG3H1mBwrBvxAo55T2Tx9WJRv8EWUDxOzVOBBHHoU0CJCWKFHxPQPceO2aCc/y7xzpBn5eFT+frmJhOzhNlh1rVKU5t0O1iyTh02GRGEWJJ5E7/00DOu+YolzoR7mhOKUZKiWyOqVGRNFVutDVI8NVVV63LtVGTSuHpcBq0Re/uE9b72tc//NNPfP9dnYj98MN3vJs93ldkRSSSrpERWlaUeD5zu1REIImxzAceHr8d9seXNTGJI7T8Fz8vaKOsAHg/MXmHk0blXGFdN5ZQJ64aPA8xcvlSdSguFvIyYQ01XdONq0VKB07UcXAzp+PCqeXjeDzyZtPcttLoeE03mSLqlaXtgTeJEBmUGl+EtK5s1+bMKFdezhdi6nlginJha/S8M7Btdb/4Y0ND5inw8uULP3+s2qf1CnG98Q8/1Z9va+T9vPBjrtlF7+YD4hlI7xyEeTqytuT3lCLzFPDDXruQcmLpVrPLsXFHGmIeBO+X6pK11GObs2AlMc9NK4BUOnF3IwYszIOyHNOGFOEw1fPBB8GLIzfdzna5kdaNWJouAIfaRupexH7itJwoVil0ACetU+du9z/5GbPMpVH+LDsmcW8iBu5U3vval1GYlk65h5wyW7dejzV2Y+4yAGt02DS13zcO3oPocJJzVnMXO/IRpBZfW0Ow45opUZl7dqAFvOZdB97Pz9SczI7KY3BDbxjXzGtKmDbUqihfNnj+p59JucsTXLW71y5ncMzLYVAAKRlyobRr5iaGTIoru/a85FJd1wBvinM6nIS3Yvz8+ZmHQ0dhEy9rYo0bOrIfA/MhIG2vv0TBKWwN4Uk5sW386zoi1OgWqNKN4KZhv/2SN86JPVahGJa3YeXvVNhyxrou6uDwZmgou+baDMmOtVnvR0tMkx/onTmPOTfqUlcKt7g7mBZKtUzvmrGgqNMhK3GTcvKOi6/vcV031tW4xUJjOJNE8Gosx1YXaqhZnfWvETO8c0Oa0rVEv+b6TTRCKrJrfuhc7eGGUP/X+alkVPetvlgCcbV9GBSuJgTrVDmFa0wDgnw8HigmQ/uRMVwptfCnipej7RzsUtqJ0U4OUWNdVw6n0N4/TKJkE3IPz8ppfNHjY9gOQY7/0DcUOLHBw7V/JZuDSnjbG6Psqia7H4ds225D3jYsSe3m2OBhFal+8eNCNsjCuZ2IEqp9Zt+wktWX6yfJhJFURqaTk0JWhm9+cY6UM780k4GvL1ceDoHvTw8jV+Pr5czH85lDs/KNseAmT5Dugw8ZNyy/15LB9gtTnGOLRurmC6UQSx50v2xlUN76Z4wx4W9unEMq1Yo89c0DhaRcmlhzK4XFLTSaLdudcn9fb9aWhH/56TMAlzXzR77j6XG/uVWCQjt/Y+S23oaORcNMOH7ALx6u9TrRMuEWP4pvcRMlZ1RbjlWjptAKjZQisWxoK4QPHAnFkVooRimJk/OD2vtBFrYn2LrBCLk2V5Mbe54Ww2TX1jmvOPNv8ic8QRXp+V0klrDfYB+C8s2HA43dh0XjsMzQmpLX1zPOeXK7rmPcyCmC86zNXOV2Wsm5sLZQ6p8/f+K8Gq5po5bgyF748rX+fjwmvnk6sZ4b7ezxQIq3EfKKGMc4845qgsLzhTQ7yqlFM5jDT+xarVItgcULtNwM5yJ+9uM9mNX9f2u24PFyZZocx2bp7X0Vmne9jguVPtMbndvrmVtcR1ZIzoVUMsupPv93331H2Ryvr7/Q7xHiFHUywiLJdVhVmsYiS6m056GLvG9Y97WvkiIPx9qYH9Q4B4e1HJgtVip5NxsyM5x68tAMJbwaosuwWHYegg9jeOkwSin0VA1xjm3Ney1UjGhlZIGYL6grQ0uzlsx53XMdb9fClvIIi59cjQFZAT/2RCPHQg5toOqVh/nArVFOz2djzRvWdb9Cy2FsJiYOvPghTQgeJqcj+iOuiRgTcwtr/rJmXmNhtYLvmYdb5irnoTmMW232eu1iVF2y60GzCrccq+0/1ZBg21aOPcdMlI1CXvt3EWtwba/X1KgyEj+Oa2n6an2jPS+kQZu1JKRtG3vchBC3ROwD+OCYyg4sJFP8FMZxySkhVuj+K2UVSoxDQ2m55rNlMXqc0gFlWsIwhHGl6shLEwOpKhtxnGN2D1Sty97kHji6GL9v5lVno3tH8K9yHOrfeSCPTB6Pktm/XHWe42QsvUGSjvo0rYsVch5zCpwXnOoIIsUgUwZvUoLnMfiRoWGmxGKYE4rsN6PK1e4IURUYq+wnrOiQu9ZBrAmJndNanVP6xKMel84XLRgFG8nKpVnBF8q+QUn72fokpmZM9ONirTl7fmkJ9Or48MGNcLWpeArQLOmxUmORsrSiThRxnvP12t6EMqlwahvBq8DBOX53PNBZmPM0890hjVygzSVykTFxqAGNjkCfPknVRr1BCs2URjdGKKRgY6IhpXZvfTNK1jbilAnNa9/NrgrUu44oK7GUajYBiCsky0x90y33wuK+9iWqNTAZWH/5xLwIh0NFVqYQwMqbplvJJbNt3Z1IiNcLnGbCVAv05fgV5yZ8m7KZCCXlXVzsqgDWGndcvUdT3B3YslEkcZw7ulNYTguhCZ7DdMNEuPVhUimY96gIueVDaKJuEK7z2430Rps3BccR5fS+vsZt87ycHbfW6ASvzG7B2nUdfWL20zA2+PJ8ZktlFBaLX7gycY2vXBqK9OXlI+/ffcfv/1AL/I9fXnlePxG0pyQKsgm5iQeKBbDActz1o2XNY1BzOB5Q4NwazvN64fv374dewtJGMYfR0J9SanC2MVyUpnkBScQWeOp1IsfM89dPALy+fOWD/2ZoipbpUBkHLQtJm/lM36d9cDh1g60gJmCCtU12vSVKvpDFYWmoXOvNoGs3q+Vpu++BSi0a9/7n1y8s7uu3s2IxUqtSr0EJKGt3TnSRI7pnMFLF8b32UVE0eKQYpZ2jJYHzNlCIrRRQYe5OigA5k3wfRAtbSoMpYpqI4rFWnBsNHGqvGRXMwWHUPoVLicxhakHQkEvmljd8N4+KCbUy0CYDVD2mHS2ug55ej5kqk7gx8NBQw5hdN2mSwsMy4dpnOK8baMapjhygl8uNNSnH9phYhIJSGtqWkhFcHTADbBmsGLkNpgVlMs93bd9eDjN+PfPa0JzbWjDTMQTWVPBOuKaehwjzNBG3zNZMa+YWcK+xI0RwnCesvadrzESDpZtP5Qo9dJTrIFCcsV4bIycZW1yZmzPnpIo4GRlSx2VCY6zzLtfr4cy2FqwN7rw51hiHNsoVKLojQrP/9duQu0bovu7rvu7rvu7rvu7rvu7rvv7NrV+/FQPWmN7YKQtvDJp3++Q3E4tiuy21V1c7fdHdLa0UrmscyevOBw7eDYtSADUhvLEQVPX0SZqVOpEY2UVWUYqRBO8FLzKssCt7r+JL0hEfbeSYsrvGaYd5qMMPwYaVtWUHYuSBfAnuzURWqG4rHTaFpjHK3d1lz6aY3NReY0PFBnSbzLhthS+vdZI8h8DjcuTD8TTek0fInfrmKyQ9MjKyEF3ZbX1znbp0ugsxMc+Bh8dTe/6J00H5998+YdSJ6jQ/8t/+7m84r/Xn//7PP/HzZWXr9rM548OBrfNGs7XvvL+moVazVaBOcnIqHcRCUMTvdpGxFJRKHek8nweZKsrfzqlkFbr3bQDrSiEfI2Z1eq13jdB9vVk5FUrjop/jyk+fv/CHv/kBgOPhiDqGBq6kqh10Q1SSUe9w04K2yWBoHNece0K5YJYGHUuc1myzRn1DHMEvxOZymB3MbubD+0rPiuuN6fR+aIQKCQk63rOqo7R8o9hRca3J8H0ynBqS3OkMxSvFMs/Xhh6bVPpEQ6ku6cb1pMMpChFSjgRfp52n+ch1W4dD5fX6wmsyJMMLjUp7vbJF5Zt33wLww4d3vJxXGmOVY/AUTYMdMAXHNM2INeQ2RzYrg7YhFA7Lwtr2ipgjP3z/w6CJOCfEGElNt2SWEYwQlkr9oYJxMRVKc8fLLpOtsBzqHhvCBx6OR0K3rC5rtZptLIdSCjlBatTIuG344HhogSW2ZS63yBbrd/n54y8Ep2Qgdhe49q9+95xX79sAACAASURBVBpBAA2ZR33NkOvsg+5Id1/3RUV7vzZ0cZkm5uAGPV7UkUvCN9fe4DzXso36a8LjklAUSjvH1y1BTsNd9uAF/LRf2+tKSobrdPfJEYofVDcvCyI7Y0fEkYsb9/BsBe8N30TY3jlkrUSXrVFBMiCuozywbcbluhK6/s/ViJM43PASrijWEHArhvoynOpKFHTxTI2mFnOqkSmXy3h8ECVrGfbWoJQivHbKlzi8SDdoq6haLuRuXR6EZQqs7ThZLOgMx6bf+nq7kS5weKhMgTW+Vke+bs8dHVvJTO1nKYXbNeKzG1qnZg08XgNVtk0GQp1ZKVnZOuLjFPW6W4CXwrZGtrgja855yB2FNzAdaGAqG4WC5EphrN9fVU3121UuBREdtaxfPGq7NtN3yOxXXL+JRkid7dCUCKK7sKqUWgSnRj2wmDHdM2GwgupcYcv2mExhnuZBJVAEdTJ421EyzZEd2Ol4ud28Nquvr9aNCyrBY8/0qY4D3RpWrTY0CgM2FROQspsbqNSGqhdEOUM2Sr+rS31+15sMa6/StTBWYV1rx0Gk4IpgPXcIIYUaBNubAJPMLLI3LlIfnxpM6kRwrnBs4rxUChkbDaJq5bvGXgwhdbPrnNhcsJza8QCxzHM0PrR8nof3J0QLrykiLVPgDx8+8Hd/90ekWdo+r/8Pv/zpl10ESfXEz81a0cyYgx+NcCwJVTe+C4sOt+hoIA9m3LC9cdZKUYylQNMenNlQ3C4Y3S6UEpFGwRGtzblvzZr+BqDb+/rtrFgyl14Yq+PLy43nL9XW9cPDO0SMqV1TTuum36lzRTzz4zcgGWsaj2k5UlIkx10fqC7QqOhoEaRsrJf6Gkwe9Z65GR08PH1DCMIx1hvo6/MrKWbc0uh6MWFJxg05xZXslHmadqliBt7QXXCekiLXpoUpJZM17JoiE5z3mDRbae95f3ri+Nj0OKWwbpmvX6te5xbhHK88tfwvNz9wff2IlMy5Z33kjRgzjbnGh+9/4NvXC3/+5Uv9g9nXJqDplJyDLa0E63qsjdf1Sup5FgYvt20UVDodWW8bp4fH9kVmtvM6RNpTOKABsExu+1XZZgSY2++scYOSB11vXjyCJ7Xfj3mi5BvavlsNnmKCtaBHscTp4YGl6cFu5wuTn/h0fh3nly/Gmm7QM+kKbAWkaVy9P9T8qtwLCYe6PEwiKs/xvu6rriTVkKUuI2cdw0sTh1kmtoGGC3XP6lbsq2REtf7Tw0elDkNdo6j64PAmrG2/Wg6B5G235M5GwpB2HU5TQC2z9bpiLUQdM11mlUop7luRc0yHgEXjpdHGMoJz+8BcRbgl2SnyTiiyW1kHU3BCKW8K/ixjqLKIoKpVY02ltX253MbA/ZyM6xbJqQz5woOfiXmPThApXLPDWd131Sewgu/W5cHjkSE18KKcFs+na32+z5dITon0uUoNJNdg2l4cm1T6n7AbW6CwScJ1/adQs4K6Dim13qg3nXgKZdR0kyon9dzaUKWUWuvOzX5b1ZjnhbI1HbgZlnfZQHGCUjgcd7CiFKn/tEHfdPTgjMu5/nw6BbTUbCYA14VZv+L6TVR4k/rhFodk1MnQ45ANyXtqbXYVEdAeaIhh5VadNbqmwzuc7kiGtqaiN1uK4ERGblD9tT1VSk0wk32KqwK2O9dpFoqV0bRoUVD713k3JjUgdaBQAklog5cmfC24xvPGOnt11wRB2Sc3NACjP53VSfGuRahJwyUbyj5pqXz0jpQ5Hk8TSwsDTDHW3CZ5OwW2mhRMkxaJDuFcNYzYXV+sGCLC3DbEEGYuMXNOtSiQTdniRrxt/J+//11744E//fQj0gtFE+YgbHFvSre0b8wINUm5XVQUWNnNEYyM111LtZVcw9/GcSttwr6/7227gshu4JcKE8qh5XRk04pSUj9HaP7393VfAMHPzFM9lz6/Xji/bvzjn38E4Jtv3/Pu4QFt170eAuIVbS5MpWgVsuouHs05kVMemkNRh0nAt0K4lBu36ys5ddcwrQL60VQ4RMPgz7vgqxawnd+3eCNb2jWT4lDnK4pd+uClELON/eb2/7P3ZjuyHEma5ieiqmbmEXE2MpmZVT1dNRg00Jiref/3GGAWdFdXZnclk8lDniXCFzNTFZkLXSyyH2B4gHK5ISOOh7stbqKiIv9yu3Db+5JfiyMCWOsUzlp5jm/e1Of4j9+/5cObd4ROhlFjzSs/N+EU0YU5zOytWnqzKH9498Avt5Wp/U3eF74+X/nz9t8B+N33P/CHH74fLulfL1dKseFHUUrm1+evTC1f3a7Gbb/ycKpGso6ybht72zg9zBOTOkoj+mJMp0hs0585Brb1zFps8KtOE4T0MKbJtmWs5GpcCKQUUXe8FYnmuX5yy/NBakc706Z7NhFDIcdaeCxpwt+95+lWN0Jfv5y5nZ+Jtgy+qWlBcj6MXy2jIqPxZ14RFbFxIPdead3jHkAS5/1TU2iTmeJlCApJUHJJXNuk5SKZOYTxzCVRUoy422i6olQvwV6gu3HLeXBuY5I61exrdKlT7p6/rlabp50nHFUpkkl9kiKpmo32pq8JEiLbXihNSS6oYm7sbfeUFKbFh+iWVBLdQOhQhGJG6AJY2tb/zoGchBhh33tz1Kt/WG/AlhWxKqZQWv7I4mSFqYtCbLD5NrhOb9PMNC9ct67YZ4RgvG2blBQTQRPXa22S3ErhMcKkTUgqCF5ubG0kHkIgSGAb180RDURXLHdOT1X+DU3d4JSUh5OOjW0xJUYfvkJ7KVzyjVflN0mV0BTftq2uS+WVAFkhMLXJW4zCRiEgg6+1m2B7Jrf6OYRqtto52mWrdXxq6hryDXCw7xyhe9zjHve4xz3ucY973OMe/+7im5gIIelQU6OO+g+vmp2i1YkYquRhNh8j0SgBF2E3GR2I2MacvSNaBXeUrU0qkkaS6IGpVkVcxq7QUcSOqUId8xxdElPFi3Q1yWOa1T+s/rbynbqKHIpGr74+QFYHD1Wjv716GxpLhzpax+z3/3bcrUh1gXfpkpaBqAHZGHj1qnR3OBnbXijuaFNCmcJMyEqHlBecGBjYzYxWaFnv8vZRc5+kiFCaet24jiJs7efbWrvQV3H+7VPF4X+5Zn78f37G2nG/WRa+W6bRmd4x8q0waDlaZcz7VMsz5DIa12ioU6wu4Y1WxbjD572ObIsfnK/iWxPS7BLdhlp1y4aqxpJLZpPe4Tpxj3v02MqVBrnm7RLZXPnaYJd/+/gJpPD2zXugSrKG00QqdSJQimNSn+s+RXBzUoiEVCEVqGK+DVf04sK+7rg1qGZ4wL0wNQn6KJHr7TKgvlOaSNOJ214hFikkAop2KEpQQopkybRUwLZlzpeVqam6qSpzTEO6VbVK8Vub/hZ1NCuL1mOWsFDEsAYRW4vz5frCda3HsEyOzAvQ/ZQip+UN//TwbviPCM5lvXJ5rhDAX7/8hMbv+V9+/w8AfPz8K19fzjw2yN+2Zm7bzrVBxrCMplNVaqPyc5CqfATV8X7Nmb1BXmMMzDExNZnxXz/9wsvtyjzNnM9NCVP+yOx5eIWkNGFycBKVhISCNo8n33cwIdgBIcTKWN+ISs5+cBxDJISZx/DU7mXiVwnk5090OqgWARFKW3C81BzX7022Qtnt1dpx5zTe44irw9wQFzJpnbZ0nokKocCp1SWmK2lOhNh5xo0nopUnXf+o/b5NmEsRtqBIe87Wy17X4fb9jJMSXChrR3FUpMvU4Vv7hkbIrQYo+8oU0lBrve0FcvXKCe3BOyVh241t8HGElMJAiojVc+11xLYWfN3ZG7hDiYgd9iMhRPZr6WjUqgJMIXFMnHwuWFRS6XL7RjHF2yTkZjsxGNJQPpdrYc9lTEpO88QP79KoZbds7A63dkzLaihhIAVmtUbNaZB9FCs2/MJcq3R2NGUdkzBHlHGdxB3Ph/S+mbFmG/6TxWHfq/0LVCqBJB3T5aiV29UpHLlUqGSvr9SMKQWUo2bbKIj6UKbb1dACj/OYYXMuNjhjUg7V6N8qvomNkCvE0uX+Yi0SutQeseHp+6FWnkv/MtQRrzbV16E8QOCQ5ytevwBdIrCoIEE4oHAVBtYXFvFKkM/tmFyswlZebbQcRuXcTQfbodTjkliJfGMjY7T1rJ2zI65cG4k2iTCL4NoXUGcXGZssd1A7PC/cjfN+qw9/Owdp9J3ND4ntYGUQCkNS8prHQVy3FS2wNHGFqNIgh/06GGQfCSoSkehIW2g9ZMTDgNy8nG8kjYSW4CQ4p+UEJfPnT7W4WdefIURKKyxWEb6b5mG+9WgRy2cuPQEFR3HKkL3s16leF0GZNFW/ISBKIcurEblbTQ5ywAhLI/51CGF0o5gNiVyViWxG3zot8ts/qPf4duJ63vnShAgWVTQGro2g/+PHj8xL4s3DB6DCTSMVigbgwVqjJ+Gx47Incj6kX8EJOHsnBueNFOLRiMnOtp85nZrvkCrb7cr1VjcZy3JiWZZh8vn4+Mg8L3x6qd9vc7BcqkBMOwamwCTzOEeNAUUOMrFVOEo/pmxOxLi2HLluKx99H4aspUDJQmmQwK8GiUJHIz9OUHzFSxr+I3nf+TA/8KHJiF+L8fGXX/njD7UQ+O7NW/Z1Z9vqeVxXI5sMroyIgxm3reaaNE28e3tiastcSo6akToX4bQgGljb+z2fX7hcN6b3J27No+n88oWyzSxN3CCmxH65se3P7VbVtUG7jC8VVr21XOL7Tt4LtPVrWhaiCtLOUVJCQ8DbBnF+WvhhqmIKv3yq3Kjz1zNGxBuXSnBMC6GLPnht+o3GH/d8dY8jfHdyg+qe7cqU4uALpmiEFEip1zATqo41mkHeMpc1s4iQmpBAqL4er/jLxnpzppafYoi4CFMXnxJnVuPa0os26HorE4gqnL0Mf5w5xVrvtI1X9lKl7bMPOWvRypvrOVM0Vsn70IvrZlzahVVUWSXgDdpbqCIEb+fDCzJMR9M3+5Uv1xuluVC7CA9TglhYc+ffFFAfIlyTKzIpDy3fbGtmdxty2Y9x5ncP75mW+hnP64XiAXtpObQYZS/Edl1DiMzFufQcu+9ghdLhzCJEc7SUQ5BBBPeANQihuXIp+yvRLuchBaw18tZcOGTGatgruXWRuuEcHmZu1Zux1Vsrxrs4ozpxbevL2TeC6LAI2IqiBnu3fjFndxlGs11Y6LeMb2IjlMSRVihYcUrOgwMUJKDBB8EM8+qKO1yKlYAjGg9xBPc2SXglNOB1AlN/VsorjkjzMh10nh3Itg5PDETrZsx7cR4wNfJYeHw4wfYCvFohCd5utpvXXcqgvlQBh+EaHCrjqHcDsmj16WkkNheQBJYPZamAEgduHEyqSZm3L33VepehTLfvpX7le9dEm0pU+1mphqt732TGAGZs7Yv6tRhTSjylrjADhOrKDFA0EkIgxT6RqtMiDQmXhqv1wkN8ABqR2wPXfR3FCmqIlIGxn5OgIXC+HklVtLpNA8gu2LKNQjO7YpYHqbuIEvbK7+oJa7Oq9d+nc1HBSj4Kz2IUUaw97C/XRlK/xz2AVVe+Plfc9lecpyXwvjUTHpb/wNsPf2RQ3KKw9zEmEDSxsyM9t1CbIjXH1PfMl8zNIDQBEVvPWIH91heOXygSOY0FEZbTidKUx/AN98MjI+/OPCs0Y789F6ZiaAqVF0TlCkxRhts7Wrhu+TCnFiWXMngquxnFdryRaLdcLbC7M1oQCDHytHQFpBu77JyaitytFPK6EpPTBNj4fL3w/cOJ77+vm8jy8YXL+SPrQ53O6BJY0sRPL5VPc96qoeDeNjKiiskVa7nkuw8f+OHDwxCDOU0Ty5JIbcK7lyvb+UpMVeXy7fsPvH3nqMeRw7Ld2HJhal3gjNYJU8PgV05BYW0Glbdy493Te1Zvx7RvFWff1o6H9x94+/Yd1jZvSZR93Si5Fz+BLJm3bx6quhfwV5yXl3V4PklQrAndAEyyYJ5ZmzLYflm5xz16xJSGYJKUwqbH9HDbC66ZPu0RFDcbTZdHUZJoU+A9cpZK5ehA7QcnOQSLzGsjp09m99X5WjJz964JTi420DJaQHcdDdVzCMxSxqTWc63zlsQrMYMqLTW1/LScAnkreMt5JQCmo2GOGWmOlK5kJk5QwdsxFgcNeniW3a6I6CD8u1PFFTgErEJSHpDhG6RSRSNi21Q+TY8UgVt7Li/bjf/3bz/VDRWge+Af/+P3/LFdF9vgpVzZu2FrcdQzsV2HU5j5eFuHGqiXQLaMihIf+uQq4oVh2rrednIuQ0BLBaY5jUayF8O2nS4B6KJkqxucem8zVpTY+T4KFhJT831kFz493zAX5lfNoK2UUdvGkDDV6jdFXyNC5ZkBEn/7CfadI3SPe9zjHve4xz3ucY973OPfXXwTE6EKUurqRQ0Y0iFkUZv09CFtnUSHok62OsEJUkY3sstOy+Dr1N0/nV+jgquMrmxxa/LXHY7XOS/tz6X2U4Zqj9dXahspJVUsUDt21jsrXicsXd1OpCo9jbFV027vEqghUPyVfK20m9OmNUUj5nlAS0JQJIQBU6s8JkfR8ZnBhdLUnepHBkSUstcOxSkslGjDJbh4nbb0yZdnJ8grV/RSx9pd5MNFkN2hScU+zZGdfdybKKF6MokzdanN+I6oCUsNFuSKqw4YYsSqN0juMuEOdtwrL17vi/XpTmbNDJf167YzxzAmhiKCSZOP7NfWhHXLwwdqTkIWITfoiSJMMdJBr9t+9+W4xxF/+7pybj4M7oWkgrytXb7TaWKZJ5bGY9HgWNnYu9y2ZbwYBRlqjCEbrpFtb1NxUfAvlW8CyO6UvbDemt/NlJhOC9rUzmJKWFk4PVRZaCGjJNZLla4+P98om9fnggrp2NYVCTKkpY3A5htmdaoUrPumjYcdtzA6yd7+pis77a7EnHnz0KVjFQrsjacUo7Be8+A5PTwsxBS5XK9crx1OZ2ybcb7V9/x8fmYz5/O18YxO73n/IDxf6nmu+9eq6tSmcU59lt81qfK3j5G3jzNPj/X1SzqhakMZ6uV8Y9szb5sKXYxPuBWkXPEGdVy3lRu30QVelkTZziOV6C1jeedjk/j+v//0P0DSwMc/nk788Q8/8NSgv5fzF9LpcfgMRZ2RdCK0qVbZnok4WoRTU6b75//wOz5+vfDpl/oZ++q4Zz481Gnbc7mwX3a2cz2oT+ffHmpyj28nTkscw5y8Vb5zGNOWjHlh7zWPGWpCac91EWdKE1Oc0Pa7rcC+b2xt+mKWMQ7eblIhig+ucBRndSfvr/g27jRFeUSp9iYdSXLd2AjkvddGxuOUKuy0/U4VCELqkONca7xSDhVMyz5UeoPCPEVKOJTokurgAK1eeCg6ZPKDKmkKlM4/9PoZRYQxZCp14tRRP9kya3aCdnTAhAYhX+pBrMXYdmVrPMpSjO0vO/Ncn+NTjLx59zjQBM/Phb9eVh7ahT1rpQTENrUqpSKACD58foIL2Xf2rSuSVl5qR7+cojLPccCJkyryMHPZak2oUvlFnVYSbGropo6eMSRkyt4ROlpVMbOTlvo3M5H1krm2utL6NRtUE1DLg6f2DQyEvpGNkHEIF0gtXvtGyLwKJUiHtUEljrqPn5Uqsd2Jv65O9oo9pb2qigocuEkvHGIHVEhbHO8ZUFH8lQFrJaA2/CjdELXjahsgzsOQwDXRBg9pDyb6d15FVoW/xzjYvRqfahtBmmeqLkF70HGKyRhOB8A1VFwsdVNWPZfG3mks1uMXYuxe2DpnyApT0MaHgZyNZZoYit57rkTfdk5hSgStm8524rgb4t1foMLOxse189yLI6FDZkKVrW3YWxGQvVA6sS7vVfK7JbhSNsqWhz8TDpqEU5egvBpznNg6ZvWW8aXK+wKkWDeG/kqSfVJhC5HgfeNsiOUhEuHN6LaPbjtE7h73APAgLM0ErwBxksFhu1w+cbv+wGlpUtZENEwjV6hWeXhf1yFTH6cFN2Ga6nO0bYXz7YDVpqnKLBepBX22zMObD8yNIxQ0Mp0eBjmZciPnxKVVGh8vnzmb0RPkd2/ecNk29j3joS8BGxOJop3IK/WBHs2kAmrsA8KqRPdhori5cc4bp0bsfQqBL+sLuYPRb0acMg+xHTNCmGZCmodJ63bL/PXHX3l+qRu4pIllmvn8/LX+XEr1yWgQjH/8ww/czi98/NpMXqPwx+/e8o8/VEPW9x/e8zBPgxuKF3YRpBWBU5op2dkuHW58RQLk4qy9gZWdeZnHeX75+TPX2zqgJCEI55ev/OnnXwH4Lx/PXHIYUO4HnvmnX1/4335fzW7fvJ04f74MA8PHdx94+v4HwtTFNKqZpeUySMTrvrJE5Y+//129n59/Yd9i51Az2cKv1wv/7aePQPU8ucc9epg4a2ssWhFs39jbhuBhmXiYlsEvTNNEiMqlmbzc9h3NhRw24vB70SqFPZ6BKq4SWr4yN86l8vH6C0QOm45TFBRl2w5OpIfO84b5IWE7zJ2LXF+BqQ8SPxjmMiClSOOAv6JQuIN2S5XirLc8TIpjipgb1rkwzXLl4CDVtrd0AqNBydWao4tNlSJogb2fptTGd5e3flk33Pvmk0qniBCa0k4Mwq83p3z9BMD3D4H/+IfveDhVqO6f/CPzFc4DZ+08aiScGgdp37nlXJvNrQmyTYV5CgPKdg2Z4Ayo72kK1VJgpIhCJHBqnEVTQ9UO4SgNBGFw12NUVrEhIZ4Q5hjJZuP7MYWJSSOy1QbWrRhkhpdR8YJoZGk7oNObg5v6W8U3sREyt1FI0CY5neDvTT2td+QQaRrwbdNiUjH3GKE51KYQwRgcoWzG9byNRX06TUjyoXsvorj54ZkhuZm6jpFQPZY2lRKtNcXAODaXolpo1+OqD7Hj1vGjdRJV+gJrXvlAfcTjofny9MnIVAmwQ3yhMKG1AwB1T2bD2L0Zh0qdir1eB1+1aoJUP4A+8RI10GOaMoVCCjZMxDIFDVU9ql2AekX6BqJCPUltCmZq1VOjJd2zZ+YQcdXDbMtzvcf98FTIVkjjUj/wsl05tSIxpUjRAK1TPaXISSPPuZKZH5aZp2Xm15eauCcXTlUjq90brc2SYkeSFOUhJbL2DpdRyqGDH4pX1ZhWiMRvQOf+Ht9OnMLM3oQ0dhfKDnsn4WYjSjw6ieIgx+RWVYixenuNb5VUzmEnjdr1RvCVYUoWAiqJqQsV3FaWZamGqNRpshpDqMBlRkWwtuCuBbbdaEJlPC6B7x6e+Pn5E6U1mJSIYEhbMEPZuG6Ne0lVZ6wT7qMJUrIN4+NbMS7Z+PSlLn75BOtqnKnP6dtT4s18YmnHlHNhD8qUFmLLP/suFNuZG45fIpzSNHL9dSv8fL4Q2qT2H35I/OH79/zwvhYOOcDvP7zn3ZvqIzTNC3nbOV+bO7w5SBq8p/N6Y91XmvAd07SgRDy/DJNW4oK7cGleH1+fr/zl51/5+GvdrG175rwaX3ujThJxzqPJtu3wX3/+hVubIP7D799ymje2NpXX6W/80z9+5fff183bPE0gGQk+8rBK4HZ54XJuHLBdsFK4NmW7fXd+/PWZny9t+jbffc/ucYQWoz/8U0hs6FgLz9eCeWF+aCpx0tTg2ncvxcRuzuYb3qlnEtmdJjhV31Pdj8axKJPL8PxRVUSP9XS1nYd0NAsErR5evQTECMlHI/e2OdtWQGDpTYxYUTnXljM9G/OsYw1HHTMd/GbcENFXk47MSuh2OjwVxx+M3Pg3IQZsFbSds0etfjrGQKNkK+TsxJaPYnCmFIeS3cu+N+XNNvLYndXyaDzPWnlXvW/x1/PK+U9/4d1jnRDd3JjmJ5bGE38IxnPW0RROSUFT3aCNBpUzNXQRgBQhPUw8NhXAECr/axlN3kjej/rbvTbZl+apOEkCPzZG1VtThwnqmgvbzdBorO1EStl4ipGFQ/wir861KauyC3EJnB7bRuj02+erb2Ij9PrLoFpv6biRXgvYLrXn1Ul0mJmKhKosh43mpUnVEjkkTAOXfRsPVlFnJrC2L0NoEsupS8UKVTWljVmLOZL8lfBBNd1M0glosTL6gMYdJmJsXsht5LiEidDGu/VNpHYwOlrL6pfRrE+lrE27+pQiYG6HkawL8koRzl3bRs9GAdXfqUP4AgIeDklvBfyVkaMEokiF5lBJjRqEFDsk0DHzUZhEqYaqXVpRJDAHH8nHrGAaSCGMTSTmqMahIHJbM3txHksfva4U2zm3h38mMuMsS5sgAQ9RCV2utr4rL6OjlSAyEp65E1XxIOTRsaobTu33d3Oeb4W53Zo41YWiFyJDRv0e9wCwlTQfGwi7lSGFfZpnUpyHopeJoeKHr3JxQDHb2Zvbe9k39u2Mt2JFShV2b3UEEiKGHHKjopRyJoYqKuC21+lO23x5SEguw6iu3ArbBucv7bncr/zh/SOigdKOwdKOug4B/7LBet1IzeVQHxYwWEsttkOuktwdevKUIrPMo3Hzkq9kK0ynpvj2/j3RDWtQuS+b45pYYmFtlcMpCsQ48tO23piXR373tk5Tfvz4K5db4aF1RL9eVn74buHDm1o4TGlmioI1J/c1O17g3BbgGCNxOuSyIwnRC8tSN1IxKPvtVuFBLectQTg/7/z3v1bD3L99/cTX58LPl3av1CkhDrd5L852M2I3oQ4T2Wb+/LlOtX56fqkSu60DG6LyX/7tI//5n38A4D//r//Em6cT+3XHWtd1XXdk38d65Kq4zLxc6nn+17/9zOfbztvHugHMf9cJu8e/95jSVM3dqcgRsXCo0VpFoazXJmaEMzW9SKilhOB1Le8w/FDtgXOrZUyEbc/NTBhUEkHq+9TXR0IQ9qZUULbM2RhCT1NURHRIOk+lQsDWbuNhzULjlWCDU9V7rY+RGsm/iyk44J4PtTNzVIzYjnlPgaCOdmGDx5klBHITNnjUCkXb9Ki3VGI1RWnTNhev9wAAIABJREFUtEmMWQXrG4DdOe8r5n2zFljLcQzbuuNRDuGKKEPmGiDvhU8FXtY64S4BTq58/67mt9+9O/HxehtQYd2cNQRKDIMOYblw3o+m/9unxMNpeWXTUvh8vnJru84Y684n597IqwIKuUOeixLVR/1mQas0epcEJ7JJxhByk2g/54wvxmNqk68lss8V2QDgOaAqQ1WObyBf3cUS7nGPe9zjHve4xz3ucY97/LuLb2IilHMeU4aiClqlWgEQIcTBs0K8wuY6v2r3AkiTmq6/M2sTpTZVyFL47t1bbo18vK+Z677x9qlNFcQxscPstGHOpBPQJMKeB/dFI0yv+DsSvAJLdh9olheHVIxrn5MG46SOdONYcawc41+QBuHvXKjaAQ59kCJg6mPKJcUpgQOHi1G6yMHwLqoS1/0VxSoUb3AJguFFGC5ixXAZSr+Yh0bofg1LLGM0LKrMomxDsEFZVEjdR6gRgKM4W8PqBmma9I0jlEKdrE3djSs4IVePpXoOSlEjar8uhqTAU3u/z7czJsqH97Ubuu+53s9xYY8uer8S5rnKhLafA05UhvS5Wf28AckZ1/ge94CQEkvr6Gcp3DwT2nOdvGD7hf2lQeeCgpdhoGm5UPaVXLYhlKJuFboxJq0VglCa3LXEiRRmHoZfmYL58NMRDQQvA5IRtwrx+OlvlTPy48dnrnkfWHWZnFs5sYTIpU1PxBUx4dYEQy6XK89fLpyaf04KAVchts+47mdKlpEj5ziRHLR1FjeDLDLOcd82Uop8aaaKqhBC5mpnrtd6DCEopxBHd/rzbSdcPvHmsUtwe10b2nU6hSoFe4oP9ZhfLvy3Xz/ypmHsf/+HP7Be18rpAZYlIFHZcr13s8PNhOeXX8c5lD1zu67VOgAIZvzt44/8y19+rsdgIFNkflvbm7kU8lbYm7iC7xUt0AVjghTevHvDmyaZe345wyQs3ZPFlbIX/s9//SsAn3658b//p3/m++/fUXrnV0CnR9yrWIZmg1X41x//BsCff/oZlocGW2FMs+5xD4A951ey9k6a4ljj9735lHWCdQHbjVubcAaHvTQRq6m+x2OIxCSDE5Q3Z9ucqUF1qy2IcG5EFMmFh3TwmTMBLwc8rxRDXY41O1S+TSgdguakOVVoW0f1WPUUSlOrG7zyekvr7Ze9kEsh9IlRqESHgQpyYY7KY/MRchVu7uwtT1/3zJozZUxsCpILISqxfaYVJQJtEMJtK1xumdOpTbaSsu1loHyKV64Mbbqy5kAMVXQG4JphzTeeWj02TxMvFPRc7TtKNNQD//xdRQLEFPj50wt/+/xM0+Zhi4G8O94nPAWsGHFp0uQ71SOo1YC3W2GaIvOpQeX2Ot27tZwcBaZwMDj2W6HgPLap/CkKUwhspuy9jFwzWyk8dG8qr8ihwSGTAA7W0Ahr/u3FqL6JjZCIjI2N0ZRL+jfWna2UQ23NgVecjVIK2ZwleC06AC8FMzkWM1FW39HGyUpZmgFe55EIjgyicMqhFsWNmCfB0T0Mvg/umPjwgnAzzK1qsmuHzGRchNwUkL76lTkJoZOs91KTjnc4Xj2mYWAodSPU4XiB2Px62mjXrRnpHRshxFF/pZimTpGCvPIVMjGm0JWiAA3jQXUvEJRLK0Ru2413bxfEWoKjQnY6vC94rBurfjOsIMIg6j1OE3vOKGHcz2rRmNHBmQBEBlQuuBDDzNpFJPbMxQtL4yk9TqGpXtXrdL0V9u0yNnvTHBENA4dr7hXaiBxiCF5wk+ExIFR+1RDX0Kpi2Iu67oF0j3tAVRUsDQrnWn0SeiGh4pxfPqIvh0hKEF4JcVTX7WIQpXN8JsTz8BAzdzAOk04JmCp7W9SXN++J0zRerxrwIPV5BDaBv/z4I//2Uy3ev1wyITnTqRHyrXDZd2Y5eEpRJ7Zt50sTHvjyfGYOM3Pj9IRsbJaxDiddnb3s4xmy7cpNA9YaGCJOEOXUiiMLgbMVYsOeq1fPtPO6Dyht2YTbrWC548+NpAyVt33d60az5f95iTwskdta78V//dc/8el65Xcf2vt5dZnrMLR9NW7nLwNyc5qVyImXS+UQ5bkwJSVOR1NtTgtv3r1leaqcoOs5Y+ZYM8J2g6RhCMyclgTmfG2b1DAlpngoYj08PYCWw29OhSkeQhh/ej5z/b/+hf/jP/0zp4fGNw2BbDfO53atEf70l5/5l1/rBu42Keu2DVGI5N/Esn6PbyRsd5h6UwWCBvb8qtEc9FBsw9lzIXivERzUCEWGyebFjYXTaOqGUKHrnZcbtarPzt7NSKsKmbTaaNLAEmUom63ZSbMioUPqazNBRxOzkHcQjUPtLkj19RmKuFSOd1e8VQ2EaWJJPR8pZlW5rf79jswPg1O0W23+aG/cZON6zkzTIYqz55q/c9/gNRvkW8tXlr1ydZo63o5hTaUPwE2gONaOaRJlllSTIfW5VqrSHFRI/iSMBtenlytLmpjW+u/fT498/xj5co5cGycjifM0zdAUJ/dtx63wpVkh3radl70MP0qIFKd6yFHhwTHosfYEJwjDb27PjmGs13pQH04RELa9cG07QstgUri0HJqyV5Xmdm+MUsUVZFSOv3l8GxnTx7JQ+RyvDFOr/PHBpREaV6UrlqColipE0F/kqSofv5KFjhIGVjM+ThTWwbdRr5pufbPlUmqx38c7m1XVjLYrLtQuxkxPFu0mi473TCKIR6b2hfz8svLlEnhou7EgNcl0cQS8PmhdzraIN0nv9plS2ItTWsd2ve3MKRHnTmYOqFvlErSFPuKVX9ULfql9oTx4SIphY/KBSCX/tYf/MS1ET1iTvBWpGzYZ3U6jiAzZTHNj9zC6wOaOoGTLg9PVRMXH5klUqyJM50rVQ2bu+GOq5PDl1jD5JAQnhdoC+cOHN3y9nrm0ZPQmRYoql62bozqbQ2RHu1qeKBsc+GExQmQUEtUdnkESOrT67nEP2K1g1gmywkOKfHhbv48Pj0uVeG2koKR1Wj36OA4lC0kdbWqL5IbpHk2NKhJT2lOSYlUj6mvXMiXCdKpFClDWDXXjcq4F/U8f/8qf//zjIK++eXsiJUUbTrzshW3fEI1jY7OXjdt1ZW2bCg2R5XHmTZOidje8bGh7z+iQ5qPQCNOMm/LSOoklb1V4oS2oNzOSG9LzWzFsLxRzSpObtWx8uW0Dj55CIAVla8/yPAXmZeHU1PJ+//4Jz4W//FQ3KZ+vG28fvyNQ3+/T12eiRjarVUBVktTBZTiniXlamZvJa0wJVa8GhalLjWdSnDlNder0t5cveAiIvVINjK+aKjHwfloIexOFsJ30yrl9s1Lvc0cGaFU0LY2b8LSc+LJd+S//9m98/1gnW9+9eyAm4dw6qJ+/Xvnr1xdiawPLba0FXUtTWzm+R/e4B8E7hblOgsLG1JqVKUTcNqyLvZRSDezbn+bdiCHwMCe29uzbnnExYstxcVZEyhAUgcC7x2VwbNe8s+5r5e9SGzHrNuHSpaoNKfth2+GGKITWiH6MJ7bNqxpbyw0h1o2SD/EDuO0HKmZSOMU0Vm4zYy8HbzJNqU6ouohTzkQJo/bZ9r1yINvrszjFqXYhw1A1IOqE1oZVNcIUya1WMUI1hi/dCqSeVy+YhJ4/2lQ9VNnx1GrGEBLRjVs7xiyBkgI/P9dm1c+fviIilOJ425xtARYSSxMgmGME24Yi8nUvBE28tJw6Basqpm1IoEnQKY7mubiRs79CCRmiZdStOcswme6S6/OsxHg02NfcuOZdkfTmnDehLZnNpuG3jfsM/R73uMc97nGPe9zjHve4x7+7+CYmQiGmoboWqJ4cdgwpqtzpa44QjA7rNLVdKkroZqaqTKrD/2Wn6di3bkLxwiTTAbeTOqWwbvhEoOTMtanymDuPyzK6hCkIweQw2jRBpfFMXpmXuhlLkzJ9R+1udk6PVv3tw5y0nVJXy+t41v5+pRTUI+emVvTz5y+8fVx4r5UbE0RZS2EOryQjVZEpDvUhbRMhGxfX/64LDQqexwg7aUBNxpjUmiD5EGoRKq9hwPsUMWe3Lkt93MSpnwdOxNnbdUixSl1Lx49qlSFPbY++K1B2rs3XIMTKEfuuy/gSmecZaaP/qKlNrhoUKRh5L3Vy2HhIEhz06JKtucpveh+j90vTz5N73ONVuAwlQfXAEiO/f1OVzeYwV+PSDnewMjxoatRcEZomZH2NYOLD18pFMJzYPH7CnHCP6K1+5upG3ArrWpUS1/XKDnz8W/Wj+PHTL/x6NaSp9jwtiaw6VMdSEgTjmne21gm2Yjzftv4SphRYApTWGxaEFGBv3bs0T8Q5Mi19qiqoRx5Cf30ixTi8koJKm4t0SBj4pFCU1LqPOWRkg9I6z5K8Skc3qfzTdEJS4PGhya7GiW0rXJqu72k6sURlW5uMdAjcrAyvENJEUatdUkBKzV97U8IrxTgtbxAVYtPUvm2fcITH1s1+mGY0RSw2lcDiEALnlky8ND5Gy2fn3Xk3H7DrzY3gMiTAzSrQWDvaQHbiJLxcMz//WqGNb34SNM08N9Wt27oT58hTgy3OMXK1Ql+OXta7oeo9jljLZUw2gs9YisxTX48rrH9vD37QSJoEXzvktRBmIaWjVllpNVdz1chSlWhPpz7tLaDO3OolVDGZ2LvXB612Ch16bkzFiY1brCjZy/C6CZ4oAhqO2mPfjChKaXXENTshHBSL4I6YszUOJKXghCHVP5Nq/dfeL4ZARNE2hfKw40nZe11C5U8Xk+6FTJxq/RmbN1rZM7kYW4Pxu9WaqGhTrVShGIMmYG5/R10ASDEO8/kUArfd8Ta9Oa+FcruQUvs8A6RwfrFOuWYuxi3LoEzM0YgpcO1rUMngVdEO6uRs3cowt13mBuPtasRUCxe1QyEwqA4T1JyNYsYtG3NT9j2dqk3ttnb4sCPFhldkmOBBGDVb/gYKrG9iIzQlwXOT2iuFXcOQRXSgiHFI7DWibCO5PemMbXArN9YGL3CE874O8yyRhoFN7eaq4YPxAkLAJQ9MKl4XrDw4QYKY/J2vkLsPKcaxtivjSS3iEAsTdeY4TVVGd3gbUX13DpHr9kYDOi5/B3Orr3TmBoX74d0TUwykPlY0q7LjVsYIEqojfQ/vct2dP6OQ0EFSzFLqPzUMjsVImgxri3Zuh9fP+/iU8QkY/mqjVL0w8n6Meys0D/KA74UKVRl6ngEJDLKxKCxhQdroNuBgMlCLz/nG7j4MWi9zxjH2tvlzlCSVmdSTmko1CevMHw2VINoFGmLwinNt/x75drCs9/jtw1WwvtEWeJgSb5f6BU0i4OWQXm9Q0CPXVwd0kUMoxZUGk+vPleFMNNcuQpwxF6wVwutto+iFT18+A3C+XvjycqN56hGlQvRKl3QODQTbigD1modcdBDsgzvvovLQFq99L5TdsCbJLRLwkJiagEPRyi1ILTe4V45i59mp1H8bvh3UTcdo9KgQJNbiKh8w1phgir3An7DdxsK/7YbJypQqnyYuM2XbkCbAkIKCGzaAPeHYcFE9yx6XiYfGUwIn6WGUHUMiTTNT0iGHrfmB1b5wa8cYJLDdMmvnBYjgZngTb0mqqDtrg8MUca5lHxtMDcL0Stinux502K6KM6lSvLA33P+/3Dby5wuh5cw37x6JIR55Nkr1rmp669f1zmm8xxHJT+yN57pRBZNaKmFJkRASna6x7jfy1UeDhKQQI9ecB3QtSsBwtrZTCXkHbDRMizjPl41lORqLMSa2Vp+pG2ERcrcL0AqW73CrFCLszrX7ptlWm6yqR6NmEkKT2e6HiQuxNTmyFaxsROn1VmSOMjYZMVQo7t7zU5BaK22tTtmrOHj3dsvFGrcqY+0415JIRE6t2Z2jcl5vg29lRVAN4xjUqhCXl859CkSVIehQrG4sOh8nqqLk8XMphRcrpFyhvmlJbOtGSqdhZrpuhpkh7f4tqTaae2P46XFh2425v343QqhwSKgbTLEwxKuCwC7G3vJ+cMWkjDyeVAlSSCajmX1+2VDxwWF1QjWQzm2DF2sp3ms4+QYMoL+JjZBonQQAWMloSOPGmilqOrxqshslF6x5Q7z73Tumt4lPn41f+2KFUzKspW5z193xCZ5CVR+aqWIIRzHjhFF2NJLaPA0vEIrhgTFhWkTrhqYbAQavmFkO0zAH3PS4wKK42tgIJYTizt5FBKR2EftRuCmIVX4BtcFcrJBaJ2eaFiYNg5+TzcjmuJRh8CVWuyIeuoBD5+PI8e+qg4/lpfFzUt+NRehTH6pZqfrBmAnS3Y46Ebyqg3SeVLDaSbns+zBZDRPcroVT29BZdnIpQ8EtijZvpEZq1MgkBZlb19g2RKa2OYZikbUU9lvt6i7hVJNmL24kIGps5uMzxEJNPq1TI5qQsI3kISaVn9WubX/o73EPgLfpxDXX3FKsENWZ2nOpoYm/9I18+5v+1NTJs+Ec30dQosRXrZ5cBTzaFCLFmbxloP7888e/cj1fmRpv5fliXAuEtsgX6rOd2kSouCFuo9BQqCIngZGPZC+UeGDkl7yT92NKvpdMIuKtFWhYVcPrWPJQeTJyVOe1M/R3vSJDeivRqvrkum9svftcqs/HQ+sMOxmJzt5MDh9S4rvv3/HHD++B2tV8/rqR90O4Yt32DslnQ6vvRfcw2yunsYvqiGbE85AkvVIqT4g4zmO93vjl0y/c2jEwGeftNng4ErQ1m+rrn6aZlITUFv2HUpCSjw1n0KoC1zeMXS10NMAq7zWrMbUO6++XRH6QMbEmFwQZzSILXnN07/LO98bNPV5FqjUPQLTaGL62h2RbdxZ1Yujc5pkNY4rHmr6tBZnS4LIQjFSESxceKBuoE7zmGxNl3ZytkxqNWvWOzb5gO6RWP8Wk1Z9wGL8LxMBk/RmpBszrbSM28ZWkge2Vgb2qV2NQrblgIZGjsJW+eYNJXxmuxoBk59YFINaNkzihcbhNI2aG9clH8wYqQZm7Kq5UcYatrQVr7rnkFeHZnNgV+Qg8zWkgTW7ZkGKDX4hUr8Ny69demSzU5i+1gWxFCO3zn0KCNzNf1pWtN2ZcMdvIpSskK3EOfGiGuR/evsHch+/i5XZjWxVpNd/5AjkyOEUKiBpLu+7MRtnl4AyF6pH3KAHXLh4GexZ6PyamalA/db+l7GjQIQTWG9S/Zdw5Qve4xz3ucY973OMe97jHPf7dxTcxEaLQxA8hx4hI1ZUHhhyzv5oyqGcua92Ff/r6hXmZWMlDkWgthfRG+Z4KobjtO2U3OiAiqpNN6dooLsLuQp/QSevV9o28hapId26cIY8Bog6Z6AFt8CouDTSXGj/kraXJNOuYO1WcbdtZ5wLbXlDt2M7G6elcg5zRzBj9msDmmaP7ILUVbFr5R+24JMgBQO+f20cdDarSVeBijChVFaRel8xeQoX7ANELoumQmaZOiw4uTeUB9AlKKQXbje2Wubb79fbdiafTafAmPn954Zrz4BI8PgiLhkPNpRQCPqTQ81a5UEs4oEjXbSdsjUOUZ0I4JL6jglr1ThpdeTVCjFxvXUqzGlUNeUd3CEpofYI1H/DCe9xjs31IME8Kp9PENHVPsSbGP56J19DX/hvD7Jg4itYuYp8PVQaRoU1N7breOH/+NNCjD6eF63UbXb3PL19gmQZM1k3RIFjD51XepVa/IirXD7Oak7qCUardy0G9I0DwTnWq3MB0QGiCdwXJ9u9ez6A/M0h1QuuTWXcqJzL3Z8yQImxb4dxyw0IgpFdczq3msg9PVT3th3cP/PE//I65KUY+f/nCp+ev7D1xO9zyDW2TMPyGljD4EepGWb+yN1U5UZjS1AX+2PJe8+seWZs8/59//Bs/fy64HkvlnCa0ww4dVteh4JclkMNEagZwuXELXssRB3z4oYgKiBDkgBFV2HAitCbsmiucsk+2TGgwlANm6Bz5awr3/uY9jgiqaPv+bW7Yug012+hV9bX7NuZSESVLm0ZmAd12rOzsHYIaU4XLt+fKtTDFcPDeUEIqWIPlq4SKqBmePFWVtf9crHK/+/sVjPJqSlCKU3IghjQmqZuXim9pr4sxIcGgD39FCFMitbVbzMl6qDdWCL8NLnIJQjYGV2ovAqKkBtOdpKAiJBxpPKLJYdvyoGQEraibkSPbdLfXV2bOl/N1nNcpJm4Gc3teg1ZF5H5OXgoSjuk0VuvKOKbuyhICaxB6stimC54T66XWtlc30gpb425OT45EJT3UHLrEmdtSeF7rObx5t1N2Duny9jnDLqLUqVSH9zUcEEEStzYZ8+IVStjqUHcFD2MimF3Q/ThPvoF89U1shMQh9ocK6iLdRpFZMyLpWASoN7Ivhud957JtaIzkTr4zqVKF7To/LTMlGUtbINMcuGwH9rLSYqzBvCCXjNkBAZME21p4af46F8l893Z+Vcgo7oLBIcnd6TgDVqWoKqVDZto6NrZF9bk7MPYYxTpMrJqW2e5oOCAZKmHgVYW6qBazwT1Qqf4W/RjcDfyQCTep3kI9OaRQsbC9gFJV3JRLOa7901QO+B4CamND6C5sJYzvtYQd3WGOwksj4+1rwacySNfZSpWXbIt4yYWS/JWnj4FVKcl6ThXOsvcHE0gp8LRUsvqSJnZWaEaPWQy08Xykwy0z7nEIRUjeIR9QkxAgqKOvJCPvcY8et90IrWHx/TLx+3fvhieCmuEizYi4wSfk8AuDmi9CxVW03zhFnNxwGAlly4XQvuOXr4Xr9QKhQuEepweup8LLpyqO4FNimtIwhJbYYL+dhSpVtL4fQR7iDTK4eWLN7aKT9pNUgZG26CfXJrbSiiEJzRuk5W2rZn8c71zl+jvEoibDwd0jV+gJVt+7vknh6XQaMr0SM28fFv7j738AKi/SNXO+Voz8L5+/cL2VAZNFBJdI7CIC8wyW2Np1zHllq2cFwCQJL8rWLsxjqrnxfM78jx9/BOCvX58pOtOhulFbjg/HBs8phHZ/t7yy5mnAqJ0qnNP5E4SCYWPTks0pCI+twRVDLVaLG9o5XeKoHYWD4LgLQQ4JdzGt/A+AtHCPe/TY1gOmthcjqRC8SzpHbtmH6AAiRGXwVoS60d/2A9YvxQluPHaT81Bl53NXH6ptHGjf6ZSU3YxTy0/F62a/m37uItWwuR3CrRQ2Owr+PYN5qUVVq9lmc/LEqEVkr2Dj0psemmFTJHR7Ecddh9BBkR0kjI2QmrCXwrkJr5RiBOIreHzGNXF65VG4FWctfjTYRStdoTVtN9sJqqNGiyqc0sTefYhUSe5jg2AqvDslbm3zlnMhi9BOgSiR2+rDKuT2vCI40+lo6pcykTejU8NFoVD4cm2coJ8+MU2JeeqG9oF1K2MjvN+MSYTSukMalIkw+IhZIUc5YNhqrNczFmrjq15bw9QJHYKMI+osoee8av/Sm+FRf3so7zexEdLw2mfDcQljQY5M7F6GDw0iECD3QteF4K0T2f0nouJFsNbeLFbZMQ99d59S7fh1u1ytF8KGWlHitjlrcwvvuO7OnSnFKMXGn4sDUh/KvgAKtVuawrFJqP5HfQpRPYTieBMhx2MqFahFRmr/7qkprr0qGlzimJwVMhoCQawW+VTT1YV9eJ6YG6o63OA1OqZObl0Q2zPZClPrRIPjwQZeNBe4bQZTU3zTuU5T6B0SQSQPknaQSJwDt3Vjbh2o6RRhhtIMvh6mE55eOV9Hb93qll60PuRdWcVd2a6Z0BRqUko8auRhGK0pt+1VV0Xb3RA42tfKZlY5UMCuVo18e9IzJ+7WRW1Gx/ge9wDY884y1y/F796e+O5xoTN8AtTHoQ9q24+jreJ1WvQKSd7+5+DWmSrX5wtfLj8BsJzeU/aMSVVP0xgpdnQi45SoVkVtQTVvfbrekXv1MfTHQI7ngcpRfP01DyK1+zr+uOYvfbV5M6M6xAPEutXqpNy60dOxcaL+OIRWdlau2bjkndxU294/vOHD+w/EVlAtpxNvHxbevnlqb2Gst43PH+sG8K+fPzMtCw9zF6SZ2LOzN85Q2XfAB1+LECgFcqsSxB1NgYfGxQpRKQ4vtwtfmiJfbmIXJfcpuaNueOMMFerUrE90HGOzjUwXmYCpHTtUs0G3cHSVYy08OyKiejFWZc3Q1pKolRS+t8+IJeDm4zMDAZIPTsWSev6+xz1amdNRHiXjFti3LoBUKoKmFbZLDIgXrm0ims3Yt9pUXZpAlaNEKYRWwMYYyRTCK//AUGSITZVcYDO2rpIpjqr3PQ2m1Vetq9mW4ki24b4VEdYQq3BLq1U2DYTsx0alcW16nSEiLcW1pm7jK1urI7ZciDEM81IXsOJI3xCaVT+zhjJappndC2su7E3kIe+CRiV3fzarDaGe46rQVUWjQOXCpCkyt2PaRHHPw9fRc2Y5PTE3YYt9Mwo21EOJkDRC+/zdCu7O7eIHp3EzrJRXnkxQNu99Yc7rxqw7sd3vnOs973z4JcWKgGn5bvedx9NTFbAAlui4CXNHHZnzqczsGE8t72ybUdwP8QyvzZ7xmVsmBMidy85vH7/9TOoe97jHPe5xj3vc4x73uMc9/n+Ob2IiNIVUVYh66CGvnL38TwdZFXKkdxu8jt3MM9OYGnhVSuqwsQI7mS9bHzmuzSm9wTza6K/zUEScm61cmx/FW32DBXg6dYnUyobpO17XijCJDiJdsS1g6kM60UUwc0rrmmhwzH28Xj0S2bleru0Y4LQk9oG5d+IkAyPrSMW+dygeilpmL4XctDFTCmwljHGwqeLOwQEqXuUQORRkaguzd0WE6IfK3BSEOR0OwTFU9b29TeK+emES5SFO7ZiMslc1u7V1YeOtkFQHLG0vK0Hn4SKNVQ5DR9ms5pwsHHAeF5aHiaHYtwshlaEcZbpUFRLr8tyKmVEqALfdr4BmG/dm9/r/nR5Rle+U0nC1Kt9Cz+Ie30qkqJyanOiHxxOTMGRci/xPE6AW8uq/B2jakZDEAAAgAElEQVSq/1Y7xgqAy5b5+Msz/lAnHfND4Lplzlt1FH/79B2TRmJ7ziwoYAOG5lZzi76axrxuu1XM+usjAkQqSq7/SJ3+/P006fUUyer7D16SVZuChvvvn9En+d5wwL43+F8yliKsrUMNsFCVN9++rdzOd28fWUKgw9Jenp/59PLCj881R+4kntLDgNHW6dMxqa/X4FB0E69qfd3ORHY4xYchj//4+Jb1duXTlxfWPiV3p9g+PE16aunw9uJOkuqkDhB1YpoOHuVecm3JjzxdoSOdK7qkyCkGTg2tkIJCiPXfe45zRzxj1mwN8l75XAOGrdSU2uEsHaxzj3tANBvTRHcFZHBwFFjmiU6rixIqNGrw0ZwoxobgbRKhGthF6niTygW+lYI21dU0R2IKeOiTDkNTGJMPMxr14JhauNccArBtguUyntPpITJb5Q2ZdCSIklIZa7MEwVxH3ViyV9htywUpCVMSpjb5mA0mUbrV0WbGknTAk295Q6yQYs3BMSYu68q2lqHQFq3ydzqXfFHlUg6epZtwzUbs0tMhoDi3lk23PbOveUxKQohc1hu5Jd1ljsQQCB0Sq8rZ18HZnpfYJkI2YNFzUGKUwZu82f/H3pvuSJIkeX4/EVU1M/c4Miuru2u6d3ZnSYBLLpcEH4KvxBcl+GGxyyGGe8z09FFVmRnh4W5mqir8IKpq0csHqATaBWg0oiLD3U5VOf5HQUQOYHQAorC2g4wBXnYb0vwnAqqu1Nzv3dvblZv0dVt5WM6khhoqxZiniq23oXAck1sEMKBwxrrbkPU3jDQf1i8DFfULxjdRCJnbegFtURcl9IepmRcOLCi1Cc92EhyIVrBK6WT36j4fXfY5SkbNuG4OdwiDi38UU0pAU+eQwJaN3KAGooYEWNrlmkLAOIqSiicMER0vGiJYqMOIygwIgnWNeYPMPgwLJ1W0JurSHpZdMCKlE2JFvXjqeHgL1JwHEdilF33x2Js7lspCjEcyU4uS1xufG+nx6WEihA7eASGx7hkNfgzPy0TQyGsTicAqz+cTp3GO0cUcGkwkZuExTTwvDmXZbefHlwuPD8tITkKAOaUBZfs5F962zEO7d8s8YyqUttgkEW75ABKlWbF9GolmFKXkzdUl/CSZNB5FT3W54nqAdIiqbMWY2ig3qHFhG4toQlFN5K2f550jdI8jHmbh+0fPHL7/7gMSDxl7GuxN/5uBf3/2+nPo4LW+ATgXMLfN6/Pnr/zT5688FvfP+fR8Y9s2btdWQtVXLi+vA6tuVRx+0X+2hof/b4qxo8h5d1AD+dbERN5xmYxjbegQ3I53t+JNnY4kyZZZ0nxAebXzkjpBFqggdkjNvl0zxXYeW8H36fnMMimRZmRdEm9rITeYxrpuWDY+nJ0rtWw7qcBeu9fH5sfTm1EaiVGYmvRrLca6r+TOTdg2vtY3ut/qy/aVP37+iZ++vnFpa9q2v7lfUitUTmkinmYk97XBjbQ7BWiSREwyZH5hQvSdpYAEJOiQNp9iIoQwNuJtvXFdN/Zy+J6JBuYoYw1NokiMoxBCDNHh4UsePkr3uAdeNHdPsjChwvDaEgkukd9zmWjoFNgbZ0RywVQ4R+XWBIlUXLr+2iGmxSjFhihTydW9+lqDwaLLOk8DTgVr3bn1xLgIIoGHqRtIw3qBDlgSCYQkaEzDpLPkHaoO/gy1FVPdw1W8gdmV5EMQas3M5muNTjNTiqNxczLY18y1W6qYkGultGMsa/Y2S7EBl5tCbDyYxgdV41nUPSSBWgL7atSeA4ZKrG6x4N9hzFMgtIJxDmCqaC+0mhdP6o3lHbQcvPEgStJIPO/DsDlkRQmY+b1aQnJueFtLtmpca2Fua8da9IBKt/PbShkeQLMmJtMh0rXEwLZvfGnWNJdLpqiBuEktwHnuz0PbO6KhJZM7NzP6dw6jcf3LvfKXiG+iENpKGR02Feek1LHJV2jO69C7fvKOZ1zdK4ZjilRwwYCejNxKdR5RJwCaO6u/7+rtWtBGLrZcQOo7NbXAWfMgxBqBGI7kR6ohUgmio6thYkQ9jPMQQL2qB+9G7uXQlO9qcc9tAy2TUkPC2gNH/+w+zTGQEIZSh5YIITo5ryVUrgFXx+IgmxMeP546yTZwy5XHyROua37hdt2Ymx9AOgsxRJ5Phy/RImmc91oLtdahc09UrttG3n8CYE7CeQ78IAtvrVDJVjjFdBh28cA/fv7Mz63Y+rXCeZm5tXv3+euNWjKnczdZPPGQlK37NYmRdBpkTwOixmEgZ9WTsHLLQ9Xmy+2FvSrfn9u1r1AlkPuEMBumNhbR634vhO5xxL/73See2/N4jr72/OUkhDGNNkCqjKlqBawWF1jpk4u9gghrSzR+/HxhN6W0RKLUSkgzS1s71uvO23Xl0hoe8/OjM1nknbmplTGFCKIUnyG3Y1Kw3ivosx7tB9s+wzCRUQAhrSnVzmtfM7kIW+sSV4xT5JgQmfmG3SWUrEBVSltjX15vxB1+Nc/8+uMzAH/zq4+c54g1cQNKZVtXUmoKkVOgSGCOfp1eGsb+9OC+QnMtXLaNzy/e8KoipGkmNrPT0yLU8MTLVyco/sNPL/z844/cOo9AE1NQwiJoO+55emCeAh8fXLnu09MJDYHcOqZq1a97u9Yll9EY8qtraC2UVqxNwFYLZfN793J7c4+zBuK/bplqBZEy9i8R4U2OZLZIwQhDoU8NditH0+2Q/rvHPdgkcG6IixMCtQyuDCFRm98guDBHzjbWkqCV8wR71sE9jkGdD9xVenPF6rH+EDxf60gUSYIbHffGsu+5XVWMtg7NraoJU4RNWKu/56eU2PdCzWXwbVQCRqK0/GeS2HwUmwiAgEZhaznh9W3jPCvX4J/5wESKxmnw6ZTP+9t4d5aUyDPNvw12E5YYqPGY5k4xgDDW6XWraHz33kZB1jJyvmourtBV4s4hkCJcu5gLxqRGbD5B61pY8z6En0IyzkscqKJaIMQEWtE2dZJg2FZIUy+uJqpVcruWsQi5HGim8+SKlV3pd10ze61jr8lk59t3LtVNWPNOse7dppQbnGbB2ndYVdDA1l17d78WsU3bZBKgjgnhL18G3TlC97jHPe5xj3vc4x73uMc9/grj25gI7YXYOo+7Nk5K7NKhCrWMqUaoStkOiedcXC1tkeiSibiELQOBCpfViLHycTlqz1qOGjDjU6Lhr6M+vnvqSmdRmpR1/2OfFmlXvVDxbpwJpXUDK7UpL/VxjLCXfUh6pxhJElmbduv1tvnIOnS/nCtpy0xNCrUGZWUbSmanORLDzNdb6zbkSlGlWOX85KOOgDTZqnbg8058npk6F2EvvF4v1DaNWoJ7BnXVpborQYw09XOoLqHWOz9N0rWrv8xqZKus474CAl9uN+bm+6NAMSW3u/O4zHz/8EBZ2vh3ScQYeGjneZ0j+60MmGPejDJx8CGsEDSxdQ+CWkhqvO2tAxIC1/XK5W3jUX3ylWthL5l9yMz6vVva1EpLYSvGuUMAuXdY73HE//C7H5AGH01B4B0syTEaHO+cCVY7eKJNhMxBYx26VsUoNbJ11SSEmCLffXCuzDxNlFrQrqY2L/y+fuVybf4VYYUloOGA5YoccOJSXAmx+4t1af/3YcX8ndJjouNqazaOu2BYg4qcQmK3zHVrU/ig5FyGjHiIEQuwNnJNTIltX7k0DuQsge8+THw4L/zQzvPD4xkJsO0NW24bFgPT2X8v60rZrs0/DazsbBus2xf/+eMjn57OQyXu88uGXd6w5kO0XoyfX174v//xn9vvL4R44vzQJkaz8P13H3lYFqR1PAkJTQtP3XcjBUopY0XIdaVk46efXwD4hz/8RLXC+eTrWVJl3XZemgrdeZ6IGkfXOGBUKwNJkE0JweHgHZ4C4kpc4xnyDvv+TtbfqFzbQjx9Cy3We3wzMQVlbludiBItOF4NuGbPVfa1TRk24RZ2nibfrysu566T8NAmFRRX1A1tvYkqWDr8c0wN1YBZ5xBVtCauXYLejFAM6dQDMuzGW4NzBSopycjRttvONWcwZelisgS2dWfrMuDRpyGdriCqBDP2NpZKqpTC4PI9nGZOUxrwvWrCanUoDT+eI28lHz5qEohViA9K7YpqYogKT216cjFzZbrS+c7usdjXefcCq5R3tI+8c1z7pFQpA9FTivO6X65t6rU7j7SrRebsCr4SFHmHhj0vC6cGr9vyDsGITVmzFGHdy5iCTyIoSuw71O62CafTqf37wl52LtdGK1ElhcMrciExTYVZD4OGRFPg7bks7sMZew6P+gSxw7K/AcDNN1EIVQRrBcNed17XdWwCj/NC0jQu8lqy+/E0nksuxnly06ruzYApc1L2pp0/SyXZgXO3rs49iiFricAxdg0xoK2omSSwwSCDvU8WABAhipJEMGl4dCpJh+g3mYIWo0vtl7hjufLy2jHzhSiV706+ae974sXWIUkZp9gWmpbwl4BI5bGtcBqNDeNWj0113zMZG+IFYZqcXNdexG0PPE5PnHqClJSnrbKVt3GaKjKKEOc/yCh8tJkfdczq1QpVDrPAYMpadl5fb5S5/bckrLYztRF2tMCyLMRWpIToieN56pjUhbftdRRfsybEhLc2qt3qhhUj9qK0rOwlE9tBnCUwpROyKIt2guiMrDuvjXyOOsik3/8YIykJsSWmnz7cfTnucUSIx7MSrK87HVJWm1R+X4tcuGDYpao3KMzerVcSPbEepsILcVI+PvlaEIJidnBlttcb23obcrNf3m6cbGJujR4NSin1kO5voJTxff+/MsiLsXdQcWf3uEuq/0X14+0ePedlZirKbfszAHtVzinRlKjZSybBkMC9Xm7s241TWwd+OH/k15+eeFhm5sYRKvvO/nobQji7Kug0oCAl71zXr7w2T4w//OmF//LzF760pse//e0P/K//438/vNb2+srL5cb1jw6F++n2lde3la1B5b7/1TPLMvGrR3+/P354YElncjGk8ZREhRiVU2sGpSmhIQ6Cby0TpQjbzf99sRt5N/bGgdTknInc4LUlQngHEwJPTru/XG33ySoHFLsV1rk9Q8EEzAZ/tGC+Dr/jrN7jHj0u+Ybl9t5OiogetICyU+U9TMkIZpQGwT9NAfbMdS3u5YM/jykcnLVAW1t6QmvNJLW/I9lhub3ZrQqlNWv858n/W/u9vG1sEhj6SLWCKPMpjmZAUiVFmIb/kVJLPUQeVNlyHZ5hqpFllpFfPczJuUnt8277ym3P5AbdXeuGwOAG1lrJClqNune4nDKlxN46D6nJ3HfUoUZlmQ//wnyrbBm2vp5ZW9vbQeTczGS3Tq/w69yzSL8Myto9yMQ/6yQFSsufcyHnSjtsaqmEosMjMe+Fa37v0+iDgFbLMZ8CZG8wA6TJCBaRW/u84PYEPRfeuZGzEorxcPY889cfzly2ws+vnkfetpVpmg4vSDPKnrEGF+5CHr9kfBOFEGaDnBdEmNuLAXg2HmVU9jfLzJaORKMaeVvRUxpqGiGq48LbPwlLJOdwvKiiTflnyHtw28sw8IpBqaJot8qqhpWK9gmBOsC+F0LSOqcZe6cw5ipM3dMwmXHdMrc2bXlcZqLqMLYKwagcD+zDshAqfP7acLJUljkwx+4dAWzbwKoXKmmemKOwNZfgpC4MkHpbw3xx+nz1ruxPXy88TBOn5OIGUwo8LzMvl04+NtbC6BYEM7LxF14iiI1F1czdMN7VTcwp8v2HM7RrebndKHVHmjJdiBNLPLyIcq0ojpdtX8qSppE4BHX1le+bO/znHEghk9oSqfHEW1lJXcFmmSmTMC+Hw3Mu8GrCpXEyrAhme7eh4izKl1thbvf7lO+F0D2OCMSBmS4iGId3RCU0r7C+QfuG1pOCoIaYks2Gn82uwc2Y2/P29HzmsSbmNqG0WqklUxtePSblh++e0C++0fzDn/7M18vEhw/+Hi9LcqXE5ns2RUE0jvdUzLp10VgjVcUbGL2jar75b+092m7uFN+bS/Vp5l88f8+/+dvf+jFF+PBwHvzBrWQul3VwYy43JT6deXzwd+n5dOLhdKLUndrew31f3Wy0+XuV/UIpmf3mzaJcDZWFvfp5/7i98rJWbpuvLf/nP/7Mbf2P4xj/+OVCljxME6c0Mz8+cm4H+Xia+PT4zPNT635b5Y+ff+LlcqPPXx5OC5+eZs5Ld2KPfq16kqcbISjn5rHy/HjmbTvOodZKDPB48r9PEltD6RDmCZVR5Ph62ppJ2n1bmrpn66JV8ySqjGVdiHp4qtg3kFjc49uJScLw38nZ2OrGtXHULKsjWfo/FoDA1h6u/bpRrJBCHMIoe3FETG9WawoNEeO/r+qqvT2HC+q+Z100IARhTomydfSMgNTh4/dWK1LqyE41uiFxFaG8q7ZyNvbSGw7KPMcxyY2S2SZ5p362UZnYWtNkv7lCY23Np63srGumtAl2serKwENp1qc/WBgGzqVUSi3Dh9EAy0Lsr3IUCMLataayiwr0f79W42Q21sT1Vvyd1q5A4w2plvKR8QJlqB2HSC2FW2FwvCqVXHdS6QrHiV3LuNYlC8XkULYz42o7jw9+HZ4fHrhtmeubPx+hujKcteZS0G6m2qd5ShF4KZmXr6/tWmUCkbVzPak8LRMyOK8baYmU1T9j6TCnXzDuK+Y97nGPe9zjHve4xz3ucY+/uvg2JkLIUFBSM0I4lMhKFXLe+fLms7l9r8QH97MBVxJKVVER1DpnxweincMTxEek3e8mlcN1HbyjNqtyeWvqHZPjaLdW0U5LRSSOSYeKtK7dGIWQGuZ/dBBQitSB3czB/UdiO1GlyaI2RbalJu80N0iGCSxl4vmhwc5eL2h6ZBKv9LcSEFZ+/5PDPq77G7/6+MTDw2ngZJFIMnPJR7wbbSHShlAsCZZZmZt8o9RCFRn40VSNervx3Eaeps7JCu8w6MUMqR1n67Cf2kGfUgElhmlwJh5S4FoPCgUiFKvUrtgnlZjCUJ8SYNKJfajCFdacsaaS8hCVmpXQ2jBhjjyWE2HqcuwQ5weK4QosuKv0x+9mUpNTf7tcMYn8quFinx8nTq83vt785l3zxj3u0cOsEKxPZt+rWbpijk9N2/MXXPa+K35RhR0jF2NrWPAsKxqnsV49PT5S6zq6VNUgpkhsngIi8HF+QBr07feff+atCuut+4Ft3PadTx+dWxM1+jvb3mt/K32S2zmMvpYJUvqU283R1s3fmdfXN8q2D/7hNEXKVPju4wcAPj6cCEEHLFbE+PhcuN0u7aLNzInx4teaMclQMrHBe0NQSt5Zm6v9bQuIGbkrFNWdkFwLE+B5ObN+XDmV7vc18c9fv1LalVseZ07TM9q5BmXFYuCxTdr+1a+/Z4rCn1+dY/T17ca2++y52zlYvhLlmfMyj/t5ihOxtWnFoqvxtfVsCYkwZ+rgNIKEOJzYbcvtGTnga9WUW2ueavNqE5UBfcO8+973yJwL5Z2nk1WHFW5dVrebwtzjHkCcA3PqipLFIVidx1IiKpXUFdwEtMrgbWzVSCnxPC1c7ZCSBofVgU9sJMjBoS4OveoWGG52IpyW5nVzSjymiWubUny5XKkIj20iLhjXfKitUZWawWJm28vx3wAdOP1ANmVua6iJMVPZu7Q1zu35fO0QVuEc4+AEva3FFRvbO5XmmWpCbnt/qD7J2inj/Ypqf2HlshXD9p3c6BFhE4hl0CFQYTaGhcpUKzEYW+NGVanMKZAaF2vb3WupA5FSzqw5oF1uew6U3bhsDjXzay1IEDe1BJ+or2VcJ02RKDB1SxAVHsI0YDxfX1bEMlP7jhii71fWVQShah3rW0WYgUtRrKG2Xt4yE8at33+F1+tGT6Oel5kY4TT772+dVP4LxjdRCD3EeGwcpXFQutmSKtu2DQLsjz9eeJTE46lLLSaiRbKEoVNutZDLzluDdZyCIFEG7rFt+QPeoKIQjU6B1eJQhS63rRKRkI6f8WSmy0NGgaKKmA2N+GqBL5fbGB+fkqIamJdWNFApUgiNK1PEfXcW85dow0lwz43k9vp6Yb1lUsOjWqkQomNQgbctuklZfWfSSmUlY+3anWJAauapEXmnIMRwkNyKgYbIhydPoC6XN0qMLG3MairU6sRo8MWBXNi7cZoKkQPbXszIObutYrsw82mGUgf/Sgn8+PUraxuTnk6Bj+HspqvgsuSqR1LgGuRjwcIK62ZE7bKZzreQkZFVRNUNvob05o21MAwKv153vnuaO3qPHz594H/5V7/h0iS9/9OPP3OPe/TIArH7e1G9MdL2ldUqgrmIAuBS/4c8aTGHwu3iZFvwDTDVwtyS7fPDI7nMgxOkCs/piSV5EfJ2vbHXwkPbSP7uX/wN//nPPxJa1yUA3338jjD35EbJ5ZDE1dhMRs2wcviJIAfcd887Xy6vrI37MofI93/zHb/71a8A59NE0ZHg7/vGthWsw2XEIcOxvfcqlaCJ3O1ka4UQiOcHpP1NLm6Q+OXLVwD+8PXC0+mZ1K7Ly9uVP/70E1vbUTfck+z7Dy6//Xw+cVu34XeCuczJpUGBVYRlSnxsEMLTPPHj55/5/KUZtDapfQ0CbT257pm43VySHPfxuNUdGsTZrLKVzNeLN1XW3TH6fT+jOkG66T9wK5UoNgrnoAJi5JaQTShqgWBu8gjulSbtPgLcxCHK7/Q4MIlszWphCXcfoXscMc2R55Z3XDfjeq2jmanJGna3rWcxEt5Zh0zVOcDX6qR7cMPMfTckdAirJ8ejEqretGDweB3S33m/qhEVHTyVhHDbC1t7B1IMzDEOzlsu1Xs4WdDWDag49L/nW3upvpZ1mJrihU6DjFnJBE3c1o4J25lPYUDtruvOHJTSUuJShT2vgwcVFW77TqmV1HmSaSLb4QYXqOwiSCtCornoUm+WhRTItQyuemqws85rEgyJ07AtDM0wtRu/57pDdP9IgNu6I9ULrTh1GG2llkrrp7PVTK4H7FC3lXNS0im17wxcNzucx+oKyPg8qe5d2eF+mYoh5HfnsAnMUbm1NXItLqolUy/odn78ch2el9d1J2pgOTd43TcA5f0mCqGkehBLKm5I1d8prcQpcWoP03KK/Olyg9mT+d+kZ5RAyZVa20RnL7yt2zDOi9NElESgE1bFVSt69mKu7vHhoWnKq/rLPfCoiRi0i2BgVLTaeFERcXagMrp2lMKWM1vriJ7jM0sUtv6ZpogJuZESnSUjo0Nh3UupvbcfPnxkW9/IDRObIqCBp8WnGB+WB+bZOxbbOxkOQcai5wTcMDbYlGaKFqb2Iu4GNeShTPdwmpnSNJRTokWybQOPigokIbXO9l4q2ZSU+mK1e5H17n4qEN8VoSLKOSauN08kilW2UljSUcxVZRTCVhWNDPPJaIEQCnsjIM65olqJrcCsBOcu5XUUnRLcM6WbP4ZirLedS9PBDz984N/9T/8bjy0B+3//6Q/c4x49lDCmEkoTPeiJbPN76UVHLo5l74qUFhQxRamkvqCEyJwSS1MSWJaZdVdUjoQ+TifObeOwn34krBAe/N9/2DeCxcER+fTxiafTPN6JtWSq5eEdshsQlBDDECaoTeGoq5ltObOvlYem9vjbjx/49a8e+L55/iznEyVnyuZ8nW0tIEbs5OQUiDEOI75SK3veDuWgtKAq1L3wdvNCJOfMl7cLv/+zT2j+tGf+/p++su/+e9OA6sI8d85PYJoCc9u0o+3uzN4aYGvNGHWoXv7m8Zmn+czDh2Yglr3DnDtx3IrbvVmky5QWCpfryj/92ZshP8evvG63cW0LSraMtcmZZSOI0rYebltmfSfeEkQQVaIeE8Ugxrl1gZPKUPWTseYZVTnMtdUTlMFHVUX0MBSP/PKJxT2+nZBivLSGRt4K9k5OY1qEUGX48E1tutMJaJJ8mnzJ+/CpktprnNbwJCNFj4Q2Qc4HyX8Sda+a9h23txufc2FvjZ6aC7mU0aiuzEjV4c0WohKDq8x1E2kVo1QGl0nF1c6ORg58rdtQ0nyKC2KRtfaGReXrHAbPbque7V1za5pY9KlYOiYhsylZ94ObtxeEiqa+HhnEaai6SSmocSBkiPhf9BsjqEEK0/h5XRXtHCQymZ2i/vs4RWQvlM4tzS7esJbCY1s/phBYzUaOV2tljoGmv0DZr2ya2BtfJ1TBpAwlvGKFKJGtTZiKVKYQB4fMsk8AeyMQrV6QWmBvG9Be3TZc6FMqfzYa4AazSjZ4vbY1MP7yjZv7inmPe9zjHve4xz3ucY973OOvLr6JidBW8pB2reY66Rq6CpNXoDQY0w+fHil7IXT8qCmrZQhKF1f88eef+fx65UPzj5hPC1MAa0pje828vNxIjZ9jGghRiHsbL8pODe/kts192TsUDjH0GHJ4F1UraBhjTSuF5yVC9O7jkgL1nbqUifdl+r+vVgmBMZrFBJPK2rsiCA/zaXypafCpVDsomQVToZR9dA6FgFgdHQqN4tOcPl4uhdt1JzWPjCkqpRRCw7/nWBxb2yYpb+vOTy+v47yfHk7eQWoTotfrG9sOT8/eRY4xEASmdx1QxDs81kdnJjw/PJKaxPdleyNyQI1QwyhDhheN1FrHePjrtqNqvFy8M70vJ07Lgqh3wFQEJbCWcsCZgiEp8LE9H7kYP75eeGk8pcuaySXz8PQdAL/73W+4xz16BHEYA3QJ/UMKNoqyF+HWxgzrvrPulTj5873EiCiITkMVLk2JeQ5DklRFUczXPdpUd5qGd9p8nig58/ufPwPwhz99gWCc23t8nmfmEJA2bQ6qVJu5bf7z9fXV4QynaXCZrPEqT226klJieT7z3bO/I3/7m19zPs0ss7f1atnY1xt7U58KEknTNN5jDS4tWxrs7fp2odaMnnw9rMB+W3l9eR1qQ2vJ/PnrKy8vjTuwXjFNpPadpyXx6enMQ5PbDiqIVnLj/gWJfJgTZW4SXg0AACAASURBVO7TZCAEpoYeOE2Jc0qENp350+sbX67rgKlpAEwQbEDhRIS8Gf/YplQajFxtQG7A1Zu651hQ91brMr9TDCSFraEVdhUeYmDqmJ52fzviQcVY2+dfm3eHiHJapsH9NHAvu76kqmI4nt+v7fHZ97jHy3UbcHgVeHhQ9sbPybViomNqkeuOigxls1PzBcxVxnsy4e9KR59XApYPNEwN1ZUpG+/NrLBmow1qieIy0t1vR8V5MR0+/OVyc5uM7hlUYIoRMxleakUcet9fgqgBRR0+BpANre/QMJNQbHU1Onwq/vX1laS+Zl5yaeibNs2JFSEOLt9rrkyTEG2itunvhkPyb29tmjYFUoxY407dciWG6DQGYLeVaZqpDZ5XrZKrMnfF2w5PbjlfpJD3MnhKkgK1FFevAyYNJBVkK2NSVkWxEGB4MhmlGqEhFGxKWIXrpedHrsY5NdVLy5nbLTMtbS0JkYJRW1o6M7OGTLeWLCbsRWgCef43xW1QaKql+14oBfbdr20SoZY8lDPDN7BefROF0L7LGAciweEDHXVWI4U65EXlYeK8y+Dz1GwEp+gPMfRfffiOoBPLGFkqKSjWSLPr6tCqOKBzkVlkGA5ec2DdN06py6o696bjLKXxVEPoBUYg54wVowy8o7FEpTZoCeoSlf2BTAjFjL2Th83la3v+X0uhYIPrEkTIlWYWCyKRoIXl1Dd9gRDQGphq50IpYINvk4JDdva2iedcuOaCXXwc/OF8IoqMl98QJzT3a01h3TYuW2f2Vj48PPHUzFBjUn56fRsy1CEpKoZI9Jccx/+KRnJb0KRUQlKezp7svNwWJg3snZhZRkXUHg//+a14knB723leFk7dd2iKxGBDXAENlFowy8M/ZK5G8oE+AI/TTDkVro1b8F///JX/69//Ry5fX9p3co97jMhWEOmLeBceaHjoUllLHZKpW3HS6NKEDuZiTFNCU2BqWPM0RUTlnaBCRaO2T/e1RjWOZlBKiVwLf/jJk/PLzVjiMvDz//znz3z/8ZF//ZvftGN44+vPV7bOa9mNW1nJe2XqpH8Kj6eFjw2/8HiaiQoPD86nOZ8mEOXWvCHKfsFqHpCCaZ5ZppnSTWElsFbYVy+U9u2KSOLS/v5tzdxuGy/XnR/be/a23ni5FS63DolJTCkMCOEPf/M9f/P0NBKBOQbmKbI30ZM0nXn56Uf+/OpwZEOoptRWAGarfLm+cWuwj8/rxsrhe1ZNUISqLsriF8Yhg53/INUhP6XxsYoVKIWb9DXTpcj7mquaKBKYrV9nhwWHLuSDQ5b7eldzxarweiv89NKMFKdEmtLgGtRqmB2+K0EMR0o3juw7IYZ73EMw9i7aZBtznFjafkuBvZQBNd9rIYmOHOG6F6R6k6ZbBlRtaPfabTWayWf7fQgRE7h0Ly6r3K6FruERRFlCdEM2aMJWlbe2PpVcUanEDsUTIRRlrXmYsk4EktqwPHGTHXuXkwkiYSTbl9vmsvdtzY3FRQ6u7O0Y3fAzdfGYIKjC26XB0PaCFrdN6LoSb1bIex0N+BCFUgrSqgRVY7cjlzWArVC7D1BV1r2Su1gCldOS6D4HmisxJXIvUnNBiMzvuFRBncM1hCmkul/TX/iS1cE8mbU3qFsO2CxfttylroUpCaE14WIQtmwD5iipkjahtr+f1K/VtjKOO03q8Mr2zCWh8aZk3KopCVNrupX6y69X30QhZOQxAVBR0HeEeykki+ROVCk7pR4mVWhFWrnauTFmhU/Pp7HBWYGsOlSWEOE0B2qvvGMgqJFi9+SJvF33wd8pWgk6EWIXdIAlKn1EpFmINTqJv22AuWaUwtYfQFPmwOj6GkoVG90CaUaMXVxhvW1UraSGUS2lsOf6zp3XDce6v06VSrldiaJMDXO6WyVIYuniBhrdJbq7CiflbNMgLaq6MWzvbu+luBnk4FwHvv/4xGPDky5JSFHHdE4l8OnxROg+ILhQQS6V0rw/Yji7C/RwlXaRhU6Anid3Xe98hnU3VPSYUmXvmDxHT9DC+Y2kR8EZQ/DEsZ1zKdXtjtDBCRL8RW3IXHQ2XvbElzZV2n7aWP/9P/Gf/tF5Ad89J/537nEPj2w2VONEhCqwlf7OwGZhEGBz9Q5e77iu+8Z8Wljm5fCiqYWocXT4rRZUdUxBJfi+1pH9ghHkMDetbBhGF9953Teet32oQ54fH9nWnT9fXIQgUHlM7qz+/J2/N1NILFMa6mjLlJCow5iv5ILIjTCU6yKq8+heTlMizjPSio7b5ZWt2lhL0vyI5Z01r+2chJiUk0Wets6n8sTFpvYdFtAk/PC9K9N9Op/58aevbE3g4flxIk1wa6Im07Ty489f+GMzqdYqGJnHs0+h/u7Td1wuN760CdTLupGBaRQp5nTPcshaBlGCOHfHP5Rm1Hh0s1Wc99V+7VOl9s/TUEBt6501HkMnSPc1qSvCibCXzMvlbXCXtJun9u/Q4Fy0PiSnNp6rHMdwj3u0OKcwuMenEJ2z0/ZfDcokwujyIgSxYXx8uwq7OUl+6vy/qpRswzg0JkOUwZvbb9krpd4QVeGcdLxTcfFJjfWmSansObO3ai3qhIQDFURTZ5NaObddW9UwDcOLLZdKjL6mgCNBcq5DTVa1+fw0ssy1Nu5OW5djCGyax3WINUKQwXcOWttEVjFta6RlqpQxydpX0AXq2hXVCrbLSPR1CtSIX2+g7krIlX6hkgSodXBtJAVCGfZMqLgvYz/GYgVV50pa4zRueYdSuq4FFoRQhNzFxySwLHEcwxVjX+uYpBUij8nRSOCiEUUZ5vK1+gRpb+O9C4WAMYdA7jwlFd5KOXiQkxKkDA7rLYtzI9t5ddTALxn3NfMe97jHPe5xj3vc4x73uMdfXXwTEyERGRwhMVcH6TC1YpXKPjpymzkuvNdwe60EqRQzaufLKBTZ3b8GQCJYGXLJMcIpLuytwzZP0b1B2tQhFgM7oCRzimSr1Pbvy809G84N4x9CxUSIwTHeANYgZqmNcEpQCIp1oKw4X8iGdCJYlUPuESGkgDVN52qGUNu5N7ntUunFtAYfrRoHfn3HpRv7ZExLodoB+yhWiNGhPdAGXFLcEZnWaUQPMpQUpiVyqn5MKkac0oAt1lKwauPzNfq0R2od4+QgmVJldItyofGcOh+rUkXQDoXTiIihfXpnQq6F2joW53lGydxaN2rL2R2ju0pmBUyIKgPXauJyxr3TUkWhVk7tGG5Efrxd+fObT4Tsv8L/wT3u4dH1vgA2XO6/tpZ+UZ/WhlNXJAyEFJFwqCDGFHz60D7PpeWlIwuQEIdCk4dzAa12P53KPC08nxzf/qevK7VUpjYVfTjN6BT4w8U5RH/38Df8i9/+wKlxZT6/vHC7FT48feSpfYboRghxeFiEEEkqo7MokgkhoKm/++qO72198wlsIEU/hn3bse2NlDpf0N3lz/EjAGk6kbeNfd95ffHp7n/5w49c6xdibuvyMvHr50f+u3/5t/43ISJVeXnxic4cEtQyeov7urFtO+SuQhRZSyY02Ee1iIYD91+LETQMuLIGn+SUfKwNfq6M9cdvi43roiE452v8gd/bDskxc4+p3v3GWne733sxKAcc+bYVKkJKE1V8sjVHl9CNoatx+qxQOkqiZjI61D3l/cHf468+5sm9YADUXJV3bTwWucBNrnyc3TJj3SrXvLM02NJ5TrxpcR5ex1cFmM+K1e5NZJRayT0XQQlRRsc/BCAddiOl7hQV5gZDMwSJkdM7xE4FrMO9srGyNZXIA15VzCce4NPyKoZ1XncxeOcXqVEdIqjvIGFVujgkFcgmQxm4aMWqDgiZqiBSKcawJ0kxgcjB086VUo7p7zkmbjG43wIQkjG9s4pRgzRBbMnRuu+ITGMKpTi/s6eMQWm2DG2SZgETn+BJs5OR3Sh2TFvMYNFIHiMPn+b0KZZEz6Gn2CkcRiwMxeVNKmIM1bmtFDQb+R1HNgYlzoFt61woIdQwznOW8hd2NAvS0EYNXpx/ee7BN1EI5d0GoR+tCGngnGsxqmRSM6kqBtd3iXW04i+OGO+hhlLDmPYWancRBJx4hwixw+tw36EeJfvf9NsTaRCJ2m90Ya2Vpc2Gw+lMzbV9TyetuZ9Ph65RyvCMABq5zdB2C6pkqEYtDvN4y5lTjNTOOGQnigyeU21+JX3sGqIbZanKIWGLoe8KISv+AvRrK+28ujFsFwTuq0MIBckMU7IaKpFpeGLEUgh7Hr+P0iAefUe2gFghRmWODZOMkjPDO6SYX88uVR6IJNWROCQJiNSRWBRcqfxIRwtVldDgMnvOGGFwkjQEaq0NqtQWJIS9HF4ean7vSiuEJ1O2alxem17/5ZeXd7zHtxMqTeIfqBKa8EdvwgSiKqGZhMaUSEGQ/p7bRgjqBX+HTKhi5v8PLlxg9TDlLPsGHIZ1tRoSEs8N8vW03LjtO6m9I+eHhRCFl6tDPaUap6cTf3v+HQCf3l74+csXQoDYiqsqQlD/HzAaB6EVRhogxIUwfIEc+tGbJkLByrHZnZ/O5PXwChFRqkUXtsGbNiEIt9vG5WfnOt1eLgStfHjw8/rtD9/zr3/9Gx6aMWzJlW3fyQ18/vB05vXtlRiO67RaPe5NdjjZ1ghb23YloHRMTwrRE5x+Y8VFL2JgbNKYG572a19wuW19BycWY0gDO7zuwNDTkquxNRmtDOrCB+L8o9q5os4Ze3pQpuFT58fV10jB4US9eaimRITQn5e/KOPu8dce25rHE7GacppkFAiSKjPz4NRu1tjXpXP9tHEX48hdrLrQU+fY1ndcHnA+s9XxmjFZ83HsfjqSKGUbL0U1ZaMe5s7qz3LtCZuYixxUY9/aeyMOx+vQ3RDFaQe5v81GmmDtWterscw6RJZSSmQrzKmvX0IyHfBSCV7ISe50CXOBKxtHhWh0jk77iluFPdfhcRjTQiw2fBcrxi3vnJpwzmSZLSupUQlOJxel6AWlSW28pQ7dxW0/WoM/qLDWnWoV67yhpEQNg9MTxZjV6PnSmt1T6dbM4q1WJBtb41yrwc2U2igZn6ZEDVBaNbbXlue2mzcHJc3KXnV40r3lwpLmAQ8upmw5c23Y7XkJ5CrD66jvGb9kfBOFkFodHX6V0AoN/12t3lHrJPlc2sPYiO9BIIsb2I0E3xmrh1qaNuW3YfLTOgXS+TyCoeRWhJQpIkm6NQhR3R3e2gN5Pk/MOR9cmJy9U/C+8yew7plrx72acguZU+uoFmvuy+2Y11qJWphbh/aRDNgoKmrxScatdKxn8fMcMFpzfwmO7rRIJaBD/S44/YrcE66mY38oIBkIhOZfUkgImaW/BCqIWPcso6qThqV1hoqp4+H7700JRGKqg9SYd2Pb61B/8bJExyZfLTcvD/9tEvHEcHRmulpSb8lGV1p6a/4AW2aaI49NaUpVKVKwrZJ3/5slmasu9eJKXA2qd3/MCqVWtMnW1G6sdI97AJljU1cECUrphpuoG4X2zW5KbojX17OioMEduxu+fdsrMdSDAyI+ZaidwJybx8ZB1qNKJrYs4LunhctNKcNXBoIZof1eQoWyDTGFKU18//w9uW7jM82cl7T0wkcEiRNx7g2H8JeJh0au2zuuC4LGNJRFghqm0UmzeKGw7TuXpoRW7UbJhc+fX/jxc+Pm4Yannz74l/zt97/iw/cfCO39u+4Z0cBDUziaTycutxd+bgIMOe98uebRqRbLiDCMaX/6/JWgR0cWvKDofjzBfE0MfkJ+nNV/6Etk52X2gtEn+TZ8N2o17xR3h3uco9h3Hg1NzKDvVVKRELxAA05zcv6rFp949aeqylCjEo0urHMYkmACt849uC9X93gXb7kOfnTC3EOxd/Qxshl7X7+iEEzYenP0tjdF3vqO9B/YSp9+wBKUQhg8yFoL9i7/KlKxjBt9giu4xmMmvrUpqHTXTgmOiJn6fhyJu5de2xg7tanHoXTi5s3tPLd9I+XK1FJcUz/j1KbiIpVTDEO5s4qQ952uA1V3P94+dTXzAi+YEPp5mjeW+3WwUlwEpV2n63ZrIhLt2iuUotQ2bdHigi9p6g0wo9yM0tZ9UUeu9GPIBlhl7+tXyx+lKEWOCfSUwPqkAKGUw5z55bbztmYa3Z28FQKHYb1YIFAHh/u6ZyJhCNQ8xcg2RWrbuzSo8+GlsDy29eoayKXw0PaCW85kk2F+a6LOH29rXqOl/qLxTRRCISmlXeiqDm+SQQgzINANgav5xKMT33Pw6Y0ZY3Mxa+PZduWnoBhxGHgZtB2sEZzr7nLYrbiKopxUKb0SVyWYOZkN79immEZys5fiibrGcUXztnHbC1+6q/kmzCdBcRjIzVYe5xMmzQQ2b60Y9ELodPINrbYq+yKJvBqXppB0YuIU0yC1ZYNZhaQyVElEvTDpi96t+tl3I1kzP+bevWy6dl6t48kNquRBBC4gDOngIIIyUbtxlmWKyLhOio+S11yHwkytkMs+4HiqFSUyWSd+Z+8sjGvd/tdUuQxDNFMazFGqT7629nmvW+ZBjHMb9Z4QqrVzfH9dgrL3NbSuYHGQHKfZVbm0qyncuMc9RgiKtCaITDMSApP582YiaFSmdBDXRQTTOv5Wo2+W2hJ8rcHfnYEdEVJMlNi6fMzk/fh97+f25sCHxxOfPn7g1hTaimUelhPntulbzlxzITRp65o3Qows6UzN/eGObkrYp73z5LDetgaWXKnbfkigzmeQchRvQRANA/6y7jv7th4CNGZs+42Xqyu6XS433q5v3G6F54/etPi0LEzTiY+PvkbGSSnbNq61xZkffveRy7VL5L6S/xiOdV+MWyn0hXmiQpUBh/mnL29M76b02bzA7BP0oK6MFQS6X7xhTFJH0uYNqQPcVtQ7xYwJoe8PPT97uW2c5sjSlaREkVKP/C37twzStgi1SlOv6lMj73CFRhQ38c/pfX6trky49Sn6nfl7j3chQZhasu3/pw4dA7YNrrki3RA6CqEapv3nwF6rT0yaRHwMwte3OhrP2YxpOhA5Frxx0OX+33Im73UUANSdNCdi7HYmxYv79ryn6uD6rSm6PaUJNHDLhWlpuUoR1j0PAr5oZC/F4Tw4NC6HMIShrE1duzhVCC4CdVu7SICLj/SJkDV4q76jKmARVT3gcxh1tdGwKtLga32qpD7hHdLWt9aMblVInCO5CHufAGXza9S/Uyq5CLU1ojW4gfPIY0qF0KBxbS+p2ShFBk1kxbDCaLgbcJojuU/GaqBKRVvzKANIHPfytm0sxGEQvZnw/Ji49aKm+n4Ugw049xwEC5FpacpzRdmysbXvrGUHhGnu6KZffiJ0XzLvcY973OMe97jHPe5xj3v81cU3MRFSPaAHdS/eF2hVdLGGubZuQmUUq9jwoYkI2irTPlqFWAXp+utmiMnATRZcNrHXoYEKJkMC1awSRJiHLLRLSvfJyt7Ar13QQczcQKwe2EkhEkPhOTVuk7pcdQdllCZB2LsLLjUYyLXJy6qgMg2/kskiF3nl9z85UbgU+PXzwqemc3m1nSqBqgthaCc2OdgO6yiFJAFt+v0SnFPTRSCserdTBwl3pxgDYx/nyIRLjft1A0wHWdmkNqHYAzZSaqHWyqXdvxCSkxzbdcjVUGpvPLe/C+P3oi4A0Q0OzaQ9A308bKgETsm7yq/BmDRxbcS9oDuagsMa23dU8+MckMDccM5L74oUoii58ZhuG/e4xxEa0IbTlgbNlPEACynEQWxvRg7H76NDzCg2pPRTgrwfXTwVh/kOHkqam/9MWxN3Q02HnP/T9MiyzOTcOqx7JoSIpmMaE1VJfcFLiWrGvr85bA+YUiJIGMcQYmKvsL047My0Ms2R1M4rlxUNygHvdn3a/p5SjW0vY2quKZDiid998mO8nQt7vpJzwfA17PH5geU88/Wrizysby4SMTe+VZpPWM0sDc7yshq3kjlN/ve6FsAOCI5oEzpok/3iAgN9ij64kXYgBaIEJlVqg7pZLiynidDQAtv+xnVfBzz4lBIhBubWLU9tit6n7rlmcmXwKaxU5232xyO7ZcKYog+p9ANK5GbbMqDYmUoueUy0RZTXvHNtHdfH6ZvY1u/xjYQZWOvWb2IE5ejw50qtmdSlrJutx9ISk1p8HdIk1CY68rY16Gx7hk2MtdiwrFAqagfyJIkyTZHmV0+UgFUdkPppEp9stJeqlIKpYO0PdjZCUkRBG7G+BkgpDD6gmRAUzk2cJVvldbs5fBefglQYk3mtlZqO6XAp5vC9viabORysnZPUZisinrOAw31rMeo7vqDasa5QjBjCwPlvubgQS1t/1lwIzb8IYEkzqrD1pBBrQlEtv2reR9ver6ugFp2v2fNlcYGxbpQdJBBiGiJdW8mgdUyV5hjJpSBtknYTMDJRu0F0pFQldYSDVd7yTikNflwLIRqXWxmWAg+L86GuzbQ3aCBOgWtjQ+y5UR46IqsrMfyC8U2smG9bZ4jgxUvU8fMwh2ubmZvJKdX6jfAEV9S63yAi0jTo+0MvqCT2rmamrpYxRpDVbREHttoKNRsN7dIIcvrO88c9G2wM1CJQsHcvP1TmFJga5t5MCe6MCECoTsDt2MwwTYANP51QFLQObySKG2U9NUDl6zWzl0y1liSEQMmBkoTYVUWaCWw3R6u1YLX6Z+P4TmtGruCwHbM6KidRJW+Fy82ToQ9ywmYn5raDcijIUHxzDlGHx1QpmIm7Vw+ndkfDj6K0GrvsaCcwS2TNO9PgdzkQrycBakJkI0Q/7xojZd84tURlCoLljT80k9iXKfHxwyPTfJg9drW90r0URB2W2DILU3eXv5W/TJjucQ/wRHVou+BNkE6uV42uqCZtaQ1exMuAS6gXG1IPeJ0ZGg6suWfv4VCgLO5h0RXZxIQrb6PYitNEKXl0F5K6QWuHaMSY3PS5S0zuGdThMqnhP3PJhDQTm0plKZk//enP/P6ffwLg4fHErz59z/ncNuElIszOCwJUJ5z3365DUBDhrXURZAOVOKByYYpYeORy+4m3zZs7cQks88TcjkmlkEIgxt54cc7P9ep+SOe08G/+7f/M3/+H/weAL5evrGb0BWgSqGpog9WKGkgd/J4lTEwSRmKSVFBVojHgcnuszDGyNvjLbc/cchn70xITUXQI80RxkZ7OgHyc3afNGv4lSBj+UNAEa4K+E19wyJ6TovvzUal2+ORtubJu61jXTyEQMZoZPCnc16t7vItiA85ONUqwAdcKzXi0tIJhFoN3ENeyVcKsoMLW1o8d4XlOA66+l8q6F1L3QKxCxUbDdFElI8w9LxFBTclDXTZ4bt66KrFEtn1/18BQshilysgjJvV3JrfiKVRIB5IXy4JY5NxU5qIaWVxYC0AsUXa4Nl64v2+JZUCaBcwhXu0gqLur7vbiaFaBJAOWH8ScA90N6yukYswNApYmQ2tla15rU3APsn5O67aiqux7M1i1QhD3OAKouzHPwnxu170WqpPTHTKHn55JHXtHNGHLuUGGXdk3aaD15ynZ4cS9AZaWiXOMvLUFbqrCjg1lu1pdqa6rlWl1+KRYPvjxKv5vmr/nnguahalBIR9nb7r3/SjGXx6Y9m0UQmVn0b6pOwI+t6RgV68zrePprckeSsd1N6xmLY4RxTGs1Q6Cl9+UgraENqigEli7Co8CZqMQMjFyOBzJ5ymwV+2Kz94NMRm4WiRgZlRTd4CHpnTGkIn2Y7Fx80utiNk70zxXqavtvNdaMHsbG2oKAdHI989uLngKF+Y5cH7ouPHAmgGxUZlnA5oLOfhAxGwfRaTV5CTngbNt7vZdMcYCGoXzw4Nft9YR6dLW1Zo4xFh9vIu5D/1Wv5cFQ9vLnGtFTMfL7UWVDQJzNQNRQluAUtDG32r3srq54GhE7zuFOl6yT+cJK7CMhXzFskDYhipcqOrqLK3D9boZ15cbn5uT+ylFwnQo14W7WMI93oVSiW2TlxS88dI3Qw2kGMbzDkat9TBDtQNb3x/iwwC4tUy1dVt7D8SacEr/M/X3ML5ba4IeWPMpKNMpIa0Y8+aHkTffYE2FeU6kOPF6fW3HFZBQXVETuL6+8R/+8z/y9793CfmH88S//PyVv/3drwD47W9/y6SKNDXPaX4CCvvNGxBmKyrGtSnXbTljJjw8uALcaUmEOHN+/Ehs3CbK/8feey1JsiRpep+qmblHJKuqQ5pMAzNLBBDIAiJ4/1fAPSAQYGcxfHr6dNHMjAh3M1PFhZHIfoE9JTKhd1kVGenUTMlPjMteSH0CdDwoIcWZKOzFuJye+ePnVpz9+PiO3/7+r/m7bvK6lR3lyr+p2taLaVHQO7yjt3SfEh/uliZhTaP5mDul1MknbZ3vZggIbR2ORSc6wBCqX4nfY38a9+oQl5Z79Xu+aOBSCnsd4hr05+WqkGUFcu/+AmR3zltmjLSrCNnq/I6IIvFaZK7fgQrTLb6fEJEpn724YMUnj8wbiXHmPqIBketE06RChVyvyqkhBHL1ayPZnaiFbR88lIAusKxjkgGX8z73U5Ou8jYSfKt4vcppEwNCQcbkRSpikSSpr4Wt+Araejr9ICjqsA8epXNMOhuoISjF6uTGVLroTb2Ku2jwmWdYdXKVqU4M1gzqqxCGvHVsDdSRJ+JNflzTyFWaqb1e+jHFZoHyeN8tCxCsGC9DPEGElK5NYiuRAmxdOSyFpuA30pE1KBdr8tvjPLMVvDJVc4u3ojROmXEliUxD3b1WkkAax5QCa7w2x20vTWCj/3zeKinC4dAREaYowjGlmcua1bZmd6RRCErEp1jCsUurfytX5NCvHb9+KXaLW9ziFre4xS1ucYtb3OIW/53ju5gIJU2z8k4De9pHmIdiFIS8j2lPIKq8kdtOE+o0AHbFmqT2GK0WafLMYzzs5uxVeH5t3cochaeUrmprtXFbRpXt0Kcmo4IVovJmgtRUhfz6bTfaBwAAIABJREFUkd61tSkpqRK774PP70gpMNq4rUvsBBlyjk61PPk2q0Q2LaRDV1YJKymkidnPwP0iVKlsozsdlG23K4RPA5accdujpC7vejV1RQTvXWGvRuCKUUUcdblKWUvT+59wQA1UuU5SYpSGjw0LoXcvi1TclHMf/6bUoETXi1mIxHHBCbEp9g1OUKZ0HfvrZM2AQusqB4Wdyof39/1erixLIAaust8OuxVeXtsx/NvHb3x8vkycrNwvrGFhHdypOOTjbnELAJ3y/Rqa59mAImjQth4MqFwIRE2UAQ21zod7sxYgDfo5OEAuBu5zUhtjwmsld4W3vGeULrVMm3BLWDgcGk+u7hunbydOlzbteby7Z13StAc4rves6xHbd6xPPsrlBfLO1t/1z99OnLfC0qczP7yP/PjT71iP7b2KaWVNaU5bqBvIlQMZUsQ0zjW1FqHWwknamrsu76FuBA1cLu3d3QGNCemTMV9WtO7UrZ33uRZyVbRPtv6P/+v/5v6//b+snWN03p2Iczy29/VxucO9mSNC4yrUuvPtuX3fp+2Z94cPPHaepdWGKjCkTb9p6ALBJxfqeEg8ClQf63AArqqYjSSpc2P13jgffDDRwBoDql2typ1KnbBIFW+eZh3rD3CphbPtcw1c4oG7lNhKu27nXDkG49ix3OE7UGG6xfcTIkYaCC+EUnRyZZJ2Tm+fJop3M+C+FsWjQqkokTq4d3tl18pdt5dwDY0rPNYCwO2qbnZILUe7dJJIQKi5TruKJUYM4XkgcLSyBEcWnZ8v1qBgI7eQ9ofRPqltU/EwJZn3Cl5Lm2jReHVUm1YiFSj5PNOOY0isQefky6qQi4MP3yFtuYhC7hOay1Zw9TcTZcejsHY0SzRnszr5oWGJUPOEJaorL75T+kK/iLIVm7BEcZp/2bh3Hf0UJvSucTRLrdMAtXrjjw7ajboRxDkM+NmS2Gu5QiOXQLJA6qqWl63wWpjIgNdLRXLB+/ROREmq6D7498oeG8+79PHcmhLBmWumGRCFra9neWuWBcNkvJbrc/NrxXdRCB0CE1oiTufa9KJDFKdOaMGWm2HmQBKcdu9JxlXzvbpQvEwujNeCSpgvXpKAepgmdvlSIC3E7qZsWwa8acIDYs3QbogxuDTo3Rg/mo+67WpUtkShmE/MvNeOL73qOTS+TF88SjVOXq/cmBC5W5o5VjunZnwVR8KVAiqJyyD6dtMsqzqJc6Uxta/uyKKoLm8EGwpBJnqvaeW3eoxxM8yFPMbJatwj1F6sLaH5+wxSb3XDCXPRTbEVUV6vEMBowl6cbx2S83BYeLg/4N3Aq9YGI5qWKT5ghtcitA1Wh0R3k78d52xlwf3MofMKlvWAIOxlm94escuhn7up2Ou2E4S5GLg3qNH62OF55ZZY3OIaDhPWEWJzy7z6TTgll8kn1CWxxHiFmngnykvjJY5vVL1y0aq3zWNAXLVLkNj8m4VlTRyP3SsL5XK58OVLExn4+uUz+37ih59+A8C6rjiVpfMLj8cHQgy8ns5NdQXIVTnoMmFoh8OB3/z0gffvOw9leWI/v/ClH/Jvf/4RR6nWMfb1TClNdh66nw6w9sWgvdc6k6lcMoe48PXLVz7+uR3362Xn6fmZn96/B+Dp6ZG75UBKrfjatRJr4evayZtFydXo/Sp2g+gL75b2+ac1NTjwlHoVLgW+dsuCPz1/Q8T5mw8fAEix4dm3t74rQVEPSE8cY6gcY6C84Q22XGnA1traNeCPboZKIHZGtARliYH7vobu1bjU/SpoYxkhsIRA6c2ixQPL4YFTt05YUmQVJWx9/TqfcVkI02Lg13dqv8X3E4ZPw18nEIQJOxuNilH4g+FeJ6exmqEhNLuKgd40Z3GZsH3LRs1Gmc2DBpcastIXr6gLaR15g3A6FXKXrl5iJKQFKa1JsuVKduGp5z47teUQ1ZHRMEggaYKJiQhRdSb4mFFr5TyI49mJoiy9eEOEIJGtS3QXg1h85gAgHA6B2o1G3RUhkLFpN+K1Nm+hcJXfDxKwnvMlHKmBow5uciWIch4QZmlHnkZuhFNy7QT2Bu8LUTj0ogQbQhL9CKM0/k01lnS1dqnZJtXAzQmJKawjbmSctTfRtHO4R0UYg7V1svvVJFN8iVOEouKYV/Zh5RCcVSMqce5XWCWGxMgsrRpr53m1iw17jFeBjuG8+yvGd1EIBfW5EZg7W7ZJKBVzkso0Ac3VQLUnw1Cskq1yCEoMvbNnBeGKmbc+HRrKPJKVnY37uy40sO3srtwP/o4IojYx14I05ZXh20CrocbtM5Pu7eBXd2W9mu9BbxSKTJW4oTLn/SU6b2c+fzmxLO2YPrzvuPGxPpXmzzOMz3BHwz67fyqCVcNdZndRxFlinERcl25iNVzQvX3/+BPigseAjofcKiLOOvxIaml8nf4Le96RGGdl39TzylwYUlAMIa6R133rh114d3fH3bElO4FmmDoKmaCBGHQSvWspxKDUXvBtNTfC36Dt1ISnOsnrh7sAWSfO1qXp6r9eynSkj8cDh5B41/lVl/3IljN7F0vIETwpoavI3fktsbjFNQSndn5ZsJUQwsQ/59I6XEN1LEUll7ZpAu1dqf2lm0qItasfXjcEdyd3A00vW+PM9U08pYj5ia1bdZ++fuHPv3zh9dQ8ekJMvP/xh1koNf7IkYenzvULiX17/QvBF42tNksyJl0Lj+sjH8/PAPzD13/g83Pmw1NbYw9J+O0PH7i/78VYSiBO6Bsm1Tg8PRH7z+n5hdfnb2jqWHRRcq58+fKNv//YCqE/fvnC8dPKX/3czuN/+v1vuF/vkE7+//LtzF4E6ZMQU8VUqXk0yZzX04Vz5xwd0sKCT78mNHGpma2vX2FN/HLeqLnxoH64T9wvK0GUMEynvRUrW99MXkullDoRCbsJYtfuZxAhu80JYKnGGhcOvXhbojY+6WgelWYQPr6v/Z4j1qbW0ArjqI2rCs1pfvdGUga4hMjza+H5td2r4/LrJxa3+I6iwF6veUlUYx8FxSpQr2apoUvKTU8gbyppEsIUZ3HPjQs8iqvaUBmpJ+OH1J7x0ekvuYI50s3ki7XGT6/j+fZyJi6V2osSdyc4bCMHVEXcWbr4E/R8qv0vABdzcrHZICc5ISihrw2RxuuzKSQiuEeOvS4q1dlq4WhtfaqhQPDpZ+luRFH8TcMqaUKiIEM9uBvUFx8iNRGXphwJfTIcE2nsFbliO0gvnOKycP+wzj70VjKlXpsqpasT114J3YXAlssbTnYb5EVV1uGHJEJKMhs3GoxVl5nLFmtr2/CoW2Noqn+DP5/k6tFEm0qJyJyILxl2jBhtav1WcV5znqrNMQTO+FxDvSpW8lToW5Zfv9F8WzFvcYtb3OIWt7jFLW5xi1v8u4vvYiJUNcwORHZvULheuWczVBOldwFxJ5fKZW/dg7slEoOwhDDlRos3eFwesDOrlNPGkNu4v78nWRqzSZJEPp3Pk/vyw/0HzvvlKpe9Kl6vnQBokK3BOandl6aJqvWpUg1NY37QAGS4zI+fhWJyhcK5c647+dx+4bAIMawdg97GrsXa7/TLgLqhb26heMOrjsayIK0NEcZY3Al+hXW4e8fxjo6GN8n7fpCqbWI0ugWqUwATaNyFEMKcgrkVapEBL25TtOJ8Pp2nIoxHxWpB1t6hQtvxDGhRdYIoaaicSBt5D+nrRZXiNvkT1k6sYZKBkApWrlKfbpmjLhw0cOrcAsuZuAjvH1v3535deN7O/PMvr/3CFQI+7/+8abe4BQ1OYAMuWhrsdkx+VSEEmcqLl8sZt6tnVUiRdUmNiDjl+zMSIvSJ9oTZMdYvb9OWDs8q25nL6wtfP7YJwJ//9AuXUjl0/eSnx3c8HO9ZOvxhWRZSWhEdHVah1oqG0PD9gOXA5WXvEFv45eWVv/2Xf+FfP413IqEp8eWlQUX+v3/4B+6icuzT4tO3V1yMcHxo18UdLYWle9q8f/+OkOKV67lEXl9PxBC579OSh+Mdh8ORY9d2/fJ85o+/PHPp3mrPp8rz5cSigwtTeHf4max9b4jAEnjtnegvrxdq3afq4zGtpGWZ8JejB749b/zxPKC/R+Jy4BhlIhKy5cYn7fvNuWQMmfe71ErJeUJ5A04xvyqMOlRXnsYa6k22/9y/71IrIob4gO0KUYRq8No75qetkrKxDFQPhdNWKLl9x5aFLW/sW7t359t6dYs3oSFOhdSlo1wmlKo2D53hpaUlYB4oMnwaBbXGmRvisCEoGkD783lxZUmBD8dBZmkT8yHBfDgsaAyTW3M+b6QQuOsT69N5J1efSmZtWi5ceoJ1lACxksIbv0kBF0XHumqNH6gDxaNQsk+pfJGWlwyPRMGJGiYPL4t3OFeHDBZn38tcD6ND6RDm4fvjbm3SNWgcqlhQkl89mJIKmw8lukLFp3+OVFiUiaDBnct+6rBpqDR1yKk4GSIhBs79On47XTjE0KC8E+pYG6KFoSjaJnPHruBnrKxLoHaETnZIAnufMp0uO0kiOmjRIkSH1CE4RoQgbENZODa4r1ll7zwlQVEx4oD0acs97zp3sxQjbxUZieqAg/2K8V0UQipyxVRTm+TykBQMinhlGb4cWhC7Fk7i0iBkLpMw1qg4NkeMogGC4R2zark2DHh/gEMIPC0rob8UZyucLHPsT3x07aae7fuS0Aiuw5VMFSVQvQ7dAbQK1a6wDO26AeM7Butl6L+vaeWH48OEVHiFul9lCvcO7Jo8WBeKhcFxJBlkbTKUOoQmpC0cQ7ABafLYM2nDm3fQG4lIr5U6vlOkiT5047OJi3vLITJ7Uyc4JsY2ZH+LUrLwfDqz9/Hxu4d3ZApSho9BJKqydyJ3DXLFmtJkNs2ZspYxRETS9G2pXR58kCgvm1ELvHZied2d+Kgc7iLa7+dhTQTR5tcBpOOCo7h2zxMpqOgsOm9pxS3+IsTBOrZ8vzTJ7L4+aQhoWuY7UvdGch+eQRRrogca5oYHhpYL3gn0Epr09XUzM0rdyZcOASuFbS9suW1mFefufuHpXZOmfnh45LgGtJsMi8C+b0iHnujhjqBK1eu7lvPOt+dXvnQBmb/95ROfSmV0VVIUgu2sh+EFcceCkPOln0HEvDZvDSCGhNVA6fC+gKDmnDt8L79WlrRwOBz48NiKp+zOkhI/PDbY7OcvH/m3543Xbuh8yYaaE9YO0zgcCQoLXTr/YaHUK2xNYyIqc+8wcRaFw4AKryte4bWD9p8vmcCFQ6wcerGVLVNRnr1d60s1sjUTVGgcIJzZDMpuzZKgc6OSKwVr5rLAqwqlQhl7EU1ie9rFeUDcuJSdz6fGo/zyWtCqxC7bezwmtt2o3q5LKYJr4njsK5XeoLy3uIaIs6brWiMhzmZA3Sq7MTlEVQQlXqHqrhhN4GhypLWx0J46tDyWwr4becgha4PgLwPumSvFjDLltZVanZdTe6eW2HhFuXTonVjjFNqQym6y8yH51atmb+/IYcDSVKh6lX32OgqgftbiaBRMrv8etE6agNeWoM8urrSczUaeIuBLbzKP/McA0/mze/v8yDNVBUmB2POI4i1fGU1cjUqKguUu8JAL1evVjcQa1G45dFEKmpBK7PLcVpTX3AqrOOxnRDjtmXMXj4oeEHdevvV1eLkgGlkHnQHDRKYHGSGx44RBRDLFo/HSL0v0NgE49Ou47QVZlODTqQqV0V+famKUvYw+H4i2oUW/EPVWCLVwhPEEewFEiX0DjlHYamVY2DlOEmHpnUiNgptT8KnwobQEfir1VEOXBesvzXnfuVC5O7SJwBKFY1wmAezzy4mPn3feP7Xj+/Bw1xLxoTHv/hfO8GWUFKZI/44aDLeCDyNQFNWuAkIXi6vXnzUq79/dTQGGcT2G75B1t/khltDpPXNxEleih2Y8JkNJTjgInIdohDkafT6fqbuYj0mXSGC3Ms0C0XZeYw2tVgAhjC6yd1W8OeVyFtGJP96q4d5URIYKyZ53armardW6k1SRYabmbcI09AkE6eZbQxGwPQnDXfnr6cyaIjKmNwrV68QzA+RSCIsykKBzcRydGjd233nsE8KzBQI6kx15w924xS38jc+G5EzVC0E798USgTi0PPDgrQs5HMr7xNX8ahIcYmqJhJ37dwRCyDO5TilQspBlKBrt5H0j9WnLT7/9kfuHe1KK828cjvdYNzv1vGG249bbfN5EVNStK1kCUqAWfvnWpkyft4y7cEjD78s5HBK/7UXK+6d3oEruRUq6P0BV8rmdQ5HcNu5uEO2l8vryyms3Oi5eiQ9KQKe/m9XK58vOqXcrn8+vbLbwcu7FVjaCJp4O4zQiBef9XSsAP9iFjy+XSdJeQuMJHft1XpfI0/HAPiYppVANnrdWnH0rma9fPxOxucaJOSEmwnJd86pfm2KBpqQ5iMCVvspMXH9B/dp5xttyOU2vcd4yHmppZOgoSuoF3n0SshVKF0vYVYgxsnaD3Vwq1WCNgzr+6ycWt/h+YklpJt/ny8ZWSvNWBDZzPIB04pzGJi4io6gpjsUFCTZVC71UVI1LexwxSZg5z/0fpjdWf+SLVb69FmJoz3NwA6msvTHpKZHMCX1920JTVBsKb3Q+demiVdCmLyH4VcABaZ8bkwpr6sMjnSq1JefjO81aMTeOyRf/C96T0AqZZblrX5AqtlfONlMzmoCvUEdTIzZT7JE3JAKxhqsiZAx/0VA3gxKFFEez3DELxC56cnZDPYy0lixN8Goo44UoSC5UAttQcauFIEKV0WgpTUgiDdW3JixmoxlUmtn9yBnvQyTbzl6G6WubTs9jMCet8kYSLqLmZG2qnNAK291g6xNqldb4GWgAV+ewJKR/aQi/fn716x/BLW5xi1vc4ha3uMUtbnGLW/x3ju9iIhS4qoRlDFedEItcDIhTo765undVD9q40Rzwq1Oxdgz30He/aOXyUq9a6Xtuo7rRTZBALZlLl3P8er5wPmVSh7UFU9ZjYh04S2lO4m+VgtQbcnxKGwoQ43WCY0Z2mZMuxCl2ldkVFeIa3kwTmxD3kIt0a/pOA/ZWxdt4t7c8nNbdUXWW2Z0UCnrtWOAcxJE4JLlzF6MeE6GIqPZrDsfUPIV8uEpb50D0g6zmbTrW75X2TsTQ7t+yIQFiEkLvSFjJoImXDsHZvPLD0x3vOy/AvPGUZGrpC0idkpQFwb1w6d0F6+PwMcr/05dXchUeH9qj/eP6yHIQzGQiRqq38xhqVBHl3bLw9dAhOOfMvuWpjKJyddW+xS1EdHb13AyrhdynGNUNDXHy9EIKTf56TIZFMLf2nk88VMFrYd87Ll+FJR0Iw1wtgqoROiQiFWVdEo/3rVt5PN5h4lwubbLh7hDila/oFTBivKo/eh2wrtGNjLzsZz5f2hqYd8dTnTCrD/crP757z3/8uUlNr4eFrexTSjatGbxyubSJD9an3QN6Io57nQ7nJQufPr9w3jJ/+txU2z6eN4oGlsnFbNL/o6t7yU4sF/65wzxi2vjx/kf+scPtfnk9sVebPIgVQVx56Eqcv/vhid//9CNf97b2/PL5E1E2nrv6HtokbtXS7JCqClVLg4S002rT/WuzmtxtBsYx9wVp/rimNO+lStvj6hu2ZRCZ/C+JhSUk7lj42gc82RTxRBid4NT4XUOtE5yET15tHPChW9yChngZKIiN2tS7+vO26IJaaB4mtBzBMUInpIUV6tYk3dMYhcTms/Pa/b80ZgzIdUyPhVK7HxGg5o1T3fOICKxraNYDtLWhyWH3CbkZ4tPaqHMand0M7etHtWaxMqXxO0pnqsp5O+exZooJbleIKmKYCYu0qarX5m103+F+1sQbJ18zWqFGhSrTCqR2ivW4LFYq1WzmDSNHLP29DP1eXLpcXtKIF0EP/W+IUHfn3Ce/1RRNShneSNm7el1fK0QA79O9TvPQNq1Z++8kDI9XFE/jW0MesP+gBGNO+wwjihCX63pWqndETdsuYmDSQpIqMbTJ+LgO2R0r0MU7SYuzrGvzZaLBrNPCpFzUYXr0K8Z3UQitKoSOJVkOyvZGmMDFSG82DghNSnaYp3qT3xZjEuOUlhwPUYDTa+bztzOHXsg8HleO9+vknew1Y/vOx3PbIMtmLIuzdez4V8kcxUgdiqCi1CDk8ZLQDF4dmYQx2zLpsLIMIQHv49iBDzVn2/JMqNaYEHPO/UU1uqZ7/8CaVqg+jxk3Lq4NhkPHvPpOtTfFGHB+A5NQpRUp/QPWX+KxSCpN8nFwHpvn4/XKVyDngg7cWgBUrnA+Vd4aQQpdCrM5GbR/q97ECPoiuDqsMU7PJu3HNoQuzCviQu0vuuFE1zlOpjRnIekGl0+Hhya32Rf6JmfvBAm4dlhisaZEPCUlBVLgrst7nrYNJxNHcdb9PG5xixYyuTPS+Y1jk/fhI/gGLurO9OcZtQ+ik8VYzcnu5GEWKHszVh7y/+4Ej40LCWjKPL1/nIWNuHLezyCNE7QugMaZvOd8waxOCe9K86OoJU/Rh/PLC3/69JEvW1sD4+HIz08Hfuw4tD/88DMf7peJkSiXypevZ3xpn3dW1He2DpVbDmtLJEY9oH3jz61o+fj5mT9+eWFzZ+/XqmjnJQ6iZVD24uSRSIiwqU9Yz49LA6N/6XA7cydKIvQuykEXkmZ+7Byku7sD798dufdWQOpupPptCiHIKXPed5IouX9HkMZBPUq7DlsxvJR5Xps1XqT35yEgJGVmRykqxyVdxRdKhxNPvqmyus5CKYRIUCWq8MPTu/Y3Pj9jeWPYbVQD88Lav0PNOCxxclolXNf8W9xiu5TpoVc8grTkFmCVSq7OIAbXIMQlTuimWyGYUqry0AWOXJsnzISpIRxJPPT16VIKe/EJu40R3q2JvtT03E6m1w0GHmSub4s3O4IhMb8VY98qLsaxQ+yDKBaE4p2r2ZungyqQUueR963bK+BXUQgrzhIi0mGyEPAgnHozKrl32kX738+bc38Qojt5SE/XBh0bYlRahRjiNKA/75mtKtqLEqtXWBw0zzDbjXPPp0wCW1bcx97SGJw2yQqttKwTvueIGDHEqeDgtOJv5GTqiqhOr56w0ArfnqfuuTQOfT/RvXprjvf1zDBSULwrYww6yDgGE2czIQamjHhwIMoUqUkqHBeZMtnVWsE4vEJ1IHp/xfguCiErzjIqd42IZXYf3Uxjq3UWBEm07a7DfpemhKImV6MrkV6ctJv2GJV9CQwlg6DKcQ0ceray4ZxyRfvDscZATJGXoaxhG4uv88ZxiBw0zO5DwMneDunSC5m67UhYKLHrsxPa1MuHHnskRpmVuGBkkakutWjr/11s8J4gpMS5K585rbO8dXPAKE1hz61cfX1UGuFvrDcOl71eiXJh8Gb6hMel6fX3z18wVK/XuVI5bRsDUXlcF+LSJjQAnhWTYSkLh35+S1wmrnUTx3BSfynerw8cl8g+fFkkECUS+7c8553nU+ahFyWHQ2QTI/XFRmMzaLWeNT48RdblQO7XCTM2F9x2jp1ToVHYrGFy27U1cMWGWpeALTpf7FtacYu/iBDms4Mo/kZ0QAlN0GN0Q0MEr2zTR8taIU65YsW9qZSNSUZMRw5pnR1Vs0yUMBNcjwtRulM5UM8F306UPtH2HKgm8/usbCxLmt44pVb2/UTedvLWeUkCj3d33PeJ0Id3d/yv/+GvebrrDaolkoJM3Pcff/nEf/2nj3N0+/q8o7TkAeDD433jMA28fBRCCNPL6EeH0575t+fz1QNsCbgFQl/TLnuhFqX2RkS7SsrSE6YP90/stfDnPl0+5YJ55ND3kod75U7Xabh6d1xY7w/EvjTkUriUwqGvLY9H5+m4tKter3xTC86xM30vNbNn2HNfG/JOsjBx7mtIJIW9V0p3GriLTENVr02tStK1CxzQCVKPoogoinEYiaEapwDSOUArinelVIAF48e7hd+9b4XT+6fOa7jFLYDnSyWE3gTMjnQCPcBWC8WuqBBVYRVn6WtFVSOvASuF3J/5irAk5X4dpH2wrXAuo5EDIb31VFRUZT7P7l0caxhqilIqrcIHMGfLZXrdWBB00SYq0EUQYgqUkrkMUa0Umh/laFAUeHcM1P4342aYKcfOL6xVWGJkZCs1bzwcIrn7DjlKKYWtF0pJAvveGiM2m1lQ90qMo0GlzZtt+Oeo4NgsHkJqjbHhT+nFKXJVAl6icH+IU7yqFoPqU804pcAqActDwa3gKhSr6CyOFAlp5kOlN6KvSqRtHxkDnxCFUvwqUKVt4j1y57qfSbpOYTFPQtnybPhfrIsve5h5o0YhLiA2eLGNfzWKq1r7RK/frP1NLv9rxY0jdItb3OIWt7jFLW5xi1vc4t9dfBcTIa+V3DGIpTjVbU5bmoaZXD88oYujA6cNnhJ04iJFWxU6IVoPK7JGzi+t+5lzZjkuU450O2dOeUfeSBCmFPn9Q+sUXoqxxshrx5IHgXdLIA7lDWlqZ06dSj9hMYL6hK5plwuyOroHkfVwmB49ZobWMMfBURxV5RBaFzCX0vyWuI4mI1dsZ1QliJLl6g2Ctw7qcGxWnKCR0ufFS1Uk+FRFc7fmil7H2BNS0DlRigIpBEKfZYYAxzdSraaOiVB6VyWhqEiD+QzMaqzAdXS7ptRUl+Z1ad8zOGFJhIeUpq/BVsF4410UFLFCHNDKuJJUJt54u2Re8wlqYOnXUhdY/OrjIg5ZaudStPFvsEgdY/Kp+3iLWzSVm7FWiLb1Z4iHOo3LtywdRhsSCITQYGuGs1puePaBy3anVsG9YcOjRqpspHjXf07kvUyVuJgWYogTWneuzxweH5GlT4tDgGx8/dS4N+6FB30kdwW3Bt0wzOpUNBIiSwq8795D//G37/n5pzvWwW1xQawy2HJfX174p8/PvHau3t/96YVDVH583xTcfng4IzVPmfunpyd+89M9d/dtIvS7v/qXmiFYAAAgAElEQVSZ5bhS//kX/nzqI5paqF7YOobmkp1sGR/y/dJgtH3gw3FJfLuceL20399dWYLM63KqlYcYSX3i83R3T9CFuIxzLjw/P2NdpenDsnJYF76dL5z7MQQ3MsJmfSrlcIyHqQ665Z2gYU5n7houbq5vD4dj6/L61Ycjxua2Do0zJjSoIsC57GBQauZ1+J6ZEjSQRxd/21jXyP/wmzYB+t37O3768CM/vbvv16W3vW9xC2CvRup73eZt+uOT/6oQGqcDwHfjFcc7n3qNB6pUFGfrz/BDVMyFS/ffWkLbswcic13AYhjoK1AhhjAlra1Utnr1xwkKtVzV1rw6xQwdfl9hoeBc9o3LgLbVggdh7Wvi62YcFqZarONslTnJiKosi0x/QknNv3DwMhUl7z7VPqlQPU6USJWWK6UgPPaJTskdBt2/M4x3uX+FB20TJ73mUzn79HNTNYKESZ8wmjz3Xc9dimTOGGFCDBs3cUJkPTZ1vFQ5DnVP1aaKXPqJmKKqk4NoNVPqVT3PgxCjz6kUGMVsQgJFA1upk9oQXFCX6W/Z9q428SlD+de0SaIPioUL2bgqrYo0pGY/Dy3XHPLXiu+iEJJkPHdoFNYkl8fNtlbVzNGVamgFBVcIWeOiXE1Yk0SK6+QIVRGOQZGnhhW/PJ/QKpM/8+nlwueXZ97HLoF7XEECtXNGVimkFK8meaFJSQ+4l6kQzYkox2F6JwcQ75LTHXwmOvk5XisZw0YiEpTn7cyX14aht+ORd3FFhrmWNBqjd/8Sdye7TIJPh90iqoyrpTQY2uAAOY3gNxIJ3LAqb+ShG9fhpUvg3qWVEI6kXvAVK3gB6XPVbBvUdRIWoyqIThngbLAsqXn0jJdZIiH4JO8hRkUR6XLooY2O962/eDGyoFg/7wp9VDyKvcIaItINv1Qr1Dqvm6EcwhEPPiUlU1Zycb51YvfDeuDu7jg9CgRnTQmzzr/iFre4hpdugEpby0VbIwbAPVMLlHCVnVZ1pDcfokCNAUKEPKSlN9Qcn8IniSBXTpDjeJTJDxQaHnvyKo9HDilyOPbCqlwoGKUnCWIRCWFyimptstG1NnNqaIfz8LDyvzy1Au6n33zgIDbx7u6CSYTuXXMphZM5X4YkqsCjLOTuDfLlfGGv+yy0fnMuOJnf9MXi/bvE+3eP/O7lldfuL/LptOEO535Mey0YhdDd/SRIIz0PE8RaOF8yr31Njdo2WB2WAiVjS5iwn8u+8+XjF57uW1H604d3fH4+83LpUrExkrxBVmwQea3iFii9mWQILtckTmKDygwod6iNIBZ74qEYi8vE6JtYw+37lfSdayENeODaGkObJf75ufkIncyIAbZ6haek+5X/8td/AOAPf/VbosChZx5+E0u4xZtwtSl6knCCV2Q0aNVJQZG1wzARMpWXrTVlSm1QTYsNKgbwNVeEwN2A2Efh/X2cEsuvltnP+xSIEY/YLtNCw9zIxa88XolYqbMBKxpZopKHgFZ1YnSOd8sk6ddiFIN4GFyWSqlXXkoIitm1oa7dB2lYe3gy1N7kXxJwsyksVV24X9c3cD7FreK5vBEagHinlA4Xtto5PFMq36gGW7nmeEkCPmgASySoTyicF6dU53VYDgCX6qRRtFhpudgUp2pNOLM4aRvVhb0I3v3bamnCXkOk5i4mym6zgbVEa3nzyCMR3K70hh0Q6lxTve4kXSYU2CVTtHGRBoRPrSB7QLsAh6tS63DObAWgqEwTaR18718xvotCaHN/041vD/k+sJrScNPjRimCSJwqc2bNgEr0qjFfRZooQO/aJVMIwqE/UA/vntrkoncSvRZ+OjzOgiHXynI0Dr3rG44LGnUmHtTalOP65pXwPsWAPKYtMRFdqeVKUPauRNIOvIJe/XJqrYhdzf8qyqU4x/6i12LkapNUm0pgd6YyVPGMakR9vidUNxaYfJqC4V5ntd94RhUYeu4LiyrrXUsUDsuBkAL7wHK68bLvHPvv398ndvLceENdCVpmh6O9YJVqFRvmtQIpXQmF1pXuDv1l2Is3UmF/8Zrx41U0wsV6MjReXG/PR38xc624Kjq0+4MhYSEEQfu12rXdhzHhK7XiohMP7FJJKcwXd+vqOLe4BUCteW4UJtOdav5DyResc0wsLWi4+g4himrFwzY3K/ZWmIxpr8TaOIj9eawVJEasLxYewXImjgLAjM2N2v1wvFQsKOvaGjs1NzGGNCa9brgLtTK7sNWch3jP4V1rFq0aujJTf7fdwJ2tN3Yue5suv3/o3VFrbvVbb1igiqmSe4Pjl63w+i+/8Fd9yvG/HxPLcuDnH37mj5/acf9jb4KNxCAuC7m2RKpdB6fUffrnWBH2Uuj1H4cYOB4S71M774A0UZZ+Lz5/+4rcHycHadt2chH2zos624VcC1tmGiluvhPDgsSeIFXhebvM/WhdRvHak50KRW0WSi9lw3ACrUN2jBERnebfz6dXqlf+8x9+B8Dj0z1fPn2mbpnHYzvP1/LKqdaZpB3F+PHuwLu7ZnS3EtEks+gcghW3uAXAw5quPnsuyJImFzl7a6rGmROAU1l6o6eYUbxxtEtvDIayo3oVYlo2+LhtU602hIUlrUjf80/9nY/9HQrJuVPhMg1WM6gTh+iSO6dilK4mlkNlNSUEvfJMcMSsGzLCqq3J29MtjkFZUpu0t/Os1KwzxxNzFr2agO41oy64dwSOXDrfqOcptR1jWJS9F4SSoZbQPCwZybTj/d3O7qQYOHQ+YNKmZrz1AuBShBRsKv/uuXTxqXaOBxWWFFh7I6ha5TVndKzJoSF2IszJFkGIGmYBV1JDHoyC76VkvDqqQ/kXEOXYFbJchM1somVWtWZo369DIIDqFC87SqTGSC4FH01/dzYqchl8+EAxm/k5Juj1T0xU068ZN47QLW5xi1vc4ha3uMUtbnGLf3fxXUyEquisJrGmnHY5dzx7jCypw64AEHIuvHa1IyuVh+MRUyV2POdh6W62vRN4yoU1BsJw3lbvY9hWsR5TpERn1IXVDZUwx4mqTV1tDvA0ItawlAAxafcWsSn/LBKoYpPL5Oatazj1ZB2zSpmSuY5q4P44JHAb5+gyu7ht4jWkGAtGpU6eUtAjtWQkMKcnuFMna4E2QbI8OT4qAm+disWpwpSilqjUWiZG9X5ZiO/vKf0cNTSd/DEZM+u+RHHg3wPFjSDeuV6gYgiHN5Oxdn0HBlWDE1yvWvymrXXQuyji3kZrPmBCfaw7Pl/b2G34DYhdoTGjHSRWkOh8eNcw9ikKLrB0bK4EbX+nX9tlXbjFLUZIPCAdNhtTQkOY0tQmBatOyV1JsTQXiCH57ALBAq5QO+9Eq4DY5BlJNTIrU7BRAkEN69h0yYb5xqUM+EOTyC79GDQqIgeWh6v8ezFnK8/tGDwQgrAeAmbtPPbS5Pzr5Wv7Tj3wbrl/43vWcONTyU4NU+Pcu366NgBF6muHq+DB0d7Vfbxbef/wjuPAlu8V853XvPGt2xbksqOeKH26lstGIEyseUTQsPD02DkwyVjvIz8dGjdmkcR9FN4d2v+XOriTbbKSRJBwx9fnBvv5t09fOG3PVL/yU/fcXOlNBqynqdfl3r3ezLiYz0nQYgJuE+ZTJFHJ1A6ts3Ml141iber1dLjneAwTevTnbyd++vGRn39q/kyO8PH0hUvJ/G//4X8EYP3XP/GPHz+x+bjfziKKpj4Z65zYrUMtP377yi1uMUKDYSMvUaW+UYI96ILUMuWQNxfQwDbU2HBiEGKKM5+SsDSeiQ0UR6HGOPMhVeuKbPMIOJdC7hztwzE0u5A3gwCNinYoXd4yd1w9Ey9uDc5bjfv+bj+ERDZjGZOL+5Vv5zx5Suqw7U5HA7OqNIh+RxrVbGzBuhVLy5mcK3z+ECI7yt49f2Jx9BgIKIe+Dl+2C1mEte8Fbhl3JfTc42FJ1ADWpzUV5xiVQ+fzbBfB2Kf1AqqYO6lfh7Q6InXaIODGmjoHAtg7SuitBUpzNClT9U1V2Ett6xQtjZKkzeoEEBfO7lwGV0qFEISOnEOLdmW6fqNc2EJhGdSDmNDOx59ekd648HNSFgKL2qRg7KVM1cLxN3/t+C4KocIVrrVhFDW081BSkHZh+2dTEDQm1v4PlQ0353y54J38ctB7qkZE2gNa6oW7eMU9mjVYSOqJb0qBUozXnrzY7k3WdGDyXRs8TGYpND1yAIq1IsadmYBjTfe+DvF8tPEK+hMb3bBS50guSOClXMh5FAyJGHwahSKKis+ihe6sI5MPBBpbyn+1KmmfqKPIUAd5MxbHWDXh4brJO07396LsFUTmyHqJjsZEHnKH3qCKfepKkPAXEMXGE2xGt8chba6Geb3iRVHKdAlqRm1vJSezZxybBEORRs4bBaGKsMgVxpZibES8AZ30QhIo3v07+u9oFNYheSvKadumjGOpziIylH9vHKFb/EWoxvk84o6XOjcW94B5mTwWbVZzb+p+abCO6hNDb2tAPU7j0BhC4/p148+6vWKmuHaIpldqiey5FTa77yAr2nf9uBzRsExMvhysJfl7Kxhevn3Eq3D/+APH+/cAnL584uQ7e2jJdAoNojF9j5C2RvYiorrwuFyLFGJrqBxnYyZxKZki13fuYV156iawGgLPryc+fv7K53O7OnsBYb/KzWrg3XFl6fA6V+cQjA93bV2/U2FNd9ODrFTjbllZuzjCfrqQzThfeqFlcDl/4dxf7FyFh7t7cpcWfvEdJbKb87U32rZS2Eth68nKuG0DAbiVxku6rqlnCjYbVGLO5XWfa+YlC3c7nLqc+steuMvX73+4eyQeVuy0T57ju7sD//ZV8dou9sUbN+rr1yaG8fjwO0IprP26lfMNynuLazhCPPRcZwG7KAMOH1UxXdh7YZ6r86ALtT/gGuE+KHpQjNakFcvN0mTv711IHKNeM5NakZJnYrwcAmZToJmKUQoTHmooLhWz6zEd1oWnznE8S+Xr85mH+2XC7axWRGEbollVOs9nND3b2iuTd9lEt/LI4bRlSmHA+VahbjbN49ekqIZJwZDUuaC1QQXbtYmYyITRlmLEpCzL4C2Vxt2Z3ONmZDr4g42jXWdeIroQXYlp5CEGMUzRFFXBUGSIx1ghquOJCW1MIpjrPKYqhbwJNjirMz/tnDBv1I7Z70KIItgwrsXIFUqHaReBxzVOSkeptTWahWnPgDQIouSx6zmROr2rYpQOt6Pfb371+D4Kof16VZoyztWPQrpqj/SORhJIqU5jUuJKdvgQA0N8oqpTbefYq/3l4UCWSG/qkXPhsl24X1tHbaG9RGh74HLNKMvc3JpnSJ04S5UE2HQYzgWQ2l61STrrm2Y/TFWat4hfFUJcZAoXnHPhly+v1N5h3R9WPjytV2U6r00gIowE3+ZD277fwbtG/0i7tCUn4+dAU3bZ+yKY3bC6EfxaVIBiMlROFEyoYRxDIZc8C4Qg2vyAhgCEN6LdIM0Jhg5cr/j8m7sXQi9SgxuhynVxoReTg0CoipmTenmXpU2a4uBTiGLCm0U0YWIz8cilkqJg4ZrUuXXfF72SMVEljGSm1sb0mkndrRS6xTVq3fE+zbH+qPrYBJxr8wJosHqfhbq7Y3VHNBC1dTc9BCyGicuPCOo759oTWnVKqVz2L+07S2gT8L5+HdcfWO+PpNAKgFIyLy/fOD13juRhRd3wuvfP37f32IzcGzU1PsDxzGHtHKFjag2IYaxXjZeXE3/+1iYbVZTD8UjoiUnS1tKQ/pJdSiDkSo59Kn/KnA8X7h4br6Wa81oKea+sfRF85wvFKol2XdZVSeLcD1+gpwPvHx84dFW0xIrLxl3nBLl68/AZSV18wFOYHj5P90eOy3q9V6Lspwu/fG4Fxd//y5/49tKKljFdOZWuPjX4oerkUti9K4jGSHrjYSfi8AbhUIqxl0ruCdbXlxOnTQZ3HcP58vyN/+fv/xWA//KfDgRx8lb5r3/8x/4UCT8f7/inbkabYmKJSuoIhyDKuVZev7Xi7Y+fPnKLW4w46JU/9nrKRA8c+qSkViPnMt+Jp7U1apZexOxeeKmGvOSpfvZwhMMaJ8pDSsVqxXtXRFPAKlhvNB8CRBdKn7Ju9UTOZarLSq140im2ULRSlzi8UPHdSAovZyfa4La0/Gfp73Ze4Yc1THPSFJVa6/T8ed0qSp57uYpTXbhs7T2+W5bG9xwNWxOqXb3eGqqmqe3tvWEekjbejw3BGKO6sQ+DVOvmygOtoo6XwnkkN1GgLk18hbZvLPEqOlEQqHV6/NQKlTI5j6LSGmYmlN7sPkQlhTDNufddWVefTXvLlYCw9echB2WJzt6WTEQzHpd5TrlKy9E62kpp3FHtfC+v3ryaxOfUsSKoOsvwmVInEFh7xbPt7bnbhufmd1CFfAe12C1ucYtb3OIWt7jFLW5xi1v8943voBYblW6vqr35+AywlOOY2PTCuWRjL9pU4WgjT7fY1Hh6WbdZBjPiY/fy8Eculwuld/nWqFjV2cXLAkkTSy9N06NyH9eJm81SKficKASFgs+pQzUniKBBSXHIXTc/nek3glDqlUMUpU2PRsdhXRbuDwun2ruZ7gTW2cG4nDPFQLqK3ErFiVexKqzhLk3fTKUaKGcCc7xhDKfr/VDZGx0LryRJDKzbxc8oEes4WaRNTmzeG2HfZfJ9orQO0iivRYz72DrLpV8rcecY14lpLeSmAOfjPGAzuUKPMFzKnM5hgrlPP5PYf6dMCpk3mc8+rlvccRLN6WXAlRrNyPoU6lJhK7V3fmGz5mOw9nu3dm+VW9wCAK9vOEHNF8IHBr+BFxgvpldrbuPjRRVBdEVjIHQom6kTqhCsQbjMjVL35j0GQOB0vvCld/rD4Y7HH3/Pw/sfAYjJm/xs5wz9+eOf+ed/+QfGS/Xu8QeShOkDcne4R1X55c9/5p/+tU0i/vT8Si2V331oPkB/+O3veXw4Tj+v0+nCH//4kZcuFZskcL/IPO8lOWu447WvsZfTme2odJQHKRRO+yv/8OmPAPy2fEA9cIzKz31K9Fh2zvVE6NCP4wJWlL/6zQ8A/Ke/+Wse7o7U3jKNspDrzgCw19D4VUiD+0lM3C2H2ZGNyZsnUb8OrmAPDxy6nPanz1/5+z994jkblzEpq03WdshjV8mIwX23qF9TbNDIMHiWzWMjDilZCSRdyMMeYne+nc6TR6Broljg3741mOMfXp+5Y8FE2V/b73x4fE94ivzLp8b9ERXePx1Z+kToT7/8wn/7u7/n48s3AO7vbpzGW1xjWSKXYUdRhJCcw9LtKmJg3xXpe3w2I3rlPCYItXJIjT83EDAlK8GY6mUmDUWR+qYcY6S6T36Nu1CDIV0ls3hBFEKnP1QTIs4yxlTSYGGf9tf+sxGjUHeZvKKUGqpjoFeCQdaADJn60iSdt33YslSyGblPpWIIYE4fdHDJpdkUMKY5BuFq+1GsIYJEdCqo5eJNFXdMgNxZpDQvAlpeWYtx6NLkvgvnDIO8IKHiBAbSLSJt4tyBAEUa7/rQIYLqTq51qmge1ka10M0595ytYBwe0liOWMzAoXT1vBiF7JXj4F+ZYdmnch1SaLtY51JpJYY45bLzbuTNCW/QNalPpqaljTQM0uC/azEKclVOrU7SQO1p1aX8+iqX30UhhORJxlpckBBI/Ynf3aEELv0iuxTEeCO/LOz1TI5LFzUAxAiiPL+2ouKQEvu+ceraipfSYGSD0FypBNtngh+ScqZJKkKDeD5vBdv6aPg+ERKTHJisEcqCMI09zYVc90mSDjVi1AmbSVFAfHIJCs4Pj0fu+zj5dNp5fX3hx9iShC0XzrnwY4eJxHDPGo2HXnid/NJIv9WneMFu1qB3gy8jzfC0jgWsND3//idZolO0TGGKVY9YLtcFLQohyXxwa3EOMc2FYd92jknQvshW3ziEiFqdI+eAsnshjkW13cx5TFrbYjyY4pHQFr/JrZNu3jLgd04QZxvEPHfkjTjDl8uJl29feX//yKFfO9GKhjjlaE+nM5eqDJJGVGuGlf2YytDzvcUtoImyTKhAZ+mNXoM0cRLpBsABbdy56bvQNhllhyHD2sv0Iadt/XP0d7u440sidll7r8q+v5L3BmMruXk0jCTg/LoTeCSt7cV+fr7w5dszX7tv1s9PT/z80++4Wx84PrXCJ24Fs8wvzy35+Jb/jiUsE5q7Xwp5A10677IUzAJ3w4D15x9JKjyfmvfNvSS+7RvS4X93SyRooFjb5T+dvvHh8T1PTx9gaccV4j1VnshlwPEyx7TwN3/4PQBP93ds+05MA7JqxBgIj/f9zgTEK1YGrMPY8gtLlxFHIiI7moY3EkhxcpfHz/tGlQZDLOXKaQwJ7vrakNYD5nblDgRFkvJhwqyNik3zyKCBGpxT52GeNBNI5A6dW8Sxmvn2uRUxXz595v4uojXM4uvzyxfeHVceukmdqPAffvMHTudWPP2ff/+3fHotc6/5n//q99ziFiOWQ/r/2XvTJUmOJL/zp2bm7hF5VBUKZ6PPmSVXuLIi+/4PsR+4siSH3Jlmo9mNblwFVFVmRoS7manuBzUzT5APgBLpUBEIJCszwm9zPf4HXT1bW9Px1EVOpkqtlUPjkKwmXIKwtPXt4amyFqDasJ8INZIxUhcskgkX3W6NZa2UKKSWnGs0NNdOiSTV1uLpzUsVDnMcDcdqyuUxD9/GGASt7lPTt1lxc9FLb0aXSnjamFoRos0bp3MW748zFiKXlsMVLS4+pd1PCaZZRg4otbLZ7jOE+bM+h9025RCEUoaOE2aBy1rZas+XjMniMKtVdc+xcTHMZay7TYsCZdPRHI+Y53Td/DYIQuSj5O+Bu7sb1rJSJnh45+fhXTHOD3kUJVHUhbqGiJewpIC183QoFTEd/HpjIQRh7mILxZrITD/vGVUZjcAYIoaiVYfJKmKI7XC8GDynq+0716osKszTDkP8peODKISOyZ3Tgb3iHiLjStbiDzBNdUmM0pIGAQiBixWmTo2xSJFAaX4KD5bRrQ5uTDRXKevyCUKkmo5uw0blopm583MkkStcWndBJ+Oo06hwV7kwxYWg1Z3BAYJgxbCuGmcbYrtmvKlzcXK7oQQhGKRW/c9aqTUOD6DlcKCyDiLwp/dOEtZ2Hh7PG4/r5hyZrXcvGymt0xeCO0j35OYpVx4eLtwc/CV+e0zYVFmCJxZRhMe6cuntBTVkMy4N21tKdfWY6onMT+eVX724ZW7H9O59Jr0sHA+Jnimec+bkjRQAbqKQjvIzEzJUqG06F1IlmlDa76NFouw+Q0ULJcogHCrRC5qhWZ+4nFcu6cI0NaI2ztXoz+08TVQq53Z9xaxNGttCbn5+rnENgEXAWvHv9sV14OcNmqhKnxAFRAzp7Po+CVYGNhz8ZdDVHWVasDQTYkvgUyDoE8fbRobPKzEEmkAb+XThh3c/jrXlb3//Bpsjrw6uRPa0Zn54vPDT2s1QH9jyyqeffMLvvvgnAH51/wmXbSN1h/J5YS2FtRF1c1YigdPp3L5zw2IE9WbT0+k9wWrjeML9ciROsLWX3HGeXVwhtsLLjCkYUzReNFW3w2HheJx3M1OrpCkxNdXG0/pIkMA8+3csh4OTcnuTRBwvX9tyFTWiJkMtNIaE5rIrurEBha3085Ixq8yHQJx3BVFPxHoXF1KI7mECEIVXh1u+fOENq5tFyLXydPZ3zXpZOV0u40WbCBwwpOyv3lIroXWjUooc5pm749wJZtRc+d2vf8PLG+eI/cf/8Sf+21dfDV7A+/VMlZlff+z3y68+vRZC19jj4bRSLp3H4k2X7tETRAgmbJ1TslY2Krk9VMfDzM08ESSwrrs5fAyB0pqVB4wk80h0k1W0rqi1CU8RZLY9p0uBWAaTmTnCUyls3dyZ4P3OViAEg20156E05+FSDQnC3IVSpLh3Y3vvr5LJxTnP4LlQtEpqz4yasdXK1pEjFQIztRshq1F0VzSbg3sXRmVwoMvqM6TYlAqSBU5iw+soWCBIYesFY3KD7Rz7tDiBMX5v0dBtF3WaU8KQ4UknSTikMAyn69N77m4WJMCLG19DN7IjeEYVaS42pr3hroRqQ+TGzNefQ28sBzjMC6mtmdt2Yc1QW3MqpcgyhYGWsux8LYINw29T5113nbAwuxqetIU5GmQrcGbcg790XDlC17jGNa5xjWtc4xrXuMY1/uHig5gIVZ418A334+k4ykDrqPrvxXyO06dpZjA5sAQNHacdGnekVbmbQIJ7upy2UdTIDXoQJUAMhFZpF3NX8mxb24axpIDc7mPUi63sSvkRLa1j0fdLvHOwux/599R2IFIbd+eZRnzB2LoPx2EmZeXrk8MfYkqECD92eY+zomFibRK7ooG1KmbFOTL+IXft1Q7zgIiiOYzP3N0ehtKTYuRNWRsf6+5wJMZAblOnZBGzTG83xGAE06EqdzgslCBj9GtJeV9PXC47f8tHxYXSFEO2GJCycygiAUOGrKVMLmP+2I+pVkLY+VlRIkVs/P1mLl2r7f6ZDsJdjcTk6jXg3YpTeeZ0PEfup5nlpl1fKrUa57bN5dovuMb/Eu2Zaj5du1JixD2Bnqs9ypC5FwPRgllCWjczTAeKxMFBnOYZm5cBZwj14gqOsWPTJ0QOnFtHjXIkhRsem0z0FiZKVrbvfvCfS+Gybjw9NUnoywXNCxAIs0OyHh9Wcsl8/Nr5Na/izNfffce3PznU7bRlRGBrOI+b+YYvPnrJ/eQwjbRMPJ4vPLQJ0nl74HQqY4p+Oy9sdweU5qczz3x5+xE3t/fcN0+ekgsxxuHnpZqpdePU+DPTEji+PA5ZXhGDyo49D/jiHJvHU4qYlQHRMFVScod230CgVuHU9vFCYEozVY1pah4pVXDFuDbRswrVO8zgfNa7OfL5Rw5TPNxOSCk8Pvp5ePuUqKKjI79hbUc71DsgErm7aUgO69oAACAASURBVJyjGHh8OrFaJrZ3xSmv/OlvX/PUFPvWtfLVm/dMrbP80YsjH794yR9+/RnA6JJf4xoAqnX4XNXiamSdRaZFWIux5aHRhhAcug/EKXGywmIDoYXIjNUyeL89DZrbGniJgRAOiO12FFZtePyA/9zhwms18llZG15+nvweLtrzOX8eN5OhZpfUqQlz2vMGKc558X+IHKfI0kYf73NmNu1CsNzcRm7jxHZuz3WNSGAotLmv4G6HUqvD8DUGapumyex5Io2zc1FliWGggNSUrdrgZB+XgCXh2HhKVV11bUR1NcmeNYYUuBPGewB1TrmF7uUWOW3K7U3i09eO4nnz/r0rgS4NyisRLTJsWU5aSCidOnXJ7nPXL2WaAlY37tp5i3Mk2e6ZWU1YNyM09EG2QkhwiNOuThwgSRiUi5ga1aXzrTDWvCvRif3y69UHUQitVVHrmPtKRgfmPoiQJI1xoZlRzcZDGcVTDG1Ie/CxbZSdgB/MeR79MzcpsVmg5IZ/VwimQ5o6mnNUuqx0NcdrStqxnGY2jEZdQKAVP+2YDGvJUTsus595D5kYwfZCyKzusq74P+doQ54W9YTK2h37w9MT85S4CZ6InOrmD7FWpnYTZ/URcC8KqM6d6eNei01cux+HglgYkpM5b4Awda3yqGhmh/dFqIFx3o8pYexEYwmRh6eNRGVqUorHOHHeMlsjhR2m4CPoPk7GhTJiaOTN6kXN1nZKxOW5SytagyTmFAhd8jubF0KdF1UK05xY5onYFqzNKkXKzjUowiEkPpqP4/cioNWP81J2CNM1rkFkvOR99YmjmSANetKB5GJCFeidHBGXpTeZBpcuzq+wUlnP3uTQcyZvZUjePrx/x/npgakVHVqEN+9+4JK/AuD+1T2fvP49qVdSQbnRxM29Q0FLLsxp5uVLh289nh+5nW/RnPjmjcOtfjyfOV0yXzVCvuofibKxNniWhUTdVkJLoZ4efuTd04+8OPo2ojl2/vWNw9bul3vI71kbJ8hi5XYSDtGP4amcOG0X5vsjUxeeqIoGJ2gDXIIxBxnk4Gk5cJNumRrvSFA06sDoB2mcwdpfsC7uMp7eGKhaSbGvwcKPD9/z1V//5Pu0nfj8s1cUKufGp3r3eEHrNqCQhAWzMlpgxYzvfnzLfcPc//pXH/Pi9oC2phsSmGPg/do8ntaVy9PGu3Jux2DcpsTvP3Xhi/v7O3748QeWFCiNhH1zM/H29M697IAlJaZ54qYlEveHG7789AW//vhzAE6nH7nGNXrk1YgtJ5iOiZQ3pEGfSi4kCXQUbi1GtTgML7VU1lLIKoSWi5z0QgwMOPtFFAk2jEKNQC1Gt5EREbTIkJwPEkHZ+dEGFtXzIXx9KyjW7QqjYDUAO0T+MAXnvrQm7TJNrLWytkbNIR2IIjw0KG81WAUODfI6S2KKCWk5wIYS57B7G5khBnXtQgjKQXB7hJ7hFxd1SE054HgM1FPl1GCxIZrTF9p5yNmYUmjNEMCckfTMqq35t7Ufo+dFQ+xK1UXEZG+qZS2cLwXRLu4iFIGl57IipDkgHZl9SazVqG0tSTH6OtqvxaWy6hnbfL1akl+L1MVgQiLjHpkA0xSIyZt4tfaNCDGmYVabogsnjBw/CosJx6Xfg788NO6DKIQUpbRuQlUlVOezAESbSExkdmGDn/nziDju3mxMIrqiXB3FkxOUu82cJCEQ3NGdVqQ8K2IQf5j7sEaC17pxcIo8AerCZtUMCf4d/ZLqoFHv/+K9wN4pbp8bCm7WvrVvQykCdW+jUJVRfMUQSITRNUwSUM2YhFEIlbwNx+S+37HhUvtOSDv/fpwCIrxv/iVPuRJs16gXzImRoXfDFcEI1ju0XtDKUEwKpBhY1w1rXVosE4Ixtae9hEBRHdhexJVKulCB1kCROkaGUSbnPQ0Oo3skdK+QapVTzuMhvKyFbVPsfkIWXxRDjJSy27gukrjYBYrv47nA7ZyGYENXLLzGNcDvvd6ls8YB2h8pRWx/ef0vOhsyEZcbJN4M0m21zMPDW3588z0AaTny8uNfcXryn7/75q+8PWWWxYuIXApLOpCa6txHh485YFzaM/P65h6zyvc/uj/O+9OKVveMAKh14sf3j/zp6Ym3J58yWEoEAvncu5eJ+8OR2JIXX/PSUEg6pMRHL4/jDfJwUrQYj83k85ACv331gl8fPcGfQ+L25jDW7Rf5BYdlxopysV64JC7nM6n7j8jCtCyDN3l398KVnELnB3rDbDRm2jRa+3oVAmI61lRUXTBmNNmM25tbfvfFlwD86rPA3d0d05R42xTY/vL2e+pWOTV+1ePjA2ozuSVM61YoCNoaNx/fv+L2RpiaJ12U4h3u7GtLeHzgjRZkckz/zTTz+uU9n75+6buYN96fn8gSd5PDrBwPt4Nn9tFdRJh49ZF/5z9/9hvubw48Pvg+D3mva1wDzyp6A1a0cimVmzY1nKcExYYgkCRjmdLIK7ZSeZGETWUojwUxNEa2NmUQVWKIo4GKeC7UFdlqLqjE0TCttT2rvQlcAXPPQXAV3rLVIc5AjCzLzEHhtO0NJ4xRRVhVJMLSFqRUKgX3AgKfnmDO2wZ4KhuiZUxCghrnR0hpn2qYCdrFYipsaki0sc2q6n47sQssgIVAmHvT1xXVTg39clkLOVdsTEAqFmRwtmeAZTeHR2srdtq1m6PzmTtHO28QA1sIjKoxGEbk9OQ7+eKYOMxxqBVrLKSYWbqysEVyNi5tkr8EISFctn4pDeLeWE4xOkl2iFO5h1quldDUMHJWtjUTW/4Uog8Kes4XUst/+7WTX74MuWJ+rnGNa1zjGte4xjWucY1r/MPFL1+K4QV2r8iqCWaGtAo2B6VafiZPC1NTFQFcnS0aMYcBwxALhFqHhHJAICjHBrG4sUgWpSPRdnRjC7PGReobcVhd1Q6dM+9VdGRc9O5B77q0L/nZMY7pEvv/vfkw5sfeuen8G3Hfoud7Fm2XDY/Rt9elGkW8B10w97XAZXZNdKh5qPr4uUNFDCUoo3utQfx8to7DxWAKzzCrfX87Us6a9G/nR1htCiX9II2YhIPNwxfIojqMcbTQldAgeuAj6anq6ECYGUGF2DpYYopJIKR9giRmu/R5CgSJQxVHq7JtG+8vAWlwlZtjYAlpKMZoUlTS7iFAJde6e4fYGF5f4xoN0rHff/asNSkExGT8fnCHGuxSlnvifAQBbd1KUZimidi4MtN8YElHttnxKq9evob5TOn+OdvEFIXD0acKSmVbH4Z3xKsXLzlfLkj06YwG493DhYfWmcxbhejw4Jp8G6WuxKhMDQJ2mAMv7284TA6ni0TW7cTSoLifvf6ETz7+jJ9++haAb775O1uF2KY3r+/uuVlmPrpzztHhZsFqJWefauS0gSm1gKW2XqkrRR0ODre7uT+SYuLYJmEWjTnMg4cZgvN+OpQusWCTw5jbhfqfRnLOU+jT52LG3f09fzj49/s0yYfPn730/f79558RTDif/d3y7t0PPF4K37137tQPT2/JVXn9SVOyOyZiEl698GO4v3tBLhtPzcH+xd0dn3y0DtTCZ3cvOd4s5JP//qe3b8nm8GBp1ztIIEjg1Y1/pyT49OMb/vfP/tn3SZ948/47ttWhlbdLlxO/xjXgGCNdpPA4TcxEpjZ1reJwsqF0FgwLYfAVVY1snifctAl0kYrVQm/kiwkWFRsQGbf2mvpzmmJTsG3wKgWwgTSxKs7RbvtQQ8WyjRxgqxVYPdfoPJMi3KREmXpuk5mPC7b6+lLXgkjkZbMcWANsVVnbCOgmW6MzNAVJEUjVOdU4xCzIDmMTFUoMLEGQBr2dEUoKA70k6ryn1OSLQ3A/yD6RnqtTNDo3WWQiTcMlwXOiIOPcm1ZySOM8hGpU1gHTXWsgqEOxpSOHtLLEwLp1FdPKJcCh7cMaI7cm5NjWzJg4zEZMHfUTCcaQ4lcxtLqyHDRJb63jWtkUUYySjS4FHIMgkijtPK1boQpDJjw0+e4+2bqcOlbrl4sPohAKz4jrKobqLo5gprhJYSsABCTuN5OJ++GU9lfQEvG4Fy6mhlRzzxr8Jq+y36BI8jRmCBcIaoXQ5B9FhErdFwf8wek3SyeCiTX9etpIUWSIQNAmwWHPn6hBSbY/iDYo1V50mO5FB2akkXThRF9Rat3HjwQvdkw6R8eLlN1g1YUInhdXKrtQRa0uXT1qMxzQ1z2AzEKDldj4sIWADE+VRgbvRq34AxOSDPNatYaB7ZB7zyR3M66YmIO4lxBOLnaRib5PxsRO1jMyGsIoCJP5qHlt5+D+9sDr21sudRvmtHMIBIS1NmlgdSjmbRtxL8F3r5Miax87X+Ma0Ii+48FEdRdDQPxe6pBXgkA8IpMnpyEtqBZC2I2PQ4gcbl7xRSsAIBIkczw6Af/42R2fsZJbNlPKE6fLI5emlqB6YSNxungi7E2Rjc+aOephTrw9b2hLxmVKpGkiKoODeIoRNUXaGvnJ/Uv+jy+/4OWd79PxcE+aAqk1IMp6AjXmj7xgiCmR0sTx6Gvmi8MNQXYfjjVvnE5Pz7h90mDNRghNnl4UrFLw43i4KPd39+Nciwmb7V5sAceX93X8XDaH5Iy1pdJkasa1U2SsZ1qKw3fbuv/u/U9UhLtXH2GtqlxiolTlZvKCMR0/4VUJfHLyfXx8eIUE4b55GU3R20oW+5pRWJaJQzOL/PjlHY/n09if4+0t67sH3rZr+XBZ/chKHbAcv0+M2ybW8+mrF/zq8y958865QH//25+5ObziN79ysQSpH8Rr/RofSGSE6dlLfQPWLgQUhZiE0KDrWhWrNhqTEgSZZt6tF24bTFZNSBGWxglC2zuyQ5+qP3HdV8gby5GlCUHNh0CMwtroDpeLUrONfCpZJN7uBp01FxC4CXEIEZyqYVpGsi2TMAcjzbsReyB2HQOS4CInDdp7Qpmjom1tSeLeOb3lueWKRLjpXjdB3NBed563TkI02Z1eipFSHflVMbdy6eIlYQmkCKEL54SA1Tq4UnNw/vMoMmJgVWVtxxhyIJEJzaB1XqTJXxv5md/RFBlF6eO5ks6ZevBzvxwWjuJ8Kt8Jo6pybHSKauoQwPZ1idg69p2qYBhpNJ4vm4KCTmGYRJMDaruBfYwJtAwu+mSCtvcNwLT88o3mD2LF9Iu2X0jExgs0tBdZT+6R6ASyrsyBOZZaAlF3v5uKEro+e5tS1E7A305ue9c2uUxH5gpCVzlRwjI3gp6/3KiF1XLbRWORPflxxbjkR9DHIdIKg94ZDsEVjvrPuJPRkFLxD48OpoqQ4u50DG7GJaNj4Q9qV26Z2jTHycKtG1BBw17fBfGkQcZ4Kgx8K7SF69kgyxczV5kBXKGlPONnpdhUTHoSaI4X7vwJ83MkomNxCCqEZDyvEIPZ8IlKseN/uwGlNi5Tf1gaF6h34KUxt3qxRitKW7tqOUy8kBvO2xOxdcHu0kK27IIaePF0EyIvWsdLw8Il56aQxzB7vcY1evS7V80nMkPVMgQkpDG1qBKR6TAKf+yCaUJCZJh5i7JMM8u4zxYUyMWFC8TcAFiDJ995XVnXC/e37hMkaaHmB0rzYoshcn+8p1hTGUvKAeGHti5sa+XuDqYpwqFNTkulWqQNmfjD56/5zRe/ZWkiJzEm5jlibRvnsPD27Y88Pvo2bpdbXtzfcrxpjvUI5bLu69s5+CSqrR4xTZ43iVLaJAMzshpbM7r+6P7IxMLl0hzp84oUYVu9aDhvF358OPHNT14QbKL85pPP+e3nnwJwvFmQph/aI0rEhppV4bxmvv/euVj/4823/PDTO7548ZrPPn3t+3B7y3Q8cmjCFjfzPTIJ0q5VSi85HG+Yp6lfYHKu7EJ2M+ftkdKmfyEESi1sp6aut57QLXF68OLo7fsHaoqEmIbh7jwnpjnx2Wu/3r/7/Hd8+9Mf+R9f+XHneIOteRhEv3h5xzWu0WOeA7V160/njfO5jnfaZRKmFJDgRc40B0wYKJIYvXn6Ks08tWe/5gJLGu/wIJAkcukmwuLt1k5Vs2LEJTB1w1Qx1lyJLW84pEANMt7HUZzvs5saBwrKJgzCPaJkbDQ3rcK6FqYmaLVMExIij63ZGWsAFeYhIjC5OvFwLw28v2SOQ6lT0WnPM4MoGecK9QLtIJFaC319SSlQ1AbSBPHGUVerjVFIUVi7eXwp5FrHWqIN6dR0LEhp5hBgii33JZAESq838i4U0y3pUhT/jibgcMnCRZX85Ofhpho5xfE60oYs6oTEeQpMIbJ1c++8YQJlbSpyAgQlttIhVyWkQLCAtcZxnIVN88hlU4gcQkLCvo0tMwqjV6MB+MvFB1EIqbHD1EKiWkKmpiSEeSL/LBf1AqRPf6pPG7TshDCMWcKASOSgaEhYgxpoVUQiKXRy3sYSZqY2o7xMkGvh2MxLj1Pi6cLoYGgofVzS9ie6kh2GtGQjTG2G1TIin4Q870w2EuMzAYZnInINcrMfttDWnT6MaQPSfgzBgidkz6ZKtX1nn8YEpHVE+3e4EsyA77QJ1oC68T8VcyJNFryPo43nKEXMr5UVf4imlBBxsl8/dHdHDqMYCzGxwBhBVzXOmsdDYv9LEeLF4VgP24nr572owRKZ+q2thU0yS5o4tK7IR8uBhyy8bxqSa80sIY3FP0lATUfCFD4AecdrfEjRSLKAERHigKWZK72wjRs+MSEszQ28lg0wrO7wOpEZCfpMaawSgdtmdLytK6XkIe5iXHh5+4LDrU8p8uXMpRRSSwKOSwRdx3Tn6eGJ96fz/kwFOG8rq+6T9akG5gT/7qMvAPjtp78iTravy8kn9Zf2gvzbd9/y9d/fcG5iCzdzZHvxmk8/8yIkLMJ2yTy1SUe5ZJ9OW1c3CpRghFLZrKkHbZm1FH+ZA4/1HW/fvuPr7z3h/+7hLVDYmrFjWTeKRNa23mwCf/3r3/jPd14I/PMXX/LFp6+4WZowwe3CWmdObZ9/+OkNf/nhW963SdpaBc2RP33/E3/+zmGFN4eFV/d3/OYTL0K+/OIz5nnhxa1/p9jRoTEDums8/fQDf/m7S5cvcuDm5WumJo9dyyOmQlr85X952njz0zt+ePCi91yFIEqlDBJ1TIk//Po1n7/+vZ+H7//Kv/7lO7QrgenGqvDn7x2m+Em3WLjGNfBpzbY2cY9cUXSsFaVWRAPSJh+6+eRVpq4SBmWtXKrtstFTIpgMwRC35ZAhhxwJbNs+AagqkOt4x2dRSqlD+vqwRI5hGmvROSsl20DgBDNSs8jo6ndrNiwKsRl9ZlVkVWxuU4Y0kay6XBwumZ+mNKqIaTKipiHvn6shJXJpzc9DClQxSks0okAKiuwSDlzWjISGCAKKKetWaT0P7+VG4XzZG1TBbBRjBKiEXRSF0NAyrTkVQS1SW0N+zcYxRbS9B7T6PpnYmL6ZmjdERi4TqYQBr6vaCpC2C6aKqo6JkhbhOAdCN6qNcAwRPbTzWByh0xs789SoCKrUfh6AmUjt0EdVSmUU45dVm2qg70O0X16M6iqWcI1rXOMa17jGNa5xjWtc4x8uPoiJkNkuKx3dDAK1zgFpcJP2twEnse0IbCPhEK0+sowivJhnavFxby4Zs7RLMot4Bzf00l04WWYufXqjaDS0ia9fSmWtecBddj5Tn+Y0o6tn/kYpBJDQFZghOOm1Dv8R80lLhwC2Sctzo1g/lrZN2gCqd55xcnFqlzBIIOI+Pn2TVRqArDenXVlgcKl8JLrD4QQjBSV3jGrbZh/KRBWXlByTrSZNO+CAAUGIDW88RZ+yiIlPavDJnwi70IQom8QhR6zmXReTHcOKGbVr51OdFC1dGl1R3cUSFEMvZfAKjumeWoXHcmJrREqthZMaHSYLzvfqEtwYrKaNpLnfm9e4Bvh0V8Y0R8CMMqC6M7UqTZeAwzxzPB6HyElaFi5bmygPIr9POQfvqE1WQ4NbTW3N61qvt7cfE6fbwc3bLhuzyFgsQt7QaeZdI/h///COKoHYOo3zJKxrJWxw7GamUyGGRLj1bV5s42DHwcfRUjmfz/zt278A8G9/+jvvznlAUt/pxLc//ZlPHtyX6Iu7V2jMDZrmEDEsjK4hKkiuvD+vPJ3eAPD26cKbxydyk3LVXAlzor+mppsDqE/gAKZlISJMyzNMvhaeHv05/7//839hSmk818shEVKk40lOD5mHUrE26U9TZJlmLkWxJg18fr/yw/cP/PCtT4ieHs78/rdf8LLBzywEQoqUbiT79i1/+evf+c9fO9zuYbtwEwP//ot/AuDLTz4j1yfevPeJ0Xc//cC7h0eq+IQozAlyJRKYmojDr754ze+//APfvPkOgP/61VecNZDay2W6OaC58LbB7R7O33ONa/TIZkOqOFpgSXBs/J6tBLIpIwnIhgWojWZgISLiMkMd2hQqWFXKM+hJqHXwdyxAscLSoOZzDJxr5WkdKgDMYV/frDr3OKUGrSqFknd43rJELpuhuAAC4BYocedgJxWYGJD6rRQ3PdZ9bUix0DHMWaJTE/oxobw6JrRB6jUbwcr4/Dwn9/GSSug2LQa27ebuIQo2BeYueoOQzZBm5RGssm4F2lRrToEpMvI1z+kMbZO2GAIxOl8Q4JCcfNVpBiaGaeSZownRhBoc4ujnZeJQhLVxqHOpvpp23mV0vnxpxyQWOJfLSOmmGNmSMTVZcWnorW406zmsm+vW/j7bjItBfAZJRpXarmetwhKF22O7gfIvP8H+IAqhEGxgMUWCPwDDDbw24QH/2zgl5w/VnWBWTLHAMPxKYhynianhus9PFalQO2nNmnNO1843I8pGB+0Hm4gWWLeualIpVofymZtc7QUCVndhBNuHbGY2DMDcoycN0Qe1ShAd7vKGE4Wj+OKQtYHmuv5/S726aIBpG4M2vwqziEgf5+48JDMbi8fO1GnfgSf5/f41EQq7B4rgN34cyQvDONb/3vXkdrU8V6noY9Xazl3VZwuYiHOGbB8nY4YN41j3YRnwPXEIXoe+1aLUWYmxw9YEDbtPQpDoa127OA95xbRgQG7Z6bm4QWsc+xTI1THH4P4Ap1LGtewO2Ne4BnQU1F4Iqe3k49zMAJeDCxXc3LxgmhK5QzerNjz2zpdxD4iwQ1ARTGVAJlKa/DnrcDw7sZXT+Dnp5ibELSvIuZCzkhss7fXxhrsp8tAMW9+uhUddOW3K5dKKpxj44vWBP3zm3JjPX710TH972B8en/jp3U/89797Mv7jWrA4kQf3pTBb5E9f+++/Xn7ky/uP+PiViyksh8j5dCJvvk9vHis/vH/g6elp+B8VC0SEJTnsLNwIcY5DKapWxZTBCygheANjNMAAEbStJTf3kVJ0rMHbychaiF3tigjRuGkGrSrClg3RHRqSJr9cD01o4j/+8Su+efcD//43vwPg47s7JAo/vXH43jff/sDXpxVtRrRLvCVL4D99/VcA/t+vv8KUYdw4p4nj8nIoR5WYWerMchC+/MzheP/8+a/57od3/Nsf/+TXVyOHeRpw43yphMg4D6bX9eoae9SLIa1oluQ8ua17LDY7+p743t1Iy2/8HrrUQrFKDc/6NtoKkfaZNRtqYUDELpKRYCyDOmxYYXj4IEJNwtI9EE3JxQbHSAzmZRoCSBd3XMdUhhGoAbXsBYCY92OnLuZiNDGWBoWjcl53o9EUEqgSliYSsBZO28oUPWesEpAah/G7kilqFLWxTaoyEYiNQpE1gwWW9p1aDauV2FXkLJAk7ZSKTi3oP0vlkISubltC4LJt4/dzWii5NFi1vzGqGbLrVPh6KIG5Xb/54OcqnnyBOZsSk46idZkiwSKpvUtyVoJAs5NjUyUVGSbU3VNoFEIqqAlRXUzCz4uBRLqWRjHneNXBIYuIVS6n1oCaf/ky5JffA7pwQGfWGZbLTjZu3dLO0ljtgkjYMX31WWrfC9KqPORtXIhK8BIg6PhIkN2clLaFpWHVNUXUCl1oWmIY/COARB9pdMK+uNmqMG6wSHM+fjZNUHZ1PCw2fkF7sFUpaoNrMNTl+nbNSdnPpzsiMiYlKi7bm58LHpgrMw1zR35GtRr7NE7f4Cg9Gzs971wLrQvdr1VL3qQXjF7YdRMzMyOIkFJgK/3fgnc1uvKKaUt0+gLnBMbBnRKXxO6EQouNv9O4ClOMJIlDiaWqQRTv/AKbXbzIcgZo2wefJHUi9xQj65p5++SE5a1W1lzHteq8iGtcA8DqrhjZp6Zrk4XWTUi3C/cv3CAzBEEtj86lavFsBGOA4AVMZfBxsCaM0n4MAUhxmHBCxh4v48kNN7dsb98P6ddVjfXpidikrm8OE2F74tLWklfTjEkhTjC35+Rwu/B//tO/51ef/gaAy+NbHt4ba/bC5c9ff82b9yd+avyarUSm6dm01OBcMqU1F7ZT5V/ef82Ldz75UBJPDyfO2QuKmBMyJw7HI7ctQcpNOGWYaadEfcb9DHivStpUXYsbMQ8suvl61o39LjmQi3KYepNNWFIa3dEgxmGaBt9LxFhCYBMldEPJCqJ7U20+HHjz/oHv/p//1C5Vxcxo+g4saSYcJqyrh4ZEVCO1JprEQGRCd7qyr6udgG0zTMZHrz/if/utX4unrfBfv/ovPOb2uo7K+fFEXJowhW5u8jrQCDPXuEaPZamsHfxS4KJ1THKrGlMUUks8tAoZmLtxu0Y3xDQZpveqSkXHOzmKv8f7VCGF4DzJttFARApDMCYlIQQdU6caIrkqpT2Xc0iQdlXfbXWlO0/8W54gzrBulENigroJU9h5S5ICyTqpPxOjsnWVuZwBZe4Jf/F1PNFlpf2cBO3IE5ibWMFAyMy9edV4SVFYQ+Th7O8CKcaSGFzOmisJGbluLVCDdXohIoFLZiCXpgSx4h4mwGobhP28VLwxLuWZinIUUvJ8EiCvSpwSy9QKOgkEzeTS3xWFOYXRv88AWxy/MRmNVQAAIABJREFUl2hI0oHQkuiNv4FYSr6mpQTS5LAtGws7qkulUoMgbbCwaYYpsnSlOn75uLaOrnGNa1zjGte4xjWucY1r/MPFBzEREmFojquY48j70AEhJBnQqVqyG3B2LKgqqYlgdPy5Cbxdz8Q+u9UJVRvQgYYJG5X3jHcYtg6Voksm75OQJDO1dQn7FKfLdUeJrUSWYeKKGdVsyD3OEkGema5Km1K0zkuwyGxC6h1V2X5m6qpW23Bmn+lIgiXsSnkVCHUaamcEl8oeM6k+yNqHb40v1EeW/d8HaQi13Ydo52k9v3Y6RsVKAA1ow9wXMZIaWXdeVdYGOeuwxK4AF/Yvr6rDfC2ITwMHTEiEqjpG3tWcHyatUxRFMOqASbp8d6BG/bmvgcaxD2pGioGHtfkK1eqTye4HUD+EnsU1PpRYz0bVhmuWI+EWbtvEQA6BcHvHtPS1xCAkpHRuIKhuhOkwPHVScmWkvqZVUdIS0NZh82lvJXYT4XVC9cT65NOZIoZVhsJi3SqP58zD+h7wDqtaZB6KbcrL2yNfHA581KBrn758zcsXR9786NC2f/vqv/PuvEtyP27CGgzLHaaWOW8rszQYG4olGTDSkBJTSayNd1mqwrRw2wxcuXFFoyCGteNKmBv2dZ8Nq0RsV/u0tngNmaXOOWr7pNnPYVe6E0izDBhakoBZYe5YdZpqVvt8EKNohgb3AN+chTLw73m9EJgGl6AqDm8ZfiNGNlj6aF8bbLut6xFfd1NfxyPkYmiHCcWFTz+55z/89p9ZG3b+X/77/8fDuT5DB7hfSulqeVWIVgdUroqvY9e4BkCME0t7p2c1TGw3m49CDGGoyKmIG3k2uxKNAklYppmbLsSalTUba5t8WBRqXQevDlwyuavkFi2YpAERQ9oUoL2zg0RW0ZErmW1YjTuvMgpVlMXC8DeqqhDCyBtzFiQ6lA8chlaljO+wYKA7fDg19E5/zudJiNLZglBLxeLuZxiaupvIABYxxUiMiXOD+8Y4s1Q3ogfnABGUtfEH5xSoPwfskJLufFPz87INdeNKSpFg+8Q6ph1aF0RYWgpZnnmrEZ95RZpDiZcmUW25sK51nLfzppjJMNg9zpEazUfhAOKYoQ6djNL4YZ1GgmBB26S7r4Hacrx2vxQhEJib+e2NzM7bbF+66n7f/FLxYRRCzwqCGAWTOooUM4eihP7QGNQtDxiAaXBzQq3UNmKcpglUier/4HrzO8IrWOOqtIe/mvpNNcaDSsR2oywx1FYGLwDHpndDzik4Mcyc4ezfoS6/3I3MUogYE9WHj37iq1GbRnwJiTlGeq6j4vCYDl0zCU1KfOcMmewCESBMFsAKa9e1xxx2M6Bt0kbiO+xM1Qixw9JaRdLHrGZtBN2jf7YlDmogQu5SjSmQYsTGM7T5d2p8JiLhC1wd0Dh7Vki2Cx6s88Kb1KMRulmbCKZG7Hytaqjqbr4m5g9hF2eQRGpCFV1O2JMXG5VdUUOkIn2sDi6H3grdTtq8xjUA/uO//Vd+fNdko1/c8R++/C2vX3iCP98cGn7d1waZjoDsWNcQseprSzdDxoQY8yhkXEbFhtGeFsWKsnWp17JScuapiSGs28oUA1N7OV2yoibMbS1SAulm4qPZeUufH45IDNwtM3eNkJ+18s133/LHr/8OwLtzJpeJ0ODCEThYRRvEokSXTJUGfwjRPXJ6kaIIYQnubwZuZljr8AgyAhcyE9E/B80UYTdIDTjfsUvYovYzKG8jUY6lI1tgDoHUcYgxPF/ufI141kgy9fWnf4FWQWJ0bkFfZ5/xI/0wnGnZr5X09bAvEa1x07cSmoFi7BzYnh/s/TJSBGsF5acf3/DvfvdPpCnwL//6JwB+/OnCqjDFPLYZRMYaKCiY7o70/zP++Rr/0HEpdUAzp1kI1X0QwfOgLvQEULIySSDdtmRqc4L97U3k7s7TxfePKw9PZ57aS/pFWDikBW1rieaMSBoQ1tsYqOiAj+YCSBdpcA5yMJhmX2uS+Ht+73cYMxPblseaWSVykIBMe65SJY5tKHC55AFtCwEkxgEBtFLIunu5GZApg3ue5snNSJ5TFdTXOJn6YmCs22UXuRFBqw3Qa0qRXI3aigrVSDTG+lSjoXXq2gkcEmzVRi4TiJAVa0IFMQQwHRBqRdDq4ljDGxLxT/ZdCs6remwG0Nu2kYv70vk+KVoMaRDpGB0q2YuUAky287vyljkXRVqiqnlimsXNUQfXKbBEGdzMOAeOUegMA6lCqZXcE2z55ResD6IQMgvjxdG7AqMAIBCVXfceo9rePZBWxQeJQ8zAqk+JNPSJT3BB/K40gBc+Q+XChGiw9ZspqfvdNHypibXX896RK1aHV40WQ6aASkF0G98ZRMZLPm+ebG9NiW6WiXkSijbH3zkQqw1eUjChWN39ckyRZwVBpD0og2Dt3VQiXDoOVrzI3OgdV37mhNznW2PSI4FnuhREEarAvDc3KVgjWIJFY5bI9OxamO4v5JCFSzRC0EF4jghTDLRmN8UUQZEhyZdQ0fFgJ4E57bepqIst9MXCpJdnLZkyPxddRW50n2AIcsToHYu+n1hAnnHNavXPh/awd6GGa1wD4L9998C6Nh+ZywPr+kf+r3/+JwA+W2am84o2Aq1ZU4fshXxMBH+FYW2qVC1AmMc9b4A8m6JaKZRayBfvPG7nM5fLytPF15pt3TiEyFm9MLqUQlwi9/e3/vkYOc6J+1875+QwzQSE7emJN82M9Ns33/Pnb3/kMu71xDyFMQ0t6v5HU3vNpxSposMvFZtxRco+hVeq4eRgWsIFSO3ZjQvdxGDomJY1n7Pe5bXqRWFXlGyTr33Ebf5f7+qG4MIpz4wZqTb8eDzjY1QpyZqZs+xfJyEQg6/pPVLYN6mqQ4QGaOvM3mUrGphw7D94N1aebbRWP47nptZpEl42X6I//O73LFPgX776F3746dGvpynbVpjmNk0LNJ5s+87x1ujfeV2vrrFHChHtSWhQ5yP2JnD1XKKLvVTz6WQ9+b00qRAjvH98Qqs/y1tWJjVu2/s0oxSMm/bcHm4mat6VM1NKCEZoKr3LYmy6m6gfoze01/b3501J7LzgYgZRiBJG87obh46mrgpLkGEsGpOw1mm8u6P43/d8jLk3kdtzmytBAnMzkA4hebOqc4SaeKWJsrUDCwpxAm0d+G1TVupAyITWI+nbTNGb2b0JHBCk7ip0pQYv1HpxVyErDJudYkhs+4LnKXnzXGhuBV5v+Of+LtlcmbdPrCnOq9JnE6RL3sh9khYmRAOxKXGKCVoDdzdNPGMTKIXUrnXRSj27WE9oasFRAlkrqa+BIrDFwbusQZljIJW+zvOLx5UjdI1rXOMa17jGNa5xjWtc4x8uPoiJkAQZsKUi6t4wbVwWgo/q4pCZbqPFrlgSXGo5YsSpdwfirqAGLGJUtaEmVPHphlrvowWq4E7EOGQiKFifmwawrVKjd2Bv0sQxzDw1VZTT+cx9WLibFlKTTjzl1eUcWzdSppmaC6VNpQoVSQFrrZrTI8xpZu4TJM3sI4umktL3B8f6prBPc6xhOUOahh9S1Urimdxjl9UeWFzvVoYBhXOcfN1xHkwiHFsX5lSV2fTZtKXjRGnbA5FMbConIU6U1YizoGXnJ5jkn0Hd9BkfJ0okBEhtHyeBOdrozJTgCn+jS0yXgty7D7VB3cCnrll8dDvOgzpeeGBzQ+vsPmsNe5+3/Txd+wXX2ONxi1waxJVL4o+XM8fkkLIwRT756GNCg7G5Accz6JR1BcpE97Nps1r6kyT4dDXnjn/PbNvG5exwvNPjhcenM4/nJp2vlZXCNDs0JaZInAOHo0+lprsjty9ec3/bvGoIPD2e+OntO77+xvf767fvuGSG54WasZXC2ngopWSWad6H6oi7hfcJkuPaxjOVLIDVfYouQjAhDElVJWii1rID0AkUZPhPnK0ySSQ9w6e4GtK+Pjl/s8E0AhxCILefVytEZaxXEmgcp/3zIjK4DKo+LRfHzPXddi5ln6KrQ/YGWq8fehhfSQpGHyhZ8TWqc4C0oQT6dDpMkZvbA//u978G4PZw5F//9V/4y4/vkfa+IhdulgOXprh3czj63Kxzvkwb57HDgbnGNUZYFHLj8xSMiUBq8u6ZSpIwrCSaQcZA3GQANbIp+tRU3VJkWuJ41msxJoXSIGA1F8972o14qiuXatwknxg4TDZjTdJbK5yyDdl700oBukZmiLCVyuFmYmkoDYueA9U2nSmrcjgIFnfY2d2cqLFD45RzNvpozEyYJFKaDcc8CUIccC5KxZF6LV8Tt9+IBJpAKEmEdNh53xaNo6Qh+71pdg5kM1xaS3YF3MHPcujuY+k0gcpxEaYGU6tSiW1aBg7hTxqIz5ADQSJFiyv1AZKEFITS3i2XWplRrFFaq/maE8cCVlnDPHJnFSFWHdYxEoSy7T/rbEjYeecxVKItfl36PoiRzFjbtZnmCWJl69C50HnX/vfTB2BP8kEUQlH2E5s1Up6NTecpIRJ3GWoJzfen/YjDyAQbUMMY3KBr0i7XVwmSxk1eVanVBhdGgz/cS3vxrFZdcOAZLC1GYWmwkJeHheNyy404VMVKZjlMvFruqQ0I+SQXLBhz6h4VXuTF0HlJBbHAR0eHr5TiL8ul+QhZcWEBHSPIHUMPDhmrVcdLXACmRCw7UU5pGPS+YFknKT5L+Lv/Ufu9mAxFcsVYBI4N5qNkni6FAaqLlfIMFlLxpOK23VYWAinVJmnbpBRVhvCDbzNiCtJNyRqofxdMD2QYYhlmYLFLEIOZYp2fhRe1ZrYvFmZIcCnz/p1mSjVj6skIbhK7860cytJJ1pI+gNntNT6YKFZ90QCqbpQl8pcHf9Pcf/8tL5cb5qW99LWApoFWisGwELBShldNEKGWSifGTdMBK1Bqh76duJzOnFvh8/T0wPmyDrx71YmYJpYGTZiPkcMyc/uRCyHcvXpJmo50kGhZL5zPj3z35lu++ckFFU6bsG3r8PuCSJiM2GGwEhskufFSanaPsY65F4eoDfIySiJRugxrYz4Nrow0XzTiODdqjrHv2PHY1v0ughNwSF7nPKo5P7C0DkcKEeJAlpCYkGmX9VUVNMDaiASlVuZpTwJV1PHwuhc2oXModD+OqnvjRkIgPLNJmJMf17A/CM8g2DT4sFViSwqXY+R3n33K3fQCgD/+6Y98/+MTqabRDJQpUHVjap9ZS0F0t2KIkjDZnSS2q9z/NZ6FbaN1STJvKlsrAA4xApWlN2UskM1hYuCJdVUlqnC6+GfWyZijEuMOe33uM6SbN01HYtEsMR7z/hzfHQK03Gg9F+cgLr1ggJyNVqsRQkSqG6efcve7cRnp2LFwSThnHR5jIWce88ShJYoxRm6Ce4SBiyqoFmI77hgaj6g955soW3kme5+FehaWm8DxrhUmG+jKkO+X6B5zU/+MKjynPysktcE7MrzB8nLeob+rKjq83SBEQ+a+D+rF08j5hOPBmG3m0hrNS0mUvAvrHJC2dy2XCU7yyM+gvfMEd3PnCEW0KocublWFGpTcBRtUiEsanlExisv1CwOqq6asaj1Fo2VooykW1fPhfsuFDyC9+iAKobWUoeh2mA9MhKH+UaoimgfO0mgntptKhUAW7+GnRpRLFDcNa4//1F7ipTPw6Vyb3oF1H6DOY0kWyeJ+Nf7nhaoMj6DHXFj1cTgtf3y442yZtTyxtWc/moAkHpqiiMnkBUCfokTx42h3yzQr5/VCb5o4L05G4hF/jgL3VN0YSUHAyNUnQ8NtWXwbXWjCcKW00ID9s0aqlZ+Ra6v2rmvHnhsUL9ZinCiyqxOlxsYZWYMJtRpPzUcopYk0eX83N66BSWCJkaUJE2RVVmFM/NAAYei7ebPYhMvgXhlzSNw11+rVCpvl4S8AzePlmeBDUAgaKC1TiDRX9n4gQVoS2qdUEVUbC1y4GhRe41nEGJliVw0LzDGO6XJtfCDpil6XMxIm5kYE3jR78V698+pfKIRi1Fb4GAmzla2JIeTzRrmslOw+VylEbm/uhihJPQS0FnI3dc2wlkdn3wLH24V8OY8mTdk2fnzzhm+//4mHrbuiT0zTRN66j4Y5trubsYkrE3XujE9BhNSnzCKtGOgNCfHj7I8YTdSmGxpaU4gz99Pwc+n48d4E82mNjIl1kFaI9Ath7YXa0zzrj/ReSKnsSlFmiuqzpLCpPnUOkYoiVMyeF1vapl6dOyBIiAzTaQHYJ0i1eIPN2poYkzDtQnZgAY0bUzMR/PKTj/ny9Zf8+Zs/AvCXb35kM+OAjPdVNKFaGIVRVW1J4LOJttpQuKrjPXeNa7RbszUslmg+PRiDWoPn9zvKTKLf7zUyktjmNUrZNrREYvL7bSG5KttIPIyDTYOrt6EkfGrkX6qUaiytiJnnQN50JPiT+Hb72rHEgNxAQruWAaV6oaFNzGXCCNH2BkYEq5VGPyQLzBZIbZ9jCFBt5ATgfOzcRQBM0NWG95G0gqEUHdNhCQEJRmgInGn2IrOvcaFWKjqy7GiCpH0tENxjcVcajiTLg1+YLBLCPBbIFH0NvXTBGXNPphQYhYsZxDBzaWqft5NPavR5qlN2IbB5SkzHSGyqcYnApWYv4oDjnHg049juj+mQfiZuZnihLE0Uxi9vM9ttua4VWLWObYJwnBONjsX2AYglXDO8a1zjGte4xjWucY1rXOMa/3DxQUyELFdqq2hLyKQwDRnpanh129XSggw1DvBRn5nD4jp8QcWYJaDNh4Fp8rFnh2xZ04zv40EVtqxcrE9vjBTn0WlU885gb2ic8gW252PTynkDOSzcN45QmBJLmnlzaV26ImD78CSZkGLi0jH4VphIrA2OtVWHefXOo/bO6DNZ8SQyxoqbwWwVfYaZ38QHop13lMy7uqmfJ6sgYZ+miGISO+oHq3C2wPfbUzsvgajKpW1UahhdW2gQxxDHMVQt3M2Juzlxap2XtShBw+iYBhGEMrqYZoFg066gJYpVGcdgNqNax2hWI1RNu2SluItR/37FO83GDh1ZUiIGV+UDV8WbDzejo37JBUNHt7sM7tA1ruH3T2+PzrWwhMhdkzb+6OYOgrJd/JnRnMlb4XB7B4DMUyMo6t7yRIhRyat/R80XVDfyydejclkpa6bkZ1NPE3JbO9aceX96z7l18Q7zkZSMp7/5ROnp4czxMBEbdC6lxONlpRgc2qSq1ra+dbiweAe301TClFhgwLwERU0HrK26XOM+sTbn0ZShCKcsIQwanphPhaqyy6giBAksfThMcN+ODndBwMG4bR+9kzemTubQlg5bq0HbdLj/vRGwsZa41uTOsxSjTaR3FlEM3oXVPtHGXLHtGeyHZ5YD/i8yoNtJZKhFga+503TDrz52vtbvPvkNP/3wNX/9+/f+/dmISVlL2HlH6giIDi1JErwb3bcpzrnoiIZJZq5xjR5zigPyRaQ9t61br35n1j7RNEip7ty/HIjBoeMdSh6niWj/P3tv1iRJcuR3/lTNzD0ij66qbhyLGZBDPpAilP3+H4UvuxTZ4c5ggEYfdWVGhLuZqe6DHZ7gvhMlMqEikEZWZka6e4SZ6fE/AtrPbBPv5JMDr3K1Ml9D3CGEuS5RoDAnIYsoGpRtwGjVOatO37/0eCbVQt7KpAIs2ibq0lV421qRKZ+tufGYxpR02ypmxpIGB1uwUFj7/iemBPUmEQlQK1Xl8GYLRjXDBaRPgNazEsKxX8UY2Oohrd+uqMnjQ1dPqxxoldimJ7UONVsnnR7QvmdetwzXTNShfKfcxCen0oXmMWc6YdHXWiml8jCmUqGhdsaeV7R5Mg3bAxHBduOyt7MCa3zuke1q7Xthv8bdG190KgMLbQIWwsynqjknlakuLMr0qwI4C+y6EaWdicGGe9PfL76JQui1Gg9r27xL2UlLIAwMogYiTnlTlLjbHLuKHIff5JEEZ/fKqKbMYMeJb4ybiug8OAD2N68ZnDbP88EpoS38IXzgguhB4Pes/PrlKy9fv7Kf3wHw4cOJ35yfeO3kvF2c4HLo2IvzoIF9LIrckoDyRhIVMWRsLu6tKOrXkLyh8ccdJLrfkRwCDVgTStDBp6GJCIwPaKaA10MUYPCFesXw8npj3wofnhqW92FdkCCsZWwODRufup5jlMgpCKF2SI8XisFuYeJB3Z1cCzbuQwLhDX9LRNi8TmPZc1BqLZMHAIYW4zMdRtQldp/j2u8xcGPnuUPtfrbCGoRaZW7U6xpQAo8DLqBQNLCOFMuczEFo3sodanKPIx47pAqgiiAqxDSK6oC5T17dVncuLzuXW2vKPLz7wCnEJg4zMvgCFSXfOvl9v1BrJQ/foMuNPRt7bzD89PkTHz9/xYY3iMDT+w/8x84JirLwUq+HbrxGXANfu9z219ef+bdffua1GDqk6RXAOK+DolwJUWfy4tbWZB04ttDgxVMadnKERqNG2KtRRuOmGtJtCaDxe4q1ymnAnIWW4PvcZ2srhN7A0t4q2au04mUeo95edyRQUpwlKtbXcdWeEA5oC42TNJtNJgRre+DwLpUYCEEZ2heWc0vspgHJgAR2KJHVtmf355Ik9mc0eErK+3cr//DbfwLgsn3lv//z/8trJ7NbVFJdCHGbhU+ptTWwxkXF3g+bPlSN8zprsbtawj3ehKnMQsiqYUWoQ5PZDTcfeS5LSM1HpndAVLQJHOXmoQUNAlVd2fuZHYM1bt/kMxu84SWlGAlBptT+q2WSxCkLvVEhBLTDcFddCON16FC8mpsXYH+RVWkwU8ZtNK+iMnsDzWNnLJlTEIjKrau9PD8s3LzOfKwlUwflwm61CyYdxZ9qxPadnqqiAUr2mdvU7FxzZnSHVCOKE4ZHj0dKsll0Uo1cfOYZthm7lmm2HFJEik0IfzUjRWYhld0om+FTzLrxVwNh5ra5OqWWKU1+Whce1jT37T0br9e9iXMBsfuwDW6oICAHLBJtJrPTw0ykme66k7t3XhDIQYg9L1R6bjVuWwKeE1+lnYnxG0ivvolCKAqTZFtDIKtNQtlzOhNV+eXW8PF7LdQGDH8T3pKK4WTsTlXrPjuQLRKo7IPzIc2sUPvtBzq3ZkwAOt7dBy/FnChL2yD638u+MYSjahCezw9s+wu/9GTjqQgmOpXo1vXEd2GdRlabVx5j4OubRMGtTpzsY1QuhVl5J2mL/uio9uc1Fh1O0sba8f4aUWozBp3FVcGCMViI4qGrro3XbJ3N+RwK3Ipz7ZnG+RQJIlgYn9yKuGFs/blX9joUsCDGxrN5vdW5cJJGEGdhTJGErBxYXBFCfUM2FqHGSMmD3wNEmR2LQVx+6elQAs6aOPf39lmFvd4QPXhW+37j8XTi+2EAR+Xn2yvfT9WtxNdtPwQYyp18fI8jIoZ53/TDCs4UAUgxoCxzelOz8q//9s983Npn6fe//Uf+wx9+z7pGQm8lSjOumWaBpWRKztxe20Hx5eXKT19fp1jCzRxdHnnqbuEfvjuzntfptXZ9/cKnL1+4dL5PQFiXxPXW1qnFyL6BqU+foODdDPkNx6eUg5Fj2ho1yzj0GRzH/lBcUfWj8PFIL+/6zxviipVjuuNdP2l6zXY1tcOjx9rXo5CxVnwN8YNiXdBm4NXN26BtNLRiM30dIhTi0ptH4xr7zH1wB0Xw0PaTOe1HG59rDM09IXrct4i2hpMNvk7E1Y7izdt9DDv659MD//jD7+c1/I//539yLWVes7ogmnHi4b0WjSCK2zDf7siAMeLuiIhRCL3p793jHthembw5bTVOfqNUFmAm6y7ONdc50bxY49GEengYFtrneumNxYJTRVh6bvMYBX/ovobQm70+OddyA6t1NpO0gnvhNAqhEHjdMpc+ET/FQDg1U+K89waoCCJK6gn9EkHiiZdLm8TXIMSQJg1YpE0zvOdjt3wlvt1rzDGR2Yh2aXznIdgguxO8EmOYXD0zxa3ypT/Lc2jFymk8p5pRItvoHUlhp05RATFwlcNvZ1FcmSqZoT02LBzG2Ob14K5XHWNsrn2DiiLEpHOSH3Xh+mrU7chld6+s/VmbN27VMvKzqG3vm5uJk93Zh1FtrpzTqcGLAAsBq4XozkPnGSURzmGd5tnX0nwhvX/GIoVQnWvP2YYwx98z/v5XcI973OMe97jHPe5xj3vc4x7/m+ObmAg9n88TZoZBLpWll7SXsjU/milf2jCt01PHK0Gh+DEtgTZJGJ0+VeuQsSHd2jHxo7IXIYpMztAigmXh82vroGoU3p/j5J2UmsFkVvYxVp6eF9w+kCc8L/Djy8dD1c0zquvsfv7u9EhYlNjlIOueeb1m1l5VP6wn7Lbz2qtqxVCBNDwxojXw5UDX1OZW7m7IhEa0seY+XISlaVx6V2tx7ZLafkyQ1GVKUL57XHn3eJ6uxY9JKfZ2KtUGqGOaV6rh5NnRSKq4tUnR6OIGiYQQCb177cEJ5cDJqgtRdULlbjWDCHH4cBRhz2B9RB5p3anaJ0YSIVK59t9fApgnpCpG67CXDmscPKTH05nszlN3bn/ZNsx29jxkwrnHPWbENXDbO9zBnGx5wh0sJCxGaml7x59/+pH/+8evfOpcwX/+ty/8+OO/8Z/++Hu+/833ADw+OnvesK7qZrXy+nLhL782aevPX28YJ6QrjX2/LDy/f2BJvVO478QUeDq3z6+Icrpced26MuNe8FJZHxrs7WXfqVj3zGn35EEabnxq4LbvT0W2jsO13r1Ub9CXwRlqsLW+J9Ffd3cGZGxRpbogdXSR29alMFWSECd0Hg80dUcRnfuZe5sKjaOi+aAdHCCn7e2DR9DULw8fNXH/m86fQT9Nxv7YXhNRbPiU5cqBMeRQL53y/L3b2b/v0uDcqZ9fEhwz57w0bMnvfvvMdw/v+R//8/8C4KcvL3iNqOT5eps1v5LZ1hVpnNdBXyi1Tb/mQKjxAIbfSJjy5UEgAAAgAElEQVRXc4970M7aCRkz9lKIHToel0Ts9hHQztFtL9z6lCPEwOMaCCeZeYQVQ92wkU8F77C3ThXQQAzLhLZRjVMILEu7iE2t7UkDBRJgz8ekw72yl4yMqWxM1FK47dvBm4ttCjvygofTE0GEW+g5W4WgNvNED8LJK9rzjq0Wsuvk35gVvKSZ3AQXkocJ98s1E2NEY+Q8FG+DQmxy0O3ZQjKdap5uwrKsrP3ZXreNRYQwcGZRSOngeVet5FK4dZlygoCGI78qGa9xTvPWKISkRAJrGMiidu1hQONyJpi3KTJwcUFfK2XpuW6MnNcVscEpajcycuGkFclC6e/VGgO1GmXgkXPBu8rv2vNEM9j8mJqva7PAKX0fXaNSNbOWbsvyxi/z7xXfRCEUNEyz02u+IfWgxN68ECrT4EtVu9R1+12nkUiTxGmctyt49QkrC1pbwv4GxuESDllpcUyUIAPz2iQGt9zGiUJgrxkh9WtyFvEpu5qS8vund5wl8nFro9mXW8btGDGLBLIzR5RrFN7rd+zjEHZBQyQObG6MBL3OhY4YSYQ4xNnVWEJgGx94jFpr4wFxZO6uRyLgzRBjYn1rJxKPvWVwicZ7cT63gvG5J1xBnFvN+LgEURITNYIRjmwEOrSjyVmPTdHMSFoP8QONjWfZ79PRZh47fp7YYDWd3Hm53sjinId5bmzQGZuOh23cX3tCtoTA0iUkX/qPrKK4w63LFWuXQB6UjddtZ6tMPkT6Bka39/h24mlN3LaxdwjCgVWv2SnVuPYGx4+fX9hLnBjsr3mj/vSJ5+dnfvjhdwBcXi44mb3Dai+XzF9/feXzZTQsFpaUpknwh++/4/37D5TcoCM3zzyezzw8dMPUeOLTl89cPr0AsO0bJ47fd2t8weB6cHbMGjSt34e5Y3JInjaWS5mQL6fgdqyZUjJBw8GbtA7D6buLYmTn/0ck/tv/Hp5m7TW07dVjabtjXmdi0Myg9c01tRebnB8GXuzgkzZIXj9LzDE5ihiks3IEdApZ1H5ujL9hnXv5pth4I9c/bNUGZDl4QILy+F2D3f4fH37PTx9/4V//+kt7bh7wesBlmL4fUAf2Gkfc5h7q1XF/Y+TIgD8PiCD3uMeML7fbkYcUw3FOaTQwGrdn8NEWhbpAWgf/MFLN2ffWJIWWy1RpdAIAL04pB/RNpbKsPiGtyRwLzc8RGqS1qk8p/pCUNaXZCNos8LgmbtaKmttem5FxPKBwje9s0/T+0/UrKpEwG8WCFZmNmyIVESPm9vOLJKrAsCEqW+dRdfsStPG0x8l/SkIMjnmeZslNHErmyn1YF5b1gY6apuSNik6PxLwK1DqvuRaFaninFjjCth+2HTUb67JiM59SKEbsb6ar4SERFmbDfYtKzU7yAR8WlhTRzpcXg00rdQgbSMsXbe7jlSXo9H/LLas7cuvdyPVoeC0LFCqVZTZunIqrEfv+dLWKWkV7oSTVsaqT3PktpFffRCFU35hvJQ+ohEMMoSp4mdj01hIQbCTK3rCiQeI8IAMt8R6uwyE1Xsro5glClIZvbP/g8OYgeT6fiVJ5vXUzVBrhdhRjKSrFj6nVivIkC0tStmlAmHgI6yTubsUQiZx7VySokmuZohDv1oUQlNxti7+8XMlFpkKIBkXM2Ww41gtJBRtdwOpTeEHfECP9DZ1Ke393KPRp76aODqq64uLHBod11ZGhGKLts9sX2bo4z+GxTW1oBVG2OgmHe63NS8j04IB5U+u7dm5C9eaYPFaD+Q5upG4sK6qoO2V4DMQFpbwxLOzqST5cqhtZepgwCvCH9++p1cgv7TqfJWBB+XRtieTXvKPKJHNu5iQR6pg61bsK0z2OWBRyV5gUzizyJgnVQC6Z189fAfh8feVK5LU3VTRq4+15Zd/aAbicIjUfPkDFnc2BjqGnVl7yK6EO7Hll2y5cXtvEKIQT23Xnp4+f2jXkys8vn2YSENLKq+2E116UhKb0mNriB2DfNlIMOAM7Xpr/RL9n7Qn+YB9XB3OdDanH85lTjHz80u5789rIwiPRqA3wPsjLvfHYp0J9P5K2N8+SQPvQ+41gzJjYjO+ryGHISkteDtGATvad+35Tsps6cWKtwPNRrAlIYy4NDrUqoGH6kVQrEPQNr6kXb2NcI62jPTicuRoP68rvn5uIzhJO/Otf/zvZ2p7i+42wJPauxqASSR3B4FO+05HqU4XLdRR7xx73Vr3zTWl3j3vwtAR8cDxCwGKefNngga2OlQinFPkurWQ/znQvbRpU9p5XaNsDx36EKqc1TIPobauUehROJQnilXodo9yKaCKmMcWw1kDywS0WzikgY7SyVyiNu+zam7IYXm7sdUwZTmQ9ZrcRZ1nDzAukwq0cE6LdK4uGWVTog2Au1CEsZRnDCNOQte0aHuA2UrBawRwfasQBCvt8LhW4XjI+RE1OSkxhImYuVGqplJHTWeNoDgEHrZGyFULn85zWiEbmOq+lgCm3a6Xr6HBKSjUnD6/IGMi5HNPiFDjHRBr8wxTaFGqoYpqx78KwvHcrpNB8zIAmcOGgy8gRI+IRoUwD+mJNvS9OZFJzorJ8/A0RhcE1t7//fvUN1GL3uMc97nGPe9zjHve4xz3u8b83vomJkIgfMtFBmnJab/OlrooxuoZCU7QY6mpioempa50QsJM1D52cjk6f+NEpE21S2wcYoXUJR6W958yl2KzEV22+Nw+946EqHdJwTD4+bl8JRUi94/CQAtHeyMlaYdvr7Ig+PTwDoclAAizCjvGgbQr1p/3WJChHB1UDp6ATs1qrsBnkOlSdaMpNAjach4e+9pROAdSJQxrRA4hPJRXpk7EB/yxeWSWyjZG2F7IesJFoxu7b4d+k4W+K+4YoUc7pAA9tdAWXoZBV29h7dElG56LqwAs7GKyjU32qhBrn+z/gMOO9N+tj3D7se06JhxC5eWHtE7ybV5Irt96JKTcnIITevn5aziy1UHr36d1pzMvvcQ/47fMTH0v/nGYjICzdRyhIc1G/Xdpk5OH0zPfu0w3crPD++YE1BkrnESXOCBvSP2/X2yc8BtYOst6DEDK8/9CmClaNXz59JF+HItuN6saXa1PWdC1U10OqXx1qpPQuoVlbZ4voEFRjCZFc7IBjiWC1NjgGQAyIKfvwfJC2iwy4wxKVEIR1wGY9sJdDvrYJRwlxcCibXmWDzg0OkLSLs96FlcL0OWnPVng4J25dC1asqT1NaX6aP9sY9BsN7jfgfw54tsPTRxp8V0fX1zqwOEbWNKZOoanjdbn+AbkdZ4VKg7JJJwqICKI671NT5P3zd/zwrsEgf/rlT2zlUNPbAcll4rZLrZAiGhTrYyil8SiGpUDFwJnQo6btd0yxQvj7d1jv8Q3FgWRiWQXxyDk1qGaxgufjDM+L8JAS185T8ezE1Lg0g1scSoPOrWvbrzQ1Tq93aTGvRoxp5h1ejFKZ6zBExRCsw90t585H7MiTLfPrXohr//mlTa737FhX8i0hQFRizyMy3mTC+/ZUi/FSM6mvBXFpkOCJLGny3F7eyETDhBC6Cro0lVwYPkvOKRxopXKtbGWfzzZmJVSdKJ+t7mQxbCj7WkQ98Do9ALxPwLv9SGww60Hh0G7jQecqx+SoRC59i46ifTOXiegre4Pyjq8lKSEmrGd1Vo1g0CnV7HtG1Fn71LxW51Kd2J+HeUMESc+d0toQRDKVg2ly3YSmSAzEGoF9KgNXiegb3lH1xlUbgAfGZPHvGN9EIdQQGh3qpo3sO73iNJDd2IYwQXUWTYeZHLmJHYSAvjGZWKMOhT+s9gS5/0qRBhEbeNKIgMbJGSrFqAFO5wZfiGY8pci7h2YA5RrJeePza+MDvZrxsu88LgsP5/YR3Eth9xvvHh4BOK+Rn15f+dThMLwGnpd1AkG+3DJf9heeYtugHtUpUXgZ0rG1stkxNk2q7M1UaTxCghpBInRPHY2BrW4TRpjFWHwhLu01cjHMbNZJAw865AxFBHfmwjcMsTq5RFadqxij6nBzcjkgZmgrgDYTbsNzQJxqb8iZ0mxuJ1FSwapMGGIk4Fa4Dl+OkJp/0Xivuw/CKMBiZ/uNwuhmzufbjWs1LgPDbG1bSLF7V9UdIU5p8+rO7ja9iX54euAe9xjx/dMDv+3nwOW2c9JE8FaEnFMz0wx983n3uLKo8NOlwdienk/8hz/8nu9/857i43Da0JiovTC/XPYGCbYBgTCeTmfOI8N3QzTR6yb225XPr1cuvUiRRVA9eJVNUp9ZcDRwceMODsz9tQrFKvsQNVGh1k6eBdSk4fT7MzB3qttsSCRVPpxP5L0JktheSOGNnHYFMedvUwCBnqC0F5G518BhuKhjqQvs2Vm6kYeXwlZsirsMyPNAZIQQMZfpA5ZLxazOwmr4/wyyszu9MWTkMswia4OJ9Pc7Nsfq2WhpZtvMhElDgwiNs+V8DvzDD++RXvj8+vEnllx5Hf4koV/H5Kt2rxd3pL8X46Pg8zkIovbGlFo5EeaZKJNRfo97wLUUTsuwzGiZz+CdZHNqOcziy154lQt7FzUxN+QaAZmJbRGh7BB6MtzEqOSA0bqQ90ynUbJEaYalnaey7bUJmchM1xs/b0J5Bcw59cK/1Np4xEGwDr8KoUG8bKSwIeBuLF1sahPDzdj23lCPgRj12Gv63xv+SlGM4s7tjfHsQwikfs0328mbQT2sO/ZcW3nR+TQXr5yTc35seYMFxykTSlezUYLz2OWwXQSVwLnfp5mw9XwGIAUnhmN/VE2EyOTelNLyqRhk5k+l829GDqdurCqkzi0pvTuex/tbjJOG42wwOGEzf9rMiSmiwwtJjLw5tXPMEkK0Zn4r/Tnsu6FLox8AJFeq+mHOTcvvZvH5DTRuvolC6CQ6uwHFW8VZB8GM9uAWeyMx4vkgwSmcpGm8D4dyM++mX+1XBrF0TD4cI2p6IynQzLdMBjm+PZgyXIYNns+nmYh8LYVTCKRzK1qe3FmD8ryuPHfC8uttY8uBh9gLI3NCTx4AShY+e55qapvt7GaTb/PD48qWEpfX1lnO9UpV5UGHm5c3J9/ePoiiKN1zo3czTzHCbly7a3ASwcSmMzLWzQTHdE2aUMH4XEoNrSMcjwTKvBEfoXVHRfxQafJ2j6OKrSqtQ+s+VUxQ+ZupkVlhd4i9CBEF3ohj3MSJql0BCtbTiW3fKIO46YJLI0O2e5aGTe6L8lor+XKj4uQ6TFgF3S48hTZ9U1s4BWXrn4/XUnCcdRo7co97zPjhwwfkXVN8+9OPfyW5TLXHVVrhcX5q05t0K7zeXjif2pr8h9/+hv/zv/43ns6J2601UlRa169aEze4lkKtzt7FOm6lklh47TySh3Xh4XTi1TsP6eeP3AhTCUoYqme9Q4sgveEAbSIeVFniwlPv6qZLy+3H38jWeJvTnLQazV51cDMd8UCSth89nh94/+6JT9d2Dz9/faHqMveSIFCCTOKw00QQ/I3/W+McyZz+Bx3/Tr+mlqid+9pfIyzrMQ0WVRaNsxDKNbPXSu4+YKVUVMJRzFnbQ22Sj5WIIG7sff8onTI9RB+iCEH0IPh6awCN2kNVCH0qBPDd4yPfP7/n05fG3/r8uvGyG3UaFrYXOXhRAu6teeXzT/DGUB4Vn/yL9g/NvHqqTvhxst3jHnTPHYBShK0WCo3jGIPy/nTm2rsNyVtr9qmvidfaTN2LMJuwZS8gOhUj29E74Cfdk8gqp4HI6TzfcYZ7oTcy23ls4khIc5KiGtBQ+ZRbU0WyEVHEI9qVmra9IBpYh/qsGUF18p+rGIh1/mZTAtYYZlHixQkrk89cpSX1197wSA6XYpyHSmaMbb+oxvBWC6dIVG17JS1v1MDMM08hkU4rtYs+1FoIKmzDwwkQr1P0JARhr5VTN+OW5KQAQ6JNqbh3M26aWENUQGX6LIo5pyjEZfgCBVLUxvmkNdVyrsTRcIpKY4v29yYKpyXM/S7VBbfAMvjSYaj69kZO55WDTS5nmxopMhrw1iZwqW/MGUGw6fU48q6/Z9xbR/e4xz3ucY973OMe97jHPf7dxTcxEQrqU9kn4SRR9o4bzJ4bfGtwbdy4mfPQuxMnbVOQrdiU/GtSsAe2nO6PMSSZ19Bc0kfjLFtTJTn38fE/PT7x/O6RH18+A/Dnj1+57GWOi0upPD898dwnQojgZF5y5ePWOi3bvvPpsjF8OB7XE0+nB7begbiUG/vNppOxhUpAiH0EKZJYIjx06epqBkvgu/71ZS9sVvE+YaoogdDUWgZeHScJ7BM6omR7I3M55GXHCNqsP7vhgaG4F2ar0QzM8HpMiEJ84/NRvPOQ2o8XbZM6rXAwsvRvBL6bvvzR9Y3e3h/mhLBgVFLnTtUuMTy4DEHaGHj4uGybsFA5dd8OAS7VECrBD0nunCvXIVPpzubOtQ4lsATqXDp++JfXK/e4xwx1rl8b1G2/vfDDdx84pQaHkJgoZWdQbbI75sK7tX1+/9t/+c/89jc/UPJOOrXP6OV6pXppE15a99HLztKnLaYFK3XyAS+S27IdcIa4EszwzmlsK7ZOSVXoy7z/f6tGscKGsXZ4y3dPTzyfK5e+vr7eNl5rnnueViMmplJmtYLhnNKAAD7w/v13vHtpk4+/fn3h0+fr5AVEVVLQzvlskyDzNnGae3u1NukYkt6hTXsGNA5vqN/RkU1xJejRoXWEWo2tW7k3qJ/PvSFqaN5D/Roa9yFMPqp6U6aq1adkt/aJ+fidSqWUg+sUtMG4x32KOPjB13n/3SOiwp9/+jcAts24VJvQlZs7aodQr4q01zoG61gTPT34psKExfUH16SE+5fqd07jPY6Q4sc6joEgkfPgQ1uDgQ/4VbGmNCuxrfPHh0TOG2o60S2n1ahmbH1dFXdiaIgTaEgRFeW8dAhYhVwLtecNmztBm7IcNG4MbliffHgoFJUG2QJsDc2fx2XybcS00QU6VC4GqLF26B8sZm1qcRoqlwXLB18wI8Rs7INygWAaiUN5WI0HZU6Gq1S2raAaCR2TrKF5CI21vu8FPGIdHvywrjyczvgylOgCp3OayKUvLztIxvp7sxUnaCT2actmBa95TmduwKLOQ99zs2tTDsbJEz8XyGnqYhKsUMzIgwbiDX5sg69ljRWujLxTqAFG/qUYRmHb+nsdhJiUvT/3hWbronJQCwjOdq1zoh37Pj6QSslBJc1rjOXvP8H+JgqhHSbXxbVSXEhhEOkiOzd8mNdIZWGZ8AcAcW9JwsSGK8llGjiZeIdhDIyrEsVY+ossMbF5Zu8fYN498pvzEz9fGsyjGHzabqy0xOTD4zPnuHLqRQnBuZqy3S7kPs6tpRKj8tI5Qa7OonESXl/qRi5C0SHvKKDGrScmH28XYoz4+H5sB+BIhnY3duljaIBcuFnFVVl8YGtBJRyY8Vqb5OwEyTeM/OTnHMKy7WtrMLYwCisV1I8DWGnJQ3wDMjTxCSWrW6UurXj1Yf5YayMtDtThIDGOsaoHvluWaRa51Z2fbrcG/aCRIoO0Aq9dc8FdsQ5IvmxXHpbEKZ3GXSBWwCtFBwSwEjRwHZCZoJRSGF4KGgSlzsPjY924xz1GKEboBNaVyOXywkU7/MHfEdPjNEP9+frKXoXf/e49AL/58AdEnfiwsl1v/fXgZXuZvmXP5ye+bL+y5/aaazrzcI685tHAUFyMNJLxJeK5vuGcNnPU4RtkNMw9s2nSDBBraYk4wEkL59OZ87lBe+PlCw97mhBVUSOGMGEbny4XStl5PLW1f35InM6PfP/+OwB+d924XD/y8XXI21aiQBk48QqE2oz8hry1OSo2CcvVKiIL2iuhEDunqF9Ttox6bLxIgKBsXib/oXRZ/eFZpkGpVgn9LClSEXdipxbXzpEMQckM/oM2vyQbMNnaGl+DjxOEqId1Q1NkkAZLBt5998inl1f+5a+/9mteUZza39tgQhEn9ZtOKtzqjtQw4XaeO59gntZN2GdIdFdpBVzsv3Ba7kCPexwRRbA4rEV2NAayDl5vpuhhxruLUc3fFPrCxQUrhdd6kN3f8jqCBJL65KgtMXLLxmUb5JgGqR08unMEPE7xhXSKzSS4v37ejaqB536Eu7UGbvXDQ2cNSg06cxcJinid8NGYIlJlNqJFnKJ15hmLJoILp/433Yy83eY9SQhcK3MvQb1z/5TUn10KjVJRh8y9Kbdb4alzGOPS7FNK74qtqeVKA44Xg7S1W7s8dhIktCYVtKJVRWHyopro15DKVglNaAxYz60Rt+0Fvxb2AZ9bE9Xi5GpSm0tR7TSQU4fFHZDnVhTX4WcpRhCfEOlbKbAfwmIWAkWN6nXK++/ZKfngn+JN5GwNs/2NuEx4cUr3QghoHQPrC0tFKXifRABJCDVOHKa4U9jxfVSwBdVAtUIYqm4C1XQaV4kYGgXp/Bqnstc6F8kaI2tKXHpi/OPLzkv+M1s5EuBqld7g4IdHgQW2cRDtFRHn+Xzm07UvtHXhbPDrayNRb5crSSPbMA3rXJqpfietIHntPkI1R1IKU/cebfj5X0vHzXrDoo/No5tJNIGDfs3m7b67oBWbGSEuUzlFvX38BwFRQjOrHWQ9VceKTG8RlNa9lPEnBd4UNe7NQLaMyZk7Z13IWiYJm2L9Xgc6XghvDN0qyqKJPzw1YQoLwuvPP/Fya1MZl/bTy/Adol2f9IWtISAxUobqiVnvmLbubbuviIvPRCKMju6YbFlpCic2OlTfxDK5xzcSQYTcVeD+5eePXLZC6g2M//qPkbQIf/3cmiifbsbzd2c+vG+iKVEW3GNzZ+/J9m0r/PrLR/ZL5yguymaF0JsBD0+nboA3OG4ntlr49KUVW6+WMdHZTMK8iQkNjiO183DG59+w0hoiomOa4qynE889+3j/7kz1Ohs3IYKGyNJ5dT9/+cjry1dCJ/4GVWreef/0GwD+8MH56eNXLvkQXyAIwdrPR3W8eF9yc/zS1EP7WdA8751TPygfl4joQu174NUCNftsgGnQNlEfmhKl7UFTQ0ekFzb9MdU2aR8JGepU6RyccdBL4y2OfpNrQESnWl5UbfyLmRdWrFbWpRWUa3rkp7/+K9feqAnJEYvQhTGqNTPU0vlcYqFxKlKYBV8UnSp70AyezcccrCUzMR3JbN6H7uc97gEPjwulfzbMdtYlTj7Ol9152Q0d3D1vZ2rozYf91GYJMYb5GtTCtThxHIsqvF7LRJKE0AhtcUwwI1gNSM/PkjZWyhBbENpUZQ4Ghl9aGWT6VtCIO3EYvVYhqlHzJMaBt6kzNK9HVbiO/UcU0WP6nNy4ug/6MwikoLMVXLRNnNL4eY2kNXY1vPaat93BnDz2XXdUfaqhLapYCKQuurTf9lZsjS5uMDzLNIPPUolVj8aNtgZI13RCFMrubxA5TqltQhN7s9oXZbOKzaYZxCUgfU9o/5E52RdtRcrwOgqxoaXGllkBK4VlCDpooIpPg9VM5VYaz2mwL0PQ5j/ZN6jbbuwGWx80pBDwoDz0B/UtpFf31tE97nGPe9zjHve4xz3ucY9/d/EN1GKwV5tjVU2BaIe6mldHXJHRMeu/Y8MAQ5qyT9I4v+kYLj7hC9onF0P20MTaCHBOJSpRHO8TgV9uX7nllVufSi0hEhfl+dQq+1NcWxega9rXbEhQsh9KT9dinJdEHtedIWshj2sqjno9HHuDoehUQ9vFqHV/MzlpPcEHHZOQ5vczZMWbT4eCH9LTu1XOVWf1rsQ2fhsPasI7+uTMaYpF/TlFAgSlDniM+99UzuawI2hXmmrKIYfsrehQhjLCGM1K6+C+aaKQXQ+lOst8zbC89o5rWnArDKV8UaVWI3WVLndjs4MvEc+JKIJ7e2+SCq6hKQn2KdIpJHZxrB7+SSnqlOHd697crqeUMPe4xwzLmWuXzv90ufJ5Vx6GkqIFTh7RPinRmPnwfOJ33/8j0DputezgwtfPbeL81z//Tz59vrJ374769QuUxDDl8UbN49x5Rtte+PLx0/SCMKDbq7Wf72ySyRHyLhTdfyCIoKkpUJ66zHfwCp45nT4A8PT8PS46FdygUo2pLhRj4Etaee1wvtsl81P+lfO5Tb7WU+B3H554uf0CwHUzSkgsYexfbYK/JMF87B+CaiD2Z7dEZ10C//i75sHz+/fvcDEuX9rf/Jdff+Jffv40u8JJIvDmLJEGzyide7BJ4xkMrqiKEwLohBC2va682SvGMzwG820iNGA+sZOvpP9AtoqoH/yIvXK73EgdLgOHRQQ07pV4wvtEW0IgBm2T/XJM66r4tH9YxBE7oEYpNW7pmHzV+0DoHm+imqAd9bGb80qenx3fIBpzyoEq0Z3cJ5aaEyINibH21n02R9gp++A3N3lk6efpqg0uNyZEMQhFmEq/QqVmx3vu87IVVH3yo1OCUJkT0WqN1+gGNvyNUsLrMZk3h2UNE2ZrCLVL4UP33nrjm5Z9Q5FjihUDyylONEvIBZPD08cVfDGK3ai5o1eKE4JMNT1CJRDx1P7IZjeEwLnvZ/kEuWT2Mcq1xkUayY+r8rzEOY2R0Dwso3Y5bjMup8refdS8FnIJnOLhfxRd8JDY+p73WjNPRQ7JSWn8xAHFldS4mmOgHZLyoOv8/Vsp7NK8iAAWNyqFMe4xmsWKuk7EDQgSmVSEEBrL6dTl0hXnZhXtXKtSx/7/94tvohCqZmgZsLaIWqG/11QKUWQaauaeSOvAbAu4OKe4zAQ8W+mY7oF7rLjrhHiV2vXjR+LrN2qI89BThNsbg7rfnc88PwQeU4M7JF35en3hNsjNLCQMyzunvphvVbiW2nDqNFw+u5EGfjsqUjm8RDy0RKafZkUEFfA+ol5NKesCfeHfrMHxTv0D3Z5X/1sDN+uCyeELVHHwQ6q1hUxYmvRiS2ZxVRE7NiTEmsfTgJA5qJUJI3FpUtYjKTCcSylgDb7YXjPiOOJjRM8QuIkAACAASURBVO2UcGBOi8HnYty2Jg2sV+FKxvubUa0VvY9dDMG8sN8qgyZwYiSP3QBsaXv8LsZtFnhOHRK1tARRok5JyUoTcBgeKuF/eWL3+Pcdy/nEd89tL/juYaWokPvB8fF64/Ol8tcuGvD88I4//vA9HzrUM9sGpfDly0d+/MtfAPj86ZVchcs++IUNmjW+1hAhGLWLd7zeXim14P1DHyVQ/Y3ogDSIl8+Pbd8rx/dDhNCShGuXlC9VebKdFNqh2+TsfVYA5hDMDrNmdQxn7+IKeSsUKt/ltic+rCt/+P4HLh2S8euXC7e8cRtCBwK/f/fMb54eZ7Ji3lsw/UA9P5z47Q/P/NMfWhFZt8xffvyRW23PJajwuCq1Q5ZT7ITqnmDdLLPjXHtlsHjgFGXuqYJQXbu3RvsXwxE9yMQigtnhs5Kke24Mkqp2QQUG9AiWEHh4aEI6uW68XLdpDmk5koRJNN+tNFTPaDZJax6Vmifm2EtGAqRh8iqBqDo5riEFas4MfF4YG9c97gFcbpXaoVOnGFGxWRAUjEYhHI3FljcsXVYfbbLUODye++dvSfz14k3ACUhLIIpQ+tpvkNPKyL9CaqCpkV9FEVJQai/0FwwlsIwcAWGzcjRkgxFSM0utPe97zZklCr4c3moadHJdSgkUbFp7RAm4KLmvkSVGvMpsLkRvTYsw8owlUrNT+36X3MnZqVbY+lo/a2vMnuJoliilCs+9CXLWM7tnQs+/dnN0UXx/s//YYR2iwQnKQZegcRBrzxHdW/NjwvdccK3s9RCW0KiYyvTQrNbyo+GHFLXxmi5d/IC97aNDjn83CMnI9aBLpAD5Noxsm31A7IXzEgIPS2r38kb0phJ4HN5VwSh5n/5HtdbG4147lPcbSK++iUJIgk68fK17U8QZzrXVu8HqcLAr1FqJPhZN9x18Y9CkEmlLoncsvH14jrPLKd0xF/qHw2x2FzRETjHw0Cclz2vi+/MzuU8ZXq43XsuNE+d+zRl342Fd5yL4ys7H2yupdmKuZ5YQ5uSjeCPiDS4LXpHsXPoiUYUlnPmQOreAZoj6te9g5s3Rfs+DpNtJxArjQHQEQ4h9YV3daO5JYxwDvCl8FKFy+Hi4D7+KUegEzP3w7ZD2EocKvIDVw5WY5ptMSFPxSNzbpEiGQINNJRNo07oifnCf3DECsY5krnAKytpJ25lA3De8Hh9lEdh7l9kKuDmuPt2Wt1Jw5I3jvFDd2PrGXtxIITAoFurfwEq9xzcTqs6HH5r4wR+vO5/+/DOxK3X9+dMF1cj75yYa8B9+9z2P7747gNDuXF6/8Je//Mif/tII9EmE183mfnRelK3shH5KZ8tEF2rvnGU3PMRpJlitKU6OyW/w1gyaiUjQpqw2JiEeURW2mtG+jwaVVlzRplTmCyqOd97kvu3keiNMVzyF6s1ThIZ/N1VevfGWorzj4fTAf/7N7wH43eOVbSsUGc2IwvPDM6cUZtd1WSLBA3Ft6+3p+QO/+f57Ul+IP//6M798+RXztvbfPT7z3eMTe5/MXy6Zr9fb7GaGKCwOp76PR22miqOowYytm7K25wRJAzEIGo89EA2z+VPFeyLQyeYURML0DglJSVHnZGzbMsWNtXOrrg5W6tx7cOHlckN6IhOprSlkPgnNoo32FEey0xt91ve8Xy9fKSVz6snrw3rmHvcYYVY5hbZmFIWc5+c5LQmpkPe2hs7nhXLbZ85wPiWoQs2F185zM4MlBQY9R4NQM3MyG2JD+YzUJmkz/RzcF/HWJB7JtooSgtIHSpiX7gXZ8zlvgjBVd1I/xYsYu8MptnWVa+ZmsHRhAg1KcMHmhKgl4KO4Ugm4TjtWrmVHNqaSlIQIdnjh7LSpedBAGkWGgxeblJ+ozQfoduuG86fCthm1q9EWc4LI9EcrXkiic5wTteVwY1qjKKXA3vfgqE5KJ/Yw3gdj0YRZ41sCvNY2kX7se8VNmibWEJVIEtAFrBdCW81dGW7AC4Qv18tsnhMEyxWNh0pzJEyUkLtws51FF9LSlX09gxueR6Hb0Ay3/nWQdm8v/Rrmfvx3jG+iENKgU/HGxJHqc7xfkEaZnaQ2J6lOGWpECHjvEvauBoJ4mYlBdUG8zkIoaUSkHKZ4Okam481OfDg9TFMxEeVWyhQ6+Hjd0ThknuGX2yti8Id15dQTi1sQym5c+6FcxEAhdjfSUoygcRYV1duw59oTi6coTZ1ljBvFeNkz2zQkFEYvsn3d3eNd58hZtFCtTLPHsO04OseoZg5v3JVbz1ibiSoNSuiBg1xsTlA5JkJ4E16YikqN/DygKXhXbWljpfkaaocay4MEcvBJGKy0DWdsigGhVpkKSiJCprLV0SWRDoPs11grBsRlvPeKhDaBGh8hV1hw9p68RAQjzA6X0qZFYU627h3Wexyhqix9InlaVk4hssVxgMJvf3jmP/2hiQb89off8v7dB0IaUtkv/Muf/8K//unP7NuQUE5sZeP80A6SEANJV2JfBMua2PfMS1c1KkEQCU3BDJhSkKPJUqFUaXC3flHS4VbQO42zmdGhI0UoxeZ0xr3iUucB+eXlK7fbhSFd9vz4jKhNgmy2Sn1jBvjyekXLZe7jTyfhh+cn8nAfN+d5jYQQueaWKKgsvHv3MPflc1zZLjdeSi90rpnnx3d432PTkliWNFWWci5crq98/tJgi1+ur7x45KKf+mOqLPFhdi5LEVx0TlqCNNjgEsNUaKtUzI5mkDqEajNBKmJYCIzjXEQ4pzRV4768fGbL29xDkhjIQbAu5qSUpozvXgtRG5RkQnODEpfljcSxcss7X1+bIMelFpaQiKMNHL6F1OIe30pIhPcP/UzXwOXqhC5AIupsW57iQ+c1UEKaie6WSxMZSWWqnSWEU0yzKbvvhSCRU68IghrF/TAAtjalvnYhKHNH8VkYhVPLC2qHAa3n1CDvty5KcKssS8B0IfTkxTxg+8a125WMhq8tx5Sh5TVjUmttqtqbIjkXih1wvKjN6mA0pkMG2wzTIaQSkQhL0okiNCvUolNJVxaBbuUCUF43qhlljN8aCYOH09EUDi7skvvXoe8LPV/TALkS+t7hW+FqG6cBpcvtGnLxKRt+XgIZ4Wse0zTlu3NiGJbccmErZcIYq0kTjOh7xl4h58pjb+gnDWzKMaiQirlx7ffolll0wTRy6yI2hYq6z+nd7oHFmVOnJSaytSkRtEL67x139sM97nGPe9zjHve4xz3ucY9/d/FNTIRilAktKV7JFI7+veJdsg96X04ECYPX0uBX9Q3vRHCy6pRHRrxxdfqXAUcD8/uWtRNeD65MqRnrcttf9o3dhb0cnUdB+dLx9bspe65EvfLbpz5yjsqyROKAslWjAKlX3u/XJ172bUpb19J01R8H5jUoUiu3Pla9GezljU7+cEgcXd4GwsXNJ/5XxRsEbRB749L4UqNhaNK+N8wCvRkHDj8Skya88JZV9DcgsQ6NG5hWtw7PmROjNpY9UK2tQ9HkYOd8poswHNMY4RC6cCCIT9GI0Fnhvw5/JgPKdtxjABNl2HWtacWkcNv2JokNBCKLBLST96IbF7HpFQJCNedljKW+ieHtPb6VsDfiLikqq0I6t8/SP/3DP/Af//h7Hs9tunNaF277ja8ffwbg519+4s9//onb1jELwLZf21Siv+bXbaeWOvc8y5lq1sWzmTjxMXgV74qzbxCv0Q9xmAZ61TeTWj/+N9e68Xq58OlTg+s9PJzaJPza9p+H85kUdE6sg7Zp9Oul2QP85fNnHGdJP7T7PiX8Wnk8tefwtAoU57q3dXt6EH549x4EYvcrfnnJfOYTw+n6V/tMXCKxT7QFIaY0IRjn86n9zT5lD4/PvH//jvdPbVLyp59/BPnK5t2QxEKDC9vg4zgpyYSBiAlJlXWJEyJjDlWZkr61FF7eGKKuqU15hpVCUmUJYcL5rjWjhGnqWikYgTwMLpvKzZTpVWnwZlUlDNRDUEzA++YfVVGHAfOvuqBJGFrA2f5ml77Hv/MQjVzr8LppcPSRI9TOlV77hDuXgtIkmaHB/ks1goZDICQ1SL53d5FVlLDoYYGCsEicZ7Z2EZL5+RVv+9EyjNyh5jphsw/x1KC3XbAhSeK2F1ScbYgZANEr1z4NNgmEGNA0TFwrngvSIYGPS+LqZU5zxJ3FZUJ9ozRY/7n/fgyJz/XKEo88RaNQ1dA+VTrVheJ15oUaFxZJ3Dqf5jVXSjp24YhTc50cvr04p1UYTjFxieQ9YwNzGNqzHPLbF2qjgPT9cU2Rba8sYuydUnEpOykq0qXOYxBeys4ypa3bpC6cBlTbkAp754hVLxAgd1iu2UY6reiQX0eovk+xBPeGDMrsk0t9jrEZovQP2fWSqR7m1Gorwroc9IhvoQz5+18BTe1nuOtmLyg6deyHElqd+CxaIdR/V91opUuArtAW6P6B4w90w7np/u0N520Tb9eSiTTIXSi3nOcbmZLztK7EDneoJ+Hl9srnYZ4qTi2OXWzeR4zKVvMUQ9i9uQ7nThBMlE7m6wtXdzTAw9IVQip8rXWedllD4xH1RbQgDb4ynlMIuAc8Q+04WekOwSP/CRqotRzyUqEj1oaCkVrjCfWDNHjDd4516dr9h0ci4d65BgP335OKNwmZ92c7aDalFz7TNb37Ho13NHTphgHJ8fHdgWsUoXnntnt0N0SdMKArmhAtpL6wc9kJqhSrB/dJCld1Qt9QNjHcbCoRRgmsa5rGZYOseI97tLAJjfvw/pnfv9xYOzn+P//xHwkhY71Jcnnd+PLxCx8/fgbgp58/s7siGrlcGp+mePv0lm5AeNk3rOQJ7ZWonNbEMo3nWoNjQMRESls/fYkUYRoHAr2pcGDuTcZ6PCCllQbN/etffgIgSOL79++nj1l2Z8+F53O7z3ReebRn0rndl7wGbvvGrcP3nteWzCypJzdPTwSEh8fOnfHMzTOYTud0yFzy0aiJKpyXE0/P7XfK3gyhZ/ISQ2tg2SB2CxKcNTblu3haePfpC09f2jV++Xpt+3ovamx0fGbDTDmlRIo6i4kGN7Z58NdSuBVj6QlWin2PGj9vDtb4CACfr6/cPFPH3lMiH7++zHPi4bTyxbfp3XZOwrIEkiqnYfQqjaMxBGVueePTLTNokc9ihLSgp35f977NPd5EisLeOUDS14hq5/5VWIVpuBl7g2Tre9GWMwsBYpi+P8Ei+25YXxNbbd5V42P3eIIlrVONNhej1DwFjWoWPB9CUTh41cmj/OXLledlIfRijF3wurc1OYoxjcS08tjzn+qCmFOHqpw0+N9vui/aEhf88srXrjiZQ2uAls77dlO8ew0BxARPj4Hc94jrllFPJI2cOxfvFBOf6iuXvcPzciRSuucbpFjQKpQBz3PlFI1965CwlAjuzVQa2G+FWp0wihApXf2zPYaVhe3NuaAOVpybGdLfm+jKYsJtCIEhSDFyfy/WSvcOarGYIqsTu2dTKQnXNLazXjTLfK/3DO7KucMgt9rfP7fZQC+qVGTCGIWKV2PpcLuHFBFpdBAA8cHe/vvFN1EIFStTbjaaUsz4X5tabm+ya5hvjNZKDU1xbcigIgmpb40/Wxf1IPW3jlqtI6HfmxLP6AyKoA63OtzFI+KB1PGkwXc2F251mODRZF1tY7/23xFlK2WqSRmC1MprP6XykokR1tGBEKWSDxJaEKIIdci31i6vPQUgHPOj+yc0My+00rnEBAKHltShgDQ6Ela9f38kAu1QH9OULM20b3a/p+HowREyVdbelan0Lne/B9U26VJRau8WLRL6IGssxdrey8FNkNA4SnLcZ4OwjsKoYqLHIlMBt7moqlfEZSpBZRyxho2elDCE4IfMt9bGjZiS3lo5x3Uaut2+AXnHe3w7oYF5yP/hj39E0hnv67jcrvz49WceYlOVE3U+fnnh588tGb9dDWLDVoeeTBcvbNnwXtxfc0ZVppx7TNKbGkfCbjaaBE261N+oYKpWtLYDCZp07OJpHqB4+7yrRGwSWIXNM3bp+PY//YmvtwuPvfD58vIFCJTHttYfa+G271NZ8WlZyWXn2qX0TSEpUyL1tD4QEEpobeQYErcClsvcn2KKxHhGe6dQtDVzRodVFVYN87lglTeQehBtpqI9mXk8nXn4/SOPp/Ze/HP5F2714ENUryiKDwldCagbu+XJs/RODL91PPvn6w3pnB3owixms0gRaWbatXOhvlwviAS2W7vvvQi3W5lNuUwhqhP66z2eThT1TlbvD1ec27ax9ff//2Pv3aNvW7K6vs+sqrX2/v3OOffe7rabbqCBgaggiolGSdSE1qhD4gsdCfgAbRSUKAlkiBgNmMagaIavjCjiUCMICr6NzxE1BgWjQRPBRCCIUWho+n0f5/x+v73XqqqZP+asWvucPo97L/fec5pffXucvr+993rUqrVqrvn4zjkvjplShb1HyuY5MIVEcgm3S0/Ea33gCYEo7Fo3eMnUIujiz2teuV1L131qmK1CpL8s52lmHycOlC5v6vFIZCL62q6hEPLa85lrVdaqRC+8sqg7PxvjQkHnrfHvNCV2O3oujebMIQtPTa2ctpBL4Kja8wdLiuxiJM/eAqNClEpwPSETSEHIrQR9WVEVbt304lU1kQ+1O1BrEWKSrl9eXq2EukXO1lKZq2kML7je90I5IrWS3OkaSkGk9lz0HBJKZXJ5dHOXWD06D7BLkTVXerBOMyGaYwxgIrBqYb0y2XNcV8u3aqX4RUhW/5/Zo0a7JGhWJnfEzSGRUuo5oWDtVE78ZCzHirhBOe2Uy2PtBWaqCnk99nsTSoJJukO+rNasOyJdh4tFCZQ+92EKnO8nZo+SryWjRZld5z/b8dgxcoQGBgYGBgYGBgYGBq4dngjXUS2VEsx7EDFqVfPoBwmIKFtrBGvp1yqbIa289ka3sv4LpXv4Rdzia1V4JBJky0upYk1Tb7knLUjk4rhwbFXFRLjIB8R7HeXFqAxTK6EaKiFOiOw6X7RglVHasAOB5y+uTtJNrPdRK9FdIxxVubNsjWMD0nNptBRUEupRr4P7Z+KJ57J658W0MWjIon1MIsZdV490FMlE3c5RvcdQ630U1EuON0dOUVTCSYQpEKkc3d0QxfOM2u9qM4HQaWgVrI9Bd24LkdiryKlao9jTeQLpNCCNFRE9aRYJQuz9AASQGnup4Sr2LKSwVcuLwSJwjf5bJVjVmhYRkpk7x9LLZk/xiVgmA08KFHZn1hfo5o96M9P501zctryU73n3d/Lcc1c8F61yGVW4OmYuL921OAlaCouWvk6CCseiHLxMaqSSptCjThqFGjb5Jm1N9ucVNnKp/V1FmJzXraHamvNfK+bBSyrdizvFSM70+PFVEfTZ27xwx64jFyHWheXCxvhueY5aCs96Y1l05tb5OXPY9THkqr0lwXJcCWmjeYSYmGKkSiS45/f85sRSK8eDzWVdlLKsPTASp2QR8SZvguU9SXd3Bp+YFhmzv2/dsnv19M1bXJbSc5DKVFjL2r3fMUSOVSh57Ws/JpPd4vO0P5s9vapFqKVXebNjwDxPXHlu1XqVWQnUVp1PlN3ZzOQnDWJe7kanse98Bt1Le3G18t7LBaRRbiae3iemRpUMglZ6X5bQXwADA5APBXe+c74PZLL1YwSmtCMFpbUNOhZF18KNW95PLASurjIpF4o/s4sa3Sk4dS0gTNOuV5xcRJhj7dXOJioSlbVRwIJFiKZWeTOJlYwuTZeJxLBVda0KNXrjTl+HOxGUA9F1siqVmBLVZd4+VnZz6PqUlsWarvramENkPq8cWsVJMlErjfwRSCSE1KLyScircnVxJHplujQH5pQ46ykVxj5pVCStlYKym5pMTESp/Zi5wuFw6DmLeIXb3a5RyixKdnAqXVktD2nJrQ2CcDYn9sDS+rsh7GLo9YQD3vKkld73nHq8qtxhySy1WnsF4OxG4saNiHhztnUpnDZI0SiULJTg0bwgVm03TL0VQy4rVbbcy/MUmEU7i4uiaKlcecQwlMcfEnoiNLySS++REIOwuhEBligfZOM9C+olmZ3GFgWRQNXaVQHZqqLT9kLgVFuuKKV1FM9egrmFQanWibiXK62sOfd67kstnHtZQfCiAhWu6kJsjTwTnMcZtzlYqLzubN97ERGVvWz9de6sB0qoSK/barlPDZVKrRVtFqGtuO33agqCoCS/zqxqTQp9sykmljJZnXdMKamiJ4aNeOMzf2nXSpxjL+MaiiW4SatzL0CtnbYWRcjYMcHyfaQZbF7atRQ1XqwfY6l2r7v5pF6KthmxBDScnJOEUCi+OGsVYohdgUt+DZf+uxl6SjppnlZUyEG78mJ5TKEbrVorWSw/CuB4ch8GBpBE2hndKu7OuBESufUgmyLLmlmO9jnFwP5szy7Z0/TcxW2jeNSIOl20YCVWpdHU5kSRSKJRd+nrqCGwiTNLm5Re/CVgDoZJN0ePFYJpDo5sDYmXLR/n1tkZH7hz2RX419+8RdpJp49+8Pnb3Egz1d9Zt6+ukFI5rI3nX3hqPus9bFSUclSeW81QCgme2p+TfB7KUjiUheN6YHYFK6VAign1njvrlBGpTDuTibvdniBbrqcZANusiBRODSGViVoKwR1cb37Tm3n6qWeorvzcubzk9tWR2BrTKiylcGc9culFHXKxnNX9bu/HFNbj2psxl4znRXoCdYxMceaDnpe0loymuec17UVJ56k3bsy1kkPg6GOSaH2lksClKyulZOZd4MwVz3meiSn195MulaXmLudrE1wDA1jpaNelqaKslJ5/E3LhfEqce7GXcsjUtbLc9sbtyR2R7lwBmCOUdUH8QQspsJuEsnjOYqmW/+fraiJwrIXSkkhEEZGuZ1wehBqlO3B3UdEQSK25aTHnT14yh6bbTBUlE7T1DHMerRdYIE4cau1OjqoB0UJxHU6DFWRqjqAipoO05qdaK1dFu/O8CsSzRKJ2eZJSsiIQsumqGpSytNSAYDT9tk61UMvW3DRECJP2QixarIDCguVZ3j5URGHvjtg6B1KVnn94kZUQCqSE+jgPVYlT2nKypZBV2XlhClEla2b1UuaHpRKS9O0jcHUszKcp+SlyJnufR3Pxl2pjPKyWkjHpxNR0+N1MzZnVBZSSyEm5c2nvlpmJqLHnZF/Ex5+D/UQYQhqmzhfUku3Ff/JwUelCv6ot7FZVzJ5j9672/je20OheO3vWWqW5iECVXglDonU67rztlhvU7aYAGnBHALf2O6IIL1zaw7CUwlUthJroxkuFK2Er8kBlf77nRrDE39v5wPPLRatoYAWcJPSFWwgQa1d/JCZqla68C4EghdIbk1oFosim8CAWBdmCK9XnZPNAqGxGo2LznnpyVbRGjVvxKR9fsxBdgPigjzUQKtAfbCtioQKe/sAk5k3dIkLJrrbnBZReiWS70qk3LDSxLD26QxCrkuIfc7XeJ81zZD2OrQHYdhlqY/C9SjWDqTmWVypBrYGtj5qBgY6YSLvmxVJrxHnmTT5vPcO70vuYs+d8nO+IIfD8lVVXSzKxcCRL6XklSQJryb3HzjEUAqs19QNmCYQQqZtAwoNA/TOyrdPg+7SOwO051p4QLTy923OsR257D59lrdR14ZmnrBHsbrbmoIdLz8+Rym7eMe1MXp2tgbjfc8MHcfvqQABSalH0mWNYWbw3yAu3F/Kxbv3ggvU7CiK485HLFy6Ju103ztZcSQI7z7fSnfVWoxt8k0fHmpxvsq3lAFl0vOVdnp3N7M/mLv7Oz25w6+qScjDhdGc5IlpJ8469z90LF1eUsvZ7pWFi3gnN/sua7YXe+rBMkX1KvPdg85rmiRLF5Lnfg5C2ROIUAmXd0dqVqMupKoErrxMYd8Ibz25w7spMiOZiagnth1KZRIhuZJ6lx+9hHXhyIMEcDACqmVxr7yO0rgtHkd7vcD2aE3D1PJhUhSlGy7N15TlMgZASydfA8Vg5rHVrXyUBCVOvEpd15agrN13HWw+QzqVXMrvSaktamnM0oORuOElIBALzbubgTV0z1foR+jpNGliWSnBd5Cor652rXkDkfN5bwaxWuMAj5E37iVOkFuthCRahVaRHgneelynRWCkAORcr1uVatCDWv8gNnV2M1JK5Op4UpkiB1KgoWZhJ6G7rbSSlIq0KZrCel9EjTrUqlUr0jq77Ci8cF2ZVvGgcuxC4OizMLiuKR5VbBDtKYJZE8nPuoiJBen/KhFKqUlqRnJIRKUjrRblCDdbdE+BsZ39pzL0fkPWDzr1K3CILxzu5501mXZgk9OIJ0/T4zZCRIzQwMDAwMDAwMDAwcO3w+E0xYJqguEusUiFvVcWiOtGtd+Ku7NR4jwA1NGrV1pumkyVacEaV5Bk3gOeYbNuJeqi0ccWLUHUjo0zRKF5X7uGINXhekm2fdWWt2cqcNtYGgq7avbASYF0ryU9ilLmpX1eiAHHj0AuWB9Ou0/gxHZYppb33UVBjywn0yFYUn8c2zroStPYu5yLlrrK7SPFoXCunHSwi1KrMic+wW/olVILE3q8kYB7fVkWlYrldUbrTln0QLpFePta4qVt0ptXablQSxbwZ7V5YLSXp3oaQrJdLryZYC+tJBxXbx6mPreqNGAWzeYpbD5bWJyGGilQh+6D34WTiB6490pR6NTTz0imT58ac7c84n/bsvI+QqnJxtXCRneddxBZ3Cey8VH4gcvuFA9nlS10O7HXfoxJxmqlBmZysmUOhslE5hWKR3d4nqDKHyKGvGeupFk8E3rou7KeEYNGWi8vbpHnqXrqUElULT012HW940y00CNHX3dNvmEhxhzuSeeaZI3lR1vXSx7DjbLcjt/4Wx8zlmrm8uG2fl0xMiafO505pLhVqWbrMPKqgAk/fsejKW15/k6dv3qD4a6vEwixKdnk1T9HkrlOeLfdw67shmj1S7F7ip1vubQAAIABJREFUG3tiEpbk9+ZSeWFdqSg7914/fUM45MzRq8ZVMrlM0HILso1+bSVz94mEdV8Hk6U7CaxO2YlBSSFaTgRGtYtnQlqcEUH1fm+QPGdijoGb09zvzdNnN7h14xbJj/nBO8/z7LpQmsd+KxE1MECctjWxZqtS2CIE85yQIvSauqrsYsLJMhzKytVi0qatif2cKGvlykuPlbVQjwtraBTXyHIo7HeNKleY057Ycv32RsFqqbe7ELg80KlSOVe0CNPsVLxJqKEyCT2XqahCjOx9oId6IBM5i0bNvTgu7IDQyCnRc4j8Mo/LShDYJZfjUognZaWriuWA996SkEqlitHJwCoFFyqxblXgdiFQp5YDVIkqnDsNcZ1AtJBdht7YTeSTCrcpJs73keD6k8YCQbsunFRZJ+npE0kju6Ke2y0+bisb3lJLRK3dQNN9Ww53u78pGcPq/Mzzuw6BnCtLNUrzFCZ28558aMyjYrlTjU4c7N0TJJHzFinTinGNce2uVFJLk50DN/a7rRfoE1Dv/4kwhALVEq7wZK5knEMw2pnWtSdexeDllV3VnWNiInI8KX8sZSGf5BVBW/gnREik1y/XWjnWSvVk051a6dqmGJ/Nk9V8r427eQAVMq2wwUQUz3RpeWWxeqnr7YUnErqCXnIG0Y1yIQC1h2LFall33rconjOwKeXq2/gHO+5pmXDPm+qUmDgxxYniL1DpVar15IhbM1PEm502Q0hdAetlxo2TH1qJb1Gs0aNTOKQSQmMYO0SMwuf0w6xi+VhdSUsQ8pb67ZzWyRd/sLvZ+3KgsOS1z1PRYj0FulEsW0Xv07nSPumIWj+VTmJUUCnMruyeJjIPDNQ4oTQq7wook1MRpjkhIj15dc2F5y4uuOhFUBIqlVwU7pg8ycfM5XLoJUn307kpKI32EaHURJktb6VW65m2tfsVpEinolSUA6UX/yBaQ8/idJeYC4tkW2qtUbUEzs9maD0sQkCqsndFYZ6skXFrWl3Wikpm9vydfbhB2RVqMcMpL5Xnrg4snn18VGFCqb6OL+qRcswmM502+4HjHe5cLT1XsxSoc6S+z/otveXmzOtuTZxPZz6Xldc/9RSve+ppO6drMo2qOyXrCRTdSK1R0VC6jA4aOJt37Fy72p0l9nPiztWR49JkZGBKMyk0WvWRRSpXpfWDi0yTED3B4XU3bsLJ+6yUAnnLAwghEkPq7xbBiqbHk3K1ay6sueB6JE/tZyTM7Lwn05ufeZqP+Ig39oIwH7W8gfc89zzv/qA1w33/xR0GBhqmWchLK7QRqZJ7svy6Kpei3QiJMTCH2BXDZc2UbM9naxdyLhNn+0T1Hoc1F2Sa2DfjnkRMgdkNgDoFprw10JzOIqobHWtdCiVXUjN89hGp2huXJkkcykKcIrMviilMLIsV2rLr2iG5dt1mF8wrXFxXWRU0195UfZVq7UlavZEwoVKpTt+qxZw+qTkVXNWqIp0SGFOANVJDk6FwqBWvAUBVYa6y5WQngMDignleClVPilOJQNSe76NaOC61t21JYs7ulm4RtbAuytk+9eIrV8vKbppcNwPUijNIy9eplSibk1+9gXPzXy1aWDX3glrVOnP3/Vc3vLIHLvZihsxRK8eeDGWU3/YCOi6VRGDvdMwUzUF1bO+jx28HPRmGECK9/rtRvkNXPltCcPOWigqrlP797Ars5u83ZSNQuuIbxKp/tEpzpeRePx5Ag/Hrm9Vck3CGMHmfD0vyTez8gX3PxSXHnHuljSjmndRMNxLmmFhFWT2ZL4hCrScRn0AVQU5yfKxrsI/JNu/bVzkxUHwewj12UAsa9XlwY26LlFliX0vSDiW4adXJveiJIbXD6oW0/J3qPXpaHlOLrPXCBt5Mtfc3wY0LtU7SYJXxUDbOvMpdlZ8CarlLPoqiFvVq1zQHW2SXjctbvZltm5hg3u/ep0jEmyJ2CjKiVmWpTW6b1V6ITm0k7ZjzKJYwcAoN3WCQmCCeo2tLrq+EMHPHe99cHReUSHT5dVyPZK2sRbjyh/pwlSkSuen9Ifa7iSnCMzes2tkUhGf1wM4bhx64K4YKBFvTrRdXsSp0uGcyNIdKy40JiYBa4rArREGEs2nm4M4eFVN+WnXGi+ORooW9FzKQEqm5oi3SpVeEGHs+z/OXH+Q9732OK5fr+5SY0kx25f1W2pNiYs2ZO8UNQoUQZ0ra+k+U42Ygvv/qkucudwQsqnRrv+MDz12Q4nvtunY7zua590w520Wm/cTZmeU93TzbkeZ5qy6KmhPGv9jvrKjF+Y3MwZtlH66OHA8rrQ3L+RS4c9ga5qpYA+bXebL5G24+wweff47jle2/eqPG3Bw/ZaUU5XzvDVmnQEqxN3Ks1bzrkwTOptYvBPZT4XU7M/iISj4sfOD5Z/0cC9Rd6yfOe9//HAMDDYesPUc3ocR56s/fha6kFQ6tUFRVimaiK1gVe99mNgfFB28fmEX6OkrB7PzFZclSD4SoSGnMECuE0CICuWQ0Ki4ioRSm6cRxLUKIU88VvKwrAhzWlViaIWMOWZmagzwgkjv1ZC2BnLdKinpYWZIgvqYkWPGF7Mr4rDMatt6TIQZqWMmdaaLs0szNeeq65+GQWWLt1YOt0p12j2rQTEnS5+0s7BGJ3MkWbXn+aiXNc3eiKDannZEjid1Ue/S4FEBrzyc8ZCVF66e0+s3YzYkUQtd1l7KaAdsLTIrlBTXH8QJLqXgqJ3NS9ikQ0lbMpWgmuJE6aSIWaa8W1pqtomgQ5pMiWoL24hq7KRE0nDivhVAqqUexeOwYOUIDAwMDAwMDAwMDA9cOT0RESEvo0ZZDhVpzjwiJzhZhaJa6RCub2LZfV4uqSOneyx5p6SGAhKqVwAanqaWEuJdP1wpFCU5a3cXIPgbETe8UBamFRZqXRFlr7pY5c2EOiTXUXi47SOVMQj9mQgizUfgAlvVAIPZIWAyKxnTCfFMkaPeKtNhF534Kd4V/Wq6PsJnXlh8Ue8dxc01I7/AswfNvmhukWmnatXkL8D5OHp2RIETNPbycsrKWaiFiLBQsWhGPghEC6udqnOSlKpNIj24JjcbmxwyBwlZzPkrLlfLQfojsglBaTwItREn9eYkaQDbeLV7RSTys3OauRdDa3KqcVAnUu8dc5AmI3Q48OUixV3SzTJ3C7dsWpfjgB95HWTOXHhFYckXr9rwetaDAUuvmlaMSo/QckJIqsyYuPMoUVWGGtSUgRqOo9gg2FYxObmMKkXLCLddakUKv0hSDeQaVXm+TIpb2oifd4a1tgK2rO4dLVlHOg+XrvPHWU+wk9ZYCz75w4AeffT+3zq0q5n6+wXw2k70i29XxyNW69FKzZ3FGq3BnOXR5EiWi8+KVLy2gFXc7vFAUEWGOkKbmvyu8UFfedG6Rkv35njmlnp9z53IlLisXF+Z6/mCCs/0Nbj5lY7yx3yMK1cuWaxBCjOzPZs68CmC5oaylcPD7eXVxSYgXZI+E1XVhTok3PH3LxryLHPIL3PBo3u2LO3zw+dtctouY4NaO7uWtRM5PqlweciaXgkjqmY435nM+6g2vJ3q54u/5vn/FU/uneOEFowy+sCxoTbxw2/gtt3N/iQwMsFwsRI+q6n7mDXMi9NL9yrHmTv1MItRSaGVZy6pIKBTVLl+yKvMusG99F/eJ43Hl2WdNNgRdmUIiSdM7Mvkg3O50LevZ19SzOVl1272v6/Nphhg45BbhruTsUYyWn1yVelJ2edJEjLFXSzsX4bgWPOCDFGXJBW184VKRIFx6WOqARV52TvWNyXJ1FqfaLXkhSCaG1MvvL8vR5jVsVd3mBNGjJ7VEQgxcHjziXZVdFJJHkKYEuxBpgbEgpq6srcS3VLTmXsEtxkAW7dWOU7AqeNbNsVXdjaCKek5PQSAKqaVxpIlI6JF6KBZJbtXlsPCe+r175vyMWkunHN5eMhK33PasWMelamXVwfKva4hUP6bMULJuuYvFNMpcThSwxwxpyt7AwMDAwMDAwMDAwMB1waDGDQwMDAwMDAwMDAxcOwxDaGBgYGBgYGBgYGDg2mEYQgMDAwMDAwMDAwMD1w7DEBoYGBgYGBgYGBgYuHYYhtDAwMDAwMDAwMDAwLXDMIQGBgYGBgYGBgYGBq4dhiE0MDAwMDAwMDAwMHDtMAyhgYGBgYGBgYGBgYFrh2EIDQwMDAwMDAwMDAxcOwxDaGBgYGBgYGBgYGDg2mEYQgMDAwMDAwMDAwMD1w7DEBoYGBgYGBgYGBgYuHYYhtDAwMDAwMDAwMDAwLXDMIQGBgYGBgYGBgYGBq4dhiE0MDAwMDAwMDAwMHDtMAyhgYGBgYGBgYGBgYFrh2EIDQwMDAwMDAwMDAxcOwxDaGBgYGBgYGBgYGDg2mEYQgMDAwMDAwMDAwMD1w7DEBoYGBgYGBgYGBgYuHYYhtDAwMDAwMDAwMDAwLXDMIQGBgYGBgYGBgYGBq4dhiE0MDAwMDAwMDAwMHDtMAyhgYGBgYGBgYGBgYFrh2EIDQwMDAwMDAwMDAxcOwxDaGBgYGBgYGBgYGDg2mEYQgMDAwMDAwMDAwMD1w7DEBoYGBgYGBgYGBgYuHZ4Ig0hEfnbIvJrfpjHeJuI/MArNaYnEa/mNb7Kx/5mEfm8V+PY9znX14jIl78W5xp4vPiRIDdE5ONEREUkPa4xPOl4ufdIRN4uIt/6aozplYCI/HYR+ROPexyPA6/lO2HgwxNj/Q68WngiX7aq+umv9DFF5N8Cn6eqf++VPvZrBRFR4Meo6vc+7rF8uEBVv+Bxj2HgtcGQGwMfzlDV3/24xzAwMPDyMNbvhy+eqIiQGJ6oMTU8Tg/t8A6/PIhIfA3PNe7RY8KQG4/33Nf92X8lrv+1nMMf7rme5PU2MPBScd3W78CH4hUTZiLyX4vIvxaR2yLynSLyS/37KCK/X0TeLyL/RkS+8JT64SHx3yUi/wi4BD7+3jC5iHy+iHzXybF/sn+vIvIJJ9t9rYh85X3G9vXAxwB/XUTuiMiX3o9eISL/VkR+jv/9DhH5iyLyDSLyAvB2EQkn1/kBEfnzIvL6k/3/hYj8Sv+7UVx+vYi8S0R+SER+88m2P01E/rGIPOe//WERmU9+VxH5TSLyr4B/JSL/0H/6Dr+Gz7pn7L9FRP7SPd/9jyLyhx5x314vIn/Kx/isiPzVB2z3SX5fnhORfykiv/jkt3vv110hbBH5uSLy3SLyvIj8YUD8+52IfFBEfuLJtm8SkSsReaN/fk5Efqb//TYR+QEPQb/f79evOtn3a0Xkj4rI3xKRC+BnnT4TJ/t/qYi81+f9M0TkPxGR7/Gx/PYfxj36IyLy+++Zt78uIl/8sHtwnSFDbtwlN07wa18JueHffaKI/F1/vv9fEfnMF3Ff3uDP7gsi8k9F5CvvWdP3O89P922f9//+9PvN0ck8fYP/3WTlrxGR7/d7/t+cbHvm9+hZEflO4KfeM9avFpGvPvn8VhH5yyLyPp/vP/yAa3zgvIjILxCRf+7X/04RecfJb228v05Evh/4+/79S5H/93tO7jcnn+vnf1ZEvkBEfqqf57nT6xKRHy0if9+v9/0i8mdE5Jl75v+3isi/AC7kEe8Lf17/xslv91tvHykif83n73tF5PNPtn/Uc3rfd8LAALy4NTzW70vX9wYeAFV9Rf4B/xnwkZhx9VnABfAW4AuA7wQ+Gngd8PcABZLv983A9wOfjFH1Jv/u806O+4PYy0+ATwA+1n9T4BNOxvC1wFf6328DfuDkt38L/JyTz3f9fu82wDuAFfgMv6Yz4IuBf+LXsgP+GPCND5iPj/PxfSNwA/iJwPtOjv9TgH/fr/njgO8CvvhkfwX+LvB64OwB19uvwef6AnjGPyfgvcBPecR9+5vAn/N7MwGfdp9jT8D3Ar8dmIGfDdwGftzJPfy8k2O+HfhW//tHAS8A/6kf578C8sn9/Wrg957s+0XAX3/AWN/m+/4Bn/9P82tu4/ha4HngZ/g929/nmcjA7/CxfL7fkz8L3MKewQPw8S/nHgE/DXgXEE6u/RL4iFdqnf1I+8eQG6+q3PBjvBP4XN/nJwPvBz75Efflm/zfOfDj/Rjf+pDzvB54FvgcP8+v8M9veMA8vgP4hnuu+Y/7sX4ScAQ+yX//PcC3+DneCvw/996Dk+NG4DuAP+jXvgd+5n3k0kPnxe/zT/R7+CnAe4DPuGe8f9qPc/Yy7uP9npP7zcnX+DX8PEw2/VXgTcBHYfL903z7TwB+LvZ8vRH4h8AfuucZ/XafvzNe4vuC+6+3f4DJ7z3w7/j1/cePek55xDth/Lve/x60hsf6ffnrd/x7xDP3Kj7M3w78Esza/g0n3/8cPlSh+Z337PvNbArN/wJ80QPO8WorNP/wnt+/Cxf0/vktvhjSfcbWFsInnnz33wN/8gHX8sXAX7nn2n72I6733mv828Dn+9+/EPjOR9yjtwAVeN19fuvHBv5D4N24gu/ffSPwjnvvl39+O5vA+tXAPzn5TYAfOLm/n4oJtGY8/DPgMx8w3rdhL8wbJ9/9eeDLT+7/n75nn3ufiSsg+udbPqeferL9/4kLzJd5j74L+Ln+9xcCf+vVWmM/Ev8x5MbH8QrKDcy4/JZ79vljwH/7kHsQfXw/7uS7r+RDDaHT83wO8G33HOcfA29/wDy+gw9VGj765PdvA365//3/AT//5Ldff+89OPntP8AUlvvN7dvZ5NJLmhfgDwF/8J7xfvxD5vCh9/EBz8n95uSjTn7/APBZJ5//EidG8D3H+gzgn9/zjP7ae7Z50e8L7llvmEJWgFsn330V8LWPek55xDth/Lve/x60hsf6ffnrd/x7+L9Xkhr3q0Xk2z3k9xzwEzDPz0diim7DO++z+/2+a3gr8K9fqXG+RNw7ro8F/srJNX4X9jL4iBd5jO/D5gMR+bEi8jdE5N0eWv3d2Hw97PyPwtcBn+1/fzbw9Y/Y/q3AB1X12Uds95HAO1W1nnz3fZhX41G46/6rrdrTz/8H5tn4NBH5RMwz8tcecrxnVfXinnF85MnnR83ZB1S1+N9X/t/3nPx+BdyEl32PXuo9uNYYcuNFHeOHIzc+FvjUdm4//68C3vyQc78R8zC+lPn/SB/nKV6sjGh498nfl/g65EOfhXvPc4q3At+nqvkR53rovIjIp4rI/+bUnOexCOXLkc/3vY8vYf97ZdODZNWbROSbROQH/bn4hhcx3pcqq+693x9U1dsn3/X7/Yjn9KHvhIFrjxezhsf6HbrGK4ZXxBASkY/FaA1fiFEhnsHoCwL8EEYJaXjrfQ6hDzn8O4Ef/YDfLjHqRsPDXu73nuPidF+xxPo3PmKfdwKfrqrPnPzbq+oPPuS8p9f7MRh1CuCPAt+NVYF7CqOd3cuTfti83A9/FfgUEfkJmIfgzzxi+3cCrz/loj4A7wLeKncnyH4MRj2Ce+aSu+/DD3EyByIifOgz0Bb05wB/UVUPDxnL60Tkxj3jeNfJ55c6Zw/Dy7lH3wD8EhH5ScAnYfdk4D4YcuM1kRvvBP7BPee+qar/+UPO/T4s8vpS5v9dmHJyihcrIx6Fu2SIH/dBeCfwMfLohOJHzcufxRwyb1XVpzGKy8uRzw+6jy92/xeLr/LjfYo/F5/No8f7Ut8X997v14vIrZPvTu/3w57TF/NOGLi+eDFreKzfl75+Bx6AVyoidAO7Se8DEJHPxTy7YNSlLxKRj3KF+7e+xGP/CeBLROSniOETXIECo9H8SrHE6p+P5Yw8CO8BPv7k8/cAe7Gkugn4Moyf+TB8DfC72vlF5I0i8kvaj57Q9vZ79vlyETkXkU/G+Kx/zr+/hfGk73gk5GGKyYOu4S64AfEXMSHwbar6/Q87mKr+EBZe/WoReZ2ITCLyH91n0xa1+VLf5m3AL8JyCMDuwy/z6/wE4Ned7Ps3gU8WkV/mgu2/5EOVoK8Hfim2+P/06Q+ecPi2e7b/ChGZReQ/xATAX3jYdf4w8JLvkar+APBPsWv6S6p69YhdrjOG3OBVlxt/A/ixIvI5vnYnsYTdT3rQDh4x/cvAO3wMn4jRmR6Gv+Xn+ZUiksSKufx4Pz/YnP9yP/+/h+WHvFj8eeC3uYz6aOC/OP1RrJDC1/rHb8MU7d8jIjdEZC8iP+M+x3zUvNzCIh4HEflpwL3FLD4EL/E+vtK4BdwBnhORjwJ+y6N2eNj7Qizx+5sfsu87gf8d+Cqf40/B5H5Txh72nL6Yd8LA9cWLWcNj/b5EfW/gwXhFDCFV/U7g92Oc8PdgiWX/yH/+48DfAf4F8M+xF2bGqCEv5th/Afhd2M2+jVnBreLSF2EKeQuLPsz7/lXAl4mFUb9EVZ8HfiOmMP0gpug/qknf/4B5Gf6OiNzGEqA/FUCsIs4b/LtT/AOs0MD/Cvw+Vf07/v2XYIvzNjZHL2aBvQP4Or+GB1V++jps/l9smPRzsHyA78aS7T6kwpmqLsAvBj4dS0j8auBXq+p3+yZ/EFiwe/91nHgmVPX9WOL678E4sj+G7dlo2/wA8H9hSvG3tO9d6bkD/N8nm78bS8J+l5/nC07G8Urj5dwjeOn34FpiyI1XX244dennAb8cWzPvBn4vjzbevhB42rf/eiwn8PiQ83wAc0r8ZmydfynwC339A3w5FqF7FvgK7L68WHwFRkv5N9gzce+6eiv+3LgR94swiu33Y/fms+7Z/sXMy28Efqffr9+BGWMPxMu4j680vgJLGH8eMzT+8ovc70Gyqs/pQ/ArsFyIdwF/BcvP+Lv+2wOf0xfzThi4vngxa3is346ha7wCEKPnvoYnFPl04GtU9V4axYc1xEo8/yZV/RX++eOwF/f0Ivjqr+Q4PgYzat6sqi+8Vuf94UJE/ifgXar6ZSfffTZWBea3+ee3YcmIH33/ozwZ8KjaNwAfd09e1cDLxHWRG08qROT3YjLl1zzusZzCFZjvwCgl62McxxMh/18qHvS+EJFvxwp8fOCxDW5g4DXCj7T1O/DS8KobQiJyBvwszJP3EViljH+iqj+ie6s8joUklsPzB4CnVPXXvhbnfCXgc/XtwL+rqv/mIdu9jSfcEHK61DcB36Gqv/Nxj+fDFddVbjwpcDrTjEVjfyoWkfs8VR05by8CHw6K1Ifr+2Jg4NXGWL/XC69Fh1rBwn5/DquS8TexUOXAKwixAgLvwSgkP/+e3+48YLdPV9VvecBvrwlE5L/D+kh81cOMoA8HOD/5n2Ee6s99zMP5cMeQG68yRORf8qEFDgB+A5YL9Y1YlaT3YhTG//m1G93Aq4mHvS8GBgaebIz1+8riNafGDQwMDAwMDAwMDAwMPG68Yn2EBgYGBgYGBgYGBgYGPlzwWlDjHonf95VfqFqtGNRKISEcV8sxn+cIBKr/HgLUCndHshRR6UXWJQgCqH9TA0SJRC/LXsV4N3Kyv2aleK5tjBOlhn6OGGBKkVptTMdcICjSDlADgvq/BgEJFIxeupZKCpEpxrYTuVYa+zREIUjoR6hAQAluq4YARUGL595HQbXQcvFDiFQVVLZ5EQJRBZHavxGJ/bqUSkxC9AspRakowc3jKUZCEI6L7b/mSgiB4NsLFRVF+lULKpHi/UojwiwBjVB83Fpt3ouPoaLEGBCVPibr9tvGrARJhNDmQVCtVD9lqEJgKyWWS7V9+jxWVN3iD/2QaAWC+P0VqkL1MaYQkZN5VIUv+bI/cm9N/4Fril/wC3+mij87IkLQQPTnU0IgidLE01oKSy7E9lkUrbDTwD7NAMxTRBUaFV0koBWqP4NaFOq2tquvj9olnq1Za2kETfq1NVVQgs6oF32bBNYKq1Sm2Y5xNt1gChM3vUPX697wFp57/lmef/59AOx258TzW8jRZOSdw4JqYW3iSIWkdDld1EbXllwMgRAECX4NEphDQmSi+LiOxytq2PWd6lq5OC5U32eKtm7bOfOygkKa7TW21sI+Ck/d3APwhptP8eY3vZFnnn6dz2Ph8s5zrH4Nzz5/m3WpzOdnNkbJrMslte6IyY6pU6BeXlF8rktVNGdCnOx3Mdkc/XMphUUhZ7uXl4cDOSvi8myRQiQgwY4fKRzzSq1+/DUTNZJj4Gotft0TIvRjRIE5TqzRzlFzoSyBUhabhzXz97/1nw15NQDAL/7Mz9TiL8wSBKoSXX6lHdzY7VmzPTsiCYlKaxkYiIRcOUomuu6itcCcYPHaJFkhJIrrGfmQybWCLQl2854pCtHlV9FKlUoo/o5eAyICyX4XBbQi2PlCiBCUqpXiIq9qpiLM0vQG08FMcwKTgtGURQCJtnCC65laERLBZaRopWal+Al0UkS3xj1RTV0oCqGdIpisFrW5ipPYDr6Tqprc8Lk+rCtnMZKiba9ByEGY2jWsmVoy0mRBmKilEmabhyjB5IS4tiOVWWbWUAiLy6tgOhnV3wW6kiv9fiYJ1LQi/oIKGkADuV1TBELYNDo13Xvn3yyhgNhzAVCq6amq0vU+PR65XBRx8yJqRkOi+sSdzUrJikST01MKfNOf/FOPVV49EYaQPTtNOXdl3F9EEmBdC8EXUcSU22YgCIFKQdW+B1OOVWT7LIkkkcLq54go0EwnAUqA4kZJFFe2fREJbnzVTfE4NaRE2nqTuxdBqF3g7IKds73wCPiYfQzVH2K/rjYnTRmquVCR/kBLhYKg2Y+XXHgp3UAL0sboi0KCGUVtoZERTfY2B2pR7H/+OSiqm3Emoqhmqm7GmVbdJkKhkvvxiPbPFrYvEolmQLlgrmrH6aFJEROKJwcVCV0IhyA2192Ys3loW0/BzNGqTagK4k+X3wpTOtvOwLridqv0MZjS2U1rBgY2BKTLH1Mquk+kVo4oSU1+1VwoJaPRjB60shZXcF1xKAVSCFRXdLUIGqC/9Ys27aCdBUwa2GjEllpzHqi7ULotrwUl03wwGgQRmCUQW7XZeiROwlM33wTAWz5ZgCx0AAAgAElEQVTio3j906/nve+xHqiXy8KNs3OO+QKAK8mgmegKfa0Vrbk7IIRARrsegipaK/Nk2tFunolBWKspIABrUYJmkh8TEZ6+dRNJ/hJerqi5EI7NKRYpqetPxHnm1m7mDU+ZNffRP+qN3Dy/wcWzz9nxlwMpKtGPd3a2BxZasTlVmNJNVLUrBrEEZD7jeLTrrkvmcs0kt2znKRFIFJdvpRRyqRwPRx/zSlHTwcD0MRFl9pszx8Q+RbLf6+NUyUUQKtHfXyVXlnXhuLqyqnB2tus6352ro8tcO8kxP6wf9cB1g4SENF2IgooSg8kjyStXHGmO6FArYRImX6cEoUogSOq6jAqs6+rvaZDJVn3Tz9OcCOj2O4JW6SaKusNU+/6m57UNRPyzI1OJCCEEmk9X0nyXTqbVHKqbK9rWg05N7q6gBbIbBCGYrtP0NWBCkNgMKyUCa7U1t7gIDgrR9SmmZNu7kKtFNuXLJhtBWH1izuIMshJcvhVgLmwOrlps/MkvXiohaDdaUNNjmoOLYBKirqB19blrBmztx6SmrsJUyYRaTRBh+hgBYmgvC9Mh2ymyFp8Nf9+pOa3F5V+QSiyVLNJ1dMIZc8io3yzTF5XUxpATNRTEDad8ePyFdQc1bmBgYGBgYGBgYGDg2uGJiAglKVy4l5SohBCJbpnXqsQo3ZtfVYjIRu+SYhEe2Tz+wSMKnVamArrFDdaSmWLq1nPVgijMHqoTAoRMsxNVlSWXFlixo6igLZKiZmCXqj3KFKJYaLVFcBQqheDegaQTS9ZOJZnnHQHtrpAqFrFpkTIC7hFo1JOIhEAzs0WMAsYJRbBQiSFQmxtFI1GF5lYJJEq16/eDkLPA6kfYQZxOPDsBp6210IoQTvtbCmiufUwh2BzkWim06Fpgi3tBiD457d5hdKNc2r1MTDHQHBaiSgiBxT2oEpRQ6/Y8qFH1Gn3PIkM2jtU5NRIECYHSz2E+9ObQqFJBpTt3eqRoYAAIMfQ1EcA8le3HWj1e06ifANLXWFQxqm1MPYJzKCu7ONMWQdgcgPZftmg3frxA2pyPYnH0tr/49s07qkSEheLrNklgipEUpMvZIDO7dIPlaB7Qd33/9yIIy6VFNu5c3eHi+Quq06/iLpHCzOXSouyVEEFKmxeTuWvz+lWTy83zmGoFMfpx9khHEGESq9kNsKRIjLHTYokTL+RCKa1dkLCT1L3XISSSClJt+8NxJcSlh2PSbkZrITo15dZT51R9gYur2z7fgd08G/dFnHZWFogTUZyhkBphZ5PziFAabXrJXK0ri8/LmleqhC5DpBoVNzVqSozs4uSUXtDjBbUWSl5ZDzaG45rJNXQP+pSEy7xSDo12LcxzYDfZyCbdMzDQEKidUq9OGWvR55QgxtTppbVUo583GltdbF+RTn1ThUl21Eap14rmlRA3+noi9LBC0WpRhj4iJRH7Oz8Xo/9OPWzKCTMEYlbTPRBKUz1Wi8ar61MStEfp7Qz2P2r2zwEl9SiFVou6hq5eCVmFuUXNRViBabaI+eR6xaqbjkcMjZJic6cWMuprPQgVZapOW4uFpBPZdb42H43UIzWgEpAWuq8rIeoWKWsyo8v1YPpb1h4BQoO/F9oYXRdq74pQKepUHfAIlpIaM0lMH2zvnqqm/9WufwUkapdFGpLdKwoSNj1yCpXDlV9ftXBfoxQuZKKGTsuWfUsXeXx4IgyhosrsL5rgr/H2YtlSgbaX/N0kEfGX/qZcN5WgKcOKUlRZG9WtaxAnGodsHEe0kutK8OnpWTB9MHf/10K/oCrd2NLafm7nEESlGwSmOATjv9KUF0VpJeujG3L9CTaFR5uiURAJ1PZZgik6cqowmcJ2msMD2mljiD3YoR/TDJLiT0VWJa95E0jNSPNTFOoJkc/HL50abMYHJidqv39GvYun90BPpKQKVbTf/4qSUuqGj2KK3KnhFOQkR6gpkyez0ORA7GOQu8K/7ZmiT8s9ho8yMNAR8LUCIHIXDYRoiSzFrewgSpoinu7BAiARCXSFXWthpXT5MgWTRS3nR0Pwl2DTAnCHRzP+6yajwGSA1JPVGYxl52tqqkKKUEXIjbaREkThttPOLg4HKEp2o6OoWB7QtPPLFNZc+ximGAgnThfJFer2klcqVQNrtuOl1SV9DaYo+VYiiutTnIWJi8OB0ikXcJb2pKdMwhxrQbN2SobWhZwry5XN27o7Y5EDsBlOMSSk5Uu4A2V2mpCqsBzvIHEiznaOeYJaAsy2zRJXbs7qHhygCnUtHA5GR7vKheNauqJZJVBq6cac1EBy2rQNopBiQJvykyby4cjlIXPH84zq0eg05zctl2naBcun8om6Mc0QIK+NMjiIHgMbZEqIGwShmrO1P58xcp4i1Q3/KViuMk5/z1XJyfIgWw5jLYJKpjtuREASRHewqulDlc1I0bo5r/H3e6O8ShSiBjScvGhVaInAubijMtRNk0kmE/vKVgE9zbE251Cj2KmqUf97akIFrV0Xqgi1CrWNqYrJ2O4NNcdocucumPGm0B2/zQkrba2LEOrazxHEqMDJ5XIUpZzmmoeCULYc7GppIi2vUlQIRTcbpkAulicu0ujElj+tnSLXtJ429xEJE9ryebRCDRR/PuIcqVLILU3EDdZmBEs16nZZbP8axRyD1c4GGE1YQr//gUilsPpIJtdJWxBAl8fvaH4iDCFUKNJySJRI2HiYwaI7fdNaNmsfaGprOPEgBNyb3/QGtYXXFv8Ukj9smyEkxC1BX9Vy6mI/hekepSnSzcrZFBNVEzCdly9KRruRYR4R6UaEYsUTWtKsWuZM98ScGnL2u1o0pkXGUKTWzXKXuxP8+9wEE2J2WaY89fyZHjnZPDcS6FxgUail0KsnxEjVkxiQYlbGSeGKINJ/V3XB2++SKZAV6QsVLGdJm+9cZjNc2jyIoLVsxRWKL7yTHA1kE7LJ1b+mWhWxfKEgG3/Wtt0SRtVtsTYv8d6S8h8yrwPXGap05VtEyHgWPwCZiPTcPkkCMm1KqmaESF4rqXkf2ZwQABKCOTq604TTFBCPAGm39oXm7DhxuhD77yFYyFr78YRalVyV2hJ5i6LHK/CXk/HhA7lsxQ+Q2JWTUoWiMLVE4VIpZekyNoRo8rC/QIOLilO/sKJakOYMqhWtsPhcxVgopXRZH6Iw7WaSj2Fdq+c2eDJxFKYpMjXvtmZqCd1TWUqlRqUWN6SWhbIWkrtuZK6s2QqzTNGOkeKExoBmc2+mpIS6Y/UxXVxecHW8YnHFYKnVCir4Ne7CRKlC6u+KSC2ZxRXPXZwoRblzNEPqhTuXXB0LuZ68OySQYkDcSaYqzGmH7F1bKYW6bowHGYbQwAnW9bjl7gnUsK0pZEJlY88IVgyqF4oSK3SC1F6kpOUZt1wXra43uHyJ84SUyGXLaasropHqzswalDluxVwkmfFQux+6UguoK+dF7AUd69SNhqpCkMJcbO1Xihst2xqpCpKbQWB55i0ak5hdi2xyOxEkWmEampgrlvcDFkWjICToDBpFQugOLaKClu6s1pqppXRn0ExCcqS0yEkI7CRyLM2ATJ4E39bxhNRM8M+LwjQFM1SBVVdjUMXUo1Q1iLFmmmMlryQyRXY+TyuhHlqgDJUJSZm1OV1yRGNC3ailGuOmPz/BCgBJM3qrFTabJBL6C22l1JUY2vtGKRVibWwnc9T1XKfcNcrHhiExBwYGBgYGBgYGBgauHZ6IiFDWzS4XaR5Sg1G+tJcjPd0OGp3Uq2l0F6m417QfxKIvvVRiDxX5fyxXp5eijhZQLCehXNumH+5uqG0TPHQKzq1UJYTtnHdZ6gWCavfeqXqEpsc9o3uE3ao+vR6w0HULZfgYbU7utm2NFnZKkSm0iiFGm6N7h4pXb4vd9Vz8cP57Xj386zTGXkq7jbF2plubA1UosvFaxTOEpG7XJSeh3FwLQcJJBCmQtRJ9zNMUzANVWxjWK/F1D5Z0KtzdE7GNwbxNbMkYPk9beW3l1MHOvRGigWuNhJyUT44Uzb0CTsQjJ80bVhQthTD1UC6gVIGDyzQpGSUyhbYGPDewl0gKxLo91D0W3fMk2yo+qYFaaw/khmrR8hK3EPeK5RFV9e/WTFBIvZR+hZqd323eTY1bhbcYApom2u6lGm1XYqNoTMRSSK3yHcHWfsv9pBrdhkJsEWuP3jZa7D4V5klY3YtbRVmOlxBs7pMEakicOY9fglr0y1FUjJLYyvQqSCk0Iu26LohC8hyjab/j1vSUUfw6Hz+wLJlYPPIVd6xa0KPfu2pPhIrnOVUrT35aaZMUeoQwij07fslcHjKXeuT5C8vFOuTV5nEnpGyTO89CTDuW9ejPi514yx8V5mnXryNMw785sMFyoLe1X2uhNmqnM00aY0xrcMr7KSXM3viNUVGCUmr5EHkkjRS/Kpd56XmRu2my93XbXioathes1oLm3KPJYFXlOke2FlQtC6bR82IVdCc9laCulvPTK28i9hr3Y5QakBCY5lYCvOlFG7k/Efu6tBLUW1uPyoqSqCxE8SxGKRY6dzmdFAgnrKCq6BpoIjEGgZlOzUW8UpzLmiJejVhP2S50Roo4f7/Rle0ajFXUqNpVLYqevdpdIlkuV2cXR7IpP/5ZiTWRphatsaq7sY2xrsYu6AqVtTOprURgywdDe+VBiEg8Z3/TPuXLFfLSy6cvRe7Sp58EPBGGUAm107dELSGtei3rFI0z2Q2hIEZ96/kcSvUk25a8F4NStBB7/k1E5aS3TH85t5eVePiuFREQatjq3qsoiHYDIYbEQm0l6d16k7aa7BhVLFzYetUQ3G7RbRdOSnS37WRbmEaiaeUejc7SSnxb3xAzbuyiLE8gSLzLSCTGzostpVKrdkoOBIoGalj7XKJ0a9PSAkO3OqU3cdp+r8pWTEGiJQdu3UNYciFE44wCZBULffeVZTlAbcxFWwF1G0TOhXmaCc14q1bOsfakx9rsUJsG6SQ7v0K60A1t7oNQA1so3nMTehKiWmniXopThmIxsCGdlOavmhGUKKYERBKLZqrXXzbFu5I8D6Wo0Tqs5L6XR3a6b3WjI/k5Gj0hhkDY3mXA3X+j1cm6Jw4MoPFou+HUaR9KCa7gtMIpEu7KSbQeZVuuC2pLX06ovpVsjSSwMquCMKnNQw1Gn8ut3wRmVLTVWUpFpFLr0kvpt3r/TUbmZXXKzEYN0bKQ9iZk52mi1MycWilYpdSV47GVmQ7k9dDLhseYiLLJQ1XlbD9zdu6KTZi5sdshCMfGmZeKaKCcUGSQuCkCMaKsFL//RlnsCaKIZkKM3rABdlPg4nDF6gVprnJBKZTmXHJjRoJCL9G9u8tZmDSyVO20nxoqdTrJgc13PR0D1x3NsQdYkSdOsgK8n2H7XOx9efrKK2u2YlTtEFXvSj0Q/7+8uh6hlh3SSuUXc8F26pTUSkpha6FRTY1vRo7pILU7ekLcCjz0diMxojl0Jwcp+C7dkvHE/8XHbPrJRrn3FgMn01Trus2DttLaTZtIlr/DvKUKSFOWmjwBajyRmUI4k27PBe+Z0vRUVctdb8w6UwFPeig2/dPHF1TNiXsyatPQ1u4UEQ1wUlilJqFK7MZaQEglUJoD3pqoMPVrKGipmw+ueYibvoXRGKXrUhY4KKXSq0+JEqIQ3fjen+855GAFx4DguVX1CXIwPxGGkNsZgE1OpfYGnFbBjR4hiHgFuRNl3OI3elLBLIJOJ9XNLGpQO380kFm3l3oV7mqQ6ofX3n/HHogQNiUBpA86BLxogXTloyUz94Uld9kY1k9CpVvyIdoD3KMrKgSl95dISW0eWtOM7jU4ncimS7iyoWrZyieRjXBqPJF93jZv0WnqlMWjtmiL1MLpo9vme3MWCFS4Cs37WSDmuxauujIUTiStnAqkqJbv5YsoaybXY08GDKrWFLYbX7Yopcsmy4Hql4x4HyPti99u3enLYYvItS+8fsY2sQMDDu3/h6+dbWVnDmhJtIZ2IYImtsRfMQXAev808Wsv+NVlxypWcKTRtIMWNE29xwWlPZ+taZ4ZIc25oBR7eNsbOAUTS24ggPX1SCJMqUVwlFpXsntaLGdSexItGvo1gMm7qrkrOylGqtQe4Q5UooTuwMgxgxcOsEuoSDFlp7Z0UHeuNk58mAtztBg1WB6SxnmTFjmTgvaIkbWr2Iy5ZcnUDLud709A4kRreBJE2O327M+tytp6LCx5NZnYIjhxJk2w1+YFxpoeerRGQiBWmHtvkIIEIfvzsKyFQkBDS5COhHnmqb31Z4rLwu2LF6yfG2Y4h6Z3+DivjkrRpUe7QgikknvBhiqwHiFNdxvAAwMAiakr31WEVFJPZC8Ka83dER3EdaHmX1X7V+g1AVw53rQIxcRNK/yURSwS3NNMLJ95i/BUSjkp2FDsnd0LirT3+cn7GdQiTK4XFDU51+RL0NMOjE1/AwmtH5KChO4Et5yaskVuSZ6H2TzspjeF7jS3KEo91V0UWizMJ8a6PbtBp3EmSe16Y10DVXJ3xASPAKXmyNGKFnp0roqCxi52pVr0Lu1Oilb5hWa2JvaTSI9sUbxwgbSyEpMPuenKgUBm7fn1E0j1YhgtOlVp1YpVZlDtedQircJgi/LZPASVzemF9ZxqVZlrOFoQ4ETnf9wYru6BgYGBgYGBgYGBgWuHJyQidHeoT9BuJacQiK2kIwDq/Xmc7uXJHEW3OvIWHi1bbwa1vJKeRxLVeKrN+JdoXovQLPPm4/Xt8UodrQNwqSSJWK8hs8I16LYjbqhX7VZyKy3dvCBSA/GkV03ESjXmXsJbCVVYWtSlWsTiNEhxmiIEHmWC7lKoavkJLRwc5P9n702WJDmSLMHHzKJqFhFAZfdh5v8/bYZmDl3V3ZWZACLcTFWYeQ68iBqqe44VTgSTosqAu9uim4jw8pZwZ579EcFKKsUYpGb8NT0mt+yoZEWCsDL/bqpQf+K0ua7rCGigXTpfIII1VyErOeR9rePYl28QZ2GpWrFx37U9C8g528J1IaL1X503g4c3AoC9+FpwmFsrEzaUrq9lg4kuP7/He8Q4L9VQRhQCR0LC1E7MuSAWCgbrpROM6mByQyJo2wJPXnh0IqjbpV/EuClldySbHhde3Hr6G0QRynNSuG+HHgo7LvCG4dhvsr4TQZxr+DAsuj7NB0xIYEnowgByaFYOmUesUY1nj445JVeKHNkxyq4VOUgc4rK+0y2qsqNgtIZ5HJilogSGTcePECHHnQeEAPNHXhfCTqPV1k57wsYNcpaK3IkbKLw56r5tGyRB/D44qrlE+Prt1zxuAY/ZledTD9x9ucWTG7bbDUXL+cADf//xHc+G2MzwVsuF/sfzgfvthltCJ/V54FQHCtMvG7YN4f+h1QmbcN8wyqeFADfGeQEBszhGttZ8vNer91jjfr/hR8FFEyJWKpd+AESK7R4dz3kq2BXiS812uwnm3HBYcNQEoRi37CcGSBVt/SE3uJ/L2gMMHxxcXgCQAZ7WvEpq2enqcEeXvTyC2CQlojmsMxBoF/JYQwDA5wnDfpHDZoxBDX8PX0fvuCLmfDg1xnk6CCc8F2WiiDu9KRuKCWAKwEnTYBpJ06jPUAwwuNYT5vAZq1hiS17fmeeQYIJCBB5u2Gg08g4UipN+6Xjvws0hMgF8lnJmrauxxtaaOh3AtnjdZhNu0r5STA4SCXVgIO1KFh3CnQIuWWsLFDwY1GigvMfi4OrWBZnrglAwYHDHgJsBP57WZHsu1MFPHJ8iEQKq3Yow4UT4PQCZGLl14nOxs8q/BwTt6Yq9oGwe71nys4F57a4nBya+ghNP7GVtNK5leLW+yU2hOdHZCcLU/hYhIIBk466NPjB5+QHSDkN9XteMI/CiWL8jh4s3aK3hOA0Je02CPGElTpdriTrGtfGDLvhOCGICVcI4A0fLq93szi0OQRL41VpsFAVNXOkQAygWHLug/E362lNgTFuYoq/FkmvUC+6WQBgY3cJ2T0z9rOchW+yNgS1eWCZ/WG3+lr2sY+7JDlz1ids74D3e438xjud63kQoIGsdfIdbQkHERBg8qNW13fOZdMKseUqAsy3IxFSoAt8tJJs3DPh2A1kkW7cxwG4X/50qkaxiUcyDDN6PAx8/nkvSG4xNGWPaItZ7BUn1EQ7YKrxIwsyt4Q6xfpAWXCsLUX2eCmWBliwvBeeyAo+NI6hxopbYD3+Ti9fHGFBa0DlxwP0GogjInAjgrTdlBkA+esmdNnGeBzSTDt4E6o5fvgRE4+vtDhn78qxjTWgILrCO4B0dlQCSgVnw5f4lD3FA58R/++OPuNZwHKZFx4ISBUcin4/NCDoNf//4DQDwMAVkdEAn7NAZMEKUiSuNCCLzQ5/wl72JQZAhHZSMN6fxPS5j+rLMiK1Ou5gpxJBtSeuTPOGyrdgGnoIqAUONX27pc1bfEElJ22bUmlBxQsrid/2UgN1lLTYURVqfRUxR4JKEhCdbWYfEZ46CpJUAFgke5wP7XokLYPPCS3KLmCDnmXYRN4aU901PHYu1bFwSLyT/uY2ETpgtKw+R4F2WDgUJg93as8emJtQwYdTm8Gkdjw0hKNvihlbRxisJCW58S1srItMhNB8+rpNdjGMFmIvv7Mbx2jwvModNtBBG8kBWnHk1W8w/Qw1n7VUA2C0TvhLASo+7LOSQGBjW0F6RARXDUUkrlfPkzxufIhGiVjxL0u5FEYco8PCzDTbjAbmmFYqYD9q4R4Bt4dNBALOuLFnTeYOKS6P9MCM/y5xaHMGskok8Jo7J0CoqSSJ25sbighijTPMAwAPf2TSVEPTvgCpCf+8uFnM4+I5UK1Ky5BnVAxpJynpAo5rrHt8dnxFqMNIqcYFDXQBSgGnhZNUcRt4PBXtUZdsMNRmSrcziy70eCAiw8MAs/X9VOEUita7ENQmL43Zbx0ypSFML92DBgHfQ5xT/04GKT8B1Gadx3Ce6TuTIUhtry5W4VjeOorPY986zIvLOh97jfzHky0o6BBLO6lUZGwLepBMfQlTd7MqJY8BOhxS5XQwKbf7MxhtAghsiYB8cHe0z+TubCEQYWqT/XgtXsKOpdAkA8wjxEZ85J74ysDOICVKKR0NAtjD0SrFxcc9X4ImJ6/wdGP2zZ3vaOvHJ9aKKDS3ncJlj+emXkhQc2h1oexrGvhSRfpxPAIp7/jzpBDv3ehXCKWeqImWHCR5oAACiG3YI6EvdiAjSyu32y6+/AKfhcT7x40d0mYY7Pj4+kD6zuN/u4OE4M2L6MQ2///EP/PtvvwMAno8TfL8tQZ5jgmBdZBNxYEOr591sYDsVfE/8/PnEhyv0YLD9AAAw3wFz2Lg8VEq9d5BGkap95N4cofe4DBbH4MUr8QufI/z1RheNI3GI0iMQidKHKRiCLQPWQK0s/jOKk1uk/wqMK/liftlvgfQlq+9M9dr27Bm1plSyRlkYQCchahYcuTZmJMjY2sga7ti2fcVHxXWp93d8V+uZgTHW52dBhnr9ivNhtz5PS5GJ8oKEWvJ64kdxxUnchRY1hdniZAsxeNsguRaQHtFFyqRGmINr2NzMiHbtzGPSjHV26k6Wq8LmKiaNHY1OioMOxd7U7oFvDkztjhEy7FnmtwgR1HXrWiE0L3vEtenbFL+zay4Fc2BO6/cwJHiQR3nr/fz16l06eo/3eI/3eI/3eI/3eI/3eI+/3PgUHSEzaq11sEOn40TAHzaKCsVq1YV2+8ohIwOXapUCcAMM1K1YIVy4JFFpiD5ItRjTg0OrpBGcoKpMcimYXDop0VotnRILuAstaBxnV6KLJqg2Y3VXoiK7RErs8sp8lePS2QjYSHVGJC4V+OUOpvRiZ+uG5RkdVQ5zX/hOklRjS7flES7TdW0DpoiuqDKCx9RKLVbKH/kOtYS15fuJAJZU63uFAZbfkqb0b2NNKf77CrczR1e/UU0wW1eWaKnOecEHq2WOkB0HS0uTg6Ji0keUrfka1jLC1YW6gjHf468+vm53HOma/jxPTDOMLSbi2LboUJc6WvpjyJYV/4TGBWWx5rKAaWspa+LoQnNC4cyPsBCwBakgERTg3e1Vcj46QmhMvrtBhCCjqqUMOQmyGzi71rd9AxvwfETX6QQgYu33darnelrrG+A4YLlwMxFgIZQLBDxi5LoIhJqaNlCudIhinhaqw4lSDrc673c4OUauT1/2DToVli7pGymEGKeX0l3wEXodF4Pq2dA4vzlOmvj48b2PgvYN3xImcp4GOk4cxwdmyluzaOxJ6ZFygPD453f833//7wCAv//2AzYFvK819Pl8oGg6kxjk1t0/BzCdW+Kah8AGg5IjpKbYWTDpxIEo2z7dsBvgZynyxbrf+5kZXKl3c72o+73He2z76vSeh+NUYNNCohhcbg0hY1B0Lmoes2FMhvJE7/OmkGts4/k/tUVr7Oh+iZ/qJT1Y+/WxTi1Ifv/bnRSPWOkCjWvHkuLPuEN4tL+bpSVBwc7AJdlc8Vd0V2oOGQjMuiDM2YiRggwSwxw4bGLLtcA0kDvV0TGlsERIRAyXd1IhdGTDNvrPgUAh7u4wYQ/eeO0dOa97XSfAWRqe7FyxIqNh/0TgMTr+GRLvL8ifZ3xVXE2YQuEdf7t7SgUWWoFfpNQp0TtyMdN0drgRFjgyunh26fTHwWdcOgiMHTR1/f0nj0+RCBHzwlRPi4W9YB0OODQxiEjuUHhzABVex0V+EQ4gXNq/FNCCuuAplFD4Rze6ZDtAyadWACwJZy0vCbOYPit4JswMAdrYKl64+CYUBOYmKWpibFua2uEMSGNaKaBzRfDX8t9ZiQbRguSYx8IRkrp5DGYYMjrxCfwo48Vvz61bmIM5fXxygyUK7O4VzkcraTGkuWlJB5sCLAsu57kg5efEryiTtbzfFvCVEi4QDpnyupUc8VUPznZ2+zFJ3Oz2Y3LKW7la5KHuSE2+RHXtZg8AACAASURBVPokdDs5/6/O6z+g4j6BvON7fJ7xfE4cCVNzMwgUZ5rcyakg3xcMgDc4oX1p9Jx4apGA4zWnRzJfJQvXwMiXGeA0wbgxtpwjExNi6LVFYDjsFYRP5/LuClz8HbdSkmUBPKjNz4JQKHAfG2SPz9jPJ6Zaw383AVQXrIM4YLRlvEcJXblK7DrGkrYmZOEnr4vHWq9Y9hOD0wghcRtECsYyNWT1CBwuPCWQrrXF8zoXRONEEsNrjSU4MW7JEfrbt7/BzfD3R8Da7J+/Y4iEFHhKvT5M8fHbd/x+ROLz+48HPh4/LvC7W0CYU147ZID3Xo9G6qfzZW3xqW1E6+TYmGCZvI2NcZ6O81SI1JpmkUIWd0AErtI7wfiywabhPIsrdVkw3+MvPxhLlMkxA3bfctkTOp8YafisWkXiGEMlYjMDZhonRuDv8EoIPIoxnHNAKWCwJUoCZQg5rAJ3cohs2LN49HTAj6PnVBUu0IUcivXHfEHo7QQpt+w3PIpDtf6cGcNVgflUe+FgDyGcZuA8BuKBeVw8zaI62lu/kQMEyLY4hWMMbAxYimZBHSIIM9h8z+DtJcieCLgaUOu+ZbE/akAnWXOlaHoUiWr9k/DDLGEDluBOn4dir/gYgkmOrdYXjzi15dPTaoFaFtyzGJ7XhQzGCh4VG1vESbW3TALtV8Npw7Adak8M2fM9J1y8jWMNDBro4jcgUD37mTuPnx9ffY5ECNZGofC4YFVZZDAMy323GCy2UqD0IbpgVvOX1cnQS8cAiIkYHKHcnCRV6XpDzUpoZ81UrYr4MZwFsQCoALlAsHhFjldyn8NW5QRAOnxhAWvTNLFVTwyCsZ4/hPrbdtFqh63GiCOSLOZLd8QKy7vOfpCjSLiuYZhYfiTBdV5sKbfEmtZ5ewof0DpGg1/tAcJxvjD+Gp5QMri19ONzV9eKjEMoApebV3jgvI4k0sc0hFLhrz4tO33tXxKJ7HVqEWflZa1qkTzV8cD7k4C87dfn6RNULN7j84xjLq6MsWQLJhKhJ49IjmpOOGHaKiY4C9gZ7EGqB6ILILKUMmNt4FbhYSiOh8IQ33Hb9xRgyE4IETZZBYiHa1Q+8wFnSIoiVGAdVb8QU4n3TAsT6nKJZh7BO1wRFGTYZR0OtaS2TfNYEssbiRAGqLNNEicG7ijNSsaaVe1pEiEbeluiqDxrcQUggXFv/zYCQO2vdJ4GVceWi8MYin0TaCYZExpKnEeIUPwxCV+3X7HTvwAAfscP/DgmzucfeDz+DQDwj3Pi+fG9AwNomDuyZ4cPDvUTg0qZzvL/kyBtGmpVeR0VgDF1gmlq4RmVt14tKqnMvAjQ7hARbLKUVHGX5o8+P85c3/pWvcd79LDVrOl/ry4y4zY63kJ2ELSLDYYNnvXbnAMcz5r6UvtiFpztwpkiDNdCDK1nPgj3aC6xIeqW50xVOmYICSSfdx2M89RQF8tnnnbBnAYr1Uoh+NNx1hyBA8KXqCIQQh0KOeMLtuikAjhPhZ/66vtIAN3KP0zAYOwiqHU0OELa14G3gUttG8iibzn41B1o82QKvs6cqeg3CHRSXze+BdczTxGkBMwlvBKKNVHonUcW2sjgwsEzBUAji/6ZlGyeHmeVXFHEvisaAtxX8Ukti9bXJsNxea0ANiZIBUfezzEGiL0RDEKA0MDIe/M8DvC29Xom/nqFfsb4FInQOb0zeRkZypb0NTnkEsx7JRAVvAOgC+Ri/Q6L+JsGYUtJDC/mWTIooviaJBaGg4tYl+3C6s4QvZDBKI/gJYkARVuyOx+egcrK7ikkpPJDCGwMzYfCyF6gKEQhtCBlOsYEO30hxCgFFi4QL6J46Kv6kz22rk66e2T7td9mctg5i5Z+W77f4xqOhv9FElJETIBgejEpk5QKpiQ85ndGuzonCUsKtGTg4K9JqnlAcqS7e7m41WIBim5f34z47A40LNReiGxJlzvnuayOEAOXrlWc1yIMvvSH3uMvPm4ptw8APufLWvE8CCJLplVzQ9Ws1m8eG+hphpFmpDBtlSMAEExM4g6+7wOYk5fUtXkbTgMxz4VXou/mUKclTwsC7ERpUDrHrAYEM4OPA4rB9+5KcX5mu6RDwCwtnw1nCByHZSdsMERGd+GP88BUdEWWhIJ0q9d1uwoXDd6FXsC1gxTE0smV0QB89ivEGcQDR1ZkiQUbMyzXUCdGeKbnz6leVZ2TeQzoJvjtGR2h79+/499//44fj7MTmbFv2L/ecRwRrDAEwowjE7rTJ8TDNDCOMSrBLR1rBLhCWzY8Ktx9kpoiLrlenRowE8bo4iA7AmKcl24yQ+bRsrt+nnENZalLvcd71PhzIhSiSdnRJobIQsuYBYx9FEIDVLom3Yk1RHC8YjKAybC1XJrBoG0q7LRh0IK7DweOeVyU6QCA8IXCZLgUFCs6vYFwkmDcAU+46JwnAAPrKpiPfcmuQA2nOrTUGMEQQkOBzznxwOrEYp4QuXWBtQyVy3LAYBFabASnxpGBhbFnB1u9kpSMf1KoqYq8EWcQ/KzkLaBGlvGTnxpZQ0MDGbjEtkG9WCJdEQcVZLm6MRG9VMfnOKNzX4ViIQZMW2MCzEmBKOhuqPXVCsKF3lmCuw3dBkJnxvwMqoZmgV0Ihx3LdsWjE69d/CbQeQDZEfIvP1817i2W8B7v8R7v8R7v8R7v8R7v8R5/ufEpOkJjSLT9UNAwx56HpqxgWsZ/ag6+kLUcUXUbLN2xMVRm3H1QwBa2nIhBnsZPKOy4gUuf3QLyUKIA7p7EuRjbSB5OF94IoKwB+sq8mahN7xRlepXHrZmkXzUSaLVVoxnUrKZo/WK1oUoUoCu2nhwfu0qP80u12j34V6oL2gZ2SLZRZQhszsa3M6JN2zwk8mhbd+VxBv+oCYiUsJ68jJQwQm3ZemR9ehnHIjptdSnJCcJLTv1qMgkAahOqy8to23YQvGUzhQng5ZsQDwgD7G3KG8Q+w7qBEtesDyK6TA2Zu3Qf3+M9aDCK56nnhGDDSFC2nQSb3tPaslDfJngUawlDcdbcZQ4ybn6mjC8YPjGahxJVviLslw9aSdCDQrZ1SV2X8XFh1xk4Tzh/6b8Th9kzdYcmusmF43bLSmZVRt2jM0NrDWV33HmJJZB5i0YIDXwcTxwanRTxDZsRWoCkriXKFLuOIqq38UeBkSx5bDaQeHfX1BnjJrjXXiEnTpzgFCLQCfzwE5y+Q1+2gf32DVvCXf798QP/17/+a/NTP46PEIXg0f5KwsBxnqBcI5UoqqmFkfcNhgmfZVhocNUlMEMMc4JeG9ZOl452VGd7G/CAloAIzzTBVDdstPyBhBg6l+/KGAMshFkdwU8gR/sen2fQmsaN9ii4qMkAJoG3gvpaIDJ6ngY83pg7jiBVsA+wrfVpslSBH+wEhkCvhuUX/8GJ8DbisbrPOtGwXJDBT2/cPyUi5Hgoqg369KAOFJxYiCIGymN4BhgOnh1r9ziOtv4AARoG8wDAvGP62R3xiBEZlGtosGgYPuQiC52Qv+zguJVdSNE2CKJrXbayECgPn1D16ljWsltcCMO6adTrenTlat2vWJkZ3amndFg68kMmWVyTi49UIWLWOVj4IyFEwNxfqQVYAB5gi/ux5c0eSrB5Qoc0gsFcceMdkET5aBjYl/fQhGETasPvul4/c3yKRIjNg2gPAObYhJoIzH+CoaGIfxXcZ1AcZn6VHIU5qbbJJoOdFhcGwBC0KeepjtvGTV4OL8HFEQn8uy+cPzzNRDMYj9g7n5dqBxqmoXkApobBhYHPT3F61WsvHhGQELVLZpRxekPfPLgFZdY1ZIvX+BXQ6SDhboPG+0d3OQGCXAzAhEPwoNqeIiOIdpVkDMG+jU463AFTavUrL8x+8Zzm7OM9fU3m/7/BlCtWBQ5EKTtT0DnDvGDyPSeYXzCCFKSt/rm4Wt3uJYE7w1pQIU3RanGAJaY43iHvuOI9LkNt4ngmrtkYB01ghpIZxozEJRXfGB4E1YI/uGESgccObsUjgxv1hgcAw/wCS2Owb00+JmGcpEhdA9z3G5gFM9evgSd0PoByhx/Bo5kfCed6OsZuUObGaUNqPqc4wo3gvl2MjxXHfDbkjzkSOko4hJLjxmMRfQXBMbKCJz8BFXjBaDlhzmYdfJgFT7NVkcI6vY1nHQy3BbMlAqYevTfcNsGv9y/NR5xgHDbwX38NDpDpxP/73/8Vx+9x71RnEp/z9cppBrj2kh+u4VtXUEfXRGXHee9kcBccpfo2DUbSohJwb7ggALg61OdKaoThvJKXwRLQx6kdpJ0HNZEcAHyL56n9R+CYGkI48ZUvYcx7/MXHj+cTelQSTZhOGBn5beQwnat4OiK5LwUwGlGYdKWYnwCcBE6LyyLsMLuYJSMLjTVPp4LHwGkLPrpt0jGemQJGoNyP7TwyIYg11dhwHAfcFFJFV4n4pOKL6QfszD8gRGqEeXE1oZi6fM7uTJjmsJmJ0sa4yQbzmMcTZVxd4lWcgSBD8zVsEv6DuY4TSxQ1KuAaEUOOKhbBcCqHEiWQYlfS7w+vogn1ej2gzA3TFRkQvmMeeR1V4WNg6BKfOhFeRLvHtXOZEKNU7kUktCYNPySOAn0Vx6tcv5Bzkv6VeSFVcY5VaN5NsI07hjgm6jwU0wakCu4SNDHRKtxEMb31GmytbT9rfIpEaKrC80aFAvWOI6/ScOqEBsiMmbk35OiieD5MlZHme/Psgv8B1NNiTpfAOYpzM7Qt4ngQiVAlRubB16HSICSH0iLArk9GJy7q8VBV10mM4/PrwDPBu1bvWAKvC6Swo18MvTwWG3Rg8qfECAZ1ygrOOq+QuVzVAH6R9CbAqc8TCEnLFpnADOHrkromw2Fn/z26bEvamknAvEQqTA28Sagf1T00pFnt4hVdr6Blgth8LgJIZxOkhRib7KvChbikdQpGjkHSohLTfZEZ26E5zq7rEB5mtTUxozl36QK9OULvcRmP5wnzqhymcEfpjXAoGCoXHw25yde7s9uZ61i+K5PxnNt+5kJYScMWCm755N6csLFceHeE81zi1G6AqjXOfcOG6RNn8S6LN+izcf1GwIMmfuEMPkDYbt6SbtMZA88WY4zm9CIjiwhEBkZ3c4B9bItnmeaDxRsYiaWfTC9reVQ968dcj/ozQ+2xJuo5T4gM3Pbo8Pzt1/+Cv/3yt+bn/PH4HY/ffsM/vv8GAHieT/zjx4/mToEM275hzroGMxIxWoEAPLife37mjhCpqITO4JiLewzl4IUJar0isKE/0JkgbBezbwGRXQpkAqIzlDNzvbp/iRW89shpCsZtVXURa+pZyplvjtB7XIcvZEl0Zxa32IlBY2tVXtMTYGoTdp4OxXwVTvXgBF1HlSoAwDl4vl3UZcJ0hWRApjpbZRJAUr69BUPMvsZx5Rp6PGZw88bANrb8DgCmHQ8J3wBZSYhbyOaXLPjYBGMs009yAm3astFMG07XFigZJJF4tZAUY84T5/PZxz3gGEKrowONAnpdBwWcJmYK6TD25NfUNbvaVQc1yH0VZN2BjQiaa7Kqwp5/YOaF2nYBjeCOFu9o0Abhtd/Ms7pkeUxHJD/L2HoDmSU3DIiyFHXZWD0kbKpwQ8SYfqI5SQgeumGteZwR1KrdOKaf+T5gxz1EKkpU6yoL/JPGz+9Jvcd7vMd7vMd7vMd7vMd7vMd7/CePT9ER4u0O8wcAgA6Ngh9V+3DLymhW4FwTMlIVNbp0RTKzLoxjqZqgVFEKQ52qSvl6Gam4dOnOhJdQ/LdTAh2qy2CpbNYmn1FpoCL6oDwuLLhLiG6JsjZPSZxgRg1DYyLIJpB04nObmHPhwh0BlelOVsoecsNIDEalhrZaG0zSEDC3qF63QaiHOl7xHXZwVJq58KKaXiJ7f955zD6nMQASgqeyCjPBmRsaF1B4xuMw7OUhEMXvF0hga+8iqyTuXZGAAyctXSkxgvjyT2IQBi8OEZGAyWBZTRIQyEbKgJdKl8MxF2foqg4IYGRbf3XS3lCT97gM9oWpNoM7tzeQuMMU2KSgTwu6BCC7HoFzLcNAZAeUixN0K5xatRkMZmi1RnHGUF7CmY4oMxYMdx7R8SklO/vAbvtyA3AHuQATsC2qdFMJN9pxIKSl7+Mecqd5DMIMmQNzZuXQQyJcsqQqG4NlqX/u2w2/8Df8eMS6/vHjgY9UqAMAQ3A6nS7+bxcIb/2HXVCuAdlY1UwSQDbCPkLK+nmc+H/+7d/wj+9hmPpxfkSFt2AjpnCRljrf93v4iZy5lvCoiwl0dVNCy47WmnZxFIhzx/KYSwJYj4IYFQ+KUPtTqVEFlLjWbHMA3qzMOAYDwGi1KBDDbKnrWT5Pe2H09b1evccascXW81bwyeWfQ8INuw0fodmGwKZhxkkApLnG/7HnSEB3ao0NA2NV/BO10w1wp4a5xnsDKUMJISNXuM1G4Oz3Adc0RO3YxYOAWY86a/CLu7FKAUkdq6Nj03HOMj5mbDKguZ499Yi1jEp+O+ZYdTFobMGhFL4oqAUcrONIL5fDOk+AsF8gzg5J4D0ur1vebBxy3AVB9OQcZvzGg8C09TowwJhqmNMb6ha4Al+cIXKA0b2nFWvleuShTGfN06H8lOTvGOBk0KXhDcIGSnigi2G6QCAwJBwPTxge4PQVEhCYRntFmghUvbe3q7XKzxqfIhGCPVegu+9xy/JheLpi27eGedBMWeOCSjlBPXOU2vAYAOzliUyfYQBxmyddgm2EfK035hUtRgAU5rXndbSFm3APnB5JidMSWBgIiERBumATMCwTV4oHYD0DFOC82sSmB4Y2gxshbj4QEO9Vs0acRarnucjU74BzLiqydFK2SI5BxK6vnJhw7JUIYWCDLQ6Qx6JV7efphA28SI9ICGEFgcwAU6xFzdnJhe9qsErUyZXbCZJG2OfxaU9Mi3kKqWQrF2nqQMQjQGpp7Gy9M7cLNVVY0ivxei7yAgHuS6r858/T9/hE48vYcRalURxsAiRsSSwS6I1qUwdOP5s7KCknX0UCAIBbQDUyUSfVfOhWgWds1CZ5I7l47f6N4C8+cpN/6JkSrLlmKuNpE5RBgU8NsvLU5gdOA3x+x9exPC4Ee695MgTEuiRzQWAW7GWiB8fUE7JVcYmwbwOeRRQ7DU9/wGZBYEMgQhivMOUXCE6ImFSRg90BGiE7C+DUE3Oe+OO3fwcAPPWJx3HAysto37Ab4VZrMo9IQvKkdTpMD+zjW3yeTcxYTdZaQAwmX/5wFMdVuziRwWlBmIUKLpnnOQPvV/LZ5IRBZRMRcRcnNBJIMrcP4MIXdd8AWuWY4JNZ7y1lAE2lr00r4XyP92BfvF1CmhoXdDdFnmorFEnOSz6Pygj4fBqdI18b0c9anwLtm8GyXKGeISgztrGMUkvk6WJeSkyYWt5bBnfqpEdmCjI5NQwf5Bg0wiMQSXdg60SIETLXxa3zqYCieU1BRdawTgHwTb5FkacsBywK4dpUhfADGyKwfI9qvr5k7H0LiF+fusOM+xjhE6rSCaETg0g7ViGtOLU411641zopQBaUeFpIY++yRYEHsSW4Wb8n/HyWSxBLmNevu3OAMOAlFIb0YKoCjucRXaTSv4p2UkNDAj3N3tBdhmDD3pQEMw1xnRSc8Qmcdqz4mn++fPanSISiA1ATNapbL2aWhjbNGyIxYaqTwuG3YReVr9Gdn8tEc6zEh8rxp1MEsOuLIMPVR+a1Rpja+pfEKghxMfGWFw0Qxns1kSyJaOs8mS4dHwKmn7DczKY5ps0mzMpgyFjEPHMJa6NScKAKfPTSySCwWpMSibN7ls+8eso+FKnaMhDJ7xxEMF5iCNMjYSxDL5I6z7pqlx/qIiATvmv1R+jiQeB5jvXi8CmqxWG6xvFfChohtkJ1K9MUrA7CUxSj3hAJ8SuBOD6k718eeAem2fHjdsLGe7xHj2kGabW0HadMSBTIYmNzhyZ53lCJeL7XGVCLZ6v9UwkfeuBmVUCgFBvILzTH123vz4j+kXbnYR4HHir4fmaVDgPi1pufQuCiVVuCMUONsDu6U8XEMGZ8pHmNnQ88zyfuaYM+eEQFNI37+CZhxFhFEY0Ci5ax7OMBN8eRydnTZhYiq9cxwWrQqU0mjghC4FrCAxxF34rSpoK3ActjfNgJh0JznuoEJnZQBiocUQGwlYoTInDppKOqmxUUCoKXpMtwUgEwo8zPhSMhXJo1EZx5eZ+Aw13eqssEnEDvA4IQU6hCTvBXBZd3YxAhzmwV1eCOs9dTx5zaCSQxAGeoRQLk+vMx9+/xeUYEqvHf7gLwCU7vm30b8Tx1wVVwF8JRgknu8BFefyWSBI5OQj2zlEiTFj0B4GPD4GswvZKj8JPxKA4DoMEgW/6DkaxQ5SQ4ToCHQTZZCmzZldVaf+DYBnVSAo4Y7Z6FneOIou/oiJfg03GWCNN5gl07fjlSaq+Kx6QKPxy6c8eiaidghH0PNc55PAE4ti2Fc5RAdPZaEOmZdnzlpHDn9syU7JK/dN7IevNgEMQAFE/KFDwJCu3iNnlwcyq+IuJQ3bv0mFkIWrwcdwi0CzmkDvWl2ktEsJM6UxARnNd4iAbgCjK0fxvRAIuthM8Fp05spXY3DdtYSIDiJ/3M8eYIvcd7vMd7vMd7vMd7vMd7vMdfbnySjhAagw04yAN2AUSbj81a+pqR0rKZlSoZLKFv7e2QTY/uhDTuutSC6h/q77xQiFqSzdtvJ6EHVQVM+D2nrwdT6e7zC6/EzfEovxsQdjBmcVdKda4PweHnxJnXYXp447S8LQAHd1VY5xGcloLzQeKYL2dFyXO5KlbFCVXlJVrS0hUKCu+S0tYnSl+i6/XyPmZBNFAXjA2AeldpTCmrstTtYR4ECDCfWcXVCRpjQYckJMZfmu5/LnA6dVWG+vat9rEzL6dsD5+Oel2/5/IdS6Q4/+54qcjTSzfpPf7qY+yCeWS180yI26g2a3SpW+XQY54bCpYKQAZ4LG+t45zYWAN/juh+R6clq3wjOs23xvefMCcMj/XHYAApti39wMBw1VYRE2ZsvOHHmR2D8wCPG9wI51l8mQESQQFlH+rRGSmZVDowWLB9iUryfbthE2oI2G/6gM/QVwMAZcehE2d1qVwhtLUUrJOCOSGsVZU1hhHBCiphgCZcBAhEmutsiKv6hLssF3gOeG7DppkgufbH53so+rWXSPIeaO0LZB7O51lRnTIB58W7UYOMCxSOk79aopgO2Ik+JqfVDQJqTVnHAKVoUOVLhmxgDDC8+Z9SFgitSOrAybiPggs7nvNcW8n2Kbb19/gkw5hDjQwBCwcRSGoeBr5l5NNzPp9QoZZmh1B0bl54QRzeNS09VzFL/qgEuDZUjgU5nzIGQPDYykeGQOG1VVMsMPitIsccvo8UEzwOC4CdCp0lXc0wYlRj1qbHtGy1s1hv6jq4KEzXMQ122FzRExGBnKtpFe8TDz548ooGDwT6P+Ws4cG5zq65a3SjG47HnHGl9bWHO6ik98HAdkEyzYJLX1FFDk+uZewlBOiSv2aK69prgZSUfyGRCnKbawQZ/E8KgH6BZDnCXqWtYwyYvKBzNA1kBqH9IodnMMiKn80wxmgbloknvm7fSpC0VfV+5vgUK+bA8uwJqIDDS87RFWoGLcK/x2ZT0rEwDWlpLE+egmDUXA4AmDZmcUtS1xWm9mclc0fiY/90nAASvqaLgEgBV4ggovg3BueBL53gBent1o9oZFtFpDMP3LxkYDF4AM7NtzGPVmLjLP0M/5HmtQBgA7tcJrO/bLIRnBm0jfkEg/kCV3GQL3NSguPUufx0wAiA6oJ1zJfUK65zgXIMBDKGC/f9dBB4LoIcKUGEexKxcwY+dS/j50pii+9Tcp8whOFbJVIoWF21l5GGuS8pYmY7617HpclnjOlFTvs/PBzv8ZceLNQcDzUHM4Eq+JQwJq3A2c3Cf6uhCYF150E9tx0BhSupViKHTr/g9hkD1MFKJCcrLJnqUFNIwl1AwGkOKhUUcTyMl5kg7SDewXxiJIdnG7Gmam7Cx4ziUEFmjBhfd+C+hzDBRiPMjfMYDlfcnDHqGOBw1S6ywA/M6b3WBGQjZ2SuaYNiJS4O4uNQHGptRoqN00ekoGwOgHEm90AdGKCGgVBCatUrcQpp/05MhCDw9joSFrgb7JKo8BlwlYLeCsVntCkix5rTTEwCfC7POZXYFeiy7IdB5OJRcq+rwdFgB9gFWyVCFntbwfhPB2jsHUA4yqcqz3v+uXL0Hn/lYboCY6EwW64HciYfp16x3b4EJKx4KhRlZiJZBWSm4ME1XxCAXwydnQBbcK3TLeOXTIQcIWJQBVgYHNyWF56cpIKxzWmAOgR8ES2JxKl4RcweXKiStdfgFWv/3YKCUcWEqYBHtBAfqMEDqmTNY33yWUViBnNxpSt+4iyyx++3O8OMgzuEuMZexeP8Dod1Ed9xgGgACT9mUthcfB4TgE373hSdo8SdmC246cyLV+QGt3MlqRA4lvCTQrHTOu8WEmukXEp+XQTILkrnMAeGEazic7OG8Ha5xx1qE3bUMQX0rhLAsd8x1WD5Mzes+OeNT5EIGXFrkMMNOtEbjXqQ3IszwsxgMsxMamADQhKFi5x4CoO49aYuhFR+q4f+lcpiIBgLSuFHPLL14rUYZWKUryczKC0OSbxw4PQDe1ZpNxk5aVcCYL6EBwYJ1K0/c5AANPv15AwTLGW6TLyO1ItnEuy0YTm9rw7Vcg0mMGx5EZljBrEoX0c4MJddiTGmW18HZG+mEv1YCLwJzRPhR3CWihxLJqp1TAww55pbHRrCxCJd77ctOkdS95vCmb09UrIeXAEUQpiipO5kDCgMflT3jjBxdqDBLPFcKLpqAsSGYNWlqqSoEl91wJbjc3kRvMd7AIAkLw0A9q8Ch3WBYtsG9HQ8j6jaKQHbEGxUczOeLWaH5Tzctg3sJki/mQAAIABJREFUgtIBs3NikvRmI4kNb4No3qMSyVUFJNABjILw8wlzw6P3sgk7LrwXGvA5cf+64b/88gsAYNqBeWgHFqQRnDQFkRgf56NFILADytJ8lOGMfd+wf4ki02DGPB/48Yj1Ss1AIqgkRjAABw4/eyPcWGDzxMcjeUYzeYm5NgyPZLDEDoQIaoGRz4sbfEFee4dOR4UWnuuXXNYSM2rfOUpicPi9VQEqOuq1DocKE720j819YfLFIYr+TPcqeeV6RuE7UjwAIV7CDMgOlVvwUHu5IsCoVQXZPYOqPG0QSL3Vpa7GvO/xHiAHI71saMAYuOWexsJ4kT0gxQbg7CJxzgXn7v4Se3BbLlyWkGqqDpDA2Fu8gxOp0okQImAvBUpXhWwD1gqV0fFJykmEV1k0ofJ2nNGlapDLmYT8SwGdfBV2wnw1uHUA4IdFMSuDn3mewW3J6yBZK50tSBIJAbutIsf5jFgy10RJV+oShKEhYCg0/cCg0Wm2Cvwz2SIpnlMgn8o0dlgkrTWf6wpLFq9UZzAJSRdnGgwiuRSeJ9BWt+gSM5VwVHFJS3Qru0x1yASODne+f3AWlqqQQ8HbhzJA9/UliAJgPB8SKqMprKPHhA1BpR9jLX8/bbw5Qu/xHu/xHu/xHu/xHu/xHu/xlxufoyNkq2vBxOCBxrc7HMS0NOiZwOBWKzI3mEfbdAG0StVtVTWuvBMrBZOLFGxAq66pqaOxdeYtNQ1Et4bFU8YWMAvnZHda6kG81NXiO/P9nZrbSwvS+ljXv+7UEA1Kv6TV6eAURKtqAUBksIsvB4NAgzvbdQvYhTdcJSAXPquF6XBfDvZDRmD2LzA1OFqtSF1TBnjhPkINryA+2V52w3nmeXD4CfS98oK41IU6QOCGCRnNqBTltVRznOeESFVUCdvY+u6bacApy3EaBHZKzth6pvgCx/wPrggEgGUp2x1vqMl7rHEfN/x6iw7P6QohxvMInPfHeWCTAXyNzgg7sMGb36Mw+CAMjO6+FLYeCRUwCyeGe75H3DEN7auxjfDPuUlyhJyh4q2mdqeBOU4guzHQgbE57qlm5MQgn7jtgvsevzufZ1b3ch7xBjWDZZcZ5CC/I8XxYPOAAM1rku2GL7cvPaf0UOjhmD/iHbwNzMcDuqWcNhPuQ/B4Hng8o/T79caYRnhkpfhkgsjWaAFSxb98+YJEq+BjHjCbSzkT1k7rcWEnnLwrrBMM59URYmxwVpj8AAAM+RV0hjpWdaTZCad6K2IpGI65vD9cAurIWb62APF2967fVzeZm1sJxJo7aMn6eto6EBPMkoOK7EoX4mYqjBZcXGfKDec6Lj9fjfY9PtEQVyzZL8PttoP2fN7UwMqw5PMYDZAv+wkSAIKQny5MlzB0nq3q5iM7ltkBMg/YWUtXs2ATYBYUTqObU1DfUEETTEuoZ1IdVhwhAAdvum0KxCNW3Lb+TjJqBUrdAvY3toxVLM614MYOhfEGt/A5sxF4oQtVPWKqoioIh8+YL860Dgo+VKnIzQmoL18cAfSk9nGEO1gdbou3BOb+GZzxU3aIeGzQ59n2lubRiKGC3jnwOB74dbsjgUiY2T0rOxKF5/3I80i1P8/rIi7RZatDILwgeKY6nK3ls9kZ25AXWsggh15iLmWCz3N18mkDnGEob6MBZ+0O93H+Kf76CeNTJEIEepHru6KUOLGp9WxNDePBgqYQZ3vUfQXD2ext5k+1VRumtsxYa8SNvWBeXwLlJPhdiXSEfj05gTADwzqTOGeWBli16RI4Ja/jGOPTKuD3JMJJeWCAEM1S7mN4SdP8lddECDjGgHe71xC42cb2UmLaC9/uBCgtjXgkDKSuPgWXZyVSjlMXgVr6ul4SGb8sBHle8bwvtl0QnPvHkJvtj+CE1NXfA6JT2F9CJE5N37Foyve9ouRpFUEaDk2MfSdcHg3iToA8L079OS9Z44nxHu9xGa4tYcpMsOktTQ1jPI6zg+1927FvN9y/ZJBwAjQJ5/k7ivwyFDEvsriz0w6CtWmrIRKUKpqMEZyVswwLzTDcG8ZxQjHY8e1LQRUEpx8tVPDtxvjbL/8V93HHmRC+29ixyw1Tl1R+QM1KJtwxxlgiAD7BIIy8DhH8Pxr+MFgwwZjPOIdTj9ggj4TocECDWaV9yL7PZ/Be8ufdw+ag4C4khh/2Eb46AOaM4KjnMXH6Ma29QS8wxsHJA8qXsylussO/xXXSB0KQwWcEfgDIPSDHvUGdGLx1gkMW964NmQDwThio66JZnMlkzhTKgi1ff2cBSDrxikUoxC/WKleywStKi6+t9SuwRFvDnfAe79HDzJYVBBMAg59rs4vIJ9eaY0LZIDmvd9lgqh0jAACbgwfWM+sBn2/5ZN8AHCHVjYTigsFVRuF6klecAQCjYLc0EYT7LPrC4EZwW0nEEGBsgrYeniE0UDDZEGcBVDvzQWdBAO5fvgFDIpEBgpvjhmtI4I42XdfkObFf/AhPAgSgsk5gAsZo7hROBYx7PvIghEd1raHBWZrlXcQSnjtJTjebmEbLODsDUSo/SFd8xR02CLMaA8yxVtS9sLxPlZtRXoZKphAeKG0uD4fr4lwzeTcj4l44plrDjz0LRRfzpIiuWXqNhKbdQK+hcefb8+kT+JN8ikRISF5S8cjEi6wXCOt6nin6Bd2VCOfdpT0fL7puKjVWKsHg9I4o5RTDdOoEIsYKTMKnhpejL3lgyy8fbRCQCxxnv5989LEE3d86EVIYhFaSEeF8qc/lwkSyNnVEUmCXTlkkDRcMqxomrd8xMWzaMkIjj65IyXV44OOLOjNAEJFOOqYqSBV7qbswA1tdu8DLBr2mUscgGjd2OM8MkMCRIjCr5t3gCQ8mughdcJoH1lpisWBstVgOgTl1lRdE0Klthss8QK7hCYCoBB1qYLJW6bLCK9fjQRTBxJKJS45Evl5+/kR9j88zfhwK/aNMKw13GbjfMrDdN5wKnMnl22XDv2y34OYBIPsA+YaH7yAvAzqEelM+ZgfNLBhkVQ4O9oVfV40NtLl66sHjq4CfCGbSlUMahq83wZbBzcBX+CH47Y9/x54V1bHdcp3I9cUMQry8H2CAcfMHVUPQpoQHfrl/wZfbrQVpPp5P/PP5Hd+T0P84n5CxYWRH6Dkn5nlgntzeQ7RHglSfGYUZCkEXANtgbCD88vVvcZ3c8T9+/3tzDUIwbhWfyoSx/XcQUUDzD8cILkDeSp8HJjSrx/Ea4SBJa8dsiT24lGkZ1oGkQqFy9toyIIE/0Or0A6TWHaIPJ9wuBtBUazQoVKUQqIfL7lZf29xNIA0vV58J7/Eea/gyOR8DxAxqhS9JMnwWH+47iGavLec8w7vvEj+ZAWT0WvAcBLYSoZoAblgR0hPmo1UQiQXlqljHh/T0yqPFkl4AjASwKG8XJ9os/HKa/6wOmxLePgB8IJRl2zR9FVeBWOX8mN3ZoGya2KWIYIoL6ie8cnIC56VLRbVSBmbA5rN5ST728JMrtRcutdsqRHNwpiueUgbp6r4QGXgnyOW4nS9+Th5CVqcb8rQjaSLvOJGuCcn6FHQgWopxlegEnbqLLEQc50vnei/GiteQ3Ovz2TJ/FNV2lH9uccc6RkMqc9a94z8f33/++PlH8B7v8R7v8R7v8R7v8R7v8R7v8Z88PkVHyGAvEsXhw1FQqOg3tNa5/8kzSCIDjc8oHGR0XwrWYd5e7PEemlEBac6PILSfUuHIA+86rmmiYzn+mkfLsJXNHCADi7WHDvOAEOFZyiiJ8y/uEyOgbEf3VaMbI6kutXO0f6vNquY4tcXSoGbYRsBV4vtSJpHRrdv4b3R1YB8bzCfOrBQLCIMYW3U8KPwrTl1S5US8KhTQQIE0DC2U9p7lEJ1wv6omBd40VNuqdRtwwHBjB4A9KzANHYGC6dK0coZB+mcmB9O2FJLiINfzQdHB06zCzOY8UVfMKQsiJQYXla0Fr3NIYvzzmC8t9fd4D8OBH88PAMlRu32DJFzLZ3RMq5s8zycemCBJyKtuCec6G9KlSEnUkqmnAXJr7svmDhlbw0mJHGa+/HQ0pWyb+hf/LeUdQoh53lPkN0xj0PgS0vWIirD77ArqcMAKS4uADj+ev2FLmfAxBGMMbMkxcjD+8eM79lwcbrdv+HUObAnR+Cf9EdXDnGTPeWAThvDZZvBECZnNeTl8wKEt5Tuw4fSJhweuf5rC/Gh4TMzh1Q0JTuVaj0L2V7CVJQEY3+cBSZKWAM3Z4T2VoFJY6iiIs4WPSPtEEUHYofn37WRsIsvfxIPVwI02oMDtXyqy5ktFrqE5hD4vKyjclT+qHq7zeZ4EgLYFiX6P91hDGg4v2w5mb/ALscRzlB0APw+YUPBhADhOkPsLvIqSetDNEyU4L3oDfMTz2+YzA+q6YjpKysMVFuKKs5SAu/+ZmBI9E6JKoCTAkRumOUp3VyjVIdtDTELNsS3C6pxzTrkBp4EyCBg3jnUgI2LNkOEsrrGFtYixo8yKRBC8zUbCeZ7bWo/kti1EnjvYl1qocCKNeuprdI3a73IAPNfqpnFcVNfVCMrJXyy2R7TJYLnGMcU+UB0egwXvqWThHABbX8dB4XtUqnNM0ZkuX0+m6AhWTCnZbXTeF1RSJ0Daz4OBsCGekbifdWsLqfTzETefIhHiCzTKKRbyF7PTl5+ySXtpy8IjAC+CmJMHKbnIxx567lfSv3ptL/EV+dzH8SCCjRI76I3W6p+C5V3heZ4tviK9cqgwa5HOIhmYhUPzwq/WLLHYyO75APp4we6qKVQ1CHl5TIdSe/bsEkIKO0ubz4IBxcSWP08i+FzYTAdB3bst6HYmDbh/ExNv9olHQ7ulFTNZylfHhrykZK8L2hKByE8uiKBHW3vFLwbTtenDgUHWCeA0x304vKSDLf1BaH1+KtDm+zkStJe59srxWmdT44rHB/AJJup7fJ6xbXv76zADxt5iCToNjB1fst0/BsGxtfyy2hlS0hjLXBQWcKyWXDbAtL1pRkJDKongXN8W9CC5NE24n3AnSG9ehB0Dt0xaYMBBJ7ZNcOPgx5Bq+qHFSyYI5MDj+CM+Ywzcf/kFX29f4zum4uN84vsf8fddABob/uVv/2d8hRD++fw7eGZBQhzHj7OLCioKEsL0FTiE7xAgKCEKgwu1OIKZhvfEj4/8BWPgjiOhdZJ+JyWLT6Tpc5sFMmZsg/BlfAMAPI+JUw/MCgKzNia8+DYTuv4AYJIG/8vrUjp48PJ82kKEoWAfE+GfUQWygK7QKuQZZWC11n3iAyccXjAfRPGtng/zgC52MsYMJw3hBgB+vgs377EG8baKnWZwWXFKJCHr+ZtscAyQx3omFCXiEBpY4gfMhPlcRsjOaI+fsLSihb4CY/C2Eico3KhhtG4Rk1UwOqEQHdDN+/27xMS0JuwK5FxJghEHdyaNrQdFglfRjbpj28PaAADmObEJNzTuMMZG3pYp5MDBa54PEZAZzmkde8Q4ITOLXCJg2TpyYGHoNDz0mcfk2MeXTnQ845DigoYW1WjDVkfC57SKyOGRVjHgpHYWwsxi9BDGfrtD8zvZkQUu7+swmDspcc5Wg9begT+ZQHskurPuDUDiXdizzM6YOBI3AMYaz0IW3HncEhbXQRlcqLU3GD9/vfoUiVAIzVcQkNn7+mP8Pn8iFGdndWOsskteATyMuuCgmgpytTmdBiNrDCsnv6iVgLJ50MbJ2S1oHz6hNnYFUuxJFTbQCkdzTpwibfZ3zNgMW+3OPDbHwqjCQdPxPR/gczuzq7WuhKq3F45QTLKq6Opw3LcBEHeiQwwMuTfx9zkPDMFyS07O0iLG5TW7VG4ctoxFKbL3huB7JTBZycZ6uOMcLa8lNeK3U8sqg5hnFeSyuFyyK2YGMaGWF0qVwCXwsO4PAJiGIuAST4ibSeT9VNUx/W+HG14Tof/9S9/jrzfMHJJ46OjsRpAOhMjAYMdRRnxGuG3U+Gi1cPa+mhp6djL6iXNuxaT6O9PiF1p2OSupcBqA0AqMsQVcuzshjNu2QbzIyoIhOwZvmBq/cz+hXm7rAFv4PmxfwmfIyMHbV/z+iMTn+fgDMr6FASOAu4QX2//8528AgN8ff8ePx+xCjhGgdMKy0rzRDibHL7Lh46hrd+A5GUc6p3+RDQRaHWg2fOUB5CbswrjPCb9nAqBZAdEr0N/a4d7ccShhaqjEzWdUwuvVniIq6mg3ZSODjNWxMSgOJYyLb5BduKBdUmvvtrh/tdWTefuTAVFwgy+F04lQ52IS3LPrfbjiNF9dckR1/MUXz3mpD74LN+9xGePG7enCQjCbzS+LIsra74i31zqgTzA4BA8yS5gUHl3FlSlzcloycgAk0BoAiNNQ8/Kddu1bUqJ+SiiKs0jtOc/5wAEHQ3qNM6L8jiiahFfkvKjNGgTcCmxkDqhe0DLhldOH7IZJqygc8xK4WRzDtBCbIUbzccaXG0gPtPMrx/o/UzDLlULJLqfj4C+YfkRhK4ctXSeYz4w1rrEHr8ozco3rMNfhM1Thaj8iCOx8dDfOKExiKYPCAQoRieJ+ksBcIKiiy0CsMHlhjF+6f8NTme7SeYcRTAyW+wu5gk3aXwnz2ihAFI4cHRO+5JU/abw5Qu/xHu/xHu/xHu/xHu/xHu/xlxufoiN07SIQlgx2/+6KW0O0CAsGEg7CUQGYLRlIcA3FMQCYU6OK2jjKEf4S+ZkCho9VDeAob2ApKCGS9Py80GY3zKyenqeCTaO5YdUuNqgM2Bk/n5pdjmove0K4qmNNIQ+pj6iGHgcFRqMURZgbigYE9yV05bPLlcBLhja3afDAjrMhMjdKnObCxoEdy6uIOTThL7LjoguyE52b1TY1f6ldVL+l283hfm4A3ValBQkn6TJAVgUSd0upTFVgSBKO7h4XzDHvQxMmXv6JZmDcxPx98XxoXWyqwkvXafECjvQ/QePe9YL3+NMoDTcCwcxbynpqdBn2wkMzcJi18o+lZGrbk+e4oK1A9gDz3l0CUwfRaB4diMHuzR8k9tRMzp/dMIQbex1y/wxJGJyRgg1wO0KDGgCNVKHLxfi23/D7x2zo7aFPPJ//A2f9/X7D//HtS8vs/vj+D3x/Hpgpu/RxHBAIpgSM7St27EO6iMwTmKIA7bhJ/PKrbADdQjUPwIkjoGJWlWEOBEAeMzPj633DtxHn9Xge+Hg+Mdtng0G+1Keic49W6zvOMzgSI6F1tAU028K1PW90dLUKBj1f1xcw5XUuhELcSJJyk9fuSKNe5bSUKDnW/qXcmZxWRiunsjncFq8o0A1rjTpdgwdQqqbjvV69xxr7fdlPMKXC5GVHvnou+pzBc8mYQYhw6hEdnVLyhcNtIUMKClf7qUMDoNMRASUxobqqgE3vbnHjRTg9x0hg5CBPSBlvUHeIS8v3qxpc0dwWa75cHJNnvHXQ2v9dRkO6NjbsMtacKnRLqTuyQ9RxZkwZKr+Mm4w+D6EtJMMLeUQONsPwUkcb4GGYNY/piY1uF9W3nMErHFswI8QUZ1vS1dVdbhFbDgKjAeCEB8MPzCnta2bGuNBHEw2z4kp3hdls25Y6jkUjcZAQaKz1Kmjtl/iteKa1PVl4LtXekfJ+HX957TkrrPzp41MkQu7L6IpR0sZ1lQzEC//OmTDURXYEP+QyD6Ee/JlzHvWL0IFP7EBQebgTIxMDOS3cf07i+g52BvwSjCcPpjlIppjq4SFUPWczGFt/hrrBjReBkDSwkf66gZbm/LTE5rWxH6LF2hM32rfV2j3V8FDHbqN9ONgckww+klC43yPcT2zc6YbphuUB6wCPbh+zOVikxRXIDSIjDE4BhHEXNXHOiEJSuyY2UX6qvfAiBYBlwBR4W4Lnz0HkY1A+mgzFdCwpc44YsoLC0yZghi1FJloEo2a+RJJzJVHnob9wm2Jxz/NGEAR7c/BPMFPf4xMNR4HV3at0k3OOI/guEZOoZVBvuBq7WfLWcm7j9ZFl3lPQYxlIhGT2SnxCEKE2IAPplQDtoCGlZhqgXxFAcj2cFTwP3Pbg/EAcPx4Hvmch5o/Hge/zaBNXFgKPb/AZQgWP8wP/7V//Z3ti7Jti5x1nbsjGAsDCrA+Ai4F4i/kKJEEbOPTAjgV1m244K1tqamKuL2o4L54omwh4F+zFsS4J/IsVQ5g6L9Ec89mkbR6MwdLk5bhWAWP0UYFVYPSbD6rAtvFljQs+V8F6Wta85Gg3gE7q6xCeedQQHqYRxZqSV6cFUdZLwYmiYhXfoXkuJRhDAMi7APYZfDne4/OMMQiaBVmXmGdcfLJMhCqw/cIbpp8tbvT0CbKR3Pp4zXDB0/XFpoPBYA4OorEC5E01AOW3FAQMBLCsNRMxx8t3KIRbTnCuPcYGtZhhxRd04iAI+zqGiNhKCEqiSF4XwR16Wq+RQpSiXBVHGvRcBQlHxIwF79skZMZnfhYA6HmAeeCW3mmuTzAALqTcHvuCzYIfx1rTit6UitNdn93g85JiWBjTdoAmAJzbK4ndYRa+jnsFjh52zduWRS9T6AvVxCN2qvUG0TigppVYW7kAscUIrb3nKCnwRQCLAvlF/twyrixiN0ve6Xym1GZIuNf+9Qnksz9FIjSwMlDPcn1VJCg3tsUpQXgI5WJvuWGEl0ZtmIQ5tQmqruHJ0f5zcAzifuKmWauSAIhNjFawTYlhLXMun1GdO/LzT3XMNBql7vjU8pKbmWV2XclVfPI67+oQXZoU/x97X7IlSY5rdwHQ3CMyqyUt9P/fKKmrKsPNCEALDKRnv7ftzHPa2KerKiLcbTYSwx2Cl5QPDwfOvJ6/IVsJOcfrike+BBroSTAeGKWmN2conywlgVAV4V5B4bDVbOHAhq5eWUxSPQEyv52jk0NsVUfXv1eHJ/61lFHcw9DVWzEmJgzKSozns7AVSsJXo9VgJHCuRZBGCTNUmSaDi617xaWy1DyzSqj7qoDAG4nv17+o9/iNhi/Oh/RCXM93uKh3t8ZiIblyUXBLvzDG6lDCk5OYSjw04H72ZEBWQcTiMO5eW0QjF+zsiLNAhPF4VGCRx0yxOB4iID9x8MCVScKXfuGvrxf+ekWiowzwkFZDm6pgnLiKrEwHiK1x3tMkAvXE5B/MeF1f4OzmvEjBk1s0QgQY8sC0iS+LrhHpB+acTfoHsliVL7teHrh/Puog8PX3ibOFDChMWvu6RgFmKZAaCLoCLAATZ3s8PTBAlqbSFTCptVcdEEGOw7uq6xTmts2ydkMe5boXtIyxmQER3yr0SN+z8gzS8FIC4apikU3QNi87AsVQVXChEapZFaP8vDDc4z97qGOkEd/rpcF5q+ICZeE5Y5sv+wJAWJ6JHzCewXOzKj46DmJIKYvxIxKNIsenP6Flp5dAMOeOE0jD/HnaMv1kInB+Xl9ZQC3vIxcIBb/ai7vnM7gmFEkIURTT14yaMYdVsUnD6DoLHIc8AZX1+RldiyqydKeo3lMJrrK7g/O9nHNisOCVxSFFKk5mWG2TQLL4V9McsNmFGU5UUqEFVB1zrmRtCMOgsLxOw4/g+lTBn8Jn7fDlNSQyQDT63pTI1GfOmWoXflwnvHwdlTDosYrdh8DdQsQFkYQ6SQs26OV4PniJzjkDFOI/amnIxhrKp1lji2tIkFKaswHwgFZRbIeE/aJxR3j3uMc97nGPe9zjHve4xz3+48Zv0RH68pXJMxICtiRG0g+noFEDxLIXUzHd8XXN1f61aAk2lMSx6aJEd4CxlMrMHLw5jpszbGI5/tKE2/LXeV0zOj6tAAfA3+FXjjjmpV6WXcT+AO20o6zybe3jhp/lByzb2FmxmLoU2WL7wc0xWzAOteAJeVZApyvMonsFZIeXqKse0cvRvvRDxluqvDdYAUT3i3ypxYDQgvbrU3A8uhMWFdPCuCdUxBei0EPvsVVLogO1VXWJonvXLfKU6ayedimDtilQnJXRupjbnvM6hM97K8m55d/rfv56ecd7/EZDFVJS1Sy4XLtiNojAx1jvLSj4iVuRPhD5+zMVNfzqQDt9ATTgo0uFIaXcLUsGQ6C2nleW6D7E9gmvr4lR3JvPT4A+8TiSz/N14uuff+HP6wv/vKIq96U/QDlfxHkw5uU9Bzo7cIbiVO3zYupKM7nEZwr2YY4nPTAL3+4GU8d5ZXVzMJxHzFFN6COQrHcd5rh8df/lwSGP3fDgkBR/vRLyd3iK/1Ofww77Caum9X1zAE5tuwDNmrUvfoOlKmlNDUIcKn1UsI8DB0vfz6kGd+p7Ic5gpoYQMqLTXpVnhwIppw4k7J+iE3+123tAqhtLL55+RzX350Fv53mPe9QgG83xkBEqjCV1DXcIFjxJCVDaNFzJ4lEn9HrI7M2NBADTM6C9sh48CpJb7qOAIAXtDU5LQ3clvALNS8I5t1vvjF7ZBd94SSRxTo2gSd54q/ACAMNHzU+Mx7fR79B0B+nV5+TuEBLMOkZhHJLoI2Q0YIGmGRnjDBHwkBVHzCtjlfpOQZgX5C+8zSrIU6gSziu7b1A8h4C3eExheCTkUGFw51bBRM5lprbmaQ8EVcWPoUon+ItKTjvm0KPbUBkv1iHNiYMHNDMDAoFsdf5xcFJICvFAgBNIFA/OFhAczquDbT7jtiQ6QKeCxVuJk7HQQL9q/BaJUFyPgjbFei+9oiZOoV4S9/CNqfagGualmKfhuhZu0X3j0ycUqvk2RIBoB/niI1qz9Ww4YSoaMjH1lVLX9cCHoMDuS8T9ttchRHvYtxeXNyKTmbfvTgyvmD3+3i9o8ZTib/UOTYtkYBn1eeLbF851Xg742eZoBA3YXM1PhXW1OnEG4ex2sg8CjsIQA8meQYtIpPFttYJjsthTzlycN/lHULxSi8IcE2gFDnH+EwsGRDkZ1aI/IrCYNeGVuW1tjxYPCzkXd2CznrE37yqPSaomIHfNLa+/3+MeNdQIM6EHagCJ4FnWXSZg354dEOA1rgiEAAAgAElEQVTc5HkyQxD7DI8uvBAU1BBVrqpALVZMUBX0euEhjFKBhFA9rU0SwsfHwLfv/wsA8PF8QNXwzz//AgD83x9/4q/XD5gOvCyTCBhEpIm5f79+QMF4UC3iAyaAjDXnuVOTlTXBX82/oQSp1nyHCcbA8/HIcwoBgOHS83KUHxhlsfqgkV4gGRgxQG4NqXC7cE00FJhpQDd8O3EkVh1YiEONUDD3IHzbNocGf+ut+EMAsfdawvCEGdZ5BuyjoJCDH7mIrYCMmBv2kzdo2QmQA/xYEB0PiCRtxRw1hyl1sUjTF43WRA4FdXA7fipY3eM/exhf8K9VkPBHwM3i53i7rHllR8wlWdw0Vwyiji0AAEwhp12fMQsunRf/L5OgfCdm+f3wWn8XQyiSDnJZRV0JCkElQnR58nap5yfhKtKugifRKjWXrUfRJZwojD/zmNjDG6mTO0L4GdZF44hnRiZSkQRlYpMfEgmp6UZFUxhj+zZXuHpDvxgKIApMsc+Ia5rbSUfIcxeXRhVjSAvSOBQ2CdoF/mXjUhzrmHMdtjwBQH7hTP6O2As4RieQce+30DVjJa1jSlh2/X1IyWevz7vHXOq1lrjDjDtYVZMs9qQ31XEEP5PS1873ufHXjN8iERq0gnIg/russtwYgtnVBScBm+NK5YlTFS9Ns8FeTQxbA6BfilYxCVjj1k3JCkfeXfULroSz3LuU0vQzbqTpwFtHAVG5jAwe/TvifbFKGloZ6znSfbkellB6qoSP8ri7cAPCBYB9J8iudMItDPUMJzgryeoHLkw8y1I+MbTlTBxqUmuBnap5XUo04gJoVZMAA8zwKHwp4S3Z87ru+U9FVBoOcvjeKXJtHyCW6PgUJlU97nG9aWYECPeE5XYBRHGt8l4bFs+pJmvve5Pzsb8znWjPWznuzcx7IZSqTaXFfydC99iGcfwfCDz8P44Dj1Que50KnecKtrOy00o/qPdudCdiaj7DxcfxJ3afIEAw6ERlPmYDukpFAE0w+xtO3PDA6wrPn6/T8NffhjNx4Nd8geBQzFadNCOoWZuTwgmHELy8bPSKhKICfBoQHngkRj+4L9xFF3GJrjzKwyeCjunFIwBc0yetPE5CGmUldDA8DgrjEgBfLwMe6CTESeCyKo9gwmUKsXJJNxCeXcFljgS06IicSlEtllAdra1ZF+IGvhe3wdBeSwSAqS7hCz7A7J0AXp4J2cYhitmpztne5nGFwVThHglQXLsQw2mfII5jV6w50EHtBn9PV/fYB9Ey0BSK2KGfJffgzNb6mcWA5jh68mh8FTnA0eXevYiYBkyr4JDFgULxZCeHuppAGTvk8Vl0SLmKvvHb1QEfgd8xWsVtpwiOmltsEonOFuB7J0eIIFOxeOI04crN5ZPhAHFzPiOBcKhW5yPKNKA17woRTDdus8Z5daxCWY3vYlKJBGRXHEcIRyTXz64oMlfMJ8KY6vhRCQQEpysor7NyHJMwd9xJ2QRo5V5mkBGOUtcDgVShpToBAh3UhqoMhpIl1zvmNiNZhSB3HCKNXogadbAiuxhNALG0tx48OJHF+w+xq1VgrsTvV46bI3SPe9zjHve4xz3ucY973OM/bvwWHSEG3lCC4ROU1S2mVBGqLoNBoZglAT0Dn//maZOtvsrMG1/Kq6TmwPoCVXcmftRpeF2O6Ytz5BoezEBl22+gtuy0/HRihqWUkp+sPqpSVHw70xZBOZvHJ6vMuXVjtp8VnlJ03ZfFQHRUlnqsg5Qwy0sHBBaGbOdhpu1YbpR1ztqVGQQWXCEADgYZursTR7ukX90D7lfnJNV5oS3fjh45xAsWZIDRqkx7dX+quqDZevXeZ59/noP7hidOTtFbWbSgkf1zwgHePsTd4dM8w3oG5a6x3mMfLpCUaz+GB8wjK2x0veDAUqwkAjl3lxUIK4CSSAYAI4NuymTCBKajO0BsiinH8muA44CvjiULvtShr4RGyRdY/sLXFdCDcRxwFli+6J/HB0QIf50TZ5qtXeWHU4hkmfA5Gx580CMqec3VFBwPxvOozkZMunVM7MlZzErkRPmeZQWWs7IasmlxnBAoHEd3j6+ABFZ7jSf89K5eEgvYHWce8wcLPgSg7IhHNdsh3eEmKI3srcd7rW4B40BA4GJmWOXqg0I2t2YAI8eQj1aUfBBwwTCSf3W9LsypeDwT129RWT4WgjnmnaoSU7m4FLYSuRAZqCS2R8B1G2LDDPFzoQ88qtM1r9M9X91jG2q2kCks8cCUwhvLmw1HIye28OPUgNdXF1OnRvf6ik4FHQL2tPxAgtqFwQUHHjP8bAqKrgmCbRSQwWH93k9TTF/zIUGgpGAmUM67MG8VXyDW/YBpZddcJ9S+8DziPfQLAM2OOy53sBOkeHhsOK8NeTQVZsAzu6yDD5gwiLV9ysw9mjk1D8PAOlotT1XhPnruF1iohhYCpxXqyrZDwH7Aec1XBAsPSgDqJ0SO/h4VJWDyJpkf16nmTHaG0ez7KSPUJn2u2JZdwI2wifmvbw2NsGco2DYLLsz2SlJzGDlcbMn9K4N9dmgKNph7UygYAnfgq3ndv36++i0SIWBDtaGSmH4LorXbyILguRQfyKYnIWxdzOLetCknYZHogZSMbg5bSNeaQ5N3cl2K14zFKPbpmWhVu3i1AOuofcfQ5p/yt/GJbCHWMUlKvdp+jL7O4+dY/i1rq3/6hmmlwJ2/JWSuMJM3YYGApRYcJiYT6+CH3rZp7rimr+BlRGCxoHCB89/xosbroZL3lKaPO8zZ8hhmBlebCWCKW+cmLWS66f3++ls3dV3Xtx31f3rjcftKbi1s6v8VpDD8B2qfv/41vcfvNMZYXBqmwKG/UjrUhWDT22OMc94pKGiJprh7c/PUBmDaCTfxBeKVTJEdcD5bFtqZ4WS4NAKRmYauta6YCwYYR0LORBjnZfjH9/KWuPA8BnAA+Cu2cb5CXGZmcHMcBOaWMYjij21Btit0rsUcYKhZE18PUBrBpmQqB+xkpHSsW8y/IkcbnDKunLcTa06UkrMJ62ALsndO3FEMGpBw+MNlJ4ippxJ3xiRtOW4xxzQCp8CDK/Agqc1jOjD9AvnRARIQ16XnbaMIVDJwMBkYJLCEFPIADjra68PdYQg4CRAmjLoV3WARaLRnncWKoDZhHkEc+cTB3nDMIDgv/yMmDtL2m0DMPe4RQ1gakg+7kmOyPMoC0F8wpneBJCDjVPONt+yATXBl9yRwKJ7PBetfkQ0yUbD10DsBpL1GV9h0tghAzKvlteXu4e21SXA7DIwVF5oZfDKutuEwDHosr0dSOBksobusguNYCYSWANMsiCAAcVyVIboGIdStRUqQnKVKEOd00LCQ4gbgxOmrWJhlDjl9L0i0RjLVPjoKpxVHGhEcAk75bBXBnNcyLmXJ7zxB9JPgQM2BbFlIrqsCgHlZxSBEv96mjL0OTQLCALWH2YyCUsmvu4FgMB9trUCucX+b5hFcT+61wjB1tmUA808P3C8Yv0Ui5FjvXiUQq6mhoShSOuZTcanh0lLpiY5BVSSBzKSZeqvRlVh3ughmBdsGATonXplcvWZk7TuJluFNKGSSN9IcUZpUdRpX52Erearqb2HsPVROukpi7/yan4PvjQKcR4T0Pspz7k9uWmdmgFiT7QhhDribmwLciRIlx8cz0DgGYzB3UDAoqzVlTLudbx2aL00JGNIjyHzxjjirN6Wkwgxs3kZGUWGnPs8wadUt0WUn8E9J58qbf7pyee+XslJMUBGQFnbX3r/bOWdt9E6F7rGGyAHhJAbPSEAqKJ2z3vr1Hke3OZ81T8NNBzyx4q5RnSwDQlXBQYyRugJ/fB4YH/8bf3/9DQD48+//h69TkYJvmOaxsGRwPjjMgMsg2i6B2YWvr/j5kIHnt3/gOAg2/w8A4JyG61RI4bjdMHfFIjrDF2NTKnMAepVwiuKQR6sRmV3h+dHvrQNGsPIekfAaEl7XBpcH/r0EGcgwMPDKRZ7AITrzSPLw6yuJwmv2i7wzvi8UprW8vd+DCJJmt7NW/PI2cgo1KRBGKVEk97M4XpJzYFe7LYVbKilhiZPLJJXcs7NTAZbHWpJdKXUC48CQKroRXjPEDyo4NdfovG/FQXlsVWCLmazUquoe3uMeQMU+WTjO4mX7MkLy/xU5t0Ff/owUQkBvg9NDqFA5gOF4yNaFeDftRK7x71EN9y4pxRioOx+B97AM0EQ4ijxboRhpvL6CmRBRGc1/5ujM8DbvKoFnKpeRwUj7EEN8amA8SwTFAaX2USOi5K0zSIsnWf3jVAw9BkIkK8+LOXzG8rzVFKIKfnwifwHAlgCEH5D9+1Aocc/rPhhms422GYgi0ZjNYexLzHVnHATuEMZyzuv7L1Foauu2n2+TJ1pJipfE4HN2hM4HcDhhAqs46LEf7nsxwGxZjA7FPnXr9c7+RWn43z9+i0SIo00AIO5BNBmyC5GVhJJqPDXgHDOzbvWl2rG/vUzcNQlNZl5VJwEGK2ApWkGZ+JQEoaYhGHUWHf+rBTvc4Tfwmnt2E7bFCpGcVaVPybt9G9v0JCRuAdPmZExgYJOxpIw8Ws6RK1nIl0QVyh7qHbQCIkIoDgEBuSFzzFyEzSUU7zqBVBAxJB/6YwjG4OIy9/FaQQY94YZv+YICnuZdyCQ11eXivNJ0thWxcu6tKopEJaRIjGwRWHQwQ0Gw1ip/w6PTthjT8SusCSw6cfscYStCBbo7VYoyGAFT7I7RnQfdYxsHneCGgzKANT8FWXapiJlHZ0c9TPcEEUwzBfk1vhNd1UKAffs+8BxPnFXGkwfOr/+Df/4ZwfXXyxI2ke8hFMb21iH4EFlQX7sA8lZ1Oh4Hns8QT1BEckU8AfZ+91kHLjoxUcc9QINXQSnfGW3hgRPAhFpkb0YECJYwi8cCX9L9B+I6mUWlNg8CTCcsBRhi9r8wClpCT4ShYbrHU5hhl1RsdNpovceSsGoveF7clzJUJbc3lSf4A4M9RBh6vkmdzJbERYqrrAqskTb7XAQwpq48k15gtyZpB3R5KY6CQrSinp8Ijjjn0OpQXyF724Iw9kY+p1TzpG39u8c9arjpKhYQgaHwBlb+y4exATKikTM44OsVOzPB1PCsZ/wp0Lmk9tlTTbO6qBUX+bYPoOcQIgIbMBs+HBD7qtCGnHfEEmRF6o/0o1AbzISPY0Ct2xIYQ+BXzdOh8FbdFhGG7SV3igiu8kClkLzfTdfhFvNHmpOaa1qkVKHlArsEsiY+ALh2CdvquMu8FADT6robFOSAlgqve8zd9d5fGjDro64rQPbASIRAXrq8tnkeBhy0wXQQ6CbL4pKLgy/uY/x5CnE1OFnH4zoZWILLAUNOMSB+ZMxuhB+64kInDZh0x7aCQwSPPKjrN5Aq+PVHcI973OMe97jHPe5xj3vc4x7/5vFbdIQAeoNrBV90SceSrwpGqCYu89LA3qd0bG2DgR30WD2X6qYgTfK0iwfhL+Hln5OdD+2qX7ZENzIMbRWOqBr6Wx3O62Q6wy5pxdrnOt7YQ5Vh8rzaVWM/i5/hYDuwM4hrznsnK7pGbZ42LGF8qxUZXbI+quiEoch7BMHATKnyaScYjEGF0f+p0gNPdGBB57Zj3Y7c4OAGlDLMsssGgDW0+EsHnySkOps/4dFlozJvcwJhLN1yrh567c4bOrcfh/98s3aoXcEAbPv7Pe6RQ2zCNLoW7QFRj/NIoYBNQGSaYTaEjMJ7iwleJFli8HGAjtjmZRdYgX9+Be/on39+AUR4NRwhJKCLd3TIAaHREA0BQfi5xBTshPATj0dKYV8Tf/75FZC6qwisjMEGTogWDsKHD8yyDHDgwWN5bXHMNxdFd/lBDxAdSyQC2bWubg3l3J1wF+I4zmlIGBgAmSD61tf04Vf2o6rLZJjqwExOEB+4HDCPY4jOCGP5KQXszDfhimkTrzM/74zHWMIt6idIgitY0tXhLbK6w5zfuwquxwGj4WdBcJKonVVfNceAtQw5UVTXKSGHJCEBPK84hpddECI4eDPMrY7P7hVibzBFwHHk81Mea/e4B5Ck/lwv6QTUOV3rA4gR0U1OYIMyHsrnHwCM8XwO+JlQTXV8Hk+kDyjOOTFfFyQXbRUC2DEkkSF2BUw356MRfhmgknBmx8T2PJsDA23ebCeBZAS0qjrRHHw6ye4LDU6qU3V/Fedr+QY9JTjOBfEytegmF5yPABfqWMf9AgkHIgWA24zv2tZBTn9DKkgyBRy5aUqcAibdfGOcBLAuLhSRNkf74EIx5XyVIjt7x5vHHncC9IjudFMs2BM1c+QeLeF5ed3IQebhw5SnEB3nOqf0f+u5JawB2qttXoDIEk9wjs47FEUSmsQYY5MmR/DBar1yC7e3VyKT2H59P+Y3SYSAursR7lNzRuADZgbNB/zSIAY3yI3Qy9Tu9eC+YltK6EopHpnFw6HXagfaRO8DaQramgitOmb9eXf0S+mdDKyIeekpbLAN2+Lz/wrOh+VlFOIKS9csFvfFnaH0o1hXL3SH3IGrDLmccBRRERWcLIOvweXum/s0ah8LABga51YtTTgBo+ez3k5/3xOaV6omCH35mFPXZ923ljY8BJR4vd1uaKgIJ2i1+FohMuEbhDAVBX8iS7UPQuOjf8o8gS2K9fckNcDIW7b00/fu8Z89dDSGgix8HJo/aEGo5VxgVSIx+jxq4VEwhyu5pXCAHAKmxen5Oif+9nPNXyNMDp+jgm2B0oTkQnKpgkCt2uSqMLza74uHQEjx9ysW4AGC21dwXVJZ4PvHA9c1cb4CKgcWHOMBPlO4wAjyAXxPdTSfjv/39VcXKI5jAE5I+g1+TIfqBZuVaClYRgcuYwjMH/D5F75JYOYJE06jzZW/LouEIpMImwoSxp+zuE8Km+vVn1Actt5VxYTSXP4VHkWW8iyzqXATXLV9BEfJ/Vw1kOQ2FHREYWDTTt7EFSDCcVWCmETkSr4417ScSqZZqDQlAfrUFP/pIlwIZyi01xd48ASWCWsSsGuOS8J22b35uOere6wxsIq+SoCP9xLrigDyZ19BK5C+MaoQK4EQxYm5Em538ObhE8bq6AKsI5TTuthNBjfq5xVEMCOwL7ipgBs971aliFVuHog4oITjxD0EZwrayxR/K6GUQ4LXWBD8jKUoTUCJHpjXiVE+aOMR0NMKfeYBMMOFFoyMg+NTP3Yxt95Tc5jIO+6K0Aljepy2ZDJZmMhWEsIScUzHfJx8obmKNIDDxwbNRsVl8XOouumWCAGkDsokk0RAfDQUOBoOlFDC4Dy6rYI+PUb6M+Wxs8NhqUCc+yyTqOTR8ohVohRIhYLDWsfEuBOhHG92m/FclIyhh4RrCRlcptCtI0RZ6vfFVw0M994BoBApmF2tDKU5OuuBjm5QCTLUG82lWpJ+5etpeMdThpHou25ZKNF6VySiaLfj0asLthLA4A3tu1gqKfG5Jb7AFsnEMg51DOFta3mewKqIXoAIwXIRJpEkIpYCiAYpMS/Dl08MDhwrEJyj5V5Y+1n3wj3Ot4QNPFXy9u4LIe4TtWRfJjr5BAwmXLZ4loRKdusY05wNJemNrrbWdd0ua15L6mOtrW53JSsz+zGmi3XfYNzjHj3MdGkiKWA8owoKgKaEfGl2DHgy8Bg4MjEyGVHVG4IrK4NzahQ28j1TjnmANmKJCONjmyW/4JCs8k4AdhnOUqozw1MOSFZkzS68THHlinsZMO2AOWHOHwCA8RA8IDgklOWEATWCPP+IbXp0lsvBfMDxj4/vXRl8isAN+Cu7M19qIN+CIx7R6ciIzGhAhoIfHy2rauqQ8VhqeTRATM0rulTxhOKViZAY4JOCwxDfCGPYfs0tJLF3ZSl3UEYgfDiMl3SwSyQwwUUoeeuotu4lp1MV1lKcyX/0EjtAWgDkdcki3dVFOEekUbWeRee5OohKpcLkXUkeg0LldJuj+FgEaHJCGCcmaZt+k2X9Hr/FmLStp5zv9sYpSW9SAMlh2Yqj7ID5hJ0TVpLJWeCsF408DM6nVLc33iPruEDz9UhyfHKX3zE0nHzLWIu5KggAwBPGGctkADU9d79JcpN7zwUETq5OJm9XxiclSuIcfJ/cBZFFQTYvhLnBFEvRjTniKObtYoZBcxEAnTz50EuO2C7t+Gfk9a88iGfyRUsRPL2sW2k4r3Pz4aEgbMakGvGkkzciwT3k0TsUZkmxsLrOBLUJsdHnBSzZ8IBjoc+RGD231cdtqxq/l+IzNqUw6KVcbzyv9/r0XvJfwJtfOX59KnaPe9zjHve4xz3ucY973OMe/+bxW5SOPJz24r/rf6XWoY65dQhgIT9aijnm+3bi34xQM2sZ5yi6rSquh7lfG4EqApL1RhzBW0spaiTVyss/VdZc8Al6+1JShHbA1VIYQRc8ChLhbUha+4ChMa2pkdIShIbyBFqwtZkdzJaPzWOoC6MwwLkVkF7qUB+blGb+Ow/xugwXrtaoZ2E8fLQ/yUPCwm8JuEUloK+ic0BJiNc+8jyrHWo20xy1sLuphtLVIEplltW9YfCyQUg50B3FRttJkEUHiXmrMMEAWkp28SgtdZdS/3Pe79A97hGDiDAaqA1M565+Ck8QC8wXBhs+8dW4b4JMBqmuOS8tNSirlSG+Mxp7Thqd1rfXdEduOqIqWa8vAZe+kHB3GAvcv0B5TOcMpTPHkqV3SyO+6iKBoJdjanU6DF9fJ/7MztdjEP7n50d7fVwGnKfilfA7uxxDBkbyki5z/Ji6VOSmYgzDGNKKenDH+eP/RscMIQMtRG2eTABel8MLGgLg5Y5Hc3wMlwJa3eUyGd3avUwL1iEyYHQ1p1J68vCWpr6IEq675nHwO1s00DGjTqHnQSA6QNMcTduxRAqUlKwaxFeHyAujv1W7Gf4vKnGciAEgT4+81wq/65v32IZjyb9DArXZXlorHAEADA6p6no+JbsLgw7MNAodEPi1c9QCktOCkgjlxuKVEEnEJBXTsYPdl/KrA0QbB67Ub8vfhAdAEgb0BTGlRJY0DA0YMpZ5vAJjcEPnnCZiVsuuVJrMkqR0MAd01xpcwpAx2uPMD4ZfE7C5/CI5OdLdEcpor7re00HCrRjJhKAVFE7R4zwKGsccuJjq50wN/mFN/AQHiJeVSPIZQ5Ezfewy9t1mq4a7AdGZEZHFsSaHb4asRCPQN3uHm2ijMmh6XnaAFnecHJwPmYjgGAu2qHkKI689uyXGKrvgvwHk5vdIhGhhUtUN5tRuu66BLWzOjSFd2bcEIttytdZQJS51I8zihlbq4RE09GLmCTt7S4RoLU7rSAFEsP4G/KZqDK5gpB6Wjs+pmUzbltYDu7awYG2OPTGiBugBEWDJ7o1EtAz19n24bd8K2Jo0mcphNiMAiivQ+6oNxCZrQrNISorcxoFV3xOIHVdLjpRNvJrjE2RraZlLy+Or92rC34IXT2ny5oTltWnp6+YCVSv3J2tVr+uxJ0IOQFY3mHklx3HJ4k5kMENvcMB7/KcPdV6x9XDAFUdBoR4HpjN0RnCvw4NTtA0jA9xB5cdFR6yn9eKoZqIePxIc4oZrf6/McOaCes4ocHTRhIHLDT9mYC2GTDz4EzNl7a/5T1xkcByg5Bnhcly4wImxcCY8jKGNoc/5ptzQyaDgRe1jA7GBj5UiOBi13goPmKCNsH1eQVTWs0UifCp4DHhiRP75uiDHwHWl3P9UXMqYZYAqAaUdxVuyEzwMSNhHYNWXAISwZzCSEDIcmFhryaUhE8tVhUIUXcywkikHZGxw38CmtJlg+MEtGfKJIKTvwjEG3/D0DCFqs8EH4mcyNNTNd3JpHBTsMlB5HTEBfmFYXocdKnyP//hx+AGkZ9mZPjRHPiJMApBDyxMoeb71vE0ijBTcLghprNHScUWs/wPC692nISmbnVPGViCdBtCgfke6WEv9dShbxyUh/z2jQNA2HJSmzLUNwuXoY2SEUah1UBgCJMURYhIYOPC1AJ78gEIxc+5xAE8nWB3DNUFwMO8xWPL2imo8PWkbxXUaePAKsqu2Uefdv6vtmeaRZ0IBBCwu557xfOA8r6ZsEDPEgOt69bVjibmihHgMMYdpHuSFLzz42SbTgOF4rGTOkGI+jZzzpCRVHJreS+3npMCMBK/ty8QxybvwBk1nvQo7NbneZbbdZKlfN36LRAhY11UdMNXig0UFzVcFrV13t8+7x1pQ3RLOzFw3XPb+UnAmKFse8y9+X/SGYkyq3ipgxLc2Zbpi7/D6RVc6+ktbUoFUu9uTMfLtYSkOVGXmoEzk1kH+d9hK3//u2r9gEpBT4NIRWGFi6g5Rtsba4Co0I9aExJSLdpMg88XpK/KeOFbhgGn7W3Z3ugKBcsBYiY9hiWGEfRL1lYo6znrRwyx14WZrQtiNVemn/6LEsNZ5CRPcpU1fr4w7eH8g7nGPHCSAZJI8Shmt3hEh+HXBk6fxMRhqc3klEEc10ngprNEJAmNU2XaEiXFVTB8g0LEKHacRFIxDMuCfodxUIiXGBjPFlXY8RA/8/Trx8uADXT7xwEdg73MxmlclOhW8CE6b3ZVSOJQvjFRw+/75BIHwOiPhcwR+/urIw6KQUOpF7mDlUKXJa0jkON1A15nbILBt1UsAXz/ONjA0MOZ1dnn7kAM80EWVQvyX6MQAYzpBSq1KDHbw6mLpFQTezRvpQVERL8WqwwXXIbDKvpzgChzdz89u95IghcjATP4XW/B5iuc05Bm8i7xX4oggpOfkmLmYKC4Sokg4yZf1mhIGUR+TE8HMYFzHfBdu7rHGZO2uJ4zBxpBHy4EEXzqfZ7UB8tZxzO62dfyVX0lERhUHOIKNiiYtecOdTOFNCIFdgn+zRzAeITsQXSmiFb+BJQqquvGRDRiPA57FHneLAm7FTRxdn/I8jI45b8ijUPYsXvjpBiLB8fjIzxv0uho1AqcUSlhqaNAZvB1ZwgLQE3wgnjIAACAASURBVMX1BDOu2bsMnh9nFyg2kNdQ+kIZUXMBjfPiVdF3GoZT+y3FtaDwFStuFEUU2hxsm4lvyYQv0TQ7Qge6ClzMALauuabZd3WZzRnRM8q1JoXFopFQtzI6hCWk089OzsPh3bYSPPtvI9l/37h76Pe4xz3ucY973OMe97jHPf7jxu/REaIFcTILFaVStoYV+iCzS+HVY0RUGi27k9JVOhQuK372UgvKLPa/KvRvWXAdVGW9stoMObK9s+HGqc7j7SO+vkT1yzqvVPzYFDno7QCCU7TU0wKwtndd/rt+xToGf1PPi66WQ7I6M2jgoH2/BGfBwpgr3Byjqt9DIEPeujmAdaVaQrUe72cBsBxAd+csfIES1kFbNwjIwgRRy19X/WZB4xKCWIfYbdvVUdqvDlNA4t6QjNkRKmhhtKqP9iNRWPKOSm7q7gzdY43P8eiXajCBn9zNYXaAXPDIDoDaBfkYoKsqrgo1QHV1WtUlnttVxIPIqgwKZZejq3wGNg+VM2Tj4MBbm9yIGzp32QVXav8KYQJIodPwGMXxcUyy7oI+NKC4TNW1QshfF9/wdFw4cVlg0w9/ArKUgz7oCSftjlN0gRlD1vwlPgLmceTLbAQD48x9/Hh9Ab4qsA4FPRgjobnXvHBAwAV1c4EatQpmlJ1HwxbpEAihq7zBmVzV0YccMb+YdZWSxxF8sJwrTiR3aYMwT3i7yVNCFEo5ymBgp+5YGyYA2hzrY47v9Q0EndHFr3mRJbqB+/wVD8uq6gPWkJl5d7LvsQ2d1msdCfezCiC5yVjqaD4BHP28EwUgn3JdBiq+2lTAfAJkQEJvPeOMRrWQwiDrecaEuqzQiAAiaciYXlfEdAl51Tc0TW5jAKSvRobI8xHd1VIbzuNAwbNCCrKP2fBILMqGYnHFfFn/LDyARp7Ee7dN04CHel1DmCWcFx3rGPix7oMjhSD/mwYIQUJ5rroxRKCx4hZzBQt3h9uc4p0XDu8lVKQ0V9BX9xUFB2ZMLCpC2wMU3x2UjZuMjVxx+TqmwyXUQ2u+Su9K3mNX84w9qyNkEc9ZXfugfXCpENKv7wj9FonQJlMOePKEGmlQfJ8tKWE09nxmovSGcEAtRnmBM0upgN13o9Nt+AZj8z247hdwBRqgtT9Q5l31ZQCWRp77krT/PUxYsSaXbCWvpa02WAtm/advf9+4ClhS3fuefDOrcsRD2QF+JgSrnTxAIot3k1zASoQk4WTv4tOrxclFGt9OmgGYbprxJAB7t73VAtrR984Ts19QI0Rg04EDSvay8PDFpqp2MTLpzVNkzyR3SdoGLE42ThWDxgHJKe4TimtOzG674x736DGEG3IxBkMeYxUPFDgOhycv6K8vhjPDEpY254zFbCzIgxnB/WrzviON+Oqxcwae9GxfvosV5mdDXKcr7I1B6BAaXXy4bAIQSBZuhCi1FajJxZZJAcorBAVvWXPK5QzOfV7XBRHCR0LlLp+ASiHrcNkFkLfnmDunZG0ufu4wIUBoyftP4DTFq8jGUIyNW0CIuWiWkaxHkYtaLtoQ8N4k5bJEASn5ESLfcQxpcZci7HaCYRMkgscYvTKah49GQZSDsIx/GeWp8nAGHZEsAYCSJswuzvu8ggtRPB5mwqCxeEpzAh7ch4Ilos6zr0PYKjTnFQID4etcQds97lGDhbdiY3DYmq+fgUUbk6Y4UfsI0QZ97xeRgr/WJNsDyOJhjb14PUjeJLlBAqK5JUYCImmfR/KISSz5EWYGokzmyk/QHRcM8vmZ2wBUL7TokkcC2EVbQa7/VZAKrk0VD1gEdmkfI7GHeE39nRxgh6stKoEQ3LjnPBaFH1vypACM3+LEfe5IKZeVjI0oJDekzAnMy8dRzVoOOz+Qx7burhuCR9Xxkq84DSEk44oWaLCsqSxfRqT4QvxdPRhGtU8lJN264laJ72fMHYcV81PX+Dl3X/WpmND6WpjfiRCAuOHeZg6xOFXWTUxbgA+A4sa/1cI8Ms5y4K0sty6wGcFc1kJCvgoM8Yu3CkYE00sFpV7o5rHwT90bB35qUbRKyh6cFN9lncrWDSHtSSn2uRa5OgbeKiLxu2VFZdDsYfFb8ELbqxAdKAdxVW6iv1IvHhhbcgA4R/WoJ0kKXO1SdKt7l4s49M001omySmNNcoyDXZ2u6cHfqmK3K0GZuorrTDGhNElb4cTLvZmKiTzyGCuo2yoWSJPXIudxZK5WV88JQhk8AuBHEEE1q90bvPke98Ak64q/0wBsEYfhE6qOI9XXvn184tITnoIA52VwZzCtBTXEYaJzAISaGWSJloSKIkFfKcCQPJZK1Gd537S4B2AkcM0uhJ5gscUhggFk4HGg5i3JAslKvsbbXEAGYCq0PDJw4Tg+8RxZ8rwUf80XzhnvDNQwhHEkR0gklnux+LxdZ5BoPYxQAeCajjk9OiLId38L+N3CnPmRr+3gJ1ysOYvTCIyBowIwjqpj8RPc44r2rEmJa6/PC1Bu8NqGgoSpeHN3N8yeOyjDK/Xqtn1G8JW+Uec0XK8LzOV75jgeq0xMyf2pc2RmEDOUPJJLAE+MXJRWcKpb0SzuqC5DR1737R73ON7iEEpkSKpDpm9VeZa5xbNcz5IzQYiD+L6plfGgINOiCqzUhZqHRDe58yJiwHwJFzCBfTTnbTJgfjWBvzy66jH2FGUi9xZSueCQx2e/+/AwW/YNSUIHd2eXnINHlHHmJz9wui4FOBhIDI86BkQhvQo5ag5MgrAsUS0zPNw79HM3XKd2ciXs0Lm6JywMm1cgZIA4J/Lu1pkrGArwt9zpGaqSZYzND5hPHOlaHdzUKER3EkoCgnbCyBYJZ4klTJw46LlupRtIrf8e99NQvo5GDtBI1T1EnGrcaxXgEOf3+C6T7ToGUk7zW6tDDBGaOuSbI3SPe9zjHve4xz3ucY973OMe//7xW3SEfk4ImZb2ehcReHVGsuQZfyCNSoFv0DCKasSsqgZxfC6zWtIBYHc23sEX+V+Ef/XXqWPBu6+QZ5WFtqLdajTmGbgh5Trix4JaNFZzh7/VMdA6TVBAJrYuRnQbq8obkJcdxlVqt1pYTS+BkGy1nhcAxYcUHIYwyNFG7RJeOks1LgGCXRDJM+9OWmjIvd1OIpApGqFHiEqLVgVqdYeAwNwGFKU6OgB0SVm7AKCsnOQ1IqeW7iRhCHNXSMIvClkxrxZ/XuyqSNTPzYcgyOPAB0Xb/ZQL97hHjdc1W7FtplkP88I7iwOznm+aoENw5PP4kIG/7Qufxwe4Sqgyo/6W79k0gzFh1ByojtO054Y5L9hUfM1y7iaAx5vSpEzFKzWdDw7cN3UXlTCYcQyC1YtJA6rWap3GoYx29ktiEPFNAemAGvDPr+hSCTGueeHUeFc+jqp6LniMAji9IGECBnDN1+qSpxfFg7Jr5OF4LgUBpJhPX8UR8gtPdfij5GSj8muJ+zgVODDxfJY8q+Lrx4Q2DpfxHLxB5RgCwUsvjFLo0xPnPJYKHEK1qbgJDIfw6C7VhEJsQX3P+QPH+MTn50fe2wuqDjqqYhsdd67t8YEvjWMkKSlfgfOAtZQT4KwbhzHnrDxNuuub99jGbBAWAIQcciFwPLuyGPn8GSVCIuY3SYC/E3Xn1JGWJLVecvF9CrUR62nDpyjgbW2BUh2i1cwBOWBaKogAaIV47IyI2Ky7xzCFXUfizwAcDFMGdog8pNSxAUwYe3e0meI8a86M86GOfQ4PIUh7C6jyX/XeDY72Rm8j0SdlBWNIxb1COw2YS8/7RgFw1TpPxHWfqf5IIIxjNGTQ4RBmiCwkgbvBXWGvwudxSihnF4rHG82DEpYmBSE0wQSvc/KgGTQrWxjAxgcDBR+p4qvkXbktOF49Jx3y5aNTTaOIEWd3nbjxX79u/BaJEG04SGdAnDvAJ4/XqQKNgJdhmUqBAsIFoECJ5oUrX8F0fa+26RtG0UuRYXtxs+Ebf/cNDoaClC2o3DqRlce474lUJkt7FgFv8l39vOP1Qhbal5dEnWt9muIKNawt8a+0TUjI9vQeaJARNN/EmtCunhw4z1r6OjDREhX42W/IOSeTwp8q4NztZqZYkm3RiHq/u0BDXa86CwN6groQCW1Jwg6XuC67YAOt62IebI0yQ4XHa2aElYQapaRkTZrJiyqzR3Z8fH7Hwf8LAPDSE/e4R43pDE1YyMmOJxjPnMsHIeReeT3XMr2D7ecRi8YBwdUGqgznD0gaFh4iGFiFnQsE1YkroXA/riuWKi6IhEB1tvx7QVGrAFIVmhJXOCjmwFjoKxvzgKz0+1hLYb2nAyLSYgrqitc822hULAoKR7KDpwVZdhkaaiQqBTMmj/eOBF95XsRrbq1dixrO2ogRXBb2lhiYIuDyJoKnX1lxFwgEadGIyYoHC45R81PMno/aoABzOr5Obc7PEGDa2fdv+oxfdqEugoZvCRGk5GZZPh/fjz9Awp0gwggPXgarbhqE6DR21Dkh4inokJkNG4ixvNiIoKq93jENDH7AZs5TN0noHtsQ2uxI3CG+kpDIWRa0iimSHi9D4IyBfVtjHQ5ZzqOZxayy8vSMILaYLbz68uNE4GP0O8QIhJd1gB/7bGicxD52GP7z+IBa+uzkdwYMXpBlAKDZXCemB8QdjILJnhCm9rCxEtOqC8OOmTLQQMQ+RlXs3caWIwioi8V1EMyyhHQonJVoiwEj7sg5NfnWmu8xKeF4HGtGpOBpF/Wd3Rv6z89n39/gQFj/aFhekhFL0xJUIcVBE7Z7+Tj6mKiTqBWv0dZE8Nz67h8JRQRx2yaJ1/3EtrW6hL96/B6J0E7Io6jqH9uNBEKdCchukRusF/18kTf1ssC68wqWHW2S+V8N93f6fyQ5m5pbHcfWpVqfXN0ax5YUExLdXr/gn7o1JZZQBxETzGbBGmS57TiiuZGTxXYU8WlGCAZsxEgS6OYBIE4ZgGwabEy48ucnIkGsJFOcMhHdrg6vxMo1Tnr5K/lbBUW2ZLUxpQQoqE1K2bN7k38eqB5anWdQgaU9ojgqx43zz0m68h7zCLh6EuaYoDgnCESwFe7vlQgV3j/+/fj2xLfv/8CnRBX3VbyHe9wDwDXPFiJ4DIEy8MoHWCkKOY+aKxw4HaB0cpfxDUd2dOrtiLlNumPpRrh0tnGogqCkOBtkf4DBGCV0QApYFIAAIAjOy5OMKTsZmaxJFjfejPHIAeY2Wy438tEKSAwjw5Hv7aADxM8WOlBVqBG+Mmm55iuKGiV05w5JrD+A5mSqraoseRi0VgV0GkHnxA9drukyB+SZc4E4/AJsVPct3Na6ix6RC67s5kAddDwhKDf5OM+aD08l6DS8rquPyYyguKAlzgIDz73rElXda8bPnyJZjc6ulb7ACpyZoygZ7BBYV7YJ4OfyMNMzi2B5gLlP2zisrMHsrLVGALAZVGpexj3u0cOI3tZiRwiFAMjixlLINdKIh3TFUkIDzrR1JOOZ700aBY+2fWEi2G4PsmkQGf151fkmWFWojYoJKOPuRsuoYxLDnFrwxZjgcoIyhB3swKStGBTzRQk9kWuaGOc7RdHFRhd3DXZRF7geTwczBzcISI5SxBee3W6YxsFviBnwEoYKfyb0PskBsgt0lGIuAN/EDyQC1UcWoqeGl9HI+Y2Y01+sLpwGV8sfi2NPhJDUq3l5JUGxz/A2aoXlVNUtY1pYxspvwlurKQAAzqsQzZAQcLB1/3PBWZHs9uvaZpSnKx779STs3yEZu8c97nGPe9zjHve4xz3ucY9/6/gtOkJG6AorM0WGXPKjYrDLoVUtQCThVRw1rf6ErCqde7ZS80erCmlV2LKD4gtPKiKLq+JZOWgB99wzlxqIZpu2zsA3WNyCxETxs+BY+buClWVHtLJ1BoHYupwX0AwHJ1aXeqNbVwMLw0qkcSHJ+7gJexae+6pzq2t5on0FJgBjx5EtahlROak6tDmBwZCS/YXipTMrLXFNW3YXAZVjAkAHpFzPWRLaOHMbhEFL1jJOYbVeyQD30Rwj8hNk3MoybgpXgNMPZUjc5648Z71B6NGQPYdCBsD1+DsAM4zkGnw+/8C35/9oPsTjLhfcYxtDBs7UTHWRqCy2j0NwW85UHwIvWC8AnDZxTcN5zoaqPZjhfhW8HcyOH/PEn1mdJDa4Oq58mQ8e0KmQfDMPjmOojpFHSa87TAUWK1w4MYOYMNygvt47YHHzJCV3q3JoSMf33kbopZXyHT8GMAmP9OLiEX4Vo7oUAkzyhvSbK8yAS3V57ESpGpTcJyGGEeFbur3z8cTjcMxzeTTRBzB0dU6ocDUAiA/QQXjke27GmPrCj4TKiQzAGVfP2RcwgamzK54TAlQlNq423L1V4Bghr60132j44P3IczBWqAmK8DVGcKt0U7A0167Axm4IxN4S3LVv746hgVyXymX6J00tmNCvV2G6x+8zSL3fMbUJMywfv+K15DM2+MA1vVVcAYW6gjWUJYFEXqWfTP1CBB0HCPAOr2IOFUxfz6/bRg336EgV2s4pIGY1bZopDAcc1L5kcIFBcLSiLWMeS20YDlwectdAdLoGUah8Irgt53SUjrQTAJ8Yz4C4MgODZqt/woPfd9CAXgldEwGMlk2LCMgNljDYeQWepS2akvNoG6SVATwexTe9oESY6Tn38QxeYHkEzWi7YVYXPrmebgTL1rvZCcMFyfXHRUEYrZ4HEI6DIUlMMhFMUfgsPW0JP8jSBLdALy0PqWhzlcIfwcDO0J5FYy1RAAeVUiYwZKntnRpqfcVN//X9oN8lEVJt/CAzhzdMxRFOiNUxb74R1ByzQNvdYd3MsTIJqvVgg6fG3xmpUV+BRTkFLRwksOS3C7pHlThtaNn98zuWkvY/16do/y5BSJr8Z+4QH90enm7Qn6zxltQjMBLpVR3MaEe/H5dbSjYW+iX/uaBxIVuuG9AvDE0LgkF4HNxiCcVpqu2ZOvRSXFZytyswiP1n9seOUYHjCGnguXv4UCVDSbSEofk6lEHDPknyMuuibHGXMSQLvwMM8yV2tiYECoV54uOZAZYcYBl4PkMc4Y8//ic+Pj4XXOVa1/0e9xASPPLZOGjgNMLlsTgOP/AhBk7+j0CiaNPEdsM8v/D1umAlAMOMg73hKn/qCa8iAgDCAQzBdQVE7NQroKFUC4nhwhJTABEu0w48yjzYq/hgBx5MWTxILkxCVMPzBjjoI/hDFYSrQmEYCRG7HAArnpkQ2GX4ul69qJGHgEBJ7zs5YMsvh8CYNmHueOTvVA24vOVlFRfkOSCjwpuQdX0+a64gvK6r1wZYcJcKxS9keE0H6wrghAh/e1xHpguDjhUiuCWEenGAnOJnLh6kAeN4wAsuKwY6AJpxzD+guNTaFPZBI0zAa7iByHEUXORgMC3BBnIByQHms4M29Svk1WfCUZiB4xPlOj5h+Ov6syHLyjc27h5rmGsnJQGU4n7POYuzHcRmPLUC3YExBNOo+ThuEzy2wnO9bxXwmwCO9ipiMIh0xWcI8arFng+ivZRvUMJAz3wpSEaUWB3L8sKSl9JxAIF5kwF3AkM6oGc64rxyriBD1LobAUYgHk0jmB68zudCjEUSQ7SK0+xg92VkbIA6teGzU1qPFJwvuVmsdS8sYNBesNiJQ6SpCT+uE+MYXSQxZxgVBSLiVZ8GPWcXWgAHXOC41nVx73vFIAxePHE1ACejVSX2EBhICwPbvIsk6RUrqAwu+xLHYJRVbT9VMBswywSSBc/xxNf5FwDgyR/41eO3SIQEuxgCQWtVQCykJEsPXt0wzWLRRCUWlqmI9+8cK0mIF3slPpFY0cJB+gj3295rMYS2DXiWK4HklGyYSff0JloP3L63OC9sHaT4gC8X1vgszcVXIcvOyPaFbYuabqfclcS8Ao4mJHseW3dbkmfM5UbrI4Kj2okGf6iqlcYE44VFZ07RiBalCP5RdedUgdCZr+1HdZbJoMUOjqNelWWKhbyo2UdVL3JyIQcGW0/M4zhwjGdX0+ETQoIxilicqluFpycGcyjJVQX1MZ74/PyOb398j5+fT8gQHEf8/fvnPzDG6MCReWP93eMerrHYA3hdr5hLMgoQCXGDkYs6syGW7yVKoCRQApxisTphOCfhyjntGA4z7gX34zFA03DkOxGcoeANAfkewpsbA3IM4UXKpegm1PN/HIKDg30oVso91XWoeVZhsP49ABi9B/TX9FZgu84TmGE2C0QHiEUWQzbdxqsTfJlCNfzfqMxIh0B5QnPBfMonSgE0NjFx4uwq7bgETzfIRyaURnClToTUPLr+1XEyB3z5fJAPhBxLcIYmF6ifGjROl2EMwsjMZYBAdOFVgSWH8EUrOzHieaiOdVfEKgEM7lYbzSKoBjVnDglvESbqwhsJQWl5dzARzsswr/RUmScA6kD0sN9iWb/HbzJCrKi4eUAUH+NvUeRdRWDDFR2MetaYMecLFq6bAKJbHIXnKlBorOkdrITPVRVcnSzIglXs5AuGzY9nBqqk+NCU63V9fgwBQUJhNkstc3oIvnSBiUB8vMWAtHEa6/iuTiLQfHQgTk2xjjksxaiL4ephyu6wLlAQwkR2mY8a2IFXvtxHijpVLGKWRfquetibAISQ4LLZ5zCc4XOZxLILpk/IxvX0MSBc6gRRNFOnnvsHRWG41DoNinM+Oh4jAvgYP9fs16CavdZ1DH6n9gcIDh2Nr4Hk/zsG45DAMV3FpFNfkCSt/qBfr8p7g37ucY973OMe97jHPe5xj3v8x43fonTktNcdAwPZB8YEGoQiibhF9WBXJytds5+z2pYtRGbdBa8ShjC6IjE1qgcLGsdweHNhAoK2MvufgVJUuvlb24dK+qSOJYuCywco5aZLfcMloDFVqfEjMf0r8967OyH96ptHkOHgA9UVqt/ZzmWqtvdY54kdRuYeVZeCFNoA1HDUPgdBaF03gwODQInRxwu4+OwLX1UXm974YVcHKzCOrFhw8g8KMlMV1HaIdlxgHAnB+fb9O/74/h2PR8nNnrguhWWVRX2mGla1xAljDAwZXUn5+Hji27dPfHzENj4//8AxHpDsKh0HgVn6OpRu/z3uAYSqGXM8OySKeWkrdSlOHGNAEyduIBg7JOcvNQe74cETf1eXNJUQC//+4zJ8DMFzcxA3kaiSImBql15Lct6jwzq7E5zKRbzeU3VvJTuCY5pGJ6LPKjsVBQ0xg7mtfZoHByUn5kMEgwg61+cHZPP7sniXm8xpYOOeHy+Ld56FMHNOPF8a8252YNWzu2xrPvkcz67SznnCmWFX42ZhRo1CjC95z7GGhP7Q8ukI2dy/47MzsMbhTVbfV7iXR0nwJIkJo7gGCT0oqK4TQZhwlKs6O3agGoFDwctW9ZvgoR+MWgstu+aJQJgJ9y1/EsQ6WPwtN4IfDMmONuvPK9Q9/pOHuwKevl4AQBNHIXCSilB+YuIHiGfzzYgNOoE9mlEnCOkmdB/olIbEpzptQVaJ+C2+ImbwQusBxCD21VVP1cuCVk0nmM/kxsVXmB3ujKv9AgmDN9JCnt9Vypkp6a0dPznYqRvWdDD8tHc6xDii051nyBggmquT5RydlVaqS8ntDVYG445N3BQ80OclRCBxyLHOAeeAJkyNhkHo0RxB8gGzq9vJOid8EA6xhiGSM8gnvKX3J2BLSZhcYq7JGNAU0MtAFXD/FOo4DESP5cFIgGtyWoGAyimSz5gdn9DgW10WRzhA5TM2mICpwVEAMG4foRhkFsx8ANc54SBoSgyKWXjlFFZ9MNhtEdAMACcYztbNJt88eOrmVkvRUhO+HrARN7yx4uRh4LUhvELooIz7IrmoiaCW6UR/rC/RElyIHImWCAAFvrTbpnV8/SBaaPrX5pCk2aVVHVNF97gdWg9n/y5auTvuk8CwKwMsykQsN3m5w5kxcjN/q8KPC3hkS5wlzGlzQT4GQMbQMgCTwp2uwISz4c09qTl4RmscCAiNEyEtJTHmCRHByG1BQlVypFHL8Xjg+fyGz4/g80xV4O8/cSI5GvTE8SBcV7VbCZ/PTzyfD3zLxOf58YHnx7ct8Rl4Pg8cKYsZcYpt1/HG3N9jjakAWZFsLcm9CRED48e8wpgQwEMZwoQrF69TGX9PwuWyALgpl1yL1WUMVcMreUemALFARs4V8wTUQJkwBI/FMbqKEvPELtIQhoaZtFyW1D1rvyMjBnST0bXEtCeW3DTmipeWyWfMvVoiNwTYMJzF15kpiODl2+EQHAvmNmPu84hO8ncTxnORj+0R51FEbpHw9akC1ThwQDrxcbrAomHwiIjDplnDZ9RjDm34sgeEthlI7OEDwkveP3hNwU0FAtbBbnjmXFEgX89CzWTCYSvgCpiyh0cI4h7z7llGYf3QmbQIiA2EJzhx/jotEr6GMKcDZe7j43HgBWDOgin+eqjJPX6fIcJd4CBzOKGLJg9hkBNeumIlhuORfmBuBJjCxvIRFAXmeXaRhA4GKeEtniVasUkmMk0D8AG1VbxkFsiD2yJFE2pXMcOlZwi+bO+u8QG44lkeiJxiArYg9SDvQo2Rx98qNjkecL9wprQ+mcCNlogER8Gp4HmCsooncFEHPIrDPW9PBXNwvwHgcTDO88LlxbtkKHZoHOGTe9bGwIWLGY+jkpSBabbmcTsBZcyM2oWClwRSjIrhBGAf4ISbXSZwn8uDTCKlleYpESZj/Z1DVIYqpjOCkXYhexgAJnhSFYQ0rAMG9bUKPa65KBXOUDBoxHrGCjw/PvF1FtXk18sl/BaJkMP7gdTKl/thiXW98M/qoQjWPBdKDKxbf8Vz0W9Rk1i2NwI93ts6Ht2Q919RV+QYnEdVGP0SV0D+vSot/8WZ9TP/c6pdB7ESJe6XLau4WJr0yxuoJheLt91TmYPSHXgTVMjsbev4ZIxEm+iD0/aduE579uVuTZJ8MXC494QF4+AVdVWmksa+EXCy6KzRqno4eMm0VgAAIABJREFUlvKTpflkGZ3heIIGII+YiD+OJx6DwEckMR/fvuPxfOLIpGZMg83Z3b/jGBjH6ETI3fHx8Q3fPv/AH9//AQB4fjzxeJTjMjDGwHGMxlFf1/z/7L3rcuRIji74AXAyJFVVd8/0ue37P96a7a6d6cpUBB3A+YGLe6hq9udkmlWgrVMlhcQgGaQTl+8CVV1+JvPH36iv+HmCeITCI+J6n7o6qPCYcn7Pe+JOkWxYNwkcTqH4JqlQZIiJaeXC5+n4vAxXGgkxM+zzAaqnnXh0cstxy4MfIp2IxFShxFOizzSaIG1urVi5urgeyXx/nxNfW+vRoOxIArFepzonEF1ixlpD9Qp8fXV5zRVuE9mvgImDLFpJ9zQQPGWAzwOjVd4IY1A1swFXHCRwbSUdhCZkFR3ZlW4uQxQ3edghyMLUHUjPoVmZLtIElDwnfvkzGRBaildBsPZeQ4lOHFhKUGDHwYvQ7BZ+T5UcESwMcOuzs+Qi1D4jPDZECKSV8Vg+c2qCOFMBr4qngesxuyv8eK1Xr9giPBUrETlBuHde8riufOxXwm9gFzx8NRJbv6g2mIIhnfCkuFWpz7JGo9iLEzST87blMG/nbeUJEEC0PcnI6Smf654kE6iaHLTu+9hLBfOJ1VWJoqWoxNMoxKdyym5wkI0eWBOAMRYXOfQltKcaM6VspFu7WPyeNjrmoCNW+qPAGAwt3zIQnGfneE6Gy2M9AIBBAhb0Pti8w1y6kUPkkQe3ZxBDoGCXVgVkUxAe8JGIBffgQpbsbioPt+KfOAYf7WumpFByCLb1avMwC/EpB4/kUskJ8ok5gZmLO0Nw4K2vuWi8PbpxxzLxsGvxsWSvoH9MvDhCr3jFK17xile84hWveMUr/nLxU0yEADxVhxw/qFdyeLKgBoMZNQucSjBimFmD2zw7no3VdH/6/uvkJgpXevqFQLbl6NZjQmRPf77kAmnfdh8Qen/7fTbZQc/KfFdveTrs3EaPtPvfPqj8w+qiLPjgfmD7T1JYbtumhxt7q0Hl5KygJxb7WfA9tZjMWbc8LB3lCxs6YSrdYY3gTa479sndl1x2cpgWisdxjAN///vfAQD//o9/hifJ/Z5/TpBjQLKzIyNgQHTPsf0YuJ1v0GNdC7fbDe8fv+Ljt5gInWPEmL98oWTkcVcH3TDn7ImQ6gsa94oVgxfUiYlBzLhywvm4XxgETBR81OG0XNUpZbGdCG/J6bg0JOjrLhEWjMHL3R3A7eMI9SUgfDXmUlokkW0sjYTdAtTSZNHObX5iNTF9rbtWcNCCjmiuu9sY/Xf93vBgJoKQLViDM24iPZYiIdjlSMXvOBdCy8GcCY+puPQTv1CqwN0GzuMA5/320AeIT9zKUmB6rHc9wA4ZfWoVpQGa3DCOiwxMS8mOPLif3qeBAIy2MLhAEDCENlXLOgFcXV/gGGP5rDDBoZCEpQV/iBYEkNKbiWt9D5Wp2d5rhIOPNfm3ULcyurrzqyaYpt1hZ4trofhYlyuIgCO5BrU2vuIVAPL5nhcs3QEcGDUt9pg0HskZmbqe/wDAZnBwrBVr6A0YcN6Wetpjat8zBRjRniL4U+piCF+0hp8Sw3Wpz8ZExHrNPPyAY4ZicI+UY9pa4WRwsSdOYqCJanoc92VPqNVjDZR130KpJ94EAmg0/aHeSZI/Hm9qG7IHrSqHzocAIwXXdMXDE6iOO74s7zYHQAKcuR7KjeK+32C2TIyZnEgnWTldIqr4dgP7A/YohBWlonEptgXvs/ioCeztc22UXPQ8t4eMeDbQet75MFAt+yGKChNv3iScMHnCH/VsifccSXfxaYGg2CCCPzp+ihWThCH58DvSB0YLg4+i/mwPmnMR9EkdUwHMTQ6bgfh0VlXhG9+mqGOrRvF8yKwSB9jk/5Awks37Jv+qf78/ysWyxR+hcbu2et1s63t1WwIPTiGPuGzHcqq5AfLcsCoug/vI99+Kry+79BU5B3j75bR4QotEUCyMm+RkSF1XAci4LsU9oRgPVbBtEA5Qy8e2lC8ouE+1QKX0b8tlC+PffvsH/te//w8AwPnxgUvXGJwduI0BzmxmHAP4QI92HQAPAY+1SL69veOXX3/Bx0fo1QtLoArzZIgEJ8MyCVRVqOr2eb/iFSuYrB/6lxo+7w98v8cDeqrDzuDDAAEPuWw9YEWSu8OM2ZcXYQjBGlRNOIUbS/64JnQu7gwRIIOfMK+52uSfF+G/8PNhHt33Pq3/l/EeFDC1Tl4madyT9cxH+F/UPghPMEmTrA3AYy6CLHmQhDuRIMcgwCkTGRech+CGX0AJix1vwPs48O17PsTJ8bjueOR7fIwRWPQicuc/dd+KUNKj8nVzHCBYJh4PRG3RkGfiNHyO3/+QGwjh36ZtlRAJTnEaT2aMCRSzyNwwceHIxtwgATD6vAqCH1GQHjeCGLeFyoWJi7StkIQMlxH8QRu0SDF9dhEKSwnbgmfqAyefOMaZG/kpHuuv+FmCgMVzHQDZMi+ttCeL7jcm3GGgNh6dfa2uZDmeodfMomFaemvFNkYasdf6pfm31Vi8POBWciZUisPDTBMia3TgYOtmg5tl/gWsbhEA2vxtkMlsJeOHA2y4rlx/hMBydjOJGMGz7OrugPrVuQ0TQcRajIGyVREiACVicwHwBZMGRUFXC7sk5zDXwImA0y1uqKQv4qJg6FQ8/Ft+NgcAA9Ua645rsxMAKQYOuN/bcZJUgyOf65d45MyV6ygBl19N53I/ofYN5LF2iAjgczW/EZ+b1fXDA6LU6777BVPCGMtcu7zSSFbTjDDgddEJA7w4/Lu2zY+Kn2LFdFUcZ5DfMQ0PvzDaCdngZr22HyxQRz9Y4NGVjClFJuwexlpVNFi0D9rpNhx6Gcs9PC6oHbtpvEQB4KlK153Iwocjv3IjuL1SAVUwUZPQKmS7c8v4NfYxSbT1lgguUn1AltObmnoxl2dRdRpT9Wl7L3KHE20ToCBD903AURn1hAehzb+OE7jUuyhVM1xKS4QihRZWvRBKdkcWKU6OqRNvIm0WCRDEBZodDDAgOHAkOfPX9w/8+rdfQEd8fxxvUPsXblILMwM0Go9sbpjXRKF5ZTBYBLdUlTvPM8QRzlt3ZpgEYFqKWLnC1mEPHpjjaq8q/jluk1f8JEE0cCVv7vNx4boePdF8Ow7wqcuQ0CyECupvIeEtQYYr7ytBPahTDcjjzi5fIIk7pDH00y5MW02TkWVQPbwEIQYjuUAdLJhqq5NZ4at4ImGwOizvq5uPULzz7V7fPMUcBvOx+DzsUEO7oJNFsnMcq/vJcOgtkh+7K+AXDj1xJFfqpgQywGq64gy22Z1oGoTrCp4VkJNpouUe7zORAfk6Mz7ncjthplbQi4PwXmcBwOSRfaSttSXJT63jcofLGmELW6xJ+SYHHZhY/kyENJ8tdVBiXKStEjeIY/2sNZPDYd6nNuqB/UjZqvosFD6XL8chAiaCZ/PHfjzk/hU/UQQrt5WigkHYBYWA9IKn0uBdCTQ2nyEQdAAwWp48Tvim2qqFzMFXKzFavwAMguRkg0hgdnV+9SZn+IkVAmM6YNYFwwEHDN0oYn4EJ9KoPf2cSqyqmiIOIO8tAKcH57LUG2OtXGuJFZewlkRTkMgqhODBcezmuGdDnLrx4hwW003dlFCsLM3j+Dl1UwV0wZyWjxkPDLJu6n5PhbrzjNevxwUXwlmfowNkE+PMfMQA8wsQw6jzcl1QOXoqfD0c2BrJxyCIAVqqlrgw/Fw+aBpeljzWGgmsOnqSgVU6rw0BGgPUwMdqDumkNtMmCh4R8hqbdmE6AtkFLHGcHxgvjtArXvGKV7ziFa94xSte8Yq/XPwUrW7B0Qo4TiFpukTjYihZ0CqlqEKrhnQDTAk6YzIARJEvJC1hGrr2siFJOGBiDbeKic6CjRV2ZGE396CClP2RubM6rAXe/PLXG0Isf2+9YKltHz9PDblWCHmiAWxTnH2n7HlvKNSL9q6GQrt7UO/bXILezpoQqdNSb4FDjZaC0t5Ryb9KqG0fpIAxU7ITyMqbFixtcDgGvP/6AQD4n//X/8Jvf/s3jOxuMhxvb+89dp/mCfuJv7/ud9zvv/eJHPKBt7c3fHz8AgB4f3tLWWxuGcrmRNn6rIRHfxYGwUkBSemT/4pXZKgzvif5Rc0xjmN1Q0FwWxAzTxB1TTyZQq5W2FuGNeSUF2xWnBOuFd+fg+A0UbJgojG91ForPNY4bGumH+gOLA+GYIRqW+xk/65u3TjhDbqrFPLaxSGChG1BQv7MJwwPaD5C2IGTaPFTLMCqBeNwC4U3pjgPHzRAw0GHYeZ7/P7pYL8wc82bysAYOPPG/DYNNn3b54AZVnfSNNX3Ngz+7r/DcJDEvQ4AZHHO6u4WSG57QY7P48Agxmy52TjWo9cvgRnB8rwwCQSzp3Egx1X+C3XyGRjZ53V4dscLXhPwQneO/UN04JlknUt3TFJYvn7IAQXjfs/Jvf74Dusrfp5wW+gX4uCBUOUVTgC4ERaHhLKZ9/XIsRQ5NXwdxLjtORjiuX6Vdx+QEPkI1Qe44LwI+BUpGrNvpuFNlHYW5LzyHoR0/eDwItKyFDAC25r2xmpnQHIWDSP4eJsKJm+IGVaG0wXU1CpNPnh7XzgvdAz2rCi3gYG1ygL0yLu3LAeGgE17GwTCjQhOtYZqTM5zvXqTA5dbIX9hboFT6c9O4Fi8pSank2BeGx3BL+g90U/XAwbCUUAljufPoljkZhrTXB5QmStxUAfaG3IIWJelgVE8My4zoOkqobrZFDBXmGofF/MRvM/mvP749eqnKIQAYBbOm+OCOVIeW90xp0MfxVOJC14z235Mx5XytUVAZS5DrnXBsC/jUO2iIV9OMllzX8ABgcjXv5Yz9OUr+vUl2R3+EP7HP6yEyeN9K6H3GvM+EccK6flcbPVPntjM2xP9S7H1tJNUULDtz5rU+PVoPEbOPT4mgDbJXc7l4+nvvqwchDQtLIZyQvG6sA0pzX/+428AgPeP91goKx9TxXEe8FyonSwXuDgz3x+fuHTiLaGVt+PE7XbDLaF1wiF4ycLr5va6PmqXKK+REmCIz9HlWR7jFa8AgG/z3hAMZ4eprjyXCUK8El/i8KXJl4NvxxgkSzjFAGB517hegKCbIkBBGQrKGQUKbwN9c0oD5kjw2dFiL57MvieYbi4oZWTsTsAYSL49LlKYUr8ngTGNuwBw91DwP2rtCGlq9UrGFUICy3WcISA4bpns8ECahz5AKYdtAzDVOH8IcYSxcTdNDc5o/gIhjB03u5JseFXyoxAe8CKGF3E5Ezpni6J042YJCGbSSdrjoZjiW/NHoALcupEVRkg+ozB+jJAgr6bLyYIJgZVvEEcDbeQa+rDgaxQ/TDU9iBj9iLrsgpr1M5JDYLs9JeYMKZ/fs3FzXZ94xSsqaJOudrOA3NYlbwYx7oLCAGBaCxGE5kDlGdf6HX/KPCJPqYYqO/TCKnQQcv/1/DWkN2TnW5kr9etZXOX6Z7nW7AJWN+KA/ec2lCPDqDWxLAKWWELoIvQ+H2iiP3pXraWxAzlXOdbzsXqTdMpEdMFog4OYvzsJxseWb2n8ftkYsIGJ0L7a0ETcxvp2cAintIyOX9G0LexrmD4B4G7+gAKKV5BmForGd1umxDs954B7fiYAZjfHnTR8zbz/Mr+ivxZqt3JVTwJGWRCYGowE1nDg8N0rQSH8BNC4n6IQMmgrbQw5ADj0Ht/f4fg+FXatbqZtd6FrddTQvCJmDoKZl/mfgSBwX8WUg1aiQZwXW4kgFOl2dQGfYpsm5bdxERgWppI5Fgb6z5LpL8WHL7MwIBMN8q2q/roJevoSm0sR++Yh2VNBGJS10djybjb0Vc3bHKwOaKvsv3gheXKa1gAobpOyeHKKFIyNuloyEJyWSdgxBv793/6Ov/3bPwAA7+c7bie35rxOBas19wAWohV3jYf9/fEdIErlt1j4mHjp6tcxVSsXSYTESnacKIQqum626I73IvpCkL5ixUOv9ZCnaAjUg4KBvJeLlEtgWfcci4A4cObLbwsAqLHidETrslTB4JSNmXW9uvOmRIf22cg3jfWpBWcERNYCDuEWDcDQ+PViCi7BhaflLJ65Y8DzPmOEv06RjSlFUmY95ONRiGZl8wAxt0EruUCNQH7GtAtRTJnT8scBYTD15MPUwCevvIMAIV6JCWfzRqtpEvvbdQ4LWBfvyUhBeANLvP+0EplA8yqPMeJn3e2J7nR5e5hqNlLi9amJQyiDymlQ2FJ847C+rSM05KXU9icEzWujTHmB4FVW04yYwbTUp0YWyVSCHKsz9YpXQHgpuJl5iIjIxo9VNNneOJ7rPRkO+ckwT+4ubtwfG8YmGi2ZTRJFIVGTW8YA8fLDsesC3Joj4rhB6bPvAUdwoJtLY5HnGeJ+BHLquakxBgDnACfp3/w73KTFEb72pF0BNQZSqCXWWkKZlpl7KubVZGz7f25y5nFXEs0sUChYarLlUHp0URkG1A7o93j9bYDo1oIMcMMbr2pNBXAekFqjLfA9xRUtn0j45hNliRZANGZEBG8n43dNj58ritI9pyU0/RBgBll/0ssfrdExCuKj/Zlg0Rh3BUbyQeNZxbCrJvsK0GjUBNyg0zHz8SY/QX71UxRClyn4zMoejPu8Q6/qmF241DYJ5zDorIeCwaPLoQ6rxNVSCa2r/fjgi9h7+YUQPV3jYW4oW4wsVZfEMwFZ0BSkirPqzW9ToY4259ee8DzFmoSk+XvfaKF0wF1xOyhdfPM9KBIh37e1TZSEBFf9bFuw1HV1ihGLXFXqipAcL4NBmMXYvDo1ngXhdl4IW3cpl8s220Kok9RRm8VEi4R6nEs0oS594b29/YL/9s9/4G+/hFz27e2Gwd733XGOmCrl7wsxMCfu2fX0eUHkhOaNrvYGEKWDcpw/opFdecofMcLSvjrHFqeziJUwAArJzvMYZYj2ilfEvTvKBM4nnLmLFiLCtLmS1lImy8LciDEYcKX2xTOfcZ2W0SeOp+WGCNlMKDIqVlsW0aBg2ZJ1zlluPmBFD7BtMI99Wdo6omoWawgAzFTAq0IHhDEZ3kaLUbAVzEznhLp3Q4IluqnLONTgCsxZybvBEI7xI82TQ2qKV8E2HZ+uPYVikRya5z4IQHRCxkpWFqgt1id2Xd0mSoUnL9gtgUgXDMgtOq4i8V557l2tO8MMg/C5rcOUHfYUjXDDYGk5bPOQU69EhcjBOPrpoXGqcWVCxuQ4iAICXkkec6zZvkEbeUl4Cwd8Wc44rhu/1qtXrHBQG/qCHBAL8joA91Au6z6jhZF7J60U8Piw/qg1LSaeR6dbDL90yV9TpOL1vLU54TL7mczCIKVWYnRcYJInFV+Y9MSAmOAz0DJXKkoahVlp5xUmIedf+ZIeUZhVjTENk4ESs4p7HahFtpbTrkmmwk9uBbjIFlKeIasG8s8wZD4XPDhsCXL6Igw2gbd6p+Miw3EL9MqQAWbBMeqzOKMBVUI7oT6Ds87LEaITXZxdgE+Ohk5blBCED7Dc8kwqPj8vjPYMcAwSSC4ek1KUoc71NBAxNA3AOSdjDedLOHFPfyKJhQ908++UEw7HI/PC8xhgcD/f1L/DbGAUdLvlIH5c/PhS7BWveMUrXvGKV7ziFa94xSv+i+OnmAgxMzS9aC4NT455RY12JUxgGds9w9XUHHCGYcnHIuvb7ki4hURqEbzsjzAv28xN4amG2rqtBGS3EMDOY87fp+wWPA1fn2exX8K9CIxrKkG+IBYthd3beMLArZ9txyEJsVmNFYI4bxyegn3Ed+wMJ+7qXmC52xvszoE6254gw5qcFLSwhA8WlHD9fUg+oqWACSkXnB2J28l4O3/Bx3t2SY4RW6gOqjDUriY9igjOjw8gu8i/k+Dz8cCV238nDk5QdqqZTwgdoA3OyAi8svWRP0fABXl1kv9/PsdX/PXCXeHVYRuSkqMJsaihb/nzpIhBTwBUQ8jAACoYBgjwjWekn4DxsgggSWGF7NKJwex5eWKmJjwLxZW+ZO8VsNlTjlZzZcC4pF4dgxYW/AEDcZsBBFnZD0zkJFYdNgUPj+8FhHGMtQY8ZkBUj5q+BPl/oCZKA2aA4oB9e+R5BR5OLbmN00DOeMv79hEnDcXxERYMBiihKLDoaLvUmurgudYn8+iQlqkiG8FtCfuPI1eIuZk7DgKJ4EjzyJMA1eULRE6YZuBehz2JwvEejxnrZL3M7sFzqI4rKQ4YNCdt5gL2sIgoo2rBEfyD4mZeCRvaoJXuho/kX01eU7tXvCJQIRHhbSq9dqgbzAHO9co46Phtiorgzbmv/MaJMAS4rDhqE/CBY/MbtMbrAsewhK32DkGZUFZ/BE74a/FYBiKjykmJESAOf6x1lCsJK16l5BRnP1BDUy7cQ1ymJj5HsAFX/uRpf9JIOg8LlHZODgiYubev0skD05aoiSWVoSY25gYRWd9fCr8sxFMQMD/3De2kNaWqfMpA0/C9JmlXWITVZO42bvhdJ3QuWxYeAnoycRWAYz+AsAYxuwLeDcAoJMO9pzMOgEDJQ4qzvHJrc8NQgnZC52DSEMkpg2cGThDGvj5tCCq34HH2887+PA/7r4yfohACMx7f4mTc1XBdVycS6sEPWUVIGEq1kpl7XvPUHKCgg6yHT/hFLL8c5ihCFl+M8sZb4bltrF9ZDsBffBrCSOtPjmtbDLqQ8fVdFEMLeuKRrcf3hKRV73u0ka69f9Sve3oA7Xm7EC1sL/bfR5IotxLrP0n8e5xcb9hEutqRp6pwbQeUeGHr4ogpFEdqMXl7O3Ectx6bh1GkQKQURRy7CJLIwMfHL/jIBepdBv6/f/3vFrQZgyGyPIKEGUICdsaC9MVJYnr+fMujSUjgkoRkpIrXK17RwXhcmbybgIUwi/EKS3hYfK+kCAx3XkvBfoUSgdNclFwA597GIAnuUYl3IOBR9RRnj8KkOUYcEApqiFdc38cIJcZrTjRwH5kbHIBs4gfIl02LkA/IwZil1uiKUx1Vc4RwiuI2CmqCUP+phsWIwqybJIk9ubzgMA7nka2VDLcwXU31IedoiNxrsQgi1FI8olCjbNEJOATWyQ4RAcdiXjIR4Eff5y4G5hOKEhc4QyXpRk0LHD4wsWDWwAFyw4HlZzL9vmAhDJBdeGRSZ2maWBmWuEN8YmQBOg34l87uTsk4MW3iUO7kZOoDUw1nQeFuAd3jVl1SuM7wvgPwdn55QL3iLx5bEYOAeXol7+miVbClQcBIx5z4/eDPGhYsVjzYxg2rhYPZ249LiCDZnAEAkgHHKjIC2rt3kz2/r7VhZj6WcGNB8iIXd8mFQoClcm0N1d1G7hoBghZrIeYQH+hCJ9bElasIxHWZowqB3FodjeAhjAMs7jAc5grprglSmq75DHhM7QaG3idoERHglBzoUnRTBbCoC8wJGy6Ta71wn5afD3DXCfDELx8nfIeX6b2VI8dxw8DREOdPvUMf3E2WI9dptZWY+gYRFIpCdbXLNXaszgsNMGs0BxvqHXlsrbwhrOO9TjMJQNqJ9M/gW/9TFEIEh2YScGlc9Fyfi3twTQqfiiwStoKBESd5qQWVGIL13zDiBgaCG+NfEnii9axzVBGyyMrxS6WkovEgfyoAChP7nGwXV+C5WKj31P2b5+KsOstPQk9rn2P31xXU++Pbn3iIBXRhTmsiE3usT4puhCQib91N2zoUURItYnicl2XA2nvXPKgkH0OKOhUkSGb87deQt/7v//4/8PfffmtXdJ0TIkdINgJ4PO45LazFQUAiLbX529//BhdpzpCMAzKOnggJBtglP5s6Mw4iRzGVDAZ17S5uKNisz398rXxf8ZeO3WgPKbLRGGsWCK9CX53hk1ZDhLodA8/7f4BgqnjkejXGLfiLKRXb12FNYmWEwloXNgrPexmIptDAwMhCqjUxa9ByHLjrHU7U95mqwWxxgmJDhH5E2IyHW8lGj+TcbWuFs6y1wKN4KNnWiVTrXEQCIHH6vr8nA5WtLDn7XE+y0dMNDEesQTn5Iglu4GWF4Y/1b28uEXs3OMxqbcxuKDtEGGNLRmChwFTTu+94xOS83tMJg8dK2lzBcAxqG0SoeksLgx0yloS3EIH8E5rKeeNkCIVqaXE7XRUnHyhlcmfAmfD9fvVnc46B80i1KdrsEV7xl4+Qyq68wWEuoOKk1c1RvBd2uHNL2BNCVMp9aVQeHkbrnOsXiYBoNuzDM2+oIoMu2kbl2bdhbpSIQ2tEDiB44ruuqyHktvmgLmTMOaZYVbiwwox7uapmyjo+Bhgt1dyqaK04E+tVT10lOtHKaXpNlJxE6nzwfimggGV3aLiGumfxCc1wv2YLPbkrjo+zeZRAGM4fZWcSyVNzPWUgGhx5LEaW+5TniWNarNeE5zpO5iA/0RLe6tAUgwEA9gFn7enNYMI0x62EK4igZvCa0hABNHox9mxGjeJgkwAmKSgc2zidcLFj8FqHA/yU14MTnKkbfX9UI/uvj1er+xWveMUrXvGKV7ziFa94xV8ufoqJkAfIMf77cfVEBoiOBG0mn57KalIVqzvUUq6vNxhy2oXj8OTilIJR6YXtnB7FMgplRGexsJjlWdMqrc4w6V0OWcgcWiw52Ri/dKeYLN+vpg7Z8Si999zHVkxFbL8q1VC523yFSKPj2duPzqo6WqpVWPBwhdQ0xbOBitXtIZLmOxjF2HyBSexp7kXEcXx13L3l1XVhT05CHqUQwwU4pXD9MUX6JSdC7x+/Bma/OEFMuOY9PUwA04nPz4nbe/qPHAMkjpGyNkqM29vAOGN7t7d3vB/vGFjmbKHmwuuzwDOukCEt1QkgzAphfR741WF9xRbuS63RLK+qUiIjAmgubLmfoIGWY3ZIG32WKqHahLHi0MadAaBNzcxjCrBMysAMKJeyj+C0s183UtiFhgo7YvK0bYWxAAAgAElEQVRCm6pmvK/h9++P9aP2pQCULrhZX/tMEuqL3aW1mN6W8TFxwnLXRDwmMnkaLH7mR/F5LAk0hDUQqinMwmUwLU6iEIEOabgKI6T9a8IDYggRrGTyqxNbEyUqeHFJ6xuMvGFuQEjhHpCeDjMxhOaCSZNjTgaNxODDQcTt8UMW26j1KYfm/awQhPrmTPPTOR0ghuVnd10PABYS2jklCmiQwxIPrtNx0ezp2iEDt/P8Isf+ildECG9mvBRTj5o6cGBwW95/sMS1XugZnwAzTjEc/BZ/44aTBq5cXxSGgxhW6o06Im/YESsbAocHw212NhP7svKQg0LifmpOrdghxnCn9FMDQBOqdwxf95nr8nFkKKahIaiuZSVQa2TkSy297w7DOkYzBW3MluDkEaZiWwPzNCWaaXL4YTbMbFrQCnJydgjj1/ez79s5LfIjXbL3kW/lBEfjs3g8Au1CcsPBgMmVn0PAEcMMZKEBnADK4zZV4CL4NvGJNSvWvAfN+MzzGEgcx0EQXapy7toIB7BAbDRs99LPUKmDwXMCpGbQhy0UF9c6Hps4JXzVmAvy9+NHQj9FIXSZ9cU1mHCZL9KaE8I7Jr43si+TNEpYmW8EMdonsU8FDxCwuk2CPh5Ott20fbNkkSKcGPi88dOKt7gjA9xF1jMEzpsDVKXXZuMZPy3/ifp9314lrJHkUxIPwOkP58FACRupm0K/7E1+Ta19lLEslSyrJ/xvQeVow/DH+riOgFECD/sxEY5N9zeksyeOvJOO88Dt4x2//PprfH8MGDwIl4iFhAAct5B/PBw4zmsbxTLgo5OZQxg41z4dtzec41zwEGcIOIvaSoxy31aJt+CPefQB6avz8EdY4yv+ukG2DOnKNLlFBShkQrtpwsBxKHTWg+gAk8MxGyXGdHTDAIj7lnFssNrg/xXAYWJCjHq9C5EBxZlrxY0GPvHAlQIOFxSDRhf71/UADcJ0B5Ifox6JSMEbhN+zQMvk2x1u2vA8GcGhq6aLJ1+ncA5EDmHudZwBDI29BwBjiuLuYKBc0VOatRZuU8IQXn45Qn2M8SbxzyEFcXUMeMPOIB78hiwgzINf2vYAAEAMpltuHxhjYLg0fGWcgrs+8K/7tzgPF+M4CO9nYXDCInc9zAeIGJKF0ikDRIs/YepgZ/wrobz/+/NfUANGJh53/UTkVgZY7hcDKld7vagZGISRcOJDRkCcu//0Ekt4xQpNewggmge+QVyLDlS50FTPfCpfZgGrwibhSr6NDAGpbg0Jhpm2KTCQb1e3BGfDqBo7ZjBdULogN1AT/iOXwxJlwgiJaDKceV9qKMQ0fNiMQ9zlC8apIF5p/d7Hbc4wcMNwGQ4Z3B49DMY4BuaV9xKtL+aLR+kMpGYErjmhV3JkchtRWMRx3d5+C6pH7oOqwsAYKXVNeIBFFn9Lg/AwChPLDIdiZP7mMAgbBkkXjW54giEKBSSwRWzUopjJZ4GSxbktvXQP1O9VawkrbLOriTO5Mk/y4Kpevo5b0r6kBDiIkyLRaDoHzVUoS7l4/8D4KQohM28TuDEI86IuQuA1SYkoHs4ivmenlLE5sYeiziIIVqUdwUhBkXp/IC+efMu8jqpLx3mDVbE0WEKBpPfL0vGYVrVBcaFWl2PR/P48qfZ8if785eWjk3+/Zi7bNoiSQFuFXDx0998JqKZ9+Ul1VHPB3AqbhdTFtv/e/7V797kDO+0JZDAyHHLDv//zvwEA3s4DPBi38623oTrbM8NnKJD0gufAdbwtzD7yTarWYsE5pLvdY6wiqbZvFMWa/+FMrEJnL3zYWxaiX3/FKypsuytEsihqNcuYotR0ht0BXabEYR4qYD8hid02j4dZ+S4MF5AwHqmwJnZEVzdNpYMftJu2enArM+Eftw9AtE2LTz1AvAiyMgTGwOETl5cRscPIlleITRC4xM3y7xbfxnPcI31vWHRRy3uND6jzWq84VOlUKwkwGDNYF0nayDBAoJwaEUWi0QpWRriw/N2GMMDcanlkhocRaCa3ijh8nKoakwOYkTwAMQk2mjiPmCa73yGQSP7ys7hfn/i8z57wyEkwVsz5mftwA0jw1hxIgbo3T0nnJ379+KU77t8+v8HUQxAIwVtlCGavf7HWz4vgpbBHI1LF/J2Tj/Amql4PQl3v4Fq/8IpXdLguxVtQPe/iW6ufrVSmfq2/TqcQdMFeAHj/khDhYUvMpVXIcpsDBHNvU1cF4RTutWa1bvNfR6wtUlw+xfRsAqdpsLqF6lred8Jp4Lk1kiOl27YZSV1+r5lJVvEVk6yZ22d4FAC5D06RNzmoKx83w5wTVxlAz8iXSqzk/e2A+wRJFC7jUMw5WshgKuCY4HIz5VBI7vPiHtykmua4QqGr+eQArsxinvpDS/iLUoCrP8/MMWsax3ny1+AhuElU5riKbB7l950XV7En8cxLfcH4vCt3q+Ks1q48LiXYNr17EiX7QfHiCL3iFa94xSte8YpXvOIVr/jLxU8xEeKwagcADCKIWXcPnGJ8uWrG4Ai1qE+NbxzoSYjX1GON+/ZJS0yR1vcxJVlVbm2ueQDTUp0up1YMqC4oO/I1WruQEyFanZieYK03XjVy9URp4fkaErfv9ZpN8N4CQHQ+mHa19qhyGWhYhj/N0f64Fw5JLlO94thFLlP6Y9deezoegLJDk53pQzDGiX/842/45z///rSvrRJnis/P7+0jdbu9ASy93WkeWvs9IIw9Kh+PMQaIFkxIICCX7Rhqgrj3nZ6nivFfsr6n5ymQ/wQdi1f8XNGKSOwxlWiloDt4rElw+FUJPFXGxhiBdbfZuPXBAxDCmepBhw9MPHBYTkaOA6DAyQMBzX1oKB0CgBhAKtCc9H6bd7hbc2fcDdPX+4EPDDpC0i27djCF6+btsE1M4zt7mpr3yLRbyYxBgsHFy3SwUcMf1C5Ml4Tjxd+yOXyuaRrDcl0vqek4r22dAH+S9i3rhITYBzzPbUGYzZ9gIkTJ7SpuAzuYBignLwbH3S8cMFC2RI/xBuEZSksICByPN1B+nhOc2419mNcdctygee6+Px44x8T3lCH/f/7jG6AXbmecp7fbG6YRHvfiBVBAS4a0BxPIMGSsaRs4PUrymnPGgSX3T6/16hVbPFkmUip25QM1wWrN1xDiQNM0F8FwkwPMB4CCocXUoiCn5J4clOQkcqVj8frDDW4L6ibMcX9pTWtibbFtR5mo/b7IBYIHTB0z70sZAjKDbjYrTNQTolpG6j3NAiJbqnEA4wAaBaK1v3UeIHBFqMcBcChsGtwIn/elhuburQonJMBBON7i3j7f3qB8QXOS7w99yjsDPrtN2dUa9goE8oiTKgIA85owcRTGZ1AQ1RWKHiohFXFriu6W63BOiwcDU2G55jkYA4JZdg8IP8pb/X1yxlrFmTzAzVSfU0hhM43N4sagao3iCZ7kcz5lvLyPGvP9A+OnKIRkS3xPVkxSqJesawpZd+EDALTJvJYEAa0xKHmKB9Sn50/Y8zBz2nyDKEa/bbBJeYOs+WJA61rP3b4UIoSLFOeavCKnux2Lo7K5Ga7cvN+3WWk1siTrbwMKUw91SdjgOsSneTYima/zBZRJLJ6lyHvrcRMFfngrv2iJRlCe57qomTlmqpVoOKepWM1VGb9+/Ia//fIbdpemt7cPcEJNSBX3S6FHEgqPM6CLJd9JBDPD4xGL8Hl+QGRB54gk4Cy5fcF4LmoQQgxLSL3ODPcot8uibRV9clj6Yr77ir96bGWyASTroc3EYF6+Da6GaQqppDaUEgBfMLEwPqYgLgMAPbcX3Eu0ZJOVzgYBEHj5qEniOr3mFb4ZBfVkBw3BmZLzj6mAKdS94XNsDiFvvHslKfsdQ7sbs8eOqLWDYZ6OxREKQFds5/DYZyrOkTmuAA83dI2ZmjBcuxAFZZ2XsD2oxg4ZMJwb5hG6vAtqMU0TNpbrW5qz1R4fRIALHglzM5cg+jJajvakeKDbdtyuhCvJxeoB6y7/pce8Y4BbCv1ywL5/x+cjiy0znCJNXv5Ux3V/YOb6dpyyemFZfI1xQBCSxUA8E28iOIrPBcZwbl+h12r1iqcY3NQDQzROLlrP/EhiszAyINxJ7wDi+epMMMyGZGEEtLXygEkWULK6TbMzMfIaVwOcl/Q1m0HdoIXInwQ5pUUEzB1qipn3DJlkTscNOb4shAhaapqSq1T3XWaFyPtyTgaRQspXKPOlVZgQXAlHG6WlYMMj4cgE6KXYrNKi+QyGZFNWZEDepPnMbhfmVHhB51jSlHWJ3CjpZuNxwHQjXEg0iqvQuo1oiJUogZtDlUBi7Zt4HAw14P4oIZXg69RWxRxKK6UJFvhsU9hjZJZatHGOZrcnnO+yCZIlmqN0B+HE5Rcsz5UgnoG1T87ZYCuuZn5WZRBpL0PVCB5HmwkaDESB3QYCN+7AbrvXiSuwGpNPRYVTkwCBvF8Jiyhn7UzxtMVmK6eLO1VWQDn5qBuAopBq/9GcOPm+yS9Rhdli3KQy1FOLVbAzcqJ0WkXIE3HlT9/ky8tZ/y0Zh9jA2KcdWDeFiz+d23Ch9l4sqIyI6u8LT7yavGBaBaM6MBFdmMc9cfsiT74hqoZv337HmeIIb++/4P1t+QQNIVzz0SpN72/vQR7caxTaPzvamw995E/HFVTM7ft1/tbrWzf8lVm8YgvmRbJ1Z0C3Ml/e4bquQSfLVTYfCrNbGTjyIX65QeZowZXveGDIgUeS3t01ppT5QCSOts8owiscyoknRyhBFc4eCAfz2/GGo+5L+z1IxM5PXVjafYX82u6QEhABtkUw7rVqRVqsLuU4TmRgNswmVAsY1kbY13SofmnEsICFlyGq2t6tARDiB7P94QzDV3JE+eyoZhKXL1uTtAGeDivRCL4wnIE0I3TSnOx5N8UUQcQuv1wCQeeFz2QT38DAGF0YORGu+8Q9H+7XvOM7NoYoE+b2WQ43HMKg25nnLbrQBPT1oTaj4bN1WAcLRil/IUQudN7zs8MrXrFiM7MEgtN4VDKNI6aovtaOaavhUS3F3ag9Ll1ZDYhqTVRDNPOa4lRTJiZPWYes5gGUIcqrYZGT3l5VOZO5TV1scN4rJR5MBJGV64Swk8OLC3MOMJYQAVNklFs/HY6reZaqhMc0eHKGnKQnYa2VaxqG7clpHG8nxm1Aclqs8wIf271PUby0yqXFOmD5++5h8FrrmeY5bAcnjudKN5olG2QUxQYAXNNgiuWTBETTqwQaKHwgl+iWArDOr6KR1KcZjmgYPcqgXk6YAT5X88nxgLm06AObAaZxHcXJa0/JOA+RmJaqaRWGPzJeHKFXvOIVr3jFK17xile84hV/ufgpJkJCaE5Q4U5rrGYb/h7YFCY2HLT3PxGlIL31OgNzur3ncpVJDyE4nkYJ5M+lMTaVE4pOZb9Kgas0YE1JqNAj24SHnvcAtNSn3J/5OMVpeWL1bNLVq6+8duLPuCyydWJ4vVv/61hwPiZ6nn7kRKiOgZ4kp6Pxur9lTZ96L81ApjDzJ8UquENn4fgNn/dvkMTMmxvGOHGct9x/htnElZ3q94+PwAfvEt1P5zbPw9ZFDtjQglcGLG7nP9S8aJ0pX6yv10joFc8xJ6YknMsSOtodOIU4L9VLTAyinqoaFCDBSYwy1iZzyLb8qBNwWCqqAfCwEyjPnjkNE9oTHzOP7mrBRccAk62J0nQwTjxapJ/BPOB+YV6P/FlCw66YKoin21ohdSm4KJT7QBT3auNdiHPJrEmZpxdPQshkwO1algY2A7dOMSWOvzFc11pYH7kyn8WNEcfDBw5a0tQHM6YX7CzWOMkTOw7GhMESvufm8NMauiJypoNAPnMAkDCEFx/HFDC/8NCCOnpAbPLR+XDHfHzintA2MgHGgg0dEHzHJ27jI7bnBp/WCqeXG4y1fYvmFQqlxIBdue6q4ROK9yOmRh/ngUMAqo6qKaYRrqKA4RWvWOFYMvYe0JhNApnAvp6GLpWzLOnjP9kg9kwkf7SwLAmnX5YkMSHynhCF982RstA8HGoXIOW9Vpi1mt4khEuulQ9xMGVWzqOAj5WQ5NcjYWssMccpZBEnKmhZEgDXXVFulO4EdWv0CpGAPCS6a1kWIYxDcKZK3HgLBdxSiBQ5womR1nTGTQutB3ICJz80jrPWzMyFXQNGu8FyTSfGrbzdqNU+a6LnZnnuYhvTnnOYQQwat57G2XzAFEhhu/4g66yyhXR2ccrAAx9jYJ6x3l3K0MvxNqhh1pcDpH8y5anBVjl5ps0B+59cY//F8VMUQszLIBNgzEubaCVMgK0UtaFk6wfxhbFIokRgXuNgAsFtyUgXwuwZRmZffrBwkJ4gtTbm+5NjIA9p1zY49f0vVpJTCXsYDj5j2STHuQBQouGj6Yxxcy4RBX86BtoLobX+NCWh9ntTkFz7Xl/rFDQRvMbcBSGrUqf3GL5+vSvStR+WEpPavhrMjGteeGQCdv/9jod9YtxCTnsMxvl2tnQmwXHe3nAr4iQxStwgXi+Y2/aee8HmCe0r6UvUZ7+dL8piaJPzDChjvvyfaZq/4i8ZTkushA9OXlBe3whOW5NtOCBN7WchAxAH8dGGn+NICeUUDIEcsHl1cnJdCse5jI8tZWL7AUlgN3DzegzYmhSTHILPBZcw4IEZSX09AswAMxSbDkbY6hiAwyeCafvBl3sG665DbMn7PeO+PQBKedoRzQsH4FdhxS3+Xxh6OeDQxpAzwlOjvEI41LPxntC2x3XF+xaz1ylMMYpv6JyS2iUqUOt0Qe2Co0SkKNcmVwk565LD1juECY/8rMwCOiKU4i+isEvBmeTJIRD92EymDU4HvmfhBL8wzoFZnhtHMKuuzzsOLr+3eBYVoNt9Aj4aFqRqUHMcZVrtr1LoFStCynrLGzZxIXeF+jLIHE4QWMNLq/m62RNmGqvw2gYGAGo+cxivU9+3Q4qrnKsEA7ALeuV6JsEpoRRjiCf0EuZ/XIrBgku1G+RkgIF7jWOnAOh1zhfCKFVETDUYtAvAAYm8pZNz4HYAVxm5z0icyvSaMEBsoGFtoMoHQ05pvrM+NI1Mqwh5hM9OfxAOmxdoRJPXAmPWhdE4EvKfS6yqB0xQlvAOgaBJ4CE+oBZw4c6HSHLtz+OUI9bUzGGGMKbN5aEphCEDl24sagbKD1ycMdVa7EchMFn7KC5gnrHu1hpJhDce8DKVLhGehjBrwLuLQ7TcTn5Y/BSFkIx1I5oDzjMMtwDA4qHa9U87tK8oDlDPeKgKjfrdTOCb9B8Tg0VL86wY9pKBNt2C3A6tx3z9FlAP00qui+tEWekvECrtnRi3RM2vt4xOyjo+pq1wKsJ0Jxb5/z6mSEr86W9y34sb9aV8KtL119Kujyt/VYvMTAQBL3NATxWmSgpzP6qL5Az8/nhAvn3vwgZvhs/PCZuREF3XxC+//oLfymB1HBiyCIhuF8CEIxckc8XwJY4QqlJbZ+i5KguSZSVtnVpy8rqWWMITJ6iL1tck6BV/DB6LfEpk4LHpqjhBBiBazQTGMQTaS63AcQHm4JzgXPaI4uVI7sq3CXLFrXDbzJh2wbQ6i47d+JglHpaNXScD01hYcyMwXVicVIbShE3HzPXjc0YBcubfzPQU65XBMgEq/g0DoM0kMZ3ja7IhIMBHT4iMUrigHqB5rnRrBjlHeVkePsYMYqRJdBQcZGsdrxSjFY88f1q1XE6o2tMpEyWd5c8Tn82opksuqnNac1bJ7mBeikgsDDaGlmqcGcCEs6ZzPuJRo2W+zRDM7iKTC3T7/pAbjuNA7TQrgEvxeMxgLgOgG6diYBVCDExb53oIjAg0Yx/u9h2veEVF5JuZrJsGV651gRhDloeeVxOnp9WAzSuKlUqIqijXEjTiUEvLZFwvizxk1H0aamhlABzT4E0szOJZW5MBE2A+luE0EF5Gt7FyC/NgKPmmOHZdCkojQ0+TrZmLnlAgQjo3gcLp2DAgoZBWhs0uDpZbc4RsapytMTDOPK4hcKz1hHy0kmecOwGGdl6qjztgjN17zZlCqQ81yNFeC4QOGF3A3Jr/RrjyPT7nA0KMk8/mNnn14GpyH2Sp4O0AuPQOZsZstVAHu3Yjj9JDUWd+lvMBkPSzSvXCdZ81zInGuiCnRnmuWWBjdA5PRlAycD2/hJOrla//BGnWq3X0ile84hWveMUrXvGKV7ziLxc/x0SIpKcOgXHU5+nM14qRsCSdCYlADfhaR3YHt2+680g5Oel5kDsUC07FiBPjW6laE5/4hha+LsOyg9rjXwpxxfUuBjhvneNEbvT2CYPRevAAYRC6dUPquYfbMdEC33nh9dnTBfrpdG3H8CfRgNA/luaE1ZFllB59dYHjc2i9+C/vQCDoZfgud3zMt9wGBxTyLbpDv/7ygbe3d7z/Ehj68zij65odCoPCTddnRUD5GcX3Dmxa/PW+/d/ZcWbfVOKKV7QBC2NCtH2++2f/E2BYX/HzhGMpc5EzbKLV15wM7IxC+joIU9c9BFKABUSOS4ufE6pgyCkSk2OcZ29TiMCX4VFNPM77LHeCySHMfR8SEQYdUE8cd17p1pMWh9CJSffm7g2EN5ckpOvyMufJ3TbAaPba4t3n/Hpm1n9bjPPj7yXkb8HFUyKYEVQpoF4AmA6IrOnLtAuKgVlQL3Oc4nWaFmqvFK5kACR45HkN5TpuzzGhAJjNHMeoGfyynj7HusPR7y44Hcfa0i7oSnjMR6+7AdXhNSlTg4/FiXSduJ03SEphwximE+8pp87DYXY1xv9Sh+sFGgRPHprwATjDvTrPGlCi4k4l1/TKZ+jc1LVe8QpWaj7hxzHCe6fl1uKf5sIwbT+P56tiwAygfu5PALKSFXKE5nxhujxhTwtJ40SL352vFFz+RoxH8twAAELgAcis6Qw1uqWV6NhjejO27RnDpKSoA6K8UEEBWxsFWZWY2Myc+Ey7IEKQmmIpBdczYWl2O/NUafB6AJCFQq6XCmUqvPUpJAOUwcVJPG+hDJfngCg9yGitbyhfTADwCTNeXPXkrVNKfHviqB6wtiVgp/RSrDVUk9fYGMJQfdvgswYs2HReKiM/m4eHBHjlnUIMHss8hjMVU2jySgF3wVRvpxjO36vzMlVhU1GqgyI/vgz58XsAPBHr1CwgV22iV//kDZAQjCeUWhc1Xx7NG1T8KTlGPIgXg8ewITnhHuINJGsz+5YX3rEqK0TR48tAkCldf/aCbjMrDczm8iNihLeGb4WQ8xIvYEgi9vI9NTC5u3cSI6FxVZi4JxzmT8/OlszskMCvX5fPh1Oclyeu1CbgYEi5zS15cjgej4nPR3h13K9fcZzUC9Lt7R3jOPCR4gjvtxsGy4IIUsBtWiKXOSCEjTetz3FdLwGv4X6dErKzw+n2k1G46f6+tr0V2694RYWIbDAzCXJ73QVpXjfqAeqGx7xw5oPlYManXnCMhsme/AZVDwEEADIMA+ciqGJiEmHkw87U8HAFEv7hTmk6uO5jHo5BATfFNXHd/9VEYdfgADjWfXRIFFOziikF2G2DADIGj7VmWkDZ2gzVCE7cgrrBN3J4QjTEJLxGNgPEgK0McMlX68TlCk8e0fvxDhB3gm9gXHfF7dfE2HPc/YVNN4/EpmDWrgHRqQTsEMIgxigeJlN4WpRMtVqoI8ho36fHZaBLG2IzwZhEeE+c//ADd73j8/s9P4sJgIGWITd8+/7A9YjXx2Dcbu+4MokUm7jIu1AWKI7bgV9+eXta6//j/i8cRz2uw/ujgfwXY+rs4tyuVyH0ihW+QfLdJqYyRtpTVC5Uz8NB2aCtQl48eIG+BIqMjszDVhsXRhuEvgqhXEucMci6+KJsZL5nLv5JDnOAxlbVsHcfm7KBYUarJjCHjCUmZUj79+L0u4Hd2w8saAbc95SqBtS/ipRxwOYMojYQbKKJ5noSE0AK9yvWCUSOB2ZYFjLHiFzDrNZZgpP2eRrCkdfolm9tvG9Q+gl4KRdwmI52QuUNj0OeIufM4cp3kxDPkf09eHmnESi8iRb+PzY3+8RF3pbn5ZAD4+Tmf1ny9/vRlPUw+bE1xA1qugyhBZgKZF8OMuTJY7MoCj8yfopCKC6yqtwBYgFbYT2j+FkP5Oe//c+b9b4lu15bBtDzjC5+HOGcu4vEGf6IG9wnK09vHNdacIhaPapEBrZqDMt7iPNx3WofFDfF4hiFyoo8j0IWP7qMTPt6piT/Pv/sT4Zpf/LfX3+6CiHb26GOVIOqV5+3XwtcL4BZwLoa/vV74NZl/L/4+99/64X4MQ3n24HzSJW4MxaBdoAmh7D0jSskENo4QlH2rGkPnqc9nApx9b91uPvR10SofpLHsB33K15RwQRQPijMJy5d3hAMARPhfuVEBb48GgDc5wOkBGPrycbdYgLeJsMemOql5eH47e3EZ1YZ3+4EqAUGHfHQhll7r8EZqg7yuOcmCYhuaxrjATu/bPlJPBwQs+geA3Bz8JBWqoMDqyyKe0a25mVHT8byLqxJhz1w2QXOLi+TYAjDBgEtEiGQbVR/zRm5Qj1ghYNYW6pMGgpvFY5s/lhNsGMKNIrfc8U9TmOtb8BqVplGE87n1UTvSx1Q6+8VIbzz3cuz544HHr22MDlEqKdQ7hbFWXlGqcG+f+9Cy49IQq08gcaJeVeYC/752zsA4F//8YlDZNVFAC4F3kulyQx6zVXo8o9PLF7x84QTd5PEaODttgyfyaIRUEWOekxyS/nM2QESGLhoJ2AB/KI1AUoeShHyy4+sG6QzmrrV2GEK+vSj+TRxj3Kqr9ndMV1beZOSJ84u3eQgDwPXykXYKSZH5UdpEz4Gzkyyj8EwdzyKz8OEC7NzwOFHNKVbFCUU46qeGFpN2NvyveE0P76KDygwuvpcMhg8pIVSGJxqublGrmQuvmoebBeY9tz8zvu7Ck7yajZTc6OANIavPNSjX9Y4IgUMd3CTwF9gcAgAACAASURBVAIhUHmoEMF1cUdV77DpOFLV901uMJ9r3Zf8DBSYnSATaOOH0mcAm9JmCCDGIdzvudG8fli8OEKveMUrXvGKV7ziFa94xSv+cvFTTISklb2ity/MW2dRoVhYz69D/55BPHUnCzZV6m7P4LavQLDwSH7+HYaDasRZ2+PtD339HJ4TmZ2zk75F/qXWtPUnEFrcAU+43xo0eXZhn/d1wdBiMlO/z5TdDPd2LfeC730Z+LSLNOLENX6Uoju67/PT8MRbNLePcR+8rd9d0z3PSdU9CQ6/f/8d7x8feP9Yl94hJ0ZOhJhSv78mteQBC2w5dQGTtPxnqOXxk18TsLkY5ySIvtb8DW/cj3SDxO0H/p9OHV/xVwxhxOQCAJRTVjUnlCKweS0sunPexwmt0gnxA24K66nBBDxUggCAXJ4QEzDg++cM3DUA1glyA5esKsf1vd+XxAzS5MbwAI/EJyAuZ3UF++LbcC4+5ZcT9xl1Z3jqDK5KDVUFgFBjy8uhvBaoWHq0eS0DhIGBKbUPFDAd0229GnGnlmSthDN8SebyYGBqqxHdbYKOC470ICMGyJqfRU7Br8rz5FzrSnWuY40vBaWCN1vCcICAlJgvBVIhAo6jFZLUCDcIkLwkdgdUMXMfjYI/9vZ2y+NmfL9/9oQJEBxhypTXS6g02WPi+7ffAQDfPi9c19XXh5PBp0Pyw/h9Tny7Jt7fgod5vEbYr9jCfbaK2uCUrW/hxLC7UC54qeEghpasnAguU4zNhzGuXW94FDFB2HGW96M5xB2efl4XTRC8kZwwy2lIKVBKQOlKqZE1rQUq/wJIFe5zQbqYQEZrduIWOUDD6UZQl0qRbT7g4J5aCTzW5qI1IXhSrum9ZgZ3xsG5tsDgfoH9CAsEANNmeLQVB5GReUauZwKwasPS5qUpQ16YJAKz9OQE7hCRVvQDMa6pIF0ooeDa5OTMQ9k41szcBAWKpxSOWSdgHuqc+a7ncQKI41QfIDUM2dYWOJDoAhEBWSiMAsDFGmv9UdBvx5wWuXK+hdARE/DZh4EBwVU5/PwWKpe5zjv9+PXqpyiErjmb4OnwgFfnxaViwFUQKHSC+kyIf0KJ9X80gTVBAwUDsdScX3Lb/ET5AcJ7ZhVC/ePcPGfBU1XNglLt2Mssb9aB7uY0eMJiQc3iHm7S2yqQ6rxUcRS/EKmPYoMQcokZUL8F2qQLK9ffkpU/XIK0n4d4X6/zkLvM2wicdggZIU3TqPcpBB0MjpJfJDzuD3z//g0AcLudmLp8o4YI4OhxslF4pBSUjlkQ/1t4+TiuHbRT56EWJn7+HGpf10FmIbV/dviTk/OKV2QhVJ49QhgkDRrTOeM+7vs30etV2PMAOAqMEs8nlkBENOJCQBLmdwBw+cQ9bvB8T09Z6boHvHm2QJpTm7csq5rhsgvUMqwEIOT7aTNEjUj4ClMBYwEAhwywUAs4EMd95vXU9oR0tHNsLBaVNIgA4BClAZAcJMLh0j4SPiOhOspnwxVTdSFU3SGDQSXFn+dL2ifIYYw2aGWrvszzetjweRjYCFcSptmzaULe0LbgYjq0LQgAnd878biMwOoNlQQJQLQ8NeYEDbQMLzwafXVeLwWOBdrFHcA4D5gD//c94HdkwHSDz5LyjaL1exWQeoGJ8T2bTd9eYgmv2MLdlm2HMQwKkoLuniFtn/eETeAi6/s8rs3MxQou6hdEjhY5AZ1QimYHkHxnRBNjBbVvjBBFnlBLBSxl+FcO+NTMZIOSg4wh1fRo8RHrrzR24+pYD3lrchAMjOJVAtg41gH/M5SvGiX9sc4bC0MIcDWU+j4zwAc1pBkay17vkoffW50mz5PDbQ0yMbecbrAATlCrtSbtCdo7kmGEzYsyCkAH1hqnM/KfXHedeeWn+Vfmsz9L9wHmE70TlR9u3e2ABHLvEwgtx00p7kCyBGPiE5wthgGM9ExKXyk64rznwj9+gkTrpyiEfv+847rWTRAw8UXQp004g/GcwOdQAjV/qYjKeylhPD0aqAqUVWQ8c48CH+q8kffQz90sBLwvvjXJ8W3K4PCtS9tvvf33VpOUiv/aDw7eytNa8nVDju4KmscFG9yhegN/qrYpu53tN5Lv3+fGo7PQCkm1TGz3SA5gcnvYxCCi0KT6QLAKJWMHZ3tAJ/D757fuDhH/CiLHsfEoaCsYNRe4Oi+SogdLyICDLL6ypW1ns67bndOwXl7F9fOn5OlNtAqi10joFSvEBiQ7ZpGsU08wZVBCvbPpAg3xg1xLdFK4eruDuBTbGM4M2VQbHdqTDPEb/nYb7VdxvyvmljiYAZdqT50YjskMpYVNF4w25jO1/8Peuy1JjtzYoguAk5GZ3S2NtEeaOfv8/88dO0+SujKDdAD7ARdnVGted5dZE2ZdnZEZvDlJd1wW1gIzYNuEZJ/RiQg4WrBQGHrpIZKNYuG3dBS0sq+ZsEjWmiIpmaQgpg7mgNIeWZo9Mgh0WDcouzMYin2PY3xNgE363TbKrGrpl4hAzZpdaowH3sfWuP8DGpNViZXCQ9qtO3UHDp894ekZkZOQw7JU9jxO6KV5GAPYIBjlaKhCT4CpAh2OrG4SG2zjHabW984J2NmhtaBpprIe8f3dBx7CeJM3/Ct7D77pgagq1rzNmRnOe/N4x/F1dg+G/gY3cdsf2egiDh/CLwBlw4aDoyJR2jVACxsDwKETtG9RXa0+EuxQ8pUQDSYCePUogmHMvW6yG8xtJYNCqb2DEHPLBKr19mHFUmdgir67QnYQL5KU+JxO4tWn9kWEUsnQJlfgTC1XwsoURFvrosUgLUY3ohEZCfKu9oMUqhPnkfMshe/Qu/BItjf3QcUCJa6NqMgX4xsyCezr6+GrSb33BPaV0K9rNPcmbAAyOKnq2h7yt9dASH1v0prSvvxNorgeF4sL4wzO1AHQbIKDTQb2TaDTL35k+ZXVE/aM6lcFykIxR10qY7+33T1Ct91222233Xbbbbfddtsfzn6IitDXoZ2BY6GM0i8MIxwlybarjkwWZr6PKaPakjCOAmYVg1HGp/XZL/Sl6xCrjFTVxS42UEax174U4jxiHjNLKf5dhuKan7DLOUbQf+GYb62if182jF6ahRNnNxAEBG986HUM+ppWIeu31SqPi7sekb8vplCj96JqdskleI5V7ZmIgrqRCNQMMcFIcxyRIf0wh5vhmTAQkYGxbS/06cTUuFjBqhyhro+u9zrBcRemlate0LqMa5ZE8uauffh1u98/YXHbD2QTE2dl9RKKWhIY6gE5q2oOIzSFWgpHPDvWDG+FkYbgQGRfAWCwwnVViBQTdnr366jH83lkldUtMnqj4aAUc+Z3VdRnsrMF5CKYfdwv8+ql/GsJ1eWGfIVmxsLo+wscmSnosytLHBCzNU/3e1k4cU/2JLpA+DjmC+JSgwdkrKL4+XQcdmLLc9op+gSQvQjsBINHlQeRnR2gZp8CAUQOzT4Ac8FUw5b4+CkerHHG0LoX2xt8TsxsqrCngnfCyF1++AbdDWdSgNMxsZOBHtnvJQw9FgyEiDAGdxZU5xkZ3aqATwLRhM5P/OsZkgOfXxMbD9SCtAngKt3HYWo4ARx5XRvf+c3blg3eACR3MTkAaUismcKNuxJy2gHhDdIVo4mBwIkt1D9BVbsqQGRwGjAtSGr4cJxrvmwCmwYtOHHqnnU1xgF16nci5gpDdQDpBLYhWUlIzbH8VrExMnNofxVyaAFzYh+YidA5ckwGYNfqjUVFB6tKYbRB8nhTJ4gstH9qLBE+kOV1zexn7qoVefiOF3I9EjQskZUxlcDVFmIaV0Zr7XAScF5M9DU5jma6jhEy8PLJhkDV4Ymw4iPn2e7lNNDGDR+GWfR0NURnjVmeBMDcWm2nOcRHE32aE7aiN/crK+nCQ228wUFBBQ7ANa6j5zz8/vZDBELwS9nMPKu3WYZNnvOqcJr7CkTiNy8LOIBeoBc9djkPKzAi4AIby36hi8hU4MTrxW0egjrdPE79YLHoX2OjAl81vMqLQXsd8yUoCRhbl27NXyD3i0u3HA1apVNkrGLIEnVeNyMZGK+BwIKu1XhcOSCizFol8Nf3wi3Ps/bHeZ3XcbnoB4CiNB33NiE1NCBEeH8PAdWff/4Fj7f33uacJ4jXizooBML4Eo35JeC8Xl0f9AJ1I0T5+wrZQ5aw6fqla/8W/aZQfNttbdMV+6ieN8XpC1suJnCaq5eGRicEgFigiRwEaSx49CMqKJ3v8yTI5kGtDGDIgJeOGBK+ptrzjzBjUMJREOzSZobq+1GKt7YXS3M4BySlFqOVFqhAyAMO1+sjwSYuvTAe0NjqqYZAC1IK5Pu6Aif3aMpuEhwLOAwxt3OjNLDxZVFXDabs3GZn4IEPaAYlz3nifE7ssud1C4C91w41xaR5mecYGwtKZkf9BMNaRNbHwLQT58nwFL1gNpCssWMHBrZekMwjwKSE99HmMGFoBZ3PJ+DeiZxt7JHESmjcGNFfdnSQa5huMAZGBlPvTuCxYerzck4bjoKTnwoM7obnt+3HWNZv+zHM3GA1AZmDYItmmg2Gs6HmLFvkFQrllv3UAsC1nOEQJ7XW9kgYlqwZhJ1QQoxzHrCTMBLyymZBI31xS4QBssLcK9RX7x7pgHJqJDa5FMPbCwoemMHUvZrlpbRoJ28tMQLkUm+LpIvYwbxh+leeg2MIkCjcSAKBQNOjb70vmzpZRJYtHA31tQ4g4hg1n+451o7drBPXZAIjX8HdOYExoM8qChh0WASmSNprEN5ltY6YA7KtPm5zCjmAvN++V4YsYdkmgJzda85ZVahOha8z5+0ihBADKa1kCzmmn/CnwrecZy3Gi0so1Q0YvFouKBKI5EUOVP1qv5/9EDOmy2K9YAcg3NoP59NwYr00USm5ZBo9FtmiQ+h9wleQYfX9yjhw6ElcIl9jWk8T0oeoh8kyaGpmlWCNWpD+aOgHLRYTBwBDM4A0grL36QBRBzKeAV9XQsgjC+PrHAiAlPifTQiN3q+5w3ni+6oSETUryeBgSakMKdd4tgsU3PzXhEAFeHGOFShUQEngC1NeRJzUSsFuiscWePl97L0/HoRffg6xx7/+6S94f7y1AGFlm7iYolpDaE1wLxUgR05wK6NxDWMMkcmiy9hXgHqJi2L//ffv0km33Xaxj/29ne/Pr08YDmiy8Dxt4jEenQU0hGNM6UQUsRFf+oGmp+teTHPTIE7NLEY8UjtivWeONTcQOHQ66km20IW4pgoqp5iboyhMZlXec05cZAmhPFJZXIZH4JWEC0xxMUvXgyO7SJdj+lXstCpa9YXoZzRvFw2ugSr/NTWYznkC5NhGzQUe1TFd5/wx3iBJriBkqRuUc8MQgLird64Wgt15koMZDl0EDhy9VNO1nTj3GQt7OgK0Z4hnlUH/ggIYdS8kHBl9hicZGiihGxU32+CuTUCzbQPOq9pHGrlwFuBPj0gWHXTgsIktCWPEBScMfhx5nYxHaSzFQXDbbW18IRwBQDg72WmWoUMlNLatGo7zFwTgwNQB19XbAlbQi0xnsIfhsq/mZ9AIvqpyS3hA9nMlljPJXILS5/OEE2NPpkUWgtAA+OJHmcNUse/ZXa0KQNBsZ3AwxoUYhWPeLKF1jzO5Ej2ZnX3ylGLNl/YeGAjK6H6ZzLa3KTzI2Jq5Ls63Gdw49ut1UgUz6spYXIPkZxJg6rmS38zxy6pWy4gkPazncbLUbiu9to3gQ5rVFIMiuXTRifLTm/hCsIGZwY+4t+/OEGacReKFByaO5Wq7A65QMoiV70oY+wpS3YMZ7yxG0rFBaOkI2Q9QErpr6Lfddtttt91222233XbbH85+iIrQJtwJiKjwXDFhBibuZH1AmlZ2ND5zIpsKhhFZjo7yCJ09jc9Bf72INoLFRC4wycxjfnemlXE1GFFj24vxDcDlPF+jTM3vdSBdMLg658u/9eP3GPxLPgSLJa+2j3Hwl73ZC+TLXcGwoNcFkst9HTYw/JdzzPP2698vw2iUONBLJUVFsOdAfrx/4C9/+TM+fvrAx8dHj905T/z5P/4KAPjTn/6Mx/sHtiybbyJg5q4qMUvCGPOYbmD4/9Q6hers6ft9PeHXEtDlOutevP79FfN3221hz3ngzH6MEzN0ego6dcnMhVFCP/oBjiycIahTATAEQgH9AgClCafSNgPmcWBa1HFqH4al/TGdwMqN8xYeIJ/JLJdJOywyWxfAK3NY+PWGAWcmkRhm2udAznC2vk4CZZKV+hhJBhWf7ZWJ0xOGtyreDGLCtNmwVzLgNOteKQaw74yRivPHCRx6dD8pMbDtA4/C0A/G/ng0xl7nieNYfZpTj6jS59wytgdcWxg+eqzMQKSwhLuwc2qhrZ6wCQfOzGaC8LY/WrH+4YY3EexvcQ7HoXBzzDyJOScc1vOTWmikNcTwnYNKnQhIzaXz0/CcT3xkhnzIhnl8tZ6S7Y+AJeV4H/MHSLHe9sMYCbVvlIXcQKQAAIXv1QgM88SDXeaabL3pJVUI06xhakQech/NwZ2bd4/1BhmGLiAFFVkfwxDwqyKdk/EOEseW56gguB0pcVKTpEdHdLGjJcqDL4s7wSEN5b3C2WL++x7/7q6r8utRZZqWlV0wmAYES4soUCRrXqZ0hS5FpmCJq3NwznVh+ZVrFJA9lgBltdkHBQipNk/freYvmsHMqfsAfzWWEUa2NOc4/aHyr80hyn3/3Q06g+00riHm5b6VYpimkBkaZV924LFRQ+9inif4Y8PWlXUC71HZq/ubXURxfy3gcd5j+/v7Vz9EILQT9Z2KZtXA4QOAsmKQgGaJc0VZt0Q/CWhU02q+S/AHXb5z+X/gOmw9geB4+PqBC9hJYTW/h0iFLg+/CLha6dD4BUpyucEN/1j82PkS1JsZcLuabKZHhXorByWhL4XpT1qEy5mtSaAeOIdBaG8Yx6KTp8tWFz/fiwJyjUM0YtfnOAe5DGjgdldJ9LEP/PxLvDR//+t/4v/9+//Gx8+/9AC4GYRHU1A+Hhv2tw2PhLdAosl60VaWWGpOmmYwtsbcv1xI/o++u76iW39Bvl3jYu8NUQNVlfM4hxsid9syx1pIGAKFJXQNcApceCPfKHDaBcdKEAkuLTwgHtGMmy/eRo+gny4K7mkJ9c35TQOCVtuHmPLyPIg5KJtbK4LBZA3HMop9Ml7p98M3SDptPaM3r/uMUt3jAosNOtdFjx0ELvHJLPomq2+ASMDw6A1AzdEMKHWvgXGc6xh5nRZU1B9vAQn72An//Bfhq0kiHKd502m/bxtw6XvCCM0yypMSFhgTRonbHl8hfJqiiVOfcFUQG0bi14U2+IbWQOHBwGlQzn4uOJxOHM9PAMBj30AP6rUIFKQXtZ5xdmvUVKNJjV1Q8DfZMHbCeRK+nkfeL8s+sfjOt+MTOq2b022GAG81K9sdCN12Mbqs4dFgPVp7y4YHFKrSuaXvU30wkwAaCYEvbS0F5ZwCAAQD0+i+SFQc1eg6xyYMdeljuK1wQLNxvnptthH9MKaxg+kKKY2vSlaTYRs7jq9472jsiA4h7stUctC8pjvRfU4cDtfLmk+8MjmeUN4rOZPTjF7H8lVKqqRedY/keifYZ4xO9X2QMJYGZe1zQZhZNhBmQxANG4z1pQ/cdJG/GEusJ8daTIQj6da9mXyAnDrQJY15tto8/CT47uDSaRSBq3ZPEXkko5UjqHkTCTHv1jORpEpfa4O5gzRIZ2qchNH3xjySezVwshUA8fezHyMQGoSuq7hDp/dCRDyDm70a89RqCQYQzX7UFaR6pCwbc1e1JTDrdUSPh/jiGZN6SVzkPOCXQOjVmBlm1A+0eehTONAY+eQ66AFO3gKsKYn6N3WORqshOhZLX5fENVHZZfvaMj4fOBGaIblo+w6QNH40yBkWdvM3ASIqw1tO3W+DAJc1gREi+Ck9sSGMv/7lz/jb3/4bAPCXP/8FP/35z3jfRwdnqopNNvAjHv738Y797b0z0sUGc2V9w2Uc7H8KSi6Cqo7VLIisWK0nAQC9csZFMchfRpReB+W229ocs9nWgi1pTfJKAvaZrGgAIHAfKDGJIcGsZghx0DAKXHhlbbd0S9KBtzOJVTpnkhVMW0+sG3Bmhm1SvPEVfCEJUKoPJXoGKZntMujIRrp6v6KH8btkkq9EjiFEEZeD5S+5pUrSaGHR1UHmqRcSpABMFKKuJY7oNbOnQySEjRg+y7lhCBs8+7HICfOwTibxARznEocUEZzHgeElCOl4suKNK9ByHCDsKbL47WsCpBji2DLYkk2iV7NZIyQdkbxyVSgmHlVB4oFB3Mmlp31Fy0V2H7/vexAA5bg8zwMGw3v1QzAAnoAR/MwqkjrYufVKTjvw7euAaa4uEtpKNcvR/7Bu3fbHND2xKh0EwM+uDpN79M5V8tMdIkunb1KwyvllTWbZsZFdGCANCu1+6CHc8wcAQBiqjNOeeVBA+JE9MbkNEdDzob74V4xgb3CnVdjJ8+baxgHzExUphdZgkCjkhYZTlc7KnBPBKVlzpCKYpXJ7UtAQWDnz5tGbwwOlqErk0RvZDn4GQhW4MMPEYPn9qRM8PjoYm26Yk7C95XusCjLGLF9YNfpuZGGONpEmVokkW8y7hWaKYpE2AsEmw9yhWfZmQ/Q5bSks+wYM4xY/dVc4LXbeSQrVhQQ4yTHElx+qsRZswv18CBPcCEOKyEJh5l0xMkzwg3ux8B+gSejuEbrttttuu+2222677bbb/nD2Q1SEyJqdD04MZ29sutCG5zkb4zk2xpxo3R/2KBdeM/yMKjlm5g/UKu5AsH44ZCX6ycHsXYJUosgcXGBuAX8rXKS9QKmiRymhI82Tm8mHxp0J2H118RAStV8ZV3qFa1EoIVelxBBA3SofqxrEpfuUnJAwFVnVFIrOgMqahBi9tQox5fh1RZsC18/996D57b4nBL1iJRyJCeKMj58im/nff/8b/utv/4X/+MtfAADbtmN/2+CKC9Xvhsf7B0aWQ/f90f1BAJJlyS4EfpF1LoVoJgLImnJXGqTTAxefih2maLOvBcPXoc6hWjeUMv3dJew7wXrbxRgbnBK6CwLEsVll1AgnKZouPqnfveBcPuDT4WzNluN0BCw2H7Tn+QSYMtsYVW+dRzO2RblYGp4XcGJauH9oTKgFiYXBebE+QZqkH5Xqq/7AmvOEBEboarLklfhljgwh95wjdTFTxTU5lKPnB4j3elzgxgQB8YCr93ziiH6EghlOcpzuOLIyQgZ802BQAwBSCy2TnKC+/fqFsW09fx3PGVDazKjqqaGfkj1H+9hBc0LP1AXxE8IE4UfDEp92pKB8VZFOfNpshlFBzE1v7+85ogbQQE1pBxRQw9k9GgFTqXHbsEEGY9sS5mYMcscujIIoiBzQk4osCu473oQaUiIigCwmQrkwEt52G3gx6Abr6uzKhxtHJbZ1zwC4XmC1sVhGH1HNDdZskL1PLBQGWfTAUfayzIZaFYV8+hY5YQSSjhZXdfU6FJzLCXCBO2WvJBLW69D0nwavykycd6KCCtmmno3aed6DUk8tPga6hdvPBKW2oF8YGKNxKOQLciMqJjdENS12XxCZLERddMzg3jIHrice22NBbHzChVdl18LnHBcHRLFgtEk8DNkBrbneal5eG4hw9ym55d5rrDn+0axaCSROOhu2yBnEq/JP7NCL3I1T1OMJF4p2z5aKS58sERoiGLpRy60a6/J+N/shAiHnC7CSwrHghEvQjCCndBegCZ+q0p8BgMVAF2aVQyDMLyvzFfpk33vCC5US2+c/L/S0dHlpmF754RE0s5d3NyAmxIuSO/tOrksUXdDiXp76FZ+FS28RttQfqcDIErryAlSLv18mPVd/CYyMVsDXW+VHQVBtFzymkMMVxDAY184kMeDnP73h//nf/wUA+F9//U/85//6G3755U99DUS0ePcR5eL9sWPbo49oly2oMcvEAnprS5yLeeFoawy/F0ldULqXX7/8/AKeu+Df/i0U7hI4fb/r2/7YFnP6gmQoJawCSMhtKW8A4gwybUJjPZJOdgCSwVTAT3ZoPafziCRDZofULSigG/7JqctT5xPA7yUOmGJ1BT2h6CepNV0onmnV6lRE9BHxIto2PiDYUTPQtCeUufUjJAOnpcsRtNQNDbYI9CrpsiUNvs8UTgaD3XGSLlz/dKhaOztAOAbPJKYgA9QvfUt8AnBsFHOJmmIjWmKBHFi9IofhnfA+Hq2Z8Twnvo5vKBWLx9iDypoUlr/1Y+T+amI/Qc7QvPBNHGNDU8F+zSeAgS17IE91sAIjV/ttCEQAyoMGTW/0MsUvCG/7jsMc/5ihaXJ+Gh5vD7ztsY8B4DlDgwiItUPh0WuLlVS87TYAAG2A1QyUgH1Z62aJQgMAeEIzUQwAjAiaHLjMP957ygOk95HBvCtOdZRUJnPoYnH9HX5JqaRWJK6JnPLkM/mgMx/qdUQjxoQ1iYn5BPHoc6z0Tvczj+VJIc/MXhI/BFyDmJckNvL1jx7E0ssJLSJbUgn6DJ8u5x8ThpgsYgFY+nBxzqGRuEYyDr+uUTjmyJpryBzD0TT5nH6K8QU2bQ6zFfhGz4UvGCMIbA6pVhMPopZKuhEE8CVmu4WC1Bq3jGK84HqeCX3nhmqHbMLym8IVvjjH89qfj2v8+rvZjxEIOS0SAaJYHCxZwygi6pU9iKilBVgJAEfFZOnZVLP7q7PcL1b9e2FSuTatNTt+vwecDkJlWBVEfMHsx2JOF++5pobyFIwiFHuloP/uCbjSxH13zoQgcGj4N8nLs0QVvb2cJ+Uu1z4cuGRg45vXBOI1oOhD1RxZQVb+4uOnD/z33/+Gv//97wCAP/38F7y//YR9L1Vqg4jg0q4FAmHf984WMQ2wM5R6ML+zGDd/+c3le0TIZqbfbBf/ox6W615iJC4MMfjt43IHQLf9OxNBHhgIaQAAIABJREFUk3n4nKG1ky/RxoJphKMXZMfhKxFp80hGScJnCslRzgT17hkcOA0zG1ThDsKAj8rCKdQV3sIxDpAVlDySNMM7Q+dPhsnsKrqbZsOsQOYF3z6WwrwQY3bIAAACttm9BkIbzvnEWbpCHJUIoqhSmE24aWv6uBsOM1j3AhqAqNAcRwnJBsvTqEwySRDnpDgpEWMXwkzv5sEPkDK8dIV2gVwcLLBDVdc8Joynzf6+q4Bkw58yaNm2HXOeoTXkNTdEcFbi2jwYDxC+soqkE3AybFwOGeHz+IR7BGeDAJaBPcVRx9jhdkBS9FQ8WPLOnLPP02EmcJvgryPvruHr61c805HYRbCPHbOywGfoDn0Wi9xvJ9Hb/sAm2+y+FLcBJ19MjQKAvAlFonByruSojNQlQ/f3TQf4JY0fKd1Z2lmDQRtjywTowI5zKCir5lMdk5p6IZjSiGBFvGKKJiJAErqwgGW2x+Qe/Sp7kbtYMs+Vr8MMIsE8cg7dOBzumiucQHZhseRE33Qv4An4WBEGE4AB2AR1M3km22veHe9gXAKj6ThdOwAMf+vZ1TSWQDuV7igzwU37Glh2mJ7ZwQggkTK0CvuYBhzHijHgeKmEuRPO07qnlTJ6qkTNEM5ApapaobVW64BysF5KVfbJI3HVWbi4KrpUstwpknAXny8YSqk3ueTGV6vr72g/RiBkllQWUUQhd6z8RVQ9qvJBg0BGK/s1gCcxjkutjTJVuVrkKWPa5Zxciy99Hvn/CieoWVEiA0uXoAaXflkzDySKr0WYLV6Q5a+/ssjBPYKpS8ATL+WKUvIRy88KJl6Zmmy4rqoXUVGI22IsQgTqdNknNDKYQCJtaAXkCk+nbGUw7BLIEyzIFvIXv/zyM/7617/hff8JAPDYHhjbem2ZGPvYwbz1VZo7hAWcVSBB0GU3W94ZAe1ionuNjdbP1xIevd686w/fx8JAjv3l84qV1kHot8/HbbcBBd2qoIUCdlZzizt8UjvbygoWgub85kwQCkfASsScBWADJxMZNKBu2vnCCAhQgoXuYPJCvkU1gpYDzIj3Qc9ccBWgfVUxdozMyPpiYTLF1AV52XaGOYMa0idQDBwpdvoGgap34+6mAh4G42Q6g7V6e5wExXl7QcA8Aw6DthgpYXtwC6hiTuipeEsq6qnAwYZZSTAwaCdISRBIkgwUGQxFFWoRrHhkdCuAIMLj8cBjFFRuwDbG15w4j4KznDFfXO6fbwOU4pBfqhiOzqDa08A7gfJe7pBoup4xLuc8ImBraimGGTebXgSmhPNkTKtq2sAGuhBZGI554DwLviJ4yIbFo3PPXLddbPKlOhzCpFYVIs1ygl/e0wsj7lTLxDOWuHvg+ldClbNpv1A6cGyMhoBNN9hkIBM/ZgKILPp/c+BwzKzCDhGMquoCYNqgHqyX9Q44OdgJR38mDPHlbBvw9Gc7L2yaKJ7VukB6KRTBI1goWmkKIplK0Ls5wEf4WxmwMTmGe8N/MQEVWuyensReGbkIE0CjA8Cpipj6Yy7RGULOPpJI5Xhi26STbqAI3mo2mxZz2T5GJ8VUT8AMtEUymtzA7HBa1bpBW1TPEEsK27EEvkkw7cAuVWU3bGNAEip5zAmWS/KJCMJ7+Ir1jFW2vXy6Cfjz2YPNHJTtv0Hx/I72AxSlbrvttttuu+2222677bbb/u/aD1EROi/NpwTGc2qLSqkaLDOkAAAH9iF4y7LGU4/Ah/qquISolbSeRAldNa0qCSbNznAMMM5LKW9SVHCa1TUbmatqwTbgdrZGxk4C8w0ODSw/sr/GJtDVlcgwdHKSGebU2E1KkZ8qqxKQZASXkoY7qlZG7NhooGqg6i192ONqBrD40lcCZTSfp4CojlknSQRxhMqoWvYBrOZAJmAk9O2nn36CDMGW92LIyD6pgpoItn0k8UPF3K1A0uMUpa/K0lrQ8l6gb+aXSiwIAsFomsxsKm+CB6qr6nGIzocLpUJjold/lftVLPZS7vtuTG+77TkX+IiUuyIDRK+gndbPks0TOgkz5699k6StBnS7vLFknWk8U2uiKJbVTuhzkQqwSMgGyILj0QUQZe44z0V5Kj8z6CSMlgdgTFBWsFO8lGOOLUpvJ4Y49RzpbjjB3WSr/gWMgY+9KjyEp88LbINyLqn5z2OOT+IDmEM96GJlL8ifR4UoYTx6OMyp4XkuDHbCn3IghAinA5YHJez4tAPVDPWODRv7EoukeM8tq9ZqJ9436Wz5pzrcFQ/e4SN6mYyiVbnmUHMDk8Z2AB47YZMNZ17X420DD2lSGyeC8oQXhNANogzNytp5KL4dimdCk/bB2IcCrPBH/G4AGEzQC6b5/PrqeVfGDgbwyy8xL1txId92G4DDtVdfdscw6p42B8NorZaSKN9VbQ7UTTz/3YQI5h2uq/LhbNh77sDL8hqVZV9Cx07wrwNWfeDCGGMHcxCOuMVcNvIdMst+aEMTzMT7ldANAGBAnTEKYprrfUNxqUhrCjLvIF6+T7RjLAgPOwHkl76lmJ9AgFtWd8/ober2QVT1rOZ1A4lctCMJsFW5Fwr9ryamoCCm4m4CopAfaO0kxlXA1ZW7MldrhRjBBxo9YO7gPWCCAKKS7Re4sXlUlEoiyg27bCiJgp02MAiTSqw7LoMK+JOQN0pvMobWQX4lvFLwRpCqSqU3xr7m5d/bfohAyM2gKZ5lavg8DEWRY7bECoFVVqvfWfUD/RtndYHO8hZdmuMHRjsO6to3uDYMtBW/bn8JtELUtRYmx0bxsnNhMfMl9etOYa+Ird9o4lwAWqXyedU6urz44R7oZctw96NqvSYH/25o3L//7B2UEEdgwbnoa27c4qYZFHWDdI5M6VaoKdwtWEoQ+GJgQPzCZJe9VHwJjBx6IX2IAV5xEGWDYV13BTRXaBx63K7/9o/fweWov7XgKbju87K/tZPbbgvbMBpCpm6xvPZrGyw7lQz4VMXzMDxKsA4BL9BTg+0rNoKyQbl0YRxQ775ZnvEO7ElFNvZ3nHwuKFTqaxSG321C5oRICtUdgnNH6BkhtLzMTogZOB36MRC4+q1XRIAcM7c58cQOgGbs83kqdDzxU/a+MDEGHE7pjDuFWGhBmD0IZooF0zmIZEQEXuJ+bjhPdO/Llyrexgh9EAAP2UDY2kE6CCBV+JFrx3jiZ97hiX9XU4gD7zkOwhKN2laQHOCxv+FpsX8+Cefp+BWf4LxuZgGJteaJn8HAR+k5bAgSiyZDeLxhuPT3zQbm8yubxwHHAdYV5M7zCQVA+SzszFAY5nRIkVtsDhZrSLJAwI8HtHWGZnSxftX9v4Eety2LRGH8bK4wu4Y05TOEjSQNa9InD22aYG4rf4ggfEk8m4SeGi2GNb2uu6ohVNw+gIVIcMLjQ9lwkcG4Jxtc+YSWPXq+EH7K5V3VO2GX9TxgawRuZzt6/DWOA0CwRetDJ1gZGCsxHSPklzYBZCtDzJ9xjfmdnvz39lf6uhwL2oaA7bZvk/j7FShpDH4l/SWChatAPOCLJIUpmEDpEkxsAhdugisSBsgwE0bLYIxx7U7XKDI0U49DmKuVKp4XtQ6cySMp067Sys30GujpMC9pR4EMhtT6JBLjWv74HQiFnZdQA+bgVAwvY+JFn8wMJkAz66dmWNyQtU3u73KzXsdao2JUuG4yCPGr6+u1H+BaOaj9MXhlVdyg9JXBTR0Bqca8AqGXKkV0Kb7088RE0W9mvlDlvFu66plVwZav1EWMihLbW/01SKhmBy75p46t/OUlm9OSPrsyrqFm3q8uRYZYE1/8+e0L3379xM8f8XmIBWNJiU06ARAwSd+jYqhZr6JDfb0Mdc49KtnYWUxR6+e653WB9fmVLTB2mxPDKjPFtdO6v365/2t33z9Xt90WgYYXM5BZOBr5jJxmGGNVsHkS3oZgZDPq9Akjgsp6B8wVNhmcDv/zOCPL332QAtBAdc0aT7ie3VcJJ5xqlwUa2HnrBnybIT5YTD+DRxAJDEbNbc+ZddOiliPg82tiZp/RNgAa3uvlpKBi6F4aOeEWjEMAIJzZ0JoLpgLMyBgFc04IGQirmRgznIt6fx8yIALsXEruDtUDv+Y5yeCo9rTaH+NznLFQA+24VUS57ZHU2YrQwTc81fBeZAn7gM6Bf3z9GoEaACLDJO8qlbBgPk+AF4EDQbFJ7dMxzwMzK0BmB/xpQMakvG3pY1Xy6Q2bWxNZgCju3w7A33OjE5+nwz37rzxmUMnnYwzG8TzwLZvVd74DoduWqZ/gdPXYM3DpLuxYB5tIxUNKs3x39qjo8KUiZG44db+spwaa3hVLyZjphdjgXEGFbI7HGLCRyQIisG4rSBlBXa2VoGCCSFSm1pRH2WcY+5wOPGRVjwXIfub6u8GdW1w5dtz59kjUyGvl12GLKtvSKTHqpIeQQECdeDBoj1uMrOOchMdWvTHh6zZTZ7ZmFbKoSijVMwlmfFz8M/XoqSw3UlgwzXFMAyXpDe0S5BZUhDAh1q0pxkwbYzDwSFSPKrJ6lGsNCbABQ2OxmXrCvKcvKIdUzGL9IoApycqWT+bGF59bwqmbn3lZAyA0Ysvx+/tX94x522233Xbbbbfddtttt/3h7IeoCA2izm5BCCLeGTl4BJ0VmRMI7tbwiQWNwysWjrwZ1zj/a9w+Xqs/BEk+9Nw8y3pyqcaEek5hYJNN5FIuBEmiJBfFNl/KLykLiu+BfIuqnl6rVinQ2iXJ/K+LrAmBe9XT+Y55jgqPunYcVNb+sk3ZkCuUL77MhM78kOfRsiL09fWJX7/9iqlnb2IGnIl/F9n6PK8XR6CujXEyuDWdJ424p83YR1D+LTTu5RJyhF8uqTNcWQm6Vo16TFaljy47q3vSZfIfoHR7249jX3NCioLZLWAgBYk1wmna9NlMDDufhfKAjBD/20kWA9LT4OKYWXWYBowLFawTABvQZ8LxUvi4/q6umPBO4woLmA1aWhDMgG+LyjoR9ButJ5+ZgwXumZTessMJGHvs821sMDZYZhYfbxs2WSnVUx16zGYfYh7RH1P4Pbfoz8lXipkD0kdoTZPHYADS4qNMjjltiTFvAzudizacBHMqnkmR+7aF6sU8nnlIgcOw80d8/eMnsFjj49k96a1z3Cige29vD1j1IPLEYYavQiC4weZEzcTEDEhAc4Doa5pqvQ4McvjbogR3n5imnf0NiCVha7z8wKkT7EdT2H6divOpvWrJvgWrVa7e9qWww8FZdeQL49Ztt7FvYLuscLTELp3PgPWnf3XajL6SgsOzwP2M/pUqx6QOfMGn1Mo/KWhmFmEvBdn9Tbo6I3CQLci9qmFiLmH30+GsC4rHsaifptiqEu9ZfbbyPQSnW8OJjQIWVsghcgazt/6jg8A0QMnjPKeC1hQKQEAipSsac9FpAGSxn5Fj6oRaiWenkGxV8nkD6IjqPYBp5V81jjqoxgs9wKEHNoptzxRfZl3xZhIIjeX7ztBqc8eCF6tj4+VPnxzDVPT9JAyMgaNKYZZIpIKpueM8aGEQIYBOWCGyRHI+XgguSFQEt9ZvIOjmeH6l6P0gnO7QrJqzTmDbMLov/Pefr36IQMhpgFpUk7AN4EGlSnziVL2g3wJOVj1CJf5lmO2MgLOS2QMdJdKGTM1X2NkgQKc1VC6CL2lIGBHBwP2SmMZLehEYxuYBs2yI10wR1g7gAk/aTWsZVvnloTdHQwCLElraGRKE8nA5XFJVybhkB+CSk1K+KBLF6Ap8PFkHVuAYodUKjOI1XUKycQ5UeBg4nLR7E3799omfP58tWEgjXpAlMKaAKZQcko9aXP8VkhfnWEFnTASAI3sNYGCfa2LO6baHyZH3tQKfFHy9xDDsWabtWOnfvXhXeF06aO042r/5/m1/VDN1eC6wThH8Vx+L6wAGX+ClHMH9LHwqRUChgFYTSD6zlgviYxvYtkvzKWWzcMPMGG7WyYMQSGWUkBBxzAFbBRi7wJVxJIVz7CYo7CWDAgwGWGFF5KBHBBZSXPuMz+Nf2HPRfxtBmTqLcEY2bG+OWRh+s3hTWxjZAoGREeEYhCHZ//edCOLeSBHDLitQ2XYBmywIoAWxysd7QMiO4wke7y2iaOeJfRt4e6s+JoXP2fkPtRAjKCrraRqOIC1I3+eXA+y9T94ITBc1eI6k3eevn2tseUFy1IHpBygv6v3xwGMAX2d+fyKoakdh+E9AHVPfcJzf8v4K5H2ggD+uhufpS/ReHfuD8JE9ZrI4gW+7LUhCynmGB41zPp8bMTyTuPFdDurqficsEg8+G/7rxHDX0E8DoNPh5jlnASSZ26j1dlCINZcz7RXjVPIz4FpFv+wlFl8v2Un4omydHAVde6YI9HJhBYvuWpOsZeTfhylA3MpoJd9RAYCM9CPKfzMCjF58QDDCj8xJzhlBFFCaci1EWr1NAGNrIgInA6aBc5xwevZi1ugrhKj9SiEGjJf34QwzwqlFhY7W76m+7BKCriKAe8xJY4vP+2YLk4e8R451b/PPlbCSISmJkvfaLDQ+e4pJv2kAZ/tkBnbH420RLOjhyKUjNK18dpLM/Pf3r36IQMjgmHVzq4GsbyzDTZtZQ9whIBQb+ySDmeLqyHp2/9XCQeBs9qvVTLvqAxRDikO64hMOeDnnjsScXnCUVxYVJ46MLKjh6rOckza6FmYWo139NVkMrrUHf90EVQ8BkAQCvLYni5eWV3MdeeHJa4e502tf0jVoyC+1+CnH969MdqA1DqcZDjsxi9hiKiZPnLMqQoI5J7a9EKbX671EMpfrin4Be/l+nM/Ck7rbEuGi17qYU1bvKqsMRvQZrcKO48JKh2tYVgOxWkl7jG67Lc1APR9xlG0xqzleGUO4gxCdwVrm3bcSjfJzaslqgB8bxFev3y4CYonKAQAoYdBitTSOSkuRgw1IMPIUEYEAsNHUT3Mqns9j+e4qID+CXS5/5+fEtYuaZOA8J57P+sbA/vaOLY/xdf4KndyNwsxbZluLAckhJHhU74wYlAmU1zQk+gZVHVaORPVLJxsew7CPRbRyPBWk2vMNKLQ5qop16MRpX/iPnyMw+uWXn0AWuk0AQHqCnFv34zTHTmsWPecTz1MxiaD6lffaMYiwtaq0ALLDs7/BXQFjaAWhCG230nASi6TK28/JMvfY8K9vn9339PG+4bAnsr0nGAlF4Dig+Uzs7zse2xs8A9lfj08QbXjPY/JuwYq11LZx221ldBWsB5Ih9Yp2KKn1rBiQoAmUyLN/OhK5QBCI2POiV8gAdm/R6Bd/A5FkJkEzMMS5zK7OiEV68+gJzuHEzdhmx8T2LmBEhTjOc3+JtsgmJtCJZyZ68W2+O6WsNK/PRARyW/5J6lLKXpXcCNTczk7Klg9ZY6nwTEjnZcAgQqu4QgwXb6KdyHx7V19CiomatVcoqlg1/6k6lKwrv8QzkAG8NRkC2EEsK0EOg9EEcfpgU2B0YXQzvIJl0np7WiLaAMAWxD7t6BoAJ7Au0hvSHM9iH+YIEEsbahBhmsGy1+rKzPd72Z06uu2222677bbbbrvtttv+cPZDVITI7FKFYIhwM3GIj4hgm/I0WOIWdWxUCK5sacjKn/GK5iNeX5F7t41gwavoJS5clIGJDF09RKQB5essy4zKi69KBxNnVHzJvHyXlXHijrwlv9s0iJTVjwskMKpcax9MhEuiGeBkVatMjAWtr69dvkDEvjc1v55iUkGucaX877t6UkNVzuPM+5fVOp2YOjGK7gpY19Dn9FKL6aO09hFlmvgCUzO6ZLC+65Rq4F9/v87YX7ZxunRXJVzwWl0D9Jou+vcDdtsf0r6mYtT8IwB2wrDIuCk7nubgs6rRExttzcqkbBgk+Bhj8T2ywYhh9ZwNgurZFWUhDihwZ1wdwlvPgacbxAxCoQZOanBoZ+T0K+o0lu8pUcBdvubEnoxplpgI06qqZ1U3J5gxolBzJsRvmgREhGr7qMoXvl3IoT47e7kJQdTgWSGaU3tOp6zAMoXOWUE/TIEnKfyZ1RkChiwG0c0ZPhhUeDx3PEQgjc0FSBxbwvsGDRzH2ZX/UydOd+xJbT6dIUPg59GZZQdjE+l5/csP2PwEuldh4nkCbKVrdmZlPj7/vL8Doph5/7+en1AYzmKh8wnAAy4CwIgx5wl2xUiNJlKG0Wx69I02sBAoH0IGwchWVZ3u/OZty1wVnNl3J4JNhSRUagIYoG4LcObwAwqBww5XDch5QdsQlRLuSgeF1lDBYDX/yz9/6cROS8dMKPogpfCmYDwv/T6mgcep+WEbA4KBSY4tCxt2BjNavequBB7eKDMiAOarTSAp7b3wWZgvUiKhPbktNAgHZffUI/8+AGIIU8/TprH/mr/cFEHtWdelYBWolE/CwEzdTACrye/M69xAoIbvkQN2Ll/JPKpJzWTne1TP9AlJH0uVoNOaYXKqY2wPDIkKtM8vqOHiP6ffKuXjEWSsfnWiqnoVzG1kyWdtH/72XNIxhKhqN4SZACE8Sh/OCK4GzrVH6H9wSP8v2g8RCJn7aljdNoSQVQOgoyforEAoiB9bR0jLQVjl3yrjLuBYaN/UcLN9F5ck3KuaixPktqp/HqXCeu8NUaZd/TmccCw0JGtjRqDkF+QvmtIK9sExgVya1BRXHBvy5yuEbv2RiLL/IMvHKLErauregvzhcp3kl5cAAC5l8mzfeS1tV/SzDtzXPSjEZOvPp01s2F8pKD0FXVeUgSvZAeVJ1SJuCTm0Ljcn6cQSaoHDWnTsEqet/eHydRicIrBqaNylnL3O6SUUik/NO347Frct82nQ7rsrxzPfUAYeRC3i6QiI2HnkwuQWL6oA1eQxhmDwaBFO8kCmF3wWzNDTOjBi9heSGKYR2PUWZw7NDm+H2DGIwXsFLQ6fAU2hgld5NO0Xnl14IN6muk7CwWeLK+88QB+jha8JkcRqoWSKeVNLFFZDSqDmQ2JP+AqhVFiFKJIoOcGcDvg8wdkXucsAeAdV4sUZmI5HekfMgAhjFpnL0/Dzx9tqHD5n9hXF9h9vOx77o4UhP4ihUzH1wGNLLaItyC9a0JsJ28c79Mx+q5MxhuH9EQP3r6+JnaT1mR5vBNl2PGcKtGo0HBe08jwnDAa7iAtu4wHxCSvHEIpDL87HxiAhWFJ477aDSHGWE/dc5DW33UaDoNkL6IMxNu4FkkGYpg1bkhkN+9XAzgj4LPGCy0GjGf8s34QdpmgyBeIQa9ZMmogHgUtFKZa9NEcmMOYZ800TZrGAlMBJMDI2AnyCjeEa53X6Cfjs3mMWCtrpYnDIJG6TbhGBXWCj4FuEjQ3lAlvpMlaQwwLY8+IzziBTuWgykTkIK0myScwl1dvEBOiwbiUgCbIGLR9lhjZYBTEGgfm5WhuofKg43jTDGDtW9HcmvC8CUQAY/IBBIUXgYB4kETn/gBhwQKT8SopMOa8kMRMt/0uzS6oIG0yjz6z9LGo/sUSjiRniDE/4rzMgbvjUEu/miIa7Heb3tx8kEIqsJgBgntHPkc/vzgOHLuCl+Uzl2nUjYgm/1Eo4MX+l1WAOw+WBXEF27APhMK/ySwZT7XhEAFYLZpzf2oOmN06J8QRq/9Y4WPLoW6kX021GMJPOiYKzoS8zNRoZk/LFzRNbW+/AIJw+L44IR+Dnc/UfUUwQ1oFJXGs1ByMrYY31JQZfRMYMofRewmdUWOLKyO4bfnp/g51LU+PafBXBogG2HEPk8Yq4Iuo1i6jCSXElJwjhW+9xIcjSHUFOYEYY9SiTRMBHK6iNypp2A+GgupbaZzwBPdaow9W4/Dgv7G2/vwmvPjZyj8fjKtYlglE4clYIG856hE4Dk0XzcjE3uccimc6HzhkZ1SJnMQ8Bz6pQZzJjxUkO0AnNKIYtChI1F2myGVn1NTGDRcC8SAEYBBkD2ArHH9pbVUWyaWBdLHIyKJJQOQ2KMIR59V1OgjCD34qZILKjPTOOCObUL0EGxZtY+xhiGNseuiKILDOB8TyCaOB0xkYDylm9otDUqSoWmYBt4Eymu18/n1Ay/OXnnwAAP739FP2MmR1/0w1PBXjfIRkIPcSgtPWafRzPIHN5/1P84v0J1xNixbrlGBcR2NMOnAdhS92Oz1Px9fXZ85+fioiNi+hgjUEFRz89dpx2rp4xMKCAWDhQv+pnrhWcx1jClrfdxgTII9ExwjDTZpGLHhGvAmaQTE3rrK8KpbayQ2jNFedcq7QUU23OT6q5Ta6f+xjgjVGPLxNAPFDMKu8M2Mbt24QGEHUFKoTeA9rSqcp51SKMWWVs0lleM4WrYdF1pk9S2W1hNNMNcvr2SzewJZSmBZUYIIs4oqq5YIREYs03ucmFAdkcfR0CxsYMSl/Ft0reL79z8HYhtwKGODT7omQAUO3tBQZnh5LAaoERhl2SYoMfMFdMO/LC3uNoUv5Wjl8ne/P3RUbmBleNtQGBELjo5qbvHWuNbJWcJjhZaz6pxvlUAZCS8K/G+keQabxT3bfddtttt91222233XbbH85+iIpQZMEKez5B5hiPyKARhXq4VOnOJaL9opK1yHY2ji3N+x9U2WFhqLv/JP68iGqt/3WsCiQK+VLftyv987LOBPRhX7GWoJbMQABmvbUiBB700x2Zx5gswg56qYQJLNir8q/mwMjMTY9rVl4WQCYzBbwyEAAudNmvMDOmzGhUsrtgfZklGfuG7e0t4IyIKtmVypGIEw7jXfEhvEbfVZW5qgtfx5ZQrE4F4eGEx+U9RDLINeQw7g37Gvi150UhGnktejnKqlIl8LW2/AEyFrf9OPb22Jv6U/UMutHSFUK8MINi/mJIpsAijfYQwWP/gJp3lu48ZrAz7VWpZexjgLoSMuHDuyKgpiBiFP59YwbJaK14NscQwZbv6dMApQHNb+xMAcdYCdSkurclMcBRPq6K0HFGpfmRxyCTSx033iAhdCZSbUIgoFkV7gCfjMKaEydaIQxjAAAgAElEQVQun9DKCYHB6HHeOXR9tLKdHN098ggo3M/bjnMavj0/8/shaVBvtbvh8/zCyEl0DMYGwZkVk3/gHxAe2DyZ7WCAK375eMejJmoRTJ0NFdmGYDPutUON8eWEb8noNgZj/3jH+ZlwvOMJGYzzM/7+r88ndgBbZujPwdDDs8qYcFyfGMx4SLDfPeex7guywq0KLWYvBCSxMPn77y/LcdsPZNPQ/TlsAQsrqmPmXA+z/8y5Ki81nzF8AsxUbXEQBp6hGQAgqsXqBnmLSqsdZ/SuJNoFDJBpVxLoIZjzbP0cwKHnXKgRLLgVAOgZ81IgNbLSMRiC1c4QEL+5fDxikHCzEcepUq/l3O9T+SXZBFloGk7IWb6XjihgzdMhpdmT1RsqHnv1Fwa2Qgi1K3IG2mWRyAXteP9dPWRaCoHiA+YL4rzxDhLB17/+meM4QMxgXf1b4Oy1LNRMVdnyAZCxYR52mSTjkksChSlaPEoxhWxgE+lx/vX5hV12XEcv8BELeRStDmgWQQYl2qhuaIxNu6o/gH/1QwRC0XRWRhg8GmnCiAGVHLUHCEqE4yV0WU47cHGqLwEPEb04vtc2mSBL4IVfz7fwWrqjFS1d4quLI/0dDTShNICqvEtwWF+XjAHHhYJSQm9kVBnVJs6pHZikX4L1LEV0V8eTfBAjJrhc/6X/poFgq0EnYYArGIl2q/pmOFsXmC2IGFtid3fZMWRrSA8bYds2bInZH/ve16lY9dRRNwVVRvVF55iBS/V3cRbA6dITZFilXstAyPNRHgCEBrydhLxMNxiVTgHDLw5XuBGj7zj13buM0223pUUzcfxMbjDaMLkc/n9i9zccHg3+Hw/BeaB1hJwNmJ9BNZ84blPHY4SoIJBzw5z4+gx41ccm4MfAZkXbuoONuhdGJMQKW18CGnCYatKdATEux+QBgbniS0/omQkGVciQnmedHMoOHAU7iwlw5IL6nM/Aq7dqYiyHTaHrAsISQ4URNhCKxRVkeIgALti2CK+mKb6OL3h6TEwMVsFnnsP75tDxgGXS6zCHGfD2U5BEhB6FgPokFKctCOwvb+8ADJp4+WMa3oiB1HNyduyPgbf3N7zlu/9pClHGM+F3dDoGO7j0lTiegYNzPhLGPI5e9N/eNhyHtkP2gOIx9u6HIAL8wRhJ2HCYYriAVXEkvO5zKh4s8LP0Sww2t+5TE1GwMTRhjTv9EMv6bT+IDWJUFKKaXsOlL5gVQOmckYFoAzUTgmHfQy7kzK8cM+Bh7AWTDWKo8xnvALOABN1HZ+JgeYAfOVfME04xJwHAJIcdx6KZZoogqQMKSl8GWC0S4Z3M/BzrPi1orodDv48kZyHKNoIMnDS8PepDjkhWdUIrYGuNiqcIwoi8SbiUDsDR/TgQfUHRkxHksRKsqo7jQsIlgbZbPp5Er3ndGxkDbjP6SgFAJ1ROPP6UvTfHhE7AZWCUAD2dMFD3UAeM2lqiAPJMTc2cS8yzNeoSGV2TxOyY8+xgLPqZVm86U4hSu60+NJLog6zEXSgl8GpFSH+6oXI/gH/1Q8yYIX66svGmwewGhIr6MU/MMxYFRdy0Yv4xrmBiVV9Wm0qXMgC6FEKcXl6CaErjiyNsIF9Zv2Zaq5gl6xz1hdrqxWHOClT1ElFVJqoCRADxapplEQgLHonFZB74ek58pRMAwnIqgMi4XMPHYlLza7UEl59iJ9Ecd3m7fZ32YlFZ53zVpyAKR2hL/LwIBbd+a4nkddPK7ISOkV3yIJE9uH4nGPTWpV3VmUsD6qrJpH7i0FSPh4OIm0nF2V8Cxk55AB3oek1GnURh8IWAYVAwvyyto2vYfNsf3fScUK1Am7DttBZ1/sBj23pusBl9eiVot403bI8NToZ//DMqGbwNDKFehOc8wUqhDQTAORyRUlUn3qBzXrDjhI0GZjc4Mx7b6MXL3TFhODOwOikSR8TAXgQNNCAb93s39cT79oD+FPv49vUEY4NkuUGxgViwV6oZCvWJ9Dvw08cD4oSvbNznDXjbHp2ZftoZDo8SnrmAHscznI90sL75hLi1no4ZAecTeyU5hkHGQBJi4fATp554Zi+nmeJtCH799i33P/Hnjw+4hSOh8xP/0m/4+CUqL3s2LrM6fpWcK84Yvy1Z4badYFjrz9MIcMHP8kvef8d5qYDv+xaK8nlOjyF4PAa+SsgWhMfbAzO9TD0mnBmDpYOp9+Hw3ZvIYvMdeBt4r0Zvm/inHtDPDCD3qtvddhtgdIIpA/fsT+y17cz+wa6MBD1CVxQ8NYR8NhmCKuLdfaxEMBs1N2wQR51d5WSKNXeVrAUPInSXkVIQrVQQA4IJNXJHmMEyIgjJ6osgXKmN1rp/qoK9xJMtkhKVYU0GXeR1GSyTozlXsAaoiFdS2AUrsHGDE4M27h5rd4a5NWkJGYE3WsQDHsLbpfdmRCBbCSoGQbfXnps4fJ6jzlgS8sWf7rDTo8SX58hJRNBJfArxXKv7x46dN5QwrB4WCabqn8cB49EVIDOCCbpHbJCAhodeGgDVIAqz0gxijgS8oIkrLIa71xIHQYw7eU0SxBh1TmKX6PF3srtH6Lbbbrvttttuu+222277w9kPURFy08j2AYFLJ2/M4jc9cU6FZ1RcLGdVDTGEFg9jMc+pAxu4KyNEkaDlzhwWfM77+yjWNQBgiYC4sYt1zDCT6ClZ52/ZH8O49gkRX2o2lLjVZrsL3YchVQEibMJ4S+z4PgQD30CZObSxwdSgmeE4LcciI/+iqL7CLZ0RrCk1tEGNcmGJixplFYjIDczc1ReiqNZVVSvwrlRkV60DMJItRBISd86qYlF8x7n7AIgYyp6wwTzvS7UNZAjq8iu0TbpUa24BDdE4xpca3h/vaPyeI/HExcUfWzpZ41wJ9KK14ZXj7QyGZhWxTuqmo71tGVOTq+EwxvmcGFtRgyrmpcL9nMDYHG9vCRelAVhk1N7esg9SJwiKWQgLJ0AY79XbsjE23hqTrwAe+95zh5PC+cQoqAptULfFEgeLvqG3yixasEC5t15Q6Ido4xWUCPo813u0MYYbqGBrbABrQ1Ee24bH/lPDclUPfJ1H9+OMbYB3gWZG93CNeVO5vzOfB3jfeuwk4cxVTRu74J/H0T09gGEXB++pE3Q65vyC5v7OOTFpJmwPsPPEr////9fQ3rePB96I8ci5/DgUX/aJ8QWUYMk2JObNHEungABXlUpNwc7NqgQ6cdrR1NdfXwI6Jx45bt/c8Pw88Kg5UwRf354N1XY1nGqYIrCkm92F8OAHPI/hYOA0fEreOyI8+A32FhnXPpfbbgPgtGDexLGaNmJ1BnsjZ6mWPTL89Q56UUoLoRZxthM8RjOwebLytoaPE3D1hTyg5u1HcPgtDc+iEwC/qFQwLdbLMTh9m+WbwBVG6KqCa8Czlo4QQ4zq1YcaoNO6J1LEQbyD6j2eB5xCpwzIas1crJqezpW7wxBolOoBL82xUx2idmlX59BXa+RJSI9wVvbVqfcR4+ZAVlgAAHPCXdrfIiRDX7PSbeE3maWOGzBdoOqQKukQX/yY1Qax4FOCOGxWuUboqz0SrswWVOdfxZhsDhdDMzI7AdDwIQsFkbIw0vA8i7Et1ITHM9PP5BUO9DvZDzFjui0P3jwom8+EwpFR8rXXoMXEfxXHVESZtL7D+cBW4GMwTMcSqgIXm2J8JsB9dlCBwtAWsg5V5rtCzK4PF7IHCf0doqTZvRwn4CjprMjSHiobQ1YPkE083h7QdIZUHZ/fPjFLPDCngNfuqtefYpSu550l3ytk0BoPFxA4uryYQMJO1mSwi+A9oRc8HpCxY8+XZpOB6QqqQAgUpVtejxkRQ4RaM+VlEIEUOr1QW3vgWVc/lsF94nnEZPQ1J4YwxlaiiQyQrnHx1zG62irs0+tvPMC7L+N0221pRhPbiPf4Y+whRscFa2OcSt0r8z4IMq6U9Y5TZwjMpfOxjUdQreZis5HgV9MmUpnmIJztWLAImAxHvmenKjbSbgB2JkxVTC8oKABaqmr7PoIYYepyJAD4nMtBSlHE0hkSZez7trSMti3e7Qwi3h6Cbdsxs9fg/7T3bluSI7mymAFwMjKre8+S9P+/qKMj7ZmuDNIB6AEXZ87o+XQtldusqa6sjBsZpDsuBrP7vjA9hnOBkF299Qb0MVgMClPWDLpex8ANYCTXjVjgt8Oq+HM5PjBaqOK+QqJ15vzO4YJTpIe6XxgAD9zv8g5xTDBm7gNzvqF84r//inmuzx8npgP/0i985AYx7gOHHD1fNafj6/7rsY4D53muuUg/QDRwWdDxyAj/IkeOYuFDTnwcH123Ub1h5rjK/8QNB6WxbMmrD8Z9G+6vnLkwgpwUNBlkgIj7Md+wsbHgCsya3+C0+Wi97Nz1iqXGER/Ujp0yHHB/QSmuaeOIt7y2eQ+S2zJIlceemu/hy57EyAEy2IOGxrw+AzLeq+DcTNMuwB/JFTe9LT6CxXpR/pIYcDd4UVApPNOkjGVN0mKjZl0G+Gkk6pGMVUG+Iz71LjRETrJmeiDxqDouY8EgaS81NwtZ6XWr/9s0hSJocXVeRs6318xkiNzcSIrZFUUaE8VZw5dOmHr1/Ojx8YqXawnvVALv4HjA1B5jIJxF4qQMwkK6vPaWLL6X5UGMfwhcuDoKMYtl3nQ7wKFskKJn5rmovedXGBL6JRIhUwvNd0SFbcKa28leExx19YRhqPWmj/zOnjdvBNS9yefvqX9v3/TbqR70aN9Q/6J+8r6RCd+/O+boMNSlAwSvdcjy/nCPm7suwOOIC/DdHjyA6sQ7K6YEx8fHK2YHEANvDscsWXtDzNY8yiiUA4JtgvhvCUCnRyuniGNrqfy0yaL1fHlUPHgM/PnnD/wf/wgPjT/++AN//PHZcwOXz+8mWR5KIXRyu0THvJF3RTUqImsmKN53beaVq/X6hwjSKgh8XxdOGTjOj3x9Dm8XftyorTu35jrivw/VJX9UsIjgmJ0IPYUVNjZ+jBeuVAmbduHH6wOa9+HtMZhq1S0FQWzCpa4lg4vDLfwVgOjQvF6Ocu9+Z7fmLiduAsjeHRhMFfi0rhyqG1QNo+/TuNfPTFoUDCfGO4tLrhP/JQNv8Z6Lyxuk+eqDBPSxeN46Ncz5KGd+iKFQ3OVpMRVkhlnBOxFkHKtgFLsvUkQO0xR+GS5M/Hn8iOcwY/iEVrJkDghBr3jSv0y/qcIBFhVWzU7JdUPPgR+pKgc1fL1nJxnTDUxniirEff02gtYM4GVgCPR2/EQkRxf9xOf4ALIL9fV1ww/HyEBj+Al3w79SgGHOG0oHrpTl+vnXP+F8Qmklpf+cP0OdCxFo2USbvCoM5zgxTPCmeE35MkxYS/xNGFwPIM0hXQ1iiwHB/7bub/zeGCLQ3JddSoky4xQJVbJiSwwHjAwlV6sg3HaD7MZqbQhILQpAyP1TqOd34HEFVndYKDwUO9d3h/gN49iznWLv7XEct/REzMIPYhYZbv0Z1GYWoKpgOgAsJTslh4nh01NYIDO+ukeUFO6jCzvhU+pdp3GP2LLV5dKINCaYKq7kNDQtoYIB9jU/KCT4ef1c3RNmyENEAABOccw8jz4PwLU9EPnkMLvN6au0kgXlvkAji/XKy9NJJIyn6zURcdzTpFWwEkpL9dFOIE0w5ITlDDacYeQYeR4mZ1RdNCLPmNGs38NTvKcNw52hYt2dc/U0ns2ff4Hlakd4GxsbGxsbGxsbGxu/HX6JjlA4F1erjqLVXxxVj0peZdUjB4IqiXTL2ZiHXruAYYTlF4TgwT6oktkBerQZaHRmD3goFz0oYnCsFmi2i9EfOShvbqtiwUJRwS3Kn32fzyEPQkNxcSGE9z3bFX0MwV9f7378z1vxnsuFPWamHr2TKlw80uvvpDg8/j3VpyQ6WS3BnfS/p6cPKCgxAPDxxx/4xz/+gR9//Fc+f8CcW71qzp8wU5xHqjwNpIwvt/IcQNEqfnTbmB5zTP7w70nYN1W5dKQvf5OvL/ylDkr+sp4TLNLzE4NDoUR8fPd5Wg2+rJesua9Fuqx28N+varLx6+Dyu1Ut2YHrupb8uzk+ZeBM+oQy4TbCqCohHAzDBHX39DxDOr+p35jgg3FKqcAdUD9Q6oXqM+gpZa+DoH0oFy3kDjn9+sA5EzRKQZVPvOnGQUdLMrNIcObzQWQOsK9uKMd60bMD2aZdnmHJC8+u1Bl8vGrHx1pkgFqtNQN8DAgdmNnpuN5vuGmvgTGX+Zi/ccXQpYBkErNMryw1Kivk4Zs2KSrGddfP+4bBIKl6SVMB06ZJf90X3Bhwxx/pA/XxekHd8T//+p8AgL/eX/iv+cLHP/43AEE9+Xrf+B//5/8Vv7++MD4+8JGf2Qbhmj973f44P0L9M797ccN1vcOXBcDHeMHc8S/cOEohS068jgOeleHDEXYEWupVgByEl/wJALhpzzRuLBjb2vM99nnLtcSJ4z6u3xsgfKAk3sQ1u6grXnJXgEfPIJoAZLo8a9wBHihGvM0ZPjdlK2RBr+K85kkGyIoaFp0TFupZGzXPDhUv4zMm0GBQdbnHGZy9ou6Kg29Az4zHiOGPGWt1gEh7rbinJR0vOyXJPAKnCh3SykR4rWlMUJ0dVxzkUEezXxw3iKTn3w/EiEPHIUJQODgprlM9WfnZSRuSPkXZBcszVMyBUAO3oOiVHCcJ+NQHzZpg0FatxDji2K6aL4xoVou2aBMG9LxpxeaE0Y9nj+8szjMArUh0xbaYea4QandQgmYX/aQTfgioupTz71fl/SUSIVDIFwIxWEXusCJRWyQ01aJk4pQnzAtaPTcZR4/4sEOwgm+DgZWaa95kJ/9GZusb3eDgZ0BeczPPFh7xko2um4/QEtchSdnOPDFw697+EW4OVe/WrjnnBbaC8Tm1+aXv24Iz3sZnBneswTpYkgOXIAPcYtEqKWqmDDLyc3NQ1RZlMA6yLmhrumAFcRLUkZxTuq8vqN7QJAubR2v6M2lq9CfAb4ccAqmgjhxGCivpX6YIwPqbQUs1xqmPz1cBFJEDNnHljTyviZ8KgP/VryCDAUrOPkskOPSkwq3rIt8lz1G7Un2TKv8FOrcbvxCIpIsDTBGWJ0EAQxiv82jpajbgNCD3DRyc97l7bz4iBHd5FFqC6vDzKtlnx58fHy0wYm5QLD77a4S3l9f6ZSGR+xxAJCDJXoD7BIxzqD+u+UMiibF8jdOWmUB8JAEzmgLoHoaGRTet+ccWbODY8FsS1yNI4OT2kirMHVMNljRDOQR2HmtNu+Jc8FERFaD+7mCHEJKtrZDLjuErQQxKHOF1xlpAEoaFNa9FbrnWx+N1Al/3DDnyXoMusEvP63wcf4AG9Xqk9w1xx+sVa96/9Au33RjFl/eYqxwpjMHMeM/3miOwKBSVb5ET8OWOAcdECjbIgAhh9qyBY9AKLJ1DYGOmjO+xiR4bD5A9ChZw3JfhthI9OTDEQ/wEWdR9xEIEwMm+GbWbTwx+oaxADmKA5DG+ABi09EVixsjWHArXiEALMiyL83jP7/PWYRWC3KaTNkYH3LRN7+WOJKKHM+ON2r/NeAIacRYQcRaTgzs+iz9as8vTB7IOgmJmiTjWTSDkrcdxdBx4TcdLjhZuun3C3VpMihDGse3v5iOo/l7UupA4ePXjFXN6zzTC45QVdZhHiFHJeIHb4iOEnkqQIciN3JYE4BhToEzwnBx6+0Mg6/42y07TEPvRI67ld6/7Vp5Dz/i4Dq9OpuX39pAq9wvLz/IXMID+JRIhd+uNZSotVbP4ZdAg19kF2Uowaj6IsDbd+k5qg9TUkF+qYNEdovU9ZcdndYi4XihfMeZYKvkKDm1l3cwOOUJNqDs+hJwJKhWSDBaqC5Gfp4auAQpd+zzOOWOTtPbEqGN9Xm3P7gk/Olr1Hll9qCFrikpLJUqtzNK/zwy9bppM5q5MfOjnX4ArfubgMAE4Xy+809nd3CEksM9MamE4/hGVo+bleyRwz2E7w0rWwjvNu/pt0Ois1VdDDqdVuYn/Gq47wrzxZpw4MXJ4uS+l/5hBegaJkRza+sLz4Y9VcWMjMYb0lSIggFfxgZ0hYNxzmV/yYd0RIg6hFoJ2FW9Ozc0x144Zryzp23EIoHZ3kqIc1coSIaHkZFdAH0Ubb5UeJ4aSY9zVUbohMFxOrQ50yAmmhwoTx3BzVScZDleCZEZH4wQeTu4pSLnuIA9/sLp35nTMStAQa0UZKVfSSExRra65SgGGrEoiKdCmQUAu9N6ePIMAU+6ZIIOBiXCeySbwA6rLbT5c/bznooSAl0WluSrmehl+zhvvfE2G4boYX1/RIfo8D3x+HOAs5H1+DHx+/gh1QAD/47//H7jJ8lRhAMbQ/C5uVdAkDDnzu40SK8FRKl23Ofx2XO0YnpXjKuRl1fZMr6PX2D5CGwvC3t5a7ACGY9xNh4ChbWNivtoUNfEMJtgM18USPjkHg+cqI64CcGU6yXzp+Wh5FGwBY45mQXelcq15KvE+/zwQ68bDO9HsDSfv52j+rY1ivTo2EReYpzdgHmmM2TiOSvhowG6PuRvE2iPimLOKyJ6JmOPIzuxtN+y2DuhZjpgFrNkoHzBxrIa2x7kpw9T8AqovReT4r/ED9xXxFF6O1zk62bNUxjtfmQjJGTGlOFKkMua0HvPORms2Oo7Yk3WzhMEAB9XMWMfFdV4iHivRCPZ8UX883dDzP0/UHH/MMj3kMxwRx9ePTP/55P/F2KWjjY2NjY2NjY2NjY3fDr9IR2j5CJVMYqt1eFYNM3+8PbmcVT2l1UqtOm21WEtmVWc+puUds79Ej8f70ljr6mp3kBiO1e1hJohIa9bDGVMvHLQoYMchOHi1mOM4vDsjSg4Z0spO0x23UX9mU81OSlVVgs7nj1pJ9DD6U2cVZunWOwjC0tUBEYpj0+VCHJLZddzhpVPFG046S6nBfL0V97xwZCX78xwwn+0bRMT48flj/fyTYP/IDtC3uSN01UTVAH+v6jaF+lHLVnI8lrMSrRbdo9fHRz5foXNiZkfonW3d1yf363G9ZX1diCpOf33u35RLHPqdDke7XrCxwM/us0j43eR9/74m3L7w+fEJIIpnhwzc73c+V8AkMEFTHtY8Ytw34zUw+AwJJwC47qCHtuY/g8iLgg2mcDgvSql78fzrHog18yjH81T4+eCjZ3pAGh2GZ1PZHJwd6yPXF6FSesq7pKjAnF2pnnlkANwyrj4Affuid3mcG/BoWvR0w+mMV3ZC3kdIgOuTRkvSNA7PKm0dgtAA3IOTDoBJILx+TxZd89foBRKXTZxZ6Z5m0bEjBuV+9DVv/Ovnz54VIHeYUp9LYwUm4TPpd3+eBDkPpNUIbjWoaq9ftXb2/pXnxsq/RIJuyOD2eCInmC0aIjHwvt9LLpuii1Vr2KQiQW5shH9OtYuFQ9bZqrObLJVQXQPMFewKR6nZvvASwfX0fdGYq7Om4HP4llXXSQyg1eEJX6KnVjQDPDrOaNW1JsQVZyNjnepA8OoekAPDx5qXgYGMuyPE2RHy0nCmG87ymJVygCa0LApgoHGshnPGayxFAcvPYw63mrEWKBSvj1gbVB2s6K73DQsabnWob4t7uMc8kslU7RQmfOlfJdiHecUMTh/TETM/NXzlPsMHygZ8Vjw1AYxWGMUI76WaGHU3sFuMZeR7MgjgWmskGA6ruQd1e3xHDpazQ6L6rPA1D59fItDXUHh0knE/lKJ9l1fD3x9f/RKJUNDAHkIFD+lrOL6ZmXImKU0D4fSccXoEunFTcXtgBB+9blRP3tuis0R/r1MKiovDHsnYM0YIdcklfGAWfhyDF72ubum+uSm8PYrfSYLknOaNrDMWjPy9NTe1LpZFCwOQcpfc70TIBeOhCEHJTKnOI3mcp5nPkdSMf3piPO2SHA4y7wFD0/D0KANEN8VUxXnE7z8//wQRrdYvhWznnIqjFgOymPsqaV8F3Ca85IYlObP5mdUcZvHvQJh9mRvO9DIyNdzXG/NnfKb3/QW6GJ9XBKI+zpw3ezbeFwu5Tp7BsMbLqa8hPP67sQEAf/1845T0rZIREv9FfZIIkj/L7NQcc04cKelsUAgPHGN00mB2R2KRG+yP4xMmDreSkQ7ugWkVixwswDHqnmG4EcpizDwMDu++kTU2stY9EMAZJ42yfgAoOPw1ZyQU93+vgaA0ja5CTMn852tSBOr1fOTPVUQxD2rcbZUAEMgNw639JyCGSQZLnv/HeeK6Z69fDsNxfjzW1PidNc2WY3HOteLImUjOQMNBmJh4pw+HMGG44K+cUWIPAQdiflgvzCjS5Hm47khKP1Lym4kw9ca7ktBbYZdB8j0POUFY8xG3Tej6ZiJJI46Zn/weaERRb1ZgqZRFry7dZPCy9hbiNWf7r+vvHz7e+HWgBEh7AQIwBqOo44ZptqSvmcDkkB5Ai2IogdesgYSksvTQvoFI24yUICAnKFXx+gvkgpE+MoPDOqT2W7IYO2Ap6i4FHczKg0xxkwA+Wzpa+AV1heR9FzLQszhv8cpmoFJsIAsPyrxHol68fBtfBExb6x/MQlili0ex7t4GkOR7TgOLQL+s32P6krF3t1hHM5Z7exSgxJLyKh6iWe0XVwXYUpVwkFH7wX28Tsz5F2qBc43ky/DGkcWjQwQX7DH+EN9VKcKwWXgooeT8Y26yiksGwwjzovh9FqtKuIUxssgViZMqB+2NtPeKwQN+a18fxFE8qgQRB4HUQ9wCgJ9/f3z1iyRCxVusRsESImieaP+Y9YKe+aCsH6xNuSoKndVK8DObp+q0VJ7y8cyMdlFHiDXUwLyBmtMOAEOOvHGr1BhB/1Mlbs7wQ6ohRSaOvbTGb5CVEi2RCIXr7OOMm5TR7N1USOodVB3kD+MyigSPseaQqu7Y4gd5gxS7l/NzVKOs5omeZmuAfZvvAXzdJB43Isr5/TggQ/D5GUnKn6DzrVoAACAASURBVD/+xBgDet+4e5FMRRKphdhjQXwYlxFWYjwRg8Ezu0xmCnfH6EB0YtLdVZVbb/z8+RMfRwyan8cLdDAGrwpVvce6wr5fQYRY+P/DaHVjA4C8JNQrEZUtArVC0gmB6Rt/aVyvL/mAMzBy0RciDDpghFZXvO6B29GzMjIGQIYjBT9uuQBHzxndmFG8yAtY5wTIV2CRCc1DNw54XM/kwNsn2FfAjqxUdveEPIL8DqAIgwfIqwgyQTRSvRJwJwhx+4O9bwXpGgTm/Dw1nBx/Mzi053EIDCGJ4WsAP68rfC+OavkIxtAe/J1RoF3rtOe8Zs0PSpyjUkwyzYCvFlkZUJ7Iug4+B+MQwn3fuDqZuHEcL1R105TCWPYVx/3f7wv8vvH5+swvQ3HIgTMFHoZccBDunGNSV7hrsxacwqutzCiZs+ClDp4VEHFWXB9FLqZWyqScoSx9B93r1cYD5CuJJo9iqXq0LJ3iWqpVYFpU/60UVKNtGzOMNdOjCqNjJUapKEc9oB+JfBWrebxSGbYKOTM8EPOxzIA7rzjDItbomWy3FIpZsQswwg8nX2WAoMx9i5g7YNYdb1MKEZkq0joAUK+55nEDaRmdmYHHmkkiMggThMqIFbBBj4J0vB4Yy5so1Yu7g4SIAWu9Y4v47MobN2a2l3DFwAB0mcAOGjD/wEyPH+EBGQaoYbzKpIfAdndcqZekiETG0eqgYYCvJIXMMFuhMpk3NUc5s+tQxSiK7t6j3gXkelXtIff4ruURN4oM1CARkUMfLJtKBP9O/P09qY2NjY2NjY2NjY2Njf/F+CU6Qgx/ZPJZoW/37+hCOFbl8RurqToo5N0l8qS6VaIZ7b3F63cvWttqo7oz2snYk8dY/jHGKKcZILNoLHoX2HB4dJIqU1YKl/JSEAQBPARH68nGsTaH3vCtStLdmfb8AZis5bSNQqmqVVQQMwNBXskKqCsI1MwTs6jMlmzvyPNShM/QjEdXIJhjZqlc0MmjO9MePecJHqOrn+eIDsznR9BGzuOVnRfH+w76iZpjDMYYxSceOA5ZbSlmkFnzEN0cNyss/U6kfE66Gn7jut6wohEpcKni6yt48ufnG0NCtekp/hYKWfke3SF71gUWrXFT4zae+DgEUhcgI/0pqqshcD3wVVcX/8QBhVPJx79CGY3nw827KKxxnX29L5gr9J0y9beGD0Z1TpxhE7i8Zmck1ROfHU3rKm+uVs2HjzmAoLEtejpnzyMpE2bZ4a6Ozhn046bzRU/jyLVGrNQ9A1MnyDQ45wCID6gDN4rqa03XoVQ5s1TmLIXQF58wTFiteaoALcU+goftQNGRa10v1UvUz/F6EwalG6Pltx1vI7yOmHsaI+agruta0r9CQavJyvLH58CAQ69yXjecH5/dnTGNfWcmZ58RHZ8lfW3ZzXnwFxi9oBFxuK47QaTolJZ7k/d7grxVvA6WWCfLE2rs+ubGE9/XBk++Q/2OfHVrohtx9j0FumF6RRzTarIM4HpsoBTc9eoaeHZ0ysfRFMbe8ZVryGeXnUmMN6DjEqTScjWYbrdUhJNeA8OJzXq9IUxIGwzEgToA04g76DggEFB2Zhf1tai+OQfUxx1MICq+MY2Q/BaNWUQkfdhuSHnuPCTCgZw9n4rqN4wz3u/JuDG3prgSCDBplV74F0wEP5LG+KX/BLlDSrWXBIQBHtp0YLsdPL3XaT4zlkwGTajGXU86TJB8uJQmozNW312MqSyqHNW8BfoQgrbra0YfPsHs0NxcBg642epC3gTQgBw1L/n3x1e/RCJEGN1uhGvIqlaSoRUlrAs2Bm3XXRfiCWiNeCAuPXuIQvKjFXf77GQh3h+AxZAZALgETUSqnSzc6Vi8nEVbsqWxFaSxwS2mGoWk/b/xuOtzuKdkQwUaTnDmxyBSeRcl1xw5xVSLCQXv0nr42FP+ei16TAS4PTTia/alAip8WxLL9LUyJ6Wck6p2MkcSdB5lsPqJ1/nCURf8OHGcJ15H0EREThguzEv7c45x43ydOHKu6HwRjoMX/z1ld+tGVpu43xfqTj98gIV7hipoLFdL7KoFNeSuxOu+gY9s9lMNp8d5rDa5QZNyWedtgEGPK+SRQW389jjl+LckhnBfmYi7YzrgdxUjwjvoo7jpPHHP3NgzAAd9gTFBuVmdPPBT/xWmmQhK9hjoggS7BJ03ueq9sdaeHYOVy5/CKda8WmMphBKYOMyqkTMpsL7vQkZ1FQMYQanp+eiI3nHnZwQZBISPKtyME8oKS6rJbTHX2LK87lACXAhHvoaDgr+e69Xb7pbWjY/NQaF5kKAH2aLqalI4fL0Hkff8IRGDaUDRWrM4MOBHvhwD96VwYpyfcRwigmnLz20I4Afj/letT4q3KWYFVj9v/Px54/yI9/jxSo+0FD4YHLOhPRObholF2yYP0QMS7ySV3nF+y3DSSHEwg3Km4gBDCfiq83j/AsYcG78MQmBk+eEQjt7TQwSqw5C4P1k78QcfYAqRk9oFBxNgB8hrlCBpbG1WGrPEK5g+ANf2uhl5T9U9EMVZ4JX3+XRAwatoUmEPcRdPYr7ySGoa4t5QWzPalIb2yVk2u+DmsMyuRKtoXpV0j5npGnewiJK81lYPk1KfDD9LbCrECbg/Z4gneM9dUFKPk/LM6aeUa8lUhdr6zMYDDG1qHNML8Imvu2YYJZOvuM9vTVlzItxXFagMRBOWScbLRjYJ0kDVQ6zbe3aTYU6Q8vFUA3x5rfmgbwIPRAzy2UIZlsncQeh42I0hQrB3vMdfPDF44CW134XBr+a6rNtQNcCPJDM6IeihONARQ/vPahhWU8hpzft0HdDtexYLVNQfsEgWVlLs/b5AbEIQtJIKcywQVan0nJ2p1xcwVLwVWPJFYQj+Zb29+Qpm4AT29ZmI48atQIPIMzl8HMPzv0rd6QIA7kB+da4EFAljJ4ExTNzmWxzHvoQqQhDhnUmGsobTez2bB+R4YeTg9+t14sf5Wh4ZHx84XyfGUcme4n2/cf11oxyh5xhQvWGpssQgKGP5oHF4DtWsgdmdQ3aPxDdk6OIYRTDGic6joWCWpfaiFgawdPfNzOQIA7jyO9I0vM0FKytk/27AurEBxJxPK/0AgEgrJU6aEOalymPRJa6OAY8RKw85rAJXJmCua0zzWlzmfxkC2+KiE1cysiqw1dEcBNwRTcej3WE2F6/bGcYKYsXiiue9mDeWQuC6iihWgVQiKfbt5zVkgBRrVuo4oUawvo8vfB6Cmd1msgHFhLZPCVIU4lF2YAK7rISAGS5Y4i0eHSmqpBQOIsGsaqgDxxhY1aU4R54+IOFYT495iFhBXx+jE92pBrNVNFEPA8KrlDEZYF3CFirh03TmQPRPvXF9vXFlZZoPAfvAqAIXMY7HeTcy8Aiz2hqypiFgtZ7HilmqUCoFYsZAjcCVKH//qjZ+czhNUIZ6IYxwr94JDxDbip3Sm6eJK1deg7wG6pEFXu+ZEAHUYWWsblFe5Z6jjHnDCpSJBeNec5WGmG+s+16Eo8BU95gQdBIYBs9ExiVnI+s55xHXf8cRiIWxjK2dAObVtRANhd86JkcIVdUMJAnM0lwWWSzleFlKDyY/BOLe83+HSLSx0nAVY2Rcka+p8ZlKEfk1Bq5LcWbS4hbGptpbQcxqMa2Y18CYVqyYiIsFhpmfcxCBj7PPvXvsP108coKMD1yeprBOEFJAa4Z1APxQCIRFd08rDlWQPOJUU5w0AGLcHcNPYEZMCwBH7kUl+sDZf8PNj5//XvwSiRAe9AXyqLBW4EzMgFBn0dEifXTnsmpZlY18wa60xU+r2r/wCG97862s2gGivrGJGE6PwMQd6pZqczm0RlFxrQtOLcb6RgXfiIuu53TzIq7OVnWMVguynlebfrZtH4cRAdaqdkJHDyADQc8LKah1rgBvGpoRp1NxVoWJMNO4rM4LEXoIbgzB58eBz3RJ/zg+Y9NOSbcfnwPnOHqQfF435j0xbfb3d9uN9/0G4b/yNU+IUA/nhVzkeKjvcbZQ86YZoepURB45Tnx8OO5ZN/INGSfO8+hz8DXfGDqh6Wwmw2A8OhU2KBxLMtKTUuNdNfv7b9SNXwiOvk8HZ8WsggLk/lumeuRgGmilH6TQByu+3rXpRg5uKbAgMsD8wjGyizQpO5rx9kFbWWtk3O+2VCxpZLIfjyd3nHL0BnvPK5Tu8GqzPyIDG3rNvM0WrReVTHnfl9FZ9q4cCjiKOaPEYSg6x7nJf7wIaif+2Z1a4NKJmUqUAEBa4VjSWVKUpsQPaESxaFFuLAQSWk47KH/Vff7SCRV7SLxSLodpZJsbSdGTg44jEHH89c/4DF+34xhH03RckfSZ+EyfrxOHHLiulKwejEEHpOS3bwNj4LPMc5N+w5UYM4HJmjo5fYI01/M6LgLA3GrqBvpmlHhNBWx2gjhGtbg2NgBj7yCUQBj8EKMqpdmipmuIjCxJeo3AO0MHIIxGb7YVV4RiSaszVgDcRdzBEF9KZvdtUFuqYgyKzkLtv2aAL+rsnA4Sjk5q5W/O4Od17oa8cfKto2Ndndiu3DQNPpOmYoWwgYc000RTkU0kn58qmEwepqkIAQYCYSRDJvKTsU7UdMxhzbApyv84KuZzsEgXYFmio6Md63I0ArLzr3DYnB2HCtJSQAivKlhpxH86qwAVp2IRohjX/V6iE0RwoqYLQyIOIqvnU46SWH/XLKPPM3OMHRhZx9jDXrjxBUmGA6kCdq+OITOQe1bg71+vNpl4Y2NjY2NjY2NjY+O3wy/REfKsya+fMlNOEKxZIU3VqIS2/3x4wyTlrCqNBk8aSdHScibnUbggWJtQOQw0CX4uKoJjdXeUIp8tOVunaGmGMVl2W7wMTrMaIBQp/5PGAeoqb/RmVycoDuUx0kgEcWpO7JB4raVZT1EReVRIiaI1vGiHKUqRNJwZ3eIHLzGMTGuoWiSqR1WRfR2CYwwc2dMWGWCypgkNEbzG0UOP095QvUPUoVq1UJChZ3i+7nec76xIfR4n5OSWyBUiMDE4S9ckaRZWHe4h+EN+wBH80+t+Q+RonyFOgrHbxJW92wEAQ3tmQjU8EYZUpaYKYPn7bzLEG787zBd1ZFL2eqqq5wzFkkcGBc+8DIKhBtc3/Lk+UXK78yHX9QWWj/bOMhWYL/qK5NrQHkAwOILiAsQ1T+CWRJ1QuMlj1jk63E6Lb+7k2c0u+ihVy7nfg2kN+bsRhMOrJ35WTHacdd9qUE8tf284QGz4yM94DweNA/PnG57riWajpdZ48TVnAGTxVmOZi3MdVGQtDr4I2K3X5WkThntVnoeEkEH58yAouFrVT3eQMugC3veDkfDwZoMzBgnklbQPim+6bBIOEdhD5Nc8OlIlj+0c/nVFTbp5Vtu9X9/N0yy2ZgsQPL8qmZvj9kdFHhx0ltoU2zh8YwM4cfZa4GAYO7gDKnxjmajdAAzWszEEpTvoct2hFHApvOSr5ghhvmRYlWg1Ea7sEuXvb43Yp/ZVZorhOSxOZ5jBp0WGxaiCMC8KfLPlvf9h9aqf/63jtPh7rUfm4YdUXfQr+8Q1NUAE4bzPEPM54BRZqFnjOuaKSafGJ695dnKQrnkrlgEw96yyETAOXtQw46BS5ycXJhhd3WET55xXzyPVWIcV6BkgIoDFH4yaGOkoSqARg0Qh/pDb9tGjCKQpvt/eM6j2fx4DIXzpFvXO3aGyhCiYBHKewFf+7AqMT7j8jBdRIKKwojb+/VzeXyIR0tU9RLC5Fi0pPDGeRLZoeVbCUGpuZYIa/xZhrOemSwao0QpGyrCzboIZHNa+hTg4qJwGYLE5L2rKoODxL/qaNZ2uIElzK65mvV9f9FTiB/meCIPTtenS4884TiNfQ4w5CFy+HA7PhGytbNFK/u4q8ZwtIAphgl4MbFH14udQoOuP5IR5K95pm848YCfhVT4f6XCv6cFxXxbqR+PAkYGCzjfe88bPv+KmMCf464VxxMzQYIff91KtkRNjrABMcgiyZi4+Xh9h5pjn+Yf/ANHDWTnSLJhNzPc7P9fEPWm1i51A46NNx2r+a7GWNzYWSLypT26OCxMzeeEGTjGOrj7kOrTmzW69Qc6d/JvHvSdlQDjfOHJIGYgNUdW/i5740xSYADpA6Q4eptOMWYGHGVwZZ77ekZ5ng7w9dJzomzIUi8d9UbUlpmX6iQhUiAlSFNQvw/xSvPI+P48BIe1ZqakGtS+8v955nghOI9Ze+8rjYsgYeHHRxg44rAdznRnTdBV6OM5F6q7gZMGNrzZRPPUDarNd18OvjmCdKETCUq9P6pg+MY0gr0xspsS3VsqZwuDLQUlvmfcdoUZSAE8XfAG4qmCF9FTJ7+pkwm3LD0WSFmI08/cDBIMwYLkeiSFEa2qQMi6YRbOm2AVeSVmWRxFxYwNAU+G4/AnLdGqkRFuuZywvgK2LgDWTMgTLP8cUmIse1RWanuuOgmspJ56u8HM0bXZIDCvUjI8Zgf3AITXHFGMGFQMyM6aHYENd9AOcSox5n3EoSK4gLu6RFQdohEWV4AkByjCtQrLCxyrIE7KgXNkcZ3JHwKgEjULUybQEGQwEzeAPkdjQWKt0jB5DczbGOO/zEqiRkORqWuIQ0JRQWatPRXP5YQIR3JIDXhznVMrM13RmqGoYmAKYHgrHLeLFjslYiZHe8bssPPs1I7auogzFWt51vRnvz4eDc3b8PW/gJ3pkgowAXC2AFl5FV393wCf+bvwaiZB/u96yCpFJTBUlvyX4/vgxqhFMqxBWvy3paQaiMuuLa8mPql3MhDxd07Pi0EZP8QZtPDokZ3FyM/Qk0DYPNbmb9Jg7IQLsmeARyJ5DafSNe17/qQQxqrHWFdh7xhBc3+ge23p4m+XGTpnK93mJv1bA1RWV7pxlgaiGGhG+w7dmtHRduEzxnnFedSrk48Bnyt++3xeur7k4wmZwZhwncCSf90svvK93y1t/zjf+S//E548/AcTjCICXTLZ48ParqlIDYnlexjgAwqr6ErDqrYghcmI4y+IozzfUDDmSASYPHm5VaiBZ5KoO0U6INhZ0XkvGHQeggKVpnvqFMT460HA32DTc+fPEhDBhsuOo6ysGPrpDOegDRApK+WTSG6yP6zH/Vh0jx4D5XL/3eJ9K9F/HGftkmeyZ5bzPkqKO+efHrJMb3LWVMwcO3PpeBQqPDvW8Sm471sW35ZyTGj7OF4jXeZmTWvLZdMDthimBU7r1dQqIDauxQRAOQ2YgNvVLvRnlkhLgtdxc9w1FBiPxJjkd2moL34tHuTRWkiIisQ8MxlHsACY4DJIWASwTagrO7xuHxGB3LtRvugFDF36IIxir8+we+1QrnJIBZL0Ri0SBidzB+X3dMwp3ld8QcQQVpZzpjgPcAZpZSntvbCDDzRZ3uUFGvcerTYTBfHVAI/FfDB3gZE6FtEfHhmeHRwMC86eYdRRkz7MKN3GtVgDvDxZJvCeDRVs9jMaIbm/+XilMlNlXMfsmgpxALg3QqSAhkD2ET5gg1XSgAX14ZrA7pr77Pj5OgU5r4SiRCWJ5rAOxpD98ZeN4iVqRj8XAugqsph6z0WcfSBRXKyk1ADY7PpseQgltAutxDCWa4pKvmT+/xoBLiFu8Uzp/OIGUV8dGbwwWdMLoFoyGUg6Gg/zuYhDc4/jeUajmkL3o2azpnoWaZAG9TpBQFLRzLondgUGYGWANiWkvSXlOhYFZ2mi2ikB/J/aM0MbGxsbGxsbGxsbGb4dfoiNkK0kGkB2ZzlBjjqW5oc/SGoJi0V6Cj/KmkX+ndmOl8uIC4UWFm5qdmkdWDACzuOPMCG31+PXZldT4U59GqPVfolZPq2MClnqdpzY7dcs6aXKdmkYbrOgtnGaDw4v/HsfXbBWOVi+VMhyyI2SPyks9VNa/ONCUi6Alcnd0KE1nq3V7vTXYY0W5wY0Lip/yFwDgX/cbgxjnR1xWhww4XnCy7hbDHfd94euv6AgJMez47JmgS39iyA+MrPv+GC/wWJ5NhOiSlVoVVeXVHx0jLHU+Lm4lqH1biBk6r6btmBtudXhWVV7HjcWbW9/exgYAHMcHLLukOi84jm/+FYb5TfXQHzS1MQgghjg1DZVyyqUNfbOT2/4UTFFBy+tQdYKJuyvFiDmlJnaaQx/3QDyG8EoaG6tjWnoCUXWAYhGumSHAg9lR8zdmOMfqbKjG2lWy0MIHWAQzq4JfWipR8fo/3z/x8/2zu6vTHF8+IQfj4/VR7xg0vqpOzxvytBQww0nL4ctcMc2XlxoLnBlSBqwek5xSstI0ATBuXdXQkMzO8+qpQGrl0REKWSSMO9fAc/wAHQatLxQK5qXSBAfIpddQrk50qTjR6kQBWQ1n6n3ATOF2QUii2whAXo45NZkHAIhx4G6ZcBhhDoLdsabe8++vsG78OnCba+9Pio3pupaCBr6UY8lW7EQpVz9YWllMlHHhWvQqxJRHsTJCQWyxX9L1rEObAcac+lBpVdi9Yhn38OKpGHAS4YRjgroj7TrhxN2ZMCKYabM+1D3iwOwyyYiu1gpDQn22uljDYy04mr4lMJKH/H8cKAkeTKHn0ce5c/aOK9xipkiSQRMfhR5y2ASnB51PS+l4HYNdq2NkGY8dFb9RzAkaAVLyn3ZD1bvb4gj/oupAW3bsqxNGEkwj6zUxYqqOnS2+u1ojGZbz2vkZ1TCviWNQnwekd1J15gmCw9fPpg4/VnxVflR/J36JRMhdl249Ugq7ONkUge9T2nhgJU5aATQMszafTCqkOK1Jt2NLUoXEjV+vOQ6K3mf+LMGja8ln9Ql2wizqASZEuKkKTACcQaBFVau7bvHv4mYtWq1rDvzVP8TnqjEVi/u4vUaC28K4W267EoMMAixDFl68fuLFY43z7MmUeyZHN2qKSOEYYzkEmwYtpMQT4B7OxdUW/fGBcwx8VQt0Aj4I18/4+U0Tny/AToFJfU7FOQaO//0fAGLGZ7xOcHLu//zxJz4+P3HmzJCMARZp2k/o5nsnKjEWzkvq2iOAXOS4nBijxfMX4pDmTVrPnA74hVwj8LYUUshgyJ+eMRu/Pb7+ejftluTAl14teUomwKE9p5HbTxh/IgdeY5IoVzLk35++VYCproQABBHpYFmBYOLmJm8UkrfWgYnF+pTrlV6K+Z74qgTCkB4UBvLaMHnNHyKDEXhv2kKEl7zWZ0g/jErm1IE5tWm3NghfOuG5fl0enkElG30eAibDIEHmc7g1zWhLhAbJi17DfDiI8LNEa9RBmhFKnme2RSEUPtBO6gB0Ig0E16Js7mvW5iCcNKC3Q7Mooh4CCzUfQfMN1zdmzYjxwMtHs19o+DcTaoIH3Sh5jGIOY+p1GxpiCTbKVwh44QQxIx0BMIjhfsPSV0XnGxOE8RHvenrMneVytrxSNjaQcXv7yhB8Gqy8aCTusUo64r5fc8XkhuEH+EGfU9KMdZL2qjPWQylvwNmGnQAgrjDiNX/jVbyutScNzTt2ymJ4FYLSC2cwmlJHwsEMrc+kETku7yIGgyGlOU+E6dY0WxkHXiK4aM1YD1nlpCiI+Jo7z6WIGcvjchFe488Z8V3NYzkDB07cM9af6ROfr4+g3ufTw+Q+E76vGzxWIZrh4NfRsuQTE4NGU1/dPc21seLnnOvsGfpBuK8vIOfdZUjMXnbRX2FzzRUSYi8pK4Mwtb0ee9MJfXrSUQjERJRVXO0DgAI58xXfq0DzmgjhmEdy9QvMNP4iidDz77GJdOyNONkd1lpswv1FQmFEMS9mK1AIF/JH34bRV0vMwqw5I0IOAj8EGLCeCXcOdY4ORML0s5IRFkrfB3TFgpjjc9a7eAQf1VViCvEDf95LptBWCiIMLIWQEIPw9i5yIdyIQcM+Tz3ks87nMxdDViKpFilKLqk/nlDzTvkZn90uIKoSdy4mP79u8Ofim8IINLkNDmlICrUMlLeRjAOfn3/iVZv4MTDVcL6yA/TjT7xer6UcxStMXEe0viN6/K/Og+ds0zrxdT1Upcb/rcljmNPQ/iUai3uJK/z99YqNXwlvxUqq5xUVreqSEsK7t/5BLLeI3PQVmExgIZx9jUoWPfI1nXHbu2caRU6MRwdIEZx4LRNP9yCQawXboV53tVIUQK+xVMXATXav28Cd8bSYlyM431WYGePIWcu6Lx1MyQdHqKYxqBXYpnly7tdcJtHopeY4Bj5AgLxQQ0GmFxirUswCEFvOTkYVmOnsGaGDCLfTCttuAtzSpwIAootO/FGnGeJ3K2ZFBwg5mBojN3IK+FxzRj5DWOV8pWqlTZi9cFZiJNG5v0pJymL9GC0gM4FDQjEKAOYE2zomiEBNYVcGNyK4MDH4aB8OuGIQY2b3+1bHcFn+RxRD3Mgu5fy2tm387iCSjoXMHLfaKoVy7J1tK6QMksf1aVmMVelAjZizsJjX+Kx6RVzD1Apu1Qm5cweP63MgPICqCGPmMLGeJ0QG8lWwHVCAHCdTsHMA3POGO3fhZWRnqz622oTrI74SwXTCqj8oPmk020UVgM8e8BcRfICXaWt6rx5Af4bVX0pxKE7PnZo9huOiN8ZRRTHGAeBdcUjOC7Xo1hHzRT2PMx1jrKKKT49ZpSoUmWI4w3l5QSLn0mu5UVCYW/uZ5+UCaHaBK+YXpee/jBw2vYtsYThN4IrfoBhyYGbVmAAMHkE8ShNp+AD8gmfjwX3C3XHnXiCHANe9Cjb89ydCe0ZoY2NjY2NjY2NjY+O3wy/REYKtLNjI/72pEWgGWTHqi7MYamlRjaw2Z7XrFlXOXB/0qWq8Nt8ueNsPeVhydOs3PiL1ZwQmzGjxxImDC14tF2RXglZ7F+zBH6mODpWP0eMzOLrqYvlS9QUdQWRZvSqKP9oQGHkO/+PE/Wd5sOvAHv2qVoxBdEta3cVDttppVVhhaM359/snyGbP65wvB52MVzotH+cL5/HCkNHKTuc587zGGQAADFFJREFUcL6opapPOXE68OP8EcfBIe3bynMEMMa3DtD6lkvV5HnQlv2gelQem6/ZA50TZgbLiup917xQdQwJ833h/Q7O/fYR2nhizhucEs3mBgfDObqJ0IFsTwMI/wmB4UhKmIuD2ZLuVNftDZJF57RpoayT7ePpBtMb5EXN1XA5H0kfhcJccWeVzrLLWxVbx8z1rDoh4Z3DENBYVU0Gt8SpGfAaHzilKqQEn9ENB6LiehL3cQV9L5oycV7CgV159d2h3mvNfU+QOOz6ibtpHXfMSp15bqfC1Vf1ml6YZk1LBAMfH4vCehtFdbL8TszhNuDZrfH7Ak6A8phMYy+o+ULiG1/XG84nJqr75jg/Xjjzu7hVMQ7vava8FGDHmZXkeTj4ZijiuzgggBomxRylu4IwHj5pQf2tzhmDQz6X4nwAQbmZ7L3/MJ2xyml13xRmwF0V9GPXNzcWTK0lmWkQXmNgVuc3BhFQl4zfEbfYt6FshiX1DADIDEHTz2uWBSzUc3LGAD8k4klivrrWr/DyWlLYQFJ1i6bmsV9PW/S6IRL2h173icRsc8lpCwPM0PQD4JyarBGL6JoTRnZZnQEla1queTBXRj1+3qGQljEgaYxvTJKOf8wVcAbnvew1n53L03RgyOhOLZPgXz6bMRP0wJrwjL/6g+l7suS8VMUwgN6G51hAfAdrlkkvAp/es9NCBIX0HM4xBD4Vy5Uu1m3pvcGSCpxrpMS+UN2biBgJZ7acLg1Zc4FAq3OPCVLpSC1o295z4mQEH9zK0DWf9Hfil0iE3BeRyZJ7vriZBPDiPALIhGf9bETRRu0kIr6sMgJlI7g9/HIIy88n3iRlVR90K6Lu2JET2H35EBHDYX2BunpeOGuzcqTvx+NGc+v4COYAMX3z6MGKxcOPxxGmRciWLPDgdka62NQUiuSq+LX5IeI5xWHNv/f6QwyH9oLFeVpnr4EElrWpOsUHpzzur5/hyVOt3x+HYOjE+ccfAIDXxw+cr08MkebuCp0YL2STGDgOwfk6caQGPb8OyHE2fSWkPr/nd9xC3/ldPah9ixpXx2wZ7ODRBtf8fwQac97Jmc4Eb9643zeulJCcWz5744HjlN5I7J5xT9asvBqOYc3JdgjcDFx8rvK8Yo5NDcGpjzUnjYoPwpiC4nmYBHWlDVOt1sh8SXDIxLdPmkfhxR/LuwOWwXncGiG7WpRVyg25gp1jxN8tr/1hDh60Zoos7jOTeP5JhA86cOfQ7nQLemmtuU64o8QQx4iJ963wceAqbyEDXq9XBw7hj+M9jwMtAYQayo3gYzwo0Pyg7BA5pji4ZrEYmHLjrscz4ZiOOz2gPo4fAByXeosbwG4ITrzTAJpYcdBHJ4R8xBLP5ZlBMRbeW/vtgBK4LgAaMd9QgjxuGKAOwDjXcDxmqCERrD7ns2DWa6JQzKsyJf1Ft1jCxgPivfdBCTx4rRV9paaQylAwo+WUb/++vy5YFxScKQOb8ujJQKaMi73WqFXYoXuNJoBrtmfNRDJ3uQMkE2qOy3TN/toLGA40de0EdHbhmXiCeEC5CjWRyFCuBWqGe6458WNwWqpksocjksEaHOZItCIhWAIzUUjONZRjjrP83xixjnglUzLANtf96SMLublGZqzzbczcZdH8iQDWfj4TAz7gfrVoxOsVCWKd3dsqdcmX4Hhemd5bHkdJ8RspQKM9NCOZmf0ZHVHA147PNJNT6dfAjEC3R6sJIF+S3jrfED46WbMVYv5t+CUSIZGlmhPVAGqlH8quSiWNl8bpLCdvAWG4AzB4BRJGmPow3pOMpB+O5HIO6JWcVQ/DrpFVv+NgCDNer8WTvS5tzqqrBt+91pbboHrjHNI8fpDHBpYXnDhBSbpCMTgSi7sHUBysj80vhnn6PvwKI5G4UJFrjD8TL8QN+FDDc0MowKzDiFuqByNnCklU5fixYCJVrLzKFACRxmKWL3ip4+DZRmp6Tfj5Wi7FzPg8B+Q4+znCgh/nR/tyjDEwxoGRgcTJJ6Br5oe7q/ZIRv7NTPKZphAEjO9dLXeH2sQ7efg2Y6GeOXx8T8N9v7uj+P5647//+//GdZdB5d/PYd34dWC39X0MfIHo1UkMwLjo6kB6CGMwINk9ZraueEr6b7kpzJY/hAvH0GvdA6b4GMejo5PN5XzHKPKs4CWCnGwrNAgo0zykGTOtRIgRhY8KNIiy/9wbZq0j674kECh54TcMip892Evg9NapKm+JtnCetYmpDtEJm6uS6Lh7aHoQQ8hXtfMOj6FOAInDwyR/Vna4LqNGGY7X8eqKox7AsA9YiSdIrOND43u47IKa42ta7xXjGDDcmF6V5iM6dPVt10BwbwaGpxAUUfWwn15G6KKdw4BnoPn/EXNSDnr2wzjXxDrXE3B2ePkHsf/ni2z8tnCjruiLAGDreMr7/7k+pTJkJUqDqFXQHq8IH9JzI7cToAODqhqUiraVlHjGFl2oCd+Z+pljkHgF0skJWqyQAweokyEAGHjn0pLzf5h5S61iNfMyTK1CuqdnDbEAVgWg+L2BIamm9tY3Th/w9EJSjWTBCZAWuTnCE0mycyvIgnYldHEeumiS9/4hH3UaYLSSL7flida/n7NngtS/AHx2YUc4kktV9H7kHNVv69ehbwyrFkf+tzmlXBIBYcix4u+Yc/++KLktrzcGPcSkHsHoYEi2GSNhW4yq+ySQj1i4gC6s/534BXKxjY2NjY2NjY2NjY2N/7X4JTpC3HJnWJST1haP0mdV3KR0DBPB7QzJ5JbYlpXpAikHmIoe8YqOabO7NVNu+L3kldlTbajaqDl3IqtMGFSrRyv3gmDeBiSvlY9Qamk5R8r27yqKRMemjjKrmT0rlQpO5VhupPCnpwbQMy9AHqpTU1biOCnV0NZzokl815nFU7aXkxpTFYqoKiw2KVPM4yx2Xj6upIPJYKqYWvrxUTE9x8NXQwR8HDjP1RE6jgHJyqq0jn5VibFaw31U+Pbzs1tkAEC+3Jlvxbxv3NcbV9JbzIOTXC7S9/vG+3q3/8b1/sI///uf+Ovrq44cGxsN9p6LMwyAZUmAOjCVYNnqdSfgJbizo3A65wJ1tMIaXIKKWzx9D9qWFi1VFUqyvImcwW5L0hlx3RdXnZFr5EN2GsDD28gASvnrfIQgKMVV1VVVEL2ApJZMKFwX6YtgOT9Y1UyHGYXsPGJt0Mca/PwcQFB5SQ58vf/qqizTAZ+Eo2iEThAWlMy4cVBh2sGeFEoGKZrGCLXNOs4DDMPd6yGI8SYH55zABxxvv2HZ0f4xXvhpFwiGV6rE8aFgEEbSzkiBCevv/+ABtbtlxAGvEng8P70empaNqrbXnECUaJf6p7dvXkvUIqiRrSAqCHn1WiOnxxxUPX53sDceOIRw8Fqf3vfV3URDUa9ifbI7VpNWMuPkaeL7fWwwHEm9HSAcp60ZIQVY+VucNrFoawMHpmhz8N2DckvFkaJURysVXwcmJ4m/PcOO4NKOv/IjvaKTXPEXRYxWqnJOAiP0XAq7xyzyv/nrvK180U64WMcEdhuYB8brwFUxnP8EKfXsEyPi1Od4BIxakQ0aa7CPR8cI1F10E//WEdIMi6k7Sh8gwpqBFILZG5OAUTGbTpA6KMcVBmcnpth1Big91IyhIHcc6f1oGHCiRfeLFQsrUrXsCNX6NYKWSBM958EEnIsKWWyAGiU5EPOjBf4F7EnIv21UGxsbGxsbGxsbGxsb///HLnVvbGxsbGxsbGxsbPx22InQxsbGxsbGxsbGxsZvh50IbWxsbGxsbGxsbGz8dtiJ0MbGxsbGxsbGxsbGb4edCG1sbGxsbGxsbGxs/HbYidDGxsbGxsbGxsbGxm+HnQhtbGxsbGxsbGxsbPx22InQxsbGxsbGxsbGxsZvh50IbWxsbGxsbGxsbGz8dtiJ0MbGxsbGxsbGxsbGb4edCG1sbGxsbGxsbGxs/HbYidDGxsbGxsbGxsbGxm+HnQhtbGxsbGxsbGxsbPx22InQxsbGxsbGxsbGxsZvh50IbWxsbGxsbGxsbGz8dtiJ0MbGxsbGxsbGxsbGb4edCG1sbGxsbGxsbGxs/HbYidDGxsbGxsbGxsbGxm+HnQhtbGxsbGxsbGxsbPx22InQxsbGxsbGxsbGxsZvh50IbWxsbGxsbGxsbGz8dtiJ0MbGxsbGxsbGxsbGb4edCG1sbGxsbGxsbGxs/Hb4fwEd2bauaYTKqgAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 864x648 with 9 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"data.show_batch(rows=3, figsize=(12,9))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To create a `Learner` we use the same function as in lesson 1. Our base architecture is resnet50 again, but the metrics are a little bit differeent: we use `accuracy_thresh` instead of `accuracy`. In lesson 1, we determined the predicition for a given class by picking the final activation that was the biggest, but here, each activation can be 0. or 1. `accuracy_thresh` selects the ones that are above a certain threshold (0.5 by default) and compares them to the ground truth.\n",
"\n",
"As for Fbeta, it's the metric that was used by Kaggle on this competition. See [here](https://en.wikipedia.org/wiki/F1_score) for more details."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"arch = models.resnet50"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"Downloading: \"https://download.pytorch.org/models/resnet50-19c8e357.pth\" to /home/ubuntu/.torch/models/resnet50-19c8e357.pth\n",
"100%|██████████| 102502400/102502400 [00:01<00:00, 100859665.66it/s]\n"
]
}
],
"source": [
"acc_02 = partial(accuracy_thresh, thresh=0.2)\n",
"f_score = partial(fbeta, thresh=0.2)\n",
"learn = cnn_learner(data, arch, metrics=[acc_02, f_score])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We use the LR Finder to pick a good learning rate."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"LR Finder is complete, type {learner_name}.recorder.plot() to see the graph.\n"
]
}
],
"source": [
"learn.lr_find()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYsAAAEKCAYAAADjDHn2AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzt3Xl8VdW99/HPL/NISEgYMpAAgjIJSsS5TlXRWlBbLbbeavXW2161t7XtfeztfVqvHW97vbWDt160dnqq1qG1aLWoVXAWggzKPJOEBEICCSRkXs8fZ6OHGEiA7LPPOfm+X6/94px11j77tzjJ+WXttfba5pxDRETkSBKCDkBERKKfkoWIiPRJyUJERPqkZCEiIn1SshARkT4pWYiISJ+ULEREpE9KFiIi0iclCxER6VNS0AEMlPz8fFdWVhZ0GCIiMWXp0qW7nXMFfdWLm2RRVlZGRUVF0GGIiMQUM9vWn3o6DSUiIn1SshARkT4pWYiISJ98TRZmNsvM1pnZRjO7s5fXR5vZy2a2zMxWmtnlXnmZmR0ws+Xedr+fcYqIyJH5NsBtZonAfcDFQBWwxMzmO+dWh1X7d+Ax59wvzWwS8CxQ5r22yTk33a/4RESk//zsWcwENjrnNjvn2oFHgTk96jhgiPc4B9jhYzwiInKM/EwWRUBl2PMqryzcXcD1ZlZFqFdxe9hrY7zTU4vM7NzeDmBmt5hZhZlV1NXVDWDoIiISLujrLK4DfuOcu8fMzgR+b2ZTgBpgtHOu3sxmAE+Z2WTnXFP4zs65ecA8gPLy8pi4P+yW3c2s2tHImWOHMSwr9bD1urodG3btY2VlI9V7D5CSlEBqUgKpyYmMzc/krHHDMLMIRi4ig5mfyaIaKAl7XuyVhbsZmAXgnHvTzNKAfOfcLqDNK19qZpuACUBMXnXX2tHFc+/V8OjiSt7e0gBAgsHMMXlcNmUUM0pzqWlsZevuZrbWN7N+5z7eq27iQEfXYd/zjLF5fPPySUwtzolUM0RkEPMzWSwBxpvZGEJJYi7w6R51tgMXAb8xs4lAGlBnZgVAg3Ouy8zGAuOBzT7GOmCcc+xt6eDd6kZWVO5lRdVe3t7SwL7WTkbnZfD1S09k5pg8Xllfx3Pv1fLt+asO2T83I5mxBVl86rQSppXkcHLxUMqGZdLR1U1bZzdtHV0sWFXLT17cwMd/8RpXTi/kH88dy/AhqeRmpJCcqNnQIjLwzDn/zt54U2HvBRKBh5xz3zOzu4EK59x8bwbUA0AWocHuf3XOPW9mnwDuBjqAbuDbzrmnj3Ss8vJy5+dyHy3tnSxcF/qCf2Pjbjq7HcmJRmKCkWBGW2c3B9q7PtQbGFeQyamjc7nq1CLOGDOMhIRDTx1t3LWPtbX7KMnNoGxYJjkZyf2Kp6m1g/sXbuJXr22hrbP7/fLs1CSGZaVQkJ0a2rJSGZmTTumwDEbnZVCSl0FOev+OISLxz8yWOufK+6znZ7KIJD+SRUNzOy+v3cXzq2tZtL6O1o5u8jJTOP/EArJTk+jsdnR5W1pyIukpiaQlJ5KdmsTkwiFMKc5hSJq/X8y1ja1UbGtgT0sHe5rbaWhup765nbp9rdTta6NuXxtNrZ2H7JORkkheZgrDslIZlplCnrflZqSQl5lMflYqI4akMXxIKsMyU0lM0NiISLzqb7IIeoA76uxpbufJd6p4ftVOKrY10O1gxJBUri0vYdaUkcwsyyMpik71jMxJ44qTC49YZ19rB5UNB9je0ML2hmZ2NrW9n1R2NrWytqaJ+ub2Q3ooByUmGCOHpFE0NJ3CoWkU5aaTl5nKkLQkstOSyU5Lor2zm8YDHTS1drC/rZOx+VmUl+WSf4QBfBGJLUoWnrW1Tfzm9a38eVk1bZ3dTBw1hNsuOIGLJ41kStGQmJ55lJ2WzKTCZCYVDjlivQPtXdQ3t7F7fyiJ7GpqpbaplR17W6nec4AlW/fw9Moaurr71xsdm5/JjNJcxg3Pojg3neLcDEpy08nLTInp/0+RwWjQJ4sdew/w1cdW8ObmetKSE7j61GJuPKuME0dmBx1axKWnJFKckkFxbsZh63R1O/a1drCvtZPGA6GeRGpSAjnpyQxJTyY9OZG1tfuo2NrAkq17eGntLh5fWnXIe2SmJFKSFxpDKR2WQemwTMqGZVI6LIPCoek67SUShQZ9shiWlUJLeyd3XnYSc08rYWhGStAhRbXEBGNoRgpDM1IOmRcdbkZpLjNKc/mn80LP97V2UL33AFUNB6jc08L2hhYqG1rYsruZRevrDjn9lZKUwMRRQzi5KIeTi3OYVjKUEwqyPjQxQEQiSwPcEqjubsfOfa1s3d3CtvpmNu7az7vVjbxX3Uhze2hm2ZC0JE4tzaW8NJdTS3OZXJijGV0iA0QD3BITEhKMUTnpjMpJ58xxw94v7+52bN69n+WVjSzd1kDF1j0sXPfBki5FQ9OZOCqbKUU5nDehgGnFQ9X7EPGRehYSM/a2tLO8ci9ravaxpqaJNTVNbKrbT7eD/KxULjppOBdPGsF5Jxbo4kSRftJ1FjIo7G1pZ+G6Ol5cs5NF6+rY19ZJQXYqn5xRzLXlJYzJzww6RJGopmQhg05HVzeL1tXx6JJKXl63i65ux+lj8rimvITLp44kI0VnXUV6UrKQQW1nUytPLK3i8YpKtta3kJmSyMdOHsXsaUVMLcrp97IqIvFOyUKE0MKOS7bu4fGKSv76bg0t3gyr4tx0JhcO4ZTRuVwyaQRjC7ICjlQkGEoWIj00t3VSsW0Pq3Y0snpHE6t3NLF5dzMA44dnMWvKSC6bMoqJo7J1hbkMGkoWIv2wY+8Bnl9Vy99W1bJ4S2gtsPHDs5gzvZDZ04oYPezwV7OLxAMlC5GjVL+/jefeq2X+8h0s3hq6SdUZY/P40kXjOXOs7kwo8UnJQuQ4VO89wF+WV/PbN7ays6mNmWV5fPmj4zlTt7OVOKNkITIAWju6+OOSSv5n4UZ2NrUxrWQonzl9NFecPEpTcSUuKFmIDKDWji4eq6jkt29sZVNdM9mpSVx5ShFzZ5YwuVD3QZfYpWQh4gPnHBXb9vDI29t55t0a2ju7Obk4h0+dVsLsaYVk+3xnRJGBpmQh4rO9Le08tayaR5dUsrZ2H+nJiVxTXsxtF57A8Oy0oMMT6RclC5EIcc6xoqqRP7y1jT8tqyY1KYGbzxnDLR8Zq56GRD0lC5EAbNndzH89v46/rqwhNyOZfzx3LJ85fbRuqiVRS8lCJEDvVjXyowVreXXDbtKSE/jEqcXcdM4YxmlZEYkyShYiUWBtbRMPvbaFp5bvoL2zm2tmFPOtj0/S6SmJGkoWIlFk9/42Hnh1Mw+8spmi3HTu/dR0ZpTmBR2WSL+ThW4nJhIB+VmpfOOyiTz2T2fiHFxz/5v89wvr6ejqDjo0kX5RshCJoPKyPJ77l3O58pQifvb3DZz/44U88Mpmmlo7gg5N5Ih0GkokIC+v3cUvF21i8ZYGMlMSuaa8hM+eWap7a0hEacxCJEa8V93Ir17bwtMrdtDZ7Thz7DCuO300l04eQWpSYtDhSZxTshCJMbv2tfJ4RRWPLtlOZcMB8jJT+OJ547jx7DKSE3XGWPwRFQPcZjbLzNaZ2UYzu7OX10eb2ctmtszMVprZ5WGvfcPbb52ZXepnnCLRYHh2GrdecAKLvnYBv795JlOLcvjes2u4/Kev8uam+qDDk0HOt56FmSUC64GLgSpgCXCdc251WJ15wDLn3C/NbBLwrHOuzHv8CDATKAReBCY457oOdzz1LCQevbh6J3c9vYqqPQeYPa2QOy6eQFl+ZtBhSRzpb8/CzwX5ZwIbnXObvYAeBeYAq8PqOGCI9zgH2OE9ngM86pxrA7aY2Ubv/d70MV6RqPPRSSM4Z3w+/7NwE/cv2sTTK3dw4YnDuemcMZylGzFJBPl5GqoIqAx7XuWVhbsLuN7MqoBngduPYl+RQSEtOZE7Lp7Aa/96AbdfOJ7llXv5zINvM+veV3ln+56gw5NBIuhRs+uA3zjnioHLgd+bWb9jMrNbzKzCzCrq6up8C1IkGgwfksYdF0/g9Tsv5MefPJmWjk7mznuLp5ZVBx2aDAJ+JotqoCTsebFXFu5m4DEA59ybQBqQ3899cc7Nc86VO+fKCwoKBjB0keiVlhy6JmP+redwSslQvvzH5fx4wVq6u+NjZqNEJz+TxRJgvJmNMbMUYC4wv0ed7cBFAGY2kVCyqPPqzTWzVDMbA4wHFvsYq0jMyc1M4fc3n87c00q47+VNfPEPS9nb0h50WBKnfBvgds51mtltwAIgEXjIObfKzO4GKpxz84GvAg+Y2VcIDXbf6ELTs1aZ2WOEBsM7gVuPNBNKZLBKSUrgB1dPZfyIbL7319W8vWUhX75oPJ85o1TXZsiA0kV5InFiTU0T3/3ral7fWM/Ygky+eflELpo4IuiwJMpFxUV5IhI5E0cN4f/dfDoPfrYcHNz82wpuffgd9jTr1JQcPyULkThiZnx00ggWfOUjfO2SCSx4r5ZL7n2Fl9fuCjo0iXFKFiJxKDkxgdsuHM9Tt55NXkYKn/vNEu58ciUH2jX0J8dGyUIkjk0pymH+7WfzT+eN5Y8VlVz1P6+zrb456LAkBilZiMS51KREvnHZRH5942nUNLby8Z+/ptNSctSULEQGifNPHM7Tt51DcW4GN/12Cfe+uF4X8km/KVmIDCKjh2Xw5BfP4qpTirj3xQ185bHltHVqHEP65ueqsyIShdJTErnnmmmcMDyLH/1tHTubWvnffygnJz056NAkiqlnITIImRn/fP4J3Pup6SzdtodP/vINqvceCDosiWJKFiKD2JWnFPHbm2ZS29TKVfe9zua6/UGHJFFKyUJkkDtrXD5PfOEsurod1z/4NlV7WoIOSaKQkoWIcOLIbH5380z2t3XymQffZldTa9AhSZRRshARACYX5vCbm2aye18b1//qbRq0ppSEUbIQkfedOjqXB284jW31Ldzw0GKa2zqDDkmihJKFiBzizHHDuP/6Gaza0cgdjy3XhXsCKFmISC8uOGk43/zYJBas2sm9L64POhyJArooT0R6ddPZZayrbeJnL21kwshsrji5MOiQJEDqWYhIr8yM71w5hRmluXzt8RW8V90YdEgSICULETms1KRE7r9+BnkZKXz+dxXU728LOiQJiJKFiBxRQXYq8z5bTn1zO1/+43K6NOA9KClZiEifphTl8B+zJ/Pqht38/KUNQYcjAVCyEJF+mXtaCVefWsRP/76BV9bXBR2OeO54bDm3/K7C9+MoWYhIv5gZ371yCuOHZ/HlPy6nplGr1EaDTbv209rZ7ftxlCxEpN8yUpL45fUzaOvo4raHl9HZ5f+XlBxZTWMro4ak+X4cJQsROSrjCrL4/tVTWbptD/e9vCnocAa1zq5udu9vY0SOkoWIRKE504u4cnohP3tpA8u27wk6nEGrbn8b3Q5GqmchItHqP+ZMYeSQNL7yx+VacDAgNY2hpeRHqWchItEqJz2Ze66dxraGFr771zVBhzMo7fSSxQj1LEQkmp0xdhi3fGQsjyzezgurdwYdzqBT692kaqR6FiIS7e64eAKTRg3hG396l/06HRVRtY2tpCQlkJuR7PuxfE0WZjbLzNaZ2UYzu7OX139iZsu9bb2Z7Q17rSvstfl+xikixy41KZEfXD2V3fvb+N9Fmh0VSbVNrYwckoaZ+X4s35YoN7NE4D7gYqAKWGJm851zqw/Wcc59Jaz+7cApYW9xwDk33a/4RGTgTCsZyuxphTzw6mY+c3ppRE6LSKhnEYmZUOBvz2ImsNE5t9k51w48Csw5Qv3rgEd8jEdEfPT1S0+kuxvueX5d0KEMGrVNrRFLzH4miyKgMux5lVf2IWZWCowBXgorTjOzCjN7y8yu9C9MERkIJXkZ3Hh2GU+8U8XqHU1BhxP3nHOhnkUcJIujMRd4wjnXFVZW6pwrBz4N3Gtm43ruZGa3eAmloq5OC5uJBO3W808gJz2ZHzynqbR+azzQQVtnd0SmzYK/yaIaKAl7XuyV9WYuPU5BOeeqvX83Aws5dDzjYJ15zrly51x5QUHBQMQsIschJyOZL104nlc37GaRVqb1VSQvyAN/k8USYLyZjTGzFEIJ4UOzmszsJCAXeDOsLNfMUr3H+cDZwOqe+4pI9Ln+jFJKh2Xwg2fX4JxulOSXg9dYxHzPwjnXCdwGLADWAI8551aZ2d1mNjus6lzgUXfoT9VEoMLMVgAvAz8Mn0UlItErJSmBL104nrW1+1i4Tr0Lvxy8ejtSYxa+TZ0FcM49Czzbo+xbPZ7f1ct+bwBT/YxNRPwze3oh9zy/jl8u2sQFJw0POpy4VNPYihkMz06NyPGiZYBbROJIcmICN587lsVbGnhHq9L6YmdTK/lZqSQnRuZrXMlCRHwx97QSctKTuX+hrur2w8GrtyNFyUJEfJGZmsQNZ5bywpqdbNy1P+hw4k5tY2vEBrdByUJEfHTDWWWkJiUw7xX1LgZabVNrxKbNgpKFiPhoWFYq15aX8Odl1dR6s3fk+LV2dLG3pSOia3ApWYiIrz5/7li6HTz0+pagQ4kbtRG86dFBShYi4quSvAwunzqKRxZv50B7V987SJ8OXpCn01AiEleuP300+1o7eWbljqBDiQs7I3z1NihZiEgEzByTxwnDs3h48fagQ4kLNRG+ehv6mSzMbFzYWk3nm9mXzGyov6GJSLwwM66bOZpl2/dq+fIBUNvYSnZqElmpvi7CcYj+9iyeBLrM7ARgHqHVZB/2LSoRiTufOLWIlKQEHl68LehQYt7OplZGRPhuhP1NFt3ewoBXAT93zn0dGOVfWCISb4ZmpHDF1FE8tWwHzW2dQYcT02oieDvVg/qbLDrM7DrgBuAZryzZn5BEJF59+vTR7G/r5OkVGug+HjubInv1NvQ/WXwOOBP4nnNui5mNAX7vX1giEo9mlOYyYYQGuo9HV7dj1762iE6bhX4mC+fcaufcl5xzj5hZLpDtnPtPn2MTkThjZnx65mhWVjXyXnVj0OHEpN372+jqdtE5ZmFmC81siJnlAe8AD5jZf/sbmojEo6tOLSYtOYE/vK3exbE4ePV2tI5Z5DjnmoCrgd85504HPupfWCISr3LSk/nY1EKeXrGDlnYNdB+tIK7ehv4niyQzGwVcywcD3CIix+Ta8mL2t3Xy3Lu1QYcSc4JYFwr6nyzuJnQv7U3OuSVmNhbY4F9YIhLPZo7Jo2xYBo9VVAYdSsypbWolOdEYlpkS0eP2d4D7cefcyc65L3rPNzvnPuFvaCISr8yMa8pLeHtLA9vqm4MOJ6bsbGxleHYaCQkW0eP2d4C72Mz+bGa7vO1JMyv2OzgRiV9Xn1pEgsETS6uCDiWmbKzbT1l+RsSP29/TUL8G5gOF3va0VyYickxG5aTzkQkFPLG0iq5uF3Q4MaGzq5u1tfuYXJgT8WP3N1kUOOd+7Zzr9LbfAAU+xiUig8A1M0qoaWzl9Y27gw4lJmze3Ux7ZzeTRg2J+LH7myzqzex6M0v0tuuBej8DE5H499FJwxmakayB7n46uGLvpMLoTRY3EZo2WwvUAJ8EbvQpJhEZJFKTErlyehHPr9rJ3pb2oMOJeqtrmkhJSmBsfmbEj93f2VDbnHOznXMFzrnhzrkrAc2GEpHjdm15Ce1d3fxluRYX7MvqHU2cNDKbpMTI37fueI54x4BFISKD1qTCIUwuHMKT72hW1JE451hd08TEkZE/BQXHlywiO8lXROLWVacUsbKqkS27dc3F4exsaqOhuT2Q8Qo4vmShuW4iMiCuOLkQM5ivU1GHtbomtEpvVCYLM9tnZk29bPsIXW8hInLcRuakcfqYPP6yohrn9Hdobw7OhDppZHYgxz9isnDOZTvnhvSyZTvn+rxTuJnNMrN1ZrbRzO7s5fWfmNlyb1tvZnvDXrvBzDZ42w3H1jwRiRVzphexua6ZVd6XohxqdU0TpcMyyE4L5ialvg2pm1kicB9wGTAJuM7MJoXXcc59xTk33Tk3Hfg58Cdv3zzg28DpwEzg295Nl0QkTl02ZSTJicZfllcHHUpUWr2jKZCL8Q7yc/7VTGCjt+hgO/AoMOcI9a8DHvEeXwq84JxrcM7tAV4AZvkYq4gEbGhGCudNGM7TK2ro1vIfh9jf1sm2hpa4TRZFQPhlmVVe2YeYWSkwBnjpaPY1s1vMrMLMKurq6gYkaBEJzuzphdQ2tbJ4a0PQoUSVdbVNOBfc4Db4myyOxlzgCedc19Hs5Jyb55wrd86VFxRoqSqRWPfRicPJSEnUBXo9BLnMx0F+JotqoCTsebFX1pu5fHAK6mj3FZE4kZGSxCWTRvDsuzW0d3YHHU7UWF3TRG5GcsTvux3Oz2SxBBhvZmPMLIVQQpjfs5KZnQTkAm+GFS8ALjGzXG9g+xKvTETi3JzpRTQe6ODVDTq1fNDqHU1MKhyCWXDXQvuWLJxzncBthL7k1wCPOedWmdndZjY7rOpc4FEXNrnaOdcAfIdQwlkC3O2ViUicO2d8PrkZyTylU1HAB/ewCHJwG6DPayWOh3PuWeDZHmXf6vH8rsPs+xDwkG/BiUhUSk5M4PKpo/jTO9U0t3WSmerr11TU27K7mbbO7kDHKyB6BrhFRN43Z3oRBzq6eHHNzqBDCdzqmtDg9sSAexZKFiISdcpLcynMSdOsKELjFSmJCYwryAo0DiULEYk6CQnGx6cX8sr6OhqaB/dNkTbVNTMmP5PkAO5hEU7JQkSi0pxpRXR2O559tyboUAJV2dBCSV5G0GEoWYhIdJo4Kpvxw7OYv2LwnopyzlG5p4XRShYiIr0zM2ZPK2TxlgZ27D0QdDiBqG9up6W9i5K89KBDUbIQkeg1e3rotjlPD9LeRWVDC4B6FiIiR1I6LJPpJUMH7ayoyj2hHpXGLERE+jBneiGra5rYsHNf0KFE3MGeRXGuTkOJiBzRx04eRYIxKHsXlQ0t5GelkpES/FXsShYiEtWGZ6dx7vgCnnyniq5BdlOk7Q0tUTG4DUoWIhID5p5WQk1jK4vW7wo6lIiKlmmzoGQhIjHgookjyM9K4dHFlX1XjhOdXd3s2NtKSa6ShYhIv6QkJfCJGcX8fe0udjW1Bh1ORNQ0ttLV7XQaSkTkaHyqvISubsfjS6uCDiUiDs6EioZps6BkISIxYmxBFqePyeOPSyrpHgQD3dsPJgudhhIROTrXzRzN9oYW3txcH3Qovqvc00JSgjEqJ7j7bodTshCRmDFrykhy0pN5dEn8D3RvbzhA4dB0kgJemvyg6IhCRKQf0pITueqUIha8Vxv397mobIieabOgZCEiMWbuzBLau7p5vCK+exdVe6LngjxQshCRGHPSyCGcc0I+v3h5I7v2xec02ua2Tnbvb6c4Sga3QclCRGLQ3XMm09bRzXefWRN0KL6o8lab1WkoEZHjMLYgi1svOIH5K3awaH1d0OEMuO1Rdo0FKFmISIz6wvljGVuQyb8/9S4H2ruCDmdARdNNjw5SshCRmJSalMj3r5pKZcMBfv7ShqDDGVDbG1rITEkkNyM56FDep2QhIjHrjLHDuGZGMfNe2cy62vi5OVJoJlQGZhZ0KO9TshCRmPZvl08kOy2J/3h6Fc7FxzIglQ0Homq8ApQsRCTG5Wam8C8XjeeNTfUsXBf7g93OudBNj6Jo2iwoWYhIHPj06aWMyc/k+8+uobOrO+hwjkt9czsHOroYHUUX5IHPycLMZpnZOjPbaGZ3HqbOtWa22sxWmdnDYeVdZrbc2+b7GaeIxLaUpAT+z6yT2LBrP49VxPYS5tE4bRbAt7uAm1kicB9wMVAFLDGz+c651WF1xgPfAM52zu0xs+Fhb3HAOTfdr/hEJL5cOnkEp5Xl8t8vrGf29EKyUn37evNVNE6bBX97FjOBjc65zc65duBRYE6POp8H7nPO7QFwzg2uG+yKyIAxM/7t8ons3t/GvEWbgg7nmB1MFtG01Af4myyKgPCVvqq8snATgAlm9rqZvWVms8JeSzOzCq/8Sh/jFJE4ccroXK44eRTzXt1MbWNsrhu1vLKRoqHppKckBh3KIYIe4E4CxgPnA9cBD5jZUO+1UudcOfBp4F4zG9dzZzO7xUsoFXV1sT8LQkSO3/+ZdRLd3XDP8+uCDuWoNbZ0sGj9Li6bMjLoUD7Ez2RRDZSEPS/2ysJVAfOdcx3OuS3AekLJA+dctffvZmAhcErPAzjn5jnnyp1z5QUFBQPfAhGJOSV5GXz2zFKeeKeKNTVNQYdzVJ57r4aOLsfs6YVBh/IhfiaLJcB4MxtjZinAXKDnrKanCPUqMLN8QqelNptZrpmlhpWfDaxGRKQfbrvwBLJTk/jBc2uDDuWozF+xgzH5mUwtygk6lA/xLVk45zqB24AFwBrgMefcKjO728xme9UWAPVmthp4Gfi6c64emAhUmNkKr/yH4bOoRESOZGhGCrdfOJ5X1tfx6obYOEW9s6mVNzfXM3taYVQt83GQxcvl8eXl5a6ioiLoMEQkSrR1dnHRPYvITkvmr7efQ0JC9H0Bh3vw1c18969r+PtXz2NcQVbEjmtmS73x4SMKeoBbRMQXqUmJfP3SE1lT08Sfl/UcLo0+T6/YwZSiIRFNFEdDyUJE4tbHTy7k5OIc7nl+Ha0d0XvPiy27m1lR1cicaT2vLogeShYiErcSEkIX6u1obOXBVzcHHc5hzV++AzO4YtqooEM5LCULEYlrZ4wdxqzJI7nv5U3s2Hsg6HA+xDnHX1ZUM7Msj1E50bV4YDglCxGJe9/82ES6neP7z64JOpQPWbWjic11zVF5bUU4JQsRiXsleRl88fxxPLOyhjc31QcdziGeX1VLYoJx+ZToPQUFShYiMkh84bxxFOemc9f8VVF1z4uNdfsZnZdBbmZK0KEckZKFiAwKacmJ/PvHJrFu5z5+/9a2oMN539bdLZQNi64VZnujZCEig8alk0dw7vh8/vuF9eze3xZ0ODjn2FbfTOmwzKBD6ZOShYgMGmbGtz8+mZb2Ln7x0sagw6FufxvN7V3qWYiIRJsThmfxyVOLeXjxdmoag51Ku60+dKOj0nz1LEREos4q9kR3AAANsUlEQVRtF56Ac477Xg62d7F1dzMAZToNJSISfUryMri2vIQ/Lqmkak9LYHFsq28hMcEozo3ei/EOUrIQkUHp1gtOwLBAxy621jdTnJtOcmL0fxVHf4QiIj4oHJrOp08fzeNLq9hW3xxIDFtjZCYUKFmIyCD2z+ePIynB+NnfI9+7cM6xLUausQAlCxEZxIYPSeMfzijlz8uqWL9zX0SP3dDczr62zpgY3AYlCxEZ5L5w/jiGZqTwhd8vpbGlI2LH3epNmy3LV89CRCTq5Wel8r//MIPKPS3c+vA7dERo3aiD4yQasxARiRGnleXxvaum8trG3XznmdUROebW3c0kGDExbRYgKegARESiwbXlJWzYuY8HXt3C+OFZ/MOZZb4eb2t9C4VD00lNSvT1OANFPQsREc+dl03kwpOGc9fTq3l1Q52vx9pW38yYGFjm4yAlCxERT2KC8dO50zmhIIt//sM7bPBxhtTW+hZKY2TaLChZiIgcIjstmV/dWE5qUiKf+80SX5Yy39PcTuOBjpiZNgtKFiIiH1Kcm8Gvbihn9/42Pv+7Clo7ugb0/bfG2EwoULIQEenVtJKh/OTa6SzbvpevPb6C7m43YO99cGnyWLl6G5QsREQO67Kpo7jzspN4ZmUN97+yacDed2t9M2ah1W9jhZKFiMgR/NNHxvLxaYX814J1vLFp94C857b6Fgpz0klLjo1ps6BkISJyRGbGD6+eypj8TL70yDJ2NrUe93tu2d0cUzOhQMlCRKRPmalJ3H/9DFrau7htAJYE2RZDS5Mf5GuyMLNZZrbOzDaa2Z2HqXOtma02s1Vm9nBY+Q1mtsHbbvAzThGRvowfkc0Prp7Kkq17+NHf1h7z+zS2dLCnpYMxMbKA4EG+LfdhZonAfcDFQBWwxMzmO+dWh9UZD3wDONs5t8fMhnvlecC3gXLAAUu9fff4Fa+ISF/mTC9i6bY9PPDqFvIyU/nCeWMxs6N6j20NsTdtFvztWcwENjrnNjvn2oFHgTk96nweuO9gEnDO7fLKLwVecM41eK+9AMzyMVYRkX75949NYva0Qv7zb2v5v395j66jnFL7/tLkMZYs/FxIsAioDHteBZzeo84EADN7HUgE7nLO/e0w+xb5F6qISP+kJCVw76emUzg0nfsXbaK2sY2fX3cK6Sn9m9n02oY6khKM0TE0bRaCH+BOAsYD5wPXAQ+Y2dD+7mxmt5hZhZlV1NX5u+iXiMhBCQnGnZedxN1zJvP3tTu57oG3aGrt+8ZJS7ft4bGKKm44q6zfySVa+JksqoGSsOfFXlm4KmC+c67DObcFWE8oefRnX5xz85xz5c658oKCggENXkSkL589s4z7r5/Be9WN3PqHI8+S6ujq5pt/fpdROWl85eIJEYxyYPiZLJYA481sjJmlAHOB+T3qPEWoV4GZ5RM6LbUZWABcYma5ZpYLXOKViYhElUsnj+T7V0/l1Q27+b9PvYdzvY9h/Pr1Layt3ce3Pz6ZrNTYu5WQbxE75zrN7DZCX/KJwEPOuVVmdjdQ4ZybzwdJYTXQBXzdOVcPYGbfIZRwAO52zjX4FauIyPG4tryE7fUt/OLljZQOy+SL54875PWqPS385IUNfHTicC6dPCKgKI+PHS4Lxpry8nJXUVERdBgiMkg55/iXR5czf8UOfnbdKVwxdRQJCaFptf/42wpe37ibF+74CMW50TWwbWZLnXPlfdWLvb6QiEgUMjN+9MmT2bH3AF96ZBlfemQZWalJZKUmUdvUyjcuOynqEsXRULIQERkgacmJ/OrG03hqWTX1ze3sa+1gf2snBdmp3HTOmKDDOy5KFiIiAygnPZkbzioLOowBF/R1FiIiEgOULEREpE9KFiIi0iclCxER6ZOShYiI9EnJQkRE+qRkISIifVKyEBGRPsXN2lBmVgds6+WlHKCxj7Lw5709Di/LB3YfQ4i9xdHfOgPRhvDHx9qGI8XYnzpHirmv5z0/i2hpQ29l0fJZHOn1Y/0sovnnqbcy/W73rdQ51/c9Hpxzcb0B8/oqC3/e2+MeZRUDFUd/6wxEG3q055jaMNDtOJrnPT+LaGlDNH8WR3r9WD+LaP55OpbPQr/b/d8Gw2mop/tR9nQfj3t7j4GIo791BqIN/Y2hLwPZjqN5rs+if7H09/Vj/Syi+eeptzL9bg+QuDkNFSlmVuH6sZxvNFMbokc8tCMe2gDx0Q4/2zAYehYDbV7QAQwAtSF6xEM74qENEB/t8K0N6lmIiEif1LMQEZE+DdpkYWYPmdkuM3vvGPadYWbvmtlGM/uZmVnYa7eb2VozW2VmPxrYqHuNZcDbYWZ3mVm1mS33tssHPvJD4vDls/Be/6qZOTPLH7iIDxuLH5/Fd8xspfc5PG9mhQMf+SFx+NGGH3u/EyvN7M9mNnTgIz8kDj/acI33O91tZr6NaxxP7Id5vxvMbIO33RBWfsTfm175Nc0q2jfgI8CpwHvHsO9i4AzAgOeAy7zyC4AXgVTv+fAYbcddwNdi+bPwXisBFhC6/iY/FtsBDAmr8yXg/hhswyVAkvf4P4H/jME2TAROBBYC5dEWuxdXWY+yPGCz92+u9zj3SO080jZoexbOuVeAhvAyMxtnZn8zs6Vm9qqZndRzPzMbRegX+C0X+l//HXCl9/IXgR8659q8Y+zytxW+tSOifGzDT4B/BSIyMOdHO5xzTWFVM/G5LT614XnnXKdX9S2gOAbbsMY5t87PuI8n9sO4FHjBOdfgnNsDvADMOtbf/UGbLA5jHnC7c24G8DXgf3qpUwRUhT2v8soAJgDnmtnbZrbIzE7zNdrDO952ANzmnTZ4yMxy/Qv1sI6rDWY2B6h2zq3wO9A+HPdnYWbfM7NK4DPAt3yM9XAG4ufpoJsI/SUbaQPZhkjrT+y9KQIqw54fbM8xtVP34PaYWRZwFvB42Om71KN8myRCXb4zgNOAx8xsrJe9I2KA2vFL4DuE/or9DnAPoV/yiDjeNphZBvBvhE5/BGaAPgucc98Evmlm3wBuA749YEH2YaDa4L3XN4FO4A8DE12/jztgbYi0I8VuZp8D/sUrOwF41szagS3OuasGOhYliw8kAHudc9PDC80sEVjqPZ1P6Is0vBtdDFR7j6uAP3nJYbGZdRNaq6XOz8B7OO52OOd2hu33APCMnwH34njbMA4YA6zwfsGKgXfMbKZzrtbn2MMNxM9UuD8AzxLBZMEAtcHMbgSuAC6K5B9PnoH+HCKp19gBnHO/Bn4NYGYLgRudc1vDqlQD54c9LyY0tlHNsbTTr4GaWNiAMsIGkoA3gGu8xwZMO8x+PQeHLvfKvwDc7T2eQKgLaDHYjlFhdb4CPBprbehRZysRGOD26bMYH1bnduCJGGzDLGA1UBCJz8DPnyd8HuA+1tg5/AD3FkKD27ne47z+tLPXuCL14UXbBjwC1AAdhHoENxP6a/RvwArvh/tbh9m3HHgP2AT8gg8ubkwB/p/32jvAhTHajt8D7wIrCf3FNSrW2tCjzlYiMxvKj8/iSa98JaH1f4pisA0bCf3htNzb/J7R5UcbrvLeqw3YCSyIptjpJVl45Td5//8bgc8dze9Nz01XcIuISJ80G0pERPqkZCEiIn1SshARkT4pWYiISJ+ULEREpE9KFhLXzGx/hI/3oJlNGqD36rLQarPvmdnTfa3WamZDzeyfB+LYIj1p6qzENTPb75zLGsD3S3IfLIrnq/DYzey3wHrn3PeOUL8MeMY5NyUS8cngop6FDDpmVmBmT5rZEm872yufaWZvmtkyM3vDzE70ym80s/lm9hLwdzM738wWmtkTFrpPwx8O3g/AKy/3Hu/3FgFcYWZvmdkIr3yc9/xdM/tuP3s/b/LBIolZZvZ3M3vHe485Xp0fAuO83siPvbpf99q40sz+YwD/G2WQUbKQweinwE+cc6cBnwAe9MrXAuc6504htLrr98P2ORX4pHPuPO/5KcCXgUnAWODsXo6TCbzlnJsGvAJ8Puz4P3XOTeXQ1T975a1hdBGhq+kBWoGrnHOnErqHyj1esroT2OScm+6c+7qZXQKMB2YC04EZZvaRvo4n0hstJCiD0UeBSWGreA7xVvfMAX5rZuMJrbibHLbPC8658PsMLHbOVQGY2XJC6/m81uM47XywCONS4GLv8Zl8cP+Ah4H/Okyc6d57FwFrCN2PAELr+Xzf++Lv9l4f0cv+l3jbMu95FqHk8cphjidyWEoWMhglAGc451rDC83sF8DLzrmrvPP/C8Nebu7xHm1hj7vo/Xepw30wKHi4OkdywDk33VtyfQFwK/AzQve1KABmOOc6zGwrkNbL/gb8wDn3v0d5XJEP0WkoGYyeJ7SCKwBmdnD55xw+WKr5Rh+P/xah018Ac/uq7JxrIXRL1a+aWRKhOHd5ieICoNSrug/IDtt1AXCT12vCzIrMbPgAtUEGGSULiXcZZlYVtt1B6Iu33Bv0XU1oaXmAHwE/MLNl+Nvr/jJwh5mtJHTTmsa+dnDOLSO08ux1hO5rUW5m7wKfJTTWgnOuHnjdm2r7Y+fc84ROc73p1X2CQ5OJSL9p6qxIhHmnlQ4455yZzQWuc87N6Ws/kSBpzEIk8mYAv/BmMO0lgresFTlW6lmIiEifNGYhIiJ9UrIQEZE+KVmIiEiflCxERKRPShYiItInJQsREenT/wc8UkBY6dZ64gAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"learn.recorder.plot()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Then we can fit the head of our network."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"lr = 0.01"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"Total time: 03:30 <p><table style='width:375px; margin-bottom:10px'>\n",
" <tr>\n",
" <th>epoch</th>\n",
" <th>train_loss</th>\n",
" <th>valid_loss</th>\n",
" <th>accuracy_thresh</th>\n",
" <th>fbeta</th>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <th>0.125128</th>\n",
" <th>0.110038</th>\n",
" <th>0.944010</th>\n",
" <th>0.904893</th>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <th>0.112533</th>\n",
" <th>0.101303</th>\n",
" <th>0.955964</th>\n",
" <th>0.910774</th>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <th>0.100574</th>\n",
" <th>0.093255</th>\n",
" <th>0.955187</th>\n",
" <th>0.918653</th>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <th>0.096056</th>\n",
" <th>0.087997</th>\n",
" <th>0.954983</th>\n",
" <th>0.924016</th>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <th>0.092320</th>\n",
" <th>0.086761</th>\n",
" <th>0.956400</th>\n",
" <th>0.925110</th>\n",
" </tr>\n",
"</table>\n"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"learn.fit_one_cycle(5, slice(lr))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"learn.save('stage-1-rn50')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"...And fine-tune the whole model:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"learn.unfreeze()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"LR Finder complete, type {learner_name}.recorder.plot() to see the graph.\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYsAAAEKCAYAAADjDHn2AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4wLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvqOYd8AAAIABJREFUeJzt3Xl8VfWd//HXJwlh3xO2hFV2ZFEC4gJ1F22rtaLFaa1LlXZaa6czWu2002ntWKuOnbZTf1Ot1WqrUvdSN1CrVkWWhE0CREJYEtZAICRA9s/vj3ux1xi4NyQn9yZ5Px+P++Cec77nnM+Xm9xPzvd7zvdr7o6IiMjxJMU7ABERSXxKFiIiEpWShYiIRKVkISIiUSlZiIhIVEoWIiISlZKFiIhEFWiyMLPZZpZnZvlmdkcD22eZ2QozqzGzORHrzzGzVRGvCjP7QpCxiojIsVlQD+WZWTLwEXABUAQsB65293URZYYBPYBbgQXu/mwDx+kD5AOZ7n44kGBFROS4UgI89nQg390LAMxsPnAZ8HGycPct4W11xznOHODVaIkiLS3Nhw0b1sSQRUTal5ycnL3unh6tXJDJIgMojFguAk47gePMBX4RrdCwYcPIzs4+gcOLiLRfZrY1lnJB9llYA+sa1eZlZgOBicDCY2yfZ2bZZpZdXFx8AiGKiEgsgkwWRcDgiOVMYEcjj3EV8IK7Vze00d0fcvcsd89KT496FSUiIicoyGSxHBhlZsPNLJVQc9KCRh7jauCpZo9MREQaJbBk4e41wM2EmpDWA0+7e66Z3WlmlwKY2TQzKwKuBB40s9yj+4fvlBoMvBNUjCIiEpvAbp1taVlZWa4ObhGRxjGzHHfPilZOT3CLiEhUShYiIhKVkoWISCv2/Ioins0pIuguBSULEZFWqrq2jvsW5vH8iiLMGnq0rfkoWYiItFKvrt3FztIKvnbW8MDPpWQhItIKuTu/f28zw9O6cs6YfoGfT8lCRKQVWrHtAKsLD3D9mcNISgq2CQqULEREWqVH3ttMj04pXHFqZoucT8lCRKSVKdp/mFfX7uTq04bQtWOQg4f/g5KFiEgr89jiLZgZ154+rMXOqWQhItKKlFfWMH95IRefPIBBvTq32HmVLEREWpFnswspq6hpkdtlIylZiIi0ErV1zqOLt3DKkF6cMqR3i55byUJEpJX43bsFbN13mK/PGtHi51ayEBFpBdbtOMj9i/K4+OQBXDRhQIufX8lCRCTBVVTX8t0/r6JXl1Tuunxi4ONANSTQZGFms80sz8zyzeyOBrbPMrMVZlZjZnPqbRtiZovMbL2ZrQvPnCci0u7cvyiPvN1l3DtnEn26psYlhsCShZklAw8AFwPjgavNbHy9YtuA64AnGzjE48B97j4OmA7sCSpWEZFEtXjTXh5+bzNfmTGkRcaAOpYgH/2bDuS7ewGAmc0HLgPWHS3g7lvC2+oidwwnlRR3fz1crjzAOEVEEtLBimpufXo1w/p25d8vGRfXWIJshsoACiOWi8LrYjEaOGBmz5vZSjO7L3ylIiLSbvxi0UfsLqvkF1dNpktqywzrcSxBJouGemBincopBZgJ3ApMA0YQaq765AnM5plZtpllFxcXn2icIiIJZ/fBCp5cto0rp2a2+DMVDQkyWRQBgyOWM4Edjdh3pbsXuHsN8CJwav1C7v6Qu2e5e1Z6enqTAxYRSRQPvlNAbZ3zzbNHxjsUINhksRwYZWbDzSwVmAssaMS+vc3saAY4l4i+DhGRtqy4rJInlm7lC1MyGNK3S7zDAQJMFuErgpuBhcB64Gl3zzWzO83sUgAzm2ZmRcCVwINmlhvet5ZQE9SbZvYhoSat3wUVq4hIInn43QKqa+v41jknxTuUjwXaY+LurwCv1Fv3o4j3ywk1TzW07+vApCDjExFJNPvKK3n8g61cOnkQI9K7xTucj+kJbhGRBPL79zZTUVPLzecmRl/FUUoWIiIJ4sDhKh7/YCuXTBzIyH7d4x3OJyhZiIgkiEfe30J5ZQ3fTrCrClCyEBFJCPsPVfHo+5u5aEJ/xg7oEe9wPkXJQkQkAfz6bxs5VFnDv104Jt6hNEjJQkQkzrbuO8SflmzlS9MGM7p/YvVVHKVkISISZ/e+lkeH5CS+e/7oeIdyTEoWIiJxlLN1Py9/uJObZo6gX49O8Q7nmJQsRETixN352SvrSe/ekXlxmFe7MZQsRETiZGHuLnK27ue754+ma8f4DkEejZKFiEgcVNfWcc9reYzs142rshoc9SihKFmIiMTBo+9vZvPeQ3z/4rGkJCf+V3HiRygi0sZs2XuI+xd9xPnj+nPu2PjNq90YShYiIi2ors65/bk1pCYn8V9fOBmzhiYVTTxKFiIiLWj+8kKWbi7h3z87jgE9E/dW2fqULEREWsjO0iPc/cp6Th/Rl7nTBkffIYEEmizMbLaZ5ZlZvpnd0cD2WWa2wsxqzGxOvW21ZrYq/Ip1OlYRkYTk7vzwhbVU19Xx8ysmtprmp6MCu7HXzJKBB4ALgCJguZktcPfIubS3AdcRmkK1viPuPiWo+EREWtKC1Tt4c8MefvjZcQzt2zXe4TRakE+BTAfy3b0AwMzmA5cBHycLd98S3lYXYBwiInF1pKqWu15ez+TMnlx/5vB4h3NCgmyGygAKI5aLwuti1cnMss1siZl9oaECZjYvXCa7uLi4KbGKiATmkfc3s6eskh9+bjzJSa2r+emoIJNFQ/8j3oj9h7h7FvBPwC/N7KRPHcz9IXfPcves9PT0E41TRCQwBw5X8dt3NnHe2H5MG9Yn3uGcsCCTRREQ2d2fCeyIdWd33xH+twB4GzilOYMTEWkJ//fOJsora7htdmJOahSrIJPFcmCUmQ03s1RgLhDTXU1m1tvMOobfpwFnEtHXISLSGuwsPcIf3t/C5VMyEnKq1MYILFm4ew1wM7AQWA887e65ZnanmV0KYGbTzKwIuBJ40Mxyw7uPA7LNbDXwFvDzendRiYgkvF+/uZE6d757QeJOahSrQMfEdfdXgFfqrftRxPvlhJqn6u+3GJgYZGwiIkHaVFzO09lFXDNjKIP7dIl3OE2mJ7hFRAJw/6I8OqUkcfO5I+MdSrNQshARaWYrtu3nlQ93cePMEaR16xjvcJqFkoWISDOqq3N+vCCX/j0Sf6rUxlCyEBFpRs/kFLKmqJR/v2Rcwk+V2hhKFiIizaT0SDX3vpZH1tDeXDp5ULzDaVZtJ+2JiMTZr97YSMnhKh67dHqrG1U2Gl1ZiIg0g492l/HYB1u4evoQTs7oGe9wmp2ShYhIE7k7P/lrLl1Tk7n1wtY9rMexKFmIiDTRa2t38X7+Pv7twjH06Zoa73ACoWQhItIEe8oq+OGLaxk3sAdfPm1IvMMJjDq4RUROkLtz2zNrKK+s4am5U0hJbrt/f7fdmomIBOwPi7fwzkfF/OCz4xjdv3u8wwmUkoWIyAnYsOsgd7+6gfPG9uOaGUPjHU7glCxERBqporqWW55aSY9OHbhnzqQ290xFQ9RnISLSSHe/sp6Pdpfz2A3T28xAgdHoykJEpBHe27iXxz7Yyg1nDuczo9PjHU6LCTRZmNlsM8szs3wzu6OB7bPMbIWZ1ZjZnAa29zCz7Wb2myDjFBGJRXllDbc/t4YR6V35XiufU7uxAksWZpYMPABcDIwHrjaz8fWKbQOuA548xmF+CrwTVIwiIo1x9yvr2VF6hPvmTKZTh+R4h9OigryymA7ku3uBu1cB84HLIgu4+xZ3XwPU1d/ZzKYC/YFFAcYoIhKT9/P38sTSbdx41nCmDu0d73BaXJDJIgMojFguCq+LysySgPuB26KUm2dm2WaWXVxcfMKBiogcT3llDd97dg0j0rryb2107KdogkwWDd1L5jHu+03gFXcvPF4hd3/I3bPcPSs9vf10NIlIy7rn1Q3sKD3CvXMmtbvmp6OCvHW2CBgcsZwJ7Ihx39OBmWb2TaAbkGpm5e7+qU5yEZEgLSnYxx+XbOVrZw0na1ifeIcTN0Emi+XAKDMbDmwH5gL/FMuO7v7lo+/N7DogS4lCRFpabZ3zk7+uI6NX5zY79HisAmuGcvca4GZgIbAeeNrdc83sTjO7FMDMpplZEXAl8KCZ5QYVj4hIYz23ooj1Ow9y+8Vj6ZzaPpufjjL3WLsREltWVpZnZ2fHOwwRaSMOV9Vw9n1vM6hXZ1745hltdkgPM8tx96xo5fQEt4hIAx76ewF7yir5j8+Na7OJojGULERE6tl9sIIH3yngkokDmDq0/XZqR1KyEBGp5/5FedTWObfPHhvvUBKGkoWISIR1Ow7yTE4R154xlKF9u8Y7nIShZCEiElZX59z5Ui49O3fg5nNGxTuchKJkISIS9vB7BSwpKOGO2WPp2aVDvMNJKEoWIiLAh0Wl3Lcwj9kTBvClaYOj79DOKFmISLt3qLKGW+avJK1bR35+xUTdKtsATasqIu3ejxfksmXfIZ66aQa9uqTGO5yEpCsLEWnX/rp6B8/kFHHzOSOZMaJvvMNJWLqyEJF2qayimhdX7eDe1zZwypBe3HKe7n46HiULEWk33J01RaU8uXQbC1bv4Eh1LRMG9eDXc0+hQ7IaWo5HyUJE2o3/enk9v39vM507JHPp5EFcfdoQJmf2VId2DJQsRKRd2LrvEH9YvIXLT8ngJ5dNoEcnPUfRGLruEpF24X//lk9KkvH9i8cqUZwAJQsRafM27z3E8yuK+MqMofTr0Sne4bRKgSYLM5ttZnlmlm9mn5oW1cxmmdkKM6sxszkR64eaWY6ZrTKzXDP7RpBxikjb9r9vbiQ1JYlvfOakeIfSagXWZ2FmycADwAVAEbDczBa4+7qIYtuA64Bb6+2+EzjD3SvNrBuwNrzvjqDiFZG2aVNxOS+u2s6NM0eQ3r1jvMNptWK6sjCzk8ysY/j92WZ2i5n1irLbdCDf3QvcvQqYD1wWWcDdt7j7GqCu3voqd68ML3aMNU4Rkfp+/eZGOnVI5uuzRsQ7lFYt1i/h54BaMxsJ/B4YDjwZZZ8MoDBiuSi8LiZmNtjM1oSPcU9DVxVmNs/Mss0su7i4ONZDi0g7sXF3GQtW7+Crpw+jbzddVTRFrMmizt1rgMuBX7r7d4GBUfZp6MZljzUwdy9090nASOBaM+vfQJmH3D3L3bPS09NjPbSItBO/enMjXTokM09XFU0Wa7KoNrOrgWuBl8Lrot17VgREjvObCTS6zyF8RZELzGzsviLSPlVU1/LDFz/kpTU7uf7M4fTpqsEBmyrWZHE9cDpwl7tvNrPhwJ+i7LMcGGVmw80sFZgLLIjlZGaWaWadw+97A2cCeTHGKiLt2IZdB/n8/77Hn5Zs46aZwzXmUzOJ6W6o8B1Mt8DHX97d3f3nUfapMbObgYVAMvCIu+ea2Z1AtrsvMLNpwAtAb+DzZvYTd58AjAPuNzMn1Jz13+7+4QnWUUTaAXfn8Q+2ctcr6+nRqQOP3zCdWaPVPN1czD16N4KZvQ1cSii5rAKKgXfc/V8Dja4RsrKyPDs7O95hiEgcVNXU8b1nV/Piqh2cMyad+66cTJo6tGNiZjnunhWtXKzPWfR094NmdiPwqLv/Z/hOJRGRuCqrqOYbf8rh/fx93HrhaL51zkgNDBiAWJNFipkNBK4CfhBgPCIiMdtzsILrHl3OR7vL+O8rJzNnama8Q2qzYk0WdxLqe3jf3Zeb2QhgY3BhiYgc36bicq59ZBklh6p4+Noszh7TL94htWmxdnA/AzwTsVwAXBFUUCIix1NTW8e1jyyjorqW+fNmMCkz2oAS0lSxDveRaWYvmNkeM9ttZs+Zma73RCQu3sorpmj/Ef7rCxOVKFpIrM9ZPEroGYlBhIbs+Gt4nYhIi3ty6Vb69+jI+ePU9NRSYk0W6e7+qLvXhF9/AHQDs4i0uMKSw7z9UTFfmjaEFM2b3WJi/Z/ea2ZfMbPk8OsrwL4gAxMRaciflxdiwNxpg6OWleYTa7K4gdBts7sIzTUxh9AQICIiLaa6to4/Zxdyzph+DOrVOd7htCsxJQt33+bul7p7urv3c/cvAF8MODYRkU94Y91uissq+fKMIfEOpd1pSoNfwgz1ISLtw5PLtpHRqzOfGa2O7ZbWlGSh5+lFpMVs2XuIdzfuZe60wSQn6eunpTUlWcQ8kZGISFM9tXwbyUnGVerYjovjPsFtZmU0nBQMUO+SiLSIyppansku4vxx/ejfo1O8w2mXjpss3L17SwUiInIsjy3eQsmhKr582tB4h9Ju6YkWEUloa7eXct/CPC4Y35+Zo9LiHU67FWiyMLPZZpZnZvlmdkcD22eZ2QozqzGzORHrp5jZB2aWa2ZrzOxLQcYpIonpSFUt35m/kj5dU7nnikmapyKOAksWZpYMPABcDIwHrjaz8fWKbQOuA56st/4w8NXwFKuzgV+amUYLE2lnfvryOgr2HuIXV02hT9fUeIfTrsU6n8WJmA7kh4czx8zmA5cB644WcPct4W11kTu6+0cR73eY2R5CY1EdCDBeEUkgC3N38eTSbXx91gjOHKnmp3gLshkqAyiMWC4Kr2sUM5sOpAKbGtg2z8yyzSy7uLj4hAMVkcSyq7SC259bw8kZPfi3C8fEOxwh2GTRUONio57NCE/l+kfgenevq7/d3R9y9yx3z0pP1yC4Im1BZU0ttzy1ksrqOn419xRSU3QfTiIIshmqCIh8eiYT2BHrzmbWA3gZ+KG7L2nm2EQkAbk733/+Q5ZtKeFXc6dwUnq3eIckYUGm7OXAKDMbbmapwFxCEyhFFS7/AvB4eEpXEWkHfvO3fJ5fsZ3vnj+ay6Y0utVaAhRYsnD3GuBmYCGwHnja3XPN7E4zuxTAzKaZWRFwJfCgmeWGd78KmAVcZ2arwq8pQcUqIvG3YPUO7n/9Iy4/JYNbzhsZ73CkHnNvG0M8ZWVleXZ2drzDEJETkLO1hKt/t5Qpmb34443T6ZiSHO+Q2g0zy3H3rGjl1HMkInG1q7SCeY/nMKhnJx68ZqoSRYIKsoNbROS4auucf/nzSo5U1/Lnr59Obz14l7CULEQkbn77ziaWFJRw35xJjOynO58SmZqhRCQuVm7bzy9e/4jPTRrInKmZ8Q5HolCyEJEWV1ZRzS3zVzKgRyfuunyiBghsBdQMJSIt7kd/yWX7/iM8/fXT6dm5Q7zDkRjoykJEWtQrH+7khZXb+c55o8ka1ife4UiMlCxEpEU9tWwbw/p24VvnnBTvUKQRlCxEpMUcrKhmScE+LpowgJRkff20Jvq0RKTFvJNXTHWtc/74/vEORRpJyUJEWswb63fTp2sqpw7pHe9QpJGULESkRVTX1vHWhj2cO7YfyUm6Vba1UbIQkRaxfHMJBytquEBNUK2SkoWItIhF63bTMSWJmaM0n3ZrpGQhIoFzd95Yv5uzRqbRJVXPArdGgSYLM5ttZnlmlm9mdzSwfZaZrTCzGjObU2/ba2Z2wMxeCjJGEQnehl1lFO0/oiaoViywZGFmycADwMXAeOBqMxtfr9g24DrgyQYOcR9wTVDxiUjLeWPdbszg3HH94h2KnKAgryymA/nuXuDuVcB84LLIAu6+xd3XAHX1d3b3N4GyAOMTkRby+vrdTBnci37dO8U7FDlBQSaLDKAwYrkovE5E2pFdpRWsKSrl/HFqgmrNgkwWDd1I3awTfpvZPDPLNrPs4uLi5jy0iDSTNzfsBuBC9Ve0akEmiyJgcMRyJrCjOU/g7g+5e5a7Z6WnpzfnoUWkmby+bjdD+3bRTHitXJDJYjkwysyGm1kqMBdYEOD5RCTBPJ1dyNt5xVwycaAmOGrlAksW7l4D3AwsBNYDT7t7rpndaWaXApjZNDMrAq4EHjSz3KP7m9m7wDPAeWZWZGYXBRWriDS/F1YWcftza5g5Ko3vnDcq3uFIE5l7s3YjxE1WVpZnZ2fHOwwRAV5as4NbnlrJacP78uj10+jUITneIckxmFmOu2dFK6cnuEWkWS3M3cV35q9i6tDe/P66LCWKNkLJQkSazVt5e7j5yRVMzOjJI9dN09AebYiShYg0iyUF+/jGH3MY3b87j90wne6dOsQ7JGlGShYi0mRrig5w42PZZPbuzOM3TKdnZyWKtkbJQkSaJG9XGV99ZBm9u3bgiRtn0Ldbx3iHJAFQshCRE7Z13yGu+f1SUpOTeOJrMxjQU2M/tVXqfRKRRnN3Xli5nTtfWocBf/766Qzp2yXeYUmAlCxEpFGK9h/mBy+s5Z2Pipk6tDf3zpnESekayqOtU7IQkZi4O39aspWfv7oBB378+fF89fRhJCVpGI/2QMlCRGKyaN1u/uMvucwclcbPLp/I4D5qdmpPlCxEJKraOue+hXmMSO/Ko9dNIyVZ98a0N/rERSSq51cUkb+nnNsuHKNE0U7pUxeR46qoruWXb2xkUmZPZp88IN7hSJwoWYjIcT2xdBvbDxzh9tljNSdFO6ZkISLHVFZRzQNv5XPWyDTOHJkW73AkjpQsROSYHn53MyWHqvje7DHxDkXiLNBkYWazzSzPzPLN7I4Gts8ysxVmVmNmc+ptu9bMNoZf1wYZp4h82t7ySh5+t4DPThzIpMxe8Q5H4iywW2fNLBl4ALgAKAKWm9kCd18XUWwbcB1wa719+wD/CWQBDuSE990fVLwi8g/LNpdw18vrqKip418vHB3vcCQBBPmcxXQg390LAMxsPnAZ8HGycPct4W119fa9CHjd3UvC218HZgNPBRivSLu3fudB7n1tA2/lFdO/R0d+cdVkDeUhQLDJIgMojFguAk5rwr4ZzRSXiNRTUV3Lf7y4lmdXFNG9Ywp3XDyWa08fRudUTYkqIUEmi4busfPm3NfM5gHzAIYMGRJ7ZCLyscNVNcx7PIf38vfy9Vkj+ObZI+nZRZMXyScF2cFdBAyOWM4EdjTnvu7+kLtnuXtWenr6CQcq0l6VVVRz7SPLWLxpL/995WS+f8k4JQppUJDJYjkwysyGm1kqMBdYEOO+C4ELzay3mfUGLgyvE5FmcuBwFV95eCkrtx3g11efwpypmfEOSRJYYMnC3WuAmwl9ya8Hnnb3XDO708wuBTCzaWZWBFwJPGhmueF9S4CfEko4y4E7j3Z2i0jT7Smr4OrfLWX9zjL+7ytT+dykQfEOSRKcucfajZDYsrKyPDs7O95hiCS8t/L2cNszqymvrOGha7KYNVpNuO2ZmeW4e1a0chqiXKSdqKyp5b7X8nj4vc2MHdCdJ2+awej+3eMdlrQSShYi7UBBcTnffmoluTsO8tXTh/Lvl4yjUwfdFiuxU7IQaeM27z3EnN9+QJ07D10zlQsnaJhxaTwlC5E2bE9ZBV99ZCkGvPDNMxme1jXeIUkrpWQh0kaVVVRz/aPL2VtWxfx5M5QopEmULETaoKqaOr7xpxw27Crj4WuzmDxYo8ZK02g+C5E2pq7Oue3Z1byfv497rpjEOWP6xTskaQN0ZSHShpRX1vDdP6/i9XW7ue2iMXoqW5qNkoVIG1FYcpgbH8smv7icH39+PNeeMSzeIUkbomQh0gYsLdjHPz+xgpraOv5w/TRmjtJT2dK8lCxEWgl3Z1NxOe/n72NfeSWHqmo5XFXDwYoaFq7dxZC+XXj4q1mM0GRFEgAlC5EEVnq4mpxtJby1oZi38vZQtP8IAGbQNTWFzqnJdE1N5uKJA/mvL5xMz84aXlyCoWQhkiDcnZWFB1haUMLa7aV8uL2UbSWHAeiSmswZJ6Xxz2efxGdGp5PRqzNmDc0RJhIMJQuRODtUWcNfVu3g8Q+2sGFXGQCD+3RmYkZP5k4fzJTMXkwd1puOKRrLSeJHyUIkTkqPVPPLNz7i2ewiyiprGDewB3d/cSKzJwygd9fUeIcn8glKFiJxsP3AEa5/dBkFxYf47KSBXDNjKFOH9lbTkiSsQJOFmc0GfgUkAw+7+8/rbe8IPA5MBfYBX3L3LeFpWB8EsoA64Dvu/naQsbaEujqncP9h9pZXUXKoin3llRyuquX8cf0Z0rdLvMOTFrJ2eyk3/GE5R6prefxr0znjpLR4hyQSVWDJwsySgQeAC4AiYLmZLXD3dRHFvgbsd/eRZjYXuAf4EnATgLtPNLN+wKtmNs3d64KKN2jllTXc9Fg2HxTs+9S2n768jgvG9edrZw1n+vA+x/zr8sDhKlYWHmBtUSmj+nfnvHH96JDc+BFbqmrq+Muq7SzdXMLV04cwdWjvRh9DTsxbeXu4+YkV9Ozcgef++QxNPiStRpBXFtOBfHcvADCz+cBlQGSyuAz4cfj9s8BvLPRNOR54E8Dd95jZAUJXGcsCjDcwpYer+eqjy1i7vZTbZ49l7MDu9O2aSt9uHamrc/68vJAnlm5l0brdTBjUgzNO6os71LpTV+ccrKhhdeEBCvYe+sRx07qlcsXUTL6UNfgT99ZX19ZxuLKWrh2TSYlIJuWVNcxfto3fv7eZnaUVpKYk8WxOEZ+fPIjbZ48hs7euboJSU1vHHxZv4e5XNzCmf3cevX4a/Xt0indYIjELMllkAIURy0XAaccq4+41ZlYK9AVWA5eFE8xgQs1UgwkgWYQGXVvDmSP7ct7Y/vTs0rz3qe8tr+Sa3y9j055y/u/LpzY48cytF43hW+eM5MVV23ls8Rb+tGQbSQZJSUaSGV1Skzk5oydzsjKZMrgXEwb1JGdrCfOXFfLwu5t58J0ChvTpwpHqWsoqqqmoDl2AmUGfLqmkd+9I326pfFhUysGKGmaM6MPdX5zItGF9ePDvBTz0900syt3FTTNHMG14H/aVV7K3vJJ95VXU1DkTBvVgUmYvRqR1JSkptjb1Q5U15O8p56PdZeQXl5PRqzOXTh5Ery6f7rh1d7aVHCa9e0e6pLa9brTFm/bykwXryNtdxvnj+vHLuafQrWPbq6e0bebuwRzY7ErgIne/Mbx8DTDd3b8dUSY3XKYovLyJ0BVJKXAfcA6wFegAPOjuf6l3jnnAPIAhQ4ZM3bp1a6PjLCw5zJzfLmb3wUpSkowZI/py0YT+XDRhAP0a8Zefu7OjtIJOKUl079SB1JQkdpVW8OWHl7D9wBEeuiaLWaObfwiGPWUVPJeznbU7SuneMYXunVLo0akDnVMlzyGJAAAMpElEQVSTOVhRQ3FZ6Iu/uKySjN6duWnmCKbUG656x4Ej3PvaBl5cteMT61NTkjCgsiaUfLp1TOHkjB6cNTKNc8f2Z9zA7h83mdXWOdlbSnjlw538LW8PhSVHPj5OSpJRU+ekJidxwYT+zJmaydShvVlaUMJbeXt4e8MedpRW0CHZOGVIb2aOTOPMUWlk9urM5r2HPn7tLK1gdP9uZA3rw5TBvRJ+WtDtB47ws5fX8/KHO8ns3ZkffnY8F03or05sSShmluPuWVHLBZgsTgd+7O4XhZe/D+Dud0eUWRgu84GZpQC7gHSvF5SZLQZurNff8QlZWVmenZ19QrHW1Tmriw6wMHc3i3J3UbD3EEkGZ41K54pTM7hw/AA6px77i2nL3kN877k1LNtc8vG6o1+0HZKTeOS6aUwf3ueEYmtJG3eXcbCimr5dQ1ci3TqmUOeQv6ecNUUHWFNUysrC/azdfhCAgT07ce7YfqQkGa+u3cWesko6piTxmdHpTMrsyaj+3RnVrxtD+nRhw64yns0p4i+rtrP/cPXH5+zWMYUzR/blrJFpFB04wnsb95K74+CnYktNTiK9e0e2HwgloQ7JxskZPTl7dD++eGoGg/vErwnN3VlVeIAlBSVs3XeILfsOsXXfYXaWVtCpQxLfPHsk82aNSPjkJu1TIiSLFOAj4DxgO7Ac+Cd3z40o8y1gort/I9zB/UV3v8rMuoRjO2RmFwD/4e6zjne+piSLSO5O/p5yFqzewfMrtrP9wBG6dUzh4pMHMPvkAZw5Mu3jX/raOucPi7dw38INdEgOfSl0SU2mrKKasooaKqpruTJrMCdn9GxyXIlkT1kFb28o5s0Nu3l3415q65xzxvTjs5MGcu7YfnQ9ThNLZU0tb23Yw7qdZcwY0YesoX1ITflkJ/2+8koWbwqNfzQ8vRsj0royqFdnkpOMA4eryNm6n+Vb9rN8Swkrtu3HHc44qS9XZmUye8LA4yb25uLufLi9lJfW7OTlNTs/TmJp3VIZ2rcrQ/t2YXjfrnxxaiYZvToHHo/IiYp7sggHcQnwS0K3zj7i7neZ2Z1AtrsvMLNOwB+BU4ASYK67F5jZMGAhodtmtwNfc/fjtjE1V7KIVFfnLN1cwvMrinh17S7KK2vo1CGJmaPS+czodF5YuZ2crfs5d2w/fnb5RAb0bH8dllU1ddS5x+2v5qL9h3l+xXaeySmksOQIXVOTOf2kNGaNTmPWqHSGNXIq0cNVNfzqzY2s3V5Kp5RkOnZIomNKMklmlB6p5sDhKvYfrmLfoSoOHK4mJcmYOSqNz04axPnj+jXYJyOSyBIiWbSkIJJFpMqaWpYWlPDG+t28sW43O0or6NEphf/8/AS+eGqG2qHj7Ghif2nNDv6+sfjjPpMhfbpwzph0zh3Xn9OG9zluUlu8aS+3P7eGwpIjTM7sSa07FdV1VNbUUlvr9Ojcgd5dUundtQO9uqQyJbMXF00Y0Ow3RYi0JCWLAB1tqkrr1lHDMiQgd2frvsP8fWMx7+QV8/6mvVRU19ElNZmzRqZx5sg0hqeFmooyenWmoqaOu19ZzxNLtzG0bxfuvWISp43oG+9qiLQIJQuRsIrqWj4o2Mff1u/hzfWhq8KjUpKMTh2SOVRVww1nDufWC8e0SJ+HSKJQshBpgLuz+2AlW8N3LG3Zd4i95ZV8adpgpg5N/DvWRJpbrMlCTwZJu2JmDOjZiQE9O6mpSaQRGj+wkIiItDtKFiIiEpWShYiIRKVkISIiUSlZiIhIVEoWIiISlZKFiIhEpWQhIiJRtZknuM2smNBESZF6EppI6Xjrjrd8rPdpwN4mhNtQXI0tF0vd6q9rL3WLXG7Ouh0rjsaUOda2pv5cqm7H19Sfy7Zct6HADe7+1+Pu7e5t9gU8FG3d8ZaP8z67ueNqbLlY6taI+rSpukUuN2fdYq1fY+t2vPhj/exUt2B/Ltty3WI9RltvhmooU9Zfd7zlY71vqliPdbxysdSt/rr2UrfI5easW6zHa2zdGlqfqD+XbbluxyvXlusW0zHaTDNUSzKzbI9h4K3WSHVrnVS31qk11a2tX1kE5aF4BxAg1a11Ut1ap1ZTN11ZiIhIVLqyEBGRqNp1sjCzR8xsj5mtPYF9p5rZh2aWb2a/tohJuM3s22aWZ2a5ZnZv80bdqBibvX5m9mMz225mq8KvS5o/8pjiC+SzC2+/1czczNKaL+JGxRfE5/ZTM1sT/swWmdmg5o88pviCqNt9ZrYhXL8XzKxX80ceU3xB1O3K8PdInZnFt2+jqbdtteYXMAs4FVh7AvsuA04HDHgVuDi8/hzgDaBjeLlfG6vfj4Fb2+JnF942GFhI6JmdtLZSN6BHRJlbgN+2obpdCKSE398D3NOG6jYOGAO8DWTFo15HX+36ysLd/w6URK4zs5PM7DUzyzGzd81sbP39zGwgoV++Dzz0iT4OfCG8+Z+Bn7t7Zfgce4KtxbEFVL+EEGDd/gf4HhC3zrwg6ubuByOKdiVO9QuobovcvSZcdAmQGWwtGhZQ3da7e15LxB9Nu04Wx/AQ8G13nwrcCvy/BspkAEURy0XhdQCjgZlmttTM3jGzaYFG23hNrR/AzeFL/kfMrHdwoTZak+pmZpcC2919ddCBnoAmf25mdpeZFQJfBn4UYKyN1Rw/k0fdQOgv80TRnHWLK83BHcHMugFnAM9ENGN3bKhoA+uO/qWWAvQGZgDTgKfNbET4L4a4aqb6/R/w0/DyT4H7Cf2CxlVT62ZmXYAfEGrSSCjN9Lnh7j8AfmBm3wduBv6zmUNttOaqW/hYPwBqgCeaM8YT1Zx1SwRKFp+UBBxw9ymRK80sGcgJLy4g9IUZeambCewIvy8Cng8nh2VmVkdo/JfiIAOPUZPr5+67I/b7HfBSkAE3QlPrdhIwHFgd/sXOBFaY2XR33xVw7NE0x89lpCeBl0mAZEEz1c3MrgU+B5yXCH+YhTX35xZf8ewwSYQXMIyIDilgMXBl+L0Bk4+x33JCVw9HO6QuCa//BnBn+P1ooJDw8yxtpH4DI8p8F5jfVupWr8wW4tTBHdDnNiqizLeBZ9tQ3WYD64D0eNUp6J9JEqCDO67/sfF+AU8BO4FqQlcEXyP01+VrwOrwD+CPjrFvFrAW2AT85mhCAFKBP4W3rQDObWP1+yPwIbCG0F9FA1uqPkHXrV6ZuCWLgD6358Lr1xAaByijDdUtn9AfZavCr3jd6RVE3S4PH6sS2A0sjEfd3F1PcIuISHS6G0pERKJSshARkaiULEREJColCxERiUrJQkREolKykDbNzMpb+HwPm9n4ZjpWbXiU2LVm9tdoo6maWS8z+2ZznFukPt06K22amZW7e7dmPF6K/2PQukBFxm5mjwEfuftdxyk/DHjJ3U9uifikfdGVhbQ7ZpZuZs+Z2fLw68zw+ulmttjMVob/HRNef52ZPWNmfwUWmdnZZva2mT0bnkfhiYj5B94+Ou+AmZWHB+9bbWZLzKx/eP1J4eXlZnZnjFc/H/CPAQ+7mdmbZrbCQnMgXBYu83PgpPDVyH3hsreFz7PGzH7SjP+N0s4oWUh79Cvgf9x9GnAF8HB4/QZglrufQmhU1p9F7HM6cK27nxtePgX4F2A8MAI4s4HzdAWWuPtk4O/ATRHn/1X4/FHHAAqPJXQeoSfmASqAy939VELzp9wfTlZ3AJvcfYq732ZmFwKjgOnAFGCqmc2Kdj6RhmggQWmPzgfGR4wE2sPMugM9gcfMbBShUT87ROzzurtHzlWwzN2LAMxsFaExgd6rd54q/jHQYg5wQfj96fxjDo0ngf8+RpydI46dA7weXm/Az8Jf/HWErjj6N7D/heHXyvByN0LJ4+/HOJ/IMSlZSHuUBJzu7kciV5rZ/wJvufvl4fb/tyM2H6p3jMqI97U0/LtU7f/oFDxWmeM54u5TzKwnoaTzLeDXhOajSAemunu1mW0BOjWwvwF3u/uDjTyvyKeoGUrao0WE5nMAwMyODiHdE9gefn9dgOdfQqj5C2ButMLuXkpoKtRbzawDoTj3hBPFOcDQcNEyoHvErguBG8LzKmBmGWbWr5nqIO2MkoW0dV3MrCji9a+Evnizwp2+6wgNKw9wL3C3mb0PJAcY078A/2pmy4CBQGm0Hdx9JaGRS+cSmtwny8yyCV1lbAiX2Qe8H77V9j53X0SomesDM/sQeJZPJhORmOnWWZEWFp6V74i7u5nNBa5298ui7ScST+qzEGl5U4HfhO9gOkACTEsrEo2uLEREJCr1WYiISFRKFiIiEpWShYiIRKVkISIiUSlZiIhIVEoWIiIS1f8HMPlluO1aD5oAAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"learn.lr_find()\n",
"learn.recorder.plot()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"Total time: 04:00 <p><table style='width:375px; margin-bottom:10px'>\n",
" <tr>\n",
" <th>epoch</th>\n",
" <th>train_loss</th>\n",
" <th>valid_loss</th>\n",
" <th>accuracy_thresh</th>\n",
" <th>fbeta</th>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <th>0.097016</th>\n",
" <th>0.094868</th>\n",
" <th>0.952004</th>\n",
" <th>0.916215</th>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <th>0.095774</th>\n",
" <th>0.088899</th>\n",
" <th>0.954540</th>\n",
" <th>0.922340</th>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <th>0.090646</th>\n",
" <th>0.085958</th>\n",
" <th>0.959249</th>\n",
" <th>0.924921</th>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <th>0.085097</th>\n",
" <th>0.083291</th>\n",
" <th>0.958849</th>\n",
" <th>0.928195</th>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <th>0.079197</th>\n",
" <th>0.082855</th>\n",
" <th>0.958602</th>\n",
" <th>0.928259</th>\n",
" </tr>\n",
"</table>\n"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"learn.fit_one_cycle(5, slice(1e-5, lr/5))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"learn.save('stage-2-rn50')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"torch.Size([3, 256, 256])"
]
},
"execution_count": null,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"data = (src.transform(tfms, size=256)\n",
" .databunch().normalize(imagenet_stats))\n",
"\n",
"learn.data = data\n",
"data.train_ds[0][0].shape"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"learn.freeze()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"LR Finder complete, type {learner_name}.recorder.plot() to see the graph.\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZIAAAEKCAYAAAA4t9PUAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4wLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvqOYd8AAAIABJREFUeJzt3Xd41GW68PHvnQ6kkwRCEiD0LiU0EQRUBHXtBdfeu7vr7h71eI77rq67urbVY8WCysqufVUsiHTpoUhJaAktpAOppM/z/jETDCFlkpnJFO7Pdc1F5lefh18y9zxdjDEopZRS7eXn7gQopZTybhpIlFJKOUQDiVJKKYdoIFFKKeUQDSRKKaUcooFEKaWUQzSQKKWUcogGEqWUUg7RQKKUUsohAe5OQEeIiYkxvXv3dncylFLKq2zcuLHQGBPb2nGnRSDp3bs3qamp7k6GUkp5FRE5YM9xWrWllFLKIRpIlFJKOUQDiVJKKYdoIFFKKeUQDSRKKaUcooFEKaWUQzSQKKWUcogGEqWU8kG780p5YdFu8ksrXX4vDSRKKeWDthwq4uXFe6istrj8XhpIlFLKB+UWW0si3SKCXX4vDSRKKeWDcooriAkNJjjA3+X30kCilFI+KLuokviIkA65lwYSpZTyQbnFGkiUUko5ILu4QgOJUkqp9imrqqW0spb4yE4dcj8NJEop5WNyiysAtESilFKqfbKLrF1/4yO0RKKUUqod6seQaIlEKaVUu2QXVyAC3cI1kCillGqH3OJKYkKDCQromI94DSRKKeVjsjtwDAloIFFKKZ+TU9RxY0hAA4lSSvkc66j2jumxBRpIlFLKp5RW1lBaVaslEqWUUu1zoutvB41qBw0kSinlU7I7eAwJaCBRSimfklPUsdOjgAYSpZTyKTnFlR06GBE0kCillE/JKa4gNjSYQP+O+3jXQKKUUj4kp7iyQxvaQQOJUkr5lJziSuI7sFoLNJAopZTPMMZYR7VHaiBRSinVDqVVtZRX13Vojy3QQKKUUj4jp4MXtKqngUQppXxETgcvsVtPA4lSSvmIHDdMjwIuDiQiMlNEdonIXhF5pIn9U0Rkk4jUisiVDbaPFJE1IrJDRLaKyDUN9iWLyDoR2SMiH4lIkCvzoJRS3iKnqAI/gbiw4A69r8sCiYj4A68Cs4AhwLUiMqTRYQeBm4H5jbYfB240xgwFZgL/EJFI275ngBeNMf2BY8BtrsmBUkp5l5ziSmLDOnYwIri2RDIO2GuMyTTGVAP/Bi5peIAxZr8xZitgabR9tzFmj+3nbCAfiBURAaYDn9oOfR+41IV5UEopr5HTweuQ1HNlIEkADjV4n2Xb1iYiMg4IAjKArkCRMabWkWsqpZQvyinu2JUR67kykEgT20ybLiASD8wDbjHGWNpyTRG5U0RSRSS1oKCgLbdVSimvY4zxyRJJFpDU4H0ikG3vySISDnwD/I8xZq1tcyEQKSIBrV3TGDPHGJNijEmJjY1tc+KVUsqblFTUctwNgxHBtYFkA9Df1ssqCJgNfGXPibbjvwA+MMZ8Ur/dGGOApUB9D6+bgC+dmmqllPJCOSW2MSQdPD0KuDCQ2Nox7gcWAunAx8aYHSLyhIhcDCAiY0UkC7gKeFNEdthOvxqYAtwsIltsr5G2fQ8DD4nIXqxtJu+4Kg9KKeUt3DWqHSCg9UPazxjzLfBto22PN/h5A9bqqcbn/RP4ZzPXzMTaI0wppZRNjhuW2K2nI9uVUsoH5BS7ZzAiaCBRSimfcLiogriwEAI6eDAiaCBRSimfsK+wnN4xnd1ybw0kSinl5YwxZBaU0zc21C3310CilFJe7kh5NcUVNRpIlFJKtU9GfhkAfWK7uOX+GkiUUsrLZRaWA2iJRCmlVPtk5JcRHOBHQgcvaFVPA4lSSnm5jIIy+sSG4ufX1Ly2rqeBRCmlvFxmYbnb2kdAA4lSSnm1ypo6Dh097rb2EdBAopRSXu3AkeNYDPTVEolSSqn2yCywdv3VEolSSql2ybAFkuQYLZEopZRqh4yCcnpEhNAl2KWrgrRIA4lSSnmx+q6/7qSBRCmlvNQvkzW6r1oLNJAopZTXyi+toqyqlr5xWiJRSinVDicma4zRQKKUUqodMuona4zTqi2llFLtkJFfRucgf7qHh7g1HRpIlFLKS1l7bHVBxD2TNdbTQKKUUl7KncvrNqSBRCmlvFBFdR2Hiyo0kCillGqfzEL3z7FVTwOJUkp5ocwCa48td65DUk8DiVJKeaGMgjJE3DtZYz0NJEop5YUyCspJjOpESKC/u5OigUQppbxRZkGZ20e019NAopRSXujAkeMeUa0FGkiUUsrrlFbWUFZVS3yEe0e019NAopRSXiavpBKA7hpIlFJKtUducRUA3dw8x1Y9lwYSEZkpIrtEZK+IPNLE/ikisklEakXkykb7vheRIhFZ0Gj7eyKyT0S22F4jXZkHpZTyNLn1JRJfDyQi4g+8CswChgDXisiQRocdBG4G5jdxiWeBG5q5/B+NMSNtry1OSrJSSnmF3OIK4PSo2hoH7DXGZBpjqoF/A5c0PMAYs98YsxWwND7ZGLMYKHVh+pRSyivlllQS2TnQI8aQgGsDSQJwqMH7LNs2Z3hKRLaKyIsiEuykayqllFfILa7ymGotcG0gaWqCfOOE6z4KDALGAtHAw03eXOROEUkVkdSCggIn3FYppTxDbkmFx1RrgWsDSRaQ1OB9IpDt6EWNMTnGqgqYi7UKranj5hhjUowxKbGxsY7eVimlPMbpVCLZAPQXkWQRCQJmA185elERibf9K8ClwHZHr6mUUt6ips7CkfIqj+n6Cy4MJMaYWuB+YCGQDnxsjNkhIk+IyMUAIjJWRLKAq4A3RWRH/fkishL4BDhHRLJE5Hzbrg9FZBuwDYgB/uKqPCillKfJL63CGM/psQUQ4MqLG2O+Bb5ttO3xBj9vwFrl1dS5k5vZPt2ZaVRKKW/iaV1/QUe2K6WUV6kf1X66tJEopZRyMk8b1Q4aSJRSyqvkFlcQHOBHZOdAdyflBA0kSinlRXJLqugeEYK146pn0ECilFJeJK+40qO6/oIGEqWU8iq5JZUe1T4CGkiUUsprGGPILan0mJUR62kgUUopL3HseA3VtRat2lJKKdU+ucWetcRuPQ0kSinlJTxtrfZ6GkiUUspL5BR73mBEsDOQiEjf+gWkRGSqiDwoIpGuTZpSSqmGcksqEYHYMM9az8/eEslnQJ2I9APeAZJpep11pZRSLpJXXElMaDCB/p5VmWRvaiy2aeEvA/5hjPkdEO+6ZCmllGosxwO7/oL9gaRGRK4FbgIW2LZ5zkQvSil1GvDEUe1gfyC5BZgIPGWM2SciycA/XZcspZRSjXniqHawc2ErY0wa8CCAiEQBYcaYp12ZMKWUUr+oqK6juKLG47r+gv29tpaJSLiIRAM/A3NF5AXXJk0ppVQ9T1yHpJ69VVsRxpgS4HJgrjFmDHCu65KllFKqIU8d1Q72B5IAEYkHruaXxnallFIdpH5Uuzc3tj8BLAQyjDEbRKQPsMd1yVJKKdVQrodOjwL2N7Z/AnzS4H0mcIWrEqWUUupkucWVhAUHEBps18d2h7K3sT1RRL4QkXwRyRORz0Qk0dWJU0opZZVbXEk3DyyNgP1VW3OBr4AeQALwtW2bUkqpDuCpY0jA/kASa4yZa4yptb3eA2JdmC6llFIN5BZXemT7CNgfSApF5HoR8be9rgeOuDJhSimlrOoshoKyKq8vkdyKtetvLpADXIl12hSllFIuVlhWRZ3FeHcbiTHmoDHmYmNMrDEmzhhzKdbBiUoppVxsf2E5AAmRXhxImvGQ01KhlFKqWT/tLcRPYEzPaHcnpUmOBBJxWiqUUko1a8XuAkb1jCKis2eu3uFIIDFOS4UPKT5eQ0V1nbuToZTyEUfKqth6uJizB3huR9kWh0iKSClNBwwBOrkkRV7u2rfWMqBbKP+YPcrdSVFK+YCf9hZiDN4bSIwxYR2VEF9QVlVLem4JB48ep7rWQlCAZ62rrJTyPst3FxDVOZBhCRHuTkqzXPpJJyIzRWSXiOwVkUea2D9FRDaJSK2IXNlo3/ciUiQiCxptTxaRdSKyR0Q+EpEgV+ahLXbllmCMNaCk7j/q7uQopbycxWJYsbuQyf1j8ffz3GZplwUSEfEHXgVmAUOAa0VkSKPDDgI3A/ObuMSzwA1NbH8GeNEY0x84BtzmrDQ7Ki2nFAA/gSU7892cGqWUt0vLKaGwrMqjq7XAtSWSccBeY0ymMaYa+DdwScMDjDH7jTFbAUvjk40xi4HShttERIDpwKe2Te8Dl7og7e2Sll1CRKdAJvWLYckuDSRKKccs310AwOQBMW5OSctcGUgSgEMN3mfZtjmiK1BkjKl14jWdJi2nhCHx4UwfFEdmQTkHjpS7O0lKKS+2YncBQ3uEExfmmQMR67kykDRVoedol2G7rykid4pIqoikFhQUOHjb1tVZDLtySxjSwxpIQKu3lFLtV1pZw8YDx5ji4dVa4NpAkgUkNXifCGQ7eM1CIFJE6nubNXtNY8wcY0yKMSYlNtb1D2JfYTmVNRaGxIfTq2sX+sR20UCilGq31RlHqLUYj28fAdcGkg1Af1svqyBgNtY1TdrNGGOApVgnjQS4CfjSoVQ6SVpOCQCD48MBmD4wjnWZRymvqm3pNKWUatLy3QWEBgcwumeUu5PSKpcFEls7xv1Y13pPBz42xuwQkSdE5GIAERkrIlnAVcCbIrKj/nwRWYl1ed9zRCRLRM637XoYeEhE9mJtM3nHVXloi7TsEgL9hX5xoQBMHxRHdZ2FVXsL3ZwypZS3McawYncBZ/bt6hXj0Vy6+K8x5lvg20bbHm/w8was1VNNnTu5me2ZWHuEeZS0nBL6x4WdeOgpvaMJDQ5g6a58Zgzt7ubUKaW8SWZhOVnHKrj77L7uTopdPD/UeYn0nJIT1VoAQQF+TO4fw9KdBVhr5JRSyj6L0/MAz54WpSENJE6QX1pJQWkVQ3qEn7R92qA4cksqT7SfKKVUa2rqLLy/+gApvaJIiu7s7uTYRQOJE6TbRrQPiT85kEwdaP02sVR7byml7PT1z9kcLqrgnqneUa0FGkicIi3bWuJoHEjiwkIYkRih3YCVUnaxWAyvL8tgYLewE+PRvIEGEidIzykhIbJTk4vOnD0gli2HiijTbsBKqVb8mJ7Hnvwy7pnaF+uMUN5BA4kTpDVqaG9ofHJXLAY2HjjWwalSSnkTYwyvLcsgMaoTF42Id3dy2kQDiYMqquvILCg7paG93uhekQT4Cev3HenglCmlvMnazKNsOVTEXVP6EODvXR/N3pXaDvb99hw+ST3U4jG78kqxGBgS3/QaYJ2DAhiWEMH6fbo+iVKqea8vzyAmNIirUpJaP9jDaCBpweebDvP6sowWj0nPqW9ob371svHJ0fx8qJjKGl3LXSl1qu2Hi1mxu4BbJiUTEujv7uS0mQaSFgxPiCCzsJzSyppmj0nLLiEsOIDEqOaXsB+XHE11nYUth4pckUyllJd7a2UmYcEB3DCxl7uT0i4aSFpQv0byjuzmBxTWN7T7tbAMZkqvaETQ6i2lVJPWZh7h3CHdCA85teenN9BA0oL6QLL9cHGT+y0WY5sapen2kXoRnQMZ2C2MDbqOu1KqkaPl1eSVVLX6OeLJNJC0IDYsmO7hIc0GkszCco5X1zXbY6uh8cnRbDxwjJq6U1YVVkqdxnbmWms8BnVv/XPEU2kgacWwhHC2NRNI6quqUnpHt3qdccldOV5d12I1mVLq9LMr1zrF0iAtkfiuYbYG96YWqFq37wgxocH0ienS6nXGJlsXp9HxJEqphnbmlBLdJYjY0GB3J6XdNJC0YnhCBMZwygy+xhjWZR5lfJ9ou6YyiAsLoU9MF21wV0qdZGduCYO6h3nVlCiNaSBpRX2D+7ask6u3Dh49Tm5JJROSW6/WqjcuOZr1+45isej6JEopqLMYduWVenX7CGggaVW38BBiw4JPaXBfl2ktWYzv09Xua43tHU1JZS278kqdmkallHc6cKScyhqLV7ePgAYSuwxPiGB79smBZO2+I0R3CaK/bY12e4yzlV60G7BSCn5paB+sJRLfNywhgr35ZRyv/qXBfV3mUcb1tq99pF5iVCd6RISwTttJlFJAem4pfgL9u9n/hdQTaSCxw7Ae4VjML/NqZR07zuGiCsb3sb99BEBETrSTNLeOe0V1HXd+kMrt76fqWu9K+bidOSX0junilfNrNaSBxA7DE+tHuFsDyYn2kWT720fqjUvuSkFpFT+k5Z2yr6yqlpveXc8PaXn8mJ7Hgq05DqRaKeXpduaWen21FmggsUv38BBiQoNODExct+8IEZ0CGdS97Q1kM4d1p39cKHfN28hjX2w7UV1WfLyG699ex8aDx3hp9kiGxIfz9Hc7dcZgpXxUeVUtB48eb9fniKfRQGIHEWFoj4gTPbfW7TvK2N7RLU7U2JzoLkF8/cBZ3DE5mfnrD3LBSytZsjOPa99aS1p2Ca9fN5pLRibwp18N4XBRBXNWZDo7O0opD1Dfe3OgBpLTx/CECPbkl7G/sJwDR44zoY3tIw2FBPrz2IVD+NcdE6ipM9z6XioZBWXMuXEMM4Z2B6zdii8Y3p3Xl2WQW1zprGwopTzEzhxbj61mlun2JhpI7DQsIYI6i+H9NfsBmNCG8SPNmdCnK9//djIPTu/Hh7ePZ+rAuJP2PzprMHXG8Mz3Ox2+l1LKs+zMLSE0OICEyObXMvIWGkjsNCzB+q3h4w2HCAsJcNq3iLCQQB6aMbDJiR+Tojtzx+Rkvth8mE0Hjznlfkopz7Azt5SB3cPaVUXuaTSQ2CkhshNRnQMpr65jbO9o/Dvo4d87tR9xYcH8+es07Q6slI8wxrAzp8QnGtpBA4ndROTEvFvj2zC/lqO6BAfwwPR+/HyoiL35ZR12X6WU6+QUV1JSWauB5HR0IpA4oX2kLSb2jQFgs675rpRPOLGYlQ80tAMEuDsB3uSqMYnUWQzDbQGlo/SJ6UJYSACbDxZxdUpSh95bKeV86Tm+0/UXNJC0SZ/YUP77gsEdfl8/P2FkUiRbtESilE/YlVtKQmQnwkMC3Z0Up9CqLS8xKimSXbklJ00cqZTyTvWLWfkKlwYSEZkpIrtEZK+IPNLE/ikisklEakXkykb7bhKRPbbXTQ22L7Ndc4vtFdf4ur5oZM9ILObUBbaUUt6lvKqWjIJyr1+DpCGXBRIR8QdeBWYBQ4BrRWRIo8MOAjcD8xudGw38CRgPjAP+JCJRDQ65zhgz0vbKd1EWPMoZiZGANrgr5e3e/WkfdRbDuYO7uTspTuPKEsk4YK8xJtMYUw38G7ik4QHGmP3GmK2ApdG55wOLjDFHjTHHgEXATBem1eN1DQ2mV9fObDmogUQpb3WsvJo5KzKZMaQbo3pGtX6Cl3BlIEkADjV4n2Xb5oxz59qqtf5X2rKylJfTBnelvNvryzMoq67lD+cPdHdSnMqVgaSpD3h7h2a3dO51xpjhwGTb64YmLyByp4ikikhqQUGBnbf1bCOTIsktqSSnuMLdSVFKtVFOcQXvrd7P5aMSGdDNd9pHwLWBJAtoOOghEch29FxjzGHbv6VY21bGNXUBY8wcY0yKMSYlNja2jUn3TCOTrO0kWr2llPd5efEejDH89tz+7k6K07kykGwA+otIsogEAbOBr+w8dyEwQ0SibI3sM4CFIhIgIjEAIhIIXARsd0HaPdKQHuEE+ftp9ZaXOV5di8Wi86SdzjILyvg4NYvrxvciKbqzu5PjdC4LJMaYWuB+rEEhHfjYGLNDRJ4QkYsBRGSsiGQBVwFvisgO27lHgSexBqMNwBO2bcFYA8pWYAtwGHjLVXnwNMEB/gzpEa49t7zIF5uzGPfUYi54eSWrMwrdnRzlJs8v2k1wgB/3T+/n7qS4hEtHthtjvgW+bbTt8QY/b8BabdXUue8C7zbaVg6McX5KvcfIpEg+2nCI2joLAf46ntRTlVbW8PiXO/hi82FG9Ywkv6SKX7+1jvOHduOxC4bQs6vvfStVTdt+uJhvtubw4PR+xIQGuzs5LqGfRF5mVM9IKmrqTizTqTzPlkNFXPjyT3y55TC/Pbc/n9w1kcW/P5s/zBjAyj2FnPvCcp5duJPKmjp3J1V1gDkrMgkLDuD2KX3cnRSX0UDiZUYlWfueazuJZ9qRXcyVr6+mzmL46K6J/PbcAQT4+xES6M/90/uz9A9TuWhEPK8uzWDWSytZm3nE3UlWLpRdVME323K4ZmySz8yr1RQNJF4mKboT0V2CtOeWh3p/9X6CAvz4+oGzGNvEqpfdwkN44ZqRfHj7eOoshtlz1vLo59sorqhxQ2qVq72/ej/GGG6e1NvdSXEpDSReRsQ6E7A2uHue4ooavv45h0tG9iC6S1CLx07qF8PC307hzil9+GjDQWb+YwV5JZVOTY/2FHOvsqpa5q8/yKzh8SRG+XabmE4j74VGJUWydFc+JZU1Pl1c9jb/2XyYipo6fj2ul13Hdwry578vGMysYd2ZPWctj3+5nTdvSGnXvY0xrNxTyLbDxezMLWVnTgn7j5RzVUoST106DG+aAMIYwx0fpHLgyHEuHZXAZaMS6BHZyd3JarNPUg9RWlnL7WcluzspLqclEi80smckxsDPWirxGMYYPlx3gBGJEQxPbNvCZ6N6RvG78wawcEce323LafO9a+ssPPzZVm58dz3PLtzF5oPH6NW1C+cN6cb8dQd5cdHuNl/TEVW1dRjT/tLQD2l5/JieT50xPLtwF5OeWcKv31rLt+34v3GXOovh3VX7GNMryqfm1GqOlki80MikSAL8hFV7jzC5v2+M2vd2Gw8cY3deGc9cMbxd599+VjILtmbzv1/uYGLfrkR2brlqrF5VbR2/+dcWvt+Ry4PT+3HHlD6E2Uqpxhge/mwrLy/ZS4/ITswe17NdaWuOMYZVe4/w+eYssosqyC+toqC0itLKWvrHhXLjmb25fFQCXYLt/5ipqbPw9Hc76RcXyve/mUx2USVfbD7M55uzuPfDTfzx/IHcN63tYzHKqmp5efEeFqXl8dp1oxns4iVuF6XlcuhoBf89q+MXwnMHLZF4obCQQMb3iWZxep67k6JsPlx3kLDgAH51Ro92nR/g78czV4zg2PFqnvom3a5zyqtqufW9DXy/I5fHLxrCQzMGnggiYG1Pe+qy4UwZEMtj/9nO0l2/rLhQUFrFe6v28dgX2yivattiaVW1dXySeohZL63k+nfWsXRnPnUWw6DuYVwxOpHfnNOf4EA//vc/25nw18X8+esdHDxy3K5rz193kH2F5Tw6axAB/n707NqZ35zbnyW/n8qlI3vw7MJd/N/iPXan1RjDl1sOM/25Zby1MpPC0ipufW+D09ujGnt75T6SojsxY2h3l97HU2iJxEtNH9SNJxekcfDIcZ8a3GaMoayqFosFIjp7R/vPsfJqvtmWw+yxSXQOav+f1NAeEdw5pQ+vL8vgkpEJnNU/ptlji45Xc/PcDWw7XMzzV53BFWOaHNdLoL8fr103mmveXMN9H27iofMGsHx3Aav2FlLfFl9Va+G5q86wK40/puXxyOfbKCyrYmC3MP5+5QguPqMHIYH+Jx3323P7s+lgEe+v3s+8NQeYt+YAN53ZmwfP6U9Ep6afa0llDS8t3sPEPl2ZPujk9er8/YTnrx6JnwjPL9qNAR48p+U5q3bllvK/X25n/b6jjEiMYM6NKQT6C1e/sYZb39vAx3dNbFNpyV6bDx4j9cAxHr9oCP5+3tM25QgNJF7qnEFxPLkgjSU787h5knc25pVX1fLT3kKWpOezM6+UwtIqCsuqqKq1EBTgx7cPnkW/OM+fJfWzTVlU11r49XjHq45+c05/vt+ey6NfbGXhb6c0G5ieWJBGWnYJr183utVvvaHBAcy9eSyXvbaav3yTTlJ0J+6d2o+LR/bg65+z+b8le5ncP4ZLRra8ysOmg8e4b/4m+saG8uI1Z3BWv5hmG/FFhDG9ohjTK4rHLhzMi4t28+6qfXy+KYuHZgzk2rFJp8zM8PqyDI6WV/PYhYObvK6/n/DsVWeAwAuLdmMxht+c0/+UY8uqavnHot3MXb2fsJAA/nrZcK4Zm3TiQ/2V60Zz+/upPPCvzcy5YYzTZ4h4c7l1AOLVY5NaP9hHiCONYt4iJSXFpKamujsZTnfO88voEdmJebeNd3dS2mTB1mw+2nCIdZlHqa6zEBYcwBlJkcSFBRMTFkzXLkG8snQvY3tH8+7NY92d3BYZYzjn+eVEdQnis3vOdMo112Ue4Zo5a7lvWl/+eP6gU/YfOFLO9OeXc8uZvfmfixovOtq8vJJK8koqGZ4QceLDt7bOwjVz1rIrt5RvH5zcbOn24JHjXPbaKroEB/DFvWfStR1TfezILubJBWmszTxK39guXDuuJxef0YO48BAOF1Uw7bllXDQ8nheuGdnideos1rafTzdm0SMihBlDuzNzWHdSekXx/Y5cnlyQRl5JFdeOS+K/zh9EVBNdsf+59gD/85/t3DChF09cMrTZgGixGKpqLXQK8m9yf2Nbs4q4+JVV/Oac/vzuvAF2nePJRGSjMabVroRaIvFi5wzuxtxV+yirqiXUBUV0V8goKOP++ZvpGd2Zm87sxbRBcYztHU1gE98K//bdTn7aU9hiFY+7rck8QmZhOc+3owG4OeP7dOXiM3rw9sp9XD+hF/ERJ3d9fW1pBv5+wp1tnHKjW3gI3cJDTtoW4O/HS7NHMuullTzw7818evfEU55F0fFqbn5vPbUWw9xbxrYriIC16u5fd0zgh7Q8Xl26l798k85fv01nUr8YausMAvzejgWf/P2EZ64YwaR+Xfl2Wy7/Wn+Q91bvp3OQP8er6xjaI5zXrx/D6BZ6S10/oRcHjx5nzopMfs4qYtrAOKYOjGVEYiS1FgtrMo7wQ1oei9LyqKyp4193TGBYQuu98Z77YTdRnQO5fbJ31hK0l3d8+qgmTR8Ux5wVmfy0p4CZw+LdnRy7vL96P4H+wqf3TCQuLKTZ4246szfz1h7gL9+k8c2Dkz22rvnTjVnghTIHAAATeElEQVSEhQRw4Qjn/v//8fyBfL89l+d/2H1S+0XWseN8timL68b3JC68+f+/tkiM6szTl4/gvvmbeGHRbh6e+UspqKq2jrvmbSTraAXzbhtH39hQh+4lIpw/tDvnD+3O3vwyvtxymC82HybrWAX3Tu1Lgp3jRfz9hMtGJXLZqETKq2pZvruA5bsKGJYQzq/H97Lr9+WRmYOIDQ3mu+05vLxkDy8t3kN0lyBqai2UVtXSJcifqQPj2HKoiJveXc8nd0+kTwv5X5t5hBW7C3jsgsEndXo4HWgg8WIpvaIIDwngx/R8rwgkxRU1fLoxi1+d0aPFIAIQEujPI7MGcf/8zXy2Mcsj65sra+pYtCOPmcO6n9LY7Kik6M7cPKk3b63M5NZJyQzpYe2u+sbyDETgrrP7OvV+F46I56e9SbyxPIPVewtBBAFKKmrILCznpdkjGd+nq1Pv2S8ulN/PGMhD5w1gd14Z/eLaF6S6BAdwwfB4Lhjetr8BPz/hjil9uGNKH46VV7NiTwHLdxcQHODHjCHdmdi3KyGB/mQWlHHVG2u44Z31fHrPxFNKiGCt4nx24S66hQdzw0T7BqT6Eu3+68UC/P2YOjCOpTvzvWI6jE9SD3G8uo5b7ewccOHweEb3jOS5H3a1uYtqR1i5p5DSqlouameX39bcN7UfEZ0C+eu36RhjyC2u5OMNWVw5JtElI70fv2gos8cmEdk5iIhOgYR3CiQhqhN/u3x4qw3xjhARBnYPc2upM6pLEJeMTOCFq0fyt8tHMG1Q3IkvB31iQ3n/1nEUV9RwwzvrOVZefcr5S3fls/HAMR48p7/Tv1R4Ay2ReLlzBsfx1c/Z/JxV5NEjaOsshvdW72ds7yi76prB+gHz2IVDuOL11by5IpOHPKzxcsHWbKI6B3JmX+d+U68X0TmQB6b358kFaSzfXcCK3YXUGcM9Z7tmcaROQf787fIRLrm2txuWEMFbN6Zw09z13PzeBp69csSJddctFsOzC3fTM7ozV6d4Xsm5I2iJxMudPSAWfz9hcXp+6we70Y/peWQdq+CWNnZVHtMriotGxDNnRQa5xa4dRNYWlTV1/JhmrdZqqqOAs9wwoRe9unbmiQVpzF9/gEtHJvjUuCFvMrFvV165dhTp2SXMeHEFs15ayRvLM3h/zX7Sc0p46LwBLv1d8GSnZ659SGTnIMb0imLxTs8OJHNX7SMhshMzhnRr87kPzxyEMfD4l9sdmsPJmZbtyqe8uo4Lh7umWqteUIAfD88cRGZBOVW1Fu6b5ty2EdU2M4Z2Z9Uj0/nTr4YQHODH09/t5M9fpzGwW1i7ZzXwBVq15QPOHRzHX7/dyeGiCrt7vXSk9JwS1mYe5RHbtBdtlRTdmYfOG8DfvtvJN9tyuGiE+/9gv96aQ9cuQUzoc+qaI842a1h3pg2MJSGqU4u9hlTHiA0L5pZJydwyKZn9heUs3JHLWf1jPLZnYUfQEokPmD7I+i2/pbm3jDHkl7qnamjuqn2EBPox24GeV7edlcyIxAj+9OUOjjbR2NmRjlfXsiQ9n1nDuzt9VHRTRIS5t4zjL5e2b0JI5Tq9Y7pw19l9GdqjbTM++xoNJD6gb2wXBnQL5S8L0nlyQdpJH7TGGH7aU8iVb6xh3FOLmbf2QIemLbe4kv9syeaK0Yl2z2jblAB/P/5+5QhKKmv489c7nJjCluWVVFLXqEfckp35VNS4vlpLKW+hgcQHiAgf3Dqey0YlMHfVPs7++1JeWbKHFbsLuObNtVz/zjoOH6tgdM9I/vTldpZ2UHvK4aIKZs9Zg78ItzlhcZ9B3cO5b1o/vtySzY9prp/5eE9eKZOeXsKN7647qcvnN1tziA0LZlyy66u1lPIGGkh8RPeIEJ65cgQ//G4KE/t25bkfdnPju+vZf6ScP188lGV/nMq828YzOD6c++dvYkd2sUvTs7+wnKvfWMORsmrm3TbOaXX7907tx6DuYTz2H9evc/72yn34+Qkb9h3jkldXsSu3lLKqWpbszOeCYd1P6zpxpRrSSRt91KaDx9hfWM4Fw+NPGiCVV1LJpa+uwhj44r4zmxyl66jdeaVc9/Y6ausszLttvN3jRuy1NauIS19dxQ0TevHnS4Y59dr1CkqrmPT0Eq4em8jloxO5e95GyqpquXB4PJ9szOKTuycytreWSJRvs3fSRi2R+KjRPaO4fHTiKaNsu4WH8O7NYymtrOHW91IprXTut/qfDxVxzZtrEOCjuyY6PYgAjEiM5LJRiXy6MctlI97nrdlPjcXCrZOSGd0ziq8fOIv+3cL4ZGMW3cNDGOPBgz+V6mgaSE5Dg+PDefW60ezOK2Xac8t4Zckeio6f2hOqvKq2TYMAP0k9xFVvrqFLcAAf3zXxxMhfV5g9Lony6jq+ccE63pU1dcxbe4BzBnU7USXXLTyEj+6cwF1n9+HhWQPx02otpU7QcSSnqakD4/jozgm8snQvz/2wm9eWZTB7bE9GJEaw+eAxNh48RnpOKXUWw40Te/HwzEHNriZXU2fhLwvSeH/NAc7s25X/u3ZUu6cat1dKryj6xHbh4w2HnD4txWebsjh2vIY7Gk0FHhLoz6OnyRrcSrWFBpLTWErvaN67ZRzpOSW8tSKTD9bsp9Zi6Bzkz8ikSO6d2peSiho+WHuApbvy+fsVZzCx0bxS+SWV3D9/M+v3H+WOyck8PLN9gw7bSkS4OiWJp7/byd789s8c25jFYnhn5T6GJ0Roryyl7KSN7eqE3OJKjpRb1+JuGAw27D/KHz/5mf1HjnPtuJ7EhgaRnlvKrtxSDh49TkigH3+/8gwu7uApIvJLK5n4tyXcPjm51ZJCVW0db6/cx6R+MYxMimz2uB/T8rj9g1Remj3SpTPeKuUN7G1s10Ci7FJRXcezC3cxd/U+BEiO6cKg+HAGdw9j5rB4p5UI2uqOD1LZfLCINY9Ob3bCvMKyKu6et5HUA8eI6hzIV/efRVJ00xMfzp6zhgNHjrPiv6adthPwKVVPl9pVTtUpyJ/HfzWEe6f1JTQ4wGPWXLgmJYlFaXks3ZnPjKHdT9mfll3CHR+kUlhWxf9cOJiXFu/hrnkb+eyeM09Zh3t1RiFrM4/y3xcM0iCiVBvoX4tqk5jQYI8JIgBTB8YSFxbMx6mHTtn3/fYcrnh9NXUWw6d3n8ntk/vw8uxRpOeW8MjnW0+aSfijDQe5+d0NJEZ1Yva4nh2ZBaW8ngYS5dUC/P24YkwiS3cVkF9i7aqcUVDGffM3cfc/NzGwexhf3T+J4YnW8SzTBsXx+/MG8OWWbN75aR9VtXU8+vk2Hv5sG+OSo/nq/rMIP83W21bKUS4NJCIyU0R2icheEXmkif1TRGSTiNSKyJWN9t0kIntsr5sabB8jItts13xZRLRD/2nu6pQk6iyG15dn8F+f/sx5Lyxn6c58Hpzej3/fOYG48JPXh79vWj9mDu3OX79N55JXVvGv9Qe5d2pf3r91HNFd2j+xpFKnK5e1kYiIP/AqcB6QBWwQka+MMWkNDjsI3Az8odG50cCfgBTAABtt5x4DXgfuBNYC3wIzge9clQ/l+ZJjujAuOZq5q/YT5O/HTWf25r5p/YhpZiyLiPDc1Wdw+WtlHDp6nDeuH83MYfEdnGqlfIcrG9vHAXuNMZkAIvJv4BLgRCAxxuy37bM0Ovd8YJEx5qht/yJgpogsA8KNMWts2z8ALkUDyWnv0VmD+G57LjdO7EViVOtL0YYGB/DZPWdSVWtpNuAopezjykCSADRsAc0CxjtwboLtldXEdnWaG9UzilFtnP8qLCQQ103iotTpw5VtJE21Xdg7aKW5c+2+pojcKSKpIpJaUFBg522VUkq1lSsDSRbQcBKkRCDbwXOzbD+3ek1jzBxjTIoxJiU2NtbuRCullGobVwaSDUB/EUkWkSBgNvCVnecuBGaISJSIRAEzgIXGmBygVEQm2Hpr3Qh86YrEK6WUso/LAokxpha4H2tQSAc+NsbsEJEnRORiABEZKyJZwFXAmyKyw3buUeBJrMFoA/BEfcM7cA/wNrAXyEAb2pVSyq10ri2llFJN0hUSlVJKdQgNJEoppRyigUQppZRDTos2EhEpAA402BQBFDdxaOPtDd83t6/h9hig0IGkNpcue49pal9LeWr8vqmfOyJPrR3nrHx527NqvM2en70hX972O+jo54U3P6texpjWx08YY067FzDHnu0N3ze3r9Exqa5Il73HNLWvpTy1lMcG+XN5njoqX972rOx5Pt6YL2/7HXT088Kbn5W9r9O1autrO7d/bce+5q7VHvZcq6VjmtrXUp4av28pv+1l73U6Il/e9qwab3P1s7L3Wqfb76Cjnxfe/KzsclpUbXUUEUk1dnSV8ya+mCfQfHkTX8wT+Fa+TtcSiavMcXcCXMAX8wSaL2/ii3kCH8qXlkiUUko5REskSimlHKKBpBki8q6I5IvI9nac2+xywCLygG354R0i8nfnprrVdDk9TyLy/0TksIhssb0ucH7KW02bS56Vbf8fRMSISIzzUmxXulzxrJ4Uka225/SDiPRwfspbTZsr8vWsiOy05e0LEYl0fspbTJcr8nSV7TPCIiKe347iSPczX34BU4DRwPZ2nLsemIh1/ZTvgFm27dOAH4Fg2/s4H8jT/wP+4GvPyrYvCeukoweAGG/PE9bVReuPeRB4wxeeFdbZwQNsPz8DPOMDeRoMDASWASkd/Zza+tISSTOMMSuAow23iUhfEfleRDaKyEoRGdT4PBGJx7YcsLH+RtQvBwzWmYufNsZU2e6R79pcnMxFeXI7F+brReC/sH9BNqdxRZ6MMSUNDu2C7+TrB2OdbRxgLSevWeRyLspTujFmV0ek3xk0kLTNHOABY8wY4A/Aa00c09JywAOAySKyTkSWi8hYl6bWPo7mCeB+W7XCu2JdP8YTOJQvsS51cNgY87OrE9oGDj8rEXlKRA4B1wGPuzCtbeGM38F6t+IZS0s4M08ez5VrtvsUEQkFzgQ+aVCNHtzUoU1sq//mFwBEAROAscDHItLH9m2kwzkpT69jXTvG2P59Husfs9s4mi8R6Qw8hrXKxCM46VlhjHkMeExEHsW6XtCfnJzUNnFWvmzXegyoBT50Zhrbypl58hYaSOznBxQZY0Y23Cgi/sBG29uvsH6wNrcccBbwuS1wrBcRC9b5dty1qLzDeTLG5DU47y1ggSsTbCdH89UXSAZ+tn0QJAKbRGScMSbXxWlvjjN+/xqaD3yDmwMJTsqXiNwEXASc464vZg04+1l5Pnc30njyC+hNgwY0YDVwle1nAc5o5rwNWEsd9Q1oF9i23411tUewVnMdwjaWx4vzFN/gmN8B//aFZ9XomP10cGO7i55V/wbHPAB86gvPCpgJpAGx7siPK3//8JLGdrcnwFNfwL+AHKAGa0niNqzfUr8Hfrb94j7ezLkpwHasSwG/Uh8sgCDgn7Z9m4DpPpCnecA2YCvWb1nxHZUfV+ar0TEdHkhc9Kw+s23finVOpQRfeFZYl90+BGyxvTq0N5qL8nSZ7VpVQB6wsKOfVVteOrJdKaWUQ7TXllJKKYdoIFFKKeUQDSRKKaUcooFEKaWUQzSQKKWUcogGEnVaEpGyDr7f2yIyxEnXqrPN4LtdRL5ubbZbEYkUkXudcW+lmqLdf9VpSUTKjDGhTrxegPll4kCXaph2EXkf2G2MeaqF43sDC4wxwzoifer0oyUSpWxEJFZEPhORDbbXJNv2cSKyWkQ22/4daNt+s4h8IiJfAz+IyFQRWSYin9rWx/iwwfoSy+rXlRCRMtvkiT+LyFoR6Wbb3tf2foOIPGFnqWkNv0w0GSoii0Vkk1jXuLjEdszTQF9bKeZZ27F/tN1nq4j82Yn/jeo0pIFEqV+8BLxojBkLXAG8bdu+E5hijBmFdcbcvzY4ZyJwkzFmuu39KOC3wBCgDzCpift0AdYaY84AVgB3NLj/S7b7tzrnkm3upnOwzigAUAlcZowZjXXtm+dtgewRIMMYM9IY80cRmQH0B8YBI4ExIjKltfsp1RydtFGpX5wLDGkwY2u4iIQBEcD7ItIf6+ysgQ3OWWSMabgWxXpjTBaAiGzBOgfTT43uU80vk1tuBM6z/TyRX9ZDmQ8810w6OzW49kZgkW27AH+1BQUL1pJKtybOn2F7bba9D8UaWFY0cz+lWqSBRKlf+AETjTEVDTeKyP8BS40xl9naG5Y12F3e6BpVDX6uo+m/sRrzS+Nkc8e0pMIYM1JEIrAGpPuAl7GuMRILjDHG1IjIfiCkifMF+Jsx5s023lepJmnVllK/+AHrGh0AiEj9NOARwGHbzze78P5rsVapAcxu7WBjTDHWJXP/ICKBWNOZbwsi04BetkNLgbAGpy4EbrWtm4GIJIhInJPyoE5DGkjU6aqziGQ1eD2E9UM5xdYAnYZ12n+AvwN/E5FVgL8L0/Rb4CERWQ/EA8WtnWCM2Yx1htnZWBd0ShGRVKylk522Y44Aq2zdhZ81xvyAtepsjYhsAz7l5ECjVJto91+lPIRtZcYKY4wRkdnAtcaYS1o7Tyl30zYSpTzHGOAVW0+rIty8ZLFS9tISiVJKKYdoG4lSSimHaCBRSinlEA0kSimlHKKBRCmllEM0kCillHKIBhKllFIO+f+FKk4F4ElbxwAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"learn.lr_find()\n",
"learn.recorder.plot()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"lr=1e-2/2"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"Total time: 09:01 <p><table style='width:375px; margin-bottom:10px'>\n",
" <tr>\n",
" <th>epoch</th>\n",
" <th>train_loss</th>\n",
" <th>valid_loss</th>\n",
" <th>accuracy_thresh</th>\n",
" <th>fbeta</th>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <th>0.087761</th>\n",
" <th>0.085013</th>\n",
" <th>0.958006</th>\n",
" <th>0.926066</th>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <th>0.087641</th>\n",
" <th>0.083732</th>\n",
" <th>0.958260</th>\n",
" <th>0.927459</th>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <th>0.084250</th>\n",
" <th>0.082856</th>\n",
" <th>0.958485</th>\n",
" <th>0.928200</th>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <th>0.082347</th>\n",
" <th>0.081470</th>\n",
" <th>0.960091</th>\n",
" <th>0.929166</th>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <th>0.078463</th>\n",
" <th>0.080984</th>\n",
" <th>0.959249</th>\n",
" <th>0.930089</th>\n",
" </tr>\n",
"</table>\n"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"learn.fit_one_cycle(5, slice(lr))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"learn.save('stage-1-256-rn50')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"learn.unfreeze()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"Total time: 11:25 <p><table style='width:375px; margin-bottom:10px'>\n",
" <tr>\n",
" <th>epoch</th>\n",
" <th>train_loss</th>\n",
" <th>valid_loss</th>\n",
" <th>accuracy_thresh</th>\n",
" <th>fbeta</th>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <th>0.082938</th>\n",
" <th>0.083548</th>\n",
" <th>0.957846</th>\n",
" <th>0.927756</th>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <th>0.086312</th>\n",
" <th>0.084802</th>\n",
" <th>0.958718</th>\n",
" <th>0.925416</th>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <th>0.084824</th>\n",
" <th>0.082339</th>\n",
" <th>0.959975</th>\n",
" <th>0.930054</th>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <th>0.078784</th>\n",
" <th>0.081425</th>\n",
" <th>0.959983</th>\n",
" <th>0.929634</th>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <th>0.074530</th>\n",
" <th>0.080791</th>\n",
" <th>0.960426</th>\n",
" <th>0.931257</th>\n",
" </tr>\n",
"</table>\n"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"learn.fit_one_cycle(5, slice(1e-5, lr/5))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZIAAAEKCAYAAAA4t9PUAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzs3Xd8VfX9+PHXO3tAQsKGAGHKnhEnCIoKLqx1YN2zjk5r+6NVq1+tLbbWqtXaulDUilaLYsUNCiobAdkECBA2hBGyx+f3xzl3nzuSm5sEeD8fj/vg3nPPPfecJNz3/az3W4wxKKWUUvUV19QnoJRS6timgUQppVRUNJAopZSKigYSpZRSUdFAopRSKioaSJRSSkVFA4lSSqmoaCBRSikVFQ0kSimlopLQ1CfQGNq0aWNyc3Ob+jSUUuqYsnTp0v3GmLbh9jshAklubi5Llixp6tNQSqljiohsjWQ/7dpSSikVFQ0kSimloqKBRCmlVFROiDESpdTxoaqqisLCQsrLy5v6VI4rKSkp5OTkkJiYWK/XayBRSh0zCgsLadmyJbm5uYhIU5/OccEYw4EDBygsLKR79+71OoZ2bSmljhnl5eW0bt1ag0gDEhFat24dVStPA4lS6piiQaThRfsz1UASwqvfFvDBip1NfRpKKdWsaSAJ4fUFW/lo1a6mPg2lVDNx4MABhg4dytChQ+nQoQOdO3d2P66srIzoGDfddBPr16+P8Zk2Lh1sV0qpCLVu3Zrly5cD8NBDD9GiRQvuvfden32MMRhjiItz/p4+derUmJ9nY9MWiVJKRSk/P5+BAwdyxx13MHz4cHbt2sXtt99OXl4eAwYM4OGHH3bve+aZZ7J8+XKqq6tp1aoVkydPZsiQIZx22mns3bu3Ca+i/rRFEoYxTX0GSikn//fBatbsPNKgx+zfKYMHLx5Qr9euWbOGqVOn8s9//hOAKVOmkJ2dTXV1NWPHjuXyyy+nf//+Pq85fPgwZ511FlOmTOGee+7h5ZdfZvLkyVFfR2OLaYtERMaLyHoRyReRgJ+OiIwWkWUiUi0il/s9d4OIbLRvN3htHyEi39vHfFpiOIVDJ4copSLVs2dPTj75ZPfjN998k+HDhzN8+HDWrl3LmjVrAl6TmprKhAkTABgxYgQFBQWNdboNKmYtEhGJB54FzgUKgcUiMtMY4/3T3AbcCNzr99ps4EEgDzDAUvu1B4HngNuBBcAsYDzwUayuQynVPNW35RAr6enp7vsbN27kqaeeYtGiRbRq1Yprr73WcZ1GUlKS+358fDzV1dWNcq4NLZYtkpFAvjFmszGmEpgOTPTewRhTYIxZCdT6vfZ84DNjTJEdPD4DxotIRyDDGDPfGGOAacClMbwGpZSqsyNHjtCyZUsyMjLYtWsXn3zySVOfUkzFcoykM7Dd63EhcEoUr+1s3wodtseMjpEopepq+PDh9O/fn4EDB9KjRw/OOOOMpj6lmIplIHEaYYj0YznYayM+pojcjtUFRteuXSN8W/+T0EESpZSzhx56yH2/V69e7mnBYK0Uf+211xxf9/XXX7vvHzp0yH1/0qRJTJo0qeFPtBHEsmurEOji9TgHiHSZeLDXFtr3wx7TGPO8MSbPGJPXtm3YSpFKKaXqKZaBZDHQW0S6i0gSMAmYGeFrPwHOE5EsEckCzgM+McbsAopF5FR7ttb1wPuxOHmllFKRiVkgMcZUAz/BCgprgbeNMatF5GERuQRARE4WkULgCuBfIrLafm0R8AhWMFoMPGxvA7gTeBHIBzYR4xlbJuLeOKWUOjHFdEGiMWYW1hRd722/97q/GN+uKu/9XgZedti+BBjYsGfqTNeRKKVUeJoiRSmlVFQ0kCillIqKBpIwdB2JUsplzJgxAYsLn3zySe66666gr2nRogUAO3fu5PLLL3fcZ8yYMSxZsiTkez/55JOUlpa6H19wwQU+04ebkgYSpZSK0NVXX8306dN9tk2fPp2rr7467Gs7derEO++8U+/39g8ks2bNolWrVvU+XkPSQKKUUhG6/PLL+d///kdFRQUABQUF7Ny5k6FDh3LOOecwfPhwBg0axPvvB65KKCgoYOBAa55QWVkZkyZNYvDgwVx11VWUlZW597vzzjvd6ecffPBBAJ5++ml27tzJ2LFjGTt2LAC5ubns378fgCeeeIKBAwcycOBAnnzySff79evXj9tuu40BAwZw3nnn+bxPQ9I08kqpY9NHk2H39w17zA6DYMKUoE+3bt2akSNH8vHHHzNx4kSmT5/OVVddRWpqKjNmzCAjI4P9+/dz6qmncskllwSthf7cc8+RlpbGypUrWblyJcOHD3c/9+ijj5KdnU1NTQ3nnHMOK1eu5Gc/+xlPPPEEc+bMoU2bNj7HWrp0KVOnTmXhwoUYYzjllFM466yzyMrKYuPGjbz55pu88MILXHnllbz77rtce+21DfOz8qItkjB0iEQp5c27e8vVrWWM4Xe/+x2DBw9m3Lhx7Nixgz179gQ9xty5c90f6IMHD2bw4MHu595++22GDx/OsGHDWL16tWP6eW9ff/01P/jBD0hPT6dFixZcdtllzJs3D4Du3bszdOhQILZp6rVFEkIMS50opaIVouUQS5deein33HMPy5Yto6ysjOHDh/PKK6+wb98+li5dSmJiIrm5uY5p4705fb5s2bKFxx9/nMWLF5OVlcWNN94Y9jgmxIyg5ORk9/34+PiYdW1pi0QppeqgRYsWjBkzhptvvtk9yH748GHatWtHYmIic+bMYevWrSGPMXr0aN544w0AVq1axcqVKwEr/Xx6ejqZmZns2bOHjz7yJO5o2bIlxcXFjsd67733KC0tpaSkhBkzZjBq1KiGutyIaItEKaXq6Oqrr+ayyy5zd3Fdc801XHzxxeTl5TF06FD69u0b8vV33nknN910E4MHD2bo0KGMHDkSgCFDhjBs2DAGDBgQkH7+9ttvZ8KECXTs2JE5c+a4tw8fPpwbb7zRfYxbb72VYcOGNWq1RQnVLDpe5OXlmXBztJ1MeGoenVul8uINeTE4K6VUXa1du5Z+/fo19Wkcl5x+tiKy1BgT9gNQu7ZC0BESpZQKTwOJUkqpqGggUUodU06E7vjGFu3PVANJWPpHq1RzkZKSwoEDBzSYNCBjDAcOHCAlJaXex9BZWyHoMhKlmpecnBwKCwvZt29fU5/KcSUlJYWcHMfSUBHRQKKUOmYkJibSvXv3pj4N5Ue7tpRSSkVFA0kY2hWrlFKhaSAJQcdIlFIqPA0kSimloqKBRCmlVFQ0kIShQyRKKRWaBpIQRLNtKaVUWBpIlFJKRUUDSRiaikEppUKLaSARkfEisl5E8kVkssPzySLylv38QhHJtbcnichUEfleRFaIyBiv13xpH3O5fWsXu/OP1ZGVUur4EbMUKSISDzwLnAsUAotFZKYxxruS/S3AQWNMLxGZBDwGXAXcBmCMGWQHio9E5GRjTK39umuMMXWvVKWUUqrBxbJFMhLIN8ZsNsZUAtOBiX77TARete+/A5wjIgL0B74AMMbsBQ4BWqZQKaWaoVgGks7Adq/HhfY2x32MMdXAYaA1sAKYKCIJItIdGAF08XrdVLtb6wE78AQQkdtFZImILIkmU6iOkCilVGixDCROH/D+n8vB9nkZK/AsAZ4EvgWq7eevMcYMAkbZt+uc3twY87wxJs8Yk9e2bdt6nL6W2lVKqUjEMpAU4tuKyAF2BttHRBKATKDIGFNtjPmlMWaoMWYi0ArYCGCM2WH/Wwz8G6sLTSmlVBOJZSBZDPQWke4ikgRMAmb67TMTuMG+fzkw2xhjRCRNRNIBRORcoNoYs8bu6mpjb08ELgJWxfAalFJKhRGzWVvGmGoR+QnwCRAPvGyMWS0iDwNLjDEzgZeA10QkHyjCCjYA7YBPRKQW2IGn+yrZ3p5oH/Nz4IVYXYN1HbE8ulJKHftiWiHRGDMLmOW37fde98uBKxxeVwCc5LC9BGvgvXHoQhKllApLV7YrpZSKigYSpZRSUdFAEoYOkSilVGgaSELQERKllApPA4lSSqmoaCBRSikVFQ0kYWg9EqWUCk0DSQi6jEQppcLTQKKUUioqGkiUUkpFRQOJUkqpqGggCUGHSJRSKjwNJEoppaKigUQppVRUNJCEoctIlFIqNA0kIYguJFFKqbA0kCillIqKBhKllFJR0UAShtGKJEopFZIGkhB0hEQppcLTQKKUUioqGkiUUkpFRQNJGLqORCmlQtNAEoIuI1FKqfA0kCillIpKTAOJiIwXkfUiki8ikx2eTxaRt+znF4pIrr09SUSmisj3IrJCRMZ4vWaEvT1fRJ4WXX6ulFJNKmaBRETigWeBCUB/4GoR6e+32y3AQWNML+BvwGP29tsAjDGDgHOBv4qI61yfA24Hetu38bG6BuscYnl0pZQ69sWyRTISyDfGbDbGVALTgYl++0wEXrXvvwOcY7cw+gNfABhj9gKHgDwR6QhkGGPmG2MMMA24NFYXILqSRCmlwoplIOkMbPd6XGhvc9zHGFMNHAZaAyuAiSKSICLdgRFAF3v/wjDHVEop1YgSYnhsp6/z/h1FwfZ5GegHLAG2At8C1REe0zqwyO1YXWB07do1sjNWSilVZ7FskRRitSJccoCdwfYRkQQgEygyxlQbY35pjBlqjJkItAI22vvnhDkmAMaY540xecaYvLZt29b7IjTXllJKhRbLQLIY6C0i3UUkCZgEzPTbZyZwg33/cmC2McaISJqIpAOIyLlAtTFmjTFmF1AsIqfaYynXA+/H7Ap0iEQppcKKWdeWMaZaRH4CfALEAy8bY1aLyMPAEmPMTOAl4DURyQeKsIINQDvgExGpBXYA13kd+k7gFSAV+Mi+KaWUaiKxHCPBGDMLmOW37fde98uBKxxeVwCcFOSYS4CBDXqiSiml6k1Xtoeh60iUUio0DSQh6BCJUkqFp4FEKaVUVDSQqBNOaWU1M74rpLZW+y2VaggaSMLQj5rm59k5+fz543X1fv2/F27jl2+t4OnZGxvwrJQ6cWkgCUHzCjdPf/lkPf/4chO5kz9k3e4jdX69K2H0k59v5HBpVUOfnlInHA0k6pg2Y9kOn8eHy6rYXlQa8jXJCZ4/+6827ovJeSl1IonpOhKlYi0x3goKFdU1nHT/x+7tGx+d4H7OX+HBsoBt1TW1VNcaUhLjY3OiSh3HImqRiEhPEUm2748RkZ+JSKvYnlozoYMkzVp6svVdqKSixmf7oi1FjvvP+n4X//xqk9d+BwC4/uVF9H3gY8fXKKVCi7Rr612gRkR6YaU16Q78O2Zn1UxoPZLm5+ZXFvs83mZ3Y9X4zcB6bf5WjMNq0gWbD/g8fn3BNopKKvl204GAfZVSkYk0kNTa9UJ+ADxpjPkl0DF2p6VOVIdLq0JOy529bi8ACXFCnMCW/UcBqKyp9dnv49W7HVsl0+ZvDdj2xgLPtsrq2oDnlVKhRRpIqkTkaqxMvf+ztyXG5pTUiehwWRXf5O9nyMOfctIDznk4317iqZP23t1nMK5few6VVlFTa/jjh2sD9i+r8u3uqqpxDhJ//WyD5zWVNY77KKWCi3Sw/SbgDuBRY8wWu2rh67E7reZD65E0jhunLuK7bYcAqKpx/pn/5p2VAPRok87AzplkpyexfPsh3l1WyIff7wrY3791URpBkNh+sJTMtMy6nr5SJ7SIWiR2LZCfGWPeFJEsoKUxZkqMz63J6TqSxuMKIpHYvL8EgKz0JA6WVlJR5Rwg9hZX+Dz2bm2se2S842su+vvXEZ+HUsoS6aytL0UkQ0SyseqpTxWRJ2J7akr5yky1elOn3TwSgOy0JKpqDMuCBKH731vl87i43Fp8+NSkoaQkxvPRz0fF8GyVOnFEOkaSaYw5AlwGTDXGjADGxe601Ilkn1/LAeC1BVup9hvT6Jqdxtl92zG6j1U6OSs9CYAZ3+0IeL2T3UfKAeiQkQJAbuv0ep+zUsoj0kCSICIdgSvxDLafELQeSeztPBS4QPCB91bxyrcFPtuqaw3xcZ7+xux03/ke/7x2BLeN6h70fUoqqgFomWK9znuFe1aa51g6c0upuok0kDyMVTJ3kzFmsYj0AI77jHc6RtI44oL8oP/w4VqfqcBrdx3xeZydnuyz/+CcTO67sD9/vWKI4/GO2osWW9iLGOPihFR7JXvvdi2ZOLQTAH3u1+rNStVFpIPt/zHGDDbG3Gk/3myM+WFsT001V5v2HSV38od8sXYPh8uiT3p49QsLgj63p9jqjjpw1Or++sJeRwLQ2u7acunUKhWAH47IcW+rqLaCR8H+Ev5mT/NNT/akQWmRYgWVlKR4bj4jeGtGKRVcpIPtOSIyQ0T2isgeEXlXRHLCv1Idj1Zstwa3b3l1CUP+79OAVeV1ddTucnLy1083sG73EeasD0yumOUVSJISfP+UB+dYU3jnbdgPwE2vLGaH3YXmSqsCngH8hZsP0DU7rZ5XoNSJLdKuranATKAT0Bn4wN523NMhkkD+iQ1XFkY+dddfudfU3XfvPJ3/u2SAz/PvLC1k/JPzuPc/KwC47tRu7ufSkzzn4b/Y8MGL+wNw67QlgGd8BHzHRvbYA/A927Zwt04A9trblVLhRRpI2hpjphpjqu3bK0DbGJ5Xs6C5tpy9vsA3zcjB0sp6H8v7tSd1aMmkkV1C7j+8mydXqIhw55ieQOCkiM6tfFsX1V6tJvEakykutwLM/5vQ1ydb8Mg/fhHhFSilIg0k+0XkWhGJt2/XAprl7gTln+Bw1Y66F5dyqajytCRaJCeQnBA6jfuEgb4p3n5+Tm/H/bK9ur2enZNPUUnoYFdqt1iuOaVryP2UUoEiDSQ3Y0393Q3sAi7HSpuilHt9Rn24ki1OntDXve25a4bzq3P7OO7v363m6qbyH9/wHjP5yyfrg77/x78YRZ/2LTizdxsAzupz3De0lWpwkc7a2maMucQY09YY084YcynW4sTjnlMq8hPZHoegcSiKri1X/qsebTyLAycM6shPg7Q0/IkI028/lXfuPC3guf/99Mywr+/bIYNPf3mWe23JeQM6uNeq+C+IVEo5i6bU7j3hdhCR8SKyXkTyRWSyw/PJIvKW/fxCEcm1tyeKyKsi8r2IrBWR33q9psDevlxElkRx/hFZtu1QyLTmJ5pH/rcmYNus73fX+3gP2GlMqh1+xq3SIkswfWqP1rRrmRKwfWDnTNq08J0i7JrNFYproP5gA9dz//fCbYx45DP9cqKOO9EEkpAj0SISDzwLTAD6A1eLSH+/3W4BDhpjegF/Ax6zt18BJBtjBgEjgB+7goxtrDFmqDEmL4rzD+vrfGvq6KvzC2L5NseU/60MzLIL9W+5uWZt9WzbIuC5oV18i3A+86NhdT6+95jLmb3a8PKNJ4d9TWt7oePJj35e5/cL5XczvudASSUFB0LXlFfqWBNNIAn3yTESyLcXL1YC04GJfvtMBF61778DnCPWlBoDpItIApAKVAL1H9GN0u7DOhXUxbUI8C57tpTLkfLga0FCOX9AB8CaseXvmR8N5/27z3A/7tcxo87H906pMq5fO9q0SA6xt6W1Vytmb3HD/+7HPv5lgx+zLv7xZT65kz/0mXqtVDRCBhIRKRaRIw63Yqw1JaF0BrZ7PS60tznuY1dgPAy0xgoqJVgD+9uAx40xrnJ3BvhURJaKyO3hLzF62hHhMeakdmSlJfLr80/igYv688hEa93Hpn1H63W8iuoa0pKcZ2q1SE5gSJdWXH+atXakfUZg91U4KYmeP3HXOEg43u+zemfsvr9sPVDS6N2ms9ft4c8fW5MPXpi7uVHfWx2/QgYSY0xLY0yGw62lMSZcUSynri///zXB9hkJ1GAFq+7Ar+z8XgBnGGOGY3WZ3S0iox3fXOR2EVkiIkv27QtcFV0X2qftUVFdQ1ZaEiLCLWd2Z1jXLADufmNZyNcdKq3k3v+sCPgWXF5V67NA0MnDEwdSMOVCd46suth/1DMRwL3gsPww7PwOVr0Lc/8CM38G8/8B+9aDMeS29swAS4yLptEe3Jb9JZz1ly/5++z8mBw/mJtf8QwreleGVCoadf+fGblCwHt1WQ6wM8g+hXY3ViZQBPwI+NgYUwXsFZFvgDxgszFmJ4AxZq+IzMAKOnP939wY8zzwPEBeXl5UkaA5xpHXFmzlk1W7ef3WU6ipNZRUVpPh8I17+fZDfLp6N78Z39fhKHVXWV3rM7XW9Y1/V5juv1++tZw56/fxztJCCqZc6N5eUV0TMKW3QZQWQdEWRpXNJjd+D93i9nDKF0fhw+1Q6rcEKjULlr1qpSXNyEF6nc2EuCy+qR1ASWX9uuwqqmtIiItzd60V2MW4XIpKrNxhX27Yy8/HRTZDLVralaViJZaBZDHQ2y7LuwOYhBUgvM3EqgM/H2ttymxjjBGRbcDZIvI6kAacCjwpIulAnDGm2L5/HlZm4phqbnHkb59t4KkvrOTLOw+V8fzczbzybQEb/jDB50P+41W7ueP1pQDcc24fEuKj/3ZdUe3bgqhPTY+qmlr3KvK1u4o5EGaxoCNjrIBwYBMUbQ68lVtpW55Kgloj7KQ18cl9oPvFkN3Dc8vKhaR0OLgVNn0B+V/A6vd4LukINUY49PkQ2DcBep4DnYdDXGRB76T7P+bc/u154XprPsj6PcU+z7smATRmjfgFm30D6MDOdR9zUspJzAKJMaZaRH6C9T0vHnjZGLNaRB4GlhhjZgIvAa+JSD5WS2SS/fJnsXJ5rcLq/ppqjFlpd2/NsFNcJAD/NsZ8HKtr8FxLrN+hblxBBKyiTq66HfuPVtCpVSpHyqt4fcFWd184QGlVDRkNEkhqfGZCeQenDXuK6dM+cNB8xfZDPkkXC/aX0Nve7/sdh4O/mTFwdI9zoCjaAhVe4xcSB5ldrOAw8IfuQPHmpgQemlfCDaP78rsL+gV/r6xukHezdaup4uCGb5n2xlSurtkIX06BL/8EKZnQY4wVVHqdA5nOeUtdA/Sfrdnj3ubKkjxxaCfeX77TvX6mrBFbCTdOXezzuLqmmf1hq2NWLFskGGNmAbP8tv3e63451lRf/9cdDbJ9M+BcbOIE1dIr0eC7Swv5ydm9+Nmb3/GlX7bc0ooax66vuvi/D1azYHMRZ/Zq47P9qrwuvLVkO9uLSh0DycRnv/F5fO7f5rq7t4RaeqUUw5Z5gYGiaDNUeXUJSbz1gZ/dA7qcAtk9PS2LVl0hwXfNCMAPe9VS0Wor13olewwrPpHMk0bznJSyq1tnpkzIgc1zIH+21WpZ8761X5uTrIDS8xzodjokWWMrM5YFVmx01aQf2qUV7y/fyX47LX5jtkj8rdtdjDHGJ/eYUvUR00ByvDDNrnPLY79Xmdq/fraBbm3S3WnevdW3r9/b1G8KAN96HgDXn96Nt5Zs55ZXl/iMf4A1USGOWjpygG5xe8iVPXST3fDmG1C0mbUpm0ih0jMJPD7J6m7K7gHdR9mBorv1b2YXiK9bMExKiOPGetQZiYsTyqtqmb54O/83cQDJA39otXSMgb1rPd1gi1+CBf+A+GTodjqL44exdFcPIIshOZ51MG8u2gZAx0yrZspTn1utylgGkhnfFZLXLZsuIdLjH62odpzNtr2olPy9Rxnbt13Mzk8dPzSQRKC5dW15e9pv1s/63UdIS0oIWJVdWlHTYN8+N+71neqbmZpIPDV0kv2Q/7mnNVG0mZr9m1ibvIVk8QSycpMIRb0guwdv7etJ6y79uGjMGXawyIl4HKKxTH73e34z/iSqqg1dW6dB+/7W7fSfQmUpbP0WNn1B2dpPOfnwHE4GdidnsfzQMPh+N/Q8232sdhnWOhbXmElxiFos0dhbXM4v31rB8K6t+O9d1lqclikJFJdXs/Kh83h2dj7/mruZw2VVjoHkkme+5mBpVcAXA6WcaCA5hizdWkRRSRWt05OCDlAfLK0KaDEA/G/lTi5+5mu+vHcMuW1CD5Cv2nGYAZ0yAoJOAtV0kX10PbAbFqxzB4ucos2sSy4gUWrgdXvnxDTI7kFxy568tbcvBaY9v7l6Ahe8vpM9ZLH5rosQER697yNu7tSdi3o2zKyyhnRWn7Z8tWEfM77bwYzvrO4q1wdrTa1hW1Ep3dukQ+9x0HscT3MD7325iFHxKxkdt5IzqxbCu7MxCO8ldWdu7WC6FqeTQDXV9n+9LtmpDXrOxhgmPDXPnV5m2bZDfLJ6N+cP6ECcCDec1o2MlESGd7OmbR8qrSInK/A4ri8i5VUxmlWnjisaSCLQHNaR7D9awQ+fmw/AyblZtMtIoWfb9ICUJfl7jpKWFPhr/c/SQgAWbjkQNJDM33SAP32wnJI9m3h0dBqntjrsM26xLnkbCWInMvwYSGppdTt1GMSilDP5YHsqU26daLUsWrQHEZat3cOU9UuY+ZMzyM5pxW4+BHB/E66sqXXXTW9ufndBP77a4LwG6b4Z3zN98XauOaUrj/5gEAAfrNjJLlrzds1Y3q4ZSxy1vHxuHIlb5pCy7Uvujn+f+P+8x7LkVL6tHcjc2sGsr27YLD9HyqtZt9t3hti3+fs5f0AHa6KE/bNuZVeG3H24nIGdrfxjCzYfYNLzC/j8Hs/SrCNlVRpIVFgaSCLQ9GEEDnq1QGpqDa3TkxzzXi0qKOK0Hq0DtrvK2Ybq2rrmhW9Zm3wjycnVsNDemJJpDWp3zuPZfcPYWtueS88ZxehTToH0NmAfb/HnG5i+eSOPdjnNJy1JiT0G4B/cVu884s6llZoUm0V/0XJK2+IyfbGVtOGNhdu497yTyEpP4rBfd2ItcexsMYgdXXrybP5YOqeU880V8VSsmMWg9Z8zPn4xVL5Exd/+zJsHejP2gkl0G3E+JAfmHYuUU92V8qpajDFUek3d7pBprd5/e8l2xvVvD3jGbcY94VmWdaS8mnY6S1iFoYEkAtPmb+XhiQOb9By8P5yXbTvE6D5tGdQ5M/T0WS+V1VZLwnvKZ3VNLbsOl9MlO41v8/dTSxyPVV/NAdOSs049hcvGjYa0bPf+r679jNN7tmb0OcMDju9qVZRX1fjURHeVuHV1t718Yx43v7KEa15cyBUjcnxe2xyd2asNpZXero59AAAgAElEQVTVLNsWvJzw1qJSstKTaJ+ZQrHf+FFGagLlVda4yPO3j4NOmRxofTbjV86lp+xkdNxKLq/ewFXxX5L66afweSJ0PdUzG6zDIHewDmdl4aGA1ghYXyKqaw21BpLs6drd7PU/roACgZMoAI6UN2wGZHV8ap5fBZuh8qoax1ocjcU/zfr8Tft58/ZT3Y+9WyHz7YVnv3BYMX20wvPB8PTsfEb9eQ7bi0r50YtWE+Tlmgm8X3sm+zIH+QQRsIKRU7p2gFQ7X1ap3ywkVyBxtUjycj3HdHW3Neeuk/TkeJ9ryp1sdc2d7TWbqcJeC5LvFUR+dnYvwCrlW+aX4Tg9KQEQNpnOTK2ZwHXlv2ZoxfNM6/0UnHqHtSr/84fgX6Pg8T7w3x/DyrfhaOhUP5c88w2/eWdlwPaCAyVU2F8kkr1yj2WnJ/lMJPl87d6A1xbXMxmnOrFoiySEpPg4dwW/C56ex+Z9Jax7ZHyTfPC5WhQuVTWGFskJXJmXQ0lFDQ9PHMCIP3jSno/r155fjOvDtad24/Qps92vP1JWzZuLtvHxqt3u/v/lDtOFdxwqc99/bX4BU78toKK6xmflvDdXHqyv8/fxg2GehXquD+F0O9BkpCTSKi2RQ17dQKlBkjY2B+lJCY7f8r/euN99/7vthzjFDuSdMlOY8+sxVNUYnp6dT3F5FWWVNcSJp5qjf84wqzsqib9s6Mj119xo5Ws4sgs22etWNn4KK6dbO3cY7GmtdDnFce2Mv73FFe7ff5LXAtK0pPiw08KPaiBREdBAEopXj8LmfdbCuIrq2iYJJE6FnwD+fLnz+kxXDqw2LZJ9gtCBkkqemeM7Zfinb34X8HrvD/oH3l/tvh8sU69rseMv31rhDiTbi0p5wk4M6L0C/pIhnZg2f6v7cbh66k0p3SFR5N4j5e4vGABTPlrH7aOsnKKX53UhOSGepHhDnFiB2/Xzdo1POR0T/KYCZ3SEYdfAsGt4bs56TkvdwdDKpdaiyG//Dl//DZJaQO4oO7Cc7XhMsFrTpXbA8A7a6UkJlFaEXsfyx1lruXBwx5D7KKWBJIQ4h65p/5ZBY6nyK/vqlDH3vP7t+dROy7HXa6Git31BtnvLTE0MmuAvWG99RmrgWoSZK/xzdFr8v5EP6+Iw/7SZcFqM6lR7ZWuRVazKNd4jItQaAoI2eOrJ33h6rju9jYt/ChqAxz6xjlEw5dcw+tdQfgS2zIVNX7Bt0Qd03fARAF8ltWNu7WDm1g5mfm1/fnVxHv/3wRoEOGBnQXYV7QJISw7fIvFumSoVjI6RhBDnMMjp/4HeWFzv+8ilA8lOT+LZHwUOeP/jGs+2RVuKAp4H2BymbsglQzqR2ybd3afu71CZ8+BrRqonOLhqbATL5eT9jXzJ/eMYFEH526biaol6c7Wg7h7rKe7lKla1bndk9UsKplzIgxf354GLfIuGbtgdQV2XlAzodxEV4x9ndOWTjKn4K5XnTWGj6cxl8fN4IekJVqXdwU3r72Ja77l0q9jApc/OA6BNS08gWbermHleXXRtWybTuZW1ruVPl1lTmutTTEydeDSQhOD07bvpWiTWh3L/jhkse+Bc95RNbwnxcfz71lMCtruyvHZulUpRaehupPMGtCcrLZGdQb6JBltS06edZ6qsq4tmcYFzMPPODxZJxcKm5JSf7Fp7YsKgzpnu7L4uW73K6MY7NWm9iAiXDfOt9XbxM19TE2GxKyt/l1BgOnJw4E3cWvVrhla8wNWV99mr7o8yevs/+SD5fpYk38lTic+Qs3UGFO8GPAkjb5y6iKVbi9hXXMGFgztSMOVCrh7ZlXP6tgtdT1spm3ZtheC05qKyiVokz9qpUJLCZPAd2d2aFdXXaw3E+3efyaItRczbuI/n524mt3WaY93wH5/Vg4sGd2JJwUGWbT3o3p6dnhR2HCMuTvjDpQO5/71V7DlSTmZqItl2Wd5LhvgW00y3Z3BdPCRckc2m94Phnfl49W6m3TySyupabp22xP03kJQQFzCLra3XN37vgPDLcX0cj+800WDnobKQ+bFcXIkfAb7Jt1oWVSQwv3YAjLsQxj3E658vZsns/zI6fiWj4lbS5vNv4fNfQLv+vNEig03lLdmdn8Wb+VmMisuiW3U8lHWAlFZkpSfFtEKkOn5oIAmhOYyRlFfVEB8nLLK/3SfEh/6OmBAfx2u3jPTpkoiPE07r2Zpl2w5SXWsoOFDKOX3b8cW6vaQkxrHukQls3FNMD3t66p4j5Rwpr+b5uZv446x1Pse/8mTn1OngGbc5729zWfi7cyipqKZDRgp/vdJ3QoBrskJ1EwXlujh/QAd3nZe1u3w/VJPi4wOWeDxslx72590K8+Y01jVn/V6uPy0X8M2qYIyhqsa4x1i8p+be8/YKx+Ob9La8V3sm79WeiVDL+p/kkLRlDmz9hkFlBQyo+p5W4tV9t8y+JaRyf0JrNpS3oPbtfsRldoaWHaBlR/tm308KH/DU8U8DSQhOLZKtB0od81DFSt8HPmZEN89gdCQzxkb1bht2H1ff+N1jrPUOvb3Sv2+zB479g0jfDi3p2yF4n7n3uY3761e0z0xhQKcMdxErF1cwbKrxprpyfXBnpSUFbPfuvrp8RI47uy/Af+86ncv+8S0QPJCICGf1actFgztSeLCMp77Y6NN9eNRrJlf331oVGb741VkUlVRS7LBYcECnDH59/knux94ZBQxxJOUMg5xhMOoeCgoPcckz35BCBe3kEO05yK1Dkjm/K1C8i4Nb8jGlBZidy2HDx1Dt0N2ZkukVWDp5AkyGV8Bp0b7OWZvVsUUDSQhOseLufy9j8oS+3HFWz8AnY2SpVzdTl6z6J/nzni0VFwcFjzpndn38iiFMeGqez7Yr83K478L+jvu7eH+7Lq6oprKolMGdAwfSW9rnEelYQHPhSoTokpQQ5zM29PgVvi2v4V09XwCcMuy6vHrzSMBqfT71xUafmVKDHvo0YP9z/vpV0GN9+LNRPo9DpXnp1c5qgZaTzDbTnm2057ZBI2BABwBWfLeDX7y1nNnXnEWPNulWrfvi3VC80/53l7XepXiX9Xj/V9a/xn/Gn0B6WyuoZHTya9l09GxPzbb+MNUxRwNJCE6ztsBajNaYgQSsBX1Xndw1qnK5Y07ytFT8v117a53u+9zgnMyg61W8+beWKvzqu7uM7J7N9ad148bTc8MeszlJSYzn3TtPcyfPTIqPIy5OyH90QtB1PvFxQk2tISNIi8SbKxA/P3czk8f3paYBkoV6f3n4922+EzH8U9M8NWko59lBBDwz8Y6UV1vfqlJbWbd2ITI119ZC6X444hVsir2CzeEdULjE2sdfXKJXkHFo2bhaPMktI04boxqHBpIQgv2p1vr9B39h7ma6ZKcyfmDDLtzyXstRXl0bdXJD7xlSmQ7rPlzS/NZ5nORQ9dCJfxcW4BhIEuLjmjx3WX2N6OZJ8eJKN5IQH0dCkB7H5IQ4SitryEwL37Xj6i5t0yKZHr+bFWZvj99O6Et2ehLj+gXO5GvhFcD6+03lFRH6dmjJut3F3HNuHyYO9Z1B5lpzsvNQmTvBZlhxcdCinXULpboSju52btkU74R962Dzl77llF0S0/0CjF/LpmUHaNEBEp3T+aiGp4EkhGBfevy7ZB6dtRagwYsA/c1eFe56T/+FanWVnpzAP68dwXfbDnLdacFLz/ovGOzfqf5rCcLNMjsW/fEHg/jdjO/day5Cca2lyU4Pn8oErBxem/YdZX8Ey0lcfhyidez9u/T/vQJ8/IvRAdtcerS1Ejve9cYy3rnjNJ88aVFLSLLKI7fqGnq/iqPOLRtXi2f7IuvfGoeFtqnZXgGmoxVc0rIhNct6LjXL9xavH4f1pT+5EIINqEfS41BaWU3/33/C6D5tmWb3gdeVf5LIlMToP5THD+zA+IEdwu/oJdIuqH4drZaLaxowOLdIjnU/OqUrPzolzAegn1Bdid4S4sRnLQpAt9ZpAdt6tE13XCzpz3vcqq7dot6B5/J/zudPlw1iZPdsd/LJRpHcApJ7QZtewfcxBsoOOrRsvILP3jVwdA+YEBM8kjPs7ju/IJPmH3S8H7fSiQRoIKmXSPquj5RZs23mBimMFIkR3bJ4b7knzUhT5Pg6r3/7iGeotUpLomDKhRhj3IFkiddEgRPR23ecxqerd0f8u3OluPFWeDBwttTbPz6Nj1btdifDDCaa2YX+r/3tf7+nZXICf//RMO5/bxUf/XxUyEkEjUbE+rBPy4b2ztOvAWv8puKwFXTKDkLpQc/9soNQVuT7+NA269/yQxEGIKdAEywQHV8BSANJCMHihff6h2/zHQYNaZj1Jv5pSppillOLCAaJ/Xl/AG3ZH/5b8/FsaJdWkY8vYGUf8M9v1bdDy4CFgW1aJHPdqcG7J2OluKKaF+ZtpvBgGQs3FzlmWGi24uI8H+Z1UVtrjdX4BJpDVrp/p0B0uNCzLVQASmoJaVkhWjtOQSirWQYgDST1UGn3e1fV1HLvf5wXgpVXew2U17Putf8q+vKqxlt3cVqP1szffCDigfZg/GeAqdD+dd0ILvr71z7b7h7bi7veWAZYEx/qWue9b4eWjqleInFu//Z85tdKcn2haaosD40uLs4zY60u3AHIO9Ac8moR+QWiugQgV7dayG43OxC17gVxse3N0EASknMLYO2uI/xx1lpO79manYc94xgb9xRTUV3LzkNlPqkyRjzyGasfHl/nd/dv1WSnN943kTdvP5VFW4rI61bHb29+vBNJqvB6t/eMP/z07F68+m0Bp/dsTUpiHOVVtTx19dCQi0KdhBpQD+eF6/N4f/kOfj59uXvbgs1WloW1u45wwaDoZiruPFRGamI8WcfjFw6fANQ98tfV1kJlsUOLx+/mev7wDq8A5JC1+77dEFf/9WeR0EASgn/XlndBpufnbqbAr9vmvhmr3KlMvJVUhq754KS8qoY3Fm5zr0MAuHxElzofJxquvF318ZfLB7PrcLk77YqKTHJCPH/+4WDm5e/n7rG9+NV51ir19KQEyqsqIx60b0jBWjN/n53PxKGd3Qsb66q8qobTp8wGGn7G4zEtLs7KGJCSSb0CkH+gSYxtEIEYBxIRGQ88BcQDLxpjpvg9nwxMA0YAB4CrjDEFIpIIvAgMt89xmjHmT5EcM5YG57TyGTz3Hxh1CiIuN01dxAWDOnJFXmTB4B9z8t21Qz6/ZzSJ8XFhs8k2J5Fepwp05clduPJk35/fqzeP5D9LttOuZeNnS/YuEeBve1FpvQNJU5Xx/SZ/P7lt0iOavn1M8Q5AWbmN+tYxCyQiEg88C5wLFAKLRWSmMWaN1263AAeNMb1EZBLwGHAVcAWQbIwZJCJpwBoReRPYHsExG4x/x1ZVFAPoc9bvY876fRF/wHpXy+vVLrpxCnXsG9g5k4EO6WYaQ6xmZpXVo6UerX3FFVxjlwG48fRc7r+wX1TZIpQllj/BkUC+MWazMaYSmA5M9NtnIvCqff8d4ByxpvwYIF1EEoBUoBI4EuExG4zx69vyTjESay2DlGNVqrF5J5z8f+P7cnZfz6r1YJU0I1Fa5fmyFKwQW0P7Ot/To/DKtwUsbKT3Pd7FMpB0xmpBuBTa2xz3McZUA4eB1lhBpQTYBWwDHjfGFEV4zJi5za7L3RiC1fVWqrG19Uqtc+eYnrx848ncOcZaTe8qjrVxTzH3vLWciurIA0uJV734K/81n/eX74jqPD9dvZvbpi0JWZ7Af7ynLuergotlIHHq0PfvLQq2z0igBuiENdr0KxHpEeExrQOL3C4iS0Rkyb599VsU6H/guAjHKLyLSt1/Yb96vbfmpFPNhVPXz012toN73l7Bp6t38/in6/nvdzu47qVFER/Xv2vr59OXR1Wj5vbXlvLZmj0B63BWbD/EnHV7ASj1e8+mGqc53sQykBQC3gMCOcDOYPvY3ViZQBHwI+BjY0yVMWYv8A2QF+ExATDGPG+MyTPG5LVtW78uKe+erWCpPmb9bBTv3nmaz7Z7z/PUg7jVrxVzKEypW5c/f7w+wrNUqvGleK2of23BVlokW9/069JF5VRPZd9Rh5xZdXTdS4vctW5qaw0Tn/2Gm15ZDAQGryMaSBpELAPJYqC3iHQXkSRgEjDTb5+ZwA32/cuB2cYamNgGnC2WdOBUYF2Ex4yJBLs1kuDXKunfKYMR3bK5cLBnPn1mWiK/v6g/Pzs7MD/Q32fnc8U/v+VgmNK1wdKSK9UU7rugn09+Me8U9PM27qdNi7pNS96yv4Q77UWW3r5Yu5fDZYEBJhzv8cxtRaX8/v3VAJz1+ByffTbsKfZ5XUmFBpKGELNAYo95/AT4BFgLvG2MWS0iD4vIJfZuLwGtRSQfuAeYbG9/FmgBrMIKHlONMSuDHTOG1wBYA99/umwQAJ/dc5bjNNxnrh7m/s+VlZbIzWd25x67ZfL1/xvLbydYNRxe+noLiwsO8ut3VjJ73R4+XrWLkY9+HjSlyvcPndfg16VUXd02ugd//MEg92P/kgErCg8BcP6AyFKmPGDnYvN3/3uruPDpeY7PheKfTujL9VZX1vYiTzdXaWUNL369xWc/DSQNI6YjusaYWcAsv22/97pfjjXV1/91R522BztmrLi+43w9+Wx3/Y7ubdJ587ZTufJf8332FRH6tG/BisLDAdMlc7LSuHVUD/70kad07edr9/D52j10yEhhb3EFB0oqfMq0ZqQkUFVjmkdSPKXCcK12L4swjc/+EF1YhQfLeOLT9SQnxnP3WE+r/sOVuxick0mX7DSMMXy5fh+n92pNckJ8QHLUXYfLA2ZdOr3nUQ0kDUInUNdDsBXf/7ouj0cuHUj7jMCCOsEWE7q2u+pWuGSkJjKhjunelWpqkU4HXrfb08V015ie3HRGrs/zT8/O5y+feMYJSyurufvfy5j0/AIAnvtqEze9spi/fbYRsAba/W3a51vU5ay/fBmwj7ZIGoYGklDqOEzRITOlzhlZE+KtQFLlN1ulpKJapwCrY04kgWT3Yd86O78Z35cHLw6e/n3PkXIes1vzOw6VkfeHz8nfYwUJ/xo9L9+Y575fsN+3hovLNV5jPd5TkFX9aSAJwRVHGmoq7vCugdlDXS0S/8y+Ryuq65XCXamm5D0r6sOVuxj44CfsOlzGox+ucY8DBsuYHcwpf/yCV+dvdT/ef7TCPSDvX1phQKdM95e5W6ctcTzeIa/B/GJtkTQIDSQRcIojX/+/scz7zdg6HcepdoOryp132vmK6hqqaoxjaVSlmovzB7T3qcDYMjmBsqoa1uw8Qu7kD7n3Pys4WlHNNS8s5IV5Wxj7+JcAbNxb7Hi8ub8O/P/kXyXU5Qt7XYj/DK/s9CSflfhOEuLEXd5Au7YahgaSEFLtufJOVeZystLokp1Wp+O5BuydeHcJHLXntmsgUc3Zv67LY/0fJrgfn9azNYUHy3j8U2tsw7XqfbOdJdu1UHBYF+fSBF1bpwWUHZi30blwnMtRr3UgOVmpJMbHkeH3/8x7thnAE1cOZekD5zIyN5ulWw+6W1Gzvt/FP7/aFPL9lDP9pArhrdtP5dM1exrsA71VavC59t5dAq6ZJDpGoo4FL16fR7uMZK61kyHOtlsL/obYlSJX2lOFp908MuDLmH99k3DdYK6V6skJcVxov9Z/0eHAzp76LV/8yjN935Wt+38rdzKye7a7eNjVI7sGfOmrrK6lsqZWv9wFoS2SEHq0bcEdZ/VssOOFanIf8FqguMOu0d0xM3D2l1LNzbj+7Rmc04rcNukR7e8qBje6T1u6R/iaYJZtO8ih0koqqmvdPQiXDvOk3xvXrz2DvLIm9/Sqj5Nm7x8nwusLPGMw+4oDu9NueXUxAx/8JKpzPZ5pIGkmXLVHAIrsNCptm6D2hFL19dgPB4d8fsX2QxHN6jq7bztG9wlMa3T/hf0Cuqn2Flcw9OHPAE9g6N4mnZ5trQB1pLwKEaF7m3R+d0Ffn9f+76dnAtbgu3cp7P1HA7NOhOtiO9FpIGlE/vUkXH/IALsOl1FaWc3KwkMcKbO6tupbZ1upptCvY4ZP6hQn8zcfAHB3Qzl5+caTmXbzSEbmWuu1MlISWP+H8dw6qodPmhZ/3u/t6klwtern3DuG20f79i50tbvVSiqqfQLJkhAF6tbsPBL0uROZBpJGlJ2e5FNSdECnDPfj1xds46K/f80lz3zjzgcUqjKdUs1Rq7TQX35cH8Qffr8r4mMlJcSTnOD5oN/46ASGdGnFLWf6lqFNTfL8fzmrT1syUhJCln5IiI8jKSGOkkrfQPL4pxt4Y+FWx0zERWFy5J2o9JOqCXzwkzMpqawOmA3mmgq8fncxCXES9tudUs3NQb/s1vN+M5b5mw4wf/MBZny3w2e1ejiuQOKf2iQxPo737z6DmSt8E397/39pl5HCyofOD/se6UnxlFXWBCxsvG/GKl6ct4XubdJ55kfD3NtvnbaYdY9M8D/MCU8DSRMYlBO6ZKqr+e807Vip5sx7Ye2mP15AfJzQJTuNgZ0zmfGdp3DVQxf3D3usZdsOhXzetRbEZWtRSR3PFtKSEiipqOGpzzcGPLdlfwlb9pdww8ueGiv+C4djadr8Atq1TGb8wODdgM2Fdm0ppWLCO79cWpJv6/q8AeHzyJ3jVdLXSWuv1PWdW6Xyw+E5dTxDSE+OZ8ehUvYWB08iubjgIJ3ssZbGzH/3+/dXc8fry3wm4jRXGkiagdzWgQsbR/Vu0wRnolR0OreyMlh/9esxPtvbZfjOQAy1ONflrJOsmVsXDHL+8M5O8wSSbyaf7ZgsNZyWKYks2xq65QOeKcsfrdodkBcvFr7d5JkldvKjn/PEp8270J0Gkmbg37edGrBNx0fUseitH5/Kf+44jW6tfdeHpCUl+JSd9m+hODm9Zxu+mXw2/7hmhOPzbVsm84txvZn9q7Pqfb4JcUJlHQPDysLD9X6/SPmXAH56dn7M3zMaOkbSDHRqlRqwbYE9TqLUsSQnK42cLOfUQd7T2SMd/+vs8H/D+xi/GNenbifoZ6FXaeDnrxtBfJzw3JebWLL1YNDXbNlfwohuzmleGsJOv5rzxwJtkTQTb//Yt+77b8b3DbKnUsem8+1xEf9B8uaiR9t0zunXnnfuPJ3/3nU6vz7/JHdaF291zV5cF7W1htOnzObHDvVVjjjUuG8uNJA0E/07efIBFUy5kGvrWNdEqeYuMy2R31/Un3fuPL2pT8Vt3SPj3fez0z3jOMO7ZnH32F6s2O4ZP3nhek+tk8EPfcKBEFUe6+topW+X1q/O9bS4PvCb7tycaCBpJlokJ3B233bceHpuU5+KUjFz85ndo86v1ZC8FyI6TQD46xVDAGuF/LleZSCOlFfzzaaG7372HxuZ4JUB4L4ZznXumwMdI2lGXr7x5KY+BaVOOP07ZrBm1xHHctgTh3YiIzXRcRal08r3aB31CyTtMpJp1zKZvcUVXDa8c5BXNT1tkSilTmj/ueM0Ft13juNzCfFxnNu/vU/LxaW6po61uL18vmYPf/54XcD2o36FttKTElh03zgA/rtsR8D+zYUGEqXUCS09OYF2LSNbgzLEKytFRQQtEmMML87bHFDJ8dZpS/jHl5uo8KqMWlRSyfvLfYOFUyupOdJAopRSEXpykifvVnwEU5iXbTvIHz5cy+g/z3Fvc9WuB9+urOGPfMY0r9r0xxINJEopFaF0r4WURyvCT8dNjLc+Yg+XVfH+8h0YYzhQ4pntVXDAyg+2vag05HHuGtOThDjBmPp3p8WSBhKllIpQu4wUHrdncrnqBoXyh/+tdd//+fTlfJN/gN+8s9K97YfPzWfrgRJGebVYnAb2M1MTqa41lFSGLwwGcO2LC3ltfkFE+zYEDSRKKVUHl4+wkkM+Myd82pJFfkWyrn1pYUC1RVdpbYAfn9WDF2/Iw1+WnVfsYAT1UIwxfJ2/nwfeXx1234YS00AiIuNFZL2I5IvIZIfnk0XkLfv5hSKSa2+/RkSWe91qRWSo/dyX9jFdz4VOEaqUUk2kf8eMsPv86MWF7vu/ndDPXcRrvFeGZFeRO/91Jk4iaSk1tJitIxGReOBZ4FygEFgsIjONMWu8drsFOGiM6SUik4DHgKuMMW8Ab9jHGQS8b4xZ7vW6a4wxS2J17kopFUpmaiKHy6pYsf2QYxoVlzW76lead/0fxpMQ5/me76r+WFoZPkjsL2n8tPOxbJGMBPKNMZuNMZXAdGCi3z4TgVft++8A50hgNrergTdjeJ5KKVUnrtX5bywMPssq2AD6fRf044swGYuTE+J9pv66BvlLIxgj2W/XL0lKaLyRi1i+U2dgu9fjQnub4z7GmGrgMNDab5+rCAwkU+1urQccAg8AInK7iCwRkSX79u2r7zUopVSApyYNBeBQqWfmVv7eYpZts7IGPzN7o88Aure83Cx6tm3Ba7eM9Nnep32LoO+XFkGL5MH3V/HBip0csMdRKqtrA8oUx0osA4nTB7z/3LWQ+4jIKUCpMcY7ycw1xphBwCj7dp3TmxtjnjfG5Blj8tq2bVu3M1dKqRBc6e0/XbOHV77ZAsC4J+Zy2T++payyhsc/3eCz/9iT2vL4FUN48OL+DLW7wkb1bssHPznTvc9HPx8d9P1c9VtKKpxbJPl7i3l1/lZ++uZ3fL/DUy8l7w+f1+Pq6i6WubYKgS5ej3MA//SVrn0KRSQByAS8pzlMwq81YozZYf9bLCL/xupCm9awp66UUsElxHu+gz/0wRpuPKO7+/Elz3zts298nDD1Jt/Wh8ugnEx3epZQq9jTku2urSrnQHLUK8A89+WmMGff8GLZIlkM9BaR7iKShBUUZvrtMxO4wb5/OTDb2CtuRCQOuAJrbAV7W4KItLHvJwIXAc03JaZS6oSzce9RWqV5MgmPD1PnvV3LlLApWtJdXVsVzl1bFUECTAp1WzQAAAtOSURBVGOJWSCxxzx+AnwCrAXeNsasFpGHReQSe7eXgNYikg/cA3hPER4NFBpjNnttSwY+EZGVwHJgB/BCrK5BKaXCyUpLpLi8yj17a0hOJoM6Z4Z5Vd24Sm8HW5Do1FLp26ElM+5qnNovMU0jb4yZBczy2/Z7r/vlWK0Op9d+CZzqt60EcC7grJRSjahNiyT2H63kYGkVZ0yZTYtk6+O01lhZfJPi46isqaVPu5ZRv1dcnJCSGEd5kJZHuV+AmXLZICaN7Br1+0ZKV7YrpVQ9zL53DH07WEHiSHk1Ow+XA1YQKamoZmzftrx2y0juHtuzQd4vJTE+aCAp89ueGN+4H+0aSJRSqh4yUhLJyUoN2L5lfwkb9hylRXIio3q39RmYj0ZqYjxlQbq2/ANJenLj1izUQKKUUvV0Wk/fBIveKVFapjTsh3lqYnxAwHBxBZiPfj6Kq/K6MLZv4y550ECilFL1dPMZucz/7dnux729FhWmJQVWVYzG5v0l/G/lLsfnXF1ePdu24LHLB7vzdTUWrdmulFL1JCJ0zPR0b7XP8Ezjra6NTe2Qqppa9xhIaWU1981YRUlFNckJcY2aFsWbBhKllIrS7y/qz/aDpe6ZWwBHysIXvqqPQQ99wrpHJvDtpv386AVP5uBIMg3HigYSpZSK0s1nWivbV+04zBOfWelRMlMTQ72k3sqrajn3ia/YuPeoz/b6ZhpuCBpIlFKqgQzsnMmWP13AByt3cV7/9g167LP6tOWrDVYCWv8g0tR0sF0ppRqQiHDJkE6kJDbsgPfz14dei/2rc/s06PvVhQYSpZQ6BoSbidWigacb14UGEqWUOka8c8dpQZ+LpOhVrGggUUqpY0ROVlrQ5xqriJUTDSRKKXWMaJ+RzI2n5zquF7m6EZM0+tNZW0opdYwQER66ZAC/GX8Sf/tsA/ecexKb9h1l8/4S+rSPPstwvc/LriN1XMvLyzNLlixp6tNQSqljiogsNcbkhdtPu7aUUkpFRQOJUkqpqGggUUopFRUNJEoppaKigUQppVRUNJAopZSKigYSpZRSUdFAopRSKionxIJEEdkHbK3ny9sA+xvwdJo7vd7j24l2vXDiXXNDXm83Y0zbcDudEIEkGiKyJJKVnccLvd7j24l2vXDiXXNTXK92bSmllIqKBhKllFJR0UAS3vNNfQKNTK/3+HaiXS+ceNfc6NerYyRKKaWioi0SpZRSUdFAEoSIjBeR9SKSLyKTm/p8GoqIFIjI9yKyXESW2NuyReQzEdlo/5tlbxcRedr+GawUkeFNe/aREZGXRWSviKzy2lbnaxSRG+z9N4rIDU1xLZEIcr0PicgO+/e8XEQu8Hrut/b1rheR8722HxN/8yLSRUTmiMhaEVktIj+3tx+Xv+MQ19t8fsfGGL353YB4YBPQA0gCVgD9m/q8GujaCoA2ftv+DEy2708GHrPvXwB8BAhwKrCwqc8/wmscDQwHVtX3GoFsYLP9b5Z9P6upr60O1/sQcK/Dvv3tv+dkoLv9dx5/LP3NAx2B4fb9lsAG+7qOy99xiOttNr9jbZE4GwnkG2M2G2MqgenAxCY+p1iaCLxq338VuNRr+zRjWQC0EpGOTXGCdWGMmQsU+W2u6zWeD3xmjCkyxhwEPgPGx/7s6y7I9QYzEZhujKkwxmwB8rH+3o+Zv3ljzC5jzDL7fjGwFujMcfo7DnG9wTT671gDibPOwHavx4WE/sUdSwzwqYgsFZHb7W3tjTG7wPqjBdrZ24+nn0Ndr/F4uPaf2F05L7u6eTjOrldEcoFhwEJOgN+x3/VCM/kdayBxJg7bjpfpbWcYY4YDE4C7RWR0iH2P55+DS7BrPNav/TmgJzAU2AX81d5+3FyviLQA3gV+YYw5EmpXh23H3DU7XG+z+R1rIHFWCHTxepwD7Gyic2lQxpid9r97gRlYzd09ri4r+9+99u7H08+hrtd4TF+7MWaPMabGGFMLvID1e4bj5HpFJBHrQ/UNY8x/7c3H7e/Y6Xqb0+9YA4mzxUBvEekuIknAJGBmE59T1EQkXURauu4D5wGrsK7NNWPlBuB9+/5M4Hp71supwGFX18ExqK7X+Alwnohk2V0G59nbjgl+Y1k/wPo9g3W9k0QkWUS6A72BRRxDf/MiIsBLwFpjzBNeTx2Xv+Ng19usfsdNPSOhud6wZnpswJrlcF9Tn08DXVMPrJkaK4DVrusCWgNfABvtf7Pt7QI8a/8MvgfymvoaIrzON7Ga+lVY38Juqc81AjdjDVTmAzc19XXV8Xpfs69npf1h0dFr//vs610PTPDafkz8zQNnYnXJrASW27cLjtffcYjrbTa/Y13ZrpRSKirataWUUioqGkiUUkpFRQOJUkqpqGggUUopFRUNJEoppaKigUQdF0Skxs6AukJElonI6WH2byUid0Vw3C9F5ISp9x0JEXlFRC5v6vNQzYcGEnW8KDPGDDXGDAF+C/wpzP6tgLCBpKmISEJTn4NSkdJAoo5HGcBBsPITicgXdivlexFxZTudAvS0WzF/sff9jb3PChGZ4nW8K0RkkYhsEJFR9r7xIvIXEVlsJ837sb29o4jMtY+7yrW/N7FqwjxmH3ORiPSyt78iIk+IyBzgMbHqa7xnH3+BiAz2uqap9rmuFJEf2tvPE5H59rX+x87NhIhMEZE19r6P29uusM9vhYjMDXNNIiLP2Mf4EE8yRKUA0G896niRKiLLgRSs+g1n29vLgR8YY46ISBtggYjMxKpXMdAYMxRARCZgpR0/xRhTKiLZXsdOMMaMFKtw0IPAOKzV44eNMSeLSDLwjYh8ClwGfGKMeVRE4oG0IOd7xD7m9cCTwEX29j7AOGNMjYj8HfjOGHOpiJwNTMNK0PeA/d6D7HP//+3dT6hNURTH8e9vgqQeSTKi5M8AEZFI/sWAmQFSyIiiUFKSKJkYmDAiRHpF+RMRRVGvR/4kJEMTBjwpf0PPMtjr5sQ9qCvqvd9nck7n3n3P2uf1WmfvXWsPyr5tz7bvJW0FNkvaTymfMTYiQtLAvM8OYGFEPKtcq+vTJGAMMB4YCjwGDv/RX8V6BScS6yk+VpLCdOCYpHGU8hh7VKocf6WUzR7apP184EhEfACIiOr+Ho2igHeBEXm+AJhQWStoo9Q0ug0cVimydzYi7tfE21457qtcPxUR3Xk+E1iS8VyTNFhSW8a6rNEgIl5LWkzZ0KijlGaiD9AJvKEk00M5mriQzTqAo5JOVvpX16dZQHvG9VzStZo+WS/lRGI9TkR05hv6EEptoSHA5Ij4IukpZdTyI1FfUvtTHrv5/j8jYENE/FTkL5PWIuC4pL0RcaxZmDXn73+IqVm7ZrGKsknT8ibxTAXmUZLPemBuRKyVNC3jvC9pYl2fciTmWkpWy2sk1uNIGkvZVvQV5a36RSaROcDw/NpbyralDVeANZL6529Up7aauQysy5EHkkarVFcenvc7SKnYWrfP/dLKsbPmOzeAFfn7s4GuKPtQXKEkhEZ/BwE3gRmV9Zb+GdMAoC0iLgIbKVNjSBoZEbciYgfQRSkv3rRPGceyXEMZBsz5zbOxXsYjEuspGmskUN6sV+U6wwngvKQ7lKqpTwAi4pWkDkmPgEsRsSXfyu9I+gxcBLb94n6HKNNc91Tmkl5S1lhmA1skfQHeAStr2veVdIvyMvfTKCLtBI5IegB84HuJ9N3AgYy9G9gVEaclrQbac30DyprJW+CcpH75XDblZ3sljcprVykVoR/U9OkMZc3pIaVy7PVfPBfrhVz91+wfy+m1KRHR9b9jMfsbPLVlZmYt8YjEzMxa4hGJmZm1xInEzMxa4kRiZmYtcSIxM7OWOJGYmVlLnEjMzKwl3wD0UB3V79se0wAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"learn.recorder.plot_losses()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"learn.save('stage-2-256-rn50')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"You won't really know how you're going until you submit to Kaggle, since the leaderboard isn't using the same subset as we have for training. But as a guide, 50th place (out of 938 teams) on the private leaderboard was a score of `0.930`."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"learn.export()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## fin"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"(This section will be covered in part 2 - please don't ask about it just yet! :) )"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"#! kaggle competitions download -c planet-understanding-the-amazon-from-space -f test-jpg.tar.7z -p {path} \n",
"#! 7za -bd -y -so x {path}/test-jpg.tar.7z | tar xf - -C {path}\n",
"#! kaggle competitions download -c planet-understanding-the-amazon-from-space -f test-jpg-additional.tar.7z -p {path} \n",
"#! 7za -bd -y -so x {path}/test-jpg-additional.tar.7z | tar xf - -C {path}"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"61191"
]
},
"execution_count": null,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"test = ImageList.from_folder(path/'test-jpg').add(ImageList.from_folder(path/'test-jpg-additional'))\n",
"len(test)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"learn = load_learner(path, test=test)\n",
"preds, _ = learn.get_preds(ds_type=DatasetType.Test)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"thresh = 0.2\n",
"labelled_preds = [' '.join([learn.data.classes[i] for i,p in enumerate(pred) if p > thresh]) for pred in preds]"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"['agriculture cultivation partly_cloudy primary road',\n",
" 'clear haze primary water',\n",
" 'agriculture clear cultivation primary',\n",
" 'clear primary',\n",
" 'partly_cloudy primary']"
]
},
"execution_count": null,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"labelled_preds[:5]"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"fnames = [f.name[:-4] for f in learn.data.test_ds.items]"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"df = pd.DataFrame({'image_name':fnames, 'tags':labelled_preds}, columns=['image_name', 'tags'])"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"df.to_csv(path/'submission.csv', index=False)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Warning: Your Kaggle API key is readable by other users on this system! To fix this, you can run 'chmod 600 /home/ubuntu/.kaggle/kaggle.json'\n",
"100%|██████████████████████████████████████| 2.18M/2.18M [00:02<00:00, 1.05MB/s]\n",
"Successfully submitted to Planet: Understanding the Amazon from Space"
]
}
],
"source": [
"! kaggle competitions submit planet-understanding-the-amazon-from-space -f {path/'submission.csv'} -m \"My submission\""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Private Leaderboard score: 0.9296 (around 80th)"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| apache-2.0 |
masasin/spirit | notebooks/03_pre-analysis.ipynb | 1 | 5235913 | null | mit |
ernestyalumni/servetheloop | packetDef/podCommands.ipynb | 1 | 22537 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# `server/udp/podCommands.js` - from node.js /JavaScript to Python (object)"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# find out where we are on the file directory\n",
"import os, sys"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"/home/topolo/PropD/servetheloop/packetDef\n",
"['.ipynb_checkpoints', 'reactGS', 'podCommands.ipynb', 'podCommandparams.pkl', 'react-GS_node_to_py_to_YAML.ipynb']\n"
]
}
],
"source": [
"print( os.getcwd())\n",
"print( os.listdir(os.getcwd()))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The `reactGS` folder \"mimics\" the actual `react-groundstation` github repository, only copying the file directory structure, but the source code itself (which is a lot) isn't completely copied over. I wanted to keep these scripts/notebooks/files built on top of that github repository to be separate from the actual working code. "
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"/home/topolo/PropD/servetheloop/packetDef/reactGS/server/udp/\n"
]
}
],
"source": [
"wherepodCommandsis = os.getcwd()+'/reactGS/server/udp/' \n",
"print(wherepodCommandsis)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## `node.js`/(JavaScript) to `json`; i.e. \n",
"\n",
"## `node.js`/(JavaScript) $\\to$ `json` \n",
"\n",
"Make a copy of `server/udp/podCommands.js`. \n",
"\n",
"In this copy, comment out `var chalk = require('chalk')` (this is the only thing you have to do manually). \n",
"\n",
"Run this in the directory containing your copy of `podCommands.js`:\n",
"\n",
"``` \n",
"node traverse_podCommands.js \n",
"``` \n",
"\n",
"This should generate a `json` file `podCmds_lst.json`"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Available `podCommands` as a Python list; `json` to Python list, i.e. `json` $\\to$ Python list"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import json"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"f_podCmds_json = open(wherepodCommandsis+'podCmds_lst.json','rb')\n",
"rawjson_podCmds = f_podCmds_json.read()\n",
"f_podCmds_json.close()"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"<type 'str'>\n",
"<type 'list'>\n",
"104\n"
]
}
],
"source": [
"print(type(rawjson_podCmds))\n",
"podCmds_lst=json.loads(rawjson_podCmds)\n",
"print(type(podCmds_lst))\n",
"print(len(podCmds_lst)) # there are 104 available commands for the pod!"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"GS_Heartbeat\n",
"LGU_PositionChange\n",
"LGU_SpeedChange\n",
"FCUPod_Off\n",
"FCUPod_Stop\n",
"FCUPod_PowerLatch\n",
"setBrakeDevelopmentMode\n",
"FCUBrake_DisableDevelopmentMode\n",
"FCUBrake_EnableDevelopmentMode\n",
"FCUBrake_MoveMotorRAW\n",
"FCUBrake_MoveMotorIBeam\n",
"FCUBrake_BeginInit\n",
"FCUBrake_MLPSetZeroLeftBrake\n",
"FCUBrake_MLPSetZeroRightBrake\n",
"FCUBrake_MLPSetSpanLeftBrake\n",
"FCUBrake_MLPSetSpanRightBrake\n",
"FCUStepper_SetMaxAngularAccel\n",
"FCUStepper_SetPicoMetersPerRev\n",
"FCUStepper_SetMaxRPM\n",
"FCUStepper_SetMicroStepResolution\n",
"FCUBrake_RequestDevelopmentMode\n",
"FCUStreamingControlStart_AccelCalData\n",
"FCUStreamingControlStart_AccelFullData\n",
"FCUStreamingControlStop_Accel\n",
"FCUStreamingControlStart_Brakes\n",
"FCUStreamingControlStart_MotorsRaw\n",
"FCUStreamingControlStart_Lasers\n",
"FCUStreamingControlStart_ForwardLaser\n",
"FCUAccel_FineZero\n",
"FCUAccel_AutoZero\n",
"FCUContrast_StartStream\n",
"FCUContrast_StopStream\n",
"PowerAStopAllManualDischarging\n",
"PowerBStopAllManualDischarging\n",
"PowerAPowerLatch\n",
"PowerBPowerLatch\n",
"PowerAChargeRelayOff\n",
"PowerAChargeRelayOn\n",
"PowerAStreamingOff\n",
"PowerBStreamingOff\n",
"PowerAStreamCurrentTemps\n",
"PowerBStreamCurrentTemps\n",
"PowerAStreamTempLocations\n",
"PowerBStreamTempLocations\n",
"PowerARequestRomID\n",
"PowerBRequestRomID\n",
"PowerAStartCharging\n",
"PowerAStopCharging\n",
"PowerBStartCharging\n",
"PowerBStopCharging\n",
"PowerAStartDischarging\n",
"PowerAStopDischarging\n",
"PowerBStartDischarging\n",
"PowerBStopDischarging\n",
"PowerARequestBMS\n",
"PowerBRequestBMS\n",
"PowerARequestCooling\n",
"PowerAStartCooling\n",
"PowerBRequestCooling\n",
"PowerBStartCooling\n",
"PowerAStartRepressurizing\n",
"PowerBStartRepressurizing\n",
"PowerATestSolenoidPin4\n",
"PowerATestSolenoidPin8\n",
"PowerATestSolenoidPin16\n",
"PowerATestSolenoidPin22\n",
"PowerATestSolenoidPin23\n",
"PowerBTestSolenoidPin4\n",
"PowerBTestSolenoidPin8\n",
"PowerBTestSolenoidPin16\n",
"PowerBTestSolenoidPin22\n",
"PowerBTestSolenoidPin23\n",
"PowerAToPowerB\n",
"PowerBToPowerA\n",
"PodSafePowerNodeA\n",
"PodSafePowerNodeB\n",
"ForcePreRunPhase\n",
"FCUHover_Enable\n",
"FCUHover_Disable\n",
"FCUHover_EnableStaticHovering\n",
"FCUHover_ReleaseStaticHovering\n",
"FCUHover_EnableHEX\n",
"FCUHover_DisableHEX\n",
"FCUHover_SetHEXSpeed\n",
"FCUHover_StartCooling\n",
"FCUHover_StopCooling\n",
"FCUHover_OpenSolenoid\n",
"FCUAuxProp_Enable\n",
"FCUAuxProp_Disable\n",
"FCUAuxProp_SetSpeed\n",
"FCUGimbal_Static\n",
"FCUGimbal_FullBackwards\n",
"XilinxSim_Start\n",
"XilinxSim_Stop\n",
"XilinxSim_Laser0On\n",
"XilinxSim_Laser0Off\n",
"XilinxSim_Laser1On\n",
"XilinxSim_Laser1Off\n",
"XilinxSim_Laser2On\n",
"XilinxSim_Laser2Off\n",
"AutoSequenceTest_Start\n",
"AutoSequenceTest_Skip\n",
"AutoSequenceTest_Kill\n",
"AutoSequenceTest_Restart\n"
]
}
],
"source": [
"for cmd in podCmds_lst: \n",
" print cmd"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"## Dirty parsing of `podCommands.js` and the flight control parameters "
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"<type 'str'>\n",
"19296\n"
]
}
],
"source": [
"f_podCmds = open(wherepodCommandsis+'podCommands.js','rb')\n",
"raw_podCmds = f_podCmds.read()\n",
"f_podCmds.close()\n",
"print(type(raw_podCmds))\n",
"print(len(raw_podCmds))"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# get the name of the functions\n",
"cmdnameslst = [func[:func.find(\"(\")].strip() for func in raw_podCmds.split(\"function \")]"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"funcparamslst = [func[func.find(\"(\")+1:func.find(\")\")] \n",
" if func[func.find(\"(\")+1:func.find(\")\")] is not '' else None for func in raw_podCmds.split(\"function \")]\n",
"#raw_podCmds.split(\"function \")[3][ raw_podCmds.split(\"function \")[3].find(\"(\")+1:raw_podCmds.split(\"function \")[3].find(\")\")] "
]
},
{
"cell_type": "code",
"execution_count": 46,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# more parsing of this list of strings \n",
"funcparamslst_cleaned = []\n",
"for param in funcparamslst:\n",
" if param is None:\n",
" funcparamslst_cleaned.append(None)\n",
" else:\n",
" funcparamslst_cleaned.append( param.strip().split(',') )"
]
},
{
"cell_type": "code",
"execution_count": 38,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"106\n"
]
}
],
"source": [
"print(len(raw_podCmds.split(\"function \")) ) # 106 commands\n",
"\n",
"# get the index value (e.g. starts at position 22) of where \"udp.tx.transmitPodCommand\" starts, treating it as a string\n",
"#whereisudptransmit = [func.find(\"udp.tx.transmitPodCommand(\") for func in raw_podCmds.split(\"function \")]\n",
"\n",
"whereisudptransmit = []\n",
"for func in raw_podCmds.split(\"function \"):\n",
" val = func.find(\"udp.tx.transmitPodCommand(\")\n",
" if val is not -1:\n",
" if func.find(\"// \",val-4) is not -1 or func.find(\"// udp\",val-4) is not -1:\n",
" whereisudptransmit.append(None)\n",
" else:\n",
" whereisudptransmit.append(val)\n",
" else: \n",
" whereisudptransmit.append(None)\n",
"\n",
"#whereisudptransmit = [func.find(\"udp.tx.transmitPodCommand(\") for func in raw_podCmds.split(\"function \")]\n",
"\n",
"\n",
"# remove -1 values\n",
"#whereisudptransmit = filter(lambda x : x != -1, whereisudptransmit)\n",
"\n",
"rawParams=[funcstr[ funcstr.find(\"(\",val)+1:funcstr.find(\")\",val)] if val is not None else None for funcstr, val in zip(raw_podCmds.split(\"function \"), whereisudptransmit)]"
]
},
{
"cell_type": "code",
"execution_count": 47,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[[\"'./binary'\"],\n",
" ['udp'],\n",
" None,\n",
" ['liftName', ' liftDirection'],\n",
" ['liftName', ' liftSpeed'],\n",
" ['value'],\n",
" None,\n",
" None,\n",
" ['data'],\n",
" None]"
]
},
"execution_count": 47,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"funcparamslst_cleaned[:10]"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"113"
]
},
"execution_count": 32,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"raw_podCmds.split(\"function \")[4].find(\"// \",116-4);"
]
},
{
"cell_type": "code",
"execution_count": 42,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# more parsing of this list of strings\n",
"cleaningParams = []\n",
"for rawparam in rawParams: \n",
" if rawparam is None:\n",
" cleaningParams.append(None)\n",
" else:\n",
" cleanParam = []\n",
" cleanParam.append( rawparam.split(',')[0].strip(\"'\") )\n",
" for strval in rawparam.split(',')[1:]:\n",
" strval2 = strval.strip()\n",
" try: \n",
" strval2 = int(strval2,16)\n",
" strval2 = hex(strval2)\n",
" except ValueError:\n",
" strval2\n",
" cleanParam.append(strval2)\n",
" cleaningParams.append(cleanParam)\n"
]
},
{
"cell_type": "code",
"execution_count": 43,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[None,\n",
" None,\n",
" ['Flight Control', '0x400', '0x0', '0x0', '0x0', '0x0'],\n",
" None,\n",
" None,\n",
" None,\n",
" ['Flight Control', '0x3000', '0x76543210', '0x0', '0x0', '0x0'],\n",
" ['Flight Control', '0x1', '0x1234abcd', '0x0', '0x0', '0x0'],\n",
" ['Flight Control', '0x3030', '0xabcd1245', 'data.powerNode', '0x0', '0x0'],\n",
" ['Flight Control', '0x1400', '0x0', '0x0', '0x0', '0x0']]"
]
},
"execution_count": 43,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"cleaningParams[:10]"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# get the name of the functions\n",
"\n",
"#[func[:func.find(\"(\")] \n",
"# if func.find(\"()\") is not -1 else None for func in raw_podCmds.split(\"function \")];\n",
"cmdnameslst = [func[:func.find(\"(\")].strip() for func in raw_podCmds.split(\"function \")]"
]
},
{
"cell_type": "code",
"execution_count": 48,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"106\n"
]
}
],
"source": [
"# each node js function has its arguments; do that first\n",
"podfunclst = zip(cmdnameslst, funcparamslst_cleaned)\n",
"print(len(podfunclst))"
]
},
{
"cell_type": "code",
"execution_count": 50,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"podfunclst[:10];"
]
},
{
"cell_type": "code",
"execution_count": 51,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"106\n"
]
}
],
"source": [
"# each node js function has its arguments; do that first\n",
"podCommandparams = zip(podfunclst, cleaningParams)\n",
"print(len(podCommandparams))"
]
},
{
"cell_type": "code",
"execution_count": 52,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"(('PodSafePowerNodeB', None),\n",
" ['Power Node B', '0x3000', '0x76543210', '0x0', '0x0', '0x0'])"
]
},
"execution_count": 52,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"podCommandparams[-2]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"So the structure of our result is as follows:\n",
"\n",
"Python tuples (each of size 2 for each of the tuples) \n",
"\"\"\" \n",
" ( (Name of pod command as a string, None if there are no function parameters or Python list of function arguments), \n",
" Python list [ Subsystem name as a string, paramter1 as a hex value, paramter2 as a hex value, paramter3 as a hex value, paramter4 as a hex value] ) \n",
"\"\"\" \n",
"\n",
"Notice that in the original code, there's some TO DO's still left (eek!) so that those `udp.tx.transmitPodCommand` is commented out or left as TODO, and some are dependent upon arguments in the function (and thus will change, the parameter is a variable). "
]
},
{
"cell_type": "code",
"execution_count": 53,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[(('const bin = require', [\"'./binary'\"]), None),\n",
" (('', ['udp']), None),\n",
" (('GS_Heartbeat', None),\n",
" ['Flight Control', '0x400', '0x0', '0x0', '0x0', '0x0']),\n",
" (('LGU_PositionChange', ['liftName', ' liftDirection']), None),\n",
" (('LGU_SpeedChange', ['liftName', ' liftSpeed']), None),\n",
" (('setBrakeDevelopmentMode', ['value']), None),\n",
" (('FCUPod_Off', None),\n",
" ['Flight Control', '0x3000', '0x76543210', '0x0', '0x0', '0x0']),\n",
" (('FCUPod_Stop', None),\n",
" ['Flight Control', '0x1', '0x1234abcd', '0x0', '0x0', '0x0']),\n",
" (('FCUPod_PowerLatch', ['data']),\n",
" ['Flight Control', '0x3030', '0xabcd1245', 'data.powerNode', '0x0', '0x0']),\n",
" (('FCUBrake_DisableDevelopmentMode', None),\n",
" ['Flight Control', '0x1400', '0x0', '0x0', '0x0', '0x0'])]"
]
},
"execution_count": 53,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"podCommandparams[:10]"
]
},
{
"cell_type": "code",
"execution_count": 54,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"try:\n",
" import CPickle as pickle\n",
"except ImportError:\n",
" import pickle"
]
},
{
"cell_type": "code",
"execution_count": 55,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"podCommandparamsfile = open(\"podCommandparams.pkl\",'wb')\n",
"pickle.dump( podCommandparams , podCommandparamsfile )\n",
"podCommandparamsfile.close()"
]
},
{
"cell_type": "code",
"execution_count": 56,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# open up a pickle file like so:\n",
"podCommandparamsfile_recover = open(\"podCommandparams.pkl\",'rb')\n",
"podCommandparams_recover = pickle.load(podCommandparamsfile_recover)\n",
"podCommandparamsfile_recover.close()"
]
},
{
"cell_type": "code",
"execution_count": 57,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[(('const bin = require', [\"'./binary'\"]), None),\n",
" (('', ['udp']), None),\n",
" (('GS_Heartbeat', None),\n",
" ['Flight Control', '0x400', '0x0', '0x0', '0x0', '0x0']),\n",
" (('LGU_PositionChange', ['liftName', ' liftDirection']), None),\n",
" (('LGU_SpeedChange', ['liftName', ' liftSpeed']), None),\n",
" (('setBrakeDevelopmentMode', ['value']), None),\n",
" (('FCUPod_Off', None),\n",
" ['Flight Control', '0x3000', '0x76543210', '0x0', '0x0', '0x0']),\n",
" (('FCUPod_Stop', None),\n",
" ['Flight Control', '0x1', '0x1234abcd', '0x0', '0x0', '0x0']),\n",
" (('FCUPod_PowerLatch', ['data']),\n",
" ['Flight Control', '0x3030', '0xabcd1245', 'data.powerNode', '0x0', '0x0']),\n",
" (('FCUBrake_DisableDevelopmentMode', None),\n",
" ['Flight Control', '0x1400', '0x0', '0x0', '0x0', '0x0'])]"
]
},
"execution_count": 57,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"podCommandparams_recover[:10]"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"## Going to .csv \n",
"\n",
"`@nuttwerx` and `@ernestyalumni` decided upon separating the multiple entries in a field by the semicolon \"`;`\":"
]
},
{
"cell_type": "code",
"execution_count": 79,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"tocsv = []\n",
"for cmd in podCommandparams_recover:\n",
" name = cmd[0][0]\n",
" funcparam = cmd[0][1]\n",
" if funcparam is None:\n",
" fparam = None\n",
" else:\n",
" fparam = \";\".join(funcparam)\n",
" udpparam = cmd[1]\n",
" if udpparam is None:\n",
" uname = None\n",
" uparam = None\n",
" else:\n",
" uname = udpparam[0]\n",
" uparam = \";\".join( udpparam[1:] )\n",
" tocsv.append([name,fparam,uname,uparam])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Add the headers in manually: \n",
" \n",
"1 = Command name; 2 = Function args; 3 = Pod Node; 4 = Command Args "
]
},
{
"cell_type": "code",
"execution_count": 80,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"header = [\"Command name\",\"Function args\", \"Pod Node\", \"Command Args\"]\n",
"tocsv.insert(0,header)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The csv fields format is as follows: \n",
"\n",
"(function name) , (function arguments (None is there are none)) , (UDP transmit name (None is there are no udp transmit command)), (UDP transmit parameters, 4 of them, separated by semicolon, or None if there are no udp transmit command )"
]
},
{
"cell_type": "code",
"execution_count": 69,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import csv"
]
},
{
"cell_type": "code",
"execution_count": 82,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"f_podCommands_tocsv = open(\"podCommands.csv\",'w')\n",
"tocsv_writer = csv.writer( f_podCommands_tocsv )\n",
"tocsv_writer.writerows(tocsv)\n",
"f_podCommands_tocsv.close()"
]
},
{
"cell_type": "code",
"execution_count": 77,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"#tocsv.insert(0,header) no need"
]
},
{
"cell_type": "code",
"execution_count": 83,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"#tocsv[:10] no need"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.11"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
yugangzhang/CHX_Pipelines | rheadric/XPCS_GiSAXS_Single_Run_Oct12_with_Bin_Funcs.ipynb | 1 | 4642917 | null | bsd-3-clause |
taslug/esp8266-hackfest-july-2016 | notebook/TasLUG July 2016.ipynb | 1 | 1435 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# TasLUG July 2016\n",
"\n",
"## ESP8266 Hackfest"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Agenda\n",
"\n",
"- 6pm Arrive and Setup - order Pizza?\n",
"- 6.30pm - Introduction to ESP8266\n",
"- 7pm - Hack Hack Hack\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Coming Up\n",
"\n",
"- NOW until August 5th - LCA2017 CFP is Open!\n",
"- July 29-31 - GovHACK\n",
"- August 12-16 - PyCon-AU - Melbourne\n",
"- August 18 - Hobart Meeting - Andrew Elwell"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# https://git.scriptforge.org/TasLUG/esp8266-hackfest-july-2016\n",
"# https://pad.taslug.org.au/p/esp8266"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.10"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| gpl-3.0 |
CompPhysics/ComputationalPhysics2 | doc/pub/week13/ipynb/week13.ipynb | 1 | 2539 | {
"cells": [
{
"cell_type": "markdown",
"id": "347cc549",
"metadata": {
"editable": true
},
"source": [
"<!-- HTML file automatically generated from DocOnce source (https://github.com/doconce/doconce/)\n",
"doconce format html week13.do.txt --no_mako --no_abort -->\n",
"<!-- dom:TITLE: Week 14 April 4-8: Neural networks and project 2 -->"
]
},
{
"cell_type": "markdown",
"id": "5332a94a",
"metadata": {
"editable": true
},
"source": [
"# Week 14 April 4-8: Neural networks and project 2\n",
"**Morten Hjorth-Jensen Email [email protected]**, Department of Physics and Center fo Computing in Science Education, University of Oslo, Oslo, Norway and Department of Physics and Astronomy and Facility for Rare Ion Beams, Michigan State University, East Lansing, Michigan, USA\n",
"\n",
"Date: **Apr 6, 2022**\n",
"\n",
"Copyright 1999-2022, Morten Hjorth-Jensen Email [email protected]. Released under CC Attribution-NonCommercial 4.0 license"
]
},
{
"cell_type": "markdown",
"id": "be4ffac7",
"metadata": {
"editable": true
},
"source": [
"## Overview of week 14, April 4-8\n",
"* We have two project groups based on the selection below\n",
"\n",
"a. Neural Networks and Boltzmann Machines with [material](http://compphysics.github.io/ComputationalPhysics2/doc/LectureNotes/_build/html/boltzmannmachines.html)\n",
"\n",
"b. Path integral Monte Carlo project\n",
"\n",
"**Schedule.**\n",
"\n",
"Since the majority of you plan to work on neural networks and Boltzmann machines, we will have lectures on this topic for the rest of the semester.\n",
"We meet each Thursday at 2.15pm for theory lectures and discussions till approx 4pm. The remaining three hours are dedicated to project work."
]
},
{
"cell_type": "markdown",
"id": "f061009d",
"metadata": {
"editable": true
},
"source": [
"## Alternatives for project 2\n",
"1. Fermion VMC, continuation of project 1\n",
"\n",
"2. Deep learning applied to project 1, either neural networks or Boltzmann machines\n",
"\n",
"3. Hartree-Fock theory and time-dependent theories\n",
"\n",
"4. Many-body methods like coupled-cluster theory or other many-body methods\n",
"\n",
"5. Quantum computing and possibly quantum machine learning\n",
"\n",
"6. Suggestions from you"
]
}
],
"metadata": {},
"nbformat": 4,
"nbformat_minor": 5
}
| cc0-1.0 |
littleowen/Conceptor | Speaker.ipynb | 2 | 3679167 | null | gpl-3.0 |
mne-tools/mne-tools.github.io | 0.21/_downloads/6035dcef33422511928bd2247a3d092d/plot_source_power_spectrum_opm.ipynb | 1 | 11555 | {
"cells": [
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"%matplotlib inline"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n\n# Compute source power spectral density (PSD) of VectorView and OPM data\n\nHere we compute the resting state from raw for data recorded using\na Neuromag VectorView system and a custom OPM system.\nThe pipeline is meant to mostly follow the Brainstorm [1]_\n`OMEGA resting tutorial pipeline <bst_omega_>`_.\nThe steps we use are:\n\n1. Filtering: downsample heavily.\n2. Artifact detection: use SSP for EOG and ECG.\n3. Source localization: dSPM, depth weighting, cortically constrained.\n4. Frequency: power spectral density (Welch), 4 sec window, 50% overlap.\n5. Standardize: normalize by relative power for each source.\n :depth: 1\n\n\n## Preprocessing\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Authors: Denis Engemann <[email protected]>\n# Luke Bloy <[email protected]>\n# Eric Larson <[email protected]>\n#\n# License: BSD (3-clause)\n\nimport os.path as op\n\nfrom mne.filter import next_fast_len\n\nimport mne\n\n\nprint(__doc__)\n\ndata_path = mne.datasets.opm.data_path()\nsubject = 'OPM_sample'\n\nsubjects_dir = op.join(data_path, 'subjects')\nbem_dir = op.join(subjects_dir, subject, 'bem')\nbem_fname = op.join(subjects_dir, subject, 'bem',\n subject + '-5120-5120-5120-bem-sol.fif')\nsrc_fname = op.join(bem_dir, '%s-oct6-src.fif' % subject)\nvv_fname = data_path + '/MEG/SQUID/SQUID_resting_state.fif'\nvv_erm_fname = data_path + '/MEG/SQUID/SQUID_empty_room.fif'\nvv_trans_fname = data_path + '/MEG/SQUID/SQUID-trans.fif'\nopm_fname = data_path + '/MEG/OPM/OPM_resting_state_raw.fif'\nopm_erm_fname = data_path + '/MEG/OPM/OPM_empty_room_raw.fif'\nopm_trans_fname = None\nopm_coil_def_fname = op.join(data_path, 'MEG', 'OPM', 'coil_def.dat')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Load data, resample. We will store the raw objects in dicts with entries\n\"vv\" and \"opm\" to simplify housekeeping and simplify looping later.\n\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"raws = dict()\nraw_erms = dict()\nnew_sfreq = 90. # Nyquist frequency (45 Hz) < line noise freq (50 Hz)\nraws['vv'] = mne.io.read_raw_fif(vv_fname, verbose='error') # ignore naming\nraws['vv'].load_data().resample(new_sfreq)\nraws['vv'].info['bads'] = ['MEG2233', 'MEG1842']\nraw_erms['vv'] = mne.io.read_raw_fif(vv_erm_fname, verbose='error')\nraw_erms['vv'].load_data().resample(new_sfreq)\nraw_erms['vv'].info['bads'] = ['MEG2233', 'MEG1842']\n\nraws['opm'] = mne.io.read_raw_fif(opm_fname)\nraws['opm'].load_data().resample(new_sfreq)\nraw_erms['opm'] = mne.io.read_raw_fif(opm_erm_fname)\nraw_erms['opm'].load_data().resample(new_sfreq)\n# Make sure our assumptions later hold\nassert raws['opm'].info['sfreq'] == raws['vv'].info['sfreq']"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Do some minimal artifact rejection just for VectorView data\n\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"titles = dict(vv='VectorView', opm='OPM')\nssp_ecg, _ = mne.preprocessing.compute_proj_ecg(\n raws['vv'], tmin=-0.1, tmax=0.1, n_grad=1, n_mag=1)\nraws['vv'].add_proj(ssp_ecg, remove_existing=True)\n# due to how compute_proj_eog works, it keeps the old projectors, so\n# the output contains both projector types (and also the original empty-room\n# projectors)\nssp_ecg_eog, _ = mne.preprocessing.compute_proj_eog(\n raws['vv'], n_grad=1, n_mag=1, ch_name='MEG0112')\nraws['vv'].add_proj(ssp_ecg_eog, remove_existing=True)\nraw_erms['vv'].add_proj(ssp_ecg_eog)\nfig = mne.viz.plot_projs_topomap(raws['vv'].info['projs'][-4:],\n info=raws['vv'].info)\nfig.suptitle(titles['vv'])\nfig.subplots_adjust(0.05, 0.05, 0.95, 0.85)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Explore data\n\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"kinds = ('vv', 'opm')\nn_fft = next_fast_len(int(round(4 * new_sfreq)))\nprint('Using n_fft=%d (%0.1f sec)' % (n_fft, n_fft / raws['vv'].info['sfreq']))\nfor kind in kinds:\n fig = raws[kind].plot_psd(n_fft=n_fft, proj=True)\n fig.suptitle(titles[kind])\n fig.subplots_adjust(0.1, 0.1, 0.95, 0.85)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Alignment and forward\n\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Here we use a reduced size source space (oct5) just for speed\nsrc = mne.setup_source_space(\n subject, 'oct5', add_dist=False, subjects_dir=subjects_dir)\n# This line removes source-to-source distances that we will not need.\n# We only do it here to save a bit of memory, in general this is not required.\ndel src[0]['dist'], src[1]['dist']\nbem = mne.read_bem_solution(bem_fname)\nfwd = dict()\ntrans = dict(vv=vv_trans_fname, opm=opm_trans_fname)\n# check alignment and generate forward\nwith mne.use_coil_def(opm_coil_def_fname):\n for kind in kinds:\n dig = True if kind == 'vv' else False\n fig = mne.viz.plot_alignment(\n raws[kind].info, trans=trans[kind], subject=subject,\n subjects_dir=subjects_dir, dig=dig, coord_frame='mri',\n surfaces=('head', 'white'))\n mne.viz.set_3d_view(figure=fig, azimuth=0, elevation=90,\n distance=0.6, focalpoint=(0., 0., 0.))\n fwd[kind] = mne.make_forward_solution(\n raws[kind].info, trans[kind], src, bem, eeg=False, verbose=True)\ndel trans, src, bem"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Compute and apply inverse to PSD estimated using multitaper + Welch.\nGroup into frequency bands, then normalize each source point and sensor\nindependently. This makes the value of each sensor point and source location\nin each frequency band the percentage of the PSD accounted for by that band.\n\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"freq_bands = dict(\n delta=(2, 4), theta=(5, 7), alpha=(8, 12), beta=(15, 29), gamma=(30, 45))\ntopos = dict(vv=dict(), opm=dict())\nstcs = dict(vv=dict(), opm=dict())\n\nsnr = 3.\nlambda2 = 1. / snr ** 2\nfor kind in kinds:\n noise_cov = mne.compute_raw_covariance(raw_erms[kind])\n inverse_operator = mne.minimum_norm.make_inverse_operator(\n raws[kind].info, forward=fwd[kind], noise_cov=noise_cov, verbose=True)\n stc_psd, sensor_psd = mne.minimum_norm.compute_source_psd(\n raws[kind], inverse_operator, lambda2=lambda2,\n n_fft=n_fft, dB=False, return_sensor=True, verbose=True)\n topo_norm = sensor_psd.data.sum(axis=1, keepdims=True)\n stc_norm = stc_psd.sum() # same operation on MNE object, sum across freqs\n # Normalize each source point by the total power across freqs\n for band, limits in freq_bands.items():\n data = sensor_psd.copy().crop(*limits).data.sum(axis=1, keepdims=True)\n topos[kind][band] = mne.EvokedArray(\n 100 * data / topo_norm, sensor_psd.info)\n stcs[kind][band] = \\\n 100 * stc_psd.copy().crop(*limits).sum() / stc_norm.data\n del inverse_operator\ndel fwd, raws, raw_erms"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now we can make some plots of each frequency band. Note that the OPM head\ncoverage is only over right motor cortex, so only localization\nof beta is likely to be worthwhile.\n\n## Theta\n\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def plot_band(kind, band):\n \"\"\"Plot activity within a frequency band on the subject's brain.\"\"\"\n title = \"%s %s\\n(%d-%d Hz)\" % ((titles[kind], band,) + freq_bands[band])\n topos[kind][band].plot_topomap(\n times=0., scalings=1., cbar_fmt='%0.1f', vmin=0, cmap='inferno',\n time_format=title)\n brain = stcs[kind][band].plot(\n subject=subject, subjects_dir=subjects_dir, views='cau', hemi='both',\n time_label=title, title=title, colormap='inferno',\n clim=dict(kind='percent', lims=(70, 85, 99)), smoothing_steps=10)\n brain.show_view(dict(azimuth=0, elevation=0), roll=0)\n return fig, brain\n\n\nfig_theta, brain_theta = plot_band('vv', 'theta')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Alpha\n\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"fig_alpha, brain_alpha = plot_band('vv', 'alpha')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Beta\nHere we also show OPM data, which shows a profile similar to the VectorView\ndata beneath the sensors.\n\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"fig_beta, brain_beta = plot_band('vv', 'beta')\nfig_beta_opm, brain_beta_opm = plot_band('opm', 'beta')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Gamma\n\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"fig_gamma, brain_gamma = plot_band('vv', 'gamma')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## References\n.. [1] Tadel F, Baillet S, Mosher JC, Pantazis D, Leahy RM.\n Brainstorm: A User-Friendly Application for MEG/EEG Analysis.\n Computational Intelligence and Neuroscience, vol. 2011, Article ID\n 879716, 13 pages, 2011. doi:10.1155/2011/879716\n\n"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.5"
}
},
"nbformat": 4,
"nbformat_minor": 0
} | bsd-3-clause |
napjon/ds-nd | p1-statistics/project.ipynb | 1 | 32267 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Overview"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In a Stroop task, participants are presented with a list of words, with each word displayed in a color of ink. The participant’s task is to say out loud the color of the ink in which the word is printed. The task has two conditions: a congruent words condition, and an incongruent words condition. In the congruent words condition, the words being displayed are color words whose names match the colors in which they are printed: for example RED, BLUE. In the incongruent words condition, the words displayed are color words whose names do not match the colors in which they are printed: for example PURPLE, ORANGE. In each case, we measure the time it takes to name the ink colors in equally-sized lists. Each participant will go through and record a time from each condition."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import pandas as pd\n",
"%matplotlib inline"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Congruent</th>\n",
" <th>Incongruent</th>\n",
" <th>diff</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>12.079</td>\n",
" <td>19.278</td>\n",
" <td>7.199</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>16.791</td>\n",
" <td>18.741</td>\n",
" <td>1.950</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>9.564</td>\n",
" <td>21.214</td>\n",
" <td>11.650</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>8.630</td>\n",
" <td>15.687</td>\n",
" <td>7.057</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>14.669</td>\n",
" <td>22.803</td>\n",
" <td>8.134</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>12.238</td>\n",
" <td>20.878</td>\n",
" <td>8.640</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>14.692</td>\n",
" <td>24.572</td>\n",
" <td>9.880</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>8.987</td>\n",
" <td>17.394</td>\n",
" <td>8.407</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>9.401</td>\n",
" <td>20.762</td>\n",
" <td>11.361</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>14.480</td>\n",
" <td>26.282</td>\n",
" <td>11.802</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>22.328</td>\n",
" <td>24.524</td>\n",
" <td>2.196</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>15.298</td>\n",
" <td>18.644</td>\n",
" <td>3.346</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12</th>\n",
" <td>15.073</td>\n",
" <td>17.510</td>\n",
" <td>2.437</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13</th>\n",
" <td>16.929</td>\n",
" <td>20.330</td>\n",
" <td>3.401</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14</th>\n",
" <td>18.200</td>\n",
" <td>35.255</td>\n",
" <td>17.055</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15</th>\n",
" <td>12.130</td>\n",
" <td>22.158</td>\n",
" <td>10.028</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16</th>\n",
" <td>18.495</td>\n",
" <td>25.139</td>\n",
" <td>6.644</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17</th>\n",
" <td>10.639</td>\n",
" <td>20.429</td>\n",
" <td>9.790</td>\n",
" </tr>\n",
" <tr>\n",
" <th>18</th>\n",
" <td>11.344</td>\n",
" <td>17.425</td>\n",
" <td>6.081</td>\n",
" </tr>\n",
" <tr>\n",
" <th>19</th>\n",
" <td>12.369</td>\n",
" <td>34.288</td>\n",
" <td>21.919</td>\n",
" </tr>\n",
" <tr>\n",
" <th>20</th>\n",
" <td>12.944</td>\n",
" <td>23.894</td>\n",
" <td>10.950</td>\n",
" </tr>\n",
" <tr>\n",
" <th>21</th>\n",
" <td>14.233</td>\n",
" <td>17.960</td>\n",
" <td>3.727</td>\n",
" </tr>\n",
" <tr>\n",
" <th>22</th>\n",
" <td>19.710</td>\n",
" <td>22.058</td>\n",
" <td>2.348</td>\n",
" </tr>\n",
" <tr>\n",
" <th>23</th>\n",
" <td>16.004</td>\n",
" <td>21.157</td>\n",
" <td>5.153</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Congruent Incongruent diff\n",
"0 12.079 19.278 7.199\n",
"1 16.791 18.741 1.950\n",
"2 9.564 21.214 11.650\n",
"3 8.630 15.687 7.057\n",
"4 14.669 22.803 8.134\n",
"5 12.238 20.878 8.640\n",
"6 14.692 24.572 9.880\n",
"7 8.987 17.394 8.407\n",
"8 9.401 20.762 11.361\n",
"9 14.480 26.282 11.802\n",
"10 22.328 24.524 2.196\n",
"11 15.298 18.644 3.346\n",
"12 15.073 17.510 2.437\n",
"13 16.929 20.330 3.401\n",
"14 18.200 35.255 17.055\n",
"15 12.130 22.158 10.028\n",
"16 18.495 25.139 6.644\n",
"17 10.639 20.429 9.790\n",
"18 11.344 17.425 6.081\n",
"19 12.369 34.288 21.919\n",
"20 12.944 23.894 10.950\n",
"21 14.233 17.960 3.727\n",
"22 19.710 22.058 2.348\n",
"23 16.004 21.157 5.153"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df = pd.read_csv('stroopdata.csv')\n",
"df['diff'] = df['Incongruent'] - df['Congruent']\n",
"df"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The experiment takes participants with two test, congruent task and incongruent task. Congruent task is word with agreeing text and font color, while incongruent is a different text and its font color. Both of the task require the participants to say it out loud the word that are being display, and press 'Finish' button to see which time do they take. The control group is the congruent task, while experiment group is ingconruent task.\n",
"\n",
"The independent variables is which makes differ between congruent task and incongruent task. ***That is words that are being displayed***. Participants are requested to say the font color of the words, which is the same for both control and experiment group. But while text displayed agree with color in congruent, incongruent is the other way around.\n",
"\n",
"***The dependent variables is time participants take to complete the task***. The time is depend on whether the text agree with the font color being displayed. We can see that from the data, on average, the time participants took for incongruent task is different than when they solve congruent task. We will use statistical test to test whether the time is significantly different."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"So what kind of paired data should we be asking? We know that in general Incongruent task take longer than Congruent task. So in Confidence Interval, we could be asking the interval in which Ingrouent takes more second than congruent, and in hypothesis we could be asking is whether the incongruent task results in significantly different than congruent task."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Our sample size is less than 30, and that would means that our sampling distribution won't be normal. We're faced with two conditions, using t-test or bootstrapping. In this case, We will be using t-test. And since this is an experiment (assumed random assignment), we can draw causation. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In the instructions, it doesn't stated anywhere how the participants are collected. There might be a convenience bias(only participants that know the experiment), location bias(city/country where the experiment performed ), or voluntarily bias. Assumed participants randomly sampled without any bias at all. The result of this experiment can be generalized to world population."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We design the hypothesis test as follows:\n",
"\n",
"\n",
"\n",
"H0: $ \\mu_\\mathbf{congruent} = \\mu_\\mathbf{incongruent}$ The time took for population to solve both congruent task and incongruent task is the same, on average\n",
"\n",
"HA:$\\mu_\\mathbf{congruent} \\neq \\mu_\\mathbf{incongruent}$ The time took for population to solve both congruent task and incongruent task is different, on average"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We're going to use **two-sided** t-statistics. This is an experiment where we have limited data and samples, and we want to test our hypothesis to the population parameters."
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Congruent</th>\n",
" <th>Incongruent</th>\n",
" <th>diff</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>count</th>\n",
" <td>24.000000</td>\n",
" <td>24.000000</td>\n",
" <td>24.000000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>mean</th>\n",
" <td>14.051125</td>\n",
" <td>22.015917</td>\n",
" <td>7.964792</td>\n",
" </tr>\n",
" <tr>\n",
" <th>std</th>\n",
" <td>3.559358</td>\n",
" <td>4.797057</td>\n",
" <td>4.864827</td>\n",
" </tr>\n",
" <tr>\n",
" <th>min</th>\n",
" <td>8.630000</td>\n",
" <td>15.687000</td>\n",
" <td>1.950000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>25%</th>\n",
" <td>11.895250</td>\n",
" <td>18.716750</td>\n",
" <td>3.645500</td>\n",
" </tr>\n",
" <tr>\n",
" <th>50%</th>\n",
" <td>14.356500</td>\n",
" <td>21.017500</td>\n",
" <td>7.666500</td>\n",
" </tr>\n",
" <tr>\n",
" <th>75%</th>\n",
" <td>16.200750</td>\n",
" <td>24.051500</td>\n",
" <td>10.258500</td>\n",
" </tr>\n",
" <tr>\n",
" <th>max</th>\n",
" <td>22.328000</td>\n",
" <td>35.255000</td>\n",
" <td>21.919000</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Congruent Incongruent diff\n",
"count 24.000000 24.000000 24.000000\n",
"mean 14.051125 22.015917 7.964792\n",
"std 3.559358 4.797057 4.864827\n",
"min 8.630000 15.687000 1.950000\n",
"25% 11.895250 18.716750 3.645500\n",
"50% 14.356500 21.017500 7.666500\n",
"75% 16.200750 24.051500 10.258500\n",
"max 22.328000 35.255000 21.919000"
]
},
"execution_count": 28,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df.describe()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The measure of tendency that will be used in this situation is mean, and measure of variability is standard deviation."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYEAAAEPCAYAAACk43iMAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAGQVJREFUeJzt3X+0XGV97/H3BxLIQQoxNxqowgXbIlppEyr+ICqD9eSk\n9jY1SZfe0taj3GVcbRc/ck9pvHa1Oba9FnCFa6/r6i0V5ahLWgWDxNZzcgSG2+hVBBJ+S9orqCgJ\n/iheIqmIfPvHfoZMDmdy9pzMnj0z+/Naa1b23mf2zCcnO/Od/Tz7ebYiAjMzq6Yjyg5gZmblcREw\nM6swFwEzswpzETAzqzAXATOzCnMRMDOrsMKLgKQjJe2UtC2tL5E0LWm3pO2SFhedwczMZteNM4GL\ngPuAxoCEdwHTEXEacGNaNzOzEhRaBCS9EHgj8GFAafMaYCItTwBvKjKDmZm1VvSZwP8ALgGebtq2\nLCL2puW9wLKCM5iZWQuFFQFJ/wl4NCJ2cuAs4CCRzVnheSvMzEqyoMDXPhtYI+mNwCLgOEkfB/ZK\nOiEi9kg6EXh0tp0luTiYmc1DRMz6xXs2hZ0JRMS7I+KkiDgV+M/ATRHxe8ANwGh62ihw/SFeo6ce\nmzdvLj2DMw1WLmdypk4/2tXNcQKNdJcCw5J2A69P62ZmVoIim4OeERG3ALek5R8Ab+jG+5qZ2aF5\nxHAbarVa2RGexZny68VczpSPMxVH82lD6gZJ0avZzMx6lSSiFzqGzcys97kImJlVmIuAmVmFuQiY\nmVWYi4CZWYW5CJiZVZiLgJlZhbkImJlVmIuAmVmFuQiYmVWYi4CZWYW5CJiZVZiLgJlZhbkImJlV\nmIuAmVmFuQiYmVWYi4CZWYW5CJiZVZiLgJlZhbkImJlVmIuAmVmFuQiYmVWYi4CZWYW5CJiZVZiL\ngJlZhbkImJlVWKFFQNIiSV+RtEvSPZLG0/ZxSQ9L2pkeq4vMYWbtm5qaYtWq9axatZ6pqamy41hB\nFBHFvoF0TEQ8IWkBsAO4CFgNPB4RVxxivyg6m5nNbmpqirVrR9m//zIAhoY2sXXrBCMjIyUns7lI\nIiKU9/kLigwDEBFPpMWjgIVA45M9d0gz664tW65MBWAUgP37s20uAoOn8D4BSUdI2gXsBbZHxK3p\nRxdIulPSVZIWF53DzMyerfAiEBFPR8Ry4IXAKyX9IvAh4FRgOfAIsKXoHGaW39jYBoaGNgETwARD\nQ5sYG9tQdiwrQOHNQQ0R8UNJNwOrI+KZD31JHwa2zbbP+Pj4M8u1Wo1arVZwSjMDGBkZYevWCbZs\nuRKAsTH3B/Sqer1OvV6f9/6FdgxLWgo8FRGPSRoCpoBLgTsiYk96zkbgrIg4b8a+7hg2M2tTux3D\nRTcHnQjcJOlO4FayPoF/BC6XdFfafg6wseAcVjJfbmjWmwq/RHS+fCYwOHy5oVn3tHsm4CJghVu1\naj3T02toXG4IEwwP38D27deVGctsIPVac5CZmfWwrl0dZNU1NraBHTtG2b8/W88uN5woN5SZAW4O\nsi6Zmppqutxwg/sDzAriPgEzswpzn4CZmeXmImBmVmEuAmZmFeYiYGZWYS4CZmYV5iJgZlZhLgJm\nZhXmImBmVmEuAmZmFeYiYGZWYS4CZmYV5iJgZlZhLgJmZhXmImBmVmEuAmZmFeYiYGZWYS4CZmYV\n5iJgZlZhLgJmZhXmImBmVmEuAmZmFeYiYGZWYS4CZmYV5iJgZlZhhRUBSYskfUXSLkn3SBpP25dI\nmpa0W9J2SYuLymBmZoemiCjuxaVjIuIJSQuAHcBFwHrgexFxuaRNwHMj4l2z7BtFZjMzG0SSiAjl\nfX6hzUER8URaPApYCASwBphI2yeANxWZwczMWiu0CEg6QtIuYC+wPSJuBZZFxN70lL3AsiIzmJlZ\nawuKfPGIeBpYLul4YKukl834eUhq2eYzPj7+zHKtVqNWqxWU1MysP9Xrder1+rz3L7RP4KA3kv4U\neAJ4B1CLiD2STgRujojTZ3m++wTMzNrUM30CkpY2rvyRNAQMA/cDNwCj6WmjwPVFZTAzs0Mr7ExA\n0hlkHb9HkhWbv4+Iv5S0BPgUcDLwEPDmiHhslv19JmBm1qZ2zwS61hzULhcBM7P29UxzkJmZ9T4X\nATOzCnMRMDOrsDmLgKQX5dlmZmb9J8+ZwHWzbPt0p4OYmVn3tRwxLOklwEuB4yWtA0Q2989xwKLu\nxDMzsyIdatqI04DfAI5PfzY8Tjbq18zM+tyc4wQknR0RX+pSnub39TgBM7M2dXywmKTnk33zP4UD\nZw4REefPN2SuYC4CZmZta7cI5JlF9LPA/wGmgafTNn86m5kNgDxnArsiYnmX8jS/r88EzMzaVMS0\nEZ+T9OuHkcnMzHpUnjOBfcAxwJPAT9LmiIjjCg3mMwEzs7Z1vE8gIo49vEhmZtar8kwbcYSk35P0\nZ2n9ZEmvKD6amZkVLU+fwAeBVwPnpfV9aZuZmfW5PJeIvjIiVkjaCRARP5C0sOBcZmbWBXnOBJ6U\ndGRjRdLzODBewMzM+lieIvABYCvwfEnvBb4I/FWhqczMrCty3WM4zSj6q2n1xoi4v9BU+BJRM7P5\n6PhgMUknAz8CtqXHj9I2s4EwNTXFqlXrWbVqPVNTU2XHMeuqPIPF7uHAXEGLgFOBByLiFwsN5jMB\n64KpqSnWrh1l//7LABga2sTWrROMjIyUnMxsfooYLPayGW9wJvCH88hm1nO2bLkyFYBRAPbvz7a5\nCFhVtH2j+Yi4A3hlAVnMzKzL5jwTkDTWtHoEcCbw7cISmXXR2NgGduwYZf/+bH1oaBNjYxPlhjLr\nojx9ApubVp8CHgKui4h/KzCX+wSsa6amptiy5UogKwpuCrJ+1tE7i6VBYpdHxFjLJxXERcDMrH0d\nvUQ0In4KrJSU+wXNzKx/5OkY3gV8Ns0kuj491uV5cUknSbpZ0r2S7pF0Ydo+LulhSTvTY/Xh/CXM\nrDs8pmLw5OkTuDotHvTEiHj7nC8unQCcEBG7JB0L3A68CXgz8HhEXHGIfd0cZNZDPKaiPxQxTuBt\n8w0TEXuAPWl5n6T7gRekH7uJyayPeEzFYMpziegHyM4CGh/aAfwQuC0iPpv3jSSdAqwAvgysBC6Q\n9FbgNmAsIh5rK7mZmR22PPcTWAS8GPg0WSFYDzwI/LKkcyPi4rleIDUFXQtclM4IPgT8efrxXwBb\ngP8yc7/x8fFnlmu1GrVaLUdcs8PjS0Zn5zEVvaler1Ov1+e9f54+ga8AKyPiqbS+ANgBvAa4OyJe\nMsf+C4HPAZ+PiPfP8vNTgG0RccaM7e4TsK5zu/ehuUC21iu/m46OE0gv+ADZ3cUeS+uLgVsj4jRJ\nOyNixSH2FTABfD8iNjZtPzEiHknLG4GzIuK8Gfu6CFjXrVq1nunpNTTavWGC4eEb2L79ujJjWY/r\npS8PHe8YBi4Hdkq6Ja2fA7xX0nOAL8yx70rgd4G7GrenBN4N/Lak5WT9Cw8C78wb2Mys1/Rzp3me\nq4OukvR54BVkH9rvjojvpB9fMse+O5h9LMLn2w1q1g1u97aqyTuLqIDvAo8BPy/pdcVFsqorc0DS\nyMgIW7dmTUDDwze4P8ByGRvbwNDQJrLW74n05WFD2bFyydMncBnwFuA+4KeN7RHxG4UGc59AJfVS\n26pZOwa5Y3g3cEZE/Phww7XDRaCa3DFrdng6fo9h4P8BR80/kpmZ9ao8VwftB3ZJuhFonA1ERFxY\nXCyrKnfMmnVXnuagt6XFxhNFVgQK/Z/p5qDq6pW2VbN+1PE+gfSiRwOnpdWvRcRP5pkvNxcBM7P2\ndXywmKQa2XVP30ibTpY0GhG3tN7LzMz6QZ7moDuA346IB9L6acDfRcSZhQbzmYCZWduKuDpoQaMA\nAETEbvJ1KJv1Jd89y6okz5nAR8kGiX2CrFP4d4AjIuL8QoP5TMBK4MFq1u+KGCy2CPhDssngAP4J\n+GDRg8dcBKwMHqxm/a6IWUSPBN4fEVvSGxwJHD3PfGZm1kPy9AncBAw1rR/D3FNIW8X1a7t6P08E\nZjYfeZqDdkXE8rm2dTyYm4P6Vr+3q3uwWjn8e++MIvoEvghcGBG3p/WXAx+IiFcfVtK5grkI9C23\nq1u7+v2LQy8pok/gYuBTkh5J6yeSTS1tZtYR/Xxnrn6X585iX5X0EuDFZPMHPdCNaSOsf3kSOLP+\nkXfuoLOBU8mKRgBExMcKDebmoL7m9l1rh5uDOqeIPoFPAC8CdnHwncUumG/IXMFcBMwqxV8cOqOI\nInA/8NJufyJXvQj4P4SZzUcRcwfdQ9YZbF3SODWenl7D9PQa1q4d7atr7W1u/TqOwgZPnjOBOrAc\nuJWD7yy2ptBgFT4T8CWWg83t31akIi4RHZ9/HKs6N2s9my+HtF6S5xLRehdyGAc+ML/3ve9z1FEX\n8+ST2fZ+vcRy5jfeHTtG/Y3XrMe0LAKS9nHgvsIzRUQcV0ykapr5gXnUUZewYsXfsnTpMsbG+vOD\n0994Z+dxFNZLWhaBiDi2m0GqbuYH5pNPwtKlnesHcLNM7xgZGWHr1ommf4/+LPI2GHyHsAooq1nG\n33hbGxkZOezfvwu7dUREFPYATgJuBu4lu9T0wrR9CTAN7Aa2A4tn2TeqZHJyMoaGlgVcHXB1DA0t\ni8nJyY689vDwuvS6kR5Xx/Dwuo689lwmJydjeHhdDA+v69jfx4o9Xqy/pc/O3J/TRZ8J/ATYGBG7\nJB0L3C5pGng7MB0Rl0vaBLwrPSprUJsIOvGN157N/S3WKYUWgYjYA+xJy/vS6OMXAGuAc9LTJoA6\nFS8CUNwHpptlzKyVXBPIdeSNpFOAW4CXAd+MiOem7QJ+0Fhven50K1sVuP14sHjAmbXS8bmDOiE1\nBd0C/EVEXC/pX5s/9CX9ICKWzNgnNm/e/Mx6rVajVqsVntWsX7iwG0C9Xqderz+z/p73vKe3ioCk\nhcDngM9HxPvTtq8BtYjYI+lE4OaIOH3Gfj4TMDNrUxETyB1OGAFXAfc1CkByAwcmxhkFri8yh5mZ\nza7QIgCsBH4XOFfSzvRYDVwKDEvaDbw+rduA8AyZZv2jax3D7XJzUH9yh6VZuXqyY3g+XAT6k6fB\nNitXT/UJmJlZb3MRsI4aG9vA0NAmsjGAE2lg2oayYxWqm30g7m+xTnNzkHVcla5f72YfiPtbLA/3\nCZh1UTf7QNzfYnm4T8DMzHLz/QTMDkM3J+fzRIBWBDcHmR2mbvaBVKm/xebHfQJmc/AHqQ0yFwGz\nQ/AVNjboXATMDsFX2Nig89VBZgXzgC0bJC4CXdRvHx79ljePwx3R3GhOmp5ew/T0GtauHR2Y341V\nVDt3pe/mI4s2OCYnJ2NoaFnA1QFXx9DQspicnCw7Vkv9lrcdk5OTMTy8LoaH17X9dxoeXpd+J5Ee\nV8fw8LqCkpq1L3125v6s9TiBLtmy5crUGZm1Re/fn23r1Q7JfsvbjpGRkYH4e5h1gouAWRs8YMsG\njYtAl/Tbh0e/5e2WkZERtm6daBpn4MtLrb/5EtEu6rdBSv2W18w8TsDMrNI8TsDMzHJzETAzqzAX\nATOzCnMRMDOrMBcBM7MKcxEowCDOuWNmg8mXiHaY56s3szJ5nEDJPF+9mZXJ4wTMzCy3QouApI9I\n2ivp7qZt45IelrQzPVYXmaHbDne+ejOzbiq0OUjSa4F9wMci4oy0bTPweERcMce+fdkcBJ5zx8zK\n03N9ApJOAbbNKAL7ImLLHPv1bREwMytLv/QJXCDpTklXSVpcUgYzs8orowh8CDgVWA48AhzyjMDM\nzIrT9ZvKRMSjjWVJHwa2tXru+Pj4M8u1Wo1arVZkNDOzvlOv16nX6/Pev4w+gRMj4pG0vBE4KyLO\nm2U/9wmYmbWp3T6BQs8EJF0DnAMslfQtYDNQk7QcCOBB4J1FZjAzs9Y8YtjMbID0y9VBZmbWA1wE\nzMwqzEXAzKzCXATMzCrMRcDMrMJcBMzMKsxFwMyswlwEzMwqzEXAzKzCXATMzCrMRcDMrMJcBMzM\nKsxFwMyswlwEzMwqzEXAzKzCXATMzCrMRcDMrMJcBMzMKsxFwMyswlwEzMwqzEXAzKzCXATMzCrM\nRcDMrMJcBMzMKsxFwMyswlwEzMwqzEXAzKzCXATMzCqs0CIg6SOS9kq6u2nbEknTknZL2i5pcZEZ\nzMystaLPBD4KrJ6x7V3AdEScBtyY1vtCvV4vO8KzOFN+vZjLmfJxpuIUWgQi4p+Af52xeQ0wkZYn\ngDcVmaGTevEf3Zny68VczpSPMxWnjD6BZRGxNy3vBZaVkMHMzCi5YzgiAogyM5iZVZmyz+EC30A6\nBdgWEWek9a8BtYjYI+lE4OaIOH2W/VwczMzmISKU97kLigzSwg3AKHBZ+vP62Z7Uzl/CzMzmp9Az\nAUnXAOcAS8na//8M+CzwKeBk4CHgzRHxWGEhzMyspcKbg8zMrHf13IhhSYslXSvpfkn3SXpVD2Ta\nKOkeSXdL+qSko0vK0XOD71pkel/697tT0mckHV92pqafjUl6WtKSXsgk6YL0u7pH0mXdzNQql6Tl\nkr4saaekr0o6q8uZTpJ0s6R70+/lwrS9tGP9EJlKO9ZbZWr6eb5jPSJ66kE2duD8tLwAOL7kPC8A\nvg4cndb/HhgtKctrgRXA3U3bLgf+OC1vAi7tgUzDwBFp+dJeyJS2nwRMAg8CS8rOBJwLTAML0/rz\neuSY2g6MpOVfI7t4o5uZTgCWp+VjgQeAl5R5rB8iU2nHeqtMaT33sd5TZwKpir42Ij4CEBFPRcQP\nS44FWTE6RtIC4Bjg22WEiB4cfDdbpoiYjoin0+pXgBeWnSm5AvjjbmZpaJHp94G/ioifpOd8t0dy\nPQ00vtEupsvHe0TsiYhdaXkfcD/Zl7HSjvUWmX62zGO9Vab049zHek8VAeBU4LuSPirpDkl/K+mY\nMgNFxLeBLcA3ge8Aj0XEF8rMNEOvD747H/jHskNI+k3g4Yi4q+wsTX4BeF1qeqlLennZgZKLgfdJ\n+ibwPuC/lRUkXWK+guwDtieO9RmZmpV2rDdnavdY77UisAA4E/hgRJwJ/IiS5xaS9FyybyCnkFXZ\nYyX9TpmZWonsPLBnevol/QnwZER8suQcxwDvBjY3by4pTrMFwHMj4lXAJWRXzfWCPwAujoiTgY3A\nR8oIIelY4Drgooh4vPlnZR3rKdO1KdO+pu2lHevNmcjO4to61nutCDxMVsG+mtavJSsKZXoD8GBE\nfD8ingI+A5xdcqZmeyWdAJAG3z1ach4AJL0NeCPQCwXz58iK+J2SHiQ7Zb9d0vNLTZUd758BSMf8\n05L+Q7mRAHhrRGxNy9cCr+h2AEkLyQrAxyOiMZao1GO9KdMnmjKVeqzPkqntY72nikBE7AG+Jem0\ntOkNwL0lRgL4BvAqSUOSlDLdV3KmZo3Bd3CIwXfdJGk12Tfb34yIfys7T0TcHRHLIuLUiDiV7MP3\nzIgou2BeD7weIB3zR0XE98uNBMB3JJ2Tll8P7O7mm6f/Z1cB90XE+5t+VNqx3ipTmcf6bJnmdax3\nqye7jR7vXwa+CtxJ9i2p1KuDUqZxsk6Xu8k6pBaWlOMasn6JJ4FvAW8HlgBfIPuPuh1YXHKm84F/\nJiueO9PjgyVl+nHj9zTj51+n+1cHPSsTsBD4eDqubiebTqUXjqmVwG3ALuD/Aiu6nOk1ZM0au5qO\nodVlHustMv1amcd6q0wznjPnse7BYmZmFdZTzUFmZtZdLgJmZhXmImBmVmEuAmZmFeYiYGZWYS4C\nZmYV5iJgA0XSCZL+TtK/SLpN0j9I+oWyc+Uh6RxJry47h1WLi4ANjDSCcitwU0T8fES8nGzys0Im\nGkuzynbSufTWlCRWAS4CNkjOJZvE68rGhoi4KyJ2pJt/3C3pLklvBpBUS7N3fjrdGOQTjf0kvTFt\nu03S/5S0LW0fl/RxSTuAj0kalfSBpv0+15hyQdIqSV+SdLukT0l6Ttr+UHqd21OeF6dZIN8JbEw3\nc3lN8b8uMxcBGywvI5t+4SCS1pNNR/JLZHM/va8xERmwnGz2xZcCL5J0tqRFwP8GVqeziaUcPGPl\n6cCvRsR5s2QIICQtBf4kPe9XUq7/2vSc76btHwL+KCIeSu95RUSsiIgd8/0lmLXDRcAGSas5UFYC\nn4zMo8AtwFnp+bdGxHcimz9lF9k9LU4Hvh4R30j7X8OB6XgDuCEifnyIHAJeRVZYviRpJ/BW4OSm\n53wm/XkH2ayPzfuadU2n2zTNynQv8Fstfjbzw7VRMJo/zH9K9n9iZjGZue8TTctPcfCXqUVNy9Mt\nzhaa37fxnmal8JmADYyIuAk4WtI7Gtsk/RLwGPAWSUdIeh7wOuBWZv/WHWT3an2RpP+Ytr2FA4Vh\n5j4PAcuVOYls7v0AvgyslPRzKcdzclyl9DjwM7n+smYd4iJgg2Yt8IZ0ieg9wH8HPgncRTY9+Y3A\nJalZaNa7U0U2L/wfAJOSbgP+P9C41/VB+0TEF8lu5n0f8NekPomI+B7wNuAaSXcCXwJePEve5tfb\nBqxNHcMr5/sLMGuHp5I2m4Wk50TEj9Ly/wJ2R8RflxzLrON8JmA2u3ekb+T3AscBf1N2ILMi+EzA\nzKzCfCZgZlZhLgJmZhXmImBmVmEuAmZmFeYiYGZWYS4CZmYV9u+QgGTqMa9vXAAAAABJRU5ErkJg\ngg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x109ba1d10>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"df.plot.scatter(x='Congruent',y='Incongruent');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The plot shown a moderaly weak correlation between congruent variable and incongruent variable."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXsAAAEACAYAAABS29YJAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAEBpJREFUeJzt3X+M5HV9x/HnizspP6SyrbpaFwPGYrXVAiq1EePYKkVK\n/BGNlmirNrEmVbFNa8Wft/+0tiYo2iamrWiwItWi+KOhLZA41P44QTwUAeE00AKyJ0ZXOU0NyLt/\nzNzdctzuzu7Od+b2Ps9HMrnvzHzn+37vlw+v/e5nvt+ZVBWSpEPbYdNuQJLUPcNekhpg2EtSAwx7\nSWqAYS9JDTDsJakBnYZ9kick2bHk9oMk53RZU5L0YJnUefZJDgPuBE6tqtsnUlSSBEx2Gue5wLcM\nekmavEmG/e8AH59gPUnS0ESmcZIczmAK50lVdXfnBSVJD7B1QnWeD1y7f9An8YN5JGkdqiprWX9S\n0zhnAxcf6Imq6vx27LGPAW4HquPbLczOPn5dPW7btm0i+2Iz3NwX7gv3xcq39eg87JMczeDN2U93\nXUuSdGCdT+NU1Y+Ah3ddR5K0PK+gPUj0er1pt3DQcF/s477Yx32xMRO7qOqAxZOaRP2ZmTkWF7cD\ncx1X2sns7JksLOzsuI6kliWhDtI3aCVJU2TYS1IDDHtJaoBhL0kNMOwlqQGGvSQ1wLCXpAYY9pLU\nAMNekhpg2EtSAwx7SWqAYS9JDTDsJakBhr0kNcCwl6QGGPaS1ADDXpIaYNhLUgMMe0lqgGEvSQ0w\n7CWpAZ2GfZJjk1yS5KYkNyZ5Rpf1JEkHtrXj7b8fuKyqXppkK3B0x/UkSQfQWdgneRjwrKp6FUBV\n3Qf8oKt6kqTldTmNcwJwd5KPJPlKkr9PclSH9SRJy+hyGmcrcArwhqq6Jsn5wLnAu5auND8/v3e5\n1+vR6/U6bEmSNp9+v0+/39/QNlJV4+lm/w0njwL+u6pOGN4/DTi3qs5ask51VX+pmZk5Fhe3A3Md\nV9rJ7OyZLCzs7LiOpJYloaqyltd0No1TVQvA7UlOHD70XOCGrupJkpbX9dk4bwQuSnI48C3gNR3X\nkyQdQKdhX1VfBZ7eZQ1J0uq8glaSGmDYS1IDDHtJaoBhL0kNMOwlqQGGvSQ1wLCXpAYY9pLUAMNe\nkhpg2EtSAwx7SWqAYS9JDTDsJakBhr0kNcCwl6QGGPaS1ADDXpIaYNhLUgMMe0lqgGEvSQ0w7CWp\nAYa9JDXAsJekBmztukCS24AfAj8F7q2qU7uuKUl6oM7DHiigV1Xfm0AtSdIBTGoaJxOqI0k6gEmE\nfQFXJvlyktdOoJ4kaT+TmMZ5ZlXdleQRwBVJvlFVX9zz5Pz8/N4Ve70evV5vAi1prZJD84+zqpp2\nC9Kq+v0+/X5/Q9vIJAd7km3A7qo6b3i/JlF/ZmaOxcXtwFzHlXYyO3smCws7O64zeYOwn9RYmVSt\nGPbalJJQVWs6Aut0GifJUUmOGS4fDZwOXN9lTUnSg3U9jTMLXDqcAtgKXFRVl3dcU5K0n07Dvqpu\nBU7qsoYkaXVeQStJDTDsJakBhr0kNcCwl6QGGPaS1ADDXpIaYNhLUgMMe0lqgGEvSQ0w7CWpAYa9\nJDXAsJekBhj2ktQAw16SGmDYS1IDDHtJaoBhL0kNMOwlqQGGvSQ1YNWwT/LkSTQiSerOKEf2H0xy\nTZI/TPKwzjuSJI3dqmFfVacBrwAeC3wlycVJTu+8M0nS2Iw0Z19VtwDvAN4CPBt4f5Kbk7yky+Yk\nSeMxypz9ryZ5H3AT8BvAWVX1ROA5wPtGeP2WJDuSfH7D3UqS1mXrCOt8ALgAeHtV/XjPg1X17STv\nGOH1bwJuBI5ZX4uSpI0aZRrnt4GL9gT98Ej9aICq+uhKL0wyB5wJfAjIBnuVJK3TKGF/JXDkkvtH\nAVeMuP33AW8G7l9jX5KkMRplGueIqtq9505V3ZPkqNVelOQs4DtVtSNJb7n15ufn9y73ej16vWVX\n1X4S/1iSWtDv9+n3+xvaRqpq5RWS/wTOqaprh/efBvx1Vf36Kq/7C+B3gfuAI4CfBT5VVb+3ZJ1a\nrf44zMzMsbi4HZjruNJOZmfPZGFhZ8d1BgZh3/3+G1Y7BGuFSYw/adySUFVrOtob5cj+j4BPJrlr\neP/RwMtXe1FVvQ1427CxZwN/ujToJUmTs2rYV9U1SZ4IPIHB4dbNVXXvOmp5CCVJUzLKkT3A04AT\nhuufMvwTYsUzcZaqqquAq9bRnyRpDFYN+yQfAx4HXAf8dMlTI4e9JGm6RjmyfyrwpIm8kypJ6sQo\n59l/ncGbspKkTWqUI/tHADcmuRr4yfCxqqoXdNeWJGmcRgn7+eG/xb6PPHBKR5I2kVFOvewnOR54\nfFVdObx6dtSzeCRJB4FRPuL4D4B/Av52+NAccGmXTUmSxmuUN2hfD5wG/BD2fpHJI7tsSpI0XqOE\n/U+qas8bsyTZinP2krSpjBL2VyV5O3BUkucxmNLxW6ckaRMZJezPBe4GrgdeB1zG4PtoJUmbxChn\n4/wU+LvhTZK0CY3y2Ti3HuDhqqrHddCPJKkDo5wv//Qly0cALwV+vpt2JEldWHXOvqq+u+R2R1Wd\nz+BLyCVJm8Qo0zhPZd+plocx+Gz7LV02JUkar1Gmcc5jX9jfB9wGvKyrhiRJ4zfK2Ti9CfQhSerQ\nKNM4f8KDr5jd++mXVfXesXclSRqrUb+p6unA5xiE/FnANcAtHfYlSRqjUcL+OOCUqroHIMk24LKq\nekWnnUmSxmaUj0t4JHDvkvv34qdeStKmMsqR/UeBq5N8msE0zouACzvtSpI0VqOcjfPnSf6VwWfa\nA7y6qnaMsvEkRwBXAT8zrHVJVc2vs1dJ0jqNMo0DcBRwT1W9H7gjyQmjvKiq/g94TlWdBJwEnJHk\n19bXqiRpvUb5WsJ54M8YfNQxwOHAx0YtUFU/XvK6hwD3r61FSdJGjXJk/2LghcCPAKrqTuCYUQsk\nOSzJdcAu4PKqumY9jUqS1m+UN2h/UlX3J4PrqJIcvZYCVXU/cFKShwGXJvnlqrphz/Pz8/N71+31\nevR6vbVsXpIOef1+n36/v6FtpGrlr5NN8mbg8cDpwLuB3wc+XlUfWHOx5J3Aj6vqvOH9Wq3+OMzM\nzLG4uB2Y67jSTmZnz2RhYWfHdQYGv4An9XXAh2KtMInxJ41bEqoqq6+5z4pH9hmkySeAXwLuAU4E\n3llVV4zY0MOB+6pqMcmRwPOAv1xLg5KkjRtlGueyqvoV4PJ1bP/RwIVJtjB4f+ATVXXZOrYjSdqA\nFcO+qirJtUlOraqr17rxqroeOGXd3UmSxmKUI/tnAK9M8j8Mz8hh8HvgKd21JUkap2XDPsljq+p/\ngd9i8G7Zmt4MkCQdPFY6sv8scHJV3ZbkU1X1kkk1JUkar1E/LuFxnXYhSerUqGEvSdrEVprGeUqS\ne4bLRy5ZhsEbtD/bYV+SpDFaNuyrasskG5EkdcdpHElqgGEvSQ0w7CWpAYa9JDXAsJekBhj2ktQA\nw16SGmDYS1IDDHtJaoBhL0kNMOwlqQGGvSQ1wLCXpAYY9pLUAMNekhpg2EtSAzoN+yTHJflCkhuS\nfD3JOV3WkyQd2EpfSzgO9wJ/XFXXJXkocG2SK6rqpo7rSpKW6PTIvqoWquq64fJu4CbgF7qsKUl6\nsInN2Sc5HjgZ+NKkakqSBrqexgFgOIVzCfCm4RH+XvPz83uXe70evV5vEi1J0qbR7/fp9/sb2kaq\najzdLFcgeQjwz8C/VNX5+z1XXdcHmJmZY3FxOzDXcaWdzM6eycLCzo7rDCQBut9/w2qHYK0wifEn\njVsSqipreU3XZ+MEuAC4cf+glyRNTtdz9s8EXgk8J8mO4e2MjmtKkvbT6Zx9Vf0HXrglSVNnEEtS\nAwx7SWqAYS9JDTDsJakBhr0kNcCwl6QGGPaS1ADDXpIaYNhLUgMMe0lqgGEvSQ0w7CWpAYa9JDXA\nsJekBhj2ktQAw16SGmDYS1IDDHtJaoBhL0kNMOwlqQGGvSQ1wLCXpAYY9pLUgE7DPsmHk+xKcn2X\ndSRJK+v6yP4jwBkd15AkraLTsK+qLwLf77KGJGl1ztlLUgO2TruB+fn5vcu9Xo9erze1XsZh165v\nkmTabahhkx5/VdV5jUPxZ1qLfr9Pv9/f0DbS9Q+V5Hjg81X15AM8V5PYqTMzcywubgfmOq60EzgR\nmNRAibU2WOdg+596HAbBOLn/VpML+0PrZ9qIJFTVmn4DOo0jSQ3o+tTLi4H/Ak5McnuS13RZT5J0\nYJ3O2VfV2V1uX5I0GqdxJKkBhr0kNcCwl6QGGPaS1ADDXpIaYNhLUgMMe0lqgGEvSQ0w7CWpAYa9\nJDXAsJekBhj2ktQAw16SGmDYS1IDDHtJaoBhL0kNMOwlqQGGvSQ1wLCXpAYY9pLUAMNekhpg2EtS\nAzoN+yRnJPlGkp1J3tJlLUnS8joL+yRbgL8BzgCeBJyd5Ild1dv8+tNuQAehfr8/7RYOIv1pN7Cp\ndXlkfyrwzaq6raruBf4ReGGH9Ta5/rQb0EHIsF+qP+0GNrUuw/4xwO1L7t8xfEySNGFbO9x2dbjt\nNdmyBY455tUkR3Za5/77d7N7d6clJGldUtVNJid5BjBfVWcM778VuL+q/mrJOgfNLwRJ2kyqKmtZ\nv8uw3wrcDPwm8G3gauDsqrqpk4KSpGV1No1TVfcleQPwb8AW4AKDXpKmo7Mje0nSwWNqV9B6wdU+\nSW5L8rUkO5JcPe1+JinJh5PsSnL9ksd+LskVSW5JcnmSY6fZ46Qssy/mk9wxHBs7kpwxzR4nJclx\nSb6Q5IYkX09yzvDx5sbGCvtiTWNjKkf2wwuubgaeC9wJXEPD8/lJbgWeWlXfm3Yvk5bkWcBu4KNV\n9eThY+8BvltV7xkeCMxU1bnT7HMSltkX24B7quq9U21uwpI8CnhUVV2X5KHAtcCLgNfQ2NhYYV+8\njDWMjWkd2XvB1YOt6Z31Q0VVfRH4/n4PvwC4cLh8IYOBfchbZl9Ag2Ojqhaq6rrh8m7gJgbX6TQ3\nNlbYF7CGsTGtsPeCqwcq4MokX07y2mk3cxCYrapdw+VdwOw0mzkIvDHJV5Nc0MK0xf6SHA+cDHyJ\nxsfGkn2xffjQyGNjWmHvu8IP9MyqOhl4PvD64Z/zAmowz9jyePkgcAJwEnAXcN5025ms4bTFp4A3\nVdU9S59rbWwM98UlDPbFbtY4NqYV9ncCxy25fxyDo/smVdVdw3/vBi5lMM3Vsl3DeUqSPBr4zpT7\nmZqq+k4NAR+iobGR5CEMgv4fquozw4ebHBtL9sXH9uyLtY6NaYX9l4FfTHJ8ksOBlwOfm1IvU5Xk\nqCTHDJePBk4Hrl/5VYe8zwGvGi6/CvjMCuse0oaBtseLaWRsJAlwAXBjVZ2/5KnmxsZy+2KtY2Nq\n59kneT5wPvsuuHr3VBqZsiQnMDiah8FFbhe1tC+SXAw8G3g4gznYdwGfBT4JPBa4DXhZVS1Oq8dJ\nOcC+2Ab0GPyZXsCtwOuWzFkfspKcBvw78DX2TdW8lcGV+E2NjWX2xduAs1nD2PCiKklqgF9LKEkN\nMOwlqQGGvSQ1wLCXpAYY9pLUAMNekhpg2EtSAwx7SWrA/wN5vR/EKkz3UQAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x109dc1ed0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"(df.Incongruent - df.Congruent).plot.hist();"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can see that is the difference is right skewed distribution. This makes sense, since congruent task is easier, there shouldn't be any participants that solve incongruent task shorter tha congruent task. And it should be the longer time it took for the participants at solving incongruent task, the less should be for the number of participants. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Hypothesis Testing"
]
},
{
"cell_type": "code",
"execution_count": 75,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[1] 8.020707 2.069000 -2.069000\n"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%R\n",
"\n",
"n = 24\n",
"mu = 7.964792\n",
"s = 4.864827\n",
"CL = 0.95\n",
"n = 24\n",
"# z = round(qnorm((1-CL)/2, lower.tail=F),digits=2)\n",
"SE = s/sqrt(n)\n",
"t = mu/SE\n",
"t_crit = round(qt((1-CL)/2,df=n-1),digits=3)\n",
"c(t,c(-t_crit,t_crit))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Since our t-statistics, 8.02 is higher than the t critical values, we can conclude that the data provides convincing evidence that the time participants took for incongruent task is significantly different than when they took congruent task."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Confidence Interval"
]
},
{
"cell_type": "code",
"execution_count": 55,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[1] 5.910216 10.019368\n"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%%R\n",
"\n",
"ME = t*SE\n",
"c(mu+ME,mu-ME)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"So we are 95% confident that participants on average, took incongruent task 5.91 to 10.02 seconds longer than congruent task. Since this is an experimental design, we can draw causation intead of correlation."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"> ***REFERENCES***:\n",
"> * http://napitupulu-jon.appspot.com/posts/paired-data-coursera-statistics.html\n",
"> * http://napitupulu-jon.appspot.com/posts/inference-means-anova.html\n",
"> * https://www.udacity.com/course/viewer#!/c-ud134-nd/l-4578095863/e-147019342/m-147300501"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.10"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
seyeunlee/AliceBob | notebooks/07_GitIntro.ipynb | 1 | 73045 | {
"metadata": {
"name": ""
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"source": [
"<style>\n",
"div.cell, div.text_cell_render{\n",
" max-width:750px;\n",
" margin-left:auto;\n",
" margin-right:auto;\n",
"}\n",
"\n",
".rendered_html\n",
"{\n",
" font-size: 140%;\n",
" }\n",
"\n",
".rendered_html li\n",
"{\n",
" line-height: 1.8;\n",
" }\n",
"\n",
".rendered_html h1, h2 {\n",
" text-align:center;\n",
" font-familly:\"Charis SIL\", serif;\n",
"}\n",
"</style>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<small><i>This notebook was put together by [Jake Vanderplas](http://www.vanderplas.com) for UW's [Astro 599](http://www.astro.washington.edu/users/vanderplas/Astr599_2014/) course. Source and license info is on [GitHub](https://github.com/jakevdp/2014_fall_ASTR599/).</i></small>"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Version control for fun and profit:\n",
"\n",
"## the tool you didn't know you needed\n",
"\n",
"#### Sources of this material:\n",
"\n",
"This tutorial is adapted from \n",
"[\"Version Control for Fun and Profit\"](http://nbviewer.ipython.org/urls/github.com/fperez/reprosw/raw/master/Version%2520Control.ipynb) by Fernando Perez\n",
"\n",
"For an excellent list of Git resources for scientists, see [Fernando's Page](http://www.fperez.org/py4science/git.html).\n",
"\n",
"Fernando's original notebook specifically mentions two references he drew from:\n",
"\n",
"- [\"Git for Scientists: A Tutorial\"](http://nyuccl.org/pages/GitTutorial) by John McDonnell \n",
"- Emanuele Olivetti's lecture notes and exercises from the G-Node summer school on [Advanced Scientific Programming in Python](https://python.g-node.org/wiki/schedule).\n",
"\n",
"Via Fernando, some of the images below are copied from the [Pro Git book](http://git-scm.com/book)\n",
"\n",
"Also see [J.R. Johansson](https://github.com/jrjohansson)'s [tutorial on version control](http://nbviewer.ipython.org/urls/raw.github.com/jrjohansson/scientific-python-lectures/master/Lecture-7-Revision-Control-Software.ipynb), part of his excellent series [Lectures on Scientific Computing with Python](https://github.com/jrjohansson/scientific-python-lectures)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## What is Version Control?\n",
"\n",
"#### From Wikipedia:\n",
"\u201cRevision control, also known as version control, source control\n",
"or software configuration management (SCM), is the\n",
"**management of changes to documents, programs, and other information stored as computer files.**\u201d\n",
"\n",
"#### Reproducibility?\n",
"\n",
"* Tracking and recreating every step of your work\n",
"* In the software world: it's called *Version Control*!\n",
"\n",
"What do (good) version control tools give you?\n",
"\n",
"* Peace of mind (backups)\n",
"* Freedom (exploratory branching)\n",
"* Collaboration (synchronization)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Git is an enabling technology: Use version control for everything\n",
"* Paper writing (never get ``paper_v5_jake_final_oct22_9.tex``\n",
" by email again!)\n",
"* Grant writing\n",
"* Everyday research\n",
"* Teaching (never accept an emailed homework assignment again!)\n",
"* Code management\n",
"* Personal website history tracking"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## The plan for this tutorial\n",
"\n",
"- Overview of Git key concepts\n",
"\n",
"- Hands-on work with Git\n",
"\n",
"- 5 \"stages\" of using Git:\n",
" \n",
" 1. Local, single-user, linear workflow\n",
" 2. Single local user, branching\n",
" 3. Using remotes as a single user\n",
" 4. Remotes for collaborating in a small team\n",
" 5. Full-contact github: distributed collaboration with large teams"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## High level picture: overview of key concepts\n",
"\n",
"The **commit**: *a snapshot of work at a point in time*\n",
"\n",
"\n",
"\n",
"Credit: ProGit book, by Scott Chacon, CC License."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Looking at my current directory:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"!ls"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"00_intro.ipynb myfile.html\r\n",
"01_basic_training.ipynb myfile.py\r\n",
"02_advanced_data_structures.ipynb myfile.pyc\r\n",
"03_IPython_intro.ipynb mymodule.py\r\n",
"04_Functions_and_modules.ipynb mymodule.pyc\r\n",
"05_NumpyIntro.ipynb mymodule2.py\r\n",
"05_Trapezoid_Solution.ipynb mymodule2.pyc\r\n",
"06_Denoise_Solution.ipynb number_game.py\r\n",
"06_MatplotlibIntro.ipynb style.css\r\n",
"07_GitIntro.ipynb test.npy\r\n",
"README.txt test.npz\r\n",
"\u001b[34mimages\u001b[m\u001b[m test.out\r\n",
"modfun.py tmp.py~\r\n"
]
}
],
"prompt_number": 1
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"A **repository**: a group of *linked* commits\n",
"\n",
"\n",
"\n",
"Note: these form a Directed Acyclic Graph (DAG), with nodes identified by their *hash*."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"A **hash**: a fingerprint of the content of each commit *and its parent*"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import sha\n",
"\n",
"# Our first commit\n",
"data1 = 'This is the start of my paper2.'\n",
"meta1 = 'date: 1/1/12'\n",
"hash1 = sha.sha(data1 + meta1).hexdigest()\n",
"print 'Hash:', hash1"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Hash: 7bb695b77966e27cfaebfa59e27a0b91f1d33813\n"
]
}
],
"prompt_number": 2
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"# Our second commit, linked to the first\n",
"data2 = 'Some more text in my paper...'\n",
"meta2 = 'date: 1/2/12'\n",
"# Note we add the parent hash here!\n",
"hash2 = sha.sha(data2 + meta2 + hash1).hexdigest()\n",
"print 'Hash:', hash2"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Hash: 543da8bac9f643ba5611897b192a16dea42d2ab7\n"
]
}
],
"prompt_number": 3
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"And this is pretty much the essence of Git!"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## First: Configuring Git\n",
"The minimal amount of configuration for git to work without pestering you is to tell it who you are. All the commands here modify the ``.gitconfig`` file in your home\n",
"directory.\n",
"\n",
"Modify these before running them:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"git config --global user.name \"Jake Vanderplas\"\n",
"git config --global user.email \"[email protected]\""
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"prompt_number": 2
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Other settings\n",
"\n",
"Change how you will edit text files (it will often ask you to edit messages and other information, and thus wants to know how you like to edit your files):"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"# Put here your preferred editor. If this is not set, git will honor\n",
"# the $EDITOR environment variable\n",
"git config --global core.editor /usr/bin/nano # my preferred editor\n",
"\n",
"# On Windows Notepad will do in a pinch,\n",
"# I recommend Notepad++ as a free alternative\n",
"# On the mac, you can set nano or emacs as a basic option"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"prompt_number": 3
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"# And while we're at it, we also turn on the use of color, which is very useful\n",
"git config --global color.ui \"auto\""
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"prompt_number": 4
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Password memory\n",
"\n",
"Set git to use the credential memory cache so we don't have to retype passwords too frequently. On Linux, you should run the following (note that this requires git version 1.7.10 or newer):"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash \n",
"git config --global credential.helper cache\n",
"# Set the cache to timeout after 2 hours (setting is in seconds)\n",
"git config --global credential.helper 'cache --timeout=7200'"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"prompt_number": 6
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"Github offers in its help pages instructions on how to configure the credentials helper for [Mac OSX](https://help.github.com/articles/set-up-git#platform-mac) and [Windows](https://help.github.com/articles/set-up-git#platform-windows)."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Double-checking the result:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"!cat ~/.gitconfig"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"[user]\r\n",
"\tname = Jake Vanderplas\r\n",
"\temail = [email protected]\r\n",
"[core]\r\n",
"\teditor = /usr/bin/nano\r\n",
"[color]\r\n",
"\tui = auto\r\n",
"[credential]\r\n",
"\thelper = cache --timeout=7200\r\n"
]
}
],
"prompt_number": 7
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Stage 1: Local, single-user, linear workflow\n",
"Simply type `git` to see a full list of all the 'core' commands. We'll now go through most of these via small practical exercises:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"!git"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"usage: git [--version] [--exec-path[=<path>]] [--html-path] [--man-path] [--info-path]\r\n",
" [-p|--paginate|--no-pager] [--no-replace-objects] [--bare]\r\n",
" [--git-dir=<path>] [--work-tree=<path>] [--namespace=<name>]\r\n",
" [-c name=value] [--help]\r\n",
" <command> [<args>]\r\n",
"\r\n",
"The most commonly used git commands are:\r\n",
" add Add file contents to the index\r\n",
" bisect Find by binary search the change that introduced a bug\r\n",
" branch List, create, or delete branches\r\n",
" checkout Checkout a branch or paths to the working tree\r\n",
" clone Clone a repository into a new directory\r\n",
" commit Record changes to the repository\r\n",
" diff Show changes between commits, commit and working tree, etc\r\n",
" fetch Download objects and refs from another repository\r\n",
" grep Print lines matching a pattern\r\n",
" init Create an empty git repository or reinitialize an existing one\r\n",
" log Show commit logs\r\n",
" merge Join two or more development histories together\r\n",
" mv Move or rename a file, a directory, or a symlink\r\n",
" pull Fetch from and merge with another repository or a local branch\r\n",
" push Update remote refs along with associated objects\r\n",
" rebase Forward-port local commits to the updated upstream head\r\n",
" reset Reset current HEAD to the specified state\r\n",
" rm Remove files from the working tree and from the index\r\n",
" show Show various types of objects\r\n",
" status Show the working tree status\r\n",
" tag Create, list, delete or verify a tag object signed with GPG\r\n",
"\r\n",
"See 'git help <command>' for more information on a specific command.\r\n"
]
}
],
"prompt_number": 80
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### `git init`: create an empty repository"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"rm -rf test\n",
"git init test"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Initialized empty Git repository in /Users/jakevdp/Opensource/2013_fall_ASTR599/notebooks/test/.git/\n"
]
}
],
"prompt_number": 8
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"**Note:** all these cells below are meant to be run by you in a terminal where you change *once* to the `test` directory and continue working there.\n",
"\n",
"Since we are putting all of them here in a single notebook for the purposes of the tutorial, they will all be prepended with the first two lines:\n",
"\n",
" %%bash\n",
" cd test\n",
"\n",
"that tell IPython to do that each time. But you should ignore those two lines and type the rest of each cell yourself in your terminal."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Let's look at what git did:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"ls"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"prompt_number": 9
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"ls -la"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"total 12\n",
"drwxr-xr-x 3 fperez wavelet 4096 Feb 14 00:57 .\n",
"drwxr-xr-x 7 fperez wavelet 4096 Feb 14 00:57 ..\n",
"drwxr-xr-x 7 fperez wavelet 4096 Feb 14 00:57 .git\n"
]
}
],
"prompt_number": 40
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"ls -l .git"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"total 32\n",
"drwxr-xr-x 2 fperez wavelet 4096 Feb 14 00:57 branches\n",
"-rw-r--r-- 1 fperez wavelet 92 Feb 14 00:57 config\n",
"-rw-r--r-- 1 fperez wavelet 73 Feb 14 00:57 description\n",
"-rw-r--r-- 1 fperez wavelet 23 Feb 14 00:57 HEAD\n",
"drwxr-xr-x 2 fperez wavelet 4096 Feb 14 00:57 hooks\n",
"drwxr-xr-x 2 fperez wavelet 4096 Feb 14 00:57 info\n",
"drwxr-xr-x 4 fperez wavelet 4096 Feb 14 00:57 objects\n",
"drwxr-xr-x 4 fperez wavelet 4096 Feb 14 00:57 refs\n"
]
}
],
"prompt_number": 41
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Now let's edit our first file in the test directory with a text editor... I'm doing it programatically here for automation purposes, but you'd normally be editing by hand"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"echo \"My first bit of text\" > file1.txt"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"prompt_number": 11
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"ls -al"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"total 8\n",
"drwxrwxrwx 4 jakevdp staff 136 Sep 12 10:05 .\n",
"drwxr-xr-x 30 jakevdp staff 1020 Sep 12 10:03 ..\n",
"drwxrwxrwx 9 jakevdp staff 306 Sep 12 10:03 .git\n",
"-rw-rw-rw- 1 jakevdp staff 21 Sep 12 10:05 file1.txt\n"
]
}
],
"prompt_number": 13
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### `git add`: tell git about this new file"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"git add file1.txt"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"prompt_number": 14
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"We can now ask git about what happened with `status`:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"git status"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"# On branch master\n",
"#\n",
"# Initial commit\n",
"#\n",
"# Changes to be committed:\n",
"# (use \"git rm --cached <file>...\" to unstage)\n",
"#\n",
"#\tnew file: file1.txt\n",
"#\n"
]
}
],
"prompt_number": 15
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### `git commit`: permanently record our changes in git's database\n",
"For now, we are *always* going to call `git commit` either with the `-a` option *or* with specific filenames (`git commit file1 file2...`).\n",
"\n",
"This delays the discussion of an aspect of git called the *index* (often referred to also as the 'staging area') that we will cover later. Most everyday work in regular scientific practice doesn't require understanding the extra moving parts that the index involves, so on a first round we'll bypass it. Later on we will discuss how to use it to achieve more fine-grained control of what and how git records our actions."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"git commit -a -m\"This is our first commit\""
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"[master (root-commit) 609a459] This is our first commit\n",
" 1 file changed, 1 insertion(+)\n",
" create mode 100644 file1.txt\n"
]
}
],
"prompt_number": 16
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"In the commit above, we used the `-m` flag to specify a message at the command line.\n",
"\n",
"If we don't do that, git will open the editor we specified in our configuration above and require that we enter a message.\n",
"\n",
"By default, git refuses to record changes that don't have a message to go along with them (though you can obviously 'cheat' by using an empty or meaningless string: git only tries to facilitate best practices, it's not your nanny)."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### `git log`: what has been committed so far"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"git log"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"commit 609a45916899c56d1e3b8fe021b907f58845e75e\n",
"Author: Jake Vanderplas <[email protected]>\n",
"Date: Thu Sep 12 10:06:55 2013 -0700\n",
"\n",
" This is our first commit\n"
]
}
],
"prompt_number": 17
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### `git diff`: what have I changed?\n",
"Let's do a little bit more work... Again, in practice you'll be editing the files by hand, here we do it via shell commands for the sake of automation (and therefore the reproducibility of this tutorial!)"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"echo \"And now some more text...\" >> file1.txt"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"prompt_number": 18
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"And now we can ask git what is different:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"git diff"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"diff --git a/file1.txt b/file1.txt\n",
"index ce645c7..4baa979 100644\n",
"--- a/file1.txt\n",
"+++ b/file1.txt\n",
"@@ -1 +1,2 @@\n",
" My first bit of text\n",
"+And now some more text...\n"
]
}
],
"prompt_number": 19
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### The cycle of git virtue: work, commit, work, commit, ..."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"git commit -a -m\"I have made great progress on this critical matter.\""
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"[master 43ed8dd] I have made great progress on this critical matter.\n",
" 1 file changed, 1 insertion(+)\n"
]
}
],
"prompt_number": 20
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### `git log` revisited\n",
"First, let's see what the log shows us now:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"git log"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"commit 43ed8dd431bde1d511934526da8414113965178b\n",
"Author: Jake Vanderplas <[email protected]>\n",
"Date: Thu Sep 12 10:09:41 2013 -0700\n",
"\n",
" I have made great progress on this critical matter.\n",
"\n",
"commit 609a45916899c56d1e3b8fe021b907f58845e75e\n",
"Author: Jake Vanderplas <[email protected]>\n",
"Date: Thu Sep 12 10:06:55 2013 -0700\n",
"\n",
" This is our first commit\n"
]
}
],
"prompt_number": 21
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"Sometimes it's handy to see a very summarized version of the log:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"git log --oneline --topo-order --graph"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"* 2d29a7b I have made great progress on this critical matter!\n",
"* 679f246 This is our first commit\n"
]
}
],
"prompt_number": 51
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Defining an alias\n",
"\n",
"Git supports *aliases:* new names given to command combinations. Let's make this handy shortlog an alias, so we only have to type `git slog` and see this compact log:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"# We create our alias (this saves it in git's permanent configuration file):\n",
"git config --global alias.slog \"log --oneline --topo-order --graph\"\n",
"\n",
"# And now we can use it\n",
"git slog"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"* 43ed8dd I have made great progress on this critical matter.\n",
"* 609a459 This is our first commit\n"
]
}
],
"prompt_number": 22
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### `git mv` and `rm`: moving and removing files\n",
"While `git add` is used to add fils to the list git tracks, we must also tell it if we want their names to change or for it to stop tracking them. In familiar Unix fashion, the `mv` and `rm` git commands do precisely this:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"git mv file1.txt file-newname.txt\n",
"git status"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"# On branch master\n",
"# Changes to be committed:\n",
"# (use \"git reset HEAD <file>...\" to unstage)\n",
"#\n",
"#\trenamed: file1.txt -> file-newname.txt\n",
"#\n"
]
}
],
"prompt_number": 23
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"Note that these changes must be committed too, to become permanent! In git's world, until something hasn't been committed, it isn't permanently recorded anywhere."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"git commit -a -m\"I like this new name better\"\n",
"echo \"Let's look at the log again:\"\n",
"git slog"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"[master 110c1bb] I like this new name better\n",
" 1 file changed, 0 insertions(+), 0 deletions(-)\n",
" rename file1.txt => file-newname.txt (100%)\n",
"Let's look at the log again:\n",
"* 110c1bb I like this new name better\n",
"* 43ed8dd I have made great progress on this critical matter.\n",
"* 609a459 This is our first commit\n"
]
}
],
"prompt_number": 24
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"And `git rm` works in a similar fashion."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Exercise\n",
"Add a new file `file2.txt`, commit it, make some changes to it, commit them again, and then remove it (and don't forget to commit this last step!)."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## 2. Single Local user, branching\n",
"What is a branch? Simply a *label for the 'current' commit in a sequence of ongoing commits*:\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Mulitple Branches\n",
"There can be multiple branches alive at any point in time; the working directory is the state of a special pointer called HEAD. In this example there are two branches, *master* and *testing*, and *testing* is the currently active branch since it's what HEAD points to:\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Once new commits are made on a branch, HEAD and the branch label move with the new commits:\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"This allows the history of both branches to diverge:\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"But based on this graph structure, git can compute the necessary information to merge the divergent branches back and continue with a unified line of development:\n",
" \n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Branching Example\n",
"\n",
"Let's now illustrate all of this with a concrete example. Let's get our bearings first:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"git status\n",
"ls"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"# On branch master\n",
"nothing to commit, working directory clean\n",
"file-newname.txt\n"
]
}
],
"prompt_number": 25
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"We are now going to try two different routes of development: on the `master` branch we will add one file and on the `experiment` branch, which we will create, we will add a different one. We will then merge the experimental branch into `master`."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"git branch experiment\n",
"git checkout experiment"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stderr",
"text": [
"Switched to branch 'experiment'\n"
]
}
],
"prompt_number": 26
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"echo \"Some crazy idea\" > experiment.txt\n",
"git add experiment.txt\n",
"git commit -a -m\"Trying something new\"\n",
"git slog"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"[experiment 2ac278c] Trying something new\n",
" 1 file changed, 1 insertion(+)\n",
" create mode 100644 experiment.txt\n",
"* 2ac278c Trying something new\n",
"* 110c1bb I like this new name better\n",
"* 43ed8dd I have made great progress on this critical matter.\n",
"* 609a459 This is our first commit\n"
]
}
],
"prompt_number": 27
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"git checkout master\n",
"git slog"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"* 110c1bb I like this new name better\n",
"* 43ed8dd I have made great progress on this critical matter.\n",
"* 609a459 This is our first commit\n"
]
},
{
"output_type": "stream",
"stream": "stderr",
"text": [
"Switched to branch 'master'\n"
]
}
],
"prompt_number": 28
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"echo \"All the while, more work goes on in master...\" >> file-newname.txt\n",
"git commit -a -m\"The mainline keeps moving\"\n",
"git slog"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"[master 0c5002e] The mainline keeps moving\n",
" 1 file changed, 1 insertion(+)\n",
"* 0c5002e The mainline keeps moving\n",
"* 110c1bb I like this new name better\n",
"* 43ed8dd I have made great progress on this critical matter.\n",
"* 609a459 This is our first commit\n"
]
}
],
"prompt_number": 29
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"ls"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"file-newname.txt\n"
]
}
],
"prompt_number": 30
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"git merge experiment\n",
"git slog"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Merge made by the 'recursive' strategy.\n",
" experiment.txt | 1 +\n",
" 1 file changed, 1 insertion(+)\n",
" create mode 100644 experiment.txt\n",
"* 3471d04 Merge branch 'experiment'\n",
"|\\ \n",
"| * 2ac278c Trying something new\n",
"* | 0c5002e The mainline keeps moving\n",
"|/ \n",
"* 110c1bb I like this new name better\n",
"* 43ed8dd I have made great progress on this critical matter.\n",
"* 609a459 This is our first commit\n"
]
}
],
"prompt_number": 31
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## 3. Using remotes as a single user"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"We are now going to introduce the concept of a *remote repository*: a pointer to another copy of the repository that lives on a different location. This can be simply a different path on the filesystem or a server on the internet.\n",
"\n",
"For this discussion, we'll be using remotes hosted on the [GitHub.com](http://github.com) service, but you can equally use other services like [BitBucket](http://bitbucket.org) or [Gitorious](http://gitorious.org) as well as host your own.\n",
"\n",
"If you don't have a Github account, take a moment now to [sign up](https://github.com/)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### ``git remote``: view/modify remote repositories"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"ls\n",
"echo \"Let's see if we have any remote repositories here:\"\n",
"git remote -v"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"experiment.txt\n",
"file-newname.txt\n",
"Let's see if we have any remote repositories here:\n"
]
}
],
"prompt_number": 61
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"Since the above cell didn't produce any output after the `git remote -v` call, it means we have no remote repositories configured."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"#### Configuring a remote\n",
"Log into GitHub, go to the [new repository page](https://github.com/new) and make a repository called `test`.\n",
"\n",
"Do **not** check the box that says `Initialize this repository with a README`, since we already have an existing repository here. That option is useful when you're starting first at Github and don't have a repo made already on a local computer.\n",
"\n",
"We can now follow the instructions from the next page:"
]
},
{
"cell_type": "code",
"collapsed": true,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"git remote add origin https://github.com/jakevdp/test.git"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Process is terminated.\n"
]
}
],
"prompt_number": 32
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"Let's see the remote situation again:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"git remote -v"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"origin\thttps://github.com/fperez/test.git (fetch)\n",
"origin\thttps://github.com/fperez/test.git (push)\n"
]
}
],
"prompt_number": 67
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"#### Pushing changes to a remote repository\n",
"\n",
"Now push the ``master`` branch to the remote named ``origin``:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"git push origin master"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": []
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"We can now [see this repository publicly on github](https://github.com/fperez/test)."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Using Git to Sync Work\n",
"\n",
"Let's see how this can be useful for backup and syncing work between two different computers. I'll simulate a 2nd computer by working in a different directory..."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"\n",
"# Here I clone my 'test' repo but with a different name, test2, to simulate a 2nd computer\n",
"git clone https://github.com/jakevdp/test.git test2\n",
"cd test2\n",
"pwd\n",
"git remote -v"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Cloning into 'test2'...\n",
"Checking connectivity... done\n",
"/Users/jakevdp/Opensource/2013_fall_ASTR599/notebooks/test2\n",
"origin\thttps://github.com/jakevdp/test.git (fetch)\n",
"origin\thttps://github.com/jakevdp/test.git (push)\n"
]
}
],
"prompt_number": 34
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"Let's now make some changes in one 'computer' and synchronize them on the second."
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test2 # working on computer #2\n",
"\n",
"echo \"More new content on my experiment\" >> experiment.txt\n",
"git commit -a -m\"More work, on machine #2\""
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"[master 8852251] More work, on machine #2\n",
" 1 file changed, 1 insertion(+)\n"
]
}
],
"prompt_number": 35
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"Now we put this new work up on the github server so it's available from the internet"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test2\n",
"\n",
"git push origin master"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stderr",
"text": [
"Everything up-to-date\n"
]
}
],
"prompt_number": 39
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Now let's fetch that work from machine #1:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"git pull origin master"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Already up-to-date.\n"
]
},
{
"output_type": "stream",
"stream": "stderr",
"text": [
"From https://github.com/jakevdp/test\n",
" * branch master -> FETCH_HEAD\n"
]
}
],
"prompt_number": 38
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## An important aside: conflict management\n",
"While git is very good at merging, if two different branches modify the same file in the same location, it simply can't decide which change should prevail. At that point, human intervention is necessary to make the decision. Git will help you by marking the location in the file that has a problem, but it's up to you to resolve the conflict. Let's see how that works by intentionally creating a conflict.\n",
"\n",
"We start by creating a branch and making a change to our experiment file:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"git branch trouble\n",
"git checkout trouble\n",
"echo \"This is going to be a problem...\" >> experiment.txt\n",
"git commit -a -m\"Changes in the trouble branch\""
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"[trouble d46245e] Changes in the trouble branch\n",
" 1 file changed, 1 insertion(+)\n"
]
},
{
"output_type": "stream",
"stream": "stderr",
"text": [
"Switched to branch 'trouble'\n"
]
}
],
"prompt_number": 40
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"And now we go back to the master branch, where we change the *same* file:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"git checkout master\n",
"echo \"More work on the master branch...\" >> experiment.txt\n",
"git commit -a -m\"Mainline work\""
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"[master 387f3ef] Mainline work\n",
" 1 file changed, 1 insertion(+)\n"
]
},
{
"output_type": "stream",
"stream": "stderr",
"text": [
"Switched to branch 'master'\n"
]
}
],
"prompt_number": 41
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### The conflict...\n",
"\n",
"So now let's see what happens if we try to merge the `trouble` branch into `master`:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"git merge trouble"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Auto-merging experiment.txt\n",
"CONFLICT (content): Merge conflict in experiment.txt\n",
"Automatic merge failed; fix conflicts and then commit the result.\n"
]
}
],
"prompt_number": 42
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"Let's see what git has put into our file:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"cat experiment.txt"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Some crazy idea\n",
"More new content on my experiment\n",
"<<<<<<< HEAD\n",
"More work on the master branch...\n",
"=======\n",
"This is going to be a problem...\n",
">>>>>>> trouble\n"
]
}
],
"prompt_number": 43
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"At this point, we go into the file with a text editor, decide which changes to keep, and make a new commit that records our decision. I've now made the edits, in this case I decided that both pieces of text were useful, but integrated them with some changes:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"cat experiment.txt"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"Some crazy idea\n",
"More new content on my experiment\n",
"More work on the master branch...\n",
"This is going to be a problem...\n"
]
}
],
"prompt_number": 44
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"Let's then make our new commit:"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%%bash\n",
"cd test\n",
"\n",
"git commit -a -m\"Completed merge of trouble, fixing conflicts along the way\"\n",
"git slog"
],
"language": "python",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"[master 0213b88] Completed merge of trouble, fixing conflicts along the way\n",
"* 0213b88 Completed merge of trouble, fixing conflicts along the way\n",
"|\\ \n",
"| * d46245e Changes in the trouble branch\n",
"* | 387f3ef Mainline work\n",
"|/ \n",
"* 8852251 More work, on machine #2\n",
"* 3471d04 Merge branch 'experiment'\n",
"|\\ \n",
"| * 2ac278c Trying something new\n",
"* | 0c5002e The mainline keeps moving\n",
"|/ \n",
"* 110c1bb I like this new name better\n",
"* 43ed8dd I have made great progress on this critical matter.\n",
"* 609a459 This is our first commit\n"
]
}
],
"prompt_number": 45
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Merge Tools\n",
"\n",
"*Note:* While it's a good idea to understand the basics of fixing merge conflicts by hand, in some cases you may find the use of an automated tool useful.\n",
"\n",
"Git supports multiple [merge tools](https://www.kernel.org/pub/software/scm/git/docs/git-mergetool.html): a merge tool is a piece of software that conforms to a basic interface and knows how to merge two files into a new one. Since these are typically graphical tools, there are various to choose from for the different operating systems, and as long as they obey a basic command structure, git can work with any of them."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## 4. Collaborating on github with a small team\n",
"\n",
"Here we will set up a shared collaboration with one partner -- choose someone sitting next to you. \n",
"\n",
"We will have two people, let's call them Alice and Bob, sharing a repository. Alice will be the owner of the repo and she will give Bob write privileges. \n",
"\n",
"**Find a partner & decide who will be Alice, and who will be Bob.**\n",
"\n",
"<small><i>\n",
"Note for SVN users: this is similar to the classic SVN workflow, with the distinction that commit and push are separate steps. SVN, having no local repository, commits directly to the shared central resource, so to a first approximation you can think of `svn commit` as being synonymous with `git commit; git push`.</i></small>"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### 1. Synchronization\n",
"\n",
"We begin with a simple synchronization example. Working together, follow these steps:\n",
"\n",
"#### Creating a new repository\n",
"- Alice: create a new repository on github called ``AliceBob``\n",
"- Alice: create a file ``README.md``, commit it, and push it to the remote.\n",
"- Alice: on github, go to the settings for ``AliceBob``, and add your partner to the list of collaborators\n",
"\n",
"#### Cloning your partner's repository\n",
"- Bob: clone the ``AliceBob`` repository using ``git clone [url]``\n",
"- Bob: makes changes to the ``README.md`` file and commit locally.\n",
"- Bob: push changes to github.\n",
"- Alice: pull Bob's changes to the local repository.\n",
"\n",
"Now Alice and Bob should both have the same ``README.md`` file on their own computer."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### 2. Dealing with conflicts\n",
"\n",
"Next, we will have both parties make non-conflicting changes each, and commit them locally. Then both try to push their changes:\n",
"\n",
"- Alice: create & commit a new file, ``alice.txt`` to the local repo\n",
"- Bob: create & commit a new file, ``bob.txt`` to the local repo\n",
"- Alice: push the latest commit to github\n",
"- Bob: try to push to github. What happens?\n",
"\n",
"- Alice adds a new file, `alice.txt` to the repo and commits.\n",
"- Bob adds `bob.txt` and commits.\n",
"- Alice pushes to github.\n",
"- Bob tries to push to github. What happens here?\n",
"\n",
"The problem is that Bob's changes create a commit that conflicts with Alice's, so git refuses to apply them.\n",
"\n",
"Bob must do\n",
"\n",
" git pull origin master\n",
" \n",
"And then deal with the conflict manually, then push again."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## 5. Full-contact github: distributed collaboration with large teams\n",
"\n",
"On large teams, you don't always want all contributors to have access to the main repository. So how do you move forward? Using Pull Requests.\n",
"\n",
"Again, we'll do this as an exercise with your partner:"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"[Brief demo of how this works on scikit-learn]"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"We'll practice this here, by having Alice now *fork* Bob's repository.\n",
"\n",
"1. **Bob:** create a new repository named ``BobAlice`` with a ``README.md`` file, and push it to the github remote.\n",
"\n",
"2. **Alice:** go to Bob's github page and click the *fork* button. You now have your own remote version of the repository, that looks like ``http://github.com/Alice/BobAlice.git``\n",
"\n",
"3. **Alice:** use ``git clone [url]`` to get a local version of *your fork* on your own computer. \n",
"\n",
"4. **Alice:** use ``git remote add upstream [url]`` to add a pointer to Bob's remote (the original)\n",
"\n",
"5. **Alice:** type ``git remote -v``, and you should see both your own fork (called ``origin``) and Bob's fork (called ``upstream``)\n",
"\n",
"6. **Alice:** create a new branch called ``alice_changes``\n",
"\n",
"7. **Alice:** add a file called ``alice.txt`` commit, and use ``git push origin alice_changes`` to push to the remote.\n",
"\n",
"8. **Alice:** reload the github page for *your own* fork: there should now be a button that says \"compare and pull request\". Click it and fill it out.\n",
"\n",
"9. **Bob:** go to your own notifications page (the blue circle in the upper-left of GitHub) and you should see a notification of Alice's Pull request. Check the diff, add some comments, and merge the changes.\n",
"\n",
"10. **Alice:** on your computer, checkout the master branch, and update it from Bob's fork with ``git pull upstream master``\n",
"\n",
"Congratulations! You're now a collaborator!\n",
"\n",
"This is how virtually all open source collaboration proceeds on Github!"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Other useful commands\n",
"- [show](http://www.kernel.org/pub/software/scm/git/docs/git-show.html)\n",
"- [reflog](http://www.kernel.org/pub/software/scm/git/docs/git-reflog.html)\n",
"- [rebase](http://www.kernel.org/pub/software/scm/git/docs/git-rebase.html)\n",
"- [tag](http://www.kernel.org/pub/software/scm/git/docs/git-tag.html)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Git resources\n",
"### Introductory materials\n",
"There are lots of good tutorials and introductions for Git, which you\n",
"can easily find yourself; this is just a short list of things I've found\n",
"useful. For a beginner, I would recommend the following 'core' reading list, and\n",
"below I mention a few extra resources:\n",
"\n",
"1. The smallest, and in the style of this tuorial: [git - the simple guide](http://rogerdudler.github.com/git-guide)\n",
"contains 'just the basics'. Very quick read.\n",
"\n",
"1. The concise [Git Reference](http://gitref.org): compact but with\n",
" all the key ideas. If you only read one document, make it this one.\n",
"\n",
"1. In my own experience, the most useful resource was [Understanding Git\n",
"Conceptually](http://www.sbf5.com/~cduan/technical/git).\n",
"Git has a reputation for being hard to use, but I have found that with a\n",
"clear view of what is actually a *very simple* internal design, its\n",
"behavior is remarkably consistent, simple and comprehensible.\n",
"\n",
"1. For more detail, see the start of the excellent [Pro\n",
" Git](http://progit.org/book) online book, or similarly the early\n",
" parts of the [Git community book](http://book.git-scm.com). Pro\n",
" Git's chapters are very short and well illustrated; the community\n",
" book tends to have more detail and has nice screencasts at the end\n",
" of some sections.\n",
"\n",
"If you are really impatient and just want a quick start, this [visual git tutorial](http://www.ralfebert.de/blog/tools/visual_git_tutorial_1)\n",
"may be sufficient. It is nicely illustrated with diagrams that show what happens on the filesystem.\n",
"\n",
"For windows users, [an Illustrated Guide to Git on Windows](http://nathanj.github.com/gitguide/tour.html) is useful in that\n",
"it contains also some information about handling SSH (necessary to interface with git hosted on remote servers when collaborating) as well\n",
"as screenshots of the Windows interface.\n",
"\n",
"Cheat sheets\n",
": Two different\n",
" [cheat](http://zrusin.blogspot.com/2007/09/git-cheat-sheet.html)\n",
" [sheets](http://jan-krueger.net/development/git-cheat-sheet-extended-edition)\n",
" in PDF format that can be printed for frequent reference."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Beyond the basics\n",
"At some point, it will pay off to understand how git itself is *built*. These two documents, written in a similar spirit, \n",
"are probably the most useful descriptions of the Git architecture short of diving into the actual implementation. They walk you through\n",
"how you would go about building a version control system with a little story. By the end you realize that Git's model is almost\n",
"an inevitable outcome of the proposed constraints:\n",
"\n",
"* The [Git parable](http://tom.preston-werner.com/2009/05/19/the-git-parable.html) by Tom Preston-Werner.\n",
"* [Git foundations](http://matthew-brett.github.com/pydagogue/foundation.html) by Matthew Brett.\n",
"\n",
"[Git ready](http://www.gitready.com)\n",
": A great website of posts on specific git-related topics, organized\n",
" by difficulty.\n",
"\n",
"[QGit](http://sourceforge.net/projects/qgit/): an excellent Git GUI\n",
": Git ships by default with gitk and git-gui, a pair of Tk graphical\n",
" clients to browse a repo and to operate in it. I personally have\n",
" found [qgit](http://sourceforge.net/projects/qgit/) to be nicer and\n",
" easier to use. It is available on modern linux distros, and since it\n",
" is based on Qt, it should run on OSX and Windows.\n",
"\n",
"[Git Magic](http://www-cs-students.stanford.edu/~blynn/gitmagic/index.html)\n",
": Another book-size guide that has useful snippets.\n",
"\n",
"The [learning center](http://learn.github.com) at Github\n",
": Guides on a number of topics, some specific to github hosting but\n",
" much of it of general value.\n",
"\n",
"A [port](http://cworth.org/hgbook-git/tour) of the Hg book's beginning\n",
": The [Mercurial book](http://hgbook.red-bean.com) has a reputation\n",
" for clarity, so Carl Worth decided to\n",
" [port](http://cworth.org/hgbook-git/tour) its introductory chapter\n",
" to Git. It's a nicely written intro, which is possible in good\n",
" measure because of how similar the underlying models of Hg and Git\n",
" ultimately are.\n",
"\n",
"[Intermediate tips](http://andyjeffries.co.uk/articles/25-tips-for-intermediate-git-users)\n",
": A set of tips that contains some very valuable nuggets, once you're\n",
" past the basics."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### For SVN users\n",
"If you want a bit more background on why the model of version control\n",
"used by Git and Mercurial (known as distributed version control) is such\n",
"a good idea, I encourage you to read this very well written\n",
"[post](http://www.joelonsoftware.com/items/2010/03/17.html) by Joel\n",
"Spolsky on the topic. After that post, Joel created a very nice\n",
"Mercurial tutorial, whose [first page](http://hginit.com/00.html)\n",
"applies equally well to git and is a very good 're-education' for anyone\n",
"coming from an SVN (or similar) background.\n",
"\n",
"In practice, I think you are better off following Joel's advice and\n",
"understanding git on its own merits instead of trying to bang SVN\n",
"concepts into git shapes. But for the occasional translation from SVN to\n",
"Git of a specific idiom, the [Git - SVN Crash\n",
"Course](http://git-scm.org/course/svn.html) can be handy."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### A few useful tips for common tasks\n",
"#### Better shell support\n",
"\n",
"Adding git branch info to your bash prompt and tab completion for git commands and branches is extremely useful. I suggest you at least copy:\n",
"\n",
"- [git-completion.bash](https://github.com/git/git/blob/master/contrib/completion/git-completion.bash)\n",
"- [git-prompt.sh](https://github.com/git/git/blob/master/contrib/completion/git-prompt.sh)\n",
" \n",
"You can then source both of these files in your `~/.bashrc` and then set your prompt (I'll assume you named them as the originals but starting with a `.` at the front of the name):\n",
"\n",
" source $HOME/.git-completion.bash\n",
" source $HOME/.git-prompt.sh\n",
" PS1='[\\u@\\h \\W$(__git_ps1 \" (%s)\")]\\$ ' # adjust this to your prompt liking\n",
"\n",
"See the comments in both of those files for lots of extra functionality they offer."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"#### Embedding Git information in LaTeX documents\n",
"\n",
"(Sent by [Yaroslav Halchenko](http://www.onerussian.com))\n",
"su\n",
"I use a Make rule:\n",
"\n",
" # Helper if interested in providing proper version tag within the manuscript\n",
" revision.tex: ../misc/revision.tex.in ../.git/index\n",
" GITID=$$(git log -1 | grep -e '^commit' -e '^Date:' | sed -e 's/^[^ ]* *//g' | tr '\\n' ' '); \\\n",
" echo $$GITID; \\\n",
" sed -e \"s/GITID/$$GITID/g\" $< >| $@\n",
"\n",
"in the top level `Makefile.common` which is included in all\n",
"subdirectories which actually contain papers (hence all those\n",
"`../.git`). The `revision.tex.in` file is simply:\n",
"\n",
" % Embed GIT ID revision and date\n",
" \\def\\revision{GITID}\n",
"\n",
"The corresponding `paper.pdf` depends on `revision.tex` and includes the\n",
"line `\\input{revision}` to load up the actual revision mark."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"#### git export\n",
"\n",
"Git doesn't have a native export command, but this works just fine:\n",
"\n",
" git archive --prefix=fperez.org/ master | gzip > ~/tmp/source.tgz"
]
}
],
"metadata": {}
}
]
} | apache-2.0 |
obulpathi/datascience | scikit/boston/boston.ipynb | 1 | 97643 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"% matplotlib inline\n",
"\n",
"import numpy as np\n",
"import pandas as pd\n",
"import scipy.stats as stats\n",
"import matplotlib.pyplot as plt\n",
"import sklearn"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from sklearn import datasets\n",
"boston = datasets.load_boston()"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"['data', 'feature_names', 'DESCR', 'target']"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"boston.keys()"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"(506, 13)"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"boston.data.shape"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD',\n",
" 'TAX', 'PTRATIO', 'B', 'LSTAT'], \n",
" dtype='|S7')"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"boston.feature_names"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Boston House Prices dataset\n",
"\n",
"Notes\n",
"------\n",
"Data Set Characteristics: \n",
"\n",
" :Number of Instances: 506 \n",
"\n",
" :Number of Attributes: 13 numeric/categorical predictive\n",
" \n",
" :Median Value (attribute 14) is usually the target\n",
"\n",
" :Attribute Information (in order):\n",
" - CRIM per capita crime rate by town\n",
" - ZN proportion of residential land zoned for lots over 25,000 sq.ft.\n",
" - INDUS proportion of non-retail business acres per town\n",
" - CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)\n",
" - NOX nitric oxides concentration (parts per 10 million)\n",
" - RM average number of rooms per dwelling\n",
" - AGE proportion of owner-occupied units built prior to 1940\n",
" - DIS weighted distances to five Boston employment centres\n",
" - RAD index of accessibility to radial highways\n",
" - TAX full-value property-tax rate per $10,000\n",
" - PTRATIO pupil-teacher ratio by town\n",
" - B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town\n",
" - LSTAT % lower status of the population\n",
" - MEDV Median value of owner-occupied homes in $1000's\n",
"\n",
" :Missing Attribute Values: None\n",
"\n",
" :Creator: Harrison, D. and Rubinfeld, D.L.\n",
"\n",
"This is a copy of UCI ML housing dataset.\n",
"http://archive.ics.uci.edu/ml/datasets/Housing\n",
"\n",
"\n",
"This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.\n",
"\n",
"The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic\n",
"prices and the demand for clean air', J. Environ. Economics & Management,\n",
"vol.5, 81-102, 1978. Used in Belsley, Kuh & Welsch, 'Regression diagnostics\n",
"...', Wiley, 1980. N.B. Various transformations are used in the table on\n",
"pages 244-261 of the latter.\n",
"\n",
"The Boston house-price data has been used in many machine learning papers that address regression\n",
"problems. \n",
" \n",
"**References**\n",
"\n",
" - Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.\n",
" - Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.\n",
" - many more! (see http://archive.ics.uci.edu/ml/datasets/Housing)\n",
"\n"
]
}
],
"source": [
"print(boston.DESCR)"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"df = pd.DataFrame(boston.data)"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>0</th>\n",
" <th>1</th>\n",
" <th>2</th>\n",
" <th>3</th>\n",
" <th>4</th>\n",
" <th>5</th>\n",
" <th>6</th>\n",
" <th>7</th>\n",
" <th>8</th>\n",
" <th>9</th>\n",
" <th>10</th>\n",
" <th>11</th>\n",
" <th>12</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>0.00632</td>\n",
" <td>18</td>\n",
" <td>2.31</td>\n",
" <td>0</td>\n",
" <td>0.538</td>\n",
" <td>6.575</td>\n",
" <td>65.2</td>\n",
" <td>4.0900</td>\n",
" <td>1</td>\n",
" <td>296</td>\n",
" <td>15.3</td>\n",
" <td>396.90</td>\n",
" <td>4.98</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>0.02731</td>\n",
" <td>0</td>\n",
" <td>7.07</td>\n",
" <td>0</td>\n",
" <td>0.469</td>\n",
" <td>6.421</td>\n",
" <td>78.9</td>\n",
" <td>4.9671</td>\n",
" <td>2</td>\n",
" <td>242</td>\n",
" <td>17.8</td>\n",
" <td>396.90</td>\n",
" <td>9.14</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>0.02729</td>\n",
" <td>0</td>\n",
" <td>7.07</td>\n",
" <td>0</td>\n",
" <td>0.469</td>\n",
" <td>7.185</td>\n",
" <td>61.1</td>\n",
" <td>4.9671</td>\n",
" <td>2</td>\n",
" <td>242</td>\n",
" <td>17.8</td>\n",
" <td>392.83</td>\n",
" <td>4.03</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>0.03237</td>\n",
" <td>0</td>\n",
" <td>2.18</td>\n",
" <td>0</td>\n",
" <td>0.458</td>\n",
" <td>6.998</td>\n",
" <td>45.8</td>\n",
" <td>6.0622</td>\n",
" <td>3</td>\n",
" <td>222</td>\n",
" <td>18.7</td>\n",
" <td>394.63</td>\n",
" <td>2.94</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>0.06905</td>\n",
" <td>0</td>\n",
" <td>2.18</td>\n",
" <td>0</td>\n",
" <td>0.458</td>\n",
" <td>7.147</td>\n",
" <td>54.2</td>\n",
" <td>6.0622</td>\n",
" <td>3</td>\n",
" <td>222</td>\n",
" <td>18.7</td>\n",
" <td>396.90</td>\n",
" <td>5.33</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" 0 1 2 3 4 5 6 7 8 9 10 11 \\\n",
"0 0.00632 18 2.31 0 0.538 6.575 65.2 4.0900 1 296 15.3 396.90 \n",
"1 0.02731 0 7.07 0 0.469 6.421 78.9 4.9671 2 242 17.8 396.90 \n",
"2 0.02729 0 7.07 0 0.469 7.185 61.1 4.9671 2 242 17.8 392.83 \n",
"3 0.03237 0 2.18 0 0.458 6.998 45.8 6.0622 3 222 18.7 394.63 \n",
"4 0.06905 0 2.18 0 0.458 7.147 54.2 6.0622 3 222 18.7 396.90 \n",
"\n",
" 12 \n",
"0 4.98 \n",
"1 9.14 \n",
"2 4.03 \n",
"3 2.94 \n",
"4 5.33 "
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df.head()"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"df.columns = boston.feature_names"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>CRIM</th>\n",
" <th>ZN</th>\n",
" <th>INDUS</th>\n",
" <th>CHAS</th>\n",
" <th>NOX</th>\n",
" <th>RM</th>\n",
" <th>AGE</th>\n",
" <th>DIS</th>\n",
" <th>RAD</th>\n",
" <th>TAX</th>\n",
" <th>PTRATIO</th>\n",
" <th>B</th>\n",
" <th>LSTAT</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>0.00632</td>\n",
" <td>18</td>\n",
" <td>2.31</td>\n",
" <td>0</td>\n",
" <td>0.538</td>\n",
" <td>6.575</td>\n",
" <td>65.2</td>\n",
" <td>4.0900</td>\n",
" <td>1</td>\n",
" <td>296</td>\n",
" <td>15.3</td>\n",
" <td>396.90</td>\n",
" <td>4.98</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>0.02731</td>\n",
" <td>0</td>\n",
" <td>7.07</td>\n",
" <td>0</td>\n",
" <td>0.469</td>\n",
" <td>6.421</td>\n",
" <td>78.9</td>\n",
" <td>4.9671</td>\n",
" <td>2</td>\n",
" <td>242</td>\n",
" <td>17.8</td>\n",
" <td>396.90</td>\n",
" <td>9.14</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>0.02729</td>\n",
" <td>0</td>\n",
" <td>7.07</td>\n",
" <td>0</td>\n",
" <td>0.469</td>\n",
" <td>7.185</td>\n",
" <td>61.1</td>\n",
" <td>4.9671</td>\n",
" <td>2</td>\n",
" <td>242</td>\n",
" <td>17.8</td>\n",
" <td>392.83</td>\n",
" <td>4.03</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>0.03237</td>\n",
" <td>0</td>\n",
" <td>2.18</td>\n",
" <td>0</td>\n",
" <td>0.458</td>\n",
" <td>6.998</td>\n",
" <td>45.8</td>\n",
" <td>6.0622</td>\n",
" <td>3</td>\n",
" <td>222</td>\n",
" <td>18.7</td>\n",
" <td>394.63</td>\n",
" <td>2.94</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>0.06905</td>\n",
" <td>0</td>\n",
" <td>2.18</td>\n",
" <td>0</td>\n",
" <td>0.458</td>\n",
" <td>7.147</td>\n",
" <td>54.2</td>\n",
" <td>6.0622</td>\n",
" <td>3</td>\n",
" <td>222</td>\n",
" <td>18.7</td>\n",
" <td>396.90</td>\n",
" <td>5.33</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PTRATIO \\\n",
"0 0.00632 18 2.31 0 0.538 6.575 65.2 4.0900 1 296 15.3 \n",
"1 0.02731 0 7.07 0 0.469 6.421 78.9 4.9671 2 242 17.8 \n",
"2 0.02729 0 7.07 0 0.469 7.185 61.1 4.9671 2 242 17.8 \n",
"3 0.03237 0 2.18 0 0.458 6.998 45.8 6.0622 3 222 18.7 \n",
"4 0.06905 0 2.18 0 0.458 7.147 54.2 6.0622 3 222 18.7 \n",
"\n",
" B LSTAT \n",
"0 396.90 4.98 \n",
"1 396.90 9.14 \n",
"2 392.83 4.03 \n",
"3 394.63 2.94 \n",
"4 396.90 5.33 "
]
},
"execution_count": 13,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df.head()"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array([ 24. , 21.6, 34.7, 33.4, 36.2])"
]
},
"execution_count": 14,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"boston.target[:5]"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from sklearn import linear_model\n",
"lm = linear_model.LinearRegression()"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"X = df"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Important functions: fit(), predict() and score()\n",
"* model.fit(): Train the model\n",
"* model.predict(): Predect an outcome\n",
"* model.score: Calculate how well the predection is"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)"
]
},
"execution_count": 22,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"lm.fit(X, boston.target)"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"36.491103280361635"
]
},
"execution_count": 23,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"lm.intercept_"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"collapsed": false,
"scrolled": true
},
"outputs": [
{
"data": {
"text/plain": [
"array([ -1.07170557e-01, 4.63952195e-02, 2.08602395e-02,\n",
" 2.68856140e+00, -1.77957587e+01, 3.80475246e+00,\n",
" 7.51061703e-04, -1.47575880e+00, 3.05655038e-01,\n",
" -1.23293463e-02, -9.53463555e-01, 9.39251272e-03,\n",
" -5.25466633e-01])"
]
},
"execution_count": 25,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"lm.coef_"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>features</th>\n",
" <th>coeffecients</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>CRIM</td>\n",
" <td>-0.107171</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>ZN</td>\n",
" <td>0.046395</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>INDUS</td>\n",
" <td>0.020860</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>CHAS</td>\n",
" <td>2.688561</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>NOX</td>\n",
" <td>-17.795759</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>RM</td>\n",
" <td>3.804752</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>AGE</td>\n",
" <td>0.000751</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>DIS</td>\n",
" <td>-1.475759</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>RAD</td>\n",
" <td>0.305655</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>TAX</td>\n",
" <td>-0.012329</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>PTRATIO</td>\n",
" <td>-0.953464</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>B</td>\n",
" <td>0.009393</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12</th>\n",
" <td>LSTAT</td>\n",
" <td>-0.525467</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" features coeffecients\n",
"0 CRIM -0.107171\n",
"1 ZN 0.046395\n",
"2 INDUS 0.020860\n",
"3 CHAS 2.688561\n",
"4 NOX -17.795759\n",
"5 RM 3.804752\n",
"6 AGE 0.000751\n",
"7 DIS -1.475759\n",
"8 RAD 0.305655\n",
"9 TAX -0.012329\n",
"10 PTRATIO -0.953464\n",
"11 B 0.009393\n",
"12 LSTAT -0.525467"
]
},
"execution_count": 27,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"pd.DataFrame(zip(X.columns, lm.coef_), columns=['features', 'coeffecients'])"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.text.Text at 0x7f79397b2b50>"
]
},
"execution_count": 31,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX4AAAENCAYAAAAIbA6TAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnWeYU9XWgN/USU6mMAwzDL13QXovQ1NQmoiKAkpRLxYE\nC9wPUAFFuSJgQRC9XhEUKxYEwUIZeu8oSEcQld6mJ1nfj31mCFKcgQkBZr/PkyfJyS7r7CTr7LP2\n2muBRqPRaDQajUaj0Wg0Go1Go9FoNBqNRqPRaDQajUaj0Wg0Go3mBmUwsAxYDTwAlAWWAIuAiYAl\ndKJpNBqNJrdJAL41X3uAEcAMoKl57G2g09UXS6PRaDTWILV7C7AZ+AaYiboI1ELN9gHmAK2C1LdG\no9FoLoE9SO3GAsWAdkBplPIPNO2cAaKC1LdGo9FoLkGwFP8RYCvgBbYDqUCRgM8jgBNB6luj0Wg0\nlyBYpp4lQBvzdWHAAOYBzcxjbTlr9jmHMmXKCKAf+qEf+qEfOXvs5BrgFWAVsAZoDZQDElGePu9x\nca8euZ4ZNmxYqEW4bK5n2UW0/KFGyx9aUMo/WwTL1APw7wscSwhifxqNRqPJBsEy9Wg0Go3mGkUr\n/lwmISEh1CJcNtez7KDlDzVa/uuHa3H3rGmu0mg0Gk12sVgskE2drmf8Go1Gk8fQil+j0WjyGFrx\nazQaTR5DK36NRqPJY2jFr9FoNHkMrfg1Go0mj6EVv0aj0eQxtOLXaDSaPIZW/BqNRpPH0Ipfo9Fo\n8hha8Ws0Gk0eQyt+jUajyWNoxa/RaDR5DK34NRqNJo+hFb9Go9HkMbTi12g0mjyGVvwajUaTx9CK\nX6PRaPIYWvFrNBpNHkMrfo1Go8ljaMWv0Wg0eQyt+DUajSaPoRW/RqPR5DG04tdoNJo8hlb8Go1G\nk8fQil+j0WjyGPYgt78OOGm+3g2MAj4A/MAW4DFAgiyDRqPRaAIIpuJ3mc/NA459CwwBFgFvAx2B\nb4Iog0aj0Wj+RjBNPTcDBvADMA+oD9REKX2AOUCrIPav+Qf8fj9DhgynQIESxMWVZuzYN0It0iX5\n7rvvKFGiCvnyFeaee3px5syZHNXft28fDRveQlRUPDff3Jiff/45V+Tyer306/cM+fMXo1Chcvzv\nf5NzVD81NZUHHuhLdHQRihatxBdfTM8VuQA2b95M1aoNiYqKp3HjNuzfvz/bddevX0+lSnVwOPJj\ns0USHl6QiIh4IiLisNujsVjCKVCgNFu3bmXnzp3Urt2cqKh4atduzo4dO/6x/QkTJhEfX5aYmOIM\nGDCIHj0evuwx2LdvHzVrNsVuj8Rmi6ZChZq59v1qcsZNQB/zdTlgF3Ag4PMWwIcXqCeaq8Mrr4wV\nw6gjsFVgvRhGBfnww2mhFuuCbNiwQdzuWIEfBfZJWNg90rlz92zXT09PlxIlKonN9pLAAbFY3pGY\nmKJy8uTJK5btmWeGimE0F9gpsFIMo7jMnj072/V79nxEXK4OAnsEFophxMuyZcuuWK5jx45JdHRh\ngfcEDojNNkJKl64qXq/3H+seOnRIoqLiBVoI3CHQX6CxwOcCsQKJAnsFbhO3O1YKFiwtFstrAr+L\n1fqaxMeXluTk5Iu2P336l2IYpQXWCPwqNlttsdmqmG0m5mgM0tPTpXjxSgIvChwQeFsgVqKjC8uJ\nEyeyPV7XO1wjZnMnZ809AKuAjID3HYHxF6gX6vHLM9Ss2VzgBwExH1OkXbt7Qy3WBRk9erQ4HAMC\nZD0kbne+bNf/9ddfJTy8VEB9kcjIBpKYmHjFspUqdbPA6oC2X5PevR/Ndv3o6KICu7LqWyzPytCh\nz12xXHPnzpWoqKYBcvnFMIrK7t27/7HurFmzJDKytUBBgd8EagqsEHhe4NmANncLRIjHU/lvY1tV\n1q5de9H27767l8A7AXUWCtS6rDHYtm2bGEaJc/qHBuLxVMmV7/d6gRwo/mDa+HsB1VALuIWBCOBH\noBmwEGiLMgGdx/Dhw7NeJyQkkJCQEEQx8y758kUCe7LeW617KFAgKnQCXYLIyEjs9qVkZE0d9uDx\nZF/WyMhIMjKOAyeAfEAqXu9BoqKu/HwjIzPHsTYAdvseYmKy3254eCTHj+8BSgPgdO4hOrpGrsjl\n9f4OpAFhwHG83pOmvP9c1+8/AGSeW+Dz+oCSewALPt8R4AwQDpwhI+PQJcc2f/5IbLY9+HyB7Tiy\nPs/JGKjzPEngdwsH8fkycuX7vVZJTEwkMTEx1GKchx1lyllkPuqjTD6JwDLgPcBygXqhvnDmGdas\nWSMeTwGx2Z4Uu/0RiYqKl507d4ZarAty+vRpKVOmmrhcXcRiGSqGUSjHZqlHHnlSPJ5qAs+Lx9NA\nOna8V/x+/xXLtmDBAjGMAmK1DhKns7cUKFBMDh48mO3633zzjbjdcWK1DpawsPukaNHycuzYsSuW\ny+/3y+233yUeT2PznG+S/v0HZauuz+eTVq06iNNZWSC/wH0CEQKPChQQ6Czwb4EoadGirXTv/pB4\nPLXNfmpL9+4PXbL9vXv3SnR0YXE4Hhab7WkJC4sWpzNaLJZHxG6vJfnyxcmePXuyfa59+w4Qu72i\neTdSS2y2ItKhQ9dc+X6vF8jBjP9CijfUmOeguRps376dzz//ArvdRrdu3ShWrFioRboop0+fZvLk\nyRw9eoxbbmlNo0aNclRfRPjyyy/ZuHET5cuXo1u3blituePfsGnTJr75ZgaG4aZHjx4ULFgwR/VX\nrVrFnDnfExkZQa9evciXL1+uyOXz+fjoo4/YuXMXNWvWoFOnTlgs2fvbe71epk6dypIlSzl+/Dgg\nuN1uypYty88//8zhw0dp0+YWBg8eDMCnn37KL79spXLlSnTt2vUf+zl48CAfffQRaWnp3HlnZ9as\nWcNDDz2B338HDsdpoqLWs3HjcuLi4v5RVhFh+vTpfPbZZ2RkeOnc+Q569OiRa9/v9YA53tn6crXi\n12g0l2Tz5s00bXorfn8N/P4/qVw5ioULZ+Nyuf658t8QEb744gt++GEhxYrF8+STT2SZYxo3bsvS\npXcCDwJgtz9Bv35uxo17JTdP54YlJ4o/71wONRrNZdGr1xOcOPECp059x5kzq9m82cM777xzWW2N\nGPEyvXqN4P33yzNq1E5q1WpCUlISAIcOHQGqZJX1eqvw559Hc+MUNH9DK36NRnNJ9u//DWhqvrOS\nktKYXbt+y3E7fr+fUaNeJjn5R6A/6ekf8NdfBZk1axYA7dq1wu0eARwBdmIYr9O+vd7qEwy04tdo\nNJekXr26OBxvoiKtHMbjmUajRnVz3I7f78fnywDym0csiMSSkpICwH/+M4K77ipJWFgpPJ56DB3a\ni3vv7Zpbp6EJQNv4NRrNJTl69Cht2tzJpk3r8fszGDDgSUaPHpntReJA2rW7m3nzLKSmDgHWEhEx\nmF9+WUvRokVzX/A8hl7c1Wg0uYqIcPz4cVwuF4ZhXHY7SUlJPP74QObNW0ShQvFMmvQqNWpc+Z4F\njVb8Go0mh3z33XdMnfolkZEGgwb1p1y5cqEWSZNDtOLXaDTZ5sMPp9G372CSk4dgsfxJePjbbNiw\nnNKlS4daNE0O0Ipfo9Fkm9Klq7Nnzxgyg+VarQMZNCiMUaNGhlYwTY7QfvwajeYfSU5Opn37e9iz\n52egHTAMEPz+CNLS0kMsnSaYBDsDl0ajuUbp3///mDvXD5xCJcprBRzGMKbTrduc0AqnCSp6xq/R\n5FHmzVtMauq/ATcQDzxKgQI/MGvWZ9SqVQuAdevW0bhxW8qXr8NTTw0mPV3fCdwIaMWv0eRRCheO\nx2JZY74TnM41PPxwd5o3V9lS9+7dS7NmbVi6tDM7drzJpEnreeihJ0InsCbX0Iu7Gk0eZfPmzTRu\n3BqfrxkWyzHi4v5k7drFWZFB33rrLQYO3EBq6ntmjSOEhZUiNfX0FfUrInz00UcsW7aW8uVL8uij\njxAWFnaFZ6PJyeKutvFrNHmUqlWrsm3beubOnUtYWBi33347Ho8n6/OwsDCs1pMBNU5gtzuvuN/H\nHnuaqVMXkpR0H273PD77bCZLlvyA3a7V0dVCz/g1Gs0FOX78OJUr1+LIkXZ4vVUwjDcYPPgBnn32\n35fd5smTJ4mNLUJGxn4gGvARHl6DWbPG06xZs1yTPS+iZ/wajYZvv/2WGTN+IC4uP0899QSxsbE5\nqh8dHc2GDct55ZVxHDy4io4dn7/ioGnJycnYbC4yMjJTItqwWuOyQjNrrg56cVejuQEZP34i9977\nJO+/X54xY45QrVp9jh07luN2du3axfz5y1iyZBnz5i3NiqR5ucTHx1OxYkUcjgHAL1gsb2G3/0qD\nBg2uqF1NztCKX6O5AXn++ZEkJ08D9uL17uLwYRfvv/9+jtrYuXMnt9zSkY0bH+P33z9n2rQD9Oz5\n6BXJZbFYmDt3Bm3bHqFQoTuoV+9bli79iejo6CtqV5MztI1fo7kBcbvzkZpaBSgLdAWmkz//T8yZ\nM51atWphs9n+sY3x48czaNAWUlMzs20dx+ksRlramSBKrrlcdMgGjSaP06ZNW2An8D7QFniPY8es\nNGt2J02btiU1NfUf2zAMA6v1UMCRvwgLu/yQzIGcOnWKffv24fP5cqU9Tc7Qil+juQF58cWh2O0W\nIPPuWYAwUlOns369h1dfHfePbdx1110UKLANp7M3MBbDuJ0XXnjuimUbOfIVChQoTOXKDShd+iZ2\n7dp1xW1qcoY29Wg0NyB+v5+mTduydm0Uqan3AF8D+4AFwBTuvHMxQ4f258SJE9SoUSNr09bfOX78\nOG+++RZ//nmU225rSfv27a9IrgULFtCuXW+Sk5cChbFax1Klypds2rTsitrV6LDMGo0GSElJYdiw\nl5gy5QsOH45CZC4QhmF0pFSpI+zdexSbrSg2224WLJjNzTffHHSZxo0bx+DB+0hPf8M8koTdHkNG\nxj+bnjSXRtv4NRoNbreb0aNH8ssvy6hc2YLHUw23uwTly59izx4LSUlbOXVqMcePv8S99z50VWQq\nVaoUDsdiINMt9CcKFSqF1+vF6/VeFRk0WvFrNDc8MTExbNy4jLVrf+Dnn5dzxx1tSE1tDbjMErex\nb9/OqyJLx44dadu2Kh7PTURFtSYi4l9UqVIBl8uDy+WhT5/H9ILvVUDv3NVoQkBSUhLvvPMOBw78\nSfPmTa7Ydv5P2Gw2KlSoAED16tVxuweTlPQ0EIPVOpnKlYNv5gGwWq18/vkHrF69mqNHj7JgwRIm\nTFiBz3cYED79tCNlyoxjyJCBV0WevIq28Ws0V5nU1FRq127Grl1FSU2tjWG8z7PP/ovBg5+5Kv2L\nCE8/PYQJEybicOQnJsbFwoVzKFmy5FXpP5BGjW5j2bJHgMwL39c0azaZxMRvr7os1zvaxq/RXMPM\nmjWLffvcpKZOBwaTnDyP4cOH4ff7r0r/FouFceNGceDATjZs+IlduzaHROkDFCsWj822Juu9zbaa\n4sULhUSWvIQ29Wg0V5kzZ84gUoSzk7N4vN4MvF4vTueVhz3OLrGxsTkO3JbbvPrqCObPb0JKygbA\nj2FsYdSoJSGVKS8QbFNPHLAWaAn4gQ/M5y3AY5zdXRKINvVobmh+++03qlSpzZkzbwC1cTpfpnHj\no8yblzfNG8eOHeP777/HYrHQpk0bHbfnMrlW/PgdwOdAJaAj8CowBlgEvA38AHxzgXpa8WtueFau\nXMmDDz7JX3/9SbNmTfjf/8YTGRkZarE01zHXio3/VZSC/8N8XxOl9AHmAK2C2LdGc01Tr149Nm9e\nxqFDu/niiynXlNI/cOAAdeo0x+FwU6RIeRYsWBBqkTS5TLAUf0/gMPCj+d7CuVeiM0AUGo3mmkJE\naN26E+vXJ+D1HuLgwTdo3/5ufvvtt1CLpslFgrW42wtlv28FVAemAIGrSBHAiYtVHj58eNbrhIQE\nEhISgiGjRqP5GydOnGD37u34fM+j5mptsVqbsGLFCooXLx5q8TQBJCYmkpiYeFl1r4Yf/wKgL8r0\nMxZYCEwC5gFfXKC8tvFrNCEiPT2d8PBoMjJ+BkoCGYSH1+Sbb16nZcuWIZZOcymuFRt/IAI8DYwA\nlqHuNKZfpb41Gk02cTqdjB79CobRFKdzAB5PUxo1Kkfz5s2zVX/GjBmULVuD+Piy9Ov3DOnp6UGW\nWHM56J27Go3mPJYsWcLKlSspWrQoXbp0yVbGrhUrVtCyZSeSk6cCxXC7n6BXr2pMmDA2+AJrrhl3\nzstFK36N5jrk//5vKK+84gCGm0d+JTa2LYcO7Q6hVHmHa9HUo9FoLoNt27ZRq1YC0dFFaNy4zTXt\nXRMZGY7D8XvAkd/xeMJDJo/m4mjFr9Fco5w+fZomTW5l/fq7OHFiOStWNKZp07ZkZGSEWrTz8Pl8\nHD9+Gr//GyyWcsC/MIxujB07PNSiaS6AjtWj0YSQjIwMli1bRlpaGg0aNCAiIiLrsw0bNpCSEoXI\nemApPt/dHD2ayu7du7NCLF8rPPPMUN59dwk+33RgFw7Hk7z33iQ6d+4catE0FyA7iv8m1A7caJQ/\n/lZgVjCF0mjyAtOnT+eRR57i5EkvLldJPJ6/WLFiPiVKlADgyJEjJCXtArqhwl71JyXl6DkXh2uF\nyZOnkpy8GCgDNMPv38TevXtDLJXmYmTH1PMm0Bu1E/djlEumRqO5AsaMeZ377nuKI0ceJSOjCadP\np3LoUDf69j0bk3/hwqXAk8C/UXsi3yc8PIbChQuHSOqLY7c7UBvyFTbbmasaaVSTM7Jr499hPv8O\nnAqSLBpNnkBEeO6558nISAT+D/gUiMHvd7Bz556schkZPsAdUNNFamo6nTv3YM2aNVxLPPvsMxhG\nF+A9bLb/Izz8e+67775Qi6W5CNkx9RxD7bz1APdyiVALGs21xp49e5g06T2Sk1Pp1u0u6tevH2qR\n8Pv9ZGSkApkJRyxAEez2H6hXr2ZWud69u/P++7eSmloEZep5lLS0W/j667LMmdOauXNn0ahRo6t/\nAhdgwIB+FCpUkOnTZxMTE8WQIcsoVEgnVLlWyY7PZxQwGKgG/AK8jLoYBAvtx6/JFXbv3k2NGg05\nc6YHfn80hvEGX345hTZt2oRaNNq27cKCBS7S0p4DNgC9ufnmaixc+D1RUSp+4fbt26levS4pKRbU\nzP8eVMirMUAcTuefLFz4PWvXbuD119/DYrEwZEg/eva8P1SnpQkhOfHjzw5lgcx7tlGoAB7BRDSa\n3KBfv6fFah0sIObjK6levWmoxRIRkVOnTknXrr0lLq60VKxYR2bMmCF+v/+cMn36PCbwuEBpgfoC\n4wWKCfxhns/XEhFRUNzu8gKLBOaJYZSQ6dO/DNFZaUIJF05sdUGyY+OfCmQaHucA/7sMZa7RXHVO\nn07G748LOFKQpKTkkMkTSEREBB9++A6DB/enTp0a7NixC6/Xe06Z06eTgXJAMlAHeAFoBMSbJTpy\n+vQxUlJeAJoALUhOfpH//e+zq3cimuuS7Ch+AZabrxdls45GE3K6d78Tw3gVlRZiDYbRnwceuOuq\nyvDHH3/w+uuvM2bMGHbt2pV1XETo1Ok+hg79lg8/vJnnnvuB227rggSYOXv2vMuUfwgqmd0pYC5w\nyCwxC5Xo7nRAj4fxeAIXhLPHJ598StmyNSlWrAojRrx81RK/a65dZgMPA1WBPkCwE4OG+o5JcwPx\n+edfSPnytaVEiaoyfPhL4vP5rlrfe/fulejowhIW1lscjsckPDxW1q9fLyIiO3bsELe7kECqabZJ\nE6u1oFSt2kBee218ltln2rSPpVy5WhIdXVQKF64oTmesQJRATYGCAneIzRYpMFJgmHg8BbL6yC7f\nf/+9GEYRgXkCa8QwastLL43O9fHQBBdyYOrJDrHAGygzzzigQG42fgFCPX4aTa7Qp89jYrUODVhj\nmCgtW3YUEZHNmzeL01lSwG9+5hcoITBQPJ4aMmzYyKx2xo+fIDZbcYGvBd43Ff8rAn0FmstNN9WS\nRx8dII8//pRs2bIlx3L26PGwwJsBci6WChXq5to4aK4O5JKNv5j5nB+YCAwA3jHfazSaf+Cvv47h\n95cLOFKeo0eVN3SFChXw+08Cg4D1wPNABiAkJX3IhAnvZdV67rkx+HwfAJ1QG7n+BYxE/RXvZMeO\ngzRoUJvx48dSpUqVHMsZEWFgtf4VcOQPPB4jx+1orh8u5cf/FGrb4KQLfJa9rAwaTR6mS5e2zJ8/\niuTkuoAbw3iezp3bA+BwOIiPL8iBA5uAH4CKKMXuBDKwWs/OydSCdGBgtlWoC8BLAKSlVeb555+k\ne/dulyXn00/346OPGnLmTAp+fz4MYzz/+c+0y2pLc31wqRn/k+bzbJSiD3xoNJp/4P77u/Pcc73J\nl68VERH1ePjhJgwZMjDr86FDn8IwdqFm/bWAaUB+DONeBg7sl1WuePFYoCdqpt8ApfgDE6NEXVGm\nq9KlS7Nx4woGDXIzYMBpFiyYRevWrS+7Pc21T3ac/RcArQHvPxXMJUxzlUZz4/Pxx58ydeqXpKYm\nYbH4cTojuPfe9jzwQI/MDTmsW7eOunWb4vPFAc8BW1BW13FARQzjKQYOvIPhw4dmtXvw4EGSk5Mp\nVapUtrJnaa5/cjsD12agIMqX349aQGh4ucJlA634NTccKSkphIWFnWPCATh16hQtW3bg55+3I+Il\nIaEJM2Z8cl6As4iIOM6cWYry6weHox022yIyMiwUKVKYL76YQt26dfH7/XTp0oOZM7/DajUoUSKe\nJUu+Jy4uDs2NTW4r/pKcu1psAfbmVKgcoBW/5obh999/p23bu/jll7U4HGFMmPAmvXv3zPq8Tp2m\nrFmz0nzXFJfLypAhCTRv3oTXXnuXU6dO0rx5PV588VVSU7cARVDbadoBtwN/AAcxjGNs2LCcTz75\nhGHDvgYWo8JrPUmrVvv46aevr+Zpa0JAbodsKA/MQMXh/5yz3j7BIpQeURpNrlKrVjOx2Z4T8An8\nIoZRSFavXi0iIt99951YLEUE9glkCPxLoLHUr99CDCNWoKtAtEBDsVqjxOFoJDBfIE6go8BbAmkC\nncRqbSKjR4+WIkUqCLwW4Jq5WTyeQiEeBc3VgCCEbPgvyrwzBfjgstS5RnMD8OOPP1KjRjPKl6/D\nyJGvXHCHq4gwe/ZsXnvtNdatW4rPNwT1V6uE39+J5cvVRvhFi5Yi8hBQHOVg93/AFg4fPk5y8jMo\nb5+1wFL8/jX4/ZuIinoA5cbZELWX8g5U/MSTOJ1OfL50lD9G5pLcTFyunO/k1dzYZCcscxJnM259\nh3Lz1GjyHCtXrqRTp+6kpLwNxDNq1JN4vd5zFlUB+vYdwLRpc/F6WyDiQnnhNAW82GzrKFSoBQBF\nixbC5fqe1FQ/6sKwirAwJ4UKxbFr13RURM45wCNAWQyjFMnJe1DLblGov2JlYBUeD3Tt2pXffvuL\n11//EL+/EuoC8StPPvnvqzA6mhuNd4DHUCafHiizT03zEQxCfcek0VyQAQOeEXgxwIyyVooVq3JO\nmW3btonbHS9w0izzsYAhdntngfJitUbJI48MkIyMDElJSZEaNRpLeHhDcbu7iNsdIzNmzJDw8FiB\n5wW+EKgu8JzAInG7o80wD/4AGW6Wm26qLvv37xcRkbS0NOnW7UGx2Rxit4fJE088c17UT82NCbls\n6gkDaqNi8rdAxeLvZz40mjyD2+3Caj0G/IXaUHWMsLCwc8ocPnwYp7MEEGkeuRdw4/UuBJ7G79/I\nlClreeGF/+ByuVixYh4ffTSId9/tyLZt69i/fz9eb1tUhtMuwDfAqzidbejTpxvFixfC4RgEbMdi\neYOYmGMsWZJI0aJFSU5O5siRI0RGRlCkSAVuuqke99xzR5ZbqEZzLRPqC6dGc0Fmz54tFku4GSvH\nIw5Hfvnkk0/PKXPixAmJjIwX+EQgReA9gVgzxk7mLH2+VK3a+IJ9jB8/XlyuXgFl9wu4xOl8TNzu\nO6RIkbLSsmUHiYsrLfXqtZJt27aJ3++XgQOfFbvdLVarRyyWwuYi8Mfi8RSQX3/99WoMjybEkMtB\n2q42oR4/jeY8fD6fFCxYUuBDUyFvkLCwGNm5c+d5ZZcsWSIQLmAXKClQQeApgSFZF40iRSqK1+s9\nr+6BAwckKiperNZXBGaKxXKzwJ1ZFwKns4e8/PKoc+p88MEH4nKVElhleg89LnCXWf5RGTduXNDG\nRXPtQC6bejSaPM/hw4c5efI00N08cjNQh7Fjx54XLqFRo0a89NLzQDgqgV0P4G1gJmrX7Q6OHs3H\n6NGvZdXx+XwcOHCAfPnysWrVQjp02ESDBhPweP5AJWBRpKdX4tCho1nvly9fzsMP9yc1NQLl1/88\n0B+1oAw22yEMQwdc0+ScB4D7A57vBRoHsb9QXzg1mvNIS0sTlytSYKM5+z4hUEhcrjpSr14LSU9P\nzyq7bt06GTlypDgchQXSzfJtBD4PMOHMkvr1bxURFZu/WLGK4nYXFKfTI2PGvJ7VVs+ej4jLdYfA\nIYENYhjF5ccff8z6PC6upMAMs80jotI0DhSoKA7Hw1K4cFk5fvz41RsoTcggBzP+7Lhz3oPaArgM\nUGEGlZPwWs4GcrsQNpT/f3lToL5AGmofgB819XksJ8JqNKHC6XQyefJ/6dOnFcnJVYGdwH2kpo7m\n558bMXv2bDp27Mibb05k8OCRiFQjIyMMlSEL1I7bjYDKAGa1/kzBgjEAdOhwHwcO9EWkP/Abzz/f\nmOLFCzNv3hKSkpKpXTuJNWvK4nKF88orI7ICqKWnp3P48H6gvdlHDFAXp/Ntbr+9HZUrxzNgwHLy\n5ct3lUZJcyMxl7MmIStqV4mFs+kYL0ZHIDOoeDOUG+gMlEMzqHvfTheoF+oLp0ZzUbZs2SIWi01g\ngcAjAiXFYiksTz31lBw/flxsNrdAOYGyAvECg8wZeSkBQyyWOyUsrLtERcXL9u3bxefzidVqM3fg\nqruBsLCHxeWKMJO4TBTDKC6TJ0+5oDyFC5cV+NSs+4eEhRWRWbNmXeVR0VwLkMuT6HWAy3ztAlab\nr9dmo26Hz+NyAAAgAElEQVRmWMAHUDP9AwGfdQDeukCdUI+f5gYkLS3titvw+XwyatQYM01hvEA7\nge0C34nLVUCeeuppgSICKwXWC1QTiyW/WK2RAv8xj7cTi8WVpZznzJkjdnusQC2B/wkkicNRUazW\n9gFmoUVSosRNF5RpzZo1Eh1dWCIjq0hYWD4ZNuylKz5PzfUJuaz4+wC/Al+j4vX0RGV/fimb9T8A\nTqBCO/8ecLwF8OEFyod6/DQ3EOvXr5eiRSuIxWKV2NgSsnTp0stua8iQ4eJy1RL4SSCfwMEs5Wy3\nPyXly9cK8PoRge/EYskvhlEl4JgIlJX8+QtL27YdTe+fjwVmCxQXpzNOKlasKfBsQPmNUqhQ+YvK\nlZSUJBs2bJCDBw9e9rlprn/IZRv//1C7SMqiDJtHUTN5Xzb76IkK67yKs3cOABGoC8J5DB8+POt1\nQkICCQkJ2exKozlLSkoKrVq15+jRV4CuHD48mzZt7mDv3q3kz5/9DKKHDx/m6NGjjB37Fmlpi4BK\nQD5gP1AIAIdjPxERBhbLb5wNLrufSpXKsXPnXiAFtTyWBJzi2LGT/PjjRpTHzr1m+fcpUmQg06b9\nlyZNbiU5uRJQFMN4hgcfzPQmOh/DMLj55puzfT6aG4PExEQSExOD1n4NlD1+svl4P5v1eqB2+4La\nxrgbtT7QzDw2icyVrnMJ9YVTc4OwZcsWiYiocM5sOyqqgSxatCjbbTz77AvidEaK211SwCMwXcAr\n0EhU5MwRYrHcI0WKlJOVK1eKyxUt8ITAQAkLi5aVK1dKs2ZtRYVeeEmgvkB7sVjyC7Q3j2XK9624\nXIWlWrUmMmTIEKlbt5VUqlRfRo58RXw+XxBHSnMjQC7P+D8AxqOmN5YcND7drLsQ5drQH9iG8vRx\nAr+YZTSaoBAbG0t6+p+omPWFgOOkp++mYMGCl6wnIkyePIVJkz5g/fpdeL07gDhgIvAQyuopwCfA\n+4gsIiPDzZgxY/H73cBxIA2LxcaJEyeYP38Wt97ajsTEV3A4imCx7KBWrTosXVoUv/811N8wH/B/\npKY+wqZNjdiypQ8NGlTm668/oEKFCsEaIo3monx/lfsL9YVTcwMxYsQoMYziYhi9xOMpI/37//sf\n67z88mgxjMoC3QX6BszIk0Xtxq0kMNH02Mlnzv6jBBoKFBZ42iz/tnTp8oCIiKxcuVKKF68iYWGR\nUrt2gqxYsUIKFCgmLlcLsdnKmncA/w7o61OB6hIRESe7du0K8ihpbgTIwYw/O9GbJqEybq3PVMzA\njzlW59nHPAeNJndYvnw5W7ZsoXz58jRr1uyi5c6cOcPnn39Ov35Pk5z8MWoZazDKczkcdYPaC4fD\nSUZGASAVtRVlCcqSuQa1VaUG8BGwlO7ddzB69AhKlqxMenocEIvVWpqyZbewdOmPzJkzB4vFwtSp\nX/HTT7eiEqqD8oT+AZutKM89F82wYc8HY2g0NxA5ycCVHVOPC6hgPjIJpuLX5AFOnTrF0KEvsGnT\ndurUuYkXXng2aKEFGjRoQIMGDS5Z5sSJE9Ss2Zi//ipNcnIH1BLVV0AToDQuV0nCwvbz1VcziIuL\no2rVmihlXxQYCDRHpa3ogkqM8gY22xyeeGIejz32JOnpZVDey/vx+x9l714vXq+XHj16AFCmTBmW\nLu1AcvJp1H/3P8DXiMzE682uH4VGc+VkbjkMu8AjmAT9lujo0aOyatUq+eOPP4Lel+Z8MjIypFq1\nBhIW1kvgK3G57pZGjW4Jadz4l156WZzO7gGmls8FbhIYL253tEybNk2OHTsmImpPgMViP2fTFXQR\n+EDgV9P801qczroyYsTLki9fMVGhHjYKbBEYLBaLU86cOXOODCtXrpTq1RuK3V5YYKzAJPF4Csgv\nv/wSiiHRXGeQS378n5jPe4E9AY/dudH4JQjq4MycOUsMI0YiI2uIyxUtkyb9N6j9ac5n9erVEh5e\nSVQkSRHIEMMoIjt27AiZTP36PWVusspU5L+I3R4jt956p2zYsOG88qVK3SQqJ+5W03ffIxAhECZQ\nUNRO3WrSuPFtUrhwBYGqonbzlhQoKTabSzZt2nReu36/X15//S2pU6eVtG59R1Z+Xo3mnyCI4W9s\n/1zkignawJw5c0Y8nvwCy8w/9w5xuwvI7t27g9an5nxWrVol4eGV5WwmKa8YRlHZvn17UPo7cuSI\n9Or1qNSvf6v07z9ITpw4IbNnz5bPPvssa9PT7NmzxTBKCvwicEJcri7ywAN9z2nn+PHj8tBD/aR+\n/VulZcu2YrWWMJV5Y1EhHGyiwiH7TJfPu6Vy5drSuPEtAvcHHO8gcIuUK1cjKOeryZuQy4q/O2qH\nSU/gEMqgGUyCNjDbt2+X8PDSf/Prbn5OtENN8ElPT5fKleuI0/mwwCxxubpJvXotguKrnpqaKuXK\nVRen8zGBWRIW1kXCwwtJREQdiYjoJBERcbJ27VoREXnzzQkSHl5AHA63dO7cXZKSks6RuUqVuuJ0\nPmS2003s9mixWocIzBS3+1bJl6+4wHcBv6+vpEGDW6VmzeYCPwYc/0ygo9jtLlm6dGlI73Q0Nw7k\nsuJfjQr7Nxe10LsoNxu/AEEbGD3jv3Y4duyY9OzZV2rUaC6PPvqknD59Oij9LF68WCIiqgfcXbwu\n0CLAzDRVqlZteMk2/H6/zJkzRzye8ufcpYSFFZbIyMLicBSUihVrSs+eD4vT+UDAzL6hOJ3hUrJk\nZbHbe59zJwB1BKLEYskvNluUPP74M0E5f03egVxOxJJiPp9C+a9dDXNPUPB4PHz66VQ8nvZERtbE\n5arLa6+NolSpUqEWLc/x7ruT+fjjD9m2bSuzZs3hr7/+Cko/FosFEX/Akf2oMFGZP/1GHDx44PyK\nJidOnKBevRZ07NiNpKR9wCOoqOJCWloap071IyMjkd27a/Lrr7spWXIDdnscakPW76SnP87evRZs\ntm9xOEoChbFa5wLbgemIzMfnq8w773zI/Pnzc38ANJrLZDIqRk87YBgqfEMwCfqVMdOr588//wx6\nX5rzWbx4sRhGcVH5ZEUslnFSuXLdoPSVlpYmlSrVFqfzQYGvxOGoJ1ZrSVEB1rzicDwmt99+90Xr\n33NPL9Mk5RU4KVBToK84HF3Eai12zgK1xeISt7uwWK2dzQXeJ8zPUsViKSQff/yx/PDDD9Kp0z0C\nowNMP2vEYiksEydODMoYaPIG5HLIhl6o3StnUDtU/rw8fX7tkD9//hwF6dLkLuvWrcPna4fygQeR\nR9i2bRAikrkJJddwOp0sW/YTQ4e+wM8/T6ZevdbYbFZefbU0YKVGjXpMmfLFReuvXLmW9PTJqBvd\nSKAPcXGv0aBBTebOLURSUqa8uxARUlKWASVQYRuqoDZkVcZqLUJsbCytWrVi3ryFnBuh/CCQRpUq\nVXL13DWai5Gdf9nkv70XoHcQZMlqX/TO3Ruab7/9lvvue56kpOWoiJXfER/fnz/+2Bm0PkWEjIwM\nnE4noLJXpaamEhkZecl6LVt2JDGxEX7/IMCPy3U3Q4fWYtCgp6lTJ4Ht2+NJTa2P2/0uXm8qGRmB\nCr0+8AyQRHj4IPbtU1FBDxw4QJUqtTl1qjMQD4yha9dOfPLJ1OCcvCZPkJOdu9kp1Aal7K1ATaAw\nap96sNCK/wZHROjatTfffbcIu70cPt86Zs/+kiZNmgSlv48//pSHHnqU1NTTVKlSh65dO7J8+UaK\nFSvIsGH/d8mgbbt376Z+/RakpZXC7z9O+fKRLFnyA263m+TkZIYNG86vv+7klltaMHz4aI4e/Q/K\nCW4BFksHrFahWLEyfPXVFGrUqJHV7oEDB5gw4W1+//0P7r67M+3atQvKuWvyDjlR/JfDT8Fq2CR0\nRjLNVcPv98uKFStk1qxZQUkgMnbsGxIbW0qiooqIzRYl0EdU1qxwgYoCU8Vu7y/x8aVlxYoVcuTI\nERFR/vzR0cXFYgkXhyO/3H//g7J161apWbOhGEa0lC1bQ2bOnClbt26VwYOfF7c7XqKiWophFJAx\nY8ZKoUJlxGYLE7s9Iqv8kiVLRETE6/XKr7/+Kvv377+gzD6fT559doTExBSX2NhSMnr0uJDuZtZc\nX5DL7py3AreYj56ojNHBJNTjp7lOOHjwoPTo8bCUK1db2rbtInv37hURkQ8/nCaGUUFU+sOtAkUF\napuvXQJ/BSysthCHI0rsdpfcdde9ZprEHwR+E7hHIEas1gix23uZi9F3CrjF5SopFku4wHKB0wKr\nxe3OJ2lpaVK7doLY7Y+Z5adLeHisrF27VipWrCUeTwlxuWLk7rsfEK/Xe875jBnzuhhGLXMT2QYx\njIoyZcqHoRhazXUIuaz4P+BsEpa3gVq52fgFCPX4aa5xdu/eLeXKVRdwCLgFHhKrtZsUKFBMfvnl\nF4mLKyvQQGCwwDcCFQQWmp45YaZ3Tqbib2964FQyP3so4LNj5rF8AsUFmooKuXDE/PwZUclYXAIF\nxOnMJzt27BCbLczsS7UTHn631KjRWOz2p819AEliGE3k7bcnnXNetWu3FJWCMbP/D6Vt24t7HGk0\ngZDLfvw9gbHAHOBdspdkXaMJGm3b3sWuXV1RIZBXAp/h9+/jyJHjVKtWh0OHOgPRqJ/rm6hUz1+g\nPHO6A3cAC4BXgfkop7VngbbADs7+f/YABVBJ4w6hnNo6o8JVPYPKSjoYSAa+Jj09HYvFgtVq5Wx6\naT+wl/37f8frvR9lgjVITu7C6tWbzjmv6OhIs0+F1bqHmJioXBgxjeZcsrMQ8ARwH7ACaIj6B70a\nRJnMi5fmeiYlJQWv10tERESuten1evn444/p2bMPImmcnbfcDyQAJVFK/QFUjMHpwEso18l9qDnM\naVQKaQeQgfJong9UR+XDLYuKp18TdZP7H+A3YAzKmW0GylXzCfP5U2AZUBqbrQkxMQfIn78Ae/f+\nQWpqNwxjI1WqpOHxhLN4cQN8viFABm53R0aObI3XK/z3vx/jcrno06cLzz77Eqmp3bFY0jCMr1iz\nZjHlypXLtTHU3Ljk9uLuCs76+ztQ055gEuo7Js0V4PP5pG/fAeYCp1tatGifK+EYvF6vNG9+uxhG\nA3OBdnXW5igV+XKOuZnKIhAj0FIgVuA9gTUCt4jKe9tGIE6ghsB/zba2mG2lC1QRcJqmnx9FhVmO\nE6gsKt9urKhYO5nmmMECA0zzUUGBD8ViqS9gF6s1TCpWrClHjx6VvXv3SuHCZSUyso54PGWlWbPb\n5OWXXxGPp7rAEoGZYrVGS8eOd8qIESNk1KhRsm/fvlz4RjR5BXLZxr/ib++X5WbjFyDU46e5AiZN\nelcMo65pH0+XsLD7pHfvx6643VmzZkl4eE2BeQK3iUp12M60uXcybefjTaXdUMAQlToxU0GfMu31\n/zG9fLoKbDMVfwWBWaKiZtYz1w1uN9cQwk07/v3mc5zAooB2x5v1C5kXgHfMNo4LpIvLda/06fO4\niIgkJSXJ4sWLZe3ateLz+aR8+Tp/a2uc2GxlpHPnblc8Xpq8B7ls418KfAkMQN07L708fX79M2nS\nfylbtiZlytRg4sR3Qi3ONcmCBStITu6DsrE7SEt7gkWLzs4dUlNT6dt3AMWKVaF69aYsXbqUXbt2\n0azZ7RQtWokOHe7l8OHD57V75MgRvF4P0A2V7eoO4AecziPAd6g4goNQdvy/zOdVAS0cQ90Fv4zP\nF476ST+CMg9VA55ExR/cg7qx3QsUBIqb9eaYzxkoM886lIloGMoUlIwyCy0H+qBi9ThITT17/oZh\n0LhxY2rWrInVasXlcplynZXR52vLzJlfc/LkyRyMukYTHNqhVrNuvwp9hfrCeUGUi2BZc4a2WAyj\nnHzwwdRQi3XNMXToMAkL6yGZUSyt1rHSsmXHrM/btOkoVmtpgWYCD4rbnV9iYoqJ1fqqwGZxOAZI\nlSp1zwvRvG3bNrFY8gl8HzBD7meaZu4SFUOnsDlzF4E/TJNPHYGe5mcFRWXWijXrtjRn9O0FHjNn\n+i8KDBRoIsqM5BeVVD3KLPu0KC+fUqI8fWJFeRBFSFhYC/NO4d6A8x8jrVp1uuBYzZw5U5zOAgJj\nBIaadxObxOHwyIkTJ4L4LWluRMilZOsPXEwxA8HcW26ew7VFy5Z3MH9+V+Ae88iXNG06hYULvw2l\nWNccp06dom7d5hw86AaicDo3sXz5fMqVK8e2bduoVKkm8ApqJv0sVqvgdBqkpmbOzgW3uwhbty5n\n69atTJv2JWlpSaxdu57du/9AzbJrmmVfRs32k4EOKJ+D5ABpOqDy4EajAsu2R21DmYCK0ClmGZfZ\nbhIQi9qsfjPwuNnORtSdxnSUh09PlLdQBCoez0BgJhbLFETKAkeBeGy2SPLl28mKFQsoW7bsBcfr\n+++/5847HyAlpRQivXC7Z9K6dQQzZnxywfIazcXIrWTrlVD/DAtqD/rHVyzZdUxEhIFy6cvkL8LD\n3aES55olMjKSDRuWMnfuXNLT02nWrBkxMTEATJv2CfAo0M8sXRy/vwUiMYAX9XM8g8+XzKxZ3zFw\n4EukpLhRP8NML57ewH9RsQJHA3ejPHi+BvKjFH074A9UKonFwBGU+WUW4AEqmP1bUIp7PPAg0BLl\nAroN2AU8BDiBz8xyFVFmpvlm3VhgMyp47URElqI8n5sAc7BYerB48eqLKn2ANm3asGvXRgYNGsbO\nnd/QrFldRowYmrNB12iCxIKr2Feo75guyNq1a8XjKSDwnMAw8XgKyKpVq0It1hWzceNGmTx5ssyb\nNy/o4QGee26YWCxPBphqVovFkk8aNGgpbvdtAq+JYdSX7t0fkhIlqgp0FrWhyi/KY+ceUQnQbzbN\nK88KVDNNLy0E8ovKfVvKXNwNzKHbQpTHT5TZ7mGBFeb7GqK8c0oIDDHNQlHmYm4RgfKiwjifErUL\n2CWw0mx3n2mi+VWU589Pkult5HCES9Omt0utWi1kzJjXxefzyaJFi6RZs/ZSp04rmTTpvzokQ5BI\nS0uTr7/+WqZOnSq//fZbqMW5KhCEnLt5XvGLiGzevFkGDHhG+vd/5oKJsq833ntvsrjdBcXj6S4e\nTwXp0ePhoCqiHTt2SHh4rFgsowU+FYejtIwcOUrS0tJk3LjXpGHDFuJwuMVisZv2fKtpV3/DVKZf\nmoo+U5kPFKczWiyW/Ka9/g7T1p9g2ut/N8slmcrcIxaLR+Ljy4rLFSlOZz5TkWfG1N8tyisowqxf\n0LzwRAk0E4uloJQvX00slgIBMohAgtjtbcXhiBaH40GBLyUsLEFstgiBSQJzxDBqSZ8+fcUwCghM\nFpgphlFR3njjraCNd14lOTlZqldvJOHhDSU8/B4JD4+V5cuXh1qsoINW/Jp/Ii0tTcLCwkW5NIrA\nGfF4ysiyZcuC2u+WLVukS5f7pVWrzucsjs+fP18Mo5ioeDopAg8IdBHYac7gZ4pahA03FXx7c3Zf\nQNQiblWB/4ny1R9qzvaLigrOVtqclZc0FXqkWCxhYrXGinLhzFTgW8zPRwhMEBXUbbrAHoH7JDq6\nsPzwww9mv/PNOr8KhEuHDl1k586d8q9/9ZeEhA7StGlzsdkC725+FpergMBLAccWSZkyNYM63nmR\nN998U9zu9nI2TeanUqlScBL9XEuQS4lYAleXKge8F9ROXs11zIkTJ1D260x7twebrQoHDx4Mar9V\nqlThiy+mnHc8MXEhKSkPoOzoACOB2kAZlP29KyoRSkNUDP/lwE0om3xds/wbqAXascBXwGvACKAU\n6ic8zazbBpHiiLyLSiVdF/VX+B3l1vm8KUNJ1M7fpUBpKlf+E8MwcLniSE29B2Xj/x273cLEia9T\noEABJk16HYCXXnqZZcv+CDjDNCwWK2qt4uwxu/26zWR6zXLgwB+kpNTh7DpnXf76649LVdEEkIBy\nYUj426NZkPsN9YUzT+Dz+aRo0fJisUw0Z0bLxTAKyJ49ey67zT///FPmzJkj69aty1G9zZs3y6OP\nPiou1+0Bs7SZ5izeL07nneJ25xMoJ8pVMkrUZqw1AmdM80wBgWmidtuWE2WHd4my9RuiNmNVFegd\nMOMeb95BfCjKNl9W1KawszNyZd8fLQ5HpGzatEnS09PlppvqidN5n8B/xOVqLfXqNZf8+YuI1WqX\nIkXKy/r162Xv3r0SGVlQrNYXBaaKYZSXQYMGm+tEowUmi2EU19E3g8CsWbPEMMqIirCaIU7nw9Kh\nw72hFivoEARTz9Uk1OOXZ9i2bZuULFlFbDanhIfHyMyZMy+7rcTERAkPjzVj0xeXnj0fydZ6waBB\nz4nbXUgiI1uIxRIpLldjcbnuFzAkLOxWCQ9vJVFRhQXKmGagYQK3CtgFbObxYn8zoSw1TTuVTLNP\nb/PiUN8042SW6y3wQsD7laIWij8TmGteCMpIWFgB2bBhQ5bMJ0+elCef/LfccksXGThwsISHx4oK\nGeEX+EhiYopJSkqKbN++Xbp3f0huu+0emTr1IxFRi+ldu/aWdu3ula+//vqyx1tzaUaNelUcDrfY\nbE5p3PhWOXbsWKhFCjpcA4rfAXyI2gq5EuVAXRZYYh6byMX9TUM9fnmOpKSkK17UjYsraSo/ETgt\nHk9l+f777yUjI0POnDlzwTpr1qwRwygqZ8McLxGn05AJEybI3LlzZfz48fLII49IfHwxgcamMm8m\nyvvmJVGhG0qZdvnBAQr8R1EhFAyB/xN4yrTLu8w2EkWtHZQUFVo5s958iYgoKsWLVxWLJVqczjiJ\nji4sq1evFhGRM2fOnBdDf8GCBRIV1TigDZHw8LKydevWKxpPzZXj9XolJSUl1GJcNbgGFH9PYJz5\nOhq1p30G0NQ89jbQ6SJ1Qz1+mhzi9XrFYrFKYAx6t/sh6dixszgcbrHbXVK3bnM5fPjwOfW++OIL\niYzsFKA0z4jNFilNmtwu/fs/I2XKVBWXq5VYrd1Mk8wIU8n/Zpb3i4qLU8M8/oKoWDlFRbl9/jeg\n7RdELdZGBjyizBn+CwLvChSREiUqi4jIsWPHZNu2bZKSkiIHDx6UatUait3uEqfTkPHjJ2adw9at\nW8XtjhcVm0cEDkhYWGRWRi+N5mrBNaD4Pagg56CCqOwC9gd83gF46yJ1Qz1+mhyyZcsWsVqjBCaK\nco1cIA5HrDidhUwl7RWHo5/cemvnc+pt27ZN3O5YUZ5FXlGumncIfC4WSwdT2RcUFSCtsamcnaKi\naIoo75+Cojx3xpl3AsXkbNC0zDsQEfggQNnfKcq90yXK9/5BUV5EfaV16zvOkXH58uVSqFB5sVgG\nmee2SwyjmCxevDirzBNPDBKPp4x4PA+IYRSVUaPGXJVx12gC4RpQ/JlEoLY53svZzBSg9st/eJE6\noR4/TQ6pVStBlO29lKhNTzGmSSW/aVYRgf0SGRl/Tr3U1FQZP36ihIVFiNtd0FTWmXcNGaYSf9dU\n2PnMGXtjgV4CO0zzTmU5uyCcbCrzTgJvinLtXC8qPWIps60GpoyVRMXk6WjeITQUcMmkSWezYs2Z\nM0cMI85s80TWRcTheFJGjx59zrksXLhQ3nvvPVm5cuVVGXON5u+QS+6cV0oxlE/dBJQr6OiAzyKA\nExerOHz48KzXCQkJJCQkBEVATe7w22/7ULFs/MAW4HPOhlfoiIp1s5qCBQtn1Xn++RcZNeplLBY7\nVarcTJs2TXjllY8QyQwYa0X9PBuiInGuRWXH+hX4GZUPyA+U4+xykc183QQVZycZFXfHhnLRrAkM\nQYV8KAY8hYqOGYVKvrKHfv0GUb9+fW6++WaeeeYFkpP7ohKyLDfb8uJ0rqZw4b7njEHTpk1p2rQp\nGs3VIjExkcTExFCLcQ4Fga2owCaZfMtZV9BJwF0XqRvqC6cmh9x2213icAwwTSifBJhX5grkF6ez\nmoSHx2ZtDvvmm2/E46koKoKmT2y2x02zTqSonbLfi4qo2cg06zQSFQXzNbPdP0W5WTpELdoOMM06\nt5nlaph3BK1N01B+UQnUh4gK8xC4YStKIM18v1cgTIYMeVbOnDkjTmeMQC2BuqIWijuK3V5ZEhJu\nl4yMjBCPukZzLuRyPP7LYQhqGvU8atfvAlRS0xGoRC52VKhDzQ3ABx9MoHLlVVitP6Ju7nyo3+BX\nQAwNG+bnl1/W0qBBAwCWLl1BUlI3IB6w4vM9bbbUDrWpbBAqPWIN1Cz7DCqI202oWf4dqAjhR1Cz\n8feA/wPKo/wKDpt1q5qvPwO6oGLq/xUg+VGUA5rTfF8ccGCxCC+8MBK/vykq0NtK4Bkslnm8+GIP\n5s6dgd0ezJtljSa45Fp+xlzEvHhpridEhN27d1O2bHUgDqVMw4EY3nqrPY899lhW2YkTJ/LUU5+T\nllYcpYgjUKYUA2WOOQmEAT+aNRyouUIpVITUP1A7YDN3vd4F3Ab0Ql1wwoF0zkb0BOVE9oPZzoNA\nCdRu31Ooi0xTYBxW61giIw1On07F53uBs5FENxIRcTuHDu00E6hoNNcWOQnLHKwZvyaPYbFYKFOm\nDP/6V28cDgMV0rgN0dGbueuuc616nTp1wudbj1Lk/YHdKGX/JypzVT9UBiwDpaiTUL/nbaibSQNl\n7wd1d7EVdYOJWS8d9dPeGVBmF06nFXXHMAsVy78YdnsNHI7uWCz5yZfvPTweBydOvIXP9zrwPmoN\nwAuMITnZRvXqjTh9+nTuDJpGEyK04r/O+e677xg+fARTpkzB5/MFta9Tp06xb98+vF7vRctMmDCO\nESMeoFGjedx99wHWrVtKXFzcOWUSExNxuZqjLH9lgAOohdYXUUtBftRWj1TUbDwZFUPHAvwLFYOn\nGSq2f1OUyWY4akG3Dupn/SLKeWwAUA/DOITd7kbF5tmB8i4WvN5/4/Wm43LF4vMV5PTpVFSMni3A\nQdRyVSTwFz7fRvburcSYMa9d9hgGG7/fz4EDBzh27Ng/F9ZoriFCvERy/TBkyHD5//bOOzyqamvj\n71/JUuEAACAASURBVPSZM5NJSCGNkBBIaKEjIIQWwIBIUZAqHQQRkeiVoqJiuYKfgAWRe1ERRYqo\nCEQFQelF1KgowgUMNQqRlkB6Zt7vj30ymVDTYBLZv+fJk8lkn33W2ZOss89ae7/Laq1NjeYpWq1t\nGR9/7xUlC8uLmTNn02CwUlFCGBoaxYMHD5a6r6VLl9Ji6aYmVB+lqHFQkHD9nKLs4Ztqcrbgfae6\nrLJgbf4GNeHqTSHF3FtN9uooZJWnq207ENBTpwugkHl2uPU5jGIPQBSF5s+PaiLXn0AdAr8SWK0m\nh3eqx7zFIUMeLMeRLT9Onz7N+vVb0GKpSoPBxvHjE6Te/20EKtA6/tLg6fGrFKSlpdFgsBI4rTqk\nXNpsdYpsLCovtm/fTkWpTuAEAVKjeYO1azcrVV8HDx5kcHAURVEUX4qauHPdnPEWijX21SgkFQpW\n3BymEGazqDeEMIq9AkEs1NDXUacz02SqQrEu36p+JalO3E4h1+wk8DsBO3W6ULU4zP9Uhz+fYlVR\nM4q9CVS/TyZwhorShIsWvV/OI1w+xMf3oV7/uHp952i1NuGSJUs8bZbkFoEKsKpHcpO5ePEidDoF\nQhoYAAzQaqsjLS2t3M/1008/wem8G0A1AAA5FocO/Qyn01mifpxOJzp16oG//noYQB7Eev99AKYD\nmAhgC0SCNhVAe2i1OTAYmkMkY+9Qe/EDsAfAeQCREPsAFYjQTxocjoPIz68Co/EMRPI2BmIj+Q8A\nYgEsh0j+tgCQjT592kFR1gFYDGAIgIcAxANYArEFZTqAtQBmQ68PxZgxXTBs2FDXNZ05cwZ3330/\nfH2roX79Vvjhhx9KNCblSVJSEvLzx0KExKogI2MAvvsuyWP2SCQlwdM3zkqBw+FgdHQT6nTTKdbD\nL6HdHsjU1NRyP1diYiJttgYUlaxI4AsGBUWWuJ+UlBRaLFXdZvekUNqcRSCAWq2dGk1LAlOp0dg5\nePBQzps3j3FxcdRqLRRFU7wJLKcojvKQ+nQQpIZptlJUvJrIhg1b0dc3TH1KqEGxm7gahaZOGoFt\ntFp9mZ+fz0mTplCns1DsISiw62eKHb61CIykzRbAAwcOXHFNzZu3p8EwkWIPwEf08qrKlJSU8hj2\nEnPHHXHUaOaxYOezxRLPN9980yO2SG49kKGe24OTJ08yNrYrbTZ/1q7dnD/88MNNOY/T6eSgQaNo\ntUbQ27sLbbYAbt26tcT9ZGRk0Gi0UpQ4LCiJGElR+/YNajTuZRW/YGhoNC0WP2q1/Qk0p9Dluc+t\nTT6FPHNrCumFGhQx+1DWr99MlVv4n9p2NQErjcZAenvfRUXxZ2Jiosu2PXv2qPLKzxD4gELvZw6B\n6uoNQE8vrxAuWbKEGzduZEZGBtPS0qjXK3TPG3h59eaKFSvKc/iLze+//05f32q02zvQZqvLtm27\nMicnxyO2SG49kI5fUp5s2bKFjz8+mQ89NJ7Lli3jX3/9Veq+Xn/9Ler1AQQGUSRQR6kx6UcpJJcL\nd9VqtVUoCrIUJHc7qI64wNEeV2f0HSkSvanq+2cI2Gi1dirydGEy+XHjxo384osveOLEiStsS0pK\nosgJ9CewhMAfFLmD3er551CjqUKbrSWrV6/DY8eOUa83s7AQ+yACVvr71+AXX3xRliEvNefOneO6\ndeu4ffv2KySkJf9sIB2/pLisXbuWjRu3Y506LTlnzhtXrAJZtmw5LZZgAi/QYBjJoKDIMksO79q1\niy1atFKd9mQCD6qzajtFcvcQgVjqdDYCJ92c9zSKRG4cgeeo04XRx6caIyPrUiSC3UNI0TQYfFmY\n/N5NRanC3Nxclx3Hjh1jfHwf1qzZlIMGjeb58+dpMPgTeEQN3UwgcNdl/doJnKVeP5n9+g3nc8+9\nREWJphCE66/au4GKEsC9e/eWaZwkkpIA6fglxWHz5s2qKuYqApuoKDGcPfv1Im1CQqIJbHM5PqNx\nCGfPnl3mcx86dIgmU1XVWY5UZ+x1KGL21Qk0o9UaTKHEmaOGbKpRqzVw7ty5nDr1SY4YMZqKUp1G\n42h1pr5cfRpYScDOnj370mIJpLd3ByqKf5EKYxcvXmRwcE3qdM8T+I5G42g2b96ejRoV6AJVoQhD\nhVOofpJiJZCNQjl0Ixs1akeSXLNmDXU6Mws1+UmjcQLnzJlT5nGSSIoLpOOXFIdhw8apceyC2exm\n1qnTskibKlVCWRiTJ7XaaXz22eeK1X96ejp79hxIi8WHVavW4MqVn7h+l5iYyEIBNSNF0na+my0/\nsLBgio6AjQZDbY4ePYFHjx5lkyax6nEFRVl2qGEZLYEgentX5dmzZ7l27VpWr16fJpOdDRrc6UrQ\nbtiwgXZ7G7fz5dNsDuC7775LkQh2qOGdEQQiqNP1pZCGfodALs3mgRw3bpLbOIVQJJhFWMpqvZvv\nvvtuOXxKEknxgHT8kuLw0EOPUqN51s35fU6TKahIAfBRoyaom632E/iSFktAsZPI3br1pV7fgsAL\nBFZQUQK5Z88enj17ljqdN8VqnGCKdfl3qSGcbIpY/ZMUCdsV1GptrFevFadPf4HZ2dmMiKhPjeYJ\n9fjCMIzR2J4REfXYs+dAHjlyhBcvXlRvXAsInKVGM49Vq0YwMzOTW7duVVcqFeQLLtJotDMpKYkm\nk7/bLH8+ASONxhBqtRYaDFaazX6MjY13lZRcv349+/cfQJMpkFrtNFosvVm7dlNmZGTclM9NIrka\nkI5fUhz279/vtpLlNYoNUTOoKNVdhcCzs7M5btwkBgbWZK1aTYudtDx9+rQafulLEcP3p043mP/+\n9785ePBoNbzjpJBd7qXaoFBs0FLUrxYExtNm6+BagXPs2DEqSrAabqmt2p1N4AvabAFFEs+ffPIJ\nxa7cwpuD1VqXP/30E3Nzc9m0aVsajV0JjKHR2JBNm7Zmp07d6esbQYOhPUVJRm+KJK94IrJa/Zic\nnOzKhUyePJ1WaxQNhkk0m2syJqYJx40bx+XLl/PChQvl/IldyYYNG3jXXX3YufN9/PLLL2/6+SQV\nF0jHL7kRWVlZ/P7775mYmMiAgEgKLftNqoNbxO7dB5Sp/3/9a5rq8OnqU6utzrfffpsxMW1YWJmL\nFMsn71Gd/kYKXf/uFEswH6FG481vv/2WJHnhwgUajTYKTf5DFMs8tfT1DePChQtZo0YD6vVm1q17\nB9u160KxGzddndnvoEZjc8lNvPfeIur1PtRq49WbXi31+wM0GKozNLQWTaYORW4cihLKo0ePkiRP\nnTpFk8mbhauJjlGjsdNqjaWXV2cGBUVedfVQebFx40Y1R7OIwAdUlGCPrSaSeB5Ixy+5HkePHmVo\naBTt9oZUlGr084ukqElb4OBeYf/+I0rVt9Pp5MqVK9m48Z0E3nLr8zsaDAG8dOkSBw4cRb3+EXXG\nn0egJzUaO02mGNWJequz+IJlnDH09Q3liBHjmZmZyaeemkGrNYo63WRarS3Zo0d/nj9/nj4+wRTl\nFYcSqEaNxoeiiEsDdeYfRI2mOqOjmzAlJYVms51CyoEUpRXDKfR9qhDYRrPZi2ZzAMUKHxLYTqvV\nj9nZ2SQLnphqul3jpCI3O51uOvv2HVqeH10RunXrR5FzKDj/Enbo0POmnU9SsUEJHL+sJnEbMmzY\nwzh1agQcjmkAsuFwtIJGMwHknxCKmK+iTp3JJe6XJIYOHYtVq35AVlZ1ADMBdAJQBQbDUxgzZgis\nViveeGMmkpLicfJkXWRmXgCZASAH+fnHIaSZL8eMc+eewbJl65GePhaffPIBYmNbICkpCTVqPIqu\nXbti6NAHkZ6uBfB/AJoDWAdyF4Tsc1sITf9VIHU4ciQB48c/DlEzIEY9hzeAhgCyIArEJCA7Owda\nLaHVxsBqjUZe3mGMHz8Wx44dQ3R0NCIjI2GzERkZb4EcCiElMdFltcPRFsnJ25GRkYGvv/4aeXl5\n6Ny5M3x9fUs8thLJPx1P3zjLFafTyZ9//pnbt293JQM9TdWqNQgspViF4iDwCnW6QAITCSQQ+JyK\nUqXEyo6///47LZYQCqXLi+rs10KTyYtDhjxYZBfp999/z6CgSGo096uz/rM0GMJpNAZSp6tBkfD9\nnMB4AjEUydYLNBgsRezKz89no0ataTCMUGfrDxBoqfZJ6vUdKVb7LHabGW9lzZrNGBhYQw0zkULI\nzZ/ARxRLNhur15BLg6E3g4OjaLXWoZdXfypKAD/99DOSQsDO1zecGo2BVmsAzeb26nFZtFh6cdy4\nRxkRUY9eXp3o5XUP/f3D+Mcff5TL5yhCPVVlqEdCUoZ6Kgx5eXns1q0PrdYI2u13MDCwBg8fPuxR\nm06cOEGTyY9AfQI1CdxFg6EFjUb3pY3Z1Gr1Jd75uWPHDtrtdxA4QLEWvwWBAHbs2L1IX/PmzaPB\n4E2xoud3t/P+H/v1G8wlS5Zw5MhxjIpqTp0uisDf6u8P0Gr1c/Vz5swZrlu3jkZjQYJ6rXojq0ng\nJwLPqU7ch0ITKFcNHY2lt3cYf/nlFwYFRVIkkk3q9wAK6YdFbna9So0mkkCW+vP3tFp9eebMGQYG\n1lDDVm/TYolmo0atqddbqNcr7N79fo4fP4kGw0OuvrTaf7N7937l9nnK5K6kAEjHXzFYsGABFaUD\nC6SFtdpX2bp1vEdtio/vQ53uGRYIeQFxjIqKocXiR+BrAn/TYBjPtm27lrjv9PR0dflkKIHX1XNk\nUVFa8/33hZTxrFmzqdUGEJhNoDML8wD5NJvv4Zw5c4v0FxFRj0bjMAKv0GQKYr9+A/nTTz9x7NhH\naTDY1Dh+cwJPUazyeYZC08dH/SqI8ddSbzSR6k3Pm+np6XQ6nfzggw9oMgUQeJJa7SM0mXxoNA5R\nbxKkRtObOt39bjcCJ7VaA59++mlqtbUItFPP+xttNn+uXLmSd9zRmc2bd2aNGvUue9rYxAYNYsvt\n85RICoB0/BWDiRMfp9B/L/inP8iAgBoetSkioiELNxqRwFscPHg0161bx5CQaFos3uzSpfcNZRnS\n0tL4xBNPslevwXz11bmuGX2nTvdQbLo67naOGZw69Unm5ubSYLBQFE15j8A+9SbRgVptNOvUacY+\nfYZy6NCx/OWXX0iS58+f54wZLzAqqjHN5mharUNpNHrTaGxA4EuKnb656nlOEzDRYPChCO8sUr+s\nFKGjthQKnfHU6wO4f/9+1/Vs27aNY8dOYMuWsezYsTt9fUNosdSmydSKBoOdOp0PRSLYSa12NiMj\nG9Bi8aVQFt1IsQ9hCA0GhRZLEIEVFKGqQPUJ4jxF+Kc3J06cfPM+YMltC6Tjrxi8//77VJSWFDFf\nJ3W66YyL8+yqi969B9NgmKTOZjOpKB35+utvlKiP7Oxs1q3bnCbTMALvU1Hac+DAkczOzqZOZ1Rn\n8i+pzjiNJlNDLlu2jOnp6aqo2WrVAa8iMIYajY0tW7ZSHeZ8ajQv02r1d2ndbNu2jVZrLQo1zzyK\nvQGzCCSyqJaOkzpdFer1NhYWURlE4EW3No8QiKSi+BbJuWRnZ7NOnWY0GoeqTxDVVLVQG4FnqNF0\nJ2CiXm9hzZoNOXPmTFos7k8BFwjoGRYWQ7GyqOD9zwhEU+wy1rNHj/7Mysoq189UIiGl468wOBwO\nPvDAGJrNfrTZIhkZ2YAnT570qE2pqamsW7c5rdYIms0B7N17EPPy8krUx4YNG+jldYcrFAJcpMFg\nY2pqKvV6E4Ff1Jl4TQJejIu725WQbdasHQ2GBALzKJKpsQSep1YboTrpAof5PO+6qwdJcuXKlbTb\ne1NUAGtAsdyyLYUqZiCBD9XXU1mrVmP6+VUjMEXtJ47Aerd+l1GrrcKYmDtZr96dnD79Bebn53P9\n+vX08mpJEXrq6PYU8Zp6IyPN5v4u/Z3FixfTau3l1u8parUm9u49mMAbbu8vJdCNwEHa7UHl+2FK\nJG5AOv6KxYkTJ7h///4iypCeJD8/nwcOHODRo0dLVZP1yy+/pN3uvrEpl0ajN//++28++OBEKkpr\nAu9Trx/M4OBIpqen8/jx4xw5cjw7d76Xdeo0odlsp0YTTaGpLxynSLBmuhyuXu/Dc+fOMTk5mYri\nTxGvf5ZijX9nigRyXfVG4EegJvv2fYBr1qyhSNS+SBFWaqc+dZ2jydSSBoOdYv37ZipKLCdOfIKJ\niYm02+MIdOLl4TkRqiFNptF84w3xdHT+/HkGBUVSr3+MwBIqSnMmJEzhrl27VFtfI/A2xYawtTQa\nx5ZrUlciuRxIx1+xOHbsGH///fcK4/jLSlpaGoOCIqnTzSDwLrXaGFavHsXk5GQ6HA7OnfsG7767\nP8ePT2BqaipPnz5NP79q1OmeJLCEVmsj9u3bn3b7PW4O1kGxc/dj9SuQihLp0gUSom5WAsdYkAwW\nydx/sVAVcwNr1GjI1NRU7tixg3Fx3dmmTTxjY7tQpzNSpzOyZct21OkmuJ33CO32QKalpTEgIJyi\nsEt9iipdTrX/5gTm02YL4JEjR1zj8Ndff3Hs2Im8++7+nDfvbddNdPfu3ezXbzhjYu6kXm+iVmtg\nbGw8z50754mPS3KbAOn4KwYOh4ODB4+m2exPm60ma9SIualb+ItDTk4OExKmslatZmzVqgv37NlT\nqn6OHTvG1q3jqNHYCDxNnW4S7fZAHjp06Iq28+fPp8UymIU7cf9Lvd6szow/IHCEev0kioRsC3U2\nv5Bmsw9Pnz7t6qdx47bUaAoUPLOp00VQp7tXvWl8R6AK9fpwmkzefOWVuUVsyM3N5YULFzhw4EDq\n9UPcHP+v9PUNIykKzoibS1uK3cNVCXhRp/NleHh9/vjjjyUeJ4fD4drpK5HcTCAdf8Vg0aJFlyV3\nn/F4cnfEiIdosdxFUVVqEa1W/1LvLbjzzniK+LpwohrNM7znnr7s0WMgu3Xrx6+++ook+eabb9Js\nLhBlG06gIYFRNJuDGBgYxSpVqjE+/j6+8spsWix+9PZuT4vFj++8s6jI+fbt20c/vzB6e7eh1RrJ\n+Ph72aRJLK3WutRovCgSqSRwnIoSwqSkJNexaWlprFWrIS2WThTLPB8jsJCKEsXZs18jSe7du5ca\nTbDr6UFIRi8lsIOK0opTpz5TqnGSSG4FkI6/YlARl3NaLN5qPJ1q3HosX3vttVL1JcTWvnW7vv9Q\np6tCIYO8iIoSzDVr1vD48eP08qpKoWUT7hbHP0Gj0cqLFy+6+jxy5Ag3bNjAY8eOXfWcaWlp3LRp\nE3/88Uc6nU7m5eVx48aNarH0QjE1m20AP/ywUF561qxXaDINUG8+xwncQy+valy2bLmrTUpKCo1G\nHzV09CTF3oDCJ4PAwFqlGieJ5FaAEjh+7U104Lc99etHQ1HWAcgBAGi1qxEdHe1Rm/R6E4ALrp+1\n2gswmUyl6mvIkPugKE8A+BnAduh0z8HhuB/AWADDkZn5GmbOnI+wsDAkJIyHRrMYQCgAi9pDNej1\ndpw/f97VZ0REBDp37ozq1atfcb7s7Gzk5uaiffv2aNq0KTQaDfR6PeLi4uDl5Q3gG7Xl33A6dxYZ\n64MH/0BOTgMAGgBhAObAbDZgwID+rjYhISEYPXokrNZ2ALYDOOt29gswGo1YvHgxXn31VXz//fel\nGjOJRHJ1PH3jLDfy8vJ49919qSjhtNubMSgo0uOSDbNmzVZrxM6nXv8IAwNr8OzZs6Xqy+Fw8Lnn\nXmJISG2Ghzdgkyat1ZUsBbPkT9mqldip3LnzfeqTQADF+vtsArMZFla7WNIQL7/8Kg0GC41Gb9at\n2/yKZbHffvstbbYAenu3osUSwCefnOH63aVLl+jl5U+xWWw/hUxzb9533wNXnMfpdPKzzz5jQkIC\nFcWPWu0TBN6kooQxIqIOrdY4GgyPUlGC+OGHH5Vq3CSSmwEqUKinJYBN6utaENOorQDmQ0y9roan\nx69ccTqd3Lt3L3fu3HlTRNrOnj3LTp160mCw0Ne3Gj/+eOUNj1mx4mMOGjSajz02hadOnSrT+Xfu\n3MkxYyZwwoTHuHjxYlU0bDFFxa0wV7nFQYNGUat9nqJ+by0COtpsIVdNBrvz22+/MTS0QCf/BAs2\nwt15Z5cr2p45c4bbtm274ua6ZcsWarUxFNW0/AiYCVThmDFjr3vuo0ePcsKExzhkyIOcPHkyrdZ2\nLKzYlUS7vWoJR6soeXl5nDv3dQ4Z8iBffXXOP2bVl8QzoII4/skA9gLYqf68BkA79fXbAHpf4zhP\nj1+lolOnnjQax6nLD3fRYql6zdUnFy5c4P33D2NQUBSbNevAn3/+uUzn/vrrr6koVQnMokYznTZb\nABcuXMiOHXuxbdt7+Omnn7ra/vHHH/TxCabJNJJG44O02QK4b9++6/afkZFBf/8wAveqyyoLniTO\n0GLxLrade/bsoUZTjQWKnSLZ7s02beKK3ce8efNoNrsXlsmiTmco1T4IUkwIune/n4rSicBbtFji\n2blzz1L3J5Gggjj++yBm+bvUn0+6/a4ngHnXOM7T41epMBgUCrkA4ZCMxkc4e/bsq7Zt27YrjcaR\nFIqY79BuDyxSqpAUDqm4zqdFi84Elrut6nmBI0Y8dM32KSkpnDt3LufMmeOqYnU9fvrpJ3p51VdX\nDrVh4W7aVYyIiCmWjaTYsBYcHEWxTPQNAq0J+NForMJvvvmmWH38+uuvVJQAAlso5KEnsG3bbsW2\n4XIOHTpEiyWYhQVncmi1hvPXX38tdZ+S2xtUkOTuZwDy3X52D+1cgqh8ISkjdrsfgN/VnwiD4Xf4\n+fld0e7SpUvYtWszcnP/A6AugFEg78SWLVtcbV58cRYUxQdGowX9+g1Ddnb2dc+dlZUNoPBcpB8y\nMq59TEhICCZNmoSEhASEh4ff8Np8fX2Rk/MngK4A/AE0AdARwGDMmfP8DY8vQKfT4cCBH2AwfA/g\nKQC/AngGublPYfnyVUXaJicnY/PmzUhNTcXp06eRkDAZAwaMxN69v2Lp0oUICBgGozEUsbFHsWrV\nh8W24XKys7Oh09kgisEAgAFardcNx1wiqQxEoHDGf8Lt/V4A3rzGMZ6+cVYqVq78hBZLVRqNE2i1\ndmLjxm2uumEoJydHFUg7zYKNVDbbnVy7di1JcsWKFVSUOgSOEEij2dyTDz2UcN1zv/HGW7RaY9S4\n/VdUlFCuW7euXK+vb98HKKQZJqhLQeNpMFhvqB56NWJiWlMIxBVo4/+Ljz8+xfX755+fSYslgN7e\nsbRYqrBKlVBVa/8/VJS6fOGFmeV2Xbm5uaxVqxENhskEkqjXP83w8Hpys5ek1KCChHqAoo5/DYD2\n6usFAO6/xjF89tlnXV+bNm3y9HhWeJKSkjhnzhwuXrz4uo5j6tRnqCj1CfwfzeY+bNCglav90KFj\nCbzpFsP+gTVqNLrueZ1OJ2fPfp21ajVjvXp3FiuxXFLy8/NZr15T6vV1CIyixdKMo0dPKFVfX3zx\nhZp8fpE63ST6+AS7Qk6//PILFSWYwF/q9U+hKEBfMB6HabX6luel8dSpU+zRYwDDwxvw7rvvZ0pK\nSrn2L/lns2nTpiK+EiVw/NdaWVNeRABYCqA1gCgACyGebX8HMAZXN5Rkhblx3VIOHTqEl1+ei7S0\nDDzwwL24995r5b9LB0msXLkSW7bsQkREKB5+eDwURQEATJs2HbNnn0Ze3n/V1u+hZctl2L17Q7na\nUBpyc3Px9tsL8L//JaNVq6YYMmQINBpNsccrOTkZhw8fRnR0NE6dOoXlyz+F1WrB2LGjXfsFVq1a\nheHDFyE9fY161DwAuwEsUX8+A5OpBrKzL97sy5VISoVGowFuvk+/aXj4PuoZkpOT6eVVlVrtDAop\ngQi+8857t+z8Z86cYVhYbVqtPWixDKfNFuASSCsvtm7dyilTnuQrr7xyXcGyP//8ky+++BKfemp6\nEdkFd5KTk2m1+lGjeVQNxVx9vObNW0CLxZ/e3nG0WPy5cOHVx/TAgQPq08BhdYa/iELh8z8EdtBi\niefQoddf/nktMjMzuX//finSJrmpoAKFekqDp8fPIzz99DPU6R5zCy1sY3h48VeulAdpaWl8//33\nuWDBAh49epRZWVnFrrubmJjIZs3i2KBBLOfP/88VK4OWLl2mrmJ5libTAwwLq83z589f0c/Jkyfp\n6xtKg2EcNZqnqCgB3Lhxo+v3P/74I2Nju9Fo9KcQdatGUVx97RXjlZKSQrPZl8AfLJDMMJt9mJqa\netVrWLBgIc1mb3p5RdNuD+S7777LNm26Mjr6Dj722LQixeKLy+7du+njE0ybrRZNJjvnz/9PifuQ\nSIoDpOOvfEyePI3A026OP4khIXU8YsuFCxfYrl036nRGGgwWPv/8y9dtv2nTJipKEIFPCXxNq7UO\n33prQZE2gYE1CexwXZ/Z3J+vv/76FX39619TqdMluI3DJ2zYUNSoPXz4MG22AAIDKQq4ZFBo70wk\n0IOhoUXHa+fOnfT2vsOtL9Jub3hdlc2zZ89y3759zMjIKO5wXROHw6EWhfnclSdQlED+9ttvZe5b\nIrkcVJDlnJISMGhQfyjKAgAfANgIRRmNceOGesSWESMmYPfuEDgcl5CXdwgzZy7CmjVrrtl+4cKP\nkJn5JMTWjS7IyHgTb79ddKljZuZFAIX6O3l51XHp0qUr+jp3Lh0Oh7tOT3VcvCjarVmzBrm5fQDY\nAAwCoECENIdBo9mFsWOLjldUVBTy8pIB7FHf2QGHIwWRkZHXvBZfX1/Uq1fPlfsoC2fPnsWlSxkQ\ni9gAoCZ0ujbYt29fmfuWSMqCdPwVhEaNGmH9+lVo02Y5GjZ8HjNmDMHTT0+9Jed2Op1YtWoVXnvt\nNezYsQPbt+9Abu4UAAYAocjMHI7Nm7df83iTyQCNxj3peRFGo7FIm169esFsngDgMID1MBrfR9eu\nXa/oq3//XlCU2RDqHgegKI9jwADhOA0GA7TaixD7AtehcJvIakRFhV8xXv7+/li2bBEUpStsvNE8\nQwAADJNJREFUtkhYrb3wySdL4OPjU5LhKRXp6elISHgSubnZAHao7/4Nh2MPatWqddPPL5FUNjz9\nxHRb4XQ62bv3IFqtTWkyTaCihDE4OJrAEtd6f7P5Xlet2QLy8vI4Y8a/2aFDT9577wAqih81mpco\nBM2CuGbNmiLtMzMzOXz4Q/TzC2dkZCMmJiZe06bFiz9kWFg9BgTUYELCVFdN4NTUVAYEVKdO9yiF\npn81mkyNGBoadU0ZZ1KItB08ePCa4Zvc3Fw+99xL7NChJ0eNepipqalct24du3Xrx+7d+3Pz5s3F\nHU6SYkxjY+PVYvSvUxR1aUyzuSqfemrGjTuQSEoBZIz/n8f27dtZvXo9mkw2tmzZqdwqeW3bto1W\na2036YCj1OlMtNkCaLP1o80WywYNWl3hNAcMGKEWNfmUen0CAwPD+cADozlw4ChOmTKVfn5htFi8\n2afPkHIVp0tJSeHDDyewT58hfP75F7h169Yyx+P79h2iFqf5lAbDo6xaNYwWSxCB9wj8lxZLQImc\n/9mzZ2k0erFQG+gUFaUZ58+fXyY7JZLrAen4/1mkpKSoSc1VBM5Tp3uW0dFNykXQ67PPPrus9q2T\nZrMfk5KS+OGHH3LVqlVXbArLyMhQdwFfch3n5RXHzz//nFu2bKGihBD4nkAqzeb7OWDAyDLbebNI\nT09X9Y4y3Hb0hlFU3ioYkwXs0WNgsfu8ePEi9XoLC2sBO+nl1aLcdzVLJO6gBI5ffxMduKSc+O67\n76DVtkSBoKnD8SyOHXsdZ86cQUBAQJn6btGiBRyOByFi5u2h1b6J4OBgNG7cGE2aNLnqMXRtsHNP\nEelAEuvXb0Bm5mgAzQEA2dmvYP362DLZCIhNXBs3bkRmZibatWuHqlWrlrlPQFyLuJzL011Fr83p\nLP5kymazYcSI0fjoo67IzBwOk2krwsM16NChQ9kNlkjKAen4KwFVqlSB05kMIBdi43MKnM4ceHl5\nlbnv0NBQJCauxMCBo/H338dRv/4dWL16bcEuwKtitVrRs2cffPVVX2RljYdevwM2WzLi4uKQnJwM\ns3kPCrXGDsDb27dMNmZmZqJ16y744w8HNJqq0GofwfbtGxATE1OmfgHAbrejW7ce2LixH7KyxkKv\n3wa7PR9ZWY8jK8sJIB8Wy9OYNGnJDftyZ8GC19Cs2bvYsuU7REXVwRNP/LfUlc4kktsBDz8wVTwc\nDgfj4++l1Xon9frHqSgRfPnlV8v9PCUJHeXk5HDatGfZqlU8Bw4c5dKZSUtLY2RkDC2WXjQYHqXF\n4u8qul5aZs16hWZzH3XNPqnRLGCLFp3K1Kc72dnZnDJlOlu1iuegQaP5559/cvXq1ezQoSc7duzF\n9evXl9u5JJKbBSqQVk9pUK9B4o7D4cCKFStw/PhxtGjRAnFxcZ426ZpcvHgRS5cuRXp6OuLj49Gw\nYcMy9Td27ET89781ACSo7+xDSEgfpKQcQGZmJqZNew47dvyIqKgIzJnzIoKDg8t8DRJJZaMkWj3S\n8UsqPEuXLsWYMbOQmfkNAB8YjQ+hZ888fPzxInTp0gs7dpiRnT0aev03CA5ejf37f4TVavW02RLJ\nLUU6fkmF4OTJk/joo4+Ql5eP++/vi9q1a5eqLUlMnvw0XnttDgAtWraMRWLiCuTm5qJ69drIyUmF\n2GwGeHnFYuXK6YiPj7/JVyeRVCyk45d4nOTkZDRt2gaZmffC6bTAbP4Amzd/hebNm5e6bU5ODnJy\ncmC32wEISYSQkEjk5p4CYAFAeHm1wmefvYTOnTvfgquUSCoO0vFLPM7IkeOxeHEAnM4Z6jsL0bFj\nIr79dnWZ2l5O796D8PXX55CVNQJG47cID9+DvXt3wWw2l9/FSCSVgJI4fqnVI7kpnDuXDqezhts7\nNXD+fFqZ217OypWLMW1ae3TpshJjxtjw3XffSqcvkdwAuY5fclPo1+8ebNjwDDIzGwFQoChPoV+/\nq1fbLEnbyzEYDJg+fVr5GS6R3AZIxy+5KQwaNACpqX/j5Zf7wuHIx5gxwzFlymPFajt69LBrtpVI\nJGVHxvglEonkH4CM8UskEonkmkjHL5FIJLcZ0vFLJBLJbYZ0/BKJRHKbIR2/RCKR3GZIxy+RSCS3\nGdLxSyQSyW2GdPwSiURymyEdv0QikdxmSMcvkUgktxm32vFrASwAsBPAJgA1b/H5JRKJ5LbnVjv+\n3gCMAFoDmApg9i0+/01n8+bNnjah1FRm2wFpv6eR9lcebrXjbwNgnfr6OwBXlmOq5FTmP57KbDsg\n7fc00v7Kw612/HYA6W4/Ozxgg0QikdzW3Gqnmw7A67LzO2+xDRKJRHJbc6v1+O8D0APACACtAEwH\n0P2yNochk74SiURSUv4AUMvTRlwNDYC3AexQv6I9a45EIpFIJBKJRCKRSCQSiaT80QF4D8B2ANsA\n1PesOaWmKoATqJwhrCSITXWbALzrYVtKwzSIjYHfAxjmYVtKyjAUjv1uAFkQK+AqA1oU/u9uBVDb\ns+aUGCOADyD+drYAaORZc0pES4i/GUDE9gs+g/momPXUr6AXgHfU1+0BfO5BW0qLAcAqAAdQ+Ry/\nGcLxV1Y6AFijvrYCmOE5U8rMPACjPW1ECegKYIX6ujOATzxoS2l4GEJNABD/tz960JaSMBnAXogb\nFiD+/tupr9+G2Cx7TSrKGvrVAMaqryMAnPecKaXm/yAG/C9PG1IKGgFQAKwH8A3ETKIycReAXyEm\nDGtReBOobDSHeNp950YNKxBZALwhZpjeAHI9a06JqYfCTaUHAYSicjxtHYZYJVkws28KMdsHgK8g\nbsKVhvcBpAHo4mE7SspwAE+przeh8j3uxgAYpb6OgvijqiiTguKwEOKfVw8xazvgWXNKzWcQT7yV\nCT2AzQD+B+AMgDs9ak3JGYPCG20riE2lwZ4zp0REANilvk5xez8OwIe33JoyEgjgKACLh+0oCVsg\n/vg3QTyt7Ia4jsqCESLcU8B3EDOfysLLAB5z+/lnAP4esqW0+AD4zdNGlIInAbykvq4GMWs2es6c\nEqMDMAcitzgTwH4AJo9aVHwiUOj4T7i93wvAm9c7sKLM6oZAJOcA8ejoROXa0dseIs7cEcLpDAVw\n2pMGlZARKBTMC4F41K1MIavtELFmQNhvBXDWc+aUinYQYbbKhhWFMiznIXJdOs+ZU2JaAPgWQFuI\n/MRfAHI8alHp+AmFT4vdUBj2qdBYIBJEWyCSFT08a06Z2ITKl9zVQzwablW/WnnWnFIxC8AeAD+g\n8oUKAeBfACZ62ohS4AOxqGEbxJPuAM+aU2J8AWyA8DvfonKpBkSgMLkbBRF12AkRuqoUq3okEolE\nIpFIJBKJRCKRSCQSiUQikUgkEolEIpFIJBKJRCKRSCQSSYViMoA/UXl2UQJAFQixu/WeNkQikUgq\nI3shdhNXJonldqh86pQSiURSIegA4FOIHdB7ADSA2FVZQCKAxgDugZDR/VZt/+xl/TwHIfz3JYB9\nECqegNCCKtCTmQlxc2kPMVNfDTFrfxDAcgjtlnFXsfFx1badah8GCLmO01ex4zfVvqUQCpaJELvU\nd0DIfABit/FuiN2Xn6rtOhTDppfUfr6DeEqSSCSSSskSAHerr7dB6KnsBFAdQjlxF4TO1B8AAtyO\neeayfp5FodZ6Zwi5WgA4gkLH/zIKHf9vEDozLQEch5CyiIDQQXGnAYSTLtCk+RRAd7WPZVe5niMo\nLPDxKoBH1NchAJLV18koVIWcCCHzXRybjkCMixHixiCR3JCKItImkRRQBUJk6lEIR+0NYAKE/shQ\nAA9AVHwKgBAH+1s9bhuurk9S4CBPoqgCaQHux/wGIcubBnFTyQdw4SrH1YZw/A63c9+oatz/1O91\nUCig9ad6DVXV7wXCeO793cimwRA6ReshdHMkkhsiHb+kovEAhJOPh7gBtIQI0XwNId53L0TI5G8A\nXiiUXy6JDnw2xGxbAxEyKoDFPP6AapdO7aMdCh37tShQm92PwkpJoRDO+hyEImqQ+n57t/6uZ5MR\nwP0ABkJosA8HEFbMa5Dcxug9bYBEchmjIJx/AVkQoZQhEDF0HYAM9XcTIOL3aRCTmINX6Y9Xef2K\netxRCKfL67S9/DUgZuEfQ8TWtRAz9NUQDvtqjtr9vX9DPLH0hVClfRBiFj8GohCLU7VpOERI6Xo2\n5aptC+r0rkdRXXaJRCL5xzEVhbH6D1H0hiGRSK6BnPFLKjMXIWa7mRBJzhXXby6RSCQSiUQikUgk\nEolEIpFIJBKJRCKRSCQSiUQikUgkEolEIpFIJB7n/wGDpWiNyJ0eGQAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f793c8fd490>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.scatter(df.RM, boston.target)\n",
"plt.xlabel(\"Avg num of rooms\")\n",
"plt.ylabel(\"Housing price\")"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array([ 30.00821269, 25.0298606 , 30.5702317 , 28.60814055, 27.94288232])"
]
},
"execution_count": 30,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"lm.predict(X)[:5]"
]
},
{
"cell_type": "code",
"execution_count": 33,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.text.Text at 0x7f793756e090>"
]
},
"execution_count": 33,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYQAAAENCAYAAAAPAhLDAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXeYVMXSh9/JaWdJu+ySc5CMSBAkKggY4CIGQEDvFRAR\nM2YviFwxIqKifioGTJhAjAgoqIiCqCCCEhVJkuOycX7fH312WQSUsMsA9vs88+yEPn3q9M50na6q\nrgKLxWKxWCwWi8VisVgsFovFYrFYLBaLxWKxWCwWi8VisVgsFovlb3HF4ZzfAdud5yuAkcALQAxY\nCAwCFAe5LBaLxXIMCWIUQn4mA62c508CXY+pRBaLxWKJC02Bn4EpwHSgGbA63+fnA4/HQS6LxWL5\nx+M9xufbDTwIPAdUAz7+0+e7gCLHWCaLxWKxcOwVwhJgmfN8KbAZaJjv8yiw7RjLZLFYLBaOvUK4\nHKiHcRyXxiiAT4DWwEygE8aUtA9VqlTR8uXLj6GYFovFclKwHKgabyEOhhcYD3zuPJphTEczgK+A\nZzlw5JNOZoYOHRpvEQoVe30nLifztUkn//VxmBGbx3qFkA30PsD7bY6xHBaLxWL5E+54C2CxWCyW\n4wOrEI4D2rRpE28RChV7fScuJ/O1wcl/fYdLPHYqHwmOOcxisVgsh4rL5YLDmOftCsFisVgsgFUI\nFovFYnGwCsFisVgsgFUIFovFYnGwCsFisVgsgFUIFovFYnGwCsFisVgsgFUIFovFYnGwCsFisVgs\ngFUIFovFYnE41tlOLRaLJe7EYjG+/vprduzYQePGjSlRokS8RTousArBYrH8o8jOzuaccy5i1qxF\neL1lcbkWMWPGR9SvXz/eosUdqxAsFss/ivHjxzNr1mZ27/4R8AEv0KvXlSxcODveosUd60OwWCz/\nKFasWMnu3W0wygCgPb//vjKOEh0/WIVgsVj+UTRqdCqRyFvAJkB4PE9Tv/6p8RbruMAqBIvF8o+i\nS5cuDBz4L3y+igQCqVSu/B6vvfZMvMU6LrA+BIvF8o9j5cqVZGWBywUbNmwgMzMz3iIdF9gVgsVi\n+UcxZswY3n57DrAa6Q+2bx/IGWd0jrdYxwVWIVgsln8UEydOAnoARZ13Lmfdut/jKNHxg1UIFovl\nH0XJksnAB0C68857uN2BOEp0/HDIxZfjjCTFWwaLxXKCsGjRIqZMmUJCQgKXXHIJ0Wg077NVq1ZR\npUoDsrNDQCqwhFtuGcx9990bN3kLC5fLBYcxz1uFYLFYTiqmT5/O+edfQnb2xXi9q0lJWcb338+i\nSJEieW3eeOMNBgy4gYyMTNq1a8G7776Fx+OJo9SFw+EqBGsyslgsJxUDB95MWtpzZGY+TlraJNau\nrc///d//5X3+008/cfnlg9i2bSR79rzDZ59tYsiQO+Mo8fGDVQgWi+WkYuvWLcApea8zMk5hw4bN\nea/ffvsdMjIuA3oDZ5CWNo4XX3zlWIt5XGIVgsViOano2LE9weDtwAbgLjyeUWRlpZOTkwNAMBjA\n7d4OZAO7gO34fP74CXwcYRWCxWI5qXj66dF07hzE7a4KfExOzh0888wPdOt2KZLo3bs30mtAAlAE\nOIurrro8vkIfJ8TLqVwSmAecCcSAF5y/C4FBwJ89yNapbLH8A8nOzmbZsmWEQiHKly+f6yT9W5Ys\nWUKDBm3Ys2cFEATSCYer8t1303n33Xe55ZaHgC+ACsBAkpI+Z+PG5YV3IXHiRHAq+4Cngd0YQUcB\ntwOtnNdd4iCTxWI5zvjjjz+oU6cpp53WmZo1G9O9e+88s8/fkZaWhtdbFKMMAIJ4PEXZvXs3L7/8\nCtAfqOF8PpxNm9YXyjWcaMRDITwIPAmsc16fCnzuPP8IOCsOMlksluOMfv2uY8WKduzevZz09N/4\n+OPVPP30//39gcApp5xCsWLg8dwN/IzHcw9Fi2ZTq1YtcnKygTnsNUT8gE3rZjjWCuEyYCPwifPa\nxb7LmV0Yo57FYvmH88MPP5KVdSlmigiRlnYBc+YsOKRjA4EAs2Z9Qps235OSch6tW3/LrFlTCQaD\n9O3bF/gaaAJcAlxC0aKhQruOE4ljrRYvx6jls4AGwItAcr7Po8C2YyyTxWIpZDZt2sTUqVPx+Xx0\n6tSJSCTyt8fUqFGNtWsnk5NTH8giFPqQ+vXPPuRzli1blmnTJu33fqlSpYDSGHdlJlCO1NQZh9zv\nycyxVgit8z3/DLgSY0JqDcwEOgHTD3TgsGHD8p63adOGNm3aFJaMFoulAFm6dCnNmrUlM/M0YBdJ\nSUOZN+8Lihcv/pfHPffco7Ro0Z4dOyaRk7ONJk1qMWjQVUctz5IlS4GLMAYLgDWsXTv+qPs9Hpgx\nYwYzZsw44uPjmbriM2AAZsXwDOAHFgH9sFFGFstJw9lnX8C0aacTi90EgN9/JVdfXZSHH77vgO2n\nT5/OwoULqV69Oq1bt2b+/PmEQiHq1auH2330Vu5XXnmFAQPGsHv3Z0AYl+sxGjZ8i3nzZh5138cb\nhxtlFE9PStt8z9vESwiLxVK4rF69jlisad7rzMymrFz52QHb3nbbMB577GWyszvi9T7NpZd24Kmn\nRheoPD169OD996fz7rvV8PlSCAa38uqrHxfoOU5UbHI7i8VSqAwePIRnn11GevprQBrhcCceeujf\nDBw4AIBp06Zx4413s2XLZtat+52cnBUY1+IOQqEafP/9DGrUqFGgMknil19+Yfv27dSpU+eQfBon\nIifSCsFisZzgfPLJJ7zwwhuEw0FuuulqatasuV+bBx+8h99+u4wPPzQBhJdffjUDBvQD4Pvvv6dL\nl56kpT2FcfDezN44k0T8/gps2rSpwBWCy+U6oKz/dKxCsFgsR8Sbb75F377XsmfPHbhcm5kwoRXf\nfvvFfpN3MBhk8uTXSU9Px+Px4PP58j57++2J7NnTD+iGKVgzBONS7AO8C/xG7dq1j9k1/dOxuYws\ncScrK4unnnqKIUNu5a233sKaBwsOSQwfPpISJcpTvHg5hg4dUWDjO3Tow+zZ8yxwFdJd7N49gLFj\nnzlo+2AwiNfr5dlnx9GlSy8GDryO7OwsvN5NuS2Ae/F6b8HtTqB8+WFMm/YeRYsWPWifloLFrhAs\ncSUnJ4czzzyfefNySEtrTSRyN7Nnf8fDD5981aviwVNPPcP9979OWtoUwMVDD/UgObkEV1898Kj7\nzsrKwmwdMkhR0tO3kZ2djddrppbly5fzzTffkJKSQrt27bjjjrt59NFJpKVdj9e7gKJFXyUazWb7\n9mvJyalAOPwITz45ht69ex1y3qI/s2rVKubMmUPJkiVp2bLlAfvZunUr48aNY9u2HXTu3JHTTz/9\niM5liQ+ynJzMnDlTCQm1BVkCCTbK54to+/bt8RbtpKBNm/MFbzpjK8FEnXHGOQXS90MPjVY4XFcw\nTTBBfn9xBQIJcru9atGig1599VWFw0mKRi9UJFJLXbr0kN+fIPg9T55w+AI9/PDDuvnm29Wv39Wa\nMmXKUcn0ySefKBxOUmJiFyUk1FTXrj2Vk5OzT5utW7eqbNnqCgR6yeW6U6FQit58862jOu/xCvuH\n8P8ldoVgiSs7d+7E7S7N3q9iCTyeEGlpaSQmJsZTtJOCpKSiuFwryLUSuVzLKVGiYLLD3HDDNXg8\nHp57big5OdmsWOEiI+MboCpz5tzIN98MIDv7I6AFkMH06c3IyckEwnl9SGEikQj3339DgcjUs+cV\npKVNANoBGUybdjrvv/8+559/fl6b559/nvXrG5Kd/TIAe/acxbXXDqB79wsKRIYTGetDsMSVZs2a\n4XYvBJ4DVuD13kzVqlVISUmJt2gnBG+//TZ16rSgevXGPPzwo/v5B0aMuJ2EhIfx+a7C57uahIQH\nuPfeOwrk3C6Xi+uuu5off/ySPn26kp19OVAL8JOVdSfZ2buBZk7rALFYI5o0aUYodDEwA5drDD7f\nJ5x77rkFIk8sFmPz5tXAGXnnzM5uwu+//75Pu4ULfyI7u2K+dyqwceMfBSLDiY5dIVjiSokSJfj8\n8yn06TOI338fzqmnNmL8+HeP2H58vLNu3TomTZqEy+Wia9eupKamsnLlSl599TUkccklF1O1atVD\n6mvq1Kn06XMNaWnPAFGGDh2E1+vh2muvzmtTo0YNfvxxDhMmTEASF1/8DRUrVizw60pJSSEYnM7u\n3THMfeYCvN4ixGIPEYvdDPwCfMDo0e8yceIHfPDBXaSmJjN69KeUKVOmQGRwu93Urt2ERYtGE4sN\nAVbgdr/PaaftW/zGfLeeAToAlYBrsffGJxZxtsRZLEfP0qVLVbRoKYVCvRUKXapixUrrk08+UTRa\nUl7vYHk81ykhIVnz588/pP569PiP4PF8/oFXVbp0Fb366qvatWvX3x4fi8W0ePFizZs3T3v27Dmq\na0tPT9dpp7VWQkILhcOXKRxO0osvvqhq1RrI6w0rEEjQuHEvHNU5DoUVK1aocuW68vuLyO+P6Ikn\nntqvzejRo+X1NhakCIoLmqls2ZqFLls84DB9CCfKbZhzbRbLiUv37n2YOPEUYrHbAHC7h1Oq1Ous\nWVMFE3IZAhLo3HkzH3ww4YB9SGLLli0UKVKEK6+8jnHjUpDuwhQgbI/b3Y5weCepqev59tvPKVLk\nwP6CnJwcunW7lGnTvsDjKUrRotnMmjWVcuXKHfH1ZWZmMnnyZLZs2ULr1q3z9iPs2LGDSCSCx+M5\n4r7zI+kvV5C5YxSNRvH796+VvHz5cqpXb0gsdilQDbiXwYN7MWZMwabIOB443J3KJwpx1bIWS0HQ\nvHknwbv57ujflMdTXFBLUFJwkaCcUlKqHfD4zz77TImJJeTxBBUIRDV69KNKSEiWy3WX4BTBOKff\nmPz+3rr77nsOKstTTz2lcLi1YI9A8niGq23b8wrr0guEbdu2qX37rvJ4/IpGk/Xcc88fUT8PPPCA\n/P7L8/0fZqtUqQOP+YkOh7lCsIYzi+UIicVifPPNN0yfPp0dO3b8bfsuXc4iHB4JrAXWEAwOQwoC\nqzAVvCYAC9myZQcLFuxbCObXX3+lXbtz2bGjEzk5l5GR4eeWW4YyceKrDBq0m3B4G9DIae0iM/NU\nVq8+uKN0/vzFpKWdR26JyZycC1m0aPFhj8HhkJ6ezo033k7Tph249NJ+/PHH4TlyL710ADNnFicn\nZws7d05j8OA7+PLLLw9bjrS0PWRn5y/Dkkx6+p7D7scSP+KtaC2WfcjMzFTbtucoEqmuxMQzlJRU\nTj///PNfHpOTk6NrrhmiYDBRwWCiLr64l/z+cs7qQHkPr7eZLrjgQq1Zs0aSsYuffXYXwZB87cbK\n46mot99+W5LUt++VCgYvEuwWrFI4XENvvvnmQWUxK4RWgjRnhTBM7dqdL8n4Fn744QdNnTpVGzdu\nLKARkzp27KZQqKvgQ/l8Q1SuXI1D8nXkkpCQJFibNwZu920aPnz4Ycsxf/58hcNJzv6MbxUOt9Wg\nQTccdj8nAhzmCuFEId7jarHsw+OPP65QqL0gUyC5XI+qadOzFIvFtHDhQn311Vd/O9k98cRYQSlB\nqmPuiQmmC4rK7e6npKRyuuyyKxUMJsvjKS14Pp9CmC6XK1nffPONJGnXrl0655yL5PH45fdHNHz4\nSElSRkaGNmzYoFgsts+5s7Oz1bVrT4VCpRSNnqLy5U/RqlWrFIvFdNllAxUOl1ORIq0VjZbUrFmz\njnq8Nm3aJL8/UZCedw2JiS310UcfHXIf5cqdIpiSZxYLh8/Vk08+eUTy3HffffL7S8rtLqb69Zsf\nlmI6kcAqBIul8Bk8+AbB/fkm6F+UlFRRXbv2VDhcTomJjZSSUklLliw5aB+nnNLM2eX7o6CmwCOI\nOkpB8novl8+XLNgqeElQRTBf0E9QQuFwqTyFkEtWVlbe5D9u3AsKBBIUCBRTuXI19lvBxGIxLVmy\nRN9//73S09MlSR9++KEikdqCnc51vatSpaoe9Xht3rxZfn80b0UCMUWjp+vjjz8+5D4+/vhjhcNJ\nCgYHKBI5S3XqNFVaWtphyzJv3jyFQsmC9wU/KRTqqH79Bh92PycCWIVgsRQ+L730ksLhRoJtgpi8\n3ptVu/apCodb5Dlq3e5H1KTJmQfto1at0/Pd8UowVNA777XLdZPc7qZ5EyiMECQIzhJ8J3hJkUiS\nli9fvl/fCxYsUDicIljs9PWEKlSopQULFmj9+vUHlWnMmDEKBgfmkylDbrdnvxXGkdClSw+FQp0E\nb8rvH6TKlese9oT+008/6bHHHtP48eOPOFR22LC75Xbfmu8aV6hYsTJH1NfxDlYhWCyFTywWU79+\ng+X3JyocLq2aNRvpqquuFtyTb6JZqWLFyio9PV1XXnmdypQ5RXXrNtfMmTMlSS++OF7hcAXBy4Ix\n8noTFQw2EswRTFAgUEyhUAXBFqe/FwS+fK+lYPAKPfbYY/vJ9/zzzysS6ZVPlpjAq4SEGgoEimj4\n8PsOeF2ff/65I9NaR5E8qWrVGhbImGVkZGjo0BFq27arBgy4Vps2bSqQfg+Xhx56SIFAn3xj86VK\nl64RF1kKG6xCsFiOnp07d+qJJ57QiBEj9jPL5GfDhg1auXKlsrOzNX78eEUijfPMLR7P/3TGGR3V\nu3d/BQKdHHPPGwqHk7Ro0SJJ0ptvvqUOHbqrS5demj17tm6++S5VqtRADRu21owZM3TNNTc7q4LK\ngtKCIoIleZNZONxVzz777H5yTZs2TZFIDcEup+3XgkRHMaxVOFxeX3311QGv6Z577pPfH1UkUkGp\nqZW1ePHighnU44RNmzYpNbWyfL4rBP9TKFRaL7/8SrzFKhSwCsFiOTjr16/XsGHDde21N2nGjBkH\nbLNz505Vq1ZfodC/5PHcrHA4VW+8cfCInVxisZj69BmgYDBJ0Wh1lS9fU1dffa0gIFiX7450gEaO\nHHnIMv/nPwPldld0FEKSoKzgUfl8/VSmTDU9/PAj6t69r26++Q5t27YtT5bevfsrEqmqaLSLIKz8\neyAikcv0zDPPHPScW7Zs0bJly5SZmbnfZ9u2bVP37n2UklJVDRu20nfffXfI13K8sHHjRg0ffo+u\nu+4mffbZZ/EWp9DAKgSL5cBs2LBBJUtWkM83QPA/hcOl9dprr+/X7sknn1Qo1GUfk0JKSuVDPs+v\nv/6qhQsXql+/K51JPMVZHeT2d7569eolyUzca9eu1ebNmw/aX3p6ui68sI88Hr+83oA6dTpfl18+\nUHfc8V/17dtf4XBTwbPyeC5VkSKl9cor5m73/fff13nnXaB//esCFS2aKnjPOf9mRSKV80xXh0vL\nlh0VCPzH8U88r8TEFK1du/aI+rIULliFYLEcGBNq+O98E/NM+Xwl9gl93Lp1qxo2bC6oJOglWCNY\nr3C4+AH7XL9+va69doguvPAyvfji+Dzn68aNG5278mqOuaes4EFBX0Gyhg4dqq1bt6px4zYKBpPk\n90fVu3f//XL35yczM1PZ2dl5r9PS0uT1BmWikHL9BE0UCJTVuede4PgCRsnrHahixUopISFZRYo0\nVShUUjfeePsRjeGuXbucc2bljWM02k2vvvrqEfUXLzZs2KChQ+/WNdfcqOnTp8dbnEIDqxAslgNz\nxx13yeW6I59CWCpIVThcUrNnz1ZOTo5OPbWlfL5/C74Q3CKoJr//QnXrdmlePzt27NA11wxRixYd\nFYkky+sdLHhG4XBtDR06QpI0bNhwRwnMEEyV2Xx2qqC8gsFkzZ07V5dc8m/5/f0E2YIdCodb6Ikn\nDj2ufufOnfJ6Q4KMfNfUWfC043yel8/53EsjR47UF198oaVLlx7xGGZmZsrrzW8Ciykh4XS9++67\nR9znsWbjxo1KSakkn6+/YKTC4TIaP/7leItVKGAVgsVyYObOnatwuKRM/PmPMuGb1wo6q3z5OurR\no69CoVKCnHwTbA21bt1BO3fulGQ2dDVseIYCgd6CgYJz87VdqVCoqCZPnqzk5GraN2/Ri4IiSkhI\n1oQJb0iSKlVqIJibr82T6tCh62FdU/v2XeTzdRfMEjzgKKE1MnsaVub17fVep/vuO3Bk0eFy5513\nKxKpJbhfwWA31a3bLG8fw4mAiTLqu49JsHTp6vEWq1DAVkyzWA7MaaedxptvPk/XrpeRlRUBLgS2\nA1tYtepO1qx5lZycnUAmJsdPjIQED61bN6dx47OQxEUXdWLp0j/IyJgJPA3kz4ETJTMznYsvvpY9\neyLA5nyfbcLl8vLFF5/QoEEDAMqVK83KlVOA04AY8AkzZ37Knj17CIVCh3RNEye+Qv/+1/Daa+ch\nVQOeJhC4keTk6mzefCV79owEluL3v8x55808muHLY/jwu6hfvxYzZnxFxYrNueqqgQQCgQLp+1iw\na9dusrJK5XunFHv27I6bPJbDJ96K1nISMWHCGwqHS8vsNPYJtjtmnSRBPUEbwfMKBC5U5cp15Xan\nCD4WTJXLVVo+X4pjr//NMQU9IfhSodDZ8nqLOs7WlwURwb2CYYIkBQKl1Lbtubrssiu1aNEivfLK\nK3K5ighaC+oLWiohoUpeSOrh8O2336pRozYqU6amevfury1btmjw4CGqUKGu6tdvecQO5JORefPm\nKRxOFkwW/KhQqIP6978m3mIVCliTkcXy90ybNk19+vSXy+WTSadwhuBtmdxEDwrqqVmzVqpcuYFg\nfD7zwttyuYrL5eoj+EDQQR5PCVWv3kQdO3YReAULHL9ATUFVwZlyuVrK5UoSPC2Xa4QSEpI1ZcoU\nBQIlBBMcX8PPCgSK/GXEUS4FsXP4n8zHH3+sGjUaq1Sp6ho06EZlZGTEW6RCAasQLJZDxyR4O1cm\nGmhOvol/lPr1u1rFi1cWjMn3/rOC4nK7UwVnCgYrGOyo005rIRNVVF8mH9HNjj2/nlyu2nK5igs+\nydfPbera9ULdeedwhcNllJj4L4VCKXr88f0rfOVn48aNatWqszwev4oWLZXnj7BYDgS2YprlZCU9\nPZ0FCxYQDAapU6cObrcp5xGLxXjuuXHMnv0dNWpU4tprBxMMBg+pz4yMDO688x7Gj5/Apk3Fycl5\nEdiE39+VM844ja++mk16uoBbAQ8wEvABVzjPAd4E+gLfATUx9YMbAr0xfgYB5TH1Dpo7x4zE4xlN\nz57nc+WVl7NmzRpq165NrVq1/lLe1q3PYfbsKmRl3QcsJBQ6j1mzPqZhw4b7tJs8eTIzZ86ifPnS\n9O/f/5B9EpaTC1sxzXJSsnr1apUvf4oSEuoqEqmoM888L2+Zf/nlA53NWWMUDHZRkyZtlZWVdVj9\nZ2Vl6frrb1VyciUlJpaS31/F8TF0lUkdUUZQwfEzhAWX5d3tu91XyuWqmu/uX4Lqgkfzvb5MbndV\nZ5XwstNPDUFEXm9Iw4bde1C5br31v6pYsZ7q1m0ht9unvekopEBgkEaPHr3PMcOHj1Q4XF3wPwWD\n56tBgxYnrUnE8tdwnJuMPMA44EvgC6A2UNV5/TkwlgNrs3iPqyXO1K17uiA3Q2WmgsEOeuihUU6e\n/ajjGJYgW5FI7SN2omZnZ8vnCwlWa+9mr+aOEnA7ymGUoKJcrmaKRs9R0aKpcrsj+UxO3wpC8no7\ny+wRSFMweLZatmwntzvZcVqXckxLtQVvKRKpesBU0DfccJvC4ZYy4amvCUIyeYkkyFEk0lovv7w3\nhj4rK8vZOLZX/hNtn4Cl4OAwFcKxLqF5Lia+7gzgTuBe4GHgdqAVRhl0OcYyWY5zfvzxRxYu/Bm4\nyHnHR3r6+dx33+OMG/cCbncQSHA+87B7t58ePS5n1apVh32u7OxsYrEcILfEogsoDlwCZAOTMF/b\nt3G7v2PMmO54vX5isW5AB6AC0JJbb72O1q09BAIp+P2pdOhQjI8+mkxSUhjYCHQDlgH3AVeSlnYW\nc+bM2U+e8eNfJy1tDOZnchmQjcvVHr//KiKRdtSq5eLCCy/Ma5+VlYWZB1Ly5He5yrJr167DHouj\nYc2aNTzyyCOMGjWK33777Zie23Ji4XH+9gVeAFbn++x84PEDHBNvRWuJAzk5OXr22WfVpk0HuVwl\nBTc4d+x7BM0ElysUqq6yZWvI6x0oky/oAUEFud13qFGj1kd03nbtznM2Li2W2VAWFvyez/xzltzu\nf6levaaqVaup3O4ygkdkaiP8IJ8vqk2bNikWi2n9+vX7lKH89ttvnUik7Hz9XSK/v4ZefPHF/WQp\nV66WoKegi3PdW+X1NlK3bt31yiuvHNAU1KJFB/n9/QXLBC8rGi2p1atXH9FYHAnLli1T0aKlFAhc\nIb9/gKLRklq4cOExO79lLxznJqNcXgC2Ae2BNfnebweMP0D7eI+rJQ706PFvhcPNBQ8JWsjE/Fdx\n/iYK1gs+VcWK9VSnTlOZRHLnyKSk2CGfL3RE592+fbsuuugylSxZRcnJVeRy+QW/OpP3DkEJValS\nW6FQCUdhTBU0FIwUbJfPF9b27dsP2Hd2drb8/rBgeZ6JC2qrfv0mB/R7vPzyK0646mf5FMiLOv/8\nngeVf8uWLerSpaeSkiqoTp3TNWfOnCMahyOlZ8//yO0enievyzVK55578TGVwWLgBNmpfBlmTTsH\nsyU0lyhGUezHsGHD8p63adOGNm3aFJpwlviyaNEiJk2axFtvvUFW1u9AUWAwUAG3200sth0oBVQH\nstm8OUyDBi1ZsiSTzMx3AD/wASVLljui8ycmJjJhwvN5rx955DHuvLMF0B6XazYXX3wJxYtHeegh\nH9DHafUs0JVw+H0uuqgPiYmJB+zb4/HwwAMPcPvtbUlPvwSf72uqVo0wZ84XeL37/xx79erJmDHP\nMXfuV0htAPD7v6ZixdIHlb9YsWJMmvTKEV17QbBhw1ZisfZ5r6XqbNz4cdzk+ScxY8YMZsyYEW8x\nDpnewG3O80RgBTAFaO289xQmn8CfibeitRQyzz//oho0aK2qVRvJ709UMPhv5667rXKTt7lcNeXz\nVZMpEvOwcwe62HndX5AsEwnUVh5PdJ889zk5ORo3bpyuueZGPfPMM/tkDT0U5s6dq2eeeUbTp09X\nLBbTHXc+3rIDAAAgAElEQVTcJbf7hnx37V8oHC6lxx8f+5cZS3P59NNPNWLECI0bN+6ANQfys3z5\ncpUoUVbR6HlKSDhTFSqcErdqY4fCk0/+n8LheoJfBCsUDjfRAw+MirdY/0g4zk1GIUww9kzgK+A8\noBoww3n9LDbK6B/HSy+9rHC4sszO33cEqYI3BTcKygnOFtwtU1dgk0y6iZgzEf8hOE8w1om+CQgG\nKBSqrg8//FCS2dV70UV9FQ6fLrhP4XBLdenS46C7fWOxmMaPf1l9+16pu+4adkDzz/LlyxWNlpTb\nPUwm02kFPfvsuLzj58yZo/fee++Q6gTEYjG9/vrruummW/T0008f0HS0adMmTZgwQW+//bZ27dp1\nOMN7zInFYho6dIQSE1MUjZbUkCF3HJKStBQ8HOcK4UiJ97haCpEmTdoLJuW72x4rE5b5H5m0Dm0c\nn0FpmVQQUZldwncLigrKO++VEFwoaCC3u5rGjh0ryTg5Q6EUwW6n/z0Kh8vsVxpyzZo16tKlp4oX\nr+DsGagvkzU0qN69++ynQH755Rf9+99XqVu3PnrnnYmSzGTYq9cVikQqKTHxbCUkJOvTTz/9y+sf\nNOgGRSL1BSMUDrdV+/Zd7ARqKRAoJIVwFtAfqIu5yz/WxHtcLYVIy5bnCF7JpxCuFpySbxWwx1EI\nM53VQk/BpYJiglVOm+KCb5S7TwFO0YMPPihJmj9/vqLRmvn6l8Lh2vs4W3fv3q3y5WvK47nNWWWc\nJ+gjk+dooaCELrro4I7cXD788EMlJNTJp3ymKCmp/EHbb9y40dlHsSVP9kikmr7++uvDGsOsrKzj\nfuVgOfZQCPsQRmI8Z/2BxpiNZRZLgXHXXdcSCl0PPAY8hMv1LPt+jz2Y7StlgGeAqUAtTNrockAO\nJo31qU57Hz5fY6LRKAA1atSgWDFwu4djYv/vJS3tNx577BknZh/mzp3L1q1RcnKGOef+ArNHIITZ\nP9mPN9+cQFZW1l9ey8qVK8nJaQ6EnXfasXnzanJycg7YfteuXXi9UYzj3Mju8ZRi586dfz1o+bjn\nnvsIBsMkJhalXr3T2bRp0yEfa7EcLl84fz9z/n4dBxnirWgthczMmTPVrduluvjiy/Tggw/K5Soh\ns+9giuBiZzWwTCaVdKJjIkp0zEpDHF/DHTJhnD/I7y+h+fPn5/W/bNkyp32is/poKre7hL744gtJ\n0ldffaWEhNoyxXEucMxPH2vvbuVz5HZ7tXv37r+8jtmzZyscLiuTGltyuR5XtWoND9o+Oztb1ao1\nkNd7u2CFXK4nVbx4GW3duvWQxm3ixIlyuYoJWsmU50xU48atDulYy8kPhWAy+goTGvoZ5lZtVkGf\n4BCI97haCpHdu3erdOnKziQfVnJyKfl8UcElgnYytY3DjmJIcCb+XwWPO+/fKvi3M9l7BQnyeML6\n4Ycf8s6xevVqGWf0GmeSnyMoLp8vqtNPb68VK1aoUaNWCgYvEjzpbITLzVnUWi5XabVrd+4hXc+o\nUWPk90cUCqWqTJlq+uWXX/6y/Zo1a9S27XkqVqysGjZspZ9++umQx+7sszsKOuYzr02S2130kI+3\nnNxQCArhQuAnYAMwD+hV0Cc4BOI9rpaj5Ntvv1XnzhepZctz9dxzz+/joK1T51SZRG8jHCfx2TIO\n5ARBDXm9UZUoUdmx7RfPN/lJ0FTwqfP8VkepdBBUVbVqDfJCOjdt2iSTBygmE6mUKnhBsF4ez92q\nUqWeduzYoTvvHKZu3XrrgQce1qRJk1SlSi0lJ5fXpZf2yyujeSjs3LlTq1atOuzw1sOlU6fOgjvz\njccqud3RQj2n5cSBQnIqlwOaYHL4xoN4j6vlKFi4cKEikSTnjv5thcM19Oijj+d97nYnOcog6EzU\nJWTCT6sIKsjlaiV4VWa/QYJgqzP5ZQgqam9d4secVcITgiwFAm319NNPSzLRP9WqNRRcL+PAbplv\nEo0pFErVqlWr4jVER8wHH3zgVHRbIkgX9NYZZ5wdb7EsxwkUglN5GDAQs6v4QUxieIvlkHnhhZdJ\nSxsADAK6kZb2Ag8//FTe5yZl+0PAh8A6YDImhqEcsArpQyAVqIOpQ9AWGIHJkZibtO1T4H5gDOYr\nu4KMjDasXPmbcw4Xn3/+IW3aLCUUugqXawWmdjLAJnJydh10d/HxTOfOnRk16k78/lNxuRJo3nw9\n7733erzFspygHIpCOB+TjRTgYue1xXLImCId+W9UYrmFOwDo0aMjJmtJOvAJJlqoAqbgjBsTYVQU\nk/bqXsw9ySbge9xuDyYl1o3AA5iciacC3xKJTKBJk9PyzpOamspnn73H7t1b6dTpdCKRdrhcdxCJ\ntOK6666nSJEihTMAhcy1115NevoOMjP3MGvWJxQtWvTvD7JYjpC5QMB57gdmx0GGeK+8LEfBokWL\nHJPRaMHrCoer6bHHxuZ9Pn/+fJmC9Gc4PoE6jr3/KcFp2lvvuL6gruMrqCFoJJ+vuEKhYjJ7FCST\nNC5BXm9QQ4bcedDdyNnZ2XrppZc0dOgwvffee8dqKCzHCdOmTVOdOs1VvnwdXX/9rX+bPuREhULw\nIfwHWAK8AyzC3IIda+I9rpZDJDMzU+vWrdvPmTpnzhxVq9ZACQnlVa9e87zIm4yMDHXs2E0u1y3a\nG+LZV3CW8/phmfxE58rkK+rgRAuVFURVvnwtJSeXc/wL9QSJ8vuLaPny5fvJlp6erilTpuj9998/\naDbSQ2XNmjX68ssvtW7duqPqx3Ls+eGHHxQKJTk3Gd8pHD5TAwdeH2+xCgUKyamcDDQFkgqj80Mg\n3uN6UrBr1y7NmDFDX3/9daFEv3zwwQeKRIorGExSsWKlNGvWrLzP+vQZoFDoLMFUuVwPqkiRVH3+\n+edKTa3sVBGbms/J+6rMXoFnZUpXJggqyVQuC2pvOcsbBCH5fCUcR/NYwfUKBmto4sSJ+8i2fft2\n1azZSNFoEyUmtlNKSiX99ttvf3tNWVlZ2rx58z4rjeeee0GhUHFFo43l9UbVqlUHffLJJwU3kJZC\nZdiwu+V235zv+7ZMxYqVjbdYhQIFqBDucv6+9qfHqwV1gsMg3uN6wrNq1SqVKVNNiYlNlZBQU82a\nnak9e/YccX/r1q3ThRf2Vb16LdW//zVatmyZYxb6yvmRvaciRVKVlpamnJwcp6zjlrwfYTjcQ6mp\nVeVyPSG4SdDdiRraLbP3oJ48nuKOKSk3T1E5J6roR5l0EvUcReER3OKsEk4VVJXLlaiOHS/Iywp6\n8813OEVvTMiqxzN8vxz9sVhMd901XEWLllaxYmXUtetFCgQS5Pcnqnz5mvr555+1du1ahULFBT87\n17JAEFUolKpXX33tqP5HlmPDgw8+KL//8nwKYbZKlaoWb7EKBQpQIdR3/nYF2uR7tC6oExwG8R7X\nE56zz75AHs/dyi3KEgx21YgRI4+or927d6tChVPk9d4s+FSBQG/VqtVYiYn5QzmlhISqWrRokWKx\nmHy+sGBdPoXQ1ZnI9zhK4Dxn8g8JLpLf30Jud9CZ4HfK7EDuK2gss0HtIsFQmX0Jic7KoazgPpmd\nxklyu8/Saae1liR17Xqp4Pl88n2uWrVO3+e6HntsrMLhBs5k/7OguuAumR3HY1W+/Cl644035PHU\n2uc6jV/jaVWsWO9o/02WY8CGDRuUmJjqmCAfkseTov/7v2fiLVahQAGGnc53/g7BpKfOfcw8/Pnc\nEm+WLFlOTk5n55WH9PSz+emnZUfU15w5c9iyJUp29v1AWzIyxrF8+UoyMn4C/nBaLSM7eyOpqam4\nXC4GD76GcPg84BW83iF4vV9j8gR9gMn78wpQAq8XfL73yMr6gVgsBRN+moDZJD8IWIqJKjobU201\ngvnOe4GamH2TbwI1iMUqsGDBd2zdupVWrRoTDj+PCVPNIhB4ihYtGgMwceJErr9+CKNG/R9paf8F\najiPkcAPAEhXsmbNSvr06U9OzmpggXOd32Kin2qRkZF+RONpObasWLGCzMxsTFTbT7jdVfjyy2/j\nLdZxwaGEnW4GrgU6Yn6FHQpVIkuhcNpp9fH7X8CEcKYRDr9Os2YNjqgvj8cDZLD35iObWCyDRo1q\n4/PVIBo9h1CoBaNHP0SxYsUAeOihe3nggf/QqdNk+vbdQ2ZmGtAdM+E3ACoCW7njjptp0OB0pIEY\nhfGRIzOYWkoBTJzDvzEhqNsw1s0fgOaYr2k2Zt9CSWKxLEKhENdcM4hu3arj86Xg9yfRrNk2Hnnk\nXoYOHUHv3rczenQJfvttJyZ+IpclGGUEJsQV0tPrYBLstcKExp4F3EI4PITLLutxRONpObZ89NHH\nZGT0B14ExpGV9SqTJ78Xb7FOGF4Anv/T41gT75XXCc+mTZtUr97pCodLKxAopu7dex+xYzkjI0N1\n6zZTINBH8LJ8vgZyu4vJ7b5FgUBXpaRU1rfffrvPMStWrNDkyZO1YMECrV27Vh5Pbm6iZMH/Cb4T\n3CS3u6hjAqogU/MgUVBbZmdxGUHlfKaauwTV8r2OOT6FhwRh+f2ldeut/9XmzZt11VXX68wz/6Xb\nb/+v1q1bp1gspszMTMe3sdY5fqEgIo9ngHy+AfL5EhUKlVc02k2hUJK6dOkqU8Ut5vhDHhJEVaFC\nPf33v/cUepoKS8EwatQoBQI98n1vPlPZsqfEW6xCgQKOMqoLVCnIDo+QeI/rSUFOTo5Wrlx5SFW8\n/o4dO3boxhtv09lnXyi/v7jgi7wfWDDYVWPHjlV2drbefPNN9e7dR35/ESUmdlIoVEq33HKXfL6I\nTPTQv/P9MDMELsd2n+a8N91pd6ejDCKCl51H1FES6U7bnU7bavJ4Oql///7avXu3qlSpJ7//SsEb\nCoU6qFu3XpJMviGjELLzZIhEOqpnz5564IEH9Ouvv+rzzz/X66+/rqVLl2ru3LlyuRJlajE8LWgk\nv7+YLWZzgrF161alplaR291dcIv8/hJ6++234y1WoUABKoT/YTKdzsPUQo4n8R5Xy0Ho2fM/ziS9\nVnsn9uv0n//8Rx07dlMoVM+ZyKPO3fU8BQIp8nhCjiO4jiBLudEepq9TnEl3gkziOpfAL+gkE2lU\nTCYJXjOZCmmtBSOdlURPwa8Kh8vo66+/1pQpUxSNnq69CfF2y+dL0ObNmyVJzZu3l98/QCYX0IuK\nRktqzZo1B73ekSMfkNsdltebqmCwiL788sujGr+cnBxb2OYYs3LlSiUkJAnOEVygQKCi7rvvoXiL\nVShQgArhK0x94zCmIkk8ife4Wg5ARkaGPB6/THbSroK3ZEpfBgSJCgYrOyach2V2EP/XuYN3yUQT\nBR2TUV3B5TIRQ8Vk0luPkzEbFZOJLqruHDtYcLUqVqzoHPuHjMnpEoFPXm+S/P4EjRo1RpKpYBaN\nttpnFeL3J2rjxo2SpC1btqhLl55KTq6k+vXP2M/UdSA2bNigBQsWHPVEPmHCGwqFisjrDapq1fpa\ntmzZUfVnOTT+97975fVene87MV/JyRXjLVahQAEqhE8P8jwexHtcLQdgr0IYLZOZNCyzmWyUTLqJ\noEy6iRzBYpn9A5WcSf4TwZOCbs7q4b+C6wRX5vuhfqu9PoPtznGNBH653V5H+ZR0zlVC4Nbnn3++\nT5rqnTt3qmzZ6vJ6bxF8rFComzp06BrHUTMsXrxYoVCy4HtBTC7XKFWtWj/eYv0jGDHif/J4rs33\nPftJSUkV4i1WoUABhp26DvLc8g9DEtnZ2fu97/f76dGjD8Hgy5hw06rAN8BbwEWYbKQrMYFpHTB5\nETdjIoDaYyJ0ZmBKVD4CjGXfkt1h9kYYJQKlgd+AFcRiN2JcXDOBu4EfATedOnXh9ddfzytZmZCQ\nwJw5M+jW7Q/KlLmR0qWX07RpQzIyMgpkbI6UuXPn4vGchYmwciFdx8qVP7N79+64yvVP4OKLLyIU\nehVTsvV9IpFLGTSoX7zFOu7ZgUlkNxtTsDb3+VdxkCXeijburF+/XjNmzDhgjp7CICMjQzNmzNAd\nd9zh2FvdSkqqpAYN2uiKK67OK/GYlZWlu+++VyVKlHHu0ovIOHfNBjizWaycjFP4WZlooahMVNEA\np30fwWNyuUrnW2VMdXwCXQSZMvUREmT8CxL8LhOBNMF53sHp9xLBKapbt1le1E8sFtOZZ56nUOgc\nwTiFQl3UsmXHuDqDp06dqoSEWjIb8yT4XqFQkYMm47MULPPnz1fnzhepWbOzNXr04yftuFOAJqOK\nf/E41sR7XOPKBx98oHC4hIoUaa5gMEkjRjxQaOfatm2bfvzxR9Wu3UShUA1nwp4rU7O3p+BD+f39\nVatW430yRGZkZCgcTnbMOvkrmtWVcfyWc56fnc9/UEQmFcVmp+1KGedxfUEtx1yU63MoI+MELCKz\ns1lyuQbI7S7mnDPkmJgk46SupUcffVSS9PPPPzt1jjNl6iQPld9fQt9//32hjePfEYvF1L17HyUk\n1FJCQk+FQsl6/fUJcZPHcnJCISW3izfxHte4kZGRoUikuPbmCFqjUChVCxcuLPBzjRhxv/z+BHm9\nKYIkx67fTyaNQ3ntDc+MKSHhlH0csEuWLFGRIqnOhH2lYL7gXsfOP0LGV5CrKJ5xJvvPBP+RSWWd\n4fgJfII2MpXTXnQUxMa888Jp8vtbKRS6VEWLltINN9yiYLC1ozRyo5UkuFS9epnw0h9//FEJCVVl\n0lpUEdwmaKJGjVrGde9ALBbTtGnT9OKLL2rRokVxk8Ny8oJVCCcXq1evViiUkm+ikxITz9GkSZMK\n9Dzvv/++QqFy2luE/hFBTZn6BD/JmH5yJ9wcJSRU17x58ySZesnVqp0ql+thZ/Iu7SiCJMFrMs7i\nB/NdwyLt3VAWc9qfLhNW2kcmPHWmzF6EgPbuM5BcrjPVo0cPjR07VuvWrVNWVpYT+hoV3O7I+K0g\nUY888ogkY9aqUeNUR7mszltFJCTU07Rp0wp0HC2W4wmsQji5yMzMVJEiKY6pQ4KlCoWS8+oJHC1Z\nWVm68MI+zr6AsEz4aJrz8Ak6y5h6KsokoHtLgUBvNWx4htasWaMGDVrI5SoqEzL6lGOWedBZKTSR\nyUj6sKNc1jsT9qVOX28I5jmrj1Sn/R4Zk9GXzvV2l/EjzJLZGVxcTZq0zZN/x44dmjJligYNutqR\nwy2IqGbNBsrKysprt3TpUrndYeU3ZyUmnq+33nqrQMbRYjke4TAVwl9FDz1/sMkZk0jmWOJc2z+T\nL774gnPP7Y5UjKys9Ywe/RADBlxRIH3/738PcO+9U0lLexeTIK4HJlqoOdCbQMBPhQpluOKKS1m8\neBm//voH9erVYNiw22jevD2LFzcF+gETgYcxX6l0TPnLWpj6xqOBHEwNYzcmH5EHE4X0FVDM+WwL\nJnfR55h8QaOB34E7gMpAJWAICQld2LlzI7/99hvNmrUjLa0MsdgOypTxcsUVl1CxYkW6du2K1+vN\nu05J1K/fnMWLW5OdfR3wJdHoIH7++XtKly5dIGNpsRxvOKVqCyRK9DTnMQHzi68BXIbJCHWsibOe\njT+7du3SwoUL83bYFhTt218geD2fOecTud1lFY2W1Pvvv681a9YcMAJjyZIlCofLa18HcmMZ/0FU\n+dNBQAOZdNWZMjuCi+Qz3fzurExukEljERH45fFEFA6XVeXK9RUM1neOleAV1ajRSJLUsWN3eTz3\n5JmxgsGLNHTo8INe67p169SqVWclJCSpatUGmj17doGOpcVyvEEB7kP41nmUwNyu/YJJdFf2CCd1\ny1EQiUSoXbs2xYsXL9B+q1evgN//KXu/N1OpVCmRbt068euvv1KyZMncu4x9cLlcZGbuAPY472QD\nW4FumNXAbc5nX2CyhjYCfE6bSkAZ57iyzuNd4CfMyqQeXbtewPbtK3nyyQdIScnA56tJQkIHEhNv\n4OWXn+L9999n9uxZ5OTMxKw0ziY9PZXFi1ce9FpTU1OZOfMDdu7cyNKl39OsWbMjHTaL5aTkUJYS\ns4D/AnMxv7ybMYVyjgQfMA6TNzgAjAAWYxRNDFiISXr/Z63mKDvLn9m0aRP33vsg8+cvpmrVMlx1\n1ZVs2bKF7du306xZM1JTU//y+K1bt1KpUl22by+B2RS2CGM6KgmkUbp0iCVLviMcDvPHH3/g8Xh4\n++1JXHvtDWRmAlTHLBw/cnrsDozBbGP5DQhi/u0hzCa0IFAHY2I6C/gEuAB4H9gJ9AFq0LlzOVas\nWMEvv/yB5AJi+P07mDRpAgsWLGL48CdJS6uN2ZD2FGarTH8GD+7LmDGjj3pcLZaTgYI0GeVSA5iM\nWSFM5Oj2IVwGjHKeFwNWYW4NWznvPYmp0PZn4r3yOi7Ztm2bypatLrd7gEwoZw1BggKBmkpMPEfR\naEnNnTt3n2OWLFmiWrWayO32yOdLVunSNeVyBRwH732CFMH1jikoR9BF7dqdrdatOysQKCafL9GJ\n/V8suFZmX0EtmWRztWT2DQSdh19m81iC45guLvDKVEGLOu+HZPIW5ZqX7pbbHVGnTv+S231ZPjku\nFnRQkyZnyu8PC36ViUyanu/YR9S7d/8jHs8lS5Zo9OjReuqpp/I23lksJzIUUpRRdeAcoByHVlTn\nYETYW3GkBLAc4zXM5XxMGaw/E+9xPS556aWXnN23uRPiGmcSzrW3v6oaNU7La5+VlaUyZarJ7BpO\nkikpOdmZtGOCiTIhoDPy9TleUExud1en3z2CtjJ7DAbK5C3aIZOIrpRMNNFZMmGqa51+/+d8HnHO\n+6zjN/hNJgppWr7z9VfPnr3UuPFZgg/zvf+WIFWVK9eX2+1zZGkleDevjcs1XP37Dz6sMdy0aZM6\ndequhIQUuVxF5PX+S+HwhSpdumpeAjyL5USFAvQh5DIYc+c+ArgQYw84UnZjahhGMXUO7/yTDLuA\nIkfR/z+KzMxMYrGEfO8kYP7/uUPamrVrV+V9+vvvv7NlSxrGjt8cuASj56sCNwClMKaeFzAWvAxM\nsJmbWOwqjOknCAzAlL5MwlQr646pXBYF1gG/Ou+VwqxWrwLWYvwMtYFrHIlSMNbI3sADwNWEw+9w\nzz3DqVKlLDDekSMH83WJ0axZQ1q2bI+pmtYDE+8wFhiBz/cw11wz4JDGbvXq1XTp0pOyZWszZUoS\nu3bNQXqK7OxZpKU9wsaNZ/LII0fzVbdYTjy8f9+ESzAmnWkYc8/RFh8tB7wDPAG8hpkJcoliZpb9\nGDZsWN7zNm3a0KZNm6MU48REEvff/zBPPPG883o1JklXI+AeTBK4DUAqXu+jNGrUhHfffZcZM74k\nEgmwZ882jC0foAkmke1oPJ4uRKMT2LYtC2PFm4yZiIWxGn6ISUgnjN1/HsbfEMEktBsJDMTo9OYY\nn8B9GFfRJIwPoRVGSXxLYmKU3bv/RU7O1bhcLfF676VChdKsXLmDatVOoWLFShiLYimMEqqGxxNi\n0KB+1KpVi+TkKmRnfwYUx5TWXEO/fr2pXbv2347hrl27aNq0LevXX0Asth2zKPUA5TGJ+b4gK6sW\n69f/cjj/Gosl7syYMYMZM2YU6jly6yJ85rz+8ij6SsE4kdvme28y0Np5/hRmFfJn4r3yOm549NHH\nFQ7Xk8kv9IWCwfIqV66GXK5icrsTFA4nyesNKhAoqjp1mmrIkNsVDlcXjJTLdY5MTqA9jinnKkEb\nhcPVNHz4vWrWrJ3jC2goU5FspWPnv8mx+TcXnCaTlygsqOr4HEKCDfnMO7do72a2pk7bPvuYfypV\nqq+bbrpDTZq0V8+eV2jkyPsVDjdxzF6NZTbE3e2YobrK7++lBg1a5G0269//GoVC7QU/CN5ROJys\nH3744ZDGcOrUqUpMbOGYnYLaGwKb41zfkwqHq2jixImF+a+0WAodCsGHMBgTO7gKE0py01H09SjG\ndvBZvkc9zC3rV8CzHNgjHu9xPW449dS22rtrWYJx6tKll3JycrRlyxbFYjGlpaVpypQpuv76m+R2\nB/JNeDGZKmMTndcfqESJqpowYYKaNm0nr7eXowQmObb+6TK7las4k/5zgkdldhavd/qYILOv4BHn\n9TYZ5/ItMknn6jq+g/vzybxQpUpV3+e6unXr4/Q/QSaXUe7+huVyuQK64YZb96lzkJGRocGDh6hM\nmVNUq1azw0pBMWPGDEWjDZxzjJRJozFMHk87uVxRRaMl9cgjYwrsf2axxAsKQSH4MFtOL3Im72IF\nfYJDIN7jesx45pnnVKVKQ1Wu3EBjxjyx36awM87orPxROS7XiP0iaz7++GOFwyVlKo95tdfJLJmU\nEc8LMuXxdNWFF/aSy1VE4FFuFtHc5HDG2fy4TPRRcWfiLyezySy3XY5MuoiQcqOcTNGaMs4KoZhM\ntbNkmYR3GwQdlJxcWX/88UeezDfeeKv8/n4y0VK98/WfLo/Ht08aiqMlIyNDdes2UyDQS/C8AoF6\nqlGjrsaOHav09PQCO4/FEm8oQIVQCmM8/hoTZVQDOAWYU1AnOAziPa7HhNdfn6BwuLJMYrcvFQ7X\n0LPPjpMkrV27Vqee2koul1cm4dtpgmYKBqP7ZT6tU6e5c5cv7U0Y94tMxFBUxixURMWLl5PbnSA4\n15m4f85bSXi9Z8jrDSkQqOHcQU8RvOAohSTBJqftREcB1BIMclYPHmdVkSrY4rQbImM6isqUxByo\n009vnyfzli1bVKlSHYXDzRyl8pZghfz+y3XmmecX+Fjv3LlTt956l7p2vVQPPjiqQBWOxXK8QAEq\nhH9hTDpb2WvemY7xXB5r4j2uByQWi+mzzz7TSy+9VCDpqE0aiZfz3R1PUvPmnSRJjRu3ldd7m3O3\n302mOP09gnqqXbvJPsVeKlTI9THkmnCaORN+EZl9A9UFqQoGT3WUw+sy5SzLC4YKOsvlSlTnzt2U\nlFQ5X18S3OUcU9xRSikydRLOkElOV0R79yCcn+84Oe/nKohdcrl8+1z/rl279M4776hv374qVqy8\nwrWJOIAAACAASURBVOFknXfexdq2bdtRj63F8k+Ew1QIfxVlNNF5dMbUKdyNqWG49khn9ZMJSVx+\n+VW89danuFyNyMm5iaeeepg+fS494j6j0TAmQiiXP4hEQkhi3rwviMU+wrhyZmG2cESAG/jpp7Lc\ndtud3H//vaxZs4Zt2zZiwjKvw6SP+A24H+Ozn43ZArKI9PRimN3Cr2ICv6pgNqKvRVrGzJnnEwrB\n3vQUYL4G6ZjIn5aYENfngJq4XIuRIphIIz8m/mC50+8EzNct0enneyTfPtcfiUTYunU7b745nbS0\nKwgEFvPTTz/h8XiOeEwtFkvBMgy413k+Abg1DjLEW9Hux6xZsxSJVBHsUm6O/0Aguk8VscPl/9u7\n7/CoqvSB49+ZTDIzd5JJAkmA0CGAFOlIh+AqIIKVsui6IDZc+6Ii/LCgK5ZVV7G3VXQFKyCICBZY\npBhQAZHeFFhqIBDSy7y/P85NE0QCSYaE9/M882TunTv3nnMH7rn3lPesWrVKfL4YMQPHHhLLiikM\nwBYdHS9mkpyVdvVMwV13rkCCNGzYSkREunS5QEw7QYSYKSjriBn8FSfwql2Pf5VdTSQCy+1ta9rb\n+sXMfyACN0mdOvXtp4A3BR62nw5629tGiOmptEkgV7ze+vaTQZz9FPOavU0du7qoupieStcJVBfL\nijrmHERH1xYzvabJn2VdIuPHj5fJkyfLJ598EtRpL5WqbCiHRuUff7OscyqLyEcffSR+/2UlqkTc\n7ijZv3//ae137dq1ctdd98gdd9xdohvljBkzxLJixeu9xq6WeVTMiGIzEY3D4ZUHHviHuN0RAhfa\nF++CAuMCMSOF64ppZO5hX7jTJTT0LmnfvqdcfvnlUqNGbbvKSASetS/gI+zvRQtcLyZkRa59XE+x\n6qS9Yur+Lbs66Tp7farAMvF4oqRZs/YSFtZRoL+43bHy73+/fUz+TfoL2idEQkL+JKGhseLx3Cw+\nXyfp3/8KLRSUOkmUQ4GwAjO6CEw9wLKyPsBJCPZ5PcbWrVvFsmLsO+yAOByvSJ06TUs9WfeiRYuk\nT59LpHPnvvL662+e8Ptr166V1157TSZOnGjHE4oUM/mMCOwRn6+RxMXVF2hoPwkUr/f32QVIlpip\nMX0C0dKsWfvC3j5bt26V2rWbSHh4S7vA2GZ/P1NMr6FZUtR9taVd8ETYBYclpq2ijl1YeMU0Qn8n\n0EOqV68vycnJ8vzzz8uDDz4kixYtOm4er7jiL+LxDBXYKiYshUtMb6W6AneLz3euzJs3r1TnWKmz\nFeVQIFyHiV88HTM0dURZH+AkBPu8HteMGTPFsqLF5fJIvXrNZf369aX6/ooVK+xCxcQUsqxm8sIL\nL5/Ud7du3WrH9CmostojISHnS58+fcTh8Nt36Pn2502lqIqo4IIeJpZVT3766acS+83IyJD58+eL\ny+Uv8fRjnjIixTR6j5Giqqi1UjRVpoiZG7mtQHMxjdTtBe6TsLD2UqtWM2nQoLX83/9N/N25jNPS\n0mT48OukWrW6UqNGfTHdVZPEVEv1kLCwNvKf//ynVOdZqbMV5RTcLhbojAleEwzBPq+/KxAIlBgw\nVeDgwYNyySXDJTa2obRr1+u4o2hHj75DTJ/77vaF82Zp3Lj9SR+7Xr3mYrpnbpKCEb0hIeeKGUzm\nsS/gkQJ97Tv6gvEIGwR84nb7jxvVMxAIiN8fL2YwWbbAl/ZTQLR95x8hZsBZQddWj5QcqXyPmK6q\nI+zlpfZ3ZwmsEMvqKuPGPfiH+bvmmhvFjIOQwv04HNGyZcuWkz5HSp3NKMPgdvfbf6dhAtrdiQma\nM/WULulVlMPhIDw8/Jj1/ftfyRdfRHPgwDxWrhxB79792b9/f4lt9u3bjQkSNxZzapdy+PChY/a1\ncOFCXn31Vb799tsS6z/88C38/lsICemBCQI3i/z8XZgewhmYmU47AR/jdKYSEtLBXtcNl8vJyy8/\nT1RU1HHzNGbMTZgpMS3gevt7LTDTVURgei5ttb/hx4SmEmAf5p/MDkyPqc/s/A0HBgEdych4iXfe\n+fB3z2mBatX8hIRsL7ZmOwkJjWjcuPEfflcpVbba2H8TMbGGir8qWrAL2lJJSUmR0NBwKT6NZETE\nQPnkk09KbHfllVeJmZC+6A44Li6hxDZjxowXn6+xWNZ1YlkNZMKEklNEPv74E3b9/Rz7bv5fdhVR\nnpi4QF5xOl0yZMhfZdq0adKpUxcJCQkVhyNUPJ44saxYueiiKyQtLa3EfrOzs8U0EjcSM3ahppge\nTvcLhEtoaGNxOn0Ct9gxksLtp5EwcTj8MnToUAkNrWZ/f6iYhua37XzOl4SEP34S2rlzp1SrVltC\nQ28Qp/NusayY3217UEodizIch9DWfh1zcS7NAc5GHo8HkTzgIGbmsQAie/D5fCW2q1MnHofjIEWT\nwR0iNja28PNt27bx0kuvk5m5ARPVcz///Oc5jB49itq1a7N69WoefPAxoD1muAiYB7knMcNFlgL1\ncLsPc9tt17NixUrWrhXy8z8DBpOV9TZwDnPn3sWFF17K0qVfMWvWLKZO/ZSoqHAsK5SMjH2Yp41n\nMB3OXgbyyM3dg+mRvJSQkAXce++dREZG0q5dOy644AIWLlzIRx8tx0yL6QE2AO2AvVjWczz22POF\n+Vy5ciV/+cvN7Nr1C+3adWTatNepVasWderU4eefV/Duu++SlZXN5Zd/w7nnnlsGv5BSqrTG2K95\nwHuYIPhvYWIZV7RgF7SlNnbs/WJZLQUeF693kHTs2PuYMQpbtmyRiIg4cTrHCTwtllVTZs6cWfj5\nsmXLJDKyY4nGXb+/lfz4448iIvLyyy+L232pmF5FBXGIdojpIdRXzHiAJIEnZOjQa8TjqWk3AMfa\nd/0F+00WcEuPHheKyxUt8Lw4nf8noaFegavtBuK6dmNxPTE9lJ4s9v2JEhZWT7zeOLnnngkiIjJ1\n6lRxuX7bkO2Wjh27y4IFCwrzuH//fomMrCkwRWCnuFzjpHnzjqXuraWUOhblcAM//zfLX5X1AU5C\nsM9rqQUCAfnoo4/k9tvHyLPPPiuZmZnH3W7Lli1yxx13y3XX3SILFy4s8dnhw4fti+UnYnoMTZPo\n6PjC6p0ZM2aIz9dBYKTdyHujQIxERdUSGC9mxjIRp/MeCQkJFzO2YLnAYDED0KbZVUvf21U+z4oZ\n1JYokCtO56USElJP4Ge7Kupi8ftjpGHDNgILil3sJ4gJkZ0sPl8DWbJkiWzZskW83hi7QTlf4Amx\nrBrHFIqfffaZ+P19SxQcHk+M7N69u3x+GKXOIpRDgfADRRFO4zj9CXJORbDPa6llZWXJV199JXPn\nzpXU1NRjPs/Lyzupu+CkpCSpXr2egFNiYurLDz/8UGIfffteJj5fO3G7+0hIiCVDhgyV9957T7ze\nmgJPidM5VrzeamIGoxVFEDVPEZH2HX+kmFhGBdFLWwt8I9BTHI4wAUuczlgJD4+V7777Tt588y2x\nrAYC7wg8ZT91mNHN4eFXydtvmwFns2fPFr8/ThyOEGncuI1s3br1mPwtWrRIwsNbiBnsJgL7JDTU\nOu45U0qVDuVQIFwGbANW2n/7lfUBTkKwz2uppKamSosWnSQioqP4/b2lZs1GsmPHDhExc/j26NFP\nnE6XWFaUvP76m5KUlCTduvWTZs3Ok/vue0Byc3MlKytLAoGA/P3v48TnSxCPZ5T4fA1l/PiHShwr\nPz9fJk2aJB6PX7zeP0l4+CCpUaOhfPzxx3LDDbfKnXfeI336XCAmEF3BHAMHxHRNvUXgDjHdSPOL\nFRi9xASma2hvmy8u151y/vmDRMRMRj969M3Srl13CQurLmbU9FsCD4jHEyvff/99YfoCgcAJw3nk\n5+fL+ecPEstKFHhAfL7mct99D5TDr/L7du/eLfPmzSuTAIVKnUkopzbfEMzUl6F/tGE5CfZ5LZWx\nYyeI231N4QU4JGSiDBw4TERE/vSnSyU09BYxPYLWiscTLx5PpJhYQYvF7W4rbnd1cThC7Dt7S+Cg\nfaHeL253tOzatavwWHfddZ89anli4QXd5bpHRo36mxw4cEDefvttcbv99pPAnwVeEhMp1S+wTmCN\nmDEGNwisFofjaQkJ8UuNGg0E/lGskNgq1avXk3nz5ollxYjPd42Eh3eWli07idPptwuRGyQ0NFpm\nz54ta9askaSkpN+tKisuNzdX3njjDZkw4X759NNPy+13OZ558+aJzxcjkZHni9dbS/7+93EVenyl\nyhPlUCD0Bn7GTH05ETNyuaIF+7yWymWX/UWKT2ID30rz5l1ERMTrjbTvusWu3/+7OJ1d7OXNdl3+\na3Zh8rWYBtzdhdsXb1T++uuvxedLsOv859qFzNcC90mXLhdKTExdsawrpKjb6BV2wRAjpgupiJkx\nrJ9Ae4mIqCM9e14kGzdulJdeekm83r5iwlYcFXhT2rTpIbVqJQjMt7+bJ2FhTSQs7KJiTx/zxO2O\nEcuqJxERraVu3Wayc+fOYP4cvys/P18iImIEFtlpPyQ+XwNZunRpsJOmVJmgDAemFfgHplDYixmp\ndEvpr+dnl549O2JZUzChovNwu1+lW7eOAERH18DUvgEEcLl+wOksmDX0fkxI6xswM4meD7TETAKf\nD0zD6TxE06ZNAdi4cSN5eR0xXTqvxwwcuxv4iqSkZSQnx5CRMRz4AhgJHMTpHIzLlU9IyCDgXOBV\nYDSWtZfPP5/GokWf07RpU6677jpiY3diBp1VJyRkDM8/P4lDh/ZiBrsBhJCXF0tubiuKZj5dTnb2\nOWRkbObo0dXs3j2cUaNuL9PzW1aOHj1KVlYmJow3QDQOR2e2bt16oq8pdVb7r/13gf13YRDSEOyC\n9oSWLFkil156tQwYMEzmzp0reXl5Mnz4KAkNDRe3O0p69OhXGN6ioMrFsq6V8PAe0qZNN6levY64\nXH8XE77CEjOvcUGk0FgxXT6dAuGSlJRUeNyZM2faTxD32U8JVxS7U58o0EHgHLuOf7pAXYmLayS/\n/PKLLFiwQFq0aCMul0eiomrKlCnvlsjTp59+KpbVVMzgtjwJDb1ZBg4cJr16DbDTmism8mmEOBzR\nYqKepojT2UrMvMsFT0erpXbt5hX6e5ysQCAgcXENxEwQZKrFLKumrF69OthJU6pMUIYD0wpsAR7H\nzKoyDhOzQNmWLVvGBRdcSmbmw4CHBQtG8f77rzBixFBatmxEo0aNGDZsGE6neRjr0qULd911Ez/9\ntIauXQdw9913c+DAAR5//BkWL/bw008x5Od3Ay6kqAy+APiQAQMSWbRoMQ8++BQRERbJyXswYabW\nAKswA9IK7tT7ArMxvYSbYAavXY7Pt4j4+HiuuuoGduzw4HYPISdnLjVqFA2IA/j226VkZPwVMycS\n5ObezbJlfVi3bgX9+w9m5UoPZsDZJESW4XT2weUSEhKasn37dDIzbwTcuFzTaNOmVbmc+9PlcDiY\nO/cT+va9lKys+8jLO8gTTzxJ69atg500pc5YYcDNwEvAbfZyRQt2Qfu7hgwZ+Zs74o+kZs3m4vM1\nlbCw28Tnay4333yXiIgcOXJEGjZsKV7vEHE6x4pl1ZDp06eLiIle+sYbb8gll1whTqdbTC+gK8V0\n64wWGCVO5232E8Q/BDrZr5fETFITJaYnUap99z5c4CYxXUxDBEaJx9NPbr/9XnnnnXfE5+stRaE1\nvpSaNRuXyNfkyZPF6x0oRb2P/iOtWnUVEZH58+eL39+r2NOIiGXVkW3btklubq5ceulw8XprSHh4\nE2ncuPUZP6YgOztbNm/eLEeOHAl2UpQqU1TAwLRgCPZ5/V2DB4+wL8oFBcIMcTiqSVHPoMPi9cbJ\n5s2bZfLkyeLxDCm27UKJj28qCxYsKNZzp7s0aNBSLKurfWG/SYomrRGBFwUKYgfFipmnoLtdIJxn\nr/eL6Ur6tcAQcTgixOuNlL/+9SbJzs6WJ598UkJD7yq2zxQJC/OVyFdmZqZ06NBLwsPPk4iIKyQi\nIk5WrFghIiZst8/X0G5wNmMHwsLC5dChQyJiqmK2bNkia9asOa0Z5JRSp4dyqDJKAS4FNmJCaoKZ\nH0EBt9wykjlzhpGZGQF48HjuAnxkZVWzt4gkNLQuBw8eJCXlMDk5xSN1NiYt7QjXXns7GRlvAQOB\nAIHAxdSp8z927+5MZmYa+fkTin0nAdOI3B5TVocCQzFDRL4DjgA5QHdgMD6fm02bNhAfH1+4h+7d\nu+NyDSY3tytgERLyGZ079yqRL4/Hw7JlXzF//nzS0tLo2fP5wn106NCBfv26M29eL7KyeuPxfMrt\nt48hOtqMX3Q4HBqRVKkqaiGmMrv4q6IFpXT98ccf5aOPPpJ169adcLv58+dL796DpHv3AfLOO+9K\nTExdMeMK0gXelejoeElNTZWkpCTxemsI/Fdgl3g8g2XYsGslPDxWinctdTjGywMPPCBz5syRG2+8\nSbzeZgI/CWwUE6KipRRFDjXVVObJ4KgUzXAWI15vlBw8eLBEWnNzc2X58uXSrFkbMbGOOorTGS6f\nf/655ObmSkZGxkmdm/z8fPnggw9k0qRJMnfu3FM+x0qp8kMZVxn5Mf0gg63CT+SECQ+LZdUWv/8y\nsawa8sorr5/0d9esWSMJCW0lJCRUGjVqLStXriz87JNPPpH4+KYSEREnf/7zKElPT5f+/a+U0NC/\niZnAZrNYVj355ptvRMRUvzz55DNSvXo9iYqKl/PPv0hq1WoiTufldv1+QByOMeLxxIoJOTFJoKvA\nnwTayt13jy88dmpqqrRp0008nsZi5ljuKHBI4EOJjIwXl8sjISFh0rv3ADl8+HDZnUylVFBQhgXC\nrcB2YDPQv6x2eooq9CRu3LhRvN44gX1SMGDs92YXKwsHDx6UHj36icPhEofDL5YVJ716DSgMdyEi\n8tBDj9oXbLd063ahJCS0kZCQBhISco7ExTWUWbNmidMZZjc0v243GG+S6Og6hfu47ba7xe0eUViQ\nmPaJW8XEJKonpotpjsDVEhfX5JinC6VU5UIZDky7GmgGdMUE2T9r7Ny5k7Cw5phYfgAJhIbGsnfv\n3nI5XrVq1Zg792NiYmoDE8nI+I4lSzrTq9dF5ObmMmPGDJ588h3y8raSn5/GihV12LbtV/Lzh5Gf\nP4SjR3PIzs7hhhuuxeFohRmkFgKk4XIVRRtZs2YT2dmXYH52B3AJpjno35jxhvGYNon72b//MEOG\njCyX/J4qEeGLL77ghRdeYNGiRcFOjlJVzokalTMxrZPJBC+GUVC0bNmSvLy1mAlmugGzCAlJ55NP\npvO//+0nMbEbQ4YMweFw/MGeTt7q1avJzo5DxJS9+fn3k5z8Dlu3buW//11KRsZIisYE3AfMxQwP\ngczMDjz++GRmzXqXDz/sxJEj4wkEGmFZTzBhwpjCY3Ts2IrvvnufrKxLMAXCW7hcK/D5QklP95OX\nJ/b6JKApixYFv4NZeno6s2fPJjs7m3nz/susWUnk5/fC6XyasWNv4oEH7gt2EpU6Kyz4nffBUOGP\nWnPmzBGfr5q43dWkWrXa0rhxS/F4zLgAn6+VjB17f5keb9WqVWJZ9e1xA2aUsttdTXbu3CnPPPOM\neDyXF+v3/45As2KNyrOkffs+IiLyyy+/yE033S6DB4+QDz74sMQx0tPTpXv3vmJZtcWy6kr79j1l\n7dq1kpqaKnXqNBMzUnqI3dj8H4mKqlWmeSytQ4cOScOGLSU8vK94vYPFjMH4zs7zHnG7/ZKcnBzU\nNCp1JqMM2xD2A1MxM6YXzJw+zV53ujpTVMgkAIuBRZjBb8e77Q7KyczNzZV9+/bJzJkzJTy8S7EL\n8j5xudySnZ1dZscKBAIycOBQsayeAv8Qn6+jjBgxWkTMhbx1664SHt5NwsMHi2VVF48nyu7J9IFY\nVj2ZOnXaSR9n06ZNsnHjRsnPzy9cf+TIEWnQ4Bxxu1uJy3WDWFbNk95nebnvvgkSFnZdsYLveYEB\nhcvh4Q1l06ZNQU2jUmcyynAcwlB7Zw5MBLTCi3NpDnAc9wJ/AdLs5WeA8ZgC4WXMmIdgTNN5DJfL\nRVxcHFlZWTgcNSkqq6oBTnJycggLK5uB2w6Hg5kzpzJlyhTWrdtIu3Z3ctVVVwFgWRbLly9g3rx5\npKWl0bv3s2zevJlHH51MTk4et976NEOGDD7p4zRp0uSY9X6/n/XrVzJt2jSSk5NJTJxFp06djrOH\nirNjx15ycjoWW3MeJtBfDg7HFHw+qF+/fpBSp5QqC1dgngqW2cu7in12CeZ//G8FtZTds2eP+P01\n7N47a8Xtvk569Oj3u9tv2bJFOnXqI35/DWnfvpds3LixxOeLFy+WJk3aS2RkLRkwYEil6c2zd+9e\nWbJkSYWFonj77SliWa0F9gpkSFjY5WJZNcTpDJGEhLaydu3aCkmHUpUV5TRBTllrQFGB8L9i688H\n3j3O9sE+r7J69Wrp2LGP1KrVVIYMGSGHDx+Ww4cPyz33jJfLL79GnnvuBcnPz5fMzEyJj08Qp/Mp\ngV3icEyWuLgGhfMgb9++XXy+GIGPBXZIWNjoExYuZ4pp0z4Qr7ea+P3niddbTd54461yP2YgEJCx\nY+8vHB8xaNAwycjIOKmpR5VSpS8Qyq6bTOk0wLRHdAV2YmZjA1NddAEmiF5x8uCDDxYuJCYmkpiY\nWO6JPJGsrCzatOnGL7+0JSenJ5b1JsOGteaOO26iZ8/hHD26rnBbv789X375Cueddx5Tpkzhllvm\nkZ5e0BSTR0iIj/T0VNxud3Ay8wdSUlKoXbsxmZkLgdbAJrzermzZsqZESIzyEggEyM/PJzT0rOrs\nplSpLVy4kIULFxYuT5w4EYJ3nT9pDSh6QpiFmYAH4BVgyHG2D3ZBe4w5c+ZIRES3Yg3NR8Tl8srP\nP/9sjxpOtdeniWXFy4YNG0REZPr06RIeXvx72yUszCrRwFtWNm7cKC1anCcul0caNGgly5cvP6X9\nrFq1Svz+lsUad0UiIzvL4sWLyzjFSqmyRDnMmFZeChI6BjM151JMI/fHQUtRKeTm5gLhFBW+HhyO\nEOrUqcOwYVfi8yUCE3C5WuJyhXLjjWNYtWoVF198MU2aOPF6BwIPYlnnM2nSpML5Eo5n06ZNjB07\nnjFjxrJq1aoSnwUCASZN+ifnnNOZDh368NVXXwGQk5NDYuIA1q+/hry8A/zyywQuvPASUlJSSp3X\n+vXrk5e3B1hhr1lDTs5mDWCnlAqKYBe0x0hJSZHY2PridE4S+FY8nj/Ln/40SERM3ff7778vbdt2\nkbCwXmLm7H1VwsNjZdu2bZKZmSkvvviijB8/Qb744osTHmft2rUSHh4rDsdYgQfEsmJkyZIlhZ8/\n9NCjYlkd7WN8JJYVK0lJSbJx40YJD29kj2u4T6CHuFx15N133z3B0X7fzJmfimVVE7+/lXi90TJ1\n6vuntB+lVMWhkjQql1aFnLwZM2ZIy5bdpHHj9vL440+dsPFy69atMmjQUKlWrbHExNSX66+/tbDh\nuIDXGymwp7Caxe2+QZ577rlSpemqq64Th+MxMZFT1wk8L4mJlxR+XqdOC4Hvi1XnPCx33nmP7N+/\nX8LC/AKDBQYKLBB4VCIja8qBAwdKd2JsKSkpsnLlykrTK0qpsx2VqMrojLJgwQKuuupm1q4dz9at\nz/Pww//hn//813G33bt3Lx079uSzz5pz6NATJCf7mDr1/WMmZw8JCaVouAU4nUdLPW4hNTUDkVSg\nEabNfTzbthUdxzREHyl2jMN4PGHExsZy1123AzOAD4BEYDz5+V348ssvS5WGAlFRUbRt25Zq1ar9\n8cZKKVVOyr0kHTFitMC/it1pL5KmTTsdd9sXX3xR3O6ri237q0CE1KzZqMRTxSOPPC6W1VzgDXG5\n/i5xcfVLfXc+bdr7dsiGz+1jbZLQ0OjCEbpTp04Ty6otMFmczvHi99eQ7du3i4gZaW0ioB4sTGt4\neF/58MMPT3BEpVRVgT4hnBqfz4PDcbDYmoN4vZ7jbisiBALFe3KFAE5SUlJITk4GTGNvbGw1Wreu\nwTnnvMqoUTmsWrWMmJiYUqWrZ88ehIZawEX2miZ4vd1Yt850ax0+/M9Mn/4m11zzM6NHZ7By5VIa\nNGgAmJHWN930NyzrYuBdQkNvIzr6V/r3D3Y0c6XUmeiM759qswu78rN582Y6dOhBWtr1iERjWU/x\n4YdvcvHFFx+z7e7du2nWrC1paXdg+uVPAprj9U4nNTUZl8vF6NF38u67y8jIGIXbvZhGjTawcuXi\nUo81yMnJITq6JhkZnwNdgD1YVgeSkubTqlWrP/x+IBDgxRdfYf78xTRoUIsHHxxX6kJJKVU52RGZ\nK8t1/qRVyOPVpk2b5I477pYbb7xNFi1a9IfbNmzYRpzOWHG7W4vHU70wumh6erq4XB6BFLuqJiAR\nEV3l888/P+6+1q9fL5dddrV07z5Annlm8jGN2bNmzRafL0YiI3uI1xsrjzzyRNlkWClVpVGGwe3O\nOh6Ph6ioCNzuUHy+E88c2qRJE7ZtW8Xy5cvZuXMnbdq0ISEhATBjFByOEIpmH3UAUWRlZR2znx07\ndnDeeb1JSxuDSDNWrnyE/fuTeeyxiYXbDBo0kC1b1rBhwwbq1q2r/f+VUuWisjxK2IVd+fn1119p\n27YrR48OJj8/Gst6mdmz3+f8888/pf316TOQZcuiyc6+DYdjEdHR/2Lz5jUleugEAgG6detNUlJj\n4G177VYiIrqRmrrvtPOklDq7lbbKSBuVbU8//TypqX8lP38yZhrLF7nnnkdOeX+zZ7/P8OERxMYO\nw+G4nyNHUuja9QJ+/fXXwm3eeuttfvxxByUnpBPy8vJO+biff/45CQntiItrxA033E52dvYp70sp\ndXbRAsF25EgagUDtYmtqc/Ro2u9u/1s5OTkllsPDw7njjhtJS8skEPiR/Px0tmwZysUXDyvcJBa6\n2AAAC+FJREFUZtGi5eTm3gDMBh4DPgEGkZsbYNmyZZTWDz/8wODBI9m69TEOHPiC997bxs03/73U\n+1FKnZ20QLANH34ZlvUkZp6eNVjWGK6++vI//F5SUhI1azbC47GIj09gxYoVhZ8tX74ch+NioDng\nIBC4h3Xrvi98AmjWrAEez2pgIbAReBQIJT9/NF9++VWp8zBnzudkZ18H9Aeakpn5ItOnzyj1fpRS\nZyctEGz9+/fn5Zcfo379W6lZ80ruuKMfEyaMPeF3UlNT6dfvMvbtexqRXPbseZy+fS8lLc08WcTH\nx+N0/ggUPD0sx++PweUybfl33nk755yzB4fjMmAHkAx8gsezierVSz8aOCIinNDQ4vMN7cLniyj1\nfpRS6kwW7N5bx5WUlCR+f/sSYaH9/tbyww8/iIjI0aNH5aKLrpDw8FYSETFMLCtGZs2aVWIfOTk5\n8sgjj0hYmF9CQm4Wy7pEmjRpI0ePHi11eg4ePCjx8QkSFjZS4GGxrFpBnxdZKRU8VJIJckrLztuZ\n5ddff+WcczqQlbUeiAX24/E0Z9OmVUyc+ARTprwJOGnduj1/+9tIevXqddz5jAFWrVrF/PnziYqK\n4uqrr/7Dbq+/5+DBg7z22uukpBxh4MCL6NWr1ynnTylVuZW2l5EWCKdp3LiHmDx5CiZ43ALGjLme\nmJhoxo2bao8u9uLxXMOIEfG88srxg+UppVR50AIhCBYvXsyGDRto0aIF3bp14/LLr2HmzPOBawu2\noHnze1i3rvQ9h5RS6lTpOIQg6NGjB9dffz3dunUDICGhLmFhiymovnM6F1O/fp0KT9f27dvp1KkP\nPl91WrbszE8//VThaVBKVR4auqKM7d+/n1279uJ0fkFoaGPc7iZ4PBt46aWFFZqO3NxcEhMHsGvX\ntQQCH7Bu3RwSEwewfftaIiMjKzQtSqnKQZ8QylB6ejqdOvXm44+jycp6DYejBU2apPPBB2+xbt06\ndu/eXWFp2b59O4cOZRMI3AvEAdcSCDRg5cqVFZYGpVTlok8IZWjx4sWkpFQnL+9pAHJyLmT16moM\nGjSS0NAW5OX9wOzZH9KnT59yT0tUVBS5uYeAQ0A1IJPc3F1ERUWV+7GVUpWTPiGUIdOAU7zrrxAI\nBMjIWMKRI1+Qnj6NoUNHVEha4uLiGD36Jny+Xjgc4/H5Eunfvydt2rSpkOMrpSof7WVUhjIyMmjV\n6jx27Tqf3Nw+hIa+Sn7+LwQCG+wt8nE4wsjJyS4crVyeRITZs2ezevVqEhISGDZsGE6n3gModbbQ\nbqdBlpyczLhxE9m06VcaN67F++9/RmbmUqA+DsfLNG78Kps3rwp2MpVSZwEtEM4wzz77AmPHjsPl\niiAqysc333xGs2bNgp0spdRZQAuEM1BaWhopKSnEx8cTEhIS7OScstTUVGbNmkVOTg79+/cnPj4+\n2ElSSp2AFgiqXCQnJ9OuXXdSUpoi4sfl+pqlS7+mZcuWwU6aUup36EhlVS4ee+wp9u27gPT02WRk\nvMfRo/dz223jgp0spVQZ0gKhChI5vWk4j2fnzn3k5rYrdox27N6t8z4rVZVogVDFvPjiK1hWFG63\nlz59BpKSklIm+73ookQs63lgN3AUr3cS/follsm+lVJnhjOlQHACrwBLgQVA4+Amp3L65ptvuPfe\nx8jKWkEgkMbSpfFcc83oMtn3yJF/5fbbLyMsrAkuVyyDBsXw5JMPl8m+lVJnhjOlUfkKYCAwCugM\njAMuK/a5NiqfhAcffIhHHslH5BF7zf/w+ztw5MjeMjuGiBl9XZl7Syl1tqisjcrdgS/s90lAxyCm\npdKqWbMGHs9KikJnrCQmpkaZHsPhcGhhoFQVdaYUCH4gtdhyPmdO2iqNkSNH0rRpCuHhfbCsa7Gs\na3njjWeDnSylVCVxpkQ7TQUiii07gUCQ0lJpeb1ekpK+4dNPP+XIkSP06fN/JCQkBDtZSqlK4kwp\nEJYAg4CPgC7AMVN7PfTQQ4XvExMTSUxMrKCkVS5ut5uhQ4cGOxlKqSBYuHAhCxcuPOXvnymNyg7g\nJaC1vXwtsKnY59qorJRSpaShK5RSSgGVt5eRUkqpINMCQSmlFKAFglJKKZsWCEoppQAtEJRSStm0\nQFBKKQVogaCUUsqmBYJSSilACwSllFI2LRBOw549e1i7di1ZWVnBTopSSp02LRBO0T33TKBhwxZ0\n7Xol9es3Z/369cFOklJKnRaNZXQK5s2bx5VX3k56+lKgOg7HKzRr9ibr168IdtKUUqqQxjKqAD//\n/DO5uRcB1QEQ+QtbtqwJbqKUUuo0aYFwCpo2bUpo6NfAUXvNLOrWbRrMJCml1Gk7UybIqVQGDhzI\nsGHzmDatGWFh9XA4dvDxx58FO1lKKXVatA3hNKxfv56DBw9y7rnnEhkZGezkKKVUCTpBjlJKKUAb\nlZVSSp0iLRCUUkoBWiAopZSyaYGglFIK0AJBKaWUTQsEpZRSgBYISimlbFogKKWUArRAUEopZdMC\nQSmlFKAFglJKKZsWCEoppYDgFAiXA+8VW+4CfAcsBh4IQnqUUkpR8QXCc8AkSkbfexkYDvQAOgNt\nKzhNQbdw4cJgJ6Fcaf4qr6qcN6j6+Sutii4QlgA3U1Qg+AE3sN1engdcUMFpCrqq/o9S81d5VeW8\nQdXPX2mVV4FwHbDmN68OwIe/2c4PpBZbPgroTDNKKRUE5TWF5pv264+kAhHFlv3A4XJJkVJKqTNO\nIjCt2PJKoBGmGmkO0Ok439kCiL70pS996atUry2UQnk9IZxIQUILjMb0OgrBtCGsOM53EiogXUop\npZRSSimllFKqUnACrwBLgQVA4+Amp8x0xuQHTHXYYmAR8BIlx2hURqHAu5j8JAGDqDp5DAH+jcnL\nt0BLqk7eiosDdgJNqXr5+xHzf28BpuNLVcvfOMz1cgUwgiqWvysw/wHBXERnBjEtZeVe4CfMjwYw\nC+hlv38ZuCwYiSpDI4Fn7PfRwA7gU6pGHi8F3rDf98bkq6rkrUAoMAPYADSjav379GAKhOKqUv4S\nMfkB8AETqWL/Pp8GhhZb3hWshJShKzCl9jJ7uXieLgFeqPAUlS0fEG6/rw5sxdxtFqjseQyx/44A\n3qbq/X7PAn0xd9DNqFr564wp6OYBX2PC5lSl/E0CHsXcOH+DGftVqvyd6cHtfjtwLZ8zP81/ZDqQ\nV2y5+CNcGpV/YF46Jh8RwEfABEr+ZpU9j/mYguA5TO+4qvT7jQQOAPPtZQdVK3/pwD+BfhT1biyu\nsucvFlMIDMbkbyql/P2C0e20NH47cM0JBIKUlvJSPD8RVI2BeXUxBd+LmDEnTxb7rCrkcSRQA1iO\nqYYoUNnzdi2mS/gFmJhiUzAXmQKVPX+bKOqXvxk4CLQr9nllz18ysB5zw7kJyAJqF/v8D/N3pt9t\nLwEG2O+7YOreq5qVmPpogIswjT+VWQ3MHea9mDtpqDp5vAbTaAeQiXla+J6qkTcw+UgE+gCrgL8C\nX1B18nctphoaIB5zgZxP1cnfYqC//T4esDBVY1UlfzgwDSFL7FfT4CanzDSgqFG5CbDQXn6DSt4L\nAFOVspuinhwLgNZUjTx6gQ+A/2LyMoiq9/sVWID5/1aV8ueiqAfcIsxNZlXKH8ATmCfX74ELqXr5\nU0oppZRSSimllFJKKaWUUkoppZRSSimllFJKqTNVIrAf0x//G0zsqVt/s00/4IaKTZZSSqmK1hsT\nC6ZAGLCdyh3rRqkTOtNDVygVLL8N7ObHhKr4CjNa+UtgFPCY/fkETAz6lcCN9rrbMCNEl9jvlVJK\nVUKJwD5MldHXmJg+F9nLl9rbjMAUCO0wcWQcmPkEngJaYCbRcWBCZn9N1Qm9oqqoMz3aqVLB9A0w\n/Dfr7gU2/mZdU0z8GAFygbsx83jUt/cBEIWZB2NTeSVWqdOlVUZKld5vQ7BvANpT9ITwhb1uLSZy\naB9MULWqGK1XVSH6hKDU8Yn9OpntVmMKgSWYm6yXMBf/rzFVSR7gO0wUWKWUUkoppZRSSimllFJK\nKaWUUkoppZRSSimllFJKKaWUUkqpquH/AdJgtZG2qwzJAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f7937580d50>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.scatter(boston.target, lm.predict(X))\n",
"plt.xlabel(\"Price\")\n",
"plt.ylabel(\"Predicted Price\")"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.6"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| apache-2.0 |
zlpure/CS231n | assignment1/features.ipynb | 1 | 355838 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Image features exercise\n",
"*Complete and hand in this completed worksheet (including its outputs and any supporting code outside of the worksheet) with your assignment submission. For more details see the [assignments page](http://vision.stanford.edu/teaching/cs231n/assignments.html) on the course website.*\n",
"\n",
"We have seen that we can achieve reasonable performance on an image classification task by training a linear classifier on the pixels of the input image. In this exercise we will show that we can improve our classification performance by training linear classifiers not on raw pixels but on features that are computed from the raw pixels.\n",
"\n",
"All of your work for this exercise will be done in this notebook."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import random\n",
"import numpy as np\n",
"from cs231n.data_utils import load_CIFAR10\n",
"import matplotlib.pyplot as plt\n",
"%matplotlib inline\n",
"plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots\n",
"plt.rcParams['image.interpolation'] = 'nearest'\n",
"plt.rcParams['image.cmap'] = 'gray'\n",
"\n",
"# for auto-reloading extenrnal modules\n",
"# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython\n",
"%load_ext autoreload\n",
"%autoreload 2"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Load data\n",
"Similar to previous exercises, we will load CIFAR-10 data from disk."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"ename": "MemoryError",
"evalue": "",
"output_type": "error",
"traceback": [
"\u001b[1;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[1;31mMemoryError\u001b[0m Traceback (most recent call last)",
"\u001b[1;32m<ipython-input-2-09809c4bd243>\u001b[0m in \u001b[0;36m<module>\u001b[1;34m()\u001b[0m\n\u001b[0;32m 19\u001b[0m \u001b[1;32mreturn\u001b[0m \u001b[0mX_train\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0my_train\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0mX_val\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0my_val\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0mX_test\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0my_test\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0;32m 20\u001b[0m \u001b[1;33m\u001b[0m\u001b[0m\n\u001b[1;32m---> 21\u001b[1;33m \u001b[0mX_train\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0my_train\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0mX_val\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0my_val\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0mX_test\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0my_test\u001b[0m \u001b[1;33m=\u001b[0m \u001b[0mget_CIFAR10_data\u001b[0m\u001b[1;33m(\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0m",
"\u001b[1;32m<ipython-input-2-09809c4bd243>\u001b[0m in \u001b[0;36mget_CIFAR10_data\u001b[1;34m(num_training, num_validation, num_test)\u001b[0m\n\u001b[0;32m 4\u001b[0m \u001b[1;31m# Load the raw CIFAR-10 data\u001b[0m\u001b[1;33m\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0;32m 5\u001b[0m \u001b[0mcifar10_dir\u001b[0m \u001b[1;33m=\u001b[0m \u001b[1;34m'cs231n/datasets/cifar-10-batches-py'\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[1;32m----> 6\u001b[1;33m \u001b[0mX_train\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0my_train\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0mX_test\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0my_test\u001b[0m \u001b[1;33m=\u001b[0m \u001b[0mload_CIFAR10\u001b[0m\u001b[1;33m(\u001b[0m\u001b[0mcifar10_dir\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0m\u001b[0;32m 7\u001b[0m \u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0;32m 8\u001b[0m \u001b[1;31m# Subsample the data\u001b[0m\u001b[1;33m\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n",
"\u001b[1;32m/home/zengliang/winter1516_assignment1/assignment1/cs231n/data_utils.py\u001b[0m in \u001b[0;36mload_CIFAR10\u001b[1;34m(ROOT)\u001b[0m\n\u001b[0;32m 23\u001b[0m \u001b[0mxs\u001b[0m\u001b[1;33m.\u001b[0m\u001b[0mappend\u001b[0m\u001b[1;33m(\u001b[0m\u001b[0mX\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0;32m 24\u001b[0m \u001b[0mys\u001b[0m\u001b[1;33m.\u001b[0m\u001b[0mappend\u001b[0m\u001b[1;33m(\u001b[0m\u001b[0mY\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[1;32m---> 25\u001b[1;33m \u001b[0mXtr\u001b[0m \u001b[1;33m=\u001b[0m \u001b[0mnp\u001b[0m\u001b[1;33m.\u001b[0m\u001b[0mconcatenate\u001b[0m\u001b[1;33m(\u001b[0m\u001b[0mxs\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0m\u001b[0;32m 26\u001b[0m \u001b[0mYtr\u001b[0m \u001b[1;33m=\u001b[0m \u001b[0mnp\u001b[0m\u001b[1;33m.\u001b[0m\u001b[0mconcatenate\u001b[0m\u001b[1;33m(\u001b[0m\u001b[0mys\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0;32m 27\u001b[0m \u001b[1;32mdel\u001b[0m \u001b[0mX\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0mY\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n",
"\u001b[1;31mMemoryError\u001b[0m: "
]
}
],
"source": [
"from cs231n.features import color_histogram_hsv, hog_feature\n",
"\n",
"def get_CIFAR10_data(num_training=49000, num_validation=1000, num_test=1000):\n",
" # Load the raw CIFAR-10 data\n",
" cifar10_dir = 'cs231n/datasets/cifar-10-batches-py'\n",
" X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)\n",
" \n",
" # Subsample the data\n",
" mask = range(num_training, num_training + num_validation)\n",
" X_val = X_train[mask]\n",
" y_val = y_train[mask]\n",
" mask = range(num_training)\n",
" X_train = X_train[mask]\n",
" y_train = y_train[mask]\n",
" mask = range(num_test)\n",
" X_test = X_test[mask]\n",
" y_test = y_test[mask]\n",
"\n",
" return X_train, y_train, X_val, y_val, X_test, y_test\n",
"\n",
"X_train, y_train, X_val, y_val, X_test, y_test = get_CIFAR10_data()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Extract Features\n",
"For each image we will compute a Histogram of Oriented\n",
"Gradients (HOG) as well as a color histogram using the hue channel in HSV\n",
"color space. We form our final feature vector for each image by concatenating\n",
"the HOG and color histogram feature vectors.\n",
"\n",
"Roughly speaking, HOG should capture the texture of the image while ignoring\n",
"color information, and the color histogram represents the color of the input\n",
"image while ignoring texture. As a result, we expect that using both together\n",
"ought to work better than using either alone. Verifying this assumption would\n",
"be a good thing to try for the bonus section.\n",
"\n",
"The `hog_feature` and `color_histogram_hsv` functions both operate on a single\n",
"image and return a feature vector for that image. The extract_features\n",
"function takes a set of images and a list of feature functions and evaluates\n",
"each feature function on each image, storing the results in a matrix where\n",
"each column is the concatenation of all feature vectors for a single image."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Done extracting features for 1000 / 49000 images\n",
"Done extracting features for 2000 / 49000 images\n",
"Done extracting features for 3000 / 49000 images\n",
"Done extracting features for 4000 / 49000 images\n",
"Done extracting features for 5000 / 49000 images\n",
"Done extracting features for 6000 / 49000 images\n",
"Done extracting features for 7000 / 49000 images\n",
"Done extracting features for 8000 / 49000 images\n",
"Done extracting features for 9000 / 49000 images\n",
"Done extracting features for 10000 / 49000 images\n",
"Done extracting features for 11000 / 49000 images\n",
"Done extracting features for 12000 / 49000 images\n",
"Done extracting features for 13000 / 49000 images\n",
"Done extracting features for 14000 / 49000 images\n",
"Done extracting features for 15000 / 49000 images\n",
"Done extracting features for 16000 / 49000 images\n",
"Done extracting features for 17000 / 49000 images\n",
"Done extracting features for 18000 / 49000 images\n",
"Done extracting features for 19000 / 49000 images\n",
"Done extracting features for 20000 / 49000 images\n",
"Done extracting features for 21000 / 49000 images\n",
"Done extracting features for 22000 / 49000 images\n",
"Done extracting features for 23000 / 49000 images\n",
"Done extracting features for 24000 / 49000 images\n",
"Done extracting features for 25000 / 49000 images\n",
"Done extracting features for 26000 / 49000 images\n",
"Done extracting features for 27000 / 49000 images\n",
"Done extracting features for 28000 / 49000 images\n",
"Done extracting features for 29000 / 49000 images\n",
"Done extracting features for 30000 / 49000 images\n",
"Done extracting features for 31000 / 49000 images\n",
"Done extracting features for 32000 / 49000 images\n",
"Done extracting features for 33000 / 49000 images\n",
"Done extracting features for 34000 / 49000 images\n",
"Done extracting features for 35000 / 49000 images\n",
"Done extracting features for 36000 / 49000 images\n",
"Done extracting features for 37000 / 49000 images\n",
"Done extracting features for 38000 / 49000 images\n",
"Done extracting features for 39000 / 49000 images\n",
"Done extracting features for 40000 / 49000 images\n",
"Done extracting features for 41000 / 49000 images\n",
"Done extracting features for 42000 / 49000 images\n",
"Done extracting features for 43000 / 49000 images\n",
"Done extracting features for 44000 / 49000 images\n",
"Done extracting features for 45000 / 49000 images\n",
"Done extracting features for 46000 / 49000 images\n",
"Done extracting features for 47000 / 49000 images\n",
"Done extracting features for 48000 / 49000 images\n"
]
}
],
"source": [
"from cs231n.features import *\n",
"\n",
"num_color_bins = 10 # Number of bins in the color histogram\n",
"feature_fns = [hog_feature, lambda img: color_histogram_hsv(img, nbin=num_color_bins)]\n",
"X_train_feats = extract_features(X_train, feature_fns, verbose=True)\n",
"X_val_feats = extract_features(X_val, feature_fns)\n",
"X_test_feats = extract_features(X_test, feature_fns)\n",
"\n",
"# Preprocessing: Subtract the mean feature\n",
"mean_feat = np.mean(X_train_feats, axis=0, keepdims=True)\n",
"X_train_feats -= mean_feat\n",
"X_val_feats -= mean_feat\n",
"X_test_feats -= mean_feat\n",
"\n",
"# Preprocessing: Divide by standard deviation. This ensures that each feature\n",
"# has roughly the same scale.\n",
"std_feat = np.std(X_train_feats, axis=0, keepdims=True)\n",
"X_train_feats /= std_feat\n",
"X_val_feats /= std_feat\n",
"X_test_feats /= std_feat\n",
"\n",
"# Preprocessing: Add a bias dimension\n",
"X_train_feats = np.hstack([X_train_feats, np.ones((X_train_feats.shape[0], 1))])\n",
"X_val_feats = np.hstack([X_val_feats, np.ones((X_val_feats.shape[0], 1))])\n",
"X_test_feats = np.hstack([X_test_feats, np.ones((X_test_feats.shape[0], 1))])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Train SVM on features\n",
"Using the multiclass SVM code developed earlier in the assignment, train SVMs on top of the features extracted above; this should achieve better results than training SVMs directly on top of raw pixels."
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"0.105775510204 0.111\n",
"0.125551020408 0.114\n",
"0.41512244898 0.419\n",
"0.252040816327 0.271\n",
"0.413816326531 0.417\n",
"0.408653061224 0.415\n",
"0.413734693878 0.413\n",
"0.40887755102 0.403\n",
"0.332408163265 0.34\n",
"lr 1.000000e-09 reg 1.000000e+05 train accuracy: 0.105776 val accuracy: 0.111000\n",
"lr 1.000000e-09 reg 1.000000e+06 train accuracy: 0.125551 val accuracy: 0.114000\n",
"lr 1.000000e-09 reg 1.000000e+07 train accuracy: 0.415122 val accuracy: 0.419000\n",
"lr 1.000000e-08 reg 1.000000e+05 train accuracy: 0.252041 val accuracy: 0.271000\n",
"lr 1.000000e-08 reg 1.000000e+06 train accuracy: 0.413816 val accuracy: 0.417000\n",
"lr 1.000000e-08 reg 1.000000e+07 train accuracy: 0.408653 val accuracy: 0.415000\n",
"lr 1.000000e-07 reg 1.000000e+05 train accuracy: 0.413735 val accuracy: 0.413000\n",
"lr 1.000000e-07 reg 1.000000e+06 train accuracy: 0.408878 val accuracy: 0.403000\n",
"lr 1.000000e-07 reg 1.000000e+07 train accuracy: 0.332408 val accuracy: 0.340000\n",
"best validation accuracy achieved during cross-validation: 0.419000\n"
]
}
],
"source": [
"# Use the validation set to tune the learning rate and regularization strength\n",
"\n",
"from cs231n.classifiers.linear_classifier import LinearSVM\n",
"\n",
"learning_rates = [1e-9, 1e-8, 1e-7]\n",
"regularization_strengths = [1e5, 1e6, 1e7]\n",
"\n",
"results = {}\n",
"best_val = -1\n",
"best_svm = None\n",
"\n",
"pass\n",
"################################################################################\n",
"# TODO: #\n",
"# Use the validation set to set the learning rate and regularization strength. #\n",
"# This should be identical to the validation that you did for the SVM; save #\n",
"# the best trained classifer in best_svm. You might also want to play #\n",
"# with different numbers of bins in the color histogram. If you are careful #\n",
"# you should be able to get accuracy of near 0.44 on the validation set. #\n",
"################################################################################\n",
"for i in learning_rates:\n",
" for j in regularization_strengths:\n",
" svm=LinearSVM()\n",
" svm.train(X_train_feats, y_train, learning_rate=i, reg=j,num_iters=5000, verbose=False)\n",
" \n",
" y_pred=svm.predict(X_train_feats)\n",
" y_val_pred=svm.predict(X_val_feats)\n",
" \n",
" train_accuracy=np.mean(y_pred==y_train)\n",
" val_accuracy=np.mean(y_val_pred==y_val)\n",
" print train_accuracy, val_accuracy\n",
" \n",
" results[(i,j)]=(train_accuracy,val_accuracy)\n",
" \n",
" if val_accuracy>best_val:\n",
" best_val=val_accuracy\n",
" best_svm=svm\n",
"################################################################################\n",
"# END OF YOUR CODE #\n",
"################################################################################\n",
"\n",
"# Print out results.\n",
"for lr, reg in sorted(results):\n",
" train_accuracy, val_accuracy = results[(lr, reg)]\n",
" print 'lr %e reg %e train accuracy: %f val accuracy: %f' % (\n",
" lr, reg, train_accuracy, val_accuracy)\n",
" \n",
"print 'best validation accuracy achieved during cross-validation: %f' % best_val"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"0.427\n"
]
}
],
"source": [
"# Evaluate your trained SVM on the test set\n",
"y_test_pred = best_svm.predict(X_test_feats)\n",
"test_accuracy = np.mean(y_test == y_test_pred)\n",
"print test_accuracy"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAAHpCAYAAACiDWlbAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvXecZNd13/m9L1Tu6tzT3dOTZzAABpEIJEGCQZKhRJq2\nbNlrr22tZEsfSbbl9a4leR0+XGf7I0vyaiXbK1OmFSzJSStZllYiDQYRBEAQAJEnhw4znVPlqhfu\n/nHOe1UznNADcjBDuX6fzwDVr169d88N5557orHW0kcfffTRRx999NHHzcG53Q3oo48++uijjz76\n+EZEX4jqo48++uijjz76eBvoC1F99NFHH3300UcfbwN9IaqPPvroo48++ujjbaAvRPXRRx999NFH\nH328DfSFqD766KOPPvroo4+3gTtWiDLGfNAYM3+729HH24Mx5rwx5puucv39xpjjN/msTxpj/v7X\nr3V9vB38jzQOf5hoNcbcZYz5ijFm2xjzV253e75WXIu3/I8IY8zHjTG/fJ3v3zDGfOCdbNOdAmNM\nbIw5eKvfc8cKUYp+Eqs/ZLDWPmOtved2t+NOQH8z6OMdwo8Bn7HWDlprf/Z2N6aPrzuuuU9aa++z\n1v7BO9mYm8Et5oHviPxwpwtRfdwAxhj3drfh64U/TLT0sTP0x/wdwT7gzat9YYz5H3IP6M+7Ox9f\nhzEyX5eG3AC3fQGpJPo3jTFvGmPWjTG/YIzJXOW+HzfGnDHGVFRF+cd6vvseY8wXjDE/YYzZMMac\nNcZ8W8/3ZWPMJ4wxl4wx88aYf2CMeUc6+EYwxswYY/6LMWbFGLNqjPkZY8xBY8zTxpg1vf4rxphy\nz2/OG2N+zBjzKlC7gxnh41eO65Vm2qvRYox52Bjzkpoffh3I3T4SdoabHUdjzC8Be4Hf1jn9N24v\nBV+N642DMeYjaiLaNMY8Y4y5v+e7KWPMf1aazxpj/mrPdx83xvwnY8wvG2O2gO95Z6m6Om5A6/cb\nY07rOP6mMWaq57unjDEntB9+zhjzOWPM990WIq4CY8zTwIeBn9N59u+NMf/SGPM7xpgq8CHlj7+k\n43XeGPO3e37vGGN+Uuf0WWPMX1Yzye3mOQ8bY17Vfv+1ZM+4wVjFxpgfNsacAk7ptZ82xizruL9q\njLlXr2eMMf/cGDNrjFnUPsveFkq77f9xY8yCjuNxY8yH9ausMeYX9frrxph39fwm1fT0rL1f13tf\nNMY8cFuI4TIe+N+0PT+qY/R9xphZ4Okr9wv9XS9NjjHmbxmRDbaNMV82xuy+yrveb4yZM7fCtGmt\nva3/gPPAa8A0MAQ8A/x94IPAXM99fwLYpZ+/G6j1/P09QBv4PkT6/EHgYs9v/1/gXyKMcQx4Hvj+\nO4B2B3gF+OfatgzwBHAQ+GbAA0aBzwE/dUWfvax9lr3ddHyN43oZLYAPXAB+BHB13DvA37/dNN2i\ncfzw7W7/NWi65jgADwHLwKO63v680uLr3y8Cf1t/tx84A/wRfe7Hda1+VP++7fP3BrR+GFgFHtT7\nfgb4vP5uDNgGPqZz4EcSPnS7abqCvs8C36ufPwlsAu9J+h/4JeWRBURrdbLn/h8E3gCmgEHg00AE\nOLeRnvMID9+lvOUt4AeuN1b6uxj4faUjCzylc3VAvz9Kd0/5aeA39d4i8FvAP7qNNN8FzPW0by9w\nQNdTA/hWXXv/GHjuir76Jv2crL0/rvP8fwfOAe5tHssP6+d9Okb/DsjrGF22X1yFph8FXgUO69/3\nA8M9430Q+DZgFnjkltBwuzrvig75/p6/vx1hul/VeVf87it0GfH3AKd6vstrB07ovxY9zBr4nxAf\ngdtN+3uQzei6DAlh0i9d0Wffc7vb//UY1ytpAZ4EFq541he5s4Wor2Ucv+l2t/8abb3mOCAHkr93\nxXcn9DePAxeu+O5vAr+gnz8OfO5203cTtH4C+Kc914u6Ee1FhMcvXvG7Oe5MIer79PMngX/X852j\n9BztufYDCX8Enr5iHX8zd4YQ9Wd6/v5nwL+6xlh1gL36dwx8sOf7D+u8fTdgrnhHDTjQ8/d7gXO3\nkeZDwJL2v9dz/ePAp3r+vgeoX9FXvULUsz3fGeAS8L7bPJZJ+/bp3NrX8/2NhKgTwEeu8exYec95\n4J5bRYPHnYGFns+zyKnnMhhj/gLw15GTLcgCGeu5ZSn5YK1tGrHWlRANgA8s6jWj/+a+bq1/+9gD\nzFpr496LxpgJ4P9CmHsJOTVsXPHbBe583HBcr3LfNHDxiu9nv56NugX4WsbxTsX1xmEf8D09ZjqD\nrLFphHHtNsZs9HznAL3OrXda1O21aDX63UvJRWttXWnbrd9dScs3wrrsbfMYoint5YezCH3w1TTe\nKWO33PO5gbRzhK8eq3WEloS+hZ7vP2uM+Vng54C9xpjfAP4GcggvAC+ZrteHwzvkY3M1WGvPGmP+\nV+D/BI4ZY34P0SRBz96H9EXOGONcyY8U6fhZa60xZgHpuzsJN7OG9iDatGvhrwG/ZK29qYjwm8Ht\ntmsn2NPzeR8iHacwxuwFfh74YWvtsLV2GHGU3Mmknkc0UaPW2hH9/ZC19rbZgnswjyzeK8fhHyOb\n0TFr7RDw5/hqWu070L6vFdcd1x700rJIl4En2Pv1bNQtwNsdxzt5DK83DnPAP9T1lKypkrX2PyB9\nce6K7wattR/tec6dRve1aLWIcLU/uWiMKSIHs4v6uz1X/G7mlrXy64fe/l8DAmR9JthHV6hc5HKa\n7tS1aBH+sj+50DNWC1fc1/3D2p+11j4K3IuY834U6ZMGsm6TeTxkrR28tSRcH9baX7fWPkl3DP7Z\n23hMOl+NSIgzXJsvvxO4Gi/ovVZHBFogdTYf7/l+HtHSXevZ3w38cWPMj3yN7bwm7hQh6i8bY3Yb\nY0aAvwX8ul5PNpwishmtqSPZ9wL37eTB1tol4FPATxtjBozg4C1xMLt5vIAwqX9qjCkYY7LGmCcQ\nrUUNqKqT3I/ezkZ+DbjRuF4NzwGhMeavGmM8Y8x3ISaiOxlvdxyXEJv9nYjrjcMngB8yxjwOslkZ\nY75DN60XEHp/zBiTM8a4xphjxphHbw8ZO8L1aP114H8xxjygjsX/GHjeWjsH/A5wnzHmjyqdfwXx\n0/mGgWor/iPwj4wxJWPMPkTjn+Qe+o/AXzPGTBtjhpB0CXcqfo2rj9VVtWfGmEeNMY8bYzygiRy2\nYyu2oH8D/AtjzLjeu9sY89Q7Q8ZV23qXMebDRhzoO9re6Fq3X+dRjxhj/pgKI38dofn5r29rbwq9\nPDCxEvXiFKJZ+3Ydp7+D+Jwm+ATwD4wxhwGMMfcbY4Z7nncJMYH+iDHmB28FAXeKEPWriKBzBjgN\n/CO9bgFUFfeTyGAvAccQR+XroVea/QtIx7+FmFP+EzD5dWr724YysI8CR5DT/Tzwp4C/BzwCbAG/\nDfyXK3/6Djbz7cJyg3G9ymestQHwXcD3AuvISeJK+u8ofA3j+E+Bv2skovR/e+dafGNcbxystS8B\nfwn4WTVtnUKj7LQvPoI4n58HVpANqcwdihvQ+jTwd4HfQLQzBxCfSqy1yb0/gWgv7kYcldvvLAU3\nxI34xY8gmpdziNn1V6y1n9Tv/g2yhl9DTGW/A4TXMBW9U7gqPdbaz3CNsbrG78oIfRvIXF1DxhLg\nxxG+9byRKNJPIc7dtwtZhF+sIoLBOPB/XOPea/JXxEH+TyPBBf8z8MettdcSxt4JpDwQCei4cj+o\nAD8M/AKiUaxyuWbxpxBB/1PGmG1EqMonP9dnzAPfAvy4uQWRs0YdsG4bjDHngb+oC6CPPvro4xsS\nah5ZAP6stfbzt7s9twJGUsf8K2vtgdvdlj5uDsaYjwOHrLV/4Xa35Q8T7hRNVB999NHHNxyM5Ika\nVPNRkl/pdppHvq5Qk+y3q7lyNxLh9Ru3u1199HGn4E4Qor4RTFN99NFHH1fDe4GziNnyO4GPWWvv\nNHPe1wKDmKU3EHPem4gg1UcffXAHmPP66KOPPvroo48+vhFxJ2ii+uijjz766KOPPr7hcMuTbf7m\np3/bep6UHPL9DBnHl88OeL5EM7quh3Hks5fxcDTBmRNZbGLtcxwcR2Q+45BkJCWKLVEkwQVhFBHH\nEjRio4gwkM/tDoQagOA4MZ12B4BWENAI5PGNZsC2Xq+1GgSh/Paf/NBfumEuqp/+V79ml5dW5F2t\nkGxWggMymQyZjNAbx5Y4ljY0Gk22mnV9V4tmvQVAp9EhDpL2G0nqAMRxSBLNahxLNiN1GXO+Sy4v\nfZvNemRz8q5sPgOeNNtam/aJ67rkcjltm0++IOk3fuyvfN91aQzjmkY5BJg0AtWSRqP2KjNNb5Sq\nJY5t8olL2w0ATiyvMJIrAnBpZZWO0rZ7TKLDC/k8xyaHpM3EPUGvhrdr/fXc4evS+N4jE9b2RNcm\nY+UYJ51rsY0vi7+NkwAli9INruNgnN6zSTIOcTpPHWO689r2UGTTq5dRaq2l6MuYv3dwhPLwCADj\n9z2E7Uif/uC//OUbztM/+71/xkqUMGSzOfIlGX/jwuTMBAD7D+zjvqNSBm+gUGZsWPLZNhtNRock\nTU6n1WRuUaLGl9dXGCxL4J3r+7zy+osAvP7WK1RqMseb9TadIJQ+I8L3ZZ6uLVdYXdoCIGiFBEGQ\n9kMmK1HMIxNFGjW5/sJnnrkhjT/0A3/etlqynhYXF5makvyue/Yf4N5jxwAYHR2lq4C3tOpifdtc\n36Q8WBJaPIOva8jzfSLlB9balA81mk0qW5sAVLY2GB6WyOpCocgbb7wOwHalwvqm3HPy1Mn0vcZA\nGMkzY+uRzL2XX3r9ujT+1//wqxagurXNT/7fPwfA/KWLPHD0qDzLddja3NaXQBBKv2cdF0d57JnZ\n8yRJJC2G0ZLwqz/9sW/jwH5JFxU0qkK75+Bq+rOTx0/z9IuvAnB2cYUBHaPBYoajhyVKfWp6msEx\nmUvT+w8xPCopfXwn5M0XvwTAx3/yE9elcfbccVsYkt85NuST//r/AeCLL3yJwTHp4x/6S9/P8OAA\nAL/4H3+Fjvbrx771ozgd6dff+8LneOB+mctPPPoYsc4vJ4pS+p2etepkM8RKq+u66VqPoohkataa\nMUsbkuez1d5mICt8zLguVvv3iUffc8N5ulFt2ygK0zY4+jbHmu7YWJt+Nsame6S5RtnXKIpSXnWt\ne2QvUH4WW7QJBEFES4kMidN+6e2fdjsgVh527Mj0TnI02uR+Y8DaZM4BJuVuPXc7Pbz+sk0FbM/r\nHBlfY0nXTWzAKO1O73Wn+yjXgjVJUKm9PJeCdfWqxXWTb5wdJVe95UKU67pd4ccYjHaecWzaqXEc\n4yWTJQq6A+eYrkDlGrqpDLsbm2tirCMdELugY0bodCcgBrxQN3NjQYUQa2JiZBZFHUvOlxcEkZtO\n6p3A4JDxRZipVdtUKuvShjBMGVc2m8XzZPNwHENOBR43Y8goXU0snYYIcpGBTkeIiaIOVgUN10Cg\nglYchCmT7HQ8Wm2hK9NyceXxuK6L58swu2RIVo1nXLI7HH1Px8PiXaNXuoKT7RGuWmFXCF6tNnju\njZMAnD9/gWxWGpjPZnE8eX67KbQ/dPcRfE8a59heIerWIbaWbtS2STe7mLgrmF9h+k6Fqzi+jPE5\nev3K+xMhKjbmqkwueQ8I8+oKb5ZCTja6u8sDEIjg5L36pZSx7gTWRrRa0se5XIFMRp5ZqW+SMPTt\n7U2On3gTgMHyIBvjspll/QyxkfeGQQCujNmBvUcYHRwFwM+65HQs15eWWZp/C4AgjBjQDW+7vk4n\nkH6oN2q0Wk2hsR31zDObbnjba9vYeOfF3B999BEWFiRP5OLiIqH2+cTELg4eOgLAxvo6oa6bYrHI\nxXVJ+HxxfoHDWREGRseGiWNpg+Hq42XjmHxeDiWdVo5EeHNdN/08NzdHXWkE0jkWx5ZIhSgct/v5\nBhjZI0Fxp8/9AWdnJQn36Ogwm1sijDY6bY4cuRuAhx59hEjftzI3R8aR+bRd26LW1LZag6N8qR4a\n3njzLADrixJFvu/wwfTg9PSzX+FStaY0OoQ6X42XIZdLosoNgQrMmxubJEw740QMFIo7orETBBS1\nux0Mw6MivBcHcmQLwmejHkF7cmKMpPvy2QzFsrTl2N2HmZwYTdvrGj3QhhFxJGMb2+46dWMXRwV8\naxziZP1hCDoiaGcdh2Ed842gRk6ZdxAHON7Ot9M4Bmt1vtvLDUKX842eA1z81UJU7+deoct13a/i\nP937lJ/Fcc+8M919Oq0IA1EY0e5IXwWd8JrPvDah+r+w+zvbKyCZOBVnLBZj9KBpIxLFgcXBGpek\nVTZud5+tG11sYsxlB1NHrxuM9m9kXayn8gcWowd8YyNiq/uujXEKuaRHdkTirS/7cplmIl1TMtjp\n5Z6OjOUvUAEsFYS6m7PjOL0/TTcAxxhIGLGBSAchA4QqaLXDUAQpfaZRydTzQgomEVoc6vHOJ0vQ\niVLBptFoU6vJZhOFYUqj77VxdZG5joOb04ElwgbyLt/4iUBMFHaIrUxeS4RxkhMGGCfSZ3r4mnbM\ncWM83cA81+KpNJ3NeOR00eeyOfKquSoN5CmXB3ZEn6W76LrCuaWTMIHY4qZMz6bMZ2G9ysV1Ye6z\nC8uceksy79c2F8lqm/KlMsMjoll5112iiTowMgCqCbKmR1VzjdOVqsnklt4vepnNDWg0kLYbbI+A\n1LP4exjI9RjZtYSuK+9Lrl3t9Gjt5SelgmpwR3AYOizpajJDQ0Q3keJl7979dDodpdehXhNtQ9Bq\n0WnIplrZ2KJdkc8buVWqNRm/sbFRtupaacPE7BqTBN+jY8Pk3Ly2OWJ8SDRXowPjtLdlXY5PTeHn\npE9W15ZIvAhMBIWMbopxkLKsTqeTnngtPq67c6+DOLYUVMM6MjKCq+t+aHCY3VOSrHn2/Bxra2sA\nlAcHWV2RQ8/Kyjr5vNAyOjpCItPGcURvWqREY7axsUG1Iv1jbJxeX1hYoF4XLZzrujSbIkQ1Go30\n+b7vEzSETzTqjcvm2fWwtCga799/+jNUdPzyuQyoUDCzZy9PfOibATh87D5cK2NwvjTAuVMn5J6p\nGTY2pCrPwECZlTV55ssvvY6vm9LWlvQPhTxBR9UV2Tx5FYDb9ZCWbsBDg4PkVYhyTIZSXvjKrrFx\ncgVhUGGrzvDY6I5otHFMuonHMU9+6H0A3P/4/UTavqnhKUp6CvzAe99DpJv02Ogwka6nQsahrPzO\n2jgV7lynuzeEYZQeMh3jECcCjTUkQx44DtVY1kRUb2I8mVNePoejzCnn+7hqddgJ2q2ussB4poev\nxj3apx7hvedzL8/oheM4l/GQXuVF7/1RqgGN03nnGAdf1yJxLHsXItB2VIiKQrtjYT/B8rzwjJWF\nZfKuzAWDTZULfsbD6Po2vs9AUdoQdmo06rK2WmEbLyv7hesaVi5dkLa1YiZ2i+a02qhhdMA8Y0Qd\nhYy70dycmewg+VHNhWt8Yp3XcdhkbVmStjeaVR5/37sByA+O7IjGvk9UH3300UcfffTRx9vALddE\nRXGM0dOydd1UY2Bj01UUODY1n4SW1BxiMKk2wdiuYqFbRxisMdjkC0uqejbWpDZS44Cnkm+AgxMn\n/ism1aBkvK60HmcdvqoK2nWwvr7F1mZFnt8J6eo9TNqeMIwJAlFDRlFEuB2lxPiqZSAEG3VNRIlt\n1vN89ECN65L6ahRyLtmcSNm+75DRk1k2kyGnaul8Pp/6QRWKBQYHxX9l1+Qok7smdkRfqhO5QrOT\n6A7a1pLRvis6Me1Irp9bWOGV18Wks7JlaK3Lac6PWjRCOd1MT0zy1LsfAeDoPtEUOK5hqyXPy3qG\nvH/9U7rp+a+19qZMXAniOL7stHa1z70nul7TW+/1a6m7r+WjcL37bO860M9hKc/g408AUJyYJtJ+\n3AlWVlYpD4pJxXMNJhStlG8N9U3RasTtABuKT41xYenSIgC7pseZ2i9aJj9v8GW6k/dzDJcl+X/W\ny6b+gJ1mxK5R0VYNFAY5O/8GAFHL0lGzbafSJqNqerIZMRMCe/bMpBroxcUVirm0dNYNcfbsWS5d\nklNlpVKhWBR6h4aGKRZFQxJFljNnzunnCFXWUK81eUPn68joCOWy+ke5pFpex3FSLdP29nZq5tlY\nWyVRmTYazXR+DA8PE6hWdWtrK70eRSE2TuZSRFP75Eb4zV//VQA+//nPpnNlfXOLimpThobH2FwW\n8+SC62IjWXONygaxtnWwVCCrKmxrDLU50ZSVim2GB6WvN6oywHPzF1lT3nbwwEEyG6KhCsImRrVf\nI4PFrrYiqqSaw0whx+79Yh6NbIv9Bw/siMZOp4PrJiZcl1Zb+vvC/FnwpH2lbJlCRnjZwuwFVhdX\nAXjXu9+LUZ74hc9+Gu/D3yI0l4epqatEsZTFouYhz8XzExMhYt8DTNzVRlvfTf3Cgno19WUbHBkn\naxJTUUx8E0qaer2B5yX+iVlIrAjO5RqkXlxNE26t7blucF15Zhx3/YMdx7lMO55ok3p/GxNjVByI\nwohWS8az0wkJ1McsDCPim9RE1bdk7DYXN+moJsrDpuspl8viqr9nfiAPKiu0altUtmWuNcIGVu+J\n44Cl86e0bTGZnLS5E8a4Oqa1VpMwULMzIUb311xxnNiRNrjeIFGoe3Ns2dxS7fvGBpcWRHt2aIea\nqFsuRIVhmJrY3DhO7b9iwOtKKonfmHVI9WNRT93sXq8I2yNQWdeQSBhOGKeWHw/S62EUEpNMKLoL\n1NrUR4jIEOlDM25IaszdAdqNempjx9D1QTImNUtEYZw6p0ZhV2i0RISJo5wxuNoG37fp4Liui64N\n/IxLNivtL5WyqYCUzWZSJ/N8NsNgUZjNYHmAvPoRlEpFhkfEYXtycorx8d46jtdGYmu+wjiViorV\nAAI1Se7Ouaxsy8I5dfwtlk/KpjTlFwkiYWIbxmdoRFT77330XezdLUXE27rQ682Iz78pzrgPHR7k\n8JhM/NhyVYueyNRdVXfi8L1TweWraesysl4/g6/6zVUEqt7rV/7uas+5lk/DZf5RPap8t9pk+Vd+\nVa87xMi8u+e7b5yEuLpRTQ8WxWIBo4uu0+ywVBXGUSoWUt+kequBk1FTh+MwMiFzZ2O7wvKCmMAu\n+JcYLolwNTY0zcaaCGCzs8s8/NC7AJjcPc3a78jzL11cJl3gDoSxrL+h0aFUiBqbGKVWESYY2Zh2\nsPO0SxcvXmRlRcxThUKB/Qdk4z5y5C6yahKw1rCyIgw6iiJMrJu+l6GjKv7XXn2dqWlR/U9P76JY\nTH5r0zlYLBYZmZG56zmGCxcuALC2vp769BWKxXSz7HVotzZOzf7GOGSzveXAro2XX3kZAMdzyepz\noyhK/cyWlhd5/otS/OHIgYOMj8nYdMI2jpqhxsfGCJUPr62vc+iw1G994L77OXP6DABVNUF24hhX\n29ZqdYML8lmXovoDzeyexGofGlxyataqb69Rr8pBLZvN0FR/qhshji1u6tjss7gkgvx/f/q/01H/\nuOLHykyPPgjAmROnuHD6PAB7Dhxi79HD8k7fo6W+X5VqFWt0A3VzqQuI67rpPuF5OYLEfyaOcZzk\nYOhBVZ7TnLtIR4WKQ5OHcVXQjo2l0dn5PG002jiOOnKHlkgPwBm/Kwi5PX691naFIvFakXZmXafr\nnhLH1NU3zstkyKjTe+8BMY7jNGjG2q57jee6qWN5u9VK+y2MQqIombSGm/BykS1Uzaw+GbIaYObY\nOLVeusYjo/MybDeoqm4hiEIi3WH8XInttvZ/owUqCF1cOc1bF8WHrzAwwrG7JIhgfGiYqKrzt13H\naD87YYOgIfuKzXoYT/rH8Xy8AZnX546/Sf6sPPPQsXt2RGbfnNdHH3300UcfffTxNnDLNVE27kbA\nhZFLkITem57oAevgqUjsYLvhnnQjIW2Ps6+1URrZ1wg7qeo/47o4qrNyrMV1klO9IYlsdOk6tFtI\nTzzGWhK9fhyG3IzI7RDhmETTZYnixNk3wiZRIJFN1ffYHkds1+2a7XyD5ycnOkuif3Ncg+cljngu\nOVVXF0u51FwxMDCQfi6XiuyZlhPg1NQuCqqJcj2TplzIZPI7jj64OrrjkSMmo/SsNSKefUmiuyqz\ns+xTLdt+p05Loyp2Z/OMa5TR4twa8xfl9JSEvgetDpVl0XR0Bh4gHp2Rh5u4q7LsUepYoBOqGjgy\n6QnZ5fKUAdfDldqk9NnX0EQ5jpNG2115fy+uGtXVo0bv1aLZnnb0vjfqsWX71iEOxfRmC3km/8R3\n34CyLjqtNrVKorFzidQE0wk6VCv6zDAir5qHZrNJLMoSLpybY1lDu0M65LKq6cyVGVCziolPc0kd\nSUvlIgePiCnn3mP3MzQmWqyf+pmfYHZBtAa5YjbV6tRa9XRsT5w+nUZqxsbQau/8hH9+9lLq4L1r\nai+Hj2hag7GJ1Jn8xIkTtPWZruumkyOyMb5qdlfW1mkH0oZ8MU8mK2toYWE2NTlMTY6nGqo9+/dS\nb0pnNdstlpbEpLa6sZ467JaKAzSb+l7PI5eTz83tahq5eyOsrQsNw4OD6XoxdPvI2Jg40RwYB/SU\nPzAwytSAjFOr3mBD0y40Wk0W1fw3OjJCfbeYZr3X5dmDI8O8/777ALg0v8RQWXhM0GkyMSpjumt6\nF7myfM6UygSaMmL93HG2508DUA9d6sM7M8tW660k+BNroTQgvMx2sgSqIXEsNOsyPu26T7Mjc/aZ\nL75C9jV556nzG1RaXwHgxdcuMKza74cfup+9h/bLCzyXto5JdXud8uReAPxMnkJHeFDl5edZfFZS\nd1RXl6jkJM3CgYefIM5qpGzOT6O+d4J20A1qimxAoNrzbOzgJhFqkO6Fke2myHEcg6tass21JZqq\naWksr7D0FWnnRifgj/zp7wdgYHxEeAiyz3Uj+Ezaz8YALZ1DUQvPSdK3dAPDIsBeheddC5aYKJAX\nhG2wRdX4+j6+Rr46tklDU/xEXkymJJq9ThzhKB8KwybVmka4Gp+hUen/1skqv/Vp0bq23QJPPih8\n5YPvepiOjDsVAAAgAElEQVTpfTKOYSsiULrIVom3ZgEoDfrkdL80JkYte5yan2VwYufuA/COpDgw\nqTDjud0wStdziZUZhXGUpH7A2B5Tl4lJpY0ev5Moioh0s1ne2CJUFfz0rlGy+vw4DFIJzNquABNH\ncY+JrUOgjDKMgtS0EEZxavfeCQZLeVLzn7GpQBVie4Qxm6Z3sK5JTYqZjJvah12/63vRG5nh9OTU\nymS8HiGqwMCA+HkMDAyIbR3I5vJk1I+kNDDEoPrBuK5JI+1uJt1Sas7ryWMkpOliNIZ6EtI9u4hd\nkhDzY+UC+bwylnob35V3l6OI+LTYtU02h68+CehG4sUxkzo3tk+eYTEn349Mj5LJdgXspC2OcVhT\nxv38uRVmhqVP7t89SD6Z4TeQoq4Uiq7mB9WLawldybOufE7yrORaeiAwbkpJHMdp1IrjuD2BkDGO\n9nUQtSlNyaay78//RSY++C3XJ6wHYRzRbAszCjY7tHTTd42T+tzhwPguya00FEecnxOms7y8hl8X\nusZ3jZLRKJr9e49QX5e+P/nmadZWRYg69sC9fO5znwXgxKkzfNM3fwiAyelJLlwSfyQ8KGvqg5WF\nNdp1FerCsJtry5rUT3AnWF3bSsPtw8hhbV3Mi5ub27z44pcBeO65Zxkakk3fGIiSg04ckXUT/xhD\no6lReJs1tlXI3Fxfpl4TAWRtZT41ifu5YqrXd32XfFHasLBwkYfUrDkxPsmXvvSiPqeGr/49xtTT\nlAg3hPKTkXKJkm442UyGukb6Odayd0Z8CydnZtg1KWNpHIOjO+bUzAzNV18DwPM8Dt4l5q/ltVVK\nBWn3HjVl3nvP3akZdHV9nX0H5dnlUoGyCpC5Qo6C5gobmt5LTfv8jc/8NzLqYlBpwubczjbgar2W\nCtdRFDM6IoLdhz/wrfjqG1PMl/i3n/xlAJ75g+dpazTZ6+fniXQ9ZXNZFrfENNNpdxgoCR88cfIt\n7nlQBMMjdx/l0jmZ4+dPnOWv/vBfBqBQ77DwlS/K9Wf+gIKaImMT8fqsbsRnj3PwPjH5lDyXzE2k\nOGi2Wik/CKOYQOd4uxWRcZP0LoZOK/GjDXF0L8wXcqkQtbS2zHpNIi3j8/O0X3wFgNn1ddY//DHp\nh6EB4mRu9kYg0rMNWJtGj2cyWSIN+W8HndRU3OlE3VxuO0Bs4nReZ30XnQo0tlZAn58t+2TKGnnn\nZFXdAo6fwdW53mxs0ajInCoMDKbtGcmUeOxu8ac9sdFkdkV89/77s8/zQFXuP7xnkqCjpr06oH6g\nptzEz6ifaezQ0EPIdnULGyet2Bn65rw++uijjz766KOPt4FbrokyJiYONVFZPkc20bq4hihJtkmc\nap+i2Kaq6byq1uGrc2Ak+W4yvp+ezsIw7MkxamkmSe56DkBRGKaJ9oIwIFRn59iG3cznYZRqyXaC\n++49wtqWSL7rm9tUquJY3e600twkYSdKk2fGManGwfUMiZ+753UTijrGxSQOj65JncMLxVzqhFoo\nFNLTaD6fT7Uj9UaDM+cuALC0skKxlOS+GWLPTBIxVaDrPH99WTrRmjTjNBE6Lg6bVTmVrG1WWJ+T\n5HzthYsMaGSPqTep6Qk+rlSIE3WxNeCKqtzN+JjElJFkCPV9Aj39bnRCWuokOLh7hv0PihlwZLyc\nHqOqzZBXzsj73zxzgdmSRFVE9gAP7RGNQ+EGMz2Keh03zVW1Rr3zr1cT1Wt68zzvMufwa0X5JXBc\nw/S4OuvmfRYuaQbvIE7ngo1djI5V7vABjnzfDwEw9tiTrJ+TzNhDI9PXJxDJ6F8ekPmSy2dS7WYh\nW6Bckn569F2P8YEPfljaEAa88ZYEBjzz7DOsVyUCarw8wrhmMq9t1jmlCRqXLi1RzMsY7poYYX5J\n7j975iyPPConRs/NpNGe1Uo9zaHUanQkSz9iYsskyVjzOaIdRq6BOGznVHPZ6bRYWpJIvUuXLrK9\nLWt0eHg4dfaOoohYzfiSRVxN6MYn6Lj623W8TGJiiUnM7HPzlzh3QTK350uD6Sm9Xq+nZrvdM3t5\n8sknAahU6hw6dFhpr6VZ3L2sy9r6+o7oS3JgzUxNp3nePKdruC4WS0zvFvP3gXuOUtLxXrowy9qq\nONwfPXaM3/qt/wpArVrhj/3JPwHAc1/8Ir4GreyeFG1nLpvhzeMyB4oDeUqaMHNm7x4G1Km61ahS\n1VxTtbV1VpbF5Li2sc4Djz0qn0+8RTazMzPJ9vYWieo4jk1qhvvghz6E48i4/f7vf4o3TojZzisP\nUFHzZL5UYlp5nDWk88v1PKYnRaMVNmq8rlGYeD5n3pT8dcdPnGb3r34CgMfH85SUH+3fvYfooiQ2\nXalssrUu2tbTrz3Pg0fEbOS16hjl7+h7rodms5nygSAIcL0k51aOgmoxfcelruu+1QpT07GfcUk2\ntd0HD7CrI/Rmds1wRpOkXmq20ijldqeDxv3gu37qKN6baJTeSD0LgVpiOmFEpPur67rp3rkjWPAc\nWbsjQw5RUyM7g20GdX6NHdxNVud0bb1BWx3RPQPNimjY6rUa7bbsKe2oxZ4R+e344Bj37ZH5OrZn\niLcWZVyWozovHRfTXqVWZ3pE5uyUnyEJBq5XV0Ed761bZuGiuiGUynjm5sSiW59sE0sUd0s+2MSE\nF4TdIB1jIDUZxVRVdZfxMzhONzGYTYiLIwJVwZs4ppBNGGJIkPgmWcuaRolZGzFSLKVtCNQeG9kw\nfa/B0lI1ZzVoUdi5eZt9e6cZG5eFvra5xfqGbIS1Ro2OMtZOO0oZa9yTIDQM26lPlHFsEsiI6/r4\nGs2QL2QpDchEKxbzqS+E63qpWTCfy1FUgarRbLKpTGVpdQ1H+fPKxlqa1O3w3r2pyjybuf40SFJI\nbLYtrgq+9U6HC6siIFU212mdl0nbWZinvq3Zk7croKpUPwqpKUMIHS8Np3VjB0fHNc1mb2McHV+v\n0SCnidDc6jYVZfLvH3sgzXI/u7rBC8oU680meWXWn33pLdZrEnn00fvL16VRBJ6U4vT61VIOJNdT\ns52NU989h64g7LoeYaI+NnSz7xsnfcNo2ee7PiIpC4ZHZ/jN3/0DAI4fP50K0VHUZmifJJV7+O/8\nE8ozIkh2WrVUSN8JjGvIKyOO4iBljl4mx0MPPwbAkx/4JnZNiUCWyfocOixZvh96+GFe/IqU7Whv\nbVGryNq6dGmFzXURllqNGlOahLM8UGS/lvZpNCOMcq+jd93N5z4vZr4wjNMM/Y7rgZp7fdfw6ENi\nbpncM8bs2fM7prFYKrB7RkxYu3dPMToqAnUcd8vNFIvFVOAJgyCdd67jpENvrZNmSq83Ago61u1W\nK00EWxoYJtB13GxHbG+Lycf3fQpFEYwffPAB7r1X/LJeeeXVVPApFEq029KGZtCiUq3uiL7EJdAx\nTurPmclkGR4TOscmJxjdJZv4vsOHKGn25e2VFVoXZS0OFEssLS9rH+1ielrud7HUtFRPIfGfarZ4\n6CGJghsYKLE0L2vxnvvvZWhUeF47XyDWebh8cZ5LczJeG/UOF2ZFyNxYW2b62MM7ojGKgjTRJdbF\nzwgNcwvnWF2VjfULz3yZlqZScfJ5OokQ5XjUNXFsvdWkoFHKNrIYFYocz6dZVT/MbI577pOortmX\nT7L9jPhQbeZDXE0cG7ouUUPmuBdG3K1903ztK7xck37MRJaMLsUPPfrJG9IolTxUUIxiqlpmZ2lt\nke2NxFy8yqb68W1urDKqvkATu8aYmhJz69DAIJNaWmdgsMzIt3wAgIUzZ/jt3/0dAJ76ru+iUJbf\n2jDsVmOwNk2dgjFpssrIds2LOH6aUNTGcU/qiRvDwWFkSPq8s7aOowesoalDFMdFEPKLRayup2I5\nQyZ5b9gm7si+cPzEy7xxRgTdyen9jGmqkvxwkVJThKt7xmbwhqRPTl9aYG5eokw328vsH5fxanQ8\n9k/JHlmPV9NIwO1ajg1N43HPPfd1E3zvmM4++uijjz766KOPPm4a74Amqps3KYxDOkHXMbi3yGGs\np0HHIVVbysEwqb1gUpVniMXVqBM3dNKoOiKLo/amMAzw9BTSCQICNb+EUUSs2irjdBNlOEbMFwDt\nyFB2du5A55iYnGpIxkcGUpNGtVmkoyfVKIwJ1CEuCAKadXEErVaqaUkJSVIn/VCrV7m0LKrZTMbn\nrrtEIzAyPZ46etbrdUI1lQZtg6+RM/tnpjiwVzQCjUadjjrPe65DQeulhWFMNrOz3DSNtrSv2rZs\n6kmh0gxoRvLudtzm4qac7BbPzhKp423NJS1HMVIsUh/UArbWpKfCbC6fnnqtXvMcn0yS/6pQpKDl\nIorlQebb0p+vnl6kpGrgz335FVaWJZdMHFpcjRarhS7zX5ZSFx+9/8h1aTQ92tBeXGnOS+tsuS6+\nmqYH/CyenkfCOErNZDZ2yA/JySfjmzQPUr0epdEyB3fvoqPOlxdn58im9tKutsoAuQnRFpSn9xOH\nyXh6DE0fvC5dl9FoDRfnpJ88H3x1YC3mipQK0me+n6edlIZxuzUkZ3bvpTwg8+v0G28wrw7nWxtb\nJP602YzBVdoXlxcZGJTTrwljzp0W08vE6CQzam5a21ih1UwcZ2OKJdG8FvM+Sxoxtra1QtDYeXTe\nk08+wZ494vw8PDxCQcusDAyUWF1dTe+75x5xCD5z5gyNhmhfjHHT2ptRGKcBIp7J4Kt203U9Robk\n8z1HDzGq2hjHy/L662JaPXf+XBpt994nnkwduqvVWmoGrmxXCDSiNJ/Pp22+EZL512g0KCp/2z0z\nzqTmqzKukybS9B2fjq7dyX370+ixIOgwofni7jq4L62p59iI2YuiaWq2uzzjqe/4NgB+5/d+nzU1\n0X7n+Fh6As8XChQ0Os9bXU3r2LWsx9K6aOcmpvZTLO8seWEul+kmXw5jfvv/E43Ky6+8guvIeOYK\nQ9gN1YRXN3G0XlZ9q0ZNr1vXsO2KVSObzabXfS+mpSW1jp88zce+/TsBqH3g/WTULcEpZqlaWZdt\nu0XsqUuK9diXL6T9yFsSiRxGcVqjbSfIZHPpWD777Of5zDOfA2CzUWFrXbRtzVqdUNfi+MigFqKX\n4KMhDZ7ZPTnJ/jEZ+7Cc57F3idaz7hX5xV/6RaFlaJgDh2W+z0zuuSLwPLEAkVp9LKSaqCCyaRCX\nE8eXlT+6EYxxiALZF6ob5yhP7ZcvCjncovCbjJsh7qj7SxgQKW9r1DdZX5ex6AQVljVYaWbPQd44\nLkERd+0dYnjXsHaow0FfPodhxIYmD55fW2Jby8dsbEYsb8q4T4yVyWhkZTssMj4uZtlqfR3inbsP\nwDuSsTxKTR1hFOGrTdvSZQjiU5JEpUFeI0TEmpFk9vbZUtV/qZhjQMOGFzcu0dYFP1QsUdQItXo7\nZK0im3nGK3TTCxCQzXXbkEbqWWhoEjVrHBx23pGO53YLKJtMGj03PDqUFkDtNf+0Wy22t2WQt7cq\nbGmCtLNnz3D8uGz6586fYnV1Ke2fXbtEVXns2DHe//73A/DYY49dljAzMT0VC1lGtB6d53mXRZ0l\nviCO4+xYNfvqsjCTxUZApMynvr3Nlm50xYzhUk3UoSvbm4zoPZ3JUTbOiy+Bn8kQKQNsB12G41gv\nzSKbJGL1cgWKZRG4CgMlisqg3XweRyfTb3/mWXJqxp1bOMOlRVlkw+VBFlTNnxnchW01dkSjVBnv\n/n256U79+ByTRuB4ntdV41qLrwcF3xg6yuyyWQdfN9C4HeNr5Ne+fWVy6uNG0OG1l0/ocyKqGrY9\nXMzT0XqM20GQMr7N9Q30VZSHR/CCnTM1G0YkTHNibILJCZkjg4MTDGofWxt1E5rG6RGGsBOkPkuD\nI2Np8dkwiqnqXK6Wt9REDidOnuTgwf1yTyvknJrk9h46zD1HpfbfM19eJMk9EnVCXA3fCYOY02cv\naKMdcu7Owv+l/TEbG5oI9MJ5pqbEtLd//yEWF0WAzGazqRC1sbFBs6E1KmOPKEzqZ0Z4GWnbXUfv\nolBOMr1bRobkc6mYYWpGzKx79h5kl9bme+PNN9JUtA8+9Agn33wJgMr2Nm31C+x0glRYHRoZ4t57\n790RfZsadbRZGWBwSDYixzUU9UARhQGNiqzFjfUNsuofFtuY/YfFH8vNeLz7vWJaK2c8NvUAMr17\nipZGOifjNTo6ygHNNN5ptykPq7DtuVw4JQXFDx29hymNCGzVm0xPa73Fyd3k1CerlM9iop3x1NjG\naXTmmdPn+MIzEiVnPI+VZfG92r/3bh588HFp6/m3mGto2gzPo9XQaKwwwtGFk8t5qTDeNh0KI5rt\n/NIin/u8mNAffug+ltUMG41OYEIRGLPuEjnkmYUty+wzkvA014lx1eRrjI9zE2Uuzr76AgUNsfcd\nwz4Vco6NjdDRCNqzx9+ior5y2YyXusJsbqyyrkJCtV5nfVHrHOYL5NQ1wvWKdNR/6T/9h3/PwaMP\nAPDn/twP4OrhLwzD9KAWA/Qk80ytaj2Fso0FbkKIwlrmZmWOrJ99hUO6N++amCFb1AN8HBFp2orN\nlWU2tFbny688z/E3JZo2n3U4sEfWx/Z6yJkzcljxmkeZHJd9sbTLI69rbsjzuGu3+onlsrS0wkBg\nPM6vaZRtvcORPSKIHty/h4WG9NXWxjbDkzsrlJ2gb87ro48++uijjz76eBu49ck2bZw6bvqekzrT\nyQG0W6ojOe0TR8Q2KaFicVTOq7Yj5lQ1PJiL8JM8UZsbVNTE0x6JGdWTj2daLKg5bHB4ht2ax8TF\nJdDTcjOEdpoDI2Qj0Kg3p4UbVXZMo+NnMeoUa6Io1WL4rptK3I7jUNTIliAMeKsqjnJnzpzk2Wef\nBeDFl15iczOJ0onSBH/5XI5TpySv0qlTp/j0pz8NiCbqW75F8gQ98sgj3H+/OEhOT18eqdUbdfZ2\n8NKbIvmb2DAwLBqL7bUNXntJcpLcdXBPajIMbYSfODu3OjTUVNXymvg63vmBYlo9vFguY1Q72dR6\nTX4BoiRPTG+ZgijCV+f58mCOC6dErduqb5M3+s6wRqway8h0yGSv71DeRU8txyuQGNaKvseY1hZz\nsWk9xnLJw1VtSRhE+Jrsc2AgT1WDG1wvy4iejh54+H46mnfmxIlzJFZVYyx79DnVrSqB1ni8sLiW\nLtRTb71GpynPvP9djxNoJOvQyI1NJU++7/FU3dZqNchov2c8H8fV5H3baxjty5afw0u1QIZ2K9Ek\neAwOitOteyBDdUtoWbl0idkFMfPNLi5wSSPjZqZ3s7Ulp+tKvcbAsGgk41aAr32bK+ZoN2WeNiLI\nuBqZayzOTZhJnv3i5ymrebg0UKKkGr+LCxfY2BDNwtjYBHs1Gd/xEyeZn1tRCk2PRjzEataadquG\np2OaKxcYVLO0DTtsb8nJttU+y+KiaGbDwFKvSZ+89eYJzmudPjCp9qnVaopjL1CtVnn55Zd3RF+5\nJLQNDg2nJWoWl1c4rZqj7come/aKuXT+0jx1NZdeXFyirdHK9993jCfeI477YaPOa69KUEY2P8DB\nA6JZS7S8U5NjlAoyBw4dmGHfQdEiZnOFNJBlanqGWCMWNzcqDE9IPwStNgPq2J/L5QjbO9MKtxsh\nSRDYcy+8xMqyWBT27t/LqDoqH3/9AoWCjEN5cIBySTTytdpaWofOjTwKJaEjl/cpqXY7MiHFQWn7\nzJ4Z5tSE54U+u8ek705ut1i9JPOlHW1z+IDw1COFAh1HTNPFcJsoMYUSYuOdb6fP/OYvky+oqX/6\nKLtm9ks7RwZA590bLz/L6pJo8ien96Z7Z6vZBtV2m8Cw0pR2Hjx8GE+DlOKBAmGiuVqZY1stFpVG\nlaxGpXU6nbS0SmSdND9SHIdp6SwwqSYqirtlzHaCmIi2lmtxnCxBKPMvbm1iW0lZp4hqVcyXjUaF\nM+ekxubzL36BrQ25Pj25m13Dwjvz2RLLZbE6nD4/z+nTMnaHHzZM7xNT5vDQKJ6aXAvFEpvqqD9a\nKJLXrNDTU+OMj8hYb1SqbG3Ku6JmA8PNaaJuuRDlOKTJNl3PSc1qvT4oURSlan0yfposD/x0N23V\nthkfEIbou4aNDVFr750Yxw01UqgVsrmt6RG8NvmcTNJmtUKgTME6EIUiIHXqFVxXOtvPeuSSekRR\nm6I9tWMa5+Yu4msm8Gwmi6f+Wm3i1A+m0+nwzDPPAPCVr3yFLzwrn0+ePkmj0VtTyqT/D5ThRmF4\nmQBUUwb92c9+li984QsAjIyMpELUk08+yaOPSmjxgw8+mJo0epNARlG0Y3NeWyezm8nR9Lt1tJLI\nszDoEKoga2NDSyONVoIGzSQrdqNBKSlMOlCk05bF6LuZJNgpNRc5uHgamRaHEUbnjBOTquQHhkex\nuol47Q7lJNt5p0NOQ41dVrHt7R3ReC1YazHaT2FsqdaFEeR9H6Nh+K3AEmko9XAhx9SYqIkDICpI\nf5WG8+T0/ue+8CotjcbxXY93vV8iau6+734qWyJEv/nKc7TbSdTKMIH65PjWUtPfzp07Q74g79q3\nA1ryBYfDB8SHamJsgkJOfvviy6/TVsGsVt0k6gjjc10/9b/zXJ+WmqKCIEwFgEy2QFbXa7sTsLUt\na6veaNKpSd+3wjYl9YGoXqqyXRFa4tBKBQFk32up6T4yDq4engaHBug0dpiIEjBhi8kxMS3ddddd\nlLXg9qkTrxF0pN8efPDD7N0jQtSuyWkc96S2J0z9N6WSgIz7/Nw5MupPdPToUTot2YwNsKw+Qttb\nF1KfqzCK2NA1c/LNN1m8JCkgcrlsuiEFQSetbBA7Ma0dmp1z6mvVqDWpa+qPE2fOsaERsbmCj6dC\n+bmzp1jc0iLThTI5NUUf/43fJezI+/7oH/022i+8CkBhwGV8l2xWY5phfqScYX1VNq2PfORb2btf\nzE6Ol2NKowCzhQF8LTw9NLHCkBY2b6xtpnUYMxmPsgreN8L21hYdPRw0mg0cLSC7MH+RTkvW/PDw\nblxHXTdqFepqwgti8Lxkn+geDhwvg7Ii6s2IuvLcZu1iejh4afkk5wZlDOM4StNOtDpNzi3KPV+q\nNzgSSgffXRijoL5SuZxHVN95pGyrtklQUwG8EdFZlz52Bvw0AfTywhkqmqF+YmKSbJLyJ4qw6r8b\nRlBX89/m+lo6ZwulUpqAdXqwzPiYrLlq5RKhJ+PgeTk8nSwGl7rylfW1xTSVwcDAADlN3BzjEt1E\nioPYWHbtEuEz9rI46je8tXSBjCaadTJZYuU9GxsXeeU1iQC+uDiPY4TeM/PLDA+KwBPVN7Ga0b0a\ntWkp32288TIdNL3K5AEm8onSxDKtEbHlXAkvFF6Sybi8dVKE4fOLyzz2sBwqxooZLsuJtAP0zXl9\n9NFHH3300UcfbwPvSHReogEMOxbN2o/jOhIdh+RoSnKeNNcuUm/JqapdrdFJ6uoMjKbOuPVmk7wv\np1y3NYK7IKpwe2KW+Uik7ODwXdx7lzgeOnFAXrVDQ4N5cpqzJm77uBmRUrc6AafmxcE3MnVMtLVj\n+sLYpPluwtikUvzmxjIvfOk5AF544QXe0sSFjUbXVOg4Tursfa3kjKKpSy6SRvv4np86ja+srPD0\n008D8PTTT5PTU8sDDzzAU089BcBTTz3FfVoHa3h4eOf05USqb0cx7S1pe7Pe7FZaxxBpNrd2RFq5\nu1VvpFGXxjpETe2X9UY3uWqUSelPEgnmc/nEx5EgtNRqWm+sE5HTeywejk5fJ4oxGtVmXAfHyIkk\nsm06qqW8EXody03PH8aY1Lk6wsFTE1gh41NUR2jPAV9NtQP5PJFGCm1X66zWNJnrdodOICc9J3Zp\nqWnjgQeOcuzofgD8cJsk2czDjzzMiVNiDjt78nmGD8vp/sA9x5hpizYpmy/0aG1vjNjtUGvKugkX\nW2nE2dz8bJoItpDJUkfuiSObnkKz2Vyq4vez2dT0Wq3WqKkWYLtaTZ1ZYwu+OjX7xQzlYemfMBMx\nf0noMq5PoLmSWkGTkRkx/bSjkGBbc7/F9qZMCA8/9BATE0miyCxRkJgoIg4flpxhdx090k3oWyji\na560qT0zaemkCxcupGvLc32CQO5fXl6koLmXXNelUhGNxvzcIg09+YdhmJrQg06T+TnJlWSxaTSf\n53lpgkzfxITRziIQkzIa883FVNMQRDFHDsmceO+7H+J9T0jOr1dfe5PZVXVXiGBzS7Qa41MzfO5z\nwpc+8tGPMDYmpp7YWEpDmvhVTXgzk2OMT4ue88TxU3zq05KMslAa4u577gbgwQceSgM+MrksE3v2\nS191QjaWNRlpZpLA3Vn5nmzW0G5V9Nl3M6u5plZWV9CAUiZ3F1JNVKWSwc9Kv25ueIShmp+imCgU\nHlWvdh2kG003rb1a2aylQQCeE9OormgbMtQqMiZ+NkNTcxatbQXUVBs/dGAfe/LqxJ6F2trOXUBc\nY/HVurDd3GKlpg7kQ2Vq6mhtQ5NqizuNJqhVI2q3CNVMVhoo8MjDUlbo8OHDPP6IWCCee/a51GKR\nzYzjqIvM05/6z4wVxTKR8fJMaqRsvdmmpvMpjrvrrVEoUB4UrWS2WE5zHe4EDt0cX1HOS2vY1Tc2\n06SagfWoN4UvvvjK85w8IXvw5maVQknGq1TOsbgt+bhWV1ZZ18Suh/btZkQ1zcsry5x49fPSn0vn\nUneDkem93PuAJPrN5wZo1qVP3njrdRY1MenRg4c4emA/ABcunCa4ybIv70B0XpCa5MIgxEn8hYxh\nXbNZz6+u4yrzii58kWhV1N9+Y4tsoD4lmTIMyuZ0/MIGg7vUf2nqGNaThd9cWGE7SX62a4zWpkSd\nFAoOzUQYq3rkdKMajkPK+4WBtFsVJhqSoKuzOUu12NwxjTPTo5xUn6Uv/MGLvPqKqMcvzJ5PI++K\npRJl9aWIsak5J47j1I4dXqceWxJG4RiHWJlBaDtpRMjYyAhHNA3CBz7wAQY0HP1LX/oyv/JLvwLA\nJ5XDkH8AACAASURBVH7+33JYI3QefOgBvv07vh2A7/zO77gufZGOX7sZYFTV6RiXcY2McJ0cXhI+\nFjTxdfOJwyahCjdBBqxumKEbk1H1v5/Jk1ETRV4FEYNLZVX6zRiPdknt/zYGVV3HUUghSUZp3G7u\ndSdJFQGBbe0487ztyd5rjMOwFkvtNDppluSRUo5RFeQHSz4FNdVlMj5ju2QeZX2HxXVp++z5TRpt\nrTdXLvLedx8F4MCBg9TULGkcjyCSuVlttnn9LfGV297YpqHpQOaWl3GHRDAIq1sU1efH2Jh4h2Yg\ngEp9m1w2iYALaatJoNrcYv118RuIOh12zQgtUWzJ5aS/y4OD6eEgExWoalLG9fVNNjQku9UJGNSa\ndGuVddxMktokYkv9HuJ2TKgMPYydtHC0n3PJlZMErJa2lc9BtUO7s3PGPT6+KzVRVCq1VMj0spm0\nEHcYhqnJJJfLpgkwDx8+yCUV8OI4TDeTRrPD0FDXt25+Xjb1QqGQRtnWapU0O3YURV3fqh7fxiDo\nUK8nCYAtJc347fsOvr8zo0ClkVRDCHD08JHPF6hoguJTb55k3x4xyR277xiNN4SewV37qepvm7Vt\nTr0sQtTGxjpl9Q+KbEQ2k5iDZBwP3fsutmsyP3/u53+NS4uy2d//wD18+csvAFD/jjXe/63im5kv\nFNi9b780NmqztS48uFKpUrgef+vB1MQw1aqascYGmNAo0ouXLqU1DzEtqVoAZHKDFEuyXsvlYY6/\nJWaafK6I5+kmHkJB54LrGmpqlrfWpvy0EzSlmgIiOBvkt3Ho4HryrqDo0NTozMlveorKsviLRmWX\nfLxzn1MTO8TK992CS1BVYb8NoW7LNpPDK8i8mJmaYs9uMY0tjY/g6IHmyQ88yfs0Wjuby1LSpNLP\nP/sse/aKWbtRa/H8M+J3Oz69i+K0jOep2TleeSlJ9Oxx4JAIxeWhkdQ03W63yahJP1saIExSn/O9\nN6YRmF0SQeWtL3+WjAq9GIelqkRc1jsxTT3QLK5dYn1b1lybAi1VTJQHPeYuypqrVitMj4iA1GyE\n6eEv62XwrQppa7PUN2TerW8tsaJz8OjdD7B/30HtzxnyrkaOFopsrojc0Gm3cLL9ZJt99NFHH330\n0Ucftxy3XBNVr7XSemuOQ7cujfHZbsnJ6HdfPc2qlpGItjbwrEi+w/ndlI1Io9Nhlbs1b0eeFrNa\nETyqbjO0T04q4YEHiNSxrt5uM3tCTltjcRWjFetPR0XK2p7xi3PYGfHoH3v3UQbVc3/r+CrOkdEd\n0/gLP/8zaa6RM2fOkNfIgD/5XX+Khx4W9equ6SlaqoKdu7jAmZNi2nv9lZfZ0OiBAwf2c/fdchp4\n4403eP1VOeW4nsd73i2myccee5xz50RTN7cwx/ve/z4A3vfEExw7JrTs2bsHo3rv6tY2zz0r+TZ+\n6qd+hhMnxYm2OFDk3Lkkauj6SE2MxknNXFEUMzo2kV4eVzVveXUNT6MfXZfUGTI2gJ6Ws8USuSRp\nZb2KVY2So5qRaGOLjKqWs7jpmBYLAzhNUcdm4oiGzo1OJkNLTQURASYp5eOYHSfAs9aman3HiNYJ\noGZcdmmOoJGyT15NVEODA5QGNV9QuYSvCVaXlzbZrEpfHDq4l8a2nHjHxoZ4z+MyPutr2xS1jE9m\ncJqXXpYxKY1M0LFy4l1aXWJ2XiLdqq02K7MXAPi1f/0TTEzKidTi02nLuvmhf/Avbkjj0uI6uYy0\nuTw6SLkkGpiM5/H6lyS668LcGXIl6e+p6f1oaiscz6Wl2qcgNDR1fGrbW1Q0yMPGEGuiusKAR0eT\n9/m+31WRuxZU6xI2A1TJRxiHrMzLOjDGSU01nm/IDXRraN4IURQzOqrJW21PQl/PJZNPSicV0zVa\nKpVSzeX6xirbmlsuioPUbN7pBGQ0hHJmZibNN3Xx4sUe7ZOl65AapaV/DKRRn/V6Pa35GUURxZKW\nxWm0CHaY7yspM5PP59L52mo1iNVh9lSrRfR7Ytb/s3/mT3L3XTJXttouZETDeObkSYxqaINOm5Fh\n1ZAbS1m1dVOqWR0ZGuHZF0VrcOjBD9JGImIPHnuU7TVxhv7s7/0eUSzvX7i0zv/P3pv9Wpbd52Hf\nWmuPZ77zULfm6uru6nkQ2aQomRQpaqAgRRKs2IbhxDZiJIEB/QEBgrzaCZAAefGrg0AJBCeMJNuC\nJIuWKM5ssufu6hpvVd26daczD3taQx7Wb69ziiKrTjXQejq/lzp1cO45e6+9ht/0fV9ZDNlYXcLG\nJpWLxiNoOd89VmIOo+y4MiaxsmLn6Wg0Rqtp9/pebwRO+8LayhY8Yce123kAsJLrC5iMqJtcB1Cx\n3RfiegxB2e/RcAhNwKdA1KFLXdWcucZmaI0J8bcFYQVjKre9d+0atrbsM6xsNSDT+Xiw7PcDISF9\nU9+gb+z9LleXkdGa7rE2nnnacnT9s//6n+AsoXuH/a7jJVzf3ASjVpU8y1xDfhgGeO01ywW2f/sO\nrl2zZbKVFYP927sAACEVUuJYjOIazp+yGR4FiVtX79AYSoxp/ubHHMbM7zIYaFy/bzNRf/7d70ET\nf193lKBLLQDMF/BJC1YiREQZv6jaQEpVqEJ7KEg+LBlNkEV2/AdJjpDaDSKmERC346joQdH5kh0f\nIKAs1o9++F383u/+QwDAudPPQVCFpX10DEbfkymFiD+ZW/SpO1En7buo0iCleYSCEEptJl0atRZJ\nvLdrN+JklCMnUkZ0EoiImHC9FlrK9vHEZgxDDMsNtoHa9235THCOygoRMwK4TmWGDdlFjXoJPlRV\nNKnctD7uo7NPQqFhgRWaLIcTgaefAFb9+uufcSip4+NjPEdaWV/58lddTXgwHrkeiEvPPI3f+PVf\nse/3uuiRMOrmxgZ2duymM+i08fabNl2ujcEbn/2svc6d0xgRsiSTGVYJuhqEoWO3lTJH2X5Qbzbx\ny5Rqf+nll52m3vrWOpaX53MUJTk3Wstp6pJhKkxpDBT1jFQnYxg6HC6BwaeF02zUEJ7YMpdOpSOF\niw2HJtK5mBB2dSXgleWQWgRZErSqqb6dAZAQuqVoFsgIkZTpDJWAUJkyhWLzlfM45+DUKxd7Ag1y\n/jg8LJFDtdyK4ZXiz/UYMTkh9XqE7piYoXcuoT+0c200ynDleduH01xewg++ZzeyG1dvO0K9N37j\ndzAiB7RzYxetZVsiNTJHQiWHkHEIKoG120fwCelWbaxhlM9fv69ENXTbdq49ODp2ZcRW2HS9OuA5\njttlScvDqTNElxEAkspq41HqSoF5lrveOD8QODqx31+txfBo7LM0m9JscAYIJ5rpdKrCIIJM7efT\nrJiyoMe+64Obx1568RXX12SMQRTTc/S4g3PnWe5oRZJMohTi7vU64MIxjbprVkq6MtzJyQnahNoa\nDAYuwLA9TqXO55Rg2Pc9p51nEa1lj5Z2ZIuFNmjU50OuRUQyvNRsutfDyRgjur5KtYowtON1594h\nfvHLXwQAZLnBjdvW6Vn3U6Qbdp8sxj1wciiiWoylpp3TSy3SWtMKfUJcPvPaZ8GoH2j70hVXTmxW\nOVZX7bx99/1r+PrXvw4AqIURfpfEjbe315GO59MHBCQ09YgpWSBN7d8xxsBQkjRqjIfktOiOe+ZK\npQipHKMLjcAnElkVWt1DAHFd4ZVXbbB6586e67kyCGCM/f4ik07vEQDSsb2eIDYISVT35jvvYr1u\nn+3ZjR2wwfw9UVIzCAoeN3a2AdqL67UGMm2vuRppXH7KOlEXL5xxvXsiaKFC0Q1XErt3bDCsOBz6\nNhLAjauWTR1J4dQdmCdwgcp8Vd8Hp+fpeT4i2n8HSY46tZ6MJmOMSwRcOp6O/xxmNEch7Pcsn30J\nH7xnKXEKVsXSlm096fX3IYlS5dy5lyCpzWVtuYWASLf9ehN3rtk2B4MTXNu3tA8FGOpEjrqzvIqQ\n1vq4L5FRL+RgMMRThCLdv38Pf/3NPwUANH5jC0clrYEAdgit29lN5j4zSluU8xa2sIUtbGELW9jC\nPoF9+o3ltz5CRiniYmUDQ4oqCpZBUOr/fJbjR5wa9+IGAkrl5oMOPEr9G1ZDR5E8CDyYzHrNfjuB\nP7J/uyQ0YkYRCVMQsN59J96ACWwk0Rvn2CPdumv1JYQtG2kfPfAgOPFPiHW8/44tHf6LOe7xjTd+\nHi+88LK95jxDCaXr9fowzEYnw9HINdBpZhCTNMxyq4kaEej1ByNkt3bp/QY+88bn7ee1srUxAIPR\nyCmTN+MlFy2nk5R+2zZ9RyRtw9g0hb6xvYqNbcp0GIlp+eHRfFGs1E4ycDpKgjEnKV/kEhn540Jw\neNTAeklJBIReKuIlBJTdW+rnEMxmMnilCkMlJkMElH6jhbxuo7Hh2WegqSE0+PgteBRxszBGTFmb\nlU0Npm1UERugWqUI/fAI/pz6gJa1jEqCTEFSJGOYAgvs+yurdSgaq1qjAgp+MRgOEcR2rj311FNI\nJrYp9v7BCbbO2Ajnb779LjilqreuvIKYoqY0A5KkJBNlDum2tr4FQ7+l8wSMsqeRH6JKTebr2+ex\nkm3NdX8A0D3punJsrhXywkbmsqLw1FmL2hwmR+gRiuvubhuHR7Z0dfbsGfhUNhgMM3iUBZmMJxY8\nAsCYArLUikxzeNR4P+j14fv282EcuDkb+IGToPAjAUkRoODcaWMOxhPXYDqPHR8foyAU0+rqqkPq\nXb3xMXoEZNnqT3Dt+i4AoJBAhSJeaIWVZZuBOT48xGA4oPuCK1/euXMHY0L4KKncdXoedwg+KRU4\nLzMjEgNCeWVZ6hB/jDHHbaThubX0OFtbsuUszrmbQ1euXHElxl635zjlsrzAPmnhfeELn8dXvmRb\nC75xKsb/9r+8BQC4d/MjvPq6zXIvb65jfdOuqWps7ysd7aPo2gxWIip46TP2s5A5DEl0/PyXv4xL\nVyx/VLTUQp84q/74330d779rWxJWlj6P3evzce/5QTxFzIFjjzJFMk9haK4lkxRG2efWqAUYU6mZ\nC40mARQCHuLBMWUfZeiQtS+9+AL+wT+xbRB/+Ad/hd1bFu2VGAkjKWNjIoiSwFen0FRuzaVGWLXf\ns7q1jvHYXk9dNBAvzUvsa7MfE9qvV7iPCiO9w0TjDBFvrldaOLNlKxOTQR+gfSjLUvgV4nryOf7T\n9/6zvUyPIyG9vxt3b+DkxJKeRpohIY1VxAL+ss3UZ3mO8dhmjvM8w/V9+5yHowwn9AwneepK2QIG\nYfAEeRfDUScS1M3NZ8Fgn1dzeQk+tezcvuljTOfus1deweFtyp7lXdQ8mxVVQQOtJgFr0iEGxFuW\nZhk80t1LdQMeZaWELByKXMFz635jfRWKMpzvXvsA5y7aOVtohYNjO8c6x3vY3JpKqc1jn7oT1R91\n0YS9qNpGjEl/FwAw6h6hvmlrvFsbK1jqE1NzewJGRFxYWUdBCAmPB6CsMwwYDG0URhkUKzZdN1xe\nQUT9IpU4njoYmkOQYxaPBhju2XSg0Rk4lX4GmYecaqoDGaF/tWQOf7x9+1vfQwmfC4LAEZ4J4UHT\n+9oAoFKB4QyDIRGMdfvuOoUQToPt7p6HCvVtBMGUBsD3O2gSK/va8rL722QycRt0s9nE0jIh3jgD\nJyoJXRTOUdDMe4ho7VFmqAQo/BCKDk8YOMJFzYAqfVfoVSAlQWVnEp2SKeR0uDW5B1HSTBQGjPrh\nSi6MrNeDJLI07kfWYQOA5gpSSjmnnCOjPpDJ8RCmZn+rSoK/AGDYVPvtccZmiEhblQibLSKQBINH\nG3o1EkjLe2IGVSrzJcc5GpH9pXG6j7V1u5hrrSXcJjbs53/uK7hwxfYoFJMREkKVfPNP/x1uXqU+\nk7Pn8fEHtjS9sX0arSW7Ue7vfoyAyptaFgBpkOk8/Zks6z/Nzu5sOYhyKiXywj4nIRkSIrxLsxRD\nEuwsJjHee8setjevfYilFetgbG2fx5kztmzQ6XRwTBqKhZ44fS9TaAg6gyLmIaaNOMtyB3UO/QpK\ntVpZSHjUk8g9z4no5olEMZ7fier2jp0T8fzWM84hfP/dd1x5pt/uYzSy+8Hp0+fw/HOWpPZHP/ox\n2g+IvVxqSEJQep4PXSJL0zE0kZEqpeCTs5ROEozLvpkghGsd4QKHhxb5s7e358p5nuc55CDnAcbj\n+VCWNdoT7h8eokfIwDiuYImoCXr9Lg4P7PPY3NhA+9g6RT9+802wV+19vvPuR673J0/GqNXsmtra\nWsHSComED2xQ8uGPv48Gt59dXa9gMDyk8Rnj1Ss2QGifHOPqH9p52+228cKLVqdN5xIfv22dqL/s\nt6HVfKSptVoLgU9lWGawsWbXwWuvVLBJZ8bevQe4e9c6iEEQOATfeNTD+XPW8eDSYCzt8+mOq64n\nZ2lzB2tb9jubrTXEoX3NsAddEAlnJmBozQU1Hyuk1FBkAh0qA318dwRBzmYUNdCozd+7lxQ5TGrn\n6RpnqFNpF4UlLwZsv1bJUn7//j3kys6RWrOOzVV75t3tH+ODw136zD6++ePv2fG5cQtpybivDURs\n19P9BwfoU/tIlqTOWY3iiPhpAB8CkpCpcRC686ZVi2fQeY83xoHXnrflzp3WNo6OrPPTHx8hPyEU\n/Wode9TasbVzDlur9jne/vi7qNXsfjORHGeJhiP2xhhM7PXHPHB+QH84dMSbsiiQEju/kgY9Wute\nUMXowK7vU5cznN+281erFJwRrcSwBj33qWFtUc5b2MIWtrCFLWxhC/sE9qlnos5duQgR2OhmyDRW\nN21a7vT2BlTTliKGyscLpDvUUR1I8iI940NRAyszElKVyJbCqU97mkFQg3M+7GB0bNPateVlBB5x\nGuU56pQ6TQZdbJESemAE2oQaGkkNQw2vejjAS882577HQb/v5CKklPApWyI8D8w10XIwQgNoZRx5\nphDcoYMY4y6K1gZIqGk4LaaNbsLzkFNUrNLMqc4naeqilmQygYb1rDf8NYSEHGPGoMyYMaMAp1H4\n6JLXMaV5q9U6BGX6wABB5TnNBEDlGn/nInTfZvFUvwdN0Ez/uEsQPUC2amDEE+UFIRhFnT5JTaha\nHRlxkyRHe1ClpEscowf7HI+7h/DpOU7a9xGeIa2kesOhPkeTBF4wL0+UgU+pTt8IHHYJHVgNXcZJ\nKTlNbXsaE5Ij2d5s4OxlGyHfuHYbPnHT+MJHj1TnfX4EfdlGOJ3DPXz7P38DAHD93e+htWzvO510\nUSQ2yr1/q+ckE8IwxGhAfGNZFQd3LTozHY2RJqVk0H/72HsMfI4iI4RSKNCgCFNoD8dH9jpbqzHy\ngnhheB1GEy9ROsDeXZsi93gFFQJ2HNx/gILWluKZC8sqURUhyXVEbOK0Lg3jiGmuKKmcdFCoA2SE\nehLcw4i0Kzl8V4aZx6IoQByTNp+W+JgaUmvVistubGxsokHl4nq9iZx0vHqdQzcORV6AGXttHuPQ\nVKrL8gSSMqDCE+Al2pgzmLJUZyyPGQC01ppoEQ8TF3DAjjRJYKicHgQcWpcahY+2slQ2GA1dJvjD\nj6+iTjp226e2sNqy0fzhwSHMO1SKh0KzYdfIzZu7WFmy+/Dt2/u4TyjQC0+dg0dR+ICawG9cv4nc\n2EzNP/7VX8GIJJ3u3rmF6zS279+8ifa+3XfjIERzzU6Cy09fRkoZrfaDO3jtjS/MdY9CeGA0roEv\n8MUvfoHueWJ1uwCc3llHvW6f8+7uPhLKpnmC40u/aGWUbl//CMMSiTJoojO0f/ve7X1864f2+T84\nHiEMbdnomVPriOjM+P57h/Cadv15FQ+GkDrLS8vICH3shQJbW+cAWHQb955AV47DATIGgyFKrZ5s\nmDr5lbgeO4Lbthzi6Ngi3fxhiAOas2++9w5uEOJ6dNx1GSQtABlRlkyEaJF2LBcemKRSqdEQhOIO\nWAjFqN1EK6yv2fnx0osvIaCSe+wzyOLJmq5zyjovN1rIqQyep33UiYfMtNawtG6zpR/8+If45V+2\nnIVrm6sYUqP+B++/ieGJLbcpk+L8Ges33L6+57KFWmt0Cf3dHw5haL+phLGTRFImQ61lM1qvvvoa\nNkuetkKgsmzfbx8f4fAJAALA34ET1dw+jYM9ewjf3Wvj6bN2AB4MBji6bx9+PslwaUKb7K0THA8o\nXZ5JJLRhSa0gVclurJGU7K1KQ5hSyFgiKr2TqAJG4r9+7MEQsmHCwzJrCe0LJFTjDVdb4HRYL7U9\nnN6an2yzWo1cuS0MQ+cIpbJwEPtABAjDEgnhuY3e8z2XUi2KwtEg5FkOowkRMlPOAzNYISLIM5vr\n7rcYYwio1MaEcdB0z9dOWJILDkanHDfAvLWgE0LBySxHa72kNfCciLABoMkpCte3IYiNdtTtwlBp\nthZX4EcEB26swj9lWZCTMEafDtt2Kc4KDUklyMxMMCKB2+Gg41i/02yMs6TjtXXhIoYHNo2dTQbo\nUv/KyWEX1eX5kV2SDsGJTHGKxEp7wwnq5EQZP0KTBE15UIGm57Z1YRsfvG/7PVjBsX7eImp+8Nbb\nduMHII7v4dt//kcAgBsfvY3ugV0TS40aDM3lXvvE9dikaYE79+ymGYYhfHJGpdJg1BdSZCOYYn5d\nOWEYVpeJqJMDYWznQpoo9LokZNyqISbCxZOjAhcv2vXa6/gYEuqw6ns4oRJVIDQ8Ym4fFYlDt2mt\nkZMj4fkeMiqNFQaQ1F9i50/Jbp+ioKBBMu0IToVv4AXzb1Pj8dj1QR0fHzv6EM/zEJB+5s995nXc\n37OH/ve+/12k5HQnyQhh2R4FiZDmt1YpSr7PNM0da3Y1ChBT39fSyhqMsmMyGk1cL14Y+i5IOnVq\nwxF+npycuNIeZwZxPJ8TVYvs5565cNqhzSbjETyiGBh22uh07KFhwLB5ypZ9WiurDgX6ygvP4Dt/\nY8uce3v3EdO6jOO6Yx6/dc1SsOzvH6J12joTo2HXrZGsKNBcseO8o+HIc+txjPVtW07rd09w+XlL\nMFt74zXsXHpmrnvkzJ/uU9xDiyhG4ooPo+37y0t1rK8TZcONe7hxwxIlwxhsbtg56yNBJ7Olzb4Q\nSCK7pj+++wDmP9g9Je1rtMdlP1UVa8Ss32wwmKp1HodJipwCTi4G2DlvP3Px4g42N+34BlEEJuY/\nM772W7+Jkt/jg6N9MEHzaPM0jtrWkZe6wPe/b/e17rCNJCUtSlWgT1qlDBzBwP5uNSmQ0F4fbixB\nrNk+TTkcO93LAAqCnCghtRM/1+MMIa2PVEmsEVpwe30DEenCBoGYW2+1tDIJkg7GSKjnNUKILer7\nSodDSDq/6/oE779ptWA3z5/FrTvWSd+//xEKCiIvnDuPjS17dhztTefjKE2QlOh0Y9zZpplGSvQI\namTwtb//2wCAF597HYL2pLjqz7TaeG5fn9cW5byFLWxhC1vYwha2sE9gn3om6o++/k3s3rMRWpJL\n/Pg9S+o3GIyRUXnrYj3CM9QAKk5GkGPrXXYlc0rnidHIKdU8AcOYXisIeBQa6sDHmDiKkuUGRN02\npomoBkGeZiIBkGfaCBQ2l20qN6pH6IyoET2q4Did3+N+5cUXHmoOL5u3J0UORelYxthMw7mYloWE\ncOU/pbVTydZauyxTEIYI6fNJksDj02bAKkmlgDGnMeYFAoWZIoUYRZf5OHclAKW547hZWXl0tiZT\nVB5LUiy5sgxzJVWhGW637TN+950f4AsNigSVwYjS+dm4jxqVgNSZSzjq2ZJff/8Q5qUrAIAuZRrb\nR3cgSeNNoUDZ853J3JEYGi1QEArQ8yvoUGOuOkkcT1PSm8CbU1qOcw5DpdH11VVsEUIjk/tY37JR\nWS8JoLh9DlWV4MxpG4lf/+ge7t629/P5X/gK7u3buby8fRlBZKP4qx99gGtvWdJTleYIKbOUFbkD\nZnHFXQTlCQFOPDKBB4fmDARDWEZNRfqQztXj7PTmFgrK7GotkdNrrgxaJBNkZI6AsmEwCUrVnHq1\nigrxDzUbVYyowbQS+SipqvyCOcBAoQySwq4zLjg8mr86VWA0xxlnjmsIHAD9bpbl4DQ+QRRAF/Nz\nYQ2HAzSJ4+b69esYjWxqnjHm0HP7+/fw3e9ZtfjDg2M0mnaSRLFwzdpR7CGu2HT/cDDBygqhoUSE\n3d3bdF8AK7mwshSayjxpNkGtbu93NB7Ao3sRnkGFNOk2NpYd0rXd7qHIi7nu79lnLwOw/FPHD2yW\nZdj3wKmJWPg++rn9vc3tU3j6KcvHE4UhqpTtOnN6FR/U7GfGXQGDMkMeQlJWdEDcUKvrWzh11maW\n2kfHSLLyOgU8Snd32j0UVOb5zJd/AUsbtjzz7W/9FTYo43D+4iVMxt257jEIIghR7o8B4sj+pqc4\nOKg1gXloNUjyamUN24Qq/Ju/+Q48WqOnd87i1r7NYOyPC9w5tms0nUxw+5bNWpw6vYNzL9sxuj88\nRmefnlV9G4IQzn7oA6U00+QODJH87t+fYL1ps9TMs9n5eW11Yx0ZZZPGt69jMLJ7RrAlUKPS7HDS\nR0hnw6nlFeSJXR+dUR8xNbQfdHsOrb3drGKPdOVGaYpS9TNgM+AYz0dCbTGjfIKM5JgY4zh/7pz9\nntUVbFA2t0hSxznIuIDbgOcwxgBBhLuT8QkiQtqf27qAkJCGo50zuH3btic8tV7F1fs2o//d7/81\nEklyUuOBa2FZW9nB2ipVA4SPjJrJNzY2LEsygP5w4GSdfBh0KYultcDmhn3Wsd9EsEqVFF9C0lli\nwGGeMBP1qTtRu70EI+q54ZUIK2ct+eDZesNp8qxXgPZ3LCvuj9oTXKNywtjjDjqfMw1VPj/DSjk+\ncM+HLp2TqAJD7LtpNXbijUHgQxAjrBEGjYbdNNdihhqliiVjrg9myBmy3vxO1FKj5pwoM5NKbPh1\nV9IoYdeAZXAunSgpJfJ8WpLxeEnpwJzj5Ae+gzOvrSwhpzR+Mknc5ssYc9cQxiG8kFjAhcCIQLj4\nvgAAIABJREFU4L/dTsfBqu2ctL+1snLqkffne0Q5MfZcrVn4wjlRWZZh/9AiHu+ODrBNyLpzYRUq\nIfg79zFU9i/u37sBxe24hxub2GvbstWA+oG0zl19Pk3GTow4ihpoxLbfo+5FqBzZjf54kGBAZcPh\n4T4K0kkUgYBU86FJAuEhp99hLMSDQ5t6bjRXIDx7raNMoLVjHT6GXXTpoLl2dR8rS9bpOmof4+Yd\nW6rbOv8cbt/6EQDgxsfvgdPijCPPUU8Izt2SZQzwqf+ACw6v7NHT0x66NE3QJ7LHIIwerbf4E8a1\ngU9ODvM816PnRwp5QGOmDARtlI1q5Ag/oTN3PZwDrHTetHKfaVUq8ImkdJhlYKT9BwNoKtnGAmBU\nJpMeg/HK6xGOzZsLgaAULpVTUt55jDHmWMQPDw8xofkOpp2O4rvvvo0HD+wzkoUCVToQhsKheqSU\naFAfSbUWYXPTOlHbWxdxQOg3KRNkdM0a3AUrQeCB/F+k6dgFcEHgo7lk9yRjasjoh6MogJTzOcMr\n1KuitIaksrkxgCakZb0aY42EpauNCvbv2APq6OAezp62paezpxq4eOEcAODGR7fQ3iN494M9TIjB\nWhAK8PXPXcTqptXbjAIfivaMa9dv4ujABk6tRgsvv/Ciu5av/8Ef2HH+3rextWkDWZYP4c952gRB\n5ETEPREAzF6LJ6e9UhwedEnUGgFPXbQl9A/e+xATWv+N9SbqVKLabDLc8e37S6vLMJrK5ibH1nm7\n/7X3I7R7dhzjKMOzl2zfzu1rb+GEhJSLbIBBxz6rleoGXnjJlihFIAiCPZ9NxmMMaZ7evncL92lO\nffjh26iSTmN9dQl1mi/V2ENR9tSaAlXybKJcYZnQ6aPBGKB1JpSCpugmS3P4pSh8MXURttZWsUrI\nx2aziXVCwG2ubaBKz9+eQRS0MbiAfz4zOKE+Lq3HaFI/klEFOlTaqy01caGw8+v9j3/g+lKVBCJO\nLOImAadWmMOjDhizQYwXBwi03ScuXrzoeszanRPUKFgZdnuQdygpozzcJLqMy2vXcI5aFYQfOiR0\nvbmEg/58zn5pi3Lewha2sIUtbGELW9gnsE89E3Xh5ZegKBXHGcP2Fnl/nMNQNG5UgTdjG7G8451g\nSKnpXCkwVqZvNQxFdAwMwpSpOA5FORHBJRil7HnGIYgNMQgFfJTNdBwxZWmiigNFQCsPAYVKocgQ\nhE8Q/RoFjrLJ2kzlIgrpdNxmRdp9DoBKV0YWMHLKg2McXxGDzEtkjYakt5VgZQ8cikI68kTP81yU\n4Hk+yuhhMk7R7Qzo8wY9atI+ao9c2vIzn3n0/XmU1h6cjHDrA8sbdPqpF1AhhNNkPEGSEYfJxg6O\nKDO4IRggCPG2tQ2P1LelCVC9YMsSO6+/jMNvW62vvOSgKSRCQUR6S6uIKcsUMh8oGxXTFAcknZKa\nAD4h3IpDIJvQfGt6KPL5nmMoPBdRnHS70Mam1H/+pS/CEEpLBAYb52wmqr0f4ht/9Yf2GqsRPJ+y\noaaOddLEeu/b/x63btkG5lYlRkB1u8DnLnwxjDlEjQFc1o3NiK4xzkB99pCZxIjKq0FePFEmSsO4\npkkOjpDQaoVMoKhklk5y1IhTRuYTDEj7r9XwYegz+/sPMCaCUJUXGBIqphktuRJC1Q9cubgoJAzN\nCe5xePQ60RI5ZYeYJ9waSlWOPCXeJAVEXjj3PUZhhOFwKi9SAjgKmSEi3UOtpUOyer5AWAIyoCHK\nSD70EZYIUk+4zNL62jrWSGopzY9Qbdq/ldJHnhPydWSQ0vVHcQWMHl4hM5hSWc7A8bcFgYdqdb66\n8+nzl+geFLINm1n52AApkSY2a7Hjw/LD0AEb9m/exs0bNiv13/yz38av//3fAwB850fX8MG7Nlv6\n3MUa9k/s5zNm5/+Vl06hRjqP8AQ4jWEchti9bpu5w0CAkc7Zndu7uHvzOgCgGnKIssQ57KO+sz3X\nPfphxUkwWR1FKplxn/Y2AGAO2ALGXXP8uXM7GA5t+WZluQFN2cHlZoBLW/ZvdebDHX0hsERrV9Z9\nJJSFbQUckW/HwmMDQNvsRKMS4le//MsAgN/6rd/ExratfBgop1c6j3V7PUzorDq9tYmMWkwOHjxA\n98A+y2jShXpA2adQI6KzQY8nUMR9FMgYE0EIXa0dkMkvlJNBEZUQrdiOz/rSimsaX15edqXvSqXi\ngEme8BxvHmPM8Q8aYwjhPZ8ZAxRUuu92TsCJYLMz7KJUj1ldWcL2aVuK9VsbWO7YzFVr83ncuG0b\ny8P2XfAKzYckxYAa7DNVoLVsKxOMw+1DS/UaJiP7vA4PjjCiaoj0PZz0LLfYzdsf4OTElg7r9YpD\nQvcGHQDz3yPwd+BEGcMRkLif73lISKSRMwZOnoXOJfZTGmwDlA6ANAasREVwuJ4VxoV7yEL4Dt3G\nVA5NhGSCh/CJvM/zOHwj6HrgmJdFoFzvBdPTdL8wQCjmT9JFUQhFJQebZi8PxZkDjrEpks7A9Xpp\naAjn/Hju3gUzqNPGyoVwUFRjpsglP6y4Po8iz+CRY5YVKXLqUcjyzMGSh8MBej1ioh1nc5e6/JCE\nUuUJ7v7QsuOe7N3E+ecte3ElXkLpFUQaGHmkRcY1ym6rAArxWeso80kdoz7pFh0coEq6c9uxTat7\nNQ5eIv9yCUmLYCTHSDBF0JXoSyNyjA/s4hh3BtAlQiUMnRDl4ywQYto3l+WYkMPQ7R6jd2KvdXlj\nBwNC1X345g/x0TX7m1EcoLZsU+pLcoA4KFFvE1RojldC35YmAIcyBWzZqOxTYzNzRGkDQ/10nDEU\nxDisjXFaZxoKoT9/2VkJwBDNBBhzsP1CFZA0fzvtERrby+6a+4T6qkQVlAXc63eP0evb909vLKNJ\nPRzVSlwS6yPPlStfJjpHOdUkh6MDqRgGnpc9esaJwvqxcD0QIvAgymuew6rVOnxyuopcwZDjGgVV\nxKEtk8RhHRM6hHq9PupVe/2NZgOBXxLc+m7NFTJHo2nn7uapdayur9C4hWg0yr6pFKFHmomDodOx\nbNSaqNBh5nuee9ZZmrqeKFbhM87Bo22Z0JWTJEVIfXLbZ86gTYSnzCj41CaxffYM4oYtB60fHLrn\n7TdWsLpjyVJ/75//9/ijf/O/AgC+840fYBTaefzb/5XVvFs5tYODe7sAAK0nCGisnn32aQyIdPLu\nrQ+RjGyJ+cL503jq8jkAlhSySb1kXHBHhfE4E17gHCQ/8FFGkEYY11dq10l50Au3bt743Gdwl0o2\n48kIKaFXozAAAe8wESHGxILv8xByYtd6BdoRZnpK4dr71ukM/Qq+9mtfAwBcunQJ585ZdFitxqFp\nXfrh/I4+ABTMOATnxa3T8Eu6mLTA3qENvCbtHkCtLazuIaXjeq227gTMO/cfYEi0GbVKBYrGuBpH\n2KQS1db6BjaWSJuvWnOi8GEUurYSz/PcfPc8f0q1o7UT8S7/P7cZgyCye0lrOXQUI9UVAUXtLUwH\naBDtUbi2hSUqL24tHUHRXr9yahNXP7A9jJ3OITIahzCqQSnrOH14deDaEIzWODq2vWHjcY6c5tKr\nn3kBZ9ZssC0FcP+IerWv7bvxPOhNsHbq/Pz3iEU5b2ELW9jCFrawhS3sE9mnn4nSgCwjao9ZDgcA\nHAYyLaPfHk4IFaOZfoi+qES6+cE0s6S1dtpmURzAJ4SPTlMweh2EgUvZM2PgkZfKfAanXDKT9fID\nA88rayyAz+dHPRWFRC5JvkIDmn5LKaDTabvvbDZtFJllCRBRk27o4/jEfiZLC4fYKLIxnrpgaelF\nEOLBkUVvZLl0qetqEKNGPDWryzVUK/Q4DXNEmMIYNKsUAUQCyy3rcXMvQjBn9LTastFBsp26iLPT\nvoPkBzYCai6dgqTG1q1aAwGV304G+1gmOn0+7kPdt9EB9xk4ITAPP7yDWNrrzqkRMpn0kVPqItUF\nRqSPlBmJlOR76ltbkETImHSPkWd2/hijygon5DiHN2cpyMDAp0iMgTn+n6OTIxQUqZqD+zjatdHp\nqHeMTULmdIcSu3s2qkmzDC3KIF68eAEfF1Zhffv0M07b8MHuB+53tVYueczBnEyQgXHzl3NWcgxC\ngMH3y2ylcmM2j/mMQ1F5o1AKkkAJAReoUpnmhAkIauqu+R7qNUJGBRFCWh9BOETo2/cb9QZyymK1\nlpZdZC6QIijRSpq5z1QCH2k+zUandGOZ1qDeVxRQiIl7ikNA5U9AYqiAO7sW5CALhXrdZmJ8L4SW\nNqrPM+2QZVlaIEvtvUTrFdRIF208HltSXABJIhEE5bqBQzUqxaAlRfIMaFSJT0cIgAhX65UmaoTy\nC8MQIa05z/MwGtkyDGPsoWj/UWZKyZ8iQ0rkpL1eDwNq1OVQOLNq12sYhzi4bzOn7eMjl7V+991r\nWN22ZcFf/KUv4s1v/hUA4Bvv/gi//z/+PgDg2VffAGAbqW/fshnXu7v3cfEpm4V56soVvPyK5Wnb\nWA9dFiOK60gp06q1dlUCaIOolDZ5jHme91AJqeTI44y7cZrNRM3mAlbX1rC3Z0tC/cExNHHthULD\nF9RCAR8ipP3RN9CsJFVVAPH0BQHHMukUfvlLr+IKSdw8eHCATsdm4ITgaJLM1JPyJ4nAR0qI4rQ3\nQEYao8gL+IR8zdMUkqojvMegqLG8LRL0S10hLhFQ5ltygTPULnP2zBnsnLIlqnq1hoDGUEnpULBC\nTHmfgiBw+ybn/JNnn2aMMQZNkmLVahMh9c6Mun00qFTerNRcC47IFEI6R1txFcslWOd+Gw8oO5el\nQwwpoXnxqQ1srdlndOvmNQx6NisltcCIABJMTrBOQLIXz2xiiRMSl1cQNu16zdMh2gTW6fVG2Nh+\nskzUp+5E5blyBwPzAnCvZMzWGBEp4t29u25DCcMIKJEqDK5MFsWR21iTdAQQdNLzBSLamDQMDBGD\nWWLLKTqoJLYTQeT6iEYj6ZA8Bj4yKikqrTFW8+t1ZVnmWMWPTjrOAUhyiQeEYPF9H5WK3YjH4xF0\nOQ6+QJfI8fr9kevhqTUaOB5R2Yd76FNvwzjN0KLywIX1FjaotLCyXENATNCj4RDdE6qrRyGaLbt5\nBfDgk8PSafdxiwjqLj790iPvr0JO2OapbXg0vr3OCXqHdnM9PrwFTQdj5vmoUF/JkEkwEplmoxHM\nNbu5pfU+ZIV6mG7sI6GNIqXFLT0OVicB2pMOOiQ4WV/fgk/lFpk8gIcSApvYUwxAuBQ7B1sIAfEE\ngplxWPYC5TB0cHcPe6iQxhkCieGQHEGPQyh7jc16gPu37L0lkwxf/bItc8pxF+cunbN/Wl3D7js2\nJQ0pUbLcVRsNJET2Z5R6SHex3NQMYw74o1ThSmOcK9f/Mo8Jw21UAwC+7xoCVZoiohJbvVF3ZV4B\ngyo5k2AcBW1wQRhieanUhCxsUAAgzwu3ocRhhIR6ySrVypQEFwxVKjeNJxPwUpiYc0yo1O/7U8I7\nJc1Mn+DjrSgKpIRerdVqiKJSz4yjoGeqtcbp06cBANvbW6gSRJwx5nqosixzMOlGvY4N6oNqHx27\ngCwIPIemRRg6IWbheVgjosNWs+VQtkpp1yemtXZ7j1LKwdofZx6V0yrw3V7heb6bN7W44lB/vU4X\ny9Tz0ogjHBAbexhUMaZyptESp69YTb1RofDqG1akuGyjGPQ7bt964ZWXsLpuy32MB8gouAE0MnII\nBp2B60PyfQ+K9ovm8jKqxFL92Hv0PHeIc87dOmBgU4eKc5TOkzFTZHLg+VijktCf/Pv/ByHtXc2W\nhxeesQ7G3t2Og+o3V+qu6aIoODghyRvVELKw+2YUK9zft+ubMYbtbeucrK6uIAg89/6TWJFmLpjw\nfR87G3Zcq9UKupvledB3rRiq0BB0v6HnO13VarOCCpWiVltLWCcHulqpulLdrJNeqVbBSoePw6Hh\nPE+4vYSxKf3N7L0ppR56/3HGOMMSCXq//Z0fIi4DEcOwfMYGN1Aax4QOTSZjeHWbaEiZ7xB8e/sH\nGI7L4ExgqW7ndD2u2b5gAJM0xYQc4EIJ+PRcrjx7HheJ/mJ7dQ1DKuMqPsH2ti0jrm1cRK1qr1Pj\nAPwJC3SLct7CFrawhS1sYQtb2CewTz0TlebS8ackkwmKnPw2ZjAa2khmMkqmERqMo2D3WYAKZSd8\nnzndpHq1gSAmqRQvgEyokTiOwMMpRX3JWSOE59BBigGKGlWNEcjyEkFUICEvNc9zMG9+j/tf/et/\njZdefg0A8PSV52w2DcBgkuIvSSPtzt07uHDeNnN+9o03sE68M3E1Ru/ERh7/6c/+AopqGn/vC2/g\ntSs2rdgbjPCtP7cN3Tdu38UVItz7pf/uX+D0jm3GHvQ6+D//5E8AAH/5F3+Bftdmov7hP/ov8du/\n85sAgIMHh/j+D2w25E//w5+h17PlsK/9zj965P0V1JwZeB52Ttm09nJrHZN1+7p7coIBlSSLTgcD\nKvkpo1E+7lwr91wzw9ChhmXRqIOR/IgSNpqVKJx7z9IaTi/bsd15+rLTJ/vwe38MldlyojGBbUAF\n4NcFgrAk6mNzz/BK4KNMWhlIMEqpi0Bh1LWl1HzsuyhOGkATWCEKPHCKZ7NJgg6N63KVochsBNXu\nXMP6jh0vz7+ISov4zIZdXP/wHfudjLlSsC4M8qJEtXLHgeIHPny/bADlYE/QdB0EgYt+tVZI6dpU\nmiErsxrcagQCwHg8QErZmzxTqFHGJgxD5LrkJ9OuTC0L6crvlShClcpb4By9AUXUSruS1iRJpmUD\nxhCV3GnaOHV27XMXbc5jP0lqW5qZadRPkgQZ3Tvn3GU3tFEO2TeLdt3eOoUlkgG6evUqmjUbRadZ\n5loJGAc6B8f0YwatFmmDwUyv3wCS2XHL89xF+J7nuazU46xWt+ULGSQwtEji+glG9+65+8+kXfud\nXtdJeSw3GmgQoSqUxP07u/TbIeqRzW49/fSzuHvHcvCklM0p8gkGNCa613PN0I3mWVQqdkzyhsbB\nkLjeum2HPA6jCJVTdn+qVBuuDeFxNltKsq+nFYXZDBVzxI/CnR+MMZw5Y9fZ5WeuwKNs65kz53Fq\ny2Yf9cvT5y9CH4aXkh8Cwq0thjy3+9G9u3toUUZvdXXNoTxLIEr5uyUXoJPoeoQFXEBRRYEHAWqU\nDms2mzizZcfMKO2ycLmaApWCgMMrz0jfd4ScURA6HjjP990a4kI4DVfGXIEVnM/KuExBLcYYN552\nnKfztKzozGMGQEwl3I31DfhUoTBqWoUajkbw6Kxt6xQH9+2e3htlOOzZ15trO2i89gv2ekyKpQZl\nNDmw98DO1wuntqC3Nuht4TjRzp/bwHhAVRJU8SHxw+X5PbyiLNK6UQlRIYkfEY3xBMk2AH8HTpRS\n2jlRRa4cco1z5hBkQRShRnB5MIKAA3bQqdQTBtMJq6RECWZhnDuUiqe5O+Sq1SoUOV2F1A616HsM\nZYeFAXMTUyrtBEGN0XiCfRthELrepyzLHTomDBheftFqR6lihIhYWjdW67hMBG9RGMCjmvDrz13G\n4YE9sF+8dBqnCT4dFmNcWLMbt0ha+Ax9p9QZjo4tKmfQ7WGVtKxO75zF5z5rU84vv/yyI8jM8umm\n/2u/8qtYXlqa6/6qBI9lzHMEf4IJRNQ7UwmrqMR2I+4rBtWzZYMUGhFRHLRVjiqtV3H5eTx1xt7/\neHyCw0PbZ6RIVDMdHGPSt6+XVy/g/BVLaDcZdnFw22p6jbpdlLhzv8qn+6yZokmMxyCC+ZwMqTOk\nVE5imJZ/A3+K/FFaw6PXYtrtAa2NS+vLbIJrV21PzuZqAwUJyz7/8vPondhNYf/uTRzct71SaTJ5\niGhR8JKlnoOYBh46SIzhKOjzsoDrxZvH4jh2qNZkNJgiXP0AnKgjmvUIKIVx/QC67G8xcBtro9HE\niKDrjBnsnLbPUqYZeid2/g6LkXOoDOOuxGaMcQ5hrVbDhDbTJM0Q0nwKwBxaUDOBYE7kGmBHqSxj\nBEHgnl2WFtN5YaY0JEWRI83IqZuMXVtBs9l0pb319XXsk/7njWvXUaWDQQiOScmUbxiGpDGptXbO\nmJQFfFoDs6WQWcLdWq2G8XiMeaxkse+1j9A+sk7bsNtxqL/Dbs85CErmWCLHqX3UcftSrzvEmMS7\n+90Bbn68CwCIKj4+/PBdAMBuhe59bRXLhLDzBVCrkXi0Tt1hU22soqVK4ssYOpk6otVKnV6HDv38\nOLPsHlNNUO6cJfZT0XncUscDsMismMqPX/3lX4cu2fS9oCS0hqnGYM5xYigcKttD6VJoZgAqnTbr\nyzO/y13P7mxP0Wypdh7zfB9VlD2YFrENAL7wHipZlq+VMpCyDFzgEMhWkaJ0ljynDBD4ATA73005\n3ws39/0ZFB7AAKIcYkKAl9/JudsLVSFnHNfHmzHGnceXL192fV+jwQhjWjeVVgtdEly+1h3gNrW/\nNCt1vPy8dXKeuXgREacS9fEd9E8O6B49FNr29k3SART1PLSWlh1xb5IUqPtU1hQNbK3Z+dvt9HDr\nlm1n8QLftRUkkwGaq/Odi6UtynkLW9jCFrawhS1sYZ/APvVMlJTSZUKMz6eII8EcL0xYidFcoVJd\now4YG7XKiURSpl0rIeqkcdXt9sFLlkxVgFFGq1By2kjKOGQxLUWUHrRUcEgSQXgowEYzuqTV11NU\nwTz2u7/7OwjLbI3wkVHEEAqNN155DgBwcWfdRbYXL513jbzJZITLZ2zDY/xrX8HubZvF+OpXvuKi\n97ixjt9q2izTD3/0Y3zuc5+z9wKJPqU8feHj9dd/zo6z0lhesiWW9fU1p+B9emfHNbkWkwJZNl/z\nfF6UjaK2AREAOPPgeyXSctqIOB6MkVMkOhoNcEyoOV3k2KT7X0s7MG0b3fTaDyBgo/wwt9HxnesH\nrqlXjnOkpCs16rVRKHsvzOfwqzZ68CseGGWc/NAHJzJVeIDGfClFwzFt5NYcPnE6MRgU9Dx9EUCZ\nkgAT01ZpPm0IjwMPA8oODk9O0KTGyn67DUkN2DovXCN+4DGEIWUZmXakmkxw5DQGWTZFuDLGkBe0\nnrSBeYJ5GkWhUz33PA+M1sqkSFxKnTHmMrhRGAB6Wm5T1GycZnDyG93uCUaUwatXqm6daa0cwsrz\nhWtOLgrpot84jl02xh9NXGaaceEyYEabuTmUACAvCldWyfPcRfJZWriMn5TSvQ4CH31C9QDaXfNg\nMMA50hKDMfjoA5sBZcY4YlJoDlD5pN0b4PDQZmAbjQqShDJUSrpMFGPMRfXVatWVF8fjsYucH2cd\nQhEdn3SRJvZvxsMJ9vcteqk/GTuCwyxLHZCAg6NG6+/02hK69D2N5buQlA0MA4HdkLKNJD2y9zHQ\npIz1xtY6opIXa5gimZD8VDJBNrQlbKNycNojlNHokkbmOEvgEUDj9M6zj7xHITxXtjfGzgc7ftzN\nOyGmGmcGzGWi+EwpLYxmSoHafQSG+U5nzTDAo/OJa0C4TDPcZzyhXMVittTIGJsigaV8IkkU3/fd\nXGOMuWyrLwQE3YOU0mWNmNaI6PuFmJYvldHgM9k5l8Gb0WSdzbzKQkLR3C/yAkVhP1OtVh03lzHT\nezGMuYy1HeYna6D3qb3GJAWSxGZbk2wMUMtFEXj4iABHdzs9XHzWnperUYxXnrcViO31ZXSO7bmY\ndgqYiKpZxkCXWe1G3XF1JRIYyLIsWwcIhVwNPbx61qJL89Nn0Rnbs+ntG9fw4ccfAwAacYiXScpn\nXvvUnagin26mSpmHatplDlNwb0o7AAtTBoB0OJpu+j5DSqLAtUYdnDr9PW0gR/ZgDWpwqIss1zA0\nKRiflhA0GMapfT9kHgSlcnNZuMWK+SskAIBJNiX0mkXhrTTWoeggVFnuJqbQQEIbYH+UQmu7iZ10\ne7hLKJBv/PW3HKQVMI7RVqscijZcoxWqMyyzJWPrcNiD79mNdNDvuN9lqGFMKL/jgza8ORd9SUvB\ntEFIDoovps8viAKAW0egtbmJftuWGXIwB3cupMLewB4y2Z33gHul09XDufP0nay8rymsOZ0MkGc2\nDeyHntMEFIEHv073XhEQETl3IXMOFfOZ2zAeawYzDOEaUVRqdxnXfxB6U5SLAXMHlMeZm2vGCEy7\nDBRGHTsWH7/dc/OiUq0joPEq1Ah6BqpdIsjyiUThCFwBhnKjNBCUdvdCD1E4/8ZdKOUEsQPft4cJ\nAKY8KJ9wwxoOVi2ZQUSCr4ILx0pfXVrBCpH3ffDWm1BUWlB5hpB606K4BulKfhyKnLFknDhHXJup\nyHalWgFL7DVkeeEQc1JNndh5zPd9N3dmUV6BH7reJM65c7SCMHCagGBwvUlLS0uuz+6tt97ChN5f\nXl56mKCQXn9w9ao7pC9cuOjoUoqigEdOVJqmKIjZezJJkdD9Br4/PeEfYweEZDo+aiOltXz1+nUc\nkVMkfN+VBvNCTg9GGIzpHgLOsEW9jRtbm2gRTJ8Zg4zKmYd7RBOhUuiC0GjbqxiMiN5hMkZKoq0C\nCt0D68RpFI5E2Q9CJzadJRk068x1j5wLJ3qrtXYs/p43FeWeRZDpGclYw9i0rMZmhnWm5mJ9o3K9\nGldCB3+45Dr9Wzaz/h5+TrOO0JM4GEopNwd933e+nlTKlWbBmCuriZkePQMz7dsxzJG2cs5nVCs8\ndz2+7z/0uixZS6XcuSiEmLYnGD3tfZLSraE0SZ+oP5Ezhjo53e/cuI73P7K9n5PxxOkecs9Hn65H\nGIPewS4AoFsUuHf3qr1mj0NSX67MEzBTXsN0DnAxRWgmuQT3ShUCAUVOVBj4ALtLf8vAaX1XAobz\nm7adqBJFaFGP59z3+USfXtjCFrawhS1sYQtbGIC/k3KewjS1Ix7y1gvyEI0CIpKG0UbCUDapurGO\ngLxFqTPIEv0AH6ZUqJ4kIDARvDhw1O8cAppRFsLAyT8wPk2pK6lQZGXJRCPNiWciyVyHOVMcAAAg\nAElEQVTj3jy2t/fAlXMajQaCgDxrJlwp8+iw7aKN8Ug7XqksL9zfHjzo45vf/CEA4P/+v/7YRZFS\n5fAJOvYLX/gctohThIFPU62Ai9hv3d7F0ZEt1bTbPaTEnyGLAgdUcuh1++53f+Mf/ONH3p8pSyti\npvwpuGUThc2IeJQR2RQeuseWU6d7so+QmnCjGndolsn4ZBpFKoX79ynaooxA3IynDYzCh6A5wAVA\nVTYgZGAxNWZWOERI3xFMNcmYMAjEfJkawTQEkUMKziELG7UzyVwzvjEMZR+30moaPRYGXqmL5wmX\naQki4aJZLji0ss9h2J8AipBo4DOIuWkKVAiB0GWZDEpZrsALEDCSEfE9eP78cVAYR05rTxmNkHjX\ndGQgKUPCtIdJQg3+giNlZZapgEeZK6UUJK2PZrMJQ9nWoshd1i4IPKezxTkDfQT1Suwi7UEyQZ5O\ns0xlWSIIAyeFJBTA5mxIBqwGWLnHNBoNl5VKktQ1scdxhH7flp88T0xLHXLaDsAYw7vv2ibr0I+w\ntGpRccsrq67M3ut13b3kRYqdnR37+TB035nnKQ7aNgMzGAwwGAzc9589e4auLZtbEuW7f/Nte92c\n45jALLv399waSSezpcGZ8g64y+ofDUe4Sw28mzsbaK1S6X9jEyE9v5yyjoVKMKZrvvrBVdz8E4sS\nPrd1BttbtuG81WqiQZlJwxSYV86TAppKwDovYJ7gOZZm96jpmVHuG8aUsIW/nQUqs0PTv384g/So\nBvCfhlD7yfd/2udnMz/z2Oz3aD3N/Phimj0VQkzJRWeuZzbDKrWGKPdkxh+6hoeJSa35vo9Go+He\nn+UtKyWyBBPueoqicOdulmUzcJr5rE6yQ2tbGzgzuei+c9Zmr+9nE3uWQIOfrWzn2it+1rNmbNqz\n8TN+3/c8PPXUpZ/xCz/jd58EUbCwhS1sYQtb2MIWtjBri3Lewha2sIUtbGELW9gnsIUTtbCFLWxh\nC1vYwhb2CWzhRC1sYQtb2MIWtrCFfQJbOFELW9jCFrawhS1sYZ/AFk7Uwha2sIUtbGELW9gnsIUT\ntbCFLWxhC1vYwhb2CWzhRC1sYQtb2MIWtrCFfQJbOFELW9jCFrawhS1sYZ/AFk7Uwha2sIUtbGEL\nW9gnsE9d9uX1L3/RlAKJMFOhSGYeVsQuyd4VA2okG7C2tIzjzgkAYJwWcLKDHgcnan8BOCkLrTVK\nMQCtpuKmVsRS0yUYR/2u1fT9hz+jwUl2ZPejq4/luf/clz5vSgmUM/UVrG9bCQTJJJix95LkGvs9\nEh3utHFybAU7s0yhSUK6QSDASNR3R+ZIjJUsOFYMnaN9AMAgz51Qcr0awW+t29+KlrEc2esfHd1H\nQsK7vuAoSKZCSQlG+iHnL19BtWYp+f/s//t/H3mP/+Zf/b4BAE9wlI/MDzwo0tvReQZe0vJzAT+M\n3OuSD19wDuZEP2ep/RlmxUABwEBBkeSN0gaFIvkbrZ0QKNcGqpSUYBqKhHJbK2dw4dJLAIBLTz+D\n5RX7LHwvfuQ9vnv90LRHdF1CICABZ6ETJ6gsYBCRzEoc+JAkEzQ8PkCjuUS/v4IRKdr3Tg7gRfbZ\nhrUG7t6x4pdJkkKQHM3qyhpiGq/hcIQktfIfGgxx1Yp3SlSQl/e3uoRVkiDJxwkqJAf00vNnHjtP\n/4f/+X8yEYk8V3zlZHjCKABDKYbKEHilvAQHaA7af+3nm80QsW9lcRoRoCZ2HAadARJ6tvVGDS3P\nfj4KDDRdnZIMaWLHNlceUiXc+0WpgcwYpG8/Mx6nKEgw/J/+y//9sfdYa26ZUsVBa/2wXMeMsOvs\nPlTaw7Id0zlq9xW6fhiU85Vp6cRKN9Y3sbt7BwAQRiFGwyH9rnah6t+WERF/6/1k0n/kPf7byw0D\nAFs1jU0S3Y6YRD2y39GqMQhun6ViCty3X1dIYJiQQGvGoAxJi3COgu6nOy4wzmm86D3VuAj52msA\ngMFf/xWO6Jke5gGWx3Zd3O76kDUSba3VcEjyOs1sgpDEkCdCQ9Ca/rcn+SPv8f/46+umFJkVgjsR\nXjAGn2RcuBBgrJybHE4lSgBuwJkPTXuUQTGVFGGe+1vGpsK12mgnWM5mRMULWUDT/q6NcZ/njKNU\nR86zDBnJ7fzL/+LnHjtPv3/1mpmVMpmacfskMCtzAxg3Jx+WRpmVwinvnf0UqRz7mjkJNDANU46z\nypGTvI8wcNegjHFyMFxw5CSK/tVf+pV59F9MKR8jpYSUdnyUUlPptYdeSxQkhyb1VNbnpH2E/Xu3\nAQCrG5to1O2e3qw3USOhct8Xblw49yC8UsJL/HQZnRmpoEeIR8+lcfOpO1GzStTaGIhShRtTXSNj\nzDQlphVaFXvw/PyLT+OtH/cBANdGAyC0OmzK6OnMMz9dI8hw4w52KaU7lLk3vWXFlVsQSmu3UMyM\nQzWPNXiM+uaW/U8txjCwv6EL4HjfOkujURc6s6dE/8EtZJ49dFm0irWm/d1GDdg/shO5yBW2AnrI\ntQrywh6ck27PTbT1s8/gwjMvAwAe3LsDNbFj9dwrb0AeH9hx++hDHGo7eRutBta3rF7X6TPncXp7\nZ74bTElHyyi3WXmVGIJOIKMUOG1KgmsE5O4KaCd0xDSclhpjzOnkCeFBkGNX6vKB8ekmrs2MXp2B\nmnmt1VT3KaOpvH/vLk56dpzry8toNJsAAP8xM32kGDJRoe/m6HW6AICkfR/50DqwPjeI6RCp+Bwg\nTcF0MkA66QEA9u7eRL9vtefGwyEUjRcPfEzI2ZhMEudEnRweIwjsfM+KAm363eN2B4y0/KLmGeyQ\nYzhUEU6G/XIQ0IztGLz06Nuj6x8jpzmyVm06FfNJPkRI4xMK3zny4L7TDfS8AEEU2/eFQEZe0ShX\nmIzs/BoXEQa5da5uH+zi88+ds9df8Z3SvBLczRVfC/CMDipu4NF6zaQEyDkMTDDVwJzLjNOc/MnN\n8SGttfL1T/l792pWEsu9NtN5ajS+8ktfAgC89fbbOHf+LAAgjmL8+MdvAwCEN93cjZk9MNlDh9+8\numtfsssXDZ9BkKM5SnJwcnaNZMhprNNcg9McyqTGgJzUcWFc4Mk9G7gCwDBhGJOsmWSlzmUbt/7j\nXwIAmmYEU9DYFoAkJ7xWW8UNCsje6x2iSeuyxYBAlN+nIcychQ9joCTt1wDglV7ojGOrGBib/t99\nsxDgdFjneRcIW/S3gKY5ywVzZ8bs2DPD3JkEAyiQQzVzaQzW8QT9qzQ5V0pNnb15bhHaOToPK69N\nnXQ89Gr6QfPwuz/hRE3nqfuUmX6TMQzG/e40qaExTUaYIrOCtrBndnlmBkEIM59fAcCeuxmdeUop\naBorpeTUcdIaRUHBuNaQ9Jl2u427t68DAN5+89u4dfUdAECtUUelas/C9Z0dXH76RQDApYvPYGNr\nGwAQV3wY+k7DtdOX1Vq758v5VGdwNpnzk87VPPapO1GcMXASE9Vaw5txomajRCdRrDU2l+zEf+rU\nOpIDO2D9kwMcpVZwk4cVGBJh1YYBKDdZNvWtjHGHdiA8mJnfzdVUXNgNJIAyhLVRzvyT5flnzqGx\nap2iUHCEPgnzqiGwaR2/VLbwH//MCprCqyCu2nuUzEetYg9v5AmytnWiro2GOCBR5ktf/TLOr1vv\nu5iMcUKfMWCI6Pm/rCZYok2ivttDft+KnnpDDn3mFwAA59/4LF58xgrfbq5vwqTziZ5yYZ+OmMlE\nCTEV4A08323WnmAQJAAsIKdRlTHgvBQaFg99T7lvefRCQDinV2rtHKdcarexGa7hDidmwOkzvmCf\nqEhtfIO8FN2UGkVhHR4tU4TMnixcK8jUbtBJquHT5j5MUuQDG3EfnXRxdGwdlUlawGj6W67g+3bs\n81xCcBKMTQsnWJykKdod64wNRmNktBHwXgbetOugtrYCXW4EfgAE8wtly8kRPn7Hbkbi0iVsnLVO\ntCxS1EPrIAkoF6lKA0QUEDDBoOjQyrWAz2jOKolU2TExHkfv2M67Vr2B1RV7sBb/P3tv/izZcZ2J\nfZl5l9rrVdVb+/W+oBuNhQQJoAERXCBiIFALKVuyKIU0MdbIy3hsaWxLE46wI/wvOML+xXYoZias\nGFHWPlpIjWiSorAQBEFsjW400Gigl/f67e/VXnfLTP9wzs16DwSIakSAP9VBBOKhcOvWzby5nPy+\nc74z2gWEx/3gI2CPzcYGXt63nnRFnI3RiLlIqTEG5g7e53vn7f4F8QAanZuF82zeO+MPbE78P5UA\nLA/Ir3zly/jZp54EALzwwvN47LM0z178wcvjgudQMA4A2++gffAz/zhb9vk0n2lEPLeGiXZF2JME\n0GmOOI1/J9ESOdA60ECag66ehObn6qcSUcaOLH+WpRmkoXWiG2pUDBeJFhZb7Ayv1kJc5vH/7t4Q\nJ/m7XqhQsDnSbz+4cux7zPd9sB8Gzy9Ab16kZ13/IexZ6m9/5rhDUoWVbnzZuIvOS/8PACDa2UDz\nn/weAEAWa5A6R7f8AyxFbu8tCiz0ftTiYNFcgDbfLKHPhZQoBMGPXPOBZuz7efAADKz40Y6y/M97\nn/P9vk/XH/zu2ATgkCjr/rQQCIo0p1XoQ+ToHMZOlOePEbxJzBhzEEnbV+zYoX9aO8dsd6+Ni688\nDwB487UXsbtFh9do0IHP7cqiAXoJHerbW9fx7sUfAABenFvGoRNnAQB33fsA7ruPwIV6tQ7DxdKF\nGDtMxpgDjvR+R+pObRoTNbWpTW1qU5va1Kb2EexjR6KsUO405EkfgmkcISlGhy4yjroQUuH4EqE6\nFTGAp8nrhE6RMNUhVA9hjWKBEJSQMceUSUByPJXKNHSWc6SA4BORzlKAvWkrFQR7qZ4S8FUOzRp3\nEprEnnp8GT4IuUhNiIgRhGgUwmcqIk1DaElUR+Z5Y09cWuyM6HRZqZXROEzoQK3dg2DEoeYPcXTx\nPD1nkuHkIn339sBDaun0U75+FZ3hFQBAVysMCnTPlfkhQklxZcerEo06IWDbt9dw8+ob1ID/6jd/\nbPtKfEIRSCEZ8ikVw7EnD+NOVZ70IB0vP0aLhLDw/ByNkO40b412cQUORRTKxU1Za/fFUGkoz10E\nGD59QsMTOfSewUEXk9IH3DafuQedxIj6FO9h+tvwYhp3g34P7T36u9PZc3FzhUodmtvT6faw3SY6\nb5hYKEbfhEnh+zn3b5HEdM1Ou49igdoxGA6w2yaUMUkzNwbFYIiF9jJ9Hp9EscSokQpcTMMk5usR\nupsbAIDLnT4WFhYAAI1qDQGjh76SyBi1VYUKVECIb5rGjr4UQQGC3/FoOMpDezBXr2Jjk/6eqVSQ\nvyp4gmOJiCrPEYTAWPDPIo4yaO4ro4xDBbUF0smBGnq+fQj3fjTpA0/wjiYZ/1sIuPeb6syNQWNT\nfOHzhDj93v/4P+DZp78LAPiX//JfYHWd+nZzcwOK1zMag/n43d8QeyAga1I0aofjKiMjoUOOt7QF\nwCNKuNvtQqf03FEMpDmqCIERz4ehscj4cz8VSHnuxEYhYm4vY9TRaoMiT6OeBjoZo6AiwIhp6JVk\nCN2m9W/eeGh4dL+qAHxueqgltJhsPnpKQXj0Rc/3Ea3ROrX36rcxz/Omf/op2NIsAEAJ5eh6efUb\n2L1M70SUlhHmfeyHbj0VUrmx4Og7HERI3kvr5Nfvf01aa0hGkQuq5JD2SUxiHKN3IGZJvP84PRjX\n9P7j5oPG94Hr931u9tGjSiqonK43hQPYlebfSKx5L/f4Y+0A4mQ0tM7pvPHf1gKrKxQr+nd//TW8\n9cozAADPWoQc++Qp6UI3BOQ+himE4hZtr13D6g0aJ9//7jfwqcd+GgDwM7/wKzh25IR7hiwbU3j5\ns+0fAx8FkfrYnSghFXI8W1jp3oGBdVwlrSf0PxpFDzO0buON11/BpSvEiw77Q5xepkW/XCxhfvkk\nNaDcxMWrbwMAbm2uI+XNTBlAchCwXyjB5I6WChxVFAYeTJZDwhpuPxJEX0xqUXcNIw4q1F6IfkaL\nSyoCMOmBgqdw+DTBjf0rqxiSPwXf8xHtUBBqrVTD4TOfAgD0RgkCQTvSrUEEe4MC6xYLHo4cPUX9\ncGgWq5vkIHXOHQJOk0PVS3rYiakfij2JEzOnqU9K29ha5ZirkXTB0B9mIcPU1hoUOY6mWPDhe/S5\nUgaCFxCdCgjh8/UWmuksC+1iCTzlId89hRnHJOQbqpLWbbpKGMiQBrmBRJLlXH3g6FdrMxhe9L2e\nht4XXPnjoe99bZQF+BzkrIIAMX9vY2sd7Y23AAD9YeScnO3dtpuEx5cPoVqkQVvxgMUzRwAA3cRg\nt0OHgEE/drROoRBgGLf58yF6feqjNEvQH9AmkWnjxnLSbePyKy/R/SuLuO+TRO1JFSBh2nESq4UF\ncFw5bty4iStL1K5HH38MKt+ElEWWzyH4iBL6O04ylCshf27gcd9rE6NWzWNEUvT6TOvEMY4tUGB8\nq+pRfBwontEFs0oDj4PYhW8Apg186cH0+D1nGYycnEJ4rx2gMlxQ1Phvi4ObTB6rF8cjZEwpFotF\nKEVj/dzZ8/hf/5f/GQAldiwt0pr0mc89hv/+d/81AKDT7brkjw8efeLH/t8PstuCwgP6KkTFp9Ul\niTUGQ+qvYV/C8poWpQJRTssJgYQdp9jAUSgBBDKeu4kcX5P7Hqkw8Lh/vMxDPEvOfNhaRmeN4j3t\n3gYW+fl60uAYx7T6MgaKtDHLvoE2kzn8SkhYXq+llPC9PDlHoZwSXZxe/A+4ePkqtydDq0Vr2bl5\nDwn/zOLsIUhFzwIhofg+Zt/73r+ZCnEwViofF1JKF7cJ2AMHPI9DVQA4x2AyO0gj5vekfef9Hab3\nc4V+dH2zP3L1wfsd/O74P4W7r4Z0T2eFcNcYISHvIFbYGI39iVs5qJFkmXvuq2+8jq//5b8HAKy8\ncwn+vkPyaERrpCc9CKaR9TByzp/0Qng5hSoLKJVprGVxilee/jYAYGtlFY8+/hQA4KFHPotajRIg\nTGYgP2Bdeb8Y6x9nUzpvalOb2tSmNrWpTe0j2MeORCmlIBkl8KXnghgzZAci5Q2f+uqBQJnTcodS\nYmOXTv7VIMCF+whROXXXWczO0Wk/MyFWrtGJ+o2bb6PEgbCB8iAYwRjuAqpCp/difQ5a5Wm8Bgjy\noHcPOqcxjHYZPpOYtCPkCUSqIBGmBDNJEyMtEn0WdTUOHyYE6calHWg+jQfVJpaKdJoNbIxSSDSl\nbC5iuEXetGkuY23lHXr+QwvorNAJsFi4hRmWNfDqM+iPKBNtoQp8bp6yBZVVaJfo/qYYYuvGJWq7\niBxK9GGWB+ZZm8LzCXGREg5RkEpinIYHOApPCuQItzFApnNqM0PAJ7iCHziEKj/leMK6kygEEDHK\nJ4WARk6rCOxPEVfeOPXZnQfF5KcJ5flATN9s72zhyqWXAQBv/PA5bK2/436TE9FQKZdwfJ7e7eG5\nOkoFOhHNtJqozxHN0BnG6DPi+NwLr2NtnRIjLDxYzn4JPIk4Z7WtQspI22DQdyf3NLXYVfTdzfU1\n9Lp0QvODAPVCYaL2AUBBFeCDTuaLzXm8c+k6AODUqXM4dIKwhOFoBMOnu2iQwHJvBqF081XZFD7D\nhtLX8BR1yvZeHx1ujB4J3O7TOwwLAiVvnH6cI8GwGsIm3A/KDSFlBcBB+Ebb8fUT2H7qRUp5gLIY\nI56Cxw+gpYCQ+Wk5QZ6kcur0MTz0IKHC995zHvUKoWqfPHcPzp87AwD4h6e/hY31WwCA7z3zXWwy\nMhNnGpYDnYU1H5zPdAd0c25rkp5jYAPYHUIho+4Qo3gs+ZJnwUXaIua1V0u4ZzJWQjiaz7rsPAjh\n+Covv1YBigOyy6qCAgfsXhMFbMW0fjRsil6XEPFWxcfRGqFlFSthmdaM4gFEOin1LBxLIQTR+wAh\ngnFCQe4zAbDAIQtRMkC2R2h+u7iAQkCIRKHegOVxRDkg4wSC98uMlFIeCH7ev3bsD0jO0RXP85EP\nWmMMkmSy9ZS+ME7VDIPAoZ6Z0QcCy38kCQL4QPySrjV471UHwCprkfeDhcV4aonx/e1BRG1/JqvF\n5GjbfiRKa42EJWGMELh69U0AwJ/+4f+N3VVikorFkvuulBJpSu9XwcJw3+rR0H0OFcDPk7ICHx6/\nawGBgOntjevv4E/+3f8BALj21iV8+Zd/FQCwtHgYY1Dt/Xt0UmrvJ+REjemVPB7CWOk+VxAuG6Ba\nq6DHOjuNchFf+RJlY5gkRa1GG0atUUW9ShP1pRdfx823yTFolRUWZujzZqmInTZBv12dARmnhXdT\n2DJBv6ZQdunzVmCsHWIzRy9OYn/13V3c+4l7AQDaVjEY0kseJgaRoZepjQddonsunDuO3lu0MUdZ\nH1GZnBxbrSOu0PMvt8rIFKVsmkoFon4PAGDU3UDRUlzOUq2F1uwcAODNt65h5RbB2w/c/2nUTlEM\nVRrHaMVEscQ2wRpv0jeuX3MpoR9mgyEtUEFgICS9gygeutTUGVmG8vJYNx84EM+U67RYN5mtMbD7\nMqVyGFzm3LSULvZAWwPN72VzaxOFEvWPFYDQeZyNHmdw3TlDAgAwNkPGm8VgNMQoY4pNeIBHE3Vn\ncx0d1jhqNep47MIDAID5RhkD1uKq1BtotMiJWt9+C9ffpQyTWzeuYXWdxrWGjxLHQZVLgZM7qFTL\n7u84jhFyzMvxc3fj7H0XAABHT59HdYYgac/3oLzJF7WZchEzvMEVhYe9Hm1IL3zve/jyEsUQ1KoS\ngh3CfqIhXayUQZHj/jyVIeRFCpUQCTtOw1EKmW/gCTDQdJ/tyGKGabKKX0DKC6IUAmFI12htkHGf\n6ySD4LWhWg5h0skpBOC9SU/jDUPu20T3ERaw7Kw26hV89au/DAD48s/+HA4fooNIFg9R4QXetxJX\nr9B6Y7IE5RLNh+3NdQQcmGPtOJNKiEmz0iZz9t9YI7o3TSzAcgNGaxePY4REkNN21rg2S20hee1V\nwoPMY4KEHWsseRK53h0sO1ES8HOtpWYD7zJV+P133kV3lxz7s60WquwMn1BAWTBdG2mAnR5rh3cU\nM5Q7MEopaMlxn1UP4ExBJRSOLtPa194L3YGjAA0eatjsDnGEQw58CPdO9m+OHyQv8UE0H2V1sQaR\nkk4rT2t9R1mW1loU+QB05PARbG1TDOb23vY+CvoDwhHeO6TysAb3L/qui/Kz+++IA3tb/sQ0YvNM\n9RS5xAHsONtZwx6gAydpY94/SZLA8Jxrb3fwzb/6GrV39V34DF5kWQafD9dpmiJhJ93zQoz6tH9L\naxHm12QGo1yPTSpH1wbFEMUyZQYrL0A6pLCY57/9lxgN6Ppf+rV/juXDx6ldH0DDet5k7tGUzpva\n1KY2talNbWpT+wj2E9CJkpDBWKMpP40I+PD4COQJCclZQIuNJryEvM5CQUI2CTWyBqhy8oAvM7S7\ndAp66bUfwmeF3iMnllFiKrAc+AiYzit2upAcGDgYdLDNgpZy9ihEmSgwCzgtCqHVjwia/Tj72t+9\nilPXyeP+xIVH0WhQVoEKhNOJ01HmkIUzn3oAioMv00RAJHS6rFUrqIH+vqsCiBYhHeuDFaR9ClAO\nigHO3vsgAGCm5GFtm/pqlAYYcFDvYPsm3vg+oQadXgeK0aB2p43GSaIUF86cwPbNlYnaVypS39XK\nAWpFeu693QGU03KRTk1XeXBKv1miYXRO4ygXtKutdtfEceyuySk5PwgxinNUKEHC4nlRbFCseXzv\nFDkbKWCQMsysjXYoxp0E70pjEfJJZnHpCCo/RcjMiSNHcOn73wEAXBx2EfGpxkeEk8cJqVheXsTt\ndaIzoAJ0ODvv7as38NpFQi36vaFTT4awLjsxiTIXtKoLHgKm0oRQjn755COfw8OfpeBILTz4jAIJ\nY5AxdTyJKWEwiFhNvTtAwjzO9uq7eHiVKKqHHr4LvYjGkVA+JAd+F4s+KizsqWGcbk5mBHqDXJUY\nUHzKPbo0j0KBxTx1Bo8zKdPIIGVkqVT2waLbMCaGULnuVwIVUhsNNLw7CGalB//R07IAADHOFKpX\nCVl67DMXUGH098KFh/HVr34VABANYtx49xr3G1Dl9SnOEke33HvfeVjWZtvc2MS166sAgOdfuoyY\nx6+YEGGa1Db26H2HUG7+CSkQ8mlew8Lw2djuR5msdeutEoDiPipIH1muLeQpxKxxp/i0LwMfQjPa\nVqvgjTUS8X3n6hV4Ma1JBT2LM/zuyqMhEo5tyOIMPqPFCgYGkyUISCVdoLXneej0qM2m10bBZ5S3\n3cHpYxTkvrR4CG2muK+8ext1Xlvj/mCcAV4oQrKQoxDSjZEDosoCECb/fEw9flAmFyHt9HeWZSjk\n2W0TmBUJkDHlayQqLFba7q65TF9jAxgWLs6kgDCMyGWUiQ4AsTLIuL+tsPAzfm9WAIwIGjFG6g0A\nwfcvZhoBNz+WAUacPCFkBunEzTBGuvYhrJOY1gY6zROBMkQJ/f3Nv/8L3HqHtL9KBd/pmhkDJ845\n6g/QrDb5oQUg6NmCchU6Vz43qUOxlBSIOClnpGN4vNd6XgC/QH3rG42rF38IAPgzC3zlV38LAHD0\n6LH3zcqc1D52J8rzfJhc1kAIt3nIfRCphESZs5uqtRbSNkFuxip4nEY7yCwGGXXw2uXLePs6TeZR\nMsL8HDlavhSYmeEYpNEQQZEWx6MzTVy7SlTXTKkEk9Emsbt3G34p98xKcNweJgXXyYqBRLXEEOOg\njY0eTeher4s9LhlSLBRx/yfJKXrr0sto93gT0hZxQhtb1ypc8ImqaVqDTR50tVIV1WWKB8viBPUq\nxUUMRyP0OvTdWrGIc6eZUhxcxahHG4AeGkR5hkSi0dum+5/6xKeQdfsTtS/fcGoFhSJTAlnoO/i3\nqBTSvExLFjsqgNTkWXU7DB01lOzj/LXOEHO9D8GbemJSxLzAbO11EcfkEB5amPYnruIAACAASURB\nVIGXb7pqvODpzDhFbGMOblyTsrK+kgj8PK6qglLhOABgaa6FrevE3zdrFQx75Lw3yj58zv6UXgAw\nDff2tevY4Ti+LNWO2jTJyGU8aa2R5ardUkFzfyVR4LJHtneLKJToPR89eRZhjRzzOEnHFQDiCHfA\nkAA+sLBMc+XWsOMEP30f+M53ngMAHDu+gEKZPhdi6DZem0WOGjLwMRiw+n57gEGf/va9gqtIMOi3\nUQoXub0p+iMa74n04DON0dcpdI8WxIIn4PGG63ueExQd9Me08ST2I2Kb+fuXApZFQZvNGv7Vf/df\nAwA+++jDjhKfn51FzGmz/U7ftbdZr6HGm1yiU9Rny3zvFKscn1gIfJw6fgwAUb2318jZllIdUHl+\nP/mFOzHNS7YQCp7I076tc6gsAD9/Z7AuZMKHheeUtgWyEh9GWg0UeRMLCwH6vGl7fPBKtcSI51wv\nk9jc2nFtr/r0o0vREPOWS0tZDcNrRLxPzFEab2LZGCskLD9rpg12VmgtW1QS5Sodel+7cQOlCq1f\n58/UMdyhtXK7r3HsCF2zvnYL3c0bAIB64xOw7MhDCCdtI8w4RghCIK8tJve9H2PGEi5KjeURqGQJ\n/W4YFj8w2+t922jH4r6jfh8zdfruTkFhr587Vz5yFWFlMkexJRIw+bu3FgHTUZ4BEi8PQ7AIeE0M\nNaC40k4qgRGDCyNIxHlAnNSApP60Bi6bnT7InxmTL6gAskw7ij7TAk//f38HAHjp2W84+RMBiRMn\njgIAbq6sYGebZEKalSZqDHD0+j2UK7T+BYUCEq6KUJ0JEXIc1KDfQxbT51EcYcD0X6FchuCSWaEX\nIklp73/9pWdQKNL6+kv/9L900j8fxaZ03tSmNrWpTW1qU5vaR7CPn87z1LhgoxVjqkVJVwJGQVC9\nLADPXb6G8wt0Gj97/DwSRp+uvfUOuh0KFL99622AYcJz587j1i26597uDgYsXNlszOLta6StVK/W\n0JylrLe9nV3MzpAHKnoDKEalhl6IUa754d0ZnGd1hpvv0Gnp6qVLiEYEcyslXfDg55/4IjwWK2y0\nmjh8nE9UL70KUaHActW8F2mYw7pdLJyhk+3s3Y+iyjXghAJiDmIejWLMHyOEKhrG2OAA+7deugSZ\nkUe/GLTQ3aV2rYwktvqUTdRaOIr7H/rcRO3LEUPf913QZhgWXLZd1Ss42LaXRa5enF8MoZieCnwP\nHiNRUSJcncIsE/Cc1AoHk3ohQq4F1ulazDA6U6sUIBi6LhVDB3jFkXEnXl+O6y/dyalJBcohIUIJ\nWJXXjKvgxF2k77X21gsQPF6OLh9Gf0hj8+q7q7i1Qsjoyy+/ht0drrsXRU73pBgq7HV63MwAqctE\nVMjFXzs6RY2R1PpMCwk/z167i3keU54XOE0uKQTKxckphFhrZHxu0sK6TJtiMcQa13h85umX8DM/\n+xnqE9+gUMz1ejQkX58mCnu71JYsBQKfnsEauMDyJBohZKXFYjGEx1k0w2GEzAmySQw0IyJpjAoP\nLmk1Ita/0iID13D+SCYcKmNcEPs//61/hl//DcrS2VpbRZF/QGuLYoFQpmGYOGHgzBpkOb0Uegi5\nT4bdAaIhnd6TOEGrSXO01ZjB7dU1buJYG28/SrY/i/BOLEcPpQU8R63ocdC8sa6kkicl8okhhXC6\nbuVGDVGV7qNrJdgdOsHr2LhA4AGvVcarIOY+aacKFc42Pn6siGJGiKunNTqMdJjhEJ7JM/8ylxQi\nrJyYCtqfGaeNhlU0vm6vt7G0QOPi5x4771CU9voqCkxdPXnhNG6tUphC5/Yqrv/N/0a/3/1lFOaP\nAwB2V95Cb41DGbLUiQAXi1WUF08AAKrLd8Er53RSCk/mwr7jRBidZS742PM8R0VNYtrIMZpkInhc\ne7NRDrHTzxkaBcHoqQcNWC5OLsZMiTIEIgGAbwQArlWnDITJwyckNI8DayS8iBN5pIYV/MzWuAxz\nY0tjNgH7tNbuGIlKkfF3L7/5Op7+j39C7c1iGEbuJSwefugRAMDS8hq+/td/Re2yPja297izND79\nMCVWKeXj8mXKxg+KVfT7tA6lBvB5nIoY6HP4iyr4UK7GonRoYcEPcPX1FwAA3/pGCz/7ZVoPih9h\nsfn4s/N8n4IlAIRCOemA1I4hUhjrUpG1p3Blhzqg9/wVlD0aRL31m4g5VkMbgVJIi3Kv03dU0qkz\ndyHXyNzb2cb8AtEJ7XYHtSptxJ12DwFTh4tKIIoJ9qtUalhnWDu13h0tcIN+D32ugA0AM02CHj/x\n4IM4dw9RbKWwCJ9FKJePnAA0LVy+FNjbpoW4XBjghU363Lu3hS8tU8xNpV4DNA32/Wm0pVKAAr/0\nSh0IOePLryhsv/lNAEB86QpkxOniQRFDjpuKBkNEXG39wyzn6H3fd3IVtVoVnS4N4E5/iFaTYhWM\nHyBhJ8YLfEg/r6Yt4aucJpJIWLbA9wBwHbY8Y08KiSFn9czNllHh9HJlLAIWGIQQSDhTTlrtavT5\nKoGxd+5EJSaD8vPio8ZJUHQHXcR870arAR1Tm8/cdTcKJXrPV956Fy++RDXp1tduu7p7gMXMDDnF\nwmq42ws4Gs4TFpLj+FKTYsC8frPZgmQ5CZ3EiPssPFdrQuZ1wpSE1pOnVW/tDSADmgetxaPo7dGh\nJO70He366itXcM99d1Eb71mC4BWaMpGoHzqdATxFzxaoANqMs97O3kWxVdYmSAd8QOn30OD4hjDw\n4eXxYFogY8V9TwgkJk9pFkjB6ujCus1jYnO1wcaOSxLH+E+/8osAgN/+7f/GUWGt2TlUK+T8SBk4\n2QHle64ga5xmGDGlXA6LSPjvXreLIdN/zeYsSg06DD366KN46y06VGWZxr7y6nccb/FeC/NxY61b\n64zdR2CL/en7gJV5HJtCxrF0fS/AZo/aUPDKGPKcKjSqqB2lNecYF1NeOnIeitez4TPPIt6m723c\nuoXVyyQAu74wgy6HIXgb25jp0RjWVo/rkRrh5G0+zKiPxqKRbdD8L6oKOm0aU76vUOfD8O12BMV8\nZjTooM0FwMuBj0KXnKV3//b/gg3oepsMoSO6RgnrxDclLAQXuS/OHcXsg18GAMzd9YirwqBhYbM8\nu3RcISPLxkV1JzGNscxGd28Te7dIqfvQ/Q+gHNJ4HPUzWJFnNxtHCydynCWnrHDVAwwkZEbv0uhx\nEelMCih2/Ot+GZVtWkuu/+AvMd+iMX74049jTZFs0EZ3cKC484Eaknewpmptsb1HsaLf/eafIR2O\npVlyFXSjNSTTrHff/Um8/SY5SHsbe/ADumZpfg6PcJWAa1fecnutlQoxO0uLy/MYDenddXcM7B7v\nbYl2QsImS520h/QUVWEA8A9/++dozNDcfezxx+84inFK501talOb2tSmNrWpfQT72JEoAzgRrEB6\njgICrAuQpSSq/MSrkDKVsz7M0OKA7flGAymXgljdiTBkL/LW7XXkhZNGSYYKZ/WMogwzDUIBwkKK\nNqMmswvz6LYpOHK2VkKRg8kzxOCyVDCFGdyBHAYazTmnX1Sr1XH67nMAgKXlZUfV+J6PWplOa/1R\nG2BYcWF+AXFCzzNTSKFCOi3NHW2g1CToXNoMmavd5O2TpVdOW0kqgypnMgblz2B+nsri7LReQswF\nzU5lFl3Bp7FmA6NuZ6L2eXnWlElZWBMQVqBWoefb6vaxu06/MVOvI2fT+u1dl21WrdQgOVVxd2cc\n0F4IQ9Q4O4rZBmgTQfEJuloJUSxypgXGIoHGWliOMrdh4M6tUqb7UMQ7EUw1UDnVbA2yNNc3yRDy\nuz115gwWmjSmms2Gg+/7/S4G/TGtkw9rpeA0zwCLmVqOoilXUw8wSPOIWyWQcMaT9AIstAgBmJ+b\nQRjmiJ5xfQMJF7g+id3eGMBKev5ao4B+m1AUIfrweY6OBhlefZXE7xaOzqNUZp2dwIPv09xqzCj4\nQZkfIXCZaGkSI/apT9q7m9hdJzh+c30PxTINiiMnDoHjkSlgPJ+71iI/MprMwJhc2BPu5D+ZyQNU\nhNGEnBw/cgj/xW/9UwBAq1lGZ5dOxTMzs67OXZIkiPP+h4XvEdpm9yW4SCkR9+meyShzAa+bnQR7\nPWrvhQsX8OKLlAX08iuvjfXP3nPGlQdidyd7jwXmXDwIqByRBKGSrs18KyPGBJr1JLpMuWepRfnM\nfQCAcz/9JFrLVK9TVsoI67RG5ZhKpkvYYWT15MOP4LNHKXzg0vPfx//5g+cBAM9dv4EqB3x//sTd\nsDcpjELvrDr0SVoLPSGKcbAMj8KRu4jK6bRfQ8Rj/+ZOHz4nIBX9IhJG6gfdBOUarYOeV3E6Xt1h\nhBFT8YWCRYHXnFLBg88Q8SjKsM1zYrjyBq5tUOhD3N3EoU8+wX1acGCM7/suWP5OUCiARTV5DzA2\ng4lYiy/exDynrK72M2Q8SFIIGKYvRTbOINMQSPIMcGkQSBqngfAxw0LSFZvBG9Fan66uY/QuaRSG\n119Gy6e+miso2BZRmTvRNWTJeI0+wMpMiCYCQJLEuPjSiwCAG2++hkKuZWbHtWnjUYLeHs3FSqWM\nKtP+o7rm2qvAkeNLUOyqdHd3ETOKaPaAmOk8u9hCgUMb+qoIjgJCGqWQgXa/a1wcfYCQE89gMzz9\nrb8EAJw4cxeOHD0+cRuBn0RMlPRcho+GcCuHr9QBATOr88yRcd20xGp0OIM7hMCxJYrij43EBkOS\nwzRDg6m6ODUuQn+mMY9On7OkjHEpu1YKFMocE+UrlCuchj3SCJkr7gYpdGFcE+nD7PEvPukUuJvz\nc5ido/grP/AQD2niBtJHltLLnyvXsRTQwvXAIyeRjpjaKwYI67zJnTkOcFq1hoDHfxPSnS+4xglE\nWpNB82KXJTEUt7Fx9kGkoEVNrGzjMDs+o3oDt7PJsvOkzSFrAbg6eoDglGU/nMH3XiA6S2IVhw8T\nLKxkiNGIaUh9GzWub/Xuu2tIOfPw5JFDqAS0cdUqDN8emkHJp34YjUbIR34KgyQmT1dID5Id1MwC\nWU5tKA/G5Cnek3vCJd9HL86V2QVU3jYohBz3UG020CjxbyYjVLmWXKkgYVzfJwh48QoDHykvrkp5\nKO5L3skfTcoAJuKMmjiDYN2GaNjF2uq73F9vY4bHflEJ50QZmwF2cgfD8yvueQa9Pk6dJuqtVjmP\nlAvLBkEFh1m6QXl1xLzxxt0UxtB8MvAwGpHDYDPlNu299ha21+hA0GvvIfDpvWpvHnWfC1+/tYMi\nb9Gd7XWcPUftKpdCl7YtjHKZlyLTkOnkC7cQYt97N8gVyJ/44uP49KcoOzaJIxdXGFQqNMYAGLNP\nHDCOnA8uoFz6utEx4ojGdBxnWLlNh4c/+5u/Q4ep8l/4+Z/HhQskjvr6pTfACVw/qryw/78nbGKY\nUytSuNg4YaWjmzwAGVNbVowV24cqQPkk0bSz99+P8Dgdsja9Oi6+RZTX5sYmRnu02faYPt7dG6LN\ntP+DjzyIn/rdLwAAKp+V+OEjFMvy59/9O2x3KQZsvtrEw+xoDbt9SF7zPIwPgpNYTlBaY9E4dBwA\n8OYAaJaonfONKjg5FtVKGcUyx8P4AW68Q07CTK3uHNXOMEIhdzbSBIMk/yGLOs/XaqWEkNPh270B\nbm9Qm1ae+RNIdqhb930RMhdhFMLJlhhj7igExAqN3FVNM40+1z7cXL2J5l1ELW3tJIh4YTPKczVo\n/SxzFJLyPSg+ZAalAqoMLqDXgenSuK6bBCuvfA8AEO9to9Yih/fsZx7F7DmSvElbCwhYDDoIgSHH\nFtt9Cuc4UAz+w21jYwOv//BZAIDMEiR5djKsC+uJ4xi3WfV/bqmJEjs21ZJFxmuqVB662yQfsnLj\nmnOuhp0OEqbTtzY3UazU+PlDlCv5ASNGHDHQYLRTsC8EISvO00G+zQ7zpddfwtzC0sRtBKZ03tSm\nNrWpTW1qU5vaR7KPXycKwsnM6/0UHsYwoZTS1U+DsU7MTkKQ1g6AtvEhmAYKggIaTHUUUoM6I1Fq\nH6Td6/b2ic55qDG11++0Ua1RkGsgNRpcJqZUshjGdP9OrwNTmJ+4jadPHEK9ToHVlWYTHDeLXmcX\nWyvXAQC1ag3HjnPtP7WIwi6dWr0kdQHEUbUAeYROIV6r5U48EhaWEQprMgjmy4zJXOZjluqxUFkc\nIWZ5e0DBX6C+SrfaQI9OlWGtgRZn/H2Yffs5yjybmy+i2eJA9orvxEONqGD+KJ1otrd3gCK9j8PH\nTuAHPyBaY3VtG/OWTvM3twYoMO261uljhlmu+cPLfD85zggMxrXhsjRFlDkhFyfsmFmLROd9Ysc6\nUXeQ/KSkgDeO1IXM66mlfciE+nLU3UW/Q4GSZ++9HwOGki9fvuxqes3OtlAuc6A8MnQ4CNLzMpic\n58R47AshHOUZJ9p9XiwW3cm929lDxnWnYLSrK2ah4QWTa9MstkpI+oQgaV/h6CFG+1DBdocDLvtd\n2Gt0kr9x4wqsybPkEkRMh1jjwUR0faBCpCx+tzvsIuTkiUoQoqM5ESQsIvJyMcQ3UCnQ+NCDHl65\nfB0A8NCDd+P8WUIwBSwEo5+Eut6hTlReL84kmJunsf+f/covo8To7M7WikvQEBhTMfs1gDKjMWSE\nqlguubmYJBHyani9/gDf/Na3AADf+ta3sXSY0OUoinDXXYT6LCws4MZNOkXnJS24YRO3ab95jJAm\nEnnpSAgtqN4gAAWJNgcj+xBIBc2f+rl7kR6jOfrCVgft60TFmaCIS4zc3HznbZQ4rGKO18u1nV3E\nLHT42c9/HgOGcIrlWXzuF34JAPC9y5dx/RYF0l9auYWA578I66hyEH5D3AkSNS7RkiQJmvPUr0v3\nfRG9m08DAI4EAebqNM8qlSoSSX+vrK7B8rZWmFkA4nzMbqM1Q+tdqaiQMiXkewESRj0TFCECmluN\npoLmcbS2toXtl78BAKgeOY/SLAXdmyz9yCKNFqnLqIwywJshRDbzgFKVdMuqtQgd1uXyjYbHtKOp\nKSxw7EN1kECtUyb2cG0D3U16l72kj8oiraetU0exfD+9+0rtPEosBo3GMiJOjomVQm9E93n6uW/j\n+s3b7klzrTFjDGa4D3/hsSc/tI23Vm6ivUX3KRXLxEQB6EdDt15qbbDboTVpbX0VC8u0/2UWsIb2\nC+UZrKzcBACsru3CY9q/F3Xhca1crTNEeW2+OMFclfrnRLmKV1iQOrISBabAQ1863ltb67KK33jl\nJTzw0GPcgiMf2kbgJ5Gdp+04FWmf+qkx5oD6a54B5kkPljcbC8BjFdWBlQhELomQQjGWWykWMMM8\nfn84cGnJjfl5bG8S1G4yjSFTJl5YgOJ4jko5hB+w6JpNMVOm+5eHI+T5VZNYWKrA43pjyleIeHMd\n9vZcraf5+VncfYhS5aNLq1ABTfogrAMVjjs5OQM9y9kVygIZb2BmXy0jrV2MiDZjbjlKEvQY2hxG\nI4z4GTwVoMiijWjWoTn7LxymKJcnoyz3BtSP6XYZ7RGnO7f7iGJ24EwKn+nP2dYcbtymiX/z9h6u\nXyeYdBQn2OwQPTVKUiwt0n1UMcDCMaL5BGeptft9FDgdHdjncEjPxRFEOoOfjyUYF2tnjYH4CPiq\nFICXO+ECSDn2pOgZBEX6nW0TY4br1rVaDdy8TgtWt9NFhQVQwyB0m2W/HyMHe8vlClIuMpqm48WX\n6pDS/f3Adw5VvVZDmzNPdre2MOCFptWc3Ve/Kns/ce4PtHS4Dg90n3LFw+4WLZqvr28jmaGxma3s\nYnCTUn8XjtZw9jQtxIuHWxCcEeurKrIBvZNyWETM4nebmyXs3iQKZLjZwTrPuaAeIBvSWC5FPXRY\nHiHVHoYRtfGV165h5RYJI54/exwLc7SRSBiYOynUu49yUJ7Fb/zGrwEAHn30glM6juMUJZ4TWTau\neTYajRBFXDzc8zC3lIuFagzZGfA9zxXhhlT43OcfBwBUmotIuDDq0tKSW9uOHTuG6zeILhNC7Nt0\n31dY/UNNeOPCxrmwqdWZS5c3QmLEvImRHvyTRNvtVuu4dPF1AEB7r+ckX7JGHTrPigwkhlyLDEUW\nMK6Xce4eKjp84YufR8SHWq9vcf+nHgUAfOGLX8Iff+0P6FmSDK+9fQUAUPV8zHFGrjYZipiMehbC\nuioG2CcF8cAXvoTBiyReHAxXkPK4i0bSUZihD+iw4Nrf3aNDTGu2jiJXWxj1+pjjA2SjUUMvpRfx\nzlbm0vxb1QIO5YKv7RF22UkcXX8F5dYR1++CaSkphBMIncRWVm/A5wzXgajggTMPAQAWl8pAQIf8\npeUAaUZrTFnECNjxSNZW0blJc2V7dRWahSXr5RD1OXJ+l4/fj3CZHHl/bgl+Nac7x1m2RheQxvT3\nMO7h0mUaH1fevIJN7jetNRI+nGdZdkcSAHtbt5GMGCxQwlUrqRbLkPwM/UHi7h9HEQ6fYsHa+Tnn\n5LS3t7G7Se9dKOFkPoSUqDEIorWBz2NGZwY7DLg8LKu4i6neV+LM1e3M/JGLbVOejwIffDdWr+ON\n1yk05X7OrP8wm9J5U5va1KY2talNbWofwT52JMpXnqvNlBkDua+S9n79ibyWmlSSqomDdCZcCJ3v\no8oQM3Z66DFNktgUCes73XX2LCSf5G+urkAFBAcWhETg5QJmFmXWhTE6RsRBoulwAMN1yAJl0E/f\nv7Lz+9lobwXQrAekDIa7pL9jBh3UGKFYaC4jeZcQmubiURQV1wazKUbz9HdSljCsQ6TSsQhjlkTQ\nCZ3YbRoj4xNYonWuOYpRkmDIQdxpmmHEqJRNElRmCLKttxpQMZ/SUgO7M1lg+fI89xc05vnvWrWE\n6zcIqk2GGrtb9HzrqzsocTbb/PwiKiUOKN5dRZTRM9XqVfS6hIgUwibmWtRHo+4W3y9CFOeaUsKd\nGAI/wIhPEsM0gse0RRZFTphSa+WQqDuqiOIpBHlJjiwD+NQcegbWY22sahlLRwl2n2m20OFTexgW\nkfH49TyBhGFlKgmRi1UKp2WjtXF0pbUCOi83ZIGAs8Aq1SqSXERPKZg8YHRfIPk+nc6JTJsRlhhd\niUYatTkaC8erHt5u0zMcO3MUap6e/9OP3IVqmTWdTBe1FqEXnbZErOj0a6TF8sm7AQD3P1jDcIuo\nq2effxVtArqwvtFG1idK+OTcDPwm9fNOBlQXiWYwaYz1G3S6fub6bVRqNI9PnzyKQ6z3NpkJZCxQ\n+OQTn8N/y+VdgsBHzKfiSrnqsjxHo5Gj80ajEXzOFmwtzGNvj+bH1tYWLGe1Kj9wgqiLh5ZRnz3M\n/XY3NjdZ4HZx/LwnTpzAs899n9poxnQWJWbcuZkc1c+4PhoIRU2YekoqNTQXGPGODNpz9Cw/fPcm\nAkaxms0aZluEqK7oFAkj25VaDbJMY2KWM5Qe//RD+OJTPw8AmFs+hoTRZ68QIOJMxqBexn333A8A\nWH/7MnZG1G+DRhP33vtp+u5oiL2LL0zURpob4/I4kvePVCr0UhrwpSyD4mD/KDXoc/jC5tY6Kox+\nJZ1tWNBYqBRLiDiZYH1tE4MBtb+6eAgNTngp7t1Cd0DzcpRKFD2agM1GHRs7HHC//g4aSZ7GbZHT\nsgLiALPyYfYfv/OPqBQI/VgqN3FijtboIyeOwPJ+JrZvorhBJacGOyu4fYsQTX+ni6DCge7LDdSO\nn6c2Li+iXONMy1IDYM2rztDgyjWiw7bb22jzPtHd2kV3l/akzZ1NrGzQ3O3pCLMV6ttHHnoYPc48\n/sfnn0OqJ6fWdzc3XSiPMXB1DK3JAL5PKSi5cVkoVNBllPrQoVnscgatgA9IWg/SNMHmBu2voe+j\nWqO52BsMoPie3Z02aswANaoWVtLcfXuQurXZWu2SAiw0JKOCsCneeI2QKHz11ydq58cvceD70Axz\nS6WcgrAU4yKTQioEYV6MWDiRMCktSpyJ1PQT1C1twmu9ATJO5elmBoO8VNtqGzFDeoMkQyOkiSJN\nB5LFE6v1GRc71W3vYZiweJtJUeQF1BMSxk4+IXrtTficVbDy5hUnXBj3t3Hu3CcAADNJASuvE1zq\nnz4LcZhgy141hW3yYhAPEffIkTA6geAdMk1ixLwwZWmEjB2qLEtcUc9+pPHqKwSjt7t9HDlCGQZF\nXzlYurjUhKkzdbjeAaI8ReXHW666HcfaFXkMVYAlXoijWowopvb3eglqzJv7gUK7TYPW84socPZH\nrVnB0jxTqgWB7VWOGWGnKEoTpHk9KC+Azuh7o9ggYUpM6wwppzX3hyNkJpe2EE4p+07ScUnoMxfp\nzJyoqETqYmyq9TrK7JCqYgVeIadkC84BCwKJHosNKunB2lyZXcPoHPpX4/gJIZywp+cpFFkI1vM8\n1Jimnp1tIvTzwssxAo4DUL5yVMwkVqsXEUU09ltzhzC3QPephz7Kt6kvw7iLI3UqcD230IQvafMY\njuAEUPtpimqT7nNzpYfnvkNK+Z97/JO4+5OUJl0Y7CHkWLyv3P8E9l74LgCgvPU2Bn1aBG/dfBOL\noMNQJahgnuUC2nsD3F6lxXT11qt48IHJ26hNhqUlcvZ+53d+GwuzHGORRfvqn/lIY67llyTuIBUn\nCeYW6LvFUhlbW9T292oMCo7JqNbqkBFnZw0TLC7QbzUbDZf5c+Hhh/D1b1DNsN29PRdfkt8XuDNn\nylG5Rux7JoWUaZbdmQaapzk7LrN4e4f6ceHu+3DrBgkZak9QAVwAwyTFPfcSbfHUU0/hzMnjAIBl\nlj1ozi+62NLt3Q5yxdgsGeHf/7t/CwB45i/+HPexGniUSeyxE3D33ffisSe+BADwNjbw7KXXJmqj\nJ6VTiIeUsLzZeX4Bt1hQcW+tj7PzHDPYH6DPjk0Sj1A/RM9elAZZXmxTJ+CScViab2GbBTk7A4s6\nr7+z9RBbe+QIb+wpHOOarF4xRK5sOti8Bc2HWFUsQuZDU9o74mf7UYQwMFcrLAAAIABJREFUyJXS\nLXwOIHnr0mvocdxl99ploE2Hj4VmDSfPUrvqcydQaBHlJ2tVWM4oTFURiaH+CXygN6J59uzzL+KZ\n7/0jAOD66jvo5T6gsahW6but2RY2OrlzIrCwSGP5V3/+5zFkivvq229ghQ8Kk1inG8GVuDAGKndu\nTYaUD46hV4RgB2lmfgH1Cq2pg63bzrmqN5tYXaPftRkQcwiAp4oo1GivmV1cxPV3KFxkfWsbRz9B\n81ifaqHfYXpfAtEGtaWgNbTh1H+t4LF8izUW7e3tidsITOm8qU1talOb2tSmNrWPZB+/TpSS8Dm7\nI8sylzklhHCeqZLSCbGNIODzyf9Us4ATIcPH0GhzcCoOH0FxhmDqcw88hHk+NVUKZXznuySf/93n\nn3MBlq1yHRVGJ6y18FkXRAkAHGwKpTBkPZpBZmHV5DpRlVoLSY/FzEYDlFivotFo4cginQrl9RG6\nG3SqePH6W7j7Cz8DAIiPV8Dl8pBmMfoszjjY23J1gV597TJSRgHOnT2BJut8DIdDWEarwtIMylwe\n5Y03rqJaJY8+8SUACk70SmWUGTHLQg3LlN+HmavVphQS1lIySqDIGXZJGjv9psAPx+iL7kOyUKfC\nEIcXCR377BcewcwMjYkb1y5ih9tc5FNuFCUIOCtPitSVO/A8HxkjUSZLIRlpUlKhP2T9o6FFoZ6P\nsYmaR9fuyyIVlsQ3AQo2F6wtYsMCcvg+TWNUmdYplUouYHg46iFlYSDpjalFq43LOoUQsCIXTBWQ\n3O6SV0bIQbEQEotc9qc1vwSfs/A8hbHYprDQ8eQ6UY1mA8MRj31vLFCoTIrj8xxo3TPY4aBS4Rcw\nz9Rbllr0uYxLraGQ8FzsDCQ2OjSmvv7N63j2WfpuL7J4bY2+2zjTxN2f/WUAwOji09i9TYhIiABq\niU7UcRagvcHlnuQQlRn67t7uO9gdTl72RUqLX/zFXwAAPPLII8j0uDZYTttlxiBmMdU4SZHw5635\nBZT4ZBtFqcsgEko6LSxoi5iR9STNnDiqMEC5SHOuFBbc4Hv0kYfx5JMUfP5Hf/THEDLPOhwjSRb7\naop+iOXrpxQSKd8gVR72WKT34ijF4NJVAEBxZga1Fq2T3cEQN9Zo/bEeUGCBw8HeAL/7e5Rl99Vf\n+zWH9FpGf4f9xGX9ehbweG3++p/9BZ7/Q6qFVtzexahPW8nSwjEsLZMe14XPPo75eRrDQbmGsD43\nURuN1q7GmZDS6QYqIXD+UVo3X/rLqwg481khQ5k1206ePokGa+1t3l5xfdyLaG0CgMZcDTGLuW5u\n7qHKOksztRmUPEIhNnc6iBg59z0PPie69LdvId4h2rl65J68ShCktXekE9XbehfLDdobRsMN/PGf\n/hsAwO29DmZmKdP713/2SRyfJb2xSqUEzUKaaTCHlNFQpTxYzmS1qU8vCcA7K2/itUsvAwC+9Z1n\nsNeldqU2RoFpviTN8NVf+U8AAGdOn8G/+bf0DKurN/Daa/Tdt69dgWA0L0mGMHeAfI9GAyQpzY9S\nELpECCFrSJmWDf0QPs+bzBgsnSJUdNUUsHCYxs6tW7fQG3BiSqWMBqNnc4fmcfTUcb5mA5vbtPac\nOrKAhQqtK0/f7gIFXsPiEd68QUlS50/Oo8Kaf0oVUCjkdJ7FsLc7cRuBn4ATtT+FW0rp6qPlaYoA\npxYzfSOEgsfxKDPFIqoqz1ATuO8BGlCHTp/HkdPE+9cbzQO/F/Om8uIrryDhWnvDTKPMm1AaDRwX\nWi6GMFw4sz+MsZPQMw1VER5nz01i5foM2ms0sXzlORbp+InzCCKGMPe2UK4TXRHOLkLywmTTAKMB\n1wIyGjFTbJsbW9japJij77/wMhbnCV791Kc+hV6f2vjMc6+g06HvPnzhQTx8geIPTp05je6ABQTj\nIYZcv2jv3XdgCzRBg97kTtRgQM/q+75zTDIdw+f32mzOYDjiRXlgMWpzWn+YYpazrBZaFRw7cggA\nkPY2cHmF4NneYBc+T/wo4zixyEKzExOGPjJ2dIVSbgOTVjtnWGjrFL0L2j8gcTBp2rEUYrxB7atL\nprVByiulVyjD8rMkoy6qNVqMFpdmscvir0kaQCou1KtTF7MkjXBOlBXS1VOzQkDyjwVeAR6nLtdn\nmjjJhY8bcwuosoxHoaAgxb4CqGpyMNloCY/7bJQOULScITmSKHMbd9tArbTAz1ABQO8pDBRmA6YN\n0MXeHjn40bCCoeFxMH8flhZZEf/2Giyr2F+8eBHLj9HiuHDPeQTLNAZr4hH4XHMx6Wm02jTOOqsb\nSG9QXEK3v+qKb09iZ06dwG/8OhUTLfi+k2jIrOYYNX6n7ET1e33UGuQMz87NYsCyBv3ewGXqjUZD\nR1eXfOWyiZTnwc+rZwsg4oMEhHBcXbPZxG/+5j8DALx+8RJef/0yAKKp368w8YcaU8LWACk7NKY2\ngyUu4npxYwe9dXo3SScBAqKt3rl6BQnXy7PKR6vO2XeNkpNnWVvvYJcPg6MRXSsM0GBauVIuuHYt\nLi7jvnsoVGG4t4f5EyTcOnvXOdTmaE1WEujxQbBRKsA0GhM1Mc0yeCw1IADnUGmtMcsHsUOf/hIu\n/tn/DgC4Z05jkeP1lNV47TUKm5htNdzmuLO2A2bKUSj6GOXZf502hn0WNU4tum1qvzIR5mYoM3W3\n3YcTlE9HSDoUm2QO3zd2Kqw9EPP2YXb/mUUYTXGhw8EeInZq19p9pGUaD6vDLkqW+rKXAhGr72u9\n6+Rl7ChFe4e+W/QqWGVJgb/5+z+lrG4At9Zuo96g/SwMPTf2b9++jk6Hrt/dK0DxXlsINeYW6Po/\n/6uvQfn5Xj1ErTZ5mIuU0h0O4mgA3+Oag0HFidoWZuqocHyXD+2Ag5nlw2iz4OvazRuwfJAPKjWA\nHV3fL+Hda0Th7bRX8MhpWnuaQ4NKXlOvUsXtMj3/6vURNjh2t1Qe4KF7Kb7VDxT6LMxdDIuw6s5q\ndU7pvKlNbWpTm9rUpja1j2A/ATpvLGCnlHI0BgCXoSSlRMif+5BQDLve2huhdZLQi0c//SBOnqeT\nT6E+48TYtNFQ+XF/n9aPrySSvOp1kqKXV7vPYhhDXnBdJbA5NJ9ZbOW0QWsRgTe5HsbO2i0o9kej\nKEZrjjzcxZkjsKuEhklLtCIAIO7BdsnL1kMfWT/XDNIwjMhFcYJ5zhr50hOfw/wSaZPMzjbwyqsX\nAQA3btzC7i6dZnzPQ7FESMGRU6fhcSmV3o6GqnCAZCyR7XAttwTI0sk87iTO6xp6Lih/FEVIWcdq\nfnEWzVk6Bayu3kBQZM2sYKwNMtuqI2K06vrqJmSBhl6tXnG6V8LkVJOCzst+KA8pa/R4VrsAz9Ar\nOLRICu0CJPupdtTanZhSAop/0/cUDAc1ZkERfo01i7IBEkt9FmiN+VlCFkfHYodieaEPw1pMUbzn\nnkVr7WhJ6Skgr3tmreujIAwRMEV69NhRLC/TSbhUqaHENaX2Z7WmUrpkiEksGmmoEj2PXxAIuaZU\nWRoopmAPn1nEgGvPRWhDKdZ5CSNAEhqzupIhafMJc5Bg6QgF5nb1GlCgcXrsaIgkyLNuVuFxcKeo\nea58TC0owUSUSCHTBNLSXCw3+g59OHv8fiecN4l96akncP+9lC2odQyVozVZ6gR9k1GK9i4L8MUx\nTrBwbxzH+MEPfkDXawuPx4AxZlzqJfThM+UqpXR1QXf3etjaorZUqlVUmFpX0uITnyCdpd/5V7+D\nf/17/xMAYDgcHQgyn9jy7KhMY8joy4Vf+XUUPk0o/Xf+5M/Rf2eb25zB57nY77SR8mk7LFVRKtC7\nbC0sQzG9s7HTRp8zGHOgplGrI2a6s7uxjgrr6TzwhccRMPW5srYKn5NJYisgc8o9GsLwuntrfQUb\no1wA+MebUBKa10Ep1YGst4wz7M498FPobZIm2c1n/xCjPoUsGGtchuXSocMOYZDIUCnltRmtQ4IX\nGkUwiI3d7hAVpn6WTxxGkbP/0nhnXGYFAvFgz/1Wvl5DwLEpk5gyvQMZ49UGvaf5QhXbe5Ro8wd/\n/AeYbxIdu3z4OJqM6pcqIQQn4Wxs3cbFVylgP0tJWBoAkmyEUome3y9I+AGvbaFGkXXv7jo7h2ef\n+1sAwMuvlBzCWiwaBDznBvEmdESDoVL3EJrJx2y5UoVAyN2TQTEtqLMMISO4gVdAuVzl3y2iKHMt\nvT666/ROfZmOhZXTFOUy3bNcGmGmRuP17uOz6HEtxSUhsdCk8ZhUyxj16J43N25CsIjy4cUGalzL\nNI5jFJjSHQ4GKFQm3/uBn4TYphxPCKWUw74E4Aq+KqnGC4rRmGFZgE/eexaffYQyhY4cPerif7TW\n8POJJRR2WNX1jTcu4/d///cBAG9euYSfvkBpt7MzS7h2lcTSrDaocYeN9naRxHSftcSiX6Tfrc3M\nunibScyzCVIWbEujGDWOiVIjgZjpNim59hyAzVs3UB3Sb1XuXoTJxf76XSTDPPtNospppnNz8/BZ\nBXgYxYg4Iyj0fRSYUlvf2MbF14gqqDZaKOZildrAZy4dgxTRHottCgmtJ+O3d5i6aQqLIj9TqVJ3\nHDesQok3TGsSRFyDcGZ2zoljrm5tujijaqOGIK/3pMZq9QlTsXGaocDYuzZjOH80jFBnZykQEr0O\nOWXS8zEc5sJ7GvuZ2EnDFKzWLpFECAXJ2U6+mkWS0G8m/V2YlDZfoTKU+Jpms+4WIKEkhrzhdnp9\nMHuGNNUus0oIBSHHG0OuXJxlxlFXrbkWAqagi6E/dhgxFq+1UkAnk8dEZVpA6ly6QSGU5GgX/XEl\ngULZQxRzUeBuGzqhPq6WJPZY+Xf1xhALDdrAP/PQIfRZxmKkM8wWKJ6g4gNnD1W47QoSu3lHoBmw\nMKKKoJgC0SqGLrLoY8lgWODsSO3BTphFCgBPPvnTY/kIk1A6D4B42Ifm+oD9zhC72/Q8x04cceEG\nFy9fwje/+U0AwOlTZ3DsGGXQaq2h2Rn2w4ITgo3jGClrjPiFEIvLdOBTgXeggHleS/GJJ57AU089\nBQD4o//3j13cnzFmYkovjx2NU43Dn/8nAICH/vN/gR/cJIqpNrcEv0wFpK1NXSzlsNdz8hhp3MfV\nd2k9PHLqbkhuT5QlLiaqyE7WoNfH33/9rwAAr118CXMLtJH/zJM/h1NniaL1Fg6h12ZqKh667Kkk\nofp5APDsP/4DVtZWJmqjtXB7BpAecKJyKZPQkzh34XMAgG+/8NcYRuR4HDm8iOUFoieHwwFusPJ2\ntVJ0NUfb7RFqnBo/u9xEqUyUWSft4UiVqOzFVgjNUgCjKHbP06gUIbJxSMF+iQN7Byr0QmiXlukH\nvjscNosF1Jj2jAcZtnaJEr+1vgbDGW0ysegOaF7OH57DHlNgtze2cO999E5malXEvE/0++N1KCgI\nGEvvp1AQbg8YDHpu3sACo2gcQ+wKECYCZsJC2QAw25rHSpHWTpNqJ4hsjHY0eJomWN9gAVUp4cu8\nzq52gtFpnLi+NdqgwLFMpaqH81xnsNms4D/8A4UAnPv0KXi8B790dQ/PvET3v7HWwcOfoOzhe8/M\nY9hnEdEkhmJ61Pc9FDi+cFKb0nlTm9rUpja1qU1tah/BPv7aeZ439nAxpvCEsc6D8wWgGPk5dfY0\nnnicThjn7zqF0P//2XvPWMuy7Dzs2+Gkm19+r3JVh+ow0z15xBnSNINBi6REgLYB2zAgwABh0QIM\nE4YAGTBt+JdtGLAA/bAAA7YhmSYskQI4Q9JikkhO4oTmzHT3dKqurlz1crjxxL23f6x19rklyV23\nGmj+uguYntu3z7vn7H12WPtba31fLRtgvHqMUgp7D+mE8S/+6I/x+1+lk9KP3noLDx8RxNvvdWA+\nS7B+K1K4eoE81iLLcfCIiMdmeYVhRV0wkjE6mxSGE1I9FRKVVyUse/0XL17GDick5kdnPpFeygCG\npWpamxdRaia6FM7rw0kd+uuTJPYhn7K00HFNTCqhOPn46rVn8Cx/bne76DB8W6aZhz+TdgcBV2+o\nUECuNJUKJetKPcnq099wMoNkxCkIQrQYuev3ezBMpLm61kNW1tplxhPyRaFCzFUYUTtBxve2xqEX\n10RqfDIwgDXMR1NKPwaytMSkRvYgkXESsA4MHIeaSDuNH1wAi2qUSfH4iULWULtQHgGFrWBmHHqU\nKQIO97RbkU8yPzw+9qRyUkiPokmpvZSFNQ7Kc6FJ1MV2SauDi1cJ/VhZW0GL0bhASX/9PGJh0YQC\nFzEnAMXjKzQOltuSh8rzuVRqhiETyaTZDDHrkxW5w6MHdCp+sDvEWp9O7198aQe7I3rHs5lBh8NH\npipRv4g8cJjyOEBRIGbUua0ciqzmasnhuJLO2AphTR5pcqTlYgUQAPCpVz8BcDK5hIHl5NrpZAzh\nqD9PDk89Wry5uYmzU0JRvvH1r2Nvj9YPrRoJnrW1NaQzJrt1woeaIRRSRh11EGJrZ+Cfo0FPmpP7\nxvo6fvVXfxUA8M1vfgv3H9AaFgTBwpVdM0azbWsFyWWS9fjD73wfeywLNFhZRcQIqTAOew9prcvy\nqQ8Vh3EHLUZigjCCVHX1VeErGLlgFL/7ld/Bb/wfhO47UUHwvHj7jTfxK3/n1wAAz1//BATz1Z0c\nn/hCmXI6xNf/5A8BAG9851tY1Yu1sX4GgCSSfDqI1j5iUZUFjn9E3EerwQQ7TFa5ttZGycneu/uH\n2D0gxCYIFHIOJ5aFxtY5QquECHDIRJqPHh5gY50lxKYWCc+JyXQKWRMfmwoWXK3rhI97OiHg3OJE\nlJVQXhKyKAvfRq0krOfICrGyzuuaBAquQH7rtVuYcOrJucvrGHDB0njWwoCLBKwZ4XCfIjQP7jxC\nkRLC3e1uwKGRVWvGnfMJ59IJv2pakJJh/QdPkTuPtc1tJDzOpmczONAzxzrwVctpPsS9+/ReRif7\nmKVclBRHOGFNwKpySNO6mMZgbYP2nbXVDkpOAWmPDD4taE3qHXaQ71Jb7t+Z4LXXKSx4+eI6Pvki\nySDN0ikKRhQdHKq81qYV6A3WF28k/ipyouZyOKSUgA/hAZoHS0sJvPIysa7+zV/6m9hYpY431nrR\nViWV30D/7E/+BX77n1B57Wvf/TbOTmmw0N5dM84Cr71LC0helHhumzq4mM1wwHlBhYwwlOR46MEG\nophejoV5Kn3Q9uAieuSj4doLn8cgpn+ZTo+hNgnOVEGMNg9kkXYRtnmT7nZg2LFM2h0odhjagwI1\n+WORZl68U2qFF14i5/DZ557xwqhWCJRZzWpuYbkSSYkA+Ygr9QqLNjMvx4ghisU2p5jpEpSWcHWu\nWKiRcxXl8eQUKZe8B60AJVcpWWTY4BLnXq/tRV8LM0FWMslpK4FhhzVk/b1ERv69C2d8W2xVYMZV\nQ0qFiHmzqKz18XYZCF8S/TQSrxIOTR37vFC280SapYMnNzVW+JwJN7AYMXt5VZU+JGKdmyNUlHOU\nC7LhX3AAeFPe2NzC1g6XhMchAt6wQiU9tcPJ2alnNe/1epBPASZLWO+wtYIIzG+LMi/heNc0eYmS\n302rJRFxbPTOu/eRTuk5/62f+hK6XMFi8xP0amoKUyCdNtpwtSPhpPOhFGcMNGskVkXm9ewcbCP+\nW5VeaFcIAWMXzzXpdBKYiqvnpIDhfLrR8BRFSePr4OQYn/70Z+hexuF7f/l9AMB7N95Hu02b6O7u\nHmY8pr/4xS/4qsmz4RlWuSL47OwM779PdAKXLl9BxRtqFMeQkkPuYYiK6QKMq/ASr3P/5a/9Gv6H\n/+l/BACcnJz6TfpJVtMxxBt9fOMHPwQA/O7//pt45TOUL/rsq68iYmepSnPMprUAtoLkd/mJz3wB\nl599AQCQJC3/nqqq8rqPdWXwH/7e7yDmw9/q2hZSXjNu3XwPX/nt/wcA8Eu//B9hPKbvj8+OAK4i\n+4s//WO88d1vUT+4Akl7sTCJMcYftpVq5o0SwmsHpqM9zG6RGDHSKY4MOcitlkPEYfAszTBhcmBr\nV1AW1HdHe/votTlvU0pPCHx6fIyYK8hQKOQzmgeHh8coa8LfIIHqsAPmbBN2nKvIXMRSq7xOn0Rz\nEDKIYAxX3kHX0wbOFTCct7hybQdffoloM9bXVjAe0nM+e+1FrG8xWW9Q4vmrlM5y/coRZjPaI8Mo\nm8snnsvpAlDzSzuDJoSnpK+UdnBwZvE2xkkb/T6T3WZjpBNOucjP/BrmHAA+aI5nY7xzk+bT1tYO\nVrmCVEcxJu9SuHal38MFXj+u7TnkIef1ThXOnbB+KXLcHdG68uath3j2GVpTX7y6hSJntY+8fEw9\nJecUlMIKbOxcWriNwDKct7SlLW1pS1va0pb2kexjR6IqY7yHLvw/yEJGpb78pS/iF3/uZwEArVYC\nN4c+1afTG2+9i9/8R/8IAPBHf/CHOGZVZwjjk5Sr0iFmCvyVrXMQffJAXbKCdz+4AwC4/cEt6BbB\nn0OXIFin6odubwDBlXqlkE9zqEArANbXyOPuxKs4fUSkdtG48vjnaTTFumFuljzCxNLpIXYz5Kyd\nl+ZT31dlmSPl5EFnCmRcNWNBqBYAmKL08KoVEoIRGy00hCaUBJVAeEadPh6PgB5XNoQr0Asmlg9Y\nvmN/9xDHD6hta+s99Ad0sk1HY2SchCmiENvrlHzaG0To9Ops7RRRm0OzhUOLQ5hJHKPK6PQXcoKr\ngvISKVqi0TgyJeI6ATBu1wcYjM9GSKd00poUMSIugnyaRE9jyqbvi9yjaVpIlIwCHR3sw3JF4mpH\n+RNvt9dDt8sVZ70OuixdMB7PYGQdipBAXdkyJ/sihfYJxpvbOx7dMpUhjSkAk9EQRweUCP3BB7d8\nkvOVK5exubm2cBtjLdHiZ1au8iEYIRtkbDqZgItj0e4FGB3RSX5yWuF4n8bgJz8rcXmD0OJIlv4k\nncQh6jz3x/KkrUHAibMyUAjqPNU09XNdSuHDBs44jBhBEUJ6dGQhE9brpTmrUDAScef2LYy4iOTS\nlWfRZcLaO7fv4rXvE6KT5xW0rhFChdGI2vvWW+/h6pUrAKiitR6Djx7tei6pZ5+/DsXJsnle+FCg\nUiGM4UIAARxxEUyn1cYv/HVKDP+//8k/g7XzHfb/b4ZjQJktcY/JJrV0GDMSGoYhBkwC+/6juygZ\n6YtaHbRWaF52B2uYTgm1Xl1dw+bmpv99zajUDSZqHA5PMOBijtPTE49K9DptvPVDQvCef/5FbF+4\n5u9/6z3Se7vxzluIuBpqo9tDuyY0XMhqnUnjq95cVSFgPdRsluHeA9oDzHCI8zu11qbzfGD9/irW\n1+j9dJLIr5VpmuKQ94+NnS30uJhjZUejM6DwWeCmOD6mKsfKWLRq2FYnSLrUX8JWXlrKmhLyKTYN\nawDF3GxSBXPrQQDFkJBxzn/vAGhGz1a2BpABjc3h2cT/jkaI4cEx91uGFrM476x1MQ4ZHYcCao5G\n16yRQojmXk6gweQpbYC+bzRuF7EgCLCyQnvw2eFD1O5Gno/8/qrC0If2LAQKftf7h8dQTEwbVBUu\n8fpRBh3U2I8RJS7uEHLcRowJRWVxczzGt04JST13dRNbO7Q355NTVIxMK0fVqwBQWefTR7qDTaxz\nJfyi9rE7UaHWUHMLZVXrk5WVF6p95eUX0eJwjC1LVLwonx4d4Nt/Rgzkv/kbv4G33/4RX5NBoR4U\nDgnnZ5zbuYT+Br20breDiO91tr8PyXDsWaGgOXeotX0euk3P4JxFUFf/QcA+hbBriBIbmySkqlID\nN2QW41xSDAhAXs7gOP9KZBOIgCZ3VRiILsOWStFmDiB0CpYdIRtGkLapTKy1rIRzcBxCMIGCFvVk\n0nBFrQMYoc/UCiJXnrSsN1hDsWC5quaFottNmIARCCKJjCt/tBI+32ltfc2X1sKVUDXzdxjA8O1C\nO5cDYiw0P1NdadbtdpAyO3YxS6F4AllTIuIxU5gK0zFdU5YVRsxomzvhQ8YCi21MADCdDL2zVBUl\nTllEutvt4OSUPj94tIuVFerLTtTGhMf1oJdgpRalXV/FMVd+TWYdjJn0rTQFHFfXWDSLowoC9GtC\n0q0d9LgqSlSGmK8BFKbA8T4t6JOzqQ9p7j48wKuvUngI//aT2xhKC83Loy1yTHlOtHsDOA4dKmcR\ncSn4bDTG3Q9oMZKujZ/40if5GR6i6lB7k1YEjjKgyB0EC3kqpTy9A1Fp0L1aUQBdi5JK58ejtRaa\nveJKSB/OeZrKNTLnF0c4652FR492USraVH7y6lVP6vfGG6/jhEVYkyT2VAZB0LAYnx6foixqx+wK\nWi0+9KQpVriSyln4ClEppSdHhRM+18RB4d33iK39977yFXzx80R9sN5fwd7RYizJE577+WQKu0H9\nePXSRRi/2TokCTvixkBx2KS/uoGVbcq3c074+XXhwgXf17PZzPf1/j7lo+ggQJudqFan41nrR2en\nGDOz8813f4SdS1cAkBNz/84dAECVzjDgfMdYyblw+YebMcZfSuFcHkcQvsI16q5hmlzgZ/0B+l16\nV73hKaYzPky22rh8jg7J6ysdT22zsbECxaLiZTlDr09j+bw1njxTCo2ED+RXL297kfAHUwnJTr0q\nK38QNdY+Vb7Qpf7qY2SrjQNjYF1dxWYbVntnPUFlNZxh5ikgpM+LdA4At1ECSNUB/zH8qcY6i9I2\nv1/PUWdt4yzxf6NrjA9ZWmubMN8CpqTGzkUacwf79zAZ0fMEKoZWnFcG4fOAHQDBa32WjXDvQZ2H\nCKwwlUgBiRmPgbtCYuU96v/zK220I2r7N/ZHCNbo+gvrfeQlE8dK5WlmrDN+d5BQMDyvzl17EREf\nZBe1ZThvaUtb2tKWtrSlLe0j2MeORCUyQMXwpIOArBNzzQhrLIE9/fa38HvfpiTBZz7313CDOZ3+\n+Ve+ije+8xoAYHh6hDorNrcWISMSq5vbWLtwBQDQX930ULuZnKFTeim9AAAgAElEQVTDCY5v3/oA\n8QqFPTpXXkQ84BCIkj6B2dqmCk1o+Rg3yZOs11+DEuS9ysPMJ+864SAYKZIoUSV0KmzpCII5eqoy\ngz5hRKfnGu6mskLAfVVYibDWR5IKJeqkS3gyO0ABKSd0ZxUEo3B6ECFmdODc+gXsjynZ/uDRDawn\ni2lZ5TOm4u8miNvUzmmWgg/tWOms4hmuKpsUI4y5wmI2nSEAPXdn0IHkhMB+p42MT7Q2yxudOj5t\nCKn86SfQAWLuNystSj61FGWFOjYc6AAxE+w5E0C6p0EuyL7zne9iMqJ2vvDc85hMKAwUKI0Hd4nf\n5mQ0QsRhmmNTgqPIiLRAFNQSOCtY4fDANDNehkhr7asPrbPQnIwdhAESJtI0psKDeyQfdO/BXfz0\nv0Mh7mefeQ5v/+gdAERyytEKpHmJ0Xi2cBurfIaKj8tRLKHrMJkgFAIABhtryDgx+9037+LhbUIb\ntla2cf1ZOtWnhUGL564wwvMvAc3JVgiBgtGbqioQcnvjsIWKQ9NxqFAy0WqWF8g5rBsEoSdPHY/H\nyOqBtpA5rgwErJUeCTw9m2Bth8a7cMDd21Sx8967b6PFYeQ4iT15bZaWkEwUqAKFnCtB7927j2vX\niGvm3LkLHkH43vdeqxVZEAYBtrapry5fvDwnexV5HbrT01PMTpjnbK5S+Ul2YGpONYsZk+C62Pl+\nz7LMIyJ5WUKzVmZ/YxsXLlPIbX1lzYdOkzjG7i6hjc46X9lXoz9CB74auNcfoLIUBqvSAjPWvLx7\n+yaeZdmryTTDw/v3+Rkzr+83q3IgXOyEryA88qeDRsZJSYk60OTKMV66yDIfw2uYcpjmzfd34Th8\n+uw1YMDpGjpMqOIZQBzHDanxZIaqoDXRVPCh9dI4z/WlghYEk0C2SviEZCUqCFcjP3bhkCwA7B/s\n+ipe65xHYyphUXLGuXNNsYV7TJtPwLlmntWksEIIWB77UpBuLQBY6x77nToka63zYXchhL/GOgFb\nX2+tT4pwzuEpitahlMJgjaJEz770Ck6OKRXEQMDw3myrEn6nlQ2xsjAGhvdgpSOceOmvwL+7mQhQ\njumaRyd7CBkl6273IR2tMeks9Wuetca3xTh4XyQrDfpbTGa9cX6uqGgx+9idqDNXwXCYTDuDtqON\n6rNrLVxXtHn88fd+iNtMCLnyzl188A6RRr7/9o884RZc6dlY25vbOHeNynvXz12E4FwEV1UQBb2E\n8f4D3OcSydbqNkoOPwRrm5C84do8heaZUpUlTD1pICCegn12Y+MZVKdcnTaceSqGylZQPFFaOsao\noI25HaxCcBl2bi2SUb3RCq+PVM1mHjqtAgHJIRwpJWRUi5jCV3hU1iE9ZiLNTCHiijphnS9rj3SI\nHrOX7996G9PiEbfgP/nQ9jnfHuMrzwKpEXdocb2ycw59Dn2cjQ+RsNOTlpknnoxN7FnpXVGhzYtV\nbiyqwpepAABOTw7R79AmGgUhSoaxc+NQ1FTKVsDUJbkQ2OCy1NMRoDlM9TQT/l/+yZ/j9Jgchnu3\n7nsyuHPntv1GbwqL92/Q5lulY+xsUMim337Rl/ZHQYgBhwf2DoePCcb6EIWUnqhUK406Hra/+xAz\nHu/vvfcOXn6JtPOuP3fNhx+kcr6az1nhN/1FLJQOijchLYCQN5VZ1bC8j8dj3Gddw+O9AlcvUBXX\n5QsDHO5TKKrXkpCcO1QZieGUw2ci8IePomjKtpUAUM8nW/m8BCGcb/t8LeVsOoOqc7eUeiohabjm\nvRdZjimXgpcGiKKEv8+w9+gRf07R7bT9n7d57JZ5CccHFKUb8szh2RD3mNhSqcBXiL722veRscP8\nyiuvYHOTNu+bN2/6CrGXPvUqNjZonK6truGYqRWGo9FjNDAfZiPdVE0pJiGtOgZO1IzLGTqrdEg8\nd/V59NZpE3vuhRdx/fmXAQAXtrdQ/0zUihAxE6Ozwk/2NpMkShH4UMfO+fPY2KJ2vfPGG5jl1K69\n/Ue48RaxZk9nKQ4PqJKqqCpM60kdKCBcrI1U4t9s4jUFg7EG4MPk6cP3oU5oPP74F17EiCu/fvDW\nB7j7gObxy2GAGVfYHRxPfJpBp6WR8FiYlhUspyWEQYyAD5xpNsUjJoGcTVJ0E3qGdmezIQcuC/8Z\nFk9Fi3OvPPb5RVJKqmAFbciqnguioVqZT02YLwS0zsGK2nGSHmgwznrKBRmouZC4gLQ1U/rj1jha\nwufyOtvQqggQbcailiQJZqxfu33uEl785I8BAN770V8gn1FoT86FFLUQ8EnTsvlsTOXbHyiFitew\nIFBwNYO/cCg5xafKJ5CKU2GKzFM6mDknyhqLlA8h7d4mnv8E6c72+oOnoo0BluG8pS1taUtb2tKW\ntrSPZB87EpXDImH0YL2c4Mc3CYId6Bh/wHIiu1EbXQ753bp9D7c4nJdNJhCKT+CtHtZ2KJHw4jPP\nI2YOCSuV99GryuEvmfPFjk+wskMyDHLjApIWoQbOVl4zTgKIGaq2UmFakz1ai0gt3jX91R0M36PT\nlykNpK4rSyzaqxRCUIM+jlhzKS8CjAu6Zm94gIR5SpLz6zBdhqvTKao697oToeLqG1MZ2KTWIxKY\ncQhqklcQQ65qnDkkdVJ6kaDksEQE6blaLl//LE7u3l6ofVVdgVLkyBhF6LY6/nRweHgAx6ehrJgh\nY32rdDaD4hOyzQu4kkNYUeyh7E6nAyEICZjxib3ba3miSWMcxlM6ZQ7TDClzvQx6Kwj5tOFK4yFt\nKayvFnua80QrjnHMz/Tm6294Is27tz6AZuSyBJAzz0g31mgHzB0znSHhcJUSDeuLKSufVFyWlVd5\nZ2yKPgvpw3xZOkGHE3FXux0UU3q3R/sPMRpyGKWcgqNtcKZAp724zlNZWUSeN9QiZ9S2hEbOSf27\nh6e4dZPCMdMTg/YO/f7FnR7CkMI3VIBRa2sBOb9XKxVKRhWN4ao/bqPnPCtLjxxbW8EylKoCgYAr\nZAQkijrBV4qnCq2jMh6JKvMCEw53drorHolKpzOMuVggCrVPAZhMJh4ZC7X2VaFGNCTBVWV84UC3\n0/VhR2Msbt2i+XRyfIoDrv7qtBO8/gahNA8O9tGrEdZWgtv7tGZMqxxKLfgeWXMSwiFgiaheHICj\nGihGpz5RHs4gnRAScOOdd7B3j95rJ0k80hokoZ8vtjL+8/CIkAJblgh5/L9/44ZHUA8O95HzuB2P\nh/jeNykdIy8y5Cn1uVYSmauTnqUvHHiSVVXlgUlKrm5CURC8dicbuOeIz+fujWME/G5bz3wZobsD\nAPj+uzdxrs9yRnGEOCCEzuQRTlLqu7Nh7vVAhdLod+h7iQoFh/SnwwnKKY2L1cE5JIy629LBsJSO\nlGrh9gEkQ9O0q0F7lLM+vQGYW8MEfJ84YC4pvSnCkFJCeRSlQYysMT6xXAoB5eWnmrDdfD9bp31I\n2Fn7GKfdU+kDBiFCU5O3hnjmWeI3hLR47y3SqMzGB9CK10VrIBj9FUo3Se/OeU+lKHNork4XACom\n03XGomKyXmcd4haNbxmGyDhVQaomNGytQ7tPe/NLn/4yts9f8n1Sr4uL2sfuRLWswau8QHxu5wJ2\nmbn4dw+HGPEm2AsCmJwW6MxZ9M9TfLK9vo6YN4nB1jY6A4KmdRgi57ASjIHmcGGalzhh0reNtfNY\nY0I5JwLUCQsC8GEyJwQKrmZwovleQQILkt8BQLk3AZiYzxoJyU6jjkL0VpmYLWhhwgvASriFDris\neK0Nd8CiwGUByaXdR3vHmDFTc+vyjoecszRDydUGVlpkvGDlOdDmkKhFhYr72aQaY4Y5VTzwG3Cs\nE1y4+PxC7asHs5TSLyAEsVKfTosJKtbks6JCTcUbSiBg6DUbnSFiUdbpyHgNplayhpzbVlcmtlsh\nhkPaCIrSYlrr0glgfZP6UwqNIqtzBwSm3DCrQ18F+DRkm2GoUDCRYD5r2MizdOwdxzBpIWInJ5IR\nJmOqqZ1OJthYISddQkDMiWWOh+QIFcZ62ga4ppJHCOlZtYdnJzhjagVXFnj3Tdp8D/Yf4CHTZkxn\nBiVXfFa2wqB7feE2ZlYiqoWdpUbG+YBTZzHm6saD3TNoXic/98olJCFXQM4O0OLFq7LKM2efZRVm\n7O2XQnnCSa2DJiRgCgh2TsYm830Lof0iCFf5PA9rHCxvTnleoiwW1+six5XuVZYWBX++cPEiIq5a\nOzo+wdEpvTupdcMqL5QPZ0kh5ghfm4o/Z+FzvW7fvuOr84qyQsJ5mvcfPsAdzm37iR//MjRXHn/r\n619HxX+71u/hvdtMYSIEhTYXMMmHvjhIMOU5tHfvA6RMsPno/nvYO6Bw7HQ4hmMHwQHeAZKAX9+E\naljAhXN+d5Y8h8six7VLdBgVQuPoiObl+Z1tvPMu3cdWBYZMeOzgfFjLCec14ayycAvGZa2xDd3F\nXK6OENILMLfWdvDK3/jbAIBiOvGHw7DVwcUTqmT9yj/87/HwfZpDn3t209MttGKNCa9XrioQ1ake\nrT7aTMNiszHanCu3N8uwz+kUvZc3EDDhcFkaP8ZNVXp6iEXsYtiZa9c82aaBlY1j40NLDo/lJs07\nlvPdOk+J4J2iuYCTmPPAnHU+H0lK5Q951md9AU6KuUo9t/A7BJiJ31BfFUWOhPNpn3nuk0haNG/e\nf/PbGB6Scy+V9U6jdQ6G18sgCCHrw7izfryWVQHD+zeldtSVhgZpNuH+aOhRrLWo2OVpb1zG9ZeI\ncHewsuX7WWmFPgtrL2rLcN7Slra0pS1taUtb2kewjx2J+pnVBM9wAvLbJznenJJ3mSUdzxdTZBmm\nJ4ScqDjBhetEjiWl9HpPTlBiMwCU1kFyuM1UFlUNGSuN658i7pVur9/ovEHCcoJzJQQl84Iq22qe\nGikEwpr23gqf0b+IFbtDyFovzhhI1vmpqhzDW5T82E4GKBJq47sPbvhnqBINyTT/5WiCLKQTTzG0\nODyi8F+iJVprdNIqNfwzz0Y5qmOW6NAttPma2FbIGL3Rsxlmirz16dEJcsVVL0rAnpC3/vP49z60\nfYpDg5PJ5DEeoBlXU82KHD3H8jlaN1UqTkPUpIMhUHGlXjqrfDjv9GzXw9E1T9OemyIK6/CGgOR7\nxsIhNnSfWVrBcpLpKE2h+D4IWyj8SfjxU96H2f27t8CAAVQr9PxbOhCQzGkitYDjMBOs9IhglqY+\nSTTLc1/Zl6ap1wGrjOWwFunoKdlU1FRceZLOZjDMNaQFcP/uHQDA0cGePwFa25B/ZsUM47P9hdoH\nAOOsQqioz2IjMeLQ2zDLMTyksTY7G+OVlwgJfvH6JuBqotMKJZ/6xrMCKcP6UyORcdt16DzCVlam\nSUi1aE7spmoIYp3xlXQmzyDKOhE9QplX3IcF0lldgfpkqyxQcKg8y6zXn7x0YQtjRovvPXyEE67a\nUypCXdegdAzFcwU286hRFAQepTbwcmkoigIHBxT2SrPcH0mdgC+GSLMMn3qF5De+9ud/BsFr2MHu\nI3zwPhUpaCE8UvckC1qMuOgIVtbkhTn2OKw/LXO/Zm7s7GDKVYWVNf9KuKl+CYb+ByIf9ASEjit9\nrcFbnDR+/fmXscOJ5ffu3UTGMlMCzhMmCggfgxJKQDCzatiKve7ek8zYhsPHYU5vVTh4rKIq0Yrr\nRPGu3xuqqsQGV0b+8n/+3+C3/pf/FgDw5v27WGcizVBLZGOao4fHM5QxoSIX1tfAdHeYlBM/xg9O\nJwgZgV8/fx3G1e0oEMia16jwPE6L2KTIG8kYzCdvW1/8YecQJ5IEFXPf16EueGQJgB+nQkiIx1As\nTzg19+qND+cB8GvYY0jUPNLlGuLNRUxK5SuAnUNT9WYMLpwndLPT+Sk8ekBh8KNHd3G8R5+dyaHq\ndVcqv45Krb0MlDXOI8dCNGtqVkwgbMMjqVRD0HzuAlXWXnnmRfQZgYyjBDKqCwfaaLe6C7cR+Ctw\nol7ureKfPyRRz3sqgWLnQTmLnCHS08Njz0o8WF31ORDGGD8QHNxjg077kAC8rpyTAp0+h1W08kKO\n1rlGq8c0C7IS0g9A5YSv/kud8Vpsi5iKW7AcCspMjpDjSeM0x+EuVfK0ncBsnQbFo/v7GHLegu61\n0O9RrL4VdmFWOGQSxogSghXTtIJi4LUEYLgqR1YaCWvhKSc9YeJEVBjyZhzoAoM1iv0G3QTSV6VM\nMAkXYyz/hV/6WwCA119/HSdMQillXQDOpaI8gCs0E1YogaJecJxDmjYaTA3Jm4Ow80smx7qrenLI\nOp0GQgDpiPNvIGCYmRq6Q4KeAISMEXPeCQmWLgg/G/iyalMVKJm9PkGMDochh8OR13oTZYyEve5H\nu/vY2iaS15PRDHd5vJ8OT6G5Imk2ziG4j2AqFDz2kzD0rN2R0jjlZxjnTVl/lpe+PDsIQl/GrJyA\nT5xbwCZZ6akgynKGI66qc1JjyA711XPruHqB2ptnByjr2KgM4VhnclgI5PxeMyv9O45MA8dXVeXn\nsYTz4staa5TM0VBWuXdEhbFw7DjFQQDHOZJl4ZDni4fzpNKeaqCsDPpMN7G5tYnhTVqg79y94/M8\nhBD+2Wihnq+C4gOWlL7kH3P5K8Y0RISmMp7sNg5CCN6QDg4OsMJrUtJq4YhDbXdu38JsWudqLL7W\n5DyGHAQK/hyv9rHDOZ8iCtHp0fh3lcGd29TmNEsRczhTKQXFAs+iTGHYKXeVQcW5cYarh8uiwJQP\noG+/dwOS7zkaHvqKxSAKqbKv7rO6ylkpaK78C6P4sQ37w8z+K3k3bi5vp3aonHONEDQakeIgCFFx\nSHx18zx+4Vf+LgDgt//+38PvfZPImq+dX0WvQ6vXbGqRfkA5uGZ0giPeV8osxcP7tHbLySmuffrf\npd985hP+AOhss44JOK8NuoiNhIFTTUiubldoLQKfm9TkKQmIho5ACjjX9MN8t9ZkknDCr6vW2cZB\ncnM5TkJ6ckvn3NwhQPg1fF4YWwjxVKErrQKvCRmGCTLOQxNSAhnT3fT7SBKqGu31Vrx27GR86gXm\ns+nIp3oExkGKukJ7Pl8OMDVxLyJIPmCHSRcD1m+9+txLOM/kn71uF5bfl9Qagvf7VtL2Tteitgzn\nLW1pS1va0pa2tKV9BPvYkag/2j3CTUenwVCVgKMTzmxcIGdIPUkS9DaYAFOIOcTJoWZ20FpzPRDj\nFeyBaqU9JX+kA6DmjBLw9PbSCZ+MFqoQKeufOekQMMRtK+PhUq01Fj/7AhsvbaHKKOk9TzOEmiUI\nTI6KUSMBhTVFz3PuC9InzaUm8wmsUZhAceKyKY3XgCqrFFbVycoVyrwRKFP++GD9qQJOQHimOIGY\nyRyjsO1J3axtKmCeZJ985fMAgJ2dq0hZK4za1KCE8z/WfN/8UwhONP032by2Iv51fqc5jjmgRrZE\nMFc0YuDqNyYEEsbkt7e2fNLwk+w/+A//Y9y48S4A4PTsBMfHVF114eJFfPYzxCFy984dPLhPCcOB\nkl6uZpQaTBk4knEPn/j0FwEAG+ev4XREhQK7+/vY4erSJO7i7JROZVVZYmebkuVfeOF5fMCn4rt3\n7/kEbGNKlJx83253fKLyzs4Ots5dWKh9AJDmFc4kJ8i2YqxvnafvZylaWxQW3ugCgeMqF6dgFYVA\njscG4zruFWsYTtgsIGEZwa2M9eGN+Yo6C/gwQ2msT8zWgfAnZ2elTwgv8jHCiMds1EI6fYoSAakg\nGO2WOkCf5XjiOPbodb/fx/kL1G/Hx0eYcihMa+2rj6SU/vqyLEkDFIBQob/GVhUKrkS1kAiZcDWJ\nYh8Onk1n+MsfvE6/CevJP4XSHoGaX8+eZFWd3oAAmrXwti5cRmuT3mUpgSkXm5wdHSNkyafO6iYC\nTpR2UiDghHNtq0Z2w1iU3J6C+X2ybOr5zcIw8bFM40rkxZj7CpCyCdvU61mgNOI6nC8UrFsM+aak\n8gYRnJ/+/p9UIUSfpYBqWCNhee0r8hznr1Fx0b//d/47fOervwEAuPneD2HuEVoco8Iq98XwwQNo\n/hyFEVpbNEa+8JO/jKtf/AUAQKu97tFoJ4Qn6guEgFTNMz/JeiryCChEg0Q52axl0s4TbDaIE622\nc+vtXCGNqBF5yDkUSzZrr7Pw2RZzSJqZ07i1wv0bkSgpJBbHTB8nAnXOUbEJaG0IuJoZ0vk9bHtz\nB+ssgVVWBXLeO4cnpxgOqVhgfHbiIwbzvoKtCmju/6TTRadH835j6xI2Nyk9qN/vIWQ0VkB4EF8H\nAcKEw+RB6KuxF26nW3DyLm1pS1va0pa2tKUtrbFlOG9pS1va0pa2tKUt7SPY0ola2tKWtrSlLW1p\nS/sItnSilra0pS1taUtb2tI+gi2dqKUtbWlLW9rSlra0j2BLJ2ppS1va0pa2tKUt7SPY0ola2tKW\ntrSlLW1pS/sItnSilra0pS1taUtb2tI+gi2dqKUtbWlLW9rSlra0j2BLJ2ppS1va0pa2tKUt7SPY\nxy778n9+9dvuZHRG/yKlVxhXSiJgKnrpzJzqgYJj6YjKWVS1JIETc7T3c8rTznpBUDjn5RmME0gs\n+YiBTiAKkus42b8J9EkKIIwHyFl52wkDwaKn86KOv/6f/vwTufw/+7mfdLV8jNICij9HcejV2aWU\nUJp+tF0CgsUPs8BBapbFWb2Eion133/7dSiQxMrK+gA7F14CALS6A7z8Igk2PvvMK0hzuub07MRL\nnKytbniKfTjnZVge77um337x565+aBv/i//5f3PA48KgwolGQXv+YkF3oVu7x79nl13ZRqTUzGmG\n1x69cw5S1VoG0oubusd+04EFRUgYs5ZNsICs36MAKhar/Ad/7z/70Db+13/78+53/+QWAOD+3hgv\nv0TyA596foBv/yVJwGgBFCX9XuFyvHyVpIqqIsAP3qVrfu5LF/CNN0hSwpkCP/YqSbqUxuDojJ7x\nzu4EtiJpjgs7bShu6/5RgeGIxsXVCyGev0DCmbd3h5iyGOePvXQOG+s0XvaOM2Ql/c7/+ltvP3Gc\n/vrf/RU3OSAB6TJUKFfod954+z0vVpoeT/DG90moNdIBdj5xBQAQrCWIAnrO7toq4phEbq8//wmc\nnJ0CAOwkx+eufQoAMJxOcPPsPvVP5XB1+3kAwCdfuo4H77wFADiLQpydHQAARsf7sDlLz2ysoGJV\n9ZkpvAzQP/71f/DENv71X/ySs476MM9TGB4vUgtEMa8lhUI2o89xz2J7kySbLq5fxsmYhMHDSMGm\n9LdvvX2XJD4AqBCYzmjN6KxuY32dxkkrjtHpk3TE7PQR3rn5HvWnFVAsi2Mr4UV7oQTaA+rD1a1V\nP0d/5x9+9UPb+OUvv+wA4PathxgN6d1DKAiWkAlCBc3vyZQlBMskSSm9forSGkVVCydXfq2TspGj\nqmV7tBYAz6GiKPw800rDGBZ8ta5W24K1jSiz1goZS3cURXOfqjQf2sav/eO/7xIWCIayMGDB7UDC\ncQe22j2sct/H7R4GWzRX0jRDUdD7CUXoxXbLovRyNGEYomTRZWskzo5oDGppIMHvttOB4bZmWYle\nt8fXW0xYuqfVaZOYLoCDvT1sr9M1/ed+4onjNAgHLgprUXHt31mv14Lh5yyKApbFjoVz0CzpopWC\nZiFoIaQXA0/LCpWr35+A8IK8zos/B1EEybJIRVmRIDFYlstvsM36K4WEDuqX61CyHNDR/Q+e2MZ/\n+uZDJ1jaJtAaMd83kICQfC/R7CnOOjhWm09nJd7+0R0AwNnJGDKg20WdEFeff4b6IQq9vFkAAc0q\nOt0QiHKS1VqJY/zFG28CAG6dnuGnf46EpEMnvG9RSoC7nJ6B++HnX95ZSMfnY3eitKsQOBoISihI\n7jTrjG+EmFOxFhBeC8846ye+hPQLkAWalz+ndO2s9fo/yiqvnVcYA1HQ9VkRIkbtpJUIWcJHWIfC\n1T35uBbck6wsM4AXnco0DkJlcoQhdXEUBV4vKLUlUkOLS5lbBJI24OrkAI4X3FgUyHihOzs6w/D4\n69xeg/SEHMJObwOvffcvAAA/fO3PoCPqw8//2M/g85/7afqdKPHaSlJKCFer0ZtG8fsJpuqFeM4F\nk8JAiEZh0Os0CYG5l+bvYF2jMK7nHC0hhB8Twq/movltIf1CKITwWk/OWVj/vuA3C6UUUDt7wkIs\nqIK4dzDxvx2GGqtd0oxrx23M0j0AwM5qguMTWkRcJJGW7ICXQFGPWSuRxAHf3qDK6Zr19T6OWKOt\nMhW6bd70lAKvpZCa/hsAtOIO4oSVyAMHHZDmUysJcTykZ9gfzrDSjRdqHwAcxxncKjsVosKsRb+z\n89mLOLxNG8nDG49gJY3NZLWL7oA07LIyx+kxPf/a5jqcoOc8S8e4eJUWtTgXCFjhcnt7G4eWdAPD\nOEQlaeP57o2/AKb0/exMI4x5AuoK4EU/DwwqSxpuUJXfDBax2XQG8EKstPDrRJFVEP7QBu8sVIWF\n5bYgqJC0afOO4wjTkjQErXAoMtp0O0kMxdenZ/soWvSONlcvYcfRPG7F+xhcovd1o2jhrG5K5lCy\n/mAlKrTbdE0UhI1z9QTbf7QPAGjHMQLeSPMSyFl30JnKH0K10ohDao8xBgnrhqWzFMrU1zsU3BdO\nz20HtY6ac3QyAc3x2kFyDhBodNEKbpcQzYZUOgvJG7+zJaxdbE29c/cEnT7168p6C+vbpIMWtTSy\nEWmone7dwP7Dm9TOoItnrr8KANjYuoA4oLlblBUMzydTlshzep9xGHmdw+FsjN29RwCAc1ur6HSo\nj1SgkbMz1un1/AFVaY243reEw2xKcyKKAlTsmC1iQmgU/M6yvESrTfO4MoCoHRitveNp5triHBBG\n1D+B1l4rMDPN+7EQEHwsdXRD+n0r4FwNNDgEtbah0jDcrqosYfh6HUXQfI2wDl5IcbFW+k/z52mp\nFKSslVUbnUQn3GMH79rRrcoK6YwOkaGJoHjcO61guQ9bUsrb4OgAACAASURBVKPFY21DFdCGnKiw\nqJCe0Tva3zuBrcc6lL+XMRbOzGkEyqcL0H3sTlS7kyAvabHu9doYzWggl8Z5JERI2eAjzvitWkv4\niSeFhaxfrJBwjDKVgEefyLniyY8KlheTUDlMp9SpKulB1gPHlWixd2ysha0HnSCPdFETQsCwwyOk\nmBMureD8AmQAwQKl7RjtFi1uDx8couCTbS+J0eNNZXMwwGhKG8/D4wkSvj5JWrh79x4A4Hf+2f+F\n/UcPAADD010/MP/0D38L+Yz6/Es//jdw/8E9/2yDPqEPG+sbzQnjCRYqer7CFAjYWZTCkYgxW/3O\npJSPTYTaMRFoRKClM35SSxn8a1KjQsLPOmMrj3hBNJias5UXArXWQfNziSD081y6EmrB+XDrwdCf\niqwB2hEtamUuMJrSZN5aayHnNocOiNgpns1K8F6FyaxEzhtKvx/i8CzlloUIeVy0I4m1LrXEVBar\nHXJUhu0CB0f12Nd+Y1LKeWf8cDxB5Q9vBkm02DsEgKPUQPNGWqZTDNMhAEDECdCn37/46jX0N+lE\nnZ8MEYT0PHlm/CKr4gAypOcfT4ZQLD67s70De0xjdrDaR3dMv7OyvobdfRqDB2cPUByTw1bCoc3C\nn1oqjzi5zGKNBUTb7RjTvBG9fqI5IGShXUiDKmdxb63RTRqh5NmYftOWAqWhzw+PbkOCXmQrb3lE\nU4caJ8fk+LX7EVqMkgRCQFlaVzbwAOcsLdZx4HDxIqFM7ROLr98nL8o4BWNZkFwD+YTue1JUiLut\nhZona3Q9UOBuRyvUXrzZmALbO5sAgIsXz6HfoecYDoe4eOkiAGA0HOHwgN7Bg90D3N2lz9O88KhZ\nWa9nxkLRqQdxHPu5XZaVn9v0f40YeY0WzS0PkFJDLSjQ+2DvIQZZm5+phVM+fESxxvlNWr+efeZF\ntLorAIDJrMKjh7QO3r//EHGL/naw0kd/QNcXeY5A15GGFOMxvTdrBDbXCYnsdjtIU/o+6XaxNljl\nNklUfEjK0qkXGi6rHD1GH6eTMUZjPmQs0Ma4FUFrGqeT6RRBxPsQDCzfSwqJiOdrZmd+b9NhCMXX\ntzoxypSROkhsdGneZFmGLK2FxNEcRFyDFMJZj+RIqbwgttaiQS2VQH0ocXD+QL6ICSH8Ou//ndtV\nI070cM0huXZWgyD0jldZWrD/CAndjC9jYUuaT3uHh+hrnpetAjqnw0bS6eGkpHmWQ/i/lVJC1cCN\nrfzaL4RoIlsL2jInamlLW9rSlra0pS3tI9jHjkSZYgZhyCOOdAfdqD7pcPgN5OF6KBG2CRo5QNSf\n7Rw4KATqkKqERe2mSsBDz8I5iBpKNhIq4nAIHASHF611SBlxEpAQljx6Yypo9RRdI4V/flMZWA4h\nRUHooUFjLSYTQoegHCJGFgaDtm9XXlgcT6ivpLQY9On5T2cKo5RdcWewxaexKztdPLxDOS5BIHxI\naTgc4mtf+38BAKPxFDfe+SH9ztkhul06Xb3w8ufQG9Cp5Zd+7r/60OaNxgShV2XhcwCEa3IspBD+\nwEHwf3Oy8E69UP5vi3SIgOF0HXVQQxDONu+lscdPBs1nh/oyIaUP2hWVATi0Z7Opz0l7klVFCcfI\nVhgpZHkdBqhQ+hyPJlTrjEWkCAqIBi2Ee4TAPNof+bCBMC0YhsKmaQYhqc2DXoB1OkRjd79ClvE8\nMPCn/iBQSDmfREmB1S6HfuIAo0MaR0JbGLt4CKHMcpxwKCpsCThHzz86m/rfWXt2CxeeofySW2++\ng9blVf8MnRn1QyktqpSfwcU4PuA8opnGqiQE7/DwAJ0eIVFChZjN6ITfiUOULWrLTBvkfIoedDfx\nwuUXqY1OYrNH5/n1lXWIOFy4jdY5CD7NGmc9iCk1tQEAukkLw2M6nZrK+bwdIS0kx6JmkxSxovuG\noYTjd32wP8LqKrVRtxJcWKHPGyKF4NN1pVtIAprfn1jJ8OiAvv/BaQalaTzEMoGZMkoWRAixWBu7\nbUJZHJrQinQVVnrUp5cvP4cXX6Kcz/PnttFuEcJVVRUin4+qMOb3sXt4jD/+828CAN69eQfTac7X\nM+qopEdwAh3MAQvChzjhgPkpW1VNyE/ruTD7gnY6vI/JjPp1MFvDoE9jIQoT7N+nPLt+7xirm/T9\nzuWLuPYCtbm0JXYZnT88vofS0ERTUmJze4ueS6Rodzi3S7RhMuqLYjbBhMNzRgj0GXaJ2z2okN6/\nMoFHKGMR4OSI1sYw0FhZXVm4jf2NHqIOrePBcISE80rKKkfBc6LTaiPkvjelQqtHqKIzgJHUx4Ot\nNUwe0fyLHLDF+X0P7u9BctgLEqgjVFoJH/4DLELOPVSRQMCRCSEkyqreb+BzfIWzKBeNO4MBJo8y\nNd87OGheF5WOUNUoqjUe6ZRSPoZ01tEFYx1MRddEocTpkN7du2+9hRbP0fthic+/RO86LTMc8juy\npoWMx+w7774FxXP0+isv+9xJNXffRe1jd6JG41PvYJyeDNEf0MKqlMXRISWkRlHiEzfn8o/hTJP8\nbKXzIR4nJKx3riwixY22DpY3qtIaBDUGKBzWtwnino4myOr8FamR80QRWY6jXZqgD3cfYnNra+E2\nZlnq832EUEh4MGot/aYYhhohO3JBoJCl9WINtDv0GnZ2Yow5HDI8zXAw4UEkBFohOwZlifPnrwIA\nXv3Ul/Ht730fAJBOp7A8U6wUGI4oVPONr/2BdxoFLE6PHwIA/vLbB2jzggx8uBMVccgljKzPMYEV\njzmaPrHbzTs6wiejU/4b/a2OAn9NEMV+UteJn86Yx6Df+fwpn/8Gh6AeKHNhPgvlYWBtQs6/erKt\ndCLsHtECGgSaVioArjI+jt5PAgS8ESeRRsRh4bNRhg7nL41mGXpt+v7iVgenI3aENFByjkVeCkRR\nvTEZlHXcwzkffpSy2ciCQCNgp3t//wwhOyErvcgvcIuYDiRmnIt3Opxgq0+Juc5kSPmgE7sEORc9\nrDyzDZvUYQYLV+fASAMoTgCtUqyv0dzqyC4qzkUY2iHqGOfByQFmHOoaJH2IFucaBRVGBYc7wxjJ\nKs05lc0w5TBcUgo89/y1hduYFyU0b0hCuTrNCnlRYspRwU7chuZNsawqSEvvazScoRXXoQKF6ZQc\nRWOAdos2sDzP0OmTY9Jtaawl9JxBIFBYei8noxJdTlu4uCbwpat0/ciUeETdAwUNHVP/WMCHgp5k\nQdTkcdSOy7WrV/DcNQrVbW1t4dLlSwCAlf4qhOC8ujBCWRT8twYiICclaffxiyE99xc+dYj3P7gD\nALjxARVZnJ0NofnAA6FQ8NhwpfHJT87YJudFSFy5TM9y8eJFRJwf+OaP3sTx8elCbTRuBPCzTs4E\n8jF9joK2X+POhjnu7tIB8vV3buD8FXL8N89t4vKl89QXa8/4NJG7t2/j9gcfACCHrt8jB2ZtJYKu\na1hMhVaL+kVq5fckGQQ+9JPIFrJpndtYol4CoySAVtFC7QOApN9Ga4X2QicsFOf/FNnU7206Dr0T\n2kKMmPeV4fEQgzX621a7DWspF6/Xa0PxvBTKQvGeIRSQxHU6SAQl6vXUIeLQdxwHPj/KOUrQB4Cy\naNZiaw2KBXNMATpcY24dny8Aqx228fgUu3vk5Gysb6DVrvuwapL/55yoPM19rlc3jDH2+WnCH1ir\nSqMT0Psdne2hOKLCNtVJUOQ0lm68dwMF703XX/mEz8c9PDxAnCwWWvftfKqrl7a0pS1taUtb2tKW\nBuCvAIn6xjf/COfOnQMAHB+doNsjVOPw8BATTqz8zKc/h/MXrgAAbElJgACghULJiWNFlSHLyDuW\nUiJmaLooK3+St3Bg0AVV0oWK6F6ZdTgq+URtFKoxJYnqbIaKaQf27+/iwX2qekuHY4wf7i3eSKGg\nUcPWEiGfWlpRBMlQiI6BOKETcpYWOD0jxKnILJyjk6DWCnGHTgMGwPiQj63OoRXT8yudQMfUrrQA\nur1tAMDe4RFE0IRBa//YuKJJEhQKjk8hWkvE4WKvX8oO/5bxIRGhLGxBbRDOIOWTozUWJSMoWgeI\n48R/ru8tdFN6bKFhmNZBKoZUhfVhWSnnQoXGeVxawPmwqZgjcXAOcBzOEyKCYeTlSaakQ2nqxHeg\nxSfAdFZB8z07rcQnh2sFjxqNp5lPPl9fjRGrujrKoNvm0nglofjkfjosYQxXbbYU1tcJ5Xi4P/Yn\nXmObtiqtMOWxH8cJej06KTlrMU4Xax8AjPMcYYch+0Lj3g0qw7cBsHKOUKDx2RnCmE7jRjggp/uG\nYQRXn2xDhZWQQhfpiYVgSgHdkbj9PlVMHWfHCPrULhlYuFYND0o4jsWnxQS6zSHecIq3HrwOAOhF\nCqGhNqaJxPH7tE5cv/izT2yjKQ1sVSfnSwRce29tiYjLpK/sDBDwmNs/meHcCiFyNx/eRqG5DF43\nJeI6CmBBqNTmRgfdAa09m10FBqWQ5Tk0J6UnvQ3YivptNj7GIKLfeX4jwP6UqwXLFHlB61x2WviQ\n8ZPMVnUIzeH6s1QV+bM/81NIuCBFCOERZqFkPY0QJzEkt6coS3TiuvilxIXz9A5WV1ZwnkNeLz5H\nv30yHMPUBSEqwHhUVzrt4+iIEJCiKBFx2HBtbR3PP/8cAEKiMl6/D472MRyOFmqjcgJa8ty2M1hL\n/ZRmxyjrKuBZ2CD7SYx779M1D+/u4va7tI5fubiN8+cJlQplBzc/eJvadHyMbpfGZhKF6DCyu7Gx\nhotXLtP3gzVIRuDzysHWyHkcoeJE5dHJEDGHmgUsxryv1Pj+h5nQAoLHWpzImkUCrqoQJzT/onYC\nWSeZB8AqJ8nn47HfD7Y311Bw5XmQhLCSNsAtu4os5z5U8IU3WkloXRcHAXWufxRoBLreIy0EF6xU\nSjahNCd9uHsR087Aoqb4CSHr1BlXouKimd///X+JR/cJKfqxL3wRn/w0jbuyqCD5efJqRrQ4AFxu\nsLfLe3M+QMrh59EkQ5v3vxgG4zHN1yLPkfLa6ToKJfsW3VDhaMg0Q/kMqqDr//RP/8xXG//yZ64s\n1s6Fe+Qj2vdf+xZ+IOoKtQpd5tuYTjIPRw9PH+HFl18BAFy59Cw6XFGSTVLsPaQQW5aeYZbWvCgS\nSUJDdW/3BJOiriDKsJMwNG8ssj6FvfDCZyFDum8EAXl4BwAQP7gBU7GjEsZoaRqAO2ttFMXim1Mr\njlHzRAnhfOVdHGqUHFIsK4uQF24hpYe/rW34lybjFCFD6+1+iDXL/ZAa9Ltc2Ze0sbpK3EMWJVYG\n1A9RoHzlGD1HHV7UHh42QiCoOUIqCbkgNFtXixCPR+0IAeWQqnrE5AQVVx0d7e/h7IwGpBUS/QGF\nelrtNbTXKAdL6woBL1CQDsaXu3Luka2g2Bs22Qx5ToM9jPqQMbWX+J/YyXAStfesUEGhphiQKHij\nepKdnmWow41SOFj+u1JGiDn0Np1mvmozLywMT04FgQcHtLlM0hKfenGDr1F4dEALa7cTY8A7rpQj\nX5KuQu3L7fPK+vCTENKHr6u8RMzVglcub+GY8wAKAxTVXAnUE0wMc2QlPfPm9jrSCf2OC4XfVI4f\n3kUnoHcTBW0Eda7fMMWYq+TEWgeGF+IqFLg3oRyU9/duYLJH4eLeoA/D+QdSOF/tlRYpCq46zV2O\nkCkCZuUJghZX3JYGxYg6Yn82hNqntv+tn36yE1WZEsZwyKlSCDi0Z63wfFw7Gz28cJFyR05GObSi\n9hZliocjqurRikI6AG0qsabx3Q1j7PRp/p3vFrBDciSmp1MEAc37VAOG81okZuis1E5XAgkaD3mV\n+0QiWzokncVCCAlvhr1eD3/ts5+lZ2q1Ad48gyDwYZAojFCx05VlGiGHayrjELGjrOdoDay1MMyv\ns71KfbKzvYmcKwJ1GPuwx2g0wphDkEo1dDJxkvixGgYCgvPKBv3B4lVPZQRVp4jZqQ9hClWiy5t7\nGLcxYqfFzXooc86/iyKccWXym0e3cfNd2nD7gz5OjinFYTotUHJYZ2NdYlhQWLAqU7T5kK+zAq1V\nWruidg8Bh8NgyoYuoGo4zFZXVqD04nQjnSRCFNe5VTFS3ieSbgLJVXs2LzCpnYE0heYKskvXLviD\n1MH+LtbXKDdMhBLHEwqN9VfbGMg6DOseT5VAU6FWrzdSoslLthUcgwtSSSi+PnD66Zwo4SgNB0SP\no2uKEZS+2u7ocIzDfXqPJ8dnONyn+XR4vIegzlQQgOM9qCwLfP1PvwYAWO20cekqOb1FWSHkXLWT\n9Az7J9Q/kSww5XEq9AjTQ5rfkS0wGzFdjTXIuXr/YG8f5y4tnj5A7Vna0pa2tKUtbWlLW9pT28eO\nRPWSFsXoAHRbfc/MGjmJ0tLt07TErfcJat1I2mizZ52YCooJJE/PHDodOgH2+j3PSrtyroNNDm+1\npEN4Rp7s+9/7LrIP6BRyfmcH4SZDpMqh4jBDP7qCik9ewWAFmNFJRZ8d47BGvRZpY+jgGMVIYoVe\nt2aTBSY5Q+iFQcEVdkrphnE2kj7EGQTa81/BWEQhef29tsC188w70zuHgEOZw7MjrG8SMnPx0jns\nH5FHX5UlSk4UrsqqqYIUDWNyO5H4yU9vLtQ+xUSJEk0CqdQJnKN7bA1iXLxEEOidmxZHB9Tv4yyH\nk+ztlxZnt2/TZ5th4xwlv25eayPnY2ddnReIEo4Tju34GLsPCOnIW2sYXHkWABC2Gs4aLQK4Onle\nVghqsjop/fdPsmHacKYEkUbEJ085d3rO8syHENuBxgZzblXV2CewDqcVjs/oPWx0VzGa1v+lRLfN\n5H0t60+D6bTCiaD+LSvnKxOjMERU86IFGgOuzlOwkIzYxZGElovzRF0arGLm6KQ6KwXiASFmYSJQ\nDOldXunu4JKmEPFWe4CoZp8PZphUnFDbCTFidO6krVA6Rh6zIVYY4RApMBkychU4FFxNFAcCsaNQ\n4LTQ0Bzq6va7vqpuOJoABbVrMj1E0F480dPaCgXzPkkoSO6fOAphHSfnD2dYa9G7u7YV+yTXbnwO\n371Nf3s8LQFOvo5jgS9epuvPrcWIOCl9fHiCw10KRVTGIubHPDk7wRlXUNpEYJ2fYb2n8Mkdeo/f\nuln4woEwlEg6i6EYL3II7/yF89jiarAkCiE4+bvTaSOKaibs0HOzWWd9knen00LIYfbZLPWVc8Za\nZKdEPKkt9UOROwRJn+/eJOoncYSIq5uklKh8xbOB4kKfMptixm2sTFN59SSbFEDBiEcrlv8fe2/W\nJEly34n93D3uiLzr7Pse9AwGmMHJA7Q9yJXZmkQzmd70IJPJTF9DH0QfQHpbsyW1glErkiC1WAIk\nOCAHA/ScPX1UddeZWXnG6Yce/B+ePS/obJgNn8qfyrqrIjM8PPz4/y4IZyLYwKMq49YgQeDZMTud\nLtbv06xycL7iEoORhSebosD5xL6X3AtBRUNokzgvtGzQw3DXrjGrssTiws5jF5NTGEIRdrdHLmlj\nb3vkIFLVNPDF5irSwBeIaBxpACXNWczzURGEXiyXrUUTGBhmpO6OsxgJqTHPTk5xOrZj0PgecoKR\n+1tDp8xk3DhlsJbaqSdh1ibJVlNOlVHGYFo5n1nbTgvO4IWbbxkYY06I43EgCltzVgnZUie0wGpp\n55VaLp3x8nxyBmbsd67LErK0z1rJEvMzq0bEcoWk9dEqSlfZy1dzfPy57as7V3YAEqlMnz3F7MAK\nEDqxj+mF7bf//OO/wq1ti5JMJ3NHAdi0fe2bqH/3J/8ekqzf86LE+YXtMGNCqNE1AEAdZ7iS2Jdj\n3jB8cUbRF7zEM9/e9On995HSBL3MEsRUhh74AsPEdt4w1HjxyPIqeiKFRxuS2FOIDixXgwU+MuJG\ndLMB5gtaLMMMt67axWN28BJJ2tn4HhnzEBKHppdkuNIn9UDI8OjQTkZR1kd/QJu97gj7u1Q2jnoY\nDO2mMUkThDShCdZAUNxB6iunzluqBPDtxLBcTiFu2U1UZ/gQy7zdODWoia90fnaM2dSWqxW0M2rc\nGvQxD7Y3uj+P2dK3NGvXXGE8J8t9cOcKssx+j2q7g2FkX+RVWaE2tn+Zl+LkwKpz6nKFffqdq/EK\nS4ouaTd+Qkss5/ZFiXQB5dkXYtUoyIl97osJR5dgTSkiV4oGU6iFvU5gAGnKje4xDGKEYSs559A0\nZhvDnHqnk8QIfIri6cXYGZIpZaPXXCnPAMTJGfYjPLhhX85KSqe06WSh4yUoxVBL++9VpZ31QxIE\nAEEO3Ftz7gKPA3VrDaI2dmQHAPbWDq57ts8mhys36fc9HyMqhb998yY6yr5nVb6CIL5TGMeolP39\nUkvUDT3XqAOfFuT42hVI2ow9eTrB05NWqVdBxvb756FBSHD9KNkBo7HFa+Xkx7xOcX3Xlull02BM\nUSybNMMEtG5VQACCVlm0NpCcFQ1WNIl7UkPRGLkyiPDfxnZzf74sUdLk6+sGAY3NcnaABXFN8tJA\n03NsDIOq7HPPiwY5QbRnLEAWtOafwH//PTvnPbi5g58/tov68aRA3Wy2wbh9w/79/v4euj2CtiGd\nSb8fhEhIXRT4HjziPTa1RNjainhrI0Pf8xHRvJqvcgiyhWml9XXdIGiJM8KDoT70hYCg+1JKwXNm\nm56TiBd1iQkpsCdn59ByMyioEgINHSZkqVFJe+1QZI7jeHy6wrXrlu+0yA/Q1O26wtfmvLLC4oIW\nX5M4paxiPk7H9rA9Hm/hyjV7mKy0QW9kKQpXru+jRzstLjzMZgQFTsdYTO145EZha5vsF/zAubNv\n0pRh7tDgCTge26qoYCgVJ00yVIvWnLqGL1qLihB5Tu9llICYAQjCBNOVHcvTiyVigujB4UwyJdMu\nmcO8GgmmteOeMiHgRL8GzjAanGEtid6sJQS/ZlGABdEHGl07o2LBNFZL+x7MF1MsCWJrVgUYt/f4\n5MsvnbLUg8KI7quaL3FyaDf9YS9z9jPaGByeTOj7C2iidyzOJ5ie2Oc73N3GgmgRf/F//T/40Xcs\nnchIBvGGAN0lnHfZLttlu2yX7bJdtsv2O7SvvRL1z4/PMKHsmkYa1HS62791A1eJaPvi5BSavECm\nZYUPn1h1hb/l4emZ/fenUjjysDEGggjYcW8Lu2Tbz5san35s/U0SL8Cob3egw/NTZ4zoJT6GVAqd\nedqZduYnx0iEPYV2ugMUy+nG97gsFbw2CuCVPL5olKFP6jkvGyGjPLYg7kIRhKdZiCXFvtSyQLfb\nqka6CAgfiPs9DOhvBwzwvTYP64rbfZd1g5x260Zx1FSFGy9WmFzYU1RRlW0RA4YHqNRmp9+cTjda\naZtnCKCp50gJCt0a3kXTVhuXOQSdpDI/RE6k/0aVGPVJTcMjDAdkGlhdQFA8QVsM94zBcmFL6bwT\n49odW40UfgcffmKhvX/+zRd4+L0fAgBu3H8HNVV/jJFQbZhuVUPJzc4JnVhgnrcnWOlIv40Beqkd\nO900wrBrT+17wwwd8jRJYw+9tCXsN65ypWvlYIBlUSNKWgGEAaEcqBuFTvsaGuFK3qN+Bk3f/Xw+\nRyvKqhuFixl5TwnmoL1N2pfLMSKqmNWLBsGCqg5zhgd9e6K+zTrIKRy5KFao6ORfogaHfU7bWzsQ\n3D5LVnFogh+gCkiq0tzyPfgksDiYa8xIlZbnOZ6ft/EoPm7t2PGeZByfkJHiy+kYN//UKrzGTw9x\nuHi28T1qrV0MTRCETlkURRFiqliXtcKspKqjLiAEBRbXGu0BfCuKsZR2DpjNz7DM7T2Wq8Kd/Bu9\nlmYIz7O5mQCkbsAI0uIBQ0R5bFUDzMc2nPp7V4e4R4rkn318jn/+/HSj+2sNMztxhCSy42NeFMjI\nuDHrDhC1cISqHLFccOFMIgMeOhGK1ga+1+an+fAD+14qElb4vkTgckENmGjVqd463ko2Np4Jdo5p\nzRM97mE5s8/69OURxIaZIRfzlavsszhw+ZMV0/BJtbdYXUBTZYYHCZZLO8dBC0d+jyPhcuI4FPpd\nmkO3d7AgcUNZSRwdWLKxln0sZ78CAGxtv8D9B9bAc//6HoajIV1fISGKyfGLp/iUjIyjKEaaWnj1\n1v73X3uPZdEAczt/Rr6AaH3jEh9dmldkqVATrCqE72JcimWBgKBUAw5JGY/Ic6RUefTD0FUElTao\n6R3VWrsqu9b6laBpD2sn4XVGqmAcvBVEmXWQ8SaNMWaV1gCK+QWePLNzetHU+AapP40qUVD81MuX\nJ3gxsuulj8hlkMZhiCFRfFS+RDGx1c3VbAZGFa100HPxb4KHYMK+D18czbEE5RKKFB/+xlJKdhe5\nQ2WEYpiNSWQj2RtXlr72TRQTIbK0NZyMHBYf+Qr30vbr1rg+sjBDGih88SsbqttEXeQUDqmOzmEq\n+0Ku5lOANlHLwRXc+f3fAwDs7W7jF4//AQBgtm/i9x/YRHmjJDxKee2mPs4JCz2cXODavl2gZ9MJ\nntEqnsLDGeXNbdKCzg4Yp9yeKEBDEtVjZNC0KWJBgILcnLXooGzs4Jov5vBo0ks9H4pelIuiRN2Q\nE+3pBDsEXe1tjdAj7PfqKESvb695sahwfmEnhsVKQtGLEngB0lb5Iwwi2mxEfgDGN+MLCVIvCWEQ\nOL+BGhfndkHIy3vobdnSuvJ7+Oxzuxhe2x64oEwlJRLKQ4NsUNP9N6sVGE0CLVwbeAJ+u7uNYuze\nsS9cLEIcEUTk1QrPPn8KALhx79uvwK8GZdM6z5duQ/O6tlotnTQ+jgMMaIP/xfESXdogCW4wpJ9T\nz7gk8jT1cGPPQntH53OkJHtO/MAF6YaZjxkdFGYLjV5KNhCCo0Pho0xw9GgC7Xd8xLRZDnztJNbG\nCGd6GcYpvM0RBDQXBUpaPLKmj+KYyutxgGs3HwAAfF+jWNhJbZlfoB0hAZPISPkahR0YMnHUzNj4\nAVj4b0UmfZ4fop9SALjmEGXLk1li2doyVCU6gR03OkF41QAAIABJREFUI2TIYd/pF+MC//TTD2yf\nyBW6N7ON75EZGzYMAEEQuDywRjaQje3DsqhRtS7lrHCcwVxKrIhrWRQ5CjKsrRdLJGRPEqYJPIKL\nAqlBCDCkZqhoA9nPuAun11WO2di+x3UgcCYtXDG7mOL+Q3vNP367hz1vMw5m65weRKHj4/h+AC9s\n+S8BTGtvouDgGg3jFLSF1jYvEUDa6TpTUT8MkZEJZUn8UMG5Mx+UynMqryAIXAYb5xyaxqQ22tnP\nVFXlVM5NI1+JnPjtrZIGVWttoxQELelpFMKjz2EGeHxg+zVJfcf9AmMuwULUr4Qec4aSeJbCAxKC\nlLOkgyW5sM4mc1S57V/TCFTLTwAAz798hpt3LYXC94CM+Gtbox1s0+ZKG4XjFyeb3SCAMPRcBp8y\nhoKzgbJRziE+XxVWpQs7N7QJHCIKkfXbDNQBzk/sPLxazjFoXc3DwFn/1KVCWdrre56A8FoYca1Y\n9YRYk5/M+lExrHlTRmNtcr1BY8xmVgLAcr7EJ48spUYJD7euXaPrN8ipYHF6PMazxN7LTtdHr7Xq\nMFhbnnOgatW9q9wpjOuyBqfJvpoXLn2kYEBAvLhYZXgxsRu5cXOIuqYFv5Lu2ckwRJ1vRgFp2yWc\nd9ku22W7bJftsl22y/Y7tK+9EhWlA3CfTDIFwKncWNYGIEggTRN8+9s2NyvQFR7fuwUAKJZzmNiW\nSINODe1RnlNTgflUIq9WiMnTYpQIiJwIyXwXgkzUHn38BFuUyO0hxq9+87H9DkXh1DtKNrhBp7M6\nz7Ewmx/xd979H9ClzxoNekjpOr7gYPxV4i/BTLWEopPwTo+5k5vRCozO/o3mSNoKngCK2v58fD7H\nMrQnJ6lipEu7K1/mEs530WhnnBZz7iJDBr3uK3l3wkW1vLaJVlWh0SKAsWC4ec2WXhsl8fGXFnJ5\nfLrAAZmYTadPcfOaJa97aYgBlbt1UTsf/6YqnTkp91sSug8/Jpgn6CCkZ9HNEly5YU8Vg60MB2N7\nqjg4eo6dK3eoh5krOWutHBH+dS30PERk1nbtSg9h0JK9FRKq/MWRcJUi3/exKlu1XeqifphhLheR\nMYkeXVMGPkoy1+v0Qkd+Dj3mYEGfM2x17M8X8wXGdIrfHXVw2nriaA+haMcFh36Dc1A+WSFqc/qW\nC9SnlnxZDxM0pLy7KEtMLlrfHA3mYIO1ukpKCU5VMs4FcoJ187Jy4yMKY2RE6BSBAiNI//TsGJpg\njKYsMfbsWFmeMWR71pT3zu5tjI9syT7bibCYb2bSCNjKSVt98n0PHj2XopAgiyxwrRCRohDGYLqk\nF4dpSEmK4bKELEghWkkYOr3HaQDfb0nUDIa3FRgGEOxRFBXmHXv9ydkSORlUju7uYjy2Y+ajR2fW\nUBXA/Yd38c61eKP7WxD5XjPuqkJp1oUkMNzzY6SJPcHncwCUldhUlfNhg2cQiA5dR8An08r+0Aer\nSRRC1QGmJDz6f659GIJ3X507OOcQRFrngkOSdxnnHA8fWkjsv/zd32My3YwikWQDSElE/rKAoutp\nBmStBNJIaKo26MqgKm0fh0GALGyJ/MxVovLlHJUTZEhUFSmZzSkEVfc4F2iqVranMKfvG54Gzq8w\njH0EQQuBAT6ZKW9tj9BJuxvdn/1b5qLCyqLGakFZjhoA9bGpG4AgYs049m/a6s3bbz/Acm7f0aqu\nnGdUGgPb+2SaWzc4XbaqWb3OpGNASGM5CH0Imtu1WkdqMcBVGVUj1xl2Zq1C36QxozGgPvEaieXc\nrlWrqoEhJAINA6fK7nI+xYSqaqNoB5rEHKpcoqExuDIFzlakRtQlelShqsoaPG6rXnMUczt/9Pe3\nMdyzCEiU9lHMbQVP8QXmXx5S/yiUVAlmUuI//4c/BwD8b//rv9/oPr/2TZRRymHUWhrHP/D4utSc\nhj6WF1YtcfL0E4SB7eCjqkac2puuX7wAqBzdiT3EzH71vGlgCjspizDG1r4daEHaAaOJvjJA1S7a\nUqIuWgm0AqjkyQxDRNyAoppA+ptDCMdf/gKnVFp/wn3EJLuMo9AZ3HlRgqCVHgchGBmz+dxD09jB\nLhgcjCUR0RtlswLb8rvmPkriOx1OK5gJOZ83ChXBUVKvAz+1geMLKanWgZCcbVyYVcZ+hjHGqXoi\nX2N3226QziYLfHG6tooY3LwFAHjx8T+D0Uvx4O4NJ3fVgedkrYYbwGuNN2nBZgKGNoH9OIZHL3RZ\nzh1HAAGHT5vni+ND7F+3z72pJXhbovZrMLbZJmrYjdEf2LHWSQOXc9fPArfJTZIIQ7pclkbwWjc4\nbRDSxJomnuOHTOYVJPW9CLlzLz+bSCcVj0IPIEfm3UGCTmvpMa9xPqWQ0UFvHawN41z8q3KFqtk8\nEHQUjwCy7lCzJWqaZE/0Ap9+aaGLvU7kFIJMhE7qXOUrVOQyPJuPrYcBAC9MUOb257ysHWdGg6FD\n0IJXlLggdRNbTdEK5jtbPfd8JtM5vIHdZO9lXewShLTsapy/geJYG7a2pTAS7cHF4xwRLXhXRxl6\nKUmjkWJZWINQZpaoKlKllSsw4nOw3gBIKSVAlchzO3bTNETao/fScCiCkaPUwyCxv7+3FaFc2eeV\nehrpFfvvv5kscPjcTvSd7imieLNN1JfP7Xd9+851MN1aJHQw2CZT26yPwwO7OBw+/RzXr9uDzvbW\nAJzGZZZl+OTZobve2w/tAXZ3dxeSIPd4ar9nUxYugUBpiX7W+nEbl69mjHbh4nbeWWdd7u7az792\n9aobA69rhnFEZMbre6HbLObLFarKjt/AY/DIHDkFh0fzqYFA3oaH1w1C4nilnQ4YUSVqWYA3rSUK\nAxOtZcwKAdlaVOXU3UcYpODM/nsjG8SUr5d1Mocyff7ZMQLavN390f/42ntcLHM0ZH9SrUoH/4IL\nJy4UEJB0Krl25yZ+8IeWtgKZgyvb9/PpOVRpN4S9LEROELQfxkjoAFEb43hcAYeDgTljFmYFUCkN\nJlozaLY2yfSEcwvnwoDpzfMBmVF48tTSYg5fnmFJ/Lx5tcTP/8nC9bnFnG2fTMcYEyy9t50iI7Ps\n/d0hclJoMp+B71HQs9bIaE01TQXQgYwxjXM6eOkkQUrjt99NkBiCdNMBpsd2zzGrL+CRstaTtTNr\n3bRdwnmX7bJdtst22S7bZbtsv0P72itRge+5jDGttPMfgZZot99Zx8fBsYWDvnj2FC9e2OrFtJAI\nSNkCLpDQKbfDfPgtE9/U8KlCFccRtunkw7vbLntHG+2qA3XDYVQLS1SOVKokcHJi4aEXTx5DdW9s\nfI+rgw9eiVnhKFsIIYrhEwE+iFMX7RCnPSSZ/Z4y6oIRsZwFgUsp99SCIAILc3EykNMS8Dwi5wc+\n2kfI0LhyPXu14moMOClUtFFot/0MfGO1jOCk/jDMmZyypoGk7/386AxPKCl7dOM6hjds31WywvzA\nVjiyMHYnoAYaOUWICN9HQPCIJk+i5apAUVIcD6/Q0Dg5Oz3DdGI/p9PfQV5Sn8ym4ETYtadWyobi\nEmbDStTWIIWivmkaCU1w3u4ocR4rgnsuKysMfEe+rJRGRH5EV3dTCBpTJ5MSPkFv20noTpgBL8FJ\nvRUID4LKe4OOD5/IkYtVhSiw42Wrn6Cq29NmhCwlNRUXGF8sN7o/AHj57Ag9ymmcnZzhgkxBRVlj\nTF4towDokP+VYhEU2tOygqTy+tn4EIzbKlMYdRwRlgvPqQ4Xy5WDugzj8GgS6MURDBFkWRTggsru\nRnCAqrY932CXKtC/MVMU+eYRTNqYdRVWG3htyc8HRmSCe6XvgYX2Hkf3/jUWv/prAMCnH/wENYk/\n8kWBs3M7RhsTodez1adhZDCArQIkYoZux/ZbNhqAx6SqWpVATVWpyEPaISNNrdpbxLWrPaxIuTYZ\nzwF1sdH9ffbYwkqrP/yBg3F8nyEg/57AD/AZmdr+4uc/xx8LW724d/cuvBaGNBrnY2u6Oj4/Qxi9\nDwBY5gVmBLu2RHERJQ4S9RWHaeckIZBQdS7Pc5dJBsYcPAamEVJl4b33vo1nzzcU62jjoqa48OGT\nKIhzf00DaHKsCFFoao1u2gqWPDfulGBYUlVKFwsXh+P7HIruwzQNaqpuCe6tISRloOjnqphDkS8a\nuECR25/LsgGne5VKQ72BUraqahBDA3lRIaF79MMQnFAWlQMeITeziwn+8Wc/BQBs9zPkCzte5vMz\nXN+xVJVOlEESZu17Hro071f5HAkp3fa3tp25rDIML84t/WVZFdBUgYbwwGl2i/21R53hcCrhTdqn\nv/kIB8/teH3+cooXp/azbt2+hudkoJwMMnzzXQv5nh6ewqeKrBQeLsjHKUtCTA+swCzQY2d2O17k\nmC3s7/AqRUBCKbVYuGqxOg+RUQ5ub5QglhYGnZxIyIIQoMhD6+gad2IkyebmvsC/hDqPGWfWpY2C\nIX6LbNZ8Fc4VJlM7KD7+7ClWtFBu726jIXxYGY0uPeSrUYCGcst0UyBgLX5bYUk5OcPhDQjnhL0G\nrmRToybcX+m1iq0oaxydWIZ+t9fF9E1UCMJzHAFutOMdGQ0HvQRxAkMbP9k0jsvCmHAQm2HMBZFq\naaBpsalN7QxLvcY4HNswgyXh/EVVu3thnEG0CxiEu6YyyrlyewxgYjMoqFU7yVfcbp/Pz6BGdqEr\nEMJLLAxQNICk593duoYOvchh2kNA8BeHj5ocaFkpEVA5XVGfnIzP8IIy2K7s9lDP7Pccz2dYkN3C\ncHsPeW6vvZotsaAFyQQhNO16pGq+8ux/W9saZKjI3HK6YAjpZQ65hmkVWFIjoBeYMYa6aWXd62Dm\nUPiQ9O9K2AkPAHzOUZN7fTcUSMh8MoCHUc/23cWsQUl93Qlj/Mm/tlJpwSWOCBb1OJAlZHLYMLcx\n3aTdu/4WTokHcDQ5R0i8wnTYQ0Nck9lqBcMtJBAkHIwm33lZQRX2vYz8AB5NOkVRuXJ86IfwCHY+\nn5xBUccl2QBRaGGV/e2reDKxcv4vj5+DkeotihJk2k5qu2mMhA5PzfQUwmx+j4BGQHJxy/Fo1agK\ne0N7L+dnY+jc3u/+e0PEXSufjnp7Ts7/7PAZLog/FvY86IhsO2KNDgWbNwo4mtIm9uwFEjokdYcZ\nQtotzVclvKUd63EcOA5N1gkga7twLnLpFI6vay+O7ebn6GyKvR0La+RNA0GKopu3e/jjf/uvAACD\nboDrOxZyj5IUMTm/K2h89zvfAQDcu/cAI1KYvTg+xeELMi+kTVm6NXAKOyHgGDFN0zjagucHbnNj\n2Pp3gsQHpzn4nXfewePHjze6R6YlGtlCghwssPOD5/nu4M24B0EbXg/SvefFsgIjR3Ht1c4OJvAj\nNKame/MhaVxwzRASFFjkDaSk+VoItHbhnDVQsBst2XAUdHibL2cwjPiMQYhCbZbTCQBNrWCCdrPJ\nEVBfijDEdGLfPy6lk/lXqsDZ1I6RF4fP4TvneLYOfOccIVmkSFWhQweXMPGQ0nWu9RJn8rksKpTE\nebxoFM5JlSvSDiIaKxpwBQiAORuBTdr+sO+sGEp5iI9/ae0g+tev4AWNsy8eP0ZFa/aV3evu+T5+\n+gSRb3/+4vPP8MWv7N9+/1oP99+38+KHT3McPLfzGVv4uElzbVZeYMTsNauVQTqxnXVvZw88ts/3\n5mgPKdFIJteBksypu90uPPFm26JLOO+yXbbLdtku22W7bJftd2hfeyWqkbXb3SutwaiGaSTQUNQB\n0xr5gvKC5gW2aAcdHB/iZEk+L/kKmkxZcl3Daz16Ih+GiG9GMZRUoWqkcqqvq8MuRn0LP9Tzc1cd\nAtNo6ATFoxTHFI9ytcORV5tDCJZwTV4a3HOEdubH8OiE7yUDMCqj8iBDyweW2jjvE27WpGR7iCZ4\nSSmn5PEUQ0ynXAbjoimqqoFu7fmZcf5BjAPyFXWFbtVqjDky6OtanzLWLsZTMDpJj6szHBCpvTvc\nQUYVBQU41QnzfHBSV57PK/Q79nunYccZ/60WhTudlynBrI1EUxFJ0CiUVLWaLWvMV/bnbL+PdGIr\nF2fHkzXMwDyAFJceM4DaELJkzHmsnE1OURMc4wUMIQkOGi0RU9ldCO6UPxzMJa/XxRJ98pGZVRXm\nFGMg8xWuDexp8+7tPhgp+LT2wEnBeWUYuXzF7UGKW9et0ubxwUtH6K8q6Urtihun7NuklYsKJfVf\nDQNBJ+1KATOqeg61RnluCZdJolHSyfbJbAVFJnc9H9gl70EvlJhO7Qk2DjNkW5bgLJsCjMivxWru\n4B7OOAqadXr39hHv2vHhez4UyUt9AcQdW50z4ycw1eYYghDMRepoJUFFCYSeB065a4cnU0Sk5hRe\njJ1tEiXcvImLc3uPV0dXkcT2NNsfGmz59hn5tUJrRWgEh6TKW6kbnLwkwvn5Cjs7dCrOItSEgeTz\nBerCjpPu7gBeRhXI4zFib7Nq2/GZrUT9xV/+LUqCI7Sf4d3vWB+5wdEBOqQm/eaDO+iRKjmMIlRN\nW8URGAzIoFh4Dv5MkhSa4GSf4LE4jq0gBYBWxlUWVGNQ0FzLOAPauYSZde6k7zlhRa/Xw40bG1Ik\njHE0C3ADSc+Naw7wFr1grlrCdANGVXjZKNQ01uqqhKHqUxxqDGgN+KM/+j0ElJf3xW8+wcvntk85\nC21sE6yJZTunCGFgWnENE+BU5X8Vvi6KEkpsrlwT3HPVJ6XWPnBKraO1mrqETxVBI/ja/4554ESl\nqBqJ4zOClOMA22RoLHWDiJ7V/iBzop56MXHGsRfzFSTl1+7FiVuPp6scjDz7wBkaua6S5svNSdes\nylEvbN/2eYUfPLTv3MGjR3h6YCvrRTXHFpny3t/pY05Vx1m+gqDnnkY+rm7ZZ/0gC9CnHM63791C\nTR5spSpxPaM+WRTYo0p2znzsebaC/u72Ns7IZ/Dv/r+/AbpWDXz73lt4MiNUoS5wjTysNm1f+yaq\nLGoHAWmt4J6HUm6hinzuSv8IBSZjOxl503M0NX1FZpDTRB95Cltk1CmkcFk3Xpyhd/WW/fU4Rkbr\ny7t3d5xC7ekMzqjz6nbH4fpnC2A+sR0czpeY5G8A/sI4Sajvx45DoLWEoYGgmwqcIA3mpTBUilbM\nh99izoZDkvJONRVaHIn7ga2lw6qAKpowfANU1LeVXkvQmTGuLCoYc5soo42bALQxDiJ8XVss7Iuj\ntGlFYuhv7bnJLdcMhiA0ztaZUMJjYJHlnhyefIodUgBfuzpETdLdJ4cn2G8sLNgqQl4ejpEQxBd6\nPqYEcX325SFiCo7NBHN9kpeFU3rGQeAM5ACGcsPnaBhzjIY0jZyrryci+ARDNpV0C4oX+g42kLJC\nQxBx6ANRan//6XmJ4XVr5vr9t3ZwJWo3EhKc1EeG+ViRum3UCZ25nh+FDiaTkr/yDhlkZEJXNBKx\n3Bx2bnSNnEz3mBAIaLOXbfcBWpDqUoGT0eJqfAq9Z7l72L2Kk7H99/l0Dgj7rvQyCUPqqdls4XLl\nlK7B6WUvpYaizewir6FpAQsHPeT0O5abQkGhKLFFC1iYJsg2z3UFXrG4kMqgIkhuENq8NwDY2t3D\nN35ouUK377yNU2Pv5dFf/kecP7cww63dLYxoA6llCUmOz0vJUM9pMTPKKbXSXuKsFepViZcUQBzP\nJUIaJwEUfOJHpWCAIPNd7aEqNzPbbGMBf/bBr/BPH/4GANAd7uJ/Jmhib9SBKkjCLgTy0o6tpNtz\n+Xw2YJvmzFXucuHqusHWVTte68LOwWVeOAhbBKGjY2gGd2BlYDDtHkoIB+dDSiiSsiul0eu1uszf\n3pgI3CHQQKGNldCQaEMClW7s5g12A946V4Mbl+VoKu0g9Pmiwe62fW92hj1UK7uIX9kJ8ekj2kSF\n22g/2OjaKaUbyWEMGeIaA95SMSAB3W6Qp9Abhp0DQNJNUdHSJgLh7BqMMvDocLaqG8iM7lF4EC3V\nw9QOVkuzCB5BdXmlQVMlfL62mjBgxIcFLs7ObcA3gEZ7YLQOJamP62QF4BclqormfMkhdUsxUZDF\n5sWFbz98gIfGZmCiVBiP7Wbvy8NznNFaKxKGi88tb7YjBfYIZn52fIzZS/suQte4umPHTpBPcfzU\nwsL+nYd4923Lp5oux+ATS8dRDZBuXQdgixRhZD/36nYXamrv63ocY0Ymz3J6jBs37XUOj49xcna8\n8T0Cl3DeZbtsl+2yXbbLdtku2+/UvvZKVF410O0OWmu0pShTG0g6yUhdOjId4xoVlTO1ZFBUUZFa\nIyeS4pVuDwNh/3a8WiKmcuD+tT38we9b0lmUdN0JdrqCg7qiMMG737C+KJ2uwPHEftbZFEiplJ0v\nc6g2IGuD5nuxy2gyRgFUTfLCBLz1L+EBFFXSDAw6lMfWTwN8/56FbaJeD3/1y6f2vmZr8rlSau1Z\nI+DKq40UaKivXiX8CeavT4yagVNlqM29a6/JXVT3b29K2r4WgkHSfUrVuFNxU5eIyF+FaaAxlPHU\nKMRU3xFhiJCgTc19vJzZE8HBvEROUMAZnVpNw3F3h4jqVYOXY3u9eaGwTadJzhQMlc8NNw4G9T0G\nn7fjTUKLzZ5j0VRu3IUBdwpHqSSo4g2tNUqqSKRRgCBsy/rCjevIC5xfUBYyXLttI2v+m//uj6CO\nHwEATk7PEJCPkB93sCCVnK4bq1IDwMPIRZOMJ6cupwxYj2XGGMJwcxOlvFqioOiLMArhxxQhkkXQ\nZHSqjEYQ2nvMuilWQ/sclGboPfim/dzxFGcr+50PX44hyCB2tczBiGib+h4a8qQyHkfRmutFKQJS\nEy06viM7r1Yr8D6RsVWME7pmemUH/XpzCIEzDtlWP6SBJnhGeAIhndjf+ua/wXt/aI30BABwijWK\nOkjCFkLIATJ8fHmyxKwtMgjhqq6+8KDb/C2jMRwQcbsfo6YKaFM1yOlnL4mhCGquKwBUbW3gY7nc\nMIKJIJq6qEGFYKyOTvHjP/+PAID3v3kbW/ffsr/LBSISIbw4OsYvPvgIABAEMf7VH34PABDFESYz\n+ywvJhMYr527qBIMD6wdk0HgvMIq2YC3FXcl4STYnL0ilAF88k6qq/orY/i33yR3cB5jr4gnmHGe\nUUJ4LhdQaQXeKj7hw6fKWTfsI8+JyhAwzOg9Ozk6QuzZMbU17IBuA0enJxjsWJFByLir1OtmXYHn\n3INq6RFN5SD9TjfFhogsAMALBBRVukKPw29fjzCCJkiLb/fhU6Vzvlo4X64k8l0f502JkDDFl0dz\nyMpClqNBhoi86xZ5iX6HDFP9EIY83sDWoqNqNYNuY8+SEJwTgqINNNr4Jo16Q/NiALh76xZUYz/r\n8aNPMSSIeOvdBzg9seKSs9OXmJNS+6IEqgNbZbpYzTChipCcrRzJ/CwMMNyhKlPYx9YWxcecJUh3\nyYj5Wylkx1ZUF7ML3B3Y/im7I1QU25XtR1gcW+g+P5li64H9bnujEYT/ZrWlr58TpSQkLSqc86/k\n8DT0EoxGHciGzDMXJYZkeiiLEjU9BFEzdLYsN2f32hDsyAYN69g4Y8Ys8PFg1/5O2kkxJg6HVHBl\n5X4WQdCi/fjFAkdUVizrJa7etH/bTD0sSQ21UePChTQKPwRIms6jzMFnXtiB6Fho5M5+g/dvkfLH\ny3BzaH/n7tvX8PjEvugvxjkCui8h1sakjWxQNa2xnXIZdFIbd1/aMGePYAwcts8Yd3wOJjyYDTdR\non3DDcPZuS2ZHj4/dOZsGkBAmzafcVSttFZqhGSO+f6dEfoDy9v45UcfY05w3u33v4cVlY6XxA3a\n7Y3QGdg3eilX0LQR3d676rKqmgDwI9s/Qeihpo3eKl9CeC08Wjr47XVtli8db4BzHwFxnKRusGjl\n2xAoSUUV5D6UsZ9faYWMJilZS7SeCNu9GMeHdpw++kcf37hpJ+hktIuUNj9hOnJmtEaWkG3YZ5jh\nlCb9xXzuIOvFsnT5VdpwsDdwEH73/XegV3RAabawtWUn3O7+Dna27bNhzw8QktHl9etX8WsKoq1N\ng+5tcp+/OoIhS4TZOMOSHIRRd+HVBJlFGa727QbsxekxzqYWMrl55y6yezYvby/xwWgRMoNtNzeo\nC4Wnx3acRbseBv7meJ5SVvkEWDS03WQ2SkMrmicaH0//7icAgHD/JhIKN9279xC6sXywZZGj1PS3\nXoA8J7m7lKhanXcjQaI99DuBC48GGKRsHfklErLLCDoZDI3x2gQoW7uJUjte5+vaNs2Nqs+war/T\nssLTL62U/C//359ilxaZ3d0dhBnB6Z8/x5//3z8GAHgiwK3bdvG5du2Kmz939vcwvbAcE04bPGGA\nitR5xaJAQRSMRjbOiFUphWiNvzkFsIBAu8vUpnH5g69rRmu0JEAD84p9DINhrcXCK31cNy5/VDCx\n5sgKjohsJ4zPHEdvucpx+xt2DJ4dP8WdW7a/Pn/8SxjaPIThFjxOXEipHN1EtN8PdmPu7Hu0Qb3h\nXAMASRY6g14dB+jH9nAoG+kMPNM0Rk40Aa/DITzLH0yjGHMyhFzMl4hoCpgfTvHycEV9MkKvZ6/p\n+wKmhfAqiYb6p1bGcW1rrVz4NoLAhVLXVQ2fkcrdq1u/642a1tJt9F++OIOkDVi/34daUfiyEej1\n7eZHhTEe/sDCeeP5HEcDq9D+1kMgpOSHi/EppgQLBqbBBR0AVkWChbZrQ8Ua6KXlN8/OzvH4QzuX\n/NVfl5iTins1W6FHVJNaGyS/+CUA4Ef/9o/QGbY5rJu1Szjvsl22y3bZLttlu2yX7XdoX3slqq5q\ntF4tUkoIgleM1CiJ2BV09tG/YmGP4GiG63coquDBAj//W2uE1xMMmrb9g/v3kVyjTL1CYve2JYWl\nWQ/9HburPR9PIOg0xeA5Rd7hWY4vju1ufTpbgZX2hOzVR1hN7N/2e1tIizbe4PUt6Ow4nxIhPAR0\nqhC+j7YyaDgHp1L8pOziJ4/taWBRLfDOjj3IQUasAAAgAElEQVRt/C+37yCOW38O5nKKpPHd6Y7x\n9WlMaaAhRmdjDNqDkOAaioiKTLPWwsXmyrXKImbgmc1OTq1PjFJwypEszWwYIgCpFTyqvmRhAEnf\nuzECKbP3dmV3hNNzezo4PjnB9VuWcCjTbSQEha3N6hRyTvEkqwpFZa8d93dcHy7Ozx08MNjfxYxU\nI8yPnDqwblYb+yhpoeDRSbmSBYxpSeAecoKdQxE4Ir9Zaiiqfy9NA5a0CsgGjNSTw17HGZ2evzyE\nukJ5ZVJiRuMxqjVKgr0CX7jIlbJpcDGxVZHFfIGExkWjFAzdU1XVjpS+0T3mElukyor8AL3E9l8Y\npijHlIY+zaEIsuxOF8iomrTNmFNxBf0Q0dCO8b0be2uCL/cRU5VUHZ3CUPRCPNzCPqkaH9x/C4Yg\nE66UU1VpbRw5uGQSNbf9Mxxk4Gxz8rxS62gjwDjos5YGcyK9H3z6GbSwxo87SYYOPa/Bgx+hokrj\n+cEjGOqHDBHm5GEl6wYeVWNYoFptAwooNHVLqgfKFUG6sYeUKgJMAB6NX2/3PlROnmPJMQw2E0Ds\nj8jkNE4xperCfLpCQf5pP/v53+HaDQtl/OiPfgRF1aJOv48dgjuiMHbq4yfPDxysPxwO0NP2eTf0\n/0VZQtP/N6p2ggvfC3BBvkJSKVTU5500RURjuKoqVDTH5/kKTb2Zj5KUyolDGGMuu80Y4yJ9jNGv\nRFspCL72BmujTJRsXAQUMxyCxtFsvoSheTPLEjy4Z+eio5MFHh9Y0+ckjjGf2+sIL3HVzbrRzhOu\nrhtXlfI9D/wN/IWklohaU8fIh6Y5S3vcVc+NbmCoiqnBHR0jDgWSwI6DtNcBJ2qEnM7QLOxcMp2t\nIPw2isqHrGkNrksUpHatJUNNVamg18OqaXMGS2jqn3xVQFP1NAr8NWy7QdPGeqkBQDrYxjmhGEup\n8OFj6+90Pl3hnDI8q6pE7tl3pdE+jg7tvyccOD+yY31ydopOZsfmv3v7OuYk8qjmGv/hP1kz0jCs\n0RvZKu/4YoWGql6CS6zIWFUrBoHWNUDiO5QDG0TJG+WRAv8CmyhZNQ7H1ko5V2LuJ1gwO4iendeo\nY1um3n/wDcSJfZh7V3dw9md/Zq/jh3Dm0yJD97aFH0StkI5sB/hJjJgygmJPISbOx7PTBT5+Tnj4\ntIYk5UlYvUQmiCOSpijbSckYvHXvysb3KHjozBPTNMa8btUsgQ3EAyDirstouqgCCMoCMlrhYmIn\nl2aV4+E1W2L86UchcoJehA/34gIMFW3YmDJuglGvKO20Ya60rLWBR666BnDPgnHuIL/XtUCQFBcM\ne9t2gr5/K3GKsbwqnYJj0EnQ0Hc5n67QIZO6KPDx7NhCpEm3AxBvYV5JZ4rK24xFUaIgCHj8Yowq\ns88iGfZRatpc5SX8wG6kr9+/B9XCpn7o+sTHG+Q8+QqSOAomYHBaPcNQLikjDBoBfVdpGsxpMa1N\n46DFWhvU9HLOpcG1jp3s9raGYMQbOzob47/+o+VH3bs6xC3if4UeRxvZOCs0Xp5ZOHqWF20OKQBg\nVbSqKP+NrDh2wy14W61sm6NLE3SadPDyxG7YChbhlMadd7zE7tDmV13xI+cibZR2rsdCeG6jarRB\nTAvJJD9yztFX7j+EeGJhzRQ+MkYqrUA4XkvgB64uXvo1dG+d96jewOAveEWdqZV0xqc5GMqA+vlb\nP0BDB4OLconJ80/t34YJzNAuqP5yATa3cEKXcZxRiHDMNSLaEMpaOi6i4nztBL2qEYZkqpkEbpOp\nAXgjK/PW3esoVpYXgrgLXm+2iUrJZZFDoUfzWxr1URDkvFpN8dOfWqhysZzhm9/6rv0eWQd/8Pt/\nAMDC+m2oc5yELt/OaO24UJLexfnk3KnwyrxATT9zLtC0PMTAR0NjclwU2G0VnYDb0DSNdrl0mzTR\nwoMwMGYdaNz6A7fvOACEYQjVeg0Y4xZBLeHSAJSsQPQw7O3vo25abhVHRO/B9957iG6fDrEiQFmS\nSq7SaFibEgB339DG0SyWReUoHZu0ptFEjLPXlM6h3UOF1rjUwGt36ZxDUVpEXhRIaQMWcgFNvLMg\nTRwfs5EKJYVVX1yskMY0xzLu7EMCA5ceoP0QM8p4nJUlymK9Zjc0n3m+QLA5ewAffvQIv/zlrwEA\npydTp1ovmwYfPrLzwfF46TYhEdP47MnfAgBeni2wIEf61DPOHNcTDLdv2TH6jz//0HESnxxPcOOu\nvceLsxMcPrPcqlXtgdFzMap0qk+tGUrZzusM5xeWkrAqa2Thm22LLuG8y3bZLttlu2yX7bJdtt+h\nfe2VKK0lFBH0eDJAcsvCdsMruxiQuWLKCvQ7dj93Y8tDTOncp8+fQHfsDnQ+nqJDOVtynsPs29L0\n8cUEUUbxEpGPl4c2N+rsYoImseTBj88Vnp8RPLM8RtzYUmI/8+CHazOziE6wD27t4OH9zbPzKlmC\nlbb0+M6d7+LLqT1xldyHR8RWz/dd6dewBoK3xD2FX5MF/v/+f/wY779rlTV3+wKPSAGlmsD1oWIM\nkqAzBePM3jSEI+Y2Ujm6MTOAoUw68UpCuDIastmsiqHolKkVh0f4ZBZwILD93klCdyL3fY5KtiTP\nFSSVwcfTGnNSbsEXOB/b/oq2O+hm5JlEp0MTBC55+yT/EhWz378fpajouyxWJc7H5PVy7y5U2yd1\nuVbPmArObOk1LY1ip7TRZu1blsUJrpKaDDBOsaWkRkVGfj60O44kcYCyLZerGvevWujq2o0rAEFy\nHx1/ib/4p88BALcPhvjh23asZSHD23Sa+uVnL/EPv7antSjxUdIzlJVxkGLII5Ry86Mh1xZuAYAw\nCBC3poheiMnSvhO1ZOCprfIueIh7I1t5jDmD30ImnLnqCgCnXBI8QE6eYoenMzy4Tynst+7j+TNb\nyl9IgT0SGJTFElHcmpeuxy9Xa8Vh0zTOO2vDu3QCCwHuPMuU0ZhSNWlelpheUHbcJ4cQ4bqq5pMy\nylSAlrYCq4WP0f4d6p8KZUFk1tXKVU89HkCTz1WUeoiICBtGARLKIhxcvYFo31IPlrWGJniJ+T6W\ny9lGd9ft2mtVUq8zNz2OUWDHqFIG3/+e9cAKohgffWQVef1+H0ncpWv0IAgK7/X6CNvqk5SO0L2i\nStXhs+c4P7d9la9yzMlTKut28M1vf8teezCApKrBLz/4AJ9/8QUA4L333kNMilyjrBfYJo1z5mBD\nxgxUWz1ncFCt5wk0rYlzI11FyGgOJ+bjHmq6jmDAN999BwDw2RdfAo01hb1zLQQjKJWjxqBLVXe/\ng0efW8j3N589w2DHvjeDXhde+66HgfMBbBq4itkmrWkqNAWNEV+AEZRW1bmrOpsMUIq8x6rGRYtJ\nqVyGqWFwsVlR1sN8Yp8bMxzThZ2rpssSO0Py10s8mxUHoIHBIm99xGLEKUGEvEZKlVRPMJjWgFQz\n1PPN/MwAG0X2d/9gCdvL3KD1zG0Ux8GhrcKOL5aol/a9HEQBOqmtktV5DeG184BGrUgAVlX44jFV\n7Zp93L5jRQFeNMP+wM4l03GJOQlfFIvdWApUAxG0PmAMMVVGo6yDrGv7R3gBmPdGxnT/AhYHwsfw\nG1YavXvvHQT9tpRYoSnspmhV5EhLW04LmgIffWbL64fjJd790/8JADCdL7Fc2c5eigTDvn0J+tv7\n2O3bySEIMzxf2Fv69THHSWmVJlWQIlH/BAC4t1ug27Mqo7JWjsvkex5u37Abs9tXdxB5m/Mw/DDC\nzaHt+L1RgiclLU7ag6EHpbl1/AUAbhQkSbgrCRwRVvx/fvgIf/uznwEA3rl3F6PU3tcKKWRq73ch\nBWpaOJlp3DUbrdfbBfYKdwBwGy2plTMiNAzupXz9/ZHEGT5eHFO2VlhjRFlFxmhE5MCtlMZ0Yvu9\nLnLUtBE8fnyEdM8uyInvoSLTtnpyhnreSvzJPoFLNGTIWMu1K3AcR2jqtiSs0UYAp4EH80oIrksM\nZhHqDXkYN3evOmhsUdRukoq9BCnBN2EQOnXHRbVwLuIQHkpyAY6jAD6FFAeeh17XjvdPXh5hhzaA\nTTnH9b2uu4//8shO1qOsj60dO9N8/PwAx1P7TmyJDhKyRKibHIUzWDVuw7hJ29vddQZ8YRiuORx+\nhPipha6qogDPaEFmPrpb9p1gTMOjj1IMTjGltXY5jZyHmBC3apJLJCP7t2HWQ03GkiezHN9oJy+9\n5rIAcLBdEgYuf1L72i2Qm7RGShjQoc1bu3GHvo+LC7txf/7kN+6Q8fLoCbRqjQ4lQrJciKMIPsHg\ngodQEQWUJimGoT2cybpygeECAsXSjnttmIN9kyhAllnY2etsYUG2FXVVIwzJ/qSpHbz2ulbJ9n1f\nB/3WdQ1JKuZeb4C3HrwNALh77wGeEsdnPJmgRaGSJEaX3Pl7vR4icqdezOfgtOC8ePIUAPD3P/0p\nJpMJ3ZfB7Xv2EPzDH/4A/S27GTbG4JT69ujoJb54bDdRaZbhe9/7of0dzaA3zAc0r069DG5zDcBx\nnIwx6zGiteN1CcHBKMAXxjgFXK+b4OTMQtZ//Rc/wXe/aTfF23/6ruMkelzA4y10zHH00v7+6fkS\n6cg+QyMSlKSYy1dLRMQ78j0feAOlrDEaadIqemusiNNZ1Qo+bWqbooamea1u5NpEmHGXq1pJ7eae\nKIjcBmA8PnE8K+YLZ1h69eoDFOR0/+izx9C0Adu/mYGna4W1Ii4b08wpzJMghs42hyxv37uH7/7g\nBwCAP/tPP8HJOalJK4bJqZ3bylXuNuBKr1CE9meT+G4DWUiNNCErn6ZEsbL9/MWLMxxOaE+wWGCV\nt9xShrRDKQSKo9/moKJxdg3Mj9AZ2APu/vVruP9NW7zwgsApFjdtl3DeZbtsl+2yXbbLdtku2+/Q\nvvZKFCtzTJ9aWIKHIXZDu+O70hXQZDl/FNzAM2FP7JMnj/GysKf0/q2HELu2XLd/ZQ+CTCzjOkdO\nsS/fvr6DOrCl1h8/O8c/HNuT8OEnj/Hyc+ud4huJ79+zu87v3us5m3yttCMoekIgplK+1toS/zZs\noTb47oN7AIA/eO8eniu7I/7ytIRoPU64B6/1OAGcaqs4fY7pgS25q3qO5wd2h57Px3j3XXui7GZD\nMII4Kj7Aqo3WQO0qaRrmldgXW1kDSN3SloeBrxzzGNvshJ9QJhFTHPBIDWEaLAkObJRcxy40Ckcv\nngIApvMZaiLrd8MEiwsqsQoBRachpgwWbdWMTtmKG5zRZ5+cT3Ft2578ua7BiFmqGIOkE6Fg2pn6\nMc7cfSmt0WxobBKGoTvZh2HqPE1CzhESCT4MIkiq/I3nKyhSsPg8QEBOez5bE619AB/SGBSBQkjf\nKxEM7xFcvFyWzsAuED1cELkzCgPsjCiGwVt74sRJgIJyJhtmEIabn4OSMAKPW48x4UwUWRCB07F+\na9QHp2f5+KOPXaWIMeGUdIJzJ4ATgrnYF0BjQc816vewfYUqj1EAP7QVnsVy6UiupV4TxoUQrjIq\nwNZkcmbJsJs26zFE77THwVhrRgt0U6qGHT1GRpDi1u4+BFXkVvkZyorS32XjcsXiuOvGV9XkyCv7\njkZhiiTsUf9wRN7IfY/WZ8zjPiRVpabLCVRDp+UgQ90Sf8/PkZebQV1uVjIMrKIquvHAoxZ+MQ6+\nD/wA9+/cBwDsbs3xV3/5VwAADoNbt+md4sZVHUxTYzaz6MAnn9k5qWkWiMmIqJINatkqm8coqILQ\nNBJPH1v04OT0ANdvWyHIjbu3ESe24uXBx4LIu69rnHM3L9uxtlYmK5eRV0FQafRV/0FtNHgrEDFw\nlIXZvMEZ+Zn94R+8j+8RbUI2CwR+S0Q3Dp4LIh/atOpjAe6n9O9dl41agUMre/2ylPDWKPRrW6eb\nIc0ovinnKDhVYIyGpnlwdjFzOYRMMETUl34QONPjwBcAVdtUWSMjJahWA/SGlEsZ+WjmtkralCso\nqoaqmsGjathilsOjNY+BoSTFH4eH7rYd16qpkW9YMQWswvwHv2crUR8++gTCs1DwdJwj0HaNF1s9\n1ITzVXmJhOD9vC7A6FkUVYX5yvaP1gqMU6XOCyAJ+xSdbXQzEsp0Qgx3LXJjKo1dMixNWONU3AvD\nkBDEeeP2VfTJG0qbBkK9WSXqa99EqeUcam4778XJUzRPbd7T1ls38fglGWL1bgBd+8Bl9wZG71su\nRdzNUNOEeFgp+O3E3Xg4PLOD6JfzY4DMGhcvnsGfWZfTW/oE20Pb8f1OivffstBCN9ZuU/GViZt7\nUKpVcmhnSrlJa5bHqCtyahY5Hu7anw/PCvitSZvB2iHcwNkOxHHsFulVXjkDzPP5GE+ePKFPeI6G\nBtR7v/8n6GR2AhxPC7ScH/3qwqMUDC3MjHNniQB8tTS+Kddkm6zffQRYLu1LGsXChYHCSLRJr8ID\n3nnnLn2Axq9+8SEA4NrOddy6b0vov/6HDzDcsYvYrbfvQ1Ffu8v5AWYndmwcfvYlrl0hF2GvBqPF\nYmtvCwePLVThBxxRsi7hC7qvujaosF6of1sbL5ZObQjmI2xlQMw4GfDk4gLzmV0EC2Pc82ScuZef\nm/UGIw59NLRRkA3DbGnHo8cYulRiZsagNhRKGwaIA7q/boaQpOJSNs7wMAp9hAQ11oVG8wbZeQyA\nIjhPygacyB2CcQT0c7Gsce+mff8+/uCfMaVJMwx8BGYN67bvzatDyEBiTtyerN9FRA7FDAzXrtkx\ne/D8wKn8lNJuUQwC5lynwbkbT5zxr/CvXteM1vBoc9hJfQja3FZ1g4Qm01o2OD+1EDoXHhIKAt7e\nuYOiIhfj4gJFbg8As+UZ4shOskIEKEv7TJerl0hp7ul2RkgSO4c1dY08bzlOGh5t0nwvcD9XTYEF\nmQHPL2Yu1+51LSV4eD5bQdOiF0cBBHFYRsMhwnYsijU/jHOGgCD3LEsQkFKqLis0FPCdL5b4+NOP\n7fWJpzIajVxw82KxQEFh0//1r38Cn1zuYYAit+OkG4WI6XnlFxc40k+pT0p8/OjDje7RE8LB6UpK\ntynSWjrLCg7lMuxehYSNhsuhU9ryxezPypmh3ri+jdCz7xNXEoxc5EsW4kOac4f7BhXBwsbAwbMc\n3BoqA2DJ2sAVRjul6Wb3yNEQ/MQApB0L10u5gqS8w9DjCNv1yfeQBO2Gijs6CIPlMwGACjm6noXi\nR0kIdMguQCkkFKAc+R4qUt51so6zMEEYOS5WWVTObJMzz/FBFFeoN4RkAUAZg9nCblzHk2MsyRKj\nqhpI1Zr4cpfSIEMDtCHCFwsHQXYHGQD7/kVRhIwUz1G34wyfPc9zilsv9LC9bw9wqBSGNEd1ocHP\nWuUu0Nuym6ikE0DTwUMrAfUGlirAJZx32S7bZbtsl+2yXbbL9ju1r70SVUgJ01YpljVOHtky8Uez\nE6zoRLdqHsG0p24/AU+IKR93Ydpdf78Pk9idddrtYkV+JUcHj9E8/RUAIFm+xCizu/JOEuA7VNFi\nrAY39sRYVh5aSyXGpDvFcC5dWV9r/Yph3+vbdo/jxi6ZfwqJu1v2VPHzgKGmkjBn4hWlkIEh0lwy\n3MO9b1n/luPHH6BYEDlVSRydHtH3AQYDS4a/v5uioMy4Fy+XMF5rzvlKlUlrRyBngFOdvZpdZYz+\nKoHztzQ9tVUhgwApKWK41GBUORBao62IMQgYOi0GHsfurq0iTWcXqKQ93WohURryntGFg19CGo4c\nHDnFGnR6GbZGGd1jCUXKzf6oi9MjIu0bhTbsjjED0cZOMANfbPYc54sCi7n9zEIxeGQKO+pl8F2m\nokJeSPodwKNxXTcNQtGqAxW415JcEwQhEUAbgxdUkfUCDw0plfwAEBQv4jON5cp+B48DPTL/bCSw\novvjjGFIJf5E8Dc6GUZpgpyuP58vUNDJLYwTMLqXRmlH6PQ6ffz8AyvI2Bt1sUWn1iTrubEUhiFi\nitZopHTZgg/feuBUe5px9Hr2nT7AIVYkKvDFumrHOIOkiodU7CtVvjfglUPKxlUEsk4fjLVeZg3G\nMyLLGgN4pLwrl5iS+iyQDQZbVPXspggD+7wWy3MURNw2xQoeVSWEHzszydlijPnSnrp9L1r7uunG\nwbvc89ByVhngRA+LVYGyfDPSdaebIGrhZGEgqJr91oO3sXfFUiAUjKswai0RkArxypV9ZOQzVOa5\nE1QIxlFQtbRckQq1LBC09yLhIN3lYuIeCxfCmfsmaYAlKW///id/4/LhDFPO5+h1rSwqlxWqdQ0e\ntGTy2pn6GmYgafxqzr8ikmnnceaJ9TxuDDzqi9AXaCMny1xCxLay8fHBDH/+N7YSJ8Ij1GVrtqnh\ntYbRde2qQGHkg5uW7G3g681J1x7zEFM8WNE0ECRGMRkQ9ux8F4X+2hyZMwvd4av0daZqNPR9NPv/\n2Xuzn8uu607st4cz3fGbq+pjVbGKxSqOEilTs2VL8dCdbnfQQYBGAiR5MZCHfmjkLcl/ECDPcRIg\nQIAOOh0YDXQCtNux23ZktS1ZomSRNAeVWKx5+ubvjmfcQx722vvckg3WLQIU8nDXA/Hx1r3nnL3P\nHtb+rbV+P4MehayjNEZBPGJlWSCLXBs3dragpFuHt5nBkLQxp0aipMIewxC0YwXjAPdV0xyyuzzX\nl1IKY0Iuh8M11ETEm/Q0ciKHNYahonFxZrCGDlUPr+UbAYmPuQzvVyuFmBLvu8NuIBRlYCjIJ9BG\nIaWwlZAxUiILja1FRohfzzB0aA6whchQ06gnOBeXsc8/J0o1YRwbawOL+P7DfQhDEPAgRkTQacwS\nNFNXAaanEn6PiA/7yGlzjHs9qNL9tjcbQxN5prYlYnK0Xrx6ETs7buBU5QReRdZoFvS6GGtDWoy1\n8XZrW6HLZez8VoaMwkymqdGV7recWxhiMVbagFF5jAVgCTs1gqOz6SoJvrS5AVE7J0qrGiXB7A9P\nZ2Ejv/VoDyhdjtludgYPKzeoi7LtZ8bajYfBgtFuptRCubi1S4csKyrdnZUFemuuT+cmDyXGjAlw\nchbBBE4o9+l4/xAqd/cYnUxhpSvrn80qlORQnZifOY0tABHlfUmZ4OTA9cOcKbxL1ZrD9SEGGxRC\nEA2UcPcfTSbISLxW6RqgsQTWMlY/zYqiAaPfdSPAUGdO5yV8GZBRCDlZXWFD3lyjNORiHg7Nqrwq\nUSpfxs5wTLH/RItAQigER5dyMsq6wHTuYHceAREoF41ZMCL7i4RETOHVommc+PGSxhhDRguHBZDQ\nMxhrA0lfVVaIiRB3+8wOGoLyNze3w4bsBV7db9v+PTo+DmLj6+trC3lNPJTRN0qhImJIFokFcvGW\nOJbxdvNjC2K0y1q3R0zQwqCqyOnNG5Q1zTmlkGZEyCoEDOUWldN9PJ6TZma0BpGQ9pjsQggffiiD\nvpoQKSzlxFTVHH7SNXyObsflfCRJJ8w5A4QwCbMCgjYJEcswrp5mWwOq6LMKff97btGhiuMXXrgW\nSH0r00BQmHA+n8H7Gevrw/C+67LyURNorTEnXbL5gdv8LDeYkyPqCDDdc2bdDpLU510CNa1tTV1A\n03qhmxLHlGMFbrFOVYpPM2sthPDVxS31hRASdkHMPoSUWZsHaYwJf0ech0orbWwgf71+4z5GR26M\nbPYSpAM6xHU3IWnsG6tw4bzLqxmdHALM51Y2gQhUKQ0pfcm8faaD96AzwPqGe2ej6QSjsXPAs1gi\nI4cqyWIkVDkppURN+V3T+Swc4LjVqGmfAOfQNL7SNIP21A0c6FAY2CQZbOY+H0ZrGFKFdT5XiFJa\nh7tx8NTqqg7VsTri6JDe3DLGgHB4+tKXvoSDE9dGZYApUSWMR7PgRPXX1gOFx3w+C9WXqE0gzS3K\nMoSi1zYHgYpGCoG0cO+3yOfwpagySkLagjUGEeWASWVarU6tURPZrda2rYJc0lbhvJWtbGUrW9nK\nVrayz2Cff2J5UwbdOs5Fq4+Vn+L00FUu9fpdnH3OJYIN1zgiOl0LpSDpFJToGl1L0hr7+8ik5xHS\nUHTy6XVifPUNVyX32isvkW4fMD4FLMmsNI0O1SuMMTSqlRTwyKw1dmkOJQDopQKmcie3Wb6Ov3HN\nwmRag3ueKGvhpeosFiBZxVAGwr4aHeE8cRUl6HQImUlqcEpubpIB3nzZefe5Bo7ed4n047oIHjT3\nNwEczwpr/6c9+C+fPJdTFUyTGDQFnVClDRpuMBaRTwqGQU7VH3t7pxCUeGm1xd4DFzYpiwqWwIzD\nfIQpJWvryl1PVQp9quDK1jl+8M7bAIB+b4gr15ykRK9jMa8dmrW3/xhauL+VaQJMbrWFrpdDMcqy\nQE6IRJbwBd4rBkXjJa8aSEpU7kmJiP5WxsAf85ls+1vD+PxolHkNRt9HkhDCBYiYh1clBUPlZVBk\nBE2QlpYtghFxgZhCaY1Sz6QrF0VReO9pmiIn3iqtDXaJw+vg8R7WKJzw4pXLuPGJS7RdW9tERlVA\nXMqAMjHGAvfUrVu3wr06nU4gH1SNCif22WyGx3tuzL5w8Tz8QHXoA7XXcjRU5MEEIJ+B/E7KCBlV\n32rVoKKxyCygaxeqEpzB+krDOAlkm0VRI6IE7fHpQ5SkNxbHWaiCZGkHHUrYzZIMjEIdVT2Bn+Cc\nMWjrdbliREmPni2BpMou1WgkRG7YGQxRT5ereup1E2pDjB7p8DFtwAkR3Lt3F/ASSDHDHiX2Ptjb\nR9Zxvy2reUAVszQJ3FA3rl/H3RuO44kTAmkSBgLwwBmQ0T23zqwjJR2V+XwO7sPTWqBDXFuqtJiW\nLnzcKI1ySfkeIViIBDS6gaQIBOdwAp5wa5znAOOcPzEePVrFjFsDADe+CmpnlTc4OnaFBaauMC1d\nCO/uwQwzmhOvv/oCnjvjkKL52R4SClnbBQRMKwufS86YgODLz8UsytChcdHJ+mHPe3D/DvanpBnX\n76BLOqxZlrVhYWtDikbCY3S7lO4gBAziIQgAACAASURBVFJGYWptA4rMTQom3XdYto2edIjg5Phh\n0Bll0OhRqIsLGUL9puKYU4i+0jX6zyDdY60NIbONjQ3EhKrVdQO94cLm0+kcBVWmMimREnfaoBuj\n8lV7pcJ06tZ3aXh4F2AMDD7UywLi20m6UJrekQZKShMwVkP5McNkWHerogpailIyKPb/s3CeNm0F\njtIGpnYVL005DtUS1TzHwQM3qEdHpyHwzxgHowErk/iJUFQo/WQcCTFav/b8JWyS4zE9OQjM0ZzJ\nsOFLiZaMDQAhg9BGB2ZcrTWWThgCcP32PlJalN45XMf7+xSWkAKRLug5W/27OIpDHlBV55jN3HN2\nRYOs7wbRvJiikG6RLXMDX2T209MZ3rtNIQcb1hQACEKhXCBUN2ltQm4K5zxAztqa0LdPs9OJC682\nSgWonGvHHgu4CevpAQAZQjybO11sDoidelZCUBVMGic4mjjG2s5mirv3nNc5OnELrtURBDnP55/f\nQnRMOl7jGe7fvwMAuHL5LAxpOuXVCD7dwuXkuM+zJEUnWU4/L4oENolksjYlxmMXTpQyQkoVc4Ms\nRU0OVQMTHBgZsRD+e3wyQpb5vLw0aH3N8jrMNmkY0pQq14TGjMjyJEeA8pVRmFH/cm3gS0o1c2Sl\n7h94YE9ero1tGE4pBUnjRXKJ588T8y/jsDTY+sNeKGM/2D/ESy+66koN/YQT7kMvg8EAlSYaC61D\n+EhpFRiyr127GioEheDBAYukRKgs5jJQd1SNCeSGy5gQgKXNoyksNIVchbBIaQFV2iCO/RpjQg5b\nrSy0r9IxBowmVzk5xcRXbqYDJKfuO2d3U+xeJF1HM0ReuM2Pw7TCt6IN2zEuUHlaDhEvUJI0kEtG\ngiqf76c4LFG+dLmEoLDlwxsfYo90w2LJYLW732nD8NKbXwIARLEACzQACg2FJE9PTzCh1IiYHCQr\nELQCx6MR1rdITJkrzGbu8KMaFpJKJJNgNMyktLi46/pn7+AYEeWrPs04Z2DkCDJukKbeibYhLcPq\nZkE3VId1SQgRwpPWLJAOm9apkFEW8qBEhyGlcNgmm4ElbvzGMQ9M5p2OBIQ/AbdjU0YR/GnQHU+X\n17Gcz6fQB5RnZVsh6/O7Z1tKGs4wnjgn+OTkMLD7b+9sEbkn0E97yCIfdk7RJVJbrRps0zyOZISU\nDpa1smAN5SNBA8zN75izEMrMS4U9ymurG4WUqlqzboqYLe8yFEUZcj+zNG33PFg0tHYmwwGqzI3d\nsqrB4KsvbQhxK8nRG/i8WANBB1xjGaRoaYlqyukSigWnyDCGymcVMKAJm6EM86+u6kCVED2LOCDZ\nKpy3spWtbGUrW9nKVvYZ7HNHopRSoVKMcxEST7WpwanKLOEcdUmcLKcFaoISrV0ghGQMkk7gg8Eg\nwIRJzPHFLzpCuWuXz1FiMXByehRgV84l2jxxHkCmRbJJrQ0knRillE+ohD/NhGC48ZjkQPIPcETI\n0ryqkRE8GQuL7aH7++WXnkOPkjKv332EgzsOlflgPME3vuIkcr597QXcyd3x5PHtGnnjE+hYkHqx\nRsCX+1hYGOKGanTbNgYE797qNvmRmeUTy/eP79K9ZXgH1tqQ8KsXSEthJQydFk8nJyhLl1iaRh2w\nmsI1aYYkolMDSjx33iU99vrudMUhoIkkszMAzncdQlQWBjWhM0JyRKkfGw04XU+CoyKdJTQ1Gr0c\nA97GcAO9DUeAWZRzRM+5sLBFiaZyJ+46L9AljaVur49iRnpOtQpjB8khNkkiQucjzEeONpSBIZ/7\nk5LCcEDVbZFGoTzcHCESrYJ7XXmNPAZG/TtXJSoKe0qWIs6WPwfNZ/PAucQZB194/55P6NLzz0PT\niVpEMb7y5bcAAIO0E8InxpggFWKthabnP3fuHHrDjfAdD0VJIUKo+dq1a4E8ky0knHMhUFIoZVLM\nAwGVtTacZpexNIvCGtNUJqAGWcoDkq1yix6Fiytt28RZJsK9hJTo0xzN54DO3XfKqoKXnLxXKxgq\nirjw/C7WiK9HqTyM3yiKwaXrq0Y1LWdU1IGu3LxHXQQ072lG0o1olIYiyKXmHCKkBAAJrQOGAxmF\nHl+59jIuX3EEk5xF8NUPFjbojCnTIBm21b4AYOsagtDC9TiFmRLpYSIRe+3FCOA0Pquyarn3BEfj\n9UKLGvWS6L7SdSDeFYKHpF9jLARabjqPrDZNE4ohmqYBhyc1FqElqqkhKJRqWYRKeQJPEYhUz+z0\ncIZIGqUAmE+Q12ohuZ2FsWm0gfRoSaOfSTuvP+hj66y713g2wSlJZSVRFJKx004H60O3luwfPA6I\noZStJmsjAaNIcspwWEEErJHEJsmaSBFjROSZRVMjp/VsphtwT9QpBOZUET06zUNBBucCjIqGEhmB\nPQMvnQvJUkg8iVH5cLrkIY3GwiKKfdWhCIUAVV7CECQXi9ZvkDJqNfWYhaKqUKVM+G2tdFjZtLHI\nKNVEc4GCiqFmdQ5Bn/eTOHCO1aZ5lvoA90zP9vVnN601LOUKWFVCVxT7V3Wo4mAhn4YWXJqcTdMO\n3k6ng4yEahvVoCTY+VtfeQtvenJH3saKLRaqfWDhq0qklE9UdfhKIcAEDSXGeIg/L2MvXdhGRiRh\nh6c55APSx+ohMEgKcAw77nm2hhwbXTdx379hcJy77xznDeKbTgj2y1/9Gr7zihdXvI8/fseFvGZz\nHfrLGh7aC9iwQcacYfHxQ5ksfiHXa8lFzTMjRBGDolWcgQV6CClFIKrkHPDJZefOb0DRAgjThNy1\nvCoxWKPyUtag1yOHgio/hIwgIs86XsBQCGNjIwuEqMzUYeCDyZCDEqcJFHnMBibkMz3N0iiGoDEi\nrMBw4BYgZeZAzz3XVI7gozpxNEC24cbjfD5DRE7UxvqWo1wAsP9wDk5hzjRdXDiAqvQ5HDqEOWGA\nghynRunAYm0igS5B6sNIoKIchVlZBT27ZczUFXIi+DPWwMDTQjDkFFKMZBJYmEXEMaRQZr8rcXJK\nPPJchJCltTY47HEcI6MOssYgohCC4DKM0yzNAj2CrsqQ76S1Dnkt82Ie8rWUUkiSZxAEtQxl7ccC\nh/CEooKFsSOlCGuDqkyA/rXVwdESnGNr6N7LsQH2KG8vimXI1xqdnGDmKQHyEq+95pyUuNuF0r4/\nBRg5WlZEIextGgNTujUsiy3k2nJt7PqclJi1jizjYZOBqn1KFKqqBKOQ38XL19CnMV3l80BIKSXH\n/qFz5n7+yXUfLVtwXC0ier9pp9MKgI9K8MRXUFpI6kOrbRBWns4nOB259X6iqyBg/TTjnMHadr0O\nKQTcVdwBTpB30bkOFZ+MgZFzZbGgAcctjK/YQgJLzmzdVKHv4qilajCchdxDIaIQ5tXaoC3eMtBe\ndxHmCQqZpxljPJTV9/trgV6lrppQudYog4yqyS5dvBLSJI5PjnF07PJLRSYhPOmoFUhpPg37AygK\nR5rGIi9It85oNLQOn8xm4JRbHEkG1fjqdIaUhKON0e3B2bDwbMuYUk3Yk5RSIX2ESYkodX9X0xyK\n0n1qXUFrP6ZkoCrRqhWYFrylKLKo0dB3VANU5CCVRQPm55k1sJQfpTjHjMLphTZIItfGPDewkeuf\nOBFLH2i8rcJ5K1vZyla2spWtbGWfwX4J1XkVOGW762oMRdVdQrSZ9Ro2nELNgpxGt5eGE28cC0xy\nn5Rp8Vvf/gYA4MtfvBqqIrQ2gYBNLBCtudOfJ52zre4X56EiSHABKb28gAlhhmXs5dfeRJe0/NI4\nxeMDl5SnLMOs8lVJOTRp6hUNx0lOFVZsHVmf6O01cIeUw//nf/Gv8A++8y0AwPlzZ/Ctaw4N+ckn\nY5xMyUO3HMZ6VA1goaIFgfCSc9uiUtYGin3G7NKaZB4WNsaEEx/nMnB3CMEQR76arVVUj6I0oDJa\nG7AhhXdMFKD4QuWB6DFOfHWWRU0nwkjKkChsbYOYpA+q0gaOJCY5GkrgN5BASCC2sCrEcT/V0lQg\nJV3AmpW4f4ckKpiBP/oYY0LVytHBg3CC7cgocMfUpgkyNrrWoTqIodVuA2wAAVWzoAdmLWpCq1xV\npdfu4qg93xQMktiHUXiQUFnG8tkMcyLbrJsaBcH6YMzJOwCIYxWqaa3RoUpK1Q2k15ZkLFwny7Lw\nLsuixNGhG79aqVAdy8BDKHAwGIQwsKrrhTCJQEoI9NloK/Bo4RfR06cZY6HiKEnjMLbKsgqaZEJw\nVE0L/ZtADhtDCF9Ny3FSUv9zAxiHGk3HMyQdqmJiQEGhsHuffIKMUK/nr11Fl1AfMB2q9hwiTqEL\nXqHTpT4ZJhiNlhunPg1AJDGER+gsC9WbRVGGMKqIs4DKyKSLmJBBaQUqQlZORqd4tL9H3xHY7q+F\nawKOmFTRe6yVQk5hsHpeoUuVt53UophRBTZrub+mJ+PAKcaFQI8iCU8zrdUT/H1+rmhtENP6Fcdx\nQKJ+MfXCg/MNswFtjzgPFaIaOqCDgmkIQeSZkQhccdrYMCcgZEihaGoFzdwamMRZSKFgDEHfchmT\nsq0+mxUVDBHcDvqDUHwwm+SYUfg0TmJ0qf8k7yD2CHtpQhEAj0VYnw7u3wvo4PpwLfAG5lWJ2oe7\ntUII3FqNDo3r3d1t5FRQMplNg/5gVVVgz9DGsqwxJ967ptEt4lTXaCg9xdL/A4DSGk3tK1yjsPbU\nSoWiE2Vs4E+0tkZDkY66NuFeUAyC1qqyrpDTj3tRgtqvZ9aCGV8YVQduP93wgEYua+xZSt1XtrKV\nrWxlK1vZylbmbBXOW9nKVrayla1sZSv7DLZyola2spWtbGUrW9nKPoOtnKiVrWxlK1vZyla2ss9g\nKydqZStb2cpWtrKVrewz2MqJWtnKVrayla1sZSv7DLZyola2spWtbGUrW9nKPoOtnKiVrWxlK1vZ\nyla2ss9gKydqZStb2cpWtrKVrewz2MqJWtnKVrayla1sZSv7DPa5y75c/7PftyCq9VjwICYqpQyC\njWmaQkQkYMlNECrkjEF72Q5jgnQE5xyWpDUMY0FmgFmAe8p/a+D1Tpix0CQjYY1t1Z7rGmVJgpqT\nOeZTRz8/LypM5472/h/90//mqWqE3/2Ld2ztldOtCbIDnBnEXnaBx0EMVBgGr25tBfNKEOAiCmKb\nQA1LgpnGAJoUrY1hYET5zzkWvs9aIVVdoSJJjyztBTFGbRbZ6b04BvCdb735qW38X/+H/y780Kul\nc8ahlX8+g4g+l0JA0ed1XYfn01p7JQknEhokeUSQ/vDyDYtCnmkStQLWtpUHiqWE14kUQjwhHWD9\ne2csXPO//K//+09t496f/Wt79PFt9xylQexFjDkPzy20Bae2MQEoej9aKQiSqeCaIUiIWwvrhWGb\nBjV9rDhw7msvAwCS88OFd+tEUwFST19oh5c+EYKjsV4EWoAz927XX/vtp45TcTa1Wd/JKLEIEDHJ\nQmwk2Fl3Mglb/T6a3I2vUmmMvWxPFCMm8duEpShyEjQtNaQkiSRtUJCI9zSfg5HMRm/QR0USHXEc\nBbkh1TRAbX1XAdIL9bIgBh1LCQP3DB//23ee2sbi6OfWS0cIAYAb/2jw2g6MW9SkKM+5gCRVeKUU\nOPNyIDLI04BZaC/vITnsgpyUJhkMoxuA3kvTaERRKxvl78UW5OGjOA5iq3Wt/BKAsy985VPb+CUh\naHS1c9kyBDHbuJfh3IVtAMDju3uoC1orGMI8s0CQAbEWMFi4pb/sEx/Zv/XPv9geLwZirA1fstaG\nubP425vGfmobi9nEWuobziIImgc8qp2MDgDY1A1iAJYrt/jTM3mxWvfcf0eDADDr5U5aGRNlFPx9\npTE4vPnnAIC9ez/EhCRFCquwvukkuLq9MxjsvOX+Hr4OTq9mbX3zqeP0P/+vftfOlRsX03IKTrJZ\n65sbaEr3eV3k2N4cAgBELBGR5E2Vz9CU7nnWBhs4e+4sAGBjbQdV4WSILr14FcXMSRWpomjlvqwT\nSwaA2XyMfN5QW3bafbGpcev+LQDA/tF+kN0yWsCrMf3Bv/jXT1fp/d8iC79GxhJWurVHGAav5G5g\ngkQZ0ya8Lv4LQirMK6swFuTcLDPw71UzAUOziMGE71sIWHJzLGPQXgONcVjW7mUgabpaRBC09vf+\niwdLKRF/7k4UZxycdrs0jcH9hOA8aG5xzsOEZLzV2VrcbMNmRN/x89eydjKzhQksGA+LBmzrgCnT\nkIYVEEkOm9BE7KYQzDsbGlWznOK4u077YhtlIazXlGsdRW45RvkMAPDgwb0FdXEgCYrlSRg9TNeQ\ntHGeO38RMusCcLpQfgGw2rb9Y21Y9I1VrUq9NuDhcxv03pTWkNFybfR9p7UODhIDgr6WtRYVOaMV\nfc+b19Ez1oa+UEoFp2DxHfvfcc6DnlxZlkFVu2ma8E6l4EEka3ExZ8y1zV9v8d8+zZpbtzH7/l+7\n9pYMDSmgK9bCtdIg3FPxhU3JtA6pNKbdaMSCs2xqMK+FJwD9ktMoS1+I2w3aiOAIgwsw6R2qFjDm\nnIOZVpPOX3MZY9CI6LDCEw7llelh0FA/HUzmmJeklSYNEu8gVTXq3D3nXOeAdfeNoxSW+qSsSjT+\n3QuOhBTowQWoKW6TogVdigRWeI08oAyK7Abd1P3WGBP0F5exsmmg/aKs4M9vMExgVjm9P6PKMCfq\nxsBK0tpLIsTU19K2BwYpRNiYmQaKuZvHcZyEd8MBlOS8xVEMTnOjqivSKAOiOEJFul/zPEeSujmt\njQnXf5oFHcyF71uG0ObN3W385n/8bQDA+z98Fz/+yw/dd0yr12iB8HyLh6lF52rxs9YpCcscPsU/\neWLOLTpgy7XQH6zctyPOwKU/ZaawjHQdeTtuGET73E84UQjaeU8+lw3PZS1rdQKNBCct1Tq/ixsf\n/BEA4N7N+/j4iNa3usTza+4dbqxxXPuKG7PJq7sonM+CNdIa/TQ7PDqAimhf7HZQVe76qqqD/ivj\nHGVJuou1BrfOcYqsQhL5NbnGwZ7TPuQqwuZGHwBQTGdhr1W6gqB1WCtgVrrxWxYlytI9/zx/EDRH\n87IK+pmdLEFNmrXzogD48pqyljHMmNNrtOubOBWk71hJ9DL3ubAVBFx/diIBTs6wUU17Mmh0OKBY\nBmjSt7S2E56HxV3wxF2TCRmAAyZSgL6PKIOlz51eKDl1og8r3N9pLKEev7d0G4FfghMVRRHEwimh\nPVGL1sHgIqAuTLAnN0X/fSmDIKHbeGkTlu0GwyyCWKzbvhZOuTSxONpjW6MQBGpZEoN7xMN0oU07\nSZ9maSIg/aRXDNa0G6Hxz9PkePThuwCAP/zDf4Pp3AkxbwzX0EncC+RJ2q6SdYHNNXcK+c5v/ja2\nz1+gfoiDMK0xLTJj7ZPnRbtw0rJoUbiaJodqGgDLTQh/D6XUgsP6d3930SGWUgZHuWkad0pd+N4v\nXtNvWsYY1DUJHTMLY1ony1/PGAO+4ECGzUzw4PQwxoJI6dPs7o1bKE7dKpiaFJzT7suA2I81cBg/\nlo1GZNpdKaATWrYnJcNguXe6LCLtx4hFdTCh6zAYPwa1ceMTbiGwXiDacvgdyxjWOo8c4UCwjHHB\nwkneGA1BCIwQXRS1u1dZamhLwraqROIX4lyhIAc66qTBAa/qGnWlwt+MHN44y8BJfNYyFpwupXR7\n0FkYK9a2YrGMMRR0Gk/jGHx5PxFvv/c+0swtmvmsxP7hMQBgWleYkajqmbUerl14DgBwOp1gRPdK\nogSDxDk2aZKh2+vT8whEkeuTXtJBSad3paeIIvfMaZaEDXiWT1CTiKyBCQeCNM3Q77trxoyhoTFe\nVRUauVwjw5oGtugfBOdmY3Mdna5DSr745WvYf7APALj18T4EOa/W2oAc2b81gtrrt//3t/7ZL7Dh\nM79sGTCoBUFgFg4A9on5/2nGhATnzmGwzRHK0jm/SfcSYEggmVsY7vqYA+B/x1bGwn/+9sNb69cR\nG9YybgFODvW9ow9wOLoBADgc1TiYuTX63GANHXsHAJDqCMNkxz1btImPP3ab7/OXX3xqGyfjGXjH\njVMhY5QU+cjHI8AfJoWA6rp+6K71IUQrKs+Ck15D0LgDE5CE9gy7axjNTlwbLTA5PQUANFUFTmLV\nTWPCQl5WM4CuowxQENIFq9Cj55xPclRN8dS2eZun6yi2vubaK0tcf+judfvRJhIao1nMkSbuXsN1\nDkaos5QGhuZHpjQ4d/dtYGC5+63lMogas1qAkSC2YRwx7andbg8JOVqmiVHMaA0TCk3pnicfTYIj\nV2UZfuXcRffbJdu5yola2cpWtrKVrWxlK/sM9vmH8ziHNW2YxiMG1tonUIIQlVj43Jg2P4rxFsWy\nwAJyJdvPjQkwpJAieOhcMhifv6N0+1urfWQBTHJo4Z4zSyUGvWzpNkYRd+47gLiTuNM2AGUZ3v7B\nXwIAbr33LsoTdxq4cv48OmuvAQC2tncwL5wXrOMYzJ8W8xkiQjGu376Nm/uH7vtnziFLHWyZJMkT\nITKt3Pcn02MUBNmmSRZQUQYeTviCC6wPng47A3givBpCpMaGkKEx5onwnLdFJIhxDg4b/mYL3/Gm\nTYsiJqk7/RitXL4J3PjxaJVduKfWGtI/I+dteIwvf0Y499pL+Mn9AwBAfVQh8+3UBsJ6pCxCTeGw\nolFIfd4GGDSN3yhuc8U44xA+xwkCHQoXx9pi8mAEABjMBNKeew8WNfgTCKjvd7EACXBE3J88F8M7\nT7ekE0NS+FqmETjB63muMC888hYBmtCIqg7Xb2qNGZ0MN6IUCaE9o/EUBYX/ZCSRdrp0GQHtf9so\n2KbNxwn5M1qB2/ade6RCa4OExrXReiHg9HTb2z/E2rpDcFWtEafuFBpxDd74MG+DWe7mgREJZoQC\nfHDrJmJaEgeDddT0/eFgHZLWkn5viHO7Dn3YPznCg70Hru0C2BwSyhQBWUIIOrOYzuj0ziRimrvr\nG9vYWu/Rc5Z4fPAYAHDl5W9/avt8iMZlLlj6rO3TSHAIeq+d9R188c0rAIDHdw48SA/G/m5Eyyyg\n2f4vtvBfwAbE9QljDI2/uBTYPLcBAKhqhdOjMfUDg1nyNQoRwWiHMv35n/w+Ht75PgDg67/2O7j6\n0n8KANClAo99KGewMBEsnoSfnsjiWvjYt8/CKtozOIOeOeSu/Ph7uJy5Zzj7YoMXlJs3/UwhhkPG\ntLiI/tbzAAAuEzx69HC5BgIoihkEheWtVYhpXZkXBRraD2CAZuoQ6ygR6A3d3Gp0De3zSFUV9s6H\ne/fQ1O7ZdjbXUVZu3GnLMKMcRugSoqF0EN6i5saYgDIpu4AQG4vY76OLOcpLmOEd1Bsu9/PmvZ/j\n/eturvzovTl07a6ZRUA8oDmaJZhPJtSuBpSyiXOdBJsbru1zY4EeRTrSBtbQ3qkVNKUDgHPMZw7d\nYoah36VwnrJhbev1BMq56yuVN+hk7vNs5yxe+e3Xlm4j8EtwohrVQNBAVgohCdU5UX7DYIhpY1jc\nVIUQEH4xtSaElYQQYdIYdzEAbjPzToUFQv6PaRQaijPXeR42c8F56HitTZtkaA2iJfOFAGAyHofN\n4+2fvItx4SZfUea4/p7Lszm+8Ql2L7oFrX/1GtZ33EL8+N49vPsBxWDjCKNj52hN9w8AQwm+VRVy\nX3rdHra2tgAA3e4Ar7/2KgDgjddecfEdAD9798c4Hbkwhsn6SDO3WFfzOU4P3WI9HAzw5Te+sVT7\nJIVMq0oFJwbWoqCNSEqxsD61EDFgQz4TgwWneHSjFOLEjQNtdHDGEp8pbm0Ip8pIIe65jScvm5Bs\nzcEgIz9mFvLf4PLPAPf+1ZLhvJ03LuElSvS888fvYb3yIUQTxpeOJaaF2xRirrEmKTavNSoKA0x1\nA11RsqaMYSjUlccWp7QqzOo5LgzOAwD+3Q9+ipdfugYAeOHClkvkAcD4Qr4bEPIKpYhQN+3BwrI2\ndPI0i7spoo7rS0QcPvApqhoVOULGVmGhiSBR031rY2Do82quwOD6qmoUJMH9WacbHG5jDHTlrqnr\nxud3g8cS1icHizY0qWoV8uryeQU+cPOp1DVYtPwy9c0v/wo0ze+yLDGl/KXZfAK+sw4A6HeHODx1\nC+i71+/icM8t3GuDzbB+jOc1+l33DN3OAMO+c8wa1UD5fCLewXju2piXYxxPXPhkY62H3TPOMWbQ\nQExhvqLCvY/v0fffxxpdc2NtgLxwz/k7T2kfWwhJ+aWSMxZyKauqRpzQpiH6uPT6KwCAq7f2cP09\nVzghGIMyfs1EiEdw2x6SwmxacLjcPyyE+WieK2Owue366hu//gauvuY2oVJZ/OkfOwfoo59+FMLv\nTzMuOJrSffcnP3gPH/3VdwEA8jhH9++5kHvDjyA7bj3dufZPEPe22wd+wv6ue1pwGpDj0T6OHrt3\ncm5nA+OHPwAA1AffQ5eGXX9o0Cnc2lXNZ9Ap5bwOzgEdCi/GFapq+VCXbhpwemedzgCCwrnljKGh\necYtgyrdvUaHpyEhXDKBSLaHWcHc+66bMWYT953792+iqN06FHVSaDqIqjIHF27M8iTDfOqckGJe\noLE+d6+DjNIm8rpEScUixqpwnWVMGg1fB5F2UzBJh8tMYIdC5UNhMKc0Gm6BNHP9ef/BA2ycde+0\nLAtw4cbX1noPlXfqhEHduDVDC6Di7tkaZiB67jp1aVELt+a9cOkSIhqDNz55H5pCuk2scVw75/nF\niIU1eFlbhfNWtrKVrWxlK1vZyj6Dfe5IlDUmlJxrpaEajzDIEG4TXCwkMrI2mXwx/KcZLHnK1rbh\nG2URwmfSMgj4ajAdkmgtVEiiZTJpwy3WVSv4Z/MncHAG8Qyn35s3foaUPN///f/4fWjydufTI+Qn\nrnLipa1z6G240+mj0Qhzau/o9BQiI5RpfYADgvUn+RyCrlNXdaimsdogJWRmlBcYPnJJdsN+Ak3J\ngKO9BzDKnTBUPYNg7r7NySEYLTNvqwAAIABJREFUnZYnswO8M3eoF/7Z735q+4zvdyj46mQO7vMQ\nIURbhceYDdVxlmkkPmneGlQVQdCWQfskfjRIqfg/mVN5C5foDh3itbXew+HUfXduWzQkEhzWV1JJ\nGe7Z1DVkKDoQaJgnFvh0M5nClS9cAgB07o0wp1N7bDkan3zJHdIEAJtphg0qkQXXqFL39+lojJTG\nTjeOAnS+HUU4oFMT+hlee8ud1m9OR/jj7/4FAOBb3/gSvnDNlSsnkYYmuL+2QCTdSezRwTH2H7rQ\n7kuvvIAkWT7UFWdpqOC0tYEipMjWKhRYWGsgfGVLxOGpOyxn4ITOFrat6omSBGmHqlq5gfHoljaI\nakqEbSxUm+0fcA3OWAAtHT0JVclFMQoKgdVVCUF9u4xVVR6e+eD4CPtHrq/Orm3i9SsutIC0j7uH\nHwEANrcu4tLzDhHqdTJMJw5pPBqd4NwZhxavd3vY3XZ/F0WO8dS9xws7FwDlxux4/hAZIVdVrfDo\nyIVrD49O0fchTs4gKKlXCIX7Bw4tPil0WMOeZn6JMsYGkIXbtgqxyEuAUP2sOwSjufXl7/wK9qmY\n4fTRcVsgsnBtF+ZzthgE88CbBdpydMag/FxMBH791x2a+uZbV2FjhzJsdfv46te/BAC4ff02ivny\nSE1EY9DqGHfvuvf5/o9v4KVt14b+do3T1KHwgwvfhMgoAtHMAKo6dcU2vjpahqo9wxV8kdbJwce4\nf9MlkKf1Ok5v/jsAgDR3AHEGAKDsAMXYPcPxo0NsX3IoelGc4uTgOgDg8vbzoVBgKbNtGX7aSQP9\nSW2Mq0wDIKIIEYUsm6pGQyE5zRgIREEUtRWfURQHug4hJGZ+fW9yJJm7zvHho3b+xfOARGmFUAUp\nWB1odIw1qHzyNufg4hmqgXWFRLjrD9ckDCE8UdaBkG7ADtIECaH180qBgjhI4w46hKh2+ikaSjgf\nZBE4pc7oRkESlUglOCp6tqKao6C0niQeApHbm7fOvYJBx82/h4d7KJXbL8eTKQ7n7saXEwH2DOg+\n8EtwopJEBs4HYW14QBkhVEAJaSFjz+UgwLCQJ0GbI5MCUviKCo2qbkMCwue+2HbjaWrtyuDh4quj\nE+c89LtDMLpXU1WBG0NwGaBKzjmYXlxGPt0+/JufoKBRPZ6OsTV0YQNEEuOxm/Tp7qWwkTRGoSKK\ng8HaEMcjl4szH0+xveMm7vlzF2DqtvIuif3iK9Bb71NfMaxRtc+j0xOoE7dhdDo97G6560z2PoSY\nuEViO2EwOwRhgkHp20u1z3MwCSFa+gLWUhaIxYnF2/fErAZ8ZSDnqMip5WhgqaQ3lRbd0kGpfOQc\nznjtDKRyG8/R/gx3j9w14v4OlJ9A3CDlbRWgWqhSXCx3lktOel0pRLH74davXsHxkXum6MYYhooY\n88YGLpIYHLUfm9wGR2ukORJyEPMqDxHinVSi0a4fNzfXkW67i14bbuNPvucm8zt/cw+CFqw3XzsH\nTmXcykpc/8QtiH/yp3+N53fcO3/55SuwWD5HgUsR+NLqqob1oU5tQxiHcx5CrSyKwcjpmud5KNVn\nNUNG77gTZeAe4ZcIYSXdKDC6l6prNBQW5LF0Jelw1AG2oirMhQovaBMQdWElmF4eML/38G4Yl2vD\nAc6dcSGBTtyWN9++f4iGclx2NtcwGdPBos4D71M3TTEnh8rkc2z23cFlZ3sDnDvHScgYu2ddTox5\nXGH/0I2Z01mF05l714cnUzS1m5cCwLDvQuv9bhcVbYrj8V6oOn2a+ZAYFzY4BVywkBOl6wKC3tmg\n20c+c23or2/i9a86R+evv/8+6jGVjDft+DGwIW8pbLTAL/BL+TxEg/6am6Nf/8ZlvHzNVTtK0UGU\nuYOTqufok//bH/SeyYlC4t7hS1eGeHjJXWSzM4OoXD9FZh09ynfL7/4RJh8X1J4JIh/aFwwNhdlj\nFodWadaA0bpQTSbQR27dmYkUovrA/baIcHh8BADoDBmtZUAmxuhUtG3WP8bJj1wYdq0eoSZepmUs\nSuIQij8+OATntLfVOlS4dodd+GCRairkU3cvzg06W84x4MzRLgCUdkHXPDh6jHnuQtbSxIhiN+54\nkqCgXKB8PkdNYXzOJaSieWl5WFXqRqOmsKCQMdJo+blodQmtWk47XRPwAYEZVbUeyRqRoNQOyzGZ\nUqWvTUIl3YWLuygZVQuKKNClGC7BKXdWNQqnUxoDoo8JgQXCljA994N/+X/+AS6cc/2wvtagICdq\nphvoBfDFmGdwhrEK561sZStb2cpWtrKVfSb7/MN5ugEnjpgoihERIRaXIpy0DasDJ05d1pB0KhNx\nHCDG06LG3mN3Mnj8+ADjsfPKheDYJq98c7OPM5Q82kn6gQV47/Fj/OQHbwMAfvWb3wyMs3XdsmPb\nSqEMWOLyhGIAoOoqhBx+8zf+A6QEMR6cPMSAPPdzly+jIJe1KOeIyJ2OZILZhNqSpSHsaBc5iQQH\nI3RAxHE46XW7WagaslEESZV3MeOoiNjTjA8w6BAnERjmFUG2cYZMlEu1z59+tdbtCVW02P8iYSbj\nEpJOf0JVgKaTiBAYRu5E0+cNOgQ1mKZGPncnQasc2rK5cw0TuBPGRx/cwfqZq/QcAv7gXCkDKnSC\nUioglkIIRLIlcTVmSWjWMDR0ahJbGc58xZ3aT47fhaWw1Lw2gXMkYywwaUPwcBoccIF1goy51oGB\n3EiGksKiZ7Y3EPVc+47vn2J7wxUKvPHKVUSxe4baSFjlGvjznz3Ej/70Hff53ile//qbAICulLDN\n8kmQ4+kkIKxNXiIi9QAeyZCkn2VZQM+UsQF9qpsmoH0DsYZB7EJg1UkORuhNMswgOxSCVho1XajQ\nKoRhk27niWfydZp104RKRqPaaj6jLKRYPmR59rmzWOt5DpokhC9LZXH72IXP/ubjh9jc2AUAPLez\nAa7cyfz2zdt49x2HRCSxxOuvufDfpVdfwmTsfptPRzh/waFPynI8OnD9MyszzGv3d6Mbx7sDQAgD\nTuFOZgw0xd2qssLOmlursiyCR2yfZmLx2OuzD4AA43FuQ7J+xExYZ0Zljed2HSq3/+IFjI7cmjDe\nP0FJ4UksoLge3XfAop/ojpwUAPobQ3zt6y8AAF5+cROd/hZ9vhsqCIvRCJICVdEzpEcAQDlz6N35\n/in+/hvus0FPgkm3hkzzEqq+CQDIH1+HQE7PbSH9tmYZNKHfMybAaCwnqMGlTxkxGBIiaI8SMKpq\nfnSnDmt6wyZIiBhz7fk1wLj+2uASReWS0m/86F/i8YNXlm6fSGMYKhzSqkE5c2OQc46o5xA+K1go\nUqmqCp5xP+sIaNsWRHW9kkCaoKb11hSqJfDUJWJC9jY2t3GkPBl0jNy4fmuaKoT3J4VFb91VWBrj\nojqAqwOZUWRlGWPMgoUwdRxQTJEY5CkhS5lEQsTWj2+P8Hif7mU5Up8igi4MrSV5bSF8JClOMSbE\nN6+BkxP326P9YxwdOF9hOp7iK2+5tepb3/w13Lr5QwDAvBxjXLg5PRqXGFDokGkN2yy3L3r73J0o\nVeuQR3OSz3Fy38HL1nBEseuY3fM76GQ+98kClYcYFQ4pt+AP/uRHeExOVFPbIM8QCYvBwC3MWTdB\nmrmBf+3FF/Dy1efpXhHGE9cxH12/iVe/RCWMXILTQN5/8AgnBOu/+PqrsM+A0Z2eToCENpitHuaV\n+/v+431srrnFpbexg8rDzPMJNMmyyChDVftB3YSqQGOasMFIKQLEa2AxpYGcj0dIYx83Xgfn5KDq\nCo+O3ACpZwYjIhWDZai8Colowub3NIuINLGqakTkdGqlnyBHTMjJiwSDbNyCIMp99Oi9lnWFXuTe\na9aUaHL398PDGSoKwe5S6KWOuziauvtsXngJkqrgmqoJjN6MsycYznnIj4padnr1DIzlSofKJ8E5\ntq6dc58fjDD56X0AQD7PsQHaEHX7/YZzzGmxW+cWOxTSEsYE+Y8DY0IOYP/sWUTElnvz4W0MqVLl\nrVfPAdItgqUS+OGPXbj1e999D70T16dff+EsNtdJpkQXYcNaxnTdVqCKNIJMXZ9laYTBwB1EoihB\nTvkBTWOQ175MGoisg8LPDS5jNnYh6NQkeOuLLjelP8iQ06L5zo0PMaEKvpIZoKQQveVIPU2FNYEs\nLy8rl+cDQJk6MCzLhIPx5XMUOlkfjEr8K2WhKDeCR93gyGVxD7tbLk+wn3agN1y+0+H+IZ47Tzlp\nQmBrw20kHBZbG65/Do5Ocff2XQBuQ/I5IseTCp3eJeqrfQw7lHepGhj4HKUMsZc0MoCixZqlAhtr\na0u1z1fVuUJ+yjmzHJraVtcWJeXmMAkICu9MTk8xnVC4ScbonXXrUi0Yin0qK28aWHoffvmrqzok\nRTFrcO6i66uvfvML2Oi7tifdDXTXHRkwi7oAzWcRdxFTTg/ny3KyA/XkQ9z/q3/unmn0U2yfc9eY\nFwluPCS5k6FGxt1+YASgmc+XNYHYlenWaX0wEugn7vPn0hKK5oGWAPNEs/dFCF/HogtFOZwHd0eQ\nVFnb246QdNzzbGw+h96mm7s3b03w6PEnS7YQ4JFAROtB2k0wVe4dxFEEQ85elZdIyPmMIgnGPRgR\nwWteZd0OupQja41FTs5Yt9vDsO/JYi0YjZuqqdCjQ4aqLQy1PRYpSgr/zYsKFm1qi/esrbaQz8B8\nawGAaBNqBpg+kYtOI8zowIw6QzV115zPa8ScqG0gcEB7xA9/9gnyyvkNL756CWcvujlaGImHB27P\nvnvnMUanbmxwbWEpcsx1hJs3XDrLr33ra3jtjS8AAD668RfQ1JYsiZAR9UvaScGxfAUisArnrWxl\nK1vZyla2spV9JvvckSiGBIcUevs33/9LfHTdneKuXHgRik4sly8/j/Nn3clwvZ+gIHmG8XiMj2+4\n0/iP37uF/sDBcnGSIKaQUbebodd3pzgmE9y570JDP7v5ffz1e0436s1XX8Bk7rz77/7gHfzhj/8G\nABBFFt965SUAwG7SQUZJajKSLXvdEnb/0QH6a0Qw10jEsYNjL56/gj4RYMZJhrNdhz40VY6akixF\nrxXJ1VWFkkjCmrxESlIT61ubyCgMIuIIp4QyMaWgUqpCkF30+u4ZRJNjfOROSzcOGkwmzrOWMoYg\npEsxhrpcLinZA2iLiI9Gq38nhAiIDzcN+NyhFB11AEkhskGaou8RoqLEx7dcEu7tY4vLLzgEKiJ9\nQG0ZNFH4iziBJrQwiiyUJ26VUei3pmmCpp+WKpwwGGMtr9VTrKoNPJmRsBay69p29o2raG4Seno4\nQxqTSK5pAsmdEQJzQmDWBUfMPPytwa3Xg9OQJCly72SC+BPX/gePTnD1MiXlYhpCZg8eHuGP/ux7\n7vsHNb79kkNVv/GPvwq1Tv0oASmWr1xjttUh4zFHl06GRtXY3nHvIE06uHfHkeJxwRA1ROZaGmz3\nHTqX2ASjmUNR/uE/+E/w1puvAwCmp4/w//75v3ff0QwZvBZX7R4WQFXUQVrDQIUKVAuOnDS6GMtC\nEn4k8Uxo28ef3ERBfFOccygq4Oj1t5F1XD+f2dxqK+bAkJJO38Xz53HhOXoXnIcqqdFoBC+kmnV7\nOD526Pj0wT3sT918PTk6gFcKOnfhDDbXXV/de/AAxyckPTNXEISYDPo9cAr17x+fYD5fLpl1kaQ2\nCK/DtiG0YobTIyKNff48qsKhC2VV4xERXx6N5+j2Xfs3djaREhKqlEKfQkljatfhyQQpva8Xdzfw\nyjXHb5aPpyjmbuz1X7mIuOvWbxmlMJrC6XWJlEIvDMsvqR+9/W9R3v2Ru14nwa1jt+6//ZMjDNfc\nu3o96QCWkod5O3c5a1qxWi6xlzv09P95O8eZDffb33o1ARcOCbGmwoD6UdooIIuiV+PkgEJOqq1M\nrY7nMBP3+dEcaBKH6pwcaxzsjZdsIegZKU2iUYi9RJLR7XrHDDZ3qMhDDmCI0beTtsVFvW4H0q83\nBrAUpiyKOiSEc7Sks1zGSIg30EKDRW48DntdxDHtPTgOephRJBHTPmQ0kHX7y7fRAFa5vZ/FMU6m\nbizWaMW3m0KjPHHztSt7GGxQf44moeT05v07mFPawgQRfvcbfw8A8NZXv4Qj4lW8d+cRNBWgPHfu\nHP6X/+n3AAAfffhhKBL6vf/x9/Abv/lVAMBgOEBOvF5JluDo5BEAQIrzQVJnWfvcnShtOR6SftU/\n/1f/F/p910m/9q2v4/59t1i/+/57uP5zN4iG3c5CHgvDoz3akAddDNadI1FUM8yoA9iIw/p4eDxA\n7uPAiPDhJ+7673/wAdY9A7aI8OEDF8c2zQy7lKN19uqL2HnOLXyM8ZZ4cwk7HU9RU1e+uHsZX/3G\nrwMAHh5NsffQhYISW+PRz38GAJgURdDTurT7PPqU3FNqhd6665+13S62hs4p2tzexvqW2+SyXi9o\nCArmysEBIJJxgM4jwTF+3YVYzjz/Iq5fd2W49+/fx5zyvvqDPtY2l2Rl95VbjAUtwFiIQJ5pmWwF\nTecHYDPX750+D+FJK9sqv/k8x7xw19zevYb1NTf4p1MHz6+v5dilKsVbj0YB3pZxhKxLoSC0lBd1\nUweKhbwsENNzRVEMXS63OT16PMJZWmSjiCHuepHLxpWNAxhGUcjP0ZYFTUhlAKrSRdyJYWi7sAIw\nwodZGCrrxshf/fA9vPeRg/7Ts5u4+pu/QveaQxJtwkBa/P3v/Jp7tqnCMHHPYNcYeO3zySxstPyE\nl0KASZ87A3QJ1teqwZRU6qfzKoDZjDNIckL7vQSM3t/k6Gd47SU3Hoc9g7t3HVz+8w/ew5gWtfM7\n2xg2blzrSYEZhT7z6RSMvA3LDRIKaRhjAt1InCRIUq+r2YpeL2OMMXQoZ5Bzjpy6Z5LPMJk7+pBO\nvNFqWkYi5A1d2H0Ojde8UwrTmQuxNE2Mipzk8mSMlCgEkixDQ7lbPQGcTpxz9fCuwrmLlwEAV699\nEVepR2/duoHrN9xcPJ23DnknTX20c6n2AT5LKXhRgRCz0+uGvjvaf4CTMZHDZhl2aE4N1s6EfJnh\noI+YqlLjiIccE89Cf7kuQ47I5efWkZOzd3I6xcULLqySZt1A8MlYBE4lfoLpwCFTKbW0E3X20m8B\nZ11+0Y2P3sbPHjmyzZuPp/jVS25dm1iNikRj+6JETKFjyWYQtqT7K2hKohwVGcYP3Hv4lYsRdvuM\n+otjZ80fBjMwGu91nSPr+rywKBzwbt2UePzA9Wl3cATNfEXe2aDdtoxFggdyWVUhcFfIWECmlDJQ\n60B03N/YCHpwSaQRRz6Xt4Gk3My6MjgZuXlcwgSqB2EVekS/0ekN3IERbi9JyHnTSmNzy4Vqc9VA\nW1IhYDI4aY3Rz7ItgmuOiLn3srExDMTZgkskFLbrIcX6hltLGl7h8b5zeLZ7Es+ddw772+9MAtnm\ntJSoa/fM1y6/ipeuuPf4jbfaw9ajvaNAM6R0A0kO9nx8glsfuj34H/2HbyGjgtif7+8H5xNoAlnz\n0u18pm+vbGUrW9nKVrayla0MwC8BiTLSYIsq5r75xheC1/w733oD45Gj7f/p++/j5j2H2JyOHmOe\nO286rxSmpJj+0tXXsEkaO0eHExQU9lBlhRER6smkDDw+ZcOxd+JOkgcHj3CRkpbPnDmD8+cI1u9l\n2Nlwp6lHxyNsXHHJkbAWql4+Qz+REppO1A8nOf78r10l1YOHB2gogTxjOW596MKI115+BbsUNtjc\n3MR/9Dv/GADQGQ7RHzroWgoRQpactzqAFoD1fD2wAYmKpYRdgCHXz7jE0QtXr+HbVP239+gh7t51\nKNzW1ha2z+0u1T5BVRVVXYWk7TSW0L6ChzOw2p3I7PQhUDpEyQ62wFPSe7ImnJ6q+gDrAzpNvHkF\nSez6+nDfPed8cowXrjiSvgYR9gnJVJYF6QMYhpgTKsVFqPwwxoBTkiCXsuW1eoo9fHiCfuJO6r1+\nioaggaP3PkExdm0bMgtliddIMsSeRFZrCEZVe8jAvSYWFyhZGz6d1e60OSkBQ+GSL1w8g16XUDQj\nUB7SSfKwQpcILdPH+yhKd/p9e+8htmmMJ1ESwgAvvvVPntrGOEkA4Ss+jS/iAo8STEnCR2vW9iVM\nKGhIkxSM5uKZ9QZnNt33v/fd/xudjptD3V4H5y9dpD7MMJk5VGp0fIpy5OaiFBLG80eZBoLIQo01\n6PSoaMHMISnUxWBhn0GGYXf7DDxOwxkPpHvH4xyPD934UirBMXFAiWmDAZ3S19aGMLHnPuM4S2uG\nsgYF8Vk9uv8oIME1GhiqqusNOkiHDiko5g2O99x6pssT7J5x69+V81v4+Kb77cPjoxBS7Fc1uJwt\n1T4WJJXauc4ZC9VLa+tDn1eN2/fuQUhCa7p9pD5cjhiCyvw4szgh9JBxiV7Pzam1gSf6LfD4kQt1\nHJ7MYagfJBTW1xySKTkDCBWOkz5MQ2EtpnHnvlubj08mLeHqU2zzwgv44fdvAQA+uj9GTejs1S+8\nhm/+w/8MAJB0JR4//BgA0EweQzdufHEzhTCUVaymGGy49/+111Oc5m4diTszJIIqZTcG6PT9OiLB\nCMXmqQbLiAKz0mgIUXlwInDzPqHoZxgiAvOvvPUGzs2X5xZUTQNLa1OSZqhpzYjTGBEV6RRHFif7\n7r5FeYLdC5T2EEXQtDaMT8eIpH9XDHuPXT+IlKHbJx3Ifj8gmJPRBJIQLcs4Spr3qtChPjTpZKgK\nSpWoKmiqyKyqBvUzaOdxC0BTkZFUIKotcMPAKUAQQ2Kb5t/uuV2Mifj28GQf+4cu9aeXdfH1r/+G\newYNXH3BVYVOTyeB084YC07r1ul4hKrxhKsGIJ9DMg1NvGm8yDEkZGyYJZBdlxKUJBrMPgOfGX4Z\nOVHW4My2i5f/t//sn8I0bpNY72VYIx0vJl7HuV23ge0fHuPOAwe7f/jxbTQ00CbHe/jCJQfxbsWb\neLTvOun+fo6SIHVdafDYXfPuwyPs0eKgTI0ZhUCuDofYYi6ue35zgPVtIi1TVWBKV0otvfkCwJXL\nz+OnN51zcmd2C/FjKp08OAjiy4NhH9Ga22xEdw1Xv/BlAEDcG6JPA6HX6YbqHVd+3moC+rVTcBFC\nOIwhbHjK2kBFYFlLlgaZINtw0OnljU2cv+b6sKorqCUVQX2o4AnBY2tg6aGknkNULheNNyN0KBSW\nJDE0VQqlnY5TaQWQ9jtYY85xqvJbSIWbOAPKbZs1FpY06l6+dA7b6+56Za0wo3y56bhElVPYzDJ4\n7tVIZlCqZSlf9j3WmmFEFZxplqI+dffZv/Mw5CkNeYwJMe0WsIgpH6kpFDKiVYjAEZMza2SMilYO\nYy1O/EOaJJRM72x0AU1tyhu890PHpH3ws4cgfw1DxOhTXyfTGhXl6uR1u5W+uEQb0yRBTBh20kkC\nhUajDbTxYcoFSgtj0dC8ibXBDlWQbQ1THO+RQ1J2YBPKxYszKHK64qyDAVWG7e6cxZx830kxhSJn\nUqYx/OtZW++DcdcPWTdF7NmH5wXsM4RJzmxshdDk7b0DPNp3a8m8qFBpN892z5yDoZ6r8gIdCoNP\nxlNw6pO1jbWgrnAynuCTe25+f3znNuZEJVLUNcYTX9FUoqLy8nJeYtBxG9XaaQef3KI1bJ5jRgfE\nLO6iKmrqwxpra8vlmvj3BBa0Y9EYE8gpN89v4ejQHWLAIwxScuK1Qtp1uTA7O7s4OXbOzWw2R0pU\nF3lRoUOVZ4IOCGUFDEjHcHJ8igGlRfS7HaSUZ2OUDZVsibSIaTveH8/wk5+7jXC/LsGW1COdzeah\nUmxn5ywGxLZ96crL+MpvuAOnjLqYE+3Eyf5d7D+8AwAYHe79f+y917JkSXYlttz9qDihblwtU2dV\nZumuqga6G5gGGsIIDEnMmA2MZjSYkUbykb/EB5Jj80CCQ9KMMwDImYZuAC1Ruiortbr63tBHuzsf\n9j4et2aArsiyqX6K/QBkV0ZGHOFi+9p7rYVsTGXVMp9CsXzFW28CGbg/LvsYnRa9z87GMmrrBV0m\nELoWgw5dzyNMjpMzeof75xKFxz6K4Sq8Hs2J9uW3UL7/2Vz3B7AzgD8rC9cdY0VeoOADXFXArdEl\nKvR6zHosBRJuyzDWh0bdG2ode7OhQjRY+sAaiZQZ75U2UDxO00LD48+XeYlsyPceRjCcpMEa9xz8\nKETO7L95QkDD5PR5oTUyZjAXRQkl6gN1gYM+s5/TYxifTe0bCut71K/86i/fxrvf+lW6hrCB3T0q\n8+V5ibqYlueFE589ODjEkA9J2lo3pwGNFveB5mXuWOHtOIDgNSn0DdQLCIoCi3LeIhaxiEUsYhGL\nWMRXiq8diYK28LiEsNHrImqs8H+vkNWWD1JhhU+5kRfhlDVx0jRHxKeXzeUGhoePAAANUaDLjtDP\npMWET4yD8QRHRyTAVmkfTIyDNtaxkrLpBJubdHJ++dZ18CEHS+2eE6zTWs8v0gigGQeuhFOVGWKP\nhcrKHFWNrXd2nBbFiZb4m88IIr+642GHPo5eqdFipKXdbqDNTIgwCCH4OGCFhHEHOgvwyamsNEqG\nMMuyRMaspCzLkKb058l0gn6f0LnJeIKSTyf/5ffe+bn3V5cSaxFNgPzvanhMmgSRoe/1/Qwhl/B0\nmSPhk/fqygrO2Q1chb4TIS2yYwxMLVJIvzMtNJJzIhR0IoFrKy2+Rw9ZSSf8fK2J/pju9/BshBPW\nCCm1dOUWY/QXLWl+TmgpMGTG5GrZhuIG08bNPZQpNcrjLIfy6tJmgWlV61EVaLGODHzj9LeMVEhr\nTzpYDGqLoUqixfY7a1c2XHnr8Hkfj+4TiuANKzS5WX6zE2LN+fflGHOjdZpYqBeYws1mjMixPD1M\nuNRsYJ2Ko5DSWcOYtETJEFJmCnQvMws2FIj4JHlrZx1RQOWqw+MnaNdiumqGem2uSShBfz6Y9jHk\nplXtCSdS6scCvR6d8JWX8nuKAAAgAElEQVQs0Gpzucm04efzi99GQYQnzwhl+fd/8xMcs6ba1Z1t\ndFizbHCyDzDC1oxDpyVZljM7pkmaOPLH4ek5PrpL68qdJ48w4YbgRtTk0zCdbFPWxIGxSEf0u89P\nz9Fq0DyWUkKxo3wsBPJa1FQXmDLj68tixMMswMwmR8UNvPVLxJC8+tI1R7IIpHCloSTTWNugdoUo\nDABN93BtdwUPHlC5elyVePKU0J36XWhtiRUCQHke2l2aixvLPceGioMAhlmA48kIPov4Pj8b4ME+\nvYvCEut1nuitbOHXfuv36PerFIbXtUa0BHj0LLURaHapHSHubmDj6hsAgGwywuic5lD//BijIa1L\no2QCNaJx1xmnWFume/bDECWYtCEmAJd/fROh3gKMqrDPbOe/f1Tg+uuE5r/y67+FLa6OdDevIU0/\nmOv+ABKbrhHuSZZAOS0moNOhqky8vo6ItZ467Q1I3vM8WWCL94x0dIY4qj3vgNin510hR8Sl8vF4\n4GBLKT13X/m0QMzrXBD4GPF6UFUaitlz02mKCaNeraVleOH8bGCJCpLXdqs1wONFCYmox99jSkwL\nQrUz5LC8TnTjFXzzTSrhba5eQYu1sHrLq47oZKx0rNbxeOyQ2fOTPgpmD4e+Qq9DY3aptYm9q1QN\nmpYJpKLnHymBohYDFhLefAUaF19/EiWBuiZZlanrEfGlcp5MQghUzBY5ef4UQ4aab1/dwkqXHt7u\n2gqmJ7SZTQYDlKYuaXkYsHHto4NjSBZDXF3qOtg9L0tnyDsdD1AwTdYY7Wq8jdaq6y8qi9Jd2zyh\npEWL4fSzSQbJHny+BEpuBBiXATRLH+hpjoPHRM89yULsTGkTurLSwUaTqfKVRlov9M0WBKu4T5MU\n56e0MAz7A4z6BF0n0ylSHuxZlqBgM+I8myLnAZUkqWPIeZ6CmlMJ+qJ3npM1ENIxmaTO0fC4tIYS\ntZVhkecwTLMdnZ0iN7WoaISyNjJVEn1WTC7R5Hss0WV16fXVDgqmWGlIRz/1pUY75lq338WYGXT5\ntHQmnMaYud+jUsJ9tior5NyzdelbbyAtaQEd/OBDhJwISQVHn4+VhM9JupYKJfdqlfBQcsKTWeOM\nryOrsMOTubm5jXMWtzw8SzHOmI0jQmeSGiNDyOM9UwpN/n6FAmE4n+caADQ6MVpd6mNJyhyaSzBC\nSghTe3RVzk9NQjgfRAmFgq9/eWcPe7tX6N/Cx4RNTLOyi5B7ioJgVvqlEjX3f3RbeDLiTS5P0Ghw\nUudViGP6fNw0iNhQNvIbyPvzJRgAoCuD5RXqB9xc38HnzwnWP+lP8fIusW9NaXHCa0mwfcnJYMRh\niIA99YyuEHGvxtFojMNjYg3lVYWCk6t81J8xrMrSMdSklChrE1nlQch64xEoeZO2tnRmxEEQIU/n\nu8eUmXSlEKj4lLiz2kWH+3qOnh/j1beIwXbr6jaeHzN7TEhcuUWJlikmaPq0Np7tP4XgeZlMxiiY\nzTod0rrS6y1hmNFvtpdWnPCplR4abVq3smziFOYn0wQxr9nPzkc45X5CkkGZd02V8EPuDY26TrJA\nWAldJxsC0I4q5sHzOdnotdFheYntKxnSgv3RsgzDh9+n+7+3j2Zt3K2tW1M8E8CvzWeNcYr7uRH4\n9DFdwwePcoh1lrv46BF2EnruO6nnpDXmCWuNc1YQvoJg71Vtc6xsXAEAbO69hhuvUm+oL3uODZ2m\nCcyE5tDk6A5uXaf7ffft2/jxj0ka4qfv/QjThPbRMSauR6jKp+5QrYImcq8WbC0geWwJJVCVzG6r\nLIqUD3nTQ6xsrs19j8IaoOKyY1mizOqEysBwT1rpTSEiLvNZAVtwOwsMDGczZVW6Z9sqSwi3vgtM\n+eA7mYxQ8H40OD2Cz4ae169uYmeH1trrV67Bk/X1HCDmNaYJDzahnEBPC7ygdd6inLeIRSxiEYtY\nxCIW8VXia0eiMqvh88kNUkKaOuOG8zvLsgzjYa2xchc+N8r9F7/7HUzP6MT47HCAk3PKrNO0gJZ0\nSowaTYxZYHOSptheodORZzWWWFMoyXMUKZ2IAn8VxyyW12p10G3S9XhCOVFJY8zcdiEAEAYR2nxq\nLZ4/henQNVihYLixWJcF8oJOqg1pwWgpxkWBc2ZC5CcpTsb0F5tLHtZrdtZo6vSyPv3J3zkkqkpT\nGD7ZoqpcE35Zlq6h3RgNyfitFwTOl7ACUM6p3FLxqbqqZgKbgVSoMRBfAJJ/L0lTaFkjED4iRkry\nZOqYdRNdIeUm37QwznMsYGaQCBuY8GlpXHrYT1hrpihnzJIiRcBlYhkswbKYoy+D2WnZGvKcmiNM\nlUOxXpeFcCKQXlJAM0pgLujeeEo4x3sPEl59KjYVsQUBWDtDeCYWznqhFSpsXKbT0Qd37qHos0VP\nLiGZeVdoBZZzgW8qd1I9Tz2E/A4hKphifiZJ3AyRcaPncDR0p3pYCTAiKwsNW5cjYZ3nmdUWKTN5\npPCdFciDh/cx4ubq7a1N9JYIQWg0Gg7Zk0rAT2nsd5TEckHweqpLsH4gpJCYMGNxfTNCzvd10p9i\na2U+SxSAmKJdFrX9vd/8NRyd07z/6Ucfgqse+Mbt2zDMGrLWOqaaUgoe060i34Nl5uNgOsJwwohO\npRFzSXdamhlxQUh4coYK1tpT9gK70BiLhNFxTynUy69UCq3mfPc4ZvSJHi39xlVfYSlihpav8Yf/\nz78DAPx3f/Bfodej9olKBLh6i0zozp58CpHSetLydtEf1TZbY3RbzPwMa7sRCclecePUQDRZ/PH0\nFDELc6ZlAyGzAFWUYcgMqJ+995HzXgyUcD6S84S5+NkawRIWM4UsA/kFtax6LGP2GREi5vWi6eWQ\nhkgbNjx0wreV1JBlrX3nQfJyWpgCVtC6dzaO8NlzJsV0m8hz+q2nT59jwkjX2aiP8Xh+XzlTGkif\n32WhkbO4bBwv4+yA9rwHn32Azz/5GQBgfecWXnuTdOOW169iyOuB6hXQ3EBewse1a9SM/fjRE0xY\n56zVXEP/OX3nuD+ZidF6GXwmVZRZiu3Lq/wkC/TPuPXC85xmYllWmLxQY7mFZWJRWebweF+I/QiC\n50RWVmgxAm0rIOVWgiACplOq1qzGG87XtqxKgNd0LTWShMbaYHSCszNCi+/c+ymu3KQ9+NLVTbRb\ndF+ra9tImIwwrU4heT8KrIeIn2dyfg6dzl+yBH4R3nmmcj0HSiry/QFQVgaDMdVCT09PSXUWpKJa\nUzZjkSLP2Phz0Hcb4jAp0M9qo9YAFZcfyrxyhodBZODxIF1ut9Fl6O6Vm5exzaWIZrOJ4Wkt7rXr\noHlrreurmScsBGKmK5fpBEePSHxQhC1I3kQjk0Gw95gpCiffK/MEMmXvKrmCE+4/GJSVez5LDQ8/\n+tv3AABPf/JjV8LxFWZeaALO1yiSAsJtDP4sIfQVMr7H/nkfYs5+oZr1INWsBFuUFhHXlD2bIB3Q\ne9JJBsEmvXI5RsC0ah8SkstBhwenSASVlaayiwmXPMtzlhU4PcXL1ynJMAcZpsWsDFB7Oukic5PA\nIsGEfZbiZtv1GgDClZS+LDZWliF4IZNKwT+iTfPxn/4U2RFNVNFowPJzrYQAI+TQ0xRdvhZfT1Hz\nnktdAaw+PLEKhpmUUSfEh/epx+bTJ3fxP/43/zUA4Kd/9/cQE0rw++MCdwa0YDU2m1ht0KLwx/ce\nosfmxd/e3EYxOJ/r/gCgrRTGvKj5VeWuR/rBLIkyAkU9n1BBs/Bcr9XFMnvJHR+fI2OIP242sLVF\n76rVbDmasVLK9RUKX6HD3nNFf4Ql3tiO0yEqNqgtcgFf0n8/3J/CC2kR18ZAvEAfxunJiSv/xM02\nvvMmmVf/7JMP8aPPiAU0mVrscs/P/fv3sbNGJYpmo4GcRXyl8Z3Uyp2795Dx4t5rx87P7NzznUzE\ndJKg5DVJ+T5cTdtaZLX8h4HrVxLSg+LyjLEWxsyXYOQ18VQAGys0t37zn7yOjS6r4ffPMeKD1ePz\nEZp8uNu8chsxi6sORYUb10kB/yd/80N8/DmLpT49Qczsu1f2SHixJSqccUJb5hYVs/cG0xTyGT3P\n6WiEgOdF3LD42cc0tp88fQ6fn0NeWSfDME8ILqvR2lP7BVqXONHf/AMHXQFcLLDU/oLD/T9D9ZzM\nZ2MEOEzowJSYEjEzZZvI0eDv17aCkfTOHz1t4jMW6rz+1jXc3CV5mkaoEDLjMQyabg+YJ6y1aHIS\naoxBr12DAldw7yNy2sinfZiSxCGrIsXWFr2Tl26/jLBBY/YMJQ44efjZhw9xbZcShrff+Q5GU1o/\nnh48xgozw4tphfNzZq7pxCVR2hrkfHiSnkLGLRwoi5mJurXQZt6SLO2LHq+pmGZQLI7a6bZgG9x/\nNQoQchKY5zkCBlz8SmM8pPtqXH0b9Wlr1D9Fp0P3rloKBSfpB4eH+Pw+SQuF7RI3NugdCSEcaxbC\nOsbtaFK4Xl9hcsdy94MGhJ4/GQYW5bxFLGIRi1jEIhaxiK8UXzsSJavKncqkHziH7fNxgiPOiCtT\nYYcFOd/3ApzyCbwsDFaWCI7+lbf3MGRdlfv7J/jg7iMAwL2DoZOTD4XC6hJl9K1YoGSBwts7e9hZ\nohNDVJxjOyZBwDs/+xu02DdK3bwCRm9hjHalxnkiSVLXWNxqRDg4eA4A8KMWFLOVyv4Rmk26Ryk8\n5FyqG40f4Ow9FsDcu4HVG9RIWHXX8YSRt4PzBGBods/LUDKa11haQsxsK+kplNxcfXx4hCHbPWhj\nnN+cgSFfQAArvVXcvPHS3PcI0OmpRnb0zPoJg8EAITf4NVUE5bHWTNiAxxYcRZIjYNbezl4TD47Z\n3buQOJvQ9d19RM9hNMmgI3ovjVU9s33xPFdOFF7kEKfpdOoQTmNL17zr+8Hc7DxhKlfW0cZgzKyi\n5MkpyphQi8lSDzmfOzJtZlUG9FEm9H42fWDIJ+6Btpjyd45yg5yPLKc6R0cTKhB4XZSMtPnCQ4ub\nJpd7Edqay7+BB8WCg91WDI/tQqLQR/oCmiYHh8fO1T5uhIi4ZFNCIatLx03lvh+VxWhIJ8bm8gYC\nRoQ2ltfQ4hN4t91Cg/WChJTIGCoR0qLRoOuvUKA+2PpehFaD7j0anyOvZu/W58ZWXZVIDSGb3W6I\nCdupzBOPn+872592M0WH7+Xm7i4+fULfc3Q6RljrRJVnuHp4BQCwurqCkp9PmeQIm3Sd7agFVSMg\nQjtdniAQaDYCvubK+Y1JT0KK2r/Rh2Y6bVEV8HhueF4AU39eSpRznvBrhpvvKax1axZsBeGx7YoF\nfus7NK+328ZZ5lx96TVIPnmvrfXw5O5HAIA/+qv3sPESsfb+7JP7aHHJ5W0WapyeHSNN63KfcmhS\nFDeRMGI5OTyC4abeTifElEs+y60QR2wjI4QFXgDFcM3k4sJCA3kBe7qIQllXXrZi5tEnBFBmZK/0\n9PG/RCsjRLDZWMLfvk+f+fRZB8sBtYO8cQl44yYTHeQEtdvQRw8NHrEu4T/979/BP/vd/xwAMBpM\nUPeS+1EbXrAy9/29+tJNCK/WJSyxfZXW/e7lX4baIabhw+fPYY9IdLQqgLufENKy1lvDzi7ZCjU9\njUd9et7n5wnGPFe211bx3e/+DgDg83uf4e///scAgCuXA2f5Y3SONK8JEAFszWRRvrs2bQVqrKXV\nbcKq+d+hEQKK1+5qPIHOeJ/uCGRM9IIPlHXZX3oIVN3QXuHpMSGd20ePIXKaQyvLbWys03jNS4uE\nSVPVNEHM3xl0QwxSquLoalbZSob9GRlKehgyoSduhgiZFKICDZjjue8R+EWU8/ISgiFs7VtXeptO\npzhhBlbkWZyy6vjDp/tIuKQlvBBXr75OXyQ9pFy73riUYG2D6K3eTz7AeErwcTvykHLPgTIavZh7\nU6ZjrO/QAL+8vo6IN7zVSGB5j/77uBpD1CroRflC0PNwNHLiZwIGkks4VTqE4fKJ1xkg7ZOsQbPZ\nQ5MTivHJIfr3fgoA6D/6CMfsQ3b17d9AsEkT5XicoptQ2Wa5Oka4TYqt3b1rSHlCLPWWcfCUBt3D\nh49hOdlYWlpCt0fJW6sZoN3mZDLuYHA2n2GmYC61McYlMVmZoKi4H6f0kLJRrd+M4PncK5EZSBan\nlEohqVclr4VOlwbt4bO+mwj1+y1UCw/36R29fLNEqzETQXVJkbWuv6vVarnSUVVpB9NKKecW24zC\nwCVreZ4j5g1q2omR9Qgivyt9PHhM43SYpOjwBnopVLjEkzCqCjya0HM5tQIlX+95rjGqvf4qA79i\nj64qxh/9KZUZzDjBEpu3XvEDvN6mDTe2cDD393bW4PGGsV5lOJu/goBCGFj2rWvHPqra7nCcII7p\n+nu9EIMB3WM2NIg4SfOVmBkuCw2fJR08Tzp6dpqlTpjV931X0YobAYqc7ivzBaoJLXABBLy6o0Xl\nEMzYgSqdOW+nE2FvdX7T0yIvUbLYY1GUEJz0762t4+EB/W5SlTjo03yKpMQps4GLqnLK5GVZosmb\nyss3LiNJeGEVBhMW8xRGwG+xmWtpMGTzcKMNfGb6KuUh8GsBywCKkxQhZmNTCOGEfr8sOCdHI/LQ\n4dLaeX+MIKRn9NZLL+PePVpDHn74OX7r938FANDprTnhw+nxM/zh//7HAACvuYGbN4nd9d3vvA5P\n0Ti4vEVrxnmV4vkdEiyN4ha2uaQEAFXdtCfg+iCfn0xJFgFAGMzKnUIIvICPNL5YJPlC19N/HHZW\n8oM1Tg4Geoz+UzLE/uEP7qN/wi0dV1v4/JSe/UeHEq/s0nsOVgMMWJyzrRUmQ/rFj56VjnF7+/qr\neP1t8kYts8IxJPvngxcqdX3zzTdQ8N5QFBU6m8SoDNZ2cJvFa6ONa7BDklBo+m2s8HrTH1V48re0\nZhw/e4I19rzb2L6EIVP++/1HuHmZRCkn4xLDAScYvodLeyTNG0UGmsv4z06O0e5Syf387BSKD1jF\ntIDHvxu0IgzZTHueELAQXD4r0wQVMxnzoxHCLWYaJgVSFhuOqgARS4CEzQhhrUaOAk/YaeP8PIJi\nQe2ws4Uso/e10gxwzjIbIvCdzIysKkhGR5LpyA0T3/OcgrrSQMOn74SewLyAVyewKOctYhGLWMQi\nFrGIRXyl+NqRKE00PABAVRn4ijLEOAqQc+ZolUHMFhqe76FKKHPcPzrBjWvUACl8D4ob/Vpa4hb7\n5xhDaBcAoKxwyiw/vx3i6k1qKvWLCU4P6TS1HHlob1PWeWV9EwE36RbTMZSI3HXXwpXzRJKkruk9\nDHz4rJVTag0hmZHVjpAXdPodZAmaXTr9WZ0C3ERpqzHOHxAbQ6cJdr9FsHHWWIXHZdDV5XUES3RK\nDJpNxygrtcDKOqFzv/27lxwyI6WAZmTs/Pgp9p9TRv/ssI95c+ga6izLyjWpe0rAgt7Z2ISoLIsI\nej6yjN737vKqEzmFtLB8Qs1KwOPTxKVNH+0OQf7DjBoJB4czmDkvCix3qKxSVrPfl0r9gwxKKQUu\n6qTKOU/4yTiF4rHpCw25StdX3NjDfkV//uT+UxwckT5Lrivsj+l+DiMPukUlvwIK53xdJ3mGIT/7\ns8Ig4/rfdJjh9EPy/aq0wSGfisOqwqUlOoXurDXRYATuNDUYMiNTG40l0PuYKmAczD+F45ZEWTPv\nRIKS9a+MVoDP411o+CFdZ57niNmaKYpCSEbVtDWu7FUZ7exjut0uPGa0eZ7nSkm2Mgi4gdWG0qFY\nFjkgRnxtAi32a1MeUHETarfdws5WZ+577PV6TtesKAqUPC8bngePj6HjqsKUh85St+W0kQ4Pj3Bw\nRKWdIPDRbhFytdKNsbfOY1BXGPE9Dsc5JswcbYUNpKyDoysLUzdGWwuwFo8QEg5VERK+X7M450e9\ntzdp7m+udbDaIxgyDBuoGJ2cag9QhI69/Oa3cPuNX+JrypEyaeFf/cs/xKMPCf1+/Z238ewjus+b\nyx00I/q3Mc95bG7g1g1CCn788T4ePaU5enVvA5rHUlWWiLghvTDKsTgneQUGIqCtxQvoF1+InwNf\n1cCPATTvDVpYBEyGyPo/wr2//fd07X8e4DloDP5o30fBWn6ZTHHGjPE/+qkATuh7/uBXmxglrGkY\nBfjt3yGk6M0330a9bXqBgs+UT88L4AfzEyCWOh13Z9Z6GDGKVZyfQLBX6G5VYvMatZ48SnxEYb3G\nKsRsE6SiGE+fEfNu+vgRdlap6TpUDRydsp+gH+LV10lQ+cHDz5GygG4xqdBlP9qVZSCd1qwF5UqZ\nZaERsW2YFS/Cr6SqjOJ1QloDj9fXNM/QtLTOhSZGyY3fKozQ5DYOXRbwY9YE9Hw0YnpHk+QIH33y\nAwDAa9/4LQhF7/HJyWPcPaTn0MhiV0nQukReUMUlDNpoNmidHg0zNCN6jw0vhM/7qy41dDX/3g/8\nIgyIDVxpTGvreo3azRjXr14BAPRP97G2Rg/17W+8ib/8W6rfBkEABCyMCeso5X4gIWvF5GtXEXBZ\nJwx8/PmPWDVWSIyZsfXy3hZiSwnbvcNn+MmThwCAXrODX/sW0UabjQ4Ml0aUp2Dz+aHZNMud8nIr\nDrHK9zKZJigY7q3GJyh42lT+MjJmcOmsmMGTHlyfRHLyFIPPqW8hePmXHUNNdbbRCGmhS4ZjZJzs\npdPEJauT6RSnpyzGNhxizOUTrQtn2NhZWsHW8ny0ateHJMQsifIEJikrpIsYAxZJW4m6GA/ot4OT\nAW7evAIAmBYTeLzItDs99Af0b0U5xqushF2bQB78uw/ATGo0AunKib7vu2S1LAsnVmcB16slpUSW\n0Xt/EamKp48PcPtVKp82fI0xU2fV7i7u/ewRAODoyVOsMRU2VALHDMcf2wofG1poDsockr37TOhh\nzMtOH8aZYxsjZmasfoCMF/RWu4XtN24BAB7kI/yM1eXDeAklJ2kH9x7AY6V0T0lYvr/fn+Meu902\nSi4jlmWKEftLTVPtevqiaBVZzgcar3SyH1VZuVKdBlyfox+F8DhBajRjtLi8ZYxxBxFVeq7nqhAl\nLDPylFdid5sm3dq2Dz9k2H2SI+N5UOUpdDm/2KbVelYak0CflcMn04kzydWVgeHPtOLYrR8QEn5A\n73E8HGCFzcB7nQ42Vqhkcjo8QcXZwHiSzvr1lEIzZumGJIfRM7+ugiU8wihyQrBCKMzye+tEWb8s\nru1RaXk6TVwp5sbN67h8g8o+o6TE7a1XAQDf+fa3ENXJkKkgeC1dvf4W3lE1rb/EOfczTvMKWUjr\n2KhuJbQGr79OCcTW7lV8/y8o+ZLSx+Vd2rDL3HNMRs+PYBSNBz9sII7o+yZZBm9Ocd+5o/46YVxp\nGghQTWl9P7v3rzF8xsnijRAroA36k881Sj4ArrSnOGZvw49PJF7dZe/H2Mfz5/SMLl27jl//5zTD\nrvNzBjgprstDQYS19c25Lz3wQ2JxAoBQeO89OlSdTe7hldv0G0sb6/BYWX6zHEDmdX9liZO657W5\nC7FLLSmlOcY9NmUO0cYopcT/0vY6NjaZMWwMnu5TsmG0j/MxlbIH51Mn7rvUW8aExTYbQcd5nhZF\niiic3z0AVpDgJujQvX2ZgINB0XTtL0jg+pJbnSayE5qvNgdiyQlVoeHxgSMpUjw/pnL1pdHr2GIW\n3k/zBGKZ1pJhkmCiaTyGsQfNe3BDp5CaS6LjISIWvx4OzqF5P7ZmAvOCSdSinLeIRSxiEYtYxCIW\n8RXiF4JE1VC+0RbWzIQQd7cpM93d6CFimfYwbqPJrJ715a7TdRDCI1FAAMKbNSmGYYRrbOfQ+s1f\ngc9meH/y5z/FkNHJ/f4Ar1ymbF3aGO+/T6Jr7x09RMBefm+99gaafEqMm03X1DZPFEXhShe+J9Fj\nH8DQDzFhaLuaniHkzLfT9RA16AZGSkIxgy3wpPPrMjrDYEAnhtX0Klos6na6fx/7+1RykK2mE+/T\neYmK0arj0QQVsyvCyEOboc217iV02cfL0xZiTqHGWjOrZq8BAAQQcTOyiiJoS+9gUuYIQzoBPd4/\nwtIylR+WVppImVQgpIfzM0KrbDJEzAjNt9iTalgAacbIm5RO4M33fVRcQvA8D/qibRAjnKHy3LvT\nWrv38mUxnkwdLL632UPFXoj3Hx3i/kfkzr4Rhng5pvtZLTUOmTH5g2kfx8yemxqgqJG/TCB1aJmC\n5FMZlVrp/S8vdTAc0vu88crLSLkU9cFHTzCa1sKMJ9hj64JqeQn7+/TspH6xM1Dgx2hw+XcwNCgY\n5o4aCnuX6PuV9FExqtpstSBLejfj8RhLrWW+F+sc6FXgw4/o3qWnXGlK69lzF0KwuCTZ5fRZXBSi\nwMYmjZWV9Zl7uq98qKwucSfon85HgACAZJqSaBqAJCuRXHCj7zKTNS0T8DDCaJIiirhJXpS4zA7x\nj4ocKYt/BhtruHmDEELzeY4yp+sXMDgfUol+WgCW9dHCMHCIVpLn8GrUzvcdYmoMHKqaZRkCf75S\nUI2smorQfABYv3QDl269DYBEFs2IEEw5SZAx6uD3VhC1CVn7/f/2f8DDO1Tm+4s/+b8gK2p18Kxw\nyGPNxFRKObRte3MJb9yiloGffPgYXfYkW+210J/UJJPKPfMo9NGOmDVb5K58+Z8uWD9KFs5DUpQp\nho/+LQCgOvpLvHqVntfWHvCvf0zjaFRYtNn25p/+Uh+CNYj+5kcJvvUGr1FBgcMJPYPe+jouXyKU\nWqhZyweZtXFp2s4YhfOEkMIh/GWl0WE7psF06ix3NtbXEDDyfakRoGItsXZeIedG/uP+AGpKn2/3\nApRrhJjm/THu3yfE5vykg90tWp9fuvkKJI/TT+/cga3t07SPk1Nila+trWLnBol2plWFkwGRKiZJ\nhuQF2lxgPYcWalPB1N60okLODeGeJxEx8cIvBAYntHY2/AgVs819ZZHw/nc8PkfCWm4HJ0+x0SMk\nKhQeQkZXS2GRshE8yecAACAASURBVA9gpuD0/Mz4FGcsup2IAk/PWIAbFQYMw11dncyYuHPG1++d\nB+ESAwiNhEtAYejDMAbriZmabbcV49vvEt0zEqXroDfWOGaWhoHlXiPlewhM7ZfXwm//6jfp8yLE\nh5+w6KWRWOLa76+++w1sbV4BAPy/f/bX+D/+P2JvPBtlbhO/devluanxAFF/a6aYUNKpsSJ2zFtS\n8i5pgBSnzzBmGQRpchg2Lk0LwHdMHgApl8VOH6BZ0QJgVA7j8+K1vIp2rd5aVgD3auz5DWTMFGoI\nCy4tkyo003xPxyMMs/nKJE40USjXbyKEgBfWVHiNpWWavCYbI8tpES/9Dp4e0iYjUaLRrSUefOSs\nAN32K0S8gWzQGo/vfXMXH97jZ5JVsLaeuNJtxkJKKG9mGF1PViElvAs0oHl729Y21vDk2WMApCju\nNegZf3r3AcKCBuFmFKBKBnwlwC3eIM50Az8smTobdqBrWQejkXGC6BsDXJicksf7ZDjA+jol3a2u\nj49/SAlbMCpxq0kLdppOcfqENkOxugHDZVHyDpu/RGIKi0rXKs8hOh164KtrLbTYey1NLDweX57U\nkJw4D0Z9ZEs01oSw0NzHUOQJfJ6LEtqJJBqjoXnc5FmOsmKDaFicD9mrDQlSzmYGaQFwGbaofMeQ\n2VhaR6Mxv19XUZbwWEu/KA0MbxK9bhfbfKg66o+QMrPsuK8xno74mZQoWJ2+2+lilXsPy6xAxGbK\na50eTE7XNhykWOMDU7MCpnz9wghn1l0UForLIQICRtdJpnHCpGEYuvHwZVEnN8srHjbX6f0Jr4GC\nN9jQFrBDWjeKk0NMmb3buXwVLWbmNro9XHmF1Mv7pwe4+8GPAADj81OUtR8kC3N2ux1Ypo4naYpt\nHqvffFPh7JzWs8dJhjEn/EII5+HpKaDNDMJkMoH/n7iaV4eFgMeM7vH+H2Py4H8FALSqITzusfns\nw3McP2L5Aj+D5gPk1dYEr96k8Xt73UNX0b0enWkMCxp3l7b2sLFGtHoIfEHu09bSCniRmQhEcdu1\npOgqQ6vJEjldD9OEEwzloeCxVqRDhMw6Xg4iNLZ47kZTKEvrhGdS/OCv6F0OR2OEvA4djE8Qcl/e\nu9+8gZUNSrhLU+Lv/vpP6X4PHyPjsvmzZ08R+5Q0Bs0QbWbn2SqADOeX/rkY1lrk7KPnN2IE7FgR\nKoUmjzWdagQsnbLU6bpyp1A+Kj6c9Ufn0IKu4fj0ObLLLIdUFih4nZ4kBVJdr1UGlsGX6ckhNCeu\nDQ9oBLxulQUEP/OtZcsq1vPHopy3iEUsYhGLWMQiFvEV4mtHoiwschY/DADXxFlZC8soivU9CD6x\nS6Hh1b5TquHk2AUwQ7QA57wNWJga1hUWS+yF97vffhU+S86/9/FdnPcpC9ZFhavbdML4F7/3n+H7\nP/gQAPDRR3exxt3Mly/tOSbSPFFVBnV9UUqFwKv/LBnypb+undono1NkSS1KaBzE7ykfuhYfVBKK\nBcP8wwfoNtlxem0VlccCm5MRJDd0pmmKoEcZfawkIka3VJFjzAKI/SzBgE+ao7JAoeeDLWurCq31\nhcbyACWfUKWQCLh8ITwPBUPNyg+gFMP8GlhiJlklR7h1k8qo02GEFHRiythQcLndwM4yvevziY/S\ncDnYwOn+CCGgbS0Up2bIoRCuBGxegA4klYeNzW3+Ch/7B4Q47R8NsMonRn+SYMzo22OUeDemU+41\n0cR7Z2zdU1ZQtfUJDCJbn1O0s6Cw1rrG4zQZY+tN9jQ7PQNYg+gbq6u43mDfxcrDX5/Sc/x8VCLi\nZ11k8/vmAUAhFMDlRd+XWGG/M08CgwEjl+ESDHulCSkcEpWkKQZcZtjcWsFkOnb/VjI7z9gK/Khg\nrUXG15ckGQo++Y/TBEfHhJQ01y2m0xqJ6iNuWXe/2z1i39648m20G7tz3+M4K+DzYbkstCtPSVhs\nLNP8WGpGTuMsLTT2Twg5fSdowPIYXF9fwdoyNXH7SqAo6aTabXVgCm6SL4A4ou88G09dE3uRliiY\nXBCiwjSrbXRyVA6Vlw699pSk+twcUSNry2trDi0S1kDzGnv5xi1oLtmm/VMIJyKoYHj90RdK3m98\n67sIuDR78uRzDE+ptPz40SMAwLMnj1EmNcpksco+ht9+9zVMGc27/+gA739CopDTceIayOMgQBTx\nXJQKdk4Lpp8btl7rNSxjP9aGqEb0++ef/08IC2rX8G0XlaBS1GvXFTZ3CFE5Ho/w6JCuq2EqKJ5z\nV5cszJC+//2jFoRPJbDt3etotQmVhACEwx4Evqhh9QLlPBU7BF7CQzimtXQ6OUWVcXN11celPULA\nPLmGsyMqI/f7Q2geX5uNBiSXoh4/egTL47q33MPZGZfhBsc43qeqzGR6iO/9xm8AAH7pm+9As63a\nv3n+gSvBjwZTJDy/l5ebaAVUxl9uN1+ItU43Sv/P8z1n7WagYXm85qmFx0SE8XiKkv/BKDWwXE3J\npil8bpfIphoJl+r21QHMW/TMB+cJ7nxCzPMCABrswSdnGq9VlYJ7zJE3fGTM7hG6RDHiMZA3IWrN\nqDnj6xfb1JVbyLTR4PUHUltHnxZCQdd1O2udP5u2cIwzT0hXQ66qyn3GUwrGq1kODUhOZtZ7Pn7n\neyQ0J6VEO+SJ3Yjci93bWsMf/IvfBQDc+fwxpCr4dysoMTMT/bKwVjhoXgjrejKstYi5X0RIM6uZ\na+VkdVOduaRxfW3NTdDz8wEqZhOdjY6wbAm+7YoQMZdGFChxBADdVEi5F+FseIQxJxijbIwhlxnK\nyqkpAFqgIeZLFGdyCdL1GJVlhbLmL0M4xfDKAiqihbYRx1gJ6bd7LYmSJS0mxT52L18HAHiXb+KM\nE8pH+7SZXdpr4doWfUf5bIA+5wrCwgkUSikd6zMIAnddVVm6d1FV1dw9UZXRKJntVJQGkyl73mU5\ntpnJEysP+wyvp1WCl7ncthQ2EfEhAMriCtOS8zxHyh5zlTGoWO4gz3KXOOfprGfw2cPn2OE5cXWl\niTaXRVuwuM2U5odnGTrLBHmLVuyS9Hki0xoFS0c0UCJiE9Y0raA4Mde5hcdeVr2mj4TdA3prPQyY\nIn866EPymMUYqCeUn3vOSFVKgTSlF5elOUoud95//ADnE6LJ7762BqHov0eRhc/MMC+QCOP6ICVd\n/9U88cNPH2KDxWUvr6+68m9WFmhwWW2l28TJkO6rshJ3HpJI7a0Hj/HGy8RE6/U6zjBbCB8xe0BO\nlI8me6QttTU0JzXGWtSTuvRLJ9HRbLcw4A3ytD+E4U1IeDPGohIC3pz9NIWhZ9FdWcf6Dm2wlZ4p\nk0vfh+bESQuFzVdIvVyEEQouWUBi1vvkhbjy0msAgDiKcM7lN8/yoVOGGA2oleDw4BAT7n06fLYP\nwaziIkscLbzdbmB1lU2PkxFG3NsWhKGbXy8a9SEZVkDyjki+drxGlyMM7v8vAAA1/CEC1GvxFD4L\nLfpLAh1B7+HausI7V7hEZXNUlsaszS3OJ/Ru90cNtLn9YGv7Cnwu71uoC5594j+Yfi9Q0PM6qOqW\nlEhgpculuobBnQeU8Pyb//MpVta4l+mll/DaqzQ2r918xckRHB+cYcQJwHhaYmmVpXPgOfHPIhnB\nYwmh87MCf/i/kdBq2FA4PbzHF+TjJjMPNzY2UHt+9+IIfp38ehIZ90vOFcK6cdZpddwYn4yHiHj9\n8CCRjGl8lVpDcqvC+SDBWovAjt2NLXz8AXkIJqca45Q9Vs3QiZ1KGWM64ZygGcykVkKLrO79FRqc\nxyFPK1QF5wRRAHCvm0ZEJ8MXiEU5bxGLWMQiFrGIRSziK8TXj0RV+guChzXTC4BDk6w1sz8LCfcR\nO9OVEp79wr9zLBVDpSUAkEq677e2xFKLTlW/8+vfRsGlsUbcIDU/AEWeQXKT2usvXULG+jVlaV1z\n5DwRhoFDjYQQToROygsaR8YD+ATry8hZE5gUzgqi02o77aP+2QAeoxu51rjPnkiDzEfMn5FWcnMx\nYD3p5PNHRYWckT1tKqC2Z4B0jXVWCieS+GVRl2Avil0aYyHlbPg4bSZrnRZOaX0k/C4PRxkkw5Dd\nbhcln6ghJZaWCS5OD+mkOB4n7uS/tr6C/iPSMrHWwuN3BwHUBLCLaJPFDDlTSs3NshxPJ85TyrcG\nE26UNSDiAwD4SkHUVgGyhbL2hLTSlb0qkcPwiReyhGKbFUgFobls21SOjRWHFVJmoUwHJTbZ+3Gc\nJXjGaNjrPrDC99EUORqsp9Xtdl6IAKHSCbycrmfFUyjBGj6Q7qQqhITn1+I3AHje7VzawvFzQpAO\njg4QMQtWV5UjGzRiHxO2d7HGomDUxVQGmhGqg5N9LK3xu91s47yk7wxF7ogCVvs4OiN0CDrAztp0\n7nv88OEBxhN6/uvdtkOmPSVd0/v6cgd3n1Kpo9RAn0/yw8kUbWacWVM5BKSwFqGoBULFrLFYCmjW\n+KqqHJbXqiAIAJ4beWXQaxOKKCBxfE7oYlIWDikw1iCbk+QBRjPX17dw9TYRcCbjEU6OiKgSKYmn\nzN6t8hzhLqFVQVgiZEFMM9ZfWG8tCw1G7RV0V4il2eD3W5QlBifE3mu3fHfyPz0+xp2PCMWYlAJh\njaavdrF1iZDYaf8AQ2bWSgFY89WQqBrhYylWum6ENfaL6eFfYfL4/6ZrtOezSoAAlK2Z4Rq1Oaqs\nDJSZldnrFoqkVHjGArrDLMDeDUJ11tZ3IHl+2AslvC+EwD/83/+RCJsb8BgZrYoESz0as7/6ro/v\nvHkFAPDk2T7u3CFLsz/7k3+LH/7lXwAA3vrGu/iV734HAPDGN17C02dUHv/47n3E7M+61F1yFmtx\nvOSuLAwC5IzMlHmG0zMaK+JCO8Pg/AQrHSZMhBFC9sa0wsJ/Ee8eoWE5xQj9JhqSrV5g0R9TyTLJ\nAc1VnyzXCAyzVBOJlNHQP/3+9/Hw/iO6htRDg0VTY99DwXvetMgRMKtfhtatW4UxKGqU1gi3Z0jp\nORSxLDRQ1GMgR4Xu/PeIX4hi+ayPpqqqLwg3frFMxBNMCCj+TJ5X7kaDQLrFWko52zyM52pUptLO\np0pDOl+uXseDcgqmFeratZSSlQNpM6j4f2R5BVPN/2iENFDcN2QqjRrgC8IQlpMZYQWCOrGRxgkC\nakE9IwBwfHCEqKbE6wpCzSDPklfug2kKBV4MhHSLofSUM5fVxjjI2RrDSsn0bHFRHVnMB0Sm7LIp\nhHC/p5Tnkld6j3T/F/X0JkmOkEXMPD+AZhZlrFroT1kw0kzQjWgBWevSBlaIEJM6WQkbrlRYlqkz\nUQ2CAB4rX2s92xR833fGwHmeOyXlLwsDjSZLNqSVwaRm29kKOdfjQwm8zjmZDkKnVtw3FgFfy7TK\n8YQ3MWEEZE29lgqSH46SQMEMzuV2NBOTtBV83jCSpMAjhuzX2w3EXPLzpYbPSrvtbsv1q80T/nSI\nkEuTfiWRcV+WbLbA2nqwuqLEG0AjDBDF9P6qwsCyBIGxFudDSgam0nNwdhQHCPjaqqpEyX0brVYH\nG+sEzV+7dQ05l36syoGE+nryoQ/F48OYwBnyFvkAvphf4mCl08L1y9t8nRWV7wHIUjkRvbV2G10W\nxuyPcqBWgE8MBkPqBek0FLodFvvTGnkxY4iWvDl5nkKrRSWts+HA+doVRQ5bC6vqCpL7N7utJop6\nFZ9MnUhp4Ck8vvvpXPd37Qr1h22sr2N5hZ7p8koP9++SyOKTR/dwek6b6vMnTxGE7MV47QaWuMxm\nk9T1v1ghnf+mJww6y/SdWUTv/fToKaZJXZZNkXN/5aA/duuxH0R0OAWwurGBtS1K3Ew2wBr3oXnK\ng65erIevDrdKCevYzkIYlKM7dC2f/89oJMRq9f0K9ZHKQrCBLiC1gazTX61c+5IsS5iUy0xJhCfn\nvKb5PaxvU8tBe2kdcxVtXiC/kH4AL6TNOmisu2TcNk4Qch/pxu4lvP0NYtId7h/h/n1iDz+8exef\nfkK9vHuXr+Gtb7wLAFDCImRV8+XeMp48oD4xU2ToD+iwcnb+DCXLBWitUTmpAYGPPyZmn9EWV3fp\nd4Ow4Rw4rDCQ4sL+8aXhCrEoSgPBe3ygBVq1C4YuwdVUmJHGhA8TyvooGfg4On0f9aJuUSBu0dza\n3uliZZWlOLwMlpOuRjtA0KX3dXR8iIABizCIgKB2EphiqU2f6bUDWE6ibl6TCLwXMyBelPMWsYhF\nLGIRi1jEIr5C/EKQKO8io6puDBbSdfpLKWelIWtcw7LWGg2GEquynDWc6xksbLR1wptGWwg+mRdV\n4eBSzxPOVqHSQFg70AcBsrQu//koitpCJYcQ87MQtDYOmteVdk3jnlIXHM1DaEYfqkojrpuftUFe\nW2KUJUIu84RhgIxPep5S7pBjLqBH5kIZ1FTWoXwSM3sWanetGzNnZVApqDw1T9QIysX3J8RMWFFK\ngSCYIWi1KGe704Lm386Fj+YSnbwGucZwRN/TqAQiLnk1WNckbC7h4RNCc9J86p6PgHLoZVmWzpfQ\nXnBPr8pqJuwo5dy2L1ev7kHwGFF+A2iSvtWPP3yMISMY2otxTdFn4nYIb4fYW7mKkD+jksfl7Q1c\nu0LMso8++gxFWQ8Gzx1ZNIw7eaZ56MgHChoeozfbng+vTae1RqCgAmZIKo2EkYHRaOKa0ueJrCgg\n+R5P4uZMh8UaZIw+Kek7R3NbCNTNu2mVIFxq8XXCieZOkhGGY0JvoARC1s6qUCJnAsTa2joEe1/1\ns4mzkRgeGUhs0L8VGrXbggosLGu1LHe3EQWrc9/jaitGxK/82vYGDLMj88rCMLq4IiQub1I5YTh5\nDMllhs/uPsKrN6kRe/nGFsZccgCEKwt7YYiM14m81MjyWlgyBk9XVCipRABAl8bpnJXWIGI0b225\ngzN+bsNJjkk+Xznv5dvUXLyyvulO55sbW6j4xw+e3MfuFiFO7VBifEgI15P8CMcrJEwYNTvwmOFp\nrHUIWq/bhuB1WHo1q68FGXT4Oo/xhJvwz/pTNLhM6TdiJ6S5d/U2WtyQfSQkRlNGdJVEYV8AqvlC\n8Dplba23DKtPcHL/XwEA9PGfY4nLnLpUDn0SUkNwi4Y1TFQCUFXWkTz83KBK6V6PjmIcnlPFIlrd\nwdoOzeMGs3CBF9OC+nkhhUVlCIH3PELcAcCqLZiqRv4NAiZeXLnawe42oZDvvDXG/hGtN3c+f4jv\n/wk1ig+nBTZ3afw+evIUmgWDK1PAD+uSnHQopJTmwh5sUDHKuLaxjk6XO8uVB49RSWsrBC+goSQw\nY8YNxlPkhnXXrO/GxShJkLPFWp5IpPzfPenDZ0JJUZZotul3220BKekzbX+Mh59wk7x4H++8ScjV\n0lqITofXy0xgrUff02oBLWa5t6IAnSY9h06s6yUJzWaKNvujzhtfexIlpXId+rDUHwGQKGXd71Tk\nmdv4fDWrVXq+7xIJ35tt1EWWIWPTUE957t/mRTlT1ZYeHJtYCFI8B6BNCct/TrLSmYYCFqaqFbCV\nU8CeJ4y2KLlU5ymFkBkGUkhYWTP14CjNUnluYQ08H35NdZUKRX3RdvZ87EUTXWsvgKSz/gzYL5pD\n1smVkOICBX32L60lEbN5QroanUDIzC2jrTMaDcPQlVdzbV3vg+d5s/chBEoWV5V+4MoC+ZSSBwBo\nc1IW+sBoQn+fpRY+U2A9b5YcGqth9Uz93iWQF/z9giCYW+bgyu4WjCtPxGhwKWe19x7O92mDe5Q3\nsdSmDcW3EiNWVX+upxiwiu73bu4hqA2oi0mtH4myCGE5AZbSOOZXlgCXO7RwK6NQcmll1VfocW+S\nCQWGPXoG00OLkIfsYJw6Rulc0VtHOaWFprQ5Aqbee2WAFidjod9AyYnB1JB6PwBEgQ+I2vcN8Dg5\nNHnhxlSWphiwWnar28LKOiVISoY4ZU+svLCo+IBipAB4cVfQMAnN6VYp0a3LsCcFzsrx3LeojcKD\nx/sAgG+8dN2VfEtkyCZUFiyKHO2YF+5ygpwZl1bnGLKicanXMB3Rn5vNGbVbG+DojPoTy0pjPKnF\n/ionmNkII5S1xAiEWxuUsPD5wJBNJ/D5UJUhgZozF758g5Ko7UuXXVNgXhTY26M+pHH/2MklXH3p\nBoo+rS0BMkRLXBY3lRM/jRox2k0a61ICOSeatRfeeJxiyhIAaV66g9DSxpZrBzg7H6DVZRr8xjZG\nXOr96LPHeO9j9rEbZbhw1vmKYV2bQjY8wOQ+mQs3s1PkXAquPKBeuq0Rbp5ZDWhRS6zErlUih8Rj\nrt6899BiIil52FnbxuoWJS0qCGZMzX+sJwoXRTi/PITVcL0kqCBrwdowhmDpkbLIkQsuR8NHfQpr\ntQLcjOk6r1+6hpMTuoGHT/YxYMmQzIROWmg4GWCpu8r30nHtHd1OG48ekBxElpxiqUuHp1devoHN\nTSrrxq2m64/TukDu9st5Yva+tAG2dkiQeZpo3LhJf/aCEmd9SghH/TF0Wme6U0Q+Xf/KsnDyJ91e\niJhZ0Z3251A+lTXfeAVo8dps/RAh70eBbSDndX2SVMj4+43WqNiXcJiUSJmp1zzzcLN8MYmDRTlv\nEYtYxCIWsYhFLOIrxNeORJVaQ3Jjl/IVwrrsY0tn7eBJz5W9PM+DqO1djHFu8cLzYEVdpvEdBmOt\nRc4CksZaVEUNT87OA9bOTgdKeajJXEVhXFmiLKeuDCcgUOn5gVutLevEECNEXIB7PC4vWmud15s1\n2kGVjSB0TutR3ETJWfPo/Hymr6W1Y8hp6FlzpRROV8qaWbO6J6VDYKy1KBnWpYbhWizT+8Iz+nkh\nnAaWhFK1VUHhmrattY4hpy5oSZH1Rd38bTDNZ8iVdvYXFvsDhtZZ4C0aWeeXEzciGPaIM0ZfaGyf\nCWxqrd39ep7nSo5KKUzYx+5LQ1cwfHLLKos2N0i/8tIV/NnBxwCAh9PMXddSapGwDtIn5wMsdelk\n1e0u4Zybk1Ujdh58sBLqQonV/V+TQjPSouIQT1igcteL0GYqYN5o4+MhnZpSG6HFDf2e78HYF0BM\n/Riqy2iSLlCw3QnSMXxmowo/A1j/pxF33AKRl4XTpBJKIktpzpVliU6HToDZWepK63HcRhgQwhH4\nITyeu14QIGNUp6hyeAXdeyw1uvxvw6xEm0tsmTU4Pp+/sfyz52dosyDqn/zgxzg9OeTrLHD7CrGt\n9rY30IioNBmFy+h0aBxvb6zj2QExQS+vtrHK2lwXx3dRVagYUsmLCmWNyGkLMEO3LCo0olrU1EPC\nosJ5kTtHiUBawON54iuMR/OdZ10zeW/JNUrnWQrD9Yjdvct4/IAarqfJFM0u3bPOxxhO+B17GiHr\nHvlKOguU8WSIhH3YUrZlOjvYx+CEkL242cASo4tShQ5ZWt66hPXtK/TdUuL+xx8AAIanR+gyQ7rU\n9sWFGv+jMDOhy9zCjggF1AWQMZKjTeXQD9+EEB6jvF4MRHTttrWJKbNUf/aTu/jJ+/TOR+ihu8ve\nmJu76K0RU5HGfT3PJFx58T+IF0GiAOv0l5QXOm07KaSzNRFSwfAMNAggmLmWVzNigECJlXWar1tb\nOzg6pjaEpwenkCWVdbvhbQxYi6k/OkLKVZxk4qPVovF75dJlXLl0GQCwt7ONNhMmmu2G0zHMswoI\n5vN4rKNeDzr6BK8tEaIZb/pYX6Hxt9ILYCoaa1pnEKYmieWwvK+HAtCSN+2gguC5VfhtiJDGt/S6\ngKB3LcIYKqI/G+3DjLmkWxkYU49HiYrfY2YtDlNCT7vlKfZGfw8AaM15j19/ElXNFJwpKap7Z7Qb\nCKYoZqaxxrgHae0M/xVytoHDM86DSkjjyjpfEF2sSsgLrMCAX37s+8iYbaaU5zbzoigQcHmrqmZK\nx/OElBLGqWRbt4lbo11G5fverJR2AeaMwhAtLpmU1iLivqDRhd4nrTWqegOTwjEBIWdsOSmVYzVa\nMxMsraoK2tZMHOuSsUajMTf9P+RNVRvjnksYRi4BNca4ezbGONYemQVfMOiUtVSCnSnRC4kJ96XV\n86S0JQLeFHQ1Y3daay8kTjOmp+/7s94wY5zIozFm7nKeFXAlRm01mtwX9O5bt3H3EcHlTx6f4lNm\nzAklUY3ZG67QWOVn+eFn95BwImw9r85H4BuBiHfQIIzQbtNfbHR9rG0Q1P70sIFPf0I9LHqSYYvZ\nguenE3zKG0botRCAFpdOHDlhw3lCTzN4y1QGEFogK+teNAPLMLdWPjVpABCmRJ6yfEHou4NCaeHe\nQ9hqo+TyUavVRBDQ98fNDqTgEuQkhRSFe84yrMuCGiEnyL62LuH0hEHKCuFTBQz0/PC6lgJDLs/9\n5fv3MRn0+S80ZETPSiy3cTilZ7iy/TIafLDr9do47VMS8fT5PjoxbSqmMs5RYZwlrpesGI6caqWB\nQMFrQBw34HGJfjpNYGqGmFTOX095Eqr2C+02EYTzJVH1mhZ4HposzIpOE1M2w262Olhdp43l4OlD\nDOs5qjWa9cbY9FAk7OM5GSNLaBMbnB4iGdbMJLqerKic95+WHjxmP+9cuYUu+2WGcQtjVpd+7+/+\nEsUZscIur0conlPiNJAWVs1/MP2HgoSF6X4a7UuQO98FAPTv7SPkRFXI2SE882IYQeOxqnrINLE2\nT58L3PmMrvHB3QSFoe2ytbGEdpuS1M3tlxCzlAg9i1lLwz8WL3J3pixQefU1+1C1TI+Aaz0RQkDW\nYq7VrN8Xpg3F67AnDAzPlTQ5Q8BM52t7CrevUw+cttaVZwfjY/T7lGiVGmjwGtNux4g5OfGkcOVF\n5QuXRBXZC7LzhILi3HO1GGFZsstBZoHHvNY+KCG4jUNd6F8VuABGGBaxBmBkAC3oe4wQsCw9Aa8F\nU5c+pQ+PgQkrAyetsBe3gID2VyEDeHyQkl4EvUJl6iopIN+bX1IFWJTzFrGIRSxiEYtYxCK+Unzt\nSJQX+O5kLeVcLAAAIABJREFUYAWcd5RSHmsqEYRZIxPWzlhmVTXTiRJCIOOmW50VyBhtkMoiiurG\nN+2QpaosXbmpLEvkfFJRSiHnxlkhSKyTfpcsagBCk+wLJNzKEwjqplsr3Im9AhxiVpkZa81Tijod\nAUjPgg8ASIYJxqxXoasKwta6PCVyLoV5yofHpwQBOLFNqRQyXZeOAIcACbjGdcA6RC4IgrmZa+Mx\nnVqllI4NZuwMSbyIEJEVAjfzloXTyVJKoTK1jcbMj08AaDVb7t8CxPCz/Pe+5zn4uf6e+pMXRTXr\nuMjcFEI4a6EvCw0Fv8GfrWbvsNdt4tf/yTsAgP+fvfcKkiw78/t+55q86SvLV7Xvnu7xMzCDmcGC\nswCI5VqSu+AuTcTGBrWiC1HBFz5Q1INCoiRSji4YIQUlGhEUqVhDEm5BaA24S2CxGJjxg3Ftpk11\nV5evSn/zuqOH77s3swcz6OzRAqGH/B5msrJvZh7znXO+85n///ed57i1Ja7/oTWFzlZLHp4CVx4d\njqhqovi5k4vU1MtY9z2aNfn+uVaDOQ0VzVUdHK3YOnYipK8ep+tXb7CtHFqxY6ivSOLuoyfOcN9Z\n8QCsHV+iOVeZqn8ArUYNozfb7mhU0L6UfQeTJ2CnEGthQLPkkuWVkVE09m5mFNhdaZwU8xqUKmNA\nx4xx5Y8/Li6Jkhg7VOqZSplUcau6cUysXhqDoebmXr4uWekeFqNNi+per9KgVZEbpufA3kj05Nk3\nbpK6uXfV5dbmTQD2dnxOrso4v3b5GvM6j2vzc5oIDLVKmUZd9HXQ7ZDomhuNIlz1ZLuOR5pTItms\nWK/Wc4owfn9oxSML7OwcUmtOh2eWh0e8CR66Wq1GpSLj2GkfMTefg3ueYBTJ2g0qFZpNCU/Vqk0G\nHfFG3Lr6BiMN4RnSoijEV4/42tpp+lqMECaW1pJ4N46dPE9Ql9/Z3dnhuy8KxtDezbdwtCJOPOP5\nmrdE91Cs816SUz05wQInP/SXANh0l7jy3B9I//e3iyrrJLOEOg+9cIfuQLxs7V5S0PLYNKCiVbDV\nepOFRQn5nTh5Bl+LaOyUPqZ78UTZaIDNIyuuR5Z7f12nqBb1Xac4z6wDRgGKbWbGUYA0xfii46YS\nUPYlHGmSHiU396gkNFriVTtbPlnwLCZJwlDHJ04ifC1kMTbBqle41+8w1DSLSuAxTO+B9gUHN69O\nH0TkSMWOHYdljR3rsX2v88hOlFAlGTDQMbHYIjniYJzmko29WBaHLE8pQYtZ5ClSm5+RpgChzhyf\ncnpvnihj7yVuNZOZzGQmM5nJTGYyE2AWzpvJTGYyk5nMZCYzeV8yM6JmMpOZzGQmM5nJTN6HzIyo\nmcxkJjOZyUxmMpP3ITMjaiYzmclMZjKTmczkfcjMiJrJTGYyk5nMZCYzeR8yM6JmMpOZzGQmM5nJ\nTN6HzIyomcxkJjOZyUxmMpP3ITMjaiYzmclMZjKTmczkfcjMiJrJTGYyk5nMZCYzeR/yA6d9+eef\n+TU7Jskdkwi7jlvQgxhjCgqSydeO40xNTZLLnQjsCglvwdqcLNcWdCFCUCtQ9Gma3fm+kvb+Z3/5\nl+7aAPMRx5Jov0oZ81WhRlls1KhWc9LdjMARGomPfvgJThwTegGylL0dYZrfbd+iHyrTdWWOs2fv\nk2dGPl/9DWGW/tp/eAXIKSLSoo/vFKd42yug7q03ZO2c0EM88EQJ68lDX/3nh9+3j5/41IctwMrq\nPKUgnxsKEuVKpY6jpJk2jYkioWlJswwnJy/N0oLNPk5jAiWIDEolhn3pc6zEvQ6mIJL2XZeG0kuU\nHJ9I6RoyByKl4ghHo4IRfa7aYNQT2P5BOGSkJLv//svf/r59vL13ZHMqE2BC70xBPTSpW9aOSZ7f\n+T5KJ8CE3lmbYcnpSyaeh/G7oqh3/BuAzbKCPgebQZbTM1BQJJ06efyuevq3/pu/YbNIqGSOdt9i\neVGoPdbXz9EfCJXJkCYNpSDp7r1KpOzmlXKZ1pzobxiOGCgVSL1SItE5qdYrY0JQ41JR4tJuLyRU\nnZhrljFWaaCyiPmmzG217LGxKZQ6SeYSKTVFEDgcO3YSgJ/95X9w1z7+i7/+YZsTmpZ8D6PjE0Uj\nklTaWSqVhAwdIes2jtJRuGBjZYInxS8pUTkeRhdUmiXESb5PGFC9T1LDSCl1DGN6EmNMQUOSpl5B\ntuqQEmkb+gkMImnD3/31t79vH5/6qV+yAAutBru72wB88NEH+PjTH5J2xBGdrlBEdYYJhx3pwzBM\ncHQf2Li9yeGhPFOpzrNzsA/A6Ogiw84NAHrttn5fUnBj+UGVSl32rXDUJTqSz1XLDbpDWXN+pcS5\n+88D8LN//Kf4wGMfkO8eJbz80gsA/I9/+29/3z7+h2990+ak0G98d4OvvPA7AHz8kx/hzPwpAF69\n+Ar9ttCdfOLJZ2CkBOCXX2X9gujO4sIaNhJde+3KNjduiy5bEhZb8nx1/iReSXTf87yCRDqNk4Jq\nJElSch4wxzgFPckwDAmjaOIZaf///Ff/+F31tFQq2ZwAflqS9HcTY6DREJ2tVP2CyLpUclhqKJ3U\nok/YVnqi4YiTp2SNHvUSXr4oe2+aulRL0uzt/SGdkbbJOBilgLHWxaq+93rdu/axm2FzGi5jzMR+\nBlY5WpLEkmY5iTd3nPf5uKSTZ5yFRM/s2KT8hy/+OwD+/t/573j4CaHn+q/+zj+gWp3TfiVjAntj\nCt6kdOLst5klU3qaxDHMlURnHl9tTWV8/MCNqEles0kjyjHuexpLkwbVvUoxYNaSO9qMscWkjY8s\n0XlTGHiT32LllJ5SvEEZmxNsxxF7Pdmg9npDjNJt2wyUUoqjzhHnTwsHVa/TY3PjtrxuJ/Tbsohd\n1+f+B4TTatSPufjSVf01l/cynO6QnEeIFAfZkLK0zOFWrL9rWVoPpupfqrxwYdxlqIebMWMevsxJ\n8D35LpvGhJH0P80yXOVGitOEUaKHSZaS6esYlyiVA9ZXg8t3PVw9tDyT4SL/brMYjIxPlMTEuYFC\nQpqpsWYN1kh7jZtSzg/1uw3XOxbve+ne9xhM7/Ze/vcdRlRa8Dzd+dXOmOcpmzDMJhi7bDZhgFlb\nGFFWGjtV/wC85DYlV8a9naVcvCgH5sbGHgvzSwCU6wsc7Oq2kO5jMuHN8r15kkTG0vM8XOWAwxiq\nNTHG/JLPYVs2ZccxdHQD3TkcFQvsaLjDfSdPy9ePytTL8j2nTxynrLyMm3tt4kS47VwT4aWdqfsY\n4WCt6B9ZRoAcMA4unqfGkkOxhIzvMMoPwszFUwPYdYVvD8BkMSQj/Z6UTHUtMmVSV9ocZS5RqvtN\nlmIy0dOy7+DpZdHxLKnyCWISLLqJYwpezbv2z5MDf+NwRJTJuO/0Ejb3ZK/42BMfwtO1ePX2AUcD\n+Y3bt3fYOxQjor58kqOhGGDD2FJpCt9a/6iE78t3VqvS/uGwQ0kvF15ljpV1mbtud59BfldIRvg6\nbvXWHKWyfMfZc+dZWxGex3/32c9xe/v2VH08OGxTV57J84+c5rm3pD+/+f98iYcffACAvd4tIuWS\n6z63QSWU/fSgv0PSkkvAUmuVblfm7bDTJ9N5CPyEUlnGy3MapIl8v+/4VLTt1s+KMyHLUuI4P3Cz\nglfTOC5K/4rjWFxv+jOjVCoV/IeT+8d77UPGmHfdb1zPUAq84vmRGj/hICXuyXPh0KOi63W+GbAv\nS5rbey7dUN4/6KaF0eK5LpT0om4tbjZxHpvpTYYsy4rLsPQjb7+RCwiQJpYs388ME5ujHa9R7MTd\n0hb7ZZa5PLIu+vU3f/Fn+fKz4mho72xTPyuXs9SmxWXfGFNw4gp/X/6N2fhnjcFwb0btD9yImryx\nG2PGVrcxxS36vfj73vn+NEbVuyma/P29nii54asVnL3TE3UPA3krw6hXx3FdslzRfBdPrfsss5hE\n+nvtVsi1b12WNqQGm+QWmEfBogi8cHujaCdqjMgYTNG2CWV01PBwrCEZSDvjUQXfm87AiNUrl5qs\nGMc0TdBzgmw0pKRj59iMoRpRoyguDtvMjLtmHYpn4n6Mr4Z1uSaK77teMdeuhYoSKAflEgdt2fyi\n4YCeElI7rkOgB3C7cyAsugB4OO50Ku667h0G/6S82yb3zvfu/HvSEJLXrucWnoAkiQvyZoNbbAqe\nM76tCQl2YV3dyW6aG8iWOzxXd5OaO6TdFQ/D8lKf48fkcJyba+E6smm+deU6t3dkLh987Al8NUjL\nbqcwbF3XIWjWtQ0JibZza6dLp69GggN7Ole15golXetOMCAzQn5bqz9AO5Lfurrn4FfOSttOOiS6\nye5vvsHOYXfqPtosAatGd5pgUpnTLI5wK2rkkJFPdZalhZGQWJ8sdov3Ez0hjbU4aiQYt4R1ZayG\nacDWvvS3H1l6PXnt2pRGWb6nZDKaVTmYK0FC5oy9rbm++UCcTTePkep2nEGsc3/x2k3mq6LnP/2p\nT9Htildo9+AI64kxUqnW6Ct59n63Q+KIJzGJhhyo16k/3MPp63yrJ8h1y4Vnsh/5eGX5PmfYpaT9\nGrR7NJRQ+8SZs6yurmlbM67dkD3sm89+g0j3kbvJ5WsXWVteB+DYiTIP3/9h6c/eTV6/+BIAXj0j\nzmS8B+Eebvo2AL1+m/1XRKdWWis8fOYjAGwfdRleegsAGx4wUMJmSl2sEvhWqFDKDSHPxXFFB6Nw\nRIx6wG1WOAIsFi83fh1DyX9/x6m19l3PtiAICkL1NE2LZ/LLq7Qnpd+TOUuzMbGvtXCo473VHXJ8\nVcbTr5ToHsmlJBwZ7luXvq9XOsgFHbY6fY40amCdgMzRfmXZPeX/vDPCNN6q3rFfUlhFE5d/U+yX\nrjHj83hizysnGWsNaf+5T3wK/CYArWoFR7/Tc8ak3cYxZLkhl5kimSnDoNsNjmvwp7zQ5DLLiZrJ\nTGYyk5nMZCYzeR/yA/dEwXQepPcK4b2Xl+pu3/NOD9g9fs09hRKzoVN4aDBOkfNhjCXLvRKWwj2Z\nucnYVWldnNz8nnhIvJ+5m9MhK6ZqMg/qvdt4Z3fT4ulM8znSQZVmZXWq/o1DZR6ul3uIPDSMzDBM\nGQwkjGPStLg9ZUCSW/7G4OvttlQqFbkEcZriuvK+ceSG5eAVoRQfg2fl/STMcNXLV6nUSYpri6Hk\nB/r7GVa9PBaDMdN5FN+ZizcpY++mfOvkZ/J/v9MTlX8Q+kMZl+3t23Q64plZXV1hfV3G3jWQaIhn\nb3+PcCgeumq1hq/eNb9Uwhh33Kf8d8aNmkpefesW1comAD/28VMYWtIGm+Do90erBt+VuTl24v4i\n1619+1kGPfFe+OU6rt5ObRLR13yYyIacPL8IwObNAX5JwkRpnHFwIH3345SlefF8NAIfq+Gj7Z5L\nBfFynFxfp9sWr0laapHad/cQvpt46Ujcl4CTxQSuej88U4QUHdcppjHJbHFV9UsV1s7cD0DnaI+9\nfZk73yvhoGG7xGNopc1vXN/DBgsAxG6NqC4em177gFs70t964JFuyetTqyUWG/I9Zc/DqKegZCTs\nMI1Ydf/aLIVIPBBJyQNdQ29fe5vX3hCPy839PmtrkkO0tLBchMvffvsagRGdW6h6pAPx9GXhqPDE\nOI6sm0azgTqC6YRJkd9lHJf+QOY9jmMaNfECnDhzH4l6iD//pS/TrMhY3dzYpD7XmKqPf/Dcl/nQ\nIx+VP8owSCUM2Vpq0NXcuv2D7SKs+vCHP8RKSzwtb9+4RKheFMeYIoR7cqXF3mXRqcPdmwxK8nwn\nvl3kU5paRD2T+ZxrzTPSPe2o1ydXmLJfKvaHwA2worJESSwRgynlnXvG5FmVh/myiUjJ5LMVHVOA\nfr9Pmo7DZPnm45dKJLpuMpuxuSVrrnvokWWyxzRqlscvSL6ht5pgU9Hf5IolVP11S2UGsaaD2JSg\nMs4bvdc+5nmIWCZCbA7G0fVtx5GOLMmwui6N6xY5aUykS8TZCDsve9jX/+Alruv++qml+cJL697h\nDYP8zLTOeP92KDIkMI6D50x/9sMPwYiaDHUYYyaOgHszrv4wZVIx381Is3BPxps8Ok4mRg9u44yN\nN2PG70tsK398MuH4HY0oxuq9Fud7t3GcW8MdIcK8PcP9lIXSiff8/KTkhmA4GhLoYet6pgg3JUlC\nGunBFVG87wRukYuWWkuWhyLShFS7VPLK+HogZ4l8Lsrios2e45FYzaWyEUFFc+pwyJx8MWVYHX+H\ncTJLYAy+myfhf395p57d8XdhLI3j+k42TjbNGOvRcBhy7eo1AL79nRe4clVy2a5dvUw6lEX+9OPn\n+aU/9/MA3HfhCSJks75x+3leeOEVeX5jQGlODK2P/+SPc/bsGRkP49zzxSKXzmCLB87JBhqU6zRq\ncsDeuPT1wvCrVho8cL8YEvV6jczIoe8tLtA9GOcOHRxISM4PKiwuSJ5MeHSdUA1YL6hRKuX6fsj6\nihygv/ftLZYacggcXyxRqkoulpuVcX2Zq1E4IIvl4BxEoyJnYjoxGE82VmMMSZ4Q7CREibS/5I7D\nJDZLi/kt+Q5P/7EfB+D5bzzLpiZO9xOPJJXcqus3d7l665aMYWudE6sSgrRBg0hzkfz6MkkoBuf+\nzibVlhzMN3vbhHqQrDZ8qr5eTuLBRCHI95fUyCFmDWRqUMXDhDfffBOAf3Ltuzia11OuL7O+JDkj\nK/N1apo70z3YJ7ZiALUWq6zW1VAOS/gaKhoO5NC1NisMJ2t99vfEECGLSGMxVoKggq/J2fXmAt95\n9uvS94ND8qSh7u4hebjobuIH8PXv/DYAN3dusbcjuXsH3R1+6id/DoBer0OoRv0zH/gxjq+JMfBH\nn/ppXnjpOwDs3trlha6E/3a6HruhtGUYWfwD6d/C/AotTWtI+gf0NW8qLZXJb4mVdMhQE/8T18Po\nHDYazWILHrZD0mw6Qxje+3wxxpAnnIuBNJGYrZ9pt9vkRTDGjPPpJl+nWYLed6lXa8Vc+a4l0Vy6\n9mGf716S+QwcQ6YX27mGz/GlYwC4xmVzV9ZirexTabSm7qOEwfP+ZmT5WRANGWlawTCCLNX9NRuQ\naB/nqyv4c7IfZKnFyc+zNCmMzJdffpHP/9qvAPDSt79JbyiXgaf+2M/y8Aee1HFIi9C9MQZXdfCO\n4XedIlzoWDG87kVm4byZzGQmM5nJTGYyk/chPxRP1OTr/M+pPEyGOzxX7/cGPinTlKlj32Gpvs/f\nmPTuTpZ4TnqGfpgi1Qlq9Y8s843lqT4X6w0+wysqU+JRTBzloQWDox4fWysVNw7XS3G0fJwsLfrt\nGluEFhzHKcJvod4kRlbc5gBhJjAHAPVyiYqWn/qOR6IeOjfNiPSmGMURrv6O7wb45g/jnpCXyDrj\nUJqZLEpI2d6WG90XvvRlvvK13wfg4tUbjEIt/3ddjjekT5tvXeXL/+pXAXj8R9ucuiDegu++8iIv\nfOtlAC5fG7Erl0dudTr8hT//SwCcWD/G2EN5b0r60HmHll4k97YvsfLogwAE5TkGgz0AwjilqrfN\nUlDC6hYRmXJxyw0CF+OK7pSqa9QVguLixgZHPdGVZr2O54mnoNV0OXFMbr9vXq/iaOjJrzTxNJzn\nOQFayMMoikk0hNuqeYXOTiMjp0F7IDGWNBkxX5cvbbopXj5fSTRREZlIeA8YDA753S99AYDtoxHb\nPXn/+q1DrmuRh1uuk7oSuqo1l/CrWh5frhCorpWdGntaOLF+4hShhjuvXt3moK2wCabOmWX5rJ9m\nmHS6pGvPqEckTTE6jkQJW1s7APS8IX/2F38RgFdev8LWlnhxnnriMZpaCl+vNxnsb+uAdahqu4/i\nDqNU5nukYWXP9Yvqr3JQL2o2jg4PKZsiO59Q9fzmrW3aR+JliMMh6Uj6lVkIh9FUffzRJ5/ht58V\nT9SVjRdJdG0vr6xw/6lHARj2B+xs3pQ2WpeDA9HfVmOeY5rY/vrhNj0Np5eCRcqO6JpTbrK0LGvu\nseNrlHS/GHYNITJXWXuHTPtnsjbxUPoXVeYKD7QzCMlypc0scTzdHML3pgzkkqYpozwc6Tjfc17l\nkle9TX6X67qk6uKPo7ioPB9hWV6UNVoODLF6fsKRx6EWEiSpw6Ar6/Xxsw2OLYqOu8mIU1q5OyLl\n0q3e1H28o9rYWnyNxIzihF/59c8CsPH6S/S2ZR7bUchOX/r1+OPP8Bf++l8H4PjiYlG8Yq2Hq0Ue\nLz//Ar/ymc/oGJjCY/2d7zzHIx98svjdIhLGO0N7kzIucrvX0/mHkBM1DoEUf4KUFuU7mYEiZCVx\nr+Jx+26f1X8p3vzDNkrM98s2uhcZl2a+n9yudzM03ysECe+9MCc+TN6zueYy68v3T9WW/Pc81yNR\ngypOogKzKY4yrFYdlWplaoqN1fAdatqmiuPi2TwG7VIp5SXs3rgCRX8nsVlRRbF/eMiRboTB8gpO\nJdC+ukVV32DYJ9a2uMYl0MOl0WgQeNOF8+4yAoCoZmEKG4PVwydOYl557Q0APvvFL3F1U3C/jF8h\nM2IMRNaw25E2vhl12FDMmutU+YuP/kUAls89Q/y8bOJHo6v0NST03Lef54OPPgLA2k+sSAmy/MI9\nWfvVagZq1Ja9I5KhlJz7/gLDUA5hv5JSKmmOCM44NGu8Qg/SNGFhUUrKg+o6W3sabmm3WV6SEGG3\nPypyGmrNVdo9ObRPn4mp1WQcHHc8946JyHUzjh2skQO/VjtByZu+j7tDl4NYjMCvfeOrPHRBvueP\nPrLEvOZKZWmK4+ZGvE9q8zwfuHpdwq8HwwBblZwut17HmRcDv9KaIwrl4IlMRnNevr9Zr7GzJfPe\nOTygoWNYrlS4cSgHvN9YYVeNmvp2l7WmVu0Zj0Qrze4mrZI8dxAOcSpqLHoZvX0xXEYWTh47A8Bz\nL1/kxpYcUMbL8APRxaW1M3R86cNSY5eqhuvaHZ+bW/s6RrKeq+W5Ao9tlEX4JQ3XOpawn0NJpKSB\n6O2N6xv0O1pNGQ8ZDfPKsZRQx+1u4hxt8cj5pwDY692gN5K+LS6u8OLlrwFgI0ujLGHSYThgoHvE\nxsY1Tp6Q8PLJE2eLdIJ6tcaxQN7PhsuszktV13w5YBR29ZkEE0s/vMEOpi/6cqWyWux1dtgpKhez\n2GLzqk3HpVaePl/I9/33zImKNUfSdccwQNbaoprTGDMOR7/j/eJ5LFlutKQJba3g29sfjnXNcYsL\nbxKNoRveutUj0RxARsMCjqAbGbb376FS9h1OigDRnY2Nm/ybz34RgPnOVT55Xgy2q/t7hAPpy2//\n2j/m1qasxf/hf/p7tJa14hNLpnp07cql4qD2PZ9RjgPnB5h838rs2HHj2MKwNGZc/WcxBX4bjsG9\nx9N/Fs6byUxmMpOZzGQmM3kf8kMI5737ZdmYSZeafYd/7V68NpPP3lui+nt5e96P3JFAfkd73qsv\n7y8k872YRO9ejXhnu8a3AVcRx+eOeSRZf6rfLCu6eLlSJk1zb0FY3CzTdAxM2MKnpejtCxZOKMr1\n8YX5IpwyGsX4WonnWq9wTedJhVGWMNBEyNVKnYEmnvuloMDusc4YxDBLUqxWHZaCoAjnOcZQr9en\n6uP3k7Hz1DI5ljnifmINL31XPFGbW3tUrSYYZz5Dm3vZMsKSPN9vVGmuiJfjqU8+w8KS3LIcd44/\n/UuS7H/mgRf5jS99DoBOd4/t2+LliJO4qCay3wcU9N2k38+oyXRQW86II0mQrrVOMrql3kbr4Xvi\nIXFdrwhJe65beOHSKCTT8N9e55CrG+JdyVKD0dtdr91meUWSfeM05a1XJNy5t73P+h+TvpMOyBR9\n3zqm0K0oigpPUVBq4JTuoTpv7iyDffUQlpY50JvtICrTLGlY2iZFOY7rVgkj6e/uCPa6Ml/V1gLz\ny+JV62cdltAxKVeIfPmesN8l7AnmzunVRQbqfdqJhhitFm0fDCSUDQz7fVz1wO50Drmtob3TSy7O\nlIVdn/6ZHwNga/eIzlDWzc5uh/6qeN+S8JA3L10DwPGqeBoW39nvcFtxooKgwtL6CW13g7MNPQbe\nuE67L+tu0BePgzG2wD1L4qMCOb9cNvSGCuw4THBj1Y0kHiecu06xL2ZZVqQF3E1Su8h8STxFUbmL\nyR08meXWvobwHIeDrnhzl+dWODYvidBpv83eLfFgOMYFDbG5cY8lTz0VVagq8nE0iIuEcIMFV9MC\nqobMFz2q2oh5xRjLbB9XAYdDZxVK6ol04b61pan6B4KgnyeH+57B0b0kirNxwUpmxqkRrku5rAnw\ncVwUFVg7UVXsQajzB6ZAVo+SjIO27vUWmEiu9pw8VBuQ6NwOM8vbNxUwOSjRVs9ikEL5Htai/MZE\nEZe2p3vUoaLb1qm1ZdbmpQ39gyNsLP+w/sAiX/nNzwPwf505xX/+X/zXMg5BhdvXJLT+2ovPF8dn\nmqT4JVmjx9aPFwntjqXwShlri2ptx3Fx7PgMLlhVMFOWP4zlhwJx8G5yh+vxDyHX6f+rvNM4uRfx\nXIeqHta9fp8szVGqx6FJe0eYcoyWykTFopOZwgBAcLj1tVOUmmdOis2r/JJsDMhokqKyxgAj3Rhc\n36VWV1DFBYf107KJn3owY2P3lan6l7s9K5UKaZrDOKcFdYvBw7EKX5AYoo4swP3eEcGhPFMPE2qK\nbB3GESMta/WsIVPDqKzgfW4a074tB/wwDJlryaFbCgL6uvEcDcMi/Neo1oi0lN21DslINrn20VEB\nCPqHIhMArALIKq9ffe0Nvv28UFoM4xRf9TqMBhgvh02wYHPE7BI/+ROfBOBHP/JhvvvccwD86r/7\nAiM1KH/+53+OJHkGgH//xS+zNC+hC9/376xWuwedrVQMjbpuoJ5LMpJ58r1DanXRiygxRFoaXQIy\nq2j1o0Nc1YMshSiSjXVz84Ct2/L6+PHj9NsSgnSdCrrn097fZHlZ/lhfX+NgW+ECjoUYBX103bni\nYEheG6ynAAAgAElEQVSSkHQoxknmRYT34F5/4PGnuPlNKfGvzy3z1I9IWKjqXidSw8DxfIzmYqW2\nRUONvZdeuUy9JRANx08/gnXUGPYjspGEuaIow/EUiNJ4vPayrKFm4FNVC7VWrbO5JeHLJLO4alDN\nNyq0NeRweBBzVcvOj62u4ZWmMzD+zM/9JABhYtnelTH61osXua5hyGbNZ1dDe+XKHIOBPPNbv/sH\nhLFWtjoOsaJ0l4J56g3Ry9Mnj7G9L+24ePF1edaFUqB5iNGIWHO9SqU6nla12SwuysIHnbZUPAJh\nnBQ5Oq7njdM37iJLJx7iyuYV+ZxT4pmHpGKy5JZ49drzAFy58RbJoczJfvA258oy9ufnm9g0B1vN\nSDV0Fe0eMYgUYNSDKK8ETcDoZ8u1Kp620WQZaZ7jRspaTZ4fGMO+5v2lvuHx07Iul+sl0ig3YO4u\nKRTQNvO1CmWtyNvaPSJJc4onyBHCHWsZ6b7GxAUOK0C+AM25CkPNv7OpPxFmeveUGM/zKGlo0it5\nhAOZWxtbRqmvv9ujFkh7Fht1vCnBi8c/pntGZonUPJmfb9Hdl1SCS6MDTFv0aG8vZGtXdPfhCws8\n/fAFAP79v/nXPPxBAU19+kc/xf/xv/0jAHZu3+LxhyWv8423LrOolajnzp4rEpKtHSOciyGXj8XE\nGYydSGB2psKynpRZOG8mM5nJTGYyk5nM5H3I/y/ANt+LI2j6UMX3erTeC/dnEmL/vcJ5ZuK/00hz\npVJUoWCzAnIesgJOfvLrnGxsBTsT1WOp4xb4SQLUmQMFWjJNBDW+oakenfmgRlPxWY7dd4qP/8jT\nAPzeV/8jNztyG187UaM5p9QP9YRKRdq2NFelEkx3M8zDbXEcF4nlnutSrcgNLoltgRPV3t7F08qe\n4806FaVyCVNDX+k7usMBZQVtqwUlHPVK5SEcXJ8wkREajRK8HGgyGhVYP1GaMcpd3fhUlbYkSmKi\nnK/OGNrhdCHLSfkewNfxP4wpg4CtHUnG/twXvsjFy3pzDgKGBaicoaLUEa26z/mTclP62JMf4qee\n+SMAlB2XVl3m8/zJFS5eUWqKqM0vfPpnANi4eo1QE2dtmlIAwGCLZNBppFQqMxwoXsxiswjtGa/G\n2pJ4+zZ34iKEEEUpo464zvv9DkmUJ5ZnDPR1px/SbEooqV6vs7cn4ZbllWNkOlc7t/Z48GF55uSp\nBs99QwFfMweTSb+y0MUq0WkyuEkUCqZWbKAcjMEF7ybVuUVOn5OCiWEMp84KGe5SbDm6el2+0yak\nys331Mc/zalzcss9+9g1nn9RqiPn62ts7kjI0rMlgpyc2oq3GaB9eMB8zc/fLohUl5aXGWkYae+w\njdHqv0a9Vtzko3DA2xs6Vq0KF05MB0TZUq9yikNVwVhvbx+xt71J3sCgIom61zdv0OnKmtveO6Kp\nHHnGqeJo9aPnlGnoT9ePknHoWrelSqVEXXG9wjDDIJ9LowSr+0LgWUhkTNIRBWZbHI9pSMqBTzZt\nBWIZ9lTvan6VcwtCxD7s9XDFUcGcafDwgxJufWj9GBX1mDpZRjoSj1PY6xbgtUdHBwVQqe+XCuqW\nJBmh8FHMLa7TmtOqNJtg1XNinARP9+KaO8LR9Rp6XVZrMucPnVvnm89P59mXhvoY9WhmOOwfqr5n\nKdWa7OkuKfFA+hKHllT3Qb8UFGNsscU6c1MfXycwvMPTcqfk5+QkX2Ov34ec29Q6jLQK9OPHy5SU\nx3CjB/3uPeynzrj4xjgOju7Lfq2KW5XN52jrOtvKB3n7qMeZk+LZO7PWZP6YzK95NeZf/q//EICX\nXnyRF56T4oIPPf4QcSzf+dpbl3j6RwSg9dTJY6RpXiwyNnHsHTVotghNu1hMHrlxHO61Pu+HHs7L\nD6gsy9jRQ6jZbFLTHX3asNqdeT/jEsbJar53feY9DLPv4fmZukcwJGagbOluGhRgbJlJxgCb2KKU\n2nFLRUgmhSKPxKslNJqySdUrAY4ycrs+1NToWF1a5cFTolxnl5doH4hSL5+5jxPHJc/hzYt1qqcl\np2DlmCWJZSMR3ieNvSe7ZFP6LfODOkmSO8YvryIxjAHoGIVU1Biaa87haSjDGk9c+oDnJsQjzT3A\n4ucggMq7FgQVFpcEaDKqVFhdlhBLWvbZ00qnzPWJlSQ6S7MCGC9JU5xADzbXYTiarurp+/E35jqV\nMeZeyqxla0dyTDZu3iTJrV+nVCxB1zjkfy02a/zMT38CgB//sU8Q+KLvqedx5r5zAPzpuQYb1+Wg\nn5tfpKrGw9x8k81bcqj0uh3m5+e1DeMqxmmkHCwUeQnG82g0ZPPKjEdZN7VKbZMkkxBQHA7o7kt7\njg7btJULr16Bw67Mcb8Xcey4VOrFw7jI/2lUKiSxzFVzxeHSJfns1oZlYUk2ym57m3KgOWumT5qq\noZh00QgF3e6Q0ZSl8QBuUGdzW/LTPvjEk9T0AuF2b5EqmKtX8nh7Q4yLZ+bPQlXWTaM2oKwbeqVU\nLQiRyVKOHxOE69evXKGk5KydbpczJyTkcP+DD3NwoAS/zRabCjlgHJeWhmLbncNi/VWqLYZd6e/l\njS6V0nRBgcuXpG/Hjp8gcMX6qQcuH3r8YQC6vR7ffF6eSRJbcBAaz2N7V0KMruNSLefEzItUFMC2\nWqlQ0wMzb2ejWaPRlPd6PYg7emB7KYvHxDB20ph+pCFsxwFX3u/EBwT5qW7eA1T4XeR3fvfL3NiS\n8OSFsxf4nT/4svTTr7LelNynB9aOc3pO58ozxeWu22sz7IjejQYDuj2Z57DfZ6Tha2t8EjWQypUA\nq+kE/U4f/z4xukvOxIHr+mLZASVToay5b7E5IjySeW4f1Lhwem2q/gHUyi6x5o7FYcLD94uh+Kmf\n/Clamr5wcOsye1flUnV1u83lDcmL3D5ok+RBJMfF6t7T8H0Snb/tZDRO0LXvcDDo/5MkGacGZBlW\n+VnLWcRj94sxefbkKt95S4z9Gwc9kmj64JXJEpxMQ6tkJBoiXF5c4MP3yxn25u4VuqoWoXFxtBL3\n9LFFFtZEj6rVp/iH//Z3APjWN77CT3/8RwBZZ5euSds+/ad+jk5fjec4ItALvsGOgTRxCDR5N8ts\nkaaSJsVo3okGMKXMwnkzmclMZjKTmcxkJu9DfqieqElvT5IkXLt2DYALFy4UlQqO4xSw7t9P7vAc\nmDFQ1r2EAt/pfRp/5h4r9soGr6r26CAhpwIybopX1ptnIyCoasVRkOHlD2EoKX7L6uIiD545A8Bc\ntUJZmcZdt8TqgtyWm9UGx+blhtzZfZuvXHsNgIvfvsZD5+Q26joRviPjGYURGTnFxdj63uvfJgwH\n03WvrNV5QRnj5FUhLoOBhhgNRYLz3HyLlt7gB3FKr6igabKiAG6BTQq8jpJfwdUKor1DeXYU7bCu\n1WunT52mVtYKqzSjORLvTDeKyRT3JxwNyH3yru8WIHkWuAecxkK+B5A1r8jDMsnhVNVk0KXWAmW9\nqabWxcv5BbF4VsOfTkSWyk1pMDwssF2yMGMU5qFan7MPSCgqijMivSE/9NDDPP+iJK6/8cbrPPmk\nAMnda2WpU1rAMTJ+1zauE+v8LS/1GSFz49dSjHoSbNpm0JVb/f7eDssNaf/xtUU2boruREKQqP3q\nUavIOHieYW9bvE+tdZ9IdW1+pcT6qtyWjV3AKIdbFu3haTVU5lUZ9CVuE3gG15k+YdcvNwlDGfPR\nKMbXarhqrUlN6VACN6HuyXd+5p/8c/7kn/tr8tn+FqUg545LOHtOPGw7B5uEPfH4rq0scdCRvoyi\niHPnxXNx3/n7aesc9bs9On15JkkzhoqV1GrNkVrxjDRbPomC1brOiJu3d6bq3+c/LxWba+urPPKw\n6IFLlQtn5Wa/vbfP2opQ8uzsdznSZHrP8zEaWt7bucG6egPLpVaRXLxxc4PbmhBfzTGokoRIwR/7\ng14BpHnh3HEunJLvcJOEjW35nRt7EfiiS1E1oaKeqHDQIbXTeaK+++bzVOviSdjc3qCi2E1nHniK\ntVXpZz3qECSijyalCEV1D3YZ6p4zHCVsb8u4hv0he4fyPZ3E0Nd0gXJQ4kRLPb5lChDO8uJ8sT+6\nPkUBjzUG19V92YzIIk3kzuzEnn53afqG+RX5rUcunOK+s4JhNWrv8K8/++sAPHxqgb/5134ZgPUH\nP8jGrqynL37+c/zGF78EwI3bHcK+JrqnWVEgUolTRmGeemAKL6AkV6uOZymZhrQy45FquPUj55f4\n4FkZk9987hpvH+QpHBnGTI+756Yeic6LzVJixdSycciaFrhsLzQZlUVfHr2wxuHbEk7f2D5iYOX9\ny1sx6uhkfnmJLeWi/JHzj/Bf/q2/DcALL7zML/7Snwfg85/7PAuLcn4kgw73PyjJ5416ky9/Scbt\n0pWr/Imf+zQAn/jEJ4t9/f3Ulv1Qc6ImN/0kiQtj6eDggL664hqNJgsLGq7IxiXlYuQ43/OdwBiw\nz3HvzKzPvZmTh+J7tm3yvXd58PvIynGHQHMaRr0hNa3kcMoublm+yPdTji+oK3rpUdCS/IXFBUb5\nZpq4zJfFRd2qVqlqtdrKiTMsnZDNOskiqoFsWF+9+QobR7LprZ19nA89KZVI5brL81fkmX73iOa8\nVu0ZS7ujuRrtgFu7B1P1r9OR8E616tGcU9Rf16Gk1YBxnJGleUwZtvflezdv7JBq2O7s8RXckmwU\njapHXrXsuC6hLrSR/v+w3WaklTT93j7nz8hhNrewSLMqLvnbScRQCVhjx1JSQ8vzXTzlJPNcvwAK\nvJu8Exjue2EiciNKXrtY1lekpPmjT36It99+G4BbW7tFypJrLItNOQwefegcK8tinIzCkLKCFqZJ\nVoRFHaewRyhXqwRqAPzMz/wJHn5EDOQoDosqNsdxx8TXU8j+UUacaEWV8yibHdHZ5vaIxUUJmRrv\nDPsHYhym/be4+JaEEcOwz1JDZu3GzSGhhiKs1yTMCaezEXV1o8ejhKMj2eycUohflecvPHqS/ra0\nISgbEq3Ci8IebqwE1E5Y5BVWq2X8YG7qPhrXZ6AGTzgY4ms4ubufgiu669NmvSU6cumNy2zevCwf\nHmxy/eY1AD609hTHNTxzbGeV/mUJay4ELRotmfe3377G+jHRzaNOh1jDKtu7+0VemXE9BmpEGSct\nrme1eg2U7LZkhkT7W1P1b2tT5uPtS69w46ZUOJ0792HOn5OQ8NbOHuurEgq/vrnLtoZgHc8n0PzE\n+tw8oRqpvc4+l67LuH/n1atcvipwFXN1ea/cNiSaR2f7A5Y0J2t1oUygl5hGrVpwFA77HUI9aN2l\neULtu5t0cdLpjP5j66dYWZGxXyu1uF/R4us7B5SWZOwDOyJfLQZDontBt3NUoK1v7g9465pU8HV7\nI440XaCbZAwUet13XA7nZZ09drJGty3jsrq6TAFnQkZ+sNgswmrFn01dhj0x2NpH+4wU5qG1eHeo\ng5Ln8+iDEgpulVPcWHOfYnj8gujUL/yZn+fkYxK6cuoNHqjJefmzD7o8Fsn4bHRO8txbst9eOwi5\ntp9DVCR4ebG+zQqYCsnT1XWWRWT6TGQcLqzI+frgfU2+8rKEya4dJng5uwR+YXRNI/vdPTxX1p/r\nlPDUoB6MYm7syLofJA5PPCm5vOsnL/DZq5cAuHi7z+6byiN6u02kFZfZ0RHLH5TQ54//8T9JXsh4\neHiIo3P0v/z3/y06VLRKGRfufwCA8twC39Qq6s3tXV5/XRwQx44d48H7xdDKMnvPPpRZOG8mM5nJ\nTGYyk5nM5H3IDx5sE4dxvZuLk1cPDPvUlMIjS6PCYnVMVnCp9XrdgkfI9XwqVblJGcfgOjlbdcZQ\nXdblcplYP+t4boFj4rlBkSSYYQs6CjIKN4O13BHOuxfIrfvOL+IqSFscB1Q1sdn44JbFOp5L6/z8\nR/9TAE4unuFoV26R/eGQakvcutVyjb4yxxsstbrcwNeOX6C1Klg2uBk7B+L1WLzvw3x6UW6gi2sn\nKWtYcOXEEtmbMj57B0MaWj11+a02Lz8nydClOR87XUEQA61GOmq7RLG4uGu1oADy8zwPhYki7Q1o\nKwdTP05xtDoidkukbo5J4uBrtUsQGMrqIQjqiqezNF9UcnT3d7h1U8Zkbm6Jiv5mlkVE+Y3QK0Ee\nwnPA05CMzQT7ZRqxWVZU3mUTpIeTHqoMQwE8lcXcuiG3Js8M+HO/IFg23/jWt3j1dfFszNXn+CNP\nfxCAH/3YYywty4A3qouUPQWc9KGvWEntXhtPQyuVoISnWDYkcPbsGRnfLB7T5KTJPWGbvfnWBhWl\nMilVAxpKO9IelLm5q0mZowP2duQ2noSbNNQbWm5WeHtH5r7THhWgdatLdfo9ed4veXiBjPfmxg1G\nodw2u72UhTmZt/4gYBg1tOvbYJQuqNrE8/L17VLNuRhtinsvV73M4qrurC8tUi2LTv3uK1eYV+/v\nhQWfsmLflLyQ3Z1r8tHRIafuOwuAWw6oajXb0uoJ9g90jjqD4va7vLxcFE6EUUKkFXnDcFRg/SRp\nSqj4PkniFFg2xviUjHhPApOQ2un01NfBWFxosbMroaqbG7/HKS02OeyE9HW9xqMhtRzLzQ8IShIe\nmavW6Wxf1TZZdg7Uaz0I8RT109P5XWzWWVBv6rljxwmU0qlScSGRvblU8lhaEA962C1z5qEPA/Ds\naze5dFHCwa5n8Oamq7J8/IGniXTMLmx3eKorOr5rLLFW3hk7wlHvSpZl9Puia71ul64m7L96ZYdL\nm+KJwzqESm9jnXEKBfhsHslvLTVLnE3GYa9APe0ZTlFhiWNAzxjjZIXuX7n0GoGurQcefuSufTzo\nd/mtrz4LwFw54LH7JF3jT/zEx/izupc05xcZqFet5Fc5vCzYXfuvfJ36QPr1kRMneeK4eDT32pav\nXha9+9y3b7NzIG1zXIPRakTrePi6h2UERBoTqGd9Pnq/RAo2tkNubKkH0asXnpZSyb2j2u1u8q9+\n5e/RaIi+z7fWOanFGbWFRUZV8daVlwY8/oSEpddOPsC//Gf/FIDvXL5JR8ORx+olHlYP94Lt0FXA\n1a9+/Wt897vfBeCPfPRj/NW/8lcA+Id//x9QU8/k2aUmB5flmb5T475T4uXr9we8/sqrAHztP/4e\nj+qcxVF2r/jXP5xw3mSe0t6uHOKvv/4Kw1xBSqUiJ2qSCyiO4yLU4Xl+gUgqlSPjKr9YByyzaRFL\nP3n6NK4aUQvzy0Vl3GSOi4zW+PX7ycyX9sf4eog3/DmqFXldCUIqqNGRVWj6ouy3Nq4QKSjawuIx\nFhfENeuVAjIFbBuN2vhNLRX2e+wcKgqv69MbyHfOza9Q1U1tt32bb70kh/rrr7/E29evyTNzi7zw\ndVlwb722QxbLpt8/iPFa0/Wv1ZDNYa5exaKufWtJ8w0nS0kjNTwyi9EKiGo9YL4pfV5bX8NqeXSn\nnxa8d6XMYU6JeRebqgO1MiUN9e6VXG7ckEUzt3MITT200pSI3OhJinwE1zqkSc7HRhHau5ukWUaO\nL5FOQFBYOyYaTi1FLtfmzQ2+85xsgvVGwOMKDDe3EPDYY48BsDS/woMX5FBeX2vhOnke2ByOkUPH\neBmHPZmfW1tbhf5W6018r6ptEJJjbRFpUS14bzrb68TsqvGe2h1c7xoAjlcrSEmTKKRezo2QgLPn\nZOPbP+qytaGVkalDvbWsbXAYRdJ+P1hlNJK1eHhwu+DuGnZTKqn0Zf/WgEFPDsLm+ccwWhpvHI9y\nVUKKnlcmGsnBnoZ7jOJ7yInyXOa0BL3VqGD0wOjYGnuH0selhkdNjdXUibm2KeOwOj/H6fMSNg1j\n+LZWud26fUijLmvA98u8dvmG/ppDpkfMKEroKZdca2GBRG9tt7d3qDXkMuS5lmpVxqFUCiCWy0Ha\nP2J1ZbobTVcR0peWF+jtyz6wtbXJF77wbwGwpRpeWcaxNVfH6KXjoBtCJmvK9RssrJ2RZ5arEN7S\n8SrR0qqpqjIbLLaqLGgVXDkIMBracV0wykwQBGWs7kkLrSb3qSH6yo1DSpqHZjKD6w+n6uO5tYfo\n7EiYrGVuYZ5Qw/PEAm7BMZiSw1JnacpQ00HS0YBDRee+sdsnTJQ026MwJDzPK/jRHAeamkd0FFq0\n+JAwHI2Nd8dgcjJixydT481mCWkOxdLvMkymjwNFWUqayXeGw5D2C2IgdQd7jCLRi6effoqGgjjb\nvUMObsnl2avUCiDbeBASaAXc6SDjFz4suvbo/ffzH18VXXnp4i1u7MmYjGxAJa9QMz5lXaMfOLHI\nflfm51tvbJEararOIFW4g8xmBP70N5oPn1mirWv9aOsFXrgi7azNLfOBxyW1pX12joXjspfs7G1y\noKH4djeipVyE9y/P8ei6vA5WWvzf33wRgM/+zu/z9MfFAPuJT/4Yf/E/+WX54fZNfuOffgaAY5WA\niiu6+fr1AeUT0pcL58/x7ecvAnDr5g0Sq5dj43IPGRLALJw3k5nMZCYzmclMZvK+5AfviTITFXMO\nHB5JEtwLL7xQJCyXSqXC++S6Lo6G6qrVapF8nqZZUWrled5EEnBWJL5FccSps2cAOH7iBDCuDMg9\nUVg7ga1jx1hJhoIbDGOnpigA8NyYciZu8/uW76dZU5fh0T7Rodxmu70jvvPtrwKwsrDA6bPiuThx\n8n6Uiok0ikFBwsLePkNFlrvWvkRH+YvSzC2Segdhm0irgN6+dZsXXpMw0t5+hxNrchvduTni9Zdz\nZvYSga+3MVNhdNiZqn8tDQeurcxjzUj708692hh8SkqjETojrM5fpRJQ1QrDcBiypUnmvuvj6w25\nXDWF98JryVysNAOsVhQuLy0Q6y2wMxoxONRQ4SgkzCklXKfAAkmTrEi8rtVqU/N1JUlWJMdKUvCY\n/iFPKh3GMa++IsmIX/mt32QUii5//JNPEmjY8IknP8bHnhJvUuCXC6oU13WKELS1pqh/yIBYMa62\nbm9T0fDZ8fVThTfDOk6RDGqzlJxoLbMpWTodDhbAUmuuAIG01tBVd3m1FNJsiv426y1a6jmxWcL+\nvngENm9vE2qYqF5fIiiL5+So3aNalc9WKnV2tyRButMdsrAgulYve4wUJLHqW9q74smJzzyF44ue\n+iYhtnkIz2fQFV3u7l3CrUwX6gJwjWFNk5I9HLJQ9HX9xFmeU4/TkalhXenL3FLKnHpA/XKDM+qJ\nqs8t8i/+z38FwCAc0RnKXA+GfXQJsTbvEx5Iwnk/SJnTsNebb11ie3tXx6FHqyUfaNbquFbmy4/6\nuAMByFyuxcyVp/Ni5OCZ1XqDnW1Z181Gne1d8dZuHfRZWpW9ZenYGTxNmXAjyzBHlbReEULPjE+g\n3tpHLpwmirTqMpTfWZyrU6vmCf8w1LXq4tJQ0F/juoQjLebwfN64KOPst06zfp94orOjDUy6MVUf\nn37sadq3ZH6Gq1tslEVf0uSIIPcYOLYIu6dpTBpLuwa9Phv74lHpxYb5VlPf71JXva7VG2xvi0c2\nGvWo6R611wm5oaHsC2dTfFfBIf0xB6CDQ+57sJkl0fUXkxFOyUUK4BmnSDFxPQg1rPb6rUMeflv6\n+8EPPEx3T8Zs2N3n5JOCM3f88adIdyUyEY56hJrOkg57NDqiE08MjnhgWdbTtQ+0+NZFWcffvrjN\ntT2Z44Mw4ey89OXksWV+/zVZu0epj+/kmH4UdFWNZu2ezsXHLzxIqGDHSTIkU5yu9lGbcFX0ojea\nIzsQLKwrr96grd7c2DoslqUNJ5bqdBN5v9sd0tQE9WwQsXFFxuf5Z38HN5L1dGre8PgpObMGnUPW\n12UNXL7SZnQgZ9786jr5Ht8dduiEMu+Z9UFD9DAd7+oP3Ijq9XrkjY3jEc2mbL6nTp3i6lVRBNd1\ni3wk13UJtHS8VquN4Q4sBaCi47o4E6CdjpbuJmmZBQUitNmYN2kUDkkiJR/N0sKEytKMSN/PS//z\n75zMi7mbNGpVmonEeFtmlVosr61ZYFdJQvv9q5zJ8kOrRqMhLszUGroKDhcNu0RtLTEm4e2bsjF+\n7bVXaM7JYVOuNoq8hFHSpTeQyb/dvs3WrnxPZzthtC/96bf7Bd6nYy2jUJTRCVLM3HSOSKtVOH55\nXJ1R8kpYJ+cQq5KE8kyEj6+knGkSsrktbboRbjFXkw1teWmZZlNeh/2EnrqRs0TDtd48VQUX7fa7\nlJW7q9ass6dhnmwnItIF53kpI82tiYGSbvp1Uy9yCu4mYTquyEsnCjRMZkjU8Pitr/wuv/orEjbp\n7O9z7qyWQ5frrK9JPoFfauDbnO/KFJeD74EjyPUXWFyQaqrjx84yUGRyx5SBHA3b4BQ5DVnBTeaY\nDFOws95dTq63iHOy5zQrEJBbjSr1qgJvphQAfINRwq1bsin3ByMqvhgzQkQt7fS8jLKWKCeJZWdP\n8nQ8H+p10S/PtZS0wu7CmUfoHvwBAJvXX+Xcw3Iw+L4tQrh21MUmsuk7noOpTN/HUimgOb+mffQI\nPNlL7j97iueel72n458nM6JHq8d9Xn/jmwB87BO/zLPfkNf9foc4Et3d2dogPzh7sYOnl7N555Dj\nFdmU27uXSFzZe1ZX5oty8eEwLNDm+35AkuUI1LdY0fDWsXqVUTKdng4VvuGo3WV/X+YmTkZ4oUJm\npAFNRd1O04SeVtYZt4Kj1l+W2QJJstPtsVaX+V5bmWNnWwEpNQxWLgfF3mitJQzVaC9DvTEON+fv\nR7HDjVuaX7d4gdaahG1qcz5BMt1xMxplOHnor3yETdVwy8aAnWmaFQd6lmY4qjs7nZitQxmjYysL\n9DWc1Asj5vOULJMRaK5cnGTsdUb6nTG3diQ0fdgf4Ts5Z5xHpiEta6Li0p7ZlFjXSmxTUpvnWd1d\nMutgtOQ/Iyv2g3Y34duvSXj1x/7okAryWgA15Zna0llcJceOvXEaQhYOSdpi7I/2N1lUI/34KFrr\nFvYAACAASURBVOJDH5H2f/qgw++/IQbksy/dpKqhrlv7R+zu62XWD4p9vhyUmNeqzoWFEtXG9OwB\nvU6XWPMiPWJ8LVteXmoVYfAkA1/DslfeeIs4zuuTfTw911+9ucetIzHGnHKXT//Cn5L+vvQqr7/y\nEgA7L/w2b974OgCdTszKsuxnr20fUFeeyKVGmT2FEunuHyk2Brz06nP8s8/8Y/lZx+PYkqQw/I2/\n/Nem6ucsnDeTmcxkJjOZyUxm8j7kB+6JOjzcL0JvjuPiqnX5yCOPcEaBJd+L524SdNNai8mt/jie\nCOeNKQp836esiZtpnBR0JZ2jw/FvTEDgZzYrqmjeiRN0L1VPUS+ipp6CtBvhzMutrFoLMBW5nW5c\nvEjLFRf/2vI5HKMhn0qLuRW9Fe6MiDry2q/UaFpxedqupa63S7ISl9+6Js8PDxggN4/YDFk5pQnt\nfpO0L+05/9AxHFduZr1uyFFbbl3tYWdabyVhqu7xYQcvT44uBZQc6UPYN6RaTWMzjySV+QgjS38k\nt6RBf0SkPGlBM8Hq82lvSKBu80A9Dt5Rn6CrN/neETUNG5w9f5wVpX242N7hQEM1NonxnJwixyvw\ntZIsKSrZ7ibxBNt3NqEjJddl47q4uX/t336BK9fkdteqVQi1b6ORJRqpjhtDKcdVcXhXT9Tk68w4\nzCvu0JMf+RixJsW7rv8O8DL5n2WCwd0Zc5NNI5XAwTg50J6DoyGdUeRxY+OajEM0LIo8SoFPpu3J\nkpg450SLhmTq5XW9gEC/s9fdZ6ThoFbTUlHgzTgKCbXK1tiMU8dEr196/UWW1wX/bGX1NJkWKoyi\nAVbBS53WCsNw+rVYq9eYVyyhxHiEjoaN601aLfGG3djY4pknpRon7GVUG7Iub9+6yeWLkmyapFEB\nmtvvtGksyu203R4wV5e2PXD/o3zn5TcBeOHNazzzyZ8GwC9VefuyhCPb3UFx6w6HPU6vyq2+Uquw\nsCCvrZcUvIR3k/l5Tb73S4VX+SgbUVavUFCrEARjcNx5TQrf68YM1bPiuB6eFhL4bkxFq4l9MgIF\nyu118vAGlMrqccocqjX5d+OklBSEt1LyilBhYgMSTxPB3TnK6ulYm1+gVW1O1ccsi0mN/L6lN4Fx\nNC6wMEzQdmRZURUaNBfwPfFaBH7G9iAvOnIKTLUkiikpb10QjCtcXddjX/k9+8OIWME2szihoWFB\nm6QEWv1r3IAkp+/KbJGAPY1EcYqvhU/W2qIa2RjDm7rffO43f59nHpD97r4Tq2xfE11r1HcKT5pb\nCXA0QjMaDBgNhtq2CrYlCf6+tSyq53H5rMOjH5Xf/Uu2yvOvSnrC3/3fP0OE9N1NR0XSfmpTzpxd\nK8aq4DedQsqBQ5rkhReWoeJoZXFa1HOlaUpZ58JzfDTIQn+Ucb0te8xmmJJo0n4jqLD+gBTu8Nqb\n+Fbas1ByybSg4GvP3mL1rER6em6N8lA+G9TK9LSIJ/Ic8kLD/d1Nvvp7vwlAqVzm9LpEFZjSE/UD\nN6KyLB2TttpMatCRPKi8UmWyIu+d3HmTxMEjDb31ez3inCwxSWho+WO1WisqwzIkfAXcQXx5Z8n6\n+LBMkqRYZFINNX04b9SNiNSYSVtNrCdKd/r4aY60BHajWuVIK/JubN3kgceELLHeWKCmCL/z9Sov\naUju2vYOFa0yeurBx2jMSR8v7mxyc1PyMKxnmFuWA4nSkKCqwG/7HW5vyFgFCyMe/IAYcmulKsNQ\nxnznyGeoSNl3k4Gi8g6jCjXdcD3jkyr5YxKCo5U/vlfB99VAsiGR8tvFxuVQQwtHV67h6QbYqPqs\nax+q2t96akh1XpZXVzh7Qg6wC+fPUFIk89vxkOQFAWPrt0PmKnog+Q6hGmW9Tg+H6dzP1qYFiF5m\nTRHOGw5DXn5ZANpubm2S5Rs3RXRZSthzEE7jFIZbZrOCvNnzvELHHccZV/yRkjuEgyAg36PSLC3y\nvDBZAd5osdj8ULETr6fqo2WghKbGr1PT6pc337zKvpbLl8tBvkRpVMtF7pbB8v+y92ZNkh3Zmdjn\n7neLPSL3rMzaF6CwdgPoBehudpNszmBI0zbDRUaZccwkmtFMMpl+gJ5kmleZ3mUmSg+SjEPOsEWN\nyBk2OaTYDfYKoLFVASgUCrVXVm6xx13dXQ/nXI/IagAVBQ76Kc4LsgIRd/Hr1/2c75zzfQHTeEhb\nkJPHV+4Jevbj0R3XJbW+XEfIHXCmsKjUaOH+4NpNrDNDdKcxxv4ubQzLq9tIRpTKTgbXEQsmzCya\nwCM4UaaYoMXt9uNYY6LLDVLixHFqI79y6QP0J3Rn9doJHCfuPty4cgN37lKq48UXv+TGqnFsC0vH\naEO6efgeYnaeg9oSmqtEPfLFxjb29ii9dv3GmxjHZdpthNVVWtBb9h5O1unztaaCL5hoNI9Rm5N9\nvt0hR3A0yZDz/KhFFSeoW6nWUKsz+7ysYn2VUsXtJY39/pB/m6Iime6grRCw05H2+ii4G3rC1280\n0GaF4izXUKwbGCcjCFU6IlV4XL/peQpC0gYfqRzrDRr/Y+vHcXxrc657tEghRFlmMa1g1bBOo1OK\nKQmu1hYZ6yLWWi0YSYHO7ftdJHkpOuy59zLJUvdeArNCvAJjJgedxCkOD+j5HB50sXmMO8vqDWgW\n7g6qCqWnTX3e8+8ZDz5tp8/pK+Tcevfd1y7jNpOfPnfhGLa53vDimRNY43KIoN1wBL26MC5NmycJ\nki6902acYnBAz2cwTrDEhKntpTo2NiiI+S9/7/fQXP4+AODtN67gkElax5MJ3r9KKcVWPUC9Pn86\nz/MsfKaS0BJQ5fgUqZtnMBnSvNSwk1jhjGgMjQPeX+o+sMWBS6dVxYcfUhnQ3Wt7WG7Re/n9d+8i\n42d6ZSCxcpfmusgUxrwfTOIEKae0t04fx+471M1+YnsLL71AVDTDYR/LTG0yry3SeQtb2MIWtrCF\nLWxhn8E+fyRKF9NCbmNdUawSAvkM4lRGCQJwKYcZSTb6B7t8YTVCPuICWaPd92/euIHjTDonlHQo\nljHGZUaoQ4oL0Y2B9MquEgkp5Mz35+f8iIcR0kpJaT/EWsDwYRSgyRH45kYTggtS33jvDXzhK18H\nADxWfQq9AUWC2WCMWpW6Ck6dPYf+iFGp6x/gg7eoy++tWzdxwAXVg0kKdYui5fMXtrF+giLGw40r\nGPTpXvYOD9Dcoahuda0Oj4uD67UAczc98bhkeeaiiVB4EFnZEWenaSIl4XNjQLPVRsbyCkmSwHJX\nmZACluHiSRZjr0sRfCWgZ1H1JLZW6OI2NzdxbJuj6U4dtQ5FYL/y1a9iPKTo8LXXLhHvDoBCWUxY\niqHIjetceZiZPHNq6BbAzg4hEq/95If4wQ+oEDpOxtBMwlqYHCM+9uFhF9ohTtIV8lsNl1KejXzt\nTIdoYXLHXyOE76JZYw0sx5gWBsYhssKlNywM7CPIMChPuYjdmgJa07j3ez1EnKJYadcQa4r6ktRg\nODrke8mx3CzTDxmSCV1Pu1VzZJI7OwMsL9F3Ou0q7u/RvD53oolqh9CYm7dSLLdpjp8+tYU+dzj2\nD+8CmpCosNZHoLggOWtikFyZ+x6HB/dQ4e6aNMkgTDm2FitLlAq7Iq9h95Cu7UAZtOqEHD/+VAvX\nblC3T66BHmvknT9/HudPE1x1414fly4RSd/BfhVBSKhXp97A7UuEqu0cDCA4jaiiBja3KVo+KYAT\nDU61ycJpmxnju4L/h1nBqPru7gHKdaxSrTidRSssgpDTtLHG7buEyhhPYcLnmMQFcp43o0iDgUEk\nw6HTi7MMR0rhocpoQl6MobjEIk4LXPmAjv3Y6eMIubuwWfMw5Os6e34NpzfofrMUCIKHy6EAwHBw\nAGmZG0xQY4X7R8kPaI1L/8ZJhh43p3hBCMPr1TgtXFe2lAq63HsgXVG61tqlxPNCI6zw/cUT7OwR\neqOLFCmPb606wPo63cfSmg/FKUptzCOVgDxoJfobLrWgNigdmqcZLrP23/7wGoIP6D146ekz+Gff\n/hUAwOraMdQbnI3IUwz3KTWdjsa49h6l6vZu3sXwgHUDRym2OI38pW8+6zjtnjv+Iv7T3/3nAIAP\n3/0I77z7IQBg92Af2YQQub37H6FanW+eAkAWJ5C8r/t5hqx8ptbAK7sdPYWMO6ij+D5ePMnkhXaA\n5TOEknV7XezfoiarXEn81V/9JQBA6BTL6/T9a9cNak16F4NljeuHhKRFfoBiQnvJcJhA1ghGXF5e\ngZQ0np3mMn7txRcAALXQR6WyNvc9Ar8AJ6oShtP0hplqrLU6LdTrnIKx1nXJWUvdWwAQhMFUV0wI\nlK3mnlK4fZsgxtu3b+P0iVMAgLs37+DEFjlRfuC79FySxqjVaICr1apLq2R5Cs91rBhH/gmIuUSQ\nS3v7p31E5+llalfb6PZK9udLWGrRPW6ub+Kty8Scevm961j57ncBAM32Etr88JEXOPMY1WoElQou\nfUitn1du3cCdA9rUE6vQ4+6T/fsj5BMan71rN/DEC7RJTEIfyyd4k6sHiLjWaDRWjvFY69TVrzzM\nyi56rQtkpSYYBEpVSKng4PfQ96B8uh/fVxAlOV6eIGZCvij0UOdajaRIoRlCL7jGyTcCDdYQVMqD\nx62ulUaIkB2xrUYTLz31LACgvz92jmWcxVDcHSesRq06n2CmLizAsG+v38O/+bM/BQBcfucNbB+j\nTXalUUV3wHNEaGRMudHtZ8g59x8oHxNut86zHB7n+/1AQZfi27Zw0YGBhLSlYvWMaKMQsLbsAhIz\n5J8Whs8rrHokdl0rAqQ5d9hFAkVB1xkECj57ftLzUeFuOxUJjAa0UeaWmLgBoF6tu7bwTnPFMWRn\nWQ+nT3GaIVSosYbayTOP484e7dReGCNo0niiqMO3zDSdpBCSvl8NzsP36Dip3Ueez9e5BgDXrl7D\nifMX6R5lBpPx5hpFTki70aijzumQxx9/DH/93b8AAEz6O6gu0QJ69fYujm/TWnL6secQBjSnzpw4\ngd4hOemX3/3AdTHd6WUYxBww6BCDHs31tY1t3GRSzKXjLRxwgAGToVc6Pl6E1MxLxUFzYn93Dx7o\nN/VqBQfM0r2/t4/9XXJGt06cwnDEacXDDEGFhXZrTTemB/17qJfvqJqmmcvvTtICe9wWnluFvR4F\nDq+99j72eIN/+dvP48tfJloF79ohIuazeOrMOpZadL937nTnZp4fjA5QDUrmdAU3yeUM83aRQ/Pe\n0BtO0BtPxdDLUoDCCtS5Ls9YIMvKDsJ4mgrMc2T8dgXK4oWnSUMtChQOWWw51RZg0WFxOELCzmhU\na6DOVB/k6M2/ZyipYMsaKqOdqHG92ULU5rVxFKPP3tXdQQyfaSR++LP72FilmruXl9ZQ4fOOxhPs\n36WU3/27t7A3ouO/dX2I/iGNT2epDeXT/nq9WEXwEQUxrdElNPm8T5w7hi88RQ5MnmvusAcO9/bR\n686ntwoAw9EQmul4lARyS9dgdQ5wjVNmgGsfUnnKaPcWnjhNTtETL76AL36ddAPv3O/jX/xP/zsd\nx1P49tdpjxz0+tjcJjohIR7DGjtUP3z1Ev7oT35M97XewotfJe28v//eW+jHrJ84TF0aLvIAyZQ6\nnvCciPq8tkjnLWxhC1vYwha2sIV9BvvckajHLlxw+nfGGHiMAlUqoYt6oihy6Y6i0A41qlQq084J\nKanKEVRsXtbT9rtdbDD8+dRTT2Bri6JcIafkhmmaTIvJjXEEiDIKHTyui9x1e0ghHWI2j0VhA1c+\nJKTo2Mo6+pro+VdX1lAkVKQ2HGi8+jMm5kskfvRTSglEQYBnnrhA16Atnn/hawCA0d4B/t+//vcA\ngA9v30TKT+re/RH273LXSOxB8UBk4wxX3yF0bu2LEbKya0RLBFwMKoSF5WhAaoVKMJ/UhOYIzpc1\nREySKTIxU3xvUaKEeTFx8LivLDoc3VRChZgp/dMkheR0Xr1RR32Z4OiTaxQhXTi1jbUlQkykBcYM\n1fe7fUfC6YUGZ7bpWT978Tx+xCSYoxQIoxrfr4av5iuE1KZAGfHeuXMLly/R8e7evoMXvkCQ93/9\nBy/gjbcITXztZ2+j1aRrPHHyJGrMpZIXGij5syKP5GQAwFqXCp1VCpeQLl1aaI3clEXpAmamW9Bp\nPAKueNSa6d/zmK88p4M2jgeImIhR+hGytGz4qKBRdnT1R2hwmjrTAn7JFxb4qFS400oLpBNKO68u\ntVFr0jNcW2/AgMbnxr6AYDjz+IkVfLRL99gdhdjoUKq2Ij2EVUrhGSExSTn9cHgTvf780e8bV3dx\n4qkv03EwhijTZMY6ospebx/LS1RI+usv/zK+8CyhD3/8p99x8h6tVgdbx6gQvd5sQ7E8zdKGh83T\ndC/9SoSfvfkmAODeSMByg0hrYxkrZ6kAXHkRND+j920NV3eYZ00J19gxKYDCzNf1lDHnzWF3gK11\nRgyFQMxNG6kukHJKbmNzFdhj3ieTo9mkReT+QRdV1uWU2Rgxc3IttxqoMnlviabePzhEzM8iLQxu\n7xA6c/PeIWIuqfjBT9/HY08SSWm7XcPgPq1DWfcqioD505SH6pwR/jhNEXLnGi3JHOsLCe3kviwy\nRkZ3D4aIuWygXgvgc4lGkVskKevEGe0yEM1azRH8ZgJYXSYE41e/chFfeJyud2dnD3wY7PVjgJsn\nhJIoLI3B1naC6hLrWFoB+wjNSMJax29YrTWQpzSnRru7iBN6HnmSoxjR8wujCCl3cF6918X/8kd/\nDQC4t9vDyy8RMqNHBzhkpPDSrX388B1Cka/fGIF5LtEcTmBvUhrrT394GfX6/wMAaLdarut3eXnF\n8fhpY9zac3hw6PQaf/zWf/TQe7TSOOknazQKzVx+6QSWO7gHE+BvXqEGIdPdxz/+FWq42nr6WeQF\nvffnt2tY3aQsS5Hn+NZXCSWzNgdYXzQIFFCWP8hT+O533+fr1zh9gX67v3cS3/sh7bs/e+NtdHgt\nfOn5x6H52saTHH4wXwlIaZ+7E+V5nmMgV0q5FJuAdZCq7wcufZZlBRJeXNI0dRu1FMI5YICF5h1m\na3sbE+56W91Ywd4BQdlFUbiXZjQaIQhKIjTh8uTK812X32Q8cR0SAgJFMb8TVRiDwz1afN67/hE6\nK7SJDgaH6DMp+PV7PaSK2zoU0Gdyuu+99jqu3SMHbH2phZiJ5e7v7uP996l7YOdwgr0h3eNokAJM\nWqegIFA6lhaTAY3V3uUYa6dpU19uNJ3emzEFhKDzhn7D1dw8/Aa5fTnNUHAqKbAV+GVH5czikesM\nKdfIwBoo7l6pV31UfXbaTB0ed1FWQoU2b+bbrB+2uuShGtG1VSuRW3w9XyEIyy5AuHqgE+sdvMos\n5VmcYlTW/VhgnPXnu0WbAZo7bazGxgZt7tl4gHdZ5HJrs4Hf+Ef0kj958TSEJAftqScvOEFTbQHr\naiwyiFJ3ShtXjwQIN/ejoOKcel0YVxtD05udJQEcydvZ6R/zu1BAGPoIIno2B4exo6vwgwAeU27A\neuhwd0pqG5j06H1Ceogap4W1qcJwWik3EyTMph7U19Ht0lzY3T+ErygNEHg91Kp0/N3dHdiQxra5\nvAnB6U6jawiZ9d7aCYbd6wCA/uEh7nfn6yIFgCv9CvZ12amZQPLzt0ZB8lw8trmGb7xEIrmRr3H6\nJKUEfuM3/3P8q+/8OQBgf6ePe30uB0iuIuB35TAucJVb0JHlsCuUKuisVV2dmxA+DNMCGBE4Rvq+\n9l0QEnkCY0FrRu77rjP0YVYKFQ/GObZ4+R6PU/R581xe28bGKm0ae7t7GPTp3M1mC0JRnUied+FZ\ncpS1BuKS7qATos4B7A6nf/a7I4yZSkHbDAk7K1YJlPm52/fGePcKjfOXnjgFAQpADu6+jSiiueT5\nq66u76EmlKOekcJA6LKucOo4pZMxxkzDcG+v61LljUhic5mpLHZ6br9pN6t4/gvk6J07dRJpPOJj\n5jjB2m2nj604HdbhYIAGqxB0h5kTRKZeWhZHH0+wUlLkYP66NgCQyjohawugw93XwrPIObWb6gwZ\nv6NKCPDrAW0lJkyu+p2/fA2H96iO78UzHexxm/+b14d47wY5Y3EiIXiuxIMJ3wUxrh9wqu76vZEj\niIW46mqIjTEoiwmU8uF5JZv3w+2wf+BSXcIU6LPuI4RB4NP9/u2PL+ONq+TsvfxLzyLcoHqz3XEf\nAevO6lCgwlqOgzRFXNA112s+kozmfTos4DPz/uZGC889T+/0333/DXzwIR3/mee2cf0u1VZd+egA\n33yGguOL57aguS7LD4JHYmUHFum8hS1sYQtb2MIWtrDPZJ87EjWZTDCZTAuYy+JOAeGkW7Isd1IT\n1lpHq0/cTVOv0OOiQiklxhPyuLUBegOKsNI0cUSBWmt3zDiOHSeV73kzMb10iFaaZkcK4ItHiCq0\nTYAK+aM91cdmmwu89/dQcB6uHhQoKuTtZqGHWpVRl9VjaHQo+gubHr7/k++5cejzuN24vkM6GuDO\nEjXt4CrJ5wAL5DS2vVsaGcvB/JOXvwjrUST52s8+cN01hY2hzXyF5SUBXyWIXFRojYbkCMVTHhQX\nfId+BWhwp1xWIGNUschSRygXhD5adYrIj622cO4kpeW21yiCXG5X0OZUWa1WQ4U7KsJmAI+7yGyR\nwjIHzGqzig4Tct7txXD1miaf6iE+xAoDlG11W9tb+Oe/97sAgOHBLi69+VMAwM9+9H1M+pT6eea5\nl3DyLBUwh1Frmp7zJFJOrcSjAfyQ0Qk5jejStICnmEyyUnUdfHGaIC9Kbig506V6tLDcaVEauEh7\nHrt97wAhI7JKSOx36R2qVVsYj8tuwQpqDYLyvdyi0abi6u7eEIKRRCUj5Ia1rJIImWH5myBBkVOU\nuH9YoMHEjK1WDZOE5l06vgYbEEy/3G4Dls8VRgDroo0GN5HHrPdoPPhq/uj3Sk/iz14hyP4LJ1ew\nwRJEVd/D5gbNs82VJs6eoVQdbIZ7zO/0h3/053j9jct0nUkGtwRYCctwvw6b0Jyu9VBBwem/QlYQ\nlaupFUgynqdSwGPiUGUMbMJlCzDwmUNNCYksnw+lOXacUv/V1jqu3yKUsF5vomBOneWlFTx2gbua\nRinGHvPp6TH6PbrPwItQpFwSUGjkjGynSerIFEPm3vOiFJnN+HchCj2rD8cEs0EFzWXqQFzbaMAm\ndF039vewt0vdYrW1FeSMejzMstTC+DwfYWD5QcTjMQZdSh0PB0MMh3S83e6wzPthc6WGk8fpOSda\noN2hVN250ydw4gRxetUqETxGe0w+AatKwea5Q3k9P8QydwInmUV3VDaLZI6PKM9y15VrrALmV32B\n7ytkaXm/GVh6FfXIx2abSZatxZBLGawukHLKr9VYQZ0lVIo4Rb9HF/2Dy13cOSBk5srOCGlSdiMK\nWG5CkK6EGoCYao4CVLRNnwu3XwJwDVe+H6DemK8EBCA0upRuQZHhoxvXAQA5NJRHe94rP3od5y+c\nAgBcuLiFpGC0Kk6dbNsgKaAYkfOUQcIPSeWZ62a2AsiLEgku8EvfpHfgjbeu4jLL6Dx2YQnf/FVC\nn/p//oZbU0NfISvRORhYzK9HCvxCtPPGLv9cFAVyrq+ZZQ63dqZGRAqX/rP2wU1Cuu9oB6MCosy7\nAo7xWYjp9hkEEQre/PMim6nlEW4DM9q4Ftii0DPOycNtbW0Lb90lCoLDRGEnpZc7qvuIuQZp/WQD\n51pENpcbDZ3RZNw6toKoShO8s9RErUMPf2fnFk49QWmPWsfDiNN52sIxII/iDLrUINK5o1DwlYTi\nNu/9gwOcPMeCsoXEndsE8T7+xAZaTNz3MCtFhHWhobnGQHoGkCUthXLbvJQKkjcWP/IQ8KKsgxA+\nO8H1Wg2rS+T0PHZmFU+dp8Vtk1tvW7UAPndDWSGcPlWSZoi5u0LqAuDuNU8FiBh6F6qHMCyvxUOR\nzekMi4DromgxWWUC0OPrDZw8Rtd16bUG3r9CKdb33r6E5RXaiCvVjoOAhQQ89uLyeIAhd/jESR/l\nJA+DOo4xeWMQ+EiKaa3UrMs3DSCsI461Fg/UQc0PPQthELGA9MZKHa+/T8FHJRrBD+h+wyiCFDR3\ndBo7XbzltfOu68mKqUB0rgUgWaMyK9z8qFdCJ6ac5QnGE9rAoRO0mVIgNz4C1oxbbq9iEnM3VNxF\nKXqqixxPXjwz9z2OZIB//zrVfHzw4TW8/DylcM4ea+Gja/TsfulLTyHiYGuYKfzxv2Mn+fJdTLjm\nCF4E6ZeUJxZSlPUWwq0TqZHIS2oWkSMttQ6tdelqpSSqrOUYQJcyZ9DCI/03AEVeIGi057q/46eI\nauFr3/zHeOunfwcA6B3sIeL04f7ePn722qsAgIvPfgntFp271+9DSUqthZUGMsNkhCpAJWeG/2JK\njFytlqUHfUfF4MkAWVLW+ClE7Ggtra3gxV/6FgBgs9HH8P51+in2cYu7qNtiA5mZk9x3nKHCm2YU\nTLvqer0e7t8jp6w3nDjNzcE4RamImmtgjWssq9UIGxu05h7fOu7SiRK2LJ9BnhauLjYXEgU/E6kk\ntjYozWcsULLgehMJxc/WCuGC8KzIYeYtjwAQBdLVOEVhAI/rVrMsRXeP1ugkEyh4bzu9HmFvl4Pw\ncYL6Mj2zwzzH+1z3NoitSyl6noJfHrPIYTlAob2jLKkxmF0/yuVGWAE7A2qUf5six2Q0n2g9APzd\nT99Ayh2Uy7UqQsklGq0WXmWm/7OnVvHtb5FjE4R62nmMzBFnh8KgFrGuqkqhM9arHGkUZurgeVxe\nEeoAW5u0tx0/tYEhi6gLAzx2gdJ8L+5n2LlJ69/uYR8+136KWgNWzNcpW9oinbewhS1sYQtb2MIW\n9hnsF5DOm8K/Ukpk7JkqMe1GEWKasLDGoGBE4Ch52RQ1stbOFL5Z52XTv6d/T8k2jx7LTIcb+gAA\nIABJREFUydBghm5fG/d5oQsUxfzeqJIRkJEXvHMjhfAo2t/cbkBymmmnGGHIfEi1wMLjNM9BnGGp\nSl5zwzTQ5s4ooapYZZWE0Ukf4wH9tjsaIWbkQnhtF+3DzzFkDz3TBW5zB9/fvvY2jt+lYr2LZ57C\nsSX6ztbpBtqd2lz3N4rpN0JUITkF4UWZ6y6xxkf5NKWcRuHCChhTyvlIeIyOBX4FMUPTd+7fRcRI\nRrxL0fhas4UKF5tbX0CwPIlVEUzKkX8xhs/fOSw0ejwmE5tCeaUOlTd3mFCKqgCsz8XzUyg4lGl1\nZQkHe1x0HU8wZGmEpZV1B4UrZV0XW/fwPt67Sp0n93Y/cvP0hS98HWdOPsZjJKcSCNJzHT660C4V\nKQRgSu08IQCUBfDTzpl57NxWEzXOOQ1GBVbu07t52B/AM/SMKyt1V6ypvAKSx17IVQgu3BRWIGZk\ndDK5D8Xp5UAEaLM2XBh1MBjRcfr9+xA8PrX2RdQ6lCKc2DoqOTVVdHemBJXVsI6Ux6rRaSCqbsx9\nj8srqzjs0pjc6/bwA454dX4SZb5ldWMbglOEP3n1Hfz53/wQAJCaKsCFsyUaDgA6zabRuNFTyR4r\n4Htl15ZyXEKeUk6GpdGouy5haXNoW8pS+ShhqY2NFhrN+VDhUmbk5PlnUWlSGvX9S28hG7JkzqQP\nyZ1tXtBGvXxHrcWYUVzPr6DDBe7LDYXtBh3n4OYQWw0qRbh85ToAYGt93UmAZFkCw+evNDqugaK2\ntIa7O5SiXasqRG1C0BvjAO99QOm3rn8wd8dznhhMeJxESyLJ6HeHvQnuMmnkQXfgeMsmWUGSJwD6\nwxTHjtG6trq2ghY3Sfi+7xoLiiImrjYelxIRhBCuoF0IYGmJ9fIEIbQAMEkSKP671mwiK8quZIPM\nzI9ENWp119ihlEDCqJrW2nXrpjGwwjyajUodhyFd2+37XSyxlt+tboE7A9qrPAksMVnoiY0V3O3T\nnnHQy3B0ISy7HQU+liBUCOR5qeGpXMeqhYTW87eyFNLg3RvUkd7rjtFi/sBGtYndQ5ovTz95Ae9d\npcJ439Pw/LLpSyDg92a51UbE68dSpwYwilroADmjiGkewzLnXDWqImNh2NAzOP9FTjWv1JFwOvrs\n6VUccqfpJB6hxu9MkfkYjeZrRirtF6Cdd5TJtVxcNOXq6EMBVx9FLMzTFN6s0LCd1vq7zjvS5nOH\ncXC5ktLpjRltphPBWvfCSU+i4NZrcqBKQctHUUEi4dVyoy1GGoj5gdfqqFaYckEEKExJKJoj5xbi\nw+EeBlz/MeyOscr58LBSwLIIZ61TYGmFFrdOXMXhkBc1naDaZBbiIseV92nB2u0adAec7tQ5HjtH\ni+TpE+cRnOH6AjtlPH7o/XHHR9ULHat7miQQpbOitKtJsELPMHZbR4gHAJa7fIweQ3KXYJYomAld\n07BOjt9ebeBy6cITaKzQQlhvdeBzqqyIu0j42d2YFLizQ5tInOVwPKnWIJ1bd806p1soz21WRghE\nnGoJ2svI/XIx1djZZ6K61SGWeAM1SrvNVEVLUBF3oi0JeB7dZ3tpAz5vYtIUjs00T1NH4KkNUJYT\nEMl+SThI1wpQaknY+cHkcZzjoE9zMEkNlpZo486NxZDJCpO4h1t3WHswtWjVGFL3fCiup8oyjWFM\nc1DnY6y16PnUai3kmpx6YyV0qVtYeRwryzR/4Vdguc2ooiwEp8aGwyHay5Q+CSsbsCEdsyJ9ClLm\nNE8p+OysF0mA6/dpYU3H7+KXnqN6okp7E31OS/3dj19FwhtqXuROvNcYc6SWU5Ut7jN8qKHyIEoV\nU+lBsAhupVJx3cZ5XmA4Lus3LVJee1qdFaxvUnBTjzzEw/naqhs1ur5RWoVmXbwvvvBViJxSFivL\nTSwfI+LLe90EAZMJt1pNSMn6dko73cRzJzewWqP3UmYn8dgTz9OJfHpeX251kPOiOp4M8Pc/fA0A\ncOPWLkZJSWRax/f4czNpo8WBo4gsDK9hd+7eRehNA+dPM99rIOvxGi0zjBJmxN8fYH9AjtNwkqMo\nHRgLR08zGWcog4yNjS2nZGABV05gdOIcp0wXbr2KIt+t+9LCKS+02k1UuBbIAJD8uVKBY4rPcouJ\nnT/w3t0fo8LakhU/RMokvoUKMREsAF6M8Mxx7rQcTmCYrmUSH+DSB7Te5Zlyguf1VoFzp2i/Ge6N\n0evROzrDqDKXCTFTLmOnXfRCCITh/PWJf/A7v4033/8IAIkpv/06Uf/cLSaIOH32ox+/hqxMaxuJ\niJ1A5SlYLsFZW2qi16XPH7/Yxi4DClUvQBSVY5Ii4SKzSZri5i0Kzmw+wpnTFLTpfIScS4uioApw\nin44HiFicucsiaHzRTpvYQtb2MIWtrCFLexzt88diYqTxKXhZoI4wFpH7jXLJUV6edZ9x/FESQVZ\ndsX4nvutkh48VRaiG1eACwsnyQBpXSEshIBiyHCWuBB2Cm1KSCcvMI/t3N515JEQAumQIoNLP+kC\nmrzjMKgDjL6kZoySkmN5tYann6PowW8dImW0wuQt7A2oQF2rISRDlXlewGdJhEZLIjUlZDvGhLXk\n8tgHxnT9zZrCheOs6u5NkHCEoZVyhXgPM48jo0pYc9150BqatZAMLFRJGJmnmHDaMk8zKEZ3ojB0\nXCWjycg9J5OHMIwWDUKKxjq1GmoRowlFjhqrqa9sxE6L0LcxYu6YunLtNq5+xESmEFAlKaT0Eaj5\nUpYWcKiCMRrjlCNVaHicZvI6W9h+msYiTQoUPB97oxTt5pQA0/L86mxu4YyiCGc07CJPCXFsdVZg\nJLfmFNZF6FICBcPoRngudaIE4MmSVMbClB0pZspZM48FQYj+pOyqS7HNBHbtVhU37zGHkBSuAHSt\nVXN8aZNkgCLmztciRr3K11bZhPBojCe5jySnsQorEYIqjefyUsMhIlFYgceIVjVQqIdU6Bl4PhQd\nHklRQEWESkV+WIKcc5kpNEohMqMiZIxK7I5SvP4+8cX8+sRiaAn5udMdIqzTMyomCgkTA1erFScJ\nlaQpBD8LKZRL4VnpOXTcDyOM+NllxRiVSsl5NUWfxkmGepvQp/bqhtMMe/+99+DP2ciyvUa/DyoB\ndg/o3IfKYmONou0Tp07j1XfoXeiOCwSSnndVKVxglGJjbRkVbtxo1qvwLSFutYsvYO3YKQDAiw1C\nuaQfOukiawqcPPUUjdvOLkYTGsMPb97D9euEyu73QoyZwyhNLDpNQnGzkUaezFeUnFdqSLkhpNAS\nB0PmHhvEGExKvibpOMaU1qjy/TRaNVS5mzeIKqhw6s2aAjp37ZZImQ+qs7yOlXUieQ0bVQz7dE/3\n7t6DHzFqkaQwJYolpdvP9g97GDE5aWEkskeAJHSRYcJF0Z32huvyHGcZMt4zVtt1wKN59P6Nm4g1\n368fYFwWwAsLxftKJaxhwOSceweHjqxXfAIO9Ulaf2aG92/276KwR9DZh9lqNcKz3AX74dnT6ISE\n5j1+ZgtLbVrfdw/3cI91LK/fPkCPO0hX11ZQb3BDlPGwe4eaRUwC3LpGzQVKdVGt8/4SBQi5E7e9\ntIyf/OhNPtc2zp6idU5niVsvhQpguPvv1q17qEfc9JUkiGrzdyACvwAnKi8KBw1KKafOkhAOgoWA\na7UUM117hdYu5SctIDgfq7U5cpzSrLXumKWTBZQp5p+vp8qSwn1PCum6NAjCfAT2Wa8CC5q8wijs\nMytxrQXUWjQp4vQQkyG9BEWmkHNL8s69Ce7cpsXl3PM1bJ+kSbq9nqGxRC9Wf6KRaYLrhymQjOnz\nuJsh49ZbKX0nvCm9DFLRNaytd1DvcGpB9CBY+dGDD3/OzakW0uSM/AoKdtqMzkhvDtT9wdJxiPMJ\nYmZMhrEIOW0FK6C5diYKQnhembYySHncsxEtHnvdfSwxY27oeeiz0O9er4elFqVM1johbEAnPegN\nkfCimykPsnS8PbiumoeZNhrlLi5UiMJMmYgls+sav42NE8ycWxQYDei6kixHyhpRNSMB7pKsNwSy\ngtvbvSpSbivPbIz9Pi0EEhUoJp6zQrq0KISAnpmDYqZWYzat/Si2vNxErUHnur/bRcQbT7tVg+K0\nR2+UIGInp1VrYJKxUzTuYcAwOjwFZWjhG6Y1xDF3xQQSIdfohbUqIJmmohpBsoMahFU0GmXtU4RQ\nld26hes6lVa6Lp08t0fqkx5qxpJ3CSIHNNzBqaWP67v0vP7wj/8Cv/ItEhz96O4eJuXzhYQfcSo2\nCFDl4CyoRK4GLM8LWHaK/MhztXB5XsyUGFjEk5H7u/y83VnC8jot1vsHh+jtE2ln7+YHOHf69Fy3\nV6bhVmQNJZdHlilkBY31a2/ewMGQHA3hSdSr9P3Hzh7HU9yZVIskdaiBeHRLVv9obQXg93KZu12N\nBSYTeu7jXoZmg9KsW8dPoM3ULPfv7+LuDq1hkYjRY0dkEud45llOg3k1ZPF8TpTqVIEWp+1zhbzL\nKgkqQqZLSppiGhhrg3ad51qrAemVaTvt1nrI6fqutcHaMeoIrreXp2GIDFBbojHy+zn2Dij95Esg\nLXX3IF0qPs0NJpxqNJDQcv7t9OTWMmJeDxKdIeH33kiDNi+ZRaHx/XcpbdcrfCcsHbUCpDGN8WpN\noV4hR/Xq9UN0d8vu2xaG+ZDv99FIecUn1EpR/dj8XeuH/S5yTrE988RpPHPxFF1zM0CFN5/BpIUC\n3A1cCHRZjD4IPQgOUl9980OkZykAePkbz6HRpGub5Bq9EX3//s4edgY0Vjdv9rHL9U5fee5pVDnl\nlwvpOse9SgcVTuGNRxbtNs1rqTU8Pu+8tkjnLWxhC1vYwha2sIV9BvvckShCh0p+J+nIMGdRKWAK\nGxJCNUWZpoiQdJpss4SD5b9L0xypzBbjzhKKGWOmBcSfIkNgHkEHySo7QwLpOUK6teNVXHyBIjEN\nYDIidCVPDPKMIpjJuMDeLn3/7dcz3PiAPP0nnjrEuaeoIFyEAXbuUNRy884Y+wOWqkl1SfkBz5PT\nDi4LSK7/s57Bm1epuC+Awuoy/Y9apQKbzff4FaezdG6hGUFTkAg5mvClcLxa1sDJGUhIlwbJc4Mq\nQ+utdseRp03GfVi+jCZD/739PewPKT2w0mpCcqF2POojz2ispKmjza0rjXoTS0tcMK98xAmhAKEK\nHVr2MCu0cd1wRihXWO6J0BV4KyUdRB6GFgFfVxb3kWt6PnGSQWUleuojsPSsAq9w3WdJTpqGACBF\nAemzsJUXTtEwazDD9lhmqGBn+M+o2WL+eRonmXs2aytNWI6cR0mOYcwF55l1RLNpNkKdSfdWVtqI\nfEISxmODPs9l4eVY5uemKh1All1fIQpOlY8zD03WqVru1MAAGPJcIysJW72K49/xQLpnQEmaO/89\nLrXbSBKKwMdxhkCVHEgGkgvOv/eTt/DRXUrt9cc5DjkFUmRwup2FMa6I1gsCRBXuVpIKHiMRGhKF\nKYlPrZMh0nmOjItTK1Hkiuo7K5vI+EGmgYeYpYKM5ztplYdZ2ZAihUGLC/p74xA3b5WFxinadXrP\nTp1cwxPnKVV1fLkBBUIFkknsEP4CAj53JimvAiXKguIpD1/EHZ1epwXDZQWjQR/LHZobp7c3sLlK\nSEEWx+iOaf4MEo02I59RECCL5yuer9YrMIwaFQkQcmNHa30LE+7UO9i7jwkj1ErBdep6YdVx5KnA\nhygL/JMEA26eUF6I5jIhTv3RCAWn9saZQcydqdarIEeZlhwBqixFiOExgamFcqlOLTzkdj7UGwCE\ntljnNHI31fC5ul36CoKJi4OKh5wL2itCQXKns40Ejh+jZ7wdSFy/QXp2RsCVvAz7sesonReFejCr\nU342+7maE9kHgF73ACUU2AkLNBt0v0oKpIxQ2SKH4LRaxYvQWOfu5zRFypxz2+0qLnybSI5PnWzA\n573WWAkhmHPuXI5bt6jL7/J7d/HNbzwLAFhZq2HAKLKSBZK8JB3N0eHu9Pc+uI5f/iY1Y7TqIarh\nlGh0HvuFaOeVNvswjJlSCjz4YGadHGuP/gYgB+yT4MYjBJ4oW5H1EUdq+h1ZIv9HugjJkZt/smyc\nWMfXvvQiAKC708WPfvr3AIBKlXKvdJMalSV2YOzEpRHv3c5gD5gormewd5cWiZ/uDvDhR/Ryi7ZB\nj9t583zagRj5/rTLSyk4EeA0c/d7Z2+EjxhqVwDOn+JFTVkcMHkb/vtPvz+Pa150IR0LbqQEPO4u\nCX3lKCGksK6zzvM8R4MgFEHVADBMRg5mt0K6/n3ep1BrdTDhtmoZRPBZOy+JR/CqNIbNxjKqHndD\niS7qAacWdeaY7dMsQ5HO50TlxrhuDSssSpDWAC5NqoydMqAL46gcbBhgyLU0uckdDYQxBinXFFkZ\nwueuNIEQggktrTDQJVmsNk5DTQrhWqCtMdAlCZ2YBY/tJ9Y1fJxpqVz6od/L0BuXc8q696DTqKHO\n5KphWIPnlQuKRBKyltwgRlbQb5XnQZUbAKZtQJmG65ypNyKE7Dl5QkOYmRQYO3JCymkXkJQuC6uU\nwlEK0k+3NInBayxSncPn969QgC2DuUodN+5yOtVTzmErCuN0O8fjsQvmwjBEreykqkSQ5SYXhahU\nuasnK7DPbdsGhWvV7jRrWF8iJ2BjY8mN+bDXxYjneHtpCft7+3PdX6kdmcQpDnqldtwhLNOEnDuz\ngicfo5Th2VPriHggJ/2BY6r2w9CRROZ5ioLnrpIK9bLOqKwBMsYFozKUWGaxXmsaCP0pueiYN8Ve\nP8FHd2m9uXq/C8UT6/jGKlaY3Pexh9xjo1GHLYW4KxE8RV2VYaOD2jI5hfVbH6F7SGMWBR6aTZpr\nqagh4W7OGB4K3ogn4xS395mSZHkVHa4/GI4z18W9P+xhwo7WZDLBHj8TT1q02REubIFRTPcqvQps\npXTYqmhFc9JUALh/0INdJgepgILk8c61dutNWuRIuBygUAprmhy89aoHyfPx/Q/v47DHotZh3alC\nxMnIBXyPmvb/D2Vpnrp9VCqBOKNAQSnp3mk/8jHg2l8DQLNLkpsctQY906++8ARGY5rrSdyHsFyX\nauSMwgMQcqr7uRfOQ/HczLIESpXdlJH7GyrA44+RA9ZeimAUzZNxZhA8wnoDLNJ5C1vYwha2sIUt\nbGGfyT53JEpKOUN6OUWfPimCnkWAqAh82vU0e8yPswe7Cko0RpviCBJVHlMXU46p2c+N0TB2fuK0\n7TMtnD1L3Sz+xdMoGlTsNop30d2l6EeFGmlGKR9pIzQZcld5hOE+KUvrrIDH0hGTnofRW3wNtRzh\nKo3L+skmllYpuq4EVVRmeFA081Dt7w1x/T0u7uwWEKWESj3H4T7d8NPbT+KZ58/OdX+WUZA4zpAw\nkuFXI6iAUIqwEiEbUqRQFAEmHG0LoRExqlGtVpBmdG/GKpcy8jwPAcPaowkjO7lG94D+f5JMUKtw\ndFWMXUpsmGokBY1nVGugyYWfo8EYmrukhnEGnc0XheX5VGdPSANZIlFWwJRUolJj2l+qYTn1IZTv\nOuliC1hbdtspCO4ylFY4pMViNvVqMA0Zp12kVjwgf+SQqCkaJsUM19oc9tO376DK0ZoxQMjppI21\nGqpVno8idNGd54WYJFxQm2Wue7FWW0EQ0udhVEdQYYLNMHK8PBAKyiuJOuEK9ZPEwvdKIrGp7ITR\nBtZRnhauq9NTakqGOIelcYKQ0c+qB5g8Li/HdTUaa9wzLTILq6eElOW6ZMy0eaXb7eKQj9Os19Dq\nUBq5qSQi0Lhpkzq5HxUqpIwch55wnxeTPgrWVRz1DmA4tRCFPpI50yQfXadi5xu3drDH/G1+VMH5\nM9Sdd+5kCys17qg8vIMBIzHjYexS654/RaL6wyFKBLsWVdBoVHksplkCpcp3wbjCXCUlugeMLI9j\n3LpPjS+3bh3g1n1aC/bHuZP5esdXWF6icfvWc//Fp96jkN60AFj56HBBda3VwebJUwCAx555DjEf\n21PSobYeLPyQ19BAuQL6rJ5DrlIKeuJJ3BvSGH108z4q3EwQeB5Y2hDdTCLjDlEbBtCNVb6GABXH\nDeajLUskqgLPn5/PrBfnsEyS6Yc+XNMzpHtX+qMYKXeINtsZzmzSe5ZOJrj8HvO0mQb8JqfBpUTK\n+oS5naLp89rsnvxJJS+Poil78Qu/7pDdQk/JgwmJmlqWsjZjELp3Ls9zl05XnnKSXJPJ0Gnr5jkc\nKWiaJlgr310UU149KLd2Bn7k0q8GAs9+kVP91iDXvE5YoNnYnvse6TePsAgvbGELW9jCFrawhS2M\nbJHOW9jCFrawhS1sYQv7DLZwoha2sIUtbGELW9jCPoMtnKiFLWxhC1vYwha2sM9gCydqYQtb2MIW\ntrCFLewz2MKJWtjCFrawhS1sYQv7DLZwoha2sIUtbGELW9jCPoMtnKiFLWxhC1vYwha2sM9gCydq\nYQtb2MIWtrCFLewz2MKJWtjCFrawhS1sYQv7DPa5y7602su2pI6XUqLUExZSOGp/zIgMSzEVWRUz\n0hcP0s/PyjNMhYOnKhif9lsnJQMcoZ+fZW8v/965c/2huiEXz56z4zFJkEziCSxT4693mnj64jkA\nwPHtM06kd3Wpidev3AQA/M0rP8RgxGrkAFY7RO3fajVQMuxneYKMJQ4EJAyPm/AVIhZaDMMq/IBk\nB4IwQMRSBlEQQTLVvef5iFjhXMipfM6f/N//8lPv8Tvf+Y4FSPpDa5Y6ARDMiJSWYxqG4RH5ndLo\nmbKgrh7AWrqfPM+hWbHdlj69rKBg4V76/9pdv2LpCmMMfL738nsAyRK4axQCkiUrfv8P/ptPvced\n+4dunr7xxhvY3yfx0a99/WswpcwKpJNoscV03kEAksWIxYzY52g0wv/5f/whAOAv/uxPMemRTMd/\n9s9+G//J7/wOAGBpYwO+8t1vP05u4UEl9aMC3fTZ8eMrD52nL331rFUspeAHITw+71K9hQrPhfWV\nJp5+iiRi+6MRuiz8eeaJVXgsmhz3R9jdIbFdFQErG3Scmx/FSHMWxA7qaCyTnM/p0ydhYzr+wW4X\nBQs0p5lBzGKuBmNYzcruGSAsC3fLAAXLsvwP/+J/fOg9Ht7uluL1EJ4E1MxzKdcecXSc3XogLAQv\nicIKCBTT37of4xOldo6sH9MPj4iiH/m7/IrWTqViaav9qfd49uKTtjxBKX8hpUK1ThIWBgY+S4VY\na9Go03ri+Z4Tg9e5QJLQYZIsAS8JsNYgYJFsxce2xiJneZo8LxAE9Lk2BQp+b6v1Knp9kn0JfB8T\nlh4JPN/JvqwuL6HG1/Jn//Jff+o9rq0v2dnn49YTC0jLUkjQyBUd+/iFM3jupa8CAFqrmwhaJMCs\nVQMFy/JEURvNGsm+NKp1RKVklR/C53UMZiqjZIzFYExSILuDPvZj+nuiLUwp6wQBzYt0nhWleg7+\nr//2Gw+dp/djY92+BXFkLTk6i37+vZ/R+f4HaQsL4JGkdme/u1GRDz3zX/7VX9qExcY9KeDLUvZF\nOfkVKSUUSx4pARhe9wtjIGf8hlkfwl2/EJClgLmYfsca62SLjNVO7J5+S/8o8nz6/lnr9o9KVHHP\n9CsvfmWu0f3cnSijJaQsnRYJywro1lhoW2520mllWSFnp82RG51++vFm7dHvmXKSPqAJNJ2MR/Xh\nZzf/R5HDCcMAaZrw8S2OrXYAAC9/48s4dow09XLVxrVrHwAAlpc7+MpzpAouvRD/7q/+LQDguYsn\n8ctfeRoAUKtVoRRr+xiN8YSdtHGMvQGd6+7+EN1uj28M8FjZWwUegio7UWEFAS+qSnoIePFQUnyi\nBuEnmbXWTXhPeRBmqq9V2qxTK6Vw/482/FKbrkq6bwAkMmSgRbrQpWab716ywPcRs/4SINxGYK2d\n0ZazyLLMXUP5HVjr1NEfZu43AIIgmHlpFVQ5TlrjnUvvAACuX7uGZpMW5aWVFRw/cRwA0G63Efg0\n9teuXcPfv/IDAMCdu/fg8ev2+huv47kXedFfWkJUi3iMpHvh53ei5l9Fl5ab0LzoZDlg2JnxvAD1\nKu2klTBEKSgphcBSpw0AWFtdQf+QnP1eb9+906EfIEvJ+YExiFg7LzNAwbqFplDwODDy/QCqdJZF\ngXJpzoocplxkhUQypkVNFyks5tOVA0ijq9QlFMY60c1PcpyOjGvgQZVafkY7vU0hyKmif8yc7IE1\n4uMcpNk15uedKP7bGMg55QH393f4+gyMKYNH4Z6HsNYFDlJKF2h4SsH3+V2EQp6VJzTwA95YrEDB\nm55bO6WE5GenBIAi5vMXM3pvBgm/f0VeuFVb5zkunDsNADh3/CL8SnW+m8TRsTzyOc8FYQV82j5w\n98MdbG6TE3f87HMIWht0flVFYWk+hpUGanz+Shgh4PWlEgQIymBMGygxXVOUsjwuGaTP+oHSd++c\nLizSnDbcLM1g8vk1HpWSTr9QzIZeYo69Rzy4Psx92o871Nz2qApxlbCFzbUtAICnBIJSgtSbzstZ\nByn0BErXLMuymX1k+n2llNunjTGALfeDo2tn+VsK0KfHKe8hThLk7LAZa9z+0WzUcbi780j3+bk7\nUZBToMnyvwGKUhqMlgxii9KNFxCYrpnSCQkKaWF50TeYQk52ZgbZB5yg0nl68NkfcZZmPn8QsZrX\nokqAvGCxRGXw1S89BQBoNwNUavT5hx/edALE41EXu/v093Irwu/95rcBABe2m6iyYG2WaVgWXVxZ\nWobnU3RVqdTAmosYjDPs7pPYcaanaNU4KZyQprYC1YjGbamzgnFC95ik6dxO1Kzo5OzkVPwK+r7/\ngHhluREVKJ+rlNIhREpgBmkyUCziqXXG5wB8dggLMXXElFQIgoCPPRWzLopiBo0URxwiM+ebX17b\ng9eqiwI+L7hxHOM73/nXAIC/+5u/doKqFx5/Ai997esAgF/99q/C403s1o3ruH+J1T6RAAAgAElE\nQVSPNz0rofjZ3rxzG7s79wAAleBLsCw4CnkUSXWR1YwQd/n/pv99BCdqqQ2r6Bq63QniMY23sBIe\no5tBELh5FE8mqLUJPRgPExS88cbjCYqM7rFSrSD0yAmsRhq5ps+z3CDyGNWwAfK8FKUG3FsnLMop\naGEheHGwxiJnUdK8sPBmEMeHmRUCVkznwscje0d/U86XcX+ASY+CkmanBY+FsQGJj/NVf35miZnP\n3YOcrlUz35n9igU+9vgfZ9X1k/wbC11MEVePB9IT0iG7RVG4jSLVBcBixKZI3TUpYWFZZFopH5ub\nvOlx4JVlGdptcqR1obG3ex8AcNjvAfxeaCGBCo1V1AgcsiNshvUTJHK+dfY8xpPxfDf5SSYAsEC3\ntAbscyNJc1x9/yoA4Plv/CpWWvReZjaA4bUlqtRQr5ET1ahUUPVLpH7GiTLT+hZdGPS90rnUhGoC\nyAoLze/B7Nrke75Do+exQlv33tsjgT0+3luZhY1m5hSh1z//9aMY1sfbIyNRM0EA5ghsPN9HvV4D\nAFSiABWfnc88w/Ub1wFQ0Lm8zICCgAsASvFh4KgY+INOVLl0amNn4V+3B0klZ94zC8OBulASnipR\nVQ3JAVOuNfJHEFkGFjVRC1vYwha2sIUtbGGfyT53JEpIMQOzAUlObuFzFzfwa196EgDwb753CVdu\nU4QTeAoFQy1GwEHQSgDgVISGgYv37NQrN0LAzCAKR67jYyLSj/v3Z7Fqo+E85YbfQKdK1xmEVYy5\n9uDmh5fw/LMXAACb622EFYrS02QMy/lYYQpIn6IoX1pkjBplhQ/N9ShChygYKQj9Ks6eXeLjjKAz\nSntZpdDtUl1Cri02j9F3ljvLOEwpMvjg+nVYU6bJPt1mUZ7y76Io4HHq5kiqbjaqEhKqrEmZ+U6W\npNOIQE5TEUFI0aGGdeiX1tpBuVobpGnqjjcbkZQR4Sw8TP//ETFoHI12rHFgKEyhEXP9Wr97gP7h\nHgBgPJ6gys/zpa9+GcmYxv69y+8gTeh6fS+E5Tkymoxx+dJbAICnn3oS22doXnjyaHT3cXNz9rNH\nSTkDQDWMoCJCDAJVxb1kl46jtUt7mUK7CDbwfYfCjYc5snEJb3oAI07JxKDVpu80KhX0RzQ3a5UI\n586cAQAc29pGjxHTJE7c2AphYcX0fS1r4oo8c/UQvgAeXn0xNTtTU/JgND4du+kcVVLhtVdfAwD8\nxb/6E5gxIVH/6D/+DXz527/GxwyO1Lp98rlnaypnPp85v0vhWeu+P3vND7NTz77k/i6RKCmFe06+\n9ByKmqapS1PkeQbNqbh43IcveY3NEuwxWiqtxtYxSoU9//zzAIB6o452i5AooXxcvUEI6g9efR09\nrhnSXgAvovlfrXUQMLLniRSnTlE5Q+rXcPX21bnuUXzCYFgBGFnWqRkITihIodA9oBq93mEXz3yR\n0uwFFDQjJlElQLNG19ioVBHwuxh4ApKPKa1wNVeZkMgiGtNmLKAKOk6mFHJe96wXIWMoJEsGsNn8\n6TxPCmiHXIoj8OiR259dAz5hCtqZ/1+ic5ShmaJVn2TzvFqza/ujmDYZspz2GM+ziMoa5SLGK3/9\nl+7Yv/U7vw0AWNk8hpT3ttnzSSmPlG6UVy2EgOA8uMRsFmqapZACEIq/D1Fm/2CVguG5kSQFpCzR\nYu1q/ea1z9+JOrKpCtS4ivHZMyexvUG1Q194fAXbG7S5e0ED127Si5pmYzeo4wzOQZLGoKweLcwM\nxGimA/zzuXS+hAfgTzvzfz6r1Rt1KEOL1fmtFWyt00LUWl7B377yE7pmYXDy+Aaf0yBPuJYpHcLj\na2g2N9BorQAAdnfuIvBorNaPbWN57QQAYHXzGGJOdVTrDYzHtKkP9vZhGeq2ymJvhzb4a1eu4i47\nqFev3ED7LKWdVo6dgx3feKT7LIpiZnIKt9FZa48Uc5fZtCDw3HM4PDzE/h5d02jQh89f6nQ6aLdb\n9AOuR8iNhc9wu1LKHdsa49KAUsqpo2OtS8kYY47UR4lHrPt68Jxaa8CjaznY30MaUxrWU9NN7GD/\nPu7euQUAePvtt3Dn9m0AwE9+/COEvOAqP8Akpd8WusAbr9PG/fi5C1jZpHqquh85ZwYzTuesHU2b\nAkLMXy+01lkDeFxjP8cgpDoSm2coctowkjhGwU59FARuDsbDHLbg70wACXZs0xCTIY23KSQE1zmG\ngUTEtTaVyEd9m+5xOBph/5AcKguNoigLy+Ec6zRN4ZWbgTWwxXRhnctcZsS6dL8QU29MWgnD68rO\n/i1854//CABw9d03sb1C69CVd17DE1/8AgCgvbY1U9wsadPjMxyxOTwh+3He1Xw/BQCcOnUeAM1L\n9y5K6QpspfRcDZ+1FtoFGhomp/kXT/Yx6tEa271/D/t89vFgiLfe+BkAIOJ0+ssv/xOcPUN1TY1m\nBxeefA4AsHniDP7+VfpurgIEdXJcvKDhnCBlR1haJcdl0L+HwbA3511+gtlp+YYRwqVsIIB0Qg7d\ntfc/wLd+5WUAQK0aQruGF4UKB+SRpxDyxhoGCkqUG7EAuGTEFxamoM8ngY9c0HsTKB8xpyV3732A\nndu0hu4f3kO7c4wv9MxDb0UCMGK6NtmZlO+s0z2PlTVoCm4JpbGaHh3/oAr0B65xXtOW0mMAlY94\nguZUPk4QCZqvP/jRK9jr077wm7/zu7hw7jE+l4FrEBFyZp2brSucnouGSsx8n991Na3ps3Zarxt4\n1v1ehqELQowFIOdfU4FFOm9hC1vYwha2sIUt7DPZLwiJ4n9Y4PgKFaEuNRRu3SYYeT0AvnSREJhK\nZw17j60BAHS8gzSmKHeYeNDc6pwUBhOOJEdphsGEvN3DUYrugKIEYQV0XrZLWugywodFVhaRWQtV\ntsxaD5ohPWkLh7LMY2udNlSThvLsqRPY2iDE6fad69i5/xEA4OknHkeaUCR4+9ZNJPz3aqeFMKAo\nrrm0jajGxaz7e4giGqvO6jpOnL8IAKgvL6FStjMbIGFqhf2o6SLtaj3E0ipFfYHfwKXL1FF2b3cP\n/YDG/PEnnsRSdXOu+yvrJbUw0JpRAaWQl3/rsoi8jCDKtIzF7Vt3AABXr17DcEioWZ5PoBmBqNYi\nrG+sAgC2tqiodXl509FfGA1X9KylBlDSIdgp4mDtTPQ9LfbUWj9S/FVGKbNIlNEGB0x38KMf/hB3\nbt/iLxuU+YQsz3DzFlFW/G9/+L8i4ZTj4eEhIk7zST+AHdPVpAkwHA4AAJfffhtPf+lFAECzvQSt\np+XHH0fdYa1xEaYuCmhdzuvlh95fu9rGIObi3qKAz5F8JfQdymutcW3GQeBPU4wyQhBRYW6nOcBH\nHxLatlVZgULZ0WVQrxGSY5TAcEDjdu+uwHKH3ul2q4m9fYo8PeVhZYWuezhOsH+fPqeUYtmFZaGL\n+dMkn2QW1kWkN29cx//3V38BAOh1d3D/3hUAQFoMYDla3rt3AzffuwQAaK1sTek3jsSdj1qa+yk2\n50Q9s0bo/WQ8huR5Hvg+BNNVKD880i2bcDpZ6xy2IDSl1x3iyh16NqPdG5CMiiuT4fCA1pNXXvk+\nAEKwfuu3fgsAsLaygk6Fnm/tuSfx1s8ITb19sIOT27SWeGEDZX91s1JD0qd5sn/rA9S8f9hzFKAm\niPJfpkwFC0AwenrjvcsYdAnpPLmyjJTfj2oUosrpuWroIWIkKvAFlOtsBKBLpMtAMJVB0mmjd0gp\n+rfe+Al+/Dffoft+5zWMD2jODrIMx86+AAD4n/+7f/rI93UkH/IxTSTALPJydM6FfP2RNO6nmQFS\nblM1/wFQqAevZR4jVI2LyY1Fxp2Mb7z5Ft56m/aka9ev48fvUmnD377yI/zWP6XU3u///n/lUnjG\nGEdBADyIiJmf+0zMFPx7apoNMWaKPgk7g0RJ5bpvda6hHxFx+8U4UbMn5DNKncJnvM7TE/hli2G4\njGaN0jvBZIB60HKXqpqUXxfKg8xpUlshkCtyQkRzE/d4w+u068hiOvNgmGAc0wY+SQscDum312/e\nxOX/n703i5Usu67E1jl3jHl4Y77Ml3NmDVnzQKqKFCmSGizZsuB2G267YVimuw3JgD/95f4xPHzY\nhuBGG2jbUEOA0RBlknKr2WqZ3VKLLJESSZFF1ZyV08uXbx4i4sV853P8sfc9EVmqrIwsqgh/xP4o\nRgZfRNxz7xn23muvtd+jQzFJLYwUbSDdUYqhmj1Jd2p5AWWbrqFU8NDmWpn33nsbi01iN62u1NBp\nUQ1KEIxQYLptklmoN8npKi+uIUkCvh6g1aLN7fQ4RBRw/dJgiDu3adMveD4sSRtD/+QEYz4gt+/d\nwanTBJ/U6lU4Hh3kZ9aWoV36nv2NGyhfms2JsnKgXaXQDFtKu4AozuuTtHEolEpweEDj3NvaxSHD\nilGUosAbsOd6iNgZ6nY72D+klPjGxg0AwEsvvoLz5y/zb8qccQ9LSKNfEwRjA/k5jn1faneadaj1\nbBu3ERfi38mdiiRJ0O+Rw3Owt4Nuh+ZXnKaIcwdGKHT5b3qDgalBKJVK8Ir5c9YocN2IIzTATudx\n+xD9k7w26SLyr0yzDIoZbXGSIGQJjTAMMRrRcz7pnKDXJx2nxx77ew8dY9n3kfLNTOLU1BF4rmUO\nEseW5neTcQbPIUe+VqlDJfQ3jVITt5NNvoYWykwpr9eaqPN8bw/aCCJaZ+PjNjJNzzhLyyixo7W6\nehHNJq3vm7dvoLXLdZGWDY+dmTiJEWePCOdN1Ux8mIVhiNdff4P+Ro9xdECOvuMImE05DbF1kzb6\nC0+/hGKD9h6d6Un9hfggpPDhpQQPMv3AfzzYrjRoDmV11+hBCSFMfaK0XaR5AKAyowelMokDHufd\nzevo75JzM+50kYzz2khtZCZ6Ia3z7/7l6wYSrBQ8PPfM8wCAkg2kA1rb13/0PTz7OLEGL55aMnIN\n1VoZb+ySI9pttVGpVmYb5ANNGMcG0NC852go+HxodnZ3cf1tOpQff/opePxMbMuB7+WyBhJMWIZt\nacgcztOsBQdAuRbaLFnwxhuv44++QY7TX33vNfQPNgAAXhrBzueY5WBpYWnmkXDIwv+dYuJOj/YD\nZ+c0ipz/nSMUNEvAjLMExQKzER3HOP6hmv7wT8+mS3lsyzLwa+ekjYMTqmE7Oukj4vV09+42/rv/\n4X8EAHT7Q/zmb/4GAMD3fagPYcyRPuFfr9ciKQN6P1OZ2dunGd1KaaT8fgaJOM1LCWLDbp3V5nDe\n3OY2t7nNbW5zm9vHsE9eJ2rKtNZGbbtsA1XBIn1lCx67c/0whbbp/dU0RQZWtlYWUpcLXmUAPyJP\nVlguxjFlbOJRgNMMGzSrHuwliqIhV2B79NoRwOCEovfXX3eQ7twBACwsLkE7lE0aRimG8ewpvUrR\ng8WRm6Ni3NmliO+41cPLP/MsXVuSGgVy2ypACLoeJRwDk0ip0O1QViKKQrDAOW68cwN3bxNctH71\nKmKGKZeXF9BlFezN2xtIOPKP48CoBi82FwBWB68VBcol8tjvtgNsHc2m2xKwWm/+vwCzfQyUpOB6\nNJWiYIx336EIvtc5QblMmYaKWzZF4VoJ2JLG77mA5ujy6JAKnf/8u99Hp02ZnccffxI+M8qEkBC5\nkuKUyq9jO5Pic6nvS/1Oa0Z9pH0gHWyil0xheZkizOeefgav/+WfAwA6/Z5hdCgFk+GpVWrI40S/\nWITg3w/DkREnLXoeXNZrCqMAxweUFdjd3sRBm+Zmv9/HeJC/7mHA2afRaGSeQxzHRk36N37j4Zmo\nUsFDgVWjtVKQPObRaGDYhUkkMezTvW80F+AynOdbNpoLBLm7QuHUCt2Tje1NRFz4/eyzS6iWCZ5z\nCx66vC4zJ0bm0rPNdIZy5QwA4N7mNm7dJsZWf9BCwjphUilTkK9tCxqPCANNE5ruEyal8V68fAWv\nfu5LAIDTywv4v37nH9N9GB7CYhJBlMTY473h4O77uFKncaXCmilr9GFZqQdmqMQHUlofYU5GWYei\nZyNVAX+vgmDB2qJXM8KQgA2rTPex3TnG/iZlerfu3MQhZ/0GgxCKmZbSnYLlGfpMIXFng0oS7ty6\nhcevPgkA6LRb2GTx4KOdu4gGlKE9v/wymPgHLRXqPN9WT61PiebOYuJDXk9kKQnWFh94F1BxgH/9\n/3wVAOC5Nn7hV38NALCw0kTBpbVYtAGX55QrACvPbtlAxFPtreub+L//2TcAAH/0B19HZ5uy/24W\noZL/mu0iljRf1s4/js996d+ZeXQKk0cuptiZ03DeB3NHJhElJtkPR2WIGRFIM2U0r6RI4TEzOoOF\nOIfHZ77Cqd99xAxrbo7toMiZ+KLnoN+hOXfz1i10uTi/Nw6NYGmhXEaqaR7/L7/1W1g5RYX6/9Hf\n+Q+NsCyxr+n7rans1nSHkmk9qyzNjH6kmn5fAXmVQJyliDjrmKTqkUVFf0pOVL6RaVR5IpcLEg4f\nqo5twy/Tzd4MFIYRQW+2b8MCbe7bA4FRm95f82NcqtCNd50UfVbt3u/fw7hOm3u/VEaCvK5FQ/Fk\nH6cWtvYIM8/6J/jsE5SmL1crcDjd67k2Rnp2gb9SqYCNO5S2HjgZ3r5Jh2Kt2sS5dYLV7m7uodGk\njfhw/xgRP6l+v4vh8McAgObOPQzZ+YmSFBnXMAyGu7B5ZxoMe/D5oLpz+31krArdOTiEkHSYaUtC\nMrvm5o1jdLg25fL6ErRFzsvCuWtwKrmY4EdbwlDrtOhZmiRmISuVQbO670m7hRYL8gGAZZntzUgZ\nUJ1GTjH34TEsUSrQe0mS4Pp12vCjKMVFpsqXqzVodsLzxQmQMOCkxY+8j1k3a23btNJ6/m8ASLME\nJWYPlsql+9LGedsUSI1Ske6rLYVxLgf9HsDX2xsMkTI7r1EpoljPnZkEdzfIkTjuDnBzc4fHHQE5\nc03dzzKbdgwfJfUcBSHqSww7+x5cFhNM0gQRy2kknmXYKbbjodaguRZnGgHDfFJaKHJQUikUMWAo\ns3XcRoGd6TAbInPo2pbPN+EWCcI7GQQ4Zuek31eITao9RKVM8z0eRQjZWYDvosStSP6mLEWCK9cI\nLtZRgnKN7sl41MZwRL+7vLiKSo1+t7V9A1euEVNPOLVPBBmZtd4kF2gcBwkChngzreFxeUA4pfCS\nJAm6LB66vXUPf/lDYtPt7x1gxGw2IiPxYasyI2xartA9cWzXQCnv37iJp56hYM4vFFGr0brQWmNz\ngyCu3gsdlDgo1EJhiYUULQe4w3/zcPsgQDK5N3lQLS1hxFmna2DSJMbuLYLzfvu3NrFxi/aRX//y\n38ezT1BdadFyTd1WlmkMuG5sr93Ft75HdV5f/b2v4Obr36W/ifuwLZblsBUUB3KJ8NC4SE7lL/x7\n/wmuPPPSjOO7vw5KaT1xnIQwMgUQuC98mJ4hMu8WoagrBUAOhm3nTHg16SgBOdX74+NP3ulAZLa/\nx5QAtsbtW7TPvfPuO7jy+OMAgMXlNbz2baq/S9PMiCmfDIf42te+BgD4pV/8BawsNj/0Nwy7XgDy\nQ8aWKWXg6OlOAkpMCegKCZmzNS3LlInManM4b25zm9vc5ja3uc3tY9hPpbA89/48x8FKjaIUR2oU\nCuTxVXwbEbOSwlAhTCgFfSNKkbB+QxgqjBn9Oz5JsdtnDRpbYjAmMbhBlGCXW1k0KiGOj5mBMuhh\noU7eerO5iCpH4+cvNbHgcCuW3ggchEKFMcbR7BH+6ulT2Nqgaz44PsbOMcEw1556GpXyJNuT9woM\noxEyTiFv3dtGmlL26bHHLsFhSDGIJYYs2qh012QfuqMIjsWtRESGYolhhixCMKbfFbYHtDnzNgzQ\nanNrmCSB4Kaw68+dNj3eHma51pJt20b4UmUZPI7+dne3sbtLEepw1EPEGRcpJXrcmNTzivC8PKMw\niQ6yTJqIslalaGMcDDAaU9bx1q2baLcJ4rxw6SrOnqc2EtN9/KYF2KSUpmVAkiQz60RNC7SRFgm9\nDsPAaHFdv/4u+gx1uY6PhEMZ2xbwOMOaJJHJJo5GIyj+G6UUJD//1AWkpnsRh2O8x+zJhbU+gijX\nwbJhMS3ShoTgVhq2bU/a4FiW6dk4i1mWbYrbPddFidmfSZpSqgBAqVxBvUGwnbBdpPxskixDwKxD\nz/cMC69SLCMa0vPeureNmFmnpYoL7dCaDpIAtRX6rX5rhHCQs4mKcDgL4loSHqfmB6lGr0/fE6oE\njppKrzzMPiLQzqNo23Zw5TJlov7gK1/BYpPWRLN6CaMeraFSsYQyt2zS8TFGXPzvrTQBJleQKM8D\nNKMe9VJnTBDs7RERxi9XkIPWiVboc+uW/YMbE4HNOMFJl9bf7vY2dnZp3wiCyJA1iEHFsLjrwWLB\n2yJn5VWS4uiQ9tGbtzfwz75BENeFCxfwt5m1t72zg51NWv8He9tYWSQ0wC145vkmUYwyZyNnM23+\nN4dsHNeBw+zlaqNm1oFSCo0GsRY7rRbGfRqz0gpvfu+bAIA/dBI4v/KrAIBrl69BMhHo1v4+/vDP\n/hQA8O3v/BluvEWIQjzsw7XpDPBsmIy2goOYoc7K8jo+/cV/GwBw6dpzGMWzEyAEph75dFE0gDyZ\npLUhC/61O5NrC0JrRFEuTJyixMxt17NND0x7QmSGEj9ZIvVRGHqW1nDy/pNao1yh7PsLL7yEL/08\ntTob9Af48es/AgB0egN4vCctLi7jjb96EwDwzW9+E1/+9b8LAEjT5D5Nrcxcj5xk5zCB9qTjTLKU\naWowVAvCZK5sBThpDgtK9JxHc4t+qnCebVso5I1xbQmbaymSKEUAcq6yNEPITLTN/gCtgEThzhV9\nVOrEAlJOA0eMqfZbPfTHdPMKpSoSPsBFPzT97JSqolmmA/rcpQtorl+gyxqfoLVDWHev1YGO6TuV\n1hhFs2+KK2fW8eQLRFN/6423MX4zZ/u4Blrq9/vosqpulsUolGnRN5oL6La5nqHgw7LoPvRHqVF3\nz7IU4xM+VMZHqBZpg1s+tYaMu90HyQgWM6kUbNy6TZutJYTpaj4WJayfIidk+ewyUt5gH2Y+93yL\nognbwnNdZCFBArduvI/dvS0es4STayIIaRRrwzCClOSMSAuTHniZQBTlAo15I95JSjVTKY6OafPv\nDYZYXKaxlEqlKeqqgiUnUzlfQK7rzpx+bneOTa1Rq9UyTtx719+Gyw5Mq90yMKJtj5DEdN3loo8i\nL/40TTEekqOVJtFEHFRI2JwyVkkEwTBcqVI0dShZlhrmmm3bxunSWkBMjW9ayXfmmi8AqZZYWqY6\nAw3gFlP4M6XhMQTj+0W4/BwWlk/jItfAKD3psaaCAG0WTt3a2TKYw3AwQp8P4VJh2UC5re0WuuSD\noFxZwfISQdyVchNCsZhuexfHLFzYP+4atoy2HHSCzsxjnMUcy8Fb79K637pzC5UqXbPtuKZ35WAw\nRrJIwVmSpTjYvA4AuLB43ijPA5Pz78HlTrNBILPuNnc3CQpdObMOi/vVnQxHuHGb3u+0Oqbvned5\nE0HY/gAq3+6FAy04SBTajMF2XVg81wt23ldMwWZob3FpBd967TUAwB998//FP/hv/gEA4Etf+CL+\n8F/8CwDA9r27qHND7WLJNX0ko3GIovcosGwO02SwucarUvWxeIrKL5oLTTi8h0ghzAF9fv2UWVu2\n1MgYgrazPn70PXKWtt5/F8sLLHxsS8gWwUzVYA+nfQqAOuEAir+/VCwg5bXeD1NkPq3RS8+9jDMX\nCZbq9YcQIg9ozj90dDa0aZQNCAPbWdCmVlHfB1Hd77xIvj/j8Qg7LLvS63Wxskr746lTp+F5EwHJ\nLO9Na8m/9l2flDmOjTLvl8NwhMUlCs6+/OX/3Oz/169fh8c9dJ2hQJH3j4WFBRMMfOV3fxfXrtF9\nfvlTnzI1r/fxGafY1dOw3WA4NsFxsVSa1M7qSTcLKQScXBbkg4zIGWwO581tbnOb29zmNre5fQz7\nqWSi8oLiKEqQcdRdLHrIWBhT2lW0hix+Vl9C1aHo4fvvb6HNReMXnj+HaoG8yEqjjCggj/VYpFDM\nAirIGCrPmqSh8S4Ty8frNykUvrXbw5lzFEWfb1gonFCmCxqQFkVK4+EIo2T21GypVEONJf+ri120\nBzSuVreHDl9/pVLBPrcGUWmGkD3iWrOJiDWsCn4BSZZHgMIUJQsIo2mhlYLgRH4QRSjwNQdqDEfR\nfWssLKHJRelhOMJIUNZL+qdRKVH7mP2NXfzcz8ymE5VX4NmWPaX7IbC9T9mnVvvAKOVTViVPjWqj\nt5RllLqlC9Emc1StNuAyEysvyKZCcYr2oniE4xYVqjvuGFFE2aJyuXhfO6GYWWpiSnMFmJ1R8q/+\n1TcNDBdwaxcAuHt3A/GY/u1AwWZ4WWthWm14jguLx6y0NoWhQimjI+PYEh5n6IRKoZmJdvrUMgpN\nYpSGsJGX60tLwsr72SlxX+FpbtOF/rPY0to5nL9CEV2l0cB3XvsWACDLAtjWpG0IWHtsaXUNlx6j\n/pbRaIjxCWUu+8fHJrIN4tgwE1UmMRrQ8wkrIRzFrTKUj7jPz6e+gsVLPwMAWKg3ELeokL67vY14\nxH3IRjFUDgO4GunU85jFHhhJ5pBMkmHzFjHLut02NJNOvJJv5qLnFpHxHIRVwsneJgBgfdiGxRlx\nrdKpgt3pn5lknx6V0fQwS3meawAtfh53tnexvUfZ2lKxhBoTWBzHMXDvqTNnjX7T4cGeER4FMngs\nQmm7vsl8NFnTyQKwuER726uv/iz2WQPv+rvv4jvfoYLgq5cuo8aZIJ0laLdpvQoLGHJ/PZVmqHIB\n/8NNGEam59lYXKQC9qWlJoolymyUPRt1Jmf4vm/Edm3LNmNwHIExt5qJ4xj7rT0AwBvX34HDkP/p\npVW4fAz+7MsvI/nUywCAzd0dJMzYisch3n2PCtRPxiNUF2m9Lp1eQ48ZtBl2vRwAACAASURBVJ1O\nG5ZZm5966AhtUI9QAFBCG7FH+YHpkqtikYLZpIg6L9hutY5x8+bbAICtnU2cPUtIQ5oqI15suQUD\n2T5iR5OfyKIowpBZxUooNBuEBrlTZSG+7xv/oOjZWOXs76c//RKWl+k+37l7F9/4A4KRL124jEaT\nzjNobWBNpbNJ8lIKw9z8+td/H5ublOH+8pf/M5w6RWdenCZTnE5hMslZqv7/1ztPCxiBtLIH+Kxa\n6zkuLK6BSRWQsgMgHBu1Gk3wM8sV6IAWweLyCgTXc0SpgsfYeCVWCJiS0ht0kTF13vU8s4GkcWqa\nmHZHAY7eokl3XQJPLtFG+eRjl9Dt0SHfDqMHNjL+MCsXCvA5PVmrVODzAn1vcw/PPknQ4UK9ilGf\nrm3Yi3DIdQbd4RaCgH7r8WsXzMJyCw2UHYZPshHCmA74U/U6alVmDQ1TFJnRlIgGOge0qRZSF36F\nJmNnmCKIuM9ZUsDWMdVH/coXlvHC5ZWZxmecG9uZsPPSEFu7BCGkOoDDNUFRlBjVbWDS80gKa4qa\n6sLhHoqAZeCjvLmwtARs7tmWpikSpsBadoy9nU0AQKVSgMNpda2zicJ4Onlu06ydh9mPf/wj8x2W\nZWNlhRZwksaIYjoIxmFoNgXLsuDmqrhSmnTycNDHmP9GQsDllHq1UgbYcdJJCMFOgi0Emg16Vq1R\nBJXmUJ2AzOkjWtzHzjM03Syb9A+bwV753BdRYUbVcbuNOM1pw5NtQGmNYi6DoCV2WXF+2DpGyur4\nURRgyK8HYQDNfcW0FogjmrNZqmFxHFJ0SsgSnh/2ErZCWru7eyM0YxYd7Y7RD+gDqZBwOK0fqxjy\nEXYpMc1D+oAznR+0vZMubtx4DwDQ6fVQWiDJBZXaRgW8Viqhx/WVtWoFNRYxHI9HqPEenmlM1bPM\n9hw+Ll08t2qV971qBTudHR5D37DzbNeDZEffcl1YPC+r9Qa6xwSLNpqLWFklaCUMR8ilH3uDwHRA\naLDDc+70aVTrtE9cuHgJa3ww7+3t4uCQnKVLFy6YQ308GmA4zOU7QrAaC4qFkqmje5hpnZk+oKVi\nAc0FupZKxUOpQJPBkjGSkBwYZCNkSb5XZhjzvt8fDEwAWC5UcHxEe99gOILN8PvhcRuChZUX6w08\ncYn26198+RUsNgl23tzexf4e7a2H422srPEEkH3s71PdThInsIxj+h8/dIxiqirqg1qYegqoyqZe\nq6nPKt4T93e3cPcuQ9O7t9Af0BgtyzFlGEsrp80+KDQmrLRP2LTWZr4XCgUjakr7Fr2/urqKVYYg\nsVDHv/srvwyAzu/8mi987jMmGXH73Tdx7hwJuyZJgoz3MMfz4Pq5bJCGzWfK1r0dfOtbBEEvNBfx\nn/76rwMAbEeauletMNXwfro2djabw3lzm9vc5ja3uc1tbh/DPvFMVMWzsc7p2IWChbUqRyn9MWyu\nrMviIQqaPEHpJCiyF/nLP/ssok9RV+dBrNBiNCjuj9CocYGz56BQ4BYRqYdjZtekugrJnaK9QgWK\nw9l4ODDtR0ajFO936HfXghRh3vOtWAEyf+Yxep5nivgKhSIqLDA56A8hOcrRogDBrSy8gsK5c6R9\nlG3vodunNHOUZPAK9NmV6hkEXCSfjDvQGWU3akVhtED8VCJmRp5MFDwWcDzpxZBcKNwbu1hZp/F+\n9jMX8YXPPw0AuHSuCYk8azPbNNBam0zUoN/DMRd8C6GhMVWoKqegR4440kQhzSFSoWA7OWvNQsRk\np4SJBie9E6yurPOvCmjNzLc4w82b7wMA1s6cRoMLVdNskt5WWWZyArZtmwLGhxn9HWdmbMvoXnm+\ng2hMY94+OMQ4ycUIM0guihZam7YpWRxDczbMd3w4XPhtCWFauni2B8URVPu4g9opynQVPB8xw91S\nWNQ4kG6wYRlS0WReUK8hxOxRU/94DyOGRlvbW/A4pY6CD4sLgIW04HmU7djbPcLGXYK703GImMUS\n0zTDUYeFWq2GEVQV2kaN4ZbnXn4BnkeR5Htv/RVCzjL1hyVsXydIyBtuw+6RkGNwfAjEOTPOg2Qx\n2jhIpwpwP75Ni/G1Oy1scTGu7RcgPWb3jkbIQGN0IRAydFZ0LSwsUGZS2Z7JIkoxa/7pb85GMV1f\nu3tiejQqDVicfcq0xoBh6bSbwrJzyNk2bMO15Yu4cPE8AMoqnnCvuRu3Nji9BjhctF6oTsQ7bRso\nevR8q5U6rl69CgA46XZxxC2t+sFZnCtSycBgMEK5ymK71dJEw+ghVizZJsNXLHmGxe0XPIMohIMR\nDru0b4ZRhJD3lnEYIo4ZhosSWLkGXbmCHpcTOI6DKu95o1EbY+7PurmxhZMjmpvdK108SZwKNFdq\nWF2jcdxq34ZXoPseBjsYM2U8S1JYj1CSPClrzqE6snTq/QnnOGdRkkkQ2xEADg920W7TPjwcnGA4\nIlKL75VQ56xzudqEyyxx9YHv/CRNyIkWU5wksPPetBAm81Or1fDcs88AALJxH4rX3He/9xdYP0MZ\n4mLRN8X27bKLZEAZ1fdv3MAP/pI0Fsu1Jp598UUAQD8MYLEPIaVt2N9f/erXsb5OWaxf/KUvIeW9\nXEBOiCEztgmbtk/ciXr1ymmcWaJFUPUl1uu02IdhgKxAm1dx6TwCbj569PZ7OHuBUsa1hapRWJaj\nCIMe/U0YxbCZlSakQLVO6V7PcREyM6o3HqPBPekUFDRPujiBgeqqtQoOWRjy+tY+1rhxcGmh+Egp\nOtu2TU83zxFYbNL1SJWaA0bDRqVLD791vGscuYuXruLwiN7v9vpYZFX2ZrOMmuKJH3tYqNOjCkYt\nI44nfWFqzEbjFJ0hOxL2CFdOU4r085//FF78FO0GVy6vwnEY3tLABHH/aMvx6yRJDHsnDEOMx9y/\nUGfmfceRyBOcSaIMO0hpjTAmpzAY9M0YSoUKpMxlLFiJOxkbaC9LbGTMUrSkxNEhbdatVhvlGsHB\nuQAnAEAIA9sAMAyPh5nv+abmQAmNdKqmpdOh57NzeDzpeZhG8K28p1gRdZbuSIISFENUvlfCgPsZ\nBmFkFIQ93zUq7cNhgJDhP79RMAsesAybSkMb+pcQwtDTU5XBeoSJ+sff+H0U2blWAAoMmYVRgIQ9\nvDiT2NmnQ3V75wh9rlvM4gwRU7i1kMg44LDdIhBzcOC5KNYIJrK8MmpNWt+nz5xgGBD0dDJMEZwQ\nRFhJb2N4RE5xr93G+ilaN7WqB46FoBKFLH3U3nkfbTubu2i16JmuXTqLHtdxjQc9SK4POkoCFFiw\nNo1ClIrksJfKpYmC+iMojef2k9ZI9dlB2utcR8DQr8pSFFms2JaW6Z03rdyvpMDFCxSYPPX4Y8Yp\n7/V7pnb05q0N43QlfNQedLpYW6H7EIVDXDh7HgBw7YlrqFZpD/ud3/kn6Ad0XdJxwPEBipUyarw3\n245lHKCHWWNhwliVtkKf65qieISU+zeeHJ1g3KO5GacKEY8nwkSBXE5JkA/GA6Q8jxxLIQ14vqca\nioPtLElw4y451/3xGO9wj9KFpSbGKTlglboLyLxjQAtpRNeQxjHUI9D/Y0xgO0xB0LzKp15PLEfu\ntQAidkKC0RABS4zc3ThEvU7z4KB0Fxt3yPE/e/Yylir0rKiWcWq//Mk1OB9oicowYjV1z7Fg8Tmi\nLQta5PtrhrU1us67N47x2p8R9JaEGcIR1aF12wc4s0L7SsFSOH+J5EkqBQ/1Mj27fm8f3/sef1b6\neOc61Tw+//wLqDAEfufOHXz/B98DAHzuc5+BnUtkaGXKMTKVIXkUSRXM4by5zW1uc5vb3OY2t49l\nn3gman2hiBUu3j67Wp5I5qcKUS64GKZwXPobS3exfzcXbrPgcC+rimthqUqRrWcV8Nw1KgDcP2pj\nY4uiyjBJjM4LbI0ye6mDUWBSraWCh5Sb0jmWC8cmz/3GThcj1pV68mwNRW9211xrAa1zCCfDi0+T\np/wn/+Y72NwlOOTq5SuoN0mELkkidE4oY1aqr6BYokLF7e191OvMYJBj1JuUTVKJg5QboAurDo+j\n4o3NIxz16P5YlRKW65RGv7f5HqSijM2XPv/vY+38Gb7SbFKcOFWQ/DBljLzAjwoCzYdMaGRJaeAg\npRXyRJAQ2vyN1hlnqYBRkKDAY9AixWBI0VzIcJHn2Tg4oFR9ltome6bhIM4hv+4JznA0ZjnWpL2L\nZRkIUSl1X7+/jzQx6fzNkowAgIPDPbzFRIRYCVRYM0dIYbITiwt1VDljmoSxgUTCIEHCrVsilSBX\nkZGyDMEw43A8Qp/1uvzaginyToQFk2bKUlMEaUlpso9Ka7jW7C0K9vf2YOWMT9tCwPdvMIoB1nQ6\nbO8gDGn9BWFmsoRSThgsEBYMd0AEsHOYxBYYDWheh2GASyxoiUTgzJkL/J0FpBlFzp+5vI6gQ3fl\n+38xNvC7a/mQmt63JeDas7dg+ijLL/lg/9CwQ/1yGYMuZ1GgYDHkFIcxXIZKi0UXDc6oOI5NbTrw\n4HUznW161FYZDzMD1cHGuQt0f9vdAbF5QVCrk+uRpRIur51SwcelCwRlrCwvYWmJGaFhgO/+OfWD\nzJIUMbdA2d2hbOG9OELx09TOpFQs4ktf+AIAwLItfO1rvwcAeOuNv8LCIu1hnuuazHWtVjM6ZlLK\nKUbgR1u57CDJqwNAxfwAcHA4xGBE9zINAYt7/inpQVTp+aycPZvXySMajdBlpCGLI9g5wznJMOJx\nZhDQRtZOYsDQXrC1C8GttuwNG81VGt+Z9TVUG1V+BikUM6VTlRjyxyymppKY939KfMir+9+RAoZ4\nAQlUGNUou1XUqzlLMsbRAT3Dw4M9LDEhICd5AVxg/gkWmSslkPN8bCmQ8lkgtTKaeVBAp0373w9f\n/xFCVrxuVhewt0/kK89KIED3P47HeOMNas2zv38ImfcmjWPc3aSs9uLp8+h2KZX9rW99Cz4XnMdx\njBs36G8ODg9x6hQjVVMtvzKVTvWEnc0+cSfq3OU1LC8TpJUlEaKEN3HXgsWNceMwM+m05dVlRKx6\nfNJpYfeQJgKyBKfPUDr66ZdfRaNGkyWLI/Rb3Myw3UKoc5ZUD5ZLDpJX8IFKftiECKOJ+KfDOeY4\n1jjg3nwWhnj6XGPmMWZpiv4JQY1R5xAvP0k006g/xDtMjT17dh1nr1LvpjBNjXrw0koJjz1BmPCf\n/+A7WFwh56dSvgXJacViqWLEFrVlYcRsu1ZXoBvTAlq59Bzee/vbAIB//Sdfw4++T+97voP/8r/6\nTfqt1eWpjV/PvH4m4o4TLBugnoEAEMeRSb+Px2OziaapQs4WjaIU+R5aLpdQNJ9VBnKTMnfWiGpK\n3xEZsb1xGCLLN06lDJvOcaWBB5Mkuo+VNasEgG1JiHwhgfotAsDRwRFOTshJl24R7TYt7IrvocYM\nJseyEDJsp3UK28qht9Rce3+cIWB4xXEsI0g6GI/Q4+9fOatgsXJ4pARgGDUZbNN4NTOwhNATZfVZ\nzPVc+Ezh74/GCBl2HAYKPVZlD4IYGdfxWbaPArOhRKaN4r5SyaT5q5RQGTPyYoWIHeHBcIR7TLtf\nqjdxeoXqZ+KxRIVhoCuXLqJ4mQ72pZXncMD1KCJLMEy4z1qSIGJIYGZ7wMTO3y6WS1g5TbR9KQQC\nFvf1bAWbn8vi8gKaFZqjtUrZsH20sKYg14fbTA6U1jMfwHm/umK5hlLBzz+OlDf+brdnDoFqyTdB\nRL2yiAWmmC8vLuH0Go1fSIkeM5/efPNt3OD+ZiF/7tK5s/jsK58BAFy5dNkwOg8ODrBxhyATrVI8\ndvUKAODqlSuo5+vCcSZMJ6WNg/owazTKCLjWKE21acSeRZZh0llQkILno4RZK8X6CjKXgtV4PES1\nTK+HG9eBkMapbQ2lcmdCwlQkaQHBm1QAAfh0r9cWzmA8os86vQRXnqDvtAs+xgWG64OxKV2YxR7V\nd5kO77QWcLlheLFcMeULp5YWYbHKuqUV+gNyTlqdI2jet6Vrme9RuJ/xN31NfxNuP+3/vI+LDG4u\n8SIn+7Lv2XAYNt89PEKJa/GOuz10T8gRWlkoocOdIt5+730MuO9jEMUY8jw5PukhYnn3p196BQHX\nxb355lsYDAbmmnY4ODhqHaO5TBDhdNcHpbSRV5nV5nDe3OY2t7nNbW5zm9vHsE88E3V2qWZEDHuh\ngG3ljKMMGYcYlnDgs/S77ZXhF0iX5PTqKt5RLCR2cIz2gLzOOBoi6lPUWrQ1GmWKKsajHvZaVBSL\nTMDjrEUwDEwRmeu5yJhVpVRmIg8hBBL2QN+628VSZfYWBWmWoXVAGaTdu1uocsT36ReewaBHEUy/\ndQCvwpHg2SvocNar12vhzDox9Wp3nsSf/ehdvrYCzjISVak2IblwvTsa494WwS13bu/ixc//bQCA\nY2t890+p9UISDXAY0ff/0698BdeeocLyv/Uf/K0pTaDZY6G8CDXLlCladV0XRe6F1e93pzI+GhlH\nPXGcQKv8s6n5bdtyMORi3iTOTA+/XJprNBohL34sFl14RYqLoiiZCOBFsclg2U4KzdG3zhQKHKVN\n65E8zBoVH/e2KEopV+uGiAClDMNvEIwRsPBmZf2U6UM3HIfQnHKLkgQJzy8tFWxmbXrKy/mLBDPm\nmliujZij/iyKTI88CYrwAUCq2DDCtFKEZQAoeB5871GWsEbI7K4oTdDp8bocRhiM807nAhZD6EpI\nJHoC2Sa5FpdSBouQWuRIILTODAQyHml+jkC/28GQ5/IoHuDU8zTfF08tQUQUeT65dAUv1yn72293\n4X//LwAAN+7cQnD71iOM8eEz++yF86hy0Xt/0DeZPdciTSgAOL+2iEXWYyu6Dmx+1hDO1C88OpPn\nw0wDMxeo12p03Wmm0DkmqCqIYlSYBXd6dQk721TE77gOVs5QSUC1XMIiixSePn3atBfSWuNFZjWl\nCri3RYXVBZ63Lz73LK49QQxpx7aRZjRvi0XPZKIvX76Il196AQDQrNfNXgsNOIZw4sB1ZoNllVZG\nwDUIY+rtCMBxXcR52w4ow9iy0xRJjzIV22++geISZTe9egVM7ENqW6bXYCamBHn15GkKIaA5++/U\n17H49C8BAL702Z/FW699FQBw78a3sSBJzPTy+pOIua1MGEWP1McSeirbo6e5d8CHQXrivmvWsHnP\nrNWbpqC9sdRAxC2SbCFMD9PhqGcyUbbvG062nPpNDRiY+kEriKDpfM4/PP+yd7CJu3mvR8dGhVu+\nuZ5tykk8WwKC7mF9oYkRa7Ntb++g4NPcSS0HWy3KSsX7HdPnM4wTHB9PdLEqvH+0W21cvUJQ940b\nN9Ht0hlcLBYx4v375u1bWGXyVb/fn0D0Qhjm46z2iTtRe/t7YNQACWwY2VyVwWEHplCAUQoulkrw\ni/S6sFRHL6DFsd8b44nnabG/8f49/OB1EjnzPB9HfBgMRhlqPm0yfrkKnzeKKBwiivODPYRm6DDN\nEhRYRC/NYtMvLU01do/7M48xyxQG3DB1e+cQxS4dHou9ARYatLnZwsK7b74FADj7+LM4dZ7gjY33\nXgf4eH3y6Vdxc5vgon/57R/h8YtUF1QqVjEMeXIdHMFRdCI9/9SzWGG2Yxy24DGd14KE5nqO4+Nj\n3Nvc5Fue3SesOPP4+LDIBDHXAMD2fPh8r6NoB3wbYWmNhGmqUtiGni6kNFBgGifG6XAgkdN2cjps\nYbEKj6nU/cEQIU982/WwuMzPt1CCYtaeLWykDA1bH+glN6sTtX37Om7fIrr9S596FTHXMvmWhTLT\ngwfjjhlDv99HELKURTiCbU+aIfeYLRPHMRTXLNkQpqeZSlLDYJKObXrz2QAsFp0tOS4kU4IdR6LA\nfRELxYJJvIdRiPQRmp6mSTLZ+6RExA7paBwhSye9o1Sa30tBSsCgbTWXVsjS2MgvCCmR5M8YE6kH\nqBQyV18vaHR7VIsQjw/g5lISftPsQBoScOlwEo5reqQVG3Wsn7sy8xiBKQhtSuxPa23ebyw0UWeH\nQkEh5LVVLltosHNVLRdQY8abzjLYuTistKcOEv2o5LwPv85HsFx4tlwuw2Umr2sLDHrclzOOUM4l\nX+IYLj/v9bUVNLlJr+e4ps5MawWfD58v/tzPIWFIKq+rKnoeLJ6HSRybMr1yqYgXn38eAOC7Fs6s\nneLPyfvUw32GHH3Ph5iRnjcKYgwZslGZhsWBgm9JxCm9n0bKBGhSSbis6ql6HQQMvQUF16hhi3Fo\nNphUSdj8+j4IS2ko3pfKhQJc7vv22vdfQ2eXeidaGMPl4P90aRGw8h6fytR0zmJxMILDwd40PCxp\noRnLmalpGBlHKEtT01w4TRKMc6mLVENn+V6aImJx38Ggi06bkg5VlSEvWpWWNH0gpe0YmQxy6Sbr\nZuJc6YnsygxO1Pb2bbzxHq37SqUAi88R33ORssPZrFVMiUG5WsJhi85d6dqocO3ZIIxM6UacpgjZ\nOYyTDIvLtE8sNBtG/PWHP/wBnrzG90TpKRFlaWR2/vkffMNIXvgF18DOWgOL9dpDxzZtczhvbnOb\n29zmNre5ze1j2CeeiQqkj4g7hnu+B5WnS4VAmVkFjufA4qIzaI00Yq9TSAibsgBLq2uolSmqKVcq\n+NG75OF2TkYosYhco1qFk7ObsgjBCXm7tXIR4HYz4ThBnxlEhZJGmRlWg0EMxdmHUsFHtz8jqwvE\nyHK5Dc29e/cgczG+a0/BcnIWhYdSkaCC/vEhJL9fqSyhz0y9hdUreOXzlEL+51/9h/j265S5sgBM\n+///1meJLfPYpfMIepTO9BZL+Pu/+V8DAP7J//4/4e7mO3RPGk3DkrJnTKf/NcsLyy0JMINKKRtV\n1gQCbOi895OQkDLXYMlMlB9HGRKOFi1kcLngulQqwjNME4b+hECf+w+OhgPDEFtZOY3HnqBebivL\nq8jjSFtacPxJJmhatn/WwvKj7Q0s11hgUCr0WIAwCcemW7zt2KbocDAYYG+fmJeWlAYeUSrDyTAv\nMtcQyNvRaLgcxju2gwI/C6km7LOi72GhTpmQhZVFCNC9S4PIFFxWazVsb1OK/K9u3Ebr+Him8eW/\n63FK3dEO0l2K2MMwhsif61SRs4aC4AJNZTlG0DRLYwiGGrVlmWh2ugeVSmNIzlo6mYbN86CoHBQS\num/D7tuo5oxbx4JKaIxII5S8fJ+w0Dh3YeYx0nXnVzPJ9pC+Fl1/o1nHqVPEVgqCASoVXhdpCFtz\njz8ZIE04U+7X4TKDdrpv2Udew5TO2HTG6cN66k23x3iY5UxZ33dREpxFL3iIObJXaYwFjqSTJEHE\n+k0qTUxrKmu6az0sQ8pwXB8xZ+xzId4sSZGxELJlSdMfrlwsYHWZCqzvbRbh8xp2HQcOwy0F3zdF\nw1ppgwA8zIrlGnS+jyfxhMwiNXyX2d2WQMpMMy2k0e4S0MgrRqJxbLJfXiaNzpJ4QN8TrRUEX/u4\nvQnxztcBAHEIhANCCM4s11Eo0f0djvqQerK/JDNq0gHAH37td/Hzv/wrNCxpATxGlSYm+6RUhp1d\nKjHY3d010KhSmZnLYTjEeEzPfuPONpYqdE9OLRaRcBa50z7Gt1/7E/qs0KZ8wnEco294Zu2MEaIU\n0prKUFmw+Z7YtoN33yYEaOVnP/vQMSbxCGHKfU+zIjwuE7D8GmJupRWGGufPUKZZI8Uh60U+de0i\nfv7nP8XXf4IgoLN5aWkJR7znSSFx8TyLVmeBYXRvbhzjrTfeoGsQjkEnXNc2pSYbt+5ijckliyt1\nU+aQKUBkudDzbPaJO1GOX4K2claSY2juDia47iBMEDJDJghCjBkXTYXExh73mOv00OcmpqeaPl54\n7DwAoD8IjNJ1mmWoM9V2HMc4OqZDQhQcBENK3bmOjSrT1EfjEDEfiq4UWGQa82A4RqZnvzVBOESZ\n2YJOsYz9jU0AgOffQZuFGrXwTc+fhWUHo5Cu+fC4g+VcSMwFnnmKmHo/eO0MdnbIuVJywpywLWnU\nrjdv38YgpQPp4jM+fu3vfhkACYp+7ff+IQDg2aeu4qmnn+VPS+ADODjwcImDPB0qpZzIB1g2/CId\neq5XgtLc+1DYZtPVeiIxMB5HJp0uRUIijQCaS3VDfT5q0bNun/QxDvI+ehYWF+j+rK+vm6aU5XLZ\nCHzGcWwkFqwpiQMp5cyVX49fPIdETHr4HXO9STQeo8S9EBdrNXT7hM0nYYDjNr22bcs8T8uSSIzE\ntoBvREUt1Cp0vxr1GrJ8w1UZwOOoVAuo1bkx6mIJ4YjmZqffMf3jjna7+LNvk6jcu+/fMlDnLOa5\nlmF0DU9inHTpsxmEaaCcpImRi1ASBiZVlmuek9ATSjA1/swPMGkOKKE1Up0fDBmWG3TgVr1FrK/R\na98RgKJr8JweUu67Vy4U4Epau92TPkrVszOPUWuNBz30/JoLBR9rDD9t3nkPdk5TTwIohpEcXULE\nNZWrqxdglwlqTPXsrNYH/f5PYgXuUekLIGPY3BUSK02qt1TQhh1rlYvY2yeG5Hg0QIkDPcf1jHOh\ndTbpIUbFWZj8F0SlErZ5L2fYObaFHteaFFwXJY/mlRDS9A71PM8c9lmWzRzETavLS3sCn2YpAP4O\n4U5YqmqKWyaFuE/0Mhf0z8REI5z5ph/6u0boMgkw3id4XwkfRd7rLl26Bp+D/93DTQP/ZVmG8axy\nKgD+19/6LdM8d9A7xpjrhuM4Rsb3TEqBHu83wXgM19xXHz6L/pbLRUhOUtTqPvIGDYlWRrz4+GjH\nCAZv7dwz+3MUhchi2ttPr5zCuXVaZ7Zto8DPs1gow2GB3mp9Ef/nb/82AOCLf/wnDx3jQqOOa1fJ\nyfEsaUoerIKEWmB4XGs4DXrWl69exPe+QzXQzWYRS8v0NwsLywh4LK5rQ3O9bJpm0KBgNwi78Avk\nQzzz7BpOWNh6c7uPcpHG4jgu0pShwCzAgOvHiolCkL8fK4Rx/aFjk2uCCAAAIABJREFUm7Y5nDe3\nuc1tbnOb29zm9jHsE89EuY6E5syJq2PYMfltYZZhNMxTzQIRR/Lt3gjdAXmF/SDB1jFlkAp+CTcP\n6LWKxliwKVNxYeU0llgG/sZbbyHmAMN3LLisI+JZ0hSLtU66hhVoWzYGJ/SdjUYFHdaTiKMYyp/9\n1vT6A4xYpG15/SI2bm8CADY2trC2zMVrxRL6JY4iXQc2wwNhkpl0o6UUGszsO7V6Bjs7xNSbLjSM\n0wzv3LoDAMhOrUFnFCXclW/jT//lHwEAVlefxm/85v9Mr5cSFIs50zDFRFnuo2Xdpi0vmLwvy2NZ\nKFdoDMsrp9HvUopVq9BwlqTM4Hl0X1QmELLAnRYCpQqLU2aZScMeHVEmKtOAx33xPNdHkQs8Pc8z\nRatSCtO+J4pi07twGhaZFSIBKOM0YIjKq0xYQLZjocQRlLtQN61A9g+PEHCRr0xSRPzadV3TI09A\noL5IUU2jUkCFC9TX19cNcy1NElTzQkaZ4ejgHgBgqV5A95h0XjpHx2gu0Je+e/Murt8iDaXWIID1\nCHGQgILDWly9kzGGnPFV0oLii870pMWMShJiEwDQNiDyLIDgvwOQKgGLw31LaGQ6zzZMGDiQFha5\nf2a1UkXRCFdWDeSnowF0RvuBbdeRpnR/TrotWO7shZ7UIudh4rES67lOUppg2KK5W6uWAMWpf13B\n2ceJyLJ09jFk0s1/wDTp+GBO6ifJNM362WKutRON4PBHKtVFyAbd9/ZJyyzxKAow5NIFz/FMNsWy\nHANLa0wyUQKaejaCCnLp/9dGv00LTPpiAgYWWmwsQOaPWkqTRcqyzLx2HAeeN1s/UqGFIcBICOSK\njY5XQIGFE4ulFCcs0hiNI1PvrBWQ5sQFDaP9pgQm16jxEf0Yc7jVRsKtxRKlsMpEhMcevwxoyor0\nB20EDKNGUWx6Gc5i7VYL775LWZdB5wCjEc193/cNxGbZjsneFHwHQ9ZKsqENmWOsUsroAlhqFsxz\nDdIEMRdRn3QOYUm6b8HgBAnrukVBgHqJ9uGge4S7Y8os2lIY2DZOUgxC2tsq9dN45+13Zx7j5SsX\n8dzLBNUVLIki93aV0jKlG6nKIJlwE/Q8/P5X/hgA8DMvv4jPvEJlK1E0NkzsTqeDtVXaU5VSZt+K\noyJOODMqhYNf+HkiPfybP30LrRY9oySKDTkmTgOMApo/jlcGPC49iBVc/9HW8SfuRFmOjYUC909S\nGSTj2J7WCDp0aKYKpleaZwk0WawtyfqmjqSx0ECPm1y+tzfGY5wCtIs9HG5tAgBWVldw1KMJfrR1\nZDa5OI5NKrReraCs6IC+t3uA4w7BNpARDpiRd/rcBUg1+4I4bp3g6IjSrpntYYlhu/bWPXS69J0N\nS2N3i4TshErh1akmwxI+tnfpGs7563BZ5NHlFOoHTQA4YDXWonRxqkhQ1/H2Ft79ASm5nnlMobFK\n93C1WUVO7u2fHMGxK+aLcifD5zT/gyz/uyRJTHreth3jRDUXVxFxunU8So0DZNvSbIZZdmJqooql\nMgLuabX7/gbGOYTiTDYMj8UNPa9o4AmAnDf6bhvTiflkSgTUwBmWZaDIh9nhcQuhRffcifVkkWcZ\nklwwTimzCC3bNk1PLWiz0WdpaA5EaUmA67lqiyvGiSo1FmEXKnztCksNer2zs4uFJjkMhUIdoxGl\nqjuDDJlH17C518Y4yudI2fTjm800xgybD0cBUr5mbVtGiV5KMVX7lBolc4gJk0dM9YwjMlHeg0og\nB1AVFCTXZHiejaLPB2s6xhHXPcg3T5CXQjYaC4izXDU4wGDIB4mzgM0tWh8/M9sQpxo0q/tq4qYp\n4seHBHPdu3UTMqY1eu7xq3jli79IvxvGOMW1GijVjWMsoT5UpvZBtU9/01Zgup0KxkZhwZHKwNnF\nQgEeyzHsHhyixqULly9dNg6IbTsAQzpCWBMnSQukBjpjiDNNJ+vJtkzgoqENtD7odozIapl/D7g/\n6HoUk9IG8to0WHBt2rszpUzNXXNpEc1FgoVH/SHGrKExHIwQc0CTpikUv1Yz7gO5EyWEDdui+9gs\nV/DFV74IAHj6ylNoH5PETKIURhE5P2EYzt4dAVQLGuR1QWliBCQt1zWq4ipJzb7muQ48fn5pmmHA\nNZvNWg0Vft5xOELEe5KGhufmkJlCloT5S5OwsIVEk3vqSWmZwGgYZUgNTDkpw7AswPdnl/45ONxD\nfEz3p1YpYbVB86XklVFiOLJSrKDKavMLtYZ5/9L5q3j22ssAgCiMjIBsmqWGYRfFMXQO6WYpYoa3\nh8ORmSfPPvUS/tH/Rsr6G1steCWG9pAh4LN5uVE3JUcHRwew7Efr1TmH8+Y2t7nNbW5zm9vcPoZ9\n4pmo5VrBQAjS8kxEVxYSVRa2C8MQXdY5OT7uoT8kL7juAQsstOjGXezd3QQAjJIYbWbqPR1nuMie\ncvnUGcTMVJCYFCcGYYiIBbSCMIRWucc6QJuhQyUl1s+fBwAsrpzC4b2bM4/xpNtFyFGFdG0snaZe\ndfFoAItTp91RhIQhvyjYgLIpC7d84UUIbhPSbu/CKhM06fkVCM5iCGT3Rbb5PdxsHaNXyoUXBxgw\nNLLbu4OFRS48FJ9Cr0NFsaO+DcsieFFKy6B463mPswfYRENDG3aQEMK0ollfP28i29s3h8h1r6Io\nMswapZTRuGl1BiZDpJSC51E0lIv3FXzLRNOeW4DLEFqSxCaipExULupnmX6IKWAiNsuyZmbnScfD\nsMttfxKNwWjMY0gQcSp5MB6b95NMG5RVaWFYOpP8DOmYdPoES521fBSYzajtAkSufePa4OWBwTDE\nlSskjHpwPEJ3QGNN7BoOKaBDYpXhlSid7Sht9HxmMct2oBmu6fYHpoAVWhjmlIaeaNCoFOYeyxQc\n9EFKOQUBCWhuoZFqAZshdClS2DZ959rqApYXKMPmeEU0KzQfk0GI92/ROhsFNyA44yCcCoKYnvlh\ne4zdPSJP/J3/4u/NPNaPsiiKsLlBkOjdWzfxxFmKkM+dPo/HP/0qAOBkcxvjEbN1y8oU3s9iszDy\nPuzfs5gtcs22DAlH5If726gu0BgWFheR8AYRjMe4wFnxi+fPweFslWtZRvtHZdroeWloKM5YxJxZ\nzrIMhsc3JWKktDItaJIkMYK8ruuarL/WE40e2549K1wu14zga5SlGPO1xKOxeQrSseHaeSsvgZg1\nz8Q4hMjyPpMWtMgzZ7PKC+fMVA2fGb+f+8xn8MtfINZ0qeBCMJY2HIfoB7wfqBhhPLv46uqpBUSc\nxer0uzhqU2YpExJVzljHSWSKwxuNBhxm8cZRiJBbITm2BafCGSqlEef9RKENIUZLgSFnn4J4orkE\nS6PDJTXS0gYpCBMxJT6pEHPG2q8FuHJ5dqZsu9PB9V2CLKUtsbpKmk7lahFFroBfKFexyP1i7+3d\nhWZW6CgMcXREcJuABdvJkYkCPN47S9CwOdPpWPbUOlPQTHR68QUbNUZ9/tv//h9hj0tGfMsHQvqt\niuXh7HlaJ8vlGnx/kk2dxT5xJ6pRLELl1Ezt4YQnSxyNjDKoays0S3RT+ycSFb5JF1ZX8exl2hy6\n3SHONojefnfnALe3uWnh7UNsH9Dr0wsteNWcaq6gmWF30u9AZMz+C0cYsUDhvcMhXIZVXnzls1hg\nNeDDVh+VyofDaR9m97a30R8QHjsc9tHu0PXsnQxRYRXKRqkGzZDlaBAhAz1M4WxhhRsE905OYPlE\nX3d9H48/QTUZd26/iSTOU8UTJkoiNA7HjJOPRtg5ocOmWCzis698GgCwstTA3h7BIbblGDhMSMsc\nnA9zoiKGgErFoqH7q0yhwLRm31kw19fvDXB0wA1sRyOkuaqkFqYxcRbGyBvpVcslFHOmCbPXbFua\n33EczzhulmWbVH2SJHAZ2tA6NTlVJbRha0KKiXzCQ2zvqAWd0/xliJDZgYlS6HO9Qn84hMqV1Msl\nRLl8QxiaVDiEmMAfwkWHBd2GYYr6IjW8jJMYWS4C6DjYP9zmsRbQH9K1//iNHxqGYi/O0OfXzXoN\nlQY5IRu3b8F5hFxyrd5Eh6U7eoOxka7Q02w7lRmldIEJfKIzaZoOazXZZOWUM62VhpZ0/dJKsMa9\nqS6dO4MqC1dK24bD9UWeV0PBoXWwfe8mlKR51g9aaPXocBJuGUuLs/exZNlOfjXVNBkCmgthur0u\n7myQ87Z/vI/zDH2vnT2HlOelX28g5Jo0sZRCsfMpMV1n8/Dmwg9ynKYdrUeROMibT8fRJDAUNvWj\nBICC56PDTqctLayfob3FEsLIHThy0oUgDiNMwgFtaPqKoZEsTREZwVUFy88dJBi4qFatocwSH5VK\nxUhkjMdj0z3AsiyCEWcwadmoVGgvrljSCIAOh0P0WEhzOO4hYafFtX0IO3fkNQRyIcrYQNP3393J\nHno/F1EbWFvpBA7XGl29fAGrS0t87xyk7ESNoxhDdqL6/RBhNCkpeJidXV+A5s4DaRyb88N1HLNn\nJUmMXZZRCaPYXGYUR1habOZXbDoJSMsyavE6y2Dn3Q8sgchicWNbmPqxwSBAr0v7QbVeQsxOVJYJ\n0/MzyWIjeyH2t/D4pSdmHqOQFhyuLU50hsPjI77+MrJ8rxcaGTs8lhfj7FWGiHUH17dIpkDHqXlC\nruua8yDLFCzB8guWO5HqsG0jYOo4Di4+RvfqV3/tVfwf//j3AXCcyDdi1Olh+UkKXs9cXMEwmMN5\nc5vb3OY2t7nNbW6fuH3imajDbgSfGVrVokSNW7ocj7oIuXN8iAw676VjSZRYK2d1sYwKF6TK5RpS\nSR5xr9/E9iFFAO9vt3F7i6DAvf4IS07eKkMgTWh4h8cdjAL6rSzTGISTFO/zj5E2xtrqIjY3qNg0\nysJHin7vbNwDOFrr93oYcIp0ECbYPaJrW66WsMRFfFYUw2cYZni0BTdnvPk1WJKYah4SLDMjZEta\niKcC2mnykeR/KK1gcRR95fJFPPvccwCAcZRhd4/GZdm20VYCBBKOMF59yPisKVFLm39DSQ2VZ380\nUClzd/liFb5LkX2gAyQRZcrCcWiiwlLRNeKcy4tNE1l4HOUK6RgYTmCiTWVZExZZFIUG5rNsCSHy\nlgUCqc5FPRXEjIXXiRKocNFhuVaHz4J6t+7eNQwcLYg9A1Afr4AzAQrCFBtbQkLInOGkkHH6ptXu\nmKJux3FMxBuEEbrc92tlcQXvvk994u5tbaM3pOh0r9U14oOu4yAc0/zSKkU6e/CLOEmxxz0ewzg1\nka3WylwPtILWOeyipiDLbNKxaaqHlkoBm7WDJDQqBRr7hTOn8dTVSwCAZrkMxffBK1oYDOj6TzoB\nItaG8lzXZIVtLzY9BIXro16bPSusIIyoop56DaGNrtCoP8LmzU26D0EGlfK99cqwc7JCoYqjIQkd\n+v0efIYcKHubZ5AeDsmJB2SrPi60N07y9hcKmtdiuVxBjVm9yLTJHK+vnUaVSSM7W1smc9ts1NFs\n5h3sE4xHAV+rNGsxv54kisDt4eBNZwG0Nj0ll1eWUeFMo+04phh6cXHRsPyINDLbWmz1T1BkLaZC\noYRSmeZFqVKBN+A9/egQ45DWTXt8bKDmRCXI/yGEnvyk0maNCgIuze/lLFINbcSgfb+Il54ldtjj\nVx83+5HlOEYgdnnpDEbcgmQ0jtAfzt4q7Nq159A6ZDQCx7D4PLAdadafEBoDZlfaloWMs/pZlsHj\nrN7KwhICzogPxyOUWQfOtYuw+ZoHwcg8k1KhgE6HiEnDQTQRUnYtU0yuU6AgPf7OARKeAME4wFJz\naeYxjsI+ggFlcyvlMizO4luZhszZlEkKzefQxfVzeOm5Z/j/iBEy3KnjzAh+xTGQGSomDIyr1P0t\nnvJ9hZAM+vNq3cLSMs3T3XvHOOnRZ19/5130Eiq7KJeLOLM0uy4d8FNwonQ8QsYzOZEJRkOmuWuY\nRRjHgSEB1UsWCkUWHyxZKDL90S1aiHhBuoUCMoecomKjgc99jjaEcBzgzQ1qvtnu95G0yIFJkhgl\nTiuHkcJqmW7ekxdX0ajQNdy9cQMnLJ640HCg09nouACwsbGJGjtIURQYBVmltDlQ93tDdHizqhV8\nVJnBtlBI0e9xXyP4GPbIiSo7CiVmbRVffhWbuzSurb1djMJhfncNXGFbEo9x08Xnn3sB4xHXSxwc\nm/Sw49hTDZcl0mQ2DD9X455m22g9YTspPRH4W1ldRcSHfJaEpgedtG1kjOMrTWl/gOp0LKOePGF/\nTddeTbPtphdKLr0ghDCCcNKaTOksy2auw3C8onGQGvUaxi1yYOI0hZX/PoShDYdJatLcgDSerYac\ngrfSCbMxDpHw+D3XNu6JSlNzoFmOh/+PvTeNte3IzsO+qtrjmc8d333zwKkpdrNntoa2JcFyQ5Hg\nKHHHUWIbsAJnVAIHCZDhZ/4IARwjToI4iBQYjhJEsaLEURwpsiVZanWrW+yR4tAkH4c3vzvfM++5\nqvJjrV37vJab75ABBQM56wd5ebjPPrtq17Bqfd9a3/2HtwEA83wOLXmumDkGPbpmkSygGZruDQYo\nstWrJAdBAM0bSWVFs41Y6xYmEuWuWyXc31SGcCkjb0lPK2DYI/QFblwh3sMnnn0SfZ5zoZAw3D+z\nZA4voHc7GmVIc1q8tNWwzCvrtroIA4bl0SQIrmIWTfkFYa3bIAWE41tobbFg3uUnPvlDkOxcvPLt\nb+P8E5SR1+tt4j5n/U4nh/jUn/lRAEDqfoX+9TgH6Xthu1Ucqveyh7ymqSqHx+NMlAYpQ0n5bIqC\nS4mcv9BzwtzJfI7Mo6efzQ6QJAQtd9p9t15J4UGpRyG3osidrimMRsGUhLIs4fPaPBgMnEC2EFSK\npG5XraPpebFzUB5nR5MTdFjoOKoyhAU5KnHUco721raA4DXi9PQYaUbjSIYWhudrnhQo0jrLT7hi\nsRACbhcXsqYAQkCiw5SOFz7zQ/jCj/8kAGCjv+2Ez8sywaIWGlYeel1yKrY2p0jy1Qvf/tQXfw4j\nhre+8vv/GJ9jeF9JDydHBOHdu3cbdQqmUgK6quFL3+mN5nmBgteV0/EIoSKovxeGrgTFZDHHlItN\nd+KWE3qvTOW0LrN8AcPC6cIo+B7Nv0F/AwPuk63hObTC1Q80QeQhYGpOHHhQoPdSlSUmE1pfZ5Mz\nbHB23t6TV1EwbaHIExeM8EXofIKyyF2pHCEbPVIllePuCiFhuWzQIktRJjVvDfjUpwmObAUxjrk6\nwOF4ivIBUVCMyGHEahSQ2tZw3trWtra1rW1ta1vbB7APPRK1tXfJFePTxRyV4UyLPHOwRBD52Oai\nhL1WhBaTzJWk0B9A9Ux89oJPR3NU7DWXeQlTS7S0d9Ht0SlhMslcds0LH72KnQ2KMjw8mjh4qhcp\nd6qokgyXNzk8vdEDgtUjUQf7hzAVyy5o4363rr8CAFZIZHwqzOYLnNUhWGGw1WUCoJyBD/U4t30N\nr75BdaVmyQwhE9Tb7XgpEgVXmO3ShYu4ePEqAODsdAyj65MNHOzleV4DjclG7+5x1hD59CNZdTWR\nTwjB2XLAzvY26zMAYejDqjryoR0BMs8L5AxLWKH+RE0s73uy6tQSJLf8+64e01KBP2OMa+OyXtrj\nTPoBfC4GmGQ5Ts5YV67QroiesYA21v3dcMmb56PTd9k8F3dxlqauFlqn03aaeq04RKfPdX0eHKLi\nk2dv2EbMEEkUawwHBO0+eJihPyCIJmwFODpcvTbN5UuXcJbQu3nptfsQGauq+xIRF4JNU4OCoxrK\na5IPjFmCRmzlstV2hkNc2KXT+LAf4+pFPpkPOsi5dk9uPEQ9gkelEg623dyKkeR0Gjfw0OGsQ60r\nRCxvUpkKi2T1NnpSuwQBIaQrDklZoDS/B5sD/Mt/7S8DAIJY4Pd+6zcAAN/61tdwfEZRgKvXbuDg\nDhU+jaIYV598CgDQ3j2Pivvke0+gq2Tkfb/rV7WDU86urXLYGjbTHrb4VD07OSGJJQCAcNEFawsH\nrSfpAgnDRN3OBjyPIaCwDZ8j5HWB26jdcjJAeZkj4YhGnudOQqjX6SFNF3WjkCZ17aTCFdiUQrma\ncY+zyWzsCkJGeQafszY9r8n8U0rB4wzeVr+HOsOi0hVMyHC670HXkqxZBZT1XmKheZ6FYYxBn8jM\n164+jU98nBJynrz2JHZ6NOdsKTAv6qzcEjP+e7aYI03raLhC/H1q+/3T7MqTz+LyDRpTvY0NdLs0\nP5T0MDmlRKDf/Uf/N248SclUi/kEb36XCl3mWeYi+UEU4YQzzvKshDZ1xrIP5dUZzh2kGc0zDym2\nWfOwqHJUnGSlpMTGkKKTly5exxZne37msz+I69cJ4ej3Bjji+mqr2HSe4a27hKD0+z2XUAJr0OVE\nCGk1Nln2bDxb4GREkVZ9NMdxQnB6lSmnDSmEcW2PoxiK53enFbqCnL4fuD1lluUIFL3rTtTFC5/9\nJADgEx97Af/Tr/x96re8guaEJREaFPL9zcsP3YkKoxCy3uwCz00kUxYYcCi00x+i02JIQC4Vy6tK\np31klILlAo22qDBk0eFAZzg5oHTlNx9MEfJk6okM558j3Z5uKF1WV78dYzylFzKeFTD8Ax3fB9M5\nsJjNgWh1hn6apk440VMeEs7YyLMEdehfub8AKwQM4/bHxyOcMox493Afu5vUJw+Pz/DK22/Sc/LA\nAiiEWW/MwloMOhQKHfQ2kHEFamGkS2cui8zBpr7vQ8kGOhMrBiKXHZF64fc8z/EKpJQOcpNSYucc\n6ZJFrRiKHTgN64pTtrRBh9N443YHkh0wr9a/W4IpAeuyepbhPCGEaxc5h+xELWWafa8Y8XuZhkTB\nJK/pZOFSgovKoqwXXymdUyHEkuKgaKAuoMmgsrap/LuYJ7j/gBagfn+ImEPtl/a2MDqhRTMtcoRt\nmvxWJIi4cm6nF8BnQV7ICr06E6vl4eRodVJUpBQ2+/TdjZ6HMqP2XruwgysXaBEfjaeYLGpNPYnj\nU3ImzyalcyAFSmxyFuxHb1zE+S2CEPq9GILLWySzOaKQ3nHU6WPI1ySLKVq8sbZbPm4/4Kwq4aPN\nGTuL2Ryyrtrs+8hWhIEA4Btf/RIk6zKmSY4bT9NGtbO7g/0D2mzeevNNnJ0SbP7w+D6idj2O+pgy\ntPXKay87MWJ7UuGN10gM/IVzF+CEDNHwo4x51IH6fg7V/9fsvJxFkYVWKLi4ozg7wzu3SMVgNh6j\nyHjc9DcQxvUBLcdsSmuU1gaHrDBQFnfx5JMEcVy5sYfOkByHiB1drTUqXa+FFuWMfjOdz2GYK+P7\nAQxDsVWRYcEOWpYV0HxYgpGI4xW3m6pCwtW5s/nCHdA8P3DZsWWlXfmULMvdwUUIAcVwcStuIebD\nsMlLgHXilFRQ7ICd37uCj3FRx6uXP4LtTcpmbAcRwGVTZpMG6qpsgVlBDuNkPsZ4RM7JaHKENF2d\nEyVsw9G6cv2pBkbVJQ7u0eFZCYtd1g1dxCGOBrR+HB8fugzR0PeQ8WFoOs4waTOsCYGIHaT5Isfk\njOd0S+P8BUr5Pzw6RMDcp82NHnZ3ad3e2dh2MN/0+AR3HK/Nx6qFIgBgNF3gaMr8x7yCL+qyLkDO\nh8g4DHD3iPrw7Tf3kSt2UPMUc4Yvi1S6SvppluJgRP2sK42CKTIXdjcd1SLPcnjsbE8XKSkvAOj4\nHTx9lbjCP/S5H0erRXvnwfERZqd0n429FlxZlxVtDeetbW1rW9va1ra2tX0A+9AjUb60jlBblNpJ\nRPQ3N1ydEQUPlkPNuUkcTNRqtVFxeDJLZpiy6nyaA9OMoz1JgvGESYjSos2h3Fj1UXCkZH+UQLA3\nOklyzJm5P2z7CL1aH0lC19EEKVF9f3GlP2F5lmHC9YCElPBZy8JopwZC0bX6lgaObO8uBFAsFpiw\nptrNu7fxqNfPxGUjYTl65nsxJPfheDZ1IfBO1UHKJMcoaAiGnvJctAdKQsoVVdX538rzHJxGRGSO\nsqmG1GeMQcSEYkiB8zUx0lfoDwmuiVstVxtqPB5jkVCbTZ1qVhXupKWUclGuZZjP87xHIL+GGP1o\nQdBqxfS1PC9Q1skHRUF1WUAZbS7IoA3EP+Uk9j0Kasu8YzeWrbU4OKCI06VLF3HhiasAgMuXLuLe\nHYoipHmO+YIiIUcnD+FJOh3FYYSDnCJCh4cJlOK6KkpiNn8fel1Hx1hMKFvm8t4m2lzk9PqlXewO\naYxs97vwODNKQ+KlV18HAExnDxwc22lFuHH1ErXl/C4ibmNRZI68HSqJTYYgw6jtCnvGcduNlaos\nXGaRsRrzhKGiLEPBkLCMIpept4r92q/+CiTP6fl8gV0ufPsDzz2PW3dvAQDu3XnHZQQNNvrY5uic\n32lj5wJlFN698y48cHYQBPbv03fT2RjHE6YhKIGII63t/hCVrmsSGXh10kzZRKBhSzSD4/3LoQBA\nu0XPaqugqVelLRLux6DVg2JOwGi+wJSh0Nn8GLdvve2un3FEqRV3cOk6kemNsJhxxvQ8aSgDtRVl\n4aLih4fHTQatkA7yiwMPrShwn9eacNZal2H1OAvjaImEbqBZq67MF7CaoboKrjikqQxQZ64ZC867\ngElKF1HxfQ+KEwj82McGS9bsXriEdo+oGIEfQ/Jkr4oMOa+hWTZHUVI70myCkzOKCB2ePMAspf4o\nitxlt61ijWAVYD3f1c1LZgtMTk7c/00SQikO9g/w6ms0F/O8wIXzHO0PFDY5WjWfp6h4jo7mIwQ5\nvctkUSLkYpVPPvkcAs5gzxYVEkYvep0uJL+f09OHLqFkNDpyz6akh4Aje3/pX/mrj21jEAbwOFkH\nxgNYzkZ6qn5dMMrHfU6WEDrHuScYqgsDV/OqKpokhjA85wjnUghURU0mb4pH51nu1ulOp4VkTm08\nPBjhcMq1qswcYDm0yXyG5JDlsKocT134ZwzOa/U3kcw4Sy4n+YfnAAAgAElEQVSfoGKOk+/FDewh\nCvjsDPgqpBkC4Gw8dRjvIknd4vX2wynGM+qYUAGmrlYbBJjNat0kgaKoOzsAJ4kgNQKtmJ2KwGv0\npwIfEZdfyAuNySRbuY2fv3wFKYd+i8rAMDariwIZw3a5KWF4MEprHZSmRRM89IV0sUHh/gFE0kPI\nEIIqM3CBc3RVjIi5Cxs7W2hxWn6723XQSNTtIeZNMVIeQl70wziEvyrva0lHrnZKrLVuYAshXGE3\nIYTbMD3PR79PG2l/0Mfly1QVVkjpMmXm8zlGY9rYZ5zqr4usqYgtpON0+WHsngVCOnhJGw3hNc5K\nbUVRrMw7Mda4hTtLU0wZkjCmcZwsrOOgAfi+mX+PVJfXNeSpH8ksrIVFR6Mxbt+hYpsPDkc4GZND\neTaaw+eSHq3Ix6Q+QGQWQLPBmPcx30PPR8D9d+3iOWz16J6dyHMadt1BFz1O56+swOQC8STefvcB\nDG8SVy9cxHPPEEx2bmvTbZrzdFbrFaM/HOLCRUoVthUVoQVISLzuE5QFKp4rnU6Mbpec2DxJXSZS\nkRTY2F49rbrd7bjsHS8QODwkXsXpyQlMXbrBlvD5YKGrCrMJbVTnNofQXDS2rLQT7+13Otjfp3f0\nG7/+q3j7LhezFBY9hl8H23tOi3Bne4BrT5JjsrlzGQHDiwZoiHSU+0iP8z6qoZ/nzV8Ii/EZFS7e\n293B1hZtpJ4Xumr/lS7AMos4nWXIWDNUSon2Bm1Ww8EAIy7C+d23Xl+C+GvnI1ji/AmkvJ7tn5w2\nXEvfw5zF2yPh4WMfIR5Ptx9jwU6ZFwpIbzUno9cdurlobAXN485Yjbria1VWbhxpbVzfG2OWqu8b\n9+yeD8SOV9rFoMUQdLyJyGMIvWr4XLMqxzyhdWmejHDIenn7B+/ibERQcJ6nrr+U5zlHchULpHA+\npRVNpuyw18ef/dGfAAC88IM/AsUT82tf+yNo0HptjcXP/PM/DQCYjEf4hV/4zwEAiyTBx57/cwCA\nLJvgLh8a0qTEvftcqTt+iC984ccAAJ+alciZInP16iX8+Z+gz4Mggqqz4oPQUUA8z4cfrHbwBoBQ\n+tji0jcCFoIDE0ErcA54kZduvSyyBdKE9Vz90JXn8BWQzrksw6QRtfaUQug3Y9pBurZyVBM/Ano1\npUTEOJvTPP6dL/8aers0rvZsjDmvGacnh5hP/uQB4r1sDeetbW1rW9va1ra2tX0A+9AjUaPxCAUX\nuvRsBWFr1WWLkolvfqsFRHQystZiMR3xdzNXl2Q8r3AyJkjj9GwKzaFBrTxXC8YUmSOXWaNQVU3G\nRs1vjMMIGz0+hWrrtKjCVhu1SlQgNFpidWL5f/8jP+YUpNMigeWaJbbMUWr6PCs0DGcn2Cp3tW8s\nNDwmzfkihqmrA0oLxbpPvhci5KwZvf8OSiaUBmEb0dNUnKz3xLOQtWZcKwQ4uwlxG4q/C60hapJ2\nt4cVOdcobV1fp4Hw/MCHEk1RyTpqZnRD5lZC0BEQdGrwFdePMQaKyaKBF7vTRL/LEZCydCdRKWVT\nIFQ2RS2NUE4HzhgDU9TEUgmfkwtWrRFFv6OQMPQxn8+hq7rgHRzJWWv9SKbicmHC71f/p+6LLM+X\nolsW9+5R1sor33qAu/foZHs8XmBR1GTjEEVB7cjSxOn3CeE1Woaw7ysSFUUtJFzoMkkXGHD9r3M7\nG+h2iWRZaQ1RF/6DwPVL5wEAuxtvYcyQ9ZW9XfRrArzVLsKj/ACWT4kbO3tQDGmdjk4w47nbOt91\n7y0vEnfKjaMIcYvGgecpCK7j4/khqnJ1mEQGPiTD2lIr+HUEFwKo14NKPFLvrC5EWGUJijlFzU2Z\nYcHyD0Km8Hx6zjde/TYSfkeVttivC3h+5zsYsBbohXNb+O7L3wQAfOTZj+OH/sxP8LOFLrOvKgs0\nRTsNVgyYQnGEtt1uo8Pw843rN9zYlZBocT+WRmHOUSYjA1y+8TQA4NzOLuYLHotWuwy26WKKOOB1\npmpgklqvsjIWXqeOcPdRFHWRTkCyvEfsd5zWGjwFy3BaUeUw6WrvMQw6kC57xriogjXGQf66qhzh\nvSxLp51pTKMzKoSEx5l9UdRCp01jvN/bQq9FEdYobCHntftkcgjN90ySCUYjgt/39+/i7j2C3Kfz\n43pJQxxH8Bk6llW5chILAEhjAJek0lACpBTwOCs3brdd1OXzn/+z+OSnqPhnVZbY26N5+ZWvfBlP\nPP2Mu+/zn6DswmtXLuN//OW/BwC4d/8ennqaornbOzv45376XwAA/Mxf/Fk37gLfx+4O9YmQakkS\nyv0JKcXKCRAAMGwNcHVI0eiopVDwGq2lajRVtXYJQrnqomLqTydoYxhTFCvwfBftyfMCKe9/RVog\nVPROW1ELkjPDTFtD85qU68z9bjAsXca8BHDpItFLLl58GrMFPc/oZIZL3LermvggabZrW9va1ra2\nta1tbf9/tzWct7a1rW1ta1vb2tb2AWztRK1tbWtb29rWtra1fQBbO1FrW9va1ra2ta1tbR/A1k7U\n2ta2trWtbW1rW9sHsLUTtba1rW1ta1vb2tb2AWztRK1tbWtb29rWtra1fQBbO1FrW9va1ra2ta1t\nbR/A1k7U2ta2trWtbW1rW9sHsLUTtba1rW1ta1vb2tb2AexDl3355T+aOFl7KWUtCA0pRVOCXQr4\nXE5eLonTSknyFADQ6bSd/IcUy6XoAb7NI58L2WjVSmFRqwhIIZpnAKBQy3sICP6CFM09n4rx2Dr3\nDw5SW8sFeJ7CyTGppb/51tdQapK7mM3HcNrdymA6JXmJ7Y1r2Nq6CgC48+Bt7B+SaOR0OsH+g2MA\nQDqZ4okn6JrNrS6GG1QOfzJLcXhI12Rp5oRHdVmh3SYJikuXLiLLSeKhKHLs7WxxGzWSCZXP/3f+\n3f/uPdv4Lr9AD0CtSiPQSBUIAAX/j4ODDO986+/Tc8++i3lJz9E69wXMjr8LADh78GW0uiRB4Qdz\nxIpkfjosW9MePAGv98PcJye4dfPLAIAr5zdw+y3qz6//wZfhKRYxns1hWPYhyxaYssSIlAKaZTmO\njvffs43/5X/8X9vNYa2MHkNrlhsaPcT+Pkk+TMZHzZjyVCMd4sRoWAKDPxdCONkGGvuNeLJohB5I\ngby+ph77YvlzD5703d9wUholDk5Ilfy/+l/f+x0CwE/87BetYIUCqyTg01dascK1HZLcWWQVpiwx\n04p9BCy5kWQWma2FSBXaLNuj8xJlRX1VGYnNTerDK5evImP5o9sP7iBPSOy43xtgb5fkJWI/wiIj\noe/xfIq9nV0AwPnt8zg6pXbd2b+N0YiEdn/5b/2dx7bxxd/4X6zvk2zGZDzFIiPZk/3DB2izzI3n\neUgX9GymKDA+IXHW2PNx4Rw9v7EVXn/jJeorY9BpU/+UWQmw9AqERmWor3rdLsBSRdMywO2S5tkI\nQ0QsayGEcHJGWlt4kp5T+oCK6b384i/8++/Zxv/s53/SAkAc+AhZiiY3FiULqLbaMeK4FlcuELL8\nkxcGiBSNobODfRifrvcDH5ubJMYrpMRiRv2ScP94fiOjVKW5W5uN8jDc3eV+8JyEly0KzPh9dcII\nJ8c0tyup0GZ5p3/jb/7We7bxX/+3fsrentPa9PEvPIfB5oDvLeEJknEp/QVEzALEsPBZ3qWyMyhL\nf8NKGEs/pXwPCQtNm2NA5CxT0woRDOm5zhZnmI9onP7R//EGdELXfO5nnsbGJbrn9GQO3aVnCzsW\nSrDsiw1hWD/nv/iX/pvHjtPx0S0bBnRPpRRKXqd0peHxewriGIplZayQJMcCQJvSSe4YXcHyd8ej\nU5we035wdHCMkxPaY+49eIg790iIe5GkkIrWWSl8CF5LAj9AFNdSTgaHxySy/e6tW7AsHLy7u+fW\np1//v37tsW38wzdP7OiM5tbN+6c4Kll+TPlOvkgI4eSzlFJub4Y0bu201rrnlEI4sXQICctxoEgp\n9CO6T0ta8NSAH7Ywz1jKpzQwLO2mhEHE65/RFQpWTs8RoOI97uc/v7OSxs2H7kQJYVA7UUI0oS8J\nAckbiYR0+neAdY5QludIWAW812vzvehGTlpJkEI0QJu55F8Q1qLeMKQAJG8GAgLC8jXCPvJsjZY2\nPdWq5gcWAWhCFEWFW3deBgAcnryGNKOB3O60EIW0WEkVotcjzZ+tnQGUJN0ea0t0O23XbztbdL0p\nFk4l/e7dO1gkpOSeZhoPHx7QM/gSgyHdc5Ia11cnZ3eQJrRwx2EXhieEMRaDwcZK7ZO1nN/S+6O+\nZs1CCFR836I0SNnxLascnRb9RnL2KiYH36bnaLVgJD3r2dkIsqIJO+TF0m/NEYEW+SuXn0XgU9++\n9c3fxrf+8OvUVzqF5qepigwsb4d0MYfljQpCraxJFgYRhj161m6r55wozxZYTGhhKrM5JPer8r1m\nksM2Y1CIxomS0v0tpXSHBgjhFiNYuXSYUOQkgXS/pKgXFx+ydqKUB94XsEgTt6mtYkJoWP6ysRa+\n4I0kCsBrNfJ5jvmC2j5bVOAzBoyxAGs5KqmQ+9wPUqCWKNzsb+PyhYsAAK0rLJIp/65F3KIFemtz\nE1tDGteBlPB5ISt1jg7rsllrkbNm5mKxQMIO2Cr2x//gf8B0ShvMbLog/UYAuiyQssNWlRXAC7cf\nhhh0eHGXBrde065/lKZ3mhYVqh6NTQkLyw67sBoxr1vyXgbZpnbNw8uY81y3cYiCJeO0ySAVa3VG\nPhRPLGM0ymw1nccTdm7aVYAea6xl2qCq9RTLHFWt+2kqCNbCq6xAsqB+1B7gt3nz9yQSTf0irUBh\n2CEGtTHwQ0wWfCjRxmlKtgdDnI5pXnh+AM2Ot4JAbuh++TxFzmub9oAin63Uxmro4/nPkH5Z3PVQ\ngbXP+gFKUBssNAKfnAFhC2h+bt8P6iUdAkBV0fUmlxAz1tFTPqKL1P5KVCgsPXvYEpgdUD/mY43u\ngN7h6E6KYz7Qbl1vYZM1PrUoIXhTFvCg5Up7Ll9vYdiRMAbwAmpLEHluDZCqOTAJIWDrNUYqBHx9\nVeSN5ucswT3W4Tx8cIAsp3ZZDWxvknbeuV0fXZ5nvh8g5/e5f3iKuw9pHT46PMRiRvvWxnCAC+cv\nUXu1RZrmK7cxn48wbNNzPnX1EvK7dM9ZoSF5/n3vQVOpeu2E0yKMwtBp7UkhIHneWFH/A6hMhTQr\n+D4WFc/LNC9R2XqdVvXQgPIAaLpn5Cmo+mCaF+6eq9qH7kTJpYElpYDH/62WxAzlUtRICAup6g3J\noCiz5nMXWWruKyVceESKpkFSwt1fCANZXyPhHDYp4Dzc5c0Pwq2xK9nZ6W0MBjRI4zDCbELe9+jk\nAFbQoAt9hZMZCVq2OwO0WcB1OjtDltAEHZ0ewhh6sVvDPjodGoAnRwuw5iLyvHCnu9kiR8CnmevX\nL2FzawgAuHZ5G0fH9+i7Z7cRB3RifPbpF/DcsyRWGYUKrbCzUvvqrlB22WEVkDzYtDBYLOjv8ckY\n04IWqEhdQyDp/Z1NX0Oe8+lW7SA3NKHSdAoDWqwubpBQq/ALeLxJl0WCr//+7wIAvvP7v4UFL+hC\nKLQ4cpWlcwSsCiosnGCq1nplwUxjNDRHVGArN14sAL3kiVl3vybsKdEoiC7Na/q7/t7S58oL4NUq\npnYppmcbgWWBpciopxqna2k+WSHe13yPWxGKnMaX8DyEIT8DFN55SO8jLzTqs4QSgOBon1CVE3b1\nlcRWj/q+321BcXTg3Pkb7pT74GgfZxyRqKoK3Xa9cHvu1F2YCuANsh0F6HCkSOclJixCniYJhF1d\n2HV6fIbZjMV4lY8BO+CBJzFl8XMZ+FARjdF40EXcomcuywxZzptuaVCwYHFhQ5QeP5vO3NrQDQMo\nnq9thEgi2lzn3ha0IudFCg3NY2mRp67PAyVhFM0HaA8+2iu1r9S8yZcV0pwFeIV064DyhBN517pA\npdlB19YdJIPAQ4uP6iTmSvOlrCqYhB2qOrIEQM+oT6IgRMlK7i2hkPJYQqGBnPrcD1vwq3oCKKR8\n79kiRYudnsfZ3icvQXVYODoyLvJQmhSK/0OJAM2srNy6JBGh4Hmc6wSWnavA9BC3qI+EZ1EIet4y\ny2Gr+mAkMD2iyGWeF+hzf91/awweRrjy3BARR/qKUkDXG7Q1biNexWxVwtYDSSoo7hvlBRAc8aUj\nfj32LUzdrVbUQU/keYU04fZmOTw+De1duuz+NhBOFDrNc8w5IvfWzZt49bXXAQCj6RRdPig88/QN\nXLv8eQC0nx0e0X62//DQ7d+rmNQFlEfXb3T7OLdJa0B+ksDIxomqN3a7BCV5UkAw8hQoCWHrfVrC\n8piyJMHO3WPdgQkwLlpsrXZrpxLL8X8Nn52xbhwiZZHzUluk+v05UWtO1NrWtra1rW1ta1vbB7AP\nPxKl4CAVKa3z1pe9dtk4oxzaayC2OGb8dimCJKTAEr1kKUIloNxvCQhp3ecNT0U2+Ooj91ziUy1x\nolaxL3/l17G9TTyPixcuAqBTTrfVR6npFOfLFs5dJr5FZYHTU/Lub9+5jTikU+jbb72JnE+XTz9z\nA3lGr2c8mqHIObpSWSQV3V8pCY9xrNFo7GChbsvHnCENX+5gZ/M6AGBv50lcPP8s94nGvVv36fNL\n792+epAoNPBnicbz9wBkjDvPJgfw+UQeqw5MSb9R6AiJJn6UMD7aIXPINtro7f4YAODZH/wC9c9s\nH/duvgEA+Af/29/Fu9/9DvXD6RHKgk5d1kpkPkdSpETOUA1sA4sIuvC9G8eWJlMkCUW5PAVUJf3O\ndHKMqkz5N40LLRlrG36YWIKmhXTRIQu4U1AYxegxPNDtb7r7VGUFzaHqskhR5Aw5VboJUME2Udsl\n+I76f/VTk1IelE8/7HnKjX1dahg+ffnKa077EBCq5pQoF3YXxkLWESpr0e3R+O13Ozhjnl2WJw6u\nCIMArRZHZjyJ0lJ703QBaLp+a7iLjS7D0eUpYKkfWoGEL1eLYABAeOEjMAmF9avKos0QcTIbwzIU\nFrc7CHlQ2yrHGZ9CUxVhJmqYR+NgRs8wKwA9m3BbLC7tUWTXdPoYckQ5ExXeOKLr90UML6LQhRQF\nCo/6OYw8hEHdlhYqjnQpqyG9crUG1qdkTyHlqBGCCAFDv4FSQMHRe60BjlwJbWA5GiGlhJbUzrRK\n3Ck/avdQLcO3AOZ5Ac3riopbKPi9JIWGCGpIUEEzNJJWGiXfuyyBjCEWWA/CBis1sXeujYwRCAMN\nzeupthawPn/eQGmB13IQmLYFDEcqTGnQEhSdj9CB4nZkmMNz0R4fJcOZyvNQpvQeqiJ3tABjJHzm\nAKaTCvE56pu8ShxvUQgJYcKV2gcAyXyKNkejW+0Ygu9vhQLcs1kX/bXCQtXQoRQAR3jC0EANeR32\nPPghjcfxfIGTU4ouPzw4wJ17tA7funUbb715EwBwfvccnv/kJwAAVy9dRK/X4bYXyBmenc3miEJ6\nb1ubQ8yYM7eKFWXpnr8sBCSvB560DvoUUizxm5vYvSes2/vzPHOcaSGBqu4TNIF5TwpISfePwwAd\nnn95pbHgiKkVDe3CExa9Nq1Jw26MjLnFyhgEcvX3CPwpOFGq8YkgpYBaInsvd550sJpFxXDM0eE+\nWhENNCVMA71J6zg/6hEOCmCkdvfxHiHp1vdHA//JhgQsxRIks+TUrWK3776EkzMavPf32+gwwXsw\n7CDNmrDifE4ckUVWOM6H5wmUFQ3MMFSwvHiNR6cYjWggR/4AVc12g0IrpvtbqTHjjWE2m8BjcmWe\n5lgseAPzdpEl1IdHR8d4400id2fJDN24v1L73MIqBDiAj0IDzFlFAAnDzl/s97C9/REAgJ68jFJT\nv8S9G8D4VXo+E2Agmbzs97DNZOR+jzr9D776Gv73v/tLAIDpyT5yDlcXRQld1k8AVLIO/QYoS96E\nrHEwmNEaq7lQQJpOMBrR96bTfeeUZcnCkYH/hC1NZgfDSeE+V16Ado8W8d5gE3GLFilhDZKUxkKa\nTFAWteNUuM1LyRAhE0wFGjhPCuEWpvdri8UC4PtXIncwZRCG8GtoT1hIdsythfstoaXzR4UvMc14\n08xKBG0iUc/TDJOEYLgkm0Ix3ykOQ7SYExXHIWq8sDIFqora7geecwePR/tIMnJaLAoYuXp7f+yv\n/4cOKp1MpmgxRHh8fAzJA9kWBQw7yZP5BAevE6RxNpniNKWN52x2hodjOgBleYlS81wMFMaaHZBw\niNbVqwCA2wf7ePkBbVQ2tNjc5cU6DpGXNEenp8dukzt3+Ul4DBFK4UGb1U5tCW8IlYxcUownS3Ri\n5tKZAvUiG/htx6uTkPBaDCVGoeOJeH4EP6T1RHV7MCm/j9rBTioIxpG0tQ5iydIEcQ2zVcKN28Jo\nTApq4+u3Ju7zzWHbOQqPs8Jk8Bg/M1o77gpgYJjIrzwffg3hC7g5J4RwfKGW7KFaUHtsZWDZOSnL\nwo3xIAqapA0hUTinz7q1Q5cVSgZtDt9cwHTo/0RDjVbU52cuoN4HsJMkCYJW1/1WPb+t1bCo+T8+\nJPMWdVnheEwH71JblDyWp9MJjo6IJnLn7l28e/sO/f3gAA/3ieO0mM0wHtfw+AI/+rkXAAA/91f+\nMjY2aH2aTsYYnRL8vigrx4P1pULkM3zpByiDZv19bBsLA8V7+ayYYZrUQQ35CAWn3vuVgjuYKxgI\nTtZSS5xTiSUKDuB4YlII8HkPuzubGDLP8XQ8Q8r0F2stDK89rTBAj2H80AN6LT486RTWfp/1/vvY\nGs5b29rWtra1rW1ta/sA9uFHogAX4SHeWAOfNR6oIKgElKGkOapx984tXDpHmWjy0nmXCglh62gm\np5TT39Zol/Hiq4YQLeoLwVGspWiYt3TCr03IR/i7j7XpZIqQf82GFoWk50+THJMJZaRUpcDBIaXK\nh1GMy9cuAAA67bZL4e622tjbJsin3W7h5JjSvEfHM8RcssBXISqOkhQiR8BpncLzsH9MmXq9qIN2\nQCcMWyZYjOlEcvudDCf8DOd3z+EHfuS5ldo3uk9kS6UkLJ8KTamhmaiZCAExphP8ViAwSeldpmUO\nhQ1u8zlIEESXTo6ReATdXHvqUy4C8St/5xcBAF/6zf/TlSyoSoOcs4qEtTD171vrygRIIeAxtGd0\n1SQOSNlEqB5j08kJxBJM6qI9tskSAZrQ8/KYkkI2kVTA/aYvJJIZl7iYTepvwfMUMk69T5MxUJ88\npXApzXHYh88p4Z5okjCw9LtYihStYlVVQdSRqKKEZXij0oDH4Xs/9FDW0b4lZrwnpTvFwRcQnM7d\njSN4EUVUJos5ziZMJteFg5eVas5qRVkgTel9jscTBBwBU36Mszn11Wt3buLsbMR95X1P1ux7W+fi\nUwgZflCzOTyfYfBWAM3ZSuOTM8wmdM+J8XD7mH734cN93Hr3XQBEuK5PvHmeo+TIsbAa9XsM2x18\n86VXAADHZ0eO9K38NrZPaS5GcYwioahanmXYuEDQ+mw4R6fHpPcogF6RzJrxc8CPEAcNvFNyZC2H\ncWtZGEZohZzFZSuX+WSFhcfvxhcCYQ0lQTo6geEU+l6nDTAMly0ylx0RhwH8Jh8dhp+lzEscn9LY\nHi0Ebt2nbLFY+vj4R6+u1MYKc7RFn9tmUXC2X+h7UEyI17aAz+R9Yww0R4tDv4204OQAYVCF1I5C\naAScACF0AFvU9xGAovHuhzEqzshUqkEvrLEw/M4XJxqbM2p3e68La+qoNzDkBJ5VzAqLyjB0qHMo\nW5fBUA6umi3mGI9o//jt3/lt/JN/8jsAgKjTw5yj85Pp1GWv5nmOhPcGY4CA4dZkPnWRpX/tr/0c\nvvjTP0n/UeSYMMn85OgYkylFx7M0dXO0KAqXkZcmqaMerGKLSsLjSOiiqFCYev3zUWMEnpINIiUA\nxWu3Bwvoeh1tksSiKEBaUzqMcWUffCkQ8TiOPA8ej/WtjS7GE4oE50a4kgjddhuhz1G+IkOfob0s\ny6Gr1ddUetYP2eqUcIA6qIHPlnhRxjj4LPAUBGc/9HsdeF7NvTAu1CeUcA7SMhT40jdfRouv+cSn\nPwpTt040WWVyifvkyabmhHD/oH+9D0oUYLr43Cf/HABAiwO8ffstAECeKdy/M+W2bOPaBXJa4laI\ngjPVxouJy27aGvZxdEgLer4QSKb0FHEwgKdoozq3M8Dp4V36WSgEPBCkZ1EZ2pCSFKg4iy2UU9iU\n7nP/zhtoc3rrzTDE1RvEj9rau/aezcve/ib9hlJLjgNQMXZcScDnsK1nNUw6479jnPHEnKTfRdAi\nx074XXS3qD2B38Ov/dLfoWd65TUAgO8LpFxjKE0S5Fwyoapyl71oLBzMZoyBxw52q91xC4Dv+6hm\nq4VmyyJDWdfzgb/ktCzxEpbm1vdmc9bOhjYWo7Mp/z4gON1cmxwZO1fTReNI6DJHwm2NWgHO7ZJz\nfWEvdg6j8B/dYN3zLHHUVjFPOIoMAAlVQwildvV0jJJNH5umVovDbgGUmYZmZ2x7Yxv1qWS6mCHn\nrC4hPMffiqIWfIZnirLCLKH2FlWJTouc6cCPcHxGh4bj41PXP+1W+xEn7HH24MXfdP1TVRoBL6bz\n6RQzhnYOj09x6yFBIA9Op7h5kzgik/HYlUHodDqIojprr0TGn+siw2BAPCtPKZQlp8dHAaqkzj7V\nEJocieT4GAFvltJ6mPKCvud3YS31aZ4XLm37cVYv/KHUaDPvI2wHDn6rTI52UEN7FUrm2AlfwOqa\n0CcQcHZiUmZIFzR3Ou2e+52abhAMe2ixk5wHKUantK5oYxwPS1sgqPtK+Oj0eMObZEjYce0Nz6HV\nXs3JiMV5SE1rWWlnUIL/LkoUXOIg9DqNA2MqQNTZVTPoGub0Y3QC4qqmcoGMD2ZhMEBlaY4qM0DB\ndAo/ilw7rLDETwKVM9F8yC+yEoev0fNE/Rhb5wjKtk4pi4QAACAASURBVMUZtnrPrtQ+gADteuzk\nWQrPq+t5xRjxwftv/7e/iJc5e25//wALpoNURkLXDolS7pBpjXUwWVVm8HjuPvPUE/irf+VfBQD8\n8A9+Dtmc7j9dzJ3TVVnjuJxGWBS89szTFBnXIMuqws37VWyclAhj6qscHkxNv1ASkuFxCTiHXuvC\nHaqGrY7LsEuSBP0eOdWbW1u4/5Acc6WNo7n04hY2GZJ79aU/xnPPPQUAiFs9+Lw3lEbD8HpZ5Bkq\nhinDpaBJrxUhYz7xqraG89a2trWtbW1rW9vaPoD9qcB5j4br+G9w9ggAqaQ7bQpbubDcR599BmXG\nmRllgZBPT1Io+Etlcwxn+9x843X4jN48//GPQPl1lWe7VK/KQNcnQ+VB1YRg0XjYAoD/PrKe+v0r\n2Lt4FQBwZ/8Ax8d0Ct3oX0UU0unhwvlr2NmkU9F8OsPDB3TqPpmMXIVhJRNsDum0Nhhs49pnnwAA\nZLnFfY5QPfHEDezfoYroX/r930SRUh/OK42SiZNxGCBnT/+55z+KHpNB375zDwXoebQ5g+Yw+ePM\ncvjCWNu8P6VgNJ3gFCxUnbkFi5jJ/ZnNcXTyJj2f6eLcE0RoPHxwF7dfo9P/r/3ir+KNP/4WgOY0\nG4VtFBmH5HUOw0Q/baoGlgUcBKxNVZcbQqcdI+d3rbVGq9NdqY3GmKVq7E1FcabX0udCQNTFXCFd\nPReJhnRdlBYXLtMpSIkEk1Mieh4dneCQiZv7owmqGorUFiNuq/AVJpzluMgqtGIikj771PNoxxQN\nMNKvueEw1rgI60pmrSNNWqtdG5WSS/VojItuaq0dcdNa60j9tjLwQ4qCdDtdFBx9StIEOZ9ahRDo\n9LlCuB+44npZmjr4QQrpsvasAB48pKrK6bzJ7EuTrImGrWD3fu9XkHBRtTAMIZgEPl8YnHBRwrNF\njpfvUSTq3XHqIldSSmxvbzft5fUpDENXw6oqMhwd1RGzYxexzEsNz6Pxe/n8BQejjXUBwXDwdJZi\ngyFwzweUx5FGwBVBfZz5vE5utEN4DKFFoY+YIczJWY4djjYjT5FxFDcUoYO8qzJzRU4DTyCZ03oV\n9ktYU9eS4khVskDByTHDQQ9tJuzmuXE1x4xQMAyJJVmOVpv7EBWyujjjIMFotL9SG0MRukrwVhSu\nNpUVBgHPP18FqDghQ8Ogw4VHy7RCXHF2VVxgmhIsPJ0s0OJEGq1GkB2OXPsCbT3k+yxVz7bKJWEI\n5blij2VRYXpAn2cjg/ZT1B+L0mBv68JK7QMAz29DchajqYyrOO97ERKu1v7VF1/EQ478xXGELkdA\ni8qi4tpW6WyOk0OCjvNFCo/hzm43wgs//IMAgP/0P/mP8PxHfwAAcHJ8hKJexJWE5KjlxvYW+htE\nvciLvEmsyTPX/0VWUtbwimaVj6SGh6GaaJuyMI7CYCF5fVWeQMRrT78du8xzabVLBKmyBC1+Zr3I\nXMLK6f4+vvYS7SPf/sYf4i9+8WcAAJ/93I+4KK9EQ+VZJAv4XNDZ70TwA5ob7XaE7j97cN73OlE1\n16RJk/aUbCqQwza8KWsR11lDVjtuhKk0wC9E+go1Ynjp8mWEXOwPS1VIk8UMJYdyh8Ohq7StBFxR\nxUeeGYD3Ppyow/0x3niTnIXbB28ADM899wOfxvMf+xwA4Osvfgvf+gbxJ955+xbuPqRMnnMXzuPy\nVVp0/EjhM5/9cQDA9etPoiyoYbdvH2GwSQPcyl20Oaku8Aa4f0Acp+P5DAtOLGl1W9jj1O6t7V0U\nXE4hDD1s8n2kasHzV2uj5EknpXSbIYCmOrxQLq04K3Icz2hSPzh5DacppY6KNnD45lcBAC/9o9/F\ngNNXg+kxQnYQsoQWc1tVUJyZVlWVy1ahqtmNFEDNg/AB58SNRmMonny+70OquqDke1tVlQ7GAoJG\nosXa7+EdsRNnPUh+z1VpMJkwPOB7uHiN+n50fIYj5qmNzk4cz0vYyvGOci0x5UXKVBUkZ9HoSqOq\nbrvPn3vmkwCATmf4yHPb9+FE5XnuHJIw9JrqvZIL3YHmQ10gT3nN5mGsbb4b+Dh/+TIAoN/vo2A+\nVZ7n7nrP86h6NPdhvTlVWrtrOp0OYpaaKKsKJ2fkZOqicnytXFeP8BUfZ11fYMibZVmVGJ1x2Qo/\nRGm5knmVIOGyFVJKhOwQGmO4+CSNtfpgZ62F4YNEHATO0RqdjRxHyfNjPPkkSRntbW/h6AE5hHlp\nkPBmvygLxFy1O0lOYSWN+3bcg10xOy9mCC/yBKK4Lh4p3YZfVMZBcR1PgKsowFPCrXvWGGQpzbWi\nyKD5osV8jgVDQx7DY7Myw8aAU9/LgrMr6X6CVRrSUqNkh7MoS8dZ6XYH6PH7feJ6F+1wvlIbK5m4\ndaaYW8y5GHG330XoU9/nZYacN9ZuvIkgI2cm+dIDnJ/RwSm9nCL7AWrH9tYOqrqYri7RUkwtQBua\nHcBCZ1A1R8+zMKJ23jyH5Ve6gq15O6WPXNP8vnBuG5sbV1dqHwBIrw3fo2cO/dipaNgS8Biqa0Vt\nRDE5IXmRYzKus8yarGMPAhf2qE82un18+lO0Tvzoj38en/3MpwEAg34XU/6uMAYB752tdgeeX3Ox\nqDcAmgfNYav53Fr5vqp5bwwHmEzpnWtjnXxQpx3AMBSbJonLxg+CAAE7PNliBp+d/shTznmbnJ3C\nMCwdQDgKyFe/9CW8/QqVwqmKGb7zbVLHuHrtOsIOrcdKwmVlwlh3+EtTIOTPlVQY9FYrfFvbGs5b\n29rWtra1rW1ta/sA9uFr58lqqUaTdRCMp5TLFpFCLxErhQtZ51mCjLXzhFDY59Pd1tYQWxsDvj5w\nRZ2kUvA77Fl7Aj7f/81X3sS9eySD8i9+8adchoHwFCR75cI25DIJi+ac/njPe3vQwXjEYsFJjnN7\npB929dolVxzujdffxd07fE0lELQoC+/8pWdx+doNatf2Jj7yUSq3n2U5Xn+LM38Oz1BIOl21N1qQ\nMUF+O5eewtdfoRDm/ulBU0p/LJBM6fT4e3/wj3F5a8Dt9eBxxlccDrC5sf3YtgHLEjtNDaTlfxZV\niemcTjpHZ3dxcEbE+qycYDairL3QaLz0NSYEFhme+fjHAACf/swLiH7n9wAA33mboK+iKCDqLBCr\nl4jd1kFNy2FlErFkwm0UIS9qHS0fXrBagT9tSpScDRJYDVlnWy5l5y2LC0MIR2ocj+a4y8Xshptd\nHB3eBgCcHd118iVJVrjsLV96EEwqnReZG2mDMMYuh6c3WjFK/l2dzaE5igU0NWUIXlz9ZNhpxy5q\nVOnS9Zk2ZumenoMKiiJfKpQr4fH1yvews0NjRymBnCMtWZrAcB9G7VYDiVqDnLMRx2fHDhYUEC5S\nuFikLjuo1NolCrwfUjkApIUGKwahLAoUOct4+MDxnJ7tznGCed7UFRo7wWqJmGuwKekj5npvvu8j\n4FPx7s4QmhMEBHwsFhS56m8O4TPM8OI3v+lIw1JalHxyzq3AbMYZUPMpPF4DZkmJyFsRJlmSqQI/\nR5bP0GFZHU8KlEwKLkwFV9lNGeiayJ5oVIKeT1cWPkOBtiqc/liH6/N12hFaPIdMqV3moxQCPJTg\n+SEER3PEbIqCYdMqV7hx/QoAGs95crZSEw3KJitUeejFFDWSyiA3HK3WBhstWmcrzJHepHu3vn0X\nbc783W1fwKLg97nRQ1XQNcYC85wg2bDSjsAsPEAxH0QY62r2qUA4uScrBARHDe+/foy9p6l9Tzzz\nWZwe81pz7vFtFFLBC+tIou/WAGOtK1yqhIRfR9KFwZijOrZM8cSTRPX45Mc/gY8//zwA4PmPfQzX\nr1KSULfbQsY1v2bTCRYL+m6WZih43FjbZL1JIZcyZySqWtJLaxeVp/m6espVJ1QwNbE8z+Er1l0M\nAMWIUewJF/2tqhJtLjyN0iCdN1qLy5D+Posp/8GXv4qbN28BAIpkjpTnlq80JrzvvPTSd/CJTxMa\nJIMW6hp1QilXTLWsKhdRDuMOlFg9Gxj4U9HOa1KCAdNwagSawQvpMq3SNHWK3KPxGV769h8DAHRp\nHA/qyuVdnOeqwZvbQ7S6jHUXhcvqUDBu0Q+CGB0O8XuwTmtIRf6SCDKgam4EmhIKqzhRP/vFH4fH\nwqILcxGaX9TRyU0c7lN4fDQ6c1WMP/P5H8E8oYG8u3cF5/ZoIg43tzFKaSI+eHCMoEPlHfb8AN+9\nRVDHO/ceYGtAGSGbl55Hb4ecqLO0gBR1VkoOpeh3HxzeRLtFYp6bW5sY9OnvrcEVtFu1I/reVvNl\nqPji0iLOXbNIprh/QKnho/EhNvq06ClsQnPRz2kywP27lGkSmQX8iBb9a088h+7XX6L767f4B40r\n0rcsEm2tdQ6N1sY5d7qqUPEE9cMIkjPilJRu0X+cSSGa8glVyQqVtHA0hfyWqt2rRsg6CCP0e+Tk\nRqHE6SFN7LPTfYzZMUiSzAkmAwJtLnCYSThYe2fYxzbfx1M+Wiwee/HKFZdVqZRynCghmpILq5g1\nDcepLAvnOHnKc1l7RVEtZT1qB8lZbVAwT6Xb7zlIY5EsMJ2SE1JVpVvs4ihusvMCH/MFO0h5hoh1\nwgLlQXEG1Gw2ccVohfQA7ltdGsdNWsX6caOpFqkQEjTvb51l2B/RRnIwzpGUDPXnC+ekx3HsCjgG\nQQtbWzTPpJSoqjrrUGAwoPHdbvdxdETzcvf8Lg5PCNqpdNUUatQGrRbr7intHNTT42OEA5rffhjD\nrljioBai9pREHLG237xCUVfsh3bVprXOEQUMzUIjqNcHIcBJezDWB1hfTxmgx7xEjw+1rcAH2CHM\n8twdNFudDgp2hisNx7eSVqDgSurTqUanS+N5cjZz2aCPtUqiqsV5swqtkJwibRQK5tPFfh+eoQNH\nqkfAIb3bKNOY+JyFZzrwWLvTiASiRnIqCR91uYMSPnPZjNXoD2meBaGCrUVvQ+m4hxYCFa8T+aLC\nk3vE86zm1/DqXZoHf+Gjjy9iHLdj57yqMHBcNPgBCh48WZ5jfEoH76vnz+Mv/Zt/HQDwwqc/haef\nJuh4e2fH7VCV1qjYQVosEndPoTwEEfWVFRLCFfet3DUWxtEgPCEgmWJQWuOculJXzrFcxZLJiZvf\nASr4/E6zaYaAC13GYYjAo2eryhIhp8v7XoApj+MoCjHnotLf+PrX8ZUvES3k+PgUYcyanFI6jnWa\nzHHnFq3BrW4Pn/gUvaN2HGPB3DMr4NY/YyqkNZdTBUv6qKvZGs5b29rWtra1rW1ta/sA9qFHokxV\nYDqh04OSHgZ98jp9P3Dse9/3kfHR6LVX38Drr9/kz0OAw5nd3gY6nNlycHKGnKGU0WSEVq1TlaeQ\nOUceSo3DGRGqC2HR3eHik14T9ZLGPBJ9Ws4clO/Dvzy/uwMHbdkhZiWFIR/uj2AEtffCpSdw4QZ5\n393NXYy5FkW7s4nhBsme3L1/hJtfehEAnYovnd/m5ykwTwmO9G2E+CKRend2XsC/fY4iS3duv4IF\nS2Uob4p2izzrnQ0PHYYKdrfO4dJ5qlXViS4iDFcj0DnIyNqlMvvKRUGMqVzo+JmrH8Ez10mM78Xv\nfBN3Dun9feObr+LghN5HFBi8epPkZ5KkwsWrVIAweJkiUkU5XyquFjuIZTQ+c5GOIBCOnG2scVGk\nqihcVDoMY2izWmjWD1ouKomycOKJVnkOglbKR5f1pYT0oEsaa1EZIe5Q3wdhjumYohPHozOMmair\nq6aWlYV1+nEtJV3yxCCO0OaiqqHfQbdL739v+4qLzj5K7BSrSgMCACaThQvHCzRFNY0xrr1lUTgI\nLQh8N1fKsnQRoQ3O4gGALMuQ8rtPkwIdjpiR9AoTcKWC5RNyJ4rR7VIEdHtrG32GL09O7qHN0iWm\n1E67kP57RV05AHoxR1WHHKSHKUec7pwucIflH0aZQMr1izwB9Dj6F8dN9Gxra9MRzquqchHQPMtw\n8TxlYY1GE2wMOSoVx0DJkhJ+iJSziouiguBI1N7uOSy4KVmaYnbGc3p4DkG8uVL7LK97RhckiQLK\nHsxY883zFRKGGBUMCl7HenmBVpejip5FxsU0BSziiOv3QKIbMVzO63GeJC4CmeU5ZA2bxwZlrW9n\nY5dkARu5pJDDwwMMNri+3d4W8nS8UhuN9pyeXaBiRJYiUYsiB0p6t0mVotBULy8KI5wc05p7vZTQ\nnKH2x2cziDk9rx8vHETvywjwGPJXBh5rruVFhWFd7HijhSLhCKiUMA5OMigLmjfdwTVsblIm7ot/\ndIrCXy2yDwBeEIGDkhCVdmPtwcERfunv/c8AgJs3b+Iznyai+H/w7/08PvkcZdjFrbar15TnOUqO\nmFWVdpElqQQUR1W7UdiM3zxDUdbwWe5I3UZrt5YopWDLWqtVu3mvK+2yZlexaZa4dvnSoJhRtDDu\nxKg4C1kXCXy/zsqO3Jrkh76Ldr/y2qv4yle+AgB46623AM5Ib/uRg82FFK6W1GJuHaE9XSQ45ezF\nzeHQ1dzTZhljEiiYHqIXcwS836xqH7oTNZ9N8Q9//f8BAEynC5zfoxD5+Qt7GHLK5sbmJirGE269\ne88VKxxPZjh3gRYsYX0cH1Fn3HrnDTxxnTbeyxc2EDH21g17SLnC68PbdzFiCGE6K+CHnO2Tp5AM\nT3nCNvpTS5mDwtpmQ13BmXrn1hgR8yda7RYOpzRAXvz2KfKEvj8YDtDisPHJaYIFcw/uH7yDXp82\nYG0UQn6BcbsFcIHC+wcZUl6gN3db6PRoMTy3vYHzG7QBnN87j5vHxMtphxKbXbp+o5Pi8qDGnwMI\nRZuW9CKn6RXhvSf/lBfowJPw68wtWKdFJVWIc0Pa8G9cvoLf/SPicv3KP3wR794m/Ho8eohOq+ZZ\n9LH/gNKdr+xdwsO7BAXW8K61TZFHrUts71zn/hGwps5WKWCZ+2SMRMUlHUQBV8W2LCuEvEk/zpSn\nXEkMa62Db6SQkDzJL165hoB5L6PjEywYtshLDZ/f2+6FPcwW5ESleYk5h4m1BTxe+KQFLI+72PfQ\nCekdDnt72DvH0O5gB60WLQpR1IEQTeVYxxEzq6fGUz8ZxyVTnucyGouqBOu3kiBoXUKh0i6rTgDo\nMjTT7/VciD9LF8i5MKYQwqUca20QBFzRfrHA2FUg9x2sE3ohKn6H+w/vu0qgoadcxeEg8KG81QWI\nR+M5bMDZnlWJb9ylUgZfv3OMgxnDMJVxVbpbrbZL5/c8heGAHMRev+8y8oh7RrZYjPE6a+3FcQc9\n1kY82j8EeLPZ3tjE4SH9blomyFlncHO3DY8PguP5AgUv9IkaA3q1LNJ6/MMAZV63x0fBm16n08J4\nSmuglAJcpxJVDoxrMfSoDcvjOM8WiJkrJaSHkOeAx+tems3cvJSihaqsx0MAw45OGLUQsA5g6PdR\nI+jj6RhnU1rbntjdQavdON/vZbmeomQoR6kBRlxVu0IOxVCdNhVkXKtNeDhiR3urLLDHzzWePEAn\no0Nm2w/hMxSaFqlzJGSgXWax7/egIuZ2CeHgLQy70AyXirKikioALj11A4cn1Hff/u4hPv6ZrZXa\nBwDGCpdlJhRw+yaVrfmbf+tv4ytfpYP0X/jJP4+/8Td+HgBw5eJF5CysPZ3OHsnJrR0ka41zcrS2\nkKbmCjd7mJDS8YA9CXi2uUf9XaMNDGpOooGstUCXuJOrmPYCCFb6fnjrHbz8h38IAHjm2afx5MfI\nIfRE5MopLJICbS74Oh5PcOcOcWRffuUVx5eM4hiC12a7ROlQSiHs0HoZxzFyVg3RlcbN75JmazI+\nwydZcLkywu21RlcoeF4VVYny/dXaXMN5a1vb2ta2trWtbW0fxD70SFSRpnhwlyIkp6dT3HrnNgBK\nqKtJq1EUIeKS7VJ6aMUcXo86eHCXrl90J9jbJU9/2I0xOaJMrzfGDxCxMnqnNcSFXSKcB7eFqzeV\nTgv0uJbG/8veezzJlqX3Yb9jrk1flVX16vn2dqZnMB4YAiNgACEEUYREgARCWFAKkaGN/gYttNFK\n/AOIkCK4oCJkQqJAOAEBEYyB4aC7p73vfr58Vfprj9HifPdkvhHYL19HNDfKbzGT8yYzK++95557\nzvdzQikU1AKsq2KZwSfYSl6e9jECwKM7GT9562PvaZEkCe6SMuDeyQRd2n1VAPq08o3jFJV2uyvG\ncr/r7nd7HgaQDF61UIchSlruvvvZR5Ad8mqJLBh1ic4nI3xy15HpLnW2sdNybeY8q1C13fvTMIfS\nbpdaVWMYOj+9weebxL3xutsZ/fwv/iqixjRxNvHQni5rPHPNQXi9dgsP7rtdeCeV2Bs2xNISWlEr\nvihxiyAvJt7AgsiiFXXbsKIa0UZ5X6Fr15/EnFSAFxcX3uvG/f9LjxNJbezZbIpSrQcFaaMhAurS\ngXnydhinGO6687O7fxnzyYj+DkPZqFwYsL3nxtdwb98rsE7OL7Cga1jpemnkt2KRGYYtPP3UVwAA\nN28+h1aH/GuY9AnuYBK8aRVx4cmdjPHH2hkmSQhVNxmVy88yMN+y51jCl7XS0LyB/DR2CMbjjKMk\nCG8+m/muXafT91EpQgh/T4zPz3y8RKctveEdExLHJ444e//OIWrybQlC7jPSpBRIW+tPU63+EOe0\nk/zs5BT/9mPXvb6baZ+blYYCXcrKCqIWBO3M2+0uOp0mhiaEpW16EAQ4aQQCiwwtguekrFES7JXl\nGTR1+XaHQx9RpbVGTRd7Oplh96qbw/JSo8ooWoPNUVbr4bKtlOC0QPgcyzTugnGC55j1499qCyhS\nlekAirrQVgzQHboOTT6b+PxNHkgwSxl8NSnBeIKKoNWt9pZXxxodIggaaDtCRb9fyhYiggdbaYrD\nE3e/nF/McHlvPbhLhgzMND6ADMmWG1Och1Ag1aOQgCBDTqExJfXqea2Rztwcd5rOPNrBggQNsi+4\nRC9y16E0CzSc/kAYKEsmv0WJMHDXeawrGDINFar2Br43n3kB77zvxsXxyQSCrT9OL8YTr3q7c+cO\n/uAP/gAAsDPcxn//3/23AICXX37eoyx37z1wIgAAzBpvULmaOWXt0jdOQ/sO1WqXaVWc03wazTes\nKK+tn0+XPnlOyPIYyjULn9l3cniEt153dI1PPvoQ3yfl3Xe/93dwTmNkNM6wveWuyxs/eQ2fUY5l\nEATY2yaR1c4lUDMSFxcjnEzcs7auax9Vw8G8KpsxjjMyOR5uDVBT57vd6aNqYFCjljQH6cg8j1Nf\n+iIKpl4CY0xiVU6k6Qafz3LMs8aIjUFwt8AIggABSWenWuMK3YRXL19aBv6yGnOa0LNigXfedSZb\nH33IEdNkki0qfO97jqF/ut8Hp36zsdY7oTK2HICMYeU8PnoRVWqBjB6otx+c4D1a+FVgEMzBVruz\nXeQkt7525RoY4fBxEkLSjaKrHMLztWoExDMIOXDjmpv0OBcUggoc3r+NFh1jEsX44d9xUs5B1AIq\n9zDIC4V7p25RI/YKCN7kL5XgYr0wyVi48/LE8y9iRqHI5WziFz+9yOLaZTfIO9s9/Pbf+zYA4JV7\nN5Bbtyj43d/9Z3jnHcrGYzFGUwclvvfxLWyTXUXdQGirDtUWWCzcePjVX/s1f9f/q9/7PczoBhJC\nLHF7vRxviom1lRZaa0834jJETKqPwXAfjOC8LMuQkUoky0tktOAF5wgD10oWPMbVGy8AcEaGgq7z\n2dmR57AYrVHTpDYc7uPSFWdx0entYmlsB39jSyE9F4UxicZdVsrAPzDXKaOtX5wqpfxiKQwjRAQd\nG1gP+XEG/wBttRJv1GqtxXzuzsNstgCjmTJOIn97p60EGbllX1yce2sIKSXiaAnPNdYj8+l86Wpe\nVogJ9tLK+PzMderW8QU+OHbzwVu3z/BgTA/dQKLVcvdyt9P2waiSRxAE/0Y8Qhq690gmMKcsvPF4\n7B2l+90tb5EiuYCkndf27g5AHKH9rT72d9zDYG9vF0d0/00ri5qUUTIIPIWhrjVstl56QEx/rwID\n4+48am0QkXt5yAFNyqfJvICgkN463MHw8jMAgEJLKFqI29Y2KoKt2FYf3Ubxd+A2ZPPjeygy9/uD\nnRAR8U/rkqNYEHeuHfiwbB7E+Op33Kbgzc/OkZGthGAhpFlvrE7nUwRoHoIV4siNx9JUCGijE4TG\nP9yNEZ4390k2wm3trtVHM4bufTcvXevEKBvjXx4iIYm9MRyFpQ1tBA/JitqiLt38ltVHSBr1alnh\npa+7DSoL9/H6m85k2aoCj5O4Op5M/Zw1ny/wwx/+svudV695WHuelVjkS8WqaR5K1nqTaMZXrAmW\ngmkH3Tc8Ua199p97xjWpD3/7fbX6/FtdXAE/NTc/oriyMARlP//Uc/jkppvn7t6/g9//P38fACBs\nhMtXnS3D26+/4V3wT44PMZ8tLQ6aiUXVNYpZRn+AYU6L53a7jZS4eA6yJOWdXZrPRnGECzL0LSqN\nlPibSisYMjgNIolAPN6yaAPnbWpTm9rUpja1qU19gfr3AOctYBSpOEzl1S+MwSuNViyH3G60Ibtp\nA03/T16UuHfkILz9vT0wam32um30+m5F3+9EWFy4HdGnnxxgNFvQdzK88ZqDpO7f+gRXn3Ur3+Br\nTyOh9nSr6/woAKfqagz7ZPhoMuRn9489jLGYV3jr7Q8AAOeTM2+fH8UJerTyvXr5CkKKOgmTFFt9\nBwX121vo9VxHo9/vo6bzFhhgnwh3rXYbQePnAYWQdtFJmiKl79SmwrR2u6tSc+jardznRYmtNqWU\nGw25Zmv27//OP6LzInBGpOlKFzDKfe/1azvobJE3igiws+d2HN+4/ApmC3cMP/z5X8C77zrCuWAM\nXTrOViv26pKG5G+XHWr3t0rX8fnmN7+OK1edwd6d27cxGze5WGPf5WEMXlFmjVn6rzyinG0ZwRCd\nAQZb5OEjAhwfu3GXtFPfPciLGjmZCkZpiKBpWJuntQAAIABJREFUH3N4mHSwcwlPGEegHG7v+J2t\nVhqSSNeXLj+JFvmcGRi/O5QyQEgdsCCIfOvfYgk7cyHXjrUBgCwrG19ahGG4hPCEhSQTtqpWSxNc\nzn1H7vLlPeyQwjWvSihN6tI0wmXy1uFJC5Ah/Xvsz5s2Ci2CQDqdDlLqCBV5geOTYzqu5QUPggAl\nqXcqrjwsuE79ybt3cDRznz2ZlpDUdY6SBH2CdoIggCZYU3DhTTWTOPFk8qzMUBAUW+Q5Op22P64J\nQbpRFHpln+EMihqT7VaCRd7sqI+QEeycdoY+PyyE9BErSmkIsd44lQ0WKiSUdq/no1PsDrt0PCm6\n5G81vDHE9o6DohelRa7c314UBRqucZCkIH4zPn0wxWDgvufJZ74FAOCygwnBgFqwpUrNWoTU/QLT\nnjoRxDF2r7m/ubc7xOkxRZVgfWPYlPfQapHXXBWgmrlugwkNFHNzeqXHCMN2cypQEkXDqAoFGb6e\njhRu/4V7/5VnQsQddz/VhcbRqesg9Xp7aB6Do+kISlGWY9hBSV2ROJsh6jiaSI0IWe3m2b957Q7u\nfOwI4aHOIOz6fmYA/Fi4du2aJ0jXtfKws5DxUtix2lFnq9Oj9f/DwvqukVwRoJgVfz9tjYc13Xub\nbt7yNeD9q/8/Non2MeTATFuv8hv0t/DSy85g+f79B1A0p7//9vuoCvedF6dnXkDDlEVC3fEwCDAj\nZV85z3FK3lmtbhularykAvBodZ4gPzxVo6Yu5UcffYSQnp2zz+7g+hM3AQD9wRZCyvBUSoObx7yO\nj/XuL1CffHgXKnNtObUYQcbuJmViJeKXMRjbqD6Yb/3rWoM1LVLGcHrqFgaLeYmIfvruTh/tFuG3\nqo1uy02UnUGJ7sCNhFY7QYs4TuX4HA9+8mMAwHuTT9G75OwFnnn+K5BDuoH0ArYxIlxDeXx8PkMY\nupYhFwK7Q/ed09mFh+1C4TL8AOD9999G1cxcIgAXpA4SMRKCOnqDPvqk/OlEbe8uHQaBfwiFofTt\ndSmkvxGtAKomY84Adeakxd94Zht/94cO8ot4AmEaF+zPr51rzlLh4P33MCd8uSxy7JDqb7BzCSBj\nSMs5+tecmq4btPDZ+04ZETDrOQNVnnsH6O1uD3cP3MNWkcEit3p5LBYI6WbiTCGk1e1v/dY/wBkF\nwf7VX/4IxltVLB/IFnbFhPDzKwgTdDruYg8G+56vN7o4xGTieDXzhYShcbeYzryyLGmFXrVnrIZp\nlILWIiZTTXQHsHpppCnIsqDf30MgG8g4WMn9iyHpuIUMfDvbgrlwVLhg3yb7ap3SCtB0H0RR5B2T\nC62xIBWVMBK6kecJhn7X3a/tdg+WFl2zyQQVQeidVoBrWxR+W2u0CMaq8wlygui73RTdtvueNOki\nJLXdyegYxuR0vNJnRXLB/KJUa43ZbL1rCAAfTI2XTKeDyJ/nVqvtVXhaa1jecHgkwmj57004cqu1\nVO21Wi3EDZ8xkcgLUrZVGSyZeS6yColcqkKb75EywO6uW5C3tveRkQovtEuLCaWUhxzWLc65X/Rr\nXaOR4Sm0kbTdImb/5kvglM9XTieAcb+p04sg6F6rqhJT4nsJHuF8nNHxOJi1E3Vw9aXvAwBMfgRe\nubmkKicQUZP/mMEHDAQcVeUWLlevXca777psz6wqINa0AIhD6X8fExVU0AR011ABLd6DHU93qHQO\n1O6anGeFZwtFaQvHH7lxffjhAYYvuvdvJzcR04YgU+dg9KBPJVAbkuTHbfR7dP1lC7fJ1b4bBDgd\nu/H11t1XoYkTF8ah57auU2EYriR5LBc8jp+3TCRo6uHFi/U5ss4Aeckl9bwmo8BIRWh17Xml2lpv\nZAyDJb3G+v+ABVCzFWXqyu94HDjPGo0mWGKR13j5a85Z/d3338PFW85E++j4CDX9nrwovKK3qnJv\ntWKsQkjq+kSHaFMINpPLjFtrFDTZxoRx5O0RYI3nQY0uzjGmDVCRl3jrTZe1d/XaDb+garU7fkO+\nbm3gvE1talOb2tSmNrWpL1Bfeifq3bc/xKLJD5ucIKAOTKvTXyoDLPOdB+ja78attW6XBbhlJ3Wl\n8kzBSrdSPj45wyRya8HzszHa1KVh1iKg92sITEhtIhYz7A8cRPfU1ZtYUNfg/qdH2KvIxKvDoSlh\nO12jE8Vk5DtLoeC4su+Uap9+8q6PYkmDAGmLILw08uaG4BKzudtdLbLSk8+r8wKTmdtFSR4hp47K\ndDL10SPgHILgSCEEuG/TBtAUfaLKKV686Qil/+CH/w3i0EGHTKu128+TB7cBAOODj8CofcrtHFuk\nPBSoXZsDAJJt79MDrfHxh47on7QUdijD7/hsAk0774vpDDefdufrrTffp+NaRs0Ya/HUMy7ioJWk\nUKTgGgy6HiplzK68n/ldF1CuHVMQxyliUl1BMGSF202PJqeYz137uK5rKOV2/MVU+xZ5KLmHwIpi\n4cd7XeQQaKJP0qVRHefOSBZAHLcgqVsig9jvxMIw9IRnd71pv8MZWNOyD6PH6kQpXfuMyvFoBEFd\nMoul/1cccMSUmzaZL7z4o9cdYjZz4/T8bIKcdnf9Th8R7Xh7add7dB2enixVb63W0nRv5feen5+g\nJNPHIBLQTWamKn12YgN5rFth0gWnHXUYSERNjIkMliojzhBRxzeNUoQrKuHGLDQMQy8iCILAx2kc\nH59hkbnOzaA/wBOUDXfr3gEuDl3Hcr/fQURdrP39SxheImVw0sdr7znFUdwZYHvbTS5ZlnnIYd2y\n1qIomviqFJzy5bqDmwC9PjiZwGqCv+oCSctdgySJsJg2UKLyzYgwDCFpF974es0Y8OHHztRyf7eN\nm3uuq8bTGEVG83o5gbSNL0+JkxNnqlvkpc8km0nlDTQfVbkqUdO4MDrzuXztcAfaujGb1zPUNJYD\ntFHQHHqeFwBd24hbMOqy3f7Lc6S7DpKLOzkiyiJV47GHGcuxxfm/JSFQbWEoSqq73UF55mDnQmm8\ntO/G5Bw9jC/c3CClARfrdzCcOnYJmzdlLfycZe0yt3Q14oljyfU21kA38JNZRiQxuzTJNHUN1SjS\ntVrCfysI8kM9NMZgGryXMf/7HgfKAwDGzZJ6IDmOjx1y8PzLL+KTWy7ia3tvCXF3+i1MJu56WV6j\nIjdSpuG7Z51egqef+wZ9KffHXpYlTgmZKMsMkpABGA1GvcmqrHH3trv/Ll++7M/Pg7ufoaLx9vwL\nL3mF7rr1pS+iyjr3wbgybflJ3OpyicAyBks3oTXCyzc5l6hoEWWshNGkqhMSjAzinFKBYCAwLKw7\nGUnIIGhoTKYzHBy6k6cW5yieca7dl+9dICPJ/GT8Pvb33KT2zFdeRPuSg7DWsU8TqP2aSMCi33MX\n4elnn8e9B26wzC6mXvbMQoU+OV/3OgHqDhlLmo5fi8AKNGFPWkj/wFZmz/9dy7U3TJSQEGSuxiyH\novN2aaeH/+q3fhMA8DOvPA/bLEo1AxoX7EfU8YfOLZbpCm2SFeuwRE3XYHp2G50dd75E/4qXxx7c\n+Qhvv+Wg09FihLTtFrjVgyN/UzzzXBdf+5Y7pg/fdeeqLJeu49dvPIFf+pUfuGO3J6ipbT+blDgl\nQ0OrquW5ZdxDey4fbq1DRK0rZHnj+A7/HVpXKIjLlC8WqAtaLM20hzBYYLBND8p2t+fb6EZVnp8F\nxj2/wXJ4uEoI4WGjKG4hDBs598PO5M3ihAuxhC5FiYfIY4+oKJK+Ra6U8JOjkCFCohPsDRNw+h9a\n1dgm88kwDHE+dg+M7TDAzetOLToYxNiVlFW21cYF8cTmAMqUeEStDiyNzSCUmC0cNHJyegxNHCQh\nJSJSgRrFvVLTWosoWp8TpRcLWJqUK2XA2TJIujmjUkoEzeKMMc/Ji9kyAw6MI6FNTwzgiPiY+WIC\nQ8Z8J6fHyAiy/PW/95/gf/kX/8K9p6yQ+Ywu5h33a66R0bF/cusuduihzjlHtSac1ygY5/M5LAXh\nsrgDHboNyvmkRmzdYmWSX6AZfmEoEAVuXlKsRpMj22qHqIkzGQZLyoEmRawRAQribn18J8P5yC3K\ntiPpzSutSZA2e2BwLOZuPMymmb/Pa6vgXVwfUTKQiGlTErBtb2UASG8wqsISi7k79wFPUdHmTjEO\nS69FDbTIgX1yxyD/kKgSLyTID93xZZ+eA5RyMftshPldd50DXXk37weffoIRcXLSvRu4Ebj3HPVu\n4M2Ju7aS548Vlm2MeWhR4m0H7HLDxDn396j7b/d+pSsf9K2Uejhbsvkeo6Do4ldKefPSsq68Es2a\n5U3BwJa5oFwATRbiSuCwtdZzBtep6egEoLmwrkrcvefMM5MwwPe+72glYZwgolw/DeD01M0x5Wzi\nLX6qqvSvAY1Wu7H5CL2SzlgL3oz7yQyNjwqzNZpHnrUG56dukRyHDGVJ51ADx0dk5P3JJ/jq151L\n/PdevrbWcW7gvE1talOb2tSmNrWpL1BfeidqPD2HbVj2nSGEXrZ9lytxBsuaaAHh1XxhFEP71TcD\n5xTRYgJvPGaM9Lsdoy3oLYhhERE00m3FuP6C65RIeRlGOjLowdEFurHbhVzZ62Gn51q8s4nCJHY7\nwxfWOMZ8MfPqnXwxQ03Gd+1WAsYaSCbClHZxWTaDmbtj1O0FUtqpMhEg9OaJCobIlYIH3myRSwHf\nIxXwERohk5B0OVVd4/jM7bSGgyfw479xykTBSuxuu95av9XBaO5ap89d/vwVd5lTOj0ChNSyTsMY\nOW1KyvMj2MR1LAZM4uzImau+/dpfY2/ozrtmAQJxx39n08HWE4YPXnP/bmjXIoMAL331awCA3/jP\nfgM3n3E7yHnxPsrS7eTT+Bn843/yXwIA/qd/9rv44EOnttEwK4qWhyxOPrdUVSCbO9K8UTkkqcwk\nD9HtOaEAs2c4HbljK+clTAMDFAEq6lbBdJbNIWZgiOxoLSCoc8ctA2t8SXiAiIjQoVySTc0KDCkE\n9zFEzHLfhzdqmdq+Tllr3S4TQBBwP45kwBCE7oIMhjECimrodnZw9Yq7fmFg0SeT18FwiOt75Bml\nxwi1O2/n52OcTNzvTlttXGsP6A8bgI43DgOcTEicUGZoU7enrEqYJiKnKqGbYDHLYYPHibaxCOgY\nwyDw502CeZVfGIbe2DXXpRdqyDiCoC4cZxFaXXdOTs6PvSHjzas3MDp3cNXh6TH+8Pf/CABQ1TWe\nedYJKj79+BZAXZqq1lgQLFjZOUK4Tk85PsctH4Wz/jTckF45Ayq6h+JkiFlOENN0jD5BrWdnZwCN\nrXavCwY3VtJQoCjddSrVklusigUODm6780K5ce1uGyUpqRaV8/QDgHt1jZDGz97+Djpddx1tzYER\ndT1yhRaRgI0tINdUklpWQDXiCR5Ccvcdi2yOmuDJJOiAGhjIFxmYbnI0sYSxDLzSDVri6A33u7on\nc3DqqNjTGFmT6bbIERL94kBriMJdK1toT37uBAVSuHnzUv0BXh3RfXz9qjfnXKeKovIw4iq0Z631\nkVDaaN+p5YJ7wRWDhmmMIuvKRzAxa1a86Axqel3WlTcdLusa2neilt0nxrjP9pSB8OrN2Wzm6RHd\nbvexIL1/83//K1jqhmV55ikAqiq9yXVR1T6GptJLZIWvoAsW1neisizD2eFtAEAkQsTUxQ/DEJyo\nLRxAtnB/a3p+iD4paNtpjISe9w9uZz7zszcYott3KFQSCPzVX/w5AOC/+M1fXes4v/RFlKotfNKi\nyv0Ft6Ze4fBIb3RouYIll+RaK0jCtyttYeiCK2tgvfJAQJF0t1ACecNZqYE6dH+gF9cIqT3cibbQ\nzIgxl+g0TtBVieOymeh7YGp947SiKLx6bme4i5MDtyi48/H7iBqTxDjAZORuvpQFOD5yk8GJnXll\nV6eTQvgHxlLaHUQtxJ4rEyCgwcIC6blVmjHfTo7jGBlJxF9/5yP8bx86k8uz83P82g9/4N5zJcTt\nW+53Pvf1b3/u8S1KgkQC6flqkkUAKVlGZYH8xC0u6vYDfPrBWwAAYULcuOL4WGmrj6OX3QJoMhsh\noyTWQgc4+NRNYoauy80nn8A//q//iTsnLYXz0WvueHkFxshxHQrPvuBM7377d/5z/NP/4Z8CAKaz\n2YoJn11bTaK18ZLzPM8gaFwwBB6eDILUK+ms5D5rr522PT9L6covnK3lfhGntfK8F60VqtBN6L3e\nNiLSxltYrwplYJ5TxBA4YgCc0qZqJsRi4UNg1yvmf4MxxrtMMxEgpYVTUgdIO+644q0hdi85yGkx\nm2FI0F6/v40JwUdBtYukdFy246nChNRqvd1tdEgCX1ntlYadOMVs6ia4XneIc1qQzOfZQzYVwrfj\nmbcjWKeCMPT3Tbvd9sfLwBCQMakU0puIRnHs8/6CIPDnHJYhp0zAyWiEgmC7CWqfi3d+cY6IpNG/\n9y//L1y/7vhRrVYXTz3lxqZRDBnBTp1BG9/71s+577n4azw4dcf+OGqghuNVKoEkdYvUtLOD8cSN\np7wsEJAC09QVCgpr1RbQNE/qRCLP3bU/Hs28U/ygE/kxnTemoFWBgK7j4mzk56rtwQAxXdN7RxeY\n3nEwybNPPIny0HFTjNXeKHU2Kx5yyv68KgsFSeNRcwNDqQyWAyHx9aSNUZO7eq20v0eFXJqYcnBU\n5HwurVNQAsCrH3yCPbIV2Q5D5DTWTi1H2HebzPOsxlxTAHVxhhKkvg4Dn3sa6wtskbq03b7mIfd1\najabr2y2HIUBcJuJMGpUuUsT4SiK/Li2xnjTVqOVz4I1qvKbj7rWHo5URjsuFABlDLRtOE58RSGo\nERG3WFU1RsRfquvaw9FSBn6Duk7de/cNPxfnVYkxqfSjQKJDG5f7Dw6gaFO4e+mSC/IGUM4nfoOV\nZZnn1hVFgQlxl+MwRkCL5Ha7DZlE9LeWC0XOGUrR5MgGGHTc958eH+L2Hcf1e/HFr+LGi65dcnBw\ngpOD+2sfI7CB8za1qU1talOb2tSmvlB96Z2oNEpgaZU9n47BQcaKTHuiJ7MhDO38Dee+pWcUQ0Lv\nT7lERTCfMCEkJ0WTlBBEsISVyFlDCLZYlBQ7Mbc4MU1C/BgJqXGCKPJ+MUCN7afd7uSZsItwzVR1\nACiKuY+CmM8W6KXu97/wzJO4f+RW9GdVgbjXEDsNLP2G+XwBRd4sySwDJ3JtGDJESWM2VqNFO9BW\nHPqWZJAkfodvGMe8cp2u559/Cd/adTDMa2+9h3ntfs+Dk3PsDJ26pioV7t8/WOv45oU7F1uDHWjj\n/obkDIKuQbT1BI5O3Xe998f/IxgRVXe3nvbdqk6a4OYNt8t798MIhnZ5hTG+1dwQDC9dvu4zwm7f\n/RuUtYN/gpijRYR8VPdgLtznrj9xGc887aCUn/zkjWWkBR5DUWK5b1vX1QK6USHyAJb8rYzSHl62\nAQeCJnqIo24MUazxZHKtNRR50LjUdjJyLOYw1LmaLy78jlTK2Hc0pQy9ak9x4SE8axnqRpFSzKCq\n9SPHjbVeWCClQLvTdF00mrbwdQg8F1NG3uUnEe+Sb8ugQDl3x/vMpXvI6DerYBdD6bpS1/I5cuGu\n8ekiwujCjf1UCSTG7SSz42O8/74zXT04PPRqHM6XxHvYZe6lUyqtv/vlnHuifqfTwYyiIxyUSfOK\n0X5X3+12fSeq1Wr5bokM4Hf7+XSM+dhFDB18co4FxdmAcR8rZAwwok5zq9XFeOy6TKFIwIlUf2l4\nAz/zze8BAO7fneL4wqXaB2G4oih9RJGnHI8GuHTzeQDA9GIOISh3MBCYkDoUSmE2d+d9kk2gKnfv\ntPe2oUlNfHF+gTF5INlL2xgMHPRRkEBA1XMfLSSFAaP5OBBuDgeAVhKgUJRJ1oqxmLpzfnD8wBuN\nMmYRx+spSSMMoaj7rVWFiLt5s6gnEJxI8LwDBnc8xtQ+AodxBk5dCMEtqgYVrkvMp5TXyTSm9CyZ\nlTnmdD15p4c2GRab6QPk5H1XdZ5EPXa+WboqcTgm5e5ijP0n3fc88bU9aLN+T+L49HQFute4OKcM\nOK3QJVPYxr8McNB0M5MppXyGoaoqr0bVdenHUUMeB9z04iFOa/38yLjwULIQHFW19A1s5s0kSbyR\ntFLqofc8qnq69F1OaQzKpvvLNa71XYd7K7rm45UGwy72qfOt8y2/Dqjr2p+r8XiMESlLORPoUm5u\nmiRerXlweoqA8nd3doZokZdiHEjMR25OGp8e4oCUelcv7eHdn7wKAChKjW7r0VFvq/WlL6Je/PYP\nYUhe+eDuB7jznuPnLCZHDU0CAsq3xDhn3p2ZMQZND9u03fHiDqbgJdMhZ5AEMSVBjJhRsGggYFnj\nyMwhSPUk4wiscSYfDBAm7oR1kgi97UsAgKoKYNRj8DCQ+4FZ5QuU5MA6vTjCk0/eBACcnLztTeBs\nKLxLdf/SLs6PnSLBFrV/uFbMel4ClwwLekj3rYGiE5FwIKXFmIhaODl5AAA4e/0dvPiKcxw2MsGN\nZ12r8srV65iTi/v0Yow71M58VLXa7rcGIkBRNTlpQHtwif72EBOC50z1sVdFzhYLRGmTUQUIehh+\n9eXn8Nqb7rceHU9QVU0+m5sUk1YHM3oQhCFQEgyR5zkkLVwSHgChm3jSXhsvfsUtGl9/7S3PKVh9\noD6qwjCGpcytrK4wowm3qmpY4rdwHiBoFG3tAJwexCIOEdD4qooamr5H6xqcPhuIEJoWi4tsjLom\nnsli4nAKAGGYQNJDUvDAu/cCS3kzYxyGJs2yWECp9U0aBXdqGMA5+fZ6ZCAZcQreBO7NR+g/IN5b\nqcFL93p4TSCjifvoeITr+27BsLUzw/H9jwAAxZShvUW2HNKgT7zC4/cKpJW7brePTnH7wE1klkm/\naDTGevNJd97dnCEDCW3WhyyTJHloEdU8VPI89xNxEEiEYsmPalIC0jTFhCTxVtde9lznC59pudXv\nIaLFwCzLkBHkpw33PAyllF88BC2GPoVKt5MEjJR93/zGy/jjP3fcC2Pt0jDxERX13ENmeP05yNA9\nKM6OP8CCoJLxZAxBVgKRYH5Mp2kfluYQowwyWiRNZ1O/eM3zzENDCZ3DohpB0gK7LBbY33f3fBxy\nr7yKA+E5LnmRIaLcw952H7OFO5+z2RyT6XitYyzVDCHROGpVoNTNhgY+iy/X50gbUlQtkNFiWdXl\nUgFuAIXGBoF7GkdeZJjTb6mqhb+Pn7t6029QzhYLKOJiybQHxZyBaW4nOGVka/BShKeecgkK/V4L\nVb0+LHt4crRCNWB+vFtYTCjAnM2X1j9VVXvlWhgn6PUah3oG06gRGbxSHUwuF1RKLflXjKNouEnG\nYGfHqYqNMd4yQ0r5EE+vWDEsZuvKnQH0tEJBZqS2rtBurmNR45e/4ygkN5+8iR+/6hTcR6fH+PbL\nbmNgiwIzuhejKPJqXa0NPrxLvNTK4OYlpxKez+coaexm2QwdyvncHnTRTugZpGvkMzevJyHDz//s\nNwEAw50h/uY19xteePGr2O483iJqA+dtalOb2tSmNrWpTX2B+tI7UYNrL0NTG6+zewWDrmtVvvHq\nn2M2dS1vIUJE1D2QgiMghYyUISwReTv9LQRkDiiDCN22Y9OnrRQtIqClaRsRZX1FSQxGeWBhECIU\nFB0SLjN2RBAhoN2+ZBwNu90CUFh/VzGaHKLbcTCGZRLnU+oyzOYImpZtOcecVtZBHAMUC2E7PYS0\nE+T9jve3sIZ5y3wdROC01dMhg2kURGEERqnmiFrYobiVT+4e4c/+0rUnuTV45QX379ev38DhkSPF\nMm3RbnXWOr4bV90ubDQ9hwWdu9YA29fdruFkkmE+c92F3b3rKIgIOs8LsObad3ewt+uIt3md4Tvf\ndjvqP/2zv8bZiXv/hNSCV69fg6BuW6+9h+HQ7fba8Q4Y7SyjiKHWrutxMXsfSZc6MsJzsMG5QERe\nRY8qDeUjdzIe+l3ZeDrGeO66d4IHSKjFH4URYurqyCjyBphChjAl86+b38ss8zmQggUoCzIqzCQC\n2cTaMA8LA9IT1PlyaHrCNQBUdY5qXRgIQLcVQpBAoa4CgOCHIrcIIvc776JGRpCJvJjAjCje5XbL\nmwCWhcJ3nnW7yl/sMfz4Vbe7e/ckwSR3x7XICiwWZPCnOLaaxPRqjtHI3R9xGiOkTlQQcO+1Vte5\n72ZoMISPETWxu7u3snNmviuVZZn/dynbSAiiCMPQ77qVUigKIvkzi/mMOidGIaQO6DzPcIkgh6/u\n7eHswnVDLy6mHgp87/33sEuxIs8++QRSul9Ho1N8/PF7AIB+v40W5VgeHZ2jla63++3vu9zPEhE+\nec8pUkNbY0qxPUdHBz4fU8aB7yJpVaFNCqSyKHzUS57lSGinrpVGRuKKiJRmvW4bNd3DgQD2dtwO\nP40TLJqunbJg1EG/ffszr/iSXHgT3H6/i153vXuxrBaoVBNF00ZEc19ZVrA0SBbFxHd2bZZCl41p\nm/F5kkYmYCKm7wkhKQNwsTjE7MIR4ZXW6Gy5uTuIEozO3Fhe6Nh79tn5p7DcfTa7vIvt77v5MB5q\nWEJBVC5QhesrZU/Pzjzx2xjjx6CU0vs7WcCLIbTWXm0HrbxvFbMGKXVGO63Uj/HZYg7rCfaAIk+k\nk6Mj7/3UHfT9/cE59xCetdZ3J1dhdsG5R4nWqV7I8TSNVxZHePNjN16vXr+CK0N3f2y1YoQ0drba\nKXZJIZ8O2si6bn4dDof+3irLEscX7hrt7F7Gd19xKu6iKHCPcjhHswk0+U4G3KAi4+Sd7S288tIP\nAACqyr3opyw1Pv7IZSAW2RxQ60OWwL+HRZTNF+CNdJ1LXH3GuY0OrzyJumrY+iGkaMJWg6UqTUpI\nuoGiOPHhpkIEiIgLxDiDpInYMqDRZnImvCSUM7bMGsIyW81YQDU5fXwpHYfR4I8h5Rxlh7ChO5ZW\n2kav7wZCP9nCx5865VIYMFzZc63Tsqzf5ZayAAAgAElEQVRQEd8iVJGHcGaLkc/9kivHyNMIspEz\nS+HdkGEVSlJjnE8rjOnaZ7KDgiY+W9e4degG0WsfHEA/7RYkgyRCvSaGv7vvJo15NoJUJIXfeR5h\n2y2Iq8NTWJrE2ls7yEv3IDWm8vBbp93BZEJOwiLCS0+7m+tP/uRHuH7dBRZ/9RWXrfTz338FAeV8\nCb2Ndt/dcDevfw00byKIJLLc3UzTj88RRaTaq5RXybzw/Nfw8//BD9Y6xrt3P8SlbfdwFBze4kCZ\npaNzK0nQjsnROkggmjHIpFfXSJEtDemshaIbsq5qb3hXlznyhitiajBanKjWAEFE3y9TCC8Jf/g6\nLSc77eHfdSoIpOdrRaGBDKndrwVM7b5zomuUzWQ9r5G23N8ezTIEpMwKrMar7xHMFxxiQbYGo6LC\nGXE7oAwWuTveTFuMiXcSsMpDokZZaLaEXpv7vtdLQbc0xrMM+Wx9yHK4ved5UFoBCXFcxuOxh0zm\n87kP3Y3Ttn+A1XXtA6un03PM524RdXBygF7Hfc+syDC67R7wRV2iTXSAV15+BvdogzLJGMYj91nB\nJRQthk/Oz7zqrdXt4+mn3abi/Hzm4eBH1Sktah+cHuP+LcfpiAKBnBRjSlkPQ7KwxhOXHQdyXguf\n5lDkY+RkprmoFLZ77rxHMMhoAyRp0Les9FLz/e0+LtEcZrRBTgu3fhKh7rlxe+foAiM6/9V8im0K\nnh4OOmil60Hr7XjL0w5mxQhT5c5rXRjskx1LoWuU1t3/s9MzxKJxY09QExUjTtoQNHHOszOcnLnv\nLLMR5gUlWAiJfco2fHB4Fw+OafxCoiErZvNzcObev8guo64c/HttuIsLyhKFDn2awjp1cHCAU/ps\npWoMttzitNtpLw02V/IzJQcY2aXMFzM0yHeVl+iRvc4snaOg8aUMEDS2OIDnqeVVjQ5ZlVhr/b0i\nfspUkzdmp0HguUlCiLXVzgBw46UnsTt08G8QJZgRL/KVb30V8cCNhYXKUTW85CSE6FIuLK8RtN1v\nitLIK1ittD68vZWm4GTbkUTwKsJ+r4sehU3vX9r3iyXGGLb7PXrd9crdOGnj2eeeBgAcHp/ilVee\nX/sYgQ2ct6lNbWpTm9rUpjb1hepL70Rd3d9aQhocsJzah8I3jYgM16yE2UNBPtwq/+9LdYL2u0dn\nqEgxGGCe4MjBPBHdwqn+mvc3X8RhGk4vtFl2qNzn1lcE7e8GaHXcKvvSfhfbCe3Wihg7Q0d8e3D/\nFJOp2yUcHB7j+MQZWF6/dgWjsdvRVfkIaOIfGLxiEfUctomjSFvQzJ1DFnJElIx+NCkxJfJulLSx\nt+cMIrN5AU3k5g+OCkwKR8p7+vIObn28njrPKNcVKmuLCXlKPt3f8vEjZ/c/Q9ioKzVDReZ8ve4W\nugNq4YsMjLoOVy89iX7fnaN/+Pf/Q1hySH3hRecppc0ZWuRDVC5yTE7db561e6gIbpFRgJq58xlH\nAsOh26F+9+d+Ad/4piMt/kf/8d/FZdqJP6qsXeDkxO3skyDF9sB1v/qDPiYE54UixjZBIu32FhiN\nZcsc4RsA8mIBSwomxhhAJrLG1D7aiAsBWLebWiwUauU6d52aod8n0UPIvTGm+y7+0H+71xL8MfZB\npVKIqTMYygBZvhxrjG4ErTkM7d6LogCjLqmuK2/GpzkDI5+h+uQ9nBJsN1/E2Bm4sbbXS3xX45Pj\nCdq0wxS2hQWhbYfHU1SNWahdGowGkiGi3xmHEpVYvxOVxEs10Xw+9/EmQiw9cbTWnnSrlHoI8muM\nMVVd44T8oLIsR0wUgCRKMSNS9kef3fL+RMcX5+j23JiZzjKUBE2PJjNo5j473NlBQIKYLM+wSzl0\nURQiDNaLYLpz1wkyDo/PPfF2MptCUSc4TQVioj3EgcE2eX510MJ9IiZfjE9g6XpPphNUrUap2PJU\nCtuYxGqGhObaKEmxTV32+WKOLeo+WaWgCTIxdYmmsWCqGpd33X2u6wlMla11jCWbej+q/KKEKdxF\n3BoOYeAGTyCAuOVgOAWDunbXKkm7sOTLZVmNkrrCo4tTlJRLasoCOXWO9wct/MbPfh0A8OGtO7j1\niYuemmQ1BMF/sBqKxA3ntz/F6W2ij+xMUFdkZirb0Gb9cToej1ES9CYC6XM1i2rpM2dKC8apw80M\nQvL/YtxiTiIGo4WH/BQcDA0A0MZ7oWmlwIkPMNzZ8X6CQgjfjamqagnbCe7hM6Uqf99IKR+rE/Wt\nX/oFDMh3azbL0L/qUJCtS10knWa8Rwi6rjv09jtv4xfpteQVbOMpKSMkNKY7UiJquWv0kzffxg+/\n78jhdV1Bxe6zL+UVvv2KQzfCMIQiBdvFxQQJdY6VqhGRwAxM4sUXXD5rt99Dr7ce7NzUl76IghT+\nwlqswGp2yfnhzEDSexjgLXTdxfNGCN6oOwykV4BZax96sDSWBcqah5QEzL9/FQ4BGuoTt9bn01nL\nYR9jsHzjhSfx5FNu0bK9PcDde65F+urffOhNzs7HC5QVtUijyE+4k+kCZeXeE4aRH7yruUmAAif8\nwVbAIqd2ueAQlFMViBjDJjQ5FEhI8mz1HFZTS3sa4gPCkw/uH2B2frzW8R3ccZDk/Xt3MWGUf1cD\np/edWeebP/kL7GxRsDEPkMZuou31h5AJGeLJMwwuN0Z5Q9jKDeDvfOPrmOcO+phNxvQdCjwkjpnm\nMGR8Oj2fN2sSZNMFFiBeg5nhpZfdwumHv/SP0KEHtrIW2WQ9RRBjBjHlbNXFAhen7kHZSrrY6brf\nEidtRJGbQJOkDRlQgK8FlKFMQVsCXmhlvDO7DBg4LUjSdgfbO5fpPUun4DhOEMfu+6WIvEs94wys\nac0z5hcblXZ8wnVLKYuQHpiCM8zOGpVOiagJ7ISEIgNP7ew/6bPaS/6jNMHEuofmH75W4TZlWi60\nQismBZQ2qEmtNC8tzIw4CoKhpH8XwoA3RrxsCUvWiqGiax5HHK0r6ztBM8a8clcp5dWLUgYoaYPC\nOfebsNWHghACivDiLMs8b4gxxxcCHM8namwGYkCZJpj4BEdn7r6c5hUimodOzkcw9JCLWik6faeq\nOj49w3vvfeR/M18zd+3OnVvu82djzCYOerJGYzhwY/TK/h5asskhnaAq3Pgv6xKjE4KeROBsLQDw\nlcX96WiEHm0eVMNBURaW4MGtfhc1wYD5dIIWmXDmtUJKr4ftCGR+j73udSQJOUSfjRCKZsx/fo3P\np2in7oEYRSkSOmeiZzDLiUfLE2x33YNvhLsYk5pXsBX+IGfIadOlTe3ds7XR3qR4UlX48RsuJP1n\nn30K6mccrPP+vSPMyRJ+UlyC6LnjGO7vor3nPttOt2EiN9fV8xicraewBABdK3Q77rMWxMkFUFcK\nmhZUDDV4k05gFRqxbrcVQiY0N0Q970qvLVDRwszUJSQ9MOuiQIdg1e2tAUYjd66KYmmkmaapX0RN\np1MfDL66+WCM+Q3KOjWtLGYn7m9pZZGT0vfWmx96A9ck7uHiws2dk1GF0QVtjPspOg2Pstb40V86\nw2UZBDgbucXwyfkENS2QZJjAEn0g7XShaRDkZe1pEUmaoE0K8CCQ3rRYa4vhjtsc97a2vFp33drA\neZva1KY2talNbWpTX6C+/E7UCnwG2J/qMmH5etV/4qf/v7+lGo+p1c9aaz2ZfLWstb77xBh7yIBx\nVZHw8O9e3w/jwfEIliCQ2/fPcHBEWWLzEc7GROhbAEnsdnmBjL2RZl1pxOR3EsWJ70QZa30iN/eg\ngctNapa+HMyr3xIYCEak0MpAENTVlxaMWLrKMB/roOsFSsqGelSdzx3sN62maA1vAgDeev3PcXzL\nxbuMpg8QRG5n0Wr3sL1F/lGSY0FGmTYaQXYJKqiAULr3ZGMLDurQEDSZVWcwtDuu7RxRvEzkDmWT\n+M0xJfNHY9qIIkfM7HQTP96stjD6p67rv6OM1t4AVVvtfXfy8RjRqfv3pNvDzhV3/HHc8h0kzgWE\nauAwgVq7nZI2le+88pVuUhi1vfdWHLW9Ok/KwEN4Lk9r6ZeGJkoG1kcnBdp4Q851StcWC/LzquoC\nBRGthQihfVaf8ZEJUkpoIpzXVY0JmdyJeY0pvedDbpGktDNvC5/3eHJRQxA5NU0TVNRtLWrtuzqd\nXoK+JEjIGA8Pc8ZWmnkWqB/Ds22lA52kKWazJl6nh3Mi8oZh4HfU1tpltl1Vea+q0Wi0jIxZ4QAw\nZnwHZtjbhiQI5+6owEXtxkl/0AeoA3b/4Aic1FOWM9w/dPfS7Tv38PEtB+n3+1dW5sjPr6Mj9/nj\n0xEWBBkmscQ3X/kqAGA8Poem2CwWVaipEyOsRY+6FwsjkBERfavXRkgq5tOLCQIyeGwSWhgYLEFZ\nXJdYjJ0Kt5emKKZunFfzOWJSAQ7iZVNx5+pV/Ot/8yP3ehB709pHlcoNjhbuOLtRD1aQmrPuQ1qC\n5yuJixPyejITgFNW2jjznYcwiGBorNV16a8nuPVjs6hr/NFP3gEATEaH+O7LLq7nOy/+HCrjvmes\nGO4QpJy3LfpPujE7LqdgNc3dNvQiqHXq7PjEd0KiNEGH8t24DL1QKhGAoPG1tz3AU085MU5Rlnhw\n6rqQC10io1w5XdU+Q1CbyvuCWWOwIBHA9OLcd+FqtYwWu3Tpkr8PZrMZwmhpwtm8hzH2WGabtw/P\nkWVu7Hzwwce4e8fRMvLFBJJ+w2Br35PkD08m+Of//H8FAFzZ6WN3Z5d+Q4C//ivn4zQZTzEnsU6/\nk+DeoYOou70uzsgE9dNbd1BMKXpIq4eQqsZYd2ul48SF9K/1SsbmuvWlL6I4Y35yZIw91BpsXnPG\nvEQcWAHwVt7z0CKHwRsOMrYMUYSFx5bZT3+G6t/lYP3TWO/jYL+fHE5xf9K4qEpwavGHYYyK2ooV\nShRzd8G3+kM08qO4HTeedeCMe3M1a+HDZYV1mkLAwQqN+6w2LoMQAJg2kJQR1LIh6owwc8sgqGXb\nlRYxOaJPyjkWp+uZbVaBm9Bkf4EOmSkuJvcQdByc9/ylLurSPaB4OEAQucWQNQyckxswsyhL91ld\nL9AK3CIqiWNwgjkTmsxT3fJy93l5hJJu3HbCEIUEJ5Z6qSDhKYKQAlDBPHRrlPbGdY8qCyydxk2N\nnCCtMivQI4VXxLpeDad0Be2vc4iQFCNaK1QEA1S1BCeoKwwYQnLX7fZ20ErdpCll5A05wYW3uFjl\nBdoVM0ZrDTi5jouqWma9rVGlUpie0YRbV36fIGQFQxljWudQNPkmSYKUzFI5595KpKwrNJgNZxoV\n2XUsdOml8UWuIel6JinQzEvWSliCwxizPnRaCAnmZcwVLAXQqlrDqPWVslIKfx0ZM4ibRYFOkNN9\nEMaRP5Z2p+Phv6qu/YN2NpktF+PW+jlGhMAWTcTffP5pbFHW5TsHY7xJVh1WJmBkLHhychcnr79O\n5yFFTnyqvCjBOVmMGI0VDPhza0wQ3vHJMQIa/1f3r6AmvtHJ0SGu7rj7r9VvIZZk5cAF2nGzgDZQ\ntLiMAw5NC77uVse7is8oaDgvK9y47KD6JOAYnTgI3W4NPHxSLKZ+IzBIA3S7Dn6b1TXOZu53DXcH\nMHw96DkJe8gnpETTBTjBsMPOAK22gy0nizMsSOY/3LuO7WuOJzO7mPn7cjqz3rBW1aW3WwAsLF/K\n/xcEgf3k3jGuX3WwjmUVuik58Q/3sFW675lYjh2iGpwcn6GgUPE6qBCK9cdpXVbeQDKMIu/szZVB\ni1SUwyRAQr9/O2F48PEHAIDX3/8UgriZ3Uv7S0uPPAdv5jDOMSNFHgOQ0PxUZRkYLTLnee5h7cVi\n4V9HUeSfu0ot7wk6dWvX//H7fwROm7/z8wu/oEqDALFsqA3bGE/dM2IyyfHWW+4Y37G15wkKGfnA\ncCECVMTXK6sL/M//+78EAPzgBz9AQfY7b737AV769V9x7+dARYafWmt/H08mI28L0u0P0O66BkcY\nBJ5Ltm5t4LxNbWpTm9rUpja1qS9QX75P1GqHiS3jKxwh/PPbn4wtbe+Nefi7zCok16S/GwOBJSSw\n2k362/7W5+WqrZ25BkBbCaUaY88Imnb1SnNYIhtGaeB9RPJqhDxz/97tbKOduB2PYMsMLWstIjJ/\n5Fiqsqw1nlisjV7uEhhDTb+5LnN/fkqlIam/HnINkB+NqnLkxXpqmbvnbic9XViMMtd9EtwgptRv\nKRcAQYkLHEMoR34NZRtJSJ1Hy2GU2xnFso126AiHSU8jI1hRym06bwHKmoxJ5QLZ3JFJZdBHEJIK\nqBA+ygfaICRIlFl4SLQocsxnk7WOsSwLBI0Aghlw6jBACvTJw6XTansfIVWXnrRsTISQfkscpx6q\nU2q5+w1k5LMBg3CZkeeUOA0+y5edKKxCzcZ3WC0MoJaJ9VysfwvP5jMIIjlbZhGREisIBBQRvKMo\nQJI08CJ3GUsAgjCApHOSsMADzHWpAeHek0QBoiZeKdC+gzibZpD0t4wBSlLt1ar2ESpaawRBAyVZ\nT3wWgvmO1jplrYFqXBKZRkJ/t8o4BuQ3pmGRUDep3W57Qq01BgHtkAMees4A5wwxwRsSyo/pViKx\ns+W6Sc9Ljo+J3LywISRvyORDTE9u0flvPIgchNoiY2AOA2bW8/tqun6MC9y44bq53/3aM75bd/PG\nHmK6ZsOtNuKATGAtMCRFVHaRIyXCd7fXQU2eZcPhLiSNxQuae1qdFK3Efcd8OsWCsJcoKSApmxTl\n3HujCSn9OKkrhV7b3Ts39i8h7a9nKGoKgwEpnHkgoC1F6MQ14iY600T+WsXRNq5+3Ql7Dj85xnTU\ndJ85BBH8jVaevB+EKTR1M+qigKbO7pXda9jfcZ54qhrj6Nx14EfzKV6kSLBn966B3Xfz1dPnAWpJ\nRPvor5D1G3+hG488Rh4JtFqNUp352344aGGXYkfKbI5bZCD5o9fewojg07Q/xHbHHdfx4ZGfkyLO\nvL+XBls+M7Ty0VqBlDCmeWYYxHQfdAddb8JZ5CXyhetEhlLC0P3EGbyyb53aGQ5xdOQg6zgOEZDi\ntphn4HSvb+1egubuvgiiAO008Z9XRMXQlkGQISysQGPyxgOBHxMUe+/wHLvXbgIAZlmJwdB5/rVb\nCQKCWaVgHqeeTcfe066Vpt5PTEjxOEwe972P9/bHr1otoShu4YNFAetNBrlYCrUZHNcHcIZuq13u\nh46tMdBaCRblQkA0H7Dum5oyfwv3ydplg3fVKuFxy+QzSFLGWW1RUr6clhJdkksmceglrfP5AgVl\nWrEcHloIg9QbmymlvEkYZ8JP9KucLmuVD6m0YP5m6qoKMZ2gKbMYUUsdifQmg520i2effXmt47t7\ny01KZQ7M5hRuahniLmH3KUNEk7UxGmHorAI6nRQdUuppJcADkmFHEix0+HiYxigp6yuWFHwrY7Tp\nhrt6qcZ83vA3KiSkROEmQdGE+BrpYT5rl2GbZZ6hXnOhaAGvpDTaeGfeMIr8QjVfZBAEj5RBBuYN\n6hgaSlEQpghItSeCBIJwScaFDyjVdQWmljYIHuLGUgmzeievjlML69RFIEibrW/F0eu1UVOOZcBj\nBLJRwEXIcuK9BHJFAr2UOgvBl2HKWvkAW1Vrzy9R1mBBtgntdoyQbAEyFDC0mdCm9jeytQKkNEee\nVxCSOBzaoEMwogi4//51qqxK1ATFxnHg3bgF556rE8cx4mSpMmq4IEVReHUe5wwBTaxJGGFInJWE\nc6R03e8fHWA2b7hVy5BorY03602SLrb67sFcloU/nw4CJkPXuvZj9lH15DW3uOhuWTx53cFKO90I\n56fuYT5oBYiDJvHBIqDFX73IEdLCbrfXgSWjVSkC6GYxbSySZrG45SC5UuWew2aNXs5JQnjTmXYa\ngpEEnckAFPmJNI1w87K7p5+6ug0u1nPXZ4EGuZ5A8ggtSdB3aFFTkoC2ORaZ40SZizGeeNktXA7e\nOcP0R05NrJSCbcaylB6Kd4t02ogY4CtP3QQA/PrPfRfbHXdtH5yOMCYlYlTk+JTuuVsXx0goQ3Ir\nSjCgObDTOkd3/gEdwS8/8hjzxdRvpIQU0KR8nZ8e4o0Tt3jLytIbIkftLrZ33TjiQsDSYrbf6/nn\nX13XyGiRXSvln7Uc1r+WwvGfAGD/8hVYWmgdHp8sTWq1AaNNlQwtlgxFg0Cszxf6zf/017widrFY\neFXgxfkI4ykpg22FMHbnPG1JGLPcJDCCF61mHqJlgnnVsmUckj57MprgePahP5+vvu74ul956Xn0\nyPmcQftgeWaNDztmIkAjEjZGe87purWB8za1qU1talOb2tSmvkB9+XAeCzwploF788FVpZ4Bg2rI\n5xYIGhInWxpvPgTNoSFbu/+1JKjDe0lZy+CdNME8rGZXlG4W1hPUrf0pESHW3/120hYaxEFrg5bP\n/pNYrtsZtCGjwyBCd0s2Jwh57nY8MQsREkEz4CG0bs7bUh0kOF+xsQ9910BrA0bneU8Y9Gk1PRMh\nFLX6Yw7ImgjwNkaLr7eryC7c+8rCoqJcOKuNV/pVmQKoW5PlBuDudSu1CAQpeLSBJBv/rb5AJ3BE\ndBkF0NQdabyK2mmMPnUismoG3rQQbBdSkpFnK0WXuiGBGUI2xpfWLjtH+QLt9noQgjIMWdlAdTVy\nIuaXpfIKuNwyFNS9kaqEpFiQKEoR0k48jFKERHKXMvTESs7FSpfJrnSfsNJ1WipN2U+Zzj5EO6Z/\n19qgfAwSpFHWm3MaY5DnRELV3JtAVnUJRXBhsGKuV1fa+6jBMt+xaY4NcPzoxaIx+DOIqBOllYWm\nI1BaQTZ5YGppsNlOE6/I1MwuYX/DHovMyhjDZOLup6KQsJX7u3Eco6J7QkrhO4RCCE8sD8PQQ4G1\nLpCQb9jeoIPLlAq/lSZezFFbhSm10nSpocjbyljjr5EQETpEhm6nZkWdbJHRfV8rRYbDj66Xn3KG\nhR/dvUBKc1o2nkERaTdKIh9Fw63wcyDnAhlBNHHcxw51yLWxyAguM6r2cUeNOiusJKjJDBEE4KKB\nB5mH07g0MGS4V+UlDHf3glI1Xnjadc6G/QT1mjmPF+Nz3Bg6JVqQKQ8xnp9NMMud6oolEoy6EJ0E\nSDvu937lV55CTh3/0zunyCnHtJ2GSBoTS8PQTQiGvfYsvvnsTQDAoMXxyS3Xzbhzds/7GCrD8QEZ\nIoecIaZr2IkSbBEheX/vMlqnzgj1W2sc4+L8HCFBWjIIkFOH8vTkCEa539/t95ESSgEhIKgbdnlv\nz2c/VmWFi5GDpSbjCWwzvqRA0HihwSCiTLpeu49BIxCZTHFw6OC289HYd7XjtOXhv3xm0KK5OI0j\nnB4frXF0rnqJgCZC+6WtFOHTrpMmwhgHpw7d+OtX38fla06F99yz25gShHp0eoFjUiDOFhUqtVwr\n1HSfMcthGgqGtaipnaTLEn/8p/8aAHB8coKfeeVFAMCN65cQUBeRWb4U6xiFxlzbGP1QBM46xb4o\nhLWpTW1qU5va1KY29f/n2sB5m9rUpja1qU1talNfoDaLqE1talOb2tSmNrWpL1CbRdSmNrWpTW1q\nU5va1BeozSJqU5va1KY2talNbeoL1GYRtalNbWpTm9rUpjb1BWqziNrUpja1qU1talOb+gK1WURt\nalOb2tSmNrWpTX2B2iyiNrWpTW1qU5va1Ka+QG0WUZva1KY2talNbWpTX6C+9NiX3/6Hv2ObBHqj\nFRQFbVrLEATLoNMmSDeOY+RzZwn/wTtvAxQJourShxlyxqDJJl9ygaAJeWXGJ2UEUkAbFzOglEZF\nifLWwkdcGGNR0Xcmaert3vM8Q0R29a/fPnxk/svZqLJN8HEgGMCbcFkX/eJeL+NphBAPxdj8bVWU\nJf7wT/4EAPBnf/r/4N4tF9jLAOztugiKneEQCaVeh2H4/7L3prGWZVea0Lf3Ge88vHmIiBdjDpGD\n006XKz1V2eVS19SgKgrREt3NjxYC1BKNEPwBIUD8aIEEPxB/ECAhJNRdDV1dFF2VNZfLLjttZ2Zk\nph2ZkTG/ePN799353jOfvfmx1tn3patx3LA6SyC99Sdf3Dz33LP32Xvttda31vpw4SJRQly/cQPr\n6+sAgJXlZYinM28/bYz/v2lrrwF8fLgDAPifv/XbuLh0EQDwD77+Gz9xjP/Zf/gPdIkZzQWI+gUA\nkjQxRNlIU0zHRPUyDcZwfJr7cq1pSLM9SyLTCV8eQxZksJYPj6kafM+DzUTGWaoM1UgUTxGHRMFh\nS9uQicZphmqdaDqEJRHHRAshFJAm9Jz//f/2j5+6Tv/L/+a/1SvLRLFgh1MkR7Smnhx1sFBdAABU\njvdxkjMN0c1XIVwi6Vy9fgOCWeeVyDHungIAdj++D31K1Br50QGu+TSW4PEDHPN4V158EfZ7HwIA\nGl/6LA54vAffehfR3hP6rZLAvkfUFP3Viygv0/MgTHCyQ0z2t9775lPH+Df/1m/q1WWiWUmTFCHr\nm4X2EmoVeheWpQ15rlI5Tu5+HwCwod+DxYzvaahw3Kfn79Q+j84pjfd4bxulCr0LaZWQCVahCXB9\njT7vTRPcf0T0Fd1BB4KpV0rlEn7mS28AAMbdU2zfI8Lar//yN/DFr/4cAODv/zv/wU8c4//yP/y7\nGgAmpz2UajRHQRLh+JBolJI4Q69H769ab8Cr0Jx+9zvvYmvrAgDg9c+/hNs/ugcAuPPwGFFE7+9z\nr2yhXifi4bfeug0AuPnSliFrvn37MS5dof20vLSEwyOiAJmMh1hgwuJmvYo4GPOzJDg6pv1SdiRq\nTdJb/9P//oc/cYz/6T/8X/XUprn8WDQR1+jvF+opfq3ORMtuAKnpfQqpDU2XlBIW05dowFD0yPEY\nLut04ViIijPjjG7UWkPw9XmeGgLcXFgQTHmkVY5CXWpo6EI3QKNg7vmZb/wbT12nX/3N/1wL/oJt\nuZB89ugzbE9CCEPjos9SQgkBeYITjSQAACAASURBVJa0XP5VqqhPENUrPfscGlIUa18ZQuyzKl6p\n3NAxFd+h/ypopnv643/8Xzz9XATOkLPNxEFBsvJJ0f8vf5/9tzrzt8bsB7SCIYFXwnCBE51bYX/o\nM9drjX8hW4tWZj63ys5c3G+fPndeFs/Y35WGYO4ar+SixpvDdW0zUNuSaNaIZXo6HGD3yWMAgKVt\ngA2eXClonso8z+FYM36yKCBGduW6qFTp/tl0aniBlM6R8MEjhIBgY0ZrbZjUs1zBVp9gK3uKKCid\n8bMJgNnCxZlXIKWc8aWdWeAADJufkBKTMR2ij7a30R+SMnr73Xex/ZDmwXMcw2VUq1Vx4SIptWtX\nr2I0JgVz584drK6uAQBe++xn8MLNFwAAlWoFMFyBArZ8ttf//wWKoGIOldZGAXSnI+yM6BDpDIcI\nQjLCdTrFg4OP+Ju/8RPva4sEOjMU9ej36X5BEKLi0XzbWsNiBVTyPcTMBXZ0fAyXecQWGzVIyZs2\nzaCYzymROQYjeq5mrYp6lQ4dleVGEUutELGxD6SwHVqznlRIYzropmGI4YSMK8f1DQfcPHI6HuP1\nL30ZALCysYIop3tW7tyHk9Az7O09wIQNm4bjI54S83rJkkg5cC1tid6U1iZKFm5+/gYA4PDDCCdH\n9N3WlQtwpnTPSSeEl9N7W65WsMK8hKfdIRJegtFyEw1NnF6Dw33UVmh+ppaEZc/HfwgAR0+eoLlA\nhl+SRkiY7b4/6OPJQzLGsiwzzPR5liHp7gIA1i8LWJL2rnSAghAzVRox6wwNgThhJ8mKZ9xdUQRE\ndL2fK0hem77twmX9tLy8jGaVxjjZ20fNpXUlpzF620/mGl/JonmPdB/TPq2n3mgMS9H6W1ts4/Rw\nGwAw7Qe4+fxVAMD2QhnhkHnn0inGE5qL0bgD12UOPEtBWsyJKMhQT/Mpaszx1hsc4ZKguR2MTrC7\n9wAAsLRQhyVIb5VdFyk7wWVfYutKEwCw+2gbFT3fe/yevY4aGzCtkyM8mNJ6/2BUxtYGraOvLNpG\nwUohIHnrusKCZxW8pECcM4/mcAhlszFbrUEwvyAsC+ZYlhYs3hOyvzM7yEtNJGzgW5Y7M3LIrDDP\nPT/bKpBBGMNM5YBk3WpZ8syeFmc4XKX5W5z5XEPNPj/LLytmfKvCgtGVKtfIWd8IKSHZCdDIodiA\n/Ctq/gyfp3iK839WpJrpaDr/+Hb57KxVSsNmPlIpBJQxAj/xALO5FRp5MS4tZnyeZ6wrMpxmBqTh\nyPvEwDSEuV7Nxqw1YMY4H7fsp25ERXkG26WHatZqqLNh49iWifwIoU3USErLWL4Xty5iMCAl3u8c\nzyZG61kk5wzhrHQdY9HHcYxczwyt4nNxdtOcmdMsy84QGQtYz7BYLEugePtCzIiVf5xT1BAf6xkB\nrQaRKgLAh7c/wu/93u8BAH74ox/hpc+8BgBotNqYBD+kcVkWAo5WDMcj9Abk6e3v76PBRqnneXAc\n8iTf/+AWPvu5VwEAb/zsG7h+4wZf4889PvP84lnUxKcrUggM2bD4y/sf4d4+edZPeju4ukQed7tU\nxwePfjjX/ZoVD5pf2HA0xfHRIQCgWq2hwSTGvhCw7MKQsNAdk3I/uPsQNivuqufA5gNaCg2vRAcQ\n/BJ6+xSd8G0LCzVSytICBB/WcW6jz2s2UwprHFHxpEbObKiTKEG1QobW6WiMGu+neSQPU3R36fC8\ntHEJmiNvF6/Z6JzQAds73Ud7ZQsAMD09gbdAz6lLwvB55yrHiCNRCMaortJzXln7GiaHZAxEe8eo\nPqG9mw8inPAY8yc7EDEf1K0SJCvB0uoGEDGh7HgC7FI00RV1VJgsdh7p7D6G5Cjf4uZFxBzN23v8\nCBM2YsNpAJedOddx4DPxcZq7EGwg6VxCKybBPu6hyWTg7fVVZDl9N1IWXL6+AmCZHTUIDdWmqEu2\nsIgy/1azUkf5lIygFcvFYoujgjvH+LAznGt84x6TdVt1RCGvg5MJqhV6B7JZwWKbItIHhweQ7Ny9\n+so13Lr1AQBgNOhhY5OIgR/t9zFkZ+3w8AhaU3RLMdkthDJnSqnkwuZI3XDYMyTFli3hsMGfJBHq\nHDUdjoYos06q1nwE0WiuMY4eP8EpG8KbRwfImuRUB5MQex47HG3HRPy1klD8flSSIeTzoFGrIWdH\nx3YcpKw3+2EI7+IWAMARgOYDHXmIvLtNwx7sIiuMk2iE3KN3JVtrEHzoQ890otb6r0RPfpJEcWwO\nbtvKITG7Z3EuWlKaQ0RLaUiqpZSAiSalBu2gfxfOv4CUM32d8TyoLIdm4nbLniEiSmXIco5wn9Hz\nFJFSfEcFkc9HIg0QWXNuDL9Z7pAtBT68TUTPh4eHWFmhuX311VdR2I/C/CrMOQ4AOc7ytQsTfcqV\nMgaVpSVU8R0hoPmXLa0g9Sw48glDq7i/kBDi2QiIz3OizuVczuVczuVczuVcfgr51CNRtUYDlTJ5\n4wuLLZTYatZZhozx1TzLUObcHg0LKedBVSoVNFsUDu4cHBjYC1IY3BKACZdXXBshR7SSNEaUEGwg\nIOCzNygA5NnMGjWhUCGM9SqEMLlb84miCBTYSjYhJxjYUSllwoTiDB4rpEQU0Xh/67f+CX73d3+3\nuCMuXnsOAHD1+nWcnFBkZDIamjyYJEkwHJMXORgO4LCJXiqVjDfjOTY+ev89AMB73/sBvvrVrwIA\nvvFLv4yl1fVnGOOnL8WcKKVgFbkKWpyZqzORMA3Y7JldX1hBj6GKiuOhXaMowOPJAwyGwVy/LbLc\n5EckUYLJiGDhsl+Dz3lNnlDGC0rzHJq9Ps/3TGh+OBzC47VgaYUkpncbWxMMRxRtWGzU4PA1tlTG\n40qgEUcR37OMss2/ixSKx16uNmAJWtedQR8lb36vqbK2gGEBdaocgiE8BzaigKJ6ajBFJaYn2j7c\nx5UXXqcvVyVkzvMzniLqdOj63jHiPkU6N2++Bv8yRTr7nUNEBxStSjoD/OhuiQcZQ7i0F5d//nWM\nuhRJHQ0CaJ6JykITOKb32dIKemm+sDoAeLZAn/dKs9lCmVVcPAjQalGUZej4UOyZQwC+1QAAnIQt\nLPCaypSPkqQoyuVmFeUJPWdSq0OX6PNwGuDSmOaz1vAx4ChlqkO8skrPnDsOMo4i6jyHE9LvuqU6\nIo8gy3KWIM/ne4+ZLqIUNgokA7aDU34+Z1TBwjp59qejIYYMhS2uLaA7pGd9snsAu0o62XE8VEqs\nG7WDkKNbpRLBjo1aExzkgedVkDHkrXKBhdYSX+tiyjosTiJUfB678BBHdH2zsYCj0+5cY/Q9HysH\nDwEAvShB75giuG6WYnmV9rbUCzABJCGgWA/G0yksjg04KkNa5ERZAgnPReDYsHkfJPsHsDPWEWlo\nIhV5miIOaL/m3gRekyY7yTPoxop5zhmcIQw8NI+kSWDydnKRQErO7xKzfUZ5tKwHxSwdBOIMvAWF\n5F+AmpyNJn0CxjqTppLFyQzm0zm0zs5cxvOQZ7Pf0jnwDJGoEgxAA4orcd6wdKD5bP7WH/0RUob3\nb732WWxyXu/W5gY2Nul8arYbs2eGQFxAgVAmLKUtIOcXkGsFq4Asc2HSJbQWsHj/OBAQBVIlc2TF\nc+aa8FW+ah751I2oxVYVHhswdp6bQ8WxbYNj50ogixjOswRsfqxUJWjWaQL9chWCjSuN1CScO1Ki\nxXBLxZJIAgrZSjlbgAIWlEloz6DVmYV55mA2ts+ZxPW5RCkDQUqBWTLgmcUrIAxcpISCVYQepcQR\nJ2h+8MEHCEe0oZubm1i9cAUAsPfgY7z8CkF7XsVHntHYw2mIzjEdVN1OB1OGK9IkRsa5NdM4Qn9A\nn2dBho01grq++rUMSUiL1y1584/1X5LoMwbrTDhsbAnsn9Ah7UiJRoPWgCudM+8IqHFew4ubl42i\nr5YqeOs+QXjHg1O0avPlYdCGopu4jgWbD0SFHFowPGdLTCZkXO3uH8Dx6N7Nko9wSsZPvVRBmQsX\nwnBqDP9oOkXOOX1QM+NdaxjjOslijBl+crySCdO7CtBsFCfSwojzkXSWwX0G2Ll9ZR0257eMsjF0\nTN/tdroYd8hoQb+DIORE8WiMfES/lY76KJXpAJuMBwh7dH1yvIujuwQdb61fgbdE72rh4iUoTmJP\nOn10SjSH0f4eymUaV/3iJjgFBTsfP0DESchHuzEShmovWGW44WDuMa5vriPjXL/yJEDdoXd0ud3G\nAV8zERoln66Rlo0opGc7mLQQWKQ4a1YZG1u0/168fBEuG0tWuQZ7kcY13N9DvkP5VKcPHmLA6yGz\nJSIuLqj2uwjZGE4ch9MJgLLKUeNDa1SuwZ7TafPY+FFxCuXQc1ebJURdOvA7oyP4TYIhm0sNRLzm\nVqptXL62BQDYP+5h2SKDcnGhDbRpvbqWQpLQPVfYwXLcMizeqysLS6hWyKltNBdh81hOuz1oNgJW\nllsYD+hZ9g5GsDg/cG3Fg2XPdyjp0QTTRgsAYF15Dqsf/wAA8Fo7wufWNmj8UkIz7GLnGmGffnPa\nPUGjRs8YuA6K9ChIBavOkPtkhPw+FVWodAqLE+eF7cJl4zHMIvSPCfo+OOrBb9N7dtrLaG6RYyEu\nbMBl/IlSNOYaHgAgTwJIA//mKIqvICQ0ZjlCxvGGheKEEhpw2LHLcxhnTgiYM+/HE6eNg5qnJmdX\nn8kr1T8Gc52FBU1idq4gnwG0tAADsQkhzXh1DkymtL8tITEckk79y+++jcoHPwIAuGmCeoNg/BvP\nXcPNl16kv198EdUmOR+ZhjF+dJYgKxBobZExxHOoiwIBlSHjPRdMhkgTshWmyQjDkFIPhpMOtKLr\nN774r801znM471zO5VzO5VzO5VzO5aeQTz0SVXGksV6lymfhHqVNKaqwz4YeFcKQvPrxeIqUIYf1\ny1uwi2qZYIJjrmbxpYTD0aTheISYzVEpnTOhUAtuiSz3UsU1cFgwDaAK81XNoiKWPFsVMYd8Iun/\nTGRLiFlFAoT5f5YAQvbw/+nvvYnjDkWTarU6mlXy5MdBiD4nLntuySTQOZUqGj5DdZaLS5eo+iZN\nUqQZeZ1xOEXMVYpRGkMlNMbntrbwtV/4GgDgzg9u4c+e7AMA/s5/9PfnH+szyCe9obOJjrPE+lwp\nWEWJLn9264e3cetDSjysVUr4ys+Q57exunr25mbapZRolsmD/O72B3j3wfsAgFAnePH6Z+d61l4Y\nmShBkGfQLq2XzBJQVlEoYEGy5+lI2wR7bSFNonLNc5FzRIsgP3rKRtmHZ5P37zmuqRa1HBsJh9GC\naIqQE5WVyA0ULKRdXA4FjWnK8IPSsJ+hOs+LU/gcgXnv7e+gahPEFkU5eqfkdXdOnuBoRFFAPU1w\n50++S2O8vY2Vy7TWsiRBMKQ1K3SAB4/fBQDkVoJqgyCezVc+A/Denex34HIlWscTmMQBf36Mrecp\nwmqHU2BC69dpLWDXou/eyCZAZzL3GJee20DI0bxKx0KU0j47kAG6U9r3URygsUKQjOM4sDgp2vYc\nTHiP2r7Ctc9QJOr6i8+bknK/VIVfpUhHEr6C0SlFqL77T34L+3sEI9YrVaNjbBkDKXndQakKN6Ix\n9pMI3oRbAfghJEd4niY2R8omKoPmOV1Z2oQlyDuf5AksmyJLqyvLyEPSAzXXw3PXCWqdJvdhufTu\nWw1Aa0YKpG3wly5Dz5MgxIUWRYVeunYFokG/MwjGODmiNfPo8b6J6Ft5iG6HW9Tc70Lx/aZxBe36\nfFFhf6EJq6jirrl4oUZRvc/XQuSH9JvT0RCiKI6xJUas78LxBCHDQ1v1KlyrqHpLkKf0XHkygOZi\nAq1iRBypl9JCym058iTCoEuff3j3CLlF633r8gBZhSKRtdUVCE6uf6bSPAB5NACK6mjLhhb0XvUZ\n2E6eSSyniNTsfHIdgpSjIPrEGVO8h7MIngBMpMvKU+SWMp8XEZtMKIMM0ffPlroVuGOGZ0mf3+vd\nw/EJoSz93gjXr1A0KRkLvP026YxOp2sqmK2Kgynv3WGvi2G/R/d5/Ahv/fk3AQCXr13BV77+dQDA\n8uoKPvr4DgBge+cJUoZBy9W2aaHglhxcfI701sblDezsUluRjz6+hTSn/acwhbS4Ml8pcF0C/pU5\nI1GfuhFlC2lwy1xpzKLW2uREBWFg+jhlKkXC1TtpqmBz2LK9tAQ+4+C0m7C5dDnodBAUGz4KkPFp\nk+YKsigRdz20WBGsrS6AIXv0e3083qYqoCCIYHOZujzT02keUWdKTunvs2FU/q/QJg/GsR28e4vy\nlP67f/hf46u/9DcAABcvXcSH7xE0cu3GC7MckWoJnkcPfenSJmo1UoCD7gBD7gljezYqLTIkquV1\nLLTIGKtVy1hjWKW53MJ4hwynN//RP8KgTwv2X6YRpc8M+mxvrFzlmPLB0h+M8N13CXJ7uLeHps/9\nW3j1fvutt6C4Aub6tev4xle//BN/U0hhDBff9vDi5WsAgI8P7+AxV+09Td750X3CYgFAWoh5Y/vK\ngsXbxIGEz3BYpVRGxsaP4zuoVuiAUHmKyZDhJ61g82EQBYmp9jk+PUI4LfKjWgZC8L0ySny42RqQ\nPCZ1BlqW0oLHuVvSksbwm0f2v/021r9A+Ut3P/gBspScldxyEDHEbdsu7Ba1xyi1HCCi3x6OQnxw\n6xYAIByewgpojBUnQxSSsnv04BZsSc+/c7SNLOXDOZNYuEz3RBhhxFDtrUffx+kR51b5Jdg+zU97\nuYXdZYKTxqMQJe7RNI8oW5hKrUE4xojn+SQJYfO+XFlaRo0h4nKpjLRGh24Upch4jZZrApVGUdmV\noOTxOyqXYbECka4Nl/M9P/Orv4DmQ1prbg50jslw2r3zEBdPqT1JGRacMhlLg2YJwxod/O3xCTpz\nnsIFzFlySwgYy+hNBhDsRCzVltHg9hkV20GWsHERBMhTGmetWjbpDSXfh8djC6cxYt6DLju2jmWh\nyhV25UoNDzjfbPdoDz7D1kEUoHtC66FqxcaILVeACech7e5OoVc25hpjv+SjVRgGngc7555q3/sh\nBm1aC6HSkNw6x6r4CPi5H3T3sf4ZMhYtkSNP+KAcD5BxJTOsDILzoILeMRR/t95qw2ZjJskVgoz2\n1pHyYPO+rA1DVPbuAwCmW8+hxEaXVvqZzgydDlFkFwkhDBwKaZsqvFzAGFFCWuYsyQSQJwQ/ZSmM\nY8flgvznj1WA8/sua42Mszek0rBSdvgsBavQM3pmdGmlIFQB/6lnMKGAv3jnt5HndK7v7pzg4S45\nxva4ir3HNIdIA/hsTPZHPXS5Gt9Lc7R5j0qVI2dH5MEPP8S4R/qmVq/h6JCMtCgMkXH5sFepo16h\n9+XYwJPb1AeutbGAqETPE6gpctB+sEWKMp+vlrDgV+bPwQTO4bxzOZdzOZdzOZdzOZefSj71SFSc\n5iaJbBJGiDnEn2YKCWfo51luGgs6roUyW5G1ug2nSEq3baiil5RKsbJOnu3haIg84uoSSyJh6CqV\nwiQHW64DzyHzu+p6yKdkyS5Vy6g8T17L/Ufbpj9Els46nM8juRJn+lLAVAZQk9mZdzLiJnTDnRP8\n/u/8MwBAMBqixl2Ch+MxpmGRWOwi40ZxrmtjYZGSeq/duIbLl6mCoX/ax1t/+T26zzRAkRgdhlOE\nDNv4rsSYu2x7dQ9ejb06FwjKz2ZDn+1v9eOfFyIouxEA0B0O8dG9RwCAH318DwfcW+jwpIttTsj1\nPAfJkKIFI/ZChCXQ5Ejaqy88h0WGELRWM4gWQF70hgFwZYkiF5kW+D++//sAgMFgjBNO2n+aXL+8\nNYPPLAtdbrYpdQq3GJvWcIqKOc9DzI1R01yZkHeeRKZpnWNZGDFsO5xGyIqokQWcsvfbLXVQZQg3\nhoWM4R6hyrMkeilMc7pc4RNVQPmZhNCnSdwf4vQxweBiPMJkQKnWoRBAmaDGleVLKJcoWuI4tun/\ns5IqdEdF1+4UkaQ93YsCtDgiULcBS9K4Tva3UVqlRrCx0Lj/nW8CADYrDVNVGU5H6O5QFdbaxjV8\ncIeSSq2Kj+svfw4AsJ5mmPzFH8w9xvbyRXQnFG3dm+wgS2mylhtLBtLfunQJ9TolrdqWiwG/63bL\nx8Y69Vvy7QjLawTn+X4Tldoi/4JEFBQVnwK9Dv3WJOrhaEDzY3k+vvg3CTZf+cIbuPfP/i8AwKWd\nhxhv0d69ePMaHt2hRrD5vRGqHDF6moyHpLtU4uI779Nvo27j+ZepkjdUylTKLa8volam5w5HXVR4\n/GsrbVM4E4Yxci7SCYOxKWaoV0lfriwtospR/Ec729g/pUhUbimsXFjhGfHx5C7t51duXkbCCbux\nztHhVIVH97rY25uvOm8hjBG79HzZ4T4i7l6+nNiwT2jduVJC8J6wxxr1Yv9NXdQ48X867SHYp4i3\nX/LhucxIkExNYUQwGJh0jGq9BqfM60JUUGmM+btDjLias7F2CWJK47t76/to/eIvAwAs24PO5z8z\noONPdNJWRWqLtKE5Ii4ty+g7paTRT1JKpDFDe5ZjUgaUmjXe1NAmQqW1MtGtRGukvCfsXFN2Nl00\nq9RT6kwPJQV9JhH9WRouD6Zdk6pRrZdwwgwJx3d7yBlat/PEFEqNp1OMOXIptIRMODrklyD42Rq1\nMhYapJ8m4xiSq1p920XEaQ6OnkLzHrVsCUT0/A8OH8Lh/X3xuSuwqlzll0aYDOhdW14M2PNXIAJ/\nDUbU9m4HIzaikmxWzq21QpWrIhqNKsr8t+1Y8Hw6tiwLxpBQKjfUGkJIuNz5t7K4gCjhELfQmCaz\n/IniBdqWMBBYueJiYZErPJTG3YfbAICq7yHn6eiHI6Tp/C0O1Nl8JyUguJpLnOl+KiQw5mZvf/LN\nP0XAFVa//Cu/hMvXSFn/4O13MDG5TImB82zbgs8QglIZ+mMyNsr1CpwCWoiEaYQmJUz1YhxF8BdJ\n2bWcCmLeWP/q3/u7+OM///bcYwT+arPNWTfaGYB50uvjB1xh8Sd/+Ra2d0np9nr9Wbv+M8alzFPk\nbFCMeAM5loWNNTpsLmysz8pYc4UCuE+zHDs9goK2u8dY4irOw2EPY670vLz8PC4vXp1rbJubF89U\n12jkbOBPp2Oj7HItjIJrLS0gYXtue2cXinMLdJbC4QqQarkMj8vhr118Dls3nqcxWwqPP6YDdNQ5\nMc0Mg1EfAVevdnsCD9joWmjWUeWmmlpYiOKiPF8+Uy5GYAm8c4fg4qqvMOKycPhlNJfo8KjVqqb7\nuu04Z6pONcq81i5e3sJknQ7W3Se3MeXnt7MMNVbKy2sreO4lykc76Q6wO6G1X/FcdDkXSFQ8Ax/t\nP3qAnYfUAbu2sYkbL3+R/obA3sNHc48xy3MEk8Jpm6JUI2Pgl37lG2hxA8fO8TFaLS6VtxxsXrwM\nAFhoVlHxmFoKCRaXSU8ICICNZ9vxoCLao0k4xeFjOqQ//OiH6E5Ix3iVFsZcxfm1r38ZKzbd88Gb\nvw/BLSlWaxJ7DBdNWxdx8eTBXOMbcZfyPAIGnMbwG7/5b2JhnYzgH7z9Np7cpbyPIAzxhVeJrWBx\nacHoUpx0MeAq4CwW0CBd5zkSuaL116xy+sPyEvr8vkKtsMh0Uh8+vI8Rt8VwfAubG/T766ur2N+n\n96V1ZhrGnhyMDKPC00QsNLA6JbgnUj6ijS0AQOf4ITZOGf7NQijeOHajBsm5YmtXtxBqeufffedt\nWD1K13jphWsAQ1fxsIO4cG4GAUq8rtMkNlCw43hot2jPXVqu4skhN32exlhfp/f86MFH+IBTETZv\nPI/lzStzjQ8ABBITIFBKmc7nGvmsqaaYGVEE5xVG1KxJpiXPVJJbeuZkam3eKxlXJJnUKGqcLaXM\nmrAt2zilQmuT2ZDr3HT3V1qZ3MB5pNvvocLQmI48TLq0tp7s9mGnDBfrDFOGXJ3FMl54kVIxov0T\npD363PZ9+C6NZWOlhhJXZU/HCoqNqFxnEILuL3KFEVf8dYIQzTZXa4YBkjE51TWvibUXaI2P0hSx\n4mrHUQLfn58hATiH887lXM7lXM7lXM7lXH4q+dQjUd1RhJwT0xzPRY17EpVLLlpMD2ALZRpfSSln\nBIlZBoetYI2iBT39bTkcxVpdR4+rK9qNBWifrNeTXh+WxUnAlTJWl8nqLHvAzVcpufbb3/ou7twl\nD1BYHjKOJkVx8om+GU8VQYnjAJBDm7EIMYNeMqXw6BFBF++8/X382jd+AQDw2Te+jLsH5F198P5t\nlJgOxJMSOuLqvMYiHn5A3x1Mx2CnC1e2rqLDiXWOlKhVigRlF7UyzW2j0cTSInmDa0urOB5SSH1x\nw8L1K/NFaQr58VBu4Q0FcYxv/oCqLX7/T7+F+4+2AQBJHM8oCQRm86JmpLuTPEPEHrXi6E+9tYCc\nYa3f/udvmqKA6xcvmOiXkAIjnp97hzuYhjTGcqmEn718k+4dRegG83m/bnPVNPi0LYFLnGzb754i\n5wqfRKUmsuhWyljkCr6T4RAnnCAdTqaoMs1Rq7mAxgJVFH7mjZ/DhSsEHWfJFBFTbUTDISy+f63q\nIWHPcBwkOOQKxbLn4ObNmzw3bQiHPGFf2qb32DyiXBsP9ikyuLxWw8ShfbnUqGFlhSIMruvCZzJw\nKa0Z75QAnIQh99zDpauvAAAGNRsPjgnK6Q0zqBElqy/HGhVui1WOFFa570+p4qO8RhV8znILnfsE\nL/YPT9DiaOLKhUuoLdD1lWoDS298ae4xWvBQzendlYQNm3VPniksLdO7KPkeag2KRK1vXjbEtL4r\nkEyp+kvnMYqiYbtUAVBUc834w6JgiAlD9KXyArbaBCM5XgW+T8+QTMfw6+QhX/61n8PglCJyo5Mu\nKhwNsoUF2581FPxJksS0Vt743Gcx8eldLi0tot1mwmbHRmWNniNzbewe0jWvv3gF169TxM3xS7hz\nn5LdkygxFX9xFBtao1a9+sS+tQAAIABJREFUws8mcMyJ/Uvrm4ZqKYONmBPbp6MeXrxKkeMonJie\naYlSONwn+NGyI6xtVuYao5rs4OGQ1rhyK1ir0Dv87i/+HVzsbAMArr/7LVziar/Nz38B1gJFG7TO\ncMQQ6+GjXThMDXNTCYwHpPuiXh9JUKSSKDjMHQghDLQpbAfNJr2TFy62UfaYJ3MyBIMF8HWO93/w\nNgDg0XvvYOOzXwAAfP7rv/7UMUbh2HAWCiFntGRnOfVSbRLLLds1sKPKAbCuUnpWAU4UJyRSSENd\nZsmzuluhooviqwSJ4l6ByptR/ZyhVbMsAcURrVznz9QLC0KaquJuf4zdHU61US2kFq39RE6wco3S\nNd74xueR8frr7TRw71tUqCEnEV69Qvt19WILjzsFAXsI3+HoKjTyokmpzmcNjDUw4fWoVI6ci2D2\nHz2CrlOkOfUzcI9ZyCRCmj5b38RP3YiyHBvVEm2IeqOMKhtRjoRp+iW0gm0VXVph8kskYPKUhChe\nJRCnGmOGB6IgRpNzL5IkQT7mMmmvZPjhyp4DndBEamnhD96kHItUSTjMyzWcRmdaIgg8S5BOqsws\nNGpUxp8LYapYtx8/xp0fEcz1hc+8inKdS767h8giWggvvfgydna423KtiqBLm771/A2UOMS4/+iJ\naV56cH8HA644EVqjzhDn+vo6NjdJqXW7PQw516hz2kGD84sm4ym++MUvzjW+iHPRRK7NZpdS4tEO\nhcr/6T9/E3/xfTKiJtPQEEIjzzFhpZvmGVBU09izjW9poFFhrjNujGlBwuJD6869e/jtP/hDAMC/\n97f/FqpcyZbnuWm2+euvfRkZr5mjQRdNNiA7/SESNV+ewjQKjVKr+zWsbW4BAJaW15EH3MQ0DZBx\nvpMlJVxBiqBdqWAMOmgypVDjA9S2LIQMz6VKFdXESDNgyrl7J6MxSmx06Uwh45zBcR5izCFplH10\nOvQOY+Fg8QI1TBW5gP0MzTYr9QqWrtJeKS+W4EnOgyovoVpiQmSlYNlnSqy5WFi4LmrcODEejNB2\naY6//NxruMAwmTzpQ7tM3BxO8PiYDKQUM0UspUB7gX63troCMaH5vH9wApfn7dLWVZSZc9BvVnH1\n86/NPcZkGGFFMT+n38A7AzpQb916H0tc8ddqSNRLNMZG2YbFELHte/AdMkCEyEwzScoFKXKIRsi5\nRYPvl7G4ep1+2J1AW6Tb1tcvYIkJwHsnx+hw08Zc2Wiu0LsbTiIkLZrz/HSAIRtgT5MLWwR3LF+8\niM9aNF/f++M3cf2VzwAAypUyqnzfSytrGLI+efikg6/+DMHJaRDg+KTI/QHCgHRjYGtT8l5lvRWO\nAwwYZm+4DhxWaO1GEwM20K6ur6POeX0f//Bj9Hukk3qDMSYjWv/tFR+bq0tzjTGLIkwCmstxlKHl\n0xo5qCqMbnweAPDc5ga2bHruSqVuKshknEJ7dOBWPAf9onmt60BzJ/4sTjBlI6pcsuC6xRljGa49\nLTLjAFZc2+QO1RyBowGfJVmGccCpCGmGR3/wRwCAf/+/evoYVaaQicJoOcPbKqUxlixLmlYoSZrP\nkPszVc9nK+bkjzlUhVOo9axqzwKwxDmPlbUVfHRCDlAcTkz1n5SW6WqgoKF532dpYnIz55HmYt04\nGW7JQy7J4U/FBBev0lpY3tjAS9xKZG1zFccn5PRWb24iZ91p3enjCzfJAQ0cD49PuILPzeA3uPp5\nmiE3rXJsiCLloVRGxEbpdDyE5vcbTWJMh2RDeL6FWp30TR5oaGaEmFfO4bxzOZdzOZdzOZdzOZef\nQj71SNT6ast4euWSC6doxQMgz2fwXGZoWZRJcIujBGlWNMHKjTWd5bmBdSqliqn+2zs+MNxjtXIJ\njRp5amXPxoSTGuORRrlCXs6VjUu494gs8VwpWAVHgLRgulvOISqLZ8nkFlBk+yoNSB5jksRY5WaR\nk96hgfY+fvgYrVWyxC9sbODqFQq5/9GfvIkL6xRN+sqXv4Rf+5VfpbFnCXyGkaCBmGkdHj58gLtc\n7XN0dDSD2oIpum/N+uwsLZEH8PwLL+JLX6jONb7TkOauUapgyPP47W+9hf/7zT8FAPR6IxM+tQEE\nXL0ihTQVmFmaIeeKR9934XGPmYrvIwj4c4aRdBAj4sq3puvhPYYK3335Jr72xhsAgJ3BKR51yBO+\nvriG0yl5PLce3kHAUSxb2/jqc6/MNcbJdAwrZJgmDLDI8EijVoPjswetc9PQNIkCHJ2SR+QIFzXu\nzTOaTJHw2hmFIfrcjNH/+GOsbJE3BaeM2PJ5bhND2eHZElOOCkRJBpvX0erqEnxOYE3iBB73rKmU\na6ap4zyystxGc4vGVV9pwvY4+jvMgD7dx/McwwPpujakKBoCCogKV/hMQ+Tcy22z3sTiNU56Xx2h\n61BS8UcffYwRw3zlegu5YIqT8QgljqQ6zSYE94HLHAf1RdofrfYSplwF5tsKC6uX5x5jMFCoWhSh\nbFUWIYYUBTrudDHsEuTqKo3FGr2veNgzdCQ6T5FzxFpKhaTgbxS2aU456veRJwyzV2pYvUCRqIV1\nBzlHbFuttonYHne2kXA/vJNOD6cjumYwPIW/TM9wcHwMifk8fMVwx0cPd7GxQXDEhYUm3vnOd+iZ\n1hawtE7z6NsC909o799+6228dJnWcd33sLzAVEo2cJIx944KYDPUY/P76p328P4tSp4XJQuVCj1z\nSWdYXeE0gXob771Duufk5ARDrrb1vTJaXFVcLgm06u25xtif+tjUtI6GUxfVgPR4J9jA1jFFFl9v\nJsxdB1i5guLIg3BdJBxGKVfL8JluSFoCPkecRlKannBSWDMarUkIWaL3H44jKF1cow2t1LA/RIPT\nI/LaEia8TgeTBMuV+WEgoeUMtlNnqt4shSIUpc6U4QrMqvOEELOWdkKb6JnS2kDNkBKGHlII01S6\nBmC1zrRF0ykSjqpmaWoao1q2dSZ1RsNmrsssT81vzSMf3vkItqB31K41cfN1guiDUQUNjpZWmh4O\njwliOzqK0TultZPZEarcAPP1z21hieH9h4PERMrbDQ+C+0WejEIUvC/VRgOupDUzmGQmup/lwlD/\neUqaIoJwMsC1dYrQL1y7iiAczz1G4K/BiGpWXaQxLUxbZ7C4qZjKgSAk5TIJQtOpNNfK8I2laYYi\nWOaWfXPIVsplo4gHvT4e3n/A1yeocGVf2bVQ4UPClrlZFFGisLxI4cxXX30Of/6dtwAAx6cagi08\nrSQg5s+JyrU2XdnTJDW5PbVKBYMhHbTT8RAuGz+1Wg1NzgcLMw3JyjpLIrz0IoXc//Lbf4YyN3Kz\nhYDHoWVLa9gc4i1XynA4X2h9dRVf+Dx19o7jeFYSn2eI2LAMgtBwLi0uL+GESWSfJq5H379z7yF+\n53cIWvvR+x+DdQ9s38M0IkU8DQKkaVHxYSHh347jxOTGWdAo8XPYno2Dh6SIagw1Nuo11LiKsGoB\nJz06CG69+yN85WfJiLpQX0CJ19Lu4BQNn+bz+Y3LeHJKpbQNrwqvyHd4ikg56xScJAlOOQ9kMh7D\n53v4rg2PS/6lslDxCRIJ/TFU0UJjaRUNztU4PjxAd0TzshEEyHkN1kp13LhKOU6nx0e4f49gXiky\nOLzLwzjEEnfVrjSqhhx5cXEZTSZYTvMMcTp/6LnVqiHjrv/rzVXkbLBNsikCdnRKJReKqwsty4Ij\nuVIPEjYbvkk7xSAiI1f3cwxGVC4+Pt5Hj7t2j6I+ph1aICuWRsZrv+mVILgr+7DTwylDP9ovY/UK\nGSS27eDh+zQn09N9uO58uTQAUI0kSrz2+0uXcImfU8kM4ZRJhH0bMefcjUd9kzJgjQamohdQUJxu\nUKrUoW3SB6fHh3AMEULJNDuttxrmUHdcx5Sat9prmI7okIinBzjtkT7oDqYoF5WPdQc4mU9x7x9S\nW4qjwwGWFsiIunhlE5custHW6yLep7U7yHKUE/rtweE2vvVNaofy+us3jUFR9hw4/O4lcuRszHUG\npBsOj0+Q9GgOS+MhajZd6zVq0Lz0PnjvR+j16flLpZLZR67joc/pBmsbm8Y5fpqshF08PKT7NdDD\nrngZADAMTvEfv0R7y4ldRLyfcqXhcHV3NAlwsE/7f6ldhy3p82Q6QjIueFVtA5nFuYCe0JgbVdu8\nc0sJ5FzNl4URnrtChunKygKmRQWtlmgyv1urVsLByfFc4wOATCXGqVRKQXCTT0tpSC6xT4UNyVVj\nZVFCzO9J5zEsVZDwSlh8NpDtaDA5ZHx2WkLC42X9qtC4yc/8+3u7JjdMWhIFYJhnsxYHAgJZUKRE\nSAg9v8kQDDO0FxgSbfrgIxuVpkSdUzjGQVpkeaA/OMGYbYKaX0OV01wurNXYuAROR4Fp6+LIBKMe\nvWtHhcYosoWHOldWdkYZwrAwpF3kedF+JjPv2iuVsMDXC5GgXJ7vzCjkHM47l3M5l3M5l3M5l3P5\nKeTTTyzPlaGTi6MIY26INZzGGDE3XJbP0DPLFvCZj6jWnEWffN9DiSMCjgBOOVnz/oe3iZMPQLtc\nMkmCjgQkNz/LUwvjmD0MrXHzeUrOtK0EAfP0aUhjmSqtn4kj6NHukWELDyZD9A4ooXZ1aRHH/Jxh\nHMErKhMdF07Bx+YUdT9AmkSocaPRf+vv/m34zG0mIUxgTAKwTN+kHEmR6CdgegaVSiXz/FoB9XrL\nXFI0BdVaIVHRXOP7oz/8JgDgD3/3mxgP2JuDRMCNQePJaNZDKsuRcvQps6xPRMSKirwMCjm789OR\nRnuBIitFQv7B8SkyjuZ5dmaSXXudXRyfUjL7aTzA3T2Ciy6vbmGRoz8Xllp4+SLBoMNJgHsnFP5/\ncf3CTxzj0tISMg5VCw2IIpytFGJ+ljSNkBRzn8TodCgCs/1kGxFTDnzxK1+H5jWepgr1RVqPL730\nMspF1Vsa4QpDMbWf/0UscbPVBw8/wn5IkSutJfwKeYxOuYKlVUqKXl7dRMIe8mA0QvIMkag8jRAP\n6Prq8gZC/mowmkLyszmuj7zoN2a5hofNgjDVagv1NkYn9B4++uH3MGSIRYSxWROJUMgihjI9ifYl\n6ldUay1jn3uHHXQHCLjpXnV5HWsMQ0X9Qww6dP9RdweDPoX4/+3f/NefOkYvd1BieKrbbuHq4iUA\nwEn/HkYDSmxdqS9g2Kd3l8UxwJClEBYcjialaQTJxBz1DMhA9zw53EOJrxmPxmY/XbxxE/UNgh0t\nS8DjyMjy+mUcPyHoviwzxOy2ttsbKHHPKL8ywmm6+9SxAcD2E/K8Dw9G2NulaM3d7QeocmWuVAAG\nnEzdqOFnXqJnCjvH+OafEv2FtGIsrxC0J7IE3JcX7VoJU9aHx1zhdudOH1ZGF6xXyxCadOrdvQ66\npzQnUZQbMDLNUky46CfLMgNDr6wsGU7Up8mv64f4H8cUcdvvhsCQ9na5FuC4QvsmuryCfMJpH50u\n/CZdszsd4eN9rri2FarMkdc5GSJjqFZEOSYhRyFkjgo39j2dxOh26HfXlpuY8r7Xwsb6hS0AQCWM\nMeYoZt6LYXMVr8gSHA/n53hUWpvIiYCAdBnayxW8lKPdiQ3FdEzaUwZ+jyGRM/RGnK/F+sUsGqPz\n2RmjctQ46fx6vQqP93e5WofiymgNbUrJlVIGucmzdMYvK/CJZsdPk+XVmnn/vW7frIv1lRVMuOF1\nFGskDLeNRgGqfFbZOVDmQg0nVxhxkVUyzhFx8VgU9zFi2rOSY2HETWbDQYAVhp1znSKMi2rRzKQE\nKaSGZmrz0oaxUaTUSLP5ipEK+dSNqGkYojckZToOQiRpYagI80Is2zEVfCVPosQ8NrWKa/jDoLUx\nlna2d/Bkm5SOY1uolGkD2dICrxskSYzTCZerKomMiUhfemEZr71CmPD33nuCU1YEWtomp+EsifA8\n8ujxtskjgVAYn5KC7nYOUKlQmLBSrRkrQaUpIq72SJVGxmOcBlOU+OBst1qwUECfs3wJ3/dNTpTn\n+2eqNLRpznmWQ0kICa0L/jplNpllSUzHAeaRN//xmwAI9y9+L0piTJjcNE4SSF0QfVqmTDjPYJrI\nKZ1DcDg6jgNIPogWF5fQ4gP8gJsq1us1hAmth0xayFhxT8IhTkZ0uB6kfdze+4Ae0J6g1SLF05/k\n8Li1xWnWxc7gIx7Fz/7EMdq2DY9L3S0hZ6SbWpsGhEkcYMDN/nYfPsTpMRkDSZaguUxG2sbGJQjm\neep3uljbJKz9xpVr2N3bBgA8vPchUubmu379eaxfoZy4u7sP0BnRnDaaq7h0/SW658V1lLnZZhjl\n6PN+UnlmQvnzSMl1cfKYuwbX95FzfD1UMZZrpLxgWXC45N22HOPcZFIaI2raH2H3HhF/nhzeBdiQ\nK9k+XIbERZbDZiPBSmN4Fr1PbXuQXIVXb1gA5y9VN9ZR45ySxx/dRR4V0ItA5+GducdYjWPsN5jo\nOY6xyM88sC34Hv2W51eRsWIdZ7Pyb8epIGR4cdTrYHFpmZ85Rq4Yrh5NcDKhOQymA1i8NkQ6QoOr\nSyvNReQMk7h2CeMhV2hmNixe92vLVzF+SG0GahMbx87CXOO7c5d+u1JuoMJdxdMsRu+UDpm6V0K/\nSwfUaDTA514hSHgahdjbJShxb28XS216B5YGatxs0l5oYswG62RC9xOORDomvbi9f4xMMN+pslHn\nKktrFBmVmWWzSjOlFC5tkdHTajXmbmB86WiM/+Rl2k+DhRK0ov087gfwfXq+958cYWWZKiCdRoJh\nSmMuuQIVj57x1sM9vLxK+jSaxijzfI3DAToBc2NmCcp1elfvPe7jiJ2MxeUJGuy5vv7ShVkuZKbh\nMPFzxc0gOeWi38vgO/PvRUu6nyBeLxxjuC5Cdp6d9gak4IrlXGNlkXTAWElMudVFcvAAOefcQcPo\nrTCYmKo6Swh4nD7Szcs4OKCzsG9pZAWhuq1RK9JHbNvsCaUUtOHuFJ/g8XyaXNhahso4jzLOsXmB\nHcemiyyn+VSpRpYUDU5XYRdYeaRxkVsN9I92MTjinOZ4EdmU9lNvOEIw5TQEJ8fRKfNEngYoNSll\np1ot4XjIHKE5oHgNapmjtcStUKo+ch5vrjXyoi/DnHIO553LuZzLuZzLuZzLufwU8qlHop7sHxkq\nC23ZM+4xy0LJnzXDLKJPnhSGq0dqZfjyoCWOjijEfO/uPRMo8Ms+Bkw/4FqAXTTn1ClKNaYCaDq4\nwb11vvqz15DE5LX82V/8ACFHZqRjo7AphfirjSV/kgyOd007/NryIsoVTsYVDiyOGiUqhcUJ1zrP\nkHKDRd9xcdojr+/d9z/EG18izi3PK8OxySJWKjON0LIMSIrKkiwzEJ4UwlB0KK1xpumHSRiUUkIU\nfIKWgx5TSDxNcoZC4zRFwFUwWisorgwTeY6UPYssE9A8j1k+ozNQuYLHEac8jhEVAIBfwoULBLkk\nTEMy6HewuLTG82AjB3kYO6cj7HGS+frFNfyNN36O59nCiCMXQgARJw8KV+CVGzfmGuPB4SE89jBL\nnm+e1bIAxZG1YecUT+5SVCQYdNGukseYq1lybjQe4sJliixdijITFldpgqNtorL4oz/4XUQMyXmV\nsukpZFdqaHPTy/XlVfO5lj5OOXE3jhLTh6vsV8x+mkcsy8bR0axa7cYrVLnYaDZNjyyV53A5ed6S\nAmCYUkobCVdpfvzR2zjaI8jEAWBx2D1XGTymXvDsHIngfVBqwPVortIkQ4O5r6QdQ3DUcG1zDSlX\nCu3vPIHg+Sl7JYTp/BWIS2GEvSZ5mDruweb97S2vm2a6ifaBpChqmWLCyf8QFvoFf6NQ8Bkiq2QK\ne4cUAdre3sHBYxp7NhlgjelvFqo+NjdpHVvCQW9COqbSWMPuMa3f7tQ2++HR/vuYvk+R1LU4RKs6\nX+XaAlcwbqyvEw0SgDAZYoEbiVY8H4fMrzcNUnz8mOCp6WiKBe5FVa+UEAe0X1zHR42hx7LjIB9w\npSjrlVq9gjHr1+NxgPY69wTLFKKA97AlkPF8UkFGkVTfQrtN4xLSmjsSNZ1EaD2g9d7cnwJtiqJI\n30HOMC8gIfldyTRHiatFrSjDBab9eWes0CvTOD9+dIoa9+bb8lLc5UR+Syjc3qP7PEwEDhJay22l\n8RvcBLLiCUTc2HcyznHIFWRl34Hkc6s3HEM8A3feysqaqaAWQsz6GJaqOHbod8OVS7A0jX0h0Vhd\nYJ0USyhBEKRfXkLG6RP9QR8tjsCMjk9gcWQ9no6RcjXqh7FCjyuZQz+EKvhZfRvLTNHzifNPnOGF\n1TApGfNIq9VEmhTvXJioeZSHJuJULvuwzyTAK5uvjzVUj/5+vHeEBx8SFF9qA7UqjfH4NEPEUHN/\nMEVnwAUraYSNU4oory9twCsxrYzwEHLfQiVzTJm+6bRvwS8KSpRAms2vb4C/DgJiZcHmMHqpXDJ8\neb5jwWV8wLFh8g+EEpjwpu0lCYJigfQH6HPFFLQ2kJZUMQC6puwCVcY5b15fxVe+sAUAuHKtjY0L\ntEB0ZuO3/s/3AAAfPj6ANuyygFRc5SAyU10zj/S6JyhxKNQqeWhweNy1JcCHBGwbIcNSKo5QYlLE\nk84uQr+oDJCmss11Z7RoWusZr5GAwcOzPDtj7M06pROmXfAdaWNEQcxGZUmJXn++6rwhG05xkiBi\ng8ImAJ5/WhnIMM0yKF6QaT7jbNJ5DskVecKWxhA86vbROSWl/yKTQfffPoUrCyJNgQq3D5gmGW7d\nogOsudw03cNTnSNjAlcp5SwUrZWB6J4mWZYj5KaaQ4xgMS5s2xoZ86CdPHliGm8u1MooswLNcxua\ncy9Gx7vI2GDfvHoDXcby4zhGlQ2VhUodfVb0aRgjZSz/4tollNkosmQOu4gTa8BhQ8Wvl+AW3Yqz\n3JCPziM7e/szgyRVKDMM3mg0zX0c2zZGmtA5ElY6ll3Gk0dkQO7tfgSnWMtKIGdDy9YJ6sxx1Wo2\ncRDQflpYv4r2Ah3gUZwCKGqvIywtESTULPtIUprnpaVlnPbpPpEQyDC/4o5LFSyxQe1PQ2huJRHB\nx/42wa9ZkOP680TYe9Q/wpNtUtBlT0JxPlWlVMLpPhmcnYHG/n0ygA/2dtDnEuiFMEbMJfFBOEH3\niEm1S3XYZSZJ7UcYPCbn77sPHqPpFCSvGWRR/ReMIbly8GnSWiB4ajI4RZkPpQvLDeQMD6d5iiUm\n4G2kKRDR3rKtKVbXmWcsyRBzi2bPcuBwQqcjLDicw2Lz0eDqEerc0HAyDdDmNISy5SG02TkuWxhP\nybAI4tAwRRyd9FBv0vofBzEe3N+ea4y1ag2Sn0NmGugwNGrlsETR7BcQXEUqbAua84IUgCaTSzfD\niuErTd0y3tyn+1xIhhizY3+cZLjJ+ZRlzzf5nH42RTUtoKgGjruUonHYHWLC8BPaddisi8MgQP4M\nfKuVyqyKUUqJnPOA/cYqrlygxqmBqiPg/KuVRh+1AeXWiczF4ZQM/M0Ll1BjA6k/HJoWNhYkTvpk\nHG4/vIulTTJ+T/b7OJxyQ+p0CM8umnAqZGw8WNas/D9OEqRqNq78GeC8ex8dYDwh47M3HKDoPB1H\nGjHzmy4tLaDKecBJHEPymhZRhKvMzFAKPXzwmDkjD+7jjddpfip+CYMefT6YJpiwmpgkCgfMBrC4\nmJm2Sr7lI+cq6tQGHu3Qvq9HARoV+t2yrJoOAvPKOZx3LudyLudyLudyLufyU8in3yeq2YBf9G4q\neabHilQ5BEM6aRgg4D5R3eHUNF8MkxjTKXl9eRKhXibr23Wr0Dldf2HDw5ULzLPlaCw26LdevbaA\nV69xonBjjJwjJe9/GGNvSJ83ltfR3aEwvRSyYLh4pigUyaynzHjQh13lG5V95EWVn0gw5Bb4t7/3\nPVzmhLsHDx6g8QWiXymVamYePL+MiKvSpCUM7YSQNh48oGjMt7/97VlVHICYK6OiKDoTjSFvAgAs\n2zZUBo1GHQvt1lyjK76v8tz02aBSDforzVLE7K2kWQZVYK1nEiYtKZFwY1ChcqScLO+7Nm7fIv6p\n5WXyoJc2LuHJPUoIX19dRdH7pFSu4fY7lHx+47kLuHCFvKs8y0yfLq1NpxQopUwC99Nkob0Alc8q\nUrKEIhLBuI/9bfIAs8kYzTJHigQMfFou+cgYfhoe7+J0l97P4qVraBf9wCYBlE0e7wsvv2Z6zWgh\nTR+11aU2OodU2dleapvQPOzSjM0d2nBLaqWRxPNDCLV6E6tMB1QpV40HqzU1HQQA1xLQnER7985t\n3Ll9GwCwubGFboeeLZoM4NfIS0Q+q2MtlX24Fve4URJtpmNa2rxqqvycXEKwp1fNFTym7ilLwOEI\n2wuvvowfbtM6fXy4A+nP7xkObQ9eRjpjKR7isEYwl6NzLE3pGQ4fdBCc0JwPowSKe/REwwARR1Gc\noyHCE1qje+UMDkNX67IMt0HRrWbagRPQeMdRjgPmJUyzDA5Ta4w6FpY5Wfv15iKmHBltpzH2m1x5\nZe9gKZ6vsmvIPadUkEAz/LzQKqHR5MR02wNshs3TBLGk9VHzbLQ5zUBCQbLqz5X4xH71uVebXyG4\nSKg+2gxr2r4PyZValbKHOldAZUpjkffu5SsRhlz4cLB/iF2mhjo6BKqV+fgB+/2u4VG0hAWLI6OZ\nkFBOAS9rE22XKjdRlERlkDyeGgR2udr1jdoq7o9o/b6yXMa3dhj6mSjscW+iv3dzGV8CjePkZISS\nVexRoHNAkSjLllhp0J5u1ktwuadQEkUQ8weFEYRjkwIiLWmKmbIgRpk5CcvlKmLuy6TsZFYAYFWw\n1iTYv7bYMonlC6sLprJ2oVRC1aE5vNB4EZd4zfYXPSQ3m/xbq0jTLQDUJNqcJULg+IiiNHGamLMt\nVwrPULSOh7ePEDLMOg0j2KwDKl4NOqJ3NIrHEM2iGljD5rCRCwfNBUKPSolEvU6oyf3TI5xwQVOt\nUodTovdrZxY2tmjv8bXEAAAgAElEQVSdfOVzi1hkrk4cx1BP+OxUJVgciXrptU20rzNsGitYHE8q\nOZ5BleaVT92IWmlWTOmkFDky7jAaRjFGnAMzDQITtoxzwGGlliWR6fjtSRdgRdNqV3DpIm3sX/35\ny9hapkHf++hjVFy6vlWOUJwvpdDD7Q/JWPrOuzZSiw7fratXcdzhUsswgW0XGLXEs6wWKYEgoLEE\nnS6eBBRGHQz6mEaFAaKxtEih1ne+dwu73MDObVTQeUCbO5O2aTz22mt1M28OrBk8l+emS/nOzo4p\nG7VtG+MhQQKTyQRXr17l+3wW3//+DwBwk882LZytS5cxnU7nGp9QRRMz8f+092XNkmXnVWsPZ8zx\nznVr7u7qbvVoqSUhNAcQxg+AjeEnEAG/wH+FV94cQYSDF0MgCIQwFgpJLbll2Rp6rqpbdavukPfm\ndOY98LC/szOrDaqsimg/nfV0uzrz5Bn22fvb3/ettdDK4NbaQLdBlNZoLR+1NdBtSTIIAeoV0kzB\nUkATCIblgkpnlxOA+t5+8TNHwf69r/0DSBrI5+fnENSfNN7ax4svO6p8ncUoKS0dxtazyJjFmqyC\n3piu2ktSz2i0RqPJ3LmefHqCjFL5W/0URDhDwFcCq2EoEdHkXpdLTB66QM9CY3zgAokwSn2/03B7\n7D31wJnvDTw9vu9ZadtbL2FEQY7hITiV+Zg1MKotpdE93hBp2sMeqeYzcC8pYbUFp7FvjcJvf+WE\nLt9790e4JKZpNj2B5FR+CkMvAREEHBGVXhgaNCRuGA8PcP0VZ/Qt+mNo6o0IAuYXuTS1UPTsq2IO\nQWyo7YN9HJCkwL3FBewzkGXO4x72iPacGoGcJkfLjGcCKq2gPnaLe3B4E2bbzQej5RINyX6MUCGu\naTxEgCWPzVHTgA2oT8WEiGtXrjp9cApF7QCVldjdc89rel4imLv54FUu8CFzCwNXFV6N3UT/eLCL\nnQ37MHaIjl/LGgdUIt3e2/I9Z2EU+4VLRBI7o7bfiYETa7TO517QWCNERiUsGXOE5L8pEmoxEDF6\nNPZGW6NVTyWzSMjfsGoYRmM3tyVpgPnCzanjcYp7H9913x2l6KWbBVFbf/RdjMhnr7qYwV4SC3g6\nQ0Nm7RbM0a0A5JOpLzlxvjLe3euNMFu2zgcC//y6+/3LbA5GbNFXrw9x79zN3X/6Nw/x777ryryB\nDTHP3Ng8m1xC0Q57b9RDQmvMzoAjJNbszmiIesP5FMATZsHGACEtxdligZ++95cAgHT3FmpS/L6e\nBuhTYH6+bLB/lcajvvCMWCkDjGh+v77dx/tt/2YxQ0kyAsXFGd76ouuFFGIXf/ljJ8BqYGFpDKpG\noVwQ61RxBIZKq89QygOAb3/9DhjdtyiIkdCGKYnilagtaxCQvEMUS+iq3SAKpMROP/rxJxgN3TN9\n4+p1/N63nSD1h3/1MUSPNn+G4/V3XBvFt//4DTQLd8x7PzoCD9yYaWoDTnPttcNt3LrpNh6zmYIl\nUVPO/TKwMbpyXocOHTp06NChw3Pgc89ERcyiJNGyZZljvqQ0+rJA3TZDGgBkLxGnIRg1L+pGwVAp\nKUw03viC05m4fW0HWyP33a1+gItTsppYVJjTLnfRcJD7AXpBg7uXLmKd1ANosnAYpBG2xy6if1w8\n9iluwYUv/22CH/zgf/rodX/3EJrEFh88fOjF6y7PpxhSw+fSAmHbEK4b6GOXOu0Ph3hIlgWvvfYF\n7zfGeAJOeh5aa9y548RC/+RP/sRnoozWXiPEGIshNVdKGeA73/4O/ftKzt9ahu//4C82u0Da5aVc\nouXzLesSkG1JQHspfsaYb0q0wvgylIHFd3//ywCAK9d38F///EcAgJPjR6iI2ZM9vOt+5zc9vPa6\ny2I0yyV6ZFOws7uDisq4P/z+D/HaxGV2Xv7SDd+Qr9d8FZVS3sYCr/7uS4zDGLZtJucWd6kkd/TR\nhwCxxsJ+hKC1tJBypQ0Gi5AyZ3XVwFZuR6rm5ygpQzC+8iKiyO0kLRt6Abj5fIai9Rq0DbaHlAkA\nkMZUMpMxWKvmajRAuyZt7Io5swEapSCClnW4evWNWYnozaczfPrxh/T3BG0ljZkMAaXCA4TeDT1I\ngVC4e19WDczAXePeC2+iv+OeT2mEz/Jq1fiyqZQCpS/jz7BDXpfWWuySz9rrN15CfrH5Dn9ia+zS\n3yUPIIk1eljl4JXLOKTMoE+ivFXYg6KxwxjQp/vyctADp515UeWoyD9sUJdYFO6mzJoSVyihqCcN\n5mP3H5nmGHB3r67cuYHFe7911zudYczcG/TQLLFPO+2d4SG43iyjOKYs2PBwFy+RF6PSGSrKPknO\nEJJekRAcQxpP0tYoZ21GuYeSynKXJzPM5+6cBkPpNNIA3D9yGchKMVzZJZZiFCAeU3aUCa+1FUUD\nnx23tvGitUEQ4NYLTuwzjDiWi2Kja3z5n/1jT+ywYL69whqNmtYPDQXRapiVtdcHtIL55mRuLd78\nW8eAPHnwHrZ+7cbRg0UGOaAsmooxJmLkQS/Gf/mZIwF8640rOBy5zMmkyBDFrQdcjK2xy2jJ0SEE\nZTFv3jZo5puRAwCAIwTz/n0MnMp245BDErmhmHwC1epB9Xo4IlXUAkA8c9WFk+Wxr4JYC3zxi67p\n+vbXv4mj953n4fn5Ofo9dy3zxcJXR3Z2d3F6SnpgYN6r01qDgMavCELPHzLWrmlGPR1vf+FlhETs\nCHngRZON0Aiokd4RkoiYIgJwanMpLQMjvbrd2xbxL1y15oXXb+FLX37HXftHC5w9IN9VCez2XKvC\nC9tfhunT2nTYwy9D911d5YippH3r8C28tHPb3c+eQqshGvL+yi90Q3zuQdTkcoEl1aWzskSjV2aA\ngmr3oQw8Jb/Ol1hckp+WKnHtqpsS33ztGm7ccOm3bF7gbOqO+YOfXSCgwVjV10HvMmTOEJ9T1/9i\nir0bLj0chgxTmjSK5RLX99zxh3HoS0KzRYaL6Wb0fwA4fvAIDU0coYyhial1ucjRC+jlS1PUrd9Y\n3eAeTdwjNoQg+iwTDBWxod79yU+wf+BKL8PhENmS3nSjUBOVVggOTZNhXdcoyb+urmtMiar86PgY\nEQn81XWNgj6T54XvXXgaLqkv7Vp/5AXlzha1p/67RqQV00S27DGjPWOwN0rw5W848cibL12HpYnu\nP//H/4XJiXtopOiA0wcPsL3lntfh/j7OTt2E/stf/BzbZFx5+/pNPLjnouR0P0Q8aPtmGET7+8yA\nbViWjaMIjJgq2XyCI+qDiiRD2E4oMAh4y1yDN1EWjCOkXpcw1WhasdFigfLSMbya/hhy6CbcRgQA\nmWuWZYGC/BX3hn1Uu26MN1XlKdAiDFY5ZgNfvzeA9+PbBHVTQNDEFEUB4PvIFGqSsSiKBWZEkWfQ\niGjiZlwjaINmZRBQUKG1Rkm9eCKIMdxxsgyD7WuwbX8R57CsNU+10NRjwdjqHhaLuWPwABgPRiAS\nG670d1A0m5csd4uZ96Q7ZhI1lZl3VYElvVu7guGAygwndYFw5jYxPB253kgAsdGIiE064MyP114Q\nIqVAqwwjTKh0pXmK88fuPVGDB3j0yDH1Rr0xrm+RqvWyhqQS1BlnCCkKGPSGOIqHm13fjgtSb964\ngz7JIsyXFjGNJ+gGumrnE/heSmstxiO3+E8va9w9cucXYxssJ4bZ8sLXJhT1rJQaSKkHCEzDtt6O\nZY45Gb+nowYydmO+rAQk3Z/haN9phABodAGRbLYA10XpBV+jIIAh2QzBOYJBy15NoWkuM0kI3pa1\nrYFqFbYlw/bbbuP28Qc/xYz610wvxZdbRWsW46Nz945GCRDQIjuvGhySw8RvPrjAO6+6IGTnxddg\nae6u8ikMBdrMWCQUqGwCY4w3IAbnaGjDHDY19ihQqaRCa1CYNA2kF8FlOLrvEgc7O32cXLjzr8oK\nmkrupxdnvl3DSou6Vd/fGvr3e7q49CVZ6+ws6OxW6wqM9e8u1qVzNsDNrS96KSLOxarnStg15wy2\nJm7NIenFT1kDTa0g4oUASJ0JfV0zJH23nr32lZdw8sBdSz2J8PBTt76eP5ijv+XGYG0XUHRvZcBx\n7XCH7onBKSVfYC0a6cYSt9b3tt188XcLNLfoynkdOnTo0KFDhw7Pgc89E3U8maNuyztM+BRm0gvQ\nI82obDHH5NSJwqEusUs7piju484dJ2A3GA1xOqFOfNFDRSWNiwUwJAaUthJGthpKFUzj/p4vDCZH\nlEo2FkVGHkrGYovS41vDATRFykfHjzCZbp6avXXztr+u4XCI03MX4RZlBdZK2hsN1WZulEVC7JNK\nWUxOXJPr7u4uesSE+f73/wcq+nwaJxiRHYxWDYq69VezSMguR0qJgjJ+y+XSN1cLIfxu/9q1a7hC\njcXj8RjbG7LzcirHni0uIEnrKBQSS0rnCyGe8JprGYDGaAgq47z2pRcwpLJAUeR44/ecIGWvH+Dd\nHzoG2M9+5Bohy7LCfOHu/+PjI69bdOPmbfRI4LKyCvO5O6+Tx1PsRO45Gm18mp8BkHyzfUIYSQjK\nIB49vIuYdi8Hd25CUtm5ygrfRA3As8ySuAdJ4y5KI1SULtd1A7Vw2bKLRwE4sQbk1hXY1srHrOwi\nQi4RSvJukxEspeZYxP0uThjWGppD0T3eFErlEJRV05xD07PkHJ6BE4YcresBDyUiGl9cK1+ytdBg\ndJymseDUVC9liD4J4QVh4nebnK8YfC5z1jrEW0jK/AySPqZTV1rIFo+9hlVdNWAban0BwKhYgpMA\n31E/QU3PK8jOcTZ2mcDXlgtEpC13AWBImUv0x7igLMOn1QIjaqiexwOckC5dGJa4oKZrm6RIKItc\nGIVL8vQ6+eiuF45dlg2+dN2RPO4MxtBUrqhUiQllycbFHDPSinsa5jP3e+b6Gisy6UNRlq3KC2QL\nl4UuihwBaZmNBylukjfh3tXruEeEmnufnGJs3Wde2EkwoexFWbrxduvl17F/y7UhzB4/xOmJy9qF\ncYprh2S70usho7Hd1ACnMRxECTJqx9Asgow3YwgEUQxJ77zhDJzIChwMhuY+jRqWMuxBEINTqdkY\n5USI4TKsJw/eBwBcqgjHywVd5218bcvNP4oJ1HccWeVPf/0z3LnunsO17RR/9lNX1t4WDW7ccVn0\nZrqEnjq7nv7WGAF554Wm9EzyTRAHkU8uM85hiFQRNQojIo7ktoamxunEVAjJcqcwGjs7ZA2Thrh+\n2zVU13Xt2zUm8/OVgC6zKHVbpSg8Y5oHgS+9Gmv8eHrCYxXWkTJAFl7P0HQ9ze97XcFG61a3l2xe\n20yU9WuVMcYzdMG1Jy6pXCC3JJhZAHfPf+XuyXXgJjENT//3p/jkrptrf/gTibe+7uKGmb1A0zLV\nG4OIrKWmdo554RrOJeNQdA5Wc8A8w0Xi7yGIUuAAlUCEZE6AEi6AOTl2/T/T8xMc7rsF/c7tm9jb\nc5Pdsih9LTprNCQnPzVtwIiyI0WAkhYtpSuU1F8zW+Yoq5ayrnAyof6iNVbJwfa2Z5tZDu+fs3dw\nBacXmwdRX//a1zxNmDFANW6CfsBPVordbNWHImER0SJxPrl8wqcopuut6go5UTmbTAMUCPV6KQbj\ntt9JIqCSw9bWlu8FWiwWnhYchqE/5v7+PvrEJjHG4JLE2J6GhH57XuaQlOYNhVwZIZvVy6W0RtSW\nfbTBaNtd51e/8TZ6pCStKo2YzvuNd17G4Q03GSsajnc/vo9LWgjyyxl2ieoqmfS9A8Uyw2ziPjO8\nInHtRTd+DPQT9AopN5u4hQxRzl06+OL0HNsUyI/SENRChypK/D0Ow9D3gTDG/TUXZQVNPX1cBkhT\nN2ZzVWJJafehXFskLEM6cGWZ3vYWtolBljU1JAVpsjYoaTGqBQOj79baoGk2F6JUSvkgWErhU/OM\nMy+Q2BuOcfvFlwEAR/cYBC30plgF5oHgK4Nuxv3kqwzzgnpM8CfkN8zaGF+pIWNFU4fAoOcmxMnF\nBA8ekFxA3aB8hmsULIAkGQ4JICNG2tzWEEPqScxzTFJif463EJy7wEQHEQqSDVguT6DmbpLV6Rbm\nkXvnLphGCfcsuDXejDjKLnBJBLujKTxTNklinFKPy+5oC9vkAXbDAg2VpqLlDHvFZqV1C/f+LrMc\njJPBs4ydUSWAvZ0B9rfcGCqyAgWpMnMZgpMAaG/Qx1e+6cbctPoJHvzGla6vja/geEL9fyMXcL39\nlW8isO6cm+USI1rZhuMd9If0vOZzKJqPo2QbPVKk19YgoQDtcrr0vVdPg2QAbLu4czDq+eF2CRO6\nMr9GgHDgSjNxnELTGLFVjpqeeZktkF26wHxeWujIlfCkMchIlV81GjEtmt86vIX//qmTVvk/v5yh\nppLm1771JuraHX/6+BMc0FoVDfqe1ToeRHj7W/9ko+sDgEAIX64H3KYGACLB0Ws3qtHK/SGyAQLR\nMp0NWI8Y7FwibZludhVYrzPM1t85YeBbLCxbSefArt5F9/n223bVR2v0s1Tz8OHk7sqTDtYLdSpt\n/f38rBdfKyQMARS0ebWXAhmVnKfFFO99RLJEEnhw6jYDeamwoE39rz+8D5Cw7PxyBtXeDMtwQmPw\nF/fuwXD3wnIFKE7no4UXtv7j72x2nV05r0OHDh06dOjQ4TnwuWeihAwhqHEsSQNk5Hd0dvwAYeCi\n1C++/SpeuOU6661WMJTiT9Je29APDuZ33UYb1JQmvDi5QJ9S9kVV+ayUttZbGMRpgDR1O8nBoI8e\n7UJDKX0TmbEWNWVZLONet2oTlFm+agIWHOO++60kSZC3zX2q9lnCRhk0xKqrmxq7uy7TEsexZ6Ls\n7OxgZ9ft6Mw8x5tvvAEAOLh1A3vUcF7XNb73ve+5YzYNXnzRpaifZOFZnzHJ89zvBrMs89mqpyEM\nWjZY5HW+OOcIKbNWaeWvXysD3rJOOMfeVbfj3d0foaBGVIZVVlgbg/7APY9/9AdfAQD8zXs7eJ90\nvbKLc8yo8fqTux9hQOXXqi6Rzd29vfXmgWefNI3yTZEMFmJDZ3UjY68FowxAQxOSCZ89DQfBakcn\nhM8CKqX8TniQ9FDXbjdfNcans5dlBU1ZtPziMaZ07lwE6F91WlJiuI/9kcuWfPjRb/Czn/4VAODs\n4SM8PnPN9fHuGKND95miKJGRJc2//pf/4qnXyJkEo1qdtfaJbBInITwOibe/9FUAwM3btzG/dCny\nT371HirKCDRaQ1BNkTMGRdfFeYSAtGDCKIKm6aVpmid2nN4zTK+EHrW2sJTv7/dGaMWh8jzHPJ88\n9dpahI3G/dYORFjsVm7sDC2DpnJLvTzzmZY4m2GPvmu5REzM2uvgKBv3jupijl0qU46qDJWmdwgM\nE7I7GUuFwNcfgMa48x9yjkPyhhyOr+H4I6cBVBuDsx2XcY8HW1DL842ub5ey9GVdQ1D5fri7hUFK\nthWJ9jptWhnkbfM1uLdGKRVDQlm5L339m3g3c59/OFugJI2+N8hXcWdnF9PWZy6IIQM3nhdZAbS2\nHL0h9sakP8b7OKcM99HxXSxn7v6U5cy3HjwNcZr4bAnjHPnMsauqxacQY/Ifja9hcebumQolOJGU\n6nyBnNiuebbA5ZkrPy4vTtDfdmvM+clj5D13TUf5Ar+971pJAmbw60cu+7gzSPGHr7uM00txjiRz\nLRdbV7eRkFgcY044GACu3HgBX//GH250fQDQVLVvAQEYLFVrZlajprYCowQKoh1yXSOgknslOajC\nBs3VWvZpvQxl0JbNzZoCsbDwGWhlrdf3A7ykn5sb1qyz4N/RZ9OJ+vmHx5740hgFRd/XcAKt7W+1\np825WGtV0ChJQ66Xp5iT2O2sXMLecwxKHgLTE/cuVnmDWrWlzAq/vEcei5n1bTrCcmRkd/Tg/AIm\nIg250kKTjRUTDGzDFpAWn3sQlYQBmtan6P5dlGR+uD3q4+ZNR4G+cmUbs7l72YyBFxYE454w0NQK\nC+ozaBrljRB5o8HpBmhtENHL1B/1ENPiHAYB4qQthyXgtIQXZYmGHmwgI0/xrJXauF8IAOazmV8Y\nAilQkXjdoN/3/Uj3Pn7fD8w46UPTAJFCrmrXxiAnplM1r6C1O84Wj3x5ILvbuAkMABgwo0mqVRVv\n0QZOk8kEU+rviuPY91yFYejNQZ+Gm1fd5PPx/bv+ZdTGeNkFppU3keRCgKM1l+zh8KYLECtbw5Tu\ny8si8xTmJAz9yz/eahdj5pXbX3jlOh6TQejF9AIXM7egNsrg9h03cd94dYxKu2CirrVfmJUykGYz\nteu5Bh5PXGp4UdWwVLLJMgtLwVKZFwjpeY7XTHvruvJKwUEoEVH/Wq0U6rYnRDXIyC/q6N4DZKWb\nKF9+7W1f6lrkFcY07pbLAn/+vf8GADg/OUNNs6YcpBDkNWXN302H/y4IHoDz9pVn/vm5VP5q0epR\nmWa0tQWrbwMA+nGA937qhPlUU3t5C6WVn5j6EYemDZAyprU2dBsD28oarEsrGAje9r5YNE17LQJJ\n0sodMC9nsglsWeFy180rl0mAAQmyynCA9MwF5vtMY0nBpCguUYbuemdaI6Py/oXRqKm354FoMKPy\nTzA+wLJ079MxNyja+1A16NG1j2QA3XPPMZAMYUzq5VmApE8MzWKCBzTnnR3ewL7ebCpuS2hxKsAp\n4MmKEpkhf8ezqQ/6BZOQISnC90dQFNhBczB6L8Zbe4iG7h39q198iJdevg0AuPWikyaomtoHt5ZH\nkNQPlkQpJAXMlocoaM+ZZzMcP3KlWGsUYnIyTpPU9508DVwIRPRulY9+hdS4dz4XKZC5ICfUBZId\nJ7pYGw5TE82/KcDbUqCq0KPN1dUbh1hST9RZxfDLyQcAgA/O5+jddpIx//QPfh9/OHFCs9XRb8Fo\nMxbEEQJ6nlIY8NgdU8YDL82TRhGegSgLaw1saz0KgNOzqbhESS+OhERD44IzC8bankTueycFzFor\nyVoQZVdB1Hq9af1d5LC+zxHGQqzV6tr5QGsFH7HJNWPiDbAsa39PtDW+nOeSJDSm1kuQxoKv9XuW\nrE1MGEQD96ndrSEMvYtMAumeexb5vcd+8yzTfWjTthBZhKmbs/NJAUuCuKph0BTEGm1h2pYja3x/\n76boynkdOnTo0KFDhw7Pgc89E7XVS/Crjx1DgpkKb7/umlbHO9urbMnl0mv7BIH0TWe10iiorDZf\n5qjpb8m4FyJM+hE4cxFoPxmgT428o1Hfa9xEUYhGkUibqrzdhdKNb4S1gNcXaZoGKfn0bYLpfOYb\n7oJA4mTiMiezxdw3dfMgAtTa1qPNXHAGQ+cmwwB1s9J9WtBONd29gXtn7m87neI+WR9EYYSDq46Z\nYa3BfRLqNFqDU6muKkpfdtre3vbNwUopPHz4cKPrOyBG3+PJGc7PXQpdBoFvDjdNA9kyTQIJRrH5\nwcEIV2+7bNfJdIqI7Ftmy7lnpA2TCA1ZgjSUeetvMdy65YosN14ZgVwHcH50AQuXwdnbHeLNb7gy\n2OgwwpQac21joOgeamUgws1Klj/7za8xOyZvuCxDK1TUCxk0sROhLQLaIRd57u+r4AKMcuEsCnC4\n77IN8/MzmMadF69rzC4oi4YQL77gdr/L+aW3Hnrri1+BJCG/awdXcZWECvNQokfidGDMNfIDYEJ6\nkcxNIETos09SSp9GF4J7sULB+Uog1cI3nB/efBH3jtx4eXB037uwczBIarrevXoTe4fX6NyYH2sM\nqxJeo9T/syTqSgitAJ9GUbTWNnpjhiUA9OoMfcr+ZcsG44KsQdIe8sadf5SM8JFyzyWMJMLUZWLy\npI+SshhlEKLPXNYnzSrUpBs34in6oZtjTNLHXuHObXfxMQIqjcTxHs6pFC/mM9T33Pkcnf0tXp67\nd/Sd4RhX6B5+cPIhxsVso+sbkDIkFwrGUJlZJuhRdiSUYz9epxczzyCtFYC6Fds0aCyx/KzBiDLS\nOhlg/0Un4Glpl17nBTgxMYNkCE3Hy6sGFWmLcWnASLtuscygqZHe6MJryU2mjzduSjaqRGWoXePs\nFPXENb7H/T56JOZqqwUMseSGh1+AVcTmDAVkSUzKOMSQhHrvvPYGLk8dseP88UN88qk75q13ruKP\n/s2/BQDs7u2iPnE+psc//DMcfeiEOoNoCEGEAx6G4DR36bqGIV2mdP8l9OTmGQwZyJXmEmOeKAUu\nfa8DZ3xVYoOBoc8wA8+YY2A+8w8D/93WbqX9zBNobdiwInpxbmFImNYa67NbLpPf6v6ZZ8pEWRN4\n8VbOrPfNtTz02U29lp20xvqMPjNA6DPlFrvbRIjiHJMmpsvgiBL3rOMkRK3cmA7SGKLN7OoSpPeJ\nKOVeC9CWAk29Ips1vGUjAgzPVrb83IOofsQwHrqX8LXX30RAA3CxyL1AWtob+H6n5SLDhMQ2a6N9\nOpALhhGZY/aiEBEFXUkSeLbdsN9DRCKADAaMgitr1ROpTtsuPJbB0EMr9eozUnDvLbUJZvO5F9uU\nUqBcU89uA5UsLzBM3UAIghBA65VlMCaJhihNcHpOPRzDAWK6FsMFNAVFQSB8ScaCYUE9V1VZ+vNn\nnOPqVVfSeOP1152YKeHdd53Z7+npKUoqOz4NbcC6v3eACZW8oDWi9rhRDEZ1/IBzr/Z+/c0dhDs0\n6TYlmlaEdDn37DSLAYqcehha6YbU4JW33MJWQuGtb7leryq/6hf+0U4fnAron9x7BEllXFOVYLpN\n5QIs2uylf/fnPwejyZ+VGRZ0bBuG2KVjR0yjaqnczRKyFZC0BopKyggk5Mw9E204gja4shYhCd4V\njcb7R65mf3RRQJA/1o0Xv4CDPWJybY/xnW9+0333vXfx8MIFr5VSaGdKyaQXh9wEjAnfE8UYX5la\nW+MnAmatl19ggkO1nmRhDzeJCm5l7FXsd7a3sE9B42A8RkxjXKz3Gxp4xfJGrd6z9VKkEBxV1VLT\nNVbtegbPcE9UV3gAABOzSURBVInQDOBU2t1b5jikezVFgJqe4zLPUNLEej3axZWlC2CmwmJA7QZb\n83PcaNlcguMe9bmNZAhBvWFzrrBP89B+kqIg4+bMagRtOUFrXLl0gVOydwMmcwv5siowog3WkAc4\ntptdZDtnhmGIhPz80rCHfkJ9Ls0MZ4/c+1TVGgEt/jJMYFvTYQU0tOkoqyVU7eaBg+s3AQrGJi1z\nVxvf16KsQEONnYYHkFRS0gyYTV3P3vnjCS6obBpwjcXM3RMuFEajzbzzpG3ASc1999brmJL8w8n7\nP0Yxc/d+MBxCUrAYpmMEA9fjFYccYStcahkacg+wTQ+7247Nd/PlV/Hal79B1xSA0WJdLJcItxxT\n+Oo3/hWS/dvuXhx9CEVSFvn8HBXJP0S9MQYHrt9t9/odBHrzPlqGtWCJr1TZuVjrGXxiDRLrX169\nu5BoD2SM9f/+pJMBe4Kttx4ItXIwhpvPfKetxVsf69m/c9zfjboWzkkDbe8TrU9M+Y02Y8xfr7UW\nzJKAsWFg1BAdqhpXt6gkXtaeBcuFhKCa6HYsEBi3ThWlRU7jjukSI9oYJYMQRrrPzLPGC5xKwf2N\nqHXtz3lTdOW8Dh06dOjQoUOH58DnnokaD2N8+Z233I9FEhWVbmoNLGkHqC5mvmxnG+3ZYL0k9S71\n/UGCEXlrRYKBessgOPMeZlopVKb1bRJo7cEapX2pTus1PQxt/U6ec46G9GWqukZebL6rqJp6VSZb\ny2gNh0Pv6Wa0gabde6MaNGQXIKVAQ+WHJEl9qSYOI+xvU8PrPEdVtEJuCQqV+WO2GbAokEjJoTov\ncmQLtxs9PTlF7X2tVkw9KaUvNT4NbWr4ysE1zFs7mYdHaB9CIAO/TxLaeFHN/Vd2oeh/KK39vqpR\nDeZ0f4M4RhC0DbluF7zISkhiwIRgqKW7V70oxfaYGq/z3DM0a1sgiSjLMys8gzBILaTerJzXZEuA\nUvOMS8xox/XxJMNpuymrCujGnXcvCXF132XLdFNBZy57GmiNrX2y+tm/BkUWHMJWSOgGHM9muHvh\n/r1MthESa+qDe/cRU3q6zzkOaOf+nXe+ip/+jWt4vXfyCDWNX7u289zoGpsCirJtUg7B4MaL4o0n\nW0gpV4QBwAvOcCFxixpwb958wZffw0D6JlQw7stAWhu/2yTJPncfhPDN9k6Dpt05G89WsnAaNgCc\nrpXafGe4FBIVlTriugICapJv5hjR757mF0gDyuKwAJZKaUEqISgrw5sK3CdaU0jKujZWw9Rk34Q+\nCsrscZ6iR+N41mTOKwyASgaYzRz7qzl4GeNDVy4Lpg98CUzmGcpwMwJEazMi4gSSmu8byzEh0g3T\nCpaanRvLUZDVSY8rJDS2goDB0PMrq8aLRIahxYyO0+u7Y8eB8CSYWhlUxIBa5iUi21YVLvH4oSut\nzS6WWBIDeHtrG5dEfBlv9TG53EyM0tYlWEjjDhyjXVe21zbA2QPnaZmdP8KdO+79qJcTBKSBxa0B\nb1OgLABfmep5DaJUx0iJWXhyOUVNDMaAMWjSGlKaYfyaEwoqyxKLU1fqv/b2d5Fsucxr2B9BUosC\nVIWamJ2bwJjVOmEth6FsCbgAo6wkExzcZ45XnGbO2aqJ3az/uyUvus/cz7Xskf2MHlRL0DLNah5h\njK2x8yxs2wEP+xkG4FNQLb2VTBQEq8yaqSHa7JOxMKQHJfmKSMY08x6bgdUYjd3zLc4LgKoBRlgw\nIhTs9w22Uje+P6imMEXbKK59kBMHHDm9ZllT+NKe5BIhpb5FEIE9A1kH+HsIojhnkLRIZFmJCyp1\nzLMKJbH2lFl5cfUGPfRpce+FIRIapDIK/GfiQELQhKtU4ymYdk0YzBgLXa+zDVZpzqZ9CJbD0KSQ\n50tkuTu3vCg8a28TGAb4aX5N+TUIAs+AGw6HKHMSgStLqHYhBDw9vq4qGPr70cNj4MB910Cj3+v7\nz1eUxm6axpfkCgAXNMEqpXBJfVmffPSRFyzd2dnxgVOSJE/Uo38XNK2FMghxSCrF+XyKkliCkjOE\n1DvToER6w01QYSqREdtwWRgfHCsNf98bpZw3HOBpyuPhENO77jfT7Qg8daUswSS0bsXbANP2IAiF\nUtF4CABNhriZWiA/3kyokdsGop2wROT7FTJrkXuxx7YgBwQ1x8Ul+S0xi1i5NPS2DHD1ikvxh/0h\nZvcpuKpL2JpYiIMd9KifxEjpJ6YP7n+CnCaFK2nfs/9ypXyfV8AkWCu6x+0zsfPyYuKvK445JCcJ\nDWu9mjCEgCD1Z8YMtFnzLRPtIrzyurSwfnPAmPCl47qu1yyxrDcf5Zx51p7W8MGYtsyzcpkwPoAB\nkzCsLX0/HQsWwFDZWFiNUlD/UnmOPep1YELA0HjlxqBWrVhvjcC0MidARU+7MfCBpTEWQrWGYAI1\nldbnUGA0C9TxFvKhY7Tm8gzZpQuiHp9/hIOUepr6Y2xTUBcwhk2lfUvqk5TQ4FTmkmGMuFVRVxIB\nvVtBqqGKdmMQeHHcpiwxK9w9ms4NesQevLIV+o3knKRoyjDywW1WNiiqtpxt0FCANJ2coibJlirL\noEr3TCdnpf88FjnUho/RVhky2pRolSOi8tzWwSFaOf1Hvz3DX//w+wCAg5e/ils7rn+QSQlDz5NL\n4b3bHNObTkBYWDKjtsU5PvlrJ4NQIsBo6H4rlgGu3rxO111geOD+3n7hjVVvl61gcupV1TUi+QyF\nHZ770pgrs7cuDwaeuQYOw9o+Wrba0PB1v7lV2Y9xtpKXYeuuoWwV/Fju5xLDVz1OjLHV3Kr1Eyri\noPfPfXbzIOr6buzZuIP+wJcU83yJHvUuM7YqZTphZJpXao08b9tiDCpaOwtkiMiPlkmLgNo1vvDK\nAZrWVLsooGjDIE2EgaHnLmuAWp2TIPQq8aap0VC/4CCJkMSbbWhadOW8Dh06dOjQoUOH58Dnnoma\nzBZe1yjLC1StWKMQGPSJURIG6JH2zaDX92nXRHJEQWtx0aw5kisY26ZCDaxpG2RXmaimVl5kizEG\nQ5mlLMuwzF32pq4VarKJaWrld9TgHMEz+HUxIcDX059rzXRtJG6tRUzXGCYxgqhleWVIKTukm8Y3\ntala+Wu/nE/RRujHxxe+XMUYW0sJ25X1gTEomcsAcSmwteV2v4PB4AmLGb4h66kiTaOsLH3pZjwa\nYU5bS2ONZ5GMD8bYe90xtC7LCmeTCZ2rwNZ263FoMV+48+slEZghTRjhMmyxkLhcumd0MpN48W2y\n+xEaFSOWpcgQEfOuUSt9LRZpVLUrJ9SV9j6DT4dd7ejAV/wMISBo5yOshWz1Ao1B0bLMuEAtqZwo\ngSmx2BJ2jD3a1dzeO8QeNfle621h+sldAMDiYu5V7kpV4yOyQrrvamnuuq1FpdrMFfONsFwboNm8\n0dMY7bNb6/2h2mg/9oWxnuQRhMJnYLhda3hlzNs5GGNXnxFyjXDEva8f4wyrG2qfYOS12lBuLNPx\n19L6TqBv893vUZiipgZfHQzAKFMkmhI1jdeFCCFHLqNaZwXmZNOUIYAmwseMhRDSbVsfyR4ehq50\nVKgMQ8qGnMoEksZszYExZbfs+BoWLYFmOMQ1ElAVqsT70yN3nNrgCy2jNx5hnAw3ur6TB66sJK7u\nIyUNJCE4OI1R8ACWrpnLGCE1nDe6weWMMqdg0OQrOgxT2IE770rGaMijbFm4TNQ8E45IAMAECTQx\n9YRoUJPQaCo5Svp9zivUVO5cXExxjbI5vUGIutws861U5plZIkxg6JkwNcX2lvt9+crbuCD9n2S8\nD0ul/aopPNOUw8AS85kxC9lqgzHhs54JV8gm7p37i3d/gauHjpCDqsA//IYT/93bPcDu3i6d3BwB\nazOvBppaAIoyx9mZu2c7G1xjEMKX3hgz8KlgK554z9pynsvArXV4t3MVg29n4Xy1HjC20oN6Ilu9\nlkxab1xnnIPbNvu0KttxDrRFGbd2bD7fxFL4TDNU479Z1SU0ZXkDIfza0VQ1mG1Zddy3qlhrvX6b\nHfUwJC9FJkIMtt1zvHltB/MLd//3zxiaHs3ZuYaaUuuEaJD2SEsKxpNsKsZRUiaqXJao+OaZb3es\nzxl3j8/8hBjFCUYjt5D2k9BT3sOAIyXhtjiKPMVQCkBRapbBgLepf6PRJtG01uBt/0QQQrcLu1nV\nh5dZ7n3i8ixH3QYbFmuU7wABvVhBGHpRxU3AGBBQSUprhfWpolUFl4FcBTCN9sarWitkVNZslPYD\nzcL4st2N69eQUyCjmmPfV7bObGBY+SBZWM+M6qU9JJQ6revanw/nfGO66pyEPqfLJWry82PGYEj+\nf1opGFrkozTGnPqAzDRH0ZYYmxKSFGIX8wptJZFJCU5l2ooYUGezGVTqxgabhyiW7v4UIkNMhqoM\nCtYLWWrPUrRTgQUFaE1VocyfFCH9/0FDtC1RYMaAtyKK1kDT/RZsJWjHwL0XIuMShkpdRjIUlbvm\nrTjBmy+4Hpir4xE49cdVIsDOoXu2D4sKlqjqqnGikwBQYZVSt3BGrO5vBu85rPST0dBTIHiIJHa9\nQJwHa7HJanLURq8kDgzzmwAGrII3ISFao2+lVgxaLj7jv+Vl9J4oG6yPu/bzSunVv9tn7L1YwzyR\n0JS+t9E+MrpXY20hW5eD8Rj20EmtPLj/AZh1C+0iHWBcuQBgmKQoBy6wKcMe5r68yCBCd38ybmC0\n+/yWrrArXFksX8wwamnwQYAd6r+JtURIQTXLH2BCKuWjcoFren+j65ucOBbcIFr1+sXjEjv7ToYk\nDCPE1B+0Ewy8AGFVZDAULAbCKXsDgFUKJRmyG1UioOchKECJWIycmIZNECMmN4bJgykuz925jEYR\nhuNWZJWhR/6c06nF7dtUHksCxMT8exp+/uMf+k11nCbo9VoWYoiwbemIEtx+1ZkCM8FgMrdxYQy+\nr7SyqzlUNbUP6q3lvkQpuUIKt+l648YASrtNHxcl+MwxaEeHb2Jx6a61KZbIiam3WOY4fuTWlek8\n98Hrm3+8wUWalXq7NdaX89bZdgxs9e9sJYlgrfWlvTaAcv++llBgzPchWmu9rI81q7+BVTuAtdab\nkDNmPTvWWgYuVomAZ5E4uPcw838LIVYMQaYRhrQBZcqvVbpuUJXuWWijn2DttXNhKCQ4BTlBlPp1\nt1BARK4Cew1HGbQBs8a9wpVr0/EAe9suGM7KEm1VPtcl2ta2HCu/wk3RlfM6dOjQoUOHDh2eA58/\nO2+847MHaRwioZ1EEkjIVn0L1tuASLaSsbeWrzSRzKrcIhj3u40wWPmZGazcsJd5junU7bYWi8wL\na4EJL0QppfTiiYGUPksTRiHCDT3XAGfp0e7YpRAQfBW5txE0ZxyGMmwBGNCmk9Oet4mxHDBt6zJn\nOD1zu6KiqlFQY51qms9o/dBJMPjsiZTSn08QBr75nDG2Vs7ZfFcxmzpxz0prlEXLNjNIvGBm6LNj\n1gBT0rpSkfXsFVtbzC/crn25LNGn3XJdl5Ck19Ea1mlmUGhiupQRZnM6dqzRj12JxdgGMd3DKAhx\n/NA96+npDNOJy5ylfYF6uVnj9c7hHoS3QABqyhrxUPjdb1mUPhvKGPdeUk2jYGlbE9jV8wcETiZu\nZ2Vy5Y+/MA3O24we4956YeWl5RgjrQ6VNfCWGarRfuw/i2YL4HSrtF5lmdpGTGM1FDWQB1IjoXus\njfbvbhAEa59nq4ZwbdZ2s2qVPVs7N6Wa1XeNgaLU/DoxoqxXFhFlVXlih9HakUc2RD1/7DXIVLyH\nGXf3OWY1ThmVfGSEnIQue7aB8vpRUxxSo/CwseDkG8iCBWLtijShKtGnrOfg8hFqKntdHx4gpXvL\nyim2GhqnUQ+9yGUd0rxGOXTsUmsEGL1LDxanKOab+QOeXpD/X11gZ+7ep/3rzJNldvavICVByiSS\nMHSv0zQFJ5Zdnk1RViQCywVCtILAAspQyZ2a0/syRkilpqxWODlzli6PHj9CRhlfjQZb2y5z9dZb\nb3hrqUePTtFQBn04SsGJNfg0/Pv/8J8wIK/TJE7QH7j7Nx6kCGhei9MAKWX1+sM+drbIZicMPfNr\nNl/69WOxWKA/dCVZbQXywo27XixQl+55hmGKkBOzeHsMQRY9jyZLZLnLaIkgAQvISucwxUvXaA6K\newijzdjOAKAajjb7yxhfK8NpMKqgGMBXWRgYAmrwltagYlQpEatsNLNrLQn8M5lcn+UVq3XUlr65\numEBeLvustXawNay1I7Zt/ElIuJipb0oV5WYIIigicDAzCohHrEQnDJUTMBbprl1ixrFwSDoG5ZL\nBJQHmmoL0JiNk8Qzt6216I1dNrQQDEcn7p1pjPGlfm0jv16OU/aEruImYM+SnuvQoUOHDh06dOjg\n0JXzOnTo0KFDhw4dngNdENWhQ4cOHTp06PAc6IKoDh06dOjQoUOH50AXRHXo0KFDhw4dOjwHuiCq\nQ4cOHTp06NDhOdAFUR06dOjQoUOHDs+BLojq0KFDhw4dOnR4DnRBVIcOHTp06NChw3OgC6I6dOjQ\noUOHDh2eA10Q1aFDhw4dOnTo8BzogqgOHTp06NChQ4fnQBdEdejQoUOHDh06PAe6IKpDhw4dOnTo\n0OE50AVRHTp06NChQ4cOz4EuiOrQoUOHDh06dHgOdEFUhw4dOnTo0KHDc6ALojp06NChQ4cOHZ4D\nXRDVoUOHDh06dOjwHOiCqA4dOnTo0KFDh+dAF0R16NChQ4cOHTo8B/4vn1GswG121MQAAAAASUVO\nRK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7e6a940>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# An important way to gain intuition about how an algorithm works is to\n",
"# visualize the mistakes that it makes. In this visualization, we show examples\n",
"# of images that are misclassified by our current system. The first column\n",
"# shows images that our system labeled as \"plane\" but whose true label is\n",
"# something other than \"plane\".\n",
"\n",
"examples_per_class = 8\n",
"classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']\n",
"for cls, cls_name in enumerate(classes):\n",
" idxs = np.where((y_test != cls) & (y_test_pred == cls))[0]\n",
" idxs = np.random.choice(idxs, examples_per_class, replace=False)\n",
" for i, idx in enumerate(idxs):\n",
" plt.subplot(examples_per_class, len(classes), i * len(classes) + cls + 1)\n",
" plt.imshow(X_test[idx].astype('uint8'))\n",
" plt.axis('off')\n",
" if i == 0:\n",
" plt.title(cls_name)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Inline question 1:\n",
"Describe the misclassification results that you see. Do they make sense?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Neural Network on image features\n",
"Earlier in this assigment we saw that training a two-layer neural network on raw pixels achieved better classification performance than linear classifiers on raw pixels. In this notebook we have seen that linear classifiers on image features outperform linear classifiers on raw pixels. \n",
"\n",
"For completeness, we should also try training a neural network on image features. This approach should outperform all previous approaches: you should easily be able to achieve over 55% classification accuracy on the test set; our best model achieves about 60% classification accuracy."
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"(49000L, 155L)\n"
]
}
],
"source": [
"print X_train_feats.shape"
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"0.505\n",
"0.531\n",
"0.556\n",
"0.574\n",
"0.59\n",
"0.589\n",
"0.6\n",
"0.6\n",
"0.579\n",
"0.595\n",
"0.598\n",
"0.588\n",
"0.57\n",
"0.571\n",
"0.574\n",
"0.574\n",
"0.57\n",
"0.57\n",
"0.565\n",
"0.564\n"
]
}
],
"source": [
"from cs231n.classifiers.neural_net import TwoLayerNet\n",
"\n",
"input_dim = X_train_feats.shape[1]\n",
"hidden_dim = 500\n",
"num_classes = 10\n",
"\n",
"net = TwoLayerNet(input_dim, hidden_dim, num_classes)\n",
"best_net = None\n",
"\n",
"################################################################################\n",
"# TODO: Train a two-layer neural network on image features. You may want to #\n",
"# cross-validate various parameters as in previous sections. Store your best #\n",
"# model in the best_net variable. #\n",
"################################################################################\n",
"maxn=20\n",
"best_val=0\n",
"for i in xrange(maxn):\n",
" net_exp=net.train(X_train_feats, y_train, X_val_feats, y_val,\n",
" learning_rate=1e-2, learning_rate_decay=0.95,\n",
" reg=1e-5, num_iters=1000,\n",
" batch_size=200, verbose=False)\n",
" acc_val=np.mean(net.predict(X_test_feats)==y_test)\n",
" print acc_val\n",
" if acc_val>best_val:\n",
" best_val=acc_val\n",
" best_net=net\n",
"################################################################################\n",
"# END OF YOUR CODE #\n",
"################################################################################"
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"0.564\n"
]
}
],
"source": [
"# Run your neural net classifier on the test set. You should be able to\n",
"# get more than 55% accuracy.\n",
"\n",
"test_acc = (best_net.predict(X_test_feats) == y_test).mean()\n",
"print test_acc"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Bonus: Design your own features!\n",
"\n",
"You have seen that simple image features can improve classification performance. So far we have tried HOG and color histograms, but other types of features may be able to achieve even better classification performance.\n",
"\n",
"For bonus points, design and implement a new type of feature and use it for image classification on CIFAR-10. Explain how your feature works and why you expect it to be useful for image classification. Implement it in this notebook, cross-validate any hyperparameters, and compare its performance to the HOG + Color histogram baseline."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Bonus: Do something extra!\n",
"Use the material and code we have presented in this assignment to do something interesting. Was there another question we should have asked? Did any cool ideas pop into your head as you were working on the assignment? This is your chance to show off!"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.11"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
timestocome/Test-stock-prediction-algorithms | Silver Winner Jane Street Stock Competition/graph-and-plot-feature-correlations-v2.ipynb | 1 | 2743687 | null | mit |
kecnry/autofig | docs/tutorials/3d.ipynb | 1 | 228907 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Plotting in 3D with autofig"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"import autofig\n",
"import numpy as np"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"#autofig.inline()"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [],
"source": [
"t = np.linspace(0,10,31)\n",
"x = np.random.rand(31)\n",
"y = np.random.rand(31)\n",
"z = np.random.rand(31)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"By default, autofig uses the z dimension just to assign z-order (so that positive z appears \"on top\")"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAagAAAEYCAYAAAAJeGK1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzsnXdYFNf3xt9haQIKKNgVC7aIit0YRcUea8RuYolfsPcOMfaK2GPDHnsXNdFoYsESo8aCYsOCDQuoSC+77+8PsvNzZYEFFhb0fp5nHp2Ze++cWXbnnXvvuedIJCEQCAQCQU7DyNAGCAQCgUCgDSFQAoFAIMiRCIESCAQCQY5ECJRAIBAIciRCoAQCgUCQIxECJRAIBIIciRAogUAgEORIhEAJBAKBIEciBEogEAgEORJjQxuQXuzs7FiqVClDmyEQCASCDHLlypVQkvZplct1AlWqVClcvnzZ0GYIBAKBIINIkhSsSzkxxCcQCASCHIkQKIFAIBDkSIRACQQCgSBHIgRKIBAIBDkSIVACgUAgyJEIgRIIBAJBjkQIlEAgEAhyJEKgBAKBQJAjEQIlEAgEghyJECiBQCAQ5EiEQAkEAoEgRyIESiAQCAQ5EiFQAoFAIMiRZJlASZK0XpKk15Ik3UzhvCRJ0lJJkoIkSbohSVKNrLJFIBAIBLmPrOxBbQTQKpXzrQGU+2/zALAyC20RCASCLGfHjh1wdnaGjY0NOnTogDt37hjapFxNluWDInlGkqRSqRTpAGAzSQL4W5IkG0mSipAMySqbBAKBIKs4ePAgevToIe/7+fnh4sWLuHv3LqytrQ1oWe7FkHNQxQA8/Wj/2X/HkiFJkockSZclSbr85s2bbDFOIBAI0sPSpUuTHXv16hV27NhhAGs+DwwpUJKWY9RWkOQakrVI1rK3TzNLsEAgyAJiYmKQkJBgaDNyHCqVCidPnsSVK1e0nhcv1RnHkAL1DECJj/aLA3hhIFsEAkEKPH78GK1atYKlpSVsbW0xYsQIxMfHG9osg3Pjxg2MHz8exYsXh6urK8LDw7WWa926dTZb9vmQZXNQOuAHYKgkSTsA1AUQLuafBIKchUqlwrfffovbt28DAKKiorB06VIoFAosXLjQwNZlP0+ePMH27duxZcsW3LyZ5KBsZJT0nu/q6orQ0FDcuHEDACBJEjw9PVGzZk2D2ZvbkZJ8FLKgYUnaDqAxADsArwBMAWACACRXSZIkAViOJE+/aAD9SF5Oq91atWrx8uU0iwkEAj3g7+8PFxeXZMfz5s2L8PBwJP2MP2/evXuHPXv2YOvWrTh9+jQAwM7ODnFxcYiIiECdOnXg7e0NFxcXkMRff/2Fx48fo1GjRnB0dDSw9TkTSZKukKyVVrms9OLrkcZ5AhiSVdcX/D8k4e3tjZUrVyI8PBzt27fH/PnzUbBgQUObJsjhREREaD0eHR0NlUoFhUKRzRZlD7GxsThy5Ai2bt2KI0eOID4+Hvnz50fbtm1x+/ZtPHjwAGXKlMHatWvRpUsXWaglSULTpk0NbP3ngyGH+ATZxOzZs/HTTz/J+5s2bcLNmzcheqKC1Hjy5AmWLVum9VyHDh0+O3FSqVQ4c+YMtmzZgj179iA8PBx58uRBp06dUK9ePfj5+eHw4cPInz8/Fi1ahEGDBsHMzMzQZn/ekMxVW82aNSlIH/b29kSSh6TGdu7cOUObJsiBJCYmcvHixbS0tKQkSbSxsdH43tSsWZMvXrwwtJl64/r16xw/fjyLFy9OADQyMmKLFi24adMm3rp1iz/88AMlSaKZmRnHjx/Pd+/eGdrkXA+Ay9TheS96UJ85KpUKYWFhWs9dvHgR9evXz2aLBDmZa9euwd3dHZcvX0b16tVRrVo1bNy4EQsXLkTVqlVhbW2NWrXSnDrI8Tx9+hTbtm3D1q1bERAQAACoWbMmxowZg27duiFPnjyYM2cOPDw8EBcXh++//x4zZ86Eg4ODgS3/wtBFxXLSJnpQ6efbb7/V2oMCwCZNmvDgwYNUKpWGNlNgQKKiojh+/HgqFApaWFhwwYIFPH78OCVJ4rfffkuVSmVoEzPNu3fv6Ovry0aNGlGSJAJg6dKl+dNPP/H27dskybi4OC5evJgFChQgALq6uvLKlSsGtvzzAzr2oAwuOOndhECln/v377NUqVKyKJmamnLhwoUcNWoU8+bNSwB0dHTk0qVLGRERYWhzBdnMH3/8wTJlyhAAW7ZsyYcPHzIsLIzFihWjvb09X758aWgTM0xsbCz37t3LTp060dTUlABYoEABDh48mOfOnZOFV6VScdeuXSxbtiwB0MnJib/99ttnIcw5ESFQAg3i4+PZtWtXAmBAQIB8PDw8nIsXL5YfUNbW1hw7diwfP35sQGsF2cHr16/5ww8/EADt7e25detWqlQqqlQqdu7cmQB4+PBhQ5uZbpRKJU+ePMn//e9/8vyZubk5u3XrxkOHDjEuLk6jvL+/P+vWrUsALFKkCNeuXcvExEQDWf9lIARKkIy5c+cSAB8+fJjsXGJiIvfv389GjRrJE8WdO3fWeMsUfB6oVCpu2rRJHsbq168fQ0ND5fMbNmwgAA4ZMsSAVqafGzducPz48SxRooT8HW7evDk3bdrEDx8+JCt/584dduzYkQBoZWXFGTNmMDIy0gCWf3kIgRIkY+nSpcl6UNr4999/2bt3b5qYmBAAa9euzW3btjE+Pj6bLBVkFUFBQWzWrJk8rPvnn39qnL9//z6trKxYqVIlRkdHG8hK3Xny5AnnzZvHKlWqaHgZLly4MEVPw5cvX3LQoEFUKBRUKBQcPHhwrh7GzI0IgRIkY926dQTAixcv6lQ+JCSEkydPpp2dHQGwWLFinDNnDsPCwrLYUoG+iY+P59y5c2lubk5jY2N6eXklE6D4+HjWrVuXpqamvHr1qoEsTRu1s0Pjxo1lZ4dSpUppODtoIzIykjNmzKCVlRUBsGPHjrxz5042Wi5QIwRKkIzt27cTAP/666901YuJieHatWvp5OREAMyTJw8HDhyY6sNAkHO4ePEiq1atSgCsV69eij3oyZMnEwB9fHyy2cK0iY2N5b59+5I5OwwaNCjNYejExESuXbuWRYsWJQDWrVuXZ86cyUbrBZ8iBEqQDD8/v0xNfKtUKh4/fpxt2rSRh1Nat27NY8eOiXmqHMiHDx84fPhwSpLEvHnzcvny5SlO/vv7+9PIyIjNmjXLMUsOlEolT506RXd392TODn5+fsmcHT5FpVLxt99+k1+sypYty127donvag5ACJQgGX/++ScBcOfOnZlua+PGjaxRo4b8NvvVV19xzZo1uWLe4kvAz89PjozQoUMHPn36NMWy79+/p4ODA/Pnz8/nz59no5XauXHjBidMmKDh7NCsWTNu3LiR4eHhOrVx5coVurq6EgDz58/PxYsXpyloguxDCJQgGRcuXCAAbtiwIVPtDBkyRGOxr6WlJQsXLiwPu3h5eeWIB92XyIsXL9ilSxfZZXrfvn1p1unVqxcBcP/+/dlgoXaePn3KefPmyUORAFijRo1UnR208fjxY37//fcEQDMzM06YMEGEJsqBCIESJOPGjRsEwOXLl2e4jevXr2uNSNGhQwfu2LFDXk9iYmLC77//npcvX9bjHQhSQqlUcvXq1bS2tiYADho0iO/fv0+z3pYtWwiAHh4e2WClJu/evePatWuTOTt4eXkxMDAw3W2NGzeOZmZmlCSJvXv3ZnBwcBZZLsgsQqAEyQgKCiIAzp8/P8NtrFixQqtAFSxYUC5z4cIFduvWjQqFggDYsGFD7t27Vyx+zCICAwPZoEEDeaj17NmzOtV79OgR8+XLx/Lly2fb+h+1s4ObmxvNzMzkIbhBgwbx7Nmz6Z4fiouL46JFi5g/f34CYLNmzfjvv/9mkfUCfSEESpCMkJAQAuCUKVMy3MaxY8e0CtTXX3+drGxwcDDHjx8vT3CXKlWKCxcu1HkeQZA6sbGxnDp1Kk1NTWlqasoZM2boPM+SkJDAb775hsbGxlney03J2aFr1646OTtoQ6VScceOHXIElCpVqvD3338XDhC5BCFQgmSEh4cTAMeNG5fhNpRKpTyMp96MjIx46NChFOtERETwl19+Ybly5QiAefPm5YgRI/jgwYMM2/Glc+bMGVasWJEA2KhRo3Sv55k+fToBcO7cuVlkIRkQEKDh7CBJEps1a8YNGzZk6iXlzJkzrFOnDgGwaNGiXL9+veid5zKEQAmSkZCQQAAcPHhwptoJDw9nvXr1CICVKlVKFo0gJZRKJQ8fPsymTZvKD6yOHTvy1KlT4s1XR969e0cPDw8CoK2tLdetW5fuz+7ChQtUKBRs3Lix3h/sT58+5fz585M5O/j4+GTaceb27dts3769/JIzc+ZMRkVF6clyQXYiBEqgFVNTU/bt2zfT7aiDieriJaaNGzdu8Mcff5TnIapXr85NmzYJV+AUUKlU3L17t+wt2b179wyF5/nw4QPLlClDGxsbPnnyRC+2qZ0dmjRpkmlnB228fPmSAwcOpEKhoLGxMYcMGcJXr17pwXKBoRACJdCKra0tu3Tpkul2vv76awLg3bt3M9XOq1evOG3aNBYqVIgAWLhwYU6fPp2vX7/OtI2fC0+ePGG7du0IgCVLluSRI0cy3Fbfvn0JgLt27cqUTbGxsdy/f38yZ4eBAwdmyNlBG5GRkZw2bZocmqhTp06Z/r4JcgZCoARaKVasGNu0aZPpdhwdHQlAbz2e2NhYbty4kc7OzvIalv79+6cZ2PZzJjExkUuWLKGVlRWNjIw4atSoTOXr2rlzJwFkuAetVCp5+vRpenh4JHN2OHjwoN6+C4mJifT19WWRIkXk8Ey6eiYKcgdCoARaKV++PBs3bpzpdgoUKEAjIyM9WKSJSqXiyZMn2aFDB3m4qFmzZjxy5EiOCcGTHVy7do21a9cmADo7O/PSpUuZau/Jkye0sbFhmTJltKaeSI2AgABOnDiRJUuWlOcOmzZtmmlnh09RqVQ8cuQIK1euLIcm2r17t5if/AwRAiXQirOzM+vUqZPpdszNzWlhYaEHi1Lm/v37HD58uDzEU6FCBa5YseKzztkTHR3NCRMmUKFQME+ePPT29mZCQkKm2kxMTGSjRo2oUCh44cIFneqonR2qVasmOztUr16dCxYs4LNnzzJljzYuX77MJk2ayNFIli5dKuYjP2OEQAm08s0337By5cqZakOlUlGSJBYqVEhPVqXO+/fv6ePjQwcHB9l7bcKECXqb5M8pHD9+XE453qJFC62JJTOCOlHl9OnTUy33/v17rlu3TsPZwcHBgZ6enrx165ZebPmUR48eyaGWzM3NOXHiRJ0iYAhyN0KgBFpp3rw5S5cunak2wsLCZBfz7CQhIYF79uyRoyYoFAp269aNf//9d7baoW/evHnD3r17EwDt7Oy4ZcsWvQ1rXb58mcbGxmzQoIFWl3K1s0Pnzp1lZwdbW1sOHDiQ/v7+WTas+vbtW44dO5ampqaUJIl9+vT57F44BCkjBEqglY4dO2qEJcoI//zzDwHoZS4ro1y6dIm9evWisbGxHMli586dmR4Oy05UKhV//fVXOSFk3759NVKvZ5bIyEiWL1+e+fLl46NHj+TjSqWSZ86coYeHB21tbeXeS5cuXfTq7KCN2NhYLly4UL5u8+bNc3RyREHWIARKoJWePXvSysoqU21s3LiRANizZ089WZVxnj17Rk9PTzkWW4kSJTh//ny+ffvW0KalyoMHD9i8eXMCSanXT5w4ofdruLu7EwC3bt1Kkrx58yYnTZqUzNlh/fr1WT6splKpuH37dpYuXZoAWLVqVR47dixLrynIuQiBEmjF3d2dkiRlagjJy8uLAOjl5aVHyzJHVFQUV69ezUqVKskpQIYMGZLj1s3Ex8dz3rx5zJMnD42Njenp6ZklObT27dtHAPzuu+/o7e0tu++rvQKzytlBG6dPn5Y9EosVK8YNGzaI0ERfOEKgBFoZMWIEATAmJibDbagntTObVyorUKlUPHr0KFu2bCk/kNu2bcsTJ04Y3F35n3/+kb3i6taty+vXr2fJdW7fvk1LS0uam5trODtMmjSJN2/ezJJraiMwMFBeYJw3b17Onj1bhCYSkBQCJUgBT09PAsjUXIeLiwsB5HjnhFu3btHDw4Pm5uZyxOt169ZlSpwzQkREBEeOHEkjIyNaWVlx2bJleu9BxMXF8cCBA3Rzc6ORkZEsCgMGDOCZM2eydQ1ZSEgIBwwYIIcmGjp0qIgMItAgRwgUgFYA7gIIAjBRy/mSAE4CuArgBoBv02pTCFTmmDlzJgFkymNKHUU7tTTiOYnQ0FDOnj2bRYsWJQDa29vz559/ZkhISJZf+/Dhw3I07/bt2+vVU03t7DBgwADZ6UDtNNK1a1fGxsbq7Vq6EBERwalTp9LS0pIA6ObmluOGWAU5A4MLFAAFgAcAygAwBXAdwFeflFkDYNB///8KwOO02hUClTkWLVpEALx9+3aG27C3t9drmKPsIi4ujlu3bmWtWrUIgKampuzTp0+WeJGFhISwa9euBJJSr+/Zs0dvQ4y3bt3ipEmT5HVhkiTR1dWVU6dOpYmJCevWrcv4+Hi9XEsXEhISuGbNGjmQ7ddff81z585l2/UFuY+cIFBfAzj20f4kAJM+KbMawISPyp9Pq10hUJlj9erVBMArV65kuA1zc3OamJjo0arsRaVS8ezZsxrDYY0bN+bBgwczPfSmVCq5Zs0aOVbdwIED+e7du0zb/OzZMy5YsCCZs4O3tzefPXvGqKgoVqpUiVZWVgwKCsr09XRBpVLx0KFD/Oqrr2RvRH0KseDzJScIVGcAaz/a/wHA8k/KFAEQAOAZgHcAaqbQlgeAywAulyxZMss+tC+BLVu2EADPnDmTofrqnFI2NjZ6tswwPHr0iKNHj2a+fPnk+G9LlixJd7w6Msk5QT0/V6lSJfr7+2fKtvfv33P9+vVs2rSp7OxQsmRJrc4OQ4YMyVbHlUuXLrFx48by4uJly5Zla69NkLvJCQLVRYtALfukzGgAY/j/PahAAEaptSt6UJlD7X589OjRDNV/9uwZ8V++n8+JDx8+cMmSJXIK8Xz58nH06NEaC1xTIjY2ltOmTZNTr0+bNi3D8z9qZ4cuXbrIzh22trb08PBI0dnh0KFD8rxTVvdeHj16xB49esiLez09PUVoIkG6yQkCpcsQ3y0AJT7afwigYGrtCoHKHMeOHSMA7t27N0P11VEkateurWfLcgaJiYk8cOCA3DswMjKim5tbijmO/P395bVXLi4uGZrbUyqV9Pf354ABA+QFx2ZmZuzcuTMPHDiQqti9fPmS9vb2LF68eJYuTn779i3HjBkjhybq27dvrnGSEeQ8coJAGf8nOKU/cpKo/EmZ3wH0/e//lQC8ACCl1q4QqMzh7+9PAPz1118zVF+dU6h9+/Z6tizn8e+//7JPnz40NTUlANaqVYtbt25lXFwc3717x4EDB8rDnb6+vul25b516xY9PT2TOTusW7dOp16JSqVi69atKUkST548mcG7TJ3Y2FguWLBA9hJs2bIlr127liXXEnw5GFygkmzAtwDu/efN5/XfsekA2v/3/68AnPtPvK4BaJFWm0KgMse///5LAFy1alWG6s+YMYMAOHToUD1blnMJCQnhzz//LHsv5s+fn3nz5iUAduvWLV3u6s+fP+eCBQtYvXp12dmhWrVq9Pb2TnePZOnSpQTAiRMnpveW0kSpVHLbtm0sVaqUbOMff/yh9+sIvkxyhEBlxSYEKnPcuXOHALhw4cIM1e/Tpw8BcNGiRXq2LOdz7949DS86MzMzenh4MDAwMNV64eHh3LBhQzJnh4kTJ2Y4Y3BAQADNzMxYs2ZNvbv7nzp1SnbFL168ODdu3ChCEwn0ihAogVaePn1KAJwxY0aG6ru6uhIADx06pGfLci6JiYlctmyZnHp9xIgRPHToENu2bSuLVatWrXj06FF5niouLo4HDx5k165dZWcHGxsbenh48PTp05mK7BATE8MqVarQwsKCd+7c0ddt8tatW/I95cuXj3PmzMmSOIECgRAogVbevn2bqWEhtUNAZlOQ5xauX7/OunXrysNc//zzj8b5u3fvcsiQIbSwsJBj3rm4uMhzNmZmZnRzc+P+/fv1Ftlh5MiRBMA1a9bopb2QkBB6eHjQyMiIxsbGHD58uAhNJMhShEAJtBIbG0sAHD58eIbqFyxYMNOhknID0dHRnDRpEo2NjZknTx7Onz8/xXU+gYGBHDVqlCxKAGhiYsI2bdroPRPt0aNHCYAdO3bMtEt5REQEp0yZIocm6ty5M+/fv68nSwWClBECJdCKSqWiQqFg//79M1RfnXU1u+O8ZScnTpyQU683b95ca2SG58+f08fHJ5mzw5w5c7hixQrWq1dPjo3Xq1cvvfQ4X79+zcKFC7NIkSJ88+ZNhttJSEjg6tWr5dBE9evX5/nz5zNtn0CgK0KgBCmSN29e9ujRI931oqKi5Bh2nyOhoaGyE4idnR1//fVXjV6K2tmhWbNmsrNDiRIlUnR2uHDhArt3706FQkEAbNCgAffs2ZMhhwOVSsX27dsTQIa96VQqFf38/ORh2nLlynHfvn0iNJEg2xECJUiRwoULZ2gd0/3794n/ooF/TsTFxXHGjBnyEF2fPn3kHkpKzg7u7u46Ozs8efKE48ePl+PzlSpVij4+PumKwLBq1SoC4OjRozN0j5cuXWKjRo3kv9/y5ctFaCKBwRACJUiRMmXKsFmzZumud/r0aQJgxYoVs8Aqw+Dr6ysvxAXAJk2aMCYmhmfPnuXAgQPlyA6mpqZ0c3Pjvn37Mjy8GRkZyV9++YXly5cnAFpZWXH48OFpBne9ffs28+TJw2rVqqX72g8fPmT37t0JgHny5KGXlxfDw8MzZL9AoC+EQAlSpEqVKvz666/TXW/btm3Ef5G/czsJCQn8+eefZWH6eLO2tpYjOzRp0oRr167VS0RyNUqlkkeOHGGzZs3k63To0IGnTp1KNtwWFxfH6tWr09zcPF0OF2FhYRw9erQcmqhfv34iNJEgxyAESpAidevWZbVq1dJdb86cOQTA77//Pgusyj7+/vtveR5G22Zqasr58+dnywM9ICCA/fv3l51PnJ2duXHjRrmnNH78eALgL7/8olN7MTEx9Pb2locTW7VqlWWp5QWCjCIESpAirq6udHR0THe9/v37EwAnT56cBVbpH6VSyQcPHtDPz49z5sxh9+7dZTf51LYKFSpku62vX7/m9OnTWahQIQJgoUKFZIeNNm3apOnIoFQquXXrVjmun7OzM48fP55N1gsE6UNXgTKG4IvDwsIC0dHR6a4XHBwMAHBwcNC3SZlCpVIhODgYt27d0thu376NmJiYZOWLFSuGXr16oWrVqhgwYACioqI0zvfu3Tu7TJext7fH5MmTMX78eOzcuRMLFizApk2bAAD58uXDzZs3UaVKFa11T548iXHjxuHKlSsoUaIENm3ahO+//x5GRkbZeQsCgf7RRcVy0iZ6UElcunSJnTt3ZrVq1Thw4MB0LZzt1q0bra2t031NdeZUQ4U5UiqVfPToEQ8fPsx58+axd+/erFmzphzFQb2ZmZmxWrVq7NGjBydOnMgGDRrIvZLdu3dr9EZOnz7NChUqEP/lNxo2bJjB486pVCp26tSJQFL6dLVLe9OmTXn48GHZc/DmzZts06aNHJpo7ty5IjSRIFcAMcT3+fLvv//KLs/qrUSJEjpP5Pfr1y9DKdvV0bw/Dfejb5RKJR8/fswjR45w/vz57NOnD2vVqiVHPFBvpqamrFq1Krt3784ZM2Zw3759vHv3LhMSEqhSqbh27Vp5LmbAgAGpfj7BwcEZyqKbFaxbt44AOGzYMJJkUFAQR4wYQSsrKwJgmTJlWL9+fUqSRBMTE44YMSJTC3cFguxGCNRnzPfff6917mTo0KG8dOkS7927x1evXqUY5Xro0KEEkK51MCqVisbGxgTA4OBgvdyHSqVicHAwf/vtN3p7e7Nv376sXbu2/CD+WIiqVKnCbt26cfr06dy7dy/v3LnDhIQEre3euXNHXvNTsWLFDKe3NwT37t2jpaUlK1eunKw39OzZM7Zo0ULuUZmYmNDDw+OzDzsl+PzQVaCkpLK5h1q1avHy5cuGNsOgNGjQAOfOndOprLm5OaytrWFtbQ0bGxtYW1vjyZMnuHv3LoYOHYqCBQsmO//xfr58+WBsbIy3b9+iQIECAICYmBiYm5vrbC9JPHv2LNkcUWBgICIjI+VyJiYmqFChAr766itUrlxZ3hwdHWFsnPZ0aXx8PObNm4eZM2cCADw9PTFx4kSYmZnpbKshSUhIwDfffIPr16/j0qVLqFq1KgAgMTER69atw5QpU/Dq1SvUr18f7dq1w2+//QZ/f38oFAp07twZI0eORL169Qx8FwJB2kiSdIVkrbTKCSeJXEjDhg21CtTYsWNRoUIFhIeH4/379wgPD5c39X5QUBBevnwJAFi+fLlO17O0tISFhQUAQJIkfPfdd1pFLV++fFAqlQgLC0NISAiePn2Khw8f4u7du4iIiJDbMzY2RoUKFdC6detkQmRiYpKhz+T8+fNwd3dHYGAgGjZsiNWrV6NSpUoZastQTJs2DZcuXcKiRYtQtWpVkMShQ4cwYcIE3LlzB+XLl8eqVavQoUMHSJKEiRMn4sqVK1i8eDF27NiBnTt3om7duhg1ahTc3Nx0EnWBICcjelC5kNDQULi4uOD27dvysfbt22Pfvn1QKBRp1l+wYAHGjRuHa9euwc7OLpmIadu/f/8+/vnnHxgbG6NIkSJ4//69huikhampKfLmzQtbW1sULFgQtra2qfbcPt23tLSEJEnJ2g0PD8ekSZOwcuVKWFtbw9vbG/379891HmxnzpxB48aN0bx5c/z++++4cuUKxo4dizNnzsDe3h5Tp06Fu7t7igL+4sULrFixAqtWrUJYWBhKlCiBoUOHwt3dHba2ttl8NwJB6ujagxIClUuJiYnBunXrMGzYMHTv3h1bt27V6aEcFRUFNzc3HDt2DM7Ozhg7dix69eqltSxJhISE4NbDZEaUAAAgAElEQVStW1i/fj127NgBCwsLmJiYIDw8XC6nUCjg4OCAEiVKoEiRIrCzs4O1tTXMzMwQGRmZouiFh4drDPGlhkKhQL58+TREKzo6Gjdv3kRMTAwqVaqEzp07o0SJEimKnLm5uVaRMzTv379HtWrVEB0djUOHDmHx4sXYuXMn8uTJgzFjxmDcuHHIly+fTm1FR0dj69atWLx4MQIDA2FhYYG+ffti+PDhqFChQhbfiUCgG0KgvgBUKhXMzMzQp08frF27Vqc6zZs3x4kTJzSOLV++HJ06ddI6R/T+/XuNspaWlmjZsqXG0Fz58uVhamqaoXtITEzEhw8fUhQwbcdev36NoKAgREZGQpIk6PodNjExSbOnltq+WnT1CUn07NkTO3bsQPv27fH7779DqVSiX79+mDZtGooVK6a13osXL3Dv3j04OTnBzs5Oa7vHjx/HokWLcPToUQBAmzZtMHLkSDRt2jRHCrXgy0EI1BdCiRIlULVqVRw5ciTNsleuXEGtWsm/E58+5BUKBRwdHTWcFfbu3Ys9e/Zg0KBBWLFihV7vQVeUSiVWrVqFSZMmITIyEsOHD8eMGTNgZmaWqqClNXz5/v17JCQk6GSDNqeT9Ircx3ND69evR//+/WFqaor4+Hi0bt0a8+bNS3FRLkmMHj0ay5cvR2JiIszMzODl5YXJkyenaPPt27exZMkSbN68GTExMXBycsLIkSPRq1evdDm7ZCehoaHYsGEDgoOD4eLiAjc3N52GrwW5AyFQXwh169ZFfHw8rl69mmbZ/fv3o1OnTlrPeXp6wsnJCZUrV0aFChWS9RRatGiB48ePY+bMmfDy8tKL7ekhICAAHh4e+Pvvv1G1alX4+vqiTp06emmbJGJjY3UWtJSOKZVKna5naWkJa2trKJVKvHr1CgBgY2ODb775Bl999VWqInf8+HG4u7sna/PEiRNo2rRpqtcNCwuDr68vli9fjufPn8Pe3h4DBw7E4MGDUbhw4fR/cFnEw4cP8c0338jOPADQtm1b+Pn5iZ7fZ4KuAmXwdU3p3cQ6KE06duzIggUL6lT25cuXNDExSbZ+ysXFJc266uCqvr6+mTU5XcTExNDLy4vGxsY0Nzfn3Llzc2QeI5VKxYiICD579oy3bt3i+fPn+dtvv3H79u1ctWoV582bx0mTJnHw4MFs2rQp8+XLpxE93draWl7flJFt4MCBOtsaHx/PrVu3slatWvJ6qt69e/Pff//Nwk9Id3788Uet9/j7778b2jSBnoCIxadfgoKCYG5ujuLFixvaFA2KFi2K169fIyEhIU0X7UKFCmHevHkYPXq0xvGyZcumeR31m36hQoUybmw6OXnyJAYMGID79++jWbNmWLVqlU62GgJJkmBlZQUrK6sU541u3bqF8ePH488//5R7qLNmzYKnpyeApDnFiIiIVD0pN2zYoOGgoiY9Q3UmJibo2bMnevTogfPnz2Px4sXYsmULNm/ejEaNGmHkyJFo165dtg2pqVQqPHz4ENeuXcO1a9ewe/dureUGDRqEVq1aoWLFiqhQoQIqVKiAkiVLiqG/zxldVCwnbdndgwoMDKSzs7P8FteqVascFVZmxowZBJCuaAIHDx4kAHbu3JnNmzcnAPr5+aVYPiEhQX67v3jxoj7MTpXQ0FD269ePAFigQAFu3rw5V6clf/78Ofv3708jIyOamJiwa9eulCSJrq6uaWbkValU9Pf3l9O9a+tlKRQKXr16NVM2Pn78mGPGjJF7dmXLluWSJUv0Hv4pKiqKFy9e5Jo1azh48GDWr19fa+SQT+8RAO3s7JLdv5mZGZ2cnOjm5kZPT09u2rSJFy9eTDNbsVKp5PLly/n111+zfv36XLFiRa7+juU2IEIdZR6VSiVnP/1469SpU7bZkBbquG3pEY5Hjx4RAOfMmcOwsDA6ODjQxsaGDx480Fr+2bNn8r0/fvxYX6YnQ6VScevWrXLMv969e+eol4H08uHDB06ePFkOZtutWzdevXqVpUuXpq2tbar5phITE7lv3z7Wq1dPfhC7u7vzzp079PX1ZdGiRQmApUuX5q5du/Rq89KlS1m2bFk5CO2oUaP48OHDdLcVEhLCo0ePcu7cuezevTsrVapEIyMj+bskSRLLly/PLl26cNasWTxy5AifP3/Of/75J1msyWrVqjEuLo7R0dG8ceMGd+/ezZkzZ/KHH35gnTp1NIZM1VuhQoXo4uJCd3d3LliwgIcOHeL9+/eZkJDAESNGJCs/ZswYvX2OgtQRAqUHLl68qPVNTqFQMCIiItvsSI3ff/+dALh//36d67x+/ZoA+NNPP5FMioxuamrKGjVqMCYmJln5f/75R753bef1wcOHD9myZUs5GGpuzmUUHx/PFStWyLmnGjZsyL///psk2bt3bwLgnj17tNaNjo7mqlWrWK5cOQKgjY0Nvby8+PLlS41yiYmJDA0NzbK3/sTERB48eJBNmjQhABoZGbFTp0709/dPds3ExEQGBgZy27ZtnDBhAlu2bCnntVJvFhYWrFu3LgcMGMCVK1fy/Pnzqf6Grl+/zn79+rFJkyacOnVqmoGQVSoVQ0JCeOrUKa5evZqjR49mmzZt6OjoqCGKAGhsbKy1J5onTx6Gh4fr5fMTpI4QKD2QkkAB4KVLl7LNjtS4fv06Ad0zrpJkZGQkAXD06NHysZUrVxIA3d3dk5Xfv3+//JDRNwkJCVywYAEtLCyoUCg4YcIERkVF6f062YFKpeKBAwfk9B0VKlTggQMH5Af69u3bCYA//vhjsrphYWGcMWOG3HssWbIkFy9enCNehK5evcq+ffvKQ28VK1Zknz59+OOPP7J27drMkyePxm+jSJEibN26NSdOnMgdO3bwzp07Bk1hEhsby1u3bnHfvn2cM2cOO3TokOLv+s6dOwaz80tCCJQeSGmIT725uroyICAg2+zRhro35OXlpXMdpVJJICkFhRqVSiVHSd+4caNG+V9++YUA6ODgoC+zSZKXL19m9erVCYC1a9fmtWvX9Np+dvL333+zYcOGBMCCBQty5cqVGt6GwcHBtLa2pqOjo4boPHr0iMOGDZOHAZ2dnbl161aDeyqqVCo+ffqUhw4d4owZM+jm5sZSpUol+w0ULFiQnTp14vz58/nHH3/w1atXBrVbF+Li4rRmVi5atGiKEfIF+kUIlJ4IDAyUH6IA2LJlS44ePVpjIrdVq1YGc9FVKpU0MTFhv3790lXPwsKCP/zwg8axyMhIVq5cmXny5OGNGzfk456engTAevXq6cXmyMhIjh49mkZGRrS0tOTixYsNniQwozx48IBdu3aVe5iTJ09O5liQmJhIFxcXGhsby7m0rly5wu7du1OhUBAAmzdvzuPHjxtkoj4+Pp7Xr1/npk2bOHr0aLq6ujJ//vwaD++8efOyQYMGHDp0KFesWMHJkyfTycmJQFKiRw8PD966dSvbbc8o3377rcb9mZiYpDjsKtA/QqD0TFBQEJ89eybvv3nzhj179tQYy27durU815CdlCxZkq1atUpXHTs7O63OHnfu3GHevHlZrlw52ROqb9++BEA3N7d0XSMyMpJr167lxIkTefDgQSqVSv722290cHAgALZp00ZvuaWym9DQUI4cOZImJiY0MjLi//73Pz5//lxr2dmzZxMAZ86cyaNHj7Jp06byXGavXr0y7YGXHt69e8dTp05x8eLF7Nu3L52dnZN5zZUsWZLt27fn5MmTuXfvXj548ECrt6FKpeKff/7Jdu3ayb+Dli1b8vfff8/RHnGHDx8mALZo0YKzZs3inDlzMuQEIsg4OUKgALQCcBdAEICJKZTpCiAQwC0A29JqM6ct1L169Srr1q2r8QNv1qxZtibJq1evHqtWrZquOg4ODimK2u7du4n/vBVVKpX8QB06dKjO7b9+/Vqe6P94CEXtXbVr164c/RBLiZiYGM6bN4/W1tYEwG+//TbVYd5//vmHCoWCFSpUYNWqVQmAlpaWHDlyZJZ7RD58+JD79u3jzz//zA4dOsgvBh/3GqpVq8Y+ffpw0aJFPHnyJMPCwhgZGck5c+awWbNm7N27Ny9fvpzm9e7du8ehQ4fKWY8rVarEVatW5bj5xOfPn9POzo4lSpRgWFiYoc35YjG4QAFQAHgAoAwAUwDXAXz1SZlyAK4CsP1vv2Ba7eY0gSKTHgY7d+6UH8BqryEXF5dsGbbp1KkT7ezs0lWnUqVKbNiwYYrnR44cSQD08fGR5+FmzJihc/vjxo3TOm/XvHlzvn37Nl225gSUSiV//fVXlixZkgBYo0YN/vnnn6nWefHihcbanUKFCnHWrFl6v/+YmBhevnyZ69at47Bhw9iwYcNkbte2trZs0qQJR40axY0bN/LatWtaMy4rlUp+8803GnVNTU11fuF6+/Ytvb295c8pf/78nDRpksbog6FITEykq6srjYyMclWW5c+RnCBQXwM49tH+JACTPikzH8D/0tNuThQoNVFRUZwyZQrNzc0pSZKcIr1evXo8cuRIlgnVkCFDCICxsbE616lVqxZT+yzj4+NZv359KhQKeQJ/zZo1Orf/9ddfaxWojz0HcwsnTpyQ5yFLlizJLVu2pLrA9sWLF5w4caI8dFa0aFH6+vrqxUX/9evXPH78OL29vdmrVy86OTnJ81jqrWzZsuzUqROnT59OPz8/PnnyROfv3m+//ab171a7dm3euHGDjx49YmhoqFZx+5iEhATu2rVL/h4YGxuzZ8+e8hycIVAPtU6bNs1gNgiSyAkC1RnA2o/2fwCw/JMyB/4TqXMA/gbQKoW2PABcBnC5ZMmSWfah6YvHjx+zS5cu8gSyetFhjRo1uG/fvjSjB6SXWbNmEUjfIloXFxdWrFgx1TJPnz5lgQIF5IfUwYMHdW5f7RH46bZ8+XKd2zA0AQEBbN26NYGk9Uje3t6piszt27fZv39/jTmdxo0bZ+jvrVQqeffuXe7cuZOenp789ttv5R66ejMzM2OtWrX4v//9j8uXL6e/v3+m1/EsXLhQ699N22ZmZkY7OzuWLl2aVatW5TfffMPWrVuza9eu7N+/P0eOHMmff/6Zw4YNY61ateSRBScnJ86bN4+BgYEMCQlhVFRUlo8ynD9/ngqFgi4uLrnWIedzQleByspYfNrCDvOTfWMkDfM1BlAcgL8kSU4kNZIQkVwDYA2QFM1c/6bqFwcHB+zatQunTp3CiBEjcOPGDRQsWBBBQUHo1KkTnJyc8NNPP6Fz5856iSNWtGhRAEBISAgcHBx0qmNpaYno6OhUyxQvXhw+Pj7o27cvAKBAgQI62zRmzBjs3bsXMTExGscDAwOhUqlydMbb58+f4+eff8bGjRuhUCgwatQoeHl5ab1/kjh37hzmz5+PQ4cOQZIktGjRAqdPn4apqSmaN2+Ot2/fas3ZpCYqKgoBAQG4fv26HI8uICAAUVFRchl7e3tUr14dvXr1grOzM5ydnVG+fHm9pnWPi4tDQECA1nO1a9dG37598eHDB0RERMjbx/vv37/H06dP5WMpRXe/efMmJkyYgAkTJsjHjIyMkDdvXuTNmxf58uWT/5/SsdT2raysNH5X79+/R48ePWBtbY2tW7eK2H25iKwUqGcASny0XxzACy1l/iaZAOCRJEl3kSRYl7LQrmyjcePGuHLlCnx9ffHTTz/hw4cPcHJywsuXL9G9e3dUqFABnp6e6NmzZ6YeNGqBevHi0483ZSwsLDQegClRunRp+f/btm3DN998o1P7zs7OOHv2LLy9vREUFIQ6derg0aNHWLFiBaKjo+Hr66vXh6s+iIiIwPz58+Hj44OYmBh0794ds2bNQpkyZZKVVSqVOHjwILy9vfH333/DzMwMHh4eGDlyJJo0aYLY2FjExsbCy8sLS5cuhb+/PxwdHfHy5UtZhK5du4br16/j3r176pECSJKE8uXLo23btnB2dka1atXg7OyMwoULZ2mqiTNnzmDAgAG4c+cO7O3t8ebNG/lc/vz5sWHDBlSuXFnn9sikFCafilhERARev36NEydO4Pjx43jz5g1MTExQrlw5lCpVCgDkOm/evJHrxMbGput+LCwsZNEKDQ3Fu3fvULt2bUyYMCHdQpjRZJyCzJNl+aAkSTIGcA9AUwDPkSQ6PUne+qhMKwA9SPaRJMkOSQ4TziTDUmo3t+aDevv2LX7++WesXLkSJiYmaNSoEQICAhASEoIyZcpg0qRJ6N27d4Z+DDdv3kSVKlWwbNkyDB06VKc6ffr0we7du9PsRW3fvh09e/aU9/38/NCuXbt02wgkZc/18PDAhg0b8N1332Hbtm05ImFeQkICfH19MXXqVLx58wYuLi7w9vbWmm8qJiYGmzdvho+PD+7fvw9bW1sMHjwYw4YNQ6FChTBkyBCtCR0LFy4MpVKp8eC3tLRE1apVNYTIyckJlpaWWXq/H/P27VuMHz8e69atg62tLby9vdGnTx8cOnQIJ06cQNGiRfHjjz+iSJEier+2SqXCsWPHsGjRIhw/fhySJKFdu3YYNWoUGjVqpCHICQkJKfbcUjr24cMH3Lt3D3fu3IGNjQ0sLCzw4cMHREZGpstOU1NTvfXuLCwssjynVUJCAqZPn46NGzciMTER3bt3x8yZM7P1e5UWOSJhoSRJ3wJYjCSPvvUkZ0mSNB1J449+UtJfygdJ7uhKALNI7kitzdwqUGoCAgIwYsQInDx5EsWKFUOrVq1w4sQJBAcHo0SJEpgwYQL69++frgd3WFgY7OzsMGnSJMyePVunOoMGDcKqVaugVCpTHW7z8fHB2LFjYWlpCTs7O4SHh+PKlStaexW6QBJjx47FwoUL0bRpUxw4cABWVlYZaiuzkMTBgwcxYcIE3Lt3DxUrVsS8efPQrl27ZA+RsLAwrFixAsuWLcObN2/g4OCAUaNGoX///rL9f/31F5o1awZtvymFQoGWLVvKw3POzs4oW7aswYY6SWLbtm0YNWoU3rx5g169emHhwoUoWLCgQey5efMmlixZgl9//RVxcXGoVq0aRo4ciR49eiRLnqkrt2/fRs2aNeHo6IiLFy8iT548AJKEMSoqKkVR00X4Pt5PTEzU2SYjIyNYWVmlS9RSO6ZtuFL92/6YTp06Ye/evRn6HLMCkbAwB6NSqbhnzx55XUr9+vU5ZcoUed1Q4cKF6ePjw8jISJ3bMzU1ZZ8+fXS2YcyYMQSQ5jVGjx4te4alFVRWV1QqFWfOnEkArFu3rkHWo1y4cIENGjSQ3b9XrVqlNcyNtlBE27ZtY0JCAmNiYnjixAlOmDCB1apVS9WhoEWLFtl+jykRFBQkp1kpU6YMjx07ZmiTZF6/fs0ZM2awcOHCBJJCKU2dOjXdIZRiYmJYtWpV5smTh4GBgVlkbdJ3OTo6mq9evWJQUBCvXr3KM2fO8PDhw9y+fTvXrFlDHx8fTpkyhaNHj6a7uzu7d+/ONm3asGHDhnR2dmbZsmVZsGDBZBHcddksLCxYqFAhOjo6snr16mzQoEGy4LhAUuT4nLQoHob24suq7XMQKDXR0dGcPn068+TJQ0mS2L9/f65YsYJfffUVAdDe3p5z5szRKSdPqVKl0vUQnDx5MgGk+cPv1q0bjYyM2KBBA5KpB5VNL8uXLycAVq5cOcUoDPomKChI9rC0sLDglClTtH6+n4YiatGiBf/44w/euHGDPj4+bNWqlUaQVBsbGwLgiBEjNEJj4b8FsadOncqW+0uN+Ph4zp49m+bm5jQ2NuakSZMYHR1taLO0EhcXx82bN8ufpZmZGX/88Udev35dp/pDhw4lkP0ZoDNLfHw83759y+DgYAYEBPD8+fM8duwY9+zZww0bNnDJkiWcOXMmJ0yYwMGDB/P7779nhw4d6Orqytq1aydbjP3xpsuC6+xCCFQu4smTJ+zevTuBpPTfPj4+3LFjh5wo0dbWltOmTUt1gWf9+vXp5OSk8zXnzp1LAHz06FGq5Ro2bEgjIyN27tyZZOpBZTPCli1bqFAoWLp0aQYFBWW6vZR48+YNhw8fLocmcnd354sXLzTKqFQqHj16lK6urgSSQhG5ublx1qxZ7N27N4sUKSL/2PPnz89u3bpx7dq1ck6u7t27U6VS8f3795wyZQobNGjA7t27GyT81aecP39ejp339ddfa8RazMmoVCqePn2a3333nbzg2dXVlYcOHUrRfV+dkLNLly65MlpJRrhw4QK7deuWbE2cestpgXCFQOVCzpw5I4tSxYoVefToUR46dIh16tQhkJQ8ztPTU2sSv86dOzN//vw6X2vp0qUEwJs3b6ZarnTp0gTAIUOGyMfUQWXNzc11fqNNjUOHDtHc3JyFCxfW+4MzOjqac+fOlUMTtW3bNtk9x8fHc/PmzXIoInNzc9asWZOVKlXS6AU1btyYs2fP5qVLl+S1NCEhIbSzs2PJkiXTzFlkCN69e8eBAwdSkiTmy5ePK1eu1Ps6vOziwYMHHDlyJPPmzUsALFeuHJcvX64RHf7p06fMnz8/HRwccuTfQ5/Ex8dz27Zt8vPB2NiYvXr14oYNGzTWL1pZWeWoYVxSCFSuJTExkatXr5a/YO3bt+f9+/d57Ngxec7EwsKCY8aMYUhIiFxv2LBhBHRPKKhLJl6VSkUzMzMC4PTp0zXOqYPKOjo6ppleWxdOnTrFvHnz0tbWlhcuXMh0e0qlkps3b2aJEiUIgDVr1uRff/2lUebDhw9csGCBPN9hamoqR/8AkuLJjRgxgkeOHNGal0mpVLJly5aUJImnT5/OtM36RB1+S31vXbp0SdZjzK2Eh4dz0aJF8suTjY0Nx40bx4cPH7JRo0ZUKBQ8f/68oc3MMt68ecNZs2bJC7ft7Ozo5eWlMUweGRnJHTt28Ndff82RQi0EKpfz9u1bDh8+nAqFgqamppw4cSI/fPjAU6dOycFbzc3NOWzYMD59+pRz5swhAJ2jMquT5508eTLFMmFhYfLDevXq1cnOfxpUNrNcuXKFdnZ2tLCw4B9//JHhdo4fPy73RB0cHLh161aNXsPVq1fZtm1bmpiYaAyDFChQgD169OD69etTTceuZsmSJQRAT0/PDNuaFTx+/FhOJ+Hg4MDDhw8b2qQsITExkfv27aOLiwuB/4+B+XGes8+Jmzdv0t3dXXamcHJy4tq1a3PsPGJqCIH6TLh58yabNWtGIClT6ebNm6lUKnn+/Hk5DI96+AkAz507p1O7fn5+BJDqwysgIEB+eB84cEBrGXVQ2QULFmTo/j7l9u3bLFGiBE1NTbl379501b1+/TpbtWolv1UvWLCAMTExjIqK4tGjR9mnTx/a2tpqeDZVqVKFs2fP5r///puuoa8bN27IoYYMnVxQzafZiceMGaOzJ2huZ+3atfLfVO0dun379hzzt8koSqWShw8flp8BkiSxXbt2PHHiRK6eXxMC9RmhUqm4f/9+eUijXr16ctDNy5cvs2PHjvJDt3Hjxrx3716abZ44cYIAuGvXrhTLHD16VG43pYn+j4PK6itCdHBwMMuXL08jIyOuW7cuzfLPnj1jv379KEkSTU1NOWrUKJ46dYrz5s2jq6trsp6So6MjFy5cmOFUENHR0XRycqKFhYVOn3V28M8//8i9xlq1ahksgaYhePv2LUuUKMECBQrwypUr/Omnn+Qh8uLFi3Pu3Lm5LrVGREQEly9fLi89sbS05LBhw3LM9y2zCIH6DImJieGsWbPkNTn9+vWT56H27t0rP4CNjIzYo0ePVB0gLly4QADcsGFDimXWr18vt5mat9+zZ89ob2/PIkWKaMyLZYZXr17JD1wfHx+tZcLDw+nl5SW7e9etW5ft27envb29bLd6Tkk9gXz37t1M2zZ8+HAC4Nq1azPdVmb58OEDhw8fTiMjI1pZWXHJkiVfVDBUlUrFTp06EQAPHTokH4+Ojqavry8rV64sz9sOGjSId+7cMaC1afPo0SOOGTNGduopVaoUfXx8cuQ8UmYQAvUZ8+zZM/bq1YtAUipub29vvnz5kgD4v//9jz/88IPsburm5qb1bfr69esEwF9++SXF68yYMUN+0Kc1zn3ixAkaGRmxcePGenNnff/+vewY4uXlJQ9pxMfH08fHR855pBZstaNDxYoVaWdnJ7voe3l58eXLl3qxSZ2OQl/zbplh//79LFasGAGwQ4cOfPLkiUHtMQSrVq2iev2ZNlQqFf/44w95OBxISjL5xx9/GPzvp0alUtHf359ubm4aueT27dv32b5sCIH6Ajh79ixr1Kghu9yampryhx9+IJm0IPV///uf3INo27athsdeUFAQAXD+/Pkptj9o0CDZTVUX1NEhJk6cmLkb+4ioqCj54dK5c2f26tVLY4EsAFatWpWDBw9m79695d6Tg4MDlyxZotX7LqO8evWKhQoVYrFixRgaGqq3dtPL06dP5WHdYsWKcf/+/QazxZAEBATQ3Nyczs7OOuVCu337NgcOHCh/fypXrkxfX1+DORmoFyOrf8PqaDBfwvCsEKgvhMTERK5du1Z+MBcoUEBjGCs4OJiDBw+WcxS1aNGC/v7+fPHiBQFw6tSpKbbdvn17mpiYsFy5cjrZolQq2aZNGwLpyx2VEk+ePOG6devYtWtXjXkkIyMj1qtXjxs3buTFixc1QhFVr15dDkWkT1QqFdu2bUtJktLMpJtVJCYmcunSpcybNy8lSeLw4cMznf8ptxIdHc3KlSvT0tIy3cN2YWFhnDNnjtz7tLOz408//ZRtbvivXr3i9OnTNcI5TZkyRW/D47kBIVBfGO/evZPXRZiYmHDcuHEaD6/nz59z1KhR8tujOq332LFjU2yzVq1aNDMzk8Mc6UJYWBhLlSpFa2trPnjwIF33EBERwcOHD3P48OEai2TVwx7qf1u0aMGzZ8/KYZjUx44fP55lwzYrVqwgAI4bNy5L2k+Lq1evsnbt2gTAatWqGTQzbY8NdQsAACAASURBVE5g4MCBac6hpoV6oav6czUxMeEPP/zAK1eu6M/Qj7h27Rr79esnry10dnbmhg0b9JJpObchBOoLpEuXLsyXLx9btmxJICkI6oYNGzTcp1+9esUJEybQ0tJSLpNSOvoiRYrQxMSEbm5u6bJDHVTWycmJ06dP5+jRo3n8+PFk5RITE3np0iXOmjWLjRo10uglOTk5sUaNGjQyMqIkSfTw8OCzZ8/YrVs3uYxCoeD333/Pa9eupf/DSgeBgYE0Nzdn9erVdRpK0ieRkZEcO3YsFQoFLSws6O3tnaNC1hgCtUNQjx499PJColKpeO7cOXbp0kXvc0CJiYk8cOAAmzRpIruJd+zYkadOncoxc2CGQG8CBWAoAFtdGsuOTQhUyowYMYJAUoRyPz8/li1blgBYp06dZG7ioaGhVCgUsijUrFmT+/fvl8UsISFB/rEOHjw43bZ4enpqzBMB4LBhwxgcHExfX1927dqV+fPnl88VKVKEffr04fr16+np6Sk7QLRr147Xrl3TCEWkHq50cnLi69ev9fLZpURsbCydnZ2zPCq2No4cOSIH/2zdunWacRO/BIKDg2ljY8PSpUtnyfDm48ePOXbsWNmLrnTp0ly0aFG6rxUeHs7FixezTJkysjPTqFGj0j2q8LmiT4GaCSAIwC4k5W2SdGk4qzYhUCkzb948ApCDrsbGxnLu3Lm0srIiAPbu3VtjnN3GxobfffcdZ86cKa8bqVKlCnfs2MHg4GBZPKZNm5ZuW1q0aJFMoD7e8uTJw1atWnHhwoW8efMmExISuHHjRhYvXlxey3PkyBH6+PjIxwoXLszZs2fz7du39PX1pZGREStUqJClaQTGjh1LAFy5cmWWXeNTXrx4wa5du8r3vHPnzi/6bVtNQkICGzRoQGNj41RDdOmDiIgILlu2jI6OjrLAjBw5Ms1ILZ/GCyxbtiyXLFnyxc4VpoReh/gASABaAtjxn1jNBlBWl7r63oRApcyvv/5KAPT399c4/vz5c/bu3Vv2yJs7dy5jY2NZrFgxtmnThmTSD9Lb25uFChWSveDUYqItzFFaqH+gn27ffvst//zzT42hsj/++EPOp1SqVCn+8ssvHD9+vPwWW7FiRa5duzbZ8Nru3btpYmLCEiVKZMn6luPHj8u9uOwQCKVSyZUrV8r3PWDAgM9u/Utm+PnnnwmA8+bNy7ZrKpVK+vn5yRHujYyM+N133/HMmTPyd0KlUvHkyZPs0KGDRsR1Pz+/z9ZNPLPofQ4KQDUkZce9A2AlktKzz9e1vr42IVAp8+effxIAd+7cqfX8hQsX5AlhR0dHFi1alE2aNNEoEx0dzSVLlmgMvw0ZMoRxcXHpsqVmzZpaBers2bNymevXr8vzZba2thw/fjz79OkjD+E1aNCABw8eTDUE0bFjx2hhYUF7e3u9uueGhoayaNGiLFSoUJYPI5JJLtP169eX3Z91DVn1pXDq1CkaGRmxefPmBovGrnZyUH8/q1evTnd3dzmNSXpzVn3J6HOIbziAKwCOAegCwOS/40YAHuhyEX1uQqBSJjAwkAC4aNGiFMsolUquX79e7ilZW1vz9u3bycqpA6Gqt5IlS/KXX37R2ePowIEDyTJ7Nm3alGTSOp6+fftSkiSamJiwe/fucgw9SZL43XffpSsa9fnz52ljY8N8+fLpJdySSqXid999RwD8/fffM91eakRHR3PSpEk0Njamubk5Z82ale6Xgc+d0NBQFitWjPb29tnuir1+/Xo6OjrS2NiYrq6uvHr1Km/cuMFGjRrJvSUjIyM2bdpU6+9IoB19CtR0AA4pnKuky0X0uQmBSpn379/r7AodHh4urwMxNjbmqFGjNNJmeHl5ycIyb948eSy+SJEiOsexO3nyJN3c3Oji4sI5c+bw5cuX9PT0lF3d1Smv1W+fHh4eGQ5FdP36dRYqVIjm5uY8cuRIhtpQ4+vrSyDl6AT64vjx47IjS7NmzXj//v0svV5uRKVSsX379tnysvApe/bsSTYC8HFKFnUPqkqVKgSSsgu4u7unmWNNoEeBymmbEKiUUalUtLCwYK9evXQq37x5cxYvXlxOzWBvb09fX18mJiayb9++cg8oKiqKCQkJ3Lp1q0Y6+rlz5+qUjj4+Pp7Lli2Tww+VK1dOztNka2vLn376SS+hiO7fv89SpUrR2NiY27Zty1Abd+/epYWFBZ2cnLJsfcqrV6/krMT29vbcsmWLcIJIgeXLlxMAx4wZk+3XVs87fbo5Ozvz7NmzGnNQf/31F9u1ayf3qpo3b87ffvst1yaHzGqEQH2hODo60tXVVaeyHTt2ZKFChUgmuTSXL1+eAFijRg3WqVOHFhYWzJs3r0YdpVLJ3bt3y04N6nT02ibzVSoV9+7dK0dktre3lx0AsiIUEZkUp/Crr76iJElcsWJFuurGxcWxZs2aNDMzY0BAgF7tIpM+j3Xr1snzez/++KNBQybldK5du0YzMzPWrFnTIMOe6t79p1vt2rX5119/aXWAuHfvHocNGyavM6xYsSJXrlyZ4cj5nytCoL5QXFxcWLFiRZ3K9uzZUyPOXlxcHL29vWUPPBMTE5YqVUprXZVKRT8/P9npIl++fPTy8pLT0Z87d06e9LewsNCYWN6+fXuWLjYNDQ2V7Zo9e7bOvZNJkyYRAJcu/b/2zjssquPr499Zlt5sCFjRYEHFrrFhibHEqOirBjUYNWoUNbHEDkYj+BMrGmMvGFEUe+ya2KJGUCzYkKAgqIAGFKWz7J73D9gbygIrbAPm8zz3eXbvzp17hrLfe86cOfOLym0KDQ0VNtZr1KgRXb58WeX3KE8kJydT48aNyczMTGuhTw8PjyKXSlhbW9OUKVPoypUrBTyld+/e0apVq6hOnTrCg9y8efOU2gizIsAFqoLi4uJCFhYWSrWdMGECiUSiAl/gsbGxgqCIRCLy8vIqNNwlk8no7NmzQukkY2NjwWPS09MTQh59+vTR6CZrHz58EEI0s2fPLva+ly9fJsYY9e3bV6U2pqWl0aJFi8jAwIAMDAxo8eLFGq9GURYZP348ASA/Pz+t2ZCcnJwnzKenp0deXl4UExND69evFyrtA6AaNWrQDz/8QNevX88jVhKJhA4ePCg8rInFYhoxYoTa13HpOlygKihTpkwhAEqFzuSVJ/KLT2pqqjAhLA9H1atXj44ePVrol/fr16/zbJwoz8j7v//7P7WXIiqMtLQ0waZx48YVuiZFvuGdqrPELl26JIRNu3XrxrO8lCQgIIAACJX5tU1gYCDt27dPoffz4sUL8vHxoY4dOwp/97Vr16aZM2dSYGBgnv+XoKAgGjFihJBk0alTJzpw4ECFLF3FBaqCIt+aQpmK2/JyRPl3G5VvxQGAJk2aRLt37yZbW1sh2+zRo0dC29TUVPL09CQjIyPhGiMjI7KzsxNEbuLEiVor0yORSIRFykOHDi3gvchkMqFqQ+4N70pDfHw8jR07lgBQlSpVaOfOnTwJQkkiIyPJ0tKS7O3tlUrA0SWeP39Oq1atEsLL8rnW2bNn061bt4S/gRcvXtC8efOocuXKwhKOlStXVqhF2VygKijyBbKXLl0qtq18/6b8G91duXJF+Af7+eefSSaT0bFjx6hz586kp6dHIpGIpk6dSitXrhSSHuRfxsuWLaO3b98SUXbRWGdnZyG0MXbsWK1sWS2VSoVdcHv37k3JycnCZ7/99hsBJas3mB+ZTEZ+fn5CtqKrq6tGFvmWFzIzM6lDhw6kr69PwcHB2janVERERJC3t7ew1xMAql+/Ps2bN4/u3r1LMpmMkpOTadOmTdSoUSMCsrd1nzp1arnZ1r0ouEBVQGQymfBUtm/fvmLb+/j4EIACZYL27dsn/FNt2rRJ8DDkh3y7gNzx961btxY6txISEkLDhg0jxhiJRCIaOXJkHi9ME8hkMvr5558JAHXs2JHevn1LT58+JTMzM3JwcCh1llV4eDh9/vnnBGTXXzt//ryKLK84yD361atXa9sUlfLPP//Q0qVLhcxX+VILDw8Pun//PmVlZdHp06eF+pWMMRowYABdvHix3HreXKAqILkLvCrzT75lyxYCUGD/m1WrVgn9FJXJJK+E3qJFC6UqODx+/JhcXV2FLTSGDBlCd+/eLfF4S4K8QkazZs2oTZs2pK+vXyobMjIyaOnSpWRkZERisZgWLFigtR1ayzIXLlwQklTK89qh0NBQWrJkCTVt2lT4P3JwcKBFixbRo0eP6OHDhzRhwgQhZN6iRYtyuWcUF6gKiHxyWdmFjXv27CGgYHHZmTNnCv2MGjVKoTg1aNCAMjMzac2aNcLWGC4uLgXChYoIDw+ncePGCZPFAwYM0OgGfLt37xayCxcsWFDifq5duyZ80XTq1IlXECghb968IVtbW7K2tqbXr19r2xyN8fDhQ/rpp5+EEJ/8wWnJkiV048YN8vLyEuZ+5bvuqmJBuy7ABaoCIhcWU1NTGjFiRLHtjxw5QgDo7Nmzec67uLgIYTxPT0+FAjV06FCh/evXr2n8+PHEGCNjY2P6+eeflfIinj9/Tm5ubkJKe58+fQqIpTq4du2a4MXZ2tp+tLC8e/eOJk6cSEB2LcPNmzeX66d+dSKTyejLL78kABU2LCqTySgkJITc3d2FkmJy72nJkiW0atUqYS7LwMCAxowZo7XMWFWhEwKF7P2jwpC9Rce8ItoNzfmltC2uTy5QhdOpUyeyt7enhg0bUvfu3Yttf+7cOQJAR44cyXPeyclJmMuKjY0VMvJyh/byb4BIRBQcHCys96hbty4dPHhQqRj6q1evaPr06UKNvu7du9OFCxfUEn9PTEwkOzs7qlKlCgUEBJCZmRlVqVJFqXUpMpmM9u/fLxTa/eqrr/Lsr8X5eNauXUsAaO7cudo2RSeQyWR0584dmjdvHtWrV0/4n2vdujVNmjSJevfuLXj/PXr0oOPHj5fJhyOtCxQAPQDPANQHYAAgBEATBe3MAfwFIJALVMnJyMggQ0ND+vrrr6lbt27UsGHDYq+5evUqAQUXQ9avX5+sra2FKhMvXrwgNzc3cnR0pEGDBhW5FYRMJqO9e/cKhWh79OhB9+/fV2oMcXFxNGfOHKFMTKdOnej06dMqFSp5DTy5KN+8eZOqVq1KZmZmRabmR0RECCn8devWLXVBWg7RnTt3yMDAgNq3b0+ZmZnaNkfnkMlkdOvWLZo1a5ZQkQIANW/enLp27SpsRGpvb0/r169XedkwdaILAtURwLlc7+cDmK+g3VoA/QFc5gJVcm7dukUAaP369TRixIg8JYwK486dOwTk3ZBQJpORkZER2djY0CeffFJie5KSksjd3Z0MDQ1JJBLRlClTCqy3Koz4+HhauHChkMLetm1bOnbsWKmfFPfu3UsAaMKECXnOP3r0iGrWrEkGBgZ09OjRPJ9JJBJasWIFGRsbk56eHs2ePTtPmjqnZCQlJVHDhg3JwsKCb4OuBDKZjG7cuEEzZswQHv4ACNEAebh51qxZ9Pz5c22bWyy6IFBDAWzP9X4UgF/ztWkF4HDO60IFCsB3AIIBBNepU0ddP7Myzfr16wkA3bx5k3788UcCUOxCxydPnhAAWrNmjXAuISGBAFC1atWoU6dOpbbr2bNnQjWHKlWq0IYNG5ReOf/u3Tvy9PQU/gGbN29OAQEBJdqlNDIykiwsLKhhw4YKBSYyMpLs7e1JJBLRrl27iCh75b88Nbhdu3Yazzgsz4wZM4YAlLjqfEVGKpXStWvX6PvvvycbGxtBrOTJSiKRiIYOHUrXr1/X2TR1XRCoYQoEan2u96IcUbKjYgQq98E9KMW4urqSoaEhZWRk0OrVqwkK1jfl58WLFwSAvLy8hHMPHjwgILvA6+DBg1Vm3x9//CFs1eHo6EiXLl2i7du3U/PmzcnW1pa+/fbbQjOUkpKSaMWKFVS9enUCsitE+/n5KS10WVlZ1KVLFxKLxXTr1q1C28XGxlLz5s0JyN6rijFGZmZm9Msvv/Ctu1WI3JMdO3astk0p82RlZdHly5dp8uTJwv8HctZSAdnFmf39/QuEUJOTk+nVq1daslo3BKrIEB8ASwDxAJ7nHOkAYooTKS5QirG3txc8HvlC2+KqSci9pfnz5wvnzp49K/yRu7m5qdTGzMxMWrduHVWqVElhZqCjo2ORYbyUlBRau3Yt1ahRg5CzIHb79u3FbsUgr5ixbNmyYm308/MTsgobN26sVNo8R3mePn1K5ubm1KhRIx4qVTFZWVl04cIFmjhxohB1kB+VKlUiDw8PevPmTZ6EpCZNmtC1a9c0bqsuCJQYQASAevgvSaJpEe25B1VC4uPjCQDNmDGDiLIrcwOgvXv3Fnldeno6AXl3jt25c6fwR7148WK12PvmzZtCRSp/ynthdm/atInq1q1LQHYts40bNypczBgUFER6enrUrVu3Ir2g6OhooSxTzZo1qVWrVgSAvv/++zKZJaWLZGRkULt27cjAwICHS9WMRCKh8+fP0+jRo8nExKSAZ5X7sLS01HgdQGUFSgQ1QURZAKYCOAcgFMABInrEGFvCGBuorvtWRIKCggAAHTp0AADUqFEDABATE1PkdQYGBhCJREhJSRHOvXr1SnhtbW2talMBAFZWVpDJZAo/i4uLK/Z6Q0NDTJo0CeHh4dixYwf09fUxefJkfPLJJ1i7di1SU1MBAMnJyRg5ciTMzc3h5+cHPT29An1JpVKsW7cOTZo0wYkTJzBt2jSEhoYiMDAQw4YNw/r16zFmzBhIJJLSDZqDhQsX4tatW1i5ciVatmypbXPKNWKxGL169cKuXbuQmJiIU6dOoXfv3nJnIA/v37/HsWPHtGClEiijYrp0cA+qIAsXLiQAQvZOUlJSHo+qKMzNzWnkyJHCezc3N+HJKv/6KFUybNiwAk9yenp6JdrQTSKR0J49e8jBwYGQs+p++fLlQhWMgIAAhdfduXOH2rZtS0D2Nt7556eysrJowoQJBIAGDhxY7srNaBL5mrv+/fvr7MR9RSD/mkb5sXXrVo3aAW2H+NR1cIEqSO/evcnGxibPP76FhQW5uLgUe621tTU5OzsL752dnYVsoKLWO5WWyMjIPAsRRSIR+fj4lKrP/NvRy4Unf/giKSmJZs6cSSKRiExMTGjVqlWFJlzIZDKaM2cOIWcBcVnbAkIXiIuLI2tra7K1tRV2XOZoh3nz5hUQJ0NDQ42XmOICVUGQSqVkaWmZR2SIiBo3bkxdu3Yt9vr69etTr169hPdt27YVkhDUvT4lPT2dDAwMqF27dhQREaGyfqOiosjU1FQo1yTfjj4+Pp5OnjwpLHr88ssvlV4z4u3tLazJ4l+yyiOVSqlv377EGKOLFy9q25wKT2pqKg0dOlSYi7KysqJjx45p3A5lBUqs3gAiR938888/eP/+vTD/JMfW1hYvXrwo9noTE5M8c1AxMTEwNDQEoL45KDkpKSnIzMzEZ599hnr16pWqrwsXLmDLli1ITEzE8+fPkZaWhmvXruH9+/fw9PTE0qVL4e3tDalUiurVq+PAgQMYOnQoGGNK9T937lxUrlwZkyZNQteuXXH+/HnUqlWrVDZXBHx8fHD27Fm4u7ujR48e2janwmNsbIyDBw8iOjoacXFxaNmyJQwMDLRtVqFwgSrjBAYGAkABgapRowaCgoJAREV+CZuamgpJBVlZWYiLi0P9+vVhamoKU1NT9RkOIDo6GgBQu3btUvWzd+9ejBo1KjskkIOjoyM6duwImUyGiIgIhISECEL84cMHXL9+HZ06dULNmjWVvs93330HS0tLuLq6okuXLvjjjz/QoEGDUtlengkODsb8+fPRsWNHLFq0SNvmcHJRp04d1KlTR9tmFIvasvg4miEoKAgikQht27bNc75GjRpITU3Fhw8firw+twf15s0byGQySKVStXtPAAQPr7QCtWjRojziBAAPHjzA8ePH0blzZ0yZMgX16tXD33//jWvXrqF79+5Yt24d6tevDzc3N0RFRSl9LxcXFxw/fhxv3ryBk5MTQkJCSmV7eSUpKQkjRoyAiYkJ/P39oa+vr22TOGUQLlBlnMDAQDRr1gxmZmZ5ziubam5qaioIlDzFPD09XaMCVZonuaysLDx79kzhZ//3f/+He/fuYdmyZbhz5w46duyIzp0748yZM7h58yb69u2LzZs3w97eHt9++y2ePn2q1D2/+OILnD9/Hunp6ejWrRuuX79eYvvLK5MnT8bTp0+xbds22NnZadscThmFC1QZJiUlBQ8ePMCnn35a4DO5QMXGxhbZh4mJiRDik4tZSkoKbGxsVGxtQVThQYnFYrRq1UrhZ506dcLDhw8xb968Ak/w7dq1w++//4579+5h8ODB2LVrFxo1agRXV1eEhoYWe98uXbrg8uXLMDQ0RK9evXDu3LkSj6G84efnhz179mDChAkYNmyYts3hlGG4QJVhbt++DalUWmD+CchOkgBK5kF9+PBBYx6UsbExqlSpUqp+Vq1aJSR2yBk4cCCuXLmCTz75pMhrW7RogQMHDuDhw4cYMWIE9u3bh6ZNm2LYsGHFhu9atmyJq1evwsrKCgMGDMCBAwdKNY7yQHh4ONzc3ODg4IC1a9dq2xxOGYcLVBlGniBRlAeljEBJJBJIJJI8bTUlULVr11Y6k04RMpkMkZGRMDIyApBdZeLo0aP4/fffP6rfJk2aYM+ePQgLC8PYsWNx7NgxtGzZEs7Ozrh161ah1zVs2BDXr1/HJ598guHDh2Pbtm0lHktZJzMzE8OHD0dWVhYCAgJgYmKibZM4ZRwuUGWYoKAgWFhYwMHBocBnynpQ8i+R1NRUvHr1CmJxdmKnJgWqpISGhqJ79+4YP348bG1t0bBhQzg6OmLQoEEl7tPe3h47duxAeHg4Jk2ahLNnz6J9+/bo27dvoXNNtWrVwtWrV9G6dWt89913WLFiRYnvX5aZP38+7ty5gzVr1sDR0VHb5nDKAVygyjCBgYFo164dRKKCv0YTExNUqlRJKQ8KyBaomJgYIdymboGSyWR4+fJliQQqPT0dixYtQosWLRAUFISff/4Z9+7dg56eHoyNjVVin52dHTZt2oSIiAhMmzYNV65cQZcuXfDZZ5/h0qVLBbIGq1WrhosXL6Jbt26YO3cu5s2bV6BNeebMmTNYs2YNBg0aBDc3N22bwykncIEqo7x8+RIxMTEK55/k2NraKpUkAWQnRrx69QoWFhYAoPYkidevX0MikXy0QF26dAktWrTAkiVL0LlzZ9y/fx8//fQTDA0NkZaWpvKwUs2aNbF27Vo8f/4cs2fPxs2bN/HZZ5/ByckJZ8+ezSNCFhYWOHPmDAYMGIDly5fDzc0NUqlUpfboIrGxsRg9ejRq1aqFHTt2lCpky+HkhgtUGaWwBbq5qVGjxkd7UHIPRN0e1Mdm8CUkJGDs2LH47LPPEB8fD19fX1y8eBGNGjUS2qSlpanMg8qPtbU1VqxYgaioKHh4eODBgwf44osv0L59exw/flwQKmNjYxw+fBiurq7YsmULvv76a2RmZqrFJl1AJpPhm2++QUJCAvbu3VvqhBcOJzdcoMoo8i02FCVIyJELVFGhJrnH8fbtW7x7905jc1DKroEiIuzevRuNGzfGrl27MGrUKDx58gRjxowp8KSempqqNoGSU7VqVXh6eiIqKgqenp6IiIiAs7MzWrZsiYMHD0Imk0FfXx+//fYbpk6dioCAAAwaNEhI5S9vrFy5En/++ScWLlyIrl27atscTjmDC1QZJTAwEPXr14eVlVWhbWrUqIH09HQkJiYW2kbuQckFg4hgYmJSYOGvqlHGgwoPD0evXr0wevRoVKpUCX/++Sd2795d6JjVEeIrjEqVKsHDwwPPnz/H8uXLERcXh6+++grNmjXDnj17IJPJ8Msvv+Cnn37CmTNn0Lt37yJ/D2WRoKAgeHh4wMnJCR4eHto2h1MO4QJVBpFIJLh9+3aR3hOgXKq5/Av95cuXALJThbVd5igzMxNeXl5wdHTEX3/9BXd3d9y/fx89e/YstD+JRIKsrCy1e1D5MTc3x5w5cxAZGQkfHx8kJiZi1KhRcHBwgK+vLzw8PODj44Pr16+je/fueP36tUbtUxfv37/HiBEjYG5ujr179wqeN4ejSrhAlUEePHiAtLS0IuefgP9SzYtKlJB7UPI2qampGqkiER0dDUtLS5ibm+c5f+3aNbRq1QoLFy5E27ZtcffuXXh5eRUrPGlpaQCgtbU3JiYmmD59OiIiIrBx40ZkZmZi3LhxaNCgAYyMjLB161Y8ePAAXbp0+ajaf7oIEWHSpEmIjIzEjh07Sl1LkcMpDC5QZZCiFujm5mM8KPlW6+/fv9fKGqh3795h4sSJcHJyQkxMDLZu3Yq//voLTZs2Vao/uUBp2oPKj5GREdzc3ITt6MViMdzc3LB48WKMGTMG0dHR6Ny5s1LllHSVXbt2Yf/+/XBzc8PgwYO1bQ6nHMMFqgwSFBQEAwMDtGzZssh2ygiU3IOKj48HkC0UmhQoIsL+/fvh4OCArVu3Yvjw4QgNDcWECRMUru8qDF0RKDkGBgb49ttv8eTJE/j5+cHCwgI7d+6EiYkJ/v33Xzg5OeH27dvaNvOjCQsLw9SpU9GsWTOsXr1a2+ZwyjlcoMoggYGBaNWqVYH6c/lRppqE3INKSEgQEiPULVASiQSxsbGwtLREv379MGLECBgbG+P06dPYt29fiUKM8iw5XSuvIxaL4erqiocPH+LAgQOoU6cOMjMz8fbtW3Tu3BknT57UtolKk5GRgeHDhwsPFbryMMApv3CBKmO8ffsW//zzT7HzT0B2uKlKlSpKeVCJiYlCdpy6BSoqKgpEhMOHD+OPP/7AnDlz8PDhQ3zxxRcl7lPXPKj86OnpYdiwYbh79y6OHTsGBwcHZGRkYMCAAXBxcUFCQoK2TSyWbKspjAAAIABJREFUOXPm4N69e1i7dq3SoVcOpzRwgSpj3Lx5E0DRC3RzU1w1CbnH8f79e1haWgJQbxWJoKAg9O3bF0B2Bt/t27exfPnyUu/eK/egdFWg5IhEIjg7O+Phw4fw9fWFoaEhDhw4gJo1a2Lu3Ll48+aNtk1UyIkTJ/DLL79gyJAhmDBhgrbN4VQQuECVMZRZoJub4qpJyL/Qk5OTBbFShwf14cMHTJ06FR07dhS29diyZQtatGihkv61ncX3sTDGMGbMGERERKBevXrIyMjAihUrYGdnh+nTpws/I13g1atXGDt2LOrUqYNt27bxUkYcjcEFqowRGBiI6tWrK71LaXHVJEQiEYyMjCCVSmFgYABAtQJFRDhy5AgcHBywYcMGDB48GDNmzAAAle60qushvsKoUaMGgoODBY+4Zs2awnb0kydP1npKulQqxahRo5CYmAh/f39UrlxZq/ZwKhZcoMoQRISgoCB8+umnSj/F1qhRQ5iULwz5XkryPlUlUNHR0XB2dsaQIUMgEonw+++/4/Dhw/jw4QOA7G0qVEVZCfEpokqVKvjjjz/Qq1cvPH36FCNGjECfPn2wadMm2NvbY9y4cUpvR69qvL29cenSJSxevBidO3fWig2cigsXqDJEeHg43r17p/T8E6Bcqrl8O3R5JYbSljmSSqVYu3YtmjRpglOnTmH69Ol4/PgxBg4cCCA7xdzKykoQRlVQ1kJ8+TEzM8OJEycwZMgQ7Nu3D1WrVsWtW7cwaNAg+Pr6olGjRhg1apRG10/9/fffWLRoEbp374758+dr7L4cjhwuUGUIZRfo5kaZahLyMjVpaWmwsbEp1RzDnTt38Omnn2LGjBlo1KgRbt68CR8fH6FiRHp6OsLCwgS7VEVZDfHlxtDQEPv378e3336LXbt24X//+x/8/PyE7ej9/f3RtGlTfPXVV7h//75abUlMTMTIkSNhaWmJPXv2QE9PT63343AUwQWqDBEUFATGGNq1a6f0Ncp4UHJBSkpKKnF4Lzk5GTNnzkS7du3w5MkTrFmzBkFBQWjTpo3QZufOnahRowbCwsLw8OFDzJ49W2Wb+pXlEF9uxGIxtm/fjh9//BFHjx5F//79Ubt2bezZs0eo4n706FG0aNECgwYNQnBwsMptICJ89913iIqKgq+vL2rWrKnye3A4SkFEZepo06YNVVRat25NzZo1+6hrnj9/TgBo6dKlhbaxtbUlAGRlZUXOzs4fbdfx48epdu3aBID69+9Pz58/L9AmJCSEGGMEIM/h6+v70fdTxM8//0wAKCYmRiX9aRuZTEZLly4lANS+fXtKSEgQPouMjKSJEyeSgYEBAaC+ffvS9evXVXbvrVu3EgD6/vvvVdYnh5MbAMGkxPc996DKCKmpqbh///5HhfeA/9Y0FeVBSaVSiEQiJCQkfJQHFRMTg6FDh2LgwIHIysrCoUOHcPz4cdStW7dA2/379yv0lvbu3av0/YqiPIT4csMYw4IFC7BhwwbcunULXbt2FX6HdnZ22Lx5M549e4YffvgBly9fRufOndGzZ0+F29F/DI8fP8a0adPQokULrFixQlXD4XBKhFoFijHWlzEWxhh7yhibp+DzmYyxx4yx+4yxC4yxgt9sHADZcztZWVkflSABZM9rVKtWrUiBkkgkYIxBJpMptUhXKpVi48aNcHBwwJEjRzB58mSEhoZiyJAhCjcR9Pf3R0BAgMK+VDW3oauljkrL5MmTsWfPHoSFhaFLly549uyZ8FmtWrWwbt06REZGYvbs2QgKChK2oz937txHC1VaWhqGDx8Oxhj279+v0iQWDqdEKONmleQAoAfgGYD6AAwAhABokq9NDwAmOa/dAAQU129FDfGtWrWKAND9+/c/+lpHR0fq0KFDoZ8bGxuTSCQiALRhw4Yi+woJCaFPP/2UAJCjoyPduHGjQBuZTEZ//fUXjRs3jszNzQkAmZmZKQzx7d2796PHo4gJEyaQSCQimUymkv50jZMnT5KRkRHZ2NgU+jfw77//kru7O1lYWBAAateuHf3+++9K/0ymTJlCAGjHjh2qNJ3DKQCUDPGpU6A6AjiX6/18APOLaN8KwPXi+q2oAjV06FAyMzOjrKysj762T58+VKdOHYWfSSSSPMJx6NAhhe1SUlJo7ty5JBaLydjYmLy9vSkzMzNPm2fPntGiRYuoXr16BIBEIhH16dOH/P39KTU1lfbv3y/Md5mbm9PixYs/eiyF4erqSqampirrTxe5cuUKWVhYUOXKlRU+GMh59+4dLVmyhCpXrkwAqEWLFnTw4EGSSqWFXnP06FECQC4uLuVW5Dm6gy4I1FAA23O9HwXg1yLa/wrAo7h+K6pA1apVi3r06FGia8eOHUv6+voKv6BevXqVx6O5evVqgTZnz54VRKd379707Nkz4bP379/T9u3bycnJSeijSZMmtHz5cnr16lWBviQSCT19+pSSk5NLNJbC6N+/P1WtWlWlfeoit2/fJisrKzIxMaHz588X2fbDhw/k7e1NVlZWBIAcHBxoz549JJFI8rSLjo6mypUrk52dHSUmJqrTfA6HiHRDoIYpEKj1hbR1BRAIwLCQz78DEAwguDBPoDzz8uVLAkDz588v0fXu7u4EgN68eVPgs5s3b+YRqH/++Uf4LC4ujkaMGEEAqHr16uTv708ymYyysrLo3LlzNHLkSDI2NiYAVLVqVZo6dSrdunVLo0/gcXFx1K9fP8H+/v370+vXrzV2f23w5MkTql27Nunr6xfq8eYmOTmZfHx8BO/V3t6edu7cSZmZmZSVlUVOTk6kp6dXpFfG4agSXRAopUJ8AD4HEAqgujL9VkQP6vDhwwSAjh07VqLrf/31VwJA9+7dK/DZsWPH8ghUbGwsSaVS2rp1K1WqVIkA0IQJEyghIYFCQ0Np3rx5VLNmTQJAYrGYBg0aREeOHKGMjIzSDrNE9OjRo8C8Vu/evbViiyaJioqihg0bkkgkUnrOKC0tjTZs2CAsCahbty59+eWXBICWLVumZos5nP/QBYESA4gAUC9XkkTTfG1a5SRSNFC234ooUHPmzBHEoyQcOXKEANCZM2cKfDZ16tQ8X+4WFhbUvHlzISR08uRJ2rBhA7Vv315o07p1a1q3bp1Cj0yTREVFFRAn+aEovFjeeP36NbVq1YoA0OrVq5W+LiMjg7Zv3y54VIaGhuTj40MpKSlqtJbD+Q+tC1S2DegH4J8cEXLPObcEwMCc138CeA3gXs5xvLg+K6JAde3alezs7Ep8fWBgoMLsLIlEQmZmZgq/4EeOHEmDBw8WFoPa2NjQrFmz6MGDB6UdjsoIDw8vVKAULRYujyQmJgrzf+7u7kqHVxMSEqh27dpkbm5On3zyiRDGXbFiBSUlJanZak5FRycESh1HRRMoiURCJiYm5OLiUuI+oqOjCQB5enrmOX/nzp1Cv+DlT9YuLi50+vTpAhPruoLcg8h9tG/fXttmaZSUlBRhHm7y5MlFZusRZS8DGDx4MAGgU6dOUVZWFgUEBJCjo6Mwn+jl5cUTJjhqgwtUOeHu3bsEgHx8fErcR2ZmJgEgNze3POflwpX/YIzR2rVr6d27d6U1X+2EhYVRs2bNBNubN29O4eHh2jZL42RmZgoJLSNHjiywBCA3GzduJAA0Y8aMPOelUikdPXqU2rRpQwDI0tKSFi5cmKfMEoejCrhAlRM2b95MAOjvv/8uVT9WVlY0aNAgIsqeLA8ICMiT/Zb7mDhxoipM1yj37t2jkJAQbZuhVaRSKbm5uREA+vLLLyk1NbVAm/v375OhoSG1bt2a0tPTFfYjk8no9OnT1LFjR0LOIuu5c+eW++xIjubgAlVOGDNmDOnr61NaWlqp+mnevDk1adKEJk2aJGTnmZqakoGBAVWrVo0AUJUqVcjd3V1rGXmc0iOTyWjBggUEgLp27UqJiYkklUopPj6ekpKSqEmTJmRqakphYWFK9fXnn39St27dCAAZGxvT9OnTK0QCCke9cIEqJzRu3JjatWtX4uujo6Np6dKlZGpqKoTvevbsSbt376Y3b94IISEAtHHjRhVaztEmK1euJABkZ2cnLAuQJ8T89ttvH93fX3/9Rb179xbmJidPnlxhElE4qkdZgeLVzHWYxMREPHny5KMLxKakpMDPzw+ff/456tatC3d3d4jFYjDGEBERgT///BOjRo0Stl6X7/eTkpKi8jFwtMOsWbMwf/58PH/+HK9evQKQvWcXANjb2390f/ICtEFBQejduzc2btwIe3t7jB8/Pk8BWw5HlXCB0mFu3rwJAHkEKj4+HgsWLED37t0xfvx4PH78GAAgk8lw+fJljB07FjY2Nvjmm29w+/ZtTJw4ETdu3MD3338PIsqzHYW8wnmdOnUA/FcRnFM+iI+PV3h+165dJe6zffv2OH78OO7evQtnZ2fs2LEDjRo1wjfffIMnT56UuF8ORxFibRvAKZygoCAA/23xnpKSgi5duiAsLAwAcOXKFezfvx+urq44e/YsoqKioKenh759+2L06NEYMGCAsGXC3bt3AWRv/S7f80n+ZC3fv4l7UOUL+R5Zyp7/GFq2bIlDhw7h0aNH+N///oe9e/diz549GDZsGDw8PODo6Fjqe3A43IPSYQIDA1GtWjXUr18fAODv7y+Ik5yUlBRs2bIFlpaWWL16NV6+fImTJ09i2LBhefbzUbT1u/y1vH8uUOWLoUOHftT5ktC0aVPs3bsXoaGhGD16NA4fPozmzZtj8ODBuH37tsruw6mYcIHSQU6fPo3PP/8c586dg6mpKf79918AwD///KOwvaOjI0JCQjBz5sxCNxxUJFByD6pOnTowMDDgIb5yhrOzM+bOnQt9fX0AgL6+PubOnQtnZ2eV36thw4bw9fVFeHg4Jk6ciFOnTqFt27bo168fbty4ofL7cSoGXKB0jBMnTqB///64cOECpFIpoqKi0KNHD0gkkkK3e3dyciq238I8KHNzc5ibm8PExIR7UOUQb29vREdH4+LFi4iOjoa3t7da71evXj1s3rwZERER+P7773Hp0iV06tQJPXv2xOXLl7NThzkcJeECpWOsWLGiwD/x48ePsX79euEfPT/37t0r1vuxtrYGY6yAByUXLlNTU+5BlVNsbGzQo0ePQr1rdVCrVi388ssviIyMxKxZsxAYGIgePXqga9euOH/+PBcqjlJwgdIxoqKiFJ7/8ccfUbNmTVy6dAmVKlVCtWrV4ODggJYtW+Lvv/9G69atsXfvXly9ehXh4eFISkrK8yUgFotRvXp1xMbGCudiYmKEFHPuQXHUgY2NDVauXImoqCgsWLAAISEh6NOnDzp06IATJ05woeIUCc/i0zF69OiB3bt3Fzg/b948iMVixMXF5TnCw8MBAGFhYXB1dc1zjYmJCWxsbIRDKpUiODgY27Ztg42NDV68eIHmzZsjMzOTe1ActVKtWjUsXboUs2bNwvr167F27VoMHDgQLVu2hIeHBwYPHgyRiD8vc/LCytoTTNu2bSk4OFjbZqiNqKgodO3aFdHR0cK56dOnw8fHR2F7mUyGd+/ewd3dHVu2bEHLli3h4uKC+Pj4AmKWkJBQ6H3FYjH09PTQpUuXPKKW/6hSpQr/IuGUmg8fPmDjxo1YvXo14uPj0aRJE7i7u8PFxQV6enraNo+jZhhjt4mobbHtuEDpHikpKTh06BBevXqFzz//HO3bty/2GiLCggUL4O3tjcGDByMgIEDI3pIzbtw4+Pr64saNGwgODsbUqVPRr18/1KtXDwcPHsT79+9Rs2ZNxMbGFrpWRl9fH9bW1kWKmPwwNTVVyc+DU35JSUnB1q1bsXLlSsTGxqJBgwZYsGABvv766wJ/v5zyAxeoCggRYfbs2Vi9ejWGDRsGf39/iMX/RXEXLVqEJUuWICYmBg8ePECfPn1w6NAhDBkyBIMGDUJgYCDi4uJAREhOTi7ggSk6Xr9+DalUqtAeMzOzAqJla2tb4Fz16tXz2MmpeKSnp2PHjh1Yvnw5Xrx4ATs7O8ybNw9jxoyBoaGhts3jqBhlBYp/K5QjGGNYuXIlsrKysG7dOojFYvj5+QkhE3nGXmxsrLAGSlEWH2NMSD9v0KBBkfeUyWRISEhAbGxskUL26NEjvHv3rlC7q1WrVqxHZmtri0qVKoExppKfF0d3MDIywpQpUzBhwgTs3r0by5Ytw6RJk+Dl5YU5c+Zg/Pjxecp0cSoGXKDKGYwx+Pj4QCKRYOPGjRCLxfD19YWenl6etVDydHP5OXkWHxF9lACIRCJYWVnBysoKzZs3L7JtRkYGXr9+XUC8cotbeHg4rl69ivT0dIV9GBgYKBVetLGx4V9oZRADAwOMHz8eY8aMgb+/P/73v//hhx9+EBIsJk2aBDMzM22bydEQXKDKIYwxrF+/HhKJBNu2bYNYLMb27dvzCJTcg7K1tQWQ7UHJZDJkZmaqLaRiaGiIOnXqCMVpC4OI8OHDh2LDizdv3sSbN28gk8kU9mNhYVFkaFF+WFlZ8Yl5HUMsFuObb77B119/jUOHDsHLywuzZ8+Gt7c3Zs6ciSlTpsDS0lLbZnLUDBeocopIJMLmzZuRlZUFX19fiMViLFq0CMB/HpSVlRUMDAwAZHtQQPaktbZj/owxWFpawtLSEo0aNSqyrVQqxb///lusmIWEhOD9+/cK+5B7gYWFFXO/t7Cw4CFGDaKnpwcXFxcMGzYMx48fh6enJ9zd3bFy5Ur88MMPmDZtGqpUqaJtMzlqggtUOUYkEmHbtm3IysrCtm3bIBKJIBKJBA9KvkgXgJBxl5qaWqb+4fX09ATxKI60tLQ8IUZF82ahoaG4dOkSMjMzFfZhZGSkVHjR2to6T7FeTukQiUQYNGgQnJ2dcebMGXh6emLJkiVYs2YNpk6dihkzZqB69eraNpOjYrhAlXP09PTg6+sLiUSCLVu2wNTUFLGxsYiJiUHLli2Fdrk9qPKKsbEx7OzsYGdnV2Q7IkJiYmKRHllsbCyuX7+O+Pj4QqshVK5cWSkxq1atGl9bpiSMMfTr1w9ffPEFLl68CE9PT3h7e2PdunWYNGkSZs+eLYStOWUfLlAVAD09Pfj5+SErKwuHDh1CUFAQEhISCvWgKjqMMVSuXBmVK1eGg4NDkW0lEkmxIcaXL18iODgYSUlJCvvQ09ND9erVi03Ht7GxgZmZGQ8xIvt31LNnT/Ts2RNXr16Fp6cnfHx8sHHjRowbNw5z584tdq6To/twgaogiMVi+Pv749q1a4iLiwOAPE+aFcGDUgf6+vqoUaOGkIBSFCkpKXj9+nWRKfkPHjzAH3/8gaysLIV95C9fVVSIUT6/WN5xcnLC+fPnERQUBC8vL2zcuBHbtm3D6NGjMX/+fGG/M07ZgwtUBUJfXx/9+/fH9u3bASDPhnLcg1I/pqamqF+/frFfmPLyVUWFF+Pi4hAWFlZk+aqqVasqJWblpXzVp59+ihMnTuDu3bvw8vLC9u3b4evri5EjR2LBggVo3Lixtk3kfCRcoCoYtWrVEl6fOnUKnp6eWLhwIfegdAiRSISqVauiatWqaNq0aZFtMzMz8ebNmyJDjM+fP8eNGzcKffgQi8V5ylcVlZJfFspXtWrVCocPH8ajR4+wdOlSYTv6r776Cu7u7nw7+jIEF6gKRu5QVIcOHfDTTz9BX18frVu3BgBERERoyzROCTAwMECtWrXyPHgURlJSUrHp+Hfv3sXZs2c/qnyVorkzKysrrdfSa9q0Kfz9/bF48WIsW7YMfn5+CAgIwKBBg+Dh4YE2bdpo1T5O8fBafBWMU6dOoX///gCAyMhIfPvtt7h06RIMDAyE1OrBgwfD39+fp0lXUOTlqwqr9pH7KG35KhsbG1SuXFkjiR+RkZHw9vYWslr79esHDw8PdOzYUe335uSFF4vlFCA9PR3Tpk3D1q1bAQBbtmyBk5MTmjRpUqCth4cHPD09NW0ip4xRWPkqReJWVPkqa2vrIkOLqixf9eLFC6xYsQLbtm1DRkYGevbsiYULF6Jbt26l7pujHFygOAUYPHgwjh07lufcl19+iVOnThVo27hxY4SGhmrKNE45R9nyVXFxcUqXrypqzkyZ8lWxsbFYvXo1Nm3ahNTUVDg5OcHDwwO9evVCeHg4NmzYgKioKHTv3h3fffedME/LKT06IVCMsb4A1gHQA7CdiLzzfW4IYDeANgASALgQ0fOi+uQCVTLCwsIUZjGZmpoqTIxo1aoV7ty5ownTOJw8SKVSYcPN4qrkl6R8VX5xy8jIwNq1a/Hrr78iKSkJzZo1w7Nnz/Lsida5c2dcuXKF12xUEVrfboMxpgdgA4BeAF4CuMUYO05Ej3M1GwfgHRHZM8aGA1gOwEVdNlVkXrx4ofB8SkoKzM3NCywiHTdunCbM4nAKoKenB2tra1hbW6NFixZFts1fvkpRaFHZ8lWNGjVCcnIyHj16VKA6yPXr13Hy5Ek4OzurbJyc4lFnFl97AE+JKAIAGGP7ATgDyC1QzgAW57w+BOBXxhijshZ3LAO0a9dOobfUpk0b/PLLL5gyZQru3buHSpUqYdq0aZg8ebKWLOVwlEeV5avi4uLw9u3bQktXPXz4kAuUhlGnQNUEkPux/SWATwtrQ0RZjLH3AKoCiFejXRUSS0tLrF27FhMnThTi+xYWFli/fj06duyIu3fv4u3btzA3N9d6ejCHo2o+pnzViBEjsH///gLnW7VqpS7zOIWgToFSlDea/9FEmTZgjH0H4DsAvL5WKRg/fjy6d++OY8eOwcTEBC4uLqhatarweVmqYs7hqIuFCxfi3LlzeVLoP//8c/Tt21eLVlVM1ClQLwHUzvW+FoCYQtq8ZIyJAVgCeJu/IyLaCmArkJ0koRZrKwj29vaYNWuWts3gcHSWJk2aICQkBFu2bEF0dDS6d+8OV1fXclEOqqyhToG6BaABY6wegFcAhgMYma/NcQCjAdwAMBTART7/xOFwtE3t2rXh5eWlbTMqPGoTqJw5pakAziE7zXwnET1ijC0BEExExwHsAODHGHuKbM9puLrs4XA4HE7ZQq21+IjoNIDT+c79lOt1OoBh6rSBw+FwOGUTHlTlcDgcjk7CBYrD4XA4OgkXKA6Hw+HoJFygOBwOh6OTcIHicDgcjk7CBYrD4XA4OgkXKA6Hw+HoJFygOBwOh6OTcIHicDgcjk7CBYrD4XA4OgkXKA6Hw+HoJFygOBwOh6OTcIHicDgcjk7Cytr2S4yxfwFEaeHW1VBxt6LnY6+4VOTx87Grj7pEZFVcozInUNqCMRZMRG21bYc24GOvmGMHKvb4+di1P3Ye4uNwOByOTsIFisPhcDg6CRco5dmqbQO0CB97xaUij5+PXcvwOSgOh8Ph6CTcg+JwOByOTsIFisPhcDg6CReofDDG+jLGwhhjTxlj8xR8bsgYC8j5PIgxZqd5K9WDEmOfyRh7zBi7zxi7wBirqw071UFxY8/VbihjjBhjWk/BVRXKjJ0x9lXO7/4RY8xf0zaqCyX+5uswxi4xxu7m/N3304ad6oAxtpMx9oYx9rCQzxlj7Jecn819xlhrTdsIIuJHzgFAD8AzAPUBGAAIAdAkX5vJADbnvB4OIEDbdmtw7D0AmOS8dqtIY89pZw7gLwCBANpq224N/t4bALgLoHLO++ratluDY98KwC3ndRMAz7VttwrH3xVAawAPC/m8H4AzABiADgCCNG0j96Dy0h7AUyKKIKJMAPsBOOdr4wzgt5zXhwD0ZIwxDdqoLoodOxFdIqLUnLeBAGpp2EZ1oczvHQA8AawAkK5J49SMMmOfAGADEb0DACJ6o2Eb1YUyYycAFjmvLQHEaNA+tUJEfwF4W0QTZwC7KZtAAJUYY7aasS4bLlB5qQngRa73L3POKWxDRFkA3gOoqhHr1IsyY8/NOGQ/XZUHih07Y6wVgNpEdFKThmkAZX7vDQE0ZIxdZ4wFMsb6asw69aLM2BcDcGWMvQRwGsD3mjFNJ/jY7wSVI9bkzcoAijyh/Hn4yrQpiyg9LsaYK4C2ALqp1SLNUeTYGWMiAD4AxmjKIA2izO9djOwwX3dke81XGWPNiChRzbapG2XGPgLALiJazRjrCMAvZ+wy9ZundbT+Xcc9qLy8BFA71/taKOjSC20YY2Jku/1FucllBWXGDsbY5wDcAQwkogwN2aZuihu7OYBmAC4zxp4jOx5/vJwkSij7N/87EUmIKBJAGLIFq6yjzNjHATgAAER0A4ARsgupVgSU+k5QJ1yg8nILQAPGWD3GmAGykyCO52tzHMDonNdDAVyknBnFMk6xY88Jc21BtjiVl3kIoJixE9F7IqpGRHZEZIfs+beBRBSsHXNVijJ/88eQnSADxlg1ZIf8IjRqpXpQZuzRAHoCAGPMAdkC9a9GrdQexwF8k5PN1wHAeyKK1aQBPMSXCyLKYoxNBXAO2Rk+O4noEWNsCYBgIjoOYAey3fynyPachmvPYtWh5NhXAjADcDAnLySaiAZqzWgVoeTYyyVKjv0cgN6MsccApABmE1GC9qxWDUqO/UcA2xhjM5Ad3hpTTh5IwRjbh+ywbbWcObZFAPQBgIg2I3vOrR+ApwBSAYzVuI3l5GfN4XA4nHIGD/FxOBwORyfhAsXhcDgcnYQLFIfD4XB0Ei5QHA6Hw9FJuEBxOBwORyfhAsXhcDgcnYQLFIfD4XB0Ei5QHI4OwBhrl7PnjhFjzDRn36Vm2raLw9EmfKEuh6MjMMa8kF1KxxjASyJapmWTOBytwgWKw9ERcurB3UL2flOdiEiqZZM4HK3CQ3wcju5QBdm1Ds2R7UlxOBUa7kFxODoCY+w4snd1rQfAloimatkkDker8GrmHI4OwBj7BkAWEfkzxvQA/M0Y+4yILmrbNg5HW3APisPhcDg6CZ+D4nA4HI5OwgWKw+FwODoJFygOh8Ph6CRcoDgcDocfWrjlAAAAIUlEQVSjk3CB4nA4HI5OwgWKw+FwODoJFygOh8Ph6CT/Dzc3JSJScRYZAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7eff1d93c2d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"autofig.reset()\n",
"autofig.plot(x, y, z, i=t,\n",
" xlabel='x', ylabel='y', zlabel='z')\n",
"mplfig = autofig.draw()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To instead plot using a projected 3d axes, simply pass projection='3d'"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAagAAAEYCAYAAAAJeGK1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzsnXlYVHX7/9+zMeyrigKyIyHgCi6pmeZuguaupGluJLa4VfRkZZk9aVZKZfGoaWqm/kxQE63UzCUFl0fBjX1HdpgZZpjt/P7ge84zw+ybM8J5XReXOMs5Z4aZ8z73/Xnf980gCAI0NDQ0NDS2BtPaB0BDQ0NDQ6MOWqBoaGhoaGwSWqBoaGhoaGwSWqBoaGhoaGwSWqBoaGhoaGwSWqBoaGhoaGwSWqBoaGhoaGwSWqBoaGhoaGwSWqBoaGhoaGwStoGPp9tO0NDQ0NCYCkOfB9ERFA0NDQ2NTUILFA0NDQ2NTUILFA0NDQ2NTUILFA0NDQ2NTUILFA0NDQ2NTUILFA0NDQ2NTUILFA0NDQ2NTUILFA0NDQ2NTUILFA0NDQ2NTUILFA0NDQ2NTUILFA0NDQ2NTUILFA0NDQ2NTUILFA0NDQ2NTUILFA0NDQ2NTUILFA0NDQ2NTWLoPCgaGpuCIAiIxWLI5XKw2WwwmUwwmUwwGHqNm6GhobFhaIGieSqRy+WQyWSQSqXUj6IoMZlMsFgs6ocWLhqapw8GQRg0JJeeqEtjNQiCAEEQkEgkkMvlAAAGgwGpVAq5XE6JD/mZJh9PEAQYDAYIgqCESzHaIoWLFi8amieGXl82OoKisXkIgoBMJgOfzweXywUArYJC3t7+flK4yMhL3XPkcjmcnJxo4aKhsQFogaKxWUhhkslkaG1txd27dxEbG6siGEwmk4qotKFJuMh9CYVC5ObmIioqSuk+xVQhmS6khYuGxvLQAkVjc5DCJJVKqfQck8mkflf3eFNhMBhgsVgAQP1Lbptc72q/fyaTSaUK6XUuGhrzQwsUjc1AEASkUqmSGDCZbZUQLBZLryjJ3GiKlMi1LbFYrFa4aIMGDY3p0AJFY3VIYSLXhRSFiYQ0OWjbhqkCoGsf7R+rLZqTSqWQSCRK99HCRUNjGLRA0VgNRas4oJ/xwdKYmi7UZdAghUuds5AgCHC5XNqgQUPzf9ACRfPEkcvlVCoP0C5MTxJLHoM+zsKsrCwMHDhQ6TnqbPG28n7R0FgaWqBongiaaphs6URrSIrPnPsk/1U0agDKBg2xWKz0PNpZSNMZoAWKxqKQJ1mymBawPWGyVbStc2lzFtLrXDQdBVqgaCyCOqu4pYTJXNu0RgRlDLqchRKJBGKxmBYumqceWqBozIqiMN28eRN9+vQBh8Ox9mF1CmhnIU1HgxYoGrOgroZJLpc/FREJydMSQRmKPs7ClpYWPHr0CJGRkUrOQnXCRYsXzZOCFigak9BWw6RvCyIa69DeoEEQBGV3BzT3LKSdhTRPClqgaIxCnxqmp02gOmoEpQ+KZgtdPQv1cRaSIkYLF40p0AJFozeGWsXJNB+N7aNvJw7aWUjzJKEFikYnxlrFyQav5j4WS53YOvMJ09T3lXYW0lgCWqBoNKI47oIcCGhIysbcKT4yBdd+//QJzXQsJfyGOAvz8vIQGhpKCRWbzabShOS/NJ0LWqBoVDBXDZOlBIrG/FgyMlWHunWu5uZmymDT/vNHPpZ2FnYuaIGiodA27sIYaIF6enjSAqUJfXoW0s7CzgMtUDSUMJWUlMDHx8dkYSIxt0Cp2x553DweD87OznBycoKTkxPs7Ozok5MBkLVPtoq5nIX0OtfTBS1QnZj2VvHi4mL4+fmZbfuWjKAkEglKSkpQWVkJHx8fdO/eHUKhEHV1dSgpKYFYLAaLxaIEixYu7dhKBGUMtLOw40ILVCdE07gLc385LSFQra2tKCkpQXV1NXr27ImhQ4eCwWBALBbDw8ND6fFSqRQCgQACgYAWLh2QJhhrYYnUraHOQolEgpaWFnTp0oUWLhuBFqhOgjXGXZhzzUgkEkEgEODOnTsIDAzE0KFDqZSUJhFks9lwc3ODm5ub0u3ahEskEqG0tLTTCZe1Iyi5XP7EUoyaPvd8Ph/V1dVwd3dX27OQdBaSv9POQstDC1QHx5rjLswRQQmFQhQWFqKxsREcDgfR0dFwdnZWeZwhr0ebcGVlZYHFYmmNuJydncHhcDrUyakzCZS2YyCjJkV0GTRoZ6HloAWqg/Ikx11owhSBEggEKCgogEAgQFBQECIiInDnzh0zH6EyZN2Nj4+P0u3tI67i4mJIJBKw2WyVVOHTKly0QLUJkOLASBLaWWg9aIHqYKgTJn2/+GRrInOdKJhMpkqqRBc8Hg8FBQUQiUQIDg5Gly5dqC+0tXr7aYq4yDULPp+P2tpaFBUVaRQuOzu7J37chkALVJvQGHIMtLPQ8tAC1UEwRw0TKQDmFCh9BaWpqQkFBQWQSqUICQmBh4eH2o4Rmta0rHGC5XA4GoWLjLhqamqeCuGiBUpzBGUMpjgLGQwGOBwOLVygBeqpR9u4C0NhsViQyWRgs83zsdBHoBoaGlBQUAAACAkJgbu7u8bHahIoW0ubcDgcuLu7q7wWXcIlFovR0NBgFeGiBep/a1CWRJezsLW1Fbdv38aAAQOo+zqzJZ4WqKcUfcZdGAopUOZCk0ARBIH6+noUFBSAw+EgLCwMrq6uRm/vaUGXcNXW1lot4qIFqi2Cstb0Z/L7K5VKweFwKKHUNg2ZNGgornGRPx0FWqCeIhSt4g8fPkRQUJBZF+Ut3fmBIAjU1NSgsLAQDg4OiIiIUOvI00RHbXVECpednR169epF3a4t4nJ2doajo6OSq9AUaIEyb4rPWKRSqVIGw1iDxieffIItW7ZY+GgtDy1QTwHqrOJ8Pt/sxZWWEiiCIPD48WMUFhbCxcUF0dHRcHR0NHh7HVWgNKFvqrCwsJA6sSm2eyJdhfpgCwJl7ZSVoSYJSx2DPiKpS7j++OMP8x+cFaAFyobRNu7C3Ok4wPwpPgaDAR6Ph6tXr8LDwwP9+/eHvb290dszREDr6uqwe/du5OTkIDIyEq+++io8PT2N3rctoUm4xGIxJVyPHz+GQCCgUkbq7PCKWFsgbCGCehJrULpoH0EZCoPBgFAoBJfLNeNRWQ9aoGwQfWqYLCFQ5oqg5HI5ysvLUVRUBAaDgdjYWLN8YfSNoOrq6jB69GgUFhYCAI4dO4b9+/fj/PnzHUak1GFnZwc7OzuVlk/6CFdLS4tRUa25sIVmtbaY4jOGpqYmFWfp0wotUDaEIVZxW4ygZDIZysrKUFZWhm7duiEqKgolJSVmu5rTV6B2795NiRNJYWEhdu/ejbVr15rlWJ4m9BEuHo+H+vp6VFRU6BVxmZunKb1m68fQ1NSk1Q37NEELlA1gjFXcliIoqVSK0tJSlJeXw8fHB4MHDwabzUZLS4vFx22oIycnR+3t2dnZZjuWjoCicMlkMtjb28Pb21uviIs0aZhLuOgIqg06glKGFigrYopVnM1mWz2CkkgkKC4uRlVVFfz8/DB06FClL7i1BhZGRkbi2LFjKrdHRUWZ7Vg6GoomCX0irqqqKiXham/OMPQkawtrULYQxUmlUpNTrY2NjXQERWM8msZdGII1IyixWIyioiLU1NSgZ8+eePbZZ9V+sa0lUK+++ir27t2LkpIS6jYul4v58+eb7Vg6Gvq4+NQJF1n2wOfz0dLSoiRcdnZ2KqlCTcIll8vNViBuLLZgkqBTfMrQAvWEMPe4CxaLpVL/YCosFktr7zyRSITCwkI0NDQgICAAoaGhWq84LSFQ+mzP09MTBw4cwIgRIxAVFYUePXrg999/x7/+9S/85z//sbqd2RYx1mbOYDBgZ2cHT09PJQOKonAJBAJUVlZCIBBAJpOpFS5biKAAw7riWwJzpfhogaLRC0uNu2CxWGhtbTXHIVJoEpSWlhYUFhaiubkZgYGBeOaZZ/Q6fkvUVekbNZIdFxYuXIhly5bhrbfewu7duxESEoLk5GStz7V2TZA1MPdr1iZciqlCUrhaWlrA5XLR1NRkUqrwacdcAhUeHm6mI7Iuneuv/wQhreIikQj5+fkIDw83a8+4J+HiUxx5ERwcjN69ext0/OYurDVkey0tLQAAR0dHMBgMbNmyBUVFRfjss88QEhKC2bNna90HLVCWgcFggMvlgsvlKglXbm4uXF1dweFw9Iq4Oqpw0Sk+ZTrmX9mKtK9hYjKZaGhoMPuX35JrUDweD/n5+RCLxQgODoaXl5fR6R9zH5++AiUUCgEADg4OANqKW/fu3Ytx48Zh5cqV1NoZTRvWFmWCIMDlcuHu7q5XxCWTycDlcpXaPTk6OpokXLbQpYRO8SlDC5SZ0FbDZIkPviUESigUoqqqCjweD8HBwTZX1KrvGhSgHEGRuLm54fDhwxg9ejTmzZuHP//8EyEhISr7sIUT1ZPG2gKlaQ1KU8TVXrjKy8vR0tJCCZditKWPcFm7kwYJHUEpQwuUiZhz3IUhmFOgyM7iMpkMLi4uSq3+bQlt4tH+5NI+giIJCAjAoUOHMHnyZMycORN//PGHzQmxNbB2HZKhJgldwkWaM7QJl5OTEyUGtuDgIzFVKJuamlRKBJ5WaIEyEkuMuzAEUwWKIAjU1dWhoKAAdnZ21BpZfn6+GY/SvBiT4lNXUxIbG4vvv/8eCxcuxMsvv4xff/2VMlV01gjK2hGEuVx8isLl5eVF3U7OWtIUcdnb20MikaC5uVlJuJ5Gmpub6QiqM0JaxY2pYTJ3CsVYgSJHXhQUFMDJyQm9e/emRl6Yu/ODudGW4iMbZJInOU0RFMm0adNQUFCAjz76CK+//jq+++47m0jxWAtbSPFZcv8MBgP29vawt7dXK1z19fVoamrSO+KyZSQSCd0stjNhqlXc3JNqFbepLwRBoKqqCkVFRXB1dUWfPn1UogtbHwioLrqpq6tDfn4+ZU4hCAIODg4oKytTeo66v9Xq1auRn5+P/fv3IzQ0FGvXru20EZQtCJQ1Tv6kcLm4uMDZ2RkREREA1EdcAoEAcrlcSbhIc4Y5jt0cIt3RPru0QGlB27gLQ7CmQMnlclRWVqK4uFjnyAtLGC/MiWKKjxQmLpeLiIgI2NnZUeIiFAqp11FdXY2srCwwGAw4OjpSLXmcnZ1hZ2eHr776CiUlJdi4cSOCg4MRFBRkzZdoNWxBoKy9f0WR0RVxkcJVVlZGCZe9vb2KOcMQ4TKHg0/x+DsCtECpQZ9xF4bAZrMhlUrNGnbrWo+Ry+UoKytDaWkpunbtipiYGJ3jwi0hUGRazlzrCy0tLbh+/Tq4XC6VniQXxsm/laOjI7W//v37w9PTEzKZDC0tLRAIBGhoaEBZWRlaW1vBYrHwwQcfYMmSJVi+fDm2bduGyMhIk47zaZxFZQsCZU2ThiGDAvURrvr6eiplrq9wmUOgRCJRh0nvAbRAKWHIuAtDIAXqSSCTyajO4t7e3hg0aJDeHactkd4i04amvo/19fV48OABJBIJBg4cqDQqnrx4UDz29iYJFosFFxcXuLi4KG1XKpVCIBBg586dmDVrFpKTk+Hi4oLAwEAq0jJk/eFpnUVlbYGytovQVHu3NuESiUR6CZc50pwdqZM5QAsUgP8JU2lpKXr06GF2q7gl+ua1RyqVoqSkBJWVlfDx8UFoaCj27NmD7OxsREVFYdmyZTpPkJY4QRnivFNHfX098vLywOVyERISgurqaiVx0oRQKKQcXdpgs9lwc3PD0KFDcfjwYbz44ovYtGkTfvvtN7BYLJX1B3t7e6U0oYODg1K92+bNm5/KWVS2IFDW3L+lRm0wGAw4ODjAwcEBXbp0oW5XJ1zNzc2QSCS4c+eO0anCjlQDBXRygWpvFS8qKoKvr6/Z92OJ0RgkYrEYxcXFqK6uhp+fH4YMGYLGxkaMGDECBQUFAICjR49i3759uHTp0hO/ijekuFYRRWEiU3l8Pt+gQl0HBweDTnpDhw7Fu+++i40bN2LJkiU4evSoSo0NeVLh8/mora0Fn8/H/fv38c8//+DixYuUOaM9tj6LytoCYW2e9KgNdcJVU1MDHo+HHj16GJ0qpCOoDoCmcReW+oJaIsXX2toKkUiEzMxM+Pv7Y+jQodQXLDU1lRInkoKCAqSmpuLtt98263HowlBnYH19PfLz82FnZ6dkgQcMS0EKhUKNFnNtjBs3DkKhEFu2bMHatWvx1VdfUZ8L8qTCZrNx9+5dpKen49SpU6iqqtK53ZCQEIjFYnA4HJsUgs4uULYw7oM0UukbcZHC5eDgAEdHR1y+fBkikUivDIM6MjIy8MYbb0Amk2HJkiV45513lO4vKSnBwoUL0djYCJlMhs8++wyTJk0y6TXrotMIlL7jLizxRTVnik9x5AWbzUZsbKyK+UHT1frdu3fNcgyGoK9AKQpTRESE2i+Zoc1ijRn8xmAwsGbNGpSUlGDPnj0IDQ3FqlWrIBQKcf78eaSnp+O3335DY2MjGAwGBg8ejBUrVuDcuXO4ePEiYmJiUF1drTSLyt/fHxMnTsS9e/cgFovBZrOV0oS2UF/T2QWKrHuyJtpMErpShXw+H/n5+cjKykJhYSHOnz+PoKAgjBs3DitWrNC5b5lMhpUrV+L333+Hn58fYmNjERcXh969e1OP+eSTTzBr1iwkJibi3r17mDRpEoqKikx+3dro8AJlSA0TeTI198mCzWabPBqjpaUFBQUF4PF4CAoKwjPPPIMbN26oPWFHRUXh6NGjKrdHR0ebdAzGoEugSGHicDiIiIhAa2srUlJS1K6dGRKNGRtBAW2fj5SUFOTk5OC9997DBx98AC6XC4FAADabjeeeew5xcXGYPHkyWCwWEhIScOXKFcybNw9ff/01BAIBdu/eTb2GxYsXK6UKFeckVVVVgc/nQyaTQSgUIi8vjxItc9XX6AMtULYx7t3QiypF4froo4/wn//8B1wuFytWrEBRURGampr02s7169cRGhqK4OBgAMCcOXOQlpamJFAMBgPNzc0A2lKJPj4+Bh2rMXRogZLJZJBIJHpbxTkcDiQSiUUESiAQGPVcPp+PgoICCIVCBAUFITIyknoNmmzhy5Ytw759+5TSfMHBwVi6dKnO/ZnTFg5oFpX2wuTs7Iy6ujqta2dPIoJqbGzEgQMHkJGRQUWiUqkU3bt3x7Zt2zBhwgSqz9m9e/cwe/ZslJSU4OOPP8brr79OGTO0GSI4HA48PDyU+qXJ5XJkZmbCw8NDbQqnvTHD3GJCC5T1x72bq1FseHg4mEwmJTb6UF5ejp49e1L/9/Pzw7Vr15Qe8+GHH2LcuHHYsWMHBAIB/vjjD5OOVR86tECR6PvBs5Qd3JgUX3NzMwoKCiCRSKjO4u1PIJoEytPTE5cuXUJQUBBV63P8+HG9DBLmsoW33x6JojA988wzSrZvTWtnS5cuxYoVKxAQEKD3+ygUCvV2M5WVleHEiRM4ceIErly5ArlcDldXV8yaNQsRERHYvHkzpFIpRowYQYlKRkYGXn31VRAEgUOHDmHixIl67UsbTCYTXl5eKjZloVBIGTOqq6spC71iNwMnJydwuVyjRcaaAmUL4mgrEZS1Rm2ou/Br/zf5+eef8corr2DNmjW4evUqXn75ZWRnZ1tU2Du0QDGZTIM++JYSKENcfI2NjVTD1uDgYK1dibUV1np6elJunurqahw7dkxl0VPbNs21YEwKVENDA/Ly8tQKE4mmtbNTp07h1KlTANrey+DgYISGhlI/wcHBCAwMhI+PD3XcQqEQPXr00Hhcubm5OHHiBNLT03Hz5k0AQNeuXTFlyhTMmjUL48ePp9b2Bg0ahPj4eMyaNQtnzpzB3r178d5776Fnz5745ZdfTC7sJVH3WSULjx0dHdG1a1fqdrlcTi2YNzY2KhUeK4qWs7OzQXVw1sDaRbrkMXRmgfLz80NpaSn1/7KyMpUU3q5du5CRkQGgzfEqEolQW1uLbt26mXTM2ujQAmUoZIrP3OgSPoIg0NDQgPz8fLDZbISGhuplFdXV+YHD4SA6Ohrl5eX4/vvvsXr1ap3dJMzdj6+1tRUPHjyAk5OTRmEi0bR2NmTIEAiFQty5cwdSqRSPHj3Co0ePVB5nZ2eHwMBAhISEoKioCEVFRTh//jxCQkLg6+uL7OxspKen48SJE3jw4AEAoGfPnnjttdcQFxeHwYMH4+HDh/D391d6n0aMGIEdO3YgMTGRKkMYMmQIDhw4oCQaTxImk6m18JjP56OmpgZFRUWQSCTgcDg2Z8wgsQWBsoUIyhwXhsYKVGxsLHJzc1FYWAhfX18cOnQIBw8eVHqMv78//vzzT7zyyiu4f/8+RCKRxT//HVqgDL0itGQEpW67BEGgtrYWBQUFsLe313kCb48ugeJyuZBIJEhKSsLy5cvx//7f/8PcuXNN2qa+kBGTSCSCv78/AgICdD5H09rZsWPH4Onpibq6Ovz444+orq7G33//jdu3byuJqVgsVhGv+Ph4tfvy9PTEm2++iZdeegl+fn46T5Djx49X+v+JEyes7vpSB1l43P4CR9OMJLK2hjRuKLaJelLQAtWGVCo1yxqUMbOg2Gw2UlJSMH78eMhkMixevBiRkZHYsGEDYmJiEBcXhy+++AJLly7Fl19+CQaDgR9//NHiUTfDwCr/p65VLtmjTR9Ia7C/v79Zj0EqlSIrKwtDhgwB0CZM1dXVKCwshLOzM4KCguDk5GTwdgsLC2Fvb68xldWvXz906dIFJ0+eRFhYGPz9/XHp0iWtH6q7d+8iICAArq6uBh8PAKVUHtn5wcnJCd27d9fr+fX19UhNTcXdu3cRHR2NpUuXUmtnBEHg6tWr1Kj2pqYmXL16FRcvXsTFixdx69Yto8TV3t4eQUFBCA4Ohru7O/r06YPIyEgEBwfDx8cHDx48wOzZs1FcXEw95/PPP9fLvqsvMpkMt27dQkxMjNm2qQvF2poHDx7Aw8ODmkTc3phhb29vsZMR6V60hsuUJCsrC/3797eqSGVmZiImJsak9/mFF17AxYsXNTaEtiH0epEdOoIyFA6HQy1AmxMWiwW5XA6CIKjO4m5ubujbt6/RVmigLc2j7YRsZ2cHiUQCe3t7LFmyBJs3b1Y6wWs6VmNO8prWmGpraw1KGXp6emosJm7/xXVzc8OECRPw3HPP4fTp0zh48CC1VtUef39/DBs2DMOHD0dUVBTkcjny8/NRUFCA/Px85Ofn4+rVq6ivr8eBAwfUbiM8PByvvvoq1q9fj/Xr1yMgIMAs5ghNr8/SKFqUuVwutZYml8shFArB5/PB4/FQVVUFoVAIJpOpYswgu8ibgrU7mZPHYO0oDjD9M9CRZkEBnUCgDLEmWyrFR3bbvnr1Kjw9PbWOvDAEXe5ALpcLsVgMoC19tnXrVqSkpGgVKEPXoHSZHyw1Y6qxsRGnT59GWloazpw5A6FQCA6HgzFjxmDkyJF4//33sXz5ckycOBGXLl3C5cuXcfToUfz8888AAF9fX0qwpk+fjtDQUDAYDFy7dg0ikQhVVVVYs2YNVfcBAA8fPsT69eup/8+ePRsAEBcXh+DgYISEhFA/3bt3t/pJ11gUhUgRmUxGGTPq6upQUlKiUnhMipchaynWbhQLPPmJ2Jago82CAjqBQBmCuQVKJpOhvLwcpaWlkMvleo28MARdBcAcDoeqv+rRowdmzpyJQ4cOobi4WOOakL4RlD6uPMC8AvX48WOcPHkSmzdvxoULFyCRSODo6IgJEybgxRdfxNixY+Hu7o7Kykq8//776NKlC0aPHo3Ro0cDaKuNyszMpAQrLS0Nhw8fBgB0794dw4YNQ1hYGEaPHo2LFy+iublZyQxBWuTz8/Px22+/4fjx4wCA9PR0lWN1dHRUEi3F3729vZ/KkyGLxYKrq6tK+lcikVDGjMePH6OgoIAaL6PPYD9biV46Ck/jZ0sTtEApYC4XH9kZvby8HD169MCgQYOQmZlpVnECdIuJnZ0dFUEBQFJSEg4ePIidO3di8+bNap+jS1BIYWKz2XqZOphMpknvaXFxMdLT03H8+HFcuXIFBEHA3d0dM2fOxNSpUzFmzBg4OjoqtbAi11HaF+o6Ojpi5MiRGDlyJIC2tlFZWVmUYJ06dQoikQifffYZ9Zy4uDjU1NTAy8sLnp6e8PT0RGxsLObMmYNz585h+vTpiI6Oxv79+1FVVUUJGJk6vHDhAtLS0pSOw8nJSUW8AgMDIRKJbKImyFA4HA7c3d2V3GNk1oA0ZpSWlioVHiumCW2hSNbamCPN2dFmQQGdQKCeZB2URCKhRl74+vpiyJAhVKrD3B0aAP1cfIoCNWDAAAwbNgx79uzBe++9p7bfnSaBIm3wLBbLILehMRHUgwcPcPz4caSlpeHWrVsAAG9vbyxZsgRhYWFITExUqe1R/DuT64i61vfs7e0xfPhwDB8+HABw+/ZtPPfcc9T9jo6OSE5OBgB4eXlh2LBhVFowMjISo0ePxrZt2/DGG2/g7bffxv79+zFo0CClfRAEgbq6Oty6dQt79+7Fw4cPqc/EuXPnqCiMxNnZWSVdSP6/a9euT414kR01uFyuzsJjHo9HTRVQjLhMKTw2BLJPpzUxVw1UR+pkDnQCgTIEYyMoxZEXPXv2xNChQ1VSGaT4mTOKMjSCAoBVq1Zhzpw5OHDgAJYvX65zm4rCFB4ebpANHtBPoAiCwK1btyhRevjwIQAgICAAb7zxBuLj4zF48GCwWCxcuXJFZ+GpohNNX8jOEI6OjtixYwdmzpwJiUSCmzdv4vLly7h06RLOnTtHpfPc3d0pwRo5ciROnTqFDRs2YNOmTUrbJdc21q5dqzQnKigoCP/9738hl8tRUFCAR48e4erVq1TPxT/++AO//vqr0rZcXFwowWovYl26dHkiJ3NTpwWrKzyura1FU1MTvL29wefz0dTUhIqKCohEIpXCY9KYYU5sIcVozSJdW6bDC5QhX1pDr/ZbW1tRWFiI+vp6lZEX7SENDdYWqClTpiAgIAApKSlYunSpyvEymUxIpVKThUlxe+reU5lMhitXriAtLQ1paWlUFXvv3r3x7rvvYurUqeidgyrNAAAgAElEQVTTp49RJ93203S1QRAEvvnmG6ozxOeff46hQ4cCaLtgGTx4MAYPHozVq1dDKpXi9u3blGD9/fffSq7BHTt24NSpU9i1axf69u1LnXB2796tdojhnj17sHbtWnTt2hUDBw5EZGQkBgwYQB1XTU2NitMwPz8fZ8+eBZ/PV9qeq6srQkJCEBQUpCRcISEh8PLyMot4WWpaMNnFwdnZWSWqJwuPBQKB1sJjR0dHo0/wttBFwlx9+OgIqgOj75dYKBSisLAQTU1NCAgIQHh4uM7nWmJooT4C1d5EwWKx8Nprr+Htt9/G2bNnMWHCBKX7RSIRKioq4OLiYpIwkSi6KFtbW6k1mRMnTqCmpgZAWxX78uXLER8fj7CwMKP3Ra7f6BtBicVivPXWW/jpp58oM0RjY6PGx7PZbMTExCAmJoaam3Pnzh1cvnwZZ8+exYULF1BQUIBRo0bBxcUFQ4YMwfDhw3Hx4kW129M2xJDBYKBbt27o1q0bJZiKr7O6ulqteJ05c0alMbGbmxsVcbWPvAwRFk1Ca+q0YG0RjLbCYzJNWFFRAYFAoFR4rChcuqIjWynSNTWCamxspCOopw1zpj0EAgEKCwvB5/MRFBSEiIgIvbdvCQu7MREUALzyyiv4+OOPsWPHDkqgGhsbkZeXB4lEAi8vL7P1lxOJRDh79iw+/fRTnD59Gs3NzWAymRg+fDjeffddTJkyRamLsjnQJ4Kqra1VGZPB5XLR1NSk93oEi8VC//790b9/fyQlJaG8vBwREREAgG7duiErKwu///67xudHRUVRvxtijmAwGPD29oa3t7dKyQBBEHj8+LFa8frtt98o8SZxd3enej7GxMRoFa+cnBy1x7N7926w2Wz06dMHffv2VVpz0gdjUmx2dnaws7NT6prQfqhfXV2d0sWKYqpQsSN8RxEoOsXXSWh/siCHgYlEIgQHByuNvNAXcw4tVNymPoW67V+Pm5sbFixYgG+//Rb//PMP2Gw2WCwWevXqBbFYjLq6OpOOq6GhAadOnUJ6ejrOnj0LkUgEOzs7vPDCC4iPj8fkyZPN3sOrtbUVUqkU9vb2Ok0SmsZkmIqvry+uXLmCcePGQSKR4Pr166ipqdFYd/b7779DJpNh+PDh6Nu3r8n7B9rEq3v37pRtXhGCINQ6DfPy8nDp0iX8+eefSo93d3dXEixN6e+qqips2LCB+r+vry8lVn379kWfPn3g5+en9j2uq6vDt99+i9zcXMTExBi8ptX+tasb6kcWHgsEArWFxywWCxKJBK2trWYpPDYGc7U5ogWqg0NGOhwOB01NTVRNR0hICDw8PIz+8FoixadrzYy0nIrFYhX7aUJCAr777jt8+eWXSE1NpWpb6uvrjapbqqysxMmTJ3H8+HH89ddflCNr3LhxGDx4MJYuXWp0+6T2KApua2srCgoKqAnDYrGYMlnw+Xw0NzcrNUbVNSbDkMJudURFRWHPnj2YPXs25s6dS6XnEhISEBQUhKtXr+L69etobm7G1atXcfXqVQBtf6uIiAhMmDABw4cPR2xsrEldRtTBYDDQo0cP9OjRg3IuAqDW1nx8fFTEKz8/H+np6RCJRGq36eTkhFdffRX29vbg8/ng8/koLi7G1atXcfr0aepxHh4elFiR4uXp6YkxY8ZQacPTp0+bZU2rPYqFx4qdt2UyGVpaWvD48WOIxWLcv3+fKjxub8zQtyO8sZirUWx4eLiZjsg26PACZaigcDgc1NXVoby8HAAQEhJilqsSS6T4dL020pChKFBkKo/FYmHs2LE4c+aMUhrQkFZHBQUFVI3StWvXQBAEPD09MXfuXEydOhWjR4+GTCZDfn4+JU51dXVITU1VOzFX39dMEAQkEgkKCwtRV1eHoKAghIaGUvU0ly9fpl5/eXk5tT6Rnp6OlJQU+Pj4YP/+/ZQhwdyMHz8e//73v7Fu3TpkZWXhhRdewPbt25VGgcTExEAul+OXX37BjRs38Pfff+Ovv/6iarDs7OwQExND2doHDRqk1NnBVDedIgRBgMViwcfHBz4+PhgxYoTS/XK5HJWVlcjPz8edO3dw4sQJSlgFAgG2b9+u9HgvLy+EhYVRU4h5PB4EAgFu3LiBCxcuUI9T55o1x5qWvrBYLLi4uEAsFoPBYCAkJATA/wqPBQIBHj9+DIFAQBmc2hszzJUaNGaabnvoCKoDQxAE6uvr0djYCKlUivDwcLNd8QOWSfHpgrzqE4vF1JwpJpOJXr16wdXVFW+++SbOnj2LXbt2Uf3vtEVlBEHg/v37lB38v//9LwDAx8cHy5YtQ3x8PEaMGKF0tUkWZwLQOTFXHxgMBvLy8lBTU4OAgACEhYVRPQlJYSWNIWTLIbFYjDfffBP79+/HwIEDsWXLFtjZ2SEzM1PFxkz2TDQVxVHZwcHBSlfH5HjuxYsXIyMjA+vXr8f8+fORk5MDV1dXyiV46dIlXLlyBVu2bAGbzcbAgQMxfPhw9OnTBx988AGKiooAmO6m07X+xWQy4evrC19fXzz33HNISkqCSCRC3759YW9vj7S0NBQXF6tEX3fu3NHa6URTSYc284glaL8GpU/hcVlZGQQCgdrCYwcHB4PX1Mzl4qMF6ilDV5ShOPLCwcEBXl5e8PX1Nas4AbrbElkCMmrKzMxEt27dEBYWpvS6Ro0ahcjISGpWFIfDUYmgCIJAVlYW0tLScPz4ceTl5QFoO+muXr0a8fHxiI2N1fiFVBQ8TRNzU1NTNTaIJZHJZCgpKQGPx4O3t7dWS7/iGpQmMwRJ+/lJtbW1qKmpQXl5ucrVsr4nndzcXMyfPx9dunSBt7c3UlNT0b9/fyQkJFCPmT59Onbu3Ikvv/wSL7/8MmUFJ9d7FixYAIIgUFxcrCRYX3zxhdp9mhJ5GNO9wt7eHmvXrsWaNWtw+fJlzJ8/n+rQUV1djVu3buHGjRv47bffcOfOHYO2nZ+fjy1btigVKpvqJtWGPuKgT+GxQCBQmnjs6OiolCbU1hGeNkmop8MLFKB+XYF0OxUWFsLFxQXR0dFwdHREXl7eE50JZQ7UnWAaGxspG7efn5+SY4yEwWAgKSkJiYmJOHbsGGbPng0mkwmxWIwLFy4gPT0daWlpVLozOjoa//rXvxAfH4+oqCi9TmqKAqXpyvju3bsany+Xy1FaWorS0lL4+vrCzc0Nvr6+WsWCdG4VFRUhISFBqxmivY2Zw+HAyckJrq6u1NWyohus/bTa9ovqdXV1mDFjBlpbW3H8+HGEhYVhwoQJeP311+Hv7091qmAwGNi8eTNeeOEFfPzxx/jqq680vh53d3cEBgZSRayarPDGRh7GtldasGAB3n33XSQmJqKwsBDZ2dm4ffs2KioqlI595MiR6N+/P/r164d+/fohKCgIcrkcOTk5mDFjBqqqqqjHczgc5OTkUNE5Sbdu3dT2NQwODlbbEcUQTGm1pG3icUtLi8bC4/Yd4c0lUMbMgrJlOoVAKSKXy1FVVYWioiJ4eHiodBZ/0kMLTYXJZCqdYMhUHrkgDkBrf645c+bg/fffx9atW+Hi4oJff/0V6enpaGpqAgAMHjwYK1euRHx8PJWjN/T4SIHSNDFX3RwguVyOiooKFBcXo3v37lTbKH1MHOQV7KRJkzSaITRBvo/29vawt7dXcYORJ52GhgaUlpZCLBZTRaMcDgdLlixBUVGR0hrX4cOHMWrUKCQkJODPP/+kar1iY2Mxc+ZMHDhwALNnz0ZZWRlu3ryJ7OxsZGdn4969e0rd1F1cXBAZGQmJRIIbN26oHLu6ixB90FegqqqqcOvWLdy+fZv6IdcvP//8c7i7u6Nfv36YNWuWkhip2zaLxUKfPn3wzz//4PPPP0dJSQkGDBiAxYsXw83NDaWlpSo2+YKCAmRlZamkBr29vTWKlz5z1uRyudm7UzCZTI2Fx+RnqLa2lio8bm1tBZPJhJubGyVghgpWc3MzHUE9rZAnvJKSEnh5eWHgwIFqT9xsNtsiY98ttQZFbrelpYUSJjKVl5mZCQAaU4s8Hg9nzpxBbW0tamtr8dJLL4HFYqFv375YuHAhXnzxRWrEubEoCtTAgQNV7g8ODsbSpUup/5Mzs4qKitClSxcMGjRIaU1Ll8uOIAjs27cPQJtz7JdffjFbTZemkw65NrFy5Upcv34dy5cvh7e3N+7evUs9ft++fZg6dSqmT5+OXbt2oaqqCtnZ2cjLywNBEJgyZYrSawwODsaoUaMQFRWFqKgoREZGIiAgAAwGA/X19Rg1apRK66TFixcb9brUCZQ6MaqsrKTud3d3R//+/TF9+nSkpKQAaEttGtqs1NPTEwsWLEDPnj2V0niBgYEIDAykOtGTkI2Y1dV5Xb9+XeU71r17d7V9DYODgylTgkwmQ3NzM3766SezmE60wWaz1XaEz8rKQteuXSESiVBZWUkZe7hcrt6p5o42CwroJAJVXl6OwsJCdOvWTefICw6Ho9FSawqWsJkDbcJ7+/ZtsNlshIaGKlXcK5okSOrq6nDq1CmkpaXhjz/+UBGv4uJiPHr0SOvMKENQFBSyMerq1atRUlKiNDGX7I5QUFAADw8PjRcQ2gRKLBZjzZo11P/Pnz9vcL2VMTZzOzs77Ny5E6dOncKiRYvw+eefA2hbi7l58yb++9//IicnBy0tLSgqKsILL7xAPVfxRDVkyBBs2rQJvXv31nrl7+npifPnz2P37t2UG3Lx4sXUCdVQh19lZSUuXbqE9PR0SowU026kGM2dO5eKjEixBICIiAisXLkSBw4cMEokDZkHxWazERQUhKCgIJX7pFIpSkpK1IrXP//8o/L98/HxQXBwMFxdXXHlyhUqdWquFk6GQBCESksqgiDQ2tpKpZrr6+upLiGKxgy5XP7EjvNJ0ykEytHREYMHD9YrZH5aUnxNTU3Iy8tDS0sLIiIi1I5UJ0/wxcXFyMzMxPHjx3Hx4kXIZDI4OzsjLi4OU6dOxbhx4/D666/j8OHDKp0GTIX8wrW0tODIkSMYM2YMPv30U+p+xZ5zLi4uOoc5anIZ1tTUYO7cuZT92cfHx6hiYGPWYg4ePEjZwz09PTFv3jzk5ORQLjvyuMPCwpCbmwug7TM5bdo0lJeXw8/PDydPnqTSmYDu7gqenp5qDRG6+uVVVlbi9u3bStGRohh5eHigX79+mDdvnloxUsecOXOwdetWbN26FfPnzweDwUBrayvEYjH1L/m7utvz8vLg4eFBnZAVH9/+eZq2RabJ2m+f/FfdxWFFRYXSepkiT9LuTtL+PWYwGBpTzYqFx/v27UN6ejoaGhqwaNEiREdHIyoqCqNHj9arfisjI4Nq3bVkyRK88847Ko85fPgwPvzwQzAYDPTt2xcHDx40/QXrAcPAq8WncmSjVCrVO3ppbm5GcXGx2nURU5DL5bh27ZpKXzVDIYWJdHyVlpaiZ8+ekEqlSvVFY8eOxapVq3Dz5k3quV5eXnjxxRcxdepUjBo1SkkIbt68iWeffRZr1qzB5MmTzRZBAcCVK1dQXFyMRYsWYd++fZg1axaAtqLg3NxcODg4IDQ0VK86kDt37iAoKEgpHZSTk4OXXnoJJSUl2LhxI06ePAkej4d//vnH4GMtKSmBnZ2dWsEH2tb47t27R60T/fjjjyqPcXd3p1JzZHouIiICjo6OIAgCiYmJKl9wLy8v1NXVYe3atZg+fbqKKYP8UYz+5XK50klZKBQiOTkZJ06cMPh1BwYGon///ujWrZtagVAUBXViYGr3EX1gs9lUiyPSUUf+rni74v0cDkfltvaP3bVrFx48eKCyv5deeknt39cSZGZmIjY21ujnC4VCvPjii/j++++RnZ2Nu3fv4uOPP9aZ8pPJZOjVqxd+//13+Pn5ITY2Fj///LNSmURubi5mzZqFc+fOwcPDA9XV1UoFz0ai15Vgp4igDMHSZgZjURQmxVReRUUFampqEBcXp1Rf9OGHH1LP7dWrF3bs2IFhw4ZpjCIHDBiAoUOHYteuXSp5f3Owb98+uLm5YcqUKWhsbERubi44HA4iIyMNcmG1fx9Pnz5NWbIPHjyIyZMn4+jRo0Z3YSBTfDKZDAUFBdSXPScnBzk5OSgpKVH7vEWLFmHixImIjo6Gj4+PxoiDwWAgMDBQ5XbyBL9161ZkZGTAyckJYrEYIpEIQqFQSRykUqnGqMBYioqKlCI+XSd4cl4TeTubzcaxY8cAtPV6dHV1VSsU6gSkpKQEzzzzDBwdHTWKjZ2dncX65eXm5qoVKGNNJ9aAdPCRvSH15fr16wgNDUVwcDCAtmg4LS1NSaBSU1OxcuVKyiFoBnHSm04hUE9yaKG5IYUJgMoaE9Bmkti7d69KfZEijx49QkJCArU46+LiAjc3N7i4uFC3ubq6gsvlorGxERs3boSdnZ3Sfa6urka3e6mqqsKFCxewYMEC3L9/HwCMLoQmBz8SBIHt27fjnXfeQc+ePXH06FH06tULQFs6UVMEpI6Ghgbk5OQgOzsb165dw6NHj5CXl0e5AYG21Fd0dDRefPFFREVFwcfHB0lJSaitrcWpU6cMuvptb6FuT3Z2Nnr37g0ulwtXV1d06dJF6aReUFCgcxvtiYmJwYYNG9RGICKRCM3NzYiIiKBEw5hU58SJE7F06VJEREQgMTFR7+fduHED/fr1s1rD1vj4eJw9e1ZJoE0xnRiKTCYzuf+fsTVQ5eXlSs2a/fz8cO3aNaXHPHr0CAAwbNgwyGQyfPjhhypTECxFpxAoQ7CUi89QdAkTCYvFwr1799Te5+npifr6eri4uGDYsGFoamoCj8dDZWUlHj16hObmZrVrTteuXcPYsWNVbndwcNAqcO1vJ3//7rvvQBAEoqOj4e/vr5RPNxRyfWPFihXYu3cvhg4dil9++QUMBgNbt27FvXv38PjxY/j5+ak8VyqVIj8/n0rPZWdnIycnB2VlZUrvZ3BwMCZPnozo6GhERkYiOjoa3bt3V+r/N3XqVJSVlWHfvn0GiVNdXR2uXLmi9r5ly5ahoqICp0+fxo8//ojw8HBUVFTg9u3bOHv2LPbs2aNxu4sXL8awYcPg7e2NxMREar4W+Zpu3bqFsrIyzJkzRyWKbmhooNr+mMKMGTOwZcsWbNu2DQsXLtS7dY+1BwY6OTnhzz//xN69e9WaTiyNufrwGTMLSl1Wp71YSqVS5Obm4sKFCygrK8OIESOQnZ39RCzttEC1w9JfFF01J/oKEwk5UFBxcB5JfHw89uzZg5SUFMyePVvt8yUSCXg8Hpqbm9Hc3Eyt4cybNw9Dhw5Fc3MzJWzkY5qbm8Hj8VBaWkrdro/zce3atVi7di1VCKtN6NpHb+TPw4cP8cknn+DevXtISEjAN998Az6fr9RCCQCuXr2KU6dOoaioiErP3b9/X+k4vby8EB0djalTpyIyMhJRUVFwcXGBvb09fHx81L4GgiCwatUqXL58GR999BGmTp2q83Ursnv3bjQ0NKjcTk7oLS0txcmTJ1VGx7dn9uzZWLt2LXr16qXyefr7778ph1/v3r0xcuRILF++HElJSSgqKsK4ceOouUnOzs5mSxWyWCy8++67WLRoEXbv3o2kpCS9nmdsobC5kMlk8PLyeqKGCEWsOQvKz89P6WKmrKxM5bPv5+eHIUOGgMPhICgoCOHh4cjNzTVpzUxfOoVAWfPDrwjZRkjdh9FQYVLc5pw5c3D8+HGlE3RwcDCmT5+OPXv2qJ0JRcLhcODp6UldLaampiI4OBjV1dVK9Um6EIvFlHjV1NTg4cOHqK2tRXZ2Ng4ePAgvLy8sWrRIrdAVFhaCx+OhqanJoOj1+PHjOH/+PFpbW1FbW6t0n0gkwty5cwG0RcXh4eFUBwwyKurWrZvKZ6O8vFzrWuHnn3+OQ4cOYcGCBXjzzTf1PlaSv//+W+3tAoEACxcu1Pi8CRMmYPny5RgxYoTOolJ1Dr/ff/8d06ZNw+effw4vLy+88sorVIun+vp6tLS0oKmpiWrPo86UoQ/kPrZt24ZFixbpVShrbQyxuVsCa/bhi42NRW5uLgoLC+Hr64tDhw6pGHimTp2Kn3/+Ga+88gpqa2vx6NEjas3K0nQKgTIGS1zVketbigLV1NSE/Px8EARhkDCRkKmZS5cuITU1FXfv3qXqi8gFfUN6AHp4eGDixIk4duwY7t+/Tw3g0wW5ZlVbWwuZTIbx48ejW7du1Fj5rKwsqrOFNsj1EFKwyN8PHz6MI0eOAADCwsLw/PPPU5Hd9evX1W5r4MCB2L59O8LDw83SKeDIkSPYtGkTnn/+eXz55ZfU50Nb3RFBECgrK8Pt27fxwQcfUBch7dEkzBkZGRgyZIjJJ9CuXbvi5MmTmDFjBt5++23w+XysXbsWXbp0gbOzM5qbmxEQEEB1Oairq0NxcbHSeHXyR1sXbyaTieTkZLz88stITU01SsQ7G9bsw8dms5GSkoLx48dDJpNh8eLFiIyMxIYNGxATE4O4uDiMHz8eZ8+eRe/evcFisbBlyxaDh1IaS6cQKEOFhqy1MfeirWI3CVOFiYTNZkMgEMDT01Ol4SpZ32LomtqsWbNw7NgxfPPNN1SXAG2Qoy9qa2sRGBiI8PBwMBgM8Hg8HDt2DIMHD9bb+UPWfZCPJ80QR48ehb+/P7788kvExsYqbe+zzz5Tci2SkOtIhkCaMNrzzz//IDExEeHh4di3bx9lGFFXd/T9999j5syZePDgAW7fvq23BbtXr16YOXMmpkyZgr///hvr1q3DvXv3zGb5d3d3x/HjxzFv3jx8/PHH4PP5+PDDD6mLMfJip/1aFNkpg8/no7S0FC0tLSAIAg4ODkrCxeVywWAwMGXKFERHR+Orr77Cq6++atFGr+bA2hkWcwmUsbOgJk2ahEmTJindtnHjRup3BoOBbdu2Ydu2bSYdozF0CoEyFHJOjbkFis1mo6mpCY8ePTJZmEi0zW9SHFhoCIGBgRg7diwOHDiAjz76SOPVklQqRXFxMaqqqhAQEKBypX/s2DG0tLRg0qRJRgm+WCzGqlWrlMwQPB5PRUCWLVuGffv2KaU43d3dzebCKigowNy5c+Hq6oojR44oXanu3r1bqeUQ0NZB4ptvvkG3bt0wcOBAnD17Vul+FxcX8Hg8AIC/vz8WLlyIKVOmQCqVUtbmsLAwpKamYtOmTZgxY4bZFqSdnZ1x+PBhvPLKK/jyyy/R3NyMt99+W+tJ2s7OTikNDPyvWFRdM1RnZ2dqzWvnzp1Yt26dWY7dUphjvIop0J3MNWO9xKsNYwmreXNzM+rq6lBSUoKQkBAMHDjQZHECtAsUeZVv6JgPFouFZcuWQSgUYvfu3Sr3y2QyFBYW4tq1a2Cz2Rg6dCj8/PxU0lD79u1Dly5dMHz4cIOn9NbU1GDixInYu3cvEhISkJGRQa0ZtT+heHp64uLFi3j//fcp+6uhgxBJ2m+/oaEBM2fOBJ/Px88//6xUw1RRUYH9+/er3c7EiRPxzz//qIiTnZ0dnn32WaSkpFCOwnXr1sHf31/pcRwOB5s2bUJdXZ3GERvGYm9vj59++gkzZszArl27sH79eoONEuSUWrJRa58+fTBo0CD07dsX3t7eGDVqFJ555hl89dVXOH/+PO7cuYOCggJUV1dDIBBYXRRIrG3QADrXLKidO3eiX79+YDAYtxkMRiGDwTiv7fGdIoIy9ANoToFqbm6mGoJ6eXmha9euZhEmEm0CpThR1xCYTCaGDx+O3r17Y+fOnXjzzTfB4XAgl8tRVlaG0tJS+Pj4YMiQIRq/WPn5+bh8+TKSkpLA5XINEijFzhCffvop3nrrLepvqKlXnqenJ9asWYO8vDxkZGSYxSIsFouRkJCA3Nxc/Pjjjxg8eDCANvHctm0b/vOf/2gU/7t37yotJMfExCApKQljx47VO+U1btw4jB49Gt999x0WL16stv+csXA4HKSmpsLZ2Rk//vgjJcCmNhtls9nUsL+NGzdi1qxZuH79Ol5//XUqTVhdXY2WlhYwmUw4OjpCIpGgvr7eKFOGqZgyasNcdKZpuitWrMCKFSvAYDBiAZwDoDVv2CkECjCsCag5aqEUhYkcG19YWGj2hrH6pPiMiaDkcjlWrlyJlStX4tixYxg2bBiKi4vh7e2tV19DsqP4ggULIJfL9RYoxc4QR48exeTJk5Xu19SLj8FggMFgUHVdxn7hyc8JQRB444038Pfff2PDhg146aWXUF9fjx07dmDnzp0QCAQYM2YMVq1ahZUrVyrVUgFQ+n9BQYFRtV8MBgOffvopnn32WWzYsAE//fSTUa9JEywWC19//TUA4Mcff8ScOXNw4MABk0+WJOPHj8fAgQORkpKC5cuXo2vXrkr9EWUyGXg8HhobG5VMGe1Hqzs5OVlMRCyx1mwoUqnULBHUUzYL6msA5wiC0NqXi07xqYHD4RgdQTU3N+PmzZvIzc1FcHAwBg4cSF3ZWCJ1qE8EZajYkiIwd+5ceHh44LPPPoNAIEBsbCxCQ0N1ipNMJsP+/fvRt29f9OnTR+sYeRKCIPD111/jpZdegoeHBy5cuKAiToDuCw3FabrGQG7/iy++wIEDBzB//nwsW7YMn332Gfr06YMvvvgC/fr1w6ZNmxAVFYXVq1dTYuTo6KgyM6uhoUEvcdKUaurduzcWLVqEtLQ0XL582ajXpA0Gg4H169cjKSkJf/75J6ZNm0bNAjPHtpOTk9HU1IRvvvlG5X5yvcre3h5hYWHo378/Bg0ahN69e8PT0xMSiQSlpaW4efMmMjMzqQa8tbW1EIlEZkkTmiO9Zo5jMHUN6mmaBfV//Q0DAHyk67F0BKUGY4REXcSkbruK7XPMgaVSfPX19cjLy8NLL72EXbt2obGxUe/0y7lz51BeXo7Vq1dT29MmUOrMEJpcf7r+jqZGUECbtXvjxo2IiYlBUFAQoqOjqeLa0NBQ5Ofn47333gPQ1jVS49AAACAASURBVK/tnXfewZQpU1BZWYkZM2YAaHPkZWVlGX0Mirz33ns4cuQIkpOTcf78eYtEE0lJSfDx8UFycjLi4uJw7Ngxs1iJx4wZg0GDBuHbb79FYmKiSupVXRcJfUwZ5eXlaG1tBZvNVmqoa+igP1sQKHOYJJ6WWVA3btzA1q1bASCBIAidaZVOI1CGYMhMqObmZuTn50Mul2sUJhJLDC3UJlBsNptqDaQPBEGgrq4O5eXlcHBwQL9+/eDv74+9e/ciJSWFWoPRxU8//QQOh0N1r9AmUDU1NZgzZw4uX75MdYbQ9kVjMpkaI0KCIEyOoG7fvo3169cDaBsi115k8vPzMXjwYKxatQqTJ0+m1pm+/fZbakzB/Pnz8d133xm1f3V06dIF69atw/vvv4+ff/4Z8+fPN9u2gf9Fb0lJSXBycsKbb76JiRMnIj093aCehupgMBh47733EB8fj5SUFGzYsEHpfn3bHJGmDNKYQSKRSKiCY8VBf/b29koWeAcHB7URakcQKFsxnOhDSkoK6uvrAeD8//09sgiCWKLp8Z1GoAxtGKsrLUYKk0wmQ2hoqF7htSWGFmp7XQwGA3Z2dnpFUA0NDcjNzYW9vT18fX3B5XLh4OAAX19fTJ8+HUePHsXmzZvV9rhTpLGxEenp6XjxxRep1JamqEebGULba2q/LblcjvLyclRXV1MNP8mu54b83XNzczFz5kyV29lsNp5//nlMmTIFkyZNUjpBAkBiYiIOHDgAANi8eTNWrlyp9z71ZcWKFdi1axc2btyIqVOnmrVDg+L7tGjRIjg7O2PZsmUYP3480tPTERAQYNL2n3/+eTz77LPYuXMnVq5cqRSZmdqHj8PhUKYMEoIgIBKJKFPG48ePIRQKKZFTFC5bMEmYSySt7UbUB4V+kv30eXynEShD0JbiM0aY9NmupdAlUE1NTcjNzQWLxULv3r3h7OyMsrIyJSFNSkrCL7/8gp07d+KTTz7Rur8jR45AJBJhwYIF1G3qIihdZghNKAoUQRB4/PgxZUIICgrCX3/9BaCtgDYzM5Na51D8aX8yKCkpwbRp06hhgiRxcXGIj4/HuHHj1DovCYJAbGws1e35yJEjGD9+vF6vQ922tMHlcvHxxx/j5ZdfxldffUWlGM1BeyGfOXMmnJycsHDhQkyYMAHp6ekICwszevtkFDV58mRs374dH330v6UHSzSKZTAYcHBwgIODg4opg4y2amtrUVRUBKFQSBlsFDtlPEnRMlWgRCLRU5HeMwZaoNRAFuoqYoowkVhDoLhcrlqB4vF4yMvLg1wuR1hYmNIJmMViKT0nNjYWQ4YMwa5du5CcnKx1fWffvn3o3r27Ujd0RYFqPybj2LFjBs3dISOjuro65ObmwsXFBQMGDKBeJ/lF79OnD8LDwyGVSqkr6crKSvD5fMjlclRXV+Pq1avYsWOHyj62bduGhIQErZN9pVKp0hrJtWvX9G4LpQldV8BxcXF49tlnsX37drzyyivw9fU1aX8k6iLNSZMm4ciRI5gzZw7Gjx+PtLQ0k4Z4jhgxAs899xy+//57JCUlUcLxJDuZs1gsqukwSVVVFQQCAdzd3SEQCFBSUkKNVVfXl9BSUYop2zW2k/nTQKcRKGNnQpEncplMhpCQEJOsnNrWiyxF+whKIBAgLy8PYrEYoaGhal+Puohn1apVmD9/Pg4cOKCxiez9+/eRmZmJ1atXK+XUye0ZYobQhFAoRFlZGXg8HqKjo6lUFxmBkGuH5BoUWZfj5uaGGzdu4OTJkzhx4oRKtAQA8+bNw2uvvQYAlN1Z3cmzqalJaYaOsTZyQyFt588//zw++ugj/PDDD2bZrqZU6PPPP4+0tDTMmDGDGgSpq8u6NpKTkzFhwgR89dVX2LRpEwDrj9qQy+Xgcrnw8vJSST2SfQkbGxtRVlZGmTIURcvJycnk9Jypa0hPSw2UMXQagTIENpsNkUiEW7dumUWYFLdriQiKTHupO8mQAiUUCpGfnw+BQIDQ0FCtDi0mk6kipPHx8fDz80NKSgpeffVVtScVxdqn9turqanB/Pnz9TZDtEcgECA3NxctLS3w9PTUeDWv6OKTSqW4fPky0tPTcerUKVRUVKg8nhy1PnfuXHz99deorKxEQ0MDSktLqStpxXWL2tpaxMTEUM+vqal5oumVAQMGYO7cufj555+xfPlyDBw40ORtalurGzx4ME6ePImpU6ciPj4ehw4dwsiRI43az7PPPotRo0YhNTUVq1atQvfu3a0uUJrSa0wmk/qbKyKRSMDn8yEQCFBRUUGZMsi+hORnRZMpoz3mMDjQEVQHQN8IioyYWlpa0Lt3b7MWv+lTD2TsdjXVUnA4HDQ0NOD27dsICQlB165ddb4XZKGuImw2G6+99hqSk5Px559/qgw0lEqlOHjwIAYNGoRnnnlG6b68vDwkJiaivLxcbzMESWtrK/Ly8sDj8ah1kPajNRT5P4cQVq9ejb/++kvt7CU3NzesWrUKvr6+SExMxLBhw7B9+3ZwuVy4uLhQFyVA25U0uW7xxx9/YMmSNsORi4sL/vrrLzQ2NlLrFqakaQw5UX3wwQdIS0vDu+++izNnzpicdtJlJunbty/OnDmDuLg4zJgxA/v27cPEiRON2ldycjLGjh2LL7/8Ev/+979tQqAM6V7B4XDg4eGhdF4g3aPk50SbKaP9VGpzFAobOwvqaaDTCJQu2qfyhEKh2SuzLZW/VjfGQywWU50rCILAkCFD9N6/plTkokWL8Mknn2DHjh0qAnX27Fk8fvwY//rXv5RuP336NBISEgDAIDOEYof04OBg9O7dGwwGA/X19Sri2dDQgNOnT+PXX3/FiRNthenp6ekYOXIkfH19cevWLeTk5MDJyQmJiYlISkpCQUEBJk2ahJCQEOzfv5+Kgtq7BJlMJlxcXJCWlkal/8aPH4/9+/eDx+OBz+ejpqaGat3j5OQEFxcX6oRkiH1Y37+Pj48P3njjDWzevBnHjx/HtGnT9N6HOvRxO/bq1QsZGRmIi4vD/PnzkZqaiunTpxu8r8GDB2PMmDHYvXs33njjDbDZbKun+EwVCAaDAUdHRzg6Omo0ZdTU1KCwsBBSqRRcLpcSLi6Xa/Lrp1N8HQBNX0BzrjFZC0VBkUgkKCoqQnV1NQIDA6kPriHiqCnS8/DwQEJCAn744Qc8fPhQqb3/vn37YG9vT9m0Fc0QPj4++Pbbb/VyuMlkMpSUlKCiogL+/v4qHdJJAamoqMDJkyeRlpaGv/76S6Wf2alTp5CSkkKJT1JSEt566y107doVJSUlmDNnDhwcHHDkyBGdBanJycnU2JH169dTIszlcpXWnsgTEo/Hw+PHjylTDVmTQwqXvb29yRcrr7/+Ovbu3YsNGzZg4sSJWg0dutDXjh8YGIiMjAzEx8dj8eLF4PP5WocsaiI5ORmjR4/GF198gXXr1lk9grJUHZQ6UwZBEErjS6qrq8Hj8ZCZmWm0KYMWqA4IKUxSqVSjWcAWOh3rA+m6e/z4MSorK+Hv74+hQ4eCyWTCzs4OfD7f4O1pSkWuXLkSP/zwA7755hts374dQFvK7dSpU5g2bRrc3d1VzBBff/21zgapBEGgvLwcxcXF6NGjh9pGtHl5efjll19w/Phx3L17F0Bbk9g5c+YgLi4OI0aMwNixY5GdnY2JEyeCw+FgyZIlWLt2LTXGuqmpCTNnzqTqtUJDQ5X20T6CmjBhAq5cuQKgbbQG2SlC0/um7oRE1uTweDxUVlYqjaUgRcvQtQgnJyd88MEHWL58Ob777ju89dZbBj1fEUMmyvr4+CAjIwPTpk3DqlWrwOfzDa77iomJwYQJE7B3717MmzdPpa7sSfKkC3UZDAa4XC5lzGhubkZ5eTnCw8MpU0ZDQ4NBpgxTZkHZOp1OoPQRJuB/abP2OWNTIQfimeuqkbxqv3v3LhVxKH6A9S3UVUSdSYIkPDycSnF9+OGH8PT0xKFDhyCRSLBgwQK1nSEaGhoow0F7CIJAdXU18vPz4eXlhUGDBlHvOUEQuH37NtLS0pCeno579+4BALp164bExERKlNhsNgoLC7FmzRpkZ2cDABISEvD2228rFZlKJBIsXLgQ9+/fxw8//KB1EKBMJkPXrl0pU8u5c+eUzBH6oqkmh7S/83g8lJeXo7m5Ga2trZDJZErCpe0qevbs2di5cye2bt2K+fPnG+yIJJHL5QZdiHl5eeHEiROYOXMm3n33XfD5fKxfv96gbSQnJyMjIwM7d+5UO2zySWHtQl1y7ViXKYPP56O8vBwCgQByuRwODg4gCAJ3795FVVUVYmNjDd53RkYG3njjDchkMixZsoTqhNKeo0ePYubMmcjMzDTqO2AKnUagyJOdRCLRKkwkZC2UuQWKFD5TxwqQ3RNKSkrAZrMRHh6u9kpUUx2UNnSZOZKSknDmzBns2bMHa9aswU8//QQ/Pz94e3tj+PDhKp0hNG2vvr4eubm5cHJywoABA2Bvbw+ZTIaLFy8iPT0d6enp1Nj68PBwrFu3DmPHjoWbmxv69u0LoK1r+L///W/s2bNHSVS//fZbpX0RBIF169bh3LlzeOeddzBnzhy1r43siK74+bh3757ODhqGojiWAsD/Z++7w5sq+/fvNG3SlaaUVeigdNHSFgq0DKEUZxER9EURWSqjwLcIiAoiQ/Z4UVFA5WXJFJXNC8iQUWSvviCF7kH3SEeSJs3+/dHfczwno9lttdzXxaWk4eTkNHnu8/k89+e+qTtpf39/iEQiSkkol8sZkes8Ho8aJHVwcMDatWuRkJCAVatWUc7k5sKSTgGfz8fRo0cxduxYrFq1CiKRCCtWrDD5ONHR0Rg+fDgOHz6MxMREm810mYvmdjM3ZnPUmCgjPz8fDx8+xLVr13Dx4kWsXr0akZGRmDJlilHCUqlUSEpKwvnz5+Hr64vY2FiMGDEC3bt3ZzxPJBJh48aNJtuc2RqthqAcHBwQEhJiskWMvSTh1hIU2X/Jy8tDhw4d0LdvX+Tn5xt8viUVlLF5rZdeeglhYWH4/vvvMWTIEDx48AC9evXCCy+8oNcZQpughEIhMjMz4eDggIiICDg6OuLixYs4fvw4Tp06Ran0YmJiMGXKFIwcOZJqYYjFYmRlZaGsrAxffvkltm7dCplMhhEjRuCzzz7D7Nmz9XoPbt68GTt37sTo0aOxYMECg++ttLQUcXFx1N+Li4t17mrtBRaLRfnN0UHfs8jPz6ek9G5ubvDx8cFrr72G3bt3IzExEREREWa/rqWtbDc3N/z666/44IMPsHHjRojFYnz99dcmVyQLFizAyZMn8Z///MeiCsAWaG4vPkt8+IgoIzw8HOvWrcP777+PlStXwt/fH6mpqYxK3RBu376N4OBgyktyzJgxOH78uA5BLV68GPPmzSMGr02OVkNQAMzq9duboMwF3danbdu2iI2NpUjOmKO5rSsoYiw6c+ZMSsmVkpICf39/vc4Q5HgSiQSZmZmQy+Xw9vbGtWvXsH79epw9exZ1dXVgs9mIi4vDyJEjMXz4cMYwLAGJbjh8+DAkEgkSEhLwxRdfoFevXlAoFJBKpTpOFydPnsSiRYswYMAAfPfddwYX45SUFMaMT3V1dbMbiQKG3b2JQiwxMRHnzp1DUlISvvnmG4aK0BT5uzV7rVwuF7t378aMGTOwc+dOiMVi/PDDDyZ1HqKiovDSSy/h8OHD+PzzzxkBj02F5iYoW6XptmnTBm5ubiYPUhcVFTG+X76+vrh16xbjOSkpKSgoKMDw4cOfEVRTwJzIDWsyoRqDuW4SGo0GFRUVyM7OBp/Pp1phph7TEoIyZbEaO3Ys5s6di9LSUgBo1BlCqVRCIBAgJycHmZmZuHDhAi5fvgyFQgFnZ2e8/PLLGDFiBIYNG2ZQUScUCrFx40Z8++23EIlEGDx4MJYuXUrtI5Hfq0QiYSjr7t+/j8mTJyMgIAA//fSTwaHaY8eOUQPG3bt3x40bN5pUIGMuSRD5O4/HQ6dOnShyKigowIABA3Tk79p+hPS7dmvFQE5OTti6dSt4PB527NiBuro67Nq1y6QB5mnTpuHChQtYv369TR3gTUVzz2HZIk3Xkiwofesg/TOgVqvx0UcfkeymZkOrIihzYItUXUPHNZX4BAIBsrKy4ObmhujoaIMREmw22+C5cjgcsxN1TUFdXR2D+M6cOaOzICmVSly5cgXHjh3D9evXkZqaCo1GA09PT7z11lsYOXIkXn755UbbrnV1dfjhhx/w9ddfo6qqCrGxsZgwYQISExN1nkt68+Q6FRQU4J133gGXy8WhQ4cMkt+6deso65333nsPSUlJfwv1Jh2ffPIJJVy5efOmjvyd7uxN5O/E/aC+vh5yudxk9wN9cHBwwNdffw13d3d8++23GD16NH766SejLfXAwEAMHz4cBw4cwMcff6yjqrQ3mlup21xZUL6+vigoKKD+XlhYSCldgYa9p0ePHmHIkCEAGlrfI0aMwIkTJ5pUKPGMoAygOVt81dXVyMrKAofDQWRkpNEvOZvNNphfRSooW34RSUwGwWuvvUZ9QYgYZe/evfjtt9+Qm5sLoCHTaOrUqRgxYgTi4+ONtoDq6+uxY8cO/Pvf/0ZZWRmio6Oxc+dOPP/883j48CHjuQKBANu2bcODBw+otpxQKMTo0aNRVVWF48ePG3TjHjt2LE6ePAkA2LBhA0aPHq0T3/53gIeHBxYtWoQ5c+Zgx44dmD59OvUzNpsNPp/PsMMhZC4Wi1FaWorc3FwoFAqrvOZYLBaWL18OHo+HlStX4o033sDBgwcbvbsnd+onT57EunXrsG3bNssvwt8Q1rb4LLVKio2NRWZmJnJzc+Hj44Off/4ZP/30E/VzPp/PcGwZMmQIvvzyy2cqPnvCnAXanNBCc9BYaCFdPBAWFmZ0doh+TEMtPi6XC41GY5NYaeCvmAyRSMR47NChQ7h9+zaOHj1K3ZkFBwfj448/xiuvvAJ3d3eTfOMUCgV2796NNWvWoKioCOHh4fjmm28wcuRIKqyQ/qUUCASIi4tDTk4O9djly5cxbtw4pKam4ocffsCgQYN0XketViMsLIxqUZ44cQJDhgxhvK+/GyZOnIitW7dizZo1eOeddxpVqtLdD0pKShAWFgYul6tX1qzRaHSGSA3dsZMIeTc3NyxYsACvv/46jh49atBMV61Wo1u3bnj77bdx8OBBfPLJJ00609PclbItKijA/Pfh6OiIzZs3IyEhASqVCpMmTUJERASWLFmCmJgYjBgxwupzsgVaFUGZA3tWUNrtOLFYjMzMTKhUKp3oC1OPaSz2nQz9WQrtmIyhQ4fi4MGDABoWGWJnFB4ejkWLFuFf//oXwsPDwWKxUF9fj9TU1EaPr1KpcODAAaxatQq5ubkIDAzEjz/+iNGjRzPuMLX3Ebdt28YgJ6DheiYnJyMpKUlv+mx9fT1jr+zevXtUhWXOPqUtYYsK19HREatXr8Ybb7yBdevWYe3atWa/tj5ZM93ZW1v+ri3IIPs5SUlJ4PF4+PDDD/Hqq6/i+PHjjBYS/dgODg6YP38+Dh06hLVr19JD7eyO5k6jtZagrMmCGjZsGIYNG8Z4bPny5Xqfe/nyZYtew1q0KoKyNHLDlnB0dKRiySUSCbKyslBfX4+QkBCLbZYaq6BIK00ul5udwlpZWYnt27fj4cOHyM3NRUpKCthsNgIDAylyoi/ot27douaT6Ghs0Ver1Thy5AhWrFiB9PR0+Pn54YcffsD48eP1tgG1FYZkMFcf/vOf/+Dp06fo27cvoqOj0bNnTyiVSoZaLDc3l7E31dx31NbihRdeQEJCArZu3YrJkyebFDRojBwNDZHK5XLKj1AgEEAikVBSeXd3d7z++utwdnbG9OnTqeDDgIAAxjEIQYWEhGDMmDE4cOAA5s2bZ3W2likwd0DZHrC2xfdPdjIHgObNOm7B0BdaaAuQKI9Hjx7h4cOH6Ny5M2JjY63OmTJEpuTuylwln1gsppRyR44cQUpKCoCGLxS5m+rcuTNOnTpF7RvcvXtX77H0ydY1Gg1OnjyJfv36Yfz48aitrcU333yDR48e4YMPPjC4R6VNdo2FHSqVSpw5cwaLFy/G66+/Dn9/fwY5HTp0SK+Cq7nvqq0FEXwsXrzYpOdbulBzOBy0bdsWXbp0QUREBGJjY9GrVy/4+vqCzWajoqICwcHBWLp0KYqLi/Hiiy/i+vXrkEgk1DWmq+jmzZtHDR83BZpbYm6Lc/gn+/ABrYygmruCkslkKCgoQHl5OTp06IB+/fqhXbt2Vt/FGZOZk9c2B//97391WmcAMGrUKAwdOhQsFgsnTpzACy+8gDFjxsDHxwebN2/Wu7hrJ+qeP38ecXFxeOutt1BSUoK1a9fi8ePHmD59utF2hfa1SkxM1Lkrp2P48OG4desWZWJLx1tvvYUuXbrA398f7777LjZs2IA//vgDtbW1jZ6DPWBLUgwNDcXkyZNx+vRpJCcnm/TatpJas9ls8Hg8dO7cGaGhoejduzc+/PBDHDhwAHV1dXj33Xfx22+/4c6dO7h37x5lrFtbWwt/f3+MGzcOR48ebbQythWa20UCsL61+6yCaqWwJUHJ5XKkp6fj3r174PP58PLyQocOHWzWXjCFoMytBvWRE9AQ0Hf9+nU8//zzVPXi5OSEGTNm4MmTJ7hw4YLOvyEE9ccff+Cll17C66+/jszMTCxduhRPnjzBnDlzLJ4F8fLywvz58w3+PCoqCpcvX6Zakm+++Says7MZ1kU1NTU4ffo0vvjiC4wePRpDhw5FVFQUJkyYgK+++goXLlyAQCCw6PzMgS3bTZ999hk8PT2xYMECo3N39pZas1gsvPzyyzhx4gQ0Gg3mzJkDjUaDnj17wsnJCSwWCyUlJXjw4AFeeeUVsNlsLFq0CJWVlaivr7dbRdsSKihr8U/OggJa2R6UOXBwcLD6i6FUKpGXl4eysjIEBAQgJCQEcrmcCtWzFYyp+ADzK6jg4GC9ZNO+fXsIhUKd1NxJkyZh1apV2Lx5M1566SXGz+7evYt58+bh7t27cHNzw/z58zFnzhybRZtcvXoVjo6O8PX1RV5eHvV4165dkZ6ejl9++QVAQ9Dfxx9/jPXr1+tIyTUaDfr06YNu3bqhqqoKIpGIsl8i8Pf3R3R0NPWnV69eRqM6mgtt27bFvHnz8Pnnn2P//v06v6/mQN++fXHq1CkqnffAgQNwd3eHj48PVcH17t0b48aNw549e3Dz5k34+fnpuHrzeDy4ublZXfU1N0HZ4sbgn97ia1UE1VQboiqVCvn5+SgpKYGfnx8VfQHYp3XYGJnSRRLmYNSoUTh9+jRjmC8wMBAVFRXw8PDAyJEjGc/38vLC+PHjsW3bNmRkZCA0NBQPHz7E8uXLcfLkSXA4HMyZMwcff/yxSV5hpkKtVuP8+fMYNGgQdu3ahR07diA1NRURERH49ddfKXLav38/Xn/9dQAwqCi8d+8e7t27B6DBMZ24dsjlciiVSkilUly+fBknTpyg/o2fnx9FWD179kSvXr1s+v6sQWJiInbs2IHly5fjzTffNDi20JTDqlFRUVTw4dtvv42FCxcyfPhYLBbmz5+Pn3/+GXv37qV+f3T5e0FBAeWOT+TvdPd3U9HcBGULF4tnBPUMJkOtVqOgoACFhYXw8fHRm2lkrtWRtTBXJKHRaFBSUgKFQoFdu3bhypUrSE1NRVRUFF599VX069cPkyZN0utqkZSUhG3btmHWrFlo164dDh06BCcnJ0yfPh0vvPCCXWYrUlJSUF5ejo8++gienp6YO3cuVCoVY+7mypUriI6Opv4eERGBI0eO6BwrMTER0dHRuHbtGioqKvD48WNGpcVisdC1a1f4+flBLpdDoVBALpfj0qVLVJIvAPj4+OhUWpZGYVgDDoeDlStXUvtrS5YsafJz0IeQkBCKpJYtWwZfX1/GHqGfnx8mTpyI7du34969e+jTp49R+btAIEB+fj4UCgU4HA6j2nJxcdFLBC0hasMWPnz/1CwooJURlLl3iSQXydiHSK1Wo7i4GPn5+fD29ka/fv0MzjY0tazVVJGERqNBZWUlsrKy4OnpiY4dO6JTp04YOHAg9Zw1a9ZAo9EYbBeR1yIqv/fffx8LFixAly5dqNA/W+Ps2bMAgJdffhkajQYCgYBhl5OamqoT5TB58mTs27ePcrkAGtqBn3/+Odzc3NCjRw/06NEDQEOP/8mTJ0hNTUVqaioeP36Mx48fM4QUXC4XfD6fIq2ioiIUFRXh1KlT1HM6d+6sQ1r0eBR7VTHDhg3D4MGDsWnTJrz//vvw9/fXeU5zSK27dOmCs2fP4pVXXsGUKVMgFovxwQcfUD8nMS6rV6/G4cOH9R6DLn/39vYGwEysFYlEqKyshFQqZcjfyZ/mFknYYkj3WQX1D4M5g5ikHWfoQ0yqjby8PLRr144RttdSQEijsQqqpqYGGRkZcHZ2pjz/MjIyGNJwjUaDvXv3olu3bjqOyQUFBVi7di12795NPTZ58mR89913Nn43Dc4R+/btw/fff4/IyEicOnUKfn5+CA0NRV5eHkUs5LxcXV2hUqmoqpXFYoHP5+PixYsYMmQIBAIB5s6di0mTJsHLywsymYzx+fD09MSAAQMwYMAAxrUoKiqiCIv8Nz093WD7tri4GMXFxTh9+jT1mLe3N0VYwcHB8PPzs7kXHYvFwurVqxEXF4cvvviiSYdgjcHb2xtfffUVVq5cidmzZ0MsFuPDDz8E0FCFfvDBB9iyZQtu3bplch6RdmItAQn2JCa6ubm5kEqlcHR0hEajoUjLGj9Cc/GMoIyj1RGUOSCuD9rSZ3r0hZeXF2JiYqwOILQF9N2Fk3PXp+ITi8XIyMgA0OAAQd+j0I59v3btGnJycrBq1SrqNUpLS7F+/Xps27YNcrkcb775EIuztAAAIABJREFUJhYtWoSxY8fi3LlzNrNxIdC2NTp06BAAYNy4cbh58yZeeeUVAICLiwtKS0up11ar1dBoNIz/enh4ICwsDA8ePMDs2bMppaEpNy8sFgu+vr7w9fVFQkIC9bhCoUBWVpYOcRnK6yotLcWZM2dw5swZ6rGOHTsyqqzo6Gh06tTJqkWzR48emDBhAvbs2YPp06c3W/icPvD5fPz3v//F6NGjsXDhQohEIixYsAAsFgtz587Frl27sGbNGhw7dsyq12Gz2fDw8ICHhwf1WGFhIZRKJdzc3CgjXalUCjabreP+bo9Ky1YtvmcE1UqhHblB2mDZ2dng8Xh6oy9Mha1bOmSB1f7Ak4qO3uKTSqXIysqCVCo16GChHfu+Z88esNlsjB07FgKBABs2bMD3338PiUSCoUOHYsmSJejduzeAhsTdDz/8ECdOnGCYylqLLVu26JW/37t3D/v37wcADB48GKdPn2ZcW7LPQL82arUanp6eEIvFlMhErVajpqaGahOR1Fr6MRqDk5MTwsPDdVwQRCIRHj9+TLUKCXnpU3OWlZXh7NmzVOsSaBBs0NuD0dHR8PHxMevzs3jxYhw5cgQLFizA77//3qx7L9rw8PDAkSNHMG7cOKxduxZisRirVq2Ct7c3pkyZgs2bN+PGjRuMKtYWUKvV4HK5aN++PUPYolQqKUFGSUkJxGIx1Go1w4+Qx+OBw+FY9R22VQVlKzVsS0SrIyhLWnzAX9EXrq6u6NGjh1UZLuS4tmwHEvGFNkHRW3xyuRw5OTmorq5GUFAQ2rdvb/ALRh+uFYvFOHz4MPr164ft27dj48aNEIlEGDJkCL744gudhWPs2LFYsmQJNm3axCAoa0g5JSXFYKR5WloaAGDChAlYsmQJ6urqGL5wht6fh4cHxGIx5QafkZEBBwcHhIaGUq0fQtL0FiH5Y+oiz+Px0K9fP0blQqpwQlj379/H48ePkZubq2NSXF5ejnPnzuHcuXPUY+3atdOptHx9fQ1e344dO2Lu3LlYvnw5Dh06hNGjR5t07vYE/Xvo6uqKn3/+GZMnT8bmzZshEonwzTffYM6cOdi5cydWr17NEKLYAiqVSu8NpqOjIzw9PRmViUajoQQZtbW1KCoqgkwmg5OTk477u6mfC1sQlCVZUH8ntDqCMgdOTk6oqalBbm4unJycEBERYZP4b0ImtiQoQ1HypMVXWFiIO3fuICAgAN26dTNKFHS14b59+1BXV4fr16/j+vXr6N+/P7744gs8//zzev+tm5sbJk+ejC+//BJ3795FTEyMwQrPGGQyGdauXYv169c3Ks/fvHkzRowYAZFIhNzcXNTV1VGb6DweDx4eHjqtGtLSvH//PoAGdZm+Lzu9NUj+ANaRFovFgre3N7y9vfHiiy9CIBCgpqYGAQEByMnJYYgyUlNTkZuby1jQKysr8fvvv+P333+nHmvbti2DsKKjo+Hn50f9rpOSkvDjjz9i6dKlGD58uNVBedZC28GCy+Vi165dSEpKwu7duyEWi7F161YkJibim2++wR9//IG4uDibvb45n0cisnBzc2OIW4ggQ1v+ri3I0LcFYIsWnyVZUH8ntDqCMvUOXigUori4GCwWCz169DA5+sIU2GMWSp98Xa1WU20kpVLJmMcyBgcHB4jFYmzatAmffvopgAZ59urVq/HKK68YvY7Tpk3Dhg0bsHnzZuzatctsgiK5UomJifjzzz+px9u3b4+KigrGcw8ePEi5MmtvjItEIohEIhQVFVGtGrJ4kEqFzWajV69ejVaT5HkE+va1yGuS82ez2dQxTb3ubDYbISEhCAkJwRtvvEE9XldXh7S0NIqwSLuwvLyceo5AIMCFCxcYA9ZeXl7UfFZ0dDQmTZqEZcuW4bvvvqN+r80FfXNAjo6O+OGHH+Dm5obt27dDIpHg66+/xvbt27F69Wqd9q01sAVBcDgceHl5wcvLi3pMrVZTggy6/J3L5TJIS6FQmG3gTMff3TPSFLQ6gjIGsViMrKwsKJVKeHt7U95itoS9CUqj0aC0tBQ5OTnUh9jDw8PkRVIul+PAgQPYuHEjysrKADSoqu7evWvy4uDn54d//etfOHToEFavXq3XMFYfNBoNZDIZ1q9fj3Xr1lES7traWsyfPx/vvfceunfvTj1/586dOpEBBGw2W6dVo1KpUFBQgIKCAqqCTUtLY0Soe3h4gMvlGnX4Jq9BQCcpjUajl7gsqbaAhjvyPn366GRqVVZW6lRbT548gUQiAQBUVVXh0qVLuHTpEuPfrVixAtnZ2UhISKD24Jpabm5oUNXBwQFfffUVeDweNmzYAKlUivHjx2PLli1ITk6mUl6thb0GdemfJQKyr0nc3ysqKlBdXQ0nJycIBAJGbIm5bb/mdmS3J1odQRn6ZZLoCyIc8PLyoj5EtkZj7uPWHrOyshKZmZnw9PRETEwMnj59CsC0QV2lUomffvoJq1atQn5+PuX+nZOTg8OHD5v9RZg5cyYOHjyI//znPxg5cmSjBEWI9MGDB5g2bRoePHiAuLg49OzZE5s3b8aoUaPwwQcfICwsjPo3PB7PrL2UmpoaZGZmwt3dHf369aNcMrp27YrQ0FCIRCIIhUIUFRWhvr4eHA6HQVqurq4mkZb2omus2mKxWBYPb7dr1w7x8fGIj49nvF5eXh5DSZiamoqsrCzG7+Cnn36iUlQ9PT0ZIoyePXsiMDDQrotfY04KLBYLy5Ytg4eHB5YtW4aioiKwWCysWrUK8fHxNjmvphzUpcvfyRB5eno6OnToADabTZnmZmdnQ6VSwcXFhVFtOTs767xna7Kg/i5odQSljfr6emRnZ0MkEiEoKIjhLm7PTChbu0koFAqkp6eDx+OhZ8+e1P6CPhWfNtRqNQ4fPowVK1YgIyMDfn5++OqrrxAXF4dRo0ahR48eDCcGU9GvXz/07dsXO3bswKuvvmqQoEjV9NVXX2Ht2rVwcnLCV199hYCAALz99tuIjY3FtGnTGOQEAGPGjDFpoZJKpVQgZHh4OLWPSCTHIpGISpel7y/IZDKqRVhRUQGJREJJkAlxmSJBNtYiFIvFKCwsRPv27RnjAA4ODmZXWuTfBQYGIjAwEMOHD6cer6+vR3p6OlJTUxmR8EADeV++fJkRTMfn89GzZ08GcQUGBtpsUTfF6ufjjz+Gm5sb5s2bB6Ahc+zChQs6fo+Wvn5zD+pyOBy4ubkx5O8ajQb19fXUsHFJSQnq6+upbo67uztqa2up7sI/Ga2WoGQyGXJyclBTU4PAwEB0795dZ7GzJ0HZ6rgkjVcsFsPHx4eRdwQ0PqhLMpmWLVuGR48eoVOnTvj222/x/vvvQyqV4siRIygoKMCsWbMsPr+kpCS89957OH/+vE52E1mgHz16hOnTpyMlJQUDBw7Eli1bIJFI8NJLL8HX1xfvvvsuNeMUHh6OuXPnYurUqdRjhqBQKJCbm4uamhoEBQXpGLuSFoyhmHftO16gYVEhpFVYWAixWEwNehLS4vF4RgUwJL4+JycHQqEQISEh8PDwYFRa5P+t3dcicHZ2Rs+ePdGzZ0/ExcWhT58+iImJwccffwwul6vTJqytrcWVK1dw5coV6hgeHh46pBUUFGQRaZnqRTd9+nTweDwkJSVBrVZj5syZ6NevHyIjIzF58mTG/o85aG4vPkMqPhaLBRcXF7i4uOiVv4tEIuzatQuXLl1CZWUlxowZg+joaPTr18+gcEkbZ86cwezZs6FSqTBlyhR89tlnjJ+TfT9HR0e0b98eO3fuRJcuXax7wxag1RGUUqlERkYGKisrERAQgLCwMIN34fYMLbSWoOrr65GVlYW6ujqEhIRAJBLp/bLp8+LTaDT4/fffsXTpUty7dw/t2rXDunXrkJiYSHnsyeVyHD9+HI6OjhgzZozF5/mvf/0LCxYswM8//0wRHVl45XI5NmzYgLVr14LNZmP9+vWYPn06ysvLqX2l2NhYzJ07F0DDQO7WrVsxadIkcDgcRluLDrVajaKiIhQWFsLf3x8hISF6f8f0CspUODo66vWEIwtHeXk5srOzoVQq4erqqrOvRd5/YWEhCgsL0aVLF4SGhjLOT9++FlEP2mpfy8/PDzNnzsSXX36JhIQEzJ49G4MGDaJ+rtFoUFBQoDN0nJGRgT/++AN//PEH9Vwej0dV2URFGBwcDAcHBwgEAuzcuZMy8KUTijlBiePGjYNarUZSUhKKi4tx9OhRHD16FPv27cOlS5csIqmWQFDmvD5d/r5u3Trcvn0bBw4cwNy5c/HgwQNkZmaaRFAqlQpJSUk4f/48fH19ERsbixEjRjD2dnv16oW7d+/C1dUVP/zwA+bNm0cZ9zYlWh1BKRQKuLq6on///ka/zPaqoNhsttnu4gTkrpt4zpFZJolEordtKBaLAQBHjhyBs7MzoqKi8PXXX+PatWvw9PTEsmXL8H//9386QhCRSITLly/jtddes8qdm5jFLlmyBMnJyXjttdegVquRlpaGadOm4f79+3juueewZcsWBAUFQSqV4p133kFRURFcXFwoH7Y1a9Zg1qxZUKlUuHDhAgYNGqSjgKIPUrdv3x6xsbGNbjiT9ywUCi1+f8BfM1XabRqJRAKRSISamhoUFBRAJpPBwcEB9fX18PT0REREBHg8nt32tYyR1ty5c7F3715s2bIFM2bMYEihWSwW/P394e/vj1dffZV6XC6XIzMzU4e4rl27hmvXrlHPc3d3R3h4ONLT06nre+TIEQahmNtiKy0t1XksNzcXO3fuxCeffGLycQiaO/LdWoKsqamBl5cXunfvziAXY7h9+zaCg4OpbsuYMWNw/PhxxjHoRNe/f3/s27fP4vO0Bq2OoNzc3BhhdY3BXs7jlhAfPcLD0F23NukJBAIMHToUAJCRkYGlS5cCaLgGn332GebMmWNwyO/EiROQyWQ2yRGaNGkSVq5cifnz52P//v0Qi8W4cuUKHB0dsW7dOsyYMYOyVkpMTKSi48lMCV1Gfv/+fVRWVuq094RCITIzMyk/QVMcPoy1+KwBfW7G29sbEomE8jf09fWFTCZDbm4uJBIJHB0dGZWWKcOexva19M1rkX9HSMvd3R0LFy7ErFmzsHXrVsycOdPo++JwOIiIiEBERATj8draWh1T3fv37+sMHdMJxVyCMBSTYk36bnMr4KxN07VkSLeoqAh+fn7U3319fXHr1i2Dzyd7yM2BVkdQ5sBeH15zCIq0q/Lz8w1GeAD6yXTbtm0Mx26CpKQkiqwMYf/+/fDy8mJ4zVkC4sbA4XCQm5tLnQ+Hw8HOnTvx3HPPUa2OFStW6MRgXL9+HT179qT+TtwUyHkRkUt9fT1CQ0PNGgkgFY+1FVRjUCqVyM3NRXV1NYKDg/W2ohQKBbWvlZ+fD7FYDBaLpTNkbEx+bMq8lva+1ptvvomNGzdi7dq1eOeddyyulvl8Pvr374/+/ftTj7333ns4evSoznMJoZibh2QoJkV7b/PvguYKK9Q3P2XoXPbt24e7d+8iOTnZ7NexBZ4RVDPAFIKiG9K2b98e/fr1a3TjXR9BGbqzNBTnTpCWloY7d+7gnXfesdiKhX4nv2PHDqrVSCCXy3H37l2Eh4cjPz8fJ0+exL///W/GczIyMnSiMs6dO4eAgAB07doV2dnZqKio0FFfmgpnZ2c4OjrapYLSaDQoLi7G06dPKZfyxvY6tYc9VSoVQ8UlEokoPzhCWsQPrjE0Nq8lEAiQnZ2NhQsX4oMPPsDq1aup34Gl81p0REZG6iUoQijaThLGYCgmZdKkSRadX3NWT+RmwRpYmgXl6+vLCCItLCxE586ddZ73+++/Y9WqVUhOTm42OXurIyhLPpS2HmI01joUCATIzMyEh4cH+vTpY9KHQ590PTIyknL8piMqKqrRY+3duxcAjKrk9IFOTEDD9TbUmsnLy0NISAiuXr2qQ05nz57F06dPUVpaSi3GMpkM9+7dw7vvvou7d+/C19cXffv2tXgBZbFY8PDwsHkFVV1dzZhFs8TSis1mg8/nM2TEGo0GdXV1EIlEEAgEyMvLg1wuh7OzM6NFqG9mhg65XI6MjAxoNBr07NkT/fv3x5EjR7Br1y5Mnz4dISEhOvtahEzMIS1jhGLuHJKXlxcuXbqEnTt34tGjR4iMjKRiUsyFLQjCGthC4m5pBRUbG4vMzEzk5ubCx8cHP//8MzUPR5CSkoJp06bhzJkzzRK2SdDqCAqwzDDWHr552qitrUVGRgY4HI7ZhrT6SC8xMRF79uxhVEyBgYGYOnWqweMolUrs378fMTEx6Nq1q8mvr4+YyCIZGRmpN3QuKiqKcjMgaNeuHbKyshjzW6T99dNPP0Gj0aBbt27g8/lgs9mQSCRGjWEbA4/HsxlBkXkrtVqNiIgIq2xs9IG0/dzd3dGpUycAf83MkGtUUlICqVQKJycnnSFjAMjPz0dZWRlCQkIYsvuVK1fizJkzWLRoEaONZkyMARie1zJGKOZWUOSYlggitGGLuHVr0JxRG46Ojti8eTMSEhKgUqkwadIkREREYMmSJYiJicGIESPw6aefQiwWU0nH/v7+OHHihFXnawlaJUGZg6YgqLq6OmRmZkKpVKJbt24MNZip0I7HABq+zFevXsW2bdvw559/IioqClOnTm30jvP8+fMoLS3F559/btLrau9v0ImJYMqUKdi7d68OUY4aNYpRzSUkJOg4VnC5XCgUChQUFODOnTvgcrmYOnUqVCoVhEIhwxiWviC7u7ubtAB5eHhY3eJTqVTIy8tDZWUlgoODdeat7An6zAz9TpfY6hDz3NraWshkMri7u6Nz585UxU0WyeDgYEybNg2bN2/G77//Tg3CWrKvRYjHwcEBnp6eBgmlOUmiJUjMmzOscNiwYToWYcuXL6f+n25C3JxolQRlTgWlnQllCxDvM7qLhfYdrbkwVJV5eXlh/vz5Jh9n79694HK5ePvtt/HkyRODzyPXj7R/Gmv7eHl5ITk5GTt27KCIcuLEiYyh4k8++QTLli1j/Du5XI7s7GyIxWIEBgbi3r17GDRoENX2ohMtGWIUCoUoKCig9ryMCQ08PDz05jKZAuJ5mJeXR82TtJScJQ6Hg7Zt28LFxQXV1dXg8/kIDAykBBna5rk8Hg+JiYn46aef8Nlnn+HmzZsGF9DG9rXo81rGokrUarVNAy3NwT+FoP7JWVBAKyUoc0BSdW0JhUKB+vp63L9/36CLhbmwhSReIBDg5MmTGDlyZKMffHo7j77oNAYvLy98+umnEAgE2Lp1K4Octm3bhrFjx1J/V6lUePr0KcrKyqhh6jt37qCqqsqgqlBfhg8ZoBUKhQyhAVmQCWnl5eWZeIX+AmnH8ng8i/eZ7AmVSoXc3FxUVVXphFJqXyOyryUSiTBhwgR8++23WLFiBSZOnGi2ea4581pSqRTu7u5QqVRWiTEsQUuwObL29f/pWVBAKyUoc8jAlsO6ZOEtLi6Gg4ODScPCpsJUt/DG8Msvv0AulxucfWpsn8kUCAQCDB48mEEInTt3pma1iHIxNzcXnTp1YgggSMKsOcINfQO0arUaEokEQqEQFRUVUCqVqK6uxoMHDxjqOEPCFOLgIZfLGb5+LQX0a0iqOmPEQnfeXrZsGX777Tfs2rUL48ePN2iey+Px4ObmZvT3r6/aIonOCoUC/v7+je5r0Y9hSzR3BaVSqayuoP7pWVBAKyUoc2ALuyO1Wo3i4mLk5+ejc+fO6N+/P27dumVTZaAtjrVnzx74+PjghRdeoB4jrTxriIng22+/1alWiouLsWPHDkydOhWZmZng8Xjo06ePjnz63LlzCAwMRHBwsNmvSwcZUCXEEhAQgIsXLyIoKAhisRjV1dV4+vQpZDIZpY4jw7NlZWUoLy+3WNZub4jFYqSnp8PFxUXvNTQFTk5OWLNmDUaNGoVdu3Zh1apV1M/0mefSCc6YeS7d4ikoKIixZ2ZoXwtgqggNVWrmorkJytoWX2vIggKeEZRRWFNB0WeZ2rVrh759+1KtIEsTZu2Fhw8f4n//+x/mzZtHnRMxNCULsaXEBACZmZnYsmWL3p/98ccfePnll9G9e3e9yreysjLcv38f06dPtzkp8Hg8akEkCbfAXw7rtbW1KCkpgUAgoJzMa2pqoFKpwOPxjEZwNAXoprOWimzoSEhIwIsvvojvv/8eU6ZModSc1pjnSiQSpKeno02bNujbt6/O597Yvpa2EMPafK2mjNrQB1u0+IDmd8KwN1olQZnb4mssqsIQBAIBsrKy4O7ujt69e+tY7xDiaykERWafJk6cSC3YHA4Hjx49Ap/Pp1pfluy13LhxA6NHjzZ4Hfv06dNonAdRFL388stmv7Yx0A1j6S4ULBYLCoUChYWFcHFxwaBBg8DhcBhVRFlZGaRSKdhsNnV9SOurKRY/+jCwPvsrS8FisbBmzRr0798fixYtwv79+w0+15h5bmlpKf7880+oVCpqNKCqqophnmsIluxrmTqv1dw3hyqVyqr2XGvIggJaKUGZA3NbfEKhEBkZGXB0dERkZKTBWRgSMNgSPmQkQfe5555DUFAQ9UWPiopi7NeQMDW6m4GHh0ejpHXs2DFMmjQJPB4PR44cwZw5c3Tk5h9++GGj53fu3Dk4Oztj8ODBNnvPBHTDWDJNL5fLqfBKbfskfVUE3aooLy9PR/Zuam6UOSAiDQ8PD7uINCIiIjBp0iRs374d165dw8CBA03+t+S9i8Vi1NbWIjQ0FB07doRUKtUxz+VyuYzrZEpFaor0nZCWUqlk7GWR//+7t/hqa2v/8VlQQCslKHuIJCQSCTIzMyGXyxEaGmr0w2OP0EIWi2XRbMlvv/2GyspKLF++nHqv5A6Uvl8D/OXSLRQKUVlZidzcXMohnlQRHh4e4HA42LRpExYsWICgoCAcOXIEPB4PX331FS5evIiioiL06NHDaJ6PUqnEhQsXEBcXZ9bgsqmgG8aq1WrKvaJr167o0KGDSZ8VQ1ZF2q0vwLjs3Rjo5GlvkcbChQvx66+/Yv78+bhy5YrJnyuxWIy0tDS4u7szyJNungv81UalV6S2Ns8F/qqs6MQlFovB5XKhVCpttq9lDqwVSVgzA/V3QqskKHNgbA5KJpMhOzsbQqEQwcHBjDvrxmCPKA8iNTfni6bRaLB79264urrijTfeMLrPRHfpprsZkGiJqqoq5OTkYNOmTThy5Ah69uyJH374AVVVVaivr8fgwYPNUuLdvXsX1dXVFtkumQLS4nv69ClUKhU6duyI2NhYq++u2Wy2RbJ3Q21UtVqNwsJCFBUVITAw0GTytAYdOnTAp59+isWLF+PAgQMYN25co89XKpXIycmhPOKM7YWxWCw4OzvD2dmZYVJra/Nc+veBuMo7ODjA398fAGy2r2UOrG3vP6ug/sEwt4LS1+JTKBTIy8tDRUUFAgMDER4e3mzydQJCUKa0e8jdZElJCc6ePYt33nnH4g88nbT4fD6WLl2K48eP49VXX8WcOXMgFArB5XIhFArx5MkTqjVI5NyNXTdt93Jbg1yrwsJCvPbaaybFdFgKU2TvOTk5VEVKqgiNRoPc3Fy0bdtWr8DAnkhKSsKOHTvwxRdf4I033tDbstZoNCgvL0dOTg78/PwMBkSaCkvMc+mVuz6QAMbi4mK9Q/HGokpsTVrWtvhqamqeVVDPoEskZJapqKgI/v7+Fs8ykT0oW8KUY2pLeX/55ReoVCpMmDDB6tevrKzE6NGjcevWLYwfPx4TJ05EaGgoJcmm+8bV1tZS+xB0Obf2UOjZs2cRFBSEoKAgq8+PDoVCgezsbAgEAgANw6v2JCdD0Ja9Aw2/I6lUSpkGy+VyODk5UbZFhNyNmcLaAlwuFytXrsT48ePx9ttvo127doiMjMSUKVPg5eUFiUSCtLQ0cLlci6XtpsCYeW5VVRXy8/P1mucqFApKQWioOjZnX4tu6cRmsy2a17JFBfWMoJ6BsiXSaDRULlOnTp0wYMAAqz5g9tiDMnZMYj9D98zbt28fAgICGHHfliAnJwdvvvkmsrOzMWPGDMyePRs+Pj6ML60+3ziyDyEUCikLHqJQkslk+N///oepU6fazFGe3ioLCAhA3759AdgntNBSkIqktLQUISEhaN++vcHrRIZnCWnZQ/YeFxcHZ2dnKhPo8OHD2LNnD/bs2QOFQoFu3bo1y2JpzDyXhFgSD0KVSoWysjLKPNfW+1rmVFvWqgifEdQ/GOZ8gTUaDRQKBW7cuIG2bdsiNjbWJneJlsrXG4MhuyNDDhD37t3DkydPsGjRIqvaFnfu3MGoUaMgEomwfv16TJkyxWRVGX0fgj64KZPJsHPnTgBAWFgYbt68CQ6HwxBiuLi4mO1kkZWVRc2k0ReIlkJQlZWVyMrKQseOHRlOGoauk1wup0irvLwcEokEbDabQVrWyt537typNxn30KFDWLlyZYvxHwT+ugkSi8WoqKhAQEAAfHx8GPtadINh7XktY6TRmPTd0JAxOS9t0rI2TdeSLKi/G1olQQGmGcZWVVVRLuP9+vWzaQvI0dGRijS3FbQJypg1EZl9ovvgmYuDBw9i2rRpcHZ2xrFjxxAfH2/xsejgcrm4ceMGnJ2d8d5778HFxYVSfAmFQkrx5eTkxCAtfRVEXV0dMjIywGaz0aNHD7i4uFA/a4pUXVNA37w3NbIeaDCFbdeunUHZOxEZkMWYXCtzZO+Ggi8LCwtbFDkBDTc26enpAIDevXtTYxzEPJe+90RXWhYXF+uY55LPlCk3W3SXCwJD+1pSqRQqlQoKhcJgVIkxPKugWjFEIhG1WERERODRo0c2nzOxhbmroWOa4plXX1+PgwcPIj4+Hl26dDH7teRyOdasWYP169fD398fx48fR0hIiE3eB/CXvDw+Pp4iFH0zSCRWQigUUhUEyUJydXVFbW0t6urqDLahSKunuSqH0++mAAAgAElEQVQoelRHSEiIReF72rBE9k7+6Nu4j4iIMJjn1VJAt1EKDg42KbrekNKS7GvRxyhcXFwYpGVM3APotgg1Gg1KSkqQn5+PoKAgavtAO6rElH2tZwT1D4e+CkoikSArKwsymQwhISHUB8Aerg/2UPERayLtfSZ9+O9//4uamhqzxRFkQV25ciV+/fVXxMTE4ODBgzZP3bx9+zZqamqMysv13RnL5XLk5uYiJycHzs7OUKvVlM8fEWIQYiKpuk1NUHTlm4+Pj92jOhqTvRPHBxK2SK8g1Go1evfuDT8/P0ZMuLOzM95//327na85EIlESEtLA5/Pt1rlqG2eC/y1ryUUCi02z5VKpZSYRHuwWl9UibEW4TOCakWQyWTIyclBTU0NJUGlf9AImdjS9cGWKj5CtK6urkhPT0d5eTn4fH6j0tu9e/fCw8MDI0eONPk1SktLkZGRgU2bNuG3337Da6+9hh9//NHmybHAX/Jyc+efqqqqkJWVhTZt2mDgwIFURUDaXtohh4SsqqqqmixATywWIyMjw+7KN2Ogy959fHwA/CV7r6qqQnp6OuRyOdzc3LBt2zacPn0a2dnZqKurw+XLl7F7926bpNtaCpVKRX1vw8LCGKRiS9DFPR07dqQep+//GTLPdXNzQ0lJCYqKihAaGqq3QjbX0kkul+PJkyd2+d61NLRqglIqlcjNzUV5eTkCAwMRFham9w7IFo7m2rCVio/ezmvbti0GDBhA3e1VVVUhLy+P4fRAqoWLFy/i/fffN8mdoaamhrq7XrFiBW7cuIFp06Zh/fr1dpvJOXfuHEJCQhi5UY1BKpUiIyMDQEPEvPb70tf2Ikanbm5uqKysxO3bty1O5jUF9EFWU9xGmgMsFgvV1dUoKipitMqI7ZNQKERNTQ1mzpyJ5cuXIzQ0FP37928y2TsBkeB37twZMTExzWKaqm//j26em5eXR5kMe3l5UVW6qZ6W+lSEjx8/xuzZsxEVFWWTdnBLR6slKFIN+Pv7Y8CAAY0uQvZox1l7TEP7TCwWC66urnB1dWVYypBhUIFAgO+++w4ajQYDBgyg5mr0bQYT+ybiTj1u3Dikp6dj5cqVmDNnjt0WhZKSEjx48AD/93//Z/S55CaDBPOZ86UlRqdt27aFSCRC//79qb0a7WReuirOXF89+t6Dv7+/1YOs9kJtba1Bx3HymSIVxC+//IL+/ftj4cKFOHDgAIqLiyGVSu0ue5fJZMjIyIBarTZLTNJUcHR0BJ/PR01NDerr69GnTx/weDzU1dVR+6TE05K+r2VsaF2hUGDDhg04deoUvv/+e8TGxjbxO2setFqC8vDwQP/+/U2a5ran64O5sCQ0kO704O3tjUuXLiEkJAQjR46kNoNzcnKgVCqp54nFYtTX1yMkJAT5+fkYNmwYampqsGvXLrz99tsWvWdTcf78eQCNt/foi76fnx/69u1r8ULI4/FQVFQEQP9eDXExEAqFOgIDuou5PtISCoVIT09vscm7QMPil5WVBYlEgu7du5vk7xcQEIANGzZgypQp2LZtG7799lsA9pO9kznEgoICnSyplgShUIi0tDS0a9eOsa+ob1+L2IMZMs+VSCTo0qULUlNTMXv2bCQkJODq1astwmC6qdBqCcrd3d1k0rFHi8/cxdTaNFuCGzduIDs7G8uWLdMZciQ9/aKiImoR2bNnD1asWAEOh4P9+/fbJfJCG+fPn4eLiwvi4uL0/rympgYZGRng8/k2WfT5fH6jIgl9LgZ06x26RJmQlouLC8rLyyGVSu26P2IN6CQfEBBgsMVtCGPGjMGZM2ewfft2DB06FK+++qpdZO/EfJbH4yE2NtbqJFp7gL4fZgrJa980ArrmuYsXL0ZKSgpqa2sxdOhQBAQEIDc3F2FhYU3xlloEWt5vugXCHkO1poI++GdMmWcK9u7dCwcHB4bxp0ajoXzgOnTogIEDB4LNZmPnzp1YvHgxfHx8sHXrVnTo0AH/+9//oFKp4Obmxpg/stWiQZeXa7dv6uvrqbm0iIgIm20S83g8CIVCs9wq9JGWWq2GSCTC06dPkZ2dDQ6HAzabjfz8fEYF0RIWWEOO4+aAxWLhm2++wc2bNzF9+nTcvn2bISIgMEf2Tv9cubq6oqCgAFVVVQgLC7M6iNFeqKqqQkZGhtX7YfRh7KdPn6KgoACJiYmYOnUqHj9+jJSUFNy4ceMZQbUGmPMhcnJysvlQrSnQtiaydrO+rq4OR44cwUsvvURVTcQOxsXFBb169QKXy4VGo8HSpUuxfv16REdH4/Dhw9RdHsA0OKX31MniYs1CfOvWLdTW1jLae0TaXlFRYZZjvKkgcmqJRGIV6ZEssDZt2iAuLg6Ojo7UXA0ZLs7KyqKulTEHc3vAXMdxY2jTpg22bduGYcOGYcaMGTh8+LBJ3y1jsvf8/HxUVVXB0dERnp6eqKqqgkKhMHlwtimgUCiQmZmJ+vp69OzZkzEAbimkUilWr16N27dvY8+ePejevTsAID4+3mZD8H8ntFqCMgeGHM1tAX3SZlu187Rx7NgxiMViTJgwAfX19cjKyqLyq0gLSi6XY/r06fjll1+QkJCAPXv26LQr6AanJORPeyEmqj/tfRpjpEWXl2s0GpSVlSE3Nxc+Pj4M6x9bgu4mYQlByWQyZGZmQqFQ6FR2+uZqDBG8dqaWLRdiWzuO0zF48GDMmTMHGzZswLZt25CYmGjRcRwcHKjqAQAGDBgAZ2dnvYOz2i7mTb0vQ35vAQEB8Pb2tsm1vH79OubNm4fx48fj0qVLLaLSbm48uwImwB4iCXJcen6TvYiJYN++ffD09ES3bt3w4MEDBAUFMWa+ampq8O677+LKlSv44IMP8M0335j8JTG0EBPSog+CEtIiizF97+Hs2bPUvMi9e/fg7u5u91khemghqSxNAT3gMCgoiHJtNwZ9BE935tYXBEmulSXXoSkcx5csWYKLFy9iwYIFGDx4sNltKPp+mHbelT5DWH3pvNou5vaQvcvlcqSlpQGAza5lXV0dli1bhtTUVPz8888IDQ21+pj/FLRagjK3xWcvgiK5MPYkJqDBbfzKlSsYOXIk+Hw+wsPDGdVIYWEh3njjDTx58gRLly7FJ598YvU50EmLPghaV1eH2tpalJSUUJJhd3d3SKVS/PnnnxgzZgyys7MRFhZm18RYAjpBmQoyh9OhQwebBBwacuYmSi+BQMCw3dHO1NIHuo2SvR3HORwOdu7cieeeew6vvfYaBgwYgB49elCxHI2hrq4OaWlpcHNzM2k/jD5KQfa86AIDEghJl7035tVoCugEaqqVkinHvHLlChYsWICpU6fi22+/bdYY+paIVktQ5sBeLT42m01l/dhCAGEIAoEA69evBwB89NFH8PX1Zfz8wYMHGDVqFCorK7F9+3a8++67Nj8HAkOVllAoxKZNmwAAPXv2hEKhQH5+PrUQmzt7ZA7MMYylDwTbat/BEAwpvUj1UF1dTWUgkZkaQlpisRhZWVno1KmT3W2UCNq3bw8ej4fS0lIcPXoUR48exd69e5GcnKyXpNRqNXJzc1FZWYmwsDCrBpcNpfPSvRqJ24O5svfGbIoshVAoxKJFi/D06VMcO3YMAQEBVh/zn4hWS1DmEIGtjV2JNZGzszMeP36MNm3agM/nm2xCaSqIpQ6bzcalS5cQERGBmJgYxnPOnz+P8ePHw8HBAceOHcOQIUNs8tqmQqPRoLKyEikpKTh48CDYbDbEYjGCgoLA4XAo7zNS3dDbg7YiLVMqKLpQQ18ia1PBUPVA3EMEAgEeP34MtVpNhfVVVlba/LNFh0KhwL1797BixQpUVlYyfpaTk4MdO3bg008/ZTxeXV2N9PR0eHt725VA9Xk1mip7d3BwoFJ4DdkUmQuNRoPff/8dixcvxqxZs7B169YW5wjfktBqCQowLXKDPM9WoO8zBQUFwdfXl7rDKywspHrpZBHm8/lm97llMhmys7MhkUgQEhKClJQUFBQUYO3atYz3smfPHsycORPe3t44evQoIiIibPY+TQFxjZfJZJg7dy7y8vIAAKtWrcKBAweQnJzMqPYMDczSWzg8Hs/sL3xjFRRdgt+pUye7CTWsAYvFApfLhVQqRU1NDSIjI+Hl5UUFHNINTrlcLkOIYck+jUqlwsOHD5GcnIzk5GRcu3atUZXrn3/+Sf2/QqFARkYG5HK53StQQzAmey8qKkJtbS2kUimcnZ3RuXNnsFgsq2Paq6ursWDBAlRXV+P06dM6nYxn0EWrJqimhCEBhHZbgn43XFNTg6dPn0IulzM2yw0pvEgcfVlZGbp27Yrw8HCwWCzs3bsXjo6OeOedd6jXWL16NVavXo3IyEgcPXqU2qxvCsjlcsq5IDQ0FFu2bKHIiUDfnXdjA7P6SIteaTVGKqSC0iaouro6pKeng8PhUBL8lojq6mpkZGSgffv2DALVF3BIT5stLi6mXLnpe1raQZAajQbp6ekUIV25cgXV1dUAGmTmL730EuLj45GVlYXvv/9e5/yioqIos+G8vDx07doVHTt2bFF2T0T27uHhgby8PIjFYvTu3RtsNltnRICutjRFuKLRaHDq1CmsWLEC8+bNw7hx41rcTU5LxTOCMgOWxI6bq8zT55xM99IjtkT0L4qHhwckEgkKCgrQuXNnxiJVW1uL48ePY+jQoejQoQMUCgVmzpyJffv24YUXXsD+/fubbABSrVajoKAAJSUlDAI1FIhHv/M2BEOkRe6GiZ8eESHoIy3yb0mLj/j7VVdXIzQ0tMXGGsjlcmRkZEChUCAqKsok4199+zT0KHkiLiCtwpSUFNy8eRPl5eUAGgZpBw4ciCFDhiA+Ph49evSgrmNVVRXOnDmDnJwc6tiBgYEYO3YsUlJS4Ozs3GLtnoCG70paWho6dOiAmJgYhk0RgSG1JRGuaMveKyoq8Omnn0KtVuP8+fOMecJnMI5WTVCmtviAvyThppb4tpSM0zfL6Qqvuro6lJSUUAs5h8OhJvPJl+XIkSOQSqWYMGEChEIhxo0bh4sXL2LChAnYtGlTky0WFRUVyM7O1qt6i4yMtGkgniE/PVI5PH36lNp3oLcEibIwLy8Pfn5+CA4OblF3+QT0cL6goCC0b9/eqvPkcrlQKpW4c+cOVSWRipbD4SAyMhLDhg1DbGwsYmJi0LZtW72KOC8vLyQnJ2PHjh34888/ERERgYSEBBQWFtpdRWgNVCoVsrOzIRQKERkZ2egsnCG1JV32/vTpU8yYMQMcDgfFxcUYN24ckpKS9LpsPEPjYJm6QP9/mPXklg6FQkERiDHcv38f4eHhRnvmtrYmMgTiNA4AwcHBcHNzoybxyb6DSCTCzJkzUVpaioMHD2LWrFlITU3FwoULsWDBgiZZfIlQg8PhIDg4WK/7dFVVFeLj43XuvA2pv2wFQlpk3yYhIQGzZs1Cu3btqHaPJcam9gQxn/X09ERgYKDFIpGqqipcvXqVIqQnT54AaCD3Pn36UM4F/fv3pz7zCoWC8dkiijh65UCCIGtqapCeno4OHTqgS5cuLeoa0kFsinx8fODr62uT70RpaSk++ugjuLi44PXXX0d2djbu37+P2NhYLFy40AZn3YBJkybh5MmT6NChg94uhEajwezZs3H69Gm4urpi165d6N27t81e30qYdKFbNUEplUqT1XkPHz5E165dGzX91LYmspdiiljVhISEoE2bNgafm5GRgV69eiE+Ph7p6emoqKjA3LlzMWzYMPB4PEo52FgSqDXnmZ2dDZFIZFL2UVVVFXXnHRUVhcmTJzdJ3g05z8GDB+OVV17Brl27qEpLJBJRlRZ9j6Y5SIvuON6tWzez58PEYjGuX7+O5ORkXL58GQ8ePKC6B1FRUYiPj8fzzz+P5557zqyWLz0IklwvuVwOBwcH+Pr6ol27di2O5IG/bIpkMhnCwsJsItZQq9U4cOAANm7ciJUrV2LEiBF2vQm8cuUK3N3dMXHiRL0Edfr0aWzatAmnT5/GrVu3MHv2bNy6dctu52MmTLowrbrFZw4aczS3twME8Nf+TXFxMQICAhAaGmrwNQQCAXbs2IEDBw4AAJKTk+Hu7k758JFQNXq6LLkTpkeiW/Ie1Go1ioqKUFhYiICAAHTr1s2k43h5eelIke0JenxDQEAAPD09IZVKqYwoOvHTr1deXh51vehCDHuQPDlPSxzHZTIZbt26RVVId+7coYbNQ0NDMWXKFMTHxyMuLs4qb0OiiGvTpg3KysqoEQFXV1cdGbe9giDNhT1sioqKijB79mx4e3vjypUrjd442gqDBw/WERfRcfz4cUycOBEsFgv9+/dHTU0NSkpKzHJLaW60aoIy54Opz+6oKYhJ22lcO0hOGwKBAEOGDGG0y9hsNg4dOkTFV+hbhOntG5LjQ1d3mSJJFggEyMrKQtu2bY2eZ3OCBPN5enpS8Q0kaVgfDJEWuV50krclaZnjOK5UKpGSkoLLly8jOTkZN27cQH19PQDA19cXY8aMQXx8PIYMGWJzxSYZZOVwOIzz1E4vJu1n+h6gtlejPUlLJpMhPT0dLBbLZjZFarUau3fvxtatW7Fu3TokJCS0mH3LoqIi+Pn5UX/39fVFUVHRM4L6J4Jud9QUxAQ0LKSZmZlwdXU1Wea8Y8cOBjkBDXstN2/eNJivBDS8P+2BRhI+V1tbS0mSyRwNmdHicrmQSCTIyMiAg4MDevTo0SyzLaZAJpMhKysLMplMx9SVRG6YCkdHR51ZGnq7Kycnh7FHY05lSlSENTU1Bh3H1Wo1UlNTqZbd1atXKYJt3749hg8fTintunbtapfPJ92LsFu3bo1WDcSVXJ9wRTtyw9bD2PawKQKAvLw8fPjhhwgNDcXVq1dbXOaXvu2blkKepuIZQZkIYndE9pjsuc8klUqRlZUFhUJhth+dNZJtbWiHzxG/M1I5FBQUQCQSQaPRoEOHDujYsWOLrJrUajUKCwtRVFRkUPXG4/EoKbWl0DcASictMjxtiLS0HcfpKkKNRoPs7GyqQrpy5Qrl2sDn8ylRQ3x8PLp37273hYhIstu1a2fx8LKx9GLiIKLRaHSGsU39nEmlUjx58gQuLi42CztUqVTYvn07du/ejQ0bNmDIkCEtcuH39fVFQUEB9ffCwsImnXe0BVo1QZnb4iOWMfbqnyuVSuTl5UEgEFDu2ObC1pJtOshgMZfLhVwup/KZvLy8IBKJUFVVhby8PCgUCp1sqOaafamqqkJmZia1kBpa2Bpr8VkDQ6Sl3U51cHCAQqEAl8tFeHg4+Hw+ioqKKEJKTk6mYuldXFzw3HPPUS276OjoJrsxUCqVyMrKQl1dnVFJtiUwFARJSEtferG+KBeNRkPt2Rqr7sxBZmYmZs2ahd69e+PatWs2f/+2xIgRI7B582aMGTMGt27dAp/P/1u194BWruJTq9VGTWBJO08ul1N3dHV1dXBycqLaXNZa+6vVahQXF6OgoAB+fn7o3LmzxQRob8l2dXU1MjMz0aZNG3Tt2lXvHSl9sJj8oQca8vl8s+6CLUF9fT3llN6tWzejbccZM2bgwIEDqK6ubtK7YeLxV15eDg6Hg9u3b+Pq1au4c+cORUhOTk7o06cPXnjhBQwZMgQxMTFN7mpBr+66dOmCTp06NWvVQI9yIQpCtVoNNzc3cLlcCAQCeHl5ITg42CafM6VSie+++w6HDh3Cxo0bMXDgQBu8C+vw7rvv4vLly6isrETHjh2xbNkyaj2bPn06NBoNZs6ciTNnzsDV1RU//vijjhdnM+KZzNwYNBoN5HK5wZ81ts9E358RCoWor6+nPPQIaZmyCVtZWYns7Gy0bdsWAQEBNmlB2EOyLZVKqTyn0NBQk1wL6DC0oNBFBbbYJFer1cjPz0dZWZlZ6bvz58/H5s2bUVlZ2WR7aLm5uTh69CgyMjJw//59pKamAmhwfO/VqxcGDRqEmJgYdOvWDUqlUke4os+WyB6QSqVIT0+Ho6MjQkND7ZrNZQ2USiUyMzMhEAjg4eEBmUym47hiSTX/+PFjzJ49G3FxcVi6dKneWb5nMBvPCMoY9BGUpQIIuoceIS7tVpeHhwdFQCKRCJmZmeBwOAgKCmqxwgJ62zE4ONimLt6kdUNIXttHj8/nmzVDQ9wqvL294e/vbxbZrVq1CqtXr0ZOTo7dJv4lEglu3LiBCxcu4Pz580hLS6M+Z927d6dadoMGDTLoukBujMgfknlkjtrSVNCtqWzl5m0v0G2K6IPBdGsics2USqVJQZAKhQIbNmzA6dOn8f3337ek6uOfgGcEZQpkMhkA+yjzyJdDu9VFXiMgIACdOnVqcUOMAFP55OvrCx8fnyY5T7olESEt+qCsPvm2RCKh7vBDQkIsusPduHEjFixYgAcPHiA4ONgm70Uul+Pu3bvUHtKtW7eoG6IuXbpQLbu4uDirSJEuXBGJRJBKpeByuYzq1FzSEgqFSEtLg5eXF7p27doixS8A06YoPDzcpD0heguafNZIenFBQQGkUinatm2L5cuX49VXX8XChQtbbNX4N8YzgjIFZFbE3g4QKpWKaj116tSJckkWiURGF+CmRk1NDTIzM+Hh4YHAwMBmN/ekzxwJhUJIJBI4OjrC3d0d9fX1kEql6Natm1V3+Lt27UJSUhKuXr2KXr16WXQMEkNx+fJlXL58GdevX4dEIgEAdOzYET169MDgwYPx5ptvomvXrhafqymgkxZpQdNHBHg8nl7SUiqVlANIUyUaWwpb2hQRP73Lly9j69atePToEXg8HsLCwtCnTx989NFHNpeRnzlzBrNnz4ZKpcKUKVPw2WefMX7+9OlTvPfee6ipqYFKpcLatWsxbNgwm55DM+KZk4QxlJaW4uTJk+jduzeCg4Ntsv+jDXol4uPjg379+ulUIvQFOCcnhxJhkL0sW7ZtGkN9fT0lb+/evXuLUShpzxwRF4jc3Fy4u7vDxcWFisWg7wGaE9BnKHKjMWg0GqSlpVFKuz/++AM1NTUAgLZt2yIhIQEDBw5Ely5d4O3tjbCwMLP37iwFl8tF+/btGTM/9KgN7XwoEm6Yn58Pf3//Rp1Kmhv0TKno6Gib7AmxWCw8fvwYa9aswVtvvYVTp07B0dEReXl5uH//vs1FKSqVCklJSTh//jx8fX0RGxuLESNGoHv37tRzVq5cidGjR2PGjBl4/Pgxhg0b1qhzxD8RrZqgWCwWysvLsWrVKkqK3KdPH/Tp0wexsbFW26AQxRufz2/UCUDf0Ke+IVlLRBimgFR35eXl1JxQS4VYLEZ6ejpcXFzQr18/xjXQF9BHD3+kxyBow5RUXaBB2ECGY5OTk6nZKXd3dwwaNIgajo2IiEBJSQkKCgps4jhuC+jLHpPJZBAIBMjMzIRSqYSTkxMqKiogk8kYoYYtBfawKZJKpVi1ahXu3r2LvXv3Mkiia9eudql2b9++jeDgYAQGBgIAxowZg+PHjzNem8ViUTdMtbW1f7sZJlug1bf4CEig2u3bt3Hr1i3cuXMH/6+9M4+K6rz///sOAyKrgIIoKphhBtRABgaXGhtMczQhSptUjVZFv+5pj6AnkWqNShKTat3OCTQmLg1RG1yTo00V14TTRMuMW5WyDYILCLLpDNswMHN/f/i7t3dggDtwZwGe1zmeo+bKPDOE+7nP835/3p+KigqMHj2aLVpRUVHw8vLq8oeioaEBarUaFEUhNDRUkKdmrgmDMRVwTRhM0bJEK6BpGk+ePEFJSQmGDRuGESNGOKQeBvwvJFer1XaYrtAW5gbMfF5arbbD4Y/nz5/H22+/DYVCgTfffBPLli2Dr68vysvLWQ0pKysLDx48APD8Zj9x4kS2IMnlcvYBhJs43pEV3xHg9goxjse2zdharbbdlOfOCr21aG5uRn5+PkQiEWQymSAPZzRN49q1a0hOTsaCBQuQmJhos+/VyZMnkZmZiQMHDgAADh8+jOzsbKSlpbHXlJeXY9q0aXj69CkaGhpw6dIlREdH22R9NoBoUD3FaDRCrVZDqVRCqVTixo0baGpqwpgxYxAdHQ2FQoEXX3yR/WGtqalBdXU1r6RxITBnwuBat729vTtsKtZqtSgsLIS7uzteeOEFhxWBaZrG48eP8fDhQ0H6bxitgfuZ1dTUYNWqVSZJEl5eXvD390dRURGA57tchULBpjVMmDCh3c6CSUZvaGjoVuK4Lamrq0N+fj6vsR3chyPmiNBWRctaMUX19fX48MMPkZeXhy+//BKhoaGCfF2+nDhxAufPnzcpUEqlEqmpqew1u3fvBk3TeO+993Dt2jUsXboUOTk5DvsQaSFEg+opzNOaTCbDwoULATw/ertz5w6ys7PZXiMmJLS4uBifffYZYmNjbfIkxh2exmz/jUYjexNhooi4JoyBAweirKwMzc3NkMlkDpcfxkWj0aCwsBBeXl6CTWKlKApubm5wc3Njp5tu3769XcyRVquFi4sLlixZgqlTp+LVV1/t0PrNHWduSYK7PWBcbxqNBmFhYby+/x1NeWaKFjOkT6/Xs5NlmV89efBhYorc3NwEiymiaRpZWVnYsGEDVq5cidTUVLvc8PnEEB08eBCZmZkAgEmTJkGn06G6uhr+/v42Xas9ITuoHvKPf/wDGzduxPjx4xEcHIxbt26107MUCoVdO+9bW1uh0Wjw8OFDPHv2DGKxGAMHDmSPBZnQV0e5qer1ehQVFbHuPGvvRBISEszGQ8XHx2PHjh2s3Z2maXh4eLCfm4eHB2txZ3ai9nY8dkZ1dTXUajWCgoIEG87HpW0vIHOkamnRslZMkVarxQcffIBHjx7hyy+/RHBwsCBftzu0trZCKpXi8uXLGD58OGJiYvDNN99g7Nix7DVvvPEG3nnnHSxevBh5eXn41a9+hbKyMof5Oe0hZAdlCzw8PHDx4kWTPpa2etbBgwdRUVGBkJAQtmDx1W+VBv8AABgrSURBVLN6Ck3TqK2tRXFxMYYOHYrIyEiIRCLo9XpWm+GaMLjOQVsf+3FnSY0ePRr+/v42+WHsKL8wKioKQUFB7J+5QaYPHz5ETU0NDAYD/Pz84OnpCZ1OBycnJ4c7gmHGTADP35O19KOOdlrMkWptbS0ePHjQTgfkNsrW19cjLy8PPj4+iImJEaT/iqZpXLx4EZs3b0ZSUhL27dtn9++RWCxGWloapk+fDoPBgCVLlmDs2LHYvHkzFAoF4uPjsWvXLixfvhx79uwBRVFIT0/vK8WJN2QHZSOMRiOKioqQnZ3dTs+Kiopi9SwhHVPMuPUBAwZAIpF0emPqzITBLVrWath8+vQpCgsL4efnZ/PGUEvyC5n5XPfu3UNQUBACAwNNGouFHP7YU7hDGYXUb3qKOR2wpaUFNE2jtbUVISEhGDp0qCC70draWmzYsAEajQZ79+7F8OHDBXgHBAEgJglHh6tnqVQq3L17F2KxGHK5nC1aoaGhFt+s9Xo9K9ZLpVKLRnhz4ZowNBoNO/qg7TFXT55GdToda3GWyWQ26xNqC5/8QuY4z8XFBaGhoR3uMLkjNjQaDRobG23e18bsRLy9vfHCCy84bBIE8FxrzMvLg6+vLzw8PNgZUcwDEjcRg2/Romka33//PbZu3Yr169dj3rx5dt81EUwgBaq3QdM06urqcOPGDbZoqdVq+Pn5mfRndaRncecehYSEICAgwCqj57k3X24UEXMD5rNj4A67c/TeK6PRiPv376OqqgpSqbRbmoi5DD1uk6xQ/UYGgwHFxcV4+vQpwsLCuv1wYgsMBgOKiopQX1+PsLCwdo3hHaXidxX+WlVVhXXr1oGmaaSlpVktW5HQI0iB6gtw9SylUgmVSoXy8nITPUsul+PChQvQ6XR4+eWXMWrUKJs+MXOTMJgdQ2epDtXV1SgqKkJAQIBJsKcjwjSxdieAtivaGgoY63Z3dUBmrUxPmyPrFcxamZxHvms1F/5qMBhw8+ZNPHnyBC4uLvjuu+/w4YcfYtasWQ79GfRzSIHqq3D1rPPnz+PcuXMIDAzEuHHjEBMTYxU9y1K4JgyNRoPm5ma4uLhAp9PBxcWFt8XZXjDzpGiahkwms8ln2ZELzlxjMRe9Xo+CggJ29pUjJT+0hYkpYqZFC7FWpuF2165dqKioYAdqhoWFITU1VdAEfqDrDD0AOH78OFJSUkBRFCIjI/HNN98IuoY+AClQfZ3Lly9jy5Yt2LFjB6Kjo3H37l3WhMHoWS+99BKrZ0mlUrtoEQaDASUlJaiqqsKQIUNgNBrZsQdtx5HYWyvhjpiwZJ6Utehs+KOnpyf0ej2qq6shkUgcvj/myZMnKC4uFvT42Wg0IiMjA6mpqdi6dStmzpwJiqJgMBiQn58PmUwmaE+iwWCAVCo1ydDLyMgwiShSq9WYM2cOrly5Ah8fH1RWVjr898YOkALV12lpaenQ1txWz7p+/TrrkuOjZwkBdworkzjNXStzXMPstBgTBlcU76kJwxKePXuGgoICDB48GMHBwXYvlh3BOAnVajVEIhFEIpHZz81R1s/EFDk5OQk68LC0tBRJSUkYNmwYdu7cafXkFgC4du0aUlJScP78eQDAn//8ZwDAhg0b2GuSk5MhlUqxbNkyq6+nF0P6oPo6nTmaKIqCl5cXpk6diqlTpwL4X/Ye05/11Vdf4fHjx+36s7y9vXtctLgW9+joaLM3JW4SBmP/ZXqNmMbi+vp6NqnDEhOGJej1eqjVauj1erz44ot2cxLygRkRX1NTg3HjxsHb2xvA/4Y/MkG5TOhtd4c/CgE3pio0NFSw3ajRaER6ejr27duHHTt2YNq0aTbTmsrKyjBixAj2z0FBQcjOzja5prCwEAAwefJkGAwGpKSk4PXXX7fJ+voapED1IyiKwtChQxEfH4/4+HgApnrWhQsX8Omnn6KxsZHNG4yOjkZERARvraC1tRXFxcV49uwZZDIZewPli5OTE7y9vU3+HdeEUVRUZNaE0R0tg9snZMvG4O7CzD8KDAyEQqEwKTbcOCsG7vDHBw8e8Br+KBSNjY3Iz88XNKYIAO7fv4/Vq1dDJpPh559/trmOae7EydxMLbVajR9//BGlpaWYMmUKcnJyOozKInQMKVD9HJFIBKlUCqlUapI3yOhZ6enpuHPnTrv+rLZ6FjfUc+TIkQgNDRXsxmduHAk3cbu0tBTNzc1spA5TtDrbYTKJ497e3oLeQK2BXq9njQWRkZEYOHAgr3/n5OSEQYMGmdwYW1tb2aJVXFzMDn/k7rQGDhzY7e8dTdN4+PAhysvLERYWJthN2WAwYP/+/Th8+DB2796N2NhYuzxM8MnQCwoKwsSJE+Hs7IyQkBDIZDKo1WrExMTYerm9HqJBEbqE0bNu3rzJ9mcVFhbC19cX0dHRGDx4ME6ePMmaNeyRR9c2nUCj0bBmAubG6+npCaPRiHv37rG9N46cOM4t+tbc4bW0tLSbWMzsUC1pLObGFAmZBlJYWIikpCRERUXhk08+sesRLJ8MvczMTGRkZODrr79GdXU15HI5bt++LbibsJdDTBLdpSsbaXNzMxISEnDjxg34+fnh2LFjdg2etAfMNNn33nsPeXl5CAsLQ2lpKYKDgwXXs3qyRsaEodFoUFtbi+bmZnh5eSEwMNAuugxfGhoa2CMyiURi86JvbmR8R+M1jEYjSkpKUFNTg/DwcMGO3VpbW5GWloZTp07hs88+w+TJkwX5uj3l7NmzWLNmDZuht3HjRpMMPWZERmZmJpycnLBx40bMnTvX3st2NEiB6g58bKSff/457ty5gy+++AJHjx7Fd999h2PHjtlx1fYhNTUVgwcPxty5c0FRFLs7Yazu169fR0NDg8n8LEv0LKFgpvC6ubkhJCTEZIghY8JwhOw8wDS1QiaTOYxu0dEgQ7FYjKamJvj5+XWZ92gJubm5SExMxCuvvIItW7Y4dG8XoVuQAtUd+NhIp0+fjpSUFEyaNAmtra0YOnQoqqqqHFpgtxdcPUulUuHOnTtwcnKCXC6HXC6HQqGATCaziiWaG/vTmWGDyc5jihZzxNU2O8/aMIG5AQEBgqdWCE1rayuKioqg1WoxdOhQtsG4tbW1XWOxJfqeXq/Hnj17cO7cOXz++edQKBRWfBcEO0Js5t2Bj42Ue41YLIa3tzdqamrs3tTpiLi4uLBuQOD5k3h9fT3bn7Vt2zYTPYvpzxo2bFiPhHpu4nhMTEynX8vZ2blDE4ZGozExYXCLllDHbi0tLVCr1dDpdA5vcweexxQVFhZixIgR7YYzchuLKysrce/ePRgMBnh4eJjk55l7IPnPf/6DpKQkxMXF4aeffnLYKc8E20EKVBv42Ej5XEMwD0VR8PT0RGxsLGJjYwGY9mcplUp8/fXXePz4MUaNGmWiZw0aNKjLz7mpqQn5+flwdnbusP+KDwMGDMCQIUPYEFuuCaO6uhrFxcWsCYMpWh3deDuCO4nXWuG+QsKNKZLL5WZ3lRRFwd3dHe7u7ggMDATw/NiSScUvLy9nI6Tc3d2RmZmJqKgo/Pjjj7h69SoOHDiAiIgIW781goNCClQb+NpIHz16hKCgIHZabdvRDAT+dNSfxehZFy9exLZt29DQ0IDw8HCzelZTUxM7Mbi7ieNdrbHtqHjujffx48cWNccyfUKurq6CjbO3FtxEkO4UUpFIBE9PT3h6erIN2UajETU1NaiqqsKmTZtQVVWF4cOHY+/evYiPj8cbb7wh+Pvgk6EHACdPnsTs2bOhUqnIEaOdIRpUG/jYSP/617/i7t27rEni22+/xfHjx+246v5BS0uLSd7gnTt3IBKJEBgYiJycHLz//vuYP3++XW/23OZYcyYMT09PVFZW9mh0hy3R6XQoKCgQPKaosbERn376KW7cuIEvvvgC4eHhaGxsxO3bt2EwGDBlyhRBXoeBj/kJAOrq6vDmm29Cr9cjLS2NFCjrQUwS3aUrG6lOp8PChQtx69Yt+Pr64ujRoxg9erQgr93VU97u3btx4MABiMViDBkyBH/7298watQoQV67t1FWVobExETU1NTg5ZdfRkFBAQoKClg9KyoqitWz7Gk4YPqMKisrUVFRAZFIZDL00dvb22pj2LsLN2VDyJgimqZx9epVJCcnIyEhAYmJiTbJDORjfgKANWvW4LXXXsPOnTuxc+dOUqCsBzFJdJe4uDjExcWZ/N1HH33E/t7V1RUnTpwQ/HUNBgP+8Ic/mDzlxcfHmzzlyeVyXL9+HW5ubti7dy+Sk5P7pcUdeO56W758uUnOGXMcxeQNHjp0CGVlZe36s/joWUJSWVmJxsZGTJgwAW5ubiZWd8aE0dVYDVvR2NiIvLw8uLu7C5qyUV9fj5SUFOTn5+P48eMIDQ0V5OvygY/56datW3j06BFmzJiBnTt32mxthI4hBcqBUCqVkEgk7G5s7ty5OH36tEmBYoJfAWDixIk4cuSIzdfpKIwbNw7jxo0z+TuKohAQEICZM2di5syZAEz1rEuXLmHbtm2or69vp2fxjRDiC2P+KCkpwahRoxAWFsYWxQEDBsDf358dw8CYMDQajWAmDEvhTjkWMqaIpmlkZWVhw4YNWLlyJdLS0my+o+3K2GQ0GrF27Vqkp6fbcFWEriAFyoHg85TH5eDBg1YRk/saIpEIoaGhCA0NxYIFCwCY6lmHDh1i9Sxu3mBP+rMYNyFjs+9Ku+GaMMy539qaMJiiJVQSRl1dHfLy8uDr64vx48cLVkA0Gg02bdqE0tJSnDlzxm7H0V2Zn+rq6pCTk8M6SysqKhAfH48zZ85YfMy3adMmDB48GElJSQCAjRs3IiAgAImJiT1/I/0MUqAcCEvs60eOHMH169eRlZVl7WX1SZydnREVFYWoqCi8++67Jv1ZSqUS27dvR0FBAXx8fNr1Z3V28+buQqRSaY/cnebcb1wTxv3799HQ0MCaMJiiZUnYq9FoRHFxMWprawWNKaJpGhcuXMCWLVuwZs0aLF682K46YExMDNRqNUpKSjB8+HAcPXrUZMqtt7c3qqur2T/HxsZ2W4NaunQp3n77bSQlJcFoNOLo0aNQKpWCvI/+BilQDgQfizsAXLp0CZ988gmysrIcTlzvrXTUn9WZnsUYMXx8fEBRFP773/+ioaEBfn5+gu5CuJhLKOeGvVZUVKCpqQkDBgxgtayOTBjPnj1Dfn4+AgMDu2xmtoTa2lqsX78eWq0W586dY4urPRGLxUhLS8P06dNZ89PYsWNNzE9CERwcDD8/P9y6dQtPnjyBXC4nQbHdhLj4HAg+Fvdbt25h1qxZyMzMtKnITHgOs+Pg5g1qNBo4OzujpaUFO3bswPjx4wXXsyyFiR7i5uYxJgx3d3dUV1ejqakJ4eHhgiVX0DSN77//Hlu3bsX69esxb948h45rsibHjh3D1atXUVFRgUWLFrUzXRGIzbxX0pXF/bXXXsPdu3dZnWLkyJE4c+aMYK9Pmhkt4+zZs9iwYQPeeust+Pv7Q6VS4e7du6AoCi+99BJrwpBKpXadOcWYMEpLS/H48WOIxWKIxWJeEUR8qKqqwvvvvw+KopCamoqAgACB30HvgpnOzMRY2cJK38sgBYpgGaSZ0XL+9a9/ISwsjI1EAtBOz1KpVO30LIVCgeHDh9tsh8EMPTQYDJDJZHB1dWVNGIzdva6uDhRFmfRoeXh4dHr0ZzQacerUKezcuRNbtmzBb3/7W4eOa7Ilq1atwqBBg7Bt2zZ7L8URIX1QBMvgY3MHnruUkpOTSa8IYDbxoDM9S6VSITs7G4cPH0ZpaSlGjRoFhULRTs8SCq7Vve3QQ64Jg4GPCcPV1RUikQgVFRVYu3YtvLy88MMPP5CwZA5GoxH//ve/rdIv2Z8gBYrAQpoZrQfTnzVjxgzMmDEDgKmedfnyZWzfvp2d9MvssiIjI3lNszWHTqdjg3P55v11ZcK4f/8+VqxYAQ8PD1RUVGD58uX4/e9/b9Xi1NvSVXJzczFjxgy89dZbRCfuIaRAEVhIM6NtEYlEkEgkkEgkmD9/PoDnxSAnJwfZ2dn4+9//jnXr1kEkElmkZ3FjiqRSaY8dZM7OzvDz84Ofnx+cnZ0hkUjg7++PdevWITc3F4sWLUJERIRVHlh6Y7rKmDFjUFxcbLfX70uQAkVgsWUzI8E8zs7O7DDHVatWddifNWjQILZgcfWsvLw8aLVaDBo0SNCYIqPRiPT0dOzfvx9/+ctfMG3aNJtoTSRdpX9DChSBxZbNjAR+dKRnVVVVsf1Zhw8fxqNHj+Di4gKtVos//elPmD59umDOsZKSEqxevRrh4eH46aefBGvm5QNJV+nfkAJFYLFlM2NH8LG5Hz9+HCkpKaAoCpGRkSZFtD9AURT8/f1ZPSsvLw/Lli1DVFQUoqOjcfv2bXz11Veoq6vrkZ5lMBiwb98+HDlyBHv27MErr7xic4ceSVfp3xCbOcFh4GNzV6vVmDNnDq5cuQIfHx9UVlaygav9lYKCArbvhgtXz1KpVLh9+zZEIhEiIyPZoiWTycweAxYWFiIpKQkKhQIff/yx3cbQ8x2TcenSJaxevRpZWVn9/v+HXgLpgyL0LvjcjJKTkyGVSrFs2TK7rLE3w9WzVCoVlEplOz0rMjISZ86cwalTp5Camopf/OIXdl0zSVfps5A+KELvgo/eUFhYCACYPHkyDAYDUlJSTOZBETqGj561fft2hIeH4+eff4arq6t9Fwx+x87r1q1DfX09Zs+eDUD4dBWC/SA7KILDcOLECZw/fx4HDhwAABw+fBhKpRKpqansNTNmzICzszOOHz+O0tJSTJkyBTk5OYLNLiIQCDaB1w6qfyY5EhwSPmnuQUFB+PWvfw1nZ2eEhIRAJpNBrVbbeqkEAsEGkAJFcBi4Nne9Xo+jR4+2cw7+5je/wQ8//AAAqK6uRmFhIdsjQyAQ+hakQBEcBq7eEB4ejjlz5rB6A6MpTJ8+HX5+fhgzZgymTp2KHTt2CD5rJzMzEzKZDBKJxGzQ58OHDzF16lTI5XJERETg7Nmzgr4+gUB4DtGgCBajUqmwdOlSKJVKGAwGjB8/HseOHcO4cePsvbQew8fqvmLFCsjlcrz77rvIzc1FXFwc7t+/b79FEwi9D6JBEawDk4f2wQcfIDk5GQsWLOgTxQkwjdZxcXFho3W4UBQFrVYLANBoNGanHvd3utqFNjc345133oFEIsGECRNIgSeYhRQoQrfYvHkzLl68iOvXryM5OdneyxEMc1b3srIyk2tSUlJw5MgRBAUFIS4uzsRlSPhfwOu5c+eQm5uLjIwM5Obmmlxz8OBB+Pj4oKioCGvXrsUf//hHO62W4MiQAkXoFrW1taivr0ddXR10Op29lyMYfKJ1MjIysHjxYpSWluLs2bNYuHAhjEajrZbo8PDZhZ4+fRqLFi0CAMyaNQuXL182+9kT+jekQBG6xYoVK/Dxxx9j/vz5ferpl4/V/eDBg5gzZw4AYNKkSdDpdCYhuv0dPrtQ7jVisRje3t6oqamx6ToJjg8pUASLOXToEMRiMX73u99h/fr1UKlUuHLlir2XJQh8rO4jR47E5cuXAQB5eXnQ6XQmI9/7O3x2oZaEwBL6L6RAESwmISEB3377LYDnE1izs7Px6quv2nlVwsDH6r5r1y7s378fkZGRmDdvHtLT0wW9uS5ZsgT+/v4dGk9omkZiYiIkEgkiIiJw8+ZNwV5bCPg2XDPXtLa2QqPRwNfX16brJPQCaJq25BeBQLAyWVlZ9I0bN+ixY8ea/e///Oc/6ddff502Go30tWvX6PHjx9t4hZ3T0tJCh4SE0MXFxXRzczMdERFB5+TkmFyTlpZGr1y5kqZpms7IyKBnz55tj6US7AevmkN2UASCg/HLX/6y093E6dOnkZCQAIqiMHHiRDx79gzl5eU2XGHn8NmFLl26FDU1NZBIJNi9e7dZKzqBQNLMCYReRkcmhMDAQDuuypS4uDjExcWZ/N1HH33E/t7V1RUnTpyw9bIIvQyygyIQehk0MRgQ+gmWRh0RCAQbQFFUMIDvaZpu55SgKOpLAD/SNJ3x//9cACCWpmnHOecjEASA7KAIhN7HGQAJ1HMmAtCQ4kToixANikBwMCiKygAQC2AwRVGlALYAcAYAmqa/AHAWQByAIgCNAP7PPislEKwLOeIjEAgEgkNCjvgIBAKB4JCQAkUgEAgEh4QUKAKBQCA4JKRAEQgEAsEhIQWKQCAQCA4JKVAEAoFAcEhIgSIQCASCQ/L/AMKIi5bR5/aBAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7eff1d93c110>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"autofig.reset()\n",
"autofig.plot(x, y, z, i=t, \n",
" xlabel='x', ylabel='y', zlabel='z',\n",
" projection='3d')\n",
"mplfig = autofig.draw()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"If the projection is set to 3d, you can also set the elevation ('elev') and azimuth ('azim') of the viewing angle. These are provided in *degrees* and can be either a float (fixed) or a list (changes as a function of the current value of i)."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAagAAAEYCAYAAAAJeGK1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzs3Xlcjen/+PHXadEiNams2VosFZWlUtnDGCGTxIx9yDbGMGMZs8ky+ExjGfs0tmGQsiXbRHZFNNkpYSoxVBIttP3+6Hfur6MTJ6JjXM/Ho4fc5z73fZ3ivM91Xe/rfcmKiooQBEEQBHWjUdENEARBEARlRIASBEEQ1JIIUIIgCIJaEgFKEARBUEsiQAmCIAhqSQQoQRAEQS2JACUIgiCoJRGgBEEQBLUkApQgCIKglrTKeL4oOyEIgiC8LpkqJ4kelCAIgqCWRIASBEEQ1JIIUIIgCIJaEgFKEARBUEsiQAmCIAhqSQQoQRAEQS2JACUIgiCoJRGgBEEQBLUkApQgCIKglkSAEgRBENSSCFCCIAiCWhIBShAEQVBLIkAJgiAIakkEKEEQBEEtiQAlCIIgqCURoARBEAS1JAKUIAiCoJZEgBIEQRDUkghQgiAIgloSAUoQBEFQSyJACYIgCGpJBChBEARBLYkAJQiCIKglEaAEQRAEtSQClCAIgqCWRIASBEEQ1JIIUIIgCIJaEgFKEARBUEsiQAmCIAhqSQQoQRAEQS2JACUIgiCoJRGgBEEQBLUkApQgCIKglkSAEgRBENSSCFCCIAiCWhIBShAEQVBLIkAJgiAIakkEKEEQBEEtiQAlCIIgqCURoARBEAS1JAKUIAiCoJZEgBIEQRDUkghQgiAIgloSAUoQBEFQSyJACYIgCGpJBChBEARBLYkAJQiCIKglEaDUQFFREQUFBRXdDEEQBLUiApQayMvLo0uXLmRnZ1NUVFTRzREEQVALIkCpifT0dG7dukVmZiZ5eXkV3RxBEIQKJwKUGrl79y4A8fHxZGdnU1hYWMEtEgRBqDgiQKkZDQ0N7t69y5MnT7h27RpPnz4Vw36CILyXRIBSU1paWqSkpJCdnU1WVpboTQmC8N4RAUqNyWQyNDQ0SExMJDMzkydPnojelCAI7w0RoNScTCbj7t27aGhokJCQQFZW1juRkp6Wlsbs2bPx9fVl9uzZpKenV3STBEF4x2hVdAME1cgDVa1atYiLi6Nx48bIZDKVnpuWlsaKFSs4f/48zZo1Y/To0VStWhWArKwsACpXrlxubU1LS8PZ2ZmEhAQAtmzZwpo1azh9+rR03xd59OgRWlpa6OnplVubXldmZiY6Ojro6OhUdFMkGRkZVK5cGW1t7YpuiiQ9PR0jIyM0NTUruimS1NRUTExMVP7/IqgPEaDeMZqamty5cwcrKyvy8/Nfen5aWhrt2rXjxo0bQHGwWL16NUePHqVq1aqkpKRQVFREnTp1yq2NixcvloKTXEJCAosXL2by5MkvfX5SUhJ6enrUqFGj3Nr0um7cuIGpqSkmJiYV3RRJfHw89erVo0qVKhXdFMnVq1dp0qQJurq6Fd0UycWLF2nVqhUaGqoPGGloaKjVh5H3lQhQ7yj5/NTLrFq1SgpOcjdu3GDVqlVMmTJF+lRZlv+8L3Pp0iWlxy9evKjSfeSvrTzb9LpEm1Snbm16lZ+TSEpSD+rzr0h4Iy5evKj0+IULF97YPe3s7JQeb9q06Ru7Z3lIS0tj7ty5DBgwgLlz54p5M0GoYCJA/cdVRLAYMWJEiTkICwsLRowY8cbu+brS0tJo06YN06dPJyQkhOnTp+Pu7i6ClCBUIBGg/uP8/PywsLAocbxmzZpv7J5paWlSpqGmpibTp0/n+PHjKiVIVJTAwEClQ6GBgYEV1CJBEESA+o+rWrUqx48fZ/To0QC0bdsWKysrxo4dS3h4+Bu5Z0REBAAffvghBQUF+Pj4qHVwgtKHQjds2FAi4UMQhLdDBKj3QNWqVZk3bx7a2trUrVuXvXv3UqNGDXx9fYmJiSn3+x06dAgDAwOGDBkClP7mr05KGwqNj4/Hzs6Ozz//nIiIiHd68lzMsQnvGhGg3hOVKlXC1taWc+fOUadOHfbu3YuBgQHDhw/nypUr5XafgoICDh8+TNu2bXF0dATebEJGeVE2FCpPMy4qKuL48eMMHDgQOzs7Fi5c+M69uYs5NuFdJALUe8Te3p7Lly+Tm5uLlZUVYWFhAAwbNozr16+Xyz1iYmJ4+PAhHTt2pG7duhgaGpaadq5O5EOh/v7+9OnTB39/f+Li4vj6668B0NXVpUuXLshkMqZOnYqlpSWjRo0iNja2gluuGjHHJryLRIB6jzg6OlJQUCAFjGbNmhEYGEhWVhbdunUjOTn5te8hn3/q2LEjMpkMW1vbd6IHBcVBasqUKWzYsIEpU6ZQvXp1Zs2axa5du9DX1yc8PBwfHx+2b99Ohw4dWLduHS4uLrRv356goCCePn0KqOdQWkUsNxCE1yUC1HvE3t4eQOFTf4sWLVi6dCl3796le/fu3L9//7XuERERQY0aNWjSpAlQnM4uryH4rurcuTNbtmzB3d2duXPnEhAQwK+//srly5eZOHEicXFxDB48GGtra6ZMmULr1q3VbijtXV2bJrzfRIB6jzRt2hSZTMa5c+cUjrdp04a1a9cSFxdHr169yMzMfKXrZ2dnExkZSfv27aUKFU2bNqWoqKhc57kqgqmpKRs3bmTmzJlERUXh5OTE5cuX+emnn0hISGDlypXUqlWLRYsWkZiYqPBcdRhKGzp06Du3Nk0QRIB6jxgYGGBtba103sTb25slS5YQExODt7c3OTk5Zb7+yZMnefr0KR07dpSOyT+5/xeGkjQ0NJg0aRIHDhygcuXKeHt78/XXX6OhocHgwYM5efIkHTp0UPrcin79hw8fpqCggK5duwLQsmVLtV+bJggiQL1n7O3tuXDhgtItOz777DN++uknjh07xqeffkpeXl6Zrn3o0CEAhTdpW1tb4N1INVdV69atOX36NL169WLJkiW0b9+e69evI5PJaNeundLnVPRQ2pIlSzAxMWHz5s04OjqSlZUlgpOg9kSAes84OjqSk5NDXFyc0scnTpzIpEmT2LNnD8OHDy/Tup+IiAgaNmyoUBnd0NCQevXq/acCFICxsTGbN29m0aJFXL58GRcXFzZt2qQ0Xb2ih9JOnTpFdHQ0w4cPR09PD3d3d65cufLa842C8KaJAPWeUZYo8bwZM2bg5+dHUFAQEyZMUGkX37S0NGJjY5UOcTVt2pSLFy/+Z3YDlmfpDRw4kAcPHhAWFkatWrUYOnQoU6ZM4a+//sLf35+qVatiZGTEsWPHKrS3smTJErS0tBg5ciRQPOcIcOLEiQprkyCoQmy38Z5xcHAA4Ny5c/Tv31/pOTKZjIULF5KRkcHKlSv54IMP8Pf3f+F1jxw5QlFRkcL8k5ytrS1hYWHcuXOHWrVqvf6LqEDyBa/yNUUhISFYWFhIQWn9+vWcOnWKDRs28OTJE3766SfS09MrbB+p5ORktm3bRp8+faSfvaurKwDHjx/Hy8urQtolCKoQPaj3jImJCebm5vz9998vPE9DQ4NVq1bRrVs35s2bx8KFC194fkREBBoaGrRt27bEY/L5l3dhwe7LlLbg9c8//yQwMJDVq1eTkpKiEMTeVM1DVaxYsYKCggI+//xz6ZipqSk2NjYcO3aswtolCKoQAUoN/PLLL1SrVu2t1XlzdHTk3LlzLx1y09bWZuPGjbi7uzN16lTWrFlT6rkRERG0aNECY2PjEo/JA1RFZ7KVh9Lm0v744w8OHz5M3759iYqKwsbGhs2bNwMQHBz8Npsoyc7OZvXq1bi4uNCqVSuFx9zd3Tl//jwZGRkV0jZBUIUIUGWwb98+GjVqhJWVFXPnzi3xeGJiIh06dMDR0ZFmzZqxZ88ela77xRdfoK+vT25uLufOnSM/P/+NztfY29uTkZHBP//889Jz9fT02LZtG46OjowdO5Zt27aVOOfmzZvcuHGj1BRrS0tLdHR0/hMBqrQFrwkJCXz44YfUr1+fgIAAvvnmGykxIjIykiNHjrzNZgKwceNG0tPTFXpPcm3atKGoqIjIyMi33i5BUJUIUCoqKChg7Nix7N27l8uXL7Np0yYuX76scM6sWbPo27cvf//9N5s3b2bMmDEqXVtbW5tbt26hr6+PlZUV+fn5REdH8/Tp0zKneqvi2XkoVRgaGhIaGoq1tTWDBw8uMWSlLL38WVpaWtjY2PwnMvmUZenVrFlT6qGkpqaydu1a+vbtS1BQkHRO165d+d///vfWeslFRUUsXbqU2rVr06tXrxKPu7m5AcXzUIKgrkSAUtHp06exsrLCwsKCSpUq0a9fP3bu3Klwjkwmk6owPHz48JUSAipXroyuri7NmzcHirPtcnNzefTo0eu/iP9Pnsl38uRJli1bxvjx419aM87MzIywsDBpm45nP3kfOnQIXV1dWrduXerz7ezsuHr16hsJuG+TsqKyZ8+e5ejRo4SFheHi4iKd+3xFjh9++AF9fX3i4+PfeDsPHjzIlStXGD16NNra2iUer1WrFpaWlmIeSlBrIkCp6Pbt2wrre8zNzbl9+7bCOdOnT2fDhg2Ym5vz0UcfsXjx4le+n5aWFpUqVaJly5ZoaWlx8+ZNsrOz+ffff197+M/c3BxjY2MCAwNZsGABe/fuValmXJ06ddizZw8GBgZ4eXlx/vx5CgsLOXz4MG5ubujq6pb6XDs7O/Ly8kpdf/Uueb6obNWqVZHJZHh4eHDo0CF27dqFk5MTUJxs8rymTZtSpUoV1q5dS1pa2htp45IlS9DT02PYsGGlnuPu7k5MTAyPHz9+I20QhNcl0sxVpCwoyOvNyW3atIkhQ4bw1VdfERkZycCBA7l48aLSNylVyWQytLS0aNasGadOneLx48dkZ2dz+vTp1wpU+vr6PHjwQOHYjRs3cHV1pVmzZnzwwQcKX0ZGRtL38+bNY9y4cXTt2pWJEydy//59GjZsyJkzZ0q9X6VKlQDYuXPnS8soZWdno6mpWS7V1cvL48ePSU9Pl17HixgbG/PLL78QFRXF6tWrpTqEPXr0oKCggD179pCXl8eoUaMYNWoULVq0oF27drRt2xZTU1OV2/To0SOysrLQ0lL8b5yYmMi+ffvo1asXN27cKJF1KGdubk5+fj7r168vkUTxqh4+fMi5c+dK1P2rSI8fP+bs2bMl/r+WRl9fn8aNG7/hVgmqEAFKRebm5iQlJUl/T05OLjGEt2rVKvbt2wcUl8PJzc0lNTWVatWqlUsbNDQ0sLS0JC0tDXt7+9eaz9DX11d6/NatW9y6deuFz61cubJUnfz7778HilPIDxw4gKmpKaamppiYmGBiYoKpqSlGRkbUrFmTCRMm8PjxY5o1a/bC68vn48rr51Ye4uPjMTExKdOCW3t7e/z8/Jg4cSKrVq1i165dGBsbM3bsWE6dOiUF9LNnz3L27FkWLFiAk5MTvXr1okePHtSrV++F1798+TJ169bFwMBA4fi6desA+Pbbb1/4RmtkZMTs2bO5c+fOS38nqjp37hyNGjV6YW/6bTtz5gxNmzZV+YOiqoFMePNEgFJRq1atiI+P5+bNm9SuXZvNmzezceNGhXPq1q3LwYMHGTJkCFeuXCE3NxczM7Nyb4tMJkNHR0dpPT1V2dvbK50LMTIy4uHDh0DxepkOHTrQrl07ioqKSE1NJS0tjfv375OamsrBgwel5x09epSjR48qvZeWlpbUM5g/fz6JiYlSEDMzMyvxfVFRkTTEqS40NTXR1tZ+pTbNmzePdevWYWBgQL169Vi6dCkmJiZUr16df//9FwMDAwYMGAAU9zCnTZvGtGnTcHR0pFevXvTu3ZtGjRqp1KaMjAw2btyIh4fHS4OOlZUV5ubmnDx5stx+1hoaGlSqVEmtfnfyNpVlJONtJbMILyYClIq0tLRYsmQJXbt2paCggGHDhmFra8sPP/xAy5Yt6dmzJ7/88gsjRoxgwYIFyGQy1q5dq7afxsaPH09ISIjCMQsLC44dO0Z8fDxBQUGEhIQQHBzM9u3b8fDwwNfXl3Hjxkmf2J8+fYqhoSEADRs25M8//yQ3N1chiD37/e7du4HihavyIFgaQ0NDqlWrJvXIXvZVuXJltf1ZGxgY4OrqSlxcHCdPniQsLIxZs2Zx/vx5oHgIasWKFfj5+XHp0iXOnz/Pjh072L59O9OnT2f69Ok0btwYLy8vevfuTbNmzUp9rWvXriUrK0tpavnzZDIZbdq0Ydu2beTm5qpVr0cQAGRlnMf4bxRTUzNPnz7F2dmZX375hVatWhEdHf3SP9u2bftaPajCwkLMzMyoXbs2lpaWuLi4MGLECIUhrPz8fA4dOsTmzZvZuXMnjx8/Rk9PD09PT3x9fdHT06N79+40b96cmJgY2rRpQ2hoKHp6ekrvOWXKFBYtWsSdO3eoXLkyaWlppKamlvi6ceMGmZmZPH78WOH4i16vrq6uSoHMzMxMGqoryyfqq1evSs99FT///DPff/890dHRNG3alMLCQkJDQ5k1a5ZC+r2lpSVbt26lcePGFBUVce7cObZv386OHTu4du0aAA0aNMDLy4umTZvSvXt3jIyMgOLfl42NDTo6Opw7d06l17dq1SrGjh3LgQMHcHd3f6XX9qyzZ89ia2urVsFOvn9XWXtQpf07FsqFSp8mRQ/qPaWhoUGzZs1ISUlh0aJF1K1bt8Q5WlpadO7cmc6dO7NkyRL27NnDli1b2Llzp0J1hBEjRpCWlsZ3333Hp59+SlBQkNLUZvki14sXL9KmTRtq1qxJzZo1S5x348YN9PX1qVGjhnSsqKiIjIwMhYB1//59Kcg9+31cXByRkZEv3MVXQ0NDYZ5MHnxK+16+nfur8vDw4Pvvvyc8PFyaD/Hy8qJnz57s2LGDWbNmcfnyZRISEnBwcGDRokX4+fnh4OCAg4MD/v7+REVF4e/vz99//82CBQuA4jVYXl5e9OrVi7S0NBITE1m4cKHKb8bywrHHjh0rlwAlCOVJBKj3mIODA5GRkSqlGevp6eHt7Y23tzcZGRns2LGDUaNGATB69GgpYUS+TceaNWtKvEk+H6DKQiaTYWxsjLGxMdbW1io9JycnR2kQe3748d69e1y5coX09PQXZkYaGBhIQetFc2jyL0NDQ2kozt7eHjMzMw4cOMDEiROla2poaPDxxx/j5eXF1q1bGThwIFA8BDt+/HiSkpIwMzMjLS2NYcOGKWTkGRkZUaNGDZYvX87y5cul42ZmZjx9+lSleSBra2uqV68uFuwKakkEqPeYfMHulStXsLGxUfl5H3zwAR9//DFjx46lc+fOdOrUiS1btpCSkgJAUFAQQUFBXLhwQSGYNGnSBA0NjbdWUUJPT4+6desq7R0qk5+fT3p6utIgFh8fT05ODpmZmaSmpnL+/Hnu37//wp6Vtra2QsC6f/8+ERERfPfdd9SpU6fE8GPv3r3Jyspi/fr1UvCvU6cOgwcPpk6dOiXSxR8+fEi3bt0ICQlh5syZrF27FoBPP/0UIyMjunXrRu/evencuXOpWZsymQx3d3f27dtHXl6e0p6vIFQUEaDeY46OjkBxurK3t3eZnnvs2DEKCgr45JNP6Nu3L+PGjSMhIYFNmzYxa9YsoHhBavPmzfH19aVPnz7Url2bhg0bqm3JIy0tLapVq0a1atVo0qSJwmPK5qCKiop49OiR0nm0Z7/S0tIU6h4GBASU2gZjY2NMTU1xdnbm1KlTwP+ljStz6dIlateuTX5+PhoaGhw7dkxKsti6dSubN29GX1+frl274uXlRbdu3aTEFjl3d3e2bt1KbGxsua2HEoTyIALUe6xJkyZoa2uXqCmoioiICADat28vHbO0tOS7775jypQpNGrUiJSUFGJiYoiJiWHq1Km0bduWq1evAsWT0K+zgFkdyGQyDA0NMTQ0LFGfT5k7d+7QoEEDfHx8mDRp0ksDW7Vq1bh3794Lr7l7926MjIx48uQJUFxBwszMDFdXV9q3b090dDTHjx9n+/btbN++HW1tbTw8PPDy8sLT0xMTExNp7unYsWMiQAlqRQSo91ilSpWwtrZ+5QDVrFkzpYtptbW1uXjxIj169ODEiRN8+umnUlV0OScnJ6ZMmUL37t1LHX76r6lZsyZNmzblwoULKi+MLSws5P79+3z66acl5olkMhldunRRqJq/Y8eOF1bqyMvLY+/evezdu7fEY9OmTcPc3LzEfJo6rWkS3i8iQL3nbGxs2LFjR5nWwaSkpHDlyhW+/PLLUs/R19dn27ZtfPjhh2zatIkNGzYwf/58JkyYwKpVq7h48SIDBw7EwMCAHj160K9fPzp27PifnwPx8PBgwYIFJCUlKdR2LI2GhgbVq1dn4sSJJQJUUVERMTExQPFw6unTp5HJZGRnZ78wOSQlJYX9+/crvd+gQYNKHDM0NFR5PVpWVla5bRWTlpZGYGAgFy9exM7ODj8/vzJV8hDefSJAvedsbGwICQnh0qVLtGjRQqXnvGx7DTkjIyNCQ0Pp1KkTgwcPZtu2bUyePJlVq1bx1Vdf0axZM4KCgggODmbTpk2Ympri7e2Nu7u7tB3Ef408QB04cIChQ4eq/Lxdu3ahoaHBpEmTmDdvnnT87t27QPFmkOvXr+eTTz5BX1+fevXqvbRUEvzfWrcePXqUeExXVxc3NzeqVq0qDTvGxsZy//79F1alr1SpkkKqvrJ1aM9+b2JiUqJ2X1pamsKuxCEhIfzxxx8cP35cBKn3iAhQ7zlbW1ugeFuPsgQobW1tlYKImZkZu3fvpmPHjvj6+hIWFoahoSE3btxg9uzZ+Pr6kpaWxrZt2wgKCmLlypWsXLmS2rVr079/f3x9fbGzs1PbKhFl5ebmhp6eHgcPHlQ5QBUUFLB7927c3Nzo06cP8+bNo1q1aqSmpkoleapXr46fnx/z5s1j2rRp+Pr6ligiq4x8rdvx48dxd3fHx8eHWrVqsX37dhITEzl48CBNmjTBy8sLLy8vaWhSns34/NfFixeRyWQ8ePCA1NRUbt68SXR09Au3i5HJZFStWlUhcCUlJZXIWrxx4waBgYFMmTJFpZ+b8O4TAeo916hRI2QymcqbFxYVFXHo0CGcnZ1LFCktjXybjk6dOvHxxx9TVFSkkMlnYmLCiBEjGDFiBElJSaxcuZK9e/cSEBBAQEAANjY2+Pr60rdvXxo0aPBKr1Nd6Orq0qZNGw4ePEhBQYFKVb9Pnz7NvXv3+Prrr7G2tkZDQ4MePXqgo6PDsmXLAOjduzfW1tbMnz+fzz77jLlz5zJt2jT69u2r0j0cHBwwMDAgPz+fefPmMXfuXGJjY6UqFnPmzGHOnDk0aNCA3r1706tXL1q1aoWlpaXCdUqrJCEvgVXaAusbN25w9OjRl27H8l/YlVlQ3budRiW8tsqVK1O/fn2VA1RcXBy3b9+mY8eOZbqPtbU1u3btklKz4+Pjyc7OLnFenTp1GDZsGLt37yY2NpZvvvmG3NxcfvzxR5o0aUK7du1YtmwZ//77b5nu/6alpaUxd+5cBgwY8NLNHzt37syDBw+k+aOXCQsLA8DT0xNdXV0sLCy4cuWKVMuvatWqrFixgj/++IOwsDAWLlxIVlYWQ4cOpXnz5gQFBXHv3r0Xtk9LS4vWrVtz/PhxioqKkMlkODo6MmPGDM6fP8/ff//NDz/8gKGhIfPnz6ddu3ZYW1szYcIEjhw58tKyW7q6utSuXRt7e3s8PDxo3bo1JiYmPHjwgKioKCIiIqRhw1q1akk9++c1bdpUpZ+Z8N8gApSAjY0N58+fV6m2nzy9vKwBCooXBm/fvl36+4EDB154fuPGjfnxxx+5dOkSx44dY9y4cfzzzz9MnDiRBg0a4Onpyfr160vsXPu2yedLpk+fTkhIyEs3f/Tw8ACKi+aqYteuXdjZ2Ump7DY2Npw8eVJKmpDf59y5c7Rp04aqVaty+fJl5s+fT2ZmJoMHD8bS0vKl7XN3d+f+/ftSzb9nNWnShGnTpnHq1CkuXbrEnDlzMDc3Z/ny5XTt2pX69eszevRooqKiSixeLigoIDY2luXLlzNw4EAsLS1p2LAhQ4YM4bfffqOoqEiqPnL16lUSEhIIDw8vkbpvYWHBiBEjVPqZCf8NIkAJ2NrakpOTo9JutxEREVSpUoWWLVu+0r1cXV2ZOnUqAH379iU1NfWlz5HJZLRq1Yqff/6ZhIQE9uzZw8CBA4mOjmbEiBHUqVOH/v37S9mIb1tgYGCp8yXKNG7cmNq1a780QANcu3aNuLg4PD09FZ5fGh0dHQYNGsSXX37J4MGDuXz5Mh9++GGJpAZl7Xt2PdSLWFpaSj2n69evs2DBApo0acK6dev46quvqFWrFg0aNMDZ2ZmOHTtSo0YNXFxcmDBhAmFhYVhYWDBlyhR27tzJnTt3OHPmDIsXL6Z///7Ur19fmpM6fvw4/v7+9OnTB39/f5Eg8R4Sc1CCVDUhNja2RAWFZ+Xn53P06FHatm2r0gR8aSZMmMDcuXMB6NmzJ/v27StR3aA0mpqadOzYkY4dO7Jo0SL279/Pli1b2L17N9u3b8fQ0BAvLy98fX1p3779W9nZtbTKGKXNl8i3h9+wYQMPHz6UqpErs2vXLqB4N96ioiL+/vtvhbp7z3N3d8fAwIC1a9cSFRXFhg0bSp0rfL59LVu2RFdXl+PHj6vcUzE3N6dnz56YmZlRvXp1goODyc/P586dO9y5c0fh2v7+/rRp00bldVVVq1YVCRHvOdGDEqQ6fC+bh4qJieHhw4evNLz3LCMjI6k+XkxMDN7e3i/dBl4ZXV1devXqxZ9//kliYiK///47zs7O/Pnnn3Tv3h0LCwu++uorTp8+XW5rc5QpLZ37RfMlnTt3pqCggMOHD7/w2vL5p9DQUOzs7HB1dX1hRlzz5s1ZtWoVv//+O0lJSbi7u5faq3y+fTo6Ojg5OUnzUMoUFhZy8eJFAgMDGTJkCI0aNcLS0pIBAwYQHBxM/fr1GTRoEAEBAXz33Xf07NkTXV1dzpw5Q+/evenXrx/r1q0jLS0PHvdpAAAgAElEQVTtha9bEED0oASK67+Zm5sTGxv7wvNeZ/7peU2bNiUrK4uvvvqKadOmvXCbDlUYGhoyYMAABgwYwL///iulrS9dupSlS5fSoEEDfH196dev3wuHyMqqqKhIaU/pZfMlHTp0QCaTceDAAXr16lXi8YSEBJYuXUpUVBRQvCuvfIPMGTNmAMUJLs9uKfLsPQcMGICzszMDBgwgLCzshec+y93dnaNHj3Lz5k0sLCzIzs7mzJkznDx5ksjISE6dOkVGRgZQvN6pRYsW+Pj40Lp1a1xcXLh161aJLL6srCz279/Pjh072Lt3L3v27EFTU5N27dpJW448u7WKIMiJACUAxWnGz2ZwKRMREUHNmjXL5Q3ezs6O3bt3079/f9LT0wkICJAmyl9X9erVGT16NKNHj+bmzZsEBwezefNm5s6dy9y5c2nWrBm+vr74+PioXOm8NMHBwfz111+MGDECc3NzLly4QNOmTUts/vg8ExMTWrZsSXh4uPQzv337trSL8ZkzZ6RzW7VqxYoVK7C1tWXfvn3ScXnlhkaNGvHJJ5+UuKe1tTVHjhxh2rRpLFu2jA8++IDCwkIeP35MeHi40vbJt5Z3d3fHysqKmJgY8vPzpTa7u7vTunVrXF1dad68OTo6OgrPv3XrVolrVq5cmY8//piPP/6Y3NxcDh06xPbt2wkLCyMiIoLx48fj4uIipa+rssBYeD+IACUAxQEqLCyMf/75h/r165d4PDs7m6ioKLy9vctl0eyze0PNnDmThw8fEhgYyAcffMAXX3zx2teXa9CgAZMnT2by5MlcvHiRzZs3s2XLFr799lu+/fZb3Nzc6NevH71798bU1LRM175//z4TJ07EwsKCefPmlbmmoIeHB3PmzGHq1KmcPXuWEydOUFRURO3atfnyyy/ZtGkT2dnZHDx4UJq3Wbx4MZUrV8bR0VHK4hs9erS0PcfzdHV1mT9/Ph06dMDPz0/KeLx58ya1atXi2rVrnDx5UuohJSQkAMWZgenp6fTv3x9XV1dcXV1p2LDha//udXV16datG926dSMvL49jx46xY8cOQkNDpd9T8+bNpYXBDRs2fK37Ce82MQclAMUBCkqfhzpx4gRPnz4tl+E9+L/5D3nlgYULF+Lj48PKlSv59ddfy+Uez7Ozs2PWrFlcu3aNQ4cOMWrUKK5du8a4ceOoX78+Xl5ebNq0SaUNHKE42SM1NZXly5eXKThlZGSwbt06Fi1aBMCiRYu4du0afn5+HDhwgPj4eL777jsyMjL48MMPpeB0+fJlDh48yKBBg3BxcZGuZ25u/tJ79ujRQyE7z8PDAz09PRwcHBgzZgxBQUGYmppK9RUNDAykuaahQ4dKC7rLk7a2Nh07duTXX3/lxo0bRERE8MUXX5CamsoPP/xAs2bNaN68Of7+/pw/f/6NziMK6kn0oATg/zYvjI2NVTonomr9PVVZWVmho6Mjzd9oamqyevVqHj16xMqVKzE1NeX7778vl3s9TyaT0bp1a1q3bs3PP//MoUOH2Lx5M6Ghoezbtw89PT08PT3p168fnTt3Vpp1tmPHDkJCQvDz86Ndu3YvvWdWVha7d+8mODiY/fv38/TpUypXrgwUb6x48+ZNhczI8PBwnjx5olAjb+nSpQCMGTOG06dPS8dLKzqbmppKVFQUkZGRnDhxQunC4Pbt2/Ptt9/SsmVL9PT0gOJFuwEBASQnJ6sU/MqDhoaG1FObN28ef//9Nzt27FCoYmFhYSH1rFq2bPnOb9civJz4DQsA0jYLpSVKRERE0KhRo3J7w9LS0sLGxkYhRVtbW5uNGzfSokULZs+eXS7zUS+jra1Nly5dWL16NYmJifz555907tyZnTt34u3tTb169Rg7dixnzpyR6t6lp6czfvx46tSpw+zZs0u99pMnTwgNDWXgwIHUqVOHQYMGcfDgQby8vAgJCSElJYWePXuiqakpXVtu165daGtr07VrV6B4MfDGjRvp1q0b1tbWCjsgm5ubU1RUxPXr1/njjz8YNWoU9vb2mJub06dPH3755Rfu3r2Lt7c3ixcvxszMDIAaNWpw5MgRDhw4oJCc0qZNG6C411wRZDIZzZs3Z8aMGZw7d46YmBh++OEHDAwMmD9/Pm3btsXa2pqJEydy9OhRlRaYC+8m0YNSA2lpaRVeDFUmk+Hg4KB0iE9exXr06NHlek9bW1uCgoIUthrX19dn2bJlfPbZZ4wdOxYjIyM+/vjjcr1vafT19fH29sbb25sHDx6wY8cOgoKCWL16NatWraJGjRr069eP8PBw/v33X3bt2kWVKlUUrpGXl8fhw4fZsmULoaGhPHz4EB0dHT788EN8fHzo1q2b1HOC4nTz0NBQTp06JQWG/Px89u3bR9u2baU1UqtXryYnJ4exY8cCKNQkHDNmDJGRkdLmhpqamjg4OPD5559LPcVatWpJ5ycmJvLzzz+zc+dOvvvuO+bNm8fRo0dZt24ddevWxcXFRdqd19fX9838sFUkk8mwsbHBxsaGadOmkZCQwM6dO9mxYwfLli1j2bJlmJmZ0aNHD7y8vGjfvr3Yv+o/RPSg1MDOnTuxtLQkKyuLc+fOkZuby+3bt8nPzy9RNuZNcnBwICUlpcQurvK1OuU1vCfXtGlT8vLyiI+PVzhepUoV1q1bh5WVFYMHD1a5JFB5MjY2ZujQoezbt4+EhAS+/vpratSowcKFC7l06RJQXMT1+vXrFBYWcuzYMb744gsaNGhAjx492LhxI87OzgQGBpKYmEhQUBB9+vRRCE4AnTp1AhTLHp04cYL09HR69uwJFAc9+RYbR44cwcPDQyGRRb555Pfff8/evXv5999/OXHiBAEBAXh7eysEJyjeLBKKEyV27tzJTz/9RHR0NM7OzoSGhmJkZIS9vX2J/afUgaWlpdRzun79OvPnz6dx48asXbuWnj17UrduXYYNG0ZoaOgrra0T1IusjBOP7/Us5b59+xg/fjwFBQUMHz5cKtnzrC1btjB9+nRkMhn29vZs3Ljxpdd9+vQpzs7OBAQEYG9vT0xMDHXq1OHmzZsYGBjw8OFDqlSpQnZ2NvXq1eP27ds4ODiUGBZ6Fffu3aOoqIjq1auzY8cORo8ezcaNGxWC0aRJk9i4cSOXL19+YdWDsjp69Ci+vr4sW7aM3r17S8dTUlLQ1dUlJyeHXr16kZ6eTlBQUIVuR/7PP/+gqakptcHU1FRpmabWrVvj5eVF9+7dMTExUenarq6uVKlSRdpE8Pvvv+f3339n2rRpJCUlsX79eoXza9WqhZOTEzt27AAgOTm5TBUz7t27h729PWPGjJHm+WJiYhg1ahRJSUkMGzaMgoIC1q1bx4ULF8qU3Xjt2jUaNGjw1nsxqamp7Nu3j927d3P8+HHy8/PR09OjU6dO2NvbM3jw4BK93dJoampiYGAgzckJb4RKQ0ZiiE9FBQUFjB07lvDwcMzNzWnVqhU9e/ZUmAuIj49nzpw5nDhxAmNj4xI9kZeRyWTo6OigpaWFubk5d+7cwdHRkejoaOzt7Tlz5gyVKlWioKCAlJSUcslqevz4MUVFRRQWFlK9enUATp48qbDW6fDhw9jY2JCdna20Avmrkq/DiY6OVshKe/ToETk5Oejr67NkyRI+++wzPv30UwIDAyss7TgrK4uFCxcCxQkepX06z8/PJysri9TUVJV7v82bN2fr1q18//33/PPPP1Jv6qefflJIBPjhhx9wdnamZs2aFBYWSgHq2rVrGBsbl+n11KpVi6ioKKkcUc2aNdmwYQOzZs1i9erV0nn79u2TenmqyM3N5d69e2+lxNTzOnXqRKdOnXj06BFHjhzh0KFDhIeHExYWxs8//4yzszOdOnWibdu2fPDBB2RkZBASEkJ8fDzW1tb4+PhgZGSErq6uylvJCG+WCFAqOn36NFZWVlKF5X79+rFz506FABUYGMjYsWOlN4tq1aqV2/21tLTQ1NSkRo0aJCUlYWdnVy6Tw0lJSRQVFVG3bl0aN25M5cqVuXPnjvS6bty4QXJyMp9++qnCay0v1apV4+7duwrXvnHjBvr6+tSoUQMbGxv27t1L586dGT9+PAcPHsTKyqrc2/Ei169fZ/LkyZw9e1b6e9OmTRk5ciR9+vShfv36HD9+nKCgILZt28aMGTOYO3cuXbt2xdfXl48++kghDT0zM5NTp04RGRnJyZMnpSHU33//XTpHJpMRGhqKhoYG3bt3Z9KkSUybNk16/Nk6d4WFhWX+3bi5uREWFkbDhg0VsgdDQ0NZtWoVn3/+OQCzZ89m3LhxKl83JycHa2vrEvtBvW3Ozs5MnjyZx48fs2TJEi5dusTevXs5duwYmpqauLq6cuXKFakXHB4ezr59+6SCtOUxOiG8PhGgVHT79m2FdF5zc3NOnTqlcI68GribmxsFBQVMnz6dDz/88K2283VoaGjQrFkzhUw+eXp5ea1/ep6dnd1LN6GTb9Ph6enJRx99RERExBtPf05MTGTr1q1s2bKFv//+Wzo+atQoRo4cWaKobtu2bWnbtq20nfvmzZsJCwuTir1qa2tTp04ddHV1uXr1qvQGWLNmTbp06cJff/2Fra0tPXv2ZM6cOURHR2NnZ8fgwYPR1NRk5MiRCvdLTk6Wvr969aqUYKEqJycngoODuXjxorQGDooD4/Dhw2ndujUtWrQgIyODYcOG8euvv6pdr+LJkyc8evSIzMxMHj9+rPDno0ePpK/4+HgqV65Mhw4dOHjwINnZ2Uortosde9WPCFAqUjac9nzmXX5+PvHx8Rw+fJjk5GTatGnDxYsX+eCDD95WM1+bg4MDy5cvJzMzE0NDQw4fPoyenp7CEFx5srOzIyIiggcPHrxwmMrNzY3Nmzfj7e2Np6cnBw4cKHPlh5eR1/DbsmULkZGRgOIi2BUrVjBkyJAXXkNTUxNzc3NcXV2ltU9QnOjw7JYcw4cPZ8KECVhYWEjVzW/cuMHevXupX78+tra23L59m61bt/Lxxx+XCMjPBqjLly+X+bXK59Kio6MVApScra0tffv2ZcuWLWzcuJF9+/axadMmldZ8vcjTp09LBBD5l7JAoyzgyL/KkkCkoaGBoaEhVatWpX79+ty9e1fpfl1ix171IgKUiszNzUlKSpL+npycXCI7ytzcHBcXF7S1tWnQoAGNGjUiPj6+Qif3y0q+YPf8+fO4urpy6NAh3NzcStRcKy/ykkeXLl2S9iMqTdeuXVmzZg2DBg0q8zYdpUlPT2fnzp1s2bKFI0eOSHNxY8aMwcfHh7y8PLp06YKHh4fColm5rKwsTp8+LQ3XnT59WionpKurK9Wua9SoEXfu3GH//v0cP36c33//nb/++ou+fftKC4J//PFHUlJSGDduHDKZjN9++438/HxpuO1ZzwaoK1eulPl1Ozg4oK2tzalTp5QWjU1LS1OotJ6enk7Xrl355JNPGDZsGFlZWUoDh3zBcXZ2ttJAU9agUqVKFenL0NCQatWqYWhoiIGBgcKfz5737PkGBgZSD/PZebG5c+cyffr0EvcUO/aqFxGgVNSqVSvi4+O5efMmtWvXZvPmzSUy9OSlcoYMGUJqaipxcXEldgVVd/JP07GxsVSpUoXU1NQ3NrwHiiWPXhagAHx8fMjMzGTs2LF4e3sTGhpa5myrR48eERYWRnBwMOHh4eTl5WFsbMzgwYPx8fGR9rvKzs6mVatWVK1alW+++QYonvuRB6PIyEhiY2OluUAzMzM6dOggrT1ydHQskc02adIkEhMTCQkJISgoiICAAAICAhTO6dGjBzk5Ofz+++84OTnh7Oxc4jXIPyy5uLhw9erVMr1+KA6eDg4OREdHK308MDBQaZLPxo0bX5iZqqGhoRA0DA0NMTMzK3NQqVKlCvr6+uWyPvDWrVslruPn58cff/yh0KsVO/aqHxGgVKSlpcWSJUvo2rUrBQUFDBs2TNr+oGXLlvTs2ZOuXbvy119/YWNjg6amJj///LPKqcbqwsbGBm1tbWJjY6VdWN9kgGrcuDEaGhplGlr57LPPyMjI4Ntvv1V5m46cnBz2799PcHAwe/bsIScnBwMDA/r06UPfvn3p1KlTiWDi7+9PQkICbm5uLFiwgPPnz5OYmCg93qhRIwYOHEjr1q1xc3PD0tJSpTfUunXrMnHiRCZOnMiVK1cICgpi8+bNUiXwadOmkZeXR1paGvPnz1d6jeTkZAwMDGjRogVRUVGkp6eXebfZVq1asWzZMqXDq6VtwqipqSkF5B9//JGuXbsqBJgrV65gZ2dX4UkSLyPfsTcwMFDlCvTC2ycCVBl89NFHfPTRRwrH5HvzQPGc1Pz580t9U3kXVKpUCVtbW86dO8e///6LiYkJzZo1e2P309PTw9raWlr8qqqvvvqKBw8eKGzT8Xxttry8PA4ePMiWLVvYtWsXjx49QkdHh48++kiq6vBs7ysnJ4czZ84QGRnJokWLpE31Tpw4gba2Nvb29vTp0wdXV1dcXFzKZQ6sSZMmTJ8+nS+//FLaEykuLk4aJlyzZg1Pnz6lV69eCsOZycnJVK9eXUq7v3LlCm5ubmW6t5OTE8uWLePMmTN07txZ4TE7OztCQkJKPOeHH37A3t6e4cOHM3PmTAAmT54sDZ9VdEWUshA79qo/EaCEEuzt7Vm3bh2XLl2id+/eb7woZ9OmTdm3bx+FhYVlutez23QYGxuzYMECqapDcHAw27dvJz09HS0tLTp37oyPjw+enp7SG/39+/cJDw+XhutiYmKkXqPcmDFj8Pb2xsDAQKpX+CbIF+kCDBs2TFpzFRMTw+HDhxk3bhwfffQRvr6+dO3aleTkZBo0aCCtV3vVAAXFSyieD1AvGgKrWrUqp06dYujQofj7+3PkyBHWrFlDzZo1X+m1C0JpRIASSnBwcGDdunUUFhaWe3kjZeSf1m/dulWmOTv5Nh0ZGRmsWLGCFStWUKNGDe7evYtMJqNdu3b4+Pjg5eVF1apViY+PZ+vWrdIc0vXr16VrWVpa4uvrS+vWrQkPD2fHjh0KWXuvMs9TFvJ0dICFCxeiq6vL9evXMTAwYP/+/QQFBbF79262bduGvr4+2dnZaGpqYmlpCbxaokSDBg0wNTVVqIwu97IhsNq1a7N3717mzZvHrFmzcHJyYtWqVe/ckLag3kSAEkqQZ/LBm51/kns2k0/VAFVUVMT58+cJDg5WqLp99+5dfvnlFzw9PUlJSSEyMpKRI0cSFRUlLcrU0tLC0dGRL774Qhqukw+vxcbG8sUXX9CpUycGDx5czq9UuSdPnrB//35pjVdubi79+/eXhhB79epFr169yMzMZOfOnfz888/ExcWRlJSEq6srAOvXrycgIKBMQ2wymQwnJyeioqKU7qT8siEwTU1Npk2bRps2bRgyZAg9e/bkk08+kQKsILwuEaCEEp6dc3obWYjyAHXhwgWlqdzPunbtGlu2bCE4OFhaGO3g4EDv3r2l/ZK++uorpk2bxpMnTwAwMjLCxcVFyq5r1aqV0g0Gnz59ip+fH3p6eixbtuytzaccPXqUR48e4enpyZ49ewCUVnA3NDRk4MCBWFhY0KlTJ2xsbKhcuTL37t0jMzMTW1tbfH198fX1VShV9SJOTk7s2bOHhISEV67Q0aZNG06fPo2fnx8bN27k2rVrrF+//p3LYBXUj6hmLpTwtvfXqVevHlWqVCk1c+zWrVsEBATg7OyMvb09s2fP5tatW9SvXx83Nzdyc3Ol4CQnk8n49ddfOXPmDHfu3GHnzp1MnTqVdu3albr7bUBAAOfPn2f27NnUq1ev3F9naXbt2oVMJqNt27bSsZSUlFLPl6eYjxs3jj179khVz588ecKcOXNwcHDA2dmZ+fPnK6zdU0a+Ru/5qihlZWJiQkhICOPHj+f8+fO4uLiwdevW17qmIIgAJZTwbBmYtxGsZDIZtra2Cqnm//77L0uWLKFdu3Y0btyY7777TmGvqqdPn3Lr1i0iIyPR09Nj7NixbNiwgVOnTmFtbU1BQQENGjTAzs5OpcSLS5cuMWfOHNq0afNW18IUFhYSFhaGs7Mze/fulY4fOHCg1OfIF+nKi/t269YNKB7mi46O5uuvvyY9PZ1p06ZhbW2Nh4cHgYGBUlbis1q2bIlMJlM6D1VWMpmMvn37Eh4ejpmZGZ9++iljx44t1wLDwvtFDPEJJUREREjfx8XFlag7Vx7S0tIIDAzk4sWL2NnZYW1tTVRUFIsXLyYkJITTp08rLS9lYGCAs7OzNFzn5ORUYhuF3bt307FjR3x9fdm9ezetW7d+YVvy8/MZOXIkWlparFix4q1uJR4TE0NKSgqjR49m6dKlWFpaUq9ePSIiIigoKFBaFVweoOTFiOWFYq9evcqwYcNo2rQpM2bMICoqiqCgILZu3cq4ceOYMGECnTt3xtfXF09PTwwMDDAyMsLa2prQ0FDS0tKws7PDz8/vtdYDOTg4EBUVxbhx41i1ahWRkZFs2LDhjRQbFv7b3qsAJc/0Anj48CH169eXiqEK/+fZABUbG1vuASotLY02bdpIKczPrreZNGmSwrm1a9fG1dWV1q1b4+rqip2dnUL1bWXq1q3L3r176dixI7179yY8PPyFJWwWLVrEmTNn+N///idlxb0t8uw9TU1Nbt26xfz588nLyyMiIoLY2FhatGhR4jnJyclUq1ZNKj/1bKq5nIaGBq6urri6uhIQEEBERARBQUGEhoayd+9e9PX18fT0pHv37qSkpPD48WNCQkIICQnhjz/+kKp6v6oqVaqwZs0aOnbsyJdffombmxu//PILQ4cOfafWSgkV670a4hs1ahSxsbFER0djbm7OxIkTK7pJauf27dtcvXqVQYMGASjdAv51BQYGKqyveV7//v1ZtGgR165d4/r166xfv54xY8bg4ODw0uAkZ21tza5duygsLMTT01MhpfxZcXFxzJgxA2dnZ2k79bcpLCyMRo0aSXUFBw4ciIeHB0CpOwknJycrFI81MjKidu3apaaaa2tr07VrV1avXk1iYiIbNmygU6dObN++ncGDB/P48WOF8+VVvV+XTCZj0KBBREZGYmVlxZgxYxg0aBAPHz587WsL74f3KkDJjR8/no4dO740Y+x9JO9R+vj4YG5urrD1RnkpLRkCiif+v//+e3r16kW9evVe69O2g4MD27dvJzMzk48++kihwGpaWhpz5syhffv25Ofn87///e+tb7KXkJDApUuXqFevHkePHmXIkCFUqVIFGxsbateurXKAguKKFKqshdLX16dPnz4EBweTmJhI8+bNlZ5XnlW9GzVqxNGjRxk5ciTBwcG4uLhw5syZcru+8N/13gWotWvX8s8///Djjz9WdFPU0qFDh9DW1sbV1RUHBwdiY2PLZefeZ8nTyp9nZGRU7tsdyLfpSElJwdPTk9TUVGmI0d/fn/T0dAoKChg6dKjS7RfepLCwMKB47ykNDQ1Gjx4NFPc8OnXqxKlTp6SSR3I5OTmkpqYqDVC3b98uU+/E2NhYygB8XnlX9dbT02PRokVs3ryZBw8e0L59exYuXCg2BhRe6L0KUGfPniUgIIANGza81Ynwd0VRURGHDh3CxcWFypUr4+DgQEZGBv/880+53sfPz6/EGhkLCwucnJy4ePFiuQdE+TYd165do2fPnixZsqTEEGN5DWuVxa5du9DU1CQhIQFPT08aNGggPebh4UF+fj5HjhxReI68F/h8gJLPQ5W14kVpv4s3lcno5eVFVFQULVu2ZOrUqXz88cfcv3//jdxLePe9V+/SS5YsIT09nQ4dOuDg4MDw4cMruklq5dq1a6SkpEjVI+Rbb5T3PJS8jI6/vz99+vTB39+f48eP4+joSGpqqlTxoTz5+PiwZMkSYmJiWLlypdJztm/fTlZWVrnfW5nU1FROnjxJQUEBeXl5JfZ86tixIzKZrES6uXxd07O7O8P/ZfKVteRRab+LN1nVu379+oSHhzNp0iT279+Pk5OTwt5TgiD3XmXxrVmzpqKboNbk2XvyACUveRQbG0uvXr3K9V7KyujIh5Xi4uLeyELZZ7fpUCY2NhYrKytGjBjB6NGj32jx0z179kjDW82aNSuxZbupqSnNmzcvMQ/1sh7Uq9Tkq4iq3tra2sycOZN27doxbNgwunXrxjfffMO0adNUToQR/vveqx6U8GIREREYGhpKqc3y6t1vIpNPGXmAunbt2hu7R2nFby0sLPjtt9+wtrbmf//7H40aNcLPz6/M24CoSj7/BPD5558rTQaRbwOfkJAgHSstQBkbG1OzZs1XClAVycPDg9OnT9OxY0d++uknqVK7IIAIUML/l5+fz9GjR6XdZKF4st7e3v6NZPIpY2VlhY6ODvHx8W/k+kVFRVJxVTlLS0tpWGvQoEEcOXKEiIgIunXrxvr162nRogU9e/aUCqqWh+zsbKlnZGZmRt++fZWeJ083P3jwoHQsOTkZDQ0Npb07VTP51E2NGjXYtWsXM2fOJCoqCicnJ3bv3l3RzRLUgAhQAlCcQJKZmVmiermjoyMpKSlKt/8ub1paWjRp0uSN9aAmT54sfZ+VlYWPjw8JCQnk5ORIcy4ymQxXV1eCgoK4cOECI0eO5NixY4waNYouXbrw559/8vTp09dqR0REBDk5OQCMGDGi1MrfLi4uGBgYKMxDJScnU7NmTaXDYE2aNCEpKYlHjx69VvsqgoaGBpMmTeLgwYMYGBjg7e3N119/LRX8Fd5PIkAJQMn5Jzn5PNTbGuazs7MjISGhxMaBryslJYXFixcDcP78eTQ1NVm1ahVdu3Zl7ty5LFq0qMRzrKysWLRoEdevX2fs2LHcv3+fzz77jCZNmvDLL7+QkZHxSm2RV4/Q1tbGz8+v1PO0tbVp3749hw4dkn4eycnJJRIk5F41k0+duLi4cOrUKby8vFiyZAnt27cvdZG18N8nAlxnqnwAACAASURBVNR77sGDByxfvpylS5dSpUoVzMzMFB6XZ/K9rWE+Ozs78vLyuHnzZrlds6ioSEql7tSpk7RNeqVKldi0aRNubm5MmTKFtWvXKn2+iYkJI0aMICoqiuXLl1OlShW+/fZbrKysmDRpErdu3VK5LQUFBdKWGj4+PtI+VKXp3Lkzjx49kqqNJyUllZh/knvVTD51Y2xszKZNm/j111+5fPkyLi4ubNq0qaKbJVQAEaDeY2lpafTp04cFCxaQmprKo0ePaNOmjcKCVSsrKypXrvxWAxSUby/gjz/+kL7fsmWLwmP6+vps27YNBwcHxowZw7Zt20q9jq6uLkOHDiUmJoYdO3bQsmVLFi9ejK2tLQMHDlSpOsKpU6ekdT/Pp5YrI5+HOnDgAA8fPuTRo0cv7UG96wEKioda/fz8OH78OLVr12bo0KGMGDHirS0DENSDyOdUY0VFRWRlZZGfn8+dO3d48uQJ165dIzs7m6ioqNe+/h9//EFiYqLCsRs3btCjRw9atWpFpUqVqFSpEllZWWzdupUWLVpIxypVqoSOjo7C3+Vf2trar1yiSL69R2RkJI6Ojq/9Gh88eMDIkSOB4jmoy5cvKz1vxowZjB07lkGDBnHnzh2cnJwUHs/KyiI9PR1tbW2guFc1c+ZM4uLi2Lx5M9u2bSM4OBh7e3v69euHq6ur0sXgv/32G1CcWl5QUEB0dPRLX0OtWrXYuXOnVLS3sLCQ6OhoHj9+zOPHjxXmo6pWrUpkZKRK130TMjMziY2NLdeyUYsXL2bhwoWsX7+eI0eO4O/vX6bNFR8/fsyZM2dU/jepr6//Rir4C2UnK2NmUvku8RcA2L9/P4GBgQwdOpQqVarw8OFD9PX1ycnJwdTUlPT0dOrXr09SUhK2trZcvXoVNze3196rafDgwS/sMbwOXV1ddHV10dHRUfqnrq4ulSpVKnFMR0eHBQsWADB37txSn/uyY/I3Iw8PD2l4LDMz84VvUklJSXTp0oX09HR27tyJi4uL9FhcXBympqalLmBNTk5m+fLlrF27lszMTKysrBg3bhz9+/dHT08PKP7A4ejoSEJCAuvXr8fLy0uln+WECRNYtWoVv/32GyNGjODPP/+kZ8+eXL58mbp162JgYCCd6+npya1bt15Y7/BNio2NpXHjxm9ky/egoCC+/PJL8vLymDNnDsOHD1cp6ERHR9OiRQuVq8fIZDI0NDSk35vwRqj0aUH0oNSAoaEhGRkZVKpUCVtbW2JjY3FyciI6OhpbW1uio6OpU6cOd+/excjICA0NDbS1tV+7XFOzZs2UBqivv/6azz77jCdPnpCbm8vKlStZs2YNkydPpmXLluTm5pKbmys9Xta/P3z4sMTjyrK1pk6d+sqvTUdHp8Q13dzcSgS15//evHlzQkND6dy5MwMHDqRVq1bo6OiQnp6OmZkZZmZmpT7/m2++4auvvmLTpk0sXbqU8ePHM3PmTEaOHEnfvn357bffSEhIwMjIiHbt2km9sZfp0qULv//+Oxs3bgSKKzHIf/9aWloK17GxseHIkSM8efJEIXC9LfJ/m6q+trIYMGAALi4uDBw4kIkTJ3L06FGWL1+OsbGxSm0qy/8XUSNQPYgAVQb79u1j/PjxFBQUMHz48FLfQENCQvDx8SE6OpqWLVu+9LotWrQgLS0NTU1NKlWq9Nb2y/Hz85O2YJCzsLBg4sSJCj2FkSNHsmbNGqpXr15qcdHXVVhYyNOnT8nNzeWzzz5j9+7dHD16FF1d3VID3ouC4J07dxQWw7Zt21Z6LDMzU+lzn7d+/Xr+X3v3HhZj/v4B/F3NVERFDhsRKelcVqTddT7mtHxDa50W1VdtWcfWOpZyWIUQfaUcQl2K3aRyWqe1K6RIodKBDqsSSjrOzPP7o2vm16iYqZlpsvfruly7zTzzPHfJ3PN5Pvfnc4eGhjbr++H/Hb569Qo+Pj7w8fERPFdaWgpDQ0N8/fXXUFdX/2jCVFVVFZS183eaf/bsGWpqapCXl4fq6mp07txZcCx/B460tLRGe0m1dfr6+rh+/TrWr1+Pffv24f79+zh+/Pgnm1KStokSlIi4XC5cXV1x+fJl6OjowNraGlOnTm3QJfTdu3fYu3cvhgwZ0kqRiq5z5844c+YMTp06hdzcXJiZmcHR0bHBbSxjY2Ow2WwkJSVJLRZFRUXBm6ytrS1iYmJQU1PTYC5IVD/88IPg/3Nycj5ZLccwDGprawXJ6urVq1i4cCGAultL5eXlaNeuHZSVlcUaNVZVVSEuLq5B2XxlZSXi4+PBZrNRVVWFyspKkRcCL1iw4JPHfPXVV+jQocMnR4yS/FpFRQUVFRXgcDgifR/NpaKigp07d2LEiBFwdHTEmDFjsHr1aqioqCA1NVUiXYGJfKAEJaK7d+9CX19fUK7s4OCAqKioBglqw4YNWLNmDXx9fVsjTLFpampi6dKl6N27d5PH8G89ymotFL8MPDU1FV9//bXYr4+LixOUJXt7e38yOQF1Ix5+kUdtbS1ycnLw1Vdf4fbt21i/fj0OHTqE/v37Q0tLS+x45s6dK9Q1mI/FYmHPnj2YMWMGlJSUwOFwGk12hYWFsLe3FyzuBeravX///feCZQH81+Tn5+PkyZMAgEmTJjW4jVpdXY23b982SKaVlZUSva2lpKTUZFKTVELs3r07jhw5Ajc3N2zfvl1wbUl1BSatjxKUiPLz84XKe3V0dAST73xJSUnIzc3F5MmT20yCEpWFhQVOnjyJ6upqQatxaenXrx8UFRWb1RuqtLRUMMLQ0tKCm5ubWK//sB09AGRkZOC///0voqKimpWgTE1NG01Q1dXVmD9/PtavX48ff/xRUCTTsWNHoePOnz8vlJwAoKioCNXV1XB0dGxw/KVLl2BtbY1jx46JFWdTCVKcEeOLFy/QoUMH1NbWChLih8eXlZWhqKioweslOfLit0+R9Sa4RLIoQYmosdsv9eeKeDweli9f3uRiz7bO0tISx44dQ2pqapNdWCVFVVUVffv2bVYl2tq1awVN/gIDAz+aTHk8HgoKCvD8+XPk5OTg+fPniI6ObrQdfVpaGn744QfExsaKXd3l5OSE48ePC51XT08PV65cQUxMDPz9/bFmzRp4e3tjyZIlcHFxEVqM29TPIT09vdHHm7snH4vFQocOHVpUXHH//n2YmJg0q4qPw+E0q/AmJCQEycnJDc4n6eaXRPYoQYlIR0dH0IsHqCsr7tGjh+Drd+/eISUlBSNGjAAAvHz5ElOnTsW5c+dEKpSQd/wtj5KSkqSeoIC6Rac3b94Ej8cTufrqjz/+QEhICIC6LZsmT56MwsJCQfLJyckR+v/c3NwG++o1VaBiYGCA27dvY+7cuQgPDxerSo3fcykoKAiPHj0SmutzdHTE4sWLERsbi927d2PXrl3Yu3cv7O3t8dNPP8HS0rLJERj/VuiHjIyM8Oeff6KiogLt27cXOc7WxmKxwGKxoKamJtbr3r5922iCknRXYCJ7lKBEZG1tjYyMDGRnZ6Nnz54IDw8XlP0Cde3K6zfaGzFiBHx9fT+L5ATUlaQrKCjIbB5KV1cX7969w4wZM2BjY9PopDfDMHj9+jVycnKQmpoqtK/d1atX0blz5wa3xhQVFdGzZ0/06dMHQ4cORZ8+faCrqyv478mTJ+Hp6dkgnvHjx2PcuHEICAiAk5MTgoODxSpb/ljPJUVFRUyePBmTJ09GQkIC/P39cfr0aYSHh2PEiBFYsmQJ9PT0GozAZsyY0ej5jIyMwDAM0tLSJLLYWd41NUKVVldgIjuUoETEYrGwf/9+jB8/HlwuF4sWLYKJiQk2btyIQYMGSa38Wl506NABBgYGMklQb9++RUREBIC60v4LFy7g4MGDWLp0KYqLi4VGQeXl5Y2eY+jQoUKJh//fXr16fXT04+zsjNDQ0Aa3+WpqarBx40ZUV1fj8OHD0NDQwO7duyW+JGDQoEEIDQ3Fli1bEBAQgJCQEFy/fh39+/fHtGnToKioCEtLSzg6OiI/P7/Rc/B3QXjy5Mm/IkF9bIRK2jZKUGKws7ODnZ2d0GNeXl6NHvs5trC2sLBATEwMuFyuRLey+VB4eLhgvzq+wsJCbN68GUBdBVufPn0wceJE6OrqIi8vD+Hh4QDqtqnJyMhoVjED0PDNztDQENeuXcOhQ4egrq4Of39/lJaWIjAwEJqamoKYJK1Pnz7YuXMn1q1bh+DgYAQEBCAqKgrdu3eHhYXFR0vS+QmqqW2dPket0RWYSB8lKCIyS0tLREREICMjQ7AxqTQ0Nfk/btw4hIeHC82rVFRUwNraWvC1j49Ps5MT34dvditXroSdnR18fX0FbTrKysqwfft2dOrUCcuWLWvR9T5GU1MTK1euhJubGyIiIuDv74/Nmzdjx44dmDx5MlavXg1zc3Oh13Tt2hVaWlptuu0GIQDtZk7EUL9QQpqamvz/6quvGkz6e3l5CVqiGxsbS2XeoX379vD398fo0aOxY8cObNq0SaQ2HZKkrKyM77//Hnfu3EFMTAy++eYbREREYPDgwejXrx9cXV0Fu9ArKCi02e66hNRHCYqIjN8bStrzUA4ODoIte/gam/S+c+cO9u7dK/h6586djXaalQQVFRUcPnwYU6dOxe7du7FhwwacOXNGpDYdkqSgoIDRo0cLtp4C6tboBQcHo2/fvggNDQWXy4WRkRGysrIaFIkQ0pbQLT4isi5dukBHR0fqvaE0NTURFRWFqKioJie9q6ur4ezsLNj9YPLkyRg9erRU41JWVsbJkyexcOFCBAQEoLq6GlFRURgzZgwWLFiAjh07YuzYsVKNgS8oKAiFhYVCj/EX7m7duhUsFgsMwyA9PV0w8iWkraEERcRiaWmJv/76CwzDSHVTW01NzY9Oem/dulUwx8Jms7Fjxw6pxVIfm83GsWPHwGazcfjwYdTU1CA6OhpjxozB7NmzERsbK9SmQxru3Lkj6Cv1IUVFReTk5AiKKGbNmoXr169DW1tbqjERIg10i4+IxcLCAm/evMHz589bLYYHDx4IbSXl7u6Ofv36yez6LBYLwcHBmDdvHo4fP47NmzcjOjoaampq+Pbbb6WygwHDMLh8+TLGjRuH4cOHNxg98fF4PKEKv+fPn8PQ0BCOjo5ITU2VeFyESBMlKCIW/roaWS3Y/VBNTQ2cnJwErUm6d+/eKuXFSkpK+N///oclS5YgPDwcPj4+OHv2LHg8HiZPniwo3GgpDoeDiIgI2NjYYMqUKUhMTMSKFStw7949oe2QgLp5ukuXLmHhwoVCWw3V1NQgNDQUX375JaZMmYI//vhD5J3TCWlNdIuPiIU/n/HgwQNMmzZN5tf39fVFcnIy+vbti+zsbHh5eUFdXV3mcQB1t9P27dsHZWVlHDhwALW1tQgPD8eMGTMwceJEXLt2DT179mzWuauqqhAaGordu3cjKysLXbt2haenJ5ycnAQN+o4ePYqrV68iPT1daJ5u2LBh8PHxafTaly9fxuXLl2FmZoaffvoJM2fOhLKycot+DoRIC42giFh0dHSgpaXVKiOo1NRUbNu2DYaGhiguLsbAgQMxb948mcdRn4KCAvz8/LB8+XJERUVh3759OHbsGAoKCjBp0iSh7a9EUVpaCl9fXxgaGsLNzQ1cLhf+/v5IT0+Hh4eHUPdYDQ0NLF++HCdOnICHh4dQEYmWlhYWL14MoK7xIn+PSL5Hjx5h8eLFGDBgAPz8/PD27dvm/xAIkRJKUEQsCgoKsLCwkHol34c4HA6cnZ3BYrHQrVs3lJeXw9fXt8Vt7yVBQUEBW7duhYeHB+Li4hAUFISAgACkpaVh2rRpgt3VP+bly5dYv349DAwMsH79enTt2hVHjx5FamoqnJ2dxd5BHfj/HSUGDBiACxcuIDExEY6OjkJryQoKCrBu3Tro6+tj1apVyMnJEfs6hEhL6//rJm2OlZUVCgoKUFRUJLNr+vv7IyEhAd9++y1u3bqFWbNmwdbWVmbX/xQFBQV4enpiw4YNuHLlCk6dOoUdO3bg/v37DZoN1peZmQk3NzcYGhrC19cXpqam+O2333Dv3j04ODi0aF1X/T35gLqFzPv27UNWVhZ+/fVXQfNNACgvL8f+/fthbGyMuXPnIiEhodnXJURSKEERsfHnoWR1my89PR1eXl4YMmQIsrOzoaqqCh8fH5lcW1zr1q3Dli1bcOPGDfz+++/w8PDAzZs3MXfuXKG27w8fPsS8efNgZmaGoKAgjBkzBlevXsXVq1cxceJEiZTwN7Unn6amJtzd3ZGSkoLffvtNaO0Wj8dDZGQkvv76a4wePRrnz5+XaKddQsRBCYqIjb+jhCxu83G5XEEbjbFjxyI+Ph6rVq0S6m4sb1avXo1ff/0Vf//9N65duwZHR0fExMTAyckJ169fx9SpUzFkyBCcPXsWDg4OuH//Ps6cOSPxEaG2tjY0NDSa3JNPUVEREydORHR0NJKTk+Hi4iLUnfevv/6Cvb09LCwsEBQURLtSEJmjBEXEpq+vDzU1NZmMoAIDAxEfH48VK1bg6NGj6NWrF5YvXy7167aUu7s79uzZg7t37+LevXtQVlZGWFgYJkyYgJs3b8LFxQWpqakICQmBiYmJVGIQZ0++/v37Y9euXcjKysLu3buF9kPMyMiAm5sbDAwM4OXlJdNbu+TfjRIUEZuioiLMzMykvmlsZmYmNmzYgIEDB4JhGOTl5WHr1q1tpkvsokWLMHToUDx48ECoc+/cuXOxa9cu9OnTR+oxGBkZ4dmzZw06BzelY8eOWLp0KR48eIDo6GjY2dkJbje+evUKW7duhYGBAVxcXJCWlibN0AmhBEWax8rKCpmZmSJVqDUHj8eDi4sLamtrsWHDBvj7+8PW1hb29vZSuZ4kvX//XlBwcPv2bcHj2trasLS0xOHDh+Hv7y+TWIyMjMDlcpGRkSHW6xQVFTF27FicPXsWKSkpWLZsGTQ1NQHU7fkXEhICCwsLzJgxAzdv3qSFv0QqaKFuG8Tj8VBSUiKRyev3798LWqeLQ19fH0DdPMWQIUNaHEd9FRUVCA8Px40bN7By5UocO3YMVVVV2LhxI968eSPRa4mqqqoK7969+2jxwuvXr3HkyBGEhITgzZs30NPTg5+fH2bMmIHY2Fi4u7tDQUEBurq68PDwAIvFwnfffdfsmKqrq1FaWipUfPEh/m4T9+7da/Z+fJ06dYKHhwfc3Nxw5swZhISECEZPsbGxiI2Nhbm5OZydndG/f3+8fftWrhb/cjgcvH79WuQlCUpKSkJzcaT1UIJqIzgcDmpra5GYmIiqqioUFhZKJEG9e/euWa/r0aMHAODvv/+W+K2qzMxM+Pr6wsDAAIaGhvDz88P06dPRvXv3Jvegk7aKigowDNNoocDLly9x4sQJnDlzBlVVVTA2NsYvv/yCkSNHQklJCW/fvoWtrS22bduGX375BR06dICmpiZWr14NHo+HMWPGNCumyspKlJSUfPTvkL94NykpSSIfJMaNG4exY8ciISEB4eHhuH79Ong8HpKTk+Hq6opu3bphzpw5+M9//oMOHTq0+HqSUFtbi6KiIpErI1VVVSlByQlKUHKMP7KprKxEYmIieDwejI2N8ejRIxgbG4PL5bb4Grm5uWAYBr179xbrdf369QObzcY///wjKGeWBIZh4Obmhurqahw5cgRubm5QV1fHnj17BP2PWsPTp08FnWrrP+bn54ewsDBwOByMGjUKq1atwsiRIxt9MzQyMkLfvn0xZ84csNlsKCkpYd26dTAyMmpWknr06BH69Onz0TfTAQMGQF1dHcXFxRL9ezI2Nsb8+fPx/PlzBAUFISQkBK9fv0ZRURH27NmDkJAQLF68GC4uLq1ecVlaWooBAwaItaibSuvlA81BySEul4vMzExUVFSguLgYysrKsLa2hoqKitAmoK1JWVkZJiYmEq/kCw0Nxa1bt+Dk5ISUlBQkJSVh7dq1rZqcPnT37l3MmjULlpaWOHHiBKZNm4a///4bsbGxGDVq1Ec/qU+ZMgWRkZHgcrmora1FTU0NZs2ahfj4eKnEKu3uurq6uvD29kZmZiYCAwNhYGAAACgrK8Pu3bthZGSEhQsXynznEfJ5oAQlJ9q1a4eamhrcv38f1dXV6NixI9q3bw9DQ0MoKSlJtfdSc1lYWODJkyeorq6WyPkKCgqwZs0a6OnpYcmSJdi4cSP09fXh6uoqkfO3BMMwuH79OsaNG4dhw4bhwoULWLRoEZKTk3Hy5EkMHDhQ5HONHz8eZ8+eFWxfVFFRIbU2HUDdKCojI+Ojc1Ut1a5dOyxcuBBHjhxBXFwc7O3toaSkBA6Hg/DwcNjY2GDChAm4ePEiFVQQkVGCkgN79+5F165dAQBmZmZo3749unXrJpdJqT5LS0twOByJ9BliGAbu7u4oLS2Ft7c3Dh06hKKiIvz666+tOuHO5XIREREBBwcHfP/994J2F0+fPsWBAwcEIwZxjR49GlFRUVBTUwMAvH37VqJtOuozMjICh8PBs2fPJH7uDykoKGDo0KE4ceIE0tPTsXbtWnTr1g0AcP36dUybNg0DBw7EkSNHUFVVJfV4SNtGCUoOLFmyBC9evICysrJcVT99Sv3WGy0VERGB8+fPw83NDZqamggJCcHYsWMxceLEFp+7OaqqqhAUFAQzMzPMmzcPRUVF8PDwQEZGBrZu3SooEmmJYcOGITo6WjCHVFhYiIkTJyI/P7/F567P2NgYAKR2m68pPXv2xKZNm5CRkYGQkBBYW1sL4li6dCkMDQ2xbds2lJSUyDQu0nZQghLDhQsXYGhoCH19fWzfvr3B87t27YKxsTHMzc0xevRokbvOtpWFpx8yNzeHgoJCixNUUVERli9fDj09PWzevBk7d+4Ej8fDzp07ZT6KbKrdRVxcHNzd3YXaXUiCra0tYmNjBWuMXrx40aw2HR8zYMAAALJPUHwqKiqYM2cO/vzzT9y8eRMODg5gs9koLCyEp6cn9PX1sWzZMqmMHknbRglKRFwuF66uroiLi8Pjx48RFhbWYBNOKysrJCQkIDk5Gfb29lizZk0rRSsbHTp0gIGBQYsLJVasWIGSkhIEBgbir7/+wrVr1zBv3jzBG6ssfKrdhTSLU6ytrREXFycoCX/69KnIbTpE0atXL3To0KHVElR9gwcPxtGjR5GRkYGNGzdCW1sblZWV+N///gdTU1PMnj1baHEz+XejBCWiu3fvQl9fH3p6elBWVoaDgwOioqKEjhk5cqRgNGRjY4O8vLzWCFWmLCws8OjRo2aXvP/++++IjIyEs7Mzhg4dijVr1kBTU1Nm++1Js92FOKysrHDx4kXBXOSn2nSIQ9qVfM3xxRdf4JdffkF6ejpCQ0MxdOhQMAyDqKgojBw5EsOHD8fZs2clspSCtF2UoESUn58vtJ5DR0fno3MFwcHBrTZ/IkuWlpaoqKgQeysdoG7nhWXLlqFXr17w9vZGUFAQnjx5And3d2hoaEgh2v8ni3YX4jIzM8OlS5fwxRdfAECjbTqaa8CAAUhPTweHw2nxuSSJzWZj5syZuHbtGm7fvo358+dDRUUFd+7cwZw5c2BqaooDBw6gvLy8tUMlrYASlIgaK41t6k3sxIkTSEhIwOrVq6UdVqvjF0o0Z+PYVatWobCwEAcOHEBNTQ22bNkCU1NTqe23xzAMbt68KbN2F81hZGSEy5cvo2fPngAgaNPR0oWjRkZGqK2tlet5HisrKxw6dAiZmZnYsmULdHR0kJ2djRUrVsDAwAAbNmzAP//809phEhmiBCUiHR0d5ObmCr7Oy8trtJLrypUr8PHxwblz56CioiLLEFsFvzeUuPNQcXFxOHXqFBYuXIixY8diy5YtePPmDXbu3Cnx22o8Hg/R0dEYMWIExo0bhz///FMm7S6ay8DAAJcuXRKM2MPCwrBy5coWrR9qrUq+5ujSpQtWr16Np0+fIjw8HMOGDRP8bvTv3x+Ojo4SWdpA5B8lKBFZW1sjIyMD2dnZqKmpQXh4OKZOnSp0TFJSEpydnXHu3DnB2o/PXZcuXaCjoyNWJV9paSl+/PFH9OjRA9u3b0dKSgoOHTqEadOmYeTIkRKLrba2FqGhoRg4cCBmzpyJtLQ0rF27Funp6TJrd9Fc/fr1w5UrV9C3b18AwMGDB+Hl5dXs87V2JV9zsFgsfPvtt7h06RISEhKwePFisFgshIaG4ssvv8SUKVNw5coVWvj7GaMEJSIWi4X9+/dj/PjxMDIywqxZs2BiYoKNGzfi3LlzAOo6qZaXl2PmzJmwtLRskMA+V5aWlnj48KHIbxRr165Ffn4+tm3bhsDAQMGcj4eHh0Ti4be7MDIygqOjI8rKyrBjxw5kZGRg06ZNgkIEeaerq4vLly8LFgNv27YNe/fubda51NTUwGazERwcjO3bt4u9e31rMzU1RUBAALKysrB9+3b06dMHly9fxuTJkzF48GCcOHFC5J5XpO2gBCUGOzs7pKenIzMzE+vWrQMAeHl5CRLRlStXUFhYiAcPHuDBgweCxPW5s7CwwJs3b/DixYtPHvvHH38gJCQE06dPh6enJzZv3ozi4mJwuVzMnTu3RW+cJSUl8Pb2Rv/+/bFq1Sq0a9cOgYGBePLkCZYtW9Ymd6jW0dHBpUuXBBu9rlmzBkePHhXrHCUlJRg+fDhqa2uRl5eHzZs34+uvv25zSQqoa/3x008/ITU1FWfOnMHo0aPx6NEjLFmyBAMGDICvry/evn3b2mESCaEERVqMPw/1qdt85eXlWLp0Kbp16wYDAwNkZWUJPZ+VlYWgoCCxr5+bm4vVq1fDwMAA3t7e6NOnD8LCwvDgwQMsXLiwzc8Famtr4+LFizA1NQUAuLi44LfffhP59UFBQRL7WcsLJSUlTJo0CTExMXj48CH++9//oqysDOvXr0e/fv2watUqThVvjgAAFPNJREFU5OTkAKi7pbxjxw7MnTu3TY4e/80oQZEWEzVBbdiwAS9evIC/v3+DN0w+cTZMffr0KRwdHWFkZIR9+/bBxsYGsbGxuHXrFqZPnw4lJSXRvwk5161bN1y8eBGWlpbg8XhYsGAB7ty5I9JrU1JSGn1cWpvTypqhoSH27NmDrKws+Pn5QVtbW9DReObMmViyZAk8PT0RGRnZpkeP/0aUoEiL6ejoQEtL66OVfLdu3cLBgwcxY8YMTJ8+XTAa+JCZmdknr3f37l3Mnj0bVlZWYre7aMu0tLQQFxcHa2tr1NTUYNWqVbh3794nX9eSn3Vboq6uDldXVyQnJ+PcuXMYN24coqOjUVxcLHRcWx89/ptQgiItpqCgAAsLiyYTVEVFBZydndG5c2fs3r0bAODk5AQ9PT2h4/T09ODo6NjoORiGweXLlwXtLuLi4vDDDz80q91FW9apUyfExMTAxsYGVVVV+O677z45EnJycmpQsfixn3Vbp6ioiHHjxuH333/HhAkTGj3mcxk9fu4oQRGJsLS0RH5+PoqKiho85+XlhczMTPj5+QkaD3bu3Bm3bt2Cp6cn7O3t4enpiVu3bgn2o+Pjt7uwsbHBlClTJNbuoi1TV1fH+fPnMXDgQJSWln6yTUfnzp3h6ekJABgyZEiTP+vPkY2NTaOPf26jx88VtXwnElF/we7YsWMFj9+5cwd79+7FpEmT4ODgIPSazp07N1lazm93sXv3bmRlZaFr167w9PSEk5OTxHcUb4s6dOgAf39/rF+/Hjdu3MDEiRNx7do1wQ4UH0pMTAQAnD59Wq66E0ubk5MTDh06hIKCAsFjn/Po8XNDCYpIRP1CCX6Cqq6uhrOzMzp27Ii9e/eKNDdUWlqKw4cP4/jx43j16hV0dXXh7++P+fPnCzrQkjqqqqo4ceIElixZgosXL2LSpEm4cuUKunTp0uDYGzduYMCAAf+q5ATUfQgKDAxEYmIiUlJSYGZmBkdHx3/F6PFzQAmKSIS+vj7U1NSE5qG2bt2Kp0+fIjAwsMlP9nwvX77E/v37cejQIZSVlQnWtNjb28tsR/G2SFVVFadPn8bcuXMRHR2NadOm4cKFC0Jrvt68eYOHDx/CycmpFSNtPerq6lizZg0UFWlGo62hf/lEIhQVFWFmZiYoNU9KSoKvry/GjBmDBQsWNPm6zMxM7NmzB8ePH0d1dTVsbW0xb948TJgwAdra2rIKv01TUVHBqVOnsGDBApw9exbTpk3DqFGj8PTpU5iamqJ3795gGAbDhg1r7VAJEQslKCIxVlZWOHjwIEpKSuDk5IR27dohICCg0Vt7ycnJ8PX1RWRkJHg8HiZNmoSVK1fC1tYWWVlZn22puLSw2WwcP34cXC4XUVFR+PvvvwEAkZGRgtYl33zzTWuGSIjYKEERienXrx8AYODAgSgsLMS2bdugq6sreJ5hGNy6dQu+vr64ePEilJSU4ODggJUrV8rdjuJtEYvFgqWlZYNGmqWlpejateu/ZgNj8vmgBEUkoqSkBHv27AEAFBYWAgC8vb3x5s0buLu7Iz4+Hr6+voiPj0e7du3g4uICd3d3ud5RvC1qqg2Furq6jCMhpOVo1pBIRFBQUIMW9+/fv8evv/6Kvn37wt7eHk+fPm0z7S7aqqZ2jRg0aJCMIyGk5WgERSSiqf3eAAhalltZWSE9PR0rV64Ei8UCi8UCm80W/D//63fv3kFVVRWampoNnm/sT/1jlJSUGj2nqM+zWKw2Pf/l5OSE48ePN9jrsFu3bnj9+jWVV4uA+kvJD0pQbQyXywXDMBLpfcPlclFcXIzu3buDy+W26FwmJiaIjIxs8nlVVVWkpKSAy+WitrYWHA4HHA5HkLzkiZKSUoMExjAMlJWVoaysLEho/OM+lQCbSqj1r/OxczZ1joKCAmRkZEBDQ0Po+ICAAJw+fRrh4eGorKwEAOzbtw8xMTG4ceOGVJOUkpISSktLwWazpXYNcbFYLOTn5zfaAbsxW7ZsAYfDgZeXF629a2WUoNoIHo8HhmHA4/GgpKSE+Pj4Fn3S4/F4qKqqApvNxvv375Gdnd2i+CwsLNCjRw+hFfv1zZkzB3PmzGn0OS6XK/hTU1ODyspKsNls8Hg8weMcDkfouA//fPg8j8dr8Fj9rxt7vv4x/Gvzv+Z/IOBwOEJxVVVV4f3792LH1hqysrKwadOmJv8eJIHH46GoqAiqqqpys+6IYRikpaUhLS0NKioqnxwhX7lyBSUlJTh69Cg6d+6Mjh07okuXLrhw4YKMIiZ8lKDaAIZhwOVyoaSkJNTSorm3ojgcDqqrq6GqqiqxlhQaGhoICAhAZGQkzpw5g6qqKsFzPXr0wJQpU5qMl//Jn5+ENTQ05Oo2G8MwqKiogJqamkTOx+PxhJJccxIw/7GKigqw2ewGx5w/fx4ZGRkNri3tEn4lJSWoqqqiqqoK7du3l4u/RwUFBbRr1w61tbWorKz85O/9jh07ANQ1h3z16hXKy8vB5XIxaNAgSlQyRglKjtW/lcdisTB48OAWny87Oxtv3rzB4MGDoaysLIkwhYwbNw7bt29HcHAwHj16BDMzMyxevPiTt5V4PB7u378PExMTwbodeVFaWoq8vDy5LIVPSkpC//79GyRPdXV1wQax9Y0YMaLJDVQlqbi4GC9evICVlZXcjKSAup31U1NT0bVrV+jq6n40gd68eRM8Hg+nTp3C/v37sXHjRnz77bcyjJYoiHmbiGYPpaCmpgZDhgyBn58frK2tcffuXXz55Ze4f/8+vvzySzx8+LDFc0QMw6CqqgqKiopQVlaWi0+29dWPTd7wPyTIY2y1tbXg8XgNugaXlZXB1dVV6JZrjx49EBAQILOS85qaGkFs8vT7xv/gx+VyRboV+fPPP+Pt27d49+4dqqqq0Lt3b2hra9NIqmVE+oWgEZSc4c9P8Hg8sFgswS7ULcGfK+FP8Mub2tpaMAwjl7EBdT8/eUxOQN0ttcYKTdTV1REQEIDo6GhkZWVBT08PU6ZMkel6KDabjerqatTU1DRIoK1JQUEBKioq4HA4qKyshIqKykf3e9y+fTuAukRVUlKCjIwMlJaW0i0/GaARlByoqanB4MGD4efnBysrKyQnJ0tsIr22thY1NTUSnW+SJB6Ph8rKSrmZr2jM+/fv5Tq+iooKuSpKqI9hGEHRizx+AOEXCykqKoo80vPw8EBBQQHevXsHXV1dqKioUKISn0j/mOTvN/pfiP8hgV8EIYnkVFtbi8TERHA4HLRv314uk1NNTQ3u378PVVVVuX3zLy8vR3p6utzGB9Ql0LS0tNYOo1H8AoVXr17h2bNnrR1OA4qKimjXrh0UFRWRm5uL58+ff/I1O3bsQGhoKPT19VFWVobi4mK8evUKgwYNarKDL2keGkHJAS6Xi+7du6N3794SeyMsLy8Hm82Wq1srH6qoqADDMBKrjpMG/i2q+u0r5A3DMHjz5o1cL8Jls9nIz8+X6/0A1dTUkJWVJVbPLB6Ph+LiYhgZGeHy5ctSjO6zI9IbHSUoQgghska3+AghhLRdlKAIIaQZLly4AENDQ+jr6wsq/eqrrq7G7Nmzoa+vjyFDhiAnJ0f2QbZxlKAIIURMXC4Xrq6uiIuLw+PHjxEWFobHjx8LHRMcHIxOnTrh2bNnWL58OTw8PFop2raLEhQhhIjp7t270NfXh56eHq5evYqCggJ88803QiOpqKgoLFiwALt27YKXlxfOnDmD0aNHi1QpSOpQgiKEEDHl5+ejV69egpHUzz//DBsbG2zatAm9e/fG9u3bBcdYWVkhISEBurq6mDBhAr777jsoKCggISGhtb8NuUcJihBCxMSvfuaPpLp06YJbt27B3d0dI0aMwKZNm5CWloaAgACMHDkS7du3BwAYGxsjNTUV+vr6mDVrFkxMTKS6u3xbRwmKEELEpKOjg9zcXMEoKT4+Ht27d4epqSmioqLg7u4OXV1dREZG4vHjx+BwOCgtLcUvv/yCESNG4OXLlzh8+DBSU1OxZ8+e1v525BYlKEIIEZO1tTUyMjJQWFgIHo+H2NhYmJmZITMzExoaGjA3N0fPnj2hqKiI4cOHQ0dHB0pKSsjNzYW+vj569OgBdXV1vHjxArNnz4aVlRXMzc0RGxvb2t+aXKEERQghYmKxWNi/fz+2b9+O8PBw2NraolOnTjh79qxg95YBAwbg+fPnqKqqQkVFBYqKiqCmpobMzExUVFRg8eLFGDRoEExMTJCYmAhzc3NMmzYN5ubmEtkk+nNACYoQQprBzs4O2dnZ+OKLL2Bvb4/nz5/j3bt3MDc3R15eHhQVFWFgYIBJkyZBTU0NysrKKCgowKVLl1BQUICioiJYWVkhNDQUERERyMzMxKBBg3Do0CEsXbq0tb89uUAJqo1rC4sFPxXjrl27YGxsDHNz81Ytw/1UnHyRkZGtVoUlSoynT5+GsbFxq03AfyrGFy9eYOTIka16W2vRokXo1q0bTE1NG32eYRi4u7tDX1//oyMa/kjq559/xvXr12Fra4uysjLs2bNH0EUgISEBPB4PWlpaUFBQQLdu3WBgYIDo6GgcPXoUXC4XCxYsQHJyMvbv3w8bGxu8ffsW//zzjzR/BG0DwzDi/CFyhMPhMHp6ekxmZiZTXV3NmJubM6mpqULHBAQEMM7OzgzDMExYWBgza9YsuYvx6tWrzPv37xmGYZgDBw7IPEZR42QYhikrK2O++eYbZsiQIcy9e/fkLsb09HTG0tKSef36NcMwDFNYWCh3MTo6OjIHDhxgGIZhUlNTGV1dXZnGyDAMc+PGDeb+/fuMiYlJo8/HxMQwEyZMYHg8HnP79m1m8ODBnzxnTEwMo6+vz7BYLGbFihXMqVOnGFVVVWbfvn0MwzCMn58f07lzZyYuLo7p3r07c+/ePcbLy4vR0NBgxo4dyxw8eJAxMjJiuFwuM2rUKJn/fsmYSDmHRlBtWP3FgsrKynBwcEBUVJTQMfzFggBgb2+PP/74Q1AiKy8x1i/DtbGxQV5ensziEydOANiwYQPWrFkDVVVVuYwxKCgIrq6u6NSpEwDIfPdwUWJUUFBAWVkZAKC0tBQ9evSQaYwAMGzYsI/u/h4VFYX58+dDQUFB5BGNnZ0dMjIyEBUVhejoaKxatQo6Ojr48ccfsXHjRty6dQssFgvjx4/HnDlzMH/+fPj4+MDHxwdsNhumpqaoqqrCq1evAECuW7zICiWoNoxf4sqno6OD/Pz8Jo9hsVjQ0NBASUmJXMVYX3BwMCZOnCiL0ISIEmdSUhJyc3MxefJkWYcHQLQY09PTkZ6ejq+++go2NjYyb6InSoybN2/GiRMnoKOjAzs7O+zbt0+mMYpC3N/b+uzs7JCeno7nz5+Dy+UiOzsb69evx5MnT6Curg4FBQXs2rULjx8/xsiRI6GmpgYdHR3Ex8ejqqoKXbt2RV5enlDivnfvHszNzVFVVYX379/DxMQEKSkpEv++5Q21fG/DGhsJffipS5RjpEmc6584cQIJCQm4ceOGtMNq4FNx8ng8LF++HEePHpVhVMJE+VlyOBxkZGTg+vXryMvLwzfffIOUlBRoamrKTYxhYWFYuHAhVq5cidu3b2PevHlISUmRq47Akvh3w5+fGj9+PLhcLqZPn44LFy5g48aNGDRoEKZOnQo/Pz84OjqioKAAYWFhiIiIwJ07d6ChoQFtbW3BuaytrTF16lSsX78elZWVmDt3bpPzZ58TSlBtGH+xIN+Hn7rqH6OjoyNYLCjLxnaixAgAV65cgY+PD27cuNEqTRY/Fee7d++QkpKCESNGAABevnyJqVOn4ty5cxg0aJBcxMg/xsbGBmw2G3379oWhoSEyMjJgbW0tNzEGBwcLRnZDhw4V3NaSp2aGov7efoqdnR3s7Ozw3Xff4eTJk3j16hVCQkKgq6uLwMBAAMBff/0FhmHw448/wsXFBe3bt8eRI0canGvjxo2wtraGqqoq9u7d2/xvri0RdbKKoSIJuVNbW8v07duXycrKEkxIp6SkCB2zf/9+oSKJmTNnyl2MiYmJjJ6eHpOeni7T2OoTJc76hg8fLvNJbFFijIuLY+bPn88wDMMUFxczOjo6zKtXr+QqxgkTJjBHjhxhGIZhHj9+zGhrazM8Hk9mMfJlZ2c3WSRx/vx5oSIJa2trGUfX0D///MPo6ekxRkZGTHl5eWuH01Ii5RxKUG1cTEwMY2BgwOjp6THe3t4MwzDMhg0bmKioKIZhGKayspKxt7dn+vXrx1hbWzOZmZlyF+Po0aOZbt26MRYWFoyFhQUzZcoUmccoSpz1tUaCYphPx8jj8Zjly5czRkZGjKmpKRMWFiZ3MaampjK2traMubk5Y2FhwVy8eFHmMTo4ODBffPEFw2KxmJ49ezKHDx9mDh48yBw8eJBhmLqfo4uLC6Onp8eYmprKRUXdlClTmJMnTzLe3t6Mq6tra4fTUiLlHGr5Tgghcu748eP4/fffcfbsWXC5XNja2mLbtm0YNWpUa4fWXCJN6FGCIoQQImsiJSj5KZsh5DOzYcMG+Pv7C75et27dv2dymxAJoBEUIVKSk5ODGTNmIDExETweDwYGBrh79y60tLRaOzRCWptIIygqMydESvr06QMtLS0kJSWhsLAQVlZWlJwIEQMlKEKkaMmSJTh69ChevnyJRYsWtXY4hLQpdIuPECmqqamBmZkZamtrkZGRASUlpdYOiRB5QLf4CGltysrKGDlyJDQ1NSk5ESImSlCESBGPx0N8fDwiIiJaOxRC2hwqMydESh4/fgx9fX2MHj0aBgYGrR0OIW0OzUERQgiRNVqoSwghpO2iBEUIIUQuUYIihBAilyhBEUIIkUuUoAghhMglSlCEEELkEiUoQgghcokSFCGEELlECYoQQohcogRFCCFELlGCIoQQIpcoQRFCCJFLlKAIIYTIJUpQhBBC5BIlKEIIIXKJEhQhhBC5RAmKEEKIXKIERQghRC5RgiKEECKXKEERQgiRS5SgCCGEyCVKUIQQQuQSJShCCCFyiRIUIYQQuUQJihBCiFxiiXm8glSiIIQQQj5AIyhCCCFyiRIUIYQQuUQJihBCiFyiBEUIIUQuUYIihBAilyhBEUIIkUuUoAghhMglSlCEEELkEiUoQgghcokSFCGEELn0f9TunPNDeEJ0AAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7eff0c6e1ad0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"autofig.reset()\n",
"autofig.plot(x, y, z, i=t, \n",
" xlabel='x', ylabel='y', zlabel='z',\n",
" projection='3d', elev=0, azim=0)\n",
"mplfig = autofig.draw()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"When provided as an array, the set viewing angle is determined as follows:\n",
"\n",
"* if no i is passed, the median values of 'elev' and 'azim' are used\n",
"* if i is passed, then linear interpolation is used across the i dimension of *all calls* attached to that axes\n",
"\n",
"Therefore, passing an array (or list or tuple) with two items will simply set the lower and upper bounds. If you want the axes to rotate more than once, simply provide angles above 360."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAagAAAEYCAYAAAAJeGK1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzs3Xlcjen/+PHXabOULcaSskRE9p2GZB072SlTWkaYsTWjwSTCMPY9oiF7SNaRQdYsI/nIEpUlslekfTu/P/qd+9vRopVwPR+P83DOvV7nON3vc133db0vmVwuRxAEQRCKG5XPXQBBEARByIoIUIIgCEKxJAKUIAiCUCyJACUIgiAUSyJACYIgCMWSCFCCIAhCsSQClCAIglAsiQAlCIIgFEsiQAmCIAjFkloetxdpJwRBEISCkuVmI1GDEgRBEIolEaAEQRCEYkkEKEEQBKFYEgFKEARBKJZEgBIEQRCKJRGgBEEQhGJJBChBEAShWBIBShAEQSiWRIASBEEQiiURoARBEIRiSQQoQRAEoVgSAUoQBEEolkSAEgRBEIolEaAEQRCEYkkEKEEQBKFYEgFKEARBKJZEgBIEQRCKJRGgBEEQhGJJBChBEAShWBIBShAEQSiWRIASBEEQiiURoARBEIRiSQQoQRAEoVgSAUoQBEEolkSAEgRBEIolEaAEQRCEYkkEKEEQBKFYEgFKEARBKJZEgBIEQRCKJRGgBEEQhGJJBChBEAShWBIBShAEQSiWRIASBEEQiiURoARBEIRiSQQoQRAEoVgSAUoQBEEolkSAEgRBEIolEaAEQRCEYkkEKEEQBKFYEgFKEARBKJZEgBIEQRCKJRGgBEEQhGJJBChBEAShWBIBShAEQSiWRIASBEEQiiURoARBEIRiSQQoQRAEoVgSAUoQBEEolkSAEgRBEIolEaAEQRCEYkntcxdAEARBKDi5XJ7ta5lMhkwm+9RFKjARoARBED6BnAJIdq8zLlM8//Df9+/fA6ClpZXtuVVUVChRokQ+S/75fHMBKjU1laSkpEy/Jj78hZHV+oKuEwSheMtLEPkwgHy4TC6Xk5iYSHx8POXLl8+0bX5kdT2JiopCRUWFMmXKZLk+q3J+Kb7JANW3b1/2798vLfuwKqxYltV/9vPnz9HS0qJMmTIfPVfGY3z474fny2k7RfBMTU1FVVUVSP9FlNVxcjrHx9Zl9VoQipPCCCAZ/42JiQFAU1Mzx4u4TCbL1UX+w7+f2NhYXr16Rfny5YusmS27a8vX4JsLUACRkZHShT6vEhMTKV26dK72/9gXOqdfNlkt9/f3p2XLltK6jF/I7AJqbsr4sYAWGRlJhQoVlIJiTjXOrNblN0iK2umX52NB48N1H6uFvH79mu+++y7L/fMj4/cmKiqKtLQ0NDU1P3qhz8/37WsOHp/CNxmgPpWPfSnz+qWVyWT5Dqy5kd0f/8OHDylXrly+9s24Li/vNyYmhtjYWKpUqfLRbT8W0LKrlSr+zVhrhvTaaXFo7o2IiMDV1ZWbN2/SpEkT7O3t0dbWztMxslKYzViK12/evKF8+fKF8v388HMKCQmRAlRh10JEACneRIASJDn9kaqoqGRqVixKqampxMfHZ3vBK+zaKcDr16+Ji4ujRo0aQOFetLJr7n3z5g2VKlXKtDwiIoIuXbrw4MEDADw9PXF3d+fcuXNUrFhR6dgffkbZ3UwHCA8PR0dHp0DvJavP5enTp5QuXZrSpUsXaTOW8G0RAUr4IhV27RT+LwirqRX+n0VOtdNKlSplCqibNm2SgpPCgwcPcHV1Zdq0aUrHVVdXzxSksnv/YWFhVK9evciCSG6P++7dOy5dukR0dDRly5alQ4cOlC1bttDLJHzZRID6ykRERODu7s7t27cxMjLC2tq6UJqFhILJ6b5GVhf2O3fuZLn9nTt3MgUjNTW1PAWcz1kbCQ0N5c8//2Tfvn1oaGhINcukpCSGDBnC77//Tp06dT5b+YTiRQSor4iiWejhw4cAeHl5sX37dnx9fXMMUiKoFT9GRkZ4eXllWt6oUaPPUJrC4efnR//+/YmPjyc1NZWEhASl9bt27cLb25tDhw7RoUOHz1RKoTgRqY6+Iu7u7lJwUnj48CHu7u7Z7qMIai4uLnh5eeHi4oKpqSmRkZFFXVwhB9bW1tK9MIXatWszduzYz1SiggkNDaV///7ExMSQmpqa5TapqanExMTQv39/QkNDP3EJheJIBKivyO3bt7NcfuvWrWz3yU9QE4qetrY2kyZNkp47OTl9tCZcnP3555/Ex8fnatv4+HgWLlxYxCUSvgQiQH1FjIyMslz+9OnTbC8O2QW1FStWMG7cONauXcuNGzd4+/ZtoZVTyJ0rV64A0L17dxwcHL7Y4PTu3Tv27duXbc3pQ6mpqezdu5fo6OgiLplQ3IkA9RWxtramdu3amZZfvXqVTp06ERAQkGlddkEtOjqanTt38vvvvzN16lRq1apF48aNGT16NAsXLuTYsWM8ffr0i02hUtylpaXh6+sLQM2aNT9zaQrm0qVLaGho5GkfDQ0NLl26VEQlEr4UopPEV0RbWxtfX1/c3d25desWdevW5eDBg9y7d4979+7RtWtXfv/9d6ZMmSJ1pba2tmb79u1KzXxVq1aladOm/Pvvv6SlpUnHrly5MufOnePw4cNK52zSpAmNGzemcePGNG3aFAMDgyLpqv0tuXXrFq9fvwagVq1an7cwBRQdHZ3nHzJyuVzUoAQRoL422traODg4SK/Hjh1Lt27dePr0KaVKlcLFxQUfHx82bNhAnTp1MgW1Ro0aMXbsWLS1tXny5Al///03bm5uREZGIpPJsLa2plu3bkRFRXHz5k1u3rxJYGAgZ86ckc5ZsmRJGjZsKAWuJk2aYGRklGO2ZUHZ6dOnpedfeoAqW7ZsvrKmiHFRgghQXzkdHR28vLzo0aMHqqqqWFtbs23bNr7//nsWLFiApaVlpqCmoKenh5OTE926dePRo0ds2rSJZcuWsWLFCnr37o2trS0zZsyQMh8EBgYqBS0PDw+pBiaTyahbt64UsBSPypUrZzpvREQEa9eu5ebNm7Rt2/ab7PaeMUB96U187du3JykpKU/7JCUl0b59+yIqkfClEAHqG2BoaMiePXvo378/Z86cYf/+/Tg6OjJp0iSOHTvGmjVrcsx5p6GhwYgRIxg1ahTXr1/Hzc2Nffv2ceTIEerVq4etrS0jR46kc+fOdO7cWdovPj6eO3fuKAWt48ePK43vqVq1qlLQ0tPTw9raWmpyPHHiRK7Gcn1NYmNj8fPzA0BdXb3AqYk+t3LlyjFkyBB27dqVq44SqqqqDB06VNSgBNFJ4lvRvn17Nm/ezIMHD3B2dubo0aNMmjSJEydO0LZtWw4dOpSr47Ro0YL169cTFBTE3LlzSUhI4Ndff8XQ0JCpU6cSFBQkbVuqVClatmyJlZUVy5cv5+TJk4SHh+Pv74+7uztTpkyhYcOGBAQEsHTpUn788UelgcYK31q394sXL0o1Dl1d3SJNEPyp/P7775QqVSpX25YqVQpHR8ciLpHwJRAB6hvSv39/lixZgr+/Pz/99BOzZ8/m2LFjaGlpYW5ujr29fa5vTFesWJHJkyfzv//9jz179tCmTRs2bdpEmzZt6Nu3LwcPHiQlJSXTfqqqqhgYGDBkyBDmzJmDt7c3oaGh3L9/n71799KwYcMsz5fTWK6vjaJ5r2TJkl/8/SeFOnXqsHTp0hy3UVVVRUtLi0OHDol0RwIgAtQ3x9bWFgcHB3x8fJg8eTIdOnTAz8+P0aNHs2PHDjp06MDFixdzfTxVVVV69eqFt7c3/v7+2Nvbc+PGDSwsLGjcuDGLFy/m1atXOR5DJpNRtWpVevbsyeDBg7Pc5ktO8ZNXp0+fpn79+iQlJX01AQqQen8aGBhQsmRJypYtS5kyZShbtiwlS5Zk1KhRXLlyRaQ5EiQiQH2D/vjjD0aNGoWHhwd//vknZcuWZf369ezYsYPY2Fh69+7NH3/8QWJiYp6Oa2BgwKJFiwgKCmLFihWUL18eFxcXGjRogI2NDVeuXPlod+OsxnJ9ySl+8io8PJygoCDq169PWlpaoXaQiIiIYPv27Zibm7Nw4cJPms4qICCAI0eOAOk598LCwti2bRvr1q1j27ZthIWF4ebmJmpOghLRSeIbJJPJWL16NS9fvmThwoVUq1YNKysr+vXrR5s2bZg4cSIrV67k5MmTuLm55fn4WlpajB07FisrK/z8/Ni4cSP79+/H09OTZs2aYWtry5AhQ7K8J6Gtrc2///5LvXr1qFq1KjY2NlK392+BYnCu4kJdWAEqIiKCjh07SlN47Nu3Dw8PDy5cuPBJPtv58+cD0LFjR6k23LNnzyI/r/BlEzWob5S6ujrbtm2jefPmTJkyhWPHjgFQpUoVPD09WblyJY8ePaJz587s3r0712lqMpLJZBgbG7N161Zu377N9OnTef78ORMmTMDQ0JBZs2Zl6hAB6alx0tLSGDJkyBed4ic/Tp06RcmSJalWrRpQeAHKzc0ty/ml8vMDJK8y1p7s7e2L/HzC10MEqG+YlpYWe/fupUaNGlhZWUm532QyGVZWVly4cIFmzZqxceNG+vXrx+PHj/N9Lh0dHWbOnMnt27dxd3fH0NCQVatW0axZM4YOHaqUtSIkJAT48geo5pUivZGxsTEvX74EyDJ1VX5k18kkMDCwUI6fk3nz5gFQvXp1+vXrV+TnE74eIkB94ypXroyXlxelS5dm+PDhBAcHS+vq1KnD8ePHGTt2LFevXqVDhw7s2LGjQPn3NDQ0GDJkCD4+Ply8eJEff/yRc+fOMXjwYFq0aMGaNWu4du0a8OUPUM2r//3vf0RGRtK1a1cePXqElpZWodUes+vi3bhx40I5fnauX7/O0aNHAbCxsUFdXb1Izyd8XUSAEqhbty579+4lISEBMzMzXrx4Ia1TU1PD3NyckydPoqOjg729Pebm5rx586bA523cuDGrVq0iKCiIBQsWIJfLmTFjBosXLwbI9fQMX4tTp04B0KVLFx4/fkzNmjULZfbbBw8esG3btkzL9fX1sbW1LfDxc6K496Surv7NdHTJL7lcTmpqKsnJySQmJhIfH09MTAzv37/n3bt3REVFERERwevXr3n58iXPnz8nPDxcWv7w4UNCQ0MJDg7m3r173L17l9u3bxMYGPjFzkbwTXSSOHXqFAcOHJASmKqrq/Pbb78xbtw4pSm3c/OIi4tDRUVFmqq6MB7weafhBmjVqhVbt25lxIgRDBkyhGPHjimN5G/WrBnnzp3D2dmZ9evXc+XKFVavXk2vXr0KfO4KFSowceJExo8fz6lTp6Su5ubm5rRv3x5bW1v69++f54zYX5rTp09TtWpVGjRowKNHj2jTpk2Bj/n+/XtpbNkPP/xA9erVeffuHY0bN8bW1rZI7+9lrD0NHjw4x2wln0NaWhppaWnS7L6K13K5XFquWJbVQ7FddtvK5XISEhJITEwkOjpaWpYTFRWVPD/kcjkqKiqUKFEiy/UymSzXg6SLm28iQBkZGaGpqUlKSgrx8fH4+/vToUMHypYti1wuz/ah+EJlfCQlJREXF5fluvw+ckMulxMXF8d///0nLcsY3BQPxRfyw+W5edSrV4/Zs2fj5OTEkCFDWL9+PSVKlCApKYnnz5+joqLClClTaNu2LY6OjgwfPpyRI0cyc+ZMtLS0CiVYd+/encqVK1OmTBmMjY05dOgQY8eOpUqVKlhZWWFlZSV1ICiOIiIicHd35/bt2xgZGeU6j+D79++5cuUKQ4cOJTY2ljdv3hT4HlxKSgrfffcdAKVLl8bb2xs/P79PNs5Ice8J0jtH5HSxz+mRlJTEo0eP8rVvTmQyGcnJyQBERUVJfzsZL+6qqqqZLvYqKiqoqallCgQZt1VsFx0dzZs3bzA0NJTWFbawsDBkMlm2KbG+5Clxik2AOn78OJMmTSI1NRUbG5tMqU7CwsL48ccfefv2LampqSxcuJDevXvn6thVq1alatWqQHoSypiYGAYOHJivcqamplKhQoXP0rPsv//+o3Xr1gCZAlxWwTWr5R97jBo1isjISFasWIGTkxOLFi0C/u/Xplwup2XLluzbt48FCxawa9cuLly4wNy5c2nSpEmBg3VMTAyvXr3i+++/Z8SIEQwfPhxfX1+8vb1ZuHAhixcvpmPHjgwYMIDGjRtnG4wB6UKRVW01YzBXLI+PjyclJYW0tLR8Bde3b99iZmYmdSbx8vLCw8ODI0eOoK2tneU+igvw2bNnSU5OpnPnzjx69Ago2D24tLQ0pQtWWFgYcXFxpKamSr/mC/Px/v17rl+/Ll2A7927J/UMrVevHikpKVy5ciVfNQRIb/XIz74fa5l4+vQpqampRXa/MyEhAVVVVTH9TD4Vi08tNTWVCRMm8O+//6Krq0vr1q3p37+/UtqbefPmMWzYMOzt7blz5w69e/eW/pC/RRkvrIVtzpw5REdH4+7ujr6+PgMGDKB69eqZfv3t3r2bffv2MXXqVKytrZk6dSqOjo4Faorz9/cH0nP+VatWjTp16tCxY0f++OMPrl69ipubGwcOHODMmTMYGRlha2vL0KFD0dTUzLJmmlVNWLH8w5ry27dvSUhIUKpZZxXos6s9u7u7Z+rp+PjxY8aMGUP37t2pWrUqVapUoUqVKpQqVUpqArpz5w779u0DoFKlSlKqo6SkJKUac04+/C44OTlJaauOHTvGvXv3UFFRITExkcePH3/0wp7XgBAYGEj9+vXR1NQEYMmSJVJZHBwcMDY2zv2X4APh4eFUr1493/sLX65iEaCuXr1K3bp10dfXB2DEiBEcPHhQKUDJZDLpD+7du3dffIbn4kwmk7F06VJevnzJypUrSUlJoUWLFlluO2TIEDp06IC9vT1Llizh5MmTbNy4EUNDw3ydW9GLUPFdyFimtm3b0rZtWxYsWMCWLVtwd3dn8uTJzJ49m1GjRmFjY4OBgUG+zgvpTWIqKipUqlQpX/s/f/48y+UBAQGZZjOuUKECNWrUQFNTkyZNmkgZ3rW1taUb2t27d882N2FG6urqSgFq6dKlXLhwAYAbN24o/V/4+fkVSc+9jD+Y/P39pdpTxYoVGTp0aKGfT/g2FIsAFR4ejp6envRaV1dXGpOj4OzsTI8ePVi9ejWxsbGcPHnyUxfzm6Kqqoq7uzv9+/dn3bp1tGrVKts8eTo6Ohw4cAA3Nzf++OMPOnXqxJw5c/jpp5/y3OauCFA5pbypXLkyv/32G1OnTuXo0aO4ubmxfv161q9fT5cuXfjpp5+k+a8+JSMjI6WpRDIyNTVl8ODBvH//nidPnkiPW7duSVNrAErTlQwePJj69etTo0YN9PT0lB46OjpZNhsdP36cmTNnAunZIvL7Q6EgMt57srKy+mJv0AufX7EIUFndxPuwyWLXrl1YWloybdo0Ll26hIWFBbdu3SqSm45CulKlSrF7925MTEz46aefqFKlCt9//32W26qoqPDTTz9hamqKra0t06dP559//mH9+vV5ap4JDQ1FS0uLypUrf7RrrJqaGgMGDGDAgAHcvXsXNzc3du/ezenTp6lZsybW1tZYWFhQsWLFPL3v/LK2tmb79u1K2TF0dHSoVasWvr6+XL9+nUmTJvHHH39ITWH//fcf//33H46OjkyePJlatWoxefJkAGrUqMH9+/fx9fXN9DeiqqqKjo4Oenp61KxZEz09PWJjY1m7di0AU6dOpW/fvp/kfWd07do1/vnnHyD9O1HU3diFr1uxuLrr6ury5MkT6fXTp08zNeFt3ryZYcOGAelzGyUkJBTKWBwhZxUrVmThwoVoa2szcuRIbt++neP29erV4+TJk0yfPp3z58/Tvn179u7dm+vzBQcHY2BgkOf7aw0aNGDZsmUEBQWxePFiNDQ0cHJyokGDBtjb23P9+vU8HS8/tLW18fX1xcnJCTMzM5ycnPDz8+P48eMcPHgQfX195s6dS9OmTdmwYYM059Ply5cpXbo0M2fOZOzYsRgZGdGqVSt8fHw4f/58pt58FSpUYOjQodStW5dXr15x4MAB/vrrLyk4ASxbtgw9PT06dOjAiBEj+O2331izZg0XLlzgxo0bREREFEnvLsW4J4C+fft+c4OthcJVLGpQrVu3Jjg4mIcPH1K9enV2797Nzp07lbapUaMGp06dwtLSkrt375KQkCB1oRWKVtWqVfH09KRPnz4MHjyYkydPoqurm+326urqzJw5k+7du2NnZ4e1tTVHjx5l2bJlOfZ+TEtLIyQkhD59+uS7rGXLluWnn37Czs6Os2fPsnHjRnbt2sWOHTto1aoVdnZ2DBo0iBIlSuT7HDnR1tbGwcEh03JTU1M6d+7M4cOHcXFx4ddff2XNmjUMGzaM06dP8/3331OiRAnkcjmPHj3ihx9+AMDd3T1TvsKoqCjq1avHxo0bgfSeYpUrV5bWz58/n/DwcMLCwggLC+Ps2bNERUVJ652cnADQ1NSkRo0aSg89PT3pebVq1fLUTHr9+nWp9gQwbty4XO8rCFkpFgFKTU2NNWvW0LNnT1JTU6VfkU5OTrRq1Yr+/fuzdOlSbG1tWb58OTKZjC1btnz2wa3fkiZNmrBjxw4GDx6MmZkZPj4+VKhQIcd92rRpw8WLF5k1axabN2/m0qVLrFu3jq5du2a5fXh4OPHx8QXq6KAgk8mkKeifPHmCu7s7W7Zswc7OjhkzZmBpaYmVlZXSvc+iJpPJ6N+/P71792b37t38+eefSlkz5HI5ERERxMbGSrWm7Gqsitx6KSkp1K9fX1r+6tWrLKdKj46O5smTJ/j4+KCpqSkFrydPnhAYGMiJEycy1ajU1NTQ1dVVClqKR82aNdHV1aVkyZLS9osWLUJNTQ2ZTIa+vj6mpqYF+rwEoVgEKIDevXtnGtc0d+5c6XnDhg3zNJGeUPg6d+6Mq6sr1tbWjBw5Em9vb6ULVFY0NTVZvnw5vXr1YsKECQwaNAg7Ozvmzp1L6dKllbZVJIktjACVkZ6eHrNnz2b69OlSZ44lS5awbNky+vTpg62tLSYmJoV6zpwo0kcNHTqUOnXqEB0dzfnz5+natauUTFURoLLreNGoUSPkcjnDhg2Takd3797NMjhBes3SyMiId+/eZTlQNykpiSdPnkhBSxHAFI8rV65ITZIZValShRo1avD06VOlXozGxsa8e/eO8uXL5/nzEQSFYhOghC/D0KFDefHiBTNnzsTW1pYtW7bkqhmoR48eXL58mcmTJ7Nx40Z8fX1xc3NT6r6u6MFX2AFKoWTJkowcOZKRI0dy/fp13Nzc2LdvH4cPH6Z+/foMHz5calr7FEqUKCFd3CdMmMDq1auZPXs2gDSZoLW1NR4eHkrjq2rVqsXYsWNxcXGRerOePHmyQJnPNTQ0qFOnTra9J9PS0nj58mWmwKUIaB92sXd3d8fd3Z2yZctm2XyoeFSpUkV0dBKyJcvjjdIvN2fG/5eUlETbtm05d+5cvvYPDQ0tFpkkPqVr167RokULpQvJ77//ztq1a7Gzs2Px4sW5bm6Vy+Xs3r2bX3/9lbi4OH777TccHBxQU1Pj119/ZcOGDTx79oykpCSioqKKfIbViIgIPDw82Lx5M2FhYZQuXZpRo0ZhZ2dX5F20o6OjqVGjBqNHj2bt2rVEREQoBZkBAwYwa9Yszp07x7Rp06hevTrh4eGsXbsWdXV17OzsAFizZg02Nja5OmdRpDq6evUqnTp1okWLFly/fh09PT2mTJmSqSammEIkIw0NDXR1dTMFroxd669du5ZjmSMiInBzc+PWrVs0atQIOzu7XP99FnUmicjISF6+fEmDBg2K5Pjwf6mOsmuuVlzjP9ba8Ynl6oIhalBCvsyfP5/nz5+zceNGqlevzpQpU3K1n0wmY+TIkRgbG2Nvb8+CBQs4ceIEGzZsIDg4GB0dHbS0tD7ZdOQVK1ZkypQp/PLLL3h6erJ161Y2bdrEpk2b6NSpE3Z2dvTu3btIUtWcP3+etLQ0unTpIpXF0tKSLVu2YGFhwc6dOzl8+LCUzeLChQsYGRkxc+ZMqQu+paUl1tbWhV62vJg/fz4aGhro6Ohw/fp1jhw5onRfTCEhISHL5sOwsDAePnzIhQsXSElJUdpHJpOhra2NgYGBUpd6RRDT0tKiV69en22mYKFoiQAl5IuKigobNmzg9evXzJ49m6pVqzJy5Mhc71+jRg0OHz7MunXrcHZ2pmPHjsTFxdGpU6ciLHX2VFVV6dq1K+3btyc5OZlNmzaxY8cOzM3NqV69OmPHjsXS0rJQe46eOnVK6syhoJhmY+3atUyZMoVZs2ZJWRkWLVpEuXLlpOa0Ro0asXz58kIrT35cvXoVHx8f+vTpw5kzZ+jatWuWwQnSf8EbGBhk24SbmprK8+fPMwWvmzdv8u7dOwIDA4mNjf1omRQzBU+fPr1A7034/ETjr5BvJUqUYOfOnRgZGTFhwoQ8Z/dQUVFh4sSJnDt3ThrMe+7cOaX5qD4HAwMDFi1aRFBQECtWrKBcuXK4uLjQoEEDbGxsuHr1aqGMITp16hT16tVTGkj86NEjqbmpbt26mJubS+tcXV2V7vX4+Ph88mwZH5o/fz4lS5akUqVKxMTEFGhKd1VVVXR1dTON3Vq4cCEBAQG8efOG8PBwLl26hKenJ7a2ttk2LX+KmYKFoicClFAg5cqVY//+/VSrVg0LC4tMOedyo2HDhmzatEl63a5dO6XxNJ+LlpYWY8eO5dKlS/zzzz/06dOH/fv3061bN0xMTNi+fXu+J1V88OABDx8+pFWrVtKy1NRUnjx5onQ/5PDhw6ipqXH37t1Mx/j7778/66SOV65cwcfHB2tra86cOYOenl6hzA+WHZlMRvny5Xn69Cmurq64ubll+0OhqGcKFj4NEaCEAtPR0cHLywt1dXWGDBmSaWBpbih6qTk4OFCmTBns7e2ZNWsW7969K+zi5plMJsPY2JitW7dy+/Ztpk+fzvPnzxk/fjyGhob88ccfSpn1IyIiWLx4MZaWlixevDjL+2m+vr4ASgEqPDyclJQUKUC9fPmSAwcOUKFCBXrGjeJjAAAgAElEQVT27JnpGLNmzaJ58+Zs3rxZmteosEVERLBw4ULMzc1ZuHCh0ntR1J5atmzJ48ePsba2LrIa3Zs3b1iyZAkNGjRg6NChXL16FXt7e86ePZspsfCnmClY+DREgBIKRf369dmzZw/v37/HzMwsz2moFGOgLCws8PPzY/jw4Rw9epQOHTpw/vz5oihyvujo6DBz5kxu376Nu7s7hoaGrFy5kqZNmzJs2DC8vLzo0qULLi4ueHl54eLigqmpaaYgdfr0abS0tJR6dymCdK1atYiIiKBTp04kJCTw+vVrwsLCgPQURsePHwegefPmlChRgokTJ9KsWTM8PT0/OklfXkRERNCxY0ecnZ3Zt28fzs7OfP/990RGRnLlyhVOnDiBjY0N3t7eaGhoKDVHFpaAgAAWLVpEnTp1mDVrFqVKlWLFihU8ePCA5cuX07ZtWy5cuMCcOXMYMmQIc+bMER0kviIiQAmFpn379mzevJkHDx5IM8PmVnBwMBoaGtSoUYMyZcqwaNEili1bRnx8PH379mXmzJkkJCQUYenzRkNDgyFDhuDj48PFixf58ccfOXv2LJaWlplqkA8fPsTd3V16nZKSwtmzZ+nYsSPq6urSckWAqlmzJu7u7llO3xEVFUW7du2kVFPXrl1j9erVxMfHM2bMGNq3b8/x48cL5R6Zm5ub1DtOQdEBQVF7Gjp0KEeOHKF79+6FFhSSkpLYvXs3nTt3pn379vz777/07NmTY8eOcePGDcaNG6c0IFlbW5vp06ezfft2pk+fLoLTV0QEKKFQ9evXjyVLluDv74+lpWWmbsPZCQ4ORl9fX6mJyNTUlCtXrtCrVy9Wr15N586duXnzZlEVPd8aN27MqlWrCAoKokqVKlluo0hNBOnzJUVHR0vdyxUUga1WrVpK22e0atUqPD09GTBgAAEBATx69AgbGxtu377NggULCAsLY+DAgXTt2rXAmVeyK8OZM2c4ceIEtra2Ujf4wpjzKTw8nDlz5mBgYIClpSXBwcE4ODiwfft2PD096dKli0hv9o0RAUoodLa2tjg4OODj48PkyZM/+mteLpcTEhKSZffj7777jl27drFmzRoeP36Mqakpy5cvJzU1taiKny9yuZytW7fy6tWrLNdfu3aN/fv3k5yczKlTpwAyBajHjx9TqlQpKleunG0tIDk5GTs7OylzuaurK5A+NcrUqVMJCgrC0dGR//3vf3Tt2pVBgwblO6g3atQoy+VPnjyhZMmSjB8/nr///pt27dpl27X8Y+RyOefPn2f06NHUq1ePP//8k+rVq+Pm5kZoaCjz5s2jatWq+Tq28OUTAUooEn/88QejRo3Cw8ODBQsW5LhtREQEb9++zXZ8jEwmY8yYMVy8eJEWLVowe/Zsevfuna/OGEXh/fv3jBkzBicnJ1q2bEmNGjWU1mtpafH27VusrKwwMjJi4cKFaGhoULduXaXtFGOgZDJZllkXateuTUBAAOvWrZNm2nVzc+OXX37h/v37QHqvSmdnZ+7cucOECRM4deoUbdq0YcyYMYSGhubpfdnZ2VGtWjWlZTo6OoSEhGBra8v58+eJiIjIV9by2NhYNm3aROvWrenevTuHDh1i6NChnD17losXL2JhYVHcMh8In4EIUEKRkMlkrF69mm7durFo0SL+/vvvbLfNbQ4+fX19jh8/jrOzM9euXcPY2BgPD48imdcot+7fv0+XLl04ePAg48aNw8fHh3PnzuHk5CQNOh49ejT3799n7dq10jQfSUlJWFlZcfPmTan8igAVHR3NkSNHABg7dqw0t5Svry/VqlXD3NycS5cuScd3c3OjSZMmDBo0iNOnTyOXy6lSpQpLly4lMDAQCwsL9u3bR5MmTVi+fDnh4eG5em/a2tqYmpoik8no27cvc+bMoV69epQsWZJp06axfv16qlSpgpmZWa4/r9DQUH777Tf09fWZOHEiUVFRzJ49m5CQELZs2ULbtm1FM54gEQFKKDLq6up4eHjQvHlzpkyZImVE+JAiQH1Yo8iKqqoqU6dO5fTp0+jq6jJx4kRGjRrF69evC7XsuXH48GFMTU0JCwvDzc2Nv/76C3V1dWlOqCNHjmBiYsK2bduIjY3FwsICFxcXIH2Q8+HDh5kyZQodOnRg3bp1vHjxAl1dXTp27Aikd5ZYsWIFW7ZswcHBQanZTyaTsWbNGgC6d++OjY0Nvr6+9O7dmzZt2uDh4UFiYiI1a9bEzc0Nf39/+vbty+HDhzEyMmLGjBlERETk+P5SUlLw8fHBxMSEffv2YWJiwpkzZ7Czs+Px48cEBARgbW2NhoZGjsdJS0vj+PHjDBgwACMjI1atWkWTJk3YuXMnQUFB/P7779neuxO+bSJACUVKS0uLvXv3UrNmTaysrLhy5UqmbfISoBSaNm3KuXPnmDhxIkePHqVdu3bZBsDClpqaypw5cxg9ejQVK1bk5MmTDB8+PMttZ8yYQVxcHCtWrADSxz+pqKhw//597t69i5WVFVFRUTg6OgLpM0crmi63bt2aYzlq1apFmzZtCAwMZOXKlYSEhODs7Mzr16+xs7OjXr16LFiwgNevX9OgQQP27NnD2rVrad++PcuWLaNBgwb8+eefxMTEZHn8c+fOERERIdWQ5s2bR8mSJZk6dSrr169HTU0txyS1UVFRrFy5kkaNGjFw4EDOnz+PjY0N165d499//8XMzEypF6MgfEgEKKHIVa5cGS8vLzQ1NRk+fLgUkBRCQkLQ1tZWSvmTGyVLlmTBggUcPnyYEiVKMGLECH7++Wfev39fmMVXorhgL126lB49enD27Nkcsxa0b98eU1NTNm3axMuXLzl16hQtW7akQoUKVK5cGXNzc27duoWFhUWmfV+8ePHRziCK6U/Onj1LpUqVcHR05N69e2zatImqVasyd+5cDAwMGD9+PHfv3qVBgwb8888/HDt2jHr16jFnzhwaNmzI2rVrSUxMVDr2gQMHpEkWL126xMmTJ7Gzs0Mmk7F//34GDhyIjo5OpjIFBgYyYcIE6tSpw/Tp05HJZCxevJgHDx6wZs2abDtfCMKHRIASPok6derg6elJQkICgwYNUsq3FxwcXKA5oExMTKTBvVu3bsXY2JjLly8XRrGV3LhxAxMTE3x9fXF0dMTT0/OjswpD+tQk8fHx/PLLL4SFhWXqvaemppZlUB0xYgTNmjVjxYoV2TbHDRo0CFVVVXbv3i0tK1GiBObm5ly+fBkfHx+6du3K33//TfPmzXF0dOTff//F1NSU8+fPs2fPHrS1tZk2bRqNGzfGw8OD1NRUUlNTOXjwIMbGxlStWpX58+dLPQXd3d1JTk5W6hyRkpKCt7c33bp1o3Xr1ri7u2NiYsKhQ4cIDAzk559/FpMXCnkmApTwybRq1QoPDw/Cw8MZMmQI0dHRpKSk8PDhwwJPUli+fHnc3NzYunUr796944cffmDOnDlZzgKbHzt27KB79+68e/eOPXv2MGPGjFxPtNeuXTtMTU2l/IIfTnkfGhqKt7c3gJSiZ9euXfz1119oaGjg5OREgwYNGD9+fKZch5UrV6ZLly54e3tnGsgsk8kwMTFh//793Lx5k59++ombN2/Sr18/WrZsyZYtW+jZsyf+/v64ubkB6T33WrZsyW+//carV68wMzNTqj1VrFgRNzc3GjdujLGxMS9evGDBggUMGjSIsWPHcuvWLSZNmsStW7c4cOAAPXr0EBMSCvkmvjnCJ9WjRw9Wr17NzZs3MTc3Jzg4mOTk5Dzdf8rJoEGDuHz5MqampixdupQuXbpkmWg1t5KSkpgyZQr29vbUqVOHM2fO5Csh6owZM6TnLVu2lJ7HxMQo3b9SNHf27NmTcePGce3aNQ4ePEi3bt3YuXMnJiYmdO3ald27d0tNciNGjCA6OlpKgZQVAwMDVq5cye7du5k3bx7v3r3D3t4eAwMDFixYQI8ePQgMDGTZsmVERkZK46zKlSvHvHnzpNrToUOHePbsGc2bN8fS0hIDAwPmzp1L+fLlWb58OaGhoVJqIkGZXC5HLpeTlpZGamoqKSkppKSkkJycTFJSEomJiSQmJpKQkEB8fDxxcXHExcURGxtLTEwM79+/5/3790RHR/Pu3TvevXvH27dvpW0iIiKIiIjgzZs3vH79mtevX/Pq1StevnxZrLKw5MU3MaPuzp07Wbp0KZD+JXnz5g3lypVj5cqVeT5WYmIiqqqqqKmpIZfLlbrEfux5bpdl9zwyMlK6T5Ofc+X3vM+ePUNHRweZTFbgYymer1u3jpUrV1K2bFmio6NZu3YtPXr0kLaLiYkhNjZWGqSZ1/cjl8vZvn07Li4uyOVyHB0dsba2RkVFJdv9IyIiSEhIkNIIPX/+HBsbG/z9/Rk4cCDLly9HU1MzX59tcnIylStXBuDSpUscPXqUW7du8d9//0ndvmvVqsXTp08ZPnw469ev50NPnjzB3d2dLVu2EBERQaVKlbC0tGTUqFF06NCBXr16sWvXrkz7wf/Nqurn50e7du1ISkriwIEDrF69moCAADQ0NBg2bBj29vbo6upmmmG2Xbt2eHp6Ko3xUlVVpU+fPlhZWVGhQgX09PQoUaKEdC7FBbmgr8PCwtDT08t2/ceOldP2CQkJpKWlUbJkyWy3LQhFEMo4pkvxd5Tx+1KQ1zExMchkMsqUKaO0LuP3sGrVqlSqVKnA76cQ5WosQbEJUMePH2fSpEmkpqZiY2Mj9WrKyNPTE2dnZ2QyGU2bNmXnzp15Pk9hT/me8fPL+OX+cFlunn9s/8DAQOkGc26Pld9yZVwWEhKCvr6+dOEvyLEyLps7dy6enp4AeHt7U6dOHWl9XFwc8fHxmT7nvH62Dx8+ZPbs2dy5c4eWLVvi5OQkBb0P90lISCAlJQVNTU0CAgKYNWsW0dHRTJgwgaFDh0p/8Pn5bG/evMmkSZMA0NTUVMpTqKWlRVpaGnFxcQDMnTsXY2NjspOUlMTZs2fx9vYmKCgIFRUVKUnsoUOH0NLSynbf2NhY6UKmEBgYiKenJ+fPn0cul6OhoUFSUpI0u29WbG1tMTMzo0qVKshkMl6/fo22tjbq6uqFduFVPL937x6GhobZbvvhsrwc+/nz56SlpaGnp5fj8fJLTPmerS8nQKWmplKvXj3+/fdfdHV1ad26Nbt27ZJGy0P6jfRhw4Zx+vRpKlSowKtXr6RfpHlR2AHqU/rvv/9o3br1Jz/vtWvXaNGiRaHfS0hNTZU6GcydO5fJkydL6yIjI4mKiiqUpqLk5GSWLFnCX3/9haamJkuWLGH48OGZLj6vXr0iNjaWY8eOMWvWLLS1tdm6dSvff/99gcswd+5clixZgra2do7T2ZcuXZqHDx9SqlSpXB3X39+fzZs3s337dmnZihUrGD16NGXKlMm0vZ+fHx06dMjyWKGhoaxbt05q3suOYpxVrVq1pGUBAQHUr1+f0qVL56rceZFTmQvq6dOnpKamZqoxFhYRoLKVqwBVLO5BXb16lbp166Kvr4+GhgYjRozg4MGDStu4ubkxYcIE6YKWn+AkFC+qqqrS/ZjZs2fj5eVVJOdRV1fn999/5+TJk1SuXBk7OzssLS0z9YyLi4vD0dGR33//nRYtWnD+/PlCCU6QPr1G7dq1adKkSY7bxcXF8cMPP2BmZoatrS2Ojo789ddfbN68GW9vb86fP8+dO3d48eIFSUlJtGzZUspbpzB58mRq167N5MmTCQoKynUZ69Spg5OTU5br2rVrJz2/evUqjRs3ZurUqVmmZBKEwqL2uQsA6VmMM0Z/XV3dTAM6FbnGjI2NSU1NxdnZmR9++OGTllMofOHh4bRq1Yro6Gjs7Oz47rvvpEwKha1ly5ZcuHABJycnNm7cyKVLl1i7di3du3cnNDSUESNGcO/ePaytrVm4cKGUlqigIiIiCAgIYOzYsejo6HDmzJkct5fL5dy7d4+IiAip2S87ZcuWpWLFikr3FzQ1NYmJicHV1RVXV1dUVVWZNWsWY8aMyTa7fFBQkLR9Rurq6jRu3Fjqtl+5cmUWLFjA/v37WbduHVu3bmXixIl069YtF5+EIORNsQhQWTUzftj8kpKSQnBwMGfOnOHp06d07NiRW7duibEVX7Do6GhevHiBmZkZ48ePp1u3bowaNYrjx49nSlJaWEqXLs2SJUv44YcfGD9+PIMHD0ZPT48XL14gk8lwcXGR7hUVlrNnzyKXy+natSsdOnRg8+bNPHv2TFqfsdnv8ePHSmOr4uPjiYyMlHpoKR4Zl0VFRSnVBj+ch0uR+WLOnDnSMn19fcqXL8/169dzLHtycjJv376VXr9+/RobGxtMTExwcHDg4sWLLFq0iHXr1jFt2jR++eWXImnmE75NxSJA6erq8uTJE+n106dPM41Q19XVpV27dqirq1O7dm3q169PcHDwZ7knIxQOxSy6BgYG1KhRg/379/PDDz8wePBg9u3bl+v7MPnRrVs3Ll26RO3ataXv3pw5cxgwYEChn+v06dOoqqrSsWNHypUrh5+fn1RrU3S+2L17N8bGxpkG/pYqVYrq1atTvXr1bI+v6JiguJdbvnx5Dhw4IAWwx48fs2bNGqXu9h9ORJgTxbaLFy+mX79+rFu3jr///puzZ89St25d+vTpw82bN3F2dmbDhg3MmDEDS0tLkcZIKLBicQ+qdevWBAcH8/DhQ2k2zf79+yttM3DgQHx9fQF48+YN9+/fR19f/3MUVygkH+bga9y4MTt37uT169f8+OOPREdHF9m5o6Ki+Omnn5SWzZ07l3Xr1pGcnFxo55HL5Zw+fZrWrVtTrlw5IL3G5ObmRlpaGvHx8dK9t7xkBc+KqqoqQ4cO5fbt2yQnJ9O8eXO6deuGtbU1AQEBXLx4Mcu5lZYuXcrTp09z7BWrqqqKhYUFtWrV4q+//iI0NJTFixeTnJzM0aNHefv2LTVr1uTdu3f8/PPPNG3alN27dxfqFPTCt6dYBCg1NTXWrFlDz549adCgAcOGDcPIyAgnJycOHToEQM+ePalYsSINGzbE1NSUxYsX5zl3m1C8ZKxBKZiYmODq6kpwcDCTJ08ukgGGt27dwsTEhBMnTjBt2jSioqK4c+cObdq0wdXVle7du2fKF5hfwcHBPH36NFN6oxYtWtCrVy/++ecfKdtFnz59Cnw+xaDfPXv2AOnj9nbt2kWnTp0wNjbm1atXDBgwgM2bN0tZxKdNm0aTJk0YNWpUtsdt3ry5UnN62bJl+fnnn7l9+za7du2idu3aPH78WLpn9uDBAywtLWnXrh3//PPPZ50SRfhyFYtu5p+S6Gaed0XVzdzS0pITJ04QHh6e6Z7jokWLmD9/Pv3792fr1q1KU8EXhKenJz///DNqamq4urrSr18/ad2LFy9wc3Nj1apVqKio4OLigq2tbYHGwqxfv57p06dz8uRJ2rRpo7QuICAAExMT6XV+a4wZxx7J5XKaNm3Ks2fPmDBhAn///TevXr2iUqVKWFlZ0aJFCwYNGiTtm5SUhLe3N+vXr+fSpUtA+n26DztnnDp1KsexWQEBAcTExLBx40a8vLwyJblt3749Li4u+eoVKbqZ50x0MxeEIhASEkLdunWzDAC2traMHj2aQ4cO8dtvvxX4F3hycjK//fYbNjY26Onp4evrqxScAFRUVLCwsODcuXPUq1cPBwcHzMzMeP78eb7Pe+rUKcqXL6+U3kihefPm+T5uVhTTp9+/f5+YmBgWLVqEnp4emzZtIiQkBBcXl0zzLikySCxbtkxapmiWU1zQGjZsmGNwUmjZsiXbtm3j7t27TJ06VWrShPTsGd26daN///7cuHGjMN6u8A0QAUr4LNLS0ggJCclxIO7UqVMxMzPDzc2N5cuX5/tcL1++pF+/fri6ujJgwAB8fX2pV69etts3aNCAU6dO4eDggK+vL23bts3XGK3ExEQuXLhA586ds60BFkaPt5iYGNzc3GjVqhU9evSQlhsbG3Px4kXMzc0/+utZ8f4CAwN5+PAhixYtkppXFdPHBwYG5qo8NWrUYMGCBYSGhrJs2TKle8UnTpygXbt2WFhYSE28gpAdEaCEz+L58+fExcXlmMVcRUWFDRs20KlTJ5ydnfOV2urKlSt07NiRy5cv4+LigoeHR5YZFj6kyCLu4+ND+fLlsbS0xMbGRqnLdW7OHRcXl+n+U0YZm9LCwsJyfWxIr4E6OjpSt25dfv75Z96+fYuzszOPHz+mVatWPHz48KPzSUF6zcvLy4tGjRphYGBAhQoV+OWXX6RMLt27d8fd3Z3WrVvTtWtX9u3bl6uOJFpaWowfP15KpZSxeW/v3r00bdqU8ePH8/Tp0zy9b+HbIQKU8FkoOiF8bJqNEiVKsGPHDoyMjJg4cSInT57M1fHlcjlubm707t2b5ORkvL29mTRpUp7vJ7Vt2xY/Pz8sLS3x9PSkffv2nD17Nlf7nj59GgBTU9Ms13/YEWPJkiUfPaZi+nQzMzNatGjBunXraNq0Kbt27eLevXs4OjpSpUoVRowYwbNnz7hw4cJHj3nr1i1CQ0OV7k1duHCBO3fu4OzszOHDh7l16xaTJ0/mzp07mJubU69ePebNm5er5k9VVVX69+/PyZMn8fPzY8SIEaipqZGamoq7uztGRkY4Ojp+dAp64dsjApTwWeQ2QEH6lA/79++nWrVqWFhYZJoT6UPx8fGMGzeOadOm0ahRI86dO0fnzp3zXVYtLS1WrVrFnj17SEpKol+/fjg6OhIfH5/jfqdPn6Zu3brZ3oA/cuSI9LxPnz5s376dx48fZ7ltVFQUq1evplmzZgwbNgw/Pz+sra2lSQkHDRqEmtr/DWscPHgwKioqUm++nOzfvx9Q7ubu6uqKhoYGY8eOBdLTIC1cuJDQ0FBcXV2pXLky8+bNw8DAAAsLC27cuJGr+4QtWrRgy5Yt3Lt3j19//ZUKFSqQmJjIihUrMDQ0ZP78+UU6I7LwZREBSvgsPhwD9TE6Ojp4eXmhrq7OkCFDePjwYZbbPXr0iB49erBr1y7GjBmDj49Ptr2b8qpXr15cuXKFvn37sm7dOkxMTPjf//6X5bZv3rzhxo0bOTbvHT58GEi/+M+cOZOUlBTGjBmDpaUlixcvJjIyksDAQH755RcMDQ2ZOXMmqqqqLFy4kKCgIJYvX66UUDmjatWq0blzZw4cOJBpKveMFM17hoaGUk+z8PBwvL29GTx4cKacl6VLl8bS0pLLly/j6+vL4MGD8fb2xt7enk6dOrFp06ZMmSyyUr16dVxcXAgJCWHVqlXUrVuX9+/f4+LiQsOGDVm9ejUJCQlERESwfft2zM3NWbhwYY6JdoWvT74DlKurK82aNaNZs2bUrl0722YMQchKSEgI1apVy3FqiA/Vr1+fPXv28P79ewYNGsSbN2+U1p86dQoTExPu3r3LqlWrWLNmTaF3ra1UqRI7duxg3bp1hIeHY2pqypIlSzLd61EMKv9w9lyFZ8+ece3aNSB9Hqhq1apJ03x4eXnh4uKCoaEhxsbGbN26lU6dOuHl5YW/vz/jx4/PVYqv4cOHExUVxb///pvtNnfv3uX+/ftKtSc3NzdSU1Oxt7fPdj+ZTEb79u3ZunUrISEh2NnZERkZycSJE9HX1+fXX3/NVScITU1N7OzsuHnzJl5eXnTu3JnXr1/z66+/0qBBA5o1a4a7uzv79u3D2dmZ77//XgSpb0i+A9S4ceO4ceMG//33H7q6ukydOrUwyyV85UJCQvI1zXv79u3ZvHkzjx49YujQocTGxpKWlsbixYsxMzOjdOnSHD9+HEtLy8Iv9P8nk8kwNzfn4sWLtGnThrlz5/LDDz8opQ86ffo0ampq2Y77OXbsmPS8Vq1auLu7Z6p5JCQk0K5dOwICAti7dy/dunXL01i0gQMHUqJEiRyb+T7MYpGYmIi7uzstW7bM9Zi7KlWqYGVlxY0bN9i1axdNmzZl9erVNGrUiH79+nHs2LGPdtZQUVGhd+/eHD9+nCtXrmBubs7Lly95/fq10nYPHjyQpqcXvn4FbuKbNGkSXbp0yTSmRBCyk5CQwOPHj/MVoAD69evHkiVL8Pf3Z/DgwQwfPhwXFxc6duzIuXPnaNWqVSGXOGu1atXi6NGjzJ07l+vXr2NsbMyWLVuk9EZt27bNtsegonkP0nv7Ke4DfUhHRyffKb3KlStHr169OHLkSLb3dQ4cOICBgQFGRkZAesB69eoV48aNy3OHEnV1dQYNGsSJEye4fv06dnZ2+Pn5YWZmhpGREcuWLctVR4imTZuyadMmevXqleX63HZ3F758BQpQW7Zs4fHjx8yePbuwyiN8Ax48eIBcLs/1/aes2NjY0LdvX/z8/PDx8eHnn3/G29ub7777rhBL+nGqqqpMnjyZM2fOULNmTX755ReaNGnC8+fPs23ei4qK4ty5c9LYqFu3bnHnzp0st1XMoJxfw4cPJz4+XkoZltG9e/e4ffs2gwYNkoKRq6srFStWZOjQoQU6b8OGDVm1ahUPHjxg2bJlaGhoMGPGDOrUqYOdnd1HO7oA2dbgGjduXKCyCV+OfAcof39/lixZwvbt2ws9BY7wdctrB4msHDhwQOrGDek37zP2YvvUGjduzJkzZ/jll1+knnjZzeXk4+NDamrqR5u9ateuLfWiy69evXpRtmzZLJv5Pmze8/f358qVK1hZWRXavbty5coxfvx4/ve//3H06FF69OjB9u3bad++PSYmJuzatSvbThx2dnaZao/6+vrY2toWStmE4i/fkWXNmjVERkZiampKs2bNsLGxKcxyCV+xrJLE5lZKSgqzZs3ixx9/pFq1aly4cIFu3bqxaNEi3N3dC7uoeVKyZEnmzZsnXdyXLFnC+PHjM+XYO3LkSLaZJRo2bIiZmRlOTk74+voWOOdjyZIlGThwIKdOneLVq1dK6w4cOEDt2rVp2rQpkF57UtBkgEUAACAASURBVFFRKZIAIJPJ6Nq1K56enty9excHBwdCQ0OxsrKibt26zJ49W2nKHUjP+n7hwgWsra0ZMmQIc+bM4cKFC58lD6bweeQ7QP399988e/aMGzducOPGDTZt2lSY5RK+YsHBwWhoaOQ5QeebN28YOHAgq1atok+fPpw5c4YmTZrg4eFB8+bNmTp1qlLng89BkR5IMfni9u3bMTY2xs/PD0gfo3Xy5Mlsa49Dhgxhy5YtODg4FNqFePjw4aSmpiqlawoJCeHmzZsMHjwYmUzGmzdv8PT0pF+/fkWWOFWhZs2azJs3j5CQEDZt2kStWrVYtGgRhoaGjBgxAl9fX2lMlba2NqNHj2b79u1Mnz5dBKdvjGibEz654OBg9PX185Sh3N/fn06dOnH+/Hn++OMPduzYISUj1dLSYu/evdSsWRMrKyuuXLlSVEX/qEuXLpGQkMCgQYNwdXVl27ZtvH//nl69ekmpk+Li4jLNRQXp085YWFgUepk6d+5MlSpV2L17t7TswIEDAFL2iC1btpCYmMi4ceMK/fzZKVmyJObm5pw/f54LFy4wcuRI/vnnH3r16kXz5s1xdXUVg3a/cSJACZ+UXC4nODg4T/eftmzZQs+ePYmJiWH//v38+uuvme57Vq5cGS8vLzQ1NRk2bFihzeeUVx+mNxowYACXL1+me/furFixgjFjxgDpmR4UBg4cSN++fUlJSZECR2FSTGR4+fJlKTXRgQMHqFGjBi1atCA1NZUNGzZgaGhYoIwbBdGqVSs2bdpEaGgo8+bNIzY2lsmTJ6Ovr8+qVasICgr6LOUSPi8RoIRPKjIykrdv3+bq/lNiYiI///yzlEnh3LlzdOvWLdvt69Spw969e0lMTGTQoEG8ePGiMIueK6dPn6Z+/fro6upKy6pWrcrevXuVcu3NnTtXeu7h4cG2bdto2LAhCxcuzFNC2txSTGR4+vRpHjx4wPXr1zEzM0Mmk3H06FGePHmCvb19gea+KgyVKlXCwcGBoKAg9u3bR5s2bfD29qZZs2b06tWLgwcPkpKS8lnLKHw6IkAJn1Ruc/A9e/YMa2trtm7dyogRIzhx4gS1atX66PFbtmyJh4cH4eHhDB48uEinjf/Qy5cvCQwMzDK9kUwmw9DQUHq9efNmAKmXmqqqKvPmzSMyMjJXSWPzqlWrVujr63Py5MlMzXvr16+nTJkyOc6o+6mpqqrSt29fjh49ypYtW5gwYQL+/v4MHz4cQ0NDFi1alKnTh/D1EQFK+KRyE6DOnj1L3759uXfvHkuWLGHDhg15mjepR48erF69msDAQMzNzaUp1YtSREQEDg4OQPo4p6zS8SiSw966dUta9uDBA3bu3IlcLqdbt2506dIFV1dXHj16VKjlk8lkjBgxgsePH+Pi4oKuri5t2rQhKCgIX19fLCwscjUNyedQo0YNli5dyoMHD1i9ejVly5Zl9uzZ1K1bFysrK65evSqmlP9KiQAlfFI5jYGSy+WsWrWKAQMGoKamhpubG3Z2dvlqdjI3N2fWrFmcOXMGe3t7aZbYohAREUGXLl04ePAgALt378bU1FQpSMnlco4ePUrLli3R1NRU2n/cuHFYWFgQERHB/PnzSUlJwdnZudDLqWjmU3TikMlkuLq6AmTZaaO40dLSwtbWFn9/f06cOEHfvn3x9PSkU6dOGBsb4+Hh8dEM88KX5fONbPyEwsLC/l975x0W1bH///fCLr3bhVgARQVRUZQbRVGjKCJRRCyxICgSS/wmV9REwRZbYpIb470xMaBgQ0WRRQUVgzUaIGIEyRVUDAKKAsLCUrad3x/+zrnbd+mrzut5znP6zOe0ec/MmZkP8vLyQFEUBAIBTE1NkZiYyIyTJp/7UrdOj5dGO2xrzLlNWZfeJhAIUFhYKHNMa8dPURTq6+uRn58PFoul1j5twrtz5w4sLCzw/PlzPH/+nNnP5/OxY8cO/Prrr3B1dcXGjRthZmaGe/fuaW2v/L7x48fj3r17OHnyJPT19REWFqb2fKFQCIlEIjP+G0VRGgXyyJEjCqOrFxQUYPz48XBxcYGpqSlKSkrw9OlTGBoaYuHChcxxe/bswfnz58HlcnH9+nWEh4dj0qRJOH36NMaOHatytHJpmiLgDg4OuHTpEmJiYjB06FCUl5czTeFVha9uXl1djezsbOjr62t1vKa59DXV19fjr7/+ktnepUsXbNq0CcuWLcPJkycRHx+P0NBQhIeHY8aMGZgzZw5sbW01xlVZWQmJRMK0KG0J26Xn1dXVaGhoQGVlpcw1yV+jqmuXXlc1F4vFYLFYTMdv+f1vMqxGFo3fyHL09evXkZSUBBaLBYlEgqtXr8LNzU2mSa38w1S1XlFRAWNjY5kqJ23Pbeo6ve3x48fMPwtlL3drrT948AB9+/aFnp6e1raqWh8zZgwsLS1lxqKjO2zm5+dj8eLF2LRpE/h8Png8Hnr06NGsa5VIJAgKCsK5c+ewfft2pWPM0esvX75EbW2tzL8ubT7yoKAgpS7h9fX1tfJoq47AwEBYWlrC0tISFhYWzJyeLC0tYWNjAysrK5iammq0l+5EfOnSJeTk5ODTTz9FfHw8fH19lR5Ppw/q5hRFITs7Gw4ODjA2NlbINGgThrp5dnY2XFxc1B4nEAhw/vx5xMbGIjMzEywWC+PGjcOCBQswcuRI6OnpKT3v1atXkEgksLGxkbFVm2tWdo3y6/X19aitrYW1tbXa41TNtTmO7ntnaGio8rg+ffrINNzRAbRST50pQaWkpGDVqlUQi8VYvHgx1q1bp/S4+Ph4zJw5ExkZGVoPCurp6QlPT08Ar0shI0aMwNdff90kO8ViMaytrdulw+DTp0/RtWvXNo+XzWbDysqq2UNaiUQiPHnyBIGBgUw119mzZ7F06VKIRCLs37+fqYYSiURgs9kwNjZutv3R0dHw8/PD+vXr0b17dxnXEtLQudXG5jydnZ2VCtT69euxatUq8Hg89O/fH/X19Th06JBMX6egoCCYm5uDx+OhsLCQcdNBc+LECa3t0NfXlxEu+bl0n6KpU6cyCZuNjQ2Ki4thaWmpIHLa5sb19PRgYGAAQ0NDre3VFjabrdX3FhoaitDQUPz555/Yt28f4uLicPnyZTg6OmLp0qWYP3++gpsSuuTRo0ePFrcbeJ2hLS0tZXxttQaFhYVgsVgq/Z69yf/ndEKgxGIxli9fjkuXLsHOzg7u7u7w8/NTqN6orq7Gnj17MGLEiHaylNAc/v77bwiFQjg6OkIsFmPbtm3YvXs3evXqhSNHjrTaIKDGxsaIi4uDt7c3QkND0alTJybD0hKEhITg8OHDMtV89Dh6HA4HFRUVqK+vxz//+U+ZVoWBgYGYP3++wqCo8fHxCAsLYxp3FBYWQiwWo6qqCjwej5nodbq0Sa/T85cvX+LRo0eoqqpSGBeQFicAMq0ONYmc/JyeSkpKYG5ujq5du2pVkmtNBg0ahB9//BHbt29HbGws9u3bh/DwcGzcuBFz585FWFhYswfhJbQNOiFQ6enpcHR0ZKqvZs+ejcTERAWBioiIwJo1a1qlGS6hdSkvL8euXbsAvB4Vws/PD9evX8fEiROxf/9+WFtbt2r8HTp0wOnTp5khiFJSUhgXE83FxsYGaWlpiI6ORk5ODlxcXBAcHMzk+s+dOwcA8PX1xbZt25jzVA0pFBAQgH/84x9MrrtHjx7IyMiAk5OT0uM5HI5GQRAKhXB3d1fZ4XXs2LEYNGhQo0ROFU0ROQsLC1hZWTHbWkLkrK2tsWrVKqxcuRKXLl3Cjz/+iKioKPzyyy8YNWoUwsLCMHToUDLYtQ6jEwJVXFwsUzy1s7NTGK4mKysLT58+ha+vLxGoNwy6lRtdwqCbW69atQqbN29uswSiR48eOHXqFCZNmgR/f3+kpqa2mDt4Gxsbppm5PElJSbC1tUWvXr1w5coVODg44NGjR2r7ddna2qKiooIROXd3d3z11VcICAjAgQMHcP/+fTg7OyMkJARdunTRaF9ZWRkePHiA7t27o6SkRGF/hw4dsHPnTrVhCIVCVFVVKYhYVVUVcnNzYWRkhLq6uhYXOTabjW7dumklctJiR4ucnp4evL294e3tjUePHmH//v2IiYnBvHnz0LlzZ8yaNQuLFi0Cl8tlMhihoaFk3D8dQCcESlkdqXTuSSKR4NNPP8XBgwfb0CpCSxEdHa3Qyg147YqhrXOvAwcOxNGjR+Hv748ZM2YgJSWlVROiZ8+eISMjA6GhoUhOToZIJMKQIUM0ChTw+t8Ll8uFn58fAGDNmjXYuHEj05T69OnTOHz4MG7cuIEOHTqoDYvL5YKiKLi6uioVKG2qVzkcDjp27IiOHTsq7MvKyoKTk5PG/mrqRE7VvLi4uMVLcn5+frh06RJKSkrwww8/4IcffmDOi4+PR2xsLBk5XQfQCYGys7OTGWq/qKgI3bt3Z9arq6uRk5PDjBP2/Plz+Pn5gcvltpn3VELTuX//vtLt0h1W25IxY8bgp59+QnBwMObMmYPExMQW838kDz26uq+vL/bu3QsLCwumKrtnz54oLS1Ve76XlxcmTpyIixcvwtTUVMEtfEFBAX755ResXbtWbTinTp1Cx44dsWTJEuTl5cm4p29LH0vqRE4Vv/32G95//31mvSki19iSHO1aXtN9JbQuOiFQ7u7uyM/PR0FBAWxtbREXF4ejR48y+y0tLVFWVsase3l5Yffu3USc3hBUtXJrzx/VAQEBeP78Ob744gssXrwYMTExrRJPUlISrKys4OLigrS0NPj7++PZs2dgs9mwtbVVKlAUReHhw4dIT09Heno6Ll++DAAK4kRz9+5dtTaUlpbixo0bCAoKgrW1NW7cuIH9+/cjOzsbAwcOxJIlS96okkJTRE4eWuQePHiAiIgIpX3AiGv59kcnBIrNZmPv3r3w9vaGWCxGcHAwnJ2dERkZiWHDhjFVHIQ3E3Wt3NqTFStWoLi4GP/+97+xZs0arFmzpkXDr6ysxLVr1zBz5kxcuHABQqEQH3zwAb788ksYGBjg22+/hZubG3g8Hv744w+kp6cjIyMDGRkZePXqFYDXzbednZ3VJpYJCQnMvxNlcLlcSCQSpnm9jY3NO18yoEWuvr4ew4cPVypQxLV8+6MTAgUAPj4+8PHxkdkmPeKzNFeuXGkDiwgthaZWbu3Jtm3b8OzZM+zfvx+WlpaMO4yW4MKFCxCJRJg6dSpiYmJgZmaGbdu2MS7ht27dCjabLTM6t42NDUaMGAF3d3cMHz4cbm5uMDc3x4sXLzBo0CCIRCKlLtKHDRuGLVu2YPXq1Qr/9RISEmBjY4MxY8YgIyOjxa7vbWHOnDngcrntVu1JUI3OCBTh7UZdK7f2RE9PDz/99BPKysqwe/duWFlZ4ZNPPmmRsM+ePQtjY2MMGzYMCxcuhJOTk8J/N5FIhKFDh2LJkiUYPnw4HBwclDav7ty5M/75z39iy5YtTEnIxcUF06dPx/z585GTk4PIyEh89913yMzMhK2tLYDXrfeuXr2KefPmgcPhtMh1vW1YWVm98dWebytEoAjvPIaGhjhy5AgmTJiATZs2YcCAAWr9TmkD7dp9/PjxSEtLg1AohJmZmdJje/bsqZWri2XLliEqKgqZmZnIzMxkGnakp6cjJiYGH3/8MV69egUHBwfExsYiMDAQXC4XYrFY5egZhNeQak/dhPRQIxDwuiFOVFQUOnXqhPnz5yMrK6tZ4V25cgV8Ph++vr44c+YMzMzMVHqr1baxiImJCSIjI1FYWIiffvqJ2c5isbBo0SI8ePCAKSUtWLAAXl5eiI2NhaWlJePht6mUl5dj586dmDdvHnbu3KnUnQiB0NIQgSIQ/j9dunTBjz/+CA6Hg4CAAKV9t7QlKSkJ+vr6GDlyJC5fvoxJkyYhLCwMvXv3ljmue/fujWosMmvWLAwePBi7d+9GeXm5zL6ePXuisrISX3zxBQDg9u3buH37NmxsbGBgYNDkaykvL4enpyc2bdqE+Ph4bNq0CaNGjSIiRWh1iEARCFLY29vjxIkTqK6uxvTp02W6N2iLSCTC+fPn4enpiVu3bkEgEGD69OlMY5HIyEj4+/sjMjIS//73vxv1r0NPTw/btm1DVVUVduzYobBfX18fkZGRyMzMZLYVFBRg6dKlTXbcuH//fpkGBMD/+gkRCK0JESgCQQ4PDw9ERUXhyZMnCAgIUNn/SBW3bt1CRUUFfH19kZiYCFNTU+afFt1Y5ODBg1i9ejUsLCwabZ+npyd8fHwQHR3NOICUx8XFRWYQ2JiYGFhYWKCwsLBRcT18+FCmT6I0pJ8QobUhAkUgKGHq1KnYvXs37ty5g4ULF8o0BdcEPdbgmDFjkJqaCm9v7xZxGyLN1q1bQVEUIiMjle6vrKzE9evXMXv2bFy6dInZHhQUhK+//lqtCwahUIiEhAT4+PjAxcUFeXl5So8j/YQIrQ0RKAJBBYsXL8bq1atx8eJFrFq1Siu/OhRF4ezZs3Bzc8Off/6JhoYGTJ8+vcVt69OnD4KDg3Hu3Dlcv35dYf+5c+cgFArh7+8PT09PvHjxAsOHDwfw2itAx44dFUaxKCwsxKZNm9CnTx/MmTMHGRkZCAsLw+XLlxUElvQTIrQFpJk5gaCGiIgIPHv2DIcOHUL37t2xfv16tcf/+eefePr0KYKDg3HmzBmYmJhgwoQJrWLb559/juPHj2PdunW4ceOGTAfdhIQEmJqaMnFbWFjg2rVr2L59O7Zs2QI+n4+ePXvi0KFDMDc3x/79+5GcnAyJRILBgwcjIiICs2bNgpmZGXg8HkQiEQYOHAgnJyfST4jQZhCBIhDUwGKxsGfPHpSWlmLXrl3o1q2b2lZ3tCv7sWPHYufOnZgyZYrGEb6bSseOHbF69WpERkYiLi6O6UvF4/Fw6dIl+Pn5KZR8vLy8EBISwviikvbuu3DhQixZsgRDhw6V6SyckpICoVCIzz//nPSnIrQppIqPQNAAh8NBbGwshgwZgs8++4xxQKiMs2fPom/fvnj8+DEaGhrw4YcftqptYWFh6NGjByIjIxk3HMnJyWhoaFAQE4qicOfOHXz22WdgsxXzposWLcKwYcMURrLgcrkwNDTExIkTW+9CCAQlEIEiELTAzMwM8fHx6NmzJxYtWqTgUBN43eLtr7/+YjrnGhsbt3qibmRkhC1btqCoqIjxaXT69GmYmJjA29sbAFBRUYE9e/bA1dUVq1evRlJSEmbMmIHU1FQZVyheXl5YsmSJTIOQ+vp6pKSk4IMPPlA5EgaB0FoQgSIQtKRTp044ffo0zMzMEBgYqNC6jS5ZjRs3DhcvXoS3tzdMTU1b3a7AwEC4u7vj66+/xuPHj3HhwgV4e3vj3r17CAkJQe/evbFmzRqIRCKEhobi0aNHiImJwahRo+Dg4ICamhqmwcOhQ4dgZmaGR48eAQDS0tJQU1NDPAoQ2gUiUARCI3BwcMDJkyeZKrTnz58z+5KSktC9e3e8ePEC9fX1mDZtWpvYxGKxsHPnTlRXV2PQoEGor69HQkICvLy8EBcXh0mTJiEpKQn379/H7Nmz0alTJ5nz2Ww2fvjhB9y8eZPZ5uzsjN27dyMxMRF6enqYMmVKm1wLgSANESgCoZEMHToUsbGxKC4uxowZM8Dj8fD8+XOkp6djypQp4HK5MDIyatN/NnRJTSgUAng9QndERATy8vJw/PhxTJgwQcENhzxDhw7Fq1evMGbMGADAhg0bcPDgQfTv379ZzgEJhKZCBIpAaAITJ07E3r17kZ2djXnz5iEhIQEAMH78eFy4cAETJ05s9X82tbW1OHz4MDw9PeHh4SGzr6ioCOvXr2fcbmiLsbExLly4wFwPANy/f19mnUBoK4hAEQhN5KOPPkJERASuXLmCtWvXwtLSEnw+H3V1da1avffgwQOsXbsW/fr1w7Jly1BYWIjw8HDs3LmTOebatWvNimPy5MkyTdDnzJmD999/n2kpSCC0BaQfFEGnoCgKFEVBIpFAIpFAJBIx25RN0uc0dz+Px4NAIGDGq5NIJCrPp7dPnToVv//+Oy5evIiqqiocOXIEBgYG6NGjB7KzszXGy+fztfJyKxAIcOPGDZw9exZ//vknAGDQoEFYsWIFPD09weFwsHXrVgCvB5RduXIl9u3bB319fSYMPT098Pl8ZGZmgsViQU9Pj5nk1wHg8uXLcHZ2RkBAADZv3ow7d+7A2toaZ86cgZubm8w5QqEQNTU1kEgkKsNV5oiRQFAHEahWpiUSUnqfSCRCRUWF0v3aJKZNTcRra2uZ5sjant+cxIjFYkEsFkMkEqG6uhosFkvpRB/b2P0AmERYfp+enh44HE6jwvXx8cHFixcBAL/++ismT54MFxcXrc7PzMyEu7u7yntRUFCAgwcP4tChQygrK4OVlRWWLVuG4OBg9O3bF8Drflr19fXIyMjAlClTMHr0aKxduxYFBQWMC3ta9G/fvg1XV1cmAyCRSGQyBPR07949lJSUYM6cOZg/fz7Gjx+P0aNHAwCmTZsGPz8/bN68GSwWCxKJBHV1dSguLoaenp7KcLV57sqEs7a2FtnZ2UqFtLHr8ttEIhEkEgnEYjERUR3knRCoy5cvIy4uDmKxGAKBAGKxGLNnz8b69eu1SuSlaWhowIsXL5R2dFRHUxJS+f20QGl7rqpEuLFx19TUoHfv3tDX12+UCDSHiooKxjtsW/HixQvU1taiW7dujTrvypUrMut6enpajx6h7F6JRCKkpKQgKioKly9fBgC4u7tj69at8Pf3VzrwbGpqKmpqajB9+nTMnDkT+/btw6ZNmzBjxgyYmpqCxWIxz08b31D0+H7z5s2DnZ0d7OzsUFdXh3Xr1uH7778Hl8sFl8vFf//7X/Tq1QtZWVlwcnJq1qgZ8oJGr//xxx/o2bOnyv3Sk1gs1nic9HpdXR0kEglevHihtYg2RhgbGhrA5/NRUFDQYsL6LonoOyFQzs7OCAsLA5vNhkQiwbJlyxAREQF7e3utE1t6/ujRI1hbW7fLOGRVVVVwdHRs83j19fVhYmKisRXYu0h9fT0uXboEX19f8Pl8pKWlMQO4enp6NiqskpISxMTEICYmBiUlJTAzM0NISAgWLVoEV1dXteeePn0aHA4Hvr6+MDQ0xJdffomPPvoI33//PePAsDFwuVz07dsX/fr1Y7axWCzs2rULQUFBGDJkCACgX79+2Lp1K+NOpDnQIipdLQm8fv+a4pZEG4qKiiAWi5mhn9QhnWnVVgB5PB4aGhpgaGjIbBMKhVqJrapj5KH9fD19+hQAZMSNXu7Vq1ejM166gM4IVEpKClatWgWxWIzFixdj3bp1Mvu//fZb/PLLL2Cz2ejUqROio6O1eqkAoGvXrujatSuA1w+zvr4ezs7OLX4NhHePtLQ08Pl8jB8/Hhs2bMCgQYNQWlqKuXPnIiUlReN7JpFIkJqaiujoaCQnJ0MsFsPFxQXh4eEIDAyEubm5RhsaGhpw7tw5jB8/HlZWVgAAf39/eHh44JtvvsGiRYsalTg9fPgQubm5WL16tdLcev/+/VFdXY2ZM2ciJSUFERERiIiIwOPHj1tt3EFdQDrDKi+iqtDX14dAIED37t1bza7CwkKwWCy89957MgJKz8ViMTgcTqvF35roRJZYLBZj+fLlSE5ORm5uLo4dO4bc3FyZY4YMGYLMzEzcu3cPAQEBWLNmTTtZSyD8j7Nnz0JfXx9sNht8Ph8rVqzAqVOnQFEU/P39mVytPC9fvsR3332HBQsWwN/fH6mpqZg1axZSU1Nx8+ZNhISEaCVOwOsqbB6PJ+PWg8V63XmXz+czjSe0JTExEQDUjiPI4XBw5swZpKSkMNvs7e1Jc/R2hi4xsdlscDgcGBoawtjYuNG/JHQFnRCo9PR0ODo6wt7eHgYGBpg9ezbzkdCMHTuWyZ15eHigqKioPUwlEBho1+6jRo3C1atXYWBggEmTJmHgwIE4cuQIysrK4O/vj4qKCgCvq4hu3LiBRYsWoV+/fti4cSPYbDZ27NiB//73v9i3bx+GDx/e6H8MCQkJYLPZmDp1qsx2Dw8PBAQE4ODBgzJj7mmCy+XC1tYWQ4cO1Xisl5cXysvLmRqKOXPmYNiwYWhoaGjUNRAIytAJgSouLsZ7773HrNvZ2aG4uFjl8VFRUZg8eXJbmEYgqOT27dsoLy/HhAkTkJKSgvHjx8PS0hLAa2+6P/30Ex48eAAfHx989913GD58OHx8fMDlcjF16lScO3cOBw4cwPLly5v8T1MgEODs2bPw8vJSGsbWrVvBZrMVqsxVUVJSgt9//x1Tp07V+p+jqakpEhIS8J///AcAkJOTA0tLS2RmZmp/IQSCEnRCoJR5KlWVizx8+DAyMzMRHh7e2mYRCGqhXbsbGhqipqZGpnMuRVHo1asXACA3NxcbN24En8/Hxo0b8ddff+HgwYPw9PRsdousq1evorKyUqXX3t69e2PZsmW4dOmSjOt3TdfUlMFhZ8+eLZOxHDVqFIKCgrRqHUcgKEMnBMrOzk6mrr6oqEjpT8XU1FRs27aN8U9DILQXtGv3IUOGID09HRwOBz4+PqipqcGBAwcwevRojBs3TqYU4u3tjc8++wydO3duMTsSExOhr6+v9n/R2rVrYWNjg88//xxisVhjeNbW1o1ugUjToUMHpjk6AMTFxcHExITp/EwgNAadECh3d3fk5+ejoKAAAoEAcXFxCjm4rKwsLF26FFwut0U/cAKhKdy7dw+FhYVM9V6XLl2wadMmODk5YdWqVSgtLcXatWuRk5ODyspKzJgxA1FRUfjuu+9azAahUIikpCSMHj1a7WCu1tbWWL9+PXJycmQaNcjz6tUrXL16FT4+Ps1q9cVisbBp0yaZ/159+/bFV1991eQwCe8mOiFQbDYbe/fuhbe3N/r374/AwEA4OzsjCgYGbAAAHKhJREFUMjISXC4XABAeHo6amhrMnDkTgwcPJv5pCO0K7dqdy+WiuroaRUVFiIqKwrBhw3DkyBHcv38f69evh52dHfT09LBv3z6MHj0amzZtwtGjR1vEhuvXr+PVq1cqq/ekWbJkCRwcHHDgwAHU1NQoPSY5ORkikajFvAA7ODigtraW8ewbGRkJIyMj8Hi8Fgmf8PajM20PfXx84OPjI7Nty5YtzHJqampbm0QgKCU/P58pDfz3v/8FAAQFBWHVqlUqR74wNDTEkSNHMHnyZKxYsQKdOnXChAkTmmVHYmIiWCyWVpk1AwMDbN++HbNmzcK3336LyMhIhWO4XC6MjY1bpNMtjZ6eHo4ePYrff/+dcePRuXNnHD16VMElPYEgj06UoAgEXUcgECAhIQFTp05VaH7t5eWFPXv2aByWydLSEqdOnUK3bt2wYMECZGVlNdkekUiEpKQkjBw5El26dNHqHD8/PwwcOBDfffedQivZuro6XLx4ERMnTmyVzrYjRowAj8djRkKZO3cuXF1dGf9VBIIyiEARCGr4+++/sWXLFgwYMAALFy6UEZVRo0YBAMzNzZm+Tpro1q0bMyxRQEAASkpKmmTXb7/9hrKyskZVx7FYLHz88ceoq6vD5s2bZfalpqaitra2VavODQwMkJOTgyNHjgAA8vLyYG5urtVo7oR3EyJQBIIcYrEYycnJCAgIgKurK3bv3g07Ozvs2rULH3/8MaysrMBisXDjxg0Ar/9HjR07VmuRcnJywokTJ1BdXY1169ahrKys0TYmJCRoXb0nTb9+/TBr1iwcOnSIcdsBvK4uZLPZCtXsrcGMGTPw4sULZt3T0xPz5s1T2t2E8G5DBIpA+P+8ePECP//8MwYOHIhZs2bhxo0bWLBgAa5evYpTp05h37592LVrFyorKxUS04KCAkRHR2sdl4eHB6Kjo/Hs2TMEBASAz+drfa5YLEZSUhI8PDyaNADoli1bYGBggHXr1jFuXM6fP4/Ro0fD2tq60eE1BQsLC9TX1zPDMMXHx8PY2Bh///13m8RPeDMgAkV4p5FIJEhLS8P8+fMxevRo7N27FxYWFti9ezcePHiAH374AUOGDEF0dDQKCgrUhpWTk9OouH19fbFy5UrcuXMHCxcu1Pp/zO3bt/HixYsmt7br2bMnVq5cibS0NFy4cAHXr19HRUVFi7Xeawzh4eF4+PAhs+7k5ITt27e3uR0E3YQIFOGdpLy8HHv27IGbmxs+/PBDJCcnY8qUKYiJicGtW7cQGhrKDFsEaCc+Li4ujbbDz88Pq1evxsWLF/F///d/WlVznTlzhjm3qYSHh8PGxgaLFy/G8uXLAfzvn1pbQ/uamjNnDoDXJTzSHJ0AEIEivENQFIVbt25h8eLFcHJywoYNGwAA27Ztw4MHD/DNN99gyJAhCsMPicVimVy+Mnr37o3g4OAm2RUREYGPPvoIhw4dwrZt29QeK5FIwOVy4e7uDjs7uybFB7xuBainp4eysjI8fvwYADBz5kyt/6O1NCwWCwcOHMDt27eZbZ07d8bJkyfbxR6CbqAz/aAIhNaiqqoKx48fR3R0NHJzc8Fms+Hr64vg4GCMHj2aGY5I+sc9jUgkwpIlS5CdnQ1zc3NUV1cz+6ytrTFy5Ei4ubkhODi4yQO+slgs7NmzB6Wlpfjqq6/QvXt3lWKXkZGBZ8+eYcWKFU2Ki2b//v0KjTMeP36M/fv3Y+3atc0KuzkMHjwYfD4fHh4eyM7Oxvz589G1a1c8fPjwjXUZQWg65IkT3lqysrIQHR2NkydPora2FnZ2dtiwYQMWLFjAuIdQh1AoREhICM6cOYOQkBBs2LABBw4cQE5ODlxcXJolSvJwOBzExsZiypQp+Oyzz9ClSxdMmTJF4Tja31Jz/xepqrLMzs5uVrgtgb6+PjIyMnD27FkEBATg+fPnMDMzw9WrVzFixIj2No/QhhCBIrxV8Pl8nDp1ClFRUcjKygKLxcLEiRMRHByMiRMnau0JVSAQYNGiRUhKSkJYWBh27doFFouF1atXt5rtZmZmiI+PxwcffMDELZ0gSyQSJCYmws3NDT169GhWXC4uLoiPj1fYPnDgwGaF25L4+vqioqKCyQSMGTMGfn5+OH78eLNHgSe8GZB/UIS3gr/++gurV6+Gk5MTVqxYgeLiYqxevRrZ2dk4efIkJk+erLU4NTQ0YP78+UhKSsLKlSsZcWoLOnXqhNOnT8PMzAyBgYHIy8tj9v3xxx8oLi6WcevRVEJDQ2Fvby+zzd7eHkuWLGl22C2JiYkJfv31V2ZoKXo4pidPnrSvYYQ2gQgU4Y2loaEBJ06cwKRJkzBixAj8/PPPcHNzQ2xsLHJzcxEZGdnokkZDQwPmzp2L5ORkfPbZZ/jyyy/bPLfu4OCAkydPoqGhAf7+/nj27BmA/7lib4nRHmxsbHDjxg1s3rwZAQEB2Lx5M27cuNFiVZYtzSeffCIjSv369VMYDYPw9kGq+Ag6TXl5OaKjo3H//n04OzsjJCQEr169wsGDB3H48GGUl5fDysoKK1aswKJFi9CnT58mx1VXV4dPPvkEt27dwpo1a7B+/fp2q0oaOnQoYmNjMWvWLEybNg2+vr745Zdf0LVrV1hZWbVIHDY2Nu3aIKKxdO3aFfX19Vi2bBmio6OxY8cO7NixA6WlpTJdAghvD0SgCDpLZWUl/P39mQ6yp0+fxu7du1FXVwfg9QCk27dvx7Rp02BsbNysuPh8PkJDQ3Hr1i188cUXWrtIb00mTpyInTt3Ijw8HH/99RcAoLa2FmPHjkVaWprOlnZam//85z9Yvnw5M2hvly5dsGfPHlRUVDANWEJDQ9/Z+/M2QQSKoLPEx8crjN5QV1eHoUOH4ocffmhSx1hl0H7Gbt26hZUrV+qEONEo66xKD6vUmg02dB1nZ2fU1dVh9OjRyMjIwCeffMLsi4+PR2xsrE5XWRK0g/yDIugs+fn5SrffvXsXy5Ytw5IlS/DNN9/g3LlzePTokUZ35srg8Xjw9/fHzZs3sXbt2nZrJCCRSJRO6pqDi8ViZqIoSu30NsJisXD9+nXMmzdPYR/dp4vwZkNKUASdpU+fPrh48aLC9v79+zNNro8fP85sNzQ0RN++feHk5IR+/fqhb9++6N+/P3r37i3TybOiogJRUVG4e/cu7t69i+LiYmzbtg0zZ85EVVUVampqoKenBz09Pejr6yv8h5JIJADQpP9TFEVBIpEwc6FQiNu3b4PFYjFx6enpgcVigcVioVOnTkrD6dq1K/Lz85njWCwWI0TycUjPhUIhRCIRE46ya5Dfpuk627vJd319vdLtutCni9A8iEARtIZOmFWhLqeubp+yBF8oFGLChAngcrl4+vQps71Hjx6IiYlBhw4dAADFxcXIy8vDw4cP8eDBA+Tl5eHcuXMyfXw4HA7s7e3h4OAAW1tbJCQkyIyiYG1tDS8vL1RXV6OqqgqvXr2SSdhV2U/bKy0OtFgoWwbACB89mZmZyYiMPP7+/jh37pyMg0FbW1tMmTIFdXV1MqUtaXuloeNisVgwNDTEnTt3ZOJUZqcy6NKYMvGrq6tjRkZXdo/UbWuuwL0JfboITYPVyOL/G19XIBAIMGLECFy7dq1J5z969AjW1tYtUrfd2AQ/MzMTzs7OYLPZMrlsZedRFCWzT35dU7zSCdCDBw9QX1+vkLhK2yCf85dP8Oi5dLUTHb6qRE8oFILH4+Hs2bMoKChA79694ePjAzMzM5n7I3+fKIrCy5cvUVhYiKdPn+Lp06coLCxEYWEh08BCnuXLl2PJkiVgs9nQ19eHvr6+zHXKhy8WixlhoJdFIhGzTyQSyeyTPl76uqVtl35G0s+qpqYG58+fZ+6Br68vLCwsmOOk7ZS3W9U7ouz+yd9/eln6GqSfoyrRVfYOaBI+AErfAeD1WIj/+Mc/ZMKQXq6oqMCYMWOYMQWB1326rl27xmRkVFFcXAyxWIyePXuqPa6pVFRUoLS0FP3792+V8AGgsLAQLBYL7733ntL99P01MjJqNRuagFaJ0TsnUBUVFRg9ejQuXrwIY2NjmQ9OFdIJyZMnTyAWi2FmZsYkZMom+kOVD0NZAqAqkZZffvnyJQQCgcK50qgSBnk0CQltv/xcPjz5BFbZJJ2QS5c0aOj7RVdxSc+l46WFQpXoKUvg6H809PL69evx+++/K9wPT09PfP7550pFQ95eaXuUiYP0nJ7YbLZS8aNLX/RcXvhosZP+36RK9OQFUP45KUvgVZX26Ena1qaKn7J3XP46pTNV8qVR6fjk46WXeTweEhIS8PDhQzg6OmL69OmwsLBQEF958ROJRLC3t1fqV6slSn+vXr0iAqUcrQTqnaviy8zMxLNnzzB9+nQ0NDTI7NPX10dVVRUAgM1mw8TEBKampujfvz9GjhwJAwMD5gOhExr5j0bdT2llCb78hy+fuEknal27dlUpHABkEmXpxEpZwqYqwaPDkbdb22og6eOlj2WxWDIlP+lER1mY0tVF6kRPvhqODkdeLOj76ObmplSgBg8ezHzg8vdTmejJ32fp+yj9Dqhalr9f0vdN3bsh/U4om0vfY+mw5e2lRU+Z+Mlfn1AolHmfpJ+R/DWoew+kj5EWOgMDA5nMiDoBVFbqoygKVlZWWLhwocyzEggEMs9EHj09PXA4HBQVFaGkpESh9KftO6/sHZF+L7p06aJQ9akszKZUfTa3elTXeedKUMqg70FDQwNSUlJQWVkJkUiE+vp6CIVCGBkZwdjYGNXV1aipqUF1dTV4PB7zz4LH44HP50MgEMiEaWhoCHNzc7x8+ZJJJOmwBgwYADc3N5mcNZ24yIuONgmb/MetKmcvPyk7V3oZgMIHp6xkIr1OJ3qqSnrKEgFV1TfS90DZPnnUVTMCr1vthYaGyvzT6d69O3788UeYm5sr2CyfqMqXklVtk888yGdg5AVWVWZCm+pB+WVl74eqUp+qkp8qEVT2ftDXIF2tqaz0J/1eyF+jKvHTVCNAPyN1JUF1VdOqUHZ/1T07ZSU/de+EpnefDlu6ZC0SiRQyFPR953A4kEgkEAgEzNTQ0MDMu3XrhlmzZqm83naAVPG1B9IvdX19PaqrqxEXF4e6ujqIRCKmFZWlpSVMTExQU1ODmpoa8Pl8RvjoSSgUylSLGRsbw9zcHGZmZqAoCpWVleBwONDX14epqSlYLBYmTZoEMzMzpQmLsvp9dQma9LKyD11e+JQJnLIcsXRCrarqRz4hUyZ60vecFltViYD09fF4PJw5cwYPHz6Eg4MDpk2bpiBOmp6vupy1qoRNmdBKl5TkqwTll+lMjvy9peOSFzFloqeqlCR/b+WFUF2tgLKSn7YZJPra5M+Tfm7ydijLDMkn3PJiKP9s5G1X9l5Kv5N8Pl9pdbOy6nhl4qtMjOXvq/z9ysrKwuPHj1FeXg6RSAQjIyO89957MplZOoPLZrNhaGgIAwMDpfNevXrBx8dH5XvdDhCBehuQTuykRezOnTu4efMmk6tisViQSCTo27cvBAIBamtrUV1dzcxramoUPmK6NEdXZZqYmIDD4YDH4zEJh6GhIYDXLaW6du0KDofDfBzS/w+kE3ZNibgmIaRzn5oET101kKpqQWkRlE685QVPOqGg7ZG3A4DMsrQddHiqRENeUKTtll9W9V6out+0XfKZB3XiRz9X6YnO1MhfB22/dI6+MVWGykpNykqA8ttFIhFqampkwjIwMJCxRSQSQSAQMHOhUMiUJOh1+lzpd0e6upHD4cDAwIBZlkgkuH79OtMFQSwWY8yYMbCzs5MRASMjI3A4HGZZXiToycDAAEZGRjL7OBxOk6r43mCIQBEUoZ+3SCQCn89nqirp6dGjRzh16hSTCBgYGIDNZqNv374wNTUFn89HbW0t6urqFDqKSn+QxsbGzIdKT3SiJ51oAkCvXr1gbGyskJgpS4DlS0j0dhrpqhbpubqPXb6EKJ1DViZ+9FyVAEon4vKiId9YQrp0pKkqiI5XlcjJ5+ClS+zy/8iUZSjUiQO9LBa/9i5cV1fHvAP0v1npaiV1pRr6vsiXpujaAPq9MTExYd4dQ0NDiMVi5OXloaGhgREaHx8fdOzYUSshoN9l+WdPaBeIQBFaH/r9EQgEqKmpYQSPx+PJrFdXV+PPP/9EWloak+BZWlrCwMAAo0aNgpmZmUwuHIBMbl46Z0vPlSVK9KSvr6+QQMqXSjSV1JRVEUoLEovFkkl85f/ByFeVKft/pGy/9H2l45EWKB6Ph5s3b6KmpgYNDQ0QiUTo0KGDQpWodOlPXghU3UN1pQH63ldVVaGhoQEU9brjr6OjIxwdHWXCe8dKA4TGQwSK8OZBv4/0/ztlgicvfHTV57Vr11BZWQmJRAJ9fX1YWVmhS5cuCAoKkhEVPT098Pl8GBkZMSKjrhGCfOMBHo+Hy5cvo7KyErW1tUzVqnTpSLo00Fgh0LZaSE9PD7W1taipqUHnzp219ndFIOgARKAI7zbSpRD6XxwtbNnZ2ejWrRssLS3VioChoSEpDRAILQ8RKAKBQCDoJFoJFBnNnEAgEAg6CREoAoFAIOgkRKAIBAKBoJO8lQKVkpICJycnODo6YufOnQr7GxoaMGvWLDg6OmLEiBF48uRJ2xtJIBAIBLW8dQIlFouxfPlyJCcnIzc3F8eOHUNubq7MMVFRUbC2tsbDhw/x6aefYu3atWrD1CR43377LQYMGABXV1eMHz8ef//9d4teE4FAILyLvHUClZ6eDkdHR9jb28PAwACzZ89GYmKizDGJiYlYuHAhACAgIACXL19WOayMNoI3ZMgQZGZm4t69ewgICMCaNWu0slWT8NHEx8eDxWIhMzNTq3AJBELr014Z13ephuitE6ji4mIZvyh2dnYyI1fLH8Nms2FpaYny8nKl4WkjeGPHjoWJiQkAwMPDA0VFRRrt1Eb4AKC6uhp79uzBiBEjNIZJo43wnThxAgMGDICzszPmzp2rddgEgq7RHhm91sy4NjfextYQ6TJvnUApKwmpGk9N3TE02gieNFFRUZg8ebJGO7URPgCIiIjAmjVrtHY2ps0LnJ+fjx07duDmzZu4f/8+/vWvf2kVNoGgivbKFLVmRk8drZVxbYl4G1NDpOu8dQJlZ2eHp0+fMutFRUXo3r27ymNEIhGqqqpUunBvjJgdPnwYmZmZCA8P12inNsKXlZWFp0+fwtfXV2N4NNq8wPv378fy5cthbW0NAOjcubPW4WtKiAoLCzF27FgMGTIErq6uOH/+vNZhE5pHez2b9swUtVZGTxOtlXFtiXgbU0Ok67x1AuXu7o78/HwUFBRAIBAgLi4Ofn5+Msf4+fkhJiYGwOti/7hx41SKjjaCBwCpqanYtm0buFwu46JCHZqETyKR4NNPP8U333yjMSxptHmB8/LykJeXh5EjR8LDwwMpKSlaha1NQvTll18iMDAQWVlZiIuLw7Jly7S2PTg4GJ07d4aLi4vS/RRF4ZNPPoGjoyNcXV1x584drcNubdrb9tZ+Nupo7UyROloro6eJ1sq4tkS8jbFN13nrBIrNZmPv3r3w9vZG//79ERgYCGdnZ0RGRoLL5QIAQkJCUF5eDkdHR3z77bdq6621EbysrCwsXboUXC5X6w9Pk/BVV1cjJycHXl5e6NWrF27fvg0/Pz+N9efavJwikQj5+fm4cuUKjh07hsWLF6OyslKjzdokRCwWCzweDwBQVVWlVMxVERQUpFYsk5OTkZ+fj/z8fPz888/4+OOPtQ67tWlv21v72aijNTNFmmitjJ4mWivj2hLxNqaGSOdR5dxNxfROcu7cOapPnz6Uvb099eWXX1IURVERERFUYmIiRVEUNX78eKpz587UoEGDqEGDBlFTp07VGKZQKKR69+5NPX78mGpoaKBcXV2pnJwclcePGTOGysjI0Bjub7/9Rk2cOJFZ3759O7V9+3aZY5YuXUodOHCAWR83bhyVnp6uMeyTJ09SISEhzHpsbCy1fPlymWNKSkooFxcXytbWlrKysqIyMzM1hitNQUEB5ezsrHRfaGgodfToUWa9b9++VElJSaPCb03a0/a2eDaqOHHihELcK1askDlmypQp1LRp0yiBQEA9fvyYsrW1pV69etXsuDW975WVlVSHDh2onj17Uj179qQMDQ2pbt26afUtqUOb7/fOnTuUvb09lZeX16y4Ghvv3r17qaVLl1IURVHHjh2jZs6c2WLxtyBaac5bV4JqDXx8fJCXl4dHjx5h/fr1AIAtW7YwJanU1FSUlpbi7t27uHv3LlNSU4c2Jb2moE2Jb9q0aUhLSwMAlJWVIS8vD/b29hrDprQonR07dgxBQUEoKirC+fPnMX/+fMZranNpbL2/LtHatrfns9E2V//hhx+Cw+Ggd+/ecHJyQn5+frPj1vS+W1paoqysDE+ePMGTJ0/g4eEBLpeLYcOGNStebb7f8PBw1NTUYObMmRg8eLDCd9ha8Tamhkjn0VbJqHe4BPWmoanEJ5FIqE8//ZTq378/5eLiQh07dkyrcLUpnQ0YMIAqLCxk1nv37k2VlpZqbbu6UoiPjw91/fp1Zn3cuHEtVgpoCdrT9rZ4NqrQJlefnJxMLViwgKIoinr58iVlZ2dHlZWVNTtuitL8vkujbU0EodXRSnOIQBG0RpuEaNKkSUz1YW5uLtWtWzdKIpFoHQep4msabfFs1NFamSLCWwsRKF1kw4YN1L/+9S9m/YsvvqC+//77drSocWhKiO7fv0+9//77lKurKzVo0CDqwoULjQpfXSJ/9uxZatKkSZREIqFu3bpFubu7N+9iWpj2tr21nw2B0IJopTnEYWEb8+TJE/j7++POnTuQSCTo06cP0tPT0aFDh/Y2rd2ZM2cOrly5grKyMnTp0gWbN2+GUCgEAISFhYGiKKxYsQIpKSkwMTHBgQMHmv0voaV4k21/G8jIyEBISAjS09MhFosxfPhwHD9+XGWzf0K7Qzzq6ioTJkzAV199hdLSUvzyyy+Ij49vb5MIhDeeDRs2oL6+HnV1dbCzs8Pnn3/e3iYRVEMESlc5fvw4fvvtNzx//hwLFy6Ej49Pe5tEILzxCAQCuLu7w8jICL/99hv09fXb2ySCaohA6SoCgQADBw6EUChEfn4++ZAIhBbg+fPnGDlyJAwNDZGRkQFTU9P2NomgGiJQukxYWBisrKze7D4KBIIO4efnh9mzZ6OgoADPnj3D3r1729skgmq0Eih2a1tBUEQikeD27ds4efJke5tCILwVxMbGgs1mY+7cuRCLxXj//ffx66+/Yty4ce1tGqEZkBJUG5ObmwtfX19Mnz69xccHIxAIhDcEUsVHIBAIBJ1EK4EiY/ERCAQCQSchAkUgEAgEnYQIFIFAIBB0EiJQBAKBQNBJiEARCAQCQSchAkUgEAgEnYQIFIFAIBB0EiJQBAKBQNBJiEARCAQCQSchAkUgEAgEnYQIFIFAIBB0EiJQBAKBQNBJiEARCAQCQSchAkUgEAgEnYQIFIFAIBB0EiJQBAKBQNBJiEARCAQCQSchAkUgEAgEnYQIFIFAIBB0EiJQBAKBQNBJiEARCAQCQSchAkUgEAgEnYQIFIFAIBB0EiJQBAKBQNBJiEARCAQCQSchAkUgEAgEnYQIFIFAIBB0EiJQBAKBQNBJ2I08ntUqVhAIBAKBIAcpQREIBAJBJyECRSAQCASdhAgUgUAgEHQSIlAEAoFA0EmIQBEIBAJBJyECRSAQCASdhAgUgUAgEHQSIlAEAoFA0EmIQBEIBAJBJyECRSAQCASd5P8BEQuD2gfgoSEAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7eff0c667d10>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"autofig.reset()\n",
"autofig.plot(x, y, z, i=t, \n",
" xlabel='x', ylabel='y', zlabel='z',\n",
" projection='3d', elev=0, azim=[0, 180])\n",
"mplfig = autofig.draw(i=3)"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [],
"source": [
"anim = autofig.animate(i=t, \n",
" save='3d_azim_2.gif', save_kwargs={'writer': 'imagemagick'})"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can then achieve an \"accelerating\" rotation by passing finer detail on the azimuth as a function of 'i'."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAWQAAADuCAYAAAAOR30qAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzsnXlcTfn/x58t2uxUBiGhIWsq0lhGdib7OsPYGWMbM/NjMGYYBmMZjGXMGMMoEmIKKWSfyJ7KEi1KhEq0L/ee3x897vl23UqluGY+z8fjPtzO+Zzz+Zxz3df9nPfnvehIkoRAIBAI3j66b3sAAoFAIMhFCLJAIBBoCUKQBQKBQEsQgiwQCARaghBkgUAg0BKEIAsEAoGWIARZIBAItAQhyAKBQKAlCEEWCAQCLUG/mO1FWJ9AIBAUH52iNBIzZIFAINAShCALBAKBliAEWSAQCLQEIcgCgUCgJQhBFggEAi1BCLJAIBBoCUKQBQKBQEsQgiwQCARaghBkgUAg0BKEIAsEAoGWIARZIBAItAQhyAKBQKAlCEEWCAQCLUEIskAgEGgJQpAFAoFASxCCLBAIBFqCEGSBQCDQEoQgCwQCgZYgBFkgEAi0BCHIAoFAoCUIQRYIBAItQQiyQCAQaAlCkAUCgUBLEIIsEAgEWoIQZIFAINAShCALBAKBliAEWSAQCLQEIcgCgUCgJQhBFggEAi1BCLJAIBBoCUKQBQKBQEsQgiwQCARaghBkgUAg0BKEIAsEAoGWIARZIBAItAQhyAKBQKAlCEEWCAQCLUEIskAgEGgJQpAFAoFASxCCLBAIyhSlUokkSW97GO8EQpAFAkGZIEkSGRkZvHjxgp49e77t4bwT6L/tAQgEgpKRkJDA5s2buXHjBi1atGDKlClUq1btbQ8LAIVCQVpaGjk5OTx+/JiEhIS3PaR3AiHIAsE7SEJCAm3btiU8PByAPXv2sG3bNi5evPhWRVmSJDIzM8nIyODRo0dYWFjw8OHDtzaedw1hshAI3kE2b94si7GK8PBwNm/e/JZGBNnZ2SQnJ5Oenk5cXByPHj16a2N5VxGCLBC8g9y4cSPf7UFBQW94JLmz4rS0NFJSUoiNjUVfX1/MikuIEGSB4B2kRYsW+W5v2bLlGxuDJElkZWXx4sULoqKi0NPTE7Pi10TYkN8CmZmZKJXKQtukpqaSlpaGmZnZGxrV/4iLi6Nq1aoYGhq+8b7v379PvXr13ni/ycnJZGVlUb169Tfed2xsLObm5pQrV67Ix4wZM4atW7cSGRkpb7OysmL06NGkp6cX6RxKpZIHDx5Qt27dYo9ZdXxmZiaPHz8mLi6OOnXqlOg8gv8hBPktoFQq0dUt/OEkMzOTpKQkatSo8YZG9T8SEhKoWLEixsbGb7zvR48eUb9+/Tfeb3p6+lv7AXz69Cmmpqav/D+RF1NTUzZs2ECfPn3Q1dVFR0cHf39/TE1Ni3wOSZJ4/PgxlpaWJRg1sm+xmBWXHsJkIRC8o0RERADw6aefolAouHv3brGOT0hIwNXVlZEjR7J8+XISExPLYpiCYiAEWVAmJCQksHz5cvFlL0OuX7+Orq4un3/+OQBnzpwp8rEJCQl8+OGH/PHHH+zbt4+FCxfSvn178Tm9ZYTJQlDqJCQk0KFDB3kGt2/fPnbs2MG5c+e0JnDh30BQUBDvv/8+zZs3p1atWsUS5C1btsifj4qIiAi2bNnCnDlzSnuogiIiZsiCUqewL7ugdMjJySEkJISWLVuio6NDx44dCQwMJCMjo0jHh4SE5Ls9ODi4NIcpKCZCkAWlzrv+ZX8XzC137twhIyODVq1aAdCxY0cyMzO5ePFikY5///33893evHnzUhujoPgIQRaUOs2aNct3+7vwZVeZWxYuXKjVttXr168D//M77tSpE1A0O7JCoeDatWsa262srJg4cWIpjlJQXIQgC0qdSZMmUalSJbVt9evXfye+7GvWrHknzC2qiDyVIFtZWVG7du1XCrIkSXz11Vf4+PgwYcIEjI2NqVmzJosWLRI2fi1ACLKg1KlWrRr169fHzMyMtm3bAvD5559r7Zf98ePHuLq6MmbMGFatWpVvG20zt1y/fp26devK91RHR4cOHTq80o68evVqNm/ezODBg1m+fDnp6en069ePOXPmaO3n819CCLKg1MnMzOTmzZv06NGD48ePU7t2bbZv365VScqfPn3Kli1b6NmzJ/Xr12fBggWF2l+1ydwiSRI3btyQ7ccqVHbkwMDAfI/buXMn3377LR07dmTr1q1yvgkRYac9CEEWlDohISFkZ2djZ2dHuXLlmDRpEqGhoZw6deqNjuPlxbm7d++ydetWevfuTb169Zg+fToBAQEYGBgAoKury9SpUzUiBbXNthoVFUVSUpJG3orC7MjHjx9n8uTJNG3alD179mBoaEhMTAwgBFmbEH7IglLn6tWrANjZ2QEwfvx4li1bxsaNG+ncufMbGUN+vtALFy4EoHLlypQvX17OXwGgr6/Pxo0bGT16NPPnz2fLli0EBwfTvHlzJk6cqFWP8yr78csz5ILsyNeuXWP48OHUqFEDLy8vqlSpAiAEWQsRgiwodS5fvoy+vr6ckczU1JThw4fz119/ER4eToMGDcp8DPn5QgOMHDkSU1NT1q5dq7Y9JyeHmzdvArk2cG0OjnjZw0KFyo584MABMjIyMDIyIjIykv79+6Ovr8/BgwexsLCQ2z948AAQgqxNCJOFoNS5evUqzZo1w8jISN42bdo0JEnit99+eyNjKMgX2sfHR0OMVdy5c6csh1RqBAUFYWpqSu3atTX25bUjx8fH07dvX5KSkti3bx82NjZqbWNiYtDT06NmzZpvauiCVyAEWVCqpKWlcfPmTVq3bq22vVmzZnTq1Int27eTnJxc5uMoyBe6MH/igoIltI2goCA5Qu9lVHZkPz8/Bg0axL1799i2bRvt27fXaBsTE4OZmRl6enplOl5JksjJySnTPv4tCEEWlCpBQUEoFArZfpyXadOm8eLFC9zc3Mp0DLGxsYW6fs2ePRsrKyu1bfXq1WPYsGFlOq7S4MmTJzx8+FDDfqzCysqK9957j59//pnAwEBWr17NwIED82374MEDzM3NgbKJTpQkiYcPH+Lr60tSUtJrn++/gLAhC0qVlxf08tK7d28sLS3ZuHEjkydPLlb+31eRnp6Ot7c3rq6u+Pv75+tiZ2xszJ07dzA3N+eLL75QW7jr16+f7G2hzbwcEJIfcXFxAEydOlXOBPcykiQRExND+/btefz4MR07duT+/fvA6yeDSk9PJzMzk5ycHDIzM+nRowcnT54s8vG+vr7MnDkThULBhAkT+Oabb9T2R0dHM3r0aJKSklAoFCxfvpzevXsXe5zaiBBkQaly+fJlDA0Nadq0qcY+PT09pkyZwpw5czh69Cg9e/Z8rb4kSSIwMBBXV1f27t3LixcvqFSpEm3atNHwxf3tt9/49NNP5cf8lxfu4uLiSEtLe63xvAlUC3oFzZCXL18uv7eysuLkyZPEx8cTHx/PkydPiI+P5+nTp9y+fZv09HSOHTuWb4WW4mZ+kySJxMRE0tPTuXXrFrq6upiYmFC/fn3i4+OLfH0KhYKpU6dy7NgxLCwscHBwoG/fvmr27yVLljB06FCmTJnCzZs36d27N1FRUUXuQ5sRgiwoVa5evUrLli0LLEc0evRofvjhBzZs2FBiQY6JiWHXrl24urpy7949dHR06NKlCz169ODq1au4u7vLbW1tbdmzZ8877UmgUChITEzk6dOn/PLLL0CuX/Hu3btlgX369Cnnzp1TO+6rr77K93zVqlUrkkmiKNGJCoWCrKwssrOzefz4MQYGBrRu3ZpLly4V4co0uXjxIg0bNpRNSsOHD8fLy0tNkHV0dHjx4gUAz58/p1atWiXqSxsRgvwWuHjx4itr6uXk5JCTk0NCQsIbGtX/SE9PJykpqdiLPampqYSFhdG3b18CAgIKbNe1a1e8vLxwd3fXmJ2lpKTke2xGRgb//PMPvr6+XL16FUmSsLCwYMKECXTq1InTp0+zYMECDdvxypUriYmJkX1uCyI7OxulUik/7pclSqWS5ORknj17xvPnz3n8+DHu7u68ePGCpKQkjdeLFy80TDBffvml/L5SpUqyQAE4Oztz4sQJABYsWEDlypWpWrUqaWlpXL58mVOnTqkJctu2bfON7qtcuXKhn6MkSSiVSiRJwsTEhCZNmpRYiFXExsaq/XhaWFhojG3hwoV0796d9evXk5qayvHjx1+rT21CCPJboE2bNq+0n8bHx5OQkPBWVv6Dg4OxtLSkYsWKxTru9OnTSJLERx99hJOTU4HtTE1N8fLy4vz584wYMUJtX0BAgHysJEmcP38eV1dX9u3bR3JyMpUrV2b8+PGMGjUKBwcHPD09mT9/PtHR0Rr9/Pzzz/l6F+SHymTx8mJfUVAqlTx79kzDLKB65d2uehX2g1ylShXMzMyoVasWrVq1wtTUFDMzM4yMjFi4cCFNmjRhx44dmJmZUb16dYKCgujevTumpqacPn2amjVrMnbsWDw9PRk5ciQ+Pj78/vvvsrA1bNhQniVv27aNHj160L59ezW/bSsrKxYvXlyoDVmhUJCRkSGbUUqD/Gz/L3uTuLu7M2bMGL766ivOnz/PqFGjCAkJKdU1ibeFEGRBqXHlyhUg/wW9vFhbW9OjRw/c3NxYtGgRVatWVdsfHR3Nzp07cXNzIzw8HF1dXbp06cKoUaNwcXHB2NiYS5cu4ezszIULF+Tj9PX1+f7770lLS2PZsmV06dKlRNehVCpJSkrKV2DzE9v4+HgUCkWB56tcuTJmZmaYmprSsGFDTE1NMTU1xdzcHFNTU54/f46trS116tTB1NS0QHOPyiQxc+ZMObdGeHg4AwYMwMjIiIMHD1KzZk2Sk5N58OABWVlZ8g96zZo1mTFjBsOGDaN169bMnTuXtWvXUqNGDapVq8a5c+e0IjrRwsJC7WnmwYMHGiaJrVu34uvrC0C7du3IyMggPj5e9hh5lxGCLCg1rl69Svny5Ys0q582bRp+fn5s376dWbNmkZqaipeXFxs2bJA9NSpWrEjXrl356aef5EXC6OhoFixYgIeHh9r5mjdvzp9//knz5s1xdnamdu3aWFtbA7mzrsIEVuVK9vTpU168eEF8fHyhfrOVKlWSBVWV1S6vwJqZmcnbzMzMXum9cfXqVZo0afLKKt8vh0w/efIEFxcXkpOT8fb25t69eyxZsoRDhw6Rnp4uH+fj40OnTp3UTFAxMTFyCDloT3Sig4MDd+/eJTIyktq1a7N792527dql1qZu3br4+/szZswYbt26RUZGxlupFl4WCEEWlBpXrlyhVatWRbI9d+3aFWtra+bOnUtoaCheXl4kJydjYmIi20STk5M5fvw4Q4YMwc/Pj61bt7J27VoNO7GNjQ3jx4/n8OHDbNiwQbZ7tm3bVhbd7OzsAsdSsWJFqlatStWqVWnUqJGamOZ9qbYZGhq+3o0qIdevX6dcuXLY2NiQkpJC//79iYiI4L333mP48OEkJiZiYGBA7969GTZsGNOnT6dx48Y4OztrnCsmJkYtjFpb0NfXZ8OGDfTo0QOFQsG4ceNo2rQp3333Hfb29vTt25fVq1czceJE1qxZg46ODtu3b883SOZdRAiyoFRISEggMjISFxeXV7a9f/8+O3fuJCwsDAA3NzfatWtHz549uXDhAkeOHFFrHxERQaNGjQo8382bN/niiy80thsaGmJra5vv7DWvwBoZGb2WDflNERQUhI2NDaGhobRr107e/vjxYzp16sTw4cPp37+/nDzI29sbT09P0tPTNWbfMTExhfoyv0169+6t4Vf8ww8/yO9tbGz4559/3vSw3ghCkAWlQt6AEEmSSElJUVvIioqKYsuWLdy+fTvf48+fP8/58+eL1eeCBQuoW7eumtguW7aMbdu2ER0d/a+wKaq4e/cuN27cAFAT459++okhQ4bk6/rVqVMn3N3dCQwM5MMPP5S3Z2Zm8ujRIz766KMyH7egeAhBFrwSSZJITU0t0GvgyZMnsp1v9OjRTJo0iczMzFee187OTl4IdHZ2pmvXrhw5coSzZ89qtG3evDnBwcFYWFjw+++/5/sYDrnC3qJFCw0xfv78OefPn5eDR5ycnDTKTGkb8fHx7N+/H3d3d40fq7Zt23Lq1KlCH9U7duwI5OZHzivIsbGxAFppsvivIwT5HSchIYEtW7YQEhJCs2bNmDRpUpFWx18W2Lzvw8LCyMjI4NmzZ/K2vItEL5M3q1u3bt1IS0vTeKQ0MzNj1qxZjB49murVq8vbo6KisLGxoXbt2owZMybfWbK+vj7BwcGMGjWKVatWUbly5XzH8eDBA27fvs2sWbPkbeHh4Sxbtox9+/ZhYGCAJEno6OiQlZXF4MGDmTt37htJB1pUUlNTOXjwIB4eHhw7doycnBzMzc0pX748qampQO493r9//yvtpvXr18fCwkIjP7LIg6y9CEF+h8kvCfuWLVtYvnw5GRkZ+YqtamZbWJiwgYEBpqam1KhRg8aNG2vYXPP+rRKLmjVrkpSURGZmpizGNjY2jBo1iuHDhxeY4tHS0pKePXvi6uqKq6trvm2qVKnCr7/++kr7tCoYQjV7DggIoG/fvqSnp8s+s3lxd3fn77//xtvb+63ajnNycjh69CgHDhzg4MGDpKamUqFCBYYNG8bw4cPp3LkzTZo0ITU1FWtra9zd3Qt0jcuLjo4OHTt2ZN++fWp2ZCHI2osQ5HeY/JKwx8bGMmrUKLVtBgYGsoBaW1vj5ORUoIuWmZkZUVFR1K9f/5WBIUqlkrNnz7Jq1So5m1dISAhTpkxh5MiRtG7dutBZnCRJ+Pj44OPjI29bsWIFnp6eatFZFy5cKNLjtb+/PwYGBnzwwQeEh4fTt29fUlJSCmyvUChISUmhb9++HD58+I26TkmSxIULF9i9ezceHh4kJSVRrlw5evbsybBhw+jTp48soIGBgbKIHjt2jAoVKhS5n44dO7Jr1y41O3JeQX78+HHpXpjgtRCC/A5TUBJ2FdWrV6dPnz707NkTJycn3nvvvSKd91WPwhEREbi5ubFz5045QxjA0KFD2bJlS5HcwoKDg5k9ezYnT57EzMyMp0+fUqVKFa5cuSKL8YcffsipU6e4devWKwVZqVRy8uRJnJycMDExYdmyZYWaWfKSnp7O+vXr1Vbyy4qbN2/KIqy6d7a2towePZqhQ4dqmJvCwsLo37+/3K5GjRrF6i8/O3JMTAy6urrUrFlTCLKW8e7HGv6HKSgJe//+/Rk7diympqbs2LGDjz/+GEtLS2xsbJgwYQJ//vknt2/fLlYV6OTkZP766y+6du2KjY0NS5cupUKFCvz0009MmDABgMWLF2uI8ct5dm/fvs2UKVNo27YtAQEBfP3114SGhjJ9+nSSkpLkgI9GjRrx119/oaOjw6FDh145vtDQUJ48eUKXLl14/vw5+/btKzR6Li8KhYKDBw8WOpt+HWJiYli9ejVt2rShdevWrFixgsqVK7N06VLu3r0r1/J7WYzj4uJwcXHh2bNnAAXmNS4MlR359OnTauOpVasW+vpiPqZtiE/kHWbSpEns2LFDIwfBpk2b5C93fHw8Fy5cICAggICAADw8POQE8dWrV6ddu3Y4OTnh5OSEra2tmqAqlUpOnz6Nq6srf//9N2lpaVSrVo3PP/+cUaNG0apVK3R0dOjfvz+mpqbUrVtXbXz52bgXLVqEJEkMGTKExYsXU6dOHdasWcP69evVjnV0dKRGjRq0adOGw4cPs3bt2kJn7v7+/gB06dKF8+fPY2BgUGiS+pcpV64cV69elesAvi6JiYns37+f3bt3yyHP9erVY/bs2QwfPlwte9nTp081jk9OTqZ///48ePCAESNG4O7uXmDKzcLIa0dOS0vDxMSEmJgYYT/WUoQgv8MUJQeBqakpH330kexzmp6ezuXLlzl//jwBAQGcPXtWnoEaGRlhZ2eHsbExT58+JSoqiufPn6Onp0evXr0YOXIkvXr1UhNtSZK4evUqdnZ2GoKZn41bkiTGjx/Pxo0bCQ8Pp0uXLly4cAFDQ0M1VzkfHx8SExPp3bs333//PTdu3Cg0kMHf359q1arRsmVLPD09izX7V6HyYigpaWlpHD58GA8PD/z8/MjOzsbU1JTPPvuMYcOG4ejoWKSIsqysLEaMGMH169fZtGkT4eHhQOFJ6QvjZTtyTExMqf3wCEoXIcjvOMXNQWBsbEyHDh3o0KEDkDsLvnnzJn5+fsyfPz/fCCgXFxf69euHra2tRl6GmJgYnjx5olFDDwq2cSclJfHbb78xd+5ccnJy6Nq1q0YKxYSEBDZu3MiAAQP4/vvvOXz4cIGClJGRwblz5+jduzd6enpUqlSpRKG0qrwOxSEnJ4eTJ0/i7u6Ot7c3KSkplC9fnkGDBjFixAicnZ2L5BGhQpIkPvvsM44fP863337LuHHj6N27N7Vq1SpxoEteO3LLli1JTU3VeJoRaAdCkP/DqBbC3Nzc+Pvvv4HcGXXz5s1p1qwZ2dnZnD9/Hi8vL3l/7dq1ZROHk5MT9+7dA8De3l7j/M2aNWPfvn0a269fv46npyctW7Zk69atalUu8rJ8+XJu3rwJwJ49e5g3b16+7S5cuEB6errs7tauXTuysrKKdS+ys7Pz/VHJD0mSuHTpErt372bfvn08efIEfX19unfvzrBhw/joo49KJO4A3333Hbt27WLs2LHMnz8fSZIICgqiTZs2JTofqPsjqxYIhclCOxGC/B/k3r17uLq6snPnTh48eIC+vj69evVi1KhR9OzZkzt37qjlQ37+/DkXL17kn3/+ISAggEOHDrF37161c/r5+VG+fHnatGmDiYkJkGvjXrdunbwoBaCrq0tkZCTffPMN8+bNw8DAoEDhfv/99+U0i7dv36Zjx458/vnn9OnTR80lL6/9GHLTXQ4ePBh3d/ciLezp6enh4uLySneyO3fuyB4SKlOMk5MTCxYsYMCAAZiamr6yr8LYvHkzK1eupFevXqxfvx4dHR1iYmJISEh4rbwTOjo6dOrUib1793Lnzh1ACLK2IgT5P4LK88DNzU2OhmvZsiVffPEFw4YNK9QHt3LlynTr1o1u3boBubPJ69evExAQIJtLfv/9d37//Xf09fWxtbWVZ9DGxsakpKRgZmbGw4cPqV+/Ptu3b8fBwUE+f36Lk7q6uhw+fJhKlSoxe/Zstm7dysWLF7l48SKGhoZ069aNgQMH0qdPH06cOEGDBg2wtLSUj587dy5///13kTwnjI2NmT59er77YmNj2bt3Lx4eHly7dg2Apk2bsnjxYoYOHZpvPbqScPDgQWbNmoWDgwNubm6yB8TLKTdLSseOHdm5cyeenp6AEGRtRQjyvxiFQsHJkydxdXXFy8tLzhs7ffp0Ro4cWeJZV7ly5XBwcMDe3p5ly5bRvn17li9fLs+gAwICWLduHevWrZOPefjwIRUrVmTXrl0aC0qqxUkXFxc5t4VSqcTPz48xY8awZs0a9u7dS+vWrZk8eTL79+/Hx8dHzR3OxMSEpKQkOdNZgwYN8Pb2VovUyw99fX28vb2pV6+eHL2YlJTEgQMH2L17N2fOnEGSJOrUqcPXX3/N8OHDC3Q3LClBQUF88cUXNGjQgP3796uZO15V1LSoqOzIXl5egBBkbUUI8r+Qu3fvyiaJ2NhY9PX16dOnD6NGjaJHjx7FWmQqjIiICJKSkrCzs6Nhw4Y0bNiQ0aNHA7lmkZeFKzk5mbZt22JmZqbmbteqVSuqVatGp06duHLlCn369OHq1auyf66BgQHdunXj8OHD7N+/nwEDBpCens7Ro0cZOXIk2dnZpKWlUadOHbp06cKAAQNwcXHBycmJwMBAli9fzt69ezVyWVhYWHDv3j2SkpLIyMjg6NGjnDx5kiNHjpCVlUW1atWYMGECw4YNw8nJqUxKBN26dYvZs2dTqVIlvL29NZ5UgoKCqFq16mvPxC0tLalTpw4xMTFUrFiRypUrv7Kuo+DNIwT5X0JSUpJsklCVNbK1teXLL79k6NChZRIWrJrNvryg5+/vz6RJk+S/Hz16hKGhIZcuXZLd7U6dOoW3tzeQazJwcHCQk+BkZWUxadIkFi1axJkzZ+jUqRN9+vTB09OTkydPymHF/fr149NPP2Xr1q388ccf+Pv7c/jwYXx9fZk6dSrOzs4MGDCA5cuXs3r1arVsb+3atSMnJ4datWqpBVyozjtixAi6du36ymofr0NsbCwuLi7k5OSwZ8+efPNpXL9+nRYtWrx2AnaVP/LOnTupXr36vyah+78NIcjvMAqFghMnTuDq6oq3tzcZGRmYm5szc+ZMRo4cKdddKytUgmxrawvk+vHOnz+fzZs3yzbQsWPHyjXzOnXqRKdOneSxh4aGyiaOvO52x44dIzQ0FIAePXpw9+5devToga6uLocOHaJPnz5yW39/f9q0acPIkSMZOXIkmZmZ+Pv74+npyaFDhzh69CjTpk3jww8/ZODAgfTt25fo6GgWL16ssTC5fPlyJkyYUKxcESXl+fPn9O/fn7i4OFasWJGvSSIhIYGYmJgSRejlh0qQHz58WCrnKwxJkpAkicTERIKDg+VcJ4LCEYL8DnLnzh1cXV1xd3cnNjaWcuXKySaJ7t27l5pJ4lVcuXKFevXqYWpqyoULFxg/fjzh4eEMGjQIe3t75s6dS79+/fI9Vk9PjxYtWtCiRQs+++wzAAYMGCBXC6levbosHI0aNaJOnToolUq2bdvGlClTaNq0KVFRUURFRTFs2DD5vIaGhnLFiaysLE6cOIGnpyeurq74+/szdepUua2VlRVr167F29ubEydOYG5u/kbEODMzk6FDhxIcHMyWLVvkeoEvo1rQK63KHqpq3sV1CSwMpVKJUqlEoVAQFRUlBx6lpaWho6NDQkICFStWfGW9QEEuQpDfAoGBgQVGkj1//pyDBw8SHh5OvXr1GDhwIJUqVSI5OZmTJ0/i5+fHrVu3gNzqzdOnT8fZ2VnOEXzp0qXXHl96ejpJSUmF1sZTKBTq6r9UAAAgAElEQVRcuXIFW1tbxo4di4eHB+XLl2f+/Pk4Ozvz7bffYmJigpGRkVzj7lWoZlFt27Zl2bJlBAUFybmNq1atKmcpa9OmjVp+4CdPnnDy5EmNPBqJiYmcOHGCixcv5ttfVFQU27dvl2en8+bNo0aNGmUqHkqlkqVLl3L69GnGjx9PgwYNSExM5MqVKxo2atUCnCRJRb6HhfHo0SP5fUBAAJIkkZaWVuJzq2bBmZmZ6OrqYmxsjIGBAba2tnIFmUaNGpGUlFSsOoS+vr7MnDkThULBhAkT+OabbzTa7Nmzh4ULF6Kjo0PLli01CqG+s6huahFfglIgLS1NysjI0HjFxsZKVlZWEiC/3nvvPalfv36SoaGhBEg1atSQZs2aJV25ciXfc5TG69KlS9LTp08LbXPt2jW1cXbv3l2KiIiQMjIypPj4eMnQ0FAaMmRIsfpt1KiRBEjW1tbytg4dOkiVK1eW4uPjpcuXL0uAZGRkJLm4uKj1X65cOalt27bSuHHjpL59+0otW7aUdHV1JUCqXbu29OWXX0qBgYFSenq6lJycLB06dEgaN26cZGpqqnGeyMjIMru3s2bNkgBp0qRJUnp6upSRkSEFBARIz54902g7bNgwycjISEpJSSmVvo8dOyZfZ2JiopSamiqdPn26xOdLTU2VEhISJH9/f8nf31968eKF2r9539vZ2RXpu5GTkyNZWVlJ4eHhUmZmptSiRQspNDRUrU1YWJjUqlUrKTExUZIkSXr8+HGpf0fLgCJprMj2pkXkl/shLi4OLy8vatSoweLFizl27BgzZszAwsKi0ErKZcnjx49ln2TIrevm5eUl13U7evQomZmZ9O3bt8jnzM7OJjIyEoDIyEjZTW3q1Kk8f/6cnTt30qxZMxo1aoS1tTW7d++mSpUqWFlZsW7dOkxMTAgMDOTPP//E29uboKAglEolDRo0YMGCBYwfP15eHCtXrhxdu3Zl06ZNREVF4ePjw8cffyyPo379+jg7O7Nx40a53FFpsH79etasWUPfvn3lismFERQURPPmzUstK5vqCQOQF361jYsXL9KwYUOsrKwwMDBg+PDh8pOCii1btjB16lR5beLfVDtRmCy0iMLyG0dHR7NgwQIWLFigtl1fXx8TExNMTEwwNjbO933eV0Ft8r5XRe+ZmZnJZgfV4/SlS5fo2rWrWiKg3377jVGjRslJjby8vDAwMKBHjx5FvvbIyEhycnJkU8SDBw+oV68eLi4u1K1bl40bNzJx4kT69OnD2rVrOXDgAElJSSQlJfHdd9/x/PlzjIyMcHBwoG7dulSoUIErV65w7do12UZdo0YNNXe7li1bUq5cOZydnbGxsWH8+PFytN/NmzcJCAjgq6++wtHRkUGDBtG/f/8S++/u27eP2bNn4+joyF9//VWoOQhyExWFhYUxbty4EvWXH3kFWeW9om3Exsaq3WMLCwu1YgWAXK38gw8+QKFQsHDhQnr27PlGx1lWCEHWIgoKIR4yZAjdunUjPT2dtLQ00tLS1N6r/k5NTZXfJyUlqbUrTirK/Hg5G1teIiIi2LJlC3PmzCErKwtfX1+cnZ2LVUT07t27QK79+MSJE7INXU9PjylTpjB37lyOHz8uJ6ofOXKkfKyDgwPDhg2jX79+Gn2mpqZy8eJF2d3u+PHjcl4OExMT2rRpQ7t27WjSpAmNGzfm119/ZcqUKUycOJFu3bpx4MAB/v77b/7v//6P//u//6Nt27YMGDCAAQMGFNk3+PTp04wbNw5ra2s8PT2LZKMODg5GqVSW2oIe/C8x/XvvvadRZ09bkPJZW3n5SSInJ4e7d+9y6tQpHjx4QIcOHQgJCZGDgt5lhCBrEQXlN163bl2RCpcWhlKpLFDQXxb38PBwjI2NUSgUpKenc+fOHTmnREEEBwcDueLz/PnzYpkr4H+zHpUgR0REyMmCVDO5/M4ZFRVVaCWU8uXL07lzZzp37gzkfplDQkIICAjg/Pnz/PPPP5w6dQrIDddWuQquXLkSJycn1qxZw+rVqwkICODAgQMcOHCAb775hm+++QYHBwdZnOvXr59v/yEhIQwdOpTq1avj7e2tVuC1MEorZDovMTEx1KxZk86dO+Ph4VFoXcW3hYWFhdpM/sGDB7IpLG8bR0dHypUrR/369Xn//fe5e/euWjj+u4oQZC0ib37jy5cvY2lpydy5c19bjCFXbMqXL1+kLGTBwcFYWlpSoUIF3Nzc2LZtG3p6esyZMwd9ff18Sx2phMzLywtdXV05/3JRCQsLQ09PDzs7OyDXxpmVlYWHh4faI+uwYcMIDQ0lJCSEvn37FrkslQp9fX1atWpFq1at+Pzzz5Ekifv373PkyBHOnz8v+z9Drhte7dq16dixI05OTowfP54VK1YQGBjIgQMH2L9/P/PmzWPevHm0bt2agQMHMmDAALmKdUxMDP369UOpVPL3338XK9ru+vXr6OnplWqYtioxfceOHXFzcyMwMPCVdRPfNA4ODty9e5fIyEhq167N7t27NTwo+vfvj7u7O2PGjJGrpL/NIrWliRBkLUOV3zg+Pp6EhIRSEeOS8PTpU8aNG8fBgwd5//332bp1K/b29iQmJuLm5qYxi584cSJKpZJDhw7Rrl27Yi+0hIWFYW5uzuXLlwFwc3PDzc2NmjVrMmPGDNm9rmrVqtja2hISElKiJPQvo6Ojg6WlJQMGDKBHjx5YWVmRmJjI6NGjOXbsGLGxsezfvx93d3cg1/3O0dERJycntm/fjlKpxMfHh/379/Ptt9/y7bff0qpVK5ydndmwYQOSJOHl5VVs08P169d5//33S80FT5IkoqOj6dWrl5zX4uzZs/Tu3btUzl9a6Ovrs2HDBnr06IFCoWDcuHE0bdqU7777Dnt7e/r27UuPHj04evQoNjY26OnpsXLlyiI/eWg7QpAFGpw4cYIVK1aQmJjIjBkzWLRokSwMhVUpOX/+PHFxcXz55ZdF7isrK4tjx47JkXp5cyP7+PjQqVMneQFs165duLq6youFZfXIXa1aNby8vOjSpQtXr17l7NmzpKamylGF58+flwNYDAwMaN26NUOGDMHAwIBHjx7h5+fHzz//LJ8vMDAQCwsLrK2ti9R/dnY2ISEhDBo0qNSu6fnz56SkpFC3bl0sLS2pW7euVgoyIAf25CXvU5mOjg4///yz2j3+tyAEWSCTlJTErFmzcHd3p27duri7u8uzqbwUVKVElZviVfZjpVLJP//8g4eHB/v37ycxMVHet3DhQq5evYq/vz+dO3dWW9CZOnUqx44dY//+/UCunVWhULzSY6Ek6Orq8ttvv+Hg4MCMGTPw9/enXbt2fPXVVyiVSsLCwtSy2xUkDrq6uixatIhFixbRtGlTBg4cyKBBg2jcuHGBfd++fZusrKxStx/D/7K8dezYEQ8Pj9de7BWULsIPWQDk5o+ws7PD3d2dfv36cfr06XzFuCDyPprnzUucd39wcDDz58/H2tqabt26sXXrVlq2bClXrd64cSMdO3bExsaG1NRUjRL13bt3V/OiiI+P13CJKk2sra359ttvuXDhAr/++qu8XVdXl8aNGzN+/Hi2bt3KrVu3iIyMZOfOnRrnyJtRLTQ0lMWLF9OqVStsbW1ZvHgxoaGhGqYXVcrN0vawAHVBVs3EBdqDEOT/OKmpqcyYMQMXFxcUCgUHDhzg22+/LXZOh9DQUCIiIjRmx1FRUaxYsQI7OzscHBxYvXo15ubmrFixgvDwcI4cOYKjoyOA/EivWqB5OUhGV1eXJk2aAP+rDnL48OHiX3QxmDVrFra2tnz33Xca48lLzZo1iY6OBmDgwIE8fvyYw4cP8+233+Ls7KyxmHrr1i1+/PFH7Ozs+Pjjj1m6dCnBwcFyySYoe0GG/4m/QDsQJov/MAEBAUyYMIGIiAiGDBnC2rVrqV69uuzCVlQSEhL4+uuvgdxZ6927dzlx4gS7d++Wq5NYWVkxb948hg8frmFLVbm8WVtbEx4eLnsphIeHywlxVNSsWRPItYk2bdqUw4cP8+OPPxb/4ouIvr4+v/32G05OTkydOhUfH598I+zc3d2ZO3cu7du3588//8TIyIguXbrIPxw5OTncuHFDzd0uLi4OgPv377Ny5UpWrlxJo0aNZJ/sKlWqkJCQwJYtWwgJCaFZs2ZMmjSpRAu9Lwuyyo78XxTkzZs3s3nzZiD3/5GlpSUnT558y6PKRQjyf5DMzEx++OEH1qxZQ5UqVXB1dWXIkCElOldCQgIdOnSQZ4+//vqr/Hhfo0YNpk2bxrBhw7C3ty8wVPju3btUrlwZc3NzwsPDC5whS5IkmyguX75Mr169OHLkiJqIlwUtWrTg66+/Zvny5Wzbtk0jek6V/9nGxoa9e/diZGSkcQ59fX1at25N69atmTZtGpIkERkZSUBAAN7e3oSFhXH79m1ZjAGaNGkiRyNCbrTfjh07OHfuXLFFOTo6mgoVKqgFT3To0AEPDw9SU1NLXJT1XeSzzz7js88+Izs7G2dn52ItQpc1wmTxHyMoKAgnJydWr15N9+7duXLlSonFGPLPvwHw6aefEh4ezqpVq3BwcCg0b0NYWBjW1tZym/feew8TExPCw8PV2t26dYtHjx4xevRodHR0uH//PlD2ZgvIrdHXqFEjZs2axcCBA1m+fDmJiYkEBQUxfPhwzM3N8fLykvMrvAodHR2srKwYOXIk33zzDefPnyc2NpaVK1fKbWJiYjTyCKuiIouLygc57+fQsWNHcnJytDavRVkzc+ZMnJ2dcXFxedtDkRGC/B8hJyeHZcuW8cEHH3D//n02bdrEgQMHZBNASSloUSgtLa1ISXEUCgX37t2jUaNG8jaVWKmSDak4ceIEAOPHj+ejjz7i3r176OnpvRFBTklJIS0tjczMTHx8fFi4cCGOjo64uLigq6uLl5fXa9epq169OrVr1wbgwIEDBXqrFNekBP8T5Lx06NABQGvDqMuS7du3c//+fb7//vu3PRQ1hCD/BwgLC6Nz584sWrSIdu3acenSJcaNG1cqZXwKiiQrarWS6OhoMjMzNezKDRo00Jgh+/v7U7lyZezs7Jg6dSpZWVkoFArOnTvHs2fPSnYBReT333/XyPwWHR1NQkICe/bsKbWIurweFgUt6hW3EkxOTg4PHz7UEOR69eppdV6LsuLKlSusWrUKNze3MqmT+Dpo12gEpYpSqWTjxo20adOGGzdusGLFCvz8/ArMu1ASJk2apBG2qorcKwoqm+nLgqyKmFMJbVZWFmfOnOHDDz9ET0+PTp06yZU2FAoFR48efd1LyZfU1FR+/fVXVq1ale9+e3v7Us2aFhQUhLm5OTVr1nzte6vi4cOHKJXKfGfwrVq14vLly3Ky//8CGzZsIDExkc6dO9OqVSvZ7VIbEIt6/1Lu37/PpEmTOH36NHZ2dmzdurXQYISSUljkXlHI62GRl7wLe3Z2dgQGBpKamip7Lejo6DB16lQ+//xzAA4dOqRWyul1efToEZs2beKPP/7g2bNnVK1aNV/RKu1It6CgIFq2bImOjs5r31sVL3tY5MXW1hZfX18uXLgg39t/O9u2bXvbQygQIcj/MiRJYseOHXz99dekp6ezYMECZs+eXaZ19gqK3CsKYWFh6OjoaHhJvCzIKvtxXtEYMWIECxYsICEhgaNHj5Kdnf3a1xkSEsLatWvx8PAgOzsbR0dHvvjiCz744AM6deqksYBZt27d1+ovL3FxccTFxamlFn2de6uiMEFWmUVOnz79nxFkbUaYLP5FxMXFMXjwYCZPnoyFhQVnzpxh/vz5b6zoaUkICwujbt26Gkl08voiQ+6CXr169dQe4Y2NjWUXtOfPn6tVri4OkiRx5swZJk6ciL29Pbt27eKjjz7i1KlTnDp1iv79+2NmZsbQoUOB3PSPpqamAIwbN67UKiqXRcpNKFyQa9asSb169f5zdmRtRQjyv4T9+/djZ2eHj48Ps2bN4vz587Ru3fptD+uV3L17N9+kO3Xq1KFcuXJERESQlJTEpUuX6NKli8ZC5OTJk+VcFsX1tsjMzGTHjh04ODjw6aefcvXqVT7//HNCQkJwd3eXIwgBXF1dWb58OR9++CGhoaFyPg1JkvItwlkSVAt6ZSHIOjo6sgfHy3Ts2PE/Z0fWVoQgv+M8e/aM0aNH8/HHH1OxYkWOHTvGsmXL8g1O0DZSUlKIjY3NV5D19PSwtLQkPDyc06dPo1Qq5YT1ebGwsGDgwIFAriAXJSVnYmIiP/30E40bN2bSpEkkJCQwe/ZsTpw4wc8//6yxkHb06FE+++wzmjdvjoeHB4aGhrRp04YRI0YAuS5U/v7+JbkFagQFBVGxYsVSz+2rSkxvYGCQ7/7WrVuTk5ND//79Zf9qwdtB2JDfAtnZ2a90t8nJyUGpVBZayPTYsWNMnTqVR48eMXbsWH788UcqVqz42sVPlUolOTk5ZV5E9datW0CueULVlyRJ8vv69esTHBzM8ePH0dHRoX379vmOafLkyezdu5eIiAhCQkIKXLyMiIhg48aNuLm5kZaWRtOmTVm4cCGDBw+WS169fP5r164xYsQIatWqhaenJyYmJnKb77//Xs6TPGXKFAIDA4udAwT+d7+vXbtGs2bNUCgUcpHX0iA6OpratWtrXJtCoSApKUnOVHf27FnOnj3Ljh07OHny5CsXDxUKhVryJMHrIwT5LXDjxo1XzuSys7PJzs4mOTlZY19aWhqbNm2SSwKtWLECR0dH7t27VyrjUwVBlEVay7wcP34cyPWYuHbtGpB7bar3FStW5NGjR3h7e2NtbU10dLScwCcv5cqVo3Hjxty+fZs//viDTz75RG1/cHAwHh4enD17FkmSaNOmjVo4d2hoqOzTnNef+eHDh0yZMgVdXV1+/PFHedEtL2PHjmXbtm1ER0czbdo0Zs6cWez7kJycTGBgIJGRkbRu3Vq+/pIgSRI5OTlkZWXJr9DQUOrWrcvOnTvlbZmZmXIu6rwlkyD3h2vJkiWMGjWqSH2pTB1BQUFkZGQQGRlJdnY2Ojo6pKSkkJOTUyrFBP4LCEF+C9jZ2b1yhqyqGPL++++rbf/nn3+YMmUKkZGRDB06lLVr15Z6VRFVCaeyLu/j5+cHgIuLi1y8NCAggDZt2gDQrl07PD09efz4MaNGjZK358fs2bMZN24cN27cYN26dSgUCry8vFi3bh2BgYEYGBgwatQoZs6cKfsv5yUuLo60tDTZXKCqmJKWloaPjw8ffPBBvv02a9aMo0ePEhsbi6enJ1OnTsXR0ZHMzEzS09PJyMggIyODzMxM+f3Lr7CwMPlp4dq1a/j4+Gi0yXt8enq62t8vnzu/WWt0dLRcfbsoPHv2rND7Dbkz5IyMDK5fv44kSTRu3Jhr165RoUIFJElCqVRy//59/P39NVKpCvJHCPI7QkZGBosWLZIFeOfOnaVaUeJtEBYWRvny5QtcbDIzM5PfP3nyhMTExAJ/fAYPHiznhLC1tSU2NpYXL14A8MknnzBmzBiqVKlCWloaZ8+eVROy9PR0njx5QkpKCuXLlycxMVF+jDc3N2fbtm1s3rw5X4FMT09Xi+DLz85dHCIiItSqpujq6mJsbIyxsTGGhoYYGRnJr6pVq2JkZISxsTFGRkYa+w0NDQkPD2fPnj00btyYWbNmqe0vV64cv/76KwcPHtQYR3GjAXV0dDA0NERPTw8zMzOioqIAaNq0KWlpacWysfv6+jJz5kwUCgUTJkwocNF03759DBkyhEuXLmFvb1+s8WorQpC1kISEBH755ReuX7+Ok5MTjo6OfPnll9y8eZPevXuzadOmYhf3fNMolUqNmdvLs8a9e/cCyJUrMjMzuXXrFmfOnOHZs2dqSXR27NiBp6cnjo6OKJVKjZlhXv9g1WxTxc6dO/NNHl8Unjx5Imdwe/llbGxMlSpVsLS05NixY2rHzZgxQ0MgX36p9kdFRbF+/XqCgoK4efMmlSpVktsUJR9IYfj6+rJnzx4WL16skURHZatW5bJWUZJowNJCoVDIlWEsLCxwcHCgb9++2NjYqLVLTk7ml19+oW3btm9lnGWFEGQt4+V0lqqQ4AoVKrB582Y501lRyMnJKfSx+eVHX1WbqKgojI2NCxTVwo5V7cvKyiryNY8ZM6ZI7VJTU7l06RKmpqayID548ECeCedHp06dcHZ2VhNB1YwyryimpKSgVCpZu3YtJ06cwN7enjp16tCiRQsmT578SrPQxYsX5aTvenp6jBgxAltb2yJdl2qhsFWrVmXiYQH5+yADVKpUqVSiAUuLixcv0rBhQ/k+DB8+HC8vLw1BVgU8FRTS/q4iBFnLKCidpbm5OadPn+bo0aMF2iJfFsjSXKnPO9t7eeZXpUqVAvcVNCtMSEhgzpw5ODo6smTJEnn/zZs3adeuHbNmzeLQoUMa4+jevTuurq4cO3aMtWvX8uLFC3R1dalVqxYPHjzQaG9mZlakSLe4uDhWrVrFiRMnqFChApcvX+by5cscOHAAV1fXV+YgVrnBubu7o1AomDx5Mv/880+RgnIyMzO5c+eOWoReaaFaBC0sE11pRAOWFrGxsWpjtbCw0CjTde3aNWJiYvjoo4+EIAvKloLSWUZERBAXF5evvbBy5crUqFGjUFviq2yNeWeNUVFRNGjQQJ6JGhoalnpWLFUo9JQpU2jfvr28/cWLF9SpUwd7e/t8BTk7Oxs7Oztu3rxJ+fLlmTZtGlOnTsXDw4OFCxdqtC+qLXT37t1s2LAh3yxzERERcj+WlpbUrFkz3/uxePFivLy8SEtL48aNG6xatYq5c+e+su+IiAgUCkWpB4RA7gzZxMTkrc14i0t+3hh5nwiVSiWzZs1i+/btb3BUbw4hyFpGs2bN2Ldvn8b2RYsWvbFZTHZ2Nu+9916ZelkUlOVNxaRJk9ixY4fa04Kenh5eXl7UqlWLJUuWMH78eDkhfH7ti2oL9fHxYf78+TRp0kQuI/Uy+/fvl6PzDA0NqVu3LvXr18fS0lLtNX78eNavXw/AsmXL6N+/v1wHMD8SEhJkcQkODi504bIk5JeYXpuxsLBQc8N78OABtWrVkv9OTk4mJCSEDz/8EMh9sunbty/e3t7/ioU9IchaxusIy7uEKstbw4YN891frVo1XF1d+eKLL7h69SoKhYL333+fr776iiFDhmhEnZU0M9rFixf55JNPqFmzJps3b2bp0qX5ths7dixOTk5ERUXJr9DQUI4dO1agj21WVha2trasWrWKBg0aYGlpSb169TAxMQE01wv+/PNPTp06VaISTQURExNT4I+eNuLg4MDdu3eJjIykdu3a7N69m127dsn7K1euTHx8vPz3hx9+yKpVq/4VYgxCkLUOlbCsW7eOa9eu8cEHH7zVRZayIiwsjFq1amnMwiVJIiAggLVr13Lw4EEkSaJHjx7MnDmTzp07FzrTK64t9N69ewwcOBATExP++usvfH198fPzw8jIiIyMDLmdlZUVP/74Y76fQWZmJjExMURGRspCvXr1arU2qgKwKmrUqIGlpSWpqaka6wWqEk2l8TSkUCiIjY19p7K46evrs2HDBnr06IFCoWDcuHE0bdqU7777Dnt7+wKrqPxbEIKshVSrVo3p06fnGxjybyEsLEytbFNOTg5eXl4sWbKEW7duYWBgwOjRo5kxY4bGCntp8PjxY1xcXEhNTcXX15czZ86wbNkyHB0d2bFjB+7u7kWaaRsaGtKwYUO1mf6SJUvo3Lkz165dw9DQkBcvXrBixQp0dHTUZti3b9/O95wlKdGUH48ePUKhULx2aak3Te/evTXyTP/www/5tj116tQbGNGbQwiy4I2Tnp5OdHQ03bt35/79+8ycOZMzZ86QlpZGxYoV+eabb/jss8/KzNc6JSWFAQMGcP/+ffbs2UNISAgLFiygefPmeHl5Ubly5deaoero6LBy5Uo6dOhAkyZNCA0N5fDhw/j6+qrN8JcvX/5aC5Gv4lUubwLtQ2R7E7xxwsPDkSSJv/76iyZNmuDr60taWhqQ6289Y8aMMhPj7OxsPv74Y65evcovv/xCYmIi06ZNo1mzZmzZsoXKlSuXSj8ODg58/PHHXL9+nS5dunD69Gm2bt2q1qa0SjQVhBDkdw8hyII3yo0bN+QAiqysLI28C48ePSpRmfuiIEkSn3/+OUePHmXevHmYmJgwefJkmjdvjpubG5UqVSrV/hYvXoyJiQlPnz7FxsaGuXPnqnkQqNYLJk+ezIABA1i0aFGpL+iBEOR3CSHIgjJHkiT8/Pzo1asXbdq0kWfDBeXnPXDgQJkkS1+0aBGurq6MHj2axo0bM2HCBGxsbPDx8aFKlSql3l/t2rX5+uuvuXLlCt26dSM1NZXp06ereWVUq1aN0aNH8+effzJnzpxSd3kD5MRNAu1HCLKgzMjIyGDbtm20bt2afv36ERAQQM2aNeX9BYVXX79+nUaNGvH9999rpLssKVu2bGH58uX07NmTLl26MHbsWKytrTly5IhcjqksmDVrFhYWFnh6ejJp0iR8fX3lHMplTUxMDO+99x6GhoZvpD/B6yMEWVDqxMfHs3TpUqytrZkyZQq3bt3CyMgIHR0dHj16JLc7d+6chg21Vq1a/P777zRq1IiffvoJa2trJk+ezM2bN0s8Hm9vb2bOnIm9vT3Dhw9n3LhxWFlZceTIEczNzUt83qJgbGzM0qVLefDgARUrVqRBgwZ8/fXXbyQdpSooRPDuIARZUGrcu3ePGTNm0KhRI3744QeePHki78vIyKBJkyb8+uuvGBgY0L9/f+zt7Tl37hyLFi1i8ODBLFq0iE2bNvHpp59y+vRpTp48Sa9evdixY4c8yz5x4kSxkp2fP3+eTz/9FEtLSyZOnMjEiROpW7cuvr6+arP1smTIkCE4OjqyceNGvvvuOxITE/nyyy/LvF8hyD1gR5AAAB/ISURBVO8eQpAFr4UkSZw7d44hQ4bQvHlzfv/9d9LT0+X9hoaGfPLJJ5w5c4aAgAD69OlDVlaW7IOsCuZwc3Njzpw5agtr7dq1w8PDg+DgYCZPnsyZM2fo3bs3jo6O7Nq165Ulpu7cucOgQYOoWLEiM2bMYPr06dSuXRs/P78CczCXBTo6OqxatYq0tDT8/PyYNGkSnp6eeHl5lVmfycnJPHv2TAjyO4YQZEGJyMnJYe/evXTo0IGuXbvKUXUqLC0tWbp0KeHh4WzdupU2bdqgo6Mjh0wXJ5y3YcOGrFu3jnv37sl25XHjxtG4cWN+/vlnnj9/rnHMo0ePcHFxISMjg+nTpzNnzhxq1KiBr6/vWxEpe3t7PvnkE3bt2kX//v2xsLBg5syZaiWjShNV5jshyO8WQpAFxSI5OZn169djY2PDqFGjuHz5srxPR0eHXr168ffffxMaGsqXX36psWBWEkFWUb16debOncudO3f49ddfqVixIvPmzaNBgwbMnj2b+/fvA7kZ4/r3709sbCxTpkxh2bJlmJqa4ufnh6WlZckv/jVRucH98MMPbNy4kbi4OGbPnl0mfQmXt3cTIciCIvHgwQPmzZtHw4YN+b//+z+1YqPVq1fnq6++4ubNmxw4cICePXsWWCD1VVneioKRkRFjx47l6tWr/P3339jb2/PLL79gY2PDsGHDsLa2JigoiJEjR7J582aqVKmCn59fqSd/Ly61atXi//7v/7hw4QJJSUl88sknuLq6cuHChVLvqyh5kAXahwidFhTK9evXWbt2Lfv27SMnJ0dtX9u2bZk0aRKDBg3CyMioSOcLCwvDzMxMTpv5Oujq6tKzZ0969uzJ9evXWbNmDR4eHvL+v/76CzMzM3x9fQvMKvem+eKLL/jzzz+ZP38+p06d4vjx4/z0008MHjwYY2PjUutHzJDfTYQgvwWSk5NfmfA9LS2NrKwskpOT39Co/kdmZiYHDx7kzz//5Ny5c2r7jI2NGThwIGPHjqVly5ZAbjjyqxbYVNy+fRsrK6sCr0uhUJTomhs0aJCvC9vTp085fvw4VatWLVTwVCWp3sT9XrBgAZMmTZJ9o8eOHcuCBQtKtfpFZGSkXFygsHtd0vutOr44Hi+CVyME+S0QHR39yv/ImZmZZGZmEhkZ+YZGldvnkSNHcHNzUzNJQO5Ma/DgwfTp00f2hCju2HJycoiKiqJp06YFHpuVlVWia/bw8GD9+vWYm5uTkpJCVlYWPXv25PLly3z11VcsWbKEwYMHM3jw4Hxn5+np6SgUiiL/sLwOLVu2pGXLlqxbt469e/fSvn17/vrrL5ycnIpch+9V3Lt3D3Nzc7n6c35IkkRGRkaJ/49JkkRqaippaWmUK1euVEuG/VcRgvwWaNq06StnyPHx8W8s/WZ8fDy//fYbv/32m5rvsK6uLh999BGTJ0+mc+fOr13GKSwsDIVCgaOjIy1atMi3TUBAQIH7CmL//v38/PPPGBsb8+LFC4yMjDhx4gStWrUiOzub/fv3s27dOrZs2YKrqyuffPIJM2fOVLNjx8XFkZaW9sbszJs2beKDDz5g165dfPPNN4waNYqVK1dy6dKlUjFdJCYm0rBhw0LvpUKh4PLly8W+33mPz8jI4OrVq2RnZ3PlyhUyMzN5/vw5kiS9M1VKtAmxqPcfJiwsjGnTptGwYUMWL14si3G1atX48ssvuXPnDnv27KFLly6lUlPvdTwsCuLs2bOMHTsWSZJIT0/H0NCQw4cPy/XpypUrx7Bhw/jnn384evQozs7ObN26lRYtWjBo0CDOnj37Vh677ezsGDlyJO7u7jx69IilS5dy7949lixZ8trnViWmf1P2Y11dXQwNDXFwcEBfX5/Y2FjS0tLkoruCoiME+T+GJEmcOXOGwYMH07JlS/744w/5S/PBBx+wY8cODh06xNy5c0v9C13agnzz5k2GDBlCZmYmABUrVuTgwYPY2dlptNXR0aFjx47s37+foKAgxo0bx/Hjx+nWrRvt27fn4MGDGouWZc0PP/xA+fLlWbt2LUOHDqVHjx6sWbOGK1euvNZ5Hz9+THZ29htf0NPR0fn/9u48qskr/x/4OwurCK4omGrBIGURdTSC60jpCC7ELqjUfQSFFtcz7gtfte6n7rhMkaljqSi1VRxA6mhdj1ZktB2B0USlyCYKNlCRQJb7+8NfckS2gNmAz+ucHDV58jyfRHjn5j73uRd8Ph+enp6wtbUFl8tFdnY2MjIytBNKkYZRILcRSqUSiYmJGD58OEaPHo3k5GQwxmBnZ4e5c+ciIyMDFy5cwKRJk3Raur45JBIJ+Hw+XFxc3npf+fn5CA4OhkwmAwC0a9cOSUlJGDx4cKPPdXd3x4EDByCVSrFq1Srk5uZi/vz5CAoKwt69e412IlUzDC4rKwvff/89YmJi0K5dO0RERNQ78ZIuzGGEBYfDgYWFBf70pz9BIBBQ/7KOKJBbufLycuzZswceHh6YMWOGtvXl4eGB3bt349GjR9i7dy+8vb0NXotEIoGLi8tbB75MJsOECRNQUFAAALC1tcXp06cxdOjQJu3H0dER0dHRkEql2LRpEywsLLBs2TIIhUKsWrVKe7WbIS1cuBDdu3fHunXr0KlTJ2zevBmZmZnYvn17s/dpDoH8uqauYJ6WlgZ3d3cIhUJs3bq11uM7d+6Ep6cnfHx8EBAQoL0gqDWgQG6l8vLysHLlSgiFQixfvhx5eXng8/kICQnBuXPncPv2bURGRup9UvaGSKXSt+6uqKqqwqRJk5CVlQXg1UUi33//PUaMGNHsfdrY2GDq1KlISUnByZMn4e3tjZ07d+K9997DX//6V/z6669vVXNjx46KikJhYSF27dqFsLAwjBgxAtu2bdO+xqbSBHLPnj31WapRqFQqREVF4ezZs8jOzkZCQkKtmf4GDBiAjIwM/Pe//0VISIjBrnY0BQrkVubOnTuYOXMmPDw8sGvXLpSXl8PZ2Rlr166FRCJBfHw8Ro4cafQz4L///juePXv2VoGsVqsRHh6OK1euAHg1cdHJkyfh7++vlxo1o0ouXLiAq1ev4sMPP8SJEyfg6+uLMWPG4Ny5cwY5Afj+++/Dz88PO3bsQGFhIQ4dOgQ+n4+IiIhm9WtrAtmYEyjpS3p6OoRCIVxdXWFpaYnQ0NBakzD5+/vD1tYWAODn52eUbzLGQoHcCqjVaqSmpmL06NHaGdKUSiX8/f1x/Phx3L9/H6tXr4azs7PJatSc0Ht9pemmWrlyJb777jsAr1YbSUxMxAcffKCX+t4kEokQHx+PrKwszJs3D+np6RCLxRg4cCCOHDmiPZGoDxwOB1u2bIFcLseaNWvQu3dv/N///R8yMjKwb9++Ju8vLy8Pjo6Oer3yz1jeHB0iEAi0XVN1iYuLw5gxY4xRmlFQILdglZWVOHz4MAYMGICPP/4YV65cgb29PaKiovDrr7/i7Nmz+PDDDw12kk5XpaWl2LVrF4BXLaDnz583eR979uzBnj17ALwaypaQkIDAwEC91lkXFxcXfPnll3j48CE2bdoEmUyGyMhIuLu7Y+vWrSgtLdXLcfr3749p06bh+PHjuHnzJubPnw+RSIT169fjwYMHTdpXS54Hua5vIPV9m4uPj0dGRgaWLl1q6LKMhgK5BXr27Bk2btyIPn36YN68ebh//z58fHywf/9+5OTkYMeOHUa5oEQXpaWlGDFiBE6fPg0AOHLkCIYPH96kUE5MTMTy5csBADweD/Hx8Rg3bpxB6q1Phw4d8Le//Q337t1DXFwcunbtinXr1sHNzQ2LFi3Cw4cP3/oYmmFwS5cuBYfDwd///neoVCpERkbWWgy2IS05kAUCQY2FYPPz8+v8Znf+/Hls2rQJZ86caVVLVFEgm6nff/8dsbGxmDZtGrZu3Yrnz59DIpEgKioKbm5u2LhxI8rKyhAaGoqLFy/i5s2bCAsLQ7t27Uxdeg2xsbF49OhRjfsePXqk88rSFy9eRFhYGIBXYXz06FFMmDBB73XqytLSElOnTkV6ejpSUlIwbNgwHDp0CN7e3ggNDcWNGzeavW8nJycsW7YM6enpOHHiBDw9PbFixQpcu3YNhw8f1mkfFRUVKC0tbbGBLBKJIJVKkZOTg+rqahw/fhxisbjGNnfu3EFERATOnDlj8CW4jI0unTZDpaWlGD9+vHY4z8mTJ7F9+3bt4PqePXtizpw5mDlzptn/QGZmZtZ5/927dxt97t27dzF58mQoFApwuVz84x//wCeffKLvEpuFw+EgICAAAQEByMrKwp49e5CQkIDTp0/Dz88PCxcuhFgsrnca0vosXLgQcXFxWLlyJaRSKe7duwdHR0esXLkSQUFBjY6caOkT0/P5fMTExCAwMBAqlQqzZ8+Gl5cXoqOjMWjQIIjFYixduhQvXrzAxIkTAbz6fThz5oyJK9cPCmQzFBsbW2ts5cuXLyEUCrFt27YG5xs2N97e3jh58mSt+/v27dvg8x4/fowJEyagvLwcHA4HsbGxmDx5sqHKfCteXl746quvsH79ehw8eBCxsbH49NNP4eLiggULFmDGjBk6f3OxtrbGqlWrEBkZic2bN9d4LCIiAqmpqQ2OkGkN8yCPHTsWY8eOrXHfhg0btH8/f/68sUsyGuqyMEP1tSr79++PcePGtZgwBoC5c+fWmrDH1dUVc+bMqfc5z58/h1gsRmFhIQDg4MGDmDp1qkHr1AcnJyds2LABUqkUu3btAmMMixcvhlAoRHR0dI0Vtxvy5MmTOu+/ePEivv322wafa24XhZCmoUA2Q/VdNddYq9IcderUSbuydKdOneDg4ICrV6+iU6dOdW5fXV2NkJAQ3Lt3DwAQExODWbNmGbHit2dnZ4fPPvsMWVlZSEhIQJ8+fbB9+3a4u7tj7ty5jV7wUd8Hsp2dHZYuXVpvYAMUyC0dBbIZmjt3Lnr16lXjvsZaleZMs7L0/PnzUVZWVm+gqFQqbN68GdevXwcA7N69G+Hh4cYsVa94PB4++ugjXL58GRcvXsTYsWPxzTffYODAgRCLxbhw4UKdw7zq+0CeNGkSZDIZFi9eXO8x8/LyYGVlha5du+rtdRDjoUA2Q506dUJycjLmz5+PkJAQrF+/HteuXau3VdlSaPoFU1NTaz3GGMOSJUu0V+F9+eWXiIyMNGp9hjRkyBAcP34cmZmZiIyMxNWrVzFu3Dj4+vri7NmzNSYTqq+bZ+PGjYiMjMSpU6dw6tSpOo+Tl5cHgUCgl+lSifHR/5qZ6tixI8LDwxEfH4/ly5e3+DAGAB8fH/To0QMpKSm1HtuxYwcOHjwIANiyZQvmzZtn7PKMonfv3ti9ezcePHiAdevWobi4GF988QUGDBiAHTt2QCaT1ejmefMD+YsvvkDPnj2xaNGiOi9KacljkAkFMjEiDoeDsWPH4ubNmygpKdHe/+2332LNmjUAgPDw8Aa/krcWnTt3xooVK3D//n2sWrUK9vb2WL16tXZV7/LycixfvrzWB7KdnR3279+P4uLiWleoqdVq5OfnUyC3YBTIxKiGDx8Oxhg++ugjbN26FadOnUJERASAV4t/TpkyxcQVGpe1tTXGjx+P69evIykpCSKRCPv27YOnpyemT5+OjIyMWs/5y1/+ghkzZuDYsWNIS0vT3v/06VNUV1dTILdgNA6ZGE1paSnWrVsHALh16xZu3boFDocDxhhWrFiB1atXa0/otTUcDgeBgYEIDAzEL7/8ol0AVbMI6qJFi+Dr64u4uDhkZmZqV9mOiorCnTt3YG9vTyMsWgEKZGI0sbGxtVY41owyOHPmDFJSUlBZWQl7e3vweDzweDxwudwaf755/+v/fv2+Nx9/8743t6+srIRSqUTXrl3r3V7XOpqyPY/Hw+PHj2FtbQ1bW1vweDx07doVW7ZswcKFC3Ho0CEkJCQgJCQEFhYWNVbF7tatGwoKCrB69Wrs27ePArkVoEAmRlPf+NouXbrAwcEBjDFt4FRXV0OtVkOlUmlvr/9b8/eGtlGpVCZZwNRQXg9j4NXaeV5eXoiNjUVISEiLnpievEKBbESMMZw6dQocDqfReXwrKiqgUqneam215lIoFFAoFHo9dmlpaY0Tea/7/PPPsWTJEjDGcOvWLZ3WxdMVY6zOIH8z1IuLi1FRUQEnJyeo1ep6n6MJ+eZ8UNS3z4KCAnTs2BE8Hq/e/SQnJ0MqldZ6fb169UJRURHmzJmDzp07AwCOHTuGyMjIRkfmaH6+5HJ5s4bJMca0N2MveNBaUSAbQVBQEIqKirSD9tu3bw8HB4c61wvTtBKVSiWsra2bNXfw21AqlVAoFKioqNDbL1lZWRnmz5+vvRT6dc7Ozujfvz/S09OhUqmgUCiQnp6ul+M2hUqlglKpxLNnzxrdVrO6Mp+vn1+f/v37Q6FQwNraut73XCaT1RnI3bt3x/Tp07Fnzx7tPBZbt27F0aNHERMT0+gSXQqFAleuXIG1tXWzxy5zudwmTQ9K6kejLAwsMDAQ9+/fh1QqRceOHfHOO+/g0KFD2LZtGzgcTo0bYwxyuRwAtP2Jb25jyJtarUZ1dTVsbGzA5XL1tt+UlJQ6w3jgwIHYv38/HBwcwOFwoFKpwOfzjfqaNTcejwe1Wm2SY1tYWIDL5UKpVNa7jVgsrjUvsLOzM4KDg1FeXl7rvS0sLERycnKjx7aysoKVlRXkcjlUKlWz6meMgcvlorq6ulV1EZkCtZANJCgoCIWFhcjNzYWdnR0EAgE6dOhQZ6sYeNUyraqqgpWVld5aXk2hVqshl8thY2MDDke/Xz/fnA9Zo3379jVacEqlUrtWmrG9Hi76fv26sLKyQmVlpfZE35vs7e2xf/9+/Otf/8KjR4/g6uqK4OBg2Nvb1zpRqlHf+/4mPp8PLpcLuVwOtVoNCwuLJr8HjDH88ssv2g8W6sZoHgpkAwgMDMT//vc/lJSUoEePHujYsWO9QcwYQ1VVFdRqtbZlamyMMVRWVsLKysogx3d1dcWlS5fqvF9DrVZrW+WmwuVyta10Y+NwOLC2tkZlZSVsbW3rfB/s7e3rnPVOl/e3MVwuFzY2NqiqqoJcLm+w+6Sh18AYw+3bt6kbo5moy0KPgoKC4O3tjevXr0OtVkMgEDQYxmq1Gi9fvtT+MpgqjOVyOSwtLQ0WRMHBwfV+3dZQKpUmCcLXaU6qmQqXy4WlpSXkcnmTvvrr8v7qQvOhwOPx8PLly2YHqqb7i8vlQqFQUDdGE1ALWU8UCgVGjhyJH374AcnJyRCJRA1uf/XqVVhYWGDQoEFwcHAwUpW1nTt3Du+++y769Olj0OPcvHkTcXFxuHv3Lvr27YuwsLAaowASEhLwySefwNLS0qB1NKSiogKpqanalShMJTs7G8XFxfD399f5OY29v01VVlaG7OxsMMYwZMiQZu1Dc6IUqHvxUlIbp4lvFL2rdQgKCkJBQQGkUqn2axuPx4NAIKhze80oCgcHB5MMa9NQqVSQy+UmX4ePMYaKigrY2dmZvI4//vij0ZEJhsblciGTydC+fXuTduHY2NiguLgYdnZ2b/3traFhj22ETv+RFMiEEGJ4OgUy9SETQoiZoEAmhBAzQYFMCCFmggK5AbNnz4ajo2O9a5wxxrBgwQIIhUL4+Pjg9u3bRq6QENKaUCDXIy0tDf/+979hZWVV59nhx48fo1+/fjhy5AhsbGwwa9YsfPbZZyaolBDSWlAgvyEtLQ19+vRBcHAwPv30U1y4cAEymQzZ2dnabRITE9GvXz88ePAA3t7eOHHiBPbu3QuZTIaioiITVk8IackokP+/14NYJBJh1KhR+PHHH5GbmwsHBwckJSUBAPbt24fJkydj2LBh6NWrF1auXImysjI4OztDIBCgoKDAxK+EENJStflxyGlpaViwYAFycnIwadIkPH36FBKJBCKRCAMHDsS5c+dw7do12Nvbw9vbGxKJBDY2Njhw4AAmTpwIa2trKJVKnD9/HsuWLcP27dsxcOBAU78sQoh5oXHIjVGpVIiKisLmzZsxatQoXLt2DQ4ODhg2bBhyc3MhEAhgYWEBR0dHTJkyBTweD9XV1VAoFJg9ezYAICwsDKmpqZg+fTry8/NrzSlACCG6arOBnJaWBhcXFxQVFeHUqVPo1auXNoiFQiGePHmCmJgY3LhxA0+fPkV5ebn2sujKykpYW1sjOjoau3fvxnvvvQeZTAZbW1s4OTmZ+qURQlqoNhnImpbx8uXLERoaimvXrkEmk0EoFKK4uBiurq4oKSmBRCIB8Gomsm+++QYvX76Evb09+Hw+unfvji5duqBLly7w8PDAs2fP8NVXX9U4jjkNm0tLS4O7uzuEQmGds889fvwY/v7+GDBgAHx8fJCammqSOoBXJ009PT3h5eWFKVOmmKwOADh58iQ4HA4yMjIMUocutezcuROenp7w8fFBQEAAcnNzTVJHVVUVJk+eDKFQCF9fX/z2228GqaNNe31dLB1urcL169fZ6NGjWWJiIgsLC2ORkZHMzc2Nff3118ze3p4tWbKEde/enVlYWDCBQMBWrVrFADAul8vs7e0Zl8tlXbp0YZ6enszCwoJ5e3uzH3/8sdZxLl++zP7zn/8wLy+vOutISUlhQUFBTK1Wsxs3brDBgwcb5PUqlUrm6urKHj58yKqqqpiPjw/Lysqqsc2cOXPYgQMHGGOMZWVlsV69epmkDolEwvr378+eP3/OGGOsuLjYJHUwxlh5eTkbMWIE8/X1Zbdu3dJ7HbrW8tNPP7GKigrGGGMHDhxgkyZNMkkd+/fvZxEREYwxxhISEgxSRyumU8a2yRZyQUEB3nnnHQgEAuTl5cHX1xfFxcXIysqCWCzG3r17UVJSgkWLFiEvLw+5ubng8XjIzMyETCaDk5MT2rdvDy6Xi6NHj+Lu3bsYPXp0reOMHDmywSkQk5KSMGPGDHA4HPj5+Rls2Fx6ejqEQiFcXV1haWmJ0NBQ7agRDQ6Ho10KSDNqxBR1xMbGIioqCh07dgQAODo6mqQOAFi7di2WLVsGa2trvdfQlFr8/f21K6n4+fkhPz/fJHUkJSVh5syZAICQkBBcuHCBptXUszYZyJofIpFIBKlUiufPn2P48OHYu3cvLl26hOjoaPTp0wfV1dXYvXs3bty4AWdnZzg6OoLD4UAoFCIxMRF3795FaGhos+vQfDBoGGrYnC7HWbduHeLj4yEQCDB27Fjs27fPJHVIJBJIJBIMGzYMfn5+SEtLM0kdd+7cQV5eHsaPH6/34ze1ltfFxcVhzJgxJqnj9W34fD4cHBxQWlqq91raslYZyLdu3YKPjw/kcjkqKirg5eWFzMxM7eOaljGfz0dMTAw2b96Mn3/+GdHR0cjLy0NVVRUsLS0xefJkJCcn48WLFygsLERAQADEYjEuXbqEQYMGvXWddbUuDDH/rS7HSUhIwKxZs5Cfn68dNaLvJXh0qUOpVEIqleLSpUtISEhAeHg4ZDKZUetQq9VYvHgxduzYodfjNqeW18XHxyMjIwNLly41SR3G+nlty1rliiEikQhisRhr1qxBZWUlpk2bVuPEmqZlnJOTgw8++AA9evTAsWPH4OXlBQDYsGEDunXrhn/+8584f/48jh8/jh9++AGJiYl6rVPzwaBhqGFzuhwnLi5O2xodMmQI5HI5SkpK9NploEsdAoEAfn5+sLCwgIuLC9zd3SGVShtdgUWfdfzxxx/IzMzEqFGjAABPnjyBWCzGmTNn9PJB3JRaNM6fP49Nmzbh8uXLsLKy0msNutah2UYgEECpVKKsrOytViUhddC1s5m1sJN6mhMTgwcPZkqlstbjKSkpzM3Njbm6urKNGzcyxhhbu3YtS0pKYowxVllZyUJCQljv3r2ZSCRiDx8+bFYdOTk59Z7US05OrnFSTyQSNesYjVEoFMzFxYU9evRI+75kZmbW2CYoKIh9/fXXjDHGsrOzmZOTE1Or1Uav4+zZs2zGjBmMMcaePXvGBAIBKykpMXodr/vzn/9ssJN6utRy+/Zt5urqyiQSiUFq0LWOmJiYGif1Jk6caLB6WiGdMrbVBnJRURFzdXVlHh4e7MWLFyapITQ0lHXv3p3x+XzWo0cPdvjwYXbw4EF28OBBxhhjarWaff7558zV1ZV5e3sb7JeescY/gLKystjQoUOZj48P69evX52jRoxRh1qtZosXL2YeHh7M29ubJSQkmKSO1xkykHWpJSAggDk6OrJ+/fqxfv36seDgYJPUoa9GShulU8a22kunxWIxQkNDkZOTg6KiIsTExJi6JEJI26VTZ3ur7EM+evQo+Hw+pkyZApVKhaFDh+Knn37C+++/b+rSCCGkXq22hUzaprVr16JLly5YuHAhAGD16tXo1q0bFixYYOLKSBtHq06Ttue3337Dxx9/jNu3b0OtVsPNzQ3p6eno3LmzqUsjbVvb7bIgbde7776Lzp07486dOyguLsaAAQMojEmLQYFMWp3w8HAcOXIET5480U6TSkhLQF0WpNWprq5G3759oVAoIJVKwePxTF0SIdRlQdomS0tL+Pv7o0OHDhTGpEWhQCatjlqtxs8//4zvvvvO1KUQ0iStcnIh0nZlZ2dDKBQiICAAbm5upi6HkCahPmRCCDE8WuSUEEJaEgpkQggxExTIhBBiJiiQCSHETFAgE0KImaBAJoQQM0GBTAghZoICmRBCzAQFMiGEmAkKZEIIMRMUyIQQYiYokAkhxExQIBNCiJmgQCaEEDNBgUwIIWaCApkQQsxEU5dw0mmSZUIIIU1HLWRCCDETFMiEEGImKJAJIcRMUCATQoiZoEAmhBAzQYFMCCFmggKZEELMBAUyIYSYCQpkQggxExTIhBBiJv4f7Q/IP3INSmIAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7eff046cf0d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"autofig.reset()\n",
"autofig.plot(x, y, z, i=t, \n",
" xlabel='x', ylabel='y', zlabel='z',\n",
" projection='3d', elev=0, azim=[0, 20, 30, 50, 150, 180])\n",
"anim = autofig.animate(i=t, \n",
" save='3d_azim_6.gif', save_kwargs={'writer': 'imagemagick'})"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.15rc1"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| gpl-3.0 |
sympy/scipy-2017-codegen-tutorial | index.ipynb | 1 | 11665 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<h1 style=\"text-align:center;\">Automatic Code Generation with SymPy</h1>\n",
"\n",
"<img src=\"intro-slides/sympy-notext.svg\" alt=\"sympy logo\" style=\"width:100px\">\n",
"\n",
"<h3 style=\"text-align:center;\">Watch the video of the tutorial online</h3>\n",
"\n",
"[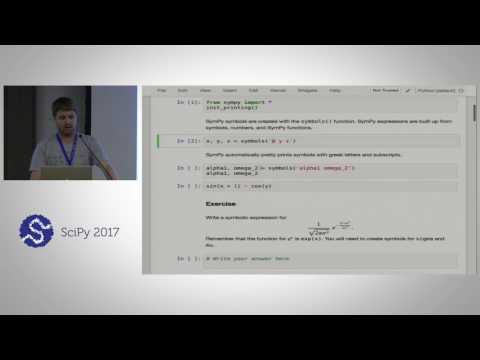](http://www.youtube.com/watch?v=5jzIVp6bTy0 \"Automatic Code Generation with SymPy | SciPy 2017 Tutorial | Jason, Aaron, Björn & Kenneth\")\n",
"\n",
"This tutorial will introduce code generation concepts using the [SymPy](http://sympy.org) library. SymPy is a pure Python library for symbolic mathematics. Code generation refers to the act of converting a SymPy symbolic expression into equivalent code in some language, typically for numeric evaluation. This allows one to use SymPy to symbolically model a problem and generate fast numerical code for specific platforms that executes that model. This is a powerful tool that is useful to scientists in many domains. Code generation allows users to speed up existing code, to deal only with the high level mathematics of a problem, avoids mathematical errors and typos, makes it possible to deal with expressions that would otherwise be too large to write by hand, and opens possibilities to perform automatic mathematical optimizations of expressions.\n",
"\n",
"SymPy supports generating code for C, C++, Fortran, MATLAB/Octave, Python, Cython, Julia, JavaScript, LLVM, Rust, Haskell, Mathematica, Tensorflow, and Theano, and can easily be extended to other languages. SymPy’s code generation is used by libraries such as PyDy, pyodesys, sympybotics, pycalphad, and many other programs.\n",
"\n",
"You can run this tutorial online with [Binder](https://beta.mybinder.org/v2/gh/sympy/scipy-2017-codegen-tutorial/master?filepath=index.ipynb). Otherwise, follow the instructions in the [README](https://github.com/sympy/scipy-2017-codegen-tutorial) to install the tutorial materials.\n",
"\n",
"## Instructors\n",
"\n",
"- Björn Dahlgren, KTH Royal Institute of Technology\n",
"- Kenneth Lyons, University of California, Davis\n",
"- Aaron Meurer, University of South Carolina\n",
"- Jason Moore, University of California, Davis\n",
"\n",
"## Learning objectives\n",
"\n",
"Attendees will be able to:\n",
"- write SymPy expressions describing mathematical functions and identify the\n",
" function arguments and outputs,\n",
"- use the SymPy code printers to transform SymPy expressions representing\n",
" common domain specific functions into multiple output languages,\n",
"- use the SymPy code generation routines to output compilable C code and use\n",
" Cython to access these functions in Python,\n",
"- generate custom vectorized functions with the three SymPy functions:\n",
" lambdify, ufuncify, and autowrap,\n",
"- create both custom code printers that make use of specialized C libraries and\n",
" common subexpression elimination (CSE),\n",
"- subclass the core SymPy printers and create a printer for a custom language.\n",
"\n",
"## Outline\n",
"\n",
"### [Introduction](intro-slides/intro-slides.html) [5 minutes]\n",
"\n",
"**Description**\n",
"\n",
"Introduction of the topic, speakers, and software.\n",
"\n",
"### [Intro to SymPy Expressions](notebooks/01-intro-sympy.ipynb) [25 minutes]\n",
"\n",
"**Description**\n",
"\n",
"Writing common domain specific mathematical expressions with SymPy.\n",
"\n",
"**Motivating Examples**\n",
"\n",
"Long expressions, Matrix operations, and Loop Fusion from classical mechanics, chemical kinetics, nuclear dynamics, and materials science.\n",
"\n",
"- Expressions\n",
"- Reminders on common gotchas\n",
"- Floating point representation\n",
"- Undefined Functions\n",
"- Derivatives\n",
"- Matrices\n",
"- Matrix Symbols\n",
"- Indexed\n",
"\n",
"### [Code Printers](notebooks/02-code-printers.ipynb) [30 minutes]\n",
"\n",
"**Description**\n",
"\n",
"Printing expressions in multiple languages (C, Fortran, Rust, Julia, Octave, Javascript, etc)\n",
"\n",
"**Motivating Example**\n",
"\n",
"2D interactive plot in a Jupyter notebook by Javascript injection\n",
"\n",
"- [15 min] Code printing\n",
" - **Exercise:** Codegen your own function\n",
"- [15 min] **Exercise:** Plotting SymPy Functions with Javascript\n",
"\n",
"### The Easy Way: High Level Code Generation [55 minutes]\n",
"\n",
"**Description**\n",
"\n",
"Generate python functions from symbolic expressions.\n",
"\n",
"**Motivating Example**\n",
"\n",
"Generate a Jacobian function for a chemical kinetic problem.\n",
"\n",
"#### [Ordinary Differential Equations](notebooks/20-ordinary-differential-equations.ipynb)\n",
"- [10 minutes] Refresher on ordinary differential equations\n",
"- [5 minutes] **Exercise:** write an analytic Jacobian function by hand\n",
"\n",
"#### [Lambdify](notebooks/22-lambdify.ipynb)\n",
"- [10 minutes] Introduction to ``lambdify``\n",
"- [5 minutes] **Exercise:** Create a function from a SymPy expression\n",
"\n",
"#### [Chemical Kinetics Introduction](notebooks/25-chemical-kinetics-intro.ipynb)\n",
"- [5 minutes] Governings equations for systems of ODEs in chemical kinetics.\n",
"- [5 minutes] **Exercise:** generate a function evaluating the rhs of an ODE system\n",
"\n",
"#### [Chemical Kinetics Symbolic Construction](notebooks/32-chemical-kinetics-symbolic-construction.ipynb)\n",
"- [10 minutes] **Exercise:** construct SymPy expressions from a simple data structure\n",
"- [10 minutes] **Exercise:** derive a Jacobian symbolically and generate a function evaluating it\n",
"\n",
"### 10 Minute Break\n",
"\n",
"### [The Harder Way: C Code Generation, Custom Printers, and CSE](notebooks/07-the-hard-way.ipynb) [55 minutes]\n",
"\n",
"**Description**\n",
"\n",
"Convert SymPy matrices to a C program and speed up numerical execution by extending the printer with common subexpression elimination.\n",
"\n",
"**Motivating Example**\n",
"\n",
"Evaluate a chemical kinetic ordinary differential equation and its Jacobian using C.\n",
"\n",
"#### Section 1\n",
"- [5 minutes] Introduction\n",
"- [5 minutes] **Exercise:** Load the ODE expression, compute the Jacobian, and inspect the results.\n",
"- [5 minutes] Printing C Code\n",
"- [5 minutes] **Exercise:** Generate C code for the Jacobian expression.\n",
"\n",
"#### Section 2\n",
"- [5 minutes] Extending and Customizing Printers\n",
"- [10 minutes] **Exercise:** Construct custom exponential printing and symbol names.\n",
"\n",
"#### Section 3\n",
"- [5 minutes] Common Sub-expression Elimination\n",
"- [15 minutes] **Exercise:** Generate C code (w/ CSE) for the ODE and Jacobian expressions.\n",
"- [5 minutes] **Bonus:** Compile and execute the C code.\n",
"\n",
"### [The Easy \"Hard\" Way: Cythonizing Your Code](notebooks/08-cythonizing.ipynb) [1 hour]\n",
"\n",
"**Description**\n",
"\n",
"Generate C code to evaluate an ordinary differential equation and and its Jacobian and wrap it for use with SciPy’s integrators. Additionally, demonstrate how one might access external C libraries.\n",
"\n",
"**Motivating Example**\n",
"\n",
"Integrating the water radiolysis system of ODEs.\n",
" \n",
"#### Section 1: Introduction to Cython\n",
"\n",
"- [2 minutes] Explanation of Cython\n",
"- [3 minutes] Example: writing Cython and compiling in a notebook\n",
"\n",
"#### Section 2: Generating C Code with SymPy's `codegen()`\n",
"\n",
"- [2 minutes] Review the water radiolysis system\n",
"- [2 minutes] First exposure to `codegen`\n",
"- [3 minutes] **Exercise** generate code with a cleaner function signature\n",
"- [3 minutes] **Exercise** generate an even cleaner function signature\n",
"\n",
"#### Section 3. Wrapping the Generated Code with Cython\n",
"\n",
"- [5 minutes] Overview of the wrapping process\n",
"- [3 minutes] Explanation of the build process\n",
"- [3 minutes] Explanation of the wrapper code\n",
"- [3 minutes] **Exercise**: use the wrapped function with some random inputs\n",
"- [3 minutes] Use `odeint` to integrate the ODEs using the wrapped function\n",
"\n",
"#### Section 4. Generating and Compiling a C Extension Module Automatically\n",
"\n",
"- [3 minutes] Overview of the `autowrap` function\n",
"- [5 minutes] **Exercise**: explore the `autowrap` generated files\n",
"- [5 minutes] **Exercise**: use the wrapped function with some random inputs\n",
"- [2 minutes] Writing a wrapper around the wrapper\n",
"- [8 minutes] **Exercise**: generate a function to compute the Jacobian\n",
"\n",
"#### Section 5. Using a Custom Printer and an External Library with `autowrap`\n",
"\n",
"- [2 minutes] Overview of `CodeGen` and `CodePrinter`\n",
"- [2 minutes] Explanation of fastapprox library\n",
"- [8 minutes] **Exercise**: implement a custom code printer to use `fastpow` instead of `pow`\n",
"- [3 minutes] Including `fastpow.h`\n",
"- [3 minutes] Using the new function and proving it worked\n",
"- [2 minutes] **Exercise**: compare outputs of the callables using `pow` and `fastpow` functions\n",
"\n",
"----\n",
"\n",
"The attendees will come away with a powerful set of tools that will allow them\n",
"to develop high performance numerical code using Python that compliments NumPy\n",
"and SciPy. This tutorial will be ideal for users of the SciPy Stack that would\n",
"like to increase the performance of their Python code, get into some of the\n",
"depths of how low-level languages can interact and be used from Python, or to\n",
"learn a new technique for expressing mathematical models in Python.\n",
"\n",
"# Bonus Materials\n",
"\n",
"- [Radioactive decay chain: Tc-99m](notebooks/23-lambdify-Tc99m.ipynb)\n",
"- [Chemical Kinetics: Using a Cython template](notebooks/40-chemical-kinetics-cython.ipynb)\n",
"- [Chemical Kinetics: Using a Cython template & another SciPy solver](notebooks/45-chemical-kinetics-cython-vode.ipynb)\n",
"- [Chemical Kinetics: Using a C template and an external solver's C API](notebooks/50-chemical-kinetics-C.ipynb)\n",
"- [Chemical Kinetics: Adding diffusion (mixing hand-written & generated functions)](notebooks/60-chemical-kinetics-reaction-diffusion.ipynb)\n",
"- [More Cython Examples](notebooks/cython-examples.ipynb)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [default]",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.3"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| bsd-3-clause |
goddoe/CADL | session-1/session-1.ipynb | 4 | 32631 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Session 1 - Introduction to Tensorflow\n",
"<p class=\"lead\">\n",
"Assignment: Creating a Dataset/Computing with Tensorflow\n",
"</p>\n",
"\n",
"<p class=\"lead\">\n",
"Parag K. Mital<br />\n",
"<a href=\"https://www.kadenze.com/courses/creative-applications-of-deep-learning-with-tensorflow/info\">Creative Applications of Deep Learning w/ Tensorflow</a><br />\n",
"<a href=\"https://www.kadenze.com/partners/kadenze-academy\">Kadenze Academy</a><br />\n",
"<a href=\"https://twitter.com/hashtag/CADL\">#CADL</a>\n",
"</p>\n",
"\n",
"This work is licensed under a <a rel=\"license\" href=\"http://creativecommons.org/licenses/by-nc-sa/4.0/\">Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License</a>."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Learning Goals\n",
"\n",
"* Learn how to normalize a dataset by calculating the mean/std. deviation\n",
"* Learn how to use convolution\n",
"* Explore what representations exist in your dataset"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Outline\n",
"\n",
"<!-- MarkdownTOC autolink=true autoanchor=true bracket=round -->\n",
"\n",
"- [Assignment Synopsis](#assignment-synopsis)\n",
"- [Part One - Create a Small Dataset](#part-one---create-a-small-dataset)\n",
" - [Instructions](#instructions)\n",
" - [Code](#code)\n",
"- [Part Two - Compute the Mean](#part-two---compute-the-mean)\n",
" - [Instructions](#instructions-1)\n",
" - [Code](#code-1)\n",
"- [Part Three - Compute the Standard Deviation](#part-three---compute-the-standard-deviation)\n",
" - [Instructions](#instructions-2)\n",
" - [Code](#code-2)\n",
"- [Part Four - Normalize the Dataset](#part-four---normalize-the-dataset)\n",
" - [Instructions](#instructions-3)\n",
" - [Code](#code-3)\n",
"- [Part Five - Convolve the Dataset](#part-five---convolve-the-dataset)\n",
" - [Instructions](#instructions-4)\n",
" - [Code](#code-4)\n",
"- [Part Six - Sort the Dataset](#part-six---sort-the-dataset)\n",
" - [Instructions](#instructions-5)\n",
" - [Code](#code-5)\n",
"- [Assignment Submission](#assignment-submission)\n",
"\n",
"<!-- /MarkdownTOC -->"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<h1>Notebook</h1>\n",
"\n",
"Everything you will need to do will be inside of this notebook, and I've marked which cells you will need to edit by saying <b><font color='red'>\"TODO! COMPLETE THIS SECTION!\"</font></b>. For you to work with this notebook, you'll either download the zip file from the resources section on Kadenze or clone the github repo (whichever you are more comfortable with), and then run notebook inside the same directory as wherever this file is located using the command line \"jupyter notebook\" or \"ipython notebook\" (using Terminal on Unix/Linux/OSX, or Command Line/Shell/Powershell on Windows). If you are unfamiliar with jupyter notebook, please look at [Installation Preliminaries](https://github.com/pkmital/CADL/blob/master/README.md#installation-preliminaries) and [Session 0](https://github.com/pkmital/CADL/blob/master/session-0/session-0.ipynb) before starting!\n",
"\n",
"Once you have launched notebook, this will launch a web browser with the contents of the zip files listed. Click the file \"session-1.ipynb\" and this document will open in an interactive notebook, allowing you to \"run\" the cells, computing them using python, and edit the text inside the cells."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a name=\"assignment-synopsis\"></a>\n",
"# Assignment Synopsis\n",
"\n",
"This first homework assignment will guide you through working with a small dataset of images. For Part 1, you'll need to find 100 images and use the function I've provided to create a montage of your images, saving it to the file \"dataset.png\" (template code provided below). You can load an existing dataset of images, find your own images, or perhaps create your own images using a creative process such as painting, photography, or something along those lines. Each image will be reshaped to 100 x 100 pixels. There needs to be at least 100 images. For Parts 2 and 3, you'll then calculate the mean and deviation of it using a tensorflow session. In Part 4, you'll normalize your dataset using the mean and deviation. Then in Part 5, you will convolve your normalized dataset. For Part 6, you'll need to sort the entire convolved dataset. Finally, the last part will package everything for you in a zip file which you can upload to Kadenze to get assessed (only if you are a Kadenze Premium member, $10 p/m, free for the first month). Remember to complete the additional excercises online, including the Gallery participation and the Forum post. If you have any questions, be sure to enroll in the course and ask your peers in the \\#CADL community or me on the forums!\n",
"\n",
"https://www.kadenze.com/courses/creative-applications-of-deep-learning-with-tensorflow/info\n",
"\n",
"The following assignment breakdown gives more detailed instructions and includes template code for you to fill out. Good luck!"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a name=\"part-one---create-a-small-dataset\"></a>\n",
"# Part One - Create a Small Dataset\n",
"\n",
"<a name=\"instructions\"></a>\n",
"## Instructions\n",
"\n",
"Use Python, Numpy, and Matplotlib to load a dataset of 100 images and create a montage of the dataset as a 10 x 10 image using the function below. You'll need to make sure you call the function using a 4-d array of `N x H x W x C` dimensions, meaning every image will need to be the same size! You can load an existing dataset of images, find your own images, or perhaps create your own images using a creative process such as painting, photography, or something along those lines.\n",
"\n",
"When you are creating your dataset, I want you to think about what representations might exist in the limited amount of data that you are organizing. It is only 100 images after all, not a whole lot for a computer to reason about and learn something meaningful. So <b>think about creating a *dataset* of images that could possibly reveal something fundamental about what is contained in the images</b>. Try to think about creating a set of images that represents something. For instance, this might be images of yourself over time. Or it might be every picture you've ever taken of your cat. Or perhaps the view from your room at different times of the day. Consider making the changes within each image as significant as possible. As \"representative\" of the thing you want to capture as possible. Hopefully by the end of this lesson, you'll understand a little better the difference between what a computer thinks is significant and what you yourself thought was significant.\n",
"\n",
"The code below will show you how to resize and/or crop your images so that they are 100 pixels x 100 pixels in height and width. Once you have 100 images loaded, we'll use a `montage` function to draw and save your dataset to the file <b>dataset.png</b>.\n",
"\n",
"<a name=\"code\"></a>\n",
"## Code\n",
"\n",
"This next section will just make sure you have the right version of python and the libraries that we'll be using. Don't change the code here but make sure you \"run\" it (use \"shift+enter\")!"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# First check the Python version\n",
"import sys\n",
"if sys.version_info < (3,4):\n",
" print('You are running an older version of Python!\\n\\n' \\\n",
" 'You should consider updating to Python 3.4.0 or ' \\\n",
" 'higher as the libraries built for this course ' \\\n",
" 'have only been tested in Python 3.4 and higher.\\n')\n",
" print('Try installing the Python 3.5 version of anaconda '\n",
" 'and then restart `jupyter notebook`:\\n' \\\n",
" 'https://www.continuum.io/downloads\\n\\n')\n",
"\n",
"# Now get necessary libraries\n",
"try:\n",
" import os\n",
" import numpy as np\n",
" import matplotlib.pyplot as plt\n",
" from skimage.transform import resize\n",
"except ImportError:\n",
" print('You are missing some packages! ' \\\n",
" 'We will try installing them before continuing!')\n",
" !pip install \"numpy>=1.11.0\" \"matplotlib>=1.5.1\" \"scikit-image>=0.11.3\" \"scikit-learn>=0.17\"\n",
" import os\n",
" import numpy as np\n",
" import matplotlib.pyplot as plt\n",
" from skimage.transform import resize\n",
" print('Done!')\n",
"\n",
"# Import Tensorflow\n",
"try:\n",
" import tensorflow as tf\n",
"except ImportError:\n",
" print(\"You do not have tensorflow installed!\")\n",
" print(\"Follow the instructions on the following link\")\n",
" print(\"to install tensorflow before continuing:\")\n",
" print(\"\")\n",
" print(\"https://github.com/pkmital/CADL#installation-preliminaries\")\n",
"\n",
"# This cell includes the provided libraries from the zip file\n",
"try:\n",
" from libs import utils\n",
"except ImportError:\n",
" print(\"Make sure you have started notebook in the same directory\" +\n",
" \" as the provided zip file which includes the 'libs' folder\" +\n",
" \" and the file 'utils.py' inside of it. You will NOT be able\"\n",
" \" to complete this assignment unless you restart jupyter\"\n",
" \" notebook inside the directory created by extracting\"\n",
" \" the zip file or cloning the github repo.\")\n",
"\n",
"# We'll tell matplotlib to inline any drawn figures like so:\n",
"%matplotlib inline\n",
"plt.style.use('ggplot')"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<style> .rendered_html code { \n",
" padding: 2px 4px;\n",
" color: #c7254e;\n",
" background-color: #f9f2f4;\n",
" border-radius: 4px;\n",
"} </style>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"execution_count": 1,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Bit of formatting because inline code is not styled very good by default:\n",
"from IPython.core.display import HTML\n",
"HTML(\"\"\"<style> .rendered_html code { \n",
" padding: 2px 4px;\n",
" color: #c7254e;\n",
" background-color: #f9f2f4;\n",
" border-radius: 4px;\n",
"} </style>\"\"\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Places your images in a folder such as `dirname = '/Users/Someone/Desktop/ImagesFromTheInternet'`. We'll then use the `os` package to load them and crop/resize them to a standard size of 100 x 100 pixels.\n",
"\n",
"<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# You need to find 100 images from the web/create them yourself\n",
"# or find a dataset that interests you (e.g. I used celeb faces\n",
"# in the course lecture...)\n",
"# then store them all in a single directory.\n",
"# With all the images in a single directory, you can then\n",
"# perform the following steps to create a 4-d array of:\n",
"# N x H x W x C dimensions as 100 x 100 x 100 x 3.\n",
"\n",
"dirname = ...\n",
"\n",
"# Load every image file in the provided directory\n",
"filenames = [os.path.join(dirname, fname)\n",
" for fname in os.listdir(dirname)]\n",
"\n",
"# Make sure we have exactly 100 image files!\n",
"filenames = filenames[:100]\n",
"assert(len(filenames) == 100)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Read every filename as an RGB image\n",
"imgs = [plt.imread(fname)[..., :3] for fname in filenames]\n",
"\n",
"# Crop every image to a square\n",
"imgs = [utils.imcrop_tosquare(img_i) for img_i in imgs]\n",
"\n",
"# Then resize the square image to 100 x 100 pixels\n",
"imgs = [resize(img_i, (100, 100)) for img_i in imgs]\n",
"\n",
"# Finally make our list of 3-D images a 4-D array with the first dimension the number of images:\n",
"imgs = np.array(imgs).astype(np.float32)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Plot the resulting dataset:\n",
"# Make sure you \"run\" this cell after you create your `imgs` variable as a 4-D array!\n",
"# Make sure we have a 100 x 100 x 100 x 3 dimension array\n",
"assert(imgs.shape == (100, 100, 100, 3))\n",
"plt.figure(figsize=(10, 10))\n",
"plt.imshow(utils.montage(imgs, saveto='dataset.png'))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a name=\"part-two---compute-the-mean\"></a>\n",
"# Part Two - Compute the Mean\n",
"\n",
"<a name=\"instructions-1\"></a>\n",
"## Instructions\n",
"\n",
"First use Tensorflow to define a session. Then use Tensorflow to create an operation which takes your 4-d array and calculates the mean color image (100 x 100 x 3) using the function `tf.reduce_mean`. Have a look at the documentation for this function to see how it works in order to get the mean of every pixel and get an image of (100 x 100 x 3) as a result. You'll then calculate the mean image by running the operation you create with your session (e.g. <code>sess.run(...)</code>). Finally, plot the mean image, save it, and then include this image in your zip file as <b>mean.png</b>.\n",
"\n",
"<a name=\"code-1\"></a>\n",
"## Code\n",
"\n",
"<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# First create a tensorflow session\n",
"sess = ...\n",
"\n",
"# Now create an operation that will calculate the mean of your images\n",
"mean_img_op = ..."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# And then run that operation using your session\n",
"mean_img = sess.run(mean_img_op)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Then plot the resulting mean image:\n",
"# Make sure the mean image is the right size!\n",
"assert(mean_img.shape == (100, 100, 3))\n",
"plt.figure(figsize=(10, 10))\n",
"plt.imshow(mean_img)\n",
"plt.imsave(arr=mean_img, fname='mean.png')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Once you have seen the mean image of your dataset, how does it relate to your own expectations of the dataset? Did you expect something different? Was there something more \"regular\" or \"predictable\" about your dataset that the mean image did or did not reveal? If your mean image looks a lot like something recognizable, it's a good sign that there is a lot of predictability in your dataset. If your mean image looks like nothing at all, a gray blob where not much seems to stand out, then it's pretty likely that there isn't very much in common between your images. Neither is a bad scenario. Though, it is more likely that having some predictability in your mean image, e.g. something recognizable, that there are representations worth exploring with deeper networks capable of representing them. However, we're only using 100 images so it's a *very* small dataset to begin with.\n",
"\n",
"<a name=\"part-three---compute-the-standard-deviation\"></a>\n",
"# Part Three - Compute the Standard Deviation\n",
"\n",
"<a name=\"instructions-2\"></a>\n",
"## Instructions\n",
"\n",
"Now use tensorflow to calculate the standard deviation and upload the standard deviation image averaged across color channels as a \"jet\" heatmap of the 100 images. This will be a little more involved as there is no operation in tensorflow to do this for you. However, you can do this by calculating the mean image of your dataset as a 4-D array. To do this, you could write e.g. `mean_img_4d = tf.reduce_mean(imgs, axis=0, keep_dims=True)` to give you a `1 x H x W x C` dimension array calculated on the `N x H x W x C` images variable. The axis parameter is saying to calculate the mean over the 0th dimension, meaning for every possible `H`, `W`, `C`, or for every pixel, you will have a mean composed over the `N` possible values it could have had, or what that pixel was for every possible image. This way, you can write `images - mean_img_4d` to give you a `N x H x W x C` dimension variable, with every image in your images array having been subtracted by the `mean_img_4d`. If you calculate the square root of the expected squared differences of this resulting operation, you have your standard deviation!\n",
"\n",
"In summary, you'll need to write something like: `subtraction = imgs - tf.reduce_mean(imgs, axis=0, keep_dims=True)`, then reduce this operation using `tf.sqrt(tf.reduce_mean(subtraction * subtraction, axis=0))` to get your standard deviation then include this image in your zip file as <b>std.png</b>\n",
"\n",
"<a name=\"code-2\"></a>\n",
"## Code\n",
"\n",
"<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Create a tensorflow operation to give you the standard deviation\n",
"\n",
"# First compute the difference of every image with a\n",
"# 4 dimensional mean image shaped 1 x H x W x C\n",
"mean_img_4d = ..."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"subtraction = imgs - mean_img_4d\n",
"\n",
"# Now compute the standard deviation by calculating the\n",
"# square root of the expected squared differences\n",
"std_img_op = tf.sqrt(tf.reduce_mean(subtraction * subtraction, axis=0))\n",
"\n",
"# Now calculate the standard deviation using your session\n",
"std_img = sess.run(std_img_op)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Then plot the resulting standard deviation image:\n",
"# Make sure the std image is the right size!\n",
"assert(std_img.shape == (100, 100) or std_img.shape == (100, 100, 3))\n",
"plt.figure(figsize=(10, 10))\n",
"std_img_show = std_img / np.max(std_img)\n",
"plt.imshow(std_img_show)\n",
"plt.imsave(arr=std_img_show, fname='std.png')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Once you have plotted your dataset's standard deviation per pixel, what does it reveal about your dataset? Like with the mean image, you should consider what is predictable and not predictable about this image.\n",
"\n",
"<a name=\"part-four---normalize-the-dataset\"></a>\n",
"# Part Four - Normalize the Dataset\n",
"\n",
"<a name=\"instructions-3\"></a>\n",
"## Instructions\n",
"Using tensorflow, we'll attempt to normalize your dataset using the mean and standard deviation. \n",
"\n",
"<a name=\"code-3\"></a>\n",
"## Code\n",
"\n",
"<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"norm_imgs_op = ..."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"norm_imgs = sess.run(norm_imgs_op)\n",
"print(np.min(norm_imgs), np.max(norm_imgs))\n",
"print(imgs.dtype)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Then plot the resulting normalized dataset montage:\n",
"# Make sure we have a 100 x 100 x 100 x 3 dimension array\n",
"assert(norm_imgs.shape == (100, 100, 100, 3))\n",
"plt.figure(figsize=(10, 10))\n",
"plt.imshow(utils.montage(norm_imgs, 'normalized.png'))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We apply another type of normalization to 0-1 just for the purposes of plotting the image. If we didn't do this, the range of our values would be somewhere between -1 and 1, and matplotlib would not be able to interpret the entire range of values. By rescaling our -1 to 1 valued images to 0-1, we can visualize it better."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"norm_imgs_show = (norm_imgs - np.min(norm_imgs)) / (np.max(norm_imgs) - np.min(norm_imgs))\n",
"plt.figure(figsize=(10, 10))\n",
"plt.imshow(utils.montage(norm_imgs_show, 'normalized.png'))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a name=\"part-five---convolve-the-dataset\"></a>\n",
"# Part Five - Convolve the Dataset\n",
"\n",
"<a name=\"instructions-4\"></a>\n",
"## Instructions\n",
"Using tensorflow, we'll attempt to convolve your dataset with one of the kernels we created during the lesson, and then in the next part, we'll take the sum of the convolved output to use for sorting. You should use the function `utils.gabor` to create an edge detector. You can also explore with the `utils.gauss2d` kernel. What you must figure out is how to reshape your kernel to be 4-dimensional: K_H, K_W, C_I, and C_O, corresponding to the kernel's height and width (e.g. 16), the number of input channels (RGB = 3 input channels), and the number of output channels, (1).\n",
"\n",
"<a name=\"code-4\"></a>\n",
"## Code\n",
"\n",
"<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# First build 3 kernels for each input color channel\n",
"ksize = ...\n",
"kernel = np.concatenate([utils.gabor(ksize)[:, :, np.newaxis] for i in range(3)], axis=2)\n",
" \n",
"# Now make the kernels into the shape: [ksize, ksize, 3, 1]:\n",
"kernel_4d = ...\n",
"assert(kernel_4d.shape == (ksize, ksize, 3, 1))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We'll Perform the convolution with the 4d tensor in `kernel_4d`. This is a `ksize` x `ksize` x 3 x 1 tensor, where each input color channel corresponds to one filter with 1 output. Each filter looks like:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"plt.figure(figsize=(5, 5))\n",
"plt.imshow(kernel_4d[:, :, 0, 0], cmap='gray')\n",
"plt.imsave(arr=kernel_4d[:, :, 0, 0], fname='kernel.png', cmap='gray')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Perform the convolution with the 4d tensors:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"convolved = utils.convolve(..."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"convolved_show = (convolved - np.min(convolved)) / (np.max(convolved) - np.min(convolved))\n",
"print(convolved_show.shape)\n",
"plt.figure(figsize=(10, 10))\n",
"plt.imshow(utils.montage(convolved_show[..., 0], 'convolved.png'), cmap='gray')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"What we've just done is build a \"hand-crafted\" feature detector: the Gabor Kernel. This kernel is built to respond to particular orientation: horizontal edges, and a particular scale. It also responds equally to R, G, and B color channels, as that is how we have told the convolve operation to work: use the same kernel for every input color channel. When we work with deep networks, we'll see how we can *learn* the convolution kernels for every color channel, and learn many more of them, in the order of 100s per color channel. That is really where the power of deep networks will start to become obvious. For now, we've seen just how difficult it is to get at any higher order features of the dataset. We've really only picked out some edges!\n",
"\n",
"<a name=\"part-six---sort-the-dataset\"></a>\n",
"# Part Six - Sort the Dataset\n",
"\n",
"<a name=\"instructions-5\"></a>\n",
"## Instructions\n",
"Using tensorflow, we'll attempt to organize your dataset. We'll try sorting based on the mean value of each convolved image's output to use for sorting. To do this, we could calculate either the sum value (`tf.reduce_sum`) or the mean value (`tf.reduce_mean`) of each image in your dataset and then use those values, e.g. stored inside a variable `values` to sort your images using something like `tf.nn.top_k` and `sorted_imgs = np.array([imgs[idx_i] for idx_i in idxs])` prior to creating the montage image, `m = montage(sorted_imgs, \"sorted.png\")` and then include this image in your zip file as <b>sorted.png</b>\n",
"\n",
"<a name=\"code-5\"></a>\n",
"## Code\n",
"\n",
"<h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Create a set of operations using tensorflow which could\n",
"# provide you for instance the sum or mean value of every\n",
"# image in your dataset:\n",
"\n",
"# First flatten our convolved images so instead of many 3d images,\n",
"# we have many 1d vectors.\n",
"# This should convert our 4d representation of N x H x W x C to a\n",
"# 2d representation of N x (H*W*C)\n",
"flattened = tf.reshape(convolved...\n",
"assert(flattened.get_shape().as_list() == [100, 10000])"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Now calculate some statistics about each of our images\n",
"values = tf.reduce_sum(flattened, axis=1)\n",
"\n",
"# Then create another operation which sorts those values\n",
"# and then calculate the result:\n",
"idxs_op = tf.nn.top_k(values, k=100)[1]\n",
"idxs = sess.run(idxs_op)\n",
"\n",
"# Then finally use the sorted indices to sort your images:\n",
"sorted_imgs = np.array([imgs[idx_i] for idx_i in idxs])"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Then plot the resulting sorted dataset montage:\n",
"# Make sure we have a 100 x 100 x 100 x 3 dimension array\n",
"assert(sorted_imgs.shape == (100, 100, 100, 3))\n",
"plt.figure(figsize=(10, 10))\n",
"plt.imshow(utils.montage(sorted_imgs, 'sorted.png'))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"What does your sorting reveal? Could you imagine the same sorting over many more images reveal the thing your dataset sought to represent? It is likely that the representations that you wanted to find hidden within \"higher layers\", i.e., \"deeper features\" of the image, and that these \"low level\" features, edges essentially, are not very good at describing the really interesting aspects of your dataset. In later sessions, we'll see how we can combine the outputs of many more convolution kernels that have been assembled in a way that accentuate something very particular about each image, and build a sorting that is much more intelligent than this one!\n",
"\n",
"<a name=\"assignment-submission\"></a>\n",
"# Assignment Submission\n",
"\n",
"Now that you've completed all 6 parts, we'll create a zip file of the current directory using the code below. This code will make sure you have included this completed ipython notebook and the following files named exactly as:\n",
"\n",
"<pre>\n",
" session-1/\n",
" session-1.ipynb\n",
" dataset.png\n",
" mean.png\n",
" std.png\n",
" normalized.png\n",
" kernel.png\n",
" convolved.png\n",
" sorted.png\n",
" libs/\n",
" utils.py\n",
"</pre>\n",
"\n",
"You'll then submit this zip file for your first assignment on Kadenze for \"Assignment 1: Datasets/Computing with Tensorflow\"! If you have any questions, remember to reach out on the forums and connect with your peers or with me.\n",
"\n",
"<b>To get assessed, you'll need to be a premium student.</b> If you aren't already enrolled as a student, register now at http://www.kadenze.com/ and join the #CADL community to see what your peers are doing! https://www.kadenze.com/courses/creative-applications-of-deep-learning-with-tensorflow/info\n",
"\n",
"Then remember to complete the remaining parts of Assignemnt 1 on Kadenze!:\n",
"* Comment on 1 student's open-ended arrangement (Part 6) in the course gallery titled \"Creating a Dataset/ Computing with Tensorflow\". Think about what images they've used in their dataset and how the arrangement reflects what could be represented by that data.\n",
"* Finally make a forum post in the forum for this assignment \"Creating a Dataset/ Computing with Tensorflow\".\n",
" - Including a link to an artist making use of machine learning to organize data or finding representations within large datasets\n",
" - Tell a little about their work (min 20 words).\n",
" - Comment on at least 2 other student's forum posts (min 20 words)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Make sure your notebook is named \"session-1\" or else replace it with the correct name in the list of files below:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"utils.build_submission('session-1.zip',\n",
" ('dataset.png',\n",
" 'mean.png',\n",
" 'std.png',\n",
" 'normalized.png',\n",
" 'kernel.png',\n",
" 'convolved.png',\n",
" 'sorted.png',\n",
" 'session-1.ipynb'))"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.4.0"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| apache-2.0 |
dk14/machine-learning-exercises | MultiBandit.ipynb | 1 | 1246802 | null | mit |
quantumlib/Cirq | docs/tutorials/shor.ipynb | 1 | 38600 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {
"id": "cedf868076a2"
},
"source": [
"##### Copyright 2020 The Cirq Developers"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"cellView": "form",
"id": "906e07f6e562"
},
"outputs": [],
"source": [
"#@title Licensed under the Apache License, Version 2.0 (the \"License\");\n",
"# you may not use this file except in compliance with the License.\n",
"# You may obtain a copy of the License at\n",
"#\n",
"# https://www.apache.org/licenses/LICENSE-2.0\n",
"#\n",
"# Unless required by applicable law or agreed to in writing, software\n",
"# distributed under the License is distributed on an \"AS IS\" BASIS,\n",
"# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.\n",
"# See the License for the specific language governing permissions and\n",
"# limitations under the License."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "ici9I7XIYArD"
},
"source": [
"# Shor's algorithm"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "abbe82620fff"
},
"source": [
"<table class=\"tfo-notebook-buttons\" align=\"left\">\n",
" <td>\n",
" <a target=\"_blank\" href=\"https://quantumai.google/cirq/tutorials/shor\"><img src=\"https://quantumai.google/site-assets/images/buttons/quantumai_logo_1x.png\" />View on QuantumAI</a>\n",
" </td>\n",
" <td>\n",
" <a target=\"_blank\" href=\"https://colab.research.google.com/github/quantumlib/Cirq/blob/master/docs/tutorials/shor.ipynb\"><img src=\"https://quantumai.google/site-assets/images/buttons/colab_logo_1x.png\" />Run in Google Colab</a>\n",
" </td>\n",
" <td>\n",
" <a target=\"_blank\" href=\"https://github.com/quantumlib/Cirq/blob/master/docs/tutorials/shor.ipynb\"><img src=\"https://quantumai.google/site-assets/images/buttons/github_logo_1x.png\" />View source on GitHub</a>\n",
" </td>\n",
" <td>\n",
" <a href=\"https://storage.googleapis.com/tensorflow_docs/Cirq/docs/tutorials/shor.ipynb\"><img src=\"https://quantumai.google/site-assets/images/buttons/download_icon_1x.png\" />Download notebook</a>\n",
" </td>\n",
"</table>"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "EDjKq6XBYArE"
},
"source": [
"This tutorial presents a pedagogical demonstration of Shor's algorithm. It is a modified and expanded version of [this Cirq example](https://github.com/quantumlib/Cirq/blob/master/examples/shor.py)."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "dwpxc9cfYCfR"
},
"outputs": [],
"source": [
"\"\"\"Install Cirq.\"\"\"\n",
"try:\n",
" import cirq\n",
"except ImportError:\n",
" print(\"installing cirq...\")\n",
" !pip install --quiet cirq\n",
" print(\"installed cirq.\")"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "0f-6DbifYArF"
},
"outputs": [],
"source": [
"\"\"\"Imports for the notebook.\"\"\"\n",
"import fractions\n",
"import math\n",
"import random\n",
"\n",
"import numpy as np\n",
"import sympy\n",
"from typing import Callable, List, Optional, Sequence, Union\n",
"\n",
"import cirq"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "Ock9kZvcYArL"
},
"source": [
"# Order finding"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "zqqm2kBXYArM"
},
"source": [
"Factoring an integer $n$ can be reduced to finding the period of the <i>modular exponential function</i> (to be defined). Finding this period can be accomplished (with high probability) by finding the <i>order</i> of a randomly chosen element of the multiplicative group modulo $n$.\n",
"\n",
"Let $n$ be a positive integer and \n",
"\n",
"$$ \\mathbb{Z}_n := \\{x \\in \\mathbb{Z}_+ : x < n \\text{ and } \\text{gcd}(x, n) = 1\\} $$\n",
"\n",
"be the multiplicative group modulo $n$.\n",
"Given $x \\in \\mathbb{Z}_n$, compute the smallest positive integer $r$ such that $x^r \\text{ mod } n = 1$.\n",
"\n",
"It can be shown from group/number theory that:\n",
"\n",
"(1) Such an integer $r$ exists. (Note that $g^{|G|} = 1_G$ for any group $G$ with cardinality $|G|$ and element $g \\in G$, but it's possible that $r < |G|$.)\n",
"\n",
"(2) If $n = pq$ for primes $p$ and $q$, then $|\\mathbb{Z}_n| = \\phi(n) = (p - 1) (q - 1)$. (The function $\\phi$ is called [Euler's totient function](https://en.wikipedia.org/wiki/Euler%27s_totient_function).)\n",
"\n",
"(3) The modular exponential function\n",
"\n",
"$$ f_x(z) := x^z \\mod n $$\n",
"\n",
"is periodic with period $r$ (the order of the element $x \\in \\mathbb{Z}_n$). That is, $f_x(z + r) = f_x(z)$. \n",
"\n",
"(4) If we know the period of the modular exponential function, we can (with high probability) figure out $p$ and $q$ -- that is, factor $n$."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "nIzO9TeZYArM"
},
"source": [
"As a refresher, we can visualize the elements of some multiplicative groups $\\mathbb{Z}_n$ for integers $n$ via the following simple function."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "zHFjRmNbYArN"
},
"outputs": [],
"source": [
"\"\"\"Function to compute the elements of Z_n.\"\"\"\n",
"def multiplicative_group(n: int) -> List[int]:\n",
" \"\"\"Returns the multiplicative group modulo n.\n",
" \n",
" Args:\n",
" n: Modulus of the multiplicative group.\n",
" \"\"\"\n",
" assert n > 1\n",
" group = [1]\n",
" for x in range(2, n):\n",
" if math.gcd(x, n) == 1:\n",
" group.append(x)\n",
" return group"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "kFp5r6wpYArS"
},
"source": [
"For example, the multiplicative group modulo $n = 15$ is shown below."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "5eQq1tJBYArS"
},
"outputs": [],
"source": [
"\"\"\"Example of a multiplicative group.\"\"\"\n",
"n = 15\n",
"print(f\"The multiplicative group modulo n = {n} is:\")\n",
"print(multiplicative_group(n))"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "zQnZOQuTYArX"
},
"source": [
"One can check that this set of elements indeed forms a group (under ordinary multiplication)."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "OCjTjXAGYArY"
},
"source": [
"## Classical order finding"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "NwZUENkWYArZ"
},
"source": [
"A function for classically computing the order $r$ of an element $x \\in \\mathbb{Z}_n$ is provided below. This function simply computes the sequence \n",
"\n",
"$$ x^2 \\text{ mod } n $$\n",
"$$ x^3 \\text{ mod } n $$\n",
"$$ x^4 \\text{ mod } n $$\n",
"$$ \\vdots $$\n",
"\n",
"until an integer $r$ is found such that $x^r = 1 \\text{ mod } n$. Since $|\\mathbb{Z}_n| = \\phi(n)$, this algorithm for order finding has time complexity $O(\\phi(n))$ which is inefficient. (Roughly $O(2^{L / 2})$ where $L$ is the number of bits in $n$.)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "v3GfJ0POYAra"
},
"outputs": [],
"source": [
"\"\"\"Function for classically computing the order of an element of Z_n.\"\"\"\n",
"def classical_order_finder(x: int, n: int) -> Optional[int]:\n",
" \"\"\"Computes smallest positive r such that x**r mod n == 1.\n",
"\n",
" Args:\n",
" x: Integer whose order is to be computed, must be greater than one\n",
" and belong to the multiplicative group of integers modulo n (which\n",
" consists of positive integers relatively prime to n),\n",
" n: Modulus of the multiplicative group.\n",
"\n",
" Returns:\n",
" Smallest positive integer r such that x**r == 1 mod n.\n",
" Always succeeds (and hence never returns None).\n",
"\n",
" Raises:\n",
" ValueError when x is 1 or not an element of the multiplicative\n",
" group of integers modulo n.\n",
" \"\"\"\n",
" # Make sure x is both valid and in Z_n.\n",
" if x < 2 or x >= n or math.gcd(x, n) > 1:\n",
" raise ValueError(f\"Invalid x={x} for modulus n={n}.\")\n",
" \n",
" # Determine the order.\n",
" r, y = 1, x\n",
" while y != 1:\n",
" y = (x * y) % n\n",
" r += 1\n",
" return r"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "n3J_akErYAre"
},
"source": [
"An example of computing $r$ for a given $x \\in \\mathbb{Z}_n$ and given $n$ is shown in the code block below."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "Lvs1wwgPYAre"
},
"outputs": [],
"source": [
"\"\"\"Example of (classically) computing the order of an element.\"\"\"\n",
"n = 15 # The multiplicative group is [1, 2, 4, 7, 8, 11, 13, 14].\n",
"x = 8\n",
"r = classical_order_finder(x, n)\n",
"\n",
"# Check that the order is indeed correct.\n",
"print(f\"x^r mod n = {x}^{r} mod {n} = {x**r % n}\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "9U7ajXpEYArj"
},
"source": [
"The quantum part of Shor's algorithm is order finding, but done via a quantum circuit, which we'll discuss below."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "D3JqmaE-YArj"
},
"source": [
"## Quantum order finding"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "sdm5KtkiYArk"
},
"source": [
"Quantum order finding is essentially quantum phase estimation with unitary $U$ that computes the modular exponential function $f_x(z)$ for some randomly chosen $x \\in \\mathbb{Z}_n$. The full details of how $U$ is computed in terms of elementary gates can be complex to unravel, especially on a first reading. In this tutorial, we'll use arithmetic operations in Cirq which can implement such a unitary $U$ without fully delving into the details of elementary gates.\n",
"\n",
"Below we first show an example of a simple arithmetic operation in Cirq (addition) then discuss the operation we care about (modular exponentiation)."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "I9wao-eNYArl"
},
"source": [
"### Quantum arithmetic operations in Cirq"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "03iL9sDpYArl"
},
"source": [
"Here we discuss an example of defining an arithmetic operation in Cirq, namely modular addition. This operation adds the value of the input register into the target register. More specifically, this operation acts on two qubit registers as\n",
"\n",
"$$ |a\\rangle_i |b\\rangle_t \\mapsto |a\\rangle_i |a + b \\text{ mod } N_t \\rangle_t . $$\n",
"\n",
"Here, the subscripts $i$ and $t$ denote <i>i</i>nput and <i>t</i>arget register, respectively, and $N_t$ is the dimension of the target register.\n",
"\n",
"To define this operation, called `Adder`, we inherit from `cirq.ArithmeticOperation` and override the four methods shown below. The main method is the `apply` method which defines the arithmetic. Here, we simply state the expression as $a + b$ instead of the more accurate $a + b \\text{ mod } N_t$ above -- the `cirq.ArithmeticOperation` class is able to deduce what we mean by simply $a + b$ since the operation must be reversible. "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "4QRBj3-vYArm"
},
"outputs": [],
"source": [
"\"\"\"Example of defining an arithmetic (quantum) operation in Cirq.\"\"\"\n",
"class Adder(cirq.ArithmeticOperation):\n",
" \"\"\"Quantum addition.\"\"\"\n",
" def __init__(self, target_register, input_register):\n",
" self.input_register = input_register\n",
" self.target_register = target_register\n",
" \n",
" def registers(self):\n",
" return self.target_register, self.input_register\n",
" \n",
" def with_registers(self, *new_registers):\n",
" return Adder(*new_registers)\n",
" \n",
" def apply(self, target_value, input_value):\n",
" return target_value + input_value"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "XxOfZE6yYArq"
},
"source": [
"Now that we have the operation defined, we can use it in a circuit. The cell below creates two qubit registers, then sets the first register to be $|10\\rangle$ (in binary) and the second register to be $|01\\rangle$ (in binary) via $X$ gates. Then, we use the `Adder` operation, then measure all the qubits.\n",
"\n",
"Since $10 + 01 = 11$ (in binary), we expect to measure $|11\\rangle$ in the target register every time. Additionally, since we do not alter the input register, we expect to measure $|10\\rangle$ in the input register every time. In short, the only bitstring we expect to measure is $1011$. "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "R5eN1c-GYArr"
},
"outputs": [],
"source": [
"\"\"\"Example of using an Adder in a circuit.\"\"\"\n",
"# Two qubit registers.\n",
"qreg1 = cirq.LineQubit.range(2)\n",
"qreg2 = cirq.LineQubit.range(2, 4)\n",
"\n",
"# Define the circuit.\n",
"circ = cirq.Circuit(\n",
" cirq.ops.X.on(qreg1[0]),\n",
" cirq.ops.X.on(qreg2[1]),\n",
" Adder(input_register=qreg1, target_register=qreg2),\n",
" cirq.measure_each(*qreg1),\n",
" cirq.measure_each(*qreg2)\n",
")\n",
"\n",
"# Display it.\n",
"print(\"Circuit:\\n\")\n",
"print(circ)\n",
"\n",
"# Print the measurement outcomes.\n",
"print(\"\\n\\nMeasurement outcomes:\\n\")\n",
"print(cirq.sample(circ, repetitions=5).data)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "Q2ZlalhkYArv"
},
"source": [
"In the output of this code block, we first see the circuit which shows the initial $X$ gates, the `Adder` operation, then the final measurements. Next, we see the measurement outcomes which are all the bitstring $1011$ as expected."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "jEnqlr6pYArv"
},
"source": [
"It is also possible to see the unitary of the adder operation, which we do below. Here, we set the target register to be two qubits in the zero state, i.e. $|00\\rangle$. We specify the input register as the integer one which corresponds to the qubit register $|01\\rangle$. "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "aT5BGnbnYArw"
},
"outputs": [],
"source": [
"\"\"\"Example of the unitary of an Adder operation.\"\"\"\n",
"cirq.unitary(\n",
" Adder(target_register=cirq.LineQubit.range(2),\n",
" input_register=1)\n",
").real"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "ncekGfXdYArz"
},
"source": [
"We can understand this unitary as follows. The $i$th column of the unitary is the state $|i + 1 \\text{ mod } 4\\rangle$. For example, if we look at the $0$th column of the unitary, we see the state $|i + 1 \\text{ mod } 4\\rangle = |0 + 1 \\text{ mod } 4\\rangle = |1\\rangle$. If we look at the $1$st column of the unitary, we see the state $|i + 1 \\text{ mod } 4\\rangle = |1 + 1 \\text{ mod } 4\\rangle = |2\\rangle$. Similarly for the last two columns."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "EqevQK8OYAr0"
},
"source": [
"### Modular exponential arithmetic operation"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "U3A2OnVTYAr1"
},
"source": [
"We can define the modular exponential arithmetic operation in a similar way to the simple addition arithmetic operation, shown below. For the purposes of understanding Shor's algorithm, the most important part of the following code block is the `apply` method which defines the arithmetic operation."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "Yt3iyR3uYAr1"
},
"outputs": [],
"source": [
"\"\"\"Defines the modular exponential operation used in Shor's algorithm.\"\"\"\n",
"class ModularExp(cirq.ArithmeticOperation):\n",
" \"\"\"Quantum modular exponentiation.\n",
"\n",
" This class represents the unitary which multiplies base raised to exponent\n",
" into the target modulo the given modulus. More precisely, it represents the\n",
" unitary V which computes modular exponentiation x**e mod n:\n",
"\n",
" V|y⟩|e⟩ = |y * x**e mod n⟩ |e⟩ 0 <= y < n\n",
" V|y⟩|e⟩ = |y⟩ |e⟩ n <= y\n",
"\n",
" where y is the target register, e is the exponent register, x is the base\n",
" and n is the modulus. Consequently,\n",
"\n",
" V|y⟩|e⟩ = (U**e|y)|e⟩\n",
"\n",
" where U is the unitary defined as\n",
"\n",
" U|y⟩ = |y * x mod n⟩ 0 <= y < n\n",
" U|y⟩ = |y⟩ n <= y\n",
" \"\"\"\n",
" def __init__(\n",
" self, \n",
" target: Sequence[cirq.Qid],\n",
" exponent: Union[int, Sequence[cirq.Qid]], \n",
" base: int,\n",
" modulus: int\n",
" ) -> None:\n",
" if len(target) < modulus.bit_length():\n",
" raise ValueError(f'Register with {len(target)} qubits is too small '\n",
" f'for modulus {modulus}')\n",
" self.target = target\n",
" self.exponent = exponent\n",
" self.base = base\n",
" self.modulus = modulus\n",
"\n",
" def registers(self) -> Sequence[Union[int, Sequence[cirq.Qid]]]:\n",
" return self.target, self.exponent, self.base, self.modulus\n",
"\n",
" def with_registers(\n",
" self,\n",
" *new_registers: Union[int, Sequence['cirq.Qid']],\n",
" ) -> cirq.ArithmeticOperation:\n",
" if len(new_registers) != 4:\n",
" raise ValueError(f'Expected 4 registers (target, exponent, base, '\n",
" f'modulus), but got {len(new_registers)}')\n",
" target, exponent, base, modulus = new_registers\n",
" if not isinstance(target, Sequence):\n",
" raise ValueError(\n",
" f'Target must be a qubit register, got {type(target)}')\n",
" if not isinstance(base, int):\n",
" raise ValueError(\n",
" f'Base must be a classical constant, got {type(base)}')\n",
" if not isinstance(modulus, int):\n",
" raise ValueError(\n",
" f'Modulus must be a classical constant, got {type(modulus)}')\n",
" return ModularExp(target, exponent, base, modulus)\n",
"\n",
" def apply(self, *register_values: int) -> int:\n",
" assert len(register_values) == 4\n",
" target, exponent, base, modulus = register_values\n",
" if target >= modulus:\n",
" return target\n",
" return (target * base**exponent) % modulus\n",
"\n",
" def _circuit_diagram_info_(\n",
" self,\n",
" args: cirq.CircuitDiagramInfoArgs,\n",
" ) -> cirq.CircuitDiagramInfo:\n",
" assert args.known_qubits is not None\n",
" wire_symbols: List[str] = []\n",
" t, e = 0, 0\n",
" for qubit in args.known_qubits:\n",
" if qubit in self.target:\n",
" if t == 0:\n",
" if isinstance(self.exponent, Sequence):\n",
" e_str = 'e'\n",
" else:\n",
" e_str = str(self.exponent)\n",
" wire_symbols.append(\n",
" f'ModularExp(t*{self.base}**{e_str} % {self.modulus})')\n",
" else:\n",
" wire_symbols.append('t' + str(t))\n",
" t += 1\n",
" if isinstance(self.exponent, Sequence) and qubit in self.exponent:\n",
" wire_symbols.append('e' + str(e))\n",
" e += 1\n",
" return cirq.CircuitDiagramInfo(wire_symbols=tuple(wire_symbols))"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "NKCFPDa9YAr6"
},
"source": [
"In the `apply` method, we see that we evaluate `(target * base**exponent) % modulus`. The `target` and the `exponent` depend on the values of the respective qubit registers, and the `base` and `modulus` are constant -- namely, the `modulus` is $n$ and the `base` is some $x \\in \\mathbb{Z}_n$. "
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "-6VgDqbXYAr6"
},
"source": [
"The total number of qubits we will use is $3 (L + 1)$ where $L$ is the number of bits needed to store the integer $n$ to factor. The size of the unitary which implements the modular exponential is thus $4^{3(L + 1)}$. For a modest $n = 15$, the unitary requires storing $2^{30}$ floating point numbers in memory which is out of reach of most current standard laptops."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "aLPqY6gtYAr7"
},
"outputs": [],
"source": [
"\"\"\"Create the target and exponent registers for phase estimation,\n",
"and see the number of qubits needed for Shor's algorithm.\n",
"\"\"\"\n",
"n = 15\n",
"L = n.bit_length()\n",
"\n",
"# The target register has L qubits.\n",
"target = cirq.LineQubit.range(L)\n",
"\n",
"# The exponent register has 2L + 3 qubits.\n",
"exponent = cirq.LineQubit.range(L, 3 * L + 3)\n",
"\n",
"# Display the total number of qubits to factor this n.\n",
"print(f\"To factor n = {n} which has L = {L} bits, we need 3L + 3 = {3 * L + 3} qubits.\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "JUoP7b2BYAr_"
},
"source": [
"As with the simple adder operation, this modular exponential operation has a unitary which we can display (memory permitting) as follows."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "KVIxkUhaYAr_"
},
"outputs": [],
"source": [
"\"\"\"See (part of) the unitary for a modular exponential operation.\"\"\"\n",
"# Pick some element of the multiplicative group modulo n.\n",
"x = 5\n",
"\n",
"# Display (part of) the unitary. Uncomment if n is small enough.\n",
"# cirq.unitary(ModularExp(target, exponent, x, n))"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "RlLEpUbPYAsC"
},
"source": [
"## Using the modular exponentional operation in a circuit"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "Tq9LhevvYAsD"
},
"source": [
"The quantum part of Shor's algorithm is just phase estimation with the unitary $U$ corresponding to the modular exponential operation. The following cell defines a function which creates the circuit for Shor's algorithm using the `ModularExp` operation we defined above."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "9RPcq0o8YAsD"
},
"outputs": [],
"source": [
"\"\"\"Function to make the quantum circuit for order finding.\"\"\"\n",
"def make_order_finding_circuit(x: int, n: int) -> cirq.Circuit:\n",
" \"\"\"Returns quantum circuit which computes the order of x modulo n.\n",
"\n",
" The circuit uses Quantum Phase Estimation to compute an eigenvalue of\n",
" the unitary\n",
"\n",
" U|y⟩ = |y * x mod n⟩ 0 <= y < n\n",
" U|y⟩ = |y⟩ n <= y\n",
"\n",
" Args:\n",
" x: positive integer whose order modulo n is to be found\n",
" n: modulus relative to which the order of x is to be found\n",
"\n",
" Returns:\n",
" Quantum circuit for finding the order of x modulo n\n",
" \"\"\"\n",
" L = n.bit_length()\n",
" target = cirq.LineQubit.range(L)\n",
" exponent = cirq.LineQubit.range(L, 3 * L + 3)\n",
" return cirq.Circuit(\n",
" cirq.X(target[L - 1]),\n",
" cirq.H.on_each(*exponent),\n",
" ModularExp(target, exponent, x, n),\n",
" cirq.qft(*exponent, inverse=True),\n",
" cirq.measure(*exponent, key='exponent'),\n",
" )"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "2KdE9tshYAsG"
},
"source": [
"Using this function, we can visualize the circuit for a given $x$ and $n$ as follows."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "Ug17LWJXYAsH"
},
"outputs": [],
"source": [
"\"\"\"Example of the quantum circuit for period finding.\"\"\"\n",
"n = 15\n",
"x = 7\n",
"circuit = make_order_finding_circuit(x, n)\n",
"print(circuit)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "xDRxEMRlYAsL"
},
"source": [
"As previously described, we put the exponent register into an equal superposition via Hadamard gates. The $X$ gate on the last qubit in the target register is used for phase kickback. The modular exponential operation performs the sequence of controlled unitaries in phase estimation, then we apply the inverse quantum Fourier transform to the exponent register and measure to read out the result."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "XuRRIrnXYAsM"
},
"source": [
"To illustrate the measurement results, we can sample from a smaller circuit. (Note that in practice we would never run Shor's algorithm with $n = 6$ because it is even. This is just an example to illustrate the measurement outcomes.)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "zGb2AbE1YAsN"
},
"outputs": [],
"source": [
"\"\"\"Measuring Shor's period finding circuit.\"\"\"\n",
"circuit = make_order_finding_circuit(x=5, n=6)\n",
"res = cirq.sample(circuit, repetitions=8)\n",
"\n",
"print(\"Raw measurements:\")\n",
"print(res)\n",
"\n",
"print(\"\\nInteger in exponent register:\")\n",
"print(res.data)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "MXKgsP_xYAsQ"
},
"source": [
"We interpret each measured bitstring as an integer, but what do these integers tell us? In the next section we look at how to classically post-process to interpret them."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "_7ZMlsRiYAsQ"
},
"source": [
"## Classical post-processing"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "-MHQF1x4YAsR"
},
"source": [
"The integer we measure is close to $s / r$ where $r$ is the order of $x \\in \\mathbb{Z}_n$ and $0 \\le s < r$ is an integer. We use the continued fractions algorithm to determine $r$ from $s / r$ then return it if the order finding circuit succeeded, else we return `None`."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "pKQ59vB6YAsR"
},
"outputs": [],
"source": [
"def process_measurement(result: cirq.Result, x: int, n: int) -> Optional[int]:\n",
" \"\"\"Interprets the output of the order finding circuit.\n",
"\n",
" Specifically, it determines s/r such that exp(2πis/r) is an eigenvalue\n",
" of the unitary\n",
"\n",
" U|y⟩ = |xy mod n⟩ 0 <= y < n\n",
" U|y⟩ = |y⟩ n <= y\n",
" \n",
" then computes r (by continued fractions) if possible, and returns it.\n",
"\n",
" Args:\n",
" result: result obtained by sampling the output of the\n",
" circuit built by make_order_finding_circuit\n",
"\n",
" Returns:\n",
" r, the order of x modulo n or None.\n",
" \"\"\"\n",
" # Read the output integer of the exponent register.\n",
" exponent_as_integer = result.data[\"exponent\"][0]\n",
" exponent_num_bits = result.measurements[\"exponent\"].shape[1]\n",
" eigenphase = float(exponent_as_integer / 2**exponent_num_bits)\n",
"\n",
" # Run the continued fractions algorithm to determine f = s / r.\n",
" f = fractions.Fraction.from_float(eigenphase).limit_denominator(n)\n",
" \n",
" # If the numerator is zero, the order finder failed.\n",
" if f.numerator == 0:\n",
" return None\n",
" \n",
" # Else, return the denominator if it is valid.\n",
" r = f.denominator\n",
" if x**r % n != 1:\n",
" return None\n",
" return r"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "A9cGZBaEYAsU"
},
"source": [
"The next code block shows an example of creating an order finding circuit, executing it, then using the classical postprocessing function to determine the order. Recall that the quantum part of the algorithm succeeds with some probability. If the order is `None`, try re-running the cell a few times. "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "CTFqzZRdYAsU"
},
"outputs": [],
"source": [
"\"\"\"Example of the classical post-processing.\"\"\"\n",
"# Set n and x here\n",
"n = 6\n",
"x = 5\n",
"\n",
"print(f\"Finding the order of x = {x} modulo n = {n}\\n\")\n",
"measurement = cirq.sample(circuit, repetitions=1)\n",
"print(\"Raw measurements:\")\n",
"print(measurement)\n",
"\n",
"print(\"\\nInteger in exponent register:\")\n",
"print(measurement.data)\n",
"\n",
"r = process_measurement(measurement, x, n)\n",
"print(\"\\nOrder r =\", r)\n",
"if r is not None:\n",
" print(f\"x^r mod n = {x}^{r} mod {n} = {x**r % n}\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "OvHORjsfYAsX"
},
"source": [
"You should see that the order of $x = 5$ in $\\mathbb{Z}_6$ is $r = 2$. Indeed, $5^2 \\text{ mod } 6 = 25 \\text{ mod } 6 = 1$. "
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "u5BzQWsLYAsY"
},
"source": [
"## Quantum order finder"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "c-4fTF_TYAsY"
},
"source": [
"We can now define a streamlined function for the quantum version of order finding using the functions we have previously written. The quantum order finder below creates the circuit, executes it, and processes the measurement result."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "Qwo3s-AsYAsZ"
},
"outputs": [],
"source": [
"def quantum_order_finder(x: int, n: int) -> Optional[int]:\n",
" \"\"\"Computes smallest positive r such that x**r mod n == 1.\n",
" \n",
" Args:\n",
" x: integer whose order is to be computed, must be greater than one\n",
" and belong to the multiplicative group of integers modulo n (which\n",
" consists of positive integers relatively prime to n),\n",
" n: modulus of the multiplicative group.\n",
" \"\"\"\n",
" # Check that the integer x is a valid element of the multiplicative group\n",
" # modulo n.\n",
" if x < 2 or n <= x or math.gcd(x, n) > 1:\n",
" raise ValueError(f'Invalid x={x} for modulus n={n}.')\n",
"\n",
" # Create the order finding circuit.\n",
" circuit = make_order_finding_circuit(x, n)\n",
" \n",
" # Sample from the order finding circuit.\n",
" measurement = cirq.sample(circuit)\n",
" \n",
" # Return the processed measurement result.\n",
" return process_measurement(measurement, x, n)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "setIOHrMYAsd"
},
"source": [
"This completes our quantum implementation of an order finder, and the quantum part of Shor's algorithm."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "PvoEWimKYAsd"
},
"source": [
"# The complete factoring algorithm"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "_GIl9R48YAse"
},
"source": [
"We can use this quantum order finder (or the classical order finder) to complete Shor's algorithm. In the following code block, we add a few pre-processing steps which:\n",
"\n",
"(1) Check if $n$ is even,\n",
"\n",
"(2) Check if $n$ is prime,\n",
"\n",
"(3) Check if $n$ is a prime power,\n",
"\n",
"all of which can be done efficiently with a classical computer. Additionally, we add the last necessary post-processing step which uses the order $r$ to compute a non-trivial factor $p$ of $n$. This is achieved by computing $y = x^{r / 2} \\text{ mod } n$ (assuming $r$ is even), then computing $p = \\text{gcd}(y - 1, n)$."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "XvRmVZRLYAse"
},
"outputs": [],
"source": [
"\"\"\"Functions for factoring from start to finish.\"\"\"\n",
"def find_factor_of_prime_power(n: int) -> Optional[int]:\n",
" \"\"\"Returns non-trivial factor of n if n is a prime power, else None.\"\"\"\n",
" for k in range(2, math.floor(math.log2(n)) + 1):\n",
" c = math.pow(n, 1 / k)\n",
" c1 = math.floor(c)\n",
" if c1**k == n:\n",
" return c1\n",
" c2 = math.ceil(c)\n",
" if c2**k == n:\n",
" return c2\n",
" return None\n",
"\n",
"\n",
"def find_factor(\n",
" n: int,\n",
" order_finder: Callable[[int, int], Optional[int]] = quantum_order_finder,\n",
" max_attempts: int = 30\n",
") -> Optional[int]:\n",
" \"\"\"Returns a non-trivial factor of composite integer n.\n",
"\n",
" Args:\n",
" n: Integer to factor.\n",
" order_finder: Function for finding the order of elements of the\n",
" multiplicative group of integers modulo n.\n",
" max_attempts: number of random x's to try, also an upper limit\n",
" on the number of order_finder invocations.\n",
"\n",
" Returns:\n",
" Non-trivial factor of n or None if no such factor was found.\n",
" Factor k of n is trivial if it is 1 or n.\n",
" \"\"\"\n",
" # If the number is prime, there are no non-trivial factors.\n",
" if sympy.isprime(n):\n",
" print(\"n is prime!\")\n",
" return None\n",
" \n",
" # If the number is even, two is a non-trivial factor.\n",
" if n % 2 == 0:\n",
" return 2\n",
" \n",
" # If n is a prime power, we can find a non-trivial factor efficiently.\n",
" c = find_factor_of_prime_power(n)\n",
" if c is not None:\n",
" return c\n",
" \n",
" for _ in range(max_attempts):\n",
" # Choose a random number between 2 and n - 1.\n",
" x = random.randint(2, n - 1)\n",
" \n",
" # Most likely x and n will be relatively prime.\n",
" c = math.gcd(x, n)\n",
" \n",
" # If x and n are not relatively prime, we got lucky and found\n",
" # a non-trivial factor.\n",
" if 1 < c < n:\n",
" return c\n",
" \n",
" # Compute the order r of x modulo n using the order finder.\n",
" r = order_finder(x, n)\n",
" \n",
" # If the order finder failed, try again.\n",
" if r is None:\n",
" continue\n",
" \n",
" # If the order r is even, try again.\n",
" if r % 2 != 0:\n",
" continue\n",
" \n",
" # Compute the non-trivial factor.\n",
" y = x**(r // 2) % n\n",
" assert 1 < y < n\n",
" c = math.gcd(y - 1, n)\n",
" if 1 < c < n:\n",
" return c\n",
"\n",
" print(f\"Failed to find a non-trivial factor in {max_attempts} attempts.\")\n",
" return None"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "migE2tNYYAsh"
},
"source": [
"The function `find_factor` uses the `quantum_order_finder` by default, in which case it is executing Shor's algorithm. As previously mentioned, due to the large memory requirements for classically simulating this circuit, we cannot run Shor's algorithm for $n \\ge 15$. However, we can use the classical order finder as a substitute."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "1RN4SqfDYAsh"
},
"outputs": [],
"source": [
"\"\"\"Example of factoring via Shor's algorithm (order finding).\"\"\"\n",
"# Number to factor\n",
"n = 184573\n",
"\n",
"# Attempt to find a factor\n",
"p = find_factor(n, order_finder=classical_order_finder)\n",
"q = n // p\n",
"\n",
"print(\"Factoring n = pq =\", n)\n",
"print(\"p =\", p)\n",
"print(\"q =\", q)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "PTZTrPU1Zrad"
},
"outputs": [],
"source": [
"\"\"\"Check the answer is correct.\"\"\"\n",
"p * q == n"
]
}
],
"metadata": {
"colab": {
"name": "shor.ipynb",
"toc_visible": true
},
"kernelspec": {
"display_name": "Python 3",
"name": "python3"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| apache-2.0 |
amueller/scipy-2017-sklearn | notebooks/21.Unsupervised_learning-Non-linear_dimensionality_reduction.ipynb | 1 | 8426 | {
"cells": [
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"## Manifold Learning\n",
"\n",
"One weakness of PCA is that it cannot detect non-linear features. A set\n",
"of algorithms known as *Manifold Learning* have been developed to address\n",
"this deficiency. A canonical dataset used in Manifold learning is the\n",
"*S-curve*:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"from sklearn.datasets import make_s_curve\n",
"X, y = make_s_curve(n_samples=1000)\n",
"\n",
"from mpl_toolkits.mplot3d import Axes3D\n",
"ax = plt.axes(projection='3d')\n",
"\n",
"ax.scatter3D(X[:, 0], X[:, 1], X[:, 2], c=y)\n",
"ax.view_init(10, -60);"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"This is a 2-dimensional dataset embedded in three dimensions, but it is embedded\n",
"in such a way that PCA cannot discover the underlying data orientation:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"from sklearn.decomposition import PCA\n",
"X_pca = PCA(n_components=2).fit_transform(X)\n",
"plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y);"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"Manifold learning algorithms, however, available in the ``sklearn.manifold``\n",
"submodule, are able to recover the underlying 2-dimensional manifold:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"from sklearn.manifold import Isomap\n",
"\n",
"iso = Isomap(n_neighbors=15, n_components=2)\n",
"X_iso = iso.fit_transform(X)\n",
"plt.scatter(X_iso[:, 0], X_iso[:, 1], c=y);"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"## Manifold learning on the digits data"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"We can apply manifold learning techniques to much higher dimensional datasets, for example the digits data that we saw before:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"from sklearn.datasets import load_digits\n",
"digits = load_digits()\n",
"\n",
"fig, axes = plt.subplots(2, 5, figsize=(10, 5),\n",
" subplot_kw={'xticks':(), 'yticks': ()})\n",
"for ax, img in zip(axes.ravel(), digits.images):\n",
" ax.imshow(img, interpolation=\"none\", cmap=\"gray\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"We can visualize the dataset using a linear technique, such as PCA. We saw this already provides some intuition about the data:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"# build a PCA model\n",
"pca = PCA(n_components=2)\n",
"pca.fit(digits.data)\n",
"# transform the digits data onto the first two principal components\n",
"digits_pca = pca.transform(digits.data)\n",
"colors = [\"#476A2A\", \"#7851B8\", \"#BD3430\", \"#4A2D4E\", \"#875525\",\n",
" \"#A83683\", \"#4E655E\", \"#853541\", \"#3A3120\",\"#535D8E\"]\n",
"plt.figure(figsize=(10, 10))\n",
"plt.xlim(digits_pca[:, 0].min(), digits_pca[:, 0].max() + 1)\n",
"plt.ylim(digits_pca[:, 1].min(), digits_pca[:, 1].max() + 1)\n",
"for i in range(len(digits.data)):\n",
" # actually plot the digits as text instead of using scatter\n",
" plt.text(digits_pca[i, 0], digits_pca[i, 1], str(digits.target[i]),\n",
" color = colors[digits.target[i]],\n",
" fontdict={'weight': 'bold', 'size': 9})\n",
"plt.xlabel(\"first principal component\")\n",
"plt.ylabel(\"second principal component\");"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"Using a more powerful, nonlinear techinque can provide much better visualizations, though.\n",
"Here, we are using the t-SNE manifold learning method:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"from sklearn.manifold import TSNE\n",
"tsne = TSNE(random_state=42)\n",
"# use fit_transform instead of fit, as TSNE has no transform method:\n",
"digits_tsne = tsne.fit_transform(digits.data)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"plt.figure(figsize=(10, 10))\n",
"plt.xlim(digits_tsne[:, 0].min(), digits_tsne[:, 0].max() + 1)\n",
"plt.ylim(digits_tsne[:, 1].min(), digits_tsne[:, 1].max() + 1)\n",
"for i in range(len(digits.data)):\n",
" # actually plot the digits as text instead of using scatter\n",
" plt.text(digits_tsne[i, 0], digits_tsne[i, 1], str(digits.target[i]),\n",
" color = colors[digits.target[i]],\n",
" fontdict={'weight': 'bold', 'size': 9})"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"t-SNE has a somewhat longer runtime that other manifold learning algorithms, but the result is quite striking. Keep in mind that this algorithm is purely unsupervised, and does not know about the class labels. Still it is able to separate the classes very well (though the classes four, one and nine have been split into multiple groups)."
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"<div class=\"alert alert-success\">\n",
" <b>EXERCISE</b>:\n",
" <ul>\n",
" <li>\n",
" Compare the results of applying isomap to the digits dataset to the results of PCA and t-SNE. Which result do you think looks best?\n",
" </li>\n",
" <li>\n",
" Given how well t-SNE separated the classes, one might be tempted to use this processing for classification. Try training a K-nearest neighbor classifier on digits data transformed with t-SNE, and compare to the accuracy on using the dataset without any transformation.\n",
" </li>\n",
" </ul>\n",
"</div>"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"# %load solutions/21A_isomap_digits.py"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"# %load solutions/21B_tsne_classification.py"
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| cc0-1.0 |
pombredanne/https-gitlab.lrde.epita.fr-vcsn-vcsn | doc/notebooks/expression.sum.ipynb | 1 | 2715 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# _`expression`_`.sum(`_`exp`_`)`\n",
"# _`expression`_ + _`exp`_\n",
"\n",
"An expression which denotes the sum (or disjunction) of both series.\n",
"\n",
"Preconditions:\n",
"- None\n",
"\n",
"See also:\n",
"- [automaton.sum](automaton.sum.ipynb)\n",
"- [polynomial.sum](polynomial.sum.ipynb)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Examples"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"application/javascript": [
"IPython.load_extensions(\"AutomatonD3Widget\")"
],
"text/plain": [
"<IPython.core.display.Javascript object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/latex": [
"$a \\, {b}^{*} + {a}^{*} \\, b$"
],
"text/plain": [
"ab*+a*b"
]
},
"execution_count": 1,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"import vcsn\n",
"ctx = vcsn.context('lal_char, q')\n",
"exp = lambda e: ctx.expression(e)\n",
"exp('a*b') + exp('ab*')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Of course, trivial identities are applied."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/latex": [
"$ \\left\\langle 5 \\right\\rangle \\,a$"
],
"text/plain": [
"<5>a"
]
},
"execution_count": 2,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"exp('<2>a') + exp('<3>a')"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/latex": [
"$ \\left\\langle 2 \\right\\rangle \\,a$"
],
"text/plain": [
"<2>a"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"exp('<2>a') + exp('\\z')"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.4.3"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| gpl-3.0 |
rajathkumarmp/BinPy | BinPy/examples/notebook/Sequential/FlipFlop/SRLatch.ipynb | 5 | 15877 | {
"metadata": {
"name": "",
"signature": "sha256:4819bbe8a5a2d640fb7430b44d6f07599ae9c25e7c65861336ca306e42b147ba"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "heading",
"level": 2,
"metadata": {},
"source": [
"Example for SRLatch"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"from __future__ import print_function\n",
"from BinPy.Sequential.sequential import SRLatch\n",
"from BinPy.tools.clock import Clock\n",
"from BinPy.Gates import Connector\n",
"from BinPy.tools.oscilloscope import Oscilloscope"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 1
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"s = Connector(1)\n",
"r = Connector(0)\n",
"\n",
"p = Connector(0)\n",
"q = Connector(1)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 2
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"# Initialize the clock\n",
"clock = Clock(1, 4)\n",
"clock.start()\n",
"# A clock of 1 hertz frequency\n",
"clk_conn = clock.A\n",
"\n",
"enable = Connector(1)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 3
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"# Initialize the sr latch\n",
"srff = SRLatch(s, r, enable, clk_conn)\n",
"\n",
"# To connect outputs use s.setOutputs(op1,op2)\n",
"srff.setOutputs(A=p, B=q)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 4
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"# Initialize the oscilloscope\n",
"\n",
"o = Oscilloscope((clk_conn, 'CLK'), (s, 'S'), (\n",
" r, 'R'), (p, 'OUT'), (q, 'OUT!'), (enable, 'ENABLE'))\n",
"o.start()\n",
"o.setScale(0.015) # Set scale by trial and error.\n",
"o.setWidth(100)\n",
"o.unhold()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\u001b[0m\n",
"\u001b[0m\n"
]
}
],
"prompt_number": 5
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print (\"SET STATE - S = 1, R = 0\")\n",
"# Set State\n",
"s.state = 1\n",
"r.state = 0\n",
"# The same thing can also be done by --> srff.setInputs(s = 1, r = 0)\n",
"while True:\n",
" if clk_conn.state == 0:\n",
" # Falling edge will trigger the FF\n",
" srff.trigger()\n",
" break\n",
"print (srff.state())\n",
"# Sending a positive edge to srff\n",
"while True:\n",
" if clk_conn.state == 1:\n",
" # Falling edge will trigger the FF\n",
" srff.trigger()\n",
" break"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"SET STATE - S = 1, R = 0\n",
"[1, 0]\n"
]
}
],
"prompt_number": 6
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print (\"RESET STATE - S = 0, R = 1\")\n",
"# Reset State\n",
"s.state = 0\n",
"r.state = 1\n",
"# The same thing can also be done by --> srff.setInputs(s = 1, r = 0)\n",
"while True:\n",
" if clk_conn.state == 0:\n",
" # Falling edge will trigger the FF\n",
" srff.trigger()\n",
" break\n",
"# Displaying the output using the connector instances\n",
"print (\"[\", p(), \",\", q(), \"]\")\n",
"\n",
"# Sending a positive edge to srff\n",
"while True:\n",
" if clk_conn.state == 1:\n",
" # Falling edge will trigger the FF\n",
" srff.trigger()\n",
" break"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"RESET STATE - S = 0, R = 1\n",
"["
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
" 0 , 1 ]\n"
]
}
],
"prompt_number": 7
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print (\"INVALID STATE - S = 1, R = 1\")\n",
"# Invalid state\n",
"s.state = 1\n",
"r.state = 1\n",
"# The same thing can also be done by --> srff.setInputs(s = 1, r = 1)\n",
"while True:\n",
" if clk_conn.state == 0:\n",
" # Falling edge will trigger the FF\n",
" srff.trigger()\n",
" break\n",
"print (srff.state())\n",
"\n",
"# Sending a positive edge to srff\n",
"while True:\n",
" if clk_conn.state == 1:\n",
" # Falling edge will trigger the FF\n",
" srff.trigger()\n",
" break"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"INVALID STATE - S = 1, R = 1\n",
"ERROR: Invalid State - Resetting the Latch"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"[0, 1]\n"
]
}
],
"prompt_number": 8
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"print (\"2nd INVALID STATE - S = 0, R = 0\")\n",
"# Invalid state\n",
"s.state = 1\n",
"r.state = 1\n",
"# The same thing can also be done by --> srff.setInputs(s = 1, r = 1)\n",
"while True:\n",
" if clk_conn.state == 0:\n",
" # Falling edge will trigger the FF\n",
" srff.trigger()\n",
" break\n",
"print (srff.state())\n",
"\n",
"# Sending a positive edge to srff\n",
"while True:\n",
" if clk_conn.state == 1:\n",
" # Falling edge will trigger the FF\n",
" srff.trigger()\n",
" break"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"2nd INVALID STATE - S = 0, R = 0\n",
"ERROR: Invalid State - Resetting the Latch"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"[0, 1]\n"
]
}
],
"prompt_number": 9
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"# Display the oscilloscope \n",
"o.display()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\u001b[0m===================================================================================================================\n",
"BinPy - Oscilloscope\n",
"===================================================================================================================\n",
" SCALE - X-AXIS : 1 UNIT WIDTH = 0.015\n",
"===================================================================================================================\n",
" \u2502\n",
" \u2502\n",
" \u2502 \u250c\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2510 \u250c\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2510 \u250c\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2510 \n",
" CLK \u2502 \u2502 \u2502 \u2502 \u2502 \u2502 \u2502 \n",
" \u2500 \u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2518 \u2514\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2518 \u2514\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2518 \u2514\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\n",
" \u2502\n",
" \u2502\n",
" \u2502\n",
" \u2502\n",
" \u2502 \u250c\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2510 \u250c\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2510 \u250c\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2510 \n",
" S \u2502 \u2502 \u2502 \u2502 \u2502 \u2502 \u2502 \n",
" \u2500 \u2518 \u2514\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2518 \u2514\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2518 \u2514\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\n",
" \u2502\n",
" \u2502\n",
" \u2502\n",
" \u2502\n",
" \u2502 \u250c\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2510 \n",
" R \u2502 \u2502 \u2502 \n",
" \u2500 \u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2518 \u2514\u2500\u2500\u2500\n",
" \u2502\n",
" \u2502\n",
" \u2502\n",
" \u2502\n",
" \u2502 \u250c\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2510 \n",
" OUT \u2502 \u2502 \u2502 \n",
" \u2500 \u2518 \u2514\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\n",
" \u2502\n",
" \u2502\n",
" \u2502\n",
" \u2502\n",
" \u2502 \u250c\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2510 \n",
" OUT! \u2502 \u2502 \u2502 \n",
" \u2500 \u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2518 \u2514\u2500\u2500\u2500\n",
" \u2502\n",
" \u2502\n",
" \u2502\n",
" \u2502\n",
" \u2502 \u250c\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2510 \n",
" ENABL \u2502 \u2502 \u2502 \n",
" \u2500 \u2518 \u2514\u2500\u2500\u2500\n",
" \u2502\n",
" \u2502\n",
"\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\u2502\n",
"\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\u2500\n",
"\u001b[0m\n"
]
}
],
"prompt_number": 10
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"# Kill the clock and the oscilloscope threads after use\n",
"o.kill()\n",
"clock.kill()"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 11
}
],
"metadata": {}
}
]
} | bsd-3-clause |
cathyq/practice-code-a-day | Search Insert Position.ipynb | 1 | 3141 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Search Insert Position\n",
"Given a sorted array and a target value, return the index if the target is found. If not, return the index where it would be if it were inserted in order. \n",
"[Problem from LeetCode](https://leetcode.com/problems/search-insert-position/description/)"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Input\n",
"nums = [1,3,5,6,7,8,10]\n",
"target = 4"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"# Method1\n",
"def search_insert1(nums, target):\n",
" \"\"\"\n",
" :type nums: List[int]\n",
" :type target: int\n",
" :rtype: int\n",
" \"\"\"\n",
" left, right = 0, len(nums)-1\n",
"\n",
" while left <= right:\n",
" mid = (left + right) // 2\n",
" if target <= nums[mid]:\n",
" right = mid - 1 \n",
" elif target > nums[mid]:\n",
" left = mid + 1 \n",
" return left"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [],
"source": [
"# Method2 \n",
"def search_insert2(nums, target):\n",
" \"\"\"\n",
" :type nums: List[int]\n",
" :type target: int\n",
" :rtype: int\n",
" \"\"\"\n",
" return len([i for i in nums if i < target])"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"CPU times: user 8 µs, sys: 1 µs, total: 9 µs\n",
"Wall time: 15.7 µs\n"
]
},
{
"data": {
"text/plain": [
"2"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Output1\n",
"%time search_insert1(nums, target)"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"CPU times: user 10 µs, sys: 1 µs, total: 11 µs\n",
"Wall time: 14.8 µs\n"
]
},
{
"data": {
"text/plain": [
"2"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Output2\n",
"%time search_insert2(nums, target)"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.2"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
spm2164/foundations-homework | 06/Homework-06.ipynb | 1 | 11608 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Submit this and your other two notebooks (Spotify + NYT) to GitHub by Monday morning. If you're struggling with the previous assignment I recommend trying this one out instead, it's a lot simpler! I'll send out some readings later in the week, too.\n",
"\n",
"HOMEWORK 06\n",
"\n",
"You'll be using the Dark Sky Forecast API from Forecast.io, available at https://developer.forecast.io. It's a pretty simple API, but be sure to read the documentation!\n",
"\n",
"1) Make a request from the Forecast.io API for where you were born (or lived, or want to visit!).\n",
"\n",
"Tip: Once you've imported the JSON into a variable, check the timezone's name to make sure it seems like it got the right part of the world!\n",
"Tip 2: How is north vs. south and east vs. west latitude/longitude represented? Is it the normal North/South/East/West?\n",
"\n",
"2) What's the current wind speed? How much warmer does it feel than it actually is?\n",
"\n",
"3) The first daily forecast is the forecast for today. For the place you decided on up above, how much of the moon is currently visible?\n",
"\n",
"4) What's the difference between the high and low temperatures for today?\n",
"\n",
"5) Loop through the daily forecast, printing out the next week's worth of predictions. I'd like to know the high temperature for each day, and whether it's hot, warm, or cold, based on what temperatures you think are hot, warm or cold.\n",
"\n",
"6) What's the weather looking like for the rest of today in Miami, Florida? I'd like to know the temperature for every hour, and if it's going to have cloud cover of more than 0.5 say \"{temperature} and cloudy\" instead of just the temperature.\n",
"\n",
"7) What was the temperature in Central Park on Christmas Day, 1980? How about 1990? 2000?\n",
"\n",
"Tip: You'll need to use UNIX time, which is the number of seconds since January 1, 1970. Google can help you convert a normal date!\n",
"Tip: You'll want to use Forecast.io's \"time machine\" API at https://developer.forecast.io/docs/v2"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import requests\n",
"api='53343f8442d30d598f50f5910124610a'\n",
"url='https://api.forecast.io/forecast/'\n",
"# this is the lat/long for cleveland, oh\n",
"lat='41.4993'\n",
"long='-81.6944'"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"response=requests.get(url+api+'/'+lat+','+long)\n",
"cleveland_weather=response.json()"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"The timezone for the request was America/New_York\n"
]
}
],
"source": [
"print(\"The timezone for the request was\", cleveland_weather['timezone'])"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"The windspeed in Cleveland is currently 3.45 mph\n",
"While it currently feels 84.11 it is actually 80.73 degrees F\n"
]
}
],
"source": [
"print(\"The windspeed in Cleveland is currently\", cleveland_weather['currently']['windSpeed'], \"mph\")\n",
"print(\"While it currently feels\", cleveland_weather['currently']['apparentTemperature'], \"it is actually\", cleveland_weather['currently']['temperature'], \"degrees F\")"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"The moon in Cleveland is currently 5.0 percent full\n"
]
}
],
"source": [
"print(\"The moon in Cleveland is currently\", cleveland_weather['daily']['data'][0]['moonPhase']*100, \"percent full\")"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"The max temp in Cleveland today was 80.83 and the min was 69.61 which is a difference of 11.22 degrees\n"
]
}
],
"source": [
"max_temp=cleveland_weather['daily']['data'][0]['temperatureMax']\n",
"min_temp=cleveland_weather['daily']['data'][0]['temperatureMin']\n",
"print(\"The max temp in Cleveland today was\", max_temp, \"and the min was\", min_temp, \"which is a difference of\", '%.2f' % (max_temp-min_temp), \"degrees\")"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def temp_feeling(temp):\n",
" if temp <= 32:\n",
" return \"freezing cold!\"\n",
" elif temp <= 50:\n",
" return \"pretty cold.\"\n",
" elif temp <= 65:\n",
" return \"a little chill.\"\n",
" elif temp <= 75:\n",
" return \"downright nice.\"\n",
" elif temp <= 85:\n",
" return \"pretty warm.\"\n",
" else:\n",
" return \"freaking hot.\""
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Here is your high temps for the week, including today:\n",
"Day 0: 80.83 I would say that's pretty warm.\n",
"Day 1: 86.4 I would say that's freaking hot.\n",
"Day 2: 85.63 I would say that's freaking hot.\n",
"Day 3: 86.8 I would say that's freaking hot.\n",
"Day 4: 77.82 I would say that's pretty warm.\n",
"Day 5: 77.5 I would say that's pretty warm.\n",
"Day 6: 82.15 I would say that's pretty warm.\n",
"Day 7: 88.47 I would say that's freaking hot.\n"
]
}
],
"source": [
"print(\"Here is your high temps for the week, including today:\")\n",
"for day, forecast in enumerate(cleveland_weather['daily']['data']):\n",
" temp=forecast['temperatureMax']\n",
" print(\"Day\", str(day)+\":\", temp, \"I would say that's\", temp_feeling(temp))"
]
},
{
"cell_type": "code",
"execution_count": 73,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# coords for miami florida\n",
"lat='25.7617'\n",
"long='-80.1918'\n",
"response=requests.get(url+api+'/'+lat+','+long)\n",
"miami_weather=response.json()"
]
},
{
"cell_type": "code",
"execution_count": 74,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"dict_keys(['precipType', 'dewPoint', 'precipIntensity', 'humidity', 'apparentTemperature', 'windSpeed', 'ozone', 'time', 'cloudCover', 'icon', 'windBearing', 'temperature', 'summary', 'precipProbability', 'visibility', 'pressure'])"
]
},
"execution_count": 74,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"miami_weather['hourly']['data'][0].keys()"
]
},
{
"cell_type": "code",
"execution_count": 75,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def is_midnight(hour):\n",
"# hour=datetime.datetime.fromtimestamp(int(time['time'])).strftime('%H')\n",
" if hour=='00':\n",
" return True\n",
" else:\n",
" return False"
]
},
{
"cell_type": "code",
"execution_count": 76,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def time_to_hour(time):\n",
" hour=datetime.datetime.fromtimestamp(int(time['time'])).strftime('%H')\n",
" return hour"
]
},
{
"cell_type": "code",
"execution_count": 89,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Conditions in Miami for the rest of the day:\n",
"20:00: 86.31°F and clear.\n",
"21:00: 85.05°F and clear.\n",
"22:00: 84.26°F and clear.\n",
"23:00: 83.44°F and partly cloudy.\n",
"00:00: 82.94°F and partly cloudy.\n"
]
}
],
"source": [
"import datetime\n",
"print('Conditions in Miami for the rest of the day:')\n",
"for hour in miami_weather['hourly']['data']:\n",
" clock=time_to_hour(hour)\n",
" print(clock+':00:', str(hour['temperature'])+'°F and', hour['summary'].lower()+'.')\n",
" if is_midnight(clock):\n",
" break"
]
},
{
"cell_type": "code",
"execution_count": 108,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def date_to_unixtime(date):\n",
" import time\n",
" unix_date=int(time.mktime(datetime.datetime.strptime(str(date), \"%Y%m%d\").timetuple()))\n",
" return str(unix_date)"
]
},
{
"cell_type": "code",
"execution_count": 123,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"On Christmas of 1980 it was partly cloudy starting in the afternoon. The high temperature for that day was 41.58°F.\n",
"On Christmas of 1990 it was foggy in the evening. The high temperature for that day was 32.27°F.\n",
"On Christmas of 2000 it was mostly cloudy until evening. The high temperature for that day was 42.25°F.\n",
"On Christmas of 2010 it was foggy starting in the evening. The high temperature for that day was 41°F.\n"
]
}
],
"source": [
"# this way of looping through dates is pretty terrible\n",
"api='53343f8442d30d598f50f5910124610a'\n",
"url='https://api.forecast.io/forecast/'\n",
"date=19801225\n",
"lat='40.7829'\n",
"long='73.9654'\n",
"while date <= 20101225:\n",
" response=requests.get(url+api+'/'+lat+','+long+','+date_to_unixtime(date))\n",
" christmas_weather=response.json()\n",
" summary=christmas_weather['daily']['data'][0]['summary']\n",
" max_temp=christmas_weather['daily']['data'][0]['temperatureMax']\n",
" print(\"On Christmas of \"+str(date)[0:4], \"it was\", summary.lower(), \"The high temperature for that day was\", str(max_temp)+'°F.')\n",
" date+=100000"
]
},
{
"cell_type": "code",
"execution_count": 115,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"'Foggy starting in the evening.'"
]
},
"execution_count": 115,
"metadata": {},
"output_type": "execute_result"
}
],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "IPython (Python 3)",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.1+"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| artistic-2.0 |
henry-ngo/VIP | docs/source/tutorials/01_quickstart.ipynb | 1 | 7865547 | null | mit |
logrusFr/CNAM-public | UASB03/uasb03-Choix_modele_previsonnel_catastrophes-public.ipynb | 1 | 318034 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Projet CNAM-UASB03 - \"Prévision\" des catastrophes naturelles en France\n",
"\n",
"## Partie : Choix parmi les modeles conçus\n",
"\n",
"\n",
"\n",
"Dépôt du projet :\n",
"\n",
"* https://gitlab.com/logrus_fr/CNAM-UASB03\n",
"\n",
"Auteur : \n",
"\n",
"* Fabrice DUNAN <[email protected]>\n",
"\n",
"Tuteurs CNAM : \n",
"\n",
"* N.Niang, M.Crucianu, P.Rigaux"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## ATTENTION\n",
"\n",
"Ce notebook est un véritable cahier de brouillon. Il a vocation de donner des résultats \"techniques\" sans tout expliquer. Se référer au rapport pour plus d'explications."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Initialisation des outils Python\n",
"Cette section initialise les outils, bibliothèques et parametres necessaires pour l'étude."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### imports"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"import sys #only needed to determine Python version number\n",
"import os\n",
"import glob\n",
"import re"
]
},
{
"cell_type": "code",
"execution_count": 279,
"metadata": {},
"outputs": [],
"source": [
"import pandas as pd\n",
"import numpy as np\n",
"import sklearn as sk\n",
"from sklearn.utils import resample\n",
"from sklearn.model_selection import train_test_split"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"IMPORTS SERIALISATION"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [],
"source": [
"import pickle as pk"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### IMPORTS ESTIMATION QUALITE"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [],
"source": [
"from sklearn.metrics import confusion_matrix, recall_score, precision_score,accuracy_score\n",
"from sklearn.metrics import roc_auc_score\n",
"from sklearn.metrics import roc_curve\n",
"#http://scikit-learn.org/0.19/modules/generated/sklearn.metrics.precision_recall_fscore_support.html#sklearn.metrics.precision_recall_fscore_support\n",
"from sklearn.metrics import precision_recall_fscore_support\n",
"from sklearn.model_selection import cross_val_score,cross_val_predict\n",
"from sklearn.metrics import precision_recall_curve,average_precision_score"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [],
"source": [
"import matplotlib\n",
"from matplotlib import pyplot as plt#only needed to determine Matplotlib version number\n",
"# Enable inline plotting\n",
"%matplotlib inline"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### options pandas"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [],
"source": [
"#https://stackoverflow.com/questions/11707586/python-pandas-how-to-widen-output-display-to-see-more-columns\n",
"#pd.set_option('display.height', 1000)\n",
"pd.set_option('display.max_rows', 500)\n",
"pd.set_option('display.max_columns', 500)\n",
"pd.set_option('display.width', 1000)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### versions bibliotheques"
]
},
{
"cell_type": "code",
"execution_count": 280,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Python version 3.6.6 |Anaconda custom (64-bit)| (default, Jun 28 2018, 17:14:51) \n",
"[GCC 7.2.0]\n",
"Pandas version 0.23.3\n",
"Matplotlib version 2.1.1\n",
"Sklearn version0.19.1\n"
]
}
],
"source": [
"print('Python version ' + sys.version)\n",
"print('Pandas version ' + pd.__version__)\n",
"print('Matplotlib version ' + matplotlib.__version__)print('Sklearn version' + sk.__version__ )"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Reglages OS dependants"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"posix\n"
]
}
],
"source": [
"print (os.name)"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [],
"source": [
"windows_path = 'C:\\\\PFD\\\\Data\\\\git\\\\_PRV\\\\CNAM-UASB03\\\\donnees'\n",
"linux_path= '/home/user/Bureau/CNAM/git/CNAM-UASB03/donnees'"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [],
"source": [
"if(os.name == 'nt'):\n",
" os.chdir(windows_path)\n",
" intermediaires_path = os.path.join(windows_path,'intermediaires\\\\')\n",
"else :\n",
" os.chdir(linux_path)\n",
" intermediaires_path = os.path.join(linux_path,'intermediaires/')"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"/home/user/Bureau/CNAM/git/CNAM-UASB03/donnees/intermediaires/\n"
]
}
],
"source": [
"print(intermediaires_path)"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [],
"source": [
"import warnings\n",
"warnings.filterwarnings('ignore')"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"/home/user/.local/share/jupyter\n"
]
}
],
"source": [
"from jupyter_core.paths import jupyter_data_dir\n",
"print(jupyter_data_dir())"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Import et exploration des données\n",
"\n",
"Cette section permet d'importer le fichier de données initial dans les outils informatiques choisis(python et ses bibliothèques)"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"CPU times: user 1.03 s, sys: 112 ms, total: 1.14 s\n",
"Wall time: 1.14 s\n"
]
}
],
"source": [
"%%time\n",
"#CPU times: user 5.41 s, sys: 500 ms, total: 5.91 s\n",
"#Wall time: 7.13 s\n",
"#index_col=0,\n",
"meteo_cata_DF=pd.read_csv(os.path.join(intermediaires_path,\"meteo_stations_catastrophes_alt.csv\"),encoding='UTF-8',sep=',',skip_blank_lines=True, header=0,skipinitialspace=True,parse_dates=[1],infer_datetime_format=True,dayfirst=False)"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"<class 'pandas.core.frame.DataFrame'>\n",
"RangeIndex: 453643 entries, 0 to 453642\n",
"Data columns (total 16 columns):\n",
"numer_sta 453643 non-null int64\n",
"date 453643 non-null datetime64[ns]\n",
"t 453643 non-null float64\n",
"tn12 453564 non-null float64\n",
"tx12 453564 non-null float64\n",
"n 453643 non-null float64\n",
"raf10 453643 non-null float64\n",
"ff 453643 non-null float64\n",
"pres 453643 non-null float64\n",
"tend 453643 non-null float64\n",
"rr3 453643 non-null float64\n",
"u 453643 non-null float64\n",
"geop 453643 non-null float64\n",
"vv 453643 non-null float64\n",
"ht_neige 453643 non-null float64\n",
"iscatastrophe 453643 non-null bool\n",
"dtypes: bool(1), datetime64[ns](1), float64(13), int64(1)\n",
"memory usage: 52.3 MB\n"
]
}
],
"source": [
"meteo_cata_DF.info()"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"0 2006-12-06\n",
"1 2006-12-06\n",
"2 2006-12-06\n",
"3 2006-12-06\n",
"4 2006-12-06\n",
"Name: date, dtype: datetime64[ns]"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"meteo_cata_DF.date.head()"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>numer_sta</th>\n",
" <th>date</th>\n",
" <th>t</th>\n",
" <th>tn12</th>\n",
" <th>tx12</th>\n",
" <th>n</th>\n",
" <th>raf10</th>\n",
" <th>ff</th>\n",
" <th>pres</th>\n",
" <th>tend</th>\n",
" <th>rr3</th>\n",
" <th>u</th>\n",
" <th>geop</th>\n",
" <th>vv</th>\n",
" <th>ht_neige</th>\n",
" <th>iscatastrophe</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>7005</td>\n",
" <td>2006-12-06</td>\n",
" <td>289.85</td>\n",
" <td>291.85</td>\n",
" <td>297.55</td>\n",
" <td>63.560525</td>\n",
" <td>0.0</td>\n",
" <td>3.1</td>\n",
" <td>101250.0</td>\n",
" <td>-50.0</td>\n",
" <td>0.0</td>\n",
" <td>90.0</td>\n",
" <td>0.0</td>\n",
" <td>20866.014525</td>\n",
" <td>0.0</td>\n",
" <td>False</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>7015</td>\n",
" <td>2006-12-06</td>\n",
" <td>293.45</td>\n",
" <td>291.85</td>\n",
" <td>297.55</td>\n",
" <td>50.000000</td>\n",
" <td>0.0</td>\n",
" <td>3.1</td>\n",
" <td>101690.0</td>\n",
" <td>40.0</td>\n",
" <td>0.0</td>\n",
" <td>61.0</td>\n",
" <td>0.0</td>\n",
" <td>20000.000000</td>\n",
" <td>0.0</td>\n",
" <td>False</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>7020</td>\n",
" <td>2006-12-06</td>\n",
" <td>289.05</td>\n",
" <td>291.85</td>\n",
" <td>297.55</td>\n",
" <td>63.560525</td>\n",
" <td>0.0</td>\n",
" <td>6.2</td>\n",
" <td>101850.0</td>\n",
" <td>-130.0</td>\n",
" <td>0.0</td>\n",
" <td>88.0</td>\n",
" <td>0.0</td>\n",
" <td>20866.014525</td>\n",
" <td>0.0</td>\n",
" <td>False</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>7027</td>\n",
" <td>2006-12-06</td>\n",
" <td>286.85</td>\n",
" <td>291.85</td>\n",
" <td>297.55</td>\n",
" <td>63.560525</td>\n",
" <td>0.0</td>\n",
" <td>1.0</td>\n",
" <td>101240.0</td>\n",
" <td>-100.0</td>\n",
" <td>0.0</td>\n",
" <td>93.0</td>\n",
" <td>0.0</td>\n",
" <td>11000.000000</td>\n",
" <td>0.0</td>\n",
" <td>False</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>7037</td>\n",
" <td>2006-12-06</td>\n",
" <td>290.45</td>\n",
" <td>291.85</td>\n",
" <td>297.55</td>\n",
" <td>63.560525</td>\n",
" <td>0.0</td>\n",
" <td>2.1</td>\n",
" <td>100340.0</td>\n",
" <td>-20.0</td>\n",
" <td>0.0</td>\n",
" <td>81.0</td>\n",
" <td>0.0</td>\n",
" <td>35000.000000</td>\n",
" <td>0.0</td>\n",
" <td>False</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" numer_sta date t tn12 tx12 n raf10 ff pres tend rr3 u geop vv ht_neige iscatastrophe\n",
"0 7005 2006-12-06 289.85 291.85 297.55 63.560525 0.0 3.1 101250.0 -50.0 0.0 90.0 0.0 20866.014525 0.0 False\n",
"1 7015 2006-12-06 293.45 291.85 297.55 50.000000 0.0 3.1 101690.0 40.0 0.0 61.0 0.0 20000.000000 0.0 False\n",
"2 7020 2006-12-06 289.05 291.85 297.55 63.560525 0.0 6.2 101850.0 -130.0 0.0 88.0 0.0 20866.014525 0.0 False\n",
"3 7027 2006-12-06 286.85 291.85 297.55 63.560525 0.0 1.0 101240.0 -100.0 0.0 93.0 0.0 11000.000000 0.0 False\n",
"4 7037 2006-12-06 290.45 291.85 297.55 63.560525 0.0 2.1 100340.0 -20.0 0.0 81.0 0.0 35000.000000 0.0 False"
]
},
"execution_count": 17,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"meteo_cata_DF.head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### DISTRIBUTION VARIABLE A PREDIRE"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.axes._subplots.AxesSubplot at 0x7f692524e208>"
]
},
"execution_count": 18,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAY0AAAEMCAYAAAA4S+qsAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAF2RJREFUeJzt3W2sXdV95/HvL3ZIUTMBApcI2aZmgqWGRI1DPMSjvKFQgaHRmEogGc0UK7LkNoJROqmmmL4Y8sQoGalhRCYgkeJiMm0dhjSDlXHq8fCgKjMJYAKBOJTxDaTBAYGJDSVlQorznxdn3XJ8Offe5Yf4mNzvRzo6e//3Wnuvg678Y++9ztmpKiRJ6vGmcQ9AkvTGYWhIkroZGpKkboaGJKmboSFJ6mZoSJK6GRqSpG6GhiSpm6EhSeq2cNwDONJOOeWUWrp06biHIUlvKA8++ODzVTUxV7tfutBYunQpO3bsGPcwJOkNJcnf9bTz8pQkqZuhIUnqZmhIkroZGpKkboaGJKlbd2gkWZDkoSRfa+tnJLkvya4kX05yXKu/pa1Ptu1Lh/ZxTas/nuTCofqqVptMsmGoPvIYkqTxOJgzjY8Cjw2tfxa4vqqWAfuAda2+DthXVWcC17d2JDkLWAO8G1gF3NiCaAHwBeAi4Czg8tZ2tmNIksagKzSSLAZ+G/jTth7gPOCO1mQTcElbXt3WadvPb+1XA5ur6pWqehKYBM5pr8mqeqKqfgZsBlbPcQxJ0hj0nmn8Z+CPgJ+39ZOBF6rq1ba+G1jUlhcBTwG07S+29v9Un9Znpvpsx5AkjcGc3whP8iHguap6MMm5U+URTWuObTPVRwXXbO1HjXE9sB7g9NNPH9XkmLN0w/8Y9xB+qfzgM7897iFI80LPmcYHgX+V5AcMLh2dx+DM48QkU6GzGHi6Le8GlgC07ScAe4fr0/rMVH9+lmMcoKpurqoVVbViYmLOn06RJB2iOUOjqq6pqsVVtZTBjey7q+pfA/cAl7Zma4E72/KWtk7bfndVVauvabOrzgCWAfcDDwDL2kyp49oxtrQ+Mx1DkjQGh/M9jauBjyWZZHD/4ZZWvwU4udU/BmwAqKqdwO3A94C/Bq6sqv3tnsVVwDYGs7Nub21nO4YkaQwO6lduq+pe4N62/ASDmU/T2/wUuGyG/tcB142obwW2jqiPPIYkaTz8RrgkqZuhIUnqZmhIkroZGpKkboaGJKmboSFJ6mZoSJK6GRqSpG6GhiSpm6EhSepmaEiSuhkakqRuhoYkqZuhIUnqZmhIkroZGpKkboaGJKnbnKGR5FeS3J/kO0l2JvlEq9+a5MkkD7fX8lZPkhuSTCZ5JMnZQ/tam2RXe60dqr8/yaOtzw1J0upvT7K9td+e5KQj/59AktSr50zjFeC8qnovsBxYlWRl2/bvq2p5ez3cahcBy9prPXATDAIAuBb4AINHuF47FAI3tbZT/Va1+gbgrqpaBtzV1iVJYzJnaNTAT9rqm9urZumyGrit9fsWcGKS04ALge1Vtbeq9gHbGQTQacDbquqbVVXAbcAlQ/va1JY3DdUlSWPQdU8jyYIkDwPPMfiH/7626bp2Cer6JG9ptUXAU0Pdd7fabPXdI+oA76iqZwDa+6ndn0ySdMR1hUZV7a+q5cBi4Jwk7wGuAX4d+BfA24GrW/OM2sUh1LslWZ9kR5Ide/bsOZiukqSDcFCzp6rqBeBeYFVVPdMuQb0C/BmD+xQwOFNYMtRtMfD0HPXFI+oAz7bLV7T352YY181VtaKqVkxMTBzMR5IkHYSe2VMTSU5sy8cDvwX87dA/5mFwr+G7rcsW4Io2i2ol8GK7tLQNuCDJSe0G+AXAtrbtpSQr276uAO4c2tfULKu1Q3VJ0hgs7GhzGrApyQIGIXN7VX0tyd1JJhhcXnoY+P3WfitwMTAJvAx8GKCq9ib5FPBAa/fJqtrblj8C3AocD3y9vQA+A9yeZB3wQ+CyQ/2gkqTDN2doVNUjwPtG1M+boX0BV86wbSOwcUR9B/CeEfUfA+fPNUZJ0tHhN8IlSd0MDUlSN0NDktTN0JAkdTM0JEndDA1JUjdDQ5LUzdCQJHUzNCRJ3QwNSVI3Q0OS1M3QkCR1MzQkSd0MDUlSN0NDktTN0JAkdTM0JEndep4R/itJ7k/ynSQ7k3yi1c9Icl+SXUm+nOS4Vn9LW59s25cO7euaVn88yYVD9VWtNplkw1B95DEkSePRc6bxCnBeVb0XWA6sSrIS+CxwfVUtA/YB61r7dcC+qjoTuL61I8lZwBrg3cAq4MYkC9qzx78AXAScBVze2jLLMSRJYzBnaNTAT9rqm9urgPOAO1p9E3BJW17d1mnbz0+SVt9cVa9U1ZPAJHBOe01W1RNV9TNgM7C69ZnpGJKkMei6p9HOCB4GngO2A98HXqiqV1uT3cCitrwIeAqgbX8ROHm4Pq3PTPWTZznG9PGtT7IjyY49e/b0fCRJ0iHoCo2q2l9Vy4HFDM4M3jWqWXvPDNuOVH3U+G6uqhVVtWJiYmJUE0nSEXBQs6eq6gXgXmAlcGKShW3TYuDptrwbWALQtp8A7B2uT+szU/35WY4hSRqDntlTE0lObMvHA78FPAbcA1zamq0F7mzLW9o6bfvdVVWtvqbNrjoDWAbcDzwALGszpY5jcLN8S+sz0zEkSWOwcO4mnAZsarOc3gTcXlVfS/I9YHOSTwMPAbe09rcAX0oyyeAMYw1AVe1McjvwPeBV4Mqq2g+Q5CpgG7AA2FhVO9u+rp7hGJKkMZgzNKrqEeB9I+pPMLi/Mb3+U+CyGfZ1HXDdiPpWYGvvMSRJ4+E3wiVJ3QwNSVI3Q0OS1M3QkCR1MzQkSd0MDUlSN0NDktTN0JAkdTM0JEndDA1JUjdDQ5LUzdCQJHUzNCRJ3QwNSVI3Q0OS1M3QkCR1MzQkSd16nhG+JMk9SR5LsjPJR1v940l+lOTh9rp4qM81SSaTPJ7kwqH6qlabTLJhqH5GkvuS7Ery5fascNrzxL/c2t+XZOmR/PCSpIPTc6bxKvCHVfUuYCVwZZKz2rbrq2p5e20FaNvWAO8GVgE3JlnQnjH+BeAi4Czg8qH9fLbtaxmwD1jX6uuAfVV1JnB9aydJGpM5Q6Oqnqmqb7fll4DHgEWzdFkNbK6qV6rqSWCSwXO+zwEmq+qJqvoZsBlYnSTAecAdrf8m4JKhfW1qy3cA57f2kqQxOKh7Gu3y0PuA+1rpqiSPJNmY5KRWWwQ8NdRtd6vNVD8ZeKGqXp1WP2BfbfuLrf30ca1PsiPJjj179hzMR5IkHYTu0EjyVuArwB9U1d8DNwHvBJYDzwB/MtV0RPc6hPps+zqwUHVzVa2oqhUTExOzfg5J0qHrCo0kb2YQGH9eVX8FUFXPVtX+qvo58EUGl59gcKawZKj7YuDpWerPAycmWTitfsC+2vYTgL0H8wElSUdOz+ypALcAj1XV54bqpw01+x3gu215C7CmzXw6A1gG3A88ACxrM6WOY3CzfEtVFXAPcGnrvxa4c2hfa9vypcDdrb0kaQwWzt2EDwK/Czya5OFW+2MGs5+WM7hc9APg9wCqameS24HvMZh5dWVV7QdIchWwDVgAbKyqnW1/VwObk3waeIhBSNHev5RkksEZxprD+KySpMM0Z2hU1TcYfW9h6yx9rgOuG1HfOqpfVT3Ba5e3hus/BS6ba4ySpKPDb4RLkroZGpKkboaGJKmboSFJ6mZoSJK6GRqSpG6GhiSpm6EhSepmaEiSuhkakqRuhoYkqZuhIUnqZmhIkroZGpKkboaGJKmboSFJ6mZoSJK69TwjfEmSe5I8lmRnko+2+tuTbE+yq72f1OpJckOSySSPJDl7aF9rW/tdSdYO1d+f5NHW54b2XPIZjyFJGo+eM41XgT+sqncBK4Erk5wFbADuqqplwF1tHeAiYFl7rQdugkEAANcCH2DwaNdrh0LgptZ2qt+qVp/pGJKkMZgzNKrqmar6dlt+CXgMWASsBja1ZpuAS9ryauC2GvgWcGKS04ALge1Vtbeq9gHbgVVt29uq6ptVVcBt0/Y16hiSpDE4qHsaSZYC7wPuA95RVc/AIFiAU1uzRcBTQ912t9ps9d0j6sxyjOnjWp9kR5Ide/bsOZiPJEk6CN2hkeStwFeAP6iqv5+t6YhaHUK9W1XdXFUrqmrFxMTEwXSVJB2ErtBI8mYGgfHnVfVXrfxsu7REe3+u1XcDS4a6LwaenqO+eER9tmNIksagZ/ZUgFuAx6rqc0ObtgBTM6DWAncO1a9os6hWAi+2S0vbgAuSnNRugF8AbGvbXkqysh3rimn7GnUMSdIYLOxo80Hgd4FHkzzcan8MfAa4Pck64IfAZW3bVuBiYBJ4GfgwQFXtTfIp4IHW7pNVtbctfwS4FTge+Hp7McsxJEljMGdoVNU3GH3fAeD8Ee0LuHKGfW0ENo6o7wDeM6L+41HHkCSNh98IlyR1MzQkSd0MDUlSN0NDktTN0JAkdTM0JEndDA1JUjdDQ5LUzdCQJHUzNCRJ3QwNSVI3Q0OS1M3QkCR1MzQkSd0MDUlSN0NDktTN0JAkdet5RvjGJM8l+e5Q7eNJfpTk4fa6eGjbNUkmkzye5MKh+qpWm0yyYah+RpL7kuxK8uUkx7X6W9r6ZNu+9Eh9aEnSoek507gVWDWifn1VLW+vrQBJzgLWAO9ufW5MsiDJAuALwEXAWcDlrS3AZ9u+lgH7gHWtvg7YV1VnAte3dpKkMZozNKrqb4C9nftbDWyuqleq6klgEjinvSar6omq+hmwGVidJMB5wB2t/ybgkqF9bWrLdwDnt/aSpDE5nHsaVyV5pF2+OqnVFgFPDbXZ3Woz1U8GXqiqV6fVD9hX2/5ia/86SdYn2ZFkx549ew7jI0mSZnOooXET8E5gOfAM8CetPupMoA6hPtu+Xl+surmqVlTViomJidnGLUk6DIcUGlX1bFXtr6qfA19kcPkJBmcKS4aaLgaenqX+PHBikoXT6gfsq20/gf7LZJKkX4BDCo0kpw2t/g4wNbNqC7CmzXw6A1gG3A88ACxrM6WOY3CzfEtVFXAPcGnrvxa4c2hfa9vypcDdrb0kaUwWztUgyV8C5wKnJNkNXAucm2Q5g8tFPwB+D6Cqdia5Hfge8CpwZVXtb/u5CtgGLAA2VtXOdoirgc1JPg08BNzS6rcAX0oyyeAMY81hf1pJ0mGZMzSq6vIR5VtG1KbaXwdcN6K+Fdg6ov4Er13eGq7/FLhsrvFJko4evxEuSepmaEiSuhkakqRuhoYkqZuhIUnqZmhIkroZGpKkboaGJKmboSFJ6mZoSJK6GRqSpG6GhiSpm6EhSepmaEiSuhkakqRuhoYkqducoZFkY5Lnknx3qPb2JNuT7GrvJ7V6ktyQZDLJI0nOHuqztrXflWTtUP39SR5tfW5IktmOIUkan54zjVuBVdNqG4C7qmoZcFdbB7iIwXPBlwHrgZtgEAAMHhP7AQZP6bt2KARuam2n+q2a4xiSpDGZMzSq6m8YPKN72GpgU1veBFwyVL+tBr4FnJjkNOBCYHtV7a2qfcB2YFXb9raq+mZVFXDbtH2NOoYkaUwO9Z7GO6rqGYD2fmqrLwKeGmq3u9Vmq+8eUZ/tGJKkMTnSN8IzolaHUD+4gybrk+xIsmPPnj0H212S1OlQQ+PZdmmJ9v5cq+8Glgy1Www8PUd98Yj6bMd4naq6uapWVNWKiYmJQ/xIkqS5HGpobAGmZkCtBe4cql/RZlGtBF5sl5a2ARckOandAL8A2Na2vZRkZZs1dcW0fY06hiRpTBbO1SDJXwLnAqck2c1gFtRngNuTrAN+CFzWmm8FLgYmgZeBDwNU1d4knwIeaO0+WVVTN9c/wmCG1vHA19uLWY4hSRqTOUOjqi6fYdP5I9oWcOUM+9kIbBxR3wG8Z0T9x6OOIUkaH78RLknqZmhIkroZGpKkboaGJKmboSFJ6mZoSJK6GRqSpG6GhiSpm6EhSepmaEiSuhkakqRuhoYkqZuhIUnqZmhIkroZGpKkboaGJKmboSFJ6nZYoZHkB0keTfJwkh2t9vYk25Psau8ntXqS3JBkMskjSc4e2s/a1n5XkrVD9fe3/U+2vjmc8UqSDs+RONP4zapaXlUr2voG4K6qWgbc1dYBLgKWtdd64CYYhAyD545/ADgHuHYqaFqb9UP9Vh2B8UqSDtGczwg/BKuBc9vyJuBe4OpWv609R/xbSU5Mclpru72q9gIk2Q6sSnIv8Laq+mar3wZcAnz9FzBmSVM+fsK4R/DL5eMvjnsER9ThnmkU8D+TPJhkfau9o6qeAWjvp7b6IuCpob67W222+u4RdUnSmBzumcYHq+rpJKcC25P87SxtR92PqEOov37Hg8BaD3D66afPPmJJ0iE7rDONqnq6vT8HfJXBPYln22Un2vtzrfluYMlQ98XA03PUF4+ojxrHzVW1oqpWTExMHM5HkiTN4pBDI8mvJvlnU8vABcB3gS3A1AyotcCdbXkLcEWbRbUSeLFdvtoGXJDkpHYD/AJgW9v2UpKVbdbUFUP7kiSNweFcnnoH8NU2C3Yh8BdV9ddJHgBuT7IO+CFwWWu/FbgYmAReBj4MUFV7k3wKeKC1++TUTXHgI8CtwPEMboB7E1ySxuiQQ6OqngDeO6L+Y+D8EfUCrpxhXxuBjSPqO4D3HOoYJUlHlt8IlyR1MzQkSd0MDUlSN0NDktTN0JAkdTM0JEndDA1JUjdDQ5LUzdCQJHUzNCRJ3QwNSVI3Q0OS1M3QkCR1MzQkSd0MDUlSN0NDktTN0JAkdTvmQyPJqiSPJ5lMsmHc45Gk+eyYDo0kC4AvABcBZwGXJzlrvKOSpPnrmA4N4BxgsqqeqKqfAZuB1WMekyTNW8d6aCwCnhpa391qkqQxWDjuAcwhI2r1ukbJemB9W/1Jksd/oaOaX04Bnh/3IOaSz457BBqDN8TfJp8Y9c/YMenXehod66GxG1gytL4YeHp6o6q6Gbj5aA1qPkmyo6pWjHsc0nT+bY7HsX556gFgWZIzkhwHrAG2jHlMkjRvHdNnGlX1apKrgG3AAmBjVe0c87Akad46pkMDoKq2AlvHPY55zMt+Olb5tzkGqXrdfWVJkkY61u9pSJKOIYaGJKmboaGRkrxl3GOQdOwxNHSAJOckeRTY1dbfm+TzYx6WBEAG/k2S/9DWT09yzrjHNZ8YGpruBuBDwI8Bquo7wG+OdUTSa24E/iVweVt/icGPmuooOean3Oqoe1NV/V1ywE8f7B/XYKRpPlBVZyd5CKCq9rUv/uooMTQ03VPtdL/aT9P/W+D/jnlM0pR/bH+XBZBkAvj5eIc0v3h5StN9BPgYcDrwLLCy1aRjwQ3AV4FTk1wHfAP4j+Md0vzil/skvaEk+XXgfAa/gn1XVT025iHNK4aGDpDki4z4+fmqWj+iuXRUJXknsLuqXklyLvAbwG1V9cJ4RzZ/eHlK0/0v4K72+t/AqcArYx2R9JqvAPuTnAn8KXAG8BfjHdL84pmGZpXkTcD2qjp/3GORkny7zZ76I+D/VdXnkzxUVe8b99jmC880NJcz6Hyil3QU/GOSy4ErgK+12pvHOJ55xym3OkCSfbx2T+NNwF5gw/hGJB3gw8DvA9dV1ZNJzgD+65jHNK94eUr/JINv9C0BftRKPy//QCQNMTR0gCQPVtX7xz0OaVj7PbQZ/7Gqqt84isOZ17w8penuT3J2VX173AORhnxo3APQgGcaAiDJwvZM9keBdwHfB/6BwReoqqrOHusAJR0TPNPQlPuBs4FLxj0QaSZJVgKfZ/A/NscBC4B/qKq3jXVg84ihoSkBqKrvj3sg0iz+C7AG+G/ACgZTb88c64jmGUNDUyaSfGymjVX1uaM5GGkmVTWZZEFV7Qf+LMn/GfeY5hNDQ1MWAG+lnXFIx6iX2/MzHk7yn4BngF8d85jmFW+EC3jt5xnGPQ5pNkl+jcFP9h8H/DvgBODGqpoc68DmEUNDAPj7PTqWJTm9qn447nHI357Sa/xBQh3L/vvUQpKvjHMg852hIQCqau+4xyDNYvhe2z8f2yhkaEh6Q6gZlnWUeU9D0jEvyX5e+4WC44GXpzYx+MUCv9x3lBgakqRuXp6SJHUzNCRJ3QwNSVI3Q0OS1M3QkCR1+/9vjIOEc2PozwAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f692522add8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"meteo_cata_DF.iscatastrophe.value_counts().plot(kind='bar')"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"neg: 53502 11.793855520750899\n",
"pos: 400141 88.2061444792491\n"
]
}
],
"source": [
"meteo_cata_ko_DF=meteo_cata_DF[meteo_cata_DF.iscatastrophe==False]\n",
"meteo_cata_ok_DF=meteo_cata_DF[meteo_cata_DF.iscatastrophe==True]\n",
"row_nb_pos,_=meteo_cata_ok_DF.shape\n",
"row_nb_neg,_=meteo_cata_ko_DF.shape\n",
"print(\"neg:\",row_nb_neg, row_nb_neg/(row_nb_pos+row_nb_neg)*100)\n",
"print(\"pos:\",row_nb_pos,row_nb_pos/(row_nb_pos+row_nb_neg)*100)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## REDUCTION INDIVIDUS"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Choix:\n",
"* classification (kmeans ou CAH)\n",
"* PCA individus\n",
"* **selection sur la nature de la catastrophe**\n",
"* **downsampling**"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### DOWNSAMPLING VARIABLE MAJORITAIRE"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {},
"outputs": [],
"source": [
"meteo_cata_dwn_pos_DF= resample(meteo_cata_ok_DF, \n",
" replace=True, # sample with replacement\n",
" n_samples=row_nb_neg, # to match majority class\n",
" random_state=123) # reproducible results"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {},
"outputs": [],
"source": [
"meteo_cata_eq_DF=pd.concat([meteo_cata_ko_DF,meteo_cata_dwn_pos_DF])"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"<class 'pandas.core.frame.DataFrame'>\n",
"Int64Index: 107004 entries, 0 to 268418\n",
"Data columns (total 16 columns):\n",
"numer_sta 107004 non-null int64\n",
"date 107004 non-null datetime64[ns]\n",
"t 107004 non-null float64\n",
"tn12 106996 non-null float64\n",
"tx12 106996 non-null float64\n",
"n 107004 non-null float64\n",
"raf10 107004 non-null float64\n",
"ff 107004 non-null float64\n",
"pres 107004 non-null float64\n",
"tend 107004 non-null float64\n",
"rr3 107004 non-null float64\n",
"u 107004 non-null float64\n",
"geop 107004 non-null float64\n",
"vv 107004 non-null float64\n",
"ht_neige 107004 non-null float64\n",
"iscatastrophe 107004 non-null bool\n",
"dtypes: bool(1), datetime64[ns](1), float64(13), int64(1)\n",
"memory usage: 13.2 MB\n"
]
}
],
"source": [
"meteo_cata_eq_DF.info()"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"True 53502\n",
"False 53502\n",
"Name: iscatastrophe, dtype: int64"
]
},
"execution_count": 23,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"meteo_cata_eq_DF.iscatastrophe.value_counts()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### UPSAMPLING VARIABLE MINORITAIRE (non utilise)"
]
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"meteo_cata_up_neg_DF= resample(meteo_cata_ko_DF, \n",
" replace=True, # sample with replacement\n",
" n_samples=row_nb_pos, # to match majority class\n",
" random_state=123) # reproducible results"
]
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"meteo_cata_eq_DF=pd.concat([meteo_cata_ok_DF,meteo_cata_up_neg_DF])"
]
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"meteo_cata_eq_DF.info()"
]
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"meteo_cata_eq_DF.iscatastrophe.value_counts()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### JEU DONNEES FINAL\n",
"constitution des predictives et de la variable à prédire"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {},
"outputs": [],
"source": [
"Y=meteo_cata_eq_DF.iscatastrophe\n",
"X=meteo_cata_eq_DF.drop(['iscatastrophe','date','numer_sta'],1)"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"0"
]
},
"execution_count": 25,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Y.isna().sum()"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"t 0\n",
"tn12 8\n",
"tx12 8\n",
"n 0\n",
"raf10 0\n",
"ff 0\n",
"pres 0\n",
"tend 0\n",
"rr3 0\n",
"u 0\n",
"geop 0\n",
"vv 0\n",
"ht_neige 0\n",
"dtype: int64"
]
},
"execution_count": 26,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"X.isna().sum()"
]
},
{
"cell_type": "code",
"execution_count": 258,
"metadata": {},
"outputs": [],
"source": [
"#on complete les 8 valeurs manquantes ....\n",
"X.fillna(inplace=True,method=\"bfill\")"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {},
"outputs": [],
"source": [
"X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size=0.2, random_state=42)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## CHOIX DES ALGORITHMES PREDICTIFS"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### FONCTION AUXILIAIRES"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {},
"outputs": [],
"source": [
"def plot_roc_curve(fpr, tpr, label=None):\n",
" plt.plot(fpr, tpr, linewidth=2, label=label)\n",
" plt.plot([0, 1], [0, 1], 'k--')\n",
" plt.axis([0, 1, 0, 1])\n",
" plt.xlabel('False Positive Rate', fontsize=16)\n",
" plt.ylabel('True Positive Rate', fontsize=16)"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {},
"outputs": [],
"source": [
"def display_scores(scores):\n",
" print(\"Scores:\", scores)\n",
" print(\"Mean:\", scores.mean())\n",
" print(\"Standard deviation:\", scores.std())"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {},
"outputs": [],
"source": [
"def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):\n",
" plt.plot(thresholds, precisions[:-1], \"b--\", label=\"Precision\", linewidth=2)\n",
" plt.plot(thresholds, recalls[:-1], \"g-\", label=\"Recall\", linewidth=2)\n",
" plt.xlabel(\"Threshold\", fontsize=16)\n",
" plt.legend(loc=\"upper left\", fontsize=16)\n",
" plt.ylim([0, 1])"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {},
"outputs": [],
"source": [
"def plot_precision_vs_recall(precisions, recalls):\n",
" plt.plot(recalls, precisions, \"b-\", linewidth=2)\n",
" plt.xlabel(\"Recall\", fontsize=16)\n",
" plt.ylabel(\"Precision\", fontsize=16)\n",
" plt.axis([0, 1, 0, 1])"
]
},
{
"cell_type": "code",
"execution_count": 33,
"metadata": {},
"outputs": [],
"source": [
"#precision_recall_curve(modele_ada,probas_pred=1)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### **RF ET BOOSTING RF**"
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {},
"outputs": [],
"source": [
"from sklearn.ensemble import RandomForestClassifier,AdaBoostClassifier,GradientBoostingClassifier"
]
},
{
"cell_type": "code",
"execution_count": 35,
"metadata": {},
"outputs": [],
"source": [
"# forets aléatoires \n",
"modele_rf=RandomForestClassifier(n_estimators=100, random_state=42)\n",
"#methodes ensemble\n",
"modele_ada=AdaBoostClassifier(n_estimators=100, random_state=42)\n",
"modele_gbm=GradientBoostingClassifier(n_estimators=100, random_state=42)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### APPRENTISSAGE"
]
},
{
"cell_type": "code",
"execution_count": 36,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"CPU times: user 13.3 s, sys: 71.6 ms, total: 13.4 s\n",
"Wall time: 13.4 s\n"
]
},
{
"data": {
"text/plain": [
"RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',\n",
" max_depth=None, max_features='auto', max_leaf_nodes=None,\n",
" min_impurity_decrease=0.0, min_impurity_split=None,\n",
" min_samples_leaf=1, min_samples_split=2,\n",
" min_weight_fraction_leaf=0.0, n_estimators=100, n_jobs=1,\n",
" oob_score=False, random_state=42, verbose=0, warm_start=False)"
]
},
"execution_count": 36,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"%%time\n",
"#en upsampling\n",
"#CPU times: user 37min 9s, sys: 6.21 s, total: 37min 15s\n",
"#Wall time: 37min 16s\n",
"modele_rf.fit(X_train, Y_train)"
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"CPU times: user 6.67 s, sys: 12.1 ms, total: 6.69 s\n",
"Wall time: 6.69 s\n"
]
},
{
"data": {
"text/plain": [
"AdaBoostClassifier(algorithm='SAMME.R', base_estimator=None,\n",
" learning_rate=1.0, n_estimators=100, random_state=42)"
]
},
"execution_count": 37,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"%%time\n",
"modele_ada.fit(X_train, Y_train)"
]
},
{
"cell_type": "code",
"execution_count": 38,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"CPU times: user 9.22 s, sys: 12.3 ms, total: 9.23 s\n",
"Wall time: 9.24 s\n"
]
},
{
"data": {
"text/plain": [
"GradientBoostingClassifier(criterion='friedman_mse', init=None,\n",
" learning_rate=0.1, loss='deviance', max_depth=3,\n",
" max_features=None, max_leaf_nodes=None,\n",
" min_impurity_decrease=0.0, min_impurity_split=None,\n",
" min_samples_leaf=1, min_samples_split=2,\n",
" min_weight_fraction_leaf=0.0, n_estimators=100,\n",
" presort='auto', random_state=42, subsample=1.0, verbose=0,\n",
" warm_start=False)"
]
},
"execution_count": 38,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"%%time\n",
"modele_gbm.fit(X_train, Y_train)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### PREDICTIONS"
]
},
{
"cell_type": "code",
"execution_count": 39,
"metadata": {},
"outputs": [],
"source": [
"modele_rf_pred=modele_rf.predict(X_test)"
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {},
"outputs": [],
"source": [
"modele_ada_pred=modele_ada.predict(X_test)"
]
},
{
"cell_type": "code",
"execution_count": 41,
"metadata": {},
"outputs": [],
"source": [
"modele_gbm_pred=modele_gbm.predict(X_test)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### **ESTIMATION QUALITE MODELE RF**"
]
},
{
"cell_type": "code",
"execution_count": 42,
"metadata": {},
"outputs": [],
"source": [
"modele_pred = modele_rf_pred\n",
"modele = modele_rf"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Matrice confusion"
]
},
{
"cell_type": "code",
"execution_count": 43,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[10013, 791],\n",
" [ 373, 10224]])"
]
},
"execution_count": 43,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"confusion_matrix(Y_test,modele_pred)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### ROC"
]
},
{
"cell_type": "code",
"execution_count": 44,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"0.9457938671458329"
]
},
"execution_count": 44,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"roc_auc_score(Y_test, modele_pred)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### ROC CURVE"
]
},
{
"cell_type": "code",
"execution_count": 45,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAf4AAAF8CAYAAAAuF9n2AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzs3Xd4VGXe//H3NxWpIhAUUYooLqgkyIMggmtdRGnSLbuiAooiPGJDdl11XVQsLKyoYPnp7trpIuBasICglARXedRFFEGFgHSBtLl/f8wEQkjCJMzMmfJ5XVcuZs6czHw5Yj65y7lvc84hIiIiiSHJ6wJEREQkchT8IiIiCUTBLyIikkAU/CIiIglEwS8iIpJAFPwiIiIJJKLBb2bPm1mumX1RzutmZpPMbI2ZfW5mbSNZn4iISLyLdIv/BaBrBa9fApwc+BoKPBWBmkRERBJGRIPfOfcRsLWCU3oC/3B+S4Gjzey4yFQnIiIS/6JtjP94YH2J5xsCx0RERCQEUrwuoBQr41iZawqb2VD8wwHUqFHjzFNPPTWcdYmIyBFwDnzO4QDnHD7nP+acw1H6eeDc4mP7X/cf81HitTLOL/k5Bz8/cH60McDMSDL/n/7nJY5h+Arz2L35J4oK8gC2OOcaVOWzoi34NwAnlHjeGPiprBOdc1OBqQDt2rVzy5cvD391IiIxwOdz5Bf5yCv0kV/oI78o8Gehj7zCogOPSxwveV4w5/jPK31O0UGvF59fUHTkURvq7um0lCTSk5NISynxlXzw4/TUZP+fZb2+/5ykg89JSSItOfmQ90xPKX3OwY/Nymr3HrBixQq6dOnCMUfX5sUXX6Rbt27rqvp3j7bgnwPcbGavAmcBO5xzP3tck4hIhUoH7f7gLBWCpUM0r4ywLCto8wp85ZxTVCKsD7xe6Iu+Nm15QVscnP5j5Qdt6dAsK2grPqdyQRstnHOYGW3atGH48OHceuutHHfckU19i2jwm9krwG+B+ma2AfgzkArgnHsamAd0A9YAe4DBkaxPRGLD/qAt8JFXVFRma7RkQJYMxfKC9uBzyg/aslrR0R60BwVgSvlBW2HLNqVkCCcHd07geGqyxUzQRpNPP/2UW2+9lZkzZ5KRkcEjjzwSkveNaPA75wYd5nUH3BShckQkSEU+VyIEyw7avJJ/FlUQtGWec2h39CHnxELQFodnuV3IyQdCNrms1w/uZj7sOSUDtsRxBW1s8/l8jB8/nj/96U8cf/zxbNy4kYyMjJC9f7R19YsIFQftId2+ZQRt6VZpeUF70FhuDAWtGQeNnZYdigcHYlkhGsw5JVvC6aXHbxW0EmIbN27k6quv5t1336Vfv35MnTqVo48+OqSfoeAX4dCgLR2u5QVtyeCsKGjLGvM99JwD71EUI0F7UHCWCt/0MoKzdGiWfU6pY6W/JyWJlCQFrcSnu+66i8WLFzN16lSuv/76sPw7N3/vemzTrP7YUxy0xYFYUWszr4LJUiWD9uBWbvlBW1aoR3fQJpc99lo6aMtq/ZYRtAdPpio7aEufo6AVCZ/8/Hy2b99ORkYGW7ZsITc3l1atWlX4PWa2wjnXriqfpxZ/gigsOkz38P5ALDqk9Xlo9/ChLdTSQVtyolRZnxWNQXsgNMsP2tKBWF7QpqdUdM7BE6DK+iwFrUhi+Pbbbxk0aBDJycksXryY+vXrU79+/bB+poI/TCoK2oNmD5cTtHmlwra8oC37Pt3oD9oko0TYHRp+5d2GE0w3c+mgLTm7uLwuZQWtiETayy+/zA033EBycjLPPvssSUmRWUxXwX+Edu0r4Jr/t4wftu4hr+DA7OUoy9kyg7aie1wP1yItHbRljuGWEbTFLeaU5GhbLVpEJDJ+/fVXbr75Zl544QU6derESy+9RJMmTSL2+Qr+I7Ts+62sWLftkOPFQVuytVlR0BavEFVei7R0N/Phgrb0ZyloRUSig3OOTz/9lD/96U/cc889pKRENooV/Edo0848AHq0acT9PVsraEVE5BDOOV544QUGDBhAzZo1WblyJdWqVfOkFqXTEdq4Yx8ATepV5+jqaVRPS1Hoi4jIflu2bKFnz55ce+21/L//9/8APAt9UIv/iOXu8gd/Rm3v/iOKiEh0+uCDD7jyyivZsmULEydOZPjw4V6XpBb/kSpu8R+r4BcRkRKee+45zj//fGrWrMnSpUu55ZZbouLuIQX/EdoYGONvWDvd40pERCSanHvuuQwdOpQVK1aQlZXldTn7KfiPUO5OtfhFRMRv5syZXH/99TjnaNGiBU8//TQ1a9b0uqyDKPiPQF5hEb/8mk9yklGvplr8IiKJau/evQwfPpzLL7+cVatWsWPHDq9LKpeC/whs3uXv5m9QM53kJO/HbUREJPJWr17NWWedxVNPPcXo0aNZvHhxyHfUCyXN6j8CmwLd/A3rqJtfRCQRFRQUcOmll/Lrr78yb948LrnkEq9LOiwF/xHYuCMwsa+WuvlFRBLJzp07qVGjBqmpqbz88ss0bdqU4447zuuygqKu/iNQ3OI/Vi1+EZGEsXTpUtq0acODDz4IQMeOHWMm9EHBf0T2d/VrRr+ISNzz+Xw89NBDnHPOOQBceOGFHldUNerqPwIKfhGRxPDzzz9z9dVX895779G/f3+mTJkS1RP4KqLgPwIbdQ+/iEhCWLduHcuWLeOZZ57huuuui4oV+KpKwX8EcrVqn4hI3MrPz2f+/Pn07NmTDh06sG7dupht5ZekMf4qcs7tb/Hrdj4RkfiyZs0aOnXqRK9evfjPf/4DEBehDwr+KtuVV8ie/CKOSk2mVro6TkRE4sVLL71EVlYW3377LTNmzOD000/3uqSQUvBXUW6JW/lieaxHREQOuOmmm7jqqqvIzMwkJyeH3r17e11SyCn4q2j/4j0a3xcRiRtt27blnnvuYeHChZx44olelxMW6qOuIt3KJyIS+5xzTJo0iXr16nHVVVdx3XXXeV1S2KnFX0W6lU9EJLZt2bKFHj16MGrUKObNm+d1ORGj4K+i4hZ/hoJfRCTmfPDBB7Rp04Z///vfTJo0iZdeesnrkiJGXf1VtEktfhGRmPTVV19xwQUXcPLJJ/PWW2+RmZnpdUkRpRZ/FW0MLN5zbB1N7hMRiQV79+4F4NRTT+XFF19k+fLlCRf6oOCvsuLb+TJqqcUvIhLtZsyYQbNmzVixYgUAV111FTVr1vS4Km8o+KugyOfI3eVv8Wfodj4Rkai1d+9ehg8fTp8+fTjhhBPiZvW9I6Hgr4JfdudR5HMcUyON9JRkr8sREZEyfPnll7Rv356nnnqK2267jcWLF3PSSSd5XZbnNLmvCjbt35xH3fwiItHqjTfeYNOmTcyfP5+uXbt6XU7UUIu/CvZvzqNufhGRqLJ9+3ays7MB+OMf/8h//vMfhX4pavFXgW7lExGJPkuWLGHQoEH4fD7WrFlDWloaDRs29LqsqKMWfxVouV4Rkejh8/l48MEH6dy5M2bGG2+8QVpamtdlRS21+KtAwS8iEh127drF5ZdfzrvvvsuAAQOYMmUKderU8bqsqKbgrwIt3iMiEh1q1qzJMcccw7PPPsu1116rbdKDoK7+Kti0Q4v3iIh4JT8/n7vvvpvvv/8eM+O1117juuuuU+gHScFfBZt2BSb31VHwi4hE0po1azj77LN58MEHmTNnjtflxCR19VfSvoIitu8pIDXZOKa6Jo+IiETKv/71L2688UZSU1OZOXMmvXr18rqkmKQWfyXlBsb3M2pVIylJ3UoiIpHw3HPPcfXVV5OVlcWqVasU+kdALf5K0uI9IiKRU1RURHJyMgMGDGDXrl3cfPPNpKQouo6EWvyVtFG38omIhJ1zjokTJ9K+fXv27NlDzZo1GTVqlEI/BBT8lZSr4BcRCavNmzfTvXt3Ro0axfHHH09eXp7XJcUVBX8lbdyhGf0iIuGycOFC2rRpwzvvvMOkSZOYPXs2devW9bqsuKI+k0ratKt4Zz6N8YuIhJJzjrvuuovatWszb948MjMzvS4pLin4K6l48R519YuIhMa6deuoXbs2devWZfr06dStW5caNWp4XVbcUld/JRUv3qPgFxE5ctOnTyczM5ORI0cC0LhxY4V+mCn4K8E5t3+MX8EvIlJ1e/fu5YYbbqBv3760aNGCP//5z16XlDAU/JWwY28BeYU+aqanUDNdoyQiIlXx3//+l/bt2zNlyhRuu+02Fi9ezEknneR1WQlD6VUJm3ZqYp+IyJGqWbMmAPPnz6dr164eV5N41OKvhOLFe3Qrn4hI5Wzfvp0HHniAoqIijjvuOFatWqXQ94iCvxI2FS/eo+14RUSCtmTJEjIzM7nvvvv47LPPAEhKUvx4JeJX3sy6mtnXZrbGzO4q4/UTzWyhmWWb2edm1i3SNZZn/618avGLiBxWUVER48aNo3PnziQlJbFo0SI6duzodVkJL6LBb2bJwGTgEqAVMMjMWpU67Y/A6865LGAg8GQka6zI/nX6a2mMX0TkcIYMGcLYsWPp168f2dnZnHXWWV6XJER+cl97YI1zbi2Amb0K9ARWlzjHAbUDj+sAP0W0wgoUT+7TGL+ISPmcc5gZQ4YM4ZxzzmHw4MGYaRvzaBHp4D8eWF/i+Qag9K+A9wL/NrMRQA3gwsiUdnibtEGPiEi58vLyGDNmDACPP/44HTt2VNd+FIr0GH9Zv/K5Us8HAS845xoD3YB/mtkhdZrZUDNbbmbLN2/eHIZSD6XgFxEp23//+1/OPvtsJkyYQEFBAc6V/tEu0SLSwb8BOKHE88Yc2pV/HfA6gHNuCVANqF/6jZxzU51z7Zxz7Ro0aBCmcg8oLPKxZXceZtBAY/wiIvv985//pG3btnz33XfMnDmTv//97+raj2KRDv5lwMlm1szM0vBP3ptT6pwfgAsAzOw3+IM/Mk36CmzenYfPQb0a6aQm6zYUERGADRs2MGzYMLKysli1ahW9evXyuiQ5jIiO8TvnCs3sZuBtIBl43jn3pZndDyx3zs0BRgPPmNn/4h8GuMZFQZ/RgYl9au2LiHz33Xc0a9aMxo0b89FHH5GZmUlKihaDjQURb7o65+Y5505xzp3knPtr4Ng9gdDHObfaOdfJOdfGOZfpnPt3pGssy/7NebR4j4gkMOccEyZMoGXLlrzyyisAtGvXTqEfQ/RfKki5u7R4j4gkts2bN3PNNdcwb948unfvzsUXX+x1SVIFGqwOUnGL/1jN6BeRBPTBBx/Qpk0b3n33XSZNmsTs2bOpV6+e12VJFajFHyTtzCciiWzr1q3Url2befPmkZmZ6XU5cgTU4g+S7uEXkUSzbt06Xn/9dQAuv/xyPv/8c4V+HFDwB2mjgl9EEsj06dPJzMzkpptuYteuXQCkpaV5XJWEgoI/SMUtfo3xi0g827t3LzfccAN9+/bllFNO4dNPP6VWrVpelyUhpDH+IOzJL2TXvkLSUpI4unqq1+WIiIRFXl4eHTp04PPPP+eOO+7gL3/5i1r5cUjBH4SSE/u0DKWIxKv09HR+//vfc/rpp+tWvTimrv4g6FY+EYlX27ZtY8CAAbz33nsAjB49WqEf5xT8QSge389Q8ItIHPnkk0/IzMxkxowZrFmzxutyJEIU/EHQxD4RiSdFRUWMGzeOLl26kJKSwuLFixk2bJjXZUmEKPiDsFHBLyJxZMaMGYwdO5Z+/fqxcuVK2rdv73VJEkGa3BeE3MDkvgyt2iciMWzz5s00aNCAvn37Mn/+fH73u99pwnICUos/CGrxi0gsy8vLY9SoUbRs2ZIffvgBM6Nr164K/QSlFn8Q9m/Jq+AXkRjzzTffMHDgQLKzs7n55pvJyMjwuiTxmIL/MJxzB7bkVfCLSAz55z//yY033kh6ejqzZs2iZ8+eXpckUUDBfxhbf82noMhRu1oKR6Ule12OiEjQ3n33Xc4880z+9a9/ccIJJ3hdjkQJBf9hFK/ad2wdtfZFJPqtWLGCatWq0bp1a55++mlSU1NJSdGPejlAk/sOQ9vxikgs8Pl8PP7443Ts2JHRo0cDcNRRRyn05RD6F3EYCn4RiXa5ubkMHjyYefPm0bNnT5577jmvS5IopuA/DN3KJyLR7KuvvuL8889n69atPPHEEwwfPly36UmFKhX8ZtYS6AzUA15wzm0ysxOAX5xze8JRoNcOtPi1eI+IRJ/mzZtz3nnncccdd9CmTRuvy5EYENQYv5mlmtk/gdXAVGAccHzg5SeAP4anPO8d2JJXLX4RiQ7ff/89AwYMYNu2baSlpfHSSy8p9CVowU7u+wvQAxgCNAFK9iPNA34X4rqixv4teTWrX0SiwLRp08jMzGTBggV88cUXXpcjMSjY4L8S+JNz7nngp1KvrQWahbSqKKLFe0QkGuzZs4dhw4bRr18/WrZsSXZ2Np07d/a6LIlBwQZ/A6CiXy3jMhXzC31s2Z1PkkH9mhrjFxHv3HrrrUydOpU777yTRYsW0bx5c69LkhgV7OS+dcD/AO+X8Vo74L8hqyiKFLf2G9RKJzlJs2RFJLKcc/z666/UrFmTP//5z/Tp04eLLrrI67IkxgUb/P8CxprZGuDNwDFnZh2BW/FP9os7+1ftUze/iETYtm3bGDJkCFu3buWdd97huOOO47jjjvO6LIkDwXb1Pwi8B7wBbAkcWwgsAj4E/hb60rynxXtExAuLFy8mMzOT2bNnc8kll+i+fAmpoFr8zrlCoLeZXYR/Bn8G8AuwwDn3dhjr85SCX0QiqaioiAcffJB7772XJk2asHjxYtq3b+91WRJnggp+M8vAv0jPO8A7pV5LAuo753LDUJ+n9q/ap1v5RCQCdu/ezbPPPkv//v15+umnqV27ttclSRwKdoz/Z6Aj8FkZr2UFjsfdnrW5gTH+jFqa0S8i4fP+++/TqVMn6tSpw2effUaDBg3UvS9hE+wYf0X/AlMAXwhqiTpavEdEwikvL49Ro0ZxwQUXMHHiRAAyMjIU+hJW5bb4zawmULKfqb6ZNSp12lHAFcCmMNTmOY3xi0i4fPPNNwwcOJDs7GxGjBjBLbfc4nVJkiAq6uofDdwTeOw4cBtfaQb8NZRFRQsFv4iEw+zZs7nyyitJT09n9uzZ9OjRw+uSJIFUFPxzgY34g/1JYDzwXalz8oDVzrmyxv5j2q59BfyaX8RRqcnUrqbdi0UkdFq0aEHnzp155plnaNy4sdflSIIpN9GccyuAFQBm5oDpzrkt5Z0fbw7sypeu8TYROWIrVqxg5syZPPDAA7Ru3Zr58+d7XZIkqKAm9znnpiRS6IO6+UUkNHw+H48//jgdO3bkxRdfZPPmzV6XJAku6D5sMzsFGAy05NBNeZxz7tJQFua14hn9Cn4Rqarc3FyuueYa5s+fT69evXjuuec45phjvC5LElywC/icCXyMf/b+icDXwDH4V/D7CfghXAV6ZdMu3conIlVXVFTEeeedx7fffsvkyZO58cYbNWwoUSHYFv9DwFvAICAfuMo5t9LMugHPAneGqT7PbFKLX0SqoKCggOTkZJKTk3nsscdo1KgRZ5xxhtdliewX7AI+bYAXOLBQTzKAc24e/p35xoe8Mo+VnNwnIhKM77//ni5dujBp0iQAunbtqtCXqBNs8KcDu5xzPmAr0LDEa6uBuPuXvX+dfrX4RSQIb7zxBpmZmaxevZpGjUqvdSYSPYIN/rVA8b/kL4FrSrx2FRB3G/RoVr+IBGPPnj0MHTqU/v37c+qpp5KTk0P//v29LkukXMEG/3zgosDjB4GeZrbVzHKBPwCTwlGcV3w+R+6uwAY96uoXkQqsXLmS559/njvvvJOPP/6YZs2aeV2SSIWCmtznnLu7xOMFZtYZ6AtUBxY45+aEqT5PbPk1jyKf45gaaaSnxN2mgyJyhJxzLFu2jPbt23POOefwzTff0Lx5c6/LEglKsC3+gzjnljrnbnPODY+30Adtxysi5du6dSt9+vShQ4cOrFixAkChLzGlSsFfkpm1MrNXQlFMtNB2vCJSlkWLFpGZmcmbb77JI488QlZWltcliVRahcFvfmeY2WVm9ptSr51uZm8AnwOXhbPISCtevKdhLQW/iPg9/PDDnHvuuaSmpvLJJ58wevRokpKOuO0kEnHl/qs1s2OBxUA2MBv4wsxeNLMUM3sicPwy/Dv3tYhEsZGyf/EetfhFJCA9PZ2BAweSnZ3N//zP/3hdjkiVVTS57yEgE/grsBJoBtwBfAh0BF4DbnfObQh3kZG2cf+tfBrjF0lkc+fOxefz0aNHD0aOHAmgZXcl5lUU/BcB9zvnHio+YGZfAG8DTzvnhoe7OK8Ur9qnxXtEElNeXh533nknEydO5Le//S3du3dX4EvcqGiAKgN/V39Jxc/jajJfaVq8RyRxffPNN3Ts2JGJEydyyy23MH/+fIW+xJWKWvzJQF6pY8XPfw1POdFBwS+SmL7//nvatm1LtWrVmDNnDt27d/e6JJGQO9wCPhebWcmJe0mAA7qa2aklT3TOvRzq4rywr6CIbXsKSEky6tVI87ocEYkAn89HUlISTZs25c9//jNXXHEFxx9/vNdliYTF4YL//nKOP1DquQPiIvhLLt6TlKTuPZF4t3z5cq699lpeeeUVWrduze233+51SSJhVVHw/6aC1+LW/nv4dSufSFzz+XxMmDCBMWPGcOyxx7J7926vSxKJiHKD3zn3dTg+0My6AhPxzyF4tuRdAyXO6Q/ci78nYZVz7opw1FKW/av2aXxfJG7l5ubyhz/8gQULFtCrVy+ee+45jjnmGK/LEomIoDbpCRUzSwYm479VcAOwzMzmOOdWlzjnZGAM0Mk5t83MMiJZoyb2icS/J554goULFzJ58mRuvPFGzdqXhBLp9SbbA2ucc2udc/nAq0DPUucMASY757YBOOdyI1mggl8kPhUUFLB27VoAxo4dy8qVKxk+fLhCXxJOpIP/eGB9iecbAsdKOgU4xcwWm9nSwNDAIcxsqJktN7PlmzdvDlmBGwOT+7Rqn0j8+O677+jSpQvnn38+e/bsIT09nVatWnldlognIh38Zf1q7Uo9TwFOBn4LDAKeNbOjD/km56Y659o559o1aNAgZAUWt/g1xi8SH15//XUyMzNZvXo148ePp3r16l6XJOKpSAf/BuCEEs8bAz+Vcc5s51yBc+474Gv8vwhExP6ufs3qF4lp+/btY8iQIQwYMIBWrVqRk5ND//79vS5LxHOVDn4za2FmZ5lZVX5tXgacbGbNzCwNGAjMKXXOLOC8wGfVx9/1v7YKn1VpzjmN8YvEidTUVL7//nvGjBnDRx99RLNmzbwuSSQqBB38ZnadmW3A3wL/BDg1cHyamd0QzHs45wqBm/Fv9PN/wOvOuS/N7H4z6xE47W3gFzNbDSzEvwPgL0H/jY7Azr2F7CvwUTM9hZrpEb3hQURCwDnHM888w08//URycjLz589n3LhxpKamel2aSNQIKvjN7BpgKvA+8AcOHqv/FBgQ7Ac65+Y5505xzp3knPtr4Ng9zrk5gcfOOXerc66Vc+5059yrwb73kSpevCdDE/tEYs7WrVvp06cPQ4cO5amnngIgJUW/wIuUFmyL/3ZgonPu9xy6M9//EWj9xzot3iMSmxYtWkRmZiZz587l0Ucf5b777vO6JJGoFeyvwycBb5Xz2i6gbmjK8dZGje+LxJwZM2bQr18/mjVrxieffEK7du28LkkkqgXb4t/KwbPxSzoF+Dk05XgrV8EvEnPOO+88brnlFlauXKnQFwlCsMH/FvBHMysZ/i5wf/0oYHbIK/PAxv338GuMXySavfnmm3Tt2pX8/Hzq1q3LhAkTqF27ttdlicSEYIN/bODc1cBc/IvuPBp4ngrExYDapv2r9qnFLxKN8vLyGDlyJD169GDTpk1s2bLF65JEYk5QwR9YL78tMAloAPwIHAO8CJxVvK5+rNPiPSLR6+uvv6ZDhw5MmjSJkSNHsnTpUho1auR1WSIxJ+h7XZxz2/G3/MeGrxxvFc/qV4tfJLo457jmmmtYv349b775JpdddpnXJYnErKCC38zGAf9wzn0V5no8U1jkY8vuPMwgo5bG+EWiwc6dO0lKSqJmzZq88MIL1KxZk+OPL72vl4hURrBj/COALwO74Y0ws9DtihMltuzOx+egXo10UpMjvYWBiJS2bNky2rZty4gRIwBo2bKlQl8kBIJNuAzg98Bm4HHgRzOba2b9zCwumscH1uiPi7+OSMzy+Xw8+uijnH322RQUFHD99dd7XZJIXAl2ct9e59xLzrlL8O+odxdwHPAasMnMngljjRGxUdvxinguNzeXbt26cfvtt9OjRw9ycnLo1KmT12WJxJVK92k75zY55x53zp0JXIB/5b5rQ15ZhBUv3pOh4BfxzJ49e/j888956qmnmDZtGnXrxsWioCJRpdI7WAS69nsBVwEX49+wp7zlfGOGWvwi3igoKOCll17iD3/4A02bNuXbb7/lqKOO8roskbhVmW15f2tmzwGb8G/U0xC4DWjknOtR4TfHgI07/Iv3HFtHY/wikfLdd9/RuXNnBg8ezHvvvQeg0BcJs2Bv5/sBOB5YD0zGf2vf1+EsLNJyd6mrXySSXnvtNYYOHYqZ8dprr3HhhRd6XZJIQgi2q/8d/GH/YTiL8ZK25BWJnLvvvpsHH3yQDh068Morr9C0aVOvSxJJGEEFv3PuunAX4rVN2plPJGKKW/f33XcfqampHlcjkljKDX4zaw984ZzbE3hcIefcZyGtLIL25hexc18haclJ1K2uH0Iioeac48knn2Tbtm388Y9/5Pzzz+f888/3uiyRhFRRi38p0AH4LPDYlXOeBV5LDm1pkbNx/6186ZiZx9WIxJetW7dy3XXXMWvWLC699FKKiopITo7ZHxciMa+i4L8E+L/A426UH/wxb5Nu5RMJi0WLFnHFFVewceNGHnvsMUaNGkVSkpbEFvFSucHvnHu7xOMFkSnHG9qOVyT0Nm/ezMUXX0yjRo345JNPaNeundcliQhB3sdvZqvN7PRyXmtlZqtDW1Zk7Q/+Wgp+kSO1Y8cOABo0aMCMGTNYuXKlQl8kigTb53YqUN6qGtWBlqEpxxtavEckNOYPdSx+AAAgAElEQVTMmcNJJ53E9OnTAejatSu1a9f2uCoRKakyg23ljfGfAewIQS2e0a18Ikdm37593HLLLfTs2ZMTTzyR008vs4NQRKJARbfzjQBGBJ46YJqZ5ZU67SigETAtPOVFhoJfpOq++uorBg4cyKpVqxg1ahQPPfQQ6enqPROJVhXN6v8JWBF43AL4Gvil1Dl5wGrgqdCXFjnaoEek6pYtW8aPP/7I3LlzufTSS70uR0QOo6JZ/dOB6UDxve1jnXNrI1RXxDjnyN3p78hQi18kODt37mT58uWcf/75XH311Vx22WXaQlckRgS7ZO+gcBfilW17Csgv8lG7WgpHpWlREZHDWbZsGQMHDmTz5s2sW7eOunXrKvRFYkhFY/x34N+YZ2PgcUWcc+6R0JYWGRrfFwmOz+fjscce4+6776ZRo0bMnz9fgS8Sgypq8T8EfABsDDyuiANiMvj3j+9r8R6RchUWFtK9e3cWLFjA5ZdfzrPPPqvQF4lRFQX/Uc654ln85d3DH/M2BbbjzdDiPSLlSklJISsri549ezJs2DDtaSESwyqa3JdX1uN4s2mnFu8RKUtBQQF/+tOf6NmzJx07dmTcuHFelyQiIRDU5D4zaw7Uds7lBJ6nA3cBpwFvO+eeDV+J4aVb+UQOtXbtWgYNGsRnn31Geno6HTt29LokEQmRoIIfeBL//fo5ged/Af4X+AbobWbJzrkpYagv7HL3b8mr4BcBeO211xg6dChmxuuvv06/fv28LklEQijYJXszgY8AzD+4dw1wt3OuNf6JfzeEpboIUItf5IC5c+cycOBAWrduTU5OjkJfJA4FG/xHA1sCjzOBesDrgefvACeFuK6I0e18Iv619gEuueQSpk6dyocffkjTpk29LUpEwiLY4M8FmgceXwR855xbF3heAygKdWGRUFDkY8vufJIM6tdM87ockYhzzjF58mROOeUUfv75Z5KTkxkyZAipqalelyYiYRLsGP9c4K9mdgowFHi+xGutge9CXVgk5O7yz+hvUCudlOTKbFQoEvu2bt3Kddddx6xZs+jWrRspKcH+OBCRWBbs/+l3AbWAAcC7wAMlXusPvB/iuiJC3fySqD7++GOuuOIKNm3axOOPP87IkSNJStIvvyKJINi1+ncCV5fz2v+EtKIIKl68R8EviWby5MlUq1aNJUuWcOaZZ3pdjohEUKX69sysFtAeOAb/Fr3LnHO7wlFYJBxo8WvxHol/GzZsoKCggGbNmjFlyhSSkpKoVauW12WJSIQF3bdnZn8Efgb+DbyGv8v/ZzMbG6bawm5j8ap9avFLnJs9ezZt2rTh2muvBaBOnToKfZEEFVTwm9lNwP3ATKAbkAVcEnh+v5ndGLYKw0hj/BLv9u3bx4gRI+jVqxdNmjRhypSYXGdLREIo2K7+m4EnnXM3lzi2CnjbzHYAI4CnQl1cuCn4JZ6tX7+e7t27s2rVKkaNGsVDDz1EerqGtUQSXbDB3xy4pZzXZgPXh6acyNKWvBLP6tWrR926dZk7dy6XXnqp1+WISJQIdox/K9CynNdaBl6PObmBMf6G2pJX4sTOnTu5/fbb2b17N9WrV+f9999X6IvIQYIN/ln4F/DpZyU24jaz3vg37JkVjuLCaXdeIbvzCqmWmkTto7RwicS+zz77jKysLCZMmMDChQsBKPG/q4gIEHzw3wV8hX82/x4zW2dme4BpwNeB12PKxhL38OuHo8Qyn8/HI488QqdOnSgsLOSjjz6ie/fuXpclIlEq2AV8dpjZ2UBvoDP++/i3Ah8Cs51zMbdWf64m9kmcGDNmDOPHj6dPnz4888wz1K1b1+uSRCSKBd3HHQj3aYGvmKfteCXWFRUVkZyczI033kiLFi24/vrr1XslIodVYVe/mQ00s6VmtsXM1pjZX80sLgbENxVP7NOqfRJj8vPzufPOO+nduzfOOZo2bcqQIUMU+iISlHKD38z6AS8DxwKLgT34x/IfKO97Yonu4ZdYtHbtWjp37sz48eNp1KgRBQUFXpckIjGmohb/rcBbwMnOuZ7OuTOAh4ERZhbz23ht1AY9EmNeffVVsrKy+Oabb5g2bRpPP/00aWlpXpclIjGmogBvCTzlnCvZpJgEHAU0CWtVEbBplxbvkdixa9cubr31Vk477TRycnLo06eP1yWJSIyqaLz+aGBLqWObA3/WBb4LS0URUrwlryb3STT76quvaNGiBbVq1eLDDz+kWbNmpKTExTQbEfHI4brsXSWPxwSfz5G7yz+5r0EtTe6T6OOc44knniAzM5NHHnkEgJNPPlmhLyJH7HDBv9jM8ou/gL2B45+WPG5mecF+oJl1NbOvA3cJlLvwj5n1NTNnZu2Cfe9g/fJrPoU+R93qqVRLTQ7124sckV9++YXevXszYsQILrjgAq6/Pia3whCRKFVR8+HhUH+YmSUDk4GLgA3AMjOb45xbXeq8Wvg3Bfo01DWAZvRL9FqyZAn9+/dn06ZNPP7444waNUq36YlISJUb/M65MWH4vPbAGufcWgAzexXoCawudd5fgPHAbWGoQcEvUSstLY06deowa9YszjzzTK/LEZE4FOnb8o4H1pd4viFwbD8zywJOcM7NreiNzGyomS03s+WbN2+u6NRDaNU+iSYbNmzg73//OwBnnnkmn3/+uUJfRMIm0sFfVp/l/omCgfUBJgCjD/dGzrmpzrl2zrl2DRo0qFQRWrVPosXs2bNp06YNd999Nz/++CMASUkxv0yGiESxSP+E2QCcUOJ5Y+CnEs9rAacBH5jZ90AHYE6oJ/gV38rXUPfwi0f27dvHiBEj6NWrF02bNmXlypUcf/zxh/9GEZEjFOl7g5YBJ5tZM+BHYCBwRfGLzrkdQP3i52b2AXCbc255KIsoXrynYS0Fv0Sec44LL7yQxYsXM2rUKB566CHS09X7JCKREdEWv3OuELgZeBv4P+B159yXZna/mfWIVB3Fy/Vq1T6JJOcczjnMjBEjRjB37lwmTJig0BeRiIr4aiDOuXnAvFLH7inn3N+Go4biWf0ZGuOXCNmxYwfDhg3jggsuYMiQIQwYMMDrkkQkQQXd4jezhmY2zswWmdlqM2sVOD48HIvshEteYRHb9hSQkmTUr6Hgl/D79NNPycrKYtq0aezcudPrckQkwQUV/GZ2KvAf4Eb82/O2BIr7yVsCo8JSXRjkBmb0Z9RKJylJC6NI+Ph8Ph5++GHOOeccfD4fH3/8MaNHH/aGFRGRsAq2xf8o/k15mgHdOPi2vMVAxxDXFTYHuvk1vi/htXTpUu666y569+5NTk4OHTvGzP8mIhLHgh3jPxe4yjm3PbDsbkkbgeNCW1b4aPEeCbcffviBE088kbPPPptPPvmEDh06aNldEYkalZnVX1TO8Xoc2Lwn6hXP6NfiPRJq+fn53HHHHbRo0YLly/13oHbs2FGhLyJRJdgW/3LgaqCsZXT7AEtDVlGYFW/Hq8V7JJTWrl3LwIEDWbZsGTfccAOtW7f2uiQRkTIFG/x/BRaY2ZvAS/iX2e1iZsOA/sB5Yaov5Pbfw6+ufgmRV199laFDh5KcnMy0adPo06eP1yWJiJQrqOB3zr1rZv2BvwGXBg4/jn+53f7OucVhqi/ktDOfhNqaNWs4/fTTefnll2nSpInX5YiIVCjoMX7n3AygCXAGcCGQBZzonJsVptrCQsEvobBq1So++OADAMaMGcOHH36o0BeRmFCplfuccw74Iky1hJ1zTjvzyRFxzjF58mRGjx5Nq1atWLlyJcnJpW90ERGJXkEFf6Cbv0LOudePvJzw2rmvkL0FRdRIS6ZWtVSvy5EY88svv3DttdcyZ84cunXrxgsvvKAZ+yISc4Jt8b9aznFX4nHUB//+bn7N6JdK+umnn2jfvj25ublMmDCBkSNHKvRFJCYFG/y/KeNYPeAyoC/wh5BVFEb7g1/b8UolHXfccQwYMIArr7yStm3bel2OiEiVBTur/+tyXvrEzIrwr+G/JGRVhYm245XKWL9+PTfccAMTJ06kRYsWPPbYY16XJCJyxCqzcl95FgI9QvA+YVe8eI+245XDmTVrFm3atOGjjz7i66/L+71XRCT2hCL42+HfsS/qafEeOZx9+/Zx00030bt3b5o3b87KlSu59NJLD/+NIiIxIthZ/XeUcTgNOA3oDTwTyqLCZaPu4ZfDGD9+PE8++SS33norDz74IGlpaV6XJCISUsFO7nuojGNFwI/ABOC+kFUURrkKfimDc46tW7dSr149brvtNjp16sQFF1zgdVkiImERbPAfVcaxAuecL5TFhNv+LXk1uU8CduzYwbBhw8jOzmblypXUqFFDoS8ice2wY/xmlgbcC5zmnMsr8RVToV/kc2wOTO5rUFOT+wQ+/fRTsrKymDZtGtdccw3VqukXQhGJf4cNfudcPjASqBH+csJny+48fA7q10wjLSUUcxolVvl8Ph5++GHOOeccfD4fH3/8MWPGjNHSuyKSEIJNwFVAq3AWEm7Fi/dkaPGehFdUVMTs2bPp3bs3OTk5dOzY0euSREQiJtgx/juAf5jZGufcu+EsKFy0eI+88847ZGVlUb9+fRYsWECtWrW07K6IJJxgW/zPA0cDb5vZLjP7r5l9U+Ir6lc40Xa8iSs/P5/bb7+diy++mAceeACA2rVrK/RFJCEF2+JfwcEb8sQcbcebmL799lsGDRrEsmXLuOGGG3jwwQe9LklExFPBrtU/MNyFhNv+W/nU4k8Y77//Pr169SI5OZlp06bRp08fr0sSEfFcuV39ZrbWzNpEsphwUld/4jnttNO46KKLyMnJUeiLiARUNMbfFIibfnEFf2LIyclh8ODBFBYWkpGRwfTp02nSpInXZYmIRI2EuaFds/rjm3OOSZMmcdZZZ/Hvf/+b77//3uuSRESi0uGCP6Yn9BXbm1/Ezn2FpCUnUbd6qtflSIht2bKFnj17MnLkSC6++GJWrVpFixYtvC5LRCQqHW5y331mtiWI93HOuT+EoqBw2L94T+103cIVh/r27cuSJUuYOHEiI0aM0H9jEZEKHC74M4G8IN4nqnsGNL4ffwoLCykqKiI9PZ0JEyYAkJWV5XFVIiLR73DB38s591lEKgkj3coXX9avX88VV1zBGWecweTJkxX4IiKVkBCT+0p29UtsmzVrFm3atCEnJ4ezzz7b63JERGJOggS/f7RCLf7YtXfvXm666SZ69+5N8+bNyc7O5sorr/S6LBGRmJMQwb+/q1+38sWsH3/8kX/84x+MHj2aTz75RLP2RUSqqNwxfudc3PxSkKsteWOSc4733nuPCy64gBYtWrBmzRoaNmzodVkiIjEtbsK9Imrxx54dO3YwaNAgLrroIubOnQug0BcRCYFgd+eLWc457cwXY5YuXcqgQYNYv34948aN49JLL/W6JBGRuBH3Lf7tewrIL/RRq1oK1dPi/vecmDd58mQ6d+6Mc46PP/6YMWPGkJQU9/9MRUQiJu5/ouoe/tjSpEkTLr/8cnJycujYsaPX5YiIxJ24D36t2hf9FixYwOTJkwG47LLLeO211zj66KM9rkpEJD4p+MUz+fn53HbbbVxyySU899xzFBQUeF2SiEjcS4Dg18S+aLRmzRo6derEY489xvDhw1m8eDGpqdo5UUQk3OJ+tptu5Ys+27dvp3379jjnmDFjBr179/a6JBGRhBH3wb9phxbviRaFhYWkpKRw9NFHM2nSJLp06cKJJ57odVkiIgkl/rv6d6nFHw1ycnI4/fTTWbBgAQBXXXWVQl9ExANxH/wbd2iDHi8555g0aRJnnXUWO3fupHr16l6XJCKS0OI6+AuKfPzyax5JBvVrpnldTsLZsmULPXv2ZOTIkfzud79j1apVdOnSxeuyREQSWlwH/+ZdeTgH9Wumk5Ic13/VqDRnzhzefvttJk6cyOzZs6lfv77XJYmIJLy4nty3UffwR1xhYSFffvklbdq0YfDgwXTp0kVb6IqIRJG4bgbnKvgj6ocffuC8886jc+fO5ObmYmYKfRGRKBPXwb9xR/GMfi3eE24zZ84kMzOTVatW8dRTT5GRkeF1SSIiUoa4Dv5NuwKr9uke/rDx+XwMHz6cyy+/nJNOOons7GyuvPJKr8sSEZFyxHfwB1r8DXUPf9gkJSVRWFjI6NGjWbx4MSeddJLXJYmISAXienJf8eI9GuMPLecczz77LO3atSMrK4spU6ZgZl6XJSIiQYh4i9/MuprZ12a2xszuKuP1W81stZl9bmbvmVmTqn7W/jF+BX/IbN++nQEDBjB06FCmTJkCoNAXEYkhEQ1+M0sGJgOXAK2AQWbWqtRp2UA759wZwDRgfFU/r3hnPgV/aCxZsoTMzExmzpzJQw89xJNPPul1SSIiUkmR7upvD6xxzq0FMLNXgZ7A6uITnHMLS5y/FLiqKh+0O6+Q3XmFpKckUfuouB7RiIgPPviACy+8kBNOOIGPP/6YDh06eF2SiIhUQaS7+o8H1pd4viFwrDzXAfOr8kGbSmzHq67oqnPOAdCpUyfGjh1Ldna2Ql9EJIZFOvjLSmBX5olmVwHtgEfKeX2omS03s+WbN28+5PXi4NetfFU3f/58zjzzTH755RdSU1O57777OProo70uS0REjkCkg38DcEKJ542Bn0qfZGYXAmOBHs65vLLeyDk31TnXzjnXrkGDBoe8vj/4dStfpeXn5zN69Gi6detGYWEh27dv97okEREJkUgH/zLgZDNrZmZpwEBgTskTzCwLmII/9HOr+kHF2/E2rKVV+ypjzZo1dOrUiccff5zhw4fz6aef6t58EZE4EtFZb865QjO7GXgbSAaed859aWb3A8udc3Pwd+3XBN4IjM3/4JzrUdnPKjnGL8G7++67+fbbb5kxYwa9e/f2uhwREQmxiE93d87NA+aVOnZPiccXhuJzNmmDnqDt3r2b3bt3c+yxx/LEE0+wb98+TjzxRK/LEhGRMIjbJXsV/MHJzs7mzDPPZODAgTjnyMjIUOiLiMSxOA5+Ld5TEeccEydOpEOHDvz666/cd999uu1RRCQBxOXKNj6fIzewTn9GbU3uK23r1q1cc801vPnmm3Tv3p3nn3+e+vXre12WiIhEQFy2+LfuyaegyHF09VSqpSZ7XU7USUlJ4dtvv2XSpEnMnj1boS8ikkDissWvzXkOVVhYyOTJkxk2bBi1a9cmJyeH1NRUr8sSEZEIi8sW/4FufgU/wLp16zj33HMZNWoU06ZNA1Doi4gkqLgM/uLFe47V+D7Tp08nMzOT//znP7z88stcdVWV9jwSEZE4EZfBr1v5/B555BH69u3LySefTHZ2NoMGDfK6JBER8VhcjvEr+P169OjBtm3buPfee0lLS/O6HBERiQJx2eLfuDMxJ/c555g6dSrXXnstzjlatmzJuHHjFPoiIrJfXAZ/8eI9idTi3759OwMGDGDYsGGsX7+evXv3el2SiIhEoTgN/uIteRNjct+SJUvIzMxk5syZPPTQQ7z99ttUr17d67JERCQKxd0Yf15hEVt/zSc5yahXI/6Df+/evfTu3Zvq1auzaNEizjrrLK9LEhGRKBZ3wZ8b6ObPqJVOclL8rj2/efNm6tWrx1FHHcWcOXNo2bIlderU8bosERGJcnHX1V/czR/Pi/fMnz+f1q1b89hjjwHQvn17hb6IiAQlDoM/fhfvyc/PZ/To0XTr1o3jjjuOyy67zOuSREQkxsRdV3+83sq3Zs0aBg4cyIoVK7jpppt49NFHqVYtvv6OIiISfnEX/Llx2tX/888/88MPPzBz5kx69erldTkiIhKj4q6rP55a/Lt37+b1118HoHPnznz33XcKfREROSJxF/zxslzvypUradu2LVdccQVr164FoEaNGh5XJSIisS4Ogz8wuS9GF+9xzvG3v/2NDh06sGfPHt577z2aN2/udVkiIhIn4mqM3znHxh2x2+J3ztG/f3+mTZtGjx49eP7556lXr57XZYmISByJq+DflVfI3oIiqqclUzM99v5qZsbFF1/Mueeey0033YRZ/C5AJCIi3oi9dKzAph0HJvbFSmgWFhZy77330rp1awYNGsSQIUO8LklEROJYXI3xF4/vZ8TI4j3r1q3j3HPP5a9//StLly71uhwREUkAcdXij6Vb+aZPn871119PUVERL7/8MoMGDfK6JBERSQBx1uIv3o43uoN/xYoV9O3bl5NPPpns7GyFvoiIREx8Bn+t6Az+Xbt2AXDmmWfyxhtvsGjRIk466SSPqxIRkUQSV8FffCvfsVHW4nfOMXXqVJo0acKqVasA6Nu3L2lpaR5XJiIiiSaugn/TLv/kvoZRNLlv+/bt9O/fn2HDhtGuXTsaNmzodUkiIpLA4iv4o2zxniVLlpCZmcmsWbN4+OGHWbBgAccee6zXZYmISAKLm1n9RT7H5t2B2/miZIx/zpw5JCUlsWjRIs466yyvyxEREYmfFv8vu/Mo8jnq1UgjLcW7v9ZPP/3EihUrALj//vvJzs5W6IuISNSIm+DfGAW78r311lu0adOGK664gqKiIlJTU6lTp45n9YiIiJQWN8FfvGqfFxP78vLy+N///V8uu+wyGjVqxOzZs0lOTo54HSIiIocTN2P8+1fti/CtfL/88gsXX3wxK1euZMSIEYwfP55q1aJjjoGIiEhpcdPizw0Ef6Qn9tWtW5ff/OY3zJo1i0mTJin0RUQkqsVN8Edy8Z5du3YxfPhw1q9fT1JSEv/617/o2bNn2D9XRETkSMVP8Edog54VK1bQtm1bpkyZwsKFC8P6WSIiIqEWN8GfG+YteZ1zTJgwgY4dO7J3714WLlzI73//+7B8loiISLjETfCHu8X/+OOPc+utt9KtWzdWrVpFly5dwvI5IiIi4RQXs/qdgx17C0hNNupWD+3GN/n5+aSlpTFkyBDq1q3L4MGDMbOQfoaIiEikxEWLv6DIB/hn9CclhSaUCwsLGTt2LB06dGDfvn3Url2ba6+9VqEvIiIxLa6CP1Qz+tetW8e5557LuHHjyMrKwufzheR9RUREvBYXXf0FPgeEZtW+6dOnc/3111NUVMTLL7/MoEGDjvg9RUREokVcBH9hoMV/pOv0FxYW8sADD3DKKafwyiuv0Lx581CUJyIiEjXiIvgLihypVD34v/zySxo3bkydOnV46623aNCgAampqaEtUkREJArE1xh/JYPfOceUKVNo164dd911FwCNGjVS6IuISNyKi+AvLPKP8Vdm8Z5t27bRr18/brjhBrp06cK9994bpupERESiR1wEf2Vb/NnZ2WRmZjJ79mzGjx/P/PnzadiwYThLFBERiQpxMsZfucl9DRo04Nhjj+WNN96gffv24SxNREQkqsRFi98BtdJTqJFe/u8xP/30E2PHjsXn89G4cWOWLl2q0BcRkYQTF8EP0LCCxXvmzp3LGWecwd/+9je++OILAK3AJyIiCSl+gr+MiX15eXmMGjWK7t2707hxY1asWMEZZ5zhQXUiIiLRIS7G+KHs8f0BAwYwe/ZsRowYwfjx46lWLTw794mIiMSKuAn+kjP6fT4fSUlJ3HbbbQwePJiePXt6WJmIiEj0iHhXv5l1NbOvzWyNmd1VxuvpZvZa4PVPzaxpMO/bsHY1du3axdVXX82YMWMAOOeccxT6IiIiJUQ0+M0sGZgMXAK0AgaZWatSp10HbHPOtQAmAA8H8947139N27Ztefnll6lRo0YoyxYREYkbke7qbw+scc6tBTCzV4GewOoS5/QE7g08ngY8YWbmnHPlvWnRr9u59eruHNuwIQsXLqRLly7hqV5ERCTGRbqr/3hgfYnnGwLHyjzHOVcI7ADqVfSmRbt+4YKLfkdOTo5CX0REpAKRbvGXdfN86ZZ8MOdgZkOBoYGneW/Pm/tF/fr1j7A8qUB9YIvXRSQAXefw0zUOP13j8GtZ1W+MdPBvAE4o8bwx8FM552wwsxSgDrC19Bs556YCUwHMbLlzrl1YKhZA1zhSdJ3DT9c4/HSNw8/Mllf1eyPd1b8MONnMmplZGjAQmFPqnDnAHwKP+wLvVzS+LyIiIsGLaIvfOVdoZjcDbwPJwPPOuS/N7H5guXNuDvAc8E8zW4O/pT8wkjWKiIjEs4gv4OOcmwfMK3XsnhKP9wH9Kvm2U0NQmlRM1zgydJ3DT9c4/HSNw6/K19jUiy4iIpI44maTHhERETm8mAr+cC33KwcEcY1vNbPVZva5mb1nZk28qDOWHe4alzivr5k5M9Ps6CoI5jqbWf/Av+cvzezlSNcY64L4eXGimS00s+zAz4xuXtQZy8zseTPLNbMvynndzGxS4L/B52bW9rBv6pyLiS/8kwG/BZoDacAqoFWpc4YDTwceDwRe87ruWPoK8hqfB1QPPL5R1zj01zhwXi3gI2Ap0M7rumPtK8h/yycD2UDdwPMMr+uOpa8gr/FU4MbA41bA917XHWtfQBegLfBFOa93A+bjXwOnA/Dp4d4zllr8+5f7dc7lA8XL/ZbUE3gx8HgacIGZlbUgkJTtsNfYObfQObcn8HQp/rUYJHjB/DsG+AswHtgXyeLiSDDXeQgw2Tm3DcA5lxvhGmNdMNfYAbUDj+tw6LotchjOuY8oYy2bEnoC/3B+S4Gjzey4it4zloI/LMv9ykGCucYlXYf/N00J3mGvsZllASc45+ZGsrA4E8y/5VOAU8xssZktNbOuEasuPgRzje8FrjKzDfjv5hoRmdISSmV/bkf+dr4jELLlfqVcQV8/M7sKaAecG9aK4k+F19jMkvDvSnlNpAqKU8H8W07B393/W/w9Vx+b2WnOue1hri1eBHONBwEvOOceM7OO+NdoOc055wt/eQmj0rkXSy3+yiz3S0XL/Uq5grnGmNmFwFigh3MuL0K1xYvDXeNawGnAB2b2Pf4xuzma4Fdpwf68mO2cK3DOfQd8jf8XAco+0oQAAAkJSURBVAlOMNf4OuB1AOfcEqAa/nX8JXSC+rldUiwFv5b7Db/DXuNAN/QU/KGvMdHKq/AaO+d2OOfqO+eaOuea4p9H0cM5V+V1uRNUMD8vZuGfrIqZ1cff9b82olXGtmCu8Q/ABQBm9hv8wb85olXGvznA7wOz+zsAO5xzP1f0DTHT1e+03G/YBXmNHwFqAm8E5k3+4Jzr4VnRMSbIayxHKMjr/DZwsZmtBoqA251zv3hXdWwJ8hqPBp4xs//F3/18jRpjlWNmr+AfjqofmCvxZyAVwDn3NP65E92ANcAeYPBh31P/DURERBJHLHX1i4iIyBFS8IuIiCQQBb+IiEgCUfCLiIgkEAW/iIhIAlHwi5TBzK4J7IxX1teFlXyv6wPfF5F9DczsgVL1bgvsVhny21vNLCXwGX8scexyMxtVxrkXBs49J9R1VFBfi1LXosjMfjazf5pZhcuaVvCebc3sXjM7OtT1ikRCzNzHL+KRfvhXxipptReFVEHHwJ/1gGHAK2aW5pz7R6g+IHAvd0cOXiv8cuAc4G+lTv8sUNOXofr8SngAeAtID9RwD3CqmXUM7OtRGW3x30v9AqDlfSXmKPhFKpbjnFvjdRFVEdipCwAz+zf+JWlHASEL/tKfc5jzduJfidAL35ao80MzS8e/gUwmoFURJaGoq1+kiszsKDObaGZfmtmvgS7kOWbWMojvvdrMcgLft8PMPjez60udc56ZvW9muwNf882sVVVqdc4VADlAixLvX8fMngzUnW9mX5vZyFI11DazJ8xsvZnlmdkmM3vHzE4JvH5QV7+Z/Qu4EmhSont9TeC1g7r6zWyqmf1kZsmlPrNa4Jo8WuJYhplNCZyfb2b/Z2bXVeVaBKwM/Hliqc9+wMyyzWynmW0xs/fMrH2J168Hngk8/a7E37FxiesxNnAt88zsRzN7JPCLhkhUUItfpGLJ5t/wqZhzzhUFHh8V+Lof2Ii/S/0mYImZnVreXgZmdi7wIv6u8NH4lzttBdQtcU5PYDr+dbivwP9L+l34d5A7wzn3YxX+Ls0IdE0HwnY+cAbwJ/zd7z2Av5lZPefcPYHvmQj/v71zDbWqiOL478/1g+UjEzSJMCk/RBpGIYnZwwizB9XNIC3NMO1D3ciSykgS0x7mix6kUWE+SlNSCsEHipn2sIRKrDTUbkhm4iNLMx+x+rDm6HZ77rlHvWp01g+Gc8/Mmtlrzxzu2rNm7Rl64ocyrccPWOmGH4BVjOFJphNQnfL+rkN2KjAI38t9USb/NvwM92lJ1xbAp/g2pc8AtfgWpW+mpYuJZd39kbRLnxty+ecC4/Dlnab42R/LJV1mZt8BHwIXAE/hSxqFPdELYz0DuBF4EfdudMB/H22Bu45DzyBoeMwsUqRIuYQfi2tF0ooSdaqAJvh+2Q9n8gemuuel70OBrSXaEW7cFubyW+BnUIytR/dR6XqNUjoHGJnyxiaZ29P3vrm67+CGumX6vhZ4qcS1GqV2hmXypgO1RWSvT7LdMve5EZiWk5sHrM58HwHsBS7MyU0GfgOqSujXPl1zQNK1Cf6gsRmYWU8/VuEPGxuAcUXGs11OvnvKvzuX3z/lX3K6f9eRIplZuPqDoB6qgc6ZdIR7WVJvSV9K2gUcBHbjXoBS7v6vgFaSpkq6WVJ+9nwRcD7wbnIdN0peh93ASuDqMnU/kNIW4HFgPD5zJ7VxEJiZqzMdD4C7IqPr/ZKGSrpcUoP9zzAzS9erltQEQFIr4AaOjEPoCXwG/Jzrj4VAa0r3dYG38b7YDSzGZ/T980KSekj6WNJ2vH/24zP8cq7RE39ompvTs+DNuKqMNoLgpBOGPwhKs8bMVmXSukKBpGrctbsG6IMby874rLxxXQ2a2RLc7dsOPxp2m6RFkjomkdbpcwqHjXch9cSXFMqh8LDSHmhmZkPMbF8qawlss6Mj2rdkygEexNe0B+FBcFsljZN0Rpk61MdUfBZ+R/reB/+/9F5GpjVwHUf3xYxUXk5/jMD74lpgYvr71ayApM545P8u3EPQJcmtocR45vRsjHt8snoWzkYvd9yC4KQSa/xBcPz0Btaa2YBChqTGuEu+JGY2C5glqSlu1EYD8yW1BQpHwz4BLC1SfV+RvGLXKBWtvgM/5rNRzvi3SZ/bUxt/4ksTQyW1w19vfAGf2T7NCWJm6yV9AfTF1/T7AkvMbHNGbDv+uuBjdTSzro78LLWZ/lgmqTkwUNIkMysE+t2J31evbJ9IaokvKdTHdtzoX1NH+eY68oPglBKGPwiOnzNxd3CWezkGT5qZ7QY+ktQeDyo7G98nYBNwsZmNaSBd8ywDHgV6Ae9n8u/Bjd/KIrrWAmMk9QM65ssz7MOXO8plGvCKpO74DLtfrnwBvg9BrZltO4Z2S/Ekfu/D8WBCODyeh84ql9QDD/j7IVO38OCVv8cFeLBmEzNb1kB6BkGDE4Y/CI6fBcBr6bWz+bjRegj4o1QlSc/hbt+leFR4W6AGWGVmO5JMDTAneRBm47PJNkBXYKOZvXyCus8DPscj49vghu0WPKhxpJntTHqsBObg7u49eABbB+CNEm1/DwyQ9ADwNbDXzNaUkJ8JTMAfAPYAc3PlY3FPw3JJE4AfgWZ4LERXM6vmGDGzXyRNAgZLutTMvsHHswaYLGlKan8YR8/UCxs41aTXFw8A35rZYkmz8TX+8fiGReBLOjcBQ8ws/xZBEJx6Tnd0YaRI/8XE4aj+9iVkqoDnccPwF27IO+GBY29l5PJR/bfiAV+/4rPHTfg6eptc+1fia8478Vn4T/i6dpd6dB9Fip2rR+4s4PWkx37cZf5ITmYsbrx34YFxq4GaTHmxqP5muBdhZypbn/KPiOrPXWduKptah64t8VcLa5OuW4FPyLw9UUe9QlT/fUXKWqd7+iCTNzhdYy9uuLsDK4DFubrPpnH/Jze2VbgnZXUas9/x/RNGA81P9+86UiQzQ2aHvFpBEARBEPzPiaj+IAiCIKggwvAHQRAEQQURhj8IgiAIKogw/EEQBEFQQYThD4IgCIIKIgx/EARBEFQQYfiDIAiCoIIIwx8EQRAEFUQY/iAIgiCoIP4FXsAoQ6edwXYAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f69124f98d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fpr, tpr, thresholds = roc_curve(Y_test, modele_pred)\n",
"plt.figure(figsize=(8, 6))\n",
"plot_roc_curve(fpr, tpr)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### PRECISION, RAPPEL, F1-SCORE, SUPPORT"
]
},
{
"cell_type": "code",
"execution_count": 46,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(0.9281888334089877, 0.9648013588751534, 0.946141032759578, None)"
]
},
"execution_count": 46,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"precision_recall_fscore_support(Y_test, modele_pred,average='binary')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### SCORE EN K-FOLD CROSS VALIDATION (validation croisee en K passes) "
]
},
{
"cell_type": "code",
"execution_count": 47,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.52806122 0.59209027 0.99186362 0.98184598 0.97869913 0.98901099\n",
" 0.98415123 0.96913232 0.95390335 0.90700547]\n",
"Mean: 0.8875763566114621\n",
"Standard deviation: 0.16603401419701555\n",
"CPU times: user 378 ms, sys: 68.2 ms, total: 447 ms\n",
"Wall time: 1min\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele, X, Y, cv=10, scoring=\"precision\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 48,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.96710895 0.97084657 0.95700935 0.96037383 0.96186916 0.9588785\n",
" 0.96336449 0.96242991 0.95925234 0.96074766]\n",
"Mean: 0.9621880755977135\n",
"Standard deviation: 0.0039049458902022404\n",
"CPU times: user 371 ms, sys: 76.1 ms, total: 447 ms\n",
"Wall time: 1min\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele, X, Y, cv=10, scoring=\"recall\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 49,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.68312323 0.73557522 0.97412481 0.97099121 0.97021116 0.97371168\n",
" 0.97364693 0.96576948 0.95657036 0.93310339]\n",
"Mean: 0.913682747139938\n",
"Standard deviation: 0.10350925606418922\n",
"CPU times: user 346 ms, sys: 104 ms, total: 451 ms\n",
"Wall time: 1min\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele, X, Y, cv=10, scoring=\"f1\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 50,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.69320837 0.80238174 0.99718674 0.99546884 0.99507157 0.99596574\n",
" 0.99644652 0.99165931 0.99138267 0.98061771]\n",
"Mean: 0.9439389210946635\n",
"Standard deviation: 0.10116658312273903\n",
"CPU times: user 382 ms, sys: 72.6 ms, total: 455 ms\n",
"Wall time: 1min\n"
]
}
],
"source": [
"%%time\n",
"modele_score_roc=cross_val_score(modele, X, Y, cv=10, scoring=\"roc_auc\",n_jobs=-1)\n",
"display_scores(modele_score_roc)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### **ESTIMATION QUALITE MODELE ADA**"
]
},
{
"cell_type": "code",
"execution_count": 51,
"metadata": {},
"outputs": [],
"source": [
"modele_pred = modele_ada_pred\n",
"modele=modele_ada"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Matrice confusion"
]
},
{
"cell_type": "code",
"execution_count": 52,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[9231, 1573],\n",
" [ 639, 9958]])"
]
},
"execution_count": 52,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"confusion_matrix(Y_test,modele_pred)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### ROC"
]
},
{
"cell_type": "code",
"execution_count": 53,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"0.8970528453544777"
]
},
"execution_count": 53,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"roc_auc_score(Y_test, modele_pred)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### ROC CURVE"
]
},
{
"cell_type": "code",
"execution_count": 54,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAf4AAAF8CAYAAAAuF9n2AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzs3Xd0lGXexvHvnUkBAgGkKL0IoiAkARZBBNe6iNKkW3ZtgKIIr9jQLeq6qFhYWFHBcnR37XQRcC1YQFBKEhBWXUAhEZHQCekz9/tHJhBiEgaYmWfK9Tknh5lnHiYXI/LL3Y21FhEREYkOMU4HEBERkeBR4RcREYkiKvwiIiJRRIVfREQkiqjwi4iIRBEVfhERkSgS1MJvjHnFGLPLGPNNJa8bY8x0Y8xmY8x6Y0znYOYTERGJdMFu8b8K9Kni9SuAtt6v0cDzQcgkIiISNYJa+K21nwN7q7hlAPBPW2IVUMcY0yg46URERCJfqI3xNwEyyzzP8l4TERERP4h1OkA5poJrFe4pbIwZTclwAImJiV3OPvvsQOYSEZEI5bEWjwfc1uLx2JJfvdc81uL2lDx3l7l25L7S3+e95u9N8GOMIcaAK8Zgi4vI27MDd1EBwG5rbYOTec9QK/xZQLMyz5sCOyq60Vo7C5gF0LVrV7tmzZrApxMREccVuz0cLnCTU1jM4YJiDuWX/Hq4oJicMr/mFLiPuZ5zzD0lr+UUFnO8I2sM4PJ+HU9sjKFmtVgS42OpmRBLYoKLmtXiqJngIjE+lsSEkus1q5U+dh259+i1kl9rxLmIiSlpD69du5bevXtzWp0kXnvtNfr27bvtZD+/UCv8C4E7jDFvAecBB6y1PzucSUREToG1loJiz7FFOb+Yw4VHi3NO/tHCXHo9J7+opMB7r5UW+YJij1/zVY9zHS3C3qJby/tr2es1yxTlI4W6TIFPTIglITYGYyrqvD451lqMMSQnJzN27FjuuusuGjU6talvQS38xpg3gd8C9Y0xWcBfgDgAa+0LwGKgL7AZyAVuDGY+EREp4fFYb7F1V9Ba9hbhI4/d5Vrax17PKSjG7fFfJ3iM4ZiW8dFC7Trm+rGF+tfFOzEhlsR4F7GuUJvuVuKrr77irrvuYt68eTRs2JAnn3zSL+8b1MJvrR15nNctcHuQ4oiIRJTCYk+l3do5BUU+dX2XFvPcQrdfs8XHxhxtGcfHUqtamRZ1aRd4tWMLdGJ86bXSe13UTIilepzLr63qUOPxeJgyZQp/+tOfaNKkCTt37qRhw4Z+e/9Q6+oXEYka1lryitxHu77LtJwPF5Yfu3ZXWLDLtq4L3f7tAk+Md/2qW/uY1nO1MkU74dfF+2g3eCzxsaHZqg41O3fu5Prrr+ejjz5i6NChzJo1izp16vj1e6jwi4icgGK3h8OF7oq7vksLddnXS8euy41nlxZ3P/aAExtjynVnn3jXd2mRLzuxTILn/vvvZ8WKFcyaNYtbbrklID0bxh5vOmMY0Kx+EalMRRPLyndrVzYbvHxxzykoJr/Iv63qanExFRbfo0W58uJd2vVd+tzfE8skOAoLC9m/fz8NGzZk9+7d7Nq1i/bt21f5e4wxa621XU/m+6nFLyIhp/zEsl9PJqu86/vYce2S58V+bFYbAzXjjy69OmZJVrVjC3RifJmlXBUV7hCeWCbBsWXLFkaOHInL5WLFihXUr1+f+vXrB/R7qvCLiF+UnVh2+Jj11b9uPedUULyP6Tb398QyV4x3PfWx484VdX0nJngnnv1qzXV0TCyT4HnjjTe49dZbcblcvPTSS8TEBOeHQBV+kShVdmLZka7vMmPPx45RH93spPy4dWnLutDPa6trxLuq7Nb+9VKuo/eUL+qaWCah5PDhw9xxxx28+uqr9OzZk9dff50WLVoE7fur8IuEEbfHnnTXd/mlXIcL/DuxzBVjKpxUdmyhdlWwOUr5Ql3Sba6JZRKprLV89dVX/OlPf+LPf/4zsbHBLcUq/CIBVDqxrHS51aGCIp+7vnPKFfWcgqKATSwru/Sq/FaiR7q+jzOerYllIpWz1vLqq68yfPhwatasybp166hWrZojWVT4RcrxeCy5ReW6vsuMXR/T9V3JeuqyzwMxseyYru9y49ZHx6jLzQYvW6jjS36/JpaJBN7u3bu56aabeO+998jNzeX22293rOiDCr9EiCK352ihLizXei6zB/ixY9TuY8azc8qswfan0ollp9L1feTQjnhNLBMJJ59++inXXnstu3fvZtq0aYwdO9bpSCr84gxrLflFHt+7vvOPFu2yXd+BnFhWWfH19QCP0lZ5QqwvZ3qJSKR5+eWXGTVqFG3btmXRokWkpqY6HQlQ4ZcTUH5iWUV7gPvS9R2oiWWJ8a5yY9Sx5caoK98DvGzxrhEfi0sTy0TkFF144YWMHj2ap556ipo1azod5wgV/ghXUOw+dg/wwnJd3xUU78pa3XlF/u0CT4iNqbBbu7LW85E9wMutr9bEMhEJFfPmzeP999/nxRdfpE2bNrzwwgtOR/oVFf4I8ObX21nyzc4K1lcXU+T278SyxPhfr6euciOUX41du6iVEEeNBBdxmlgmIhEiLy+PiRMn8vzzz9O1a1cOHDjg98N1/EWFP8wVFLv5y4KNlZ7KFecqf2jH0eLs60Yopdeq69AOEZFf2bRpEyNGjGDDhg1MnDiRyZMnEx8f73SsSqnwh7n//nyIQreHFvVq8NTQ5HLnXGtimYhIIBUVFXHllVdy+PBhFi9ezBVXXOF0pONS4Q9zGZn7Aeja4jR+0/I0h9OIiESHgwcPkpiYSFxcHG+88QYtW7akUaNGTsfyiQZZw1xp4U9pHppjSSIikWbVqlUkJyfz2GOPAdCjR4+wKfqgwh/20rO8hb+pCr+ISCB5PB4ef/xxLrjgAgAuvfRShxOdHHX1h7EDuUVszT5MfGwM7c6o5XQcEZGI9fPPP3P99dfz8ccfM2zYMGbOnBmys/aPR4U/jK3/qaS1f27jJB07KiISQNu2bWP16tW8+OKL3HzzzWG9b4gKfxgrHd9PbhaeP3WKiISywsJClixZwoABA+jevTvbtm0L21Z+WWomhrH00ol9KvwiIn61efNmevbsycCBA9mwYQNARBR9UOEPW9Za0jMPAJCsiX0iIn7z+uuvk5qaypYtW5g7dy4dO3Z0OpJfqfCHqR0H8tmdU0CdGnG0qFfD6TgiIhHh9ttv57rrriMlJYX09HQGDRrkdCS/U+EPU0fG95vWCetJJiIioaRz5878+c9/ZtmyZTRv3tzpOAGhyX1hKl0T+0RETpm1lunTp1OvXj2uu+46br75ZqcjBZxa/GGqtPCnqvCLiJyU3bt3079/fyZMmMDixYudjhM0KvxhqNjtYUNWycS+Tk1rO5xGRCT8fPrppyQnJ/Of//yH6dOn8/rrrzsdKWjU1R+G/rcrh7wiN81Oq069mglOxxERCSvffvstl1xyCW3btuX9998nJSXF6UhBpRZ/GCo7sU9ERHyTl5cHwNlnn81rr73GmjVroq7ogwp/WMrI0sY9IiInYu7cubRq1Yq1a9cCcN1111GzZk2HUzlDhT8MlW7co8IvIlK1vLw8xo4dy+DBg2nWrFnE7L53KlT4w0xuYTHf7TyIK8bQobEm9omIVGbjxo1069aN559/nrvvvpsVK1Zw5plnOh3LcZrcF2a++ekgHgsdGtWierzL6TgiIiHr3Xff5ZdffmHJkiX06dPH6TghQy3+MKMT+UREKrd//37S0tIA+OMf/8iGDRtU9MtRiz/MHDmRTzP6RUSOsXLlSkaOHInH42Hz5s3Ex8dz+umnOx0r5KjFH2a0Va+IyLE8Hg+PPfYYvXr1whjDu+++S3x8vNOxQpZa/GEk+1ABP+3PIzHeRZuG0bkMRUSkrEOHDnH11Vfz0UcfMXz4cGbOnEnt2pr4XBUV/jCy3rt+v2PT2rhidCKfiEjNmjU57bTTeOmll7jpppt0WqkP1NUfRtTNLyIChYWFPPDAA/z4448YY3j77be5+eabVfR9pMIfRnQin4hEu82bN3P++efz2GOPsXDhQqfjhCV19YcJa62W8olIVPv3v//NbbfdRlxcHPPmzWPgwIFORwpLavGHiR92H+ZgfjENayVwRlI1p+OIiATVyy+/zPXXX09qaioZGRkq+qdALf4wUXowT3KzOhrHEpGo4Xa7cblcDB8+nEOHDnHHHXcQG6vSdSrU4g8TGTqYR0SiiLWWadOm0a1bN3Jzc6lZsyYTJkxQ0fcDFf4wcWTHPhV+EYlw2dnZ9OvXjwkTJtCkSRMKCgqcjhRRVPjDQEGxm007DmJMyRp+EZFItWzZMpKTk/nwww+ZPn06CxYsoG7duk7HiijqMwkD3/58iEK3hzYNa5JULc7pOCIiAWGt5f777ycpKYnFixeTkpLidKSIpMIfBo5M7NPBPCISgbZt20ZSUhJ169Zlzpw51K1bl8TERKdjRSx19YeB9O2l4/vq5heRyDJnzhxSUlIYP348AE2bNlXRDzAV/jCQnqWNe0QksuTl5XHrrbcyZMgQ2rRpw1/+8henI0UNFf4QdyCviK3Zh4mPjeHsM5KcjiMicsr+97//0a1bN2bOnMndd9/NihUrOPPMM52OFTU0xh/iNmSVrN/v0DiJ+Fj9nCYi4a9mzZJjxZcsWUKfPn0cThN9VElCXHrmPkAT+0QkvO3fv59HH30Ut9tNo0aNyMjIUNF3iAp/iEv37tiX2lyFX0TC08qVK0lJSeHhhx/m66+/BiAmRuXHKUH/5I0xfYwx3xljNhtj7q/g9ebGmGXGmDRjzHpjTN9gZwwV1tojO/apxS8i4cbtdjN58mR69epFTEwMy5cvp0ePHk7HinpBLfzGGBcwA7gCaA+MNMa0L3fbH4F3rLWpwAjguWBmDCU7DuSzO6eA2tXjaFGvhtNxREROyKhRo3jwwQcZOnQoaWlpnHfeeU5HEoI/ua8bsNlauxXAGPMWMADYVOYeC5ROX68N7AhqwhCSkakT+UQk/FhrMcYwatQoLrjgAm688Ub9GxZCgl34mwCZZZ5nAeV/BHwI+I8xZhyQCFwanGihJ0MH84hIGCkoKGDSpEkAPPPMM/To0UNd+yEo2GP8Ff3IZ8s9Hwm8aq1tCvQF/mWM+VVOY8xoY8waY8ya7OzsAER13tET+bRjn4iEtv/973+cf/75TJ06laKiIqwt/0+7hIpgF/4soFmZ5035dVf+zcA7ANbalUA1oH75N7LWzrLWdrXWdm3QoEGA4jrH7bFs+KlkRr8m9olIKPvXv/5F586d+eGHH5g3bx7/+Mc/1LUfwoJd+FcDbY0xrYwx8ZRM3ltY7p7twCUAxphzKCn8kdmkr8L/dh0it9BNs9OqU69mgtNxREQqlJWVxZgxY0hNTSUjI4OBAwc6HUmOI6hj/NbaYmPMHcAHgAt4xVq70RjzCLDGWrsQmAi8aIz5P0qGAW6wUdhnlKFlfCISwn744QdatWpF06ZN+fzzz0lJSSE2VpvBhoOgr+O31i621p5lrT3TWvs377U/e4s+1tpN1tqe1tpka22KtfY/wc4YCtI1sU9EQpC1lqlTp9KuXTvefPNNALp27aqiH0b0XypEle7YpxP5RCRUZGdnc8MNN7B48WL69evH5Zdf7nQkOQnaMzEE5RYW8/0vh3DFGM5trBn9IuK8Tz/9lOTkZD766COmT5/OggULqFevntOx5CSoxR+CNu44iNtjad8oierxLqfjiIiwd+9ekpKSWLx4MSkpKU7HkVOgFn8ISt9+dMc+ERGnbNu2jXfeeQeAq6++mvXr16voRwAV/hCUnlVS+FNV+EXEIXPmzCElJYXbb7+dQ4cOARAfH+9wKvEHFf4QVHaPfhGRYMrLy+PWW29lyJAhnHXWWXz11VfUqlXL6VjiRxrjDzG7cwrI2pdHjXgXbRrWdDqOiESRgoICunfvzvr167n33nv561//qlZ+BFLhDzGlrf2OTWrjitGWlyISPAkJCfz+97+nY8eOWqoXwdTVH2KOnMjXXN38IhJ4+/btY/jw4Xz88ccATJw4UUU/wqnwh5j0rJKNe1K0Va+IBNiXX35JSkoKc+fOZfPmzU7HkSBR4Q8h1lpN7BORgHO73UyePJnevXsTGxvLihUrGDNmjNOxJEhU+EPIj3tyOZBXRMNaCTSqXc3pOCISoebOncuDDz7I0KFDWbduHd26dXM6kgSRJveFkLKtfZ1lLSL+lp2dTYMGDRgyZAhLlizhd7/7nf6tiUJq8YcQncgnIoFQUFDAhAkTaNeuHdu3b8cYQ58+fVT0o5Ra/CGktPAna2KfiPjJ999/z4gRI0hLS+OOO+6gYcOGTkcSh6nwh4jCYg+bdhwEoFMzncgnIqfuX//6F7fddhsJCQnMnz+fAQMGOB1JQoAKf4j4dudBCt0ezmyQSFK1OKfjiEgE+Oijj+jSpQv//ve/adasmdNxJESo8IeIdC3jExE/WLt2LdWqVaNDhw688MILxMXFERurf+rlKE3uCxGlhV8n8onIyfB4PDzzzDP06NGDiRMnAlC9enUVffkV/Y0IEdq4R0RO1q5du7jxxhtZvHgxAwYM4OWXX3Y6koQwFf4QcCCviC3Zh4l3xXD2GUlOxxGRMPLtt99y8cUXs3fvXp599lnGjh2rZXpSpRMq/MaYdkAvoB7wqrX2F2NMM2CPtTY3EAGjwQbv/vztGycRH6vRFxHxXevWrbnooou49957SU5OdjqOhAGfqowxJs4Y8y9gEzALmAw08b78LPDHwMSLDhlZ2rhHRHz3448/Mnz4cPbt20d8fDyvv/66ir74zNfm5V+B/sAooAVQth9pMfA7P+eKKtqxT0R8NXv2bFJSUli6dCnffPON03EkDPla+K8F/mStfQXYUe61rUArv6aKItZaLeUTkePKzc1lzJgxDB06lHbt2pGWlkavXr2cjiVhyNfC3wCo6kdLHSV3kn4+kE/2oQJqV4+jZb0aTscRkRB11113MWvWLO677z6WL19O69atnY4kYcrXyX3bgN8An1TwWlfgf35LFGV0Ip+IVMZay+HDh6lZsyZ/+ctfGDx4MJdddpnTsSTM+Vr4/w08aIzZDLznvWaNMT2AuyiZ7Ccn4cj4flPtzy8iR+3bt49Ro0axd+9ePvzwQxo1akSjRo2cjiURwNeu/seAj4F3gd3ea8uA5cBnwN/9Hy06aHxfRMpbsWIFKSkpLFiwgCuuuEK9geJXPrX4rbXFwCBjzGWUzOBvCOwBllprPwhgvojm9lg2/FSyhl+FX0TcbjePPfYYDz30EC1atGDFihV069bN6VgSYXwq/MaYhpRs0vMh8GG512KA+tbaXQHIF9E278oht9BN07rVqV8zwek4IuKwnJwcXnrpJYYNG8YLL7xAUpJ28hT/83WM/2egB/B1Ba+leq+7/BUqWqRn7gPU2heJdp988gk9e/akdu3afP311zRo0EDd+xIwvo7xV/U3MBbw+CFL1EnPLOnm14l8ItGpoKCACRMmcMkllzBt2jQAGjZsqKIvAVVpi98YUxMo289U3xjTuNxt1YFrgF8CkC3i6UQ+kej1/fffM2LECNLS0hg3bhx33nmn05EkSlTV1T8R+LP3seXoMr7yDPA3f4aKBnmFbr775RCuGEOHxhrHE4kmCxYs4NprryUhIYEFCxbQv39/pyNJFKmq8C8CdlJS2J8DpgA/lLunANhkra1o7F+q8M2OA7g9lnMaJVEjXqcji0STNm3a0KtXL1588UWaNm3qdByJMpVWHGvtWmAtgDHGAnOstbsru19OTIYO5hGJKmvXrmXevHk8+uijdOjQgSVLljgdSaKUT5P7rLUzVfT96+iJfNqxTySSeTwennnmGXr06MFrr71Gdna205Ekyvncx2yMOQu4EWjHrw/lsdbaK/0ZLNJpxz6RyLdr1y5uuOEGlixZwsCBA3n55Zc57bTTnI4lUc7XDXy6AF9QMnu/OfAdcBolO/jtALYHKmAk2p1TQNa+PGrEu2jbsJbTcUQkANxuNxdddBFbtmxhxowZ3HbbbVqmJyHB1xb/48D7wEigELjOWrvOGNMXeAm4L0D5ItL6rJLWfscmtXHF6B8CkUhSVFSEy+XC5XLx9NNP07hxYzp16uR0LJEjfN3AJxl4laMb9bgArLWLKTmZb4rfk0Ww9O2a2CcSiX788Ud69+7N9OnTAejTp4+KvoQcXwt/AnDIWusB9gKnl3ltE6C/2ScgPUsH84hEmnfffZeUlBQ2bdpE48bl9zoTCR2+Fv6tQOnf5I3ADWVeuw7QAT0+stZqKZ9IBMnNzWX06NEMGzaMs88+m/T0dIYNG+Z0LJFK+Vr4lwCXeR8/Bgwwxuw1xuwC/gBMD0S4SLRtTy4H8opoUCuBRrXLL44QkXCzbt06XnnlFe677z6++OILWrVq5XQkkSr5NLnPWvtAmcdLjTG9gCFADWCptXZhgPJFnCPL+JrW0QxfkTBlrWX16tV069aNCy64gO+//57WrVs7HUvEJ762+I9hrV1lrb3bWjtWRf/ElBb+1Obq5hcJR3v37mXw4MF0796dtWvXAqjoS1g5qcJfljGmvTHmTX+EiQYZWUdb/CISXpYvX05KSgrvvfceTz75JKmpqU5HEjlhVRZ+U6KTMeYqY8w55V7raIx5F1gPXBXIkJGisNjDxh0HAejYVFv1ioSTJ554ggsvvJC4uDi+/PJLJk6cSEzMKbedRIKu0r+1xpgzgBVAGrAA+MYY85oxJtYY86z3+lWUnNzXJhhhw923Ow9SWOyhdYNEalePczqOiJyAhIQERowYQVpaGr/5zW+cjiNy0qqa3Pc4kAL8DVgHtALuBT4DegBvA/dYa7MCHTJSaBmfSHhZtGgRHo+H/v37M378eABNypWwV1Xhvwx4xFr7eOkFY8w3wAfAC9basYEOF2nSM0s27lHhFwltBQUF3HfffUybNo3f/va39OvXTwVfIkZVA1QNKenqL6v0uSbznYT0zH2AJvaJhLLvv/+eHj16MG3aNO68806WLFmioi8RpaoWvwsoKHet9PnhwMSJXAfzi9iSfZh4VwznNEpyOo6IVODHH3+kc+fOVKtWjYULF9KvXz+nI4n43fE28LncGFN24l4MYIE+xpizy95orX3D3+EiyQbv/vztGycRH6uZwCKhxOPxEBMTQ8uWLfnLX/7CNddcQ5MmTZyOJRIQxyv8j1Ry/dFyzy2gwl+FdE3sEwlJa9as4aabbuLNN9+kQ4cO3HPPPU5HEgmoqgr/OVW8JifoyFa9zbR+XyQUeDwepk6dyqRJkzjjjDPIyclxOpJIUFRa+K213wXiGxpj+gDTKJlD8FLZVQNl7hkGPERJT0KGtfaaQGQJFmttmRZ/XYfTiMiuXbv4wx/+wNKlSxk4cCAvv/wyp512mtOxRILCp0N6/MUY4wJmULJUMAtYbYxZaK3dVOaetsAkoKe1dp8xpmEwMwbCzoP5ZB8qIKlaLC3r1XA6jkjUe/bZZ1m2bBkzZszgtttu06x9iSrBnmXWDdhsrd1qrS0E3gIGlLtnFDDDWrsPwFq7K8gZ/S59e2k3v07kE3FKUVERW7duBeDBBx9k3bp1jB07Vv9PStQJduFvAmSWeZ7lvVbWWcBZxpgVxphV3qGBXzHGjDbGrDHGrMnOzg5QXP9I9x7Mk6qJfSKO+OGHH+jduzcXX3wxubm5JCQk0L59e6djiTgi2IW/oh+tbbnnsUBb4LfASOAlY8yvKqa1dpa1tqu1tmuDBg38HtSfMjKPtvhFJLjeeecdUlJS2LRpE1OmTKFGDQ23SXQLduHPApqVed4U2FHBPQustUXW2h+A7yj5QSAsuT32yBr+TtqxTyRo8vPzGTVqFMOHD6d9+/akp6czbNgwp2OJOO6EC78xpo0x5jxjzMn82LwaaGuMaWWMiQdGAAvL3TMfuMj7vepT0vW/9SS+V0jYvCuHw4VumtSpToNaCU7HEYkacXFx/Pjjj0yaNInPP/+cVq1aOR1JJCT4XPiNMTcbY7IoaYF/CZztvT7bGHOrL+9hrS0G7qDkoJ//Au9YazcaYx4xxvT33vYBsMcYswlYRskJgHt8/hOFmCMn8jVXa18k0Ky1vPjii+zYsQOXy8WSJUuYPHkycXE6BluklE+F3xhzAzAL+AT4A8eO1X8FDPf1G1prF1trz7LWnmmt/Zv32p+ttQu9j6219i5rbXtrbUdr7Vu+vncoKp3Yl6JufpGA2rt3L4MHD2b06NE8//zzAMTGBnXFskhY8LXFfw8wzVr7e359Mt9/8bb+5dfKLuUTkcBYvnw5KSkpLFq0iKeeeoqHH37Y6UgiIcvXH4fPBN6v5LVDgLajq0BeoZvvfjmEK8ZwbhOdyCcSCHPnzmXo0KG0atWKL7/8kq5duzodSSSk+dri38uxs/HLOgv42T9xIsvGHQdweyxnnV6LGvHqchQJhIsuuog777yTdevWqeiL+MDXwv8+8EdjTNnib73r6ycAC/yeLAIc3Z9fB/OI+NN7771Hnz59KCwspG7dukydOpWkJPWqifjC18L/oPfeTcAiSjbdecr7PA7QgFoFjpzIp4l9In5RUFDA+PHj6d+/P7/88gu7d+92OpJI2PGp8Hv3y+8MTAcaAD8BpwGvAeeV7qsvx8rI0lI+EX/57rvv6N69O9OnT2f8+PGsWrWKxo0bOx1LJOz4PPBsrd1PScv/wcDFiRx7cgrI3JtHjXgXbRvWcjqOSFiz1nLDDTeQmZnJe++9x1VXXeV0JJGw5VPhN8ZMBv5prf02wHkiRmlr/9wmtXHF6PQvkZNx8OBBYmJiqFmzJq+++io1a9akSZPy53qJyInwdYx/HLDRexreOGNMaJ+KEwLSM0v259eJfCInZ/Xq1XTu3Jlx48YB0K5dOxV9ET/wtfA3BH4PZAPPAD8ZYxYZY4YaY7QBfQV0Ip/IyfF4PDz11FOcf/75FBUVccsttzgdSSSi+Dq5L89a+7q19gpKTtS7H2gEvA38Yox5MYAZw4619khXvwq/iO927dpF3759ueeee+jfvz/p6en07NnT6VgiEeWET+ez1v5irX3GWtsFuISZXVeAAAAgAElEQVSSnftu8nuyMLZtTy77c4uoXzOBxrWrOR1HJGzk5uayfv16nn/+eWbPnk3dutoUVMTfTng7OW/X/kDgOuBySg7sqWw736h0ZBlfszoYo4l9IlUpKiri9ddf5w9/+AMtW7Zky5YtVK9e3elYIhHrRI7l/a0x5mXgF0oO6jkduBtobK3tX+VvjjJp27Vjn4gvfvjhB3r16sWNN97Ixx9/DKCiLxJgvi7n2w40ATKBGZQs7fsukMHCmcb3RY7v7bffZvTo0RhjePvtt7n00kudjiQSFXzt6v+QkmL/WSDDRILCYg8bdxwEoJO26hWp0AMPPMBjjz1G9+7defPNN2nZsqXTkUSihk+F31p7c6CDRIrvdh6isNhD6waJ1K4e53QckZBU2rp/+OGHiYvT/yciwVRp4TfGdAO+sdbmeh9XyVr7tV+Than0zJJjC1LU2hc5wlrLc889x759+/jjH//IxRdfzMUXX+x0LJGoVFWLfxXQHfja+9hWcp/xvubyb7TwVLpjn8b3RUrs3buXm2++mfnz53PllVfidrtxufTPhYhTqir8VwD/9T7uS+WFX8oou5RPJNotX76ca665hp07d/L0008zYcIEYmJOePsQEfGjSgu/tfaDMo+XBidOeDuYX8SW7BziXTGc3Ugn8kl0y87O5vLLL6dx48Z8+eWXdO3a1elIIoKP6/iNMZuMMR0rea29MWaTf2OFpw1ZB7AWzmmcREKsujIlOh04UDLc1aBBA+bOncu6detU9EVCiK99bmcDle2qUQNo55844S3dezCPTuSTaLVw4ULOPPNM5syZA0CfPn1ISkpyOJWIlHUig22VjfF3Ag74IUvYO3oin3bsk+iSn5/PnXfeyYABA2jevDkdO1bYQSgiIaCq5XzjgHHepxaYbYwpKHdbdaAxMDsw8cKHtfZIiz9ZS/kkinz77beMGDGCjIwMJkyYwOOPP05Cgk7rFglVVc3q3wGs9T5uA3wH7Cl3TwGwCXje/9HCy86D+ew6VEBStVha1kt0Oo5I0KxevZqffvqJRYsWceWVVzodR0SOo6pZ/XOAOUDpCXMPWmu3BilX2DnazV+HmBidyCeR7eDBg6xZs4aLL76Y66+/nquuukpH6IqECV+37B0Z6CDhLi1T6/clOqxevZoRI0aQnZ3Ntm3bqFu3roq+SBipaoz/XkoO5tnpfVwVa6190r/RwkuGxvclwnk8Hp5++mkeeOABGjduzJIlS1TwRcJQVS3+x4FPgZ3ex1WxQNQWfrfHsiFLW/VK5CouLqZfv34sXbqUq6++mpdeeklFXyRMVVX4q1trS2fxV7aGX4At2TkcLnTTpE51GtTSbGaJPLGxsaSmpjJgwADGjBlTOu9HRMJQVZP7Cip6LL+Wvl3j+xJ5ioqK+NOf/sSAAQPo0aMHkydPdjqSiPiBT5P7jDGtgSRrbbr3eQJwP3Au8IG19qXARQx96VnauEciy9atWxk5ciRff/01CQkJ9OjRw+lIIuInPhV+4DlK1uune5//Ffg/4HtgkDHGZa2dGYB8YSHjyIx+jXlK+Hv77bcZPXo0xhjeeecdhg4d6nQkEfEjX7fsTQE+BzAlg3s3AA9YaztQMvHv1oCkCwN5hW6+3XmIGAPnNtGe5BLeFi1axIgRI+jQoQPp6ekq+iIRyNfCXwfY7X2cAtQD3vE+/xA408+5wsbGHQdweyxnnV6LGvG+dqCIhJb8/HwArrjiCmbNmsVnn31Gy5YtnQ0lIgHha+HfBbT2Pr4M+MFau837PBFw+ztYuDhyIl9zTeyT8GOtZcaMGZx11ln8/PPPuFwuRo0aRVxcnNPRRCRAfG2iLgL+Zow5CxgNvFLmtQ7AD/4OFi4yStfva+MeCTN79+7l5ptvZv78+fTt25fYWPVYiUQDX/9Pvx+oBQwHPgIeLfPaMOATP+cKG+mZ+wBt3CPh5YsvvuCaa67hl19+4ZlnnmH8+PHExJzIKd0iEq583av/IHB9Ja/9xq+JwsienAIy9+ZRPc5F24Y1nY4j4rMZM2ZQrVo1Vq5cSZcuXZyOIyJBdEJ9e8aYWkA34DRKjuhdba09FIhg4WC9t5u/Y9PaxLrUWpLQlpWVRVFREa1atWLmzJnExMRQq1Ytp2OJSJD5XK2MMX8Efgb+A7xNSZf/z8aYBwOULeTpRD4JFwsWLCA5OZmbbroJgNq1a6voi0Qpnwq/MeZ24BFgHtAXSAWu8D5/xBhzW8AShjCdyCehLj8/n3HjxjFw4EBatGjBzJlRu8+WiHj52tV/B/CctfaOMtcygA+MMQeAccDz/g4Xyqy1ZHi36k3RUj4JQZmZmfTr14+MjAwmTJjA448/TkKCDpESiXa+Fv7WwJ2VvLYAuMU/ccLH9r257M8ton7NBBrXruZ0HJFfqVevHnXr1mXRokVceeWVTscRkRDh6xj/XqBdJa+1874eVdKPjO/X1hGlEjIOHjzIPffcQ05ODjVq1OCTTz5R0ReRY/ha+OdTsoHPUFOmyhljBlFyYM/8QIQLZeka35cQ8/XXX5OamsrUqVNZtmwZgH4oFZFf8bXw3w98S8ls/lxjzDZjTC4wG/jO+3pUOXIin8b3xWEej4cnn3ySnj17UlxczOeff06/fv2cjiUiIcrXDXwOGGPOBwYBvShZx78X+AxYYK2Nqr36C4s9fLPjIACdmqjwi7MmTZrElClTGDx4MC+++CJ16+p4aBGpnM8b+HiL+2zvV1T7buchCos9tK6fSO0aOsxEnOF2u3G5XNx22220adOGW265RV37InJcVXb1G2NGGGNWGWN2G2M2G2P+ZoyJ+pM80rO0cY84p7CwkPvuu49BgwZhraVly5aMGjVKRV9EfFJp4TfGDAXeAM4AVgC5lIzlP1rZ74kWRzbuUeGXINu6dSu9evViypQpNG7cmKKiIqcjiUiYqarFfxfwPtDWWjvAWtsJeAIYZ4yJ6o3p01X4xQFvvfUWqampfP/998yePZsXXniB+Ph4p2OJSJipqoC3A5631pZtUkwHqgMtApoqhB3ML2JLdg7xrhjOaaS9ziU4Dh06xF133cW5555Leno6gwcPdjqSiISpqsbr6wC7y13L9v5aF/ghIIlC3DdZB7AWzmmcREKsy+k4EuG+/fZb2rRpQ61atfjss89o1aoVsbFRP81GRE7B8brs7Qlej3hHTuRrWtvhJBLJrLU8++yzpKSk8OSTTwLQtm1bFX0ROWXHK/wrjDGFpV9Anvf6V2WvG2MKfP2Gxpg+xpjvvKsEKt34xxgzxBhjjTFdfX3vYNDEPgm0PXv2MGjQIMaNG8cll1zCLbdE3VEYIhJAVTUfnvD3NzPGuIAZwGVAFrDaGLPQWrup3H21KDkU6Ct/ZzhVGVrKJwG0cuVKhg0bxi+//MIzzzzDhAkTtExPRPyq0sJvrZ0UgO/XDdhsrd0KYIx5CxgAbCp331+BKcDdAchw0nYeyOeXgwUkVYulZb1Ep+NIBIqPj6d27drMnz+fLl26OB1HRCJQsJflNQEyyzzP8l47whiTCjSz1i6q6o2MMaONMWuMMWuys7OrutVv0jP3ASXd/DExaoWJf2RlZfGPf/wDgC5durB+/XoVfREJmGAX/oqq5ZGJgt79AaYCE4/3RtbaWdbartbarg0aNPBjxMqlZx4AdCKf+M+CBQtITk7mgQce4KeffgIgJiaqt8kQkQAL9r8wWUCzMs+bAjvKPK8FnAt8aoz5EegOLAyVCX5HTuTT+L6covz8fMaNG8fAgQNp2bIl69ato0mTJsf/jSIipyjYa4NWA22NMa2An4ARwDWlL1prDwD1S58bYz4F7rbWrglyzl9xeyzrvRP7OjXTUj45edZaLr30UlasWMGECRN4/PHHSUhIcDqWiESJoLb4rbXFwB3AB8B/gXestRuNMY8YY/oHM8uJ2pKdw+FCN03qVKdhrWpOx5EwZK3FWosxhnHjxrFo0SKmTp2qoi8iQRX03UCstYuBxeWu/bmSe38bjEy+SFc3v5yCAwcOMGbMGC655BJGjRrF8OHDnY4kIlHK5xa/MeZ0Y8xkY8xyY8wmY0x77/WxoTIGH0hHN+5RN7+cmK+++orU1FRmz57NwYMHnY4jIlHOp8JvjDkb2ADcRsnxvO2A0v7udsCEgKQLIUdO5NOMfvGRx+PhiSee4IILLsDj8fDFF18wceJxF6yIiASUry3+pyg5lKcV0Jdjl+WtAHr4OVdIyS9y8+3OQ8QYOLeJWvzim1WrVnH//fczaNAg0tPT6dEjov83EZEw4esY/4XAddba/d5td8vaCTTyb6zQsnHHAdwey9ln1CIxQYekSNW2b99O8+bNOf/88/nyyy/p3r27tt0VkZBxIrP63ZVcr8fRw3siUtp2TeyT4yssLOTee++lTZs2rFlTsgK1R48eKvoiElJ8bb6uAa4HKtpGdzCwym+JQlBGlnfHPhV+qcTWrVsZMWIEq1ev5tZbb6VDhw5ORxIRqZCvhf9vwFJjzHvA65Rss9vbGDMGGAZcFKB8IUE79klV3nrrLUaPHo3L5WL27NkMHjzY6UgiIpXyqfBbaz8yxgwD/g5c6b38DCXb7Q6z1q4IUD7H7T1cyPa9uVSPc9G2YU2n40gI2rx5Mx07duSNN96gRYsWTscREamSz2P81tq5QAugE3ApkAo0t9bOD1C2kFDa2u/YpDaxLh2eIiUyMjL49NNPAZg0aRKfffaZir6IhIUTmqJurbXANwHKEpLStXGPlGGtZcaMGUycOJH27duzbt06XK7yC11EREKXT4Xf281fJWvtO6ceJ/RkZJWO79d1OIk4bc+ePdx0000sXLiQvn378uqrr2rGvoiEHV9b/G9Vct2WeRxxhd9aq616BYAdO3bQrVs3du3axdSpUxk/fryKvoiEJV8L/zkVXKsHXAUMAf7gt0QhZPveXPblFlG/ZjxN6lR3Oo44qFGjRgwfPpxrr72Wzp07Ox1HROSk+Tqr/7tKXvrSGOOmZA//lX5LFSLKnsin1l30yczM5NZbb2XatGm0adOGp59+2ulIIiKnzB/T1JcB/f3wPiEnI9O7cY8O5ok68+fPJzk5mc8//5zvvqvs514RkfDjj8LflZIT+yJOeuY+QDv2RZP8/Hxuv/12Bg0aROvWrVm3bh1XXnnl8X+jiEiY8HVW/70VXI4HzgUGAS/6M1QoKHJ7+GZHydnpavFHjylTpvDcc89x11138dhjjxEfH+90JBERv/J1ct/jFVxzAz8BU4GH/ZYoRHy38xCFxR5a10+kdo04p+NIAFlr2bt3L/Xq1ePuu++mZ8+eXHLJJU7HEhEJCF8Lf0VT2oustR5/hgklaUeW8am1H8kOHDjAmDFjSEtLY926dSQmJqroi0hEO+4YvzEmHngIONdaW1DmK2KLPhzdqje5qdbvR6qvvvqK1NRUZs+ezQ033EC1atWcjiQiEnDHLfzW2kJgPJAY+Dih48iJfM21Y1+k8Xg8PPHEE1xwwQV4PB6++OILJk2apK13RSQq+DqrPwNoH8ggoeRQfhGbs3OIcxnOaVTL6TjiZ263mwULFjBo0CDS09Pp0aOH05FERILG1zH+e4F/GmM2W2s/CmSgULAh6wDWQvtGSSTEqhUYKT788ENSU1OpX78+S5cupVatWtqYSUSijq8t/leAOsAHxphDxpj/GWO+L/MVUTucpGdpYl8kKSws5J577uHyyy/n0UcfBSApKUlFX0Sikq8t/rUceyBPRMsos1WvhLctW7YwcuRIVq9eza233spjjz3mdCQREUf5ulf/iEAHCSXpWsoXET755BMGDhyIy+Vi9uzZDB482OlIIiKOq7Sr3xiz1RiTHMwwoWDngXx+OVhArWqxtKoXVQsZIs65557LZZddRnp6uoq+iIhXVWP8LYGEIOUIGWVP5IuJ0RhwuElPT+fGG2+kuLiYhg0bMmfOHFq0aOF0LBGRkOGPQ3oiSkbpxD7tzx9WrLVMnz6d8847j//85z/8+OOPTkcSEQlJxyv8UTOhr1T6do3vh5vdu3czYMAAxo8fz+WXX05GRgZt2rRxOpaISEg63uS+h40xu314H2ut/YM/AjnJ7bFs+OkAAMnNtFVvuBgyZAgrV65k2rRpjBs3Tsv0RESqcLzCnwIU+PA+EdEzsDU7h5yCYprUqU7DWtq3PZQVFxfjdrtJSEhg6tSpAKSmpjqcSkQk9B2v8A+01n4dlCQh4OiJfGrth7LMzEyuueYaOnXqxIwZM1TwRUROgCb3lXH0RD6N74eq+fPnk5ycTHp6Oueff77TcUREwo4KfxmlM/q1Y1/oycvL4/bbb2fQoEG0bt2atLQ0rr32WqdjiYiEHRV+r/wiN9/+fIgYA+c2UVd/qPnpp5/45z//ycSJE/nyyy81a19E5CRVOsZvrY2qHwo27jhAscdy9hm1SEzw9QgDCSRrLR9//DGXXHIJbdq0YfPmzZx++ulOxxIRCWtRVdyrkp7pXcan8f2QcODAAUaOHMlll13GokWLAFT0RUT8QE1bryMn8jVX4XfaqlWrGDlyJJmZmUyePJkrr7zS6UgiIhFDLX6vdM3oDwkzZsygV69eWGv54osvmDRpEjEx+msqIuIv+hcV2Hu4kO17c6ke5+Ks02s6HSeqtWjRgquvvpr09HR69OjhdBwRkYijws/RZXwdm9Qm1qWPJNiWLl3KjBkzALjqqqt4++23qVNHPS8iIoGgKkeZjXu0Y19QFRYWcvfdd3PFFVfw8ssvU1RU5HQkEZGIp8JPmfF9bdwTNJs3b6Znz548/fTTjB07lhUrVhAXF+d0LBGRiBf1s/qttdqqN8j2799Pt27dsNYyd+5cBg0a5HQkEZGoEfWFP3NvHvtyi6hfM56mdas7HSeiFRcXExsbS506dZg+fTq9e/emefPmTscSEYkqUd/Vn5a5Dyhp7esc98BJT0+nY8eOLF26FIDrrrtORV9ExAFRX/gzSnfs0/h+QFhrmT59Oueddx4HDx6kRo0aTkcSEYlqKvw6kS9gdu/ezYABAxg/fjy/+93vyMjIoHfv3k7HEhGJalFd+IvcHr75qaTF36mplvL528KFC/nggw+YNm0aCxYsoH79+k5HEhGJelE9ue+7nYcoKPbQqn4idWrEOx0nIhQXF7Nx40aSk5O58cYb6d27t47QFREJIVHd4j+6P79a+/6wfft2LrroInr16sWuXbswxqjoi4iEmKgu/EdO5NP4/imbN28eKSkpZGRk8Pzzz9OwYUOnI4mISAWiuvBrx75T5/F4GDt2LFdffTVnnnkmaWlpXHvttU7HEhGRSkRt4T+UX8Tm7BziXIZzGiU5HSdsxcTEUFxczMSJE1mxYgVnnnmm05FERKQKUTu5b8NPB7AW2jdKolqcy+k4YcVay0svvUTXrl1JTU1l5syZ2vxIRCRMBL3Fb4zpY4z5zhiz2RhzfwWv32WM2WSMWW+M+dgY0yIQObRxz8nZv38/w4cPZ/To0cycORNARV9EJIwEtfAbY1zADOAKoD0w0hjTvtxtaUBXa20nYDYwJRBZ0sts1Su+WblyJSkpKcybN4/HH3+c5557zulIIiJygoLd1d8N2Gyt3QpgjHkLGABsKr3BWruszP2rgOsCEUQt/hPz6aefcumll9KsWTO++OILunfv7nQkERE5CcHu6m8CZJZ5nuW9VpmbgSX+DrHzQD47D+ZTq1osresn+vvtI4q1FoCePXvy4IMPkpaWpqIvIhLGgl34KxoMthXeaMx1QFfgyUpeH22MWWOMWZOdnX1CIY5u3FOHmBiNT1dmyZIldOnShT179hAXF8fDDz9MnTrqIRERCWfBLvxZQLMyz5sCO8rfZIy5FHgQ6G+tLajojay1s6y1Xa21XRs0aHBCIUoP5kluph37KlJYWMjEiRPp27cvxcXF7N+/3+lIIiLiJ8Eu/KuBtsaYVsaYeGAEsLDsDcaYVGAmJUV/VyBCHN2xr24g3j6sbd68mZ49e/LMM88wduxYvvrqK63NFxGJIEGd3GetLTbG3AF8ALiAV6y1G40xjwBrrLULKenarwm8610mtt1a299fGTwey/os78Q+7dH/Kw888ABbtmxh7ty5DBo0yOk4IiLiZ0HfwMdauxhYXO7an8s8vjSQ339Ldg45BcU0rl2NhknVAvmtwkZOTg45OTmcccYZPPvss+Tn59O8eXOnY4mISABE3Za92p//WGlpaXTp0oURI0ZgraVhw4Yq+iIiESzqCn/pxL5oP5HPWsu0adPo3r07hw8f5uGHH9YOfCIiUSDq9upXix/27t3LDTfcwHvvvUe/fv145ZVXqF+/vtOxREQkCKKqxZ9f5Obbnw8RY6Bjk+id2BcbG8uWLVuYPn06CxYsUNEXEYkiUdXi37jjIMUey9ln1CIxIar+6BQXFzNjxgzGjBlDUlIS6enpxMXFOR1LRESCLKpa/BllduyLJtu2bePCCy9kwoQJzJ49G0BFX0QkSkVV4Y/G8f05c+aQkpLChg0beOONN7juuoCceSQiImEiqgp/tG3V++STTzJkyBDatm1LWloaI0eOdDqSiIg4LGoGuvcdLmTbnlyqxcXQ7vRaTscJiv79+7Nv3z4eeugh4uPjnY4jIiIhIGpa/One1n7HJrWJdUXmH9tay6xZs7jpppuw1tKuXTsmT56soi8iIkdEZgWsQKRP7Nu/fz/Dhw9nzJgxZGZmkpeX53QkEREJQVFX+FOaR17hX7lyJSkpKcybN4/HH3+cDz74gBo1ajgdS0REQlBUjPFba8k4ciJfZBX+vLw8Bg0aRI0aNVi+fDnnnXee05FERCSERUXhz9ybx97DhdRLjKdp3epOx/GL7Oxs6tWrR/Xq1Vm4cCHt2rWjdu3oWK0gIiInLyq6+tOzjq7fj4SDaJYsWUKHDh14+umnAejWrZuKvoiI+CQqCv+R8f0w37insLCQiRMn0rdvXxo1asRVV13ldCQREQkzUdHVHwk79m3evJkRI0awdu1abr/9dp566imqVavmdCwREQkzEV/4i9wevvmpdGJf+HaH//zzz2zfvp158+YxcOBAp+OIiEiYiviu/u92HqKg2EOr+onUqRFeG9nk5OTwzjvvANCrVy9++OEHFX0RETklEV/4j+zPH2at/XXr1tG5c2euueYatm7dCkBiYqLDqUREJNxFfOFP3x5e4/vWWv7+97/TvXt3cnNz+fjjj2ndurXTsUREJEJE/Bh/Rlb4FH5rLcOGDWP27Nn079+fV155hXr16jkdS0REIkhEF/6cgmL+tyuHOJehfaMkp+MclzGGyy+/nAsvvJDbb789IvYcEBGR0BLRhX991n6shXMaJVEtzuV0nAoVFxfz0EMP0aFDB0aOHMmoUaOcjiQiIhEsosf4MzJDe3/+bdu2ceGFF/K3v/2NVatWOR1HRESiQES3+EN5x745c+Zwyy234Ha7eeONNxg5cqTTkUREJApEdos/RCf2rV27liFDhtC2bVvS0tJU9EVEJGgitvD/cjCfnw/kUyshltb1Q2P9+6FDhwDo0qUL7777LsuXL+fMM890OJWIiESTiC38pfvzd2pWm5gYZ2fHW2uZNWsWLVq0ICMjA4AhQ4YQHx9eOwmKiEj4i9jCHyrj+/v372fYsGGMGTOGrl27cvrppzuaR0REolvEFv4jJ/I5OKN/5cqVpKSkMH/+fJ544gmWLl3KGWec4VgeERGRiJzV7/FY1meVLOVzssW/cOFCYmJiWL58Oeedd55jOUREREpFZIt/6+4ccgqKaVy7Gg2Tgntm/Y4dO1i7di0AjzzyCGlpaSr6IiISMiKy8KeXbtwT5Nb++++/T3JyMtdccw1ut5u4uDhq1w6vUwFFRCSyRWjh3wcEr/AXFBTwf//3f1x11VU0btyYBQsW4HKF5hbBIiIS3SJyjD+YW/Xu2bOHyy+/nHXr1jFu3DimTJlCtWrBHV4QERHxVcS1+POL3Pz354PEGOjUNPDd7HXr1uWcc85h/vz5TJ8+XUVfRERCWsQV/o07DlLssbRtWIvEhMB0aBw6dIixY8eSmZlJTEwM//73vxkwYEBAvpeIiIg/RVzhL924J7lZYFr7a9eupXPnzsycOZNly5YF5HuIiIgESuQV/qzSHfvq+vV9rbVMnTqVHj16kJeXx7Jly/j973/v1+8hIiISaJFX+APU4n/mmWe466676Nu3LxkZGfTu3duv7y8iIhIMETWrf9/hQn7ck0u1uBjOOr2WX96zsLCQ+Ph4Ro0aRd26dbnxxhsxxtlDf0RERE5WRLX4S7v5z21cmzjXqf3RiouLefDBB+nevTv5+fkkJSVx0003qeiLiEhYi6zCn+mf/fm3bdvGhRdeyOTJk0lNTcXj8fgjnoiIiOMiqqvfHzv2zZkzh1tuuQW3280bb7zByJEj/RVPRETEcRFT+K21ZJziiXzFxcU8+uijnHXWWbz55pu0bt3anxFFREQcFzGFP2tfHnsPF1IvMZ6mdauf0O/duHEjTZs2pXbt2rz//vs0aNCAuLi4ACUVERFxTsSM8acfWcZXx+cJeNZaZs6cSdeuXbn//vsBaNy4sYq+iIhErMgr/D4ezLNv3z6GDh3KrbfeSu/evXnooYcCmE5ERCQ0REzhP5GNe9LS0khJSWHBggVMmTKFJUuWcPrppwc6ooiIiOMiYozfAt/s8H1iX4MGDTjjjDN499136datW4DTiYiIhI6IaPHnF7nJL/LQsl4N6tSIr/CeHTt28OCDD+LxeGjatCmrVq1S0RcRkagTEYU/r9ANVL5+f9GiRXTq1Im///3vfPPNNwDagU9ERKJSRBT+XG/hL9/NX1BQwIQJE+jXrx9NmzZl7dq1dOrUyYmIIiIiISEiCn9lLf7hw4czbdo0xo0bx6pVqzj77LOdiCciIhIyImJyX36xm9gYQ/tGSQB4PB5iYmK4++67uZeiY5EAAA0ISURBVPHGGxkwYIDDCUVEREJD0Fv8xpg+xpjvjDGbjTH3V/B6gjHmbe/rXxljWvryvuc0SqIoP5frr7+eSZMmAXDBBReo6IuIiJQR1MJvjHEBM4ArgPbASGNM+3K33Qzss9a2AaYCT/jy3qcX/kTnzp154403SExM9GdsERGRiGGstcH7Zsb0AB6y1v7O+3wSgLX2sTL3fOC9Z6UxJhbYCTSwVQSNTWpgyTtAozNO5/XXX6d3796B/YOIiIg4yBiz1lrb9WR+b7C7+psAmWWeZ3mvVXiPtbYYOADUq+pN3Yf2cNGll5Oenq6iLyIiUoVgT+6raPF8+Za8L/dgjBkNjPY+Lfho6fvf1K9f/xTjSRXqA7udDhEF9DkHnj7jwNNnHHjtTvY3BrvwZwHNyjxvCuyo5J4sb1d/bWBv+Tey1s4CZgEYY9acbJeH+EafcXDocw48fcaBp8848Iwxa0729wa7q3810NYY08oYEw+MABaWu2ch8Afv4yHAJ1WN74uIiIjvgtrit9YWG2PuAD4AXMAr1tqNxphHgDXW2oXAy8C/jDGbKWnpjwhmRhERkUgW9A18rLWLgcXlrv25zON8YOgJvu0sP0STqukzDg59zoGnzzjw9BkH3kl/xkFdziciIiLOioi9+kVERMQ3YVX4A7Xdrxzlw2d8lzFmkzFmvTHmY2NMCydyhrPjfcZl7htijLHGGM2OPgm+fM7GmGHev88bjTFvBDtjuPPh34vmxphlxpg0778ZfZ3IGc6MMa8YY3YZY76p5HVjjJnu/W+w3hjT+bhvaq0Niy9KJgNuAVoD8UAG0L7cPWOBF7yPRwBvO507nL58/IwvAmp4H9+mz9j/n7H3vlrA58AqoKvTucPty8e/y22BNKCu93lDp3OH05ePn/Es4Dbv4/bAj07nDrcvoDfQGfimktf7Akso2QOnO/DV8d4znFr83YDN1tqt1tpC4C2g/Ak8A4DXvI9nA5cYYyraEEgqdtzP2Fq7zFqb6326ipK9GMR3vvw9BvgrMIX/b+/cg62uqjj++XYpMQQRlagxpGLIlNQsS41SijGyBkNr8oFKgjWTOGKMRaP5pIcBPsp8ZI0IFgajJmODmqb4yEdOEoMPGtSbJiqBiOEDkFZ/rH30d3+c+zu/ezn3XO896zOz55yz9/7t3zrrd+as3157/daGNxopXC+ijJ5PAn5lZusAzGx1g2Xs6ZTRsQED0vsd2TpvS1ADM7ubKrlsMhwOzDXnAWCgpPcXjdmTDH+XpPsN2lBGx1km4XeaQXlq6ljSJ4APmtnNjRSsl1HmtzwCGCHpPkkPSBrbMOl6B2V0fA4wQdK/8ae5TmmMaE1FR/+3G/843zZQt3S/QbuU1p+kCcCngIO7VKLeR6GOJb0L35VyYqME6qWU+S33wd39h+Ceq3skjTSzl7tYtt5CGR0fDcwxs9lpk7Z5Scf/63rxmoYO272eNOPvSLpfitL9Bu1SRsdIGgOcAYwzs40Nkq23UEvH/YGRwF2SWvE1u0UR4Ndhyv5f3GRmm83saWAFfiMQlKOMjicBCwDM7H6gL57HP6gfpf63s/Qkwx/pfruemjpObugrcaMfa6Idp1DHZrbezHYxs2FmNgyPoxhnZp3Oy92klPm/+CMerIqkXXDX/1MNlbJnU0bHzwBfBJD0Mdzw/6ehUvZ+FgHHp+j+A4D1ZvZ80QE9xtVvke63yymp45nADsDCFDf5jJmN6zahexgldRxsIyX1fCtwqKTHgC3A6Wa2tvuk7lmU1PE04CpJp+Hu54kxGesYkubjy1G7pFiJs4F3A5jZFXjsxGHASuA14Fs1x4xrEARBEATNQ09y9QdBEARBsI2E4Q+CIAiCJiIMfxAEQRA0EWH4gyAIgqCJCMMfBEEQBE1EGP4gqIKkiWlnvGplTAfHmpyOa8i+BpJm5ORdl3arrPvjrZL6pHOcmak7QtLUKn3HpL6j6i1HgXzDc7rYIul5SfMkFaY1LRhzP0nnSBpYb3mDoBH0mOf4g6Cb+AaeGSvLY90hSCc4ML3uDHwHmC/pPWY2t14nSM9yH0jbXOFHAKOAi3PdH0oyPVqv83eAGcCfgO2SDGcBe0g6MO3r0RH2w5+lngNEet+gxxGGPwiKWWpmK7tbiM6QduoCQNJteEraqUDdDH/+PDX6vYJnIuwOnszIuUTSdvgGMvsCkRUxaCrC1R8EnUTS9pIukfSopFeTC3mRpI+WOPY4SUvTceslLZM0OddntKS/SNqQymJJe3ZGVjPbDCwFhmfG31HSZUnuTZJWSDo1J8MASZdKelbSRkkvSvqzpBGpvY2rX9K1wLHA7hn3+srU1sbVL+nXklZJasmds2/SyaxM3WBJV6b+myQ9LmlSZ3SR+Ht6HZo79wxJj0h6RdIaSXdI+nSmfTJwVfr4dOY77pbRxxlJlxslPSdpZrrRCIJ3BDHjD4JiWuQbPlUwM9uS3m+fynnAC7hL/WTgfkl7tLeXgaSDgWtwV/g0PN3pnsBOmT6HA9fjebiPwW/Sp+M7yO1tZs914rt8iOSaTsZ2MbA38CPc/T4OuFjSzmZ2VjrmEmAsvinTSnyDlVH4BljVODv12QcYn+reaKfvXOAkPJf7bZn6w/E93OclWQcC9+FpSs8CWvEUpVelpYvLS337tgxLr0/m6j8AzMaXd3bA9/64R9J+ZvYocBPwYeCH+JJGJSd65VrPB74M/Az3buyF/z6GAt/shJxBUH/MLEqUKLmCb4trVcq9Bce0AP3wfNmnZOonp2N3S5+nA6sLxhFu3G7N1Q/E96CYVUP2Gel8fVJ5H3B+qpuV+nwtfZ6QO3YObqgHpc9PAD8vOFefNM6ZmbprgdYqfcekvqMy3/MpYF6u383Assznc4HXgY/k+l0NvAi0FMg3PJ3zxCRrP/xGYxVwXQ09tuA3G08Cs6tcz2G5/qNT/TG5+hNS/ce7+3cdJYqZhas/CGowHtg/U9q4lyUdJekhSeuBN4ENuBegyN3/N2BXSXMlfUVSfva8B7A78LvkOu6TvA4bgAeBz5eUfXMqLwCnAxfiM3fSGG8C1+WOuRYPgPtMRtZJkqZL+qSkuv1nmJml842X1A9A0q7Al2gbhzAW+Cvwr5w+bgUGU6zrCr/FdbEBuB2f0Z+Q7yTpUEl3SVqL62cTPsMvc46x+E3TjTk5K96Mz5UYIwi6nDD8QVDMcjN7OFNWVBokjcddu8uBo3FjuT8+K+/b3oBmdgfu9h2Gbw27RtJtkkamLoPT6zW8bbwrZSy+pFCGys3KcKC/mU0zs42pbRCwxraOaH8h0w7wXXxN+yQ8CG61pNmSti8pQy3m4rPwI9Lno/H/pd9n+gwGvsDWupif2svo41xcF4cAl6f3v8x2kLQ/Hvm/HvcQHJD6Lafgeubk7It7fLJyVvZGL3vdgqBLiTX+IOg8RwFPmNmJlQpJfXGXfCFmtgBYIGkH3KhdACyWNBSobA37feDOKodvrFJX7RxF0eov4dt89skZ/yHpdW0a47/40sR0ScPwxxt/is9sz2AbMbOVkh4AJuBr+hOAO8xsVabbWvxxwe+1M8yKduqztGb0sUTSAGCypCvMrBLo93X8ex2Z1YmkQfiSQi3W4kb/4HbaV7VTHwQNJQx/EHSe9+Lu4CzH0wFPmpltABZJGo4Hle2E5wl4FtjTzGbWSdY8S4DTgCOBP2Tqj8WN34NVZG0FZko6DhiZb8+wEV/uKMs84BeSRuMz7ONy7bfgeQhazWxNB8Yt4gf4dz8bDyaEt6/nW3uVSzoUD/h7PHNs5cYr/x1vwYM1+5nZkjrJGQR1Jwx/EHSeW4BL02Nni3GjdTLwStFBkn6Mu33vxKPChwJTgIfN7KXUZwpwQ/IgLMRnk0OAg4CnzOySbZT9ZuB+PDJ+CG7YvooHNZ5vZuuSHA8CN+Du7lfxALa9gCsLxn4MOFHSt4FHgNfNbHlB/+uAi/AbgFeBG3Pts3BPwz2SLgL+CfTHYyEOMrPxdBAze07SFcBUSfua2VL8ek4BrpZ0TRr/TLaeqVcSOE1Jjy9uBv5hZrdLWoiv8V+IJywCX9I5DJhmZvmnCIKg8XR3dGGUKO/EwttR/cML+rQAP8ENw2u4Id8HDxz7TaZfPqp/HB7w9Tw+e3wWX0cfkhv/s/ia8zp8Fv40vq59QA3ZZ5Bi52r02xG4LMmxCXeZn5rrMws33uvxwLhlwJRMe7Wo/v64F2FdaluZ6ttE9efOc2Nqm9uOrIPwRwtbk6yrgbvJPD3RznGVqP6JVdoGp+90faZuajrH67jhHg3cC9yeO/a8dN235K5tC+5JWZau2ct4/oQLgAHd/buOEsXMkNlbXq0gCIIgCHo5EdUfBEEQBE1EGP4gCIIgaCLC8AdBEARBExGGPwiCIAiaiDD8QRAEQdBEhOEPgiAIgiYiDH8QBEEQNBFh+IMgCIKgiQjDHwRBEARNxP8BG8AHqPNBNS8AAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f691250bd30>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fpr, tpr, thresholds = roc_curve(Y_test, modele_pred)\n",
"plt.figure(figsize=(8, 6))\n",
"plot_roc_curve(fpr, tpr)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### PRECISION, RAPPEL, F1-SCORE, SUPPORT"
]
},
{
"cell_type": "code",
"execution_count": 55,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(0.8635851183765502, 0.9396999150703029, 0.9000361532899495, None)"
]
},
"execution_count": 55,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"precision_recall_fscore_support(Y_test, modele_pred,average='binary')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### SCORE EN K-FOLD CROSS VALIDATION (validation croisee en K passes) "
]
},
{
"cell_type": "code",
"execution_count": 56,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.52097221 0.59593706 0.97970043 0.98112837 0.95954537 0.96506889\n",
" 0.95477194 0.94409584 0.94439154 0.92791783]\n",
"Mean: 0.877352948377862\n",
"Standard deviation: 0.16105758438579176\n",
"CPU times: user 337 ms, sys: 116 ms, total: 453 ms\n",
"Wall time: 32.8 s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele,X, Y, cv=10, scoring=\"precision\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 57,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.94935526 0.94842086 0.92915888 0.9328972 0.93102804 0.92953271\n",
" 0.93121495 0.92803738 0.92691589 0.92878505]\n",
"Mean: 0.9335346210071662\n",
"Standard deviation: 0.0078467246686113\n",
"CPU times: user 359 ms, sys: 83.2 ms, total: 442 ms\n",
"Wall time: 32.2 s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele, X, Y, cv=10, scoring=\"recall\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 58,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.67275858 0.73195356 0.95376055 0.9564051 0.94507163 0.94696753\n",
" 0.94284633 0.93599774 0.93557212 0.92835124]\n",
"Mean: 0.8949684361708116\n",
"Standard deviation: 0.09753719851297267\n",
"CPU times: user 355 ms, sys: 72.3 ms, total: 428 ms\n",
"Wall time: 32.6 s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele, X, Y,cv=10, scoring=\"f1\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 59,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.65381581 0.76402286 0.99316508 0.9931764 0.98676906 0.9895862\n",
" 0.9890175 0.98266781 0.98413086 0.98085759]\n",
"Mean: 0.931720917838898\n",
"Standard deviation: 0.11415972989866363\n",
"CPU times: user 338 ms, sys: 87.9 ms, total: 426 ms\n",
"Wall time: 32 s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_roc=cross_val_score(modele,X, Y, cv=10, scoring=\"roc_auc\",n_jobs=-1)\n",
"display_scores(modele_score_roc)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### **ESTIMATION QUALITE MODELE GBM**"
]
},
{
"cell_type": "code",
"execution_count": 60,
"metadata": {},
"outputs": [],
"source": [
"modele_pred = modele_gbm_pred\n",
"modele=modele_gbm"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Matrice confusion"
]
},
{
"cell_type": "code",
"execution_count": 61,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[ 9358, 1446],\n",
" [ 581, 10016]])"
]
},
"execution_count": 61,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"confusion_matrix(Y_test,modele_pred)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### ROC"
]
},
{
"cell_type": "code",
"execution_count": 62,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"0.9056669217224479"
]
},
"execution_count": 62,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"roc_auc_score(Y_test, modele_pred)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### ROC CURVE"
]
},
{
"cell_type": "code",
"execution_count": 63,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAf4AAAF8CAYAAAAuF9n2AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzs3Xd4lGW+xvHvk0mhhADSi/SioJIAB0EE17qI0qRbdm2AoghHbMiuq64LiAoLR1SwXLq7YqOLgGvBAoJSEhSwUaUTeiA985w/MgkxJGGAmXmn3J/ryuWUN5PbMeY3TzfWWkRERCQyRDkdQERERAJHhV9ERCSCqPCLiIhEEBV+ERGRCKLCLyIiEkFU+EVERCJIQAu/MeYNY8x+Y8z6Up43xpipxphNxpjvjTFtA5lPREQk3AW6xf8m0K2M568Hmnu+hgIvByCTiIhIxAho4bfWfgUcKuOSXsC/bL6VQBVjTJ3ApBMREQl/wTbGXw/YUeT+Ts9jIiIi4gPRTgcoxpTwWIl7ChtjhpI/HEDFihXbXXDBBf7MJSIiYcBtLW435FnruW1xW8/jnucKbudZi/3dtUWus3i+15ZcpHzAAFFRhihjcBmDzcsm/cBu8nKyAA5Ya2uczesGW+HfCZxf5H59YHdJF1prZwAzANq3b29Xr17t/3QiIuJ31lqyct2cyMolPTuP9Ow8TmTnkp7l+Wd2Liey8sgoeDw7r/DaE1m5ZOQUuV/k+zJz3F79fAO4PF/ecEUZKsa6qBgXTYVYFxVi8/9ZcL9ibDQV4lyFz1WMdVEhLvrk4zFFri3yGq6ok23hNWvW0LVrV86rksBbb71F9+7dt5/xG+sRbIV/AXC/MeZd4FLgqLV2j8OZRESkFDl5bk9xzi/GhUU55/f307NzOZHtKdYlFOWMYvfdfmpGFxbfuN8X4QoxLirEnSzSFWOjS722+PfEuqIwpqQO63NnrcUYQ5s2bRg+fDgPPvggdeqc29S3gBZ+Y8w7wB+A6saYncDfgBgAa+0rwCKgO7AJSAfuCGQ+EZFw5Xbb/JZwQZEtUozTswqK8u/vFy3a+YU6/7miRTs7z7tW9JmKjY7KL7AFBbig4BYvxKU8d0rRjnNRLtpFVJR/CrQ/fPvttzz44IPMnTuXmjVr8txzz/nkdQNa+K21g0/zvAXuC1AcEZGgY60lO89dpFvb031dUHizT21Jn9oVXrTL++Q1/hBl+H0r+XdFuViXd2E3dvEC/vuu8AqxLmJcwTb3PHDcbjcTJ07kr3/9K/Xq1WPv3r3UrFnTZ68fbF39IiIhIzfPTXpOse7rYi3iwlb1GXR55/qpn7t8jKtYi7ikcejf3y/a5V30fsH3xUX7r5s7Eu3du5fbbruNTz/9lP79+zNjxgyqVKni05+hwi8iYc9aS2aO+5QJYuln2OVdfDJZVq5/urljXObUMWVPC7l8bAld3nEuT1EvYVKZ5zXKx7h+N1lMgtNjjz3G8uXLmTFjBnfffbdfPlSZ/N710KZZ/SLhIzvXXViUCwruqZPASijKpUwmS8/KJT0nD3/8qTMF3dyeYlu0RV10HLp88SIeV/B4fnEu2uVdPtZFbHTkdnNHouzsbI4cOULNmjU5cOAA+/fvp1WrVmV+jzFmjbW2/dn8PLX4ReSsuN2W9JyTBfiUZVRFurFLnkx2cqlW0SKek+efxkhcdNQp3doFhfZMWtYnvyeacjHq5pZzs3nzZgYPHozL5WL58uVUr16d6tWr+/VnqvCLhLmCNdEljT+XtIyq6HXp2aWNW+eRkeOfyWJF10SXjz11TLmw8J6yxMr7NdEiwWDmzJncc889uFwuXnvtNaKiAtPTo8IvEkSKr4k+OaZc8kzuEotyTpEiHiJrossXaYX7c020SDA4ceIE999/P2+++SadO3fm7bffpmHDhgH7+Sr8ImfB7bZk5uaVPqacfeqEsdImkxW9NttPk8W8WRNd4Qy7vENtTbRIsLDW8u233/LXv/6VJ554gujowJZiFX4JayWtiS4+plzqWujik8mKXesPpa2JrlBSl7fWRIuEDGstb775JgMHDiQ+Pp61a9dSrlw5R7Ko8EvQyHPbU8eUT9mru+zlVb+fTJZ/399roksbh9aaaBEBOHDgAHfeeScffvgh6enp3HfffY4VfVDhl7NQfE10eql7cp/aBV60y7v4ZLJAr4kue6vPkieIFbyG1kSLiDe++OILbrnlFg4cOMCUKVMYPny405FU+MNddq77lAliJa6FLl6Uy5pMlp3r9zXRJe2z/bv9t7UmWkSC3Ouvv86QIUNo3rw5CxcuJCkpyelIgAp/yFmwbje/7kvzejJZsK+JrhBz8nu1JlpEwskVV1zB0KFDef7554mPj3c6TiEV/hDy095jPPBO8hl9zzmtiS6jy1vd3CIip5o7dy4fffQRr776Ks2aNeOVV15xOtIpVPhDSMpvRwC4pH5lerapW/L66YJirTXRIiIBk5GRwejRo3n55Zdp3749R48e9fnhOr6iwh9CNuw+BsCNl9Th7i5NHE4jIiIAGzduZNCgQfzwww+MHj2acePGERsb63SsUqnwh5D1u48C0LpuZYeTiIgIQE5ODjfccAMnTpxg0aJFXH/99U5HOi0V/hCR57b8uCe/xd+6boLDaUREItuxY8eoWLEiMTExzJw5k0aNGlGnTh2nY3lF65xCxJbU42TmuKlftTxVKgRvF5KISLhbuXIlbdq0Yfz48QB06tQpZIo+qPCHjJPd/Grti4g4we12M2HCBC6//HIArrnmGocTnR119YeIDbvyu/kv0vi+iEjA7dmzh9tuu43PPvuMAQMGMH369KCdtX86KvwhorDFX08tfhGRQNu+fTurVq3i1Vdf5a677grpZdIq/CHAWlu4lE8tfhGRwMjOzmbx4sX06tWLjh07sn379pBt5RelMf4QsONQBmmZudSoFEfNBOdOdBIRiRSbNm2ic+fO9O7dmx9++AEgLIo+qPCHBE3sExEJnLfffpukpCQ2b97MnDlzuPjii52O5FMq/CFgg6fwq5tfRMS/7rvvPm699VYSExNJSUmhT58+TkfyORX+ELB+lzbuEREJhLZt2/LEE0+wdOlSGjRo4HQcv9DkviCXP7HP0+Kvpxa/iIgvWWuZOnUq1apV49Zbb+Wuu+5yOpLfqcUf5PanZXHgeDYJ5aKpX7W803FERMLGgQMH6NmzJ6NGjWLRokVOxwkYFf4gt37XyYN5QnndqIhIMPniiy9o06YN//3vf5k6dSpvv/2205ECRl39Qa5w/b427hER8YmffvqJq6++mubNm/PRRx+RmJjodKSAUos/yBW0+DW+LyJybjIyMgC44IILeOutt1i9enXEFX1Q4Q96BS1+zegXETl7c+bMoXHjxqxZswaAW2+9lfj4eIdTOUOFP4gdPpHNriMZlI9x0bh6ZP6Cioici4yMDIYPH07fvn05//zzw2b3vXOhwh/EClr7F9aphCtKE/tERM7Ehg0b6NChAy+//DIPPfQQy5cvp2nTpk7Hcpwm9wWx9Vq/LyJy1j744AP27dvH4sWL6datm9NxgoZa/EFMJ/KJiJyZI0eOkJycDMBf/vIXfvjhBxX9YtTiD2IbPDP6W2lin4jIaa1YsYLBgwfjdrvZtGkTsbGx1KpVy+lYQUct/iB1PCuXrQdPEOMytKhVyek4IiJBy+12M378eLp06YIxhg8++IDY2FinYwUttfiD1I97jmEttKhVidhofT4TESlJWloaN910E59++ikDBw5k+vTpVK6s4dGyqPAHqcKNezS+LyJSqvj4eM477zxee+017rzzTm1t7gU1JYOUtuoVESlZdnY2jz/+ONu2bcMYw3vvvcddd92lou8lFf4gtb5wYp9a/CIiBTZt2sRll13G+PHjWbBggdNxQpK6+oNQZk4em/YfJ8rkb94jIiLwn//8h3vvvZeYmBjmzp1L7969nY4UktTiD0K/7Esj121pUiOeCrH6bCYi8vrrr3PbbbeRlJTEunXrVPTPgapKEFq/q2DjHo3vi0hky8vLw+VyMXDgQNLS0rj//vuJjlbpOhdq8QehDdqqV0QinLWWKVOm0KFDB9LT04mPj2fUqFEq+j6gwh+E1ntm9GvHPhGJRKmpqfTo0YNRo0ZRr149srKynI4UVlT4g0xunpuf9uQX/taa0S8iEWbp0qW0adOGTz75hKlTpzJ//nyqVq3qdKywoj6TILM59QRZuW4anFeByuVjnI4jIhIw1loee+wxEhISWLRoEYmJiU5HCksq/EGmYP1+a3Xzi0iE2L59OwkJCVStWpXZs2dTtWpVKlas6HSssKWu/iBzcsc+dfOLSPibPXs2iYmJjBw5EoD69eur6PuZCn+QWb9bR/GKSPjLyMjgnnvuoV+/fjRr1oy//e1vTkeKGCr8QcTttmwsaPFrYp+IhKlff/2VDh06MH36dB566CGWL19O06ZNnY4VMTTGH0R+O5TO8axcaiXEUaNSnNNxRET8Ij4+HoDFixfTrVs3h9NEHrX4g0hBN7+W8YlIuDly5AjPPPMMeXl51KlTh3Xr1qnoO0SFP4gUTuzT+L6IhJEVK1aQmJjIU089xXfffQdAVJTKj1MC/s4bY7oZY342xmwyxjxWwvMNjDFLjTHJxpjvjTHdA53RKTqKV0TCSV5eHuPGjaNLly5ERUWxbNkyOnXq5HSsiBfQwm+McQHTgOuBVsBgY0yrYpf9BXjfWpsEDAJeCmRGp1hriyzlU4tfRELfkCFDGDt2LP379yc5OZlLL73U6UhC4Cf3dQA2WWu3ABhj3gV6ARuLXGOBgspXGdgd0IQO2Xssk0MnsqlSIYZ6Vco7HUdE5KxZazHGMGTIEC6//HLuuOMOjDFOxxKPQBf+esCOIvd3AsU/Aj4J/NcYMwKoCFwTmGjOKjiKt3XdBP0PIiIhKSsrizFjxgAwadIkOnXqpK79IBToMf6SKpotdn8w8Ka1tj7QHfi3MeaUnMaYocaY1caY1ampqX6IGlgF4/tavy8ioejXX3/lsssuY/LkyeTk5GBt8T/tEiwCXfh3AucXuV+fU7vy7wLeB7DWrgDKAdWLv5C1doa1tr21tn2NGjX8FDdwCsb3W2urXhEJMf/+979p27YtW7duZe7cufzf//2fei6DWKAL/yqguTGmsTEmlvzJewuKXfMbcDWAMeZC8gt/6DfpT2PDbh3OIyKhZ+fOnQwbNoykpCTWrVtH7969nY4kpxHQMX5rba4x5n7gY8AFvGGt3WCMeRpYba1dAIwGXjXG/C/5wwC32zDvMzp4PIs9RzOpGOuicTUdTiEiwW/r1q00btyY+vXr89VXX5GYmEh0tDaDDQUBX8dvrV1krW1hrW1qrf2H57EnPEUfa+1Ga21na20ba22itfa/gc4YaAXd/BfWSSAqSt1jIhK8rLVMnjyZli1b8s477wDQvn17Ff0Qov9SQaBgq14dxSsiwSw1NZXbb7+dRYsW0aNHD6677jqnI8lZ0J6JQaBwYp/G90UkSH3xxRe0adOGTz/9lKlTpzJ//nyqVavmdCw5C2rxB4ENu3Q4j4gEt0OHDpGQkMCiRYtITEx0Oo6cA7X4HZaWmcO2g+nEuqJoXive6TgiIoW2b9/O+++/D8BNN93E999/r6IfBlT4HbbR083fsnYlYlz6zyEiwWH27NkkJiZy3333kZaWBkBsbKzDqcQXVGkctl4H84hIEMnIyOCee+6hX79+tGjRgm+//ZZKlSo5HUt8SGP8Dju5cY/G90XEWVlZWXTs2JHvv/+eRx55hL///e9q5YchFX6HbdilGf0iEhzi4uL405/+xMUXX6ylemFMXf0OyszJY1PqcVxRhgvrqPCLSOAdPnyYgQMH8tlnnwEwevRoFf0wp8LvoJ/2ppHntjSrEU+5GJfTcUQkwnzzzTckJiYyZ84cNm3a5HQcCRAVfget36WDeUQk8PLy8hg3bhxdu3YlOjqa5cuXM2zYMKdjSYCo8DtIR/GKiBPmzJnD2LFj6d+/P2vXrqVDhw5OR5IA0uQ+B+koXhEJpNTUVGrUqEG/fv1YvHgxf/zjHzFGB4NFGrX4HZKT5+anPfmbYrRS4RcRP8rKymLUqFG0bNmS3377DWMM3bp1U9GPUGrxO2TT/uNk57lpVK0CCeVinI4jImHql19+YdCgQSQnJ3P//fdTs2ZNpyOJw1T4HbJeB/OIiJ/9+9//5t577yUuLo558+bRq1cvpyNJEFDhd8jJiX3q5hcR//j0009p164d//nPfzj//POdjiNBQoXfIdqqV0T8Yc2aNZQrV47WrVvzyiuvEBMTQ3S0/tTLSZrc5wC32xaeyqcZ/SLiC263m0mTJtGpUydGjx4NQPny5VX05RT6jXDAtoMnOJGdR53K5ageH+d0HBEJcfv37+eOO+5g0aJF9OrVi9dff93pSBLEVPgdsF6tfRHxkZ9++omrrrqKQ4cO8eKLLzJ8+HAt05MynVHhN8a0BLoA1YA3rbX7jDHnAwetten+CBiONmhGv4j4SJMmTbjyyit55JFHaNOmjdNxJAR4NcZvjIkxxvwb2AjMAMYB9TxPvwj8xT/xwtMGtfhF5Bxs27aNgQMHcvjwYWJjY3n77bdV9MVr3k7u+zvQExgCNASK9iMtAv7o41xhy1rLes+M/ou0R7+InKFZs2aRmJjIkiVLWL9+vdNxJAR5W/hvAf5qrX0D2F3suS1AY5+mCmO7j2ZyJD2H8yrGUqdyOafjiEiISE9PZ9iwYfTv35+WLVuSnJxMly5dnI4lIcjbwl8DKOujpSqYl4oexasJOCLirQcffJAZM2bw6KOPsmzZMpo0aeJ0JAlR3k7u2w78D/B5Cc+1B371WaIwp4l9IuItay0nTpwgPj6ev/3tb/Tt25drr73W6VgS4rwt/P8BxhpjNgEfeh6zxphOwIPkT/YTLxRM7LtIW/WKSBkOHz7MkCFDOHToEJ988gl16tShTp06TseSMOBtV/944DPgA+CA57GlwDLgS+Cfvo8WntZrq14ROY3ly5eTmJjI/Pnzuf766zUsKD7lVYvfWpsL9DHGXEv+DP6awEFgibX2Yz/mCyupaVnsO5ZFfFw0Dc+r4HQcEQkyeXl5jB8/nieffJKGDRuyfPlyOnTo4HQsCTNeFX5jTE3yN+n5BPik2HNRQHVr7X4/5AsrBQfztKqTQFSUPsGLyO8dP36c1157jQEDBvDKK6+QkKAhQfE9b8f49wCdgO9KeC7J87jLV6HClY7iFZGSfP7553Tu3JnKlSvz3XffUaNGDXXvi994O8Zf1m9gNOD2QZawV9Div0jj+yICZGVlMWrUKK6++mqmTJkCQM2aNVX0xa9KbfEbY+KBok3T6saYusUuKw/cDOzzQ7aws36XWvwiku+XX35h0KBBJCcnM2LECB544AGnI0mEKKurfzTwhOe25eQyvuIM8A9fhgpHRzNy+O1QOnHRUTSrEe90HBFx0Pz587nllluIi4tj/vz59OzZ0+lIEkHKKvwLgb3kF/aXgInA1mLXZAEbrbUljf1LERs94/sX1K5EtMvbERYRCUfNmjWjS5cuvPrqq9SvX9/pOBJhSi381to1wBoAY4wFZltrD5R2vZStYHy/tQ7mEYlIa9asYe7cuTzzzDO0bt2axYsXOx1JIpRXTU9r7XQV/XNTuGOfJvaJRBS3282kSZPo1KkTb731FqmpqU5Hkgjn7XI+jDEtgDuAlpx6KI+11t7gy2DhpujhPCISGfbv38/tt9/O4sWL6d27N6+//jrnnXee07Ekwnm7gU874GvyZ+83AH4GziN/B7/dwG/+ChgOMrLz2Jx6HFeUoWXtSk7HEZEAyMvL48orr2Tz5s1MmzaNe++9V8v0JCh42+KfAHwEDAaygVuttWuNMd2B14BH/ZQvLPy49xhuCxfUiqdcjPY5EglnOTk5uFwuXC4XL7zwAnXr1uWSSy5xOpZIIW+nl7cB3uTkRj0uAGvtIvJP5pvo82RhREfxikSGbdu20bVrV6ZOnQpAt27dVPQl6Hhb+OOANGutGzgE1Cry3EZAv9ll0FG8IuHvgw8+IDExkY0bN1K3bvG9zkSCh7eFfwtQ8Ju8Abi9yHO3Ajqgpww6ilckfKWnpzN06FAGDBjABRdcQEpKCgMGDHA6lkipvC38i4FrPbfHA72MMYeMMfuBPwNT/REuHGTnuvl5bxoArTSjXyTsrF27ljfeeINHH32Ur7/+msaNGzsdSaRMXk3us9Y+XuT2EmNMF6AfUAFYYq1d4Kd8Ie/X/Wnk5FmaVK9IfJzXqydFJIhZa1m1ahUdOnTg8ssv55dffqFJkyZOxxLxylntHWutXWmtfchaO1xFv2wbPAfzqLUvEh4OHTpE37596dixI2vWrAFQ0ZeQcs6bxhtjWhlj3vFFmHBUML5/kbbqFQl5y5YtIzExkQ8//JDnnnuOpKQkpyOJnLEyC7/Jd4kx5kZjzIXFnrvYGPMB8D1woz9DhrKCGf3asU8ktD377LNcccUVxMTE8M033zB69GiionTgloSeUn9rjTG1geVAMjAfWG+MecsYE22MedHz+I3kn9zXLBBhQ02e2xaeyqcZ/SKhLS4ujkGDBpGcnMz//M//OB1H5KyVNdtsApAI/ANYCzQGHgG+BDoB7wEPW2t3+jtkqNp64AQZOXnUq1Ke8yrGOh1HRM7QwoULcbvd9OzZk5EjRwJo210JeWUV/muBp621EwoeMMasBz4GXrHWDvd3uFBXcBSvJvaJhJasrCweffRRpkyZwh/+8Ad69Oihgi9ho6wBqprkd/UXVXBfk/m8UHAin47iFQkdv/zyC506dWLKlCk88MADLF68WEVfwkpZLX4XkFXssYL7J/wTJ7xoq16R0LJt2zbatm1LuXLlWLBgAT169HA6kojPnW5HmeuMMUUn7kUBFuhmjLmg6IXW2pm+DhfKrLWFLX5N7BMJbm63m6ioKBo1asTf/vY3br75ZurVq+d0LBG/OF3hf7qUx58pdt8CKvxF7DycwbHMXKrHx1IrIc7pOCJSitWrV3PnnXfyzjvv0Lp1ax5++GGnI4n4VVmF/8IynpPTODmxr7LGB0WCkNvtZvLkyYwZM4batWtz/PhxpyOJBESphd9a+7M/fqAxphswhfw5BK8VXTVQ5JoBwJPk9ySss9be7I8s/rTes1XvRZrRLxJ09u/fz5///GeWLFlC7969ef311znvvPOcjiUSEAE9NcYY4wKmkb9UcCewyhizwFq7scg1zYExQGdr7WFjTM1AZvSVDdqqVyRovfjiiyxdupRp06Zx7733qldOIkqg95vsAGyy1m6x1mYD7wK9il0zBJhmrT0MYK3dH+CMPrFeW/WKBJWcnBy2bNkCwNixY1m7di3Dhw9X0ZeIE+jCXw/YUeT+Ts9jRbUAWhhjlhtjVnqGBk5hjBlqjFltjFmdmprqp7hnZ/+xTFLTsqhULpoG51VwOo5IxNu6dStdu3blqquuIj09nbi4OFq1auV0LBFHBLrwl/TR2ha7Hw00B/4ADAZeM8ZUOeWbrJ1hrW1vrW1fo0YNnwc9FwXr91vVSVBrQsRh77//PomJiWzcuJGJEydSoYI+jEtkC3Th3wmcX+R+fWB3CdfMt9bmWGu3Aj+T/0EgZBTu2KfxfRHHZGZmMmTIEAYOHEirVq1ISUlhwIABTscScdwZF35jTDNjzKXGmLP52LwKaG6MaWyMiQUGAQuKXTMPuNLzs6qT3/W/5Sx+lmO0Y5+I82JiYti2bRtjxozhq6++onHjxk5HEgkKXhd+Y8xdxpid5LfAvwEu8Dw+yxhzjzevYa3NBe4n/6CfH4H3rbUbjDFPG2N6ei77GDhojNkILCX/BMCDXv8bBYH1u7Vjn4gTrLW8+uqr7N69G5fLxeLFixk3bhwxMTFORxMJGl4VfmPM7cAM4HPgz/x+rP5bYKC3P9Bau8ha28Ja29Ra+w/PY09Yaxd4bltr7YPW2lbW2outte96+9rB4Eh6NjsPZ1AuJoom1Ss6HUckYhw6dIi+ffsydOhQXn75ZQCiowO6YlkkJHjb4n8YmGKt/ROnnsz3I57Wv8BGTzf/hXUSiHYFegqFSGRatmwZiYmJLFy4kOeff56nnnrK6UgiQcvbj8NNgY9KeS4NqOqbOKHvZDe/xvdFAmHOnDn079+fxo0b880339C+fXunI4kENW+bpIf4/Wz8oloAe3wTJ/QVTuzT+L5IQFx55ZU88MADrF27VkVfxAveFv6PgL8YY4oWf+tZXz8KmO/zZCFKR/GK+N+HH35It27dyM7OpmrVqkyePJmEBPWyiXjD28I/1nPtRmAh+ZvuPO+5HwNoQA04kZXLlgMniI4ytKgd73QckbCTlZXFyJEj6dmzJ/v27ePAgQNORxIJOV4Vfs9++W2BqUANYBdwHvAWcGnBvvqR7qe9x7AWWtSqRFy0y+k4ImHl559/pmPHjkydOpWRI0eycuVK6tat63QskZDj9VoXa+0R8lv+Y/0XJ7QVHMWriX0ivmWt5fbbb2fHjh18+OGH3HjjjU5HEglZXhV+Y8w44F/W2p/8nCekaateEd86duwYUVFRxMfH8+abbxIfH0+9esXP9RKRM+HtGP8IYIPnNLwRxpjgOhUnSGzQUbwiPrNq1Sratm3LiBEjAGjZsqWKvogPeFv4awJ/AlKBScAuY8xCY0x/Y0yc39KFkKzcPH7Zl4Yx+Zv3iMjZcbvdPP/881x22WXk5ORw9913Ox1JJKx4O7kvw1r7trX2evJP1HsMqAO8B+wzxrzqx4wh4dd9x8l1W5pUr0jFOG0TKnI29u/fT/fu3Xn44Yfp2bMnKSkpdO7c2elYImHljPeUtdbus9ZOsta2A64mf+e+O32eLMRo/b7IuUtPT+f777/n5ZdfZtasWVStqk1BRXztjJumnq793sCtwHXkH9hT2na+EaNgq14dxStyZnJycnj77bf585//TKNGjdi8eTPly5d3OpZI2DqTY3n/YIx5HdhH/kE9tYCHgLrW2p5lfnMEODmxTy1+EW9t3bqVLl26cMcdd/DZZ58BqOiL+Jm3y/l+A+oBO4Bp5C/t+9mfwUJJntui1moCAAAgAElEQVTy4x7N6Bc5E++99x5Dhw7FGMN7773HNddc43QkkYjgbVf/J+QX+y/9GSZUbUk9TmaOm/pVy1OlQqzTcUSC3uOPP8748ePp2LEj77zzDo0aNXI6kkjE8KrwW2vv8neQUKajeEXOTEHr/qmnniImJsbhNCKRpdTCb4zpAKy31qZ7bpfJWvudT5OFkIKtenUUr0jJrLW89NJLHD58mL/85S9cddVVXHXVVU7HEolIZbX4VwIdge88t20p1xnPcxF7Ks2G3dqqV6Q0hw4d4q677mLevHnccMMN5OXl4XJF7J8LEceVVfivB3703O5O6YU/orndlg06nEekRMuWLePmm29m7969vPDCC4waNYqoqDPePkREfKjUwm+t/bjI7SWBiRN6dhxOJy0rlxqV4qiZUM7pOCJBIzU1leuuu466devyzTff0L59e6cjiQheruM3xmw0xlxcynOtjDEbfRsrdOhgHpHfO3o0f+irRo0azJkzh7Vr16roiwQRb/vcLgBK21WjAtDSN3FCT+FRvJrYJ8KCBQto2rQps2fPBqBbt24kJOhDsUgwOZPBttLG+C8BjvogS0gqaPFrq16JZJmZmTzwwAP06tWLBg0acPHFJXYQikgQKGs53whghOeuBWYZY7KKXVYeqAvM8k+84Gat1eE8EvF++uknBg0axLp16xg1ahQTJkwgLk6ndYsEq7Jm9e8G1nhuNwN+Bg4WuyYL2Ai87PtowW/fsSwOnsgmoVw09atqf3GJTKtWrWLXrl0sXLiQG264wek4InIaZc3qnw3MBjDGAIy11m4JUK6QsGH3yda+5z0SiQjHjh1j9erVXHXVVdx2223ceOONOkJXJER4u2XvYH8HCUWFO/ZpfF8iyKpVqxg0aBCpqals376dqlWrquiLhJCyxvgfIf9gnr2e22Wx1trnfBst+GnHPokkbrebF154gccff5y6deuyePFiFXyREFRWi38C8AWw13O7LBaIwMKvNfwSGXJzc+nRowdLlizhpptu4rXXXlPRFwlRZRX+8tbagln8mrlWzOET2ew6kkH5GBeNq8c7HUfEr6Kjo0lKSqJXr14MGzZMc1pEQlhZk/uySrot+Qpa+63qJuCK0h9BCT85OTn89a9/pVevXnTq1Ilx48Y5HUlEfMCryX3GmCZAgrU2xXM/DngMuAj42Fr7mv8iBqf1hTP61c0v4WfLli0MHjyY7777jri4ODp16uR0JBHxEa8KP/AS+ev1Uzz3/w78L/AL0McY47LWTvdDvqClrXolXL333nsMHToUYwzvv/8+/fv3dzqSiPiQt1v2JgJfAZj8wb3bgcetta3Jn/h3j1/SBbGNRbr6RcLFwoULGTRoEK1btyYlJUVFXyQMeVv4qwAHPLcTgWrA+577nwBNfZwrqB3PymXLgRPEuAwtalVyOo7IOcvMzATg+uuvZ8aMGXz55Zc0atTI2VAi4hfeFv79QBPP7WuBrdba7Z77FYE8XwcLZj/uyW/tt6xdidjoMznnSCS4WGuZNm0aLVq0YM+ePbhcLoYMGUJMTIzT0UTET7wd418I/MMY0wIYCrxR5LnWwFZfBwtmhQfz1NH4voSuQ4cOcddddzFv3jy6d+9OdLS3fw5EJJR5+3/6Y0AlYCDwKfBMkecGAJ/7OFdQ01a9Euq+/vprbr75Zvbt28ekSZMYOXIkUVHqvRKJBN7u1X8MuK2U5/7Hp4lCQMFWva00o19C1LRp0yhXrhwrVqygXbt2TscRkQA6o749Y0wloANwHvlH9K6y1qb5I1iwyszJ49f9x4kycGEdTeyT0LFz505ycnJo3Lgx06dPJyoqikqV9DssEmm87tszxvwF2AP8F3iP/C7/PcaYsX7KFpR+2ZdGntvStEY8FWI1JiqhYf78+bRp04Y777wTgMqVK6voi0Qorwq/MeY+4GlgLtAdSAKu99x/2hhzr98SBpmC8X3t2CehIDMzkxEjRtC7d28aNmzI9OkRtc+WiJTA2ybr/cBL1tr7izy2DvjYGHMUGAG87OtwwWi9juKVELFjxw569OjBunXrGDVqFBMmTCAuLs7pWCLiMG8LfxPggVKemw/c7Zs4we/kUbwq/BLcqlWrRtWqVVm4cCE33HCD03FEJEh4O8Z/CGhZynMtPc+HvZw8d+HmPdqqV4LRsWPHePjhhzl+/DgVKlTg888/V9EXkd/xtvDPI38Dn/6myEHcxpg+5B/YM88f4YLN5tTjZOe6aXBeBSqX185mEly+++47kpKSmDx5MkuXLgWgyP+uIiKA94X/MeAn8mfzpxtjthtj0oFZwM+e58PeBk3skyDkdrt57rnn6Ny5M7m5uXz11Vf06NHD6VgiEqS83cDnqDHmMqAP0IX8dfyHgC+B+dbaiNirXxP7JBiNGTOGiRMn0rdvX1599VWqVq3qdCQRCWJeL0T3FPdZnq+IdHJin1r84ry8vDxcLhf33nsvzZo14+6771bXvoicVpld/caYQcaYlcaYA8aYTcaYfxhjInLXGrfbslEz+iUIZGdn8+ijj9KnTx+stTRq1IghQ4ao6IuIV0ot/MaY/sBMoDawHEgnfyz/mdK+J5xtP5TO8axcaiXEUaOS1kKLM7Zs2UKXLl2YOHEidevWJScnx+lIIhJiymrxPwh8BDS31vay1l4CPAuMMMZE3DFeBQfzqLUvTnn33XdJSkril19+YdasWbzyyivExsY6HUtEQkxZBbwl8LK1tmiTYipQHmjo11RBqPAoXo3viwPS0tJ48MEHueiii0hJSaFv375ORxKREFXWeH0V4ECxx1I9/6wKbPVLoiBV2OLXjH4JoJ9++olmzZpRqVIlvvzySxo3bkx0dEROsxERHzldl709w8fDkrVWM/oloKy1vPjiiyQmJvLcc88B0Lx5cxV9ETlnpyv8y40x2QVfQIbn8W+LPm6MyfL2BxpjuhljfvasEih14x9jTD9jjDXGtPf2tf1lz9FMDp3IpkqFGOpVKe90HAlzBw8epE+fPowYMYKrr76au++OmKMwRCQAymo+POvrH2aMcQHTgGuBncAqY8wCa+3GYtdVIv9QoG99neFsFG3ta8mU+NOKFSsYMGAA+/btY9KkSYwaNUq/cyLiU6UWfmvtGD/8vA7AJmvtFgBjzLtAL2Bjsev+DkwEHvJDhjO2fpdnxz7N6Bc/i42NpXLlysybN4927do5HUdEwlCgl+XVA3YUub/T81ghY0wScL61dmFZL2SMGWqMWW2MWZ2amlrWpeessMWviX3iBzt37uT//u//AGjXrh3ff/+9ir6I+E2gC39JfZaFEwU9+wNMBkaf7oWstTOste2tte1r1Kjhw4inOrmGXxP7xLfmz59PmzZtePzxx9m1axcAUVERt02GiARQoP/C7ATOL3K/PrC7yP1KwEXAF8aYbUBHYIGTE/wOHs9iz9FMKsa6aFytolMxJMxkZmYyYsQIevfuTaNGjVi7di316tU7/TeKiJyjQK8NWgU0N8Y0BnYBg4CbC5601h4FqhfcN8Z8ATxkrV0d4JyFCrr5W9VNICpKk6zk3Flrueaaa1i+fDmjRo1iwoQJxMVpG2gRCYyAtvittbnA/cDHwI/A+9baDcaYp40xPQOZxVvrtVWv+Ii1FmstxhhGjBjBwoULmTx5soq+iARUwHcDsdYuAhYVe+yJUq79QyAylWXDLm3cI+fu6NGjDBs2jKuvvpohQ4YwcOBApyOJSITyusVvjKlljBlnjFlmjNlojGnleXx4MGyy4y86nEfO1bfffktSUhKzZs3i2LFjTscRkQjnVeE3xlwA/ADcS/7xvC2Bcp6nWwKj/JLOYccyc9h2MJ1YVxTNa8U7HUdCjNvt5tlnn+Xyyy/H7Xbz9ddfM3r0aResiIj4lbct/ufJP5SnMdCd3y/LWw508nGuoPCjZ2LfBXUqEePSEis5MytXruSxxx6jT58+pKSk0KlTWP5vIiIhxtsx/iuAW621Rzzb7ha1F6jj21jBYb0O5pGz8Ntvv9GgQQMuu+wyvvnmGzp27Khtd0UkaJxJMzavlMercfLwnrCyYZfG98V72dnZPPLIIzRr1ozVq/NXoHbq1ElFX0SCirct/tXAbUBJ2+j2BVb6LFEQ0VG84q0tW7YwaNAgVq1axT333EPr1q2djiQiUiJvC/8/gCXGmA+Bt8nfZrerMWYYMAC40k/5HJOZk8em1OO4ogwX1lHhl9K9++67DB06FJfLxaxZs+jbt6/TkURESuVV4bfWfmqMGQD8E7jB8/Ak8rfbHWCtXe6nfI75aW8aeW5Ly1qVKBdTfFqDyEmbNm3i4osvZubMmTRs2NDpOCIiZfJ6jN9aOwdoCFwCXAMkAQ2stfP8lM1R63fpYB4p3bp16/jiiy8AGDNmDF9++aWKvoiEhDPauc9aa4H1fsoSVAo37tFRvFKEtZZp06YxevRoWrVqxdq1a3G51CMkIqHDq8Lv6eYvk7X2/XOPEzwKJvZdpBa/eBw8eJA777yTBQsW0L17d958803N2BeRkONti//dUh63RW6HTeHPyXPz0540IP9UPpHdu3fToUMH9u/fz+TJkxk5cqSKvoiEJG8L/4UlPFYNuBHoB/zZZ4mCwK/7jpOd56ZRtQpUKhfjdBwJAnXq1GHgwIHccssttG3b1uk4IiJnzdtZ/T+X8tQ3xpg88vfwX+GzVA7TwTwCsGPHDu655x6mTJlCs2bNeOGFF5yOJCJyznyxAf1SoKcPXidoFG7cU0/d/JFq3rx5tGnThq+++oqffy7tc6+ISOjxReFvT/6JfWGjoMV/kVr8ESczM5P77ruPPn360KRJE9auXcsNN9xw+m8UEQkR3s7qf6SEh2OBi4A+wKu+DOUkt9tqq94INnHiRF566SUefPBBxo8fT2xsrNORRER8ytvJfRNKeCwP2AVMBp7yWSKHbT14gvTsPOpULke1+Din40gAWGs5dOgQ1apV46GHHqJz585cffXVTscSEfELbwt/+RIey7HWun0ZJhiotR9Zjh49yrBhw0hOTmbt2rVUrFhRRV9Ewtppx/iNMbHAk8BF1tqsIl9hV/RBR/FGkm+//ZakpCRmzZrF7bffTrly5ZyOJCLid6ct/NbabGAkUNH/cZxXuGOftuoNW263m2effZbLL78ct9vN119/zZgxY7T1rohEBG9n9a8DWvkzSDCw1rJ+tw7nCXd5eXnMnz+fPn36kJKSQqdOnZyOJCISMN6O8T8C/MsYs8la+6k/Azlp15EMjqTncF7FWOpUVrdvuPnkk09ISkqievXqLFmyhEqVKmnbXRGJON62+N8AqgAfG2PSjDG/GmN+KfIVFjucFJ3Yp4IQPrKzs3n44Ye57rrreOaZZwBISNB/YxGJTN62+Nfw+wN5wpIm9oWfzZs3M3jwYFatWsU999zD+PHjnY4kIuIob/fqH+TvIMFgfeHEPo3vh4PPP/+c3r1743K5mDVrFn379nU6koiI40rt6jfGbDHGtAlkGKfpcJ7wctFFF3HttdeSkpKioi8i4lHWGH8jIGK2rktNy2LfsSzi46JpeF4Fp+PIWUpJSeGOO+4gNzeXmjVrMnv2bBo2bOh0LBGRoOGLQ3rCQkFrv1XdBKKiNOkr1FhrmTp1Kpdeein//e9/2bZtm9ORRESC0ukKf9hP6CugrXpD14EDB+jVqxcjR47kuuuuY926dTRr1szpWCIiQel0k/ueMsYc8OJ1rLX2z74I5JT1u3QUb6jq168fK1asYMqUKYwYMULL9EREynC6wp8IZHnxOiHfM1DY4teM/pCQm5tLXl4ecXFxTJ48GYCkpCSHU4mIBL/TFf7e1trvApLEQUczcvjtUDpx0VE0qxHvdBw5jR07dnDzzTdzySWXMG3aNBV8EZEzoMl9wEZPa/+COglEu/SWBLN58+bRpk0bUlJSuOyyy5yOIyISclTlKLp+X938wSojI4P77ruPPn360KRJE5KTk7nlllucjiUiEnJU+NHEvlCwa9cu/vWvfzF69Gi++eYbzdoXETlLpY7xW2sj5kOBlvIFJ2stn332GVdffTXNmjVj06ZN1KpVy+lYIiIhLWKKe2nSs3PZnHocV5ShZe1KTscRj6NHjzJ48GCuvfZaFi5cCKCiLyLiA96ezhe2ftyThtvCBbXiKRfjcjqOACtXrmTw4MHs2LGDcePGccMNNzgdSUQkbER8i3+jDuYJKtOmTaNLly5Ya/n6668ZM2YMUVER/2sqIuIzEf8Xdf0uHcUbTBo2bMhNN91ESkoKnTp1cjqOiEjYifjCv2GPZ0Z/PbX4nbJkyRKmTZsGwI033sh7771HlSpVHE4lIhKeIrrwZ+e6+XlvGsbAhXXU4g+07OxsHnroIa6//npef/11cnJynI4kIhL2Irrw/7IvjZw8S+NqFYmPi/h5jgG1adMmOnfuzAsvvMDw4cNZvnw5MTExTscSEQl7EV3tCrbqbaX1+wF15MgROnTogLWWOXPm0KdPH6cjiYhEjIgu/Ot3a3w/kHJzc4mOjqZKlSpMnTqVrl270qBBA6djiYhElIju6i/YsU9b9fpfSkoKF198MUuWLAHg1ltvVdEXEXFAxBb+PLct7OrXVr3+Y61l6tSpXHrppRw7dowKFSo4HUlEJKJFbOHfeuA4GTl51KtSnqoVY52OE5YOHDhAr169GDlyJH/84x9Zt24dXbt2dTqWiEhEi9jCv0ET+/xuwYIFfPzxx0yZMoX58+dTvXp1pyOJiES8iJ3cp6N4/SM3N5cNGzbQpk0b7rjjDrp27aojdEVEgkjEtvi1Va/v/fbbb1x55ZV06dKF/fv3Y4xR0RcRCTIRWfittWzQ4Tw+NXfuXBITE1m3bh0vv/wyNWvWdDqSiIiUICIL/87DGRzLzKV6fCy1EuKcjhPS3G43w4cP56abbqJp06YkJydzyy23OB1LRERKEZGFv2hr3xjjcJrQFhUVRW5uLqNHj2b58uU0bdrU6UgiIlKGiJzcVzC+r/X7Z8day2uvvUb79u1JSkpi+vTp+gAlIhIiAt7iN8Z0M8b8bIzZZIx5rITnHzTGbDTGfG+M+cwY09DXGbRV79k7cuQIAwcOZOjQoUyfPh1ARV9EJIQEtPAbY1zANOB6oBUw2BjTqthlyUB7a+0lwCxgoq9zbNCOfWdlxYoVJCYmMnfuXCZMmMBLL73kdCQRETlDge7q7wBsstZuATDGvAv0AjYWXGCtXVrk+pXArb4MsP9YJqlpWVQqF02D87R9rLe++OILrrnmGs4//3y+/vprOnbs6HQkERE5C4Hu6q8H7Chyf6fnsdLcBSz2ZYCirX11UZ+etRaAzp07M3bsWJKTk1X0RURCWKALf0mV1pZ4oTG3Au2B50p5fqgxZrUxZnVqaqrXAQp27NP6/dNbvHgx7dq14+DBg8TExPDUU09RpUoVp2OJiMg5CHTh3wmcX+R+fWB38YuMMdcAY4Ge1tqskl7IWjvDWtveWtu+Ro0aXgc4ObFP4/ulyc7OZvTo0XTv3p3c3FyOHDnidCQREfGRQBf+VUBzY0xjY0wsMAhYUPQCY0wSMJ38or/f1wFOdvWrxV+STZs20blzZyZNmsTw4cP59ttvtTZfRCSMBHRyn7U21xhzP/Ax4ALesNZuMMY8Day21i4gv2s/HvjAMwb/m7W2py9+/pH0bHYezqBcTBRNqlf0xUuGnccff5zNmzczZ84c+vTp43QcERHxsYBv4GOtXQQsKvbYE0VuX+Ovn13Q2r+wTgLRrojctLBEx48f5/jx49SuXZsXX3yRzMxMGjRo4HQsERHxg4iqfie36tX4foHk5GTatWvHoEGDsNZSs2ZNFX0RkTAWUYW/8Cheje9jrWXKlCl07NiREydO8NRTT2l5o4hIBIiovfo3aKteAA4dOsTtt9/Ohx9+SI8ePXjjjTeoXr2607FERCQAIqbFfyIrly0HThAdZWheK97pOI6Kjo5m8+bNTJ06lfnz56voi4hEkIhp8f+45xjWQovalYiLdjkdJ+Byc3OZNm0aw4YNIyEhgZSUFGJiYpyOJSIiARYxLf5IPphn+/btXHHFFYwaNYpZs2YBqOiLiESoiCn8BVv1Rtr4/uzZs0lMTOSHH35g5syZ3HqrT888EhGREBMxhb+gxR9JW/U+99xz9OvXj+bNm5OcnMzgwYOdjiQiIg6LiDH+rNw8ftmXhjFwQe3IKfw9e/bk8OHDPPnkk8TGxjodR0REgkBEtPh/2XucXLelSfWKVIwL38861lpmzJjBnXfeibWWli1bMm7cOBV9EREpFBGF/+SOfeE7vn/kyBEGDhzIsGHD2LFjBxkZGU5HEhGRIBQRhT/cj+JdsWIFiYmJzJ07lwkTJvDxxx9ToUIFp2OJiEgQCt9+7yLCeavejIwM+vTpQ4UKFVi2bBmXXnqp05FERCSIhX3hz81z89Pe/MLfKozW8KemplKtWjXKly/PggULaNmyJZUrh98HGxER8a2w7+rfcuAEmTlu6lctT5UK4THJbfHixbRu3ZoXXngBgA4dOqjoi4iIV8K+8IfTUbzZ2dmMHj2a7t27U6dOHW688UanI4mISIgJ+67+cBnf37RpE4MGDWLNmjXcd999PP/885QrV87pWCIiEmIioPCHx1a9e/bs4bfffmPu3Ln07t3b6TgiIhKiwrqr3+22bAzhw3mOHz/O+++/D0CXLl3YunWrir6IiJyTsC78Ow6nk5aVS41KcdRMCK1u8bVr19K2bVtuvvlmtmzZAkDFihUdTiUiIqEurAt/4cE8IdTat9byz3/+k44dO5Kens5nn31GkyZNnI4lIiJhIqzH+AvG90Nlq15rLQMGDGDWrFn07NmTN954g2rVqjkdS0REwkh4F/4QO4rXGMN1113HFVdcwX333YcxxulIIiISZsK28Ftr2RACLf7c3FyefPJJWrduzeDBgxkyZIjTkUREJIyF7Rj/vmNZHDyRTUK5aOpXLe90nBJt376dK664gn/84x+sXLnS6TgiIhIBwrbFX3T9fjB2mc+ePZu7776bvLw8Zs6cyeDBg52OJCIiESBsW/wbgnj9/po1a+jXrx/NmzcnOTlZRV9ERAImbAv/+t3Bt2NfWloaAO3ateODDz5g2bJlNG3a1OFUIiISScK28AfTjn3WWmbMmEHDhg1Zt24dAP369SM2NjxOCxQRkdARloX/0Ilsdh3JoHyMi8bV4x3NcuTIEQYMGMCwYcNo3749tWrVcjSPiIhEtrAs/AVH8baqm4AryrmJfStWrCAxMZF58+bx7LPPsmTJEmrXru1YHhERkbCc1R8sE/sWLFhAVFQUy5Yt49JLL3U0i4iICIRpi79wKZ8DG/fs3r2bNWvWAPD000+TnJysoi8iIkEjLAt/4cS+AG/V+9FHH9GmTRtuvvlm8vLyiImJoXLl4FlVICIiEnaFPy0zhy0HThDjMjSvWSkgPzMrK4v//d//5cYbb6Ru3brMnz8fl8sVkJ8tIiJyJsJujP/HPflr5VvWrkRstP8/1xw8eJDrrruOtWvXMmLECCZOnEi5cuX8/nNFRETORti1+Atm9LeuE5gu9qpVq3LhhRcyb948pk6dqqIvIiJBLewK//pd/j+KNy0tjeHDh7Njxw6ioqL4z3/+Q69evfz280RERHwl7Ap/YYvfT1v1rlmzhrZt2zJ9+nSWLl3ql58hIiLiL2FV+DNz8vh1/3GiDFxY27ctfmstkydPplOnTmRkZLB06VL+9Kc/+fRniIiI+FtYFf6f96aR57Y0rRFP+VjfzqqfNGkSDz74IN27d2fdunV07drVp68vIiISCGE1q98fO/ZlZ2cTGxvLkCFDqFq1KnfccQfGOLcNsIiIyLkIqxa/L4/izc3NZezYsXTs2JHMzEwSEhK48847VfRFRCSkhVXh3+DZqrf1OW7Vu337dq644grGjRtHUlISbrfbF/FEREQcFzZd/Tl5bn7cm795T6tz6OqfPXs2d999N3l5ecycOZPBgwf7KqKIiIjjwqbwb049TnaumwbnVaBy+Zizeo3c3FyeeeYZWrRowTvvvEOTJk18nFJERMRZYVP4N5zDxj0bNmygfv36VK5cmY8++ogaNWoQE3N2Hx5ERESCWdiM8RdM7DuT8X1rLdOnT6d9+/Y89thjANStW1dFX0REwlbYFP6CFr+3S/kOHz5M//79ueeee+jatStPPvmkH9OJiIgEh7Ap/Bv3FBT+07f4k5OTSUxMZP78+UycOJHFixdTq1Ytf0cUERFxXFiM8WflujmelUuthDhqVIo77fU1atSgdu3afPDBB3To0CEACUVERIJDWLT4M3PyALiojNb+7t27GTt2LG63m/r167Ny5UoVfRERiThhUfgzsvMLf2nj+wsXLuSSSy7hn//8J+vXrwfQDnwiIhKRwqPwe1r8xY/izcrKYtSoUfTo0YP69euzZs0aLrnkEiciioiIBIXwKvzFWvwDBw5kypQpjBgxgpUrV3LBBRc4EU9ERCRohMXkvjy3pUqFGOpVKQ+A2+0mKiqKhx56iDvuuINevXo5nFBERCQ4BLzFb4zpZoz52RizyRjzWAnPxxlj3vM8/60xppE3r3tR3cocP36c2267jTFjxgBw+eWXq+iLiIgUEdDCb4xxAdOA64FWwGBjTKtil90FHLbWNgMmA89689pVTuygbdu2zJw5k4oVK/oytoiISNgw1trA/TBjOgFPWmv/6Lk/BsBaO77INR97rllhjIkG9gI1bBlBoxNqWJNxlNq1a/H222/TtWtX//6LiIiIOMgYs8Za2/5svjfQXf31gB1F7u/0PFbiNdbaXOAoUK2sF81LO8gfrrmOlJQUFX0REZEyBHpyX0mL54u35L25BmPMUGCo527Wp0s+Wl+9evVzjCdlqA4ccDpEBND77H96j/1P77H/tTzbbwx04d8JnF/kfn1gdynX7AS6+vUAAAvjSURBVPR09VcGDhV/IWvtDGAGgDFm9dl2eYh39B4Hht5n/9N77H96j/3PGLP6bL830F39q4DmxpjGxphYYBCwoNg1C4A/e273Az4va3xfREREvBfQFr+1NtcYcz/wMeAC3rDWbjDGPA2sttYuAF4H/m2M2UR+S39QIDOKiIiEs4Bv4GOtXQQsKvbYE0VuZwL9z/BlZ/ggmpRN73Fg6H32P73H/qf32P/O+j0O6HI+ERERcVZY7NUvIiIi3gmpwu+v7X7lJC/e4weNMRuNMd8bYz4zxjR0ImcoO917XOS6fsYYa4zR7Oiz4M37bIwZ4Pl93mCMmRnojKHOi78XDYwxS40xyZ6/Gd2dyBnKjDFvGGP2G2PWl/K8McZM9fw3+N4Y0/a0L2qtDYkv8icDbgaaALHAOqBVsWuGA694bg8C3nM6dyh9efkeXwlU8Ny+V++x799jz3WVgK+AlUB7p3OH2peXv8vNgWSgqud+Tadzh9KXl+/xDOBez+1WwDanc4faF9AVaAusL+X57sBi8vfA6Qh8e7rXDKUWfwdgk7V2i7U2G3gXKH4CTy/gLc/tWcDVxpiSNgSSkp32PbbWLrXWpnvuriR/Lwbxnje/xwB/ByYCmYEMF0a8eZ+HANOstYcBrLX7A5wx1HnzHlug4Lz0ypy6b4uchrX2K0rYy6aIXsC/bL6VQBVjTJ2yXjOUCr9ftvuV3/HmPS7qLvI/aYr3TvseG2OSgPOttQsDGSzMePO73AJoYYxZboxZaYzpFrB04cGb9/hJ4FZjzE7yV3ONCEy0iHKmf7cDv5zvHPhsu18pldfvnzHmVqA9cIVfE4WfMt9jY0wU+adS3h6oQGHKm9/laPK7+/9Afs/V18aYi6y1R/ycLVx48x4PBt601r7gOaTt35732O3/eBHjjOteKLX4z2S7X8ra7ldK5c17jDHmGmAs0NNamxWgbOHidO9xJeAi4AtjzDbyx+wWaILfGfP278V8a22OtXYr8DP5HwTEO968x3cB7wNYa1cA5cjfx198x6u/20WFUuHXdr/+d9r32NMNPf3/2zv7IK2rKo5/vrOUEC8iIjGNg1vtFKGpQ0OBUUYxSNZgYE2+gBJizSSNGGPRSJBKLwaolKMYNcpLQTJKMTa8BBlpGeYkMYDSLLjJ8CKBtAQSIHP649xHfvvj2WefXRbW9TmfmTvPPveee+/53d8ze3733PO7Fzf6sSbafEqOsZnVm1lPM6s2s2o8jmKEmbV4X+4KpZz/F7/Bg1WR1BN3/W87o1q2b8oZ41eAzwBI+hBu+P99RrV8+7MMuCFF9w8E6s1sV6kK7cbVb7Hd72mnzDGeAXQBlqS4yVfMbESbKd3OKHOMg1OkzHFeCQyTtBk4DtxuZvvaTuv2RZljPAmYK+k23P08NiZjzUPSInw5qmeKlZgGvAPAzObgsRNXArXA68BXmmwz7kEQBEEQVA7tydUfBEEQBMEpEoY/CIIgCCqIMPxBEARBUEGE4Q+CIAiCCiIMfxAEQRBUEGH4g6AIksamk/GKpaHNbGt8qndGzjWQND2n7/50WmWrv94qqUPqY0omb5SkiUVkhybZwa2tRwn9anJjcVzSLkkLJJXc1rREm/0lfU9S99bWNwjOBO3mPf4gaCO+hO+MlWVzWyjSAgalz3OBrwGLJL3TzOa3VgfpXe5BNNwrfBQwGLg/J/5c0mlTa/XfDKYDvwPOSjpMBfpKGpTO9WgO/fF3qR8FYnvfoN0Rhj8ISrPezGrbWomWkE7qAkDSKnxL2olAqxn+fD9NyB3AdyJsC7Zm9Fwr6Sz8AJlLgdgVMagowtUfBC1EUidJsyVtknQouZCXSfpgGXXHSFqf6tVL2iBpfE5miKQ/SDqY0nJJ/Vqiq5kdA9YDNZn2z5b0YNL7qKQtkm7N6dBN0gOStks6IulVSb+X9IFU3sDVL2khcD1wQca9XpvKGrj6Jf1M0k5JVbk+O6YxmZnJ6yXp4SR/VNKLkm5qyVgk/p4+++T6ni7pBUkHJO2VtEbSRzPl44G56evLmWs8PzMed6SxPCJph6QZ6UEjCN4SxIw/CEpTJT/wqYCZ2fH0d6eU7gJ24y71W4BnJfVt7CwDSZcD83BX+CR8u9N+wDkZmauAx/F9uK/DH9In4yfIXWxmO1pwLe8luaaTsV0OXAx8F3e/jwDul3SumU1NdWYDw/FDmWrxA1YG4wdgFWNakrkEGJny/teI7HzgZnwv91WZ/KvwM9wXJF27A3/GtymdCtThW5TOTUsXD5V19Q2pTp9bc/nvAWbhyztd8LM/npbU38w2Ab8F3gd8B1/SKOyJXrjXi4DPAj/CvRsX4r+PPsCXW6BnELQ+ZhYpUqRcwo/FtSLpmRJ1qoDO+H7Z38jkj091z0/fJwN7SrQj3LitzOV3x8+gmNmE7tNTfx1Sejdwd8qbmWS+kL6PztV9FDfUPdL3l4Afl+irQ2pnSiZvIVBXRHZokh2cuc5twIKc3JPAhsz3O4HDwPtzco8ArwJVJfSrSX2OS7p2xh80dgKLmxjHKvxhYyswq8j9rM7JD0n51+Xyb0z5H27r33WkSGYWrv4gaIKRwIBMauBelnSNpOck1QNvAAdxL0Apd//fgPMkzZf0OUn52XNf4ALgl8l13CF5HQ4C64BPlqn7sZR2A7cD9+Izd1IbbwCLc3UW4gFwH8voepOkyZI+IqnV/meYmaX+RkrqDCDpPOAKGsYhDAf+AvwrNx4rgV6UHusCv8DH4iCwGp/R35gXkjRM0h8l7cPH5yg+wy+nj+H4Q9PSnJ4Fb8YnymgjCE47YfiDoDQbzez5TNpSKJA0EnftbgSuxY3lAHxW3rGxBs1sDe72rcaPht0raZWki5JIr/Q5jxPGu5CG40sK5VB4WKkBuprZJDM7ksp6AHvt5Ij23ZlygK/ja9o340FweyTNktSpTB2aYj4+Cx+Vvl+L/1/6VUamF/BpTh6LRam8nPG4Ex+LTwEPpb9/mhWQNACP/K/HPQQDk9xGStzPnJ4dcY9PVs/C2ejl3rcgOK3EGn8QtJxrgJfMbFwhQ1JH3CVfEjN7DHhMUhfcqN0DLJfUBygcDfst4Kki1Y8UySvWR6lo9dfwYz475Ix/7/S5L7XxX3xpYrKkavz1xh/iM9s7OEXMrFbSX4HR+Jr+aGCNme3MiO3DXxf8ZiPNbGkkP0tdZjzWSuoGjJc0x8wKgX5fxK/r6uyYSOqBLyk0xT7c6F/eSPnORvKD4IwShj8IWs67cHdwlhtohifNzA4CyyTV4EFl5+D7BGwH+pnZjFbSNc9a4DbgauDXmfzrceO3roiudcAMSWOAi/LlGY7gyx3lsgD4iaQh+Ax7TK58Bb4PQZ2Z7W1Gu6X4Nn7t0/BgQjhxP988q1zSMDzg78VM3cKDV/4aV+DBmp3NbG0r6RkErU4Y/iBoOSuAB9JrZ8txo3ULcKBUJUnfx92+T+FR4X2ACcDzZvZakpkAPJE8CEvw2WRv4DJgm5nNPkXdnwSexSPje+OG7fN4UOPdZrY/6bEOeAJ3dx/CA9guBB4u0fZmYJykrwIvAIfNbGMJ+cXAffgDwCFgaa58Ju5peFrSfcA/ga54LMRlZjaSZmJmOyTNASZKutTM1uP3cwLwiKR5qf0pnDxTL2zgNCG9vngM+IeZrZa0BF/jvxffsAh8SedKYJKZ5d8iCIIzT1tHF0aK9FZMnIjqrykhUwX8ADcMr+OG/BI8cOznGbl8VP8IPOBrFz573I6vo/fOtf9xfM15Pz4Lfxlf1x7YhO7TSbFzTcidDTyY9DiKu8xvzcnMxI13PR4YtwGYkCkvFtXfFfci7E9ltSm/QVR/rp+lqWx+I7r2wF8trEu67gH+RObtiUbqFaL6xxYp65Wu6fFM3sTUx2HccA8BngFW5+rele778dy9rcI9KRvSPfsPvn/CPUC3tv5dR4pkZsjsTa9WEARBEARvcyKqPwiCIAgqiDD8QRAEQVBBhOEPgiAIggoiDH8QBEEQVBBh+IMgCIKgggjDHwRBEAQVRBj+IAiCIKggwvAHQRAEQQURhj8IgiAIKoj/A3+B5M9jEsIOAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f69124cb7f0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fpr, tpr, thresholds = roc_curve(Y_test, modele_pred)\n",
"plt.figure(figsize=(8, 6))\n",
"plot_roc_curve(fpr, tpr)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### PRECISION, RAPPEL, F1-SCORE, SUPPORT"
]
},
{
"cell_type": "code",
"execution_count": 64,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(0.8738440062816263, 0.9451731622157215, 0.9081100684527857, None)"
]
},
"execution_count": 64,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"precision_recall_fscore_support(Y_test, modele_pred,average='binary')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### SCORE EN K-FOLD CROSS VALIDATION (validation croisee en K passes) "
]
},
{
"cell_type": "code",
"execution_count": 65,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.5191659 0.57664151 0.98838583 0.98554688 0.97589425 0.97547684\n",
" 0.97359736 0.95694604 0.95623925 0.91869621]\n",
"Mean: 0.8826590059611231\n",
"Standard deviation: 0.16892218857648453\n",
"CPU times: user 411 ms, sys: 92.4 ms, total: 503 ms\n",
"Wall time: 59.1 s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele, X, Y, cv=10, scoring=\"precision\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 66,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.94916838 0.9568305 0.93850467 0.94317757 0.93831776 0.93682243\n",
" 0.93738318 0.93476636 0.9353271 0.93775701]\n",
"Mean: 0.9408054953480616\n",
"Standard deviation: 0.0066873184210212416\n",
"CPU times: user 393 ms, sys: 72.6 ms, total: 465 ms\n",
"Wall time: 59.4 s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele, X, Y, cv=10, scoring=\"recall\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 67,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.67120391 0.71960647 0.96279962 0.96389685 0.95673718 0.95575896\n",
" 0.95514713 0.94572617 0.94566758 0.92812876]\n",
"Mean: 0.9004672626479777\n",
"Standard deviation: 0.10356201355194058\n",
"CPU times: user 387 ms, sys: 81.2 ms, total: 468 ms\n",
"Wall time: 59.6 s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele, X, Y, cv=10, scoring=\"f1\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 68,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.67375455 0.77056851 0.99526332 0.99434319 0.9916656 0.99217879\n",
" 0.99247068 0.98691868 0.98790231 0.98151926]\n",
"Mean: 0.9366584899953871\n",
"Standard deviation: 0.10947794539933293\n",
"CPU times: user 377 ms, sys: 80.6 ms, total: 458 ms\n",
"Wall time: 59.1 s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_roc=cross_val_score(modele, X, Y, cv=10, scoring=\"roc_auc\",n_jobs=-1)\n",
"display_scores(modele_score_roc)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### *Importance des variables dans le modele*"
]
},
{
"cell_type": "code",
"execution_count": 69,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([0.07201836, 0.10600016, 0.11498856, 0.06354506, 0.35909978,\n",
" 0.03830383, 0.09052431, 0.03374793, 0.02425722, 0.03686312,\n",
" 0.00648497, 0.05340613, 0.00076057])"
]
},
"execution_count": 69,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"modele_rf.feature_importances_"
]
},
{
"cell_type": "code",
"execution_count": 70,
"metadata": {
"scrolled": true
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Importance</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>t</th>\n",
" <td>0.072018</td>\n",
" </tr>\n",
" <tr>\n",
" <th>tn12</th>\n",
" <td>0.106000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>tx12</th>\n",
" <td>0.114989</td>\n",
" </tr>\n",
" <tr>\n",
" <th>n</th>\n",
" <td>0.063545</td>\n",
" </tr>\n",
" <tr>\n",
" <th>raf10</th>\n",
" <td>0.359100</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Importance\n",
"t 0.072018\n",
"tn12 0.106000\n",
"tx12 0.114989\n",
"n 0.063545\n",
"raf10 0.359100"
]
},
"execution_count": 70,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"pd.DataFrame(modele_rf.feature_importances_,index=X_train.columns,columns=[\"Importance\"]).head()"
]
},
{
"cell_type": "code",
"execution_count": 71,
"metadata": {
"scrolled": true
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Importance</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>t</th>\n",
" <td>0.048091</td>\n",
" </tr>\n",
" <tr>\n",
" <th>tn12</th>\n",
" <td>0.138567</td>\n",
" </tr>\n",
" <tr>\n",
" <th>tx12</th>\n",
" <td>0.153798</td>\n",
" </tr>\n",
" <tr>\n",
" <th>n</th>\n",
" <td>0.145986</td>\n",
" </tr>\n",
" <tr>\n",
" <th>raf10</th>\n",
" <td>0.223895</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Importance\n",
"t 0.048091\n",
"tn12 0.138567\n",
"tx12 0.153798\n",
"n 0.145986\n",
"raf10 0.223895"
]
},
"execution_count": 71,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"pd.DataFrame(modele_gbm.feature_importances_,index=X_train.columns,columns=[\"Importance\"]).head()"
]
},
{
"cell_type": "code",
"execution_count": 72,
"metadata": {
"scrolled": true
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Importance</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>t</th>\n",
" <td>0.05</td>\n",
" </tr>\n",
" <tr>\n",
" <th>tn12</th>\n",
" <td>0.22</td>\n",
" </tr>\n",
" <tr>\n",
" <th>tx12</th>\n",
" <td>0.26</td>\n",
" </tr>\n",
" <tr>\n",
" <th>n</th>\n",
" <td>0.08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>raf10</th>\n",
" <td>0.06</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Importance\n",
"t 0.05\n",
"tn12 0.22\n",
"tx12 0.26\n",
"n 0.08\n",
"raf10 0.06"
]
},
"execution_count": 72,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"pd.DataFrame(modele_ada.feature_importances_,index=X_train.columns,columns=[\"Importance\"]).head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### **NAIF BAYESIEN**"
]
},
{
"cell_type": "code",
"execution_count": 73,
"metadata": {},
"outputs": [],
"source": [
"from sklearn.naive_bayes import GaussianNB\n",
"modele_gnb = GaussianNB()"
]
},
{
"cell_type": "code",
"execution_count": 74,
"metadata": {},
"outputs": [],
"source": [
"gmodel = modele_gnb.fit(X_train,Y_train)\n",
"modeleNB_pred = gmodel.predict(X_test)"
]
},
{
"cell_type": "code",
"execution_count": 75,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"21401"
]
},
"execution_count": 75,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"X_test.shape[0]"
]
},
{
"cell_type": "code",
"execution_count": 76,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([False, False, True, ..., True, False, True])"
]
},
"execution_count": 76,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Y_test_v=Y_test.values\n",
"Y_test_v=Y_test_v.ravel()\n",
"Y_test_v"
]
},
{
"cell_type": "code",
"execution_count": 77,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([False, False, True, ..., True, False, False])"
]
},
"execution_count": 77,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"modeleNB_pred"
]
},
{
"cell_type": "code",
"execution_count": 78,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Number of mislabeled points out of a total 21401 points : 5514, performance 74.23%\n"
]
}
],
"source": [
"print(\"Number of mislabeled points out of a total {} points : {}, performance {:05.2f}%\"\n",
" .format(\n",
" X_test.shape[0],\n",
" (Y_test_v != modeleNB_pred).sum(),\n",
" 100*(1-(Y_test_v != modeleNB_pred).sum()/X_test.shape[0])))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### **ESTIMATION QUALITE MODELE NAIF BAYESIEN**"
]
},
{
"cell_type": "code",
"execution_count": 79,
"metadata": {},
"outputs": [],
"source": [
"modele_pred = modeleNB_pred\n",
"modele = modele_gnb"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Matrice confusion"
]
},
{
"cell_type": "code",
"execution_count": 80,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[9706, 1098],\n",
" [4416, 6181]])"
]
},
"execution_count": 80,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"confusion_matrix(Y_test,modele_pred)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### ROC"
]
},
{
"cell_type": "code",
"execution_count": 81,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"0.7408246300104424"
]
},
"execution_count": 81,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"roc_auc_score(Y_test, modele_pred)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### ROC CURVE"
]
},
{
"cell_type": "code",
"execution_count": 82,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAf4AAAF8CAYAAAAuF9n2AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzs3Xl8VNX9//HXyQ5kIZCETNiRTSDDFlFErIILkCCgVQPab10ANxAUK+LWxVZF68ZPFBRba4tLi4oyAay7CCJBIMMiIPuSyU4WyD5zfn9MGCOFMMDM3JnJ5/l48Gjmnkny1mLeufeec67SWiOEEEKI5iHE6ABCCCGE8B0pfiGEEKIZkeIXQgghmhEpfiGEEKIZkeIXQgghmhEpfiGEEKIZ8WnxK6X+ppQqUEptOcW4UkrNU0rtUkpZlVKDfJlPCCGECHa+PuN/ExjVxPhooEfDn6nAqz7IJIQQQjQbPi1+rfU3QEkTbxkHvKWd1gKtlVIm36QTQgghgp+/3eNvDxxs9PpQwzEhhBBCeECY0QFOoE5y7KR7CiulpuK8HUCrVq0G9+7d25u5hBBCCJ+yOzRlVXWUVdVxtKYeXV9LfWkeur4WoEhrnXg2X9ffiv8Q0LHR6w5A7sneqLV+DXgNIC0tTa9fv9776YQQQggvKqus45NteVisNlbvKsLh0MQALQt2kbf4IWJiYvjb3//Or8dfs/9sv4e/Ff/HwDSl1LvAhUCZ1tpmcCYhhBDCayqq6/h0Wz5ZVhvf/FRInd15oTs0RDG8RwJj+6cwsucInm57iPvvvx+T6dymvvm0+JVS7wCXAQlKqUPA74FwAK31AmA5MAbYBVQCt/oynxBCCOELx2rq+Xx7AZacXL7aWUhtvQOAEAXDurclw5xC28oD/PGR+7nsww9pG9uCZ5991iPf26fFr7WeeJpxDdzjozhCCCGEz1TV2vlyRwEWay5fbC+gus5Z9krBhV3bkGE2MaqfibatwnnmmWf4v8ceo3379uTl5ZGUlOSxHP52qV8IIYQIGtV1dr7eWUiW1cZnP+ZTWWt3jQ3uHE+G2cSYVBPtYqMAyMvL4+prf8Nnn33G9ddfz2uvvUbr1q09mkmKXwghhPCg2noH3+4qxJJj49Nt+VTU1LvG+ndszVizidGpJtq3bvE/n/vQQw+xevVqXnvtNSZPnoxSJ1vsdm6U8+p6YJNZ/UIIIYxUZ3ewZncxlpxcPtmaR3n1z2Xfr30s6akpZJhNdGzT8n8+t7a2ltLSUpKSkigqKqKgoIA+ffo0+f2UUj9ordPOJquc8QshhBBnod7u4Pu9JVisuazckseRyjrXWO/kGDLMJtLNKXRNaHXKr7F7924mTpxIaGgoq1evJiEhgYSEBK/mluIXQggh3GR3aLL3lZBltbFii42io7Wuse5J0WSYTWSYTXRPijnt13r77be58847CQ0NZdGiRYSE+GYzXSl+IYQQogkOh2bjwSMsy7GxfLONgooa11jXhFYNZ/YmerWLceue/LFjx5g2bRpvvvkmw4YNY/HixXTu3Nmb/wi/IMUvhBBCnEBrTc6hMiw5uSzfbCO3rNo11iG+BRlm5z37vimxZzwBT2vN999/z2OPPcbjjz9OWJhvq1iKXwghhMBZyFtzy1lmzSXLauPQkSrXWEpcFOlmExnmFMwd4s6q7N98801uvPFGoqOj2bBhA1FRUZ7+R3CLFL8QQohmS2vNjvwKLDk2LNZc9hVXusbaxUYyJtV5z35gx3hCQs5uaV1RURG33XYby5Yto7Kyknvuucew0gcpfiGEEM3QroIKluXYyNpsY1fBUdfxhOgIRvdzlv0FXdqcddkf99VXX3HTTTdRVFTESy+9xN13332u0c+ZFL8QQohmYW/RMSw5uWRttrE9r8J1PL5lOKP6mRhrNjGkaxvCQj0zu/6NN95gypQp9OjRA4vFwsCBAz3ydc+VFL8QQoigdbCkEovVeRl/a26563hsVBij+iWTYU5h6HltCfdQ2Tf2q1/9iqlTp/LXv/6V6Ohoj3/9syXFL4QQIqjkllaR1VD2OYfKXMejI8O4qk87MvqbuKR7IhFhni/7Dz/8kKysLF5//XW6d+/OggULPP49zpUUvxBCiICXX17tKvsNB0pdx1tGhHLF+e3IMJu4tGciUeGhXvn+VVVVzJo1i1dffZW0tDTKyso8/nAdT5HiF0IIEZAKK2pYucXGMquN7H0lHH/0TFR4CCN7O8v+sl5JtIjwTtkft23bNjIzM9m8eTOzZs3iySefJCIiwqvf81xI8QshhAgYJcdqWbklD4s1l7V7inE0lH1EWAiX9Uwko38KI3sn0SrSN/VWV1dHeno6x44dY/ny5YwePdon3/dcSPELIYTwa2WVdXyyNY9l1lzW7C7G3tD24aGKy3skktHfxBXntyMmKtxnmcrLy2nVqhXh4eG8/fbbdOnSBZPJ5LPvfy6k+IUQQvid8uo6Pt2aT9ZmG6t+KqTO7iz7sBDFr3omkmE2cVXfZOJa+K7sj1u7di0TJ07k9ttv59FHH2Xo0KE+z3AupPiFEEL4hWM19Xz2Yz4Wq42vdxRSa3cAEKLgku4JpJtNjOqbTHwrY+6fOxwOnnnmGR599FE6duzIFVdcYUiOcyXFL4QQwjBVtXa+2F6AxZrLF9sLqKl3lr1ScGHXNmT0T2F0v2QSoiMNzWmz2fjNb37D559/zg033MDChQv9dtb+6UjxCyGE8KnqOjtf7Sgka7ONz3/Mp7LW7hpL6xxPhtnEmFQTSbHG7Wd/ov3795Odnc3rr7/O7bfffsYP6fEnUvxCCCG8rqbezqqdRWRttvHptnyO1tS7xgZ0bO0q+5TWLQxM+Uu1tbWsWLGCcePGcdFFF7F///6APctvTIpfCCGEV9TZHazeVYTFauOTrXlUVP9c9qnt40g3m0hPNdGxTUsDU57crl27mDhxIuvXr8dqtZKamhoUpQ9S/EIIITyo3u5g7Z4SLNZcVm7No7SyzjXWOzmGsf1TSE810SWhlYEpm7Z48WLuvPNOwsPD+eCDD0hNTTU6kkdJ8QshhDgndodm3d4SsjbnsmJzHsXHal1jPZKiyTCnkG420T3Jfx5Ucyr33HMPr7zyCpdccgmLFy+mU6dORkfyOCl+IYQQZ8zh0Gw4cASL1cbyzTYKKmpcY10TWpFhNpFhTqFXcoyBKc/coEGDePzxx3nssccICwvOigzOfyohhBAep7Vm08FSV9nbyqpdYx3btCDDnEKG2UQfU2zAzHrXWjNv3jzatm3LzTffzO233250JK+T4hdCCHFKWmu2HC7HYs3FYrVxuLTKNda+dQvSzSYyzCZS28cFTNkfV1RUxK233orFYmHixIncfPPNRkfyCSl+IYQQv6C1ZnteBRZrLllWG/uKK11j7WIjSU913rMf2LE1ISGBVfbHffXVV9x0000UFRUxb948pk2bZnQkn5HiF0IIAcBP+RUss9rIsuayu/CY63hCdCRjUpPJMKeQ1jk+YMv+uO3btzNy5Eh69OhBVlYWAwYMMDqST0nxCyFEM7an8CgWq40sq40d+RWu421aRTCqXzIZZhMXdm1LaICXPUBVVRUtWrSgd+/e/OMf/2D8+PFER/v/SgNPk+IXQohm5kBxJZbNuVhybGyzlbuOx7UIZ1TfZNLNJi4+ry1hoSEGpvSsDz74gLvvvpusrCwGDx7cbO7nn4wUvxBCNAOHS6vIapigZz1U5joeExnGlX3bMdacwrDuCUSEBU/Zg/Msf9asWbz66qukpaUFze5750KKXwghglReWTVZm21YrLlsPFDqOt4qIpQr+rQjw5zCpT0TiAwLNTCl92zdupXMzEy2bNnCAw88wF/+8hciIox5pK8/keIXQoggUlBRzcoteVhybGTvL0Fr5/EW4aGMOD+JsWYTl/VKIio8OMu+sf/85z/k5+ezYsUKRo0aZXQcv6H08b8VASwtLU2vX7/e6BhCCGGI4qM1rNzqLPvv9xbjaPixHhEWwuW9EskwpzDy/CRaRgT/uV5paSl79+5l4MCB1NfXU1xcTLt27YyO5XFKqR+01mln87nB/7dACCGCUGllLZ9szcNitbFmdzH2hrYPD1WM6Oks+yv6tCM6svn8mP/uu++YOHEiDoeDXbt2EREREZSlf66az98IIYQIcOXVdXy6NR+LNZdVPxVR31D2YSGKyxrO7K/s0464FuEGJ/Uth8PB3Llzeeyxx+jYsSP/+c9/5F5+E6T4hRDCjx2tqefzH/NZlmPjm52F1NodAISGKIb3SCA91cTVfZOJb9U8i66iooJrr72Wzz77jBtvvJGFCxcSFxdndCy/JsUvhBB+prK2ni+2F2DJsfHljgJq6p1lrxRc1K0NGeYURvdLpm10pMFJjRcdHU2bNm1YtGgRt912W8A9L8AIUvxCCOEHquvsfLWjAIvVxuc/FlBVZ3eNXdAl3lX2SbFRBqb0D7W1tfzhD39g6tSpdOnShffee8/oSAFFil8IIQxSU2/nm51FZFlz+XRbPsdqfy77gZ1ak2FOYUxqMqa4Fgam9C+7du0iMzOTH374geTkZO69916jIwUcKX4hhPChOruDb3cVYcmx8d9teVRU17vGUtvHkWE2kW420SG+pYEp/dO//vUv7rrrLsLDw/nwww8ZP3680ZECkhS/EEJ4Wb3dwXd7irHk2PhkWx6llXWusfNNsWQ0PNO+c9tWBqb0b2+88QaTJ09m+PDhLF68mI4dOxodKWBJ8QshhBfYHZrv9xaTZbWxcksexcdqXWM920WTYXY+0/68xOb3dLgzYbfbCQ0N5cYbb6SiooJp06YRFibVdS7k354QQniIw6H54cARLDm5LN+SR2FFjWusW0Ir55l9/xR6tosxMGVg0Fozb9483nrrLVatWkV0dDQzZ840OlZQkOIXQohzoLVm48FSLDk2lm+2kVde7Rrr1KZlw2X8FM43xchSMzcVFhZy6623kpWVxdixY6mpqaFlS5nz4ClS/EIIcYa01mw+XIbFaiPLauNwaZVrrH3rFq6y79c+Vsr+DH355ZfcdNNNFBcXM2/ePKZNmyb/Dj1Mil8IIdygteZHWwUWay5Zm23sL650jSXHRjEm1URGfxMDO7aWojpLWmseeughYmNjWb58OQMGDDA6UlCS4hdCiCbszK/AkpOLZbONPYXHXMcTYyIZ0y+ZjP4pDO4UT0iIlP3Z2r9/P7GxscTHx/P+++8THx9Pq1aywsFbpPiFEOIEuwuPYsmxkbU5l535R13H27SKYHS/ZDLMKQzp2oZQKftz9v777zN58mTGjh3LW2+9RYcOHYyOFPSk+IUQAthffAyL1YbFauNHW7nreFyLcEb1TSajv4mh3doSFhpiYMrgUVVVxX333cfChQtJS0vj97//vdGRmg0pfiFEs3XoSCVZDWW/+XCZ63hMVBhX9XGW/SXdEwiXsveon376iWuvvZYtW7bwwAMP8Je//EUeo+tDUvxCiGbFVlblKvtNB0tdx1tFhHJln3ZkmFMY3jOByLBQA1MGt+ho56ZFK1asYNSoUQanaX6k+IUQQa+gopoVm/OwWHPJ3nfEdbxFeCgjz08iw2zisl5JRIVL2XtLaWkpL7/8MnPmzMFkMpGTk0NIiFxJMYIUvxAiKBUfrWHFFmfZf7+3BK2dxyPDQri8VxIZ/U2M6J1Eywj5Meht3333HRMnTuTw4cOMHDmSoUOHSukbyOd/45VSo4CXgFBgkdb66RPGOwH/AFo3vOchrfVyX+cUQgSe0spaVm7Jw2K18d2eYuwOZ9tHhIZwac9ExvY3MfL8dkRHStn7gt1uZ+7cuTz++ON06tSJb7/9lgsvvNDoWM2eT//2K6VCgfnAlcAhIFsp9bHWelujtz0K/Ftr/apSqg+wHOjiy5xCiMBRVlXHf7fmkbXZxrc/FVHfUPZhIYrLeyWSbk7hyj7tiGsRbnDS5mfKlCn8/e9/JzMzkwULFhAXF2d0JIHvz/iHALu01nsAlFLvAuOAxsWvgdiGj+OAXJ8mFEL4vYrqOj7/sQCLNZdvdhZRa3cAEBqiGN4jgQyziav7JtO6pcwUN4LWGqUUU6ZM4ZJLLuHWW2+V3Qz9iK+Lvz1wsNHrQ8CJ133+APxXKTUdaAVc4ZtoQgh/Vllb7yr7L3cUUlvvLPsQBUO7tSWjv4lRfZNpGx1pcNLmq6amhjlz5gDw/PPPM3ToUIYOHWpwKnEiXxf/yX7l0ye8ngi8qbV+Tik1FPinUqqf1trxiy+k1FRgKkCnTp28ElYIYazqOjtfbi/AstnGFz8WUFVnB0ApGNKljbPs+yWTFBNlcFLx008/kZmZyYYNG5g2bZrrrF/4H18X/yGgY6PXHfjfS/m3A6MAtNbfKaWigASgoPGbtNavAa8BpKWlnfjLgxAiQNXU2/l6RyFZm218ti2fY7V219igTq1JN6eQnmoiOU7K3l/885//5O677yY8PJwPP/yQ8ePHGx1JNMHXxZ8N9FBKdQUOA5nApBPecwAYCbyplDofiAIKfZpSCOFTtfUOVu8qYpk1l0+35lNRU+8aM3eII8NsYkyqiQ7x8kx2f3Po0CHuuOMO0tLSWLx4MR07djz9JwlD+bT4tdb1SqlpwCc4l+r9TWu9VSn1J2C91vpjYBbwulLqPpy3AW7RWssZvRBBpt7uYM3uYizWXD7Zmk9ZVZ1rrI8ploz+JjJSU+jUVsreH+3du5euXbvSoUMHvvnmGwYMGEBYmCyTDAQqGDo1LS1Nr1+/3ugYQojTsDs03+8pxrLZxsoteZQcq3WN9WoXQ4bZRLrZRLfEaANTiqZorXnxxReZPXs2//jHP5g4caLRkZolpdQPWuu0s/lc+fVMCOFVDodm/f4jWKy5LN+cR9HRGtdYt8RWZJhTGGs20aNdjIEphTsKCwu55ZZbWL58OWPHjuWqq64yOpI4C1L8QgiP01qz4UBpQ9nbyC//uew7t21JhtlEhjmF3skxMvM7QHz11VdMmjSJ4uJi5s2bx7Rp0+T/uwAlxS+E8AitNdZDZa4z+8OlVa6x9q1buO7Z92sfK4URgEpKSoiNjWX58uUMGDDA6DjiHMg9fiHEWdNas81WjsVqI8tq40BJpWssOTaKdLOJDLOJAR1bS9kHoP379/P9999zww03AFBbW0tEhOyG6A/kHr8Qwqd25FVgseaSZbWxp+iY63hiTCTpqc6yH9QpnpAQKftA9f777zN58mTCwsIYPXo0MTExUvpBQopfCOGWXQVHXWX/U8FR1/G2rSIYnZpMemoKQ7q2IVTKPqBVVVVx3333sXDhQoYMGcI777xDTIxMvAwmUvxCiFPaV3SMrM02luXksj2vwnW8dctwRvVNJsOcwkXd2hAWKs9WDwY1NTVcdNFFWK1WHnzwQZ544gk5yw9CUvxCiF84WFJJ1mYbFmsuWw6Xu47HRIVxdd9kMswmhnVPIFzKPuhERkbyf//3f6SmpspSvSAmxS+EILe0iuWbbSyz2sg5WOo6Hh0ZxpV92pFhNnFJjwQiw0INTCm84ciRI9x5551MnTqVkSNHMmvWLKMjCS+T4heimSoor2b5ZhsWq431+4+4jrcID+WKPu1ITzVxWa9EosKl7IPVmjVrmDhxIrm5uYwYMYKRI0caHUn4gBS/EM1I0dEaVmzJw5KTy7p9JRxfzRsZFsKI3klkmFMY0TuJFhFS9sHMbrczd+5cHn/8cTp37szq1asZMmSI0bGEj0jxCxHkjhyrZeXWPCzWXL7bXYyjoewjQkP4Va9EMswmRp7fjuhI+XHQXHzwwQc88sgjZGZmsmDBAuLi4oyOJHxI/ksXIgiVVdXxydY8sqw2Vu8qor6h7cNDFZf1cJb9FX3aERsVbnBS4UuFhYUkJiby61//mhUrVnD11VfLxkrNkBS/EEGiorqOz37Mx5Jj45ufCqmzO8s+NEQxvEcCY80pXN03mbiWUvbNTU1NDbNnz+att95i06ZNdOrUiVGjRhkdSxhEil+IAHaspp7Ptxdgycnlq52F1NY7AAhRcPF5bckwpzCqXzJtWsla7OZq586dZGZmsnHjRqZNm0ZSUpLRkYTBpPiFCDBVtXa+3FFAltXG59vzqa5zlr1SMKRrG8aaTYzqZyIxJtLgpMJo//znP7nrrruIjIxk6dKljBs3zuhIwg9I8QsRAKrr7HyzsxCL1cZnP+ZTWWt3jQ3q1JoMcwpjUk0kx0UZmFL4m88++4zBgwfzr3/9i44dOxodR/gJKX4h/FRtvYNvdxViybHx6bZ8KmrqXWP9O8Q5y95son3rFgamFP7mhx9+ICoqir59+7JgwQLCw8MJC5Mf9eJn8rdBCD9SZ3ewZncxlpxcPtmaR3n1z2XfNyWWDHMKGWYTHdu0NDCl8EcOh4MXX3yRhx56iBEjRrBy5UpatJBfCsX/kuIXwmB2h2btnmIsVhsrt9g4UlnnGuudHEN6qol0s4luidEGphT+rKCggFtvvZXly5czbtw43njjDaMjCT8mxS+EARwOTfa+EixWGyu22Cg6WusaOy+xlevMvkc7eRyqaNr27dsZMWIEJSUlvPzyy9x9992yNl806YyKXynVCxgOtAXe1FrnK6U6AsVa60pvBBQiWDgcmo0Hj7Asx8byzTYKKmpcY13atnSWfX8TvdrFyA9u4bZu3bpx+eWX8+CDD9K/f3+j44gA4FbxK6XCgb8BkwAFaOBTIB94GdgKPOyljEIELK01OYfKsOTksnyzjdyyatdYh/gWpJtNjDWn0DclVspeuG3fvn3Mnj2bBQsWEB8fz+LFi42OJAKIu2f8TwDXAFNwFv7+RmPLgalI8QsBOMt+a245FquNrM25HCypco2Z4qJITzWR0T+F/h3ipOzFGVuyZAmTJ09Ga82WLVsYPny40ZFEgHG3+G8CHtNa/00pdeJju/YAXT0bS4jAorVmR34FlhwbWZtt7C065hpLiolkTKqJsf1NDOwYT0iIlL04c5WVldx333289tprDBkyhHfeeYdu3boZHUsEIHeLPxHY0sS47BoimqVdBRUsayj7XQVHXccToiMY3c85G/+CLm0IlbIX5+j+++/ntddeY/bs2TzxxBOEh8szF8TZcbf49wMXAF+cZCwN+MljiYTwc3uLjpFlzcVitbE9r8J1PL5lOKP6JZNhTuHCrm0ICw0xMKUIBlprjh07RnR0NL///e+57rrruPLKK42OJQKcu8X/L+ARpdQuYFnDMa2UGgrcDzzpjXBC+IuDJZVYrDYs1ly25pa7jsdGhXF132Qy+qdw8XltCZeyFx5y5MgRpkyZQklJCZ9++ikmkwmTyWR0LBEE3C3+p4BBwH+A49czvwRigA+BFz0fTQhj5ZZWkdVQ9jmHylzHoyPDuKpPO9LNJob3SCQiTMpeeNbq1auZNGkSubm5PPnkkzIJVHiUW8Wvta4HJiilrgSuBpKAYmCl1voTL+YTwqfyy6tZvtmGxWrjh/1HXMdbRoRyxfnOsv9Vz0Siwk+c4yrEubPb7Tz11FP84Q9/oHPnzqxevZohQ4YYHUsEGXfX8Sfh3KTnU5zL+RqPhQAJWusCL+QTwusKK2pYucXGMquN7H0laO08HhUewojeSWSYU7i8VxItIqTshXcdPXqURYsWccMNN7BgwQJiY2ONjiSCkLuX+m3AUGDdScYGNhyXn4oiYJQcq2Xlljws1lzW7inG0VD2EWEhXNYzkYz+KYzsnUSrSNnVWnjfF198wbBhw4iLi2PdunUkJibK5X3hNe7+VGvqb2AY4PBAFiG8qqyyjk+25mHZbGP1riLsDW0fHqq4vEci6WYTV/ZpR0yULJMSvlFTU8Ps2bN56aWXmDt3Lg8++CBJSUlGxxJB7pTFr5SKBhpfZ0pQSqWc8LYWOLfxzfdCNiHOWXl1HZ9ty8ditbHqp0Lq7M6yDw1RXNozkQyziav7JBPXUspe+NbOnTvJzMxk48aNTJ8+nXvvvdfoSKKZaOqMfxbweMPHmp+X8Z1IAX/xZCghzsWxmno++9FZ9l/vLKS23nlBKkTBsO5tyTCncHXfZNq0ijA4qWiuPvroI2666SYiIyP56KOPuOaaa4yOJJqRporfAuThLPZXgGeAvSe8pwbYprU+2b1/IXymqtbOF9sLyNqcyxfbC6iuc5a9UnBh1zZk9E9hVN9kEmMiDU4qBHTv3p3hw4fz+uuv06FDB6PjiGbmlMWvtf4B+AFAKaWB97XWRb4KJsTpVNfZ+XpnIRarjc9/zKey1u4aG9w5ngyziTGpJtrFyo7Swng//PADH374IX/+85/p27cvK1asMDqSaKbcXce/0NtBhHBHbb2DVT85y/7Tbfkcral3jfXv2JqxDWWf0rqFgSmF+JnD4eDFF1/koYceol27dsyYMYPExESjY4lmzO21SkqpnsCtQC/+96E8Wmud7slgQhxXZ3ewelcRFquN/27No7z657Lv1z6WDHMK6akmOrZpaWBKIf5XQUEBt9xyCytWrGD8+PG88cYbtGnTxuhYoplzdwOfwcAqnLP3OwE7gDY4d/DLBQ54K6BonurtDtbuKSFrcy4rt+RxpLLONdY7OYYMs4l0cwpdE1oZmFKIU7Pb7Vx++eXs3r2b+fPnc9ddd8nafOEX3D3jfxrIAiYCtcDNWusNSqkxwCJgtpfyiWbE7tBk7yvBYnWWfdHRWtdY96RoMswmMswmuifFGJhSiKbV1dURGhpKaGgozz33HCkpKZjNZqNjCeHibvH3x3mZ//hGPaEAWuvlSqkncc74H+r5eCLYORyaDQeOYLHaWL7ZRkFFjWusa0KrhjN7E73axcjZkvB7+/btY+LEidx4443MnDmTUaNGGR1JiP/hbvFHAhVaa4dSqgRo12hsGyC/zgq3aa3ZdLDUVfa2smrXWMc2LUhPTSHDbKJvSqyUvQgY//nPf5gyZQpaa1JSTtzrTAj/4W7x7wGO/03eCtyCc50/wM2APKBHNElrzdbccpZZc8my2jh0pMo1lhIXRbrZRIY5BXOHOCl7EVAqKyuZOXMmr7/+OhdeeCHvvPMOXbt2NTqWEKfkbvGvAK4E3gWeApY1nPnXA22BB7wTTwQyrTXb8yqwNJSAmnsEAAAgAElEQVT9vuJK11i72EjGpDrLfmDH1oSESNmLwLRhwwb+9re/MXv2bJ544gnCw2X7Z+Hf3F3H/3Cjj1cqpYYDvwZaAiu11h97KZ8IQD/lV7DMaiPLmsvuwmOu4wnREYxJNZGeauKCLm2k7EXA0lqTnZ3NkCFDuOSSS9i5cyfdunUzOpYQbjmrZ45qrdcCaz2cRQSwPYVHybLasFht7MivcB2PbxnOqH4mxppNXNitLaFS9iLAlZSUMHnyZJYuXUp2djaDBw+W0hcB5ZwfNq6U6gM8prWe6IE8IoAcKK7EsjkXS46NbbZy1/HYqDBG9Usmw5zC0PPaEh4aYmBKITzn22+/ZdKkSdhsNp599lkGDhxodCQhzliTxa+cs6xScW7as1tr/WOjsVScT++bAFSd/CuIYHO4tIosay4Wqw3roTLX8ZjIMK7s246x5hSGdU8gIkzKXgSXuXPn8vDDD9OlSxfWrFnDBRdcYHQkIc7KKYtfKZUMfABc2OjYv4DbgReBO4E6nE/uk8fyBrG8smqWb7Zhseay4UCp63jLiFCuOL8dGWYTl/ZMJCo81MCUQnhXZGQkmZmZvPrqq8TGxhodR4iz1tQZ/9PAAJylvgHoCjwIfI1zs573gN9prQ95O6TwvcKKGlZssWHJsZG9vwStncejwkMY2dtZ9pf3TpKyF0HNYrHgcDi45pprmDFjBoAsNxUBr6nivxL4k9b66eMHlFJbgE+ABVrru70dTvhWybFaV9l/v7cYR0PZR4SFcHmvRDLMKYzonUSryHOeGiKEX6upqWH27Nm89NJLXHbZZYwdO1YKXwSNpn6CJwGrTzh2/PU73okjfK20spZPtuZhsdpYs7sYe0Pbh4cqLu+RSEZ/E1ec346YKFmbLJqHnTt3kpmZycaNG7n33nuZO3eulL4IKk0VfyhQc8Kx46+PIQJWeXUdn27Nx2LN5dtdRdTZnWUfFqL4Vc9EMswmruqbTFwLKXvRvOzbt49BgwYRFRXFxx9/zNixY42OJITHne6a7VVKqe6NXocAGhillOrd+I1a67c9HU54ztGaej7/MZ9lOTa+2VlIrd35vKUQBZd0TyDDbOLqvsnEt4owOKkQvudwOAgJCaFLly78/ve/Z9KkSbRv397oWEJ4hdLHZ22dOKCU46QDJ6e11obN8kpLS9Pr16836tv7rcraer7YXkCW1cYX2wuoqXf+X6oUXNi1DenmFEb3SyYhOtLgpEIYZ/369dx2222888479O3b1+g4QrhFKfWD1jrtbD63qTP+888yjzBQdZ2dr3YUYrHm8vmPBVTV2V1jaZ3jyTCbGJNqIik2ysCUQhjP4XDwwgsvMGfOHJKTkzl69KjRkYTwiVMWv9Z6hze+oVJqFPASzjkEixqvGmj0nhuAP+C8rZCjtZ7kjSzBoqbezqqdRVisuXy6LZ9jtT+X/YCOrV3PtDfFtTAwpRD+o6CggN/+9resXLmS8ePH88Ybb9CmTRujYwnhEz5dl6WUCgXm41wqeAjIVkp9rLXe1ug9PYA5wDCt9RGlVJIvMwaKOruDb3cVYcmx8d9teVRU17vGUtvHkW52PgynY5uWBqYUwj+9/PLLfPnll8yfP5+77rpLZu2LZsXXC7KHALu01nsAlFLvAuOAbY3eMwWYr7U+AqC1LvBxRr9Vb3fw3Z5isqw2Vm7No7SyzjV2vinWeWafaqJLQisDUwrhn+rq6jh48CDdunXjkUceITMzkz59+hgdSwif83XxtwcONnp9iEZbAjfoCaCUWo3zdsAftNYrT/xCSqmpwFSATp06eSWsP7A7NOv2lmCx5rJySx7Fx2pdYz2Soskwp5BuNtE9KdrAlEL4t71797oerrNt2zZatmwppS+aLV8X/8mup524rCAM6AFcBnQAViml+mmtS3/xSVq/BrwGzln9no9qHIdD88OBI1hyclm+JY/Cip+3U+iW0Krhnn0KvZJjDEwpRGD497//zZQpUwB4/fXXadlSbn+J5s3XxX8I6NjodQcg9yTvWau1rgP2KqV24PxFINs3EY2htWbjwVIsOTaWb7aRV17tGuvUpiXpZhMZZhN9TLFyP1IIN1RXVzN9+nQWLVrERRddxNtvv03Xrl2NjiWE4c64+Bs29GkLbNZaV57hp2cDPZRSXYHDQCZw4oz9pcBE4E2lVALOS/97zjRnINBas+VwOZaGx9weLv356cbtW7dwlX1q+zgpeyHOUHh4OPv27WPOnDn88Y9/JDxcdqIUAs6g+JVStwN/BEwNhy4ANiillgCfaa0XnO5raK3rlVLTcD7oJxT4m9Z6q1LqT8B6rfXHDWNXKaW2AXacTwAsPqN/Kj9XWlnL66v2YLHa2F/88+9O7WIjSU913rMf1Km1lL0QZ0hrzaJFi0hPTyclJYUVK1YQFiYPlRKiMbf+i1BK3YLzfvpi4L/AW42GvwduBE5b/ABa6+XA8hOOPd7oYw3c3/AnKL30+U/8ffU+ABKiI0lPTSbdnEJa53hCQqTshTgbJSUlTJ48mQ8//JBHH32UJ554QkpfiJNw97+K3wEvaa3vb1iL37j4fySIS9obvtvtvIDxzK/NXDeoA6FS9kKck2+//ZZJkyaRl5fHX//6V+677z6jIwnht9wt/vOArFOMVQDxnokT/Mqq6tiRX0FEaAjX9E+R0hfiHH3wwQdcf/31dO3alTVr1pCWdlbblwvRbIS4+b4Sfjkbv7GegM0zcYLfD/tL0BrMHeKICjfsuUZCBI3LL7+ce++9lw0bNkjpC+EGd4s/C3hUKdW4/LVSqjUwE/jI48mC1Lq9RwC4oKvsCy7E2Vq2bBmjRo2itraW+Ph4XnjhBWJjY42OJURAcLf4H2l47zbAgnPTnb82vA7HOdtfuCF7XwkAQ7pI8QtxpmpqapgxYwbXXHMN+fn5FBUVGR1JiIDjVvE37Jc/CJgHJOJcg98G+Adw4fF99UXTquvsWA+VohQM6izTIoQ4Ezt27OCiiy5i3rx5zJgxg7Vr15KSkmJ0LCECjttrXRq2zH2k4Y84C5sOllJn15xviiWuhWwmIoS7tNbccsstHDx4kGXLlpGRkWF0JCEClrvr+J8E3tJab/dynqCWvff4ZX452xfCHeXl5YSEhBAdHc2bb75JdHQ07du3NzqWEAHN3Xv804GtSqn1SqnpSqlEb4YKVusa7u/LxD4hTi87O5tBgwYxffp0AHr16iWlL4QHuFv8ScD/AYXA88BhpZRFKXW9UirSa+mCSL3dwYb9zqkQMrFPiFNzOBz89a9/5eKLL6auro7JkycbHUmIoOLu5L4qrfVirfVonE/Uewjnnv3vAflKqde9mDEo/Gir4Fitnc5tW5IUG2V0HCH8UkFBAWPGjOF3v/sd11xzDZs2bWLYsGFGxxIiqLh7xu+itc7XWj+vtR4MjMS5c99tHk8WZFyX+eVsX4hTqqysxGq18uqrr7JkyRLi42U+jBCedjaP5Y0ExgM3A1cBilNv5ysa/DyxT4pfiMbq6upYvHgxv/3tb+nSpQu7d++mRYsWRscSImi5fcavlLpMKfUGkA+8A7QDHgBStNbXeClfUNBauzbukYl9Qvxs7969DB8+nFtvvZXPP/8cQEpfCC9zdznfAaA9cBCYj3Np3w5vBgsme4qOUXysloToSLq0bWl0HCH8wnvvvcfUqVNRSvHee+9xxRVXGB1JiGbB3Uv9n+Is+6+9GSZYuS7zd41HKXkanxAPP/wwTz31FBdddBHvvPMOXbp0MTqSEM2GW8Wvtb7d20GCmUzsE+KXjp/d//GPfyQ8XHaxFMKXTln8SqkhwBatdWXDx03SWq/zaLIgsm6vFL9o3rTWvPLKKxw5coRHH32UESNGMGLECKNjCdEsNXXGvxa4CFjX8LE+xftUw5g8XP4kbGVVHDpSRUxkGOeb5LGhovkpKSnh9ttvZ+nSpaSnp2O32wkNlR8XQhilqeIfDfzY8PEYTl38ognHz/YHdY4nNETu74vm5dtvv2XSpEnk5eXx3HPPMXPmTEJCznj7ECGEB52y+LXWnzT6eKVv4gSf48v4hsgyPtHMFBYWctVVV5GSksKaNWtIS0szOpIQAjfX8SultimlUk8x1kcptc2zsYJH9t6G/fml+EUzUVZWBkBiYiIffPABGzZskNIXwo+4e82tN3CqXTVaAr08Eye4lFbWsiO/goiwEMwd4oyOI4TXffzxx5x33nm8//77AIwaNYrYWJnbIoQ/OZObbae6x28GyjyQJeis3+c82x/QoTWRYTKZSQSv6upq7r33XsaNG0enTp1ITT3pBUIhhB9oajnfdGB6w0sNLFFK1ZzwthZACrDEO/EC28/b9MqDRkTw2r59O5mZmeTk5DBz5kyefvppIiPlad1C+KumZvXnAj80fNwd2AEUn/CeGmAb8KrnowU+2bhHNAfZ2dkcPnwYi8VCenq60XGEEKfR1Kz+94H3gePbzD6itd7jo1wBr6rWzuZDZYQoGNxZzvhFcCkvL2f9+vWMGDGC3/zmN2RkZMgjdIUIEO5u2TvR20GCzcaDR6h3aPqmxBITJVuSiuCRnZ1NZmYmhYWF7N+/n/j4eCl9IQJIU/f4H8T5YJ68ho+borXWz3o2WmA7voxPLvOLYOFwOHjuued4+OGHSUlJYcWKFVL4QgSgps74nwa+AvIaPm6KBqT4G5GNe0Qwqa+vZ+zYsaxcuZJrr72WRYsWSekLEaCaKv4WWuvjs/hPtYZfnES93cGGA3LGL4JHWFgYAwcOZNy4cdxxxx3yeGkhAlhTk/tqTvaxOL2tueVU1trpmtCKxBhZ1iQCU11dHY899hjjxo1j6NChPPnkk0ZHEkJ4gFuT+5RS3YBYrfWmhteRwENAP+ATrfUi70UMPK71+13kUqgITHv27GHixImsW7eOyMhIhg4danQkIYSHuFX8wCs41+tvanj9BHAfsBOYoJQK1Vov9EK+gHT8iXxymV8Eovfee4+pU6eilOLf//43119/vdGRhBAe5O6WvQOAbwCU8+beLcDDWuu+OCf+3emVdAFIa836/fJgHhGYLBYLmZmZ9O3bl02bNknpCxGE3C3+1kBRw8cDgLbAvxtefwqc5+FcAWt34VFKjtWSFBNJpzYtjY4jhFuqq6sBGD16NK+99hpff/01Xbp0MTaUEMIr3C3+AqBbw8dXAnu11vsbXrcC7J4OFqjWHV+/37WNzHwWfk9rzfz58+nZsyc2m43Q0FCmTJlCeLhsOiVEsHL3Hr8F+ItSqicwFfhbo7G+wF5PBwtUrvX7cn9f+LmSkhJuv/12li5dypgxYwgLc/fHgRAikLn7X/pDQAxwI/AZ8OdGYzcAX3g4V8CSiX0iEKxatYpJkyaRn5/P888/z4wZMwgJOZOndAshApW7e/WXA785xdgFHk0UwA6XVnG4tIqYqDB6JccYHUeIU5o/fz5RUVF89913DB482Og4QggfOqNre0qpGGAI0AbnI3qztdYV3ggWiLIbzvbTOscTGiL394V/OXToEHV1dXTt2pWFCxcSEhJCTIz8gipEc+P2tT2l1KOADfgv8B7OS/42pdQjXsoWcNYd37hHlvEJP/PRRx/Rv39/brvtNgDi4uKk9IVoptwqfqXUPcCfgA+BMcBAYHTD6z8ppe7yWsIAcvyM/0IpfuEnqqurmT59OuPHj6dz584sXCj7bAnR3Ll7qX8a8IrWelqjYznAJ0qpMmA68KqnwwWSI8dq+angKJFhIaS2b210HCE4ePAgY8eOJScnh5kzZ/L0008TGSnPjhCiuXO3+LsB955i7CNgsmfiBK7jy/gGdGxNRJjMjhbGa9u2LfHx8VgsFtLT042OI4TwE+42VAnQ6xRjvRrGmzXX+n25zC8MVF5ezu9+9zuOHj1Ky5Yt+eKLL6T0hRC/4G7xL8W5gc/1qtF2dEqpCTgf2LPUG+ECybp9DTv2yfp9YZB169YxcOBAXnjhBb788ksA2T1SCPE/3C3+h4DtOGfzVyql9iulKoElwI6G8WarsraerYfLCFEwqLM8ilf4lsPh4Nlnn2XYsGHU19fzzTffMHbsWKNjCSH8lLsb+JQppS4GJgDDca7jLwG+Bj7SWjfrvfo3Hiil3qFJbR9HdKRseyp8a86cOTzzzDNcd911vP7668THyy+fQohTc7ulGsp9ScMf0Yhs0yuMYLfbCQ0N5a677qJ79+5MnjxZLu0LIU6ryUv9SqlMpdRapVSRUmqXUuovSik5pT3BzxP75ExLeF9tbS2zZ89mwoQJaK3p0qULU6ZMkdIXQrjllMWvlLoeeBtIBlYDlTjv5f/5VJ/THNXZHWw8UApAmpzxCy/bs2cPw4cP55lnniElJYW6ujqjIwkhAkxTZ/z3A1lAD631OK21GZgLTFdKyUL1BlsOl1FVZ6dbYisSomVzFOE97777LgMHDmTnzp0sWbKEBQsWEBERYXQsIUSAaarAewGvaq0bn1LMA1oAnb2aKoC4LvPL2b7wooqKCu6//3769evHpk2buO6664yOJIQIUE3dr28NFJ1wrLDhf+OBvV5JFGDW7ZX1+8J7tm/fTvfu3YmJieHrr7+ma9euhIXJNBshxNk73SV7fYbHmxWHQ7N+v+zYJzxPa83LL7/MgAEDePbZZwHo0aOHlL4Q4pydrvhXK6Vqj/8BqhqOf9/4uFKqxt1vqJQapZTa0bBK4JQb/yilfq2U0kqpNHe/tq/tKjxKaWUdybFRdIhvYXQcESSKi4uZMGEC06dPZ+TIkUye3OwfhSGE8KCmTh/mevqbKaVCgfnAlcAhIFsp9bHWetsJ74vB+VCg7z2dwZNc6/e7tpGlVMIjvvvuO2644Qby8/N5/vnnmTlzpvzdEkJ41CmLX2s9xwvfbwiwS2u9B0Ap9S4wDth2wvueAJ4BHvBCBo/5eWKfrN8XnhEREUFcXBxLly5l8ODBRscRQgQhXy/Law8cbPT6UMMxF6XUQKCj1trS1BdSSk1VSq1XSq0vLCxs6q1eobX+xRm/EGfr0KFD/L//9/8AGDx4MFarVUpfCOE1vi7+k12zdE0UbNgf4AVg1um+kNb6Na11mtY6LTEx0YMR3XPoSBW2smriWoTTMynG599fBIePPvqI/v378/DDD3P48GEAQkJkmwwhhPf4+ifMIaBjo9cdgNxGr2OAfsBXSql9wEXAx/44we/4Zf60zvGEhMg9WHFmqqurmT59OuPHj6dLly5s2LCB9u3bn/4ThRDiHPl6bVA20EMp1RU4DGQCk44Paq3LgITjr5VSXwEPaK3X+zjnaR0vfrnML86U1porrriC1atXM3PmTJ5++mkiI2XXRyGEb/j0jF9rXQ9MAz4BfgT+rbXeqpT6k1LqGl9mOVfH7+/L+n3hLq01WmuUUkyfPh2LxcILL7wgpS+E8Cmf7waitV4OLD/h2OOneO9lvsh0poqP1rC78BhR4SH0S4kzOo4IAGVlZdxxxx2MHDmSKVOmcOONNxodSQjRTLl9xq+UaqeUelIp9a1SaptSqk/D8bv98R68N2Xvc27TO7BjPBFhMhFLNO37779n4MCBLFmyhPLycqPjCCGaObdaSynVG9gM3IXz8by9gKiG4V7ATK+k81Nyf1+4w+FwMHfuXC655BIcDgerVq1i1qzTLlgRQgivcvd09a84H8rTFRjDL5flrQaGejiXX5Mn8gl3rF27loceeogJEyawadMmhg5tVv+ZCCH8lLv3+H8F3Ky1Lm3YdrexPMDk2Vj+61hNPVtzywkNUQzs1NroOMIPHThwgE6dOnHxxRezZs0aLrroItl2VwjhN87kBrX9FMfb8vPDe4LehgNHsDs0/VJiaRUpT0oTP6utreXBBx+ke/furF/vXIE6dOhQKX0hhF9xt7nWA78BTraN7nXAWo8l8nPZx7fplcv8opE9e/aQmZlJdnY2d955J3379jU6khBCnJS7xf8XYKVSahmwGOc2u5cqpe4AbgAu91I+v7NOJvaJE7z77rtMnTqV0NBQlixZwnXXXWd0JCGEOCW3il9r/ZlS6gbgRSC94fDzOLfbvUFrvdpL+fxKbb2DjQdKATnjFz/btWsXqampvP3223Tu3NnoOEII0SS37/FrrT8AOgNm4ApgINBJa73US9n8zubDZdTUO+ieFE2bVhFGxxEGysnJ4auvvgJgzpw5fP3111L6QoiAcEaz07TWGtjipSx+z7V+X872my2tNfPnz2fWrFn06dOHDRs2EBp64kIXIYTwX24Vf8Nl/iZprf997nH8W7Zrf/54g5MIIxQXF3Pbbbfx8ccfM2bMGN58802ZsS+ECDjunvG/e4rjutHHQV38Dodm/X7nVr1yxt/85ObmMmTIEAoKCnjhhReYMWOGlL4QIiC5W/znn+RYWyAD+DXwW48l8lM7Cyooq6ojJS6KDvEtjY4jfMxkMnHjjTdy0003MWjQIKPjCCHEWXN3Vv+OUwytUUrZce7h/53HUvkh1/p9WcbXbBw8eJA777yTl156ie7du/Pcc88ZHUkIIc6ZJx4t9yVwjQe+jl9bt08u8zcnS5cupX///nzzzTfs2HGq33uFECLweKL403A+sS9oaa0bTeyT4g9m1dXV3HPPPUyYMIFu3bqxYcMG0tPTT/+JQggRINyd1f/gSQ5HAP2ACcDrngzlbw6WVJFXXk3rluF0T4w2Oo7womeeeYZXXnmF+++/n6eeeoqICNmvQQgRXNyd3Pf0SY7ZgcPAC8AfPZbIDx3fpjetcxtCQmQmd7DRWlNSUkLbtm154IEHGDZsGCNHjjQ6lhBCeIW7xd/iJMfqtNYOT4bxV7J+P3iVlZVxxx13sHHjRjZs2ECrVq2k9IUQQe209/iVUhHAH4B+WuuaRn+aRenDzzv2Dena1uAkwpO+//57Bg4cyJIlS7jllluIiooyOpIQQnjdaYtfa10LzABaeT+O/ymsqGFP0TFahIfSNyXW6DjCAxwOB3PnzuWSSy7B4XCwatUq5syZI1vvCiGaBXdn9ecAfbwZxF+tbzjbH9S5NeGhnlgEIYxmt9v56KOPmDBhAps2bWLo0KFGRxJCCJ9x9x7/g8BbSqldWuvPvBnI36yTB/MEjU8//ZSBAweSkJDAypUriYmJkW13hRDNjrunsH8DWgOfKKUqlFI/KaV2NvoTtDucuO7vS/EHrNraWn73u99x1VVX8ec//xmA2NhYKX0hRLPk7hn/D/zygTzNQkV1HdtyywkLUQzsJDP6A9Hu3buZOHEi2dnZ3HnnnTz11FNGRxJCCEO5u1d/preD+KMNB0pxaDB3iKNFhEz8CjRffPEF48ePJzQ0lCVLlnDdddcZHUkIIQx3ykv9Sqk9Sqn+vgzjb2Sb3sDWr18/rrzySjZt2iSlL4QQDZq6x98FiPRRDr8kE/sCz6ZNm7j11lupr68nKSmJ999/n86dOxsdSwgh/IasTzuFmno7mw6WApDWWe7v+zutNfPmzePCCy/kv//9L/v27TM6khBC+KXTFX+zm9B33OZDZdTWO+jZLpr4VvKgFn9WVFTEuHHjmDFjBldddRU5OTl0797d6FhCCOGXTje5749KqSI3vo7WWv/WE4H8hVzmDxy//vWv+e6773jppZeYPn26LNMTQogmnK74BwA1bnydoLsyIBP7/Ft9fT12u53IyEheeOEFAAYOHGhwKiGE8H+nK/7xWut1PkniR+wOzfr9RwA54/dHBw8eZNKkSZjNZubPny+FL4QQZ0Am953EjrwKKqrrad+6BSmtT/ZEYmGUpUuX0r9/fzZt2sTFF19sdBwhhAg4Uvwn8fNjeOVs319UVVVxzz33MGHCBLp168bGjRu56aabjI4lhBABR4r/JGRin/85fPgwb731FrNmzWLNmjUya18IIc7SKe/xa62b5S8FWutGE/tk/b6RtNZ8/vnnjBw5ku7du7Nr1y7atWtndCwhhAhozbLcm7K/uJKCihratIrgvMRoo+M0W2VlZUycOJErr7wSi8UCIKUvhBAe4O7T+ZqN45f50zrHy3pwg6xdu5aJEydy8OBBnnzySdLT042OJIQQQUPO+E8g6/eNNX/+fIYPH47WmlWrVjFnzhxCQuSvqRBCeIr8RD2BzOg3VufOnbn22mvZtGkTQ4cONTqOEEIEHSn+RgoqqtlXXEmriFD6mGKNjtNsrFy5kvnz5wOQkZHBe++9R+vWrQ1OJYQQwUmKv5Hsvc7d+gZ1jicsVP7VeFttbS0PPPAAo0eP5o033qCurs7oSEIIEfSk3RrJlvX7PrNr1y6GDRvGc889x913383q1asJDw83OpYQQgQ9mdXfyLq9Uvy+UFpaypAhQ9Ba88EHHzBhwgSjIwkhRLMhxd+gvLqOH/PKCQ9VDOwk95e9ob6+nrCwMFq3bs28efO49NJL6dSpk9GxhBCiWZFL/Q1+2H8ErSG1fRxR4aFGxwk6mzZtIjU1lZUrVwJw8803S+kLIYQBpPgbHF+/f4Es4/MorTXz5s3jwgsvpLy8nJYtWxodSQghmjUp/gau9ftyf99jioqKGDduHDNmzODqq68mJyeHSy+91OhYQgjRrEnxA9V1dnIOlqEUpHWW4veUjz/+mE8++YSXXnqJjz76iISEBKMjCSFEsyeT+wDroTJq7Q56J8cQ11KWlJ2L+vp6tm7dSv/+/bn11lu59NJL5RG6QgjhR+SMH1m/7ykHDhzg8ssvZ/jw4RQUFKCUktIXQgg/I8VPo/X7MrHvrH344YcMGDCAnJwcXn31VZKSkoyOJIQQ4iSaffHbHZoN+51b9crEvjPncDi4++67ufbaaznvvPPYuHEjN910k9GxhBBCnEKzL/4fbeVU1NTTsU0LkuOijI4TcEJCQqivr2fWrFmsXr2a8847z+hIQgghmtDsJ/fJ/f0zp7Vm0aJFpKWlMXDgQBYuXIhSyuhYQggh3ODzM36l1Cil1A6l1C6l1FchQXoAABfWSURBVEMnGb9fKbVNKWVVSn2ulOrszTyyfv/MlJaWcuONNzJ16lQWLlwIIKUvhBD/v717D5OqOvM9/n27mwa5NCC31iAgEVHIYAsEcTQQT3gYw1EIGVRw0ChCyHh5BiVzjoaMQWMcxSsedQI5IYkaNCIiRINk4mAiMyDSNBow4wx3EK9AIw0NbTfv/LF2S1E23UXbVdVV9fs8z366au9Ve7+1qp5+a6+19toZJKWJ38zygceAbwL9gAlm1i+uWBkw2N0HAM8Bs5IVj7uzOroVrwb2NWzlypWUlJSwaNEi7rnnHh5//PF0hyQiIico1U39Q4CN7r4ZwMyeAcYAb9cWcPflMeVXAROTFczW3Qf5uOIwndsW0rtzm2QdJiu8+uqrjBgxgtNOO43XXnuNoUOHpjskERFphFQ39X8J2BHzfGe07niuA5YmK5jVW3YDYbY+NVfXzd0BuOCCC5gxYwZlZWVK+iIiGSzVib+u7Op1FjSbCAwG7jvO9u+a2RozW/PRRx81Khg189dv6dKlDBo0iN27d9OiRQvuuOMOOnTQLYtFRDJZqhP/TuC0mOfdgV3xhcxsBDADGO3uh+vakbvPdffB7j64S5cujQqmdmDfeUr8x6iqqmL69OmMGjWK6upqysvL0x2SiIg0kVQn/jeAPmZ2upkVAuOBJbEFzOxcYA4h6X+YrEA++OQQ2/ccpG3LAs4+pShZh8k4Gzdu5IILLuDBBx/k+uuv5/XXX9e1+SIiWSSlg/vcvdrMbgSWAfnAPHffYGZ3AmvcfQmhab8tsCDqd9/u7qObOpbaaXoH9uxIfp7692v94Ac/YNOmTTz//POMHTs23eGIiEgTS/kEPu7+O+B3cetuj3k8IhVxHL1+v2MqDtesVVRUUFFRQXFxMY8++iiHDh2iR48e6Q5LRESSIGen7P3sxjw5PnFPWVkZgwYNYvz48bg7Xbt2VdIXEcliOZn491V+yjsf7KcwP49zTsvNUeruzuzZsxk6dCgHDhzgjjvu0CWNIiI5ICfn6i/dtgd3GNC9Pa1a5Kc7nJTbs2cP11xzDb/97W+59NJLmTdvHp07d053WCIikgI5ecaf69fvFxQUsGnTJh555BEWL16spC8ikkNy8ow/F2/MU11dzWOPPcbUqVMpKipi3bp1tGjRIt1hiYhIiuXcGf+hT2t4a2c5ZuFSvlywbds2hg8fzrRp03juuecAlPRFRHJUziX+dTvK+bTGOau4iPYnZX/yW7hwISUlJfz5z39m/vz5TJyYtHseiYhIBsi5xP/Glty5fv++++5j3Lhx9OnTh7KyMiZMmJDukEREJM1yro9/ddS/nwsD+0aPHs3evXuZOXMmhYWF6Q5HRESagZw646+uOcLabWFEfzYO7HN35s6dy6RJk3B3+vbty913362kLyIin8mpxP+X9/ZzoKqGnp1a07WoVbrDaVLl5eVcccUVTJ06lR07dlBZWZnukEREpBnKqcT/WTN/lp3tr1y5kpKSEhYtWsQ999zDsmXLaN26dbrDEhGRZiin+viPDuzLnsRfWVnJ2LFjad26NStWrOC8885Ld0giItKM5Uzid/fPJu7JhoF9H330EZ06deKkk05iyZIl9O3bl/bt26c7LBERaeZypql/88cH2H2gis5tW9KrU2Y3gy9dupT+/fvzwAMPADBkyBAlfRERSUjOJP7a2/AOOb1jxt6FrqqqiunTpzNq1ChOOeUULrnkknSHJCIiGSZnmvpr+/czdWDfxo0bGT9+PKWlpdxwww3cf//9tGqVXVcmiIhI8uVM4q8d0T8kQ/v333vvPbZv386iRYv41re+le5wREQkQ+VEU/97+yrZubeSdi0LOKu4KN3hJKyiooJnn30WgK997Wts2bJFSV9ERL6QnEj8tf37g3p1JD8vM/r3165dy8CBA7nyyivZvHkzAG3atElzVCIikulyIvG/kUET97g7Dz/8MEOHDuXgwYO88sor9O7dO91hiYhIlsiJPv43tkTz8zfz/n135/LLL+e5555j9OjRzJs3j06dOqU7LBERySJZn/jLD1bxzgf7KSzIY0D35n2tu5kxcuRIhg8fzg033JCxlx2KiEjzlfWJf83WcLZf0r0DLQvy0xzN51VXVzNz5kz69+/PhAkTmDJlSrpDEhGRLJb1ffxHp+ntmOZIPm/btm0MHz6cn/zkJ6xatSrd4YiISA7I+jP+5npHvoULFzJ58mRqamqYP38+EyZMSHdIIiKSA7L6jL+yqoY/79xHnsGgns3njL+0tJRx48bRp08fysrKlPRFRCRlsjrxl+3YS/UR5+xTimjXqkW6w2H//v0ADBo0iAULFrBixQq+/OUvpzkqERHJJVmd+Gsv40t3M7+7M3fuXHr27Mmbb74JwLhx4ygsLExrXCIiknuyO/E3g/n5y8vLufzyy5k6dSqDBw+mW7duaYtFREQkaxN/dc0R1m5P7xn/ypUrKSkp4YUXXuDee+/l5Zdfpri4OC2xiIiIQBaP6t+w6xMOVtVweuc2dGnXMi0xLFmyhLy8PFasWMF5552XlhhERERiZe0Z/9H5+VM7mn/Xrl2UlpYCcOedd1JWVqakLyIizUbWJv7aO/Klspn/pZde4pxzzuHKK6+kpqaGFi1a0L59854mWEREcktWJn53Z8221N2Y5/Dhw9x8881ccsklnHrqqSxevJj8/OY3PbCIiEhW9vFv+qiCPQeq6NquJT1Obp3UY+3evZuRI0eydu1abrrpJmbNmkWrVq2SekwREZHGysoz/tW11++ffnLS73DXsWNHzj77bF544QUeeeQRJX0REWnWsjTx7wZgSJL69/fv38/111/Pjh07yMvL46mnnmLMmDFJOZaIiEhTysrE/8bW5PXvl5aWMnDgQObMmcPy5cubfP8iIiLJlHWJ/93ySt4tr6SoVQF9u7Vrsv26Ow899BDnn38+lZWVLF++nKuvvrrJ9i8iIpIKWZf434gu4xvc62Ty8pquf//BBx/klltuYdSoUbz55psMGzasyfYtIiKSKlk3qn/11qa9fr+qqorCwkKmTJlCx44dufbaa5M+YFBERCRZsvaMf8jpX2zGvurqambMmMHQoUM5dOgQRUVFTJo0SUlfREQyWlYl/r0HqvjvDytoWZDHX32pQ6P3s23bNoYPH87dd9/Nueeey5EjR5owShERkfTJqqb+2vn5S07rQGFB437TLFy4kMmTJ1NTU8P8+fOZMGFCU4YoIiKSVlmZ+Bt7GV91dTV33XUXZ555Jk8//TS9e/duyvBERETSLqsS/+ro+v0THdi3YcMGunfvTvv27XnppZfo0qULLVq0SEaIIiIiaZU1ffwHq6rZ8O4+8gwG9kxsYJ+7M2fOHAYPHsytt94KwKmnnqqkLyIiWStrEn/Z9nKqjzj9T21P25YNN2Ts3buXyy67jO9973sMGzaMmTNnJj9IERGRNMuaxL96S+LX75eVlVFSUsLixYuZNWsWS5cupVu3bskOUUREJO2ypo//6MC+hpv5u3TpQnFxMQsWLGDIkCHJDk1ERKTZyIozfic09UOYqrcuu3btYsaMGRw5coTu3buzatUqJX0REck5WZH4K6tqqPy0ht5d2tC5bcvPbX/xxRcZMGAADz/8MOvXrwfQDHwiIpKTsiLxH6iqBmBI3Nn+4cOHmTZtGpdeeindu3entLSUAQMGpCNEERGRZiErEv/BwzXA5wf2XXHFFcyePZubbrqJVatWcdZZZ6UjPBERkWYjKwb3Haiqpg1HZ+w7cuQIeXl5fP/73+faa69lzJgx6Q1QRESkmUj5Gb+ZXWxm75jZRjO7tY7tLc3sN9H2182sV0P7rDniFBe1on1BNVdddRW33XYbABdeeKGSvoiISIyUJn4zywceA74J9AMmmFm/uGLXAXvd/QzgIeDeRPbd099n0KBBzJ8/nzZt2jRl2CIiIlnD3D11BzM7H5jp7n8TPb8NwN3/OabMsqjMSjMrAN4Hung9gRYUdXEq93FKcTd+/etfM2zYsOS+ERERkTQys1J3H9yY16a6qf9LwI6Y5zujdXWWcfdqYB/Qqb6d1uzfzde/MZJ169Yp6YuIiNQj1YP76rp4Pv5MPpEymNl3ge9GTw+/suyl9Z07d/6C4Uk9OgMfpzuIHKB6Tj7VcfKpjpOvb2NfmOrEvxM4LeZ5d2DXccrsjJr62wN74nfk7nOBuQBmtqaxTR6SGNVxaqiek091nHyq4+QzszWNfW2qm/rfAPqY2elmVgiMB5bElVkCfCd6PA74t/r690VERCRxKT3jd/dqM7sRWAbkA/PcfYOZ3QmscfclwM+BJ81sI+FMf3wqYxQREclmKZ/Ax91/B/wubt3tMY8PAZed4G7nNkFoUj/VcWqonpNPdZx8quPka3Qdp/RyPhEREUmvrJirX0RERBKTUYk/GdP9yrESqONbzOxtM3vLzF4xs57piDOTNVTHMeXGmZmbmUZHN0Ii9Wxml0ff5w1mNj/VMWa6BP5f9DCz5WZWFv3PGJWOODOZmc0zsw/NbP1xtpuZPRJ9Bm+Z2cAGd+ruGbEQBgNuAnoDhcCbQL+4MtcDP40ejwd+k+64M2lJsI4vAlpHj/9eddz0dRyVawf8CVgFDE533Jm2JPhd7gOUAR2j513THXcmLQnW8Vzg76PH/YCt6Y470xZgGDAQWH+c7aOApYQ5cIYCrze0z0w64x8CbHT3ze5eBTwDxN+BZwzwq+jxc8A3zKyuCYGkbg3Wsbsvd/eD0dNVhLkYJHGJfI8BfgzMAg6lMrgskkg9TwEec/e9AO7+YYpjzHSJ1LEDRdHj9nx+3hZpgLv/iTrmsokxBnjCg1VABzM7pb59ZlLiT8p0v3KMROo41nWEX5qSuAbr2MzOBU5z9xdTGViWSeS7fCZwppn9u5mtMrOLUxZddkikjmcCE81sJ+FqrptSE1pOOdH/26m/nO8LaLLpfuW4Eq4/M5sIDAaGJzWi7FNvHZtZHuGulNekKqAslch3uYDQ3P91QsvVa2b2FXcvT3Js2SKROp4A/NLdH4hu0vZkVMdHkh9ezjjhvJdJZ/wnMt0v9U33K8eVSB1jZiOAGcBodz+cotiyRUN13A74CvCqmW0l9Nkt0QC/E5bo/4vF7v6pu28B3iH8EJDEJFLH1wHPArj7SqAVYR5/aToJ/d+OlUmJX9P9Jl+DdRw1Q88hJH31iZ64euvY3fe5e2d37+XuvQjjKEa7e6Pn5c5Rify/eIEwWBUz60xo+t+c0igzWyJ1vB34BoCZnU1I/B+lNMrstwS4OhrdPxTY5+7v1feCjGnqd033m3QJ1vF9QFtgQTRucru7j05b0BkmwTqWLyjBel4GjDSzt4Ea4B/dfXf6os4sCdbxdOBnZnYzofn5Gp2MnRgze5rQHdU5GivxI6AFgLv/lDB2YhSwETgIXNvgPvUZiIiI5I5MauoXERGRL0iJX0REJIco8YuIiOQQJX4REZEcosQvIiKSQ5T4RepgZtdEd8araxlxgvuaHL0uJfc1MLO74uLdG92tsskvbzWzgugYP4xZ920zm1ZH2RFR2QubOo564jsjri5qzOw9M3vSzOqd1rSefQ40s5lm1qGp4xVJhYy5jl8kTS4jzIwV6+10BNII50d/OwFTgafNrNDdn2iqA0TXcp/PsXOFfxu4EHg4rvjqKKYNTXX8E3AX8BLQMorhduAsMzs/uq/HiRhIuJb6l4Cm95WMo8QvUr917r4x3UE0RnSnLgDM7PeEKWmnAU2W+OOP00C5TwgzEabDppg4/2hmLQk3kCkBNCui5BQ19Ys0kpmdZGazzWyDmR2ImpCXmFnfBF57lZmti163z8zeMrPJcWUuMrN/M7OKaFlqZv0aE6u7fwqsA86I2X97M3s8irvKzN4xs3+Ii6HIzB41sx1mdtjMPjCzfzWzM6PtxzT1m9lTwN8BPWOa1zdG245p6jezuWa2y8zy447ZKqqT+2PWdTWzOVH5KjP7i5ld15i6iKyN/vaIO/ZdZlZmZp+Y2cdm9oqZDYnZPhn4WfR0S8x77B5THzOiujxsZu+a2X3RDw2RZkFn/CL1y7dww6da7u410eOTouVO4H1Ck/oNwEozO+t49zIws+HArwhN4dMJ0532AzrGlBkDLCTMw30l4Uf6rYQ7yA1w93cb8V5OJ2qajpLtUmAA8E+E5vfRwMNm1sndb49eMxu4mHBTpo2EG6xcSLgBVl1+FJU5BxgbrTt0nLJPAFMIc7n/Pmb9GMI93J+MYu0A/DthmtLbga2EKUp/FnVd/EtC7/5YvaK/m+LWnwo8QOjeaUu498drZjbQ3TcAi4HewG2ELo3aOdFrP+ungW8C9xBaN/oTvh89gCsaEadI03N3LVq0xC2E2+J6HcuKel6TD7QhzJd9U8z6ydFru0fPbwU+rGc/Rkhuy+LWdyDcg+L+BmK/KzpeQbR0A34crbs/KvOt6PnEuNf+kpCoT46e/ycwq55jFUT7+WHMuqeArXWUHRGVvTDmfW4Gnowr9yLwVszzO4BK4Mtx5X4BfADk1xPfGdExJ0WxtiH80NgFPNNAPeYTfmxsAh6o4/PsFVf+omj9lXHrvxOt/6t0f6+1aHF3NfWLNGAs8NWY5ZjmZTMbb2arzWwfUA1UEFoB6mvufwPoYmZPmNn/NrP4s+ezgJ7Ar6Om44Ko1aECeB0YlmDsn0bL+8A/Ag8SztyJ9lENPBP3mqcIA+DOi4n1OjO71cwGmVmT/c9wd4+ON9bM2gCYWRfgbzh2HMLFwH8A2+LqYxnQlfrrutbPCXVRAfyBcEb/nfhCZjbSzF41s92E+qkinOEncoyLCT+aFsXFWdua8bUE9iGSdEr8IvVb7+5rYpZ3ajeY2VhC0+56YAIhWX6VcFbe6ng7dPdXCM2+vQi3hv3YzH5vZl+JinSN/v6Ko8m7drmY0KWQiNofK2cA7dx9ursfjradDHzsnx/R/n7MdoDrCX3aUwiD4D40swfM7KQEY2jIE4Sz8G9HzycQ/i/NjynTFfhffL4uno62J1IfdxDq4uvAv0SP/19sATP7KmHk/z5CC8HQqNx66vk84+JsRWjxiY2z9t7oiX5uIkmlPn6RxhsP/Ke7T6pdYWatCE3y9XL3Z4FnzawtIandCyw1sx5A7a1h/w+wvI6XH65jXV3HqG+0+h7CbT4L4pJ/cfR3d7SP/YSuiVvNrBfh8sZ/JpzZzuALcveNZrYKmEjo058IvOLuu2KK7SZcLnjLcXbzznHWx9oaUx9/NLMiYLKZ/dTdawf6jSO8r7+NrRMzO5nQpdCQ3YSkP/w423cdZ71ISinxizRea0JzcKyrOYGWNHevAJaY2RmEQWUdCfME7AD6uft9TRRrvD8CNwN/C/wmZv3fEZLf63XEuhW4z8yuAr4Svz3GYUJ3R6KeBB4xs4sIZ9hXxW1/mTAPwVZ3//gE9luf/0t47z8iDCaEo5/nZ/cqN7ORhAF/f4l5be0Pr/j3+DJhsGYbd/9jE8Up0uSU+EUa72Xg0eiys6WEpHUD8El9LzKznxCafZcTRoX3AG4E1rj7nqjMjcDzUQvCAsLZZDHw18Bmd5/9BWN/EVhJGBlfTEhslxAGNf7Y3fdGcbwOPE9o7j5AGMDWH5hTz77fBiaZ2XeBMqDS3dfXU/4Z4CHCD4ADwKK47fcTWhpeM7OHgP8C2hHGQvy1u4/lBLn7u2b2U2CamZW4+zrC53kj8Asz+1W0/x/y+TP12gmcbowuX/wUeNPd/2BmCwh9/A8SJiyC0KUzCpju7vFXEYikXrpHF2rR0hwXjo7qP6OeMvnA3YTEcJCQyM8hDBz7/zHl4kf1jyYM+HqPcPa4g9CPXhy3/wsIfc57CWfhWwj92kMbiP0uorFzDZRrDzwexVFFaDL/h7gy9xOS9z7CwLi3gBtjttc1qr8doRVhb7RtY7T+mFH9ccdZFG174jixnky4tHBrFOuHwJ+IuXriOK+rHdV/TR3bukbvaWHMumnRMSoJifsiYAXwh7jX3hl97jVxn20+oSXlregzKyfMn3AvUJTu77UWLe6OuX/WqiUiIiJZTqP6RUREcogSv4iISA5R4hcREckhSvwiIiI5RIlfREQkhyjxi4iI5BAlfhERkRyixC8iIpJDlPhFRERyyP8ASpRLRTStnBAAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f69124b1f28>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fpr, tpr, thresholds = roc_curve(Y_test, modele_pred)\n",
"plt.figure(figsize=(8, 6))\n",
"plot_roc_curve(fpr, tpr)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### PRECISION, RAPPEL, F1-SCORE, SUPPORT"
]
},
{
"cell_type": "code",
"execution_count": 83,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(0.8491551037230389, 0.5832782863074455, 0.6915417319310808, None)"
]
},
"execution_count": 83,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"precision_recall_fscore_support(Y_test, modele_pred,average='binary')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### SCORE EN K-FOLD CROSS VALIDATION (validation croisee en K passes) "
]
},
{
"cell_type": "code",
"execution_count": 84,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.61744138 0.69470828 0.9785394 0.97581425 0.95939566 0.97977162\n",
" 0.97151088 0.96404425 0.84770742 0.67586934]\n",
"Mean: 0.8664802477954898\n",
"Standard deviation: 0.13954943916107906\n",
"CPU times: user 313 ms, sys: 60.6 ms, total: 374 ms\n",
"Wall time: 510 ms\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele, X, Y, cv=10, scoring=\"precision\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 85,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.56101663 0.5740983 0.57102804 0.56560748 0.56971963 0.56130841\n",
" 0.56728972 0.58635514 0.58056075 0.59943925]\n",
"Mean: 0.5736423343003405\n",
"Standard deviation: 0.011462284269150745\n",
"CPU times: user 295 ms, sys: 68.4 ms, total: 363 ms\n",
"Wall time: 516 ms\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele, X, Y,cv=10, scoring=\"recall\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 86,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.58787819 0.62867083 0.72119924 0.71612827 0.71490559 0.71372549\n",
" 0.71630871 0.72919572 0.68915021 0.63536404]\n",
"Mean: 0.6852526304154557\n",
"Standard deviation: 0.04692364553042146\n",
"CPU times: user 324 ms, sys: 56.6 ms, total: 380 ms\n",
"Wall time: 511 ms\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele, X, Y, cv=10, scoring=\"f1\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 87,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.59974573 0.72785046 0.92345298 0.92822917 0.93643357 0.94320543\n",
" 0.92028942 0.88698816 0.84256538 0.74523707]\n",
"Mean: 0.8453997375952185\n",
"Standard deviation: 0.11061126443525086\n",
"CPU times: user 308 ms, sys: 60.3 ms, total: 369 ms\n",
"Wall time: 512 ms\n"
]
}
],
"source": [
"%%time\n",
"modele_score_roc=cross_val_score(modele, X, Y, cv=10, scoring=\"roc_auc\",n_jobs=-1)\n",
"display_scores(modele_score_roc)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### **REGRESSION LOGISTIQUE**"
]
},
{
"cell_type": "code",
"execution_count": 88,
"metadata": {},
"outputs": [],
"source": [
"from sklearn.linear_model import LogisticRegression"
]
},
{
"cell_type": "code",
"execution_count": 89,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"C=100.00\n",
"Sparsity with L1 penalty: 0.00%\n",
"score with L1 penalty: 0.8285\n",
"Sparsity with L2 penalty: 0.00%\n",
"score with L2 penalty: 0.7428\n",
"C=1.00\n",
"Sparsity with L1 penalty: 0.00%\n",
"score with L1 penalty: 0.8285\n",
"Sparsity with L2 penalty: 0.00%\n",
"score with L2 penalty: 0.7263\n",
"C=0.01\n",
"Sparsity with L1 penalty: 7.69%\n",
"score with L1 penalty: 0.8273\n",
"Sparsity with L2 penalty: 0.00%\n",
"score with L2 penalty: 0.7422\n"
]
}
],
"source": [
"# Set regularization parameter\n",
"for _, C in enumerate((100, 1, 0.01)):\n",
" # turn down tolerance for short training time\n",
" modele_l1_LR = LogisticRegression(C=C, penalty='l1', tol=0.01)\n",
" modele_l2_LR = LogisticRegression(C=C, penalty='l2', tol=0.01)\n",
" modele_l1_LR.fit(X_train, Y_train)\n",
" modele_l2_LR.fit(X_train, Y_train)\n",
"\n",
" coef_l1_LR = modele_l1_LR.coef_.ravel()\n",
" coef_l2_LR = modele_l2_LR.coef_.ravel()\n",
"\n",
" # coef_l1_LR contains zeros due to the\n",
" # L1 sparsity inducing norm\n",
"\n",
" sparsity_l1_LR = np.mean(coef_l1_LR == 0) * 100\n",
" sparsity_l2_LR = np.mean(coef_l2_LR == 0) * 100\n",
"\n",
" print(\"C=%.2f\" % C)\n",
" print(\"Sparsity with L1 penalty: %.2f%%\" % sparsity_l1_LR)\n",
" print(\"score with L1 penalty: %.4f\" % modele_l1_LR.score(X_test, Y_test))\n",
" print(\"Sparsity with L2 penalty: %.2f%%\" % sparsity_l2_LR)\n",
" print(\"score with L2 penalty: %.4f\" % modele_l2_LR.score(X_test, Y_test))"
]
},
{
"cell_type": "code",
"execution_count": 90,
"metadata": {},
"outputs": [],
"source": [
"modele_l1_LR_pred = modele_l1_LR.predict(X_test)\n",
"modele_l2_LR_pred= modele_l2_LR.predict(X_test)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### **ESTIMATION QUALITE MODELE REGRESSION LOGISTIQUE**"
]
},
{
"cell_type": "code",
"execution_count": 91,
"metadata": {},
"outputs": [],
"source": [
"modele_pred = modele_l1_LR_pred\n",
"#modele_pred = modele_l2_LR_pred\n",
"modele = modele_l1_LR\n",
"#modele = modele_l2_LR"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Matrice confusion"
]
},
{
"cell_type": "code",
"execution_count": 92,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[8464, 2340],\n",
" [1355, 9242]])"
]
},
"execution_count": 92,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"confusion_matrix(Y_test,modele_pred)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### ROC"
]
},
{
"cell_type": "code",
"execution_count": 93,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"0.8277735866301252"
]
},
"execution_count": 93,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"roc_auc_score(Y_test, modele_pred)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### ROC CURVE"
]
},
{
"cell_type": "code",
"execution_count": 94,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAf4AAAF8CAYAAAAuF9n2AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzs3Xd8lFXa//HPSacloffeFAQSYBFEcBVl6cVCsezaAEVRHrGX3XUfRcXCA4+oYPm5z66dTiiuXSkiNSCISJVOQgg1deb8/kgCIUAygZm5MzPf9+vFy0xh8nUXuXLOfd3nMtZaREREJDSEOR1ARERE/EeFX0REJISo8IuIiIQQFX4REZEQosIvIiISQlT4RUREQohfC78x5j1jzEFjzM/ned0YYyYbY7YYY9YZY9r7M5+IiEiw8/eK/32gVzGv9waa5/8aCbzph0wiIiIhw6+F31r7PZBWzFsGAv9n8/wIxBtjavsnnYiISPAra9f46wK7Cj3enf+ciIiIeEGE0wGKMOd47pxnChtjRpJ3OYAKFSp0uOSSS3yZS0RE5KLkuCw5LhfZuZYcl5tsl5scl5ucXEu2y427hCP0bW42rvT9uHOzAVKttdUvJEdZK/y7gfqFHtcD9p7rjdbaacA0gI4dO9qVK1f6Pp2IiMg5ZGS72Hskgz2HM9ibnsGegl+HM9h7JIN96Znkuk8XdgNE5/8qUC4ynLqVy1E3vhx14stRr3I56sTHUDe+PKk7fuGmfj2JrxzHP//5T/r06bPzQrOWtcI/F7jfGPMxcDlwxFq7z+FMIiISwqy1pJ3IZm96JnvST7InPfOMAr83PYNDJ7JL/JxqFaOoG1+OupXLUScu/5/xeYW+bnw54stHYsyZG9/WWowx5Na/nNGjR/PQQw9Ru/bFtb75tfAbYz4C/ghUM8bsBv4GRAJYa98CFgB9gC3ASeAOf+YTEZHQk+Nys/9I5qkiXrBK351f3PemZ5KR4yr2MyLDDbXjTq/W81bueav1OvEx1IkvR0xkeKlyLV++nIceeohZs2ZRo0YNXn755Yv51zzFr4XfWju8hNctcJ+f4oiISAg4lplT7Gr9wNFM3CVMqI+NiSi0/V60wJejesVowsLO1aZWem63mwkTJvDMM89Qt25d9u/fT40aNbzy2VD2tvpFREQ85nZbUo9nsbvwav3UNfZM9hw+ydHM3GI/wxioFRtTZOv9zMeVYiL98u+zf/9+brvtNr788ktuuukmpk2bRnx8vFe/hwq/iIiUWZk5LvYdOb1K311kO35feibZLnexnxETGXbGtfSiq/VacTFEhpeNu9sff/xxlixZwrRp07j77rvPuubvDcaWcPtAIFBXv4hI4LHWciQj59S19FPX2E+t1jNIPZ5V4udUqRCVX8xPX1MvvCVfpUKUTwqot2RnZ5Oenk6NGjVITU3l4MGDtGrVqtjfY4xZZa3teCHfTyt+ERHxiVyXmwPHss59i1v+1yezi2+aiwgz1IqLOb1aL3qNPb4c5aJK1zRXlmzdupXhw4cTHh7OkiVLqFatGtWqVfPp91ThFxGRC3IiK/eMgl6wBb8nvxN+/9FMXCV0zVWMjji9Wi9U1AtW7DUqxRDupaa5subDDz/knnvuITw8nHfeeYewMP9cblDhFxGRs1hrST2efVZBL7wdn34yp8TPqVEp+lRBrxd/dkd8bExEmd6G94UTJ05w//338/7779O1a1c++OADGjZs6Lfvr8IvIhKCsnPd7DtSeOs973a3vH/mPZ+dW3zTXFREWKFr64U64gs1zUVHBO42vK9Ya1m+fDnPPPMMf/3rX4mI8G8pVuEXEQky1lqOZuaedb964Y74lONZlNTbHV8+8syCXuQae9UKUV67dz3YWWt5//33GTp0KBUrVmT16tXExMQ4kkWFX0QkwLjcloPHMvOKeaHV+umVewbHs4q/dz08v2muYLVe9PjYOvHlqBCtEuENqamp3HnnncybN4+TJ09y3333OVb0QYVfRKTMych2nXEtveg19v1Hzhz4ci7lo8LPul+98OOalaKJKCP3rgezb7/9lltuuYXU1FQmTZrE6NGjnY6kwi8i4k/nG/hS+Pp6mkcDX6JPnS5Xt0jTXL3K5Ygrd/bAF/Gvd999lxEjRtC8eXOSkpJITEx0OhKgwi8i4lWFB76cdf96/uo9M6f4prnIcEOd+DMnuNUrtFqvHRdT6oEv4n9XXXUVI0eO5JVXXqFixYpOxzlFhV9EpBTOGPhyOP+EuULb8QeOZZbYNFd44Evh7feCAl/NiwNfxL9mzZrF/Pnzefvtt2nWrBlvvfWW05HOosIvIpLP7bakHM86a7V+uokuo8SBL2GG/Ka5849o9dfAF/GfjIwMxo0bx5tvvknHjh05cuSI14freIsKv4iEjMIDX841onXfkQxyXMUv12Miw864ll54O76sDXwR/9i4cSPDhg1j/fr1jBs3jvHjxxMVFeV0rPNS4ReRoGCtJf1kzlnHx+49knFqS96TgS9VK0QVu1ov6wNfxL9ycnLo27cvJ06cYMGCBfTu3dvpSCVS4ReRgFB44EtBB3zRqW6eDHypHR9zapVe9Ba3OnGBPfBF/Ofo0aNUqFCByMhIPvzwQxo1akTt2rWdjuURFX4RKRMKBr6cMW89/cIGvuRtvZ89ojWYB76I//z4448MHz6cu+66i6effpouXbo4HalUVPhFxOcKD3w554jWIyUPfDEGasZGn318bKFr7HHl1DQnvuN2u5kwYQJPP/009evX59prr3U60gVR4ReRi5aV68q7d/0cE9wKDqXxdODL6aEv5U+Naq0XX56acdEa+CKO2bdvH7fddhtfffUVQ4YMYerUqWW2a78kKvwiUixrLUczcs8q6IVX754MfKlcPvKs0+UKP65WUU1zUnbt3LmTFStW8Pbbb3PXXXcF9J9VFX6REFcw8OWs1foFDHw5tVovVNTrVS5H7TgNfJHAk52dzcKFCxk4cCCdO3dm586dAbvKL0z/JYoEuYKBL3uKNM0VNNGVZuBL0QluBY818EWCzZYtWxg+fDgrV65k3bp1tGnTJiiKPqjwiwS0goEvZ54ul3lhA19O3a+ugS8S2j744APuueceIiMjmTlzJm3atHE6klep8IuUYdm5bg4cPft+9dIMfIkKD6N2kYJeeLWugS8ip91333288cYbXHnllXzwwQc0aNDA6Uhep8Iv4qBjmTlF5q1f2MCXupXLn1qtF92O18AXEc+1b9+ev/71rzzzzDNERARniQzOfyuRMqBg4MtZq/VCTXTHPBz4cq4JbnXyG+k08EXkwllrmTx5MlWrVuXWW2/lrrvucjqSz6nwi1ygzBwXe9NPX1P35sCXguc08EXEd1JTU7njjjtISkpi+PDh3HrrrU5H8gsVfpFzKDrwpeiI1j3pGaQeL7lprmqFqLNOlyt8jb1yeTXNiTjh22+/5ZZbbiE1NZXJkydz//33Ox3Jb1T4JSTlutzsP5p5Rgf87sOnC3tpBr6cWrEX2Y6vG19OTXMiZdCmTZvo0aMHzZs3Z/78+SQkJDgdya9U+CUoncjKPf9q/XAG+49mUsKt61SKjjijiBcd0Vq9UrQGvogEkIyMDMqVK8cll1zCP//5TwYNGkTFihWdjuV3KvwScNxuS+qJrLzVeqGiXriJ7khGKQe+nGNEa6ya5kSCxsyZMxk9ejTz58+nQ4cOIXM9/1xU+KXMycp1sS898+wRrUcK/plZ4sCX6Iiwsw6iKRjVWi++PLXiYoiKUNOcSLDLyMhg3LhxvPnmm3Ts2DFoTt+7GCr84lclDXzZk55ByrGsEj+n8MCXc63Wq1bQwBeRULdhwwaGDRvGzz//zMMPP8zzzz9PVFSU07Ecp8IvXuVyWw4czTznBLeCEa0eDXyJLXwYzekRrRr4IiKe+uyzzzhw4AALFy6kV69eTscpM4wt6ViwANCxY0e7cuVKp2OEpOxcNy8s/IUNe4+eappzldA1VyEq/KymucIjWmto4IuIXKD09HS2b99OYmIiubm5HDp0iJo1azody+uMMaustR0v5Pdq2SQXZeHP+/h/S3ac8Vz1StGFbm+LKdIRr4EvIuIby5YtY/jw4bjdbrZs2UJUVFRQFv2LpcIvF2Ve8j4A7v1jU4Z2rE8tDXwRET9zu9289NJLPPPMM9SvX5/PPvtM1/KLocIvF+xIRg7fb04hzMAdXRtRo1KM05FEJMQcO3aM66+/ni+//JKhQ4cydepU4uLinI5VpqnwywX7YuMBsl1uujSpqqIvIo6oWLEiVapU4Z133uHOO+/UZUQPqINKLti85L0A9GtX2+EkIhJKsrOzefLJJ9mxYwfGGD755BPuuusuFX0PqfDLBTl8IpslW1IJDzP0vkyFX0T8Y8uWLVxxxRW88MILzJ071+k4AUlb/XJBFm3YT67b0q15NapUUBONiPjev//9b+69914iIyOZNWsWgwYNcjpSQNKKXy5I0rq8bf7+bes4nEREQsG7777LbbfdRmJiIsnJySr6F0Erfim1lGNZLNt6iMhww59a13I6jogEMZfLRXh4OEOHDuXYsWPcf//9RESodF0Mrfil1Bb9vA+3hW7NqxNXXhPsRMT7rLVMmjSJTp06cfLkSSpWrMjYsWNV9L1AhV9Kbd66vEN7+rVVU5+IeF9KSgr9+/dn7Nix1K1bl6yskgd3iedU+KVUDhzNZMWONKIiwriulY7CFBHv+uabb2jXrh1ffPEFkydPZs6cOVSuXNnpWEFFeyZSKvPX7cNa+GOL6lSK0Ta/iHiPtZbHH3+c2NhYFixYQEJCgtORgpIKv5RKQTd/v3bq5hcR79i5cyexsbFUrlyZGTNmULlyZSpUqOB0rKClrX7x2J70DFb/nk5MZBg9LqnhdBwRCQIzZswgISGBBx98EIB69eqp6PuYCr94bH7+ar/HJTWpEK3NIhG5cBkZGdxzzz3ceOONNGvWjL/97W9ORwoZKvzisSR184uIF/z222906tSJqVOn8vDDD7NkyRKaNm3qdKyQoWWbeGTnoROs232EClHhXK1tfhG5CBUrVgRg4cKF9OrVy+E0oUcrfvFIwWr/2lY1iYkMdziNiASa9PR0nnvuOVwuF7Vr1yY5OVlF3yEq/OKR09v86uYXkdJZtmwZCQkJPPvss/z0008AhIWp/DjF7//LG2N6GWN+NcZsMcY8fo7XGxhjvjHGrDHGrDPG9PF3RjnT1pTj/LLvKJViIujeoprTcUQkQLhcLsaPH0+3bt0ICwtj8eLFdOnSxelYIc+vhd8YEw5MAXoDrYDhxphWRd72NPCptTYRGAa84c+Mcrak5LzVfs9WtYiO0Da/iHhmxIgRPPXUU9x0002sWbOGyy+/3OlIgv+b+zoBW6y12wCMMR8DA4GNhd5jgdj8r+OAvX5NKGc5fWiPuvlFpGTWWowxjBgxgiuvvJI77rgDY4zTsSSfvwt/XWBXoce7gaI/Av4d+I8xZgxQAbjWP9HkXH7df4zfDh4nvnwkVzbTNr+InF9WVhZPPPEEAK+99hpdunTR1n4Z5O9r/Of6kc8WeTwceN9aWw/oA/zLGHNWTmPMSGPMSmPMypSUFB9EFTi92u/VuhaR4WrGEZFz++2337jiiiuYOHEiOTk5WFv0r3YpK/z9N/luoH6hx/U4eyv/LuBTAGvtMiAGOGupaa2dZq3taK3tWL16dR/FDW3WWnXzi0iJ/vWvf9G+fXu2b9/OrFmz+N///V9t7Zdh/i78K4DmxpjGxpgo8pr35hZ5z+9ADwBjzKXkFX4t6R2wYe9RtqeeoGqFKDo3qeJ0HBEpg3bv3s2oUaNITEwkOTmZQYMGOR1JSuDXa/zW2lxjzP3A50A48J61doMx5h/ASmvtXGAc8LYx5r/Iuwxwu9WekSMKVvu929QiQtv8IlLI9u3bady4MfXq1eP7778nISGBiAgdBhsI/P63ubV2gbW2hbW2qbX2+fzn/ppf9LHWbrTWdrXWtrPWJlhr/+PvjFKwzZ/fza9tfhHJZ61l4sSJtGzZko8++giAjh07qugHEP0/JeeUvPsIuw9nUKNSNH9opG1+EYGUlBRuv/12FixYQP/+/enZs6fTkeQCaP9WzikpOW+136dNbcLD1KQjEuq+/fZb2rVrx5dffsnkyZOZM2cOVatWdTqWXACt+OUsbrdl/vq86/v9dWiPiABpaWnExsayYMECEhISnI4jF0ErfjnL6t8Ps+9IJnXiYkisX9npOCLikJ07d/Lpp58CcP3117Nu3ToV/SCgwi9nKejm79u2NmHa5hcJSTNmzCAhIYH77ruPY8eOARAVFeVwKvEGFX45g6vQNr+6+UVCT0ZGBvfccw833ngjLVq0YPny5VSqVMnpWOJFusYvZ/hpexopx7JoUKU8bevFOR1HRPwoKyuLzp07s27dOh599FH++7//W6v8IKTCL2couHe/b9vaOnJTJMRER0fz5z//mTZt2uhWvSCmrX45JdflZtHP+wHo11bd/CKh4PDhwwwdOpSvvvoKgHHjxqnoBzkVfjll2bZDHDqRTZNqFWhVO9bpOCLiY0uXLiUhIYGZM2eyZcsWp+OIn6jwyylJyQVNfdrmFwlmLpeL8ePH0717dyIiIliyZAmjRo1yOpb4iQq/AJCd62bRhvxt/nbq5hcJZjNnzuSpp57ipptuYvXq1XTq1MnpSOJHau4TAJZsSeVIRg4talakRU3duiMSjFJSUqhevTo33ngjCxcu5E9/+pN290KQVvwCwDxN4hMJWllZWYwdO5aWLVvy+++/Y4yhV69eKvohSit+ITPHxRcbDgDq5hcJNps3b2bYsGGsWbOG+++/nxo1ajgdSRymwi98vzmFY1m5tKodS5PqFZ2OIyJe8q9//Yt7772X6OhoZs+ezcCBA52OJGWACr+cOpu/nybxiQSVL7/8kg4dOvDvf/+b+vXrOx1HyggV/hCXke3iy1/yt/nb6Pq+SKBbtWoVMTExtG7dmrfeeovIyEgiIvRXvZym5r4Q982vBzmZ7aJdvTgaVC3vdBwRuUBut5vXXnuNLl26MG7cOADKlSunoi9n0Z+IEJekbn6RgHfw4EHuuOMOFixYwMCBA3n33XedjiRlmAp/CDuRlcvXmw4CeUN5RCTwbNq0iWuuuYa0tDRef/11Ro8erdv0pFilKvzGmJZAN6Aq8L619oAxpj5wyFp70hcBxXe+/OUAmTluOjSsTJ34ck7HEZEL0KRJE66++moeffRR2rVr53QcCQAeXeM3xkQaY/4FbASmAeOBuvkvvw487Zt44kunuvm12hcJKDt27GDo0KEcPnyYqKgoPvjgAxV98ZinzX3/DQwARgANgcL7SAuAP3k5l/jY0cwcvvs1BWOgTxsVfpFAMX36dBISEli0aBE///yz03EkAHla+G8BnrHWvgfsLfLaNqCxV1OJz32x4QDZLjedGlWhZmyM03FEpAQnT55k1KhR3HTTTbRs2ZI1a9bQrVs3p2NJAPK08FcHivvRUpUjwJzq5tckPpGA8NBDDzFt2jQee+wxFi9eTJMmTZyOJAHK0+a+ncAfgK/P8VpH4DevJRKfSz+ZzQ+/pRJmoPdltZyOIyLnYa3lxIkTVKxYkb/97W/ccMMNXHfddU7HkgDnaeH/N/CUMWYLMC//OWuM6QI8RF6znwSIzzfsJ9dtubJZNapVjHY6joicw+HDhxkxYgRpaWl88cUX1K5dm9q11Y8jF8/Trf4XgK+Az4DU/Oe+ARYD3wH/4/1o4ivq5hcp25YsWUJCQgJz5syhd+/eui9fvMqjFb+1NhcYbIy5jrwO/hrAIWCRtfZzH+YTLzt0PIulWw8REWbopW1+kTLF5XLxwgsv8Pe//52GDRuyZMkSOnXq5HQsCTIeFX5jTA3yDun5AviiyGthQDVr7UEf5BMvW/jzflxuy9UtqxNfPsrpOCJSyPHjx3nnnXcYMmQIb731FrGxsU5HkiDk6TX+fUAX4KdzvJaY/3y4t0KJ7+hsfpGy5+uvv6Zr167ExcXx008/Ub16dW3vi894eo2/uD+BEYDbC1nExw4ezWT59jSiwsO4rnVNp+OIhLysrCzGjh1Ljx49mDRpEgA1atRQ0RefOu+K3xhTESi8z1TNGFN0mVgOuBk44INs4mUL1u/DWriqZXViYyKdjiMS0jZv3sywYcNYs2YNY8aM4YEHHnA6koSI4rb6xwF/zf/acvo2vqIM8Lw3Q4lvqJtfpGyYM2cOt9xyC9HR0cyZM4cBAwY4HUlCSHGFPwnYT15hfwOYAGwv8p4sYKO19lzX/qUM2Zuewcqdh4mJDOPaS7XNL+KkZs2a0a1bN95++23q1avndBwJMect/NbaVcAqAGOMBWZYa1PP934p2xasz1vtX3NJDSpEl2oas4h4wapVq5g1axbPPfccrVu3ZuHChU5HkhDlUXOftXaqin5gm3dqm1/d/CL+5Ha7ee211+jSpQv//Oc/SUlJcTqShDiPl37GmBbAHUBLzh7KY621fb0ZTLxnV9pJknelUz4qnKtb1nA6jkjIOHjwILfffjsLFy5k0KBBvPvuu1SpUsXpWBLiPD3ApwPwA3nd+w2AX4Eq5J3gtxf43VcB5eIVNPVde2lNykXpuAURf3C5XFx99dVs3bqVKVOmcO+99+o2PSkTPF3xvwjMB4YD2cCt1trVxpg+wDvAYz7KJ15w+tAedfOL+FpOTg7h4eGEh4fz6quvUqdOHdq2bet0LJFTPD3Apx3wPqcP6gkHsNYuIG8y3wSvJxOv2J56gg17j1IpOoKrWlZ3Oo5IUNuxYwfdu3dn8uTJAPTq1UtFX8ocTwt/NHDMWusG0oDC94NtBPQnu4xKSs5b7V/XuibREdrmF/GVzz77jISEBDZu3EidOmqilbLL08K/DSj4k7wBuL3Qa7cCGtBTRhVc3++vbn4Rnzh58iQjR45kyJAhXHLJJaxdu5YhQ4Y4HUvkvDwt/AuB6/K/fgEYaIxJM8YcBP4CTPZFOLk4vx04xq8HjhFXLpKuzao5HUckKK1evZr33nuPxx57jB9++IHGjRs7HUmkWB4191lrnyz09SJjTDfgRqA8sMhaO9dH+eQiFNy736t1LaIiPP0ZT0RKYq1lxYoVdOrUiSuvvJLNmzfTpEkTp2OJeOSCqoG19kdr7cPW2tEq+mWTtfZ0N387dfOLeEtaWho33HADnTt3ZtWqVQAq+hJQLnoZaIxpZYz5yBthxHt+2XeMbSknqFohii5NqjodRyQoLF68mISEBObNm8fLL79MYmKi05FESq3Ywm/ytDXG9DPGXFrktTbGmM+AdUA/X4aU0itY7fe6rBYR4drmF7lYL730EldddRWRkZEsXbqUcePGERam/7Yk8Jz3T60xphawBFgDzAF+Nsb80xgTYYx5Pf/5fuRN7mvmj7Dimbxtfp3NL+JN0dHRDBs2jDVr1vCHP/zB6TgiF6y45r4XgQTgeWA10Bh4FPgO6AJ8Ajxird3t65BSOuv3HOH3tJNUrxRNp8Y6F1zkQiUlJeF2uxkwYAAPPvgggI7dlYBXXOG/DviHtfbFgieMMT8DnwNvWWtH+zqcXJiC1X7fNrUJD9NfUiKllZWVxWOPPcakSZP44x//SP/+/VXwJWgUd4GqBnlb/YUVPFYzXxllrWX+qW1+dfOLlNbmzZvp0qULkyZN4oEHHmDhwoUq+hJUilvxhwNZRZ4reHzCN3HkYq3+PZ096RnUjouhfYPKTscRCSg7duygffv2xMTEMHfuXPr37+90JBGvK+kAn57GmMKNe2GABXoZYy4p/EZr7YfeDielV9DN37dNbcK0zS/iEbfbTVhYGI0aNeJvf/sbN998M3Xr1nU6lohPlFT4/3Ge558r8tgCKvwOc7kLbfO3Uze/iCdWrlzJnXfeyUcffUTr1q155JFHnI4k4lPFFf5Li3lNyqAVO9I4eCyL+lXK0a5enNNxRMo0t9vNxIkTeeKJJ6hVqxbHjx93OpKIX5y38Ftrf/XFNzTG9AImkddD8E7huwYKvWcI8HfydhKSrbU3+yJLsDm9zV9HzUgixTh48CB/+ctfWLRoEYMGDeLdd9+lShXd+iqhwaMhPd5ijAkHppB3q+BuYIUxZq61dmOh9zQHngC6WmsPG2Nq+DNjoMp1uVm4fj+gbn6Rkrz++ut88803TJkyhXvvvVc/KEtI8fd5k52ALdbabdbabOBjYGCR94wAplhrDwNYaw/6OWNA+nFbGodOZNO4WgVa14l1Oo5ImZOTk8O2bdsAeOqpp1i9ejWjR49W0ZeQ4+/CXxfYVejx7vznCmsBtDDGLDHG/Jh/aeAsxpiRxpiVxpiVKSkpPoobOE5N4mtbW3+RiRSxfft2unfvzjXXXMPJkyeJjo6mVatWTscScYS/C/+5KpIt8jgCaA78ERgOvGOMiT/rN1k7zVrb0VrbsXr16l4PGkhyXG4WbSjY5lc3v0hhn376KQkJCWzcuJEJEyZQvnx5pyOJOMrfhX83UL/Q43rA3nO8Z461Nsdaux34lbwfBOQ8Fm9JJf1kDs1rVKRlrUpOxxEpEzIzMxkxYgRDhw6lVatWrF27liFDhjgdS8RxpS78xphmxpjLjTEX8mPzCqC5MaaxMSYKGAbMLfKe2cDV+d+rGnlb/9su4HuFjKRkTeITKSoyMpIdO3bwxBNP8P3339O4cWOnI4mUCR4XfmPMXcaY3eStwJcCl+Q/P90Yc48nn2GtzQXuJ2/Qzy/Ap9baDcaYfxhjBuS/7XPgkDFmI/ANeRMAD3n8bxRisnJd/Gdj/jZ/O3XzS2iz1vL222+zd+9ewsPDWbhwIePHjycyMtLpaCJlhkeF3xhzOzAN+Br4C2deq18ODPX0G1prF1hrW1hrm1prn89/7q/W2rn5X1tr7UPW2lbW2jbW2o89/exQ9P3mVI5l5nJp7ViaVq/odBwRx6SlpXHDDTcwcuRI3nzzTQAiIvx6x7JIQPB0xf8IMMla+2fOnsz3C/mrf/G/wt38IqFq8eLFJCQkkJSUxCuvvMKzzz7rdCSRMsvTH4ebAvPP89oxQGPgHJCZ4+LLjQcA6K/r+xKiZs6cyU033UTjxo0UH4cRAAAgAElEQVRZunQpHTt2dDqSSJnm6Yo/jTO78QtrAezzThwpjW82HeREtou29eJoUFW3KElouvrqq3nggQdYvXq1ir6IBzwt/POBp40xhYu/zb+/fiwwx+vJpERJBZP4tM0vIWbevHn06tWL7OxsKleuzMSJE4mN1YmVIp7wtPA/lf/ejUASeYfuvJL/OBLQBTU/O5GVy1eb8rb5+2qbX0JEVlYWDz74IAMGDODAgQOkpqY6HUkk4HhU+PPPy28PTAaqA3uAKsA/gcsLztUX//lq00Eyc9y0bxBP3fhyTscR8blff/2Vzp07M3nyZB588EF+/PFH6tTRD70ipeXxvS7W2nTyVv5P+S6OeCopuaCbX3/xSfCz1nL77beza9cu5s2bR79+/ZyOJBKwPCr8xpjxwP9Zazf5OI944FhmDt9uTsEY6Kvr+xLEjh49SlhYGBUrVuT999+nYsWK1K1bdK6XiJSGp9f4xwAb8qfhjTHGhPZUHId9sfEA2blu/tCoCjVjY5yOI+ITK1asoH379owZMwaAli1bquiLeIGnhb8G8GcgBXgN2GOMSTLG3GSMifZZOjmngm7+/lrtSxByu9288sorXHHFFeTk5HD33Xc7HUkkqHja3Jdhrf3AWtubvIl6jwO1gU+AA8aYt32YUQo5cjKHH35LIcxAr8tU+CW4HDx4kD59+vDII48wYMAA1q5dS9euXZ2OJRJUSj2dz1p7wFr7mrW2A9CDvJP77vR6MjmnzzfsJ8dl6dK0KtUrabNFgsvJkydZt24db775JtOnT6dyZR0KKuJtpZ5gkb+1Pwi4FehJ3sCe8x3nK142b526+SW45OTk8MEHH/CXv/yFRo0asXXrVsqV0y2qIr5SmrG8fzTGvAscIG9QT03gYaCOtXZAsb9ZvOLQ8SyWbj1ERJihV+taTscRuWjbt2+nW7du3HHHHXz11VcAKvoiPubp7Xy/A3WBXcAU8m7t+9WXweRsizbsx+W2XNWiOpUrRDkdR+SifPLJJ4wcORJjDJ988gnXXnut05FEQoKnW/1fkFfsv/NlGCleUrLO5pfg8OSTT/LCCy/QuXNnPvroIxo1auR0JJGQ4VHht9be5esgUryDxzJZvv0QUeFh9NQ2vwS4gtX9s88+S2RkpMNpRELLeQu/MaYT8LO19mT+18Wy1v7k1WRyhoXr9+O20L1FNeLK6S9KCSzWWt544w0OHz7M008/zTXXXMM111zjdCyRkFTciv9HoDPwU/7X9jzvM/mvhXs3mhSWpG5+CVBpaWncddddzJ49m759++JyuQgP118XIk4prvD3Bn7J/7oP5y/84mP7jmSwYsdhoiPCuLZVTafjiHhs8eLF3Hzzzezfv59XX32VsWPHEhZW6uNDRMSLzlv4rbWfF/p6kX/iyLnMzz+i9+qWNagYXeqjF0QckZKSQs+ePalTpw5Lly6lY8eOTkcSETy8j98Ys9EY0+Y8r7Uyxmz0biwprOBs/n7t1M0vZd+RI0cAqF69OjNnzmT16tUq+iJliKd7bpcA5ztVozzQ0jtxpKhdaSdZuyudcpHhXHNJDafjiBRr7ty5NG3alBkzZgDQq1cvYmNjHU4lIoWV5mLb+a7xtwWOeCGLnMP89Xmr/R6X1qB8lLb5pWzKzMzkgQceYODAgTRo0IA2bc65QSgiZUBxt/ONAcbkP7TAdGNMVpG3lQPqANN9E0/UzS9l3aZNmxg2bBjJycmMHTuWF198kehoDZASKauKW0LuBVblf90M+BU4VOQ9WcBG4E3vR5MdqSf4ec9RKkZH8MeW1Z2OI3JOK1asYM+ePSQlJdG3b1+n44hICYrr6p8BzAAwxgA8Za3d5qdcwunV/nWtahITqfuepew4evQoK1eu5JprruG2226jX79+GqErEiA8PbJ3uK+DyNlOdfPrbH4pQ1asWMGwYcNISUlh586dVK5cWUVfJIAUd43/UfIG8+zP/7o41lr7snejhbYtB4+xaf8xYmMi6NZc2/ziPLfbzauvvsqTTz5JnTp1WLhwoQq+SAAqbsX/IvAtsD//6+JYQIXfi+blT+L7U+taREXopDNxVm5uLv3792fRokVcf/31vPPOOyr6IgGquMJfzlpb0MV/vnv4xQestae7+dupm1+cFxERQWJiIgMHDmTUqFEFfT8iEoCKa+7LOtfX4nub9h9ja8oJKpeP5IqmVZ2OIyEqJyeHZ555hoEDB9KlSxfGjx/vdCQR8QKPmvuMMU2AWGvt2vzH0cDjwGXA59bad3wXMfQUrPZ7XVabyHBt84v/bdu2jeHDh/PTTz8RHR1Nly5dnI4kIl7i6VFwb5B3v/7a/Mf/DfwXsBkYbIwJt9ZO9UG+kJO3zZ93fb+/uvnFAZ988gkjR47EGMOnn37KTTfd5HQkEfEiT5eTCcD3ACbv4t7twJPW2tbkNf7d45N0IejnPUfZeegk1SpGc3kTbfOLfyUlJTFs2DBat27N2rVrVfRFgpCnhT8eSM3/OgGoCnya//gLoKmXc4Wsgm3+Pm1qER6mBirxj8zMTAB69+7NtGnT+O6772jUqJGzoUTEJzwt/AeBJvlfXwdst9buzH9cAXB5O1goKrzNr7P5xR+stUyZMoUWLVqwb98+wsPDGTFiBJGRkU5HExEf8fQafxLwvDGmBTASeK/Qa62B7d4OForW7EpnT3oGtWJj6NhQ90iLb6WlpXHXXXcxe/Zs+vTpQ0SEpj+KhAJP/0t/HKgEDAW+BJ4r9NoQ4Gsv5wpJSfmH9vRpU5swbfOLD/3www/cfPPNHDhwgNdee40HH3yQsDDdQSISCjw9q/8ocNt5XvuDVxOFKLfbsmB9fjd/O3Xzi29NmTKFmJgYli1bRocOHZyOIyJ+VKq9PWNMJaATUIW8Eb0rrLXHfBEs1KzceZj9RzOpV7kcCfXjnY4jQWj37t3k5OTQuHFjpk6dSlhYGJUqVXI6loj4mcd7e8aYp4F9wH+AT8jb8t9njHnKR9lCSkE3f9+2tXUcqnjdnDlzaNeuHXfeeScAcXFxKvoiIcqjwm+MuQ/4BzAL6AMkAr3zH//DGHOvzxKGAJfbsmD9fgD6q5tfvCgzM5MxY8YwaNAgGjZsyNSpOmdLJNR5utV/P/CGtfb+Qs8lA58bY44AY4A3vR0uVCzfdojU41k0qlqe1nVinY4jQWLXrl3079+f5ORkxo4dy4svvkh0dLTTsUTEYZ4W/ibAA+d5bQ5wt3fihKZ5he7d1za/eEvVqlWpXLkySUlJ9O3b1+k4IlJGeHqNPw1oeZ7XWua/Lhcgx+Vm0c/5hV/d/HKRjh49yiOPPMLx48cpX748X3/9tYq+iJzB08I/m7wDfG4yhZakxpjB5A3sme2LcKFg6dZDHD6ZQ7MaFWlZU81WcuF++uknEhMTmThxIt988w2AdpBE5CyeFv7HgU3kdfOfNMbsNMacBKYDv+a/LhcgKTmvm7+fuvnlArndbl5++WW6du1Kbm4u33//Pf3793c6loiUUZ4e4HPEGHMFMBjoRt59/GnAd8Aca63O6r8A2bluPt+Q182vs/nlQj3xxBNMmDCBG264gbfffpvKlXXcs4icn8cH+OQX9+n5v8QLfvgthaOZuVxSqxLNalR0Oo4EGJfLRXh4OPfeey/NmjXj7rvv1q6RiJSo2K1+Y8wwY8yPxphUY8wWY8zzxhhN8vCSgkl8/dtptS+ey87O5rHHHmPw4MFYa2nUqBEjRoxQ0RcRj5y38BtjbgI+BGoBS4CT5F3Lf+58v0c8l5nj4ouNB4C86/sinti2bRvdunVjwoQJ1KlTh5ycHKcjiUiAKW7F/xAwH2hurR1orW0LvASMMcZojNdF+vbXFI5n5dKmbhwNq1ZwOo4EgI8//pjExEQ2b97M9OnTeeutt4iKinI6logEmOIKeEvgTWtt4SXFZKAc0NCnqUJAwdn8Wu2LJ44dO8ZDDz3EZZddxtq1a7nhhhucjiQiAaq46/XxQGqR51Ly/1kZ2O6TRCHgZHYuX/1yEMgbyiNyPps2baJZs2ZUqlSJ7777jsaNGxMRoTYbEblwJW3Z21I+Lx74etNBMnJcJDaIp17l8k7HkTLIWsvrr79OQkICL7/8MgDNmzdX0ReRi1ZS4V9ijMku+AVk5D+/vPDzxpgsT7+hMaaXMebX/LsEznvwjzHmRmOMNcZ09PSzA0VS8umz+UWKOnToEIMHD2bMmDH06NGDu+/WKAwR8Z7ilg8vefubGWPCgSnAdcBuYIUxZq61dmOR91UibyjQcm9ncNrxrFy++fUgxkDfNtrmlzMtW7aMIUOGcODAAV577TXGjh2r2/RExKvOW/ittU/44Pt1ArZYa7cBGGM+BgYCG4u877+BCcDDPsjgqC83HiAr102nRlWoFRfjdBwpY6KiooiLi2P27Nl06NDB6TgiEoT8fVteXWBXoce78587xRiTCNS31iYV90HGmJHGmJXGmJUpKSnFvbVMOdXNr0l8km/37t387//+LwAdOnRg3bp1Kvoi4jP+Lvzn2rM81SiYfz7ARGBcSR9krZ1mre1ore1YvXp1L0b0nSMZOXy3OYUwA70vU+EXmDNnDu3atePJJ59kz549AISF6ZgMEfEdf/8NsxuoX+hxPWBvoceVgMuAb40xO4DOwNxgafD7z4b95LgsnZtUpXqlaKfjiIMyMzMZM2YMgwYNolGjRqxevZq6deuW/BtFRC6Sv+8NWgE0N8Y0BvYAw4CbC1601h4BqhU8NsZ8CzxsrV3p55w+UXA2v7r5Q5u1lmuvvZYlS5YwduxYXnzxRaKj9YOgiPiHX1f81tpc4H7gc+AX4FNr7QZjzD+MMQP8mcXfDp/IZsmWVMLDDL0uq+V0HHGAtRZrLcYYxowZQ1JSEhMnTlTRFxG/8vtpINbaBcCCIs/99Tzv/aM/MvnDog37yXVbureoTpUKOl891Bw5coRRo0bRo0cPRowYwdChQ52OJCIhyuMVvzGmpjFmvDFmsTFmozGmVf7zo4PlGrwv6Wz+0LV8+XISExOZPn06R48edTqOiIQ4jwq/MeYSYD1wL3njeVsCBTehtwTG+iRdkEg5lsWyrYeIDDf8qZW2+UOF2+3mpZde4sorr8TtdvPDDz8wblyJN6yIiPiUpyv+V8gbytMY6MOZt+UtAbp4OVdQWfTzPtwWujevTlz5SKfjiJ/8+OOPPP744wwePJi1a9fSpYv+MxER53l6jf8q4FZrbXr+sbuF7Qe0f12MeQXd/Dq0JyT8/vvvNGjQgCuuuIKlS5fSuXNnHbsrImVGabr6Xed5viqnh/dIEfuPZLJiRxpREWFce2lNp+OID2VnZ/Poo4/SrFkzVq7MuwO1S5cuKvoiUqZ4uuJfCdwGnOsY3RuAH72WKMjMX78Pa+HqltWpFKNt/mC1bds2hg0bxooVK7jnnnto3bq105FERM7J08L/PLDIGDMP+IC8Y3a7G2NGAUOAq32UL+Cd7ubXoT3B6uOPP2bkyJGEh4czffp0brjhBqcjiYicl0eF31r7pTFmCPA/QN/8p18j77jdIdbaJT7KF9B2Hz7Jmt/TKRcZTo9LazgdR3xky5YttGnThg8//JCGDRs6HUdEpFgeX+O31s4EGgJtgWuBRKCBtXa2j7IFvPn5TX3XXFqD8lF+PytJfCg5OZlvv/0WgCeeeILvvvtORV9EAkKpqpG11gI/+yhL0Ck4m7+/Du0JGtZapkyZwrhx42jVqhWrV68mPLzojS4iImWXR4U/f5u/WNbaTy8+TvDYkXqC9XuOUCEqnD+21DZ/MDh06BB33nknc+fOpU+fPrz//vvq2BeRgOPpiv/j8zxvC32twl/I/PV5q/3rWtUkJlIrwkC3d+9eOnXqxMGDB5k4cSIPPvigir6IBCRPC/+l53iuKtAPuBH4i9cSBYl5yermDya1a9dm6NCh3HLLLbRv397pOCIiF8zTrv5fz/PSUmOMi7wz/Jd5LVWA23LwOJv2H6NSTATdWlRzOo5coF27dnHPPfcwadIkmjVrxquvvup0JBGRi1aak/vO5xtggBc+J2gU3Lv/p9a1iI7QNn8gmj17Nu3ateP777/n11/P93OviEjg8Ubh70jexD4hr+u7oJtfI3gDT2ZmJvfddx+DBw+mSZMmrF69mr59+5b8G0VEAoSnXf2PnuPpKOAyYDDwtjdDBbJfDxxjy8HjVC4fSddm2uYPNBMmTOCNN97goYce4oUXXiAqKsrpSCIiXuVpc9+L53jOBewBJgLPei1RgEtKzlvt97qsFpHh3thQEV+z1pKWlkbVqlV5+OGH6dq1Kz169HA6loiIT3ha+Mud47kca63bm2ECXd42v7r5A8mRI0cYNWoUa9asYfXq1VSoUEFFX0SCWolLUmNMFPB34DJrbVahXyr6RWzYe5Qdh05SrWIUlzeu4nQcKcHy5ctJTExk+vTp3H777cTExDgdSUTE50os/NbabOBBoILv4wS2efmr/d6X1SZC2/xlltvt5qWXXuLKK6/E7Xbzww8/8MQTT+joXREJCZ5Wp2SglS+DBDpr7amhPOrmL9tcLhdz5sxh8ODBrF27li5dujgdSUTEbzy9xv8o8H/GmC3W2i99GShQrd2Vzu7DGdSMjeYPjbTNXxZ98cUXJCYmUq1aNRYtWkSlSpV07K6IhBxPV/zvAfHA58aYY8aY34wxmwv9CvkTTgru3e/TpjZhYSomZUl2djaPPPIIPXv25LnnngMgNjZWRV9EQpKnK/5VnDmQRwpxuwtv86ubvyzZunUrw4cPZ8WKFdxzzz288MILTkcSEXGUp2f1D/N1kEC26vfD7D+aSd34crRvEO90HMn39ddfM2jQIMLDw5k+fTo33HCD05FERBx33q1+Y8w2Y0w7f4YJVEn5k/j6tq2t7eMy5LLLLuO6665j7dq1KvoiIvmKu8bfCIj2U46A5XJbFvy8H1A3f1mwdu1a7rjjDnJzc6lRowYzZsygYcOGTscSESkzdLP5RVq+/RApx7JoUKU8berGOR0nZFlrmTx5Mpdffjn/+c9/2LFjh9ORRETKpJIKvxr6SlB4Ep+2+Z2RmprKwIEDefDBB+nZsyfJyck0a9bM6VgiImVSSc19zxpjUj34HGut/Ys3AgWSXJebRae2+dXN75Qbb7yRZcuWMWnSJMaMGaMfwEREilFS4U8Asjz4nJDcGVi69RBpJ7JpUr0Cl9au5HSckJKbm4vL5SI6OpqJEycCkJiY6HAqEZGyr6TCP8ha+5NfkgSgwpP4tMr0n127dnHzzTfTtm1bpkyZooIvIlIKau67QNm5p7f5+6ub329mz55Nu3btWLt2LVdccYXTcUREAo4K/wVavCWFo5m5tKxZieY1tc3vaxkZGdx3330MHjyYJk2asGbNGm655RanY4mIBBwV/guUlKxJfP60Z88e/u///o9x48axdOlSde2LiFyg817jt9bqh4LzyMxx8Z+NBwDo107d/L5ireWrr76iR48eNGvWjC1btlCzZk2nY4mIBDQV9wvw3eYUjmfl0rpOLI2rVXA6TlA6cuQIw4cP57rrriMpKQlARV9ExAs8nc4nhSRpEp9P/fjjjwwfPpxdu3Yxfvx4+vbt63QkEZGgoRV/KWVku/jql/xtfl3f97opU6bQrVs3rLX88MMPPPHEE4SF6Y+piIi36G/UUvp600FOZrtoVz+e+lXKOx0n6DRs2JDrr7+etWvX0qVLF6fjiIgEHRX+Uio4tEf37nvPokWLmDJlCgD9+vXjk08+IT4+3uFUIiLBSYW/FI5n5fL1poMA9Gmjwn+xsrOzefjhh+nduzfvvvsuOTk5TkcSEQl6Kvyl8NUvB8jKddOxYWXqxJdzOk5A27JlC127duXVV19l9OjRLFmyhMjISKdjiYgEPXX1l8I8HdrjFenp6XTq1AlrLTNnzmTw4MFORxIRCRkq/B46kpHD95tTMEbb/BcqNzeXiIgI4uPjmTx5Mt27d6dBgwZOxxIRCSna6vfQFxsPkO1yc3njKtSIjXE6TsBZu3Ytbdq0YdGiRQDceuutKvoiIg5Q4fdQ4RG84jlrLZMnT+byyy/n6NGjlC+vWyBFRJykwu+BwyeyWfxbKuFhht6X1XI6TsBITU1l4MCBPPjgg/zpT38iOTmZ7t27Ox1LRCSkqfB74PMN+8l1W65oWpWqFaOdjhMw5s6dy+eff86kSZOYM2cO1apVczqSiEjIU3OfBwrO5u+vbf4S5ebmsmHDBtq1a8cdd9xB9+7dNUJXRKQM0Yq/BKnHs1i6NZXIcMOfWmubvzi///47V199Nd26dePgwYMYY1T0RUTKGBX+Eiz8eT9uC92aVyeuvA6YOZ9Zs2aRkJBAcnIyb775JjVq1HA6koiInIMKfwmSkgu6+XXv/rm43W5Gjx7N9ddfT9OmTVmzZg233HKL07FEROQ8VPiLceBoJj/tSCMqIozrWtV0Ok6ZFBYWRm5uLuPGjWPJkiU0bdrU6UgiIlIMNfcVY8H6fVgLf2xRnUox2uYvYK3lnXfeoWPHjiQmJjJ16lSMMU7HEhERD/h9xW+M6WWM+dUYs8UY8/g5Xn/IGLPRGLPOGPOVMaahvzMWKOjm79dO3fwF0tPTGTp0KCNHjmTq1KkAKvoiIgHEr4XfGBMOTAF6A62A4caYVkXetgboaK1tC0wHJvgzY4G96Rms2nmYmMgwelyiRjWAZcuWkZCQwKxZs3jxxRd54403nI4kIiKl5O+t/k7AFmvtNgBjzMfAQGBjwRustd8Uev+PwK1+TZhvfv5qv8clNakQrSsi3377Lddeey3169fnhx9+oHPnzk5HEhGRC+Dvrf66wK5Cj3fnP3c+dwELfZroPE6fzR/a3fzWWgC6du3KU089xZo1a1T0RUQCmL8L/7kuBttzvtGYW4GOwMvneX2kMWalMWZlSkqKFyPC74dOkrz7CBWiwrk6hLf5Fy5cSIcOHTh06BCRkZE8++yzxMfHOx1LREQugr8L/26gfqHH9YC9Rd9kjLkWeAoYYK3NOtcHWWunWWs7Wms7Vq9e3ashk9bnRbq2VU1iIsO9+tmBIDs7m3HjxtGnTx9yc3NJT093OpKIiHiJvwv/CqC5MaaxMSYKGAbMLfwGY0wiMJW8on/Qz/kASErO7+YPwbP5t2zZQteuXXnttdcYPXo0y5cv1735IiJBxK9da9baXGPM/cDnQDjwnrV2gzHmH8BKa+1c8rb2KwKf5d8m9ru1doC/Mm5LOc7GfUepFBNB9xahN03uySefZOvWrcycOZPBgwc7HUdERLzM7+3q1toFwIIiz/210NfX+jtTYQX37vdsVYvoiNDY5j9+/DjHjx+nVq1avP7662RmZtKgQQOnY4mIiA/oyN4iTnXztwuNbv41a9bQoUMHhg0bhrWWGjVqqOiLiAQxFf5CNh84xuYDx4kvH8mVzYJ7m99ay6RJk+jcuTMnTpzg2Wef1Ql8IiIhQCfTFFIwia9X61pEhgfvz0RpaWncfvvtzJs3j/79+/Pee+9RrVpw/6AjIiJ5gre6lZK19vTZ/EHezR8REcHWrVuZPHkyc+bMUdEXEQkhWvHn27jvKNtST1C1QhSdm1RxOo7X5ebmMmXKFEaNGkVsbCxr164lMlITB0VEQo1W/PkKVvu929QiIsi2+Xfu3MlVV13F2LFjmT59OoCKvohIiAquCneB8rb5C87mD65t/hkzZpCQkMD69ev58MMPufVWR2YeiYhIGaHCD6zbfYRdaRnUqBTNHxoFzzb/yy+/zI033kjz5s1Zs2YNw4cPdzqSiIg4TNf4OX3vfp82tQkPC55b2gYMGMDhw4f5+9//TlRUlNNxRESkDAj5Fb/bbZmff32/f4Af2mOtZdq0adx5551Ya2nZsiXjx49X0RcRkVNCvvCv2XWYvUcyqRMXQ2L9yk7HuWDp6ekMHTqUUaNGsWvXLjIyMpyOJCIiZVDIF/55+ZP4+ratTViAbvMvW7aMhIQEZs2axYsvvsjnn39O+fLlnY4lIiJlUEhf43e5LQvWB/ahPRkZGQwePJjy5cuzePFiLr/8cqcjiYhIGRbShX/FjjQOHsuiQZXytK0X53ScUklJSaFq1aqUK1eOuXPn0rJlS+LiAuvfQURE/C+kt/oLuvn7tq0dUANqFi5cSOvWrXn11VcB6NSpk4q+iIh4JGQLf67LzcL1+wHo1zYwuvmzs7MZN24cffr0oXbt2vTr18/pSCIiEmBCdqv/x21pHDqRTZNqFWhVO9bpOCXasmULw4YNY9WqVdx333288sorxMTEOB1LREQCTMgW/tNH9AbGNv++ffv4/fffmTVrFoMGDXI6joiIBKiQ3OrPznWzaEP+Nn+7stvNf/z4cT799FMAunXrxvbt21X0RUTkooRk4V+yJZX0kzm0qFmRFjUrOR3nnFavXk379u25+eab2bZtGwAVKlRwOJWIiAS6kCz888rwJD5rLf/zP/9D586dOXnyJF999RVNmjRxOpaIiASJkLvGn5nj4osNB4Cy181vrWXIkCFMnz6dAQMG8N5771G1alWnY4mISBAJucL//eYUjmXl0qp2LE2qV3Q6zhmMMfTs2ZOrrrqK++67LyCaDkVEJLCEXOFPyp/E16+MTOLLzc3l73//O61bt2b48OGMGDHC6UgiIhLEQuoaf0a2iy9/yd/mb+P89f2dO3dy1VVX8fzzz/Pjjz86HUdEREJASK34v/n1ICezXbSrF0eDqs5Or5sxYwZ33303LpeLDz/8kOHDhzuaR0REQkNIrfiTykg3/6pVq7jxxhtp3rw5a9asUdEXERG/CZnCfyIrl683HQTyhvI44dixYwB06NCBzz77jMWLF9O0aVNHsoiISGgKmcL/5S8HyMxx06FhZerEl/Pr97bWMm3aNBo2bEhycjIAN954I1FRUX7NISIiEjKF/1Q3v59X++np6QwZMogiT+UAABE5SURBVIRRo0bRsWNHatas6dfvLyIiUlhIFP6jmTl892sKxkCfNv4r/MuWLSMhIYHZs2fz0ksvsWjRImrVquW37y8iIlJUSHT1f7HhANkuN5c3rkLNWP+Nsp07dy5hYWEsXryYyy+/3G/fV0RE5HxCYsV/qpvfD5P49u7dy6pVqwD4xz/+wZo1a1T0RUSkzAj6wp9+MpsffkslzEDvy3y7zT5//nzatWvHzTffjMvlIjIykri4OJ9+TxERkdII+sL/+Yb95LotVzStRrWK0T75HllZWfzXf/0X/fr1o06dOsyZM4fw8HCffC8REZGLEfTX+H3dzX/o0CF69uzJ6tWrGTNmDBMmTCAmxn99BCIiIqUR1Cv+Q8ezWLr1EBFhhl4+2uavXLkyl156KbNnz2by5Mkq+iIiUqYFdeFf+PN+XG7Llc2rEV/ee4flHDt2jNGjR7Nr1y7CwsL497//zcCBA732+SIiIr4S1IXfF2fzr1q1ivbt2zN16lS++eYbr32uiIiIPwRt4T94NJPl29OICg+jZ+uLPy3PWsvEiRPp0qULGRkZfPPNN/z5z3/2QlIRERH/CdrCv2D9PqyF7i2qExsTedGf99prr/HQQw/Rp08fkpOT6d69uxdSioiI+FfQdvUXdPP3b3dx3fzZ2dlERUUxYsQIKleuzB133IExxhsRRURE/C4oV/x70zNYufMw0RFh9Lj0wrb5c3Nzeeqpp+jcuTOZmZnExsZy5513quiLiEhAC8rCv2B93mr/mktqUDG69JsaO3fu5KqrrmL8+PEkJibidru9HVFERMQRQbnVP+/UoT2l7+afMWMGd999Ny6Xiw8//JDhw4d7O56IiIhjgq7w70o7SfKudMpHhXPNJTVK9Xtzc3N57rnnaNGiBR999BFNmjTxUUoRERFnBF3hL2jq63FpTcpFeXZe/oYNG6hXrx5xcXHMnz+f6v+/vfuPlqK87zj+/nAviCKiyI9bSpAYYixSQilStRRDo4bYCsVIxQTiD9AaA0cSTYsHq0TpDxEjpiYRbBIFiz9IYuHQoEZD1KRCggU5QEKLSqKiEhBBUC8I3/7xPBfnDnt3517u3WV3v69z5uzuzDMz3/3unn12nnnmme7dad/+8K8EcM455440FXeO/8NBewr35jcz5s6dy5AhQ5g2bRoAvXr18krfOedcxaqoiv/lbXtYv2UXnY+q5exTuuctu2PHDsaOHcvVV1/N8OHDmTFjRnGCdM4550qooir+pS+Eo/1z+/ekY/umm/lXr17NoEGDWLx4MbNmzWLZsmX07Hn4o/s555xzR7qKOsd/8Ba8BQbt6d69O3V1dSxatIihQ4cWIzTnnHPuiFAxR/z/9+Y7bHzzHboc3Z5h/Q5t5t+yZQvTp0/nwIED9O7dmxUrVnil75xzrupUTMXfcO3+Z07rSYfaxm9r6dKlDBw4kDlz5rBu3ToAH4HPOedcVaqYij/XLXjr6+uZOnUqF1xwAb179+b5559n4MCBpQrROeecK7mKOMf//r79bPv9Hrp26sBZHzvx4PyLL76YxYsXM2XKFGbNmkXHjh1LGKVzzjlXehVR8b/93j5qgZED6qitaceBAwdo164d119/PZdffjmjR48udYjOOefcEaHoTf2SRkraKGmTpGk5lh8l6eG4fKWkvoW2ufPdfQCMOLkzEyZM4IYbbgBg2LBhXuk755xzCUWt+CXVAN8CPgv0By6R1D9VbCKww8z6AXcCtxXa7t79Bzhm12+55qJzWbhwIZ06dWrt0J1zzrmKUOym/qHAJjN7CUDSQ8BoYEOizGhgRnz+A+BuSTIza2qj+/e8zcZ7r6VXXR3Lly9n+PDhbRO9c845V+aK3dT/h8Aridevxnk5y5jZB8BO4ETy2P/OdoaNOJc1a9Z4pe+cc87lUewj/lwXz6eP5LOUQdJVwFXxZf0zP1m2rlu3bocZnsujG7Ct1EFUAc9z2/Mctz3Pcdv7REtXLHbF/yrwkcTr3sCWJsq8KqkW6AK8ld6Qmc0D5gFIWmVmQ9okYgd4jovF89z2PMdtz3Pc9iStaum6xW7q/xXwcUkfldQBGAcsSZVZAlwan18E/DTf+X3nnHPOZVfUI34z+0DSZOBxoAb4npmtl3QLsMrMlgDfBRZI2kQ40h9XzBidc865Slb0AXzM7MfAj1Pzbko8fx8Y28zNzmuF0Fx+nuPi8Dy3Pc9x2/Mct70W51jeiu6cc85Vj4q5SY9zzjnnCiurir8thvt1jWXI8VclbZC0VtJTkk4qRZzlrFCOE+UukmSSvHd0C2TJs6S/jd/n9ZIWFjvGcpfh96KPpOWSVsffjPNLEWc5k/Q9SVslrWtiuSR9M34GayUNLrhRMyuLidAZ8EXgZKAD8ALQP1XmGuCe+Hwc8HCp4y6nKWOORwDHxOdf8hy3fo5juc7AM8AKYEip4y63KeN3+ePAauCE+LpHqeMupyljjucBX4rP+wObSx13uU3AcGAwsK6J5ecDywhj4JwBrCy0zXI64j843K+Z7QUahvtNGg3cH5//APi0pFwDArncCubYzJab2bvx5QrCWAwuuyzfY4BbgVnA+8UMroJkyfOVwLfMbAeAmW0tcozlLkuODTguPu/CoeO2uALM7BlyjGWTMBqYb8EK4HhJf5Bvm+VU8bfJcL+ukSw5TppI+KfpsiuYY0l/AnzEzJYWM7AKk+W7fApwiqRfSFohaWTRoqsMWXI8Axgv6VXC1VxTihNaVWnu73bxL+c7DK023K9rUub8SRoPDAHObtOIKk/eHEtqR7gr5WXFCqhCZfku1xKa+z9FaLl6VtIAM3u7jWOrFFlyfAlwn5ndIelMwhgtA8zsQNuHVzWaXe+V0xF/c4b7Jd9wv65JWXKMpHOA6cAoM6svUmyVolCOOwMDgJ9J2kw4Z7fEO/g1W9bfi8Vmts/MXgY2Ev4IuGyy5Hgi8AiAmT0HdCSM4+9aT6bf7aRyqvh9uN+2VzDHsRl6LqHS93OizZc3x2a208y6mVlfM+tL6EcxysxaPC53lcrye/GfhM6qSOpGaPp/qahRlrcsOf4d8GkASX9EqPh/X9QoK98S4Iuxd/8ZwE4zez3fCmXT1G8+3G+by5jj24FjgUWx3+TvzGxUyYIuMxlz7A5Txjw/DpwnaQOwH/iamW0vXdTlJWOOrwPulfQVQvPzZX4w1jySHiScjuoW+0rcDLQHMLN7CH0nzgc2Ae8Clxfcpn8GzjnnXPUop6Z+55xzzh0mr/idc865KuIVv3POOVdFvOJ3zjnnqohX/M4551wV8YrfuRwkXRbvjJdrOqeZ25oU1yvKfQ0kzUzFuyPerbLVL2+VVBv3cWNi3oWSpuYoe04sO6y148gTX79ULvZLel3SAkl5hzXNs83BkmZIOr6143WuGMrmOn7nSmQsYWSspA2lCKQFzoyPJwJ/BzwoqYOZzW+tHcRruc+k8VjhFwLDgDmp4r+MMa1vrf03w0zgv4CjYgw3AadKOjPe16M5BhOupb4P8OF9Xdnxit+5/NaY2aZSB9ES8U5dAEh6gjAk7VSg1Sr+9H4KlNtFGImwFF5MxPm0pKMIN5AZBPioiK6qeFO/cy0k6WhJd0laL2lPbEJeIukTGdadIGlNXG+npLWSJqXKjJD0U0m747RMUv+WxGpm+4A1QL/E9rtI+naMe6+kjZKuTcVwnKS7Jb0iqV7Sm5J+IumUuLxRU7+kB4AvACclmtc3xWWNmvolzZO0RVJNap8dY05mJ+b1kDQ3lt8r6deSJrYkF9H/xMc+qX3PlLRa0i5J2yQ9JWloYvkk4N748uXEe+ydyMf0mMt6Sa9Juj3+0XDuiOBH/M7lV6Nww6cGZmb74/Oj43QL8AahSf3LwHOSTm3qXgaSzgbuJzSFX0cY7rQ/cEKizGjgh4RxuD9P+JM+jXAHuYFm9loL3stHiU3TsbJdBgwE/pHQ/D4KmCPpRDO7Ka5zFzCScFOmTYQbrAwj3AArl5tjmU8CY+K895soOx+4kjCW+xOJ+aMJ93BfEGM9HvgFYZjSm4DNhCFK742nLr6T6d031jc+vpia3wu4g3B651jCvT+elTTYzNYDi4GTgRsIpzQaxkRv+KwfBD4L/CuhdeM0wvejD3BxC+J0rvWZmU8++ZSaCLfFtRzTz/OsUwN0IoyXPSUxf1Jct3d8PQ3Ymmc7IlRuj6fmH0+4B8XsArHPjPurjVNP4NY4b3Ys8zfx9fjUuvcRKuqu8fVvgFl59lUbt3NjYt4DwOYcZc+JZYcl3udLwIJUuaXA2sTrrwPvAR9Llfs+8CZQkye+fnGfV8RYOxH+aGwBHiqQxxrCn40XgTtyfJ59U+VHxPmfT82/NM7/41J/r33yycy8qd+5AsYApyemRs3LksZJ+qWkncAHwG5CK0C+5v5fAd0lzZf0V5LSR8+nAicB/xGbjmtjq8NuYCUwPGPs++L0BvA14BuEI3fiNj4AHkqt8wChA9yfJWKdKGmapD+V1Gq/GWZmcX9jJHUCkNQd+AyN+yGMBP4b+G0qH48DPcif6wbfJeRiN/Ak4Yj+0nQhSedJ+pmk7YT87CUc4WfZx0jCn6ZHU3E2tGb8RYZtONfmvOJ3Lr91ZrYqMW1sWCBpDKFpdx1wCaGyPJ1wVN6xqQ2a2VOEZt++hFvDbpP0hKQBsUiP+Hg/H1beDdNIwimFLBr+rPQDOpvZdWZWH5d1BbbZoT3a30gsB7iGcE77SkInuK2S7pB0dMYYCplPOAq/ML6+hPC7tDBRpgfwlxyaiwfj8iz5+DohF58CvhOf/1uygKTTCT3/dxJaCM6I5daR5/NMxdmR0OKTjLPh3uhZPzfn2pSf43eu5cYBvzGzKxpmSOpIaJLPy8weAR6RdCyhUrsNWCapD9Bwa9i/B5bnWL0+x7xc+8jXW/0twm0+a1OVf1183B638Q7h1MQ0SX0Jlzf+C+HIdjqHycw2SVoBjCec0x8PPGVmWxLFthMuF/xqE5vZ2MT8pM2JfDwt6ThgkqR7zKyho99FhPf1uWROJHUlnFIoZDuh0j+7ieVbmpjvXFF5xe9cyx1DaA5O+iLNaEkzs93AEkn9CJ3KTiCME/AK0N/Mbm+lWNOeBr4CfA54ODH/C4TKb2WOWDcDt0uaAAxIL0+oJ5zuyGoB8E1JIwhH2BNSyx8jjEOw2cy2NWO7+fwD4b3fTOhMCB9+ngfvVS7pPEKHv18n1m3445V+j48ROmt2MrOnWylO51qdV/zOtdxjwN3xsrNlhErry8CufCtJ+idCs+9yQq/wPsBkYJWZvRXLTAZ+FFsQFhGOJuuAs4CXzOyuw4x9KfAcoWd8HaFi+2tCp8ZbzWxHjGMl8CNCc/ceQge204C5eba9AbhC0lXAauA9M1uXp/xDwJ2EPwB7gEdTy2cTWhqelXQn8L9AZ0JfiLPMbAzNZGavSboHmCppkJmtIXyek4HvS7o/bv9GDj1SbxjAaXK8fHEf8IKZPSlpEeEc/zcIAxZBOKVzPnCdmaWvInCu+Erdu9Ann47EiQ979ffLU6YG+GdCxfAuoSL/JKHj2L8nyqV79Y8idPh6nXD0+ArhPHpdavt/TjjnvINwFP4y4bz2GQVin0nsO1egXBfg2zGOvYQm82tTZWYTKu+dhI5xa4HJieW5evV3JrQi7IjLNsX5jXr1p/bzaFw2v4lYuxIuLdwcY90KPEPi6okm1mvo1X9ZjmU94nv6YWLe1LiP9wgV9wjg58CTqXVviZ/7/tRnW0NoSVkbP7O3CeMn3AYcV+rvtU8+mRkyO9iq5ZxzzrkK5736nXPOuSriFb9zzjlXRbzid84556qIV/zOOedcFfGK3znnnKsiXvE755xzVcQrfuecc66KeMXvnHPOVRGv+J1zzrkq8v+kKcVgFli2PQAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f69100fb550>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fpr, tpr, thresholds = roc_curve(Y_test, modele_pred)\n",
"plt.figure(figsize=(8, 6))\n",
"plot_roc_curve(fpr, tpr)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### PRECISION, RAPPEL, F1-SCORE, SUPPORT"
]
},
{
"cell_type": "code",
"execution_count": 95,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(0.7979623553790365, 0.8721336227234123, 0.8334009648766854, None)"
]
},
"execution_count": 95,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"precision_recall_fscore_support(Y_test, modele_pred,average='binary')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### SCORE EN K-FOLD CROSS VALIDATION (validation croisee en K passes) "
]
},
{
"cell_type": "code",
"execution_count": 96,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.53538774 0.63614554 0.88172249 0.91777031 0.88083491 0.9122145\n",
" 0.88966049 0.82904609 0.87528824 0.79014879]\n",
"Mean: 0.8148219110345745\n",
"Standard deviation: 0.12206304653896215\n",
"CPU times: user 541 ms, sys: 111 ms, total: 652 ms\n",
"Wall time: 2min 49s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele, X, Y, cv=10, scoring=\"precision\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 97,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.88637638 0.89198281 0.8611215 0.86785047 0.86766355 0.85850467\n",
" 0.86205607 0.86747664 0.85140187 0.8635514 ]\n",
"Mean: 0.8677985353423328\n",
"Standard deviation: 0.01175143896730753\n",
"CPU times: user 546 ms, sys: 106 ms, total: 651 ms\n",
"Wall time: 2min 49s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele, X, Y, cv=10, scoring=\"recall\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 98,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.66755806 0.7426482 0.87130024 0.89211259 0.87419962 0.88454502\n",
" 0.87564078 0.84782609 0.86317984 0.82522104]\n",
"Mean: 0.834423147964419\n",
"Standard deviation: 0.06916582873134833\n",
"CPU times: user 556 ms, sys: 121 ms, total: 678 ms\n",
"Wall time: 2min 48s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele, X, Y, cv=10, scoring=\"f1\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 99,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.64783022 0.74865915 0.93904687 0.95078368 0.93304425 0.94799986\n",
" 0.9366446 0.91212057 0.92329989 0.8897589 ]\n",
"Mean: 0.8829187987324184\n",
"Standard deviation: 0.09654689175372212\n",
"CPU times: user 550 ms, sys: 136 ms, total: 687 ms\n",
"Wall time: 2min 48s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_roc=cross_val_score(modele, X, Y, cv=10, scoring=\"roc_auc\",n_jobs=-1)\n",
"display_scores(modele_score_roc)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### **KNN**"
]
},
{
"cell_type": "code",
"execution_count": 100,
"metadata": {},
"outputs": [],
"source": [
"from sklearn.neighbors import KNeighborsClassifier\n",
"modele_knn=KNeighborsClassifier()\n",
"modele_knn.fit(X_train, Y_train)\n",
"modeleKnn_pred=modele_knn.predict(X_test)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### **ESTIMATION QUALITE MODELE KNN**"
]
},
{
"cell_type": "code",
"execution_count": 101,
"metadata": {},
"outputs": [],
"source": [
"modele=modele_knn\n",
"modele_pred = modeleKnn_pred"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Matrice confusion"
]
},
{
"cell_type": "code",
"execution_count": 102,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[7212, 3592],\n",
" [2572, 8025]])"
]
},
"execution_count": 102,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"confusion_matrix(Y_test,modele_pred)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### ROC"
]
},
{
"cell_type": "code",
"execution_count": 103,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"0.7124101716212949"
]
},
"execution_count": 103,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"roc_auc_score(Y_test, modele_pred)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### ROC CURVE"
]
},
{
"cell_type": "code",
"execution_count": 104,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAf4AAAF8CAYAAAAuF9n2AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzs3Xd8VFXex/HPSYUASSABpbcgCCJBIhKKDXVBpFkoos/aQEVQVmzYdS3YFx5RwfKou7gWlCICrl26dAsLEnoRSCEhQPqc548ZhgQpA0zmTjLf9+vFy5k5l+QLhvnNved3zzHWWkRERCQ0hDkdQERERAJHhV9ERCSEqPCLiIiEEBV+ERGREKLCLyIiEkJU+EVEREJIQAu/MeYdY8xuY8yvRxk3xpjxxpg0Y8zPxphzAplPRESksgv0Gf+7QI9jjPcEWnh+DQNeD0AmERGRkBHQwm+t/RHIOsYhfYH3rdsiIN4YUzcw6URERCq/YJvjrw9sLfV8m+c1ERER8YMIpwMcxhzhtSOuKWyMGYZ7OoBq1ap1aNWqVXnmEhERCQiXhf0Fxezz/MovKgHAFhdSnL0TW1wIkGGtrX0yXz/YCv82oGGp5w2AHUc60Fo7CZgEkJKSYpcuXVr+6URERPysuMTFL9tzmJ+Wwby0DJZvzqawxEUkUBOIjgijudnNNy/eTs24WN5/7z2uuKLX5pP9fsFW+GcAI4wxHwLnATnW2j8cziQiIuI31lo2ZOx3F/p1GSzckElufrF33Bho1yCOLkmJdGmeQIcmtYgwljH5v3L33XdTt+6ptb4FtPAbY/4NXAgkGmO2AY8BkQDW2jeAWcDlQBpwALgxkPlERETKw+7cfBakZTIvLYP5aRn8kZNfZrxJQgxdkhLp1iKRTs0SiI+JYvHixdx9w81MnTqVOnXq8MILL/glS0ALv7V28HHGLXBHgOKIiIiUi30Fxfy0MZN56zKZn5bB2l25ZcYTqkXROSmRrkkJdG6eSMNaMd4xl8vF2LFjeeSRR6hfvz47d+6kTp06fssWbJf6RUREKpyiEhertmZ7z+hXbMmm2HWoN71qZDjnNatF16REOjdPpNXpNQgL+3M/+86dO7n++uv5+uuvueaaa5g0aRLx8fF+zarCLyIicoKstazbvY9569yFftGGTPYXlnjHwwy0bxRP16REuiQlck6jmkRFHP8O+gceeID58+czadIkbrnlFow50s1up8a4r65XbOrqFxGR8vZHTh7z0zK93ffpuQVlxpvXruYt9J2aJxBbJdKnr1tYWEh2djZ16tQhIyOD3bt307p162P+HmPMMmttysn8OXTGLyIicgR784tYtP5QoV+fvr/MeO0a0d5C3yUpgbpxVU/4e6xfv57BgwcTHh7O/PnzSUxMJDEx0V9/hCNS4RcREQEKiktYsSXbW+hXbc2m1DQ91aLC6dQsgS5JiXRtkUiLOtVP6VL8Bx98wG233UZ4eDhvvfUWYWGBWUxXhV9EREKSy2VZszPXW+h/2phFXtGhefqIMEOHxvHuQp+USLuG8USGn3px3r9/PyNGjODdd9+lS5cuTJ48mcaNG5/y1/WVCr+IiISMbXsOeAp9JgvSMsjcX1hmvOVpNTxn9Al0bJpA9Wj/l0lrLYsXL+aRRx7h0UcfJSIisKVYhV9ERCqt7AOFLFx/aOGcTZkHyozXjaviPaPvnJRAnRpVyiWHtZZ3332XgQMHUr16dZYvX06VKuXzvY5HhV9ERCqN/KISlm3e4y30v2zPofTNazWqRJDaLIGuLdxNec0Sq5XLLXOlZWRkcNNNN/H5559z4MAB7rjjDseKPqjwi4hIBVbisqzesddb6JdsyqKg2OUdjwoP45zGh+6nb1s/jgg/zNP76vvvv2fIkCFkZGQwbtw4hg8fHrDvfTQq/CIiUmFYa9mSdcBb6BeszyT7QFGZY1rXjfWe0Z/bpCYxUc6UurfffpuhQ4fSokULZs6cSfv27R3JcTgVfhERCWqZ+wpYUOp++m178sqM14+vSjdPoe/cPIGE6tEOJS3rggsuYNiwYbz44otUr17d6TheKvwiIhJU8gpL+GlTlnfb2tV/7C0zHh8TSefmCd6mvEa1Ysp9nt5XU6dO5YsvvuDNN98kKSmJN954w+lIf6LCLyIijioucfHL9hzvGf3yzdkUlpSap48Io2OTWt5C37peLOFH2ODGSXl5eYwePZrXX3+dlJQUcnJy/L65jr+o8IuISEBZa9mQsd97Rr9wQya5+cXecWPg7AZx3kLfoXFNqkSGO5j42FavXs2gQYP45ZdfGD16NM888wxRUVFOxzoqFX4RESl3u3PzWZDmvp9+QVoGO3Lyy4w3SYjxFvrU5gnExwRv4SytqKiIXr16sX//fmbNmkXPnj2djnRcKvwiIuJ3+wqK+WljJvPWuZvy1u7KLTOeUC2KzkmJdE1KoHPzRBrWinEo6cnZu3cv1apVIzIykg8++IAmTZpQt25dp2P5RIVfREROWVGJi5+3ZTPXsz/9ii3ZFJfa4aZqZDgdm9by3k/f6vQahAXZPL2vFi1axODBg7n55pt5+OGHSU1NdTrSCVHhFxGRE2atJW33Pu/99Is2ZLGv4NA8fZiB9o0OLZzTvlE80RHBO0/vC5fLxfPPP8/DDz9Mw4YNueSSS5yOdFJU+EVExCc7c/K9c/Tz0jLYnVtQZrx57WreQn9eswTiqkY6lNT//vjjD66//nq++eYbBgwYwMSJE4O2a/94VPhFROSI9uYXsXiD+376uevSWZ++v8x47RrR3kLfJSmBunFVHUpa/jZv3sySJUt48803ufnmm4Nm3YCTocIvIiIAFBa7WLFlj/d++lXbcigpNU9fLSqcTs08C+e0SKRFneoVugAeT2FhIbNnz6Zv37506tSJzZs3V9iz/NJU+EVEQpTLZVm7K9db6BdvyCKvqMQ7HhFmOLdJTe9tdu0axhMZwA1unJSWlsbgwYNZunQpP//8M23btq0URR9U+EVEQsr27Dzmr3MX+gXrM8jYV1hmvOVpNTxn9Al0bJpA9ejQKxOTJ0/mtttuIzIyks8++4y2bds6HcmvQu//qIhICMk5UMTCDRme7vtMNmaUnac/PbYKXVu4z+g7N0+gTqxz+8QHgzvuuIPXXnuNrl27MnnyZBo1auR0JL9T4RcRqUTyi0pYvnmP9za7n7fnYA9N01MjOoLU5gnebWubJVar1PP0J+qcc87h0Ucf5ZFHHiEionKWyMr5pxIRCREul2X1H3u9hf6njVkUFB/a4CYy3NChcU1v933b+nFEhMg8vS+stYwfP56EhASuu+46br75ZqcjlTsVfhGRCmZL5gFvoV+wPoM9B4rKjLeuG+s9oz+3SU1iovRWfyQZGRnceOONzJw5k8GDB3Pdddc5HSkg9NMgIhLksvYXsmB9hrf7fmtWXpnx+vFV6eYp9KnNE0isHu1Q0orj+++/Z8iQIWRkZDB+/HhGjBjhdKSAUeEXEQkyeYUlLNmU5S30v+3YW2Y8rmokXZISvLfZNaoVo3n6E7BmzRq6d+9OixYt+OKLL0hOTnY6UkCp8IuIOKzEZflle453f/plm/dQWHJonj4qIoyOTWp5C33rerGEV9ANbpyUl5dH1apVadWqFe+99x79+vWjevXqTscKOBV+EZEAs9ayMWO/94x+4fpM9uYf2uDGGDi7QZy30HdoXJMqkRV7gxunffbZZwwfPpwvvviCDh06hMx8/pGo8IuIBEB6bgEL1rvP6OenZbAjJ7/MeJOEGG+hT22eQHxMlENJK5e8vDxGjx7N66+/TkpKSqVZfe9UqPCLiJSD/QXF/LQxy9t9v2ZnbpnxWtWi6Nw8gW4tEuncPJGGtWIcSlp5/fbbbwwaNIhff/2Ve+65h6effpqoKH2gUuEXEfGDohIXP2/LZt66TOanZbB8yx6KS21wUyUyjI5NE+jqaco78/RYwjRPX64++eQTdu3axezZs+nRo4fTcYKGsaWXdKqgUlJS7NKlS52OISIhxFpL2u593jP6RRuy2FdwaJ4+zEC7hvGepXATOadxPNERmqcvb9nZ2WzcuJH27dtTXFxMZmYmp512mtOx/M4Ys8xam3Iyv1dn/CIiPtqZk8/8tEP30+/OLSgz3qx2Ne8KeZ2aJRBXNdKhpKFp4cKFDB48GJfLRVpaGlFRUZWy6J8qFX4RkaPYm1/E4g2H7qdP272vzHhi9WjvpfsuSYnUi6/qUNLQ5nK5eO6553jkkUdo2LAhn3zyiebyj0GFX0TEo7DYxYote7yFftW2HEpKzdPHRIXTqdmhhXPOOK26Fs5xWG5uLldeeSVff/01AwcOZOLEicTFxTkdK6ip8ItIyLLWsmZnrrfQL96QRV5RiXc8PMyQ0rimZ3/6RJIbxhOpDW6CSvXq1alVqxZvvfUWN910kz6I+UCFX0RCyvbsPOavcxf6BeszyNhXWGb8jNOqe8/oOzatRY0qmqcPNoWFhTz++OMMGzaMJk2a8NFHHzkdqUJR4ReRSi3nQBELN2R4uu8z2Zixv8z46bFVPGf0CXRpnkid2CoOJRVfpKWlMWjQIJYtW8bpp5/OnXfe6XSkCkeFX0QqlfyiEpZv3uO9ze6X7TmUmqanRnQEnZoneLvvm9eupsvDFcS//vUvbr/9diIjI5k6dSr9+vVzOlKFpMIvIhWay2VZ/cdeb6H/aWMWBcWHNriJDDec26imu9C3SOTs+nFEaJ6+wnn77be55ZZb6NatG5MnT6Zhw4ZOR6qwVPhFpMLZknnAW+gXrM9gz4GiMuNn1o313mbXsWktYqL0VldRlZSUEB4ezsCBA8nNzWXEiBFEROj/56nQ356IBL2s/YUsWH9o4ZytWXllxuvHV/We0XdunkBi9WiHkoq/WGsZP34877//PnPnzqV69eqMGjXK6ViVggq/iASdvMISlmw6tHDO6j/2Unp18biqkXRufuh++sYJMZqnr0TS09O58cYb+eKLL+jduzcFBQXExGgTI39R4RcRx5W4LL9sz3EX+nUZLNu8h8KSQ/P0URFhnNukprfQt6kXR7g2uKmUvvvuO4YMGUJmZibjx49nxIgR+lDnZyr8IhJw1lo2ZR5g3rp05qVlsHB9JnvzD21wYwy0rR/nLfQpTWpSJVIb3FR21loeeOABYmNjmTVrFsnJyU5HqpRU+EUkINJzC7zz9PPTMtmeXXaevnFCjLfQpzZLoGY1rbUeKjZv3kxsbCw1a9bk008/pWbNmlSrVs3pWJWWCr+IlIv9BcX8tCnLu0remp25ZcZrVYuic6n76RvW0hxuKPr000+55ZZb6N27N++//z4NGjRwOlKlp8IvIn5RXOJi1bYcb0Peii17KCo51JFXJTKMjk0TvLfZnXl6LGGapw9ZeXl5/O1vf2PixImkpKTw2GOPOR0pZKjwi8hJsdayPn0f89ZlMC8tk0UbMtlXcGiePsxAcsN47xn9OY3jiY7QPL3AunXruPLKK/n111+55557ePrpp7WNbgCp8IuIz3btzfee0c9Py2DX3oIy481qV/MW+k7NEoirqg1u5M+qV68OwOzZs+nRo4fDaUKPCr+IHFVufhGLN2R5C/263fvKjCdWj/Zeuu+SlEi9+KoOJZVgl52dzauvvsqYMWOoW7cuq1atIixMSyc7QYVfRLwKi12s3JrtLfQrt2ZTUmqHm5iocDo1O7RwzhmnVdc91nJcCxcuZPDgwWzfvp3u3buTmpqqou+ggBd+Y0wPYBwQDrxlrR172Hgj4D0g3nPMA9baWYHOKRIKrLWs3ZXLvHXuQr94YxYHCku84+FhhpTGnoVzWiTSrkE8URF6wxbflJSU8Nxzz/Hoo4/SqFEj5s2bx3nnned0rJAX0MJvjAkHJgCXAtuAJcaYGdba1aUOexj42Fr7ujGmNTALaBLInCKV2fbsPM+99O776TP2lZ2nP+O06t4z+o5Na1Gjiubp5eQMHTqU//u//2PQoEG88cYbxMXFOR1JCPwZf0cgzVq7AcAY8yHQFyhd+C0Q63kcB+wIaEKRSibnQBELN2R6i/2GjP1lxk+LjaZrUm26tkigc/NETout4lBSqSystRhjGDp0KF27duXGG2/UlFAQCXThrw9sLfV8G3D4dZ/Hgf8YY0YC1YBLAhNNpHIoKC5h2eY9nu77TH7Zlk2paXpqREfQqdTCOc1rV9ObsvhFQUEBY8aMAeDll18mNTWV1NRUh1PJ4QJd+I/07mIPez4YeNda+5IxJhX4pzHmLGutq/RBxphhwDCARo0alUtYkYrA5bKs/mOv9za7JZuyyC869M8lMtxwbqOa3m1rz64fR0S45unFv9atW8egQYNYvnw5I0aM8J71S/AJdOHfBjQs9bwBf76UfzPQA8Bau9AYUwVIBHaXPshaOwmYBJCSknL4hweRSm1r1gHmeQr9grQM9hwoKjN+Zt1Y7212HZvWIiZKN/BI+fnnP//J8OHDiYyMZOrUqfTr18/pSHIMgX43WAK0MMY0BbYDg4BrDztmC9AdeNcYcyZQBUgPaEqRILNnfyEL1md6b7PbknWgzHj9+KreM/rOzRNIrB7tUFIJNdu2bePWW28lJSWFyZMn07Bhw+P/JnFUQAu/tbbYGDMC+BL3rXrvWGt/M8Y8CSy11s4ARgNvGmP+hnsa4AZrrc7oJaTkF5WwZNOhhXN+27GX0v8K4qpG0rn5ofvpGyfE6LKqBNTGjRtp2rQpDRo04McffyQ5OZmICF1ZqghMZaipKSkpdunSpU7HEDlpJS7Lr9tzvIV+6eY9FBYfmqePigjj3CY1vYW+Tb04wrXBjTjAWss//vEP7r//ft577z0GDx7sdKSQZIxZZq1NOZnfq49nIg6w1rIp0z1PP39dBgvWZ7A3/9AGN8ZA2/px3kKf0qQmVSK1wY04Kz09nRtuuIFZs2bRu3dvLrvsMqcjyUlQ4RcJkPTcAhasP7RwzvbsvDLjjRNivIU+tVkCNatptzIJHt9//z3XXnstmZmZjB8/nhEjRmh6qYJS4RcpJwcKi1m8MYv569zd92t25pYZr1Utis6l7qdvWCvGoaQix5eVlUVsbCyzZs0iOTnZ6ThyCjTHL+InxSUuVm3L8d5Pv2LLHopKDv37qhIZxrlNatGthbvQn3l6LGGap5cgtnnzZhYvXsyAAQMAKCwsJCpKV6KCgeb4RRxgrWV9+j7mrXOvkLd4Qya5BYfm6cMMtGsY772f/pxGmqeXiuPTTz/llltuISIigp49e1KjRg0V/UpChV/kBOzam+89o5+flsGuvWU3uGlWuxpdkxLp3Nw9Tx8Xow1upGLJy8vjb3/7GxMnTqRjx478+9//pkaNGk7HEj9S4Rc5htz8IhZvOHQ//brd+8qMJ1aPootnjr5LUiL146s6lFTk1BUUFNCpUyd+/vln7rvvPv7+97/rLL8SUuEXOcyyzVn88Lu70K/cmk1JqR1uYqLCOa9pLe/+9C1Pq6HOZqk0oqOj+Z//+R/atm2rW/UqMRV+kVJe/349z81Z430eHmbo0PjQwjnJDeOJitAGN1J57Nmzh9tuu41hw4bRvXt3Ro8e7XQkKWcq/CIeWzIP8MrXvwNwfafGXHBGbc5rVosaVTRPL5XTggULGDx4MDt27ODiiy+me/fuTkeSAFDhF/F44vPfKCx2cWX7+vy931lOxxEpNyUlJTz33HM8+uijNG7cmPnz59OxY0enY0mA6JqlCPD16l18s2Y3NaIjeODyVk7HESlXn332GQ899BDXXHMNy5cvV9EPMTrjl5CXX1TCEzN/A+Duy86gTo0qDicSKR/p6enUrl2bq6++mtmzZ/OXv/xFzakhSGf8EvJe/349W7PyaHV6Da7v1NjpOCJ+V1BQwKhRo2jZsiVbtmzBGEOPHj1U9EOUzvglpG3O3M/rP6wH4Mm+ZxERrs/CUrn8/vvvDBo0iBUrVjBixAjq1KnjdCRxmAq/hCxrLY/P8DT0nVOfjk1rOR1JxK/++c9/cvvttxMdHc20adPo27ev05EkCKjwS8j6+r+7+W5tOjWiIxjT80yn44j43ddff02HDh3417/+RcOGDZ2OI0FChV9CUn5RCU987m7oG33ZGdSuEe1wIhH/WLZsGVWqVKFNmza88cYbREZGEhGht3o5RBOaEpJe+3492/bkcWbdWK5TQ59UAi6Xi5dffpnU1FTv6ntVq1ZV0Zc/0U+EhJxNGft5w9PQ9/e+bdTQJxXe7t27ufHGG5k1axZ9+/bl7bffdjqSBDEVfgkp1loe96zQd9U5DUhpooY+qdjWrFnDxRdfTFZWFq+++irDhw/XbXpyTCdU+I0xLYFuQALwrrV2lzGmIZBprT1QHgFF/Omr1bv4fm06NapE8EBPrdAnFV+zZs246KKLuO+++2jXrp3TcaQC8OkapzEm0hjzT2A1MAl4BqjvGX4VeLh84on4T15hCU98vhqAey5rqYY+qbA2bdrEwIED2bNnD1FRUUyePFlFX3zm6+Tm34E+wFCgMVD6OtIs4C9+ziXid69/n8b27Dxa141lyHmNnI4jclKmTJlCcnIyc+bM4ddff3U6jlRAvhb+IcAj1tp3gB2HjW0Amvo1lYifuRv6NgDw935q6JOK58CBA9x6661cc801tGzZkhUrVtCtWzenY0kF5Ou7X23gWB8ttauJBC1vQ1+Ji6s7NKBDYzX0ScVz9913M2nSJO6//37mzZtHs2bNnI4kFZSvzX2bgXOBb48wlgKs81siET/7jxr6pIKy1rJ//36qV6/OY489xlVXXcWll17qdCyp4Hwt/P8CHjLGpAGfe16zxphU4G7czX4iQSevsIQnPQ199/6lJYnV1dAnFcOePXsYOnQoWVlZfPXVV9StW5e6des6HUsqAV8v9T8LfAN8AmR4XvsOmAf8APzD/9FETt2E79wNfW3qxTLkPK3QJxXD/PnzSU5OZvr06fTs2VP35Ytf+XTGb60tBvobYy7F3cFfB8gE5lhrvyzHfCInbWPGfib96G7oe7LvWYSH6c1TgltJSQnPPvssjz/+OI0bN2b+/Pl07NjR6VhSyfhU+I0xdXAv0vMV8NVhY2FAorV2dznkEzkp1loem+Fu6LumQwM6NK7pdCSR49q3bx9vvfUWAwYM4I033iA2NtbpSFIJ+TrH/weQCvx0hLH2ntfD/RVK5FR9+dsufvw9ndgqEdyvhj4Jct9++y1dunQhLi6On376idq1a+vyvpQbX+f4j/UTGAG4/JBFxC8OFBbz95lq6JPgV1BQwKhRo+jevTvjxo0DoE6dOir6Uq6OesZvjKkOlL7OlGiMqXfYYVWBa4Fd5ZBN5KSUbui7Vg19EqR+//13Bg0axIoVKxg5ciR33nmn05EkRBzrUv9o4FHPY8uh2/gOZ4Cn/RlK5GRtSN/Hmz9uBODv/dTQJ8Fp+vTpDBkyhOjoaKZPn06fPn2cjiQh5FiFfyawE3dhfw14Hth42DEFwGpr7ZHm/kUCqnRD38CUhpzTSA19EpySkpLo1q0bb775Jg0aNHA6joSYoxZ+a+0yYBmAMcYCn1prM452vIjTvvxtJ3PXZRBbJYL7erR0Oo5IGcuWLWPq1Kk89dRTtGnThtmzZzsdSUKUT8191tqJKvoSzA4UFh9aoa9HKxLU0CdBwuVy8fLLL5Oamsp7771Henq605EkxPl6Ox/GmDOAG4GW/HlTHmut7eXPYCIn4tVv09iRk89Z9WO5tqO23JXgsHv3bm644QZmz55Nv379ePvtt6lVS5tEibN8XcCnAzAXd/d+I2AtUAv3Cn47gC3lFVDkeNan7+PNuZ4td7VCnwSJkpISLrroItavX8+ECRO4/fbbdZueBAVfz/jHAl8Ag4FC4Dpr7XJjzOXAW8D95ZRP5JistTw+4zeKSiyDzm1IezX0icOKiooIDw8nPDycl156iXr16nH22Wc7HUvEy9cFfNoB73JooZ5wAGvtLNw78z3v92QiPpjzq7uhL65qJPf10Ap94qxNmzZx/vnnM378eAB69Oihoi9Bx9fCHw3kWmtdQBZwWqmx1YB+siXgDhQW82SpFfpqVYtyOJGEsk8++YTk5GRWr15NvXqHr3UmEjx8LfwbgIM/yb8BN5Qauw7QBj0ScP/7bRp/5OTTtn4cg9XQJw45cOAAw4YNY8CAAbRq1YqVK1cyYMAAp2OJHJWvhX82cKnn8bNAX2NMljFmN/BXYHx5hBM5mrTd+3hr7gaM0Qp94qzly5fzzjvvcP/99zN37lyaNm3qdCSRY/Kpuc9a+2Cpx3OMMd2Aq4EYYI61dkY55RP5k9INfYM7NiS5YbzTkSTEWGtZsmQJHTt2pGvXrvz+++80a9bM6VgiPvH1jL8Ma+0ia+091trhKvoSaLN/3cm8tAziYyK59y9q6JPAysrK4qqrrqJTp04sW7YMQEVfKpSTKvylGWNaG2P+7Y8wIsezv6Dslrtq6JNAmjdvHsnJyXz++ee88MILtG/f3ulIIifsmIXfuJ1tjLnCGHPmYWNtjTGfAD8DV5RnSJGDDjb0nd0gjkHnqqFPAue5557jggsuIDIykgULFjB69GjCwk753Ekk4I76U2uMOR2YD6wApgO/GmPeM8ZEGGNe9bx+Be6d+5ICEVZCW9ru3EMNfVqhTwIsOjqaQYMGsWLFCs4991yn44ictGM1940FkoGngeVAU+A+4AcgFfgIuNdau628Q4oc3HK32GUZ3LER7dTQJwEwc+ZMXC4Xffr04a677gLQsrtS4R2r8F8KPGmtHXvwBWPMr8CXwBvW2uHlHU7koFm/7GR+WibxMZHc9xdtuSvlq6CggPvvv59x48Zx4YUX0rt3bxV8qTSONUFVB/el/tIOPlcznwRM6Ya++3u0oqYa+qQc/f7776SmpjJu3DjuvPNOZs+eraIvlcqxzvjDgYLDXjv4fH/5xBH5s/HfrmPn3nzaNYhjYEpDp+NIJbZp0ybOOeccqlSpwowZM+jdu7fTkUT87ngL+FxmjCnduBcGWKCHMabMDdTW2g/8HU4kbXcub8/diDHwZN+zCFNDn5QDl8tFWFgYTZo04bHHHuPaa6+lfv36TscSKRfHK/xPHuX1pw57bgHgG5cNAAAgAElEQVQVfvEray2PTnc39F17nhr6pHwsXbqUm266iX//+9+0adOGe++91+lIIuXqWIX/zGOMiZS7mT//wYL1mdSMieTey9TQJ/7lcrl45ZVXGDNmDKeffjr79u1zOpJIQBy18Ftr15bHNzTG9ADG4e4heKv0XQOljhkAPI77SsIqa+215ZFFgte+gmKe+kINfVI+du/ezV//+lfmzJlDv379ePvtt6lVq5bTsUQCwqdNevzFGBMOTMB9q+A2YIkxZoa1dnWpY1oAY4Au1to9xpg6gcwoweF/v1nHrr0FtGsYzwA19Imfvfrqq3z33XdMmDCB22+/XV37ElICvd5kRyDNWrvBWlsIfAj0PeyYocAEa+0eAGvt7gBnFIet25XL2/M2elboa6OGPvGLoqIiNmzYAMBDDz3E8uXLGT58uIq+hJxAF/76wNZSz7d5XivtDOAMY8x8Y8wiz9TAnxhjhhljlhpjlqanp5dTXAm0Mg19HRtxdgM19Mmp27hxI+effz4XX3wxBw4cIDo6mtatWzsdS8QRgS78R/pobQ97HgG0AC4EBgNvGWP+9O5vrZ1krU2x1qbUrl3b70HFGZ///AcLN3ga+rRCn/jBxx9/THJyMqtXr+b5558nJibG6Ugijgp04d8GlJ6wbQDsOMIx0621RdbajcBa3B8EpJLbV1DM056Gvgd6tiI+Rg19cvLy8/MZOnQoAwcOpHXr1qxcuZIBAwY4HUvEcSdc+I0xScaY84wxJ/OxeQnQwhjT1BgTBQwCZhx2zDTgIs/3SsR96X/DSXwvqWDGexr6khvGc00HNfTJqYmMjGTTpk2MGTOGH3/8kaZNmzodSSQo+Fz4jTE3G2O24T4DXwC08rw+xRhzmy9fw1pbDIzAvdHPf4GPrbW/GWOeNMb08Rz2JZBpjFkNfId7B8BMn/9EUiH9viuXd7wNfVqhT06OtZY333yTHTt2EB4ezuzZs3nmmWeIjIx0OppI0PCp8BtjbgAmAd8Cf6XsXP1iYKCv39BaO8tae4a1trm19mnPa49aa2d4Hltr7d3W2tbW2rbW2g99/dpSMbkb+n6l2GUZcl4j2jaIczqSVEBZWVlcddVVDBs2jNdffx2AiIiA3rEsUiH4esZ/LzDOWvs//Hlnvv/iOfsXORkzVu1g0YYsalWL4h6t0CcnYd68eSQnJzNz5kxefPFFnnjiCacjiQQtXz8ONwe+OMpYLlDTP3Ek1OTmF/H0F/8F4IEeauiTE/fZZ59xzTXX0LRpUxYsWEBKSorTkUSCmq9n/FmU7cYv7QzgD//EkVAz7ut17M4toH2jeK7u0MDpOFIBXXTRRdx5550sX75cRV/EB74W/i+Ah40xpYu/9dxfPwqY7vdkUumt3ZnL/y3YRJga+uQEff755/To0YPCwkJq1qzJK6+8QmxsrNOxRCoEXwv/Q55jVwMzcS+686LneSSgCTU5IQcb+kpcliHnNeas+mrok+MrKCjgrrvuok+fPuzatYuMjAynI4lUOD4Vfs96+ecA44HawHagFvAecN7BdfVFfDVj1Q4Wb1RDn/hu7dq1dOrUifHjx3PXXXexaNEi6tWr53QskQrH53tdrLXZuM/8Hyq/OBIKcvOLeOpgQ1/PVsTF6B5rOTZrLTfccANbt27l888/54orrnA6kkiF5VPhN8Y8A7xvrV1TznkkBPzj63Wk5xZwTqN4rj5HDX1ydHv37iUsLIzq1avz7rvvUr16derXP3xfLxE5Eb7O8Y8EfvPshjfSGKNdceSkrN2Zy7uehr4n1dAnx7BkyRLOOeccRo4cCUDLli1V9EX8wNfCXwf4HyAdeBnYboyZaYy5xhgTXW7ppFKx1vKIp6Hvuk5q6JMjc7lcvPjii3Tu3JmioiJuueUWpyOJVCq+NvflWWsnW2t74t5R7wGgLvARsMsY82Y5ZpRKYvrKHfy0MYuEalGMvlQNffJnu3fv5vLLL+fee++lT58+rFy5ki5dujgdS6RSOeHd+ay1u6y1L1trOwDdca/cd5Pfk0mlsje/iKdnqaFPju3AgQP8/PPPvP7660yZMoWaNbUoqIi/nfAOFp5L+/2A64DLcG/Yc7TlfEUA+MdX7oa+Do1rcpUa+qSUoqIiJk+ezF//+leaNGnC+vXrqVq1qtOxRCqtE9mW90JjzNvALtwb9ZwG3APUs9b2OeZvlpC2Zude3lt4sKGvjRr6xGvjxo1069aNG2+8kW+++QZARV+knPl6O98WoD6wFZiA+9a+teUZTCoHay2PTvuNEpflhs5NaFNPDX3i9tFHHzFs2DCMMXz00UdccsklTkcSCQm+Xur/Cnex/6E8w0jlM23ldn7alEVi9Sj+dukZTseRIPHggw/y7LPP0qlTJ/7973/TpEkTpyOJhAyfCr+19ubyDiKVz978Ip7+wr3m0wM9zySuqhr6xO3g2f0TTzxBZKR+LkQC6aiF3xjTEfjVWnvA8/iYrLU/+TWZVHivfPU7GfsKSGlckyvba+GVUGat5bXXXmPPnj08/PDDXHzxxVx88cVOxxIJScc6418EdAJ+8jy2RznOeMbC/RtNKrLVO/bynlboEyArK4ubb76ZadOm0atXL0pKSggP19uFiFOOVfh7Av/1PL6coxd+kTKstTw241dcFm7o3ITW9bRPeqiaN28e1157LTt37uSll15i1KhRhIWd8PIhIuJHRy381tovSz2eE5g4UhlMXbGdJZv2kFg9Wg19ISw9PZ3LLruMevXqsWDBAlJSUpyOJCL4eB+/MWa1MabtUcZaG2NW+zeWVFQ5eUU841mhb0zPVmroC0E5OTkA1K5dm88++4zly5er6IsEEV+vubUCjraqRgyghdcFONjQV8i5TWpy5Tlq6As1M2bMoHnz5nz66acA9OjRg9hYTfWIBJMTmWw72hz/2UCOH7JIBbd6x17eX7iJ8DDDk33Pwhg19IWK/Px87rzzTvr27UujRo1o2/aIFwhFJAgc63a+kcBIz1MLTDHGFBx2WFWgHjClfOJJRWGt5dHp7oa+Gzs35sy6OssLFWvWrGHQoEGsWrWKUaNGMXbsWKKjtVu3SLA6Vlf/DmCZ53ESsBbIPOyYAmA18Lr/o0lF8tny7SzdrIa+ULRkyRK2b9/OzJkz6dWrl9NxROQ4jtXV/ynwKXDwku1D1toNAcolFUhOXhHPznY39D14eStiq6ihr7Lbu3cvS5cu5eKLL+b666/niiuu0Ba6IhWEr0v2Di7vIFJxlW7o668V+iq9JUuWMGjQINLT09m8eTM1a9ZU0RepQI41x38f7o15dnoeH4u11r7g32hSEfy2I0cNfSHC5XLx0ksv8eCDD1KvXj1mz56tgi9SAR3rjH8s8D2w0/P4WCygwh9iXC7Lo9N/w2Xhps5N1NBXiRUXF9O7d2/mzJnDlVdeyVtvvaWiL1JBHavwV7XWHuziP9o9/BLCPl2+jWWb91C7RjSjLm3hdBwpRxEREbRv356+ffty66236sqOSAV2rOa+giM9FgF3Q9/Y2e4tdx+6/Ew19FVCRUVFPPLII/Tt25fU1FSeeeYZpyOJiB/41NxnjGkGxFprV3qeRwMPAGcBX1pr3yq/iBKMXv7PWjL3F9KxaS36JtdzOo742YYNGxg8eDA//fQT0dHRpKamOh1JRPzEp8IPvIb7fv2Vnud/B/4G/A70N8aEW2snlkM+CUK/bs/hn4s2exr62uiybyXz0UcfMWzYMIwxfPzxx1xzzTVORxIRP/J1yd5k4EcA436XvwF40FrbBnfj323lkk6Cjruh79CWu61OV0NfZTJz5kwGDRpEmzZtWLlypYq+SCXka+GPBzI8j5OBBOBjz/OvgOZ+ziVBasrybSzfku1u6LtEDX2VRX5+PgA9e/Zk0qRJ/PDDDzRp0sTZUCJSLnwt/LuBZp7HlwIbrbWbPc+rASX+DibBJ+fAoYa+h3udSQ019FV41lomTJjAGWecwR9//EF4eDhDhw4lMlL/b0UqK1/n+GcCTxtjzgCGAe+UGmsDbPR3MAk+L321lqz9hZzXtBZ92qmhr6LLysri5ptvZtq0aVx++eVERPj6diAiFZmv/9IfAGoAA4GvgadKjQ0AvvVzLgkyv27P4V/ehj6t0FfRzZ07l2uvvZZdu3bx8ssvc9dddxEWdiK7dItIReXrWv17geuPMnauXxNJ0HG5LI94Gvpu6dKElqfXcDqSnKIJEyZQpUoVFi5cSIcOHZyOIyIBdELX9owxNYCOQC3cW/QusdbmlkcwCR5Tlm1jxZZs6tSI5i419FVY27Zto6ioiKZNmzJx4kTCwsKoUUMf4kRCjc/X9owxDwN/AP8BPsJ9yf8PY8xD5ZRNgkD2gULGzvGs0KeGvgpr+vTptGvXjptuugmAuLg4FX2REOVT4TfG3AE8CUwFLgfaAz09z580xtxebgnFUS/+x93Q16mZGvoqovz8fEaOHEm/fv1o3LgxEydqnS2RUOfrpf4RwGvW2hGlXlsFfGmMyQFGAq/7O5w465dtOUxevIUINfRVSFu3bqV3796sWrWKUaNGMXbsWKKjo52OJSIO87XwNwPuPMrYdOAW/8SRYHGwoc9auLFrE844TZeFK5qEhARq1qzJzJkz6dWrl9NxRCRI+DrHnwW0PMpYS8+4VCKfLNvKyq3ZnBYbzV2XnOF0HPHR3r17uffee9m3bx8xMTF8++23KvoiUoavhX8a7gV8rjGlrvcaY/rj3rBnWnmEE2dkHyg8tOVur9ZUj9bCLhXBTz/9RPv27XnllVf47rvvADQ9IyJ/4mvhfwBYg7ub/4AxZrMx5gAwBVjrGZdK4oUv17LnQBGpzRLofXZdp+PIcbhcLl544QW6dOlCcXExP/74I71793Y6logEKV8X8MkxxnQG+gPdcN/HnwX8AEy31mqt/kril205fPDTwYY+bblbEYwZM4bnn3+eq666ijfffJOaNWs6HUlEgpjP13A9xX2K55dUQi6X5WFPQ99N3ZrSQg19Qa2kpITw8HBuv/12kpKSuOWWW/RBTUSO65iX+o0xg4wxi4wxGcaYNGPM08YYTfhWUh8v3coqT0Pfnd21Ql+wKiws5P7776d///5Ya2nSpAlDhw5V0RcRnxy18BtjrgE+AE4H5gMHcM/lP3W03yMV1579hTw35+CWu2roC1YbNmygW7duPP/889SrV4+ioiKnI4lIBXOsM/67gS+AFtbavtbas4HngJHGGG3jVcm88B93Q1/n5glcoYa+oPThhx/Svn17fv/9d6ZMmcIbb7xBVFSU07FEpII5VgFvCbxurS19SjEeqAo0LtdUElA/b8vm32roC2q5ubncfffdnHXWWaxcuZKrrrrK6UgiUkEd63puPJBx2Gvpnv/WBDaWSyIJKJfL8sg0d0Pfzd2aklRHDX3BZM2aNSQlJVGjRg1++OEHmjZtSkSEpmFE5OQd75K9PcHXpYL5aOlWVm3L4fTYKoxUQ1/QsNby6quvkpyczAsvvABAixYtVPRF5JQdr/DPN8YUHvwF5HleX1z6dWNMga/f0BjTwxiz1nOXwFEX/jHGXG2MscaYFF+/tpyYMg19V5yphr4gkZmZSf/+/Rk5ciTdu3fnllu0FYaI+M+x3umf8/c3M8aEAxOAS4FtwBJjzAxr7erDjquBe1Ogxf7OIIc8/+Vasg8U0SUpgV5t1dAXDBYuXMiAAQPYtWsXL7/8MqNGjVLPhYj41VELv7V2TDl8v45AmrV2A4Ax5kOgL7D6sOP+DjwP3FMOGQRYuTWbD5dsITLc8EQfbbkbLKKiooiLi2PatGl06NDB6TgiUgkF+ra8+sDWUs+3eV7zMsa0Bxpaa2ce6wsZY4YZY5YaY5amp6cf61A5TInL8qhnhb6buzYjqU51pyOFtG3btvG///u/AHTo0IGff/5ZRV9Eyk2gC/+RTiu9jYKe9QFeAUYf7wtZaydZa1OstSm1a9f2Y8TK76MlW/l5Ww5146ow8uIkp+OEtOnTp9OuXTsefPBBtm/fDkBYmJbJEJHyE+h3mG1Aw1LPGwA7Sj2vAZwFfG+M2QR0Amaowc9/svYX8vyXh1boq6aGPkfk5+czcuRI+vXrR5MmTVi+fDn169c//m8UETlFgX7XXwK0MMY0BbYDg4BrDw5aa3OAxIPPjTHfA/dYa5cGOGel9cKXa8g+UETXpEQub3u603FCkrWWSy65hPnz5zNq1CjGjh1LdHS007FEJEQE9IzfWlsMjAC+BP4LfGyt/c0Y86Qxpk8gs4SiFVv28OGSrUSGGx7voxX6As1ai7UWYwwjR45k5syZvPLKKyr6IhJQAb/Oa62dBcw67LVHj3LshYHIFArcDX2/YS3c0k0NfYGWk5PDrbfeSvfu3Rk6dCgDBw50OpKIhCifz/iNMacZY54xxswzxqw2xrT2vD5cc/DB78MlW/hlew711NAXcIsXL6Z9+/ZMmTKFvXv3Oh1HREKcT4XfGNMK+AW4Hff2vC2BKp7hlsCockknfpG1v5Dn56wF4OErWhMTpYa+QHC5XDz33HN07doVl8vF3LlzGT36uDesiIiUK1/P+F/EvSlPU+Byyt6WNx9I9XMu8aPn56whJ6+Ibi0S6XmWGvoCZdGiRTzwwAP079+flStXkpqqfyYi4jxfT/0uAK6z1mZ7lt0tbSeg9V6D1HI19AXcli1baNSoEZ07d2bBggV06tRJf+8iEjROpKu/5CivJ3Bo8x4JIgdX6AMY2q0ZzWuroa88FRYWct9995GUlMTSpe47UFNTU1X0RSSo+HrGvxS4HjjSMrpXAYv8lkj85oOftvDr9r3Ui6vCCDX0lasNGzYwaNAglixZwm233UabNm2cjiQickS+Fv6ngTnGmM+BybiX2T3fGHMrMAC4qJzyyUnK3FfAi1+6G/oeUUNfufrwww8ZNmwY4eHhTJkyhauuusrpSCIiR+VTNbDWfm2MGQD8A+jlefll3MvtDrDWzi+nfHKSnp+z1tvQ10MNfeUqLS2Ntm3b8sEHH9C4cWOn44iIHJOx1h7/qIMHuycr2wB1gEzgF2utq5yy+SwlJcUenFMVd0Pfla8tIDLc8OWo82mmuX2/W7VqFXv27OHCCy+kpKQEay0REbqqIiKBYYxZZq09qTV0Tuidyro/Jfx6Mt9IAqPEZXlkmvt/0bDzm6no+5m1lgkTJjB69Ghat27N8uXLCQ8//EYXEZHg5VPh91zmPyZr7cenHkdO1QeLN/Pbjr3Uj6/KHRepoc+fMjMzuemmm5gxYwaXX3457777rjr2RaTC8fWM/8OjvF56nkCF32GZ+wp4QQ195WLHjh107NiR3bt388orr3DXXXep6ItIheRrZTjzCK8lAFcAVwN/9VsiOWnPzVnD3vxizj+jNn9pc5rTcSqVunXrMnDgQIYMGcI555zjdBwRkZPma1f/2qMMLTDGlOBew3+h31LJCVu2eQ8fL91GVHgYT2iFPr/YunUrt912G+PGjSMpKYmXXnrJ6UgiIqfsRFbuO5rvgD5++Dpykg5v6GuaWM3hRBXftGnTaNeuHT/++CNr1x7tc6+ISMXjj8KfgnvHPnHI5MWbWf2HGvr8IT8/nzvuuIP+/fvTrFkzli9fTq9evY7/G0VEKghfu/rvO8LLUcBZQH/gTX+GEt9llGroe7R3a6pG6dayU/H888/z2muvcffdd/Pss88SFRXldCQREb/ytblv7BFeKwG2A68AT/gtkZyQ52avITe/mAvOqM1lrdXQdzKstWRlZZGQkMA999xDly5d6N69u9OxRETKha+Fv+oRXisKhlX7QtmyzVl8sszd0Kctd09OTk4Ot956KytWrGD58uVUq1ZNRV9EKrXjzvEbY6KAx4GzrLUFpX6p6DuouMTFI9N+A+DWC9TQdzIWL15M+/btmTJlCjfccANVqlRxOpKISLk7buG31hYCdwGqLEFk8uIt3oa+4Reqoe9EuFwunnvuObp27YrL5WLu3LmMGTNGS++KSEjwtat/FdC6PIOI79JzC3jxP+6GvsfU0HfCSkpKmD59Ov3792flypWkpqY6HUlEJGB8neO/D3jfGJNmrf26PAPJ8Y31NPRd1LI2l6qhz2dfffUV7du3JzExkTlz5lCjRg31RYhIyPH1jP8dIB740hiTa4xZZ4z5vdQvrXASIEs3ZfHpcndD32O91dDni8LCQu69914uu+wynnrqKQBiY2P1dyciIcnXM/5llN2QRxxQXOLikenuhr7bLmhGEzX0Hdf69esZPHgwS5Ys4bbbbuPZZ591OpKIiKN8Xat/UHkHkeP716LN/PePvTSoWZXb1dB3XN9++y39+vUjPDycKVOmcNVVVzkdSUTEcUe91G+M2WCMaRfIMHJ06bkFvPSf3wF4rHcbNfT54KyzzuLSSy9l5cqVKvoiIh7HmuNvAkQHKIccx7Oz/0tuQTEXt6rDJWfWcTpO0Fq5ciU33ngjxcXF1KlTh08//ZTGjRs7HUtEJGj4Y5MeKWdLNmXx2fLtREWE8Vjv1mpKOwJrLePHj+e8887jP//5D5s2bXI6kohIUDpe4VdDn8PcK/S5t9y97YLmNE5QQ9/hMjIy6Nu3L3fddReXXXYZq1atIilJPRAiIkdyvOa+J4wxGT58HWut/as/AklZ/1y0mTU7c2lQsyrDL2zudJygdPXVV7Nw4ULGjRvHyJEjdUVEROQYjlf4k4ECH76OrgyUg925+bzsaeh7vHcbqkSqoe+g4uJiSkpKiI6O5pVXXgGgffv2DqcSEQl+xyv8/ay1PwUkifzJ2FlryC0opnurOlyiFfq8tm7dyrXXXsvZZ5/NhAkTVPBFRE6AmvuC1OINmXy24mBDXxun4wSNadOm0a5dO1auXEnnzp2djiMiUuGo8Aeh4hIXj81wr9B3+wXNaZQQ43Ai5+Xl5XHHHXfQv39/mjVrxooVKxgyZIjTsUREKhwV/iD0/kJ3Q1/DWlW5XQ19AGzfvp3333+f0aNHs2DBAnXti4icpKPO8Vtr9aHAAbv35vPKV2roA/e9+d988w3du3cnKSmJtLQ0TjtNvQ4iIqdCxT3IPDvb3dB3yZl16H5m6Ba5nJwcBg8ezKWXXsrMmTMBVPRFRPzA1935JAAWb8hk6ortRId4Q9+iRYsYPHgwW7du5ZlnnqFXr15ORxIRqTR0xh8kikpcPOrZcnf4hUk0rBWaDX0TJkygW7duWGuZO3cuY8aMISxMP6YiIv6id9Qg8f7CzazdlUujWjHcekEzp+M4pnHjxlx55ZWsXLmS1NRUp+OIiFQ6KvxBoExDX5/WIdfQN2fOHCZMmADAFVdcwUcffUR8fLzDqUREKicV/iDwzKz/sq+gmEvOPI2LW4VOA1thYSH33HMPPXv25O2336aoqMjpSCIilZ4Kv8MWbchk2sodnoa+1k7HCZi0tDS6dOnCSy+9xPDhw5k/fz6RkZFOxxIRqfTU1e8gd0Ofe8vdOy4KnYa+7OxsOnbsiLWWzz77jP79+zsdSUQkZKjwO+i9BZv4fdc+GifEMOz8yt/QV1xcTEREBPHx8YwfP57zzz+fRo0aOR1LRCSk6FK/Q3btzecfX68DQmOFvpUrV9K2bVvmzJkDwHXXXaeiLyLiABV+hxxs6Lu09Wlc1KqO03HKjbWW8ePHc95557F3715iYkJjOkNEJFip8Dtg4fpMpnsa+h69ovI29GVkZNC3b1/uuusu/vKXv7Bq1SrOP/98p2OJiIQ0Ff4AK93QN6KSN/TNmDGDL7/8knHjxjF9+nQSExOdjiQiEvLU3Bdg787fxLrd+2iSEMPQStjQV1xczG+//Ua7du248cYbOf/887WFrohIENEZfwC5G/rcK/Q91qfyNfRt2bKFiy66iG7durF7926MMSr6IiJBRoU/gJ7+4r/sLyzhstancVHLytXQN3XqVJKTk1m1ahWvv/46depUrj+fiEhlocIfIAvWZzBj1Q6qRIbxSCVq6HO5XAwfPpwrr7yS5s2bs2LFCoYMGeJ0LBEROQoV/gAoveVuZWvoCwsLo7i4mNGjRzN//nyaN2/udCQRETkGNfcFwP/N30haJWros9by1ltvkZKSQvv27Zk4cSLGGKdjiYiIDwJ+xm+M6WGMWWuMSTPGPHCE8buNMauNMT8bY74xxjQOdEZ/2plTaoW+Pm2IjqjYDX3Z2dkMHDiQYcOGMXHiRAAVfRGRCiSghd8YEw5MAHoCrYHBxpjDJ7xXACnW2rOBKcDzgczob0/P+i8HCkv4S5vTuLCCN/QtXLiQ5ORkpk6dytixY3nttdecjiQiIico0Jf6OwJp1toNAMaYD4G+wOqDB1hrvyt1/CLguoAm9KMFaRl8Xkka+r7//nsuueQSGjZsyNy5c+nUqZPTkURE5CQE+lJ/fWBrqefbPK8dzc3A7HJNVE4Ki108OsPd0Dfy4hY0qFkxG/qstQB06dKFhx56iBUrVqjoi4hUYIEu/EeaDLZHPNCY64AU4IWjjA8zxiw1xixNT0/3Y0T/ONjQ1zSxGrd0a+p0nJMye/ZsOnToQGZmJpGRkTzxxBPEx8c7HUtERE5BoAv/NqBhqecNgB2HH2SMuQR4COhjrS040hey1k6y1qZYa1Nq165dLmFP1h85eYz7puI29BUWFjJ69Gguv/xyiouLyc7OdjqSiIj4SaAL/xKghTGmqTEmChgEzCh9gDGmPTARd9HfHeB8fvHUF+6Gvp5nnc4FZwTXh5LjSUtLo0uXLrz88ssMHz6cxYsX6958EZFKJKDNfdbaYmPMCOBLIBx4x1r7mzHmSWCptXYG7kv71YFPPLeJbbHW9glkzlMxPy2DL37+g6qR4TxcARv6HnzwQdavX89nn31G//79nY4jIiJ+FvAFfKy1s4BZh732aKnHlwQ6k78UFpfacvfiJOrHV3U4kW/27dvHvn37OP3003n11VfJz8+nUaNGTscSEYDGLj8AABZgSURBVJFyoCV7/eid+RtZn76fZhWooW/FihV06NCBQYMGYa2lTp06KvoiIpWYCr+f7MjOY3wFauiz1jJu3Dg6derE/v37eeKJJ7QCn4hICNBa/X7ytKeh7/K2p3N+kDf0ZWVlccMNN/D555/Tu3dv3nnnHRITE52OJSIiAaAzfj+Yty6DL37xNPT1Cv6GvoiICNavX8/48eOZPn26ir6ISAjRGf8pcq/Q527oG9k9iXpB2tBXXFzMhAkTuPXWW4mNjWXlypVERkY6HUtERAJMZ/yn6O15G9mQvp9mtatxS9fg3HJ38+bNXHDBBYwaNYopU6YAqOiLiIQoFf5TULqh74k+bYiKCL6/zk8//ZTk5GR++eUXPvjgA667rsLueSQiIn4QfJWqAnnqi9XkFZXQq21durUIvoa+F154gauvvpoWLVqwYsUKBg8e7HQkERFxmOb4T9LcdenM+mUnMVHhPHzFmU7HOaI+ffqwZ88eHn/8caKiopyOIyIiQUBn/CehoLiEx6Yf2nK3blxwNPRZa5k0aRI33XQT1lpatmzJM888o6IvIiJeKvwn4e15G9mQ4W7ou7lrcKzQl52dzcCBA7n11lvZunUreXl5TkcSEZEgpMJ/grZn5/G/36QB8GSfs4KioW/hwoUkJyczdepUxo4dy5dffklMTIzTsUREJAhpjv8EPTXT09B3dl26tnB+4Zu8vDz69+9PTEwM8+bN47zzznM6koiIBDEV/hPww+/pzP7V09DXy9mGvvT0dBISEqhatSozZsygZcuWxMXFOZpJRESCn/PXqSuIguISHp/hbui7s7uzDX2zZ8+mTZs2vPTSSwB07NhRRV9ERHyiwu+jt+ZuZGPGfprXrsZNXZxp6Css/P/27j1KqurK4/h3yzPhJco7RAgCUXQAEREUIU4MowzSaJAB4guFmIisoJgZMhiDgM6IqMQYBZyY+BgwIhEQAj6wQcmIiQ3CApQsQB6KgfAMCDR0s+ePc1uLsru6uqmqtrt+n7Xu6qp7T927+1Sv3nXP3XXuMcaMGUPfvn1p3rw5/fr1q5A4RESk8tJQfxI+2X+EX70ZZuibkFMxBX0bN25k8ODB5OXlMXLkSKZMmULt2rUzHoeIiFRuSvxJmPjKeo4eP0G/js25tG3FFPR9+umnbNu2jZdffpkBAwZUSAwiIlL5aai/FEs37GLxuqKCvszecvfQoUO8+OKLAFx22WV89NFHSvoiInJKlPgTiC3oG31FO5o1yNzQ+sqVK+nSpQtDhw5l8+bNANSpUydjxxcRkapJiT+Bp97azJY9h2nbpC7DMlTQ5+5MnTqV7t27c/jwYZYsWUKbNl/N2/2KiEjlo2v8Jfh432Eezy2aoe88alRL/2ckd2fQoEG89NJL9O/fn6effpozzzwz7ccVEZHsocRfgokLQkHf1Z1acEmGCvrMjD59+tC7d29GjhyJmWXkuCIikj2U+IuRu2EXr67bSZ2a1RjXN70z9BUUFDB+/HjOO+88hgwZwogRI9J6PBERyW66xh/n6PHYgr72aS3o27p1K7179+b+++9nxYoVaTuOiIhIEZ3xx3nqrc1s3XOYdk3qcvOlrdN2nDlz5jB8+HAKCwuZOXMmQ4YMSduxREREiuiMP8b2vTEFfTnnp62gLy8vj4EDB9KuXTtWrVqlpC8iIhmjxB9j4oL15BecoH+nFvQ4O/XV9AcPHgTgwgsvZPbs2Sxfvpyzzz475ccREREpiRJ/JPfDXby2PiroS/Etd92dGTNm0KpVK1avXg3AwIEDqVmzZkqPIyIiUholfqKCvldCQd+d32tP0/qpK+jbv38/gwYN4rbbbqNr1640bdo0ZfsWEREpKyV+YEZU0Ne+aV1uuqR1yvb7zjvv0LlzZ+bOncuDDz7I4sWLadasWcr2LyIiUlZZX9W/fe9hfp2mgr758+dz2mmnsXz5ci6++OKU7VdERKS8sv6Mf0JU0JfTuQXd25x6Qd+OHTvIy8sL+54wgVWrVinpi4jIV0ZWJ/43P9zJ6+t3UrdWdf4zBTP0LVy4kE6dOjF06FAKCwupUaMGDRo0SEGkIiIiqZG1iT/M0LceCLfcPZWCvvz8fO6880769etHixYtmDdvHtWqVUtVqCIiIimTtdf4py/bzLa9h/l203qnVNC3Z88e+vTpw8qVKxk1ahSTJ0+mdu30TfMrIiJyKrLyjH/bnsM8sbSooO/UbrnbsGFDzj33XObOnctjjz2mpC8iIl9pWZn4JyxYR37BCQZ0bsHF5SjoO3jwILfffjvbt2/ntNNO4/nnnycnJycNkYqIiKRW1iX+JR/s5I0PdpW7oC8vL48uXbowffp0cnNz0xChiIhI+mRV4o+foa9JGQr63J1HH32UHj16cOTIEXJzc7nxxhvTFaqIiEhaZFXin7ZsE9v3HuGcZvW4qUerMr32kUce4a677qJv376sXr2aXr16pSlKERGR9Mmaqv5Q0LcJCDP0VU+yoO/YsWPUrFmTESNG0LBhQ4YNG4aZpTNUERGRtMmaM/77XlnHsYITXHvBN+j2rTNKbV9QUMC4cePo3r07R48epX79+txyyy1K+iIiUqllReJ/Y/1Olny4i3q1qjO27zmltt+6dSu9e/fmgQce4IILLuDEiRMZiFJERCT9qvxQ/9Hjhdy3IKagr17igr45c+YwfPhwCgsLmTlzJkOGDMlEmCIiIhlR5RP/k0u/KOi7sZSCvoKCAiZNmkT79u2ZNWsWbdq0yVCUIiIimVGlE//WPZ/x5LLSC/rWrVtHy5YtadCgAQsXLqRx48bUqFEjk6GKiIhkRJW9xu/ujJ8fFfR1Kb6gz92ZPn06Xbt2ZezYsQC0aNFCSV9ERKqsKpv43/hgF7kb/k69WtX52VVfnqFv3759XHfddfzoRz+iV69ejB8/PvNBioiIZFiVTPxHjxdyXzRD31192tO4Xq2Ttq9atYrOnTszb948Jk+ezKJFi2jatGlFhCoiIpJRVfIa/xNLN/HxvlDQd0P3Lxf0NW7cmGbNmjF79my6detWARGKiIhUjCp3xr9l92dMiwr6Jg74oqBvx44djBs3jhMnTtCyZUtWrFihpC8iIlmnSiV+d2d8NEPf97u05KLWoaBvwYIFdOzYkalTp7J27VoAzcAnIiJZqUol/tfX72Tphr9Tr3Z1xl51Dvn5+YwePZqrr76ali1bkpeXR8eOHSs6TBERkQpTZa7xHzlWyH2vrAdgzPdCQd+AAQOYN28eo0aNYvLkydSunfxteEVERKqiKpP4n1y6kU/2H+Hc5vUZ2u2bANx9990MGzaMnJycCo5ORETkqyHjQ/1mdqWZbTCzjWY2tpjttczs99H2d82sdWn7PFZwgmnLNnMi/zC29Ff8/J5xAPTs2VNJX0REJEZGE7+ZVQN+DVwFdACGmFmHuGa3AvvcvS3wKPBgafvdsf8IBz/5KwdfGMOr8+dQp06dVIcuIiJSJWR6qL8bsNHdNwOY2QtADrA+pk0OMD56/BLwuJmZu3tJO92/dzcnnrub5s2bMi83l169eqUnehERkUou00P93wC2xzz/OFpXbBt3LwAOAGcm2mnhwT10vvRy1qxeraQvIiKSQKbP+Iv78nz8mXwybTCzHwI/jJ7mr3r79bWNGjU6xfAkgUbA7ooOIguon9NPfZx+6uP0+3Z5X5jpxP8x8M2Y5y2BHSW0+djMqgMNgL3xO3L3GcAMADN7z927piViAdTHmaJ+Tj/1cfqpj9PPzN4r72szPdT/F6CdmX3LzGoCg4H5cW3mAzdFjwcCbya6vi8iIiLJy+gZv7sXmNkdwKtANeBpd19nZhOA99x9PvAb4Dkz20g40x+cyRhFRESqsoxP4OPufwT+GLfu3pjHR4HryrjbGSkITRJTH2eG+jn91Mfppz5Ov3L3sWkUXUREJHtUqZv0iIiISGKVKvGnY7pfOVkSfXyXma03szVmtsTMWlVEnJVZaX0c026gmbmZqTq6HJLpZzMbFP09rzOzmZmOsbJL4v/FWWaWa2arov8ZfSsizsrMzJ42s11mtraE7WZmj0XvwRoz61LqTt29UiyEYsBNQBugJrAa6BDX5nZgWvR4MPD7io67Mi1J9vHlwNejxz9WH6e+j6N29YC3gBVA14qOu7ItSf4ttwNWAQ2j500qOu7KtCTZxzOAH0ePOwBbKjruyrYAvYAuwNoStvcFFhHmwOkOvFvaPivTGf/n0/26+zGgaLrfWDnAM9Hjl4DvmllxEwJJ8UrtY3fPdffD0dMVhLkYJHnJ/B0DTAQmA0czGVwVkkw/jwB+7e77ANx9V4ZjrOyS6WMH6kePG/DleVukFO7+FsXMZRMjB3jWgxXA6WbWPNE+K1PiT8t0v3KSZPo41q2ET5qSvFL72MwuAL7p7gsyGVgVk8zfcnugvZn9ycxWmNmVGYuuakimj8cD15vZx4Rvc43KTGhZpaz/tzP/db5TkLLpfqVESfefmV0PdAV6pzWiqidhH5vZaYS7Ut6cqYCqqGT+lqsThvu/Qxi5etvMznf3/WmOrapIpo+HAL9z94fNrAdhjpbz3f1E+sPLGmXOe5XpjL8s0/2SaLpfKVEyfYyZXQGMA/q7e36GYqsqSuvjesD5wFIz20K4ZjdfBX5lluz/i3nuftzdPwI2ED4ISHKS6eNbgRcB3P0doDZhHn9JnaT+b8eqTIlf0/2mX6l9HA1DTyckfV0TLbuEfezuB9y9kbu3dvfWhDqK/u5e7nm5s1Qy/y/mEopVMbNGhKH/zRmNsnJLpo+3Ad8FMLNzCYn/7xmNsuqbD9wYVfd3Bw64+6eJXlBphvpd0/2mXZJ9/BBQF5gd1U1uc/f+FRZ0JZNkH8spSrKfXwX6mNl6oBD4qbvvqbioK5ck+3gM8JSZ3UkYfr5ZJ2NlY2azCJejGkW1Er8AagC4+zRC7URfYCNwGBhW6j71HoiIiGSPyjTULyIiIqdIiV9ERCSLKPGLiIhkESV+ERGRLKLELyIikkWU+EWKYWY3R3fGK265ooz7Gh69LiP3NTCzSXHx7ovuVpnyr7eaWfXoGPfErLvWzEYX0/aKqG3PVMeRIL62cX1RaGafmtlzZpZwWtME++xiZuPN7PRUxyuSCZXme/wiFeQ6wsxYsdZXRCDl0CP6eSZwGzDLzGq6+7OpOkD0Xe4enDxX+LVAT2BqXPM/RzGtS9Xxy2ASsBCoFcVwL3COmfWI7utRFl0I36X+HaDpfaXSUeIXSex9d99Y0UGUR3SnLgDM7DXClLSjgZQl/vjjlNLuH4SZCCvCppg4l5lZLcINZDoDmhVRsoqG+kXKycy+Zma/NLN1ZvZZNIQ838y+ncRrbzCz96PXHTCzNWY2PK7N5Wb2ppkdipZFZtahPLG6+3HgfaBtzP4bmNkTUdzHzGyDmf0kLob6Zva4mW03s3wz22lmr5tZ+2j7SUP9ZvY88AOgVczw+sZo20lD/WY2w8x2mFm1uGPWjvpkSsy6JmY2PWp/zMw+MLNby9MXkZXRz7Pijj3JzFaZ2T/MbLeZLTGzbjHbhwNPRU8/ivkdW8b0x7ioL/PN7BMzeyj6oCHylaAzfpHEqlm44VMRd/fC6PHXomUC8DfCkPpI4B0zO6ekexmYWW/gGcJQ+BjCdKcdgIYxbXKAOYR5uIcSPqSPJdxBrqO7f1KO3+VbREPTUbJdBHQEfk4Yfu8PTDWzM9393ug1vwSuJNyUaSPhBis9CTfAKs4vojadgGuidUdLaPssMIIwl/trMetzCPdwfy6K9XTgT4RpSu8FthCmKH0qunTxZFK//claRz83xa1vATxMuLxTl3Dvj7fNrIu7rwPmAW2AnxEuaRTNiV70Xs8CrgL+mzC6cR7h7+Ms4N/KEadI6rm7Fi1a4hbCbXG9mGV5gtdUA+oQ5sseFbN+ePTaltHzscCuBPsxQnJ7NW796YR7UEwpJfZJ0fGqR0tTYGK0bkrUZkD0/Pq41/6OkKjPiJ5/CExOcKzq0X7uiVn3PLClmLZXRG17xvyem4Hn4totANbEPL8POAKcHdfut8BOoFqC+NpGx7wlirUO4YPGDuCFUvqxGuHDxibg4WLez9Zx7S+P1g+NW39TtP6fKvrvWosWd9dQv0gprgEuillOGl42s8Fm9mczOwAUAIcIowCJhvv/AjQ2s2fN7F/NLP7s+RygFfC/0dBx9WjU4RDwLtArydiPR8vfgJ8CjxDO3In2UQC8EPea5wkFcBfHxHqrmY01swvNLGX/M9zdo+NdY2Z1AMysMfAvnFyHcCXwf8DWuP54FWhC4r4u8htCXxwC3iCc0d8U38jM+pjZUjPbQ+ifY4Qz/GSOcSXhQ9PLcXEWjWZclsQ+RNJOiV8ksbXu/l7MsqFog5ldQxjaXQsMISTLiwhn5bVL2qG7LyEM+7Ym3Bp2t5m9ZmbnR02aRD+f4YvkXbRcSbikkIyiDyttgXruPsbd86NtZwC7/csV7X+L2Q5wO+Ga9ghCEdwuM3vYzL6WZAyleZZwFn5t9HwI4f/SzJg2TYB/5st9MSvankx/3Efoi+8AT0aPfxXbwMwuIlT+HyCMEHSP2q0lwfsZF2dtwohPbJxF90ZP9n0TSStd4xcpv8HAh+5+S9EKM6tNGJJPyN1fBF40s7qEpPYgsMjMzgKKbg3770BuMS/PL2ZdccdIVK2+l3Cbz+pxyb9Z9HNPtI+DhEsTY82sNeHrjf9FOLMdxyly941mtgK4nnBN/3pgibvviGm2h/B1wbtK2M2GEtbH2hLTH8vMrD4w3MymuXtRod9Awu/1/dg+MbMzCJcUSrOHkPR7l7B9RwnrRTJKiV+k/L5OGA6OdSNlGElz90PAfDNrSygqa0iYJ2A70MHdH0pRrPGWAXcC3wd+H7P+B4Tk924xsW4BHjKzG4Dz47fHyCdc7kjWc8BjZnY54Qz7hrjtiwnzEGxx991l2G8i/0H43X9BKCaEL97Pz+9VbmZ9CAV/H8S8tuiDV/zvuJhQrFnH3ZelKE6RlFPiFym/xcDj0dfOFhGS1kjgH4leZGb3E4Z9cwlV4WcBdwDvufveqM0dwB+iEYTZhLPJZsAlwGZ3/+Upxr4AeIdQGd+MkNj6EYoaJ7r7viiOd4E/EIa7PyMUsJ0HTE+w7/XALWb2Q2AVcMTd1yZo/wLwKOEDwGfAy3HbpxBGGt42s0eBvwL1CLUQl7j7NZSRu39iZtOA0WbW2d3fJ7yfdwC/NbNnov3fw5fP1IsmcLoj+vricWC1u79hZrMJ1/gfIUxYBOGSTl9gjLvHf4tAJPMqurpQi5av4sIXVf1tE7SpBjxASAyHCYm8E6Fw7H9i2sVX9fcnFHx9Sjh73E64jt4sbv+XEq457yOchX9EuK7dvZTYJxHVzpXSrgHwRBTHMcKQ+U/i2kwhJO8DhMK4NcAdMduLq+qvRxhF2Bdt2xitP6mqP+44L0fbni0h1jMIXy3cEsW6C3iLmG9PlPC6oqr+m4vZ1iT6nebErBsdHeMIIXFfDiwH3oh77YTofS+Me2+rEUZS1kTv2X7C/AkPAvUr+u9aixZ3x9w/H9USERGRKk5V/SIiIllEiV9ERCSLKPGLiIhkESV+ERGRLKLELyIikkWU+EVERLKIEr+IiEgWUeIXERHJIkr8IiIiWeT/AbZzy0zxD3BLAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f69101058d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fpr, tpr, thresholds = roc_curve(Y_test, modele_pred)\n",
"plt.figure(figsize=(8, 6))\n",
"plot_roc_curve(fpr, tpr)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### PRECISION, RAPPEL, F1-SCORE, SUPPORT"
]
},
{
"cell_type": "code",
"execution_count": 105,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(0.6907979684944477, 0.7572897989997169, 0.7225173314126226, None)"
]
},
"execution_count": 105,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"precision_recall_fscore_support(Y_test, modele_pred,average='binary')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### SCORE EN K-FOLD CROSS VALIDATION (validation croisee en K passes) "
]
},
{
"cell_type": "code",
"execution_count": 106,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.56614705 0.61450097 0.74907613 0.77323349 0.67779993 0.71510379\n",
" 0.71170698 0.68592241 0.72382508 0.6586577 ]\n",
"Mean: 0.6875973527111319\n",
"Standard deviation: 0.05898564912084765\n",
"CPU times: user 362 ms, sys: 80 ms, total: 442 ms\n",
"Wall time: 29.6 s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele, X, Y, cv=10, scoring=\"precision\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 107,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.76695945 0.76976266 0.75775701 0.75271028 0.76242991 0.74691589\n",
" 0.75906542 0.75682243 0.74560748 0.76859813]\n",
"Mean: 0.7586628650073268\n",
"Standard deviation: 0.00808193406783947\n",
"CPU times: user 358 ms, sys: 67.9 ms, total: 426 ms\n",
"Wall time: 29.8 s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele, X, Y, cv=10, scoring=\"recall\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 108,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.65142857 0.68342459 0.75339156 0.76283387 0.71762843 0.73066374\n",
" 0.73462373 0.71963032 0.73455483 0.7093936 ]\n",
"Mean: 0.7197573248816875\n",
"Standard deviation: 0.03105900547986481\n",
"CPU times: user 350 ms, sys: 100 ms, total: 450 ms\n",
"Wall time: 30.7 s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele, X, Y, cv=10, scoring=\"f1\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 109,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.61863541 0.69153529 0.82828151 0.84115261 0.76584816 0.79912543\n",
" 0.80227281 0.77246724 0.80830686 0.75427587]\n",
"Mean: 0.768190117436766\n",
"Standard deviation: 0.06412677633183099\n",
"CPU times: user 353 ms, sys: 76.8 ms, total: 430 ms\n",
"Wall time: 31.2 s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_roc=cross_val_score(modele, X, Y, cv=10, scoring=\"roc_auc\",n_jobs=-1)\n",
"display_scores(modele_score_roc)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### **SVM**"
]
},
{
"cell_type": "code",
"execution_count": 140,
"metadata": {
"scrolled": true
},
"outputs": [],
"source": [
"# algorithme de classification\n",
"from sklearn.svm import SVC"
]
},
{
"cell_type": "code",
"execution_count": 141,
"metadata": {},
"outputs": [],
"source": [
"modele_SVM = SVC()"
]
},
{
"cell_type": "code",
"execution_count": 142,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"CPU times: user 16min 11s, sys: 77.2 ms, total: 16min 11s\n",
"Wall time: 16min 11s\n"
]
},
{
"data": {
"text/plain": [
"SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,\n",
" decision_function_shape='ovr', degree=3, gamma='auto', kernel='rbf',\n",
" max_iter=-1, probability=False, random_state=None, shrinking=True,\n",
" tol=0.001, verbose=False)"
]
},
"execution_count": 142,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"%%time\n",
"#CPU times: user 20h 57min 44s, sys: 12.1 s, total: 20h 57min 56s\n",
"#Wall time: 21h 35min 25s\n",
"modele_SVM.fit(X_train, Y_train)"
]
},
{
"cell_type": "code",
"execution_count": 146,
"metadata": {},
"outputs": [],
"source": [
"with open(\"SVM_model.pk\", 'wb') as pickle_file:\n",
" pk.dump(all, pickle_file)"
]
},
{
"cell_type": "code",
"execution_count": 147,
"metadata": {},
"outputs": [],
"source": [
"modele_SVM_test=modele_SVM.predict(X_test)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### **ESTIMATION QUALITE MODELE SVM**"
]
},
{
"cell_type": "code",
"execution_count": 148,
"metadata": {},
"outputs": [],
"source": [
"modele_pred = modele_SVM_test\n",
"modele = modele_SVM"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Matrice confusion"
]
},
{
"cell_type": "code",
"execution_count": 149,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[10804, 0],\n",
" [ 9528, 1069]])"
]
},
"execution_count": 149,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"confusion_matrix(Y_test,modele_pred)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### ROC"
]
},
{
"cell_type": "code",
"execution_count": 150,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"0.5504388034349345"
]
},
"execution_count": 150,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"roc_auc_score(Y_test, modele_pred)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### ROC CURVE"
]
},
{
"cell_type": "code",
"execution_count": 151,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAf4AAAF8CAYAAAAuF9n2AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzs3Xd0VVXexvHvTiekEDqEFnpLaAEBxZEmCNKLCTKKVGVAihN6U6QjCNJBR0cRlBB6ExSlCgSRBEILvSaQQAgJaffu94+EeREhXOCWlN9nLdbccu7Zj7MgT/a55+yjtNYIIYQQInews3UAIYQQQliPFL8QQgiRi0jxCyGEELmIFL8QQgiRi0jxCyGEELmIFL8QQgiRi1i1+JVSXymlopVSx57wvlJKzVVKRSqlwpRSta2ZTwghhMjprD3j/xpomcn7bwAVMv70BRZaIZMQQgiRa1i1+LXWu4DYTDZpB/xXp/sdyKeUKmaddEIIIUTOl9W+4/cGLj/0/ErGa0IIIYQwAwdbB3iEesxrj11TWCnVl/SvA8ibN2+dypUrWzKXEEIIYTMGrblyM46Y65fRaSkAt7TWhZ5nX1mt+K8AJR96XgK49rgNtdZLgCUA/v7+OjQ01PLphBBCCCv75WQUg74IIWbpEOyc8tB34gIWjux98Xn3l9UO9a8H3sk4u78+EKe1vm7rUEIIIYS13U5IYfDKI/T8OpS7eb0p92pHftt/iAUjer3Qfq0641dKrQBeAwoqpa4A4wFHAK31ImAz0AqIBBKB96yZTwghhMgKth67zpAvgjm/aSHeXcYysuNLvDd1OfZ2j/tG/NlYtfi11oFPeV8D/7JSHCGEECJLuXUvmXFrwlnx5Tzu7P4O13yF+KJ9WVo1Kmu2MbLad/xCCCFErqO1Zv3Ra4xevpuzq6aRdPFP6jZpxdZV35E/v5dZx5LiF0IIIWwo6m4So9eEs+NENLe2LiP1+gmmzp7HsEH9UerFD+0/SopfCCGEsAGtNasOX+HjdUe5eyeOfPkLMnrWTBoWd6RatWoWG1eKXwghhLCyK7cTGRkSzi8Hw7m1YTqers5sPfQ73l55LT62FL8QQghhJUajZvnBS0zdfILoP38m9qcF5HFyZMHcZVYpfZDiF0IIIaziYkwCw1eHse/kNWK3LyLh2A7q1W/AjytXULp0aavlkOIXQgghLMhg1Hy97wIztp0kKdVIfldHSLzI0LFjGTduHA4O1q1iKX4hhBDCQiKj7zEs+CiHL94mIXwHb73VlYmd/XEd8zouLi42ySTFL4QQQphZmsHI0t3nmb3jNPfv3ube9i+4c/J3qrauQP68DW2aTYpfCCGEMKOTN+4StCqM8KtxJF0KI2HrbFIS4pgzZw79+/e3dTwpfiGEEMIcUtKMLPg1kvk7I0k1aBzO7CR6zSwqVKjAyp+3UatWLVtHBKT4hRBCiBcWfiWOoOCjnLwRD8A/65em8zu9WVjoHjNnzsTNzc3GCf+fFL8QQgjxnJJSDcz9+QyLd53DYNS4XjtM+aTTfDLlW5RSLFq0yNYR/0aKXwghhHgOhy/eZljwUc7eTECnJVMk4kcObfmBvP7+xMXFkS9fPltHfCwpfiGEEOIZ3E8xMPOnU3y19zxaQ1HDTWI2zeDQyQg++ugjJk+ejJOTk61jPpEUvxBCCGGi/WdjGBESxsWYROztFL1eLsmSgQNITEhg8+bNvPHGG7aO+FRS/EIIIcRT3EtOY+qWE3z3+yUAyuezY0ZgPWqVLkDjAt9TpkwZihUrZuOUprGzdQAhhBAiK9t1+iYtZu/iu98v4WCnaF88gcjF/dn07UIAGjRokG1KH2TGL4QQQjxW3P1UJm2K4MfQKwBUL+ZOxahfmDv0U0qWLEmzZs1snPD5SPELIYQQj9gREcXoteFE3U3GycGO92p5smPBOGb/8jNdu3Zl8eLFWfas/aeR4hdCCCEy3E5IYcKG46z78xoAtUvlY3pnP26dO87U0EMsXbqUXr16oZSycdLnJ8UvhBBCAJvDrzNu3TFu3UvBxdGOIU3KUvjOCcoXdqd84fpcvHgx287yHybFL4QQIle7GZ/MuHXH2HLsBgAv+eTng1p5CfpXd0JDQwkLC8PX1zdHlD5I8QshhMiltNas/fMqH2+I4E5iKnmd7BnRqgqc2U2bph/g6OhISEgIvr6+to5qVlL8Qgghcp0bcUmMXhPOzyejAWhUoSBTOvoyZUwQCxYs4JVXXmH58uWUKlXKxknNT4pfCCFErqG15sfQy3y68QTxyWm4uzgw9s2qdKlTAqUUtWvXZty4cYwdOxYHh5xZkTnzv0oIIYR4xOXYREaGhLMn8hYAzaoU5tP21fnh6yUsP1mA7t2706tXLxuntDwpfiGEEDma0ahZfuAiU7ecJCHFgJerIxPaVqOhtxM9u3dl48aNBAYG0r17d1tHtQopfiGEEDnWhVsJDFsdxsHzsQC09i3GhLbVOH54PzVbv82tW7eYO3cuAwYMsHFS65HiF0IIkeMYjJr/7D3PzJ9OkZRqpKCbExPbVecN32KcPHmSpk2bUqFCBTZt2kTNmjVtHdeqpPiFEELkKGei4gkKDuPPy3cA6FjLm7FvVsXFzgBA5cqV+eabb2jfvj1ubm62jGoTcnc+IYQQOUKqwcj8nZG0nruHPy/foYiHM1++68+st2qyc9tGfHx8OHz4MADdu3fPlaUPMuMXQgiRA0Rcu8uw1Uc5dvUuAAF1SzKyVRWcSKN///4sXLgQf3//HLP63ouQ4hdCCJFtpaQZmbczkgU7I0kzarzz5WFqJ18aVSjE8ePHCQgI4NixY/z73/9m0qRJODk52TqyzUnxCyGEyJbCrtwhaFUYp6LiAXinQWmGt6xMXuf0alu1ahVRUVFs2bKFli1b2jJqlqK01rbO8ML8/f11aGiorWMIIYSwgqRUA5/vOMOSXWcxaihTwJVpnfx4qWwB7ty5w/nz56lVqxZpaWnExMRQpEgRW0c2O6XUYa21//N8Vmb8Qgghso3DF2MJCg7j3M0E7BT0aeTD0OaVyONkz/79+wkMDMRoNBIZGYmTk1OOLP0XJcUvhBAiy0tMSWPGtlN8ve8CWkP5wm5M7+xH7VJeGI1GpkyZwtixYylZsiSrVq2S7/IzIcUvhBAiS9t39hYjVodzKTYRezvF+6+VZWCTCrg42hMfH0/Hjh3ZsWMHb731FosXL8bT09PWkbM0KX4hhBBZUnxSKlO3nGT5gUsAVC7qzswuNaju/f/F7ubmRv78+Vm2bBk9e/ZEKWWruNmGFL8QQogs59dT0YwKCedaXBKO9oqBTSrw/j/K4eRgR0pKChMmTKBv376UKVOGH374wdZxsxUpfiGEEFlGXGIqEzdFEHz4CgB+JTyZ3tmPykU9AIiMjCQgIIDDhw9TtGhRPvzwQ1vGzZak+IUQQmQJ2yOiGL0mnOj4ZJwc7BjavCK9X/HBwT59dfnvvvuODz74AEdHR9asWUP79u1tnDh7kuIXQghhU7EJKUxYf5z1R68BUKe0F9M7+1Gu0P+vpf/ll1/Su3dvGjVqxPLlyylZsqSt4mZ7UvxCCCFsQmvNpvDrjF93nJiEFPI42jOsZSXeaVAGe7v0k/QMBgP29va89dZbxMfHM2DAABwcpLpehPy/J4QQwuqi45MYu/YY245HAdCgbAGmdfKjVAFXIP2Xgrlz5/Lf//6X3bt34+bmxuDBg20ZOceQ4hdCCGE1WmtC/rjKJxsjiLufipuzAyNbVSawbinsMmb5N2/e5L333mPTpk20adOG5ORkXF1dbZw855DiF0IIYRXX4+4zKiScnaduAvBqxUJM6eiLd748/9tm586dvP3228TExDB37lwGDBgg1+abmRS/EEIIi9Jas/LQZSZvOkF8choeLg6Ma1ONTrW9/1LqWmtGjBiBh4cHmzdvpmbNmjZMnXNJ8QshhLCYy7GJjAgJY29kDADNqxZhUvvqFPZw+d82Fy9exMPDAy8vL1avXo2Xlxd58+a1VeQcz87WAYQQQuQ8RqPmm30XaPH5LvZGxuDl6sjcwFos+Wedv5T+6tWrqVmzJoMGDQKgRIkSUvoWJjN+IYQQZnXu5j2Grw7j0IXbALzpV4wJbatR0M35f9vcv3+fIUOGsHjxYvz9/Rk/fryt4uY6UvxCCCHMwmDUfLnnHJ/9dJrkNCMF3Zz5tH11WlYv+pftzpw5Q8eOHTl27Bj//ve/mTRpktxG14qk+IUQQryw01HxBAWHcfTyHQA61vZm3JtVyef690J3c0tfkW/Lli20bNnSqjmFFL8QQogXkGowsvi3s8z9OZIUg5Fini5M7uBL48qF/7LdnTt3mDdvHiNHjqRYsWIcPXoUOzs5zcwWpPiFEEI8l+PX4ghaFUbE9bsABNYrxchWlfFwcfzLdvv37ycwMJCrV6/StGlTGjRoIKVvQ1b/f14p1VIpdUopFamUGvGY90sppXYqpY4opcKUUq2snVEIIcSTJacZmPXTKdrN20vE9buU8MrD8t4vMaWj719K32AwMHnyZBo1aoSdnR179uyhQYMGNkwuwMozfqWUPTAfaA5cAQ4ppdZrrSMe2mwM8KPWeqFSqiqwGShjzZxCCCEe78/LdxgWfJTTUfcA6NGwDEEtKpHX+e910qdPH/7zn/8QEBDAokWL8PT0tHZc8RjWPtRfD4jUWp8DUEqtBNoBDxe/BjwyHnsC16yaUAghxN8kpRqYvf00S3efw6jBp2BepnXyo55P/r9tq7VGKUWfPn145ZVXeO+992TZ3SzE2sXvDVx+6PkV4KVHtpkA/KSUGgjkBZpZJ5oQQojHOXQhlmHBYZy/lYCdgr6vlmVo84q4ONr/Zbvk5GRGjhwJwKxZs2jQoIEc2s+CrP0d/+N+5dOPPA8EvtZalwBaAd8qpf6WUynVVykVqpQKvXnzpgWiCiFE7paQnMaE9cfpung/528lUKGwG6s/aMioVlX+VvpnzpyhYcOGzJ49m9TUVLR+9Ee7yCqsPeO/ApR86HkJ/n4ovxfQEkBrvV8p5QIUBKIf3khrvQRYAuDv7y9/w4QQwoz2Rd5ieEgYl2PvY2+n6N+4HAOalMfZwf5v23777bf0798fR0dH1qxZQ/v27W2QWJjK2sV/CKiglPIBrgIBQLdHtrkENAW+VkpVAVwAmdILIYQV3E1KZcrmk6w4eAmAqsU8mN7Zj+rejz8x78qVK/Tr1w9/f3+WL19OyZIlH7udyDqsWvxa6zSl1ABgG2APfKW1Pq6U+gQI1VqvBz4CliqlhpD+NUAPLceMhBDC4naeimZUSDjX45JwtFcMalqBfv8oh6P9378VPn/+PD4+PpQoUYJdu3ZRs2ZNHBxkaZjsQOWETvX399ehoaG2jiGEENnSncQUPtkYQcgfVwGoUcKTGV1qULGI+9+21Vrz+eefM3z4cL755hsCAwOtHVcASqnDWmv/5/ms/HomhBC52LbjNxiz9hg345NxdrDjo9cr0vNlHxweM8u/efMmPXr0YPPmzbRp04bXX3/dBonFi5LiF0KIXCjmXjLj1x9nY9h1AOqW8WJaJz/KFnJ77Pa//vor3bp1IyYmhrlz5zJgwAC5Nj+bkuIXQohcRGvNhrDrTFh/nNiEFFyd7BnesjL/rF8aO7snF3lsbCweHh5s3ryZmjVrWjGxMDf5jl8IIXKJ6LtJjF57jO0RUQA0LFeAaZ38KJnf9bHbX7x4kQMHDtC1a1cAUlJScHL6+212hfXJd/xCCCGeSGvN6j+u8smG49xNSsPN2YHRrasQULfkEw/Xr169mt69e+Pg4MAbb7yBu7u7lH4OIcUvhBA52NU79xkVEs5vp9OXQ3mtUiEmd/CleL48j93+/v37DBkyhMWLF1OvXj1WrFiBu/vfz+4X2ZcUvxBC5EBaa74/eIkpm09yLzkNzzyOjG9TlQ61vJ84y09OTqZ+/fqEhYUxbNgwJk6cKLP8HEiKXwghcphLMYmMCAlj39kYAF6vWoRP21ensIdLpp9zdnbmnXfewdfXVy7Vy8Gk+IUQIocwGjXf7L/A9K2nuJ9qIH9eJz5pV43WvsWeOMu/ffs277//Pn379qVp06Z89NFH1g0trE6KXwghcoCzN+8xPDiM0Iu3AWhbozjj21SlgJvzEz+zb98+AgMDuXbtGk2aNKFp06bWiitsSIpfCCGysTSDkS/3nGfW9tMkpxkp5O7MpPbVeb1a0Sd+xmAwMG3aNMaNG0fp0qXZu3cv9erVs2JqYUtS/EIIkU2duhHPsOCjHL0SB0DnOiUY27oqnq6OmX4uJCSE0aNHExAQwKJFi/D0fPyd90TOJMUvhBDZTKrByMJfz/LFL2dINWiKe7owuaMvr1UqnOnnbt68SaFChejcuTNbtmyhRYsWsuxuLvT3uzAIIYTIso5djaPtvL3M2n6aVIOm20ul2Dbk1UxLPzk5mcGDB1OpUiUuXbqEUoqWLVtK6edSMuMXQohsIDnNwBc/R7Lwt7MYjJqS+fMwraMfDcsXzPRzp0+fJiAggCNHjjBgwAAKF878qIDI+aT4hRAiizty6TZBwWFERt9DKXjv5TIEtaiEq1PmP8K//fZbPvjgA5ydnVm7di3t2rWzUmKRlUnxCyFEFnU/xcCs7af4cs95jBrKFszL9M5++JfJb9Lnd+zYQZ06dfjuu+8oWbKkhdOK7EKKXwghsqAD52IYvjqMCzGJ2Cno94+yDGlWERdH+0w/d/jwYVxcXKhWrRqLFi3C0dERBwf5US/+n/xtEEKILCQhOY1pW0/y3/0XAahYxI0ZnWtQo2S+TD9nNBr5/PPPGTFiBE2aNGHr1q3kyfP4G/GI3E2KXwghsog9Z24xfHUYV+/cx8FO0b9xef7VuBzODpnP8qOjo3nvvffYvHkz7dq148svv7RSYpEdSfELIYSN3U1KZfKmE6w8dBmAasU9mNG5BlWLezz1sydPnqRJkybExsYyb948+vfvL5fpiUw9U/ErpSoBjYACwNda6yilVEkgRmudaImAQgiRk/1yMopRIce4cTcJJ3s7BjWrQN9Xy+Job9oyK2XLlqVx48YMGzaMGjVqWDityAlMKn6llCPwFdANUIAGtgNRwDzgODDKQhmFECLHuZOYwscbIlhz5CoANUvmY0ZnPyoUcX/qZy9cuMDw4cNZtGgRXl5eLF++3NJxRQ5i6sp9E4G2QB+gNOnl/8BmoIWZcwkhRI619dh1ms3axZojV3F2sGNM6yqs/qChSaUfHBxMzZo12bp1K8eOHbNCWpHTmHqo/21grNb6K6XUo2eZnAN8zBtLCCFynlv3khm/7jibwq8DUM8nP9M6+eFTMO9TP5uYmMiQIUNYsmQJ9erVY8WKFZQtW9bSkUUOZGrxFwIy+9XSxQxZhBAiR9Jas/7oNSasP87txFRcnewZ8UZlur9UGjs7007EGzp0KEuWLGH48OFMnDgRR8fM78AnxJOYWvwXgbrAL495zx84Y7ZEQgiRg0TdTWL0mmPsOBEFwCvlCzKloy8l87s+9bNaaxISEnBzc2P8+PF06tSJ5s2bWzqyyOFMLf7vgNFKqUhgQ8ZrWinVABgKTLZEOCGEyK601qw6fIWJGyOIT0rD3dmBMW9Woat/SZMut7t9+zZ9+vQhNjaW7du3U6xYMYoVK2aF5CKnM7X4pwC1gVXAvYzXdgLuwBrgc/NHE0KI7OnqnfuMWB3G7jO3AGhSuTCTOlSnmKdpK+nt3buXbt26ce3aNSZPnizX5QuzMqn4tdZpQAelVHPSz+AvDMQAW7XW2yyYTwghsg2jUfP9wUtM2XyChBQDnnkcmdC2Ku1reptU3gaDgSlTpjBhwgRKly7N3r17qVevnhWSi9zE1Ov4C5O+SM920q/ff/g9O6Cg1jraAvmEECJbuBiTwPDVYfx+LhaAltWK8kn7ahR2N/3c53v37rFs2TK6du3KokWL8PB4+sp9QjwrUw/1XwcaAAcf816tjNczX0xaCCFyIINR8/W+C8zYdpKkVCMF8joxsX11Wvma/n38L7/8wssvv4ynpycHDx6kUKFCcnhfWIypC/hk9jfQATCaIYsQQmQrkdH36LJoHxM3RpCUaqRdzeJsH/oPk0s/OTmZwYMH07RpU+bMmQNA4cKFpfSFRT1xxq+UcgMePs5UUClV/JHN8pC+jG+UBbIJIUSWlGYwsnT3eWbvOE1KmpHC7s5M6uBL86pFTN7H6dOnCQgI4MiRIwwcOJAPP/zQgomF+H+ZHer/CBiX8Vjz/5fxPUoBk8wZSgghsqqTN+4StCqM8KtxAHT1L8Ho1lXxzGP6gjrr1q3j7bffxtnZmXXr1tG2bVtLxRXibzIr/o3ADdKLfQEwHTj/yDbJQITW+nHf/QshRI6RkmZkwa+RzN8ZSapB450vD1M6+vJqxULPvK/y5cvTqFEjli5dSokSJSyQVogne2Lxa60PA4cBlFIaWK21vmWtYEIIkVWEX4kjKPgoJ2/EA9C9filGvFEFN2fT72x++PBh1qxZw6effkq1atXYsmWLpeIKkSlTr+NfbOkgQgiR1SSlGpj78xkW7zqHwagpld+VaZ38aFCugMn7MBqNfP7554wYMYIiRYowaNAgChV69qMEQpiLyb+uKqUqAu8Blfj7TXm01rq1OYMJIYQtHb54m2HBRzl7MwGloNcrPnz0ekVcnUyf5UdHR9OjRw+2bNlC+/bt+fLLL8mfP78FUwvxdKYu4FMH2E362fulgFNAftJX8LsGXLJUQCGEsKb7KQZm/nSKr/aeR2soVygv0zvXoE5pr2faj8FgoHHjxpw9e5b58+fzwQcfyGV6Iksw9VfXqcAmIBBIAbprrf9QSrUClgHDLZRPCCGsZv/ZGEaEhHExJhF7O0Xff5RlUNMKuDiavj5Zamoq9vb22Nvb89lnn1G8eHH8/PwsmFqIZ2Nq8dcg/TD/g4V67AG01puVUpNJP+O/gfnjCSGE5d1LTmPalpN8+/tFACoXdWd6Zz/8SuR7pv1cuHCBwMBA3nrrLQYPHkzLli0tEVeIF2Jq8TsD8Vpro1IqFnh4lYoIQH6dFUJkS7tO32RkSDhX79zHwU4xoEl5+r9WHicHUxc2Tbdq1Sr69OmD1prixR9d60yIrMPU4j8HPPibfBzoQfp1/gDdAblBjxAiW4m7n8qkTRH8GHoFgOreHszoXIMqxZ7txjiJiYkMHjyYpUuX8tJLL7FixQp8fHwsEVkIszC1+LcAzYGVwBRgQ8bMPw0oAPzbMvGEEML8fj4Rxag14UTdTcbJwY7BzSrQt1FZHOyfbZYP8Mcff/DVV18xfPhwJk6ciKOj6Sv4CWELpl7HP+qhx1uVUo2AzoArsFVrvd5C+YQQwmxuJ6Tw8YbjrP3zGgC1SuVjRmc/yhd2f6b9aK05dOgQ9erV45VXXuH06dOULVvWEpGFMDvTL0h9iNb6d+B3M2cRQgiL2Rx+nXHrjnHrXgoujnYEtahMj4ZlsLd7tkvsYmNj6d27N2vXruXQoUPUqVNHSl9kK89V/A9TSlUFxmqtA82QRwghzOpmfDLj1h1jy7EbALzkk59pnfwoUzDvM+9rz549dOvWjevXrzNjxgxq1apl7rhCWFymxa/SV5vwJX3RnrNa6xMPvedL+t37OgD3LRlSCCGeldaadX9eY8KG49xJTCWvkz0jWlXh7XqlsHvGWT7AtGnTGDVqFGXKlGHfvn3UrVvXAqmFsLwnFr9SqigQArz00GvfAb2Az4H3gVTS79wnt+UVQmQZN+KSGL0mnJ9Ppl9w1KhCQaZ09KWEl+tz79PZ2ZmAgAAWLlyIh8eznfkvRFaS2Yx/KlCT9FL/A/ABhgG/kb5Yzw9AkNb6iqVDCiGEKbTW/Bh6mU83niA+OQ13FwfGvlmVLnVKPNdyuRs3bsRoNNK2bVsGDRoEIMvuimwvs+JvDnyitZ764AWl1DFgG7BIa93f0uGEEMJUl2MTGRkSzp7I9LuHN61cmEkdfCnq+eg9xZ4uOTmZ4cOHM2fOHF577TXatGkjhS9yjMyKvzCw95HXHjxfYZk4QgjxbIxGzfIDF5m65SQJKQbyuTrycdtqtK1R/LnK+vTp0wQEBHDkyBE+/PBDpk2bJqUvcpTMit8eSH7ktQfPEywTRwghTHfhVgLDVodx8HwsAK19izGhbTUKuTs/3/4uXKB27dq4uLiwfv162rRpY864QmQJT7uc73WlVPmHntsBGmiplKr88IZa6+/NHU4IIR7HYNT8Z+95Zv50iqRUIwXdnJjYrjpv+BZ7rv0ZjUbs7OwoU6YM48ePp1u3bnh7e5s5tRBZg9JaP/4NpYyPfePxtNba9PtWmpm/v78ODQ211fBCCCuKjI4nKDiMI5fuANChljfj3qyKV16n59pfaGgoPXv2ZMWKFVSrVs2cUYWwGKXUYa21//N8NrMZf5XnzCOEEGaXajCyZNc55uw4Q4rBSBEPZyZ38KVplSJP//BjGI1GZs+ezciRIylatCj37t0zc2IhsqYnFr/W+pQlBlRKtQTmkH4OwbKHrxp4aJuuwATSv1Y4qrXuZoksQojsIeLaXYatPsqxq3cBCKhbkpGtquCZ5/luiBMdHc27777L1q1bad++PV9++SX58+c3Z2QhsqwXXrL3WSil7IH5pF8qeAU4pJRar7WOeGibCsBI4GWt9W2lVGFrZhRCZB0paUbm7Yxkwc5I0owa73x5mNrJl0YVCr3QfufNm8fOnTuZP38+H3zwgZy1L3IVqxY/UA+I1FqfA1BKrQTaAREPbdMHmK+1vg2gtY62ckYhRBYQduUOQavCOBUVD8A7DUozrGVl3Jyf78dWamoqly9fpmzZsowePZqAgACqVq1qzshCZAvWLn5v4PJDz6/w0JLAGSoCKKX2kv51wASt9dZHd6SU6gv0BShVqpRFwgohrC8p1cDnO86wZNdZjBrKFHBlWic/Xipb4Ln3ef78+f/dXCciIgJXV1cpfZFrWbv4H3c87dHLChyACsBrQAlgt1Kqutb6zl8+pPUSYAmkn9Vv/qhCCGs7fDGWoOAwzt1MQCno/YoPH71eiTxOz3/R0I8//kifPn0AWLp0Ka6uz79evxA5gbWL/wqZv3M6AAAgAElEQVRQ8qHnJYBrj9nmd611KnBeKXWK9F8EDlknohDC2hJT0pix7RRf77uA1lC+sBvTO/tRu5TXc+8zKSmJgQMHsmzZMurXr8/333+Pj4+PGVMLkT3ZPesHlFLllVIvKaWe59fmQ0AFpZSPUsoJCADWP7LNWqBxxlgFST/0f+45xhJCZAP7zt6i5ee7+c/eC9gpxb8al2PjwFdeqPQBHB0duXDhAiNHjmTXrl1S+kJkMHnGr5TqBXwMPFgaqy7wh1IqGNihtV70tH1ordOUUgNIv9GPPfCV1vq4UuoTIFRrvT7jvdeVUhGAgfQ7AMY803+VECLLi09KZeqWkyw/cAmAykXdmdmlBtW9PZ97n1prli1bRuvWrSlevDhbtmzBwcHaBzaFyNpMmvErpXqQ/n36L8C7/PW7+gPAW6YOqLXerLWuqLUup7WelPHauIzSR6cbqrWuqrX21VqvNHXfQojs4ddT0bSYvYvlBy7haK8Y0qwi6we88kKlHxsbS6dOnejbty8LFy4EkNIX4jFM/VcRBMzRWg/NuBb/vw+9dwIYavZkQogcJy4xlYmbIgg+fAUAvxKeTO/sR+WiHi+03z179tCtWzdu3LjBzJkzGTJkiDniCpEjmVr85YBNT3gvHnixL+OEEDne9ogoRq8JJzo+GScHO4Y2r0jvV3xwsH/mU43+IiQkhC5duuDj48O+ffvw93+u5cuFyDVMLf5Y/no2/sMqAtfNE0cIkdPEJqQwYf1x1h9Nv4CnTmkvpnf2o1whN7Psv3Hjxnz44Yd8/PHHeHi82JEDIXIDU3/V3gSMUUo9XP5aKZUPGAysM3syIUS2prVmY9g1ms/6jfVHr5HH0Z7xbaryY78GL1z6GzZsoGXLlqSkpODl5cXs2bOl9IUwkanFPzpj2whgI+mL7szMeO5I+tn+QggBQHR8Eu9/d5gB3x8hJiGF+mXzs3VwI9572Qd7u+dfFz85OZlBgwbRtm1boqKiuHXrlhlTC5E7mHSoX2sdrZSqTfpJfi2Aq0B+4Btg+oN19YUQuZvWmjVHrvLxhgji7qfi5uzAyFaVCaxbCrsXKHyAU6dOERAQwJ9//smgQYOYNm0azs7OZkouRO5h8rUuGUvmjs74I4QQf3E97j6jQsLZeeomAK9WLMSUjr5458vzwvvWWtOjRw8uX77Mhg0bePPNN194n0LkViYVv1JqMvBfrfVJC+cRQmQzWmtWHrrM5E0niE9Ow8PFgXFtqtGptvcL3+727t272NnZ4ebmxtdff42bmxve3t5mSi5E7mTqd/wDgeNKqVCl1ECl1IvdDFsIkSNcjk2k+5cHGBkSTnxyGs2qFGH70H/QuU6JFy79Q4cOUbt2bQYOHAhApUqVpPSFMANTi78w8A5wE5gFXFVKbVRKdVFKyZdsQuQyRqPmm30XaPH5LvZGxuDl6sjcwFosfacORTxcXnDfRmbOnEnDhg1JTU2ld+/eZkothADTT+67DywHliuligBvZ/z5AbirlFqlte5juZhCiKzi/K0EhgUf5dCF9HN63/QrxoS21Sjo9uJzgOjoaN555x22bdtGx44dWbZsGV5esj6YEOb0zAtZa62jSJ/1z1JKNSZ9+d6egBS/EDmYwaj5as95Zv50iuQ0IwXdnPm0fXVaVi9qtjESExMJCwtj4cKF9OvX74W/LhBC/N0zF3/Gof32QHfgddJv2POk5XyFEDnA6ah4goLDOHr5DgAda3sz7s2q5HN1euF9p6amsnz5ct59913KlCnD2bNnyZPnxa8EEEI83rPclvc14J9AJ8ADCAX+DazQWssqGkLkQKkGI4t/O8vcnyNJMRgp5unC5A6+NK5c2Cz7P3/+PIGBgRw4cIASJUrQrFkzKX0hLMzUy/kuAd7AZWA+6Zf2nbJkMCGEbR2/FkfQqjAirt8FILBeSUa2qoKHi6NZ9v/DDz/Qt29flFL88MMPNGvWzCz7FUJkztQZ/3bSy/43S4YRQthecpqB+b9EsuDXs6QZNSW88jC1ox+vVChotjFGjRrFlClTqF+/PitWrKBMmTJm27cQInOmntXfy9JBhBC29+flOwwLPsrpqHsA9GhYhqAWlcjr/MynA2Xqwez+448/xtHRPEcQhBCmeeK/ZqVUPeCY1jox43GmtNYHzZpMCGE1SakGZm8/zdLd5zBq8CmYl2md/Kjnk98s+9das2DBAm7fvs2YMWNo0qQJTZo0Mcu+hRDPJrNf438H6gMHMx7rJ2ynMt6zN280IYQ1HLoQy7DgMM7fSsBOQd9XyzKkWUXyOJnnn3RsbCy9evVi7dq1tG7dGoPBgL29/LgQwlYyK/43gBMZj1vx5OIXQmRDCclpzNh2im/2X0BrqFDYjemd/ahVynwL5uzZs4du3bpx48YNPvvsMwYPHoydnakLhgohLOGJxa+13vbQ463WiSOEsIZ9kbcYHhLG5dj72Nsp+jcux4Am5XF2MN9M/ObNm7z++usUL16cffv24e/vb7Z9CyGen6mX80UAb2mtwx/zXlUgWGtd1dzhhBDmdTcplSmbT7Li4CUAqhTzYEZnP6p7e5ptjLi4ODw9PSlUqBAhISE0bNgQDw8Ps+1fCPFiTD3mVhl40qoarkAl88QRQljKzlPRtJi9ixUHL+For/ioeUXWD3jZrKW/fv16ypUrx+rVqwFo2bKllL4QWcyzXKPzpO/4/YA4M2QRQljAncQUPtkYQcgfVwGoUcKTGV1qULGIu9nGSEpKYtiwYXzxxRfUqlULX19fs+1bCGFemV3ONxAYmPFUA8FKqeRHNssDFAeCLRNPCPEith2/wZi1x7gZn4yzgx0fvV6Rni/74GBvvhPsTp48SUBAAEePHmXw4MFMnToVZ2e5W7cQWVVmM/5rwOGMx+WBU0DMI9skAxHAQvNHE0I8r5h7yYxff5yNYdcBqFvGi2md/ChbyM3sYx06dIirV6+yceNGWrdubfb9CyHMS2n99Kv0lFIrgNFa63OWj/Ts/P39dWhoqK1jCGFzWms2hF1nwvrjxCak4Opkz/CWlfln/dLY2ZnvFrd3794lNDT0f4vw3L59Gy8v810GKITInFLqsNb6uS6VMXXJ3sDn2bkQwnqi7yYxZu0xfoqIAqBhuQJM6+RHyfyuZh3n0KFDBAQEcPPmTS5evIiXl5eUvhDZSGbf8Q8j/cY8NzIeZ0ZrrWeYN5oQwhRaa1b/cZVPNhznblIabs4OjG5dhYC6JVHKfLN8o9HIZ599xqhRoyhevDhbtmyRwhciG8psxj8V+BW4kfE4MxqQ4hfCyq7duc/IkHB+O30TgNcqFWJyB1+K5zPvPe3T0tJo06YNW7dupWPHjixbtkxKX4hsKrPiz6O1fnAWv3l/igghXojWmhUHLzN58wnuJafh4eLA+DbV6Fjb26yz/AccHByoVasW7dq1o1+/fhYZQwhhHZkt2Zv8uMdCCNu6FJPIiJAw9p1Nv8jm9apF+LR9dQp7uJh1nNTUVMaOHUu7du1o0KABkydPNuv+hRC2YeqSvWUBD631nxnPnYERQHVgm9Z6meUiCiEAjEbNN/svMH3rKe6nGsif14lP2lWjtW8xs8/Az507R2BgIAcPHsTZ2ZkGDRqYdf9CCNsxdeW+BaRfr/9nxvOJwBDgNNBBKWWvtV5sgXxCCODczXsMCw4j9OJtANrUKM6ENlUp4Gb+hXJ++OEH+vbti1KKH3/8kS5duph9DCGE7Zha/DWBRQAqfWrRAxiltZ6hlPoUeB+Q4hfCzNIMRr7cc55Z20+TnGakkLszn7avTotqRS0y3saNGwkICKBBgwZ8//33lClTxiLjCCFsx9TizwfcynhcEygA/JjxfDvwoZlzCZHrnboRz7Dgoxy9kn4rjM51SjC2dVU8XR3NPlZSUhIuLi688cYbLFmyhB49euDoaP5xhBC2Z+qC3dFA2YzHzYHzWuuLGc/zAgZzBxMit0o1GJn78xne/GI3R6/EUczTha/fq8vMLjXMXvpaa+bPn0/FihW5fv069vb29OnTR0pfiBzM1Bn/RmCSUqoi0Bf46qH3qgHnzR1MiNzo2NU4goLDOHH9LgDdXirFyDcq4+5i/iKOjY2lV69erF27llatWuHg8Cw36xRCZFem/ksfAbgDbwE7gE8feq8r8IuZcwmRqySnGfji50gW/nYWg1FTMn8epnX0o2H5ghYZb/fu3XTr1o2oqChmzZrFoEGDsLMz3x37hBBZl6lr9d8F/vmE9+qaNZEQucyRS7cJCg4jMvoeSkGPhmUY1rISrk6Wm4HPnz8fFxcX9u/fT506dSw2jhAi63mmnyxKKXegHpCf9Fv0HtJax1simBA53f0UA7O2n+LLPecxaihbMC/TOvtRt0x+i4x35coVUlNT8fHxYfHixdjZ2eHu7m6RsYQQWZfJxa+UGkP6If88wIPVQhKVUlO01pMsEU6InOrAuRiGrw7jQkwidgr6/aMsQ5pVxMXR3iLjrVu3jp49e+Ln58fOnTvx9PS0yDhCiKzP1JX7/gV8AiwHviP9xj1Fge7AJ0qpWK31QoulFCKHSEhOY/rWk3yzP/2imIpF3JjRuQY1SuazyHhJSUkEBQUxb948atWqxeLFstyGELmdqTP+AcACrfWAh147CmxTSsUBAwEpfiEysefMLUaEhHHl9n0c7BT9G5fnX43L4exgmVn+5cuXadOmDUePHmXw4MFMnToVZ2fzr/QnhMheTC3+sjx5kZ51QG/zxBEi57mblMrkTSdYeegyANWKezC9sx/Vilv2cHuBAgXw8vJi48aNtG7d2qJjCSGyD1OLPxaoRPoqfY+qlPG+EOIRv5yMYlTIMW7cTcLJ3o5BzSrQ99WyONpb5tK5u3fvMnHiRMaPH4+bmxu//PKL3EJXCPEXphb/WtIX8IkCgrXWGkAp1YH0G/assFA+IbKlO4kpfLIhgpAjVwGoWTIfMzr7UaGI5c6iP3jwIIGBgVy8eJFXX32VNm3aSOkLIf7mWRbwqQ38ACQrpaKBQoAzcCjjfSEEsPXYdcasPc6te8k4O9gR1KIS773sg72dZUrYaDTy2WefMWrUKIoXL86uXbto2LChRcYSQmR/pi7gE6eUagh0ABqRfh1/LPAbsE5rLWv1i1zv1r1kxq87zqbw6wDU88nPtE5++BTMa9FxR44cyfTp0+nUqRNLly7Fy8vLouMJIbI3k6/jzyj34Iw/QogMWmvWH73GhPXHuZ2YiquTPSPeqEz3l0pjZ6FZPoDBYMDe3p4PPviA8uXL07t3bzm0L4R4qkyLXykVAAwGygN3SD/UP15rnWaFbEJkeVF3kxi95hg7TkQB8Er5gkzp6EvJ/K4WGzMlJYWxY8dy4sQJ1q1bR5kyZejTp4/FxhNC5CxPLH6lVBfge+ASsBfwIf27fHvkO32Ry2mtWXX4ChM3RhCflIa7swNj3qxCV/+SFp11nzt3jsDAQA4ePEi/fv1ITU3FycnJYuMJIXKezGb8Q4FNQEetdSqAUmoyMEgpNUprbbRGQCGymqt37jNidRi7z9wCoHGlQkzu6EsxzzwWHXflypX069cPOzs7goOD6dSpk0XHE0LkTJkVfyVg4oPSzzCX9Nl+aeC8JYMJkdUYjZrvD15iyuYTJKQY8MzjyIS2VWlf09vi363Hx8czdOhQqlevzvfff0/p0qUtOp4QIufKrPjzAbceee1mxv96IcUvcpGLMQkMXx3G7+fS16pqWa0on7SvRmF3F4uOe/LkScqXL4+7uzu//fYbPj4+ODhY7na9Qoic72nLh+lnfF2IHMVg1Hy55zwtPt/F7+diKZDXifndarPon3UsWvpaa+bNm0fNmjWZMWMGABUqVJDSF0K8sKf9FNn7hEOYBx55XWutTbr7h1KqJTCH9JMEl2mtpz5hu87AKqCu1jrUlH0LYU6R0fcYvjqMwxdvA9CuZnHGt6lG/ryWPZkuJiaGXr16sW7dOlq1akXv3nIrDCGE+WRW/NPMPZhSyh6YDzQHrgCHlFLrtdYRj2znTvpNgQ6YO4MQT5NmMLJ093lm7zhNSpqRwu7OTOrgS/OqRSw+9v79++natStRUVHMmjWLwYMHy7X5QgizemLxa61HWmC8ekCk1vocgFJqJdAOiHhku4nAdODfFsggxBOdvHGXoFVhhF+NA6BLnRKMebMqnnkcrTK+k5MTnp6erF27ljp16lhlTCFE7mLtLwy9gcsPPb8CvPTwBkqpWkBJrfVGpdQTi18p1RfoC1CqVCkLRBW5SUqakQW/RjJ/ZySpBk1xTxemdPLjHxULWXzsK1eusGbNGgYOHEidOnUICwvDzs4yd+8TQghrF//jjln+70RBpZQdMBvo8bQdaa2XAEsA/P395WRD8dzCr8QRFHyUkzfiAehevxTDW1bG3cXys/x169bRs2dPUlJS6NixI97e3lL6QgiLsnbxXwFKPvS8BHDtoefuQHXg14zvNYsC65VSbeUEP2FuSakG5v58hsW7zmEwakrld2VaJz8alCtg+bGTkggKCmLevHnUrl2blStX4u3tbfFxhRDC2sV/CKiglPIBrgIBQLcHb2qt44CCD54rpX4F/i2lL8zt8MXbDAs+ytmbCSgFPV/24d8tKuLqZPl/ElprmjVrxt69exk8eDBTp07F2dmki2KEEOKFWbX4tdZpSqkBwDbSL+f7Smt9XCn1CRCqtV5vzTwi97mfYmDmT6f4au95tIayhfIyo7MfdUrnt/jYWqd/I6WUYuDAgYwcOZLWrVtbfFwhhHiYevDDKDvz9/fXoaFyUEBk7vdzMQxfHcbFmETs7RR9Xy3LoKYVcHG0t/jYcXFx9OvXj6ZNm8qd9IQQL0wpdVhr7f88nzV5xq+UKgIMAl4F8gOdtdYRSqn+wEE5HC+yqnvJaUzbcpJvf78IQOWi7kzv7IdfiXxWGf/AgQMEBgZy6dIl6tata5UxhRDiSUwqfqVUZWAX4Ej69/QNgAfrlVYCGgLdLRFQiBex6/RNRoaEc/XOfRzsFP9qXJ5/NS6Pk4Plz5w3Go3MmDGDMWPG4O3tze7du2nQoIHFxxVCiMyYOuOfSfpNeVoA94CUh97bC0wxcy4hXkjc/VQmbYrgx9ArAFT39mBG5xpUKeZhtQy///47I0aMoEuXLixZsoR8+axzhEEIITJjavH/A+iutb6Tsezuw24AxcwbS4jn9/OJKEatCSfqbjJO9nYMbl6Bvo3K4mBvnevjL126RKlSpWjYsCH79u2jfv36suyuECLLeJafhIYnvF4AuG+GLEK8kNsJKQxeeYRe34QSdTeZWqXysXnQK/R/rbxVSj8lJYVhw4ZRvnx5Hpxs2qBBAyl9IUSWYuqMPxT4J7DxMe91An43WyIhnsPm8OuMW3eMW/dScHG0I6hFZXo0LIO9nXVK99y5cwQEBHDo0CHef/99qlWrZpVxhRDiWZla/JOArUqpDcBy0pfZfVUp1Q/oCjS2UD4hMnUzPplx646x5dgNAF7yyc+0Tn6UKZjXahlWrlxJ3759sbe3Jzg4mE6dOlltbCGEeFYmFb/WeodSqivwOfBgxZFZpC+321VrvddC+YR4LK016/68xoQNx7mTmEpeJ3tGtKrC2/VKYWelWf4DkZGR+Pr68v3331O6dGmrji2EEM/qmRbwUelfVlYDCgMxQLjW2mihbCaTBXxylxtxSYxeE87PJ6MBaFShIFM6+lLCy9VqGY4ePcrt27d57bXXMBgMaK1xcLD2CthCiNzKKgv4AOj03xKOPc9AQrworTU/hl7m040niE9Ow93FgbGtq9LFv4TVTqDTWjN//nw++ugjqlatyh9//IG9veVX/hNCCHMxdQGfrk/bRmv944vHEeLxrtxOZGRIOLvP3AKgaeXCTOrgS1FPl6d80nxiYmLo2bMn69evp1WrVnz99ddyxr4QItsxdca/8gmvP/w9gRS/MDujUbP8wEWmbjlJQoqBfK6OfNy2Gm1rFLdq6V67do169eoRHR3N7NmzGTRokJS+ECJbMrX4qzzmtQLAm0Bn4F2zJRIiw4VbCQxbHcbB87EAtPItysdtq1PI3fq3sC1WrBhvvfUWb7/9NrVr17b6+EIIYS6mntV/6glv7VNKGYAPgP1mSyVyNYNR85+955n50ymSUo0UdHPik3bVaeVr3QUiL1++zPvvv8+cOXMoX748n332mVXHF0IISzDHacg7gRAz7EcIIqPjCQoO48ilOwB0qOXNuDer4pXXyao51q5dS8+ePUlNTeXUqVOUL1/equMLIYSlmKP4/YFEM+xH5GJpBiOLd51jzo4zpBiMFPFwZnIHX5pWKWLVHElJSXz00UcsWLCAOnXqsGLFCipUqGDVDEIIYUmmntU/7DEvOwHVgQ7AUnOGErlLxLW7DFt9lGNX7wLwln9JRrWugmceR6tnmT59OgsWLGDo0KFMmTIFJyfrHmkQQghLM2kBH6XU4xbpMQBXST/j/2Ottc1u1CML+GRPKWlG5u2MZMHOSNKMGu98eZjayZdGFQpZNYfWmtjYWAoUKEBiYiL79++nadOmVs0ghBDPwhoL+OR5zGupWWHVPpE9hV25Q9CqME5FxQPwToPSDGtZGTdn665+FxcXR79+/Thy5Ah//PEHefPmldIXQuRoT/0pq5RyAiYAwVrrwxZPJHK0pFQDn+84w5JdZzFqKF3Alemd/HipbAGrZzlw4ACBgYFcunSJiRMn4uJivcWAhBDCVp5a/FrrFKXUIGCLFfKIHOzwxViCgsM4dzMBpaD3Kz589Hol8jhZd8lbo9HIjBkzGDNmDN7e3uzevZsGDRpYNYMQQtiKqcdVjwJVgV0WzCJyqMSUNGZsO8XX+y6gNZQv7Mb0zn7ULuVlkzwGg4F169bRoUMHlixZQr58+WySQwghbMHU4h8G/FcpFam13mHJQCJn2Xf2FiNWh3MpNhF7O8X7r5VlYJMKuDha/8Y227dvp1atWhQsWJCtW7fi7u4uy+4KIXIdOxO3+wrIB2xTSsUrpc4opU4/9OdJK/uJXCo+KZXRa8LptvQAl2ITqVzUnXX/epmgFpWtXvopKSkEBQXx+uuv8+mnnwLg4eEhpS+EyJVMnfEf5q835BHiiX49Fc2okHCuxSXhaK8Y0LgCH7xWDicHU3/PNJ+zZ88SGBjIoUOHeP/995kyZYrVMwghRFZi6lr9AZYOIrK/uMRUJm6KIPjwFQD8SngyvbMflYt62CTPL7/8Qvv27bG3tyc4OJhOnTrZJIcQQmQlTyx+pdQ5oIPW+qgV84hsantEFKPXhBMdn4yTgx1Dm1ek9ys+ONhbf5b/QPXq1WnevDmzZs2idOnSNsshhBBZSWYz/jKA9e9/KrKV2IQUJqw/zvqj1wCoU9qL6Z39KFfIzSZ5/vzzT+bMmcPSpUspXLgwq1evtkkOIYTIqqy7TJrIMbTWbAq/zvh1x4lJSMHF0Y5hLSrzbsMy2NtZ/6Q5rTVffPEFQUFBFCxYkAsXLsgd9YQQ4jGeVvxyQp/4m+j4JMatPc7W4zcAqF82P9M6+VG6QF6b5Ll16xY9e/Zkw4YNvPnmm/znP/+hYMGCNskihBBZ3dOK/2Ol1C0T9qO11u+aI5DIurTWrDlylY83RBB3PxU3ZwdGtqpMYN1S2Nlglv9A586d2b9/P3PmzGHgwIFymZ4QQmTiacVfE0g2YT9yZCCHux53n1Eh4ew8dROAVysWYkpHX7zzPe7+TZaXlpaGwWDA2dmZ2bNnA1CrVi2bZBFCiOzkacXfXmt90CpJRJakteaHQ5eZtOkE8clpeLg4MPbNqnSuU8JmM+vLly/TrVs3/Pz8mD9/vhS+EEI8Azm5TzzR5dhERoSEsTcyBoBmVYowqUN1injY7i52a9eupWfPnqSmpvL+++/bLIcQQmRXUvzib4xGzbe/X2Ta1pMkphjwcnVkQttqtP2/9u49Porq/v/465OEcL9fRW4CgoIGhYCiFkpLKaKAICpBtIqILeD3qyJUxF9Fq6iAWrFq8UKr9Qe0XBREQSvFCxXUIBdBxQa5g9wDBEJCkvP9YwZdYhKWkGQ22ffz8ZhHdmfOzH727D7y2XPmzJl2DQNr5aenp3Pvvffy/PPP06FDB2bOnKlR+yIihaDELyfZuPcIv5+9hs827QfgqoSzeKhPW+pUCXZKh+3bt/Paa68xatQoJkyYQHx8fKDxiIiUVvkmfudccFOuSYnLznFMW7qRye+tJyMrhzpVyvPINW3pecFZgcXknGPx4sX88pe/pGXLlqSkpFC/fv3A4hERKQuU3IVvdx2m/wuf8Og7X5ORlUP/9mfz/j1dAk36Bw8eJCkpiV/96lcsWLAAQElfRKQIqKs/ih3PzmHqhxuYsjiFzOwcGlSrwGP9L6TbefUCjWv58uUkJSWxdetWJkyYwFVXXRVoPCIiZYkSf5Rat+Mgo2et4audhwBI6tSYsb3Op1qFcoHG9dxzz3HXXXdx9tln8/HHH9O5c+dA4xERKWuU+KNMRlY2z/07hec/2EBWjqNRzYo83j+BK86NjClumzZtSv/+/Zk6dSo1atQIOhwRkTLHnCv9k+4lJia65OTkoMOIeKu2pjJm9mq+3ZUGwC2XNWP0r1tTuXywv/8WLVrEhg0bGDFiRKBxiIiUFma2wjmXWJh9NbgvChw7ns1j73xN/+f/w7e70mhWuxL/vKMz4/u0DTTpZ2Zmcu+993LllVfyyiuvcPz48cBiERGJFurqL+M+37SfMbPXsHHvEWIMhnVpzt3dW1ExPjbQuFJSUkhKSiI5OZnhw4czefJkypULdnyBiEg0UOIvo45mZjFx0XpeXbYJ5+DcelWYOCCBi5vUDDo0UlNT6dSpE8455s6dS79+/YIOSUQkaijxl0GfpOzl93PXsHV/OrExxvBuLRj5i5aUjwu2lZ+VlUVcXBw1atRgypQpdOnShSZNmgQak4hItNE5/l4fM4EAABsrSURBVDLk0LHjjJ37JYNe/pSt+9M5/6xqzBtxOaN6tA486a9atYoLL7yQRYsWATB48GAlfRGRAKjFX0YsWb+b++d+yc6DxygXa/zPL87ltz9vQbnYYH/bOed49tlnGT16NHXq1KFSpUqBxiMiEu2U+Eu51KOZ/HHB18z5YhsA7RpVZ+KAdrRuUDXgyGDv3r0MGTKEt956i969ezNt2jTq1ImM+QJERKKVEn8p9u6673ngzbXsOZxB+bgYRvVoxZDLzyEu4Fb+CfPnz+fdd9/lmWee4c477wzslr4iIvIjJf5SaF9aBg/OX8eCNTsBSGxak4kDEmhet0rAkXkD+NatW0e7du249dZb6dKlCy1btgw6LBER8SnxlyLOORas2cmD89ex/0gmFcvF8vuerbm5czNiYoJvTW/ZsoUbb7yR1atXk5KSQr169ZT0RUQijBJ/KbH70DEeeHMt7321C4DLWtTm8f4JNKkdGYPl3njjDW677TaysrJ44YUXqFcv2Dv8iYhI3pT4I5xzjjlfbOfht9Zx6FgWVcrHcX+v80nq1Dgizpnn5OQwcuRIXnjhBRITE5k5cyYtWrQIOiwREcmHEn8E25Gazti5X/Lht3sA+HnrukzodyENa1QMOLIfxcTEkJWVxahRo5gwYQLx8fFBhyQiIgVQ4o9AzjlmfLaVCe98TVpGFtUqxPFg77b0b392RLTynXO8/PLLJCYmcvHFFzN16tSIiEtERE6txK/7MrOeZrbezFLM7L48tt9jZl+Z2RozW2xmTUs6xiBt2XeUG1/+lPvf+JK0jCx6tKnP+/d05doOjSIiuaampnLDDTcwbNgwpk6dChARcYmISHhKtMVvZrHAc8CvgG3A52Y23zn3VUixlUCic+6omf0OmAjcUJJxBiEnx/Hqsk1MXLSe9OPZ1Kocz0N92nJ1wlkRk1iXLVtGUlIS27dv5/HHH2f06NFBhyQiIqeppLv6OwEpzrnvAMxsJtAX+CHxO+eWhJRfDgwu0QgD8N2eNMbMXkPy5gMA9G7XkPG921C7SvmAI/vRBx98QPfu3WncuDEff/wxl156adAhiYhIIZR04j8b2BryfBtwSQHlbwMWFmtEAcrKzuGVpRt56l/fkpGVQ92q5Xnkmgv4ddsGQYf2A+ccZsbll1/OuHHjuPvuu6lRo0bQYYmISCGV9Dn+vPqsXZ4FzQYDicCkfLYPM7NkM0ves2dPEYZYMtZ/f5hrX/iExxZ+Q0ZWDte2b8T7d3eNqKS/cOFCOnTowL59+yhXrhwPPfSQkr6ISClX0ol/G9A45HkjYEfuQmbWHRgH9HHOZeR1IOfci865ROdcYt26dYsl2OJwPDuHKYv/y9XPfszqbQc5q3oF/nprR568vh3VK5ULOjwAMjMzGTVqFL169SIrK4vU1NSgQxIRkSJS0l39nwPnmtk5wHZgIDAotICZXQxMBXo653aXcHzFau32g4yevYavdx4CYNAlTRh75XlUrRAZCR8gJSWFpKQkkpOTGT58OJMnT6ZixciZN0BERM5MiSZ+51yWmY0E3gVigWnOuXVm9jCQ7Jybj9e1XwWY5Y9m3+Kc61OScRa1jKxsnl2cwgsfbiA7x9G4VkWe6J/AZS0j7xa1999/Pxs2bGDu3Ln069cv6HBERKSImXN5nmIvVRITE11ycnLQYeRp5ZYDjJm9hv/uTsMMftO5GaN/3ZrK5SNn7qS0tDTS0tJo0KABu3fv5tixYzRp0iTosEREJB9mtsI5l1iYfSMn+5Qx6ZnZPPWv9byydCM5DprXqcwTAxLo2KxW0KGdZOXKlQwcOJCzzjqLJUuW6OY6IiJlnBJ/Mfhs437GzF7Npn1HiTG4o2tz7u7eigrlYoMO7QfOOaZMmcKYMWOoW7cuDz30UMRMFCQiIsVHib8IHcnIYuKib3h12WYAWtWvwqQB7WjXOLIugdu/fz+33HILb731Fr1792batGnUqRN54w1ERKToKfEXkaX/3ct9c9ew7UA6cTHG8G4tGdGtBeXjIqeVf0JcXBwbNmxgypQpjBw5Ui19EZEoosR/hg4dO86Et79m5ufehIRtG1Zj4oAE2jasHnBkJ8vKyuK5557jjjvuoFq1aqxatYpy5SLnMkIRESkZSvxn4N/f7OL+uWv5/tAx4mNj+N/u5zKsS3PKxZb4TQ8LtHnzZgYNGsQnn3xC7dq1GTx4sJK+iEiUUuIvhNSjmTz81lfMXbkdgIsa12DSgATOrV814Mh+as6cOQwdOpTs7GymT59OUlJS0CGJiEiAlPhP06K1O3ngzXXsTcugfFwM9/ZozZArziE2JvLOk0+aNIkxY8bQsWNHZsyYQYsWLYIOSUREAqbEH6a9aRk8OG8db3+5E4BOzWrxxIAEzqlTOeDI8tenTx8OHDjA+PHjiY+PDzocERGJAJq57xScc8xfvYPx89dx4OhxKsXHct+V5zH4kqbERFgr3znHSy+9xPLly3nllVc0Wl9EpIzSzH3FZNehY4x7Yy3vf70LgCta1uGx/hfSuFalgCP7qdTUVIYNG8asWbPo3r076enpVKoUeXGKiEiwlPjz4Jxj1opt/HHBVxw+lkXV8nGMu+p8bujYOCJb0cuWLSMpKYnt27fz+OOPM3r0aGJiIuvKAhERiQxK/LlsT01n7Nwv+ejbPQB0a12XCf0v5KzqkXlr2vT0dPr160elSpVYunQpl1xySdAhiYhIBFPi9+XkOKZ/toXH3vmaI5nZVK9YjvF92nDNRWdHZCt/z5491K5dm4oVKzJ//nxat25N9eqRNWmQiIhEHvUHA5v3HWHQy8t54M21HMnMpmfbBvzrni70u7hRRCb9hQsX0rZtW5588kkAOnXqpKQvIiJhieoWf3aO49VPNjHp3fWkH8+mduV4Hu57Ab0ubBCRCT8zM5OxY8fy1FNPkZCQwNVXXx10SCIiUspEbeJP2Z3G7+esYcXmAwD0vaghD/ZuS63KkXm9e0pKCgMHDmTFihWMGDGCyZMnU6FChaDDEhGRUibqEn9Wdg4vfbyRp9//lsysHOpVLc+j/S7kV23qBx1agXbu3MmWLVt44403uOaaa4IOR0RESqmoSvzffH+I0bPW8OX2gwBc16ERD1zVhuqVIvOGNWlpabzzzjtcf/31/OxnP2Pjxo1Urhy5MwWKiEjki4rEn5mVw/MfpPDckhSOZzsaVq/AY9cm0LVV3aBDy9cXX3zBwIED+e6770hMTKR58+ZK+iIicsbKfOL/cttBRs9ezTffHwZg8KVN+H3P86haITJb+c45nnnmGcaMGUO9evVYvHgxzZs3DzosEREpI8ps4j92PJspi//L1I++IzvH0aRWJR6/9kIua1En6NDy5Zzj+uuvZ/bs2fTp04dp06ZRu3btoMMSEZEypEwm/hWbDzBm9mo27DmCGQy5/Bzu/XUrKsVH9ts1M3r06EHXrl0ZMWJERF5SKCIipVtkZ8LTlJ6ZzeT31jPtPxtxDprXrcykAQl0aFor6NDylZWVxfjx42nbti1JSUncfvvtQYckIiJlWJmZuW/5d/vo+cxHvLJ0Iwb87ucteOd/fhbRSX/z5s107dqVRx99lOXLlwcdjoiIRIEy0eLfkZrOwBe9xHleg6pMHJBAQqMaAUdVsDlz5jB06FCys7OZPn06SUlJQYckIiJRoEwk/n1HMmkcY4zo1pIR3VoSHxfZHRkrVqxgwIABdOzYkRkzZtCiRYugQxIRkShhzrmgYzhjNZqc5z5Z/hltGlYLOpQCHT58mKpVqwL8MHI/Pj4ypwgWEZHIZWYrnHOJhdk3spvGYWpRr0pEJ33nHC+++CJNmzZl9erVAAwYMEBJX0RESlyZSPyRfNFbamoq119/PXfccQeJiYnUrx/Z9wQQEZGyrUwk/ki1bNkyLrroIt58802eeOIJFi1aRIMGDYIOS0REoliZGNwXqebPn09MTAxLly7lkksuCTocERGRsjG4LzEx0SUnJwcdBgA7duxg586ddOjQgePHj3P06FGqV68edFgiIlKGRP3gvkjx9ttv065dOwYNGkR2djblypVT0hcRkYiixF8EMjIyuPvuu7n66qtp2LAh8+bNIzY2NuiwREREfkLn+M/Qvn376NGjB1988QV33nknEydOpEKFCkGHJSIikie1+M9QzZo1Of/883nzzTeZMmWKkr6IiEQ0Jf5COHz4MMOHD2fr1q3ExMTw+uuv07dv36DDEhEROSUl/tO0YsUK2rdvz9SpU1myZEnQ4YiIiJwWJf4wOed4+umn6dy5M+np6SxZsoSbb7456LBEREROixJ/mJ566inuueceevXqxerVq+nSpUvQIYmIiJw2jeo/hczMTOLj47n99tupWbMmt956K2aRfHcAERGR/KnFn4+srCzGjRvHpZdeyrFjx6hWrRpDhgxR0hcRkVJNiT8PmzdvpmvXrkyYMIGLL76YnJycoEMSEREpEurqz2XOnDkMHTqU7Oxspk+fTlJSUtAhiYiIFBkl/hBZWVk88sgjtGrVihkzZtC8efOgQxIRESlSSvzAunXraNSoEdWrV+ftt9+mbt26lCtXLuiwREREilxUn+N3zjF16lQSExO57777AGjYsKGSvoiIlFlRm/gPHDjAddddx29/+1u6dOnC+PHjgw5JRESk2EVl4l+5ciUXXXQR8+bNY+LEiSxcuJD69esHHZaIiEixi8pz/HXr1qVBgwbMmjWLTp06BR2OiIhIiYmaFv+OHTsYN24cOTk5NGrUiOXLlyvpi4hI1ImKxL9gwQISEhL405/+xNq1awE0A5+IiESlMp34MzIyuOuuu+jduzeNGjVixYoVJCQkBB2WiIhIYMr0Of4bbriBefPmceeddzJx4kQqVKgQdEgiIiKBKpOJPycnh5iYGO69915uvfVW+vbtG3RIIiIiEaHEu/rNrKeZrTezFDO7L4/t5c3sH/72T82sWbjHPnz4MDfddBNjx44F4IorrlDSFxERCVGiid/MYoHngCuBNkCSmbXJVew24IBzriXwNPBEOMdesWIF7du3Z/r06VSuXLkowxYRESkzSrqrvxOQ4pz7DsDMZgJ9ga9CyvQFxvuPZwN/NjNzzrn8Drpr1y46d+5M/fr1WbJkCV26dCme6EVEREq5ku7qPxvYGvJ8m78uzzLOuSzgIFC7oINu376dXr16sWrVKiV9ERGRApR0iz+vi+dzt+TDKYOZDQOG+U8z5s2bt3bevHlnGJ4UoA6wN+ggooDqufipjouf6rj4tS7sjiWd+LcBjUOeNwJ25FNmm5nFAdWB/bkP5Jx7EXgRwMySnXOJxRKxAKrjkqJ6Ln6q4+KnOi5+ZpZc2H1Luqv/c+BcMzvHzOKBgcD8XGXmA7/xHw8A/l3Q+X0REREJX4m2+J1zWWY2EngXiAWmOefWmdnDQLJzbj7wCvB3M0vBa+kPLMkYRUREyrISn8DHOfcO8E6udX8IeXwMuO40D/tiEYQmBVMdlwzVc/FTHRc/1XHxK3Qdm3rRRUREokeZvkmPiIiInKxUJf7inO5XPGHU8T1m9pWZrTGzxWbWNIg4S7NT1XFIuQFm5sxMo6MLIZx6NrPr/e/zOjObXtIxlnZh/L9oYmZLzGyl/z+jVxBxlmZmNs3MdpvZ2ny2m5lN8T+DNWbW/pQHdc6VigVvMOAGoDkQD6wG2uQqMxz4i/94IPCPoOMuTUuYddwNqOQ//p3quOjr2C9XFfgIWA4kBh13aVvC/C6fC6wEavrP6wUdd2lawqzjF4Hf+Y/bAJuCjru0LUAXoD2wNp/tvYCFeHPgXAp8eqpjlqYW/w/T/TrnMoET0/2G6gu86j+eDfzSzPKaEEjydso6ds4tcc4d9Z8ux5uLQcIXzvcY4I/AROBYSQZXhoRTz7cDzznnDgA453aXcIylXTh17IBq/uPq/HTeFjkF59xH5DGXTYi+wGvOsxyoYWZnFXTM0pT4i2W6XzlJOHUc6ja8X5oSvlPWsZldDDR2zi0oycDKmHC+y62AVmb2HzNbbmY9Syy6siGcOh4PDDazbXhXc91ZMqFFldP9v13yl/OdgSKb7lfyFXb9mdlgIBHoWqwRlT0F1rGZxeDdlfKWkgqojArnuxyH193/c7yeq4/N7ALnXGoxx1ZWhFPHScDfnHNPmllnvDlaLnDO5RR/eFHjtPNeaWrxn850vxQ03a/kK5w6xsy6A+OAPs65jBKKraw4VR1XBS4APjCzTXjn7OZrgN9pC/f/xTzn3HHn3EZgPd4PAQlPOHV8G/BPAOfcMqAC3jz+UnTC+r8dqjQlfk33W/xOWcd+N/RUvKSvc6Knr8A6ds4ddM7Vcc41c841wxtH0cc5V+h5uaNUOP8v3sQbrIqZ1cHr+v+uRKMs3cKp4y3ALwHM7Hy8xL+nRKMs++YDN/uj+y8FDjrndha0Q6np6nea7rfYhVnHk4AqwCx/3OQW51yfwIIuZcKsYzlDYdbzu0APM/sKyAZGO+f2BRd16RJmHY8CXjKzu/G6n29RY+z0mNkMvNNRdfyxEg8C5QCcc3/BGzvRC0gBjgK3nvKY+gxERESiR2nq6hcREZEzpMQvIiISRZT4RUREoogSv4iISBRR4hcREYkiSvwieTCzW/w74+W1dD/NYw319yuR+xqY2SO54j3g362yyC9vNbM4/zUeCFnX38zuyqNsd7/sFUUdRwHxtcxVF9lmttPM/m5mBU5rWsAx25vZeDOrUdTxipSEUnMdv0hArsObGSvUV0EEUgid/b+1gTuAGWYW75x7rahewL+WuzMnzxXeH7gC+FOu4p/5Ma0rqtc/DY8AbwPl/Rj+AJxnZp39+3qcjvZ411L/DdD0vlLqKPGLFGyVcy4l6CAKw79TFwBm9h7elLR3AUWW+HO/zinKHcKbiTAIG0Li/NDMyuPdQOYiQLMiSlRRV79IIZlZRTN7xszWmdkRvwt5vpm1DmPfm8xslb/fQTNbY2ZDc5XpZmb/NrM0f1loZm0KE6tz7jiwCmgZcvzqZva8H3emma03s//NFUM1M/uzmW01swwz22Vm/zKzVv72k7r6zex14EagaUj3eoq/7aSufjN70cx2mFlsrtes4NfJ5JB19cxsql8+08y+NrPbClMXvi/8v01yvfYjZrbSzA6Z2V4zW2xmnUK2DwVe8p9uDHmPjULqY5xflxlmtt3MJvk/NEQiglr8IgWLNe+GTyc451y2/7iivzwMfI/XpT4CWGZm5+V3LwMz6wq8itcVPgpvutM2QM2QMn2BOXjzcA/C+5F+H94d5BKcc9sL8V7Owe+a9pPtQiAB+H943e99gD+ZWW3n3B/8fZ4BeuLdlCkF7wYrV+DdACsvD/pl2gH9/HXH8in7GnA73lzu74Ws74t3D/e/+7HWAP6DN03pH4BNeFOUvuSfunghrHd/smb+3w251jcEnsQ7vVMF794fH5tZe+fcOmAe0BwYi3dK48Sc6Cc+6xnAlcDjeL0bbfG+H02AGwoRp0jRc85p0aIl14J3W1yXx7K0gH1igcp482XfGbJ+qL9vI//5fcDuAo5jeMnt3Vzra+Ddg2LyKWJ/xH+9OH+pD/zRXzfZL3ON/3xwrn3/hpeoa/nPvwEmFvBacf5xHghZ9zqwKY+y3f2yV4S8z++Av+cqtwBYE/L8ISAdaJGr3F+BXUBsAfG19F9ziB9rZbwfGjuAmaeox1i8HxsbgCfz+Dyb5SrfzV8/KNf63/jrLwz6e61Fi3NOXf0ip9AP6BiynNS9bGYDzewzMzsIZAFpeL0ABXX3fw7UNbPXzOwqM8vdej4PaAr8f7/rOM7vdUgDPgW6hBn7cX/5HhgNPIXXcsc/RhYwM9c+r+MNgLskJNbbzOw+M+tgZkX2P8M55/zX62dmlQHMrC7wa04eh9AT+ATYnKs+3gXqUXBdn/AKXl2kAe/jteh/k7uQmfUwsw/MbB9e/WTitfDDeY2eeD+a3sgV54nejJ+FcQyRYqfEL1Kwtc655JBl/YkNZtYPr2t3LZCElyw74rXKK+R3QOfcYrxu32Z4t4bda2bvmdkFfpF6/t9X+TF5n1h64p1SCMeJHystgarOuVHOuQx/Wy1gr/vpiPbvQ7YDDMc7p3073iC43Wb2pJlVDDOGU3kNrxXe33+ehPd/aXpImXrAL/hpXczwt4dTHw/h1cXPgRf8x8+GFjCzjngj/w/i9RBc6pdbSwGfZ644K+D1+ITGeeLe6OF+biLFSuf4RQpvIPCNc27IiRVmVgGvS75Azrl/Av80syp4Se0JYKGZNQFO3Bp2DLAkj90z8liX12sUNFp9P95tPuNyJf8G/t99/jEO452auM/MmuFd3vgYXst2HGfIOZdiZsuBwXjn9AcDi51zO0KK7cO7XPCefA6zPp/1oTaF1MeHZlYNGGpmf3HOnRjoNwDvfV0bWidmVgvvlMKp7MNL+l3z2b4jn/UiJUqJX6TwKuF1B4e6mdPoSXPOpQHzzawl3qCymnjzBGwF2jjnJhVRrLl9CNwNXAv8I2T9jXjJ79M8Yt0ETDKzm4ALcm8PkYF3uiNcfwemmFk3vBb2Tbm2L8Kbh2CTc27vaRy3IL/He+8P4g0mhB8/zx/uVW5mPfAG/H0dsu+JH1653+MivMGalZ1zHxZRnCJFTolfpPAWAX/2LztbiJe0RgCHCtrJzB7F6/ZdgjcqvAkwEkh2zu33y4wE5vo9CLPwWpMNgMuA75xzz5xh7AuAZXgj4xvgJbar8QY1/tE5d8CP41NgLl539xG8AWxtgakFHPsrYIiZDQNWAunOubUFlJ8JPI33A+AI8Eau7ZPxeho+NrOngW+BqnhjIS5zzvXjNDnntpvZX4C7zOwi59wqvM9zJPBXM3vVP/4D/LSlfmICp5H+5YvHgdXOuffNbBbeOf6n8CYsAu+UTi9glHMu91UEIiUv6NGFWrRE4sKPo/pbFlAmFpiAlxiO4iXydngDx14OKZd7VH8fvAFfO/Faj1vxzqM3yHX8y/HOOR/Aa4VvxDuvfekpYn8Ef+zcKcpVB57348jE6zL/31xlJuMl74N4A+PWACNDtuc1qr8qXi/CAX9bir/+pFH9uV7nDX/ba/nEWgvv0sJNfqy7gY8IuXoin/1OjOq/JY9t9fz3NCdk3V3+a6TjJe5uwFLg/Vz7Pux/7tm5PttYvJ6UNf5nloo3f8ITQLWgv9datDjnMOd+6NUSERGRMk6j+kVERKKIEr+IiEgUUeIXERGJIkr8IiIiUUSJX0REJIoo8YuIiEQRJX4REZEoosQvIiISRZT4RUREosj/ASjGJtFnT62JAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f6902dbc3c8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fpr, tpr, thresholds = roc_curve(Y_test, modele_pred)\n",
"plt.figure(figsize=(8, 6))\n",
"plot_roc_curve(fpr, tpr)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### PRECISION, RAPPEL, F1-SCORE, SUPPORT"
]
},
{
"cell_type": "code",
"execution_count": 152,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(1.0, 0.10087760686986882, 0.1832676152923024, None)"
]
},
"execution_count": 152,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"precision_recall_fscore_support(Y_test, modele_pred,average='binary')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### SCORE EN K-FOLD CROSS VALIDATION (validation croisee en K passes) "
]
},
{
"cell_type": "code",
"execution_count": 153,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.99607458 0.99804878 0.99898785]\n",
"Mean: 0.9977037392210842\n",
"Standard deviation: 0.0012141053118430185\n",
"CPU times: user 683 ms, sys: 228 ms, total: 911 ms\n",
"Wall time: 11min 10s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele, X_train, Y_train, cv=3, scoring=\"precision\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 154,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.08680049 0.0853426 0.0865762 ]\n",
"Mean: 0.08623976673769206\n",
"Standard deviation: 0.000640964008802741\n",
"CPU times: user 787 ms, sys: 300 ms, total: 1.09 s\n",
"Wall time: 16min 37s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele, X, Y, cv=3, scoring=\"recall\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 155,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.15969464 0.1572639 0.1593313 ]\n",
"Mean: 0.158763280697471\n",
"Standard deviation: 0.001070549984412297\n",
"CPU times: user 731 ms, sys: 347 ms, total: 1.08 s\n",
"Wall time: 17min 20s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele, X, Y, cv=3, scoring=\"f1\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 156,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.58775037 0.59047879 0.58920838]\n",
"Mean: 0.5891458469498364\n",
"Standard deviation: 0.0011147530639906667\n",
"CPU times: user 767 ms, sys: 276 ms, total: 1.04 s\n",
"Wall time: 16min 53s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_roc=cross_val_score(modele, X, Y, cv=3, scoring=\"roc_auc\",n_jobs=-1)\n",
"display_scores(modele_score_roc)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Autres Tests à reporter"
]
},
{
"cell_type": "code",
"execution_count": 157,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"0.5547871594785291"
]
},
"execution_count": 157,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# % de bien classes\n",
"# attention trompeur\n",
"accuracy_score(Y_test,modele_SVM_test)"
]
},
{
"cell_type": "code",
"execution_count": 158,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"1.0"
]
},
"execution_count": 158,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"precision_score(Y_test,modele_SVM_test)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### **LE MEILLEUR: Random forest**"
]
},
{
"cell_type": "code",
"execution_count": 232,
"metadata": {},
"outputs": [],
"source": [
"from sklearn.model_selection import GridSearchCV"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"http://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html"
]
},
{
"cell_type": "code",
"execution_count": 285,
"metadata": {},
"outputs": [],
"source": [
"parameters = { \n",
" 'n_estimators':[1,500], \n",
" 'criterion' :['gini', 'entropy']\n",
" }"
]
},
{
"cell_type": "raw",
"metadata": {
"collapsed": true
},
"source": [
"parameters = { \n",
" 'n_estimators':[10,100,200], \n",
" 'max_features':['sqrt',\"log2\",None],\n",
" 'warm_start':(False, True),\n",
" 'max_depth' : [5,10,None],\n",
" 'criterion' :['gini', 'entropy']\n",
" }"
]
},
{
"cell_type": "raw",
"metadata": {},
"source": [
"fit_params={ \n",
" 'n_estimators' : 500\n",
" }"
]
},
{
"cell_type": "code",
"execution_count": 234,
"metadata": {},
"outputs": [],
"source": [
"#nb de jeux en CV\n",
"nb_cv=5"
]
},
{
"cell_type": "code",
"execution_count": 286,
"metadata": {},
"outputs": [],
"source": [
"modele_RF_GSCV = GridSearchCV(modele_rf, parameters,cv=nb_cv,n_jobs=-1)"
]
},
{
"cell_type": "code",
"execution_count": 287,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"CPU times: user 1min 28s, sys: 343 ms, total: 1min 28s\n",
"Wall time: 6min 36s\n"
]
},
{
"data": {
"text/plain": [
"GridSearchCV(cv=5, error_score='raise',\n",
" estimator=RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',\n",
" max_depth=None, max_features='auto', max_leaf_nodes=None,\n",
" min_impurity_decrease=0.0, min_impurity_split=None,\n",
" min_samples_leaf=1, min_samples_split=2,\n",
" min_weight_fraction_leaf=0.0, n_estimators=100, n_jobs=1,\n",
" oob_score=False, random_state=42, verbose=0, warm_start=False),\n",
" fit_params=None, iid=True, n_jobs=-1,\n",
" param_grid={'n_estimators': [1, 500], 'criterion': ['gini', 'entropy']},\n",
" pre_dispatch='2*n_jobs', refit=True, return_train_score='warn',\n",
" scoring=None, verbose=0)"
]
},
"execution_count": 287,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"%%time\n",
"modele_RF_GSCV.fit(X_train,Y_train)"
]
},
{
"cell_type": "code",
"execution_count": 288,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"RandomForestClassifier(bootstrap=True, class_weight=None, criterion='entropy',\n",
" max_depth=None, max_features='auto', max_leaf_nodes=None,\n",
" min_impurity_decrease=0.0, min_impurity_split=None,\n",
" min_samples_leaf=1, min_samples_split=2,\n",
" min_weight_fraction_leaf=0.0, n_estimators=500, n_jobs=1,\n",
" oob_score=False, random_state=42, verbose=0, warm_start=False)"
]
},
"execution_count": 288,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"modele_RF_GSCV.best_estimator_"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Estimation de l'erreur de prévision sur l'échantillon test"
]
},
{
"cell_type": "code",
"execution_count": 289,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"0.9465912807812719"
]
},
"execution_count": 289,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"modele_RF_GSCV.score(X_test,Y_test)"
]
},
{
"cell_type": "code",
"execution_count": 290,
"metadata": {},
"outputs": [],
"source": [
"modele_RF_GSCV_pred=modele_RF_GSCV.predict(X_test)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### **ESTIMATION QUALITE MODELE RF GRIDSEARCH**"
]
},
{
"cell_type": "code",
"execution_count": 291,
"metadata": {},
"outputs": [],
"source": [
"modele_pred = modele_RF_GSCV_pred\n",
"modele=modele_RF_GSCV"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Matrice confusion"
]
},
{
"cell_type": "code",
"execution_count": 292,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[10040, 764],\n",
" [ 379, 10218]])"
]
},
"execution_count": 292,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"confusion_matrix(Y_test,modele_pred)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### ROC"
]
},
{
"cell_type": "code",
"execution_count": 293,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"0.9467603053639938"
]
},
"execution_count": 293,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"roc_auc_score(Y_test, modele_pred)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### ROC CURVE"
]
},
{
"cell_type": "code",
"execution_count": 294,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAf4AAAF8CAYAAAAuF9n2AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzs3Xd4VHXa//H3nQbSkaIiShHFxUJAfggiuNZFlCbdsmsDFEV4xIbsuuq6Flxl4REVLJfurp0uAq4FCwhKSXCVR11EESwk9CCQNt/fHzMJQ0jCJMzMmfJ5XVcuZs45M3NzCLnzbffXnHOIiIhIckjxOgARERGJHiV+ERGRJKLELyIikkSU+EVERJKIEr+IiEgSUeIXERFJIlFN/Gb2vJnlmNkXFZw3M5tiZuvM7HMz6xjN+ERERBJdtFv8LwA9Kzl/MXBi4GsE8FQUYhIREUkaUU38zrmPgG2VXNIX+IfzWw40MLNjohOdiIhI4ou1Mf5jgY1BzzcFjomIiEgYpHkdQBlWzrFyawqb2Qj8wwHUrl37jJNPPjmScYmIyGFyDnw4nAPnHD5H6WNH2efgc0HXEnTOBc4FHfMFve6A9ybonKP0fWONAWaGGaTg/9P/ZaQYGIavKJ/duT9RXJgPsMU516Q6nxVriX8TcFzQ8+bAT+Vd6JybDkwH6NSpk1u5cmXkoxMRiRPOOYp8joIin/+r2Ed+oY+C4mLyS44V+fY/Lg4+FrimuJzrgo6XXlfRtcUHvuZwGOW3DKsrxSAjLYWM1BRqpKf6/0xL8R9LC3qcWnIs9YBjNcq9LvWA98hIS6FGago10lPISE098Hjw61JTSEmp/G+3atUqevTowZEN6vHiiy/Sq1evDdX9u8da4p8H3GxmrwJnAjudcz97HJOISEh8PudPsAck2+IDE2AgMR6cWIvLSaxlk2hxBQk4+M/i0hhirWG7P4mWl1hLjqVWklhLjqUekFgPuC7o2pLrDkjY6f4/01JjbaS7fM45zIz27dszatQobr31Vo455vCmvkU18ZvZK8BvgcZmtgn4M5AO4Jx7GlgA9ALWAXuAa6IZn4jEF+cchcWunMRaSYu1uPjgBFymFVtpAi5J6MHXBY4VFsdWpk1NsQqTbY2ySbS86w5IrKnlJNYyr0lNLU2sB7VuU1MwC2ebPfF9+umn3HrrrcyePZumTZvy6KOPhuV9o5r4nXPDDnHeATdFKRwRqYbioO7j/EASragbuGy3r7+ruUwCLSw+sJVclWuLY7BVG5QsD9USrbjFmlpBYi2n2zioFVv2s+KlVSsH8vl8TJw4kT/96U8ce+yx/PLLLzRt2jRs7x9rXf0iUoZz7qAEeHD3bgXdykEJ9MBx3eIKx2XzS4+VP35b5IutTJuWYhW0RFND7go+OLGmlEmsqQe1csvrglarVg7XL7/8wlVXXcW7777LoEGDmD59Og0aNAjrZyjxi5SjqLicpFhuK7S4gsRafrfygYm18gQcfG2sqVEmWYbeFXxgEi3bYj0wsVbcBV0jqMWbeohJUSLx5K677mLp0qVMnz6d66+/PiK/SJqLtX6yatCs/vjnnDtoTLZsAj2ohVvBuGx+cTnXlTMum3/A6w+8rjgGW7VlZwv7u3ZDabGmVpBYD+xWPuQYcOB4eqqpVSsSRgUFBezYsYOmTZuyZcsWcnJyaNeuXaWvMbNVzrlO1fk8tfiTWFGZsdL9k5jKn9x0cGI9eHJTcIt4fyu54u7ncC31CTczgpJfmWU8VekKPmiSU2o5ifUQs5FDWOojIvHp22+/ZdiwYaSmprJ06VIaN25M48aNI/qZSvxRVN5Sn/KW8pTfYi2uJLGWHCuuMLHun5W8PwnHWKOW9FSreldwebOHK2qxltdlXMFEqrQUtWpFJLJefvllbrjhBlJTU3n22WdJSYnOZEwl/sOwc28hf5m/ls279h00yaq8MdxYW+oTqQIWIS0HKpvQ1aoVkSTx66+/cvPNN/PCCy/QrVs3XnrpJVq0aBG1z1fiPwz//vIXZqzaVKXXqICFiEhyc87x6aef8qc//Yl77rmHtLTopmIl/sPwy859APRp34yhnY9TAQsRESmXc44XXniBIUOGUKdOHVavXk3NmjU9iUWJ/zBszvMn/o7HN+CsEyI7GUNEROLTli1buPbaa3nzzTfZs2cPN910k2dJH5T4D0vOrnwAmtbz7h9QRERi1wcffMAVV1zBli1bmDx5MqNGjfI6JDTIexg25/kT/1H1angciYiIxJrnnnuO8847jzp16rB8+XJuueWWmBjuVeI/DDm7/F39TeuqxS8iIgc655xzGDFiBKtWraJDhw5eh1NKib+afD5HbqDF36SuWvwiIgKzZ8/m+uuvxzlHmzZtePrpp6lTp47XYR1Aib+atu0poMjnaFArnZrpqV6HIyIiHtq7dy+jRo3isssuY82aNezcudPrkCqkxF9NmwPd/Eepm19EJKmtXbuWM888k6eeeopx48axdOnSsO+oF06a1V9NOXklM/rVzS8ikqwKCwu55JJL+PXXX1mwYAEXX3yx1yEdkhJ/NWlin4hI8tq1axe1a9cmPT2dl19+mZYtW3LMMcd4HVZI1NVfTZt3aSmfiEgyWr58Oe3bt+ehhx4CoGvXrnGT9EGJv9pKx/hVvEdEJCn4fD4efvhhzj77bAAuuOACjyOqHnX1V1PpGL+W8omIJLyff/6Zq666ivfee4/Bgwczbdq0mJ7AVxkl/moqHeNXi19EJOFt2LCBFStW8Mwzz3DdddfFRAW+6lLiryaN8YuIJLaCggIWLlxI37596dKlCxs2bIjbVn4wjfFXg8/nyN2tqn0iIolq3bp1dOvWjX79+vGf//wHICGSPijxV8vWXwso9jka1kqnRpqq9omIJJKXXnqJDh068O233zJr1ixOO+00r0MKKyX+atCMfhGRxHTTTTdx5ZVXkpmZSXZ2Nv379/c6pLBT4q+G3NKqfUr8IiKJpGPHjtxzzz0sXryY448/3utwIkKT+6phc2nVPo3vi4jEM+ccU6ZMoVGjRlx55ZVcd911XocUcWrxV4Nm9IuIxL8tW7bQp08fxo4dy4IFC7wOJ2qU+Kthc57G+EVE4tkHH3xA+/bt+fe//82UKVN46aWXvA4patTVXw05u1S1T0QkXn311Vecf/75nHjiibz11ltkZmZ6HVJUqcVfDTl5qtonIhJv9u7dC8DJJ5/Miy++yMqVK5Mu6YMSf7VoOZ+ISHyZNWsWrVq1YtWqVQBceeWV1KlTx+OovKHEX0XFPseW3QUANKmjrn4RkVi2d+9eRo0axYABAzjuuOMSpvre4VDir6Ktv+ZT7HMcWTuDjDTdPhGRWPXll1/SuXNnnnrqKW677TaWLl3KCSec4HVYntPkvirSxD4RkfjwxhtvsHnzZhYuXEjPnj29DidmqMlaRTlayiciErN27NhBVlYWAH/84x/5z3/+o6Rfhlr8VbRZLX4RkZi0bNkyhg0bhs/nY926dWRkZHDUUUd5HVbMUYu/ijSjX0Qktvh8Ph566CG6d++OmfHGG2+QkZHhdVgxSy3+KsrJU7leEZFYkZeXx2WXXca7777LkCFDmDZtGvXr1/c6rJimxF9FOYEWf5O6avGLiHitTp06HHnkkTz77LNce+21mJnXIcU8dfVXkTboERHxVkFBAXfffTfff/89ZsZrr73Gddddp6QfIiX+KtIYv4iId9atW8dZZ53FQw89xLx587wOJy6pq78K/FX7/C3+xqraJyISVf/617+48cYbSU9PZ/bs2fTr18/rkOKSWvxVsHV3Pj4HjVS1T0Qkqp577jmuuuoqOnTowJo1a5T0D4Na/FVQuoZf3fwiIlFRXFxMamoqQ4YMIS8vj5tvvpm0NKWuw6FmaxXsr9qnbn4RkUhyzjF58mQ6d+7Mnj17qFOnDmPHjlXSDwMl/ipQ1T4RkcjLzc2ld+/ejB07lmOPPZb8/HyvQ0ooSvxVoBn9IiKRtXjxYtq3b88777zDlClTmDt3Lg0bNvQ6rISiPpMqKKnapzF+EZHwc85x1113Ua9ePRYsWEBmZqbXISUkJf4qKKnap65+EZHw2bBhA/Xq1aNhw4bMnDmThg0bUrt2ba/DSljq6q+CzdqSV0QkrGbOnElmZiZjxowBoHnz5kr6EabEXwUq1ysiEh579+7lhhtuYODAgbRp04Y///nPXoeUNJT4Q1RU7GPr7nzMVLVPRORw/Pe//6Vz585MmzaN2267jaVLl3LCCSd4HVbS0Bh/iLb+WoDPQeM6GaSn6vclEZHqqlOnDgALFy6kZ8+eHkeTfJTBQrS5dGKfxvdFRKpqx44dPPDAAxQXF3PMMcewZs0aJX2PKPGHKKe0XK+6+UVEqmLZsmVkZmZy33338dlnnwGQkqL045Wo33kz62lmX5vZOjO7q5zzx5vZYjPLMrPPzaxXtGMsT+mMfrX4RURCUlxczIMPPkj37t1JSUlhyZIldO3a1euwkl5UE7+ZpQJTgYuBdsAwM2tX5rI/Aq875zoAQ4EnoxljRTSjX0SkaoYPH86ECRMYNGgQWVlZnHnmmV6HJER/cl9nYJ1zbj2Amb0K9AXWBl3jgHqBx/WBn6IaYQVyAy1+Ve0TEamccw4zY/jw4Zx99tlcc801mJnXYUlAtBP/scDGoOebgLK/At4L/NvMRgO1gQuiE1rltEGPiEjl8vPzGT9+PACPP/44Xbt2Vdd+DIr2GH95v/K5Ms+HAS8455oDvYB/mtlBcZrZCDNbaWYrc3NzIxDqgbRBj4hIxf773/9y1llnMWnSJAoLC3Gu7I92iRXRTvybgOOCnjfn4K7864DXAZxzy4CaQOOyb+Scm+6c6+Sc69SkSZMIhbvf/jF+JX4RkWD//Oc/6dixI9999x2zZ8/mf//3f9W1H8OinfhXACeaWSszy8A/eW9emWt+AM4HMLPf4E/8kW/SV6Ko2MfWX0uq9mV4GYqISEzZtGkTI0eOpEOHDqxZs4Z+/fp5HZIcQlTH+J1zRWZ2M/A2kAo875z70szuB1Y65+YB44BnzOx/8A8DXO087jPasrsA5/yletNUtU9EhO+++45WrVrRvHlzPvroIzIzM0lLUzHYeBD1LOacW+CcO8k5d4Jz7q+BY/cEkj7OubXOuW7OufbOuUzn3L+jHWNZ+8f3NbFPRJKbc45JkybRtm1bXnnlFQA6deqkpB9H9C8Vgpw8zegXEcnNzeXqq69mwYIF9O7dm4suusjrkKQa1G8dAs3oF5Fk98EHH9C+fXveffddpkyZwty5c2nUqJHXYUk1qMUfgpxdKt4jIslt27Zt1KtXjwULFpCZmel1OHIY1OIPQUlXv8b4RSSZbNiwgddffx2Ayy67jM8//1xJPwEo8YdAW/KKSLKZOXMmmZmZ3HTTTeTl5QGQkaHlzIlAiT8E2qBHRJLF3r17ueGGGxg4cCAnnXQSn376KXXr1vU6LAkjjfGHYH9Xv1r8IpK48vPz6dKlC59//jl33HEHf/nLX9TKT0BK/IdQGFS1r1Ft/QcQkcRVo0YNfv/733PaaadpqV4CU1f/IWzZna+qfSKSsLZv386QIUN47733ABg3bpySfoJTJjsEje+LSKL65JNPyMzMZNasWaxbt87rcCRKlPgPIUcz+kUkwRQXF/Pggw/So0cP0tLSWLp0KSNHjvQ6LIkSJf5D2Kw1/CKSYGbNmsWECRMYNGgQq1evpnPnzl6HJFGkyX2HoBa/iCSK3NxcmjRpwsCBA1m4cCG/+93vMDOvw5IoU4v/EHJ2aSmfiMS3/Px8xo4dS9u2bfnhhx8wM3r27Kmkn6TU4j+EzXklLX519YtI/Pnmm28YOnQoWVlZ3HzzzTRt2tTrkMRjSvyHsFktfhGJU//85z+58cYbqVGjBnPmzKFv375ehyQxQIn/EHLzSrbkVYtfROLLu+++yxlnnMG//vUvjjvuOK/DkRihxF+JwmIfW3YXkGLQqI4Sv4jEvlWrVlGzZk1OOeUUnn76adLT00lL04962U+T+yqRG1jK17hODVJTNAlGRGKXz+fj8ccfp2vXrowbNw6AI444QklfDqLviEqUbMer8X0RiWU5OTlcc801LFiwgL59+/Lcc895HZLEMCX+SpTsyqcZ/SISq7766ivOO+88tm3bxhNPPMGoUaO0TE8qVaXEb2Ztge5AI+AF59xmMzsO2Oqc2xOJAL1UWrxHLX4RiVGtW7fm3HPP5Y477qB9+/ZehyNxIKQxfjNLN7N/AmuB6cCDwLGB008Af4xMeN7SBj0iEou+//57hgwZwvbt28nIyOCll15S0peQhTq57y9AH2A40AII7kdaAPwuzHHFhJw8jfGLSGyZMWMGmZmZLFq0iC+++MLrcCQOhZr4rwD+5Jx7HvipzLn1QKuwRhUjSlr8GuMXEa/t2bOHkSNHMmjQINq2bUtWVhbdu3f3OiyJQ6Em/iZAZb9aJmSTWLP6RSRW3HrrrUyfPp0777yTJUuW0Lp1a69DkjgV6uS+DcD/A94v51wn4L9hiyiGlKzjb6oxfhHxgHOOX3/9lTp16vDnP/+ZAQMGcOGFF3odlsS5UBP/v4AJZrYOeDNwzJlZV+BW/JP9EkpBkY+tvwaq9tVW4heR6Nq+fTvDhw9n27ZtvPPOOxxzzDEcc8wxXoclCSDUrv6HgPeAN4AtgWOLgSXAh8Dfwx+at3J3+1v7Teqqap+IRNfSpUvJzMxk7ty5XHzxxVqXL2EVUovfOVcE9DezC/HP4G8KbAUWOefejmB8ntH4vohEW3FxMQ899BD33nsvLVq0YOnSpXTu3NnrsCTBhJT4zawp/iI97wDvlDmXAjR2zuVEID7P5GhGv4hE2e7du3n22WcZPHgwTz/9NPXq1fM6JElAoY7x/wx0BT4r51yHwPHUcAUVC0rW8Ktqn4hE2vvvv0+3bt2oX78+n332GU2aNFH3vkRMqGP8lX0HpgG+MMQSU0q7+usq8YtIZOTn5zN27FjOP/98Jk+eDEDTpk2V9CWiKmzxm1kdILifqbGZNStz2RHA5cDmCMTmqRyV6xWRCPrmm28YOnQoWVlZjB49mltuucXrkCRJVNbVPw64J/DYsX8ZX1kG/DWcQcWCzVrDLyIRMnfuXK644gpq1KjB3Llz6dOnj9chSRKpLPHPB37Bn9ifBCYC35W5Jh9Y65wrb+w/rpXuzKeufhEJszZt2tC9e3eeeeYZmjdv7nU4kmQqTPzOuVXAKgAzc8BM59yWiq5PNDl5JV39SvwicvhWrVrF7NmzeeCBBzjllFNYuHCh1yFJkgppcp9zbloyJf38omK2/VpAaorRqHaG1+GISBzz+Xw8/vjjdO3alRdffJHc3FyvQ5IkF+pyPszsJOAaoC0Hb8rjnHOXhDMwL5XU6G9SpwYpqtonItWUk5PD1VdfzcKFC+nXrx/PPfccRx55pNdhSZILtYDPGcDH+GfvHw98DRyJv4LfT8APkQrQC/u7+TWxT0Sqp7i4mHPPPZdvv/2WqVOncuONN2qZnsSEUFv8DwNvAcOAAuBK59xqM+sFPAvcGaH4PFEysa+JJvaJSBUVFhaSmppKamoqjz32GM2aNeP000/3OiyRUqEW8GkPvMD+Qj2pAM65Bfh35psY9sg8tFlr+EWkGr7//nt69OjBlClTAOjZs6eSvsScUBN/DSDPOecDtgFHBZ1bCyTUd7Y26BGRqnrjjTfIzMxk7dq1NGtWttaZSOwINfGvB0q+k78Erg46dyWQWBv05GmDHhEJzZ49exgxYgSDBw/m5JNPJjs7m8GDB3sdlkiFQk38C4ELA48fAvqa2TYzywH+AEyJRHBeUYtfREK1evVqnn/+ee68804+/vhjWrVq5XVIIpUKaXKfc+7uoMeLzKw7MBCoBSxyzs2LUHyeKN2SV2P8IlIO5xwrVqygc+fOnH322XzzzTe0bt3a67BEQhJqi/8AzrnlzrnbnHOjEi3pw/4tedXiF5Gytm3bxoABA+jSpQurVq0CUNKXuFKtxB/MzNqZ2SvhCCYW5BcVs31PIWkpxpG1VLVPRPZbsmQJmZmZvPnmmzz66KN06NDB65BEqqzSxG9+p5vZpWb2mzLnTjOzN4DPgUsjGWQ0lXTzN6mrqn0ist8jjzzCOeecQ3p6Op988gnjxo0jJeWw204iUVfhd62ZHQ0sBbKAucAXZvaimaWZ2ROB45fi37mvTTSCjYbSGf3q5heRIDVq1GDo0KFkZWXx//7f//M6HJFqq2xy38NAJvBXYDXQCrgD+BDoCrwG3O6c2xTpIKNp/3a8mtgnkuzmz5+Pz+ejT58+jBkzBkBldyXuVZb4LwTud849XHLAzL4A3gaeds6NinRwXti/lE+JXyRZ5efnc+eddzJ58mR++9vf0rt3byV8SRiVDVA1xd/VH6zkecJM5itrc8kGParTL5KUvvnmG7p27crkyZO55ZZbWLhwoZK+JJTKWvypQH6ZYyXPf41MON7TGn6R5PX999/TsWNHatasybx58+jdu7fXIYmE3aEK+FxkZsET91IAB/Q0s5ODL3TOvRzu4LxQsoZfk/tEkofP5yMlJYWWLVvy5z//mcsvv5xjjz3W67BEIuJQif/+Co4/UOa5AxIi8ZeO8aurXyQprFy5kmuvvZZXXnmFU045hdtvv93rkEQiqrLE/5tKziWskuV8mtwnkth8Ph+TJk1i/PjxHH300ezevdvrkESiosLE75z7OhIfaGY9gcn45xA8G7xqIOiawcC9+HsS1jjnLo9ELGXtKyxmR6BqX0NV7RNJWDk5OfzhD39g0aJF9OvXj+eee44jjzzS67BEoiKkTXrCxcxSgan4lwpuAlaY2Tzn3Nqga04ExgPdnHPbzaxptOLLDdqOV1X7RBLXE088weLFi5k6dSo33nijZu1LUol2vcnOwDrn3HrnXAHwKtC3zDXDganOue0AzrmcaAWniX0iiauwsJD169cDMGHCBFavXs2oUaOU9CXpRDvxHwtsDHq+KXAs2EnASWa21MyWB4YGDmJmI8xspZmtzM3NDUtwm3ftb/GLSOL47rvv6NGjB+eddx579uyhRo0atGvXzuuwRDwR7cRf3q/WrszzNOBE4LfAMOBZM2tw0Iucm+6c6+Sc69SkSZOwBLe/ap9a/CKJ4vXXXyczM5O1a9cyceJEatWq5XVIIp6KduLfBBwX9Lw58FM518x1zhU6574Dvsb/i0DElbT4NaNfJP7t27eP4cOHM2TIENq1a0d2djaDBw/2OiwRz1U58ZtZGzM708yq82vzCuBEM2tlZhnAUGBemWvmAOcGPqsx/q7/9dX4rCorHePXGn6RuJeens7333/P+PHj+eijj2jVqpXXIYnEhJATv5ldZ2ab8LfAPwFODhyfYWY3hPIezrki4Gb8G/38H/C6c+5LM7vfzPoELnsb2Gpma4HF+HcA3Bry3+gwqFyvSHxzzvHMM8/w008/kZqaysKFC3nwwQdJT0/3OjSRmBFS4jezq4HpwPvAHzhwrP5TYEioH+icW+CcO8k5d4Jz7q+BY/c45+YFHjvn3K3OuXbOudOcc6+G+t6HS2P8IvFr27ZtDBgwgBEjRvDUU08BkJYW1RXLInEh1Bb/7cBk59zvOXhnvv8j0PqPd/ur9inxi8STJUuWkJmZyfz58/nb3/7Gfffd53VIIjEr1F+HTwDequBcHtAwPOF4Z19hMTv3FpKeajSspW5BkXgxa9YsBg0aRKtWrfjkk0/o1KmT1yGJxLRQW/zbOHA2frCTgJ/DE453Ssf369ZUQQ+ROHLuuedyyy23sHr1aiV9kRCEmvjfAv5oZsHJ3wXW148F5oY9sijbX7VPE/tEYt2bb75Jz549KSgooGHDhkyaNIl69ep5HZZIXAg18U8IXLsWmI+/6M7fAs/TgbgfUFPVPpHYl5+fz5gxY+jTpw+bN29my5YtXockEndCSvyBevkdgSlAE+BH4EjgReDMkrr68Uwz+kVi29dff02XLl2YMmUKY8aMYfny5TRr1szrsETiTshrXZxzO/C3/CdELhzvaEa/SOxyznH11VezceNG3nzzTS699FKvQxKJWyElfjN7EPiHc+6rCMfjmZxAi7+JuvpFYsauXbtISUmhTp06vPDCC9SpU4djjy27r5eIVEWoY/yjgS8Du+GNNrPw7IoTQzbnqatfJJasWLGCjh07Mnr0aADatm2rpC8SBqEm/qbA74Fc4HHgRzObb2aDzCwhmsjaoEckNvh8Pv72t79x1llnUVhYyPXXX+91SCIJJdTJfXudcy855y7Gv6PeXcAxwGvAZjN7JoIxRkVJV/9R2qBHxDM5OTn06tWL22+/nT59+pCdnU23bt28DkskoVR5dz7n3Gbn3OPOuTOA8/FX7rs27JFF0d6CYnbtKyIjNYUGqton4pk9e/bw+eef89RTTzFjxgwaNoz7oqAiMafKO1gEuvb7AVcCF+HfsKeicr5xoaR4T5O6NVS1TyTKCgsLeemll/jDH/5Ay5Yt+fbbbzniiCO8DkskYVVlW97fmtlzwGb8G/UcBdwGNHPO9an0xTFu/1I+je+LRNN3331H9+7dueaaa3jvvfcAlPRFIizU5Xw/AMcCG4Gp+Jf2fR3JwKKppHhPU43vi0TNa6+9xogRIzAzXnvtNS644AKvQxJJCqF29b+DP9l/GMlgvKIZ/SLRdffdd/PQQw/RpUsXXnnlFVq2bOl1SCJJI6TE75y7LtKBeGn/Bj1q8YtEQ0nr/r777iM9XRNqRaKpwsRvZp2BL5xzewKPK+Wc+yyskUVRjjboEYko5xxPPvkk27dv549//CPnnXce5513ntdhiSSlylr8y4EuwGeBx66C6yxwLjW8oUWPNugRiZxt27Zx3XXXMWfOHC655BKKi4tJTY3bHxcica+yxH8x8H+Bx72oOPHHPSV+kchYsmQJl19+Ob/88guPPfYYY8eOJSWlyuVDRCSMKkz8zrm3gx4vik443tByPpHwy83N5aKLLqJZs2Z88skndOrUyeuQRIQQ1/Gb2VozO62Cc+3MbG14w4qePQVF5O0rIiMthfpHaJKRyOHauXMnAE2aNGHWrFmsXr1aSV8khoS+vKE+AAAgAElEQVTa53YyUFFVjVpA2/CEE33BE/tUtU/k8MybN48TTjiBmTNnAtCzZ0/q1avncVQiEqwqg20VjfGfDuwMQyye2N/Nr/F9kerat28ft9xyC3379uX444/ntNPK7SAUkRhQ2XK+0cDowFMHzDCz/DKXHQE0A2ZEJrzI21+1T+P7ItXx1VdfMXToUNasWcPYsWN5+OGHqVFD/59EYlVls/p/AlYFHrcBvga2lrkmH1gLPBX+0KJDM/pFDs+KFSv48ccfmT9/PpdcconX4YjIIVQ2q38mMBMoGfue4JxbH6W4oiY30NXfVDP6RUK2a9cuVq5cyXnnncdVV13FpZdeqi10ReJEqCV7h0U6EK9ogx6RqlmxYgVDhw4lNzeXDRs20LBhQyV9kThS2Rj/Hfg35vkl8Lgyzjn3aHhDiw5t0CMSGp/Px2OPPcbdd99Ns2bNWLhwoRK+SByqrMX/MPAB8EvgcWUcEJ+JP09j/CKHUlRURO/evVm0aBGXXXYZzz77rJK+SJyqLPEf4ZwrmcVf0Rr+uJerDXpEDiktLY0OHTrQt29fRo4cqZoXInGsssl9+eU9TiS/5heRl6+qfSLlKSws5E9/+hN9+/ala9euPPjgg16HJCJhENLkPjNrDdRzzmUHntcA7gJOBd52zj0buRAjJ7hGv1owIvutX7+eYcOG8dlnn1GjRg26du3qdUgiEiYhJX7gSfzr9bMDz/8C/A/wDdDfzFKdc9MiEF9E5ZSs4deMfpFSr732GiNGjMDMeP311xk0aJDXIYlIGIVasjcT+AjA/E3jq4G7nXOn4J/4d0NEoouwzVrDL3KA+fPnM3ToUE455RSys7OV9EUSUKiJvwGwJfA4E2gEvB54/g5wQpjjioocreEXAfy19gEuvvhipk+fzocffkjLli29DUpEIiLUxJ8DtA48vhD4zjm3IfC8NlAc7sCiQRv0SLJzzjF16lROOukkfv75Z1JTUxk+fDjp6ZrsKpKoQh3jnw/81cxOAkYAzwedOwX4LtyBRYM26JFktm3bNq677jrmzJlDr169SEsL9ceBiMSzUP+n3wXUBYYA7wIPBJ0bDLwf5riiQhv0SLL6+OOPufzyy9m8eTOPP/44Y8aMISWlKrt0i0i8CrVW/y7gqgrO/b+wRhRFwcv5RJLJ1KlTqVmzJsuWLeOMM87wOhwRiaIq9e2ZWV2gM3Ak/i16Vzjn8iIRWDTklFbtU4tfEt+mTZsoLCykVatWTJs2jZSUFOrWret1WCISZSH37ZnZH4GfgX8Dr+Hv8v/ZzCZEKLaI2p1fxO78ImqkpVDvCI1tSmKbO3cu7du359prrwWgfv36SvoiSSqkxG9mNwH3A7OBXkAH4OLA8/vN7MaIRRghOUHj+6raJ4lq3759jB49mn79+tGiRQumTYu7OlsiEmahNnVvBp50zt0cdGwN8LaZ7QRGA0+FO7hI0vi+JLqNGzfSu3dv1qxZw9ixY3n44YepUUPf7yLJLtTE3xq4pYJzc4HrwxNO9GxW8R5JcI0aNaJhw4bMnz+fSy65xOtwRCRGhDrGvw1oW8G5toHzcaV0Yp9a/JJAdu3axe23387u3bupVasW77//vpK+iBwg1MQ/B38Bn0EWNCBuZv3xb9gzJxLBRVJOntbwS2L57LPP6NChA5MmTWLx4sUAmr8iIgcJNfHfBXyFfzb/HjPbYGZ7gBnA14HzcWVz6VI+tfglvvl8Ph599FG6detGUVERH330Eb179/Y6LBGJUaEW8NlpZmcB/YHu+NfxbwM+BOY65+KuVr+q9kmiGD9+PBMnTmTAgAE888wzNGzY0OuQRCSGhbyAPZDcZwS+4l6uZvVLnCsuLiY1NZUbb7yRNm3acP3116trX0QOqdKufjMbambLzWyLma0zs7+aWUJUuylp8TfRrH6JMwUFBdx55530798f5xwtW7Zk+PDhSvoiEpIKE7+ZDQJeBo4GlgJ78I/lP1DRa+LF7vwifi0opmZ6CvVqJsTvMZIk1q9fT/fu3Zk4cSLNmjWjsLDQ65BEJM5U1uK/FXgLONE519c5dzrwCDDazOJ6G6/NqtoncejVV1+lQ4cOfPPNN8yYMYOnn36ajIwMr8MSkThTWQJvCzzlnAtuUkwBjgBaRDSqCCtZw3+UuvklTuTl5XHrrbdy6qmnkp2dzYABA7wOSUTiVGX93A2ALWWO5Qb+bAh8F5GIoqBkDX8TTeyTGPfVV1/Rpk0b6taty4cffkirVq1IS9PwlIhU36G67F0Vj8eF0q5+tfglRjnneOKJJ8jMzOTRRx8F4MQTT1TSF5HDdqjEv9TMCkq+gL2B458GHzez/FA/0Mx6mtnXgVUCFRb+MbOBZubMrFOo7x2q0q5+tfglBm3dupX+/fszevRozj//fK6/Pu62whCRGFZZ8+GRcH+YmaUCU4ELgU3ACjOb55xbW+a6uvg3Bfo03DEAbM5TnX6JTcuWLWPw4MFs3ryZxx9/nLFjx2oCqoiEVYWJ3zk3PgKf1xlY55xbD2BmrwJ9gbVlrvsLMBG4LQIxqKtfYlZGRgb169dnzpw5nHHGGV6HIyIJKNrL8o4FNgY93xQ4VsrMOgDHOefmV/ZGZjbCzFaa2crc3NzKLj1IbmmLX4lfvLdp0yb+93//F4AzzjiDzz//XElfRCIm2om/vD7L0omCgfoAk4Bxh3oj59x051wn51ynJk2ahByAc660xa+ufvHa3Llzad++PXfffTc//vgjACkpcV0mQ0RiXLR/wmwCjgt63hz4Keh5XeBU4AMz+x7oAswL5wS/3flF7Cko5oj0VOrW0Axp8ca+ffsYPXo0/fr1o2XLlqxevZpjjz320C8UETlM0c58K4ATzawV8CMwFLi85KRzbifQuOS5mX0A3OacWxmuADYHzejXpCnxgnOOCy64gKVLlzJ27FgefvhhatRQ75OIREdUW/zOuSLgZuBt4P+A151zX5rZ/WbWJxoxlBTv0fi+RJtzDuccZsbo0aOZP38+kyZNUtIXkaiKel+3c24BsKDMsXsquPa34f78kjX8Tevqh61Ez86dOxk5ciTnn38+w4cPZ8iQIV6HJCJJKuQWv5kdZWYPmtkSM1trZu0Cx0dFoshOpARv0CMSDZ9++ikdOnRgxowZ7Nq1y+twRCTJhZT4zexk4D/Ajfi3520LlGTOtsDYiEQXATl5qton0eHz+XjkkUc4++yz8fl8fPzxx4wbd8gFKyIiERVqi/9v+DflaQX04sBleUuBrmGOK2JKl/KpeI9E2PLly7nrrrvo378/2dnZdO0aN/9NRCSBhTrGfw5wpXNuR6DsbrBfgGPCG1bklI7xq8UvEfLDDz9w/PHHc9ZZZ/HJJ5/QpUsXrSARkZhRlVn9xRUcb8T+zXtiXsmsfo3xS7gVFBRwxx130KZNG1au9K9A7dq1q5K+iMSUUFv8K4GrgPLK6A4AloctogjyV+3TrH4Jv/Xr1zN06FBWrFjBDTfcwCmnnOJ1SCIi5Qo18f8VWGRmbwIv4S+z28PMRgKDgXMjFF9Y5eUXsbewmFoZqdRR1T4Jk1dffZURI0aQmprKjBkzGDBggNchiYhUKKTs55x718wGA38HLgkcfhx/ud3BzrmlEYovrHJKq/bVVPerhM26des47bTTePnll2nRooXX4YiIVCrkMX7n3CygBXA6cAHQATjeOTcnQrGFXU7pjH5188vhWbNmDR988AEA48eP58MPP1TSF5G4UKX+buecA76IUCwRt1nleuUwOeeYOnUq48aNo127dqxevZrU1LILXUREYldIiT/QzV8p59zrhx9OZJVu0KMWv1TD1q1bufbaa5k3bx69evXihRde0JCRiMSdUFv8r1Zw3AU9jvnEHzzGL1IVP/30E507dyYnJ4dJkyYxZswYJX0RiUuhJv7flHOsEXApMBD4Q9giiqD9Xf1q8UvVHHPMMQwZMoQrrriCjh07eh2OiEi1hTqr/+sKTn1iZsX4a/gvC1tUEZKjcr1SBRs3buSGG25g8uTJtGnThscee8zrkEREDltVKvdVZDHQJwzvE3HaoEdCNWfOHNq3b89HH33E119X9HuviEj8CUfi74R/x76Y5q/ap1n9Url9+/Zx00030b9/f1q3bs3q1au55JJLDv1CEZE4Eeqs/jvKOZwBnAr0B54JZ1CRsGtfEfsKfdRW1T6pxMSJE3nyySe59dZbeeihh8jIyPA6JBGRsAo1Az5czrFi4EdgEnBf2CKKkFxtziMVcM6xbds2GjVqxG233Ua3bt04//zzvQ5LRCQiQk38R5RzrNA55wtnMJFUsoa/idbwS5CdO3cycuRIsrKyWL16NbVr11bSF5GEdsgxfjPLAO4FTnXO5Qd9xU3SB0rH99XilxKffvopHTp0YMaMGVx99dXUrKnvDRFJfIdM/M65AmAMUDvy4UROadU+zehPej6fj0ceeYSzzz4bn8/Hxx9/zPjx41V6V0SSQqiz+tcA7SIZSKTlaIxfAoqLi5k7dy79+/cnOzubrl27eh2SiEjUhDrGfwfwDzNb55x7N5IBRUqOxviT3jvvvEOHDh1o3LgxixYtom7duiq7KyJJJ9QW//NAA+BtM8szs/+a2TdBXzFf4URj/MmroKCA22+/nYsuuogHHngAgHr16inpi0hSCrXFv4oDN+SJO/ur9inxJ5Nvv/2WYcOGsWLFCm644QYeeughr0MSEfFUqLX6h0Y6kEg6oGqfuvqTxvvvv0+/fv1ITU1lxowZDBgwwOuQREQ8V2FXv5mtN7P20QwmUnbtLSK/yEedGmnUVtW+pHHqqady4YUXkp2draQvIhJQ2Rh/SyAhmsc52o43aWRnZ3PNNddQVFRE06ZNmTlzJi1atPA6LBGRmBGOTXpiXskafnXzJy7nHFOmTOHMM8/k3//+N99//73XIYmIxKRDJf64ntBXQjP6E9uWLVvo27cvY8aM4aKLLmLNmjW0adPG67BERGLSoQa87zOzLSG8j3PO/SEcAUXCZhXvSWgDBw5k2bJlTJ48mdGjR2uZnohIJQ6V+DOB/BDeJ6Z7BnLU1Z9wioqKKC4upkaNGkyaNAmADh06eByViEjsO1Ti7+ec+ywqkUTQ/sl9avEngo0bN3L55Zdz+umnM3XqVCV8EZEqSKrJfUepxR/35syZQ/v27cnOzuass87yOhwRkbiTFIlfG/TEv71793LTTTfRv39/WrduTVZWFldccYXXYYmIxJ2ET/z+qn2BMX6t449bP/74I//4xz8YN24cn3zyiWbti4hUU4Vj/M65hPilYOfeQgqKfNStkUatDFXtiyfOOd577z3OP/982rRpw7p16zjqqKO8DktEJK4lRHKvTMnmPGrtx5edO3cybNgwLrzwQubPnw+gpC8iEgYJ3wTevzmPxvfjxfLlyxk2bBgbN27kwQcf5JJLLvE6JBGRhJHwLf7SGf1q8ceFqVOn0r17d5xzfPzxx4wfP56UlIT/NhURiZqE/4mqGf3xpUWLFlx22WVkZ2fTtWtXr8MREUk4iZ/4S2f0K/HHqkWLFjF16lQALr30Ul577TUaNGjgcVQiIokp4RP//jF+dfXHmoKCAm677TYuvvhinnvuOQoLC70OSUQk4SVN4ldXf2xZt24d3bp147HHHmPUqFEsXbqU9PR0r8MSEUl4CT+rv2Q5nyb3xY4dO3bQuXNnnHPMmjWL/v37ex2SiEjSSOjE75wL2plPLX6vFRUVkZaWRoMGDZgyZQo9evTg+OOP9zosEZGkktBd/Tv2FFJQ7KNuzTSOyEj1Opyklp2dzWmnncaiRYsAuPLKK5X0RUQ8kNCJf383v1r7XnHOMWXKFM4880x27dpFrVq1vA5JRCSpJXTi14x+b23ZsoW+ffsyZswYfve737FmzRp69OjhdVgiIkktKRK/WvzemDdvHm+//TaTJ09m7ty5NG7c2OuQRESSXkJP7tMGPdFXVFTEl19+Sfv27bnmmmvo0aOHttAVEYkhCd3izylp8WtGf1T88MMPnHvuuXTv3p2cnBzMTElfRCTGJHTi37xLLf5omT17NpmZmaxZs4annnqKpk2beh2SiIiUI7ETvzboiTifz8eoUaO47LLLOOGEE8jKyuKKK67wOiwREalAQif+kuI96uqPnJSUFIqKihg3bhxLly7lhBNO8DokERGpRMJO7nPOlW7Jq67+8HLO8eyzz9KpUyc6dOjAtGnTMDOvwxIRkRBEvcVvZj3N7GszW2dmd5Vz/lYzW2tmn5vZe2bWojqfs31PIYXFjno106iZrqp94bJjxw6GDBnCiBEjmDZtGoCSvohIHIlq4jezVGAqcDHQDhhmZu3KXJYFdHLOnQ7MACZW57NyNL4fdsuWLSMzM5PZs2fz8MMP8+STT3odkoiIVFG0u/o7A+ucc+sBzOxVoC+wtuQC59zioOuXA1dW54M0oz+8PvjgAy644AKOO+44Pv74Y7p06eJ1SCIiUg3R7uo/FtgY9HxT4FhFrgMWVueDNmsNf1g45wDo1q0bEyZMICsrS0lfRCSORTvxlzcY7Mq90OxKoBPwaAXnR5jZSjNbmZube9D53NKqfUr81bVw4ULOOOMMtm7dSnp6Ovfddx8NGjTwOiwRETkM0U78m4Djgp43B34qe5GZXQBMAPo45/LLeyPn3HTnXCfnXKcmTZocdH5/nX519VdVQUEB48aNo1evXhQVFbFjxw6vQxIRkTCJduJfAZxoZq3MLAMYCswLvsDMOgDT8Cf9nOp+0P6d+dTir4p169bRrVs3Hn/8cUaNGsWnn36qtfkiIgkkqpP7nHNFZnYz8DaQCjzvnPvSzO4HVjrn5uHv2q8DvBFYJvaDc65PVT+rZHKfWvxVc/fdd/Ptt98ya9Ys+vfv73U4IiISZlEv4OOcWwAsKHPsnqDHF4Tjc0rG+LWc79B2797N7t27Ofroo3niiSfYt28fxx9/vNdhiYhIBCRkyV6fb3/VviZ11eKvTFZWFmeccQZDhw7FOUfTpk2V9EVEElhCJv7tewooLHbUPyJdVfsq4Jxj8uTJdOnShV9//ZX77rtPFfhERJJAQtbqz8nT+H5ltm3bxtVXX82bb75J7969ef7552ncuLHXYYmISBQkZItfM/orl5aWxrfffsuUKVOYO3eukr6ISBJJzBa/yvUepKioiKlTpzJy5Ejq1atHdnY26enpXoclIiJRlpAtfm3Qc6ANGzZwzjnnMHbsWGbMmAGgpC8ikqQSMvGXbtCjGf3MnDmTzMxM/vOf//Dyyy9z5ZXV2vNIREQSRIImfrX4AR599FEGDhzIiSeeSFZWFsOGDfM6JBER8VhijvFrVj8Affr0Yfv27dx7771kZGR4HY6IiMSAhGzx5yTprH7nHNOnT+faa6/FOUfbtm158MEHlfRFRKRUwiV+f9U+f4s/mar27dixgyFDhjBy5Eg2btzI3r17vQ5JRERiUMIl/m17CijyORrUSp6qfcuWLSMzM5PZs2fz8MMP8/bbb1OrVi2vwxIRkRiUcGP8JWv4j0qSbv69e/fSv39/atWqxZIlSzjzzDO9DklERGJYwiX+zYE1/IlevCc3N5dGjRpxxBFHMG/ePNq2bUv9+vW9DktERGJcwnX1J8PEvoULF3LKKafw2GOPAdC5c2clfRERCUkCJv7EXcpXUFDAuHHj6NWrF8cccwyXXnqp1yGJiEicSdyu/gSb0b9u3TqGDh3KqlWruOmmm/jb3/5GzZqJ26shIiKRkXiJv7TFn1hJ8eeff+aHH35g9uzZ9OvXz+twREQkTiVeV39eyc588Z/4d+/ezeuvvw5A9+7d+e6775T0RUTksCRe4i+t0x/fXf2rV6+mY8eOXH755axfvx6A2rVrexyViIjEu4RK/IlQtc85x9///ne6dOnCnj17eO+992jdurXXYYmISIJIqDH+rb8WUOxzNKyVTo20+Kva55xj8ODBzJgxgz59+vD888/TqFEjr8MSEZEEklCJPycvvrfjNTMuuugizjnnHG666SbMzOuQREQkwSRW4t8Vf938RUVF3HvvvZxyyikMGzaM4cOHex2SiIgksIQa49+8K75a/Bs2bOCcc87hr3/9K8uXL/c6HBERSQKJ1eLPi5+qfTNnzuT666+nuLiYl19+mWHDhnkdkoiIJIGEbPHHep3+VatWMXDgQE488USysrKU9EVEJGoSLPHHdos/Ly8PgDPOOIM33niDJUuWcMIJJ3gclYiIJJOESvy5pVvyxlaL3znH9OnTadGiBWvWrAFg4MCBZGRkeByZiIgkm4RK/LFYp3/Hjh0MHjyYkSNH0qlTJ4466iivQxIRkSSWMIm/2OfI3R1YzlcnNrr6ly1bRmZmJnPmzOGRRx5h0aJFHH300V6HJSIiSSxhZvVv/TWfYp/jyNoZZKTFxu8z8+bNIyUlhSVLlnDmmWd6HY6IiEjitPhLivc09bh4z08//cSqVasAuP/++8nKylLSFxGRmJE4iT8GJva99dZbtG/fnssvv5zi4mLS09OpX7++Z/GIiIiUlTCJv3Rinwct/vz8fP7nf/6HSy+9lGbNmjF37lxSU+NvkyAREUl8CTPGn+PRjP6tW7dy0UUXsXr1akaPHs3EiROpWTN2VhWIiIgES5wWf2lXf3Rb/A0bNuQ3v/kNc+bMYcqUKUr6IiIS0xIm8edEsVxvXl4eo0aNYuPGjaSkpPCvf/2Lvn37RvxzRUREDlfiJP4obdCzatUqOnbsyLRp01i8eHFEP0tERCTcEibxR3pLXucckyZNomvXruzdu5fFixfz+9//PiKfJSIiEikJk/hzAy3+xhGq2vf4449z66230qtXL9asWUOPHj0i8jkiIiKRlBCz+ot8Dp+DRhGo2ldQUEBGRgbDhw+nYcOGXHPNNZhZWD9DREQkWhKixV9Y7APCW7ynqKiICRMm0KVLF/bt20e9evW49tprlfRFRCSuJUTiLypJ/GEq3rNhwwbOOeccHnzwQTp06IDP5wvL+4qIiHgtIbr6C4sdEJ4Z/TNnzuT666+nuLiYl19+mWHDhh32e4qIiMSKBEn8PlI5/Bn9RUVFPPDAA5x00km88sortG7dOjwBioiIxIiESPxFPkcq1e/q//LLL2nevDn169fnrbfeokmTJqSnp4c3SBERkRiQEGP81Z3c55xj2rRpdOrUibvuuguAZs2aKemLiEjCSojEX1Q6xh964t++fTuDBg3ihhtuoEePHtx7770Rik5ERCR2JETiL2nxhzq5Lysri8zMTObOncvEiRNZuHAhRx11VCRDFBERiQkJM8ZvFnrVviZNmnD00Ufzxhtv0Llz5whHJyIiEjsSosUP/qp96akV/3V++uknJkyYgM/no3nz5ixfvlxJX0REkk7CJP7KtuOdP38+p59+On//+9/54osvAFSBT0REklLiJP5yxvfz8/MZO3YsvXv3pnnz5qxatYrTTz/dg+hERERiQ0KM8QMcVU6Lf8iQIcydO5fRo0czceJEataMzJa9IiIi8SJxEn9Qi9/n85GSksJtt93GNddcQ9++fT2MTEREJHZEvavfzHqa2ddmts7M7irnfA0zey1w/lMzaxnK+zapV5O8vDyuuuoqxo8fD8DZZ5+tpC8iIhIkqonfzFKBqcDFQDtgmJm1K3PZdcB251wbYBLwSCjvveuHr+jYsSMvv/wytWvXDmfYIiIiCSPaXf2dgXXOufUAZvYq0BdYG3RNX+DewOMZwBNmZs45V9GbFv+6g7FX9uboo45i8eLF9OjRIzLRi4iIxLlod/UfC2wMer4pcKzca5xzRcBOoFFlb1qct5XzL/wd2dnZSvoiIiKViHaLv7zF82Vb8qFcg5mNAEYEnua/vWD+F40bNz7M8KQSjYEtXgeRBHSfI0/3OPJ0jyOvbXVfGO3Evwk4Luh5c+CnCq7ZZGZpQH1gW9k3cs5NB6YDmNlK51yniEQsgO5xtOg+R57uceTpHkeema2s7muj3dW/AjjRzFqZWQYwFJhX5pp5wB8CjwcC71c2vi8iIiKhi2qL3zlXZGY3A28DqcDzzrkvzex+YKVzbh7wHPBPM1uHv6U/NJoxioiIJLKoF/Bxzi0AFpQ5dk/Q433AoCq+7fQwhCaV0z2ODt3nyNM9jjzd48ir9j029aKLiIgkj4TZpEdEREQOLa4Sf6TK/cp+IdzjW81srZl9bmbvmVkLL+KMZ4e6x0HXDTQzZ2aaHV0NodxnMxsc+H7+0sxejnaM8S6EnxfHm9liM8sK/Mzo5UWc8czMnjezHDP7ooLzZmZTAv8Gn5tZx0O+qXMuLr7wTwb8FmgNZABrgHZlrhkFPB14PBR4zeu44+krxHt8LlAr8PhG3ePw3+PAdXWBj4DlQCev4463rxC/l08EsoCGgedNvY47nr5CvMfTgRsDj9sB33sdd7x9AT2AjsAXFZzvBSzEXwOnC/Dpod4znlr8peV+nXMFQEm532B9gRcDj2cA55tZeQWBpHyHvMfOucXOuT2Bp8vx12KQ0IXyfQzwF2AisC+awSWQUO7zcGCqc247gHMuJ8oxxrtQ7rED6gUe1+fgui1yCM65jyinlk2QvsA/nN9yoIGZHVPZe8ZT4o9IuV85QCj3ONh1+H/TlNAd8h6bWQfgOOfc/GgGlmBC+V4+CTjJzJaa2XIz6xm16BJDKPf4XuBKM9uEfzXX6OiEllSq+nM7+sv5DkPYyv1KhUK+f2Z2JdAJOCeiESWeSu+xmaXg35Xy6mgFlKBC+V5Ow9/d/1v8PVcfm9mpzrkdEY4tUYRyj4cBLzjnHjOzrvhrtJzqnPNFPrykUeW8F08t/qqU+6Wycr9SoVDuMWZ2ATAB6OOcy49SbIniUPe4LnAq8IGZfY9/zG6eJvhVWag/L+Y65wqdc98BX+P/RUBCE8o9vg54HcA5twyoib+Ov4RPSD+3g8VT4le538g75H8kHl0AAAjsSURBVD0OdENPw5/0NSZadZXeY+fcTudcY+dcS+dcS/zzKPo456pdlztJhfLzYg7+yaqYWWP8Xf/roxplfAvlHv8AnA9gZr/Bn/hzoxpl4psH/D4wu78LsNM593NlL4ibrn6ncr8RF+I9fhSoA7wRmDf5g3Ouj2dBx5kQ77EcphDv89vARWa2FigGbnfObfUu6vgS4j0eBzxjZv+Dv/v5ajXGqsbMXsE/HNU4MFfiz0A6gHPuafxzJ3oB64A9wDWHfE/9G4iIiCSPeOrqFxERkcOkxC8iIpJElPhFRESSiBK/iIhIElHiFxERSSJK/CLlMLOrAzvjlfd1QRXf6/rA66Kyr4GZPVAm3u2B3SrDvrzVzNICn/HHoGOXmdnYcq69IHDt2eGOo5L42pS5F8Vm9rOZ/dPMKi1rWsl7djSze82sQbjjFYmGuFnHL+KRQfgrYwVb60Ug1dA18GcjYCTwipllOOf+Ea4PCKzl7sqBtcIvA84G/l7m8s8CMX0Zrs+vggeAt4AagRjuAU42s66BfT2qoiP+tdQvACrvK3FHiV+kctnOuXVeB1EdgZ26ADCzf+MvSTsWCFviL/s5h7huF/5KhF74NijOD82sBv4NZDIBVUWUpKKufpFqMrMjzGyymX1pZr8GupDnmVnbEF57lZllB16308w+N7Pry1xzrpm9b2a7A18LzaxddWJ1zhUC2UCboPevb2ZPBuIuMLOvzWxMmRjqmdkTZrbRzPLNbLOZvWNmJwXOH9DVb2b/Aq4AWgR1r68LnDugq9/MppvZT2aWWuYzawbuyd+CjjU1s2mB6wvM7P/M7Lrq3IuA1YE/jy/z2Q+YWZaZ7TKzLWb2npl1Djp/PfBM4Ol3QX/H5kH3Y0LgXuab2Y9m9mjgFw2RmKAWv0jlUs2/4VMJ55wrDjw+IvB1P/AL/i71m4BlZnZyRXsZmNk5wIv4u8LH4S932g5oGHRNX2Am/jrcl+P/Jf0u/DvIne6c+7Eaf5dWBLqmA8l2IXA68Cf83e99gL+bWSPn3D2B10wGeuLflGkd/g1Wzsa/AVZ5/hy4pj3QP3BsXwXX/gMYjr+W+7+DjvfFv4f7PwOxNgCW4i9Teg/wPf4Spc8Ehi6eCulvf6CWgT+/LXO8GfAY/uGdOvj3/vjYzDo6574E5gKtgfH/v71zDbGqiuL478/MB2vSasBpPoQJzYdIoyAksacRZg+iySAtzTDrQ01kSSUkhGkPc1R6UAaF+SgtSSEENRSzpLKESobSMJuQzMTRrDHxEasPa189Hu/cuY6jRnf9YDFz9l57n3X3vtx19trrnINvaRSeiV6Y6wXATcCLeHSjH/796APc1QU7g6D7MbOQkJCc4K/FtSKytkSbKqAGf172I5nysant+el4ArCjRD/CnduKXPk5+DsomjuxfUo6X3WS84DJqaw56dyejkfm2r6DO+radLwReKnEuapTPxMzZfOB1iK6NyTdqzKfcwswL6e3FNiQOZ4E7AMuzOnNBn4HqkrY15DOOSbZWoNfaGwDFnYyjlX4xcZPwPQi89k3pz84ld+dKx+dyi853d/rkBAzi1B/EHRCIzAgI0eFlyUNl/SVpD3AIaAdjwKUCvd/DfSWNFfSLZLyq+eLgAuAd1PouDpFHdqBdcA1Zdp+MMl24AlgBr5yJ/VxCFiYazMfT4C7ImPr/ZImSLpcUrf9ZpiZpfM1SqoBkNQbuJGj8xCGAp8Dv+TGYwVQR+mxLvA2PhbtwEp8RT86ryRpiKRPJLXh43MAX+GXc46h+EXTkpydhWjG1WX0EQQnnXD8QVCaFjNbn5FNhQpJjXhotwUYgTvLAfiqvEdHHZrZKjzs2xd/NexOSR9L6p9U6tLfORxx3gUZim8plEPhYqUB6Glm481sf6qrBXbasRnt2zP1AA/he9oP4ElwOyRNl3RGmTZ0xlx8FX5HOh6B/y69l9GpA67n2LFYkOrLGY9J+FhcB7yR/n81qyBpAJ75vwePEAxMei2UmM+cnT3wiE/WzsK70cudtyA4qcQefxB0neHARjMbUyiQ1AMPyZfEzD4APpB0Fu7UpgLLJPUBCq+GfRJYXaT5/iJlxc5RKlt9F/6az+qc869Pf9tSH3/hWxMTJPXFb298AV/ZPs0JYmabJX0JjMT39EcCq8xsW0atDb9d8PEOutnUQXmW1sx4rJHUCxgraZaZFRL97sQ/17DsmEiqxbcUOqMNd/rXdlC/rYPyIDilhOMPgq5zJh4OznIvxxFJM7N24CNJDXhS2bn4cwK2Aheb2bRusjXPGuAxYBjwfqb8Htz5rStiayswTdIooH++PsN+fLujXOYBr0gajK+wR+Xql+PPIWg1s53H0W8pnsI/+zN4MiEcmc/D7yqXNARP+Psh07Zw4ZX/jMvxZM0aM1vTTXYGQbcTjj8Ius5y4LV029ky3Gk9DPxZqpGk5/Cw72o8K7wP0ASsN7NdSacJWJwiCIvw1WQ9MAjYYmYvn6DtS4Ev8Mz4etyx3YonNU42s93JjnXAYjzcvRdPYOsHvFmi7++BMZIeBL4B9plZSwn9hcBM/AJgL7AkV9+MRxo+kzQT+BHoiedCDDKzRo4TM/tV0ixgnKTLzOxbfD6bgNmS5qT+J3LsSr3wAKemdPviQeA7M1spaRG+xz8Df2AR+JbOzcB4M8vfRRAEp57TnV0YEvJfFI5k9TeU0KkCnscdw9+4I78UTxx7K6OXz+q/DU/4+g1fPW7F99Hrc/1fie8578ZX4T/j+9oDO7F9Cil3rhO9s4HXkx0H8JD5ozmdZtx578ET4zYATZn6Yln9PfEowu5UtzmVH5XVnzvPklQ3twNba/FbC1uTrTuAT8ncPdFBu0JW/31F6urSZ/owUzYunWMf7rgHA2uBlbm2z6Z5/yc3t1V4JGVDmrM/8OcnTAV6ne7vdUiImSGzw1GtIAiCIAj+50RWfxAEQRBUEOH4gyAIgqCCCMcfBEEQBBVEOP4gCIIgqCDC8QdBEARBBRGOPwiCIAgqiHD8QRAEQVBBhOMPgiAIggoiHH8QBEEQVBD/ArdfM7MQOAv3AAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f6902d4fba8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fpr, tpr, thresholds = roc_curve(Y_test, modele_pred)\n",
"plt.figure(figsize=(8, 6))\n",
"plot_roc_curve(fpr, tpr)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### PRECISION, RAPPEL, F1-SCORE, SUPPORT"
]
},
{
"cell_type": "code",
"execution_count": 295,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(0.9304316153706065, 0.9642351608945928, 0.9470318365077159, None)"
]
},
"execution_count": 295,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"precision_recall_fscore_support(Y_test, modele_pred,average='binary')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### SCORE EN K-FOLD CROSS VALIDATION (validation croisee en K passes) \n",
"INUTILE DEJA FAIT LORS DE LA GENERATION DU MODELE ! => resultat sous optimal"
]
},
{
"cell_type": "code",
"execution_count": 296,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.5286025 0.98738079 0.97614749 0.97413793 0.90340759]\n",
"Mean: 0.87393525959312\n",
"Standard deviation: 0.1752033889740129\n",
"CPU times: user 1.6 s, sys: 543 ms, total: 2.14 s\n",
"Wall time: 30min 30s\n"
]
}
],
"source": [
"%%time\n",
"#CPU times: user 1.6 s, sys: 543 ms, total: 2.14 s\n",
"#Wall time: 30min 30s\n",
"modele_score_acc=cross_val_score(modele, X, Y, cv=nb_cv, scoring=\"precision\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 271,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.9766377 0.95785441 0.96 0.96102804 0.9588785 ]\n",
"Mean: 0.96287972911956\n",
"Standard deviation: 0.006960847101161565\n",
"CPU times: user 1.17 s, sys: 390 ms, total: 1.56 s\n",
"Wall time: 25min 32s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele, X, Y, cv=nb_cv, scoring=\"recall\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 272,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.68594119 0.97239351 0.96800641 0.96753858 0.93031691]\n",
"Mean: 0.9048393189297055\n",
"Standard deviation: 0.1104991805421745\n",
"CPU times: user 1.21 s, sys: 372 ms, total: 1.59 s\n",
"Wall time: 25min 28s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_acc=cross_val_score(modele, X, Y, cv=nb_cv, scoring=\"f1\",n_jobs=-1)\n",
"display_scores(modele_score_acc)"
]
},
{
"cell_type": "code",
"execution_count": 273,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Scores: [0.68827536 0.99628681 0.99445123 0.99379531 0.97491813]\n",
"Mean: 0.9295453667307703\n",
"Standard deviation: 0.12088436685366487\n",
"CPU times: user 1.21 s, sys: 386 ms, total: 1.59 s\n",
"Wall time: 25min 29s\n"
]
}
],
"source": [
"%%time\n",
"modele_score_roc=cross_val_score(modele, X, Y, cv=nb_cv, scoring=\"roc_auc\",n_jobs=-1)\n",
"display_scores(modele_score_roc)"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.6"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| gpl-3.0 |
sonyahanson/assaytools | examples/ipynbs/data-analysis/grant_figures/Competition-Assay-GrantPlot.ipynb | 2 | 98677 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Couldn't import dot_parser, loading of dot files will not be possible.\n"
]
}
],
"source": [
"from assaytools import grant\n",
"from glob import glob\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"import seaborn as sns\n",
"%matplotlib inline"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"SrcColumns = ['A - Src','B - Buffer','C - Src','D - Buffer', 'E - Src','F - Buffer','G - Src','H - Buffer']\n",
"AblColumns = ['A - Abl','B - Buffer','C - Abl','D - Buffer', 'E - Abl','F - Buffer','G - Abl','H - Buffer']"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"file_ABL_GEF= \"../competition/data/Abl Gef gain 120 bw1020 2016-01-19 15-59-53_plate_1.xml\"\n",
"file_ABL_GEF_IMA= \"../competition/data/Abl Gef Ima gain 120 bw1020 2016-01-19 16-22-45_plate_1.xml\""
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"AblGef_df = grant.file2df(file_ABL_GEF,AblColumns)\n",
"AblGefIma_df = grant.file2df(file_ABL_GEF_IMA,AblColumns)"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>A - Abl</th>\n",
" <th>B - Buffer</th>\n",
" <th>C - Abl</th>\n",
" <th>D - Buffer</th>\n",
" <th>E - Abl</th>\n",
" <th>F - Buffer</th>\n",
" <th>G - Abl</th>\n",
" <th>H - Buffer</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>62213</td>\n",
" <td>19784</td>\n",
" <td>62890</td>\n",
" <td>19797</td>\n",
" <td>62821</td>\n",
" <td>20594</td>\n",
" <td>63317</td>\n",
" <td>17635</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>62497</td>\n",
" <td>17332</td>\n",
" <td>62936</td>\n",
" <td>18205</td>\n",
" <td>62927</td>\n",
" <td>18102</td>\n",
" <td>63343</td>\n",
" <td>14681</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>63194</td>\n",
" <td>12950</td>\n",
" <td>63056</td>\n",
" <td>13223</td>\n",
" <td>62794</td>\n",
" <td>13049</td>\n",
" <td>63251</td>\n",
" <td>10586</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>63017</td>\n",
" <td>10782</td>\n",
" <td>62743</td>\n",
" <td>11030</td>\n",
" <td>62841</td>\n",
" <td>10622</td>\n",
" <td>63045</td>\n",
" <td>9235</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>56558</td>\n",
" <td>10186</td>\n",
" <td>62107</td>\n",
" <td>10257</td>\n",
" <td>61824</td>\n",
" <td>9884</td>\n",
" <td>55471</td>\n",
" <td>8785</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>34259</td>\n",
" <td>9837</td>\n",
" <td>38003</td>\n",
" <td>9884</td>\n",
" <td>38786</td>\n",
" <td>9620</td>\n",
" <td>35771</td>\n",
" <td>8796</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>22106</td>\n",
" <td>9861</td>\n",
" <td>24868</td>\n",
" <td>9716</td>\n",
" <td>24637</td>\n",
" <td>9757</td>\n",
" <td>23488</td>\n",
" <td>8789</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>14589</td>\n",
" <td>9659</td>\n",
" <td>16880</td>\n",
" <td>10010</td>\n",
" <td>17193</td>\n",
" <td>9518</td>\n",
" <td>17755</td>\n",
" <td>8612</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>11475</td>\n",
" <td>9601</td>\n",
" <td>12311</td>\n",
" <td>10035</td>\n",
" <td>13272</td>\n",
" <td>9758</td>\n",
" <td>12312</td>\n",
" <td>8625</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>10505</td>\n",
" <td>9669</td>\n",
" <td>11388</td>\n",
" <td>9891</td>\n",
" <td>11702</td>\n",
" <td>9649</td>\n",
" <td>10925</td>\n",
" <td>8513</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>9771</td>\n",
" <td>9722</td>\n",
" <td>10457</td>\n",
" <td>10630</td>\n",
" <td>10585</td>\n",
" <td>9889</td>\n",
" <td>10062</td>\n",
" <td>8840</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>8652</td>\n",
" <td>9757</td>\n",
" <td>9712</td>\n",
" <td>9396</td>\n",
" <td>9653</td>\n",
" <td>9578</td>\n",
" <td>9429</td>\n",
" <td>8671</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" A - Abl B - Buffer C - Abl D - Buffer E - Abl F - Buffer G - Abl \\\n",
"0 62213 19784 62890 19797 62821 20594 63317 \n",
"1 62497 17332 62936 18205 62927 18102 63343 \n",
"2 63194 12950 63056 13223 62794 13049 63251 \n",
"3 63017 10782 62743 11030 62841 10622 63045 \n",
"4 56558 10186 62107 10257 61824 9884 55471 \n",
"5 34259 9837 38003 9884 38786 9620 35771 \n",
"6 22106 9861 24868 9716 24637 9757 23488 \n",
"7 14589 9659 16880 10010 17193 9518 17755 \n",
"8 11475 9601 12311 10035 13272 9758 12312 \n",
"9 10505 9669 11388 9891 11702 9649 10925 \n",
"10 9771 9722 10457 10630 10585 9889 10062 \n",
"11 8652 9757 9712 9396 9653 9578 9429 \n",
"\n",
" H - Buffer \n",
"0 17635 \n",
"1 14681 \n",
"2 10586 \n",
"3 9235 \n",
"4 8785 \n",
"5 8796 \n",
"6 8789 \n",
"7 8612 \n",
"8 8625 \n",
"9 8513 \n",
"10 8840 \n",
"11 8671 "
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"AblGef_df"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAcAAAAEICAYAAADIniSqAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnWe4FdXVgN9FFzUqFrBgLNGNRoxYYkGjRmPsJWoUK9Zo\nQmLv3ahEjRp7x4YajYlC7MaunwUbMajbggUbiqAgSL3r+7H2MHMPt5xbuO2s93nmOTN7z56zz7nn\nzpq19iqiqjiO4zhOpdGptSfgOI7jOK2BC0DHcRynInEB6DiO41QkLgAdx3GcisQFoOM4jlORuAB0\nHMdxKpIu9Z0QQtgbuKakeUHgOuBE4CZgc+A74KwY47DC2KHAQel9bgWOjjFWpb5BwLnAUsCTwEEx\nxq9S3wDgWmB14D3gsBjjS43/mI7jOI5TnXo1wBjj7THGhbMN2AX4HDgbuAGYjAmx3YALQgjrA4QQ\nhgDbAv2B1YCBwDGpb03gamAPYAngS0yQEkLoAfwbuBFYBLgMGBlCWLCZPrPjOI7jNMwEGkJYCLgZ\n+D0m+HYCzogxzowxjgLuAPZLp+8LXBJjHB9jHA8MBQanvr2B+2KMo2KM04ETgK1DCEti2uScGOO1\nMcY5McabgPGYMHUcx3GcZqGha4DHA6NjjCOBVYBZMcaPCv3vAv3SfgDeKukLab9fsS/GOBGYmNr7\nlYwDiIXrOo7jOE6TqXcNMCNpf0OArVPTgsAPJadNAxYo9E8r6esUQugO9Czpy/p71tPnOI7jOM1C\n2QIQ2Bn4KMb4cjqeBvQoOacn8H2hf4GSvtkxxhkhhJoEWk9gSg3jin11koTresAXwJz6znccx3EA\n6AwsDYyKMc5o7cm0FA0RgDsAdxeO3wO6hRD6xhjHpbai2fNtzGw5qpa+zBxKCGEJoFdqXwTTNIsE\n4PYy5rge8Gw5H8ZxHMeZh02A51p7Ei1FQwTgBsBV2UGMcUoIYQQwNIRwCLAGMAjYJp0yHDguhPAE\nMBs4Cbgt9d0JPB1CGAa8ijnIPBhjnJTO7568SK/FnGmWAh4pY45fpNdNgE8b8Nkcx3EqmeUw5eGL\n+k7sSJQlAEMInYFlmffLOQSLEfwUM30em7xBwYRlb+BloDsm/C4GiDGOTkJzGNAHeAY4IPXNCCFs\nk657HqZp7hhjLF1vrInM7PlpiXOO4ziOUwshzDXIVdTSkXSkeoAhhBWAD4EVXQA6juOUR6XeOz0V\nmuM4jlORuAB0HMdxKhIXgI7jOE5F4gLQcRzHqUhcADqO4zgViQtAx3EcpyJxAeg4juNUJC4AHcdx\nnIrEBaDjOI5TkbgAdBzHcSoSF4CO4zhOReIC0HEcx6lIXAA6juM4FYkLQMdxHKcicQHoOI7jVCQN\nqQjfbvjss8+2E5EJgKQmKWxNPS62AVSlbU7amrJfznkzS7ZZqlrViK/JcRynoumQAnDGjBlXtPYc\nWhIRAdC0VTGvUJ5dw+uswmu2zSy8zgTGA6ep6lct92kcx3Fahg4pACuUTDttbrP2ISLyGjAaGAu8\nC7wFRFWd3czv5XQAQgidgEOB/YEA9ADeB+4ELo4xzmjAtdYGhgMrAZcD6wLvxxgPCSEIsC/wUIzx\n6xDCZsATwHIxxs/LuPaZwN4xxlVSRfSxwMYxxv8rd37pOqcC3WKMp5e03w9sC2wQY3y5hvcunl8F\nfA2MAI6PMU4unWMt7/1T4CZgwxjjnIbM23EB6NSPAOukrXqHSBUwA5gKfAdMAL4ExgEfpddvgImF\n16mqqi0xcaflCSF0Ae4HBgBnAf8BpgMDgXOAXwK/asAlT8R+Y6thv7EqzHIBsBFwM7BCOn4e6IMJ\nknK4ELisAXOZhxDCasAhQL+S9j7Ar4GIPQy8PO9oPgQ2TPtdgZWBa4AbgN8Wzqv1/yXGOCaE8AZw\nAnBe4z5F5dIhBWBPzH43G3S2/cN0bqWpTAWmAN8Dk9Px98C0tP2A3RyybQ421y51bFVUN3dm+xTG\ndkr7nUvasmvU9B6dsX/C7LgrsDiwSB2frxOwQNqWwP6B62O2iEzGBOKX6TUTjh8CN6rqzDKu47RN\njgU2A9aOMb5VaP8khPAS8E4IYZsY40NlXm8xYHSM8cMa+qqtx8cYZwFlm+tjjFOx/8mmcAZwc4zx\nh5L2fYDPgKuA80IIR8UYp5ScUxVjLM73sxDC2cDwEMIChWsKdXMx8FII4YpMc3TKo0MKwGnMfUQU\nyhd+VeQCqSiY6tufiGk+X6fXbP8bVZ3VDB+nVRGRXwCPYGYsgEnARZiAXAFYDuhNLiwXoO5/2C5A\nr7TVZNbpBZzbDFN3WphkkvwDcEuJ8AMgxjg2hNAvxji2MGYT4HxgLeAL4C7grBjjjBDCR8Dy6bx9\nMTPoLcB7mDb5TLrMh8lU+AwFE2gafxmwOaZ5TgaujjGena55JvOaF38RQrg+vderwJ9ijK/V8nn7\nArumuZeyP6b93gv8Ddgb0+7qY1oZ51QjxvhOCOFjTBO9qKHjK5kOKQAP7NTphQ1hwx7Y3XgSPHko\nnD3Lflw1CjNfz6oZVX1GRH4CvIgJu8Uw09bRwFml5kwR6QwsDfTFbl4rYoJuhdTWB1i4jrc8UkTO\nczNpu2RFYFlMCNVIifBbC3gYOA3TmH6MCaw+wIHYet8/gc+BI7CHy8ziMQ7YCVszWw94J72W8uc0\n9o/A7sD5IYTHY4zP1zLFozFB8i5wNvBgCGGlGGNNgmlb4LMY45hiYwhhXeCn2FrepyGEF9I16xSA\nIYRl0vvfUYNGWR8PADviArBBlCUAQwjLYX+8TbCnqAtijJeHEBYDhmFPWN9hT27DCuOGAgel97kV\nODrGWJX6BmFP+ksBTwIHZeaAEMIA4Fpgdexp77AY40vlfqjnl19+r2vff/8x4CepafPB8Aqqx5d7\nDSdHVT8TkdWwm9VATKu+FNhSRAar6sTCuXOAT9P2Qk3XE5EFMWG6fGHbBeiPmVLXBUbNtw/kzC96\np9cJxcYQwmhMo8oYHmM8HDOXPhBjvDi1jw0hHAY8G0I4KcY4PoQwC/ihcG8AIMZYFUKYlMZ9HWOc\nmvWVMDLGeEPavzCEcBKwAbZeWBOnxhhHpPc6ADNjDgJurOHc9YExNbQPxiwlj6XjvwOXhRDWjTG+\nUjhvpRBCZhbtjFlZJgCH1TK3uhgDHNWIcRVNvR6DyaxxH/YF98IWds8MIWwIXI8JxKWA3YALQgjr\np3FDsCek/tgC9kDgmNS3JnA1sAd2w/sS82QihNAD+Df2g1sEeyIcGUJYsNwPNatTJ9I8i15RxyHy\np3Kv4VRHVb/H1nauLzTvAIwWkY0aeK2pqhpV9TFVvVFVz8BuMhknNnnCTmvwTXrtVdK+PfAzzFQ4\nGuie2gcAO4UQpmQbZm5X7J7RVBTT5Ip8B3SrY8xcD9AY4/eYZvnTWs7tzbzCvhv2Wx4RY8ysSvdg\nSyy/Kxk/DvtefgasCfwCeBp4IYRQo9dnHXwNdAsh1LVm75RQjsv8+phJ68QY45xk298AM0vsBJwR\nY5wZYxwF3AHsl8btC1wSYxwfYxwPDMWejMDs4ffFGEfFGKdjHkxbhxCWxLTJOTHGa9P73YTFo23b\noE+mOhY4uaT1b4js1qDrOHNJZuLfYWaazES5HPCMiJwkIo0OwVDVMdjTNsC2ItIhzfMdnA+w/9Vf\nFBtjjONijGNjjB9gSw4ZMzAvzp9RXRCsSu412VRTeE0hF3WtUZeGEnSu5RpgQq30d7ojtkywXwhh\nVtJgx2H32j1DCAsVzp2VvpexMcb3Y4zPYffGzsDBdcyxJjJfB0+K0QDKuWGtjWl/F4YQvgghRMx1\ntxf2B/yocO675O7AAYsXK/ZlNop+xb4Y40TMmaRfaV92CiVuxmVyMfbEmSHA7Yhs0ohrOYAal2CL\n/9nNrDPmgv2wiPSudXD9XJtee2AmUacdkeLQrgAOCCHM8/+atKMlC01jgNULQmAsZk26CFiodHwN\nzI914rWznRBCL+yeVZOZE8xpZ8mStsGY+X9Nqgv2w4EFMQFXH5nXdkNYEphWg6epUwflPGX3wrSy\nxzEnhvWwtaDtMEeSItMwvxOwP/a0kr5OIYTuWKRC6aLytNReV1/DUJ2NyP7AK+SftRswEpGBqM7j\nqeaUh6reKyKbYebq7CbwK8wkuo+q/qcRl70cOBP75z8e+EczTNVpWf6C3SOeDyGcAzyK3Sc2wEzb\nq2Lrx2Den6+FEC7CTOtLYTFwnxbCA4rpB0uPs5v92iGEb2uYS02aXn0hBReGECZiQux8TMj9vZZz\nXwZ2zg4KsX9nlHrBhhDewSxdh5A/6HUOIfQuzKkX9h11xaxpGT1DCL+uYe5PF5xlBmCOak4DKOcp\nYwYwMcZ4foxxdozxBcwz62xy1/iMnlicG1QXhlnf7JQFoiaB1hP7QZeOK/Y1HNXRwAUlrYsCDyOy\nbKOu6QCgqi9hN7Z3Cs29gUdF5NyGmjFV9VvM9RxgbRGpy1vUaYOkZYudMc/L7YGnMA3qDMzZ7aeZ\no1yM8X/Yg/RA4HXg7nR+UfsvxrmWHo/B7kV/xx6cajq3lNqulR2fhQnol7H749aFtbxSHgB6pWws\nYJ6ss6m+Tg6Y0w7mzzAghLBOeq8VMAH7edpewDxhd4oxvl6Y09LAQ8CDhe2B1J6xOeYR6zQAqc/b\nPISwA2anX7LgwXkrFnB6BLBSjHFcar8cW787MoTwInBljPG21LcrcFqMca0Qwl/S9Q5KfUtgawdL\nYDfUK2KMKxfm8F/g9BjjffXMdQUsmHrFaqZZkR6YKXTVkiFvApug+l2dX4JTJyKyGPAvzEmmyPPA\nXqr6SQOutUu6FsCpquoxgU6bJYRwF/BJjPG4VpzDzzDnmeUbGwhf672zg1OOBvgYppWdEULoHELY\nCFP778aeOIaGEBYIIayHeT/dnsYNB44LISyb1PyTgNtS353AriGEgcnrcyjwYIxxEhZD1D2EMCSE\n0DWEcCBmGnmk0Z9SdTpmeiilP3AvIt1r6HPKRFUnYaaf20q6BgJviMiODbjcCHLT+qHNMD3HmZ+c\nBewdQmhNa8WRwF89C0zDqVcAJi/NzYCfY1rfcOCPKbnrIZi9+lPM1ffY5A0KlgJoBGZKGAM8izml\nEGMcncYOwzS/PsABqW8GsA0mTL/BMkvs2IjA0OqoPkMeiFr0lNocuIkmeDA6kNKX7Y/dEDKqMI+4\nESJyqZTxoJFKO92fDpcXkRWaeaqO02yktb5raKXQnRDCGtiD/F9a4/3bO/WaQNsT9arxIotgHqbL\nYFpGca3xr6i2mhmjIyHmeHQD5ng0C3tIAngN2FNV36tnfD/g7XR4q6ruP7/m6jiOm0ArA1vrOzwd\nLUD1RLjHInJEy0+q46Gqt2Am0e8w4TcbW8xfG3hNRPaqZ/w7mFMAwC6SCh46juM0J5UlAAFUR2Lr\nlxnFhNWXILJ7C8+oQ6KqT2Dlaj4mD0H5Hovvul1Ebkwp0WojS6m3MJbI2GkPiNyMyGP1n9ik91gd\nkW0Lxx8iUpr0oraxKyBSRZa9SOQpRObx2pwviCyKyDmIjEHke0S+ReRpRAbVP3iea+2HyBeITENk\n5/SZ9kp9PRH5feHcMxGp0+pScu2nELku7Q9GpHFJ/UUeQ2TzkrZuiHyTtnmXROy9qwrbDETeQ+T4\nGs6r/e8m8jtELq9vipUnAI0/Ybn6FgT+V2gXYDgim7bKrDoYanGWG2BxmIIJv09T94HAKBFZo5bh\nfyF3UT+9lnOctkdpaMH8YASWLzZjXeCSMsd+gvkcFDPNzP91IJG+2BLAtsCpWHq1nwMjgesROa2B\nV/wrFg4RMAfBPlhICFhO0OJyzoVYRq9y2RnL9tR4RA4EpqP6ZEnPjtjyUxcsOXkpijlS9knbqsAp\nwGnVhHr9f7frgV8isnFd06xMAag6nvwPPAD7EWZ0A+5DpLb8f04DUNUvMSeqLEZpOSyzzxws3+Mo\nETm01MypqlOBN9LhRp4ard1QGrg+P9/HUP0G1fKc5FSrUP2K5qj+YppV6Q2+Nq7HrE0DUb0X1Y9R\nfRfVi4DfAycnH4Vy3lewWOZnUR2H6g/pM2Up26p//6pTKSSsrxfVb7Hcv43D/lfPJDk9ljAYS6ry\nH2r38s4+z1fpe7obE4r71XL+vJgz3WXUU1qtMgWgcQt5tvYNsEDTjCxQfrkWn1UHJAmzXbG6aGBP\nrWOxdb4eWGaMv8u8N4DMs60LdpNw2hsiHyFyLCIPJXPdB4hsj8hvkmlrCiIPILJ4YcyuiIxK509F\n5DlE1k19T2GFl89AZGzhPU5J+2em9zoNkc/TNe5HZOnUX90EaiyCyN3p3I8RObLMT1ee9iiyCrAV\ncGYtgvoOIFSLRxY5BJGY5vRfRPabO397eOwCDCt8B1WI7I3IYCxJyY9T26bVTKD55/8NIq8hMh2R\nd+765JNfFd57XvOiyOHJ5DoFkb8jskQdn3h3TJF4quQafdL38BimrW6MObyVwzQanuf0XmAjRNap\n7YTKFYDm/vo77ItdCgu5KOYNXQ54CJFFW2F2HQ5VnaOqR2Hm5yryYrhPpdffAq+LyPKFYf8gzzc6\npCXm6cwXzsCe4NcA/pv2j8WqweyAPYCayU5kPawo7jAs/++mmEaT3ZB3AT7CTIBZ/b9SQbQ5Fhqw\nBZaebwAmFGpCsBv2h1jOznOB8xHZtYzPVa62m+UerrlOoupsiskiRA7HCv6ehJlKzwcuTULwEywD\nzBwsEUmxBqJiWXHOx5Ya+lCoblHCBVjoxk+BN9acPv2i7lVz5Uvp99kZW7LYAfs+1yBV76mFHYGH\nmTfEYJ903ZFYCsXp1KwFVv9OTYDtiXmWl4/qV9jyS61xyJUrAAFUP8SKcYL9cS7A4hIz1sAD5ZsV\nVb0cu4lNw8JR1sHiqGYBK1Ko4JGK4mYJEFYRkdLEw07bR4H7UB2eKrTcgDk2nYTqa6g+hWkE2Vrw\nTOBwVK9G9RNUX0lj+tvVdBJ28/8e1W+omU7AAai+jerzmEDdsI45vojqCai+h+p1mICuWQs0LWsK\nIlMwAbXJ3GORB2q5/rx1EkWWwRxhphS2zBnmFExb/BeqH6J6OybwT04m3Owe9d0834El/ZgKzEkm\nxNocWC5E9VFUPwDOE1joJzNnzp1dDefvjeorqL6IWWO2Q2SlGs4DW9usKYH4/sCjqE5GdQq2hrlf\nyf1VgP0L38kMrDbohzQuN/D/sAesGqlsAWhcSl589RzsqbRY/mQz4GY8UL7ZUPPE/QVWB3JhLClC\ntka4l4gUKwGcUtgvBtk77Yf3C/tZ6NEHhbbpZDUCLXfvY4ichMitiLyAJdVoyLril5jZPWMytdcA\nVObVkl4hF8iljCCvbXgNdu/IKj7UVsKopjqJX5JXjFgLWwroij3kLQNcVE04muPMSjTfWnixTuJk\ngK61x4RPQrV4fpavt7bvaJ46icmE/VMsYUrG3dh3UixRp1gqxGJ5rB0wh8VnEOlKw5hA/gAyD35T\ntwrmB2Oxaiti6nJp4PWezJtQ22kCqvoq9mQ2BjOx7IaZRhem4B2W6gRmlQH2aOFpOs1DTVpI6XqO\n3X1FfoklV18T89Q8ETP1NUQANrQGYOlcOtVyDVD9HtWxSXOahHk6jk3bF7Vc/7n0mtdJNE1ubOFa\nGZkaNoTq5ZTWwJzGSusVNpZ5Pl8dX1Dpe2an1lYnUcnrE2YMTq83IDILC63I0maWmkEnF76biOoD\nmNb5M2DL+qdbjc7UsXboAhBA9b+Y3RzM9DEW82IqcgwiR7XktDo6qvoxsDHmFQb577E0b+vw9NpL\nbI3I6bgcha0fDUL1ClSfxh5MizRn2IJga4RFBlI9PKo2ynOCsXCgxzHHndJKN2YOzW7o5gjzGbBi\nQQiMxdbejq1hXa22eTWF0vGLlzgEDkzn1FZOrnqdRJFuWGrLe6ku1NfC1no3QaS0UEEpnUpey/2M\nS5IX2q71oo6ZPyP2ndyAFXgtrQN2MSK/bemJdWRSCaRtyfN/Amwo1cNQziL/wf+5pebmNAvlPqln\n530CDEBkfURWROSPwGF2hmRmzClAmOvZ2fSwi80ROQuRfskDdHfqcZ8HQPUsVMtN0jAYM8OOQmQQ\nIitjAf3HYOE+E8iF7jnA0ckTdGUswP2vmGAphynAYois2kj/hdLvU4G7EFkHi5G+EhiO6rhaxr9M\nobAwZlVbDLgI1bcK2xisEEIV5pCYvXdPRHoj0geRpZPH7iWYIHu8cF5fRLYu2TYrmcsA4KXaPqgL\nwAxbPM5s+GtiBVkPJP/yMjX6NjxQvllJibRPLWk+uNA/mfxpc3Px9di2TENr8pWOOR0LGH8EW2ta\nF/PqVHKPx4uxhPmjsZi4umr81TcnxdbyBmA1CX8P7FdDAHfTUP0Mc/i6HfN4fR27t+yBfZ6A6mvp\n3GsxB5vjsCWCs4E/o1qbJ2sp92CesqOxeouNqZNY3P8cC1t4GFsDfZzsoaRmRmJaXSZI9wdGozqv\nR6qZf+8H9k0POArsRV4ncRxwH/ZgtGW6T2fz+jXVayQ+CNw699oWWrMGddRJrKxk2OUgchWWL3Qm\npqZ/iz3R9MVs4Z2xHJcbo1qOmcQpExH5D+a6DjARWEZTcK9YZokbU9/BqnpjDZdwHKcRNGsybHNU\n+QDz5q3NM3b+Y9r8TqhuXtsp/iQ9LydiMTTdsNijrzAvpKmY8JsNLIIHys8PiumselG9MvjN5A4C\nvhbrOG0VC704G3Neah3MW/Yw6kmj6AKwFDO3ZRUjNgZ+l1yz98LU7i6YJrgsHijf3DyErcNmFM2g\nVeRB86vXkDXGcZy2guoNQCdEtqz33PnDIcDjqD5b10kuAGtC9X4seBYsK8RyWOzaCamtMyYM18A0\nE6cZSEKuqAVuISIrF46zpznBE2Q7TttGdUtU/9NK7301qn+o77QOKQC3nTKlObSyP2HrUAsDV6UF\n3b+SpwDKFnh3QmTrZng/x7gN+94zDsx2VPUlLPYKYN+WnJTjOB2PDikA/zhhwk1UzybScCyPXLbW\ntAPw2xSDcxjwTHZWev1bwUXbaQKqOg24utB0YEkliEwzX1JESuO3HMdxyqZDCsBuqmthJY16NPFS\ntwGPpv3LEVkcc9nfFQuWz7TAAPyxie/l5FxJnj2kDxYnmHFWLfuO4zgNokMKwMQWwJ1Nyp1XvWLE\nksBFqX0C5qFYrCl2Rir34TQRtZRSdxaaDin0fUmeW3IrESlNueQ4jlMWHVIAftWlS1aIcWcs91zj\nP6fqR+QJmfdHZKvU/l9sTTBjYSx7jNM8FJ1hthWRZQvHV6TX7lieVsdxnAbTIQXgfsstdzn5DXR/\nLIVZU9IlXY4FwwNci8iCaf/PWPBoxgGI/LwJ7+MkVPUN8rCHTuTJdAGuI0/Qe3zLzcpxnI5EWebB\nEMKxmHZTzP69NZaeahiWqug74KwY47DCuKHAQel9bgWOjjFWpb5BWL69pYAngYNijF+lvgFYlfDV\ngfeAw2KMteZzK2VWp04Ax2CV3Q/AAjIn0dg1I9U5iByMpWhaARN8R6M6DZHfU72a/OWIbIi59DtN\n469YOSqAw0VkqKpWqeoPYmVyNgb6i8jiWnttOMdxnBopVwNcCzgxxrhwYXsey5QyGRNiuwEXhBDW\nBwghDMGcF/pjZTwGYkKJEMKamKffHsASWG2sm1JfD6xa8I1YxpXLgJEhhEzrKg9bvzsUqy0FcCYi\njc9MoPomlrgV4Ii5mp7qw+SeiWDFIN1Fv3l4CMtpCJZ4oJh4OPtbCOl35TiO0xDKFYADsMSqcwkh\nLATsBJwRY5wZYxwF3AHsl07ZF7gkxjg+xjgeu2ENTn17A/fFGEfFGKdjAeZbhxCWxLTJOTHGa2OM\nc2KMN2FV2ouegOWhOhvL4PJYavkbIvvVMaI+zsVqlVnFiDz04ShMA844H5EfNeF9HOYGxp9faPpT\nYf9h8uKqB+I4jtNA6hWAIYSemJv/ESGEL0IIb4UQDgBWAWaVJE59F+iXDaV6vah3UxvpnLl9McaJ\nWPBzv9K+7JTCdRuGJVP+DfBiahmGyE5NuNbBWPxff7L1J/NaPKlwZm/gtEa9h1PKreSCbjsRWQLm\nCsf7UntvEVm7psGO4zi1UY4GuBTwLHAVVhHhUKx8x3bADyXnTgOygo8LpuNiX6cQQnegZ0lf1t+z\nnr7Gofp9mu//sDRmd6fK04251vPYdwFwGiKrpf1rqV536khEAk6TKAmM70QhPyjVvW5Lyyk5juPU\nSb0CMMb4UYxx8xjjwzHG2THG57AA8V8ApYHmPYHv035RGGZ9s2OMM6hZoPXECjmWjiv2NR7VicBW\nWJmObsDIJnhsnkxeMWIYIl2S08uh5N6JXTCTa1OLdTrm0Zs5FR0h6TtVq7T9eWrfVjwbj+M4DaAc\nE+g6IYSTSpoXwAoUdgsh9C2eTm6+fJvqZsvSvrnaUQhhCaz8zdvYGlup5lRqTm0cZqr8FXbTXBCr\n5rBGI64zmbyC8QZY4cosNvDiwplbY5qn0wRU9XNszQ8sM8zAQvf16bU75ojlOI5TFuWYQCcDp4UQ\ndg0hdAohbIF5b16BVdodGkJYIISwHjAIq3gMMBw4LoSwbAihN7ZGdlvquxPYNYQwMHl9DgUejDFO\nAp4AuocQhoQQuoYQDsTMsI80yydW/RDTBCdiQvdRRFZqxHUeJL/5noXIWnP34ePCmX9DpHvjJ+wk\nTinsn1nYv4o8J+txLTYbx3HaPeWYQN/DnqxPx4Th5cD+McY3sBRVXTFz4D3AsckbFOzGNAILIB+D\nrSNenK45Oo0dhnl49sHi9Ugm0m0wYfoN8Adgxxhj6Xpj41Edg2ln3wNLA48hsnQjrnQ0lhO0K3Ab\nIj1QnQoMKZyzMnBkE2dc8aTA+PfS4eZZPUC1pOWZh/JaIrJMa8zPcZz2h1i4XMcghLAClpllxRLv\n1JoR2RyLNeuOOchsmtYKy0dkY6w6hAAXonp8av8HuUluGrAKZspzGomI7EmeI/Q8VT0lte+LeYsC\nnKuq7hDjOA2gwffODkKHTIVWNqpPYubcOVhx2wcbXEZJ9TngwnR0LCKbpP0jyB2CelI9ns1pHHeT\nO0MdVmhTDh6MAAAgAElEQVS/h7x6xCHijkeO45RBZQtAANUR5IHU62NllBq6Znc68CamBd6CyMJJ\n2ys6D+2DyEZNnm8Fk2L/bkyHvUTk16n9B/I14qUwxyTHcZw6cQEIoHoreZaRhpdRsgD5fTEtZEVy\nT9CrgVcKZ16Ol+9pKqeSh0QU4wCL3rdHt9x0HMdpr7gAzFC9HDgjHe0CXN+gMkqqozFNEOBgRLZH\ndQ4WG5jdsNcmOfs4jUPNyejpdDggywyT2r5N+ztKXrHDcRynRlwAVufPwN/S/mDgogYGsl8I/F/a\nvwGRJVF9vXBNsDyhizZ5ppVNpuEJqUhxMo9mYTbdgF1bYV6O47QjXAAWMZfYY4CbU8uRNCTFlml8\n+2G5K3sD1yQBegZ5xpJe5Jqm0whSSMS4dLi75Jr6tYXTjmrZWTmO095wAViKaRKHkJdROhuRPzZg\n/Afk5Xl+A+ydcpEeXjjrT4is3gyzrWQyz9sFMDMzavGdY1P7WiKyYmtMzHGc9oELwJrIyyg9nlou\nw2LNyuU68iK5VyDSF9WRwMjU1gm4yvOENomryAs0n1zSnlFMnO04jlMNF4C1YZ6dO5NXeLip7DJK\nZko9CEu3tkga2wnLEDM9nbUpVk/RaQRq5uZ702FfEVkv7d9OnhrtUGmII5PjOBWF3xzqwkyX25KX\nUborZY8pZ+wX5GbPLYA/oDoOOLFw1lWIlFbUcMqnqPn9FUBVvwSeT21LYAWWHcdx5sEFYH3kZZTG\nYinTyi+jpHo3cEc6ugCRflgS8ayyxdJkRXWdBqOW2PztdLiJiCyb9q8unHY4juM4NeACsBxMm9sS\n+AJYCCujVK4TyxDMA7QH5qbfCfMUzcx0pyLSt5axTv2cm16FXCO8j3x9cMcscbbjOE4RF4DlYtrG\nr8jLKD1GOV6GqpPIg9/XBU5C9VXMUQasksTVNQ11yuIfWLJxgANFZMFURT7z4u0K7NkqM3Mcp03j\nArAhmJv9NliS62Uot4yS6qPAlenodETWxUyfWeaS7QpJtJ0GoKozgVvSYQ8sgQHkOUMBft+Sc3Ic\np33gArChqL6MeW/OwGr9/avMvKEnYPXsOmOm0FlYvGHGcM8T2mguK+yfnDw/nwImpLY1RWS1Fp+V\n4zhtGheAjUH1CSxOEKzywIl1nJ2NmYqt/VUB/bBEzv8k91hcHi+c2yhU9R3gtXS4DLBdCpO4qXCa\n52B1HKcaLgAbi+q/gGvS0RnJrFnfmBfJKxgcibno7wXMTm3nItKrmWdaKVxa2D8hvd5aaDtYRLq2\n4Hwcx2njuABsGscC7wNdMBNmzzLG/Bl4Pe3fDHwHDE3H3YHrm3mOlcI9WA5WgIEiMkBV/0cecrIY\nsHWrzMxxnDaJC8CmYGbNfbCK8oFyqr6b08a+2BpiX0xzORv4Mp3xG0TWnh/T7cgkz89bCk1ZMuyi\nM4ynRnMcZy4uAJuK6kvksWhDSFXK6xkzhjxmbX9gB2D3whn3eJ7QRnFDYX+QiCwD3Ekec7mdiCzZ\n8tNyHKct4gKweTgHGJX2b0Jk8TLG/I28sOt1mIfog+l4ReAPzTrDCkCt9mJmXu4C/EEticETqa0z\nsHdrzM1xnLaHC8DmQHUWZtb8AUtvdk29GpyVXRoMTMFyVl6POcRkGUwuLHNN0anOdYX9w1Nl+JsL\nbYeIa9eO42BPyWURQugNvAkcEGN8IISwGDAM82T8DjgrxjiscP5QrCJCF8wb7+gYY1XqG4SZDZcC\nngQOijF+lfoGYIVNV8e0osNijFlFhraLakTkWCzgfTdM0xhez5iPEDkC+x53wKqYnwhcQp46zSub\nN4w7gIuxOoGLYaEnt2IPJwtgv6u1gVdba4KO47QNGqIB3oilAMvWU64HJmNCbDfgghDC+gAhhCFY\nFYX+wGrAQFKR2BDCmljqrz0wzedLUrxWCKEH8O/0XotgAc4jQwgLNvoTtixXAw+n/SsRWb6MMTeT\n1wm8FBgBfJiOf4PIms06ww6Oqk4G7io0HYkJv3sKbR4T6DhOeQIwhHAYlv5rXDpeCMuGckaMcWaM\ncRT25L1fGrIvcEmMcXyMcTzm5j849e0N3BdjHBVjnI7FbG0dQlgS0ybnxBivjTHOiTHeBIzHhGnb\nx+oAHojlC/0RcAv11aOzMYcCX2OJtm/G6hBm3Dc/ptrBKYaSrIr9fm4rtO0jXobKcSqeegVgCGFV\n4Giql5VZBZgVY/yo0PYuluEELCTgrZK+kPb7FftijBMxgdGvtC87pXDdto85XRyajjYjd8eva8x4\n4Hfp6BdY0u1MY1kRkT827yQ7PC+Ql0kC+/0+QR5qsghejNhxKp46BWAIIVu/GxJjnFToWhAzKxWZ\nhq2xZP3TSvo6hRC6Az1L+rL+nvX0tR9U/0meheQ8RPqXMeZe8ji287A10uw7vhCRBWoc58yDmlZd\n1AI3x8zxxTVZN4M6ToVTnwZ4GvBGjPHREELmOSeYUCo1IfXEzKRQXRhmfbNjjDOoWaD1xLwhS8cV\n+9obfwI+AbphWWK6lzHmiMKYYZjmApYh5u/zY5IdmCzheMZRVDeDbiUiy7XslBzHaUvUJwB/C+wZ\nQpiEmSmXx27E2wLdQgjFQq5Fs+fbVDdblvaFuR0hLIE517wNvFPsq2Fs+0H1O/LCt2ti2V7KGTM4\nHQ0AlsPMxwA7IrJOs8+zg6KqE4B7C02DsHXWN9OxkK9ZO45TgdQpAGOMq8UYF40xLhZjXAzTTvaI\nMZ6DeSsODSEsEEJYD7vB3J6GDgeOCyEsm8InTiJ/+r4T2DWEMDB5fQ4FHkwm1ieA7iGEISGEriGE\nAzEv00ea92O3EKpPA39NR8chsmkZY57EguTBvrfTyT1v7/UMMQ2iaAbtiiUXKCbIPtBjAh2ncmlK\nIPwh2E3lU8xh49jkDQpwFSYgXwbGAM9isVnEGEenscMwD88+pPWYZCLdBhOm32A3rB1jjKXrje2J\n0zCtQ4BbEVmkjDEnYxpxJyx59t2pvS9w6vyYZAflCfKQEjBHrn9hJanA6jlu0dKTchynbSDmL9Ax\nCCGsgN3wVizxUG1dLJZvFLa2dwuqg8sYsw7wIpZI4BrMXJetne6D6u21DXVyROQULFVdxuHAbzBP\nW7AHtLVTZXnHqUja7L1zPuOp0FoC1f8Cp6Sj/RGpP7uL6quY9gdwGHABuSn0NkTcjb88bibX+MAC\n44veoD8ldzZyHKeCcAHYclwMPJX2r0Vk6TLGDCVPsn0oMCTtC/AvRLZs1hl2QFT1M+CBQlPA6gZO\nLbSdLiIrtujEHMdpdVwAthR58uvJwOLAsDISZmdJtqcDywAbY+EVYH+7hxHZaD7NuCNxQ8nx78md\nk8BCb65whxjHqSxcALYkqh+Ta3FbY6bN+sZE4Ph0NAiYRF5LsDPwFCIDmneiHY4HgS8Kx78E7gdG\nF9q2xdYGHcepEFwAtjzDydOcXYTIqmWMuRJ4PO3fCLwC/CUddwVeQGS1Zp1lB0JVZ5MSrgNz0usQ\nTCOfXTj1MhFZuAWn5jhOK+ICsKUxt9vDMI1kASxLTNd6xlRhtQLfwzxJ78XCTK5MZ3QHXsHXseri\nxvTaOb3uhYXhnFc4ZxnKSVjgOE6HwAVga6D6DXkuyvXIPUTrGvMV5rr/GZZr9UEsPCIL7O4JjEZk\nmeaebkdAVceSa9GzyAPjz6W6KfRPIrJ2C0/PcZxWwAVga6H6CLkGdyoi65cx5mNMCH6DFXt9FDiL\nvGTSwsCbiCzR7PPtGGTOMJnGfRgWZzmY3BTaCbhGRDrjOE6HxgVg63I8luuzMxbbV3/hX9W3MQea\n74Glgccwr8bH0hm9gP8hsuj8mHA7514spy1YbODiwCmq+gbVTaHrkZenchyng+ICsDVRnQbsg2kf\nqwAXljnuFWBHYAawEpYrdRDwf+mM3sB/EVmomWfcrlHVGeQm4ywO8CQR+QVmCv1v4fShItKnJefn\nOE7L4gKwtVEdRe54cTgi25Y57klgD8yrsT/wb8yV//V0Rl/gNa8jOA+ZGXRh4CMsqcBwbA11MLkp\n9EfAJS08N8dxWhAXgG2DocBLaX9Y2Wt4qiOAg9LRhljS7E2xslJgWuVLiHRrvqm2b1R1DFYxHuB9\nTIvuizkUlZpC9xSRrVp2ho7jtBQuANsCFqe2L1YQuDdwXdllj1RvwfJbAmyFufv/HNNuwLTDZxHp\n0owzbu9kZZI2I9e+98D+BqWm0KvFtWjH6ZC4AGwrqL5HnpR5FxpSrFX1UvLE2btjab7WAj5PbT8H\n/oOI/72Nu4EpmAdof+Dh1H4lpg0OJg+YXwmry+g4TgfDb4hti+vIEzdfjsgKDRh7BnlYxaHAiVgl\n+gmpbVNgpBfUBVWdihUaBtgTi6n8GlgIWw/8H9VNoSeJSL8WnaTjOPMdF4BtCcsSczAmtBbGCuiW\nF49mY/8E3JFaTsTWB/sD36W27YC/uxAE4DJyzW8oeX7VDbCiw+dgghBSTUZPlu04HQsXgG0N1S8x\nDQ5gE+CYBozNKk5kWuT5wA7Az8jd/n9LvgZWsWj+XX2FZdb5HXB16j4ViwXcj7yW4KZYyIrjOB0E\nF4BtEdV7yZM3n4PIzxowdha2DvhsarkGu5mvg5VVAjgIkYp38VfV8cD+6XBdzAnpLez/4nZgLOYU\nk3GZiPRq0Uk6jjPfcAHYdjkS8+TsiiXM7lH2SNUfMM3vDexvfAewPGbemzX3+iIVn/hZVR8G/pYO\nj077M4EfY2uq55CHlSxKuckKHMdp87gAbKuoTsbc8hVYg+qaSDnjvwN+jaVa64rlC+2Juf5nHo6n\nIXJc80y4XXMilhBbgDPJPWr3xrTpvclNoQeKFyF2nA6BC8C2jOpz2DoewNGI/LKB47/CYgM/xYTf\nA5j7/9bkN/QLEDm8WebbTkkp0gYBP2AlkdbDEo0DXIUVIR5aGHKr1FfCynGcNo8LwLbPGeTlem5u\ncJLrvILEBPIKEmOx6ueazroKkX2bZbbtFLUk41lCgR2BJ7CqGz8CbsM08A9S/8rAsS09R8dxmpey\nsoOEEH6Lld1ZDvgYOCXGOCKEsBgwDNgcc7U/K8Y4rDBuKOaK3wVLQnx0jLEq9Q3CbipLAU8CB8UY\nv0p9A4BrgdWxIrCHxRizVGGVhepMRPbBqsD3BR5CZDdUP2vANd5BZBvse+6DVY7YGPNqvD2ddQsi\nU1H9V7POv31xPWY2/g1mCj0OuBwYmPZ/i/0dBDhbRO5Qe8BwHKcdUq8GGEJYFRNyB8QYFwaOAO4K\nISyO3TAmY0JsN+CCEML6adwQLDlzf2A17CZyTOpbE3M53wNYAviS5PUYQuiBJXa+EVgEi9caGUKo\nv1RQR0X1f8BR6WgDLMn1pg28RmkFiUexOLis7I8A/6CCc1+qxVIeghUd7oGFo2TJs08HugMXpeMu\nWNC84zjtlHoFYIzxXWCpGOOLIYQumAYxGfOU2wk4I8Y4M8Y4CvM2zFJ47QtcEmMcH2Mcj62hDE59\newP3xRhHxRinAycAW4cQlsS0yTkxxmtjjHNijDcB4zFhWrmoXo09ZHyPPXA8jsgxDQpqr15BYg1s\nTfB2cnNeJ+BBRDZpxpm3K1R1IqYZK/bwNguIWM3G24G/AOPS6RuLyO6tMU/HcZpOWWuAMcZpIYQV\nsTiyW4FTgJ8As2KMHxVOfRfIUkYFLKaq2BfSfr9iX4xxIlaotF9pX3ZK4bqVi+o/MQeNt7Eb8l+B\nuxBZuAHXGAEcmI42wIrEXkGeFLozJlzXbaZZtztU9Slyp5fDMUeYWcCKwMVYrtZs/fRG8bqLjtMu\naYgTzCeYCWhL7CawPeY1V2QakGXOXzAdF/s6hRC6Yx6J02oY27OePkf1HSy59T9Sy+5YyaPyHxBU\nbyV3+PgV5uRxNnk8XFfgOUR+2hxTbqecSV6i6jRM8wOzcKyCJRgAS1lX8Zl1HKc9UrYATObIOTHG\nJ4F/YpkzSoOze2ImOqguDLO+2THGGdQs0HpiLvql44p9DoDq95gp8xjMnLkaMAqRXRtwjUvJtb7d\nsTXZo7G1V7CHnVGI9G+mWbcr1DLq7IX97pbAtOUnUvc12FrgV+l4TxFZv8Un6ThOkyjHCWbbEMJj\nJc3dMZfwbiGEvsXTyc2Xb1PdbFnaF+Z2hLAE0Cu1v1Psq2GsA5b8WvViYAvsRrwQcA8iFzSg9t+Z\nmPkTzPljaHq9K7UtALyByHllJ+XuQKjqWOD36fBXwHOYqX4RzGmr+MBxr3i5KcdpV5TzD/sqsG4I\nYZ8QQqcQwrbANthT8AhgaAhhgRDCelgwceZWPxw4LoSwbAihN1ZT7bbUdyewawhhYPL6HAo8GGOc\nhD1ldw8hDAkhdA0hHIg5fTzSPB+5g6H6NLA28H+p5TjgUUSWKmOsYl692d/sBOB4TPMZmdo6YX+7\n9xEpfTDp8KjqcHJvz5PIyyRtAvyCvPrG0uRJCxzHaQeU4wU6HssreQSWEeNMYKfkHXoItl70KXAP\ncGzyBgVzHBgBvAyMwZIzX5yuOTqNHYZ5ePYBDkh9MzABOwgLRP4DsGOMsXS90cmwmMDNsZg10v5r\niGxQxtgq7Lu/P7X8BYvd3BlLFJ197ysAbyNyYQWWU/oD8CH2Wz8UuDm1n4X9zrNyU0dLw2o4Oo7T\niogpAR2DEMIK2I1qxRLv1MpBZG/MKWMBzHPxCOAa6vtDiyyAxQX+AvNw3APVfyCyCKblFMNQPgW2\nRnVM83+AtonYw8RzmJfsLcBGmDPMB9ha7H3p1HdUdbVWmaTjNJJKvXf6mkVHQ/V2zGHjA0xjuQpL\noVa3F61VkNgReB0Lir8dka1Q/Q7V7bAMKZmmsxzwJiJXVYo2qKovkleR3x9zFpqNpUXbkby4bj8R\nOaLlZ+g4TkNxAdgRUf0v5qX779SyH/B/iKxUz7jvsETZWQWJexHZOfU9inlDZmtegsXIfUnleECe\nDzyd9k/E4jDB4ipvIzcXXygii7Xw3BzHaSAuADsqqt9i63inYibNnwGvIlJ3Rh2rIPEr8goS9yJy\nDyJLozob1b0xDfPrNGIp4EVEbkek+/z5MG0DVZ2DZTiahNUG3JhcIF6JORGBPTw80OITdBynQbgA\n7MioVqF6LqbVTcRu2g8gciZ1ueyrfoKtBWY3910xB5jfIdIJ1ZeA3ljC8mxtcS9gfEq63WFR1XHA\nwelwY2AU8C323f4Gc/oC2FBE9mz5GTqOUy4uACsBM1+ujYW0gJVYuh+RXnWM+RD4Jeat+y0W+3YN\n8DQiq6U4xMOAAcAXadQiWC7RhxFZYr58ljaAWsWM69LhUeSm0M2wtcDZ6fhGqW/t1XGcVsMFYKVg\nZXs2Js/0sg1mEh1Qx5gqVG/AMs3cnVo3xoLjz0CkO6qjsTJNl5Frg78GxiFySAd2kjkaS9rQGXtI\nyGIpT8bMoWAm5H/MO9RxnLaAC8BKQnU6qgdjN+wZWGzf/yGyfz3jvkR1DywedBzQDYsHfR2RjVGd\ng+oRmDaY1SnsgWlJozpiAL2qTsViVWcCPybPjtQFe7jIiuduKyK/bpVJOo5TJy4AKxHT6jbGEpz3\nwMIkrq7XiUX1fuCn5NreasCzaewiSRtcCbiUXBtcBxiDyJ8RKc0d265R1TfIHV92w7TAOcCqmLk5\n+w7uclOo47Q9XABWKlYgdx2sOjzAYcAziPStfRCgOiVpexsAbxbGvo3Ib1CdieqRqf/T1N8Z80Z9\nB5FfNu8HaXUuI48BPCYdg1WPfyjtL4JXjHCcNocLwEpGdQJmrjs3tfwcS6G2RRljX8YE6MmYOXVp\n4J+I3IvIsql/VfL1MDBT4eOI3IrIks33QVoPtVRyg7GE5AtiOUKfT90bYN63AHuJyC9afIKO49SK\nC8BKx9bvTgV2AiZjwe6PInJCvQ4sqrNQHYpVTs9KBe2MaYO/B2agOgTLTfpFYeS+wLuIHNgRnGRU\ndTyWHQYsAcFo7LvsBXxUOPUeEVm0ZWfnOE5tuAB0DNWR2M37f9jv4i+YRle/A4vqe1ih5AMwjWdh\nTPOzorpWYb0flvw8Y1HMI/UpRNp97kxVfZi8oPDh5InJ18aSwQMsCYwSkaVbeHqO49SAC0AnxwTZ\nBuTpznbB1u3eTjUBf15rAL3FBd6MOcZk4zfEPEXPBmaiehCwPXkhWbCA+9HJSaa0EHJ740RM+xPs\nYSALHVkVmJr2fwK8ISKrtPz0HMcp4gLQqY659++DlQDKBFU/rBbeS8AniFyJyJaIdK1h/FcpXdq2\nwMdYWrDTsNjBTVF9AFidvOgu6ZxTsQTbRyHSZ/58uPmLqs7AQiN+AJbB1gSzMkrjyb/PpYDXRGTt\n1pin4ziGC0BnXkybuwq7iW8MXASMTb3LYlXSHwO+QuQ2RHZFZMGSazyEhUxcDFQBATN3Xg9Uobon\nsCe5kwhYZYWLgU8ReRCRQfVWsWhjqOrbwJHpcDvgn1hoxEqYV2hmDl0IeFFEtmrxSTqOA7gAdOrC\nHGSeR/VYzHS3JlYS6PV0xqKYtngPMAGREYgcMDcNmupUVI/BvEuzMQdjTjK/xUyEawAPlrxzZ8w7\n9Q6s2sQwRDavM39p2+J64F9pfwiWQg7MUeYtcoehrsDDUl8iAsdx5gvt5YbitDamFb6J6p9RXRvL\nInMkljC7Cguo3xFzdBmPyFOIHIHIj1F9FROCx2Pmwd6YCXQkJgS2x6rQ/6+Gd14YW097AvgYkaGI\nrD4fP2mTUSs+fAiWFacHts75SOreHXuQyGIHBbhZRE5r6Xk6TqXjAtBpHKofo3opqpthAu1ATKBN\nx35Xm2JekR8h8hoWL/gwpvFlwffbYybBPwK3oNofcxg5AXixhnddDnM0GYPIG0nALjWfPmGTUNWJ\nmHasWJjIu9i66vdYqMnWwH/Js8WcLSI3SgcIC3Gc9oILQKfpqE5A9SZUd8Ju7rsCw7EqEmA5Qs/C\nbviPptdzgG+wtbBLsZyka6L6HqoXoLohJvD+APyHvMJCxs8wAfsFIo8jskdb8yJVC/84Lx3+EXMK\nWgP7DsA0wanYGiHYQ8Sj0n5MvY7TrhGz1nQMQggrYF53K8YYP2rd2TjJS3RTLDh+Z8yBpsjXmJAs\nhgS8C7xS2F5H9Xuswvr2WGjGtljy6VJmYIVoLwOexbK0tCpi38GzwPrABKxk0ltY9phLsDRpYEKw\nc9p/C1g7eZU6znynUu+d/qTpzD8sU8x/UjaY5TEhMBQrIwQWGJ4Jv+xJbFWsuO7FwDPAZETGYNre\noljtvWWx4rN3AtMK79g9tT8FTELkJkT6zZ8PVx6qOgv7PFMw7fh5YAtVvQkLBxmZTu1M/h2sDnws\nHbimouO0BVwAOi2D1RZ8GdWTUV0NC5jPYgvBnEEyqrC1xKx9dWA/TLN7HoupOyudcwLmaTkcSz+W\n8SNMy3obkfGIXEErZWBR1bHAVpjGuwjwkIgcpKqfY5rxIMwcXPwOegMfSRt3+HGc9ky9JtAQQhYH\nFjATzgUxxutCCIthHn+bA98BZ8UYhxXGDcU8+7oAtwJHxxirUt8gLAHzUsCTwEExxq9S3wDgWuym\n9x5wWIwxu0nWN9cVqEA1vt0jsiyWi3Rn7PfUpdCrWNmmzHmkdy1XmY1Vp/gE0yz7Yx6kpXwK/B04\nD9VJzTH9chGRlTATbaaV/gU4RVWrxJx5LgP2KBk2G9hOVR/FceYTlXrvrFMDTEJuJHBJjHFRzIV7\naAhhCyzWaTImxHYDLgghrJ/GDcHWafpjT/oDsVIxhBDWBK7G/tGXAL4Ebkp9PYB/YzkiF8FuCCND\nCNWDrJ2OhepnqF6F6lbY72lfLI5uGqYV/RgLqu+NeY3egcXWPUCeXaUL5myzE7ARJvxmYZpVcS1t\nOeBYYCIinyLyHCK3IHI8IjshsjEi/RBZEpHONCNJE9wIe+gD82j9u4gsoKpfqSUH2AX7n8jogsUK\nHtqcc3Ecp/qTdk0sD/w7xvh3gBjj6yGEJ7F/4p2AVWKMM4FRIYQ7MDPVS9gN7JIY43iYqw3+GbgQ\n2Bu4L8Y4KvWdAHwdQlgSS8Y8J8Z4bXr/m0IIR2HC9B/lfqiPPvrobyJyD/CIqn5d7jinDWBa2XBg\neMoC8ytMKOyAVVf4adrAstPcBjyHPcytjf2G1gUWx2IMF6/j3ZZN28DaZoPIt5jl45vC6zc1tOV9\ntu5Xy8fTSSKyNWblGIw9VPYVkZ2SELxPRJ7G1kAHp2ECXCsi/VT16Do+j+M4DaBOARhjHE1e5iXT\nCDfB3NhnlajK72I3KjBz6VslfVlVgX7k9dKIMU4MIUxM7f1KxgFEcpNRWVRVVe2ECWgVkVewFFQP\nAaNUdU6dg522g+o0YAQwInmUboL9xnbBBNdKmGXhGGxdcCQWUvEEVp9wHXKBuC7mRNMQBFgsbeUn\nrxaZTM1C83PgLYUxd8NBe5iJ/1wsAfmLIrKdqr6t9hBwgIjchQn4zBnmKBEZAGzpv2PHaTplO8GE\nEBbBzJOvYCacH0pOmQZkcVgLUt07bxrQKYTQHehZ0pf196ynr2xE5C3M7CXAelj6rheAr0TkThHZ\nT0RqW0ty2iLmUfoEqn8E+mKZZYoepb2x7CsPYmbR87Df97mo/grTHn+C5R/9K5bBpvQ3DLbm+D0w\ns54ZzcKccErjE8EccFbCfnvbYAHxRwDnY/9DY38LkxV2vhCe6mzXWLETvNBZZPP8I+vDWH7UewrX\n3gz4TETq0mwdxymD+kygAIQQVgTux55Y98BMUD1KTuuJ3TigujDM+mbHGGeEEGoSaD0xN/HSccW+\nslHVzHPuB8xBpwf29N8LuwHuCSAir5Jrhy/5U3U7wTy3RqXt5FRPMNMM18UE0KC0zUDkMeBe4N+o\n3kVWiUKkO1ayacu0rYcJzYUK7zYdc6yZjv1+lkvtXdNGybkfYinQJmC/29nYevYS2FrmT7CQhwWB\n9Y4lX0+YAIt0gScuFRl7hIVyjFFb8zyqE9yjtvbZCRP2X4rIrmp1HB3HaQT1CsAQwtqYgLgtxnhs\nahyRjHMAAB5rSURBVHsP6BZC6BtjHJedSm6+fBszW46qpW9ukdUQwhLYjeVt7EYxpHQKwO0N+1hz\nWYB5BWrm9iqYiWwdrBTPJBF5FPusj6jqlzjtA6vA8DZwHiJ9MW/SXbAcnN2xAPrtgSpEngXuA+5F\n9WNM0DwFnIpVa98MW3fcEotJ7JFeM77Cav59hQmjVbDsLj3SloV4zJ0d9uA4GvM+/TqN+xEmyH68\nEaz+Aqy8PUgEjoSVJsBKZ5PHRVTBd+/D62tC/x+gG/a/O0JEbgcOVTMXO47TAOoMgwgh9MZcyy+M\nMV5Y0ncP9sR7CHYDeAjYJsY4KnmBHoqZf2Zj3np3xhgvCiH8DDM/bQe8ilXO7hNj3CGZSD/A3MOv\nxZxpzsNcc2syV5XOdwXgw88+++wPU6dO/SV2A1yy3C+jhLexG+WDwIuqWpOpy2nLmJlwB0wYbsW8\nVou3sN/buLR9Utj/DFtH3IJcQ6wp72gEHsd+Lz9gwnKttJWbp3QC8OV4+GE7WPXVlB1mN5h+K3Rf\noBAfOBV7YouFwYvDrMvhoUE2jzFpG09bTvNkOU+7YsK8sdt0YFLJ9i3+v9pgKjUMoj4BeDKWs3Fq\nSdffMC+1a7Abw/fAGTHGm9O4Tlig8oHYE/htWBygpv7d03X7YNk+DogxTkh9/dN1+2NPzofHGF8u\n58PU9EcUkZWBX2PJh7eggeuJiZnYzfJR4FZVHVPP+U5bw+oVbo0Jw+3JU5DVhgJfUF04zsa0tlWw\nkItS60IVZvV4DMtf+iGmDWYCcWVMqPahFuvLTOyJ8tZ0PBB7Clsi7549EzrvBN0fLhl7OLbImIIf\nM6cbLdkoo62cc2pq60z5wqus5ZdG8j3zCsZ5BWVN7ar1rf12SFwAdgDq+yOKrfkMJBeIa9ZwmRnY\nP2ddMWCzsBviC8AFqvpmkybutCwi3TBT53qYQ01fLOSnL/ULxiKzsJttZ0zulFZymIY94P0nbW+i\nWpXqGvbChGG29cn2q2DpU2D1v6QQjpUxM0TRDluFCbzrSt5weSxAt4NW2Z2BPQTMxL77npgpuTmZ\nRu0C8hvMhD2hsH0NTKwr9KU94AKwA9DQP6KILIMJw19j94zFSk6ZjQUld0l9NSVgBnPVP8RjDjsA\nIj8iF4pFwVjcr+13UB9zsBvsFCyJRHZDHY9pa5+ntonAN/1g02iWlm5dYMrpcNFpdmNeGuhTBUuf\nCGteaMKzGgdi6ZsaGPcxGzPjZtv0tBX3i9uM9DoLE/6zyQVUJqSqMO0weyW9Fh8WJG2dSrbsQbQL\nubm0e2HrlMYV+4paZulxTe3NRRYvmgnFCcwrKIvH37WFZO0ZLgA7ANkf8Ztvvtl0woQJzzRkrFjW\nj/XItcOfM2+YyJeYOawndiMsPn3OwgL9z9IKNaNUBLZ2tQQ1C8bsdRmaKc/us5hHz0TsLn8pjDsc\n3seccL4AvjwAVrvZklBU00AXhiknwdMnwIRO9gDXq2RrrCAvZQ4mAGaTC5fu1G1FqXSqsIehqek1\n2/8h7X8LnInquy0xGReAHYDsjzh27Fhmz579Kubu/g9V/aih10pxVluSC8TSRMqKOT4sQ/UH7UmY\ndepu7UhfrlM+Il2w30VRk1wLiw1cDPu9LIQ9SNVbAPc9LBXS++n4jLQVB47A8hHW5P2xNeiVMHMl\n656D3XznpK24nlck0646k2tjxc2Z/4xDdfmWeCMXgB2AEgFY7HoJuBsThuNqGlsXqUp3f0wQ/hrL\nSFKMAZuIrQEV294C9lbVNxr6fk6FYL+rH2EaZXHrg8UbLo15ki7+NfTaGZb6v6RZ7gP8f3tnHiVX\nUe/xT/Xsk5mQxDBhSdieUBgICCqIRwUUfY+HYBQEA4qocB6b+g4HwQ2VBz4Eno8nqIAIgixxYZWg\nAkc2VzZlM1iJJEMWsxDIMvvSXe+PX930nTvdMz0zPdMz3b/POXXu7Xtv99Sdvl3f+lX9fr/6EQNN\nuCcQoUx6rIF463wdSZmTDF6sQJLOPPGhWcg9PGtyXJdrKHeo7UjZjPezRvneEaECWAZEX+Lua9Z8\n+eHOzjcja8Ml5/X+iFiGd4blaEaMMaYJWbXgZCQxQPSAtyMBzvEH/l7gTO/9htH8LUWJMMbUGbjR\nSz5dZsLzv4ErDxEdnA3MeQTmfxTevzWPzllI/xA63ysvI+suWUpFZJX2J7b59qsRbY9iMBsoryXe\nvh/W0hx3VADLgOhL/O2KFem5/f3fexQueZ/M5Z2IuL/HPfw8kkT5Z8Bdow18N5KF5GtI1pFI+HoY\n2DnvA64ALvXed6MooySMRkSjoBBGSL33/4hdk1x2KRe3AOd5799I/gEGO6DE93Mdi4pneNHKJ3CZ\nMcctSt1ziWKx9tNkPVGT21zHxnJNF94PG/tcLFQAy4CYADJXhkA3AhcAtxrpEX8AEcOFDFwrziPB\n+T8D7vbeb2SEBCG8CEmzFglhmoGOAJuBs4Gf6fygMhaMMacio6A1iOfoQu/972Pna5H1OC9i8Px1\nRBfSebtKn8fKplIFsJyGC7bzWnX1VYh7dgtwM/A7D/O990u896eG4wuBxciUiUHiwq4F1hljHjbG\nnDGShMMhi//JSJ7UxWQDg+PMDOdeMsYcPIZbVCoc7/1PkA7dZiRe8LfGmEWx873e+2uR3KMXIPPU\nSRqQaIn1xpiTgnWpKBVDWQrgx3fb7WokA8e94dC7gGcw5gcYM8t73+29vy8I1o7A8YiTTCfyPzkK\niTHeYIz5jTHm08aY5FxiTmJCuD+S+zFXz3o+8Kwx5h5jTL7euaIMiff+cSSZ9wok9OAOY8zX4kLm\nve/03l8J7IlkZ8qVWL4FeVZXGWMWGfFiVZSypywFEADvW/H+I0g+0uXIvZ4FLMOYM0I2Drz3Xd77\nu733JyENwUnAXYgFWYV4fd6EiOGSsJTSsNlCvPdLvfeLGFoIFyKNzqXGmGRaLUUZFu+9Q9YT/GM4\ndAnw4zAEGr9um/f+m0goxv8gz3eSuciKE6uNMf9pjGnOcY2ilA3lK4ARsqbaAuDLiIX3JsS6+zPG\nHDLwUt/hvf+59/4ExDI8GbEie5C5lmMQ54GNxpj7jDGnGFm1fIg/v10IFyBzjEkhrAa+iqzxdrIO\nQykjJWQgej/S0QJZxPrBXKMW3vtN3vsvIkOj15I7dHAn4CpgjTHmCmPM3BzXKMqUp/wFEMD7Hrz/\nNuIV9/Nw9B2ICN6AMbMHv8W3e+8Xe7EiW5CVKe5HPDprgeOA24BXjTEXGWOGjNfx3v/Ne/9x8gvh\nTGTZpxeNMe8Y7a0qlUnwLj4FSTIPMqf9vDHmYmPMPjmuX+u9PxtZbuxWco9QTAe+CKw0xtyu89ZK\nuVEZAhjh/WpkqPMoJIuLAU5HhkXPRtKh5Xib3+a9v817fxwihqch+Yn7kfir/0KGMr8zXG85JoQH\nIGKcbHj2A54K84O7jvZWlcrDe5/x3l8EfBp5Nuch8e/OGPN0GNbcKfGeFcExbAFwd56PrkZGQ541\nxjxqjDnWhCkERZnKlOVDvKS19UaMuRpjvoAxx2LMfOJzbN7/FjgQOB8JXp8JfB9xlHnXUJ/tvd/i\nvb/Fe38MMp9yFeJJOg04D1hhjLnJGDNUDBbe+5fCvGM+IVyI9Ly/Ndwwq6LE8d7fjCzX9H9Iom2A\ntyPP6lpjzINhLrs59p6/ee+PR+JmHxri448AfgksNcb8h85dK1OZco8DTLIOWQB1RWy7BZkzOSF2\n3U+ACykwOD4Mf54DfIGwhA0iaPcCl3vvnyzgM/ZHYrZOzHF6M/B54A4/iTLIK5Of4NH5PmR49KNI\nDtKILkTMbgcejCdxN8YcDnwLWT4sTjLJwyZkLvH7mu1o6lKpcYCVJoBD0YUMiUarhncjQvhd4BW8\n7xnuA4wsuvoZxLKMJ7F9DFnl/qHhAo6DEF6MNFZJliK9+MeAVzR4WRkJYSThWEQMj2ZgUuvXkZGI\n24E/eu99cMj6N+AyZMQkzlrEWSaaNuhFpgWeA14IZaV22KYGKoBlQPQlLmltfXzv3t4mZPXuOYw9\n/69Herrrya7bthZZGmk58BKxtQCNMTVIRpgLkTm9iOcQIbzLez+kQhtjFiANzzF5LnkdGap6BHgU\nWKGCqBRKSPLwMUQM35043YqEQ9zuvV8a5vuOR9L57RG7rg9JNH8AuRem7QBeJCuILwAveu+3FO1G\nlKKgAlgGjNECLAZ9iCW5DXgjDRtuAHM52FZxSADAwAovawfePFxu0CCEVyNzL0OxAXgYsQ4fQwVR\nKRBjzB6Ik8spSJKGOM8hVuFi5Bn7JBJHGPd63oiEYMxCxPAtDN3pXMVAUXwBWD5cp1AZP1QAy4Do\nS3ygtfVPb+7t7UOGZ6KM91WJUoekgmogu8L0uC3g+XvE9HsgdqwF/NnQ/jlYPyu7YvR6JG3VNsRB\npwPouA7mXQknroZ9+gYm9c7HWsQ6fCyUlSqIylCEIc8DESFcBMS9kD3yHN2GhAN9FknIXR+75lWk\nEX0FEct+JJ52L8TLdJch/nwPMsQ/QBhHk5dXGTkqgGXAmL9ECRx+K+JBF23fQn5h7EISXtcg8ylR\nJv28vIiMIy0ObwQZOzoL8aApJC/aJmQB1MXgnwG2FrDe2HRoXwCth8LKj8Dyw2BjlVisfcj8Ta79\nTqQxW4XO5VQURkKC3ouI4QkM7HT1AEuAO5FMSacyvEd5OzJsvwXp1NUhFuOuSFxtPjYw2Fp82Rcw\nJ68UjgpgGTAuX6K4ee+PzJOczuAholHRimQh/hHZnFS1SIBhlKajUF5D0tPcAzxP7gVRk8xFXAOP\nCGXPoS/vQuY6/x6KC9tleN8+gqoqUxBjTD0yF31K2MYFawsysPFm5LGahYyqjIY+RFyrGWhZJkmT\nfQ5bkd/8yrDf6r0v5CegxFABLAMm5Es05u3A94BDi/FxG4FrwgdGngEppMt9IXDwwPjAgtKkvQpc\nj7RKf0dMuuGYR1YQDwe/Z+GrWK9hoChG+2vGvL6bMukI6dWOR8TwcAY+Jz3I87AW2BrONSGiuCOS\nNGIiFqR/DQlxamWgOK4EVqn1OBgVwAKw1h4C3OOc2zW8nokkij4SeeAvds7dFLv+MmSuoBoJKTjP\nOZcJ5xYhcUYtiBfjZ51zG8O5g5A2fD5ieZzpnBs2lm7CvkTxijsNic2bidxfNAya3C+INuAGxCqM\nL1P/QUQIj6RwRYrjgb+Ez34YaQUKGcuch7RuuyFutC1kXWpbkBZtmDGvDmAZg63G5XjfOdL7UCYf\nxph5iLfzJxDnl0LoRYZCOxFLrgH5DTUN9aYi4pF+ZyvyfMbFcSWwthKdcVQAh8Baa5D0Sv8L9Drn\nWsLxO5GG7gxk8vzXwDHOuSetteeG4x8MH7ME+Llz7kpr7QHAE8h6Zi8iRtAuzrljrLX1wD+QrPY/\nQuYXvg3s5Zwbcmhj0n2J4lQQrZpdQ36h3L5dDQ2nw9F/gE90yJASALPhHyfBkvPg1b1k/mQGMi+T\nazsDyUwziB5ECG9BvoDRehikwh95EyKKuyCV3YmsWMa3sW6/R6yEpQy2Gtep1Tg1CZmP5iOPwVyk\nDxVtd2UEnUGyK69HcbmF9P18gdcNRwaZZl+NeKuuRZzSOpHO+FOISJbVczrp2s4JolAB/CoSM3Qb\ncKFzbkdrbROSoWTv6B9mrb0aqHLOnWOtfRK41jl3czj3UeAS59x+1trLgTnOudPCuVnIsMVOSMqm\n65xzu8f+/gvhvb8Ypp57UCZfYnBC+DDwJSRxd5z1DLSqou0q7306fEA1Ioj5RHIHYIaDnX4Kdgns\n8RLs0D1O6fHqEWefGcg42BzE4WcesHsoO0J/I3RMg21NsKlanol1oUTxl6vD605kbrJbHXRKjHT0\nGhAR6k52YkIcYQtZUUwK5FxEJCdieLRY9CGd/9eRZ3Ip8CfgWWCN9z7XuouTlnJqO0dCob2yG51z\n37LWHhE7tjfQl/hnLQM+EvYt8lDEz9mwvy/wh+iEc+4Na+0b4fi+ifeBNPBD5tYsN4KQ3W2MuQcZ\nAb2QrDW9UyhHJN7WY4xZxmBhdPl+kBbxZf8G2xuqg4APIZlo9qNIoSHdoWxEHoQ8xEV7nmGgqVyL\nmL71oTSGMs0YmsBPg3QT9DdBXzN0T4OOGdA2A7bNgi3ToX06tM+Ebc3QnooENFt6Eq9zHcu+LmSo\nTMQhCsPxQP9YrNzwHdUjgpPcJo/VIFZRZBmZ5GsDZgeonQWNM6CxGRqboKEBGhugoR4a6qCxBhpq\noaEGGqpj2yop9QZS4SYzGNNtoMvI/7fzWumsdBJCejy0eXm9HlhpoCMD3WuhehU0roemTTC9DWZ2\nwexuaOmGN3XJgMNkWay3huxoy78gv8Wzo5NhVbP+FHRVwdZa2NAAq5ph9WxoPRCWnw0rDpLnyeco\n3WgIyLhT0MPknMuVE3Ma8oDH6STrATYtvI6fS1lr65B2KzkP1Em2Tct3ruIIQy2PAI8YY+aQ7STY\n2HZPpFGrQ+KtFiQ/xxjzT3JbjaujdFVh+2woF4e4sB2Q3vuOQMtOsPsecGCDdIB264Adt0D9JsSJ\np5immCcbj5F80HIQ18t6oDnUecg3JNUh1za5v/1YYunG+BhctJ/0YDLhffF4mcRne8BErWAmlDTZ\nsJli4pHvrYipWVJkf8eVTnUGmjPQ3AdzO+BtmxAz62lkfgfkH1ZDNjC5CVH6C4y5/XjvP1GKilcK\nY+lNdTLYVbkRifeJzjckzvU753qstbkErRHxBUm+L36uognJhjcAj8ePBzf1vRkoitE2yvi/Syjv\nS3xsVx6rcZmXEIeofcxvuBkzAzi4D962Ad75OrxtK+y+ERnD3BhKtL8O+taD3zZ0/Ne4E4nMJEMX\nRK4wMogZ2INkv9iABN8ugpN7xcFIGSfGIoDLgVpr7Tzn3OpwLD7s+TLSCD+d51w0HIq1djbiWPgy\nYnGcm/hbFknHpOQgpFN7MZTtBAtuZ3IL4+5IY9uAODAlkx1jjFmHzPO2Jcq2HMfakLRZTwBtC4Ev\nwZ7Hwr51cDBSbPibNSAWzeuIKK6FTSthdRv0tEOmHdIdkG4H3wG+HegC3wmmC1LdkOqRUtUH1f1S\natLSkW6skk5TfUaOFWXYbDiLMeBNzPjzwwharrEvZezk+Y68Gbzvo9cM3G7/7nywyDNgMrI/IZ2U\ninNFLQGjbhicc23W2vuAy6y1ZyDB4ouQLPMgDjNftNY+gnyXX0ZWngZJhPK4tfYmZLjtMuBXzrnN\n4fq64EV6PZJ7sAV4cLR1rVTC8GnkPPJo/FxYGSCf1Rh5kO5MYclpBnFvKIEuYFsKVkyD9CyoaoH6\nnaF5DjRPB9MMsxthtkFM1rhPvB/FfgbSGehLQ1c/9PVCXw/0d0O6F/p7IN0HaRNGGGPbfrL70chj\nGshkYsXL58ePpTOQSYfX6dg16VAMZGogXQuZWsjUQbpOtr4O0vXgG8DXSqOcSmXT+KVMLKWfh6oM\nVHuoSsswW3Uaqnuhth9q+6C+B+o8VNVCpjr8zRror5XP76+VYz6UTF3Yrxt4zNQEQffS+FdlwKQh\nFUQhFe2npb5poM+EQjarUK+JbQ30xF73hte9QG9Ktj2pYBSloDcDPR3Qvw36NsvoQXoNpA8APgA1\ne0NtrTyzTcg2XpoyMK0LmttkXnF6p5SmbpgWSkMvNHbL/622SzpZ2ycuu8guFVMTnq8uZEKzHdgK\nfgv4zbJN9RYokAb6aqAz3LvPyP+zJiMjI8bLyi/KODIaAYy3NWcA1yFu7e3A+c65yOL7AeLs9xTS\nK78VCaPAOfd8EM2bEGeOJ5AwC8IQ6dHhc/8bsTSPc84VMA2kFIqXWLznQ9lOsBp3RYRwL8R5szlR\nch1rJn8GkAagIQNzIlPx1SLfTw6inK9DZRQpG6LGOV4i76WRdCBG09mI1yGK+Ykn3R3L63zn6oCX\nkMYlKVa5tuMxfxojPjBQMB5qeofI6ztfHAq/MpaKKUOjmWCUohEWX80ljMMJZ3SukRG0uykwoaRS\nkKrKsx87ljJgqmLHEE9ITNxHJVZ84nxiS+yayCXGmDwNYprcCVfjx8a5oVbyUC3WZ08VdBspnV5K\nRwba+6EjBalqqK+SUpeSUgvUGqj1oe/hg1XuxTKvCpZzKg2p/jCcWghz4bXV3reM421vp1Lbzsni\nUqyUASGDxuZQlGwIROSdmiIMp5IdWvXxsIhggSeNudpRHotCL6Bwg28sx+KrrhRiyA3aT0F1FdRU\nQ00Kaqtku70YqA6lBhke7UhDWz+09cDWXgmxyGcI5jMSu/sm0BIIMb4Dvrt9oXEfmN4EO2yGPbug\naRX8cKLqVKmoACrKeCGNaiR0BeWfDPO2vRSWwlWZgoQY3zTZPPhJnpjA6lQ045L1Q1EURVEmOyqA\niqIoSkWiAqgoiqJUJCqAiqIoSkWiAqgoiqJUJCqAiqIoSkWiAqgoiqJUJCqAiqIoSkWiAqgoiqJU\nJCqAiqIoSkWiAqgoiqJUJCqAiqIoSkWiAqgoiqJUJCqAiqIoSkWiAqgoiqJUJCqAiqIoSkWiAqgo\niqJUJCqAiqIoSkWiAqgoiqJUJNWlrkA+rLUHAdcD84HlwJnOuSdLWytFURSlXJiUFqC1th64H7gR\n2AG4GviltXZaSSumKIqilA2TUgCBI4G0c+5651zaOfdjYAPw7yWul6IoilImTFYB3BdYmjjmwnFF\nURRFGTOTVQCnAZ2JY51AYwnqoiiKopQhk9UJpgNoSBxrBNqGeV9V2M611ha9UoqiKGXK3LCtGvKq\nMmOyCuDLwLmJYxa4fZj37Ry2vyt6jRRFUcqfnYFXSl2JiWKyCuAjQJ219lwkFOKTQAvw4DDvexp4\nD7AOSI9rDRVFUcqHKkT8ni51RSYS470vdR1yYq1dAFwHLEDiAM9yzj1V2lopiqIo5cKkFUBFURRF\nGU8mqxeooiiKoowrKoCKoihKRaICqCiKolQkKoCKoihKRaICqCiKolQkkzUOcMSU8/JJ1tp3A99B\nkgFsAq5wzv2wtLUqPtbaOcCLwKedcw+Uuj7Fwlo7FwnpeQ+wDfn+riltrYqHtfZY4DJgN+CfwMXO\nucWlrdXYsdYeAtzjnNs1vJ4J3IQk69+K3OdNJaziqMlxb3OB7wHvBvqAXwDnO+d6S1fL8acsLMBy\nXj4p/Oh+CVzlnJsBfAy4zFr7/tLWbFy4EZgFlE1sjrXWAPcCf0Pu7V+Bb1pr31nSihUJa20j0lh+\n3Tk3HTgduMVau1tpazZ6rLXGWvsZ4CGgJnbqBqQD0wKcAFxhrT20BFUcNUPc223AKmAX4K3AO4CL\nJr6GE0tZCCDlvXzSbsD9zrmfAjjn/go8CryrpLUqMtbaM4F2YHWp61JkDkUybHwpPJtLgcOAZaWt\nVtHwSI7emiD2Huhhamdi+grweeBSwABYa5uADwPfcM71OueeBu4ATi1ZLUdHrnurRb7DS8O9bUDS\nTpZVG5OLchHAsl0+yTn3vHPuU9HrYBG+B3iudLUqLtbafYDzgLNKXZdx4GDE+rvSWrvOWuuAdzrn\n3ihxvYqCc64L+BTwY6AXeAI41zm3tqQVGxs3OufeCjwTO7Y30Oeca40dW8bUa2MG3VsQvWOdcxtj\n1x1HGbUx+SgXAayI5ZOstTsgQ73POOfuL3V9ioG1thr4CdJobi51fcaBWcgIxWvAPOA04Jowrzvl\nsdbuASxGhj4bgGOB71prDyhlvcaCc259jsPTgK7EsSnXxuS5t+2EIdKrgX2Qed2yplycYEa7fNKU\nwVq7J7AEcfA5qcTVKSYXAc855x6KHTOlqsw40AO84Zy7PLz+k7X2LmQ47felq1bRWAj81Tl3R3j9\nK2vtEmRo8PzSVavodAL1iWONyLB9WWCtbQBuBfYDDnfObSpxlcadcrEAX0Y8JONYBg+LTkmstQcD\nfwZ+7Zxb6JzrKXWdisiJwMettZuttZuROc+fWmsvKHG9isXfgWprbfy3Vi4dTxCrKCkMacSTsJxY\nDtRaa+fFjllkeHvKY62dBTwOzAAOc869WuIqTQjl8kMc7fJJk54QGvAb4Ern3JWlrk+xcc69Jf7a\nWrsSOMc596sSVanYPIxYD9+w1v4X4hSzEDiqpLUqHg8Al1trTwNuAd6L3N+RpaxUsXHOtVlr70M8\nsM8A9gcWAUeXtmZjJzgv3Y0sI3e8c66/xFWaMMrCAgyxKkcjD+TrwDnAcWGCfqrzWWA28HVrbVus\nXFLqiinD45zrBo4ADgE2Iu7mnyuXpb2cc2uADyEOTJuBa4BTnXN/KWnFikc8JOcMJHRgDXAnEic3\nldfPi+7tMKTjchSwOdbGPFaymk0QuhySoiiKUpGUhQWoKIqiKCNFBVBRFEWpSFQAFUVRlIpEBVBR\nFEWpSFQAFUVRlIpEBVBRFEWpSFQAFUVRlIpEBVBRFEWpSFQAFUVRlIrk/wH9G+KWRwM0HgAAAABJ\nRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1121331d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sns.set_palette(\"Paired\", 10)\n",
"\n",
"plt.plot(AblGefIma_df[:].values, 'r');\n",
"plt.plot(AblGef_df[:].values, 'k');\n",
"plt.text(8,60000,'Gefitinib (ABL)',fontsize=15)\n",
"plt.text(8,55000,'Imatinib + Gefitinib (ABL)',fontsize=15,color='red')\n",
"plt.savefig('Abl_Gef_Ima_Jan2016_repeat.png',dpi=1000)"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"ligand_conc = np.array([20.0e-6,9.15e-6,4.18e-6,1.91e-6,0.875e-6,0.4e-6,0.183e-6,0.0837e-6,0.0383e-6,0.0175e-6,0.008e-6,0.0001e-6], np.float64) # ligand concentration, M"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAagAAAEaCAYAAABEsMO+AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXe4FdXVh98NSFWxgZioURNdWGLs+sUWU2wx9qhYMYSI\nhmhE7LFgQ8GKFQsau8ZERcUYe4sFNaKiLlGxd0FB6bC/P9YeZu5wzr1zy7n33Hv3+zznOTOzZ+bs\n02bN2nut33LeeyKRSCQSqTY6tHQHIpFIJBIpRTRQkUgkEqlKooGKRCKRSFUSDVQkEolEqpJooCKR\nSCRSlUQDFYlEIpGqpFNzvpiI7AdckdvcA7gSOA64FtgG+BYYpqpjMscOBwZgfb4eGKKqC0JbP+BM\noDfwKDBAVb8IbesDo4G1gEnAIFV9rlLvMRKJRCJNQ7N6UKp6k6oukTyA3YBPgNOAq4FpmJHZExgh\nIpsCiMhgYEfgp8CawObAUaFtXeByYG9gOeAzzNAhIl2Be4BrgJ7AKGCsiPRoljcciUQikQbTYkN8\nIrI4cB1wGGaYdgFOUdU5qjoeuBk4MOx+AHCBqn6uqp8Dw4H+oW0/4C5VHa+qs4Bjge1FpBfmjc1X\n1dGqOl9VrwU+x4xdJBKJRKqYlpyDOgaYoKpjgdWBuar6Xqb9LaBvWBbg9VybhOW+2TZVnQJMCdv7\n5o4D0Mx5I5FIJFKlNOscVELwngYD24dNPYCZud1mAN0y7TNybR1EpAvQPdeWtHevoy0SiUQiVUyL\nGChgV+A9VX0+rM8Auub26Q58l2nvlmubp6qzRaSUwekOTC9xXLatVoLx2xj4FJhf1/6RSCQSaRAd\ngRWA8ao6O9vQUgbqd8DtmfVJQGcRWUlVPwzbssN6b2DDcuPLtCXDfYjIcsAyYXtPzFPLIsBNBfq4\nMfBkkTcTiUQikUazJfBUdkNLGajNgMuSFVWdLiJ3A8NFZCCwDtAP2CHsciNwtIg8AswDjgduCG23\nAI+LyBjgRSyAYpyqTg37dwlRgKOxYIvewAMF+vhpeN4S+KjB7zQSiUQitbEi5gx8mm9odgMlIh2B\nH5bozEAsR+ojbGhvaIjmAzNmywPPA10w43Q+gKpOCEZtDNAHeAI4OLTNFpEdwnnPwjy1nVU1P99V\nimRY76Nc8EYkEolEmgiRhQNgi0yluFgPqjQisgowGVg1GqhIJBKpDLVda6PUUSQSiUSqkmigIpFI\nJFKVRAMViUQikaokGqhIJBKJVCXRQEUikUikKokGKhKJRCJVSTRQkUgkEqlKooGKRCKRSFUSDVQk\nEolEqpJooCKRSCRSlUQDFYlEIpGqJBqoSCQSiVQl0UBFIpFIpCqJBioSiUQiVUk0UJFIJBKpSlqq\nom4kEolEasE51wEr0NoF6Jp57g4sAfQIyzMxZ6NjeHQqsVx0W7LsQjd8Uzy2gJ/8FnbbDkat7/3J\nRT+DaKBaMSLSAfgTcBAg2I/3beAW4HxVnV2Pc20A3AisBlwMbAS8raoDRcQBBwD3q+qXIvIL4BFg\nRVX9pMC5TwX2U9XVQ3Gyd4EtVPW/RfsXzvM3oLOqnpzbfi+wI7CZqj5f4rWz+y8AvgTuBo5R1Wn5\nPpZ57bWBa4H/U9VFKn9GIuUIhmYM8H/AYuHRKTznjUNHzDi0qdGtp8JjAhxzS83/Y61EA9VKEZFO\nwL3A+sAw4CFgFrA5cAbwS+A39TjlccBsYE3gW+xCPi+0/Ry4DlglrD8N9MEu9EUYCYyqR18WQUTW\nBAYCfXPb+wDbAYoZ6+cXPZrJ2MUB7KLwY+AK4Gpgr8x+ZctLq+pEEXkZOBY4q2HvItKWcc51xW4U\nNwTWAdYAVgbWwgxPu+d1mFOf/aOBar0MBX4BbKCqr2e2fyAizwFvisgOqnp/wfMtDUxQ1ckl2lz2\nWVXnAl8U7aiqfg98X3T/MpwCXKeqM3Pb9wc+Bi4DzhKRI1V1em6fBaqa7e/HInIacKOIdMuc01E7\n5wPPicgliecVads457oAy2M3ZMuHx49Ijc8K2H+nB9EI1ckkeL8++0cD1QoJQ25/Bv6eM04AqOq7\nItJXVd/NHLMlcA6wHvApcBswTFVni8h72J8NETkAG+b7OzAJ88aeCKeZHIbCniAzxBeOHwVsg3lu\n04DLVfW0cM5TWXT4bCsRuSq81ovA4ar6Upn3uxKwR+h7noMw7/FO4EJgP8w7qosZBfapgaq+KSLv\nY57cefU9PlL9OOc2BM7GjFAfbK6noXjSm55ZwP3Y7252WJ8dHnMyz3My63PDsR1Ih/3yyx3CfnOx\nEY+5ucc8oBvQE1gGWApYNjyWA3oBvTHDu1gj3mshZsJN9dk/GqjWyarADzEjUZKccVoP+DdwEuZx\n/AgzKH2AP2DzTf8EPgGOAL4ineD8ENgFm7PZGHgzPOc5PRz7F+D3wDki8rCqPl2mi0OwC/1bwGnA\nOBFZTVVLGY4dgY9VdWJ2o4hsBKyNzSV9JCLPhHPWaqBE5Afh9W8u4ZHVxX3AzkQD1Va5Avs/FGEe\nMAX737yHDTO/Gp5vwrwsQtua3vtZTdnRpsQ55zCjtQLwA8yYdScNxMguF91Wil716VezGygRWRH7\nEWyJ3WmPUNWLRWRpbCJxG2wOZJiqjskcNxwYEPp8PTBEVReEtn7AmdidwKPAgGRIR0TWB0Zj48CT\ngEGq+lxzvNcKsnx4/iq7UUQmYB5Jwo2qeig2HHifqp4ftr8rIoOAJ0XkeFX9XETmAjMznxsAqrpA\nRKaG475U1e+TthxjVfXqsDxSRI4HNsPmq0rxN1W9O7zWwdgwXT/gmhL7bgpMLLG9PzAVeDCs3wqM\nEpGNVPWFzH6riUgy7NcRCyb5ChhUpm+1MRE4sgHHRaoc51wPbP4oy1xsWOot7Lt/C7uOTAI+9d77\n3Dl+gP3mVwmbPgTWrWbjBBDex1fh8WpjzzffuUFz4PLvMZfxMfjrQfY/faM+52nWSJEwNHUX9kUv\ng01unyoi/wdchRms3sCewAgR2TQcNxi7i/4pNom/OXBUaFsXuBzYG3NZP8OirRCRrsA92EWvJ+Y1\njBWRHs3wdivJ1+F5mdz2nYCfYUNhE7CwVLBAil1EZHryAB7APKQ1m6A/HvvjZvkW6FzLMQsj+FT1\nO8wzW7vMvsuzqDHujBm0u1U1Cea4AwvuOCR3/IfY5/IzYF1gK+Bx4BkRKRm1VwtfAp1FpGc9j4tU\nP7uSDsmdghmZrt771b33v/XeH+O9v9p7/7j3/pMSxuknwHhS4/QpsKH3Pj8n2rZxbs2OcFE37IK8\nMkw80PuLvPev5z+zumhuD2pTzIU8TlU98LqIbIaNue4CrK6qc4DxInIzcCDwHBbifIGqfg4LvanT\nseiw/YC7VHV8aDsW+FJEemGu+nxVHR1e/1oRORIzdv9olndcGd4BPscutAvfh6p+mCyLSPaObTYW\nhXdO7jwO+xNBLRFsBSkV0l5b0EE+VLtjmXOAGZ38b3VnbHL6wDBvltAB2CcES3wXts3NDnkCb4vI\n85jR+yMWmVeUZCJ8QT2OibQO/hCePXCe975wYI9zbl1syH3ZsOkrYDPvfdFI17aBBZXcTs2b04Ma\nerrmjrXfAPOeRorIpyKiWPjvMthF5L3Mvm+RhhQL8HquLRln6pttU9Up2Lhw33xbsgu5UOXWRsjD\nuQQ4WEQWeS/Bu8iO9U4E1lLVd5MH5qmeByxe4CUba7xKsUGyICLLYN9nqWE8MCOaH7vuD3yEeUQ/\nyzwOxcbA9yvQh07U/z/QC5hRIlIw0ooJczBJKsKkehqnzbE0n8Q4fQts5b3/oGl72So4HQuxT3gA\n719s6Mma24NaBptjehhYCZts/zfwWywbOssMLPoE7IIzI9fWQUS6YJNx+Yn1GaQTduXaWjtnY5/f\n0yJyBvAf7DPcDMtpWgO4KOx7DvCSiJyHDaX2xnKAPsqEXztqejzZ9eRivIGIfFOiL6U8pbpCtkeK\nyBTMyJyDGaFby+z7PDb8AtTIfTolH8UoIm9iHtFAbO4RoKOILJ/p0zLYZ7QYcHPm8O4isl2Jvj+e\nCaZYH3i2jvcWaX2sT3q9uaPoQc65HcP+ybEzgW299/Waa2kTOPdLbL47wefW601ze1CzgSmqeo6q\nzlPVZ7DosdOwiess3YFkiCZrrJK2eUEpoZTB6Y5dVPPHZdtaNao6X1V3xSLndgIewzyQU7BAkbWT\nIBNVfQ27Cdgc+B/mgj8G7JY5ZRK1V2p9IvY93QqcWmbfPOXOlawPwwzo89jvcPvMXFKe+4BlgpoD\nWCTiPMzY1iAEzowC1heRDcNrrYIZwE/C4xksknEXVf1fpk8rYKHA4zKP+8L2hG2wiMZI2+KwzPLl\nRQ5wzvXDfgvJNWYusLP3vlSyeNvGuWUwJZrszd2teP9ao05bzzmrRiEiv8PmQnplIvCux5I+jwBW\nS+ZRRORibP7oryLyLHCpqt4Q2vYATlLV9UTk7HC+AaFtOWx+ZjnMm7hEVX+c6cMrwMmqelcdfV0F\nUyBYNTf0GGkBROQ24ANVPboF+/AzLLhi5Zio27Zwzn2MhVd/5b2vMxTaOXcYNsye1azby3tf2Ptq\nM9jw6D+wXMWEBcCaeJ8PnlqE2q61zT3E9yDm1ZwSMvk3xYZufo3d5Q4XkYHYGGY/YIdw3I3A0SLy\nCHbnfDxwQ2i7BXhcRMZgCZ/DgXGqOjXs3yVEAY7Ggi16YxFskdbFMOAhETmtBed//gqcG41T28I5\ntxRmnMCSvmvb12H5hMNyTYPapXEy+lPTOAFcX8Q41UWzDvGp6ixMnmcTzGu6EfhLEPgciM0JfISN\n6Q5NIvMwGZu7seGgicCTmOwMqjohHDsG85z6AAeHttmYkeuHhWb/Gdi5AcmZkRYmzDVdgc0dNTsi\nsg6W5nB2S7x+pKL8KbN8abmdgujrhSxqnE7w3l9ZiY5VPRZaf0lu6zxs2qbxp2/OIb7WRBzii0Ta\nB865/2G5g7OBbqVydZxzi2H5lAfkms4HhtY3v6dNYJ/JU5jDAam00xV4f2jR09R2rW1Tku7tCueu\nw7kH696xUa+xFhallKxPxrkTCh67Cs4twLmfh/XHcG6RoIaK4NxSOHcGzk3Eue9w7hucexyb1K7v\nuQ7EuU9xbgbO7Rre076hrTs2F5HseyrOTarHuR/DuSvDcn+cm1vHEeXO8yDObZPb1hnnvg6PLiWO\neSy8l+QxG+cm4dwxJfYr/705dwjOXdygflcBwStKwqJfLGOcumFBQnnj9Hfg6HZpnIyTSY0TmHGa\njan6NAnRQLVe8pFxleBuauqSbQRcUPDYD7Dh1iSiqTn6C86tBLyEJWP/DVOn2AQYC1yFcyfV84zn\nYtF8gs1d9sEuVmCSR9mgjZHYvGpRdsU0ARuOc38AZuH9o7mWnbGQ506YNmIej+nF9QmPNYATgZNq\nGN26v7ergF/i3BYNewMtzvakc/HX5Rudcz2xVJjf5ZrGAn/03rfPhG3ntgSyN6tJBO4VeP9RU71M\nFIttveTzlir5Oob3X9eyX03sj1u4JEftPXCnAlvj/TZ17YpdMOcCm+N9dq7xPJz7EhiNc6Pw/tsC\nr+sw9ecn8T5R6cies+bnb8mdxcuKeF8qp6w4znXCwv5LZer3x/INF8fmWG4ssc9MvM9+R++HXJYD\nsXnfuvF+Ac6Nwu6aty7a9SoiGYrymMbnQpxzvTHjtH5mH4ep+e/jvS+XFtG2saCSG0kdnNmYrNpM\nmniOtt4elIh0Cpp6kWrCufdwbijO3R+Go97BuZ1wbvcwdDMd5+7DuWUzx+yBc+PD/t/j3FM4t1Fo\newwr7HcKzr2beY0Tw/Kp4bVOwrlPwjnuxbkVQnvNIT6jJ87dHvZ9H+f+WvDdFfO+nFsd2BY4NWec\nEm4GpIZxcm4gzmno0ys4d+DC/pscUydgTOYzWIBz++Fcf2wi+Edh29Y1hvjS9787zr2Ec7Nw7k2c\n2yXz2osOnzl3aBhSnI5zt+LccrW8499jkjKP5c7RJ3wOD2Le3hY4V1Q9ZQb1l3G6E/g5VqqitbFl\neH7Xe79QasvZ9/8UZpyS4p0OeBnLdWrPgVaXEsrzBJL/5sV4/1lTvlBhAyUih4rIJMxKriYiV4rI\nmdFYVRWnYMM26wCvhOWhmJDu77C8MBuScm5jrCbUGEz6aWvsD5hcMHfDygScS1peI28otsEi236F\nVe9dn/LROw67oE7GJInOBM7BuXx4arlji/zOkotN6TIk3s8jKz/j3KFYvavjsaHAc4CLgpH6AEvQ\nnY/l6GVLjHgsafkcLOq0Dxnx2xwjsMjDtbGL29+xOY3kPNnPsyOmB/c77PNchyB8XIadgX+z6BzI\n/uG8YzGx5FnUjFRLqPmZmoHZB1MZKY55YS+E/rQaghFKRH/vzmxfCzNOq2OGaQ52o/I2sL0v4n23\nVZzbD9g3s+UdTGThO2yIu0kpZKBE5HAs9n8kNnziseGDP9FE4YSRRuOBu/D+Rrx/F7vILAEcj/cv\n4f1j2B11MiE8BzgU7y/H+w/w/oVwzE/tbH4qdnH+rpahvQ7AwXj/Bt4/jRm8/yuzL8CzeH8s3k/C\nwnJvwnKLFsW8lOk4Nx0zIFsuXHfuvjLnX7QMiXM/wAIlpmceSbDEiZi39S+8n4z3N2EG+QS8X4D3\nn4f9vl3kM7DyCd8D8/H+C7wvF+AwEu//g/fvYKXil8RKv0Bpo7sf3r+A989i6ga/xbnVSuwHNrdW\nSr/wIOA/eD8NU9IeBxyYC5ZwwEGZz2Q2psQ9mYYJKb+G3QC1JrJlUy6AhaKvT2L11maER1dMiWRb\nn/4m2h/OrUrNod9vsM8J4AK8/2rRgxpHUQ/qMOAQVb2SoEKtqrdhY9X9m7pTkQbzdmY5mQt5J7Nt\nFkkJDu8nAA/i3PE4dz3OPYP9+OrjEX9GTVHNaZQvseFZ1Mt4gZrCklnuJi0dcgV28UwEYf9Y5phS\nZUg+IxWUXQ+72CyGc72w5MzzahgvC6xYLczvNAXZZMUkwbfcZzQ1l9yYiGyW+4wWKUMShmjXpqae\n3O3YZ7JnZpsH/kXNMiS/w3Qvn8BCiOvDV6Q3CK2FxOOb6tOJ/bOwz+pbzCtYErsQb+u9n9z8XawS\n7P9wA/Z5JDyH/Z++IeSlNjVF/4QrU/pO7V1MUihSHZS6i8/PJ9hwkE2Gj8PmD57GcjyEYuXSE+pb\nYiPflw5lzgHef0eixejcVCxS7d2S+6Y8FZ63Iom0s2CN9Di3sHtzwvNgas7hJDvky4E0lPp8RvnX\nTPYrV4bEk5b/SOgfnq/GufxQ3Z+oWXJ7Wu4z1fBZP4Wpu9xfS1/zdKQVlSBxznXG9BjB5Ktwzi2B\nDa2CTWX0wTyoHX0jNeXaAMdhWp4JD2BD/ADnNjrgpwxFPagJ1BQWTTgEEx+NtD6OxOYv+uH9JXj/\nOLBqbp+mDAt3pNFQCZtjQ0N1USxIwvvXsaHnUzLzPJkeuB+QXHBtHuFjYFW8f3fhwy5QQ0vM65Tr\nV2PIH78szq2YWd887JMvGZNQswyJXXT7YTcd2RIk62FzjVvi3BqLnqYGHXLPRd9jL+zzbC0MIDW+\nSR7X9qTebR9s/mkP7/0zzdy36sK5TbFo0YSvMdWezpjnPKpSL13UgxoC3C8i22BDRKeKyJpYNdbt\nK9W5SL0oeqeb7PcBsFP48X2BKaJbCXTnOuP9HEz1XXBuBbz/tB6vUY5tcG4Ypp+4PRY08ZvaDwG8\nz0vL1EZ/zEiNx7kzsTysLpjk1bHYHyoximcA5+PcB1hgxabYHNSIgq81HVg6XPTfr0cfE/Kfpwdu\nw7nDsfDwS4EbMyHueZ4nU1eLtIjjecFYZ17JDcc+m0OwatQO6I5zSRkSh92gXIAZmoczfVwJ5/L/\n81lhXjNhfepRpqIKODA8z/HeJ0E1eXX/A733/27eblUZ5lXeRE1P/VTSfMhzqGDF4EIGSlWfERHB\ntOxmYZPvDwK7qmprumtqS9S35EX+mJOxOZgHsKGZezCX/UVCnSlsXPli4DfhQlZbCY26+uSx4cP1\ngWOwMuwHlkgwbRzefxyi0Q7HIhZ/gl1k38Dez+ULw8y9Hx0CB47G3udHwOl4n688XI47sKi7CViB\nxIaUIckuf4INTf4b06W8jXJBJMZYYBTOueDxHQRMwPtFIwq9fwfn7gUOwLnjw+vtSxqRtQAr9Pkk\nsH8IAkn6tV14ZPmIJNTYUhfWYVGlhWom8eZfgYVDfr/NtJ/lvb+l2XtVfVyEpZsk/BPYELMdn1E0\nX66BFNbiE5EVgZ6qOjGs9wcezpYZb0tELb5I1WOBDO9g0ZjlIhubox9/BXYpmEjd4jhTvXgyrB7p\nvb/QObctNasc/KidVsRNce73WIBNwldYIM3T2BDw4XjfaJmrRmvxici2WDTSXpnNA4DXRGSrxnYw\nEok0AAttPw3L02oZLLprEOaRtxYOD88eSFTIs8N7T0Tj5FYi/WwSDsM+uw7YCEjFFdyLBkmMAE5T\n1VOSDaq6JSZrcV4lOhaJRArg/dVAB5z7dQv1YCDwMN4/Weee1cMvw/OH3vsZQTB210z7TSWOaT84\n1xGTfVoqs/U2bJh8n7B+OhnljUpRNEhiDWq6egm307runCKRtof3LWWcwPtC5dGrBWdSXIncVzIs\nujEWtQcWudeagj0qwVFY3b6EL7B0jNHYfO67lBDWrQRFPai3sSivPL/CosEikUikNZAdDr0wPGeH\n9+7z3k9pxv5UF879EDg9t3UQFhCze1gfVotySrnzdse5P4TzF6aoB3UacIuI/BzL6AcLb92TUL02\nEolEWgGJMZruU9WOrB5k+x7es/zIrNLJzXh/Z4gABVDq+xlZVYDbMCfnekqr75ekkAelqndg6sgd\nMYO0X1jeWlVvrldnI5FIpAUIoeQ/CatPh219M9tmAPeWOLR94NwyWJ5cwmfA4Tj3f6Qh+KfgfX1V\nVoaQjsA9XNuOeQrrjanqo0DT5qxEIpFI89GP9Ka8VPTeHe28jMZhWIJ4wiF4/zXOJYLgr1JfIWHn\nNiOtEXUzpudXmEIGSkS6YWHlG2EJhEkGvAO8qu5b7thIJBKpEv4QnudjiemQRqVB6aKO7QPnupOG\n3wM8ivdjcW5rTJcR4GTqU0HYuaWxsjSdgEnAoIISYgspGiRxJVb7ZglMkHROeMymvJBlJBKJVAXO\n5kE2CatveO/nOZuwXzdsm0q5OmLtg4PJ6jrCsDB3lARMvEimZlad2LHXYoK8s4G9GiKJVHSIbzdg\nT1W9v74vkEdEhmKS9lnDtj0miDkGk9v5FhimqmMyxw3HvLhO2ETbEFVdENr6YQXwemPDkANU9YvQ\ntj4WHrkWwYqr6nONfR+RSKRVsQlWGgJswh5gl0z7jb7+cyttA1MkOTqz5TG8fxxT10iKgJ5UT+/n\ncNLP90i8f7khXSvqQU3HpCiagvWA41R1iczjaayS6zTMyOwJjBCRTQFEZDCwI1ZMb01M5fmo0LYu\ncDlWNXY5bGLv2tDWFXPlr8EqZ44CxopIjyZ6L5FIpHUwOLM8Ojxno8mub8a+VBt7kZYegUW9p/9i\n+pDFsGrdSXXdf1C/Ej41KGqgRgHDRWSZOvesm/Uxcc2FiMjimLU9RVXnqOp4bEItURw+ALhAVT9X\n1c+BRJkZLKLwLlUdr6qzMMXq7UWkF+aNzVfV0ao6X1WvxWTid2yC9xGJRFoP24bnL7z3XzrnlsLm\n1MHKlrxY+rA2jhmi4zJbHgsq9TuRDokW956c64l5qIthCb0D6zvvlKXoEN8umGH5SkSmkhZ7AwuS\n+EGRk4hId6wo3hEiciM27jsSeBmYmxMKfIs0wkaoWRPnrbANoC8hZBRAVaeIyJSwvS+L1tLRsD0S\nibQDgnpE77CaCML+jvQG/VrfiItoK2dHalZsHoZJPyXe06Ok5Uhqx4zd1VjZljnYvNO3jelcUQNV\nm4tWny+2N6YifBnwELAZNgR3HlbBMssMICk61yOsZ9s6iEgXoHuuLWnvXkdbJBJpH/wps5xIMw3M\nbLu2GftSbRybWX4c7x/DuT2xQpcAJ9XjXIdi0zNgRT8b7ZUWrQd1XbIsIosB81S13nccwUPKSvI/\nJSI3YCW6u+Z2705S8rumsUra5qnqbBEpZXC6Y/Nm+eOybZFIpH2wd3ieDTznnOsK/F/YNtl7/3bL\ndKuFcW5z0iAIgFODUGyS9/RvvH960QNLnmt90iKG/wIuaYouFp2DQkQOFZFJ2EV/NRG5UkTOFJHC\nVVZFZEMROT63uRum59dZRFbK7k46PPcGNYfl8m2ysEFkOWCZsP3NbFuJYyORSBvGOdeD9BrwvLc8\nnt+S3pxf0yIdqw4W9Z4s3HzNsK2YELhzS2LC4Z2B94ABjZl3ylI0UfdwbCLtVExg0WOSFZdglTiL\nuoHTgJNE5C3gTsyb2hvzoJbCAjEGYmOi/bAy3WAJdEeLyCOY2vDxpBnJtwCPi8gYbKJzODBOVaeG\n/buEKMDRWLBFb2oWJotEIm2XXUhvxK8Lz3/OtF/VrL2pFpxbB5uHSzgVM+aJ93Q73o9f9MBFzuOw\na+tPsGvzPnj/TVN1s6gHdRhwiKpeiWVho6q3YVF2/Yu+mKpOwsYoT8aM1cXAQar6MjYmvBhWSvoO\nYGiI5gObs7obeB6YiM1jnR/OOSEcOwaL0OtDELBV1dmYkesHfI39MHdW1fYsZxKJtCcGhGcP/NPZ\nENbmYZt6779omW61OMdklp8I3tNRwAqYGEN+pKscA0nVOI7F+ybNMS0aJLEyZhjyvIvlHhVGVccB\n40psn0o6VpxvS7y0kp6aqv6DMhpRqvoq6Q8yEom0E0Ihwp+H1cne+2+dczuRqnVf3TI9a2Gc+xGQ\nlac7Fef6kBqtS/D+3QLnWRe4KKzdQzoH1WQU9aAmUFNUMeEQ4H9N151IJBJpMjYlDb76V3j+a3j2\nNCKBtJUzBKtGAfAU8Bg2fdMD+AY4o84zOLc4Nu/UFSv/3r+p5p2yFPWghgD3i8g2QBfgVBFZE5tM\n276pOxWJRCJNQDaU/Lqgx5eMprzhvf+uxDFtG+eWo2ZJjZOx63jyWZ1JXQUb7XO8DAs+mY/NO1Wk\nyGPRelDlTIlTAAAgAElEQVTPhM68BIzFRGMfBERVn6pExyKRSKSRJDWMpmGRu9uTelTtMzgC/oI5\nGWASRo9hQuAdgPcpFh7eHws4AzgB7//btF1MKVwPCgtguE1VJwKISH/qEaYeiUQizYVzbjVS9YhH\nvffeOXdUWF+AeQDtCxuWG5LZchKwNWkxwePxflYd51gbuDSs3Q+c28S9rEEhAyMi22LyQntlNg8A\nXhORrSrRsUgkEmkE/TLL1+aG91733s8pcUxbZyBpQcLnMO8pMTAvkKq8l8bC0G/Hclc/AQ6qV32o\nBlDUAxoBnKaqpyQbVHVLrFLieZXoWCQSiTSCJEptATYdsQPp8F77i96zcvcnZLacgIWHbxjWhxYw\nNhdjZYsWAP3w/ssm72eOogZqDcxy5rmdmkKDkUgk0qIEpfJEDeEV7/0MYGhYb5/De2awk5SgF7D5\np7PC+j14/3itRzt3ACG/FKus+0QlOpmnqIF6m3ScMsuvMJmiSCQSqRZ2BBIJtptzybmve+/ntky3\nWgjLBzsts+U4LFjiR1gU3rGlDssc35dUZPdBTK2nWSgaJHEacIuI/BxI1B02wFQhDi57VCQSiTQ/\n2WvSPzFJn/acnLszkOicvhwe/wzrV+P9G2WPdK4bNlLWAysGe0Cl552yFA0zvwMr+NUR+/L3C8tb\nq+rNleteJBKJFMdZ+fJEofsLb4oISeSap72Jw1pwSNbjGQr8Dasw/h2WoFsbF2KVzBcA++L95xXo\nZVkKh5mr6qPAoxXsSyQSiTSWLUjzfO7JldZoj8m5W5FWgngVUxtPxHJH4P1nZY90bh/SWlqn4X2z\nX/+LqpkvCZyCuccK3AT8Hkvc/b2qvl+xHkYikUhxshpztwC7075La2TzlIZggRGLYWXuzy97lHOr\nkyYzP0oR+aMKUDRI4hIsC9tjP4BdgP2xAIkmKUwViUQijSHkOu0aVudgOnN/yexywyIHtWWcWw/Y\nKKy9iQ3pJbmsJ+H992WO64rNOy0OfAHsh/fzK9vZ0hQ1UL8F9lfVN7E7knGqeisWS79NrUdGIpFI\n87AWaSj1M1j17E3C+lu+GfJ2qoysuvgRpN7Ua6S1sUpxLrAe5pDsj/efVqR3BShqoDoB34lIZ+DX\nmMQFWGRHe8zIjkQi1ceumeWbMG8hX6ywfeDcj4FfhLW3sWt1Emp/dFmPyLlNSeeozsL7ByvYyzop\nGiTxNDZeOQ0L17xbRDbCMosfq0zXIpFIpF5k55/GAfdm1m9t5r60NBdlloeQKv48RLmK4jZEmuw3\nkboj/CpOUQ9qIJbQtTbQX1W/wrSupgODK9S3SCQSKYRzbnlsiA9gMpaou15Yf897P7lFOtYS2Gex\nY1h7Dys4uzo2ZHd0LXWbdif1sobi/bxKdrMIhTwoVf2Ymu4zWEn2Ji9QFYlEIg3gt5nlO6gpFntT\nM/elpbmQVEnjBGBUWL4B718ueYRp9Z0T1h6knJfVzBTOgxKRHTBXcQ1Mon2AiHygqu21rkokEqke\n9sks303NkPI7mrkvLYdzPbEUIICPsCTb5YBZWIJuOQ4Dfox5WUMrUR23IRQtt7EPNoY7Hqux0hH4\nErhIRI6oXPcikUikdpzJ8WwdVr/H5solrH8GTGiJfrUQ55KWcz8TODIsX4D3H5Y8wrllsMq6AGPw\n/pWK9rAeFJ2DOgH4s6qeAMwDvKqOwmpCHV6pzkUikUgBfkmqtfcgNb2pW32VeAMVx/KXDgprnwGb\nYSVGviIdvivF34ClgRmkhqoqKDrE9xMski/PeOCH9X1REVkek904WFXvE5GlgTFYTtW3wDBVHZPZ\nfzhmDDsB1wNDVHVBaOuH3Sn0xjKeB6jqF6FtfWA0Nnk6CRikqs/Vt7+RSKSq2T2z/E9qas/d2cx9\naUmGYyoRYBHWifrDMLz/tuQRFo6eBLqNwPtPKtrDelKfchtbl9i+OyZ9VF+uAZbBxjvBJDWmYUZm\nT2CEiGwKICKDsYiUn2I1XjYHjgpt62Iy8Htj46yfAdeGtq7APeG1emIThWNFpEcD+huJRKoQZ6Uk\nkgAuD0wFVgzr32B1j9o+VlJkUFj7CsuBctiN+ehajjybVPqoouXbG0JRD+oE4NaQ+7QYMFBEfoL9\nMH5f65E5RGQQJrnxYVhfHJNOWl1V5wDjReRm4ECsLPEBwAWq+nnYfzhwOjASU1W/S1XHh7ZjgS9F\npBcm8TFfVZMv51oRORIzdv+oT58jkUjVsgF2sws2KpON5rvTV0GodDNxKmnF4FtIJZ6Oo1z9K+c2\nxxwCgL+VlT5qQYqW27gXUwReEpPJ2B6YC2yqqncVfTERWQOLBDw0s3l1YK6qvpfZ9hapAq8Ar+fa\nkgnQvtk2VZ0CTAnb++aOA/P2+hKJRNoKO2eW/4WNpiS0j+E9S7BNgiG+IZWfe5pyn0HNpNxXgL9X\nsIcNpqia+XnAZap6YENfSESS+aPBqjpVJLEx9ABm5nafAXTLtM/ItXUQkS6Y1taMEsd2r6MtEom0\nDfbKLH9D6k3NxFQT2gPHYNdJsPylxEjXFi6+F7BpWD6qpcRg66LoHNQArGBVYzgJeFlV/yMiSRKZ\nw4xG19y+3bFhQKhprJK2eao6m9IGpzumcJE/LtsWiURaOc65H5GOpkzFotYS7vfe52982x7mCR0f\n1r4jLdb4D7x/tswxXbG5J4D78b5qDXnROahrgLNF5GzgXXIeT5g7qou9gBVEJLHuS2K5VecAnUVk\nJVVN4vSzw3pvYMNy48u0LXTFRGQ57A7qDSwwIi/DJLS/rPJIpK2yU2b5PmCPzHr7GN6z6ZKeYXk8\nNrw3l9RolWIwsArmdBxdyc41lqIGaj8swq5UQIQnTQwri6qumV0XkclYbtU4EVkPGC4iA4F1MJmS\nHcKuNwJHi8gjWA7W8aR1XW4BHheRMcCLWJjluDCE+AjQJUQBjsaCLXpTJRIekUik0WTDy6eSjpjM\nxwxW28a8p9PC2kxg47B8Gd6/U+aY5UgVJa7C+4kV7WMjKWqg9ql7l0YxELgCk+b4DtP5Szymy4Dl\ngeexUs43ECpBquqEYNTGAH2AJ4CDQ9vsIM90BVZFchKws6q2fbc/EmnjOJP02SqszicVigV4zHs/\ntfl71ez0B5YNy28BP8PySE+v5ZiTMY/rO6xKelXj6pNkLSI9sWGyjsCkoGreJhGRVTBV5FVzEYaR\nSKSFcc6dgCXog6WjbEw6pz7Ye39pi3SsuXBuWSxVpxs2pNcBuy4fg/cjyxyzBlZGoxMWVn5myf2a\nmdqutUWj+LpgXsufSIfzFojIbZgaRCxaGIlEmgXn3BKEZP3AZ9QM+BrbvD1qZiw5+SnSIc13sHn6\n9zEFiXKcg13zP6Jmtd2qpWgU3znYnNDvgKUwt3IX4OekchqRSCTSHBxGGk4OsFpm+QVfThS17XA5\naT7nxMzyiXg/q+QRzm1NqrhxIt7nU3CqkqJzUP2AfVX14cy2+0RkNjYndEyT9ywSiURyOOd6AEMz\nm8aTBgdAW4/ec253bCQLLO8rMUgvYUFjpY7pQJqU+xIWeNYqKOpBdQZKiQh+TBriGIlEIpXmUEx3\nMyFfSqOwsk2rw7kVSY3QAkzubcOwPhTvy+Wq9iu4X9VR1EA9BZwgIolSLiLSGTiR9iLGGIlEWhTn\nXHdq5u3cTU0R60lYDmTbw7lOmHRRUlbkLNKRq/vw/tEyx3UjVXe/p+x+VUrRIb4hmJF6T0RexhQg\n1sOs+HYV6lskEolkOQTLZQTLv7wFS/ZPuLMN1366GVg5LD8IbIuNXn1NqmJeir8CK2Gh+K1uKqao\nWOwkrNTF2VikyJuYeu4aqlrViV6RSKT1E6rmHpvZdD0mYJ2lbQ7vOfcHUpGEL7DAiE3C+kF4/1GZ\n43qTKkpcgfdvVrKblaCoB5UohdcWwhiJRCKVYiCWsA8wB1NQyE4vfIblQ7UtLHfpyrA2H9M0TUoI\nnYf3tSlmnAosgdXaG1apLlaSonlQk0ts9thQn1fV1Uq0RyKRSKNxJm6a1Za7DNOcWz6z7W7fiib/\nC2Hv+ynS3NNjSOeTnsPq9JU7dk3SaL+z8P7LCvWyohT1oPL17DthuQf7UWU17CORSJtjACZlBvA9\ncBGQV+pui8N7dwO9wvI/gN2w/K9vgX3wvjaBhJGYYfsA+7xaJYUMlKpeUWq7iDyNJc3VVlI4EolE\nGoRzrgsWLZwwEvMMlsfEozthQ1iPNH/vKohzQ7FACDAj8zbpPNTBeP9eLcf+irSy8PFlk3dbAYXn\noMrwMqYmEYlEIpXgYGCFsDwFuAOrXAAm2bMKMM7X7k20LpzbEBgR1uYAx5GWCboY78snIzvXETg3\nrI2nZpRjq6PoHNQaJTb3xHISSsu6RyKRSCNwznXGggIShmFTCl2waLYVw/a2M7zn3OLAw9j8Plhi\n8oVh/SXqrt90AJYCBFYpt1XPyxX1oMqFJ35IKG8RiUQiTcxBwA/C8ifAq6TzKa8Dv8DKRtzf7D2r\nBFbf6SFSdZ6rgf2x3K/pwN54P7uW47uTKrzfifdPVq6zzUNRA5WP0vOY6/m5qrZqCx2JRKoP59xi\n1AyNPgGbfwJQ0lpQZ3jvpzVn3yrI6cCmYflNbAjzj2H9T3j/dh3HH4UZ9HnUzBlrtZQ1UEHKKKGU\nDh9AJxEpWvI9EolEinIA6dzTJGyIK9GTm4GJDLyLDX+1fpzbhjQYZCY27/SvsH4l3tc+l+TcCqRG\n6TK8n1SJbjY3tXlQRSM/CpV8j0QikSI4053LlvE5kdQQPQtsFpaH+tqGvFoLVnzw3syWg7CSGh2A\n1zC5oroYBvTAFM5Pq2PfVkNtBuqXzdaLSCQSSdmf1Ht6GfgpNnQ1l3RO6hHaQnCElcJ4HOgetpyL\n5X2tgHmKe+H9zDrOsU44BuAMvP+6Mp1tfmozUFOAiao6v7k6E4lE2jfBezors+kM0vpF/8XUyxcA\nf20jwrCXAGuH5ReBr0gFuA/D+yLq7Odi3tbkcL42Q21isS9jlXMXIiKDRSTWf4pEIpViP1Lv6Slg\nD6ArptqdzEFd6b1/tQX61rQ4tysWRg6WbHw8aRTe3/H+7wXOsR2pQTuu1ii/Vkh9E3WHA+MwqY0G\nISJ7YeOlK2LK6Ceq6t0isjQwBtPY+hYYpqpjMscNx9zYTpiS8ZAkglBE+mFfbG/gUWCAqn4R2tbH\nlC7WwiZbB6lq2xOVjERaOc6STLOyaqOxit1gkXs/x+ZYWr+8mnM/BG4Lax5TibgGm89/Exhc4BzZ\npNxnMTmkNkXRgoVNQkj4HQMcrKpLAEcAt4nIssBV2F1Eb2BPYISIbBqOGwzsiI1FrwlsjoVUIiLr\nYhOKe2OVNj8Drg1tXYF7sC++JzAKGCsiPZrj/UYikXqxP6kA7DjSi/TbpKU1hvlWKny6EAuhzxYf\nPAl7rythwWl74/13Bc70V2CdsHwUbWPIswbNaqBU9S2gt6o+KyKdMAHIaVhO1S7AKao6R1XHYwW6\nDgyHHgBcoKqfq+rnmCfXP7TtB9ylquNVdRYWarm9iPTCvLH5qjpaVeer6rXA55ixi0QiVYKzYIFE\n3sdjRfmSnKDZWJi5Apc2f++anOuBH4XlxzEB3N+F9SPw/pU6z+DcYFLv6Xa8b5OVzZvVQAGo6gwR\nWRW7U7geCyH9CTBXVd/L7PoW0DcsC5Y5nm2TsNw32xbqVk0J2/vmjgP7kfclEolUEweRVsu9kzBC\nggUOJEEEQ7z3c5u7Y02KcwcD+4S1rzHvKTHMt2IjSXWd40jS2nxPY7Wy2iR1zUFdISKzSWs/dQEu\nFJHvM/t4Vd23nq/7QTjXVsBY7AvKh1LOALqF5R5hPdvWQUS6YOGZM0oc272OtkgkUgXkvKf52JDe\n7pgiQhIwcb/3flwLdK/psOKDiQFaAOyMRSguhmmaHlLnMJ1zx2KVzcG8r50KDge2SmozUNeTGqaE\nmzPLCwsW1vdFM6Hrj4rIP4GNsEidLN0xnS2oaayStnmqOltEShmc7ph2Vf64bFskEqkOBmDzx2Bq\n5cnc03hs7mkeMKQF+tV0WPHBJ0hFDQ4HjgRWxaY49qIuySbnTiJNwn0I2AXv8zfgbYqyBkpV+zf1\ni4nIjsCRqvqbzOYu2N3DjiKykqp+mOxOOjz3BjYsN75MWzLch4gshxX1egMLjMhHwwipdH0kEmlB\ngveUeARzsRve7li03s/C9ku99+UEq6sfE4G9izQA5B7sfe4Z1o/C+5fqOP404G9hy7+B3etM4G0D\nNLYeVH15EdhIRPbHvLHtgR2ATYCVgeEiMhCLTOkX2sDc4KNF5BHsbup40vDTW4DHRWRMOP9wYJyq\nTg37dwlRgKOxYIvewAMVf6eRSKQIg7AbSjDtuWR+ZhKwMTZPM6zEca0DKxkyljRX6RNMFPapsH4n\ntQV+mHEaTqqzdw/w+7aW71SO5o7i+xyLVjkCmAqcCuwSovsGYmOxH2Fu/tAQzQdwGVb++HlgIvAk\ncH4454Rw7BgsQq8PoQSIqs7GjFw/7If+Z2BnVW3zdx6RSLXj7OKbJKbOxm5SAd7DjBPASd77qc3c\ntabBuWWwkZ7EOM3BbspvwkLM3wcGlJ13ss/nPFLjdCewZ3sxTgCuDYbONwkisgomHbJqLrowEok0\nAc6i0c4Pq3djqSZgUbprYEKp63vv57VA9xqHcz/DvKTFw5YvsPzNYcC+2EjQFnhfWjTAhj5HYTfV\nALcD+9PaoxhLUNu1ttnDzCORSCR4T6eG1RmkVWBfwYwTmN5eazRO+2HTDYlx+i8WDLE1ZpzAZIlq\nM06Xkxqnm4D92qJxqovCc1AisjxWPGsN4BismuVEVX2tMl2LRCJtmOOAJcPyf4FfYyHmSVj5Xd77\nh1uiY43CuYuwCL2EUZjiw9qkuUv3AReUOb4jVkm3f9hyHfBHvG+Xot2FPKigZ/cWpsCwD3Zn8Gtg\nvIj8unLdi0QibY3gPSXF+b4jlTH6H9ALm6sZ2gJdazjOLYZzT5Map/nAvnh/BPBDTCevG/Ax0B/v\nF61Ebkrufyc1Tldhc1Tt0jhB8SG+C4ALVXVz7MfjVXVg2D68Up2LRCJtkqS4HlgQQQ9M8uynYduF\n3vt3WqJjDcK5lbHgrp+HLdOAn+H9LTi3FTbc1xdLzu2H91+VOMdiWLTyfmHLpcCgkoasHVHUQG1A\nGtad5RpSGZJIJBKplVDvKfGOppNG603GciI/J43sq36c2wELiU9kmhTzmF7Hub8AD4e26cBueP9k\niXN0xmSO9g5bLgT+0t6NExQ3UFOBVUpsXx9o3crCkUikOTmbVN3lc0yN5kPSpNwTfF2KCtWAcw7n\nTsdU1xNV8juxsj7zsbmjUdg8/5vAJng/tsR5umBpNbuHLSOAIW1RmbwhFDVQlwGjRWSPcMy6IvJn\n4AosATYSiURqxTnXDfhLWJ2OiUSDhVwDvIRd2Ksb5xYH/kOq7ADwN7zfHSuZ8RRpJYa7gE0ppYRh\nn8ddpErmZ2DRfdE4BQpF8anqOSIyHZtz6oZlfH+GfaAXVa57kUikDXE+qbcxG1gCm4NaK2w7wlf7\nsJYJvj6MFVwFk2faHe/vxbltsHyl5TApo5OBs8oERHTHcr+SILOT8f70Cve+1VHIQInIEqp6GXCZ\niCwOdFLVbyrbtUgk0lZwzi2FpamA1T9aDgsa6BO23ea9f6rUsVWDlWi/FZsrAyvrswXwJs4NwYbn\nOmIVwfelnPq6eWD3YKk6AMfj/dkl923nFM2D+lxE7sN07+5V1TYr7x6JRCpCMh8DqaL3q9jc0yws\nt7I6scCOM6nZx4nAL7Ew+ZswObVk+254P6nMuZbE5q02D1uOwvvzS+4bKTwHtQMm1XEp8KWIXCsi\nvxGRqEQRiURqxTm3Amn49EystM53pEN7I733H7RE3+rEuV5YaYuscRqLRR/2wJKME+N0B7BZLcZp\nKUyoOjFOf4nGqXYKGRhVfVxV/4yFT+6K/ciuAz4WkVGV614kEmnNhKTc60mvNUndtw8wceiPgXNa\noGt149wmwARMoijhbGA3YEvgBcwDXIApY+xVtnigCcc+CGwWtgzC+0sq0/G2Q708IFVdADyGDfXd\niilK7NX03YpEIm2Ec0kDAeZgYeWfkHpPx3rvvy91YIthIeR/wqLxEuml+cAfgBOAo4H7sTIhU4Ed\n8P6cktF3zi2BcwMxT2sjLHhiAN7H6OcCFA2ScNgdw++BPTDX9s6w/FDFeheJRFotzhJVk0q4C0gj\n+BLpnmepWaW75XGuB6aZd3Bm63Rs5Oh54DbsOggmbLsb3r+bO4fDhgAHYsN/iWrGAuAgvL+xUt1v\naxQNkvgYWBq7azgcC5SYVbFeRSKRVo1zbhcsMCLhCyxiLymlARZWXh05P84tj1XfPoy0gCJYzabt\nsVytZ0mVc24BBpL1/pxbGptrGwismznHXCw1ZxTe/7dC76BNUtRAnQTcoarfVrIzkUik9eNs7uaf\nmU3/AbbFhreSsufXe++fb+6+LYJzAhyFJdZ2ybU+g9Wo2hiL1FsK84KOBi7Aex+8pS0xo7Qn6Rwb\nmILEVcD1JfX3InVS1kCJyLbAo6o6FxNC3FRESu6rqv+pTPcikUhrwjm3KvA4NUPJtw3Lr2MeyPfA\n8c3fu4AZlc0xQ7Nzmb1uxeachmAl2h3wFbA33j+Cc71w7iAstyt7YZyFJeteBTwdVSEaR20e1L8x\nl/wLbGivNmK4eSTSznE2xPUSqRfxJalC+QOkwRLDvfefNHP3klpLu2IRdxuV2GM2VhbjKuBlbH5s\n19D2EjbnvjrO3R62L5Y5dkI47ia8jyIGTURZA6WqHUotRyKRSB5noqevYMNgYJ5Er7D8N2ArzKt6\nj7TMe3N1rjtWY+kELFUmz2uYcbkR76eEYb/nsBIZYEZrIvAIVhk34TtsLuoq4IXoLTU9RaP4HgF2\nz8sbiUgv4AFV3aASnYtEItVPyHUaT6pP50mTcQ/A5m3OCG1He+9nNlPHemHDeIeRRtIlzMY8pKuw\n4IelgK2Cnt4fMJ3ABZhh2p00cg8smu8q4Da8n17Jt9DeqW0OaiesAJfDNKOGiUg+X2F14EcV610k\nEmkNPEA6lAd2zZiMBRh0wOakAJ6gZvBEZTBB13OxCuAdc61vYtGF92BJtnsAl2Clg1xmvwVY35P3\n9Q1WUPAqvH+lYn2P1KA2D2oiFt2SfGkbYYl2CR67QzqQgojIFsB52KTiV8AIVb1SRJYGxgDbYEKL\nw1R1TOa44cCA0N/rgSEhaRgR6YfpZPUGHgUGqOoXoW19rBzIWlhRsUGq+lzR/kYikdpxzl0H/Ca3\n+THM41gaeBLoic1H/bGiYeXO7YgJtuaLqM7F8jafwry8/liuU954ZUmmNZ7EvKU7aC7PL7KQ2uag\nJmMGAxG5DjhcVRtcSCwYobHAYap6azAeD4nIO8ChWJnk3thdzf0iMlFVnxORwdidUHIncy9mOEeK\nyLrA5dgf5FXsR3ct8FsR6YrdJZ0OXI0Z0rEispqqVlfmeiTSCnHOnQkclNt8GfBX7L/8IBZWPg3Y\nzpfTqGtcJzpiaTCDgWVzrV8C/8MM5O4sqnrjsSCwJYDume1fAX8Hri5ZxynSbBStB9VfRLqIyI9J\n7zocljewoapeW+A0KwP3qOqt4Zz/E5FHsWHEXYDVVXUOMF5EbsYMynPYGPYFqvo5LPSmTgdGYklx\nd6nq+NB2LCZm2wvz+OaraiIpcq2IHIkZu38Ued+RSKQ0zrnBWNBBwjxgsPd+tHNuOcw4/QgLltjJ\ne/+/Rr5gByyBdgUsUOHnwKZYuYvsdcxjozCLY0Ea29Y8Ea9iaTMrYje9y2faHsK8pbvxfnaj+htp\nEooGSeyJfXE9SzS/h3kttaKqE8jcbQWPakss8meuqr6X2f0tTJARbDjw9VxbknfQF3g68xpTRGRK\n2N43dxyAkkbmRCKRBuCc2xMbrUiYCuzqvX/CObcEVk5iTcxo7em9f7KWk3XD0ln6YMan1PIPMY+s\ntiG5hWckjSQEuwY8il03+mJeVHa+7DPs+nUN3r9T4PyRehCiO3fAnIktgGHe+yuKHl9USeIMzOsY\ngXk1O2AFxy7EPJx6ISI9seG3F7AfzxG5XWZglXvBom9m5No6iEgXzC2fUeLY7nW0RSKRBuCc+w2W\niJrwLvAr7/17zrmuWAnzjTFP5kAPz+DcdtjQfWJ0ssan1E1vY1DsmvIoFm23FfAn4M+ZfTyW23kV\ncB/ez23iPrRrnHm7W2BGKZmLTFir5EFlKGqgVgV2UtW3ReQloI+qjg3KEiOoKUdfKyKyKjaPNAnY\nG5vQ7JrbrTsWgAE1jVXSNk9VZ4tIKYPTHRN3zB+XbYtEIvXEOfdLLGIvCZx6EfiF9/4751ynTnDb\nPCvix4nwwhk2FF8fMdgF4dyuTNt8aibHghnIRzCD9Bjef4JzP8Okh66kpgH8CLgGGEO11p9qxTjn\n1gH2xwRyV841v4PNRdZreqWogZpOqkT8FiaEOBaL9Nuk6IuJyAbYncsNqjo0bJsEdBaRlVT1w2RX\n0uG5NzDXfHyZtoUyIyKyHDZO/Qb2wxyc7wKmqRWJROqBc25nzDtKjMdj38ERPWDvec5tsgfs+c8g\nsnoGcKJ5UVkmYcKrUzEjsxQ2D7QK6XUoKwgwDQtWWBb7L3fItL+JXej+AbwWNPEWB/YJpS2y16T5\n2A3xlcADeD+fSJPhnFsJM0j7UVMgF+w77IQ5Bj8O267LLNdJUQP1EBY1dyg253OiiFyLiSN+UeQE\nIrI8Jp80UlVHJttVdbqI3A0MF5GBwDrYG94h7HIjcHRIFp6HaXjdENpuAR4XkTHY3dxwYJyqTg37\ndwlRgKOxocje2B1gJBIpSAfnDsWi8wDYGKY+bwZoggeGkiY3DQGOt+oHr2Dz01OwMO9VsMCGX1Oa\nt7Gb386kwQtLZtpLGSUHbBhqN/XDAiMSJmPRu9fRErJKbRhnlYH3xIzS1tT0eH1mfcncoXOoOXdZ\nJ6lg+T8AACAASURBVEUN1JGYUdgZuAITSPwQc7sHFTzHAGze6mQROTmz/ULMHb8Cc8G/A4YmkXnY\nH2N5bDy5S+jH+WCBF8GojcHGs58g1HEJQ4A7hPOehd3B7ayqMZchUjlsHqZXiUcHTL1gVoOem/PO\n37llgY3nwqb94SCfkffZDPhvZk5hGMy9KAy77QVTR8K0DvAD0hvMUszDwr+fwrykVbDo2h1z+yVG\n6V/Y3fjq2AVxAM6tjo2srJbZfy7m5V0JPIL3C+r5ziNlCPOLv8Wu1b+ivO3ID89+j0V0XgI86uv5\nnbiG5M2JSAcs8/ozVf243idoBYjIKthd2Kq5CMNIe8IK2CVGpjeljU/2sXjpEzWa+SxqvJLEedeA\nR4dati89DdiHmirRawEvwdwuwSBdAvwltO2OVfIrcdWajg3tvYcFWCX1kHbG7sLz2ngfYtp4X2FD\nhqtjBjI/95TlLdKyFoVGdCJ1EyLwBmApPxtQ+3eQZQZ2U3Ez8JCvIwiltmttXeU26mJZEVk7ltuI\n1AtLruyE/eCb+rmx5+hGTYOTD7SpL1OwhNF5WDBQl9xz0T99RyyiNa8p1+S8A/wOm8hN+CFmWRLj\ndCOpcdoMpl0PD3eyi8z7ucc3mMe1FhbRdRM22pFlDvbZdwBWCo9yfIiNhkzChgWfJZa1aDKc/TeH\nYSlBP6R8wIqnZtj/XCy94GbgXu99PoK6QdRVbqMoUe28qbBx9UpfhCt9oS93fMfwXOpH31qYFx7z\nM8u1PRLmYMZqJuYBZZ/nhkf23EnUmg+PJMLNk/7fFsMM1uLheYmwvESJR5EcIh7GrMjUzLYeMO8B\nuKen2az3/wQ/uMoUyjsuDW/eCuf2MO9yVWxobwUsuGEpbIK8rutD59z6h5jxyRqiScC7UW6ocjjn\nVsF+AqvlmuZhNxpdsd9X8n16LHryFuCf3vupNDGFym1EAOd6Y7lbK1B82KRDieXa9ikXYhupHjpR\nfO62WpmJDaF9jRnNqQvgm0Ng9WtgC58xKJ1g/jh4Zm2bJ9r4YVju+pAWsjbwOPRd1oIR6stH1DQ+\nyfI70Qg1P865QVgAQ/LbnoV5wEti17zlMru/gHlKtxWp6+WcWxGLVdgOGOm9v72OQxZS+I8WEmP3\nBNbA1IB/CryRSBC1A46hHiH1kUgz4zOPhOQGKE83MkNp07DIon/ldnLAfdBxK1N84UVM3mU2Zq3+\nw6Lid4E52NzT18DnWFTfO+EUiSfUJENAkcbhnOuJffW/zGyehhmmbKVgxYzSLUU0FUMJlq2wkeBd\nST347aiZ6F0rRaWOVsVcuY7Y+PH1WGb2NiKyraq+VPQFWzHz6t4l0sT43HOpbaXaii6Xaku82I6Z\nR2ugQd73RKzehJZou5pUyO5NYHvM6iwH8+6EJ35gQ37vYN7Qp+HxGd5HMeZWgHPuF8DdpOHgyQ1O\nsv4xcCtmmP5XRIneWVDR/lgO6jqZpilrw/1r1NRvrJOiHtQo7IZpECbE6LG8g6uwkO9f1OdFWynn\nY3cZfUgvZPnnPK7MM6R3tvmhvQ4llksND5Zqa2uU+tyqjZlYKO2MWp5nYHNI2Tm5TnWsd848uuT2\nS5Y7YPNU2Ud2HiuZ18o+J485F0OvofCzOSWM8PZw7x/s//3pkdDhQrgDS6z95ivYaj3vX22Czy7S\nAjjnOgEXYYUcE+ZjvwOHqXMcAYwrGhbunPsJ5rQcTE31jv+tBTc/B79f3PKmZmKh6oUoaqC2ADZT\n1QVB3ghVnSciZ2H5DG0fC1+t7iE+c6tLzW/V19C11n2a4jU8tRubrNGZ2RpzbZxzi2HJ69uVaPbA\niH/D8Xjvnc29JnWUZgA7+micWi3OudWwvKR8IERH7CZmJHB6karHQXNve8xbyua9zcPy1y6eC707\nmRhvkjv3bH36W9RAzSbImORYlVQzL9LSmAsew20jZXGW4PoIaXn2LG8AA7z3z4R9e2LKK6tjXtdu\nSVukdRHmhAZho2Glrvv/BQ7x3r9W4FxLY57SYdSULfoUE0a4ytv84whSIfCpQH+8H1uffhc1UDcA\no4LUkQOWEZE1sVy9+ohBRiKRFiAM65yNqcLkh4PnA+dgd86zwv7dsajV9bDhyX299zHfsRUSDMod\n1AyESPgGOBa4uq7hPOfcutgw3v7UFOl+CosAvNN7Pxfz0p7GavIBPAPs0xCB3qIG6gSsrPqT2Hj4\n85gbdxlwXH1fNBKJNA/hznl7bJhl+RK7vAz8IVtQMAwB/oMQvYfdWd9R6b5Gmp6gQH8ni+rigeUv\nDfHef1bL8YthUXiDsai8hJlY0vWl3vuXMwfsgUnPJa83AvhbQ0uaFK2oOxc4RkROwVy6TsDbqhqH\n9yKRKsU591NM67LUnfMc4DRgRFaKJigJ/J1UF+8Y731D8pwiLUgwLBdQsw5WwmTgUO99WeFs59zy\nWDDDIGrKUU0GLgWu9d5PyRzQFTg383pfAwfi/bhGvI3aDZSIOCxUcB7wZhBafS3Tvh5wiapu0ZhO\nRCKRpsM51wczPgMoHd35LDbX9HruuCWwaNV+YdPZ3vuR+YMj1U2YZ/w3pRUhRgJnlJMics6tgFVM\nOYCaMlwPYFM69/u8cLG93m2YPivYkF8/vP+oce+kltDkMMekwAQsXWKCiKwY2pYUkcuwjOJSwwaR\nSKSZcc51c86diCXDDmTR//dMrCLGFlnj5Jxb2Tk3EpMY+uP/t3fuYXJVVaL/ne5O+pUHYZIICQjm\nElYAAwQwiPJ0REFG0MFBGcERFATlKo8RBL0yDkZUZmAUEAF56OCgzngDouQijAZHEIgQEEhYvESe\ngTzIs5N+1bl/rH26Tp+uqu50V1dVp9bv+853qvZ5rV3n1F5nrb32XqH4WrZyzIpTXSLjs1i+vKxy\nuh+YF8fxRYWUUxRFzVEUnY9NvHsqppzWY+HoEsfxUXEc/7KAcvoYNgB7HhagtQA4ohzKCUpbUN/B\nxjwdjEXwLACuFJEvA7/C5t76J8zH6DhOlQjhvn+P5UMrFJ0HsBj4dBzHz6WOOwBTWCeQHwvVhblw\nvjiUgZlObRBZipSfMdCdux6bBef6YkEQURQdg7mCdwtFazEL/Po4jgt340RRazjm9FCyEvg4cXx3\nZr+J2ETBe2FpWG4l9QwORikFNR84RlXvBxCRT2JvZnMxP+R7VPXPQ72Q4zjlJ4qiQzC3XBIxlR00\nvhHLKXh9HMe50Mf0QUwxHZLabxUW9PS9OI7rZfqybYIoit6L5YzMBkL8FDi7WBBEFEW7Y/1USX9j\njOXS+kocx6tKXFAwZZhk0P0tZrFvTxR9ElNGyZJN/f4++gdblKSUgpqITd4IgKq+GvJA3Q/8g6r6\n25XjVIEQNnwg1ij8bWpTD/3/04uwCLyXoiiaEFnjcTb9x648hSm4W4YyONOpHUJm228AZ2Y2vYpZ\ny4sGHgVRFE3CZqM/m3w/0++Bz6ejOYtc9FSsLypJQ/MMNh722aLH9Gf9EPcDSiuoZAqfND1YynZX\nTo5TAYL7TrB06QeF9R6Z3VZgU3Al/+dNWKN1CzAziqJvAp/B0l8k3IMppru2NsupUz2iKJoJHIcF\nsryL/v2MMeZ2+0qRfqYGbAzTt8jn5HoF+CLwk34uXYvK2wsLkpsb1u9mYELO2UMQez3wOBbP8JUh\n7N/HcNIG+ESQjjNKhLfb+eSV0Tvpr1gSYqwzfAKwS6r811iyuRnYAPuPkv+fd2MD66+I4/ix0ZDf\nKS9hHNscbCzSCdjA6UI8C/xtsWmooih6BzaY9kCACLoOhUX/Bc9NtRRg52Gh5VMw66icc3tOwpTb\nu8N5sxZfUQZTUJ8QkcQkSxLpnSgiK9M7qep1Q5fVcRzoa3x2I6+MDsLeVAs1DuuxlOnLsKnH3oI1\nWImrpROLwFuPzUB9WOrYNcA12KDK18peEaesBEtnPpbd5CMMjMjL7wubdoXrl8KVkyFHFO2LZYKe\nDsx6Duaeb30+fdHWHwL+FcbPMkusknRgEX9DppSCepGBg7xeJx+GmsYVlOMMQpg+6B3kldFB9E8E\nl+ZVbG6zHGZBTQfeCxxZYN+lmGX0Vfq7XJ7GOsF/VK4U3M4wsf6iadhMPM3kZ6lvBsavhPYrYN7d\nML8F9t9iMQAFmQzx30DubGjcH9oj60s6O71PF9ZR9DXynT57YKHZhR4g8jPhd2HDEZrpPyt5er9l\nmKJ5CFiCBdhks0z3ZtY5hhEVWiqj7q5bezLHcfosoxlYmzAHC7Odj7lnCuWX6sUahSS9BuH4GYNc\nagPWQOyLDcBM+C3WvzTkdAlOGTFX2X5hmRfWb8vuth6LYrkNm/SwVN/JdOBYrLNod/rylRXkLkxb\nPRW+T8IU1efoP/I2Q5L7rJmBynENNn3RXcADFAs9HwWqlrpaROYDC1V1Zvg+BfsRjsDGX31NVW9M\n7X8pNjK+CUuYeK6q5sK2E7FxWtOxP+enVPWNsG0eNuhwTyzi5AxVfbAilXS2acIErLPIK6I9UkvR\nN+ACNDKw8zlND/aW+gY2RqUHS2a7J/lxLz3Y3GpXDBqJ5ZQHexF5K/0V0X5YivSCrMAyBC7EolR6\ni+0YTvJhbLLTnQeXJvcs5M6FxjvCMIMIazCThnEY9AL/B/hWtdLKVFxBhemTTsHe8LpSm67HXiqm\nA/sAi0TkSVV9UETOwmL154Z9fwmcB1wmIntj/vUjsUiRK7GJMY8RkRbs5eQSLEHoJ4BfiMgsVfVg\nD2dIBNeckFdEe2HP4tso/3+oG5vHLHGzTMNefHcgH3mV5k0sxcHVcRy/UmZZnATrF5pNf0U0jwJp\niGLsLeIlLNXwy1h/yT1YJ2IpZmCdThcwuPmcsBG4FBr+BRqSBvUgrCHcf4jnyBBjqVdOI47vH94p\nykM1LKiLsKiRr2P3ARGZgHXYzVbVLmCJiPwHplAexOaFukJVXw/7X4opncuwLI23qeqSsO0CYKWI\nTMMGL/aq6rXh2jeJyDmYsvvPSlTWqT7B5dYEtGBBBRPDMiGztIf1ROzNeDY2Zmgqo5PVN8l625w6\nf6KMCrECi9Z6LqyfBn4Ve4r18mITre5BXgntH9ZtMfZGkFU+zwMvYDHbb2ARK0NlBhZqeS5FpwFJ\nXlpWY5b0amDVOlh7Cex0LRyzMfQXtcLaE+CWH8B/N4XMyWHpHvI6O51RFamGgrpBVReIyOGpstlA\nt6q+kCp7GrNwwd5el2W2Sfg8B8s9AoCqrhGRNaF8TuY4sPkF54ywDk6GEHk0jv6pytNLC/Yn2g5z\ni08irwzasfwybZgCaQ37pzuUk6UpszRiUW/JOp0hF0ZHsZSLxO+fkMPau0QBpdfP9007Ywo3+b2G\nlcag7rDnsw175rbDrN//hYXo79oJO6+DHTbC9m9C+/PQoNgP/xcsWmUVef/qSJkKPcfAq1+Ax+fZ\nPe9TPAxURhsi+5/siynKeZiRtCf9p6i6fDN84+Y43lAGEWuCiisoVS007UY75tJI00E+hLY9fE9v\naxCRZuyhy0YodZD/AxfbtvVY52f27bZQAzjcsr7vHRC9AU0rYPxL0LICWlZBy1po2WRLcwe0bIHm\nLdDcDc1dML4bmntgXA+M74Xm3vznceF7c84+j8/BuBjGhXVTDhpjaIqhIQ4NflhHcWj043za9LGg\nAGqOCHraYVU7rJwMq/8K1u8AG3aCzTtBVxO0xPZ8zgB2y9lMEe0RTLgsitpiaI+htRcak4YyF0Vd\n3dDRAx3d0NEVlk7Y1AEdm8N6A2xaBxvXwKY3YXPOFGJcYOnC+uzTae4HfI/juHRbbYp0PPkXjhwD\no7t6w9JE/5eUtiLfW4G2XmjrhAlrYPKbsN1KmPwGTF0F262FSeugfT00r4PG9dC4AXOFJRXYTN60\n6AmCjTYRvBFbDqUbVsbxk0X3i6LpmBL6a/Iuxd2K7Y91eZwbx/Ez5ZS3FqhakESGDuwBTtNGPp18\nWlkl23pUtVNECimcNizCKXtcettWcV8Uvf9cWPQyRL3Yv7iX/D88R/F/e7qczDanvoihaaO9qe9Q\nxgnvEuuy0IDeUaMhimigv7makDzb2Wc/IcrsV+z4wcpqgUaso3AHyG0Hq5rgmXWw9El4sMOso1eA\nV3OZqaSifJBFYhUlLsWZFOclbFjBUuAR4JG4TDOH1yK1oqCeAcaLyM6q+lIoS7v1lmNuuSVFtiXu\nPkRkKtZxuRxzKZ2VuZZgbzFbxZlwzeNuLThOH8lL2nA6LLLKplaVTyt07wzRLtA0E+sjmhmWHaFj\nGjwwA+4eZ7PFP1wsc2wURY1RFM1hoDIaEGSR4mnyimgpsLTkJK7bIDWhoFR1g4jcDlwqIqdho+lP\nBI4Ou9wCfFFEfoNZ5Bdi07iAhdbeKyI3YoPHLgXuVNU3w/7NIQrwWizYYjoWz79VvGQzuA8Yy+DU\nNHHwRcYpn2TckC+LU/7Kvn0bIBfWaaOXnLk8o1xwecbB5ZksoTyxGKJ6sJSTDr9U51/f75tsT1H0\npwgbiv1+UdpLUYgmiJugpxE6G8yDtxHY2AzdLdDTCr1tkJsAcYiQiSZBwyRonAxNk6FpIoyfDOOn\nwHY7w/YzgfYwdCgGNsOG12DJMli6CJ66Gd7YbH2pU7Ao4hPCgNwpmDWbXhdKuZ7Qg+XcSyujx+Jt\nqC9puFRbQaUf2NOwcNmXCSkCksg8LA3AW7CRy82YcrocQFUfC0rtRqx/6HdYGDvBBXh0OO83MEvt\n2JAZeKtYCyc3wSM5mJw0ZkH+vs9JAwf9/5jJrLuhLOnHIfTrEENDLrSToRFsiAf8t8cGjamlocA6\n+zm7FGjwBkQ+DGXJNHL9lEUh12uyNJAP5Su0tEPcCptbYGMrbGqFDW2wfgKsmwhrJ8OaqbC6xfrT\n16eWmHzQR3YZj/UNNvdAS7f1LbZuCetO62ds7YaWLtunOaybGoMibYBcaokb7XnsDZ97cxB3Al0Q\nbQY6oaET4s3QsNnKok5gsz2DNNqxPYTzAL0R5HKQi8M6B7kuiLYAW+x8UVgauux7Q5ctjT3hVjZA\n1JD/3BBBFGU+J0tDuO3J52jgY9HQCA3joKnJfotxwLjIbtU0GNhRms1DshELgCC1PYcNxFwDva/B\nljWQ67C+wYnYuLNszqWtYTM2aWpaGT0Rx/HWBP7VDZHnJCuMiOxKsJpU9YUjoujyxXBOdaVyxgrN\n9FdsDeTngEmW7gJlyeKMCXqxF5E3h7h+CdABWWnrnGxbm95WbQtqzNAEjzRQ2MVQ7C0t7T7Kfi/k\nWirgakrcUGl3VK4hv04suPQaCpcnoheM5UjtU9DIiFOfo/AWXWBbLu4fM5KL89vTn+M4f45cPHDp\n257Ll/Wmy3IMfJvPWYNRyFgaivE0wIhqhEnjYbsms5onARNjaO+Fth6zaJoTKzhLZ1hWF9o4hmmC\n3Lj8Eo+D3Hhbx82pdXqiuWbMtIlS9zhEEPa7h+n7n77vqXsdp7/nINcLvV3Q3Q09XdDdBd2d4XMn\ndG+Bnm57LrJOjezndFmMWb2DKZyNnnV4dHEFNUTujuNboii6lfAy7A+mE6KwssbSAK9gI0wKfVSJ\n0VTKeNqa7YmiLfWONNR1+nMyaWhnZt3d7c+9U0FcQW0FwTR389wBILykhC4Y6iq6ynEqQTmTUjmO\n4zhO2XAF5TiO49QkrqAcx3GcmsQVlOM4jlOTuIJyHMdxahJXUI7jOE5N4grKcRzHqUlcQTmO4zg1\niSsox3EcpyZxBeU4juPUJK6gHMdxnJrEFZTjOI5Tk7iCchzHcWoSV1CO4zhOTeIKynEcx6lJXEE5\njuM4NYkrKMdxHKcmcQXlOI7j1CR1kfJdROYB1wJ7As8AZ6jqg9WVynEcxynFNm9BiUgLcAdwAzAZ\n+C7wCxFpr6pgjuM4Tkm2eQUFHAH0quq1qtqrqjcBrwMfqLJcjuM4TgnqQUHNAZZlyjSUO47jODVK\nPSiodqAjU9YBtFVBFsdxHGeI1EOQxCagNVPWBmwY5LjGsN5JRMoulOM4jgPATmHdmN1QDwpqOXBW\npkyAHw9y3I5h/T9ll8hxHMfJsiPwXLqgHhTUb4BmETkLCzU/GZgO3DXIcUuAQ4DXgN5RldBxHKd+\nacSU05LshiiO48qLU2FEZC7wfWAuNg7qTFV9qLpSOY7jOKWoCwXlOI7jjD3qIYrPcRzHGYO4gnIc\nx3FqEldQjuM4Tk3iCspxHMepSVxBOY7jODWJKyjHcRynJqmHgbplR0RasZkopgF/AU5V1a7qSlUZ\nRKQJuBUb7PwycJKq1sVYBRE5A/ho+PpW4NeqemYVRao4IvIvwPzw9WRV/Us15akkIvI89n8HuFxV\n76imPJVGRD4CfEJVj63UNd2CGh6nAw+r6iHAn4DTqixPJXk/8KqqHgasAd5XZXkqhqp+X1WPwH6D\n14GvVlmkiiIiRwHtqnoo8EVsyrC6QERmAg+p6hFhqTfltDPwmUpf1xXU8NgdWBw+PwQcVD1RKs5a\nLPEjwCQGn3R3W+RM4KequrLaglSYw4FVIrIIm9/yvuqKU1H2AXYTkcUicmPwotQFItIAXAZcCESV\nvLYrqOHxBHBU+Hwk9ZW644/AXBFZjk0d9XCV5akGxwPXVVuIKjAV2EVVj8bmTTunyvJUkpXA11X1\ncOz/f151xakoFwE3A6sqfeG67oMSkfnAQlWdmSqbh00quyc2b98ZqvqgiHwDs5SWAl8CrhKRxdhs\n56srLftI2cq6Xwq8E3gUc+vdpKpXicjJwALgHytegREw3PuuqueKyD6AqurmasheDkZ47x8Ph9wF\nXFJRwcvAMO/9o5j18Gg45E7gaxUVvAyM4L4fDPw10ALMFpH/rapXVkLmulRQIhIBpwCXA12p8hbg\nDuyP9wPgE8AvRGSWql6U2u9g4Ieqep+IXIzNmD4mGGbdL0ztdyn5juIVwKEVEn3EjPS+B97LGHVt\nleHeHw98EPh3rPF6qnLSj4wy/OcvCMddARxGXlnVPCO976n9dwGuqpRygvp18V0EfB74Ov19qkcA\nvap6rar2qupNWGf4BzLHPwMsEJH7gRnATyogc7kYad0vB04UkXuB8xlbb9EjrTvALPIKeqwx0vov\nBDpF5A/AidizMFYYad2vBt4jIr/F+uL+bfRFLhvleO4Jx1Y0YrcuLSjgBlVdICKHZ8rnAMsyZRrK\n8wWqr2MP6VhkpHVfCRw9euKNKiOqO4Cqfm6UZKsEI733OaoQyVUmRlr3jZj1OBYZ8XMPoKovABUL\nMYc6taBUdUWRTe1AR6asg20oCMLrXpBtvu5Q3/X3uhek5utelwqqBJuAbPhoG/URSu1170+91B3q\nu/5e9/7UVN1dQfVnOQMHHwoDzeBtEa97f+ql7lDf9fe696em6l6vfVDF+A3QLCJnYaGXJ2NT+txV\nVakqg9e9PusO9V1/r3sN190tqFRUSphP72gsQmk18Dng2LE85mUQvO7UZd2hvuvvdWds1D2K47qY\n59NxHMcZY7gF5TiO49QkrqAcx3GcmsQVlOM4jlOTuIJyHMdxahJXUI7jOE5N4grKcRzHqUlcQTmO\n4zg1iSsox3EcpybxqY6cmkNEcsBRqvrrAtt2BZ4H5qjq01WQ7STgElV9W4l9dgS+DPwNNnXMC8CN\nwBWq2lsJOUeCiEwD3qOqPx3BOY4H/qCqr4rIJ4FLVXXHcslY4HpvA34GHIgl3rsReFhV31Fg36uB\nM4FTVPWHInIccJyqnjpa8jnDwy0oZ6zxIrAD8Gy1BSlEUKB/BHYGPg7sgaUHPw9rNMcC3wY+NNyD\nQ+bV/wQmhKKfAG8vg1yluBpYEHJWAXQD80RkZnqnkF32w0COMO2Pqt4OzBGRQ0ZZRmcrcQvKGVOE\nBuiNastRgmuAZap6XKrsLyKyGvi1iFypqn+skmxDJRp8lyEdHwGo6hZgywjPWRQRmQ+8XVVvSxWv\nwbLDfghTXgkHYTmPVmZOcyVwMfDe0ZLT2XpcQTljiqyLT0SmAN8HjgLWAV8FfgDMUtUXRUSw1OTv\nBlqwVALnqOq94Xw54B+AczBr5yngdFVdErbvHs5/IJae4JclZJsJvI8CKbNV9R4ReQ/wZNi3GfgK\n+Rmk/wB8QVWfCNsXY7NNH4A1mquAr6rqzWF7C/BN4GOhXncDnw0ZjxGRC4DPAlOAR0Kdlw52bhH5\nJ8xFhogcqKqzwm90CXAG8GdVfaeIfACzDPcCeoHfA59W1VfC/QFYLiKnYIqqz8UnIrPDPTkY6AJu\nBS5Q1c7U/T0+1O+twBLgVFUtZjWfBdxWoPw2Biqo44GfJ3VMsQi4WUT2UNXlRa7jVBh38TljnVuB\nXYHDgZOwvp8I+tw5d2Bv0gcA+wEvAddlznEJcCGwD5as7Zpw/His4VoN7I+5vs4hNSN0hr3DtR8q\ntFFVF6dmir4KcwF+Opz7FczCmpg65EJMIe4JLAS+LyLbh23XYjNRfxR4F6bkbgpyfxY4HfhUqPO9\nwGIRecsQzn0Z1pdzG5DuvzkBOAz4dOjvWQj8EEsPfjQwC3s5AJgf1gcD/fqxwjV+D6wNcv89lkb8\n8szPdTFwajjXNExZDSDc46OAAf2VQcbDRGRyquxDmILqh6quxe7b0YWu41QHV1DOmCVYN+/DOruX\nqurvsLfpxMXUijXkX1DVZ1V1GebKmS0ijalTfVdV7wpBF5cB+4WG70isv+tTqvqUqv4MUyzFXGBT\nwnrdIHJvB3wS+Lyq3hPe2D8F9ITyhLtV9TpVfQGztsYDe4cG98RQr3tDvc4AHg7HfQk4P5z7WVW9\nGHgCU4Ylz62qmzB3XKeqrk7tf134DZ4AGsO1r1LVF1X191if015h31XJOrj30nw81PNUVV2uqv+N\nWXqnZxTJP6vqfar6OPA9+ivLNLsAUwmWaRpVfQx4GQtWQUTmAU2qWvAFArOui13HqQLu4nPGMnsD\nHaGBTngg+aCqHSJyDXCSiBwA7I5ZFDHWyCYRdelowCTd9TjMuvizqq5Pbf8j9tZfiKRhnoJZXJ4W\newAABARJREFUXcXYPVz/wZSs3SKyBHMzJjyd2r7BvJWMC8c3Ya6vZPty4GIRmQDsBPxIRG5OnWs8\n/QNLip27GInbDlV9VkQ2Bzfi24PMe2O/zWDsATyqqt2psvux30PI9y9m70kx2aaH9aoi2xdiVtOP\nMffe/y0h2xpgtxLbnQrjCsoZy3RTokM/NNYPAOsxl9XPMasq20h1FTlFXOD83YV2DDyMRYcdCNxZ\nQJ7ELfZ8dlugCWuok2sXkisqIW9yDjBL5U+Z4zYO4dzF6EtiJyJzMaVyJ/A7zML5IHBEieMTthS4\nTmNmTQH5ismWRO0V8wYtBO4MfX4fBj5TQrbG1PmcGsBdfM5Y5kmgVUTSVkfaRfN+rG/kUFX9tqre\nBcwI24YSqfY4MEtE/ipVtl+xnYNL7E7gH4OLsA8ROQo4DlgBPIcpuoNS28dj/WQ6BLmex6y/PllE\nZK6IvIY1sCuAmar6fLJgbr/Dh3BuKN7HlnA68ICqflRVr1bVP9Df8ih1/FPAvqG+Ce8Kcj8zRPnS\nrAjrqUW2349F7Z0BbB/ckcWYCrw2DBmcUcItKKdWOUBEsi9QD6e/BFfTHcANInIWFs12JdZAxsCr\noezvROR+TCF8ORzeDHQOIsM9WKP5IxE5H5gNfIHSfUznAvcBt4vINzGX1eHAt4DrVfUBABH5HvBv\nItIR5LwwyPTjcJ6IIko0uOR+AFwhIqdjLrCrgAdVdb2IfBv4moi8DizF+rdOAr4z2LkDG0xEmRmi\n8rK8AhwvIgeF+n0M6+dJlGtiqe0rItnjb8GCKW4UkQXAzCD7T1V1VbB6t4ZXMCW1L6b4+6GqORG5\nHfhn8r9tMfbBLFynRnALyqlVvo5ZI8nyK/IWR/oN/VTsrfd/sIi+mwlusPBmfzEWIbYMc3sdhSmm\n/UtcOxnA2Us+quuhINO3SwkdQqHfhUWp/Qx4DPg8FpJ9ZmrXC4Dbgf8I556GWXqvp2QoZYmch0XD\n3YFF6b0InBK2fQer879iVuCRwAeTEPYhnPtHWPDBo1lLMPBdzLW3COtHm4lF+c0WkbZgSd4cznNa\n+nqq2oFZtjtgLxz/jgVYnJI6f1a2ovKqahzkOLTE/guxQcMDovcSRGQSMJcCrlmnekRxPJg17zi1\niYi0Yo3v/1PVrlD2TmAx0JaaVcDZhhGRdwC/wNyaw7rnInIacIKqHllW4ZwR4RaUM5bpxAblLhCR\nWSKSjFX6uSun+iEMqn4M+MgITvMZzEJ2aghXUM6YJSihYzHX358wV8+TWCe+U198DvhSEZdkSUTk\nw8ATyewiTu3gLj7HcRynJnELynEcx6lJXEE5juM4NYkrKMdxHKcmcQXlOI7j1CSuoBzHcZyaxBWU\n4ziOU5P8fxFfmAi8ri/tAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x112167c10>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sns.set_palette(\"Paired\", 10)\n",
"\n",
"plt.semilogx(ligand_conc*12,AblGefIma_df[:].values, 'r');\n",
"plt.semilogx(ligand_conc*12,AblGef_df[:].values, 'k');\n",
"plt.text(4e-9,60000,'Gefitinib (ABL)',fontsize=15)\n",
"plt.text(4e-9,55000,'Imatinib + Gefitinib (ABL)',fontsize=15,color='red')\n",
"plt.xlabel('Ligand Concentration (M)')\n",
"plt.ylabel('Relative Fluorescence')\n",
"plt.xlim(1e-9,3e-4)\n",
"plt.tight_layout();"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAKsAAACuCAYAAABJJf2qAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztnXm8XdP1wL87L4MkMpgSQ0Ik8RZ+ZkWRlBhrqvGHlCJm\nRZDSolpDzVVESmtOzb+WElOUFi2pktZMLYRSKoYGiUxe8tbvj7WPe95997133nv3vvdunO/ncz/n\n7n3OPXufc9fZZ++91l4rmBk5OdVAt86uQE5OVnJhzakacmHNqRpyYc2pGnJhzakacmHNqRq6d3YF\n0ojI+sAo4DpgT1W9o4nj1sMftA+A41T1J20oS4Br4nleVNVjRWRV4GagJ/B/qnq5iAwFbovHTVbV\na9twacVlnw1cp6r/bsc5rlXVI8p9bBO/PxlYRVVPEpH+wO+APsDTqnqyiAwAfgv0BR5R1bPbWlZz\ndKmWVVVfUNUrgZWA/Zo5dC9gNVX9sC2CGvkpcJKqjgb6i8hmwHHAz1V1c+AAEekL/Bg4HRgNHBj/\nrPayWnsEFaA1wtdOQd0I2BNIJuS/B9wX79sa8aE/BrhFVUcB64vIyLaW1xwVaVlFpDdwIzAY+Aw4\nCNgdGAMcDTwKHAwMAy4AegC/Al7Hb0w9MEpEDgBmAScDSwH/BCYAhwB7icj7wI9VdU8RuQFYA1gU\ny1gY6/A5MBI4XlUfS1XzBFX9JH7vDtTFui4rIr2AAHwJbKiqR8frmg5sBDwe08OKywDeAm6KeYOB\n38Rr7w7sACwd96Xv10jg1/E+TI+t1VnAcGAV4E1gLrANcI2qXiUizwObA78HegNz8Af8O8AJsf6X\nqupvReR5Vd1ARM6N5zDgZFV9SkSei/d9LeBCVb0tVa/kYT0b2ClmfwqMFJFusdy5wKbA+Lj/Ufzt\n+GbqPI3KiPV/HRiBv+F2BwYB26pqg/uTUKmW9QjgCVUdg78ejlfVW4AVgNvxp/At4CJgF+Ab+J8C\nfiMnAk+q6q34H7YrfgM2xAX5RuAM4GMAEdkD+Dw+7ScAF8fzrIQL/+HAkekKJoIqIvsBvVX12Vi3\n84FXgb+pah0NH+i5uLClKVXGIGAP4BZgTVXdkYJAjwEeKzrHxcB4Vd0KWFpEtoj1f01Vt4335xbg\nW3jLltynEcAC/CGYBAwE9sEFZ9vU+U1ENgDWVtUtgL2By+K+YcC4eI7ji+r1c1xQv0zlTQUOwBuO\nhar6HtAff1iaukelylg15p0F7KaqOwN/Ab5JE1RKWNcExonIY8Cx+J8HcCWwI94vBOiuqp+oar2q\nntXEuf4LTAauBZYFamJ+SB1TC/wNQFVfxG8E+J9twEy8ZW6AiHwPf7AOiFnXAtvhQjUoCs2i1E8a\ntYpNlKGqWg/MptDCfB73j8FbnzRrAFfG+7UxsFrMfyVuZwNvqurs9HWo6su48NyHv20WAafgr+X7\n8JYvfY+ejr+bCfSK+e+o6ryY99W5RWTpWNeJuGDvIyJ7A7/AGx8BVETGxvr1iz/tF9NpSpXxrqrO\nxYX8jaJ7VJJKCeubwOWxZf0B8LCIdAd+ApwDXBiPWyAiy4hIjYj8noIAWur7RcBY/PXfI+an9yfl\nbQoQW5D3U+cpiYjshndPdos3DeJrLQrfR3iL8byIjBKRGmAz4IWiU5UqI8kLRfUEWCYKXZoZwEHx\nfl0GPNdUvYuuYR2gPrbcTwH74t2rCcD2wI9Sh6fv0UoUHsKS90hVv1DVtWKdTgTuVNW78IHVF/Gw\nmcAAYDqwdcwbQ2w4UjR3jzJTqdmAq4HJInI4/kAcjN+4Kar6cxF5QERGAacC98djrsIvwPDX+2rx\n9w/iN2MGLigrAs/jQn98PP5uYBcR+Us8VzKgSN+Q4ptzHt5PfdDHCJyJt0q/FZE64FVVfUhEXsH7\nnf3wEfzsonOWKsOa2N8feKfE/Tot3q+lgH8DdzVR5+JzvwlcKCKH4AJ0KN6P/TPet7wuOVZVnxWR\n10RkGv6/T2jm3KVI9p0JXCMiyQP9Pbw1vFVEjgMeVtXXmzlvcRlN3cNGhNzqKqda6FJTVzk5zZEL\na07VUPY+a5yj3ATXLi0u9/lzlmhq8KnA6aq6sHhnJQZYmwBPVOC8OV8fRgNPFmdWQlg/SBX4XgXO\nn7PkMgRv6D4otbMSwpq8+t9T1X9V4Pw5SyhxChGa6D7mA6ycqiEX1pyqIRfWnKohF9aMiEgvEVmm\ns+vxdabDhVVEthGRZq3tReQsEbkplX5GRLZNpXcQkb+m0mfGVQbp9IhUekQ0rm5NPbcTkXtF5DQR\nWRnYH9hIRMbFdPrYcSKycnE9cspLhy5riQK0Ac2YgUUMt97vhZv7zaehgcNYYKqIjFbVZE73FBGp\np2DRlWYobvv5dKouicHwl7hxyUO4FVZv3JTxMNw8sWfM2xI36P4EuEhE/oObLN4Q65iY431VD1V9\ntYXrzGkFHdqyquoMVb20OF9ETo/bk1PZU4GdcSPmr8wHRWQ5XIAmA0eljr8COAlfJZA+9yG4xdc4\nEUmbzB2GC+dVMX0sbk/5X3yO+CHc4DlhGnBPKn0zbr64XdHlJPU4iq8ZwekRQugTQugfQlg2hDAo\nhDA4blcIISwX85cJIQwMIfR/OYQtCKFvS+fv9AWDsbX9UETWpaH5XGK4nTbOBTgQWB5fF7WFiCSG\n3Qvw+bm0sTSqOllE3gZGqOoNqV3J0pWE7vgSm574ioRVaEixedr8WFbxA5/Uo2pVzSGE3vgiyW/i\nNsQ9cFVod/x6k0+xrW6bWBc43v/n9Zo7rtOFFW895+LGu5+l8hfjS1hewrsNibDsCOyiqotEJFlO\nAt6S1eFrufZPF6Cqf8ZtPNNcB1yP34MXgV/iKwXqgXNpLKzv4K32a5S2yUxI6nEVXZQQQjd8udCq\nwDr46oQ18e7SshRWEXQY10G/oS0cU3Z71riI7m1g9SwaLBE5Q1XPLWslMiAiuwNb4ZbvF8c1YV8L\nQgh/xwW0yzAA5g6urV2HZmSn01vWzhDUWO4UYEpnlN2ZhBBWprSgzsX760Px13s9vsDveXwVgtGw\nC9AN7xosxgepdWa2OITQM55jdXyh4DC8te6Pr7boB/TrDsusACNmxx9/AecNbqHunS6sOR3OAanv\nZ+Bjg5fwV/8bFPqhR5vZn1p7cjP7El+CNKPZA0N4GJ+hoR5u62Z2QXwrN0kurF8/do7bOuB8M7MQ\nQi98tmNg3HenmbXb80yThLAevqARgG6+fL5FMglrXMi2IvBBKaPYnDbiQtIHs087sNRkxP1WFNSA\nO+VYN+a/S8E3QfkplJfwKGafNHV4mhbnWaMTiD/h69AnJHOibSaEbQih+ac2hLMI4aZU+hlC2DaV\n3oEQ/ppKn0kI6xelR6TSIwihsQYrXRef65scPwPaUbdxeL8wC/sDGzX5mxAOJYRrGlxbOwghLIX3\nH6Fg3PxjfAk3+FTcTma2oBzlNcHOQPp6zsr6wywt6wn4qPlhXDs0Hfda0npcgDJrsGLL06QGixBG\nY/aVBosQMmuwUnVJpmmOwD2qbIa74bmmjXVzbVYIZ+EzDcPxQcqa+DzuSsD/xu1SgOJaseQ3vSlo\nxobGdOHazNqjFds79f32EMJ+wM9Secda+87fPCF0x5fpJ7xFiRUBTZFFg5WMAsE7321/6sxmYNZI\ng0UIp8dtixosQmiVBosQDiFqsAjhhyXqkgwoavDBwQe4IJWq3ykx56GSdSu6Wvx19wDwLD6vuynu\nF+AWfDDzJA21YkZpzVi5tGJ7xW09/pClX8d34/PMleRoGs5fT6QVc6dZhPV84K94n2Ya7j6mfHgL\n9yEhlNJgbY17/EgrCxposAihWQ0WZpPx1vYGzC5upibz8GmXlXFPI6Xq96+Y+2gTdStmPi4YCyk8\n9McCy+GKiKZ+U0fD/6ZcWrFN4/Zj/CHpGdPvA4dZJZ1IhNAff7MkLKDgRioTWboBj+ATtZ/g2o6/\ntKaADLRJg4XZIkLIpMHCrJQGq5hr8FdUdxq2YOn6fR7rUVy31jAznqsH7kXvcNzJWXO0WysWB1JJ\nv7gHhb5rPTDWKj/I+wkNHbbd0eqBpZk1+6mtrb27trb2gPj9xNra2ttbOH5YbW2t1dbWDmvp3GaG\nwRmZjuusT1evX8YP7oHQSnzO6oB7uKpBnYGlPpu1VnaydANWjK4nUdXL8Sms8mHWKRqszHT1+mXn\ngBJ503A7iEpzCQ3f4i8Az7T2JFm6AZ+IyDHAP/DRc3N9tJyuy+i4/ZJCX/X7ZraoiePLQwib4LMf\naa5OmvvWkKVlPQDX5x6K9zkqN2GcU0mGx20yczEb73NXDu8nTyrKnQvc2pbTZRHWvvjA4p/4wOLQ\nthTUYWSfkP/aEEIYSWE+uUfcPmFtaN1ayfb4vDX4QA7gNswKbkNDGE4IUwihuPVtRBZhvQdYBn/9\nf0Zjz8/loylNU/O/2Y4Q7iWE06KgXhjzzyhx7AaEsCsh3NislmrJ46ASeW1q3VpJ2u17ImsFpYC3\nvNfjcRBabASz9Fk/VdVSWqFKUErTNAwXwMTL8rl4QIxu+IN0EIW1Uq6VCmEMIISwFX7DFJ/sfwkP\nSgFwfpz7OwWzwrzqkskOcbuYgpv7qRUt0RuDb8dUHd6i/x2zf6SO2oeCx+xft3TKLMI6W0SuwYNC\nGO5F+Yqsdc6Ma5r2A/oRwvKYXRT3HIkv7KvHAzIchU+cL8CnYx7CfWqNAv4DvIDZY4SQPKmPY/bL\nqM9P99HOxh+OsRSCQSyprF2U/reZVXqgvD8F+UoekIJAhtCHgoLpYeBeCrEUSpJFWB+kDf7fW43Z\nZEJ4GxiBWXqtVM+iI7vhE/hv4uFoiiODFDM/bou1P1W/VioLIYRlKASnSISm1XaqbSBt9tcNH9Cl\ng/D9CG8sFgEnYmYUfF2VJIuw3oy3eKvg83KvtaLCraO0pula4FK8rzwf7/OcH7/fQGNh/YwQ9qZl\nfojbb57VjhpXA2NL5N1QIq98hDAcj3kFhamymzGbG/evTiE4xxWYtaTBA7IJ6w34TMAewMt4x3yn\nZn9RXpbF+6TdgcmYvUHjeTsotBZJpz4JIuHCbzYulb6+IjXtmnwnbpMIN4twW49Kclzqe/JmTFtb\nXYLPTnyId8cykWU2YNU4wJqvqlPxqayOw+wpzE7A7FjMWq31yGHDovTrZla5ro+P8A+JqWS6ahpm\nL8X921Gw/jq1wTRWC2QR1i9EZBegRwwHNKelH+R0DeJylcQqLVEGPFjhYkfhU51QkK+JsUI9vvru\n6tabaAVZhPVQPN7nbPz1e3jzh+d0IUp1164ukVdOTitK/xu3lQX4PoWZieMxq6cVZBHW1fGQjzvj\nc2UtrZjN6ToU9+3nmdmbJY8sB75sJjEaT2aQrsTNOQdR6J/e2JYuXRZhvQr4Q/x+Ae65JKc62KIo\nXVlbALcbSdS5AZ+xSVYfnIcrdWbTuPXNRBZhrVfVdwFU9d+Uyb9RTmUJIdTg85hp7il1bBkpDrF5\nM2azCOEbuCM8gLMx+7AtJ88ydXVHjPf5AvA/wP+1paCcDmdTCkqAhEr6AhiML4pMcwXuV2sS3si9\nRjvezC0Kq6peKiK346qwt1T1o7YWltOh7F+U/tzM/lvB8n5SlP4jZq8QwkG4N0KAE/BFmW0ii9+A\nfXHDXQEeF5FS0ZRzuh7bFKX/XuHyvluUnkgI/fCVugBTMHu4PQVk6bNOwJcTH4yvcP1O84fndDZx\nceAaRdm/rWCBW1KYWwW323gQNzpaEV/d2+5GLqvfgLXxZcj9iiqV0zVZg8Y+Vn9XwfLOKUpPwmUr\nUX3fiFm7XYpmGWBNxI0OTgFOLFGxnK7HPkXpT6xSS63dy8q3UjlzcAcke+DeacCddLSbLAOsO0Tk\nXXx5wh24D4Gcrs3ORelKGq58n4ZydANmswnhpJh+KKtVVUtkGWBdglvjnwxsBPymHAXnVJRi3/x3\nlDyqPIxPfTdgEiFsSkEhcXm5CsrSZ91EVY8G5qjqbTSeaM7pQkTP1v2Ksh+pUGErEx0CR+7HbAYF\nw+t/4qsAykIWYa0TkbUBRGQo7XHMltMRFHcBZlpG/6dt4Lyi9ERCWIWCC81WOV5riSzCehS+SG8F\nfJR3XPOH53QyexSlH69gWekVGS/jDuuSPuwsWul4rSWyzAb8VFX3avmwnM4mzq9uXpR9V6ljy1DY\nWBp2N67AfckmLkevxmxeOYvMIqwDohbrdaLlt6o25a4xp3PZgoJ3wIRye30EN5JJ28XOwpc7HRjL\nX0QF4oBlEdbPcCPetCHvuCaOzelcTi5Kv29mlbDl+DUNW9VrcHPAE2P6d5i9V+5Cs8yzHiIiGwK1\nuCHL9HJXIqf9BHfYsWtRdtlG4qmChlEw94NCK7o9hRWtZZuuSpNlnvUc3KJmGHC6iLQtnkBOpTmE\nxo1P+YXVA92lbZqvxOzfFFrVpyq1sDNLN2BbVd0ySYjI3ypRkZx2c1KJvJa8fbeOEPanocLhE+As\nQliLQjexYt5tskxdBREZDBC3S7QHk2okeLyDYUXZb5vZB2UspDuNI9icjrshSrRY6cWBZSdLy/pD\n4B4R6YV71yjuxOd0PmeWyPtjmcsoHlQ9C9xACMvi5qMAk6igc+IswvoSBW9wOV2M6BtgtxK7yucf\nwN39FLukHI/ZYkI4Ap9fnYeHT6oYWYQ1WWQWcO/Jb+NB3HK6BofS2HndDDwiZLkoHlTditm06LQi\n0WhOpsIRX7JMXY1JvotIH+C2SlYop9WcUiLvsrK5CArhuxTiuoK7WU+cqu0FDInfy+8GtYgWhVVE\n+qeSK9HQyianEwkh1OJOSNLMwo2fy1FADxp7cDkXs/fj92QG4gHMtCxlNkOWbsC9FLxrLMAD0+Z0\nDS4okXeVJa4l28+vaehSdAbJ1FQIB1CIF1ARJUAxWboBW3dAPXJaSXRiUayx+pJyecxxH6vFavWT\nMFtICBtRGEw9Rsc4J25aWEXkuSZ2mapuVKH65GTnaBoPrG62Nno7KUHxoOoh4P7os+oePAzou8B+\n5bRZbY7mWtbHVHWCiIxV1ds7ojI5reIHJfIaRxxvCyFch8fpTViE90+746tkh+KGK3tg9nFZysxA\nc8I6SkQmAXuIyCYUnjJT1dzRRScSQliDxgOrB8zs1TKc/DIaGqqAW/y/RgiTKKxkPRyzpt6+FaE5\nYd0J9231DRq+Ejqkyc9plksy5rWOEM6lYJCShCH6EDgnRr9J5lQvwazDpzCbFFZV/S9uuFtseZ7T\niQR3dFbsJPgftNdoJYTTKcz0pONlnYab/v0qph+hjS4r20uWqaucrsV4Cj5QE37RrtCWvsY/WfxX\nT0FQ78R9807HB3NvAftXUv/fHFmsrgAQkeIblNM5FJsCvosLVdsI4VgKAzOjIBN34zaydwIr45qr\nPTCb1eay2kkWDdbWeNypgSJyC/AfVZ1c4XrllCCE8D8UXPIkXG5mdW084REU5mWT0EPgY5T98dXM\nSTfw4K8irnQSWVrW84Ad8Y72pTQMHpvTsRRrij6nrZZOHn40sU9NC+r9+Lr/I/BQpADnYVaZVbKt\nIFM3QFXnxO0C3BQsp4MJIexMIbhEwtVm1rpQTyGE2KLemM6N2wdxdepUCi3uA5S2l+1wMkUYFJE/\nAyNEZCq51VWHE0JYmsYuKxfhr+nWnGg9PGLkxiX2Pg30oaHq9CngQCoZ5K0VZBHWB3D12nDgndxN\ne6fwMC5IaW63rMudQ1geN0ppKqbtLApGKQDP4TFt7+soVWoWsnQDrsXdwKxNIcJ0TgcRQjiB0nPd\nvyiRV/zjHoRwMR7aPi2oxV2HxDHG87j7oY0xu7crCSpkEFZV3Q33tNEdj9xSSQ/KOSmCLydJ6/uT\nUf8jZvZCCz8+Gg/QfAqFednkdV7sZfAFYE9gI8ymdDUhTcgyddULGIM7MajBnW/lVJjot+opCg3K\nQtz1eh1wavHBeOs4Al8vdzRuKF9Mcaihl4Gf4sEpWhWaspyEEEIWpUaWPusTeJ/1VFX9V3srlpOZ\n31MIPVpHjBGwG9xxL+xICEfi4Z5Wx5dhF8cQaI6X8D7pPZ0ppAAhhB/hg8UWuzXN2bNuqarTcIWA\nAeuLyPq41dW95apsTmNCCIdTcF1pNRAW445Xp3jIyazMBfqm0i/jQnp3Zwlp8KUya5lZ4txvbWDP\nEMIVtbW1zf62uZZ1JDANWL/EvlxYIXH8sCKujqzB56DnF20XZO4DhtDrZ3AAqUiAq0J4F7qvhC+s\nCg0n8EsxB1fgjKQgqK/gQX7v6uyWFDfCuTWEsGJcfjMTv54W69Wc1VUSO6Cfqn7l2EJEftXET7o2\n3q+rwQ0yesRt8fdS6Z54f3CV+Fk59X0wWWLZhjAfF95E0ALeF022NUC3t6HHualB71q4n/OA+5Nc\nIZ4t7i4W2iTdj8IA6lVcSO/sxJZ0MK4pG2duV1CDT8ONwbVl5+E2si12SZvrBhyC+4YfKSLbpnZl\nMvDdZN68PoRwDO4AoXusZPfUJ0n3SH164n2vdDq9v3tqW/y9JnXObqm8bhQEorPoHT9N8j5uOJzE\nihyECyrAaWBjCmZ7iYAWPyRJej4+TzoJdz3Z2RP6dXgP5nj8wbkHVxMnD+UCYDszWygizZ6ouZZ1\nMjBZRPZT1VYHF75g5szpNJ7IzinBe7gX4MScqYZC4IYtgbNdEEv9V+/hc6MvAC/G7ZudLaBxMePy\nZvahmc0KIXxO7E6amYUQtsD9YgH8DH8rnFr6bAWyzAbMEZE7KbRQA9KOL5qscOtGp19b3sXjNaUj\nAA8H3gAGArfAl929JfowHq746/O5SntAaQeXAEeGEDY1s1fwZTLbw1dTcnXJcvFH4J2d4GchhAva\nM8BKOBdfknsifpMyrWyd0bPnhCGLFo2j0Hk2Cp3o9IAjyUu/1kLqmOLXXrrPl/6UykvnF+9v6niK\n0jX4HOcXwGx8ADM79T351ONvkr74Wvs+FF7/S8VPPf6mrwO+fAx6fhs2+jLVT10BPnkDlgfoAd8d\nZlaNizX/AByLd0W2Ae41sylx3wrAMyGE9czs/e3g0/ehbhAMkoLSoyRZhPVjVX1BRLqr6l0icmyW\n2h45ZMi9qlpxlzLVSghhHG7el9Yi3vmxu+QB+NVHVSSoIYTVgO3N7DpcWP8PfwsArBFCmG1mM83s\no+CrZ78HXIjZ7YNCWID3goo1aw3IYhvwhogcBnwuIleRBxpuFyGE3iGE3+DWT8n9X4wPZreIeS9R\neql1V2YC8KsQwilRG3U4cGHcdzg+uALgc/hgUTqemtndmKV7QiXJYhtwHK5NmYA/Mbu05gpyCgQ3\n0XsBDy+aMBv3yX8OPi02H9jfzKrNaOh6XBO1SUz3ssJarQuBTUIIvQH6w901cBIh7EwIw3FnyC3S\n3NRVU+62t6IMseO/TsTgFIfjvqnSXlRm4v3hZPXFF8ChZVn/3wGEEPbFg7TtamYvBnfj/na83ldD\nCNub2T/NbNbjIWyyNfQihHVwFfFofNA4GddilVI+NaC5PusUChPNXdIKp6sSR7zrUAjJNIrG9/pz\nXPsFfn+vB35iZjM7qp5tIYTQy8wWxuQY/Nr+EEIYZWZT8KXiA4KrdS8ihHuBHbf2t/JYXJt2IGbL\nxhPOoGk72wY02Q1Q1cdV9c/4mvQtcROypYF3Wn+JSz4hhP4hhL1CCNfiU0wvAhcBW1O6URgQt48C\nG5rZEV1SUEOoiU7aiK/xD9YK4e9x78k94P3TYcho2DiEcB7uxv/9jz0S91jc+mt3fBnNx7jWb2BU\nVYN3i/4eNYzNkmWAdRO+XvwbeHSOm7Je55JKcEaGEPYPIVwZQngR+BQPPXk4BQe7zfEG/idu16Jt\nakcSwhBC+Gph4lZw3I3wOiH0OBMWdIfub8HGu4SwtpnN/RgeOQ9WPdRlY68L4DtA7+Wht7ltxMe4\nnK2A20VfTMGxG8BrwA2Z7CfMrNlPbW3tY0Xbx1s4flhtba3V1tYOa+nc1fDBu0Ej8LnmW+PNXYi/\nutvy+RSfs+7Z2ddmZhgMNHjCYCkzYyIceC2YQa1BzTCY0wPsBNjNoMelsOgksMd9kn+516HO/LMs\nsM4//PsbBv3j+T8wuNJgzQyy1qzsZJln/TDOrfYTkQPjk9JhBH9d9KdgoLF0/PTDJ+D74i3ZQgoT\n8RLrmUzGCz6Y6YUPcFbHW4LE5mAQPrGf2BP0xSeo0wqEdlEDHy32V+PPfgCDLvF6fBndAS1jGaZu\nMhPCEOBzzOZsEEKvC+CcneBazN5cK4T19oUnz4YtMHt5Qzjhcxh1CpxwTAgTX4Wf3QRMgR/fZ3bw\nySHUnAr1j8BuAR54EeasCz/Ho8EcuAssPgiGnGE2y2AWITwO7E4hyPAfgIcwe63d15VB2peura0d\nX1tbe1Vtbe2E2travlmejr59+x6DG1S83Qfqe7kwzAQ+rQHr5pocN6HzFmcxPvWRaLuq9TOvG9ha\nrrcfDxy2FNiJ8KfYUq/XC+rPg4djeoNeUD8ZrjMzamCDnlA/EX5uZnSDLVeExRPg+nj8jsNg8VFw\nV0x/e2Wo/zHcFtM7Lw/1P4VJZkYfOL4n2DHx+F5wdA+wg+BRM2M83FkDthM8ZWZcBzN6Qt1gX5DI\nb+A3Y11rGYAe3eCLrWGl1FvnGuBb5WjlW2pZs/RZp6rqFar6fVW9VFUzuQBfuHDhRGADYNg8CAu9\nNRwMDFwM1HuL1puCDUGi2mx3K9YR9PCH6wni0uW14CPchvS7Bgx2/fcVw2DBQuC56KJyDdi4DsLU\nGGRtGKxfB+HaGAFnOVh/MYR7YrigXjD0Y+j2rA9yAVZ+F7q9Fv2nDoBVP4AwLarBV4M1/gvhSdgB\n4FuwzJfA6/H4cbAmYC/FRYLDYZWV4J2pbhDDZJj2DTjzwxjQ4mDY9Ha3PzEzq6uHaY/7+CXJPNLM\nyh95uwRZugH1UXP1BrHVy6JGDSHMorAsoytSDywI0KsGutXA7IXwQU8Y1gN69IB3P4NX+8LovtB7\nEEx9GSYJXN4XRgyB66aYHb9lCI/OhMXLe8s0Y+sQbv8P1M3z1x+D4ZResHCeqx8ZAOOHw6KF8DjA\nCnBCd6hbI6QCAAAHWUlEQVSf6/76WQVOWgYWz4/draFw9mJYtLRP+bAmnDYbFg3yB4WhMGEu1HWD\nZwCWhmPWgIULvW/NR7DfVqDTYCLAs7DNgfDHG6MwXgbsC/f/wuw4gCe9K/WmmT0V79OfgW/ib0mA\n/fBptw4nS8t6I+4AYRYezj1TRUMIb7eyLgbMrYFFfbxr8DrwfB/4YkUv+37gd8vAJ2v6K/Yy4PwV\n4b3NXQf9fWDcMJixq9/Y7YFRAi8f5K47hwGD1oNnJsB9ZlZjZn3Xh6ePh3sWmA00s7UEph8Kd31q\nNtzMdh0Gz+8Pk18y293M/jgAbEd4cIrZ8QCLYLn94L6/mO0BMBe67wsPP212NMBiqP9f+NMzZqcB\ndIOwLzz4jNmRAAG67Qv3P2f2bfCO7F7wwFNmowGWgXn7wIP3me0NMADmHAZTf2t2OMBSMP9AeOhP\nZgcB9Ib5Y+HRJ812B6iDOZvC8/PNfgXwiffV1czuB3gHXrgUkqko8Ics7er9RNzngP9JZp9Z7AN0\nOOUeXSb9jkGDBm0CHDwcJm3m67i+DWy1LpyyGxyFj7BXHgP7/AC2BYKZsQtsczpslpxvDGw+HtZP\n0pvCRmOhNkmPhLW3gdWS9NIwfAVYIUnjjsyWTaVXBgam0oNJRq6eXg5YOpUeCPRO0svBqG/CyCS9\nGfzkWNgzSW8AJxwE/5ukR8B3t0316YbA3pvBJqn9+20HWyTpjWHvfWB0kh4L3z4rtf9c2OJu2DRJ\nHwMbXp0aae8AteNhSKr+Q4uud1V8QJekQ7lloL2y01SfNZT7IRGRYXgUwtXz1bA5raEl2cnsnzUn\np7PJhTWnasiFNadqyIU1p2rIhTWnasiFNadqyIU1p2rIhTWnasiFNadqyIU1p2qoRDjMxAHakJYc\nbeXkFJEsByrpRK8Swpq4B3+iAufO+XqwEtFkMk0lhHU6vib8AwoBF3JyslCDC+r0UjvLbnWVk1Mp\n8gFWTtWQC2tO1ZALa07VkAtrTtWQC2tO1ZALa07VkAtrTtWQC2tO1ZALa07VUAl1awNE5FDcC+As\nVa2Yb1cRORh3UGGq2pSL+XKVtSfuM2pLVd21guXsgLsvn6Oqv27p+HaUczju/OMVVb2rUuWkyjJV\nvb61v+2IlnUdVb0c2KzC5czHnY1V3B5BVe/GbR9+VOGitsav670Kl7Mm7hqq2ThU7UVERuOeI9tE\nu1pWERkJ/FZVNxKRVfDIcrNwJ2KG34C7RWQC7jWwkuWIqp4hIhdV+ppU9XZg3RgytJLX1E9Vfyki\nl+C+vipVzuWq+l4sp00RzzOWszbuEG8oHkOhVbRZWEVkMB7m8IuYdRQwUVX/JiIPAN9R1cUisnc8\n5uEKl3OAiIwH/tMB17Q07mu20uV8ISLH08Y4Dq0o5zgR6Y47w6tYOfHY1XDfZq2mzcKqqh8Cp4nI\n1Jg1mELw2E9xh2b/bW8fqBXl3NqeclpZ1he49+dKl3NfW8toZTm/7Ihy4rHv4AHrWk05+6zv4s07\neN+xUkFwO6qcjiwrLycD5ZwNuA64VEQOAe5S1foWju/q5XRkWXk5GciNr3OqhlwpkFM15MKaUzXk\nwppTNeTCmlM15MKaUzXkwppTNeTCmlM15MKaUzVU3J61mogalx8D41V1aguHJ7/ZDzcVvB03f7sO\n2FNV7xCRy4AzSsW7TfYBiaHH7JgvePTsx1X1pKLfXAyci1tGzVLVvWJ+N9xk8Yd4dMXRqnplKy+/\ny5O3rA0xYFJWQY3sCByhqj+PArISHt8UVT2pqcDMqX1GKriyqioegrIBIvI/wIJEqIFhIpIEad4S\nt3s1VX0R2FJE+rTiGqqCvGVtTAAQkR8C++Bmc+uo6gYisgtwejxmIt6a7QSsKyLn45Gt64FRInIg\nbja3B3AX8BIesHe6qo4XkcfiPoArY3S9R1T1bEpHBj8MSCzLDPgjbmr3YDzP3anfPQbsBdzS7rvR\nhchb1hKIyED81bwpcCEwQEQCcA6wDS6U4/FI1A/hgjQLF6KJwJOqmhaUGuB3qro5sJ2I9C4q8mpV\nHQVsLiIj4nmK2Rx4NZWeAnwnfh8K/Cu171UKId+XGHJhLc1I4EUAVX0Zf8UuD6yGC+fD+LqyxBdt\nqZawmFfi9kM8+HWaJFz6s8DwJn6/lKrOT6VfBtYUkfWAF4qO/Rg3zVuiyIW1NO8A6wCIyFrAUrjx\n8Bv4q3cb4DZKr0po0Actym+KjWLLvTEejr4U86I1f5rp+IDr90X5A/BQ7UsUubCWQFU/BqaIyF+B\nU4HF0SbzYuAvuJAEVV1Y9FPDW7XVklWcJU5vRVuAI4En8T7ru01U66/AhkXnuQcYqar/LDrnhsC0\n5q+y+sjtWVPE5dwDgauAw1T113EUPklVt+nAemwN7J6euhKRdYADVPW0DL+/Ha9/m1eSdkXylrUx\nxwHbA+uIyNPAzfh8aIcQ51kvo6hVjn3npUSkfwu/Xw94akkTVMhb1pwqIm9Zc6qGXFhzqoZcWHOq\nhlxYc6qGXFhzqob/B/7wSKl8KVBNAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1122367d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.figure(figsize=(2.5,2.5))\n",
"\n",
"plt.semilogx(ligand_conc*12,AblGefIma_df[['A - Abl','C - Abl','E - Abl','G - Abl']].values, 'r');\n",
"plt.semilogx(ligand_conc*12,AblGefIma_df[['B - Buffer','D - Buffer','F - Buffer','H - Buffer']].values, 'r', linestyle=':');\n",
"plt.semilogx(ligand_conc*12,AblGef_df[['A - Abl','C - Abl','E - Abl','G - Abl']].values, 'k');\n",
"plt.semilogx(ligand_conc*12,AblGef_df[['B - Buffer','D - Buffer','F - Buffer','H - Buffer']].values, 'k', linestyle=':');\n",
"plt.text(1.5e-9,63000,'1 $\\mu$M Abl + gefitinib',fontsize=7)\n",
"plt.text(1.5e-9,52000,'1 $\\mu$M Abl + 10 $\\mu$M imatinib \\n + gefitinib',fontsize=7, color='red')\n",
"plt.xlabel('[gefitinib] (M)',fontsize=9)\n",
"plt.ylabel('relative fluorescence',fontsize=9)\n",
"plt.title('excitation 280 nm/ emission 480 nm',fontsize=9)\n",
"plt.xlim(1e-9,3e-4)\n",
"plt.yticks([])\n",
"plt.xticks(fontsize=8)\n",
"plt.tight_layout();\n",
"plt.savefig('Abl_Gef_Ima_grant.eps',type='eps',dpi=1000)"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>A - Abl</th>\n",
" <th>C - Abl</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>53250</td>\n",
" <td>63141</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>43872</td>\n",
" <td>52725</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>31303</td>\n",
" <td>38690</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>24462</td>\n",
" <td>29540</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>21709</td>\n",
" <td>23561</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>18941</td>\n",
" <td>20785</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>17939</td>\n",
" <td>19159</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>17258</td>\n",
" <td>18313</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>17135</td>\n",
" <td>17703</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>17250</td>\n",
" <td>17936</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>16964</td>\n",
" <td>17938</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>17185</td>\n",
" <td>17280</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" A - Abl C - Abl\n",
"0 53250 63141\n",
"1 43872 52725\n",
"2 31303 38690\n",
"3 24462 29540\n",
"4 21709 23561\n",
"5 18941 20785\n",
"6 17939 19159\n",
"7 17258 18313\n",
"8 17135 17703\n",
"9 17250 17936\n",
"10 16964 17938\n",
"11 17185 17280"
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"AblGefIma_df[['A - Abl','C - Abl']]"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"array([[ 53250., 12894., 63141., 13739., 63400., 13953., 63432.,\n",
" 16807.],\n",
" [ 43872., 12797., 52725., 12068., 53561., 12777., 49829.,\n",
" 11596.],\n",
" [ 31303., 11876., 38690., 12203., 38596., 12048., 37127.,\n",
" 11445.],\n",
" [ 24462., 11368., 29540., 11254., 29405., 11867., 27706.,\n",
" 10914.],\n",
" [ 21709., 10305., 23561., 10359., 23947., 10513., 22149.,\n",
" 9179.],\n",
" [ 18941., 9813., 20785., 10048., 20759., 9671., 20375.,\n",
" 8845.],\n",
" [ 17939., 9907., 19159., 9782., 20094., 9803., 18045.,\n",
" 8713.],\n",
" [ 17258., 9639., 18313., 9788., 18623., 9717., 17424.,\n",
" 8804.],\n",
" [ 17135., 9746., 17703., 9823., 18595., 10231., 17284.,\n",
" 8846.],\n",
" [ 17250., 9698., 17936., 10016., 18799., 9771., 17618.,\n",
" 8657.],\n",
" [ 16964., 9965., 17938., 9939., 18223., 9851., 17518.,\n",
" 9041.],\n",
" [ 17185., 9933., 17280., 9746., 17532., 9652., 17583.,\n",
" 8669.]])"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"AblGefIma_df[:].values"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.11"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| lgpl-2.1 |
prk327/CoAca | 4_Slicing_Dicing.ipynb | 1 | 218251 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Slicing and Dicing Dataframes\n",
"\n",
"You have seen how to do indexing of dataframes using ```df.iloc``` and ```df.loc```. Now, let's see how to subset dataframes based on certain conditions. \n"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Ord_id</th>\n",
" <th>Prod_id</th>\n",
" <th>Ship_id</th>\n",
" <th>Cust_id</th>\n",
" <th>Sales</th>\n",
" <th>Discount</th>\n",
" <th>Order_Quantity</th>\n",
" <th>Profit</th>\n",
" <th>Shipping_Cost</th>\n",
" <th>Product_Base_Margin</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>Ord_5446</td>\n",
" <td>Prod_16</td>\n",
" <td>SHP_7609</td>\n",
" <td>Cust_1818</td>\n",
" <td>136.81</td>\n",
" <td>0.01</td>\n",
" <td>23</td>\n",
" <td>-30.51</td>\n",
" <td>3.60</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>Ord_5406</td>\n",
" <td>Prod_13</td>\n",
" <td>SHP_7549</td>\n",
" <td>Cust_1818</td>\n",
" <td>42.27</td>\n",
" <td>0.01</td>\n",
" <td>13</td>\n",
" <td>4.56</td>\n",
" <td>0.93</td>\n",
" <td>0.54</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>Ord_5446</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_7610</td>\n",
" <td>Cust_1818</td>\n",
" <td>4701.69</td>\n",
" <td>0.00</td>\n",
" <td>26</td>\n",
" <td>1148.90</td>\n",
" <td>2.50</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>Ord_5456</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_7625</td>\n",
" <td>Cust_1818</td>\n",
" <td>2337.89</td>\n",
" <td>0.09</td>\n",
" <td>43</td>\n",
" <td>729.34</td>\n",
" <td>14.30</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>Ord_5485</td>\n",
" <td>Prod_17</td>\n",
" <td>SHP_7664</td>\n",
" <td>Cust_1818</td>\n",
" <td>4233.15</td>\n",
" <td>0.08</td>\n",
" <td>35</td>\n",
" <td>1219.87</td>\n",
" <td>26.30</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Ord_id Prod_id Ship_id Cust_id Sales Discount Order_Quantity \\\n",
"0 Ord_5446 Prod_16 SHP_7609 Cust_1818 136.81 0.01 23 \n",
"1 Ord_5406 Prod_13 SHP_7549 Cust_1818 42.27 0.01 13 \n",
"2 Ord_5446 Prod_4 SHP_7610 Cust_1818 4701.69 0.00 26 \n",
"3 Ord_5456 Prod_6 SHP_7625 Cust_1818 2337.89 0.09 43 \n",
"4 Ord_5485 Prod_17 SHP_7664 Cust_1818 4233.15 0.08 35 \n",
"\n",
" Profit Shipping_Cost Product_Base_Margin \n",
"0 -30.51 3.60 0.56 \n",
"1 4.56 0.93 0.54 \n",
"2 1148.90 2.50 0.59 \n",
"3 729.34 14.30 0.37 \n",
"4 1219.87 26.30 0.38 "
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# loading libraries and reading the data\n",
"import numpy as np\n",
"import pandas as pd\n",
"\n",
"df = pd.read_csv(\"../global_sales_data/market_fact.csv\")\n",
"df.head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Subsetting Rows Based on Conditions\n",
"\n",
"Often, you want to select rows which satisfy some given conditions. For e.g., select all the orders where the ```Sales > 3000```, or all the orders where ```2000 < Sales < 3000``` and ```Profit < 100```.\n",
"\n",
"Arguably, the best way to do these operations is using ```df.loc[]```, since ```df.iloc[]``` would require you to remember the integer column indices, which is tedious.\n",
"\n",
"Let's see some examples."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"0 False\n",
"1 False\n",
"2 True\n",
"3 False\n",
"4 True\n",
"5 False\n",
"6 False\n",
"7 True\n",
"8 False\n",
"9 False\n",
"10 True\n",
"11 False\n",
"12 False\n",
"13 True\n",
"14 False\n",
"15 False\n",
"16 False\n",
"17 True\n",
"18 False\n",
"19 False\n",
"20 False\n",
"21 False\n",
"22 True\n",
"23 False\n",
"24 False\n",
"25 False\n",
"26 False\n",
"27 False\n",
"28 True\n",
"29 False\n",
" ... \n",
"8369 False\n",
"8370 False\n",
"8371 True\n",
"8372 False\n",
"8373 False\n",
"8374 False\n",
"8375 False\n",
"8376 False\n",
"8377 False\n",
"8378 False\n",
"8379 False\n",
"8380 False\n",
"8381 False\n",
"8382 False\n",
"8383 True\n",
"8384 False\n",
"8385 False\n",
"8386 False\n",
"8387 False\n",
"8388 False\n",
"8389 False\n",
"8390 False\n",
"8391 False\n",
"8392 False\n",
"8393 False\n",
"8394 False\n",
"8395 False\n",
"8396 False\n",
"8397 True\n",
"8398 False\n",
"Name: Sales, Length: 8399, dtype: bool"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Select all rows where Sales > 3000\n",
"# First, we get a boolean array where True corresponds to rows having Sales > 3000\n",
"df.Sales > 3000"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Ord_id</th>\n",
" <th>Prod_id</th>\n",
" <th>Ship_id</th>\n",
" <th>Cust_id</th>\n",
" <th>Sales</th>\n",
" <th>Discount</th>\n",
" <th>Order_Quantity</th>\n",
" <th>Profit</th>\n",
" <th>Shipping_Cost</th>\n",
" <th>Product_Base_Margin</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>Ord_5446</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_7610</td>\n",
" <td>Cust_1818</td>\n",
" <td>4701.6900</td>\n",
" <td>0.00</td>\n",
" <td>26</td>\n",
" <td>1148.90</td>\n",
" <td>2.50</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>Ord_5485</td>\n",
" <td>Prod_17</td>\n",
" <td>SHP_7664</td>\n",
" <td>Cust_1818</td>\n",
" <td>4233.1500</td>\n",
" <td>0.08</td>\n",
" <td>35</td>\n",
" <td>1219.87</td>\n",
" <td>26.30</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>Ord_4725</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_6593</td>\n",
" <td>Cust_1641</td>\n",
" <td>3410.1575</td>\n",
" <td>0.10</td>\n",
" <td>48</td>\n",
" <td>1137.91</td>\n",
" <td>0.99</td>\n",
" <td>0.55</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>Ord_4743</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_6615</td>\n",
" <td>Cust_1641</td>\n",
" <td>4072.0100</td>\n",
" <td>0.01</td>\n",
" <td>43</td>\n",
" <td>1675.98</td>\n",
" <td>0.99</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13</th>\n",
" <td>Ord_2207</td>\n",
" <td>Prod_11</td>\n",
" <td>SHP_3093</td>\n",
" <td>Cust_839</td>\n",
" <td>3364.2480</td>\n",
" <td>0.10</td>\n",
" <td>15</td>\n",
" <td>-693.23</td>\n",
" <td>61.76</td>\n",
" <td>0.78</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17</th>\n",
" <td>Ord_4471</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_6228</td>\n",
" <td>Cust_1521</td>\n",
" <td>13255.9300</td>\n",
" <td>0.02</td>\n",
" <td>25</td>\n",
" <td>4089.27</td>\n",
" <td>26.00</td>\n",
" <td>0.60</td>\n",
" </tr>\n",
" <tr>\n",
" <th>22</th>\n",
" <td>Ord_996</td>\n",
" <td>Prod_5</td>\n",
" <td>SHP_1377</td>\n",
" <td>Cust_371</td>\n",
" <td>3202.2500</td>\n",
" <td>0.09</td>\n",
" <td>44</td>\n",
" <td>991.26</td>\n",
" <td>19.99</td>\n",
" <td>0.43</td>\n",
" </tr>\n",
" <tr>\n",
" <th>28</th>\n",
" <td>Ord_2573</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_3527</td>\n",
" <td>Cust_931</td>\n",
" <td>3594.7435</td>\n",
" <td>0.05</td>\n",
" <td>38</td>\n",
" <td>1016.97</td>\n",
" <td>2.50</td>\n",
" <td>0.55</td>\n",
" </tr>\n",
" <tr>\n",
" <th>40</th>\n",
" <td>Ord_5035</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_7024</td>\n",
" <td>Cust_1710</td>\n",
" <td>4917.6900</td>\n",
" <td>0.02</td>\n",
" <td>42</td>\n",
" <td>126.31</td>\n",
" <td>30.00</td>\n",
" <td>0.71</td>\n",
" </tr>\n",
" <tr>\n",
" <th>57</th>\n",
" <td>Ord_4546</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_6327</td>\n",
" <td>Cust_1474</td>\n",
" <td>5208.7800</td>\n",
" <td>0.05</td>\n",
" <td>34</td>\n",
" <td>1547.78</td>\n",
" <td>7.07</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>64</th>\n",
" <td>Ord_4475</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_6234</td>\n",
" <td>Cust_1474</td>\n",
" <td>7640.2250</td>\n",
" <td>0.07</td>\n",
" <td>46</td>\n",
" <td>2027.68</td>\n",
" <td>2.50</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>79</th>\n",
" <td>Ord_5188</td>\n",
" <td>Prod_14</td>\n",
" <td>SHP_7252</td>\n",
" <td>Cust_1749</td>\n",
" <td>5177.4000</td>\n",
" <td>0.06</td>\n",
" <td>12</td>\n",
" <td>287.50</td>\n",
" <td>49.00</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>82</th>\n",
" <td>Ord_5156</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_7207</td>\n",
" <td>Cust_1749</td>\n",
" <td>8374.1320</td>\n",
" <td>0.06</td>\n",
" <td>48</td>\n",
" <td>2568.10</td>\n",
" <td>8.99</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>84</th>\n",
" <td>Ord_5232</td>\n",
" <td>Prod_17</td>\n",
" <td>SHP_7306</td>\n",
" <td>Cust_1758</td>\n",
" <td>21366.5100</td>\n",
" <td>0.00</td>\n",
" <td>3</td>\n",
" <td>-11984.40</td>\n",
" <td>24.49</td>\n",
" <td>0.39</td>\n",
" </tr>\n",
" <tr>\n",
" <th>107</th>\n",
" <td>Ord_250</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_346</td>\n",
" <td>Cust_45</td>\n",
" <td>8901.7800</td>\n",
" <td>0.04</td>\n",
" <td>31</td>\n",
" <td>2795.36</td>\n",
" <td>24.49</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>121</th>\n",
" <td>Ord_5423</td>\n",
" <td>Prod_17</td>\n",
" <td>SHP_7577</td>\n",
" <td>Cust_1800</td>\n",
" <td>13070.2000</td>\n",
" <td>0.07</td>\n",
" <td>4</td>\n",
" <td>-6923.60</td>\n",
" <td>8.73</td>\n",
" <td>0.57</td>\n",
" </tr>\n",
" <tr>\n",
" <th>124</th>\n",
" <td>Ord_2432</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_3339</td>\n",
" <td>Cust_933</td>\n",
" <td>3883.4715</td>\n",
" <td>0.10</td>\n",
" <td>42</td>\n",
" <td>707.17</td>\n",
" <td>8.99</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>133</th>\n",
" <td>Ord_2432</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_3338</td>\n",
" <td>Cust_933</td>\n",
" <td>15337.5800</td>\n",
" <td>0.10</td>\n",
" <td>30</td>\n",
" <td>6670.41</td>\n",
" <td>19.99</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148</th>\n",
" <td>Ord_1649</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_2277</td>\n",
" <td>Cust_498</td>\n",
" <td>3005.7400</td>\n",
" <td>0.02</td>\n",
" <td>48</td>\n",
" <td>1053.21</td>\n",
" <td>3.99</td>\n",
" <td>0.57</td>\n",
" </tr>\n",
" <tr>\n",
" <th>163</th>\n",
" <td>Ord_4646</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_6475</td>\n",
" <td>Cust_1603</td>\n",
" <td>4083.1900</td>\n",
" <td>0.07</td>\n",
" <td>43</td>\n",
" <td>-1049.85</td>\n",
" <td>45.00</td>\n",
" <td>0.69</td>\n",
" </tr>\n",
" <tr>\n",
" <th>164</th>\n",
" <td>Ord_4646</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_6476</td>\n",
" <td>Cust_1603</td>\n",
" <td>4902.3800</td>\n",
" <td>0.05</td>\n",
" <td>32</td>\n",
" <td>1438.49</td>\n",
" <td>7.07</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>165</th>\n",
" <td>Ord_4702</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_6560</td>\n",
" <td>Cust_1603</td>\n",
" <td>11823.5200</td>\n",
" <td>0.10</td>\n",
" <td>34</td>\n",
" <td>4592.74</td>\n",
" <td>19.99</td>\n",
" <td>0.40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>168</th>\n",
" <td>Ord_2973</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_4102</td>\n",
" <td>Cust_1081</td>\n",
" <td>4671.1495</td>\n",
" <td>0.07</td>\n",
" <td>28</td>\n",
" <td>947.31</td>\n",
" <td>4.20</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>169</th>\n",
" <td>Ord_3009</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_4168</td>\n",
" <td>Cust_1081</td>\n",
" <td>5718.8500</td>\n",
" <td>0.09</td>\n",
" <td>49</td>\n",
" <td>-2426.55</td>\n",
" <td>70.20</td>\n",
" <td>0.74</td>\n",
" </tr>\n",
" <tr>\n",
" <th>170</th>\n",
" <td>Ord_2973</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_4102</td>\n",
" <td>Cust_1480</td>\n",
" <td>6264.1855</td>\n",
" <td>0.01</td>\n",
" <td>34</td>\n",
" <td>1312.04</td>\n",
" <td>19.99</td>\n",
" <td>0.60</td>\n",
" </tr>\n",
" <tr>\n",
" <th>171</th>\n",
" <td>Ord_2973</td>\n",
" <td>Prod_9</td>\n",
" <td>SHP_6073</td>\n",
" <td>Cust_1480</td>\n",
" <td>5410.9500</td>\n",
" <td>0.09</td>\n",
" <td>36</td>\n",
" <td>2077.91</td>\n",
" <td>19.99</td>\n",
" <td>0.39</td>\n",
" </tr>\n",
" <tr>\n",
" <th>183</th>\n",
" <td>Ord_5157</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_7208</td>\n",
" <td>Cust_1753</td>\n",
" <td>5149.0600</td>\n",
" <td>0.03</td>\n",
" <td>27</td>\n",
" <td>605.44</td>\n",
" <td>30.00</td>\n",
" <td>0.69</td>\n",
" </tr>\n",
" <tr>\n",
" <th>185</th>\n",
" <td>Ord_5153</td>\n",
" <td>Prod_11</td>\n",
" <td>SHP_7202</td>\n",
" <td>Cust_1753</td>\n",
" <td>3457.5600</td>\n",
" <td>0.02</td>\n",
" <td>35</td>\n",
" <td>-365.44</td>\n",
" <td>51.94</td>\n",
" <td>0.63</td>\n",
" </tr>\n",
" <tr>\n",
" <th>189</th>\n",
" <td>Ord_2831</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_3893</td>\n",
" <td>Cust_1036</td>\n",
" <td>18092.6600</td>\n",
" <td>0.09</td>\n",
" <td>36</td>\n",
" <td>7917.76</td>\n",
" <td>19.99</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>191</th>\n",
" <td>Ord_2791</td>\n",
" <td>Prod_11</td>\n",
" <td>SHP_3838</td>\n",
" <td>Cust_1036</td>\n",
" <td>10351.0100</td>\n",
" <td>0.08</td>\n",
" <td>19</td>\n",
" <td>-1331.55</td>\n",
" <td>45.70</td>\n",
" <td>0.71</td>\n",
" </tr>\n",
" <tr>\n",
" <th>...</th>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8125</th>\n",
" <td>Ord_4515</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_6285</td>\n",
" <td>Cust_1546</td>\n",
" <td>4976.6000</td>\n",
" <td>0.06</td>\n",
" <td>32</td>\n",
" <td>601.88</td>\n",
" <td>19.99</td>\n",
" <td>0.66</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8137</th>\n",
" <td>Ord_2267</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_3089</td>\n",
" <td>Cust_890</td>\n",
" <td>6608.2400</td>\n",
" <td>0.09</td>\n",
" <td>35</td>\n",
" <td>2164.64</td>\n",
" <td>0.99</td>\n",
" <td>0.55</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8141</th>\n",
" <td>Ord_3368</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_4668</td>\n",
" <td>Cust_1190</td>\n",
" <td>3227.3800</td>\n",
" <td>0.05</td>\n",
" <td>26</td>\n",
" <td>192.31</td>\n",
" <td>30.00</td>\n",
" <td>0.64</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8143</th>\n",
" <td>Ord_3265</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_4530</td>\n",
" <td>Cust_1190</td>\n",
" <td>10330.9400</td>\n",
" <td>0.07</td>\n",
" <td>25</td>\n",
" <td>2914.56</td>\n",
" <td>19.99</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8151</th>\n",
" <td>Ord_3214</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_4456</td>\n",
" <td>Cust_1187</td>\n",
" <td>8316.7600</td>\n",
" <td>0.05</td>\n",
" <td>30</td>\n",
" <td>2108.80</td>\n",
" <td>23.19</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8158</th>\n",
" <td>Ord_2868</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_3950</td>\n",
" <td>Cust_1059</td>\n",
" <td>5405.4400</td>\n",
" <td>0.07</td>\n",
" <td>18</td>\n",
" <td>604.46</td>\n",
" <td>64.73</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8207</th>\n",
" <td>Ord_3433</td>\n",
" <td>Prod_8</td>\n",
" <td>SHP_4759</td>\n",
" <td>Cust_1180</td>\n",
" <td>3601.0700</td>\n",
" <td>0.04</td>\n",
" <td>50</td>\n",
" <td>174.80</td>\n",
" <td>14.52</td>\n",
" <td>0.65</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8210</th>\n",
" <td>Ord_2110</td>\n",
" <td>Prod_17</td>\n",
" <td>SHP_2885</td>\n",
" <td>Cust_802</td>\n",
" <td>4502.2600</td>\n",
" <td>0.09</td>\n",
" <td>38</td>\n",
" <td>1272.17</td>\n",
" <td>26.30</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8211</th>\n",
" <td>Ord_2144</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_2925</td>\n",
" <td>Cust_802</td>\n",
" <td>5318.8900</td>\n",
" <td>0.06</td>\n",
" <td>48</td>\n",
" <td>525.15</td>\n",
" <td>8.64</td>\n",
" <td>0.78</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8217</th>\n",
" <td>Ord_3359</td>\n",
" <td>Prod_10</td>\n",
" <td>SHP_7245</td>\n",
" <td>Cust_1762</td>\n",
" <td>28389.1400</td>\n",
" <td>0.07</td>\n",
" <td>33</td>\n",
" <td>7132.18</td>\n",
" <td>44.55</td>\n",
" <td>0.62</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8219</th>\n",
" <td>Ord_5200</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_7266</td>\n",
" <td>Cust_1762</td>\n",
" <td>4815.8620</td>\n",
" <td>0.08</td>\n",
" <td>47</td>\n",
" <td>1316.79</td>\n",
" <td>4.20</td>\n",
" <td>0.57</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8235</th>\n",
" <td>Ord_759</td>\n",
" <td>Prod_5</td>\n",
" <td>SHP_1036</td>\n",
" <td>Cust_245</td>\n",
" <td>8549.0400</td>\n",
" <td>0.03</td>\n",
" <td>42</td>\n",
" <td>2861.01</td>\n",
" <td>11.54</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8240</th>\n",
" <td>Ord_793</td>\n",
" <td>Prod_11</td>\n",
" <td>SHP_1090</td>\n",
" <td>Cust_245</td>\n",
" <td>4452.6500</td>\n",
" <td>0.09</td>\n",
" <td>30</td>\n",
" <td>-265.12</td>\n",
" <td>60.00</td>\n",
" <td>0.55</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8249</th>\n",
" <td>Ord_3470</td>\n",
" <td>Prod_17</td>\n",
" <td>SHP_4805</td>\n",
" <td>Cust_1203</td>\n",
" <td>5615.4000</td>\n",
" <td>0.07</td>\n",
" <td>46</td>\n",
" <td>1807.16</td>\n",
" <td>26.30</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8263</th>\n",
" <td>Ord_4954</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_6913</td>\n",
" <td>Cust_1694</td>\n",
" <td>7987.4300</td>\n",
" <td>0.03</td>\n",
" <td>49</td>\n",
" <td>1304.90</td>\n",
" <td>30.00</td>\n",
" <td>0.62</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8283</th>\n",
" <td>Ord_1741</td>\n",
" <td>Prod_11</td>\n",
" <td>SHP_2411</td>\n",
" <td>Cust_595</td>\n",
" <td>15168.8200</td>\n",
" <td>0.02</td>\n",
" <td>26</td>\n",
" <td>-1096.78</td>\n",
" <td>147.12</td>\n",
" <td>0.80</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8286</th>\n",
" <td>Ord_1749</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_2424</td>\n",
" <td>Cust_595</td>\n",
" <td>5176.2700</td>\n",
" <td>0.01</td>\n",
" <td>38</td>\n",
" <td>-743.45</td>\n",
" <td>35.00</td>\n",
" <td>0.84</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8292</th>\n",
" <td>Ord_1765</td>\n",
" <td>Prod_14</td>\n",
" <td>SHP_2446</td>\n",
" <td>Cust_595</td>\n",
" <td>14647.2600</td>\n",
" <td>0.07</td>\n",
" <td>25</td>\n",
" <td>5485.15</td>\n",
" <td>24.49</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8298</th>\n",
" <td>Ord_2172</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_2960</td>\n",
" <td>Cust_787</td>\n",
" <td>6648.5800</td>\n",
" <td>0.08</td>\n",
" <td>19</td>\n",
" <td>-555.98</td>\n",
" <td>99.00</td>\n",
" <td>0.65</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8308</th>\n",
" <td>Ord_2659</td>\n",
" <td>Prod_8</td>\n",
" <td>SHP_3638</td>\n",
" <td>Cust_1016</td>\n",
" <td>4744.6400</td>\n",
" <td>0.04</td>\n",
" <td>46</td>\n",
" <td>1033.38</td>\n",
" <td>19.99</td>\n",
" <td>0.52</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8317</th>\n",
" <td>Ord_2770</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_3802</td>\n",
" <td>Cust_1016</td>\n",
" <td>7535.9600</td>\n",
" <td>0.08</td>\n",
" <td>46</td>\n",
" <td>2745.87</td>\n",
" <td>19.99</td>\n",
" <td>0.40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8329</th>\n",
" <td>Ord_2160</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_2944</td>\n",
" <td>Cust_810</td>\n",
" <td>3636.3700</td>\n",
" <td>0.06</td>\n",
" <td>33</td>\n",
" <td>-176.91</td>\n",
" <td>30.00</td>\n",
" <td>0.69</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8332</th>\n",
" <td>Ord_2101</td>\n",
" <td>Prod_11</td>\n",
" <td>SHP_2875</td>\n",
" <td>Cust_790</td>\n",
" <td>10714.7800</td>\n",
" <td>0.00</td>\n",
" <td>41</td>\n",
" <td>-627.64</td>\n",
" <td>66.67</td>\n",
" <td>0.65</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8335</th>\n",
" <td>Ord_2070</td>\n",
" <td>Prod_11</td>\n",
" <td>SHP_2833</td>\n",
" <td>Cust_784</td>\n",
" <td>3905.7500</td>\n",
" <td>0.01</td>\n",
" <td>21</td>\n",
" <td>55.30</td>\n",
" <td>29.21</td>\n",
" <td>0.76</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8343</th>\n",
" <td>Ord_2178</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_2968</td>\n",
" <td>Cust_785</td>\n",
" <td>6030.5800</td>\n",
" <td>0.09</td>\n",
" <td>39</td>\n",
" <td>1197.86</td>\n",
" <td>8.99</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8366</th>\n",
" <td>Ord_3593</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_4974</td>\n",
" <td>Cust_1274</td>\n",
" <td>12073.0600</td>\n",
" <td>0.03</td>\n",
" <td>39</td>\n",
" <td>5081.87</td>\n",
" <td>19.99</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8367</th>\n",
" <td>Ord_3593</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_4975</td>\n",
" <td>Cust_1274</td>\n",
" <td>6685.0500</td>\n",
" <td>0.09</td>\n",
" <td>25</td>\n",
" <td>1653.60</td>\n",
" <td>24.49</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8371</th>\n",
" <td>Ord_2624</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_3591</td>\n",
" <td>Cust_1006</td>\n",
" <td>4924.1350</td>\n",
" <td>0.07</td>\n",
" <td>28</td>\n",
" <td>1049.54</td>\n",
" <td>8.99</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8383</th>\n",
" <td>Ord_2722</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_3731</td>\n",
" <td>Cust_1006</td>\n",
" <td>3508.3300</td>\n",
" <td>0.04</td>\n",
" <td>21</td>\n",
" <td>-546.98</td>\n",
" <td>35.00</td>\n",
" <td>0.85</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8397</th>\n",
" <td>Ord_5348</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_7469</td>\n",
" <td>Cust_1798</td>\n",
" <td>3872.8700</td>\n",
" <td>0.03</td>\n",
" <td>23</td>\n",
" <td>565.34</td>\n",
" <td>30.00</td>\n",
" <td>0.62</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>1359 rows × 10 columns</p>\n",
"</div>"
],
"text/plain": [
" Ord_id Prod_id Ship_id Cust_id Sales Discount \\\n",
"2 Ord_5446 Prod_4 SHP_7610 Cust_1818 4701.6900 0.00 \n",
"4 Ord_5485 Prod_17 SHP_7664 Cust_1818 4233.1500 0.08 \n",
"7 Ord_4725 Prod_4 SHP_6593 Cust_1641 3410.1575 0.10 \n",
"10 Ord_4743 Prod_2 SHP_6615 Cust_1641 4072.0100 0.01 \n",
"13 Ord_2207 Prod_11 SHP_3093 Cust_839 3364.2480 0.10 \n",
"17 Ord_4471 Prod_15 SHP_6228 Cust_1521 13255.9300 0.02 \n",
"22 Ord_996 Prod_5 SHP_1377 Cust_371 3202.2500 0.09 \n",
"28 Ord_2573 Prod_4 SHP_3527 Cust_931 3594.7435 0.05 \n",
"40 Ord_5035 Prod_15 SHP_7024 Cust_1710 4917.6900 0.02 \n",
"57 Ord_4546 Prod_1 SHP_6327 Cust_1474 5208.7800 0.05 \n",
"64 Ord_4475 Prod_4 SHP_6234 Cust_1474 7640.2250 0.07 \n",
"79 Ord_5188 Prod_14 SHP_7252 Cust_1749 5177.4000 0.06 \n",
"82 Ord_5156 Prod_4 SHP_7207 Cust_1749 8374.1320 0.06 \n",
"84 Ord_5232 Prod_17 SHP_7306 Cust_1758 21366.5100 0.00 \n",
"107 Ord_250 Prod_15 SHP_346 Cust_45 8901.7800 0.04 \n",
"121 Ord_5423 Prod_17 SHP_7577 Cust_1800 13070.2000 0.07 \n",
"124 Ord_2432 Prod_4 SHP_3339 Cust_933 3883.4715 0.10 \n",
"133 Ord_2432 Prod_3 SHP_3338 Cust_933 15337.5800 0.10 \n",
"148 Ord_1649 Prod_2 SHP_2277 Cust_498 3005.7400 0.02 \n",
"163 Ord_4646 Prod_15 SHP_6475 Cust_1603 4083.1900 0.07 \n",
"164 Ord_4646 Prod_1 SHP_6476 Cust_1603 4902.3800 0.05 \n",
"165 Ord_4702 Prod_3 SHP_6560 Cust_1603 11823.5200 0.10 \n",
"168 Ord_2973 Prod_4 SHP_4102 Cust_1081 4671.1495 0.07 \n",
"169 Ord_3009 Prod_15 SHP_4168 Cust_1081 5718.8500 0.09 \n",
"170 Ord_2973 Prod_4 SHP_4102 Cust_1480 6264.1855 0.01 \n",
"171 Ord_2973 Prod_9 SHP_6073 Cust_1480 5410.9500 0.09 \n",
"183 Ord_5157 Prod_15 SHP_7208 Cust_1753 5149.0600 0.03 \n",
"185 Ord_5153 Prod_11 SHP_7202 Cust_1753 3457.5600 0.02 \n",
"189 Ord_2831 Prod_3 SHP_3893 Cust_1036 18092.6600 0.09 \n",
"191 Ord_2791 Prod_11 SHP_3838 Cust_1036 10351.0100 0.08 \n",
"... ... ... ... ... ... ... \n",
"8125 Ord_4515 Prod_1 SHP_6285 Cust_1546 4976.6000 0.06 \n",
"8137 Ord_2267 Prod_2 SHP_3089 Cust_890 6608.2400 0.09 \n",
"8141 Ord_3368 Prod_15 SHP_4668 Cust_1190 3227.3800 0.05 \n",
"8143 Ord_3265 Prod_1 SHP_4530 Cust_1190 10330.9400 0.07 \n",
"8151 Ord_3214 Prod_2 SHP_4456 Cust_1187 8316.7600 0.05 \n",
"8158 Ord_2868 Prod_15 SHP_3950 Cust_1059 5405.4400 0.07 \n",
"8207 Ord_3433 Prod_8 SHP_4759 Cust_1180 3601.0700 0.04 \n",
"8210 Ord_2110 Prod_17 SHP_2885 Cust_802 4502.2600 0.09 \n",
"8211 Ord_2144 Prod_1 SHP_2925 Cust_802 5318.8900 0.06 \n",
"8217 Ord_3359 Prod_10 SHP_7245 Cust_1762 28389.1400 0.07 \n",
"8219 Ord_5200 Prod_4 SHP_7266 Cust_1762 4815.8620 0.08 \n",
"8235 Ord_759 Prod_5 SHP_1036 Cust_245 8549.0400 0.03 \n",
"8240 Ord_793 Prod_11 SHP_1090 Cust_245 4452.6500 0.09 \n",
"8249 Ord_3470 Prod_17 SHP_4805 Cust_1203 5615.4000 0.07 \n",
"8263 Ord_4954 Prod_15 SHP_6913 Cust_1694 7987.4300 0.03 \n",
"8283 Ord_1741 Prod_11 SHP_2411 Cust_595 15168.8200 0.02 \n",
"8286 Ord_1749 Prod_1 SHP_2424 Cust_595 5176.2700 0.01 \n",
"8292 Ord_1765 Prod_14 SHP_2446 Cust_595 14647.2600 0.07 \n",
"8298 Ord_2172 Prod_1 SHP_2960 Cust_787 6648.5800 0.08 \n",
"8308 Ord_2659 Prod_8 SHP_3638 Cust_1016 4744.6400 0.04 \n",
"8317 Ord_2770 Prod_3 SHP_3802 Cust_1016 7535.9600 0.08 \n",
"8329 Ord_2160 Prod_15 SHP_2944 Cust_810 3636.3700 0.06 \n",
"8332 Ord_2101 Prod_11 SHP_2875 Cust_790 10714.7800 0.00 \n",
"8335 Ord_2070 Prod_11 SHP_2833 Cust_784 3905.7500 0.01 \n",
"8343 Ord_2178 Prod_4 SHP_2968 Cust_785 6030.5800 0.09 \n",
"8366 Ord_3593 Prod_3 SHP_4974 Cust_1274 12073.0600 0.03 \n",
"8367 Ord_3593 Prod_15 SHP_4975 Cust_1274 6685.0500 0.09 \n",
"8371 Ord_2624 Prod_4 SHP_3591 Cust_1006 4924.1350 0.07 \n",
"8383 Ord_2722 Prod_1 SHP_3731 Cust_1006 3508.3300 0.04 \n",
"8397 Ord_5348 Prod_15 SHP_7469 Cust_1798 3872.8700 0.03 \n",
"\n",
" Order_Quantity Profit Shipping_Cost Product_Base_Margin \n",
"2 26 1148.90 2.50 0.59 \n",
"4 35 1219.87 26.30 0.38 \n",
"7 48 1137.91 0.99 0.55 \n",
"10 43 1675.98 0.99 0.56 \n",
"13 15 -693.23 61.76 0.78 \n",
"17 25 4089.27 26.00 0.60 \n",
"22 44 991.26 19.99 0.43 \n",
"28 38 1016.97 2.50 0.55 \n",
"40 42 126.31 30.00 0.71 \n",
"57 34 1547.78 7.07 0.59 \n",
"64 46 2027.68 2.50 0.59 \n",
"79 12 287.50 49.00 0.38 \n",
"82 48 2568.10 8.99 0.56 \n",
"84 3 -11984.40 24.49 0.39 \n",
"107 31 2795.36 24.49 NaN \n",
"121 4 -6923.60 8.73 0.57 \n",
"124 42 707.17 8.99 0.58 \n",
"133 30 6670.41 19.99 0.37 \n",
"148 48 1053.21 3.99 0.57 \n",
"163 43 -1049.85 45.00 0.69 \n",
"164 32 1438.49 7.07 0.59 \n",
"165 34 4592.74 19.99 0.40 \n",
"168 28 947.31 4.20 0.59 \n",
"169 49 -2426.55 70.20 0.74 \n",
"170 34 1312.04 19.99 0.60 \n",
"171 36 2077.91 19.99 0.39 \n",
"183 27 605.44 30.00 0.69 \n",
"185 35 -365.44 51.94 0.63 \n",
"189 36 7917.76 19.99 0.37 \n",
"191 19 -1331.55 45.70 0.71 \n",
"... ... ... ... ... \n",
"8125 32 601.88 19.99 0.66 \n",
"8137 35 2164.64 0.99 0.55 \n",
"8141 26 192.31 30.00 0.64 \n",
"8143 25 2914.56 19.99 0.58 \n",
"8151 30 2108.80 23.19 0.59 \n",
"8158 18 604.46 64.73 0.56 \n",
"8207 50 174.80 14.52 0.65 \n",
"8210 38 1272.17 26.30 0.38 \n",
"8211 48 525.15 8.64 0.78 \n",
"8217 33 7132.18 44.55 0.62 \n",
"8219 47 1316.79 4.20 0.57 \n",
"8235 42 2861.01 11.54 0.59 \n",
"8240 30 -265.12 60.00 0.55 \n",
"8249 46 1807.16 26.30 0.38 \n",
"8263 49 1304.90 30.00 0.62 \n",
"8283 26 -1096.78 147.12 0.80 \n",
"8286 38 -743.45 35.00 0.84 \n",
"8292 25 5485.15 24.49 0.37 \n",
"8298 19 -555.98 99.00 0.65 \n",
"8308 46 1033.38 19.99 0.52 \n",
"8317 46 2745.87 19.99 0.40 \n",
"8329 33 -176.91 30.00 0.69 \n",
"8332 41 -627.64 66.67 0.65 \n",
"8335 21 55.30 29.21 0.76 \n",
"8343 39 1197.86 8.99 0.58 \n",
"8366 39 5081.87 19.99 0.38 \n",
"8367 25 1653.60 24.49 NaN \n",
"8371 28 1049.54 8.99 0.58 \n",
"8383 21 -546.98 35.00 0.85 \n",
"8397 23 565.34 30.00 0.62 \n",
"\n",
"[1359 rows x 10 columns]"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Then, we pass this boolean array inside df.loc\n",
"df.loc[df.Sales > 3000]"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Ord_id</th>\n",
" <th>Prod_id</th>\n",
" <th>Ship_id</th>\n",
" <th>Cust_id</th>\n",
" <th>Sales</th>\n",
" <th>Discount</th>\n",
" <th>Order_Quantity</th>\n",
" <th>Profit</th>\n",
" <th>Shipping_Cost</th>\n",
" <th>Product_Base_Margin</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>Ord_5446</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_7610</td>\n",
" <td>Cust_1818</td>\n",
" <td>4701.6900</td>\n",
" <td>0.00</td>\n",
" <td>26</td>\n",
" <td>1148.90</td>\n",
" <td>2.50</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>Ord_5485</td>\n",
" <td>Prod_17</td>\n",
" <td>SHP_7664</td>\n",
" <td>Cust_1818</td>\n",
" <td>4233.1500</td>\n",
" <td>0.08</td>\n",
" <td>35</td>\n",
" <td>1219.87</td>\n",
" <td>26.30</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>Ord_4725</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_6593</td>\n",
" <td>Cust_1641</td>\n",
" <td>3410.1575</td>\n",
" <td>0.10</td>\n",
" <td>48</td>\n",
" <td>1137.91</td>\n",
" <td>0.99</td>\n",
" <td>0.55</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>Ord_4743</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_6615</td>\n",
" <td>Cust_1641</td>\n",
" <td>4072.0100</td>\n",
" <td>0.01</td>\n",
" <td>43</td>\n",
" <td>1675.98</td>\n",
" <td>0.99</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13</th>\n",
" <td>Ord_2207</td>\n",
" <td>Prod_11</td>\n",
" <td>SHP_3093</td>\n",
" <td>Cust_839</td>\n",
" <td>3364.2480</td>\n",
" <td>0.10</td>\n",
" <td>15</td>\n",
" <td>-693.23</td>\n",
" <td>61.76</td>\n",
" <td>0.78</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17</th>\n",
" <td>Ord_4471</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_6228</td>\n",
" <td>Cust_1521</td>\n",
" <td>13255.9300</td>\n",
" <td>0.02</td>\n",
" <td>25</td>\n",
" <td>4089.27</td>\n",
" <td>26.00</td>\n",
" <td>0.60</td>\n",
" </tr>\n",
" <tr>\n",
" <th>22</th>\n",
" <td>Ord_996</td>\n",
" <td>Prod_5</td>\n",
" <td>SHP_1377</td>\n",
" <td>Cust_371</td>\n",
" <td>3202.2500</td>\n",
" <td>0.09</td>\n",
" <td>44</td>\n",
" <td>991.26</td>\n",
" <td>19.99</td>\n",
" <td>0.43</td>\n",
" </tr>\n",
" <tr>\n",
" <th>28</th>\n",
" <td>Ord_2573</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_3527</td>\n",
" <td>Cust_931</td>\n",
" <td>3594.7435</td>\n",
" <td>0.05</td>\n",
" <td>38</td>\n",
" <td>1016.97</td>\n",
" <td>2.50</td>\n",
" <td>0.55</td>\n",
" </tr>\n",
" <tr>\n",
" <th>40</th>\n",
" <td>Ord_5035</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_7024</td>\n",
" <td>Cust_1710</td>\n",
" <td>4917.6900</td>\n",
" <td>0.02</td>\n",
" <td>42</td>\n",
" <td>126.31</td>\n",
" <td>30.00</td>\n",
" <td>0.71</td>\n",
" </tr>\n",
" <tr>\n",
" <th>57</th>\n",
" <td>Ord_4546</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_6327</td>\n",
" <td>Cust_1474</td>\n",
" <td>5208.7800</td>\n",
" <td>0.05</td>\n",
" <td>34</td>\n",
" <td>1547.78</td>\n",
" <td>7.07</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>64</th>\n",
" <td>Ord_4475</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_6234</td>\n",
" <td>Cust_1474</td>\n",
" <td>7640.2250</td>\n",
" <td>0.07</td>\n",
" <td>46</td>\n",
" <td>2027.68</td>\n",
" <td>2.50</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>79</th>\n",
" <td>Ord_5188</td>\n",
" <td>Prod_14</td>\n",
" <td>SHP_7252</td>\n",
" <td>Cust_1749</td>\n",
" <td>5177.4000</td>\n",
" <td>0.06</td>\n",
" <td>12</td>\n",
" <td>287.50</td>\n",
" <td>49.00</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>82</th>\n",
" <td>Ord_5156</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_7207</td>\n",
" <td>Cust_1749</td>\n",
" <td>8374.1320</td>\n",
" <td>0.06</td>\n",
" <td>48</td>\n",
" <td>2568.10</td>\n",
" <td>8.99</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>84</th>\n",
" <td>Ord_5232</td>\n",
" <td>Prod_17</td>\n",
" <td>SHP_7306</td>\n",
" <td>Cust_1758</td>\n",
" <td>21366.5100</td>\n",
" <td>0.00</td>\n",
" <td>3</td>\n",
" <td>-11984.40</td>\n",
" <td>24.49</td>\n",
" <td>0.39</td>\n",
" </tr>\n",
" <tr>\n",
" <th>107</th>\n",
" <td>Ord_250</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_346</td>\n",
" <td>Cust_45</td>\n",
" <td>8901.7800</td>\n",
" <td>0.04</td>\n",
" <td>31</td>\n",
" <td>2795.36</td>\n",
" <td>24.49</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>121</th>\n",
" <td>Ord_5423</td>\n",
" <td>Prod_17</td>\n",
" <td>SHP_7577</td>\n",
" <td>Cust_1800</td>\n",
" <td>13070.2000</td>\n",
" <td>0.07</td>\n",
" <td>4</td>\n",
" <td>-6923.60</td>\n",
" <td>8.73</td>\n",
" <td>0.57</td>\n",
" </tr>\n",
" <tr>\n",
" <th>124</th>\n",
" <td>Ord_2432</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_3339</td>\n",
" <td>Cust_933</td>\n",
" <td>3883.4715</td>\n",
" <td>0.10</td>\n",
" <td>42</td>\n",
" <td>707.17</td>\n",
" <td>8.99</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>133</th>\n",
" <td>Ord_2432</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_3338</td>\n",
" <td>Cust_933</td>\n",
" <td>15337.5800</td>\n",
" <td>0.10</td>\n",
" <td>30</td>\n",
" <td>6670.41</td>\n",
" <td>19.99</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>148</th>\n",
" <td>Ord_1649</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_2277</td>\n",
" <td>Cust_498</td>\n",
" <td>3005.7400</td>\n",
" <td>0.02</td>\n",
" <td>48</td>\n",
" <td>1053.21</td>\n",
" <td>3.99</td>\n",
" <td>0.57</td>\n",
" </tr>\n",
" <tr>\n",
" <th>163</th>\n",
" <td>Ord_4646</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_6475</td>\n",
" <td>Cust_1603</td>\n",
" <td>4083.1900</td>\n",
" <td>0.07</td>\n",
" <td>43</td>\n",
" <td>-1049.85</td>\n",
" <td>45.00</td>\n",
" <td>0.69</td>\n",
" </tr>\n",
" <tr>\n",
" <th>164</th>\n",
" <td>Ord_4646</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_6476</td>\n",
" <td>Cust_1603</td>\n",
" <td>4902.3800</td>\n",
" <td>0.05</td>\n",
" <td>32</td>\n",
" <td>1438.49</td>\n",
" <td>7.07</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>165</th>\n",
" <td>Ord_4702</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_6560</td>\n",
" <td>Cust_1603</td>\n",
" <td>11823.5200</td>\n",
" <td>0.10</td>\n",
" <td>34</td>\n",
" <td>4592.74</td>\n",
" <td>19.99</td>\n",
" <td>0.40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>168</th>\n",
" <td>Ord_2973</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_4102</td>\n",
" <td>Cust_1081</td>\n",
" <td>4671.1495</td>\n",
" <td>0.07</td>\n",
" <td>28</td>\n",
" <td>947.31</td>\n",
" <td>4.20</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>169</th>\n",
" <td>Ord_3009</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_4168</td>\n",
" <td>Cust_1081</td>\n",
" <td>5718.8500</td>\n",
" <td>0.09</td>\n",
" <td>49</td>\n",
" <td>-2426.55</td>\n",
" <td>70.20</td>\n",
" <td>0.74</td>\n",
" </tr>\n",
" <tr>\n",
" <th>170</th>\n",
" <td>Ord_2973</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_4102</td>\n",
" <td>Cust_1480</td>\n",
" <td>6264.1855</td>\n",
" <td>0.01</td>\n",
" <td>34</td>\n",
" <td>1312.04</td>\n",
" <td>19.99</td>\n",
" <td>0.60</td>\n",
" </tr>\n",
" <tr>\n",
" <th>171</th>\n",
" <td>Ord_2973</td>\n",
" <td>Prod_9</td>\n",
" <td>SHP_6073</td>\n",
" <td>Cust_1480</td>\n",
" <td>5410.9500</td>\n",
" <td>0.09</td>\n",
" <td>36</td>\n",
" <td>2077.91</td>\n",
" <td>19.99</td>\n",
" <td>0.39</td>\n",
" </tr>\n",
" <tr>\n",
" <th>183</th>\n",
" <td>Ord_5157</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_7208</td>\n",
" <td>Cust_1753</td>\n",
" <td>5149.0600</td>\n",
" <td>0.03</td>\n",
" <td>27</td>\n",
" <td>605.44</td>\n",
" <td>30.00</td>\n",
" <td>0.69</td>\n",
" </tr>\n",
" <tr>\n",
" <th>185</th>\n",
" <td>Ord_5153</td>\n",
" <td>Prod_11</td>\n",
" <td>SHP_7202</td>\n",
" <td>Cust_1753</td>\n",
" <td>3457.5600</td>\n",
" <td>0.02</td>\n",
" <td>35</td>\n",
" <td>-365.44</td>\n",
" <td>51.94</td>\n",
" <td>0.63</td>\n",
" </tr>\n",
" <tr>\n",
" <th>189</th>\n",
" <td>Ord_2831</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_3893</td>\n",
" <td>Cust_1036</td>\n",
" <td>18092.6600</td>\n",
" <td>0.09</td>\n",
" <td>36</td>\n",
" <td>7917.76</td>\n",
" <td>19.99</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>191</th>\n",
" <td>Ord_2791</td>\n",
" <td>Prod_11</td>\n",
" <td>SHP_3838</td>\n",
" <td>Cust_1036</td>\n",
" <td>10351.0100</td>\n",
" <td>0.08</td>\n",
" <td>19</td>\n",
" <td>-1331.55</td>\n",
" <td>45.70</td>\n",
" <td>0.71</td>\n",
" </tr>\n",
" <tr>\n",
" <th>...</th>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8125</th>\n",
" <td>Ord_4515</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_6285</td>\n",
" <td>Cust_1546</td>\n",
" <td>4976.6000</td>\n",
" <td>0.06</td>\n",
" <td>32</td>\n",
" <td>601.88</td>\n",
" <td>19.99</td>\n",
" <td>0.66</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8137</th>\n",
" <td>Ord_2267</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_3089</td>\n",
" <td>Cust_890</td>\n",
" <td>6608.2400</td>\n",
" <td>0.09</td>\n",
" <td>35</td>\n",
" <td>2164.64</td>\n",
" <td>0.99</td>\n",
" <td>0.55</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8141</th>\n",
" <td>Ord_3368</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_4668</td>\n",
" <td>Cust_1190</td>\n",
" <td>3227.3800</td>\n",
" <td>0.05</td>\n",
" <td>26</td>\n",
" <td>192.31</td>\n",
" <td>30.00</td>\n",
" <td>0.64</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8143</th>\n",
" <td>Ord_3265</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_4530</td>\n",
" <td>Cust_1190</td>\n",
" <td>10330.9400</td>\n",
" <td>0.07</td>\n",
" <td>25</td>\n",
" <td>2914.56</td>\n",
" <td>19.99</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8151</th>\n",
" <td>Ord_3214</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_4456</td>\n",
" <td>Cust_1187</td>\n",
" <td>8316.7600</td>\n",
" <td>0.05</td>\n",
" <td>30</td>\n",
" <td>2108.80</td>\n",
" <td>23.19</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8158</th>\n",
" <td>Ord_2868</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_3950</td>\n",
" <td>Cust_1059</td>\n",
" <td>5405.4400</td>\n",
" <td>0.07</td>\n",
" <td>18</td>\n",
" <td>604.46</td>\n",
" <td>64.73</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8207</th>\n",
" <td>Ord_3433</td>\n",
" <td>Prod_8</td>\n",
" <td>SHP_4759</td>\n",
" <td>Cust_1180</td>\n",
" <td>3601.0700</td>\n",
" <td>0.04</td>\n",
" <td>50</td>\n",
" <td>174.80</td>\n",
" <td>14.52</td>\n",
" <td>0.65</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8210</th>\n",
" <td>Ord_2110</td>\n",
" <td>Prod_17</td>\n",
" <td>SHP_2885</td>\n",
" <td>Cust_802</td>\n",
" <td>4502.2600</td>\n",
" <td>0.09</td>\n",
" <td>38</td>\n",
" <td>1272.17</td>\n",
" <td>26.30</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8211</th>\n",
" <td>Ord_2144</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_2925</td>\n",
" <td>Cust_802</td>\n",
" <td>5318.8900</td>\n",
" <td>0.06</td>\n",
" <td>48</td>\n",
" <td>525.15</td>\n",
" <td>8.64</td>\n",
" <td>0.78</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8217</th>\n",
" <td>Ord_3359</td>\n",
" <td>Prod_10</td>\n",
" <td>SHP_7245</td>\n",
" <td>Cust_1762</td>\n",
" <td>28389.1400</td>\n",
" <td>0.07</td>\n",
" <td>33</td>\n",
" <td>7132.18</td>\n",
" <td>44.55</td>\n",
" <td>0.62</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8219</th>\n",
" <td>Ord_5200</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_7266</td>\n",
" <td>Cust_1762</td>\n",
" <td>4815.8620</td>\n",
" <td>0.08</td>\n",
" <td>47</td>\n",
" <td>1316.79</td>\n",
" <td>4.20</td>\n",
" <td>0.57</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8235</th>\n",
" <td>Ord_759</td>\n",
" <td>Prod_5</td>\n",
" <td>SHP_1036</td>\n",
" <td>Cust_245</td>\n",
" <td>8549.0400</td>\n",
" <td>0.03</td>\n",
" <td>42</td>\n",
" <td>2861.01</td>\n",
" <td>11.54</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8240</th>\n",
" <td>Ord_793</td>\n",
" <td>Prod_11</td>\n",
" <td>SHP_1090</td>\n",
" <td>Cust_245</td>\n",
" <td>4452.6500</td>\n",
" <td>0.09</td>\n",
" <td>30</td>\n",
" <td>-265.12</td>\n",
" <td>60.00</td>\n",
" <td>0.55</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8249</th>\n",
" <td>Ord_3470</td>\n",
" <td>Prod_17</td>\n",
" <td>SHP_4805</td>\n",
" <td>Cust_1203</td>\n",
" <td>5615.4000</td>\n",
" <td>0.07</td>\n",
" <td>46</td>\n",
" <td>1807.16</td>\n",
" <td>26.30</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8263</th>\n",
" <td>Ord_4954</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_6913</td>\n",
" <td>Cust_1694</td>\n",
" <td>7987.4300</td>\n",
" <td>0.03</td>\n",
" <td>49</td>\n",
" <td>1304.90</td>\n",
" <td>30.00</td>\n",
" <td>0.62</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8283</th>\n",
" <td>Ord_1741</td>\n",
" <td>Prod_11</td>\n",
" <td>SHP_2411</td>\n",
" <td>Cust_595</td>\n",
" <td>15168.8200</td>\n",
" <td>0.02</td>\n",
" <td>26</td>\n",
" <td>-1096.78</td>\n",
" <td>147.12</td>\n",
" <td>0.80</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8286</th>\n",
" <td>Ord_1749</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_2424</td>\n",
" <td>Cust_595</td>\n",
" <td>5176.2700</td>\n",
" <td>0.01</td>\n",
" <td>38</td>\n",
" <td>-743.45</td>\n",
" <td>35.00</td>\n",
" <td>0.84</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8292</th>\n",
" <td>Ord_1765</td>\n",
" <td>Prod_14</td>\n",
" <td>SHP_2446</td>\n",
" <td>Cust_595</td>\n",
" <td>14647.2600</td>\n",
" <td>0.07</td>\n",
" <td>25</td>\n",
" <td>5485.15</td>\n",
" <td>24.49</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8298</th>\n",
" <td>Ord_2172</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_2960</td>\n",
" <td>Cust_787</td>\n",
" <td>6648.5800</td>\n",
" <td>0.08</td>\n",
" <td>19</td>\n",
" <td>-555.98</td>\n",
" <td>99.00</td>\n",
" <td>0.65</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8308</th>\n",
" <td>Ord_2659</td>\n",
" <td>Prod_8</td>\n",
" <td>SHP_3638</td>\n",
" <td>Cust_1016</td>\n",
" <td>4744.6400</td>\n",
" <td>0.04</td>\n",
" <td>46</td>\n",
" <td>1033.38</td>\n",
" <td>19.99</td>\n",
" <td>0.52</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8317</th>\n",
" <td>Ord_2770</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_3802</td>\n",
" <td>Cust_1016</td>\n",
" <td>7535.9600</td>\n",
" <td>0.08</td>\n",
" <td>46</td>\n",
" <td>2745.87</td>\n",
" <td>19.99</td>\n",
" <td>0.40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8329</th>\n",
" <td>Ord_2160</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_2944</td>\n",
" <td>Cust_810</td>\n",
" <td>3636.3700</td>\n",
" <td>0.06</td>\n",
" <td>33</td>\n",
" <td>-176.91</td>\n",
" <td>30.00</td>\n",
" <td>0.69</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8332</th>\n",
" <td>Ord_2101</td>\n",
" <td>Prod_11</td>\n",
" <td>SHP_2875</td>\n",
" <td>Cust_790</td>\n",
" <td>10714.7800</td>\n",
" <td>0.00</td>\n",
" <td>41</td>\n",
" <td>-627.64</td>\n",
" <td>66.67</td>\n",
" <td>0.65</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8335</th>\n",
" <td>Ord_2070</td>\n",
" <td>Prod_11</td>\n",
" <td>SHP_2833</td>\n",
" <td>Cust_784</td>\n",
" <td>3905.7500</td>\n",
" <td>0.01</td>\n",
" <td>21</td>\n",
" <td>55.30</td>\n",
" <td>29.21</td>\n",
" <td>0.76</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8343</th>\n",
" <td>Ord_2178</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_2968</td>\n",
" <td>Cust_785</td>\n",
" <td>6030.5800</td>\n",
" <td>0.09</td>\n",
" <td>39</td>\n",
" <td>1197.86</td>\n",
" <td>8.99</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8366</th>\n",
" <td>Ord_3593</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_4974</td>\n",
" <td>Cust_1274</td>\n",
" <td>12073.0600</td>\n",
" <td>0.03</td>\n",
" <td>39</td>\n",
" <td>5081.87</td>\n",
" <td>19.99</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8367</th>\n",
" <td>Ord_3593</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_4975</td>\n",
" <td>Cust_1274</td>\n",
" <td>6685.0500</td>\n",
" <td>0.09</td>\n",
" <td>25</td>\n",
" <td>1653.60</td>\n",
" <td>24.49</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8371</th>\n",
" <td>Ord_2624</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_3591</td>\n",
" <td>Cust_1006</td>\n",
" <td>4924.1350</td>\n",
" <td>0.07</td>\n",
" <td>28</td>\n",
" <td>1049.54</td>\n",
" <td>8.99</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8383</th>\n",
" <td>Ord_2722</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_3731</td>\n",
" <td>Cust_1006</td>\n",
" <td>3508.3300</td>\n",
" <td>0.04</td>\n",
" <td>21</td>\n",
" <td>-546.98</td>\n",
" <td>35.00</td>\n",
" <td>0.85</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8397</th>\n",
" <td>Ord_5348</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_7469</td>\n",
" <td>Cust_1798</td>\n",
" <td>3872.8700</td>\n",
" <td>0.03</td>\n",
" <td>23</td>\n",
" <td>565.34</td>\n",
" <td>30.00</td>\n",
" <td>0.62</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>1359 rows × 10 columns</p>\n",
"</div>"
],
"text/plain": [
" Ord_id Prod_id Ship_id Cust_id Sales Discount \\\n",
"2 Ord_5446 Prod_4 SHP_7610 Cust_1818 4701.6900 0.00 \n",
"4 Ord_5485 Prod_17 SHP_7664 Cust_1818 4233.1500 0.08 \n",
"7 Ord_4725 Prod_4 SHP_6593 Cust_1641 3410.1575 0.10 \n",
"10 Ord_4743 Prod_2 SHP_6615 Cust_1641 4072.0100 0.01 \n",
"13 Ord_2207 Prod_11 SHP_3093 Cust_839 3364.2480 0.10 \n",
"17 Ord_4471 Prod_15 SHP_6228 Cust_1521 13255.9300 0.02 \n",
"22 Ord_996 Prod_5 SHP_1377 Cust_371 3202.2500 0.09 \n",
"28 Ord_2573 Prod_4 SHP_3527 Cust_931 3594.7435 0.05 \n",
"40 Ord_5035 Prod_15 SHP_7024 Cust_1710 4917.6900 0.02 \n",
"57 Ord_4546 Prod_1 SHP_6327 Cust_1474 5208.7800 0.05 \n",
"64 Ord_4475 Prod_4 SHP_6234 Cust_1474 7640.2250 0.07 \n",
"79 Ord_5188 Prod_14 SHP_7252 Cust_1749 5177.4000 0.06 \n",
"82 Ord_5156 Prod_4 SHP_7207 Cust_1749 8374.1320 0.06 \n",
"84 Ord_5232 Prod_17 SHP_7306 Cust_1758 21366.5100 0.00 \n",
"107 Ord_250 Prod_15 SHP_346 Cust_45 8901.7800 0.04 \n",
"121 Ord_5423 Prod_17 SHP_7577 Cust_1800 13070.2000 0.07 \n",
"124 Ord_2432 Prod_4 SHP_3339 Cust_933 3883.4715 0.10 \n",
"133 Ord_2432 Prod_3 SHP_3338 Cust_933 15337.5800 0.10 \n",
"148 Ord_1649 Prod_2 SHP_2277 Cust_498 3005.7400 0.02 \n",
"163 Ord_4646 Prod_15 SHP_6475 Cust_1603 4083.1900 0.07 \n",
"164 Ord_4646 Prod_1 SHP_6476 Cust_1603 4902.3800 0.05 \n",
"165 Ord_4702 Prod_3 SHP_6560 Cust_1603 11823.5200 0.10 \n",
"168 Ord_2973 Prod_4 SHP_4102 Cust_1081 4671.1495 0.07 \n",
"169 Ord_3009 Prod_15 SHP_4168 Cust_1081 5718.8500 0.09 \n",
"170 Ord_2973 Prod_4 SHP_4102 Cust_1480 6264.1855 0.01 \n",
"171 Ord_2973 Prod_9 SHP_6073 Cust_1480 5410.9500 0.09 \n",
"183 Ord_5157 Prod_15 SHP_7208 Cust_1753 5149.0600 0.03 \n",
"185 Ord_5153 Prod_11 SHP_7202 Cust_1753 3457.5600 0.02 \n",
"189 Ord_2831 Prod_3 SHP_3893 Cust_1036 18092.6600 0.09 \n",
"191 Ord_2791 Prod_11 SHP_3838 Cust_1036 10351.0100 0.08 \n",
"... ... ... ... ... ... ... \n",
"8125 Ord_4515 Prod_1 SHP_6285 Cust_1546 4976.6000 0.06 \n",
"8137 Ord_2267 Prod_2 SHP_3089 Cust_890 6608.2400 0.09 \n",
"8141 Ord_3368 Prod_15 SHP_4668 Cust_1190 3227.3800 0.05 \n",
"8143 Ord_3265 Prod_1 SHP_4530 Cust_1190 10330.9400 0.07 \n",
"8151 Ord_3214 Prod_2 SHP_4456 Cust_1187 8316.7600 0.05 \n",
"8158 Ord_2868 Prod_15 SHP_3950 Cust_1059 5405.4400 0.07 \n",
"8207 Ord_3433 Prod_8 SHP_4759 Cust_1180 3601.0700 0.04 \n",
"8210 Ord_2110 Prod_17 SHP_2885 Cust_802 4502.2600 0.09 \n",
"8211 Ord_2144 Prod_1 SHP_2925 Cust_802 5318.8900 0.06 \n",
"8217 Ord_3359 Prod_10 SHP_7245 Cust_1762 28389.1400 0.07 \n",
"8219 Ord_5200 Prod_4 SHP_7266 Cust_1762 4815.8620 0.08 \n",
"8235 Ord_759 Prod_5 SHP_1036 Cust_245 8549.0400 0.03 \n",
"8240 Ord_793 Prod_11 SHP_1090 Cust_245 4452.6500 0.09 \n",
"8249 Ord_3470 Prod_17 SHP_4805 Cust_1203 5615.4000 0.07 \n",
"8263 Ord_4954 Prod_15 SHP_6913 Cust_1694 7987.4300 0.03 \n",
"8283 Ord_1741 Prod_11 SHP_2411 Cust_595 15168.8200 0.02 \n",
"8286 Ord_1749 Prod_1 SHP_2424 Cust_595 5176.2700 0.01 \n",
"8292 Ord_1765 Prod_14 SHP_2446 Cust_595 14647.2600 0.07 \n",
"8298 Ord_2172 Prod_1 SHP_2960 Cust_787 6648.5800 0.08 \n",
"8308 Ord_2659 Prod_8 SHP_3638 Cust_1016 4744.6400 0.04 \n",
"8317 Ord_2770 Prod_3 SHP_3802 Cust_1016 7535.9600 0.08 \n",
"8329 Ord_2160 Prod_15 SHP_2944 Cust_810 3636.3700 0.06 \n",
"8332 Ord_2101 Prod_11 SHP_2875 Cust_790 10714.7800 0.00 \n",
"8335 Ord_2070 Prod_11 SHP_2833 Cust_784 3905.7500 0.01 \n",
"8343 Ord_2178 Prod_4 SHP_2968 Cust_785 6030.5800 0.09 \n",
"8366 Ord_3593 Prod_3 SHP_4974 Cust_1274 12073.0600 0.03 \n",
"8367 Ord_3593 Prod_15 SHP_4975 Cust_1274 6685.0500 0.09 \n",
"8371 Ord_2624 Prod_4 SHP_3591 Cust_1006 4924.1350 0.07 \n",
"8383 Ord_2722 Prod_1 SHP_3731 Cust_1006 3508.3300 0.04 \n",
"8397 Ord_5348 Prod_15 SHP_7469 Cust_1798 3872.8700 0.03 \n",
"\n",
" Order_Quantity Profit Shipping_Cost Product_Base_Margin \n",
"2 26 1148.90 2.50 0.59 \n",
"4 35 1219.87 26.30 0.38 \n",
"7 48 1137.91 0.99 0.55 \n",
"10 43 1675.98 0.99 0.56 \n",
"13 15 -693.23 61.76 0.78 \n",
"17 25 4089.27 26.00 0.60 \n",
"22 44 991.26 19.99 0.43 \n",
"28 38 1016.97 2.50 0.55 \n",
"40 42 126.31 30.00 0.71 \n",
"57 34 1547.78 7.07 0.59 \n",
"64 46 2027.68 2.50 0.59 \n",
"79 12 287.50 49.00 0.38 \n",
"82 48 2568.10 8.99 0.56 \n",
"84 3 -11984.40 24.49 0.39 \n",
"107 31 2795.36 24.49 NaN \n",
"121 4 -6923.60 8.73 0.57 \n",
"124 42 707.17 8.99 0.58 \n",
"133 30 6670.41 19.99 0.37 \n",
"148 48 1053.21 3.99 0.57 \n",
"163 43 -1049.85 45.00 0.69 \n",
"164 32 1438.49 7.07 0.59 \n",
"165 34 4592.74 19.99 0.40 \n",
"168 28 947.31 4.20 0.59 \n",
"169 49 -2426.55 70.20 0.74 \n",
"170 34 1312.04 19.99 0.60 \n",
"171 36 2077.91 19.99 0.39 \n",
"183 27 605.44 30.00 0.69 \n",
"185 35 -365.44 51.94 0.63 \n",
"189 36 7917.76 19.99 0.37 \n",
"191 19 -1331.55 45.70 0.71 \n",
"... ... ... ... ... \n",
"8125 32 601.88 19.99 0.66 \n",
"8137 35 2164.64 0.99 0.55 \n",
"8141 26 192.31 30.00 0.64 \n",
"8143 25 2914.56 19.99 0.58 \n",
"8151 30 2108.80 23.19 0.59 \n",
"8158 18 604.46 64.73 0.56 \n",
"8207 50 174.80 14.52 0.65 \n",
"8210 38 1272.17 26.30 0.38 \n",
"8211 48 525.15 8.64 0.78 \n",
"8217 33 7132.18 44.55 0.62 \n",
"8219 47 1316.79 4.20 0.57 \n",
"8235 42 2861.01 11.54 0.59 \n",
"8240 30 -265.12 60.00 0.55 \n",
"8249 46 1807.16 26.30 0.38 \n",
"8263 49 1304.90 30.00 0.62 \n",
"8283 26 -1096.78 147.12 0.80 \n",
"8286 38 -743.45 35.00 0.84 \n",
"8292 25 5485.15 24.49 0.37 \n",
"8298 19 -555.98 99.00 0.65 \n",
"8308 46 1033.38 19.99 0.52 \n",
"8317 46 2745.87 19.99 0.40 \n",
"8329 33 -176.91 30.00 0.69 \n",
"8332 41 -627.64 66.67 0.65 \n",
"8335 21 55.30 29.21 0.76 \n",
"8343 39 1197.86 8.99 0.58 \n",
"8366 39 5081.87 19.99 0.38 \n",
"8367 25 1653.60 24.49 NaN \n",
"8371 28 1049.54 8.99 0.58 \n",
"8383 21 -546.98 35.00 0.85 \n",
"8397 23 565.34 30.00 0.62 \n",
"\n",
"[1359 rows x 10 columns]"
]
},
"execution_count": 13,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# An alternative to df.Sales is df['Sales]\n",
"# You may want to put the : to indicate that you want all columns\n",
"# It is more explicit \n",
"df.loc[df['Sales'] > 3000, :]"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Ord_id</th>\n",
" <th>Prod_id</th>\n",
" <th>Ship_id</th>\n",
" <th>Cust_id</th>\n",
" <th>Sales</th>\n",
" <th>Discount</th>\n",
" <th>Order_Quantity</th>\n",
" <th>Profit</th>\n",
" <th>Shipping_Cost</th>\n",
" <th>Product_Base_Margin</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>Ord_5456</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_7625</td>\n",
" <td>Cust_1818</td>\n",
" <td>2337.8900</td>\n",
" <td>0.09</td>\n",
" <td>43</td>\n",
" <td>729.34</td>\n",
" <td>14.30</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>81</th>\n",
" <td>Ord_5205</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_7274</td>\n",
" <td>Cust_1749</td>\n",
" <td>2546.5235</td>\n",
" <td>0.09</td>\n",
" <td>26</td>\n",
" <td>210.00</td>\n",
" <td>7.69</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>109</th>\n",
" <td>Ord_139</td>\n",
" <td>Prod_17</td>\n",
" <td>SHP_186</td>\n",
" <td>Cust_45</td>\n",
" <td>2671.2100</td>\n",
" <td>0.06</td>\n",
" <td>14</td>\n",
" <td>636.18</td>\n",
" <td>15.59</td>\n",
" <td>0.36</td>\n",
" </tr>\n",
" <tr>\n",
" <th>110</th>\n",
" <td>Ord_239</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_332</td>\n",
" <td>Cust_45</td>\n",
" <td>2157.3085</td>\n",
" <td>0.00</td>\n",
" <td>38</td>\n",
" <td>519.25</td>\n",
" <td>5.31</td>\n",
" <td>0.57</td>\n",
" </tr>\n",
" <tr>\n",
" <th>141</th>\n",
" <td>Ord_1673</td>\n",
" <td>Prod_17</td>\n",
" <td>SHP_2314</td>\n",
" <td>Cust_498</td>\n",
" <td>2027.5500</td>\n",
" <td>0.04</td>\n",
" <td>14</td>\n",
" <td>537.40</td>\n",
" <td>13.99</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>146</th>\n",
" <td>Ord_1649</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_2278</td>\n",
" <td>Cust_498</td>\n",
" <td>2209.5155</td>\n",
" <td>0.06</td>\n",
" <td>41</td>\n",
" <td>458.62</td>\n",
" <td>5.31</td>\n",
" <td>0.57</td>\n",
" </tr>\n",
" <tr>\n",
" <th>176</th>\n",
" <td>Ord_2273</td>\n",
" <td>Prod_8</td>\n",
" <td>SHP_3101</td>\n",
" <td>Cust_878</td>\n",
" <td>2899.9800</td>\n",
" <td>0.10</td>\n",
" <td>19</td>\n",
" <td>666.01</td>\n",
" <td>5.50</td>\n",
" <td>0.49</td>\n",
" </tr>\n",
" <tr>\n",
" <th>184</th>\n",
" <td>Ord_5230</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_7304</td>\n",
" <td>Cust_1753</td>\n",
" <td>2197.4115</td>\n",
" <td>0.00</td>\n",
" <td>20</td>\n",
" <td>305.96</td>\n",
" <td>7.69</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>186</th>\n",
" <td>Ord_5159</td>\n",
" <td>Prod_5</td>\n",
" <td>SHP_7210</td>\n",
" <td>Cust_1753</td>\n",
" <td>2213.9200</td>\n",
" <td>0.03</td>\n",
" <td>20</td>\n",
" <td>768.34</td>\n",
" <td>13.99</td>\n",
" <td>0.65</td>\n",
" </tr>\n",
" <tr>\n",
" <th>230</th>\n",
" <td>Ord_657</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_899</td>\n",
" <td>Cust_209</td>\n",
" <td>2343.0760</td>\n",
" <td>0.06</td>\n",
" <td>24</td>\n",
" <td>311.64</td>\n",
" <td>8.99</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>285</th>\n",
" <td>Ord_1607</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_2220</td>\n",
" <td>Cust_506</td>\n",
" <td>2980.3720</td>\n",
" <td>0.02</td>\n",
" <td>19</td>\n",
" <td>494.63</td>\n",
" <td>8.99</td>\n",
" <td>0.57</td>\n",
" </tr>\n",
" <tr>\n",
" <th>314</th>\n",
" <td>Ord_1521</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_2100</td>\n",
" <td>Cust_560</td>\n",
" <td>2230.9700</td>\n",
" <td>0.06</td>\n",
" <td>12</td>\n",
" <td>273.27</td>\n",
" <td>26.20</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>349</th>\n",
" <td>Ord_4896</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_6829</td>\n",
" <td>Cust_1674</td>\n",
" <td>2827.1425</td>\n",
" <td>0.01</td>\n",
" <td>35</td>\n",
" <td>713.88</td>\n",
" <td>4.90</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>395</th>\n",
" <td>Ord_4144</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_5772</td>\n",
" <td>Cust_1418</td>\n",
" <td>2182.9100</td>\n",
" <td>0.10</td>\n",
" <td>40</td>\n",
" <td>549.45</td>\n",
" <td>3.50</td>\n",
" <td>0.57</td>\n",
" </tr>\n",
" <tr>\n",
" <th>404</th>\n",
" <td>Ord_1621</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_2238</td>\n",
" <td>Cust_566</td>\n",
" <td>2010.8900</td>\n",
" <td>0.09</td>\n",
" <td>34</td>\n",
" <td>564.07</td>\n",
" <td>11.55</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>510</th>\n",
" <td>Ord_3848</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_5335</td>\n",
" <td>Cust_1346</td>\n",
" <td>2660.6105</td>\n",
" <td>0.03</td>\n",
" <td>46</td>\n",
" <td>618.07</td>\n",
" <td>8.99</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>522</th>\n",
" <td>Ord_142</td>\n",
" <td>Prod_8</td>\n",
" <td>SHP_191</td>\n",
" <td>Cust_51</td>\n",
" <td>2689.4800</td>\n",
" <td>0.04</td>\n",
" <td>27</td>\n",
" <td>399.93</td>\n",
" <td>19.99</td>\n",
" <td>0.50</td>\n",
" </tr>\n",
" <tr>\n",
" <th>536</th>\n",
" <td>Ord_4909</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_6846</td>\n",
" <td>Cust_227</td>\n",
" <td>2180.2300</td>\n",
" <td>0.05</td>\n",
" <td>37</td>\n",
" <td>660.25</td>\n",
" <td>3.50</td>\n",
" <td>0.57</td>\n",
" </tr>\n",
" <tr>\n",
" <th>541</th>\n",
" <td>Ord_4935</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_6886</td>\n",
" <td>Cust_1680</td>\n",
" <td>2292.1015</td>\n",
" <td>0.02</td>\n",
" <td>21</td>\n",
" <td>398.36</td>\n",
" <td>3.00</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>647</th>\n",
" <td>Ord_4292</td>\n",
" <td>Prod_5</td>\n",
" <td>SHP_5988</td>\n",
" <td>Cust_1439</td>\n",
" <td>2758.2200</td>\n",
" <td>0.00</td>\n",
" <td>15</td>\n",
" <td>966.81</td>\n",
" <td>13.99</td>\n",
" <td>0.75</td>\n",
" </tr>\n",
" <tr>\n",
" <th>680</th>\n",
" <td>Ord_674</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_922</td>\n",
" <td>Cust_212</td>\n",
" <td>2404.5990</td>\n",
" <td>0.08</td>\n",
" <td>45</td>\n",
" <td>496.89</td>\n",
" <td>4.99</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>688</th>\n",
" <td>Ord_4904</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_6841</td>\n",
" <td>Cust_1682</td>\n",
" <td>2257.8800</td>\n",
" <td>0.01</td>\n",
" <td>38</td>\n",
" <td>474.98</td>\n",
" <td>9.71</td>\n",
" <td>0.57</td>\n",
" </tr>\n",
" <tr>\n",
" <th>718</th>\n",
" <td>Ord_2069</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_2832</td>\n",
" <td>Cust_783</td>\n",
" <td>2135.9735</td>\n",
" <td>0.07</td>\n",
" <td>40</td>\n",
" <td>239.40</td>\n",
" <td>8.99</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>720</th>\n",
" <td>Ord_2150</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_2932</td>\n",
" <td>Cust_805</td>\n",
" <td>2773.0315</td>\n",
" <td>0.04</td>\n",
" <td>38</td>\n",
" <td>897.87</td>\n",
" <td>0.99</td>\n",
" <td>0.55</td>\n",
" </tr>\n",
" <tr>\n",
" <th>729</th>\n",
" <td>Ord_4826</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_6724</td>\n",
" <td>Cust_1588</td>\n",
" <td>2168.0500</td>\n",
" <td>0.00</td>\n",
" <td>5</td>\n",
" <td>416.02</td>\n",
" <td>19.99</td>\n",
" <td>0.35</td>\n",
" </tr>\n",
" <tr>\n",
" <th>767</th>\n",
" <td>Ord_2054</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_2808</td>\n",
" <td>Cust_828</td>\n",
" <td>2192.6300</td>\n",
" <td>0.05</td>\n",
" <td>37</td>\n",
" <td>660.06</td>\n",
" <td>3.99</td>\n",
" <td>0.57</td>\n",
" </tr>\n",
" <tr>\n",
" <th>775</th>\n",
" <td>Ord_5154</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_7204</td>\n",
" <td>Cust_1746</td>\n",
" <td>2610.8940</td>\n",
" <td>0.00</td>\n",
" <td>23</td>\n",
" <td>516.19</td>\n",
" <td>5.63</td>\n",
" <td>0.60</td>\n",
" </tr>\n",
" <tr>\n",
" <th>783</th>\n",
" <td>Ord_2666</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_3652</td>\n",
" <td>Cust_1017</td>\n",
" <td>2368.1680</td>\n",
" <td>0.00</td>\n",
" <td>30</td>\n",
" <td>1181.30</td>\n",
" <td>1.25</td>\n",
" <td>0.39</td>\n",
" </tr>\n",
" <tr>\n",
" <th>809</th>\n",
" <td>Ord_4279</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_5971</td>\n",
" <td>Cust_1440</td>\n",
" <td>2752.6800</td>\n",
" <td>0.04</td>\n",
" <td>45</td>\n",
" <td>430.32</td>\n",
" <td>12.78</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>810</th>\n",
" <td>Ord_4269</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_5958</td>\n",
" <td>Cust_1440</td>\n",
" <td>2405.0000</td>\n",
" <td>0.10</td>\n",
" <td>39</td>\n",
" <td>696.17</td>\n",
" <td>0.99</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>...</th>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7777</th>\n",
" <td>Ord_3414</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_4733</td>\n",
" <td>Cust_1196</td>\n",
" <td>2167.0500</td>\n",
" <td>0.02</td>\n",
" <td>36</td>\n",
" <td>684.90</td>\n",
" <td>3.50</td>\n",
" <td>0.57</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7778</th>\n",
" <td>Ord_3363</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_4663</td>\n",
" <td>Cust_1196</td>\n",
" <td>2040.3900</td>\n",
" <td>0.07</td>\n",
" <td>50</td>\n",
" <td>221.09</td>\n",
" <td>19.99</td>\n",
" <td>0.36</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7788</th>\n",
" <td>Ord_2482</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_3399</td>\n",
" <td>Cust_977</td>\n",
" <td>2252.2620</td>\n",
" <td>0.10</td>\n",
" <td>42</td>\n",
" <td>478.11</td>\n",
" <td>5.63</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7811</th>\n",
" <td>Ord_3215</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_4458</td>\n",
" <td>Cust_1188</td>\n",
" <td>2080.0350</td>\n",
" <td>0.10</td>\n",
" <td>31</td>\n",
" <td>844.90</td>\n",
" <td>1.25</td>\n",
" <td>0.39</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7823</th>\n",
" <td>Ord_4370</td>\n",
" <td>Prod_9</td>\n",
" <td>SHP_6092</td>\n",
" <td>Cust_1492</td>\n",
" <td>2325.4200</td>\n",
" <td>0.02</td>\n",
" <td>25</td>\n",
" <td>739.91</td>\n",
" <td>19.99</td>\n",
" <td>0.40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7858</th>\n",
" <td>Ord_3232</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_4483</td>\n",
" <td>Cust_1200</td>\n",
" <td>2206.1700</td>\n",
" <td>0.02</td>\n",
" <td>4</td>\n",
" <td>251.43</td>\n",
" <td>19.99</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7875</th>\n",
" <td>Ord_1762</td>\n",
" <td>Prod_17</td>\n",
" <td>SHP_2443</td>\n",
" <td>Cust_577</td>\n",
" <td>2287.1000</td>\n",
" <td>0.07</td>\n",
" <td>23</td>\n",
" <td>231.49</td>\n",
" <td>19.99</td>\n",
" <td>0.52</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7877</th>\n",
" <td>Ord_1748</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_2421</td>\n",
" <td>Cust_577</td>\n",
" <td>2503.3265</td>\n",
" <td>0.04</td>\n",
" <td>45</td>\n",
" <td>447.12</td>\n",
" <td>8.80</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7884</th>\n",
" <td>Ord_710</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_973</td>\n",
" <td>Cust_244</td>\n",
" <td>2529.3960</td>\n",
" <td>0.06</td>\n",
" <td>25</td>\n",
" <td>371.21</td>\n",
" <td>3.00</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7911</th>\n",
" <td>Ord_5012</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_6993</td>\n",
" <td>Cust_1693</td>\n",
" <td>2882.7070</td>\n",
" <td>0.02</td>\n",
" <td>16</td>\n",
" <td>303.23</td>\n",
" <td>5.00</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7927</th>\n",
" <td>Ord_2502</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_3430</td>\n",
" <td>Cust_976</td>\n",
" <td>2104.9910</td>\n",
" <td>0.09</td>\n",
" <td>20</td>\n",
" <td>165.45</td>\n",
" <td>8.80</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7940</th>\n",
" <td>Ord_3277</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_4550</td>\n",
" <td>Cust_1224</td>\n",
" <td>2185.9535</td>\n",
" <td>0.10</td>\n",
" <td>21</td>\n",
" <td>268.01</td>\n",
" <td>8.99</td>\n",
" <td>0.55</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7973</th>\n",
" <td>Ord_1694</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_2346</td>\n",
" <td>Cust_582</td>\n",
" <td>2145.0500</td>\n",
" <td>0.07</td>\n",
" <td>45</td>\n",
" <td>1012.67</td>\n",
" <td>5.86</td>\n",
" <td>0.35</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7986</th>\n",
" <td>Ord_4788</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_6674</td>\n",
" <td>Cust_1583</td>\n",
" <td>2478.4810</td>\n",
" <td>0.09</td>\n",
" <td>27</td>\n",
" <td>249.10</td>\n",
" <td>8.99</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8045</th>\n",
" <td>Ord_5443</td>\n",
" <td>Prod_8</td>\n",
" <td>SHP_7605</td>\n",
" <td>Cust_1803</td>\n",
" <td>2587.5300</td>\n",
" <td>0.02</td>\n",
" <td>44</td>\n",
" <td>401.85</td>\n",
" <td>6.55</td>\n",
" <td>0.68</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8048</th>\n",
" <td>Ord_796</td>\n",
" <td>Prod_5</td>\n",
" <td>SHP_1095</td>\n",
" <td>Cust_247</td>\n",
" <td>2780.8800</td>\n",
" <td>0.07</td>\n",
" <td>27</td>\n",
" <td>595.38</td>\n",
" <td>24.49</td>\n",
" <td>0.61</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8061</th>\n",
" <td>Ord_2020</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_3104</td>\n",
" <td>Cust_892</td>\n",
" <td>2550.1200</td>\n",
" <td>0.01</td>\n",
" <td>40</td>\n",
" <td>882.45</td>\n",
" <td>4.50</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8071</th>\n",
" <td>Ord_5350</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_7473</td>\n",
" <td>Cust_1795</td>\n",
" <td>2750.1070</td>\n",
" <td>0.00</td>\n",
" <td>24</td>\n",
" <td>600.42</td>\n",
" <td>7.69</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8147</th>\n",
" <td>Ord_3214</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_4457</td>\n",
" <td>Cust_1187</td>\n",
" <td>2143.2155</td>\n",
" <td>0.02</td>\n",
" <td>37</td>\n",
" <td>464.36</td>\n",
" <td>8.99</td>\n",
" <td>0.55</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8152</th>\n",
" <td>Ord_3337</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_4630</td>\n",
" <td>Cust_1187</td>\n",
" <td>2477.9900</td>\n",
" <td>0.00</td>\n",
" <td>30</td>\n",
" <td>747.68</td>\n",
" <td>4.50</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8239</th>\n",
" <td>Ord_793</td>\n",
" <td>Prod_9</td>\n",
" <td>SHP_1089</td>\n",
" <td>Cust_245</td>\n",
" <td>2833.1900</td>\n",
" <td>0.06</td>\n",
" <td>34</td>\n",
" <td>1409.87</td>\n",
" <td>5.01</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8262</th>\n",
" <td>Ord_4954</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_6914</td>\n",
" <td>Cust_1694</td>\n",
" <td>2455.2760</td>\n",
" <td>0.04</td>\n",
" <td>42</td>\n",
" <td>693.06</td>\n",
" <td>5.63</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8271</th>\n",
" <td>Ord_4679</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_6528</td>\n",
" <td>Cust_1587</td>\n",
" <td>2823.0370</td>\n",
" <td>0.10</td>\n",
" <td>29</td>\n",
" <td>372.40</td>\n",
" <td>4.20</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8289</th>\n",
" <td>Ord_1749</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_2422</td>\n",
" <td>Cust_595</td>\n",
" <td>2731.7300</td>\n",
" <td>0.07</td>\n",
" <td>21</td>\n",
" <td>310.59</td>\n",
" <td>8.99</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8304</th>\n",
" <td>Ord_2709</td>\n",
" <td>Prod_11</td>\n",
" <td>SHP_3709</td>\n",
" <td>Cust_1025</td>\n",
" <td>2272.5600</td>\n",
" <td>0.06</td>\n",
" <td>15</td>\n",
" <td>111.05</td>\n",
" <td>16.01</td>\n",
" <td>0.70</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8338</th>\n",
" <td>Ord_2107</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_2882</td>\n",
" <td>Cust_785</td>\n",
" <td>2409.9600</td>\n",
" <td>0.07</td>\n",
" <td>32</td>\n",
" <td>575.10</td>\n",
" <td>4.50</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8350</th>\n",
" <td>Ord_3570</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_4942</td>\n",
" <td>Cust_1266</td>\n",
" <td>2094.9780</td>\n",
" <td>0.06</td>\n",
" <td>44</td>\n",
" <td>697.29</td>\n",
" <td>1.25</td>\n",
" <td>0.55</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8354</th>\n",
" <td>Ord_3592</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_4973</td>\n",
" <td>Cust_1266</td>\n",
" <td>2614.3705</td>\n",
" <td>0.07</td>\n",
" <td>25</td>\n",
" <td>384.01</td>\n",
" <td>7.69</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8381</th>\n",
" <td>Ord_2696</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_3691</td>\n",
" <td>Cust_1006</td>\n",
" <td>2836.0505</td>\n",
" <td>0.01</td>\n",
" <td>25</td>\n",
" <td>561.13</td>\n",
" <td>8.99</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8394</th>\n",
" <td>Ord_5353</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_7479</td>\n",
" <td>Cust_1798</td>\n",
" <td>2841.4395</td>\n",
" <td>0.08</td>\n",
" <td>28</td>\n",
" <td>374.63</td>\n",
" <td>7.69</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>328 rows × 10 columns</p>\n",
"</div>"
],
"text/plain": [
" Ord_id Prod_id Ship_id Cust_id Sales Discount \\\n",
"3 Ord_5456 Prod_6 SHP_7625 Cust_1818 2337.8900 0.09 \n",
"81 Ord_5205 Prod_4 SHP_7274 Cust_1749 2546.5235 0.09 \n",
"109 Ord_139 Prod_17 SHP_186 Cust_45 2671.2100 0.06 \n",
"110 Ord_239 Prod_4 SHP_332 Cust_45 2157.3085 0.00 \n",
"141 Ord_1673 Prod_17 SHP_2314 Cust_498 2027.5500 0.04 \n",
"146 Ord_1649 Prod_4 SHP_2278 Cust_498 2209.5155 0.06 \n",
"176 Ord_2273 Prod_8 SHP_3101 Cust_878 2899.9800 0.10 \n",
"184 Ord_5230 Prod_4 SHP_7304 Cust_1753 2197.4115 0.00 \n",
"186 Ord_5159 Prod_5 SHP_7210 Cust_1753 2213.9200 0.03 \n",
"230 Ord_657 Prod_4 SHP_899 Cust_209 2343.0760 0.06 \n",
"285 Ord_1607 Prod_4 SHP_2220 Cust_506 2980.3720 0.02 \n",
"314 Ord_1521 Prod_15 SHP_2100 Cust_560 2230.9700 0.06 \n",
"349 Ord_4896 Prod_4 SHP_6829 Cust_1674 2827.1425 0.01 \n",
"395 Ord_4144 Prod_2 SHP_5772 Cust_1418 2182.9100 0.10 \n",
"404 Ord_1621 Prod_3 SHP_2238 Cust_566 2010.8900 0.09 \n",
"510 Ord_3848 Prod_4 SHP_5335 Cust_1346 2660.6105 0.03 \n",
"522 Ord_142 Prod_8 SHP_191 Cust_51 2689.4800 0.04 \n",
"536 Ord_4909 Prod_2 SHP_6846 Cust_227 2180.2300 0.05 \n",
"541 Ord_4935 Prod_4 SHP_6886 Cust_1680 2292.1015 0.02 \n",
"647 Ord_4292 Prod_5 SHP_5988 Cust_1439 2758.2200 0.00 \n",
"680 Ord_674 Prod_4 SHP_922 Cust_212 2404.5990 0.08 \n",
"688 Ord_4904 Prod_1 SHP_6841 Cust_1682 2257.8800 0.01 \n",
"718 Ord_2069 Prod_4 SHP_2832 Cust_783 2135.9735 0.07 \n",
"720 Ord_2150 Prod_4 SHP_2932 Cust_805 2773.0315 0.04 \n",
"729 Ord_4826 Prod_3 SHP_6724 Cust_1588 2168.0500 0.00 \n",
"767 Ord_2054 Prod_2 SHP_2808 Cust_828 2192.6300 0.05 \n",
"775 Ord_5154 Prod_4 SHP_7204 Cust_1746 2610.8940 0.00 \n",
"783 Ord_2666 Prod_4 SHP_3652 Cust_1017 2368.1680 0.00 \n",
"809 Ord_4279 Prod_1 SHP_5971 Cust_1440 2752.6800 0.04 \n",
"810 Ord_4269 Prod_2 SHP_5958 Cust_1440 2405.0000 0.10 \n",
"... ... ... ... ... ... ... \n",
"7777 Ord_3414 Prod_2 SHP_4733 Cust_1196 2167.0500 0.02 \n",
"7778 Ord_3363 Prod_6 SHP_4663 Cust_1196 2040.3900 0.07 \n",
"7788 Ord_2482 Prod_4 SHP_3399 Cust_977 2252.2620 0.10 \n",
"7811 Ord_3215 Prod_4 SHP_4458 Cust_1188 2080.0350 0.10 \n",
"7823 Ord_4370 Prod_9 SHP_6092 Cust_1492 2325.4200 0.02 \n",
"7858 Ord_3232 Prod_3 SHP_4483 Cust_1200 2206.1700 0.02 \n",
"7875 Ord_1762 Prod_17 SHP_2443 Cust_577 2287.1000 0.07 \n",
"7877 Ord_1748 Prod_4 SHP_2421 Cust_577 2503.3265 0.04 \n",
"7884 Ord_710 Prod_4 SHP_973 Cust_244 2529.3960 0.06 \n",
"7911 Ord_5012 Prod_4 SHP_6993 Cust_1693 2882.7070 0.02 \n",
"7927 Ord_2502 Prod_4 SHP_3430 Cust_976 2104.9910 0.09 \n",
"7940 Ord_3277 Prod_4 SHP_4550 Cust_1224 2185.9535 0.10 \n",
"7973 Ord_1694 Prod_6 SHP_2346 Cust_582 2145.0500 0.07 \n",
"7986 Ord_4788 Prod_4 SHP_6674 Cust_1583 2478.4810 0.09 \n",
"8045 Ord_5443 Prod_8 SHP_7605 Cust_1803 2587.5300 0.02 \n",
"8048 Ord_796 Prod_5 SHP_1095 Cust_247 2780.8800 0.07 \n",
"8061 Ord_2020 Prod_2 SHP_3104 Cust_892 2550.1200 0.01 \n",
"8071 Ord_5350 Prod_4 SHP_7473 Cust_1795 2750.1070 0.00 \n",
"8147 Ord_3214 Prod_4 SHP_4457 Cust_1187 2143.2155 0.02 \n",
"8152 Ord_3337 Prod_2 SHP_4630 Cust_1187 2477.9900 0.00 \n",
"8239 Ord_793 Prod_9 SHP_1089 Cust_245 2833.1900 0.06 \n",
"8262 Ord_4954 Prod_4 SHP_6914 Cust_1694 2455.2760 0.04 \n",
"8271 Ord_4679 Prod_4 SHP_6528 Cust_1587 2823.0370 0.10 \n",
"8289 Ord_1749 Prod_4 SHP_2422 Cust_595 2731.7300 0.07 \n",
"8304 Ord_2709 Prod_11 SHP_3709 Cust_1025 2272.5600 0.06 \n",
"8338 Ord_2107 Prod_2 SHP_2882 Cust_785 2409.9600 0.07 \n",
"8350 Ord_3570 Prod_4 SHP_4942 Cust_1266 2094.9780 0.06 \n",
"8354 Ord_3592 Prod_4 SHP_4973 Cust_1266 2614.3705 0.07 \n",
"8381 Ord_2696 Prod_4 SHP_3691 Cust_1006 2836.0505 0.01 \n",
"8394 Ord_5353 Prod_4 SHP_7479 Cust_1798 2841.4395 0.08 \n",
"\n",
" Order_Quantity Profit Shipping_Cost Product_Base_Margin \n",
"3 43 729.34 14.30 0.37 \n",
"81 26 210.00 7.69 0.59 \n",
"109 14 636.18 15.59 0.36 \n",
"110 38 519.25 5.31 0.57 \n",
"141 14 537.40 13.99 0.37 \n",
"146 41 458.62 5.31 0.57 \n",
"176 19 666.01 5.50 0.49 \n",
"184 20 305.96 7.69 0.58 \n",
"186 20 768.34 13.99 0.65 \n",
"230 24 311.64 8.99 0.58 \n",
"285 19 494.63 8.99 0.57 \n",
"314 12 273.27 26.20 0.59 \n",
"349 35 713.88 4.90 0.56 \n",
"395 40 549.45 3.50 0.57 \n",
"404 34 564.07 11.55 0.38 \n",
"510 46 618.07 8.99 0.56 \n",
"522 27 399.93 19.99 0.50 \n",
"536 37 660.25 3.50 0.57 \n",
"541 21 398.36 3.00 0.59 \n",
"647 15 966.81 13.99 0.75 \n",
"680 45 496.89 4.99 0.58 \n",
"688 38 474.98 9.71 0.57 \n",
"718 40 239.40 8.99 0.59 \n",
"720 38 897.87 0.99 0.55 \n",
"729 5 416.02 19.99 0.35 \n",
"767 37 660.06 3.99 0.57 \n",
"775 23 516.19 5.63 0.60 \n",
"783 30 1181.30 1.25 0.39 \n",
"809 45 430.32 12.78 0.58 \n",
"810 39 696.17 0.99 0.58 \n",
"... ... ... ... ... \n",
"7777 36 684.90 3.50 0.57 \n",
"7778 50 221.09 19.99 0.36 \n",
"7788 42 478.11 5.63 0.56 \n",
"7811 31 844.90 1.25 0.39 \n",
"7823 25 739.91 19.99 0.40 \n",
"7858 4 251.43 19.99 0.37 \n",
"7875 23 231.49 19.99 0.52 \n",
"7877 45 447.12 8.80 0.58 \n",
"7884 25 371.21 3.00 0.59 \n",
"7911 16 303.23 5.00 0.59 \n",
"7927 20 165.45 8.80 0.59 \n",
"7940 21 268.01 8.99 0.55 \n",
"7973 45 1012.67 5.86 0.35 \n",
"7986 27 249.10 8.99 0.58 \n",
"8045 44 401.85 6.55 0.68 \n",
"8048 27 595.38 24.49 0.61 \n",
"8061 40 882.45 4.50 0.56 \n",
"8071 24 600.42 7.69 0.58 \n",
"8147 37 464.36 8.99 0.55 \n",
"8152 30 747.68 4.50 0.59 \n",
"8239 34 1409.87 5.01 0.38 \n",
"8262 42 693.06 5.63 0.56 \n",
"8271 29 372.40 4.20 0.59 \n",
"8289 21 310.59 8.99 0.58 \n",
"8304 15 111.05 16.01 0.70 \n",
"8338 32 575.10 4.50 0.59 \n",
"8350 44 697.29 1.25 0.55 \n",
"8354 25 384.01 7.69 0.58 \n",
"8381 25 561.13 8.99 0.59 \n",
"8394 28 374.63 7.69 0.59 \n",
"\n",
"[328 rows x 10 columns]"
]
},
"execution_count": 14,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# We combine multiple conditions using the & operator\n",
"# E.g. all orders having 2000 < Sales < 3000 and Profit > 100\n",
"df.loc[(df.Sales > 2000) & (df.Sales < 3000) & (df.Profit > 100), :]"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Ord_id</th>\n",
" <th>Prod_id</th>\n",
" <th>Ship_id</th>\n",
" <th>Cust_id</th>\n",
" <th>Sales</th>\n",
" <th>Discount</th>\n",
" <th>Order_Quantity</th>\n",
" <th>Profit</th>\n",
" <th>Shipping_Cost</th>\n",
" <th>Product_Base_Margin</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>Ord_5446</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_7610</td>\n",
" <td>Cust_1818</td>\n",
" <td>4701.6900</td>\n",
" <td>0.00</td>\n",
" <td>26</td>\n",
" <td>1148.90</td>\n",
" <td>2.50</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>Ord_5456</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_7625</td>\n",
" <td>Cust_1818</td>\n",
" <td>2337.8900</td>\n",
" <td>0.09</td>\n",
" <td>43</td>\n",
" <td>729.34</td>\n",
" <td>14.30</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>Ord_5485</td>\n",
" <td>Prod_17</td>\n",
" <td>SHP_7664</td>\n",
" <td>Cust_1818</td>\n",
" <td>4233.1500</td>\n",
" <td>0.08</td>\n",
" <td>35</td>\n",
" <td>1219.87</td>\n",
" <td>26.30</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>Ord_4725</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_6593</td>\n",
" <td>Cust_1641</td>\n",
" <td>3410.1575</td>\n",
" <td>0.10</td>\n",
" <td>48</td>\n",
" <td>1137.91</td>\n",
" <td>0.99</td>\n",
" <td>0.55</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>Ord_4743</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_6615</td>\n",
" <td>Cust_1641</td>\n",
" <td>4072.0100</td>\n",
" <td>0.01</td>\n",
" <td>43</td>\n",
" <td>1675.98</td>\n",
" <td>0.99</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13</th>\n",
" <td>Ord_2207</td>\n",
" <td>Prod_11</td>\n",
" <td>SHP_3093</td>\n",
" <td>Cust_839</td>\n",
" <td>3364.2480</td>\n",
" <td>0.10</td>\n",
" <td>15</td>\n",
" <td>-693.23</td>\n",
" <td>61.76</td>\n",
" <td>0.78</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16</th>\n",
" <td>Ord_2282</td>\n",
" <td>Prod_9</td>\n",
" <td>SHP_3122</td>\n",
" <td>Cust_839</td>\n",
" <td>443.4600</td>\n",
" <td>0.06</td>\n",
" <td>30</td>\n",
" <td>193.12</td>\n",
" <td>1.39</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17</th>\n",
" <td>Ord_4471</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_6228</td>\n",
" <td>Cust_1521</td>\n",
" <td>13255.9300</td>\n",
" <td>0.02</td>\n",
" <td>25</td>\n",
" <td>4089.27</td>\n",
" <td>26.00</td>\n",
" <td>0.60</td>\n",
" </tr>\n",
" <tr>\n",
" <th>22</th>\n",
" <td>Ord_996</td>\n",
" <td>Prod_5</td>\n",
" <td>SHP_1377</td>\n",
" <td>Cust_371</td>\n",
" <td>3202.2500</td>\n",
" <td>0.09</td>\n",
" <td>44</td>\n",
" <td>991.26</td>\n",
" <td>19.99</td>\n",
" <td>0.43</td>\n",
" </tr>\n",
" <tr>\n",
" <th>27</th>\n",
" <td>Ord_2405</td>\n",
" <td>Prod_9</td>\n",
" <td>SHP_3300</td>\n",
" <td>Cust_931</td>\n",
" <td>1062.6900</td>\n",
" <td>0.01</td>\n",
" <td>28</td>\n",
" <td>401.80</td>\n",
" <td>6.66</td>\n",
" <td>0.40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>28</th>\n",
" <td>Ord_2573</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_3527</td>\n",
" <td>Cust_931</td>\n",
" <td>3594.7435</td>\n",
" <td>0.05</td>\n",
" <td>38</td>\n",
" <td>1016.97</td>\n",
" <td>2.50</td>\n",
" <td>0.55</td>\n",
" </tr>\n",
" <tr>\n",
" <th>37</th>\n",
" <td>Ord_5040</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_7032</td>\n",
" <td>Cust_1710</td>\n",
" <td>1637.7800</td>\n",
" <td>0.08</td>\n",
" <td>38</td>\n",
" <td>461.65</td>\n",
" <td>4.62</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>38</th>\n",
" <td>Ord_5035</td>\n",
" <td>Prod_12</td>\n",
" <td>SHP_7025</td>\n",
" <td>Cust_1710</td>\n",
" <td>416.8000</td>\n",
" <td>0.01</td>\n",
" <td>32</td>\n",
" <td>223.38</td>\n",
" <td>0.50</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>39</th>\n",
" <td>Ord_5045</td>\n",
" <td>Prod_5</td>\n",
" <td>SHP_7040</td>\n",
" <td>Cust_1710</td>\n",
" <td>1286.8700</td>\n",
" <td>0.05</td>\n",
" <td>48</td>\n",
" <td>384.38</td>\n",
" <td>6.93</td>\n",
" <td>0.49</td>\n",
" </tr>\n",
" <tr>\n",
" <th>40</th>\n",
" <td>Ord_5035</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_7024</td>\n",
" <td>Cust_1710</td>\n",
" <td>4917.6900</td>\n",
" <td>0.02</td>\n",
" <td>42</td>\n",
" <td>126.31</td>\n",
" <td>30.00</td>\n",
" <td>0.71</td>\n",
" </tr>\n",
" <tr>\n",
" <th>47</th>\n",
" <td>Ord_4659</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_6493</td>\n",
" <td>Cust_1579</td>\n",
" <td>1451.5900</td>\n",
" <td>0.06</td>\n",
" <td>26</td>\n",
" <td>435.11</td>\n",
" <td>14.30</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>54</th>\n",
" <td>Ord_4682</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_6531</td>\n",
" <td>Cust_1579</td>\n",
" <td>1909.0065</td>\n",
" <td>0.01</td>\n",
" <td>32</td>\n",
" <td>344.13</td>\n",
" <td>8.99</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>56</th>\n",
" <td>Ord_4410</td>\n",
" <td>Prod_5</td>\n",
" <td>SHP_6146</td>\n",
" <td>Cust_1474</td>\n",
" <td>605.7700</td>\n",
" <td>0.05</td>\n",
" <td>42</td>\n",
" <td>129.33</td>\n",
" <td>5.00</td>\n",
" <td>0.49</td>\n",
" </tr>\n",
" <tr>\n",
" <th>57</th>\n",
" <td>Ord_4546</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_6327</td>\n",
" <td>Cust_1474</td>\n",
" <td>5208.7800</td>\n",
" <td>0.05</td>\n",
" <td>34</td>\n",
" <td>1547.78</td>\n",
" <td>7.07</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>62</th>\n",
" <td>Ord_4410</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_6146</td>\n",
" <td>Cust_1474</td>\n",
" <td>1480.9100</td>\n",
" <td>0.00</td>\n",
" <td>44</td>\n",
" <td>489.14</td>\n",
" <td>8.74</td>\n",
" <td>0.40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>64</th>\n",
" <td>Ord_4475</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_6234</td>\n",
" <td>Cust_1474</td>\n",
" <td>7640.2250</td>\n",
" <td>0.07</td>\n",
" <td>46</td>\n",
" <td>2027.68</td>\n",
" <td>2.50</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>70</th>\n",
" <td>Ord_4607</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_6408</td>\n",
" <td>Cust_1474</td>\n",
" <td>1463.4200</td>\n",
" <td>0.08</td>\n",
" <td>26</td>\n",
" <td>350.82</td>\n",
" <td>3.99</td>\n",
" <td>0.57</td>\n",
" </tr>\n",
" <tr>\n",
" <th>77</th>\n",
" <td>Ord_5213</td>\n",
" <td>Prod_13</td>\n",
" <td>SHP_7284</td>\n",
" <td>Cust_1749</td>\n",
" <td>1633.3700</td>\n",
" <td>0.08</td>\n",
" <td>50</td>\n",
" <td>144.69</td>\n",
" <td>7.73</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>79</th>\n",
" <td>Ord_5188</td>\n",
" <td>Prod_14</td>\n",
" <td>SHP_7252</td>\n",
" <td>Cust_1749</td>\n",
" <td>5177.4000</td>\n",
" <td>0.06</td>\n",
" <td>12</td>\n",
" <td>287.50</td>\n",
" <td>49.00</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>81</th>\n",
" <td>Ord_5205</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_7274</td>\n",
" <td>Cust_1749</td>\n",
" <td>2546.5235</td>\n",
" <td>0.09</td>\n",
" <td>26</td>\n",
" <td>210.00</td>\n",
" <td>7.69</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>82</th>\n",
" <td>Ord_5156</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_7207</td>\n",
" <td>Cust_1749</td>\n",
" <td>8374.1320</td>\n",
" <td>0.06</td>\n",
" <td>48</td>\n",
" <td>2568.10</td>\n",
" <td>8.99</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>84</th>\n",
" <td>Ord_5232</td>\n",
" <td>Prod_17</td>\n",
" <td>SHP_7306</td>\n",
" <td>Cust_1758</td>\n",
" <td>21366.5100</td>\n",
" <td>0.00</td>\n",
" <td>3</td>\n",
" <td>-11984.40</td>\n",
" <td>24.49</td>\n",
" <td>0.39</td>\n",
" </tr>\n",
" <tr>\n",
" <th>88</th>\n",
" <td>Ord_5172</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_7229</td>\n",
" <td>Cust_1758</td>\n",
" <td>1239.4445</td>\n",
" <td>0.07</td>\n",
" <td>22</td>\n",
" <td>165.50</td>\n",
" <td>3.99</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>98</th>\n",
" <td>Ord_5481</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_7659</td>\n",
" <td>Cust_1820</td>\n",
" <td>2700.7800</td>\n",
" <td>0.06</td>\n",
" <td>29</td>\n",
" <td>-793.36</td>\n",
" <td>58.20</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>102</th>\n",
" <td>Ord_1557</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_2152</td>\n",
" <td>Cust_565</td>\n",
" <td>1736.5300</td>\n",
" <td>0.10</td>\n",
" <td>46</td>\n",
" <td>457.03</td>\n",
" <td>3.99</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>...</th>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8328</th>\n",
" <td>Ord_2169</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_2956</td>\n",
" <td>Cust_810</td>\n",
" <td>1321.5500</td>\n",
" <td>0.10</td>\n",
" <td>25</td>\n",
" <td>448.24</td>\n",
" <td>10.75</td>\n",
" <td>0.36</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8329</th>\n",
" <td>Ord_2160</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_2944</td>\n",
" <td>Cust_810</td>\n",
" <td>3636.3700</td>\n",
" <td>0.06</td>\n",
" <td>33</td>\n",
" <td>-176.91</td>\n",
" <td>30.00</td>\n",
" <td>0.69</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8331</th>\n",
" <td>Ord_2148</td>\n",
" <td>Prod_10</td>\n",
" <td>SHP_2929</td>\n",
" <td>Cust_810</td>\n",
" <td>2966.1300</td>\n",
" <td>0.08</td>\n",
" <td>31</td>\n",
" <td>-1456.31</td>\n",
" <td>57.38</td>\n",
" <td>0.78</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8332</th>\n",
" <td>Ord_2101</td>\n",
" <td>Prod_11</td>\n",
" <td>SHP_2875</td>\n",
" <td>Cust_790</td>\n",
" <td>10714.7800</td>\n",
" <td>0.00</td>\n",
" <td>41</td>\n",
" <td>-627.64</td>\n",
" <td>66.67</td>\n",
" <td>0.65</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8334</th>\n",
" <td>Ord_2124</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_2900</td>\n",
" <td>Cust_790</td>\n",
" <td>926.8500</td>\n",
" <td>0.09</td>\n",
" <td>34</td>\n",
" <td>382.94</td>\n",
" <td>1.49</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8335</th>\n",
" <td>Ord_2070</td>\n",
" <td>Prod_11</td>\n",
" <td>SHP_2833</td>\n",
" <td>Cust_784</td>\n",
" <td>3905.7500</td>\n",
" <td>0.01</td>\n",
" <td>21</td>\n",
" <td>55.30</td>\n",
" <td>29.21</td>\n",
" <td>0.76</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8338</th>\n",
" <td>Ord_2107</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_2882</td>\n",
" <td>Cust_785</td>\n",
" <td>2409.9600</td>\n",
" <td>0.07</td>\n",
" <td>32</td>\n",
" <td>575.10</td>\n",
" <td>4.50</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8342</th>\n",
" <td>Ord_2119</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_2895</td>\n",
" <td>Cust_785</td>\n",
" <td>1623.0900</td>\n",
" <td>0.02</td>\n",
" <td>28</td>\n",
" <td>245.88</td>\n",
" <td>13.22</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8343</th>\n",
" <td>Ord_2178</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_2968</td>\n",
" <td>Cust_785</td>\n",
" <td>6030.5800</td>\n",
" <td>0.09</td>\n",
" <td>39</td>\n",
" <td>1197.86</td>\n",
" <td>8.99</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8344</th>\n",
" <td>Ord_2194</td>\n",
" <td>Prod_5</td>\n",
" <td>SHP_2991</td>\n",
" <td>Cust_785</td>\n",
" <td>525.7800</td>\n",
" <td>0.03</td>\n",
" <td>20</td>\n",
" <td>180.64</td>\n",
" <td>6.93</td>\n",
" <td>0.49</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8347</th>\n",
" <td>Ord_3534</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_4894</td>\n",
" <td>Cust_1266</td>\n",
" <td>1735.3515</td>\n",
" <td>0.08</td>\n",
" <td>31</td>\n",
" <td>258.62</td>\n",
" <td>8.99</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8350</th>\n",
" <td>Ord_3570</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_4942</td>\n",
" <td>Cust_1266</td>\n",
" <td>2094.9780</td>\n",
" <td>0.06</td>\n",
" <td>44</td>\n",
" <td>697.29</td>\n",
" <td>1.25</td>\n",
" <td>0.55</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8351</th>\n",
" <td>Ord_3584</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_4961</td>\n",
" <td>Cust_1266</td>\n",
" <td>2502.6700</td>\n",
" <td>0.10</td>\n",
" <td>9</td>\n",
" <td>-198.80</td>\n",
" <td>64.73</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8354</th>\n",
" <td>Ord_3592</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_4973</td>\n",
" <td>Cust_1266</td>\n",
" <td>2614.3705</td>\n",
" <td>0.07</td>\n",
" <td>25</td>\n",
" <td>384.01</td>\n",
" <td>7.69</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8358</th>\n",
" <td>Ord_3582</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_4959</td>\n",
" <td>Cust_1266</td>\n",
" <td>539.6600</td>\n",
" <td>0.00</td>\n",
" <td>26</td>\n",
" <td>147.08</td>\n",
" <td>5.97</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8359</th>\n",
" <td>Ord_3543</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_4906</td>\n",
" <td>Cust_1266</td>\n",
" <td>514.2200</td>\n",
" <td>0.02</td>\n",
" <td>17</td>\n",
" <td>187.37</td>\n",
" <td>2.99</td>\n",
" <td>0.35</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8360</th>\n",
" <td>Ord_3639</td>\n",
" <td>Prod_10</td>\n",
" <td>SHP_5038</td>\n",
" <td>Cust_1266</td>\n",
" <td>2173.2600</td>\n",
" <td>0.00</td>\n",
" <td>35</td>\n",
" <td>-465.66</td>\n",
" <td>36.61</td>\n",
" <td>0.61</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8362</th>\n",
" <td>Ord_3593</td>\n",
" <td>Prod_5</td>\n",
" <td>SHP_4975</td>\n",
" <td>Cust_1274</td>\n",
" <td>1175.5300</td>\n",
" <td>0.03</td>\n",
" <td>18</td>\n",
" <td>257.59</td>\n",
" <td>14.48</td>\n",
" <td>0.46</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8366</th>\n",
" <td>Ord_3593</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_4974</td>\n",
" <td>Cust_1274</td>\n",
" <td>12073.0600</td>\n",
" <td>0.03</td>\n",
" <td>39</td>\n",
" <td>5081.87</td>\n",
" <td>19.99</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8367</th>\n",
" <td>Ord_3593</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_4975</td>\n",
" <td>Cust_1274</td>\n",
" <td>6685.0500</td>\n",
" <td>0.09</td>\n",
" <td>25</td>\n",
" <td>1653.60</td>\n",
" <td>24.49</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8369</th>\n",
" <td>Ord_3633</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_5031</td>\n",
" <td>Cust_1274</td>\n",
" <td>1169.2600</td>\n",
" <td>0.02</td>\n",
" <td>41</td>\n",
" <td>515.62</td>\n",
" <td>1.49</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8371</th>\n",
" <td>Ord_2624</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_3591</td>\n",
" <td>Cust_1006</td>\n",
" <td>4924.1350</td>\n",
" <td>0.07</td>\n",
" <td>28</td>\n",
" <td>1049.54</td>\n",
" <td>8.99</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8375</th>\n",
" <td>Ord_2772</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_3806</td>\n",
" <td>Cust_1006</td>\n",
" <td>1413.8200</td>\n",
" <td>0.10</td>\n",
" <td>47</td>\n",
" <td>226.53</td>\n",
" <td>11.63</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8378</th>\n",
" <td>Ord_2706</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_3705</td>\n",
" <td>Cust_1006</td>\n",
" <td>1361.9100</td>\n",
" <td>0.05</td>\n",
" <td>20</td>\n",
" <td>312.52</td>\n",
" <td>3.50</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8381</th>\n",
" <td>Ord_2696</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_3691</td>\n",
" <td>Cust_1006</td>\n",
" <td>2836.0505</td>\n",
" <td>0.01</td>\n",
" <td>25</td>\n",
" <td>561.13</td>\n",
" <td>8.99</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8383</th>\n",
" <td>Ord_2722</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_3731</td>\n",
" <td>Cust_1006</td>\n",
" <td>3508.3300</td>\n",
" <td>0.04</td>\n",
" <td>21</td>\n",
" <td>-546.98</td>\n",
" <td>35.00</td>\n",
" <td>0.85</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8385</th>\n",
" <td>Ord_1833</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_2527</td>\n",
" <td>Cust_637</td>\n",
" <td>611.1600</td>\n",
" <td>0.04</td>\n",
" <td>46</td>\n",
" <td>100.22</td>\n",
" <td>4.98</td>\n",
" <td>0.40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8394</th>\n",
" <td>Ord_5353</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_7479</td>\n",
" <td>Cust_1798</td>\n",
" <td>2841.4395</td>\n",
" <td>0.08</td>\n",
" <td>28</td>\n",
" <td>374.63</td>\n",
" <td>7.69</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8397</th>\n",
" <td>Ord_5348</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_7469</td>\n",
" <td>Cust_1798</td>\n",
" <td>3872.8700</td>\n",
" <td>0.03</td>\n",
" <td>23</td>\n",
" <td>565.34</td>\n",
" <td>30.00</td>\n",
" <td>0.62</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8398</th>\n",
" <td>Ord_5459</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_7628</td>\n",
" <td>Cust_1798</td>\n",
" <td>603.6900</td>\n",
" <td>0.00</td>\n",
" <td>47</td>\n",
" <td>131.39</td>\n",
" <td>4.86</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>3009 rows × 10 columns</p>\n",
"</div>"
],
"text/plain": [
" Ord_id Prod_id Ship_id Cust_id Sales Discount \\\n",
"2 Ord_5446 Prod_4 SHP_7610 Cust_1818 4701.6900 0.00 \n",
"3 Ord_5456 Prod_6 SHP_7625 Cust_1818 2337.8900 0.09 \n",
"4 Ord_5485 Prod_17 SHP_7664 Cust_1818 4233.1500 0.08 \n",
"7 Ord_4725 Prod_4 SHP_6593 Cust_1641 3410.1575 0.10 \n",
"10 Ord_4743 Prod_2 SHP_6615 Cust_1641 4072.0100 0.01 \n",
"13 Ord_2207 Prod_11 SHP_3093 Cust_839 3364.2480 0.10 \n",
"16 Ord_2282 Prod_9 SHP_3122 Cust_839 443.4600 0.06 \n",
"17 Ord_4471 Prod_15 SHP_6228 Cust_1521 13255.9300 0.02 \n",
"22 Ord_996 Prod_5 SHP_1377 Cust_371 3202.2500 0.09 \n",
"27 Ord_2405 Prod_9 SHP_3300 Cust_931 1062.6900 0.01 \n",
"28 Ord_2573 Prod_4 SHP_3527 Cust_931 3594.7435 0.05 \n",
"37 Ord_5040 Prod_2 SHP_7032 Cust_1710 1637.7800 0.08 \n",
"38 Ord_5035 Prod_12 SHP_7025 Cust_1710 416.8000 0.01 \n",
"39 Ord_5045 Prod_5 SHP_7040 Cust_1710 1286.8700 0.05 \n",
"40 Ord_5035 Prod_15 SHP_7024 Cust_1710 4917.6900 0.02 \n",
"47 Ord_4659 Prod_6 SHP_6493 Cust_1579 1451.5900 0.06 \n",
"54 Ord_4682 Prod_4 SHP_6531 Cust_1579 1909.0065 0.01 \n",
"56 Ord_4410 Prod_5 SHP_6146 Cust_1474 605.7700 0.05 \n",
"57 Ord_4546 Prod_1 SHP_6327 Cust_1474 5208.7800 0.05 \n",
"62 Ord_4410 Prod_6 SHP_6146 Cust_1474 1480.9100 0.00 \n",
"64 Ord_4475 Prod_4 SHP_6234 Cust_1474 7640.2250 0.07 \n",
"70 Ord_4607 Prod_2 SHP_6408 Cust_1474 1463.4200 0.08 \n",
"77 Ord_5213 Prod_13 SHP_7284 Cust_1749 1633.3700 0.08 \n",
"79 Ord_5188 Prod_14 SHP_7252 Cust_1749 5177.4000 0.06 \n",
"81 Ord_5205 Prod_4 SHP_7274 Cust_1749 2546.5235 0.09 \n",
"82 Ord_5156 Prod_4 SHP_7207 Cust_1749 8374.1320 0.06 \n",
"84 Ord_5232 Prod_17 SHP_7306 Cust_1758 21366.5100 0.00 \n",
"88 Ord_5172 Prod_4 SHP_7229 Cust_1758 1239.4445 0.07 \n",
"98 Ord_5481 Prod_15 SHP_7659 Cust_1820 2700.7800 0.06 \n",
"102 Ord_1557 Prod_2 SHP_2152 Cust_565 1736.5300 0.10 \n",
"... ... ... ... ... ... ... \n",
"8328 Ord_2169 Prod_6 SHP_2956 Cust_810 1321.5500 0.10 \n",
"8329 Ord_2160 Prod_15 SHP_2944 Cust_810 3636.3700 0.06 \n",
"8331 Ord_2148 Prod_10 SHP_2929 Cust_810 2966.1300 0.08 \n",
"8332 Ord_2101 Prod_11 SHP_2875 Cust_790 10714.7800 0.00 \n",
"8334 Ord_2124 Prod_3 SHP_2900 Cust_790 926.8500 0.09 \n",
"8335 Ord_2070 Prod_11 SHP_2833 Cust_784 3905.7500 0.01 \n",
"8338 Ord_2107 Prod_2 SHP_2882 Cust_785 2409.9600 0.07 \n",
"8342 Ord_2119 Prod_2 SHP_2895 Cust_785 1623.0900 0.02 \n",
"8343 Ord_2178 Prod_4 SHP_2968 Cust_785 6030.5800 0.09 \n",
"8344 Ord_2194 Prod_5 SHP_2991 Cust_785 525.7800 0.03 \n",
"8347 Ord_3534 Prod_4 SHP_4894 Cust_1266 1735.3515 0.08 \n",
"8350 Ord_3570 Prod_4 SHP_4942 Cust_1266 2094.9780 0.06 \n",
"8351 Ord_3584 Prod_15 SHP_4961 Cust_1266 2502.6700 0.10 \n",
"8354 Ord_3592 Prod_4 SHP_4973 Cust_1266 2614.3705 0.07 \n",
"8358 Ord_3582 Prod_6 SHP_4959 Cust_1266 539.6600 0.00 \n",
"8359 Ord_3543 Prod_3 SHP_4906 Cust_1266 514.2200 0.02 \n",
"8360 Ord_3639 Prod_10 SHP_5038 Cust_1266 2173.2600 0.00 \n",
"8362 Ord_3593 Prod_5 SHP_4975 Cust_1274 1175.5300 0.03 \n",
"8366 Ord_3593 Prod_3 SHP_4974 Cust_1274 12073.0600 0.03 \n",
"8367 Ord_3593 Prod_15 SHP_4975 Cust_1274 6685.0500 0.09 \n",
"8369 Ord_3633 Prod_3 SHP_5031 Cust_1274 1169.2600 0.02 \n",
"8371 Ord_2624 Prod_4 SHP_3591 Cust_1006 4924.1350 0.07 \n",
"8375 Ord_2772 Prod_3 SHP_3806 Cust_1006 1413.8200 0.10 \n",
"8378 Ord_2706 Prod_2 SHP_3705 Cust_1006 1361.9100 0.05 \n",
"8381 Ord_2696 Prod_4 SHP_3691 Cust_1006 2836.0505 0.01 \n",
"8383 Ord_2722 Prod_1 SHP_3731 Cust_1006 3508.3300 0.04 \n",
"8385 Ord_1833 Prod_3 SHP_2527 Cust_637 611.1600 0.04 \n",
"8394 Ord_5353 Prod_4 SHP_7479 Cust_1798 2841.4395 0.08 \n",
"8397 Ord_5348 Prod_15 SHP_7469 Cust_1798 3872.8700 0.03 \n",
"8398 Ord_5459 Prod_6 SHP_7628 Cust_1798 603.6900 0.00 \n",
"\n",
" Order_Quantity Profit Shipping_Cost Product_Base_Margin \n",
"2 26 1148.90 2.50 0.59 \n",
"3 43 729.34 14.30 0.37 \n",
"4 35 1219.87 26.30 0.38 \n",
"7 48 1137.91 0.99 0.55 \n",
"10 43 1675.98 0.99 0.56 \n",
"13 15 -693.23 61.76 0.78 \n",
"16 30 193.12 1.39 0.38 \n",
"17 25 4089.27 26.00 0.60 \n",
"22 44 991.26 19.99 0.43 \n",
"27 28 401.80 6.66 0.40 \n",
"28 38 1016.97 2.50 0.55 \n",
"37 38 461.65 4.62 0.56 \n",
"38 32 223.38 0.50 0.38 \n",
"39 48 384.38 6.93 0.49 \n",
"40 42 126.31 30.00 0.71 \n",
"47 26 435.11 14.30 0.37 \n",
"54 32 344.13 8.99 0.59 \n",
"56 42 129.33 5.00 0.49 \n",
"57 34 1547.78 7.07 0.59 \n",
"62 44 489.14 8.74 0.40 \n",
"64 46 2027.68 2.50 0.59 \n",
"70 26 350.82 3.99 0.57 \n",
"77 50 144.69 7.73 0.59 \n",
"79 12 287.50 49.00 0.38 \n",
"81 26 210.00 7.69 0.59 \n",
"82 48 2568.10 8.99 0.56 \n",
"84 3 -11984.40 24.49 0.39 \n",
"88 22 165.50 3.99 0.59 \n",
"98 29 -793.36 58.20 0.58 \n",
"102 46 457.03 3.99 0.56 \n",
"... ... ... ... ... \n",
"8328 25 448.24 10.75 0.36 \n",
"8329 33 -176.91 30.00 0.69 \n",
"8331 31 -1456.31 57.38 0.78 \n",
"8332 41 -627.64 66.67 0.65 \n",
"8334 34 382.94 1.49 0.38 \n",
"8335 21 55.30 29.21 0.76 \n",
"8338 32 575.10 4.50 0.59 \n",
"8342 28 245.88 13.22 0.56 \n",
"8343 39 1197.86 8.99 0.58 \n",
"8344 20 180.64 6.93 0.49 \n",
"8347 31 258.62 8.99 0.56 \n",
"8350 44 697.29 1.25 0.55 \n",
"8351 9 -198.80 64.73 0.56 \n",
"8354 25 384.01 7.69 0.58 \n",
"8358 26 147.08 5.97 0.38 \n",
"8359 17 187.37 2.99 0.35 \n",
"8360 35 -465.66 36.61 0.61 \n",
"8362 18 257.59 14.48 0.46 \n",
"8366 39 5081.87 19.99 0.38 \n",
"8367 25 1653.60 24.49 NaN \n",
"8369 41 515.62 1.49 0.38 \n",
"8371 28 1049.54 8.99 0.58 \n",
"8375 47 226.53 11.63 0.37 \n",
"8378 20 312.52 3.50 0.59 \n",
"8381 25 561.13 8.99 0.59 \n",
"8383 21 -546.98 35.00 0.85 \n",
"8385 46 100.22 4.98 0.40 \n",
"8394 28 374.63 7.69 0.59 \n",
"8397 23 565.34 30.00 0.62 \n",
"8398 47 131.39 4.86 0.38 \n",
"\n",
"[3009 rows x 10 columns]"
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# The 'OR' operator is represented by a | (Note that 'or' doesn't work with pandas)\n",
"# E.g. all orders having 2000 < Sales OR Profit > 100\n",
"df.loc[(df.Sales > 2000) | (df.Profit > 100), :]"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Cust_id</th>\n",
" <th>Sales</th>\n",
" <th>Profit</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>Cust_1818</td>\n",
" <td>2337.8900</td>\n",
" <td>729.34</td>\n",
" </tr>\n",
" <tr>\n",
" <th>81</th>\n",
" <td>Cust_1749</td>\n",
" <td>2546.5235</td>\n",
" <td>210.00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>109</th>\n",
" <td>Cust_45</td>\n",
" <td>2671.2100</td>\n",
" <td>636.18</td>\n",
" </tr>\n",
" <tr>\n",
" <th>110</th>\n",
" <td>Cust_45</td>\n",
" <td>2157.3085</td>\n",
" <td>519.25</td>\n",
" </tr>\n",
" <tr>\n",
" <th>141</th>\n",
" <td>Cust_498</td>\n",
" <td>2027.5500</td>\n",
" <td>537.40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>146</th>\n",
" <td>Cust_498</td>\n",
" <td>2209.5155</td>\n",
" <td>458.62</td>\n",
" </tr>\n",
" <tr>\n",
" <th>176</th>\n",
" <td>Cust_878</td>\n",
" <td>2899.9800</td>\n",
" <td>666.01</td>\n",
" </tr>\n",
" <tr>\n",
" <th>184</th>\n",
" <td>Cust_1753</td>\n",
" <td>2197.4115</td>\n",
" <td>305.96</td>\n",
" </tr>\n",
" <tr>\n",
" <th>186</th>\n",
" <td>Cust_1753</td>\n",
" <td>2213.9200</td>\n",
" <td>768.34</td>\n",
" </tr>\n",
" <tr>\n",
" <th>230</th>\n",
" <td>Cust_209</td>\n",
" <td>2343.0760</td>\n",
" <td>311.64</td>\n",
" </tr>\n",
" <tr>\n",
" <th>285</th>\n",
" <td>Cust_506</td>\n",
" <td>2980.3720</td>\n",
" <td>494.63</td>\n",
" </tr>\n",
" <tr>\n",
" <th>314</th>\n",
" <td>Cust_560</td>\n",
" <td>2230.9700</td>\n",
" <td>273.27</td>\n",
" </tr>\n",
" <tr>\n",
" <th>349</th>\n",
" <td>Cust_1674</td>\n",
" <td>2827.1425</td>\n",
" <td>713.88</td>\n",
" </tr>\n",
" <tr>\n",
" <th>395</th>\n",
" <td>Cust_1418</td>\n",
" <td>2182.9100</td>\n",
" <td>549.45</td>\n",
" </tr>\n",
" <tr>\n",
" <th>404</th>\n",
" <td>Cust_566</td>\n",
" <td>2010.8900</td>\n",
" <td>564.07</td>\n",
" </tr>\n",
" <tr>\n",
" <th>510</th>\n",
" <td>Cust_1346</td>\n",
" <td>2660.6105</td>\n",
" <td>618.07</td>\n",
" </tr>\n",
" <tr>\n",
" <th>522</th>\n",
" <td>Cust_51</td>\n",
" <td>2689.4800</td>\n",
" <td>399.93</td>\n",
" </tr>\n",
" <tr>\n",
" <th>536</th>\n",
" <td>Cust_227</td>\n",
" <td>2180.2300</td>\n",
" <td>660.25</td>\n",
" </tr>\n",
" <tr>\n",
" <th>541</th>\n",
" <td>Cust_1680</td>\n",
" <td>2292.1015</td>\n",
" <td>398.36</td>\n",
" </tr>\n",
" <tr>\n",
" <th>647</th>\n",
" <td>Cust_1439</td>\n",
" <td>2758.2200</td>\n",
" <td>966.81</td>\n",
" </tr>\n",
" <tr>\n",
" <th>680</th>\n",
" <td>Cust_212</td>\n",
" <td>2404.5990</td>\n",
" <td>496.89</td>\n",
" </tr>\n",
" <tr>\n",
" <th>688</th>\n",
" <td>Cust_1682</td>\n",
" <td>2257.8800</td>\n",
" <td>474.98</td>\n",
" </tr>\n",
" <tr>\n",
" <th>718</th>\n",
" <td>Cust_783</td>\n",
" <td>2135.9735</td>\n",
" <td>239.40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>720</th>\n",
" <td>Cust_805</td>\n",
" <td>2773.0315</td>\n",
" <td>897.87</td>\n",
" </tr>\n",
" <tr>\n",
" <th>729</th>\n",
" <td>Cust_1588</td>\n",
" <td>2168.0500</td>\n",
" <td>416.02</td>\n",
" </tr>\n",
" <tr>\n",
" <th>767</th>\n",
" <td>Cust_828</td>\n",
" <td>2192.6300</td>\n",
" <td>660.06</td>\n",
" </tr>\n",
" <tr>\n",
" <th>775</th>\n",
" <td>Cust_1746</td>\n",
" <td>2610.8940</td>\n",
" <td>516.19</td>\n",
" </tr>\n",
" <tr>\n",
" <th>783</th>\n",
" <td>Cust_1017</td>\n",
" <td>2368.1680</td>\n",
" <td>1181.30</td>\n",
" </tr>\n",
" <tr>\n",
" <th>809</th>\n",
" <td>Cust_1440</td>\n",
" <td>2752.6800</td>\n",
" <td>430.32</td>\n",
" </tr>\n",
" <tr>\n",
" <th>810</th>\n",
" <td>Cust_1440</td>\n",
" <td>2405.0000</td>\n",
" <td>696.17</td>\n",
" </tr>\n",
" <tr>\n",
" <th>...</th>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7777</th>\n",
" <td>Cust_1196</td>\n",
" <td>2167.0500</td>\n",
" <td>684.90</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7778</th>\n",
" <td>Cust_1196</td>\n",
" <td>2040.3900</td>\n",
" <td>221.09</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7788</th>\n",
" <td>Cust_977</td>\n",
" <td>2252.2620</td>\n",
" <td>478.11</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7811</th>\n",
" <td>Cust_1188</td>\n",
" <td>2080.0350</td>\n",
" <td>844.90</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7823</th>\n",
" <td>Cust_1492</td>\n",
" <td>2325.4200</td>\n",
" <td>739.91</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7858</th>\n",
" <td>Cust_1200</td>\n",
" <td>2206.1700</td>\n",
" <td>251.43</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7875</th>\n",
" <td>Cust_577</td>\n",
" <td>2287.1000</td>\n",
" <td>231.49</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7877</th>\n",
" <td>Cust_577</td>\n",
" <td>2503.3265</td>\n",
" <td>447.12</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7884</th>\n",
" <td>Cust_244</td>\n",
" <td>2529.3960</td>\n",
" <td>371.21</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7911</th>\n",
" <td>Cust_1693</td>\n",
" <td>2882.7070</td>\n",
" <td>303.23</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7927</th>\n",
" <td>Cust_976</td>\n",
" <td>2104.9910</td>\n",
" <td>165.45</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7940</th>\n",
" <td>Cust_1224</td>\n",
" <td>2185.9535</td>\n",
" <td>268.01</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7973</th>\n",
" <td>Cust_582</td>\n",
" <td>2145.0500</td>\n",
" <td>1012.67</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7986</th>\n",
" <td>Cust_1583</td>\n",
" <td>2478.4810</td>\n",
" <td>249.10</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8045</th>\n",
" <td>Cust_1803</td>\n",
" <td>2587.5300</td>\n",
" <td>401.85</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8048</th>\n",
" <td>Cust_247</td>\n",
" <td>2780.8800</td>\n",
" <td>595.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8061</th>\n",
" <td>Cust_892</td>\n",
" <td>2550.1200</td>\n",
" <td>882.45</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8071</th>\n",
" <td>Cust_1795</td>\n",
" <td>2750.1070</td>\n",
" <td>600.42</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8147</th>\n",
" <td>Cust_1187</td>\n",
" <td>2143.2155</td>\n",
" <td>464.36</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8152</th>\n",
" <td>Cust_1187</td>\n",
" <td>2477.9900</td>\n",
" <td>747.68</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8239</th>\n",
" <td>Cust_245</td>\n",
" <td>2833.1900</td>\n",
" <td>1409.87</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8262</th>\n",
" <td>Cust_1694</td>\n",
" <td>2455.2760</td>\n",
" <td>693.06</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8271</th>\n",
" <td>Cust_1587</td>\n",
" <td>2823.0370</td>\n",
" <td>372.40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8289</th>\n",
" <td>Cust_595</td>\n",
" <td>2731.7300</td>\n",
" <td>310.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8304</th>\n",
" <td>Cust_1025</td>\n",
" <td>2272.5600</td>\n",
" <td>111.05</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8338</th>\n",
" <td>Cust_785</td>\n",
" <td>2409.9600</td>\n",
" <td>575.10</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8350</th>\n",
" <td>Cust_1266</td>\n",
" <td>2094.9780</td>\n",
" <td>697.29</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8354</th>\n",
" <td>Cust_1266</td>\n",
" <td>2614.3705</td>\n",
" <td>384.01</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8381</th>\n",
" <td>Cust_1006</td>\n",
" <td>2836.0505</td>\n",
" <td>561.13</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8394</th>\n",
" <td>Cust_1798</td>\n",
" <td>2841.4395</td>\n",
" <td>374.63</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>328 rows × 3 columns</p>\n",
"</div>"
],
"text/plain": [
" Cust_id Sales Profit\n",
"3 Cust_1818 2337.8900 729.34\n",
"81 Cust_1749 2546.5235 210.00\n",
"109 Cust_45 2671.2100 636.18\n",
"110 Cust_45 2157.3085 519.25\n",
"141 Cust_498 2027.5500 537.40\n",
"146 Cust_498 2209.5155 458.62\n",
"176 Cust_878 2899.9800 666.01\n",
"184 Cust_1753 2197.4115 305.96\n",
"186 Cust_1753 2213.9200 768.34\n",
"230 Cust_209 2343.0760 311.64\n",
"285 Cust_506 2980.3720 494.63\n",
"314 Cust_560 2230.9700 273.27\n",
"349 Cust_1674 2827.1425 713.88\n",
"395 Cust_1418 2182.9100 549.45\n",
"404 Cust_566 2010.8900 564.07\n",
"510 Cust_1346 2660.6105 618.07\n",
"522 Cust_51 2689.4800 399.93\n",
"536 Cust_227 2180.2300 660.25\n",
"541 Cust_1680 2292.1015 398.36\n",
"647 Cust_1439 2758.2200 966.81\n",
"680 Cust_212 2404.5990 496.89\n",
"688 Cust_1682 2257.8800 474.98\n",
"718 Cust_783 2135.9735 239.40\n",
"720 Cust_805 2773.0315 897.87\n",
"729 Cust_1588 2168.0500 416.02\n",
"767 Cust_828 2192.6300 660.06\n",
"775 Cust_1746 2610.8940 516.19\n",
"783 Cust_1017 2368.1680 1181.30\n",
"809 Cust_1440 2752.6800 430.32\n",
"810 Cust_1440 2405.0000 696.17\n",
"... ... ... ...\n",
"7777 Cust_1196 2167.0500 684.90\n",
"7778 Cust_1196 2040.3900 221.09\n",
"7788 Cust_977 2252.2620 478.11\n",
"7811 Cust_1188 2080.0350 844.90\n",
"7823 Cust_1492 2325.4200 739.91\n",
"7858 Cust_1200 2206.1700 251.43\n",
"7875 Cust_577 2287.1000 231.49\n",
"7877 Cust_577 2503.3265 447.12\n",
"7884 Cust_244 2529.3960 371.21\n",
"7911 Cust_1693 2882.7070 303.23\n",
"7927 Cust_976 2104.9910 165.45\n",
"7940 Cust_1224 2185.9535 268.01\n",
"7973 Cust_582 2145.0500 1012.67\n",
"7986 Cust_1583 2478.4810 249.10\n",
"8045 Cust_1803 2587.5300 401.85\n",
"8048 Cust_247 2780.8800 595.38\n",
"8061 Cust_892 2550.1200 882.45\n",
"8071 Cust_1795 2750.1070 600.42\n",
"8147 Cust_1187 2143.2155 464.36\n",
"8152 Cust_1187 2477.9900 747.68\n",
"8239 Cust_245 2833.1900 1409.87\n",
"8262 Cust_1694 2455.2760 693.06\n",
"8271 Cust_1587 2823.0370 372.40\n",
"8289 Cust_595 2731.7300 310.59\n",
"8304 Cust_1025 2272.5600 111.05\n",
"8338 Cust_785 2409.9600 575.10\n",
"8350 Cust_1266 2094.9780 697.29\n",
"8354 Cust_1266 2614.3705 384.01\n",
"8381 Cust_1006 2836.0505 561.13\n",
"8394 Cust_1798 2841.4395 374.63\n",
"\n",
"[328 rows x 3 columns]"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# E.g. all orders having 2000 < Sales < 3000 and Profit > 100\n",
"# Also, this time, you only need the Cust_id, Sales and Profit columns\n",
"df.loc[(df.Sales > 2000) & (df.Sales < 3000) & (df.Profit > 100), ['Cust_id', 'Sales', 'Profit']]"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Ord_id</th>\n",
" <th>Prod_id</th>\n",
" <th>Ship_id</th>\n",
" <th>Cust_id</th>\n",
" <th>Sales</th>\n",
" <th>Discount</th>\n",
" <th>Order_Quantity</th>\n",
" <th>Profit</th>\n",
" <th>Shipping_Cost</th>\n",
" <th>Product_Base_Margin</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>Ord_5446</td>\n",
" <td>Prod_16</td>\n",
" <td>SHP_7609</td>\n",
" <td>Cust_1818</td>\n",
" <td>136.8100</td>\n",
" <td>0.01</td>\n",
" <td>23</td>\n",
" <td>-30.51</td>\n",
" <td>3.60</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>Ord_5406</td>\n",
" <td>Prod_13</td>\n",
" <td>SHP_7549</td>\n",
" <td>Cust_1818</td>\n",
" <td>42.2700</td>\n",
" <td>0.01</td>\n",
" <td>13</td>\n",
" <td>4.56</td>\n",
" <td>0.93</td>\n",
" <td>0.54</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>Ord_5446</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_7610</td>\n",
" <td>Cust_1818</td>\n",
" <td>4701.6900</td>\n",
" <td>0.00</td>\n",
" <td>26</td>\n",
" <td>1148.90</td>\n",
" <td>2.50</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>Ord_5456</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_7625</td>\n",
" <td>Cust_1818</td>\n",
" <td>2337.8900</td>\n",
" <td>0.09</td>\n",
" <td>43</td>\n",
" <td>729.34</td>\n",
" <td>14.30</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>Ord_5485</td>\n",
" <td>Prod_17</td>\n",
" <td>SHP_7664</td>\n",
" <td>Cust_1818</td>\n",
" <td>4233.1500</td>\n",
" <td>0.08</td>\n",
" <td>35</td>\n",
" <td>1219.87</td>\n",
" <td>26.30</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>Ord_5446</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_7608</td>\n",
" <td>Cust_1818</td>\n",
" <td>164.0200</td>\n",
" <td>0.03</td>\n",
" <td>23</td>\n",
" <td>-47.64</td>\n",
" <td>6.15</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>Ord_31</td>\n",
" <td>Prod_12</td>\n",
" <td>SHP_41</td>\n",
" <td>Cust_26</td>\n",
" <td>14.7600</td>\n",
" <td>0.01</td>\n",
" <td>5</td>\n",
" <td>1.32</td>\n",
" <td>0.50</td>\n",
" <td>0.36</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>Ord_4725</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_6593</td>\n",
" <td>Cust_1641</td>\n",
" <td>3410.1575</td>\n",
" <td>0.10</td>\n",
" <td>48</td>\n",
" <td>1137.91</td>\n",
" <td>0.99</td>\n",
" <td>0.55</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>Ord_4725</td>\n",
" <td>Prod_13</td>\n",
" <td>SHP_6593</td>\n",
" <td>Cust_1641</td>\n",
" <td>162.0000</td>\n",
" <td>0.01</td>\n",
" <td>33</td>\n",
" <td>45.84</td>\n",
" <td>0.71</td>\n",
" <td>0.52</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>Ord_4725</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_6593</td>\n",
" <td>Cust_1641</td>\n",
" <td>57.2200</td>\n",
" <td>0.07</td>\n",
" <td>8</td>\n",
" <td>-27.72</td>\n",
" <td>6.60</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>Ord_4743</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_6615</td>\n",
" <td>Cust_1641</td>\n",
" <td>4072.0100</td>\n",
" <td>0.01</td>\n",
" <td>43</td>\n",
" <td>1675.98</td>\n",
" <td>0.99</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>Ord_1925</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_2637</td>\n",
" <td>Cust_708</td>\n",
" <td>465.9000</td>\n",
" <td>0.05</td>\n",
" <td>38</td>\n",
" <td>79.34</td>\n",
" <td>4.86</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12</th>\n",
" <td>Ord_2978</td>\n",
" <td>Prod_16</td>\n",
" <td>SHP_4112</td>\n",
" <td>Cust_1088</td>\n",
" <td>305.0500</td>\n",
" <td>0.04</td>\n",
" <td>27</td>\n",
" <td>23.12</td>\n",
" <td>3.37</td>\n",
" <td>0.57</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13</th>\n",
" <td>Ord_2207</td>\n",
" <td>Prod_11</td>\n",
" <td>SHP_3093</td>\n",
" <td>Cust_839</td>\n",
" <td>3364.2480</td>\n",
" <td>0.10</td>\n",
" <td>15</td>\n",
" <td>-693.23</td>\n",
" <td>61.76</td>\n",
" <td>0.78</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14</th>\n",
" <td>Ord_2207</td>\n",
" <td>Prod_10</td>\n",
" <td>SHP_3006</td>\n",
" <td>Cust_839</td>\n",
" <td>1410.9300</td>\n",
" <td>0.08</td>\n",
" <td>10</td>\n",
" <td>-317.48</td>\n",
" <td>36.09</td>\n",
" <td>0.77</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15</th>\n",
" <td>Ord_2280</td>\n",
" <td>Prod_5</td>\n",
" <td>SHP_3114</td>\n",
" <td>Cust_839</td>\n",
" <td>460.6900</td>\n",
" <td>0.06</td>\n",
" <td>48</td>\n",
" <td>-103.48</td>\n",
" <td>7.29</td>\n",
" <td>0.45</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16</th>\n",
" <td>Ord_2282</td>\n",
" <td>Prod_9</td>\n",
" <td>SHP_3122</td>\n",
" <td>Cust_839</td>\n",
" <td>443.4600</td>\n",
" <td>0.06</td>\n",
" <td>30</td>\n",
" <td>193.12</td>\n",
" <td>1.39</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17</th>\n",
" <td>Ord_4471</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_6228</td>\n",
" <td>Cust_1521</td>\n",
" <td>13255.9300</td>\n",
" <td>0.02</td>\n",
" <td>25</td>\n",
" <td>4089.27</td>\n",
" <td>26.00</td>\n",
" <td>0.60</td>\n",
" </tr>\n",
" <tr>\n",
" <th>18</th>\n",
" <td>Ord_4427</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_6171</td>\n",
" <td>Cust_1521</td>\n",
" <td>283.1300</td>\n",
" <td>0.08</td>\n",
" <td>45</td>\n",
" <td>-141.26</td>\n",
" <td>6.81</td>\n",
" <td>0.36</td>\n",
" </tr>\n",
" <tr>\n",
" <th>19</th>\n",
" <td>Ord_996</td>\n",
" <td>Prod_13</td>\n",
" <td>SHP_1378</td>\n",
" <td>Cust_371</td>\n",
" <td>41.9700</td>\n",
" <td>0.05</td>\n",
" <td>12</td>\n",
" <td>-37.03</td>\n",
" <td>4.20</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>20</th>\n",
" <td>Ord_996</td>\n",
" <td>Prod_13</td>\n",
" <td>SHP_1378</td>\n",
" <td>Cust_371</td>\n",
" <td>57.1700</td>\n",
" <td>0.08</td>\n",
" <td>18</td>\n",
" <td>-24.03</td>\n",
" <td>2.31</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>21</th>\n",
" <td>Ord_996</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_1378</td>\n",
" <td>Cust_371</td>\n",
" <td>81.2500</td>\n",
" <td>0.01</td>\n",
" <td>11</td>\n",
" <td>-44.54</td>\n",
" <td>7.86</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>22</th>\n",
" <td>Ord_996</td>\n",
" <td>Prod_5</td>\n",
" <td>SHP_1377</td>\n",
" <td>Cust_371</td>\n",
" <td>3202.2500</td>\n",
" <td>0.09</td>\n",
" <td>44</td>\n",
" <td>991.26</td>\n",
" <td>19.99</td>\n",
" <td>0.43</td>\n",
" </tr>\n",
" <tr>\n",
" <th>23</th>\n",
" <td>Ord_996</td>\n",
" <td>Prod_7</td>\n",
" <td>SHP_1378</td>\n",
" <td>Cust_371</td>\n",
" <td>35.6400</td>\n",
" <td>0.05</td>\n",
" <td>10</td>\n",
" <td>-0.71</td>\n",
" <td>1.63</td>\n",
" <td>0.36</td>\n",
" </tr>\n",
" <tr>\n",
" <th>24</th>\n",
" <td>Ord_2573</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_3525</td>\n",
" <td>Cust_931</td>\n",
" <td>197.6100</td>\n",
" <td>0.08</td>\n",
" <td>13</td>\n",
" <td>3.46</td>\n",
" <td>7.27</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>25</th>\n",
" <td>Ord_2335</td>\n",
" <td>Prod_13</td>\n",
" <td>SHP_3204</td>\n",
" <td>Cust_931</td>\n",
" <td>38.2600</td>\n",
" <td>0.03</td>\n",
" <td>22</td>\n",
" <td>-2.34</td>\n",
" <td>0.70</td>\n",
" <td>0.56</td>\n",
" </tr>\n",
" <tr>\n",
" <th>26</th>\n",
" <td>Ord_2456</td>\n",
" <td>Prod_5</td>\n",
" <td>SHP_3367</td>\n",
" <td>Cust_931</td>\n",
" <td>109.5800</td>\n",
" <td>0.00</td>\n",
" <td>13</td>\n",
" <td>31.32</td>\n",
" <td>4.00</td>\n",
" <td>0.42</td>\n",
" </tr>\n",
" <tr>\n",
" <th>27</th>\n",
" <td>Ord_2405</td>\n",
" <td>Prod_9</td>\n",
" <td>SHP_3300</td>\n",
" <td>Cust_931</td>\n",
" <td>1062.6900</td>\n",
" <td>0.01</td>\n",
" <td>28</td>\n",
" <td>401.80</td>\n",
" <td>6.66</td>\n",
" <td>0.40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>28</th>\n",
" <td>Ord_2573</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_3527</td>\n",
" <td>Cust_931</td>\n",
" <td>3594.7435</td>\n",
" <td>0.05</td>\n",
" <td>38</td>\n",
" <td>1016.97</td>\n",
" <td>2.50</td>\n",
" <td>0.55</td>\n",
" </tr>\n",
" <tr>\n",
" <th>29</th>\n",
" <td>Ord_2478</td>\n",
" <td>Prod_12</td>\n",
" <td>SHP_3395</td>\n",
" <td>Cust_931</td>\n",
" <td>139.9800</td>\n",
" <td>0.07</td>\n",
" <td>33</td>\n",
" <td>-140.54</td>\n",
" <td>6.89</td>\n",
" <td>0.39</td>\n",
" </tr>\n",
" <tr>\n",
" <th>...</th>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8369</th>\n",
" <td>Ord_3633</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_5031</td>\n",
" <td>Cust_1274</td>\n",
" <td>1169.2600</td>\n",
" <td>0.02</td>\n",
" <td>41</td>\n",
" <td>515.62</td>\n",
" <td>1.49</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8370</th>\n",
" <td>Ord_2696</td>\n",
" <td>Prod_13</td>\n",
" <td>SHP_3690</td>\n",
" <td>Cust_1006</td>\n",
" <td>62.7800</td>\n",
" <td>0.04</td>\n",
" <td>20</td>\n",
" <td>-17.75</td>\n",
" <td>2.03</td>\n",
" <td>0.57</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8371</th>\n",
" <td>Ord_2624</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_3591</td>\n",
" <td>Cust_1006</td>\n",
" <td>4924.1350</td>\n",
" <td>0.07</td>\n",
" <td>28</td>\n",
" <td>1049.54</td>\n",
" <td>8.99</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8372</th>\n",
" <td>Ord_2772</td>\n",
" <td>Prod_9</td>\n",
" <td>SHP_3806</td>\n",
" <td>Cust_1006</td>\n",
" <td>56.9000</td>\n",
" <td>0.03</td>\n",
" <td>7</td>\n",
" <td>12.64</td>\n",
" <td>1.39</td>\n",
" <td>0.36</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8373</th>\n",
" <td>Ord_2600</td>\n",
" <td>Prod_16</td>\n",
" <td>SHP_3560</td>\n",
" <td>Cust_1006</td>\n",
" <td>106.6400</td>\n",
" <td>0.10</td>\n",
" <td>30</td>\n",
" <td>-31.95</td>\n",
" <td>1.32</td>\n",
" <td>0.83</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8374</th>\n",
" <td>Ord_2658</td>\n",
" <td>Prod_5</td>\n",
" <td>SHP_3637</td>\n",
" <td>Cust_1006</td>\n",
" <td>1082.6600</td>\n",
" <td>0.08</td>\n",
" <td>14</td>\n",
" <td>-256.93</td>\n",
" <td>48.20</td>\n",
" <td>0.74</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8375</th>\n",
" <td>Ord_2772</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_3806</td>\n",
" <td>Cust_1006</td>\n",
" <td>1413.8200</td>\n",
" <td>0.10</td>\n",
" <td>47</td>\n",
" <td>226.53</td>\n",
" <td>11.63</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8376</th>\n",
" <td>Ord_2624</td>\n",
" <td>Prod_8</td>\n",
" <td>SHP_3590</td>\n",
" <td>Cust_1006</td>\n",
" <td>1211.0000</td>\n",
" <td>0.00</td>\n",
" <td>36</td>\n",
" <td>-27.99</td>\n",
" <td>6.50</td>\n",
" <td>0.79</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8377</th>\n",
" <td>Ord_2722</td>\n",
" <td>Prod_12</td>\n",
" <td>SHP_3729</td>\n",
" <td>Cust_1006</td>\n",
" <td>34.0100</td>\n",
" <td>0.00</td>\n",
" <td>12</td>\n",
" <td>10.58</td>\n",
" <td>0.50</td>\n",
" <td>0.39</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8378</th>\n",
" <td>Ord_2706</td>\n",
" <td>Prod_2</td>\n",
" <td>SHP_3705</td>\n",
" <td>Cust_1006</td>\n",
" <td>1361.9100</td>\n",
" <td>0.05</td>\n",
" <td>20</td>\n",
" <td>312.52</td>\n",
" <td>3.50</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8379</th>\n",
" <td>Ord_2722</td>\n",
" <td>Prod_5</td>\n",
" <td>SHP_3730</td>\n",
" <td>Cust_1006</td>\n",
" <td>1008.9500</td>\n",
" <td>0.04</td>\n",
" <td>41</td>\n",
" <td>69.31</td>\n",
" <td>8.99</td>\n",
" <td>0.50</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8380</th>\n",
" <td>Ord_2772</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_3807</td>\n",
" <td>Cust_1006</td>\n",
" <td>308.9200</td>\n",
" <td>0.04</td>\n",
" <td>45</td>\n",
" <td>-143.58</td>\n",
" <td>7.37</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8381</th>\n",
" <td>Ord_2696</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_3691</td>\n",
" <td>Cust_1006</td>\n",
" <td>2836.0505</td>\n",
" <td>0.01</td>\n",
" <td>25</td>\n",
" <td>561.13</td>\n",
" <td>8.99</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8382</th>\n",
" <td>Ord_2658</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_3636</td>\n",
" <td>Cust_1006</td>\n",
" <td>120.9800</td>\n",
" <td>0.00</td>\n",
" <td>28</td>\n",
" <td>-92.85</td>\n",
" <td>5.34</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8383</th>\n",
" <td>Ord_2722</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_3731</td>\n",
" <td>Cust_1006</td>\n",
" <td>3508.3300</td>\n",
" <td>0.04</td>\n",
" <td>21</td>\n",
" <td>-546.98</td>\n",
" <td>35.00</td>\n",
" <td>0.85</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8384</th>\n",
" <td>Ord_4620</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_6435</td>\n",
" <td>Cust_1577</td>\n",
" <td>59.6200</td>\n",
" <td>0.04</td>\n",
" <td>10</td>\n",
" <td>-56.30</td>\n",
" <td>7.78</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8385</th>\n",
" <td>Ord_1833</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_2527</td>\n",
" <td>Cust_637</td>\n",
" <td>611.1600</td>\n",
" <td>0.04</td>\n",
" <td>46</td>\n",
" <td>100.22</td>\n",
" <td>4.98</td>\n",
" <td>0.40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8386</th>\n",
" <td>Ord_2324</td>\n",
" <td>Prod_7</td>\n",
" <td>SHP_3189</td>\n",
" <td>Cust_851</td>\n",
" <td>121.8700</td>\n",
" <td>0.07</td>\n",
" <td>39</td>\n",
" <td>11.32</td>\n",
" <td>1.35</td>\n",
" <td>0.40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8387</th>\n",
" <td>Ord_2220</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_3019</td>\n",
" <td>Cust_851</td>\n",
" <td>41.0600</td>\n",
" <td>0.04</td>\n",
" <td>4</td>\n",
" <td>-16.39</td>\n",
" <td>6.28</td>\n",
" <td>0.35</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8388</th>\n",
" <td>Ord_4424</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_6165</td>\n",
" <td>Cust_1519</td>\n",
" <td>994.0400</td>\n",
" <td>0.03</td>\n",
" <td>10</td>\n",
" <td>-335.06</td>\n",
" <td>35.00</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8389</th>\n",
" <td>Ord_4444</td>\n",
" <td>Prod_13</td>\n",
" <td>SHP_6192</td>\n",
" <td>Cust_1519</td>\n",
" <td>159.4100</td>\n",
" <td>0.00</td>\n",
" <td>44</td>\n",
" <td>34.68</td>\n",
" <td>0.98</td>\n",
" <td>0.52</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8390</th>\n",
" <td>Ord_5435</td>\n",
" <td>Prod_16</td>\n",
" <td>SHP_7594</td>\n",
" <td>Cust_1798</td>\n",
" <td>316.9900</td>\n",
" <td>0.04</td>\n",
" <td>47</td>\n",
" <td>-276.54</td>\n",
" <td>8.37</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8391</th>\n",
" <td>Ord_5435</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_7594</td>\n",
" <td>Cust_1798</td>\n",
" <td>1991.8985</td>\n",
" <td>0.07</td>\n",
" <td>20</td>\n",
" <td>88.36</td>\n",
" <td>7.69</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8392</th>\n",
" <td>Ord_5384</td>\n",
" <td>Prod_9</td>\n",
" <td>SHP_7519</td>\n",
" <td>Cust_1798</td>\n",
" <td>181.5000</td>\n",
" <td>0.08</td>\n",
" <td>43</td>\n",
" <td>-6.24</td>\n",
" <td>2.50</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8393</th>\n",
" <td>Ord_5348</td>\n",
" <td>Prod_8</td>\n",
" <td>SHP_7470</td>\n",
" <td>Cust_1798</td>\n",
" <td>356.7200</td>\n",
" <td>0.07</td>\n",
" <td>9</td>\n",
" <td>12.61</td>\n",
" <td>1.99</td>\n",
" <td>0.44</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8394</th>\n",
" <td>Ord_5353</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_7479</td>\n",
" <td>Cust_1798</td>\n",
" <td>2841.4395</td>\n",
" <td>0.08</td>\n",
" <td>28</td>\n",
" <td>374.63</td>\n",
" <td>7.69</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8395</th>\n",
" <td>Ord_5411</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_7555</td>\n",
" <td>Cust_1798</td>\n",
" <td>127.1600</td>\n",
" <td>0.10</td>\n",
" <td>20</td>\n",
" <td>-74.03</td>\n",
" <td>6.92</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8396</th>\n",
" <td>Ord_5388</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_7524</td>\n",
" <td>Cust_1798</td>\n",
" <td>243.0500</td>\n",
" <td>0.02</td>\n",
" <td>39</td>\n",
" <td>-70.85</td>\n",
" <td>5.35</td>\n",
" <td>0.40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8397</th>\n",
" <td>Ord_5348</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_7469</td>\n",
" <td>Cust_1798</td>\n",
" <td>3872.8700</td>\n",
" <td>0.03</td>\n",
" <td>23</td>\n",
" <td>565.34</td>\n",
" <td>30.00</td>\n",
" <td>0.62</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8398</th>\n",
" <td>Ord_5459</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_7628</td>\n",
" <td>Cust_1798</td>\n",
" <td>603.6900</td>\n",
" <td>0.00</td>\n",
" <td>47</td>\n",
" <td>131.39</td>\n",
" <td>4.86</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>8399 rows × 10 columns</p>\n",
"</div>"
],
"text/plain": [
" Ord_id Prod_id Ship_id Cust_id Sales Discount \\\n",
"0 Ord_5446 Prod_16 SHP_7609 Cust_1818 136.8100 0.01 \n",
"1 Ord_5406 Prod_13 SHP_7549 Cust_1818 42.2700 0.01 \n",
"2 Ord_5446 Prod_4 SHP_7610 Cust_1818 4701.6900 0.00 \n",
"3 Ord_5456 Prod_6 SHP_7625 Cust_1818 2337.8900 0.09 \n",
"4 Ord_5485 Prod_17 SHP_7664 Cust_1818 4233.1500 0.08 \n",
"5 Ord_5446 Prod_6 SHP_7608 Cust_1818 164.0200 0.03 \n",
"6 Ord_31 Prod_12 SHP_41 Cust_26 14.7600 0.01 \n",
"7 Ord_4725 Prod_4 SHP_6593 Cust_1641 3410.1575 0.10 \n",
"8 Ord_4725 Prod_13 SHP_6593 Cust_1641 162.0000 0.01 \n",
"9 Ord_4725 Prod_6 SHP_6593 Cust_1641 57.2200 0.07 \n",
"10 Ord_4743 Prod_2 SHP_6615 Cust_1641 4072.0100 0.01 \n",
"11 Ord_1925 Prod_6 SHP_2637 Cust_708 465.9000 0.05 \n",
"12 Ord_2978 Prod_16 SHP_4112 Cust_1088 305.0500 0.04 \n",
"13 Ord_2207 Prod_11 SHP_3093 Cust_839 3364.2480 0.10 \n",
"14 Ord_2207 Prod_10 SHP_3006 Cust_839 1410.9300 0.08 \n",
"15 Ord_2280 Prod_5 SHP_3114 Cust_839 460.6900 0.06 \n",
"16 Ord_2282 Prod_9 SHP_3122 Cust_839 443.4600 0.06 \n",
"17 Ord_4471 Prod_15 SHP_6228 Cust_1521 13255.9300 0.02 \n",
"18 Ord_4427 Prod_6 SHP_6171 Cust_1521 283.1300 0.08 \n",
"19 Ord_996 Prod_13 SHP_1378 Cust_371 41.9700 0.05 \n",
"20 Ord_996 Prod_13 SHP_1378 Cust_371 57.1700 0.08 \n",
"21 Ord_996 Prod_6 SHP_1378 Cust_371 81.2500 0.01 \n",
"22 Ord_996 Prod_5 SHP_1377 Cust_371 3202.2500 0.09 \n",
"23 Ord_996 Prod_7 SHP_1378 Cust_371 35.6400 0.05 \n",
"24 Ord_2573 Prod_3 SHP_3525 Cust_931 197.6100 0.08 \n",
"25 Ord_2335 Prod_13 SHP_3204 Cust_931 38.2600 0.03 \n",
"26 Ord_2456 Prod_5 SHP_3367 Cust_931 109.5800 0.00 \n",
"27 Ord_2405 Prod_9 SHP_3300 Cust_931 1062.6900 0.01 \n",
"28 Ord_2573 Prod_4 SHP_3527 Cust_931 3594.7435 0.05 \n",
"29 Ord_2478 Prod_12 SHP_3395 Cust_931 139.9800 0.07 \n",
"... ... ... ... ... ... ... \n",
"8369 Ord_3633 Prod_3 SHP_5031 Cust_1274 1169.2600 0.02 \n",
"8370 Ord_2696 Prod_13 SHP_3690 Cust_1006 62.7800 0.04 \n",
"8371 Ord_2624 Prod_4 SHP_3591 Cust_1006 4924.1350 0.07 \n",
"8372 Ord_2772 Prod_9 SHP_3806 Cust_1006 56.9000 0.03 \n",
"8373 Ord_2600 Prod_16 SHP_3560 Cust_1006 106.6400 0.10 \n",
"8374 Ord_2658 Prod_5 SHP_3637 Cust_1006 1082.6600 0.08 \n",
"8375 Ord_2772 Prod_3 SHP_3806 Cust_1006 1413.8200 0.10 \n",
"8376 Ord_2624 Prod_8 SHP_3590 Cust_1006 1211.0000 0.00 \n",
"8377 Ord_2722 Prod_12 SHP_3729 Cust_1006 34.0100 0.00 \n",
"8378 Ord_2706 Prod_2 SHP_3705 Cust_1006 1361.9100 0.05 \n",
"8379 Ord_2722 Prod_5 SHP_3730 Cust_1006 1008.9500 0.04 \n",
"8380 Ord_2772 Prod_6 SHP_3807 Cust_1006 308.9200 0.04 \n",
"8381 Ord_2696 Prod_4 SHP_3691 Cust_1006 2836.0505 0.01 \n",
"8382 Ord_2658 Prod_3 SHP_3636 Cust_1006 120.9800 0.00 \n",
"8383 Ord_2722 Prod_1 SHP_3731 Cust_1006 3508.3300 0.04 \n",
"8384 Ord_4620 Prod_3 SHP_6435 Cust_1577 59.6200 0.04 \n",
"8385 Ord_1833 Prod_3 SHP_2527 Cust_637 611.1600 0.04 \n",
"8386 Ord_2324 Prod_7 SHP_3189 Cust_851 121.8700 0.07 \n",
"8387 Ord_2220 Prod_3 SHP_3019 Cust_851 41.0600 0.04 \n",
"8388 Ord_4424 Prod_1 SHP_6165 Cust_1519 994.0400 0.03 \n",
"8389 Ord_4444 Prod_13 SHP_6192 Cust_1519 159.4100 0.00 \n",
"8390 Ord_5435 Prod_16 SHP_7594 Cust_1798 316.9900 0.04 \n",
"8391 Ord_5435 Prod_4 SHP_7594 Cust_1798 1991.8985 0.07 \n",
"8392 Ord_5384 Prod_9 SHP_7519 Cust_1798 181.5000 0.08 \n",
"8393 Ord_5348 Prod_8 SHP_7470 Cust_1798 356.7200 0.07 \n",
"8394 Ord_5353 Prod_4 SHP_7479 Cust_1798 2841.4395 0.08 \n",
"8395 Ord_5411 Prod_6 SHP_7555 Cust_1798 127.1600 0.10 \n",
"8396 Ord_5388 Prod_6 SHP_7524 Cust_1798 243.0500 0.02 \n",
"8397 Ord_5348 Prod_15 SHP_7469 Cust_1798 3872.8700 0.03 \n",
"8398 Ord_5459 Prod_6 SHP_7628 Cust_1798 603.6900 0.00 \n",
"\n",
" Order_Quantity Profit Shipping_Cost Product_Base_Margin \n",
"0 23 -30.51 3.60 0.56 \n",
"1 13 4.56 0.93 0.54 \n",
"2 26 1148.90 2.50 0.59 \n",
"3 43 729.34 14.30 0.37 \n",
"4 35 1219.87 26.30 0.38 \n",
"5 23 -47.64 6.15 0.37 \n",
"6 5 1.32 0.50 0.36 \n",
"7 48 1137.91 0.99 0.55 \n",
"8 33 45.84 0.71 0.52 \n",
"9 8 -27.72 6.60 0.37 \n",
"10 43 1675.98 0.99 0.56 \n",
"11 38 79.34 4.86 0.38 \n",
"12 27 23.12 3.37 0.57 \n",
"13 15 -693.23 61.76 0.78 \n",
"14 10 -317.48 36.09 0.77 \n",
"15 48 -103.48 7.29 0.45 \n",
"16 30 193.12 1.39 0.38 \n",
"17 25 4089.27 26.00 0.60 \n",
"18 45 -141.26 6.81 0.36 \n",
"19 12 -37.03 4.20 0.56 \n",
"20 18 -24.03 2.31 0.56 \n",
"21 11 -44.54 7.86 0.37 \n",
"22 44 991.26 19.99 0.43 \n",
"23 10 -0.71 1.63 0.36 \n",
"24 13 3.46 7.27 0.38 \n",
"25 22 -2.34 0.70 0.56 \n",
"26 13 31.32 4.00 0.42 \n",
"27 28 401.80 6.66 0.40 \n",
"28 38 1016.97 2.50 0.55 \n",
"29 33 -140.54 6.89 0.39 \n",
"... ... ... ... ... \n",
"8369 41 515.62 1.49 0.38 \n",
"8370 20 -17.75 2.03 0.57 \n",
"8371 28 1049.54 8.99 0.58 \n",
"8372 7 12.64 1.39 0.36 \n",
"8373 30 -31.95 1.32 0.83 \n",
"8374 14 -256.93 48.20 0.74 \n",
"8375 47 226.53 11.63 0.37 \n",
"8376 36 -27.99 6.50 0.79 \n",
"8377 12 10.58 0.50 0.39 \n",
"8378 20 312.52 3.50 0.59 \n",
"8379 41 69.31 8.99 0.50 \n",
"8380 45 -143.58 7.37 0.37 \n",
"8381 25 561.13 8.99 0.59 \n",
"8382 28 -92.85 5.34 0.38 \n",
"8383 21 -546.98 35.00 0.85 \n",
"8384 10 -56.30 7.78 0.37 \n",
"8385 46 100.22 4.98 0.40 \n",
"8386 39 11.32 1.35 0.40 \n",
"8387 4 -16.39 6.28 0.35 \n",
"8388 10 -335.06 35.00 NaN \n",
"8389 44 34.68 0.98 0.52 \n",
"8390 47 -276.54 8.37 0.58 \n",
"8391 20 88.36 7.69 0.58 \n",
"8392 43 -6.24 2.50 0.37 \n",
"8393 9 12.61 1.99 0.44 \n",
"8394 28 374.63 7.69 0.59 \n",
"8395 20 -74.03 6.92 0.37 \n",
"8396 39 -70.85 5.35 0.40 \n",
"8397 23 565.34 30.00 0.62 \n",
"8398 47 131.39 4.86 0.38 \n",
"\n",
"[8399 rows x 10 columns]"
]
},
"execution_count": 17,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# You can use the == and != operators \n",
"df.loc[(df.Sales == 4233.15), :]\n",
"df.loc[(df.Sales != 1000), :]"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Ord_id</th>\n",
" <th>Prod_id</th>\n",
" <th>Ship_id</th>\n",
" <th>Cust_id</th>\n",
" <th>Sales</th>\n",
" <th>Discount</th>\n",
" <th>Order_Quantity</th>\n",
" <th>Profit</th>\n",
" <th>Shipping_Cost</th>\n",
" <th>Product_Base_Margin</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>8385</th>\n",
" <td>Ord_1833</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_2527</td>\n",
" <td>Cust_637</td>\n",
" <td>611.1600</td>\n",
" <td>0.04</td>\n",
" <td>46</td>\n",
" <td>100.22</td>\n",
" <td>4.98</td>\n",
" <td>0.40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8386</th>\n",
" <td>Ord_2324</td>\n",
" <td>Prod_7</td>\n",
" <td>SHP_3189</td>\n",
" <td>Cust_851</td>\n",
" <td>121.8700</td>\n",
" <td>0.07</td>\n",
" <td>39</td>\n",
" <td>11.32</td>\n",
" <td>1.35</td>\n",
" <td>0.40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8387</th>\n",
" <td>Ord_2220</td>\n",
" <td>Prod_3</td>\n",
" <td>SHP_3019</td>\n",
" <td>Cust_851</td>\n",
" <td>41.0600</td>\n",
" <td>0.04</td>\n",
" <td>4</td>\n",
" <td>-16.39</td>\n",
" <td>6.28</td>\n",
" <td>0.35</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8388</th>\n",
" <td>Ord_4424</td>\n",
" <td>Prod_1</td>\n",
" <td>SHP_6165</td>\n",
" <td>Cust_1519</td>\n",
" <td>994.0400</td>\n",
" <td>0.03</td>\n",
" <td>10</td>\n",
" <td>-335.06</td>\n",
" <td>35.00</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8389</th>\n",
" <td>Ord_4444</td>\n",
" <td>Prod_13</td>\n",
" <td>SHP_6192</td>\n",
" <td>Cust_1519</td>\n",
" <td>159.4100</td>\n",
" <td>0.00</td>\n",
" <td>44</td>\n",
" <td>34.68</td>\n",
" <td>0.98</td>\n",
" <td>0.52</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8390</th>\n",
" <td>Ord_5435</td>\n",
" <td>Prod_16</td>\n",
" <td>SHP_7594</td>\n",
" <td>Cust_1798</td>\n",
" <td>316.9900</td>\n",
" <td>0.04</td>\n",
" <td>47</td>\n",
" <td>-276.54</td>\n",
" <td>8.37</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8391</th>\n",
" <td>Ord_5435</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_7594</td>\n",
" <td>Cust_1798</td>\n",
" <td>1991.8985</td>\n",
" <td>0.07</td>\n",
" <td>20</td>\n",
" <td>88.36</td>\n",
" <td>7.69</td>\n",
" <td>0.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8392</th>\n",
" <td>Ord_5384</td>\n",
" <td>Prod_9</td>\n",
" <td>SHP_7519</td>\n",
" <td>Cust_1798</td>\n",
" <td>181.5000</td>\n",
" <td>0.08</td>\n",
" <td>43</td>\n",
" <td>-6.24</td>\n",
" <td>2.50</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8393</th>\n",
" <td>Ord_5348</td>\n",
" <td>Prod_8</td>\n",
" <td>SHP_7470</td>\n",
" <td>Cust_1798</td>\n",
" <td>356.7200</td>\n",
" <td>0.07</td>\n",
" <td>9</td>\n",
" <td>12.61</td>\n",
" <td>1.99</td>\n",
" <td>0.44</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8394</th>\n",
" <td>Ord_5353</td>\n",
" <td>Prod_4</td>\n",
" <td>SHP_7479</td>\n",
" <td>Cust_1798</td>\n",
" <td>2841.4395</td>\n",
" <td>0.08</td>\n",
" <td>28</td>\n",
" <td>374.63</td>\n",
" <td>7.69</td>\n",
" <td>0.59</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8395</th>\n",
" <td>Ord_5411</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_7555</td>\n",
" <td>Cust_1798</td>\n",
" <td>127.1600</td>\n",
" <td>0.10</td>\n",
" <td>20</td>\n",
" <td>-74.03</td>\n",
" <td>6.92</td>\n",
" <td>0.37</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8396</th>\n",
" <td>Ord_5388</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_7524</td>\n",
" <td>Cust_1798</td>\n",
" <td>243.0500</td>\n",
" <td>0.02</td>\n",
" <td>39</td>\n",
" <td>-70.85</td>\n",
" <td>5.35</td>\n",
" <td>0.40</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8397</th>\n",
" <td>Ord_5348</td>\n",
" <td>Prod_15</td>\n",
" <td>SHP_7469</td>\n",
" <td>Cust_1798</td>\n",
" <td>3872.8700</td>\n",
" <td>0.03</td>\n",
" <td>23</td>\n",
" <td>565.34</td>\n",
" <td>30.00</td>\n",
" <td>0.62</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8398</th>\n",
" <td>Ord_5459</td>\n",
" <td>Prod_6</td>\n",
" <td>SHP_7628</td>\n",
" <td>Cust_1798</td>\n",
" <td>603.6900</td>\n",
" <td>0.00</td>\n",
" <td>47</td>\n",
" <td>131.39</td>\n",
" <td>4.86</td>\n",
" <td>0.38</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Ord_id Prod_id Ship_id Cust_id Sales Discount \\\n",
"8385 Ord_1833 Prod_3 SHP_2527 Cust_637 611.1600 0.04 \n",
"8386 Ord_2324 Prod_7 SHP_3189 Cust_851 121.8700 0.07 \n",
"8387 Ord_2220 Prod_3 SHP_3019 Cust_851 41.0600 0.04 \n",
"8388 Ord_4424 Prod_1 SHP_6165 Cust_1519 994.0400 0.03 \n",
"8389 Ord_4444 Prod_13 SHP_6192 Cust_1519 159.4100 0.00 \n",
"8390 Ord_5435 Prod_16 SHP_7594 Cust_1798 316.9900 0.04 \n",
"8391 Ord_5435 Prod_4 SHP_7594 Cust_1798 1991.8985 0.07 \n",
"8392 Ord_5384 Prod_9 SHP_7519 Cust_1798 181.5000 0.08 \n",
"8393 Ord_5348 Prod_8 SHP_7470 Cust_1798 356.7200 0.07 \n",
"8394 Ord_5353 Prod_4 SHP_7479 Cust_1798 2841.4395 0.08 \n",
"8395 Ord_5411 Prod_6 SHP_7555 Cust_1798 127.1600 0.10 \n",
"8396 Ord_5388 Prod_6 SHP_7524 Cust_1798 243.0500 0.02 \n",
"8397 Ord_5348 Prod_15 SHP_7469 Cust_1798 3872.8700 0.03 \n",
"8398 Ord_5459 Prod_6 SHP_7628 Cust_1798 603.6900 0.00 \n",
"\n",
" Order_Quantity Profit Shipping_Cost Product_Base_Margin \n",
"8385 46 100.22 4.98 0.40 \n",
"8386 39 11.32 1.35 0.40 \n",
"8387 4 -16.39 6.28 0.35 \n",
"8388 10 -335.06 35.00 NaN \n",
"8389 44 34.68 0.98 0.52 \n",
"8390 47 -276.54 8.37 0.58 \n",
"8391 20 88.36 7.69 0.58 \n",
"8392 43 -6.24 2.50 0.37 \n",
"8393 9 12.61 1.99 0.44 \n",
"8394 28 374.63 7.69 0.59 \n",
"8395 20 -74.03 6.92 0.37 \n",
"8396 39 -70.85 5.35 0.40 \n",
"8397 23 565.34 30.00 0.62 \n",
"8398 47 131.39 4.86 0.38 "
]
},
"execution_count": 18,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# You may want to select rows whose column value is in an iterable\n",
"# For instance, say a colleague gives you a list of customer_ids from a certain region\n",
"\n",
"customers_in_bangalore = ['Cust_1798', 'Cust_1519', 'Cust_637', 'Cust_851']\n",
"\n",
"# To get all the orders from these customers, use the isin() function\n",
"# It returns a boolean, which you can use to select rows\n",
"df.loc[df['Cust_id'].isin(customers_in_bangalore), :]"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.5"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| gpl-3.0 |
mne-tools/mne-tools.github.io | 0.19/_downloads/9cb26d39ca23b6aac4c0d201a4775849/plot_brainstorm_data.ipynb | 2 | 3257 | {
"cells": [
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"%matplotlib inline"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n\n=====================================\nBrainstorm raw (median nerve) dataset\n=====================================\n\nHere we compute the evoked from raw for the Brainstorm\ntutorial dataset. For comparison, see [1]_ and:\n\n https://neuroimage.usc.edu/brainstorm/Tutorials/MedianNerveCtf\n\nReferences\n----------\n.. [1] Tadel F, Baillet S, Mosher JC, Pantazis D, Leahy RM.\n Brainstorm: A User-Friendly Application for MEG/EEG Analysis.\n Computational Intelligence and Neuroscience, vol. 2011, Article ID\n 879716, 13 pages, 2011. doi:10.1155/2011/879716\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Authors: Mainak Jas <[email protected]>\n#\n# License: BSD (3-clause)\n\nimport numpy as np\n\nimport mne\nfrom mne.datasets.brainstorm import bst_raw\nfrom mne.io import read_raw_ctf\n\nprint(__doc__)\n\ntmin, tmax, event_id = -0.1, 0.3, 2 # take right-hand somato\nreject = dict(mag=4e-12, eog=250e-6)\n\ndata_path = bst_raw.data_path()\n\nraw_path = (data_path + '/MEG/bst_raw/' +\n 'subj001_somatosensory_20111109_01_AUX-f.ds')\nraw = read_raw_ctf(raw_path, preload=True)\nraw.plot()\n\n# set EOG channel\nraw.set_channel_types({'EEG058': 'eog'})\nraw.set_eeg_reference('average', projection=True)\n\n# show power line interference and remove it\nraw.plot_psd(tmax=60., average=False)\nraw.notch_filter(np.arange(60, 181, 60), fir_design='firwin')\n\nevents = mne.find_events(raw, stim_channel='UPPT001')\n\n# pick MEG channels\npicks = mne.pick_types(raw.info, meg=True, eeg=False, stim=False, eog=True,\n exclude='bads')\n\n# Compute epochs\nepochs = mne.Epochs(raw, events, event_id, tmin, tmax, picks=picks,\n baseline=(None, 0), reject=reject, preload=False)\n\n# compute evoked\nevoked = epochs.average()\n\n# remove physiological artifacts (eyeblinks, heartbeats) using SSP on baseline\nevoked.add_proj(mne.compute_proj_evoked(evoked.copy().crop(tmax=0)))\nevoked.apply_proj()\n\n# fix stim artifact\nmne.preprocessing.fix_stim_artifact(evoked)\n\n# correct delays due to hardware (stim artifact is at 4 ms)\nevoked.shift_time(-0.004)\n\n# plot the result\nevoked.plot(time_unit='s')\n\n# show topomaps\nevoked.plot_topomap(times=np.array([0.016, 0.030, 0.060, 0.070]),\n time_unit='s')"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.4"
}
},
"nbformat": 4,
"nbformat_minor": 0
} | bsd-3-clause |
ShubhamDebnath/Coursera-Machine-Learning | Course 5/Dinosaurus Island Character level language model final v3.ipynb | 1 | 45021 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Character level language model - Dinosaurus land\n",
"\n",
"Welcome to Dinosaurus Island! 65 million years ago, dinosaurs existed, and in this assignment they are back. You are in charge of a special task. Leading biology researchers are creating new breeds of dinosaurs and bringing them to life on earth, and your job is to give names to these dinosaurs. If a dinosaur does not like its name, it might go beserk, so choose wisely! \n",
"\n",
"<table>\n",
"<td>\n",
"<img src=\"images/dino.jpg\" style=\"width:250;height:300px;\">\n",
"\n",
"</td>\n",
"\n",
"</table>\n",
"\n",
"Luckily you have learned some deep learning and you will use it to save the day. Your assistant has collected a list of all the dinosaur names they could find, and compiled them into this [dataset](dinos.txt). (Feel free to take a look by clicking the previous link.) To create new dinosaur names, you will build a character level language model to generate new names. Your algorithm will learn the different name patterns, and randomly generate new names. Hopefully this algorithm will keep you and your team safe from the dinosaurs' wrath! \n",
"\n",
"By completing this assignment you will learn:\n",
"\n",
"- How to store text data for processing using an RNN \n",
"- How to synthesize data, by sampling predictions at each time step and passing it to the next RNN-cell unit\n",
"- How to build a character-level text generation recurrent neural network\n",
"- Why clipping the gradients is important\n",
"\n",
"We will begin by loading in some functions that we have provided for you in `rnn_utils`. Specifically, you have access to functions such as `rnn_forward` and `rnn_backward` which are equivalent to those you've implemented in the previous assignment. "
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import numpy as np\n",
"from utils import *\n",
"import random"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"## 1 - Problem Statement\n",
"\n",
"### 1.1 - Dataset and Preprocessing\n",
"\n",
"Run the following cell to read the dataset of dinosaur names, create a list of unique characters (such as a-z), and compute the dataset and vocabulary size. "
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"There are 19909 total characters and 27 unique characters in your data.\n"
]
}
],
"source": [
"data = open('dinos.txt', 'r').read()\n",
"data= data.lower()\n",
"chars = list(set(data))\n",
"data_size, vocab_size = len(data), len(chars)\n",
"print('There are %d total characters and %d unique characters in your data.' % (data_size, vocab_size))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The characters are a-z (26 characters) plus the \"\\n\" (or newline character), which in this assignment plays a role similar to the `<EOS>` (or \"End of sentence\") token we had discussed in lecture, only here it indicates the end of the dinosaur name rather than the end of a sentence. In the cell below, we create a python dictionary (i.e., a hash table) to map each character to an index from 0-26. We also create a second python dictionary that maps each index back to the corresponding character character. This will help you figure out what index corresponds to what character in the probability distribution output of the softmax layer. Below, `char_to_ix` and `ix_to_char` are the python dictionaries. "
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"{0: '\\n', 1: 'a', 2: 'b', 3: 'c', 4: 'd', 5: 'e', 6: 'f', 7: 'g', 8: 'h', 9: 'i', 10: 'j', 11: 'k', 12: 'l', 13: 'm', 14: 'n', 15: 'o', 16: 'p', 17: 'q', 18: 'r', 19: 's', 20: 't', 21: 'u', 22: 'v', 23: 'w', 24: 'x', 25: 'y', 26: 'z'}\n"
]
}
],
"source": [
"char_to_ix = { ch:i for i,ch in enumerate(sorted(chars)) }\n",
"ix_to_char = { i:ch for i,ch in enumerate(sorted(chars)) }\n",
"print(ix_to_char)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 1.2 - Overview of the model\n",
"\n",
"Your model will have the following structure: \n",
"\n",
"- Initialize parameters \n",
"- Run the optimization loop\n",
" - Forward propagation to compute the loss function\n",
" - Backward propagation to compute the gradients with respect to the loss function\n",
" - Clip the gradients to avoid exploding gradients\n",
" - Using the gradients, update your parameter with the gradient descent update rule.\n",
"- Return the learned parameters \n",
" \n",
"<img src=\"images/rnn.png\" style=\"width:450;height:300px;\">\n",
"<caption><center> **Figure 1**: Recurrent Neural Network, similar to what you had built in the previous notebook \"Building a RNN - Step by Step\". </center></caption>\n",
"\n",
"At each time-step, the RNN tries to predict what is the next character given the previous characters. The dataset $X = (x^{\\langle 1 \\rangle}, x^{\\langle 2 \\rangle}, ..., x^{\\langle T_x \\rangle})$ is a list of characters in the training set, while $Y = (y^{\\langle 1 \\rangle}, y^{\\langle 2 \\rangle}, ..., y^{\\langle T_x \\rangle})$ is such that at every time-step $t$, we have $y^{\\langle t \\rangle} = x^{\\langle t+1 \\rangle}$. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 2 - Building blocks of the model\n",
"\n",
"In this part, you will build two important blocks of the overall model:\n",
"- Gradient clipping: to avoid exploding gradients\n",
"- Sampling: a technique used to generate characters\n",
"\n",
"You will then apply these two functions to build the model."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 2.1 - Clipping the gradients in the optimization loop\n",
"\n",
"In this section you will implement the `clip` function that you will call inside of your optimization loop. Recall that your overall loop structure usually consists of a forward pass, a cost computation, a backward pass, and a parameter update. Before updating the parameters, you will perform gradient clipping when needed to make sure that your gradients are not \"exploding,\" meaning taking on overly large values. \n",
"\n",
"In the exercise below, you will implement a function `clip` that takes in a dictionary of gradients and returns a clipped version of gradients if needed. There are different ways to clip gradients; we will use a simple element-wise clipping procedure, in which every element of the gradient vector is clipped to lie between some range [-N, N]. More generally, you will provide a `maxValue` (say 10). In this example, if any component of the gradient vector is greater than 10, it would be set to 10; and if any component of the gradient vector is less than -10, it would be set to -10. If it is between -10 and 10, it is left alone. \n",
"\n",
"<img src=\"images/clip.png\" style=\"width:400;height:150px;\">\n",
"<caption><center> **Figure 2**: Visualization of gradient descent with and without gradient clipping, in a case where the network is running into slight \"exploding gradient\" problems. </center></caption>\n",
"\n",
"**Exercise**: Implement the function below to return the clipped gradients of your dictionary `gradients`. Your function takes in a maximum threshold and returns the clipped versions of your gradients. You can check out this [hint](https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.clip.html) for examples of how to clip in numpy. You will need to use the argument `out = ...`."
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"### GRADED FUNCTION: clip\n",
"\n",
"def clip(gradients, maxValue):\n",
" '''\n",
" Clips the gradients' values between minimum and maximum.\n",
" \n",
" Arguments:\n",
" gradients -- a dictionary containing the gradients \"dWaa\", \"dWax\", \"dWya\", \"db\", \"dby\"\n",
" maxValue -- everything above this number is set to this number, and everything less than -maxValue is set to -maxValue\n",
" \n",
" Returns: \n",
" gradients -- a dictionary with the clipped gradients.\n",
" '''\n",
" \n",
" dWaa, dWax, dWya, db, dby = gradients['dWaa'], gradients['dWax'], gradients['dWya'], gradients['db'], gradients['dby']\n",
" \n",
" ### START CODE HERE ###\n",
" # clip to mitigate exploding gradients, loop over [dWax, dWaa, dWya, db, dby]. (≈2 lines)\n",
" for gradient in [dWax, dWaa, dWya, db, dby]:\n",
" np.clip(gradient, -maxValue, maxValue, out = gradient)\n",
" ### END CODE HERE ###\n",
" \n",
" gradients = {\"dWaa\": dWaa, \"dWax\": dWax, \"dWya\": dWya, \"db\": db, \"dby\": dby}\n",
" \n",
" return gradients"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"gradients[\"dWaa\"][1][2] = 10.0\n",
"gradients[\"dWax\"][3][1] = -10.0\n",
"gradients[\"dWya\"][1][2] = 0.29713815361\n",
"gradients[\"db\"][4] = [ 10.]\n",
"gradients[\"dby\"][1] = [ 8.45833407]\n"
]
}
],
"source": [
"np.random.seed(3)\n",
"dWax = np.random.randn(5,3)*10\n",
"dWaa = np.random.randn(5,5)*10\n",
"dWya = np.random.randn(2,5)*10\n",
"db = np.random.randn(5,1)*10\n",
"dby = np.random.randn(2,1)*10\n",
"gradients = {\"dWax\": dWax, \"dWaa\": dWaa, \"dWya\": dWya, \"db\": db, \"dby\": dby}\n",
"gradients = clip(gradients, 10)\n",
"print(\"gradients[\\\"dWaa\\\"][1][2] =\", gradients[\"dWaa\"][1][2])\n",
"print(\"gradients[\\\"dWax\\\"][3][1] =\", gradients[\"dWax\"][3][1])\n",
"print(\"gradients[\\\"dWya\\\"][1][2] =\", gradients[\"dWya\"][1][2])\n",
"print(\"gradients[\\\"db\\\"][4] =\", gradients[\"db\"][4])\n",
"print(\"gradients[\\\"dby\\\"][1] =\", gradients[\"dby\"][1])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"** Expected output:**\n",
"\n",
"<table>\n",
"<tr>\n",
" <td> \n",
" **gradients[\"dWaa\"][1][2] **\n",
" </td>\n",
" <td> \n",
" 10.0\n",
" </td>\n",
"</tr>\n",
"\n",
"<tr>\n",
" <td> \n",
" **gradients[\"dWax\"][3][1]**\n",
" </td>\n",
" <td> \n",
" -10.0\n",
" </td>\n",
" </td>\n",
"</tr>\n",
"<tr>\n",
" <td> \n",
" **gradients[\"dWya\"][1][2]**\n",
" </td>\n",
" <td> \n",
"0.29713815361\n",
" </td>\n",
"</tr>\n",
"<tr>\n",
" <td> \n",
" **gradients[\"db\"][4]**\n",
" </td>\n",
" <td> \n",
"[ 10.]\n",
" </td>\n",
"</tr>\n",
"<tr>\n",
" <td> \n",
" **gradients[\"dby\"][1]**\n",
" </td>\n",
" <td> \n",
"[ 8.45833407]\n",
" </td>\n",
"</tr>\n",
"\n",
"</table>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 2.2 - Sampling\n",
"\n",
"Now assume that your model is trained. You would like to generate new text (characters). The process of generation is explained in the picture below:\n",
"\n",
"<img src=\"images/dinos3.png\" style=\"width:500;height:300px;\">\n",
"<caption><center> **Figure 3**: In this picture, we assume the model is already trained. We pass in $x^{\\langle 1\\rangle} = \\vec{0}$ at the first time step, and have the network then sample one character at a time. </center></caption>\n",
"\n",
"**Exercise**: Implement the `sample` function below to sample characters. You need to carry out 4 steps:\n",
"\n",
"- **Step 1**: Pass the network the first \"dummy\" input $x^{\\langle 1 \\rangle} = \\vec{0}$ (the vector of zeros). This is the default input before we've generated any characters. We also set $a^{\\langle 0 \\rangle} = \\vec{0}$\n",
"\n",
"- **Step 2**: Run one step of forward propagation to get $a^{\\langle 1 \\rangle}$ and $\\hat{y}^{\\langle 1 \\rangle}$. Here are the equations:\n",
"\n",
"$$ a^{\\langle t+1 \\rangle} = \\tanh(W_{ax} x^{\\langle t \\rangle } + W_{aa} a^{\\langle t \\rangle } + b)\\tag{1}$$\n",
"\n",
"$$ z^{\\langle t + 1 \\rangle } = W_{ya} a^{\\langle t + 1 \\rangle } + b_y \\tag{2}$$\n",
"\n",
"$$ \\hat{y}^{\\langle t+1 \\rangle } = softmax(z^{\\langle t + 1 \\rangle })\\tag{3}$$\n",
"\n",
"Note that $\\hat{y}^{\\langle t+1 \\rangle }$ is a (softmax) probability vector (its entries are between 0 and 1 and sum to 1). $\\hat{y}^{\\langle t+1 \\rangle}_i$ represents the probability that the character indexed by \"i\" is the next character. We have provided a `softmax()` function that you can use.\n",
"\n",
"- **Step 3**: Carry out sampling: Pick the next character's index according to the probability distribution specified by $\\hat{y}^{\\langle t+1 \\rangle }$. This means that if $\\hat{y}^{\\langle t+1 \\rangle }_i = 0.16$, you will pick the index \"i\" with 16% probability. To implement it, you can use [`np.random.choice`](https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.random.choice.html).\n",
"\n",
"Here is an example of how to use `np.random.choice()`:\n",
"```python\n",
"np.random.seed(0)\n",
"p = np.array([0.1, 0.0, 0.7, 0.2])\n",
"index = np.random.choice([0, 1, 2, 3], p = p.ravel())\n",
"```\n",
"This means that you will pick the `index` according to the distribution: \n",
"$P(index = 0) = 0.1, P(index = 1) = 0.0, P(index = 2) = 0.7, P(index = 3) = 0.2$.\n",
"\n",
"- **Step 4**: The last step to implement in `sample()` is to overwrite the variable `x`, which currently stores $x^{\\langle t \\rangle }$, with the value of $x^{\\langle t + 1 \\rangle }$. You will represent $x^{\\langle t + 1 \\rangle }$ by creating a one-hot vector corresponding to the character you've chosen as your prediction. You will then forward propagate $x^{\\langle t + 1 \\rangle }$ in Step 1 and keep repeating the process until you get a \"\\n\" character, indicating you've reached the end of the dinosaur name. "
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# GRADED FUNCTION: sample\n",
"\n",
"def sample(parameters, char_to_ix, seed):\n",
" \"\"\"\n",
" Sample a sequence of characters according to a sequence of probability distributions output of the RNN\n",
"\n",
" Arguments:\n",
" parameters -- python dictionary containing the parameters Waa, Wax, Wya, by, and b. \n",
" char_to_ix -- python dictionary mapping each character to an index.\n",
" seed -- used for grading purposes. Do not worry about it.\n",
"\n",
" Returns:\n",
" indices -- a list of length n containing the indices of the sampled characters.\n",
" \"\"\"\n",
" \n",
" # Retrieve parameters and relevant shapes from \"parameters\" dictionary\n",
" Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']\n",
" vocab_size = by.shape[0]\n",
" n_a = Waa.shape[1]\n",
" \n",
" ### START CODE HERE ###\n",
" # Step 1: Create the one-hot vector x for the first character (initializing the sequence generation). (≈1 line)\n",
" x = np.zeros((vocab_size, 1))\n",
" # Step 1': Initialize a_prev as zeros (≈1 line)\n",
" a_prev = np.zeros((n_a, 1))\n",
" \n",
" # Create an empty list of indices, this is the list which will contain the list of indices of the characters to generate (≈1 line)\n",
" indices = []\n",
" \n",
" # Idx is a flag to detect a newline character, we initialize it to -1\n",
" idx = -1 \n",
" \n",
" # Loop over time-steps t. At each time-step, sample a character from a probability distribution and append \n",
" # its index to \"indices\". We'll stop if we reach 50 characters (which should be very unlikely with a well \n",
" # trained model), which helps debugging and prevents entering an infinite loop. \n",
" counter = 0\n",
" newline_character = char_to_ix['\\n']\n",
" \n",
" while (idx != newline_character and counter != 50):\n",
" \n",
" # Step 2: Forward propagate x using the equations (1), (2) and (3)\n",
" a = np.tanh(np.dot(Waa, a_prev) + np.dot(Wax, x) + b)\n",
" z = np.dot(Wya, a) + by\n",
" y = softmax(z)\n",
" \n",
" # for grading purposes\n",
" np.random.seed(counter+seed) \n",
" \n",
" # Step 3: Sample the index of a character within the vocabulary from the probability distribution y\n",
" idx = np.random.choice([i for i in range(vocab_size)], p = y.ravel())\n",
"\n",
" # Append the index to \"indices\"\n",
" indices.append(idx)\n",
" \n",
" # Step 4: Overwrite the input character as the one corresponding to the sampled index.\n",
" x = np.zeros((vocab_size, 1))\n",
" x[idx] = 1\n",
" \n",
" # Update \"a_prev\" to be \"a\"\n",
" a_prev = a\n",
" \n",
" # for grading purposes\n",
" seed += 1\n",
" counter +=1\n",
" \n",
" ### END CODE HERE ###\n",
"\n",
" if (counter == 50):\n",
" indices.append(char_to_ix['\\n'])\n",
" \n",
" return indices"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Sampling:\n",
"list of sampled indices: [12, 17, 24, 14, 13, 9, 10, 22, 24, 6, 13, 11, 12, 6, 21, 15, 21, 14, 3, 2, 1, 21, 18, 24, 7, 25, 6, 25, 18, 10, 16, 2, 3, 8, 15, 12, 11, 7, 1, 12, 10, 2, 7, 7, 11, 5, 6, 12, 25, 0, 0]\n",
"list of sampled characters: ['l', 'q', 'x', 'n', 'm', 'i', 'j', 'v', 'x', 'f', 'm', 'k', 'l', 'f', 'u', 'o', 'u', 'n', 'c', 'b', 'a', 'u', 'r', 'x', 'g', 'y', 'f', 'y', 'r', 'j', 'p', 'b', 'c', 'h', 'o', 'l', 'k', 'g', 'a', 'l', 'j', 'b', 'g', 'g', 'k', 'e', 'f', 'l', 'y', '\\n', '\\n']\n"
]
}
],
"source": [
"np.random.seed(2)\n",
"_, n_a = 20, 100\n",
"Wax, Waa, Wya = np.random.randn(n_a, vocab_size), np.random.randn(n_a, n_a), np.random.randn(vocab_size, n_a)\n",
"b, by = np.random.randn(n_a, 1), np.random.randn(vocab_size, 1)\n",
"parameters = {\"Wax\": Wax, \"Waa\": Waa, \"Wya\": Wya, \"b\": b, \"by\": by}\n",
"\n",
"\n",
"indices = sample(parameters, char_to_ix, 0)\n",
"print(\"Sampling:\")\n",
"print(\"list of sampled indices:\", indices)\n",
"print(\"list of sampled characters:\", [ix_to_char[i] for i in indices])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"** Expected output:**\n",
"<table>\n",
"<tr>\n",
" <td> \n",
" **list of sampled indices:**\n",
" </td>\n",
" <td> \n",
" [12, 17, 24, 14, 13, 9, 10, 22, 24, 6, 13, 11, 12, 6, 21, 15, 21, 14, 3, 2, 1, 21, 18, 24, <br>\n",
" 7, 25, 6, 25, 18, 10, 16, 2, 3, 8, 15, 12, 11, 7, 1, 12, 10, 2, 7, 7, 11, 5, 6, 12, 25, 0, 0]\n",
" </td>\n",
" </tr><tr>\n",
" <td> \n",
" **list of sampled characters:**\n",
" </td>\n",
" <td> \n",
" ['l', 'q', 'x', 'n', 'm', 'i', 'j', 'v', 'x', 'f', 'm', 'k', 'l', 'f', 'u', 'o', <br>\n",
" 'u', 'n', 'c', 'b', 'a', 'u', 'r', 'x', 'g', 'y', 'f', 'y', 'r', 'j', 'p', 'b', 'c', 'h', 'o', <br>\n",
" 'l', 'k', 'g', 'a', 'l', 'j', 'b', 'g', 'g', 'k', 'e', 'f', 'l', 'y', '\\n', '\\n']\n",
" </td>\n",
" \n",
" \n",
" \n",
"</tr>\n",
"</table>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 3 - Building the language model \n",
"\n",
"It is time to build the character-level language model for text generation. \n",
"\n",
"\n",
"### 3.1 - Gradient descent \n",
"\n",
"In this section you will implement a function performing one step of stochastic gradient descent (with clipped gradients). You will go through the training examples one at a time, so the optimization algorithm will be stochastic gradient descent. As a reminder, here are the steps of a common optimization loop for an RNN:\n",
"\n",
"- Forward propagate through the RNN to compute the loss\n",
"- Backward propagate through time to compute the gradients of the loss with respect to the parameters\n",
"- Clip the gradients if necessary \n",
"- Update your parameters using gradient descent \n",
"\n",
"**Exercise**: Implement this optimization process (one step of stochastic gradient descent). \n",
"\n",
"We provide you with the following functions: \n",
"\n",
"```python\n",
"def rnn_forward(X, Y, a_prev, parameters):\n",
" \"\"\" Performs the forward propagation through the RNN and computes the cross-entropy loss.\n",
" It returns the loss' value as well as a \"cache\" storing values to be used in the backpropagation.\"\"\"\n",
" ....\n",
" return loss, cache\n",
" \n",
"def rnn_backward(X, Y, parameters, cache):\n",
" \"\"\" Performs the backward propagation through time to compute the gradients of the loss with respect\n",
" to the parameters. It returns also all the hidden states.\"\"\"\n",
" ...\n",
" return gradients, a\n",
"\n",
"def update_parameters(parameters, gradients, learning_rate):\n",
" \"\"\" Updates parameters using the Gradient Descent Update Rule.\"\"\"\n",
" ...\n",
" return parameters\n",
"```"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# GRADED FUNCTION: optimize\n",
"\n",
"def optimize(X, Y, a_prev, parameters, learning_rate = 0.01):\n",
" \"\"\"\n",
" Execute one step of the optimization to train the model.\n",
" \n",
" Arguments:\n",
" X -- list of integers, where each integer is a number that maps to a character in the vocabulary.\n",
" Y -- list of integers, exactly the same as X but shifted one index to the left.\n",
" a_prev -- previous hidden state.\n",
" parameters -- python dictionary containing:\n",
" Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)\n",
" Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)\n",
" Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)\n",
" b -- Bias, numpy array of shape (n_a, 1)\n",
" by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)\n",
" learning_rate -- learning rate for the model.\n",
" \n",
" Returns:\n",
" loss -- value of the loss function (cross-entropy)\n",
" gradients -- python dictionary containing:\n",
" dWax -- Gradients of input-to-hidden weights, of shape (n_a, n_x)\n",
" dWaa -- Gradients of hidden-to-hidden weights, of shape (n_a, n_a)\n",
" dWya -- Gradients of hidden-to-output weights, of shape (n_y, n_a)\n",
" db -- Gradients of bias vector, of shape (n_a, 1)\n",
" dby -- Gradients of output bias vector, of shape (n_y, 1)\n",
" a[len(X)-1] -- the last hidden state, of shape (n_a, 1)\n",
" \"\"\"\n",
" \n",
" ### START CODE HERE ###\n",
" \n",
" # Forward propagate through time (≈1 line)\n",
" loss, cache = rnn_forward(X, Y, a_prev, parameters)\n",
" \n",
" # Backpropagate through time (≈1 line)\n",
" gradients, a = rnn_backward(X, Y, parameters, cache)\n",
" \n",
" # Clip your gradients between -5 (min) and 5 (max) (≈1 line)\n",
" gradients = clip(gradients, 5)\n",
" \n",
" # Update parameters (≈1 line)\n",
" parameters = update_parameters(parameters, gradients, learning_rate)\n",
" \n",
" ### END CODE HERE ###\n",
" \n",
" return loss, gradients, a[len(X)-1]"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Loss = 126.503975722\n",
"gradients[\"dWaa\"][1][2] = 0.194709315347\n",
"np.argmax(gradients[\"dWax\"]) = 93\n",
"gradients[\"dWya\"][1][2] = -0.007773876032\n",
"gradients[\"db\"][4] = [-0.06809825]\n",
"gradients[\"dby\"][1] = [ 0.01538192]\n",
"a_last[4] = [-1.]\n"
]
}
],
"source": [
"np.random.seed(1)\n",
"vocab_size, n_a = 27, 100\n",
"a_prev = np.random.randn(n_a, 1)\n",
"Wax, Waa, Wya = np.random.randn(n_a, vocab_size), np.random.randn(n_a, n_a), np.random.randn(vocab_size, n_a)\n",
"b, by = np.random.randn(n_a, 1), np.random.randn(vocab_size, 1)\n",
"parameters = {\"Wax\": Wax, \"Waa\": Waa, \"Wya\": Wya, \"b\": b, \"by\": by}\n",
"X = [12,3,5,11,22,3]\n",
"Y = [4,14,11,22,25, 26]\n",
"\n",
"loss, gradients, a_last = optimize(X, Y, a_prev, parameters, learning_rate = 0.01)\n",
"print(\"Loss =\", loss)\n",
"print(\"gradients[\\\"dWaa\\\"][1][2] =\", gradients[\"dWaa\"][1][2])\n",
"print(\"np.argmax(gradients[\\\"dWax\\\"]) =\", np.argmax(gradients[\"dWax\"]))\n",
"print(\"gradients[\\\"dWya\\\"][1][2] =\", gradients[\"dWya\"][1][2])\n",
"print(\"gradients[\\\"db\\\"][4] =\", gradients[\"db\"][4])\n",
"print(\"gradients[\\\"dby\\\"][1] =\", gradients[\"dby\"][1])\n",
"print(\"a_last[4] =\", a_last[4])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"** Expected output:**\n",
"\n",
"<table>\n",
"\n",
"\n",
"<tr>\n",
" <td> \n",
" **Loss **\n",
" </td>\n",
" <td> \n",
" 126.503975722\n",
" </td>\n",
"</tr>\n",
"<tr>\n",
" <td> \n",
" **gradients[\"dWaa\"][1][2]**\n",
" </td>\n",
" <td> \n",
" 0.194709315347\n",
" </td>\n",
"<tr>\n",
" <td> \n",
" **np.argmax(gradients[\"dWax\"])**\n",
" </td>\n",
" <td> 93\n",
" </td>\n",
"</tr>\n",
"<tr>\n",
" <td> \n",
" **gradients[\"dWya\"][1][2]**\n",
" </td>\n",
" <td> -0.007773876032\n",
" </td>\n",
"</tr>\n",
"<tr>\n",
" <td> \n",
" **gradients[\"db\"][4]**\n",
" </td>\n",
" <td> [-0.06809825]\n",
" </td>\n",
"</tr>\n",
"<tr>\n",
" <td> \n",
" **gradients[\"dby\"][1]**\n",
" </td>\n",
" <td>[ 0.01538192]\n",
" </td>\n",
"</tr>\n",
"<tr>\n",
" <td> \n",
" **a_last[4]**\n",
" </td>\n",
" <td> [-1.]\n",
" </td>\n",
"</tr>\n",
"\n",
"</table>"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"### 3.2 - Training the model "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Given the dataset of dinosaur names, we use each line of the dataset (one name) as one training example. Every 100 steps of stochastic gradient descent, you will sample 10 randomly chosen names to see how the algorithm is doing. Remember to shuffle the dataset, so that stochastic gradient descent visits the examples in random order. \n",
"\n",
"**Exercise**: Follow the instructions and implement `model()`. When `examples[index]` contains one dinosaur name (string), to create an example (X, Y), you can use this:\n",
"```python\n",
" index = j % len(examples)\n",
" X = [None] + [char_to_ix[ch] for ch in examples[index]] \n",
" Y = X[1:] + [char_to_ix[\"\\n\"]]\n",
"```\n",
"Note that we use: `index= j % len(examples)`, where `j = 1....num_iterations`, to make sure that `examples[index]` is always a valid statement (`index` is smaller than `len(examples)`).\n",
"The first entry of `X` being `None` will be interpreted by `rnn_forward()` as setting $x^{\\langle 0 \\rangle} = \\vec{0}$. Further, this ensures that `Y` is equal to `X` but shifted one step to the left, and with an additional \"\\n\" appended to signify the end of the dinosaur name. "
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# GRADED FUNCTION: model\n",
"\n",
"def model(data, ix_to_char, char_to_ix, num_iterations = 35000, n_a = 50, dino_names = 7, vocab_size = 27):\n",
" \"\"\"\n",
" Trains the model and generates dinosaur names. \n",
" \n",
" Arguments:\n",
" data -- text corpus\n",
" ix_to_char -- dictionary that maps the index to a character\n",
" char_to_ix -- dictionary that maps a character to an index\n",
" num_iterations -- number of iterations to train the model for\n",
" n_a -- number of units of the RNN cell\n",
" dino_names -- number of dinosaur names you want to sample at each iteration. \n",
" vocab_size -- number of unique characters found in the text, size of the vocabulary\n",
" \n",
" Returns:\n",
" parameters -- learned parameters\n",
" \"\"\"\n",
" \n",
" # Retrieve n_x and n_y from vocab_size\n",
" n_x, n_y = vocab_size, vocab_size\n",
" \n",
" # Initialize parameters\n",
" parameters = initialize_parameters(n_a, n_x, n_y)\n",
" \n",
" # Initialize loss (this is required because we want to smooth our loss, don't worry about it)\n",
" loss = get_initial_loss(vocab_size, dino_names)\n",
" \n",
" # Build list of all dinosaur names (training examples).\n",
" with open(\"dinos.txt\") as f:\n",
" examples = f.readlines()\n",
" examples = [x.lower().strip() for x in examples]\n",
" \n",
" # Shuffle list of all dinosaur names\n",
" np.random.seed(0)\n",
" np.random.shuffle(examples)\n",
" \n",
" # Initialize the hidden state of your LSTM\n",
" a_prev = np.zeros((n_a, 1))\n",
" \n",
" # Optimization loop\n",
" for j in range(num_iterations):\n",
" \n",
" ### START CODE HERE ###\n",
" \n",
" # Use the hint above to define one training example (X,Y) (≈ 2 lines)\n",
" index = j % len(examples)\n",
" X = [None] + [char_to_ix[ch] for ch in examples[index]]\n",
" Y = X[1:] + [char_to_ix['\\n']]\n",
" \n",
" # Perform one optimization step: Forward-prop -> Backward-prop -> Clip -> Update parameters\n",
" # Choose a learning rate of 0.01\n",
" curr_loss, gradients, a_prev = optimize(X, Y, a_prev, parameters)\n",
" \n",
" ### END CODE HERE ###\n",
" \n",
" # Use a latency trick to keep the loss smooth. It happens here to accelerate the training.\n",
" loss = smooth(loss, curr_loss)\n",
"\n",
" # Every 2000 Iteration, generate \"n\" characters thanks to sample() to check if the model is learning properly\n",
" if j % 2000 == 0:\n",
" \n",
" print('Iteration: %d, Loss: %f' % (j, loss) + '\\n')\n",
" \n",
" # The number of dinosaur names to print\n",
" seed = 0\n",
" for name in range(dino_names):\n",
" \n",
" # Sample indices and print them\n",
" sampled_indices = sample(parameters, char_to_ix, seed)\n",
" print_sample(sampled_indices, ix_to_char)\n",
" \n",
" seed += 1 # To get the same result for grading purposed, increment the seed by one. \n",
" \n",
" print('\\n')\n",
" \n",
" return parameters"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Run the following cell, you should observe your model outputting random-looking characters at the first iteration. After a few thousand iterations, your model should learn to generate reasonable-looking names. "
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Iteration: 0, Loss: 23.087336\n",
"\n",
"Nkzxwtdmfqoeyhsqwasjkjvu\n",
"Kneb\n",
"Kzxwtdmfqoeyhsqwasjkjvu\n",
"Neb\n",
"Zxwtdmfqoeyhsqwasjkjvu\n",
"Eb\n",
"Xwtdmfqoeyhsqwasjkjvu\n",
"\n",
"\n",
"Iteration: 2000, Loss: 27.884160\n",
"\n",
"Liusskeomnolxeros\n",
"Hmdaairus\n",
"Hytroligoraurus\n",
"Lecalosapaus\n",
"Xusicikoraurus\n",
"Abalpsamantisaurus\n",
"Tpraneronxeros\n",
"\n",
"\n",
"Iteration: 4000, Loss: 25.901815\n",
"\n",
"Mivrosaurus\n",
"Inee\n",
"Ivtroplisaurus\n",
"Mbaaisaurus\n",
"Wusichisaurus\n",
"Cabaselachus\n",
"Toraperlethosdarenitochusthiamamumamaon\n",
"\n",
"\n",
"Iteration: 6000, Loss: 24.608779\n",
"\n",
"Onwusceomosaurus\n",
"Lieeaerosaurus\n",
"Lxussaurus\n",
"Oma\n",
"Xusteonosaurus\n",
"Eeahosaurus\n",
"Toreonosaurus\n",
"\n",
"\n",
"Iteration: 8000, Loss: 24.070350\n",
"\n",
"Onxusichepriuon\n",
"Kilabersaurus\n",
"Lutrodon\n",
"Omaaerosaurus\n",
"Xutrcheps\n",
"Edaksoje\n",
"Trodiktonus\n",
"\n",
"\n",
"Iteration: 10000, Loss: 23.844446\n",
"\n",
"Onyusaurus\n",
"Klecalosaurus\n",
"Lustodon\n",
"Ola\n",
"Xusodonia\n",
"Eeaeosaurus\n",
"Troceosaurus\n",
"\n",
"\n",
"Iteration: 12000, Loss: 23.291971\n",
"\n",
"Onyxosaurus\n",
"Kica\n",
"Lustrepiosaurus\n",
"Olaagrraiansaurus\n",
"Yuspangosaurus\n",
"Eealosaurus\n",
"Trognesaurus\n",
"\n",
"\n",
"Iteration: 14000, Loss: 23.382339\n",
"\n",
"Meutromodromurus\n",
"Inda\n",
"Iutroinatorsaurus\n",
"Maca\n",
"Yusteratoptititan\n",
"Ca\n",
"Troclosaurus\n",
"\n",
"\n",
"Iteration: 16000, Loss: 23.288447\n",
"\n",
"Meuspsangosaurus\n",
"Ingaa\n",
"Iusosaurus\n",
"Macalosaurus\n",
"Yushanis\n",
"Daalosaurus\n",
"Trpandon\n",
"\n",
"\n",
"Iteration: 18000, Loss: 22.823526\n",
"\n",
"Phytrolonhonyg\n",
"Mela\n",
"Mustrerasaurus\n",
"Peg\n",
"Ytronorosaurus\n",
"Ehalosaurus\n",
"Trolomeehus\n",
"\n",
"\n",
"Iteration: 20000, Loss: 23.041871\n",
"\n",
"Nousmofonosaurus\n",
"Loma\n",
"Lytrognatiasaurus\n",
"Ngaa\n",
"Ytroenetiaudostarmilus\n",
"Eiafosaurus\n",
"Troenchulunosaurus\n",
"\n",
"\n",
"Iteration: 22000, Loss: 22.728849\n",
"\n",
"Piutyrangosaurus\n",
"Midaa\n",
"Myroranisaurus\n",
"Pedadosaurus\n",
"Ytrodon\n",
"Eiadosaurus\n",
"Trodoniomusitocorces\n",
"\n",
"\n",
"Iteration: 24000, Loss: 22.683403\n",
"\n",
"Meutromeisaurus\n",
"Indeceratlapsaurus\n",
"Jurosaurus\n",
"Ndaa\n",
"Yusicheropterus\n",
"Eiaeropectus\n",
"Trodonasaurus\n",
"\n",
"\n",
"Iteration: 26000, Loss: 22.554523\n",
"\n",
"Phyusaurus\n",
"Liceceron\n",
"Lyusichenodylus\n",
"Pegahus\n",
"Yustenhtonthosaurus\n",
"Elagosaurus\n",
"Trodontonsaurus\n",
"\n",
"\n",
"Iteration: 28000, Loss: 22.484472\n",
"\n",
"Onyutimaerihus\n",
"Koia\n",
"Lytusaurus\n",
"Ola\n",
"Ytroheltorus\n",
"Eiadosaurus\n",
"Trofiashates\n",
"\n",
"\n",
"Iteration: 30000, Loss: 22.774404\n",
"\n",
"Phytys\n",
"Lica\n",
"Lysus\n",
"Pacalosaurus\n",
"Ytrochisaurus\n",
"Eiacosaurus\n",
"Trochesaurus\n",
"\n",
"\n",
"Iteration: 32000, Loss: 22.209473\n",
"\n",
"Mawusaurus\n",
"Jica\n",
"Lustoia\n",
"Macaisaurus\n",
"Yusolenqtesaurus\n",
"Eeaeosaurus\n",
"Trnanatrax\n",
"\n",
"\n",
"Iteration: 34000, Loss: 22.396744\n",
"\n",
"Mavptokekus\n",
"Ilabaisaurus\n",
"Itosaurus\n",
"Macaesaurus\n",
"Yrosaurus\n",
"Eiaeosaurus\n",
"Trodon\n",
"\n",
"\n"
]
}
],
"source": [
"parameters = model(data, ix_to_char, char_to_ix)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"## Conclusion\n",
"\n",
"You can see that your algorithm has started to generate plausible dinosaur names towards the end of the training. At first, it was generating random characters, but towards the end you could see dinosaur names with cool endings. Feel free to run the algorithm even longer and play with hyperparameters to see if you can get even better results. Our implemetation generated some really cool names like `maconucon`, `marloralus` and `macingsersaurus`. Your model hopefully also learned that dinosaur names tend to end in `saurus`, `don`, `aura`, `tor`, etc.\n",
"\n",
"If your model generates some non-cool names, don't blame the model entirely--not all actual dinosaur names sound cool. (For example, `dromaeosauroides` is an actual dinosaur name and is in the training set.) But this model should give you a set of candidates from which you can pick the coolest! \n",
"\n",
"This assignment had used a relatively small dataset, so that you could train an RNN quickly on a CPU. Training a model of the english language requires a much bigger dataset, and usually needs much more computation, and could run for many hours on GPUs. We ran our dinosaur name for quite some time, and so far our favoriate name is the great, undefeatable, and fierce: Mangosaurus!\n",
"\n",
"<img src=\"images/mangosaurus.jpeg\" style=\"width:250;height:300px;\">"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 4 - Writing like Shakespeare\n",
"\n",
"The rest of this notebook is optional and is not graded, but we hope you'll do it anyway since it's quite fun and informative. \n",
"\n",
"A similar (but more complicated) task is to generate Shakespeare poems. Instead of learning from a dataset of Dinosaur names you can use a collection of Shakespearian poems. Using LSTM cells, you can learn longer term dependencies that span many characters in the text--e.g., where a character appearing somewhere a sequence can influence what should be a different character much much later in ths sequence. These long term dependencies were less important with dinosaur names, since the names were quite short. \n",
"\n",
"\n",
"<img src=\"images/shakespeare.jpg\" style=\"width:500;height:400px;\">\n",
"<caption><center> Let's become poets! </center></caption>\n",
"\n",
"We have implemented a Shakespeare poem generator with Keras. Run the following cell to load the required packages and models. This may take a few minutes. "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from __future__ import print_function\n",
"from keras.callbacks import LambdaCallback\n",
"from keras.models import Model, load_model, Sequential\n",
"from keras.layers import Dense, Activation, Dropout, Input, Masking\n",
"from keras.layers import LSTM\n",
"from keras.utils.data_utils import get_file\n",
"from keras.preprocessing.sequence import pad_sequences\n",
"from shakespeare_utils import *\n",
"import sys\n",
"import io"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To save you some time, we have already trained a model for ~1000 epochs on a collection of Shakespearian poems called [*\"The Sonnets\"*](shakespeare.txt). "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's train the model for one more epoch. When it finishes training for an epoch---this will also take a few minutes---you can run `generate_output`, which will prompt asking you for an input (`<`40 characters). The poem will start with your sentence, and our RNN-Shakespeare will complete the rest of the poem for you! For example, try \"Forsooth this maketh no sense \" (don't enter the quotation marks). Depending on whether you include the space at the end, your results might also differ--try it both ways, and try other inputs as well. \n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true,
"scrolled": true
},
"outputs": [],
"source": [
"print_callback = LambdaCallback(on_epoch_end=on_epoch_end)\n",
"\n",
"model.fit(x, y, batch_size=128, epochs=1, callbacks=[print_callback])"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Run this cell to try with different inputs without having to re-train the model \n",
"generate_output()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The RNN-Shakespeare model is very similar to the one you have built for dinosaur names. The only major differences are:\n",
"- LSTMs instead of the basic RNN to capture longer-range dependencies\n",
"- The model is a deeper, stacked LSTM model (2 layer)\n",
"- Using Keras instead of python to simplify the code \n",
"\n",
"If you want to learn more, you can also check out the Keras Team's text generation implementation on GitHub: https://github.com/keras-team/keras/blob/master/examples/lstm_text_generation.py.\n",
"\n",
"Congratulations on finishing this notebook! "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**References**:\n",
"- This exercise took inspiration from Andrej Karpathy's implementation: https://gist.github.com/karpathy/d4dee566867f8291f086. To learn more about text generation, also check out Karpathy's [blog post](http://karpathy.github.io/2015/05/21/rnn-effectiveness/).\n",
"- For the Shakespearian poem generator, our implementation was based on the implementation of an LSTM text generator by the Keras team: https://github.com/keras-team/keras/blob/master/examples/lstm_text_generation.py "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"coursera": {
"course_slug": "nlp-sequence-models",
"graded_item_id": "1dYg0",
"launcher_item_id": "MLhxP"
},
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.0"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
csaladenes/blog | airports/airportia_ro_arrv_parser.ipynb | 2 | 25631 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import pandas as pd, json, numpy as np\n",
"import matplotlib.pyplot as plt\n",
"%matplotlib inline"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"url='http://en.wikipedia.org/wiki/List_of_airports_in_Romania'\n",
"df=pd.read_html(url)\n",
"df=df[0].loc[:17].T.set_index(0).T.loc[2:].set_index('IATA')"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>City served</th>\n",
" <th>ICAO</th>\n",
" <th>Airport name</th>\n",
" <th>Website</th>\n",
" <th>Frequency</th>\n",
" <th>Status</th>\n",
" <th>nan</th>\n",
" </tr>\n",
" <tr>\n",
" <th>IATA</th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>ARW</th>\n",
" <td>Arad</td>\n",
" <td>LRAR</td>\n",
" <td>Arad International Airport</td>\n",
" <td>http://www.aeroportularad.ro</td>\n",
" <td>TWR 130.2 MHz</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>BCM</th>\n",
" <td>Bacău</td>\n",
" <td>LRBC</td>\n",
" <td>Bacău \"George Enescu\" International Airport [14]</td>\n",
" <td>http://www.bacauairport.ro</td>\n",
" <td>TWR 118.6 MHz</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>BAY</th>\n",
" <td>Baia Mare / Tăuții-Măgherăuș</td>\n",
" <td>LRBM</td>\n",
" <td>Baia Mare Airport (Tăuții-Măgherăuș Airport)</td>\n",
" <td>http://www.baiamareairport.ro</td>\n",
" <td>TWR 123.6 MHz</td>\n",
" <td>Closed for renovation</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>BBU</th>\n",
" <td>Bucharest / Băneasa</td>\n",
" <td>LRBS</td>\n",
" <td>Bucharest \"Aurel Vlaicu\" International Airport...</td>\n",
" <td>http://www.baneasa.aero</td>\n",
" <td>APP 127.6 MHz TWR 120.8 MHz</td>\n",
" <td>Only private flights</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>OTP</th>\n",
" <td>Bucharest / Otopeni</td>\n",
" <td>LROP</td>\n",
" <td>Bucharest \"Henri Coandǎ\" International Airport...</td>\n",
" <td>http://www.otp-airport.ro</td>\n",
" <td>APP 126.2 TWR1 120.9 TWR2 121.85</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>CLJ</th>\n",
" <td>Cluj-Napoca</td>\n",
" <td>LRCL</td>\n",
" <td>Cluj \"Avram Iancu\" International Airport</td>\n",
" <td>http://www.airportcluj.ro</td>\n",
" <td>APP 125.1 MHz TWR 134.4 MHz</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>CND</th>\n",
" <td>Constanța</td>\n",
" <td>LRCK</td>\n",
" <td>Constanța \"Mihail Kogălniceanu\" International ...</td>\n",
" <td>http://www.mk-airport.ro</td>\n",
" <td>TWR 120.24 MHz</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>CRA</th>\n",
" <td>Craiova</td>\n",
" <td>LRCV</td>\n",
" <td>Craiova Airport</td>\n",
" <td>http://www.aeroportcraiova.ro</td>\n",
" <td>TWR 124.3 MHz</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>IAS</th>\n",
" <td>Iași</td>\n",
" <td>LRIA</td>\n",
" <td>Iași International Airport</td>\n",
" <td>http://www.aeroport.ro</td>\n",
" <td>TWR 119.2 MHz</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>OMR</th>\n",
" <td>Oradea</td>\n",
" <td>LROD</td>\n",
" <td>Oradea International Airport</td>\n",
" <td>http://www.aeroportoradea.ro</td>\n",
" <td>TWR 120.2 MHz</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>SUJ</th>\n",
" <td>Satu Mare</td>\n",
" <td>LRSM</td>\n",
" <td>Satu Mare International Airport</td>\n",
" <td>http://www.aeroportulsm.ro</td>\n",
" <td>TWR 118.8 MHz</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>SBZ</th>\n",
" <td>Sibiu</td>\n",
" <td>LRSB</td>\n",
" <td>Sibiu International Airport</td>\n",
" <td>NaN</td>\n",
" <td>TWR 122.7 MHz</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>SCV</th>\n",
" <td>Suceava</td>\n",
" <td>LRSV</td>\n",
" <td>Suceava \"Ștefan cel Mare\" International Airport</td>\n",
" <td>http://www.aeroportsuceava.ro</td>\n",
" <td>APP 120.9 MHz TWR 118.3 MHz</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>TGM</th>\n",
" <td>Târgu Mureș</td>\n",
" <td>LRTM</td>\n",
" <td>\"Transilvania\" Târgu Mureș Airport</td>\n",
" <td>http://www.targumuresairport.ro</td>\n",
" <td>APP 121.9 MHz TWR 125.9 MHz</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>TSR</th>\n",
" <td>Timișoara</td>\n",
" <td>LRTR</td>\n",
" <td>Timișoara \"Traian Vuia\" International Airport ...</td>\n",
" <td>http://www.aerotim.ro</td>\n",
" <td>TWR 101.1 MHz</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>TCE</th>\n",
" <td>Tulcea</td>\n",
" <td>LRTC</td>\n",
" <td>\"Delta Dunarii\" Tulcea Airport (Cataloi Airport)</td>\n",
" <td>http://www.aeroportul-tulcea.ro/</td>\n",
" <td>APP/TWR 120.3 MHz</td>\n",
" <td>Closed</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
"0 City served ICAO \\\n",
"IATA \n",
"ARW Arad LRAR \n",
"BCM Bacău LRBC \n",
"BAY Baia Mare / Tăuții-Măgherăuș LRBM \n",
"BBU Bucharest / Băneasa LRBS \n",
"OTP Bucharest / Otopeni LROP \n",
"CLJ Cluj-Napoca LRCL \n",
"CND Constanța LRCK \n",
"CRA Craiova LRCV \n",
"IAS Iași LRIA \n",
"OMR Oradea LROD \n",
"SUJ Satu Mare LRSM \n",
"SBZ Sibiu LRSB \n",
"SCV Suceava LRSV \n",
"TGM Târgu Mureș LRTM \n",
"TSR Timișoara LRTR \n",
"TCE Tulcea LRTC \n",
"\n",
"0 Airport name \\\n",
"IATA \n",
"ARW Arad International Airport \n",
"BCM Bacău \"George Enescu\" International Airport [14] \n",
"BAY Baia Mare Airport (Tăuții-Măgherăuș Airport) \n",
"BBU Bucharest \"Aurel Vlaicu\" International Airport... \n",
"OTP Bucharest \"Henri Coandǎ\" International Airport... \n",
"CLJ Cluj \"Avram Iancu\" International Airport \n",
"CND Constanța \"Mihail Kogălniceanu\" International ... \n",
"CRA Craiova Airport \n",
"IAS Iași International Airport \n",
"OMR Oradea International Airport \n",
"SUJ Satu Mare International Airport \n",
"SBZ Sibiu International Airport \n",
"SCV Suceava \"Ștefan cel Mare\" International Airport \n",
"TGM \"Transilvania\" Târgu Mureș Airport \n",
"TSR Timișoara \"Traian Vuia\" International Airport ... \n",
"TCE \"Delta Dunarii\" Tulcea Airport (Cataloi Airport) \n",
"\n",
"0 Website Frequency \\\n",
"IATA \n",
"ARW http://www.aeroportularad.ro TWR 130.2 MHz \n",
"BCM http://www.bacauairport.ro TWR 118.6 MHz \n",
"BAY http://www.baiamareairport.ro TWR 123.6 MHz \n",
"BBU http://www.baneasa.aero APP 127.6 MHz TWR 120.8 MHz \n",
"OTP http://www.otp-airport.ro APP 126.2 TWR1 120.9 TWR2 121.85 \n",
"CLJ http://www.airportcluj.ro APP 125.1 MHz TWR 134.4 MHz \n",
"CND http://www.mk-airport.ro TWR 120.24 MHz \n",
"CRA http://www.aeroportcraiova.ro TWR 124.3 MHz \n",
"IAS http://www.aeroport.ro TWR 119.2 MHz \n",
"OMR http://www.aeroportoradea.ro TWR 120.2 MHz \n",
"SUJ http://www.aeroportulsm.ro TWR 118.8 MHz \n",
"SBZ NaN TWR 122.7 MHz \n",
"SCV http://www.aeroportsuceava.ro APP 120.9 MHz TWR 118.3 MHz \n",
"TGM http://www.targumuresairport.ro APP 121.9 MHz TWR 125.9 MHz \n",
"TSR http://www.aerotim.ro TWR 101.1 MHz \n",
"TCE http://www.aeroportul-tulcea.ro/ APP/TWR 120.3 MHz \n",
"\n",
"0 Status NaN \n",
"IATA \n",
"ARW NaN NaN \n",
"BCM NaN NaN \n",
"BAY Closed for renovation NaN \n",
"BBU Only private flights NaN \n",
"OTP NaN NaN \n",
"CLJ NaN NaN \n",
"CND NaN NaN \n",
"CRA NaN NaN \n",
"IAS NaN NaN \n",
"OMR NaN NaN \n",
"SUJ NaN NaN \n",
"SBZ NaN NaN \n",
"SCV NaN NaN \n",
"TGM NaN NaN \n",
"TSR NaN NaN \n",
"TCE Closed NaN "
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from pygeocoder import Geocoder\n",
"apik='AIzaSyDybC2OroTE_XDJTuxjKruxFpby5VDhEGk'"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"ARW\n",
"BCM\n",
"BAY\n",
"BBU\n",
"OTP\n",
"CLJ\n",
"CND\n",
"CRA\n",
"IAS\n",
"OMR\n",
"SUJ\n",
"SBZ\n",
"SCV\n",
"TGM\n",
"TSR\n",
"TCE\n"
]
}
],
"source": [
"locations={}\n",
"for i in df.index:\n",
" results = Geocoder(apik).geocode(i+' airport romania')\n",
" locations[i]=results[0].coordinates\n",
" print i"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"file(\"locations_ro.json\",'w').write(json.dumps(locations))"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"locations=json.loads(file('locations_ro.json','r').read())"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import requests"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"BCM https://www.airportia.com/romania/bacău-airport/\n",
"SCV https://www.airportia.com/romania/suceava-stefan-cel-mare-airport\n",
"CLJ https://www.airportia.com/romania/cluj_napoca-international-airport\n",
"ARW https://www.airportia.com/romania/arad-international-airport/arrivals\n",
"SBZ https://www.airportia.com/romania/sibiu-international-airport/\n",
"SUJ https://www.airportia.com/romania/satu-mare-airport/arrivals\n",
"BAY https://www.airportia.com/romania/tautii-magheraus-airport\n",
"OMR https://www.airportia.com/romania/oradea-international-airport/\n",
"CND https://www.airportia.com/romania/mihail-kogălniceanu-international-airport\n",
"CRA https://www.airportia.com/romania/craiova-airport/arrivals\n",
"OTP https://www.airportia.com/romania/henri-coandă-international-airport\n",
"BBU https://www.airportia.com/romania/băneasa...airport/departures\n",
"TCE https://www.airportia.com/romania/tulcea-airport\n",
"TSR https://www.airportia.com/romania/timişoara-traian-vuia-airport/\n",
"IAS https://www.airportia.com/romania/iaşi-airport/arrivals\n",
"TGM https://www.airportia.com/romania/transilvania-târgu-mureş-international- airport\n"
]
}
],
"source": [
"airportialinks={}\n",
"for i in locations:\n",
" print i,\n",
" url='https://cse.google.com/cse?cx=partner-pub-6479063288582225%3A8064105798&cof=FORID%3A10&ie=UTF-8&q='+str(i)+'+airport+romania'\n",
" m=requests.get(url).content\n",
" z=pd.read_html(m)[5][0][0]\n",
" z=z[z.find('http'):]\n",
" airportialinks[i]=z\n",
" print z"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"https://www.airportia.com/romania/bacău-airport/\n",
"https://www.airportia.com/romania/tulcea-airport/\n",
"https://www.airportia.com/romania/cluj_napoca-international-airport/\n",
"https://www.airportia.com/romania/arad-international-airport/\n",
"https://www.airportia.com/romania/sibiu-international-airport/\n",
"https://www.airportia.com/romania/satu-mare-airport/\n",
"https://www.airportia.com/romania/tautii-magheraus-airport/\n",
"https://www.airportia.com/romania/oradea-international-airport/\n",
"https://www.airportia.com/romania/mihail-kogălniceanu-international-airport/\n",
"https://www.airportia.com/romania/craiova-airport/\n",
"https://www.airportia.com/romania/henri-coandă-international-airport/\n",
"https://www.airportia.com/romania/băneasa-international-airport/\n",
"https://www.airportia.com/romania/suceava-stefan-cel-mare-airport/\n",
"https://www.airportia.com/romania/timişoara-traian-vuia-airport/\n",
"https://www.airportia.com/romania/iaşi-airport/\n",
"https://www.airportia.com/romania/transilvania-târgu-mureş-international-airport/\n"
]
}
],
"source": [
"#reformat\n",
"for z in airportialinks:\n",
" airportialinks[z]=airportialinks[z].split('arrivals')[0].split('departures')[0].replace(' ','').replace('...','-international-')\n",
" if airportialinks[z][-1]!='/':airportialinks[z]+='/' \n",
" #manual fixes\n",
" if z=='TSR':airportialinks[z]='https://www.airportia.com/romania/timişoara-traian-vuia-airport/'\n",
" print airportialinks[z]"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"sch={}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"record schedules for 2 weeks, then augment count with weekly flight numbers.\n",
"seasonal and seasonal charter will count as once per week for 3 months, so 12/52 per week. TGM separate, since its history is in the past."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"BCM\n",
"SCV\n",
"CLJ\n",
"ARW\n",
"SBZ\n",
"SUJ\n",
"BAY\n",
"OMR\n",
"CND\n",
"CRA\n",
"OTP\n",
"BBU\n",
"TCE\n",
"TSR\n",
"IAS\n",
"TGM\n"
]
}
],
"source": [
"for i in locations:\n",
" print i\n",
" if i not in sch:sch[i]={}\n",
" if i!='TGM':\n",
" #march 11-24 = 2 weeks\n",
" for d in range (11,25):\n",
" if d not in sch[i]:\n",
" try:\n",
" url=airportialinks[i]\n",
" full=url+'arrivals/201703'+str(d)\n",
" m=requests.get(full).content\n",
" sch[i][full]=pd.read_html(m)[0]\n",
" #print full\n",
" except: pass #print 'no tables',i,d\n",
" else:\n",
" #november 17-30 = 2 weeks\n",
" for d in range (17,31):\n",
" if d not in sch[i]:\n",
" try:\n",
" url=airportialinks[i]\n",
" full=url+'arrivals/201611'+str(d)\n",
" m=requests.get(full).content\n",
" sch[i][full]=pd.read_html(m)[0]\n",
" #print full\n",
" except: pass #print 'no tables',i,d"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"mdf=pd.DataFrame()"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"for i in sch:\n",
" for d in sch[i]:\n",
" df=sch[i][d].drop(sch[i][d].columns[3:],axis=1).drop(sch[i][d].columns[0],axis=1)\n",
" df['To']=i\n",
" df['Date']=d\n",
" mdf=pd.concat([mdf,df])"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"mdf=mdf.replace('Hahn','Frankfurt')\n",
"mdf=mdf.replace('Hahn HHN','Frankfurt HHN')"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"mdf['City']=[i[:i.rfind(' ')] for i in mdf['From']]\n",
"mdf['Airport']=[i[i.rfind(' ')+1:] for i in mdf['From']]"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"file(\"mdf_ro_arrv.json\",'w').write(json.dumps(mdf.reset_index().to_json()))"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"3041"
]
},
"execution_count": 25,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"len(mdf)"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"airlines=set(mdf['Airline'])"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"cities=set(mdf['City'])"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"file(\"cities_ro_arrv.json\",'w').write(json.dumps(list(cities)))\n",
"file(\"airlines_ro_arrv.json\",'w').write(json.dumps(list(airlines)))"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"citycoords={}"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Kiev\n",
"Paris\n",
"Oslo\n",
"Basel\n",
"Beirut\n",
"Zaragoza\n",
"Liverpool\n",
"Verona\n",
"Malmo\n",
"Castellon de la Plana\n",
"Bologna\n",
"Catania\n",
"Treviso\n",
"Brussels\n",
"Bucharest\n",
"Dubai\n",
"Dublin\n",
"Rome\n",
"Varna\n",
"Luqa\n",
"Pescara\n",
"Cologne\n",
"Milan\n",
"London\n",
"Karlsruhe/Baden-Baden\n",
"Strasbourg\n",
"Dortmund\n",
"Budapest\n",
"Nurnberg\n",
"Amman\n",
"Chisinau\n",
"Vienna\n",
"Moscow\n",
"Bratislava\n",
"Berlin\n",
"Weeze\n",
"Eindhoven\n",
"Stuttgart\n",
"Alicante\n",
"Barcelona\n",
"Frankfurt\n",
"Thessaloniki\n",
"Zurich\n",
"Perugia\n",
"Madrid\n",
"Bari\n",
"Doncaster\n",
"Lyon\n",
"Istanbul\n",
"Pisa\n",
"Turin\n",
"Nice\n",
"Larnaca\n",
"Memmingen\n",
"Hannover\n",
"Malaga\n",
"Hamburg\n",
"Athens\n",
"Stockholm\n",
"Tel Aviv\n",
"Timisoara\n",
"Doha\n",
"New York\n",
"Birmingham\n",
"Florence\n",
"Pune\n",
"Satu Mare\n",
"Oradea\n",
"Valencia\n",
"Naples\n",
"Geneva\n",
"Sibiu\n",
"Munich\n",
"Glasgow\n",
"Alghero\n",
"Cluj-Napoca\n",
"Dusseldorf\n",
"Tenerife\n",
"Billund\n",
"Bristol\n",
"Copenhagen\n",
"Belgrade\n",
"Prague\n",
"Sofia\n",
"Suceava\n",
"Lisbon\n",
"Amsterdam\n",
"Iasi\n",
"Warsaw\n"
]
}
],
"source": [
"for i in cities:\n",
" if i not in citycoords:\n",
" if i==u'Birmingham': z='Birmingham, UK'\n",
" elif i==u'Valencia': z='Valencia, Spain'\n",
" elif i==u'Naples': z='Naples, Italy'\n",
" elif i==u'St. Petersburg': z='St. Petersburg, Russia'\n",
" elif i==u'Bristol': z='Bristol, UK'\n",
" else: z=i\n",
" citycoords[i]=Geocoder(apik).geocode(z)\n",
" print i"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"citysave={}\n",
"for i in citycoords:\n",
" citysave[i]={\"coords\":citycoords[i][0].coordinates,\n",
" \"country\":citycoords[i][0].country}"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"file(\"citysave_ro_arrv.json\",'w').write(json.dumps(citysave))"
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [conda root]",
"language": "python",
"name": "conda-root-py"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.12"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| mit |
keras-team/keras-io | guides/ipynb/keras_tuner/custom_tuner.ipynb | 1 | 12122 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"# Tune hyperparameters in your custom training loop\n",
"\n",
"**Authors:** Tom O'Malley, Haifeng Jin<br>\n",
"**Date created:** 2019/10/28<br>\n",
"**Last modified:** 2022/01/12<br>\n",
"**Description:** Use `HyperModel.fit()` to tune training hyperparameters (such as batch size)."
]
},
{
"cell_type": "code",
"execution_count": 0,
"metadata": {
"colab_type": "code"
},
"outputs": [],
"source": [
"!pip install keras-tuner -q"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"## Introduction\n",
"\n",
"The `HyperModel` class in KerasTuner provides a convenient way to define your\n",
"search space in a reusable object. You can override `HyperModel.build()` to\n",
"define and hypertune the model itself. To hypertune the training process (e.g.\n",
"by selecting the proper batch size, number of training epochs, or data\n",
"augmentation setup), you can override `HyperModel.fit()`, where you can access:\n",
"\n",
"- The `hp` object, which is an instance of `keras_tuner.HyperParameters`\n",
"- The model built by `HyperModel.build()`\n",
"\n",
"A basic example is shown in the \"tune model training\" section of\n",
"[Getting Started with KerasTuner](https://keras.io/guides/keras_tuner/getting_started/#tune-model-training).\n",
"\n",
"## Tuning the custom training loop\n",
"\n",
"In this guide, we will subclass the `HyperModel` class and write a custom\n",
"training loop by overriding `HyperModel.fit()`. For how to write a custom\n",
"training loop with Keras, you can refer to the guide\n",
"[Writing a training loop from scratch](https://keras.io/guides/writing_a_training_loop_from_scratch/).\n",
"\n",
"First, we import the libraries we need, and we create datasets for training and\n",
"validation. Here, we just use some random data for demonstration purposes."
]
},
{
"cell_type": "code",
"execution_count": 0,
"metadata": {
"colab_type": "code"
},
"outputs": [],
"source": [
"import keras_tuner\n",
"import tensorflow as tf\n",
"from tensorflow import keras\n",
"import numpy as np\n",
"\n",
"\n",
"x_train = np.random.rand(1000, 28, 28, 1)\n",
"y_train = np.random.randint(0, 10, (1000, 1))\n",
"x_val = np.random.rand(1000, 28, 28, 1)\n",
"y_val = np.random.randint(0, 10, (1000, 1))"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"Then, we subclass the `HyperModel` class as `MyHyperModel`. In\n",
"`MyHyperModel.build()`, we build a simple Keras model to do image\n",
"classification for 10 different classes. `MyHyperModel.fit()` accepts several\n",
"arguments. Its signature is shown below:\n",
"\n",
"```python\n",
"def fit(self, hp, model, x, y, validation_data, callbacks=None, **kwargs):\n",
"```\n",
"\n",
"* The `hp` argument is for defining the hyperparameters.\n",
"* The `model` argument is the model returned by `MyHyperModel.build()`.\n",
"* `x`, `y`, and `validation_data` are all custom-defined arguments. We will\n",
"pass our data to them by calling `tuner.search(x=x, y=y,\n",
"validation_data=(x_val, y_val))` later. You can define any number of them and\n",
"give custom names.\n",
"* The `callbacks` argument was intended to be used with `model.fit()`.\n",
"KerasTuner put some helpful Keras callbacks in it, for example, the callback\n",
"for checkpointing the model at its best epoch.\n",
"\n",
"We will manually call the callbacks in the custom training loop. Before we\n",
"can call them, we need to assign our model to them with the following code so\n",
"that they have access to the model for checkpointing.\n",
"\n",
"```py\n",
"for callback in callbacks:\n",
" callback.model = model\n",
"```\n",
"\n",
"In this example, we only called the `on_epoch_end()` method of the callbacks\n",
"to help us checkpoint the model. You may also call other callback methods\n",
"if needed. If you don't need to save the model, you don't need to use the\n",
"callbacks.\n",
"\n",
"In the custom training loop, we tune the batch size of the dataset as we wrap\n",
"the NumPy data into a `tf.data.Dataset`. Note that you can tune any\n",
"preprocessing steps here as well. We also tune the learning rate of the\n",
"optimizer.\n",
"\n",
"We will use the validation loss as the evaluation metric for the model. To\n",
"compute the mean validation loss, we will use `keras.metrics.Mean()`, which\n",
"averages the validation loss across the batches. We need to return the\n",
"validation loss for the tuner to make a record."
]
},
{
"cell_type": "code",
"execution_count": 0,
"metadata": {
"colab_type": "code"
},
"outputs": [],
"source": [
"\n",
"class MyHyperModel(keras_tuner.HyperModel):\n",
" def build(self, hp):\n",
" \"\"\"Builds a convolutional model.\"\"\"\n",
" inputs = keras.Input(shape=(28, 28, 1))\n",
" x = keras.layers.Flatten()(inputs)\n",
" x = keras.layers.Dense(\n",
" units=hp.Choice(\"units\", [32, 64, 128]), activation=\"relu\"\n",
" )(x)\n",
" outputs = keras.layers.Dense(10)(x)\n",
" return keras.Model(inputs=inputs, outputs=outputs)\n",
"\n",
" def fit(self, hp, model, x, y, validation_data, callbacks=None, **kwargs):\n",
" # Convert the datasets to tf.data.Dataset.\n",
" batch_size = hp.Int(\"batch_size\", 32, 128, step=32, default=64)\n",
" train_ds = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(\n",
" batch_size\n",
" )\n",
" validation_data = tf.data.Dataset.from_tensor_slices(validation_data).batch(\n",
" batch_size\n",
" )\n",
"\n",
" # Define the optimizer.\n",
" optimizer = keras.optimizers.Adam(\n",
" hp.Float(\"learning_rate\", 1e-4, 1e-2, sampling=\"log\", default=1e-3)\n",
" )\n",
" loss_fn = keras.losses.SparseCategoricalCrossentropy(from_logits=True)\n",
"\n",
" # The metric to track validation loss.\n",
" epoch_loss_metric = keras.metrics.Mean()\n",
"\n",
" # Function to run the train step.\n",
" @tf.function\n",
" def run_train_step(images, labels):\n",
" with tf.GradientTape() as tape:\n",
" logits = model(images)\n",
" loss = loss_fn(labels, logits)\n",
" # Add any regularization losses.\n",
" if model.losses:\n",
" loss += tf.math.add_n(model.losses)\n",
" gradients = tape.gradient(loss, model.trainable_variables)\n",
" optimizer.apply_gradients(zip(gradients, model.trainable_variables))\n",
"\n",
" # Function to run the validation step.\n",
" @tf.function\n",
" def run_val_step(images, labels):\n",
" logits = model(images)\n",
" loss = loss_fn(labels, logits)\n",
" # Update the metric.\n",
" epoch_loss_metric.update_state(loss)\n",
"\n",
" # Assign the model to the callbacks.\n",
" for callback in callbacks:\n",
" callback.model = model\n",
"\n",
" # Record the best validation loss value\n",
" best_epoch_loss = float(\"inf\")\n",
"\n",
" # The custom training loop.\n",
" for epoch in range(2):\n",
" print(f\"Epoch: {epoch}\")\n",
"\n",
" # Iterate the training data to run the training step.\n",
" for images, labels in train_ds:\n",
" run_train_step(images, labels)\n",
"\n",
" # Iterate the validation data to run the validation step.\n",
" for images, labels in validation_data:\n",
" run_val_step(images, labels)\n",
"\n",
" # Calling the callbacks after epoch.\n",
" epoch_loss = float(epoch_loss_metric.result().numpy())\n",
" for callback in callbacks:\n",
" # The \"my_metric\" is the objective passed to the tuner.\n",
" callback.on_epoch_end(epoch, logs={\"my_metric\": epoch_loss})\n",
" epoch_loss_metric.reset_states()\n",
"\n",
" print(f\"Epoch loss: {epoch_loss}\")\n",
" best_epoch_loss = min(best_epoch_loss, epoch_loss)\n",
"\n",
" # Return the evaluation metric value.\n",
" return best_epoch_loss\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"Now, we can initialize the tuner. Here, we use `Objective(\"my_metric\", \"min\")`\n",
"as our metric to be minimized. The objective name should be consistent with the\n",
"one you use as the key in the `logs` passed to the 'on_epoch_end()' method of\n",
"the callbacks. The callbacks need to use this value in the `logs` to find the\n",
"best epoch to checkpoint the model."
]
},
{
"cell_type": "code",
"execution_count": 0,
"metadata": {
"colab_type": "code"
},
"outputs": [],
"source": [
"tuner = keras_tuner.RandomSearch(\n",
" objective=keras_tuner.Objective(\"my_metric\", \"min\"),\n",
" max_trials=2,\n",
" hypermodel=MyHyperModel(),\n",
" directory=\"results\",\n",
" project_name=\"custom_training\",\n",
" overwrite=True,\n",
")\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"We start the search by passing the arguments we defined in the signature of\n",
"`MyHyperModel.fit()` to `tuner.search()`."
]
},
{
"cell_type": "code",
"execution_count": 0,
"metadata": {
"colab_type": "code"
},
"outputs": [],
"source": [
"tuner.search(x=x_train, y=y_train, validation_data=(x_val, y_val))"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"Finally, we can retrieve the results."
]
},
{
"cell_type": "code",
"execution_count": 0,
"metadata": {
"colab_type": "code"
},
"outputs": [],
"source": [
"best_hps = tuner.get_best_hyperparameters()[0]\n",
"print(best_hps.values)\n",
"\n",
"best_model = tuner.get_best_models()[0]\n",
"best_model.summary()"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text"
},
"source": [
"In summary, to tune the hyperparameters in your custom training loop, you just\n",
"override `HyperModel.fit()` to train the model and return the evaluation\n",
"results. With the provided callbacks, you can easily save the trained models at\n",
"their best epochs and load the best models later.\n",
"\n",
"To find out more about the basics of KerasTuner, please see\n",
"[Getting Started with KerasTuner](https://keras.io/guides/keras_tuner/getting_started/)."
]
}
],
"metadata": {
"colab": {
"collapsed_sections": [],
"name": "custom_tuner",
"private_outputs": false,
"provenance": [],
"toc_visible": true
},
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.0"
}
},
"nbformat": 4,
"nbformat_minor": 0
} | apache-2.0 |
softwaremechanic/Miscellaneous | Julia Ex.ipynb | 1 | 2011 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"ExecuteTime": {
"end_time": "2017-12-13T10:27:46.487645Z",
"start_time": "2017-12-13T10:27:45.440Z"
}
},
"outputs": [
{
"data": {
"text/plain": [
"randmatstat (generic function with 1 method)"
]
},
"execution_count": 1,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"function mandel(z)\n",
" c = z\n",
" maxiter = 80\n",
" for n = 1:maxiter\n",
" if abs2(z) > 4\n",
" return n-1\n",
" end\n",
" z = z^2 + c\n",
" end\n",
" return maxiter\n",
"end\n",
"\n",
"function randmatstat(t)\n",
" n = 5\n",
" v = zeros(t)\n",
" w = zeros(t)\n",
" for i = 1:t\n",
" a = randn(n,n)\n",
" b = randn(n,n)\n",
" c = randn(n,n)\n",
" d = randn(n,n)\n",
" P = [a b c d]\n",
" Q = [a b; c d]\n",
" v[i] = trace((P.'*P)^4)\n",
" w[i] = trace((Q.'*Q)^4)\n",
" end\n",
" std(v)/mean(v), std(w)/mean(w)\n",
"end"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"ExecuteTime": {
"end_time": "2017-12-13T16:59:12.902608Z",
"start_time": "2017-12-13T16:59:07.991Z"
}
},
"outputs": [
{
"data": {
"text/plain": [
"50002725"
]
},
"execution_count": 1,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"nheads = @parallel (+) for i=1:100000000\n",
" rand(Bool)\n",
"end"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Julia 0.4.7",
"language": "julia",
"name": "julia-0.4"
},
"language_info": {
"file_extension": ".jl",
"mimetype": "application/julia",
"name": "julia",
"version": "0.4.7"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| gpl-2.0 |
NGSchool2016/ngschool2016-materials | jupyter/ndolgikh/.ipynb_checkpoints/NGSchool_python-checkpoint.ipynb | 1 | 104340 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Set the matplotlib magic to notebook enable inline plots"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false,
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Populating the interactive namespace from numpy and matplotlib\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"/usr/local/lib/python2.7/dist-packages/IPython/core/magics/pylab.py:161: UserWarning: pylab import has clobbered these variables: ['random']\n",
"`%matplotlib` prevents importing * from pylab and numpy\n",
" \"\\n`%matplotlib` prevents importing * from pylab and numpy\"\n"
]
}
],
"source": [
"%pylab inline"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Calculate the Nonredundant Read Fraction (NRF)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"SAM format example:\n",
"```\n",
"SRR585264.8766235 0 1 4 15 35M * 0 0 CTTAAACAATTATTCCCCCTGCAAACATTTTCAAT GGGGGGGGGGGGGGGGGGGGGGFGGGGGGGGGGGG XT:A:U NM:i:1 X0:i:1 X1:i:6 XM:i:1 XO:i:0 XG:i:0 MD:Z:8T26\n",
"```"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Import the required modules"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import subprocess\n",
"import matplotlib.pyplot as plt\n",
"import random\n",
"import numpy as np"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Make figures prettier and biger"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"plt.style.use('ggplot')\n",
"figsize(10,5)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Parse the SAM file and extract the unique start coordinates."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"First store the file name in the variable"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"file = \"/ngschool/chip_seq/bwa/input.sorted.bam\""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Next we read the file using samtools. From each read we need to store the flag, chromosome name and start coordinate."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"p = subprocess.Popen([\"samtools\", \"view\", \"-q10\", \"-F260\", file],\n",
" stdout=subprocess.PIPE)\n",
"coords = []\n",
"for line in p.stdout:\n",
" flag, ref, start = line.decode('utf-8').split()[1:4]\n",
" coords.append([flag, ref, start])"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[[u'16', u'20', u'194'], [u'16', u'20', u'211'], [u'16', u'20', u'479']]"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"coords[:3]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"What is the total number of our unique reads?"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"1457812"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"len(coords)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Randomly sample the coordinates to get 1M for NRF calculations"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"random.seed(1234)\n",
"sample = random.sample(coords, 1000000)"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"1000000"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"len(sample)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"How many of those coordinates are **unique**? (We will use the *set* python object which only the unique items.)"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"uniqueStarts = {'watson': set(), 'crick': set()}\n",
"for coord in sample:\n",
" flag, ref, start = coord\n",
" if int(flag) & 16:\n",
" uniqueStarts['crick'].add((ref, start))\n",
" else:\n",
" uniqueStarts['watson'].add((ref, start))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"How many on the Watson strand?"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"462567"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"len(uniqueStarts['watson'])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"And on the Crick?"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"451649"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"len(uniqueStarts['crick'])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Calculate the **NRF**"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"0.914216\n"
]
}
],
"source": [
"NRF_input = (len(uniqueStarts['watson']) + len(uniqueStarts['crick']))*1.0/len(sample)\n",
"print(NRF_input)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Lets create a function from what we did above and apply it to all of our files!\n",
"\n",
"To use our function on the real sequencing datasets (not only on a small subset) we need to optimize our method a bit- we will use python module called numpy."
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def calculateNRF(filePath, pickSample=True, sampleSize=10000000, seed=1234):\n",
" p = subprocess.Popen(['samtools', 'view', '-q10', '-F260', filePath],\n",
" stdout=subprocess.PIPE)\n",
" coordType = np.dtype({'names': ['flag', 'ref', 'start'],\n",
" 'formats': ['uint16', 'U10', 'uint32']})\n",
" coordArray = np.empty(10000000, dtype=coordType)\n",
" i = 0\n",
" for line in p.stdout:\n",
" if i >= len(coordArray):\n",
" coordArray = np.append(coordArray, np.empty(1000000, dtype=coordType), axis=0)\n",
" fg, rf, st = line.decode('utf-8').split()[1:4]\n",
" coordArray[i] = np.array((fg, rf, st), dtype=coordType)\n",
" i += 1\n",
" coordArray = coordArray[:i]\n",
" sample = coordArray\n",
" if pickSample and len(coordArray) > sampleSize:\n",
" np.random.seed(seed)\n",
" sample = np.random.choice(coordArray, sampleSize, replace=False)\n",
" uniqueStarts = {'watson': set(), 'crick': set()}\n",
" for read in sample:\n",
" flag, ref, start = read\n",
" if flag & 16:\n",
" uniqueStarts['crick'].add((ref, start))\n",
" else:\n",
" uniqueStarts['watson'].add((ref, start))\n",
" NRF = (len(uniqueStarts['watson']) + len(uniqueStarts['crick']))*1.0/len(sample)\n",
" return NRF"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Calculate the NRF for the chip-seq sample"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"0.837133\n"
]
}
],
"source": [
"NRF_chip = calculateNRF(\"/ngschool/chip_seq/bwa/sox2_chip.sorted.bam\", sampleSize=1000000)\n",
"print(NRF_chip)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Plot the NRF!"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAmYAAAFJCAYAAAAxPuH0AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAGlJJREFUeJzt3X+QXXV9//HX/iCmSRbIbgJkiWDzg9Is2NCA1aRMfugI\nU62TTnU7tQVxIs7YCEE6BGyGH6mxNQzBiQE7iJF8hdZ201Z0oKgj2AoLtls0pWxESCM1EhKz3AlE\n8oPu7v3+4bBlm8QsQ3L3s5vH46977vnsve+b2T3z3HNP7tZVq9VqAAAYdvXDPQAAAL8gzAAACiHM\nOO50d3cP9wjAKOTYwtEgzDjuOHgCx4JjC0eDMAMAKIQwAwAoRJ2PywAAKEPjcA9wtGzfvn24R2CE\naGpqyp49e4Z7DGCUcWxhqFpbWw+7z1uZAACFEGYAAIUQZgAAhRBmAACFEGYAAIUQZgAAhRBmAACF\nEGYAAIUQZgAAhRBmAACFEGYAAIUQZgAAhRBmAACFEGYAAIUQZgAAhRBmAACFEGYAAIUQZgAAhRBm\nAACFEGYAAIUQZgAAhRBmAACFEGYAAIUQZgAAhRBmAACFEGYAAIUQZgAAhRBmAACFEGYAAIUQZgAA\nhRBmAACFEGYAAIUQZgAAhRBmAACFEGYAAIUQZgAAhRBmAACFEGYAAIUQZgAAhRBmAACFEGYAAIUQ\nZgAAhRBmAACFEGYAAIUQZgAAhRBmAACFEGYAAIUQZgAAhRBmAACFaKzVE/3VX/1Vvv/97+ekk07K\nLbfccsg1X/rSl7Jp06a86U1vytKlS/OWt7ylVuMBAAy7mp0xW7hwYVasWHHY/T/4wQ+yc+fOfO5z\nn8tHP/rR3HnnnbUaDQCgCDULs7PPPjvjx48/7P6urq7Mnz8/STJz5szs3bs3u3fvrtV4AADDrphr\nzCqVSlpaWga2m5ubU6lUhnEiAIDaKibMAACOdzW7+P9Impub88ILLwxsv/DCC2lubj7k2u7u7nR3\ndw9st7e3p6mp6ZjPyOgwZswY3y/AUefYwuvR0dExcLutrS1tbW1Jahxm1Wo11Wr1kPvOP//8fPOb\n38zcuXPz9NNPZ/z48Tn55JMPufa1L+BVe/bsOerzMjo1NTX5fgGOOscWhqqpqSnt7e2H3FdXPVwp\nHWVr167N5s2bs2fPnpx00klpb29Pb29v6urq8q53vStJsn79+mzatCljx47Nxz72sUybNm3Ij799\n+/ZjNTqjjIMncCw4tjBUra2th91XszA71oQZQ+XgCRwLji0M1S8LMxf/AwAUQpgBABRCmAEAFEKY\nAQAUQpgBABRCmAEAFEKYAQAUQpgBABRCmAEAFEKYAQAUQpgBABRCmAEAFEKYAQAUQpgBABRCmAEA\nFKJxuAfg2OnZ35+el3uHe4ziNOzenb6+vuEeoyiTxjdm0li/pwEMN2E2ivW83Jtrv7F1uMdgBFh9\n8bRMGjtmuMcAOO75FRkAoBDCDACgEMIMAKAQwgwAoBDCDACgEMIMAKAQwgwAoBDCDACgEMIMAKAQ\nwgwAoBDCDACgEMIMAKAQwgwAoBDCDACgEMIMAKAQjcM9AAAjS8/+/vS83DvcYxSnYffu9PX1DfcY\nRZk0vjGTxjoH9HoIMwBel56Xe3PtN7YO9xiMAKsvnpZJY8cM9xgjiowFACiEMAMAKERN38rctGlT\nNmzYkGq1moULF2bx4sWD9vf09OT222/P3r1709/fnw9+8IM577zzajkiAMCwqdkZs/7+/qxfvz4r\nVqzImjVr0tnZmeeee27Qmn/8x3/M3Llzs3r16ixbtixf/OIXazUeAMCwq1mYbdmyJVOmTMnkyZPT\n2NiYefPmpaura9Caurq67Nu3L0myd+/eNDc312o8AIBhV7O3MiuVSlpaWga2m5ubs2XLlkFrPvCB\nD2TVqlV54IEHcuDAgVx//fW1Gg8AYNgV9XEZjzzySBYsWJD3vve9efrpp7Nu3brceuutB63r7u5O\nd3f3wHZ7e3taTz/9oHUHrrsur/zZnx10/5i/+Iu86TOfGfXrG3bvTpJc/q3/l49++8sHrf/Cuy7N\nne/+0EH3W38crl9e/vez9eWsX/SZz6Tr/9xf1Pez9cWsb2hoSFNT08D9JX4/D8f6VKvp6OgY2Gxr\na0tbW1uSpK5arVYP/oqj7+mnn87GjRuzYsWKJMm9996bJIP+A8Cf/umfZsWKFQNvYV5xxRX59Kc/\nnRNPPPGIj799+/ZjMPXI9tQLr/isIYZk9cXTcnaLzxpiaBxbGCrHlkNrbW097L6aXWM2Y8aM7Nix\nI7t27Upvb286Oztz/vnnD1ozadKkPPHEE0mSn/70p/mf//mfIUUZAMBoULO3Muvr67NkyZKsWrUq\n1Wo1ixYtytSpU9PR0ZHp06dnzpw5ueSSS3LHHXfk/vvvT319fZYuXVqr8QAAhl1NrzGbPXt21q5d\nO+i+9vb2gdtTp07Npz71qVqOBABQDJ/8DwBQCGEGAFAIYQYAUAhhBgBQCGEGAFAIYQYAUAhhBgBQ\nCGEGAFAIYQYAUAhhBgBQCGEGAFAIYQYAUAhhBgBQCGEGAFAIYQYAUAhhBgBQCGEGAFAIYQYAUAhh\nBgBQCGEGAFAIYQYAUAhhBgBQCGEGAFAIYQYAUAhhBgBQCGEGAFCII4bZM888U4s5AACOe0cMs1Wr\nVg3avu66647ZMAAAx7Mjhlm1Wh20vXPnzmM2DADA8eyIYVZXV1eLOQAAjnuNR1rQ29ub73znOwNn\nznp7e/PQQw8NWrNo0aJjMx0AwHHkiGE2c+bMfPe73x3YnjFjRh5++OFBa4QZAMAbd8Qwu+mmm2ow\nBgAAb+hzzF588cXcfffdR2sWAIDj2hHPmFWr1XznO9/Js88+m9NOOy3vfve7c+DAgWzcuDEPPvhg\nZs2aVYs5AQBGvSOG2d13351HH300v/Zrv5Z//dd/zZYtW/LMM89k5syZ+fSnP50zzjhjyE+2adOm\nbNiwIdVqNQsXLszixYsPWvPoo4/m7//+71NXV5czzzwzV1555et7RQAAI9QRw+yxxx7LypUrc+qp\np+a5557L1VdfnU984hN5+9vf/rqeqL+/P+vXr88NN9yQiRMn5pOf/GQuuOCCnH766QNrduzYka99\n7WtZtWpVxo0bl5deeun1vyIAgBHqiNeY7d27N6eeemqS5PTTT8+YMWNed5QlyZYtWzJlypRMnjw5\njY2NmTdvXrq6ugat+fa3v52LLroo48aNS5KceOKJr/t5AABGqiFdY/azn/1s4HPMGhoaBm0nGQi3\nX6ZSqaSlpWVgu7m5OVu2bBm05vnnn0+SXH/99alWq3n/+9+f2bNnD+2VAACMcEcMswMHDuSKK64Y\ndN//3f67v/u7ozJMX19fduzYkZUrV6anpyc33nhj1qxZM3AGDQBgNDtimB2t6Gpubk5PT8/AdqVS\nSXNz86A1LS0tmTlzZurr63PKKaektbU1O3bsyLRp0wat6+7uTnd398B2e3t7mpqajsqco0nD7t3D\nPQIjRENDg58hhsyxhaFybDm8jo6OgdttbW1pa2tLMoQwW7ly5S/dX1dXlxtuuOGIA8yYMSM7duzI\nrl27MnHixHR2dmbZsmWD1lxwwQXp7OzMggUL8tJLL+X555/PKaecctBjvfYFvGrPnj1HnOF409fX\nN9wjMEL09fX5GWLIHFsYKseWQ2tqakp7e/sh9x0xzC688MJD3l+pVPLAAw/kwIEDQxqivr4+S5Ys\nyapVq1KtVrNo0aJMnTo1HR0dmT59eubMmZPZs2fniSeeyNVXX52GhoZccsklmTBhwpAeHwBgpKur\nvvYq/iHYs2dPvvrVr+bBBx/M3Llz8/73v3/QRf3DZfv27cM9QnGeeuGVXPuNrcM9BiPA6oun5eyW\nMcM9BiOEYwtD5dhyaK2trYfdd8QzZq/au3dvvv71r+eb3/xmfvM3fzOrV6/OaaeddlQGBABgCGH2\nyiuv5P777899992XWbNm5c///M/z5je/uRazAQAcV44YZkuXLk1/f3/e9773Zfr06XnxxRfz4osv\nDlpzzjnnHLMBAQCOF0cMszFjfvHe8Le+9a1D7q+rq8ttt912dKcCADgOHTHMbr/99lrMAQBw3Dvi\n38oEAKA2hBkAQCGEGQBAIYQZAEAhhBkAQCGEGQBAIYQZAEAhhBkAQCGEGQBAIYQZAEAhhBkAQCGE\nGQBAIYQZAEAhhBkAQCGEGQBAIYQZAEAhhBkAQCGEGQBAIYQZAEAhhBkAQCGEGQBAIYQZAEAhhBkA\nQCGEGQBAIYQZAEAhhBkAQCGEGQBAIYQZAEAhhBkAQCGEGQBAIYQZAEAhahpmmzZtylVXXZVly5bl\n3nvvPey6733ve/mDP/iDbN26tYbTAQAMr5qFWX9/f9avX58VK1ZkzZo16ezszHPPPXfQuv379+eB\nBx7IzJkzazUaAEARahZmW7ZsyZQpUzJ58uQ0NjZm3rx56erqOmjd3/7t32bx4sU54YQTajUaAEAR\nahZmlUolLS0tA9vNzc2pVCqD1vz4xz9OpVLJeeedV6uxAACKUczF/9VqNV/+8pdz6aWXDvcoAADD\norFWT9Tc3Jyenp6B7Uqlkubm5oHtffv2Zdu2bbnppptSrVaze/fu3HzzzVm+fHmmTZs26LG6u7vT\n3d09sN3e3p6mpqZj/yJGmIbdu4d7BEaIhoYGP0MMmWMLQ+XYcngdHR0Dt9va2tLW1pakhmE2Y8aM\n7NixI7t27crEiRPT2dmZZcuWDewfN25cvvjFLw5sr1y5Mpdeeml+9Vd/9aDHeu0LeNWePXuO3fAj\nVF9f33CPwAjR19fnZ4ghc2xhqBxbDq2pqSnt7e2H3FezMKuvr8+SJUuyatWqVKvVLFq0KFOnTk1H\nR0emT5+eOXPmHPQ11Wq1VuMBAAy7moVZksyePTtr164ddN/hivHGG2+sxUgAAMUo5uJ/AIDjnTAD\nACiEMAMAKIQwAwAohDADACiEMAMAKIQwAwAohDADACiEMAMAKIQwAwAohDADACiEMAMAKIQwAwAo\nhDADACiEMAMAKIQwAwAohDADACiEMAMAKIQwAwAohDADACiEMAMAKIQwAwAohDADACiEMAMAKIQw\nAwAohDADACiEMAMAKIQwAwAohDADACiEMAMAKIQwAwAohDADACiEMAMAKIQwAwAohDADACiEMAMA\nKERjLZ9s06ZN2bBhQ6rVahYuXJjFixcP2n/ffffloYceSkNDQ0488cR87GMfy6RJk2o5IgDAsKlZ\nmPX392f9+vW54YYbMnHixHzyk5/MBRdckNNPP31gzbRp0/Lud787Y8aMybe+9a3cc889ueqqq2o1\nIgDAsKrZW5lbtmzJlClTMnny5DQ2NmbevHnp6uoatGbWrFkZM2ZMkuSss85KpVKp1XgAAMOuZmFW\nqVTS0tIysN3c3PxLw+uhhx7K7NmzazEaAEARanqN2VB997vfzdatW3PTTTcdcn93d3e6u7sHttvb\n29PU1FSj6UaOht27h3sERoiGhgY/QwyZYwtD5dhyeB0dHQO329ra0tbWlqSGYdbc3Jyenp6B7Uql\nkubm5oPWPfHEE7n33nuzcuXKNDYeerzXvoBX7dmz5+gOPAr09fUN9wiMEH19fX6GGDLHFobKseXQ\nmpqa0t7efsh9NXsrc8aMGdmxY0d27dqV3t7edHZ25vzzzx+05sc//nHuvPPOLF++XGEDAMedmp0x\nq6+vz5IlS7Jq1apUq9UsWrQoU6dOTUdHR6ZPn545c+bknnvuyYEDB/LZz3421Wo1kyZNyvLly2s1\nIgDAsKrpNWazZ8/O2rVrB9332lN5119/fS3HAQAoik/+BwAohDADACiEMAMAKIQwAwAohDADACiE\nMAMAKIQwAwAohDADACiEMAMAKIQwAwAohDADACiEMAMAKIQwAwAohDADACiEMAMAKIQwAwAohDAD\nACiEMAMAKIQwAwAohDADACiEMAMAKIQwAwAohDADACiEMAMAKIQwAwAohDADACiEMAMAKIQwAwAo\nhDADACiEMAMAKIQwAwAohDADACiEMAMAKIQwAwAohDADAChEYy2fbNOmTdmwYUOq1WoWLlyYxYsX\nD9rf29ub2267LVu3bk1TU1M+8YlPZNKkSbUcEQBg2NTsjFl/f3/Wr1+fFStWZM2aNens7Mxzzz03\naM1DDz2UCRMm5HOf+1ze85735J577qnVeAAAw65mYbZly5ZMmTIlkydPTmNjY+bNm5eurq5Ba7q6\nujJ//vwkydvf/vb853/+Z63GAwAYdjULs0qlkpaWloHt5ubmVCqVw66pr6/P+PHj8/Of/7xWIwIA\nDKuiL/6vVqvDPQIAQM3U7OL/5ubm9PT0DGxXKpU0NzcPWtPS0pIXXnghzc3N6e/vz759+zJhwoSD\nHqu7uzvd3d0D2+3t7WltbT12w49Qra1J17lvGe4xgFHGsQXeuI6OjoHbbW1taWtrS1LDMJsxY0Z2\n7NiRXbt2ZeLEiens7MyyZcsGrZkzZ07+5V/+JTNnzsxjjz2Wc84555CP9doXAK9XR0dH2tvbh3sM\nYJRxbOH1ONz3Ss3CrL6+PkuWLMmqVatSrVazaNGiTJ06NR0dHZk+fXrmzJmTRYsWZd26dbnyyivT\n1NR0ULgBAIxmdVUXcnGc8VstcCw4tnA0FH3xPxwL3gYHjgXHFo4GZ8wAAArhjBkAQCGEGQBAIWr6\nR8zhWLj00kvz5S9/+ag+5q5du/KjH/0ov/3bv31UHxcYeXbv3p0NGzZk69atGT9+fE466aScf/75\n+fd///dcd911B61fuXJlLrnkkkybNi1Lly7NuHHjkiQnn3xyPv7xj+ekk06q9UtgBBFmjHh1dXVH\n/TF/9rOf5ZFHHhFmQG655ZYsWLAgV111VZLkJz/5Sbq6uoZ07Kmrq8uNN96YCRMm5Ctf+Uq++tWv\n5rLLLjvGEzOSCTNGjc2bN2fjxo1pamrKtm3bMm3atFxxxRVJkqVLl+Yd73hHNm3alDe96U258sor\nc+qpp+bzn/985syZk9/6rd9K8r9n3/7mb/4m27dvz7XXXpv58+fnd37nd4bzpQHD5Mknn0xjY2Pe\n9a53Ddx3xhln5Oc//3mefPLJ3HrrrQcdb17rtf+/7td//dfzjW98oyZzM3K5xoxR5dlnn82HP/zh\n3Hrrrdm5c2d+9KMfDeybMGFCbrnlllx00UW56667Dvn1r/4G/Ed/9Ec5++yzs3r1alEGx7FXo+tQ\nftnx5lC+//3v54wzzjgWYzKKCDNGlRkzZmTixImpq6vLW97yluzatWtg39y5c5Mk8+bNyzPPPDNc\nIwKjxC873rzWypUrc+2112bfvn1ZvHhxjadkpPFWJqNKY+P/fkvX19enr69vYPu114O8eru+vn7g\nrYZqtZre3t4aTQqMBG9+85vzve9975D7ftnx5rVevcYMhsIZM0a8oX5G8qOPPpok6ezszFlnnZUk\nOeWUU/Jf//VfSZKurq6BMBs7dmz2799/DKYFRpJzzjknvb29efDBBwfu+8lPfpIf/vCHwzgVo5kz\nZox4Q/1fmS+//HKuueaanHDCCVm2bFmS5J3vfGduvvnmLF++PL/xG7+RsWPHJknOPPPM1NXVZfny\n5VmwYIHrzOA4ds011+Suu+7KvffemzFjxmTy5Ml529veNqSvPRb/a5zRzZ9k4riwdOnSrF692tsJ\nABTNW5kcF/zWCsBI4IwZAEAhnDEDACiEMAMAKIQwAwAohDADACiEMAM4SjZu3Jh169YN9xjACOYD\nZoFR4amnnspf//VfZ9u2bWloaMjpp5+eyy677LB/gPpY8dEswBshzIARb9++fVm9enUuv/zyvOMd\n70hvb29++MMfDvpbhgAjgaMWMOI9//zzSZK5c+cmSU444YS89a1vTZLs3Lkzd9xxR/77v/87dXV1\neetb35qPfOQjGTduXJJf/FWIiy66KA8//HB27tyZuXPn5g//8A/z+c9/Pk899VRmzpyZq6++OuPG\njcuuXbvy8Y9/PJdffnk2btyYJHnve9+b3/3d3z3kXE8//XTuvvvu/PSnP83kyZNz2WWXZdasWcf6\nnwMYwVxjBox4U6ZMSX19fW6//fZs2rQpL7/88sC+arWa3/u938sXvvCFfPazn02lUhmIqlf927/9\nW66//vqsXbs2jz/+eP7yL/8yH/zgB7N+/fr09/fnn/7pnwat37x5c9atW5cVK1bka1/7Wp588smD\nZqpUKlm9enV+//d/P3fddVcuueSSrFmzJnv27Dk2/wjAqCDMgBHvV37lV/KpT30qdXV1ueOOO/KR\nj3wkN998c1566aWcdtppOffcc9PQ0JCmpqa85z3vyebNmwd9/cUXX5wTTzwxEydOzNlnn50ZM2bk\nzDPPTGNjY972trfl2WefHbT+Ax/4QMaMGZMzzjgjCxYsyCOPPHLQTA8//HDOO++8zJ49O0ly7rnn\nZtq0afnBD35wzP4dgJHPW5nAqNDa2po/+ZM/SZJs374969aty4YNG/KhD30od911V5566qns378/\n/f39B/0x+5NPPnng9pgxYw7a3r9//6D1LS0tA7cnT56cbdu2HTTPrl278thjj+Xxxx8fuK+vry/n\nnHPOG3uhwKgmzIBRp7W1NfPnz8+3v/3tfOUrX0l9fX1uvfXWjBs3Ll1dXfnSl770hh6/p6cnra2t\nA7cnTpx40JpJkyZl/vz5+ehHP/qGngs4vngrExjxtm/fnvvuuy+VSiXJL2Kps7MzZ511Vvbv35+x\nY8dm7NixqVQq+frXv/6Gn+8f/uEf8sorr2Tbtm3553/+58ybN++gNRdeeGEef/zx/Md//Ef6+/vz\nyiuvZPPmzQMzAhyKM2bAiDd27Ng888wzue+++7J3796MHz8+c+bMyR//8R+np6cnt912Wz784Q/n\ntNNOy4UXXpj7779/4Gv/7+eODeVzyGbNmpUrrrgiSfK+970v55577kFrWlpacs011+See+7J2rVr\n09DQkOnTp+fyyy9/g68WGM3qqtVqdbiHABgJXv24jFffHgU42hxZAAAKIcwAAArhrUwAgEI4YwYA\nUAhhBgBQCGEGAFAIYQYAUAhhBgBQCGEGAFCI/w9rOJxkpeIjZgAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f97ea679410>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.bar([0,2],[NRF_input, NRF_chip], width=1)\n",
"plt.xlim([-0.5,3.5]), plt.xticks([0.5, 2.5], ['Input', 'ChIP'])\n",
"plt.xlabel('Sample')\n",
"plt.ylabel('NRF')\n",
"plt.ylim([0, 1.25]), plt.yticks(np.arange(0, 1.2, 0.2))\n",
"plt.plot((-0.5,3.5), (0.8,0.8), 'red', linestyle='dashed')\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Calculate the Signal Extraction Scaling"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Load the results from the coverage calculations"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[6, 15, 13, 19, 1, 6]"
]
},
"execution_count": 17,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"countList = []\n",
"with open('/ngschool/chip_seq/bedtools/input_coverage.bed', 'r') as covFile:\n",
" for line in covFile:\n",
" countList.append(int(line.strip('\\n').split('\\t')[3]))\n",
"countList[0:6]"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[26, 42, 21, 21, 8, 16, 16, 28, 25, 19, 13, 4, 18, 35, 19]"
]
},
"execution_count": 18,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"countList[-15:]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Lets see where do our reads align to the genome. Plot the distribution of tags along the genome."
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAnsAAAFOCAYAAAD+a9sUAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xt8FPW9//H37AZIczFhQ1AkapSL1gABTbxx5OqvthQ1\nRzyx1FawqIerFFsUtcqxXqlyFUWhgKhtLVahWGvpUUEREIkkiAEMUS4CB0myJiaEQLLz/f0RWYgJ\nYUmy2ezk9Xw8eLA7mZnvZ+a7s/ve78zuWsYYIwAAADiSK9QFAAAAIHgIewAAAA5G2AMAAHAwwh4A\nAICDEfYAAAAcjLAHAADgYBHN1VBRUZHmzp2rkpISWZala665Rj/5yU/02muv6d1331VcXJwkafjw\n4erdu7ckadmyZVq1apXcbrdGjhyp1NRUSVJOTo5efPFFGWM0cOBAZWRkNNdmAAAAhJVmC3tut1sj\nRoxQcnKyKioqdO+996pXr16SpKFDh2ro0KE15t+7d6/Wr1+vmTNnqqioSI888ojmzJkjY4wWLlyo\nhx56SO3bt9d9992n9PR0de7cud72c3NzlZKSErTtQ/DQd+GJfgtP9Ft4ot/CU3P1W7Odxo2Pj1dy\ncrIkKTIyUp07d5bX65Uk1fW9zllZWbrqqqvkdrvVsWNHderUSfn5+crPz1enTp2UmJioiIgI9e3b\nVxs3bjxl+7m5uU26PWg+9F14ot/CE/0Wnui38NRc/RaSa/YOHjyo3bt3q1u3bpKklStXavLkyXr+\n+edVXl4uSfJ6verQoYN/GY/HI6/XK6/Xq4SEhFrTAQAAUFuzh72KigrNmDFDI0eOVGRkpK699lo9\n88wzeuqppxQfH6+XXnqpuUsCAABwrGa7Zk+SfD6fpk+frn79+ik9PV2SdMYZZ/j/PnjwYE2bNk1S\n9YhdYWGh/29FRUXyeDwyxtSY7vV65fF4arWVm5tbY3g0MzOzybcHzYO+C0/0W3ii38IT/RaeTtVv\nS5cu9d9OSUlp8PV9zRr25s2bp6SkJA0ZMsQ/rbi4WPHx8ZKkDRs26JxzzpEkpaWlac6cORo6dKi8\nXq8OHDigrl27yhijAwcOqKCgQO3bt9fatWs1ceLEWm3VtVP2798fxK1DsMTGxqq0tDTUZeA00W/h\niX4LT/RbeKqv384+++wmC/HNFva2b9+uNWvW6Nxzz9U999wjy7I0fPhwffjhh9q1a5csy1JiYqLu\nvPNOSVJSUpKuvPJKTZo0SREREbr99ttlWZYsy9KoUaP06KOPyhijQYMGKSkpqbk2AwAAIKxYpq6P\nwjoUI3vhiXes4Yl+C0/0W3ii38LTqUb2mgq/oAEAAOBghD0AAAAHI+wBAAA4GGEPAADAwQh7AAAA\nDkbYAwAAcDDCHgAAgIMR9gAAAByMsAcAAOBghD0AAAAHI+wBAAA4GGGviZhir0xFeajLAAAAqIGw\n10TsySNlz3861GUAAADUQNhrSt8Wh7oCAACAGgh7AAAADkbYAwAAcDDCHgAAgIMR9gAAAByMsAcA\nAOBghD0AAAAHI+wBAAA4GGEPAADAwQh7AAAADkbYAwAAcDDCHgAAgIMR9gAAAByMsAcAAOBghD0A\nAAAHI+wBAAA4GGEPAADAwQh7AAAADkbYAwAAcDDCHgAAgIMR9gAAAByMsAcAAOBghD0AAAAHI+wB\nAAA4GGEPAADAwQh7AAAADkbYAwAAcDDCHgAAgIMR9gAAAByMsAcAAOBghD0AAAAHI+wBAAA4GGEP\nAADAwQh7AAAADhbRXA0VFRVp7ty5KikpkWVZGjx4sIYMGaKysjLNmjVLBQUF6tixoyZNmqSoqChJ\n0qJFi5STk6N27dpp3LhxSk5OliStXr1ay5YtkyTdeOON6t+/f3NtBgAAQFhptrDndrs1YsQIJScn\nq6KiQvfee69SU1O1atUq9ezZUzfccIOWL1+uZcuW6ZZbblF2dra+/vprzZkzRzt27NCCBQv02GOP\nqaysTK+//rqmTZsmY4ymTJmi9PR0f0AEAADAcc12Gjc+Pt4/MhcZGanOnTurqKhIWVlZ/pG5AQMG\nKCsrS5K0ceNG//Ru3bqpvLxcxcXF2rx5s3r16qWoqChFR0erV69eysnJaa7NAAAACCshuWbv4MGD\n2r17t7p3766SkhLFx8dLqg6ExcXFkiSv16uEhAT/Mh6PR16v96TTAQAAUFuzh72KigrNmDFDI0eO\nVGRkZK2/W5bV3CUBAAA4VrNdsydJPp9P06dPV79+/ZSeni7p+Gjesf/j4uIkVY/YFRUV+ZctKiqS\nx+ORx+NRbm5ujek9evSo1VZubm6N+TIzMxUbGxusTVOxqq9LDGYbrVXbtm3Zr2GIfgtP9Ft4ot/C\n06n6benSpf7bKSkpSklJaVA7zRr25s2bp6SkJA0ZMsQ/7dJLL9Xq1auVkZGh1atXKy0tTZKUlpam\nlStX6qqrrlJeXp6io6MVHx+v1NRUvfrqqyovL5dt29qyZYtuueWWWm3VtVNKS0uDun0+ny/obbRG\nsbGx7NcwRL+FJ/otPNFv4am+fouNjVVmZmaTtNNsYW/79u1as2aNzj33XN1zzz2yLEvDhw9XRkaG\nZs6cqVWrVikxMVGTJk2SJF1yySXKzs7WhAkTFBkZqTFjxkiSYmJiNGzYME2ZMkWWZemmm25SdHR0\nc20GAABAWLGMMSbURTSX/fv3B23dvjuul87rKvfvZgStjdaKd6zhiX4LT/RbeKLfwlN9/Xb22Wc3\nWTv8ggYAAICDEfYAAAAcjLAHAADgYIQ9AAAAByPsAQAAOBhhDwAAwMEIewAAAA5G2AMAAHAwwh4A\nAICDEfYAAAAcjLAHAADgYIQ9AAAAByPsAQAAOBhhDwAAwMEIewAAAA5G2AsBe9Es+Z68J9RlAACA\nViAi1AW0RmZrtlTyTajLAAAArQAjewAAAA5G2AMAAHAwwh4AAICDEfYAAAAcjLAHAADgYIQ9AAAA\nByPsAQAAOBhhDwAAwMEIewAAAA5G2AMAAHAwwh4AAICDEfYAAAAcjLAHAADgYIQ9AAAAByPsAQAA\nOBhhDwAAwMEIewAAAA5G2AMAAHAwwh4AAICDEfYAAAAcjLAHAADgYIQ9AAAAByPsAQAAOBhhDwAA\nwMFOK+wVFhYqLy8vWLUAAACgiUUEMlNhYaFmz56tXbt2SZJefvllffTRR8rJydHo0aODWR8AAAAa\nIaCRvfnz56tPnz5asmSJIiKq82GvXr306aefBrU4AAAANE5AYS8/P18ZGRlyuY7PHhUVpfLy8qAV\nBgAAgMYLKOzFxcXpwIEDNabt3btXHTp0CEpRAAAAaBoBXbN33XXXadq0acrIyJBt2/rwww+1bNky\nZWRkBLs+AAAANEJAYW/QoEGKjY3VO++8o4SEBL3//vu6+eabddlllwXc0Lx587Rp0ybFxcXp6aef\nliS99tprevfddxUXFydJGj58uHr37i1JWrZsmVatWiW3262RI0cqNTVVkpSTk6MXX3xRxhgNHDiQ\nwAkAAFCPgMKeJKWnpys9Pb3BDQ0cOFA/+clPNHfu3BrThw4dqqFDh9aYtnfvXq1fv14zZ85UUVGR\nHnnkEc2ZM0fGGC1cuFAPPfSQ2rdvr/vuu0/p6enq3Llzg+sCAABwsoDC3nvvvVfn9DZt2ighIUHd\nunVTmzZt6l3HRRddpIKCglrTjTG1pmVlZemqq66S2+1Wx44d1alTJ+Xn58sYo06dOikxMVGS1Ldv\nX23cuJGwBwAAcBIBhb0PPvhAeXl5iouLU0JCgoqKilRSUqIuXbro4MGDkqR77rlHXbp0Oe0CVq5c\nqQ8++EBdunTRrbfeqqioKHm9XnXv3t0/j8fjkdfrlTFGCQkJNabn5+efdpsAAACtRUBhLykpSZdd\ndpmGDBnin/avf/1L+/bt0+9//3u98cYbWrRokR577LHTavzaa6/VTTfdJMuy9Oqrr+qll15qsi9p\nzs3NVW5urv9+ZmamYmNjm2TddSmW5Ha7A2qjxLJkpKDW4yRt27ZlX4Uh+i080W/hiX4LT6fqt6VL\nl/pvp6SkKCUlpUHtBBT21q5dq4ULF9aY9qMf/UijRo3SqFGjdP3112vFihWn3fgZZ5zhvz148GBN\nmzZNUvWIXWFhof9vRUVF8ng8MsbUmO71euXxeOpcd107pbS09LRrPB0+ny+gNo6dug52PU4RGxvL\nvgpD9Ft4ot/CE/0Wnurrt9jYWGVmZjZJOwF/z94nn3xSY9qmTZv8Ya2ystL/yxr1McbUuEavuLjY\nf3vDhg0655xzJElpaWlat26dqqqqdPDgQR04cEBdu3ZV165ddeDAARUUFKiqqkpr165VWlpaIJsA\nAADQKgU0snfbbbdpxowZOvfcc/3X7O3Zs0d33323JGnHjh368Y9/XO86Zs+era1bt6q0tFRjxoxR\nZmamcnNztWvXLlmWpcTERN15552Sqk8bX3nllZo0aZIiIiJ0++23y7IsWZalUaNG6dFHH5UxRoMG\nDVJSUlIjdwEAAIBzWaauj8PWobS0VNnZ2fJ6vWrfvr0uueSSsLs+YP/+/UFbt++O66Xzusr9uxmn\nnve3I6SSb+RecPqnvlsjTk+EJ/otPNFv4Yl+C0/19dvZZ5/dZO0E/D17sbGx6tevX5M1DAAAgOAL\nKOz5fD6tXLnSfxr2RA8//HBQCgMAAEDjBfQBjSVLluidd97RxRdfrC+//FKXX365SkpKGvwRYAAA\nADSPgMLehg0bdP/992vIkCFyu90aMmSIJk+eXON77AAAANDyBBT2jh496v/lirZt2+rIkSPq3Lmz\ndu3aFczaAAAA0EgBXbPXuXNnffHFF+ratasuuOACvfbaa/rBD35w0i80BgAAQMsQ0MjeyJEj5Xa7\nJUkjRozQzp079cknn/i/Fw8AAAAt0ylH9mzb1p49e3T11VdLkjp16qQHH3ww6IUBAACg8U45sudy\nufTSSy+pTZs2zVEPAAAAmlBAp3EvvfRSZWVlBbsWAAAANLGAPqBRWVmpGTNmqHv37kpISJBlWf6/\njR8/PmjFAQAAoHECCnvnnHOOzjnnnGDXAgAAgCYWUNj7r//6r2DXAQAAgCAIKOxJ0qeffqq1a9eq\npKREU6ZM0RdffKHDhw+rR48ewawPAAAAjRDQBzTefvttLViwQJ06ddK2bdskVf+SxquvvhrU4gAA\nANA4AYW9f/7zn3rwwQeVkZEhl6t6kc6dO2v//v1BLQ4AAACNE1DYO3z4sDp06FBjWlVVlSIiAj4L\nDAAAgBAIKOz98Ic/1PLly2tMe/vtt5WSkhKUogAAANA0Agp7v/rVr/Txxx9r3Lhxqqio0MSJE7V+\n/XqNGDEi2PUBAACgEQI6D9u+fXs98cQTys/PV2FhoRISEtS1a1f/9XsAAABomQIKe2+99Zb69u2r\nbt26qVu3bsGuCQAAAE0koLCXm5urv/zlL7rwwgv1H//xH7r88ssVFRUV7NoAAADQSAGFvXvuuUeH\nDh3SRx99pA8++ECLFi1Samqqrr76al1++eXBrhEAAAANFPBFd9HR0Ro8eLCmTp2qmTNnqqKiQjNm\nzAhmbQAAAGik0/qivO3bt+vDDz/Uhg0bFBMTo8zMzGDVBQAAgCYQUNh7+eWXtX79elmWpSuvvFIP\nPPCAkpOTg1waAAAAGiugsHfkyBFNmDBBP/zhD4NdT+tgTKgrAAAArURAYe/222+XJBUWFsrr9crj\n8dT6+TQAAAC0PAGFveLiYs2cOVN5eXmKjY1VaWmpunfvrokTJ8rj8QS7RuexrFBXAAAAWomAPo07\nf/58nXfeeVq8eLHmz5+vxYsXKzk5WQsWLAh2fQAAAGiEgMLe559/rltvvVWRkZGSpMjISP3iF79Q\nXl5eUIsDAABA4wQU9qKjo7V3794a0/bv38+vaAAAALRwAV2zd/311+uRRx7RoEGDlJiYqIKCAq1e\nvVo333xzsOsDAABAIwQU9q655hqdddZZ+vDDD7Vnzx61b99ed911l3r27Bns+gAAANAIAf+CRo8e\nPdSjR49g1gIAAIAmFtA1e08//bS2bdtWY9q2bds0ffr0oBQFAACAphFQ2Nu6dasuvPDCGtO6d++u\n3NzcoBQFAACAphFQ2GvTpo0qKipqTKuoqJDb7Q5KUQAAAGgaAYW91NRUzZ8/X+Xl5ZKk8vJyLVy4\nUL179w5qcQAAAGicgD6gceutt+qZZ57Rr371K8XExKisrEy9e/fWhAkTgl0fAAAAGiGgsBcTE6P7\n7rtPxcXFKiwsVIcOHRQfHx/s2gAAANBIAX/1iiTFx8cT8gAAAMJIQNfsAQAAIDwR9gAAAByMsAcA\nAOBgAV+zV15erv3799f6vj1+Qg0AAKDlCijsrV69WgsXLlRkZKTatm3rn25ZlubOnRu04gAAANA4\nAYW9v/zlL7r77rvVp0+fBjc0b948bdq0SXFxcXr66aclSWVlZZo1a5YKCgrUsWNHTZo0SVFRUZKk\nRYsWKScnR+3atdO4ceOUnJwsqTp4Llu2TJJ04403qn///g2uCQAAwOkCumbPtm2lpqY2qqGBAwfq\ngQceqDFt+fLl6tmzp2bPnq2UlBR/iMvOztbXX3+tOXPm6M4779SCBQskVYfD119/XU888YQef/xx\n/e1vf/P/qgcAAABqCyjs3XDDDXr99ddl23aDG7rooosUHR1dY1pWVpZ/ZG7AgAHKysqSJG3cuNE/\nvVu3biovL1dxcbE2b96sXr16KSoqStHR0erVq5dycnIaXBMAAIDTBXQa96233lJxcbFWrFihmJiY\nGn+bN29egxsvKSnxf0lzfHy8iouLJUler1cJCQn++Twej7xe70mnAwAAoG4Bhb3m+g1cy7KabF25\nubnKzc3138/MzFRsbGyTrf/7iiW53e6A2iixLBkpqPU4Sdu2bdlXYYh+C0/0W3ii38LTqfpt6dKl\n/tspKSlKSUlpUDsBhb2LL764QSs/lWOjecf+j4uLk1Q9YldUVOSfr6ioSB6PRx6Pp0aAKyoqOulX\nv9S1U0pLS4OwFcf5fL6A2jDGNEs9ThEbG8u+CkP0W3ii38IT/Rae6uu32NhYZWZmNkk7Jw17b7zx\nhm688UZJ0l//+teTruDmm28OuDFjjD/oSNKll16q1atXKyMjQ6tXr1ZaWpokKS0tTStXrtRVV12l\nvLw8RUdHKz4+XqmpqXr11VdVXl4u27a1ZcsW3XLLLQG3DwAA0NqcNOx9f2StsWbPnq2tW7eqtLRU\nY8aMUWZmpjIyMjRz5kytWrVKiYmJmjRpkiTpkksuUXZ2tiZMmKDIyEiNGTNGkhQTE6Nhw4ZpypQp\nsixLN910U60PfQAAAOA4y5w41OZw+/fvD9q6fXdcL53XVe7fzTj1vL8dIZV8I/eCFUGrx0k4PRGe\n6LfwRL+FJ/otPNXXb2effXaTtXPav41bUlKiDRs2aN++fU1WBAAAAIKj3g9oeL1eLVq0SHv37lX3\n7t113XXXaerUqXK5XDp06JDGjx+vvn37NletAAAAOE31juzNnz9f0dHRGjFihIwxeuyxxzR69Gj9\n8Y9/1N133+3/xQsAAAC0TPWGvby8PN1xxx3q06ePbr/9dpWUlCg9PV2SlJ6eroKCgmYpEgAAAA1T\nb9jz+XyKiKg+09uuXTtFRkY26RcfAwAAILjqvWbP5/Pps88+89+3bbvWfQAAALRc9Ya9uLi4Gr99\nGxMTU+P+GWecEbzKAAAA0Gj1hr1nn322ueoAAABAEJz29+wBAAAgfBD2AAAAHIywBwAA4GCEPQAA\nAAcj7AEAADgYYQ8AAMDBCHsAAAAORtgDAABwMMIeAACAgxH2AAAAHIywBwAA4GCEPQAAAAcj7AEA\nADgYYQ8AAMDBCHsAADiU2bFVpqgg1GUgxAh7AAA4lP2HKbJfnB3qMhBihD0AAAAHI+wBAAA4GGEP\nAADAwQh7AAAADkbYAwAAcDDCHgAAgIMR9gAAAByMsAcAAOBghD0AAAAHI+wBAAA4GGEPAADAwQh7\nAAAADkbYAwAAcDDCXigYE+oKAABAK0HYAwAAcDDCXihYVqgrAAAArQRhDwAAwMEIewAAAA5G2AMA\nAHAwwh4AAICDEfYAAAAcjLAHAADgYBGhLkCSxo0bp6ioKFmWJbfbrSeeeEJlZWWaNWuWCgoK1LFj\nR02aNElRUVGSpEWLFiknJ0ft2rXTuHHjlJycHNoNAAAAaKFaRNizLEtTp05VTEyMf9ry5cvVs2dP\n3XDDDVq+fLmWLVumW265RdnZ2fr66681Z84c7dixQwsWLNBjjz0WwuoBAABarhZxGtcYI/O9nxDL\nyspS//79JUkDBgxQVlaWJGnjxo3+6d26dVN5ebmKi4ubt2AAAIAw0WJG9h577DFZlqVrrrlGgwcP\nVklJieLj4yVJ8fHx/kDn9XqVkJDgX9bj8cjr9frnBQAAwHEtIuw98sgjat++vb799ls9+uijOvvs\ns2vNY/ETYwAAAKetRYS99u3bS5LOOOMMpaenKz8/3z+ad+z/uLg4SdUjeUVFRf5li4qK5PF4aq0z\nNzdXubm5/vuZmZmKjY0N2jYUS3K73QG1UWJZMlJQ63GStm3bsq/CEP0Wnui38HSyfiuW5LYs+rSF\nOtXxtnTpUv/tlJQUpaSkNKidkIe9I0eOyBijyMhIVVRU6NNPP9VNN92kSy+9VKtXr1ZGRoZWr16t\ntLQ0SVJaWppWrlypq666Snl5eYqOjq7zFG5dO6W0tDSo2+Lz+QJq49j1icGuxyliY2PZV2GIfgtP\n9Ft4qq/ffNs206fNyOzMk5K7BXRGsr5+i42NVWZmZpPUFPKwV1JSoqeeekqWZcnn8+nqq69Wamqq\nunTpopkzZ2rVqlVKTEzUpEmTJEmXXHKJsrOzNWHCBEVGRmrMmDEh3gIAAIBq9uO/lWvyE1L3ho3C\nBUPIw17Hjh311FNP1ZoeExOjBx98sM5lRo0aFeyyAAAAGsb2hbqCGlrEV68AAAAgOAh7AAAADkbY\nAwAAcDDCHgAAgIMR9gAAAByMsAcAAOBghD2gHub/9so3ZlioywAAoMEIe0B99u2SqipDXQUAAA1G\n2AMAAHAwwh5QnwB+2xAAgJaMsAcAAOBghD2gXozsAQDCG2EPAADAwQh7QH0Y2AMAhDnCHgAAQDMx\nFeUyzfyVXoQ9oF4M7QEAmo59189lFs1q1jYJewAAAM3F2DJf72/WJgl7QH34nj20AMa2ZfK3hboM\nAGGKsAcALV1utuxp94a6CgBhirAH1IeBPbQEti/UFQAIY4Q9AAAAByPsAfViaA8AEN4IewAAAM2p\nmT/8R9gD6sOncdEi8DgE0HCEPQAAAAcj7AEAADgYYQ8AAMDBCHsA0NJxyR6ARiDsoVUzX2yX2ba5\nnjl4lUULYEJdAIBwFhHqAoBQsuc8LJUfknvBilCXAgBAUDCy1wCm7FuZyspQlxEWTGWljAnjYQkG\n9oBmZa/5t8zmj0NdBuAohL0GsCf9QubPz4e6jLBgjx0m87/LQ13GyYVxDkUr0oredJiX5sr+E8+v\nQFMi7DWQ8RaGuoTw8fX+Bi9q8rfJHC5vwmJOE1+qDAA4XS3sjBZhDy2aPe1eVSz/U6jLAACg6fBz\naeGiZaV2J6vcuCaErTOyBwA4TS3srBBhD82gcQ96U1rSRHXUoWUdj0DdWtgLR9C1sFNgQLgj7KHl\nC+bz/qnW3cpeYwEAzkPYQ8tn7FBXAABA2CLsocUzdihP6TC0BwBoYnxAA/geRvaAVoZr9oCmRNhr\nIYwxMrZDQ01j38CE8mLt1nZhPADAcQh7DdXEAcS8s0L2f2c06TodI4Qh2OzaEbK2AQBoCoS9luKr\nL0NdQcsVwpE9s/yVkLUNAEBTIOw1gv3GEpmKJvopryCPXpmdO2QqK4PaRtA0Q9gzJd8EvQ20Psb2\nyXyxvQnWxOUEQEtmyg/JfFsc6jJOirDXUJYl8/br0pefH5/WmFAS5EBjP/4bmff/WXfTm9aF7EFq\njJEpP1T/TM1wGtd8sjbobaAV2vKJ7CfvOe3FzJEKmWJvEAoKE3w+A2HGfub3sn9za6jLOCnCXkPt\n/6r2tD1f1Lhr/3G67PWrAltfc5yqrKyqc7I978ngPkjr+5BD9keyJw4/xQpOf9+YL7bLeAsDXyBM\nP4hxYlC2//ma7NeXhLCa8OGb+6hM9kfBb6iBnyQ3S56RPXnk8fuFBwJbruCAfPfd0aA2A1p/UYGM\nt6DmtMpKmZyG78s63+wdOSxj2zKHT33mxGR/JFPV8LMW9rr3ZL733B0M9rtvyt7wfq3ppuxbmZ15\n1c9Z/HJI+GrhZ4daVdgz5WUNX7aqUvYbLx2fUFz03Q1LpqD2E7GpqpLZ8L7Mh/8bWAPfjV6Zvbtk\nKg4HVtMX2+X73qiBMcZfjyk6KOPznfDH2i88ddZ+uLz6tG8jnkAlyRzYW33jcLnsN1+VOXrEv05T\ncEDGGNmr3vLPb294X/a7/6hjRdWjf75HJtWYvz72k/fIXjyr/vrKy6TDdY8qmsPlMvv21P23752W\nq+8FyVQelfmmqO6/+XzVL54V1fvnVIztk/ny8+p1Vh6VJNkTh8scOSL7ledklr0s86/Xay9XcVjm\n22L5Zjwoc6TieF3fnda3170n+7vlzKEymaKD1be3fyrz6caT1mMve7nGpQFmZ55MaYnMts3Hp9Xx\n+DrldhYdlDm4v/b0ykr/dp902ZwN/p/XM/v3yF7z77pn3Pyx7L8tPvl6qqpktm0+6Yuv8flkdtb9\n4R3zyVr5jgU1y133PKXf+h839v/+vdYbkxN/ItDs+VLmzy9IknwPjq3+/47rq0NCwQHZq/95/E3l\nVzulwq9Pul2SZC+aJXNgX73z1KglZ4P/uLWnjpf9P3fVnGHzBtnPPh74+g6X+/er2ZpT/RguLal5\nHFUclnn/bdl3/az28rZd4/IZ+7nHZf7xV9lr36lxrJ24PlNRLvPtN7JX/EVm0/qa61s8S/bfXqy7\n1t35/oBmz3+qel98dwxJNYOq2ZnnP3Ykyf5olcye49dim1cXyPz1j7X2hT3pF7If/63sJ++R+WBl\nnXVI3z1GLShuAAASYUlEQVRnHi6vfmwWfS9wb9usyu/evJiCA/5vdjj2eDmRveqt6sdPAJcXmF3H\nXweMMSd9rjNFBf59b77YXuO4P9lyxhiZ/G017wf4fGGqKmWOHJH5ZF31/b275Lvj+urb3z2+Tvfy\nCd9T99d8vTzWlu2r9Zp84vOnn6vmsW5P/51MVZV8o/+zeh1HKqofh6e4nMpUVsrszPNvT1OxTJi+\nlcjJydGLL74oY4wGDhyojIxTf5J13ztvyV7xF+mL7bJ+MVbWFQOlrdmy//yCXI/Pl/3CNFlx7WXd\n8HOZT9bJuuBCmZwNsn56s3Rgr+yH75Jrzqt1PgEd45r3hqyICNlr35V5cbZ0bhe5fvVrWZ3Pk/m/\nr2Q2rpH57oXd9dBsma05spKSZc+aWnNFnc+rnuf238js3yPr7HNkJZ0vU1wkfVsi+7VF0vZPJUnW\nNdfLfLVTrtsmyp5ye/Vyjz4v+3eja6zSGnydzLtvynXvk1KHs2S2b5ZZOPP4368cJLP+vZrbM+dV\n6chh6YvPq09dVx6V+eN0Wb8YK/PKc7J+dqf05fbqv214X67fPyuT87GsH2XIHv2f9XdIVLRUx7t6\n1zN/lfnz81JiJ5kVfz7p4tZl/aoPwj1fSJE/kNXvxzJLF8r6yU0yb/+teqa27ar3ywt/qL+WC3tK\nn2+pdxbrl+NkXn62/vVI0jnnV7/ofn/5S/vKyvyV7HtHybpigMxHq2vPc+UgWZf1kz37f6TUy6TN\nH8s14xWZNStllr1cY17XjFdk3/2L2u0nJUv/95Vc9zwpdTiz9qhtbJx0LExE/kA69kTW7WJpx9bq\n2wHsD0ly/fc91QE9f2vN7fhppqxPN8r+aqdcU/4gtW0ne+EMad9u6byu0u58WSPvktUrXebVBdL5\n3WT+ulDqc4V0bMStZ5q0Jat2oz3T5Or3I3/AsDJ+IbP8lerj4J0V1dPunCwz/ylJknvBiupwkfeZ\n1L2H7DtvqLkNd02tfmNSXCQdKpP1s9tlTzh+jLvm/13y+WSPuVGu2X+W3BEyb/5FZuUyuV5YJsvl\nlsn7TOp0jqzYOP+TtOvBmbJfmSftzKuu4f/2Vo+A/SBK5k/PS2efK/fDc+W743pZfQfLfLxGqjxa\n47hwL1hx8if97ilSXu7xfX7TSJnvQov142GyLu4tnddV9qypcmX+Sva0KVJMrFRWWl3fA9Nl8j6T\ndWaSdHGqtGOrzPr3FHXNdTrc9geyOiXJfLH95KehL+olKzZOuri3zJJnZA29WfL5jh97J/Sh68mF\n1c8R696R+ftJjun4hBPeRB9n3XCLzMcfyEruKuu64TJvLZVZ+46sYSNkcjZI33tRd/3mUZniourn\ntog20vfftJ7VWa6MX0rtE6r79Q9Tqqd3uUiun2bK6pkmqTrQH3sOc83/e63Hjb+9R+ZJJV7ZTz9w\nvOYRE2SWPFP3dp4RL9etE6prfOW5uueRZPUdLGvoz2TXM1Lr+t0M2W//Tfou9OiiXsdfF264Rebv\nf6qxPlN4sOZx3StdOlIhfb6lur1+P5bZtlnWWUlS+wTZT0yu1aZ7wQr/bfuFP8hkfVh3cR3OlHXt\njdXH5Nf75Br3gJR4luz/mSBFx8p1/1OyHzjhNerYc9HFveX6aabM+/+S+fiD6r8lniXrigGyzr9Q\n5qNVx6er+jXKXjJH+mRd9TH3yCRZ/a6V+WClXJMfl/3U/dUzdrtYrh/9p3RWZ9kPjpU6nOl/Y+Sa\n9SfZv76lxnOOa9LDMtu3SIdKZT5YKSv9alnX/Uw6sE/2wpnSkcOy/t8N0jkXyDq3S/Vz9jeFcj25\nUPaUUdX7fOjNMv/468n7b97r+sH+3TpccFD2gqclX82zb+e8VcfzXwOFZdizbVsTJ07UQw89pPbt\n2+u+++7Tr3/9a3Xu3Lne5b76aVozVQgAgPO45r4mq107SWry0SfU1JRhL6LJ1tSM8vPz1alTJyUm\nJkqS+vbtq40bN54y7AEAgIaz5/yPrPSrpR9Eh7oUnIawDHter1cJCQn++x6PR/n5+SGsCACAViAv\nV+aEywcQHlrVBzQAAABam7Ac2fN4PCosPP7pNa/XK4/HU2Oe3Nxc5eYef/eRmZnZpOe/AQAAgmnp\n0qX+2ykpKUpJSWnQesJyZK9r1646cOCACgoKVFVVpbVr1yotreaHL1JSUpSZmen/d+IOQ3ih78IT\n/Rae6LfwRL+Fp1P124k5pqFBTwrTkT2Xy6VRo0bp0UcflTFGgwYNUlJSUqjLAgAAaHHCMuxJUu/e\nvTV79uxQlwEAANCiheVp3IZozPAnQou+C0/0W3ii38IT/RaemqvfwvJLlQEAABCYVjOyBwAA0BoR\n9gAAABwsbD+gcTpycnL04osvyhijgQMHKiMjI9QltTpFRUWaO3euSkpKZFmWBg8erCFDhqisrEyz\nZs1SQUGBOnbsqEmTJikqKkqStGjRIuXk5Khdu3YaN26ckpOTJUmrV6/WsmXLJEk33nij+vfvL0n6\n8ssv9dxzz6myslJ9+vTRyJEjQ7GpjmTbtu677z55PB7de++9OnjwoGbPnq2ysjKdf/75mjBhgtxu\nt6qqqjR37lx9+eWXio2N1aRJk9ShQwdJ0rJly7Rq1Sq53W6NHDlSqampkjg+g6W8vFzPP/+8vvrq\nK1mWpTFjxqhTp04cby3cP/7xD61atUqWZencc8/V2LFj5fV6Od5aoHnz5mnTpk2Ki4vT008/LUnN\n8ppWXxsnZRzO5/OZ8ePHm4MHD5rKykrz29/+1uzduzfUZbU633zzjdm5c6cxxpjDhw+bu+66y+zd\nu9e8/PLLZvny5cYYY5YtW2ZeeeUVY4wxmzZtMo8//rgxxpi8vDxz//33G2OMKS0tNePHjzeHDh0y\nZWVl/tvGGHPfffeZHTt2GGOMefzxx012dnZzbqKjvfnmm2b27NnmySefNMYYM2PGDLNu3TpjjDHz\n5883//73v40xxqxcudIsWLDAGGPM2rVrzcyZM40xxnz11Vdm8uTJpqqqynz99ddm/PjxxrZtjs8g\nmjt3rnnvvfeMMcZUVVWZQ4cOcby1cEVFRWbcuHGmsrLSGFN9nK1atYrjrYXatm2b2blzp/nNb37j\nn9Ycx9jJ2qiP40/j5ufnq1OnTkpMTFRERIT69u2rjRs3hrqsVic+Pt7/LiYyMlKdO3dWUVGRsrKy\n/O9iBgwYoKys6l852bhxo396t27dVF5eruLiYm3evFm9evVSVFSUoqOj1atXL+Xk5Ki4uFiHDx9W\n165dJUn9+vWjn5tIUVGRsrOzNXjwYP+0zz77TJdffrkkqX///v59fWK/XXHFFfrss88kSVlZWbrq\nqqvkdrvVsWNHderUSfn5+RyfQVJeXq7t27dr4MCBkiS3262oqCiOtzBg27YqKirk8/l09OhReTwe\n5ebmcry1QBdddJGio6NrTGuOY+z7bQTSh44/jev1epWQkOC/7/F4lJ+fH8KKcPDgQe3evVvdu3dX\nSUmJ4uPjJVUHwuLiYkl195vX6w14ekJCgrxebzNtkbMtWbJEv/zlL1VeXi5JKi0tVUxMjFyu6veK\nJ+7rE/vB5XIpKipKZWVl8nq96t69u3+dx/rNGMPxGQQHDx5UbGysnnvuOe3evVsXXHCBRo4cyfHW\nwnk8Hg0dOlRjx45Vu3bt1KtXL51//vmKjo7meAsTzXGMfb+NkpKSU9bl+JE9tCwVFRWaMWOGRo4c\nqcjIyFp/tywrBFXhZI5dj5KcnCxzwrc0mQC/sSnQ+dC0bNvWzp07de2112ratGlq166dli9fXms+\njreW5dChQ8rKytJzzz2nF154QUeOHFFOTk7Ay3O8tTzNcYwF0objw57H41FhYaH/vtfrlcfjCWFF\nrZfP59P06dPVr18/paenS6r5zqe4uFhxcXGSqvutqKjIv2xRUZE8Hk+t/jxxel3zo3G2b9+urKws\njR8/XrNnz9Znn32mxYsXq7y8XLZtS6q5r0/sB9u2dfjwYcXExNTbbxyfTc/j8SghIUFdunSRVH2K\nb+fOnRxvLdyWLVvUsWNH/8j5ZZddps8//1yHDh3ieAsTzXGMnayN+jg+7HXt2lUHDhxQQUGBqqqq\ntHbtWqWlpYW6rFZp3rx5SkpK0pAhQ/zTLr30Uq1evVpS9SeSjvVNWlqa3n//fUlSXl6eoqOjFR8f\nr9TUVG3ZskXl5eUqKyvTli1blJqaqvj4eEVFRSk/P1/GGH3wwQf+QImG+/nPf6558+Zp7ty5+vWv\nf60ePXrorrvuUkpKij766CNJ0vvvv19nv61fv149evTwT1+3bp2qqqp08OBBHThwQF27duX4DJL4\n+HglJCRo//79kqpDRFJSEsdbC9ehQwft2LFDR48elTHG328cby2XMabGiGpzHGMna6M+reIXNHJy\ncrR48WIZYzRo0CA+ah4C27dv19SpU3XuuefKsixZlqXhw4era9eumjlzpgoLC5WYmKhJkyb5L3hd\nuHChcnJyFBkZqTFjxuiCCy6QVP3gfuONN2RZVq2PqT/77LP+j6nfdtttIdteJ9q6davefPNN/1ev\nzJo1S4cOHVJycrImTJigiIgIVVZW6plnntGuXbsUGxuriRMnqmPHjpKqvwrivffeU0RERK2vguD4\nbHq7du3SCy+8oKqqKp155pkaO3asbNvmeGvhXnvtNa1bt05ut1vJyckaPXq0vF4vx1sLNHv2bG3d\nulWlpaWKi4tTZmam0tPTg36MlZWVnbSNk2kVYQ8AAKC1cvxpXAAAgNaMsAcAAOBghD0AAAAHI+wB\nAAA4GGEPAADAwQh7AAAADkbYA+BICxYs0BtvvBHqMk7p4Ycf1nvvvRfqMgA4WESoCwCAhhg3bpxK\nSkrkdrvldrvVvXt33Xnnnf6fFLrjjjtCXCEAtAyM7AEIW1OmTNGSJUs0f/58xcXFadGiRaEuKaT4\njnwAdWFkD0DYi4iI0BVXXKElS5b4pz333HNKSEjQzTffrK1bt+qZZ57RT3/6U/3973+Xy+XS8OHD\nNWDAgDrX9/DDD+uiiy7SZ599pj179qh79+6aOHGiYmJi/OuaN2+ef/5x48ZpzJgx6tGjh1577TV9\n9dVXatOmjbKystSxY0fdfffd2rBhg9566y21adNGo0ePVq9evfzLHzhwQPfff7/27dunHj16aOzY\nsf6fP8rLy9PLL7+svXv3KjExUSNHjtTFF1/sr/PCCy9Ubm6udu3apaefflpnnnlmEPYwgHDGyB6A\nsHfkyBGtW7dO3bt3P+k8xcXFOnz4sF544QWNHj1aCxcuVHl5+UnnX7t2rcaNG6c//vGPqqqq0ooV\nKwKuZ9OmTerfv78WL16s8847T4899piMMXrhhRc0bNgwzZ8/v8b8a9as0dixY7VgwQK5XC7/CKXX\n69W0adM0bNgwLV68WL/85S81ffp0lZaW1lh29OjRWrJkiRITEwOuEUDrQdgDELaeeuop3XbbbRo5\ncqS2bNmi66677qTzRkREaNiwYXK5XOrTp48iIyO1f//+k84/YMAAnXXWWWrTpo2uvPJK7d69O+C6\nfvjDH6pXr15yuVy68sorVVpaqoyMDLlcLvXt21cFBQU1gubVV1+tpKQktW3bVjfffLM++ugjGWO0\nZs0a9enTR71795Yk9ezZUxdccIGys7P9y/bv31+dO3eWy+WSy8VTOoDaOI0LIGxNnjxZPXr0kDFG\nGzdu1NSpUzVz5kzFxcXVmjcmJqZGGGrbtq0qKipOuu74+PiA5/2+E9tv27atYmNjZVmW/74kVVRU\nKCoqSpLUoUMH//yJiYmqqqpSaWmpCgoKtH79en3yySf+v/t8PvXs2dN//8RlAaAuhD0AYc+yLF12\n2WWaP3++tm/frssvvzxobbVr105Hjx7137dtW99++22j1llYWOi/XVBQoIiICMXGxqpDhw7q37+/\n7rzzzkatH0Drxpg/AEfYuHGjDh06pKSkpKC206lTJx09elTZ2dny+Xx6/fXXVVVV1ah1rlmzRvv2\n7dORI0e0dOlSXXHFFbIsS1dffbU++eQTbd68WbZt6+jRo9q6dau8Xm8TbQ2A1oCRPQBha9q0af5T\ns4mJiRo/frw6d+4c0LLHTquerqioKN1+++16/vnnZdu2brjhBiUkJDRoXcf069dPzz77rPbv36+L\nL77YP5KXkJCgyZMn65VXXtHs2bPldrvVpUsXvkMQwGmxDF/MBAAA4FicxgUAAHAwwh4AAICDEfYA\nAAAcjLAHAADgYIQ9AAAAByPsAQAAOBhhDwAAwMEIewAAAA5G2AMAAHCw/w/cpmclrhZJigAAAABJ\nRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f9809589810>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.plot(range(len(countList)), countList)\n",
"plt.xlabel('Bin number')\n",
"plt.ylabel('Bin coverage')\n",
"plt.xlim([0, len(countList)])\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now sort the list- order the windows based on the tag count"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"countList.sort()"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[0, 0, 0, 0, 0, 0]"
]
},
"execution_count": 21,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"countList[0:6]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Sum all the aligned tags"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"1562361"
]
},
"execution_count": 22,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"countSum = sum(countList)\n",
"countSum"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Calculate the summaric fraction of tags along the ordered windows."
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"countFraction = []\n",
"for i, count in enumerate(countList):\n",
" if i == 0:\n",
" countFraction.append(count*1.0 / countSum)\n",
" else:\n",
" countFraction.append((count*1.0 / countSum) + countFraction[i-1])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Look at the last five items of the list:"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[0.9965340916728814,\n",
" 0.9968470795162799,\n",
" 0.9973277622778184,\n",
" 0.9984939460215242,\n",
" 1.0000000000000862]"
]
},
"execution_count": 24,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"countFraction[-5:]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Calculate the number of windows."
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"101267"
]
},
"execution_count": 25,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"winNumber = len(countFraction)\n",
"winNumber"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Calculate what fraction of a whole is the position of each window."
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"winFraction = []\n",
"for i in range(winNumber):\n",
" winFraction.append(i*1.0 / winNumber)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Look at the last five items of our new list:"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"[0.9999506255739777,\n",
" 0.9999605004591822,\n",
" 0.9999703753443866,\n",
" 0.999980250229591,\n",
" 0.9999901251147956]"
]
},
"execution_count": 27,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"winFraction[-5:]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now prepare the function!"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def calculateSES(filePath):\n",
" countList = []\n",
" with open(filePath, 'r') as covFile:\n",
" for line in covFile:\n",
" countList.append(int(line.strip('\\n').split('\\t')[3]))\n",
" plt.plot(range(len(countList)), countList)\n",
" plt.xlabel('Bin number')\n",
" plt.ylabel('Bin coverage')\n",
" plt.xlim([0, len(countList)])\n",
" plt.show()\n",
" countList.sort()\n",
" countSum = sum(countList)\n",
" countFraction = []\n",
" for i, count in enumerate(countList):\n",
" if i == 0:\n",
" countFraction.append(count*1.0 / countSum)\n",
" else:\n",
" countFraction.append((count*1.0 / countSum) + countFraction[i-1])\n",
" winNumber = len(countFraction)\n",
" winFraction = []\n",
" for i in range(winNumber):\n",
" winFraction.append(i*1.0 / winNumber)\n",
" return [winFraction, countFraction]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Use our function to calculate the signal extraction scaling for the Sox2 ChIP sample:"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAnsAAAFOCAYAAAD+a9sUAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XtYVNX+P/D3nkHlC0zgIHZMKiq1jhikQd5+5a3n2zlm\nysnCOp3KSs27h06a1ikrs7JMxHuSml1Opkcxq9OxbynmPUgwRQ0pNS8hMBMIjAjMWr8/BgYGBhhg\nrpv363l8nNnsvddn7zV7z2fWXnttRUopQURERESqpPF0AERERETkOkz2iIiIiFSMyR4RERGRijHZ\nIyIiIlIxJntEREREKsZkj4iIiEjF/NxVUEVFBebOnYvKykqYzWb069cPDz74IFasWIFjx44hICAA\niqJg8uTJuP766wEAa9euRWZmJjp06IApU6YgIiICAJCamoqUlBQAwP33349Bgwa5azOIiIiIfIrb\nkr127dph7ty56NChA4QQePHFF3HbbbcBAB599FH07dvXZv6MjAxcvHgRS5YswcmTJ5GcnIz58+ej\npKQEmzdvxoIFCyClxOzZsxEbG4uAgIBGy8/KykJkZKTLto9ch3Xnm1hvvon15ptYb77JXfXm1su4\nHTp0AGBp5TObzVAUBQBgb1zntLQ0a4td9+7dYTKZUFhYiMOHDyMqKgoBAQEIDAxEVFQUMjMzmyw7\nKyvLiVtC7sS6802sN9/EevNNrDff5K56c2uyJ4TArFmzMGHCBERFRaFbt24AgE8//RQzZ87EBx98\ngMrKSgCA0WhEaGiodVm9Xg+j0djgdCIiIiKqz22XcQFAo9HgrbfegslkwsKFC3Hu3Dn89a9/RUhI\nCCorK/Huu+/is88+w+jRo90ZFhEREZFquTXZqxYQEICePXsiMzMTI0aMsATi54chQ4bg888/B2Bp\nsTMYDNZlDAYD9Ho99Hq9TbOnwWBAr1696pWRlZVlM198fLyrNodcjHXnm1hvvon15ptYb76pqXrb\nuHGj9XVkZGSL+/e5Ldm7dOkS/Pz8EBAQgPLychw5cgSjRo1CYWEhQkJCIKXE999/j2uvvRYAEBMT\ng+3bt2PAgAHIzs5GYGAgQkJCEB0djQ0bNsBkMkEIgSNHjuCRRx6pV569nXLhwgW3bCs5l06nQ3Fx\nsafDoGZivfkm1ptvYr35psbq7ZprrnFaEu+2ZK+wsBDLly+HEAJSSgwYMAB9+vTBq6++iuLiYkgp\nERERgfHjxwMA+vTpg4yMDEybNg3+/v6YNGkSACAoKAijR4/G7NmzoSgKHnjgAQQGBrprM4iIiIh8\niiLt3QqrUmzZ8038xeqbWG++ifXmm1hvvqmplj1n4RM0iIiIiFSMyR4RERGRijHZIyIiIlIxJntE\nREREKsZkj4iIiEjFmOwRERERqRiTPSIiIiIVY7JHREREpGJM9oiIiIhUjMkeERERkYox2SMiIiJS\nMSZ7RERERCrGZI+IiIhIxZjsEREREakYkz0iIiIiFWOyR0RERKRiTPaIiIiIVIzJHhEREZGKMdkj\nIiIiUjEme0REREQqxmSPiIiISMWY7BERERGpGJM9IiIiIhVjskdERESkYkz2iIiIiFSMyZ4HiA3J\nMC+d5+kwiIiIqA3w83QAbZFM3wMU/e7pMIiIiKgNYMseERERkYox2SMiIiJSMSZ7RERERCrGZI+I\niIhIxdx2g0ZFRQXmzp2LyspKmM1m9OvXDw8++CDy8vKQlJSEkpIS3HDDDZg2bRq0Wi0qKyuxbNky\n/PLLL9DpdEhISECnTp0AACkpKdi5cye0Wi3Gjh2L6Ohod20GERERkU9xW8teu3btMHfuXLz11lt4\n++23kZmZiZMnT+Ljjz/GiBEjkJSUhMDAQOzYsQMAsGPHDgQFBWHJkiW499578dFHHwEAzp07h/37\n9yMxMRFz5szBe++9BymluzaDiIiIyKe49TJuhw4dAFha+cxmMxRFQVZWFvr27QsAGDRoENLS0gAA\naWlpGDRoEACgX79+OHr0KAAgPT0dAwYMgFarRefOndGlSxfk5OS4czOIiIiIfIZbx9kTQmD27Nm4\nePEi7rnnHlx99dUIDAyERmPJOUNDQ2E0GgEARqMRoaGhAACNRoOAgACUlJTAaDSiR48e1nXq9Xrr\nMkRERERky63JnkajwVtvvQWTyYSFCxfi/PnzDi/LS7VEREREzeeRJ2gEBASgZ8+eyM7ORmlpKYQQ\n0Gg0MBgM0Ov1ACwtdtXvhRC4fPkygoKCoNfrUVBQYF1X7WVqy8rKQlZWlvV9fHw8dDqd6zfOAUWK\nAgl4TTzern379txXPoj15ptYb76J9eabmqq3jRs3Wl9HRkYiMjKyReW4Ldm7dOkS/Pz8EBAQgPLy\nchw5cgSjRo1CZGQkDhw4gAEDBmDXrl2IiYkBAMTExGDXrl3o3r079u/fj169elmnL1myBCNGjIDR\naERubi66detWrzx7O6W4uNj1G+qA6lZKb4nH2+l0Ou4rH8R6802sN9/EevNNjdWbTqdDfHy8U8px\nW7JXWFiI5cuXQwgBKSUGDBiAPn36IDw8HIsXL8ann36KiIgIDB06FAAwdOhQLF26FNOnT4dOp8OM\nGTMAAOHh4ejfvz8SEhLg5+eHcePGQVEUd20GERERkU9RZBvqDHfhwgVPhwAAMD/7OFD0O7TJ2zwd\nik/gL1bfxHrzTaw338R6802N1ds111zjtHL4BA0iIiIiFWOyR0RERKRiTPaIiIiIVIzJHhEREZGK\nMdkjIiIiUjEme0REREQqxmSPiIiISMWY7BERERGpGJM9IiIiIhVjskdERESkYkz2iIiIiFSMyZ5H\nKJ4OgIiIiNoIJntEREREKsZkj4iIiEjFmOwRERERqRiTPSIiIiIVY7JHREREpGJM9oiIiIhUjMke\nERERkYox2SMiIiJSMSZ7RERERCrGZI+IiIhIxZjsEREREakYkz0iIiIiFWOyR0RERKRiTPaIiIiI\nVIzJHhEREZGKMdkjIiIiUjEme0REREQqxmSPiIiISMWY7DmJzPsNsuSSp8MgIiIisuHnroIMBgOW\nLVuGoqIiKIqCu+++G3/+85+xadMmfPvttwgODgYAPPzww7jtttsAACkpKdi5cye0Wi3Gjh2L6Oho\nAEBmZibef/99SCkxZMgQxMXFuWszGiReeBq4+VZon53v6VCIiIiIrNyW7Gm1Wjz++OOIiIhAWVkZ\nnnvuOURFRQEARowYgREjRtjMf+7cOezfvx+JiYkwGAyYN28elixZAikl1qxZg5deegkdO3bEnDlz\nEBsbi65du7prUxpWdtnTERARERHZcFuyFxISgpCQEACAv78/unbtCqPRCACQUtabPz09HQMGDIBW\nq0Xnzp3RpUsX5OTkQEqJLl26ICwsDAAwcOBApKWleUeyR0RERORlPNJnLy8vD2fOnEH37t0BANu3\nb8fMmTOxatUqmEwmAIDRaESnTp2sy+j1ehiNRhiNRoSGhtabTkRERET1uT3ZKysrw6JFizB27Fj4\n+/vjnnvuwdKlS/H2228jJCQEH3zwgbtDIiIiIlItt13GBQCz2Yx33nkHd911F2JjYwEAV111lfXv\nw4YNw4IFCwBYWuwKCgqsfzMYDNDr9ZBS2kw3Go3Q6/X1ysrKykJWVpb1fXx8PHQ6ndO3qVohLP0S\nHSmjSKOBBFwaj5q0b9+e+8oHsd58E+vNN7HefFNT9bZx40br68jISERGRraoHLcmeytXrkR4eDiG\nDx9unVZYWGjty3fw4EFce+21AICYmBgsWbIEI0aMgNFoRG5uLrp16wYpJXJzc5Gfn4+OHTti7969\nmDFjRr2y7O2U4uJiF26dJZl1pAwphVviUQudTsd95YNYb76J9eabWG++qbF60+l0iI+Pd0o5bkv2\nTpw4gd27d+O6667DrFmzoCgKHn74YezZswenT5+GoigICwvDhAkTAADh4eHo378/EhIS4Ofnh3Hj\nxkFRFCiKgqeeegqvvfYapJQYOnQowsPD3bUZRERERD5FkfZuhVWpCxcuuGzd5vEjgeu7QfvPRU3P\nO3MsUGiENnmby+JRE/5i9U2sN9/EevNNrDff1Fi9XXPNNU4rh0/QICIiIlIxJntEREREKsZkj4iI\niEjFmOwRERERqRiTPSIiIiIVY7JHREREpGJM9oiIiIhUjMkeERERkYox2SMiIiJSMSZ7RERERCrG\nZI+IiIhIxZjsEREREakYkz0iIiIiFWOyR0RERKRiTPaIiIiIVIzJHhEREZGKMdkjIiIiUrFmJXsF\nBQXIzs52VSxERERE5GR+jsxUUFCApKQknD59GgDw4Ycf4sCBA8jMzMTEiRNdGR8RERERtYJDLXur\nV69G7969sX79evj5WfLDqKgo/Pjjjy4NjoiIiIhax6FkLycnB3FxcdBoamYPCAiAyWRyWWBERERE\n1HoOJXvBwcHIzc21mXbu3Dl06tTJJUGpn+LpAIiIiKiNcKjP3n333YcFCxYgLi4OQgjs2bMHKSkp\niIuLc3V8RERERNQKDiV7Q4cOhU6nwzfffIPQ0FDs2rULY8aMwR133OHq+IiIiIioFRxK9gAgNjYW\nsbGxroyFiIiIiJzMoWRvx44ddqe3a9cOoaGh6N69O9q1a+fUwIiIiIio9RxK9r777jtkZ2cjODgY\noaGhMBgMKCoqwk033YS8vDwAwKxZs3DTTTe5NFgiIiIiah6Hkr3w8HDccccdGD58uHXaf//7X5w/\nfx6vvvoqtmzZgrVr12L+/PkuC5SIiIiIms+hoVf27t2LP/3pTzbT/vd//xd79uyBoigYOXIkzp07\n55IAiYiIiKjlHB5n74cffrCZdujQIVx11VUAgIqKCuuTNYiIiIjIeziUoT3xxBNYtGgRrrvuOmuf\nvV9//RXPPPMMAODkyZP1Wv6IiIiIyPMcSvaio6OxbNkyZGRkwGg0onfv3ujTpw90Op3179HR0Y2u\nw2AwYNmyZSgqKoKiKBg2bBiGDx+OkpISLF68GPn5+ejcuTMSEhIQEBAAAFi7di0yMzPRoUMHTJky\nBREREQCA1NRUpKSkAADuv/9+DBo0qKXbT0RERKRqDl971el0uOuuu1pckFarxeOPP46IiAiUlZXh\nueeeQ3R0NHbu3Ilbb70Vo0aNwtatW5GSkoJHHnkEGRkZuHjxIpYsWYKTJ08iOTkZ8+fPR0lJCTZv\n3owFCxZASonZs2cjNjbWmiASERERUQ2Hkj2z2Yzt27fj2LFjKC4utvnbK6+84lBBISEhCAkJAQD4\n+/uja9euMBgMSE9Px8svvwwAGDx4MF555RU88sgjSEtLs7bYde/eHSaTCYWFhcjKykJUVJQ1uYuK\nikJmZiYGDBjgUBxEREREbYlDN2isX78e33zzDXr27IlffvkFffv2RVFRESIjI1tUaF5eHs6cOYMe\nPXqgqKjImgSGhISgsLAQAGA0GhEaGmpdRq/Xw2g0NjidiIiIiOpzqGXv4MGDmD9/Pjp16oSNGzdi\n+PDhiI6OxurVq5tdYFlZGRYtWoSxY8fC39+/3t8VRWn2Ou3JyspCVlaW9X18fLy1j6ErFALQajUO\nlVGkUSABl8ajJu3bt+e+8kGsN9/EevNNrDff1FS9bdy40fo6MjKyxY1sDiV75eXl1ta09u3b48qV\nK+jatStOnz7drMLMZjPeeecd3HXXXdbn7Fa35lX/HxwcDMDSYmcwGKzLGgwG6PV66PV6myTOYDCg\nV69e9cqyt1PqXoJ2NrNZOFSGFNIt8aiFTqfjvvJBrDffxHrzTaw339RYvel0OsTHxzulHIcu43bt\n2hU///wzAODGG2/Epk2bsHnzZuj1+mYVtnLlSoSHh9s8ieP2229HamoqAMtdtjExMQCAmJgY7Nq1\nCwCQnZ2NwMBAhISEIDo6GkeOHIHJZEJJSQmOHDnS5J3ARERERG2VQy17Y8eOhVarBQA8/vjjeO+9\n93D58mVMmDDB4YJOnDiB3bt347rrrsOsWbOgKAoefvhhxMXFITExETt37kRYWBgSEhIAAH369EFG\nRgamTZsGf39/TJo0CQAQFBSE0aNHY/bs2VAUBQ888AACAwObu91EREREbYIipZSNzSCEQGpqKu68\n8060a9fOXXG5xIULF1y2bvP4kcD13aD956Km5535BFBogDZ5m8viURNenvBNrDffxHrzTaw339RY\nvV1zzTVOK6fJy7gajQYffPCBzyd6RERERG2RQ332br/9dqSnp7s6FiIiIiJyMof67FVUVGDRokXo\n0aMHQkNDbYZHmTp1qsuCIyIiIqLWcSjZu/baa3Httde6OhYiIiIicjKHkr0HH3zQ1XEQERERkQs4\nlOwBwI8//oi9e/eiqKgIs2fPxs8//4zLly/bHdCYiIiIiLyDQzdofPXVV0hOTkaXLl1w/PhxAJYn\naWzYsMGlwamWkx4JR0RERNQUh5K9//znP3jxxRcRFxcHjcaySNeuXV06bh0RERERtZ5Dyd7ly5fR\nqVMnm2mVlZXw83P4KjAREREReYBDyd4f//hHbN261WbaV199hcjISJcERURERETO4VCy9+STT+L7\n77/HlClTUFZWhhkzZmD//v14/PHHXR0fEREREbWCQ9dhO3bsiDfeeAM5OTkoKChAaGgounXrZu2/\nR0RERETeyaFk78svv8TAgQPRvXt3dO/e3dUxEREREZGTOJTsZWVl4ZNPPsHNN9+M//f//h/69u2L\ngIAAV8dGRERERK3kULI3a9YslJaW4sCBA/juu++wdu1aREdH484770Tfvn1dHSMRERERtZDDne4C\nAwMxbNgwzJ07F4mJiSgrK8OiRYtcGRsRERERtVKzBso7ceIE9uzZg4MHDyIoKAjx8fGuiouIiIiI\nnMChZO/DDz/E/v37oSgK+vfvjxdeeAEREREuDo2IiIiIWsuhZO/KlSuYNm0a/vjHP7o6Ht8mpacj\nICIiIrLhULI3btw4AEBBQQGMRiP0en29x6cRERERkfdxKNkrLCxEYmIisrOzodPpUFxcjB49emDG\njBnQ6/WujpGIiIiIWsihu3FXr16N66+/HuvWrcPq1auxbt06REREIDk52dXxEREREVErOJTs/fTT\nT3jsscfg7+8PAPD398ff/vY3ZGdnuzQ4IiIiImodh5K9wMBAnDt3zmbahQsX+BQNIiIiIi/nUJ+9\nkSNHYt68eRg6dCjCwsKQn5+P1NRUjBkzxtXxEREREVErOJTs3X333fjDH/6APXv24Ndff0XHjh0x\nffp03Hrrra6Oj4iIiIhaweEnaPTq1Qu9evVyZSxERERE5GQO9dlbuHAhjh8/bjPt+PHjeOedd1wS\nFBERERE5h0PJ3rFjx3DzzTfbTOvRoweysrJcEhQREREROYdDyV67du1QVlZmM62srAxardYlQRER\nERGRcziU7EVHR2P16tUwmUwAAJPJhDVr1uC2225zaXBERERE1DoO3aDx2GOPYenSpXjyyScRFBSE\nkpIS3HbbbZg2bZrDBa1cuRKHDh1CcHAwFi5cCADYtGkTvv32WwQHBwMAHn74YWsCmZKSgp07d0Kr\n1WLs2LGIjo4GAGRmZuL999+HlBJDhgxBXFxcszbYKyieDoCIiIjaCoeSvaCgIMyZMweFhYUoKChA\np06dEBIS0qyChgwZgj//+c9YtmyZzfQRI0ZgxIgRNtPOnTuH/fv3IzExEQaDAfPmzcOSJUsgpcSa\nNWvw0ksvoWPHjpgzZw5iY2PRtWvXZsVCRERE1FY4PPQKAISEhDQ7yat2yy23ID8/v950KWW9aenp\n6RgwYAC0Wi06d+6MLl26ICcnB1JKdOnSBWFhYQCAgQMHIi0tjckeERERUQOaley5wvbt2/Hdd9/h\npptuwmOPPYaAgAAYjUb06NHDOo9er4fRaISUEqGhoTbTc3JyPBE2ERERkU/waLJ3zz334IEHHoCi\nKNiwYQM++OADTJw40SnrzsrKshkaJj4+HjqdzinrtqcQgFarcaiMIkUDCbg0HjVp374995UPYr35\nJtabb2K9+aam6m3jxo3W15GRkYiMjGxROR5N9q666irr62HDhmHBggUALC12BQUF1r8ZDAbo9XpI\nKW2mG41G6PV6u+u2t1OKi4udGX49ZrNwqAwphVviUQudTsd95YNYb76J9eabWG++qbF60+l0iI+P\nd0o5Dg29AliGW8nJycHRo0dt/jWHlNKmj15hYaH19cGDB3HttdcCAGJiYrBv3z5UVlYiLy8Pubm5\n6NatG7p164bc3Fzk5+ejsrISe/fuRUxMTLNiICIiImpLHGrZS01NxZo1a+Dv74/27dtbpyuKUu/u\n2oYkJSXh2LFjKC4uxqRJkxAfH4+srCycPn0aiqIgLCwMEyZMAACEh4ejf//+SEhIgJ+fH8aNGwdF\nUaAoCp566im89tprkFJi6NChCA8Pb8FmExEREbUNirR3O2wdTz/9NCZOnIjevXu7IyaXuXDhgsvW\nbR4/ErjuJmhfTGx63ueeBIwF0CZvc1k8asLLE76J9eabWG++ifXmmxqrt2uuucZp5Th0GVcIYR3U\nmIiIiIh8h0PJ3qhRo7B582YIIVwdDxERERE5kUN99r788ksUFhZi27ZtCAoKsvnbypUrXRIYERER\nEbWeQ8lec56BS0RERETew6Fkr2fPnq6Og4iIiIhcoMFkb8uWLbj//vsBAJ9++mmDKxgzZozzoyIi\nIiIip2gw2TMYDHZfExEREZHvaDDZGz9+vPX15MmT3RIMERERETmXw49Lq1ZUVISDBw/i/PnzroiH\niIiIiJyo0Rs0jEYj1q5di3PnzqFHjx647777MHfuXGg0GpSWlmLq1KkYOHCgu2IlIiIiomZqtGVv\n9erVCAwMxOOPPw4pJebPn4+JEyfivffewzPPPIOUlBR3xUlERERELdBospednY3x48ejd+/eGDdu\nHIqKihAbGwsAiI2NRX5+vluCJCIiIqKWaTTZM5vN8POzXOnt0KED/P39oSiKWwLzTdLTARARERHZ\naLTPntlsxtGjR63vhRD13hMRERGR92o02QsODrZ59m1QUJDN+6uuusp1kRERERFRqzWa7C1fvtxd\ncbQxvBRORERE7tHscfaIiIiIyHcw2SMiIiJSMSZ7RERERCrGZI+IiIhIxZjsEREREakYkz0iIiIi\nFWOyR0RERKRiTPaIiIiIVIzJHhEREZGKMdkjIiIiUjEme0REREQqxmSPiIiISMWY7BERERGpGJM9\nIiIiIhXzc1dBK1euxKFDhxAcHIyFCxcCAEpKSrB48WLk5+ejc+fOSEhIQEBAAABg7dq1yMzMRIcO\nHTBlyhREREQAAFJTU5GSkgIAuP/++zFo0CB3bQIRERGRz3Fby96QIUPwwgsv2EzbunUrbr31ViQl\nJSEyMtKaxGVkZODixYtYsmQJJkyYgOTkZACW5HDz5s1444038Prrr+Pf//43TCaTuzaBiIiIyOe4\nLdm75ZZbEBgYaDMtPT3d2jI3ePBgpKenAwDS0tKs07t37w6TyYTCwkIcPnwYUVFRCAgIQGBgIKKi\nopCZmemuTSAiIiLyOR7ts1dUVISQkBAAQEhICAoLCwEARqMRoaGh1vn0ej2MRmOD04mIiIjIPq+6\nQUNRFE+HQERERKQqbrtBw57q1rzq/4ODgwFYWuwMBoN1PoPBAL1eD71ej6ysLJvpvXr1srvurKws\nm3nj4+Oh0+lctCVAIQCtRutQGUUaDSTg0njUpH379txXPoj15ptYb76J9eabmqq3jRs3Wl9HRkYi\nMjKyReW4NdmTUkJKaX1/++23IzU1FXFxcUhNTUVMTAwAICYmBtu3b8eAAQOQnZ2NwMBAhISEIDo6\nGhs2bIDJZIIQAkeOHMEjjzxityx7O6W4uNh1GwfALMwOlSGFcEs8aqHT6bivfBDrzTex3nwT6803\nNVZvOp0O8fHxTinHbcleUlISjh07huLiYkyaNAnx8fGIi4tDYmIidu7cibCwMCQkJAAA+vTpg4yM\nDEybNg3+/v6YNGkSACAoKAijR4/G7NmzoSgKHnjggXo3fRARERFRDbclezNmzLA7/cUXX7Q7/amn\nnrI7ffDgwRg8eLCzwiIiIiJSNa+6QYOIiIiInIvJnifwrmMiIiJyEyZ7RERERCrGZI+IiIhIxZjs\nEREREakYkz0iIiIiFWOyR0RERKRiTPacqdbTQYiIiIi8AZM9IiIiIhVjskdERESkYkz2iIiIiFSM\nyR4RERGRijHZIyIiIlIxJntEREREKsZkj4iIiEjFmOwRERERqRiTPSIiIpUyPz8B4otPPR0GeRiT\nPSIiIrXKz4X86YinoyAPY7JHREREpGJM9oiIiIhUjMkeURPklTJPh0BERNRiTPaIGiGzsyCmxns6\nDCIiohZjskfUmEu/ezoCIiKiVmGyR0RERKRiTPaIiIiIVIzJHhEREZGKMdkjIiIiUjEme0RERERO\nIk+fhJTS02HYYLJHRERtgiwthiy77OkwyI2kMEOWmdxappj/DyDnuFvLbAqTPSIiahPErCcgkl72\ndBjkRvLzDRDTHnJ/wZUV7i+zEUz2iIiobSgvBwz5no6C3Ckv19MReAU/TwcAAFOmTEFAQAAURYFW\nq8Ubb7yBkpISLF68GPn5+ejcuTMSEhIQEBAAAFi7di0yMzPRoUMHTJkyBREREZ7dACIiIiIv5RXJ\nnqIomDt3LoKCgqzTtm7diltvvRWjRo3C1q1bkZKSgkceeQQZGRm4ePEilixZgpMnTyI5ORnz58/3\nYPRERERE3ssrLuNKKevduZKeno5BgwYBAAYPHoz09HQAQFpamnV69+7dYTKZUFhY6N6AiYiIyPsp\nHirXy+7G9ZqWvfnz50NRFNx9990YNmwYioqKEBISAgAICQmxJnRGoxGhoaHWZfV6PYxGo3VeIiIi\nIqrhFcnevHnz0LFjR1y6dAmvvfYarrnmmnrzKIqn0nNq0/i5IyKiZmPLXj0dO3YEAFx11VWIjY1F\nTk6OtTWv+v/g4GAAlpY8g8FgXdZgMECv19dbZ1ZWFrKysqzv4+PjodPpXLYNhQC0Wq1DZVzSaCAA\nl8ajJu3ZBal4AAAgAElEQVTbt/fYvir3/x+YwLpqCU/WG7WcmuutEJaGAzVuX0P1VgjAT6tFkAq3\n2RGl7dqjAu49hxcC+J//CUA7B8ps6njbuHGj9XVkZCQiIyNbFJPHk70rV65ASgl/f3+UlZXhxx9/\nxAMPPIDbb78dqampiIuLQ2pqKmJiYgAAMTEx2L59OwYMGIDs7GwEBgbavYRrb6cUFxe7dFvMp3Nw\nqbAQilbb6HxCCLfEoxY6nc5j+6p6AFZ3lS+FGVA0qmjJ9mS9qY2UErhwFkrX61xeltrrTQqhyu1r\nrN4qzWZVbrMjRNV4d+7e/ssmE8ocKLOxetPpdIiPj3dKPB5P9oqKivD2229DURSYzWbceeediI6O\nxk033YTExETs3LkTYWFhSEhIAAD06dMHGRkZmDZtGvz9/TFp0iQPb0Ed+b8Bfwj3dBTko8TTf4ES\n9zco9zrnACeVyM6CWPg8tMnbPB0JkY/x0A9n3qBhq3Pnznj77bfrTQ8KCsKLL75od5mnnnrK1WER\nec65056OgLxNRbmnIyBf5mWJB7mfVwy9QkRERKQe3pVgM9kjIiIidfL97s9OwWSPiIjaNFlcBGk2\nezoMUhPvathjsqcG8kg6zONHejoMIiKfJJ55FPLrFE+HQS4gz/zs6RC8ApM9FZBncjwdAhG5lJc1\nE6hR0e+ejoBc4cKvno6gHvm7AfKyya1lMtlztqox9EgleBcbERE5kZj1BMS7C9xaJpM9J5OpX3k6\nBHIh6eCvRHn6JC+tkxOxlzmRb2mioaC4yD1hVGGy52ylJZ6OgFxIzJ0Keb7phE+eP+OGaIjUR5Zc\ngjTxPEo+rqmrQm6+asRkz0uZx4+ELG2bj7fxeuYKT0dApFrihach3prj6TCIXMvNPYSY7DmbM6+2\nsJXQ81r8jFpedvM0aSyALL/i6TCouUylgLHA/eWyfy45k5d9nJjsqQITC/IMmXkA4suNzllXoQHm\nfzrvWdfiuSchN61z2vo8y8u+OVxNNv9GN2nMd0EgROrAZM8TWtxaRN6B9VdNbPsEcutHzlnZhV+B\ni+eds65qJZecuz5yj2bmtvLS7xDP8ZnpDfrpiFuKkadPQnJEiipNfYjZZ4/I9zEfJGqFZn4RVlba\nLu2m5IZsifn/AI6kezoM38AbNIicy7x4LkTyQk+H4TCZvsez5VdUQGxa69EYqK429uuhFV+EsqIC\nYuELTgyGmsVc2fQ8bYGX9QFlsuds3lW/BABZGZCHv3d5MeaERyA2r69658NfzgW5kF9v9XQU1Ka1\n4kRaUe68MHyENOTD/Ns5T4dRxYfPfW4mDXkofGiIW8pisucE5iWvejoEqiL+s8l+R213/MoqKYY8\nle36cuyQXnOiJ3KC1hyuHmxZMs8ZD/ljWoN/l2WXXVKueHMWihMedcm6m03jPcme9Gji78CHOO83\n14dRhcmeM7CPgsdIKSErasa9kykfQu7fWX9GZw7B4YU32IiXJkMWXHR/wc7cF2wVb0Qb2znN/nGm\nNPDazQouQiyd1+CfxbQxkGdPOb/c8jLnr7PFvOf8KD/7lwcLb+rv7LNHHiS2fgTzrCc9HUY98vhh\niG31D1y5bwfE5NEeiKgJDiZB8tdfIP672Tllms3OWY8Xnaxrk3m/QfJh9S7n7ge029f6L0JZ68tU\nbPsXxMerWr1Opygthixz8j52ct4ghbDZf83iTT+GvflJLFK6dV8x2SMbMvso8LvrBjSVR36AvFTY\n7OXEf7dAfr6h/h/yLjghKidq5l2AYt7fIa39/FrJ1ztGN3HeEy88DZH4kntiaaPkqZMoeuJe15dz\nJqeJGZxRSM1K5LefQ6b+xwkrdQJFgZj2EKRTB46uta15v7U8Uasipo2BTPmwtUF5nicTT96gQU7n\n1Etprv2AiiWvQH7xafMXbHATPXAwO1KkB8KSGQfqT3PgOb5ew5GPXnP7PHngZO+sfW5e+ALEwV1O\nWVdtUjTSAlzi+oezy9ISiNeeaWKm1ozVJuv8711kznHLC2deeq3divnC08DJY61bX/kVyNMnm5zN\n/MZMiDWJdaZ6UcueN7Uy2sOWPe8mDuyEPOeCfhfewMt+jcii31FxaH/DB4W9yc3YBnnliss6Tbtd\nne2W589AvDy1+etp1vnHy0+mbiaNBS3b5/b8dATy0H7nrKsW8fRfIDMPOn29DnMkkWt2lz07n0Pv\nOpVZOW0QcpuV1nnvrscE/vIT5PFM22nedErw9mTPjTuLyV4LyDWJEO54DJMnEkonJ3uy6HfIyoqm\nZ2xo+W3/Qulbz6PBg6KVB7NIfBHixcmtWod9njjJ1Km7qjvRzK8/65y15xyHdFK/QHnudP2Jjuwy\nL/sxUk9jrWYtUr29zv08yYbuAvT2/dsc3r4tTg3PBdvq6JMw6vaj9aoEy5tiqYM3aHgXWWaC+eVp\ndv7g+oqSZ35xeRn1C3XudolnH4f8vAWXbeutyPIlKn/Y1/S8zTnZ/HYWKDS0MCgvU7djfXVVOmk4\nGLHgOci03c5Z1yvT6/fddMUh5e4vfMXJp1TpqkuS9tfnPa3crdhel+0z15L5uS3/MeWKz3mL1+nF\nCZZbOfC4NDfuqjaV7JmnP9T8hYwFwPkzzg/GW7niuYZFxtav45jlUoH45jPb6S78FSmFgFi1wGXr\ndzZHBkKW53+FPLQfsqIc8koLLvU4s+WqRZ81L/8Cd/bHsWpzxZYPXLLeenKd/GzilmpV8iJt/mv2\n0scyIU2lrSi/ZcTzEyB3flHzfu1iu8mf+e3n7dwx7ZJfSi1bzJtyPQ+3MspLv0N8t72ROXgZ1zVa\nMqRAQ593JyRFTQ1x0NjgnD7Fzr6Sh9MgszIcWLjOwVDvS8BeX53mnKQaOdhqnWjN40fWGqDTgQO0\nVquVvHIF4t/v15vFWZdEG1Z/P4iPV0CsfANi0UsQr9hpsSYAgPnVGRDf/bf5Czq7Za+6Dl0xNlsr\niN1f27/i4Sl2D8mGzgONnx9E4kuQ21NaG5ED7MRRWpNkyv077A8dkn0UqDumpgOnPCklROpXEJ99\nDLHn/5peQHj5DytHePRuXEB+tx3yw+UNz8MbNLyJ6z7wYvpDMD/TyKjn50+7rOwGteouuAbU6bMn\nT5+EWDYPYvn8ppe93MQv7FYfLI3Ub919UeF430NZ+9myF85Abt9i+/f8XIiklx1eX4vUvkNvbaJl\n0OXqu/RyjgH5uQ0s2Ix96u6TqbPHE7PTn1T+mAacPQV55FDzV+js/dGKFi7z9IcgDtgOMF6zva3b\nkfLoD957xcN6FbeJpO6jFTA/P8H+Hz2VI7T0/GtnW2VFBcTaWnfKVpRDfrwS8otPHRsRocXfBY3v\nPFlZ6fDQMObxIyGLL7UwDkDu+qrFy7ZeE9sowcu4XsXVfX6KGxnqoImy5c8nnBqK+fkJwK/O7ydY\nr59XdR8yB/ZtvWWdVB/SVAJxILWJmZwwsKswQ9S5QcI8fiTE8xOA44ebXv53Q8sHua09ztj+nZDp\ne1q2HgCy+u4+X/ux30jyJQ+nQUyqPyC3rK6XlpyI65QnKyshj7YgaXSGyybg559sp5VaWoqknZbm\nZmlNq0/1VdaGji9nJcyygddVFSuzs4D8XPtxVI2BJ4WAzHXjowhbfM6xs9yl3+0/TcjVsTRRf2LS\n/ZD/2dRIsXXKbc3AyLWunshfLMeCrKyweeqSs8hD+yB2fFFnaiP7gjdouJeU0tIx9qej9Qa5lFLW\nnPirp5VU/cpo8FeP/Qo0vzARsgUDAMv8XOuHtC7x5iznXgpssKXHi9Q9QKqOJfnrzxDfft74orVu\nxJD7voVcswh1D0aZlQHx6RrL6x1f1l0DAEC8NcfxeJtxud9ePyEx6wmI6Q9BnjoJ+fMJmGf8tfF1\nlDTyK1jTvMNd/GdTTV8xb7mz0UlxmMePhPyliR9LGQcgtn3SvBXX+jjJ8iuQabtd34Jrh/jCzgDk\nQLMG3ja/OqPhO+mdcAVATBjV6ADrrX/meBOXcas+S2LCKMvbWl/U1cOJiL8/4pS79eWxTDsTLeXL\n385C/l51bqp7vqi6a1qsXwrx70ZGgKisU6+K0niXAkcS6mYca2LNopo+wI7k6g20CktDvrU+nE28\nMdPy/+KXIeb93fnr//Q9yE9W10yo/WO7wQG0eRnXpaSptGbg0xM/Qjw/AWLh8xCr3oSsfdAUGiE3\nWr74RVUlioS/Va2k6QNBfLwSovqpD3kXIE83MWq8vXUse836IbWr9pfLqewWDXMivthg98Moyy5D\n1jr5yNJiyGYM1il/a+AXsfVEU3WyE6LheeuttNYBdPaU9dmHYl4C5IbkRhcV/2z8pC0rKiAWz4Ws\nuglEbmngyRZVl5bl7waYx49sPN6Ljif4Yv3Shv/2+j8snx9TCcTGNZDHMiCqnrxR+zKH9fNpTxP9\nyeSPaZYfD9VfQikfQn717zoz2f+Sd3YrsyvI7CyYX5pSM6GkuIE5aw4q+Xkzk73qViMpIRa9CLm2\n7oCzDcRWaIQ8VTOIrXnBbMuLw99D1voMyawMiC83Wl5XPXJLrEuCrPqhJouLLP+qjgu5f0fNsqYS\niBVvOBSPOLjL0k+wobtznZX8X7EzsHD1ums9c1yaShodrFrWTsqlbTJXj9ls6X/b2DZUHyvVx/qV\nMoiPVtS0cDdBms3W5EdWlNt98ouYaxmPUbw0BWLxXMu8+761neerf0OsSYTc83+QtTr6y4wDlu+x\nxu6ebuaPu9aQB1IBg6UfYe3PsTx/xnqOlJdNkL+dbXgd53+FmP2U5XXtRgwn/tCUV65YnnJkJ466\n33fNZq+1u/q77oKd5NbpwzQ1rm0mextW1wx8Wl5e84dT2ZBVJ9J6y9RtnpWW5y02NriyTP3Kdrm8\n36wn5Ubjc+ADZ23qrvUBE68/C7n32waWaGRdn/0L8mBqveli2hjIr2s6KsvN6yHemu3YOvN+g3ip\noeSqzq+Zw983Mm/dFUuYX5oC+cPeJkd4l5WVtieNKzUnRmsH7KpLBLKiwuYZu/ZuqKgX98/Hmw73\nzM9NzmNV2lDyUUVTlUj832cQiXMhq5+pW2ck/gYvj9Xt1F2HWDoP4uWp9uuiep3ZWZa3lZWWJzFU\nPfZKXjzv9Ae8y0IDxKZ1lla46ktphQbrgMDy0D5Ie8kC7Ldwymzbk7y8aHvnqSwthnn560Bled1F\nmxO15T8hgAuNP0lD7P0G5mljIIsvQaxfAvH6P2CufrJETs2Pqto3aokvPrUOyiumPWT5gtr3LWRV\nYiRemQHxyvSaQmrtH/nxu9b6AgApzPWuXFh/gL33jvWt2JAM8eFy275T9vqIHdpn6aKw7V+WH3C/\nNuOzD8t5r6EnhshPLOds8/iRds+5cvfX9paqeVm7729xkSXRajTZq7Omj1dB7vqvzWDUdfuSyVqX\nG8XEv1jOn9lZkN9sa7icatWflUuFlh8KtVrxZHW/Sykhq7rZyM8/gXhhguXHaa3jzua7Q6u1KcLm\nikTBRZjfrnkv1iyCOLjL9kdbMxOf6s+SzaDRVXd3m8ePhJj+EET1jy0hIL7/DiLN0rVEfPOZpR9o\n9bo21GohawF56qTdAcnF1Aftz19w0VJfdupKmkohL15oeGxK64yy4bf29mXxpUZbWM3TH268vGZq\nm8le1a8zKWX9E0eREeJfqywnnbr9b2r3nZIC8vMNEK/MsJ2n7DLkpcKaB7bX+gKXn30MYecONvnz\nCYhP34O5el2NHGTy4gWYp42paX3ZvsX20kwDX34267hyBbLkEsyznrT2MZB1hnawnnTzayUIVXHJ\nK1csJ90f9kFe+NXmJGed9YWnbd6b35pt9zFNsqIC4t236i+/+2v7Se9vZ4HfzlpaTDXa+n+vXm9p\nMcSk++tdQjMnvmTptF5YZziYOr+Q695QUTW15tWhfda4xd5vbe7clLW+5OW6xQ3GWE+t/pLiX+/W\nH27DzolBms3AJdt+n2LCKMuv6TqtEPV+sKDqcmbty8d2ht6QlRXWAZpl1U1DYtL9ENNqhjKSB1Ih\nXp0BKSXMiS/ZPOhdVlbaH+alanus5VePpVj1fGEx8wnrjw2xtmY/Vt/YI1a+CfnJakiz2fJlcnCX\npfzxI60tnDJtd82XUOb3tuVXl7NmkeXu8A3JQOaBegm6NBZAbPtXzfvcc5ZtKi2uf2mtulFp11c2\nd/9bzym1Z/3vFqDsMsQzfwOqL+OdyYGsMy5i9dUFANYk0LrPqo59+clqiI9XApd+rz/IbfV6zLat\n/uLpv1haH40FEN9/Z5mn7vOnhdnyXNnvtkM887ealqSqFl7zlAcgqurImoj8mA7x7OMQ8xIsq/h4\nFcRnNfuvduuw/OrfEKn/sWxP3m81SWZ18bssx1Xty711z7k222jMR00lNDibpcuKnW41NT+U6pz7\nq1pIZfJC63eGeOZvNj/exT8n1VmZgHh7jvXcKnbW7RYCu1cGxOTRNT9GD9t+ZsW/VtW8KSkGLl6w\nfeZv9XdbzvH6LXt1n0dc9cNNfLAM8kAq5HvvQCyb1/D8Tah9ZcX8+rOWc0uB/cYN+cNey75c/RbM\nC56D/HSNTf/s2ld65KlsS9Jc3Y+yosI6MoK9c4v87RzEusUQK5tuxRZ7/s9yHM8Zb1l201rr8Wdp\nnS2D/HgVxD8nQrzwdM2j7qrLkrLmapedqx7WxLeiHPKS5bi0xittvw9lwUWYl8+3nIvM5qZvTmwm\nRbb2ickekpmZiffffx9SSgwZMgRxcXFNLnP23hhAF2y9KUIZdh9knX5eSr/BliZpO5SnEiDrPQew\naZpVKRAT/9Ls5QAAfu2AygpoFqyBog+zHJi7vwYCdXZbgpT/jYPyp9FA0FWQ+3ZAiYqF/GoTlEF/\nBhRAvDARiL6j3kmkMdpky68dsWZRg/tGM2MuRPJCoJnjUykDh1lbI5XHpkK5+hqg+BLEqjehjHgI\nsqG+R06m3D4Q8oe9jc+k72TtuN3ougb9CXJXC4btaMp1N7rkBhrNy0uB0DCb5K0x2uRtTV6+Vh4Y\ni6uGj0Zx7m+Wm1EAKE8mQImOtSQ4zz0Fzdwk6xe3Mu4ftl/03XvaPt+z6jiwF4PSbwjkgZ1Q+g+B\ncveo+v1xAoJsO3nf0KP+QNO1p3W62m4rqObNNUDFFYgXJ0MZM87SzWP7FuvxAVS1EFR9cdjV9Xpo\nHhpvuWGm9iW7BspsiNJ/KOT+HdDMfB3i7ecbn7l634VHAPaeXFJFs3ILxKT7HY7BZtkVmyFTPoD8\nP9txMDVT/wmx7DXL66WWY1ksmF0/jp63QTPyrxBvzrK77tqt7kDNOUmWlgBlJojZ4+otpzw6GUpY\nF6B7pMPbpXkx0ZqkapZucOiY0CZvsyTMzz3pUBmtog8DjPk17zv8DxB2tXV/al5d4fhVkgZoJs2G\nWPlm/T/8IRzKn0dDM2CYdVKT3VhcSLNsE+SnyZC7v4YSeydk2m5oJj8PseJ1h5ZXRv3V0t3hD13r\n/8ht5DtSs3ILxNJXofnTaIhFL1qmvbYKYsFzQHGR9dykPDql8WFXAGieexNiwWwoj0wEcs/Xy0eu\n/TK9gSWbzyeTPSEEZsyYgZdeegkdO3bEnDlz8Pe//x1du3ZtdLmz98a4KcI6omIBtYyZR0T1KEOG\nQ+78T9Mzku8Iugpo7IanNkqz+jMoVa3ynkz2vJVy90jHLt07wJnJnp/T1uRGOTk56NKlC8LCwgAA\nAwcORFpaWpPJnscw0SNSNSZ6KsREz77zpyFO/Ai5b0fT87ZBzkr0nM0nkz2j0YjQ0FDre71ej5yc\n5t/pSkRERI5rrM8kea82eYMGERERUVvhky17er0eBQU1HeWNRiP0er3NPFlZWcjKyrK+j4+Pd+r1\nbyIiIiJX2rixZji4yMhIREZGtmg9Ptmy161bN+Tm5iI/Px+VlZXYu3cvYmJsb76IjIxEfHy89V/t\nHUa+hXXnm1hvvon15ptYb76pqXqrnce0NNEDfLRlT6PR4KmnnsJrr70GKSWGDh2K8PBwT4dFRERE\n5HV8MtkDgNtuuw1JSUmeDoOIiIjIq/nkZdyWaE3zJ3kW6843sd58E+vNN7HefJO76s0nB1UmIiIi\nIse0mZY9IiIioraIyR4RERGRivnsDRrNkZmZiffffx9SSgwZMgRxcXGeDqnNMRgMWLZsGYqKiqAo\nCoYNG4bhw4ejpKQEixcvRn5+Pjp37oyEhAQEBAQAANauXYvMzEx06NABU6ZMQUREBAAgNTUVKSkp\nAID7778fgwYNAgD88ssvWLFiBSoqKtC7d2+MHTvWE5uqSkIIzJkzB3q9Hs899xzy8vKQlJSEkpIS\n3HDDDZg2bRq0Wi0qKyuxbNky/PLLL9DpdEhISECnTp0AACkpKdi5cye0Wi3Gjh2L6OhoADw+XcVk\nMmHVqlU4e/YsFEXBpEmT0KVLFx5vXu6LL77Azp07oSgKrrvuOkyePBlGo5HHmxdauXIlDh06hODg\nYCxcuBAA3PKd1lgZDZIqZzab5dSpU2VeXp6sqKiQzz77rDx37pynw2pzfv/9d3nq1CkppZSXL1+W\n06dPl+fOnZMffvih3Lp1q5RSypSUFPnRRx9JKaU8dOiQfP3116WUUmZnZ8vnn39eSillcXGxnDp1\nqiwtLZUlJSXW11JKOWfOHHny5EkppZSvv/66zMjIcOcmqtrnn38uk5KS5JtvvimllHLRokVy3759\nUkopV69eLb/++msppZTbt2+XycnJUkop9+7dKxMTE6WUUp49e1bOnDlTVlZWyosXL8qpU6dKIQSP\nTxdatmyZ3LFjh5RSysrKSllaWsrjzcsZDAY5ZcoUWVFRIaW0HGc7d+7k8ealjh8/Lk+dOiX/8Y9/\nWKe54xhrqIzGqP4ybk5ODrp06YKwsDD4+flh4MCBSEtL83RYbU5ISIj1V4y/vz+6du0Kg8GA9PR0\n66+YwYMHIz3d8pSTtLQ06/Tu3bvDZDKhsLAQhw8fRlRUFAICAhAYGIioqChkZmaisLAQly9fRrdu\n3QAAd911F+vZSQwGAzIyMjBs2DDrtKNHj6Jv374AgEGDBln3de1669evH44ePQoASE9Px4ABA6DV\natG5c2d06dIFOTk5PD5dxGQy4cSJExgyZAgAQKvVIiAggMebDxBCoKysDGazGeXl5dDr9cjKyuLx\n5oVuueUWBAYG2kxzxzFWtwxH6lD1l3GNRiNCQ0Ot7/V6PXJycjwYEeXl5eHMmTPo0aMHioqKEBIS\nAsCSEBYWFgKwX29Go9Hh6aGhoTAajW7aInVbv349Hn30UZhMJgBAcXExgoKCoNFYfivW3te160Gj\n0SAgIAAlJSUwGo3o0aOHdZ3V9Sal5PHpAnl5edDpdFixYgXOnDmDG2+8EWPHjuXx5uX0ej1GjBiB\nyZMno0OHDoiKisINN9yAwMBAHm8+wh3HWN0yioqKmoxL9S175F3KysqwaNEijB07Fv7+/vX+riiK\nB6KihlT3R4mIiICsNUqTdHDEJkfnI+cSQuDUqVO45557sGDBAnTo0AFbt26tNx+PN+9SWlqK9PR0\nrFixAu+++y6uXLmCzMxMh5fn8eZ93HGMOVKG6pM9vV6PgoIC63uj0Qi9Xu/BiNous9mMd955B3fd\ndRdiY2MB2P7yKSwsRHBwMABLvRkMBuuyBoMBer2+Xn3Wnm5vfmqdEydOID09HVOnTkVSUhKOHj2K\ndevWwWQyQQgBwHZf164HIQQuX76MoKCgRuuNx6fz6fV6hIaG4qabbgJgucR36tQpHm9e7siRI+jc\nubO15fyOO+7ATz/9hNLSUh5vPsIdx1hDZTRG9clet27dkJubi/z8fFRWVmLv3r2IiYnxdFht0sqV\nKxEeHo7hw4dbp91+++1ITU0FYLkjqbpuYmJisGvXLgBAdnY2AgMDERISgujoaBw5cgQmkwklJSU4\ncuQIoqOjERISgoCAAOTk5EBKie+++86aUFLL/fWvf8XKlSuxbNky/P3vf0evXr0wffp0REZG4sCB\nAwCAXbt22a23/fv3o1evXtbp+/btQ2VlJfLy8pCbm4tu3brx+HSRkJAQhIaG4sKFCwAsSUR4eDiP\nNy/XqVMnnDx5EuXl5ZBSWuuNx5v3klLatKi64xhrqIzGtIknaGRmZmLdunWQUmLo0KG81dwDTpw4\ngblz5+K6666DoihQFAUPP/wwunXrhsTERBQUFCAsLAwJCQnWDq9r1qxBZmYm/P39MWnSJNx4440A\nLB/uLVu2QFGUerepL1++3Hqb+hNPPOGx7VWjY8eO4fPPP7cOvbJ48WKUlpYiIiIC06ZNg5+fHyoq\nKrB06VKcPn0aOp0OM2bMQOfOnQFYhoLYsWMH/Pz86g0FwePT+U6fPo13330XlZWVuPrqqzF58mQI\nIXi8eblNmzZh37590Gq1iIiIwMSJE2E0Gnm8eaGkpCQcO3YMxcXFCA4ORnx8PGJjY11+jJWUlDRY\nRkPaRLJHRERE1Fap/jIuERERUVvGZI+IiIhIxZjsEREREakYkz0iIiIiFWOyR0RERKRiTPaIiIiI\nVIzJHhGpUnJyMrZs2eLpMJr0yiuvYMeOHZ4Og4hUzM/TARARtcSUKVNQVFQErVYLrVaLHj16YMKE\nCdZHCo0fP97DERIReQe27BGRz5o9ezbWr1+P1atXIzg4GGvXrvV0SB7FMfKJyB627BGRz/Pz80O/\nfv2wfv1667QVK1YgNDQUY8aMwbFjx7B06VLce++9+Oyzz6DRaPDwww9j8ODBdtf3yiuv4JZbbsHR\no0fx66+/okePHpgxYwaCgoKs61q5cqV1/ilTpmDSpEno1asXNm3ahLNnz6Jdu3ZIT09H586d8cwz\nz+DgwYP48ssv0a5dO0ycOBFRUVHW5XNzc/H888/j/Pnz6NWrFyZPnmx9/FF2djY+/PBDnDt3DmFh\nYRg7dix69uxpjfPmm29GVlYWTp8+jYULF+Lqq692wR4mIl/Glj0i8nlXrlzBvn370KNHjwbnKSws\nxMiid3QAAAMISURBVOXLl/Huu+9i4sSJWLNmDUwmU4Pz7927F1OmTMF7772HyspKbNu2zeF4Dh06\nhEGDBmHdunW4/vrrMX/+fEgp8e6772L06NFYvXq1zfy7d+/G5MmTkZycDI1GY22hNBqNWLBgAUaP\nHo1169bh0UcfxTvvvIPi4mKbZSdOnIj169cjLCzM4RiJqO1gskdEPuvtt9/GE088gbFjx+LIkSO4\n7777GpzXz88Po0ePhkajQe/eveHv748LFy40OP/gwYPxhz/8Ae3atUP//v1x5swZh+P64x//iKio\nKGg0GvTv3x/FxcWIi4uDRqPBwIEDkZ+fb5No3nnnnQgPD0f79u0xZswYHDhwAFJK7N69G71798Zt\nt90GALj11ltx4403IiMjw7rsoEGD0LVrV2g0Gmg0PKUTUX28jEtEPmvmzJno1asXpJRIS0vD3Llz\nkZiYiODg4HrzBgUF2SRD7du3R1lZWYPrDgkJcXjeumqX3759e+h0OiiKYn0PAGVlZQgICAAAdOrU\nyTp/WFgYKisrUVxcjPz8fOzfvx8//PCD9e9msxm33nqr9X3tZYmI7GGyR0Q+T1EU3HHHHVi9ejVO\nnDiBvn37uqysDh06oLy83PpeCIFLly61ap0FBQXW1/n5+fDz84NOp0OnTp0waNAgTJgwoVXrJ6K2\njW3+RKQKaWlpKC0tRXh4uEvL6dKlC8rLy5GRkQGz2YzNmzejsrKyVevcvXs3zp8/jytXrmDjxo3o\n168fFEXBnXfeiR9++AGHDx+GEALl5eU4duwYjEajk7aGiNoCtuwRkc9asGCB9dJsWFgYpk6diq5d\nuzq0bPVl1eYKCAjAuHHjsGrVKgghMGrUKISGhrZoXdXuuusuLF++HBcuXEDPnj2tLXmhoaGYOXMm\nPvroIyQlJUGr1eKmm27iGIJE1CyK5MBMRERERKrFy7hEREREKsZkj4iIiEjFmOwRERERqRiTPSIi\nIiIVY7JHREREpGJM9oiIiIhUjMkeERERkYox2SMiIiJSMSZ7RERERCr2/wE8wKsDPr5OeAAAAABJ\nRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f97cc184550>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"chipSes = calculateSES(\"/ngschool/chip_seq/bedtools/sox2_chip_coverage.bed\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now we can plot the calculated fractions for both the input and ChIP sample:"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAm4AAAFOCAYAAAA/7JG4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xd0VMXfBvBnLkkIaZBNQiAJCYRQg9J7ryIgTdoriAUr\nCNgVERQpVpASRKQIigKhI0WkKRI6EoEgJfT0sul99877RzQ/IyV3l2ySTZ7POZ6T3b137jcOgSd3\n7swIKaUEEREREZV5SmkXQERERETaMLgRERERWQkGNyIiIiIrweBGREREZCUY3IiIiIisBIMbERER\nkZWwKakLLVmyBH/88QeqVq2KL7744q7HrFy5EqGhoahcuTImTJiA2rVrl1R5RERERGVeid1x6969\nO6ZOnXrPz8+cOYPY2FgsXLgQL7zwApYtW6a57bCwsOIokUoJ+896se+sG/vPerHvrNuD9F+JBbeG\nDRvC0dHxnp+fPHkSXbt2BQDUq1cPmZmZSE5O1tQ2/wBbN/af9WLfWTf2n/Vi31k3qwhuRdHr9XBz\ncyt4rdPpoNfrS7EiIiIiorKlzAQ3IiIiIrq/EpucUBSdTofExMSC14mJidDpdHc9NiwsrNBtxhEj\nRli8PrIc9p/1Yt9ZN/af9WLfWbcRI0YgODi44HVgYCACAwM1nVuiwU1KiXvtad+qVSvs2bMHHTp0\nwOXLl+Ho6Ihq1ard9di7fYNRUVHFXi+VDGdnZ6SlpZV2GWQG9p11Y/9ZL/ad9Vqx7gCmvT7G7PBd\nYsFtwYIFuHDhAtLS0vDyyy9jxIgRMBgMEEKgV69eaNGiBc6cOYOJEyfC3t4eL7/8ckmVRkRERGRx\n0mhEfErmA7VRYsFt8uTJRR4zbty4EqiEiIiIqOTJXRtwy77OA7XByQlEREREFibPHEP64YNIrFz1\ngdphcCMiIiKyIBlxHep3QQgd9joaV7/3mrZalJlZpZbg5OQEIURpl0F3IaVEenp6aZdBRERkUTIx\nDuqimRCjnkdIliM6+Do9UHvlOrgJITjrpoxydnYu7RKIiIgsSqYmQ503HaL3YMQHtkfYzzcxuX3N\nB2qTQ6VERERExUxmZkBd8CFEm85Qeg3E1r/06F23KhxsKz1QuwxuRERERMVI5uZAXTwLom5DiIFP\n4HZKDkJupmFwo7tvLGAKBjciIiKiYpIf2mZDuLpDjHoBALDidByGN3FDVfsHf0KNwa0U9ejRA8eO\nHSvtMoiIiKgYyJwcqEGzIJyqQjzzKoSi4OD1VOgzDXi0vmuxXKNcT04o6w4cOGDxa7z22mvw8vLC\nW2+9ZfFrERERVVQy5+/h0aquEM9MhlAqIT4jD6v+iMOMnrVgoxTPKhe840ZERET0APLvtM2EqKor\nCG2qlFhwNBoDG+lQx9W+2K7F4FaK2rVrh8OHD2PevHl46aWXMHnyZDRo0AA9e/bEuXPnCh0XFBSE\n7t27IzAwEG+88QZyc3MBAMHBwRgyZEihdn18fHDz5k388MMP2LJlC5YsWYIGDRrgmWeeKdHvj4iI\nqLyTOdlQF30E4eoG8cwkCCV/1mjw+UQYVYkhxTAh4d8Y3MqIvXv3YsiQIbh48SJ69eqF9957r9Dn\nW7duxdq1a3HkyBFcvXoVCxYsKPjsv4sM//N69OjRGDJkCF5++WVcunQJ3377reW/ESIiogoiP7TN\nhNB5QDz9v9B2KjIdv1xJxludvVGpmIZI/1Ghn3EzPj+wWNqptGz7A7fRpk0bdOvWDQAwbNgwrFix\notDnzzzzDGrUqAEAmDRpEqZNm3bP59aklA9cDxEREd2bzM7Kn4jgXh1i7CsFoS06LRcLj0VjShdv\n6KoUf8yq0MGtOAJXcfHw8Cj4ukqVKsjJyYGqqlCU/JuiNWv+b6VlHx8fxMbGlniNREREBMiMdKgL\nZ0B4+UI8OQHi73+rs/JUfHwoEiObuKORh4NFrl2hg5s1iYqKKvg6IiICnp6eAAAHBwdkZWUVfBYX\nF1foPO7VSkREVHxkShLUL6dDNG4GMfzZgn9njarEF4cjUc/NHv3qV7PY9fmMWxn13+HOVatWITo6\nGklJSVi0aBEGDRoEAGjcuDEuX76MCxcuICcnB/PmzSsU1jw8PHDr1q0SrZ2IiKg8kgmxUD97F6JV\np0KhTUqJZadiYVAlXm5Tw6I3TRjcStH9Ova/nw0ZMgRPPPEEOnXqhDp16mDSpEkAAH9/f7z66qsY\nOXIkOnfujLZt2xY6b9SoUbh06RICAwPx3HPPFf83QUREVAHI6NtQP58C0fMxKANGFvp3ettFPS7E\nZ+Htzt7Ftl7bvQhZTp5k//dQ4j+cnZ2RlpZWCtUUr3bt2uGLL75Ap06dSruUYvPvvikv/VQRse+s\nG/vPerHvSpa8GZ4/e3ToU1A69Cj0WcitVKw4HYdP+/jBw9FWU3teXl5m18Jn3IiIiIjuQZ7/A+rK\nL6GMnQDRrF2hzy7EZWLpiVh82KOW5tD2oBjcrAAnGBAREZU89ehByI3fQhk/BSKgcaHPridl45Pf\nI/FaRy/464pvZ4SiMLhZgaNHj5Z2CURERBWGlBLy582Qv+2G8uZsiJq1Cn0elZqLjw5G4MXWnmhe\n07FEa2NwIyIiIvqbVI2Q61dAXjoH5Z1PIVzdCn2emJmHDw7cxv897I6Ovi4lXh+DGxEREREAmZcL\ndcU8IC0VytsfQzg4Ffo8NduADw7cxqP1qqFPgOXWarsfLgdCREREFZ7MTIc6/0MICCivfnhHaEvL\nMWL6gdto6+OMoYFu92jF8njHjYiIiCo0mRgHdeFHEI2aQowYV7CF1T/Sc4yYvv8WmtVwxJim7qVU\nZT4GNyIiIqqw5PUrUL+aDfHIUIiej92xkkN6rhEfHLiNJp4OeKq5R6mv9MChUrqniIgI+Pj4QFXV\n0i6FiIio2Mk/jkJdOAPK6Jeg9Bp4RyjLyDXiwwO30dCjCp5tUb3UQxvA4FZqTpw4gUGDBqFRo0Zo\n0qQJhgwZgrNnzz5Qm4mJiZgwYQJatmyJxo0bY8iQIThz5sx9z7l69SpefPFFPPTQQ2jcuDF69+6N\nb775pmCv1Pv9IZ03bx4mTpxY8NrHxwf169dHgwYN0KpVK8yYMeOOPVeJiIhKm5QS6i9boa79Jv95\ntv8srAsAmXlGzDgYgQCdPZ5rWTZCG8DgVirS09Px9NNPY9y4cbhw4QJOnz6N1157DXZ2dg/UbkZG\nBpo1a4Y9e/YgLCwMw4YNw9ixY5GVlXXX42/cuIGBAwfCx8cHBw4cwIULF7B06VKcO3cO6enpmq75\n7z/IQgjs27cPly5dwvr167F161b88MMPD/Q9ERERFSdpNEL++DXkkf1Q3v0Mwi/gjmMy84z46GAE\nalerjBdae5aZ0AYwuJWKa9euQQiBgQPzb8tWrlwZXbp0QcOGDQHk/yYwf/58tG3bFs2aNcOrr75a\nEKS2b9+O9u3bIyMjAwBw4MABNG/eHHq9Hr6+vnj++efh7u4OIQRGjx6NvLw8XL169a51zJ07F61a\ntcK0adPg4eEBIH/T+kWLFsHZ2bmglk2bNqFNmzZ4+OGHsXDhwnt+X1LKgjtsdevWRZs2bXDp0qXi\n+Z9GRET0gGRWJtSgmZBxMflrtLl53HFMWo4R0/ffhl+1ynipjSeUMhTaAAa3UuHv7w9FUfDqq6/i\n4MGDSElJKfT5+vXrsXHjRmzatAlHjx5FRkYG3nvvPQDAwIEDC8JWUlIS3nrrLcydOxc6ne6O65w/\nfx55eXmoXbv2Xes4fPgw+vfvX2S9J0+exOHDh7Fu3TrMnz8f4eHhRZ5z+fJlnDhxAk2aNCnyWCIi\nIkuT+nion70LoasOZeI0iCoOdxyTnG3A+/tuIbC6A15qXfZCG1DBZ5UO+uFisbSzbXRDk453cnLC\nli1b8NVXX+Htt99GfHw8unfvji+++AJubm7YsmULXnjhBfj4+AAA3n33XfTs2RPz58+HoiiYPXs2\nevXqheHDh6NPnz7o0aPHHddIS0vDq6++ijfeeANOTk53fA4ASUlJ8PT0vG+tQgi88cYbsLOzQ+PG\njdG4cWNcuHABAQF33loGgL59+0JRFFSrVg2jR4/GyJEjTfp/Q0REVNzkjStQF8+B6DUQos/guw59\nJmbmYfr+2+jo54z/e8i9TA2P/luFDm6mBq7iFBAQgHnz5gHInyAwceJEfPDBBwgKCkJsbGxBaAPy\nH/o3GAyIj4+Hp6cnXFxcMGDAACxbtgzLli27o+3s7Gw888wzaNmyJcaPH3/PGlxdXREbG1tkrf8M\nowKAvb09MjMz73nsnj174OvrW2SbREREJUE9/hvkumVQnpwA0aL9XY+JTc/F9P230SegGh4vxcV1\nteBQaRlQt25djBgxAhcv5t8B9PT0RERERMHnERERsLW1LQhQ58+fx/r16zF48GBMmzatUFu5ubkY\nN24cvLy88Omnn973up06dcKuXbuK9XvhLFIiIioLpKpC3fI95Jbvobwx856hLTI1F+/tvYWBDXVl\nPrQBDG6lIjw8HEuXLkV0dDQAIDIyElu3bkXLli0BAIMHD8ayZctw+/ZtZGRk4NNPP8XAgQOhKAqy\ns7MxefJkTJkyBXPnzkVMTAxWr14NADAYDHj++edRpUoVzJ8/v8g63nzzTZw6dQqzZ89GfHw8AOD6\n9euYOHEi0tLSADCIERGR9ZHZmVCXfAx5JQzK1LkQPnXuetzN5By8v+8W/u9hd/Rv4FrCVZqnQg+V\nlhYnJyecOXMG33zzDdLS0uDi4oLevXvj/fffBwCMGjUKsbGxGDp0KHJzc9GtWzfMnDkTAPDJJ5/A\n29sbY8aMAQAsXLgQI0aMQNeuXRETE4MDBw7A3t6+YIaqEAJr1qxB69at76jDz88P27dvx6efforu\n3btDVVX4+Phg5MiRcHJyQkpKyh1j/Pcb8y+rzwMQEVHFIeNjoC6eDeHfAOLFtyFsbO96XHhiNmb+\nehvjWnqiS22XEq7SfEKWk1sqUVFRd7zn7OxccOeIypZ/9w37yXqx76wb+896se/uTl46D/WbzyD6\njYDo0f+eNxT+jMnA3MNRGN+2BtrVci7hKgEvLy+zz+UdNyIiIrJ66m8/Q277Acpzb0A0bnbP4w7d\nSMXyU7F4u7M3mnjeuSRIWcfgRkRERFZLGgyQwcsh/zqbv6iu573vZv10UY8tF/T4qGct1Ha1L8Eq\niw+DGxEREVklmZEG9etPAVs7KFM+h3BwvPtxUuL70HgcvZ2Oj/v4wtPpwbaYLE0MbkRERGR1ZMQN\nqF/NgWjeHuLxsRBKpbseZ1AlFh+Pwe2UHHzaxxcu9tYdfay7eiIiIqpw/llUV4x8Dkq7bvc8Lseg\n4rPfIyEBzOrlC3sb618FjcGNiIiIrII0GCA3rYb88ziU12dC1Lr7+mwAkJpjxKxfb8PL2Q6vtKsJ\nG6V8LFlVroOblBLOziU/zZeKVk5WoSEiohIiU5OgLv0MsLOHMnUehOPd9+EGgPiMPHx44Dba+Dhh\nbDOPcrXOaLkObunp6aVdAhERET0gefUi1KWfQXTsBfHYKAjl3kOeN5Nz8NHB2xjUSIeBDXUlWGXJ\nKNfBjYiIiKyXlBLy0J789dmemgjRtM19j/9nYd1xLauja52qJVRlyWJwIyIiojJH5uVC/vA15PXL\nRa7PBgD7ribju9B4q11YV6sSDW6hoaFYtWoVpJTo3r07Bg8eXOjzhIQELF68GJmZmVBVFU888QSa\nN29ekiUSERFRKZOJcVCXfAJRvWb++mz2Ve55rColfvgzAYdvpmJOb1/4uFQuwUpLXokFN1VVsWLF\nCkyfPh2urq6YMmUKWrduDW9v74JjNm/ejA4dOqB3796IiIjAxx9/jMWLF5dUiURERFTK5IVQqCvm\nQTwyFKL3oPtOLMg1qlh4NBpxGQZ89ogfqlr5Gm1alNh3GB4ejpo1a8LDwwMA0LFjR5w8ebJQcBNC\nICsrCwCQmZkJna78PVRIREREd5JSQu7ZDLlvO5Tn34Ro+PB9j0/NNmD2b5Fwc7DBzJ61ULkcrNGm\nRYkFN71eDzc3t4LXOp0O4eHhhY4ZPnw4Zs2ahd27dyMnJwfTpk0rqfKIiIiolMjsTKjfLgSSEqC8\n9wWEzuO+x0em5mLmr7fR0dcFo5u6QylHy30UpUzdUzx8+DC6deuGAQMG4PLly1i0aBHmzZtX2mUR\nERGRhciI6/lLfdQLhHjuDQhb2/seHxqdgXlHojCmqQf6BFQroSrLjhILbjqdDgkJCQWv9Xr9HUOh\nBw8exNSpUwEA9evXR15eHlJTU+Hi4lLouLCwMISFhRW8HjFiBBfatWJ2dnbsPyvFvrNu7D/rVR76\nTkqJ3IO7kL12GRyeHA+7Ln2KPGfb+Th8dzoaH/QOQDNvlyKPL8uCg4MLvg4MDERgYKCm80osuAUE\nBCAmJgbx8fFwdXVFSEgIJk+eXOgYd3d3nD17Ft26dUNERATy8vLuCG3A3b/BtLQ0i9ZPluPs7Mz+\ns1LsO+vG/rNe1t53Micbcs0SyFtXobw1Bzk1ayHnPt+PUZVYfjoWZ2My8XFvX9R0Flb9/Ts7O2PE\niBFmnVtiwU1RFIwbNw6zZs2ClBI9evSAj48PgoODUbduXbRs2RJPPvkkli5dip07d0JRFEyYMKGk\nyiMiIqISICNvQV36KUSd+vnPs1W2v+/x6TlGfHY4EpWEwGeP+MHRrlIJVVo2CVlONo2Miooq7RLI\nTNb+m2NFxr6zbuw/62Wtface2Q+54VuIYc9A6dizyOMjU3Mx69cItPR2xDPNq6NSOdko3svr/osJ\n30+ZmpxARERE5Y/MyYFc+zXk1UtQ3pwN4e1X5DkVfRLCvWgOblFRUbhx4ways7MLvd+jR49iL4qI\niIjKBxl9G+rXn0L4+kOZOve+uyAA+ZMWdl1ORvD5BLzVyQsPeTqWUKXWQVNw27x5MzZt2gQ/Pz9U\nrlx4KwkGNyIiIrob9dhByPUrIIaOhejU+767IABAnlHF1ydjcSUhG5/08UNNZ7sSqtR6aApuu3bt\nwpw5c+DnV/StTSIiIqrYZG4O5LplkJfDoLwxE8KnTpHnJGbm4ZNDkXBzsMWnj/ihim3F2AnBVJqC\nm52dXaGtqYiIiIjuRsZE5s8arVkLyvtzIewdijznUkIWPj0Uib71q2F4oFuRd+YqMk1xduTIkVi5\nciWSkpKgqmqh/4iIiIgAQD35O9RP34Ho+ijE829qCm17w5Mx+9cIvNymBkY0cWdoK4KmO25fffUV\nAGD//v13fLZ+/frirYiIiIisiszLhVy/HPJCKJTXZkD41i3yHIMqsfxULM7GZmJOb1/4VK1c5Dmk\nMbgFBQVZug4iIiKyQjImAuqyLwCPGlDe/xLCoehZoMnZBnz2eySq2Cj4nIvqmkRTcPPw8AAAqKqK\nlJQUVK1aFYrChwaJiIgqKikl5OG9kJu/gxj0RP7wqIZhziuJ+c+zdatTFU80dYfCoVGTaApumZmZ\nWLlyJUJCQqCqKipVqoQOHTrg2WefhYND0ePXREREVH7IjHSo3wcBMZFQ3poD4eVb9DlSYu/VFKwJ\njcfLbWqgva9zCVRa/mgKbt9++y2ys7Mxd+5ceHh4ID4+HuvWrcPKlSvxyiuvWLpGIiIiKiPk5TCo\nK+ZBNG8HMe51CNui11rLMahYejIWlxOzMKePL3xc+DybuTQFt9DQUAQFBRUsvuvl5YXx48dj4sSJ\nFi2OiIiIygZpNELuWAf5+y9Qxr4C8XBrTefFpufik0OR8Haxw+eP1Ob6bA9I8zpuqampBc+6AUBq\naipsbLjVKRERUXkn42OgrpgHVK6SPwGhmk7Teacj07HgWDSGB7phQANXLvVRDDQlrx49emDWrFno\n379/wVDpzp070atXL0vXR0RERKVIPf4b5PrlEH0fh+g1EELD5ERVSqw/l4C94Sl4t7M3Glfn8/DF\nRVNwGzp0KFxdXRESEgK9Xg+dTodBgwahe/fulq6PiIiISoHMzoT88RvIa5egTP4Qwq/otdkAIC3H\niC+PRCHboGLuo7XhWoWjc8VJ0/9NIQR69OjBDeWJiIgqAHn9CtRln0M0eAjKtC8hKttrOu+aPhuf\n/B6Jdj5OGNu8OmwUDo0Wt3sGt0OHDqFLly4AgAMHDtyzAYY5IiKi8kGqKuSeLZB7t0J54kWIVp20\nnff3Uh/fh8bjpdae6OjnYuFKK657BreQkJCC4Pb777/fswEGNyIiIusnkxKhrvwSMBqgTJ0H4eZR\n9EkAsvJUfHUiBjeTc/Axl/qwOCGllKVdRHGIiooq7RLITM7OzkhLSyvtMsgM7Dvrxv6zXsXddzL0\nGNTvFkP06A/RbziEom0LqhtJ2fjscBQaeVTBC608UdmGS31o4eXlZfa5mv4Pv/3223d9/9133zX7\nwkRERFS6ZE4O1B+WQF23HMr496AMGKUptEkpse9qMqbtv41hgW6Y2K4mQ1sJ0TQ5ISYm5o73pJSI\njY0t9oKIiIjI8mTEdajffAHhUxvK9AWaNocHgGyDiq9PxCBcn43ZvX3hW5VDoyXpvsEtKCgIAGAw\nGAq+/kd8fDxq1aplucqIiIio2ElVhdy3HXL3Rojhz0C076F5YdxbKTn47PdI1HOzxxd9a8Oed9lK\n3H2Dm6en512/FkKgQYMGaN++veUqIyIiomIlE2KhfrsAUFUo730B4VFD87kHrqXg2z/i8FRzD/Sq\nW82CVdL93De4DR8+HABQr149NGvWrEQKIiIiouIlpYQ8vBdy83cQfYdC9B6keQJCjkHFN6di8Vd8\nFmb18oVfNQ6NliZNz7jduHEDTk5OCAgIKHgvPDwcYWFhGDRokMWKIyIiogcjU5KgfhcEJCVAeWMW\nhE9tzefeTM7BF4cjUcfVHnP7coP4skBTD+zatQs+Pj6F3vPx8cGuXbssUhQRERE9OHk6BOpHkyF8\n6uQPjWoMbVJK7L6chPf33cLgRjq81qEmQ1sZoemOm8FggI1N4UNtbGyQm5trkaKIiIjIfDIjHXLt\nUsjrV6CMfw+ibkPN56blGBF0PBpx6XlcULcM0hSf/f39sWfPnkLv/fLLL/D397dIUURERGQeeeEM\n1BmTAAcnKNPnmxTawmIz8equ66juaIvPHvFjaCuDNN1xe+qppzBr1iwcOnQInp6eiI2NRXJyMqZN\nm2bp+oiIiEgDmZMNuWkV5J8noDw9EaJxc83nGlWJ9ecT8MuVZLzSriZaeTtZsFJ6EJq3vMrOzsbp\n06eRmJgINzc3tGzZEvb29pauTzNueWW9uO2O9WLfWTf2n/X6b9/JqxehrpwP4d8A4v+eh3DQHrzi\nM/IwLyQKtpUEXu3gBV0VTfd06AE8yJZXmnvH3t4eHTt2NPtCREREVLykIQ/yp3WQh/dCeeIliJYd\nTDr/yK1UfH0yFoMb6jC4sQ6KxoV4qfRoCm5GoxF79uzBhQsX7vjtbMaMGRYpjIiIiO5NRtyAuuJL\nwM0jf8uqqq6az80xqFhxOg5/xmTg/a4+qO9exYKVUnHSNDlh9erV2LdvHxo3boxr166hbdu2SElJ\nQWBgoKXrIyIion+RqhHZ29dCnfs+RM8BUCZMNSm03UjKxhs/30BWnoov+9VmaLMymu64HT9+HLNn\nz4a7uzuCg4PRr18/NG3aFN98842l6yMiIqK/ybhoqN/OR56tHZSpcyHcPYs+6Z9zpcSuy8lYdy4B\nz7Soju51XDTvUUplh6bglpubCzc3NwCAnZ0dcnJy4O3tjRs3bliyNiIiIsLfW1b9vgdyyxqIfsPh\nNPgJpGdkaD5fn2XAoqPRSMs14pM+fvB2sbNgtWRJmoKbt7c3rl69ioCAAPj7+2PDhg2oUqUKdDqd\npesjIiKq0GRyItTVQUBaCpS35kB4+UIo2ncxOHorDV+fjMEj9aphRBN32Ci8y2bNNAW3p59+GpUq\n5W9G+9RTT2H58uXIysrCCy+8YNHiiIiIKiopJeTx3yCDV0B0exSi3wgIG+1LdWTmGbH8VBzC4jIx\npYsPGnrwWbbyoMg/Aaqq4tatW+jcuTMAoGbNmlx4l4iIyIKkPgHqmq8AfTyUSdMhatcz6fy/4jIx\n/2g0HvJ0wPx+dbjPaDlSZHBTFAXfffcdevToURL1EBERVVj5z7L9Arnle4ju/SHGT4GwsdV8vkGV\nWHc2AXuvJmN8mxpoW8vZgtVSadB0z7Vly5Y4deoUWrVqZel6iIiIKiQZHwP1uyAgOwvKm7MhvP1M\nOj8iNQdfhkSjqn0lzO9XB67cAaFc0tSreXl5mDdvHurXrw83N7dC04dfeeUVixVHRERU3knVCHlg\nJ+TO9RB9H4foNQji7+fKNZ0vJX6+kowfzybgiYfd0bdeNS7zUY5pCm61atVCrVq1LF0LERFRhSKj\nb0NdvQhQFCjvfAZRw9uk85OyDFh0LBrJ2UZ83McXPi6VLVQplRX3DG7ff/89nnzySQBAo0aN0KRJ\nkxIrioiIqDyTBgPkns2Q+7ZBDBwN0bWvSUt8AMDx22lYciIGvepWw6iHucxHRXHPPyX79u0r+Prz\nzz8vkWKIiIjKO3nrGtSP34S8HAbl/S+hdO9nUmjLyDXi81+vY8UfcXinszfGNPNgaKtA7nnHrXbt\n2pg7dy58fHyQl5eH9evX3/W4kSNHWqw4IiKi8kLm5UHuWA/5+x6Ix5+C6NDT5GfRQqMzEHQsGm39\nXDG/X2042Gp/Fo7Kh3sGt9dffx379u1DfHw8pJRITEwsybqIiIjKDXn1Yv6zbJ7eUKYvgKhm2s5D\nWXkqVp+Jw4nIdLzStga6NqiJtLQ0C1VLZdk9g1vVqlXx+OOPA8hfhHf8+PElVhQREVF5IHNyILeu\ngTx5CGLk8xCtOpp8ly0sNhMLj0WjcfUqWNi/DpzseJetItM0q7S4QltoaChWrVoFKSW6d++OwYMH\n33HMkSNHsHHjRggh4Ofnh0mTJhXLtYmIiEqSvHgW6ndBEP4NoHywCMLZxaTzcwwqvv8zHiE30/BS\nG0+09eFiuqQxuBUHVVWxYsUKTJ8+Ha6urpgyZQpat24Nb+//TX2OiYnBtm3bMGvWLDg4OCA1NbWk\nyiMiIiqHbL12AAAgAElEQVQWMisTcuMqyHOnoIx+GaJpa5PbuJSQhflHolFXVxkL+teBS2XeZaN8\nJRbcwsPDUbNmTXh4eAAAOnbsiJMnTxYKbvv27cMjjzwCBwcHAICLi2m/nRAREZUmee4U1DVfQQS2\ngPLhQggHJ5POzzOq+PFsAg5cS8ELrT3R0Zf/DlJhJRbc9Ho93NzcCl7rdDqEh4cXOiY6OhoAMG3a\nNEgpMWzYMDRr1qykSiQiIjKLTE+FXL8CMvwClKcnQzRqanIb4YnZWHA0Cl4udljQvw6q2XPLKrqT\n5j8VkZGROHr0KJKTk/Hcc88hMjISBoMBfn6m7aV2P0ajETExMZgxYwYSEhLwwQcfYO7cuQV34P4R\nFhaGsLCwgtcjRoyAszPH/q2VnZ0d+89Kse+sG/uveOQe+w1ZqxfBtl03VPniWwj7Kiadn2dU8cMf\n0dgeFofxHXzRs56uyAkM7DvrFxwcXPB1YGAgAgMDNZ2nKbgdPXoUK1asQJs2bRASEoLnnnsO2dnZ\n+PHHHzFt2jRNF9LpdEhISCh4rdfrodMVng7t5uaGevXqQVEUVK9eHV5eXoiJiYG/v3+h4+72DXJa\ntPVydnZm/1kp9p11Y/89GJmSBPXHpUDUTSgvvA1jQCOk5xmAPO3/T28kZWP+0Wjoqthg3qN+cHOw\nRXp6epHnse+sm7OzM0aMGGHWuZqWag4ODsb777+PF154Acrfqzv7+fnhxo0bmi8UEBCAmJgYxMfH\nw2AwICQkBK1atSp0TOvWrQvupKWmpiI6OhrVq1fXfA0iIiJLk6oK9dfdUD+cCOFZM39dtoBGJrWR\nZ5RYdy4B0/bfxoAGrpjWzQduDrYWqpjKE0133FJSUu4YEhVCmLQWjaIoGDduHGbNmgUpJXr06AEf\nHx8EBwejbt26aNmyJZo1a4azZ8/i9ddfR6VKlfDkk0/Cycm0BzuJiIgsRd6+DnXNV4AQUN6YBeFT\n2+Q2riRmYdGxGHg42ODLfrXhzsBGJtAU3Pz9/XHo0CF07dq14L2QkBAEBASYdLFmzZphwYIFhd77\n763CsWPHYuzYsSa1S0REZEkyOwvyp7WQRw9CDB4D0am3yZvC5xjyZ4z+ej0Fz7aoji61XUxejJdI\nSCllUQdFRkZi1qxZqF69Oq5cuYLAwEBERUXh/fffR82aNUuiziJFRUWVdglkJj6rYb3Yd9aN/aeN\nDD0Ode03EPUDIYY/C+FSzeQ2zsVmYPHxGATo7PF8K09UfcAZo+w76+bl5WX2uZqCGwDk5OTg9OnT\nSEhIgJubG1q2bAl7e3uzL1zcGNysF/8Csl7sO+vG/rs/qY+HunYZEHULypiXzVriIyPXiNVn4nEq\nKh0vti6+3Q/Yd9btQYKb5shfuXJldOjQwewLERERWQNpNELu/wly9waI7gMgXngTwtbO5HZORaZj\nyYkYtPRywqL+deDIPUapGGgKbtOnT7/rOLyNjQ3c3NzQpk2bO2aIEhERWRt5/TLU7xcDjs5Q3vkM\nooZ30Sf9R2q2ActPx+FSQhYmt6+Jh2s4WqBSqqg0PVnZuHFjxMXFoVGjRujcuTMaNWqE+Ph41K1b\nF1WrVsWSJUuwbds2S9dKRERkETIzA+oPX0NdPBuiz2Aor880ObRJKXHoRiom7bwO1yo2WNi/DkMb\nFTtNd9zOnj2LqVOnwsfHp+C9zp07Y/HixZgzZw7atm2LBQsWYNCgQRYrlIiIqLhJKSFP/g4ZvBKi\naWsoMxZDOJq+DFViZh6+PhmL2LQ8vNfVB/XdTds9gUgrTcEtMjISnp6ehd7z8PAomBAQEBCA5OTk\n4q+OiIjIQmRcNNQfvgZS9FBeesfkRXSB/OC392oK1oTGo199V7zdyRu2lbjEB1mOpuDWqFEjfPXV\nVxg5ciR0Oh30ej2Cg4PRsGFDAMCtW7fg6upq0UKJiIiKgzTkQe7ZArlvG8QjQyF6DYKwMX15jui0\nXCw+HoNsg4qZvXzhV62yBaolKkzTciDp6elYvnw5jh8/DlVVUalSJbRp0wbPPvssXFxcEBUVhays\nLNStW7ckar4rLgdivTit3Xqx76xbRew/eek81B+WAB41oPzfCxDunkWf9B8GVWL7X3ps+UuPYYFu\nGNDAFZWUkr3LVhH7rjwpkXXcAEBVVaSmpsLFxaVgz9KygsHNevEvIOvFvrNuFan/ZFoq5MZvIf/6\nE8qo54Dm7c3ateBifBa+OhEDXRUbvNTaEzWcTV8mpDhUpL4rj0pkHTcgfxHe3NxcxMfHF7z332ff\niIiIygopJeSR/ZCbVkO06QLloyAIeweT20nPNWJNaDyORaRjXIvq6OTnzO2qqFRoCm4RERFYuHAh\nbt68ecdn69evL/aiiIiIHpSMupU/LJqTA2XyhxB+pj/OI6VEyK00rDgdhzY+TggaUAdOXEiXSpGm\n4LZ8+XIEBgbigw8+wCuvvILFixfjxx9/RP369S1dHxERkUlkbg7kzmDIQ3sgHhsF0e1RCMX0sBWb\nnoulJ2ORkGnAO5290dCDS3xQ6dP0oNrNmzcxevRoODo6QkoJBwcHjBkzhnfbiIioTJHn/4D64UQg\nNgrKBwug9BhgcmgzqBKbwhLxxs83EVjdAfMerc3QRmWGpjtutra2MBqNsLGxgbOzMxISEuDo6Ij0\n9HRL10dERFQkmZQIuWEl5PXLUJ54CeKhlma188/kA7cqNvjiEb9Sm3xAdC+aglvDhg1x9OhRdOvW\nDe3atcOcOXNga2uLwMBAS9dHRER0TzIvD3LvVsi9WyG6PArlqUkQlU1fTy0914jvQ+NxIiId41pW\nR0dfTj6gssmk5UCA/CVBDh8+jOzsbHTp0gX29vaWqs0kXA7EenFau/Vi31k3a+8/+edJqOuXAd5+\nUIY/C1G9pultSInDN9Ow4o84tPNxwphmHlYx+cDa+66is+hyIKqq4qOPPsLUqVNha2sLRVHQpUsX\nsy9IRET0IGRMJNTgFUBcNJQnXoRoYt6waExaLr4+GQt9lgHvcvIBWYkig5uiKIiLi4OJN+aIiIiK\nlczOhNwRDBmyF6LvMIjxUyBsbE1ux6BKbP1Lj61/6TG0kQ4DG+lgU8I7HxCZS9MzbsOGDcOyZcsw\nYsQIuLm5FfqsrO2gQERE5YuUEvL4r/mL6DZqCuWDRRDVdGa1FRabiaUnY+HmYIO5ff3g6cTJB2Rd\nNAW3pUuXAgAOHTp0x2dcEoSIiCxF3rwKde1SwGCA8tK7EHUbmtWOPsuA1X/E4XxcJp5tUR0dOPmA\nrJSm4BYUFGTpOoiIiArItFTIrd9Dhh6HGDwGomMvCDNGeIyqxM7LSdhwPhG961ZF0AB/VLHlSBFZ\nL03BzcPDA0D+RIWUlBS4urpatCgiIqqYpNEI+dtuyB3r8/cWnfkVhIOTWW39MyzqWqUSPu7jCx8X\n05cJISprNAW3jIwMLF++HMeOHYONjQ2+//57nDp1CuHh4Rg1apSlayQiogpAXjoHde03gJMLlDdm\nQXj7mdWOPsuAVX/EISwuE8+2rI4OtTgsSuWHpvvFy5Ytg4ODA7766ivY2ORnvfr16+PIkSMWLY6I\niMo/qY+HuvQzqCvnQ3lslNmhzaBKbPtLj8k7r8PdwQaLH/NHR18XhjYqVzTdcTt37hyWLl1aENoA\nwMXFBSkpKRYrjIiIyjeZlwu5Zwvk/u0Q3ftDeXqyWbseABwWpYpDU3BzcHBAWlpaoWfbEhIS+Kwb\nERGZTEoJ/Hkc6voVgK8/lKnzINw9zWrr38Oi41pWR3sOi1I5pym49ezZE3PnzsWoUaMgpcTly5ex\ndu1a9O7d29L1ERFROSKjI6CuWwYkJUB5cgJE42ZmtWNQJXZeSsKGsET0qVsVix/zh70NZ4tS+acp\nuA0aNAh2dnZYsWIFjEYjlixZgl69eqFfv36Wro+IiMoBmZUJuWMd5JEDEP2HQ3TrD2Gj6Z+gO5yP\nzcTSkzHQVbHBJxwWpQrG5E3myypuMm+9uFmy9WLfWbeS6D+pqpDHDkJu/h6iSQuIoU9CuJj3mE1i\nZh5WnYnHBQ6L8mfPyll0k3kAeOutt9C5c2d07Njxji2viIiI7kZev5K/6wEAZcJ7EHXqm9VOnlFi\n52U9Nobp8UhANUzgsChVYJqC2/Dhw3H48GFs2LAB/v7+6NSpE9q3bw8nJ/MWRSQiovJLpiZDbvke\n8txpiCFPQrTvbtauB1JKnIrMwMo/YlHT2Y7DokQwcag0KysLx48fR0hICC5evIgmTZrgnXfesWR9\nmnGo1Hrxlr/1Yt9Zt+LuP2kwQP66C3JncH5YGzAKwsHRrLZupeRgxek4JGTk4dkW1dHSmzcK/o0/\ne9bN4kOl/6hSpQo6deoER0dHGAwGnDlzxuwLExFR+VCwvMfG1YCbB5S3P4aoWcustlJzjFh3Nh6H\nb6ZheBM3PFrfFTZKxXyOjehuNAU3KSXOnz+Pw4cP48SJE/Dw8ECnTp0wYcIES9dHRERlmLxxBeqG\nlUB6GpRRzwGBLcyaMGBQJX6+koTgc4no4OuMoAF14GJv3qxTovJM00/Fiy++CHt7e3To0AEzZ86E\nj4+PpesiIqIyTCbGQW7+HvLSOYhBT0B06AlRqZJZbf0RlY4Vp+Pg5mCDmb184VeNz7ER3Yum4Pb2\n228jICDA0rUQEVEZJzMzIHdtgDy8F6JHfyhPjoewr2JWWxGpOfj2dBwi03LxTIvqaOPtVGGX9yDS\nSlNwCwgIQHR0NEJCQqDX66HT6dChQ4cHeriOiIishzQYIA/9DLljPUTTNlA+XAhRzbzlodJzjVh/\nLgEHr6fi8cY6vNvFG7aVuLwHkRaagtupU6ewaNEitGjRAh4eHoiKisKUKVMwceJEtGrVytI1EhFR\nKZFSAqHHoW5cBbh7Qnn9IwifOma1ZVQlfglPxrpzCWjj44SgAXVQjc+xEZlE00/M2rVr8dZbb6FJ\nkyYF74WFhWHlypUMbkRE5ZS8fjl/4kFmBpT/ewGiSQuz2zobk4Hlp+PgbKfgg+614K+zL8ZKiSoO\nTcFNr9ejUaNGhd5r2LAhEhMTLVIUERGVHpkQm7+A7uXzEINGQ3ToAaGYN/EgOi0X3/4RhxvJOXi6\nuUeF3qaKqDhoCm61a9fGTz/9hMGDBxe8t2PHDtSuXdtSdRERUQmTmel/TzzYB9HzMShjX4GobN6d\nscw8IzacT8Te8GQMbuSGNzt5wY7PsRE9ME3B7bnnnsOnn36K3bt3w83NDYmJibCzsyszuyYQEZH5\npCEP8ref83c8aNYWyoeLIKrpzGrLoErsuZKM4PMJaOHliAX968DNwbaYKyaquDRveWU0GnHlypWC\nWaUBAQGwsSk7D5Vyyyvrxa1brBf7zro5OTkh7dAvUDetBqrXhPL40xA+tc1qS0qJY7fT8V1oHKo7\n2uKp5tX5HJsF8WfPull8y6sbN27AyckJDRs2LHgvISEB6enpHC4lIrJC8tolpG9eDTUjHcoTL0EE\nNje7rb/iM7Hqj3hkG1S80LoGmtc0b39SIiqapgcOFi1aBKPRWOg9g8GAoKAgixRFRESWIeNjoH7z\nOdQln8Cuez8o0740O7RFpebik0MR+PxwFB6pVw3zHq3N0EZkYZruuCUkJMDT07PQezVq1EB8fLxF\niiIiouIlM9IhdwVDhuyH6PUYlKcmorK7B3LNGG5LyTZg/bkEHLqZhsENdXitgxcq23DiAVFJ0PST\nptPpcO3atULvXbt2Da6uriZdLDQ0FK+++iomT56MrVu33vO4Y8eOYeTIkXdck4iITCMNeVD3bYM6\n7WUgOwvKjCAoA0aZNVs0x6Biw/kETNhxHRACiwfUwbAmbgxtRCVI0x23/v374/PPP8fAgQPh6emJ\n2NhY/PTTTxg6dKjmC6mqihUrVmD69OlwdXXFlClT0Lp1a3h7exc6Ljs7G7t370a9evVM+06IiKiA\nlBL440j+xIMaPlDemA3h7WtWW0ZV4uD1FPx4NgEN3Kvgsz5+8HKxK+aKiUgLTcGtV69ecHR0xIED\nB5CYmAg3NzeMHTsW7dq103yh8PBw1KxZEx4eHgCAjh074uTJk3cEt3Xr1mHw4MHYvn27Cd8GERH9\nQ169mL/jQU4OlDHjIRo3M68dKXEmOgOrzsTDwVbB25280dDDvA3liah4aF7Po3379mjfvr3ZF9Lr\n9XBz+9+GxDqdDuHh4YWOuX79OvR6PZo3b87gRkRkIhkfA7n5O8irFyEGj4Zo183sHQ+u6bOx6kwc\n4jMMGNvcA+18nLjjAVEZUGYWYpNS4rvvvsOECROKPDYsLAxhYWEFr0eMGAFnZ2dLlkcWZGdnx/6z\nUuy7skFNSkT2ljXIO3IAlfsNQ+WJUzU9w3a3/otNy8HKk5E4dTsFY1t6o38jd9hwx4Myhz971i84\nOLjg68DAQAQGBmo6T/MCvA/q8uXL2LBhA6ZOnQoABZMT/tlGKzMzE5MmTYK9vT2klEhOToazszPe\nfvtt+Pv7F9k+F+C1XlxI0nqx70qXzEiD/Hkz5O+/5O8n+ugwCOeqms//d/+l5xqxKSx/i6pH67ti\nSGMdHGzNu1tHlsefPetm8QV4i0NAQABiYmIQHx8PV1dXhISEYPLkyQWfOzg4YPny5QWvZ8yYgbFj\nx6JOnTolVSIRkVWQ2ZmQ+7ZD7v8JokVHKNMXQOjczWor16ji5yvJ2BiWiNbeTtyiiqiMK7HgpigK\nxo0bh1mzZkFKiR49esDHxwfBwcGoW7cuWrZsecc5JXQzkIjIKsjcHMhfd0P+vAmicTMoUz6HqG7e\nb+5GVWLXX/FYdTICdVwr46MetVDblVtUEZV1moZK8/LysHHjRoSEhCAtLQ2rV6/Gn3/+iejoaPTt\n27ck6iwSh0qtF2/5Wy/2XcmQBgNkyD7IncGAXwCUwaMhvP3MakuVEiE30/Dj2QR4OFXG/z3kikYe\nDsVcMVkaf/asm8WHSlevXg29Xo9JkyZhzpw5AIBatWph9erVZSa4ERGVN1I1Qp74HXL7j4BHDSgv\nvwtRp755bUmJ01EZWPNnPCoJgRdbe6JTPU+kp6cXc9VEZEmagtuJEyewcOFC2NvbF0wH1+l00Ov1\nFi2OiKgiklICocehbl0DVHGA8tREiAYPmd1eWFwm1oTGIy3XiNFN/7e0B5f3ILI+moKbjY0NVFUt\n9F5qaiqnIhMRFSMpJfBXKNQtawCDAcrjTwEPtTI7YIUnZuOHP+MRkZqL/3vYHV1ru6CSwrBGZM00\nBbd27dohKCgITz/9NAAgKSkJq1atQocOHSxZGxFRhSHD/8q/w5ashxg0GqJlBwjFvPXTbqfk4Mez\nCfgrPgsjmrjhvbrVYFuJgY2oPNA0OcFgMGDNmjXYv38/cnNzYWdnh549e2L06NGwtS0b08Y5OcF6\n8SFb68W+e3Dy1rX8wBZ5E+KxURDte0BUMm/9tLj0PKw9l4BTkekY3EiHAQ1c77sBPPvPerHvrNuD\nTE4weQHef4ZIy9qzEQxu1ot/AVkv9p35ZEwE5Pa1kJfPQzw6HKLLIxBm/iKclGXAhrBEHLqegkfr\nu2JQIx2c7IoOf+w/68W+s24lsgBvTk4OYmJikJ2djejo6IL3GzRoYPbFiYgqGpkYB/nTOsg/T0D0\nGZw/8UDD9lR3k55jxJa/9NhzJQnd/Ksi6DF/VLMvMzsZEpEFaPoJ/+2337By5UrY2NjAzs6u0GdL\nliyxSGFEROWJTEmC3LUB8vhvEF0fhTL7awgHJ7Payjao2HExCdsu6tHGxwlf9qsDD8ey8dgKEVmW\npuC2Zs0avPHGG3j44YctXQ8RUbkiM9Ih92yGPLQHon13KB8thnCpZlZbeUYVe8KTsfF8IgI9HfBx\nH1/4uFQu5oqJqCzTvBxI48aNLV0LEVG5IbOzIPf/BLlvO0TzdlCmz4fQeZjVVp5Rxd6rKdgYloja\n1Spjevda8NdxeyqiikhTcBs5ciS+++47DBs2DC4uLpauiYjIasm8XMjfdkPu3gTRsCmUdz+D8DTv\nQeT/BrZ3O3ujvnuVYq6YiKyJpuDm5eWF4OBg7Nmz547P1q9fX+xFERFZG2kwQB49ALljHVDLH8pr\nMyB86pjV1r8DWx0GNiL6F03BbdGiRejSpQs6dOhwx+QEIqKKTKoq5Mm/9xN1qw7lhbch6jY0q61c\no4q94SnYdCE/sE3p4o16bgxsRPQ/moJbeno6Ro4cWebWbiMiKi1SNUKePgK5MxiobA9lzHiIRk3N\nauvfgc3flYGNiO5NU3Dr1q0bDh06hK5du1q6HiKiMk0ajZAnD0Hu3AA4OkF5/GmgSQuzfrEtCGxh\nifDXMbARUdE0Bbfw8HD8/PPP2Lx5M6pVKzyNfcaMGRYpjIioLJEGA+TxX/PvsLm6QXniRaDhw8UT\n2LoysBGRNpqCW8+ePdGzZ09L10JEVObIvDzII/shd28EqteE8tQkiAZNzGqrcGCzZ2AjIpNpHiol\nIqpIZF4u5O+/QO7ZDHj5QXn+zQefdPB3YHuvqw8C3LgOGxGZTvOmdgcPHsShQ4eg1+uh0+nQpUsX\ndO/e3ZK1ERGVOJmTA3noZ8g9W4DaAVBemgJRp55ZbeUaVfwSnozNYXoGNiIqFpqC2+bNm/Hbb7/h\nscceg7u7OxISErB9+3YkJSVh6NChlq6RiMjiZHYm5MHdkPu2AQGNoUyaDuHrb1Zb/wS2TWF6BLgx\nsBFR8dEU3Pbv348PP/wQHh7/266ladOm+OCDDxjciMiqycwMyAM7IA/sgGj4MJTXZ0J4+5nVVlZe\nfmDb+ld+YJvKwEZExUxTcMvJybljqytnZ2fk5uZapCgiIkuTGWmQ+36C/HUnRJNWUN76GKKmj1lt\npeUYsfNSEnZdTkITTwdM6+bDvUSJyCI0BbdmzZph4cKFGD16NNzd3REfH4+1a9eiaVPzFpskIiot\nMi0Fcu82yEN78jd/n/IFRPWaZrWVmJmH7ReTsO9qMtrVcsbHffzg7cLdZYjIcoSUUhZ1UGZmJlau\nXIkjR47AaDTCxsYG7dq1w7PPPgtHR8eSqLNIUVFRpV0CmcnZ2RlpaWmlXQaZwZr6TqYkQf6yBfLw\nPojWnSD6Pg7h7mlWW9FpudhyQY+QW6no7l8Vgxrq4OFoW8wVW5419R8Vxr6zbl5eXmafqym4/UNV\nVaSlpcHZ2RmKoph9UUtgcLNe/AvIellD38mkRMg9myGPHoRo1w3ikaEQOnez2rqRlI2NYYkIjcnE\no/Wq4bEGrnCx1zw5v8yxhv6ju2PfWbcHCW6a/8bJzMxEVFQUsrOzC73fpIl5C1ESEVmSTIyD3L0R\n8uRhiI49ocwIgqimM6utv+IzsfF8Iq4m5WBgQ1eMb1sDDraVirliIqKiaQpuv/76K1asWAF7e3vY\n2f3v+Q0hBIKCgixWHBGRqWRcdH5gO3MMonMfKDO/gnCpVvSJ/21HSpyJzsDGsETEZxgwtLEO73Tx\nhl2lsjXaQEQVi6bgtnbtWrz++uto3ry5peshIjKLjImA3LUB8uwpiG6PQpm1BMLJpegT/8OoShyL\nSMPG84kwqBKPB7qhs58LKimm70lKRFTcNAU3VVU5g5SIyiQZeQtyVzDkhVCIngOgzFkK4eBkcjt5\nRonfbqRgU5geTnYKRj3sjtbeTlDM2ESeiMhSNAW3QYMGYdOmTXj88cfL3KQEIqqY5K1rUHcGA1fC\nIHoPgjJmPEQVB5PbyTao2Pv3orneLnZ4uY0nHvJ0gGBgI6IySFNw27lzJ5KTk7F9+3Y4ORX+TXbJ\nkiUWKYyI6L+klMClc1D3bAFuX4PoMxji2VchKpu+2G16jhG7Lidhx+UkNPKogne7eKOeWxULVE1E\nVHw0BbeJEydaug4ionuSRiPkH0ch92wGsrPyA9v4KRC2pi92G5+Rhx2XkrD/ajJaeTthVi9f+Fat\nbIGqiYiKn6bg1rhxY0vXQUR0B5mTDRmyD3LvNqCqK5T+I4CmbSDMeGQjPDEb2/7S44/odPTwr4p5\nj9ZBdSfrWzSXiCo2TcEtLy8PGzduREhICNLS0rB69Wr8+eefiI6ORt++fS1dIxFVMDI1GfLgTshf\ndwMBjaGMex0ioJHJ7ahS4nRkBrb+lYjo9Dw81sAVL7XxhKMd12AjIuukKbitXr0aer0ekyZNwpw5\ncwAAtWrVwurVqxnciKjYyNgoyF+2Qp76HaJVJyjvfAJRw/SN33MMKn69noptF/WoXElgcCMdOvq5\nwIZLehCRldMU3E6cOIGFCxfC3t6+YKaVTqeDXq+3aHFEVDHIqxeh7tkMXLkA0bXv34vmuprcTnK2\nAbsvJ2H3lWTU09njpdacIUpE5Yum4GZjYwNVVQu9l5qaCmdnZ4sURUTln1RV4OyJ/BmiSYkQvQdD\njHvdrBmiESk52HZRj5Bbaejo64zZvXxRixMOiKgc0hTc2rVrh6CgIDz99NMAgKSkJKxatQodOnSw\nZG1EVA7JvFzIY79C/rIFsLOH6DsUokUHiEqmPXcmpcS52Exs+0uPK/psPFqvGr56zB/VrHjTdyKi\noggppSzqIIPBgDVr1mD//v3Izc2FnZ0devbsiTFjxsDGpmz8JRkVFVXaJZCZnJ2dkZaWVtplkBlM\n6TuZkQ756y7IgzuBWnWg9BkCNHzY5GFMgyoRcjP/+bVsg8Sghjp0q+OCyjZcHNxU/NmzXuw76+bl\n5WX2uZqC27/9M0Ra1p4ZYXCzXvwLyHpp6TuZGAe5dxvk0YMQTVtD9BkC4VPb5Gtl5BrxS3gydlxK\nQg0nWwxu5IaW3o7ckuoB8GfPerHvrNuDBLcib5cZDIaCu2oXL14s9KxbgwYNUMnE4Q0iqhjkrauQ\ne7ZAhp2B6NgLygcLIXTuJrcTl56Hny7pceBaClrUdMKULj4IcDP9OTgiovLgvsHtl19+waVLlwp2\nTpg1a1bBhIScnByMGTMGPXr0sHyVRGQVpJTAhdD8GaLRERC9HoMy+mUIB0eT27qckIVtF/X4MzoD\nPdZrRKQAACAASURBVOtWw/x+deDhyAVziahiu29w++233/D8888XvLa1tS3Ym/TGjRtYtmwZgxsR\nQRoMkKd+h9yzFVCN+cOhbbtA2JgWtPKMKkJupWHHpSSkZBvQv4ErJrStAQdb3tknIgKKCG5xcXGo\nXbt2wWsfn/8thOnn54e4uDiLFUZEZZ/MyoT6y1bI/dsBj5pQhj4JNGlp8jOwiZl5+PlKMn4JT4Zf\ntcoYHuiGVt5OqMQFc4mICrlvcMvOzkZ2djbs7fOfJ5k5c2bBZzk5OcjOzrZsdURUJsnkRMj9O5Aa\nshdo8DCUl6dA1K5nWhtS4q/4LOy4lITQmAx08XPBLK6/RkR0X/cNbr6+vjh79izatGlzx2ehoaGo\nVauWxQojorJH3roGeeAnyDPHINp2g9OsJch0MG0h7hyDit9vpmLHpSRkG1T0r58/HMr9Q4mIinbf\n4NavXz8sX74cANCqVSsoigJVVXHq1CmsXLkSY8eONelioaGhWLVqFaSU6N69OwYPHlzo8x07duDA\ngQOoVKkSXFxc8PLLL8Pd3fRZaERUfKTBAHnmGOSBHUBCLES3R6HMXgrh5IJKzs6AxiUJ4tLzsPtK\n0v+3d+fhUZV3/8ffZ5LJMpPJMlkgCyVhCWQCAgaQVRatC4KPpQjWn8UqaossQusDInWh2lr7sw8/\ntlpWWbxqhV5P1aqtqAHCKpthSQIhJNFAErInk2WSTOb+/TEwEgxkQEgy8H1dFxeZzDlnvic3mflw\n3+c+N1+crqRnqB9T+4fTP1Ju5yGEEFfjisFt+PDhlJWVsWzZMux2O4GBgVRVVaHX65k0aRIjRoxw\n+4UcDgdr167l5ZdfJiQkhAULFjBo0CCio6Nd23Tr1o177rkHHx8ftm7dyrvvvsucOXOu/eyEENdM\nVZWjUj5D7fgPRESiu2s89B+CdhU33b6wusHHJ8tJL6pldLcg/nRvVyJNPjewciGEuHm1+g48YcIE\n7rrrLjIzM7FarZhMJuLj4zEYDFf1QllZWURGRhIeHg44Q+GBAweaBTeLxeL6Oj4+nl27dl3Vawgh\nfjiVk4lK/hh19ABa0nB0s19B6xJ3Vceoa3SwPaeSTzPLUcAD8SHMHRaFv15WNxBCiB/Crf86GwwG\n+vfv/4NeqKysjNDQUNdjs9lMVlbWZbdPTk7+wa8phHCPamxEHdqFSv4EqirQxoxD98jTaMaru36t\nwNrAJ5nlbM+uxBJh4OmBnejbydDhVloRQghP1TEWGr1ESkoK2dnZvPrqq+1dihA3NVVeitrxb9TO\nrRDdFd24h+G2gWg69ycKOJQitaCGj0+Wc6rUxt3dg/if++OICJCb5QohxPXWZsHNbDZTUlLielxW\nVobZbP7edkePHuWDDz5g0aJFl13APi0tjbS0NNfjyZMnu1Z0EJ7Hx8dH2q8NKaVoOnmc+v/8L/Zj\nB9EPvwvfV/4fXtFdr+o4VTY7H6SV8L9H8/Hz9uInfSN4vUeoLPbuQeR3z3NJ23m+zZs3u75OTEwk\nMTHRrf3aLLj16NGDwsJCiouLCQkJYffu3Tz33HPNtsnJyWH16tUsXLjwiv8gWzpBWWzXc8liyW1D\nNdSj9qc4Z4fW16ONfQDtZ7+kyWCkFtyaHaqUIr24jq2nKjhwtpqhscHMGNyJhHB/NE2joa6Ghht+\nJuJ6kd89zyVt59lMJhOTJ0++pn3bLLjpdDqmTZvG66+/jlKKsWPHEhMTw+bNm+nevTtJSUm8++67\n1NfXs3jxYpRShIWFMW/evLYqUYibkiotQm37FLX7C4iLRzdxKlgGoOnc7xmz1jexLaeSz05VoIB7\newQzbWAnosOC5cNDCCHakKaUUu1dxPWQn5/f3iWIayT/c7z+lFJw4iiO5E/gVBra0LFoY+5Hi4i6\nqmNkFNfx2fnetaToAO7rEYwlwt812UDazrNJ+3kuaTvPFhXl/nvxpTrk5AQhxLVRtjrUvu2obZ+A\nUmhjx6NNm4vm5+/2Maov9K5lVeBQ3/WuBfrKygZCCNHeJLgJcRNQRfnO4dC926BnIrpHnobet7l9\nGw6lFCeK6/hPVgUHzjh71341qDOJF/WuCSGEaH8S3ITwUMrhgPSvncOhOZloI36M7qXFaKERbh/j\nQu/a1qwKmi70rt0eQaCfvDUIIURHJO/OQngYVWNF7d2G2vYp+Po6h0N/NR/Nx9e9/ZXiRInz2rX9\nZ6pJigrgl9K7JoQQHkGCmxAeQCkFmcdRKVtRxw6i9U1C94vZ0CPB7bBVXd/E9txKtp6qpNGhuLdn\nEE9K75oQQngUeccWogNTleWoPcmoXVvBW4828h50P3saLSDQrf0dSnH8XC1fZlc6Z4ZGBvD0oAj6\nRMgyVEII4YkkuAnRwShHE6Sl4tj5GZw8hnb7MHRPzoVuvdwOW4XWBrblVJKcXYVBr+Ou7s7etSDp\nXRNCCI8m7+JCdBCqtBi1+3PnjXIDQ9BG/hjtiTlo/ga39q9rdLDn2yqSsyv5trKBO2MDWXBnNN3M\nfje4ciGEEG1FgpsQ7UjZ7XB0P46dWyHnFNrgO9HNfAmtS5xb+zuUIr2oji+zK/nqjJXECAPje5sZ\nGBWA3kuGQoUQ4mYjwU2IdqDO5aN2bkXtTYbO0Wgj7kGbvsDtmaHnqhvYll1Fck4lfl7OodDH+4cT\n7C+/0kIIcTOTd3kh2ohqbEAd2oPauRUK8tCGjUX3339A6xzj1v42u4M931pJzq4kt6KeO7uamDci\nmu5mX5loIIQQtwgJbkLcYOpMrrN3bf8O6NoD3dgHoN9gNG996/sqRXpxHcnZlezNs5IQ5s+4+GAG\nRQeg93J/kXghhBA3BwluQtwAylaHOrDT2btWUYY2/G50C/8HLayTW/sXVTeenxVaid5L465uQSwf\n3w2zDIUKIcQtTT4FhLhOlFKQe8rZu3ZoN8T3RTd+CvS5HU3X+gLt1fVN7M2zsiO3itxyGyO6BvL8\niCh6mP1kKFQIIQQgwU2IH0zVVKP2bXfeJLfe5lwzdNEKtGBzq/vW2x0cPFvNjtwqjp2rpV9nA/ef\nHwr1kaFQIYQQl5DgJsQ1UHY7pH2N2rcNlfa1cwmqydOgV1803ZUDV5NDcaSwhpTcKvafraan2Y87\nYwN5bmgkRp/We+aEEELcuiS4CeEmpRTkZDp71w7ugk5RaEPGoHtsOprR1Oq+J0tspORWsutbK52M\neu6MDeTxARGEyHVrQggh3CSfGEK0QhUVoL7agdq3HTQNbcgodAv+L1p451b3/bainh25VaTkVuHj\npTEqNpA37+lKpMnnxhcuhBDipiPBTYgWqOoq1MFdzrBWVIA2aCS6p34NsT1bnShQVN3Izm+cYc3a\n0MSdXZ1LT8WFyP3WhBBC/DAS3IQ4TzU2wNGDOPZtg5PH0frcjm7cw2AZgOZ95V+VKpud3d9aScmt\nIq+qgWFdTDwzsBMJEf7oJKwJIYS4TiS4iVuacjggK9153drhvdAlDm3IGLQn57a6uLu1vomvzljZ\n862VE8V1JEUFMNESSv9Io6wTKoQQ4oaQ4CZuSaogzxnWvtoBfv5oQ8ege3kJmjnsivtV2Ox8lVfN\nnjwrmSV19OtsZHRcEP89Ihp/vdy+QwghxI0lwU3cMlRVOWp/CmrfDqgsQxs8Ct3MhWgxcVfcr6zO\nzr48Z89adpmNAVFG7ukRxII7o/HzlrAmhBCi7UhwEzc1VW9Dfb0P9dV2yD6J1u8OdBOnQu++V1zN\noLim0RXWvqmsZ1BUABN6hdA/0oivhDUhhBDtRIKbuOmoxgbnzXEP7UYdOQDdezuvW/vVC2i+fpfd\n71x1A3u+dYa1AmsDg2JM/DQxlH6dDbKguxBCiA5Bgpu4KaiGejh+GHVoD+r4QYiJQ0sahu7hJ9AC\nQy67X37V+bCWZ6W4ppEhXQJ4tF84fTsZ8NbJBAMhhBAdiwQ34bFUvQ2OHzof1g5DbA+024ehm/wk\nWlDLYU0pRXZ5PQfOVLM3z0qlzc6QLiZ+MSCcxAgDXhLWhBBCdGAS3IRHUbY61LGDqEO7IT0V4no5\ne9Z+9gyaKajFfRqaHBwrrGX/2WoOnKnGx1tjcHQAzwzsRO9wfwlrQgghPIYEN9Hhqbpa1NEDzrB2\n4qjzmrWk4WiPPYsWENjiPhU2OwfPVnPgbDVHC2uJDfZlUHQAv7urC9GBPrKCgRBCCI8kwU10SKq2\nGnXkfFg7eQzi+6AlDUN7fDaaMeD72ytFXmUD+89Ws/9MNWcq67mts5E7YkzMGNyZQD/5py6EEMLz\nyaeZ6DBUjRWVut8Z1rLSoVdftIHDnasYGIzf297uUKQXfTcEancoBscE8EjfUPp2kpmgQgghbj4S\n3ES7UlUV1B9IoWn3l5B9EhL6od0xCu3p51tccqqqvonUghr2n7HydUENkSYfBkUH8MKd0cQGyyLu\nQgghbm4S3ESbUkrBmVznNWtHD0DBGez9BqIN/7HzPmt+/s22b3IoMkvr+Lqghq/za8irbKBPJ38G\nRZt44vYIQg36djoTIYQQou1JcBM3nGqoh5PHvgtrXt5otw1C91//B+ITMYaYsVqtru2LaxqdQa2g\nhqOFNYQZ9AyINPLz/uEkhPvLEKgQQohblgQ3cUOo8lLUsQOoowedkwt+1M0Z1uYsgs4xzYY0G+yO\n8z1q1RwuqKHC1kT/zgYGRhl5Kkl61YQQQogLJLiJ60I5HPDN6e961UrOofW5HW3QSLQnnkMzmr7b\nVinOVNZz+PzwZ0ZJHV2DfBkQZWT2kEi6m/3k3mpCCCFECyS4iWumbHWQnuoMa8cOgiHA2as2ZRp0\nT0Dz+m4R9+KaRo6dq3X+KazBAdweaeTuHkG8cl88NNS134kIIYQQHkKCm3CbUgoK8lAZR5xBLesE\ndIt3hrVxk9AiolzbltfZOXauimPnajhaWEtNo4O+nQz07WRgosVMzEU3wTX5emNtaK+zEkIIITyH\nBDdxRaqiFJVxFDJSURlHQOeFZumPbsSP4ZfzXbfsqLLZOfZtFccKnb1qFTY7iRHOoPZAfAg/CvZF\nJ7fqEEIIIX4QCW6iGWWrhZNpqIxUVHoqVJZD79vQEvqhGz8FwiPRNA1rfRPpRbUcO3eOo+dqKa5p\nJCHcn76dDNzdPYq4EF+5Tk0IIYS4ziS43eKU3Q65maj0I6iMVMjLgbh4Z1B7Yg507QaajsLqRjKK\n60jPLiSjuI7SWju9wvzo28nIjDs600MmFAghhBA3nAS3W4xyOJzXqZ046uxRO5UG4Z2dQW3CI9Dd\ngt3bh+xyGxnFtWTsKiCjuA5vTSMhwp+EcH/ujw8hNlh61IQQQoi2JsHtJqcaG+GbLNSpdFRWOmRl\ngDEArfdtaEPGoP1iNpV6I1mlNjKK68hIKeR0mY3OAT4khPszrIuJabd3ItzoLctJCSGEEO1MgttN\nRtXWwOkTqKzzQe2b09ApGq2nBd2wsdQ+Mp3TTf5kldo4VWbj1BfF1Daeo3uoH73D/JmUGEqvMH+M\nPl6tv5gQQggh2pQENw+mlIKyYlT2STiVhjqVAcWFENsDraeFpvsmkxMaS5YVTpXWcSrfRvGpUmJD\n/OgZ6scdMQE81i+cSJNeZnwKIYQQHkCCmwdRFWXOYc/cU6jcLPgmC3Q6iIunsltfcieMJtfHTG6l\nndzyegrSGogOrKCH2Q9LhIEHe5v5UbAv3nJtmhBCCOGRJLh1UKq6CnKzUOeDGrlZ0NhAY2w8BV0S\n+abfeHIHh5FbpyOn3EZjtSLO25fYEMVtnQ38V4KZLkE++MiC7EIIIcRNo02DW2pqKuvXr0cpxZgx\nY3jooYeaPW+321m+fDnZ2dmYTCbmzp1LWFhYW5bY5lRjg3OW59lv4Wwu6uw3cPZb6hrsnI3rx9nO\n8eTF3c+ZnoGcsWkU19gJ1+uJ9fIlLsCXcV18iQvxI8wgkweEEEKIm12bBTeHw8HatWt5+eWXCQkJ\nYcGCBQwaNIjo6GjXNsnJyQQEBLB06VL27NnDu+++y5w5c9qqxBtK1dVCUT7qXD6cy0edzcWWn8+5\n2iYKOnXnXGhXCk3xFHYdRH6MnspGiDL5EBPkQ5cgX0YH+hAT5EuUSY9eetGEEEKIW1KbBbesrCwi\nIyMJDw8HYPjw4Rw4cKBZcDtw4ACTJ08GYMiQIaxdu7atyvvBlKMJKsqhvARVVgxFBdQUFVNcZqXE\naqPEy0BxcAwlpnCKfbtTGNyXmiAvIgL0RJp86Bzgw49Meu4I8CEq0IcIo17ukyaEEEKIZtosuJWV\nlREaGup6bDabycrKuuw2Op0Oo9FIdXU1AQEBbVWmi1IK7I1gq4PaGuyVldiqqrBWVVNtraW61kZ1\nbQPVdfVU1TdR4fCmwj+YCv8QKvQBlHslgq9GeKxGmMmHsEADEUY9A4x6wo3edA7wIdTgLbM5hRBC\nCOG2Dj05QSnl9raL3klGAUppzr+b/XF+D8CBxoXDOgDQzv99flulUA5Fo6ajXueDzdsXm06PQ9Ph\nh4EAfAjQBRPgDQGhOgIMvpgC/IkODqCP0ZcQP2+C/b0J9vPCoNfJdWdCCCGEuG7aLLiZzWZKSkpc\nj8vKyjCbzc22CQ0NpbS0FLPZjMPhoK6ursXetrS0NNLS0lyPJ0+ezMqFj9244sUNZzKZ2rsEcY2k\n7TybtJ/nkrbzbJs3b3Z9nZiYSGJiolv7tdlV7j169KCwsJDi4mLsdju7d+9m4MCBzbZJSkpix44d\nAOzdu5c+ffq0eKzExEQmT57s+nPxyQvPI+3nuaTtPJu0n+eStvNsmzdvbpZj3A1t0IY9bjqdjmnT\npvH666+jlGLs2LHExMSwefNmunfvTlJSEmPHjmXZsmXMnj0bk8nEc88911blCSGEEEJ0eG16jVv/\n/v1ZsmRJs+9dmEUKoNfr+fWvf92WJQkhhBBCeIyb4oZgV9PFKDoeaT/PJW3n2aT9PJe0nWf7Ie2n\nqauZuimEEEIIIdrNTdHjJoQQQghxK5DgJoQQQgjhITr0DXgvJYvUe67W2u7jjz8mOTkZLy8vAgMD\nmT59urRdB9Ja+12wb98+Fi9ezBtvvEG3bt3auEpxOe603549e/jHP/6Bpml07dqV2bNnt0Ol4lKt\ntV1JSQkrVqygtrYWh8PBo48+yoABA9qpWnGxt99+m8OHDxMUFMRbb73V4jbr1q0jNTUVX19fZsyY\nQWxsbOsHVh6iqalJzZw5UxUVFanGxkb1/PPPqzNnzjTb5rPPPlOrV69WSim1e/dutXjx4vYoVVzC\nnbZLS0tT9fX1SilnO0rbdRzutJ9SStXV1amXX35ZLVy4UJ0+fbodKhUtcaf9CgoK1Lx581RNTY1S\nSqnKysr2KFVcwp22W7lypdq6datSSqm8vDz17LPPtkepogUZGRkqJydH/eY3v2nx+cOHD6s//OEP\nSimlMjMz1YsvvujWcT1mqPTiReq9vb1di9Rf7MCBA4waNQpwLlJ/7Nix9ihVXMKdtrNYLPj4+AAQ\nHx9PWVlZe5QqWuBO+wH8/e9/56GHHkKv17dDleJy3Gm/L774gnvvvReDwQBAYGBge5QqLuFO22ma\nRl1dHQC1tbXfW5FItJ/evXtjNBov+/zFmaVnz57U1tZSUVHR6nE9Jri1tEj9pR/ul1ukXrQvd9ru\nYsnJyfTv378tShNucKf9cnJyKCsrkyGaDsid9isoKCA/P5+XXnqJ3/72t6SmprZ1maIF7rTdww8/\nTEpKCtOnT+ePf/wjTz75ZFuXKa7R1X42XuAxwe1aKLnTicdJSUkhOzubBx98sL1LEW5SSrFx40am\nTp3a3qWIa9TU1ERhYSGLFi1i9uzZrFy5ktra2vYuS7hh165djB49mrfffpsXXniBZcuWtXdJ4gbz\nmOB2NYvUA1dcpF60LXfaDuDo0aN88MEHzJ8/H29vj5o3c1Nrrf3q6urIy8vj1VdfZcaMGWRmZvKn\nP/2J7Ozs9ihXXMLd986BAwei0+mIiIggKiqKwsLCti5VXMKdttu2bRvDhg0DnJeZNDY2UlVV1aZ1\nimtjNptdmQWgtLTUraFujwlu13ORetG23Gm7nJwcVq9ezbx58zCZTO1UqWhJa+1nMBhYs2YNy5cv\nZ8WKFcTHxzN//nyZVdpBuPP7N2jQINLS0gCoqqqioKCAiIiI9ihXXMSdtgsLC+Po0aMAnDlzhsbG\nRrlGsQNRSl129G/gwIGuzJKZmYnRaCQ4OLjVY3rUygmpqam88847rkXqH3rooWaL1Dc2NrJs2TJy\nc3Ndi9TLm0/H0Frbvfbaa+Tl5RESEoJSirCwMObNm9feZYvzWmu/iy1atIif//znEtw6EHfab+PG\njaSmpuLl5cXEiRMZOnRoO1ctoPW2O3PmDCtXrsRms6HT6Xjsscfo27dve5ctgCVLlpCeno7VaiUo\nKIjJkydjt9vRNI27774bgLVr15Kamoqfnx/Tp093633To4KbEEIIIcStzGOGSoUQQgghbnUS3IQQ\nQgghPIQENyGEEEIIDyHBTQghhBDCQ0hwE0IIIYTwEBLchBBCCCE8hAQ3IcRVSU9PZ/r06W32ejNm\nzOD48eM/6BhvvPEGKSkp17Tvli1bbvgyQvv372f69Ok8/vjj5Obm3tDXas0///lPVq5c2a41CCEu\nT9YVEuIWsn37dj7++GPOnTuHwWBg0KBBPProoxgMhvYu7YZasGDBD9pf07TrVEnLNm3axFNPPfW9\nmxnfaOnp6Sxbtoy3337b9b2f/OQnbVqDEOLqSI+bELeIf/3rX/ztb39j6tSpbNiwgd///vcUFxfz\n2muv0dTU1OI+DofjutZwvY93sygpKSEmJqbF527kz0zuvy6E55EeNyFuAXV1dWzZsoVnn32W2267\nDXCucTh37lxmzpzJzp07GT16NFu2bCEvLw+9Xs+hQ4eYOnUqI0aMYPXq1Rw8eBCz2cyoUaOaHbu8\nvJx169aRkZGBv78/48aN4/777wdo8Xhjxozhww8/5Msvv6S2tpa+ffvy9NNPYzQaAUhJSeH999/H\nZrPxwAMPXPacioqKmD9/Pu+88w4Af/3rXzl06BCrV68GYPny5XTr1o1x48axaNEiRo4cydixY9m+\nfTvJycn07NmT5ORkAgICmDZtGv3793cd9y9/+Qs5OTnEx8cTGRnZ7HUPHjzIe++9R1lZGbGxsTz1\n1FNER0ezfft2vvrqK+bPnw/A7NmziYuLY+7cuQBMnz6dF154ga5du7qOZbfbefLJJ3E4HDz//POE\nhISwdOlSZsyYwT333MOuXbvIz89n06ZNfPTRR3z55ZdUVVURFhbGlClTGDx4MECr51RdXc3GjRs5\ncuQIjY2NWCwWZs2axRtvvIHdbmfq1KlomsaSJUv4/PPPKSwsZNasWVc8X3AOY993332kpKRQUlJC\nv379mDlzJt7e8tEixI0iPW5C3AJOnjxJY2Oj64P+Aj8/PwYMGOBapBqcH9RDhw5l/fr1jBgxgi1b\ntlBUVMSKFStYuHCha1FkcPbYvPnmm8TFxbFq1SpeeuklPv3008seb+TIkfz73//m4MGD/O53v2Pl\nypUYjUbWrFkDOBfJXrNmDbNmzWLlypVUV1dTVlbW4jlFRERgMBjIyckB4MSJE/j5+ZGfnw84hwET\nExNb3DcrK4vo6GjWrVvHhAkTmg0VLl26lO7du7N27VomTpzY7Hzz8/NZsmQJTzzxBGvXrmXAgAG8\n+eabNDU1YbFYOHHiBOAMs01NTWRmZgJw7tw56uvrm4U2AG9vbzZu3AjAn//8Z5YuXep6bs+ePSxY\nsID169ej0+no3Lkzr732Ghs2bGDSpEksW7aMiooKt85p2bJlNDQ0sHjxYtasWcMDDzyAr68vL774\nIiEhIWzcuJENGza4Fri+MDR8pfO9YN++fSxcuJDly5fzzTffsH379hZ/5kKI60OCmxC3AKvVSmBg\nIDrd93/lQ0JCsFqtrsfx8fEMHDgQAB8fH/bt28dPf/pTDAYDZrPZ1ZsGzrBgtVqZOHEiOp2OiIgI\n7rrrLnbv3t3i8fR6PZ9//jmPPPIIISEheHt7M2nSJPbt24fD4WDfvn0kJSXRu3dvvL29mTJlyhWv\nL0tISCA9Pd0VYIYMGUJ6ejpFRUXU1dV9LyhdEB4eztixY9E0jdGjR1NRUUFlZSUlJSWcPn2aKVOm\n4O3tTUJCQrPrzvbu3UtSUhJ9+vRBp9MxYcIEGhoaOHnyJBEREfj7+5Obm0tGRgb9+vXDbDaTn59P\nRkYGvXv3vmIbXTpsef/992M2m9Hr9a5zuxCshg4dSmRkJFlZWa2eU0VFBUeOHOGZZ57BYDCg0+lI\nSEi4Yi3unO/FdQYHB2M0GklKSmr3yRVC3OykP1uIW4DJZKKqqgqHw/G98FZeXo7JZHI9Dg0NbfZ8\nWVkZZrPZ9Tg8PNz1dUlJCWVlZTzxxBOu7zkcjmbB4NLjlZSU8NZbbzULZN7e3lRWVlJeXt5se19f\n32a1XcpisbiGcC0WC4mJiezYscMVui7nQgACZzgFsNlsVFVVERAQ4PoeOIeUL/T6lZeXExYW5npO\n0zRCQ0NdzyckJHD8+HEKCwuxWCwYjUbS09PJzMzEYrFctp6WXPpz27FjB5988gnFxcWuei8O3Jc7\nJ6vVSkBAwDVNQGntfC99XV9f32a9gEKI60+CmxC3gPj4ePR6Pfv372fIkCGu79tsNlJTU3n00Udd\n37u0h8tsNlNaWuq6eP5CcABnuIiIiGDJkiWXfe1LjxcWFsb06dOJj4//3rYhISGcPXvW9bi+vr5Z\nOLmUxWJh06ZNhIaGYrFY6NWrF6tWrUKv1191ULrw+tXV1TQ0NLjCT0lJiSvshoSEkJeX12yf0tJS\nV7C1WCwcOnSI4uJiJk6ciMFgYNeuXZw6dYr77rvvqmq5+OdWUlLCqlWreOWVV1w/t3nz5rk1uSAs\nLIzq6mpqa2uvOrxd7nwvDZVCiLYjQ6VC3AIMBgOTJk1i3bp1pKam0tTURFFREYsXLyYsLIyR7zcr\nXgAAAnFJREFUI0dedt8hQ4bwwQcfUFNTQ2lpKZ999pnruR49euDv78+HH35IQ0MDDoeDvLw8Tp8+\nfdnj3X333bz33nuUlJQAUFVVxcGDB12vdfjwYU6ePIndbuf999+/Yjjp3LkzPj4+7Ny5E4vFgr+/\nP0FBQezfv/+agltYWBjdu3dn8+bN2O12Tpw4waFDh1zPDx06lMOHD3P8+HGampr46KOP0Ov19OrV\nC3AGt7S0NBoaGjCbzSQkJJCamorVaiUuLu6q67nAZrOhaRomkwmHw8G2bdu+F6guJzg4mP79+7Nm\nzRpqampoamoiIyPD9dyFUNeSy51vS6FbCNE2pMdNiFvEgw8+iMlkYtOmTRQVFeHv78/gwYN57rnn\nrjgL8OGHH2bVqlXMnDkTs9nM6NGj+fTTTwHQ6XS88MILbNiwgZkzZ2K324mKiuKRRx657PHGjRsH\nwOuvv055eTlBQUEMGzaMgQMHEhMTw7Rp01iyZAn19fWMHz++1d4di8VCVlZWs16vgoKCaw5Ks2fP\nZsWKFUybNo34+HhGjRrlCjZRUVHMmjWLdevWUV5eTmxsLPPnz8fLywuAyMhI/Pz8XMO0/v7+dOrU\niaCgoKu6F9yl28bExDB+/HgWLlyITqfjzjvvbPWauYvNmjWL9evXM2fOHJqamkhMTCQhIYGoqCiG\nDx/OrFmzcDgcLF68uNl+rZ3vjb6/nRDi+zQlN/IRQgghhPAIMlQqhBBCCOEhJLgJIYQQQngICW5C\nCCGEEB5CgpsQQgghhIeQ4CaEEEII4SEkuAkhhBBCeAgJbkIIIYQQHkKCmxBCCCGEh5DgJoQQQgjh\nIf4/ox7AkHxQutMAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f97cb4e1710>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.plot(winFraction, countFraction, label='input')\n",
"plt.plot(chipSes[0], chipSes[1], label='Sox2 ChIP')\n",
"plt.ylim([0,1])\n",
"plt.xlabel('Ordered window franction')\n",
"plt.ylabel('Genome coverage fraction')\n",
"plt.legend(loc='best')\n",
"plt.show()"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.12"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| gpl-3.0 |
arcturusannamalai/open-tamil | examples/keras-payil-putthagangal/linear_regression_irumarigal_ipnb.ipynb | 2 | 45056 | {
"nbformat": 4,
"nbformat_minor": 0,
"metadata": {
"colab": {
"name": "linear_regression_irumarigal.ipnb",
"provenance": [],
"collapsed_sections": []
},
"kernelspec": {
"name": "python3",
"display_name": "Python 3"
},
"language_info": {
"name": "python"
}
},
"cells": [
{
"cell_type": "code",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "Z6NDHqfRRZAg",
"outputId": "5feb84a0-b8c4-43ee-919c-d16c919e3dde"
},
"source": [
"# (C) 2021, முத்து அண்ணாமலை <[email protected]>\n",
"# இந்த நிரல் பொதுவெளி உரிமத்தில் வைக்கப்படுகிறது.\n",
"# இந்த நிரல் வழி ஏற்படும் எந்த விளைவிற்கும் ஆசிரியை\n",
"# பொருப்பு ஏற்றுக்கொள்ளமாட்டார்.\n",
"# \n",
"# ஒரு நேர் கோட்டு 'linear' தரவை ஆழக்கற்றல்மூலம் எப்படி கண்டறிவது?\n",
"# உதாரணத்திற்கு நமது தரவில் X என்ற மாரி ஒரு இரு உருப்படி கொண்ட அணியாக\n",
"# எடுத்துக்கொள்ளலாம்; இதன் முதல் மதிப்பு [0,100] என்ற இடைவெளியில் மற்றும்,\n",
"# இரண்டாம் மதிப்பு [0,40] என்ற இடைவெளியிலும்\n",
"# கொடுக்கப்பட்டிருக்கு (இது ஒரு நபரின் வயது, இடை சுற்றளவு என்றம் வைத்துக்கொள்ளலாம்)\n",
"# நபரின் எடை என்பது Y என்ற மாரியில் X என்பதன் சார்பாக விளைகிறது.\n",
"# ஆகையால் இந்த சார்புதன்மையை நாம் ஒரு செயற்கை வழி கற்றலின் மூலம்\n",
"# எப்படி கற்றுக்கொள்ளலாம் ?\n",
"\n",
"# முதலில் நமது தரவை உருவாக்கலாம்\n",
"import numpy as np\n",
"from matplotlib import pyplot as plt\n",
"from keras.layers import Dense, Input\n",
"from keras.optimizers import adam_v2\n",
"from keras.models import Sequential\n",
"from math import pi\n",
"\n",
"def எடை_கணக்கிடு( x_மதிப்பு ):\n",
" \"\"\" ஒரு நபரின் வயது, இடை சுற்றளவு, ஆகியவையில் இருந்து எடை என்பதை கணக்கிட \"\"\"\n",
" y_மதிப்பு = x_மதிப்பு[:,0]*4 + (x_மதிப்பு[:,1]/(2*pi))**2 + 20\n",
" return y_மதிப்பு\n",
"\n",
"வயது = np.linspace(0,100,512)\n",
"இடை_சுற்றளவு = np.linspace(0,40,40)\n",
"X_பயில் = np.array( [[np.random.choice(வயது),np.random.choice(இடை_சுற்றளவு)] for _ in range(512)] )\n",
"Y_பயில் = எடை_கணக்கிடு(X_பயில்)\n",
"\n",
"வயது = np.linspace(30,130,100)\n",
"இடை_சுற்றளவு = np.linspace(40,60,20)\n",
"X_பரிசோதி = np.array( [[np.random.choice(வயது),np.random.choice(இடை_சுற்றளவு)] for _ in range(512)] )\n",
"Y_பரிசோதி = எடை_கணக்கிடு(X_பரிசோதி)\n",
"\n",
"# நேர்கோட்டு சார்பு தன்மையை விளக்கம் செய்ய ஒரு\n",
"# செயற்கை பின்னலை வரையரை செய்யலாம்\n",
"model = Sequential()\n",
"model.add(Input(shape=(2,)))\n",
"model.add(Dense(units=8,activation='relu'))\n",
"model.add(Dense(units=8,activation='relu'))\n",
"\n",
"# நாம் உருவாக்கிய மாதிரி எப்படி இருக்கிறது? இரண்டு மரிகள் கொண்டதையே இங்கு காணலாம்\n",
"model.summary()\n",
"\n",
"model.compile(optimizer=adam_v2.Adam(learning_rate=0.125),loss='mse')\n"
],
"execution_count": null,
"outputs": [
{
"output_type": "stream",
"name": "stdout",
"text": [
"Model: \"sequential_6\"\n",
"_________________________________________________________________\n",
" Layer (type) Output Shape Param # \n",
"=================================================================\n",
" dense_6 (Dense) (None, 8) 24 \n",
" \n",
" dense_7 (Dense) (None, 8) 72 \n",
" \n",
"=================================================================\n",
"Total params: 96\n",
"Trainable params: 96\n",
"Non-trainable params: 0\n",
"_________________________________________________________________\n"
]
}
]
},
{
"cell_type": "code",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/"
},
"id": "AEfd3SogRchQ",
"outputId": "7dcb115e-1d46-48b9-9275-51ca9af50e42"
},
"source": [
"# இதை பயில்விக்கலாம் வாங்க!\n",
"nepochs=30\n",
"history = model.fit(X_பயில்,Y_பயில்,epochs=nepochs,batch_size=128,validation_split=0.2)\n",
"print(history.history)\n",
"loss = history.history['loss']\n"
],
"execution_count": null,
"outputs": [
{
"output_type": "stream",
"name": "stdout",
"text": [
"Epoch 1/30\n",
"4/4 [==============================] - 0s 40ms/step - loss: 52580.7227 - val_loss: 36223.4219\n",
"Epoch 2/30\n",
"4/4 [==============================] - 0s 10ms/step - loss: 23014.6543 - val_loss: 15331.5508\n",
"Epoch 3/30\n",
"4/4 [==============================] - 0s 10ms/step - loss: 15369.1748 - val_loss: 14645.9893\n",
"Epoch 4/30\n",
"4/4 [==============================] - 0s 11ms/step - loss: 11169.2197 - val_loss: 9930.8438\n",
"Epoch 5/30\n",
"4/4 [==============================] - 0s 10ms/step - loss: 9787.7715 - val_loss: 13128.1338\n",
"Epoch 6/30\n",
"4/4 [==============================] - 0s 10ms/step - loss: 11547.4434 - val_loss: 11110.4854\n",
"Epoch 7/30\n",
"4/4 [==============================] - 0s 12ms/step - loss: 9212.5596 - val_loss: 9127.3760\n",
"Epoch 8/30\n",
"4/4 [==============================] - 0s 12ms/step - loss: 8298.6797 - val_loss: 9371.0713\n",
"Epoch 9/30\n",
"4/4 [==============================] - 0s 12ms/step - loss: 8233.8330 - val_loss: 8947.5986\n",
"Epoch 10/30\n",
"4/4 [==============================] - 0s 13ms/step - loss: 8111.9946 - val_loss: 9253.0518\n",
"Epoch 11/30\n",
"4/4 [==============================] - 0s 9ms/step - loss: 8186.7178 - val_loss: 8762.1338\n",
"Epoch 12/30\n",
"4/4 [==============================] - 0s 9ms/step - loss: 7809.4087 - val_loss: 8802.0654\n",
"Epoch 13/30\n",
"4/4 [==============================] - 0s 11ms/step - loss: 7891.7339 - val_loss: 8732.8662\n",
"Epoch 14/30\n",
"4/4 [==============================] - 0s 12ms/step - loss: 7804.1973 - val_loss: 8754.6787\n",
"Epoch 15/30\n",
"4/4 [==============================] - 0s 11ms/step - loss: 7839.5366 - val_loss: 8684.2939\n",
"Epoch 16/30\n",
"4/4 [==============================] - 0s 10ms/step - loss: 7758.1108 - val_loss: 8682.7764\n",
"Epoch 17/30\n",
"4/4 [==============================] - 0s 10ms/step - loss: 7775.2432 - val_loss: 8668.5977\n",
"Epoch 18/30\n",
"4/4 [==============================] - 0s 10ms/step - loss: 7751.6313 - val_loss: 8670.0361\n",
"Epoch 19/30\n",
"4/4 [==============================] - 0s 11ms/step - loss: 7758.8525 - val_loss: 8655.2314\n",
"Epoch 20/30\n",
"4/4 [==============================] - 0s 9ms/step - loss: 7743.5117 - val_loss: 8656.5723\n",
"Epoch 21/30\n",
"4/4 [==============================] - 0s 11ms/step - loss: 7748.0396 - val_loss: 8649.9883\n",
"Epoch 22/30\n",
"4/4 [==============================] - 0s 11ms/step - loss: 7740.5615 - val_loss: 8652.7217\n",
"Epoch 23/30\n",
"4/4 [==============================] - 0s 11ms/step - loss: 7742.1255 - val_loss: 8646.7529\n",
"Epoch 24/30\n",
"4/4 [==============================] - 0s 9ms/step - loss: 7738.2573 - val_loss: 8647.8281\n",
"Epoch 25/30\n",
"4/4 [==============================] - 0s 9ms/step - loss: 7738.4546 - val_loss: 8645.2520\n",
"Epoch 26/30\n",
"4/4 [==============================] - 0s 10ms/step - loss: 7737.0469 - val_loss: 8645.6709\n",
"Epoch 27/30\n",
"4/4 [==============================] - 0s 11ms/step - loss: 7736.4512 - val_loss: 8643.8867\n",
"Epoch 28/30\n",
"4/4 [==============================] - 0s 11ms/step - loss: 7735.5635 - val_loss: 8643.4961\n",
"Epoch 29/30\n",
"4/4 [==============================] - 0s 10ms/step - loss: 7734.8608 - val_loss: 8643.4785\n",
"Epoch 30/30\n",
"4/4 [==============================] - 0s 10ms/step - loss: 7735.2568 - val_loss: 8642.9258\n",
"{'loss': [52580.72265625, 23014.654296875, 15369.1748046875, 11169.2197265625, 9787.771484375, 11547.443359375, 9212.5595703125, 8298.6796875, 8233.8330078125, 8111.99462890625, 8186.7177734375, 7809.40869140625, 7891.73388671875, 7804.197265625, 7839.53662109375, 7758.11083984375, 7775.2431640625, 7751.63134765625, 7758.8525390625, 7743.51171875, 7748.03955078125, 7740.5615234375, 7742.12548828125, 7738.25732421875, 7738.45458984375, 7737.046875, 7736.451171875, 7735.5634765625, 7734.86083984375, 7735.2568359375], 'val_loss': [36223.421875, 15331.55078125, 14645.9892578125, 9930.84375, 13128.1337890625, 11110.4853515625, 9127.3759765625, 9371.0712890625, 8947.5986328125, 9253.0517578125, 8762.1337890625, 8802.0654296875, 8732.8662109375, 8754.6787109375, 8684.2939453125, 8682.7763671875, 8668.59765625, 8670.0361328125, 8655.2314453125, 8656.572265625, 8649.98828125, 8652.7216796875, 8646.7529296875, 8647.828125, 8645.251953125, 8645.6708984375, 8643.88671875, 8643.49609375, 8643.478515625, 8642.92578125]}\n"
]
}
]
},
{
"cell_type": "code",
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 1000
},
"id": "PlqDGRz4RefR",
"outputId": "1d521454-7946-4146-fdd3-ebd77848f4be"
},
"source": [
"\n",
"# இரண்டு மாதிரிகளின் மதிப்பு எண்ண ?\n",
"print(model.weights)\n",
"\n",
"# சரி - ஆழக்கற்றல் பின்னல்களின் ஒரு வெளிப்பாடானது\n",
"# பயில்விக்கும் சமயம் ஒவ்வொறு கணமும் உள்ள பயிற்சி\n",
"# மதிப்பு குறைவு (loss) குறைந்த படியே செல்லவேண்டும்.\n",
"# இதனை வரைபடமாக காணலாம்:\n",
"plt.plot(np.arange(nepochs),loss)\n",
"plt.title('training loss vs nepochs')\n",
"plt.legend(['training loss'])\n",
"plt.show()\n",
"\n",
"# அடுத்த பயில்விக்காத தரவின்மீது எமது செயற்கைபின்னல்\n",
"# எப்படி செயல்படுகிறது? இதையும் இங்கு காணலாம்\n",
"Y_யுகித்த = model.predict(np.array(X_பரிசோதி))\n",
"plt.plot(X_பரிசோதி,Y_பரிசோதி,'+g',X_பரிசோதி,Y_யுகித்த,'-ob')\n",
"plt.legend(['pred','actual'])\n",
"plt.show()\n"
],
"execution_count": null,
"outputs": [
{
"output_type": "stream",
"name": "stdout",
"text": [
"[<tf.Variable 'dense_6/kernel:0' shape=(2, 8) dtype=float32, numpy=\n",
"array([[-0.24633473, -0.94575554, -1.4603648 , 0.99429315, 1.5480273 ,\n",
" -0.45802143, 0.8898571 , -0.52291274],\n",
" [-0.61481124, -0.27716312, -0.6273725 , 0.27302548, -0.00271033,\n",
" -0.07500631, 0.84133005, -0.3360913 ]], dtype=float32)>, <tf.Variable 'dense_6/bias:0' shape=(8,) dtype=float32, numpy=\n",
"array([ 0. , -0.6997188 , -0.75067824, 1.1047844 , 1.4316852 ,\n",
" 0. , 1.1865197 , 0. ], dtype=float32)>, <tf.Variable 'dense_7/kernel:0' shape=(8, 8) dtype=float32, numpy=\n",
"array([[ 0.5118819 , 0.5929337 , -0.26628926, 0.23462969, 0.2081911 ,\n",
" 0.36126655, -0.102938 , -0.4713796 ],\n",
" [-0.33736986, 0.4119901 , 1.5254289 , 1.1382313 , 0.9609785 ,\n",
" 0.43206942, 0.589188 , 0.40854356],\n",
" [-0.51204437, 0.96366376, 0.22415727, 0.2654613 , 0.20288908,\n",
" -0.6043953 , -0.45469815, -0.18892688],\n",
" [-0.58159137, 1.123539 , 1.1880755 , 0.85914826, 0.8593709 ,\n",
" 0.98186827, 1.061359 , 1.0659394 ],\n",
" [ 0.30114084, 1.2849146 , 1.0926507 , 1.4119937 , 1.2712843 ,\n",
" 1.4755375 , 1.5287936 , 1.280322 ],\n",
" [ 0.0629788 , -0.54151845, -0.40909925, -0.20238814, 0.10571593,\n",
" -0.22287574, 0.5090932 , -0.47234 ],\n",
" [-0.335507 , 1.0576091 , 1.2435467 , 1.1361021 , 1.3156403 ,\n",
" 0.9314005 , 0.79116386, 1.1163743 ],\n",
" [-0.27401683, 0.09433138, 0.57395095, 0.5530885 , 0.09179211,\n",
" 0.3951351 , 0.12506616, -0.39027593]], dtype=float32)>, <tf.Variable 'dense_7/bias:0' shape=(8,) dtype=float32, numpy=\n",
"array([0. , 1.5918803, 1.6467828, 1.7623268, 1.6807063, 2.0537434,\n",
" 2.1383288, 1.7738249], dtype=float32)>]\n"
]
},
{
"output_type": "display_data",
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYUAAAEICAYAAACwDehOAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nO3deZxU1Z338c+vqje62LobBAUUo7g0KCgEMcZHooKomWBMxsHEiBmXyUzyxJkkjjqTiUuSickYTXgSzcsFo2YUDWokkURxIZFEVECMshgWFxoR2gYaaOimu+v3/HFPNUXbO91ddNf3/XrVq2+du9Q5VXC/dc69da+5OyIiIgCxTFdAREQOHgoFERFpoFAQEZEGCgUREWmgUBARkQYKBRERaaBQkIwws1+Y2X919rLtrMNIM3Mzy+nsbWcLvYe9j+l3CtJeZvYOcIW7P5vpuhwIMxsJvA3kuntdZmvTM+k97H3UU5BOp2+NIj2XQkHaxcweBA4Hfmtmu8zs39OGEC43s/eA58OyvzazD8ys0sz+ZGaj07bzSzP7XpiebGZlZvZNM9tiZpvM7MsdXLbEzH5rZjvM7FUz+56ZLWpj2w4zs3lmttXM1prZlWnzJprZkrDdzWZ2WygvMLNfmVmFmW0PrzmkiW1fa2ZzG5X91MxmhenLzGy9me00s7fN7IvN1PFGM3vUzB4Iy64wswmN2vCYmZWH7Xy90bpzzeyRsO4yMxubNv94M1sY2rHCzD6TNq+Pmf3YzN4Nn+ciM+uTVrUvmtl7Zvahmf1na++bHMTcXQ892vUA3gHOTns+EnDgASAB9Anl/wj0A/KBnwDL09b5JfC9MD0ZqANuBnKB84DdQFEHlp0THoVAKbABWNRMO1L1zgnP/wTcARQA44By4Mww7yXgS2G6LzApTP8T8NvwenFgPNC/idc6ItSzX3geBzYBk8J7tgM4Nsw7FBjdTJ1vBKpDu+PAD4DFYV4MWAp8B8gDPgasB85JW7cW+Hx4775FGPoJj7XAf4R1zwR2ptXp58BCYFh43U+EzzX1Ht4N9AHGAjXA8S29b3ocvA/1FKQz3ejuVe6+B8DdZ7v7TnevIdohjTWzAc2sWwvc7O617j4f2AUc255lzSwOfA64wd13u/tK4P62VNzMRgCnAde6e7W7LwfuAS5Ne82jzWyQu+9y98Vp5SXA0e5e7+5L3X1H4+27+7vAMuCzoehMYHfadpLAGDPr4+6b3H1FC9Vd5O7z3b0eeJBoRwzwcWCwu9/s7nvdfT3RznpG2rpL3X2uu9cCtxEF4KTw6AvcEtZ9HvgdcLGZxYgC/mp33xja+Zfwuabc5O573P114PW0OjX3vslBSqEgnWlDasLM4mZ2i5mtM7MdRL0LgEHNrFvh+x+o3E20k2rPsoOBnPR6NJpuyWHAVnffmVb2LtE3Y4DLgWOA1WGI6NOh/EHgaWCOmb1vZj8ys9xmXuMh4OIw/YXwHHevAv4B+AqwycyeMrPjWqjrB2nTu4GCcBznCOCwMPyz3cy2E33zTx/Oang/3D0JlIW2HwZsCGWN2z+IKDzWtaNOqc+uufdNDlIKBemI5k5ZSy//AjAdOBsYQDTMAGBdVy3KiYaWhqeVjWjjuu8DxWbWL63scGAjgLuvcfeLgUOAHwJzzSwReis3uXsp0ZDKp9nXu2js18BkMxtO1GN4KDXD3Z929ylEQ0erib7ht9cG4G13H5j26Ofu56Ut0/B+hB7A8ND294ERoaxx+z8kGrI6qr0Vau59a+92pPsoFKQjNhONV7ekH9HYcgXRePt/d3WlwnDK48CNZlYYvm03t4NuvO4G4C/AD8LB4xOJvuX+CsDMLjGzweGb9PawWtLMPmVmJ4Shqx1EwyXJJl4Cdy8nGpe/j2jnvSpse4iZTQ87yxqi4bAmt9GKV4Cd4aB2n9BbG2NmH09bZryZXRh6Fv8aXm8x8DLRN/x/N7NcM5sM/B0wJ7R5NnBbOJAdN7NTzSy/tQo19751oG3STRQK0hE/AL4dhii+1cwyDxANP2wEVhLteLrD14h6Jh8QDe08TLTja4uLiXo07wNPEB2bSP0WYxqwwsx2AT8FZoRjJ0OBuUSBsAr4Y3jd5jxE1Ht6KK0sBnwjvO5W4Azgn9tY5wYhFD9NdJD8baJv+PcQvR8pTxINVW0DvgRcGHo7e4lC4Nyw3h3Ape6+Oqz3LeAN4NVQxx/Stv1Hc++bHKT04zXp1czsh8BQd5+Z6bpkmpndSHRA/JJM10UOXuopSK9iZseZ2YkWmUg0BPREpusl0lPol6fS2/QjGjI6jOjYx4+JhkxEpA00fCQiIg00fCQiIg167PDRoEGDfOTIkZmuhohIj7F06dIP3X1wS8v02FAYOXIkS5YsyXQ1RER6DDN7t7VlNHwkIiINFAoiItJAoSAiIg167DEFETl41dbWUlZWRnV1daarkpUKCgoYPnw4ubnNXbC3eQoFEel0ZWVl9OvXj5EjR2LWlRfGlcbcnYqKCsrKyjjyyCPbvb6Gj0Sk01VXV1NSUqJAyAAzo6SkpMO9NIWCiHQJBULmHMh7n1Wh4O7Mem4Nf/xbeaarIiJyUMqqUDAz7v7Tel5YvSXTVRGRLrR9+3buuOOODq173nnnsX379haX+c53vsOzzz7b4jJtNXLkSD788MNO2VZnyKpQAChK5LFt995MV0NEulBLoVBXV9dkecr8+fMZOHBgi8vcfPPNnH322R2u38Es60KhOJHH1iqFgkhvdt1117Fu3TrGjRvHNddcw8KFCzn99NP5zGc+Q2lpKQAXXHAB48ePZ/To0dx1110N66a+ub/zzjscf/zxXHnllYwePZqpU6eyZ09007jLLruMuXPnNix/ww03cPLJJ3PCCSewenV0s7ry8nKmTJnC6NGjueKKKzjiiCNa7RHcdtttjBkzhjFjxvCTn/wEgKqqKs4//3zGjh3LmDFjeOSRRxraWFpayoknnsi3vtXcDRDbL+tOSS1J5LGpUudOi3SXm367gpXv7+jUbZYe1p8b/m50s/NvueUW3nzzTZYvXw7AwoULWbZsGW+++WbDaZqzZ8+muLiYPXv28PGPf5zPfe5zlJSU7LedNWvW8PDDD3P33Xdz0UUX8dhjj3HJJR+9cd2gQYNYtmwZd9xxB7feeiv33HMPN910E2eeeSbXX389f/jDH7j33ntbbNPSpUu57777ePnll3F3TjnlFM444wzWr1/PYYcdxlNPPQVAZWUlFRUVPPHEE6xevRoza3W4qz2yrqeg4SOR7DRx4sT9ztufNWsWY8eOZdKkSWzYsIE1a9Z8ZJ0jjzyScePGATB+/HjeeeedJrd94YUXfmSZRYsWMWPGDACmTZtGUVFRi/VbtGgRn/3sZ0kkEvTt25cLL7yQF198kRNOOIEFCxZw7bXX8uKLLzJgwAAGDBhAQUEBl19+OY8//jiFhYXtfTualZU9hYqqvbi7TpkT6QYtfaPvTolEomF64cKFPPvss7z00ksUFhYyefLkJs/rz8/Pb5iOx+MNw0fNLRePx1s9ZtFexxxzDMuWLWP+/Pl8+9vf5qyzzuI73/kOr7zyCs899xxz587lZz/7Gc8//3ynvF5W9hT21iXZvbc+01URkS7Sr18/du7c2ez8yspKioqKKCwsZPXq1SxevLjT63Daaafx6KOPAvDMM8+wbdu2Fpc//fTT+c1vfsPu3bupqqriiSee4PTTT+f999+nsLCQSy65hGuuuYZly5axa9cuKisrOe+887j99tt5/fXXO63eWddTKE7kAbC1ai+J/KxrvkhWKCkp4bTTTmPMmDGce+65nH/++fvNnzZtGr/4xS84/vjjOfbYY5k0aVKn1+GGG27g4osv5sEHH+TUU09l6NCh9OvXr9nlTz75ZC677DImTpwIwBVXXMFJJ53E008/zTXXXEMsFiM3N5c777yTnTt3Mn36dKqrq3F3brvtts6ruLu3+gDeAd4AlgNLQlkxsABYE/4WhXIDZgFrgb8CJ6dtZ2ZYfg0wM618fNj+2rCutVan8ePHe0c8u/IDP+La3/lr723r0Poi0rqVK1dmugoZV11d7bW1te7u/pe//MXHjh3bra/f1GeQ2n+39GjPV+VPuXv6+VTXAc+5+y1mdl14fi1wLjAqPE4B7gROMbNi4AZgAuDAUjOb5+7bwjJXAi8D84FpwO/bUbc2Kwo9hW06LVVEutB7773HRRddRDKZJC8vj7vvvjvTVWqTAxk/mQ5MDtP3AwuJQmE68EBIpcVmNtDMDg3LLnD3rQBmtgCYZmYLgf7uvjiUPwBcQBeFQkkIhQqFgoh0oVGjRvHaa69luhrt1tYDzQ48Y2ZLzeyqUDbE3TeF6Q+AIWF6GLAhbd2yUNZSeVkT5V2iqOGYQk1XvYSIQGpoWDLgQN77tvYUPunuG83sEGCBma1uVAE3sy7/FxAC6SqAww8/vEPb6JefQ27c2FpV25lVE5E0BQUFVFRU6PLZGeDhfgoFBQUdWr9NoeDuG8PfLWb2BDAR2Gxmh7r7pjA8lLrK3EZgRNrqw0PZRvYNN6XKF4by4U0s31Q97gLuApgwYUKHQsjMwqUu1FMQ6SrDhw+nrKyM8nJdkTgTUnde64hWQ8HMEkDM3XeG6anAzcA8orOJbgl/nwyrzAO+ZmZziA40V4bgeBr4bzNL/axvKnC9u281sx1mNonoQPOlwP/rUGvaqKgwTz0FkS6Um5vbobt+Sea1pacwBHgidAFzgIfc/Q9m9irwqJldDrwLXBSWnw+cR3R66W7gywBh5/9d4NWw3M2pg87AvwC/BPoQHWDukoPMKSV91VMQEWlKq6Hg7uuBsU2UVwBnNVHuwFeb2dZsYHYT5UuAMW2ob6coTuTzxrbOu4CUiEhvkXWXuQAoLszV5bNFRJqQnaGQyGdHdR219clMV0VE5KCSpaGQC+hXzSIijWVpKESXud2q+yqIiOwnS0Mh/Kp5l0JBRCRddoeCegoiIvvJ7lDQMQURkf1kZSgMLIwONFdo+EhEZD9ZGQq58RgD+uSyTcNHIiL7ycpQgOi+CrqngojI/rI2FIoSefqdgohII1kbCtHlsxUKIiLpsjYUNHwkIvJRWRsKqeEj3TJQRGSfrA2FkkQedUlnR3VdpqsiInLQyNpQKCrUD9hERBrL2lAo7qtQEBFpLGtDoUSXuhAR+YisDYXU8JF+qyAisk/WhkJJGD7SaakiIvtkbSj0yY2TnxNja1VNpqsiInLQyNpQMDNKEnlsrarNdFVERA4aWRsKEJ2BpJ6CiMg+WR0KRYW6/pGISLqsDoWSRJ5uySkikiarQ6E4kc9W3X1NRKRBlodCLlV766murc90VUREDgpZHgr5ALotp4hIkOWhkAtAhYaQRESArA8F9RRERNJleSjoongiIukUCmj4SEQkJatDYUCfXGKm4SMRkZSsDoV4zBhYmKcrpYqIBFkdChANIemeCiIiEYVCQj0FEZGUNoeCmcXN7DUz+114fqSZvWxma83sETPLC+X54fnaMH9k2jauD+Vvmdk5aeXTQtlaM7uu85rXumJdFE9EpEF7egpXA6vSnv8QuN3djwa2AZeH8suBbaH89rAcZlYKzABGA9OAO0LQxIGfA+cCpcDFYdluUdxXw0ciIiltCgUzGw6cD9wTnhtwJjA3LHI/cEGYnh6eE+afFZafDsxx9xp3fxtYC0wMj7Xuvt7d9wJzwrLdorgwj22795JMene9pIjIQautPYWfAP8OJMPzEmC7u9eF52XAsDA9DNgAEOZXhuUbyhut01z5R5jZVWa2xMyWlJeXt7HqLStO5JF0qNyjO7CJiLQaCmb2aWCLuy/thvq0yN3vcvcJ7j5h8ODBnbLNkr7hB2waQhIRIacNy5wGfMbMzgMKgP7AT4GBZpYTegPDgY1h+Y3ACKDMzHKAAUBFWnlK+jrNlXe5okJd6kJEJKXVnoK7X+/uw919JNGB4ufd/YvAC8Dnw2IzgSfD9LzwnDD/eXf3UD4jnJ10JDAKeAV4FRgVzmbKC68xr1Na1wa6/pGIyD5t6Sk051pgjpl9D3gNuDeU3ws8aGZrga1EO3ncfYWZPQqsBOqAr7p7PYCZfQ14GogDs919xQHUq11Sw0cKBRGRdoaCuy8EFobp9URnDjVephr4+2bW/z7w/SbK5wPz21OXzrJv+KgmEy8vInJQyfpfNBfkxknkxdlapbOPRESyPhQAihJ56imIiKBQAKAkkcfW3eopiIgoFIjOQFJPQUREoQCE4SPdfU1ERKEAqeEjhYKIiEKBqKdQXZtk99661hcWEenFFApEPQWACg0hiUiWUygAxYl8ALZpCElEspxCAShO5AK6UqqIiEKBtJ6CQkFEspxCAV0pVUQkRaEA9C/IISdmGj4SkaynUADMjKJEnoaPRCTrKRSC4sI89RREJOspFILo+kcKBRHJbgqFoLivho9ERBQKgYaPREQUCg2KE3lU7qmlrj6Z6aqIiGSMQiFI/VZhm262IyJZTKEQ6AdsIiIKhQYlCgUREYVCSpFCQUREoZDS0FPQ5bNFJIspFIKGnoJutCMiWUyhEOTGY/QryGFrVU2mqyIikjEKhTQliTy26pRUEcliCoU0RYk89RREJKspFNKUJPKo0DEFEcliCoU0xYk8tunsIxHJYgqFNEXh8tnunumqiIhkhEIhTUkij9p6Z1dNXaarIiKSEQqFNEWF+lWziGQ3hUKakr5RKOi+CiKSrRQKaYoT+QC6A5uIZK1WQ8HMCszsFTN73cxWmNlNofxIM3vZzNaa2SNmlhfK88PztWH+yLRtXR/K3zKzc9LKp4WytWZ2Xec3s22KC9VTEJHs1paeQg1wpruPBcYB08xsEvBD4HZ3PxrYBlwelr8c2BbKbw/LYWalwAxgNDANuMPM4mYWB34OnAuUAheHZbtdcV8dUxCR7NZqKHhkV3iaGx4OnAnMDeX3AxeE6enhOWH+WWZmoXyOu9e4+9vAWmBieKx19/XuvheYE5btdom8OHk5MQ0fiUjWatMxhfCNfjmwBVgArAO2u3vq3M0yYFiYHgZsAAjzK4GS9PJG6zRX3lQ9rjKzJWa2pLy8vC1Vbxczo7gwT8NHIpK12hQK7l7v7uOA4UTf7I/r0lo1X4+73H2Cu08YPHhwl7xGcSJPPQURyVrtOvvI3bcDLwCnAgPNLCfMGg5sDNMbgREAYf4AoCK9vNE6zZVnRHFCPQURyV5tOftosJkNDNN9gCnAKqJw+HxYbCbwZJieF54T5j/v0XUj5gEzwtlJRwKjgFeAV4FR4WymPKKD0fM6o3EdURwudSEiko1yWl+EQ4H7w1lCMeBRd/+dma0E5pjZ94DXgHvD8vcCD5rZWmAr0U4ed19hZo8CK4E64KvuXg9gZl8DngbiwGx3X9FpLWwnDR+JSDZrNRTc/a/ASU2Uryc6vtC4vBr4+2a29X3g+02Uzwfmt6G+Xa44kcfOmjpq6urJz4lnujoiIt1Kv2hupDjcq3lble7AJiLZR6HQSCoUdFxBRLKRQqERhYKIZDOFQiMlqVDQHdhEJAspFBopSoXCrpoM10REpPspFBopKszDTMNHIpKdFAqNxGPGwD65Gj4SkaykUGhCkX7VLCJZSqHQhBKFgohkKYVCE4oKFQoikp0UCk0o6atQEJHspFBoQnEij227a0kmPdNVERHpVgqFJhQV5lGfdHZU6/pHIpJdFApNKOkb/YBNN9sRkWyjUGhCUWHqSqkKBRHJLgqFJpQk8gH1FEQk+ygUmlDcVz0FEclOCoUmFBfqmIKIZCeFQhP65MXpkxvXbxVEJOsoFJpRnMjT8JGIZB2FQjOKE3kaPhKRrKNQaEaxLoonIllIodAMhYKIZCOFQjMUCiKSjRQKzRjcL589tfUKBhHJKgqFZpz6sRIAXli9JcM1ERHpPgqFZpwwbABD+xewYOXmTFdFRKTbKBSaEYsZZ5cewh//Vk51bX2mqyMi0i0UCi2YWjqUPbX1LFrzYaarIiLSLRQKLZj0sRL65edoCElEsoZCoQV5OTE+ddwhPLtqM/W6NaeIZAGFQiumlA6homovy97blumqiIh0OYVCKyYfO5jcuPHMig8yXRURkS6nUGhFv4JcPnHUIJ5ZuRl3DSGJSO+mUGiDKaVDeLdiN2u27Mp0VUREulSroWBmI8zsBTNbaWYrzOzqUF5sZgvMbE34WxTKzcxmmdlaM/urmZ2ctq2ZYfk1ZjYzrXy8mb0R1pllZtYVje2oKaVDADSEJCK9Xlt6CnXAN929FJgEfNXMSoHrgOfcfRTwXHgOcC4wKjyuAu6EKESAG4BTgInADakgCctcmbbetANvWucZ0r+AcSMG6tRUEen1Wg0Fd9/k7svC9E5gFTAMmA7cHxa7H7ggTE8HHvDIYmCgmR0KnAMscPet7r4NWABMC/P6u/tijwbtH0jb1kFjSukQXi+rZFPlnkxXRUSky7TrmIKZjQROAl4Ghrj7pjDrA2BImB4GbEhbrSyUtVRe1kR5U69/lZktMbMl5eXl7an6ATtndNS8Z9VbEJFerM2hYGZ9gceAf3X3Henzwjf8Lj81x93vcvcJ7j5h8ODBXf1y+zlqcF8+NijBMwoFEenF2hQKZpZLFAj/6+6Ph+LNYeiH8Dd1jemNwIi01YeHspbKhzdRflAxM6aMHsJL6yqo3FOb6eqIiHSJtpx9ZMC9wCp3vy1t1jwgdQbRTODJtPJLw1lIk4DKMMz0NDDVzIrCAeapwNNh3g4zmxRe69K0bR1UppYOoS7pLHxL91gQkd6pLT2F04AvAWea2fLwOA+4BZhiZmuAs8NzgPnAemAtcDfwLwDuvhX4LvBqeNwcygjL3BPWWQf8vhPa1unGjShiUN98DSGJSK+V09oC7r4IaO53A2c1sbwDX21mW7OB2U2ULwHGtFaXTIvHjCmlhzBv+fvU1NWTnxPPdJVERDqVftHcTlNKh1C1t56X1lVkuioiIp1OodBOnzhqEIV5cQ0hiUivpFBop4LcOJOPHcyClZtJ6h4LItLLKBQ6YGrpUMp31vB62fZMV0VEpFMpFDrgU8ceQjxmGkISkV5HodABAwpzmfSxYl01VUR6HYVCB00tHcq68irWleseCyLSeygUOujscI8FXU5bRHoThUIHDRvYhzHD+msISUR6FYXCAZhaOpTXNmxny87qTFdFRKRTKBQOwJTSIbjDc6t0gTwR6R0UCgfguKH9GFHcR0NIItJrKBQOgJkxtXQof15bwa6aukxXR0TkgCkUDtDU0iHsrU/yx7e69/agIiJdQaFwgMYfUcSQ/vncs2g90VXDRUR6LoXCAcqJx/jmlGN57b3tzHv9/UxXR0TkgCgUOsHnxg+n9ND+/PD3q6murc90dUREOkyh0AniMeO/Pl3K+5XV3PPi+kxXR0SkwxQKneTUo0o4Z/QQ7li4ji079GM2EemZFAqd6Ppzj6e2Psmtz7yV6aqIiHSIQqETjRyU4LJPjOTXS8t4c2NlpqsjItJuCoVO9rUzR1FUmMd3f7dSp6iKSI+jUOhkA/rk8m9nj+Llt7fy9ApdVltEehaFQhe4eOLhjDqkLz/4/Spq6nSKqoj0HAqFLpATj/Gf5x/PuxW7eeAv72a6OiIibaZQ6CKTjz2EM44ZzKzn11CxqybT1RERaROFQhf69vnHs3tvPT95dk2mqyIi0iYKhS40akg/vjDxcB565T3+tnlnpqsjItIqhUIX+7cpx1CYF+d7T63KdFVERFqlUOhixYk8rj5rFH/6WzkvvKXbdorIwU2h0A0uPXUkI0sK+f5Tq6itT3bqtv+y9kNue+YtnfoqIp1CodAN8nJiXH/e8azdsouHX3mvU7ZZV5/k1qff4ov3vsys59fylQeX6rLdInLAFArdZGrpECZ9rJj/+cNbPPLqeySTHb8Exvvb9zDjrsX87IW1XDR+BDf+XSkvvFXOlQ8sUTCIyAFRKHQTM+NHnxvLMUP7ce1jbzD9539m6btb272dBSs3c96sF1m1aQc/nTGOH37+RC477Uh+9PkTWbT2Q/7xl6+ye29dF7RARLKBQqEbHV5SyNyvnMpPZ4yjfGcNn7vzJa6e8xqbKve0um5NXT03/XYFVz6whOFFfXjq66czfdywhvkXTRjBj/9+LIvXV3DZfa9SVaNgEJH2azUUzGy2mW0xszfTyorNbIGZrQl/i0K5mdksM1trZn81s5PT1pkZll9jZjPTyseb2RthnVlmZp3dyIOJmTF93DCe++YZfO1TR/P7Nz/gzFv/yM+eX9Ps0M+7FVV8/s6XuO/P73DZJ0by2D9/gpGDEh9Z7sKTh3P7P4xj6bvbmDn7FXZW13Z1c0Skl2lLT+GXwLRGZdcBz7n7KOC58BzgXGBUeFwF3AlRiAA3AKcAE4EbUkESlrkybb3Gr9UrJfJz+NY5x/LcN85g8rGDufWZv3H2bX/kD29u2u+S2/Nef5/zZy3iva27uetL47nxM6PJz4k3u93p44Yxa8ZJLN+wnUtnv8IOBYOItEOroeDufwIaD35PB+4P0/cDF6SVP+CRxcBAMzsUOAdY4O5b3X0bsACYFub1d/fFHu0JH0jbVlYYUVzInZeM56ErTiGRl8NXfrWML97zMss3bOf6x//K1x9+jeOG9mP+1aczdfTQNm3z/BMP5WdfOJk3N1ZyyT0vU7lbwSAibdPRYwpD3H1TmP4AGBKmhwEb0pYrC2UtlZc1Ud4kM7vKzJaY2ZLy8vIOVv3g9ImjB/HU1z/Jd6ePZuWmHVzw8z8z59UNfPVTRzHnqkkMG9inXdubNmYov7hkPKs37eQL9yxmW9XeLqq5iPQmB3ygOXzD75ZbjLn7Xe4+wd0nDB48uDteslvlxGN86dSRLPzWZL5+1ih+dfkpXHPOceTEO/YxnXX8EO66dDxrtuzi4rsX62qtItKqjobC5jD0Q/ibun7DRmBE2nLDQ1lL5cObKM9qAwvz+MaUYzjt6EEHvK3Jxx7CvTMn8PaHVcy4azHvVlR1Qg1FpLfqaCjMA1JnEM0EnkwrvzSchTQJqAzDTE8DU82sKBxgngo8HebtMLNJ4ayjS9O2JZ3k9FGDue/LH6ds2x7O+J+FfIcFr3AAAAeeSURBVOHuxTy5fKN+6CYiH2Gt3VzezB4GJgODgM1EZxH9BngUOBx4F7jI3beGHfvPiM4g2g182d2XhO38I/AfYbPfd/f7QvkEojOc+gC/B/6vt+GO9xMmTPAlS5a0p61Zb1PlHn69pIxfL93Ahq176FeQw/Rxh3HRhBGcMGwAvfxsYJGsZ2ZL3X1Ci8u0Yf97UFIodFwy6Sx+u4JHX93A79/8gJq6JMcN7cdFE0ZwwUnDKE7kZbqKItIFFArSqso9tfz29fd5dMkG/lpWSW7cmFI6hHNGD6V/QS55ObHoEY/tN52fs+95QU6cWEy9DJGDnUJB2mXVph38ekkZT7xWxrZ2/LbBDApz4/QtyCGRn0Pf/BwSeanpeENZfk6MmvokNbVJaurqw98wXZdWXpfkkP4FHD24L0cdkgh/+1KSyNMQl8gBUChIh9TU1bNuSxU1dfXsrUuytz4Z/Q3TNXVJakNZTV2S3Xvrqaqpo6qmjl3hEU3vX763Pkl+Toz8nHj0NzdtOlWeGyMnFuODHXtYt6WKPWkHwwcW5kYBMbgvRx8SBcbQ/n3YW5+kurae6tooUKpro8CprqsP5VHYxGMx+uTGKchN/U09YhTkxhvKcuNG0p26pFNX79Qno+mkpz9PknQnJxatm58T229bqef5ObE2B5m7k3QwUM9LukRbQiGnuyojPUd+TpzSw/p3+nbdvV3f9JNJ5/3KPawrr2Ltll2sK9/F2i27eG71Zh5ZsqH1DaSJGRzA1coPSH5OjNx4rGGnn3THYf/nTdQtZhCPGTGLHvGYYfuVgfu+Hwl5w3b3fw5R0FhYJ/2vQcO2mvpsUl8a973GR+tptm/7+5UZRK/wUd7KT5tS66U2mb6V1Ot0SWy2caPtee3O7t0WF+bx6FdO7dRtplMoSLdp73+OWMwYXlTI8KJCzjhm/x8rbqvay/oPd7FlRw35udFxjfwWvrHnxmMkk05NXZI9tfUNPYs9qZ5E2nRtfZJ4zMiJRTvi1CMnFiMWg5xYrKGsNgyHVdfWU12X3kOJeiepbdfWOzGL2pS+g07tkEntmDGcEBZJp96jHkoyGZXVJx33VHlqZ7z/TrSpHbT7vpBIhVAyVRaCKenRzrq5HfK+5/u27XhDMDWEEVFBelg19dk3968hfb305+z3Gp2vraMm7XrtNi6c/r63pl9B1+62FQrSIxUl8hifKG7XOrGY0ScvTp+85i8oKJLtdD8FERFpoFAQEZEGCgUREWmgUBARkQYKBRERaaBQEBGRBgoFERFpoFAQEZEGPfbaR2ZWTnQvh44YBHzYidXJtN7WHuh9bept7YHe16be1h74aJuOcPcW72XcY0PhQJjZktYuCtWT9Lb2QO9rU29rD/S+NvW29kDH2qThIxERaaBQEBGRBtkaCndlugKdrLe1B3pfm3pbe6D3tam3tQc60KasPKYgIiJNy9aegoiINEGhICIiDbIqFMxsmpm9ZWZrzey6TNenM5jZO2b2hpktN7MeedNqM5ttZlvM7M20smIzW2Bma8LfokzWsT2aac+NZrYxfE7Lzey8TNaxPcxshJm9YGYrzWyFmV0dynvyZ9Rcm3rk52RmBWb2ipm9HtpzUyg/0sxeDvu8R8wsr9VtZcsxBTOLA38DpgBlwKvAxe6+MqMVO0Bm9g4wwd177I9uzOz/ALuAB9x9TCj7EbDV3W8JAV7k7tdmsp5t1Ux7bgR2ufutmaxbR5jZocCh7r7MzPoBS4ELgMvouZ9Rc226iB74OVl0v9OEu+8ys1xgEXA18A3gcXefY2a/AF539ztb2lY29RQmAmvdfb277wXmANMzXCcB3P1PwNZGxdOB+8P0/UT/YXuEZtrTY7n7JndfFqZ3AquAYfTsz6i5NvVIHtkVnuaGhwNnAnNDeZs+o2wKhWHAhrTnZfTgfwRpHHjGzJaa2VWZrkwnGuLum8L0B8CQTFamk3zNzP4ahpd6zFBLOjMbCZwEvEwv+YwatQl66OdkZnEzWw5sARYA64Dt7l4XFmnTPi+bQqG3+qS7nwycC3w1DF30Kh6Ncfb0cc47gaOAccAm4MeZrU77mVlf4DHgX919R/q8nvoZNdGmHvs5uXu9u48DhhONjBzXke1kUyhsBEakPR8eyno0d98Y/m4BniD6x9AbbA7jvqnx3y0Zrs8BcffN4T9tEribHvY5hXHqx4D/dffHQ3GP/oyaalNP/5wA3H078AJwKjDQzHLCrDbt87IpFF4FRoWj8XnADGBehut0QMwsEQ6SYWYJYCrwZstr9RjzgJlheibwZAbrcsBSO8/gs/SgzykcxLwXWOXut6XN6rGfUXNt6qmfk5kNNrOBYboP0Qk1q4jC4fNhsTZ9Rllz9hFAOL3sJ0AcmO3u389wlQ6ImX2MqHcAkAM81BPbZGYPA5OJLvO7GbgB+A3wKHA40SXSL3L3HnHwtpn2TCYaknDgHeCf0sbjD2pm9kngReANIBmK/4NoDL6nfkbNtelieuDnZGYnEh1IjhN92X/U3W8O+4g5QDHwGnCJu9e0uK1sCgUREWlZNg0fiYhIKxQKIiLSQKEgIiINFAoiItJAoSAiIg0UCiIi0kChICIiDf4/dKpT3s5HwN0AAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
}
},
{
"output_type": "stream",
"name": "stderr",
"text": [
"/usr/local/lib/python3.7/dist-packages/ipykernel_launcher.py:17: MatplotlibDeprecationWarning: cycling among columns of inputs with non-matching shapes is deprecated.\n"
]
},
{
"output_type": "display_data",
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAD4CAYAAAAXUaZHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nO3df5xU9X3v8ddnf8CKqAiiSUV3ifIQMRGCmIsP07AJmJrERq9JrBQbybVSwdym7W0bk9zH3dkmtumPR4xixGz8AQqaqtVKqDFRymLSqOliDVXESMJuhIfID5WIiAL7uX+cM7szw87uzO6ZOTNn3s/HYx5zzpkzc77z6zPf+ZzvD3N3REQkWeriLoCIiERPwV1EJIEU3EVEEkjBXUQkgRTcRUQSqCHuAgCccMIJ3tLSEncxRESqyoYNG3a7+8SBbquI4N7S0kJXV1fcxRARqSpm1pPvNqVlREQSSMFdRCSBFNxFRBJIwV1EJIEU3EVEEkjBXY7Qurw17iKI1IxSfd8U3OUI63vW9y0r0ItEL/N7lfl9i5KCew0rJHCX6oMnUmtSnam+5XJ8rxTca1huDd3aDWs3gKxlESleZjAHaF/fnrU+0Pctyn/KCu4Jl/sBy6dzYSfe5njbkZO3lOKDJ5J0ucEc8lea0t+9zoWdkR1fwT3hcj9g+WrohQTu1pah9xGRfqnOVEH/gktRgaqIsWVk5FKdKVKtqWHfv/uNbqVhREYo1ZnKqlANVHsfyED/mEfM3WO/nHPOOS4jQ4q+5bZ1bU6KIy5t69p8zp1zBrxPvsfKt4+IBNrWtQ24Pfe7k/u94oRnHXr7Lyc8m/ex8gG6PE9cLSj4AuOAB4DNwAvAecB44DHgpfD6+HBfA24CtgAbgZlDPb6Ce36ZwXgwhQTq9Pq0acE7H3yo3KdNC24bNy57e3q5vt598eKRPAuR5BrJdy/3kv4uFnzsQYJ7oTn3G4FH3X0qMD0M8NcBa919CrA2XAf4BDAlvCwClg3/f4XkNpnKPEGam89LL6c6U8ybB2ZAqhczmDcvvNPNz7JpU/oRgvtt2hTs+8Yb2dvTy4cPw7JlsGRJtM9NpBYsWQINDUCq94jvXq5Nm6JLz1gQ/AfZwew44FngfZ6xs5m9CLS6+ytm9l6g093PMLPvhsv35u6X7xizZs1yjec+MGu3rHxc7vq8ebB2LYADxty58OvXt7D1mdPI/gA5TP4xbP04A3+wPM/2nL1KkBoUqTa5ufW05uOa6dmbMcT6mqXQdS2FfLfSivmOmdkGd5810G2FnFCdDOwC7jSz6cAG4EvASRkBewdwUrh8MvByxv23hduygruZLSKo2XPqqacW9kxqROvyVtZfcz+8cwLQi6UcRu9mzq2fy9qvP7BD+sMTrOcG9vD2rb9HEMQHopOpIsVIV7JyK1xLlkBHBxw+XFiFKedRh3GfgRWSlmkAZgLL3P2DwFv0p2CC4gQ1+qLqdO7e4e6z3H3WxIkDzhJVUzLTLb/48054ZyLBmxxe3jmB9V9YF6ZZHHvfj1i7tthqtKrdIkMppG9I+/r2AVOi517yNMuWweHDMLwgHV0lq5Dgvg3Y5u5Ph+sPEAT7V8N0DOH1zvD27cApGfefFG6TQWT+xevPfWey7MvWjw/zSKqhiwwm87tYaCfAtK6HPxRxaYZvyODu7juAl83sjHDTXGATsBq4Mtx2JfBwuLwa+LwFZgN7B8u3V7tRo4KTkWaOWbA+coXUsOOtFYjUgtxAn9Uhac1SaD8IqV5IHYZUdCmVKBTaWuZ/A6vMbCMwA/hb4JvABWb2EjAvXAd4BPg1QVPI7wGJbWMxahQcPJheC97UgwcHD/CZPdBSnSls4i8w8/50y8RfFFGCfB+kyvmAiVSqQlqe5eobomPNUuj6IngDwfet8jr7D9laphyqrbXMWWcRNmnK/0ud72XNPPnS/zhH3Dvv48apoQFO/scWuv+sO+6iiAyq5dtDf05zT4Rmbs9rzVLYsBi8foQlzC+q1jKV93NT4bIDcr4PQf+7k64dpNM36Xbno0ZF0abVec97YOzY7GOWyvLlZDfzEqlQmZ/TQvLmg40B423Ou191+MdtYW29dIE9yu+xgnuRBq5pHyndiaj9o22YOQcPpt+0dPpmsDex0Fq7sWOHs29f6QP7ypWwYEHJDyMSucHy5pnLA46K+soH+s+lvXVyGUob3T92pWWKZBZlyqQy0y9HcmirO6Kozcc1K0UjFaPl2y15/1nmS79E1z49OkrLxCbKN70aAjuA8csF/bWadA1HgV3KbbAUy8IZC4c9J0HQPt1H0D49GosXR/dYCu5Fi/+fThwefzzuEkitygzogw2hm3tbZqBPL6/vWZ+dlkkZ9skv0vXw/6C0QX3wuFFfHwT2W26J7ogK7kWrltp2tH72s7hLILUqX0AvtoNR2uJXnfqvB82PaXf44c0jKF2hDHeYNi29HgT7adOCNMyhQ9EGdtBkHTKkIP+48t+fZmX7bKC/qVjbnLYRTRAikk/u5DOZrVhyW7RkBv98zRj7tt+9hmW/6tsaRVGL8vzz5Tu2gnvRquUkaMTe/J24SyA1pH19e8GzGGX5u53hgHsEA+4B0EvwvY0vURFlLr1Qai1TJKu1uF73NvQelbEh+HGrq0sPjiQSvcyWLIVM/9g2p432C68NB9yLl1l/i5f6eli0KPqUS/+x1FomMv05s8EdFcbD008vXVnKorcpXMhup9/b61jdoViKJMlUdBv0XGGNPU5z50Jvb//cSqXIpRdKwb1Izz8PZ5wx9H7/9E/B9ZYtpS1P6VnOdcZ2V1ZPRmY4J0UzA33bnDZY+gvaP9pGfOnSoCxz51ZWqzKlZYZh924oZAj6+vrkpy4q4OMjVSwz/dK6vPWIaSXT5v7EM2YcS1+nh8COT9wBXWmZEjrmmPy3JSOwK3pLtPLV1o8I7BlD6vZPTJMO6HXEFdjr6oLhONwrq6aeS8F9GD784f7lN9+MrxzlUWtnkKXU8s1iBIMNqVvez2G6U5F7EMibm4MTpc3NcNdd1THOkoJ7kc46C158Me5SiFSO4XYmGkjf/AZd10b2mMUYqFPRggXQ3R2cKO3uro7ADgruRSt0VEiRWlFIe/ShhtT1Noebn4Xd04krl+6e2cmo+im4F005aJF8tfV8A3OlWlMDjvWSZffZEZawOHPnxnboklFwlxHQD12typc3z9faJffHID3fQXrymqBzYDznd+Ju8VIqCu5F0wnGfnotakm+WnkhslI3Kx4NmzVCnJ+huXMrv8XLSCi4F6mxMe4SVBLV3GtJ7nC5+eQbO93OvRmzXtj6eyUs5VAqs8NRKaiLYZHefTcI8IfU854JE1RzrzWZ470UMvaLtRu8cxT8XWVUBBYvttiGAyg3BfdhOO00NYccNQpuvDHuUkip5fYaHWzo3bR00J/yR9+ClZ0lLd9gFi9OT5tX+gG8KpK7x34555xzvFpMm5YeEqhWL73e3Oy+cmXc74SUQtu6try3kSJrmUvnO8dtdTgcXF863/l/5ox6I/bP6dy5ZXixKgDQ5XniakE5dzPrNrP/NrNnzawr3DbezB4zs5fC6+PD7WZmN5nZFjPbaGYzS/jbVHabNlXG30uRYhXS2ajgMdQ3zsceugf2tgB1wfWD98Df9MK7x42glCNXC/n0QhRzQvWj7j7D+wepuQ5Y6+5TgLXhOsAngCnhZRGwLKrCVoZazzMbPT2wcCGsWhV3WaQYxU5Xl7u9+bjm4KRo3SF4cBUeUz1n8eIgzQLZwwSkLwrsgYJGhTSzbmCWu+/O2PYi0Orur5jZe4FOdz/DzL4bLt+bu1++x6+mUSFrbrKOQYwdWwtj6yRH5knQ3O35eJuzZEl/7roSxPWjUomiGBXSgR+b2QYzWxRuOykjYO8ATgqXTwZezrjvtnBbbqEWmVmXmXXt2rWrwGLET00h++3bp29ZpWtd3jpgZ6PcWnm+3qNLlsCyZZUT2OvUeLtghbaW+bC7bzezE4HHzGxz5o3u7mZW1Dfd3TuADghq7sXcN04HDzpKzaTpdahErctb6VzYCQRt0wdqvpge6yUt3/KyZb1USncYTe1YnILeNXffHl7vBB4CPgS8GqZjCK93hrtvB07JuPukcFtCKKBJZcs3BECurPFdNs6HG7ZC6nBw/fNFkHLKHdibm/vHSs+9KLAXZ8h3zsyONrNj0svAx4HngNXAleFuVwIPh8urgc+HrWZmA3sHy7eLSPQGSsXMaZ7Td3vWydWN84OWLpktXx75blnLm1ZNQ+pWukLSMicBD1lwJrEBuMfdHzWz/wTuM7OrgB7gsnD/R4BPAluA/cAXIi91jKZN07C/aQ3qAherVGeKVGsKGHyKunwTS6dPlHK4Mpo9JXFkxljlawBfzks1dWJydz/jjHg7aFTKRR2Z4pXZqSjfdlL4ypXuzc3uWG9/Z6NZSx16y/ZZuewy7yuHmXtTU/bttdLpKGoM0olJda9h+OlP0xNk1+bJ1XRXbv19rhypzlRWqqXvpOjG+Xzhejh4EMBgbwv20D14mZow5Hb712emfCrjNHjVqr3ADsGJre99T52YSmmwjkVDzj8KLH7Vqf+6w4OrwsDer1yBHbKnq5PyUnCXYTl0CK65Ju5SJFe+3qSd3Z1577NkSXgeJNXLsmUeti6JrwIydmxshxY0KuSIjBkD+/fHXYr47NsXdwmSJfMEaT752q3/zsce5JV16TRh+QN6Q0P2MNgNDXDrrWUvhmRQzX0YLr00uN6/v2r6XkmFGGzwrnxT1xUyA9Ir6y4hzlr68uVBG3Wz4Hr5cuXX41bQ2DKlVk1jy8ybR8YUYVIBH5+qkm98l/RtBVnxKGz9eP/62Jdh36kRlG54Fi9WXj0uUYwtIyEF9n7KqRZmsNp67gnSTAOO97Li0XCaOuu/xBTY0yMyKrBXJtXcixQMoVObrWSy1B3k0q+s5l++8Zm4S1Lx8tXI2+a0ZeXYC5q6LtVL3J+/adPg+edjLYKEBqu564SqFKmX5uY6rr++kQULFNgLNdBJ0MHMaZ7T3+PUgX/YAW+fNOh9SqWhQTn0aqTgXrRarrU7pOrpLiA41bq8nYoG0TanjbPOSg9vsS59z5KUr1DNzXD99Qrs1UjBvWi1nJYx2ua0xV2IqjFQbX2gIN8/GUbmaxvvZ0y19eqnnHuRan0mpgr4uFSFQvLnbXPa2HlfimUVNhGlauvVQ61lRCJUyETTufqGA0j1Uv91Z/GrTqo1xXfjGVkXCMZNz2ybnh5HXcPuJoNq7kWq9Zq7GZx6au3V7DJ7j+Y7KZqbZ++zZil0fbHEJSyO5r9NBtXcIxX/j2Gc3KGnBxYurK2Bw/KN9ZIp1ZrKnt1ozVJoPwhd15a4dMXR0AC1QcG9aDVedQ/V4sBhQ000ndUhac3SIKh7A5X0mdHQALVDwb1otV1zz5SUgcPy5dBbl7cO2Xs0sxNSqjXVn1vvupY4g7ry6aLgXrTKqYVJNDJTLpmBPj0C40D59YFq7kuWwLJlVMRQuwsWBIG8t1cBvVapnXuR6us1C3sS5Btet319e95hd/P1MnWH0aM5YlKMOCifLmlqLVOkVavgiiviLkVlGHXUO7yzf3TcxShYbouXoq1ZChuuAa8HOwxn3QvP/VG0hRwBtU+vPWotE6EFC+DEE+MuRfwaGuCO71VPYIcjW7zkS7lkymyfTtcX+0+QekMsgd1M+XQpjNIyRTrrLNi5M+5SxMUBDwcOq85Aklljz1wecKiAc29mWd8fyso413LNNcHrXo2vvZRXwTV3M6s3s/8yszXh+mQze9rMtpjZP5vZqHD76HB9S3h7S2mKHo9Nm+JPY8Wp+Yb3VVwNcbCZigYbLz1T5j6rVkFLCxXVPl1jp0uxiknLfAl4IWP974Eb3P104HXgqnD7VcDr4fYbwv0SpDJqcPEwevb2xF0I4MhWLXn3y+1YlEffPhvns3Bh0FEr7vc6M+Vy6JACuxSnoOBuZpOATwG3hesGfAx4INxlBXBJuHxxuE54+9xwf5HI5OsxmluLz23DPmAP0lQvZsGFB+/Jmui53JRDl6gUWnP/NvDXQG+4PgF4w93TX4NtwMnh8snAywDh7XvD/bOY2SIz6zKzrl27dg2z+OU3bVrcJYiTh4HQsff9qKCJm0tpoB6jubX43B8BO/dmrO5QeII0swdpHXG3Lzj6aAV0ic6Qn2YzuwjY6e4bojywu3e4+yx3nzVx4sQoH7qknn8eTjst7lLEJWPezq0f5zdLbyvr0QudbzRX/iEBKucPZV0dsY4QKclTSGuZ84FPm9kngSbgWOBGYJyZNYS180nA9nD/7cApwDYzawCOA/ZEXvIYXXMN/NVfxV2KuBlbnzm9JI/curyVzoWdxZUmTysYILt9eoUE9Pp6GDcOXnutNkfZlDJw94IvQCuwJly+H7g8XL4VWBIuXwvcGi5fDtw31OOec845Xi1WrnSvq3MPsqK6RKVtXVvfMqmhHzhznzl3zsl7X2Ytjf01yr00NwefI5GRAro8T1wdSZLxy8BfmNkWgpz67eH224EJ4fa/AK4bwTEqzh//cTBeh0SrkCF182ltaR1w+7/9G7GPo55uSqATpVJuGn6gSGZOpfy1j5/jHs1rka8d+pzmOQOmaFKdKe6/NhVOJp35nlTO+6PhAKTUNPxApCojcFSC407aW/R98o5/niN9gjS3Vr5kSTD0QftH04Edst+TeN4f1dCl0ii4y7DNev+4ou+TNbxuTgejgVq8ZO6fPaRu5WhuhrvvVkCXyqLgXqS5c+MuQeVYu7Y0jzunec6A25ctK83xClVfn73e0BDU0hXQpRIpuBfp8cfhd3837lJUivznawZLv6SXc2c6GnT5r+PtC1FXBytWZI/GqOnqpJJpVEgZgfz57cxJLzq7O/NOdNH3SO3GtPucTZsg3cd02jTYdMqfwo9uirrgRfuTP9FojFJdFNyLNG8e/OQncZeiuqzvWT9gJ6O2OW1M2Z7ia18Deg6zKed+mzYBm+IN7PX1sGiRBu2S6qPgXqS1ayunqV38sl+LVGcq6wToUOOlr1oFX/hCenq6yskQqglj5Th48CDbtm3jwIEDcRclVk1NTUyaNInGxsaC76N27kXS+JbZ8n18Bhs/PR3cxxz3Fm//9uhSFGtYxoyBjg4F9UqydetWjjnmGCZMmECtDi7r7uzZs4c333yTyZMnZ92mdu5SFrmjROYdXrfuEPb+eyoqsDc3K7BXogMHDtR0YAcwMyZMmFD0vxelZYqmtEw+eSfNWLM0exgAb4Dn/7A8hRpCYyPceaeCeiWr5cCeNpzXQDX3oumDlil3Mgz7zB9i47ohdRgb9Vus7nBFTVeXqblZgV3Kq7Ozk4suuqgsx1JwL1r85ygqh9O+vr2/TfrG+fCvd8DeFqAODh5bUcPsQv9cpOpNmmy5lY5SO1xp3aZRcB+GyglU8Qtei77c+g9vhN6mmMvUr76+v8OR5iKtLSMZZTRXd3c3U6dOZcGCBZx55pl89rOfZf/+/bS0tPDlL3+ZmTNncv/99/PjH/+Y8847j5kzZ/K5z32Offv2AfDoo48ydepUZs6cyYMPPhhZuYai4C4jEDZvTE9d93Z8vUjHjDlyfcWKYHhm1dBlpF588UWWLFnCCy+8wLHHHsstYQ1hwoQJPPPMM8ybN49vfOMbPP744zzzzDPMmjWLb33rWxw4cICrr76aH/zgB2zYsIEdO3aUrcwK7jICBt+/PzhZ6vGem+/oyB4aQC1fak++YS6iSNGccsopnH/++QBcccUV/PSnPwXgD/7gDwB46qmn2LRpE+effz4zZsxgxYoV9PT0sHnzZiZPnsyUKVMwM6644ooRl6VQai1TpMWL4x/AqqJs/mzcJWDCBA0NIMEoo+khL/INczFcua1V0utHHx0053V3LrjgAu69996s/Z599tnIylAs1dyLdMstsHBh3KWoPe95z8DbGxvhxhvLWxapPb/5zW948sknAbjnnnv48Ic/nHX77Nmz+Y//+A+2bNkCwFtvvcUvf/lLpk6dSnd3N7/61a8Ajgj+paTgPgzh+yRlcNttwYnQV14JrleuzE6/qCmjDKRtTlukj3fGGWfwne98hzPPPJPXX3+dxYsXZ90+ceJEli9fzvz58zn77LM577zz2Lx5M01NTXR0dPCpT32KmTNncuKJJ0ZarsFo+IEizZtXunHMpd+pp8Lf/q0Cd6174YUXOPPMM2MtQ3d3NxdddBHPPfdcrOUY6LUYbPgB5dyLpIHDSq+pCXp64i6FSHVTWqZoCuylVFcXpGJEKkVLS0vstfbhUHCXWE2YEFzSOfS77lIqRiQKSstIrHbvjrsEIsk0ZM3dzJrM7Odm9gsze97M2sPtk83saTPbYmb/bGajwu2jw/Ut4e0tpX0K5Rb/CeikmDAh7hKIJFchaZl3gI+5+3RgBnChmc0G/h64wd1PB14Hrgr3vwp4Pdx+Q7hfgijnHoVRo9Q+XaSUhgzuHtgXrjaGFwc+BjwQbl8BXBIuXxyuE94+1zQgc83Lza3fcYdy65I8nZ2d/OxnPxvRY4wdOzaSshR0QtXM6s3sWWAn8BjwK+ANdz8U7rINODlcPhl4GSC8fS9wxB9wM1tkZl1m1rVr166RPYsyGj067hJUl4aGoOPR7t3BRQN5STmUe8jftCiCe1QKCu7uftjdZwCTgA8BU0d6YHfvcPdZ7j5r4sT4RhMs1mmnxV2C6tHcDMuXK5BL+UU55C/AJZdcwjnnnMNZZ51FR0cHEAzlO3PmTKZPn87cuXPp7u7m1ltv5YYbbmDGjBn85Cc/YeHChTzwwAN9j5Oule/bt4+5c+cyc+ZMPvCBD/Dwww9HWl4osrWMu79hZuuA84BxZtYQ1s4nAdvD3bYDpwDbzKwBOA7YE2GZY7VpkzoxDaWhQUFdkuWOO+5g/PjxvP3225x77rlcfPHFXH311TzxxBNMnjyZ1157jfHjx3PNNdcwduxY/vIv/xKA22+/fcDHa2pq4qGHHuLYY49l9+7dzJ49m09/+tORTilYSGuZiWY2Llw+CrgAeAFYB6SHBLwSSP/0rA7XCW//d6+EMQ4io8CeaeXKI8d7UWCXOJRyyN+bbrqJ6dOnM3v2bF5++WU6Ojr4yEc+wuTJkwEYP358UY/n7nz1q1/l7LPPZt68eWzfvp1XX311xOXMVEjN/b3ACjOrJ/gxuM/d15jZJuD7ZvYN4L+A9E/U7cDdZrYFeA24PNISS0VJB3EFc4lbqYb87ezs5PHHH+fJJ59kzJgxtLa2MmPGDDZv3jzkfRsaGujt7QWgt7eXd999F4BVq1axa9cuNmzYQGNjIy0tLRw4cCCS8vYde6gd3H0j8MEBtv+aIP+eu/0A8LlISleBRo+Gd96JuxQiUi579+7l+OOPZ8yYMWzevJmnnnqKAwcO8MQTT7B169astMwxxxzDb3/72777trS0sGHDBi677DJWr17NwYMH+x7zxBNPpLGxkXXr1tFTgsGUNPxAkfKk0ESkgkQ55O+FF17IoUOHOPPMM7nuuuuYPXs2EydOpKOjg0svvZTp06f3zcj0+7//+zz00EN9J1Svvvpq1q9fz/Tp03nyySf7JvdYsGABXV1dfOADH+Cuu+5i6tQRt1E5gob8HYapU+HFF+MuRWWogI+PJFglDPlbKYod8lc19yKNm/ZzXnxREU1EKpuCe5H2vnAuajEjIpVOwV0Gd8xv4i6BiAyDgnsBctvP1pT9J6CRMCVOlXBeMG7DeQ0U3AvQ2d0ZdxHic/golIaSuDQ1NbFnz56aDvDuzp49e2hqairqfpqsI49UZ3+HiPU96/s6RFiqdj9kIuU2adIktm3bRjUNLlgKTU1NTJo0qaj71Hxwzwzimcvt69v7lrP1AvVlKl1laG4eeMLq5ubyl0VqS2NjY18XfylOzadlMkePyx1JLmucis/8ITaum9p7yYzrr4cxY7K3jhkD118fT4lEZGi1FqmAwcd6HvDE6cb58OA9sLeFWsw/L1gAHR3Zg4N1dGg8GZFKVpM9VItu9fI3b0HvmKH3SySnuTmovSuYi1QW9VAdgLd530nSfMuLX3Xqv+7Qe1Rs5Yyf0dMDCxfCqlVxl0VECpWo4N66vDXvbfnGes41b16QeiDVy7JlcPgw1GIqJtehQ3DNNXGXQkQKlajgvr5nfd9ybl491ZrKqpVnsnNvxuoOQaqXtWvTtyug59q3b+h9RKQyVH1wz3dydMg5FNcshfaDkOqFrmvBGwgCuoK6iFS/qj+hOtjJ0cxaeqozxZTtKb72Nejp0Tyow+O463UTqRSDnVBNRCemvt6jOYE+vd42p432pb+k8QcQTISiADU8et1EqkVVBvdUZyor7VJQ08Yf3hgGdhku9UgVqR5VmXM/YiCvjfPhhq2QOkzznc7K04OafNucNnBov34/vD2x/AUdtvhTZbnUI1WkulRlzb21pbW/ZczG+fDgXaSfSk8PXHEFQC/tGJCKp5AjUlnpj+Zm1IlJpMpUZXBPtRZycrSyAmQ16+6OuwQiUqwh0zJmdoqZrTOzTWb2vJl9Kdw+3sweM7OXwuvjw+1mZjeZ2RYz22hmM6Mu9Gf+779wxRW94UiFCuKlZhZ07hKR6lFIzv0Q8H/cfRowG7jWzKYB1wFr3X0KsDZcB/gEMCW8LAKWRV3oB6//nwUWPQ6Vly+Pwtq1CvAi1WTICOnur7j7M+Hym8ALwMnAxcCKcLcVwCXh8sXAXR54ChhnZu+NttiVXFsvddni+/FYuza2Q4tIkYqq/ppZC/BB4GngJHd/JbxpB3BSuHwy8HLG3baF2yJUycG91Gr5uYtIoQoO7mY2FvgX4M/c/beZt3nQzbWoKqWZLTKzLjPrqvUptEREolZQcDezRoLAvsrdHww3v5pOt4TXO8Pt24FTMu4+KdyWxd073H2Wu8+aOLGy26BPmAArV6oTj4hUj0JayxhwO/CCu38r46bVwJXh8pXAwxnbPx+2mpkN7M1I31Sdxka48cagjXd3dxDkc6ecG1q+PzX5/+wMdIyxY4s9bsAiyuTox02kehRScz8f+CPgY2b2bHj5JPBN4AIzewmYF64DPAL8GtgCfJMQ5QEAAAj1SURBVA9YEn2xSysdDJub4c47szvvZE45V8QjFrU9PY1d5rR2110Hxx5bzDH7TZgwvPtlUg9VkepSlaNCmpVuVMdiemM2NcE774zseGPGwP792ev55ifdswdOOKH4Y1x+eTDpSGcnDOf0hnqoilQmTbM3hObmIN3iHqReCg1ix7xnByNtmljMxNPDrYHfey/cdx/s3FncP45Ro4LXpZjXREQqQ5UG9+hq7YsXDz947e55z4jLks7l9/aWJojmBvPrr89/zqCuDo4+uv+H5o47FNRFqlWVBveRq68PAvstt8RXhqam4u+zeHHh+w6UJ888Z5AO4ul/LYcPB1PpleqHRkTKpyoHDivW2LHw1ltw6qmVkzuuq4Pbbiv+fukfo46OIBjX1cFRRwV5+/Hjg9tee23w57pgQWW8BiJSOokO7vX1sGhR6Wrno0cXd0K1vj6oFY/0R+aWW+L9xyEila8q0zL19flvy0wzHDpU2iB4++1HtiE3C1InuXntMWNgxQqlPESkPKoyuC9aNPD2kZwcHY4FC+Duu7Pz13ffHfygFNMKRkQkalXZzh1gyZL+vHOp0y8iIpVosHbuVZtzV95ZRCS/qkzLiIjI4BTcRUQSSMFdRCSBFNxFRBJIwV1EJIEU3EVEEkjBXUQkgRTcRUQSSMFdRCSBFNxFRBJIwV1EJIEU3EVEEkjBXUQkgRTcRUQSaMjgbmZ3mNlOM3suY9t4M3vMzF4Kr48Pt5uZ3WRmW8xso5nNLGXhRURkYIXU3JcDF+Zsuw5Y6+5TgLXhOsAngCnhZRGwLJpiiohIMYYM7u7+BPBazuaLgRXh8grgkoztd3ngKWCcmb03qsKKiEhhhptzP8ndXwmXdwAnhcsnAy9n7Lct3HYEM1tkZl1m1rVr165hFkNERAYy4hOqHkzCWvRErO7e4e6z3H3WxIkTR1oMERHJMNzg/mo63RJe7wy3bwdOydhvUrhNRETKaLjBfTVwZbh8JfBwxvbPh61mZgN7M9I3IiJSJg1D7WBm9wKtwAlmtg1oA74J3GdmVwE9wGXh7o8AnwS2APuBL5SgzCIiMoQhg7u7z89z09wB9nXg2pEWSkRERkY9VEVEEkjBXUQkgRTcRUQSSMFdRCSBFNxFRBJIwV1EJIEU3EVEEkjBXUQkgRTcRUQSSMFdRCSBFNxFRBJIwV1EJIEU3EVEEkjBXUQkgRTcRUQSSMFdRCSBFNxFRBJIwV1EJIEU3EVEEkjBXUQkgRTcRUQSSMFdRCSBFNxFRBKooRQPamYXAjcC9cBt7v7N6I9R2H7jxsGbb8Lhw1GXoF99PfT2gnvpjlGL0q/r+PHB+muvBdeFvM6NjXDwYOnKlmYWHOvdd0t/rDjU1wevd29v3CWpDVHGkMiDu5nVA98BLgC2Af9pZqvdfVN0xyh83zfeiOqo+ZXyh6OWpV/XPXuKv285AjsEX8akBnbQZ7vczKIL8KVIy3wI2OLuv3b3d4HvAxeX4DgiIpJHKYL7ycDLGevbwm1ZzGyRmXWZWdeuXbtKUAwRkdoV2wlVd+9w91nuPmvixIlxFUNEJJFKEdy3A6dkrE8Kt4mISJmUIrj/JzDFzCab2SjgcmB1lAco5oTDuHHBGf9Sqq8v7iSvFCb9uk6YEFzMCn+dGxtLW7Y0Mxg1qjzHikN9PdSpwXTZVHRrGXc/ZGZfBH5E0BTyDnd/PvrjRP2IIiLJUZJ27u7+CPBIKR5bRESGpj9cIiIJpOAuIpJACu4iIgmk4C4ikkDmFdDsxMx2AT1xl2MYTgB2x12IMqu151xrzxf0nKtJs7sP2Au0IoJ7tTKzLnefFXc5yqnWnnOtPV/Qc04KpWVERBJIwV1EJIEU3EemI+4CxKDWnnOtPV/Qc04E5dxFRBJINXcRkQRScBcRSSAF9yKYWb2Z/ZeZrQnXJ5vZ02a2xcz+ORziODHMbJyZPWBmm83sBTM7z8zGm9ljZvZSeH183OWMkpn9uZk9b2bPmdm9ZtaUtPfZzO4ws51m9lzGtgHfVwvcFD73jWY2M76SD1+e5/yP4Wd7o5k9ZGbjMm77SvicXzSz34un1COj4F6cLwEvZKz/PXCDu58OvA5cFUupSudG4FF3nwpMJ3ju1wFr3X0KsDZcTwQzOxn4U2CWu7+fYMjqy0ne+7wcuDBnW7739RPAlPCyCFhWpjJGbTlHPufHgPe7+9nAL4GvAJjZNIL3/azwPreYWYlnhYiegnuBzGwS8CngtnDdgI8BD4S7rAAuiad00TOz44CPALcDuPu77v4GwWTnK8LdEvWcQw3AUWbWAIwBXiFh77O7PwG8lrM53/t6MXCXB54CxpnZe8tT0ugM9Jzd/cfufihcfYpg1jgInvP33f0dd98KbAE+VLbCRkTBvXDfBv4a6A3XJwBvZHw4BpwIvIpNBnYBd4apqNvM7GjgJHd/JdxnB3BSbCWMmLtvB/4J+A1BUN8LbCDZ73Navve1oAnvE+B/AT8MlxPxnBXcC2BmFwE73X1D3GUpowZgJrDM3T8IvEVOCsaDdrSJaUsb5pkvJvhh+x3gaI78K594SXtfh2JmXwMOAaviLkuUFNwLcz7waTPrBr5P8Df9RoK/qOnZrJI2Efg2YJu7Px2uP0AQ7F9N/y0Pr3fGVL5SmAdsdfdd7n4QeJDgvU/y+5yW731N9IT3ZrYQuAhY4P2dfhLxnBXcC+DuX3H3Se7eQnCi5d/dfQGwDvhsuNuVwMMxFTFy7r4DeNnMzgg3zQU2EUx2fmW4LVHPmSAdM9vMxoTnVNLPObHvc4Z87+tq4PNhq5nZwN6M9E1VM7MLCVKtn3b3/Rk3rQYuN7PRZjaZ4GTyz+Mo44i4uy5FXIBWYE24/D6CN30LcD8wOu7yRfxcZwBdwEbgX4HjCc41rAVeAh4HxsddzoifczuwGXgOuBsYnbT3GbiX4JzCQYJ/aFfle18BA74D/Ar4b4KWRLE/h4ie8xaC3Pqz4eXWjP2/Fj7nF4FPxF3+4Vw0/ICISAIpLSMikkAK7iIiCaTgLiKSQAruIiIJpOAuIpJACu4iIgmk4C4ikkD/H2j7h5/Tn5IIAAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 432x288 with 1 Axes>"
]
},
"metadata": {
"needs_background": "light"
}
}
]
},
{
"cell_type": "code",
"metadata": {
"id": "FqwUue-_ReX_"
},
"source": [
""
],
"execution_count": null,
"outputs": []
}
]
} | mit |
dtrimarco/blog | posts/product_data_071317.ipynb | 2 | 10835 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Pandas for Product Analysis Part 1: Apply and Transform\n",
" \n",
"Python's [pandas](http://pandas.pydata.org/) package is one of the most powerful tools for data analysis in the Python ecosystem. Built on top of NumPy, it makes working with tabular data quite effective and adds an astounding amount of functionality to your toolkit. Despite its strengths, there are some very useful functions that are challenging to grasp based on the pandas docs. `apply` and `transform` are two such examples. \n",
"\n",
"One quick note before we dive in: this series assumes basic working knowledge of pandas. There are several resources like [Dataquest](https://dataquest.io), [Data Camp](https://www.datacamp.com/) and pandas cheat sheets to get you up to speed if this is hard to follow."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## What are `apply` and `transform`?\n",
"\n",
"In short, these two functions are used to operate on data structures, similarly to Python's built in `map` function. We will get into the differences, but typically they are used in combination with `groupby` to perform aggregate functions on various groups of a dataset. This a direct analogy to `GROUP BY` in SQL and I am going to assume familiarity with how it works (if you aren't, [here is a decent intro](http://pandas.pydata.org/pandas-docs/stable/groupby.html#splitting-an-object-into-groups)). The major difference is that we can leverage the flexibility of Python and pandas DataFrames to do basically whatever we want."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Data\n",
"To keep things practical, let's start with event data from a hypothetical mobile game. I created some [randomly generated, but logical data](https://github.com/dtrimarco/blog/blob/master/utils/create_fake_data.ipynb) for us to analyze."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" user_id event_timestamp lat lon event_type\n",
"0 5000 2016-01-03 00:40:59 41.795738 87.517197 login\n",
"1 5000 2016-01-03 00:50:59 41.795738 87.517197 level_1\n",
"2 5000 2016-01-03 00:56:59 41.795738 87.517197 level_2\n",
"3 5000 2016-01-03 01:01:59 41.795738 87.517197 level_3\n",
"4 5000 2016-01-03 01:13:59 41.795738 87.517197 level_4\n",
"5 5000 2016-01-03 01:28:59 41.795738 87.517197 level_5\n",
"6 5000 2016-01-03 01:35:59 41.795738 87.517197 level_6\n",
"7 5000 2016-01-03 01:45:59 41.795738 87.517197 level_7\n",
"8 5000 2016-01-17 10:07:19 41.593679 87.719833 login\n",
"9 5000 2016-01-17 10:19:19 41.593679 87.719833 level_8\n"
]
}
],
"source": [
"import pandas as pd\n",
"\n",
"data = pd.read_csv('test_user_data.csv')\n",
"print(data.head(10))"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"The data contains one event per row and has 5 variables:\n",
"\n",
"* **user_id**: Identifier for each user.\n",
"* **event_timestamp**: The time each event happened.\n",
"* **lat**: The latitude of the user when the event occurred.\n",
"* **lon**: The longitude of the user when the event occurred.\n",
"* **event_type**: The type of event that occurred: login, level, buy_coins and megapack."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Basic differences between `apply` and `transform`\n",
"\n",
"Suppose we wanted to count the number of events for each user. Both functions can do this, but in different ways. Let's try it first with `apply`."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"user_id\n",
"5000 230\n",
"5001 207\n",
"5002 242\n",
"5003 190\n",
"5004 116\n",
"dtype: int64\n"
]
}
],
"source": [
"apply_ex = data.groupby('user_id').apply(len)\n",
"print(apply_ex.head())"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The output here is a pandas Series with each user_id as the index and the count of the number of events as values. Now to try the same thing with `transform`."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" event_timestamp lat lon event_type\n",
"0 230 230 230 230\n",
"1 230 230 230 230\n",
"2 230 230 230 230\n",
"3 230 230 230 230\n",
"4 230 230 230 230\n"
]
}
],
"source": [
"transform_ex = data.groupby('user_id').transform(len)\n",
"print(transform_ex.head())"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"What the heck happened here? This odd DataFrame highlights a key difference: `apply` by default returns an object with one element per group and `transform` returns an object of the exact same size as the input object. Unless specified, it operates column by column in order.\n",
"\n",
"How about we clean this up a bit and create a new column in our original DataFrame that contains the total event count for each group in it."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" user_id event_timestamp lat lon event_type event_count\n",
"0 5000 2016-01-03 00:40:59 41.795738 87.517197 login 230\n",
"1 5000 2016-01-03 00:50:59 41.795738 87.517197 level_1 230\n",
"2 5000 2016-01-03 00:56:59 41.795738 87.517197 level_2 230\n",
"3 5000 2016-01-03 01:01:59 41.795738 87.517197 level_3 230\n",
"4 5000 2016-01-03 01:13:59 41.795738 87.517197 level_4 230\n",
"5 5000 2016-01-03 01:28:59 41.795738 87.517197 level_5 230\n",
"6 5000 2016-01-03 01:35:59 41.795738 87.517197 level_6 230\n"
]
}
],
"source": [
"data['event_count'] = data.groupby('user_id')['user_id'].transform(len)\n",
"print(data.head(7))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Much better. All we had to do was assign to the new `event_count` column and then specify the `['user_id']` column after the `groupby` statement. Whether you would prefer to have this additional column of repeating values depends on what you intend to do with the data afterwards. Let's assume this is acceptable. Now for something a bit more involved."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Custom Functions\n",
"\n",
"Say we didn't have Google Analytics or Mixpanel implemented into our app and wanted to assign a monetary value to each event. Of course, we could loop through the entire DataFrame, but this can be very inefficient with a lot of data. Let's try it using a custom function."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def add_value(x):\n",
" if x == 'buy_coins':\n",
" y = 1.00\n",
" elif x == 'megapack':\n",
" y = 10.00\n",
" else:\n",
" y=0.0\n",
" \n",
" return y"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Here we've defined a very simple custom function that assigns values to each of the four event types. Now to `apply` it to our data."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" user_id event_timestamp lat lon event_type event_count \\\n",
"0 5000 2016-01-03 00:40:59 41.795738 87.517197 login 230 \n",
"1 5000 2016-01-03 00:50:59 41.795738 87.517197 level_1 230 \n",
"2 5000 2016-01-03 00:56:59 41.795738 87.517197 level_2 230 \n",
"3 5000 2016-01-03 01:01:59 41.795738 87.517197 level_3 230 \n",
"4 5000 2016-01-03 01:13:59 41.795738 87.517197 level_4 230 \n",
"5 5000 2016-01-03 01:28:59 41.795738 87.517197 level_5 230 \n",
"6 5000 2016-01-03 01:35:59 41.795738 87.517197 level_6 230 \n",
"\n",
" event_value \n",
"0 0.0 \n",
"1 0.0 \n",
"2 0.0 \n",
"3 0.0 \n",
"4 0.0 \n",
"5 0.0 \n",
"6 0.0 \n"
]
}
],
"source": [
"data['event_value'] = data['event_type'].apply(add_value)\n",
"print(data.head(7))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"That worked out nicely. Since we didn't care about event_values per user, `groupby` wasn't necessary. If we were to run this using `transform`, we'd get an error. Since it is run column-by-column, there isn't a practical way to reference other columns like with `apply`."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In the next post of the series, we'll continue using pandas to answer more interesting product questions like:\n",
" \n",
"* How much time does it take our users to purchase after downloading the app?\n",
"* How many logins does it take our users for in-app purchases?\n",
"* What is the lifetime value of our users?"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.1"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
abhipr1/DATA_SCIENCE_INTENSIVE | Week_1/DATA_WRANGLING/DATA_CLEANING_WITH_PANDAS/missing_data.ipynb | 1 | 50331 | {
"metadata": {
"name": "",
"signature": "sha256:7c0b3516450eb5c95292bb728bcec36d2a0d8595fe755ef466188af0760cfb31"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Working with missing data\n",
"[Link](http://pandas.pydata.org/pandas-docs/stable/missing_data.html)"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"%matplotlib inline"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 1
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import pandas as pd\n",
"import numpy as np"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 3
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df = pd.DataFrame(np.random.rand(5, 3), index=['a', 'c', 'e', 'f', 'h'],\n",
" columns=['one', 'two', 'three'])"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 4
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df['four']='bar'"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 5
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df['five'] = df['one'] > 0"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 6
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>one</th>\n",
" <th>two</th>\n",
" <th>three</th>\n",
" <th>four</th>\n",
" <th>five</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>a</th>\n",
" <td> 0.493574</td>\n",
" <td> 0.690375</td>\n",
" <td> 0.338309</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>c</th>\n",
" <td> 0.940038</td>\n",
" <td> 0.545834</td>\n",
" <td> 0.963170</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>e</th>\n",
" <td> 0.674076</td>\n",
" <td> 0.518232</td>\n",
" <td> 0.366761</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>f</th>\n",
" <td> 0.015938</td>\n",
" <td> 0.786997</td>\n",
" <td> 0.184278</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>h</th>\n",
" <td> 0.923214</td>\n",
" <td> 0.462628</td>\n",
" <td> 0.749403</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 7,
"text": [
" one two three four five\n",
"a 0.493574 0.690375 0.338309 bar True\n",
"c 0.940038 0.545834 0.963170 bar True\n",
"e 0.674076 0.518232 0.366761 bar True\n",
"f 0.015938 0.786997 0.184278 bar True\n",
"h 0.923214 0.462628 0.749403 bar True"
]
}
],
"prompt_number": 7
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df2 = df.reindex(['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h'])"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 8
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df2"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>one</th>\n",
" <th>two</th>\n",
" <th>three</th>\n",
" <th>four</th>\n",
" <th>five</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>a</th>\n",
" <td> 0.493574</td>\n",
" <td> 0.690375</td>\n",
" <td> 0.338309</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>b</th>\n",
" <td> NaN</td>\n",
" <td> NaN</td>\n",
" <td> NaN</td>\n",
" <td> NaN</td>\n",
" <td> NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>c</th>\n",
" <td> 0.940038</td>\n",
" <td> 0.545834</td>\n",
" <td> 0.963170</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>d</th>\n",
" <td> NaN</td>\n",
" <td> NaN</td>\n",
" <td> NaN</td>\n",
" <td> NaN</td>\n",
" <td> NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>e</th>\n",
" <td> 0.674076</td>\n",
" <td> 0.518232</td>\n",
" <td> 0.366761</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>f</th>\n",
" <td> 0.015938</td>\n",
" <td> 0.786997</td>\n",
" <td> 0.184278</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>g</th>\n",
" <td> NaN</td>\n",
" <td> NaN</td>\n",
" <td> NaN</td>\n",
" <td> NaN</td>\n",
" <td> NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>h</th>\n",
" <td> 0.923214</td>\n",
" <td> 0.462628</td>\n",
" <td> 0.749403</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 9,
"text": [
" one two three four five\n",
"a 0.493574 0.690375 0.338309 bar True\n",
"b NaN NaN NaN NaN NaN\n",
"c 0.940038 0.545834 0.963170 bar True\n",
"d NaN NaN NaN NaN NaN\n",
"e 0.674076 0.518232 0.366761 bar True\n",
"f 0.015938 0.786997 0.184278 bar True\n",
"g NaN NaN NaN NaN NaN\n",
"h 0.923214 0.462628 0.749403 bar True"
]
}
],
"prompt_number": 9
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"* Drop not available values"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df2.dropna()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>one</th>\n",
" <th>two</th>\n",
" <th>three</th>\n",
" <th>four</th>\n",
" <th>five</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>a</th>\n",
" <td> 0.493574</td>\n",
" <td> 0.690375</td>\n",
" <td> 0.338309</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>c</th>\n",
" <td> 0.940038</td>\n",
" <td> 0.545834</td>\n",
" <td> 0.963170</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>e</th>\n",
" <td> 0.674076</td>\n",
" <td> 0.518232</td>\n",
" <td> 0.366761</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>f</th>\n",
" <td> 0.015938</td>\n",
" <td> 0.786997</td>\n",
" <td> 0.184278</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>h</th>\n",
" <td> 0.923214</td>\n",
" <td> 0.462628</td>\n",
" <td> 0.749403</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 11,
"text": [
" one two three four five\n",
"a 0.493574 0.690375 0.338309 bar True\n",
"c 0.940038 0.545834 0.963170 bar True\n",
"e 0.674076 0.518232 0.366761 bar True\n",
"f 0.015938 0.786997 0.184278 bar True\n",
"h 0.923214 0.462628 0.749403 bar True"
]
}
],
"prompt_number": 11
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df2.dropna()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>one</th>\n",
" <th>two</th>\n",
" <th>three</th>\n",
" <th>four</th>\n",
" <th>five</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>a</th>\n",
" <td> 0.493574</td>\n",
" <td> 0.690375</td>\n",
" <td> 0.338309</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>c</th>\n",
" <td> 0.940038</td>\n",
" <td> 0.545834</td>\n",
" <td> 0.963170</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>e</th>\n",
" <td> 0.674076</td>\n",
" <td> 0.518232</td>\n",
" <td> 0.366761</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>f</th>\n",
" <td> 0.015938</td>\n",
" <td> 0.786997</td>\n",
" <td> 0.184278</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>h</th>\n",
" <td> 0.923214</td>\n",
" <td> 0.462628</td>\n",
" <td> 0.749403</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 13,
"text": [
" one two three four five\n",
"a 0.493574 0.690375 0.338309 bar True\n",
"c 0.940038 0.545834 0.963170 bar True\n",
"e 0.674076 0.518232 0.366761 bar True\n",
"f 0.015938 0.786997 0.184278 bar True\n",
"h 0.923214 0.462628 0.749403 bar True"
]
}
],
"prompt_number": 13
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"* Replace NaN with empty"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df2.fillna('')"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>one</th>\n",
" <th>two</th>\n",
" <th>three</th>\n",
" <th>four</th>\n",
" <th>five</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>a</th>\n",
" <td> 0.4935738</td>\n",
" <td> 0.6903748</td>\n",
" <td> 0.3383088</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>b</th>\n",
" <td> </td>\n",
" <td> </td>\n",
" <td> </td>\n",
" <td> </td>\n",
" <td> </td>\n",
" </tr>\n",
" <tr>\n",
" <th>c</th>\n",
" <td> 0.9400384</td>\n",
" <td> 0.5458337</td>\n",
" <td> 0.9631703</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>d</th>\n",
" <td> </td>\n",
" <td> </td>\n",
" <td> </td>\n",
" <td> </td>\n",
" <td> </td>\n",
" </tr>\n",
" <tr>\n",
" <th>e</th>\n",
" <td> 0.6740759</td>\n",
" <td> 0.5182319</td>\n",
" <td> 0.3667608</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>f</th>\n",
" <td> 0.01593832</td>\n",
" <td> 0.7869971</td>\n",
" <td> 0.1842777</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>g</th>\n",
" <td> </td>\n",
" <td> </td>\n",
" <td> </td>\n",
" <td> </td>\n",
" <td> </td>\n",
" </tr>\n",
" <tr>\n",
" <th>h</th>\n",
" <td> 0.923214</td>\n",
" <td> 0.4626276</td>\n",
" <td> 0.7494026</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 16,
"text": [
" one two three four five\n",
"a 0.4935738 0.6903748 0.3383088 bar True\n",
"b \n",
"c 0.9400384 0.5458337 0.9631703 bar True\n",
"d \n",
"e 0.6740759 0.5182319 0.3667608 bar True\n",
"f 0.01593832 0.7869971 0.1842777 bar True\n",
"g \n",
"h 0.923214 0.4626276 0.7494026 bar True"
]
}
],
"prompt_number": 16
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df2.one"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 17,
"text": [
"a 0.493574\n",
"b NaN\n",
"c 0.940038\n",
"d NaN\n",
"e 0.674076\n",
"f 0.015938\n",
"g NaN\n",
"h 0.923214\n",
"Name: one, dtype: float64"
]
}
],
"prompt_number": 17
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"pd.isnull(df2.four)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 19,
"text": [
"a False\n",
"b True\n",
"c False\n",
"d True\n",
"e False\n",
"f False\n",
"g True\n",
"h False\n",
"Name: four, dtype: bool"
]
}
],
"prompt_number": 19
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df2.four.notnull()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 20,
"text": [
"a True\n",
"b False\n",
"c True\n",
"d False\n",
"e True\n",
"f True\n",
"g False\n",
"h True\n",
"Name: four, dtype: bool"
]
}
],
"prompt_number": 20
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Datetimes\n",
"* For numbers it is NaN where as for Datetime objects it is NaT"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df2=df.copy()"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 21
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df2['timestamp'] = pd.Timestamp('20150808')"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 24
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df2"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>one</th>\n",
" <th>two</th>\n",
" <th>three</th>\n",
" <th>four</th>\n",
" <th>five</th>\n",
" <th>timestamp</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>a</th>\n",
" <td> 0.493574</td>\n",
" <td> 0.690375</td>\n",
" <td> 0.338309</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" <td>2015-08-08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>c</th>\n",
" <td> 0.940038</td>\n",
" <td> 0.545834</td>\n",
" <td> 0.963170</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" <td>2015-08-08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>e</th>\n",
" <td> 0.674076</td>\n",
" <td> 0.518232</td>\n",
" <td> 0.366761</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" <td>2015-08-08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>f</th>\n",
" <td> 0.015938</td>\n",
" <td> 0.786997</td>\n",
" <td> 0.184278</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" <td>2015-08-08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>h</th>\n",
" <td> 0.923214</td>\n",
" <td> 0.462628</td>\n",
" <td> 0.749403</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" <td>2015-08-08</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 25,
"text": [
" one two three four five timestamp\n",
"a 0.493574 0.690375 0.338309 bar True 2015-08-08\n",
"c 0.940038 0.545834 0.963170 bar True 2015-08-08\n",
"e 0.674076 0.518232 0.366761 bar True 2015-08-08\n",
"f 0.015938 0.786997 0.184278 bar True 2015-08-08\n",
"h 0.923214 0.462628 0.749403 bar True 2015-08-08"
]
}
],
"prompt_number": 25
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df2.ix[['a','c','h'],['one','timestamp']] = np.nan"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 26
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df2"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>one</th>\n",
" <th>two</th>\n",
" <th>three</th>\n",
" <th>four</th>\n",
" <th>five</th>\n",
" <th>timestamp</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>a</th>\n",
" <td> NaN</td>\n",
" <td> 0.690375</td>\n",
" <td> 0.338309</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" <td> NaT</td>\n",
" </tr>\n",
" <tr>\n",
" <th>c</th>\n",
" <td> NaN</td>\n",
" <td> 0.545834</td>\n",
" <td> 0.963170</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" <td> NaT</td>\n",
" </tr>\n",
" <tr>\n",
" <th>e</th>\n",
" <td> 0.674076</td>\n",
" <td> 0.518232</td>\n",
" <td> 0.366761</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" <td>2015-08-08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>f</th>\n",
" <td> 0.015938</td>\n",
" <td> 0.786997</td>\n",
" <td> 0.184278</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" <td>2015-08-08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>h</th>\n",
" <td> NaN</td>\n",
" <td> 0.462628</td>\n",
" <td> 0.749403</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" <td> NaT</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 27,
"text": [
" one two three four five timestamp\n",
"a NaN 0.690375 0.338309 bar True NaT\n",
"c NaN 0.545834 0.963170 bar True NaT\n",
"e 0.674076 0.518232 0.366761 bar True 2015-08-08\n",
"f 0.015938 0.786997 0.184278 bar True 2015-08-08\n",
"h NaN 0.462628 0.749403 bar True NaT"
]
}
],
"prompt_number": 27
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df2.get_dtype_counts()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 28,
"text": [
"bool 1\n",
"datetime64[ns] 1\n",
"float64 3\n",
"object 1\n",
"dtype: int64"
]
}
],
"prompt_number": 28
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"* Getting help"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df2.get_dtype_counts?"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 31
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Inserting missing data"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"s = pd.Series([1, 2, 3])"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 32
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"s.loc[0]=None"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 34
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"s"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 35,
"text": [
"0 None\n",
"1 2\n",
"2 3\n",
"dtype: object"
]
}
],
"prompt_number": 35
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"s = pd.Series([\"a\", \"b\", \"c\"])"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 36
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"s.loc[0] = None"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 37
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"s.loc[1] = np.nan"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 38
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"s"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 39,
"text": [
"0 None\n",
"1 NaN\n",
"2 c\n",
"dtype: object"
]
}
],
"prompt_number": 39
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>one</th>\n",
" <th>two</th>\n",
" <th>three</th>\n",
" <th>four</th>\n",
" <th>five</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>a</th>\n",
" <td> 0.493574</td>\n",
" <td> 0.690375</td>\n",
" <td> 0.338309</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>c</th>\n",
" <td> 0.940038</td>\n",
" <td> 0.545834</td>\n",
" <td> 0.963170</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>e</th>\n",
" <td> 0.674076</td>\n",
" <td> 0.518232</td>\n",
" <td> 0.366761</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>f</th>\n",
" <td> 0.015938</td>\n",
" <td> 0.786997</td>\n",
" <td> 0.184278</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>h</th>\n",
" <td> 0.923214</td>\n",
" <td> 0.462628</td>\n",
" <td> 0.749403</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 41,
"text": [
" one two three four five\n",
"a 0.493574 0.690375 0.338309 bar True\n",
"c 0.940038 0.545834 0.963170 bar True\n",
"e 0.674076 0.518232 0.366761 bar True\n",
"f 0.015938 0.786997 0.184278 bar True\n",
"h 0.923214 0.462628 0.749403 bar True"
]
}
],
"prompt_number": 41
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df['one'].sum()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 42,
"text": [
"3.0468404382793168"
]
}
],
"prompt_number": 42
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df.mean(1)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 43,
"text": [
"a 0.630564\n",
"c 0.862261\n",
"e 0.639767\n",
"f 0.496803\n",
"h 0.783811\n",
"dtype: float64"
]
}
],
"prompt_number": 43
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df.cumsum()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>one</th>\n",
" <th>two</th>\n",
" <th>three</th>\n",
" <th>four</th>\n",
" <th>five</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>a</th>\n",
" <td> 0.4935738</td>\n",
" <td> 0.6903748</td>\n",
" <td> 0.3383088</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>c</th>\n",
" <td> 1.433612</td>\n",
" <td> 1.236208</td>\n",
" <td> 1.301479</td>\n",
" <td> barbar</td>\n",
" <td> 2</td>\n",
" </tr>\n",
" <tr>\n",
" <th>e</th>\n",
" <td> 2.107688</td>\n",
" <td> 1.75444</td>\n",
" <td> 1.66824</td>\n",
" <td> barbarbar</td>\n",
" <td> 3</td>\n",
" </tr>\n",
" <tr>\n",
" <th>f</th>\n",
" <td> 2.123626</td>\n",
" <td> 2.541437</td>\n",
" <td> 1.852518</td>\n",
" <td> barbarbarbar</td>\n",
" <td> 4</td>\n",
" </tr>\n",
" <tr>\n",
" <th>h</th>\n",
" <td> 3.04684</td>\n",
" <td> 3.004065</td>\n",
" <td> 2.60192</td>\n",
" <td> barbarbarbarbar</td>\n",
" <td> 5</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 44,
"text": [
" one two three four five\n",
"a 0.4935738 0.6903748 0.3383088 bar True\n",
"c 1.433612 1.236208 1.301479 barbar 2\n",
"e 2.107688 1.75444 1.66824 barbarbar 3\n",
"f 2.123626 2.541437 1.852518 barbarbarbar 4\n",
"h 3.04684 3.004065 2.60192 barbarbarbarbar 5"
]
}
],
"prompt_number": 44
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df.cumsum?"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 45
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df2"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>one</th>\n",
" <th>two</th>\n",
" <th>three</th>\n",
" <th>four</th>\n",
" <th>five</th>\n",
" <th>timestamp</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>a</th>\n",
" <td> NaN</td>\n",
" <td> 0.690375</td>\n",
" <td> 0.338309</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" <td> NaT</td>\n",
" </tr>\n",
" <tr>\n",
" <th>c</th>\n",
" <td> NaN</td>\n",
" <td> 0.545834</td>\n",
" <td> 0.963170</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" <td> NaT</td>\n",
" </tr>\n",
" <tr>\n",
" <th>e</th>\n",
" <td> 0.674076</td>\n",
" <td> 0.518232</td>\n",
" <td> 0.366761</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" <td>2015-08-08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>f</th>\n",
" <td> 0.015938</td>\n",
" <td> 0.786997</td>\n",
" <td> 0.184278</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" <td>2015-08-08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>h</th>\n",
" <td> NaN</td>\n",
" <td> 0.462628</td>\n",
" <td> 0.749403</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" <td> NaT</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 46,
"text": [
" one two three four five timestamp\n",
"a NaN 0.690375 0.338309 bar True NaT\n",
"c NaN 0.545834 0.963170 bar True NaT\n",
"e 0.674076 0.518232 0.366761 bar True 2015-08-08\n",
"f 0.015938 0.786997 0.184278 bar True 2015-08-08\n",
"h NaN 0.462628 0.749403 bar True NaT"
]
}
],
"prompt_number": 46
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df2.fillna(0)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>one</th>\n",
" <th>two</th>\n",
" <th>three</th>\n",
" <th>four</th>\n",
" <th>five</th>\n",
" <th>timestamp</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>a</th>\n",
" <td> 0.000000</td>\n",
" <td> 0.690375</td>\n",
" <td> 0.338309</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" <td>1970-01-01</td>\n",
" </tr>\n",
" <tr>\n",
" <th>c</th>\n",
" <td> 0.000000</td>\n",
" <td> 0.545834</td>\n",
" <td> 0.963170</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" <td>1970-01-01</td>\n",
" </tr>\n",
" <tr>\n",
" <th>e</th>\n",
" <td> 0.674076</td>\n",
" <td> 0.518232</td>\n",
" <td> 0.366761</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" <td>2015-08-08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>f</th>\n",
" <td> 0.015938</td>\n",
" <td> 0.786997</td>\n",
" <td> 0.184278</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" <td>2015-08-08</td>\n",
" </tr>\n",
" <tr>\n",
" <th>h</th>\n",
" <td> 0.000000</td>\n",
" <td> 0.462628</td>\n",
" <td> 0.749403</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" <td>1970-01-01</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 47,
"text": [
" one two three four five timestamp\n",
"a 0.000000 0.690375 0.338309 bar True 1970-01-01\n",
"c 0.000000 0.545834 0.963170 bar True 1970-01-01\n",
"e 0.674076 0.518232 0.366761 bar True 2015-08-08\n",
"f 0.015938 0.786997 0.184278 bar True 2015-08-08\n",
"h 0.000000 0.462628 0.749403 bar True 1970-01-01"
]
}
],
"prompt_number": 47
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df2['four'].fillna('missing')"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 48,
"text": [
"a bar\n",
"c bar\n",
"e bar\n",
"f bar\n",
"h bar\n",
"Name: four, dtype: object"
]
}
],
"prompt_number": 48
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>one</th>\n",
" <th>two</th>\n",
" <th>three</th>\n",
" <th>four</th>\n",
" <th>five</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>a</th>\n",
" <td> 0.493574</td>\n",
" <td> 0.690375</td>\n",
" <td> 0.338309</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>c</th>\n",
" <td> 0.940038</td>\n",
" <td> 0.545834</td>\n",
" <td> 0.963170</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>e</th>\n",
" <td> 0.674076</td>\n",
" <td> 0.518232</td>\n",
" <td> 0.366761</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>f</th>\n",
" <td> 0.015938</td>\n",
" <td> 0.786997</td>\n",
" <td> 0.184278</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>h</th>\n",
" <td> 0.923214</td>\n",
" <td> 0.462628</td>\n",
" <td> 0.749403</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 49,
"text": [
" one two three four five\n",
"a 0.493574 0.690375 0.338309 bar True\n",
"c 0.940038 0.545834 0.963170 bar True\n",
"e 0.674076 0.518232 0.366761 bar True\n",
"f 0.015938 0.786997 0.184278 bar True\n",
"h 0.923214 0.462628 0.749403 bar True"
]
}
],
"prompt_number": 49
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df.fillna(method='pad')"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>one</th>\n",
" <th>two</th>\n",
" <th>three</th>\n",
" <th>four</th>\n",
" <th>five</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>a</th>\n",
" <td> 0.493574</td>\n",
" <td> 0.690375</td>\n",
" <td> 0.338309</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>c</th>\n",
" <td> 0.940038</td>\n",
" <td> 0.545834</td>\n",
" <td> 0.963170</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>e</th>\n",
" <td> 0.674076</td>\n",
" <td> 0.518232</td>\n",
" <td> 0.366761</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>f</th>\n",
" <td> 0.015938</td>\n",
" <td> 0.786997</td>\n",
" <td> 0.184278</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>h</th>\n",
" <td> 0.923214</td>\n",
" <td> 0.462628</td>\n",
" <td> 0.749403</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 50,
"text": [
" one two three four five\n",
"a 0.493574 0.690375 0.338309 bar True\n",
"c 0.940038 0.545834 0.963170 bar True\n",
"e 0.674076 0.518232 0.366761 bar True\n",
"f 0.015938 0.786997 0.184278 bar True\n",
"h 0.923214 0.462628 0.749403 bar True"
]
}
],
"prompt_number": 50
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df.fillna(method='pad', limit=1)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>one</th>\n",
" <th>two</th>\n",
" <th>three</th>\n",
" <th>four</th>\n",
" <th>five</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>a</th>\n",
" <td> 0.493574</td>\n",
" <td> 0.690375</td>\n",
" <td> 0.338309</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>c</th>\n",
" <td> 0.940038</td>\n",
" <td> 0.545834</td>\n",
" <td> 0.963170</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>e</th>\n",
" <td> 0.674076</td>\n",
" <td> 0.518232</td>\n",
" <td> 0.366761</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>f</th>\n",
" <td> 0.015938</td>\n",
" <td> 0.786997</td>\n",
" <td> 0.184278</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" <tr>\n",
" <th>h</th>\n",
" <td> 0.923214</td>\n",
" <td> 0.462628</td>\n",
" <td> 0.749403</td>\n",
" <td> bar</td>\n",
" <td> True</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 51,
"text": [
" one two three four five\n",
"a 0.493574 0.690375 0.338309 bar True\n",
"c 0.940038 0.545834 0.963170 bar True\n",
"e 0.674076 0.518232 0.366761 bar True\n",
"f 0.015938 0.786997 0.184278 bar True\n",
"h 0.923214 0.462628 0.749403 bar True"
]
}
],
"prompt_number": 51
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Interpolation"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"pd.tseries()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"ename": "TypeError",
"evalue": "'module' object is not callable",
"output_type": "pyerr",
"traceback": [
"\u001b[1;31m---------------------------------------------------------------------------\u001b[0m\n\u001b[1;31mTypeError\u001b[0m Traceback (most recent call last)",
"\u001b[1;32m<ipython-input-53-e9f0563fd4e5>\u001b[0m in \u001b[0;36m<module>\u001b[1;34m()\u001b[0m\n\u001b[1;32m----> 1\u001b[1;33m \u001b[0mpd\u001b[0m\u001b[1;33m.\u001b[0m\u001b[0mtseries\u001b[0m\u001b[1;33m(\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0m",
"\u001b[1;31mTypeError\u001b[0m: 'module' object is not callable"
]
}
],
"prompt_number": 53
},
{
"cell_type": "code",
"collapsed": false,
"input": [],
"language": "python",
"metadata": {},
"outputs": []
}
],
"metadata": {}
}
]
} | apache-2.0 |
authman/DAT210x | Module5/Module5 - Lab5.ipynb | 1 | 10496 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# DAT210x - Programming with Python for DS"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Module5- Lab5"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import numpy as np\n",
"import pandas as pd\n",
"import matplotlib.pyplot as plt\n",
"import matplotlib\n",
"\n",
"matplotlib.style.use('ggplot') # Look Pretty"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### A Convenience Function"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def plotDecisionBoundary(model, X, y):\n",
" fig = plt.figure()\n",
" ax = fig.add_subplot(111)\n",
"\n",
" padding = 0.6\n",
" resolution = 0.0025\n",
" colors = ['royalblue','forestgreen','ghostwhite']\n",
"\n",
" # Calculate the boundaris\n",
" x_min, x_max = X[:, 0].min(), X[:, 0].max()\n",
" y_min, y_max = X[:, 1].min(), X[:, 1].max()\n",
" x_range = x_max - x_min\n",
" y_range = y_max - y_min\n",
" x_min -= x_range * padding\n",
" y_min -= y_range * padding\n",
" x_max += x_range * padding\n",
" y_max += y_range * padding\n",
"\n",
" # Create a 2D Grid Matrix. The values stored in the matrix\n",
" # are the predictions of the class at at said location\n",
" xx, yy = np.meshgrid(np.arange(x_min, x_max, resolution),\n",
" np.arange(y_min, y_max, resolution))\n",
"\n",
" # What class does the classifier say?\n",
" Z = model.predict(np.c_[xx.ravel(), yy.ravel()])\n",
" Z = Z.reshape(xx.shape)\n",
"\n",
" # Plot the contour map\n",
" cs = plt.contourf(xx, yy, Z, cmap=plt.cm.terrain)\n",
"\n",
" # Plot the test original points as well...\n",
" for label in range(len(np.unique(y))):\n",
" indices = np.where(y == label)\n",
" plt.scatter(X[indices, 0], X[indices, 1], c=colors[label], label=str(label), alpha=0.8)\n",
"\n",
" p = model.get_params()\n",
" plt.axis('tight')\n",
" plt.title('K = ' + str(p['n_neighbors']))"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"### The Assignment"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"Load up the dataset into a variable called `X`. Check `.head` and `dtypes` to make sure you're loading your data properly--don't fail on the 1st step!"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# .. your code here .."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Copy the `wheat_type` series slice out of `X`, and into a series called `y`. Then drop the original `wheat_type` column from the `X`:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# .. your code here .."
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": false
},
"source": [
"Do a quick, \"ordinal\" conversion of `y`. In actuality our classification isn't ordinal, but just as an experiment..."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# .. your code here .."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Do some basic nan munging. Fill each row's nans with the mean of the feature:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# .. your code here .."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Split `X` into training and testing data sets using `train_test_split()`. Use `0.33` test size, and use `random_state=1`. This is important so that your answers are verifiable. In the real world, you wouldn't specify a random_state:"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# .. your code here .."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Create an instance of SKLearn's Normalizer class and then train it using its .fit() method against your _training_ data. The reason you only fit against your training data is because in a real-world situation, you'll only have your training data to train with! In this lab setting, you have both train+test data; but in the wild, you'll only have your training data, and then unlabeled data you want to apply your models to."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# .. your code here .."
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": false
},
"source": [
"With your trained pre-processor, transform both your training AND testing data. Any testing data has to be transformed with your preprocessor that has ben fit against your training data, so that it exist in the same feature-space as the original data used to train your models."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# .. your code here .."
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"Just like your preprocessing transformation, create a PCA transformation as well. Fit it against your training data, and then project your training and testing features into PCA space using the PCA model's `.transform()` method. This has to be done because the only way to visualize the decision boundary in 2D would be if your KNN algo ran in 2D as well:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# .. your code here .."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Create and train a KNeighborsClassifier. Start with `K=9` neighbors. Be sure train your classifier against the pre-processed, PCA- transformed training data above! You do not, of course, need to transform your labels."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# .. your code here .."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"ename": "NameError",
"evalue": "name 'plotDecisionBoundary' is not defined",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mNameError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m<ipython-input-3-7f7ed7f5f06e>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[1;32m 1\u001b[0m \u001b[0;31m# I hopee your KNeighbors classifier model from earlier was named 'knn'\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 2\u001b[0m \u001b[0;31m# If not, adjust the following line:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m----> 3\u001b[0;31m \u001b[0mplotDecisionBoundary\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mknn\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mX_train\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0my_train\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m",
"\u001b[0;31mNameError\u001b[0m: name 'plotDecisionBoundary' is not defined"
]
}
],
"source": [
"# I hope your KNeighbors classifier model from earlier was named 'knn'\n",
"# If not, adjust the following line:\n",
"plotDecisionBoundary(knn, X_train, y_train)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Display the accuracy score of your test data/labels, computed by your KNeighbors model. You do NOT have to run `.predict` before calling `.score`, since `.score` will take care of running your predictions for you automatically."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# .. your code here .."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Bonus"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": false
},
"source": [
"Instead of the ordinal conversion, try and get this assignment working with a proper Pandas get_dummies for feature encoding. You might have to update some of the `plotDecisionBoundary()` code."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [default]",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
},
"toc": {
"colors": {
"hover_highlight": "#DAA520",
"running_highlight": "#FF0000",
"selected_highlight": "#FFD700"
},
"moveMenuLeft": true,
"nav_menu": {
"height": "58px",
"width": "252px"
},
"navigate_menu": true,
"number_sections": true,
"sideBar": true,
"threshold": 4,
"toc_cell": false,
"toc_section_display": "block",
"toc_window_display": false,
"widenNotebook": false
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
chloeyangu/BigDataAnalytics | Terrorisks/Code/BT4221 - Code 2.ipynb | 1 | 2158103 | null | mit |
NREL/bifacial_radiance | docs/tutorials/4 - Medium Level Example - Debugging your Scene with Custom Objects (Fixed Tilt 2-up with Torque Tube + CLEAN Routine + CustomObject).ipynb | 1 | 30536 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# 4 - Medium Level Example - Debugging your Scene with Custom Objects\n",
"### Fixed Tilt 2-up with Torque Tube + CLEAN Routine + CustomObject\n",
"\n",
"This journal has examples of various things, some which hav ebeen covered before and some in more depth:\n",
"\n",
"<ul>\n",
" <li> Running a fixed_tilt simulation beginning to end. </li>\n",
" <li> Creating a 2-up module with torque-tube, and detailed geometry of spacings in xgap, ygap and zgap. </li>\n",
" <li> Calculating the tracker angle for a specific time, in case you want to use that value to model a fixed_tilt setup. </li>\n",
" <li> Loading and cleaning results, particularly important when using setups with torquetubes / ygaps. </li>\n",
" <li> Adding a \"Custom Object\" or **marker** at the Origin of the Scene, to do a visual sanity-check of the geometry. </li>\n",
"</ul>\n",
"\n",
"It will look something like this (without the marker in this visualization):\n",
"\n",
"\n",
"\n",
"### STEPS:\n",
"\n",
"<ol type='1'>\n",
" <li> <a href='#step1'> Specify Working Folder and Import Program </a></li>\n",
" <li> <a href='#step2'> Specify all variables </a></li>\n",
" <li> <a href='#step3'> Create the Radiance Object and generate the Sky </a></li>\n",
" <li> <a href='#step4'> Calculating tracker angle/geometry for a specific timestamp </a></li>\n",
" <li> <a href='#step5'> Making the Module & the Scene, Visualize and run Analysis </a></li>\n",
" <li> <a href='#step6'> Calculate Bifacial Ratio (clean results) </a></li>\n",
" <li> <a href='#step7'> Add Custom Elements to your Scene Example: Marker at 0,0 position </a></li>\n",
"</ol>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a id='step1'></a>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 1. Specify Working Folder and Import Program\n"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Your simulation will be stored in C:\\Users\\sayala\\Documents\\GitHub\\bifacial_radiance\\bifacial_radiance\\TEMP\\Tutorial_04\n"
]
}
],
"source": [
"import os\n",
"from pathlib import Path\n",
"\n",
"testfolder = Path().resolve().parent.parent / 'bifacial_radiance' / 'TEMP' / 'Tutorial_04'\n",
"\n",
"# Another option using relative address; for some operative systems you might need '/' instead of '\\'\n",
"# testfolder = os.path.abspath(r'..\\..\\bifacial_radiance\\TEMP') \n",
"\n",
"print (\"Your simulation will be stored in %s\" % testfolder)\n",
"\n",
"if not os.path.exists(testfolder):\n",
" os.makedirs(testfolder)\n",
"\n",
"import bifacial_radiance\n",
"import numpy as np\n",
"import pandas as pd"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a id='step2'></a>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 2. Specify all variables for the module and scene\n",
"\n",
"Below find a list of all of the possible parameters for makeModule. \n",
"scene and simulation parameters are also organized below. \n",
"This simulation will be a complete simulation in terms of parameters that you can modify.\n",
"\n",
"The below routine creates a HEXAGONAL torque tube, for a 2-UP configuration of a specific module size. Parameters for the module, the torque tube, and the scene are below.\n",
"This is being run with gendaylit, for one specific timestamp"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"simulationname = 'tutorial_4'\n",
"\n",
"## SceneDict Parameters\n",
"gcr = 0.33 # ground cover ratio, = module_height / pitch\n",
"albedo = 0.28 #'concrete' # ground albedo\n",
"hub_height = 2.35 # we could also pass clearance_height. \n",
"azimuth_ang = 90 # Modules will be facing East.\n",
"lat = 37.5\n",
"lon = -77.6\n",
"nMods = 4 # doing a smaller array for better visualization on this example.\n",
"nRows = 2 \n",
"\n",
"# MakeModule Parameters\n",
"module_type='test-module'\n",
"x = 1.996 # landscape, sinze x > y. Remember that orientation has been deprecated.\n",
"y = 0.991\n",
"tilt = 10\n",
"numpanels = 2 # doing a 2-up system!\n",
"\n",
"\n",
"# Gaps:\n",
"xgap = 0.05 # distance between modules in the row.\n",
"ygap = 0.15 # distance between the 2 modules along the collector slope.\n",
"zgap = 0.175 # if there is a torquetube, this is the distance between the torquetube and the modules.\n",
"# If there is not a module, zgap is the distance between the module and the axis of rotation (relevant for \n",
"# tracking systems. \n",
"\n",
"# TorqueTube Parameters\n",
"tubetype = 'Hex'\n",
"diameter = 0.15\n",
"material = 'Metal_Grey' # IT's NOT GRAY, IT's GREY.\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a id='step3'></a>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 3. Create the Radiance Object and generate the Sky"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"path = C:\\Users\\sayala\\Documents\\GitHub\\bifacial_radiance\\bifacial_radiance\\TEMP\\Tutorial_04\n",
"Loading albedo, 1 value(s), 0.280 avg\n",
"1 nonzero albedo values.\n",
"Getting weather file: USA_VA_Richmond.724010_TMY2.epw\n",
" ... OK!\n",
"8760 line in WeatherFile. Assuming this is a standard hourly WeatherFile for the year for purposes of saving Gencumulativesky temporary weather files in EPW folder.\n",
"Coercing year to 2001\n",
"Saving file EPWs\\metdata_temp.csv, # points: 8760\n",
"Calculating Sun position for Metdata that is right-labeled with a delta of -30 mins. i.e. 12 is 11:30 sunpos\n"
]
},
{
"data": {
"text/plain": [
"'skies\\\\sky2_37.5_-77.33_2001-06-17_1300.rad'"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"demo = bifacial_radiance.RadianceObj(simulationname, path=str(testfolder)) # Create a RadianceObj 'object'\n",
"demo.setGround(albedo) # input albedo number or material name like 'concrete'. To see options, run this without any input.\n",
"epwfile = demo.getEPW(lat,lon) # pull TMY data for any global lat/lon\n",
"metdata = demo.readWeatherFile(epwfile, coerce_year=2001) # read in the EPW weather data from above\n",
"\n",
"timestamp = metdata.datetime.index(pd.to_datetime('2001-06-17 13:0:0 -5')) # Make this timezone aware, use -5 for EST.\n",
"demo.gendaylit(timestamp) # Mid-day, June 17th"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a id='step4'></a>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 4. Calculating tracker angle/geometry for a specific timestamp\n",
"\n",
"This trick is useful if you are trying to use the fixed-tilt steps in bifacial_radiance to model a tracker for one specific point in time (if you take a picture of a tracker, it looks fixed, right? Well then). \n",
"\n",
"We assigned a 10 degree tilt at the beginning, but if we were to model a tracker as a fixed-tilt element because we are interested in only one point in time, this routine will tell us what tilt to use. *Please note that to model a tracker as fixed tilt, we suggest passing a hub_height, otherwise you will have to calculate the clearance_height manually.*\n",
"\n",
"<div class=\"alert alert-warning\">\n",
"Details: you might have noticed in the previoust tutorial looking at the tracker dictionary, but the way that bifacial_radiance handles tracking: If the tracker is N-S axis azimuth, the surface azimuth of the modules will be set to 90 always, with a tilt that is either positive (for the early morning, facing East), or negative (for the afternoon, facing west).\n",
"</div>\n"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n",
" NEW Calculated Tilt: -4.67 \n"
]
}
],
"source": [
"# Some tracking parameters that won't be needed after getting this angle:\n",
"axis_azimuth = 180\n",
"axis_tilt = 0\n",
"limit_angle = 60\n",
"backtrack = True\n",
"tilt = demo.getSingleTimestampTrackerAngle(metdata, timestamp, gcr, axis_azimuth, axis_tilt,limit_angle, backtrack)\n",
"\n",
"print (\"\\n NEW Calculated Tilt: %s \" % tilt)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a id='step5'></a>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 5. Making the Module & the Scene, Visualize and run Analysis"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n",
"Module Name: test-module\n",
"Module test-module updated in module.json\n",
"Module test-module updated in module.json\n",
"Pre-existing .rad file objects\\test-module.rad will be overwritten\n",
"Created tutorial_4.oct\n"
]
}
],
"source": [
"# Making module with all the variables\n",
"module = demo.makeModule(name=module_type,x=x,y=y,bifi=1, \n",
" zgap=zgap, ygap=ygap, xgap=xgap, numpanels=numpanels)\n",
"module.addTorquetube(diameter=diameter, material=material, tubetype=tubetype,\n",
" visible=True, axisofrotation=True)\n",
"\n",
"# create a scene with all the variables. \n",
"# Specifying the pitch automatically with the collector width (sceney) returned by the module object.\n",
"# Height has been deprecated as an input. pass clearance_height or hub_height in the scenedict.\n",
"\n",
"sceneDict = {'tilt':tilt,'pitch': np.round(module.sceney / gcr,3),\n",
" 'hub_height':hub_height,'azimuth':azimuth_ang, \n",
" 'module_type':module_type, 'nMods': nMods, 'nRows': nRows} \n",
"\n",
"scene = demo.makeScene(module=module, sceneDict=sceneDict) #makeScene creates a .rad file of the Scene\n",
"\n",
"octfile = demo.makeOct(demo.getfilelist()) # makeOct combines all of the ground, sky and object files into a .oct file."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"At this point you should be able to go into a command window (cmd.exe) and check the geometry. It should look like the image at the beginning of the journal. Example:\n",
" \n",
"#### rvu -vf views\\front.vp -e .01 -pe 0.02 -vp -2 -12 14.5 tutorial_4.oct\n",
" \n"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [],
"source": [
"\n",
"## Comment the line below to run rvu from the Jupyter notebook instead of your terminal.\n",
"## Simulation will stop until you close the rvu window\n",
"\n",
"#!rvu -vf views\\front.vp -e .01 tutorial_4.oct\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"And then proceed happily with your analysis:"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Linescan in process: tutorial_4_Front\n",
"Linescan in process: tutorial_4_Back\n",
"Saved: results\\irr_tutorial_4.csv\n"
]
}
],
"source": [
"analysis = bifacial_radiance.AnalysisObj(octfile, demo.name) # return an analysis object including the scan dimensions for back irradiance\n",
"\n",
"sensorsy = 200 # setting this very high to see a detailed profile of the irradiance, including\n",
"#the shadow of the torque tube on the rear side of the module.\n",
"frontscan, backscan = analysis.moduleAnalysis(scene, modWanted = 2, rowWanted = 1, sensorsy = 200)\n",
"frontDict, backDict = analysis.analysis(octfile, demo.name, frontscan, backscan) # compare the back vs front irradiance \n",
"\n",
"# print('\"Annual\" bifacial ratio average: %0.3f' %( sum(analysis.Wm2Back) / sum(analysis.Wm2Front) ) )\n",
"# See comment below of why this line is commented out."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a id='step6'></a>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"### 6. Calculate Bifacial Ratio (clean results)\n",
"\n",
"Although we could calculate a bifacial ratio average at this point, this value would be misleading, since some of the sensors generated will fall on the torque tube, the sky, and/or the ground since we have torquetube and ygap in the scene. To calculate the real bifacial ratio average, we must use the clean routines.\n"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Printing the dataframe containing the results just calculated in results/irr_tutorial_4.csv: \n"
]
},
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>x</th>\n",
" <th>y</th>\n",
" <th>z</th>\n",
" <th>rearZ</th>\n",
" <th>mattype</th>\n",
" <th>rearMat</th>\n",
" <th>Wm2Front</th>\n",
" <th>Wm2Back</th>\n",
" <th>Back/FrontRatio</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1.029825</td>\n",
" <td>6.305862e-17</td>\n",
" <td>2.706027</td>\n",
" <td>2.684100</td>\n",
" <td>a1.0.a0.test-module.6457</td>\n",
" <td>a1.0.a0.test-module.2310</td>\n",
" <td>910.402000</td>\n",
" <td>189.224967</td>\n",
" <td>0.207847</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>1.019254</td>\n",
" <td>6.241128e-17</td>\n",
" <td>2.705163</td>\n",
" <td>2.683236</td>\n",
" <td>a1.0.a0.test-module.6457</td>\n",
" <td>a1.0.a0.test-module.2310</td>\n",
" <td>910.404333</td>\n",
" <td>189.023133</td>\n",
" <td>0.207625</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>1.008682</td>\n",
" <td>6.176395e-17</td>\n",
" <td>2.704300</td>\n",
" <td>2.682373</td>\n",
" <td>a1.0.a0.test-module.6457</td>\n",
" <td>a1.0.a0.test-module.2310</td>\n",
" <td>910.404500</td>\n",
" <td>188.821633</td>\n",
" <td>0.207404</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>0.998110</td>\n",
" <td>6.111662e-17</td>\n",
" <td>2.703436</td>\n",
" <td>2.681509</td>\n",
" <td>a1.0.a0.test-module.6457</td>\n",
" <td>a1.0.a0.test-module.2310</td>\n",
" <td>910.404767</td>\n",
" <td>188.620133</td>\n",
" <td>0.207182</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>0.987538</td>\n",
" <td>6.046929e-17</td>\n",
" <td>2.702573</td>\n",
" <td>2.680646</td>\n",
" <td>a1.0.a0.test-module.6457</td>\n",
" <td>a1.0.a0.test-module.2310</td>\n",
" <td>910.404967</td>\n",
" <td>188.418633</td>\n",
" <td>0.206961</td>\n",
" </tr>\n",
" <tr>\n",
" <th>...</th>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" </tr>\n",
" <tr>\n",
" <th>195</th>\n",
" <td>-1.031666</td>\n",
" <td>-6.317134e-17</td>\n",
" <td>2.537628</td>\n",
" <td>2.515701</td>\n",
" <td>a1.0.a1.test-module.6457</td>\n",
" <td>a1.0.a1.test-module.2310</td>\n",
" <td>909.756967</td>\n",
" <td>185.710300</td>\n",
" <td>0.204132</td>\n",
" </tr>\n",
" <tr>\n",
" <th>196</th>\n",
" <td>-1.042238</td>\n",
" <td>-6.381867e-17</td>\n",
" <td>2.536764</td>\n",
" <td>2.514838</td>\n",
" <td>a1.0.a1.test-module.6457</td>\n",
" <td>a1.0.a1.test-module.2310</td>\n",
" <td>909.756833</td>\n",
" <td>185.904500</td>\n",
" <td>0.204345</td>\n",
" </tr>\n",
" <tr>\n",
" <th>197</th>\n",
" <td>-1.052810</td>\n",
" <td>-6.446600e-17</td>\n",
" <td>2.535901</td>\n",
" <td>2.513974</td>\n",
" <td>a1.0.a1.test-module.6457</td>\n",
" <td>a1.0.a1.test-module.2310</td>\n",
" <td>909.756667</td>\n",
" <td>186.098700</td>\n",
" <td>0.204559</td>\n",
" </tr>\n",
" <tr>\n",
" <th>198</th>\n",
" <td>-1.063381</td>\n",
" <td>-6.511333e-17</td>\n",
" <td>2.535037</td>\n",
" <td>2.513110</td>\n",
" <td>a1.0.a1.test-module.6457</td>\n",
" <td>a1.0.a1.test-module.2310</td>\n",
" <td>909.756500</td>\n",
" <td>186.292900</td>\n",
" <td>0.204772</td>\n",
" </tr>\n",
" <tr>\n",
" <th>199</th>\n",
" <td>-1.073953</td>\n",
" <td>-6.576067e-17</td>\n",
" <td>2.534174</td>\n",
" <td>2.512247</td>\n",
" <td>a1.0.a1.test-module.6457</td>\n",
" <td>a1.0.a1.test-module.2310</td>\n",
" <td>909.756333</td>\n",
" <td>186.487100</td>\n",
" <td>0.204986</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>200 rows × 9 columns</p>\n",
"</div>"
],
"text/plain": [
" x y z rearZ mattype \\\n",
"0 1.029825 6.305862e-17 2.706027 2.684100 a1.0.a0.test-module.6457 \n",
"1 1.019254 6.241128e-17 2.705163 2.683236 a1.0.a0.test-module.6457 \n",
"2 1.008682 6.176395e-17 2.704300 2.682373 a1.0.a0.test-module.6457 \n",
"3 0.998110 6.111662e-17 2.703436 2.681509 a1.0.a0.test-module.6457 \n",
"4 0.987538 6.046929e-17 2.702573 2.680646 a1.0.a0.test-module.6457 \n",
".. ... ... ... ... ... \n",
"195 -1.031666 -6.317134e-17 2.537628 2.515701 a1.0.a1.test-module.6457 \n",
"196 -1.042238 -6.381867e-17 2.536764 2.514838 a1.0.a1.test-module.6457 \n",
"197 -1.052810 -6.446600e-17 2.535901 2.513974 a1.0.a1.test-module.6457 \n",
"198 -1.063381 -6.511333e-17 2.535037 2.513110 a1.0.a1.test-module.6457 \n",
"199 -1.073953 -6.576067e-17 2.534174 2.512247 a1.0.a1.test-module.6457 \n",
"\n",
" rearMat Wm2Front Wm2Back Back/FrontRatio \n",
"0 a1.0.a0.test-module.2310 910.402000 189.224967 0.207847 \n",
"1 a1.0.a0.test-module.2310 910.404333 189.023133 0.207625 \n",
"2 a1.0.a0.test-module.2310 910.404500 188.821633 0.207404 \n",
"3 a1.0.a0.test-module.2310 910.404767 188.620133 0.207182 \n",
"4 a1.0.a0.test-module.2310 910.404967 188.418633 0.206961 \n",
".. ... ... ... ... \n",
"195 a1.0.a1.test-module.2310 909.756967 185.710300 0.204132 \n",
"196 a1.0.a1.test-module.2310 909.756833 185.904500 0.204345 \n",
"197 a1.0.a1.test-module.2310 909.756667 186.098700 0.204559 \n",
"198 a1.0.a1.test-module.2310 909.756500 186.292900 0.204772 \n",
"199 a1.0.a1.test-module.2310 909.756333 186.487100 0.204986 \n",
"\n",
"[200 rows x 9 columns]"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"resultFile='results/irr_tutorial_4.csv'\n",
"results_loaded = bifacial_radiance.load.read1Result(resultFile)\n",
"print(\"Printing the dataframe containing the results just calculated in %s: \" % resultFile)\n",
"results_loaded"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Looking at only 1 sensor in the middle -- position 100 out of the 200 sensors sampled:\n"
]
},
{
"data": {
"text/plain": [
"x -0.02735\n",
"y -0.0\n",
"z 2.619669\n",
"rearZ 2.597742\n",
"mattype a1.0.hextube1a.6457\n",
"rearMat sky\n",
"Wm2Front 788.347433\n",
"Wm2Back 161.8852\n",
"Back/FrontRatio 0.205347\n",
"Name: 100, dtype: object"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"print(\"Looking at only 1 sensor in the middle -- position 100 out of the 200 sensors sampled:\")\n",
"results_loaded.loc[100]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"As an example, we can see above that sensor 100 falls in the hextube, and in the sky. We need to remove this to calculate the real bifacial_gain from the irradiance falling into the modules. To do this we use cleanResult form the load.py module in bifacial_radiance. This finds the invalid materials and sets the irradiance values for those materials to NaN\n",
"\n",
"This might take some time in the current version. "
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [],
"source": [
"# Cleaning Results:\n",
"# remove invalid materials and sets the irradiance values to NaN\n",
"clean_results = bifacial_radiance.load.cleanResult(results_loaded) "
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Sampling the same location as before to see what the results are now:\n"
]
},
{
"data": {
"text/plain": [
"x -0.02735\n",
"y -0.0\n",
"z 2.619669\n",
"rearZ 2.597742\n",
"mattype a1.0.hextube1a.6457\n",
"rearMat sky\n",
"Wm2Front NaN\n",
"Wm2Back NaN\n",
"Back/FrontRatio 0.205347\n",
"Name: 100, dtype: object"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"print(\"Sampling the same location as before to see what the results are now:\")\n",
"clean_results.loc[100]"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"CORRECT Annual bifacial ratio average: 0.203\n",
"\n",
"(If we had not done the cleaning routine, the bifacial ratio would have been calculated to 0.205 <-- THIS VALUE IS WRONG)\n"
]
}
],
"source": [
"print('CORRECT Annual bifacial ratio average: %0.3f' %( clean_results['Wm2Back'].sum() / clean_results['Wm2Front'].sum() ))\n",
"\n",
"print (\"\\n(If we had not done the cleaning routine, the bifacial ratio would have been \", \\\n",
" \"calculated to %0.3f <-- THIS VALUE IS WRONG)\" %( sum(analysis.Wm2Back) / sum(analysis.Wm2Front) )) \n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a id='step7'></a>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 7. Add Custom Elements to your Scene Example: Marker at 0,0 position\n",
"This shows how to add a custom element, in this case a Cube, that will be placed in the center of your already created scene to mark the 0,0 location. \n",
"\n",
"This can be added at any point after makeScene has been run once. Notice that if this extra element is in the scene and the analysis sensors fall on this element, they will measure irradiance at this element and no the modules."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We are going to create a \"MyMarker.rad\" file in the objects folder, right after we make the Module. \n",
"This is a prism (so we use 'genbox'), that is black from the ground.rad list of materials ('black')\n",
"We are naming it 'CenterMarker'\n",
"Its sides are going to be 0.5x0.5x0.5 m \n",
"and We are going to leave its bottom surface coincident with the plane z=0, but going to center on X and Y."
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n",
"Custom Object Name objects\\MyMarker.rad\n"
]
}
],
"source": [
"name='MyMarker'\n",
"text='! genbox black CenterMarker 0.1 0.1 4 | xform -t -0.05 -0.05 0'\n",
"customObject = demo.makeCustomObject(name,text)\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This should have created a MyMarker.rad object on your objects folder.\n",
"\n",
"But creating the object does not automatically adds it to the seen. So let's now add the customObject to the Scene. We are not going to translate it or anything because we want it at the center, but you can pass translation, rotation, and any other XFORM command from Radiance.\n",
"\n",
"I am passing a rotation 0 because xform has to have something (I think) otherwise it gets confused."
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Created tutorial_4.oct\n"
]
}
],
"source": [
"demo.appendtoScene(scene.radfiles, customObject, '!xform -rz 0')\n",
"# makeOct combines all of the ground, sky and object files into a .oct file.\n",
"octfile = demo.makeOct(demo.getfilelist()) "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"appendtoScene appended to the Scene.rad file the name of the custom object we created and the xform transformation we included as text. Then octfile merged this new scene with the ground and sky files.\n",
"\n",
"At this point you should be able to go into a command window (cmd.exe) and check the geometry, and the marker should be there. Example:\n",
" \n",
" #### rvu -vf views\\front.vp -e .01 tutorial_4.oct\n",
" "
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [],
"source": [
"\n",
"## Comment the line below to run rvu from the Jupyter notebook instead of your terminal.\n",
"## Simulation will stop until you close the rvu window\n",
"\n",
"#!rvu -vf views\\front.vp -e .01 tutorial_4.oct\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"If you ran the getTrackerAngle detour and appended the marker, it should look like this:\n",
"\n",
"\n",
"\n",
"\n",
"If you do an analysis and any of the sensors hits the Box object we just created, the list of materials in the result.csv file should say something with \"CenterMarker\" on it. \n",
"\n",
"#### See more examples of the use of makeCustomObject and appendtoScene on the Bifacial Carport/Canopies Tutorial"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.8"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| bsd-3-clause |
thehackerwithin/berkeley | code_examples/python_mayavi/mayavi_intermediate.ipynb | 1 | 8809 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"WARNING:traits.has_traits:DEPRECATED: traits.has_traits.wrapped_class, 'the 'implements' class advisor has been deprecated. Use the 'provides' class decorator.\n"
]
}
],
"source": [
"%matplotlib qt\n",
"import numpy as np\n",
"from mayavi import mlab\n",
"\n",
"from scipy.integrate import odeint"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Lorenz Attractor - 3D line and point plotting demo\n",
"[Lorenz attractor](https://en.wikipedia.org/wiki/Lorenz_system) is a 3D differential equation that we will use to demonstrate mayavi's 3D plotting ability. We will look at some ways to make plotting lots of data more efficient."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# setup parameters for Lorenz equations\n",
"sigma=10\n",
"beta=8/3.\n",
"rho=28\n",
"\n",
"def lorenz(x, t, ):\n",
" dx = np.zeros(3)\n",
" dx[0] = -sigma*x[0] + sigma*x[1]\n",
" dx[1] = rho*x[0] - x[1] - x[0]*x[2]\n",
" dx[2] = -beta*x[2] + x[0]*x[1]\n",
" return dx"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"(20000, 3)"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# solve for a specific particle\n",
"# initial condition\n",
"y0 = np.ones(3) + .01\n",
"\n",
"# time steps to compute location\n",
"n_time = 20000\n",
"t = np.linspace(0,200,n_time)\n",
"\n",
"# solve the ODE \n",
"y = odeint( lorenz, y0, t )\n",
"\n",
"y.shape"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Rendering Points and Lines\n",
"Mayavi has several ways to render 3D line and point data. The default is to use surfaces, which uses more resources. There are kwargs that can be changed to make it render with 2-D lines and points that make plotting large amounts of data more efficient."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"####LinePlot"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/ahaefner/anaconda/lib/python2.7/site-packages/traits/has_traits.py:1766: FutureWarning: comparison to `None` will result in an elementwise object comparison in the future.\n",
" setattr( self, name, value )\n"
]
}
],
"source": [
"# plot the data as a line\n",
"# change the tube radius to see the difference\n",
"mlab.figure('Line')\n",
"mlab.clf()\n",
"mlab.plot3d(y[:,0], y[:,1], y[:,2], tube_radius=.1)\n",
"mlab.colorbar()"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<mayavi.core.lut_manager.LUTManager at 0x10f7064d0>"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# plot the data as a line, with color representing the time evolution\n",
"mlab.figure('Line')\n",
"mlab.clf()\n",
"mlab.plot3d(y[:,0], y[:,1], y[:,2], t, tube_radius=None, )\n",
"mlab.colorbar()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"####Point Plot"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<mayavi.modules.axes.Axes at 0x126e09ef0>"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# plot the data as a line, with color representing the time evolution\n",
"mlab.figure()\n",
"\n",
"# By default, mayavi will plot points as spheres, so each point will \n",
"# be represented by a surface. \n",
"# Using mode='2dvertex' is needed for plotting large numbers of points.\n",
"mlab.figure('Points')\n",
"mlab.clf()\n",
"mlab.points3d(y[:,0], y[:,1], y[:,2], t, mode='2dvertex')\n",
"mlab.colorbar( title='time')\n",
"mlab.axes()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"####Line + Point Plot"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<mayavi.core.lut_manager.LUTManager at 0x12c0bc3b0>"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# plot the data as a line, with color representing the time evolution\n",
"mlab.figure('Line and Points')\n",
"mlab.clf()\n",
"\n",
"# plot the data as a line, with color representing the time evolution\n",
"mlab.plot3d(y[:,0], y[:,1], y[:,2], t, tube_radius=None, line_width=1 )\n",
"mlab.colorbar()\n",
"\n",
"# By default, mayavi will plot points as spheres, so each point will \n",
"# be represented by a surface. \n",
"# Using mode='2dvertex' is needed for plotting large numbers of points.\n",
"mlab.points3d(y[:,0], y[:,1], y[:,2], t, scale_factor=.3, scale_mode='none')\n",
" #mode='2dvertex')\n",
"mlab.colorbar( title='time')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#Contour Plot\n",
"Let's see how long the particle spends in each location"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<mayavi.modules.iso_surface.IsoSurface at 0x12dc51470>"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"h3d = np.histogramdd(y, bins=50)\n",
"\n",
"# generate the midpoint coordinates\n",
"xg,yg,zg = h3d[1]\n",
"xm = xg[1:] - .5*(xg[1]-xg[0])\n",
"ym = yg[1:] - .5*(yg[1]-yg[0])\n",
"zm = zg[1:] - .5*(zg[1]-zg[0])\n",
"xg, yg, zg = np.meshgrid(xm, ym, zm)\n",
"\n",
"mlab.figure('contour')\n",
"mlab.clf()\n",
"mlab.contour3d( h3d[0], opacity=.5, contours=25 )"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##Animation\n",
"Animation can be accomplished with a mlab.animate decorator. You must define a function that yields to the animate decorator. The yield defines when mayavi will rerender the image. "
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# plot the data as a line\n",
"mlab.figure('Animate')\n",
"mlab.clf()\n",
"# mlab.plot3d(y[:,0], y[:,1], y[:,2], tube_radius=None)\n",
"# mlab.colorbar()\n",
"\n",
"a = mlab.points3d(y0[0], y0[1], y0[2], mode='2dvertex')"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<mayavi.tools.animator.Animator at 0x1403e6650>"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# number of points to plot\n",
"# n_plot = n_time\n",
"n_plot = 1000\n",
"\n",
"@mlab.animate(delay=10, ui=True )\n",
"def anim():\n",
" for i in range(n_time):\n",
" # a.mlab_source.set(x=y[i,0],y=y[i,1],z=y[i,2], color=(1,0,0))\n",
" mlab.points3d(y[i,0],y[i,1],y[i,2], mode='2dvertex', reset_zoom=False)\n",
" yield\n",
" \n",
"anim()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.10"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| bsd-3-clause |
alvason/diffusion-computation | stochasticD/.ipynb_checkpoints/poisson_random_distribution-checkpoint.ipynb | 1 | 239984 | {
"metadata": {
"name": "",
"signature": "sha256:f466673fe6909ac77ba73ab30879844b8e6a6408c71351215ed3b0162f72fa13"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Diffusion computation\n",
"https://github.com/alvason/diffusion-computation\n",
"\n",
"### Section003 --- Stochastic solution for the diffusion equation\n",
"##### Random distribution --- Poisson distribution "
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"'''\n",
"author: Alvason Zhenhua Li\n",
"date: 03/19/2015\n",
"'''\n",
"\n",
"%matplotlib inline\n",
"\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"\n",
"import alva_machinery_diffusion as alva\n",
"\n",
"AlvaFontSize = 23\n",
"AlvaFigSize = (16, 7)\n",
"numberingFig = 0\n"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 1
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"'''Poisson process --- Poisson distribution'''\n",
"numberingFig = numberingFig + 1\n",
"plt.figure(numberingFig, figsize=(12, 3))\n",
"plt.axis('off')\n",
"plt.title(r'$ Poisson-distribution \\ equation $',fontsize = AlvaFontSize)\n",
"plt.text(0,2.0/3,r'$ P_{p}(n|N) = \\frac{N!}{n!(N - n)!} p^n (1 - p)^{N - n} $', fontsize = 1.2*AlvaFontSize)\n",
"plt.text(0,1.0/3,r'$ P_{m}(n) = \\frac{e^{-m} m^n}{n!}, where \\ the \\ mean \\ (average) \\ m \\equiv pN $', fontsize = 1.2*AlvaFontSize)\n",
"plt.show()\n",
"\n",
"def AlvaProduct(i):\n",
" product = 1\n",
" for j in range(1, int(i) + 1): \n",
" product = product*j\n",
"# print product\n",
" return (product)\n",
"\n",
"def AlvaPoissonProcess(i, N):\n",
" if type(i) == np.ndarray:\n",
" total_Input = np.size(i)\n",
" p = np.zeros(total_Input)\n",
" process = np.zeros(total_Input)\n",
" for xn in range(total_Input):\n",
" p[xn] = 0.5\n",
" process[xn] = AlvaProduct(N)/(AlvaProduct(i[xn])*AlvaProduct(N - i[xn])\n",
" ) * p[xn]**i[xn] * (1 - p[xn])**(N - i[xn])\n",
"# print ('probability = ', p)\n",
" return (process)\n",
"\n",
"def AlvaPoissonD(m, i):\n",
" if type(i) == np.ndarray:\n",
" total_Input = np.size(i)\n",
" distribution = np.zeros(total_Input) \n",
" for xn in range(total_Input):\n",
" distribution[xn] = (m**i[xn])*np.exp(-m)/AlvaProduct(i[xn])\n",
" return (distribution)\n",
"\n",
"N = float(100)\n",
"b = 1\n",
"mean = N*b/3\n",
"rangeN = N*b\n",
"print ('mean = ', mean)\n",
"aaa =np.arange(1, N)*b\n",
"print aaa\n",
"plt.figure(figsize = (12, 4))\n",
"plt.plot(aaa, AlvaPoissonProcess(aaa, N), marker ='^', color = 'blue', label = 'Process')\n",
"plt.plot(aaa, AlvaPoissonD(mean, aaa), marker ='o', color = 'red', label = 'Distribution')\n",
"#plt.plot(aaa, np.exp(-((aaa - mean)/rangeN)**2), marker ='+', color = 'red', label = 'Gaussian')\n",
"plt.xlabel(r'$ Output-level$', fontsize = AlvaFontSize)\n",
"plt.ylabel(r'$ Number/level $', fontsize = AlvaFontSize)\n",
"plt.title(r'$ Poisson \\ process $', fontsize = AlvaFontSize)\n",
"plt.grid(True)\n",
"plt.legend(loc = (1, 0))\n",
"plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAsUAAADaCAYAAABO1D9/AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xe4JFW19/HvYoAhR0GQLHGAIQnMMExghiRXBVQQEET0\nVRRFVIRrQEW9er0mBCSJCoIIqAgiIkqQIQ5JgqCCqAQVZAZQkBxmvX+s3ZyaOtXxdK7f53n66dNV\nu6t27VNh9a69d5m7IyIiIiJSZgv1OgMiIiIiIr2moFhERERESk9BsYiIiIiUnoJiERERESk9BcUi\nIiIiUnoKikVERESk9BQUi4iIiEjpKSgWERERkdJTUCwyIMxsyV7nYZCY2WJmtoeZnWFmt1ZJ03dl\nWpQnM1vNzA4zs2vM7LBe5Cvlo+/KqwxU7iLdoaBYZIzMbCszu9XMHjaz+el1p5ndnF53pXnXm9n7\nzazp487M9gGeMLPPtX8LhtZXgROAdxTNbFeZmtmWZvaGsSyjVp7MbBng58CXgO2Bf7djXQXrrrkd\n2gfbr5F9R+Uu0j0KikXGyN1vdfetgH3SpMvdfaK7b5NemwJrAxcBJwHntbCa1Ylg6Np25LkM3P0w\nYGb6eFlBknaV6XnAkWNcRsWoPLn7k+7+OuC4NKloW9qh3nZoH2y/RvYdlbtIl5i79zoPIkPBzI4G\njgY+6u7HVUnzL2BZYJq7X9fN/JWRmR0MnALs4u6Xd2D5awH3AV9098+2e/m5dV0DLOfuEzuw7K5t\nhwSVuUj/UU2xSPvsmN5/XTTTzBYGxqePq3YlR/J64Fng6g4tf0Z6n92h5QNgZksDk+lcLXFXtkMW\noDIX6TMKikXaIHWEmQz8zd3vrpJsBrAY8Dy6Fdpx6UfIjsC17v5Ch1YzA3gBmNOh5VfMBMbR2aC4\nG9shI1TmIn1m4V5nQGRITCOOp0uLZprZOKJpxcvAh939n2a2G3Ag8E9gBeBVwCfd/XfpO0sAXwcW\nBzYA3ubu/6iy/EnAB4iA24H5wJfd/cExpq2Xx62BDwNrAt9z9zPNbC9gJ+BFYDPg5+7+jepFN3Zm\nNp5om7k98AARQF4ILE0mkGxHmRLBTGUEiK2AJ4CrzQzgK+5+Xvr+BOBTRJvQc4DTgI+nz0sDt7j7\nsQ3maWeiPJc2s28TFRrrAx9x99vT+pYEvlZtOWa2bSqTme5+t5kdCHyoynZ81d1/0mR59WRfscjw\n24D9gH8QPzwXB97v7k/m0o4HjiD+h39Jkz+ZXrcCv2imDAuWnd0HFwbOAH4KbO3uD9Yp8+y+0/fl\nLjKU3F0vvfQa44u4gM0nLl75eZsBvwTuJW7njwfOBH4LrJRJ9x7gMeDV6fOxwCbp73nA16useyZx\nQc8u63Tg3FbTEoFFI3n8KRGAHkpcYL8GfCiTfrtULq/rYNkvTTSPmA0skqZtkPL5MrB5Jm3byhRY\nI23b/1RZxrmpHA9I+TgvlccKwEPAvxvNE3A3EZx/IjPtaOARYKn0+ZvAhGrLAY4HXgJWyE2vuh0N\n5q1n+wqwPHAJcFNlPWn6oURb3aL95DpgfJq2FnBnWu8aYyjDon1w/bT9zwNLNFrmg1Dueuk1rC81\nnxBpj0p74reb2Tnp9SMzO5+4GJ0KbOjuvyJqj3YH3uru8zLL+DFxkT/KzFYHxrn7781sIrAiEQAV\n+TRwWWVZqcbw9cTFstW0328gj5sBt7n7y8RFfhzwqLt/K5P+ifS+bpW8t8PZwMbED5IXAdz9T0Rt\n3Tx3vwPAzNagvWVaGdniyvyX0//vn+7+HFE2BvzM3ecQ5bcw8MNG/s8p3xsAp7n7/2Vm3QasBOye\nOm3h7n80s03Tch7KZWsWcKe7P56bXrgdTZTX9+nBvpLuvvwImArs7u7ZvL3A6OaBZwObAHu5+/MA\n7v4A8B/gz8T/qNUyLNoH7wX+BvzW3Z/Jpa+17/R1uYsMtV5H5XrpNegv4nblfOCvDaTdJ6X9QsG8\npdO83wCTgI3T9G8StVOrV1nmHcCjwAeBiXXWXzdtE3mcCmyUpt8A3FeQft+UfnKHyv6taflfy01f\njOhg98PMtLaWKdEc4llgsYJ52wKT0t+/IgLkomXUzRPw7rSN03LTD0rTPw5MIX50ARwDPMeCNacr\np7THNLodDeatZ/sK0WRgPnBiZtqywP8j2umuWrCffCO3jEWIoPjkVsuwxj64eFrG/za57/R1ueul\n1zC/ep4BvfQa9Bewd7qonN5A2huJW+mjgjEikJoPnJ+ZNp4Izn5RY5nvShfO+el1N1VuhTaStoU8\nLpuW+Z2C9OcQNVEL56aPI8ZtvrLJ1/dyy/lNys+k3PQd0/SDCvLUljIF/gpcVef/vSjwNAVNWRrN\nUyrDp0m35TPTj8tvI1EDPS+/PqLN7XzgTQXLr7kddfLW8X2lRr6uScs/lxj/+0QimN2dNNxowX4y\nOTd9+zR971bLsMY+uHOavkuzZd7P5a6XXsP8Ukc7kbGrNJ24qlai1BFna+Bed/97QZKd03v2lupb\niDao36m2XHc/3cxuAd5E3N6dBVxsZqu7+0vNpG0xjzOIW9VX5LZ3ceCNRLOBfD5eTnloWRpdYhrw\nJNGmNKvyPykarWHMZWpmaxIPZDmzTjYnEzWGv6mTrlaetgZu9nRbPmMWIzWCFbsQt9vPKkj7Mrmh\n6RrcjsK8dWtfqWFT4sfC2919frVEuf3kxtzsHYlOlNk8NlyGdfbBWUQgusB45E3sO/1a7iLDq9dR\nuV56DfqLaI/4MrBOnXSvJoKYopqfhYiOeHOBZTLTf0P0qF8ofT44M+8twOPkOvcRPeDnAys2m7bF\nPFZqLFfOpX9Hmr5r+rw/BbeLx1DuldvZswvm3Qj8If29RiUP7SpTRm7dz8ikORhYPve9z6d069XZ\nllp5ehY4Lpd+/bTcC3PTv0B0pso3hbiHCKwhArKdG92Oannr9b5CBKK3j3E/uSq/jGbKkGjTXWsf\nnJNJv1OT+05flrteeg3zSx3tRMYgdXB6LfB3d7+vTvK5RIcZK5h3SFrOez0NI2VmqwI7AD9w9/mp\n081qme+8h2g7mx+q6QHg9+7+WAtpm8pjsmNaxtxc+v2JjkqXpk5Re3h0PGuXecBTxC3mV6Ry2gqo\nPMFuz5SunWW6DRFM3JCWuyLR5vdfue/tSIxd/edqG9FAnh4A8h21PkbUkn40N30FonPhK+VsZusQ\nQfT1adKemeXV3I46eev1vjKH+F+NYmYrmNk308fKfvJYLs2GRPvdfC1+w2Xo0cGt1j54Q5r0ZqLt\nMjSw7/R5uYsMr15H5XrpNcgvYhzb+cA5TaT/D/CazLS9gH8B++XSbpqWvRvRzvEHwLKZ+V8FDsl9\nZw3gZmBKbnozaZvJ4yopj8cWbOvNwI/S3x8hU1vbxvL/CjHe7Lj0eWOirfLjxNizCwE/bneZAp8j\nAieI5hE/ANbMfW8pYhSE79fZhnp5OhK4LvN5X6KWtKit6r5E567l0+fliCG5ngKOSuVxPqnNbb3t\naCBvPdtXiPbALxBjAFemGTFKyHnAGrn95D5Su1kiwP1Lys8bxliGtfbBo4j289l9sJF9p2/LXS+9\nhvlVOahFpEFmthDxRLpXAesQF8nniM4zv3D3T9b5/kHE2LX3E4HT48TA/Q8UpP0y8LqU5pvufmNm\n3njgE0TQ9hxx8R1HXPz+kFtOw2mbyWMa8ulS4I3ufktu3g5EkPlH4FZ3P65WubQibddxxP/h/pTP\n/yECoyPStO+6+28y3xlzmZrZcox0UJpPPOzi9lze1iFqA/d192z7zqLtqJWnhYnxcdcA/p3yc7TH\nkF9Fy/oMCz5A4gvp84eJpj4neAwN1+h2VM1bmn8QPdpXzGwn4kfD34nxgBchjs0zPXNxS//XbxH7\nyV+Imt3VUr6Xd/encsttpgxr7YNHpmmnuPtVKX3dMk/p+rbcRYaVgmIRESkdM7sHeMzdp/Q6LyLS\nH9SmWERESiU9NGV96o8KIiIloqBYRETKZo/0XnMYRREpFzWfEBGRUjCzdxMjdkwgOuU9BFzt7vv3\nNGMi0hcUFIuIiIhI6an5hIiIiIiUnoJiERERESk9BcUiIiIiUnoKikVERESk9BQUi4iIiEjpKSgW\nERERkdJTUCwiIiIipaegWERERERKT0GxiIiIiJSegmIRERERKT0FxSIiIiJSegqKRURERKT0FBSL\niIiISOkpKBYRERGR0lNQLCIiIiKlp6BYREREREpPQbGIiIiIlJ6CYhEREREpPQXFIiIiIlJ6CopF\nREREpPQUFIuIiIhI6SkoFhEREZHSU1AsIiIiIqWnoFhERERESk9BsYiIiIiUnoJiERERESk9BcUi\nIiIiUnoKikVE2szMFjOzS8zsd2Y238xuLEizn5ndm+Y/aWaXm9n4XuRXRETA3L3XeRARGUpm9i7g\no8CmwFbufntu/jjgVmCmuz/egyyKiEiimmIRkc6ZDLwv/X1wwfylgCsVEIuI9J6CYhGRzlnK3ecA\nNwJvN7MlcvOnAHO6ny0REclTUCxDqcU2nVeY2aNm9vle5FmGi5mtBDySPn4HWAbYJ5dse+CabuZL\nRESKKSiWoeTuz7n7bsA3gbuAbcxsi1yac4CNgDuBtYFvAysAW3c3tzKkpgLXpb/PBf7D6CYUa7j7\nQ2NdkZkdYGYnmNkFZjbezA40s6+b2THpx+GrxroOEZFhV8qg2MxWMbNfF9zKHDhmtrWZnWlmpfxf\nNqCZNp2PpmnzupGxYTNMx1XWGI6xKcDVAO7+DHA2MMnMNk3LXRR4rg35WwqY4O6HEoH4hcBT7n6E\nux+ekn14rOsRERl2pQukzGxF4FfAUelC1e7l/9jM3tDu5Vbj7rcA1wNnKzAu1Eybzrm5d2lQp4+r\nXhrDMbaKu2d/YJ2a3is/zrYBftuGLM4CrjCz5YAVgZvd/fzM/IWA5duwHhGRoVaqICoNf3QucFq6\n0HXCSsSFqWvc/RRgUeBT3Vxvv2uhTefQBcXduK3e7HFlZkua2R/NbNWxrrtbmj3G0o+vp3PLuI0Y\nfu0AM1uM9rUnvoWokZ6aPp+QyYcBE4Hft2E9IiJDredBsZlNN7NrMh2i5pvZ82Z2vZldmV5Xm9nd\nZvZAuo35uhZXdyiwnLsf385taIWZvcHMrjWz283shbTd/zazZaukX8vMbjCzZzLl9ISZ3WJmWwMf\nBI4wsy27uyV9rdk2nY8C8xmS5hNdvK3e8HGVgsEzgQ2BRdqw7m5q5hibRNydyDsVWA7YG9jY3f9Y\nmWFmk81sThOv7QDc/SF3fwmYAdzj7o9k1jcZWIWoxRcRkRoW7nUG3P1qYBqAmf0deA1wvLsfmU9r\nZhsAJwI3mdkR7v7NRteTag0/D+zfloyPkbtfDFycanL+DixL1GS+ExgVXLj7A8DkVLv2Z+C7wJHu\n/kIljZl9L313Wue3YCBMAb4K0abTzM4G3mdmm7r7Xfk2ne4+38weY3hqijt+W73R4yoF6LsBRwGb\nAQP31CB3f7iJY2x74JyC6WcD3yDaud+bW/4NwHZjyOJ04KrctH2A29z9PjNbA3jI3V8ewzpERIZW\nz2uKK8xsNSIgduCyojTu/idgX6I27xtmNrmJVRwGzEvBaD/ZDLibkQvo++ukf4So0TwiGxAnJwJT\nzGzq6K+VUittOucyPEFxN26r1z2uzOxrRI39O4EfjnF9vdboMbaeu/8lP9HdnyLuWkwB/tCuTKUf\nHVuSCYpT++f9GSnzjykgFhGprm+CYqKWAyIorjqYvbs/xsjt7Xc1suBUI3gI/XlBnk4ELienzxuZ\n2cwa6TcH7nD3F/Mz3P2vRPBxRNtzOWDG0KZzLkPSfKLTt9UbPa7c/Uh339zd3+juX2t1ff2gkWPM\nzNYH1qyxmMqPs2vbmLUpxJ2/bE1x5Q7BpWa2CXBfG9cnIjJ0+jEo/oO7/6dO2uXS+xoNLntnYvzZ\nX7aSsQ6bClzt7rcCN6VpH6iRvugWadYlwK7DNixWC5pu05kMU01xRd3b6qmzXLP6+bjqpMJjzMzW\nNLNrgN8BM8zsTjMb1czC3W8mfoy1s7PvKsAV2TGP0zCDxwP/TdxhO6HKd0VEhP4Miq+vlSi1K14s\nfXy4wWXvTnSy6tSIE2MxiZGa8ZPS+x41euZPo3ZQfBUwHti1PdkbWNuTxojNOZuoQX4fxe1az3L3\nMY8d2y86fFu9n4+rTio8xtz9QXef5u6Lu/s4d5/o7oWjS7j7jKK7Pa1y9zPdfeeC6R9x9wPd/TNq\nOiEiUltfBMVpjNMJ6WPVphPJ69O7Axc0uIqpwF3uPr+F7HVMus36UCYI+xHwOHEb9L1VvrYF0QSg\nmt8RZTOjXfkcUK226byzxVrTftXJ2+p9eVx1gY4xEZEh1BdBMSM9uZ0aNcUpWKk8newSd/9FvQWb\n2ZJEwH13nXSWxnO91sxuM7Od0vSlzOwLZna5mV1lZveY2acb2agGLFDr6+7PA6enj+/NB2dmNgH4\nc60gJAV9fyc68JVSq206zWw6cD99eps5jS18XRrGb+c0bUszO9/MZqf99n/NLDuqTEduqzd6XPWb\nFstwATrGRESGU8+HZEsqTScec/d7a6T7HHEh/jWwV4PLXqey7DrpPgDc7+6HmtnPgJ+Z2Qzgi8BX\n3P2zAGZ2EHCamT3m7idXX1xDpgE/zk07BTgcWI24PZ2tDa/XnrjiYWDTRjJgZjsAxwDWSPoabnH3\narXbXWFmaxJNArYGFjWzO4EP5G9hu/vNqe1n/rb/vPR6sBv5bYaZHQg84+7bm9kZxP75UeC/gEPS\ncGHLE7XfawDvgLitTowLvAB3/8gYs9TocdU3Wi3DKho+xkREZDD0W1A8qulEGjpqK6JWa1fgSODY\nJtrHrZ7en6iT7qBMPpZIr9OAHd390Uy6Sk32boyMGNGqKcSQVq9w97+Y2WXALkSgng2KpzW4zkeA\nbczM3L3meLDuPpso34Hn7g/S4BjN7j7q1nfqdPfqduerTd4L7Jn+fhlYHNgDeFPlzoG7/8vMLgDe\nb2b/5+6dfIpZo8dVP2lnGTZ8jImIyGDoeVBsZksT7WQBJprZlZnZ44gmHv8ELgYOdvdmL8LLpPeq\n3zOz1wIPuvuzKQjfghgL+ZBcQAzxGGfIPPShFWlc5qeqjLRxEhEUzzKz9TO159vQ2DB0zxE1v8sw\nWEGLFEgPyHguDUcI8YAHBz5U0JTmyfQ+g84+2rfucdVPOlCGOsZERIZMz4NiorZ0IeIC9e5Uc9lO\n49P7UzXSPAV8Nv09EXgVcKu7F7Vvrjxx6vYx5msaxaMjAPyCuIW/JjEO7OFmtg7RKa+RHuvPp/cl\n0QV7GLxANKnBzF5DPCL5gTRmbt566X2xgnnt1Mhx1U/aXYY6xkREhkw/BMWVJgvPU2c4thZVanQX\nrZbA3bNj0+6U3q+okrzSlnmsT8abBlxeJT/zzexUoj3zgWb2KaKcZje47ErA8nzNVDIQ0t2RO9PH\nyoNdCvcdRn603d/JPNHAcTVWZvZBoiNgq54G9nT35zpQhjrGRESGTD8FxXMKHlvcDpXmCY3WnO2Y\n3kddMM1sLWBb4gEjd4wxX1MZqZ0u8l2iY+HywH4p/VkNLnsxouZ9UGrxpHGz0nvR/rkRsCpRK9pI\nh8yxaPa4apq7n0g8Vrnd2lGGOsZERIZMT4Pi9KjdbdLH33RoNX9P7ys3kJ9FiCD9eUY//hdG2vOe\nnvnOTHe/siBtrfWsAIzLtG8cxd3nmtlPiSePHULcpv1gg6t4NTGSR91arDTCxjcZ++gTN7v7wZnl\nlm3s2k5wd8+PmTyLaO9edCdj9/R+Ua19q00aPq76UDvKsOFjTEREBkOva4q3JW6/OtBUYNmE+9Ly\nV6+XMOVnSWB2/qlmaczg9xIB8/fTtG2BA2k+71MpDrrzTiKC4q2B65t40tpqQFFbyVHc/So6MPqE\nu/fLGNhDI7UrXwu4I98BNI2r+z7gWeATXchOM8dV32hjGTZ8jImIyGDodeBSaTrxNHBjJ1bg7k8T\n445OqJeWkaYTRTVIGxO3VX+ZqUH6CK0Ny7YTDQTFaXzdSu/3ap3yFpBG83gN5Xv0bhlU2sKOL5j3\naWLs4I8VPcmv3Zo8rqoZ692JVoy5DHWMiYgMp54FxWnos/9KH29uYtzhVlwLbJrWWUvV9sTAo8CL\npEfimtnexJBqNzWTETObRTTDWL7Br1SC7kbbiG5BBBvXNZOvQZKauQyUNuW50hb2OTM7OC3XzOxw\n4ChieLFT2rCeRjV0XJnZQunJkOuZWWVcbgMONbMJZraMmXXrXNSOMhz6Y0xEpIy6HhSb2almdj3w\nN2AycQt2ipndmh6zuk7tJYCZvdnikcy/NrPlzewjZvZ/ZvYTM3tfwVcuIgbq365gXtZLRFOIUYGu\nuz8MvBPYLT0NbRZwaL28ZvL8EzP7KxFwLwEcb2Z/MLMP1fnqD4hxmhu9AM8kgvdfNpq3QWLxiO2J\nvc5HC44xs3XHuIyZxD66C7CVmV0H3EYMa7hd6pjWTY0eV58lxv79E3Asccw78DHiTsi/iVrabmhH\nGQ71MSYiUlY2aA9jSu3+vuzuR5rZvcQYoQe5+11mtgwxtNr0bA2umS0KPAR8292P6nD+rgROT4/X\n7TozmwPMc/fd6ybuI2a2GdHZ8kR3P7pKmsOBR/NlmzpsXkC089yUuPMwKZdmP+ALwLrEiAE3AW/o\nVkep9PjgnwF7uPu/c/Ma2fYNgT9SsG290s3jqh3aVYaDeoyJiEhtvW5T3IrJwJx0O3o14LvufheA\nuz8JPMbIo1xJ018ATgH2b6AJxcBKF/1JwLd6nZcWTABWIDoVjmJmmwBvLPqxkcah3Y0YReMu4vG7\nW+TSnANsRIxVu7a779TNkQPc/V/A/1H8v6m57Unltn+nh1pr2AAeV2MuwwE/xkREpIZBDIr/RDw4\n43XEWKGvtP9NNYYrUzx26nHAcsAeXchjrxwK3OLul/U6Iy2Yl3vP+wr1A5HJxOgBAAcXzF8KuNLd\nH28+e23xK2AzM8s3/6i37TAS0M1ud6bGaJCOq3aU4SAfYyIiUsPABcXuPjfV8E0DHnb3P2dmTwbG\nAfcUfG8e8TCMLwxIrVZTzGxN4P8B9doo96u5ufdXmNkGwGZE84NalnL3OcRIJm83syVy86cAc8aa\n0VZ5tFX6NnBkblbVbQcws6UY6QTas/wXGZTjqh1lOATHmIiI1DBwQXHGVEYPU7Yr0QHmgirfOZ4I\nPI7oYL565STgOHfvyNB2XVArMNwbuMZrNIA3s5WAR9LH7wDLEGM8Z21PY+NDd9I1wJvSuNcVtX4Q\nnAfcDSxLdE67KXUw7djjlVvQ18dVG8tw0I8xERGpodcP7xiL7YAvVj6kphMHACe4e2GNm7vPN7N9\ngCvN7Bp3v6ED+ZpL7dvgbZcZ5upT3VxvPWZ2AFF7vxqwLxGkbkb8GJsAvCPzAIVHiaeMFZXdLODC\nOqubysgIHecS7YsPJvP0QWANd3+o+S0Zrclty7qLCMwmZ/Jbddvdfa925LeTunRctawdZdivx5iI\niLTPQNYUm9kE4FXEE+gqjgX+TIw1WlV68MbOwBfNbPF2583d93H3S9q93GrMbDIREO5Zqya129Lt\n6gnufiiRvwuJcZ2PcPfDU7IPV9K7+3yik2TRD5rNiQdF1DKFdOfA3Z8BzgYmmdmmKT+LAo0+EbCm\nZrctK/2P/kIE0JVptbZ9IHT6uOqlfj3GRESkvQYyKCbaEz8B/CiNV3waUdu2WyOPQnb3R9LoA892\nOqOd5u43uPvb3P2lXuclZxZwhZktB6xIDIN1fmb+Qox+gMlccoFhCkBXIMayrWWV1L614tT0Xulw\ntw3w28azX1Mr25b1OPGo4axR2z5ohum4yurjY0xERNpoUJtPTAXmuPtFxAMEpP/cQgR5r0+fT6jM\nSB2yJjK641xR05Nl0/sT1VaUOtQ9nZ3m7reZ2a3AAWb230R74nbtK61sW9bjjGxXRdeb3YiIiMiI\nQQ6KT+t1JqS6SttdM5sB3OPuj2RmTwZWIYYoyyqqLa3crq51V2MSMeJE3qnEOLp7Axu7+1ezM9Nt\n8W/WWG7e4e4+p8Vty1qI6BCaNfA1xSIiIoNs4ILiNCzS2kBfdeaRqqYz+mEJ+wC3uft9ZrYG8JC7\nvwycVdD8pdJsolZzhO2Bcwqmnw18gxi7+N78zNQhrN4jimtpZtuyliceIpJVtO0iIiLSJQPVptjM\n3kU8DteBb5hZ0QMapE+k9sBbkgkczWwhYH/gh2nSxzJB4525ocoqnebmUjsoXs/d/5Kf6O5PESNR\nTKF+R72mtLBtWcszulZ41LaLiIhI9wxUUOzup7v7eu4+zt03d/dT639LemgKcTciW5ta6Zx2aXp0\n830AZjYduJ9M+9yMW4GNi1ZgZusDa9bIQ2UfubaZjDeg4W3LSoHvBsAdmWm1tl1ERES6YKCCYhk4\nqwBXZMcGTo9YPh74b2J830ogOC+9HixYzmVEO/JXmNmaZnYN8DtghpndaWbT8l9095uJB2bcMvbN\nWUAz25a1OTEmcXYkjFrbLiIiIl1gGnZT+p2ZrU4EtatVaY4wMMzscKLT33t6nRcREREZoZpi6Xvu\n/ndgNvD2HmdlTFKb4/cRtckiIiLSRxQUy6D4JHBoGgd4UL0FuN7df9frjIiIiMiC1HxCBoaZvRNY\nx90/1+u8NMvMViFGwtjd3Z/sdX5ERERkQaoploHh7mcAjxd1qBsAnwEOVEAsIiLSn1RTLCIiIiKl\np5piERERESk9BcUiIiIiUnoKikVERESk9BQUi4iIiEjpKSgWERERkdJTUCwiIiIipaegWERERERK\nT0GxiIiIiJSegmIRERERKT0FxSIiIiJSegqKRURERKT0Fu51BmR4mNlawJ7AdsBJwDrAZsCNgBP7\n2+uBj7v7Pzu8/lOAtYFNgYvd/cp2r09ERESGh2qKpZ12BU4gAt+n3f0M4HLg88Cv3f0c4GFgehfW\n/x93/z5wJfDWDq1PREREhoRqiqUuMzscWKNGklPd/Y/A2cDrgFvd/bdp3ubAue7+ZPq8FXBWh7Ja\ntP4tgbsW74wiAAAZlElEQVQ7tD4REREZEgqKc8xsFeAM4M3u/kyblrk1cBhwkLvPb8cyu8ndj2kw\n3VNmNgv4TWbyDsD/ApjZysBr3P0uM1vW3Z9ocz6L1r8nsHsn1icirevEuVaaN+jXJ5F2UvOJDDNb\nEfgVcFQ7T9LufgtwPXC2mQ17mc8kmixgZosQNcNz0rw9gQvMbCrw2i6sfwPgWeBJYO8OrU9EmtSp\nc600r2TXJ5GadAAkZjYOOBc4LZ0k2srdTwEWBT7V7mW3g5lNNbPvmtmXzOxkM/tSi4tamehYB7AB\nMNvdX0yf/wwsBazr7rcV5OEAMzvBzC4ws/FmdqCZfT29Ljazlc1sAzM7zsy+amYXmdkuNdb/L+AB\n4L3AD1vcHhFpo06fa6V5/X59EukWc/feZsBsOvAlYFlipACAF4HfAs+nz+OIYGdx4CrguEyb0Xbl\n48PAAe6+TTuXm1vHqsAfgZlFQWGvpG1/K/DGSttfM7sY2C/TFrjTeVgK+KS7H2Vm84j//6nufn6a\n/0ui1vcR4DB3f8nM9ga+6u7rdCOP3WBmOxLHwybAksDf3H2t3uaqP6hshkM3zrXSvH69Pg0DM3sD\n8EmiUmhjounqk8BaRc360khKPyJGb1osTf4PcC9wiLvf3I18l1HPa4rd/Wp3n+bumwEPpcnHu/sU\nd5+ZXtPdfSNgZ2BV4CYz+2i78mBmKxEjJHyuXcss4u4PA98Dju/kepqR2uB+HTjY3Z80s4XM7I3A\nU90KiJNZwBVmthywInBzJSBOXgImAh9195cy01buYh47zt2vcPfJwKfTpGt6mZ9uMrP1zeyQavPL\nXDbDolvnWmleP16fhoW7X+zuU4mO3/OAZ4BlgHdWSf9AOtetS1QGfQtYyd23VkDcWT0PiivMbDXg\nNcR4tpcVpXH3PwH7AvOBb5jZ5Dat/jBgnrtf3Kbl1XIiMCW1q+0HnwH+BrzNzI4GvggsAuzX5Xzc\nAlwNVMrlhNz8rYEz3f35zLRJwF1dyFsvvC69X93TXHTXD4ETzazWSCdQzrIZFt0810rz+u36NGw2\nI0ZDOid9fn+d9I8AjwJHuPsLncyYhL4JihkZu9YZ6Zg1irs/RvzSAnjXWFdqZosCh9ClNqfu/lfg\nOuCIbqyvlrTt04Cz3f0L7v55d/+Uu1/Q7V7I7v5QqgGeAdzj7o9k8rk+sAqjg6A9iM46w2gGcSyU\nIvAzsxWIHz7/dPe/1UleqrIZFt0+10rz+un6NKSmE+etk9PnjcxsZo30mwN3ZPrlSIf1Y1D8B3f/\nT520y6X3ejVKjdgZWAH4ZRuW1ahLgF3NbIkurrPIisQ+cF+P85E1nWg3njWDaF9+Q2WCmW0BbAic\nZ2YLpzsNQ8HMXkvs24+6e1nGWK7UTOX/9wsoadkMi16ca6V5/XJ9GkZTgavd/VbgpjTtAzXSF10P\npYP6MSi+vlaiNMxWpeH5w21Y7+5EA/Zu9oK+ChhPPIGtl+YR2z5qvGoz293MtutmZlJnuy0pDopv\nzN0+ejtwl7vfSTzBbuPu5LIrdkjv1/YyE11WOf7rXQB2SO9lKpth0YtzrTSvX65Pw2gSI3fCT0rv\ne6ROjkWmoaC4q/ri4R1pzMoJ6WPVphPJ69O7Axe0YfVTieCqm80Ffkfkfwbt2YaWpBEcTgN2A75d\nmW5m7wDWc/eju5ylKcQ+mT8JTAe+n5u2IXBpGldzF+DDHc9d9+yQ3svUPGBaeq+3zTs0mE76Ty/O\ntdK8vrg+NcLMphD9YGyMi7rD3T/ShixVlZoBPuTuz6VJPwKOIe6evBf4QsHXtgBu7WS+JMfde/4i\nHuowH3gZWL9GunHA71PaX7RhvUumZX2vTjojOn5dC9wG7JSmL0XsyJcTgdw9wKcbXPcDwG/6oOwX\nJX6xngF8FTgO2LVHeTkQuCw3bTzwD2Dz3PSZwBVET+kNe5TfKcSDQm4BLgJWKEhzBNFZYo3MtO2B\nfxKjrBQt98F0LGxVKZO0f/0JOLNoPQXLmE505rg2ffdm4D0F6b5JPAHwZmBSmrYT8GtgNnErdbOx\nrKPKd7dI672SuI04H3gifb4yHVPL9bJsany/kfPBbKIT6Mcz39uceMT51cRY2lcD2zW4zobznI6Z\nI4lhDecQbUTfALwaeAcwroXtaer8VpCnhs61Y9yOXVI+byfaLY/Pzf9w2sf2HUs5M7Zjpqltyn13\nGeDo9N1rUh4qzcj2auf+TgvXp14cF914EYHrdWm/2jlN2xI4P23PbcRTWxeus5x3A1/OTftaOi7+\nVrA/TwB+1evtL9ur5xlI//xj0o4xt066/0npLgEWa8N6N03L+2qddB8ken8C/Ax4iugBfwmwQybd\nQWl5hzSw7hvqbW8m7Q7Er8Xbxvj6Tq//18PyAlZPF6Vl0kl/PnBCQbp/EkPHLZeZ9qWU/smC9Oum\neU8BPyAuoIumeWsSY3ifVyNfywA/BZ4mOqJWxiJfMe0DO2bSHggcmdmv5xI1FucS44bvADxOtIFr\naR0NluVeaZtPq5Oua2VTJx/Nng+OAPYHfkKMS1qZf3kq35XalWdiiMLbifFMJ6RpSxGBxm9TfvI/\nMNt+fivYjobOta1uBxEY/pwIOjdJ84/MLfO6NP2iVsuZFo+ZVv83me9uTvT9uBZYJXMOug34C/FD\nccl27e80cX3qxXHRrVf6f38x/X1GKsuD0/atmqYvTzTl/EGdZZ0O7Jabtm76380nHneenfc+Yuz+\nnpZB2V49z0D659+SdooLC+ZZOrB+BPwb+Bg1fk03ud7Xp/UeVSfdzcDi6e9L03fuAF6VS7dBmvfz\nBtZ9YToYrNflr1dL+86ZwOvS3xPT//3HuTQT0vTf5qYvTTzd74mC5f4/Ru6ajKr9SSff/1TJ0xLE\nRfdl4PUF879MJlAgLrDLpr8r+/VlwEJp2s/TtOtaXUeDZXlyWs+BddJ1rWzq5KPR88GGad79RE2Y\nFaxzPvCmNv0/lwX+QLTbXTeXdmdGauPzNVJtP78V5LWhc22r20HU2q2T/n4TBQE4cXfhuXz+Gyzn\nSrDX9DEzlv9Nmr8uEXzfDyyTm3dY+u6t7dzfaeH61K3jopsvokZ+xfT3aSlfF1f+35l0J6V5m9RY\n1j3A0gXTf1XZj3LTzwK273UZlO3V8452ZrY0cQsIYKKZXZl5XU3slJ8kdpy13P0b7v5ym1a/THof\n9USZTP5eCzzo7s+amaW8VmpLHs0lXym9P0d9zxEB/zL1Ekp/ScOHreYjT1XcJ73/Jpd0h6LpHqOr\nHE3U8ORVvnOKu5+XW68RtRLV9q8TiXEwz3H3BYaqS8Nh7UpcuDCzVwHPu/sTmf36ReBdPtLm82dE\njVF2eKaG19GEmUQbxtl10u2Q3jtaNrU0eT54deVrwPs9XekyKueLauezZvP8dWAj4Bh3z+9blfG9\nr86ePzt4fsure67NaGo7zGxNIrC6L83bO71fkf2iR4//sxl93DVSzreM4Zhpepsy6zfirsirgE/4\n6AcqPZPeL29hm2rt701dn7p8XHRFetDMcx7DwAJsR5ynPuSj28VX/i8zqixrNeKBWEUja1U63M1K\n7Y4rtmFkhArpkn7oaDeFGAXDgXe7++wurnt8en+qRpqngM+mvycSJ6db3b1olIzKaA23N7Duyolw\nSRq7UEj/eBn4KICZjSNuTT5LXHCzdkjv+WAZoubnhoLpM4hj4biCeVsSbcDvzM8ws3WJW30OHJum\nGbA2sCMxSPwFmeNrReCU9Hdlv77e3f9eWaa7n0bUjrS6jrrM7DVEDeT97v5gneTdKptamjkfTErv\nZ7h70Tlm+5SnUeeLZvNsZhMZqUn/dn556Tswel/s1Pktr5Fzbavb8Qzw8fT9ZYnmOA+6+68Lvj+X\nTDDYTDmb2YY0ecyMYZsq3gJMJkYK+kmN777yA6BN+3uz16euHBd5aYSkLzH2jna3u3v+KbkvAIen\n9byGqOF+wGMs57z10vtiBfMgOhJX6xz8C6KvxJrEON6Hm9k6RKc8jU/cZf0QFFeGYnqeOsOxdUCl\nxmPRagncfS5xIoXoTAG5GoiMvdJ7I09rqlwknq+ZSvqOx7Pqf5c+7ko8evzHBbU4M4iapKKT4QRy\nDx5JF7PVgX94PL0xrzLyStHF/h3EheEF4BgzW4Roy/wwEXy/yeMxrpVtuIe4nQcj+3XRRbnldTSo\nMnB9vfGJu1Y2tTR5Pqga7JjZesRF9g53fyg/v4U8vye931RlebOK8trB81te3XNt0vR2pJrISm3k\nvkRg8oMqy9+I6BRV0XA5t3jMtLRNGe9L7xdXuUM6M+U9e45px/7e1PWpi8dFfr1zGCm/tkrn+cqP\n7Mp5Kl8jX1H5wXh/lfnTqn3X3eeb2anEKBoHmtmniLhodpNZljbop6B4jnf/MYaVWxnVft3lVQ7m\nUTu3ma0FbEs8fOSOBpa1GPFruGbNSSeZmYZGWpC7+7gmv/PW9L5ALY6ZTSA61sxx96cLvrcj0ckk\nq3LivbLKuvYh9pkfF8zbKL3/3N3fVi/TBXmB+hf4sayjmsoFbXaddL0qm1pqnQ8qT4t8luIf+5X/\n/VlVlt1sniuByKUFeVmSqJ2b5+6/y8/PaOf5La/Rc+1Yt2Pf9D5qKDEzW4bomJn98drqvtHoMQMt\nblO6C1W5Phb9TzYhzjFXu/uzmVnt2N/Hcn3q5HHRK5XzVNE2bURUjLxA9R/3UxmpSS/yXeBzRBOw\n/VL6fiuDUuhpUGxmixHtZqCxk0u7VW57rVwvYfq1PZ345XxNQZLKI6dPz3xnprtXu4i/GnjM3ev+\nEjezGcQwQGO9RXSzux9c+eDuPW9TPgSmERePfK3Ilun9uvwXzGxlYH7BrcMd0vuoGpZ0C3YicEOl\n7aSZTSWC7peJjjzQ5IMRMvt1tYtUVkvrqGNUe+J04dzf3U/PpNshvXetbGpp4HywHbA4cHn+x34a\nW/sg4i7CD9K01YAl3P3elKzZPK+d3m8smDedONdfmdZlxFBi2SdEtvv8ltfouXbt9N70dqRy3Y44\nrxaN7bo/0WE7q+l9o8ljBlrfppWImnWnuP1vtUCtHft7w9enrC4cF70yi2j+UlT7vXt6vyjT/vgV\nqQ/KuKJ5Fe4+18x+Svy4P4RotvLBMedamtbroGhbRg76Rk+u7XRfWvfqDaTdlthR5/jI4NvAK7/o\n30ucCL6fpm1LtOuqZjWgqG3SKO5+lbtv5e5bjvF1cP21SZPWBP7t7v/OTa88gvzPBd85mFy7w6TS\nZrboB+I70/v3AcxsYWKc48ot1UqTgn/VyqyZTc9NquzX1zdwp6bVdVRLtwYRMPzN3R/IzDqIGKEj\nqxdlU0vV80FSqR0sumW6E7AWcRGt3HI+iqhtqmg2z48T5XNfQbJ8u9NtGalRJTOtnee3vEbPtWPZ\njkoQOeqYSxUw+xLj9Wa1sm80c8xA69uU7ZRV1N5+VHvipB37e8PXp5xOHxddl9r3rgXcme80mM41\n7yN+IH2iyiKmUvwDIa/S4W5r4F9Vyk86rNdBceWgfJriX9EdlW5r/4GRp+nVUu0EBPGI4VWBX2Z+\nDX6EGGpqFIsRN16DHnfa18xskpk9aGa/NbNVqiSbR/Edl8npfYncMl9NDLNzUW76eqQLkbv/rWB5\nM4l2gZWarrcTw1BVnJveC/dlM1vEzE4gLlpZzdwGbnUd1VQudq90jku16AcBp2am9apsaql1Pqg3\nf5f0fmZa/0rAFu6ebRfabJ6vIu4kLZ5LtzXwgfSx0pN9D2KUhEbz29T5rUgT59qxbMfTRCfYoiYa\n/wMcWxDEtrJvNHPMQIvblMrsxvTdpXLf3YOooXyS0dfOMe3vY7w+dfq46IVK063xBfM+DawDfMxH\njypSsRMNBMXufg3xcDLQEzt7x3s0FhxxoF9PuiXR5HcPIJ6ccwGxox5IDHnzdaITyMpEj/bjiKe0\nXQTsUmVZJxMn05rjMRIntvmkJxjl5q1K1KJ8PX3eGzi1xrKmpWXt16vy7+cXMZTQo8Dne5yPE9L/\naT65JxFl0nyC3AMNiI41ZxBP4ruR9KAZokf2z0kD9+eW80rv9CrruYg0mD5Ra3E1aUzQTJqTiVqp\njTLTliBuyV0FHFSw3Kr7dZV8NL2OGstaKi3rwkz5/ArYsh/Kpk7ea50PliZuAT9a5buHp+9uCixC\ntIOePpayJnq/P0MM+VWZtidxB+64tL6JxBBbVzW5PU2d3+rsOzXPtW3YjjOIwHhy+rwwEbh8vV37\ndAvHTMvbRARkLxLDsUFUZL0XuJsaY0aPZX9nDNenbhwXue9MIY73a8b4Oq7GOs5K+boVODhNs5Tf\nF4EP1vjuLKLGv2qaXPoPpHX15Kmyenn3g2KiBuh6oo1ZZSD+Z9MON5s0AHuN7y8FfCn9PY+4iL4l\nM/+XxFN8TiI9dpE4id9XZXn/lfIxpc56r0ivwhM6ccvr9+kAO5n0pK0qaT9LXGSW7fUO0I+vdOKe\nT/S47mU+JhOB7Z218kK0Vbw+7b+XEb3bK0MgnU08PeoS4Dxg4yrLeAfRe3vLKvPXThec64iB9deu\nku6wdCxdm/bXS9K0UY9MTulr7tftWEedZc0kBvifnZbzun4pmzr5rlpuRBOBuVR5UAVxi/+0tN3X\nAG9rR1kTAcJ1Ke3lxKN1x6f1fSct52pgWrP7AU2c32psS6Pn2rFsx6LE8Gy3pTSzSYFMu/bpFo+Z\nsWzTrsSP6zkpzRFEp6z5wGHtPk4Zw/WpW8dFN1/ENeAF4kf7KYw88vk8YOsq3/kJ0fykEuO8TNwp\n+VCddS0NPAQs1evtLuur8tjHgWFmuxM9Ym8lfgl/yd0/k5n/c6L37URPnQTM7M3AWe6+ZMHyFiV2\nwm+7+1Fd2ATMbA7R23j3uolLyMxmEReOM939oB5nBzNbnqgZ27tuYhEp1Itz7bAys2uJQHtTd/9D\nm5et61OSxqb+I9FJfVK99DL4et2muBW3EL+Wp6bPJ+Tmb00EU9les5OAu4oW5tHG7BRg/9Tzt6PS\nQTYJ+Fan1zXA5ubee20rWntggYgk3T7XDrpqZWRmqxLXkAc7EBDr+rSgyggfNcdRl+ExcEGxuz/k\n7i8RvdHvcfdHKvMsHpG4CqMbqe9B7kEJOccBy6V0nXYocIu7X9aFdQ2qfguKD2J0r3URaV43z7UD\ny8y2Bx41s6Ixob8IjEvv7abr04IaHUddhkQ/PLyjVdMZ/ettBtEWKjv+5hbEE3LOS8OnvNrd/5H9\nkrvPM7PPAV8wswu9Q21KzGxNotPQzHpph4mZHUC0z12NaJu4D9GZbiGih/Q7fMGhbh4l2mLN63JW\nRzGzXYmOIa0MTyQiGd061w6B/YgHOVxSmWDxCOuvEB3LP+Tu323nCst6farGzJZiZLSMOb3Mi3TP\nwNUUwys765YUB8U3+oLD7rwduMvd7yQeBbtxlcUeT9RMHtHm7GadRPRy7frwc72S/lcT3P1QosnL\nhcBT7n6Eux+ekn04+x13nw88Ro9ritOg6+8H/ruX+RAZMt041w6644mh2VYxsyvM7Hqi89mzRGfd\nEzuwztJdn6oxs/OIET6WJcaYvsnMfp3axcsQG9Sa4ilE3vNB8XTS4PIZGwKXpqfl7EIuAKvweP74\nPsCVZnaNZ5721A5mdlj681PtXO4AmAVcYWbLASsSHRayY8guRNSI5M2lx0Gxuz8OvLmXeRAZNp0+\n1w4Dd/8T8JZura/E16dC7r5Xr/MgvTGQNcVEu+Er3P2hygQzG08Eyufn0h5L1CofC5xY63adx8D0\nOwNfNLPFq6VrlplNJmpJ9yzh7cKqHSNTR5KJjAxYnjWXPmg+ISLt16lzrTSv5NcnkQUM3JBsMpjM\n7GvAG919QmbadsSYj+u6+3259OcA73I96lJERES6YFBrimXwFHWM3Ae4zd3vM7M1zGxcZt5ZCohF\nRESkWxQUS8cVdYxMbbz3B36YJn3M3V/OfO3OXJAsIiIi0jEKiqUbijpGVjreXWpmmwCvNJ8ws+nA\n/Yx+MIuIiIhIRwzq6BMyWEZ1jHT3x83seGK4sweAz2XSz0uvB7uZSRERESkvdbQTERERkdJT8wkR\nERERKT0FxSIiIiJSegqKRURERKT0FBSLiIiISOkpKBYRERGR0lNQLCIiIiKlp6BYREREREpPQbGI\niIiIlJ6CYhEREREpPQXFIiIiIlJ6CopFREREpPQUFIuIiIhI6SkoFhEREZHSU1AsIiIiIqWnoFhE\nRERESk9BsYiIiIiUnoJiERERESk9BcUiIiIiUnoKikVERESk9BQUi4iIiEjpKSgWERERkdJTUCwi\nIiIipaegWERERERKT0GxiIiIiJSegmIRERERKT0FxSIiIiJSegqKRURERKT0FBSLiIiISOkpKBYR\nERGR0lNQLCIiIiKlp6BYREREREpPQbGIiIiIlJ6CYhEREREpPQXFIiIiIlJ6CopFREREpPQUFIuI\niIhI6SkoFhEREZHSU1AsIiIiIqWnoFhERERESk9BsYiIiIiUnoJiERERESk9BcUiIiIiUnoKikVE\nRESk9BQUi4iIiEjpKSgWERERkdJTUCwiIiIipaegWERERERKT0GxiIiIiJSegmIRERERKT0FxSIi\nIiJSegqKRURERKT0FBSLiIiISOkpKBYRERGR0lNQLCIiIiKlp6BYREREREpPQbGIiIiIlJ6CYhER\nEREpPQXFIiIiIlJ6CopFREREpPQUFIuIiIhI6SkoFhEREZHSU1AsIiIiIqWnoFhERERESk9BsYiI\niIiU3v8HE7w40Jz/pj8AAAAASUVORK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x10b97add0>"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"('mean = ', 33.333333333333336)\n",
"[ 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15.\n",
" 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30.\n",
" 31. 32. 33. 34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. 45.\n",
" 46. 47. 48. 49. 50. 51. 52. 53. 54. 55. 56. 57. 58. 59. 60.\n",
" 61. 62. 63. 64. 65. 66. 67. 68. 69. 70. 71. 72. 73. 74. 75.\n",
" 76. 77. 78. 79. 80. 81. 82. 83. 84. 85. 86. 87. 88. 89. 90.\n",
" 91. 92. 93. 94. 95. 96. 97. 98. 99.]\n"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAA1QAAAEvCAYAAABCG4B2AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl4VOX5//H3TZC4i0urFrRo3OuCiktdQqiQiaLiUkRc\n0bq0FkJ/6fdbrUCLCtoWiizqV611qwuyqWg0E1RCXKhLC4ILVlEQUVDcK4ss9++PM4FkSCDJLGeW\nz+u65grnnGfOuefMwyT3PJu5OyIiIiIiItJybcIOQEREREREJFspoRIREREREWklJVQiIiIiIiKt\npIRKRERERESklZRQiYiIiIiItJISKhERERERkVZSQiUiIiIiItJKSqhERERERERaSQmViEgamdk2\nYccgIiIiyaOESkQEMLMjzOzfZvaJma2LPeaa2auxxxuxYy+Z2S/NrMWfn2bWB/jazIYm/xWIiIhI\nGNqGHYCISCZw938DR5hZMVADPOPupfXLmFkhUAHcBpQCZ7XwMh2Br4AXEg5YREREMoJaqEREGuoW\n+1kZf8DdV7n7TcDXwBlmdnxLTuzuf3X3Xdz9mSTEKSIiIhlACZWISEMnxX5GGztoZm2Bwtjm7mmJ\nSERERDKWEioRkZjYhBHHAovcfV4TxboCWwKrUNc9ERGRvKcxVCIiG5xI8LlY3dhBMysA/gisBQa6\n+xIzOxm4CFgC7ATsAvze3efEnrM1MBLYCtgPOMfdFzdx/mOAqwiSNQfWATe5+4cJlt1cjF2AgcCe\nwN/d/X4z+znQHVgNHApMdfe/Nn3rGlyvCBgKdABmANcDA4ADCFr3fgj8yt0/MrMDgWsJxpc9DNwN\nXB3b3g54zd1Ht/Q1xZU9JVb2E6AA+A64w90X1CtjwDlAX2AxQdK8FfBLd/+mkXM26/635H0SEZEs\n5e566KGHHnq4Q5D4rCNIeuKPHQo8BbwLlBEkBvcD/wJ+UK/cZcDnwK6x7dHAT2L//gwY2cS1uwH/\njjvXPcD41pYlSAqaE+NkgkSjP0ECNQIYUK/8T2P35chm3scHCZKhk2PPmwp0q3f8bmAOQS+J8bE4\nLyBIVCfFrrcT8DHwVWteU2xfIXBf/bLAEcBS4JF65XYEngZeiXt+f2BYAve/2e+pHnrooYce2ftQ\nlz8RkQ3qxk+dZ2YPxx6PmNkUgj+u7wT2d/cqgj/UTwfOdvfP6p1jAsEf6IPMrCNQ4O5vmtkhwM4E\nf8w3ZjAwre5cse6HZQTJQGvL3tuMGA8FZrn7WmAPgsRqmbuPq1f+69jPoiZiX8/Mdga+c/dvY+cD\nuN/dp9cr9jJwMEFr0CfuvjJW1oDH3H1mLL62BMlZi15TvX13A2fElT2SoDXr1Vi8BcAjwAnA6e5e\n//35nsa7xjf3/rfkPRURkSylLn8iIoCZ7QIcBixw9zM2U7YPQfewYV6v21iMx34eTNDl7f9i25cS\ntNY83MRpdwF+YWYfArXuPpemJ73YbNkWxLg9QasQBOPDFrr7n+PKHxr72ZxuarsAf4/9uzuwHHg8\nrszOsZ8/Imihqrv2p+7+AIC7zyfoGtia14SZ9SZI2BqUdfe/mdlD7v5dbNf5sTj/z92XxJ67A/Bz\n4BIanxq/ue9VS95TERHJUmqhEhEJ1E2XPqMZZSsI/oC/s5FjB8Z+fuXuL7v7W7H1qy4Eqtz9oybO\nORpoD4wDXjezeWZ2ZAJlmxvjC+4+L5ZEdAEam9K9F/At8FoT8azn7u+4+8uxMUndgJfcfXVcsaNi\nP2fFyrYjGL9Ws5nTN+s1xX7+tqmy9ZIpgMtjP3c2s9vM7FaCcXKfAce5+yeNXKu571VL3lMREclS\naqESEQnUdffbZEIVS466AO82kRz1iP2s38XtLIIxQX9r6rzufo+ZvQacBvws9qg0s47uvqYlZVsZ\nY1eCL9mejXu9WwGnEnTFaxDHZnQmaImKP18BQaL1X2BmbPexBBNAPNfUyVrymmJlj9pE2foOJpik\n4jx3X7eZskDz36uWvKciIpK91EIlIhLoTtCisbkWqvYEY33eiz9gZm2AfsAygjFWdS4nmGHuiVi5\nK+o95ywz+8LMznH3ue5+o7t3J5jp7ofADq0o25oY6xLK+KTm58A2wAOx559vZls2cW/qa+p83Qi6\nGd5fr6WoqbL1teQ1NVm2EQXA/OYkU829/y15T0VEJPspoRKRvGdmPwb2Bj5y9w82U/xTgoklrJFj\nv4qd53KPTbVtZrsDJcA/3H1dbHKKDvWecxnBzHXxU6kvBN50989bUbZFMcacFDvHp3HlzyeYba86\n1rrUKzaJxOacRJCgvh63//ex8w2KK7vI3TeVALXkNX1KMJ16Y2Uxs4PM7JbY5kyCe9pYuZ3M7OZ6\nu5p7/1vynoqISJZTQiUiAj1jP1/aXEF3d+AGoNjMflS3P7Zu0zDgAnevPwlD3QQMM8ysLfA7YFS9\n428Av3X3F+udaw/gf4Er4y7frLItjdHMdgMOIq57Xr34X4ydcwAbJpxokpltQTAm6kuCFq66/cMI\nxjr1cPevY/u2BY6mYffDjbTkNcXKXt9I2S3M7BKCda+uju2+Htg7thZXXTkzszKC8Vetea9a8p6K\niEiWs+D3johIfol1E3uBYCa2vQi+YFoJvA886e6/38zz+xGsnbQA2Bb4Avizuy9spOxNBNN1fwHc\n7O4v1ztWCFxDMG34SoIuaAXAaHd/K+48zS7bkhhjU6dXA6e6+2txx0qAvwBvA/929zGbui+x5xQT\nTDAxANiNYGa77QhamK5392X1yu4F/BM4N25q9abO3azXFCt7IcGCvgsI1tdqCzzh7k/EletOkOx8\nRLAA7xYEdeN+r/dLsrn3v6Xvk4iIZLeMT6hi3xKOJvhldFcj0/liZmMJFpBcDvRz91mx/b8n+MW7\nDpgLXOLuq9IVu4hIPjKz64AhwIHu/k7Y8YiIiKRSRnf5i/XXv4VgIcSDgL5mdmBcmVOAfdx9X+AK\nYmu+mFkngoHgR7j7IQQJ2blpC15EJH+dRDAeTcmUiIjkvIxOqAj61b/n7gti65iMJ1gPpb7Tic1U\nFetG097MdgW+IejisXVs3MLWbDxAWEREkii2QPJmx0SJiIjkikxPqDoAi+ptf0TD2bGaLOPuXwB/\nBT4kmFHqK3dvbMFKERFJAjP7C8GEDAXAWWb2anyvAhERkVyT6QlVcwd4bTQ1rpkVAb8BOgE/ArY1\ns/OTF5qIiNTn7r9z993cvcDdt3P3o9z97bDjEhERSaW2YQewGYsJZkmqswdBC9SmynSM7SsBXqpb\n78PMpgDHAQ/Wf7KZZfasHCIiIiKSM9y90TXyJHtlegvVa8C+ZtbJzNoBfYCpcWWmEkyLi5kdS9C1\nbynwDnCsmW1lZgZ0Bxqdrtbd9dCjweOPf/xj6DHokXmPfKsX69ata7A9d65TVPQ0bdpUEXQgeJrf\n/a5qs8/L9Ue+1Qs9mvdQvdCjsYfkpoxOqNx9DdAfiBIkQ4+4+9tmdqWZXRkr8xTwvpm9B9wBXBXb\nPxu4nyApmxM75Z1pfgmSpRYsWBB2CJKB8qleuDuXXVaBu/P993DddVBS4qxbF2XdutJYqQhjxlTR\np4/z6acbPy9f5FO9kOZTvRDJH5ne5Q93fxp4Om7fHXHb/Zt47l8IFqQUEZEWmDw5ysSJsO++1Tz4\nYIROnWD48CgVFWVsGLZqFBREWLWqmkMOifDXv0JhYfC8U06p5uyzIyG+AhERkfTI+IRKJAz9+vUL\nOwTJQPlSL9ydkSOjfPvtKIYMqeC++0rp29e49NIaunQpxGxmg7I77riKysoIl1ziLFoUPG/EiArO\nOquUoMd1bsuXeiEto3ohkj8sn7plNMbMPN/vgYhIfZMmVXHBBcaqVRG23rqK+++3ZrU2jR9fxYUX\nGmvWtOx5IiL5wsxwTUqRczJ6DJVIWGpqasIOQTJQPtQLd2fEiCirVgXjpJYvjzBiRNVmx0S5O6NH\nR1mzpmXPywX5UC+k5VQvRPKHEioREVlv8uQos2c3HCc1d26EKVOqN/u8uXNb/jwREZFspy5/6vIn\nIrLehRdewyOPFHLooca22wb73J29917FPff8qcnnXXLJNbz/fiFmxtq18PLLcMghzqGHbvp5IiL5\nRF3+cpMSKiVUIiLrDRsGb70FDz2U2HnuuAMmTYJp05ITl4hILlBClZvU5U+kEer7Lo3J9XqxbBmM\nHg033JD4uS69FBYuhGeeSfxcmS7X64W0juqFSP5QQiUiIgDcdBP06QNFRYmfa4stgtaua64BdQIQ\nEZFcpi5/6vInIsKHH8Lhh8Obb8JuuyXnnOvWwdFHw9VXQ+/eyTmniEg2U5e/3KSESgmViAiXXgo/\n+lHQqpRM06bBr38dJGpbbJHcc4uIZBslVLlJXf5EGqG+79KYXK0Xb77pPPkk/O//Jv/cPXrAnnvC\nPfcE27n4BVau1gtJjOqFSP5QQiUiksfcnVNOqeB3v3N22CE117jpJrj+evjuO+eyyypyMqkSEZH8\npS5/6vInInnsxhurGDw4yoMPltG3byRl1+ndGwoLq5g6Nco995Rx9tmpu5aISKZSl7/cpIRKCZWI\n5Cl3p337Cr75ZhTHHFPBzJmjMEvN7/l585yDD65g7drUX0tEJFMpocpN6vIn0gj1fZfG5Fq9+Nvf\nonzzTRlgzJ0bYcqU6pRd6403orin51rplmv1QpJD9UIkfyihEhHJQ+7OjTdGgVIAli+PMGJEVUrG\nN7k7I0dGWbcu9dcSERFJN3X5U5c/EclDkyZV0aePsW7dhrFMW29dxf33W9LHN02aVMXFFxvLl6f+\nWiIimUxd/nJT27ADEBGR9Bs/voY2bQo54YSZ1A1lcneefHJV0pOcysoaunQpxGwmb7wBu+wCu+6a\nmmuJiIikm1qo1EIljaipqaGkpCTsMCTD5FK9uOkmWLQIbrstvdd95JFgTaqqqvReN5VyqV5I8qhe\nSGPUQpWbMn4MlZmVmdk8M3vXzK5uoszY2PHXzezw2L79zWxWvcfXZlae3uhFRDLTww9D377pv+6p\np8I//wmffZb+a4uIiKRCRrdQmVkB8A7QHVgMvAr0dfe365U5Bejv7qeY2THAGHc/Nu48bWLPP9rd\nF8UdUwuViOSVN9+EsjJYuBDahPC12nnnwYknwq9+lf5ri4iESS1UuSnTW6iOBt5z9wXuvhoYD/SK\nK3M6cB+Au78MtDezXePKdAfmxydTIiL5aPx46NMnnGQKgpaxhx8O59oiIiLJlukJVQegfhL0UWzf\n5sp0jCtzLvBQ0qOTnKX1Q6QxuVAv3INk5txzw4uhtDRoJVuUI19x5UK9kORTvRDJH5meUDW3L158\n0+n655lZO+A0YGKyghKRlqutrGRwJMLQkhIGRyLUVlaGHVJe+te/wAyOPDK8GAoL4cwzYcKE8GIQ\nERFJlkyfNn0xsEe97T0IWqA2VaZjbF+dk4F/uXuTQ6D79etHp06dAGjfvj2dO3dePzNP3TdM2ta2\ntlu/3ea774gOHEiP+fOD48Cg+fOZNWcOh/30p6HH19ztun2ZEk9rtm+7Dc49twSzcOM591z49a9r\nOPLIzLo/2tZ2srbr9mVKPNoOZ7vu3wsWLEByV6ZPStGWYFKKk4CPgVfY9KQUxwKj609KYWbjgafd\n/b4mrqFJKUSSqLaykuqxY2m7ahVrCgspLS+neuxYhlVXb1R2SCTCDbk0f3aGW7cO9twTqqvhoIPC\njWXtWujQAZ5/HvbdN9xYRETSRZNS5KY2YQewKe6+BugPRIG3gEfc/W0zu9LMroyVeQp438zeA+4A\nrqp7vpltQzAhxZS0By9Zrf43S9J8tZWVRAcOZFh1NUNnzGBYdTXR887jv9OnN1q+4Lvv0hxhYrK9\nXrzwAuy0U/jJFEBBAfTuHUyQke2yvV5IaqheiOSPTO/yh7s/DTwdt++OuO3+TTz3O2CX1EUnIvVV\njx3L8Fi3vjrDv/mGPjvsAF9/vVH5ta+9BuPHU7vttlSPG9egVau4Z890hZ03wlp7qil9+8Jll8Hg\nwcG4LhERkWyU0V3+0kFd/kSSZ2jXrgytrd1o/5U/+Qm7rFzZINm6tqiIsssvhzvvJLp4McNXrVp/\nbFBREZExY5RUJdHq1fCjH8Err8Bee4UdTcA9iGXqVDj00LCjERFJPXX5y00Z3eVPRLKIO2s++KDR\nQz/s2JHImDEMiUQY2rUrQyIRysaMofjqq6neZ58GyRTA8PnzmTZuXDqizhvPPOMUFWVOMgVBq1Sf\nPkHLmb7YEhGRbKWESqQR6vveCn/9K6Vt2jAo7i/2a4uK6DFgAMU9e3JDVRVDa2q4oapqfetT27hk\nqk7BypUpD7mlsrVeuDvl5RWce27mJS3BIr/OL35RkbVJVbbWC0kt1QuR/JHxY6hEJAtMmABjxlD8\n0kswZw5Dxo2jYOVK1m65JWWxZKopawoLG92/dsstUxVt3nn44SjvvQfbbFMNRMIOp4HDDoPvv4/y\nyCPQs2c1Z5+dWfGJiIhsjsZQaQyVSIs1mBp9+XJK33mH4tra4K/jVpwrOnBgw/FVW21F2fjxFJ9+\nejLDzkvuzv77V/Duu6M45pgKZs4chWXQDBDuzh57VLB4cWbGJyKSTBpDlZvUQiUiLdJYAjRo993h\no48obkVCVdd6tb5Vq7CQssWLKZ47F5RQJWzy5Cjvv18GGHPnRpgyJbNagSZPjvLFF5kbn4iIyOZo\nDJVII9T3vWmNTo3+yScJTSLRYHxVNEpxNAq33AKNzBgYpmyrF+7OyJFR1q4tBWD58ggjRlRlzFil\nuvhWrMjM+Jor2+qFpIfqhUj+UEIlIi2SlkkkOnSAu++G88+Hzz5L3nnzzOTJUebMCVp/AhtagTLB\n5MlR5s7N3PhERESaQ13+RBpRUlISdggZK22TSJx8Mpx3HrUnn0z1zjtnxKK/2VYvKitr2G23Qlau\nnMl++wX73J0nn1yVEd3qKitr6NKlELOZfPopLF0KBx+cOfE1V7bVC0kP1QuR/KFJKTQphUiL1D75\nJNHevRler0Xq2qKiYF2pJCc6tY8/TrRPHy36m4Du3WHAAOjVK+xINu3zz4M1sj77DJrI2UVEsp4m\npchN6vIn0gj1fW9acWEhkZ12YkhpacNFelOQ4FTfdltGLfqbbfXiu+/g5ZehW7ewI9m8nXeGAw+E\nF18MO5KWy7Z6IemheiGSP9TlT0Sazx2uvZbiUaMo7tMn5ZfLpkV/M9GMGXDEEbD99mFH0jyRCESj\n8LOfhR2JiIhI8zWrhcrM/mNm75vZHWb2czPbcTPlI2Z2lpltlZwwRdJLfd+b8PjjsHo19O6dlstl\n2qK/2VYvolEoKws7iuYrKwtizjbZVi8kPVQvRPJHc7v8zQA6AZcDE4BlZvaqmd1oZt3MrF1c+deA\n7YGHzOzUpEUrIuFZuxYGD4Zhw6BNenoLl5aXM6ioqMG+a4uK6DFgQFqun+2i0aDVJ1scfTR8+CF8\n8knYkYiIiDRfc/8qmgIsAn4A/By4A9gBuAZ4FvjSzKrM7Ldmdqi7f+7u97r7mUDfVAQukkrq+96I\n8eODvmNpnAyiuGdPImPGMCQSYegJJzCkXTvKBg4MbUKKbKoXCxbAl19C585hR9J8bdsG3f2qs2zW\n9GyqF5I+qhci+aO5Y6ieBe5z988JkqspAGa2J9A99vgZUBrb/2nsOYuAvZMcs4ik2+rV8Mc/wl13\ngaV3cqLinj03JFA33wzTpwfT1skmRaPQo0faGhOTpm4c1cUXhx2JiIhI8yRt2nQzM+AQNiRYxwHf\nApe7e1VSLpICmjZdpBnuvBMmToRp08KNY/ly2GcfeOqp7Gp6CcFZZ8GZZ8KFF4YdSct8+CEceWSw\nJlW2JYMiIpujadNzk9ahUkIl0qjaykqqx46l7YoVrHnlFUpvvJHiioqww4LRo4Pp6x59NOxIMtbq\n1fDDH8K8ebDrrmFH03IHHQT33w9duoQdiYhIcimhyk36/k+kEfne9722spLowIEMq65m6PPPM2zV\nKqK33UZtZWXYocGVVwaLK82alfZLZ0u9ePnlYJHcbEymYEO3v2yRLfVC0kv1QiR/JJRQmdn2ZjYs\nNtvf7nHHbjazPRILD8yszMzmmdm7ZnZ1E2XGxo6/bmaH19vf3swmmdnbZvaWmR2baDwi+aB67FiG\nz5/fYF+YC+o2sNVWcPXVcP31YUeSsbJtdr942ZZQiYhIfku0hep2YAmwAJgSG0dV5wbg5rh9LWJm\nBcAtQBlwENDXzA6MK3MKsI+77wtcAfxfvcNjgKfc/UDgUODt1sYi+SXf1w/J+AV1r7gCXnkl7a1U\n2VIvsj2hKi4O3tqvvw47kubJlnoh6aV6IZI/mjvLX1NWuPstAGa2FjgNmArg7l+Y2V3ARcB9rTz/\n0cB77r4gdo3xQC8aJkan153f3V+OtUrtCqwETnT3i2PH1gBZ8utZJFyZtqDuRrbaitpTT6U6EqHt\nQQexprCQ0vLy0KZTzyTLlsE778Bxx4UdSettvTX89Kfw3HPBxBoiIiKZLNEWqvpfV08CSuKOR4ET\nEjh/B4Kp1+t8FNu3uTIdgb2Az8zsHjP7t5n9zcy2TiAWySP53ve9tLycQR0a/lfLpAV1aysriT7z\nDMM++4yhM2YwrLqa6MCBKR/jlQ31Yto0KCmBdvHLrWeZsrLs6faXDfVC0k/1QiR/JNpC1cHMdnX3\npe7+tZk1+Frb3d3MVidw/uZOvxffrdAJXtsRQH93f9XMRhMsRPyH+Cf369ePTp06AdC+fXs6d+68\nvqm+7gNR2/m1XSdT4kn7ds+ecNBBXAgU7LILe+y2G2UDBrBum22oqakJPb5nxo5l+PvvE2wF3+QM\nnz+fC6+7jnXbbJOy68+ePTuU19uS7fvug9NPz5x4WrsdicBf/lJDnz7QrVv48Wxqu06mxKPtzNjO\nhs8Lbafn86GmpoYFCxYguSuhadPNrA/wW+B0d19iZre5+1VxZf7u7r9o5fmPBYa6e1ls+/fAOnf/\nc70ytwM17j4+tj0P6EqQZM10971i+08ArnH3U+OuoWnTReJ9+y3suSe89Rbsvvvmy6fZ0JIShs6Y\nsfH+rl0ZGvdHbj5xhw4d4Pnnoago7GgS4w577BF0+9tvv7CjERFJDk2bnpvaJPj8CcDnwLtmdiuw\nk5mtP6eZdSHoftdarwH7mlknM2sH9CE2RqueqQTjtOoSsK9iLWZLgEVmVveruDvwZgKxiOSP8eOh\npCQjkynIgjFeIZkzx9l66+xPpgDMNsz2py+9REQkkyWUUMWads4DZgK/As4Bvjaz2bGWopeAEQmc\nfw3Qn2As1lvAI+7+tpldaWZXxso8BbxvZu8BdwD1W8gGAA+a2esEs/zd2NpYJL/U5HErBwB33QWX\nXRZ2FE0qLS9nUFzWcO3ee6d8jFcm1wt357LLKigtzZ3kIxKBqqrgdWVyUpXJ9ULCo3ohkj8SHUOF\nu39pZicD5wOXAwcDexMkWb9w9xcTPP/TwNNx++6I2+7fxHNfB45K5PoieWfOHPj442BWgAxVN5vf\nkHHjKFi5krVz51L285/n9Sx/kydHmTULTjqpGsjiOdPr6d4dLr44yhZbwCmnVHP22bnxukREJLck\nNIYqF2gMlUic8nJo3z67Fs6dOBFuuw2mTw87klC4O8ccU8Grr46iS5cKXnllFAksAZgx3J3ttqvg\nu+9GccwxFcycmRuvS0Tyl8ZQ5aaEuvyZWbmZPW1m483sajM7NFmBiUgIVqyAhx6CSy8NO5KW6dUL\n3n4b5s0LO5JQTJ4cZc6cMsB4660IU6ZUhx1SUkyeHOX774PXNXdu7rwuERHJLYlOSjGEoG/JSuAD\nIGJmD5jZH8xsh4SjEwlJ3vZ9nzIFjjwSYssIZI127YIk8M47U3qZTKwX7s7IkVFWrSoFYPnyCCNG\nVGX0mKPmqHtdq1dn/uvKxHoh4VO9EMkfiSZUpwG93L2fu09w9xHufgEwBRhlZqdu5vkikkn+9je4\n/PKwo2idyy+Hf/wjaGXLI5MnR5k7N2jFCeRGa06uvi4REck9KR1DZWb/C7wZm4kvI2kMlUjMf/4D\nJ54IixYFLT7Z6OST4bzz4MILw44kbS655BrefbeQmTON44+HNm2C1p29917FPff8KezwWu2SS67h\n/fcLMTNmzw7WpNppp+x/XSKS3zSGKjelfFIKM7vL3TN2/mUlVCIxV18N69bBiFavdBC+xx+Hv/wF\nXkxoctGsU1kJf/1rsAhuLrruOvjuu+CtFRHJZkqoclOik1J0NLORZnaNmTW1lKSyFck6+dT3vbay\nksGlpQy9+WYGz5xJbWVl2CG1Xs+esHAhzJ2bktNnar2oqYFu3cKOInW6dQteY6bK1Hoh4VK9EMkf\nia5DNQHYF9gZuNHM/gk8DrwMfAwcDhyQ4DVEJEVqKyuJDhzI8Pnzgx0vvsiggQMBsnNNp7ZtgwWJ\n77gDbrkl7GjSZvp0GD067ChS55hjgkkcv/4adtB0RyIikmES6vJnZne7+6VmdgDBwr4XAXvUK7IO\nONfdJyUWZuqoy5/ks8GRCMOqNx7kPyQS4YaqqhAiSoKPPoJDD4UPP4Rttw07mpT76qtgfNHnn2fv\n0Lfm6N4dfvMbOFVTHYlIFlOXv9yU6Cx/X5nZEe4+z92HAJ2AnwIDgP8Bjs7kZEok37VdtarR/QUr\nV6Y5kiTq2BGKi2H8+LAjSYvaWjj22NxOpgBKSvJ23WYREclwiSZU1wCnmdkdscTK3f1ld7/V3Ue5\n+7+TEaRIuuVL3/c1hYWN7l+75ZZpjiS5ajt3ZvBvf8vQkhIGRyJJGxeWifVi+vTcHj9Vp1u3zE2o\nMrFeSPhUL0TyR0JjqNz9e+A6M9se6JickEQkXUrLyxlUW8vwei1S1xYVUTZgQIhRJaa2spLoAw8w\n/JtvYMYMAAbFxohl5biwzaipgdtuCzuK1DvqKHjvPfjyS9hxx7CjERER2SDRMVTbA78jaOka5+6f\n1Dt2MzDK3RclHGUKaQyV5LWPP6Z2v/2YdtxxFHz/PWu33JIeAwZkdeKRk+PCmvDFF9CpUzB+aost\nwo4m9SKJFsYlAAAgAElEQVQRuOoq6NUr7EhERFpHY6hyU6Kz/N0OvAR8D0wxs+PqZSc3AHeaWW9l\nLCIZavJkis86i+L77w87kqTJyXFhTZgxA447Lj+SKdgwjkoJlYiIZJJEx1CtcPdb3P1O4C7gtLoD\n7v5FbN9FCV5DJO3ypu/7hAlwzjlhR5FUqRwXlmn1Il/GT9XJ1HFUmVYvJDOoXojkj0QTqvpf+U4C\nSuKOR4ETEryGiKTC4sXw5pvQo0fYkSRVaXk5g4oarjN+bVERPbJ4XFhT8i2hOvJIWLAAli0LOxIR\nEZENEh1D9RhwpbsvjW3f6u6/jitzm7tflViYqaMxVJK3xoyBWbPg3nvDjiTpaisrmTZuHAX//S9r\n//lPevzjHxT37Rt2WEn12Wew775BctE20c7bWeSUU4K1m886K+xIRERaTmOoclOiv4YfBp4ws9Pd\nfQnQWAVpvP+NiIRrwgQYNCjsKFKiuGfPDRNr9O0bTA2XY2bMgBNOyK9kCjZ0+1NCJSIimSLRLn8T\ngM+Bd83sVmAnM1t/TjPrgqZTlyyU833fP/oI5s2D7t3DjiT1LrwQ/vGPpJwqk+rF9OnBJA35JhMX\n+M2keiGZQ/VCJH8klFDF+sqdB8wEfgWcA3xtZrPNbB7BDIAjErmGmZWZ2Twze9fMrm6izNjY8dfN\n7PB6+xeY2Rwzm2VmryQSh0hOmTQpmCqtXbuwI0m90lL44AN4992wI0mqfBs/Vefww4PvAz79NOxI\nREREAgmNoVp/ErMC4HzgcuBgoIAgybre3V9M8LzvAN2BxcCrQF93f7temVOA/u5+ipkdA4xx92Nj\nxz4AjozNONjUNTSGSvLPccfBH/4AZWVhR5Iev/kNtG8PQ4eGHUlSLFkCBx4YjJ8qKAg7mvQ77bSg\n4THHJqgUkTygMVS5KdEufwC4+1p3v9/dT3T3Hd19e3ePJJJMxRwNvOfuC9x9NTAeiF+B5HTgvlgc\nLwPtzWzXesdVaUXq+/BD+M9/4KSTwo4kfS64AB54AHLky5MZM6C4OD+TKQha5tSbSkREMkVSEqoU\n6gAsqrf9UWxfc8s48IyZvWZml6csSsk5Od33fdIkOOOM/FkNFoL5trfYAmbOTOg0mVIv8rW7X51M\nW48qU+qFZBbVC5H80az5oczsP7Gy02KPZ929yWmzzCwCbAM87e4rEoivuV8nN9UKdYK7f2xmPwCm\nmdk8d38+vlC/fv3o1KkTAO3bt6dz586UxEZ7130gaju/tutkSjxJ3b7rLkpGj86ceNK1feGF1Pzp\nT1BR0erzzZ49OyNez/TpJfzylxl2f9O4feKJJSxdCpMn17DzzuHHUydT7o+2M2M7Uz4vtB3udt2/\nFyxYgOSuZo2hMrO/Ab+ot8uBf7MhwXrR3b+vV35n4DSC7nl/d/cnWxWc2bHAUHcvi23/Hljn7n+u\nV+Z2oMbdx8e25wFd69bGqlfuj8B/3f2vcfs1hkryx4IFcNRR8PHH+dVCBbBwYdBStXgxFGbvag4f\nfwwHH+wsW2a0aRN2NOE54wzo0wfOPdcxU89uEckOGkOVm5r763gKQbe6HwA/B+4AdgCuAZ4FvjSz\nKjP7rZkd6u6fu/u97n4mkMhqmq8B+5pZJzNrB/QBpsaVmQpcBOsTsK/cfamZbW1m28X2bwOUAnMT\niEUk++Vjd786P/4xHHwwPPVU2JEk5LnnnO22q8Asv78I6tYtuBeXXVaBvhQTEZEwNTeheha4L5Yo\nTXH3q9x9P6ATcBnwONCZYIr02Wa2xMweNLM/AXu3Njh3XwP0B6LAW8Aj7v62mV1pZlfGyjwFvG9m\n7xEkelfFnr4b8LyZzQZeBp509+rWxiL5pX5TfS6oraxkcCTC0OuuY/CsWdRWVoYdUjgSXJMqE+rF\nPfdEWboUpkzJ74+zbt3gySejTJwY/r3IhHohmUf1QiR/NGsMVaw73x8a2f8hcDdwtwV9Lg4hmOK8\nO9AT+JZgKvVWc/engafj9t0Rt92/kee9T5DkieS12spKogMHMnz+/GDHv/7FoIEDASju2TPEyELw\n859DRQV88QXstFPY0bSYu/Pii1FWrRrFiBEVnHVWad52d/vJT5zPPouydq3uhYiIhCsp61BlM42h\nklw3OBJhWPXG3+APiUS4oaoqhIjCVXvCCVR/8QVtf/hD1hQWUlpenjWJ5e23V/GrXxkQYeutq7j/\nfuPssyNhhxWKSZOqOPdcY+1a3QsRyR4aQ5Wb8nhIs0h+aLtqVaP7C1auTHMk4autrCQ6fz7D3n6b\noTNmMKy6mujAgVnRBdLdGTkySjAcFJYvjzBiRFVejh+quxdr1+peiIhI+DabUJlZOzNrVtdAkVyR\nS33f1zQxo93aLbdMcyThqx47luFLljTYN3z+fKaNG9es54dZLyZPjrJwYRkbVokw5s6NhD5+KAyT\nJ0eZOzdz7kUufV5I8qheiOSP5iRKpwE3m9njBBNTvJbimEQkiUrLyxn0738zfNmy9fuuLSqibMCA\nEKMKRza31lVW1lBQUEjnzjPZZptgn7vz5JOr8q6rW2VlDV26FAIzeemlYDb8wsL8vBciIhK+5q5D\ntT3QG7iQYOr0fwD/cPfFqQ0v9TSGSvJB7eGHMw0o2GEH1m65JT0GDMiacUPJlM3jyRYuhKOPhiVL\nQHMvbNC7N5x2Glx0UdiRiIhsnsZQ5abmzvL3DfB34O9m1olg3adnzewj4D5gsrsvT1WQIpKAr76i\neP58ij/5hPVNG3mqtLycQfPnb5jxkOxpraupgZISJVPxunUL7o0SKhERCUuLJ6Vw9wXufr27HwD8\nETgBeMfM7jWzbkmPUCQEOdX3vbIy+Es8z5MpCKaJj4wZw5BIhKF77MGQvfaibMyYZrfWhVkvpk8P\n3kZpqKQkuDdhyqnPC0ka1QuR/JHQZBPu/iLwopltCZwO/NbM7gLGE4y3+k8SYhSRRDz2GJxxRthR\nZIzinj2DBGrOnKCv2Mknhx1Ss9TUwDXXhB1F5jnwQFi+HBYsgE6dwo5GRETyUdLXoTKzXYHzCMZb\nfQ/cDzzs7l8m9UJJojFUktNWroRdd4X33oMf/CDsaDKLOxxyCNxxBxx/fNjRbNIHH8Bxx8HHH6vL\nX2P69Any4n79wo5ERGTTNIYqNyV9HSp3X+ruN7v7EcAVQBEwy8wmm1kvTcEukkbPPgudOyuZaowZ\n9O0LDz0UdiSbpfFTm1Y3jkpERCQMKV3Y193nuPtvCZKqvwN9gffNbKyZHZ7Ka4skImf6vqu736b1\n7QsTJ8Lq1c0qHla90PipTasbRxVWZ4Oc+byQpFK9EMkfKU2o6rj7Wnd/yt3PBQ4B5gK/Tce1RfLW\n2rUwdSr06hV2JJlr772Dx7PPhh1Jk9yD1pdumvKnSfvvD99/H4yjEhERSbekj6HKNhpDJTnrhRfg\n17+G118PO5LMNmYM/PvfcN99YUfSqPnz4cQTYfFidfnblL59oUcPuPTSsCMREWmaxlDlpoRaqMzs\nN2b2lZndmqyARCRJHnsMzjwz7Cgy3znnBC15K1aEHUmj6lqnlExtmsZRiYhIWBLt8tcFWA70TkIs\nIhkj6/u+u2v8VHPtvjsceWSwXtdmhFEvNH6qecIcR5X1nxeSEqoXIvkj0YTqW+Bg4KdJiEVEkuXN\nN2HNGjjssLAjyQ7nnZeRs/1p/FTz7bsvrFsH778fdiQiIpJvEhpDZWaDgOfcfWbyQkovjaGSnHTD\nDfD55zB6dNiRZIevvoIf/xgWLoT27cOOZr133w2SqUWL1OWvOc4/P7hfl10WdiQiIo3TGKrclGgL\n1Z+B35rZBckIRkSSROOnWqZ9e/jZz+DRR8OOpIHp0zV+qiW6dQvumYiISDolmlBdCpwJ3G9mS8xs\nvJldYWb7JCE2kdBkdd/3Dz8MHscfH3Yk2aUZi/ymu17ULegrzVNSEtyzdHc6yOrPC0kZ1QuR/JFo\nQtUXuBgYBMwGTgNuB/5jZgvN7F4zS6j3v5mVmdk8M3vXzK5uoszY2PHX4xcMNrMCM5tlZk8kEodI\n1nj8cTj1VGjbNuxIskptQQGDp09n6HHHMTgSobYZk1SkkvuGFippnqIiaNMm6CopIiKSLomOofoH\ncLm7r4xttwOOBU6KPY4GvnT3XVt5/gLgHaA7sBh4Fejr7m/XK3MK0N/dTzGzY4Ax7n5sveMVwJHA\ndu5+eiPX0BgqyQm1lZVUjx1L25dfZs1ee1E6bBjFPXuGHVZWqK2sJDpwIMPnz1+/b1BREZExY0K7\nh++8E6yrtHChuvy1xIUXBut2XXFF2JGIiGxMY6hyU6ItVDcC95rZaDM7xt2/d/dad/+ju58A7ESQ\nYLXW0cB77r7A3VcD44FecWVOB+4DcPeXgfZmtiuAmXUETgHuAlR5JWfVJQTDqqsZ+vXXDJs9m+jA\ngaG3smSL6rFjGyRTAMPnz2fauHEhRaTxU62lcVQiIpJuCSVU7v62u58LjAQ2auZx9/+6+wcJXKID\nsKje9kexfc0tczPwv8C6BGKQPJRtfd8zMSHIJm1XrWp0f8HKlQ2201kvpk93jZ9qhbpxVOvWpa/n\nQbZ9Xkh6qF6I5I+kDLJw948IEplka+5vxPjvcM3MTgU+dfdZZlayqSf369ePTp06AdC+fXs6d+5M\nSewvmboPRG3n13adTIlnc9t1CUFd9CWxn4uWLKGmpib0+DJ9e01hYbBNoCT2c/7y5Q3u3+zZs9MS\nT3FxV6ZOreCMM06npsZCvz/ZtO0OW2zRld69K+jf/3TMUn//6mTC69d25myn6/NC25m9XffvBQsW\nILkr0TFU2wO/I2jpGufun9Q7djMwyt0XNfX8Zpz/WGCou5fFtn8PrHP3P9crcztQ4+7jY9vzCP4e\nKgcuBNYAWwLbA5Pd/aK4a2gMlWS9wZEIw6qrN9o/JBLhhqqqECLKLo2Nobq2qIiykMZQjR5dRUVF\nlIkTyzj77Ejar5/tSkqq+Oc/ozz4oO6fiGQWjaHKTW0SfP7twBJgATDFrEFv/xuAm+P2tdRrwL5m\n1ik24UUfYGpcmanARbA+AfvK3Ze4+7Xuvoe77wWcS7AA8UWI5KDS8nIG7bZbg33XFhXRY8CAkCLK\nLsU9exIZM4YhkQhDi4sZstVWlPXvH0oy5e6MGRPFfRQjRlShL3xaxt1ZtCjKqlW6fyIikh6JJlQr\n3P0Wd7+TYOKH0+oOuPsXsX2tTmLcfQ3QH4gCbwGPuPvbZnalmV0ZK/MU8L6ZvQfcAVzV1OlaG4fk\nn/pN9dmguGdPIgcdxJADDmBo164MiURCa13JVsU9e3JDVRVDZ8zghv/5H4oXLtyoTDrqxeTJURYt\nKgOMuXMjTJmyccujNG3y5CiffJLe+5dtnxeSHqoXIvkj0TFU9UdsTwL+SMMWpChwJ7FZ+FrD3Z8G\nno7bd0fcdv/NnGMGMKO1MYhkvDVrKH79dYpnzYI99gg7mux3/vlQUgIjR0JBQdou6+6MHBll7dpR\nACxfHmHEiArOOquUxBr780Pd/VuxQvdPRETSJ9EWqg51U5S7+9dAYf2DscFJqxO8hkja1Q0qzRrP\nPw+dOimZSpb994cOHeC55xrsTnW9mDw5yuuvB60rAbVStcTkyVHmzk3//cu6zwtJC9ULkfyRaAvV\nw8ATZna6uy+h8bWeChvZJyLJ9NhjcOaZYUeRWy64AB54IFhdN00qK2vYbbdCVq+eyT77BPvcnSef\nXKXJFZqhsrKGLl0KMZvJsmWweDEceqjun4iIpFais/wZ8BRwAnA/sDNwnruvix3vAgx394z9TaZZ\n/qQxNfWmys547kHr1FNPwU9+EnY0uWPJEjjwwOCv8q23BtJTL7p2hWuugZNPTullct7XX0PHjvDp\np7DVVqm9VlZ9XkjaqF5IYzTLX25KqMtfLBM5D5gJ/Ao4B/jazGbHpi9/CRiRcJQi0rRZs6BdOzjo\noLAjyS277QZHHQVPPJG2S377LfzrX1BcnLZL5qwddoBDDw16w4qIiKRSomOocPcvgZOBfsCLBOs+\n7Q0sBLq5+zOJXkMk3bLqW8VHHw26+2nQffJdcAE8+OD6zVTXixkzghxum21Sepm80aMHTJuW+utk\n1eeFpI3qhUj+SDihAnD3te5+v7uf6O47uvv27h5x9xeTcX4R2YTHHoMzzgg7itx05plBlrNsWVou\nN20alJam5VJ5obQ0PQmViIjkt4QTKjPbzszOM7Orzayfme2ZjMBEwpQ164e8917wx/6xx4YdSW7a\nbrtgMNPEiUDq68W0aWmdAyPnHX00LFgAS5em9jpZ83khaaV6IZI/EkqozKwz8B7wAHATcDfBIruP\nm9neSYhPRDblscfg9NOhTVIam6Uxcd3+UuWjj4IJFA4/POWXyhtt2wbLiT37bNiRiIhILkt0lr8a\nYDowC9gJOBz4GfAT4DvgbHfP6AVUNMufZLUTToBBgzQlXCqtXg0/+hG88grstVfKLnPvvcFEjRMm\npOwSeenWW+G11+Cee8KOREREs/zlqkS/1n7X3a9z96nufq+7D3T3Q4D9gQeBSWa2b+JhishGli6F\nN96An/0s7Ehy2xZbQO/e8NBDKb2MuvulRt3EFPreTEREUqVZCZWZlZvZRWa2e9yhdY2Vd/d33f2X\nwBXAdQnGKJJ2WdH3fepUKCuDQq2dnWq1nTox+Kab6HfYYQyORKitrEzq+detU0KVKvvuCwUF8Pbb\nqbtGVnxeSNqpXojkj7bNLNcbOB7AzN4EpsUez5rZNe7+p8ae5O7jzaxnUiIVkYYefRQuvjjsKHJe\nbWUl0TvvZPh331EzZw4lc+YwaP58AIp7Jufjbc6cYN2kTp2Scjqpx2xDK5WWahMRkVRo1hgqMysH\nhgNjgK7AsUABsDpW5G7gIeCf7r467rlPuPtpyQw6mTSGSrLSN99Ax47BTAbbbx92NDltcCTCsOqN\nh4IOiUS4oaoqKdcYMSKYje7WW5NyOokzYQLcfz88+WTYkYhIvtMYqtzU3BaqycDF7j4YgqnSgW5A\nj9jjythjhZm9CrwOLAeKY/8WkSSoraykeuxY2i5axJp27Sh9/vmktZJI49quWtXo/oKVK5N2jWnT\n4KqrknY6iXPSSXD55fD999CuXdjRiIhIrmnWGCp3X0yQQNVtfxubiGKAux8A/Bi4DJgKdCAYO3Um\n8BhQnvSoRVIsE/u+11ZWEh04kGHV1Qx9+22Gff450YEDkz6eRxpaU2+MWk29/Wu33DIp51+5EmbO\nhG7dNl9WWmfnnYOxVP/8Z2rOn4mfFxI+1QuR/NHsWf7c/ZtNHFvk7ne7e19339fdt3L3A9x9hLuv\nSU6oIvmteuxYhsfG7tQZPn8+08aNCymi/FBaXs6goqIG+64tKqLHgAFJOf8LL8AhhwRjqCR16sZR\niYiIJFtKVgM1s+5m9pNUnFskHUpKSsIOYSPp6HomGyvu2ZPImDEMiUSoOf54hrRtS9nQoUnraqnZ\n/dIjlQlVJn5eSPhUL0TyR3PHULXUu8ClZrYrcLW7f52i64jkjTVNTI+erK5n0rTinj03JFCXXBKs\nAZYk1dWgRsbUO/54ePNN+PJL2HHHsKMREZFcklALlZltZ2YjzazSzG43sz5mto27L3T3PwJ/Av6a\nnFBF0icT+76XlpczaO+9G+xLZtcz2byampogobr77qSsFPvpp/DBB3DMMYnHJptWWAgnnADPPZf8\nc2fi54WET/VCJH8k2uXvTuA0YFfgfOBh4FMze9jMyoBPgYTmdDazMjObZ2bvmtnVTZQZGzv+upkd\nHtu3pZm9bGazzewtM7spkThEwlbcsyeR889nyI47MrRrV4ZEIpSNGaNZ/tLtxBOD6eJefTXhUz3z\njNO1K2yxRRLiks2q6/anpTJERCSZmrUOVZNPNnvA3S+I/XsLgmnSzyNYCHjbWLGou5/cyvMXAO8A\n3YHFwKtAX3d/u16ZU4D+7n6KmR0DjHH3Y2PHtnb35WbWFngB+B93fyHuGlqHSrLHhRcGzRn9+4cd\nSX678Ub48EO4/fZWn8Ld2W+/CsrLRzFggJYkSYe5c6FXL6dbtwruumsUZrrvIpJeWocqNyXaQvVd\n3T/cfbW7P+vuvwB2A/oQTJneO4HzHw285+4LYgsGjwd6xZU5HbgvFsPLQPvY2C3cfXmsTDuChYi/\nSCAWkXCtXBmsTHr22WFHIhddFKwWu3z55ss2YdKkKPPng/vGiwZLahx8MHzxRZRHHoEpU3TfRUQk\nORJNqL43s/bxO919ubtPdPdb3P2/CZy/A7Co3vZHsX2bK9MRghYuM5sNLAWmu/tbCcQieSQj+75X\nV8Nhh8Huu4cdSd5aXy86dgxaCh99tFXncXeGD4/iPoqHHqpSF7S0cdq2jfLdd6MYMSJ59z0jPy8k\ndKoXIvkj0Vn+RgH/Z2YXu/v3yQgoTnN/28U3nTqAu68FOpvZDkDUzErcvSb+yf369aNTp04AtG/f\nns6dO6+f7rTuA1Hb+bVdJ1PiKSkpgQkTqDnsMKipyYx48nB79uzZG7YvvZSam26CDh1afL5ly1by\n1ltlwAxmz96dKVOqOfvsSOivL9e3r79+BN98sztgzJ0b4frrR9C169G5+Xmh7dC3G3xeZEA82g5n\nu+7fCxYsQHJXQmOoAMxsAHAZMBiocfdvkxFY7NzHAkPdvSy2/Xtgnbv/uV6Z22PXHR/bngd0dfel\ncecaAqxw95Fx+zWGSjLfypWw224wb17wU8K3ahV06BBMTrHXXs1+mrvz059W8PLLowi+C3KOOaaC\nmTM1pieVdN9FJBNoDFVuapPIk83s/wFjgEOAx4HPzewlM7vBzErMrF2C8b0G7GtmnWLn6gNMjSsz\nFbgoFs+xwFfuvtTMdqnrjmhmWwE9gFkJxiMSjmgUDj9cyVQmKSyE886D++5r0dMmT44yd24ZGxrW\ng9YSjelJLd13ERFJlUS7/PUEjge+AQ4DugEnAYNijxVm9nd3L2/Nyd19jZn1B6IEk0r83d3fNrMr\nY8fvcPenzOwUM3uPYJKMS2JP3x24z8zaECSO/3D3Z1v9SiWv1NTrVpcRJkyAc84JO4q8t1G9uPRS\nOOMM+MMfoE3zvp+qrKyhY8dCvvhiJj/5SbDP3XnyyVWcfXYk+UELENz3Ll0KMZvJ4sXwzTdwwAHJ\nue8Z93khGUH1QiR/JJpQveXuM2P/fhN4CMDM9iJIrE4C9kvkAu7+NPB03L474rY3mkPa3ecCRyRy\nbZGMsGIFVFbCqFFhRyLxOnemtk0bqo8+mrbbbsuawkJKy8s3uTbYPff8iV69oHdvuOCCNMaa5+65\n50/r//3hh3DEEfDss9A20d+CIiKS9xJdh+p2d/9lEuNJO42hkoz36KMwbhw891zYkUic2spKov36\nMXzZsvX7BhUVEdnEgsvLlwc9NxcsgJ12SlOgspEjjoCbb4auXcOORETyicZQ5aaExlABz8QmpRCR\nVJk4Ud39MlT12LENkimA4fPnM23cuCafM20adOmiZCpsvXrB44+HHYWIiOSChBIqd58E7GlmVycp\nHpGMUH+601CtWAFPPQVnnRV2JMLG9aLtqlWNlitYubLJczz+ePDHvISrLqFKRgeFjPm8kIyieiGS\nPxKd5e8i4DfATWb2gZn9zczONbMfJic8kTz39NNBc8YP9V8qE60pLGx0/9ott2x8/1p48kklVJng\nsMOC9+PNN8OOREREsl2iXf5+Afw/YASwlGCGvYeAJWY218xGm1mXBK8hknYZMzPThAnB7AWSEeLr\nRWl5OYOKihrsu7aoiB4DGu8JPXMm7L47xNYRlxCZwemnJ6fbX8Z8XkhGUb0QyR+Jzm/0IfB/7r4W\nwMx2ALqyYYa/cuBcQIvniLRAbWUl1TffTNuaGtYsXUppx46bnDlOwlH3ngwZN46C999n7VdfUbaJ\nCSnU3S+z9OoFv/89DBoUdiQiIpLNEp3lrwvwe4IFcye6+ztxx3cDfujucxKKMoU0y580Jsz1Q2or\nK4kOHMjw+fPX79vczHGSHpusF8uXw557wquvwl57bXTYHfbfHx5+GI48MrVxSvOsXg277gpvvAE/\n+lHrz6P1hqQxqhfSGM3yl5sSnZTiNXc/G3gC+EEjx5dkcjIlkomqx45tkEzB5meOkwyw9dbQrx/c\ndlujh+fNC+YYOUKr42WMLbaAk0+GqVPDjkRERLJZomOoAHD31939hbptM+thZsebmTJwyUphfqvY\nmpnjJD02Wy+uugruuSdorYrz+OPBmB19KmaWZEyfrlYIaYzqhUj+SHSWvwPMrLHVVN4FjgImm9lP\nE7mGSL5p6cxxkkH23huOOw4efHCjQxo/lZnKyuDFF+Hbb8OOREREslWiLVTTgU/NbJaZjTKz08xs\nB3df4O6jgZ8D/RMPUyS9wlw/pLS8nEFxSdWmZo6T9GlWvRgwAMaNa7DA0ZIlQZc/fWGdebbfPsiB\nq6pafw6tNySNUb0QyR+JzvLXC7gA+BnBelS/Adaa2WzgJeBTYJ8EryGSV4r33hu22YYhXbtSsGoV\na7fckrIBAzQhRbbo3h2+/x5qa6FrVwCeeAIiEWjXLuTYpFF13f60QoGIiLRGQrP8NThRsJhvCUFy\n1Q3YF1gOXOHuDyXlIimgWf4k4/zud9CmDfzpT2FHIq11yy0wYwZMnAjAqafC+edD374hxyWNWrwY\nDjkEli4NJqoQEUkVzfKXm5KWUG10YrO9gJFAhbsvTMlFkkAJlWSUNWtgjz1g+nQ44ICwo5HW+vZb\n+PGP4fXX+e+Oe7D77s6iRUb79mEHJk056ij485+hWzdH8ymJSKooocpNSZnlrzHu/gHwC+APqbqG\nSKqE1ve9qgo6dVIylaGaXS+22w4uuABuv52qKme77SrYYQd9cZPJevWCRx91LrusgpZ+yaaxMtIY\n1QuR/JHoLH8dzGykmVWY2a7xx939K2BNItcQySv33guXXBJ2FJIM/ftTe+ut3HX5ERywZCJXHN6F\n2iUzbqIAACAASURBVMrKsKOSJvTqBePHR5k4EaZMqQ47HBERySIJdfkzsxeB/YCdge+Bx4AHgGfc\nfaWZ7Qg87O5lyQg2FdTlTzLGsmWwzz6wcCHssEPY0UiCaisrqerdmxtXrFi/79qiIsrGjNEEIxlo\n3Tpn660rWLVqFMccU8HMmaPU9U9Ekk5d/nJTol3+/uPuPwAOBW4DTgKmAt+a2cfAJ8CLCV5DJD88\n9BD07KlkKkdUjx3bIJkCuHH+fKaNGxdSRLIpU6ZEWbeuDDDmzo2olUpERJqt2QmVmTU2qGOFmR3o\n7m+4ewWwO3AqcBMwBejn7jckJ1SR9Aml7/s996i7X4ZrSb0oWLmy0f1t4pIsCZ+7M3JklNWrSwFY\nvjzCiBFVzR5LpbEy0hjVC5H80ZIWqsmN7Ptf4Aozu9nM9nf3Ne7+lLv/wd37u/v4ZARpZmVmNs/M\n3jWzq5soMzZ2/HUzOzy2bw8zm25mb5rZG2ZWnox4RP5/e3ceV1WZP3D88xUQFTQVK1NEkyy1KZcx\nLZvATMGlqaamSWdymfapXLKZSnGh0rI0LG0sm9S0PZdfCyRQJtJi+1hmy6TGVGZq6iRpLni/vz/O\nuXiBy+qFe4Hv+/XiBec55zzngftw7vneZwu49eth927o3z/YJTEB8t9dv/hN/2HvvhouiSnPihVZ\nbNjgtE45rJXKGGNMxVV4DJWIHATaqOouP/vaA21V9Z0Alw8RCQO+AgYAW4EPgOGq+oXPMUOAm1V1\niIj0AR5S1bNFpDXQWlXXi0g08BFwSbFzbQyVCb7x46FZM7jrrmCXxATIb0+9nNM2r+YZz57CtFGN\nWrD33Av4v9eXBbFkpri//vUOtmyJRETYtg127YLTT1c6djzI4sW2HpwxJnBsDFXdVJmAygN8CMwC\n3vAXWFUHETkHmOad2EJE7gBQ1Zk+xzwKrFHV593tL4FEVd1eLK8XgXmqutonzQIqE1yHDkFsLKxb\nB/HxwS6NCZDu3eGqyzPY+eY8wr75hiO7djFwyRKbkCLE7d3rLAW3aRMcf3ywS2OMqWssoKqbKtPl\nT4GHgeOBBW5XugdEZIiIRFVP8QBoC3zns/29m1beMbG+B4hIB6AH8F7AS2jqnBrt+56eDl26WDBV\nC1S0Xnh7cN48cSh3Z2aSumEDd0dFkdCyZfUW0ByzZs3g97+HZ5+t+Dk2Vsb4Y/XCmPojvBLHfqWq\nS92f54tIA+C3ODP73SwiDYF1wOvAO6p6OEBlrGjzUfFov/A8t7vfcmCcqpYY2DB69Gg6dOgAQPPm\nzenevTv9+vUDjt4Qbbt+bXtV5/VyMzL4V2oqYV99RWxcHEkZGXiiokLi97dt/9vr16+v0PEvvdSP\nUaMgN9dn/8SJ5IwfD/fdFzK/j2373x49uh+33QZnnlmx471Cpfy2HRrbFb1f2Hbd3vb+nJeXh6m7\nKtPlr6OqbiljfyRwLtAfGAzsAt4AslT131UuoMjZQKpPl7+JgEdV7/M55lEgxzsJhm+XPxGJANKB\nVar6oJ/8rcufqXG5GRlkjRvHjM2bC9NS4uNJtjWKar3Dh6FtW3j7bejUyWfHwYPOOmMrV8JZZwWt\nfKZ8R45Ahw6QkQFnnhns0hhj6hLr8lc3NajogWUFU+7+g8B24ESgC84kEvcAM46lgDjjtjqJSAe3\nFewKnLWufL0MjITCAOx/bjAlwELgc3/BlDHBkj13bpFgCmCGrVFUJ6xaBaeeWiyYAoiMhNtvh7tt\nJYlQFxYGI0fCkiXBLokxxpjaoMIBVVncac2zgA3A1Tjd7xYDZ6rqkGPJW1ULgJuBLOBz4HlV/UJE\nrheR691jXgW2iMgmYAFwo3v6ucCVwPki8m/3a9CxlMfUD75N9dUh/OBBv+mlrV1kQkNF6sUTT8Do\n0aXsvOYa+PBD+HeVG+1NDRk1Cp56ymlxLE913y9M7WT1wpj6ozJjqIoQkcY4rULjAO+ivzuBR4D5\nqrrj2IvnUNVVwKpiaQuKbd/s57y3CFDQaEwgFURG+k0/0qhRDZfEBNJPP8Hq1c4azX41agS33ea0\nUq1cWaNlM5Vz6qnOPDGZmc4kFcYYY0xpKjyGqvAEkZNwWoyuB7xTVn0OzAGecrv+1Ro2hsoEQ256\nOlmXXcaMQ4cK0ybFxzPIxlDVavPmwbvvwtNPl3HQ/v3Ok3pWlg3QCXGPPQbZ2bB8ebBLYoypK2wM\nVd1U4RYqEekJ3AL8CYhwk7OBNFW15eSNqYSEJk3ghBOYcvrphB04wJFGjRg0ZowFU7XcE0/AzPLW\ngW3ShNxBg8hOSiK8c2cKIiNJGjvWXvsQ9Kc/OQ2Ku3ZBTEywS2OMMSZUVabL3/s43ecOAEuBOar6\nebWUypggy8nJKZz6tFo88AAJU6eScO211XcNE3Bl1YsNG2D7dujfv+w8cjMyyFq7lhnbtzsnACnu\nBCUWVIWW5s1h8GB47jm46abSj6v2+4WplaxeGFN/VGZ8UQMgDxiqqtdaMGVMFX3xBXz0EYwYEeyS\nmAB64gll5EhnhriyZM+dy4xvvimSZjM8hq7Ro52WR+sabowxpjSVCai2AhOB4SLytog8JSKjRaRd\nWSe505gbU6tU66eKaWnwt785ExSYWqW0enH4sDJ//gRGjiz/odtmeKxdBgyArVuVyy6bUGpQZa0Q\nxh+rF8bUH5UJqH5S1edV9TpVPReYDIQBM0XkTRF5REQuE5EWxc6zlTyM8dq+3RnhfuON5R9rao2p\nU7M4dAg2bix/OKnN8Fi7hIVB795ZZGTAypU2XNgYY0xJlQmoJvpuqGqeqi5U1b+o6nnAP4G2wEIR\neUNE7heR24BTAlheY2pEta0fMn8+XHEFHH989eRvqpW/eqGqPPpoFh5PGrNmZZbbNSxp7FhS4uOL\npE1q1YqBY8YEsqgmQFSVvLwsDh1K4/77/b++tt6Q8cfqhTH1R4UnpVDVzHL2fwZ8BswVkTCgFzD1\n2IpnTB2yfz888gi8+WawS2ICaM6cLP73v0GAsGFDMitXZnPZZcmlHu+deGLKvHnODI+HDjHo889J\nOOecGiqxqYwVK7L4+mvn9V2/vvzX1xhjTP1T6XWoKpW5SDSwXVWjqu0ix8jWoTI15tFH4dVX4eWX\ng10SEyCqyvHHT2DXrjRAAKVPnwmsW5eGSCWWGbnxRqdvmU1MEVJUlXPOmcB77x19fXv3nsC771by\n9TXGGJetQ1U3VWtABSAin6pqyK5eaQGVqREeD3Tp4qwUmpgY7NKYAPnnPzO5+WYBjrZYNGmSydKl\nUrlWjF27nPrx+uu22G8IWb48k1GjhP37j76WkZGZPP10JV9fY4xx2YcxtVtpwXBl1qGqKnt6NLVO\noNYPyc3IIHvuXMK3bqXgxx9Jys8n4diLZ4KkeL2YOzeHuLhITj55XWGaqpKefrByD9wxMXDnnTB2\nLKxZA/aGGxIyMnLo1SsSEef13b0bNm1SXnml6Otr6w0Zf6xemNLYB/m1U1nBcLUHVKq6p7qvYUwo\nys3IIGvcOGa4i7YCpIwfDyK2gGsdsHUr7Nw5k6++CtAcI9ddBwsWwAsvOBOXmKBbvHhmkW1V6N0b\nLrooSAUyxhgTkqq9y1+osy5/prpMTk5menbJaZanJCdzd2aZc7yYWuDWW52enHPmBDDTN98k99JL\nye7WjfCCAgoiI0kaO9YC8BDy4oswfTp88IE1JBpjKs8dQxXsYpgqKGv8W010+TOmXrIFXOuuXbtg\n8WL49NPA5pu7dy9ZBw4wY/XqwrQUt4XTgqrQcNFFkJICr70GSUnBLo0xxphQUJl1qIypNwKxfogt\n4Fr3eOvFQw/BZZdBbGxg88+eO5cZv/xSJG3G5s28ZrP/hYwGDWDiRJgx42iarTdk/LF6YUz9YQGV\nMdUk6brrSAkLK5I2KT7eFnCt5fbuddZnvu22wOdtrZq1w7Bh8O238NZbwS6JMcaYUGBd/ozxIxAz\nMyV88QWcfTZToqOdBVwbNWLQmDHWdasW69evH/ffDwMHQqdOgc/fWjVrh/BwuP12uPdeyMgIzP3C\n1D1WL0xVqOoxT61elTw6dOjAjh07CAsLIyoqisGDB/Pwww8TFRWyS8mGFGuhMqY6bNsGc+aQsHQp\nd2dmkpqTw92ZmRZM1XL79ytz5jhdvqpD0tixpMTHF0mb1KaNtWqGoNGjYf1658sGmBtjAkFVueaa\nCcd0T6lqHiJCeno6+fn5fPzxx3z44YdMnz69yDEFBQVVLlddVysCKhEZJCJfisjXInJ7KcfMdfd/\nIiI9fNIXich2EdlQcyU2td0x932fPBmuvho6dgxIeUzwqSpnnXU5vXppta29mzB0KMkPPcSU5GRS\nExOZ0rMngw4fJqFv3+q5oKmyRo1gwgS45x5l6NDLLagyJdgYKlNZK1ZksWwZrFxZcobgmsyjTZs2\nDB48mM8++4wGDRowf/58OnXqxGmnnQbAv/71Lzp16kRMTAwXX3wx27ZtKzx348aNDBw4kJiYGFq3\nbs29994LgMfjYebMmZxyyim0atWKK664gj17nJWVDhw4wJVXXkmrVq1o0aIFvXv3ZseOHQA88cQT\nxMfH06xZMzp27MgzzzxT5d+rOoV8QCUiYcDDwCCgKzBcRLoUO2YIcIqqdgKuAx7x2b3YPdeYmrF+\nvdMPKCUl2CUxAfTCC1l8/jn07Vv1N6mKSBg69Gir5kcfkTB8OFx7rbMIkgkp118Pq1ZlsWbNsT28\nGGOMqjJ7dhb5+WnMmpVZpQ9pjjUP7/Hfffcdr776Kj16OO0TL730Eh988AGff/45b7zxBpMmTWLZ\nsmVs27aN9u3bM2zYMADy8/MZMGAAQ4YMYdu2bWzatIkLLrgAgHnz5vHyyy+Tm5vLtm3baNGiBTfd\ndBMAS5YsYe/evXz//ffs3r2bBQsW0LhxY/bt28e4cePIzMxk7969rFu3ju7du1f671IjVDWkv4Bz\ngEyf7TuAO4od8yhwhc/2l0Brn+0OwIZS8ldjAsbjUT3/fNX584NdEhNAHo9HO3QYr+DRPn3Gq8fj\nqbmL//qrarduqo89VnPXNBXi8Xg0NjZI9cIYUyuV9ty5bNkqbdIkU51Pz1YpeH+uzNfR85o0WaXL\nl2dWuFzt27fX6Ohobd68ubZv315vuukm/fXXX1VEdM2aNYXHXXXVVXr77bcXbv/yyy8aERGheXl5\n+swzz2jPnj395t+lSxddvXp14fYPP/ygERERWlBQoIsWLdK+ffvqp59+WuScX375RZs3b64rVqzQ\n/fv3V/h3qS7ua+c3Xgn5FiqgLfCdz/b3blpljzGm2uRmZDA5OZnUM85g8vvvk9vWql9d8thjWeTl\nDQKEDRuSa7Y1olEjeO45mDSJ3PnznXrWrx+Tk5PJzciouXKYElasyGL3bqderF9fw/XCGFNnqNuy\ntH+/d3G7ZPr0ycTj0QqHUh6P0qdPFuDksX9/cqVaqUSEl156iT179pCXl8fDDz9MI3dCpHbt2hUe\n522V8oqKiiImJoatW7fy/fff07GUoQ55eXn84Q9/oEWLFrRo0YKuXbsSHh7Ojh07GDFiBMnJyQwb\nNoy2bdty++23U1BQQFRUFM8//zyPPvoobdq04cILL+Srr76q/B+4BtSGgKqi7ZXFpzOx/jGmyirT\n9z03I4OsceOYnp1N6saNTN+3j6wJE+xht47weJQ77vC+SeVU+k0qIDp3Jnf4cLJuucWpZ2vXMj07\nm6xx46yeBUnRB6AcDh5MZubMGq4XJqTZGCpTUStWZLFhg/PhjKPyH94FIo/S+M4Y2KZNG/Ly8gq3\n9+3bx65du4iNjaVdu3Zs2bLFbx5xcXFkZmayZ8+ewq/9+/dz0kknER4eztSpU9m4cSPvvPMO6enp\nLF26FICkpCSys7P58ccf6dy5M9dee+0x/z7VoTZMm74VaOez3Q6nBaqsY2LdtAoZPXo0HTp0AKB5\n8+Z07969cLpT7w3RtuvXtldFjl+YmsqTmzc72+55MzZvZsq8eXjc6UaD/fvYdtW3589/n59/9r5J\nrQcofJOKiYmssfJkf/UVAw8dIgdw9sLAzZv51513Fs4eGQp/r/qyvWJFFuvXnwSsxSF8/PFJ3HXX\nLKZNuy3o5bPt4G+vX78+pMpj28HZ9v7sG4QUl5GRQ69ekYisK0xTVdLTD3LZZcmlnhfoPCpi+PDh\nDB8+nD//+c907tyZSZMmcfbZZxMXF0eLFi2YMGECDz30EDfccAOHDh3iiy++oHfv3txwww1MmjSJ\nJUuWEBcXx86dO1m3bh0XXXQROTk5xMTE0LVrV5o2bUpERARhYWHs2LGDdevWMWDAABo3bkxUVBRh\nxdb3DBUS6p+miUg48BVwAfAD8D4wXFW/8DlmCHCzqg4RkbOBB1X1bJ/9HYBXVPUMP/lrqP8NTGhL\n7deP1LVrS6YnJpLqc0M1tc/u3RAbewennRbJcccd/YROVenY8SCLF8+ssbJYPQstf/3rHWzZEln4\nye3hw/DBB8rAgQfJyKi5emGMqV1EJCRbsk8++WQWLlxI//79i6SHhYXx9ddfF+nKt2DBAmbNmsWe\nPXs499xzC7vkgTPL37hx4/j444+JjIzklltu4bbbbkNVefDBB1mwYAE//PADJ5xwAsOGDWP69Ok8\n99xzpKam8v333xMdHc2wYcNIS0tjx44dDBs2jPXr1yMi9OjRg/nz59O5c+ca/dt4ua+d3wW+Qj6g\nAhCRwcCDQBiwUFXvFZHrAVR1gXuMdybAfcBfVfVjN/1ZIBGIAXYAU1V1sU/eFlCZYzJ54ECmv/56\nifQpycncnZkZhBKZQLnqKoiKgnnzgl0SmJyczPTskl03rJ6FjuXLYcoUZ6LPUtZoNsbUc6EaUJny\nlRVQNajpwlSFqq5S1dNU9RRVvddNW+ANptztm9393bzBlJs+XFXbqGqkqrbzDaaMKU1OJT7xT2rS\nhJRiK4lPio+3xVhruddfh9Wr4Z57jqZVpl4Emi36G7q89eKyy6BzZ5gxI7jlMaEhmPcLY0zNqg1j\nqIwJXS+9RMInn8DjjzPliScIO3CAI40aMWjMmMJxLaZ2UVV+/VW4/np45BFo2jTYJXJ469OUefOc\nerZ/P4O++oqE1q2DXDLjJQIPPwzdu8Pll8MZZzj1yXdAtzHGmLqnVnT5q07W5c9U2X//C717w0sv\nwdlnl3+8CXmqyjXXTKB58zR+/FF4+ulgl6gcL74If/sb5OSAu4K9Cb7HHoNFi+Ctt5Trr5/A44+n\nWVBljAGsy19tVlaXP2uhMqYqDh+GYcPg73+3YKoOWbEii+efh7CwbDZtCtysSNXmkktgzx5yzzuP\n7C5dCBehIDKSpLFjrYU0iK65Bp5+Gq69NosVK2DIkOyAzrJljDEmtNSKMVTG1DR/fd8LF+/t14/J\nnTqRW1AAt95a84Uz1UJVuf/+LPbtS+P44zNp1arkJ4ihOCYi94QTyPJ4mJ6ba+tTBUnxetGgATz2\nmPLkk1nk56fV/LplJiSE4v3CGFM9LKAypgKKLN67di3T//tfsn76idxVq4JdNBMgL7yQxUcfOetN\nbdsWmMUQa0L23LnM2LWrSNqMzZt5LRSmJqzHNmzIIizMqU+BWlzTGGNMaLKAyhg/vAvzeWXPncsM\nd/Ferxl5efbQWkd4PMqYMVl4PEkA7N+f7LdVoXi9CAXhBw/6TQ87cKCGS1J/Fa8Xqsrs2VkcOnS0\nPs2caa1U9U0o3i+MMdXDAipjKsAeWuu2P/4xi127nNYER+1pVSgoZcGjI//7Xw2XxHitWJHFhg1F\n69PHHyfz/POhX5+MMcZUngVUxvhRvO97QSmfLB9p1KgGSmOqg7e1YO5cWL06hz593iExMbXwq1ev\ndaSnrylyTiiOifC7PlVsLAN/+AFSU8l95ZWjY/+Sk21sVTUoXi8yMnLo1etofUpISKVly3Xcccca\njhxxjrHWqrovFO8XxlTV3/72N6ZPnx6QvL799luaNm1aeB/s168fCxcuDEjeAEOGDOHJJ58MWH4V\nYbP8GVOevDySvvySlJiYImNVJsXHM8gWVa2VvNOjX3BBGrNmCZ9+OpP27YNdqqopsT6Vdx20Xr3I\n7dePrNmzmbFvX+HxKW7XVZsFsPosXjyzRNrBgzB4MIwZAw8/rFx7rU2nbowJHR06dGDHjh2Eh4cT\nFhZG165dGTlyJNdddx0iwiOPPFLhfBYtWkT//v1LPSYuLo78/PzCbRGp8r0wNTWVzZs3FwmgXn31\n1SrldSwsoDLGj8K+719/DQMGkDBlCpx8csmHVnsorZVWrMjiuedg+fJs3n47ucLBVKiOiUgYOtRv\nXcyOjWXGl18WSZuxeTNT5s2zuhtAFakXkZHOsmH9+sHw4VmsWmXTqdd1oXq/MKEpNyOD7LlzCT94\nsMrLXxxLHiJCeno6/fv3Jz8/n5ycHMaNG8d7773HokWLKlyG8tbZKigoIDy8DoYfqlqvv5w/gTGO\ntenpmpKUpNMSEzWlb19d27Kl6uOPB7tYJoA8Ho/+5jfjFTzatet49Xg8wS5StZmWmKgKJb6mJSYG\nu2j11rZtHo2MdOpfnz51u/4ZY0ry99y5Nj1dJ8XHF7lPT4qP17Xp6RXO91jz6NChg65evbpI2vvv\nv68NGjTQzz77TEeNGqWTJ09WVdWdO3fq0KFDtXnz5tqyZUs977zz1OPx6JVXXqkNGjTQxo0ba3R0\ntM6aNUu/+eYbFRFduHChxsXFaWJioubl5amI6JEjR1RVtV+/fjpx4kTt3bu3NmvWTC+++GLdvXu3\nqqquWbNGY2Nji5Srffv2+vrrr+uqVau0YcOGGhERodHR0dq9e3dVVU1MTNTH3Wc3j8ejd999t7Zv\n315POOEEHTlypP7888+qqoVlW7JkicbFxWmrVq10xowZpf6N3NfObzxhY6iMcflOjd5v7Vqmv/MO\nWRER5LZuHeyimQAaOzaLzz5zJgzIy6vcxBO1bUxEqRNWHDoEFFtbzcZXVVll6sVbb2XRoIFT/z7+\nOJkXXrCJKuqq2na/MMHjdybhSi5/EYg8ijvrrLOIjY3lzTffLNIt74EHHqBdu3b89NNP7Nixg3vv\nvRcR4cknnyQuLo709HTy8/P5+9//XphXbm4uX375JVlZWSVasFSVpUuXsnjxYrZt20Z4eDhjx44t\ntVzesgwaNIhJkyYxbNgw8vPz+fe//11kP8DixYtZsmQJOTk5bNmyhV9++YWbb765SH5vv/02//nP\nf1i9ejV33XUXXxbr2VERFlAZ4/J7M9q+3aZGr8V8b9r79sHo0crjj2cBZU+PXlf4nbDihBMY+Pnn\n5F54IVljxhxdW80WBK526k6n/uuvTv07fDiZq6/OZMuWkg8Xxpj6o9SZhLOyQKRCX+HZ/j+cOdbZ\niNu0acPu3buBo/emhg0bsm3bNvLy8ggLC+Pcc88tN5/U1FQaN25MpJ8P+kSEkSNH0rVrV5o0acLd\nd9/NCy+8UKF7oR7tcebX008/za233kqHDh2Iiori3nvv5bnnnsPj8RQeM23aNCIjIznzzDPp1q0b\nn3zySbnXLc4CKmNc4b/8UvhzP590mxq9dlJ34glV5dNPoVcvyMs72jrgqNz06LVtTETC0KEkP/QQ\nU5KTSU1MZEpyMoMWLSJhyxay169nxjffFDneFgSumorWC3/TqR86lEz37tmsWOGk+NZbU7vVtvuF\nCZ5SexMkJ/vptO3/qyApyX8exzgb8datW2nZsmWRtH/84x+ccsopJCUlER8fz3333VduPu3atavw\n/ri4OA4fPsxPP/1UtUL72LZtG+19BkrHxcVRUFDA9u3bC9Na+/REatKkCft8JnKqqDo4KsyY8pUY\nuPnb31Lw4Yd+j7Wp0WunFSuyWLYMwsOzWbkymbQ0eOONHFQjEVlXeJyqkp5+sM5ODlDahBXhp5wC\nW7eWSA87cCAgg6NNSc506iXrX7NmB7nttmRWr4bf/c6ptzZhhTH1R9LYsaRs3lykl0xlZxIORB7F\nffDBB2zdupXzzjuP9957rzA9Ojqa2bNnM3v2bDZu3Ej//v3p3bs3559/fqmz9ZU3i9+3335b5OeI\niAhatWpFVFQU+/fvL9x35MgRdu7cWeF827RpQ15eXpG8w8PDOfHEE4tc81hZQGXqHe9YKd+bTsqa\nNbT9y19IefNNZmzeTA5OK5VNjR76VLXEDVVVmTkzi/z8NJ56agIffZRE587CiBElp7OujJycnDrz\nqXNpn4h+//XXZI0ZU6T1yqZaL1tF64W/6dS9fv4Zrr1WueaaLH79NY1ZsyZw6aVJfuu2TbVeO9Sl\n+4WpXqUuf1GJe24g8vC2jO/du5fc3FzGjx/PiBEjOP3004u0mqenp9O5c2fi4+Np1qwZYWFhNGjg\ndHo78cQT2bx5c5nTpvu77lNPPcXIkSNp3749U6dO5fLLL0dEOPXUUzlw4ACvvvoqAwcO5J577uGg\nTxfJ1q1b8/rrr5d6bxw+fDj33XcfgwcPplWrVoVjrrzlLevvUBnW5c/UO37HSh0+zLZt2wq7Rz3R\nrZvTPeqhh+whMoT56x71449wySVZfPSRt2tVMhs32sD/4kpbELjhr79aV8AgOO44uPzyLI4ccert\nhx8mk5ZWtN5ad0Bj6q6EoUO5OzOT1Jwc7s7MrNKzx7Hm8fvf/55mzZoRFxfHvffey6233srixYuB\nohM9bNq0iYEDB9K0aVP69u3LTTfdRGJiIgATJ05k+vTptGjRgrS0tMJzi/NN846hGj16NCeddBKH\nDh1i7ty5ABx33HHMnz+fa665htjYWKKjo4t0D7z88ssBiImJoVevXiWuc9VVVzFixAgSEhLo2LEj\nTZo0YZ7P+1l5Zasoqe83ZhHR+v43qKv8dlvq04fU3r1JLfbACJCamEiqzcoUsvx9+rR8eSZXXZXF\n4sWD6NkzmVmz4NlnlcjICWzfnoYTUCl9+kxg3TpbRLW43IwMXvP5NHPgmDG8MWsWqWvXljg2NmG2\nzAAAEuhJREFU9ayzSH3/fesOWE1UlXPOmcB77x2ttxERExg4MI1Jk4Rzzy1a3/11B7TWK2NCX3nr\nNJnQ5b52fm+y1uXP1El+u/WtWwdHjlDQvLnfc2ysVOjyfjL/+ONHgyLvjGn5+Wlcf/0EVJO44QZh\n9uwsxo71P/GEjUkpyt/4qmz3U8HijnzyCbnt25OVn8+MPXsK0327A1qwVXX+JqyIiEgmNjabESOS\niY1Vdu506ru/7oD+/keMMcbUjJDv8icig0TkSxH5WkRuL+WYue7+T0SkR2XONbVbaevo+O3Wl5/P\na336kPTYYyW7OsXHM9BnrJStH3LsSvsErqxP5krb551gYuXKbAoK4M034dJLs3j/fecBdO/eZObM\nyWbGDHjrrRx69XqHxMTUwq9evdaRnr7mmH+n+lAv/HYFjI9n4PLlZLduXSSYArc74F13kbtyZeE6\nbv6mYa/La14Fol44E1aUrLeHDq3hP/+BHj2y+Oorp75/9FEyd9yRjc/EpEX+R4qryv9ceftM+erD\n/cIY4yptxd9Q+ALCgE1AByACWA90KXbMEOBV9+c+wLsVPdc9rtQVkctawb60fVU5J1SuFez81qan\na0pSkk5NSNCUpKTC1b3LSi+xKviJJ+ragQN1WmSk34lFpyUmFp47OTlZpyYk6OTk5BIriaelpQX1\nb1HT+QX6Wh6PR6+6anyJ/aWll7XvyBGP9uw5XsGjLVuO1+bNPdq9u0fbtHHSnJfWo336+M83kObM\nmVOt+YcK7//HtMTEIv8f0xIT/f9fRUdrSoMGfvd5zy/xvxofr2vT0wv/v6clJhb5//aWoyr7alp1\n1wuPx6nfvvW9WbPxGhXl0QEDVB94wKPduo33+39Qlf+5iuwrq6yV3Rfq97Oq5leV95FQ/31r8lqh\nnl9Vr1XWc6cJbe5r5z9mKW1HKHwB5wCZPtt3AHcUO+ZR4Aqf7S+B1hU5V0sJqNamp+ukpCS94sS2\nOsnPm7i/fVU5J1SuFQr5lfbA9c9p00qmn3yyrn3oIU0580z/D3CdO2tK376lPtx5lfXQ3717n4A9\ngAT6gaa6HpACea1ly1Zp06bjdfnyzAqle/dFR4/XO+/M1PnzVW+8UTUxUTU6epVCpoJqw4ar9LHH\nMnXZslXapElmkZe3SZNVfvMNpGnTplVr/qEuJSmp1P+rab/7nf9gq0EDTWnWzO++q3/zmzIDraru\nC2SAVpFzEtu3D2h+xfctW7ZKYxreqb1I0kQStRdJGtMwVZ98MlP/7/9Uzz0zVXvR093XU8/5zZ06\na5bq7GnpOrJLT+3foK1e061niWtd3a1y+0LhvSJUrlWRc06PahrS5QvVa4V6flW9lpcFVLVXbQ6o\n/gj8y2f7SmBesWNeAfr6bL8O/Ba4rLxz1U9AVZU3cb8P/QF4KKiJawU9v44dde1zz2lKQoLfB64/\nNW7sN31ydLROa9XK775piYl+rzXRLYdXWQ/9DRv2KfWhv6yAoCpBRLDzC/S1jhzxaO/ezqflPXqM\n188+8+i776q+9ppHTz3VSW/XbryOG+fRYcNU+/VTPe00j4aFOfuio8fr1Vd79MEHVbOzj7ZO+bZE\njR59myYkTNXExGmFXwkJU3X06NtLlDOQ6ntAVdb/VanBVv/+Oq1HD7/7rvCTpqCT27TRlLg4//vO\nOktT+vTxu+/q7t2Dcj+bVs3320su+KOObNSiyL6RjVroJRf8UXNeeUVHRB5XZN9fwo/ToWdN1VGN\ni+Y3MjJek85J1yuGpOsNLYruu6VtvD7xcLq+sDBdb+tQ8jUO+ntFCF0rVOpFff7b1ra/hS8LqGqv\n2hxQlRsUuQHVuT7bxxRQlfZQcHNEK705wv8D/KVEVPqcqu6ryrXGVCE/55wYv/vGRsTomIiWfvdd\nRpjf9L83aKx/b9DI7747CNNJ4r8cw6Wh/3K3TNTBrfy/VoNbJeuFF6qe3+sVPSe8vSaSoOeEt9fz\ne72iF16oeuGFqkOHerR5c+dBvXnz8Tp0qKdY+sgi6WWdU7H8Kn6Ov31Dhnh06FDVIUP8pxffd9xx\n43XwYI8OHqw6eLDqoEFOmndfUpJHk5JUBw5UHTDA6T7k7UaUmOjRhATV3/3OCW7Ao1FR47VnT492\n7656xhmqnTt7NDLS2RcRMV5jYjzarJlqo0aqcLRFCVZpmzaZetZZqqefvkobNHDSIyJW6ahRmfr0\n06qrV6umpR1tcfJtaQpWS1RpRo0aFZTrhpK16f67A1Yl2BrZooXf9GmnnqrTOnb0v++443RadLTf\nfaUGaA0bakop3YAnR0drStOmfvf9KTzc/zktW2qKT9lH+e6LidGUGP/3zlLza9VKU0r5gKi8fX9v\n6r/1749hpdyLm7XSCdH+87uxQSu9Qfzv+0Mp7xU3hrXSv4X5P+em8FZ6U3jl38tuCoH3zUDkNyrE\nyxeK1wr1/KpyLd+eMaqqFlDVXmUFVCE9bbqInA2kquogd3si4FHV+3yOeRTIUdXn3O0vgUTg5PLO\nddND9w9gjDHGGGOMCQlaS6dN/xDoJCIdgB+AK4DhxY55GbgZeM4NwP6nqttFZFcFzi31D2OMMcYY\nY4wx5QnpgEpVC0TkZiALZ9a+har6hYhc7+5foKqvisgQEdkE7AP+Wta5wflNjDHGGGOMMXVRSHf5\nM8YYY4wxxphQFvIL+1YnW/jXAIhIOxFZIyIbReQzERnrprcUkddE5D8iki0izYNdVlOzRCRMRP4t\nIq+421Yn6jkRaS4iy0XkCxH5XET6WL0wIjLRfQ/ZICLPiEik1Yv6R0QWich2Edngk1ZqPXDrzdfu\ns2hScEptAqHeBlQiEgY8DAwCugLDRaRLcEtlguQwcIuqng6cDdzk1oU7gNdU9VRgtbtt6pdxwOeA\ntynf6oR5CGcx+S7AmThrH1q9qMfcsdrXAj1V9QycYQbDsHpRHy3Gea705bceiEhXnPH9Xd1z5otI\nvX0ur+3q8wvXG9ikqnmqehh4Drg4yGUyQaCqP6rqevfnX4AvgLbARcAS97AlwCXBKaEJBhGJBYYA\njwPeyWusTtRjInIccJ6qLgJnrK6q/ozVi/puL84Hc01EJBxogjMZltWLekZV3wT2FEsurR5cDDyr\nqodVNQ/YhPNsamqh+hxQtQW+89n+3k0z9Zj7SWMP4D3gRFXd7u7aDpwYpGKZ4JgD/APw+KRZnajf\nTgZ2ishiEflYRP4lIlFYvajXVHU38ADwLU4g9T9VfQ2rF8ZRWj1og/Ps6WXPobVYfQ6obDYOU4SI\nRAMrgHGqmu+7z7ugW1AKZmqciFwI7FDVf3O0daoIqxP1UjjQE5ivqj1xZpYt0o3L6kX9IyLxwHig\nA85DcrSIXOl7jNULAxWqB1ZHaqn6HFBtBdr5bLej6CcFph4RkQicYOpJVX3RTd4uIq3d/ScBO4JV\nPlPj+gIXicg3wLNAfxF5EqsT9d33wPeq+oG7vRwnwPrR6kW91gt4R1V3qWoBsBI4B6sXxlHa+0bx\n59BYN83UQvU5oCpcNFhEGuIMDHw5yGUyQSAiAiwEPlfVB312vQyMcn8eBbxY/FxTN6nqJFVtp6on\n4wwuf0NVR2B1ol5T1R+B70TkVDdpALAReAWrF/XZl8DZItLYfT8ZgDOZjdULA6W/b7wMDBORhiJy\nMtAJeD8I5TMBUK/XoRKRwcCDHF34994gF8kEgYj8DsgFPuVoc/tEnBvbC0AckAf8SVX/F4wymuAR\nkUTgVlW9SERaYnWiXhORbjgTlTQENuMsJh+G1Yt6TURuw3lY9gAfA9cATbF6Ua+IyLNAItAKZ7zU\nVOAlSqkHIjIJuAoowBlukBWEYpsAqNcBlTHGGGOMMcYci/rc5c8YY4wxxhhjjokFVMYYY4wxxhhT\nRRZQGWOMMcYYY0wVWUBljDHGGGOMMVVkAZUxxhhjjDHGVJEFVMYYY4wxxhhTRRZQGWOMMcYYY0wV\nWUBljDHGGGOMMVUUHuwCGGNMXSEiLYHzgI5ABPBf4HVV3RXUgtVCItIQuAC4FEhU1VODXKQiQr18\nxhhjao61UBljzDESkXgReRrIBtoB7wNvA52AjSIyQ0QCdr8VkR4iMjRQ+YVoGSYDjwJXE5of/oV6\n+YwxxtQQUdVgl8EYY2otEfkzzoN1KjBHi91URaQb8A6wQlVHBuiam4HvVLVfIPIL1TKISAywE/iX\nql5fXdepqlAvnzHGmJphLVTGGFNFIjIDWApcpappxYMpAFX9BPgncKWIDAnANdsDJwO5x5pXLShD\novv9tWq+TlWFevmMMcbUAAuojDGmCkTkemAiMFNVl5dz+Cvu90C0Yngf4nMCkFeol2EAoMDqar5O\nVYV6+YwxxtQAC6iMMaaSRKQH8BDwDXBXBU7Z7n7vE4DLJwKHgHUByCvUyzAA+FhV91Tzdaoq1Mtn\njDGmBlhAZYwxlfcI0BCYraqHKnB8c/d7MwARiRKR+SKyWETeFpG2vgeLSG8R2SYind3tkSLygYh8\nAIwG9gO5btof3WPiReRJEXlDRKaJY6x7nYUi8oqIxPpcI+BlCCQRiQNOoZTudO7vd4WIvCgi/3R/\nx2dEpJnPMQ1FJE1EFonIO8V+/7NFZKeIjK1svhUpnzHGmPrDZiYyxphKEJEEoDdOC81TFTztFPf7\nj+736cA8Vf1CRHYCtwB/9zn+SuB4YAeAqi4FlopIO5yp2P+pqlOKXeMu4Abgd0AG8FucSTLmuuVe\nBLwqIt3csV7VUYZAGuB+LxGwiEgL4BkgBvi9qm53028GbsOZgQ+cLplPqerH7u84nqO/4/Hu+YOB\nuZXMt8zyGWOMqV8soDLGmMrxtsa8qar5FTwnwf2+wW3ZwA1kfoPz8P5DseP7AxtUdXex9PPd72t8\nE93Z5vapar4b8AAsVVXf497DaVlKEJG8QJehGgwAfsWZfr6QiIQBzwPnAJ28QY/rEG7PCxE5Dmjj\nBlOdcX7Hn7wHquorIrIUaFSZfMsrnzHGmPrHAipjjKmcs9zvH1XkYBGJAP7gbi4HYnGmWQe4Cudh\n/Wmf408AugIP+smuH3AQZxp2X62Ahe7PA3C6471U7JgY93t74HA1lCFgRERwAro3/XSp/AvO7/iI\nqv7oHn8cTqD7V5yFdgHaAgt8zgFYViyvV3FmK6xMvuWVzxhjTD1jAZUxxlSONzD5toLHX4LTvex7\nYJmqHgAQkXBgBPBisdaQfu53fy1A/YD3vXl4qepXbp6C04L0jqoeLnauNxD8QVXfCXQZ3PzCgBeB\naD/nlWWLql7ts30GcAL+u9Nd636PEZH5OLPsHcSZcbCvd+p6Vf3cLZMAI4F3VXVzsbzaA6sqk28F\nymeMMaaesYDKGGMqZxfOmChPeQe6AcadOA/ntxcLQpJwgrPi47D6A0cotsaT21WwA866V6Xp7uZZ\nZBpvtxznA79QdGa+gJZBVY8Avy+jfBVV1vik3wD7gD+rarmvAc54t3bAfD/7uqnqrCrka+OnjDHG\nFLJZ/owxpnI+dL93rMCx/wA6A4+r6rPF9p2NE7S8Xiz9fGC9qv4sIh1EZKCb3s/9XthqJCLXuRMp\neF3gfn/DT57NcMZV7avmMgTCAGCHqn4qIjEikuyzLwzYXMFgCqCX+/0930R37Nh/qphvWeUzxhhT\nz1hAZYwxlbMQp8XpQrc7mV/uQ/bdwErgRj+HtAR2+rZaicjJQCeOjk+6BGc8FDhd9jzAu+6xMcB5\nxdZAusAt2yfFrjURZ9KJlBooQyD05Wgr2++BKJ9963AnkihORFqKyJxiyZHu9+KTbtyCs5ZYVfIt\nq3zGGGPqGQuojDGmElR1PXAPTsvTVf6OEZHROIHUbFX9o9sVrri3gJbe1h0RaQ7MxgledohIA5zZ\nAb2BzS5gj6oeFJHGOBNGFAZI7uQX5wF7ODoTISIyHegCDFTVn6uzDAGUD3zn/nwxR8c5gTM9fEcR\n8bY8edeOGgQ8BqQVyysHJwjs4XP8P4D/K/b3qEy+ZZXPGGNMPSNFx9kaY4ypCHdB2Ck444lexBl/\n0wVn/aYCIEVVPy0njynAuTjrOoXjPNSfC4wDNgEPq+o699jmwLPAzzgBwv1ucOfNKwEneBgDtAZO\nApoC24G7VLVwyvDqKkOguEHMNGAL8KyqphfbPwCnO+X3OBNHROAEh0vVz5uaOAsPjwO+BARYqaqv\n+jmuQvmWVz5jjDH1iwVUxhhTRW4rTRLOeCrFabVYW1rwUs1luRMnwOvinfXPGGOMMdXPAipjjKkD\nROQtIE5V44JdFmOMMaY+sTFUxhhTy4lIK5zpwf2tG2WMMcaYamQBlTHG1GIicj/wGc6035eKyAci\n0iXIxTLGGGPqDevyZ4wxxhhjjDFVZC1UxhhjjDHGGFNFFlAZY4wxxhhjTBVZQGWMMcYYY4wxVWQB\nlTHGGGOMMcZUkQVUxhhjjDHGGFNFFlAZY4wxxhhjTBVZQGWMMcYYY4wxVWQBlTHGGGOMMcZU0f8D\nnWElXBxHZV8AAAAASUVORK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x10ba5c7d0>"
]
}
],
"prompt_number": 2
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"'''Poisson randomness --- Poisson distribution'''\n",
"totalPoint_Input = int(200 + 1)\n",
"gInput = np.arange(totalPoint_Input)\n",
"meanP = totalPoint_Input/20\n",
"randomSeed_normal = np.random.standard_normal(totalPoint_Input) + meanP\n",
"randomSeed = np.random.poisson(meanP, totalPoint_Input)\n",
"\n",
"totalLevel = int(totalPoint_Input/1)\n",
"category = alva.AlvaLevel(randomSeed, totalLevel, False)\n",
"gLevel = category[0]\n",
"numberLevel = category[1]\n",
"print category[2].shape\n",
"\n",
"# calculating the mean\n",
"sumP = 0\n",
"for i in range(totalPoint_Input):\n",
" sumP = sumP + randomSeed[i]\n",
"current_mean = sumP/(totalPoint_Input)\n",
"print ('current mean', current_mean)\n",
"\n",
"totalLevel = int(totalPoint_Input/1)\n",
"category = alva.AlvaLevel(randomSeed, totalLevel, False)\n",
"gLevel = category[0]\n",
"numberLevel = category[1]\n",
"print category[2].shape\n",
"\n",
"numberingFig = numberingFig + 1\n",
"figure = plt.figure(numberingFig, figsize = AlvaFigSize)\n",
"plot1 = figure.add_subplot(1, 2, 1)\n",
"plot1.plot(gInput, randomSeed, color = 'gray', marker = 'o', label = 'data')\n",
"plot1.plot(gInput, alva.AlvaMinMax(randomSeed), color = 'red', marker = 'o', label = 'minMaxListing')\n",
"plot1.plot(gInput, alva.AlvaMinMax(randomSeed_normal), label = 'minMax_normal')\n",
"if totalPoint_Input < 100:\n",
" plot1.set_xticks(gInput, minor = True) \n",
" plot1.set_yticks(randomSeed, minor = True)\n",
" plot1.grid(True, which = 'minor')\n",
"else:\n",
" plot1.grid(True, which = 'major')\n",
"plt.title(r'$ Poisson\\ (total-input = %i,\\ mean = %f) $'%(totalPoint_Input, meanP)\n",
" , fontsize = AlvaFontSize)\n",
"plt.xlabel(r'$ input $', fontsize = AlvaFontSize)\n",
"plt.ylabel(r'$ output $', fontsize = AlvaFontSize)\n",
"plt.legend(loc = (0, -0.2))\n",
"\n",
"plot2 = figure.add_subplot(1, 2, 2)\n",
"plot2.plot(numberLevel, gLevel, color = 'red', marker = 'o', label = 'category')\n",
"plot2.plot(AlvaPoissonD(meanP, gLevel), gLevel, color = 'blue', marker = 'o', label = 'Poisson Distribution') \n",
"plot2.plot(AlvaPoissonProcess(gLevel, 18), gLevel, color = 'green', marker = 'o', label = 'Poisson Process') \n",
"if totalPoint_Input < 100:\n",
" plot2.set_xticks(numberLevel, minor = True) \n",
" plot2.set_yticks(gLevel, minor = True)\n",
" plot2.grid(True, which = 'minor')\n",
"else:\n",
" plot2.grid(True, which = 'major')\n",
"plt.title(r'$ Poisson \\ distribution\\ (data = %i,\\ level = %i) $'%(totalPoint_Input, totalLevel)\n",
" , fontsize = AlvaFontSize)\n",
"plt.xlabel(r'$ Number/level $', fontsize = AlvaFontSize)\n",
"plt.ylabel(r'$ Output-level $', fontsize = AlvaFontSize)\n",
"plt.legend(loc = (0, -0.2))\n",
"\n",
"figure.tight_layout()\n",
"plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"(201, 2)\n",
"('current mean', 10)\n",
"(201, 2)\n"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAABGcAAAIVCAYAAAB87ZKYAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XmcHFW99/HPb2aykBCI7OtNJMgjj4AJ6n24IiFEhsEb\n7lW8XiTjQhDvxYUEl8eF9UZZRFQMYJRFuIoC6lUeFKKSQUiiIgKGsKiAJoRNwhKEEEgymenf80dV\nTzrdNdNbdVV19/f9evWrp6uqq8/8TnX16dPn/MrcHRERERERERERSUdH2gUQEREREREREWln6pwR\nEREREREREUmROmdERERERERERFKkzhkRERERERERkRSpc0ZEREREREREJEXqnBERERERERERSZE6\nZ0REREREREREUqTOGRERERERERGRFKlzJgFmNj7tMqTBzOaa2b+nXY5qmNloM3uHmV1pZo80+LXa\n8rgQkeZkZp8xs3emXQ5pTe3+mWhmY83snWb2XTNbPsw2mYtRVJnMbE8zm2dmvzazeWmUKyxH5uJV\nqJp2ciXHh2RPkt8rqpXlsiUhq22atu6cMbODzWy5mT1tZrnw9oCZ3R3eHgzX3WFmHzGzquNlZu8F\nXjKz+fH/B9llZqcCE9z9f4ZZP83MZsX0WrHtCzgTuAw4CeiKaZ8lmvm4iDne1bzu9mZ2kZktNrM7\nzeyvZrbQzPYaZvtPmtkKM1tqZneZ2VVmtvsI++8M/7dvmNkvGvefSC2qrZ9q6z+O/dRwzDXbvr8K\nnGBm/zbc60rrUVspMRcC3wA+ELUyrhjF3P4qKZOZbQf8DDgPOBR4MY7XinjtEf+PrB9T5drJEUY8\nPmp4/VTactWqtu0XPqeaz79Gt/0S+V5Ro1TKlqE6zWabxt3b/gZMB3LA4oh1Y4DTwvU31LDvTwPP\nA0em/X8mGM/DgFvLbLMSWBLT68W2r3B/O4b1fXkDY9S0x0Xc8a7wNScCdxbGC3gD8DjwEvCPRdtf\nAPwd2C983An8GFgF7FS0bQfQB/wcOCus+9vSjrNutddPNfUf136qfc0m3vd44D5gn7SPDd2SvaG2\nUhIx3jeM4ZcbFaM4P8NHKhNwbvi/7N6gWI34f2T5mKKCdnK1x0eax0ED41RV2y9cX9FnGgm2/Ujg\ne0WzlC1rdZrFNk3qBcjCDfivsAJPHWGbv4fbHJp2ebN8I+h5/TPwxhG2mRTG8osxvF5s+yrY57vD\nfb4n7Xhm7daIeFf4ul8BPhyx/F1heVYBneGyg4GB4jICrw2Xf6vMa6lzJsO3cvVTb/3Xsp9qX7NZ\n912w/j+I+IKuW2vf1FZKJMb/GcavIR0KSX6GA78GHmj2/6MBZS/bTm708dEs8aum7Rcur/nzv5Ft\nPzL8vSLpsmWxTrPWpmnraU0F3h7e3xK10sy6CH4VAqh6WHyb+QDwlLvfN8I2h4f3S2J4vTj3lXck\n4MCvYtxnq2hEvCvRA1xiZu8rWn4zsImgoXFouOwkgt7znxRu6O6PEvSOv8/Mxja2uJKiuOq/kv2M\nqWLbwtds1n3n/TfwOjM7LGKdtC61lRrvaGADsKxB+0/kM9zMJgCHEPyK3QhptUXiUEk7eThxHR/N\nEr9q2n6Q3fZflr9XJF22LNZppto0bd85Y0GysEOAJ9z9oWE2OxwYS3DQ/CapsjWpjwHXltnmcKAf\n+F0MrxfnvvKOBJa7+99j3GeraES8K/EwQaN/l8KF7j5A8EutAbuGi2cSfND8MWI/DwLbAm9qWEkl\nbXHVfzX7qfY1m3XfwND77v8BH4l4nrQgtZUaL+zcejvwG3fvb9DLJPUZfgTB1INGds6k0RaJQyXt\n5BIxHx/NEr9q2n6Q3fZflr9XJF22zNVp1to0WUtMlIbDCOKwOGqlmXUSDOUdJBjKu8bM3gF8EFgD\n7ADsBJzm7veHzxlHkGRoG2A/4Dh3f2qY/f8fghP1JoKDLwd8yd0fr3PbcmV8M3Aq8A/AVe5+jZm9\nh+BNuhk4CPiZu39t+NCVvOZkgjdISSzN7ANAPmP/wQTzCpeZGQRzZ39cafnN7IPA3Er2Ff5C/BmC\nXtjHCOr6uwQ9sG8ujp2Z/QPBnN4LKv2/K1XuuKi1TsxsCjAf2BNYCnyRID6vZ8sJ8KPu/mS4/XiC\nYYXDleMfgZ8CR7j7Q9XEu4HeC+zq7k8XLgz/l50J3g+PhO/XKcC68GRb7Pnw/rXAbxtY3sIyjlSv\n/cD/Bha5+9fN7LXAp4DRBPNgO4H/dPeXI/ZrwHHAbOApgi9F2wAfcfd1RdtW9D5oxHkhSXHVfxX7\n2cfM7qzmNZt13xHrbwe+b2aj3H1zxHppLWorxXhOjDgndxJ87k6goEMjjhgRfBEv2/4ys/2B04G9\ngOuBq4HPhY8nAPe4+4IKy9QdxmeCmV1O8GPw64BPuPuK8PXibItc6O7/U2W8MtVOLtquouNjhO1L\nPuOrbctV235ukIrafuGyzLX/wnKN+L2iXFvOzEaHz51I0K4/rqA9fwhwE3COu19S6T4rLVuDZLVO\ns9OmSXteVdo3gpN4juBgL153EEFSob8QDCUcA1wD/AHYuWC7DwNrCQ42gAXAG8K/nwO+OsxrHwEs\nL9rXfwM/qHVbgjdgJWX8CcHJ/hSCD5mvAHMLtv+nMC5vqiKWc4Bnymyzd7jfc4ZZX1H5K9zXBIKh\nn0uAUeGy14X72QSMi3jOh8J9HtGAY23E46LWOiH4BWYC8I5w/c8Ky0/QwLofsPDx14H9RyjHJQTz\nOHeopu7SuAEnh2X6Tfg4n9jsb8Nsf164ft4I+4x13nEV9TqXoEE8sWDdw8X1Ey5/DfAL4K6i98Qp\nwLm1vg9qPQYTrvNh6yeO+q92PwSN+opfs1n3HbF+IsEX8f+T1rGgW3I31FaKs60UdU7eL3zdQQpy\nkcQZI8q3mX4QxuX9YTl+HP5/OwB/A16stEzAQwSfL58vWPZfwDPAtuHj2NsiFZYt6+3kio+PEbYf\ntq1b7jioZZ9J3yhq+4XL6vr8p0E5ZxjhewUVtOXC983BUcc08C/hvn9RzT4rKVu71SkZatNo5MyW\nOdS9ZnZs+HcHMIqgR+4Kgp7xnJn9gKDhMdXdnyvYx4/C7c4wswsJEhn90cwOJDiwnhnmtc8E+vL7\nCnsNjwYuqmPb71RQxm8D97r7oJntTfDh87y7X1qw/Uvh/RSCD7BKHAQ8WmabI8L724dZX7b8bPkF\nqNy+riMYlfC/PewFdfe/mNkTwKvu/mrEc44kmM8ba696Ps7DHRdm9kZqqBMz2xF4xd1fDp8HcI27\nF8bk9wQNgulmthrA3f9sZgeE5fhbUXFnEiTxe6Foebl4F/6/pwC1Xprucnf/QQWvMZ7gV74XCT5g\nAMaF91E97BD0yANsX2PZqlJhveZ/xfgw8Bbferjyy8D+RfvsBH5I0DB8nbsXnl/6KZ2uWtH7oNZj\ncJj/u+H1P4y46r+a/VT7ms26761Xur9oZuuAqQTnGGltaivF11aKOic/YmaPAZs9zEVSrt1Qw/89\n7Ge4BZewXePuG8PXNeBGd/9dODq3C7g23G7EMoXP34/gXF74i/y9BL+M/6uZ/Tb8v2Nri1QRr++Q\n7XZyRcdHme1HautW0parpf0MNP7zf5i2H2Ss/Vcg8ntFJW05Cy5Lv4e7Lzez1xMc0/nRIrj7TWZ2\nDUGHYy3tw4q+87RDnWapTdPWnTNmthPwRmC1u7+rzLbvJRgidq67ry5anT84DiCYWvKt8HG+R/L6\nYXa7E3CSmT0OLHP3Bxg+iV7Zbaso43YEv4hAMNz1MXf/ctH2B4X31Qxb/AeC+YIjmUHQ635H8Yoq\nyl/Jvv4NmAV8zd2fLVi+DcGwwJJGXTgMcCbwa49/vvcejHxcTAD+J/y7mjrZCbgq/PtI4FWCoa+F\ndgzvJxH8+nNZQTn6KZj7bGa7EHwgL4j4H2YwTLyLufs3gG+U265O3ySY+tPj7o+EyzaVec624f3G\nhpVqa5XU6xvD+zMLjzszGwX8L+Ceou3fR1DX33L3NeG22wPvAU4kyLyf30c174Naj8ESCdV/lLjq\nv5r9VPuazbrvKGsJzivSwtRWAmJqK41wTh5L0BF/Q8Hm5doNhSqJ0QyG/wzfo2DfhwPPuvv3Adx9\nJWF+iHDqVLkydYf31xUt3yG835ug/uNui5SNV9bbyVUeHzW1dSnTlqtxn0MS+PyPavtB9tp/5b5X\nVNKW2wu4vGB72NJOy/s5wbSeSvdZSdm20kZ1mok2TVt3zrCl93hpBdt+iuDEfUXEuvwv2y+6++9h\naK7mB4Bfejg3MMIC4Erg0vA5jwDvc/eoHvhKtq20jL8J97E98GaCoa/F3knwq33xF8ORbEdBj+4w\nZgB3uXvUG6mi8le4r4+H98X5UN5GkM9jScRzDiRogGw1nzfsib6RLSeBSq1y95MAyh0XtdaJuz8c\nPs8Ijuc7vHSu5FvC+7+5+x3h9l1hOW4s6lmfEd5H/aIyg+HjnSgz+zTwVuCtRSfyFwiGJQ6X7HxC\nwXYNV2G9HkHwq8CSouXTCT6siuviP8L7Hc3smwTvmU3h89/q7l6wbcXvgwaeF5IUV/1Xs59qX7NZ\n9x1lLcFQYGltaivFd04c7px8KMF0sKH2RwNiNINhPsPd/a7weaMJ8gvdFPUiFZapm+DX+DuLlk8L\n759pRFukwrJlvZ1c8fFRZvuR2rozGLktV8s+EzFC2w8y1v4LRX6vCFXSlnsahtr4HwTuDDtLC00i\nmMZU6T4rKVtiMlanmWjTtHvnTH6Y7ogNjvBE/2bgL8N8MOZ/JSj8EHk3wa8EVw63X3f/bzO7h2DO\n4MzwtsjM9vKixEfltq2xjIcTHPBbXT4t7B0/huDDcrihZJH/EsFQ2EgWJJ6aTDDXt3hdVeUvs68u\ngsbFOoI5l4VmEnwRjhrCd2R4v9WJyt0HCeIeh3LHRa11MpVghEzx8zoJGtbr2Tor/1Hh9t8v2s9M\nghPhVpdpHCneSTOz9wPHAoe4+9pwWQdBTp0BM/sLwa9TUXYK7//c+JJuJbJeQ28nSLRYnPS3l6CB\ne3PR8gOAV4Bed88N94J1vA/iPi8kJq76r2Y/4bD3il+zWfc9DENXfWwHaivFcE4sc07Oxzjqi1Ld\nMariM/wQgsSht5XZbqQyvRm4O+KHopmEOSAKljWiLRJZtqy3k6s9Pmr5jC8XvzraDQ1Xpu03mNH2\nX+T3ilBFbbnQPxKMOPtmxLo3uvtXatjnSGVLRAbrNBttGk856U2aN+CvBCf/15bZbleCD5SbI9Z1\nECTBexbYrmD5bQQZsjvCx/9ZsO7dBL18xxXt6zPh6+xY7bY1lvHi8Dm7FG3/gXB5T/j4fcDYCuL5\nP8DiEdZ/MNzv4QXL/pMgeVVV5S+zr13CdUsi9vV74Hfh35OBIwvW/ZxgzjUEjYWeBhxzwx4X9dQJ\n8H/D9W8pet6R4fJvFC3/IsEUp7FFyx8maFTl49NdLt7D/J9zCRo4tdxmjxC/WQQJj7cpWv6Rgtgs\nDMu6b8TzVxPMEx/2eKYBSeFGqNfXEpGYj2Ce7Trg+vDxpPyxGi5fUcFr1vo+qPu80Kj6r6R+6q3/\nWvZT7Ws2674jtvkrwVVSYnuv6Ja9G2orxdJWovw5+U/h33tT0P6II0ZU+BkOfGG4c0LRdiOVaQNw\ncdH2rwv3+9Oi5bG3RYYrW5p1X/C8YdvJ1R4fBPl7qvqMLxe/CsoQ2W4o2i72z38qaPuFj2v+TKMx\nbb9hv1dQYVsu3PbjYflmFC0/ADi7xn1W/J2nXeqUjLRpUn3xVP/x4MtOjmAeabltjWBo2aKIdR8n\naLS8s2DZ7uG+LwgfHwh8oWD9zwlygxxatK/jCJKfUe221ZYxXP5g8euFy38JPBnusxP4UYUx/Srw\nhxHWX0rQ6z4mfLwj8L0aY1xuX+uAHxft50CCRsDXw8efpCArN8GUqWvDv+cA7475mBvxuKinTgiG\nNA4Co4uW/yp83vZFy79BUfZztnQUXBw+/kT+uBsp3kndCIbU/jfhlQOK1n0X2Cv8O38FhdOKtjkk\nXH5Fmdcp9+X/rQRDR7uqKPtw9fphoj9w/z1cfnT4+AtsuQLFLcBDw7zODgXHd63vg1jPCw04DsrV\nT1X1TzCy7Ph69lPDazblviNi9HfgY2kcB7olc0NtpdjOiZQ/J18SPp7Lls/eWGJEhZ/hwG/K1XUF\nZXqI4NLlhc+5jGAK0D5Fy2Nti4xUtjTrvuB5w7aTazw+qvqMryB+NbUbGnmjwrZf+LjmzzQq+CJP\nle0/RvheQYVtufDxp8Ly7Ve03VUUtO+r3GdDv/M0S50WbZ+JNk2qL57qPw4fCyvt+iq2f5kga3Z+\n2XvCipxdtO0B4b7fQTB17HtFb54LgY8WPWdv4G6COXfUuG01ZdwtLOOCiP/1buCH4d+foMIRJMAJ\nwHMjrJ+fX08wbPZ7wD/UWP5y+/oysJIgcz8EieVuIviF6QyiOzieYMsH+v+jqDc3hmOu3HFRU50Q\nXC1jPcE85t6C5ecSXP1g/4j9HU+QQCv/a8lEgstGrg/j00GQeC5/+e0R493oG0EyyhcJfk17qOj2\nCLC2aPtrw+PmDQVlXkKQuG/iCK+zZ1gH9xH9oTGKoCFc8kExwj5HqtfrCYagFneqnRI+ZxzBL1SX\nFaw7lCB54psLlhnB1Sd+DOxd6/ug1mMwweNgxPqptv7D435zuM+jat1PLcdcs+674HnbE3yZeVvS\nx4Fuyd1QWynWcyIjn5NPI/jsLTwnxxIjKvgMJ8ir1w98p8z/UK5MnwF+W/D4eIIv/FHn2FjbIhWU\nLevt5GqPj2o/4ys5DqpuPzfqRpVtv/A5VX+mUUHbgtraf8N+r6C6ttzBBJ1q7y16nx1T9HrV7LOh\n33maoU6Lts9MmyZ/smsL4Ty23xDMUXstwUluI7CKYJjjaWWePwd4P8Ewqm0JTlRfdvfHIrb9EvCm\ncJuve5ioLFw3Bvg8wQfoRoITXSfBB8CfivZT8bbVlNHMDgIWE7yx7ylaN4PgA//PwHJ3v3ikuBQ8\nbzJBLA909z9GrJ9I8GX0JYI3zIXuvqLG8o+4rzBuFxPU8+pwP+cQnKA+Ey67zN2XFjznaOC/wv/h\nencvzvVRtzLHRU11YmbTCU5ScwkaE7sTJMl6Bviiu0cmnzOzswhO5I8RNGK+GD4+lWBo3zfc/Xfh\ntmXrrpHM7H7gDSNscpe7/1PB9p0E75vjCBpiOxJcxvPz7l5yZQUz+ynBlZH2IXh/QdBpspqgEXJu\nwbY3Ecz/Xerux1VQ9pHq9ZfAI+4+r2j5tgTDn18maNR+2t1fKlh/JMFx/CRBsrdRBOe2a7zgpF7t\n+6AR54U4VFM/4fYV1X/4mdBHcCnUw9z9iVr2U+22zbzvgue9k+Cc8Bp3L3dFBWkiaitttV2s58Qy\n5+T/Gy77trvfFmeMKmx/vZYgie/x7n57mf9jpDJ1AZeEZXoxLM9/uftfhtlXrG2RkcoWrp9DdtvJ\nVR0fNXzGVxK/qtvPjVJt2y98TjWff9W2Lapt/434vaLStly47XsI3hMPEXS43ODuP494zUrbhw3/\nzhMla3Va8LzMtGky1TljwaXilhJkJB9NMDf1NDPbgeC67ZMIgnucu7847I4kNWZ2N8EJ4NK0y9Iu\nzOwLwFkEI2QeTrs87cLMvu3uH067HCJpMLMFBL8+l22gSmXUBhJpfWonNz+1/1pPlto06WckLuDB\nZd2OcPepwEHAEWb2NoLesj53348gh8bnUyymjOxbBMNUJTlvB55Ux0xyzOzNQNRlXEVanpmNAt5F\ncL6XmKgNJNIW1E5uYmr/tZ6stWky1TkD4O6vhn+OJhiO9HfgXwkSBBHevyuFokllrgF2MrPusltK\n3cxsJ4IhliMOQZb4mJkBHyUDlxUXScmHgEfLTX2Q6qkNJNLy1E5uUmr/taxMtWky1zljZh1mtoIg\nX8bt4ZzMXd39mXCTZwguhycZ5O4DBJnM54dzBKVBzOxCgisJdALvNrO7zWz/lIvVDj5BMOf7lbQL\nIpI0MxtPMO/95LTL0orUBhJpbWonNzW1/1pMFts0mco5U8jMtie4JNhpBEmPXlOw7gV33yG1wklZ\nZnYqwSXfPp52WUREpH5hotgfE1x+8ydpl6eVqQ0k0trUThZJV1bbNJntnIGhDO4bgA8DM9x9jZnt\nTvBr0uuLts3uPyIiItLG3N3SLkOzURtIRESk+VXTBsrUtCYz2ym8zBtmtg3QTXCprJ8BJ4SbnQDc\nGPV8T/m65Lo1/nbCCSekXgbdVM+6qZ51q/wmlVEbKP6bzjGKieKiuCgmikuat2p11dSCaJzdge+G\nw4w6gO+5+6/M7F7gR2Z2EuFlJFMso6Ro8uTJaRdBEqB6bg+qZ5GtqA0UM51jSikm0RSXaIpLKcUk\nmuISj0x1zrj7A8DBEctfAI5MvkQiIiIijac2kIiISHvL1LQmkXImTpyYdhEkAarn9qB6FpFG0jmm\nlGISTXGJpriUUkyiKS7xUOeMNJWpU6emXQRJgOq5PaieRaSRdI4ppZhEU1yiKS6lFJNoiks8Mn21\npmqYmbfK/yIiItIqzAzX1ZoaSm0gERGR7Km2DaSRMyIiIiIiIiIiKVLnjDSVJUuWpF0ESYDquT2o\nnkWkkXSOKaWYRFNcoikupRSTaIpLPNQ5IyIiIiIiIiKSIuWcERERkYZRzpnGUxtIREQke5RzRkRE\nRERERESkiahzRpqK5jO2B9Vze1A9i0gj6RxTSjGJprhEU1xKKSbRFJd4qHNGRERERERERCRFyjkj\nIiIiDaOcM42nNpCIiEj2KOeMiIiIiIiIiEgTUeeMNBXNZ2wPquf2oHoWkUbSOaaUYhJNcYmmuJRS\nTKIpLvFQ54yIiIiIiIiISIqUc0ZEREQaRjlnGk9tIBERkexRzhkRERERERERkSaizhlpKprP2B5U\nz+1B9SwijaRzTCnFJJriEk1xKaWYRFNc4qHOGRERERERERGRFCnnjIiIiDSMcs40ntpAIiIi2aOc\nMyIiIiIiIiIiTUSdM9JUNJ+xPaie24PqWUQaSeeYUopJNMUlmuJSSjGJprjEQ50zIiIiIiIiIiIp\nUs4ZERERaRjlnGk8tYFERESyRzlnRERERERERESaiDpnpKloPmN7UD23B9WziDSSzjGlFJNoiks0\nxaWUYhJNcYmHOmdERERERERERFKknDMiIiLSMMo503hqA4mIiGSPcs6IiIiIiIiIiDQRdc5IU9F8\nxvagem4PqmcRaSSdY0opJtEUl2iKSynFJJriEg91zoiIiIiIiIiIpEg5Z0RERKRhlHOm8dQGEhER\nyR7lnBERERERERERaSLqnJGmovmM7UH13B5UzyLSSDrHlFJMoiku0RSXUopJNMUlHuqcERERERER\nERFJkXLOiIi0oL6+Pq677jrcHTOjt7eX7u7utIslbWTZokUsvuQSzlu8WDlnGszMfMcDX8spx5/M\n/NM/V3b7fN10bdrEwJgxHDVvHtNnzUqgpCIiIu2j2pwzXY0sjIiIJK+vr4+FCxcybdq0oWULFy4E\nUAeNJGLZokXccuqpnLdyJeelXZg2sfbfHuW8H10AMGIHTWHd5J0R/q0OGhERkfRoWpM0Fc1nbA+q\n5/pcd911W3XMAEybNo3rr78+pRJFUz23rsWXXLLVl39JxsCxL/KNH14RvbK/H1atYvH8+SV1c97K\nlfRdemkCJUyWzjGlFJNoiks0xaWUYhJNcYmHRs6IiLSY4aZ45nK5hEsi7apr06a0i9C2Xnr1ebjy\nSli9Gh57bMv9M8/AHnvQ9fe/Rz6vc+PGRMspIiIiW1PnjDSVGTNmpF0ESYDquT5m0VNbOzqyNVhS\n9dy6BsaMSbsIbWtg8BW4806YNAmOOiq4nzwZ9twTuroY6OmBxYtLnjc4dmzyhW0wnWNKKSbRFJdo\nikspxSSa4hKPbLXURUSkbr29vdx7771bLVu+fDmzZ89OqUTSbo6aN48zpkxJuxjt51bAc3DVVXD2\n2fDBD8LhhwcdNF3B73FRdXP6lCl0z52bQoFFREQkT50z0lQ0n7E9qJ7r093dzcc//nHuv/9+fv/7\n3/PYY49xyimnZC4ZsOq5dU2fNYueiy/mrEmT0i5K+7gN2BfoHPmiEEN109PD/MMP56yeHo6++OKW\nTAasc0wpxSSa4hJNcSmlmERTXOKhaU0iIi2ou7ub7bbbjtWrV/Pe97437eJIG5o+axbTb7mFc1sw\n0WwmzSQYOdNfftPps2a1ZGeMiIhIM7PhEkc2GzPzVvlfRETicOedd7J69WqOP/74tIsi7eojH8Eu\nvxx3H3k4h9TFzJzpwDpg7Wj8cSVkFhERSZuZVdUG0rQmEZEWlcvlhr1yk0gi+isYxiHxmQp06aps\nIiIizUidM9JUNJ+xPaie4+Humb58tuq5DWzenHYJ2sdM4K/AgJp2eTrHlFJMoiku0RSXUopJNMUl\nHvoEFxFpURo5I6nTyJnk5BMCdw2mXRIRERGpgXLOiIi0qKVLl/L444/zgQ98IO2iSLs69ljsxhuV\nc6bBzMyZT5AQ+EnDH83uiDkREZF2oZwzIiICBNOa1GktqdK0puRUeCltERERySZ1zkhT0XzG9qB6\njkcul1POGUmXpjUlJ59zRiEfonNMKcUkmuISTXEppZhEU1zioc4ZEZEWpZEzkjp1ziTnNmA9QFfK\nBREREZFaKOeMiEiL6uvr44knnuBDH/pQ2kWRdnXoodgddyjnTIOZmTMd2AdY2omvGki7SCIiIm1P\nOWdERATQ1ZokAzRyJjn5aU2e3amMIiIiMjx1zkhT0XzG9qB6joe7K+eMpEudM8lRQuASOseUUkyi\nKS7RFJdSikk0xSUe6pwREWlRGjkjqdPVmpKjhMAiIiJNTTlnRERa1M0338xTTz3FySefnHZRpF3t\nuy+2cqVyzjTYUM6ZdcDa0fjjm9IukoiISNtTzhkREQF0tSbJAE1rStZUoCu7UxlFRERkeOqckaai\n+YztQfUcj1wup5wzki5Na0pOflrTgJp2eTrHlFJMoiku0RSXUopJNMUlHvoEFxFpURo5I6nTyJnk\n5BMCdw03q8rYAAAgAElEQVSmXRIRERGpgXLOiIi0qBtuuIG//e1vnHLKKWkXRdrVhAnY+vXKOdNg\nZubMB24FnjT80eyOmBMREWkXyjkjIiKARs5IBmhaU3J0KW0REZGmlqnOGTPb28xuN7M/mtmDZjYv\nXD7fzJ40s3vD29Fpl1XSofmM7UH1HA/lnJFUuWtaUxXqbgPpUtoldI4ppZhEU1yiKS6lFJNoiks8\nutIuQJHNwCfdfYWZbQv8wcz6AAcucveL0i2eiEjz0MgZSdXgIJgFnTRSifraQLcB6yF7TTsRERGp\nRKZzzpjZjcA3gEOB9e7+tRG2Vc4ZEZECP/jBD3j66af55Cc/mXZRpB1t2AA77IBt3KicMzWotg3E\ndGAfYGknvmogoVKKiIjIcFom54yZTQamAXeGi+aa2X1mdpWZTUytYCIiTSLr05qkxfX3w6hRaZei\nKdXUBspPa3K950VERJpRJjtnwuG8PwZOdff1wLeA1wJTgaeBYX89ktam+YztQfUcj6xPa1I9t7j+\nfhg9Ou1SNJ2a20BKCFxC55hSikk0xSWa4lJKMYmmuMQjcxOTzWwU8BPg++5+I4C7P1uw/tvATVHP\nnTNnDpMnTwZg4sSJTJ06lRkzZgBbDhg9bu7HeVkpjx435vGKFSsyVZ5mfZzL5XD3zJRH7+f2eLxg\nwQJWrFjB5B13hE2bkMrV0wbiJeBXwEs5FixYoDZQgayUR4+z+3jFihWZKo8eZ/ex2qjRj/OyUp60\nHg+1gcI+iWplKueMmRnwXWCtu3+yYPnu7v50+Pcngbe4e2/Rc5VzRkSkwDXXXMOaNWv47Gc/m3ZR\npB2tXg2HH449/rhyzlSg3jYQ04F1wNrR+OPqFBMREUlbtTlnsjZy5lDg/cD9ZnZvuOx0YLaZTSW4\nYsGjwMkplU9EpGko54ykStOaqlV/G2gqsFTveRERkWbUkXYBCrn7b9y9w92nuvu08PYLd/+gux/k\n7m9093e5+zNpl1XSUTx0TlqT6jke+WlNWaV6bnGbN6tzpgp1t4FmEiQEHshU0y5VOseUUkyiKS7R\nFJdSikk0xSUe+gQXEWlRWU8ILC1OV2tKVj4hcNdg2iURERGRGmQq50w9lHNGRGRrV155Jc8++yxn\nnHFG2kWRdvT738PcudjddyvnTIOZmTMfuBV40vBHNbVJREQkbdXmnNHIGRGRFqWcM5IqTWtKli6l\nLSIi0tTUOSNNRfMZ24PqOR5Zn9akem5xmtaUrHzOmf60C5IdOseUUkyiKS7RFJdSikk0xSUe6pwR\nEWlRWU8ILC1OI2eSdRuwHrJ3IU4RERGphHLOiIi0qIULF/L8889z9tlnY6apDpKwm26CK67Abr5Z\nOWcazMyc6cA+wNJOfNVA2kUSERFpe8o5IyIiAEP5ZtRxLanQtKZk5ac1ufJMiYiINCN1zkhT0XzG\n9qB6jkfWO2dUzy1O05qSpYTAJXSOKaWYRFNcoikupRSTaIpLPNQ5IyLSovKdMrpik6Siv1+dM0lS\nQmAREZGmppwzIiIt6qKLLuLll1/mtNNOY7S+JEvSvv1t+N3vsKuvVs6ZBhvKObMOWDsaf3xT2kUS\nERFpe8o5IyIiQPanNUmL07Sm5E0FujRSTkREpBmpc0aaiuYztgfVczzynTJZ7ZxRPbc4TWtKVn5a\n04Cadnk6x5RSTKIpLtEUl1KKSTTFJR76BBcRaVH5kTPKOSOp0NWakpVPCNw1mHZJREREpAbKOSMi\n0qIuuOACNm/ezKc+9SnGjx+fdnGk3Zx/Pqxfj33pS8o502Bm5swHbgWeNPxRdciKiIikTTlnREQE\nCEbMdHZ2ZnZak7Q4TWtKli6lLSIi0tTUOSNNRfMZ24PqOR5Z75xRPbc4TWtKli6lXULnmFKKSTTF\nJZriUkoxiaa4xEOdMyIiLcrd6ezsVM4ZSYeu1pSs24D1AF0pF0RERERqoZwzIiIt6gtf+AITJkzg\nQx/6EBMnTky7ONJuTj0V9tkH+8QnlHOmwczMmQ7sAyztxFcNpF0kERGRtqecMyIiMjSVKcvTmqTF\naVpTsvLTmlwj5URERJqROmekqWg+Y3tQPdcvl8thZvke+7SLE0n13OI0rSlZSghcQueYUopJNMUl\nmuJSSjGJprjEQ50zIiItyN3p6OjAzJRzRtKhqzUlSwmBRUREmppyzoiItKD+/n6+8pWvMHHiRI47\n7jh23nnntIsk7eb44+Gd78R6e5VzpsGGcs6sA9aOxh/flHaRRERE2p5yzoiIyFYjZ9RxLanQtKbk\nTQW6NFJORESkGalzRpqK5jO2B9Vz/XK5XOY7Z1TPLU7TmpKVn9Y0oKZdns4xpRSTaIpLNMWllGIS\nTXGJhz7BRURaUGFCYOWckVToak3JyicE7hpMuyQiIiJSA+WcERFpQevXr+eyyy5ju+2245hjjmGP\nPfZIu0jSbmbOhDPPxN7+duWcaTAzc+YDtwJPGv6oOmRFRETSppwzIiLSFNOapMVpWlOydCltERGR\npqbOGWkqms/YHlTP9XP3oWlNWe2cUT23OE1rSpYupV1C55hSikk0xSWa4lJKMYmmuMRDnTMiIi0o\nP3Kmo6NDOWckHbpaU7JuA9YDdKVcEBEREamFcs6IiLSgtWvXcu211zJhwgRmzpzJpEmT0i6StJs3\nvAF+9CPsgAOUc6bBzMyZDuwDLO3EVw2kXSQREZG2p5wzIiKCuyvnjKRL05qSlZ/W5BopJyIi0ozU\nOSNNRfMZ24PquX6FCYGzOq1J9dziNK0pWUoIXELnmFKKSTTFJZriUkoxiaa4xEOdMyIiLSiXy2Fm\ndHR0aOSMpEMjZ5KlhMAiIiJNTTlnRERa0NNPP83PfvYzxo8fzyGHHMK+++6bdpGk3ey0E/z5z9gu\nuyjnTIMN5ZxZB6wdjT++Ke0iiYiItD3lnBERkaGRM8o5I6nRtKbkTQW6sjmNUUREREamzhlpKprP\n2B5Uz/UrTAisnDOSCk1rSlZ+WtOAmnZ5OseUUkyiKS7RFJdSikk0xSUe+gQXEWlB+YTAyjkjqenv\n18iZJOUTAncNpl0SERERqYFyzoiItKDVq1dz++23M27cOA466CD233//tIsk7WRwMBg1MziIBR2E\nyjnTQGbmzAduBZ40/NFsjpYTERFpJ8o5IyIiW01rUse1JG7z5qBzxtQnkxhdSltERKSpqXNGmorm\nM7YH1XP98tOalHNGUqEpTcnTpbRL6BxTSjGJprhEU1xKKSbRFJd4qHNGRKQF5a/WpJwzkgpdqSl5\ntwHrAbpSLoiIiIjUQjlnRERa0COPPMI999zD2LFj2XfffTnooIPSLpK0k6efhmnTYM2aqudbS/XM\nzJkO7AMs7cRXDaRdJBERkbannDMiIjI0ckY5ZyQVmtaUvPy0Js/mNEYREREZmTpnpKloPmN7UD3X\nrzAhsHLOSOI0rSl5SghcQueYUopJNMUlmuJSSjGJprjEQ50zIiItqDAhsEbOSOL6+4OrNUlylBBY\nRESkqSnnjIhIC3rggQd4+OGHGT16NHvuuSdvetOb0i6StJMVK+CEE+C++5RzJgFDOWfWAWtH449v\nSrtIIiIibU85Z0REZGhak67WJKnQtKZ0TAW6sjmNUUREREamzhlpKprP2B5Uz/UrnNaknDOSOE1r\nSl5+WtOAmnZ5OseUUkyiKS7RFJdSikk0xSUe+gQXEWlB7q6rNUl6dLWm5OUTAncNpl0SERERqYFy\nzoiItKA//OEPPPXUU4waNYrXvOY1HHLIIWkXSdrJ4sXw1a/C4sXKOZMAM3PmA7cCTxr+aDZHy4mI\niLQT5ZwREZGhaU3KOSOp0LSm5OlS2iIiIk1NnTPSVDSfsT2onuuXTwisnDOSCk1rSp4upV1C55hS\nikk0xSWa4lJKMYmmuMRDnTMiIi0ol8sp54ykR1drSt5twHqArpQLIiIiIrVQzhkRkRZ0xx138PLL\nL9PZ2cmYMWM47LDD0i6StJPvfQ9uuQW+/33lnEmAmTnTgX2ApZ34qoG0iyQiItL2lHNGRESGrtak\nnDOSCk1rSl5+WpNncxqjiIiIjEydM9JUNJ+xPaie65dPCKycM5IKTWtKnhICl9A5ppRiEk1xiaa4\nlFJMoiku8VDnjIhICypMCKyRM5I4Xa0peUoILCIi0tSUc0ZEpAUtWbJkqINmcHCQmTNnpl0kaSdf\n/So8/TR87WvKOZOAoZwz64C1o/HHN6VdJBERkbannDMiIjI0rUk5ZyQVmtaUjqlAVzanMYqIiMjI\n1DkjTUXzGduD6rl++YTAyjkjqdC0puTlpzUNqGmXp3NMKcUkmuISTXEppZhEU1zikalPcDPb28xu\nN7M/mtmDZjYvXL6DmfWZ2SNmttjMJqZdVhGRLCtMCKyRM5I4Xa2panW3gfIJgbsGEyy1iIiIxCVT\nOWfMbDdgN3dfYWbbAn8A3gWcCDzv7hea2eeA17j754ueq5wzIiKhxYsXs+2222JmrFu3jp6enrSL\nJO3ks5+FnXaCz35WOWcqVG8biPnArcCThj+azdFyIiIi7aSpc864+xp3XxH+vR74M7An8K/Ad8PN\nvkvQWBERkWHkcrmhaU3quJbEaVpT1epuA+lS2iIiIk0tU50zhcxsMjAN+D2wq7s/E656Btg1pWJJ\nyjSfsT2onutXOK1JOWckcZrWVJea2kC6lHYJnWNKKSbRFJdoikspxSSa4hKPrrQLECUczvsT4FR3\nf9lsy69A7u5mFvkz8Jw5c5g8eTIAEydOZOrUqcyYMQPYcsDocXM/zstKefS4MY9XrFiRqfI04+P7\n7ruPI488EnfnvvvuY9y4cZkqX6GslEeP43m8YMECVvT1MfmJJ+C555Dq1NoG4puAARuCOlAbaIus\nlEePs/t4xYoVmSqPHmf3sdqo0Y/zslKetB4vWLCAFStWDPVJVCtTOWcAzGwUcDPwC3dfEC57CJjh\n7mvMbHfgdnd/fdHzlHNGRCR00003sfvuuwOwZs0ajjnmmJRLJG3lhBPgiCNgzhzlnKlCPW0gpgP7\nAEs78VUDSRddREREijR1zhkLfh66CvhTvlES+hlwQvj3CcCNSZdNRKSZ6GpNkipNa6pa3W2gmQTT\nmjyb0xhFRERkZJnqnAEOBd4PHGFm94a3o4ELgG4ze4Sg+XFBmoWU9BQPnZPWpHqun7sPJQRWzhlJ\n3ObN6pypXn1tICUELqFzTCnFJJriEk1xKaWYRFNc4pGpnDPu/huG7zA6MsmyiIg0M3eno6ODXC6n\nkTOSvBa4WlPYGdIF9IW3X7n730fYvgcYTzAlaUO1r1d3G2gmwaW0lRBYRESkKWUu50ytlHNGRGSL\nn/zkJ+y3337kcjlWrVrFsccem3aRpJ284x0wbx684x1Nm3PGzK4ETipY5MBytnTW/Nbd+wu23xH4\nF+CdwFXufnOCZQ1yzqwD1o7GH9+U1EuLiIjIMJo654yIiMQjl8sNTWtSx7UkrgVGzgA3AE8AOwPv\nAS4Htgc+D/wK+LuZ/dLMPm1mB7n7Wnf/jrsfC8xOpcRTga5sTmMUERGRkalzRpqK5jO2B9Vz/fLT\nmrLcOaN6bmGtkRD4V8B3w06XG9z9Y+6+HzAZ+DDwU4LukK8AK8xsjZlda2YXEFw3KVn5hMADatrl\n6RxTSjGJprhEU1xKKSbRFJd4ZCrnjIiIxCN/taZcLpfZhMDSwlogIXA4ZensiOWPA1cDV4dXWDqQ\nICfMkcAs4GXgPxIsaiCfEPipwcRfWkREROqnnDMiIi3o+uuv5+CDD2ZwcJAHH3yQ4447Lu0iSTs5\n+GC48kp405uaNudMMzEzZz5BQuAnDX9UHbIiIiJpU84ZEREZGjmT5WlN0sJaY1pTc9GltEVERJqa\nOmekYn19fZx44onMmTOHE088kb6+vsTLoPmM7UH1XL9mSAisem5NyxYt4sxHH2X+SSdxZk9P2sWJ\nnZltZ2bnmtn5ZrZ70bqvm9neqRQsn3OmHxgYGHHTZYsWcWZPD/NnzODMnh6WLVqURAkTp3NMKcUk\nmuISTXEppZhEU1zioZwzUpG+vj4WLlzItGnThpYtXLgQgO7u7rSKJSLDKEwIrJwzkpRlixZxy6mn\nct6rr8LddwNwXsplaoDLgDsIukFuMLO3FsyrPge4wsz+PfG51rcB6wG6YNw42GMPmDQJJk/e6n7Z\no49yy5e+xHmrVg099YyVKwGYPmtWokUWERGRLZRzRipy4oknMnny5JLljz32GFdffXXyBRKREX3n\nO99hxowZbN68mbvuuov3ve99aRdJ2sCZPT2cu3jxVssMWirnjJld5e4nhX+fBDzn7j8rWH80sKu7\nfzfBMjnTCa4RtbSTmy+6hVkHvRZWr4YHH4Rly4Lbc89xJnBuxD7O6unhnF/+Mqkii4iItLxqc85o\n5IxUZLiOL/0iL5JN7p75aU3Sero2bUq7CEnYWPD3j4H/An5WsOwW4Aogsc4ZIJjWdCvgcOnJX2fW\nXk8HnTMbNgQjZ970Jpg0ia7Fi+HRR0ue3rlxY8kyERERSY5yzkhFgquFluroSPYQ0nzG9qB6rl8z\nJARWPbeegTFj0i5CEvY0s10B3P0lYKt/OhzGuznxUg0lBO7gqTE7w2WXwZ//DK+8Etz/4hdw2WUM\nvO51kU8fHDs20eImQeeYUopJNMUlmuJSSjGJprjEQ50zUpHe3l7uvfferZYtX76c2bNnp1QiERlJ\nYeeMRrhJUo6aN48zJk1KuxiNdj1wk5ntFj6O+vUi+V6qoYTAo3j61Q3wlrfALrtA0Y8rR82bxxlT\npmy17PQpU+ieOze5soqIiEgJ5ZyRivX19XH++eez6667Mm7cOGbPnq1kwCIZdcUVV3DMMcfQ39/P\nkiVLmDNnTtpFkjaxbMEC+s4+m86DD2Zw7FjOveWWVss5Y8DPgbcB1wA7Ar3ungvXvxk4z90Tu1TV\nUM6ZdcDaCbxhu9k8+ODlw26/bNEi+i69lM6NGxkcO5buuXOVDFhERCRmyjkjDdPd3c0999xDb28v\nk1r/l1GRptYM05qkNU3fbz+mH3poMI0GOHeYabHNyt3dzHqBHwIfDRfPMrOVwFiCtLz/nErhpgJL\nO9hrr11G3Gz6rFnqjBEREckYTWuSqgwODqY6RULzGduD6rl+uVwu8wmBVc8t6plnguk0Lczd/w68\nA5gD/BYYIOiUeQw4wt1vTbxQ+WlNA5uZO1ejWkHnmCiKSTTFJZriUkoxiaa4xEMjZ6Ri7p5654yI\nVMbdlXNG0vHMM7DrrmmXouHcfZBgWtM1aZcF2JIQ+KmNzJo1Pe3SiIiISJXUOSMVy3/BGxwcTK0M\nM2bMSO21JTmq5/rlpzV1dHRkduSM6rlFPfss7Lln2qVoGDObRzBq5iXgXuAX7n5/uqWi4FLa2Xy/\np0HnmFKKSTTFJZriUkoxiaa4xEPTmqRi+U4Z/Qovkn3unvlpTdKiWn9a01lAD7AReBToMbPvm9nZ\nZrZ9aqUaupR2a+X4ERERaRfqnJGKDQwMAOl2zmg+Y3tQPdevGRICq55b1LPPtvq0pn8B3unuc9z9\nR+7+FXd/P3ADcJGZHZNKqYYupZ3Kq2eSzjGlFJNoiks0xaWUYhJNcYmHOmekYho5I9I8ChMC6z0r\niWrxnDPufqe73xSx/EF3PwnY38ySv1rTbcB60Ix1ERGR5qTOGalYvnNGOWek0VTP9csnBFbOGUlc\n609rGpG7fwV4dyovPhXoSu8zOmt0jimlmERTXKIpLqUUk2iKSzzUOSMV08gZkebRDNOapAUNDsIL\nL8DOO6ddkoYxs73M7Ktm9nkzmzLMZsm/6fLTmlyf0SIiIs1InTNSMeWckaSonuvXDAmBVc8taO1a\n2H576GrpqTU/Ak4Azgf+YmZ3mNnnzGyGme1nZu8FXp94qQoSAi9atCzxl88inWNKKSbRFJdoiksp\nxSSa4hIPdc5IxbIwrUlEKlN4KW2NdpPEtHi+mdBD7r4z8L+B84A9gS8RdI88BFwLXJx4qYYSAndw\n6aV9ib+8iIiI1Kelf9qSeGVhWpPmM7YH1XP9mmFak+q5BbX+lZoAXjSzg919OXCWmZ0N/CPwZmAM\nsCRcl6yhhMA78NRTLyf+8lmkc0wpxSSa4hJNcSmlmERTXOKhzhmpWBY6Z0SkMs0wrUlaUHskA/48\ncJqZnQxcHnbE/D68pWsqsHSQp59ek3ZJREREpEqa1iQVU84ZSYrquX7NMHJG9dyC2mDkjLv3u/sX\ngM8CG9Muz5D8tKaBfrbdtjPt0mSCzjGlFJNoiks0xaWUYhJNcYmHRs5IxZRzRqR55HI5zEw5ZyRZ\n7ZFzBgB3fwl4Ke1yDMknBH5qkBeez06fkYiIiFRGI2ekYlmY1qT5jO1B9Vyf/EiZrE9rUj23oDaY\n1mRm25nZuWZ2vpntXrTu62a2dyoFG7qUdj+53EAqRcganWNKKSbRFJdoikspxSSa4hIPdc5IxbLQ\nOSMi5RXmm8ly54y0oDaY1gRcBqwBVgM3mJkVrDsH+HrRsmQMXUp7FKNHj0v85UVERKQ+6pyRimWh\nc0bzGduD6rk++XwzQKY7Z1TPLag9pjVtcPdvuPsVwLeBf8mvcPcXwmUfTLxUQ5fSHmTy5PGJv3wW\n6RxTSjGJprhEU1xKKSbRFJd4qHNGKpZPCKycMyLZls83AyjnjCSrDaY1sXUS4B8DM4rW3wK8LbHS\n5A1dSruTc85Jvm9IRERE6qPOGalYFkbOaD5je1A918fdm2LkjOq5xbi3y7SmPc1sVxhKCjymcKUH\nb7jNaRSMqUDXJmbNmp7Ky2eNzjGlFJNoiks0xaWUYhJNcYlHTZ0zZvaeYZa/pr7iSJYNDg4yatQo\n/QovknHNMq1JWsy6dTB6NGyzTdolabTrgZvMbLfwcVR+mTERyxprKCFw9t7vyxYt4syeHubPmMGZ\nPT0sW7Qo7SKJiIhkTq2X0v4cwVDeYv9uZocBZ7j747UXS+LW19fHddddN5QotLe3l+7u7qr2kYXO\nmSVLlkT2zMbx/zVKlsuWVcPVs1Qmf6xBtjtnVM/NadmiRSy+5BK6Nm3iyXXrGA0M9vfz4pNPsvvG\njWzb08NR8+YxfdastIvaKD8C5gB/MbNrgB3MrMPdcwBm9mZgr8RLlU8I/LTBxIkwfjyMGxf//dix\nUEW+42WLFnHLqady3sqVQ8vOCP9u9DGic0wpxSSa4hJNcSmlmERTXOJRtnPGzGYBnwGWAUuA3w23\nrbtfYWY/ARaY2dfcfUVcBZXa9fX1sXDhQqZNmza0bOHChQBVdRIMDAwwevTozI2ciev/a4Qsl01a\nV+HIGeWckTgVftFeRpBcpSe8vzy/0eLFiX35ToO7u5n1Aj8EPhounmVmK4GxwD7APydesJnArUA/\n9Bx8MvM++I/MeuuB8Mor8OqrI9+vXVvZdq++Cv39VXXmLL7hBs5btWqrop63ciVnXXppSx4fIiIi\ntbJyv6ia2TSCUTKvDRf1A68CC4HbgTvcfWPRc7YBrnL33thLPHw5Pau/DqftxBNPZPLkySXLH3vs\nMa6++uqK93PrrbfyyCOPsNtuu/Hud787xhLWJ67/rxGyXDZpXevWrePKK6/k05/+NLlcjnPPPZez\nzz477WJJCzizp4dzFy8O/gbOLbgvdlZPD+f88pf50VvJX1q6wcysE3gf8B/AAUAnwQ9YX3T33yZc\nFmc6sA5YOx6eWM+UKWdw8cU9zPrnw2DDhso7X8rdr1sHzz8f3PIdv11dw3bOzL/3Xua/8EJJmecf\nfjjzdXUPERFpYdW2gcqOnHH3e4EpZjYJODy8zQHOCG+bzOwugo6a24E73X2DmSnZcEYM12lV7a/p\ng4ODjB49OnNXa4rr/2uELJdNWlezJASW5tO1adOWv4vui3Vu3DjMmtbg7oPANeEtG6YCS4PPl5Ur\nz+PSfz2EWX4XjBlT3fSl7beHPfaofPtRo4Yt0kBPD4QdeoUGx45tVBRERESaUsU5Z9z9McJGiJkd\nBLwbOILgEpIzgLPDW87M/g7cE3dhpTY2zNzw/Je3SmU150xc/18jZLlsWaZ5q/UpTggMW+ehyQrV\nc/MZGLMlz+1A0X0xfflOWH5a08CEoUUb39oNS++AFD9zjpo3jzNWrtwq58zpU6Zw9Ny5DX9tnWNK\nKSbRFJdoikspxSSa4hKPmj+t3f0Jd7/G3T/k7vsAkwlG1HyLYMrT7FhKKHXr7e3l3nvv3WrZ8uXL\nmT27uirKas6ZuP6/Rshy2aR1FXfEaPSMxOWoefM4Y8qU4G+C4bP5+0KnT5lCdwJfvhvJzB4xs1Vm\ndrmZvafcFSnNrMfM3h1O7U5ePiFw14ahRWPHk2rHDAR5h3ouvpizenqYf/jhnNXTw9EXX6x8MyIi\nIkXK5pyJfJLZB909O8N4Uc6Zcm655RbOP/989txzT8aOHcvs2bOrTkh74403MjAwwMaNG3n/+9/f\noJLWpq+vjwsuuICOjg723nvvmv6/Runr6+NLX/oSu+yyC+PGjctU2aQ1Pf/88/zgBz/glFNOAeCc\nc87htNNOo6ur1gv0iWyxbNEi+v7t3+h84xt5cvNmxpgxsGkTL61Zw267786EPfeke+7coS/fzZpz\nxsyuBE4qWOTAcqAvvP3W3fsLtt8R+BfgnQR5925OsKzOfIKRM0+Oh9XrGTv2I/z4x73MmjU9qWKI\niIhIgdhzzkQZrmPGzLoJkgXfoZ6SbJk5cyZ33nknJ598MrvttltN+xgYGGDUqFG8+uqrMZeuft3d\n3Tz44IO8/PLLnH766Zn6Etrd3c19993Hsccey5TwF2eRRiqc1gTBNDqdkiUu09/6VqaPHg2/+13q\nozIa7AaCgUEHE+TbOzK8fT68bTCzXxN21rj7/cB3gO+Y2bVAYp0zQMGltPuBs9h//wF1zIiIiDSR\nmlpVZvZ6M9shYtVfgLcAPzGzf6qrZBKrgYEgK0A9U5KyknNmOLlcjjFjxvDcc88lV6AKDQ4OZm46\nWNJcJ1YAACAASURBVJaNVM9SXrNMa1I9N6kHHoA3vKHVO2YAfgV8193XuvsN7v4xd9+PYBr3h4Gf\nEqTg/QqwwszWmNm1ZnYBweW0kzUT+CvQP4aOjqc455wPJl6ErNE5ppRiEk1xiaa4lFJMoiku8ah1\neMHtwM5m9gBbrtK0zN1XAwvM7BLgewSXlJQMiKtzJos5Z/Lcnd12241nn32W3XffPe3ibCWXy2Xu\nKlfSuopHzmS1c0aa1AMPwIEHpl2KhgunLJVcg97dHweuBq62oBf0QLaMqpkFvExwee1k3QasBxhk\nxx2f1agZERGRJlNr58w7gfcT/E7zifA2aGYrgDuAZwkG10pG5Dtn6ukgyI+cSbOTYaQs4Llcjt12\n241nnnkmuQJVKJfLZbZTK4uU7b0+uVyuZORMFo8/1XOTuv9+OOigtEuRCeEU7vvD20UpFye8lLax\nceOYspu2A51jSikm0RSXaIpLKcUkmuISj1pzztwF3AVgZrsQXEp7JsGltecS5J35z3iKKHFop5Ez\nDzzwQNpFKaGRM5Ikd1fOGWmcBx6A3t60SyHF8pfS9n5yueEucC4iIiJZVfeEcXd/1t1/5O4fcff/\nBUwBbgF+W3fpJDb5joF6OlaycCntcjlnsjhyxt01cqZKmrdan2aZ1qR6bkK5HDz4YFtMa2o6+YTA\nnaMYPXpc2qXJBJ1jSikm0RSXaIpLKcUkmuISj9gvaePuj5rZScDX2PoSlJKiVkkIPBJ3Z+LEiWze\nvJlXX32VceOy0TjNfynWyBlJSrMkBJYm9NhjMGEC7BB1TYD2ZGZXuXv67Z38yJn+QSZvvxl++lPo\n6oJRo+q77+xM+z/LvGWLFrH4kkvo2rSJgTFjOGrevKFLyYuIiFSqps4ZM9sT+CTwN+Bad99qqIK7\nv2hmGlMbk76+Pq677rqhL1y9vb10d3eXXVcorpwzo0ePznTOmdtuu43bbruNFStWsM022wwbjyTF\nMWqp0So9juJ+7nBqmbfaiHI0q6iRM1k8/uKen6xjoLzCL5FPrlvHaGCwv58X16xh9913Z/2oUVst\n69p2WwbWr9+y7qWX2GXDBgZ6evQFdIvkr8wUZSghcCfn7P4yXHUVDAzA5s2132/eDGbxdPI08n6Y\ndTN22QUeeaT8Puq48tiyRYu45dRTOW/lyqFlZ4R/Z/H9obwQ0RSXaIpLKcUkmuISj1pHzvwI2A/Y\nETjfzG4Evg/c6u4bzew1wKSYytjW+vr6WLhwIdOmTRtatnDhwq3+jlpX/IWkHUbOrFq1irvvvptD\nDz10aNlw8UhSPl5ZHTkz0jFWLm71PDdOWSlHVhR3zrRDzhkdA+UVfolcRjD/uCe8vxxYtnbtVsve\nB9yydi3nFaw7L7+zxYsz/QW0bU0Flm7mK6P/iUs2DTBv3lH1X7VpcLD+Tp5q7zdsgHXrojuLNmyo\n7DZQxW+EHR01dwwtvu8+znvhha12d97KlZx16aV6b4iISFVq7Zx5xN0PNbMDgA8BHwCOI7hi03PA\nDhS04aR211133VZfNgCmTZvG9ddfj7sPu674y0gr5ZwZrmf2r3/9K29/+9u3WjZcPJKUj1dWO7VG\nOsbKxa2e545kpHpOshzNqlmmNVVbzyPRMVDe4ksuGfp1fzHBh/SZbPmwLl4Wta6QvoBmTH5a08AY\nli6dD8DKRz4Hzz3HrBlvSrZzpVH3udzInSXbbRdMuQsfL9mwgRkFjxtx33X++VDUOQPQuXFjotVf\nqTjPu61EcYmmuJRSTKIpLvGotXNmg5nt7+4PAp8ys88CRwGHEHTM/MbdfxBXIdvZcF+oRvqiH7Wu\n1UfOFF+dplDa5c36yJlajrE4nhunrJQjK5olIXCcdAyU17Vp05a/i+6jlkWtK5bVL6BtKZ8Q+KnN\nQ4tWrv4yl37kbcza9YnGTScaNy656UudncE0q0otWQIN/rIw8P3vw0MPlSwfHDu2oa8rIiKtp9bO\nmc8A54a/zF7m7g8DPw9vEiMbphEy0jSFqE6KVs85k78iUpThOm2SkvWcMyMdY4187kiq7XlvVDma\nVdTImSwef3H+wqJjoLyBMWO2/F10H7Usal0xfQHNkKFLaW99zG885EhYMj+NEqUuiV9xj5o3jzNW\nrtwq58zpU6Zw9Ny5DX/tWuiX7WiKSzTFpZRiEk1xiUdNrVZ3f8XdPwksIMg7Iw3S29vL8uXLt1q2\nfPlyZs+eTW9vL/fee2/kumKtPnIml8ux7777VhyPJGV95Ew1x1Gcz41TVsqRFe2Yc0bHQHlHzZvH\nGVOmBH8DZxTcRy2LWlfo9ClT6M7oF9C2NHQp7a1/dxs7NpufPa1i+qxZ9Fx8MWf19DD/8MM5q6eH\noy++WNP9RESkajVfStuCnyknA5PMbBzwO3d/Ja6CSaC7u5v+/n4uvPBC9t57b0aPHs0pp5yyVQ6F\nr371q4wfP56JEyeWrMuLo3Mmyzln3J0pU6Ywe/ZsrrrqKl588UX22GOPYeORpKznnMnH55vf/Cab\nNm1it912qzhu+W2+/OUvM3HiRLbbbrtYYl7tvNX861144YWMHz+eHXbYIRN1n5ZmmdYU5/zkfF1f\neumlDAwMVHUct4vps2bBwABnHXssnYceyjOvvMIPzRjYtInj16xht/CKTPll31yzhs5tt+X49euH\n1n3cjJ0nTGBw7FiOnjtXX0CzZOhS2lsWbbPNycyd+760SpS6pHIgTJ81q2neC8oLEU1xiaa4lFJM\noiku8aj1Utp7EUxhOqBg8XozuwY4w91fiqNwEjj88MO55557OOWUU9hxx60HKnV3d/PYY4+x//77\nb3WVomL1Tq3J5XK4O11dXZnsZMjlcpgZ3d3dvO51r2PJkiXMmTMn7WIBW2Kf1ZEzEBxHY8aM4amn\nnqp6pEF3dzd/+tOfOOywwzj44IMbVMLKyvHwww9zwAEHtP2HQ7MkBI5bd3c3Gzdu5OWXX6a3tzft\n4mTS9H33Zfq++8Kvf512USRuQ5fS7gDmA/fx2c9213+1JhEREUlErZPxvwXcA3yU4IIOPwVywMeA\nP5rZ/vEUT6B8x8rg4GDZDpN6c84MDg7S2dlJR0fHUEdNGob70l04UqCrq2vo/82CrI+cyavkOBpO\nLpeLNea1dq709/dnuhMsKVEjZ7J4/DWiE21gYEDHwEgeeAAOPDDtUkijTAW6NgKDbLttP/Pnfyzt\nEqWq3Tvqoygm0RSXaIpLKcUkmuISj1qnNT3r7icVLjCzTuAI4DTgV2Z2kLs/X28BpXzHyuDgYNkv\nI/VOa8p3zpjZ0Be9zs7OmvbVCIUjBTo7OzPZOZP1L4y5XK6u4yMLMd+8eXMmypG2dsw5kzcwMKBj\nYCQPPAAHHZR2KaQRhhICjwIGmTRpr5QLJCIiItWodeTMpuIF7j7o7re6+9uBq4Gz6yqZDCk3LabS\nzpn8qJday5DvjOns7EztV/glS5ZELtfImfrVM3Im7s6Z4eq5HI2cCTTLtKZa63kkmzdv1jEwkvvv\n18iZVjWUELgfOJq99tol5QKlrxHnmGanmERTXKIpLqUUk2iKSzxq7Zx5yMyOGG6lu58J7FrjvqVI\nuc6ZSobx13sZ7MHBQbq6goFW9XTyNErhl9Gurq5MfTnL+qW08+odOZN2zPOdS2mXIwvyOZjysto5\n0wia1lSGpjW1rpnAX4H+MXR0fIe5c5UMW0REpJnU2jlzKfBJM3uPmY0aZpuXa9mxmV1tZs+Y2QMF\ny+ab2ZNmdm94O7qWfTeruEbO1HOlpcKRM2l2zjRzzpmsf2HM0siZWuat9vf3D5Wl3bl7ybSmLHYO\nNmJ+skbOjGDdOnj+edhnn7RL0mrWx7GTuts/QwmBB9lxx2eVCBjlQIiimERTXKIpLqUUk2iKSzxq\nzTlzNnBMeHvVzO4AfkXQNLgPeA/wdOETzGx/d/9zBfv+b4LOn2sKljlwkbtfVG1B+/r6uO6664ZG\nVvT29sZyadVG7TdKHJ0z+ZEztX5BGxgY2KpzphFffuqJaTPknMnil+NCtY6ccffYEwLXQp0zWyQ9\ncibJ82G512pkzpkk/89CyxYtYvEl/5+9M4+Pqrz3//vJZDIJWRDCFpDNuFEXDK4FhQAdokWrdlGI\nbdX2em/rBay3y21Fer0V9LbaVhHU6s+2aoVq9fZ2oRoiGnDfwAquGFlkScIWYbLM+vz+OHmGM2fO\nmfXMJITzeb3mlTnbc57zPedMzvM5n+/nu5Q9O3fS3tJCVU9Z6yIgHAjQ3tJCYVkZIZ/PdFlVVRW7\nuroI7dnDCX4/H4wZw/TvfIfvLVqUdd96KyZ9DJfZ1E72zz9nAGuLiByUcN11UFiY2sflSn1dO7Z3\nuaAg0/eD/QPqvi70+wl5PMxasOCIKcftwIEDBw5yg0zJmWnAbGA08AU0I+Av9CyTwAHgv4QQJ0kp\nP+yZ/whwdrKGpZQvCCHGmSwSJvMSorGxkeXLl1NTUxOdt3z5coCsHh5z1a4Vkpn5plqtyS7lTC48\nZ1KNaVNTkykz6yhnskem5Izaxm7PmXQZ+GAwCPT9OOcDZtWackXOZPN7mO55TmVfuVLO5Pt3X2Hd\nqlU03HADdc3NNAC/Adbt20cDUAc0AFcBDfv2scRkmX79JarRXbv41s9/zl2QFUHTWzHpa5BS2nLB\nZf38owyBwwEK3FD3chB/ADyFPhZMGcLsk4ZBKHT409kZOx0Ox05n8kmnjYKCnBNETW1t1I4Zkx+C\nKo021q1eTcP3v8+S5ubo6VvY8z3XBE0m/1+PBjhxMYcTl3g4MTGHExd7kCk5sxN4UUp5CHhAaK9o\nzwBm9nwuQHv7gxBiB/A8cHKWfZ0vhPgmWgnv70sp25NtsGLFipiHRoCamhpWrlyZ1YNjrtq1gp1p\nTX3VcybbmOrTOJTnjNEUtbeQ7Pz1FWSa1tRXjs9RzhyGMa0pl+RMPn8PU9lXrjxn8v27r7B66VKW\nNDdzM4fJldU93282/DVbpp+nx287Orjs/vuzImd6Kya9DSHEV6WUT5rMHySlPJCDXab2/KMMgVu7\n2RNsY/V7q6KLmoML4fJz+06qk5QQiRwmagIB8Pu1T3d35h/VRmenNr17N7S3J96mF1StZvfkkuZm\nFt1zj6OeceDAgYOjGJmSM7cA9wshOoCHpJSvARt6Pnf2+NB8nsNkzVwgm7rL9wE/6/l+K/BL4NvG\nla655hrGjRsHwDHHHMPu3buj01u2bAFg/PjxRCKRqKO0YvjSmZZSxrSn2m9paYn2JZv2jdPhcJgt\nW7bw6quvMmHChJjl06ZNIxKJ8M477zBo0CDL9jZu3EhBQQGVlZUZ9efFF19k8+bNgEbOrFu3joqK\nCluOD2D37t1IKWPiqUey7V944QU+/vjjaP+2bNnCc889x8yZM23pXzbTkUiE7du3R8mD3u6P1fTG\njRsZMmRI2tur6xPgsssus6U/al4626v7LxQK9Yl49ub0m2++SXd3N3V1dQB8+OGHFBUVRX8P7dxf\nPn8PFcFk3N+uXbui10swGGTz5s1pXz/JpnP1/yTZdKHfTxOwg8PYATRx+B+4mq7tmWe1fm3PdFPP\n3+IeEsvu87Fp06aY/8f9EP8JxJEzwNeEEBcAC6WU223aV0rPPwB8hpZgHpTg+Qj8Taiz3tzs5b//\nfQmzt7wDoRBNH34I4bCmKgmFaGpu1qZHjdKmt27VpocP16Z37NCmKyu16ZYWbXrgQG16715tuqxM\nm25v16Y9Hm3a59OmXS5turtbm5ZSm5YSCgqoLSrSFC9SgstF7YAB2nQwqE1XVGjTXV3a9ODB2vSh\nQ9r00KHadHu7Nn3iidr03r3a9OjR2nRLizY9frw2vWOHtv8TTtCmt27Vlk+YoE1//LE2fdpp2vQH\nH2jTNTXa9KZN2vRZZ2nTb7+tTX/+89r0m29q0xdcAIWF7Jgxg6Z33427J13d3dp0Dn9Tamtre/1/\nVF+dVugr/ekL0871Ys8zqjN99EzfddddvP322xk/A4ls3qYKISqBIbrUJav1hgCbpJQjUmx3HPA3\nKWVcSQmrZUIIaTyWa6+91jQw27Zt47e//W0qXTFFrtq1wqZNm3jqqae47LLLmDhxYsyyUCjEkiVL\nmDBhAldccYVlG7///e8pLy/H7XbzpS99Ke0+fPLJJ7zwwgtcffXVLFu2jCuvvJKhQ4em3Y4Vso1p\nW1sbTz75JNdffz0At912Gz/4wQ8oKiqyrY+Z4t1332XVqlUMHz6cq6++ure7Y4nHH3+ctrY25s+f\nn9Z2HR0d3HnnnZx00knMmTMnR71Ljs2bN/PEE08watQorrnmml7rR1/ACy+8gN/v5wtf0LJNH330\nUSZPnkx1dbXt+8rn72Eq+7r99tuRUnLTTTflfd+5wM11dSxevZqbgcVqXs9341+zZRi+63HZyJH8\n386dGfct1Zj0KLd6X8aYAYQQs4EfAuvQxtCvAOuklKZp2j3PRXcBv5RSvp3B/saR5vNPzzLJVOA4\n4BPg06GwpS1mnWlV9TR9eXDf8JwxfgoK0g3VEQ11XxuxqK6OW595phd65MCBAwcOcoF0n4Ey+m8o\nhPgqgJRyn56YEUIMMltfSrmXWIO7dPdXpZu8HNhota4e9fX1bNiwIWbe+vXrmTt3bqZdyWm7VlBe\nHmZS/UTL9MjWEDjXnjOpxlSxk0YYDVD7ku9MJBKhsLCw3xoC5yKtyeo8J0IgEKCkpMRJayK/aU3Z\n/B6me55T2VcwGMzJvZ/v332FWQsWsHD0aGYBC9W8nu/Gv2bLMHxXuHbAAGq/852s+tZbMckzdqH5\n692M5uhyAKgWQtwqhJghhCjWryyl3Af8K/AjO3ae1vPPDLRS2scBBOIWF59eDcuWwV13wZ13wv/8\nDyxeDLfcAosWwU9+Aj/8Idx4I8yfD9/9rmYqfO218I1vwNy58LWvweWXwyWXwEUXgdcL06fD1Kkw\neTKccw5MmgSnnw6f+xyceKJWHWzMGBg5EoYNg8GDoaICBgyAoqKcEjOZ/C/JB2YtWMBCA1l+U3U1\n3jRfjmSCvhqT3oYTF3M4cYmHExNzOHGxB5mmNaUt6ZVSpvSgIoRYiWY4PEQI8SnwX0CtEOIMNLPh\nLcC/pdKWynm//fbbGTRoEAMHDmTevHlZ58Kr7RcvXszQoUOpqKiwpV0rJBr8pjowVp4zHR0dGfch\nl54zKnbLli0jGAwyYsSItGJqHIz2JXImHA7jdrv7PGmQredMb8fbIWcOI5/VmtQ9etddd1FQUMDQ\noUNz9nuo2rzjjjuQUjJ69OiYfYXDYYQQUaKxwMZBn9rHo48+yvbt2xk/fnxOf/cVps6eDVdcQeMf\n/sDeIUOY09LCiJ6KTI8LQcjv596WFlxlZczx+eKWqfV3d3czq7WViqIiQh4PtTZUa1LHfttttzFs\n2DBKS0vzEpN8Qkq5AY2MGYv2bDINuAaN71oI+IUQr6N56z0PvCql7BJCpH3xZf38ozxnPgZCsb/l\nxcXfYf78+nS75CBHUL4yi+65B1d3N+HiYi6cP9/xm3HgwIGDoxxJyRkLSa8ppJQPCCGeAu4SQmQk\n6ZVSmr1yy1gz7vV6ee211/B6vZx77rmZNhOH6dOn8/LLLzN79mzOOuss29o1gxpsmg2c0yVnDh06\nlHEf9KW0c6EC8Xq9hEIh9u7dyze+8Q3TdfT5nnoYB6N9qZx2JBLB7XYfEcqZTIiNXJAzVuc5EYLB\nICUlJXR2dtrWjyMVRrIyV/esgtfr5cCBA7jdbi6//PKUt8vkPHu93qinzU033RQljUG7BpUheDgc\ntpWcUfueNGkSy5Yt4yc/+Une0ianulxMnTcPbr45q3aWLVvG2Wefbev/QvU/9mtf+xonnXSSbe32\nNUgpt6EpgB8RQpwOfBmtUmVtz+enPZ+IEOIAmnlvuvvI7vlHoKU0HQ/sDAOL0Oz+wkyYEOo7ZsB5\nRCa/MfnC1Nmze4WM6csx6U04cTGHE5d4ODExhxMXe5DKk2uvSnqzharcYfdAvbvHtE2V780l7FTO\nZKoqCIVCMWlNuVInhMPhjGLal5Uzipzp64qO/qCcKS4u7vNxzgfyqZxRCIVCefk9hMNE9d69e2Pm\nB4NB3G53zn+j9H/zgo0b4bQ4m5G0EQqFbL9PFanb18lnuyGl/FRK+YiU8ltSyuOAcWiKmvuA5WiF\nEPKL6RxObZICzT/4FoqL93Drrd/Me3ccOHDgwIEDB+khKTkjpdwgpawGxqM9eDwGDEST8z4LHBBC\nrBVC3CKEmCaE8Egpu1JpOx/w+/2A/SSKaldfgSdX6GueM7l8Cx8OhxPGNB3Pmb4ySD8aPGfsHgxn\nkreqlDN95bz3JowpPfkiZ9L9Pcw0PzkSiTBkyBBaW1tj5geDQQoLC3NKzqT6m2srbCRn7P5feJSW\nsL/HOENKub2HrJkvpbzFstx1LvE8h1ObXAG0wpqLjlrVDDgeCGZwYmIOJy7mcOISDycm5nDiYg9S\nJlCklNt6Hjy+DawHxqKRNSvRlDU/RXs06BBC7EEjcHodSuGSK+VMPsiZVJQzyQbVSjlzpJMzVujL\nypn+7jkTiUQoKirq9Xg7njOHkU9DYIVMyJlMEYlEqKqqoq0tthpNKBTC7XbnlJzNu3LmwAFobwcb\nylLnQjmjyJ6+Tj7bCSmlaYEDIYRXCDFF6N8U5BN65UzAA9xCSUmbo5px4MCBAwcOjhBkrG7pk5Je\nE+Qq/ShXihwzKDNeK3ImlYHIkUTOJIqp4zmTO2SjnPF4PL3uOaPSmvrKee9NGO+HXHvOQGYpiZnm\nJ0spGTFiRBw5o1fO5Oo6yDs5s3EjnHqqLRVtMk0bTYSjUTkjhDhZCDHYZNFm4GzgKSHE5/PcrcPK\nGR9AAUJ8mR/9aOJRq5oBxwPBDE5MzOHExRxOXOLhxMQcTlzsQaZPe31T0msCRaIc6coZK7+YRMv0\nsMNzRhlv5trPob8pZ44Gz5m+oJxx0poO42hQzowYMSIurUkpZ/qV54xNKU1SypwoZ9Q57+vks814\nHmgTQmwQQvxKCHGJEGKglHKrlPIu4KvAvF7r3RlAYZAzzhjMLbdc32vdcODAgQMHDhykh4zImT4r\n6TVBrtKa/H4/brc7b8oZK9VLKuSM2i4b35N8pzVZDSSPRM8ZpW7q64OXSCSClDLtQbxSzvS254yT\n1nQYR4PnzKBBg/D7/XR1dUXn58NzJtVUUtuwcSOcfnrWzaj+5iqt6Si77y4F7gXcwPeAvwB7hRBv\nCCHuBn6C5vySX+jTmkLCSWfC8UAwQ1+PybpVq7i5ro5bamu5ua6OdatW5WW/fT0uvQUnLvFwYmIO\nJy72IGkpbTMIIU4G2qSU+w2LNgOXAd8XQtwhpbQsu50LXHvttdTX1+P1eqPz/H4/RUVFKZMojY2N\nrFixAiklQgjq6+sB4uaVlZVRXl5u+5tis/0nUr2oZYnKB6tKSy6XK+GAwmzfKpb5ImfUwEG9ATf2\n6ZRTTjGVzaWinEl0fLmEmXJG9aW1tZU9e/ZQVVVFZWWl7X1K55hV/9S6qcKOtKZUz3MiBINBiouL\noyRTH+KIs0Im161ZtaZckwn5rta0bt06nn/+ef75z39SUlJCfX09Y8aMyYnnzLpVq1i9dCl7du5k\n344duIuK+NGf/kRpURHhQID2lhaqqqrwud0UQdrzCsvKCPl85ut3dlJ26qnMGj8+q7K76v7MVVpT\nXyef7YSU8nXgdQAhxDC0Utoz0OiR+UAnWtXK/OJ5QNJTSrub2d+8HFwuLSXO+NdsXqJl6a6f72VW\n67/7Lhw61Lv96yf/i/KBdatW0XDDDSxpbo7OW9jzvTfKjjtw4MBBvpEROYP2CDBUCLGx5/vzwDop\n5VbgLiHEUuBRIK/kzLhx41i+fDlAdPDS3d1NWVlZSgPHxsZGli9fTk1NTXTe4sWL8Xg8TJkyJTpv\n+fLlXHDBBQwZMsRWcsZs/8uXL+fMM89k5MiRCdOaDh06ZNmuSkkqKCiwHLBY7Ru0WKr9AAnbyRaq\n3UAgQFNTU1yfXnzxRSZOnBg3ODVTzujPebLjyyWM1ZpUXwYNGoTP5+Piiy/OSZ/SPWbVP6PqIhmU\n4bHyrElnW6t+Wp3nRAgEAng8nqhqQqXhHcnI9Lo1kpUFBQU5V87oVW+pEmOZ5idv3ryZtWvXxv0u\nX3zxxQwcONBWzxk1WKhrbqYB+A2wDmjYs4c6ODxv3z4aIO15VwEN+/axxGJ9AN54g4U33ABkPkDR\nE9924mj0nNFDStkGPNHzQQgxHrgTeCnvnZne8/dZQEbgww8hEmFVw0ss/X8v4fcX4ikKsuCb5zB7\n2iSIRCAcNv9r57J01w8GbetDbTgMr76av2M1WwZ9iviqLSiABx/sk8Tc6p/+NIaYAVjS3Myie+7J\nOTnj+GWYw4lLPJyYmMOJiz3IdPRyKfB1tDdF3+v5hIUQbwMvA230hqQXqKmpYeXKldGBi9/vp6ys\nLKW3hStWrIgZBIE2yNEPANQ+1q5dyzXXXMPevXtt67vZ/mtqanj11VeZM2dOwrSmRG8t1UA1kXLG\nat8qlnrlTDIFTjZQD/jBYDBpn/QwDkaNg7N02rIbkUiE4uLi6LGpvqxZs4aZM2fmrE/pHrPeSyMd\nYiMSieByuaJqhXTJGbvOTSAQiPEb6Q/kTKaxMSNI8pHWJKXMS+w/+OADpk+fHjOvpqaGhoYGrrrq\nKlvTmlYvXcqS5mZuBpaoeT3f7ZiXbH2FbAcouVLOHI3VmhJBSrlFCPFt4JfAt/O6c71ypg1u/e1r\nnDi2nIX//SbNzXdGV2vetRCqqvqWUbCUfYsgsnNZKKQRTuqv2SeVZV1d1svyRY4KkVNypvDjj013\n6+qxKHDgwIGD/o6MnqD7rKS3B/qHRKWcOXjwYNLtzAYvVgPNSCRCWVkZu3btyryjKexfzc/GEFiv\nnLF6gLbat96nQA24cpkioVfOmPVpy5Ytlv1MpJxJdny5hF5Zovd0SXRt2YF0j1mvnEkHirhT9Cus\n1AAAIABJREFUMXe73Vn30+o8J0IwGKSoqCinfiP5RqbXrVHBlA/ljDr3gUAgZXKmqakpozctVsoc\nPRFt1zVQ2GMqrz+iQsPfbOYlW1+PbAYojnLGPgghRgE3AruAx6SUMc7UUsp2IUT+HdL1yplS+Pny\nm+jYfhI9op4ompuXcM+3L2H2+Uv7jnIGcpLW1OTzUXvMMb2T1uRyQVFRn1KmUFBA0+uvUztlSmax\nzXGKVqiuDlavjpsfLi7O6X4h8/9H/R1OXOLhxMQcTlzsQdavN/uUpLcH+kGJ3++ntLSUffv2Jd3O\n7IE/0UDWbs8ZqwGHlBKPx2O6r1AolNSMNRVyxmrfKpb5Us4oD51AIJC0T3qYKWf0MUmnLbuhlCXK\nlFX1xSqGdvUp3WNW5zgTcqagoCDjVBK7zk0gEIiSM71dOcouZBobM0PgXBKRSjFTWlpKIBBgwIAB\nOdsXJCan7PacCXk82l/9PMPfbOYlW1+PbAYoelWinTgaPWfQnndOBCqB24QQ/wf8AXhWStkthBgE\njM17r5RyxgecAR1rtwOXm67aPXg0zJnRd1JbcvW/uKkJnMFCLHbuhHHjersXppi1YAELm5tjUptu\nqq7mwvnze7FXDhw4cJA/2P7fUEq5BU3K+1O7204F69evZ+7cudFpldaUymCtvr6eDRs2xM1/6aVY\nnmn9+vWcfvrpVFRU2Pqga7b/9evXU1NTY1mKWb0pllJaPhwrQ+BEXjFW+1axNBoC59JzpqSkhGAw\naNqnAwcOxJxfhWTKmWTHl0uogbKKW319PevXr6e6upo1a9bkrE/pHrMyLs5WOWNHP63OcyKotKa+\nVKkrW9TX1/PWW2/FzEvlGjGmNeW6WpO6BtIxX4fM85OPP/541q9fHzNv/fr1XHDBBbYrZ2YtWMDC\n6mpmAQvVvJ7vdsxLtr7CTdXVeLMYoChlUy6qNfUntVqK+EhKORQ4Ha1q00zgr8AhIcQuYDe9+IKK\nM4BxAGGsqL7iMZXw1a/Cl78Ml14Kl1wCX/wiXHghzJoFM2fC9OkwdSqcfz5Mngznngtnnw2TJsEZ\nZ2gl3k85BSZMgBNPhOOPh/HjYexYOPZYGDkSRoyAoUOhshKOOQYqKqC0FEpKwOOBwsLcETM4Hghm\n6MsxmTp7NnV3382iujpumTaNRXV1XHj33XkxA+7LcelNOHGJhxMTczhxsQeZVmvqk5LerVu3Mm/e\nvBgvhu7ubsrLy1MaMKjtli5dihCCIUOGsGjRIgB++ctf4nK5GD58OPPmzWPLli22K2fU/m+77TaG\nDRtGaWkp8+bNY+fOnQnTmvSVmMzeqKfiOaP2/eCDD7J3717GjRsXE8t8ltJWb9/Vvu+44w6Ki4sZ\nMmRI3PlVMKvWpD/napvf/e537Nq1izFjxli2ZTfUeVHx93q9BINBfvGLX1BWVsZf/vIXKioqOO64\n42ztk2rnoYceorW1lfHjxydsPxwOM2DAgKzImUwGaKo/d955J8FgMO7aSwVSSoLBYIznTH+A1+vl\n4MGDLF26lPLycoYNG5ZSbPJdSlsRwEr1lmuMHTuWK664ghUrVrBjxw7Gjh3LvHnzotehneqpqbNn\nQ3s7jddcw96TTuIrO3ZoCq0hQ3i8pISQ38+clhZG9FRaelyItObd29KCq6yMOT6f5frlo0Zx4fz5\nWVdrUsS3nQgEAtEqaUcRuoQQE6SUm4D/EEL8CI1TOw8YDLwopfxj3nult2FSpsBRqu+wi1F19U3M\nn39hfvvmwEGKmDp7tlOZyYEDB0ctMk1r6pOS3vvuu49ig+xbec6k+kDq9Xrp7OzE7XbzxS9+MTr/\n008/pbCwkG9+85sA3HPPPVHpvp64yBZer5fXXnuNr3zlK0yYMAHQBtepkDNWRpyppDWpfR9zzDGs\nWbOGH//4x3H7UW3nmpwpKSmJDvC8Xi8fffQR48eP54tf/CJNTU2m25kpZ7q6umLW8Xq9jB8/nsce\ne4zvfOc7DB8+PCfHYNY3o3Jp2rRpbNq0iR/96Ee8//77vPPOO1x55ZW279vr9TJq1CieeuqpKNFo\n1UfILGVNbwic6YDY6/Wybds2du7cyfe//33efPPNtLbXX+P9iZwBmDx5Mps2bWLUqFH8y7/8S0rb\n5NtzRsXf7XanNfjPJD9Z+TbNmjWL6dOnc8cdd7BwoaYzaWhooLi42PZrYOqIEUz9/Odh3TqamppY\nu3Ytl19+Oaeffrpt+8g1QqEQxcXF+Hw+W9tV5Ex/uudSwA+BxT3/c+6XUn4I/KPn03t4DhAcNgXe\nLQBl+rsIcFFZ+QF333193zIDziEcD4R4ODExhxMXczhxiYcTE3M4cbEHmWpJ+6Sk1+zhMJ20Jn07\nxvVDoRAdHR3R6e7uboqLi6MGmHZBeTfo95+oIpMaFCUajKRKzoAWL6uqUPnynCkuLo4Z4HV3dyc9\nf8k8ZxRUu915dP43Kmcgluyy+xoyIhAIRM2IraDObybEm54gzEatEA6H8Xg8tLa2Jl/ZAOU3A/GV\nuo50BINBhg4dSltbW8oEi1laUy6VDep6zodyRhGxQohoGp6611Xqju0E3TvvQA8Ro66tI42MCIfD\ncb+tdiAYDFJSUnJUKWeklB1SyhuBu9BeUvUNqLIMM4CPgei9OBW4lerqAA8/fPQQMw4cOHDgwMGR\nhkyVM31S0mv2sKxXzpiVlzVDJBKJe9AMh8Mx5Izf76e4uDjqsVBSUpL9AWBu2pioIpNROWOGVDxn\nFLq7u03XUW1Afjxn9AM8v98fHRBZMbLJPGcUVLv+ngos+YAyzNXHTV/9Kl2fjnShr6ZiVUVH74uT\nb88ZfTtVVVW0tbWlzbwrvxmgX3nOgHZsKoXywIEDDB48OOk2vZHWlAk5k8kbFv2xCSHweDx0d3dT\nWlqaElmdETZu1Pw2iC05fyRBT3yn+r8wFQSDwaNROYPQAjgOGCuEGAC8IqXsSLxVjqFXzvgAjgEW\nIUQzNTWD+NnPrjzqiBnnLW48nJiYw4mLOZy4xMOJiTmcuNiDTMmZPinpNRtU+v1+SkpKogPjVEq8\nhsPhuAfXcDhMZ2dnDHGTizfFZuVOVQWjRKW0E6lZ9AOWZAPv7u7uqMpCH4N8GAIr1VBxcXEMoRAM\nBpOSF8b+Wg3QVbv5Vs7ofYEgnpzJpdpAxS7R9Z+tcqawsDBrUkRPzqQLVUYbrFVTRyqUKmj48OG0\ntramRM7k2xBYkbfppjVlAqNKzuPxRKvyKd+hbInCOGzcCD0pZeraOtKUIkpVlM7/wlQQCASOOuWM\nEOJYtOedU3WzfUKIR4CFUsrPeqdnOpwBrD2kfT1jAG+9tbx3++PAgQMHDhw4SIqM0pp0kt5f04ck\nvcYBmXo4V14IqT6sRyKRuHXD4TBSSrq6uuju7sbTU17V7pQUtd90lTOJCBP1IJ5qWhMQN5DLh+eM\nUr94PJ7o8av+qLgk8pwxGgKbne/eTGuyUs7kI60JEr/p7yvKmZEjR9La2mp5nq1gTGvqT+SMIhyG\nDRuWcspXb3rOpHMtp3ueIf7YiouLo/dzTpQz4TC89x6cemrPZNiyel5fhv4c2UlcHaWeM/cBbwLf\nBW4G/gJEgOuBd4UQE3qlV8a0ptAwiov3cOut3+yV7vQFZPIb09/hxMQcTlzM4cQlHk5MzOHExR5k\n/OpMCDEc+AFwqhCiHXgeeFhKedCuzqUL48OhnkRR1XuMhsFW7ZiREx6PB5/PR2FhYbQdu1NSzJQz\nat+JSmmnmtZkporRQ5EhKhVHv59ce87ofStUCpkadGWinOkraU1WnjMqnvlMa7KCHZ4zdpAzI0aM\nYM+ePRx//PFpbatPa+pvnjN65cx7772X0jZmaU39yXPGSM6o+zknFbuam2HYMK0EMInJ8r4MRc6k\n878wFai29Gm/RwHapJTf1s8QQrjQqJGfAGuEEKdLKffmtVdGQ+Cdu5kwIXTUpTI5cODAgQMHRyoy\nLaV9OhoZM0g3+zJgkRDiOinlX+zoXLowPiwrXxggbeWMkZwJhUIMHDiQjo4OPB5PlPSxezCSrueM\nIl5SMQRWJpqJyBlFhhgHcvnwnFGDfP3bd6NyJpHnjNEQ2Iqc0b9pzwdS8ZzJR1pTous/G+WMPm0r\nG1IkEolQUlJCWVlZ2lVw+ntak1LOpPpWojfSmhQ5kw7RmK3nDBD1nAHtOlBktW331MaNcNpp0clE\nZHlfhv731VHOZI04dl9KGUYrYP2sEGIx8FNgQV57NUP3/VlAhrn1G+fBW29BQcHhj8sVO231SXW9\nggKwycPIbjgeCPFwYhKLdatWsXrpUgr9fp71eJi1YIFTylsH53qJhxMTczhxsQeZKmduB/4TraS2\nBCYAXuAa4H+FEF+XUq60pYdpIBXlTKrtmHnOVFRURN8O6kmfXHvOJKrWpB8YJyNn4HBKkn5wo4de\nOaOH0XMmF2/hFQGkH+Cpqlh2ec4Eg0HKy8ttUc40NjayYsUKWltb2bNnD1VVVVRWVlJfX4/X642u\nl8xzRvl02GnSqUemyhl1fKpfxuMybmumnEm1DdVOU1MTzzzzDC+++CJlZWWW6xvbnTx5ctSLRX/u\nzfYPpDRP7TedY8gFFPG0fv16/vSnP/H666/jcrkSxmblypU0NDRQUlJCfX09brfbNnLGLB5jx46N\npsx0dnZm1b7+QXnHwYMUAeFAgPaWFqqqqvisoIBD+/bxb7//Pe0tLZSWlvLXAQM4pqSEPS0tPP2D\nHzBo0CAOAH8eODC6bWFZGSGfj6qqKnxud1y7lvN272ZYURGhujpmLViQ0AMsUYzsuGayadeonLEL\nipw5mjxngA+EENOllM+bLZRS3iyEeDzfnYovpS2ZveI38IcIRCJail4kkvyT7npSauSMHWSP3cSR\ns559bQnRZ0m4TLFu1SoabriBJc3N0XkLe747BI0DBw56A5mSM3ullP9PN/068LoQ4na0HOx7hRAv\nSym3Zd3DNGBGztilnFHkjM/nw+VyxShncpHWpG8z0WAgFeWM0S8mkRmklXImH54zapCvj6mxFHpT\nU5MpM5uO54wd5ExjYyPLly9n0KBB+Hw+Lr744uiy5cs140U1aErmOaOWKcNOu6E3BLaCMfVKHV9N\nTY3lcSkoZZDxGkynDYCPP/6YV155hfPOO48tW7Ywbtw40/XN2n3qqaeYMmUKX/nKV6L9MFtv8eLF\neDwepkyZknCe2q/6nuox5AKBQID333+f559/nhkzZiTshzpm47FMmzaNiRMnZt0Xq3N6ySWXUFZW\nlrYKzHg/6x+U1wENQF3P398A6/btOzxv5874ecASYN2BAzHzrgIa9u3TlhnWN2tDP2+J6tz27Sxs\nbqbo8ssZ87nPWd5P6V73qSLbdnPlOaOqFR5lypl7gL8IISqBv0gpzR4CDuW5TzBD9/1ZIBSh9pRS\nPMLDgvoFzPbOZtWqdSxduhq/vxCPJ8SCBbOyT3uSUvvYRfbYuF7TO+9Q+7nPZd+e2TqhUJ861pRj\n0tlJbVHR4e3CYe1Y9B+rZzwzEq4vE1FJ1lv917+yZPt2AJqAWmBJczOL7rnHIWd6YPXcfTTDiYk5\nnLjYg0zJmf1mM6WUEWC5EKIVTVlzfaYdywRGwsDv92esnNGTM6qKkD6tKV/KGSklkUjE0oBS7zmT\nqFpTqn4xfr/flAjKp+eMPqaqFPq+ffsSbpuO50x5eXnW/ggrVqygpqaGNWvWMHPmzJhlNTU1rFy5\nMjpg0pMXeuWMiiccJvlyQc5kopxRx6eH8bgUlDLIGPN02gD46KOPksbSqt3Pf/7zvPHGG8DhlDaz\n9aSUMcSF1Ty1XyllWseQCwSDQdauXZtSP6xivm7dOk7TpeZkCqv2GxoauPLKK7Mmq1cvXRp9g7ka\njRi5mcMESabzsmlDjyXNzXyroYHjzzjD8jcw3es+VWTbbigUwuPx2KqckVISCATweDw5+Z/Qh/FT\n4OKeT6cQ4mVgDZp25Z/AV4Hd+g2EEBOklO/ntFfPEVtKuxLWjl+rLfrRS1TuP5+De8bR1XV/dJPm\n5oUA8QRNMsLlCCEiOHAAWltzQ84cqeup/9ORiLnqyePps2SK3esV6l7q6eHKY+q7AwcOHOiRKTkz\nQggxVEq5x2yhlPJJIcRXs+hXRrBTOaN/0FSqgrKyMj799FNKS0tz7jmj+qoG9lZpOqlUa1IP5ZBY\n9aIetCsqKuLWyUdak145o/ecKS8vj1apsWJk0/GcqaysZP9+U34xZSjyzio9zOz60Z8jo3pJHfOA\nAQOy6pcZVCzT8ZyxSoExO+9WaU3ptGE8f+PHj7dc36pdRc4p5YzZembnK5VzmM4yuxEIBFLuY6LU\nJTvSmqzaMCNWU4Hxfi7UKdoKDX+zmZdNG0YU9Rg0W/3epnPdp4Ns282F54xKAT4Sq1dliWnAbGA0\n8AU0I+Av9CyTwAHgv4QQJ0kpP+yZ/whwdt56eAbwyeHJ0GUdtD74NnQ9E7Nac/MS7vnSecwu+mfs\nAD7VVKXeGnSn2Faty6VVW0u1vcLCvnesNq9Xq1+vH6YqpYPQCy/A1q2ApppRCNtkmN4fYPXcfTTD\niYk5nLjYg0zJmUeAZ4QQX5FSbrVYx5dh2xnDzBA4U+WM/oFXPdSWlpbS0dERV0o7l2lNyaoxqb6l\n6zljBr/fb1npJJ+GwEbPmdLSUtuqNam0pmwNgdW+rGKpH0yb+QIZlTO5LKetqqmkqpwx81xSMCMJ\nrMiZdNpIRAgZ10/Wroqz2XpWxJBVe6n2KZcIBoOW+0s1NnYZAifyRDLeu5kg1PO7ChAy/M1mXjZt\nGNHdY3xsdT+lc92ng2zbzYXnjKokZqam7OiAzZu1Ylf9EDuBF6WUh4AHhHZyzgBm9nwuQEt9Qgix\nA62Awsk579UM3fdn0Xxn9Cj9zHSz7sleWP18/ED+KB60Ozg6MGvBAhY2N8d4ztxUXc2F8+f3Yq8c\nOHBwNCOjp0Up5dPAu8DbQoifCSGO1S8XQowExmXfvfRgp3JGv64aSCtyRl8Fym7ljFK56JUzLpcr\nOrgyqyKVjudMovXUcRkftFVaV67TmtSxGKs1Kc8ZKaVltRozzxmz41RpTdl6ztTX17Nhwwaqq6tZ\ns2ZNzLL169czd+7cuL7piTE9YQa5LaedSjUVYx/V8elhPC4FK4Iw3TZOPPHE6PpbtmyxXN+s3Rdf\nfDHqx6L6YbYewEsvvRQ374UXXjDtZzrHkCsEAgFmz56dUj/q6+tZv3593HrTp0+3hZyxikdtbW1G\npbSN9/OsBQtYWF2tfQcW6v5mMy+bNvS4qbqaEdOmWRq0Q3rXfTrItt1ceM4os2ojYR8Ow8knwze+\nAY8+asuu+hpuAe4XQjwghDhXatggpbxTSnkRWiXLWuBWYDswF7BfFmnAoAcGMeh3ZfAHNGJmnGEF\ni/8BxaVASYmWzuJ2a6qKfkLMpFrh7miCE5PDmDp7NnV3382iujqumTiRRXV1XHj33Y7fjA7O9RIP\nJybmcOJiDzJVzgD8K1CElqa/UAixGfgYLeN5KpB32tlMOTNw4EAgfeVM7IOmRm6UlZXh8/lyTs7o\nqxPpyRk16NQP6lNVzqSSkqQUQcYH7UgkghAiSn7kMq3JOMDr7u6msrIyaXnkdDxnKioqslbOKI+H\nO+64A4/Hw6pVqygqKmLcuHHMmzcvxgPCzDDXjJzJpXKmvLw8Lc8Z1f+lS5fi9/s59thj447LuK0x\n5vo2Dh06xKhRoxK2ccIJJ3DFFVfwyCOP8N5771FQUGC6vpr+xS9+QTAYZPTo0UydOjXqG6OIObXe\nbbfdRmVlJRUVFSxatAjQTICHDRtGeXk5ixYtYt++fdx3332MGTMGt9sdt9+f//zneDwehg8fbnkM\nuUIgEGDmzJmMHDmSlStXsnXrVkaPHm0ZG5/Px7Jlyxg9enQ0huXl5Rw4cCDrvni9XgKBAL/4xS8o\nKSlh5MiRzJs3j+Li4qjyLpvrWD0QL7r2WlxDh9Lq8fC4EIT8fua0tDCiqooDwLLPPmNQRQVzWloY\nPHgwLYEA7YMHs3PHDq6MRBg8eDCtgQDtlZWE/H7ubWnBVVbGHJ+PET1VmIztWs37dyEYWl5OuLiY\nC+fPZ9O2bRQVFdHV1WUZIyklt99+O263O+G9kw7U9vfffz8+ny/h/WQG9ftqt3JGqS31/xM2bICK\nCq0KOfSbcX4UUspm4KoeQ+AhJsuDwLqez38JIYYAm3Ldr/27DnAT8D+jQTYTS848CwTcaJTjYTel\n6uqbmD//wlx3zYGDPoups2czdfZsx8zUgQMHfQIZkzNSym5gjhDiz8B/AGcBJwKtwH9KKX9vSw/T\ngBk5o0gUq8G6GSKRSBw5k8+0ppKSkmibRjNfM3ImUdqTaiOVtCalNLJK61LId7Wm4uLi6IDC6h9n\nOtWaysrKCAaDcdukC6/XywcffMDcuXMZMmQIjzzyCFOmTKG6582/sW/6AYzxPOYyrSkQCFBSUpKW\n5wxox9fV1cXmzZv5/ve/b7mt3hfJuA/Vxttvv82XvvQlzjjjDMs2XC4XXq+Xs88+m9/97nfceOON\nlvv0er28/fbbDBw4kAsuuIB3332XoqIiQLtPVCy9Xi9vvPEGF110UdRMNRKJ8PLLL3PxxRdz5pln\nAtDc3MyHH37IjTfeSEVFRdy+Nm7cyLBhw/j6179u2adcQakTvF4vXq+X3//+90ydOpXjjjvOdP1z\nzjmHOXPmcN1110Xnvfbaa7aV0j7llFPwer1UVVXx7W9/G9DelmSS1mR2P0+dPZupZWXw5z/DiSfG\nLd+5cyf/+Mc/ose3Y8cOnn76aa6++mruvPNObrrpJj755BNeeOEFrr766swOMgH+ec89SUtpn3fe\nedTW1lJZWcm8efNs27fX66W0tJR33nmH73znO2ltq09rsks5o9KajIT+mjVg8PbuVxBCfFVK+aSU\nch+wTzd/kJQyjgWVUu4VQjyS634tAt6gDEkEfJ3xBsEMBeooKbmS6uoqRo0qZ/78C7Ov1tSH4Qy2\n4+HExBxOXMzhxCUeTkzM4cTFHmRtnCClfFxKeS6aZLcKGCmlvDfrnmUAI2GQKYlippxR6TYul4vP\nPvssZ8qZcDhMcXFxXFoTmHu9GBUPVm0aS2mbQXn0xEvUY4mEXHvOqMFDJBKJnsNkUnyjckYZAhsH\npGowYdd50xOAirwzQnnOWJXShtylNUkpUyp1a3UdRSIROjo6Eg7s9dWarMq9Dx06NGrqbNWGIspS\nGTxGIhG6uroYP348ra2t0Tf4EJu6p45f355apldPWZWQVwgGg1lX+MoU+mMDGDZsWMJY+nw+SktL\nY+Yl8s9JF62trVRVVcXcP+p6tuW+OnRIq65iIDkVjKSqUu3oq50lU9plg3A4nJScaW1tZfDgwbaW\nrNbvP5N29Wmjdv3WKOLQqJxZswZmzEiw4ZGP/7SY/zUhxKNCiDHGBVLKH+W4TwBs4xQoLIGJhgVn\nAIVtVFbey5/+9O9s3HgXzzxza78mZhw4cODAgYMjDba5Wkop/VLKVmnXCCADJFLOpPNAauU5A9oA\nfP/+/THVmuxWzhjTmvR+MVZVlFJVziTyi1HKGeM6RuVMrj1nhBDRuKpzqM5fqp4zRhUIHK5GVVRU\nhMfjyTq1CWIJwETkjJnnTD4MgfUDsnQ8ZxRU1SOrFA61jllak0IwGGTUqFG0tbUlbQM0cuajjz5K\neFydnZ2UlJQwYsQI2traooNEiB2Y6xVoCuq73ndIfbeKUSAQwOfLu8d5dN/q2EAjZxLFsqOjI46c\nscsQGKCtrY1jjz3WlJxJ9zo2vZ83bYIJEzTfCxMY73V1L+t/56yIQjsQCoVSImdGjhyZMxI7k/85\nuVLOuN3uGOLZ74dXXoH+8gJNCDFbCNHU4683QwhRYrWulPIB4HvAEiGEuUwwh3AxlM2MhVAZNKMZ\nBE/v+fsxuCjk4YevP6oIGccDIR5OTMzhxMUcTlzi4cTEHE5c7EH+So7kAWaGwPpqTak+kKoBqT4F\nRQ0cy8rK4kifXHjOmClnElVRssNzxko5YyQScp3WBIfjqs5hMp8Eo3IG4stpqwo+LpeL4uLirMkZ\npcxRA8LS0lLTAXxves6YDZ7MYKWcUdskIib0BKHZPRYKhRg1alRCtYeRnEl2fSkCYvjw4bS1tcUQ\nGPqBuVkZcfXdTDljVRFNSklnZ6dtBEc60CtCgOgxW8GKnLHrnlXkjP5+1JMzVmXMU8bGjXD66ZaL\nlQeWQl9UzrS1tTFy5Mg+pZxRRL+dyhmzak2vvKJxa8ccY8su+gJ2oZXMvhnNueUAUC2EuLWHrImp\nuduT6vSvQF6UMnos4VzgBCjcD9VoaU3P9/w9HooGhI8qYsaBAwcOHDg40tDvyZlMlDOqHTN/EDXo\n0StncmkIbOY5Y+yrnZ4zHo8nrq18es6ofqq46pUzoVAoZc8ZiH97rldXeDyerCs2qb6pgWJZWRmd\nnZ2mfTMSH2aeM7lIa1LHnIycNOuj6ieQMKUnFeXM4MGDCYfDlu0YScgxY8YkHOArAqKyspLPPvuM\nzs5O04G5HcqZQCCAx+NJaAKbK+jVXgrDhg1jz549lvegz+ejrKwsZp5dyhkppalyRl3PQoi0DGdN\n7+eNG+G00yy3MfOXikQi+P3+GIVgLogROEzOJPoNzCU5E4lE+oxyxqxaU3/zm+mpwlQNjAeuAR4D\nBqI56z4LHBBCrBVC3CKEmCaE8Egpu+iF56sQZwKzQHaZKmcK+pszcwpwPBDi4cTEHE5czOHEJR5O\nTMzhxMUe9GtyRilBIHXljFLM6D1O9ANHRc7oPWfsHFTrPWfMSlgn8pyxImfS8ZyxSmvKl+eMGnQp\nsiIb5YzxnOsHuXYoZ/TKLLBWzugNgXtDOaPebCdTzlilNXk8npTJGSvPGbfbndArRX+d6yuTWUER\nEC6Xi8rKStrb203TmlRMjWQjxJIziZQzSn1klbaWS+jVXgoej4fS0lLL6ktmyhm7PGdXS//+AAAg\nAElEQVTa29spLi6moqKCYDAYbVNPImd9LadJzggh8Hg8+Hy+PqGcCYfD7Nu3j6qqKlPfKzv2n0m7\nufCcMavW1N/IGQUp5TYp5SNSym8D64GxaGTNSjRlzU/RdCodQog9aAROnhECpoKr0FQ5I1xHHznj\nwIEDBw4cHEnIppR2n4P+YVlKGaecSZWcEULEeHQYyRk1EFXt2q2cKS0tjaYhGD1nrMgZuzxnKioq\nTA2B8+U5o1fOdHd3R4kydf6sSh1aKWeM5IwavNmpnFHIxnOmqKgoJwN//eApU8+ZioqKpGlNVtWa\nQHu7XlhYGE3HMasyZLzGtm/fHkdg6dHR0cGAAQOAwwa5enJG9SPVtKZEyhmlDigrK8Pn8zF06FDL\nWNgNo2pGQR1zZWVl3LJces60trYybNiwGIWMIiqMqrdUEHc/SwnvvJOQnJFSxt3rxcXF+Hy+nHvO\n6Ml7q/b37dvHwIEDo4oSpUqzC/q023Ta1aee5apa08GD2unrqWrfryGl/BR4pOdDjwlwLXA2WgWn\nu/Lfq1nAQggUasoZPUn2LNARgNtug4ICrb55QYH192TLe+t7mts1vfwytRdckNl++imcktHm6K9x\nWbdqFauXLqXQ7yfk8TBrwQKmzp6d8vb9NS7ZwImJOZy42IN+Rc6oQWVjYyOPPfYY27Zt45NPPqG+\nvp6qqqqU3hZa+YO4XC4aGxu57777aG9vp7m5mfr6eqZOnRptt7GxkRUrVkQJnvr6erxeb9Jleuil\n58FgMGbQaiRNpJQxnjNWD9yppjWZKWcaGxv57W9/y/79+3n11Vepr69n4sSJOfecKSoq4tChQ3g8\nnpRSJVLxnDGmNdmtnCkrK4sjWKSU0b7pryk70ppSuab01VTUvs22q6iosKzWVFFRkZA4UoPERJ4z\nL730EitWrMDv9zN06NC4vpoZOicaQHZ0dFBWVkZjYyOPPvooBw4cYMuWLVx11VWMHTs2aVpTQUGB\naVqT2XWtBqCpKmdSvddTgf6a1bf/xz/+kccff5xBgwbFta9io38g29zaivT7eWbRItpbWigsKyPk\n81FVVcWuri46Dhwg6PcjurspKSnBV1TEiEGDiIRCtO/ezYCSEvZGIrilpAB47FvforS0lH974glK\nXC727dnDE4cO4TnmGHx79/LRfffRXVJCERAOBGhvaaGqqgqf2x0zL1xezr0uFx0HDkA4jOjqojoY\npPyb37R8gDQjYvOlnElGhjc2NvLAAw/Q0dHBW2+9FSUs7SZnQLs20mlX/eakmnaW6u9LKOThe98r\nZPXqOfztb3DOOfDii7Hb9kPcY5whpdyOjqzpHTQAdcAyrXS2oZR2pcfDqvc2sHTLm+wKdLF7P4zo\nPJlRRUNYMNHD7HGVGkEaiWifXH7P1366u8HtTn9byClp1Ktk1p498NBDfa9fvf39449h0KD87lN9\ncoR1q1bRcMMNLGlujs5b2PM9HYLGgQMH+UO/ImfC4TCNjY0sX76cmpoaxo8fD8Dy5cu59NJLY1QO\nVtAPNPUD6Q8++IAnnniCmpqa6LrLly8nEokQCARYvXo19957b9xy/XezZcaHXb1pYygUiktrMlYf\nEkJEySQrJUg6hsDFxcVREkgfS32/v/71r+fFEPjQoUNxyicrRtbsbXqytKZcKWf0AxI1kFTnSa+c\nySatyercQOw1pZQzhYWFdHV1WW43c+ZMTjjhhLjrIxwOU1lZmZXnzPvvv8/q1as566yzLPtqVM6c\ndNJJScmZzZs309DQEHcsX/nKV6IqEbO0JqVOMxoCW6XrpZPWlOp5SRXGMtqq/UmTJlm27/P52LBu\nHet+/GOWNDezDgiiDdkagKuAhn37WAKs27cvOpxrAG2ez6fN27//8LxAIH69QICGAwei8+qAhs8+\n05Z98EHM+r8x2ZfZvCXqoFavtnyANCNnjMqZXHnOJDJgNzv3zz33HKtXr+aSSy6xrQ/635B0kI5y\nJtXrePduweLFNZx1Fpx77qtcfXU1bW0vxG3b3yClNCVghBBeoBN4uXcqV9YBjVAY1Eppf6JbdAbs\nfxtu8G2gedbW6Ox9fyrj3c0/pNn9MvxbXb8zDK7NdEMjiZQvMilXhFc4rH0Ph6kNhbTpcBjS/R4I\nZL5tptsZv+fg+ROyuFayhSJockBmrd65kyUGL8Qlzc0suueelMkZq+fuoxlOTMzhxMUe9Dtyxkig\nANTU1LB69WouuuiilNpQZIfec+bNN9/k3HPPjWv38ccfp7q6mhUrVpjud+XKlUgpLZcZB2zq4V+9\n3UxkCJzMLFh/TKl4zigliBqgWx3TX/7yl5iBtl0wKmcOHjwY4xmU6G2vsYKL2kZ/rPqBbnFxcdbm\nrkbljHor3d2jPlDHpAaSegLNjJxJRzmT6HrTX1NG5czjjz9uut1zzz3HySefbErOVFRUsHv3bsu+\nJPOcef/99+N+sI19NZIzydJSOjo6aGpqMj2Wp59+OtquVVpTWVlZjGeL3+9nwIABCdOaUiFnUj0v\nqcKY1pSsfWWMu+7BB6NvylajkR43G/6aLctmnl3tKlg9QCZSzpj5DtmJRAbsZudmxowZPPnkk7aS\nM0ZVWKow/m9JhETX2TnneHntNXjtNVi69FyuuOIAy5aVsXjxFqZPD3Pddb/r18QMgBDiZKBNSrnf\nsGgzcBnwfSHEHVLKV/Lbs6naJ/hnaH43Lq3pUMchDtUcit3ka83wwD00Nz/DPbfOY/bAgt4nEvri\n997ef7Z9VFxhX1CouN1QVNQ3+nIkKHqy2K7wuuvgrbfifilcWSrHHThwkDv0O3LG6mWVSgFKBqWc\n0Q8O9QNss/UT+Q8kUpiYLTO+3UzkOZPMj8bYplovkeeMSmtKFstcKWfU4MqonFGqDKt8xlSUM8a0\npvb29qz6a1TOwGH1jCJn9L4QiTxn0vUusjo3xvNi9JxJdE6V54yx/HhFRQUff/yx5XbJPGesYCSB\n9PH45JNPErbl8/ks70n9vR4MBikpKYk7ptLSUlpaWqIqp+7ubktyRp/WtGvXroTHlOp5SRXGtKZk\n7atrL6xThRVa/LV7XiZt7DCZp4fZA6SVcmbfvn0MGzZM2053vduZVqM3YDeeU6tzY7eCR59umw7S\nUc4YjyUSEbz11pmsX/8VnnwSJk2Cc8+F+fPf4LLLBiHEqOj/ll4RjOQfzwNDhRAbe74/D6yTUm4F\n7hJCLAUeBfJMziwCXBDpOmwIrNKajgdaCwCT3yLPTgC639sOP/5x3xiMJhukFhamtF3Txx9Te/LJ\nfXbwnLd+6dJnHF8Ic/THuIRMfOkAwilkEij0x7hkCycm5nDiYg/6HTlj9SDucrmy8pyxQkFBgalh\np3651cOq2eDSzHNGr7ywMupNpIhJx3NGr5xJFMtcGQIrUqOoqIg9e/ZETV+TebJYKWesDIHtSGsy\nKmfgMDkzZMiQaL/Mzp/RcybdtCarc2O8pozVmhINVK1KaScyBNan1pmRM4q8SdZXIzmTiueMlVmw\n/l4IBAIaWWFQnKmYKPLD7/dzzDHHJExrMvMUMiLV85IqjGlNydpXZsDtuusyZPHX7nmZtBE2maeH\n2QNkIuXMyJEjAS0eylTdbr8Xq7Qmq3Njt+dKJsoZdR+m6jlj7PPbb0/kjTfO4tRT/8Rf/3oqym/6\nj3/cTVHRcODwfddPPWaMuBT4OjAD+F7PJyyEeBt4GWhDo0PyjFu1P3vPpnDD1wldfvgFhHiqFNkt\n0MxojNCUkcWTJ8Izt+a+m/lEUxM4gwUHRylmLVjAwubmGM+Zm6qruXD+/F7slQMHDhIhsxFDH0Uk\nEqG+vp4NGzbEzF+/fj2XX355WsoZ40B6ypQppu3OnTuXoqIiLr30Ul555RXT5VZ9mjt3btz+zTxn\nrFKSEvnR6I9Hbav+pqqcser3V7/61ZyabcJhQ2CjcsaKkTVTzhh9J/QpInYZAhuVM6qij/6YzGKf\nbVpTfX09b775Zsw8s2tKkQ9KCWZ1Ts8///yocsaMnFFeOkYYr0HjPRYOhznhhBOSXv9GcuaUU06x\nvF+llHR0dCS8143kjDGtqbCwMFpOXVV2GzBggOm9EQwGU/acSedeTwXGtKZk7Ssz4FkLFrCwuhqI\n1m+J+2u2LJt5mbRxnck8hZuqq/GaPECaEbHKc0ZPZOWiYlMicqa+vp7XX389Zl5TU5OtKU2qD5Ae\nOaN+h1QlwmT/C/XXmd/v5rnnZnDSSXfw4x+fhL4QmP76VP+D6uvrWb9+fZpHdWRBSvm6lHKBlPJU\nYAQwB3gIqADmAz8B7s53v+o4m9HUMqLgf1h4xY+Z9OY5FP9xNDxQh/zwS0AlrDFs9CwQKqO6+ibm\nz8/MuLwvw3mLGw8nJuboj3GZOns2dXffzaK6Om6ZNo1FdXVcePfdaZkB98e4ZAsnJuZw4mIP+p1y\nRvk6PPTQQ7S3tzNy5EjmzZvHWWedxcMPP5xSG2aeM5MmTeKss85i5cqV0Te38+bNw+v1snXrVs47\n7zw+/PBDVq9ezYgRIygtLY0uV/j1r3+NEILhw4fHLVMwKmcS+coYB8ZmAxEjCWClsIlEItGBvBqg\nq/498MADdHZ2Rvt9/vnn8+677yaNZbowMwRWyhS3251Q6ZKK54waZIN9hsBWyhl9v8yUM8bzkm5a\nk9frZc+ePfzmN79h5MiRlJSUmF5TxrQmtfw3v/kN7e3tjBkzhnnz5iGltKzWVFxcjBCCQCAQd7z6\nc2amnAkGg5xwwgnMmTOHlStX8umnnzJixIi4vhrVEIlSpPx+Py6Xi4suuojCwsK4e/LMM8/kD3/4\nQ3T/AwYMiCHi1D2lroGSkhKEENGS0EakU61JHdOvfvUrCgoKEt7rqcCY1qTaWblyJTt37mTIkCEx\n7ft8PkpLS7UHr44OFs2di+v889m+dy/3dXZSUVrKvS0tuMrKmOPzMaKqit3d3bzZ2kokHOZCvx93\nURGdxcVsr6wkHAxy0a5dlBQXcwB4q6AAFzC7u5uKigoKKit5fMAAdu/cyeZgEHd5OV8+cIAhQ4YQ\nGTiQx4Ug5Pczp6WFET3Vmozzdnd18XpLC66CAmYHAlSNGEHVySdz4fz5aVVrMt5TufCdUfswa9vr\n9bJ582aefvppKisrKSgo4KyzzmLy5Mm29kH91qWT1qSPTSrKGXU9/frXv2bz5m8wbNgmFi2qs/x9\ngcP/W7xeL+FwmNtvvz3629SfIaVsA57o+SCEGA/cCbyU776czZvcBNxbWsnZE5ew7Ffr6d73Ws/S\nm6FwtWm6U2FbG3f/6sJ+ZwbswIEDjaBxKjM5cHDkoN+RM6A9WI4ZMybmjbLP58vKc6awsJCZM2ea\nDrJUSkpVVRUXXXQRl19+OSeddFLMOl6vl7179yKEYM6cOZb7VwPHVKo1Gb1krMgZY7qIVblgt9sd\nl9Ll9XoZPHgwO3fu5Etf+lJ03Vx5zqjjUQNlvSGwMoE1Y2bNBmyJqjXZoZxJ5Dmj75eV50w2aU0A\nkyZNYsaMGVxzzTWMHTvWdJ1AIEBpaWncOS0vL+eFF17ghz/8IQDPPPNMVDljRgCq40pEzqgUPv25\nCIVCuN1uvF4vXq+XBx98kC9+8YuMGjXKsh2Ajz76iPPOO8/0mFTqjjoW4z352WefxSlnjGqmwsLC\n6DVgVIyZxbCoqCiqikrmY+L1etm2bRsVFRVcccUVluulAmNak2rf6/WycuVKampqOPnkk6PL9LGZ\neuyxTJ00CdauZfPmzbz++utcddVVpvt55JFHOP/88znuuOP4/e9/T21tLePGjQPg0Ucf5fOf/zzH\nHx+bpfHXv/6VUaNGceaZZ3LHHXfw3e9+l7KyMp577jlcLhfTpk1LenxNTU1ccMEFLF68mMsuu4yJ\nEycm3cbKcwaIiVUuyJlEyhmAsWPHcvPNN0fN4x9++OGceM54PJ60lTPq9yYV5UxnJ5x7rpeZM7t5\n4YVZvPeeh9Gj49fTk4f6/0/Tp0/ntdde49prr2XMmDH87ne/S7mvRzqklFuEEN8Gfgl8O5/7vhX4\nGmU8e7Cav3x1Jd3dE3RLZ0FoKTQTZxQ8atiwfkvMOB4I8XBiYg4nLuZw4hIPJybmcOJiD/olOQPx\ng99U3haqNsw8ZxL5FqiBdVtbG6NGjbIcZIfD4aQPxWaeM3YrZ8yIFX2KjllqSyoET7YwpjVB7KAr\nGAxalkM3GzCbpTUNHDgw2m6uPGdaWlqi00bljIqbMabppjUBUcIh0QBUX63JmNpjNMm18pxxuVxR\nYmLw4MEx7evTtoQQUUJMnb9gMJiSQsgYj0SlkH0+H2VlZZbHrN/WzBBYn9bk9/tjvJasqjUVFxdT\nVFSEECJOzWIGv9+f9vk0gxk5o2Cm5NGTM2zcCKedBmjnJpFRqz7+xnZVqpQRekLRSKymUwlNXW+p\n3o9mKYx6hZ1CLsppG+8T4+9OW1sbn/vc56LT6Zpkp9oHpRRKbX1obg6zffsYnngCDhzw8OKLp1BQ\nAK2t2qerC4JB2LsXPvoI2tu1YirBYB2XXrqJ0aMnmbatJ7z194/qWy7KmfcFCCFGATcCu4DHpJSt\n+uVSynYhRN4Pfg5lvMwXaQ+eAMHFaHXQFKZCYdhUObP/bWPRKQcOHDhw4MBBb6BfkTNGVYmxGk42\nnjPGQbgebrebvXv34na7GThwYEJyJtkAxMxzRk+aJDIENiNMjMazVt40+hQdfclnSD01KlsY05qA\nGOVMIs+ZVJQz+rSmXCpnOjs7Y45J7zljldak+mp2HFZQA+hE58KY1qQQDAZjyAO1Xytyxiqlx2i4\nmiiVDKxJKH2cAE4//XTL+zWGgDCBvg+BQIBBgwbFEbculytt5Qxo59eMpDKiu7vbloFpIiLIipwZ\nOnSoNrFxI5x+OkDUHNcK+t9LdYwKKlXKCL1Jt/56Lioq4uDBgykdX21tbfQ+TPV+tPKcAXKe1qTu\nB2WCrb/+pZS0trYyfPjw6Pq5ImeKi4sTkn8+H/zyl/D007BpE1RUlOLxTGX3bigtdbFjx3C2b4fh\nw+HEE6G0VKtuO3gwnHQSVFVphV0eeujRnlhbkzPq/jaSz9B/yRm0FKYTgUrgNiHE/wF/AJ6VUnYL\nIQYB5nLGHOIjTmEXjwO39MxRbk49heolpsqZSMj+ly19Bc5b3Hg4MTGHExdzOHGJhxMTczhxsQf9\nipxJpJxxuVxxKRdWbZh5ziRSzrjdbnbs2MHw4cMTKiDC4XDSAUhvec6ko5xRAyO7y9Tqj9VMOZPo\nQd+sL0aiwJjWFAwG0yJDjDBTzhgNgc2UM6rUs/68KKPOYDCYkAjUIxVyxmgIrBAKhaIVXFS/1KBT\nr7BIRs4Yrw3jYDTV9K1k7RiPOxE5o78XEilnFDmjSDare0hPkKg4JCNn7FTOKLWXEaWlpezfH/vG\nO4ZIeecduPxyIHHVOLBWzkQiEbq6uqJV0/RQVa701xEkr6xmRLrKGSvPGbVvhVwYApulkqrjPnjw\nIG63OyZWuSKI1DUdCkEgAKEQHDyoqWDefBN+9jOYPh1+8QuYOBG6u/fy1FN/5vrrr0dKwa23/p2b\nbz4j6W9fMBhM+BuvvzeOJuUM8JGUcooQ4lTgW8A3gCvQKjbtAQYTZUTyh3dQuWcq7ipVqafEdqHf\nVDkjNhwVFbYcOHDgwIGDPo9+Va3JSFwYS+2mMmiwUs4kS2vasWMHw4YNS2jsmopyRhEUqaQ1JSJu\n9OukktZkVM5YkUBA9K1xrt5KAzEkChw+d01NTabbpqqcUe0qA9hsUpsy8ZwJh8PRvhoHPen6znR0\ndCQ1BjWW0lbQKx7gMCmpvz6klFHSy6imUEiWjmRUzqSa1vTee+9ZXl9WSg59H/TKmQEDBiRMa1Ik\nm5WqTK8OSKWcdjgcjhKr2SJRWpNZX6LElZRppzWp3wn9NdzV1RWNjRHqetWrSfTzU0FTU1P0XKWj\nnLHynMmXcsasfaNqRvUnm+tASvjsMy3dqKUF3n4bNmwYw6pVZ3LddSdSVgZDhsCxx8I558C//As8\n8wz87//CH/4AU6fCwIGx51elH6ZCoIVCIctzKaWMub/194/+d6WfoksIMUFKuUlK+R9AFXAxcDvw\nv8A1Usq816QOo7zu9PXPpgK3Ul0doKSgSFPOzACm9/z9GOta9v0AVs8MRzOcmJjDiYs5nLjEw4mJ\nOZy42IN+rZwxDijUA2kiZYKZ54wZ0aNHUVERHR0dDB8+nIMHD1oO+CORSLR0r9XbSDVwtDIEtiKg\nUjUEthqAJlPOGAeIVu1kA6NpJRBXStsKVqW09QMQ40BXX60nE1h5ziSq1hSJROIIM4V0fWd8Ph/l\n5eUppzUZCQogej/olTNGXxxFzuzduzeu/UyUM2bHGIlE4gbWiZQzw4YNszxmFe9IJGJaSttoCKyI\nSZfLZToQ1ZN6AwYMMCWp9FD3vx3KmUzSmkpLS2HnTvB4oCdO6XjO6EmfRColRZhma26dK+VMLj1n\nIP53srW1Ne66zKQPmzbBH/8IL78M//ynpoxxu6GwUEtDikRO4fjjg1x11Xauv/40EvCUUZhVhwuF\nQklVekpdaLXM7XZH/5cdZcqZHwKLe479finlh8A/ej69CEMaE4uAj5k0aTA/+9mV/Pv/rGCbb1us\ncsYHlYMqe6m/Dhw4cODgaMW6VatYvXQphX4/IY+HWQsWOJXF6OfkjJlyJtnDYrrKmcbGRpYvX057\nezsffvghkydPprq62rJ/6m1jUVERjY2NrFixIkrW1NfXx3jOmClnrNKNzMiZxsbGaEnxl156ifr6\netNywY2Njdx///0EAgH+/ve/c/bZZ3PsscfGxNJIYBgHJmbHkm75YHU8jY2NPPzww+zYsYPNmzdz\n9dVXc/LJJxMMBhN6zpilNemNSfVpTY2Njfz973/n9ddfx+PxWPbX6rjUdWS8xtatW8czzzzD+++/\nj8vl4gtf+EKc54wVOaNUJWb7BOLmdXR0UFFRET2fZtvpB/fG+0P/V5GSZuRMY2MjDz74ID6fjyef\nfDImVmbkTCLPmUTKGf1AcdKkSab36l233krD3XcjAwEK/H5KBg6kMBKhqqdMcxEQDgTY9ckn3PjE\nE2z57DPevOce9rS2cuUvf0lVVRU7OzspdbsJB4P49uxh6JAhtAtBSWEhQb+fB3w+CsvKCPl8VFVV\nsfXgQdaWl9Pp83Fg1y6Ki4s55HYzYtAgIqEQ7bt3M6CkhHaXixGDBuFxu2nbtg08Hl787/+O61t7\nSwtVVVXs6uqi48ABCIeRXV2MrKqCwYNj1ispKSFUXk5FcXF0nurb0KFD2e7z8frSpbTv30/77t0U\nFhbyjyVLONbjYZzfT6iujlkLFjDutNOIRCIJr2czz5lE5suKhNFvq//NefbZZ5P+DtTW1kZTs7Ih\nZ1588UXWrFnD+++/T0lJCfX19XG/icnuqz179kTJlD179lBVVUVlZaXl9a7aV+22tbVFy7Kr9fVk\nZWNjI489toJgsIhw2MOsWVfidk/h5Zdhxw7o7tb+dnTAnDng9a5n6NCHKSn5LOZc/epXf+bEE0+k\npKSE0tLUfnuNJL16UZFsW/WCwIjGxkYeffTR6G+0Md793XNGStkB3CiEGAMcm2z9/MGQxgSUiV28\nJT+En77K3IOfwvnAJ7pNzoD9L30KU6ZoRkOpfgoK0lu/lz61QsDf/pbZ9kfIMWYUk4aGfnt8mZ4/\nxy/DHE5c4uHExBzpxGXdqlU03HADS5qbo/MW9nw/2gmao4qcSUXKrQapxlLaZuSMImZqamqi8/7+\n978zZcoULrroIsv+dXd3s3bt2rhtly1bxuDBg6NpTV1dXTFqkkSGwGYDEWP7y5cvp7a2llNPPTXh\nen/961+ZPHlytHS22fHryRmrfQFpETShUIiXX345WiL4hBNOiLY1d+7ctJUzVmlNqr8XXHBBwv4m\nOq7Jkyfj8XjQE0KNjY3ce++9zJgxIzpvxYoV0XjrlTNWaSLPPfccTzzxRMw+Fy9ejMfjYcqUKTH9\nGD58OF6vNzpANOvrscceS1FREZFIxDStSf3Vp1/pyZmtW7fy2muvWZ5bo5GvmXLGaAicqefMXbfe\nyjs//zk/6eigAagDGvbsYQmwbt++w/OA3wDr3n1Xm7djBw1gut4SYN2hQzHz6oCGfftM118BrAsG\ntXn79x9uIxCImXc10NDVZd03s35s20bDtm2x6+n7BFxl1jf98QUCNHR2Hja7WL2ahc3NTLr5Zt5/\n/33+9re/mZ5LK8+ZRMoZpYJSv1GZ/g6o6y2dtCb9NaXI5ZkzD7ucLl++nAkTJjB16tToOsa+6e+r\nrVu3cujQIaqrq2lububiiy82PQZjKumaNWv+P3vvHh9Ffe//P2evuWxIQiAXroHITaQQrooIKxBR\nqZeqtcpp5fTUc9qvolbPzx5rS08v2tae3tSDrZXWSy1oe7RaxQLhsgYQkPvNcMuFW0gCue8mu5vd\nzO+PyWcyOzuz2QBCxH09HvtIZuazn/nMZz4zO5/XvN6vN6+++iqFhYXk5+er5SsqUqmomM4HH0wj\nHLbh9zdz6lQh7e3XY7F0YLe38957LUyaVMOXvpTDTTdBcrJiyFtYCGvXatvbN6IdwhA4FArF3edG\nypk1a9bw+uuvx/yuUEZp1Z7afYoXEUuWLGHUqFFq+vTLUTkjSdLNwDeBaUAfoBrYB/yfJEk7ZVk+\nP4f5CwKhmhEkzZMMHTYU/vAwyDLhf50FZW1RhsC+sITbN4Xm0BHoV06fDCdO2c7D132J+YXTlPi6\n3vbp6Pj06w+HL/1xXqzj7W2fi328WlxqUulTJKA+c5/E8X32PybHuPqZZyKIGYCny8pY/PzzCXLm\nUjfgQkKvKtFLtnuqnNE+YBpNppctWxbxYAtwzTXXsGXLFsO6xSQmEAgYfnfixImsW7cOrTmsnoDR\nTmy17dIrWYzqLywspKSkJCLVq9kxbN26NaLdRuSMmOyb7Wv58uU9ImfC4TD/+BBFcy8AACAASURB\nVMc/DOt6//33mTZtGh6Px5CZNVPO6A2B7XZ73O2NVW7ixIlRfjNG5adOncrmzZuBrj4zC5NzOByG\nxy/LcgQxI9qxbt06br/9dkKhkGlbPR5PRIicgJlyRvwPSp8ePnw4qr+1fWWUrUlPiOknhdpsVgJ6\nkmffvn2MGTMmosz63/+ed30+vo8y/RB/AVZfwHW9pY7zqVeLp8vKePyVV9hjtzNjxoyIbeJcjhw5\nUj1PPQlrEsoZm812TvcBj8fDmDFjkCTpnJUzy5YtY+LEyGxChYWFbNmyJeY9SntdlZWVMWfOHNau\nXRtB8uiPQXsvbGrK4Gc/ayQc/gG7dmXR1JSOLEt0dFhYsybIgw/C1752nJQUmZUr3+WWW9JxuXzY\nbF3X4bFjx3j00T9FHWOsvhw5ciROp5OmpibeeuutuPpcf8+x2Wy8/fbbMb8rjMslSYr4vlnbtP19\nOXnOSJJkAV4BvqrblN/5uQV4WpKk/5JleflFbVwU5tGlmgkDN+LrKOb5zZPJzwebMwkK2qIMgTtq\nUviwdDaMeB+u73pYLtvYAOPHM7/os/ugbPbM8HlGj/vk80DOyDKenTtxjx+v7PtifsJh5XOx9xvn\nx9PYiNvl+vSPV0+S9WJ4APclbsOnjnMgYjzhMG67PS7iyWZglQBgPc9MupcDLityJl7Pme7qiNdz\nxszDwSxGPxwOk5KSovrOGEG0WUxyu/OcMdsWy19C2z6zckYZe/Tt1BrHdrefeBDrQV6Eg8XabuQ5\noyUKRFhTvO2NVc7Ib8asvCCNuvOcsdvthn1gllFFZPUS4XJmEMesJ020fwXJIjKaQTRhooU+9EnA\nyNvmXLI1WSyWKCI1ubNvRG3aHryQ63pLHedTrx62QADJxLtGqKq02ZZkWSYYDMY0X9aGNdlstnO+\nD4jsQ/EqZ/TXeqzrTowhozIWi4Vg0M6ZM/2oq7ue/fuv5OxZiY8+upqGhgxaW1MIh62Ew1Z8vgCz\nZ0N9/Sj8/hE89hicPn03/fptZ+zY04wbt5eMjCYkqQNJgrq6vTzzzMuUlDTT3t7Oxx9XkpExLO6+\nidWX4sWDULSYldPCSDljtm+xXhDeTqeTYDCofj+e35bLTDnzE+BO4JfAe0ANkAFcgSJR+RJKaNPr\nkiS5gQdkWb5ErJTQ0ClwWO/HnT2Rg3/dw8q6PgRaBkFZQ5RyhqQgTLkDiiKbXVZYxvNPfZv5H22/\nNBP0CzF5r61VXLMvdXsv1vHG8wmFlIlTPGW1uNyVAM3NkJHxqSkFPrWPzfbp1l9ZCcOH9+4+uNif\nXbtg0qTL9/jPFR4PxEn8hubNg9Wro9aHdS++P4+4rMmZ8/WcEZNIs7AmM1PfWORMWloagUDA9Lv6\ntp5rKm2z+sVb0O7K6dut70utUsesjp6mqI5FBohJf089Z/ShPA6HI+72xipnlKmpu77sznPGjDgy\nG09aEjHWWNQSfQIi3EivnNGTM7GORZTpTjmjD2syMwTW1jN16lRqamoiyrR1bhe1a6/kC7mut9Rx\nPvXqEUpKMp1UCyJM9L8kSap6JlbacHEuxXg+l/uA2+3m5MmTpKSk0NTUZFpOC71yJp57nSRJVFdn\ns3fveI4eLSAYdODzLWLTpj5kZdURCh0Gsjhzpi/p6alkZdUzZMhxrNYwFksHdXXVfOc74zh48Bih\nUBtz5kxl06bXKSlZz6hRo6L23diotEmEp/a0b2KV14Y1xVuv/p4Ty+BefFeo3oRCSqQIj6e/LxfP\nGUmSsoBvANNlWd6j2/wxsEySpIeA24EfAf8OZAF3XdSGquhSziRb9/CdwiA/nFoK0kGQJH64sy8/\nqU6mY10bqnLmdC6cWAqD/j/gYFSNp/xNylvueCYdvXBC4r6Y++uFx3/B+uRzAPelbkAvhftSN6AX\nwn3NNZe6Cb0SPVHk3fDww3yvrCwitOnJggJufOihT6Flny1ctuSMEaFwoT1nFixYEBXv//HHHzOu\nM32tHh0dHapyxui727dvV0M5tKm0zTIyxdpmVP/OnTuZN29exGTfqNyWLVsiwgS685wx29eiRYsM\n+8EMoVCIL3/5y/zpT3+Kquub3/wmu3fvNv1ud54z2rSv8bZ3wYIFPP/880yaNCmqnJFyxqwvp0yZ\nAsSnnJk9ezarVq2KCtPYtGlTRGjT1q1bmTJlinrejfa9Y8cORo4ciUidqyeqkpOTo5QzHR0dEeTM\nVVddxa5du0z7qjtDYKM39vF6zujJoeu/9S0eePpp7gkE+B7KNEQ4LIgcJRdiXW+p43zq1YY2PVlQ\nwIxvfIPQjh2G5/KBBx5g69atEdePMAWON6zJarWe831AkA11dXVRxIsR2ttlamudlJYqmYzGj/9/\nLFu2jv79x+H1uvB6XVRXt5GR8WUeemggra1w9Ojv8fubmTTpILfd9g+Sk1vZssVDWlob1113DZWV\nlZSVlTF1quI5c/XVXdKCnTt38vjji5g7F+z2esLhMOPGwdatErfccgtvvvmm6TGLe1BP+8as/IMP\nPsjmzZtVYizeevVKUrvdzo033sjf/vY3pk6davhdQeDqCVWzfU6dOvVyVM7MBf7XgJhRIctyO/A3\nSZLeRsni9BNJkn4my/J3L1YjBebxn/hJ5ZAtyNJ3fs78+Yr3zIoVJTz33Gq2Hcilw/c38D0Pdj+0\nn4Czz0FwPsgLDes8LXfAj398MQ8jgQQSSCCByxzCV2bx889j9fsJJyVx40MPfe79ZuAyJmfORzkj\nFAndec6ImP7ly5er3/v6178e9cZf276UlBQCgYAa0//000/Tt29fMjMzWbhwIadPn45o67lmaxJt\nE1mY+vfvz6JFi8jKyuLEiRNR5X7+85+Tm5uL0+nknnvuiTje7jxnioqKCAaD/OIXvyA5OZkBAwaw\naNGic8rWNHfuXJKTkyP6dNGiRcyZM4ft27ezfv16rr/++qjvmilntCmjxdt90a4///nPnDp1iqFD\nhxq2t6ioiKamJp5//nny8vJISUlRy+3atStKOSO+//zzz2Oz2cjIyODOO+8kIyMjos/MyD6Hw8GE\nCRPo378///u//4vL5SInJ4fFixcTDof52c9+RlJSEgMHDuS2224jOzsbm81GMBhU9/36669z7Ngx\n0tPTuf/++zl8+DAQPT5EBi4jzxktOTNmzBi++MUvsnz5csrLyxk2bFhEX3VnCKxPXW+mnNH3ya5d\nu0hPT48o8+3Fi1m2fj2vfvQR1UlJ7Pb7SerTh3s6OsjtzIj0piQRCgS4rbKSAQMGcNLnozE3l+qq\nKu4OBhkwYACVzc3U9umD3NHBrZWVZKSnI2Vl8Uo4jK+lhbK2NqwuF/d4veTk5lJWX09jXh4NdXXM\nr67GarXSlpTE8b59Cbe3c1NVFQ67ndbOdR2hEL+trycoSXzFaiVvwICItt1TXU1uXh7HW1r4uK4O\nOjqYHw6Tl5sLfftGlLNYrSQPGMCbFguhQIAXqqvVtuXm5XHK56PK6STQ1sZNp06RnJJCi83G1/r2\npWDgQPXHbvSUKZxqbubmm2/ml7/8JXa7nezsbBYtWoTb7Wb79u0RfS1MgbszBA4GgypJrL0flpeX\nM3z48G7vAx6Ph6FDh2K1WrHbHZw5E8DvT6axEWpqFOXw9u1KZnCvFxoaoLp6HhkZIbKywOGA1NSp\n2O35lJUdICmpnpSUShYuLCQc9tG//1muuy6dQYOc7N+/m9dee4XDh08xfPhwnnrqAQA1E1laWhr1\n9fW4XC7ee+89kpKSGDlyZNR4195zp0+fTr9+/Vi6dCnNzc3k5eVFlBcko/be0NraypAhQ2L2jVi/\ndOlS6urq1PLXX389H3/8sepJJsr99re/BSAnJ8ewXiPlzPjx42lra+ONN94gJycHl8sV8V1xz9SH\nIortL774In6/Xx1HLS0tUYqZy4CcGQqsj6dgZyjTzyVJ2gW8LUnSclmW936qrdNhJdt5Ehg4cCjz\n589kxYoSFi9+jdJSO37/74AfAvOhSjz8Csvx+RBywdq6qJAnl9M4W9tnBQnPmWgk+sQYiX4xRqJf\nopHoE2P0tF9mzp+fIGMMcFmTM+fqOWOUSttMBl5UVBTxINzY2MjLL79sWrdQzgDMmDGD2bNnM2PG\nDObMmUNNTQ1vv/12RFu1kwF9tqZYIU+ibSkpKfh8Pm644QYA9uzZExUmU1RUxPbt23n00UdJSkqi\nvLycDRs2GO5HQE8UXXXVVdx88824XC4efPBBw+PvDtpJntGkRZvmWY/uPGe0abRBOea5c+fyzDPP\n8PDDD6uSfT0mT57M7NmzWbBggZo9CjBUzoh6JUnC4XAwc+ZM9u7dy9GjR9X2xAprEkqEUaNGcfPN\nNzNw4EC++lXFg7KxsZGbbroJWZZ54okn2LRpE62trRHHWFRUxOTJk3nuuee44oormDFjBpWVlQAR\nxIvFYqG9vZ0+ffp0m63JarWq5+OnP/0p//mf/xlx3PF4zmgn9+fjOQPwlb59cd16K7f+9a9R27RY\nunQpU6ZMoaSkhIceeojf/e533HHHHeTk5PDiiy9y6623kp2dzdNPP016ejpf+9rXOHPmDDt37uTe\ne+9V6/H5fLzwwgs8/vjj6rpf//rX3H///fTp0wdQSL6KigoWL16MJEmsXr2a1NRUtm/fzn333Udm\nZqZhGzdu3EhDQwN79+7lu9/9btT4lWWZH//4x/zgBz+IIh4FxL6mT5/Oz372Mx577LEo0hDgzJkz\nyLJMUVERBw8eZPDgwdx+++0AtLW1RV3f8ZIz2rAm6LofPvXUUzzxxBOEwzZOnYLGxq5PfT0cOQKf\nfAL79kFb2yDq6++lrc3OT38qkZmphP336wcTJsDtt8PQoZCWpqzfsWMFQ4cOiFC0QXbnpwsffPAB\nWVkdTJumZBQaOLCIkSOv4LXXXuPJJ59Uw+369evHsWPH1P6Arvv4o48+GlFnOBxW7yPiei4qKiI3\nN5dDhw5x112R0SxasrKoqAi/38+BAwd44oknDPtUC1FvcXExjz32GKCkG1eILHtEvbW1tWjTg+uh\nv74EuZOfn8/s2bO56667GDt2bMR3hHLGSO1m9Nvy7rvvRihnHA7H5WAIHPuBwQCyLK+SJOlBFAHb\nLRe+SeZYDNwIPFtfz4oVJTzyyCrKynKBpzpL6O+pirImK+seGpJO01FAlFlw/e76i9P4BBJIIIEE\nEkjg8iJn9KoSo7CmnihnugtrMkIsTw1ZlklOTlazkoiMKIKs0U5y4vWcERMMfbYmAT0RYFROkEBi\n0m2k0InlOQNQU1NDfn4+x44di9k/sdBdP9tstqisRQLdec4IvxktJEkiOzubmpoahg0bZliv1+sF\niJqcBAIBQ3IGIseAVlki+iyW50xbW5valw0NDeo24f3h8/loaGjA5/PhcrkMFTE2m43a2tooQkqU\nFcSHNqzJyHNGH2Iirh/tcceTrUnrOWMW1qTf1/Tp09m2bVtUOWn/fuoN0tTrYbVaaWtrU/etbZfo\nI5GyvqWlBafTaUhwigxfWoiQH0HOeL1eZFmmra1NJV+zsrK6JYNra2sZNmwY5eXl1NfX069fv4jt\nou9ieRkJEqWhoYGUlBRDYgYir1efzxdxjoyu7+TkNA4eDHHkSCqHD7uQJMV2IhSCs2ehuhoaG62s\nW3ctJ05kUFNTyI4d0N6uhBpt2fIl3njDQlkZKtmi/VxxBdx1F3znO26amiooL99JKHSWO++8jdzc\nXNPjBdi9u/vQJzAmrLVKOnFeja7HpKQkw+xRZqGk+nFu1ob29nYCgYDpPUAP8RsgIK4T/djy+/0x\n751GyplQKERtbS0ul8twnGqVM0bb/X5/xHjTvjwQ94nLQDlTDhQCm3ryJVmWX5Ek6SuSJPWTZdk4\nJcWngJ8ATwIng04WLlxCXd2bKGoZgejAx4KClTz77APc/cR7tJYFo5QzHaGeGfv3NiTebkcj0SfG\nSPSLMRL9Eo1Enxgj0S8XBpcVOSMmlmLyaRTWFK9yJh7PGSOYKQPEJFZ4K0DXxF9MArREjJnnjJ40\nSU5OBromX7IsR0zm9BMvI3JGvB0X39MrdLoLawJlopmfn8/hw4d71F8C2nNnhlhhad15zhhNskEJ\nAxCTZCMIAk0/bvx+f1TYjYDD4VC/pz2m7pQzDoeDpqYmGhsbGTlyJCUlJRHtSE1NxeVyUVtbi8/n\nIzc3Vw2TEgiHw/Tt25fGxkaam5sjjlmoWsR1oA9rMsrW1J0PjD6syYws0h5jPGFNRvvC70c6dozm\nAQOivq+HIGcEOaUnZ8S+nE4nXq+XpKQkw8m8EaknCBEBn8+H0+nE5/OpYYtJSUndhlHW1tZy9dVX\nq2NQT86YjVl9W2pra6mpqSE7O9u0nKI6kzl9OsSxYxnU1uZy6BCUlYHP5+Do0fl89BFqOFFZ2Sz6\n9PFjteazebMdqxWsViUpRL9+kJsLGRkS4ECSgrhcIQYMALtd+TQ3H+OBB/KZMiUVEw5TRWmpn7q6\ndtraHHFlbIrHlwaMyRkx9mKle4eu+7jR/dSILNcToQJGZCUoY8bs/qGF0fWtV86A8hsSa6zoSVVx\nD6ipqWHo0KGGv1mCcDL7TQsEArhcXSEv2t8W4SN0GShnNgCrJUlaIsdKU2WM14FZwFsXvlnGWAyk\n4+JAcC6+OmFUrb0HzVRLZmYeZ+rUITz00I3Mnz8Ty/csYKCckXZ9PsxgE0gggQQSSKA34LIiZ/TK\ngAulnDHznDFrgzBV1U4gxEO19o2sz+fDZrNFkDN65YxWmRArW5MkSeq+tW3VP5TrSRXRDm3oQixv\nG209euXMuHHjSE5OprW1lbS0tLj6S7+PWCoBm83G+vXrueWWaKV4d54zZpOn7Oxs1efHCGIS3hPl\njFYdoh0Hos/MyCsxYaqtrWXevHmsXLlSnRwKpUxqaio1NTXqOWttbTXMwpSdnc3JkycNlTMirXZS\nUlK3hsCxVDHxlBHtEYg3rGnbtm3R12ppKeH8fKQ40uzFIme0hGVSUpKqOjBTzujHjchkBEq/tbW1\nMWDAALxeL/3791fHRizlTDgcpq6ujv79+6vqrSuvvLLbfQsEAnD4MJSXZ7F7dzUnTgQIBEazcqWi\nbgkEFOJl/37l74kT6VRVPcCPfmTBbv8SAwa0M28eTJ8u9nOC228fQ0YG9O8PgUApO3duJBAI8PDD\nD5v2869+tYXJk0M0NjZy221dRujB4BGuvPJqnE7jkCgBj8dD//79o+6NsXA+5IxWOaNdpyc2LBYL\ndrs9KiubmZIxXnJGjH2v1xsXOaNXzmhfHuiVM7G4A314oc1mU5V5ffv2NbwmY4U1AVF9o//NvByU\nM7Is10uSdAh4FPh1D79eShcbclHwEyCXsfjk5cD3O9fq1TIzO9Uy31ANgwGFwykjOs32Z/sUJrwh\nDJDoE2Mk+sUYiX6JRqJPjJHolwuDy46c0ca8n49yJl7PGT0kSVIfZrUPrqJep9Opvh0WoSpGYU3a\nh28zckZPGgniRU/OaNuuJ15AmSjo34B259+jrUeWZWpra8nOzlYnrudKzsSC3W43fRPbnXLGSAEB\ninJmzx7TRByqKsKInDELIdGHNenPXyzlTHNzsxoWI8KcUlJS8Hq9pKamkpOTw8GDB1VyJhAIGCpV\nsrKyOHnyZASBJPYv2uRwOKIMgfVvv8+XnNGrEuLN1mToObNvH6HRo+O6Fm02G36/X5106yeOog6n\n0xkRzhdPWJM4H6D4tTidTvr06RMRpiiUM2b3m7q6OtLT07Hb7eTk5LB///6I7Y2NsHKlxJYtE7Db\nlXChhgYlpGjfPtixA4YMAYcjh5YWO06nlbS0ZNas6VKvDBsGs2bB/fdDnz4+Vq9+la9+9U5eeukl\n8vPzWbhQyc5SW9uKLB/hzjtvUPdfWZnKmTNnyMvLi9nPYoyei/m6gBh72ntjLMRLzgizbC3iVc5A\nV2iT9jrXkt/aa8UsrMmInBEqq3ggCHpxzLGUM7GIbSPPmcrKSnJyckzHaTxhTXriX/v7K9J9Xwb4\nAbBLkqTjsiz/Xw++l4qiQblomEl/ahjauaQnZRaTlHSMK69M48c//kokMQNkZWYp9zWtcsarrE8g\ngQQSSCCBBC4OLjtyJpbaRbwJjYWOjg7sdnuEsWlPw3TEw6yenLFYLBFvh71eL1lZWdTX16tl9MoZ\noYjRH59oq96M1ehNcbxhTdp6eqKcaWpqwul0kpycrPpx9BTxqJPsdntE2lctjJQzekNgo8lTdnY2\ntbW1UeELAj6fj8zMTMOwpnjIGSPljNmxOhwOTp06RXZ2NpIkqeEzwngzPT2d7OxsSkpKaGtrw+Vy\n0dTUZEikZWdns3//fkaNGqVuE6FCYtIlCAzRTjF+zMgZvdmvURmtEky0R+85I9Q7ZuEiADNnzuSt\nt3TRAHv3Ehg1Kq5rUShnhNGzkecMKBNwcR7N/JiMlDMtLS0AEYomLTnjcDgBOy0tYZqaFHKlvR3a\n2sDngx07Wjh8eApPPw3Hjw9j1y4Lf/mLQsCcOaNkJ/rCF5Kx2bLZv18JJ8rMhJEj4ZZb4JproE8f\naG7289JLf8HpdHL33XeTnW2cWaW5GWy2drxeb5SiwYh8Tk1NJRwOm5oBC9jtdtra2tTwSoF4zNdB\niU/evXu3SjhcaOWMfryaKWf07YcuVZVW4aIdO3rljFFf6dvQ3t5OZmZmj8gZ6Pr9MFLOdHR0EAwG\ne+w5U11dzaRJk3A4HOp41n/nfJUzzc3NcR1nb4Ysy2WSJH0LeEOSpJ8DP5ZlObpDonE7Sjqki4bN\nTAOEcX1XCBNYyco6wquvPhBFygjUt9Qr7jrlmpUTPvuGwIm3uNFI9IkxEv1ijES/RCPRJ8ZI9MuF\nQa8jZyRJ+hMwH6iVZXlc57q+wJsoaS0rgbtlWW7Uf7c7tUu82Zr0/hPnQs7oH2ZjKWeqqqoAY+WM\nMH8EY0WLXhVj5AnSU3LGyHPGyBBYlKmpqSEnJweI9uOIF/Gok2KFpZkpZ7oLO0hKSiIlJYWGhgb6\n9u0btd3r9ZKZmRl1Ps2yNYF5WJMgvbrL1iS8Q1wulxoq4/P5GDBgAP369aOxsZGOjg5SUlKiJn+i\nH3NycqIIKa1yR0y6YilnjAyB9eMrHkNg7bFKkqSObe35iMtzZt8+Al/5Slw3LUHOiIl1PORMvGFN\nqamplJef5aOP4K23bLz//p3U1GQSCknIMgQC/4+HHrIiSV/B4ZBxOLrULMnJoPBFWeTmppGSAiNH\nJnHmzFHuvfcKsrPtZGXBqFFw/PgpNm3axn33jTE9TnG9CbWVGSRJQpZlleQzCpXR16v9awahnNEr\n5c5FOSPIkO5wMTxnAEMlz7l4zmjbEAwGyc3NjZvA1pIdgtjUK2dEBicjAkVAf88RdeXk5Kjkjh5m\nqbQFYilnwmHFYP4y8JwBQJblZZIkjUXx271XkqRfAq/LshzFakkK6/xvwH10xRbFhfN5/gEIMQmY\nTZdiZiYwkyTnN3l1yX3MnzEeWlrAYgFJivgbDocNw5o+64bACSSQwLmhZMUKVj/3HLZAgJDTyQ0P\nP5xIe5xAAhcBvY6cAV4Gngde06x7AiiWZfkXkiT9V+dyVC5Ss9AFgOLiYl588UX8fj8vvPACVquV\nvn37qulHRepmbTaMcyVnjN40ag2BtZ4zgwcPNjQE1vp/xOM5Y7RdXycYe854vV4yMjIi6olXOVNc\nXMySJUvo6OhgzZo1jB49uttsK0aIN6xpw4YNZGdns2zZMlV9sWDBAkPljMfj4YMPPuDDDz/k9OnT\npKen8/7770ec7+LiYlatWsWmTZtwuVwR20A5R0OGDFHPUXFxMcuWLePEiROUlJSwcOHCqLTf2smM\ndiIpSRKSJBEMBqMmg8XFxbz88stUVVWxZ88ekpKSIoguQaCtW7eO9evX09HRQXl5ObNnz444V2Lc\nHzhwgLVr17Jjxw7efvttFixYwPEDB/jFl79MfU0NZ44f53BeHvUdHaxYvJjTJ0/yr//zP+Tk5FDR\n1MSRP/8Zb3MzLTU1vPP444Q6TXM//PWvcTmdhINBGqurSUtLw2u381eXi8b6ehqqqnA6nfza4SA3\nM5NAaysrH38cR58+hLxe8vLyOFpfz0N//SuEQjRWV5OXl0d5YyO7f/97pI4OGqurCaamEgqHKX35\nZXVfeY2NWBsacM2Y0e140nvOCBJL9JXFYqG4uJhXXnmFUCjEpk2bmDfvFlpabJw+rShc2trg44/t\n7NpVwIYNcPy4kqWovHwsjY1XctVVcOWVHdx11xGuu85Fff1pbr31Jn71q//hv/7rMVau/IChQ4dS\nWFgYcZ6XLVtGdWffzZnz7wCsXPkcb7+9jObmZrWtosz69eujxqXAunXrWLduHQ6Hg6NHj5qW05Mz\n2kxgRtfexo0bWbt2LTt37lTHj1G9DoeD1tbWcwohBeUaTU1NVcOa2trauv2O0bVuhPPxnAHjjE3a\nvtLeS3sS1pSRkdFj5Yz4K+4n2sxqfr8fl8tFc3OzKXGlJb/Fb+HZs2c5dOgQs2bNon///ob7FuRM\na2tr1Ha9etBqtUaQX2lpaZdLWBMAsix/T5Kk48CzwBLgN5IkbQB2AMeBDmA48EVgNPBtWZa7H9CR\nOOfnHwUh9IoZCDOmfSfzv/kmdHSALEf+7fzfMjQEk4k2BN7gg6SkKDJH/Wu07mJvi1HeU1eHOzv7\nM9n2T2ubZ88e3BMn9tr2Ray7iEj4ZXShZMUKVj3yCE+XleEB3MD3ysoAEgQNibFihkS/XBj0OnJG\nluUNkiTl61bfipL1AOBVwIPBw4k+laf2YXTJkiUUFhZSWVlJWVkZc+Z0vR5asmQJAEVFRVGeM/Fk\nEdLDKEbfTDmTlZVFIBBQTVpFm4V3TSgUilJe6OsUiCesychzxufzMWjQIMN+FHUYec5s2rSJ9957\nL2LyuW7dOiRJYvr06XH0VHT/xILNZmP37t0cOnQoYp9Lliyhf//+EeeoZGu5pwAAIABJREFUuLiY\n3//+9wwfPpyysjJuv/32iPLa/6+++uqobWIiKsKaTpw4ETGO8vPzDcuDuecMoL7h1ioStPWKMKQl\nS5Ywbdo0hgwZAigE2s6dO/nLX/7Cddddp373jTfeYOzYsepyKBTik08+YdeuXRFj/BeLFzP84EH+\npamJVcAfgZKyMlYB84BVKO9ZS+rrlXVVVV3bvF5lG7Dq1Cm1/ItASV1dRB3LgJL2dmWdqAtY1dCg\n1CHKd9YfUcfJk+q6Z+vqqAXmnTqlrgNg2zYePn6ckjlzYj4gGBkCa/1+RJ9PmHANR48WsHnzBF57\nbRg2W5jf/lZRuCQlgdU6kNzcJubNgxkzIC8PHI4Gtm17iwce+BZbthyloaGF/Px+NDQ0kpwcxmJp\nx+m0RxEURuPnqaeewul0MmPGDCorKzl16hQFBQWUlZVx2223qd81Gmeivuuvvz5mOegiZ4QR7dmz\nXdl99dd3cXExL7zwguk9Ugu73U5DQ8M5ma8LaM3StaSRGS60csZMydYT5YyZp5WRkiwzM5Pjx493\n235tO/UhtloFmggvamtri/I60x+jdgwKvPvuu0yaNIk77rgj4juCcIoV1tSdcuZyImcAZFl+UZKk\nj4HfAVNRdCZz9MWAp2VZfu4c6j/n5x8FWp8ZhaRJTv4mP/nbr8AknGnFihKee241rYf/BwxSabfK\nFtx3T8UpOXn4rm8y//obI0gdI6Lnkm7Tr9u7F8aOvfhtuNR9FKt8XR384x+Xtg3xbAOFoLlY5FFr\nK6SlfebJtwvRvtUvvMDTnWSMwNNlZSx+/vkEOZNAAp8yeh05Y4IcWZZrOv+vAXKMCpl5zixbtkx9\nGNUTMwCFhYUsX75cJWe02ZriySKkR3dhTYKMEca5wrjSKLRDm4EjHuWMnng5l7CmeJUzK1eujHjI\nB5g+fTolJSV85zvfMe8gA8TrOVNeXh61z8LCQtavXx9xjpYtW8bEiRNZu3at6fmWZdmwLjEWRCpd\nl8tFMBiMGEdG5bXt1CpntG/ULRYLwWCQPn36RLTVqN6tW7eqHjs+n48tW7ZElZs6dSqbNm1Sl0Oh\nENu2bWPKlCkR5bLOnuXFpia+T5c95OrO/2Ot62n5C1XHGYN1As/V1Bg+IITDildLRQWsWzeEPXuS\nOXhwOKtWwZEjVyJJSaSnS+ze/UVeeqmN1tYXWbGiLwMGVDFhwm7uuOPvbNlSzLp169Q6S0p20d7e\nzpw5XeRlS0sSH36ohKUIo2ahchITVjF51k5Ojc6zLMtce+21QNe9KdaY1Y6zeMcjdF33ra2tZGdn\nxwxr6km9QlVh5O8Vr+fMRx99hFDOxOM5YxTCaASj0Dgj5YyZ6sWoPbE8Z7ojZ2RZJhgMkpmZSWlp\nabft17bXSMUpyHsRXmTkdaatx2q1Gp7badOmsXnzZsPvmBkCy7IcRc7of38vI0PgCMiyvAu4WpKk\nmcBdwBQgC6gDtgN/lGV59wXcZVzPPwoEHS5UM3txOOby61/P5O23IT8/8rNrVwmPPbaKsrKnYdA7\n4D0QZQjckdHBhwUbACj7YwUkJTO/6FOenMnyBSME3IWFvYsY6QVtcPeCNsS9LRzu+oRCkcvdbdM9\n63YHt9mGzyE5Y6uvN+wXaxyhx58HJNQhxkj0y4XBZ4WcUSHLsixJkmy07fXXX6eiogKXy8XWrVuZ\nNm0ac+bMQZZlKioqANSHerE8bNgwAKqqqvB4PIgwos2bN1NaWqo+1Ho8HqBr4MVattvtbNy4kZMn\nT6rbN2zYwNGjR1UzxzVr1rB3715SU1NJSkqiuLiY8vJyNZ2ux+Ph2LFjDB48WF1uaWlRH349Hg/7\n9+9XJ3Yej4ejR49GbIeuB2yxPGrUKDo6OiLa6/P52L17N8ePH8ftdmOxWDhy5IgqTwuHw2zcuBGr\n1aoezyeffEJtba3a99r+DIfDPeovbf8IGJU/ePCgSlbpz19jYyMbNmxQJ7WnT5+OmMQZnW9AVTBo\nt4v+aWlpweVy4XA42Lt3L6dPn45ZXrTX4XBQWlqqjieLxaJuF8qZPXv2EAwGcbvdEeNTtK+iooL6\n+np8Ph8dHR2UlpZSU1NDQUFB1P5lWVbrT05ORpKk6P7xevHQdcF7gJOd/9s6l9FsP9m5rqfl3Zrt\n51pebF+DBS+D2MAQVuKklmxsXMdJBrF9YxXvjPOQlOQmEICzZz2cPQv9+7sZNgza2g4TDFYxfPgo\n+vSBQGAjTqeFcePupKWlimBwNVddJTFhQiY2W5iKigo6h4RyvJrrx+l0RpzflJQUPvnkE9avX6/6\nRu3atYvdu3dzxx13qOUPHDjApEmT1PqMxo92fArzVIvFYjgeqqurI9oX73gE5foqKysjLy+PESNG\ncOjQoYjrW7tsNh71+weFIPD7/ezZs4dAIKDur7S0lPr6esaNGxdR3uj6D4fD7N+/nzNnzkTVb1S+\no6ODjz/+WL1fmZWvrKxUDaHFdkEybNmyhfr6etxuN6FQiB07dlBdXR3x/UOHDqmeReL7ghzxeDzs\n27ePyZMnA7Bv3z5SUlLU/hLlp02bpt4PxW9JWloau3btYsiQId3eH8X9vKSkhL59+zJ48GB1/5WV\nlapypry8nMbGRpUU1te3f/9+HA6H6f2zrq4uQo7s8XjYsWMHU6ZMweFwsHv3brKystTtxcXFHD9+\nXCWKPB4Pn3zyiToe33//fVpaWmhra6OpqYnLEbIsl3CRDX9jPf8o2AFsACyAnYKkM3wwdhuV9f/F\nqiMtHAxksjbQn93eCrzhs4SpAtYrX21LhmxABGI1Anma5Qooyyjj+QfvZr48AI/Pp5AfTifIMp7W\nVmXZ4YCODjyBgEIE2O3KcjCobLdYlPLt7cqyJCnbOyfl7s7deQAsFqW8xYJHlkGSlPokSSkvScr+\nLBalPotFaY/FouxPknCnpCjlAwFlOTVVWfb7lWWXSynv8ynf71ROeLxeZXtGhlK+pUVZzsxUtjc2\nKuX79lWWGxqU7f37K+Xr65Xl7Gxlua5OWc7JUcrX1irfz8tTttfUKNsHDlSWq6uV5UGDlPKnTinl\nBw/uWgbc+flK+RMnlPLDhinbjx1TlocPV5YrKpTvX3GFUr68XNk+cqSyXFYGNhvuUaOU8ocPK+XH\njFG2Hz6s7G/sWGX54EFl+9ixSvlPPlHqGzdOWT5wQFkeP14pv2+fslxYqGzfs0dZnjhRWd61S6lv\n8mSl/K5dyv6mTlWWd+xQtk+dqpTftk35/jXXKNs//lhZnj5dWd6yRSl/7bVK+Y8+UrZfd52yvGmT\nsjxrllJ+40Zlf9dfr2z/8ENle6cytafPtJ/15bIpU/DU1ERej0C4k/y/1O1LLCeWe/Pyb3/7W3bv\n3q0+E/UUnxVypkaSpFxZlqslScoDao0K/du//Rs333wzeXl5/OQnP2H27NmAIukXHVReXg50PZQK\nDBgwALfbzdtvv62SEILssNlsaocLxFp2OByMHj2a8ePHq+umTZumTr6cTieFhYVs27YNh8OB0+lk\n6tSppKamquoPt9vNvn37VFm92+2mqamJI0eOqMtlZWXqW1y3283hw4fVh3nRnqVLl0a0v7a2lnA4\nHNFer9fLDTfcoKbTtlqtDB06FHfnRK2jo4PZs2dHKFO+8IUvsHfvXnVZ25+hUKhH/SX6R5sxxKi8\n1+tl9erVUfsDSE9Pj/hOXl4e+fn5Mc+3VpWk3W6xWHC73Zw4cYKamhocDgcFBQWcPn06ZnkBh8Oh\nTrxWrVoVsX379u0Eg0GmTZvGxIkTgcjxqa2/ra0Nn89Ha2srY8aMMW2vLMtq/R999BGSJEUdb4bL\nhbumhjWiP0H9P0TXmxGxbpCuTLzltdu15WcB7dh5n2Qq6IuFLKq5gif5An9nJFtwUUoyU0ihjWTK\nKWUZt5FEDds4zhD1s58bWUmfMVfyrV9/E6cTnE5ISXEzaJASjgSwfn1fSkr2c/vtZxk/fiAez2Bk\nWWbChDbgECkpDZ19Ho7oz2PHjinH29mf//znP3G5XBGhZFarldGjRzN16lTeffddUlNTufHGG9m3\nb58aYuJ2KySnIAPcbjevvvpq1PnTjk/xf0dHR9T5GzZsWIRaxKw+iB6PALNmzWLHjh2q54y4vkEh\nAL7whS+oy2bjUb9/QL0ep02bFqHIKCwsjPAxMbv+PR4PkiRRWFjIFVdcQXFxcczyoPTP9OnT1ZA/\ns/KHDh1ix44dEdvffvttnE4n48ePZ9q0aQCdyqg5DB06NOL7VqtVVc6I7x88eFD9fZAkSb3fDh8+\nnFmzZkW1p729Xb0f+nw+du7cSWpqqvp7013//PWvfwUUhdygQYM4fPiwuv/9+/erypnCwkJqa2tV\nckZf34gRI7juuutYtWoVEH0/zMjIiGpPIBDAZrNht9sZMWJExParr746Iv272+3G5XKp98i5c+cy\nffp0/v73v/PEE0/wox/9iATOGXE9/yhYqf5XkPcIz35zKCOvuYojWz9h/7vNnDpbSXnTGdrCf+gs\n9cOur7b8EE4+Al/WhDKsAa7o/L9zyJw6PRD+d4VCqlgs6pt2d+ffiGXNOrdmm0q66Mtrl3VHdq7L\nnk7S8ULVdzksezwe3I8//unuTxOWC+C+6abI5c7nc3VZ5yXn1mXmdE+YELk8JtIo39354kpd7nyx\nqS5rQtsB3DrlrfuGG5QJVqeKMqp9PXym/awv//sPf8iqRx7BrfGcebKggBsfeqhXtO9SL+vXXer2\n9JZl9X7bS9pzqZa//e1vRyz39BnI0qPSlw7/ABZ2/r8QeMeokDYUyWazqWTCggUL2NXJwhcUFLB2\n7dqI7+3cuZN7770X6Mocog9r6gliGQKDYjRZV1enhhKJLCVGGTViecqcqyGwNmRJGEqKN8yiHn06\nZX1Yl8ViYfbs2WzZsiVi/fbt2xkxYgQ9RbyGwBMmTGD79u0R63fu3Mnw4cMjJo/inMc639pxod8G\nXeFe4nx2V15AhDJ0dHQYniMx6dG3VV/vbbfdhs/nU9M1G5Xbvn07o0ePVpdDoRAzZ86MKnc2K4sH\n0tNVRwLocieIte4G4EkkWklmGn15iIGMYQT/zlh2M57BTGYhV5PDdSxgLu/xRTq4jxn8iK28ziA+\nYgk1WAiTio8XOMkEPGzkD/yQL5OEn6/wN9J5jsf4b8ayiOXcy+Ms4jFSeZ8huJnBchbwDE/wIC+w\nLvdjvvnDGVx3HUydCuPHw4gRXcSM6GdADVcR50RcY0Z9uWPHDlWZJGAWriLCmLRjBKC5uVkN9dCH\n9hjtE1DD0sRY7e4eFas+o3KgEC5m2Zr094ie1KvtX/36c/Gc+bSzNYm02frjNzMEvhDZmkKhkBrS\n5HA4SElJwe/3R4WXGsHMc0bULZQz2rAms3rMxv22bdsi7iECItzLKEzXKFud3nPmcg1rugSI6/kH\nYB5TmIWbbOs1PPvSncz/78dY0Z7EI6+eYfWO33Hg2DDaAn/QfENzfoLz4ciz8Id5ZL47BOtyq0LM\n5Efu41httXLDveIKGD5ciY8aOhQGD4ZBg2DAAMWcKycH+veHfv2gb1/IzIT0dOjTB1wuJW1dcrLC\nrjscYLOB1aoQNAkkkMAlxcz585n37LMsnjePV8aPZ/G8edz47LMJv5kEErgI6HXKGUmSlqO8aO8n\nSdIJ4AfAz4G/SpL0DTpTSRp9V5sqWDtZED4JwmdEZEDJzMwkMzOTRYsWRWRr0hoCnws5E8tzBhTl\nTH19vUrOCG8DI8+ZWKmy4yFnuvOc8fl8pKSkREx2RBlZlk2P32KxMGXKFLxeL5s3byY9PR2LxcKD\nDz7Itm3bEJmU4kU8njM2m4277rqLiooK/vSnP9G/f3/69OnDgw8+yObNmyP2pz3nLpeLFStWkJub\nS79+/SLOtyhTWVnJ4MGDI7aJibeY9Ij1r7zyCmfOnGHQoEFRdYEyERYTc/1EUnjOmI1PUX7RokVM\nmjSJP//5z6qviVG5+++/nzKNaVsoFGLKlCmMHz8+otx/PfUUR5Yu5Z+rVnGqXz++VFvLwIEDOeH1\nUt+vHydPNnOt/zrCKVM44+vgvZT+nGkZxK8CVxCQc/kFbVgtAaxSgNdsQawE+L9QG1aLDNYOiq0y\nHWEva4PN2KVmHPYT5PXZxbDgG/SVyklJa0P2NZObl8dJn48+Tid2q5VPqqvJzcvDe/Ysh/LycAaD\nPN257midlaacHDra27mnc104NZVhN93U7QOCGEtGhsBWq9WwLx988EG2bt0aUY+Z0avL5YogziRJ\nwuVyUV9fr3p+6D1nxD6XLl1KS0sLubm5LF68WG2HuDfV19d3O2ZjjRujrErC5Fub9lp8R3+N96Re\nbTYsLQRx0B3cbjdr1qzBbrcbZkcyQrzkjJHnTHt7O8nJyVGeM2aGwLE8Z7TG6fq09QKSJKn3U0F2\niLThra2tqlrRDFqvGYg8dnGPEVmTzIx7RbvNxv1//Md/cLgzZMHoWI3qFQoxLbSkvggHFKb6CcSH\n83n+AVjJdp4E0pNSmT9/JitWlLBw4RLq6t7sLKEf54KG73T2Cs6nIHkTz/7kSe5+4iZay1ojyZnP\nYGptozfen3ck+sQYiX6JxMz58xNkjAkSY8UYiX65MOh15Iwsy9GvZxXM7e674mHZKPtGUVFRxORi\nw4YNBAIB5s6NrFarnBFv2s+FnDHL1gTKG9mzZ8+qD+Y9Uc6cb7YmfSYmvRkwKBMKSZIMlR/6fQ0Y\nMIBnnnmGkSNHqtv27NlDW1tbhBqnO8SrnGlvb6egoIDZs2dzyy23MHHiRMLhcJSCB6LPuRFEmRde\neIG77rqL7OxsdZsgRbRkW1FREQUFBWzcuJH77rvPtF7xHf1EUnjO6I/VqK3BYBCv1xtxjvTlfD4f\nhw4dUpeV8ZrEmDGz+Na3imhuhmAQmprgZGU1gUH3IBdOp6O5hbZ+gzi24wSn7cPZ2xLG7XYweTJs\n2bKO+fPd+P37GDHiGHfckYvFkkxx8UaSk5OZoZEfv/nmm4wbN071SgL42c9+xqOPPgrAb37zG777\n3fcijuu9994jLy9P9euQZZkf//jH/OAHP4gg2H75y1/yrW99K2ICK67b7qAnZ8T1rCUrjfp8y5Yt\nEefMbNKdmpqK1+tVx4hYd/bsWXXSaqQeKSoqon///lRUVPClL30pYv25IJ4xDqjXsyBiRX84HA7D\nay/eerXklxaxiAI9jDLZxcLFVM7ESqUdT7Ym6CLptOoaQe51R84IksNMORMKhQgEAiQnJxu+FNDW\nYzbuA4EABw4cMPyOUM7of8/MlDP6bIlG5yABc5zP8w8oNsA3AocliRUrSnjkkVXU1WnDP/RKppkA\nZGXdw1VXjSYpKcxDD93I/PkzsXzPAgVEp9belVC2JJBAAgkkkMCnhV5HzpwPzJQzRkhNTaVe40Yu\nYKSc6a4uPex2Oz6fL2Kdnpypr6+nb9++QNcb2p6GNcWTJru7MkbkjLacGTkl3gbX1tZGEBrQFfLR\nU3Kmu3622Wxs2bKFK664Arvdrh5HvNlbYkFMtrXHIlKd6yea4k11LIgJjTacDZR+a2tri2tMSZKD\nhoYMNmwI09IymH/+E/x+Og1wobQUDh5M4uDBr7F0KbS0QGPjbNrbreTkKMry9HRFMZ6cDKkn+9Dv\nijQyMgI4HO2MHg3B4EHuvTePPXv+xHe/+zAATz31EQ89NJP162tJTk5GdK2REkF/fKIvfT4fTqfT\ncNKrn+yJOrTEjMfjUQkELeK9HkUZbdhNPPcGMe615IxZWFN9fT1Wq1Xdh1gnxpCZeiTWRP7Tguhb\nca1rz+W5qAMFzMKabDZb1D3QCB5Pl2m2w+FQwwFjXc89IWf046e9vZ2MjIy4lDPxhjUJEttsXBmR\nM+J+k5MTI/EO0VmP9NmahHImMzMzZlhTrPaJevRqR9EvRqRPPMoZofxMhDZdPPwEeBI4FkrWKGa+\nrymhU8oABQUrefbZB5ivT7UdAsqISq0dxe/0cggPhAS6kOgTYyT6xRiJfolGok+MkeiXC4PLjpyJ\npfbQQkwg9RDKGYvFgiRJtLe3n5NypqGhIapebVjT8ePH1UxMYhKgf4AWbx4FtOFGwoxSv72nnjNe\nr9fw7a2oy+yh3mKx4PP5CAaDakYTAdG3WkPQ7hCvciYcDlNTU0Nubm6E1L8nIVRGMBoPPp+PIUOG\nRE1e9Clkzdpqppzx+wPU1zuorobWVmhvV8iWigrlU16u/K2pgdTU++jfP4jLZeXDD5Xw/KQkJXx/\n9Gi46SZ4//0PePTRb5CWBhs2rGbYsGymTp0c1aamgsc4+a/fp3GkE5/Px3XX5fPsswe45poZHDnS\nFXogxoiRMiuWIkxAqAIsFovh2NGTXeKa08NoYieUBN3BKKxJ6zkT63vaMW9GpKSmplJTUxNBbKam\npnL69Gn1ujbzXTFT43yaMCJntBP+nhLQArGUMz31nJEkSSWqk7UGQjrEe72fr3LGSMmjJ2e04Upm\nbRLt0KbsNvv90cNIOaMNaxLKmXjCmszOsVZJpe0HsWxUbzzKGfGSI0HOXDwsBj6gP/v9NxH2C9Nn\nLSGjEDDJyV+hoCCPgQPTVKWMHlmZWXi93qjU2lmZWRfjUBJIIIEEEkjgc4nLjpyJVznjcrmUBw8d\ntEoAm81GIBC4YGFN4qHa6XTS0tIS5TljpJzRLmv9C8SxnktYk5HnjB7dEV1Wq5WTJ0+SnZ0dNSkx\n69tYiIecsdlsjBo1itLSUiZMmKAe64VSzhiRM6mpqSrJICYrYmJy5gxs2gQnTyoki/aze/cc/vnP\nNKqqrsZm64Mkgc8H1dX30NSUxG9+Y2PECEhNVZID9O0Lw4bBddfBwoXK/4MGwSuvvInf7+faa6+N\nyIYjIMsWduw4yciRcufkNojDYTD2QyFcp07hHTo0wkuivb09ihwxI2dsNhttbW0R1RqdN6EKSE5O\nNlXOaOsxqsPtdlNaWmo4no2UXnqcLzkjYEakuFwu9u7dG9EWl8tFS0tLhOeMkZLBTI3zaUJco4KI\n1ZIz5xK6KWBGzsSrmHC73fzjH/+IuDf6/f5uyZnz9ZzRpneOpZwxCmsSZcVY6e58miln4iFnwuEw\nqamphionvSHwuZIz0EWYase6IJMEKa7tdyNyRm8kL5QzibCmi4cjuChlGmFepUsxI4iXxYCVrKyD\nvPrqg4aEjBb1LfVQCJRrVk6A+t3RiuPejMRb3Ggk+sQYiX4xRqJfopHoE2Mk+uXC4HNLznSnnBH1\nGfmDdAd9lhaIztYERHjOtLS0RE2S9MoZ7THGQ84IQ9/uPGe6U86YhTWdPn2asWPHRm2Ld+KhRTwT\nRLvdTnV1Nenp6arZJPRcOSPLilolEFA+wSA0N2dx+nSI5GRlORCAHTsycDr7snMnbN16DQ89BLW1\nUFY2hro6By0tcM01StKKlBTl06+f8tfvP8u4cemcPFnG6NFDuPJKFykp8MEHq2lqKufb315Ibm5u\nt211uVxUVVWZEhJ6ws507B85QiAri3aHg/bOiZVZ6JpYrw9ZMppwm5EzPp+PjIwMw7Y4HA41rbxZ\nHWb7i+faFscAxtmaYo0zI3ImVljTqFGjItYBEdmajAiK9vb2br1GPg1IkqQSsVpFQzgcPmclj/ie\nvk+N7oFm0N8bu/MUipeMjaWcOXv2rLpvo9A8iFbOyLJMKBSK+H0Q5Eys/hNjT6+ciYfAjsdzRoRZ\nmoU1xTJ2FzD6rrjWJElSiSAxto3Cmow8ZxJhTRcXhxlLkEmdS3rFzEwKCp40DmEyQDgcNgxr+qwZ\nAieQQAIJJJDAZwmXFTkTyxBYDzGB1MfZax/UrdbotMfxIJ5sTaINYtlIOROLnAFjPxntZES8xdSH\n1eiVM/369Ys6hng8Z/x+v6FnwrmQM/GGNX388cfMnz8/4lhjTdZkWQkT2ry567Nvn7LN6ezK4ilJ\n45GkdrKylGWnE6qrCzl0yEVqKjQ2ZnL11e3MnWunrOwwgwY5uOeeCZg1+Y03jjN+fCa7d59k4sRs\nxBx+1y4fwaA/7jGVkpKCLMsx1SJaos507O/di3f4cJWgSE1NVSddwWAwSjljRMwZvQWPRc6YhYsY\nhTXp6/B4PKZkUE88Z7SGwPF4SOmvoVhhTbIsR6jOxDmKRzlzscOaQDmvWuWMVo3RnYeSGWIpZ+Ih\nZzweT5SqsDtT4PMxBBbKGa1qyCwkyel0RmRcE78VYt/aLEw9Vc6IzF7dQe85o/190nrOiFTaZi8c\n9J5Oehj9ZmnJJEHeiN8uv9+vZv0SEL8ZgsSyWq0JcuYiYy+D6TKFiVbMxEvMAFisl4chcMIDIRqJ\nPjFGol+MkeiXaCT6xBiJfrkwuKzIGa1yJp6JviBftBOTC6WcMSJnRL1if9rJnEilHcsQGLomzrIs\nG6Zp1k5GjCaiRmFNRhP/eJQzQJQZsDiuqqqqqPWxEAyGCYXsNDZ2qVkCAcUAV3wqKtI4eXIQpaVX\n0t5upa2tgwMH4PRpKytWfJG33gKvV1HFBIPKX58PXC5F4XLNNfAv/wITJyq+LVocOlTJjh07WLBg\ngdp3P/3pa3z/+99HkuCFFzZz110Dyc5O4d13TzNkyBBTYgZiZ2uC6MmsGcRkOpbSIhZhp2LfPtoK\nCqK8L+x2e1ToXizPGSOyRD9RTk1Npba21jRcRP+WPlbonJFyJp7rUfhdiLbFq5zRXx+xwpq0f7X/\na5UzvcUQGBTlTG/0nOmpcuZ8DYG1qbTNxigo/SWuY0GQGJHh3YU1iXYYGQJ3h3izNcXynIn399CI\nnNGSnNrtRr5b4jdDnB9tOGgCFwdhRmGkmEl23M+rXx/D/JYqePNNsFhAkmL/9RsrZwiEYcOG7r/f\nG/4mkEACFx0lK1aw+rnnsAUChJxObnj44URK7gQS6AEuS3Im3smGeMOvJWeMlDMXynPGarVSXFzM\nSy+9RG1tLeXl5Xz1q19lxIgRUam0i4uLWbJkCe3t7axatYoFCxZFXwxDAAAgAElEQVRQVFSE1Wpl\nzZo1vPPOOxw7dozKysqIbdqJpdFEXZIkZFlm9erVLF++nFOnTrFixQq+/vWvR6RX1XrO6Ov4xz/W\n8ctfruP06Sz+9rf9ZGc7SEvLIxCA6up6Tp5Mo719DLJcjizbsFjsyLKVlJQ0bLZkQiHUjwgvCoev\nxW4Pk5zcpWYR5rdJSeD3N3L2bD2h0HwOHvSSm5tOv37ptLUpmYhGjTrGI49cSZ8+ioeL+CQnQ1Yc\n/oVatU9xcTGvvfYaVVVV7PzwQ3IaG6k7fZr13/sejvR0fHV15ObmEkpLwwGEg0Eaq6vJy8vDa7fj\nAOrr6mhvasLlcrEyPZ00p5NwMEjNsWMkJyfz6Ntvk2y1qt+1uVyEvN6IOhrr62moqsJut3Pnc8+R\nm5lJalJS1L6qq6pY+Mwz2Pv0wXv2LB8NHEgwNTWybYEAUm4uQwsKGHrVVeo5Fb5KRp4z+klwvNma\nXC4XlZWVpsoZ/UTPqA63282yZcvOKaypuLiYP/7xj9TW1lJWVsaCBQsYO3ZsjzxniouLWbZsGRUV\nFWod2utj8+bNrF27lj179vDaa6+xYMECmpqaWLt2LQcPHiQpKYlbb73V1BD4YpMzxcXFrF69mj17\n9pCamkp2djZz5yrZec/Hc2bjxo2sXbuWo0ePYrPZ1H6KVznjdrt54403sFgsFBcX8+c//5m33nqL\ntLS0qD4XiJec8Xg8fPDBB5SWliJJEvfee6+qRNGSM7FUTELJk5SUZBpGGk9Yk54U3blzJ6+88grF\nxcVIksSYMWMoLS1V1Tni2MPhcBQ5o81EplfO6Ptc9OnJkyc5fPiwaZ+ahTVpSVw9OWOWrUl7jSUM\ngS82bgBWAfMQihmJ3XxnRDPzT/rgRCl0dCiS0m7+ZnV04PUSbQgcCsOTT8ZdzyX7CyBJuHsDSdTL\n/rotFvi//7vk7ehtf939+sGBAxd//72cSHT3QAlRsmIFqx55hKfLytR13+v8/3IiaHrSJ58nJPrl\nwuCyI2f0D4exIIxrszSzd60SQIR8nAs5Y6Sc2bt3L5s2baKwsFD1almyZAkLFizA7/cjy7JK4CxZ\nsiTCAHbJkiUAlJeXs379eiZPnsywYcMitull/EaTLkmSOHbsGDt37mTixInk5+cjy/Dssy9x5oyT\nceNm0tICFRUD2LTJQnl5Mhs2TGDdOqiqgkOHvFRVTScvbwQ5ObVkZDTS0PAGM2dej93ewQcf/J3b\nbhtGbe0JTp2q5JprpiBJHVgsHRw8uJ9//devMnv2TGw21I/TCSUl67DZrMyaNSuqP0V/3H13V398\n9NFHuN3X88QTT9DU5OePfyzlmmtu6tF50kKMBW3fp3R0YPnnP7m3oUF93F3V2MjTQMnRo13rgBeB\nkrq6iHVPAyVNTaw6dSqynNfLqjNn1HX/Aqyqq1PK6+pYBpS0t7OqtZV59fWm+5oHrGpoUOo4fDiq\nbQAcPcq3f/c7fPfdx8iRI4GeKWd64jnj9XpNVQk9ydZkFEYV69rWnr8xY8YAyvXx1a9+NW5yZv36\n9SxbtozCwkLy8/PVOgCKioooLi7mxRdfZM6crlfKTz31FA6HI2Ldyy+/zIABA6L2cbHDmkSfzJ49\nW1334YcfcuWVV5Kfn2/quRJPvX/84x8jjln001VXXdUj5czWrVt55513mDZtWlRdejIhHnJGnCPt\nMS9ZsoSsrCw1ZTd0T/ZplTxm5ExPwppSU1MpLi7mL3/5CzNmzACgsrKSt956i5tvvjmirSI8KCkp\nSTXQDofDEWqltrY2QqEQDocjimDRXgsFBQVqvRDdp2ZhTVrljLbuWNmatH2aMAS+2BAhS8WAFQhz\n1bh+/PeedxSCRYMVK0p47rnVBAI2nM4QDz98Q0TIk3dKP7gqEGUI7D2QpihnejtkuXeQRJfb33BY\nebN2IesVn3D40nwEmXcp0QvIqQvxd/XWrTzd6ekm8HRZGYuff/6yImcSSODTxGVFzvTEcwaMvVH0\nypkLGda0ceNGJk6cGLG+sLCQ999/n4kTJyJk4GJiqC+3fPlyjh07xsyZMw23LViwIIqc0faDLMOO\nHbBy5a1I0hQ2bkzC71c+kiSzbp2XYcOgTx+orZ1OSYmLrCw/yclW3G4YMAB+97tnWLjQgc0WaQp4\n7NhzyLLMDTfkAyc4cmQtt902Bzijlrn22oGsWfMKCxZEx7x3dISxWo0nONr+qKioYNiwYUyfPp1N\nmzZ1HteFy9ak3VfT1q280dDA91GIFvEXYPUFXHcx6hD47enTfOOf/8T29a8DsZUz50POxPKciSes\nycxzprtr2+zaeffdd5kyZUpcnjPvvPOO6fVXVFRkuA9ZltXJtsCkSZNYv3591D4udliTUXtnzZrF\nBx98wMKFC89ZObNs2TImTZoUsU700zPPPNMjz5mVK1fG7HMt4iFnli1bFnWvnThxIh6PJyLcLF7l\nDJiTM/EaAgvF1LJly5g8uSvVfVlZWQQxoz324cOHR4WgaT1nfD4fTqcTSZKifndi/Y7o+9ToN0t7\n/RqFNRkpZ/ShsImwpouNyJTZkvQtKiq+Rnq6TMFwmdSUDzlVVUwwcIa6eiuB4O/Vb5YdeQKam5k/\ndxrIMi57EnUGYU0uq1MxcrvUJEGcfz2ffIJ71KhL3o7e9NfT1ITb5brk7VD/ClxossBmUyTUcZb3\n+Hy4+/TpFSRHb/rrOXIE9+jRcZW3VVSAjpwBsHbjJfdZQ8JbxRiJfrkwuKzImZ54zoAxOWPkOXMu\nhsBG2ZrMDBllWcbv9+NwOLDZbMgmLH6sSUkoJFNV5eLYsTTWrYPSUqitdXHy5J387W+KB0t9vfKS\nwOmsZ86clSQnt5GU5Mfp9GO3h6moqOCVV14B4KWX3uOmm26iqamJAwc+4e67rwJg+fIT2GzDDNum\nhVk79eUEYhkCm/WHWN/TbE1GEP4+WnIrqXNSIc6+dhRcyHUXow4t7IHABfWcMQpr8vl8MT1nujME\nNttfd9d2rLESz71BHxqohVhvtI+ekIMXO6wp1v0E4jPj7mm9PfGcER5asdqoX9ddf5vVZ7FYItrW\nE+XMuXrO6LM16dtmdizadNRmnjNer1dVsOivq570qd4fSRj7irbpt5spZ/TK1QQ5c7HRFc4EYSbI\nH7PT9wcapL68ujefn8sTqGEpCnX/VMQ3yyp+zvP3TWd++mGwWKhPO6NwPOtAawhcv6EK5s7tFZPG\nuP5WV0NDw4Wt12q99Md1Pn937YLJky99O8Rf8bnU8HggMbGMRg/6JbR0KXzySdT68DkmHUgggc8j\nLjtypr29vUeeM3pTRiPPGf1DaHcQD8naTFDhcNiUQBBvLYVyRpIkgkE7p04NoKEhk3DYRihk5ezZ\nsTQ0+PD7hxMK2Whvd9DcnEZTUzp1dRmsWdNBfr4XtxsU9aCXHTt2c8cdg3A6lRTPV14Jc+b8mcGD\n3VHtMMrqpO9Ls2MQ2Uy0/WhWzgixJojafQ4bFk0MXQjlDCjjQdtuf+dxi6mFdopxIdddjDq08HdO\n+ODCKGf0fS88Mtra2uIOazLynFmxYkWPlTNm41MQPcJg1QzdmQWb7cNsvBulMb7YYU3dEZfnaggc\n614Qbyptt9vNn/70J9Pr12h9PGRsrO1aP5zzUc5oszXFqkNP4ujbZjZ2RDY1bWiQPluT1+tVFSz6\nlwKxzo8eemJHEKuijp4oZxKeM5cSMxGqmYKC7/KTZ3/LCuC551azbdtRGhqWdpYzvt79194Ano8A\nCI9LhbLW6FTayamwr/xTO4ILDfelbkAvhPvqqy91E3olEm/8jdGTfrnh4f+fvXePj6q69/4/e+7J\nTLgTCFiFDlQRUYKIgDUEbAhtWluPWiXay2n79GmPJFjrafsC8eER8fScnp7TwC8q3i+VaK1WnxYE\nBnDkooIaELweGW5yCYSEJEwuk7n9/thZkz17rz2zZ2bPJZPv+/Wa18zsvfbaa3/X2pf13d9LLZZ7\nPFExZ5Y5nVhUU5OGlmUPGit8SC76kPqMNofgPRzGgr3hl8KLOZPoxIVlqpBnTlqwYAH27dsXVbax\nsRE333wHzp0rwbvvTsY999iwc2cd/v3f78G2bTfg2LFL0NQ0Bl980Qun82oUF4/D2bOHMWTIBYwd\nexozZ36AKVP+Da++uht/+csH+L//dz8eegi4805g3rxOXHHFGVx/PTBrFnDFFeKLissuuwwffPCB\noh2LFy+OOgZetqbq6mruMSxevDhqndPpxLZt22LuQ0qsPuPt85133om4BuhhOQOIyplvfetbkX0N\nvfZaLLXbI7kv2Dckv/VYlok6GDVjxmDsvHlJWc5oTaXNsgK1t7cn7dYE8FMhx1MkqI3P2267TVPM\nGYPBEDUGpHWwscvbB4CIm510m8mTJ3MzBmXScobX3p07d2L+/PkAkreciXUtSMRiIhgM4sYbb4wp\ncylalLG8tr333nuYNm1a0pYzsdyaErGckbfN6XRi48aNUds0Njbipptu0mQ5w5QkcqVnrP6RI1e+\nyF0SpXWHw2HVbE08yxmKOZM5KnEN5qEcxYbZqKsTY7AtXboZW7Y8iPPnL5OU5J+bNlt/X0Wl0n6z\n73sSIBhzwMKBIIicpKyqCpV1dVhRWYmV8+ZhRWUlFtXVUbwZgkiAvLOcSdWtSW4509XVlfDEJRAA\nfL5h2LfPj85OE86cAd54YwLa2mbg7NnbsG7dOfj9Vvj9BTCbR2DzZhuGDZuOkSObMGcO8OMfD0Fr\n6za88soLERP+xYsXo6JiIp5+WoyZ8MIL/43CwiLYbA4sX74YFRUL8M4770S9hVWTw+TJk7Fo0SK8\n8MIL8Hq9GDt2LJYsWcLN1iSvg5VpaGiItE2+bUNDA8LhMIqKivD+++/D6/Vi4sSJinJqcpcj3eep\nU6cwbtw43HrrrSgqKgKgn+WMw+HAtGnTMGrUKDz00EP4yle+gkmjR+P1IUPQZLGgrq0NtqFDcWNz\nM77qdMJrNuMlQUDA58PtTU0Y25dB6SVBgLejA987cwZFDgeMo0bhJbMZAZ8PNx0/jsLCQhSMGxfZ\n9uGmJhgdDtzu9UbVcb6lBVVNTSiw2dBuNOL4iBEotFoV+2o+cwb/09UFy5AhuLG5GRMmTECX1apo\nmzBsGEbPno0Rl1yiUM5ozdYkn3Cr9ZvdbkdbWxuGDBmiWKclW1OyMWfUxuf8+fPxwQcfaAoIPHPm\nTJSUlODJJ59EW1sbxo0bFzV2eftYsWIFd7/79++H3++Pmshm2q2J194bbrghEi8m2Zgzsa4FzKIk\nHm63G6FQCPPmzcOoUaMicbXGjx/PvV6Ew+Eoi8R4bfvDH/6AESNGoLCwEHfeeSc6OjoiljPhcFi3\nmDMsRTkPeSpt1rbf//73GDt2LKxWK26++Wbs378fp06dwoQJE7BkyRLMmDEDx48fj7I+kceckboX\nyc8rtp+HH34YwWAQo0aNUr0Gyy2d5C6JUoUqe2Ehv+by7r9kOZNZNuF9LANgL3QAAH70o3q0tLzU\nt1baD9J02yJO5zLU1CzqLxIAP5X2AOtOioGghGTCh+TCJ1G5lFVV5b0yhsYKH5KLPuSdciaRbE1a\nY87Em7hcuABs3w689hqwaRPQ3AwUFPwEL79swZgxwOjRQDBowpQp3fjRjy5BUVExiooAhwMoKgJK\nSoDHH38Jzc3NuPfe+/tcb29AVdUNin0ZjUbMnTsXzc3N+PGPf4zhw4dHrYsVEFharqysDCUlJWhu\nbkYV5yKqZjkDiA/9akoW3rq6ujrceeedUVmx5MSbILJ62Yn/+eefo7GxEYC+ljOdnZ2YNWsWbrzx\nRtxzzz3A974H3HEHdo4dC5/Ph9mzZ+PRRx/FvffeG7OuL774Anv37kVrayuqq6sjx75x40Z8/vnn\n+NWvfpVyexnPP/885s6dC6fTiYceegj33nsvd/J/6NAhvPvuuzh37lzUm+3Ozk44HI5IuVQDAgOi\noqu1tZU78WXl2baxsjUlk0qbNwbD4bCmawNrT0VFBcaPH4+DBw/itttu07QPtlzKxx9/HHUMWhQC\n6UDe3i1btkSuFclazvDqZRgMBgiCoKluVobVxYL5XnbZZYqyTAmk5XyvqKjAmTNnMHv2bEyaNAnH\njh3D9u3boywb1YJWM6SZktRizsTrT3lAYNa2Q4cO4aabbsLYsWMBiJn4nn/+edxzzz0oKirC2bNn\nFZYzUoUpa4uaWxPbTzAYxJAhQzB37lzVNloslqh7YSzLGZZaXI70ukExZ7LDCgBNAI4ZxuLWW9ej\nu3uKZK1UISO6PhUU3AanswTjxxehpmZRVLamkcNHim7f0pgzXnE5QRAEQRDpIa+UM1KFgpY4MXK3\nJjaBk8eciY4XAbz9thhw99NPgXfeEb9nzRLn8fffD1xyCfDII0/j+9//PkaPHg0AeO21jzBhwgRM\nn34Jty1WqxVGozHupMNoNMLr9aKnpwfDhg1TrJO7UvEmouwh2uv1qr7xlcacSXbixiguLsaZM2di\nKme07odpZKXHqmfMmc7OTpw5cwZjxowRFx48CEybBnNbW0TuWsYWe4stVzwYjcaU5SlH+nY6lpKL\nN5lkMWekFi5aAwKzoKG8MWu323H48GFVRQib7BUUFKjGnNm1a1dkYsxI1spDEATu+SxHOq70cD+S\nxjcBxPYz5UA2kVtjJBNzJh5sYh5L3uXl5fjoo4+i5FFcXIyzZ8/GVM5oRWr5IrUGYa5NakGrpdu3\ntbUBSC2VNk+JI1dcsN9svDBlkNQ1SG45w9rI/stjnQFAZ2cnN6W7FLWYM9L17FzkxZuRyoMCAmeX\nS+HAsx2XIYRHIQb+ZTDFywoMH34cs2ZdjJqau6IUMlJaL7QCpVCk0m7d35qehqcJeourhGTCh+TC\nh+SihGTCh+SiD3mlnEk05ow8IDB7qGUPtuLEtRc+nxWffAK89BLw2GPAxRcDV14JXHopcOutwDXX\nAPJnVa0ZaRg2m01Tm41GI5qamlBcXKyYFMszzajJgU2+Ozs7UVJSwt1PLMuZRBkzZgzOnDmDyy+/\nXLVMohNEdgyAvpYzZ8+exdmzZ1FcXCyaRJ0+DUyaBMuBA+jt7VWdmMhhEyW5yw4L+qwnbNwzeahN\nXqVBcaWT1GRjzrBjU1POBINBVYsC9pZfTTnD9peM5YwaTBGlxXIG0CdwrzxrUabjzaihFsdET5ir\nTDxlpnz/xcXF+Pzzz7llEz3XpcoZqTUIU5plKuZMb2+vohzPlQhA5L4hVc6oxZxhx8jaw67b0mPq\n7OyM6XbFa4vccsZisaCjowMAP1MTQNmacoHZcOAWzEIILMW93H2pDE7nJtTV/VRVKcMIBoNct6ZQ\ngB/AmiAIgiCI1Mm7gMC8OClqWK3WyBtNAPB4gti/fzp+9jPg+uuBX/6yAvff/yt8+9szcOONwNmz\nwNatwJ49wOOPA/feK5bjzdW1ZKSRt0XLpNNgMOD06dOi8oCzTu7WxNunVDmjxXImVWUCexMeC60T\nRLfbHWmf3pYzzJLqzJkzonw//hiYMgUwmSLKhEQsZ/x+v+JNv9Fo1F05w5QmbFIUK2ORmuVMMtma\nYvUZG1exlDPs/ODV43a7kwoIHAuTyYSenp64AYGZkkuP2DByy5lMx5tRIxPKGS0TcxZzRjr+xowZ\no3q9SPRclypX1CxnUs3WFE+JJ485w5DLR5pBCui/fqv1FdunVFksv+8A2pQz8SxnpPVqsZyRKpAo\nIHDm+AG+hR5cj/7AMGXoT6+9EiNH3o66ukVxFTNA/gQEZs8MRD8kEz4kFz4kFyUkEz4kF33IO+UM\ns/bQMoFjWWW83k788Y/AnDkmeDyTUFoKPPgg8MAD7+Pee/+I3bs/xKFDwCOPAFOnamsLLyNNrEmF\nVuWM0WjE6dOn+91uZOu0xpwJBoMxH9qlMRn0sJzRSznDkB6r3jFnzp49K8q3z6UJ6J+cJGM5I1d8\npMtyJp4MmaJAEIRIm+JZzsgVS4FAIJIyXYtyJp5bE6tHS8wZXlrqRNCinJG7NeltOZPpNNpqSCfN\nepzjPLSm05b36ahRo9DW1sZV7KTi1qSH5YxazJl4ljN+v1+xPc9aBUDUeWEymWIGBGbHyODFnfF6\nvVExpXjIt+NZzrD1sSxngGjFDgUEzizn8RJExYw0V18ZgFUoKDiNZ5/9F02KGQD9AYEXAJjf930I\nAy4gMEEQBEEMJAa1WxMACMJw/PSnFhw9Cuze3YPXXvs77rpLdL/p6enBqVPxAwLz0JKRRorNZtO0\nHxY3g2c5w4s5E89yRu2hXc16IhlGjhyJjo6OmFYDWieI6Y4509HRgc7OTowaNUpUzlx5JYD+/kw0\n5oy8bemKOaNl3BuNRoVygrlcqGVrkitt2Dq2T7VjYeMqnlsTwD83ysvLcfDgQe54TlYRx4Ifa405\nEy8Lj9Z9yl1XcsFyJpMxZ2JRXl6OvXv3Ks6RESNGoLm5WeF2mahyxmazoaWlBYC65UysPpYrd5J1\na+ru7obFYokau2qWMzy3Jl7MGXlAYIB/3+np6UFhYaFq+5g85JYzcuWM1HJG7RpoNBoj2Zx4x0hk\ngoUANqPfYsaIgoJP8ZvfzNOumEH+BASmGAhKSCZ8SC58SC5KSCZ8SC76kFfKGWbtIQiCYrIRCgEH\nDgAffCCGETlxQnRP+vTTO1BV1YVdu4BQSBlTAFB/+x+LdLo1AUjJckZrQGC9Ys4YDAaMGjUKzc3N\nGD9+PLdMohPEdFjOOBwOtLe3Y/To0WJbDhwAvvMdAP3KhFgTEymsvMFgyEjMGXksGbVycuUSm4Bp\niTkDRAd5jWUNFs9yJp5bk3RfjFTizQB85ZQcqWtgb2+vIuh2ovAsZ3JBOZPJmDPx4O2fBRFPVTlj\ntVojli/yWCipxpxh8cl6enriZmvq6upSlOEFiwb4AYF52Zp4ljPy+05XVxdsNltcmcmVOnK5aMnW\nBIjnjzTDIbk1ZQOmgHEBMMIk7MXLswyo8rwD/PBdwGAABEH8sN/yb0GAt6UJuBaKgMDevWeA3/1O\ndbtYdSa1Lp11Z3qdHnWzD0HkETs2bMCWNWtg8vkQsFqxsLY279NxE4QaeaWckU7Y2YNldzfwm98A\nL74IjBgBzJkDjB8PXHEFMGXKXmzatBqACXfdNQTf/e53FW9wpd9acblceOKJJ2A2mzF06FBUV1fH\nnAC5XC488sgj8Hq92Lt3L6qrq7npaV0uFx577DF0d3fj6NGjUeVcLheefPJJtLW1YevWraiurobF\nYlFVzvT09CAcDqtOFHlpUWPBLqzNJ0+irakJJSUl8JrNsABoa23F+VOnsOlf/xXnAVgFAeFgEEJP\nDwoKCtAmCDAGg3j9t78Vlw0dClMoFFVHsLcXbU1NCBYVYdjw4TAEAmhpbsZb99+PkSNHosnnw941\nayLleNuaHA4EvF7uupKSEpzq7kZrUxMMAP7xq19hst+PIgALe3tx2TXXRCxntLg1sb5m2Xmk/dzT\n0xPpI7WU5ImQiOVMIBCIUsix8vJxr6acYXXs2LEDzz77LJqamnDgwAHFsezZswfbtm3DZ599BpvN\nphirf/7zn/Haa6/B4XDgqquuwhVXXBG1H7fbjXHjximUM6koEaQTczXSna0pF92a0h1zxuVyYf36\n9ZGA69KxwGLOSPfPxodUOTxixAgIgoAbb7wxYcsZabYmJnutMWd27dqF119/HS6XC6dPn8awYcPw\n6quvRo6BKfy0Ws5I4QWLBrQHBN6+fTu2bduGTz/9FAUFBZFrvnS8aYk3AyjdmqRWRi6XC08//TTO\nnTuHv/71r+jq6sLQoUOxfv16xXlPljPZRpoquwzAMlw6vghVP/sOEA4D4TA27PsCa1wn4PObYTX5\nUDu/BFXTJojrPjuANR9thw9+eAMBbkBgh8kKDBsmvvHqqzPyOxQCAoHo/7wyGVznbm5G+YgROdWm\nlLZnpKDwcfv9KLfZSDEm+3YfP47yiRNzo7051C/uPXtQPnduetoLcf6weelSrPZ4+q9kfb9zVUHj\ndrtRTlYiCkgu+pC3yhmj0YgjR4B/+ifg8stFi5mLL+4v63K5UF9fj9mzZ0SWPfnkk7jkkkui6pN+\na4HVO3PmzMiy+vp6TJo0SVXhUl9fj9LS0qjyAKLKs3LXXHONohz7La/j61//OmbNmqXYp9FoxIUL\nF2C32xEveKyWiRu7sFZ6PNgMYB2AHS0tEcPqzQDWA9jh90ctWw1gh9cbtawSwObmZnGdrI51AOpa\nWnD26NHoOli5Y8dU938HgM0tLar1ypex3BZ46y0sP3EC3tWrIzFnhg4dGlMeDIvFgp6eHhgMBs39\nnAy8QJxq5YBoVyM1yxmW/Uk+ETaZTNi6dSuefvpplJaWYvLkyYpjYYrCG27of6qXj9XZs2dH/r/x\nxhsIBoP4xje+odiXnpYzuaCcyRW3Jqls0xlz5q233sLrr78ec9xLLbCk58nRo0fh8XiixtFTTz2F\nCRMmaG6D1PIl0ZgzTBk+ceJEeDwefO9731McgxbljNFoRHd3NwoKCqKWq1nOyC3KeDFnXC4XHn74\nYcU5NnXqVMydOzeyLJbrqhQ1tyZpf1itVkV/yPvSYDDA5/NF3Kgo5kym6XdlAoIAFmHoxS74br0T\nViuwYcMOLP375/B4no5s4fEtB745BbBcwNJN/wnP9X0TpJfRHxBYgOjWNAnwfmwSLWcGCm43kE+T\nBaao0arUCQaVn927xTSjwaBYjlcmG+u0luntTU+bursBo1G9TF+8PUJHBAFbwuH+Z+4+Vns8WLF2\nbc4qZwgineShciaE48eHY+/ekfjrX4Fly4DaWqUV6Pr166MmDAAwc+ZM7Ny5M/JfGtRQK7x6S0tL\nsWvXLu4bX7XyDQ0NUZP2WOXC4TB33Y4dO6Ie1BkGgwEdHR0x36gmEnNmy5o1WO3x4D70KzW29P1O\ndFm88s1pqpe3jLHa48GyJ57AsIoKzQGBgf5gu4IgaO7nZM0M3NkAACAASURBVGBWEPGsnHjKCZ7l\njCAIEZcsufLOZDLh5Zdfjnks69evx4wZM7jreWN17ty52LlzJ379619HlpWXl+P48eOKmDOZUM5I\nJ8n5HBCYBXeOFw8rlX1s3Lgx5liZN28e3nrrrcj4k54nckUAoLxGx0MaM8bv90eUBqxf5IFvpbBx\nvG3bNkU72DFMmTIlUp8azK1pyJAhUct5ljM2m43r1iS3clK7nuzduxeLFy+OLIvluipFza3phRde\niNkf8muY0WiMsroht6ZME/VqAQbhf+P45zehyP4mLKZN6A0cgT/4l6gtPJ7VWLvsZwiP2wvP7P43\n17CCazkzVrCI2RH0tghJ07ryUAh49NGcalNG6maKBI7FQnmOWmgktc5o1O1YyrN9LDnaL+Vpbq/p\nW98Cdu1SXM2MfffuXISsQ/iQXPQh75Qzzz57HT799CIsXixg+3b17Eos44wc6WQ0GcsZtXrV6lEr\nz9L5JlpOvo1aQOCOjo6Yb1S1WmMAgKnvzbR0MJlk31qX6VGHXvVKMfl8Cbk1AeKEh006k+k/rbAg\n0VrcmgBtljN+v181Doxam9nyZI6VZ8GVjpgz0m+1MszSIp9TaTMlFLNa0SNmkxyz2Rx3LDDrLLZ/\naXk196VE2qqWSpv1izxltBTWFrV2MKWWPK6UHDaOeW5N3d3dkf+BQACFhYVRbk2sfqZEY8qZWPev\nZNya2HnN+oNZzmjpD+l5zSxnpDFnyHImk0Rbzlxl/xyrJv4Haj+ZgMNdTwFYyd2q53QHWgzHohfa\nwbWcuegToxiPLYcm1QNmXab3m4brOkHoTUAlYH1Q47M2QeQbeaWcOXjQio8+uhj33/8CfvCDmzB6\ntLryQcsDfjIBgdXqVVOUqJWXPwjHKhdLIaQWc+bChQuKN7nyMlotZwJ9ASmlj+AB2bfWZfHKezSW\nS7Re3jIpocJChEIhdHV1aQoIDEQrZ7T2czIkEnMGiG85YzAYVJVy8YLpAsmNVfk2brcbl19++YB3\na+JZR+SCckZqbZUOqxm2D7X+ZmNl+/btkFttMfRQXMZLpR0r5gxri1o7mFImXn+y8SYvx1M+ypUz\nJpMJgiBEKdNiZSwTBCHKAkarckYQhEgAZ6vVikAgAKvVqqk/5PGqKOZMNmGxZgCncxluvPP7+NH/\n9xZaup7qW8/vC9uMS3G6ZXv0QicUljPORidqHqwDKgaOqwHFQFBCMuFDcuGTbrksrK3Fco8nKubM\nMqcTi2pq0rbPVKGxwofkog+pzwxziAcecGDRoj0wmXriTjiqq6uxb9++qGV79+7FVVddFfmfjOUM\nr97GxkZcdtll3HrUyktN0+OVU1s3c+ZM7kRUGnNGDWnMmXgT4oW1tVj+1a9iIcRwhAAivxNdFq/8\nzDTVy1vGWOZ0YmFNDcxmM7xeb0JuTazPtfZzMmi1chIEAQaDISXLGaPRiG9/+9sxjyXRsbpr1y6F\nuwTbV6YDAsuzNaXqgpTLAYHZZD8dabTZPsrLy2OOFbnSWjo+nE4ntm3bFrXt3r17MW3aNM1tYNma\nwuFwlHJP6takdvysLbx2sGMwGAxxlTM8izX2Xx6PyG63K9yagH5lGrNsUTvHysrKklLOsPawbZnS\nKl5/yK9hLFuT1CWYlDOZoxLX4Csox3BzGcLhz/Hv/34QLS1TJCWUdzincxlqairgsDkAafdOAHAB\nsP3FhnlH5qHyWCXqltShagApZgiCyH3KqqpQWVeHFZWVWDlvHlZUVmJRXR3FmyEGLXllOdPcbMRN\nNx1EIBB/wsF85J955hk0Nzfjoosuwh133BFlZp5MzBlW7xNPPIGOjg6UlJRgyZIlOHjwILceVr6h\noSHy4L1kyRJFHBIt5RoaGnD48GF89atfxZIlS9DW1qZqOaNnzJmyqirgyBG4fvc7nJswAbc3NWFs\nX0aklwQB51taUNXUhAKbDS2hED4wGBAKBLCopwe2ggK0CwI+MBhgBLC/pwe2IUNweygUVUfA54uu\nF8DJEydweyiEYcOHozkQQNuIEcpyfds+3NQEo8OB271e1XpP9/Tgw/PnEQ4EUNXTg5KxY1Fy2WVY\nVFODsqoqvPfZZ+jo6EjKckZrPyeD1pgzgDiWtVjOsJgzvH3NmTMHo0ePxqOPPore3l6MHj066li0\nHOtTTz2F1tZWjB8/HvPmzYsKEAyIfqvt7e26uzUxBVWsMlLljN6WM729vZony+lEqpxJl+WM2WzG\nVVddhcsuuwxr165FR0dH5NrExsJ1112H/fv3R7aRjp1wOIyioiLs2LEDDocDI0eOxA9+8ANcuHBB\ncxvYeO/t7Y2yktFiOSNti8PhwIYNGzB27FiMGjUqcgxffPFFXCtMqUJIvlw+vouKiqJSd8stUFh/\nqZ1jvGxNWgICA9FxZ9i5xuuPxsZGDB8+nHteM7dAspzJDtfgfcyHA6sC38bhw04AD0KMpMZgabZX\nYPjw45g162LU1CxCVVUZFi9vBUoR7cY0HTDvN8P9jDujx6En9BZXCcmED8mFTybkUlZVNaCUMTRW\n+JBc9CGvlDMPPODDiRMBTcoZQHz4vvrqq/H8889j6dKlOHLkCN56663I+mRTaVdUVMDpdGLXrl34\n4Q9/CADYv3+/aj0VFRWaJumxyrF1v//973H33XfDZrOhoaFBNeZMT0+PbjFnAKBs+HDxwvrSS3HL\n6kE4HMYDDzyA+++/Hx999BE+//xz3HLLLWndp8ViSchyRqqcAbT3c6JodWtiZbVYzvT08K3P2GSr\noqIikqaYd0zxxmppaSlefPFFLFmyBK+//rrqvvQOCKxFPsx9Q69sTbno1sQsGtKVqQnoV0xVVFSg\nvb0dH3/8MZYtWxY1/njBiOVj55133kFHRwcqKyvx5ZdfYsuWLQm1g1nPSN2amNVKvHMm3jkrV3by\nUHNr4rm8FRYWwuv1Aoi2FOMp03hte+edd9De3h75rzUgMGuf1GqHySqR65b82kEBgTPLKgBjMRWd\n4Qb0x5dh1jIsUHAZnM5NqKv7KaqqyiLbBoNBbgDgUCB190KCIAiCILSRV25NVVVi0MRE3rBLA0bK\nUwcnE3OGIc9+IU0Xm07kMRbULGcAxLWcSSgmxYEDQALuBsnidrsBIBKHQS3lczpgkxWtljNmszkj\n7UooeLNMQZFMzBk2oUwkc5Ucu90emYTyzg23252WVNpalDPBYBDhcFi3bE1y15VccWvKRMwZduyd\nnZ0AELk2MaSZmrTUk8y5zpSI0uC/rF9S7Y9UY87IU2nb7XaF9QrbTyAQiHv88vtOKm5NyZxrFHMm\nu9wOB1rxlb5/TO5l6A8UvBIjR96OurpFUYoZADAYDf0BgN/s+54ECMaBHVSWPTMQ/ZBM+JBc+JBc\nlJBM+JBc9CGvlDMmkzHhCYc0JoF8u2QtZ4DoB10AaZ0ESZEqm9QsDbQoZ5gFgWZrhYMHM6KckSKd\nSKcj24wci8Wi6U05QxpzJp1IrSASdWviWc6wdLhqMWfYZKunp0ezokoOSxkcy7UmHTFn4m0vjbUU\nLwuP1n3K3ZpywXImEzFnpJYhTDnDrk0MLWm8pfUko5zhWc6w44+VSlsLcks0tTIAP+YMz3KG3Tfk\nbk29vb1xM2tJlYHhcDglt6Zk5CKPOUPKmczyP5gKPy7t+yeNL1MGYBWczl48++y/KBQzAERdjgfA\nAgDz+74PQT1KPkEQBEEQupNXbk1sUhkOhzU/wLNUpX6/XzFRSCbmDEPu+69lEqIHWixnWDviuTVp\njTkDIGPKGak/I7PuyZTljMViSchSRO7WlC70cGvixZyJ52qUiuWMIAiw2+3o7OzkjrHy8vJI+mCm\nfNMj5oxWyxm9AvfKLWdyUTmTTssZqXJm6NChCsuZOXPm4Pjx43HrSYflTCAQSNpChKG35UxhYaFq\nQGBpimo1pPcdFvtF6/FJt03FckaqVKKAwJnlAL4CpRvTCgiCB6Wlw/HAA7fxFTMARg4fKVozSmPO\neMXlAxmKgaCEZMKH5MKH5KKEZMKH5KIPeaWcYUFszWZzQpYUzNpE7l6RiuWM9C0km2RmYqIutZyJ\n5dYkCAIKCgpU60nIren8eaCtDZgwIZWmJwxTIGXKcsZsNidkKZIp5UyiAYGlSgeeAjKeckbq1pSs\n5QwgKgfVlDMAolIIm83mjMScYdcQvZQoPOuIXHFrykTMGab07unpQXFxcU5Zzvj9/pTHlJZsTYnG\nnOG5NTHLGS3KGbZ9Ii5NrD16WM6w9rJvijmTOYK4FNKgv4A4XqZPL8QHH9TH3Nbb4wWuAnBYsnA6\n4P3Ym4aWEgRBEATBI6/cmtiDYaKTDWZtIp8o6OXWxJQ+mVAgsLfEgLobiMFggN1uj9kepvjQNHk7\neBC44gogA4oIqT9jpmPOJGo5k0m3pmRjzjAFiNZsTXK3pmQtZ4D+uDM85QzrZ6kySA+3Jq2WM3oF\n7uWl0s4FyxnWt2pKOD1gfdfZ2YmCggIUFBQoLGd27tyZtZgz3d3dMJlMKV2Xtbg18VLYA+qWM9L7\nhjTumRbLGel9J5FgwPJtk1Uiyu+Z0uxnRCZgVjOiGxOwEjZbM1at+mHcLR02B9etyWHV5haXq1AM\nBCUkk2h2bNiA+yor8ePp03FfZSV2bNiQ7SblFDRelJBM+JBc9CGvLGfYRDPRN6Hs4Z1nORMv9a4a\n7K0os5rJxCQd6H9LDMS2nIn30C61nIkrzyzEmwEyH3PGbDbnvFtTPEsW3mRSrkRiyhleXXoFBAYQ\ncWuKdX5I37xnMiCwnm5NuRhzBui3xkhnzBm/3x+x4JBemxjhcDghy5lkznU1yxmmnEkFLW5NbH88\nyxl5sGg1tyaWojre9UTqmpRIvBn5tsmea3LLGXZPJjKF3GomiCn+D1D1k7+JL0/Yx2iM/m8woDVw\nHLge0W5Nk4DW3V8Cc+YoyserL+3ltNZ16BBw+HBm26ZnOUEQP0Ra2LFhAzYvXYrVHg/cAMoBLPd4\nAGBApXYmCCJ/yCvlDCA+HCajnPH5fFFvZV0uF5599lmcPHkSR44cQXV1dUJpkAVBiDx86x3XYceG\nDdiyZg1MPh9OdHTAAiDY24u2piYUFRXBazZjhMOBplOn8PYDD2Dc+PHwms2wAGhrbcX5U6fgNxjw\n/5YuxbiSEmDEiKg6SkpKcC4YRKCrC76uLvzoD39AybhxkTqk5bxmMyzHj6N42DAEKiuxsLY2rTe0\ncok/YyYtZ1wuFx577DEEAgFs37497nhg5Ts6OvD2228nPH4SQWtAYJfLhb/85S/YuHEjhgwZgurq\nagDApk2bsG/fPhQUFKC6uhpDhw7VFHMmlYDAAKJizsj7r7y8HC6XCxs3bsT+/fthNptxxRVX4Oqr\nr05qXy6XC+vWrYPX68WuXbtU+0OqnElVicKuIU1NTXjvvfdQXV2dM25NQP+EPxOWM3a7PcqqjzFr\n1ixs27Ytbj3pspxJpS9cLheeeeYZWCwWvPDCC6pjyuVyYcuWLfjwww8j51hFRUWUopPF92LnkzyG\nlBa3JpfLheeeew6nT5/GP/7xD/h8PhQUFOCNN97QdL16+OGHIQgC/H4/WlpasHfvXpjN5oSuXbwM\nh+lS/hE8WKwZUUkjCD/Fjb+6FZXvNcPnM8Fq8WPObDPeObYbvrAPVsGC2kV3omr2PARvmQF4upWp\ntC1W4L/+CwiFlJ9gkL88neUCgYTqKw+FgF27Ut9vNo41FALCYVE5o6NSqFxvBdgALrfl/vuxuk8Z\nU9437Fd7PFixdi0pZ/qQPncTIiQTPiQXfci7p6ZkLGeYWxNTorhcLtTX16O0tBSTJ08GANTXi/7a\niUywpf7/ek2ApFr+HQA2Q0ySuRnAOgA7Wlqilq0GsOP8+ahlv5CuO3YMm48di19Ha6vqvlYDQEsL\n4PFk9I1Dpixn2HiQKgZijQfp+NFSPlW0xJxhbZo7d25k2YMPPgir1Rp1Ma2vr8fChQtjKmfYmNbD\nramjo4OrvGTtnTdvXmTZ5s2bYTQaE774J9IfUremVCfuvGvIqFGjcspyJp3KGaac9nq9cDgcXOVM\npmLOdHR0AIhWHnR3dyfk9iOF9e+1114bWcYbU6yc/BwDgHnz5iksVZhSv7e3N6GAwNLxZjKZ4PF4\ncMMN/bNsLderGTNm4OjRo/B4PPjmN7+paVs5cssZ+W8i3bCU2aLVjMl0Es+/OhaHD/9BXG3ZgO3t\ndyJwU1tki49ePoz5rfPhM/T2p9KWWM5YPrKJljPZJhzOrqIkW8qZQEDbx+8XP1rK+Xzxy4VC2evr\nDCpnTIcO8Zsgu1cRBEFkirx7ajIajUnFnJFazqxfvz5qIgcApaWlaGhoSGhyzR6yk2mTGlvWrIlo\n+bdAVIzch/68DFqWJVo+3jIp6X7j4Ha7IxOdTGVrSnQ86DV+tKIl5gyvTeFwGNddd52indu3b8fM\nmTNjprcOhUIpx2VxOBxoamriKmf++Mc/Yo5sQnDddddhx44duPvuuxPaTyL9wWItpWo5o7bP7du3\n58xkNd3KGbnljNVqxfnz56PKvP3223HPXT0sZ7xeryJLWW9vL4YNG5ZQXQytYypWuRtuuCHi+ip1\nuWJKfel5Ec/KSbofuWJGrW16bCuHF6eN3JoySRn6XZuWwe/vxeHDkrv0qDVRihkAODXrFHa//Ddc\nErLisKdLYTkzod0PfOMb2VdYAElNzN1+P8oLC3PKWiOhcjab7vt1f/IJyq+6KveO1WDIuAtXoLIS\n2LIFACJuTQAQTOHFU74hfe4mREgmfEgu+pAbswQdSSXmDPOPD4fD3HKhBN8kSH349VIemCQxG0yy\nb63LEi0fb5mcTL1xyFS2pkTHg17jRytMORPLcobXplhjsre3l7ueTbhZTJZUxnWsgMB6kkh/MIVf\nqsoZtX1mKjC4FphyJlMxZ6SZ5BiZspzxer1ca45kj13rmIpVzmAwRMab1OWK3TcScWuS7kdNPlqu\nV4luK4csZ7JNv9UM8DmAydGrrae4WzmsI/H7yjvxs40Po2l7e8RyZqxvOFb97FfAjByIOZPsddPt\nBmiyEM3IkSSTPhbW1mK5xxN56QkAy5xOLKqpyWKrCIIYzOTdU1Oybk0+ny8SwFVt8pTopIC9ATUY\nDLpNPgOSGB8B2bfWZYmWj7dMTjrfOEg1spmKOZPoeNBr/GhFS8wZXpvUJlyCIKgGamXKmVRdmoDo\nmDPyfZWUlHC3SeY8SqQ/9HJrUttnrihmAO1BZpOFWbx0dnZi1KhREfdRKTNnzsSHH36oqR5AHLOJ\nylDNckb6nShax1S8ckyBJbWcUXNr8nq9quNfuh+181rL9SrRbdXKkXImO1RiE05iCD6CFcDvINq3\nSjnG3e5YexuqVj6EJ667Dmsb1qIn1AObwYaaxTWoqhjYcTfoLa4Skkk/zMp7xdq1MPb0YJvNhkU1\nNRRvRgKNFyUkEz4kF31I34w2S6SarcloNKK6uhr79u2LKtPY2IjFixcnVC97yNYzW9PC2losdzrF\n3xDD/7FvrcsSLR9vmZRlTicqMvTGIVMxZxIdD3qNH62wmDOxlDO8NgHA7t27Fe2srKwEwFeEsH35\nfL6UggEDoluTWrYmXnt37NiBhQsXJryfRPpDr4DAvH2+9957mDp1atJ16k0mLGfkAYHlljNarKZy\n0XJG65iKV44dm9xyRi3mjNqxS/fjdDoVQZa1Xq8S3VaO0WhUvOAg5Uzm2IT30YxOALMgujfJ7tLh\nICCPv70VCAVEpVxVRRU2PbUJ7mfc2PTUpgGvmCEILZRVVWHVpk1Y6XZj1aZNpJghCCKr5N1TUzJW\nKsxypqCgAAaDAQsWLAAANDQ0RCYDS5YsSTheCDNP19NtI6Llv+MOGCdOxBlBwEuCgIDPh9ubmjBq\n9Gh86fWiddQonDl1CrcHgxjbl1XpJUHA+ZYW/HtTE4JGI6qCQZSMHQuMGBFVx9iSErQBqGttRTgY\nxO2BQFQd0nJesxl3CQJGFxUhmIE3DlJ/xkxZzrB+1zoeEi2fKtKYM2oTIV6bVqxYwW3n+PHj8fLL\nL6taluhlOVNYWIju7m5YrVbFvsxmM+666y48/PDDCIVCGDlyJObOnauIkaOFRPpDL8sZ6T7b29vh\n8/nwwx/+EK2trUnXqTdswl9UVJS2+qUBgQEoLGf27NkTN+6LwWBAOBxGKBRKOuZMMBjU1XJG65iK\nV47JSB5zhi2TxnCJld5dup9wOIyioiI0NjZi+PDhCV2vEt1WDi9bIilnMsftcKAVX0G/XSuLP9Pn\n7mTycYP+Cvtyx6JPbygGghKSCR+SCx+SixKSCR+Siz7k3VNTqpYzzBqgoqIi5ck0L7CjHpR985so\nCwREX+qhQ6PWtbe346mnnsJPf/pTPPHEE7jnnnuS2kdzczMeeeQRDBs2DLW1tTq0Wn+kljPpTqWd\n6HjQY/xoRRpzJtY4U2uTfNlnn30WqVeOnpYzBoMBNpsNXV1d3H1VVFRg5MiR+PLLL/Hd734XL7zw\nQtITPa39IbWcGSo7t5Ld58mTJ/H3v/8ds2fPhsvlSqlOPUl3QGAWE+rChQuw2+2RcSNFi1WhIAgR\nJUYy5zobp9Kxw6w7UlEcaB1TscrxLGfMZjN8Pl9UDCnWV7EUoqlcc/S6XvHuvxQQOHP8D6bCj0vR\nbzHD0mqXoaDgfwMGC7o56bJVfZQJgiAIgsgo5NYEZbYmvWBuTboHPD18WAzoxpk8srgOsawotMAC\nI+fag7VUI5upbE25jsFgiGRP0uMtNZNlumPOAIikMpbvi/Wzw+GA1+sFgJgBj/VCr2xNUoqLi9HS\n0hKJa5UrpFs5w9JCS7M1yS1nZsyYoencZUqMZN2aWB3StplMpqxbdahZzvT09MBoNEbcg9LdV3pB\nljPZ5QC+AlExsxn9abVXQhD+Cb/5zVUoLi4GvBAtZ97s+/YCI4ePzFqb0w29xVVCMuFDcuFDclFC\nMuFDctGHvJvRJpO2Wh5zRi+kbk26Kg8OHgSmTeOuslqt8Pv98Pv9KR1LrAl6rpCpbE25Dssyplf8\nEC3KGT0sZwB15Yx0fWdnJwCkrHDUgjR7TipuTVLMZjOGDBmC06dP55RyJl56Zj0wmUywWq0wmUyR\nmDPS7EBar41MiZGMcsZoNMJsNivGjtls1q2Pk0XNcqa7uzuqX+Jla8oVePdfUs5kjiAuhWgpUwnA\nBZa5afr0EVi58l/g7fECV8k2mg54fd5MN5UgCIIgCA55qZxJxq1pQFnOHDgAXHkld5UgCLBYLOjs\n7EzZcgbIvQdrt9sd+Z2pmDMDgUwrZ/SynGGxSOT9x/o5G8oZvS1nAGDMmDE4ceJE1pUBUtIdEBgQ\nr4Gsj1mwWBbcFwDef/99TddGltUo2XPdZrMpZJ/LljNdXV1RbcuEIk0PyHIm2zB3pjIAqwCshM3W\njFWrfggAcNgcgAfAAgDz+74PAQ6rI0vtTT/SZwZChGTCh+TCh+SihGTCh+SiD3n31JSsW1O6LGe6\nu7t1zdYEQLScuflm1dU2my1l5cxAsJxhVg6D3XIG0HfyFqvvmUJML+VMYWFhzPT1TDkTDoejAqSm\nC2aF1NPTo6typri4GHv37sWUKVN0qzNVMmU5w6yjgP5rLVNEaLWcScWtie1XrpzJZcuZtrY2RXap\nTMTWShWKOZNtZAGAEcSUKQFUVYnLWy+0AqVQBARu3Z87gcoJgiAIYjCTd8oZ3pu7eKQr5ozFYkFH\nR4f+ljMHDwIrV6qutlqtulnO5NqDtdSfkSxn+jGZTOju7tblLTXrc55MpW5N8bLsaMHhcHDHGOtn\ns9kcUSJkIuYMIB53d3e3rhP3MWPGoLu7O6fcmkwmk/6KYxlmszlKOcNcSFmGqOnTpyuCBKu1lVnO\nJKOItdlsOenWJLWckabSlp/L7HeuXY/lkOVMtpEGAQZs1p9j1c/nA4cOASYTgoGAaDkjCwgcCgSB\ncBjIw5ccuRwDYceGDdiyZg1MPh8CVisW1tZmJI1zLsskm5Bc+JBclJBM+JBc9CGvnppcLheee+45\nWCwWPP/886iurtacocVkMkWCMOqF1K3p0L59uO+JJ9B88iTamppQ0peG2gIg2Nurfdnp0yhpbYXj\nnnuwcOlS7o3cZrPB6/UOipgzZDkjoqcbWqZizrhcLqxbtw6tra344osvVM9XFhQ4E25NANJiOfPJ\nJ59g27ZtaGxsxIsvvqj52pRO0j3hd7lcePXVV2G1WvHGG2+guro64kLKSMZyJlGFisvlwssvvwyL\nxYJXXnkF1dXVAIBXXnkFmzdvxpNPPpm1/pBazsjdmuQxZ4Dcvh67XC48+uij6OzsxM6dOyNyXrdu\nXZZbNphgQYD7rGbwEar+tAP4zwAQCMBg7uan0t7ZBRgM4sdkSv5jNA787TP0LLFjwwZsXroUqz2e\nyLLlfb8zoaAhCIIgcpO8Us7U19fj2muvjfoPKFMF87Barejq6tLdcsbv9+MDtxtNTz+Nm5uasBnA\nOgA7Wloi+RQSXQYAcLmw/PBhAMobuZ6WM7n21tPtdkc0s2Q500+mlTOpujW5XC7U19ejtLQ0skx6\nvkr7mbk2ZVI5o6flDFMa33BD/+vqRK5N6UKapllvWP9ed911kWX19fWYMmVKVMamxsZGXH311Zra\nmkzMGdaOOXPmRJY9+OCDsFqtirYBme8PnuUMCwgsVQ6ydbl6neOdz1I5//3vf89i6wYTZYi4Nlm+\ngf+55EsMLzRg4rgxWLX0/wC/uh3weJWptG0OINQBhEJAIJDaJxhMbfveXl3b4G5vR7nVqizj9wM9\nPeInFOqXR4YUVFs2bcLqL7+M6r3VHg9WrF2bduWM9P5K9ENy4UNyUUIy4UNy0YfcmnmniPTBkP1v\naGjQ9MBts9kUbytTxWKxoLe3F40NDVjb1IT7IBocA8CWvt/JLGOo3chZzJlU3vwPFMsZytYkwtLu\n6jF50xJzJlXLmfXr12s+X6XKmUyMR6PRiEAgoJvlBfqApQAAIABJREFUzPr16zFjxoyoZYlcm9JF\nOl0X1fp37969UZYzWpUtycac4bUjHA5HKWZY27LRH0zZ6ff7UVBQAKDframwsDBSLlfdTBla5Uyk\nmz6rGcs24Gvvo/MWURG6D8fxTytvRsDo70+lzSxnvMAl4y4Czp1LXbGih3JG7zZ09VkFycuEQqKi\nxGLRz/ImgTpMKs8sRonymiAIghh85JVyhkdI+kYkBlarFa2trWnJ1mTum4xIhW2SfSeyTArvRm61\nWtHS0hL1cJ8ogiBEgqPmEvKYM4FAYEAEykw3emaeyYTljDSdshR2vkr72W63Z9ytCYBuypl4x5ot\n0ukqo3bMgiBEWc5MmzZN0/6ZhUmi5zqvHWrbZ6M/WBaqgR5zJhE5E+lEdGdC8Rngluhng96FPtif\nAzrLAByWrJgOXLT9EDBlSsYUExGlSGGh/m5JsmXlamUNhqzG2Am8/z5w/LhieVCHQPvxoDfbfEgu\nfEguSkgmfEgu+pD3yhmtD4g2mw3d3d26W874/X709rlHBCTrArLvRJZJ4d3ImVvT2LFjE26zFKPR\nmLOTAaA/W1OyQULzCT37KhMxZ9T6i3e+MuVMuoPXMtg+9HJrSuRYM0k6J/yxjjmZmDNs3CVqOcNr\nh5oSJhv9wZRO0pgzZrMZ4XB4QMWcSUTORDpZKX4V/oG/urAQztYSeBb0xzlxNjpR80QdUEFxTjLJ\nwtpaLPd4omLOLHM6saimJoutIgiCILJNXr3a2rdvX9T/xsZGLF68WNO2bKKpd8yZ3t5eXH7zzfhV\nSQkWQsylACDyO5lljGVOJyo4N3IWEDhVKwODwZBzkwG32x35LQ0InO2JbrZJJoW8GkyWPJky16nO\nzs6ULGeqq6tjnq/SfnY4HOjo6Ii4bqUbg8EAs9ms277iHWu2SGfMGbVjLi8vj7Kc+fDDDzVdY5iF\nSaLKGV47AGD37t2KtmWjP9QsZ4Dofsl15YxWORPpRcCtAG4Dgvxrl2A0oG5JHSqPVWLekXmoPFaJ\nuiV1qMpjxYz0XpJLlFVVobKuDisqK7Fy3jysqKzEorq6jAQDzlWZZBuSCx+SixKSCR+Siz7kleXM\nXXfdhYaGhsgD/JIlSzTHEGDKmXRka7r62mthvO02uNatw7mvfhW3NzVhbF8WppcEAQGfL+FlRePH\nY1FNDfdGbrVadUk7nOuWM9KAwGQ5o79yRq3vTSYTent7U3L7YeellvPVbrejvb09Iy5NgHjceqZY\nTuRYM0k6J/xqx1xUVITz589HygWDQc1uTclYzvDasWLFCm7bstEfPMsZnnIm12POxJMzkRnCuBTA\nQqD3b8A2KAP/BoCqiqq8VsYMJMqqqigzE0EQBBFFXilnKioqkn7AZlYA6cjWFAwG8fVhwzC1ogJ4\n/XXd6leDHUuqD/IGgyFjE2KtyGPOkOWMSKZizrB96RF8ONb5Ko85k2nljJ5ptIHUrk3pIt0Tft4x\n79+/P8qtaerUqZoDAicTc0atHWx5tmGBjgOBQJRbE8C3nMnl61wsOT/99NNZaNFgZCHEvI7DAe9Z\nReDfkcNHZrV12YBiICghmfAhufAhuSghmfAhuehD7j7pZRi9FBpSmFtTMBhE0dGjwLRputUdC3Ys\ng8FyJhQKkeUMMm85k0q8mURhbk0DWTmTi2TDVcZqtUa5NWmNIyS1nMmnc12arUnu1jSQYs4QuUIZ\ngErAdAG4SrZqOuD1ebPRKIIgCIIgNELKmT7SEXOGPUj7/X7YjxwBrrxSt7pjwY6FYs4MHjIVEJgt\nTyXejBak/Wy32zW7v+iB3m5NuUo2Jvw2my1KOXPgwIGELGcSdWvKdaQxZ7RYzuTa9ZjINZYDKAMC\nxYAHwAIA8/u+DwEOqyOrrcsGFANBCcmED8mFD8lFCcmED8lFH3LLZyWLpMNyBhAftHt6emD3eMhy\nRmcoW1M/mQoIDGTecsZqtep6fPEwGAyDynImk66LNpstyq1JnpVIjWRjzuQ6zK1JajnD3Eml/WIw\nGCAIQk5fj4lcoBLACsB0GnAi2q1pEtC6vzWrrSMIgiAIIjaknOkjHZYzQJ9r0/nzMDc3A5Mn61q3\nGnoFN85Fyxl5zJlQKESWM8i8W1O6LWek/SwIAux2e0bdmnJt3KeDbASZlbs1XXrppZotZ/JROcMC\nAkstZwDxviHvF5PJNCjGJZEKZeIn/F+Ap1cREDgUGHzpzSkGghKSCR+SCx+SixKSCR+Siz6QcqaP\ndFnOWCwWFBw+DN+ECSjM0ORST8uZXAsILIWyNfWTzzFnAGRcOZNPCgA1suXWJLWcSSTmTLIBgXMZ\nnuUMWy4f76ScIeKzAoARMPq5ljPCvsF9nyQIgiCIXCd3Z94cBEE4CqADQBCAPxwOz9Kr7nRZzpjN\nZhQdOYKer30NhbrWrA4vFWsy5KLljNvtjmhmmXIGyO0sJpkg0zFn0q2ckfYzIAYFDgQCad0nI9eV\nknqRrYDAPp8P4XAYgiDg448/xte//vW427HYLAaDIa/O9ViWM/IxOFiUhgQfbc8/q8Sv3j8CHr8y\nlXZXL/CnPwFGo/gxGJS/ecuSLZvqeh1eusjvJUTmZLJjwwZsWbMGJp8PAasVC2trczp1OI0VPiQX\nJSQTPiQXfRhoM5AwgPJwOJyS4zS7YTSfPIm2piaUlJTghNeLtuZm7Pnv/wa6u1EwdChMoRBKSkrg\nNZthARDs7Y2U17LM5HDAe+4cxoZCeKO4GN/ZsCEjN6atW7fizTffxMcffwy73Y7q6uqE08a6XC68\n/PLL2Lx5M4qKipKqI90w5YwgCIPacsblcqG+vh6BQAAbN25Mua+2bt2Kbdu24YsvvoDZbI6qz+Vy\noaGhAVarFa+88kpGxoXL5cILL7yAUCiEN998M637dLlcePLJJ2E0GvG3v/0tJ8e9HrhcLjz33HP4\n8ssvcfTo0Ywd5/bt27F161Z88cUXMBqN6O7uTijmjMlkyisFBc9yxuVy4bXXXsPWrVsxdOhQVFdX\nAwA2btyIvXv3orCwMG/HJRGT+M8/45yAOQgInYAXylTaFgtw5AgQDIqfUEj5m7csG+tDfS5YqSqS\nurqAoUOzr2jKJaXX2bPAqVPatheEpJRkOzZswOalS7Ha44ksW973O5cVNARBENlmoClnAPFRI2nY\nDaPS48FmAOsA7GhpwWaIofQi383NWM1ZxyvPW3YHgM0tLVjNdnzsGJYvXQogvTcmNlGfP39+ZFl9\nfT0AaH6YZ3Vcd911SdeRLuQxZ1gWn3yasCUC66sZM2ZElqXSV6y+G27of+XK6mO/58yZo8u+YsH6\nmbVn1qz+l8Tp2mcm95VN2HGWlpZi0qRJADJznGy/CxYsiCxzu93YvXs3Lr744pjbDhbLGd6198EH\nH4TVakVZWVlkWT6OS0ITsZ9/fn5Y/H4ZYirtw5J10wHvx1agri5dbdOXcFj8pKj8KU90e15Zv7//\n09sb/V+6zOeLvT7e9rz1abAYLU90g1hKHxVF0JbTp7G6uzuqmtUeD1asXZuzyhl648+H5KKEZMKH\n5KIPA005EwawVRCEIIB14XD48UQr2LJmDVZ7PLgPiChOtvT9vk/2zVundZl0HSMTN6b169ejtLQ0\nallpaSkaGho0P8jrUUcmYNmaBrPljN59Fau+cDic8XGRybE4UMZ9qmTrOHn7LS8vxz/+8Q8sXrw4\n5rbMcsZiseSVcoZl8zMajRAEgSujcDgcpawB8nNcEnHR/vxjhZhKW+bWNLZwKPDuu7lhGTNQ1odC\nouWIHtYr0mVmM2Cz5Zb1jo51mn75S6CxUTE0jZKA8ARBEISSgaacuS4cDp8WBGE0AJcgCJ+Fw+Gd\nbOWPf/xjTJgwAQAwbNgwTJ8+PaLFY7nXTX3BKE8AcEN8g2Dq+32irx72n/2OV166nlcekvrYjYm1\nR96+VP+Hw2EAwJEjRwAAEydOBACcOnUqyhcwVn3hcFix/ZEjR9DU1BQ53nS1P95/tsztdqO1tTWS\nrWnPnj04fPhwxtuT7f969LfW+gBEzi/p+lAopPvx/elPf8L06dN1P75Y/0+fPp2x48vm/2yd3zz5\nAuKYi7f9nj178Mknn2DGjBkQBCGn5JnK/+uvvx6hUAgnT56E2+3mjneDwZCz1+NY5+/+/fsj/U3o\nQsznHwDA3wAMA3AOgBHAqwCGQ1Tr2IHCT5qAu+8GjEa4L1wADAaUjxwp/m9rE/+PHi3+b20FBAHl\nJSWAwQB3czNgNKJ83Dhx/Zkz4vqLLxbXnzolbj9hgrj+yy/F/04nYLHAfeyY+H/yZHH94cNifVOn\nitsfOiSuv/xycf3nn4v1X3mluP6TT8TyV10lrv/oI3H91VeL6z/8UNz+mmvE9Y2NorLAYED57Nlw\nv/+++HvuXHH9u++K9V1/vbj9O++I6+fNE9fv3Cn+X7AAyKNrTnnf8xND1/pDIZT3xRDzGAzcZ+Bg\nX8KKXJIH+79//37cfffdOdOeXPmftvEygP+zZ9RcaU+u/GfLcqU92RwfqTwDCexhcKAhCML/AeAN\nh8N/7Psf1nIs91VW4sEtW3AfgAfZsr7f8m/eOq3LpOukrKisxKpNm7QfaIL88z//M3cwHDt2DE89\n9VTG6kgXbrc7MvjPnTuHF198ERaLBVVVVRg/fnxW25YN9O6rWPWFw+GMjQvWz5kci7k87vUkW8fJ\n2++RI0cQDAbx/PPPx9y2o6MDjz/+OIYOHYpFixbhoosuSls7M80DDzwAu92OX//611wZbdu2LcrN\nkDGQxqUgCAiHw4PTvDENyJ9/+paFsbLvz1EoLGecjU7ULalDVUVuupSkC+kzAyGSCZnwYs4sczqx\nqK4uZ92aaKzwIbkoIZnwIbnwSfQZyJDOxuiJIAiFgiAU9f22A1gI4GCi9SysrcXykhIsBLCcLev7\nLf/mrdO6TLqOsczpREVNTaJNTojq6mrs27cvalljY2NctwG960gX0pOexZzJt/S6iaB3X8WqL5Pj\ngvVzJveZy+NeT7J1nLz9HjlyBDfddFPcbVnMmVAolHfnujRtNk9GALB79+6o//k4Lgl1En7+mQDg\nAoDnDLji/atQeaxyUCpmANBEgUMmZFJWVYXKujqsqKzEynnzsKKyMqcVMwCNFTVILkpIJnxILvow\nkNyaxgD4W19sEROAF8Lh8JZEKymrqgK+9S24XC6cKyrC7U1NGFtSgtM9Pfjw/HmEAwHs7+mBbcgQ\n3B4KYWxfFqaXBAEBny9SPt6yh5uaYHQ4cPP587BYrbho6lR85957035jYjEIGhoaIhOZJUuWJBSb\nQI86MgFTzoRCoUEbc0bvvtJSXybHRSbH4kAZ96mSreNk9bNgtiNGjMDUqVO5ViFyWFajfFTOmEym\nSBptXt+sWLFCsSwfxyURE23PP9LsTNMB424zDv59fybbSRARyqqqcloZQxAEkYsMWLcmOVrdmgAA\nP/kJMHs28POfp7dRAN5++224XC784he/wJgxY9K+v3xHajLn9XrxyCOPwG6345ZbbkFxcXF2G0fo\nBplG5i979+5Fc3Mzqqqq8Mtf/hL/8R//gaKiopjbhMNhPPDAAxg1ahRuvfXWvDrX//SnP6GwsBA/\nz8D9KFuQW1P6iXJrAoCtwOjuYpx9/0y2mpQT0L1ECcmED8mFD8lFCcmED8mFT966NenKgQPAtGkZ\n2ZXFYgGAvHvbmwuQ5QxBDDzsdjs6OzsBAMFgEEajMe42giDAZDKht7c3766lUssZgkiJ7QDe7Pue\nBPQEu+NsQBAEQRBELjGQ3Jr0IRgEPv0UuOKKjOyOPXRrmYAQ8ZHHnGHZmvJtwjbYIc17/iJVzrBs\nRFowm83w+Xx5d65LY84QREoskPzeCoQCoaw1JVege4kSkgkfkgsfkosSkgkfkos+DL4nQo8HGDMG\niGNGrxfMcoaUM/pDljMEMfBwOBwJW84AooWJ1+vNO+UMWc4QuiGNOTMJEPbRfZEgCIIgBhL59ZSr\nhQy6NAGknNEblkseEF3FQqFQXgYJHexI+5nIL+x2O7xeLwDA4/EkZDmTj1ZyZDlD6MYCAPP7vg8B\nCGS3ObkA3UuUkEz4kFz4kFyUkEz4kFz0YfA9ER48mFHlDLk1pQ9BEGAwGBAIBMhyhiAGCDabDX6/\nH36/PyFlC1Ng5Nu5TpYzhG5ILWe8wMjhI3XfxY4NG7BlzRqYfD4ErFYsrK2ljDwEQRAEoRODUzlz\n220Z2x1ZzuiL3J/RaDQiEAjk3dv0wQ75reYvgiDAbrfjwoULcDqdmpUtTIGRb+c6Wc4QaWE60Pru\naWDNGmDYMPEzdGj/72HDRPfuBM6nHRs2YPPSpVjt8USWLe/7nasKGrqXKCGZ8CG58CG5KCGZ8CG5\n6EPePxGytzzNJ0+irakJJR0dcJw5g4UOR9ofJlwuF5599lmcOHECR44cwR133IGKioq07nOwYTQa\n0dvbm3dv0wkin7Hb7ejo6EhI0cIUGPmknHG5XHjmmWdgNBrx17/+FdXV1XSPIJJHHhA4FAK++AJo\naxM/7e39v9vagM5OUUGjpryRLdvyb/8WpZgBgNUeD1asXZuzyhmCIAiCGEjktXKGveWp9HiwGcA6\ntuLtt7F86VIA6Xvb43K5UF9fj9LSUkyePBkAUF9fDwD08J0Cbrebm7EpnyZshLKfifzC4XCgo6MD\nx44d07xNvlnOsHvErFmzIsvoHkGkhCwgsKWnCFi7tn99OCwqZJiSpqUFOH4cOHYMOHpU/P7sM/Hb\n51NUr/bAaOzp0f9YdILuJUpIJnxILnxILkpIJnxILvqQ18qZLWvWYLXHg/sArJatS/fbnvXr16O0\ntDRqWWlpKRoaGujBW0fYRI0sZwhi4MDcmhI5b/PNcobuEYTuyCxnJrT7gauv7reaaW8HLBZ1S5mr\nrwZuuEHVcibwgx8AW7cqdhu02TJ3jARBEASRx+S1csbU9+YnG297wuEwd3koFErbPgcDvJgzQP5M\n2AgR0rznN8yt6Wtf+5rmbfLNcobuEYTuSC1nzgGr/tdvgfmLohUtKQSfXnj33Vh+5EiUa9MypxOL\nampSbnq6oHuJEpIJH5ILH5KLEpIJH5KLPuS1ciZgtYrfKuvT+bZH7Y1wvkwscgWmnCHLGYIYONjt\ndnz55ZeDOuYM3SOItNJtRNW/3qdrlczSeMXatTD29CBos2FRTQ3FmyEIgiAIncjrp8CFtbVY/pWv\nYCGA5bJ1y5xOVKTxbU91dTX27dsXtayxsRGLFy9O2z4HA263O+o/Wc7kJ/J+JvILh8OBCxcu4PDh\nw5q3ybdU2nSPIHRnAYD5AEKAQbCmZRdlVVVYtWkTVrrdWLVpU84rZuheooRkwofkwofkooRkwofk\nog95bTlTVlUFfP/7cP35zzg3ahRub2rC2JISFI0fn/a3PSxmQENDQyRg7ZIlSyiWgM6Q5QxBDDyS\nydZkNpvzSglL9whCd95EJBhw6HRvtltDEARBEESCCGp+7wMNQRDC3GP57W/FVJH36WveS+QGTz75\nJE6cOIH777+fFDQEMUBoamrCY489htGjR+OXv/ylpm3efPNNvP3221i+XG4HSeQ6giAgHA7TBTqN\nCIIQxsq+P1sBnDIi7FFz6iYIgiAIIhMk+gyUP68h1Th4EJg2LdutINIEZWsiiIGHw+FAOBwe1JYz\nBKE7b0IMCjwJMJjoXCEIgiCIgUb+370PHgSuvDLbrSB0ghdzhhQz+Qf5reY3hYWFAIBDhw5p3sZk\nMpFyhiBiMR9i3JlDgFVIPitTPkH3EiUkEz4kFz4kFyUkEz4kF33I65gzOH8eaG8HLrkk2y0h0oTR\naKQJG0EMMAwGAwoLC9HV1aV5G7KcIYg4sJgzXqB49Ohst4YgCIIgiATJb+XMwYPA1KkAPdDnDeXl\n5VH/STmTn8j7mcg/7HY7iouLNZcnyxmC0Mh0oHV/a7ZbkRPQvUQJyYQPyYUPyUUJyYQPyUUf8l85\nQy5NeQ25NRHEwMRut0eyrWnBbDbTuU4QsZjf970VCAVCadnFjg0bsGXNGph8PgSsViysrc35dNoE\nQRAEMVDIf+UMBQPOK9xud5Rmlixn8hN5PxP5h8PhwL59+zSXJ8sZgoiDJJW2sLsLmDMHGDas/zN0\naPz/BQWAihJ0x4YN2Lx0KVZ7PJFly/t+56qChu4lSkgmfEgufEguSkgmfEgu+pBXyhn2Rqf55Em0\nNTWhpKsLjiuuwMKJE3P2wYFIDYPBQG/TCWKA4XK58Mwzz+Ds2bM4efIkqqurUVFREbP8k08+iXPn\nzuHDDz+MW54gBiUSyxmYCoA//hFoa+v/tLeLsfiOHIleJi0TCqkqcLa4XFh97FjULld7PFixdi09\nYxEEQRCEDuSVcmbz0qWo9HiwGcA6tvC997B86VIAuftmh9AOxZwZHJDmPX9xuVyor6/HzJkzI8vq\n6+sBgKtwYeVLS0s1lSeIQYskIPAlEyYCM2fylTByhYz0/5kzwPHjQHOzaEEjUc6Y2tq4uzX29GT0\nMBOB7iVKSCZ8SC58SC5KSCZ8SC76kFfKmdUeD+4DsJqznN7s5CcUc4YgBhbr16+PUrQAQGlpKRoa\nGrjKlkTLE8SgZzpw0dZPAbs9vhvTpZeqr3c4ohIqBCorgS1bFLsL2myZPDqCIAiCyFvySjkDqB9Q\nLr/ZIbQj92c0GAxkOZOHkN9q/hIOhyO/jxw5gokTJwIAQiF+AFNpeSlq5Qli0MLcmv4G1Dz8EvDt\nm1XjxyTDwtpaLPd4omLOLHM6saimRrd96A3dS5SQTPiQXPiQXJSQTPiQXPQh75QzAZXl9GYnPyHL\nGYIYWKidr2pK1kTLE8Sghbk1tQqo+s4tulfPrI9XrF0LY08PgjYbFtXUkFUyQRAEQeiEoPZWcqAh\nCEJ42YQJqDx6FJsR7dq0zOnEoro6eoDIQ7Zv346PPvoItbW12W4KQRAa4MWQaWxsxJIlSzTHnIlV\nnsg9BEFAOBwmLXoaEQQhjJUQgwGfEBA+QpZlBEEQBJFtEn0GyivLmcqf/ASu//5vnBs3Drc3NWFs\nSQmKxo+nNzt5DFnOEMTAgilUGhoaEAqFYDAYYipaEi1PEIOW7QAmAThN90SCIAiCGIjkleVM+D//\nEzh2DFizJtvNIdKE3J9x165d+PDDD3HXXXdlr1GE7pDf6uCA+nlwQJYz6SfKcuaYAeHjwSy3KDeg\na4wSkgkfkgsfkosSkgkfkgufRJ+B8stp/+BBYNq0bLeCyCBkOUMQBEEQEC1nvECeGUUTBEEQxKAh\nvyxnZswA6uuB2bOz3RwiQ+zZswf79u3DL37xi2w3hSAIguBAljPpRxCEMMoAfBXAW0aED6ulRyAI\ngiAIIlMMbsuZTz8Frrgi260gMghZzhAEQRAEgAUADgEIUzBggiAIghiI5JdypqQEcDiy3Qoijbjd\n7qj/RqORUurmIfJ+JvIT6meC0BEWENhILywYdI1RQjLhQ3LhQ3JRQjLhQ3LRh/xyTKZ4M4MOspwh\nCIIgCIiWM1sB9MYvumPDBmxZswYmnw8BqxULa2spqyVBEARBZJn8ijlz333AqlXZbgqRQT7++GPs\n2bMHP/nJT7LdFIIgCIIDxZxJP5GYMx0AWiwIF0wALrkEmKD83tHYiM333IPVHk9k++VOJyrr6khB\nQxAEQRA6kugzUF4pZ5ZfeSUWPvQQPVwMElwuFx5//HG0t7dj3LhxqK6uRkVFRbabRRAEQUgg5Uz6\niQ4IbEJ4wwHg6FHg2DHF931NTXiQ8+y3orISqzZtymzDCYIgCCKPGdQBgR88cACbly7Fjg0bst0U\nIk0wf0aXy4X6+npMnToVc+fOxYQJE1BfXw+Xy5XdBhK6QH6rgwPqZ4LQkb6AwCYUAlOmAN/8JvCL\nXwC//z3Q0AC88w5w6hRMX/86d3NjT09m25sB6BqjhGTCh+TCh+SihGTCh+SiD3mlnAGA1R4PXGvX\nZrsZRJpZv349SktLo5aVlpaioaEhSy0iCIIgiCzSFxB4aNGomMUCBQXc5UGbLQ2NIgiCIAhCK3mn\nnAHy8+0PIVJeXg4AUHPHC4UohWg+wPqZyG+onwlCRxYApn3DsOS2n8cstrC2Fsudzqhly5xOVNTU\npLN1WYGuMUpIJnxILnxILkpIJnxILvqQX9ma+qC3P/mPWoYmSqtNEARBDEZGvvpVLLnt51i57Lcx\ny7G4fCvWroWxpwdBmw2LamooXh9BEARBZJm8m8nm69sfQoT5M1ZXV2Pfvn1R6xobG7F48eIstIrQ\nG/JbHRxQPxOEfpz70BNXMcMoq6rCqk2bsNLtxqpNm/JWMUPXGCUkEz4kFz4kFyUkEz4kF33IK8uZ\nFZWV9PZnkMCyMjU0NCAUCsFgMGDJkiWUrYkgCIIgCIIgCIIYcORVKu18ORaCIAiCyBcolXb6oWcg\ngiAIgsg9BnUqbYIgCIIgCIIgCIIgiIEGKWeIAQX5Mw4OqJ8HB9TPBEGkE7rGKCGZ8CG58CG5KCGZ\n8CG56AMpZwiCIAiCIAiCIAiCILIIxZwhCIIgCCJtUMyZ9EPPQARBEASRe1DMGYIgCIIgCIIgCIIg\niAEEKWeIAQX5Mw4OqJ8HB9TPBEGkE7rGKCGZ8CG58CG5KCGZ8CG56AMpZwiCIAiCIAiCIAiCILII\nxZwhCIIgCCJtUMyZ9EPPQARBEASRe1DMGYIgCIIgCIIgCIIgiAEEKWeIAQX5Mw4OqJ8HB9TPBEGk\nE7rGKCGZ8CG58CG5KCGZ8CG56AMpZwiCIAiCIAiCIAiCILIIxZwhCIIgCCJtUMyZ9EPPQARBEASR\ne1DMGYIgCIIgCIIgCIIgiAEEKWeIAQX5Mw4OqJ8HB9TPBEGkE7rGKCGZ8CG58CG5KCGZ8CG56AMp\nZwiCIAiCIAiCIAiCILIIxZwhCIIgCCJtUMyZ9EPPQARBEASRe1DMGYIgCIIgCIIgCIIgiAEEKWeI\nAQX5Mw4OqJ8HB9TPBEGkE7rGKCGZ8CG58CH61olFAAAgAElEQVS5KCGZ8CG56MOAUc4IgrBIEITP\nBEH4QhCE32a7PUR22L9/f7abQGQA6ufBAfUzQWiDnoGSg64xSkgmfEgufEguSkgmfEgu+vD/t3fn\n4VFU2cPHvydhSSABAkEwG4HghgsEERUMIFvYZBgEDEtA1OFVIYCCIijLMKKiwIwg8xtHAQkM4OA4\ng4AKqIg4qAyKKKAgkUBIEAiJ7AESzvtHd9osHeiwdZbzeZ56uvtW1e1T1dXpm1O3bpWK5IyI+AKv\nAZ2ARkBfEbnJu1EZb/j111+9HYK5CuxzLh/sczbmwqwNdPHsb0xhtk/cs/3inu2XwmyfuGf75fIo\nFckZoDmwS1WTVfUssAT4nZdjMsYYY4y50qwNZIwxxpQDpSU5Ewqk5Hm9z1lmypnk5GRvh2CuAvuc\nywf7nI3xiLWBLpL9jSnM9ol7tl/cs/1SmO0T92y/XB6l4lbaInI/0ElV/+B8PQC4U1UT8ixT8jfE\nGGOMKYfsVtoXz9pAxhhjTOlVnDZQhSsZyGWUCoTneR2O48yRizX8jDHGGFMGWRvIGGOMKQdKy2VN\nm4DrRCRSRCoBDwDveTkmY4wxxpgrzdpAxhhjTDlQKnrOqGq2iAwDVgG+wBxV/cHLYRljjDHGXFHW\nBjLGGGPKh1Ix5owxxhhjjDHGGGNMWVVaLms6LxHpJCI/ishPIjLG2/GYy0dEkkXkOxHZLCIbnWU1\nRWSNiOwUkdUiUsPbcZriEZG5InJARL7PU1bk5yoiY53f7x9FpKN3ojbFVcTnPElE9jm/05tFpHOe\nefY5lzIiEi4ia0Vkm4hsFZHhznL7Pl8l1gYqzF3boTwq7m9teeHhb1Mnb8Z4tV3M3/Ly4Dz7pdwe\nLyLiJyJfici3IrJdRF50lpf3Y6Wo/VKsY6XU95wREV9gB9Aex6B5/wP6WpffskFEdgO3q2pGnrKX\ngXRVfdnZEA1S1We8FqQpNhGJAY4Diap6q7PM7ecqIo2ARcAdOG4f+xFwvaqe81L4xkNFfM4TgWOq\nOqPAsvY5l0IiUheoq6rfikgA8DXQAxiMfZ+vOGsDueeu7VAeFee31ptxXm3F+W0qL4r7t9ybsV5N\n59kvfSjfx0sVVT0pIhWAz4HRQHfK8bECRe6XdhTjWCkLPWeaA7tUNVlVzwJLgN95OSZzeRW8C0V3\nYL7z+XwcfyRNKaKq64HMAsVFfa6/Axar6llVTQZ24fjemxKuiM8ZCn+nwT7nUklVf1HVb53PjwM/\n4Ei62Pf56rA2UNHK/R2sivlbW24U87epXLiIv+Xlwnn2C5Tv4+Wk82klHGOhZVLOjxUocr9AMY6V\nspCcCQVS8rzex29fGlP6KfCRiGwSkT84y+qo6gHn8wNAHe+EZi6zoj7XEPLfNta+46VfgohsEZE5\nebq92udcyolIJBANfIV9n68WawO5567tYBysDVU0d79N5Y6Hf8vLnTz75UtnUbk9XkTER0S+xXFM\nrFXVbdixUtR+gWIcK2UhOVO6r8syF9JSVaOBzsBQZ1dUF3Vcl2fHQBnjwedqn3np9X9AfaAJsB+Y\nfp5l7XMuJZzdvf8FjFDVY3nn2ff5irJ959552w7GwdpQ+RTnt6nMusS/5WWWc7+8g2O/HKecHy+q\nek5VmwBhQCsRubfA/HJ5rLjZL20o5rFSFpIzqUB4ntfh5D8rZ0oxVd3vfDwE/BtHF+4DzmtAEZFr\ngYPei9BcRkV9rgW/42HOMlMKqepBdQLe5LdLWuxzLqVEpCKOxvwCVf2Ps9i+z1eHtYHcKKLtYBys\nDeXGeX6byo1i/i0vN/Lsl4W5+8WOFwdVPQKsBG7HjhWXPPulWXGPlbKQnNkEXCcikSJSCXgAeM/L\nMZnLQESqiEig83lVoCPwPY7Pd5BzsUHAf9zXYEqZoj7X94A4EakkIvWB64Bye/eN0s75g53r9zi+\n02Cfc6kkIgLMAbar6l/yzLLv89VhbaACztN2MA7WhnLjPL9N5cJF/C0vF4raL+X5eBGR4NxLc0TE\nH+gAbMaOFbf7JTdh5XTBY6XClQvx6lDVbBEZBqzCMfDOnPJ+l4IypA7wb8ffRSoA/1DV1SKyCfin\niDwMJOMYMd2UIiKyGGgNBItICjABeAk3n6uqbheRfwLbgWzgcWf22ZRwbj7niUAbEWmCo7vrbuD/\ngX3OpVhLYADwnYhsdpaNxb7PV4W1gdxy23bwbkjeUZzf2vKkOL9N5Uix/paXI+72yzigbzk+Xq4F\n5ouID46OHgtU9WPn/inPx0pR+yWxOMdKqb+VtjHGGGOMMcYYY0xpVhYuazLGGGOMMcYYY4wptSw5\nY4wxxhhjjDHGGONFlpwxxhhjjDHGGGOM8SJLzhhjjDHGGGOMMcZ4kSVnjDHGGGOMMcYYY7zIkjPG\nGGOMMcYYY4wxXmTJGWOMMcYYY4wxxhgvsuSMMcYYY4wxxhhjjBdV8HYAl4uIqLdjMCWfqoq3YyhL\nRKSqqp7wdhzGGFOeWRvIlATWxiq5ROR+YLmqnvF2LMaYoolq2fg9FxEtK9tirgwRsYbDZSQiDwD/\nAJ5X1UleDsdjIhINhKjqSm/HYowxl4O1gYy3WRvLQURCgfuB3sBSVZ3p5ZAQkWrAVqCBqmbnKa8E\ntAN6Aq1V9XovhVhISY7NmCvJLmsyxlysMOBX4HNvB1JM7wBPeTsIY4wxxvxGRDqJyGYRSRGRcyKS\nLSJN3SzXQES2i0iOc7nTIrJNRG70Rtx54qoGvAdMAVriaCOVBL2BZXkTM07PAX8DHqbkXU1RkmMz\n5oqx5Iwx5qKo6nRVDVbVj7wdi6dEpB5QH/jM27EYY4wx5jeq+qGqRgOjgWQc/6c84Wa5n1W1ETAY\n2ISjN+zNqvrj1YzXTVxHVfV24FVn0RpvxpNHPDC/YKGqTgByk18lJVagZMdmzJVkyRljTHnS2vn4\nqTeDMMYYY0yR2uHoMZEF9BGRa4tYLgB4RVUPX7XIPNMa2Kaq+70diIhEArVVdVMRi+S2i0piAqQk\nx2bMFWHJGWNMedIaOAN84e1AjDHGGOPWzaq6Fse4dhWBYUUs1xb45KpF5QERCQTuouQkFAYCC84z\nvz2gwMdXJ5xiKcmxGXNFWHLGSx588EHGjx/v7TCMKRYRqSIifxWReSLyX+fAd7nzmonIAhFZJyID\nnWW9RORvIjLLWT7KTZ1RzvU+EZGJ4jDc+T5zRGS5iITlWb5qUTE45zcXkf25156LyEAR+Z+I/A94\nEDgJfOYs63Vl9pQxxhhjisvZ02O38+WfnY//T0T8CyznA9Qqgb1m7gV8KTnJmX5cODnzjapmXqV4\niqMkx2bMFWHJGS8REUQuPKh9mzZtmDNnzlWIyBiPvADMVtXBwPXkvxZ8LI7kx1Jgjoi8Alyrqo+q\nagLwDPCKiNxeoM7JwOPAK8BEYBnwvao+rqoPA4eA9+W3L8zzwKwiYgAYANQGDgKoaqKq3oFjxH9x\nxn+Hc3rnEveHMcaYyywyMpJPPilRHSLM1dMO+AhAVbcDq4GaOHqA5HU78E3ui+KeuHGWne+k0kwR\n+UhEnnCW13eeaHpdRBaKyGJnL5mCOgBngUDnsm+IyKci0qTggs6TUQ+IyH9EZLbzhNQi58DCucvc\n5IxxrYgMEZEKIvKsiPyfM46RRe1IEWkJ7FPV1CLmRwANKSKRdKH4RKSSiMwQkbkisqHAibS7ROSQ\niAwv7jZ7EpsxZVW5GP16zZo1LFq0CFVFROjXrx8dOnS46nUU5MltLz1J4BhzNYhIOOCrqttE5Fag\nFnDAOa8xsFlVc3KXA9JVdVaeKo44H6OAr53r1QJOqOox53oAic7uzLm+wpH0aSUiyQCq+oOI3OKM\nIa1AqG1xJHcyCpTf63xcizHGlAOfrVzJ6pkzqXD6NNmVK9Nx+HBade161esoLnHclvmKvoc72dnZ\nVKhQLprGJVlbHCdzcs0AOgIjgNfzlLcj/+UuuSdufhCRQzhO3IzOMz/fiRunsUAf4DEcJ5VuBfaq\n6qMAInI38F8RyQZaAI+p6q/OeTtwnFDK+x7gSM6A47bV/8+57ERglYg0VNVjzrIgYBGOdsx9qprb\nnhoGPI3jbkU43+NBoBeOQX07AtOBHThuj90N+EuhvegwEDcDAefR3vlYKAHiYXxjgYWq+o1zn4/M\nsz9qO9ftDMws5jafNzZjyrIy33NmzZo1zJ49m8jISOrXr09kZCSzZ89mzRrPv+uXo47NmzfTtGlT\nqlWrRlxcHFlZWQD8+uuvdOvWjWuuuYaaNWty3333kZrqSHA/++yzrF+/nmHDhhEYGMjw4Y7k84gR\nI4iIiKB69eo0a9aMzz8vbXcyNqVUCPB/zucPAeeAxc7XgTh6zIBjXJc9qjq1wPq3OR/35ikLBnK7\nhrXHccnRsgLr1XI+1gNCcdxaMTeGMziuSQdARK4BGuE+AdMGOA1scLdxxhhTlny2ciWrRozg+dWr\nmbRuHc+vXs2qESP4bOXKq1pHSkoKPXv25JprriE4OJiEhAR+/vln2rZtS3BwMLVr12bAgAEcOeLI\n38fHx7N3717uu+8+AgMDmTZtGgBffvklLVq0ICgoiCZNmrBu3TrXe+zevZtWrVpRrVo1OnTowNCh\nQ4mPj3fNf++997j55psJCgri3nvv5ccff7upT2RkJC+//DK33XYbAQEBTJs2jV698l/xOnz4cEaO\nLLKDgrm8IlQ1JfeFqq4GtgM3ikinPMu1AtaB606MxTpxk/ekElDUSaWjzsdHgEG5iRmnY8BNed/A\neZLpemCuqr6UZ9ZmHMmK+5zL+QJvA/cA3XOTFE5ncP5/5uyJ8ouqZjljFOA/qvoFEITjJPs/cENE\n/IAuwL/czXdqD5wC/ltg3QvG5+zpEuJMzNyIY5+n5y6kqsuBRJwn5jzd5gvFZkxZV+aTM4sWLSI6\nOjpfWXR0NIsXLy5ijctfx5kzZ+jRoweDBg0iMzOT3r17869//QsR4dy5czz88MPs3buXvXv34u/v\nz7BhjnHPpkyZQkxMDLNnz+bYsWPMnDkTgObNm7NlyxYyMzPp168fvXv35syZMx5vjzEXQ1W/UtXt\nIlIZx20ZP1TVfc55n6vqDhGpDjTD2SW5gN/haMxsylPnDlX9ynnJ0r3ABlU9W2C9O5yPaaq6wfk+\nFZwx/KfAD3wb52NRyZmNzkaOMcaUaatnzmRKUlK+silJSayZNauINS5/HTk5OXTr1o369euzZ88e\nUlNTiYuLQ1V59tln2b9/Pz/88AMpKSlMmjQJgAULFhAREcGKFSs4duwYo0ePJjU1lW7dujFhwgQy\nMzOZNm0a999/P4cPO4Yb6devH3fddRcZGRlMmjSJhQsXunoe79y5k379+jFz5kzS09Pp0qUL9913\nH9nZ2a44lyxZwgcffMCRI0cYMGAAH374oStZlJ2dzdtvv82gQYM83m/m4jgTK1vdzModeyb3EqPK\nQCVVPeEsv5gTN56cVGrsfHxOVV0NbRGpCNwApBRYPrfXzKIC5TWdj7k9hPvjSD4kquovzjqri8jD\nOG4PnvsFC+G3k2CtgYOquhBAVZNU9RpVHYp73YGPVfWku5nOdldbYH3ebStGfGH81pOpv/NxaYF6\n3seRmCrONl8oNmPKtDLfd7OobrE///wzf/zjHz2qY/fu3URGRhYqP3funEfrf/nll2RnZzNixAgA\n7r//fu64w/H/Zs2aNfn973/vWnbcuHG0bds23/oFt6F///6u508++STPP/88O3bs4NZbb/UoHmMu\nUU8cDY033MxrjSPpm29kfXEM5NcNRzIl2816TXCcdSm4ni+OpM1x8t9hqaNz+YUF6mkL5ACfFagn\nAojEcRbHGGPKvAqnT7st9121Cjy8ZLqoRqJvlmc57o0bN7J//35eeeUVfHwc5wNbtmwJQFRUFADB\nwcE88cQTTJ48uch6Fi5cSJcuXejUydFxon379jRr1oyVK1fSpk0bNm3axNq1a6lQoQItW7ake/fu\nrnXffvttunXrRrt27QAYPXo0r776Khs2bKBVq1aICMOHDyc01DFESd26dYmJiWHp0qU88sgjfPjh\nh9SuXbvQSTpzRbTF/cmdhTjGvOsgIjcDdcjTJlDVDQDFOXGjqp8718k9qTTPzfveC2QDnxYobwVU\npfCJoA44ent8WaA89+DJjekPzsdaIvJXHHckOu18nxbqbPir6kZnjJWAGGC5mxiLMhDH5U9FuRW4\nBveXDXkS335nbOJ8ry9VNalAPfWAD4pRpyexGVOmlfnkTFFjtjRo0ICJEyd6VEdycrLb8tyGxoWk\npaW5fvRz1atXD4BTp04xcuRIVq1aRWamYzDy48ePu8a2gcLbMG3aNObOnUtaWhoiwtGjR0lPT8eY\nq+QPOH6UlwOIyBBV/btzXjvnY8GRHHvhaMgsdK7TH/hXnl4sRa13L1AN+GueM2TguE1lDoUbcfcC\n36rqEXHc8eE6VV2Dm4aZiAwBltpdAIwxZVF25cpuy3NiY+HDDz2rIzYWVq8uXIefn0frp6SkUK9e\nvULtpQMHDjBixAg+//xzjh07xrlz56hZs2YRtcCePXtYunQpy5f/9r9pdnY2bdu2JS0tjZo1a+KX\nJ6awsDDXJeJpaWlERES45okI4eHhrvkA4eHh5DVo0CD+9re/8cgjj7Bw4cJ8l0iZK6oN8HDBQlU9\nLSL/B0zAMa7JAdz/416sEzdObk8qObUDNuWOE5NHPxxJmBUFypsB/3PTA7gtjkvBc9s4twAngH6q\n6smZ3rsAfzy8bbiI1AFuKjB+X0HnG9OlOPE1x9Ej6K9u5jVW1Vcuok4bb8aUW2X+sqZ+/fqxefPm\nfGXffPMNffv2vWp1XHvttfkaAeBoaKgq06ZNY+fOnWzcuJEjR46wbt06VNXVW6ZgYmb9+vW88sor\nLF26lF9//ZXMzEyqV6/ulYHzTPkjItfiaDwtUNVzzsHz8mYe2wHbVPVggVX747j+e7WzN8zvClxe\n1A7HWZQtBdYb61zv2QLlNYFDeesQkfrAdfw2pkwPHGPYgOPSqHM4z2Y5ByKOscSMMaas6jh8OM86\ne6fkGhcVRYeEhKtWR3h4OHv37iUnJyd/HePG4evry9atWzly5AgLFizI1xu5YNsnIiKC+Ph4MjMz\nXdOxY8d4+umnufbaa8nIyODUqVOu5VNSfrvaJDQ0lD179rheqyopKSn5TpoVfL/f/e53fPfdd2zd\nupWVK1fm67Fsrgxn26DGeX6X/4qjp0V/HIPMuhs/zqMTNyKS944ebk8OOdsUkRTu0VsF6A28p6on\nRKSeiOQmE8Io0I4RkeuAm4GVqpo75p4vkORhYqbIGM+jH7DkAsu0x3GZ1HciUktEYvPMK058zZyP\nX+UtdF6itvMi6zxfbMaUaWU+OZM7MNyePXvYvXs3e/bsYdiwYcW609Kl1tGiRQsqVKjAzJkzOXv2\nLO+++y7/+9//AEcvGX9/f6pXr05GRkahS63q1KlDUp7rvY8dO0aFChUIDg7mzJkzTJ48maNHj2LM\nVZI7OO86Z/fhp3HcSQERqYvjmm53Z59qAf91dltN4LdBgHOv3Y4BMnH0sMktfx7HYHsdVPVI/ur4\nHKjpHPkfEakBTMORjDkoIj44uh3nNt4OA5nOs2/+OO5sUDDhY4wxZUarrl2JffVVxsfGMql1a8bH\nxtLp1VeLdaelS63jzjvv5Nprr+WZZ57h5MmTZGVl8d///pfjx49TtWpVqlWrRmpqKq+88kq+9Qq2\nfQYMGMDy5ctZvXo1OTk5ZGVl8emnn5Kamkq9evVo1qwZkyZN4uzZs3zxxResWPFbh4bevXuzcuVK\nPvnkE86ePcv06dPx8/OjRYsWRcbt7+/P/fffT79+/bjzzjsJCwsrcllz2TQjz5h0BTlP+iwC/IDD\nbnqnQPFP3EDRJ5VyEyIF2zRdgQB+uwvSQzgv8QH2FKgbYBSOHiNP5Cn7wrkdhYhITRH5c4HidkCK\nqu5yt44b8Zz/Lk3guPtU7rbdh6N388XEl9tFr+AAzE8Ar15kneeLzZiyLbeXRmmfHJtScm3atEmj\no6M1MDBQH3jgAY2Li9Px48drWlqatmnTRgMCAvSGG27Q119/XX18fDQnJ0dVVb/44gu9/vrrNSgo\nSEeMGKE5OTn60EMPabVq1fTaa6/Vl19+WevXr68ff/yxl7ew5HMeI14/Vkv7BLwIrMZxVubOPOW3\nAb8Azdys0wbYiKOxMKLAvFY4erUMBf4EvIljRP+ZQPB54hgPfIhjQLo5OK5t7ofj7M0/gLvzLFsD\nx3XPS3A07pp4ez/aZJNNNl2uqSS3gfbu3as9evTQWrVqaXBwsI4YMUK3bdumt99+uwYEBGh0dLRO\nnz5dw8PDXessW7ZMIyIitEaNGjp9+nRVVf3qq6+0devWWrNmTa1du7Z269ZN9+7dq6qqSUlJGhMT\no4GBgdquXTsdMmSIPvzww676/v3vf2ujRo20evXq2qZNG92+fbtrXmRkpNs21Pr161VE9K233rpS\nu6ZMuZQ2Fo5kx0rg6Qssd4uzvfBMEfPjgCwgyPm6Bo67FR3HcULGB3gXEOf8us76/uKmrsU4kiqV\nCpQPc65TBUfPmr/lmfcUjhNReeM5CnQsUEdLHIMWN8tTJkAn4B0gvMC+OQO85eG+vA3H+C8XWi4F\neMn5/N+A/0XG1xTHuDwPFNgP3S5hm4uMzSabyvqU+8ep1BMRLSvbYq4MEUFVPRsF0Vw1IvJHHImW\nm1R1h7fjMcaY0sbaQPk98MADNGrUyOOxBd1JSUnhxhtv5MCBAwQEBFzG6Mqmi2ljOXu/rgOi+K1X\nxS4ct60uOKhu7jrvA8+q6uYi5o/HkQjYg2NszcnO1yOcdb+mjltRIyK34TjZ1E1VNxWo50Ngp6oO\nL1AegOOuRMdwJF5GqbN3r7NH8UwcY7D8iuNSnomq+pObONvjSGLsw3G5VkUcvYIT836ZnT1/vgTi\n9PxjyOQuPx3H5UPuxoDJu1wnYCLwM7BYVVcUmO9RfM5le+HYvz/iSLi8q6rvX8I2nzc2Y8oyS86Y\ncsOSMyWTiHwORKhqxAUXNsYYU0h5bwNt2rSJoKAg6tevz6pVq+jZsydffvkljRs3vvDKbpw7d44n\nn3yS48eP8+abb17maMsma2N5n3PcniQgWm1MPWNKpTJ/tyZjTMklIsE4Rvpf7O1YjDHGlE6//PIL\nPXv25PDhw4SHh/O3v/3tohMzJ06coE6dOtSvX58PPbyrlTElRCzwtSVmjCm9rOeMKTfsrE7JIiIv\nAwOB2jgG0PsRGKiqP3g1MGOMKWWsDWS8zdpY3iciS3BcBrTM27EYYy6OJWdMuWENB2OMMWWRtYGM\nt1kby7tEpDrwPdBAVbO9HY8x5uKU+VtpG2OMMcYYY0wZ1gf4jyVmjCndLDljjDHGGGOMMaVXa2Ce\nt4Mwxlwau6zJlBvW5dYYY0xZZG0g423WxjLGmEtnPWeMMcYYY4wxxhhjvMiSMyXI3r17CQwMpDSc\n/Xrsscd4/vnni71eadpGY4wxxnjHLbfcwmeffebtMDzWpUsXFixYcFnqWr9+PTfeeKPrdWRkJB9/\n/PFlqRtK3741xpjywi5rKqWSk5Np0KABTZo04ZtvvnGVp6enExISQmhoKLt3776k9/j000+Jj48n\nJSXlouuIjIxk7ty5tG3b9pJiuRysy60xxpiyqCS3gSIjIzl48CC+vr5UrVqVzp0789prr1G1alVv\nh+YxHx8fqlSpgohQuXJlmjRpwpAhQ+jTp89F1bVr1y4aNGjg8Tr169dnzpw5F9WWevDBBwkPD+dP\nf/pTsdctDmtjGWPMpSsXPWc+W7mS52JjmdSmDc/FxvLZypVeqeNKOHXqFNu2bXO9XrRoEQ0aNECk\nZPw+On+svR2GMcYYU+6sXPkZsbHP0abNJGJjn2PlyuL3lrjUOkSEFStWcOzYMb755hs2bdp0UT1v\nve27777j2LFj7Ny5kwcffJBhw4YxefLki6rrfO2i7Gy72Y4xxpRbqlomJsemFLZuxQodFxWlCq5p\nXFSUrluxwu3yV6KOevXq6SuvvKK33nqrBgQE6EMPPaS//PKLdurUSatVq6bt27fXzMxM3b17t4qI\n5uTkqKpq69atdfz48dqyZUsNDAzUjh07anp6uqqqa9kpU6boU0895XqvZs2a6ZQpUzQyMtJV9uKL\nL2pUVJQGBgZqo0aN9N///rdr3qOPPqr333+/6/XTTz+t7dq1U1XVtWvXalhYmNttGjRokD733HOq\nqnro0CHt2rWr1qhRQ2vWrKkxMTF67tw5HTBggPr4+Ki/v78GBAToK6+8UqxtVFWdP3++RkREaK1a\ntfRPf/qT1qtXTz/66COP9ntBzmPE68eqTTbZZJNNNl3OyV0baMWKdRoVNS5v00WjosbpihXrCi1b\nlMtRR2RkpH788ceu16NHj9Zu3bqpquqyZcu0UaNGWqNGDW3Tpo3+8MMPruXq1avnWu+rr77S22+/\nXatVq6Z16tTRJ598UlVVT506pf3799datWppjRo19I477tADBw6oqmpqaqred999WrNmTW3YsKG+\n8cYbrronTpyovXv31oEDB2pgYKDefPPNumnTpiK3QUQ0KSkpX9k777yjfn5+mpGRoaqO9sybb76p\nqqo//fSTtmrVSqtXr67BwcEaFxenqqoxMTEqIlq1alUNCAjQf/7zn7p27VoNDQ3VqVOnat26dXXg\nwIGF2l+RkZH64osvaqNGjTQoKEgHDx6sWVlZqqo6b948veeeewrFu2vXLn399de1YsWKWqlSJQ0I\nCNDu3bu79m1uWyorK0tHjBihISEhGhISoiNHjtTTp0+rqrpimz59ul5zzTV67bXX6rx589zuI2tj\n2WSTTTZd+lTme86snjmTKUlJ+cqmJCWxZtasq1aHiPDuu+/y8ccfs2PHDlasWEHnzp156aWXOHjw\nIOfOnWPmzJlu1128eDFvvfUWBw8e5B+C+1UAABg8SURBVMyZM0ybNi3f/P79+7NkyRJUle3bt3P8\n+HHuvPPOfMs0bNiQzz//nKNHjzJx4kQGDBjAL7/8AsCMGTP4/vvvmT9/PuvXr2fu3LkkJiZ6tE25\nvXOmT59OeHg46enpHDx4kBdffBERYcGCBURERLjOmI0ePbpY27h9+3aGDh3K4sWL2b9/P0eOHCEt\nLa3E9AoyxhhjSqqZM1eTlDQlX1lS0hRmzVpzVeuA33qKpKSk8MEHH9C0aVN27txJv379mDlzJunp\n6XTp0oX77rvP1XMk72/9iBEjeOKJJzhy5Ag///wzDzzwAADz58/n6NGj7Nu3j4yMDF5//XX8/f0B\niIuLIyIigv379/POO+8wbtw41q5d66pz+fLl9O3blyNHjtC9e3eGDRtWrG3q3r072dnZbNy40RVv\nbszjx4+nU6dO/Prrr6SmppKQkADgGucltxdO7969AThw4ACZmZns3buX119/3e3+W7RoEatXryYp\nKYmdO3desPeRiDBkyBD69+/PmDFjOHbsGMuWLSsU65QpU9i4cSNbtmxhy5YtbNy4MV/dBw4c4OjR\no6SlpTFnzhyGDh3KkSNHirWvjDHGeKbMJ2cqnD7tttx31SoQ8WiqsHq1+zqysjyOIyEhgdq1axMS\nEkJMTAx33303jRs3pnLlyvz+979n8+bNhZIOIsLgwYNp2LAhfn5+9OnTh2+//TbfMmFhYdxwww2s\nWbOGxMREBg4cWOi9e/XqRd26dQHo06cP1113nasx4e/vz4IFC3jiiSeIj4/ntddeIyQkxOPtAqhU\nqRL79+8nOTkZX19fWrZs6fG659vGd955h+7du9OiRQsqVqzI5MmTLTFjjDHGeOD06Qpuy1et8vW0\n+cPq1e7ryMry9TgOVaVHjx4EBQURExNDmzZtGDt2LG+//TbdunWjXbt2+Pr6Mnr0aE6dOsWGDRsK\n1VGpUiV++ukn0tPTqVKlCs2bN3eVHz58mJ9++gkRITo6msDAQFJSUtiwYQNTp06lUqVKNG7cmEce\neSTfyaeYmBg6deqEiDBgwAC2bNni8TYBVKxYkeDgYDIyMtzGm5ycTGpqKpUqVaJFixbnrcvHx4c/\n/vGPVKxYET8/v0LzRYRhw4YRGhpKUFAQzz77LIsXL/Y41tzkmDuLFi1iwoQJBAcHExwczMSJE/MN\nbFyxYkUmTJiAr68vnTt3JiAggB07dnj83sYYYzxX5pMz2ZUruy3PiY3N20v3vFN2x47u63DzA1qU\nOnXquJ77+/vne+3n58fx48fdrpebVMldr+ByIsLAgQOZN28eS5YsIT4+vtCPcGJiItHR0QQFBREU\nFMTWrVs5fPiwa37z5s1dA9PlnsXxRO77PPXUUzRs2JCOHTsSFRXF1KlTPa7jfNuYlpZGWFhYvnm1\natUqVt3GGGNMeVS5svuxS2Jjczxt/tCxo/s6/PxyPI5DRFi2bBmZmZkkJyfz2muv4efnx/79+4mI\niMi3XHh4OKmpqYXqmDNnDjt37uSmm26iefPmrHSO+xcfH09sbCxxcXGEhoYyZswYsrOzSUtLo2bN\nmvkGHY6IiMhXd952WJUqVcjKyuLcuXMeb9fZs2c5dOgQNWvWLDTv5ZdfRlVp3rw5t9xyC/PmzTtv\nXbVr16ZSpUrnXSY8PNz1PCIigrS0NI9jPZ+0tDTq1atXZN21atXCx+e3fxeqVKlSZJvVGGPMpSnz\nyZmOw4fzbFRUvrJxUVF0cHYxvVp1FHS+sxjF1bNnT95//32ioqLyJTMA9uzZw5AhQ5g9ezYZGRlk\nZmZyyy235Hv/2bNnc+bMGUJCQnj55ZeL/f4BAQFMmzaNpKQk3nvvPWbMmOHqOnwpPV1CQkLYt2+f\n6/WpU6fyJZWMMcYY497w4R2Jino2X1lU1DgSEjpc1TqKEhISwp49e1yvVZWUlBRCQ0MLLduwYUMW\nLVrEoUOHGDNmDL169eLUqVNUqFCBCRMmsG3bNjZs2MCKFStITEwkNDSUjIyMfEmEvXv3FmojXYpl\ny5ZRoUIFVy+evOrUqcPf//53UlNTef3113n88cf5+eefi6zLk7bS3r178z3P7eVctWpVTp486ZqX\ne9m6p3WHhISQnJzstm5jjDFXl/v+qmVIq65dARg/axa+WVnk+PnRKSHBVX616rhYniRxqlatytq1\nawkKCio078SJE4gIwcHBnDt3jsTERLZu3eqav3PnTsaPH8+6devw9/enefPmdO7cmcaNG7uWOX36\ndL44/Pz88r1esWIFN954I1FRUVSrVg1fX1/XWZY6deqQlJR03ts/FrWN999/P3fffTdffPEFt99+\nO5MmTbqsSS1jjDGmrOratRUAs2aNJyvLFz+/HBISOrnKr1YdRenTpw8vvfQSn3zyCTExMbz66qv4\n+fm5vQRo4cKFxMbGUrt2bapXr46I4OPjw9q1awkODqZRo0YEBgZSsWJFfH19CQsLo0WLFowdO5Zp\n06axY8cO5s6dy6JFiy463tz2R0ZGBh988AGjRo3imWeecdv2Wrp0KXfffTdhYWHUqFHDFS/81i4q\nzq20VZXZs2fTrVs3/P39mTJlCnFxcQA0btyYbdu2sWXLFm644QYmTZqUb906deqcNzHUt29fnn/+\nee644w4AJk+eTHx8vMexGWOMuXzKfHIGHMmVS02kXI468sp7JiPvwGzuxp1xt1zBeU2bNnW7XqNG\njRg1ahR33303Pj4+DBw4kHvuuQeAnJwc4uPjeeaZZ7j11lsBeOGFF4iPj+frr78GIDU11TW4Xm69\nO3fuzBfLrl27SEhI4NChQwQFBTF06FBat24NwNixY0lISODpp59m/Pjx9OzZ0+NtvPnmm5k1axZx\ncXGcOHGCkSNHcs0111C5iEvVjDHGGPObrl1bXXIi5XLU4c7111/PwoULSUhIIDU1lejoaJYvX06F\nCoWbpqtWrWLUqFGcPHmSyMhIlixZQuXKlTlw4ACPPfYY+/btIyAggLi4OFdiYfHixTz66KOEhIQQ\nFBTE5MmTXSeKCrancsvOp3HjxogIlSpVokmTJvzlL39xJUgK2rRpk2sA4zp16jBz5kwiIyMBmDRp\nEoMGDeLUqVO88cYb1K5d2+17F2wb9e/fn44dO5KWlkaPHj147rnnXPtxwoQJtG/fnipVqvDCCy/w\nxhtvuNZ9+OGH6d27N0FBQdx77728++67+d7nueee4+jRo9x2222AI2mWW7cn+8UYY8zlI2WlJ4KI\naFnZFuPe8ePHCQoKYteuXfmuj/aUiKCq1sowxhhTplgbyHibtbGMMebSlfkxZ0zptnz5ck6ePMmJ\nEycYPXo0t91220UlZowxxhhjjDHGmJLKkjOmRHvvvfcIDQ0lNDSUpKQklixZ4u2QjDHGGGOMMcaY\ny8ouazLlhnW5NcYYUxZZG8h4m7WxjDHm0lnPGWOMMcYYY4wxxhgvsuSMMcYYY4wxxhhjjBdZcsYY\nY4wxxhhjjDHGiyw5Y4wxxhhjjDHGGONFlpwxxhhjjDHGGGOM8SJLzhhjjDHGmBLllltu4bPPPvN2\nGMYYY8xVY8mZEmTv3r0EBgZit8O8eG+99RYxMTHeDsMYY4wxQGRkJFWqVCEwMJC6desyePBgTpw4\nccH1tm7dSqtWra5ChBfm4+NDQEAAgYGBhIWFMWrUKM6dO+ftsIwxxpQxlpwpQSIiIjh27BgicsFl\nk5OT8fHxoWnTpvnK09PTqVSpEvXr179SYRpjjDGmFFi5ZiWxg2Np82AbYgfHsnLNyqteh4iwYsUK\njh07xjfffMOmTZt4/vnnix2Ht3333XccO3aMjz/+mEWLFvHGG28UWiY7O9sLkRljjCkrLDlTyp06\ndYpt27a5Xi9atIgGDRp4lOApCXJycrwdgjHGGFPmrFyzkhGzR7A6cjXr6q9jdeRqRsweUazkyuWo\nI6+QkBA6derE1q1bAXjvvfe4+eabCQoK4t577+XHH390LRsZGcknn3wCwMaNG2nWrBnVq1enbt26\njBo1CoCsrCwGDBhAcHAwQUFBNG/enIMHDwKQlpZG9+7dqVWrFtdddx1vvvmmq+5JkybRp08fBg0a\nRLVq1bjlllv4+uuvPdqGG264gZiYGLZt28aePXvw8fFh7ty51KtXj/bt26OqPP/880RGRlKnTh0G\nDRrE0aNHXet//vnntGjRgqCgICIiIpg/fz4Ap0+fZvTo0dSrV4+6devy2GOPkZWVBThOvHXr1o2g\noCBq1aqVr0fR1KlTCQsLo1q1atx4442ufWaMMab0seTMVRAZGcm0adO47bbbCAwM5OGHH+bAgQN0\n7tyZ6tWr06FDB3799VdXb5jcrrJt2rRhwoQJ3HPPPVSrVo3Y2FgOHz6cr+74+HjXDzvAggULGDhw\nYL5Lo1566SUaNmxItWrVuPnmm/nPf/7jmvfYY4/Rq1cv1+sxY8bQvn37827Pp59+SlhYGDNmzKBO\nnTqEhITw1ltvueYfOXKEgQMHcs011xAZGcmUKVNc8bz11lu0bNmSJ598kuDgYCZNmsTgwYN5/PHH\n6dKlC4GBgcTExPDLL78wYsQIgoKCuOmmm/j222892h5jjDHGwMxFM0mKTspXlhSdxKzFs65qHYCr\nDZCSksIHH3xA06ZN2blzJ/369WPmzJmkp6fTpUsX7rvvPlfvk7wnmUaMGMETTzzBkSNH+Pnnn3ng\ngQcAmD9/PkePHmXfvn1kZGTw+uuv4+/vD0BcXBwRERHs37+fd955h3HjxrF27VpXncuXL6dv374c\nOXKE7t27M2zYMI+2Yfv27axfv57o6GjXvM8++4wff/yRDz/8kHnz5jF//nw+/fRTfv75Z44fP+6q\ne8+ePXTp0oURI0aQnp7Ot99+S5MmTQB45pln2LVrF1u2bGHXrl2kpqYyefJkAKZPn054eDjp6ekc\nPHiQF198EYAdO3Ywe/ZsNm3axNGjR1m9ejWRkZHF+myMMcaUHOUqOSNyeabiv6/w7rvv8vHHH7Nj\nxw5WrFhB586deemllzh48CDnzp1j5syZbtddvHgxb731FgcPHuTMmTNMmzYt3/z+/fuzZMkSVJXt\n27dz/Phx7rzzznzLNGzYkM8//5yjR48yceJEBgwYwC+//ALAjBkz+P7775k/fz7r169n7ty5JCYm\nXnCbDhw4wNGjR0lLS2POnDkMHTqUI0eOAJCQkMCxY8fYvXs369atIzExkXnz5rnW3bhxI1FRURw8\neJBnn30WVWXp0qVMmTLFdVnWXXfdxR133EFGRga9evXiySefPO/2HDhwwLMPwxhjjCkHTutpt+Wr\nfl6F/FE8mlbvXu22jqxzWR7Hoar06NGDoKAgYmJiaNOmDWPHjuXtt9+mW7dutGvXDl9fX0aPHs2p\nU6fYsGFDoToqVarETz/9RHp6OlWqVKF58+au8sOHD/PTTz8hIkRHRxMYGEhKSgobNmxg6tSpVKpU\nicaNG/PII4/ka9/ExMTQqVMnRIQBAwawZcuW825H06ZNqVmzJt27d+cPf/gDgwcPdiVsJk2ahL+/\nP35+fvzjH/9g1KhRREZGUrVqVV588UWWLFlCTk4OixYtokOHDjzwwAP4+vpSs2ZNGjdujKryxhtv\nMGPGDGrUqEFAQABjx45lyZIlru3cv38/ycnJ+Pr60rJlSwB8fX05ffo027Zt4+zZs0RERNCgQQOP\nPxtjjDElS7lKzqhenuliJCQkULt2bUJCQoiJieHuu++mcePGVK5cmd///vds3ry50KVIIsLgwYNp\n2LAhfn5+9OnTJ18PEoCwsDBuuOEG1qxZQ2JiIgMHDiz03r169aJu3boA9OnTh+uuu46NGzcC4O/v\nz4IFC3jiiSeIj4/ntddeIyQk5ILbU7FiRSZMmICvry+dO3cmICCAHTt2kJOTw9tvv82LL75I1apV\nqVevHqNGjWLBggWudUNCQhg6dCg+Pj74+fkhIvTs2ZPo6GjX/qhatSoDBgxAROjTpw+bN28+7/Z8\n9dVXHn4SxhhjTNlXWSq7LY9tEItOVI+mjvU7uq3Dz8fP4zhEhGXLlpGZmUlycjKvvfYafn5+7N+/\nn4iIiHzLhYeHk5qaWqiOOXPmsHPnTm666SaaN2/OypWOy6ri4+OJjY0lLi6O0NBQxowZQ3Z2Nmlp\nadSsWZOqVau66oiIiMhXd506dVzPq1SpQlZW1nkH+d28eTMZGRns2rXL1aMlV3h4uOv5/v37qVev\nXr73zc7O5sCBA+zbt89t8uTQoUOcPHmS22+/naCgIIKCgujcuTPp6ekAPPXUUzRs2JCOHTsSFRXF\n1KlTAcfJqr/85S9MmjSJOnXq0LdvX/bv31/kNhhjjCnZylVyxpvyNgL8/f3zvfbz8+P48eNu18tN\nQuSuV3A5EWHgwIHMmzePJUuWEB8fX+huT4mJiURHR7t+8Ldu3Zrv8qjmzZu7Ggu9e/f2aHtq1aqF\nj89vh0+VKlU4fvw46enpnD17tlDDJG+DKG8jJtc111zjeu7n55fvdcHtvtD2GGOMMeXd8H7Didoc\nla8s6psoEvomXNU6ihISEsKePXtcr1WVlJQUQkNDCy3bsGFDFi1axKFDhxgzZgy9evXi1KlTVKhQ\ngQkTJrBt2zY2bNjAihUrSExMJDQ0lIyMjHxth7179xIWFnbJcbuT9+RaSEgIycnJ+d63QoUK1K1b\nl/DwcJKSkgqtHxwcjL+/P9u3byczM5PMzEx+/fVX11g1AQEBTJs2jaSkJN577z1mzJjhGlumb9++\nrF+/nj179iAijBkz5opsozHGmCvPkjNecjlvl92zZ0/ef/99oqKiCjU89uzZw5AhQ5g9ezYZGRlk\nZmZyyy235Hv/2bNnc+bMGUJCQnj55ZcvKZbg4GAqVqxYqGGSN65LGazYk+0xxhhjyruuHbry6tBX\nid0TS+vdrYndE8urw16la4euV7WOovTp04eVK1fyySefcPbsWaZPn46fnx8tWrQotOzChQs5dOgQ\nANWrV0dE8PHxYe3atXz//ffk5OQQGBhIxYoV8fX1JSwsjBYtWjB27FhOnz7Nd999x9y5cxkwYMAl\nx30hffv25c9//jPJyckcP36ccePGERcXh4+PD/369eOjjz5i6dKlZGdnc/jwYbZs2YKPjw9/+MMf\nGDlypGs7U1NTWb3acVnZypUr2bVrF6pKtWrV8PX1xdfXl507d/LJJ59w+vRpKleujJ+fH76+vld8\nG40xxlwZFbwdgDk/T5IOVatWZe3atQQFBRWad+LECUSE4OBgzp07R2JiousuCQA7d+5k/PjxrFu3\nDn9/f5o3b07nzp1p3LjxRcXr6+tLnz59ePbZZ0lMTOTw4cP8+c9/5qmnnrqkbfR0e4wxxhjj0LVD\n10tOpFyOOty5/vrrWbhwIQkJCaSmphIdHc3y5cupUKFw03TVqlWMGjWKkydPEhkZyZIlS6hcuTIH\nDhzgscceY9++fQQEBBAXF0d8fDzgGLPv0UcfJSQkhKCgICZPnkzbtm0Bx0kid5eSF6U48x566CHS\n0tJo1aoVWVlZdOrUiVmzHAMoR0RE8P777zN69GgeeeQRqlevzpQpU2jcuDFTp05l8uTJ3HXXXaSn\npxMaGsrjjz9Ox44d+emnnxg2bBiHDh0iKCiIoUOH0rp1a77//nvGjh3LDz/8QMWKFWnZsiV///vf\nPfsAjDHGlDiWnPGSvD/meRsJ52ssFGxM5H3etGlTt+s1atSIUaNGcffdd+Pj48PAgQO55557AMdt\nrOPj43nmmWe49dZbAXjhhReIj4/n66+/pmLFih7FX9CsWbNISEigQYMG+Pn5MWTIEAYPHux2G4ra\nrqL2w/m2p6h1jTHGGOMdu3fvLnJejx496NGjxwXXyztuXV5xcXHExcW5nRcaGsry5cvdzps4cWK+\n15GRkeTk5BQZZ1Hz3K0nIowfP57x48e7Xeeee+7hyy+/LFReuXJlpkyZwpQpUwrNGzlyJCNHjixU\nfuutt9qYe8YYU4ZIWbkcRES0rGyLuTJEBFW1zI0xxpgyxdpAxtusjWWMMZfOxpwxxhhjjDHGGGOM\n8SJLzhi3XnjhBQIDAwtNXbte/uvOjTHGGGOMMcaY8swuazLlhnW5NcYYUxZZG8h4m7WxjDHm0lnP\nGWOMMcYYY4wxxhgvsuSMMcYYY4wxxhhjjBeVqVtp2y2UjTHGGFMeWRvIGGOMKd3KzJgzxhhjjDHG\nGGOMMaWRXdZkjDHGGGOMMcYY40WWnDHGGGOMMcYYY4zxIkvOGGOMMcYYY4wxxniRJWeMMcYYY4wx\nxhhjvMiSM8YYY4wxxhhjjDFe9P8BFGgOCkV51+4AAAAASUVORK5CYII=\n",
"text": [
"<matplotlib.figure.Figure at 0x10b8ced90>"
]
}
],
"prompt_number": 3
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"i = 100\n",
"print ('Alva = ', AlvaProduct(i))\n",
"print ('NumP = ', np.prod(np.arange(1, i + 1), dtype=np.float64))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"('Alva = ', 93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000L)\n",
"('NumP = ', 9.3326215443944102e+157)\n"
]
}
],
"prompt_number": 4
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"''' Gaussian Distribution '''\n",
"unitD = 1\n",
"rangeD = float(100)*unitD\n",
"meanD = rangeD/2\n",
"varianceD = rangeD\n",
"print ('mean = ', mean)\n",
"aaa =np.arange(1, rangeD)*b\n",
"print aaa\n",
"plt.figure(figsize = (12, 4))\n",
"#plt.plot(aaa, AlvaPoissonProcess(aaa, N), marker ='^', color = 'blue', label = 'Process')\n",
"#plt.plot(aaa, AlvaPoissonD(mean, aaa), marker ='o', color = 'red', label = 'Distribution')\n",
"plt.plot(aaa, np.exp(-((aaa - meanD)/varianceD)**2), marker ='+', color = 'red', label = 'Gaussian')\n",
"plt.plot(aaa, np.exp(-((aaa - meanD)**2/varianceD)), marker ='+', color = 'blue', label = 'Gaussian')\n",
"plt.xlabel(r'$ Output-level$', fontsize = AlvaFontSize)\n",
"plt.ylabel(r'$ Number/level $', fontsize = AlvaFontSize)\n",
"plt.title(r'$ Poisson \\ process $', fontsize = AlvaFontSize)\n",
"plt.grid(True)\n",
"plt.legend(loc = (1, 0))\n",
"plt.show()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"('mean = ', 33.333333333333336)\n",
"[ 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15.\n",
" 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30.\n",
" 31. 32. 33. 34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. 45.\n",
" 46. 47. 48. 49. 50. 51. 52. 53. 54. 55. 56. 57. 58. 59. 60.\n",
" 61. 62. 63. 64. 65. 66. 67. 68. 69. 70. 71. 72. 73. 74. 75.\n",
" 76. 77. 78. 79. 80. 81. 82. 83. 84. 85. 86. 87. 88. 89. 90.\n",
" 91. 92. 93. 94. 95. 96. 97. 98. 99.]\n"
]
},
{
"metadata": {},
"output_type": "display_data",
"png": "iVBORw0KGgoAAAANSUhEUgAAAz8AAAEvCAYAAABrHH/xAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xm8VfP+x/HXp5K5IiUSFaGQRGY6EeIS11ymzMPFz+Ua\nryuzKyTzGLnIPLuGSNuQzFxTIYqQoYkypfr8/vjso92xzzn7nL3PWXuf834+Hutxztpr7bU/Z+/v\nWXt91ncyd0dERERERKSha5J0ACIiIiIiIvVByY+IiIiIiDQKSn5ERERERKRRUPIjIiIiIiKNgpIf\nERERERFpFJT8iIiIiIhIo6DkR0REREREGgUlPyIiIiIi0igo+RERKTAzWzrpGEREROTPlPyISKNh\nZj3N7C0zm2pmC9LLe2b2enp5P73tZTM7ysxqfI40s32AH8zs7ML/BSIiIpKPZkkHICJSX9z9LaCn\nmW0NpIBn3X37zH3MbHHgROBaYHtg9xq+zCrALOClvAMWERGRglLNj4g0Rn3SP/9bcYO7/+buFwE/\nALuZ2RY1ObC7X+buK7j7swWIU0RERApIyY+INEbbpn8+nW2jmTUDFk+vrlQvEYmIiEidU/IjIo1K\nejCCTYEp7j6hkt16A0sAv6HmayIiIg2G+vyISGOzFXHuG5Vto5k1BQYD84H/c/dvzGxH4EDgG2B5\nYAXgdHd/N/2cpYBLgSWBNYG93f2rSo6/CXAMkVg5sAC4yN2/yHPf6mLcCPg/YFVguLv/x8z2BPoC\nvwPdgUfd/bLK37pFXm914GygPfA8cC5wHLA2UWvWFjja3b80s67AGUR/qLuAW4BT0+vLAm+4+7Ca\n/k0V9t0pve9UoCnwE3CDu0/O2MeAvYEBwFdEgrskcJS7/5jlmDm9/zX5nEREJGHurkWLFi2NZiGS\nlAVEglJxW3fgCeAToB9xEf8f4E2gTcZ+hwHTgRXT68OAddK/fw9cWslr9wHeqnCsW4G7a7svcQGf\nS4wPEEnBsUSycwlwXMb+m6Xflw1zfB/vJBKXHdPPexTok7H9FuBdooXB3ek49yeSyvvTr7c88DUw\nqzZ/U/qxxYHbMvcFegLfAvdk7Lcc8CTwWoXnHwucn8f7n/NnqkWLFi1akl/U7E1EGpvy/j4Dzeyu\n9HKPmT1IXAjfCKzl7k8RF9X9gT3c/fuMY9xLXEz/08xWAZq6+wdmth7QmrjwzuZM4JnyY6Wb4PUj\nLtxru++IHGLsDrzt7vOBDkQSNM3dr8rY/4f0z9Urif0PZtYa+MndZ6ePB/Afdx+TsdurwLpELctU\nd/81va8BD7v7uHR8zYhEqkZ/U8ZjtwC7Vdh3Q6KW6PV0vE2Be4Atgf7unvn5zCV7E/Bc3/+afKYi\nIpIwNXsTkUbDzFYA1gcmu/tu1ey7D9FE6nzPaDqV5umf6xLNvq5Lrx9C1ILcVclhVwAONbMvgBfc\n/T0qH1Ch2n1rEGMLorYFoj/T5+5+cYX9u6d/5tJUawVgePr3vsDPwCMV9mmd/rkyUfNT/trfufsd\nAO7+KdE8rjZ/E2a2F5FcLbKvu99kZiPd/af0Q/ul47zO3b9JP7clsCdwMNmHM8/1s6rJZyoiIglT\nzY+INCblQ1w/n8O+JxIX2zdm2dY1/XOWu7/q7h+m5wc6AHjK3b+s5JjDgFbAVcD/zGyCmW2Yx765\nxviSu09IX/BvBGQbhntXYDbwRiXx/MHdP3L3V9N9aPoAL7v77xV265X++XZ63+ZEf6tUNYfP6W9K\n/zypsn0zEh+Aw9M/W5vZtWZ2DdGv63tgc3efmuW1cv2savKZiohIwlTzIyKNSXmTtyqTn3QisxHw\nSSWJzHbpn5nNvHYn+rDcVNlx3f1WM3sD2AXYJr3818xWcfd5Ndm3ljH2Jm56ja7w9y4J7Ew0R1sk\njmr0IGp4Kh6vKZEUzQHGpR/elBhc4LnKDlaTvym9b68q9s20LjEAwkB3X1DNvkDun1VNPlMREUme\nan5EpDHpS9QUVFfz04romzKx4gYzawIMAqYRfYLKHU6MNPZYer8jMp6zu5nNMLO93f09d7/Q3fsS\nI561BVrWYt/axFie/FVMQPYElgbuSD9/PzNbopL3JlNlx+tDNLX7T0YNTGX7ZqrJ31Tpvlk0BT7N\nJfHJ9f2vyWcqIiLFQ8mPiDQKZrYa0Bn40t0nVbP7d8SgBZZl29Hp4xzu6eGRzWwloAy43d0XpAc+\naJ/xnMOIEcwqDn/9OfCBu0+vxb41ijFt2/Qxvquw/37EqGuj0rU2u6YHKKjOtkQy+b8Kj5+ePt4/\nK+w7xd2rSlZq8jd9RwyBnW1fzKybmV2dXh1HvKfZ9lvezC7PeCjX978mn6mIiBQJJT8i0lj8Jf3z\n5ep2dHcHzgO2NrOVyx9Pz4tzPrC/u2d28C/v3P+8mTUDTgGGZmx/HzjJ3cdmHKsDcDJwZIWXz2nf\nmsZoZu2AblRoopYR/9j0MY9j4WAGlTKzxYg+PDOJmqPyx88n+uZs5+4/pB9bBtiYRZvg/UlN/qb0\nvudm2XcxMzuYmFfo1PTD5wKd03Mdle9nZtaP6C9Um8+qJp+piIgUCYvvDxGRhifdVOolYkSuTsQN\nn1+Bz4DH3f30ap4/iJibZjKwDDADuNjdP8+y70XEEMszgMvd/dWMbYsDpxFDPf9KNMNqCgxz9w8r\nHCfnfWsSY3q461HAzu7+RoVtZcAQYDzwlrtfUdX7kn7O1sTgBccB7YgRzpYlam7OdfdpGft2Al4B\n9q0wHHZlx87pb0rvewAxuelkYv6iZsBj7v5Yhf36EonJl8RkpIsRZeM/nvFFmOv7X9PPSUREikPR\nJz9mdgtxx/Y7d1+vkn2uJCba+xkY5O5v12OIIiKNjpmdA/wL6OruHyUdj4iISC5KodnbrcSEcVmZ\n2U7AGu7eBTiChfNtiIhI3dmW6D+lxEdEREpG0Sc/7v4i0aa8Mv1Jj2aUbmbSysxWrI/YREQao/Rk\nsdX24RERESk2RZ/85KA9MCVj/UtglYRiERFp0MxsCNHZvymwu5m9bmZdq3maiIhIUWgok5xWHOq0\nuDsyiYiUKHc/hRjNTkREpOQ0hOTnK2K0nXKr8Od5FzAzJUQiIiIiUi/cPes8ZJKshtDs7VFimFPM\nbFNglrt/m21Hd9eiZZFl8ODBicegJcdlzJjKt1X2OVZ8/Ndf8a++wt99Fz/oIPzBB/Gbb8aHDMFP\nOw0/8kh8r70Y3KoV3qsX3qUL3rIl3qQJ3qwZDnjr1vjKK+M9e+JbbYX36IFvskls69sX32kn/Iwz\n8PPOww84AD/ssNj2f/+Hn3wy/tRT+IIFNY89322VPH7vvc5yS/xEp07OKac4r7/uLFiwcPvg3vG+\nz5zp3Habs/POTosWTrc23zJrVgHjy/e9+P13fNYs/L778GOPjc8S8IED8T33xPfZB99hB7xPn3h8\nww3xddfFN90UX289fMUV47MG3Axv3hxv0ya2bbUVvssuDG7bFj/hBPycc/CrrsLvvBN/8sn4jCdO\nxGfOXPSzre3fW1VZ11J0i75HtGRbpHgVfc2Pmd0F9AZWMLMpwGBifgbc/QZ3f8LMdjKzicBPwMHJ\nRSulZvLkyUmH0DilUlBWlvvj2ba5w48/wnffwRdfwMMPw/ffL7q88go8/jhMnw7TpsEvv8ASS8BS\nSy3cvuSSsOaasMwy8M03sOSSTJ41C7p3j23bbAM77QSLLw5nnx1LNlVta9++8m0JSaVg2DAYPRrm\n/LoUxx0AZjBnTvysqFUrWHVV2HBDWGcduPjitnTtCgccADvuWPnHVm+aNYOWLWHPPWMBaNcu+/te\n3ed41lnxRsyaBc88Ay++CL/+yuTvvoMPP4xytGBBbP/1V/j0U7j/fvj5Z5g3D1ZYAVq3jp/ffw9T\np0KbNn9eZs+G33+HxRZbNIaa/B/kuk3qjL5HREpL0Sc/7j4gh32OrY9YRKQGanORNmYM9OwZSUjF\n5ckn4Y034NtvY/nmm3jO0kvHRejYsZHULL88NG0aj3/6KRx2WDy+/faRxJRf2Vd1AdyjB9x8cz5/\nfe4qe4+quoitzbYKj3/8Mbz5Zryld100mbPP6Zj9abu1WuQQ5YdZfOpkfmrTkVGj4OSTCxBfVdtq\ne7zaatIEWrSI5dBDYwGYMAGefvrP+2eWpblzI+F+9tlIhl58EVZfPd7w5ZaLsjppUmz77ju4/PJI\nrNu2hU6dYMUVYfJkaN48krfMpW1bJUYiInkq+uRHpC4NGjQo6RBKW00utn76Cb76KpZ334VLLok7\n4l9/vXD5/HO49FJYaaW42GvaNO6yL7MMvPMOrL12PN63L/TvH0kNVJ7IVJXgVGFQjx7ZNxT6or6q\nbXV4vGuugSFDItdcYw2gY8fKD3dC9vfCOnXkksHwz39Cnz5xrb9i+SQDJfRe1GRbpeUiU/PmsPvu\nsUC8t9XVMk2fHglTKhX/J6+9FrVBc+bE8ebOjWR/+vRYf+QRWHnlWFZaaeHvX38d+7VtGwlcptrU\ntkpO9D0iUlqU/EijVqYv/YVqc9e4/PHZs2HKlIXLl1/Co49Gs7Kvvor1n36K2pgWLaKZ2tSpsOyy\nccXcuTOsvz5cfXVcTcOi1QxQ60SmUlV89mWVXczURfJTT8o/qssvhyuvjPVOnWJbbcIrK4tKtAsu\niOvxsjJ47rm4Fi+a6+kCJz+1KhfVadIkmsAdfHAs8OeynkrFsmABnHce9OoV/3Pl/0v//W80AZ04\nEe64A377LZrcrbFGNLlcZRX44AO47z7o0CGW8psLqknKm75HREqLkh9p1FKpVOP64qrNxcz8+ZHI\nLLZYXGh9/vnCn6+/Hh1H5s6NC6pllon9W7SAt9+GAQPizveOO0ZNTXVNzlq3rl2CU+CL3BRQxTNL\nUioVuejw4fD889F/p1xtkx+Ij/TssyMB6t07EqCGel2copJyUddJceaNgCZNqu939uuvUQv0+OPx\nYb/3XlTNffEF/PBDbJ8zJzJVd/jkkygQq6226M98bog0Io3ue0SkxCn5EWloanrBMn/+wiZnt98e\n/Q3Kl0mTotameXN4+eW4IDKLu84tW0Zn7pNPjoEB+vRJrKamVslPI/P881HZlkpFZUChnXHGwgRo\nl10Kf/ySlUS5XWKJqE09/vhYYNH/x1QqRrr48ceoBvz5Z3j11UiSfv994Q0O97jx0alT3MTIXH77\nLftrq7ZIRIqckh9p1Er6bl1N7rz++GN0/v/ww+hrM2kSfPYZvP/+HyOcMWdO9H5v1Qo22QS6do2L\noJYto21Tv35xrMy70GutVRQ1NYVW0uUiQ3lrqQ8+iJ8nnQQ33fTnFoWFeq05c6Kl1RVXRIvGpk3r\n5rWSUm/loj5rkpZbLnsTO3c499wY3m/WrGi2Onp0FKZZs2L0xCuvjPPFWmvBpptGwjVpUtw46dAh\nCkCmBpoYNZTzhUhjoeRHpJjlerHgHrUwEyfC//4Xnag//TSW8ePjzu7yy8foUlOmxAVP797RAaRj\nx0h+qqqpadas5kmOamoSV1YWI3avuy4cckiMJVGXr1VWFkWxS5fo3nXaaXX3eo1WfSZG5W0asxk8\nGI4+Om6i/Pe/UTP8xBNx/nnooTjnrLQSrLdejHZXPuLdhAlRk7T44oseT83oRKSeKPmRRq0o2mrX\n5G7o9OlxAfHxx9G5YsKEaK8/YUJ0hm7dOgYYmDEjkp399oO99opBBcovZJJuilYCiqJcFMjJJ8Me\ne0TRqA9msPPOkWjtsUckQg1FSZeLQt9wMFs4BPfmmy98vPwc88svUQv08MPwwgvRrO711+Gpp6Im\neoUVIjHq0iWqC8vPa506LTrvUQnUFpV0uRBphJT8iNSXXO9s/vJLJDQffRQXDQcdtPDC4Lffohla\n69bRPn/33WNenMGDY0ABqH2Co5qaBmf06Jij84MPYk6f+rLbblGhePjhkaNXHHVZikhd1SQtuSR0\n6xbLGWfEY+XnpvJ+RQ8+GOe/N9+M4b3LE6N27WKurTXXjPPgmDHRtG6llRadgbcEEiMRKT7m7knH\nUC/MzBvL3yoJquoLNzMpcY+JOidMiD44XbrE7x99FDU3LVvGndEJEyKpad06fu66a/UjplWV/OiC\noNH4+edo8jZsWNTE1Lf582GzzeCII2KeWWkkcj0HVrbtt9/gnntiUuPp0yN7X3XV6GPkDuusE4nQ\n2mtHE7vBg+P8WbEZnc6DkjAzw92t+j2lvqnmR6SmanK3ccGCuMP54YcwdmzMFD9+fEzyOX9+zO8x\nZQpst10kO+efD/vsE31soHa1OA20KZrUzDnnxHQwSSQ+EH3db7455qP9y1/ipr00AvmefxZfHA48\nMBZY9Bw4cybcdReMGhW1RGPHRq3QrFlRW9SzZwzU0rVr3ESaPTtG3qhI/YtEGjU1RpBGLZVK1eZJ\nf35s/vwYbOCjj+Df/4YDDohRkpZaKppvHH98zLPx7bdx1/KOO6J52xdfxJ3LUaNg5Mjoo9Msx3sS\naopWZ2pVLorI22/DiBEx6lqSunePmp/jjks2jkIp9XKRuHwTo+WWg2OOiX5EL70U585p06Kac9So\nOOe+/joMHRqZ9/LLRy36xhvHUIfDh8O4cVUP010LKhcipUU1PyKVyXYX0D3uMj7xRAwT/cEH8WU6\naVIMb/XDD1HT06ZN1PLsv39M+AmqxZF6MW9eNDMbMgTatk06GjjzTFh//bhe3W23pKORopXPzZzm\nzaNv0eDBCx87+2z4178W1rw/9hhcdVWMeDl1Klx7bZynN9wwJmFeZ52YrLkyqhUSaTCU/EijVlbV\nxieeiJ/vvw9PPw3vvBNfnHPnxhdp27aw5ZYxMWi3btG8QglOg1DKIzcdd1zc8C5vNZS0JZaIuYUG\nDox5cN9+u3SLdSmXi5KVz/mxadOYe6hz50Xbfw4eHAPJfPBBnMuHDo1z+7ffwvXXx7m9V6+Yrbd8\nRLoqkp9qohCRIqPkRxq+6vrobLFFDCzw7rsLl//9LzrbvvRSfPntsAP84x8xYcpVV9XfxJ4iNfDp\np3DbbZGvWxF1s91667j2PO20GHVdRV4KoraJkdnCpGiXXRY+ftZZMGBAjKT53nvRFPm99+Drr6P5\n3OTJ0Zaze/eozmzTJp6nPkQiJUV9fqRhqKrNdea2adNi/N+hQ+HAA0ldeWV8qe21FzzySGxv1SrW\n586F7bePntrrrhuTglY3WYpqcRqEUm3Df8wxURnZuXPSkfzZxRfHTfYpU5KOpPZKtVw0SrU5Fzdp\nEoMl7L03nHcenHBC9N/8+9+jVmj6dLj77ug/tOaa8d2www6k7r8f7rwzapLmzVt4vFy/l0SkXqnm\nRxqGbKOsffpptLEZPTo6wf7vfzH6z2qrxRwUK64YowedcUZMqpc5szlE59psNTxKcKTIpFLwn//E\nVCmzZi0sthWLdFJSqVg23BBuuQU6dIjHiyU+aWRyrYXPLKDNmy/6fTBmDDz6aCRFo0bBhRfCN9/A\nnDlxs6xHj6gxevHFqCUq7/tZTrVCIonRPD9SWrJ9YcydGx0dNtkkkp2334a33oqEZqWVYgS2ffaJ\nZGe33aLjQblc5p0QKQH9+sEee8QIv8VabOfOjZZCo0bFv6tIycj1u+LJJ+GBByIR+u9/YeWVoz9R\n27aw+eawwQaRGD33HFx6afbjKTFqEDTPT/FSszcpPlU1B3jmGXj1VbjuuoWThyy9NNx4Y8zm+NFH\nsPvu0bbmhx+iL8/gwdFU4YorFk18qqMvHykRr78eA1oVyyAHlWnePJrlnX9+0pGI1FCu3wc77hjD\nbD/+eHz3fPVVTGvwzDPRVO7xx+HYY+Gyy2KQnDXXjH/chx+OqQ/cK/8OVFM5kYJQ8iPJyKUt9M8/\nw8svxwADBx0UAw8MGQJHHw1vvhnJz0MPRZIzeHAMVDBqFJx4YvV9c8pfqlWryjcq+Wm0Sq1vxwUX\nwCmnxPyQxV5s/+//omL27beTjqTmSq1cSAFV8Y9V5fcIxNxt3brFP+rLL8Nnn8XgCu+/H53hVlst\nhkTceOOoGr39djj9dLj//phGobzVivoQiRSE+vxIMipW6//ySwwl/cYbkdDcf398QXTrFs0G3KPJ\nwPvvQ//+8Zxu3WDTTat/raquBnv0yOOPEEneu+9GZehdd8V6sSc/228fAydecEH8m4uUvMq+R6ob\ncW611WL5618XdoybPTsG5Bk3Dh58MAZZcIeePeN7cr31YKONYNVVFx3SUU3lRHKmPj9Styrro3Ps\nsXEyf+ONWMaPj8lJ2rePWp0jjog20ttuu+jzK2t3rRO/NFL77BNTkvzjH0lHkruffooR6Z57LuaW\nFGl0qvrOyvyeS6WiqdzXX8cdji5d4vdmzeKG4EYbxfL889GUrqavJXVGfX6Kl2p+JH9VnVjHjImB\nBl5/PWp0XnstOn/Omxd3y1ZeGY46CgYNitkQofAThYo0UBMmxL/Y8OFJR1IzSy8dowhfdBHccUfS\n0YgkINfvrMwR59ZcM74b3SMBuvXWaOo9cmSMbnrTTXEDccstYd99Iylq2bL6ue70/SmNjPr8SP4y\n2xp//XUkOaefDttsA//+d8xu+MQTsNVWMfDArFnRR+ftt2M0nKOOWpj4VKfAJ2m14ZdsSqVcXHRR\n9KFZZpmkI6m5v/0Nnn4aJk5MOpLclUq5kPpV8HJR3fecWSQ5Z54JL7wQ/0RnnRVNxwcPjmG1zzkH\nVlkF1lorms9dfXXcfPztt4rBFzZ2kRKgmh/JTba7Q3PmRJO1l16KMXZffTVOrKuvHvPorLxyNHE7\n4IDYv2fPSICqo3l0RKr12Wdx7+DKK5OOpHZatIgE6KKLSq/mSqRO5ToPUSazaEvauXPU+qRS0a70\n++/h+uujluj88+Pm4/rrx1jzG28MM2ZETZJVaJ2lGiFpwNTnRxZV2Qlv8ODoXPDKK5HkPPtsDMvZ\nrh18+WUkP+3b5z6Pjk6sInk54ohoUXreeUlHUnszZkQXhrfein7fIlJLufYh+umnuNvw+OPx3T1+\nfNysbN8+bk7uu28kRcOGVd78XN/fOVGfn+Klmh9ZVPlJbcaMSHLGjYuE54UX4M47Y3S1TTaBww6L\nu0fls16rj45IvZkyJeZR/PjjpCPJz/LLRxI3ZAhcc03S0YiUsFy/U5deGo4/PhaI7+4jjojv+1de\ngQsvjEGHFl88bnButll873frBk2bxnOU/EiJU5+fxqhiG98FC2II6RtvjInW1l47bsOecUb0pm7d\nOpqz7b8/rLFGDLXZq1ckPtUp8hOk2vBLNsVeLo4/Hg49NOfprIra3/8eg1h9/XXxdz8o9nIhySj6\nclHd9/DKK8dw2zvuGPv+/e8xxPa330ZfoX794k7FdttF36JPPoGZM7Mfq9jfCxFU89NwVXVn5qmn\noi/OuHEx4drYsZHIdOgQk4YceWQMM73NNguPsdZaldfuqI+OSL355pv4F77uuqQjKYy2bWMO40sv\njX5AOmWIFFiu39GZI8s1abLod/4jj8A998QN0Zdegvvui5HkNt44mr1vtllcJ1R27aHaIikiSn4a\nqvITjXvMED12bCwvvxzj444bFyerv/0txppt0yae18iasJWVcOxSd4q5XAwbFpWv7dolHUnh/OMf\n8TcdfnjSkVStmMuFJKeky0Wuse+6aywQ1whnngnvvRfXFKNHLxxMoXXruJm6xRbRQmSppeI5Sn6k\niCj5KXUVTyhz58YQ0uPGxd2Yl1+OUVy6dIlOjZtsEies8kEJWrRYmPhURSctkUSlUjHOyFVXwc8/\nL7xHkXmzthSVT2y/yirR92fJJePxUv+7REpadf98zZrBBhvEss46cY0xezYMHQqPPQbXXgvTpkH3\n7pEIffklTJ0KK63052MpMZJ6ptHeSkFVJ4bTToPevaNW5/HH4cMPYbnlYiLRv/4VVl017tbkMgJb\nda/VAKVSqdK+ayd1oljLxZ13wm23xcTuNa2gLXZjx0L//nG9VHHU3WJRrOVCktXoykWuI8s9/XTM\n7TdlStQOLbFELL16wZ57RlLUtSuce26DvCbRaG/FSzU/pSDzn//LL6O97Ysvxs/x42OUli22iAlF\nN90UWrWqXfM1KNmTjEhjcN11cOKJ0TWvodl88xhM6rnnYNttk45GRCqV63XCDjvEAnE9ctZZcc0y\ndmxcv1x8cQycsMIKUeW71Vaw4YYx0ly5Ek5+pHgp+SkW2f7B3aN/zptvxkShL70U1cprrx3taHv1\niqug3r1j/yWWiMSnOjqR/KFR3a2TnBVjuXjvvei+179/DLzU0JjBwIExH2OxJj/FWC4keSoXGap6\nL5o0iSZy66wDa64ZE7KWN5V78MHo0DhrVgyisNVWsOWWMdJsNkqKJA9KfopFKhX/6O+8E7U6DzwQ\nM/81bw4//AA77ww77RRVxZlN2FZZJXsNj0ZgE2lQrr8+BgRo1qzh/gufey507Fh51wARKXKVnZwq\nPp7ZqW/ZZRdex/z4Y5zsHn88BmP6/HMYMSKm39hpJzjqqBgiUsmP5EHz/NSniuPf//ZbJDoXXAC3\n3x6jpAwaFDMX/u1v8XPWLBg8ODoQXnPNoolPVXRSyEnRz88giSi2cjFnTsyFU+yjoeWrRQvYe2+4\n+eakI8mu2MqFFAeVixzkek3SogWcckpMrD55Mvzzn3D//bDbbjEJ65prRuuXxx6L5GjKlD8fQ5+H\nVEM1P3WhsjsSo0bB/PnxT/3889FXZ7nl4o7GZ5/BySdHc7aaDHOkJEekwRs5Mlq3tm+fdCR176ij\nomnf6adHLZeINHBVXcc0axZ9mrfYIvo0P/dcDOh0ww1w4YUxL+Gyy8ZErFtvHcuYMZUfUzVGQgmM\n9mZm/YBhQFPgZne/uML2FYA7gHZEMnepu4/Icpz6G+2tfLCB2bOjY9/zz8fyxhvRlrX8H3TzzeMu\nR+ZzstE/q0ij5Q49e0bf4O23Tzqa+rHZZpH89O+fdCQikqjKrn/Kr5nK+0a/8MLCG8s//AC77BJ3\njHr3jslXy4eQrO1gULWg0d6KV1E3ezOzpsDVQD+gGzDAzLpW2O1Y4G137wGUAZeZWd3fL8xWrfrD\nD/Df/0aM+ixwAAAgAElEQVQNz8YbR6P1U0+NuXa6dIHff4e+faMfzxJLLEx8qqPER6TRevXVuI/S\nt2/SkdSfo4+Oke1EpJGr7vrHLIbLXmutuM469NBoJ/zTTzHXUFlZXIvtvXd0Hfjuu0iYKlJTuUal\n2BsVbAxMdPfJAGZ2N7ArMD5jn6lA9/TvLYDp7j6vziNLpWJyr5deit8ffTSGYmrfPtqpHnRQ3Kbt\n23fhP2+nTpXfcVCCk4hGNz+D5KSYysX110fLjiZFfauqsPbaC046KVoDd+6cdDQLFVO5kOKhcpGA\nqgZQMFv0Wuvuu2O5+eYYVOq226K7wXbbwRFHQLduamHTyBT712l7ILM325fpxzLdBKxjZl8D/wP+\nr2CvXvFOwI8/whNPRN+cG2+MkdaGDo0anJtvjtuzkybFAAUjRsD556vvjojU2owZ8MgjcPDBSUdS\nv5ZcEg48ME6zIiJ/UpNrpn33hYcfhrffjuuz8eOjXe2cOdG2dsUV4d57o6boww//XDOkWqEGJ6ea\nHzP7OL3vM+lltLvPrGL/HYClgSfd/Zc84sulk84ZwDvuXmZmqwPPmNn67j674o6DBg2iY8eOALRq\n1YoePXrE3ZpUilR6n/K7N6lUCm66ibJff43tjzwCn35KWfv20LEjqalTYf/9KVt9ddhqK1Lz58O4\ncYs+v+LxWrWiLP06WbdrXetaL4r18seSjuett8rYeWd4//1kXj/J9Q02gJNOKuOcc2DcuOTj0brW\nK1svf6xY4mn0661aQVWfx2efQYcOlB1wAHToQOr99+GBByi76SY444y4nuvVi7K994Y+fUjdemvl\nr5dKEWv8sW3y5MlIcctpwAMzuwk4NOMhB95iYTI01t3nZuzfGtiFaKI23N0fr1VwZpsCZ7t7v/T6\n6cCCzEEPzOwJ4AJ3H5teHw2c6u5vVDhW5QMelHeA++WX6J8zZkyMKPLGG9Hztk+fWDbZJPrqZD4n\nm1QKMk6KIiI1tWBBjOg6YkSMjdIYbbdd1HoNHJh0JCLSIFR2fZZ5TTd5cuw3ZkwsM2dGDdE228S1\nYKdOOQ2goAEPileTHPd7kGh+1gbYE7gBaAmcBowGZprZU2Z2kpl1d/fp7j7C3f8KDMgjvjeALmbW\n0cyaA/sAj1bYZwLQF8DMVgTWAj7L+RXKR2MrK4M2beD442PEkDXWiAEKyufVcV+Y+FRHiU/JKL+D\nI5KpGMrF5ZfHKWezzZKOJDlHHRV9norg4wCKo1xI8VG5KCG5XJ917BhLp05x92XOnOjWMGwYbLRR\nbDv4YPjPf2JgBSk5uQ54MBq4zd2nE4nQgwBmtiqRePQFtgG2Tz/+Xfo5U4DOtQ3O3eeZ2bHA08RQ\n18PdfbyZHZnefgNwIXCrmf2PSOZOcfcZ1R48lYrlwQfhvffi1uJmm8EOOyz85+jcWQMUiEgihg+H\n445beIOxMerfP+5H3XuvTrkiUocqnmDKyhY+ljmAgntMSn/PPfDvf0f/oaWX/vNzpKgVbJ4fMzNg\nPRYmQ5sDs4HD3f2pgrxIHnJq9pbr4yIidWjq1Lj38t13MX9fYzZ4MDz5JLz2WtKRiEijVNW1oJq9\nlaSCDXWdzizeTS9DC3XcRCmDF5F6VF4hPXYs/PorXHZZPN4YbyiWvxc//givvw5nnhmTvTfG90JE\nEqQTToNTsJqfYldlzY8GKGi0MkfoESmXZLlwh3XXjfFVbrklkRCKTqdOcMklsOeeycah84Vko3LR\niFVx/aian+KV64AHWZlZCzM738wuNLOVKmy73Mw65BdePdFJS0SKxFtvRa1Ph9I4e9aL9dePvsUi\nIkVF148lKa+aHzMbCbwMzAUOBjYvr14xs+WBG4G9Kq9yqT9V1vyIiBSJ44+H1q2hd299r5Z78skY\nk+ajj6Bt26SjERGpnmp+ile+yc9wdz80/fuhwPfu/mjG9n7Aiu5+W96R5knJj4gUu7lzoX17ePXV\nGPBAFjroINhgAzjhhKQjERGpnpKf4pVXszfg14zf7wfKKmx/Gtgyz9cQqTOan0GySapcPPkkdO2q\nxCebAw9MvumbzheSjcqFSGnJN/lpn55YFHf/AVg8c2O6quX3PF9DRKRRuO22qOGQP+vTB6ZNi2nZ\nREREaivfZm/7ACcB/d39GzO71t2PqbDPH03jkqRmbyJSzKZPh9VXhy++gBYtko6mOP3zn/Dbb3Dp\npUlHIiJSNTV7K1751vzcC0wHPjGza4DlzeyPY5rZRsAqeb6GiEiDd/fdsNNOSnyqcuCBcOedMG9e\n0pGIiEipyiv5SVelDATGAUcDewM/mNk7ZjaBGAnukryjFKkjaqst2SRRLtTkrXprrQWrrQbPPJPM\n6+t8IdmoXIiUlnxrfnD3mcCOwCBgLDAP6Ax8DvRx92fzfQ0RkYZs/Hj46ivo2zfpSIrfQQdFoigi\nIlIbefX5KSXq8yMixer002H+fBgyJOlIit+MGTEa3uTJ0KpV0tGIiGSnPj/FK6+aHzM73syeNLO7\nzexUM+teqMBERBqD+fPh9tvV5C1Xyy8fNWT33Zd0JCIiUorybfb2L2AHYr6fScAOZnaHmZ1lZi3z\njk6kjqmttmRTn+VizBho1w7WWafeXrLkHXRQMnP+6Hwh2ahciJSWZnk+fxegjbs/lvmgma0LDDWz\nh9z98TxfQ0SkwbrtthjFTHLXrx8cdhh8+mkMDy4iIpKrOu3zY2YnAx+4+xN19iK5x6I+PyJSVGbP\nhpVWgkmToE2bpKMpLSecAC1bxuSnZWVJRyMisij1+SleeY/2VhV3vwTYvS5fQ0SkVD3wAKyyihKf\n2ihv+jZmTNKRiIhIKcl3wINVzOxSMzvNzCprfKDqFilaaqst2dRXubjtNlh//Xp5qQanRw9YZhn4\n4ov6e02dLyQblQuR0pJvn597gS5Aa+BCM3sFeAR4Ffga2ABYO8/XEBFpUFIpeOQReOUV+PVX6No1\nHi8rUxOuXKRSsbRrByNGxMSnoPdPRESql1efHzO7xd0PMbO1gf2AA4EOGbssAPZ19/vzCzN/6vMj\nIsXkkkvgk09g5ZXh7LOTjqY0TZkCa64Js2bB4osnHY2IyELq81O88u3zM8vMerr7BHf/F9AR2Aw4\nDvgHsHExJD4iIsXmzjth4MCkoyhtHTpA27bw1FNJRyIiIqUi3+TnNGAXM7shnQS5u7/q7te4+1B3\nf6sQQYrUFbXVlmzqulx88AFMmwZbb61mWvnac08YObJ+XkvnC8lG5UKktOTV58fd5wLnmFkLYJXC\nhCQi0rDddRcMGABNmij5ydcZZ0DnzjFs+LLLJh2NiIgUu3z7/LQATiFqkK5y96kZ2y4Hhrr7lLyj\nLAD1+RGRYuAeE3M+8ABssEHS0TQM/ftHDZAmixWRYqE+P8Ur32Zv1wPfAJOBB80s80M+D7i8wmMi\nIo3aK6/AEkvEUM1SGPvtV39N30REpLTlm/z84u5Xu/uNwM3ALuUb3H1G+jHdi5Oipbbakk1dlouR\nI2OgA90WKpxddomk8ttv6/Z1dL6QbFQuREpLvsnPrxm/3w+UVdj+NLBlnq8hItIg/P473Htv9PeR\nwllqqUiA7r036UhERKTY5Zv8tDezFQHc/QdgkZkW0p1sfs/zNUTqTJl6m0sWdVUuRo+GTp2iz48U\n1sCBdd/0TecLyUblQqS05Jv83AU8Zmbt0uvZGnJo6jkREeLifL/9ko6iYerbFz79FD77LOlIRESk\nmOWb/NwLTAc+MbNrgOXN7I9jmtlGaAhsKWJqqy3Z1EW5+PlnePRR2Hvvgh9agMUWi/e2Lmt/dL6Q\nbFQuREpLXslPulnbQGAccDSwN/CDmb1jZhOAl4FL8o5SRKTEPfYYbLIJrLhi0pE0XAMHwp13xnDi\nIiIi2eQ1z88fBzFrCuwHHA6sCzQlEqJz3X1s3i9QAJrnR0SStOuusPvucNBBSUfScLnHhKcPPaSh\nxEUkWZrnp3gVJPkpBUp+RCQpM2bEQAdTpkCLFklH07D9858wdy5cojYHIpIgJT/FK98+PyIlTW21\nJZtCl4v774cddlDiUx8GDoS77oIFCwp/bJ0vJBuVC5HSklPyY2Yfm9lnZnaDme1pZstVs/8OZra7\nmS1ZmDBFRErXtdfGRbnUvXXWgdat4cUXQdekIiJSUU7N3szsJuDQjIcceAt4Jr2Mdfe5Gfu3BnYB\ndgWGu/vjtQ7QrB8wjOhHdLO7X5xlnzLgcmAxYJq7l2XZR83eRKTeTZkCa64Js2bB4hr4v14MGQIT\nJ8LKK8PZZycdjYg0Rmr2Vrxybfb2IDAFaAPsCdwAtAROA0YDM83sKTM7ycy6u/t0dx/h7n8Faj2X\neXoghauBfkA3YICZda2wTyvgGmAXd183HZ+ISFG4+27o2lWJT33ad1944AGYNy/pSEREpNg0y3G/\n0cBt7j6dSIQeBDCzVYG+6WUbYPv049+lnzMF6JxHfBsDE919cvq4dxO1SeMz9hkIPODuXwK4+7Q8\nXk8amVQqpdm55U8KUS5SqViuvx6+/XZhDURZWSxSN8rf92WWgQsugGbpb7lCvO86X0g2KhcipSWn\n5CfdpO2sLI9/AdwC3GJmBqzHwmToL8BsYvjr2mpPJFDlvgQ2qbBPF2AxMxsDLAtc4e635/GaIiJ5\nKyuDtm3hppvgX/9S86v6Up7ktGsHV1+t911ERBZV1ENdm9keQD93Pzy9vj+wibsfl7HP1UBPYFtg\nKWJ+ob+4+ycVjqU+PyJSr/71L/j5Z1h2WV2E17dp06B9+/i57LJJRyMijY36/BSvXJu9JeUroEPG\negei9ifTFGKQg1+AX8zsBWB94JMK+zFo0CA6duwIQKtWrejRo8cfVdXlQ1VqXeta13oh1t1h5Mgy\n7r0XXnwxRSpVXPE1hvWePct45BFYZZXiiEfrWtd6w10v/33y5MlIcau25sfMmgML3L3eu46aWTPg\nI6JW52vgNWCAu4/P2GdtYlCEHYDFgVeBfdz9wwrHUs2P/EkqlfrjBCZSrhDl4tVX4cADYcIEMN37\nS8TIkXDHHfDEE4U5ns4Xko3KhWSjmp/i1SSHfXYBPjOzq8xso7oOKFM64ToWeBr4ELjH3ceb2ZFm\ndmR6nwnAU8C7ROJzU8XER0Skvo0cGXP7KPFJTv/+MHYsfP990pGIiEixyHWenxbAXsABxHDXtwO3\nu/tXdRte4ajmR0Tqy7x5sMoq8MILMcePJGfgQNhySzjmmKQjEZHGRDU/xSuXmh/c/Ud3H56ePPQv\nQHNgtJk9a2YHmNlSdRmkiEgpGTMGOnRQ4lMMBg6MWjgRERHIfZLTP7j7ZHc/193XBgYDWwIfmdkI\nM+tT8AhF6lBmR0WRcvmWi/Imb5K87bePfleF6IOs84Vko3IhUlpqnPxkcvex7n4kMdfOE8BJZvap\nmV1gZrrnKSKNzi+/wMMPwz77JB2JADRvDnvuCXffnXQkIiJSDAo+z4+ZrQgMJPoHzQX+A9zl7jML\n+kI1j0t9fkSkzj3wAFx7LYwenXQkUu6FF+DYY+Hdd5OOREQaC/X5KV551fxk4+7fuvvl7t4TOAJY\nHXjbzB4ws13Tw1eLiDRIavJWfLbcEmbOhPfeSzoSERFJWsGTn0zu/q67n0QkQMOBAcSw2Vea2QZ1\n+doiuVBbbcmmtuVi1ix49lnYfffCxiP5adIEBgyAu+7K7zg6X0g2KhcipaVOk59y7j7f3Z9w932B\n9YD3gJPq47VFROrLQw/BNtvAcsslHYlUVD7qm1o/i4g0bgXv81Os1OdHROradtvBEUfAXnslHYlU\n5A7rrAM33wybb550NCLS0KnPT/HKq+bHzE4ws1lmdk2hAhIRKUVTp8Ibb8DOOycdiWRjpjl/REQk\n/2ZvGwE/A7rPKSVJbbUlm9qUiwsugP79YcklCx+PFMaAAXDvvdEvqzZ0vpBsVC5ESku+yc9sYF1g\nswLEIiJSsh56SKO8FbvVV4fOnWHEiKQjERGRpOTV58fM/gk85+7jChdS3VCfHxGpKxMnQo8eMdpb\nMw3mX9Suugpuuklz/ohI3VKfn+KV79f0xcDdZvawu99RiIBEREpFKrVw+eknOP/8eLysLBYpHuWf\n05w5Md/PGWdA8+b6rEREGpt8a36OAK4DDPgOSAHPEbVBEwsRYKGo5keySaVSlOnKRyqoSblwhy5d\noE+fqFGQ4telC5x9Nuy3X82ep/OFZKNyIdmo5qd45dvnZwBwEPBP4B1gF+B64GMz+9zMRphZnzxf\nQ0SkaL3ySjR1W3nlpCORXHXvDrffnnQUIiKShHxrfm4HDnf3X9PrzYFNgW3Ty8bATHdfsQCx5kU1\nPyJSF445Btq3hy22UPOpUvHUUzHy24cfwkorJR2NiDREqvkpXvkmP12BwcA3wF3u/mqF7csAbdx9\nUl5RFoCSHxEptN9+i8TnzTdhtdWSjkZq4pBDYtLTk05KOhIRaYiU/BSvvJq9uft4d98XuBT4U2bh\n7nOKIfERqYzmZ5Bsci0XTzwB666rxKcUHXBAzZu+6Xwh2ahciJSWfPv8AODuX7r7a4U4lohIqbj9\n9riIltLTuzfMmBEjv4mISOORb7O3FsApRBJ1lbtPzdh2OTDU3afkHWUBqNmbiBTSjBkxYebnn0PL\nlklHI7Vx+ukwfz4MGZJ0JCLS0KjZW/HKt+bneqK/z2TgQTPL/JDPAy6v8JiISINw772www5KfErZ\nAQfAnXdGAiQiIo1DvsnPL+5+tbvfCNxMDHUNgLvPSD92YJ6vIVJn1FZbssmlXKjJW+nr1g3atYMx\nY3LbX+cLyUblQqS05Jv8/Jrx+/1AWYXtTwNb5vkaIiJF5dNPYeLEqPmR0nbggZrzR0SkMcm3z8/D\nwJHu/m16/Rp3/1uFfa5192PyCzN/6vMjIoVy9tkwcyZccUXSkUi+vvsO1lwTvvoKll466WhEpKFQ\nn5/ilW/Nz13AY2bWLr2e7UNePM/XEBEpGu5wxx1q8tZQtG0bE9Q+9FDSkYiISH3IN/m5F5gOfGJm\n1wDLm9kfxzSzjYBV8nwNkTqjttqSTVXlYtw4WGwx2HDD+otH6lauc/7ofCHZqFyIlJZ8Jzl1YCAw\nDjga2Bv4wczeMbMJwMvAJXlHKSJSJMoHOtA4lg3HrrvCa6/B1KnV7ysiIqUtrz4/fxzErCmwH3A4\nsC7QlEiIznX3sXm/QAGoz4+I5Ou336B9e3jzTVhttaSjkUI65BBYZx046aSkIxGRhkB9fopXs0Ic\nxN3nA/9JLyIiDdKQIbDeekp8GqIDD4QTTojmjGVlSUcjIiJ1Jd8+P5jZsmY20MxONbNBZrZqIQIT\nqQ9qqy3ZVFYuRo7UQAcN1dZbxwh+99xT+T46X0g2KhcipSWvmh8z60HM5dMm4+EFZvZf4O/u/lk+\nxxcRKRbTpsGkSbDHHklHInWhSRPYf//cJzwVEZHSlO88PylgDPA2sDywAbANsA7wE7CHu4/KP8z8\nqc+PiNRGKhXLK6/A00/D4MHxeFmZmkc1FOWf8fTpcPXVcOaZ0LSpPmMRqT31+Sle+SY/N7n74Vke\n7wKcRIwEt6G7f1L7EAtDyY+I1JZ79PXp1QtuvTXpaKQudewIl12mGj4RyY+Sn+KVU58fMzvezA40\ns5UqbFqQbX93/8TdjwKOAM7JM0aROqO22pJNxXLx6qswdy6sqh6NDV7PnnDzzdm36Xwh2ahciJSW\nXAc82AsYAXxlZu+Z2VAz2xEYbWanVfYkd78bmJ9/mCIiyRk+HA49FPr0SToSqWtHHhlz/kyZknQk\nIiJSF3Jq9mZmxwMXAFcAvYFNibl8fk/vcgswEnjF3X+v8NzH3H2XQgZdG2r2JiK1MXt21PiMHw/t\n2iUdjdSHY4+Ftm3hrLOSjkRESpWavRWvXGt+HgA+dvcz3X0rYnCD3YAbgUnAkcDzwCwzS5nZFWZ2\nkZmNBfK6f2Zm/cxsgpl9YmanVrFfLzObZ2a75/N6IiKZ7r0XevdW4tOYHHpo1PbNV7sFEZEGJ6fk\nx92/AvpkrM9290fd/Th3XxtYDTgMeBRoT/T1+SvwMHB8bYMzs6bA1UA/oBswwMy6VrLfxcBTgLJs\nyZnaaks2meXi5pvhsMOSi0Xq3wYbwAorwOjRiz6u84Vko3IhUlpynufH3X+sYtsUounbLYUIKsPG\nwER3nwxgZncDuwLjK+x3HHA/0KvAry8ijdgHH8AXX0C/fklHIvXtsMMi8d1++6QjERGRQsprqOtK\nD2rWF5jq7h/keZw9gR3Kh9M2s/2BTdz9uIx92gN3EPML3QI85u4PZjmW+vyISI2ceCIstRScf37S\nkUh9mzUrhr2eODFqgUREakJ9fopXrn1+auoTYG8zu97MWuZxnFyylWHAaenMxlCzNxEpgN9+g9tv\nh0MOSToSSUKrVtC/f5QBERFpOHJu9paNmS0LDAa6EgMbjAEed/fPgcFm1hG4jOgPVBtfAR0y1jsA\nX1bYZ0PgbjMDWAHY0cx+d/dHKx5s0KBBdOzYEYBWrVrRo0cPytLTd5e32dV641ovf6xY4tF6cawP\nGzaMmTN70L17GZ07Jx+P1pNZP+ywMo4+Gnr0SGHp22plOl9oPcv5QtcTWi//ffLkyUhxy6vZm5nd\nBfQEZgNrAUsDvxADH9wGvACMcPe9a3n8ZsBHwLbA18BrwAB3r9jnp3z/W1GzN6mBVCr1xwlMpFwq\nleLCC8s4+GAYMCDpaCQp7rDWWnDbbbDZZjpfSHYqF5KNmr0Vr3yTnzvcff/074sBWwMDiUlRl0nv\n9rS775jHa+xING1rCgx394vM7EgAd7+hwr5KfkQkb5Mnw0YbwZdfwhJLJB2NJGnIEPj44xj8QEQk\nV0p+ile+yc8N7n5klseXAv4CrEjU/MypfYiFoeRHRHI1eDDMnAlXXpl0JJK0b76Brl1j1L9ll006\nGhEpFUp+ileTPJ8/18xaVXzQ3X929/vc/epiSHxEKpPZVlcEYmLLYcNSmttHgJjctqwM7rknyoVI\nRfoeESkt+SY/Q4HrzKx5IYIREUnaqFGw2GLQvXvSkUixKJ/z5513ko5ERETylfc8P2Z2HDGa25lA\nyt1nFyKwQlOzNxHJxe67w9y58PjjSUcixWLevJjzZ5dd4Lrrko5GREqBmr0Vr3yHuv47MZQ1wCPA\nPDN7AxidXl5297n5hSgiUvdSKXj4YXjySfj1Vzj77Hi8rCwWaZxSqVi6dIHrr4cVV4zHVS5EREpT\nvgMePAv8C/gRWB/oQwxL3TG9yy/ECG3H5xdm/lTzI9loiFLJdOqp8PvvMGNGihEjypIOR4rIt99C\nhw4ppk4to3XrpKORYqLvEclGNT/FK98+Px+6+zh3/8DdR7r74e7eGVgdOIKY72fNvKMUEaljP/8M\nt9wCxx6bdCRSjFZcETp0gOHDk45ERETykW/Nz/XuflQB46kzqvkRkarcdFP083nkkWjmpBu5UtEN\nN8CFF8Knn0KzvBqNi0hDp5qf4pVvzc+z6QEPRERKljtccQUcn26gq8RHsjnyyKj9eeSRpCMREZHa\nyiv5cff7gVXN7NQCxSNSrzQ/gwCMGRMJ0DbbxLrKhWSTSqU4/nhNfiuL0vlCpLTklfyY2YHACcBF\nZjbJzG4ys33NrG1hwhMRqXtXXhm1PqYGClKNv/4VPvtMc/6IiJSqfPv8PA/cB3QAegMbsTCh+oAY\n7voOd38jzzjzpj4/IpLNpEnQqxd8/jksvXTS0UgpuOgimDhRgx+ISOXU56d45Zv83A4Mcvf56fWW\nRBK0bXrpBnzn7u0KEGtelPyISDb/+Ac0aQJDhiQdiZSKadNi3p9PPoEVVkg6GhEpRkp+ile+Ax5c\nAdxrZmea2Vru/oO7P+ru/+fu6wIrA9vnH6ZI3VBb7cZtzhwYMQKOOWbRx1UuJJvycrHCCrD77nDj\njcnGI8VB5wuR0pLvgAdvuPsewGNAmyzbv3H3d/N5DRGRunL77bD11tCxY9KRSKk5/ni49tqYFFdE\nREpHXs3eKj2o2XbAz8DLxdLWTM3eRCSTO3TrBtdfD717Jx2NlKKysqg13HvvpCMRkWKjZm/FK9/R\n3tY2s+WzbPoE6AU8YGab5fMaIiJ14bLLoHnzqPkRqY3yYa/V6klEpHTk2+dnDPCdmb1tZkPNbBcz\na+nuk919GLAncGz+YYrUDbXVbrxuvLHy4a1VLiSbiuWif3+YMgVGjkwmHikOOl+IlJZmeT5/V2B/\nYBtivp8TgPlm9g7wMvAdsEaeryEiUlATJ8JXX8HAgUlHIqWsWTP429/gzjuTjkRERHJVsD4/6YlN\ny4hEqA/Qhej3c4S7J35fTH1+RCSViuXxx+HNN2Hw4Hi8rCwWkVyVl6Vffolh0k84AVq2VFkSkaA+\nP8WrTgY8ADCzTsClwInu/nmdvEjN4lHyIyJ8+SWsvz4ccghccknS0UhDsMUW0LMnXHVV0pGISLFQ\n8lO88u3zUyl3nwQcCpxVV68hki+11W58hgyJxGfppSvfR+VCsqmsXGy2WTR9mzq1fuOR4qDzhUhp\nyavPj5m1B/4OfA3c6e7fZm5391lmNi+f1xARKZSpU+GOO+DDD2HChKSjkYZi551h/vyoSRw6NOlo\nRESkKnk1ezOzscCaQGtgLvAwcAfwrLv/ambLAXe5e79CBJsPNXsTkZNOgnnz4Iorko5EGpqvv4Z1\n142kum3bpKMRkaSp2VvxyrfZ28fu3gboDlwLbAs8Csw2s6+BqcDYPF9DRCRv338Pt94Kp5ySdCTS\nEK28coweeNllSUciIiJVyTn5MbO1szz8i5l1dff33f1EYCVgZ+Ai4EFgkLufV5hQRQpPbbUbj6FD\nYd99oX376vdVuZBsqisXp54KN98M06bVTzxSHHS+ECktNenz8wCwToXHTgbOt5gl8Hp3/wh4Ir2I\niBSF6dNjUtO33ko6EmnIOnSAPfaAYcPg/POTjkZERLLJuc+Pmf0GrOzu07NsWw1o7+4vFzi+glGf\nH9zHxG4AACAASURBVJHG66yzYrCDm25KOhJp6CZNgl69YiLdVq2SjkZEkqI+P8WrJsnPAuAN4BLg\nuWxJUDFT8iPSOM2aBWusAa+9Bp07Jx2NNAYHHwydOkXSLSKNk5Kf4lWTAQ8cuBpoA9xgZmPM7DIz\n28nMqpgxQ6R4qa12w3fVVfCXv9Qs8VG5kGxyLRdnnBHl7scf6zYeKQ46X4iUlpr0+fnI3f+T/v1a\nM2sCbEiM8HasmTUHxgHPAi+7+++FDVVEpGaeeCIuQl98MelIpDHp0gV22AGuuSYmQC0rSzoiEREp\nV5Nmb53d/bMqti8ObAFsA+wITAeeA55297cLEGte1OxNpPHp2zfmXBk5MulIpLEZPz6SnkMPhQsv\nTDoaEalvavZWvHKu+akq8Ulv/83MvgVWBLoCSwB9ga2BnfIJUkSkpubMgXHjoq+PSH3r2hV694bX\nX086EhERyZTvJKcAmFk/M3saeA84FDDgVqC7uyvxkaKlttoNTyoFZ58NO+0EP/8M990X6zX5qFUu\nJJtcy0V5GWzTBp59NibWrWkZlNKh84VIaalJn59FmNmSwIHA/wHlE6B+D1wHXOvu3+UfnohIzZSV\nxUhbV10Ff/97XHSK1KeysoX9fN54A376CYYMSTIiEREpl3Ofnz+eYLYScCxwJLB8+uEPgcuBO9z9\nt4JGWCDq8yPSeOyzD3TrBu5KfiRZp5wCI0bAc8/BuusmHY2I1Bf1+SleOdf8mFlP4O/A3sBi6YdH\nAUPdfVQdxCYiUmMvvRR9fW69Vf19JHk77QQdOkQt5KhRYLoUEhFJVE36/LwG7AfMB4YD67p7v/pI\nfNJ9iiaY2SdmdmqW7fuZ2f/M7F0zG2tm3es6JmkY1Fa7YVmwAE44Af79b1hqqdoPMaxyIdnUplyU\nlcFRR8FXX8Hjjxc8JCkCOl+IlJaaJD9NgMnAX9z9cHf/sG5CWpSZNSUmV+0HdAMGmFnXCrt9Bmzt\n7t2B84Ab6yM2ESkut90Giy0GAwYkHYnIQostBkOHwkknwdy5SUcjItK41WSenynAP4hJTdcBJhET\nmo529ylVPG9Td3+l1gGabQYMdvd+6fXTANz935XsvxzwnruvUuFx9fkRacBmz4a11oKHH4aNN046\nGpE/22mnmHvqxBOTjkRE6pr6/BSvmoz2Ns3d7wHuATCzjkQi9G8zWxV4n0iGnnP3mRnPuw1YK48Y\n2wOZydWXwCZV7H8o8EQeryciJeiii+LCUomPFKuhQ2GrreCAA2IYbBERqX81SX5Oz1xx98lE35/h\nAGa2LrANMNzMWgFvANOANfKMMefqGjPrAxwCbJFt+6BBg+jYsSMArVq1okePHpSlOwWUt9nVeuNa\nL3+sWOLReu3W77orxdVXw/jxhTnesGHDdH7Q+p/Wyx/L53j77QeHHprixBOT/3u0Xph1nS+0Xi6V\nSjF58mSkuNV4qOucDhr9dDYCzgL6uXvTPI61KXB2RrO304EF7n5xhf26Aw+mX29iluOo2Zv8SSqV\n+uMEJqWrd++o9fnXvwpzPJULyaYQ5WLGDOjaFZ55Jn5XMSt9Ol9INmr2VrzqJPn54+BmywDfuvvS\neRyjGfAR0cTua2LUuQHuPj5jn1WB54D9K+tfpORHpGF6/nno3x+++QaWXDLpaESqd8018OCDsOWW\ncM45SUcjInVByU/xqtPkB8DM3k2PwpbPMXYEhgFNgeHufpGZHQng7jeY2c3AX4Ev0k/53d03rnAM\nJT8iDczcudCrF3TpAvffn3Q0IrmZNw/WXz8m4r3vvqSjEZG6YJrUqyhkS0DrI/lZrsIACIlQ8iPZ\nqLlC6Uql4Kyzosbnk09g8OB4vKws/6ZEKheSTSHKRSoVy5dfwvDhMfz1MssUptxKMnS+kGzSNT9J\nh9GoVVb7VpMBD2qlGBIfEWl4llgCPv4Y3nkHrr8ezj476YhEqpeZ5Hz8MXz0ETz6KOgmsYhI/WiS\ndAAiSdLdutL0009w4IHRd6Jdu8IfX+VCsil0uejdO2qAbrmloIeVeqbzhUhpqfNmb8VCzd5EGo5j\nj4UffoDbb4/1VEpNhqT0pFKwwgrQpw+89hp06pR0RPL/7d17fFTVuf/xz8Ml4AmQIJHGw10up1Ao\n0NJUqZWgiEhLoV5+ppRUi9SirWiOtbFaiaC2v6KAvQVpxQtQpKW0qIQWrRC1QkGlFKVUEaQCxcg1\nAgICWeePtZNMJkMIcZKZyXzfrxevSfbsWXtNWLNnP3ut9SyRaNGwt9g71bA39fxIUgvNzy+J4bnn\n/DChn/+8clu0Ax+1C4kk2u0iOxv69oX8fLjuOigri2rx0kB0vhBJLAp+RCRh7N8P48f7ieLp6bGu\njUh05OWBc/DQQ7GuiYhIwxs5ciTzyodyNAANexORhFBc7IOetDT4xS9iXRuR6Nq6FT7/ed/Od+/W\nME6RRBfvw94WLlzIzJkz2bhxI6mpqXTr1o1rr72WG2+8MdZVixoNexORhFZYCGvWwE9+EuuaiETf\neefBj34Eubnw/POxro2I1LtoDJesYxnTp0/n1ltvJT8/n5KSEkpKSnj44Yd5+eWX+eijjz5+veKc\ngh9JahqrnRjeew+WLYO5cyE1tf6Pp3YhkdR3u5gwAc49F158sV4PI1Gm84XUSYyCn9LSUgoKCpg1\naxZXXHEFqcGX6oABA5g/fz4pKSkUFRUxcOBA0tLS6Ny5M1OmTAk5ZDGdOnWqUmbXrl1ZsWIFAGvX\nrmXQoEGkpaWRmZnJbbfdBsDRo0cZN24cGRkZtG3blqysLHbv3g34jIlz5swBYMuWLVx88cVkZGRw\nzjnnMG7cOEpLS6sca/r06fTv35/09HRycnI4duzYGf0NFPyISNwqLoa774bzz/fprf/8Z7+ej641\npLEpLoYpU+CTn/TBz7hxausiEn2rV6/m2LFjjB49+pT7tGrVivnz51NaWkpRURGzZs3iqaeeOuX+\nFrJQ2S233EJeXh6lpaVs3bqVa665BoAnnniCDz74gB07drBv3z5mz55Ny5YtK14fWsZdd93Frl27\n2LRpE9u3b+eekIX8zIxFixaxfPly3nnnHTZs2MDjjz9+Rn+Del/kVCSeaX2G+DZkiO/tGTDAr+vT\nUAuZql1IJPXZLkIXP92/H5YuhTvu8NngJL7pfCG1VlxceUdjyhT/L1pCTyI12LNnDxkZGTRpUtn/\nMXjwYDZt2sSxY8dYvnw5Q4YMqXiuX79+5OTk8MILL9QYMJVLSUlh8+bNFcfJysqq2L537142b95M\nv379GDhwYMTXd+/ene7duwOQkZFBXl4eU6dOrbLPpEmTyAwW+Rs1ahTr168/bb1CqedHROLWtGmw\nfj385jfQRGcrSRKdO8PMmTBqFJSUxLo2IhI12dn+Lt4990BBgU/z+HH+FRRUllfLILxdu3bs2bOH\nspDc+qtWrWL//v20a9cO5xxr1qxh6NChtG/fnvT0dGbPns3evXtrVf6cOXN466236N27N1lZWRQV\nFQGQm5vLZZddRk5ODh06dCA/P58TJ05Ue31JSQk5OTl07NiRtLQ0cnNzqx07M2R187POOotDhw7V\nqm7ldDkhSU1jtePXH/7g1/J5+mk/z6chb66qXUgkDdUusrPh61/3yQ/GjIGjRxvksFJHOl9IIrng\nggto0aIFS5Ysifi8c46xY8cyZswYduzYwYEDB5g4cWJFsJSamsqHH35Ysf/Jkycr5u4A9OjRgwUL\nFrB7927y8/O56qqrOHLkCM2aNWPy5Mls3LiRVatWsXTpUubOnVvt+HfeeSdNmzbljTfeoLS0lHnz\n5lUJ1MKFDperLQU/IhJ3XnsNvv1teOop6NjRb9PIEkkW5W19yhTo0sWvbRXHGXNFpC6i8aVWhzLS\n09MpKCjgpptuYvHixRw8eJCysjLWr1/P4cOHATh06BBt27YlJSWFtWvXsmDBgoogo1evXhw9epRl\ny5Zx/Phx7rvvvioJB+bPn18RDKWlpWFmNGnShJUrV/L6669z8uRJWrduTfPmzWnatGm1+h06dIjU\n1FTatGnDzp07eeCBB2p8P3VJJ67gR5KaxmrHl+Ji2LkTRo+G2bPhs5+NTT3ULiSShm4XZvDYY34N\noPIh7+pkiD86X0idxCj4Abj99tuZMWMG06ZNIzMzk8zMTCZOnMi0adMYPHgwhYWFTJ48mTZt2nDv\nvfdWJC0AH9AUFhYyYcIEOnbsSKtWrapkf1u+fDl9+/aldevW5OXlsXDhQlq0aEFJSQlXX301aWlp\n9OnTh+zsbHJzc6vVraCggHXr1pGWlsaoUaO48sora+zdCU+WUBta5FRE4sadd/qMbtdcA/n5sa6N\nSHx47z2f8fDHP4Y332y4xB8iUnfxvshpMtAipyIRaKx2/Dh50s/zGTAAvv/92NZF7UIiiVW7yMz0\nc98mTYLt22NSBamBzhciiUWprkUkpoqL/Yr2S5b4u9pXX+3nOtQya6dIo1eeHXf4cHj0UT//p3Nn\nfUZEROpCw95EJKaOHPEBjxl8+tNw//2xrpFI/Bo3DpYv9+nfhw+PdW1E5FQ07C32NOxNROLOBx/A\n5ZdDWpof8ta8eaxrJBLfevSAP/7RB0GLF8e6NiIiiUfBjyQ1jdWOnT174JJLoHdvmDfPBz7xMoRH\n7UIiiYd2kZ0NF14Izz4LN9/ss8FJbMVDuxCR2lPwIyINbtEiGDIEhg2DwkJoEpyJ4iX4EYlX5Z+R\nAQNg5Uqf+e2hh/w2XYOLiJye5vyISIPasgUGDYI77lA6a5GP69134dJL4Wtf84kQpkyJdY1EBDTn\nJx6cas6Pgh8RaTDPPgvXXQef+QwsXRrr2og0Du+/D5ddBmVl8Ne/QuvWsa6RiCj4iT0lPBCJQGO1\nG8ZHH/mFS6+6yt+lLiryw3XuuSc+h+qoXUgk8dguiov90NHLL4cNG6BLF7jhhvj8XDVW8dguRBLJ\nyJEjmTdvXoMdT+v8iEi9KC728xM2b/ZDcjp0gK1bISMDunXTKvUi0RC61k9KCnzqU/Cd70DPnnDR\nRZXz6co/jyIiAAsXLmTmzJls3LiR1NRUunXrxrXXXsuNN97Y4HVZtmxZgx5PPT+S1LJ1NVBvVq6E\nxx+HwYNh/Hi/iGlGRqxrVTtqFxJJIrSLq6+GV17xn7cRI2DXLr9dnRP1JxHahcSfaHwm61rG9OnT\nufXWW8nPz6ekpISSkhIefvhhXn75ZT766KOPX7E4p+BHRKKutNSv2/Pgg7BiBdx0k1/EtJyuFUSi\nr/xz1aULvPACXHCBn1/XwDdVRaQWYhX8lJaWUlBQwKxZs7jiiitITU0FYMCAAcyfP5+UlBSKiooY\nOHAgaWlpdO7cmSkhmVSKi4vp1KlTlTK7du3KihUrAFi7di2DBg0iLS2NzMxMbrvtNgCOHj3KuHHj\nyMjIoG3btmRlZbF7927A30CYM2cOAFu2bOHiiy8mIyODc845h3HjxlFaWlrlWNOnT6d///6kp6eT\nk5PDsWPHzuhvoOBHkprGakfX88/Dl78MHTvCG2/A6NF+IcbwP3O8Bz9qFxJJvLeL0M9Vs2YwdKjv\n/Rk71meBu/nm+J1nl8jivV2IhFq9ejXHjh1j9OjRp9ynVatWzJ8/n9LSUoqKipg1axZPPfXUKfe3\nkLubt9xyC3l5eZSWlrJ161auueYaAJ544gk++OADduzYwb59+5g9ezYtW7aseH1oGXfddRe7du1i\n06ZNbN++nXtCxsmbGYsWLWL58uW88847bNiwgccff/yM/gaa8yMidVY+j8A5ePppn7763HP99mee\n0bwekVgqnw9UWAijRsHChT7xSJ8+lftoLpBIwykurrz5MGVKdFPTh87/q8mePXvIyMigSZPK/o/B\ngwezadMmjh07xvLlyxkyZEjFc/369SMnJ4cXXnihxoCpXEpKCps3b644TlZWVsX2vXv3snnzZvr1\n68fAgQMjvr579+50794dgIyMDPLy8pg6dWqVfSZNmkRmZiYAo0aNYv369ad/4yHU8yNJTWO1P57i\nYvjb3/zE6h/+EGbM8L0/n/1srGv28ahdSCSJ2i7OOgsuvBA2bYLmzX3wc999cPiweoGiIVHbhTS8\n7OzKTKcFBf7G4cf5V1BQWV5tm2G7du3Ys2cPZWVlFdtWrVrF/v37adeuHc451qxZw9ChQ2nfvj3p\n6enMnj2bvXv31qr8OXPm8NZbb9G7d2+ysrIoKioCIDc3l8suu4ycnBw6dOhAfn4+J06cqPb6kpIS\ncnJy6NixI2lpaeTm5lY7dnngA3DWWWdx6NCh2r35gIIfEamTdevgd7/zE6zHj4f163263fKea10P\niMSP7GyfcGTmTFi7FjZuhF69fHKEM7xuEJEEdsEFF9CiRQuWLFkS8XnnHGPHjmXMmDHs2LGDAwcO\nMHHixIpgKTU1lQ8//LBi/5MnT1bM3QHo0aMHCxYsYPfu3eTn53PVVVdx5MgRmjVrxuTJk9m4cSOr\nVq1i6dKlzJ07t9rx77zzTpo2bcobb7xBaWkp8+bNqxKohQsdLldbCn4kqWmsdu2U/5kOH4bbb/dp\nq4cO9XeSv/EN+Pe/4aWXqr4mkYMftQuJJJHbRejn8d134X/+B0aO9MkQzjkHPvc5eOSRqq9J4Lfb\noBK5XUjsROM7si5lpKenU1BQwE033cTixYs5ePAgZWVlrF+/nsOHDwNw6NAh2rZtS0pKCmvXrmXB\nggUVQUavXr04evQoy5Yt4/jx49x3331VEg7Mnz+/IhhKS0vDzGjSpAkrV67k9ddf5+TJk7Ru3Zrm\nzZvTtGnTavU7dOgQqamptGnThp07d/LAAw/U+H7qspCsgh8ROa3f/ha++13o3BnefBN+9SvYt893\nud9//5l1uYtIbJUPvfn1r/1nePNmn6hkyhSfIe7xx+HDDxX8iNSnWAU/ALfffjszZsxg2rRpZGZm\nkpmZycSJE5k2bRqDBw+msLCQyZMn06ZNG+69996KpAXgA5rCwkImTJhAx44dadWqVZXsb8uXL6dv\n3760bt2avLw8Fi5cSIsWLSgpKeHqq68mLS2NPn36kJ2dTW5ubrW6FRQUsG7dOtLS0hg1ahRXXnll\njb074ckSasPqEjElIjNzyfJeReoidOKzc35YzLJl8Mc/+sxt//u/MGEChGa4LB9rLCKJKfQzfOKE\n/8zPnu3n8nXpAnffDcOGQevWVV+nRAkiNTOzOvVKSPQE/wfVIiP1/IgkkZru5D73HCxdCjfeCF27\n+gueRYvgvPP8nAAzmDOnahm6+BFJbOHpsdu08UPgcnPh73+H730P2rXzSUxmzvQ9v86d+lyi3iIR\niXdxn+razEYADwFNgUeccz+JsM/PgMuBD4HrnHN/b9haSqIqLi5udJl6arojG5qaevt2P9n51Vf9\nBOiXXoIvfAG+9CX405+gd+/K5AU9e0bu4Wlkf7oKjbFdyMfXGNtF+NsJTZebnu4/94cO+SyORUUw\nfTq0bAmpqT4o+tznoH9/n1EOanf+aWwaY7sQacziuufHzJoCvwBGAH2Ar5lZ77B9RgI9nHM9gRuA\nWQ1eUUlYZ5obvj7UdKe0Ls+Fbz940N/BXbQIVq70wc0nPgFZWfDgg7B6tf/9+HEYMsRf6Lz/fmXg\nk4zioV1I/EnWdtGqlV+weOxYuP56uPRS2LDBzw366ld9kDRwIHzrW/6GyvPP+6QK4QmaonE+q+1z\nDSlZ24VIoorr4AfIAt52zm1zzh0HFgLhKyx9BXgCwDm3Bkg3s0+cyUGifdJtqPIa8liNtbz16w80\n2LHqo7yTJ+G993ya6T/9CR57DF58Eb75Tb+uR2amz+Q0YgRMnuyfa9UKxo2DJ5/0gU9xMSxYUPN6\nAcl2U/PAgVO3C0leydYuIp0HpkyBWbP8+eK112DXLr+g8aBBsHOnnzN0/fXQt6/vIerTxwdOt90G\na9b4mzAvvQRvv101xXYif2+e6nskXuoXD8dKtvIkvsV78NMB2B7y+45g2+n26XgmB0nkD1ei1j1e\nytu2reGOVVzs74QeOQKlpb53ZccOnzVtwwY/wfj55/2FxMKF8Oijfts998Ctt8J118GYMf4CpH9/\n32vTsqX/+cor4eab4ac/9b07e/dCjx7w85/745WU+LTUBQU+c9uMGT5VdW0lW/AjIrX/3A8f7jPH\nLVvmzzHbtsEHH8D+/X7OUMuW/hz35z/758eO9Qsjt2/vEyn07OnTbI8YATk5MHEi3HEH/OQnflju\nvHmweLF//Ysv+qBr0yY4cMAHX/v2+UDq+HE/pBfi43skXr7n4uFYyVaexLd4n/NT2zQZ4QN0ap1e\n44YbfON97bXqz735ZuTtdX0u2uU15LHqo7xXX438mrfeivycc/65V16J/Jq1ayv3C7V5sw8iyreH\nPr766jaGDYu8cvK2bfCXv/ify8oqH3fsgKef9j+Xlfnel/LH3bt978uJE9X/HTkCU6dCSgqUp7Zv\n2tQPS/vtb/3K6+3bQ4sW/sKheXP4xz/861q2hAEDoHt32LLFr9GxYQP88Ie+jNBx+nXNwKYAp9K2\nmqJiSVpqF5Vqc75ITfULII8f738PPzetXAnPPuvPgb/8pR92e/Qo7Nnjz9tHj8KqVX4I3fHjPlA6\ncsQ/f/y4v8nzyCP+3Av+PHvypD/HlpX5m0HNmlX/t3+/X6C5SRN//ix/3LXL96A3aeKH/YY+/vvf\n/lrBrPq/117bxvDhVYcKm/nerTVrqm4rt3lz5O+y8ucifQee6rux/Ll4/85vjOW1axd5u8S3uE51\nbWbnA/c450YEv/8AKAtNemBmDwPFzrmFwe//AoY450rCyorfNyoiIiIiIlEVKdV1vPf8vAr0NLOu\nwH+Aa4Cvhe3zNPBdYGEQLB0ID3wg8psXEREREZHkEdfBj3PuhJl9F1iOT3U9xzm3ycy+HTw/2zm3\nzMxGmtnbwGHgmzGssoiIiIiIxKm4HvYmIiIiIiISLfGe7e1jM7MRZvYvM9tsZvmxro/Ehpl1MrOV\nZrbRzN4ws0nB9rPN7Dkze8vMnjWz9FjXVRqemTU1s7+b2TPB72oXSc7M0s3s92a2ycz+aWafV7sQ\nM/tB8D3yupktMLMWahfJx8weNbMSM3s9ZNsp20HQbjYH16PDY1NrKdeog5/aLJIqSeM4kOec+xRw\nPvCdoC3cATznnOsFPB/8LsnnFuCfVGaKVLuQnwLLnHO9gU8D/0LtIqkF84+/BXzGOdcPPxw/B7WL\nZPQY/toyVMR2YGZ98HPW+wSvKTSzRn39He8a+x+/NoukShJwzr3nnFsf/HwI2IRfI6pikdzgcUxs\naiixYmYdgZHAI1SmzVe7SGJmlgZ80Tn3KPj5p865UtQukt0H+Btp/2VmzYD/widjUrtIMs65l4D9\nYZtP1Q5GA086544757YBb+OvTyVGGnvwU5tFUiXJBHfvBgJrgE+EZAcsAT4Ro2pJ7MwEbgfKQrap\nXSS3bsBuM3vMzNaZ2a/NLBW1i6TmnNsHTAfexQc9B5xzz6F2Id6p2sF/468/y+laNMYae/CjbA5S\nhZm1AhYDtzjnDoY+53z2D7WZJGJmXwbed879neqLJQNqF0mqGfAZoNA59xl8JtEqQ5nULpKPmXUH\nbgW64i9oW5nZuNB91C4EatUO1EZiqLEHPzuBTiG/d6Jq9C1JxMya4wOfec65JcHmEjPLDJ4/F3g/\nVvWTmBgMfMXM3gGeBC42s3moXSS7HcAO59wrwe+/xwdD76ldJLVBwCrn3F7n3AngD8AFqF2Id6rv\njfBr0Y7BNomRxh78VCySamYp+AlnT8e4ThIDZmbAHOCfzrmHQp56Grg2+PlaYEn4a6Xxcs7d6Zzr\n5Jzrhp+4vMI5l4vaRVJzzr0HbDezXsGmYcBG4BnULpLZv4Dzzeys4DtlGD5RitqFwKm/N54Gcsws\nxcy6AT2BtTGonwQa/To/ZnY58BCVi6T+OMZVkhgwswuBF4ENVHY3/wB/Avod0BnYBvw/59yBWNRR\nYsvMhgC3Oee+YmZno3aR1MysPz4JRgqwBb+AdlPULpKamX0ff2FbBqwDJgCtUbtIKmb2JDAEyMDP\n75kMPMUp2oGZ3QmMB07gh90vj0G1JdDogx8RERERERFo/MPeREREREREAAU/IiIiIiKSJBT8iIiI\niIhIUlDwIyIiIiIiSUHBj4iIiIiIJAUFPyIiIiIikhQU/IiIiIiISFJQ8CMiIiIiIkmhWawrICKS\nSMzsbOCLwHlAc+DfwF+cc3tjWrEEZGYpwCXAFcAQ51yvGFepinivn4iInDn1/IiI1IKZdTez3wDP\nAp2AtcDLQE9go5ndb2ZRO6ea2UAz+1K0yovTOvwQeBi4nvi8GRfv9RMRkTNkzrlY10FEJK6Z2Vj8\nRfA9wEwXduI0s/7AKmCxc+4bUTrmFmC7cy47GuXFax3MrB2wG/i1c+7b9XWcuor3+omIyJlRz4+I\nSA3M7H5gLjDeOTcjPPABcM79A/glMM7MRkbhmF2AbsCLH7esBKjDkODxuXo+Tl3Fe/1EROQMKPgR\nETkFM/s28APg/zvnfn+a3Z8JHqPRO1B+wV0chbLivQ7DAAc8X8/Hqat4r5+IiJwBBT8iIhGY2UDg\np8A7wNRavKQkePx8FA4/BPgIWB2FsuK9DsOAdc65/fV8nLqK9/qJiMgZUPAjIhLZLCAFeNA591Et\n9k8PHtsAmFmqmRWa2WNm9rKZdQjd2cyyzGyXmX0y+P0bZvaKmb0CXAd8CLwYbLsq2Ke7mc0zsxVm\nVmDepOA4c8zsGTPrGHKMqNchmsysM9CDUwwpC97fNWa2xMx+GbzHBWbWJmSfFDObYWaPmtmqsPd/\nvpntNrNJZ1pubeonIiKJR9lrRETCmNlFQBa+52N+LV/WI3h8L3i8D/i5c26Tme0G8oDvhew/DjgH\neB/AOTcXmGtmnfDps3/pnLs77BhTgYnAhUAR8Fl8AoafBfV+FFhmZv2DuUn1UYdoGhY8Vgsuv2Vn\naAAABPFJREFUzKwtsABoB4xyzpUE278LfB+fiQ38sMT5zrl1wXu8lcr3eE7w+suBn51huTXWT0RE\nEpOCHxGR6sp7OV5yzh2s5WsuCh5fD3oMCIKOvvgL7f+E7X8x8Lpzbl/Y9qHB48rQjUHWscPOuYNB\ncAIw1zkXut8afI/NRWa2Ldp1qAfDgCP4lOEVzKwp8FvgAqBneYAS+Ihg1IKZpQH/HQQ+n8S/xz3l\nOzrnnjGzuUDLMyn3dPUTEZHEpeBHRKS6zwWPr9VmZzNrDnw1+PX3QEd8amyA8fgL69+E7N8e6AM8\nFKG4bOAYPnV2qAxgTvDzMPyQtKfC9mkXPHYBjtdDHaLGzAwffL0UYVjh1/HvcZZz7r1g/zR8UPpN\n/KKjAB2A2SGvAVgUVtYyfNa6Myn3dPUTEZEEpeBHRKS68iDi3VruPwY/xGoHsMg5dxTAzJoBucCS\nsF6G7OAxUs9KNrC2vIxyzrk3gzIN3zOzyjl3POy15UHbf5xzq6Jdh6C8psASoFWE19Vkq3Pu+pDf\n+wHtiTyk7FvBYzszK8RnWzuGzzw3uDzduHPun0GdDPgG8Dfn3JawsroAfzqTcmtRPxERSVAKfkRE\nqtuLn8NTdrodg2BgCv5COj8sYBiOD6TC5w1dDJwkbA2dYLhcV/y6QqcyICizSurloB5DgUNUzdAW\n1To4504Co2qoX23VNJ+mL3AYGOucO+3/AX5+ViegMMJz/Z1zD9ShXM33ERFphJTtTUSkuleDx/Nq\nse/twCeBR5xzT4Y9dz4+wPhL2PahwHrnXKmZdTWzS4Pt2cFjRW+Mmd0QTNIvd0nwuCJCmW3w84AO\n13MdomEY8L5zboOZtTOzy0KeawpsqWXgAzAoeFwTujGY6/RWHcutqX4iIpKgFPyIiFQ3B9+T8+Vg\nSFVEwQXxvcAfgJsi7HI2sDu0N8jMugE9qZxPMwY/fwf8sLUy4G/Bvu2AL4atMXNJULd/hB3rB/iE\nBnc1QB2iYTCVvVejgNSQ51YTJCkIZ2Znm9nMsM0tgsfwhA55+LWa6lJuTfUTEZEEpeBHRCSMc249\n8CN8j874SPuY2XX4oOdB59xVwXCwcH8Fzi7vNTGzdOBBfKDxvpk1wWeJKw9C9gL7nXPHzOwsfDKC\nimAmSKzwRWA/lRnpMLP7gN7Apc650vqsQxQdBLYHP4+mcl4O+JTe55lZeY9O+do8I4BfATPCyirG\nB2wDQ/a/Hfhj2N/jTMqtqX4iIpKgrOr8ThERKRcsjnk3fv7LEvx8kd749XFOAHc55zacpoy7gS/g\n181phr8A/wJwC/A28Avn3Opg33TgSaAUfzE/LQjEysu6CH+hfzOQCZwLtAZKgKnOuYo0z/VVh2gJ\nAo4CYCvwpHNuadjzw/BDCnfgkxI0xwdyc12ELy7zi7DeAvwLMOAPzrllEfarVbmnq5+IiCQmBT8i\nIjUIej+G4+f/OHxvwAunCjTquS5T8MFY7/LsbyIiIlJ7Cn5ERBKEmf0V6Oyc6xzruoiIiCQizfkR\nEUkAZpaBT+kcaV0eERERqQUFPyIicc7MpgFv4FM1X2Fmr5hZ7xhXS0REJOFo2JuIiIiIiCQF9fyI\niIiIiEhSUPAjIiIiIiJJQcGPiIiIiIgkBQU/IiIiIiKSFBT8iIiIiIhIUlDwIyIiIiIiSUHBj4iI\niIiIJAUFPyIiIiIikhT+D6xHgGPoz8cXAAAAAElFTkSuQmCC\n",
"text": [
"<matplotlib.figure.Figure at 0x10bbe1550>"
]
}
],
"prompt_number": 5
},
{
"cell_type": "code",
"collapsed": false,
"input": [],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 5
}
],
"metadata": {}
}
]
} | gpl-2.0 |
CooperLuan/devops.notes | PythonScientificComputing/Job Market with Pandas Part 2.ipynb | 1 | 16673 | {
"metadata": {
"name": "",
"signature": "sha256:8ab6da390827d5b6b0aba7dd309d1580338e650a5f9500eba71b93ee309a5d6c"
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Job Market with Pandas Part 2\n",
"[\u6570\u636e\u5f15\u7528](http://pawelmhm.github.io/python/pandas/2015/01/01/python-job-analytics.html) \n",
"\n",
"\u5728 Part 1 \u7684\u57fa\u7840\u4e0a\uff0c\u770b\u4e86\u6587\u7ae0\u4e4b\u540e\u5b66\u4e60\u7684\u4e1c\u897f"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"import re\n",
"import pandas as pd\n",
"import numpy as np\n",
"df = pd.read_csv('data/job_market.csv')\n",
"df = df.drop(['link', 'description', 'page_number'], axis=1)\n",
"%matplotlib inline"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 1
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## \u67e5\u770b\u6240\u6709\u804c\u4f4d\u5730\u533a Top N"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df.location.value_counts().head(10)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 2,
"text": [
"London 203\n",
"Cambridge 42\n",
"Bristol 19\n",
"Reading 19\n",
"Manchester 16\n",
"Berkhamsted 15\n",
"Devon 15\n",
"Oxford 11\n",
"Hatfield 8\n",
"USA 8\n",
"dtype: int64"
]
}
],
"prompt_number": 2
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## \u67e5\u770b\u8fd9\u4e9b\u5730\u533a\u804c\u4f4d\u7684\u5e73\u5747\u7533\u8bf7\u6570\u91cf"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"top_locations = df.location.value_counts().head(10)\n",
"df2 = df[df.location.isin(top_locations.keys())]\n",
"grouped = df2.groupby('location')\n",
"grouped.applications.sum() / grouped.id.count()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 3,
"text": [
"location\n",
"Berkhamsted 2.333333\n",
"Bristol 4.157895\n",
"Cambridge 2.523810\n",
"Devon 7.666667\n",
"Hatfield 3.000000\n",
"London 7.935961\n",
"Manchester 2.125000\n",
"Oxford 4.181818\n",
"Reading 3.631579\n",
"USA 5.375000\n",
"dtype: float64"
]
}
],
"prompt_number": 3
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## \u67e5\u770b\u5404\u5730\u533a\u6700\u9ad8\u5de5\u8d44\u804c\u4f4d\u7684\u5e73\u5747\u503c"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df2.groupby('location').salary_max.mean()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 4,
"text": [
"location\n",
"Berkhamsted 203714.285714\n",
"Bristol 52352.941176\n",
"Cambridge 46720.000000\n",
"Devon NaN\n",
"Hatfield 60000.000000\n",
"London 62846.376812\n",
"Manchester 74733.333333\n",
"Oxford 56666.666667\n",
"Reading 41642.857143\n",
"USA 154285.714286\n",
"Name: salary_max, dtype: float64"
]
}
],
"prompt_number": 4
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## \u6ca1\u4eba\u7533\u8bf7\u7684\u804c\u4f4d"
]
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df3 = df.query(\"applications == 0\")[['title', 'location', 'salary_min', 'salary_max', 'found', 'published']]\n",
"df3.head()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>title</th>\n",
" <th>location</th>\n",
" <th>salary_min</th>\n",
" <th>salary_max</th>\n",
" <th>found</th>\n",
" <th>published</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td> WDF, Python Developer Data Focused with Java, ...</td>\n",
" <td> London</td>\n",
" <td> NaN</td>\n",
" <td> NaN</td>\n",
" <td> 2014-12-26T21:54:34.050102</td>\n",
" <td> 2014-12-22T21:54:34.049654</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td> Python Developer - Django / PostgreSQL / HTML ...</td>\n",
" <td> Crewe</td>\n",
" <td> 25000</td>\n",
" <td> 35000</td>\n",
" <td> 2014-12-26T21:54:34.054577</td>\n",
" <td> 2014-12-22T21:54:34.054197</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td> BI Developer - Python - Disruptive Technology ...</td>\n",
" <td> London</td>\n",
" <td> 45000</td>\n",
" <td> 55000</td>\n",
" <td> 2014-12-26T21:54:34.063716</td>\n",
" <td> 2014-12-26T21:54:34.063350</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td> Python Developer</td>\n",
" <td> London</td>\n",
" <td> 40000</td>\n",
" <td> 48000</td>\n",
" <td> 2014-12-26T21:54:34.067126</td>\n",
" <td> 2014-12-26T21:54:34.066736</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td> BI Developer - Python - Disruptive Technology ...</td>\n",
" <td> London</td>\n",
" <td> 45000</td>\n",
" <td> 55000</td>\n",
" <td> 2014-12-26T21:54:34.075229</td>\n",
" <td> 2014-12-26T21:54:34.074823</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 5,
"text": [
" title location salary_min \\\n",
"0 WDF, Python Developer Data Focused with Java, ... London NaN \n",
"2 Python Developer - Django / PostgreSQL / HTML ... Crewe 25000 \n",
"5 BI Developer - Python - Disruptive Technology ... London 45000 \n",
"6 Python Developer London 40000 \n",
"9 BI Developer - Python - Disruptive Technology ... London 45000 \n",
"\n",
" salary_max found published \n",
"0 NaN 2014-12-26T21:54:34.050102 2014-12-22T21:54:34.049654 \n",
"2 35000 2014-12-26T21:54:34.054577 2014-12-22T21:54:34.054197 \n",
"5 55000 2014-12-26T21:54:34.063716 2014-12-26T21:54:34.063350 \n",
"6 48000 2014-12-26T21:54:34.067126 2014-12-26T21:54:34.066736 \n",
"9 55000 2014-12-26T21:54:34.075229 2014-12-26T21:54:34.074823 "
]
}
],
"prompt_number": 5
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df3.describe()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>salary_min</th>\n",
" <th>salary_max</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>count</th>\n",
" <td> 65.000000</td>\n",
" <td> 65.000000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>mean</th>\n",
" <td> 51898.215385</td>\n",
" <td> 66288.215385</td>\n",
" </tr>\n",
" <tr>\n",
" <th>std</th>\n",
" <td> 39004.014627</td>\n",
" <td> 44160.225622</td>\n",
" </tr>\n",
" <tr>\n",
" <th>min</th>\n",
" <td> 20000.000000</td>\n",
" <td> 28000.000000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>25%</th>\n",
" <td> 30000.000000</td>\n",
" <td> 40000.000000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>50%</th>\n",
" <td> 45000.000000</td>\n",
" <td> 55000.000000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>75%</th>\n",
" <td> 55000.000000</td>\n",
" <td> 75000.000000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>max</th>\n",
" <td> 240000.000000</td>\n",
" <td> 276000.000000</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 6,
"text": [
" salary_min salary_max\n",
"count 65.000000 65.000000\n",
"mean 51898.215385 66288.215385\n",
"std 39004.014627 44160.225622\n",
"min 20000.000000 28000.000000\n",
"25% 30000.000000 40000.000000\n",
"50% 45000.000000 55000.000000\n",
"75% 55000.000000 75000.000000\n",
"max 240000.000000 276000.000000"
]
}
],
"prompt_number": 6
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df3['daysOn'] = df3.found.astype(np.datetime64) - df3.published.astype(np.datetime64)\n",
"df3.head()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"html": [
"<div style=\"max-height:1000px;max-width:1500px;overflow:auto;\">\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>title</th>\n",
" <th>location</th>\n",
" <th>salary_min</th>\n",
" <th>salary_max</th>\n",
" <th>found</th>\n",
" <th>published</th>\n",
" <th>daysOn</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td> WDF, Python Developer Data Focused with Java, ...</td>\n",
" <td> London</td>\n",
" <td> NaN</td>\n",
" <td> NaN</td>\n",
" <td> 2014-12-26T21:54:34.050102</td>\n",
" <td> 2014-12-22T21:54:34.049654</td>\n",
" <td>4 days 00:00:00.000448</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td> Python Developer - Django / PostgreSQL / HTML ...</td>\n",
" <td> Crewe</td>\n",
" <td> 25000</td>\n",
" <td> 35000</td>\n",
" <td> 2014-12-26T21:54:34.054577</td>\n",
" <td> 2014-12-22T21:54:34.054197</td>\n",
" <td>4 days 00:00:00.000380</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td> BI Developer - Python - Disruptive Technology ...</td>\n",
" <td> London</td>\n",
" <td> 45000</td>\n",
" <td> 55000</td>\n",
" <td> 2014-12-26T21:54:34.063716</td>\n",
" <td> 2014-12-26T21:54:34.063350</td>\n",
" <td>0 days 00:00:00.000366</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td> Python Developer</td>\n",
" <td> London</td>\n",
" <td> 40000</td>\n",
" <td> 48000</td>\n",
" <td> 2014-12-26T21:54:34.067126</td>\n",
" <td> 2014-12-26T21:54:34.066736</td>\n",
" <td>0 days 00:00:00.000390</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td> BI Developer - Python - Disruptive Technology ...</td>\n",
" <td> London</td>\n",
" <td> 45000</td>\n",
" <td> 55000</td>\n",
" <td> 2014-12-26T21:54:34.075229</td>\n",
" <td> 2014-12-26T21:54:34.074823</td>\n",
" <td>0 days 00:00:00.000406</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"metadata": {},
"output_type": "pyout",
"prompt_number": 7,
"text": [
" title location salary_min \\\n",
"0 WDF, Python Developer Data Focused with Java, ... London NaN \n",
"2 Python Developer - Django / PostgreSQL / HTML ... Crewe 25000 \n",
"5 BI Developer - Python - Disruptive Technology ... London 45000 \n",
"6 Python Developer London 40000 \n",
"9 BI Developer - Python - Disruptive Technology ... London 45000 \n",
"\n",
" salary_max found published \\\n",
"0 NaN 2014-12-26T21:54:34.050102 2014-12-22T21:54:34.049654 \n",
"2 35000 2014-12-26T21:54:34.054577 2014-12-22T21:54:34.054197 \n",
"5 55000 2014-12-26T21:54:34.063716 2014-12-26T21:54:34.063350 \n",
"6 48000 2014-12-26T21:54:34.067126 2014-12-26T21:54:34.066736 \n",
"9 55000 2014-12-26T21:54:34.075229 2014-12-26T21:54:34.074823 \n",
"\n",
" daysOn \n",
"0 4 days 00:00:00.000448 \n",
"2 4 days 00:00:00.000380 \n",
"5 0 days 00:00:00.000366 \n",
"6 0 days 00:00:00.000390 \n",
"9 0 days 00:00:00.000406 "
]
}
],
"prompt_number": 7
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df3['daysOnInt'] = df3['daysOn'].apply(lambda x: np.timedelta64(x, 'D').astype(int))\n",
"df3.daysOnInt.describe()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 8,
"text": [
"count 101.000000\n",
"mean 13.336634\n",
"std 12.210059\n",
"min 0.000000\n",
"25% 4.000000\n",
"50% 9.000000\n",
"75% 17.000000\n",
"max 46.000000\n",
"Name: daysOnInt, dtype: float64"
]
}
],
"prompt_number": 8
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"df3.location.value_counts().head(10)"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 9,
"text": [
"London 30\n",
"Cambridge 13\n",
"Manchester 6\n",
"Southampton 3\n",
"Surrey 3\n",
"Bristol 2\n",
"Windsor 2\n",
"Hungerford 2\n",
"Leicester 2\n",
"Devon 2\n",
"dtype: int64"
]
}
],
"prompt_number": 9
}
],
"metadata": {}
}
]
} | mit |
luwei0917/awsemmd_script | notebook/Optimization/Optimization_helperFunctions_Sep23.ipynb | 1 | 366895 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"import os\n",
"import sys\n",
"import random\n",
"import time\n",
"from random import seed, randint\n",
"import argparse\n",
"import platform\n",
"from datetime import datetime\n",
"import imp\n",
"import numpy as np\n",
"import fileinput\n",
"from itertools import product\n",
"import pandas as pd\n",
"from scipy.interpolate import griddata\n",
"from scipy.interpolate import interp2d\n",
"import seaborn as sns\n",
"from os import listdir\n",
"\n",
"import matplotlib.pyplot as plt\n",
"import seaborn as sns\n",
"from scipy.interpolate import griddata\n",
"import matplotlib as mpl\n",
"# sys.path.insert(0,'..')\n",
"# from notebookFunctions import *\n",
"# from .. import notebookFunctions\n",
"from Bio.PDB.Polypeptide import one_to_three\n",
"from Bio.PDB.Polypeptide import three_to_one\n",
"from Bio.PDB.PDBParser import PDBParser\n",
"from pyCodeLib import *\n",
"# from small_script.myFunctions import *\n",
"sys.path.insert(0, \"/Users/weilu/openmmawsem\")\n",
"from helperFunctions.myFunctions import *\n",
"from collections import defaultdict\n",
"%matplotlib inline\n",
"# plt.rcParams['figure.figsize'] = (10,6.180) #golden ratio\n",
"# %matplotlib notebook\n",
"%load_ext autoreload\n",
"%autoreload 2"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"plt.rcParams['figure.figsize'] = np.array([16.18033, 10]) #golden ratio\n",
"plt.rcParams['figure.facecolor'] = 'w'\n",
"plt.rcParams['figure.dpi'] = 100\n",
"plt.rcParams.update({'font.size': 22})"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [],
"source": [
"# pre = \"/Users/weilu/Research/server_backup/feb_2019/jan_optimization/gammas/\"\n",
"# pre = \"/Users/weilu/Research/server/april_2019/optimization_test/gammas/\"\n",
"pre = \"/Users/weilu/Research/server/sep_2019/peptide_optimization_trial_2/optimization/gammas/\"\n",
"# pp = \"cath-dataset-nonredundant-S20Clean_phi_pairwise_contact_well4.5_6.5_5.0_10phi_density_mediated_contact_well6.5_9.5_5.0_10_2.6_7.0\"\n",
"# pp = \"proteins_name_list_phi_pairwise_contact_well4.5_6.5_5.0_10phi_density_mediated_contact_well6.5_9.5_5.0_10_2.6_7.0phi_burial_well4.0\"\n",
"pp = f\"protein_list_phi_pairwise_contact_well4.5_6.5_5.0_10phi_density_mediated_contact_well6.5_9.5_5.0_10_2.6_7.0phi_burial_well4.0\"\n",
"\n",
"A_name = pp + \"_A\"\n",
"B_name = pp + \"_B\"\n",
"B_filtered_name = pp + \"_B_filtered\"\n",
"P_name = pp + \"_P\"\n",
"Gamma_name = pp + \"_gamma\"\n",
"Gamma_filtered_name = pp + \"_gamma_filtered\"\n",
"Lamb_name = pp + \"_lamb\"\n",
"Lamb_filtered_name = pp + \"_lamb_filtered\"\n",
"\n",
"A = np.loadtxt(pre+A_name)\n",
"B = np.loadtxt(pre+B_name)\n",
"B_filtered = np.loadtxt(pre+B_filtered_name, dtype=complex, converters={\n",
" 0: lambda s: complex(s.decode().replace('+-', '-'))})\n",
"Gamma = np.loadtxt(pre+Gamma_name)\n",
"Gamma_filtered = np.loadtxt(pre+Gamma_filtered_name, dtype=complex, converters={\n",
" 0: lambda s: complex(s.decode().replace('+-', '-'))})\n",
"Lamb = np.loadtxt(pre+Lamb_name, dtype=complex, converters={\n",
" 0: lambda s: complex(s.decode().replace('+-', '-'))})\n",
"Lamb_filtered = np.loadtxt(pre+Lamb_filtered_name, dtype=complex, converters={\n",
" 0: lambda s: complex(s.decode().replace('+-', '-'))})\n",
"\n",
"half_B_name = pp + \"_half_B\"\n",
"half_B = np.loadtxt(pre+half_B_name)\n",
"other_half_B_name = pp + \"_other_half_B\"\n",
"other_half_B = np.loadtxt(pre+other_half_B_name)\n",
"std_half_B_name = pp + \"_std_half_B\"\n",
"std_half_B = np.loadtxt(pre+std_half_B_name)\n",
"\n",
"\n",
"# pre = \"/Users/weilu/Research/server/april_2019/\"\n",
"location = pre + \"../../phis/protein_list_phi_pairwise_contact_well4.5_6.5_5.0_10phi_density_mediated_contact_well6.5_9.5_5.0_10_2.6_7.0phi_burial_well4.0_phi_decoy_summary.txt\"\n",
"A_prime = np.loadtxt(location)\n",
"\n",
"\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/Users/weilu/anaconda3/envs/py36/lib/python3.6/site-packages/numpy/core/numeric.py:501: ComplexWarning: Casting complex values to real discards the imaginary part\n",
" return array(a, dtype, copy=False, order=order)\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABTMAAAMsCAYAAACInja7AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzs3Xl0nPV97/HPM/toNDPad9mSvMmy5YVlABuBCQQSWrhpIMQJpGxJoElMShPntKWXlqaNs+Dg3ktuaxonISlJEwIJpkBCbDAdYTYb7/ZYXiQvsqx930bL3D8MCq4N2NJIzyzv1zk6HM8jPfMZHw4658P393yNSCQSEQAAAAAAAADEOIvZAQAAAAAAAADgXFBmAgAAAAAAAIgLlJkAAAAAAAAA4gJlJgAAAAAAAIC4QJkJAAAAAAAAIC5QZgIAAAAAAACIC5SZAAAAAAAAAOICZSYAAAAAAACAuECZCQAAAAAAACAuUGYCAAAAAAAAiAuUmQAAAAAAAADiAmUmAAAAAAAAgLhgMzvA+/nFL36hn//85zIMQ263Ww888IAWLFhgdiwAAAAAAAAAJonJMvPtt9/WY489pqeeekoZGRl6+eWX9aUvfUnBYFCGYZgdDwAAAAAAAIAJYrLM9Pv9+uY3v6mMjAxJ0oIFC9Ta2qr+/n6lpKRM6N67d+/WyMiInE5nNKICAAAAAAAAOAeDg4OyWq2aP3/+uO8Rk2XmjBkzNGPGDEnS6OiovvWtb2nZsmUTLjIlaWRkRKOjoxO+DwAAAAAAAIBzF41OLibLzHf19PToG9/4htra2vTYY49F5Z7vTmSWl5dH5X4AAAAAAAAAPlwoFJrwPWJ2m3ltba1uvvlmpaam6vHHH5fP5zM7EgAAAAAAAAATxeRk5okTJ3Trrbfq7rvv1t133212HAAAAAAAAAAxICbLzHXr1qmrq0vr16/X+vXrx15/7LHHlJuba2IyAAAAAAAAAGYxIpFIZDJuPDw8rNtuu00VFRV68MEHT7u2c+dOrV69Wrt27ZLdbteyZcu0cuVKZWVlTUaU07x7Np9nZgIAAAAAAABTJxq93KQ8M7Ovr09f/epXtW3btjOuhUIh3X777bJYLFq9erW+/vWvKxgM6o477lA4HI7K+4fDYfX09Jz1i23mAAAAAAAAQHyK+jHzTZs2adWqVero6Djr9TVr1ig9PV1r166Vw+GQJM2dO1c33XSTnn76aS1fvnzCGdauXatHH330rNceeugh5eXlqaKiYsLvAwAAAAAAAGDqRHUys6urS/fee6/Ky8v1zDPPnHE9HA5r8+bNuuaaa8aKTEmaP3++SkpKtHHjxqjkuOeee7R169azflVWVionJycq7wMAAAAAAABg6kR1MtPlcum5557TjBkzznr92LFjGhwcVFlZ2RnXSktLVVNTE5UcDofjtLL0vaxWa1TeAwAAAAAAAMDUiupkpsPheN8iU5K6u7slSV6v94xrHo9Hvb290YwDAAAAAAAAIIFMygKg98PiHQAAAAAAAADjFfUFQB/E7/dL0lknMHt7e+Xz+SblfYPBoKqrqyVJgUDgrJOhAAAAAAAAAGLblJaZxcXFstvtqq2tPeNabW3tBx5Rn4iqqipVVVVJkkKh0KS8BwAAAAAAAIDJNaXHzB0Oh5YsWaINGzYoHA6Pvb57927V1dXpiiuumMo4AAAAAAAAAOLIlJaZkrRixQo1NDTorrvu0saNG/XUU0/pi1/8ombOnKmbb755quMAAAAAAAAAiBNTXmZWVlZq3bp1Gh4e1v3336+HH35Yl19+uX7yk5/I4XBMdRwAAAAAAAAAccKIRCIRs0NMtrMtAAoEAianAgAAAAAAAJLHu7tsysvLx32PpCgz3ysaf2kAAAAAAAAAzk80erkpP2YOAAAAAAAAAONBmQkAAAAAAAAgLlBmAgAAAAAAAIgLlJkAAAAAAAAA4oLN7ABT4WzbzAEAAAAAAADEF7aZAwAAAAAAAJh0bDMHAAAAAAAAkDQoMwEAAAAAAADEBcpMAAAAAAAAAHGBMhMAAAAAAABAXKDMBAAAAAAAABAXbGYHmArBYFDV1dWSpEAgIK/Xa3IiAAAAAAAAAOfLiEQiEbNDTKVorIAHAAAAAAAAcH6i0ctxzBwAAAAAAABAXKDMTEAv72rV3/1Hjdp7hsyOAgAAAAAAAEQNZWYCqm3s14vbWtXUETY7CgAAAAAAABA1lJkJKNNrlyS1dFNmAgAAAAAAIHFQZiagTK9DktTaxTFzAAAAAAAAJA7KzAT07mRmK5OZAAAAAAAASCA2swNMhWAwqOrqaklSIBCQ1+s1OdHkyvS9W2YymQkAAAAAAIDEkRRlZlVVlaqqqiRJoVDI5DSTLyOVMhMAAAAAAACJh2PmCchmtSjNY+OYOQAAAAAAABIKZWaCyvTaWQAEAAAAAACAhEKZmaAyvQ61ccwcAAAAAAAACYQyM0Fl+uzqHRxR/+CI2VEAAAAAAACAqKDMTFCZ3lNLgNp6mM4EAAAAAABAYqDMTFCZXockqaWLJUAAAAAAAABIDJSZCSrTd2oys5XnZgIAAAAAACBBUGYmqHcnM9loDgAAAAAAgERhMzvAVAgGg6qurpYkBQIBeb1ekxNNvnefmdnazTFzAAAAAAAAJIakKDOrqqpUVVUlSQqFQianmRocMwcAAAAAAECi4Zh5gvK5bbJZDcpMAAAAAAAAJAzKzARlGIYyvXa2mQMAAAAAACBhUGYmsGyfgzITAAAAAAAACYMyM4Fl+x1q7R7S8Mio2VEAAAAAAACACaPMTGA5aQ5FIlJrF8/NBAAAAAAAQPyjzExg2T6HJKmJo+YAAAAAAABIAJSZCSwn7Z0ys4MyEwAAAAAAAPGPMjOB5fhPlZnNnZSZAAAAAAAAiH+UmQksx++UJDV1DpqcBAAAAAAAAJg4yswEluW3S5KamMwEAAAAAABAArCZHWAqBINBVVdXS5ICgYC8Xq/JiaaGy26VP8VGmQkAAAAAAICEkBRlZlVVlaqqqiRJoVDI5DRTK9vv4JmZAAAAAAAASAgcM09wuWmnysxIJGJ2FAAAAAAAAGBCKDMTXLbfofBwRJ29w2ZHAQAAAAAAACaEMjPBZfsckqSmLo6aAwAAAAAAIL5RZia4nLR3yswOykwAAAAAAADEN8rMBJfjP1VmsgQIAAAAAAAA8Y4yM8HlpDklSSc7Bk1OAgAAAAAAAEwMZWaCK0g/VWaeaKXMBAAAAAAAQHyjzExwbqdVGal21bcNmB0FAAAAAAAAmBDKzCRQkOnUiTYmMwEAAAAAABDfKDOTQEGGU23dQxoIj5gdBQAAAAAAABg3yswkUJDhkiSmMwEAAAAAABDXKDOTQGHmqSVA9ZSZAAAAAAAAiGOUmUlgbDKzlSVAAAAAAAAAiF+UmUmgIOPUZCbHzAEAAAAAABDPKDOTQG6aU1aLVM9kJgAAAAAAAOIYZWYSsFkN5aY5mcwEAAAAAABAXLOZHWAqBINBVVdXS5ICgYC8Xq/JiaZeQYZT+471KhKJyDAMs+MAAAAAAAAA5y0pysyqqipVVVVJkkKhkMlpzFGY6dKWg11q7gorx+80Ow4AAAAAAABw3jhmniQuK0+TJK393TGTkwAAAAAAAADjQ5mZJK6qzNAls/169s1mbTvcZXYcAAAAAAAA4LxRZiYJwzD0jZtK5bAZ+rcXjpodBwAAAAAAADhvlJlJpDjLrQtm+LTnaI+GhkfNjgMAAAAAAACcF8rMJDN/mlfh4YgONPSZHQUAAAAAAAA4L5SZSWbe9FRJ0p4jPSYnAQAAAAAAAM4PZWaSqSg+VWbuPtptchIAAAAAAADg/FBmJpn0VLsKM53ac5TJTAAAAAAAAMQXyswkNG9aqo42D6irb9jsKAAAAAAAAMA5o8xMQvOmeSVJe48xnQkAAAAAAID4QZmZhCrfWQK07XCXyUkAAAAAAACAc0eZmYTmFqfKl2LTa6EOs6MAAAAAAAAA54wyMwlZLYYune1X6HivWrrCZscBAAAAAAAAzgllZpJaMjddkvQ605kAAAAAAACIE5SZSerSOWmSpM2UmQAAAAAAAIgTlJlJKsNrV0WxR6/v79DwSMTsOAAAAAAAAMCHosxMYpdXpKtnYERvH+o0OwoAAAAAAADwoSgzk9hHFmRKkjbuaDU5CQAAAAAAAPDhKDOTWFleisry3HppZxtHzQEAAAAAABDz4qbMXLNmjR544AGzYyScaxZmqrNvWFsPctQcAAAAAAAAsS3my8zjx4/ry1/+sn784x+bHSUhXb3w1FHzn2ys1+GTfSanAQAAAAAAAN5fzJeZv/zlL7VkyRLdeeedZkdJSKW5KbqqMkNbD3XpMw/v0BYmNAEAAAAAABCjYr7M/NrXvqZbb71VVqvV7CgJ69u3z9Yjny9XJCJV7203Ow4AAAAAAABwVjFfZmLyGYahy+akye2wqKa+1+w4AAAAAAAAwFlRZkKSZLEYmlXgUU19ryIRNpsDAAAAAAAg9lBmYsycwhR19Y+osSNsdhQAAAAAAADgDJSZGDOrwCNJ2s9RcwAAAAAAAMQg22S/wfDwsG677TZVVFTowQcfPO3azp07tXr1au3atUt2u13Lli3TypUrlZWVdcZ9VqxYMdlRk97swlNlZk19r66cn2FyGgAAAAAAAOB0kzqZ2dfXp69+9avatm3bGddCoZBuv/12WSwWrV69Wl//+tcVDAZ1xx13KBye2DHncDisnp6es36NjIxodHR0QvdPVDPyUmS1SDUnmMwEAAAAAABA7Jm0ycxNmzZp1apV6ujoOOv1NWvWKD09XWvXrpXD4ZAkzZ07VzfddJOefvppLV++fNzvvXbtWj366KNnvfbQQw8pLy9PFRUV475/onLaLSrJcWv/O0uADMMwOxIAAAAAAAAwZlImM7u6unTvvfeqvLxczzzzzBnXw+GwNm/erGuuuWasyJSk+fPnq6SkRBs3bpzQ+99zzz3aunXrWb8qKyuVk5MzofsnsnnTvDrZHtYt39muV/e1mx0HAAAAAAAAGDMpk5kul0vPPfecZsyYcdbrx44d0+DgoMrKys64Vlpaqpqamgm9v8PhOK0kfS+r1Tqheye6FTdMU6rbqmfeaNLf/ccB/eobi5TtP/vfJQAAAAAAADCVJmUy0+FwvG+RKUnd3d2SJK/Xe8Y1j8ej3l6e2WgWf4pdf3ljif7xszPVOzCi1b+tNTsSAAAAAAAAIGmSFwC9HxbwxL6qeRm6qjJDL+1s05s1nWbHAQAAAAAAACZvAdAH8fv9knTWCcze3l75fL6ovl8wGFR1dbUkKRAInHUiFGe674bpenlXm9a/0ajAbL/ZcQAAAAAAAJDkTCkzi4uLZbfbVVt75hHm2traDzyiPh5VVVWqqqqSJIVCoajeO5EVZrq0qMyrV3a3qWdgWKkuU/51AQAAAAAAACSZdMzc4XBoyZIl2rBhg8Lh8Njru3fvVl1dna644gozYuEsrr8wW4PDEb20o83sKAAAAAAAAEhyppSZkrRixQo1NDTorrvu0saNG/XUU0/pi1/8ombOnKmbb77ZrFj4H65emCmHzdCvqhv0/JZmtXaHP/yHAAAAAAAAgElgWplZWVmpdevWaXh4WPfff78efvhhXX755frJT34ih8NhViz8D163TR9ZkKmaE336h18c1HeeYrs5AAAAAAAAzGFEIpGI2SEm29kWAAUCAZNTxY+BoRHtO9ar7z51WM1dQ3rxoYtksRhmxwIAAAAAAEAceXeXTXl5+bjvkRQbXVgANDEuu1WLy3y6ZE6afv5Kg2qb+jUjL8XsWAAAAAAAAEgyph0zR/xZVOqTJO2o7TY5CQAAAAAAAJIRZSbO2cJSryRpR22XyUkAAAAAAACQjCgzcc7SU+0qyXFr+2EmMwEAAAAAADD1KDNxXhaWetXQPqjG9kGzowAAAAAAACDJJMUCoLNtM8f4LC7z6Zk3mrQ51KE/uyzX7DgAAAAAAABIIklRZrLNPHqunJ8hj9OqJ189qU9cmiPDMMyOBAAAAAAAgCTBMXOcF4/LqhsC2TrY0Ke3D7EICAAAAAAAAFOHMhPn7ealeZKkX1afNDkJAAAAAAAAkgllJs7btGy3ls5N0yu727Szls3mAAAAAAAAmBqUmRiXv7yxRDaLoX9+8pDCw6NmxwEAAAAAAEASoMzEuEzPcevua4tU29ivf33+qNlxAAAAAAAAkASSYpt5MBhUdXW1JCkQCMjr9ZqcKDF8blmBqve264lXGpSb5tTyK/LNjgQAAAAAAIAEZkQikYjZIaZSKBSSJJWXl5ucJDF09A7pnh/sUW1jv+770+m6dVm+DMMwOxYAAAAAAABiTDR6OY6ZY0LSPHb9ny/OVVmeW//nv47oof88pK6+YbNjAQAAAAAAIAFRZmLCctOc+uFX5mtJeZqe39KsW76zXVsPdpodCwAAAAAAAAmGMhNRkeq26ZHPl+vB5TPUHx7Rql8f1shoUj3BAAAAAAAAAJOMMhNRYxiG/vTiHH32ynwdbR7Qhu2tZkcCAAAAAABAAqHMRNQtvyJfKU6LfrThuAaHRs2OAwAAAAAAgARhMzsAEo8/xa5bLs/XTzbW6+P/sEUXz/IrP8Opm5bkqjjLbXY8AAAAAAAAxKmkKDODwaCqq6slSYFAQF6v1+REie8L1xbJ77Hpd1tbtGl3myIRqb51QN+7s9zsaAAAAAAAAIhTRiQSSaotLaFQSJJUXk6pNlWGhkf11X/fpx213Xr+Hy6UP8VudiQAAAAAAABMsWj0cjwzE5PObrPo+guzNTQS0Us72syOAwAAAAAAgDhFmYkpsWxBhpw2Q797u9nsKAAAAAAAAIhTlJmYEqkum6rmZWjb4W7trO02Ow4AAAAAAADiEGUmpsyty/Llclj05bV79eq+drPjAAAAAAAAIM5QZmLKzJvm1Q/urZDTbtHXfxTSc1s4cg4AAAAAAIBzR5mJKVU53asffmW+sv0OPfSLg3r6tUazIwEAAAAAACBOUGZiypXkuvXDFfNVnOXSd586rOq9HDkHAAAAAADAh6PMhCly/E6t+UK5vG6bHvhZjQ419JkdCQAAAAAAADEuKcrMYDCoVatWadWqVaqvr1dXV5fZkSCpOMut7945R+HhUf314/vVOzBidiQAAAAAAADEMCMSiUTMDjGVQqGQJKm8vNzkJHjXz185oTXrj+iS2X797+UzlON3mh0JAAAAAAAAURaNXi4pJjMR2z5zRb5uDOTojZpOffo7O/TK7jazIwEAAAAAACAGUWbCdIZh6O8+PUOr7y6X027RAz+r0duHOs2OBQAAAAAAgBhDmYmYUVWRrn/5wlzZrRZ97Uf7tWFHq9mRAAAAAAAAEEMoMxFT5hR5tPruObJbDf3tT2u0Zn2d2ZEAAAAAAAAQIygzEXMumOHXL1Yu1MISr37+SoNe399hdiQAAAAAAADEAMpMxKRMr0P/eOssuR0Wrfr1YXX0DpkdCQAAAAAAACajzETMys9w6kvXT1ND26A+9vdbdN9je9U3OGJ2LAAAAAAAAJiEMhMx7VNL8/R3t8zQxbP8en1/p3684bjZkQAAAAAAAGASykzENIvF0I2X5GjNF+ZqdkGKnnilQUea+82OBQAAAAAAABNQZiIuWC2GVn6yVMMjEa3+Ta0ikYjZkQAAAAAAADDFbGYHmArBYFDV1dWSpEAgIK/Xa3IijMfCUp+uvyhbz29p1n/vadeV8zPMjgQAAAAAAIApZESSbMQtFApJksrLy01OgvFo6QrrU9/eLp/Hpl9+Y6FcdqvZkQAAAAAAAHAOotHLccwccSXL59AXritSQ9ugPrd6p4J72syOBAAAAAAAgClCmYm48+mqfH3xuiI1dYb1tR/t17++cJRnaAIAAAAAACQBykzEHavF0OevLdav/3qxKoo9+vGGen336VqzYwEAAAAAAGCSUWYibmX7HfrXv5ini2b69NTmRj37ZpPZkQAAAAAAADCJKDMR19xOq771udnKTXPou08d1uv7O8yOBAAAAAAAgElCmYm4l5Zq16o/ny2b1aL7HtunNevrNDLKMzQBAAAAAAASDWUmEsL86V79x9cWaEGJVz9/pUHf+tUhjVJoAgAAAAAAJBTKTCSMwkyXfnBvhZaUp+nZt5r11z+tUUtX2OxYAAAAAAAAiBLKTCQUp92i79wxR1cvzNSmXW265Tvb9Vqo3exYAAAAAAAAiALKTCQcp92iVX8+W9+9Y44sFkNf+9F+rX+jSUPDo2ZHAwAAAAAAwARQZiJhLavM0Novz1O6x6Z/+tUhXfv3W/TEKyfMjgUAAAAAAIBxosxEQpuRl6LH71+gL10/TRmpdv3L+iP6z/9uMDsWAAAAAAAAxoEyEwkvy+fQHVcX6ocr5qskx63vP1OnH204rkiEbecAAAAAAADxhDITSSM91a5H752rmfkp+rcXjun+H4YU3NvOszQBAAAAAADihM3sAMBUyvE7tW7FfP3zk4f04rZWbQ51yJdi0zULM/UX1xfLn2I3OyIAAAAAAADeB5OZSDpup1X/dNts/faBxfry9dOU43fo6dca9Rf/b69au8NmxwMAAAAAAMD7MCJJ8ODAYDCo6upqSVIgEJDX61UgEDA5FWLJ4xvr9YPnj8qfYtNVCzJ0VWWmLp7lk81K3w8AAAAAABANoVBIklReXj7ueyRFmfle0fhLQ2J6bkuzfvZyvQ6f7Jcked1WVc3L0P+6JEeLy3wmpwMAAAAAAIhvlJnjQJmJD3OkqV8v7WzVy7vaFDreK0m6+6OF+vy1xbJaDJPTAQAAAAAAxCfKzHGgzMT5qGvs14M/P6DQ8V4tq8zQP902Sw4bR88BAAAAAADOVzR6OVoZ4AOU5Lr171+Zr48uytSmXW36qx+G9Mb+Dg0OjZodDQAAAAAAIOnYzA4AxDqn3aJ/vHWWUpxWPfNGk9480Cl/ik2fWpqnT12ep/RUu9kRAQAAAAAAkgLHzIFzFIlEdKChT6+FOvTb1xtV3zoop83QjZfk6qs3Tuf4OQAAAAAAwAeIRi/HZCZwjgzD0OwCj2YXeHTbsgJt2tWmn71crydfPanw8Kj+9lNlMgwWBAEAAAAAAEwWRsmAcbBaDF29MFPr7qvUJbP9euaNJv1n8KTZsQAAAAAAABIaZSYwAVaLoX/63CwVZTr1yDN1evCJA+odGDE7FgAAAAAAQEKizAQmyJ9i17r7KnXFvHT97u0W/fXj+zU8klSPogUAAAAAAJgSlJlAFKSn2vW9O+fozy7N0Rs1nfr2rw+rrXvI7FgAAAAAAAAJhQVAQJQYhqGVnyzVsZYBrX+zSevfbFJVRbr+5lNlyvI5zI4HAAAAAAAQ95jMBKLIZrXo+58v14OfnqEr5qUruLddn/neDr20s9XsaAAAAAAAAHHPiEQiSfVwv1AoJEkqLy83OQmSwcs7W/WtJw+rs29Y1yzM1PUXZWtRmVepLoaiAQAAAABAcolGL0ejAkyiqxZkqrLEq3/+1SFt2NGqDTtOTWjmpzt1z8eKdf1F2SYnBAAAAAAAiB+UmcAky/I59P27y1XX1K/XQh3aX9+rN2o69Q+/OKgdtV36q0+UymnniQ8AAAAAAAAfhjITmAKGYag0N0WluSmSpPaeIT34xAH95vUm7Tveq2/eOkvTc9wmpwQAAAAAAIhtPDMTMMnIaETrXjyudRuOS5KqKtJVlOVSSY5bNwRyZLUYJicEAAAAAACIHp6ZCcQxq8XQFz9WrEvm+PWTjfX67z3tY9d+/3aL7rthumYVeGSzUmoCAAAAAABITGYCMaO7f1jd/cN6YtMJPflqoyTJ5bCovMiji2b69cnLcpXlc5icEgAAAAAAYHyi0cvFbJkZDAb18MMPa3BwUPn5+frOd76jnJycCd+XMhPxYNvhLr2+v0N7jvRoz7Ee9Q6MyG41dP1F2br1ygKV5PJ8TQAAAAAAEF8Stsxsa2vTxz/+cf30pz/VnDlz9NOf/lSvvPKK1q1bN+F7U2Yi3oyMRhTc066fvVyvXUd6ZBjSJy7N1ZeuL5Y/xW52PAAAAAAAgHMSjV7OEq0w0VRdXa05c+Zozpw5kqTly5frjTfeUHNzs8nJgKlntRhaVpmhdfdV6t+/Mk+LSr36zWuN+rN/3qYfPHdEu450q7t/2OyYAAAAAAAAky4mFwCdPHlS+fn5Y392OBxKT09XQ0ODsrOzTUwGmGthqU//9qV5+v22Fq178bgef+mEHn/phCyGdPXCTN1+daFmF3jMjgkAAAAAADApYrLMjEQiMowzNzhbLDE5SApMKcMw9LELsnXtoiy9UdOpmvpebTnYqT9sb9XGHa367JUFuvujRfK4rGZHBQAAAAAAiKqYLDMLCgr0+uuvj/05HA6rvb1dBQUFJqYCYovFYuiy8jRdVp6m268uVOh4j77968P6j00n9GR1g5ZWpOsrfzJdRVkus6MCAAAAAABERUyOOi5dulR79+5VTU2NJOnJJ5/UwoULlZGRYXIyIHaVF6Xqhysq9cAtZZpf4tVLO9t06+od+vkrJzQQHjE7HgAAAAAAwITF5DZzSdq8ebO+973vaXBwUJmZmfr2t7+twsLCCd+XbeZIFm8d6NQ3f3lQJ9vDSvPYtLjMp5n5KVp+Rb687pgcygYAAAAAAAksGr3cpJWZw8PDuu2221RRUaEHH3zwtGs7d+7U6tWrtWvXLtntdi1btkwrV65UVlbWZEQ5DWUmkslAeETr32zSU5sbdaSpX6MRKdtn1/2fKNVHKjNksZz5bFoAAAAAAIDJEI1eblLGs/r6+rRy5Upt27ZNFRUVp10LhUK6/fbbtWjRIq1evVotLS165JFHtGfPHj399NNyOBwTfv9wOKxwOHzWayMjI2ddLgQkIpfDqlsuz9ctl+draHhUL2xt0Zr1dfrbn9ZoZn6K/tclObpqQYZy/E6zowIAAAAAAHyoqJeZmzZt0qpVq9TR0XHW62vWrFF6errWrl07VlzOnTtXN910k55++mktX758whnWrl2rRx999KzXHnroIeXl5Z1RsgKJzm6z6MZLcrS0Ik1PbGrQU5tPavVv6/T9Z+p02Zw0ffbKAgVm+81ExQNxAAAgAElEQVSOCQAAAAAA8L6iWmZ2dXXp3nvv1XXXXae/+Zu/0ZVXXnna9XA4rM2bN2v58uWnTWDOnz9fJSUl2rhxY1TKzHvuuUd33nnnWa8dOXKEyUwktUyvQ/fdMF1fuLZIm0MdemFrs17d167NoQ59/MIs3fXRIk3PdpsdEwAAAAAA4AxRLTNdLpeee+45zZgx46zXjx07psHBQZWVlZ1xrbS0dGx7+UQ5HI73Pa5utVqj8h5AvHM7rbp6YaauXpipE20D+u5TtXpha4te2NqiimKP/vaWGZpd4DE7JgAAAAAAwJiolpkOh+N9i0xJ6u7uliR5vd4zrnk8HvX29kYzDoBzVJDh0iOfL9ebNZ16cXuLnt/SojvX7NInLs3RvGleFWQ4VZztUqZ34s+0BQAAAAAAGK9JWQD0fkZHR6fy7QCcB8MwdMmcNF0yJ003LcnT3z9xQE++2qgnX22UJFkM6boLsvTpqnzNLfLwuAYAAAAAADDlprTM9PtPLRc52wRmb2+vfD7fpLxvMBhUdXW1JCkQCJx1MhTAH1UUp+qX31ik460DqjnRp6aOQVXvbR87hp7ts2tpRbqqKtJ18Sy/XA4e3wAAAAAAACbflJaZxcXFstvtqq2tPeNabW3tBx5Rn4iqqipVVVVJkkKh0KS8B5BoLBZD07LdmvbOMqDPXlmg3Ue69dLOVgX3tOu3rzfpt683yWkzVDUvQ59ckquy3BT5PTZZLUxtAgAAAACA6JvSMtPhcGjJkiXasGGD7r///rElPbt371ZdXZ1uv/32qYwD4DzNn+7V/Ole3XdDiY429+vVfR16ZXebNuxo1YYdrZKkjFS7bl2Wr5uX5MntZGITAAAAAABEz5SWmZK0YsUKfeYzn9Fdd92lO++8Ux0dHVq9erVmzpypm2++earjABind6c2P3NFvo409WvDjlY1dYb16t52/d//OqpfBk/qL66fpsvmpCk91cYzNgEAAAAAwIRNeZlZWVmpdevW6ZFHHtH9998vj8ejqqoqrVy5cmxSE0B8mZ7j1t0fLZIkhYdH9dvXG/XY74/roV8clCTl+B1aOjdNi8p8ml3gUVmem3ITAAAAAACcNyMSiUTMDjHZzrYAKBAImJwKSGydfUN6YUuLDp3s0/bDXTrSPDB2rTjLpY9dkKWPXZil4iy3iSkBAAAAAMBUeXeXTXl5+bjvkRRl5ntF4y8NwPk73jKgfcd7tKO2Wxu2t6qtZ0iSVJDh1Pxpqfrzqws1u8BjckoAAAAAADBZKDPHgTITMN/wSERvHejUhu0t2n20R3VN/TIkXVaepkyvQwtLvbpyfoZ8KVP+JAwAAAAAADBJKDPHgTITiD37j/fqkfV12na4S+/+F8liSDPzU7Rkbro+eVmu8tKd5oYEAAAAAAATQpk5DpSZQOwaHY2ovXdIr+7tUPW+du2s7VZbz5AshpSX7lRxlkvXXZClqxdkyu20mh0XAAAAAACcB8rMcaDMBOLH6GhEr+3v0LNvNulYy4CONPUrPByR1WJoTmGKyvJSVF7k0Z9dmiu7zWJ2XAAAAAAA8AEoM88R28yBxNDVN6wXtjbrzZpO7T7arfaeYUlSRbFH37xtFpvRAQAAAACIYZSZ48BkJpA4OvuG9MSmBj3+Ur2sFkM3BHJ09YJMVRR7lOpmeRAAAAAAALGEMnMcKDOBxPP2oS794Lkj2nWkZ+y1NI9NhZkuFWQ4VZjp0uxCj66qzJDVYpiYFAAAAACA5BWNXo7RJQBx74IZPv1wxXztOdqjHbXdqjnRqxOtgzrRNqA9R/9YcJYXefT1T5RqQanXxLQAAAAAAGC8KDMBJATDMDR/ulfzp59eVA4MjaihbVDPvtms/ww26POP7tbHLsjSHVcXqiwvxaS0AAAAAABgPDhmDiBpHGnq1/efqdNroQ5JpyY1K4pTdVl5mpbOTZfNyhF0AAAAAAAmC8/MHAfKTCC5RSIR7ajt1m9eb9TmfR3q7Du1ET3Ta9clc9J0QZlPF870qSDDKcOg3AQAAAAAIFooM89RMBhUdXW1JCkQCMjr9SoQCJicCoDZIpGIGtoH9cLWFv3+7RbVNfWPXSvKdGppRbpKctwqyHCpINOp4kyXLCwQAgAAAABgXCgzx4HJTADvp6UrrG2HurTlUJde3duups7wadfL8tz6/LXFumJeuhw2i0kpAQAAAACIT5SZ40CZCeBcRCIRHWsZUP07W9EPn+zTs281ayA8qhSnRZdXpOvTVfmaPy2V4+gAAAAAAJyDaPRybDMHgLMwDEPTst2alu0ee+3ujxbr2beaFNzTrhe3terFba3ypdhUmuvW4jKfrl6QqTlFHhNTAwAAAACQ2JjMBIBxONTQp9+83qj99b062NCn3oERWQzpc1cV6ParC5Xq4v8VAQAAAADwXhwzHwfKTADRNjIa0Z4jPXr4t7UKHe+VxZBmF3q0uMynxWU+LSrzKs1jNzsmAAAAAACmoswcB8pMAJNleGRUz7zRpDdrOrXtcJc6eofHrs3Ic+uCGX4tq8zQ4jKvbFYWCAEAAAAAkgtl5jhQZgKYCpFIRLWN/dp2uOvU16EuNXcNSZKsFiknzamCDKfKclN03eIsVZawSAgAAAAAkNgoM89RMBhUdXW1JCkQCMjr9SoQCJicCkAyiUQiOnSyTy/tbFNNfa9OtA2qoW1QvYMjkqQ0j00z8lM0Iy9F86en6pqFmUxvAgAAAAASCmXmODCZCSBWRCIRHWzo03NbmrWzrluHT/apb3BUklSY6dTHLshSUZZbhRlOFWa6lOm1y2JhehMAAAAAEJ+i0cuxbhcATGIYhmYVePSXN3okSaOjETW0D+r321r0xKYTWveH+tO+32kzdOX8DK24Ybpy05xmRAYAAAAAwFRMZgJADBoYGtGx5gHVtw6qvnVA9a0DOtDQpx213XI5LPrIgkx9dFGmArP8sts4jg4AAAAAiH1MZgJAgnLZrZpV4NGsAs9pr2/e1661vz+m57c06/ktzfK6rVo2P0PXLMrSxbN8PGcTAAAAAJDQKDMBII4smZuuJXPTdbxlQBt2tGrD9hY9+1aznn2rWb4Um66cl66LZ/u1pDxdvhT+Ew8AAAAASCwcMweAOHekuV8btp8qNg+d7JckOWyGls3P0NKKdFUUp8qXYlOaxybDYIEQAAAAAMAcbDMfB8pMAImssX1Qr+3v0PNbm7X9cPdp17xuq+YUelRe5NGSuem6aKbfpJQAAAAAgGREmTkOlJkAkkVT56DeOtClusY+dfYNq/Zkv/af6NVAeFSSdM3CU0uE0lLtSvfYlZfhkMtuNTk1AAAAACBRsQAIAPC+cvxO/clF2ae9NjIaUV1jv9b+/tipZ27uaB275rRbdOkcv66qzNTlFTxzEwAAAAAQe5JiMjMYDKq6ulqSFAgE5PV6FQgETE4FAObac7Rbx5oH1N47rPaeIe2s69b2w10ajUhWi6GLZvp06Zw0lRd5VFnilcPGpnQAAAAAwPhxzHwcOGYOAO+vvWdI/72nTZt2tenNmk4NjZz6FeFxWXXxLL/SPTZNy3Hr0jlpKs1xy2JhoRAAAAAA4NxQZo4DZSYAnJvegRHtO96j3Ud6tGlXq/Ye6z3tutNu0cz8FF04w6eFpV7NLvQoN81pUloAAAAAQKyjzBwHykwAGJ/hkVF1949o37EevXmgU4ca+rTveK+6+obHvue6xVn6q0+UKD3VbmJSAAAAAEAsYgEQAGDK2KwWpadatGRuupbMTZckjY5GdOBEn/Yd79GmXW36/bYWbdzZqmnZLl0yO023XJ6nwkyXyckBAAAAAImCyUwAQFREIhFt2NGq57c062BDnxo7wpKkokyn5hSlqrzIo2nZLmX7HMr2OZTps8tmZakQAAAAACQLJjMBADHDMAx9dFGWProoS5FIRG8d6NJzW5q071ivXtrZqo07Wv/H90vpHrsWlnp17eIsleS4VZjplMthNekTAAAAAABiHWUmACDqDMNQYLZfgdl+SVLf4IgOnOhVQ9ugmjrDaukKq7lrSA1tA9q0u00v72qTdGpr+meq8rX8inz5UvgVBQAAAAA4HcfMAQCmamwf1OZQhxo7BrVhR6uONg/I47LqU0vzdHlFusqLPHLYOI4OAAAAAPGObebjQJkJALFreCSiP2xv0bo/HNfR5gFJp46j56U5VZTlUkmOS0vnpuuiWX4KTgAAAACIM5SZ40CZCQCxb3gkom2Hu7SzrlsHG/p0vGVAx1r61Tc4KkmyWqSCDJdKctyaU+jRTUtzlel1mJwaAAAAAPBBKDPHgTITAOJTJBLR0ZYBbdrZpj3HenSkqV9Hmwc0MhpRitOiK+ZlyO+xaXGZT0vmpsllZ5EQAAAAAMQSysxzFAwGVV1dLUkKBALyer0KBAImpwIATNTwyKiCe9v1r88fU11T/9jrTpuh2YUeXTjTr2sWZWpmXoosFsPEpAAAAAAAysxxYDITABJPJBJRf3hUbd1DCu5t1+Z97dp3vFddfcOSTpWbxdluFWe5VJrr1swCj2blp6goyyUrJScAAAAATAnKzHGgzASA5DA6GtGOum69srtNtY39Otrcr4a2QY2+57ee22HRghKvFs/waXGZT/OmpbJYCAAAAAAmSTR6OVu0wgAAEEssFkOLy06VlO8KD4/qSFO/Djb06cCJPu091qNth7v0Rk2nJMlhMzR/ulcXlPk0t9ij0twU5Wc4md4EAAAAgBhBmQkASBoOm0WzCjyaVeDRxy889Vp4eFR7jp4qNbcdOrVB/e1DXWM/47QZmlOUqo9dkKVllRnK8rE1HQAAAADMwjFzAADeY3hkVDX1fTrQ0Kvaxn4dPtmnHbXd6g+PSpKKs1zKSXMoP92pedNSVTndq7K8FNmsTG8CAAAAwAfhmDkAAFFms1pUMS1VFdNSx17rGxzRK7vb9EZNp/Yc6daB+l5tPdil/3qrWdKp4+lpHrv8HpvSPHbNLfLo4ll+eVNsyktzKsNrN+vjAAAAAEBCYTITAIBxaO8Z0u4j3dp1pEcHTvSqvWdIXX3Dau8ZVu/gyNj3GYY0b1qqCjKc8qfYdd0FWaqcnirDYJITAAAAQHJhm/k4UGYCACbT6GhEoeO92nXk1NH0mvpevRbqOK3gLMp0anGZT7MKPCrJdas0x62cNAcFJwAAAICExjFzAABijMVinHFMPRKJaGQ0orqmfv3mtSa9FmrXs281S2oe+x6f26q5xamaNy1Vc4o8yk93KsfvVHqqjZITAAAAAN5BmQkAwCQzDEM2q6GZ+R6t/GSppFK1dod1+GS/6hr7VdfUp/31fdp+uEtv1HSe9rN2q6GcNIdy05zK8TuU43coL8OppeXpys9wmvOBAAAAAMAklJkAAJgg0+tQptehi2f5x14bHhnVoYZ+HWjoVWNHWE2dYTV1DKqxI6yDDX16+1DXe+5Qq/IijzK9dhVnu7WgxKuFJV5l+x1T/2EAAAAAYIrwzEwAAOJE/+CImrrCqj3Zr9+93awdtd3q7h9WePiPv8rz052qLEnVwhKf5k1PVX66U/4UmywWjqoDAAAAMBfPzAQAIIm4nVZNz3ZrerZbyyozJJ16HufR5gHtqO3WzrpTXy9ua9WL21rHfi7FadHc4lRVTvdqbrFHmakOFWW5lOG1m/VRAAAAAGBcKDMBAIhjhmFoeo5b03PcuvGSHElSR++Qdh/p0b5jPWrpHtKRpn7tOdqjrQf/eEzdapE+siBTVfPSNTM/RdOz3bLbLGZ9DAAAAAA4J5SZAAAkmDSPXZdXpOvyivSx14ZHIjrc2Kea473q6B3W6/s79IftrfrD9lMTnFaLoVkFKbqsPE1LytM0b5pXNitH0wEAAADEFp6ZCQBAkjreMqC9x3p0sKFPhxr6tKOuW119w5Ikj8uq0hy3ctOd8qXYNC3LpdmFHi0s9crBBCcAAACAceCZmQAAYNyKslwqynLp2sWn/jwyGtGeoz16LdSutw916UjzgHYf7TntZ9wOixaX+VRRnKq501I1I8+tFIdV3hSbrCwZAgAAADDJkqLMDAaDqq6uliQFAgF5vV6TEwEAEHusFkMLSrxaUPLH35PDIxF19Q2rrqlfu+q6Vb23XW8e6NTmUMdpP5uRatdHFmTowpl+zSxIUWaqXR6XVYZBwQkAAAAgejhmDgAAzkt4eFSHGvq073iv6pr6NRAe0bZ3Jjnfy+O0qjjbpWnZLk3Lcqsgw6nZhR7NzE+RhSlOAAAAIOlwzBwAAEw5h82iucWpmlucOvZaJBJRbWO/9h7t0eHGfnX0DqmhfVDHmgcUOt572s/73FblpTuVm+bUnCKPpme7lZ/u1KyCFLmd1qn+OAAAAADiCGUmAACYMMMwVJaXorK8lDOu9Q2OqL51QPWtg9p1pFs7arvV3BXWoVCHgnvbx77PajE0uzBFC0u8WlDq04KSVOX4nVP5MQAAAADEOI6ZAwAAU7x7XL2+bVDHWwa0+52is/OdjeqSlJ/u1MWz/LohkK25xamyWw2ewwkAAADEKY6ZAwCAuPV+x9WPNg9oR223dtR1aWdtt9a/2aT1bzZJkuxWQ9OyXWNToGW5bs3IT1FxlouSEwAAAEgClJkAACBmGIah6TluTc9x68ZLciRJhxr69PzWZjV1hNXVf2qz+h+2t0pqHfs5f4pNswpSlOVzKNNrV5bfodIctwqzXGxWBwAAABIIZSYAAIhpM/JTtOJPp5/2Wt/giOoa+3W4sU81J/q0s7ZL+473qneg66z3cNgMpafaleG1qyTHrcvK03Tp7DSlpdqn4iMAAAAAiBLKTAAAEHdSnFZVTEtVxbTU014fCI+otXtIjR1hHW7s08m2QbX3DKntna/WriHtO9arF7a2yDCkWfkpKspyaXqOW3MKPcpItSvda1dRpktWC5OcAAAAQKyhzAQAAAnD5bCqMNOqwkyXLpjhO+v3NHUO6rVQh14LdWj3kR4daGjT/1yH6HJYNDM/ReWFHi2rzNRFM32yUG4CAAAApmObOQAASGpDw6OqberXgRN96uobVnPnoGrq+xSq71XXO5vVfW6rMrwOFWe5tKDEq8qSVFUUp8rlsJqcHgAAAIgfbDMHAACYILvNotkFHs0u8Jz2eiQSUV1Tv57f0qzttd3q6hvW5lCHgnvbJUlOm6GlFelaVOpTYZZLldNTlebhGZwAAADAZKLMBAAAOAvDMFSam6Iv/8kflw8NhEe073ivdtZ167VQh17e1aaXdra98/1SSY5bxVkuFWe5VPSef+amOXkGJwAAABAFlJkAAADnyOWwanGZT4vLfP+fvTuPjrO8zz5+zb6PNNp3WYttbV4B2RjLhgIhG1mKSZyUhgAJkDQk4W2dpX1LS9PEfXvqQBPSFBpa0qQkNMWBUEgCNthIGDCLjRfZlhfJWq19H41GM5r3DxMRxWaxLPmRNN/POTrBz/PMzCWfnIN0cd/3Tzf+UbZ6BsdU3x5UfceI9hwf0OHmYb1wqFfR8cmvs1lME+VmXqpTuSku5aU6VZrrldvBVnUAAADgveLMTAAAgGkUiY7rVG9YTV0hNXeF1NQdUlPniJq6QmrpHlV0/K0fvawWk5Yt8Kki//QZnCU5XqUl2lnFCQAAgHmJMzMBAABmGavFrJw3t5f/oUg0prbekBo7Q6o/NaJXjvXr9eMDeu34wMQzZpPkd1sV8NqUGXCoJMejvFSXspIcykxyKNVvZ7I6AAAA4hYrMwEAAAwUicZU3x7UoaZhHWkZUtfAmHqHx9Q3FFFLd0hj0ck/qtmtp7esL8n3aUWhXzkpThVnutmuDgAAgFmPlZkAAABznNVi0sIsjxZmeSSlTbo3FhlXffuIWrpDau0dVWv3qFq6Q6rvGNHjL3fo8Zc7JJ0uOFcvTtRFxQkqznTL47QoI9GhJB/T1QEAADC/UGYCAADMUjarWYuyPVqU7TnjXlvPqGqbhtTcFdJLdX2qqe3V8wd7Jz2T6rdpUbZHBeluZQTsWpTlUUW+T1YL29QBAAAwN1FmAgAAzEGZb56hKUk3XpmtoZGIDjYOqaFjRCPhcTV1jehoa1C76/r1wqG+ide5HWZlJTmVnmhXWoJdaYkOpSXYlZnkUH6qS6kJdqO+JQAAAOBdUWYCAADMA16XVasWJ2rV4sRJ18ci42rtHVV776j21g9qz/EBneob1e66/jPO45SkFL9NZbleLc72KNFjU06KU5csTGA1JwAAAGaFOVNm3nvvvers7NS3v/1to6MAAADMGTarWfmpLuWnulS56K2iMxaLqW84oo6+sE71jaqtZ1Qn2oOqbRzSC4cmb1lP9tlUke9VbopTlYsStbLIL7vVbMS3AwAAgDg368vM5uZmbd68WTU1Nfrwhz9sdBwAAIB5wWQyKeC1KeC1aXHO5DM5Q2NRnWwPaTAU0Rv1g/rt612qqe1VdFz66Y42uR1mrVqUqBWFfpXmerQoyyMX09QBAABwAcz6MvORRx7RmjVrtHDhQnV2dhodBwAAYN5z2iwTBefFxQm65eocRaIxNXQE9UJtn6pre7XjQI+e298jSTKbpLREu3wuq5YX+HRZaUCJXpuSvTalJthlNrNFHQAAANPDFIvFzjws6QLauXOnvvCFL5xx/Ytf/KK+9KUvTfz5+9//vk6dOnXe28wPHz4sSSopKTmv9wEAAIhn/cExHW4a1qHmYdU2Dam9b1TdA2Pq6A9Pes5hMysn2aH8NJcWZnm0MNOthVkeZQTsMpkoOQEAAOLJdPRyhq/MXL9+vWpra42OAQAAgHOQ4LadMXAoFovpaFtQ++oHNRyKqnMgrMbOETV1hbRjf4+e3dcz8azHYVF+mlML0t3KDNiV6Dm95T072aHSHC+rOQEAAHBWhpeZAAAAmB9MJpMWZZ0+Q/MPhcJRHT8V1NHWoI62DutE+4ga2kdU2zR8xrOZAYdWFPmVFXAoI+BQTopTi7Ld8jr50RUAACDe8RMhAAAAZpzTblF5nk/leb5J1wdHIuroD6tvaEy9wxHVNg5p2xtdeurVM89Kz01xqiTHo8XZHi3Mcisz4FRGwC6nneFDAAAA8YIyEwAAAIbxuazyud76kfSqZcn68rX5GgpFdKp3VG29YTW0B3WkeViHW4b1zN5uPbO3e9J7JPtsuqjIr/J8n/xuqzIS7SpIdyvJZ7vQ3w4AAABm2LQMAIpEIrrhhhtUVlamu+66a9K9ffv2acuWLdq/f79sNpsuv/xybdq0SSkpKef7sVPCACAAAIC5aygUUV1LUA0dI6fLzp5R1bcHVdcaPOPZZQU+VZUFlJvqVE7y6S+Xg1WcAAAARpkVA4CCwaA2bdqkPXv2qKysbNK9w4cP68Ybb9Ty5cu1ZcsWdXV16Z577tHBgwe1detW2e328/34swqHwwqHw2e9F41GmZwJAAAwR3mdVq0s8mtlkX/S9Z7BMTV0jGggGFFb76gOnBzU8wd79Ub94KTnkny208VmilMl2R6V5Hjkc1mVkmBTgpuVnAAAALPdeZWZO3bs0ObNm9XX13fW+/fee68CgYDuv//+ieKytLRU1113nbZu3aqNGzeez8e/rfvvv1/33XffWe/dfffdysjIOKN4BQAAwNyV5LP9wbbyTA2HojraOqzm7pBaukNq7hpVS3dIjZ0j2tcweMa5nOmJdi3M8mhRlluL3jyXMzvJyWR1AACAWWTKZebAwIBuv/12XXPNNfrmN7+p9evXT7ofDoe1a9cubdy4cdIKzIqKCi1YsEDbt2+fsTLztttu00033XTWeydPnmRlJgAAQBzwOC1aXujX8kL/GfcGghHVNg3peFtQw6NRtfWMqq51WC8d6VNNbe/Ec26HWVlJTmUlOVSe51VxplvpAYcyEh3yuSz8XAkAAHCBTbnMdDqdevLJJ1VUVHTW+01NTRodHVVhYeEZ9woKClRXVzfVj35Xdrv9bbewWyyckwQAABDv/G6rVi9O1OrFiZOuj0XGVd8xorqWYR1tDepYW1BtPSG9cKhPzx/snfSs22FWeqJD6Yl2ZSY5taLAp9WLE5XoZbs6AADATJlymWm329+2yJSkwcHT5xP5fL4z7nk8Hg0PD0/1owEAAIAZYbOatSjLo0VZnknXQ2NRHWkeVmNnSO19ozrVG37zf0e158SgXjrSr1++2C6TSSrL9WpxtkcZAYfKcr1alOWW12WR1WI26LsCAACYP857ANDbGR8fn6m3BgAAAC4op82iZQV+LSs4c8t6LBZTR19YL9f1a9fhXu2u69fBxqEznktPtKs016vSHI9Kc70qyfEo0cMqTgAAgHMxY2VmQkKCJJ11Bebw8LD8/jN/EJwp1dXVqqmpkSRVVlaedbUoAAAAMBUmk0npAYc+sipNH1mVpvHxmHqGxtTaM6r9DYM62TmioZGoGjpG9PyBHu3Y3zPx2gVpLq0o8isv1aniDLdWFPllt7KCEwAA4O3MWJmZm5srm82m+vr6M+7V19e/4xb16VZVVaWqqipJ0uHDhy/Y5wIAACD+mM0mpfjtSvHbtXTB5P+IPjIa1dHWoA41D6m2aUivHx/QL19sn7jvcVi0vNCnFYV+vf+iFKUlOC50fAAAgFltxspMu92uNWvWaNu2bbrzzjsnBvIcOHBADQ0NuvHGG2fqowEAAIBZyeWwaGmBT0sLTpecsVhMXQNjau4OaV/9oKpre/VyXb9eONSnH/66UaW5XiV5bUpwW5Xksyknxamy3NNT1ZmkDgAA4tGMlZmSdMcdd+hTn/qUbr75Zt10003q6+vTli1bVFxcrA0bNszkRwMAAACznslkUmqCXakJdq0o9OvGK7MVCkf1cl2/HnupXYeah3WoaVjR8dik12UlObQk36dF2W6tK09SfprLoO8AAADgwprRMnPJkiV68MEHdc899+jOO++Ux+NRVVWVNm3aNLFSEwAAAMBbnHaL1lckaX1FkqTTqzeHQ1F1DdeWWdcAACAASURBVIzpZOeIXj3Wr5raXv12T5d+u0f6/v82KjPJoYWZbuWkOJWd5FRWskOlOV4l+RgwBAAA5hdTLBaLvftjc9vZBgBVVlYanAoAAACYuqFQRPsbBvXsvh7tPzmokx2hSSs4LWbpstKAyvK8yk5yKjvZoawkpwJeK1vUAQCAIX43y6akpGTK7xEXZebvm46/NAAAAGC2iUTH1d4XVkv3qFq6Q9pxoEcvHenTH/6073aYtbzArxVFfuUkO5WV5FB2slN+94xu2gIAAJiWXo6fWAAAAIB5wGoxKzvZqexkp6QEffzSdA2ORNTUFVJrz+mCs7VnVA3tQe0+2q9dh/smvT490a7F2R6V5nq1enGCynK9rOAEAACzDiszAQAAgDgTHI3qaOuw2npG1dIzquaukI60DKu+Pajo+Oln8lKdyk91KTfVqXXlSSrL9chptxgbHAAAzGlsM58CykwAAADg7EJjUdU1B/X03i49f7BHXQNjikTf+nXB77aqKMOlinyfrliSpMXZHtmsZgMTAwCAuYQycwooMwEAAID3JhaL6WhrUDsP9KipK6S23lEdawtqOBSdeCbZZ1NFvlclOV6l+G1K9tmVEbCrMN0ts5lt6gAA4C2cmfkenW2aOQAAAIB3ZjKZtCjbo0XZnolr4+MxHWoe0s4DvWruCqm5O6Sa2l7tPNA76bWJHquWF/pVkO5Sss+mBLdNuSlOFWa42K4OAACmjJWZAAAAAM7LcCiq5q6QugfD6hoY08nOEe2u69fR1mGN/8FvG1aLSeV5XhVnupWT7FROilNL8n1K8tmMCQ8AAC4YVmYCAAAAMJzHadHiHI8kz6Tr4ci4mjpD6hseU8/QmBo7QzpwclB7TwzqjfrBieccNrM+sTZDqxYlKjPJrvREh+ycxQkAAM6CMhMAAADAjLBbzSrKdJ9xPRaLqWtgTM3dIZ3sGNF/15zST55r1U+ea514Ji/VqWUFPqUnOBTw2pSb6lRxplspfvuF/BYAAMAsQ5kJAAAA4IIymUxKTbArNcGuFYV+XVuZpleO9quxc0SnekfV2jOqQ83DemJ35xmvTU+0qzzPq4o8n8rzvVqQ5lKC28qwIQAA4gRlJgAAAABDWcwmrV6cqNWLEydd7x4Mq284ou6BsE52hHS4ZUgHG4f03P4ePbuv5/deLyV5bcpPc+mDF6eqqjygBDdncAIAMB9RZgIAAACYlZJ9diX77CrKcKty0VvXh0NRHWo+XWy29YyqezCs7oEx7WsY1KvHBiRJGQG7FmV5tCDNpWS/Xck+m9IS7KrI98pq4TxOAADmqrgoM6urq1VTUyNJqqyslM/nMzgRAAAAgKnyOC26uDhBFxcnTLo+EIzomb1d2n9ySHUtw3rhUK+eP9g76ZlEj1WrFycqN8WpklyvKvK8cjnMcljNMpnYqg4AwGxnisViMaNDXEjTMQIeAAAAwOw3OjauU72j6h48PU29/lRQ297oVn37yBnPJvlsunJpkq5anqJlC3ycwQkAwAyYjl6OMhMAAABAXBkKRdTcFdK+hkHVtQQVjozrUNOQTnaGJEk+l0VOm1nJfruWFfiUleRUis+moky38tNcslB0AgAwJdPRy8XFNnMAAAAA+B2v06qSHK9KcrwT12KxmI62BbVtb7f2nBhQNBpTS09Ij1QPT3qtw2ZWcaZbSxb4tCTPq2S/XXmpTqX47Rf62wAAIC5RZgIAAACIeyaTSYuyPFqU5Zm4FovF1NI9qq6BsNr7wqprHVZdy7AONw/rYOOQfv57r89McmhJvldLF/i0JN+ngnSXnHbLhf9GAACY5ygzAQAAAOAsTCaTclKcyklxSpKuWZki6XTJ2dAxorqWoHqGxnSsbVgHTg7p6T3denpP98TrnXazAh6bEr1WBTw2FWe6taY0UUsX+JioDgDAFFFmAgAAAMA5MJlMKkh3qyDdPel6f3BMB04OaX/DoNp6R9U7NKa+4Yh6Bsd0vC2oXYf79J/PtcrjtKhyYYLWlCaqNMertAS7EjxWpqkDAPAeUGYCAAAAwDRIcNt0WWlAl5UGzrg3Ph7T4eZh7Trcq12H+rTjQI+e298zcd9hNSkr2anyPK/K87wqzfUqyWuT12WRx2Gh6AQA4E1xMc28urpaNTU1kqTKykr5fD5VVlYanAoAAABAvOobGtPuo/1q6gqpvW9UHX1h1bePqK139IxnLWYpL9WlslyvynJPl53FWW7ZrWxVBwDMLdMxzTwuyszfNx1/aQAAAAAwE7oHw6ptHFJda1ADwYiGRiLqD0Z0rC2o1p63ik6bxaS1ZQF9/NJ0VeR55XWx6Q4AMPtNRy/Hv/EAAAAAYJZI9tlVVZ6kqvKkM+71Do3pUNOQDjYOac+JAT23/62t6umJdhVluJWWaFdagl0ri/xamOWRy26R1cIWdQDA/EGZCQAAAABzQMBr05rSgNa8eSZnU9eInt3XoxOngjreFtSrx/oVjpy58a4kx6O1pQF98OLUicnsAADMVWwzBwAAAIB5YHw8poGRiJq6QnrlaL9au0fVHxzTnhODGghGJEm5KU4l+WxalOXWwiyP/G6rclKcKspwy2JmBScAYGaxzRwAAAAAIEkym01K9NiU6LFpSb5v4np0PKZXj/briVc6dLwtqPpTQb1RPzjptR6nRTnJTmUnO3RxcYLK8rzKS3XK6+RXRgDA7MK/mQAAAABgHrOYTVq1OFGrFidKkmKxmFp7RlXfPqKhkdPDhfafHNSp3rCOtg7r2X2nz+E0maQl+T5dWpKorCSH0hMdSk+0K+C1yWU3y2RiJScA4MKjzAQAAACAOGIymZSd7FR28pnnZw6ORPT68QEdawvqaOuwXjzcp30Ng2c8l+q36aOr03Xl0mQtSHexRR0AcMFwZiYAAAAA4KxCY1EdbwuqvS/85teo+oYjev14v071hiVJDptZSV6b0gN2VeR5tTDLo/xUl/LS2KYOAJiMMzPfo+rqatXU1EiSKisr5fP53uUVAAAAAACnzaLyPJ/K8yZfj0RjeulIn/acGFBdy7D6gxEdbQ1q74nJqzhT/TYVZrhVmOFWUYZbhRkuFaS75XFaLuB3AQCYT1iZCQAAAAA4b+PjMTV0jKi+fUQnO0d08s1/rm8f0ejY+KRnMwMOFWa4tDDLo8pFCVq2wCeb1WxQcgDAhTIdvRxlJgAAAABgxkTHY2rtCenEqREdPxXUiVNBnTg1ooaOEUWip38dtVpMWpDmUnGmW/lpLnkcFmUlObSyyC+vKy42FAJAXGCbOQAAAABgVrOYTcpNcSk3xaX1FUkT1yPRcR1tDWrX4T7VNg7pWFtQv3m9a9JrzSapNNer5QU+5aW6lJXkUE6KU1lJDqapA0CcoswEAAAAAFxwVotZpbleleZ6J64NjUTU0j2q4dHTg4deOdav147162Dj0KTXXlTk141XZisj0aGsZIfsbFEHgLhBmQkAAAAAmBW8LqsW55z+NXVlkV/Xr81QdDym5q6QWntCauke1f6Tg/rt61167fjA6dc4LbpiaZLWlga0stivBLfNyG8BADDDODMTAAAAADCn1LcH9UJtn/qDY3q5rl+Hm4cn7mUnO3RRUYKuWp6s4ky3krw2mc1sSQeA2YABQFNAmQkAAAAA80tzV0gv1/Vp74lBHWoeUmNnaOKe12nR6sWJWlsW0JqSRCV6WbkJAEZhABAAAAAAIO7lpDiVk5Kh69ZkSJIa2kdUU9ur1p6QapuGtO2Nbm17o1uSlBlwqDDDpaIMt4qz3FqU5VF+mksWVm8CwJxAmQkAAAAAmFcWpLu0IN018eeugbBePNyn3XX9On4qqN11/XrhUN/EfYfNrIo8r65anqxLSxKVGWBaOgDMVpSZAAAAAIB5LcVv17WVabq2Mk2SFInG1NQ1oqOtQR1pGVZdy7D2nhiYGCqU5LOpIs+rSxYm6P0XpTBUCABmEc7MBAAAAADEveFQVDW1vXqjfkAHGod0tDWo6HhMdqtJl5Ykan15ki4rCyjAmZsAMGWcmQkAAAAAwDTwOC26ZmWKrlmZIkkKhaPasb9Hj73coeqDvdp5oFdmk7Qo26PF2R5dVhrQZaWJslnNBicHgPgSFyszq6urVVNTI0mqrKyUz+dTZWWlwakAAAAAAHNB79CYXjjUq+cP9mp/w6C6B8ckSQ6rSQ67RQXpLn3isgyV5XmV7LPJabcYnBgAZqfpWJkZF2Xm72ObOQAAAADgfLT1jOrpvV167Vi/RsfGdbBxSOHI6V+tLWaTVi9O0GVlAVXkeVWc6ZbVwupNAJAoM6eEMhMAAAAAMJ16h8b09J4utfeN6lhbUK8c7Vd0/PQ9h9Wkhdkeled5VZ7rVVmeV7kpTqalA4hLnJkJAAAAAIDBAl6bPlmVOfHnvuEx7W8YVG3TkA42Dqm2cUgHTg5N3Pe5LCrP82rVokQtyfcpL9WpRAYLAcB7QpkJAAAAAMA0SvTYVFWepKryJElSLBZTc3dItY3DOth0utx87diAXjrSP/GazIBDywt9et+KFFUuTGCwEAC8DcpMAAAAAABmkMlkUm6KS7kprknT0vecGNCxtqDq20d0sHFIv36tS79+rUt2q0mLsz0qz/epMN0lt8OiFL9NuSkupSbYDf5uAMBYlJkAAAAAAFxgTrtFl5YEdGlJYOJaS3dIv93TpT3HB1TbNKT9v7c1/XdKcjxaU5KonGSnlhf6lZPivJCxAcBwDAACAAAAAGCWGR+PqakrpJbukILhcXX2h3WkZVjPH+jRUCg68VxJjkdXLktW5cIEpfjtSvHbGC4EYNZiABAAAAAAAPOQ2WxSfppL+WmuSdfDkXE1dIyouSukmtpe7djfox882agfvHk/xW/TJQsTlJPsVEW+V6sXJ1JuAphXWJkJAAAAAMAcNRYZ18t1/TrSMqzO/rD2nBhQffvIxP3SXI/WVySpIM2li4oT5HezpgmAcViZCQAAAABAHLNZzVpbFtDasrfO3uwbHlN7b1j/+2qHtu5q16GmYUmSxSxV5Pt0WWlA16xIUWaSw6jYADBlrMwEAAAAAGCeGgpF1NgR0uGWYe061KtXjvZrJDwus0laV5GkT6zN0EVFfraiA7ggpqOXo8wEAAAAACBOhN/clv7oC6e063CfpNPnbJbkeLWy0K/LyhJVkO42OCWA+YoycwooMwEAAAAAkBo7R/Torna9dqxfJ9pHFImergdWLUrQRyrTtLTAp/REtqIDmD6cmQkAAAAAAKYkL9WlOz+6QJIUCke158Sgnny1Q9v2duvlun5J0sIst/5oabJWL05QSY5XFjPb0QEYi5WZAAAAAABgQnvvqF452q/XTwzo+QM9GhiJSpLSE+36+KXpWlceUGG6W2aKTQDniG3mU0CZCQAAAADAezMWGde+hkG9XNevJ1/pUOfAmCTJ77JoWYFflYsSVFUeUFaS0+CkAOYCyswpoMwEAAAAAODcRaLjeulIv14/PqC9JwZ0qHlY0fHTlUJxplvrKwJaV56kkhwP09EBnBVl5ntUXV2tmpoaSVJlZaV8Pp8qKysNTgUAAAAAwNwVHI3q5bo+PX+gVzW1veoPRiRJBeku/cn6LL3/ohTZrWaDUwKYTSgzp4CVmQAAAAAATK9INKb9Jwf13L5uPfFKp4ZDUSX7bPrQxakqznJr9aJEJXptRscEYDDKzCmgzAQAAAAAYOYMjUT02Esd+nl1mzr6w5Ikn8ui296fq4+sSpPTZjE4IQCjUGZOAWUmAAAAAAAzLxId14n2EdU2DulHTzeroz8sr9OiK5Yk6aLiBK0o9CszyWF0TAAXEGXmFFBmAgAAAABwYQVHo3rspXb97yudOtYWnLienezQzVfl6EMXp8psZmgQMN9RZk4BZSYAAAAAAMZp7x3VnvoB7Tk+oOf296hvOKKsJIeWFfhUnufVsgV+Lcp2MxEdmIcoM6eAMhMAAAAAgNlhaCSih7a36Ln9PWrqCk1cL8v16KarcrSuPECpCcwjlJlTQJkJAAAAAMDs0zc8ptrGIe082KunXunQaCSmtWUBfWBlioqz3CpIdxsdEcB5osycAspMAAAAAABmt66BsL73xEn95vWuiWt3fnSBPrUu08BUAM7XdPRy1ukKAwAAAAAAMB1S/Hb93Z8s1I1/lK1jbUH9+7Zm3fN4gxrag7pyWbJWFiXIamH7ORCPKDMBAAAAAMCsVJTpVlGmW5WLEvTVHx3SL1/q0C9f6tDibI++saFA5Xk+oyMCuMDYZg4AAAAAAGa98fGYjrYG9ds9nfrZ86cUHY9p1aIE3Xx1jlYU+o2OB+A9YJs5AAAAAACIC2azSYtzPFqc49GHL0nTvz/TrO37urX7aL9uvSZXn70yWxYzW8+B+Y6VmQAAAAAAYE462Tmib/64TsfagspJdugTazP1vhUpSvLZjI4G4CyYZj4FlJkAAAAAAMwfoXBUD21v0aO72tUfjMhilooy3MoIOLS8wK+q8oDy01xGxwQgyswpocwEAAAAAGD+CYWj2nmgV0/v6dKxU0F19IUVHT9deVy+JEkfvjhVBRku5SQ7ZTKxHR0wAmdmAgAAAAAASHLaLbpmZYquWZkiSQqNRfX6sQFtfbFdO/b3aMf+HklSTrJDH7goVTdcniWXw2JkZABTwMpMAAAAAAAwr504FdSBk0M60jKkHft71Dkwpqwkhz53dY7WlgWU6OWMTeBCYJv5FFBmAgAAAAAQv6LjMf2i5pR++OtGjYTHZTFLa8sCuv6yTF2y0M8WdGAGsc0cAAAAAADgHFjMJm1cl6n3r0xRTW2vnnmjW88f7NXOA71ausCnT6/P1NqygOxWs9FRAZwFKzMBAAAAAEBca+kO6SfPtepXuzsUicbkd1l0wxXZ2liVIaedczWB6TKvt5n/7Gc/08MPPyyTySSXy6W/+qu/0tKlS8/7fSkzAQAAAADA2XT2h/Xb17v06Iun1NI9KpfdrLI8rz5zRZYuLQkYHQ+Y8+Ztmfn666/rz//8z/Xoo48qKSlJzz33nP76r/9a1dXV5312BWUmAAAAAAB4J2ORcT32Uoee3detA41DikRj+s6fLtQVS5ONjgbMafO2zDx+/Lja2tq0du1aSVJ3d7fWrl2r1157TW63+7zemzITAAAAAAC8V/XtQX3xh7XqGx7T+ook/fGl6bpkYQKDgoApmNMDgHbu3KkvfOELZ1z/4he/qC996UsqKiqSJI2Pj+s73/mOLr/88vMuMgEAAAAAAM5FQbpb//pn5fqnrfV6dl+Pnt3Xo4o8r774oTxdXJxgdDwg7szKlZm/MzQ0pK997Wvq6enRAw88IL/ff97vycpMAAAAAAAwFS3dIf3XjlY9/nKHxqIxvW9Fsr5y7QKlJtiNjgbMCdPRy5mnK8x0q6+v14YNG+T1evXjH/94WopMAAAAAACAqcpOdupr1xXqv7++XOvKA3p6T7c+8f/26kdPN+lk54jR8YC4MCtXZra2tmrDhg265ZZbdMstt0zre7MyEwAAAAAATIfq2l5t+WW9WntGJUnpiXatKPTr0+szVZLjNTgdMPvM2wFA3/rWt/TII49MnJv5Ow888IDS09PP670pMwEAAAAAwHQZi4zr1WP92nGgV2/UD+jEqdMrNK9ZkaKvX1cgr8uwcSXArGN4mRmJRHTDDTeorKxMd91116R7+/bt05YtW7R//37ZbDZdfvnl2rRpk1JSUqYcdjpQZgIAAAAAgJlS1zqsHz7VqBcO9Skn2aHPX5Ory0oD8rspNQFDp5kHg0Ft2rRJe/bsUVlZ2RnBbrzxRi1fvlxbtmxRV1eX7rnnHh08eFBbt26V3T6zB+OGw2GFw+Gz3otGozKZTDP6+QAAAAAAID4tyvLou7eU6H9eaNe9v2rQ3zx8TBazSSuL/FpXHtD6iiRlBBxGxwTmrCmVmTt27NDmzZvV19d31vv33nuvAoGA7r///onisrS0VNddd522bt2qjRs3Tj3xe3D//ffrvvvuO+u9u+++WxkZGWcUsAAAAAAAANPBZDLp+rUZunJZsqpre7TzQK921/XplaP92vJYgxZne1RVFtCyAp+WFfjktFuMjgzMGedcZg4MDOj222/XNddco29+85tav379pPvhcFi7du3Sxo0bJ63ArKio0IIFC7R9+/YZLzNvu+023XTTTWe9d/LkSVZmAgAAAACAGZfks+mjq9L10VXpCo5G9fKRPu082Kuagz360TPNkqS0BLv+7yeLtHpxosFpgbnhnMtMp9OpJ5988ozhPL/T1NSk0dFRFRYWnnGvoKBAdXV1557yHNnt9rfdym6x8F87AAAAAADAheV2WHTF0mRdsTRZkWhMh5uH9MrRfv342RZ9+YFDWlnk1wcuStHasoCSfTN7PB8wl51zmWm329+2yJSkwcFBSZLP5zvjnsfj0fDw8Ll+JAAAAAAAwLxhtZhUke9TRb5P16xM0b882agdB3r0+vEBSVLlwgR95o+ydMnCBHaXAn9g2kdpjY+PT/dbnrfq6mrV1NRIkiorK89atAIAAAAAAFxoWUlO/f2fLtJAMKLq2l5VH+zRzgM92n20XzdcnqU7PpxHoQn8nmkvMxMSEiTprCswh4eH5ff7p/sj31VVVZWqqqokvTUCHgAAAAAAYLbwu6360MWp+tDFqWrpDulvHj6mn+5olc1q0m3X5MpsptAEJMk83W+Ym5srm82m+vr6M+7V19e/4xZ1AAAAAACAeJed7NS9nytRaa5H/7GtRX/2r7WqaxlWLBYzOhpguGkvM+12u9asWaNt27YpHA5PXD9w4IAaGhq0bt266f5IAAAAAACAecXrsupfbi/XH1+arteOD+iG7+7Thn/Yq8deald0nFIT8Wvay0xJuuOOO9TW1qabb75Z27dv16OPPqpbb71VxcXF2rBhw0x8JAAAAAAAwLzicVr0jQ2F+o+vVOgTazM0OBLRd35xQn/8nT36vz+p07Y3ujVOsYk4M+1nZkrSkiVL9OCDD+qee+7RnXfeKY/Ho6qqKm3atEl2u30mPhIAAAAAAGBeKs/zqTzPp9s/kKufPteqZ/Z26+k3vwrSXbqoyK/FOR5VLkxUZpLD6LjAjDLF4uDAhbNNM6+srDQ4FQAAAAAAwNT0DI7p4Z2t+uVL7RociU5cv6w0Ud/YUKj0REpNzD6/G8xdUlIy5feIizLz903HXxoAAAAAAMBsEIvF1NEX1r6Tg9r+Rree3dcjj9Oi791aqiX5PqPjAZNMRy83I2dmAgAAAAAAYOaZTCalBxy6enmK/uHGxdpyS4ki0Zi+9h9H1NE/anQ8YNpRZgIAAAAAAMwTVWUB3bWxSN2DY/rc9w/ou4/V639eOKXq2l6moGNemJEBQAAAAAAAADDG1ctT1D0wpoeebdHPq09NXF+1KEF3f3qhknw2A9MB54czMwEAAAAAAOahWCymxs6Q2vvCemZvlx5/uUOJHqtuuTpHH1udLoeNDbu4sBgA9B4xzRwAAAAAAMS7p/d06XtPnFRHf1gep0XvW5Gir16bL5fDYnQ0xAnKzClgZSYAAAAAAIhXobGoHn+pQ0/s7lBda1B/fGm6vrGh0OhYiBNMMwcAAAAAAMB75rRZ9MmqTP3nnUt1UbFfW19s129e69To2LjR0YD3hDITAAAAAAAgzpjNJv3txmL5XBbd9fAxXf6Xu/XLF9uNjgW8K8pMAAAAAACAOJQecOiBP6vQLVdnKzXBpu8+Vq+TnSNGxwLeEWUmAAAAAABAnCrKdOu29+fp7k8vVDga09///LjCEbacY/ayGh3gQjjbNHMAAAAAAACctqLQr0+szdAj1ad0y/cO6K83FmlRlsfoWMAZmGYOAAAAAAAARaIxPfhMk/5jW4vGY1JBukt3bSxSeR6LwjA9mGYOAAAAAACAaWG1mHTb+/P04Jcr9PHVaWrtDulvHz6mMbadYxahzAQAAAAAAMCE8jyfvnl9kW6+OkcnO0N6+Pk2oyMBEygzAQAAAAAAcIY/uTxLuSlO/ejpZv3s+TYGA2FWoMwEAAAAAADAGexWs/7208VK9Fh1z+MNumHLPh1pHjY6FuIcZSYAAAAAAADOakm+T7/4xnLd/oFcNXeHdNP39uv7/3tSfcNjRkdDnKLMBAAAAAAAwNty2iy6+aocPXhHhRakufST51p1/T/sVVvPqNHREIcoMwEAAAAAAPCuSnO9+un/Waq/vL5Q/cGIvvOL44rFYkbHQpyxGh3gQqiurlZNTY0kqbKyUj6fz+BEAAAAAAAAc4/ZbNLHVqdr/8lBPbG7U7/a3aGPrko3OhbiiCkWZxX64cOHJUklJSUGJwEAAAAAAJibBkci+uQ/7tV4THr8r1bKYWPzL97ddPRy/D8NAAAAAAAA58TnsuqGy7PUMzimp17tNDoO4ghlJgAAAAAAAM7Zx1any++y6Kc7WhUdj6uNvzAQZSYAAAAAAADOmdth0YbLMtTUFdKju04ZHQdxgjITAAAAAAAAU7JxXaaykx3a8liDfvM6280x8ygzAQAAAAAAMCWJHpt+cHuZUv12/e3Dx/TgM80aZ8s5ZhBlJgAAAAAAAKYsK8mpf/1iuQoz3Lr/N0369i+OGx0J8xhlJgAAAAAAAM5LTopT//7lCq1alKAndnfq5SN9RkfCPBUXZWZ1dbU2b96szZs3q6WlRQMDA0ZHAgAAAAAAmFecdov+8voiOe1m/ePWeo2OjRsdCfOQKRaLxdVBBocPH5YklZSUGJwEAAAAAABg/vnPZ1t035ONuuXqbN32/jyj42AWmY5eLi5WZgIAAAAAAODC+PT6TBVnuvXjZ1vV0D5idBzMM5SZAAAAAAAAmDZWi1nfuK5QkWhMX3voiP7m4aN68JlmHW0dNjoa5gHKTAAAAAAAAEyrpQU+ffbKbDV0jOjXr3Xp/t806U+27NNTr3YaHQ1znNXoAAAAAAAAAJh/vvjBPH3ufTmKRPFeCwAAIABJREFURmM60Diku/7rqL77eIMuLUlUwGszOh7mKFZmAgAAAAAAYEbYrWa5HBZdsjBB/+djCzQQjOgf/ueE+obGjI6GOYoyEwAAAAAAADPuqmXJWlce0HP7e/TBv3tNWx6rVygcNToW5hjKTAAAAAAAAMw4k8mkzZ9ZpG/9yUItzvbokepT+tPv7lNt45DR0TCHUGYCAAAAAADggrBZzbpmZYp+dEeFvvShPLX2jOqW7+/XT59rNToa5gjKTAAAAAAAAFxQFrNJn/mjbD301SXKS3Xpe/97UvXtQaNjYQ6gzAQAAAAAAIAhFmZ59FfXF0mS/mtHm8FpMBdQZgIAAAAAAMAwSwt8WrbAp1+/1qnO/rDRcTDLxUWZWV1drc2bN2vz5s1qaWnRwMCA0ZEAAAAAAADwpj+9Iktj0Zjuevgo283xjkyxWCxmdIgL6fDhw5KkkpISg5MAAAAAAABAksbHY/rWI8f15Kudspil296fp89ckSWz2WR0NEyj6ejl4mJlJgAAAAAAAGYvs9mkv/lUsf79yxXKT3PpX55q1J/9a632nmB3LSajzAQAAAAAAMCsUJHv00NfWaKPr07T6ycGdOsPDup7T5w0OhZmEcpMAAAAAAAAzBpOu0XfvL5I//315arI9+qnO1r1zN4uo2NhlqDMBAAAAAAAwKyTn+rSP352sZJ8Nv39I8d1snPE6EiYBSgzAQAAAAAAMCul+O369g0LFRob190/O6ZINK7mWOMsKDMBAAAAAAAwa11UnKBPrcvUgZND+slzLUbHgcEoMwEAAAAAADCrfeEDeSpId+mHv27S/7xwyug4MBBlJgAAAAAAAGY1h82sf/58qXJTnPrHrfX68XZWaMYrykwAAAAAAADMehkBhx74UrmKM936wVON+penGhWLcYZmvKHMBAAAAAAAwJyQ7LPrX79Yroo8rx7a3qJf7e4wOhIuMMpMAAAAAAAAzBl+t1X3fr5UaQl2ffexBjV3hYyOhAuIMhMAAAAAAABzit9t1d9+ulihsXHd/bNjbDePI5SZAAAAAAAAmHMuLk7QhjXpeqNhUE/v6TY6Di4QykwAAAAAAADMSZ+/Jld+l0X3PXlSobGo0XFwAVBmAgAAAAAAYE5K9Nj0ufflqr0vrJv/+YCeYCDQvEeZCQAAAAAAgDlrw2Xp+vT6TLX1jupbjxzXa8f6jY6EGWQ1OsCFUF1drZqaGklSZWWlfD6fwYkAAAAAAAAwHawWs776kQX62Kp0feIf9+pXuzt0UXGC0bEwQ+KizKyqqlJVVZUk6fDhwwanAQAAAAAAwHRbkO7S0gU+PbuvR5s+HpHXFRe1V9xhmzkAAAAAAADmhQ9fkqrRsXFte4Pp5vMVZSYAAAAAAADmhauWJ8tpN+s/n23Rqd5Ro+NgBlBmAgAAAAAAYF7wOq368rX5au4e1S3f26+9JwaMjoRpRpkJAAAAAACAeWPDmgx9+4aF6g9GdOsPDurb/31c0fGY0bEwTSgzAQAAAAAAMK9cvSJF//UXy3RRsV+Pv9yhbXs5Q3O+oMwEAAAAAADAvJOf6tLmzyySy27WQ9ubNc7qzHmBMhMAAAAAAADzUqLHpuvWpOv4qRFV1/YaHQfTgDITAAAAAAAA89an12fJbjVpy2P1Ot4WNDoOzhNlJgAAAAAAAOatFL9d37y+SJ39Y/rc9w/oUNOQ0ZFwHigzAQAAAAAAMK996OJUfe/WUgXDUf3o6Waj4+A8UGYCAAAAAABg3rtkYYLWlgZUc6hXzV0ho+NgiigzAQAAAAAAEBc+WZWpWEz6xQunjI6CKaLMBAAAAAAAQFy4ZKFfBeku/Wp3hw6cHDQ6DqaAMhMAAAAAAABxwWQy6cvX5isSGdetPzio37zWaXQknCPKTAAAAAAAAMSNy0oDevArS+R3W3Xfk40aH48ZHQnngDITAAAAAAAAcWVRlkcfujhVHf1hHWwaMjoOzgFlJgAAAAAAAOLOlUuTJUnPvtFtcBKcC8pMAAAAAAAAxJ3SXI8yAnY9u69HsRhbzecKykwAAAAAAADEHZPJpCuWJKutd1T7GphsPlfM2jLz0Ucf1bXXXqtrr71Wn/nMZ1RfX290JAAAAAAAAMwjH7woVWaT9Bf/foRCc46YlWXmiRMntGXLFj300EN64okndPXVV+uuu+4yOhYAAAAAAADmkcU5Hv3TzSUajYzryw/UaiAYMToS3sWsLDMLCwu1c+dOJScnKxKJqLW1VYFAwOhYAAAAAAAAmGfWlgX05x9boODouJ7dxzCg2c6wMnPnzp0qKys74+u+++6TJNlsNr366qtav369HnnkEd10001GRQUAAAAAAMA8duXSZNmtJv3m9S6jo+BdWI364PXr16u2tvYdn7n44ov1wgsvaNu2bbr11lu1fft2+f3+C5QQAAAAAAAA8cDrsmptWUDP7utRe++o0gMOoyPhbczKbebNzc168cUXJ/581VVXyWazqbGx0cBUAAAAAAAAmK/evzJVkvTQsy1q7x01OA3ezqwsM/v7+/XVr35Vp06dknR6S7rZbFZRUZHByQAAAAAAADAfrSlNVEbArkd3tesj335dT+zuMDoSzsKwbebvpLy8XF//+tf1+c9/XmazWX6/X//2b/8ml8tldDQAAAAAAADMQ3arWf9551K9dKRPP3yqSf/v0RMqynSrLNdrdDT8HlMsFotN9cWRSEQ33HCDysrKdNddd026t2/fPm3ZskX79++XzWbT5Zdfrk2bNiklJeW8Q5+Pw4cPS5JKSkoMzQEAAAAAAIDZ6VDTkD5/3wEFvDb96I4KpSdyhuZ0mI5ebsrbzIPBoL7yla9oz549Zw124403ymw2a8uWLfqLv/gLVVdX67Of/azC4fCUw75X4XBYQ0NDZ/2KRqMaHx+f8QwAAAAAAACYm0pzvfrL64vU3hfWlx84pL6hMaMj4U1T2ma+Y8cObd68WX19fWe9f++99yoQCOj++++X3W6XJJWWluq6667T1q1btXHjxqknfg/uv/9+3XfffWe9d/fddysjI0NlZWUzmgEAAAAAAABz1wcvTlV/MKJ7Hm/QXQ8f1T9/vlQmk8noWHHvnFdmDgwM6Pbbb1dJSYkef/zxM+6Hw2Ht2rVLV1111USRKUkVFRVasGCBtm/ffn6J34PbbrtNr7322lm/lixZorS0tBnPAAAAAAAAgLntU+sy9cGLU/XSkX7tPNBrdBxoCisznU6nnnzyybedLN7U1KTR0VEVFhaeca+goEB1dXXnnvIc2e32SUXq77NYLDP++QAAAAAAAJgfvvShPO3c36N7ftWg1SUJctrolox0zisz7Xb72xaZkjQ4OChJ8vl8Z9zzeDwaHh4+148EAAAAAAAADJHit+vz1+SorWdU//bbZqPjxL0pnZn5TmbjcJ3q6mrV1NRIkiorK89atAIAAAAAAABn84m1mXp6T5f+a0erLl+SpCX5dEtGmfYyMyEhQZLOugJzeHhYfr9/uj/yXVVVVamqqkrSWyPgAQAAAAAAgPfCajHpro3F+tPv7tPfP3JcP9+0jGFABjnnbebvJjc3VzabTfX19Wfcq6+vf8ct6gAAAAAAAMBsVJjh1nVr0lXfPqIjLRyjaJRpLzPtdrvWrFmjbdu2KRwOT1w/cOCAGhoatG7duun+SAAAAAAAAGDGXb4kWZL0PJPNDTPtZaYk3XHHHWpra9PNN9+s7du369FHH9Wtt96q4uJibdiwYSY+EgAAAAAAAJhRSxf45Hdb9fzBHqOjxK0ZKTOXLFmiBx98UJFIRHfeeaf+6Z/+SWvXrtVDDz0ku90+Ex8JAAAAAAAAzCirxaS1ZQHVtQbV1jNqdJy4dN4DgI4cOXLW66tWrdLPf/7z8337acE0cwAAAAAAAEyHdeUBPfVqp54/2KNPVmUaHSfuTPs089mIaeYAAAAAAACYDqsXJ8plN2vri+26bk2GrBamml9IM7LNHAAAAAAAAJiP3A6LPrUuU/XtI3rq1U6j48QdykwAAAAAAADgHNxwRZYS3FY98NsmhcaiRseJK5SZAAAAAAAAwDnwOq26+eocdfSH9YuaU0bHiSuUmQAAAAAAAMA5um5NujIDDj20vUUDwYjRceJGXAwAYpo5AAAAAAAAppPdatbtH8jV3zx8TD9+tkV3fDjf6EhxwRSLxWJGh7iQfjfNvKSkxOAkAAAAAAAAmMvGx2O64bv71NId0rZvXSKblU3Q72Q6ejn+hgEAAAAAAIApMJtNunJZskbC4zrYOGR0nLhAmQkAAAAAAABM0SXFCZKkV4/1G5wkPlBmAgAAAAAAAFNUlueRy27WK0cpMy8EykwAAAAAAABgiqwWs1YU+rX/5JBC4ajRceY9ppkDAAAAAAAA5+GShQnadbhPb9QPatXiRKPjzGtxUWZWVVWpqqpK0ltTkwAAAAAAwP9v796D5KzrfPG/u3syGZIMIazcxEhIJAmBoCBMNNIBFXHZctcbCBoERCA5sshCAQpuZRHdwhIDiFHgrJRBdxWKy+8HmgUVXDgzi+SsLHKtAWXDReR+SwiQYWb6/JFkdEwg3TCZZy6vV1VXwfN90v3p8Kl5ivd8L8BA2Hvdvpn///Ins/cuE1MplwquaOQaFWEmAAAAAGwuu7x1XObO3Co33vFMKqXkSwdPTesWYrfNwZ6ZAAAAAPAmlMulfPNzM7L/7K3zi98+k7/7+n/nJ//nsaLLGpGEmQAAAADwJjU3lXP2EdOz6NBp2Wp8U8675sH83/udcD7QhJkAAAAAMAAq5VI+0rZtliyYlZbmcs6+8oG8vMYJ5wNJmAkAAAAAA2jHv2rJ/zro7Xn0mTW5+OePFF3OiCLMBAAAAIAB9ql9t8/ub5+Qy/7PY7nn4VVFlzNijIows729PWeffXbOPvvsPProo1m5cmXRJQEAAAAwglXKpXzl0Gkpl0v5+uUPpKu7t+iSRoRSrVarFV3EYOrs7EySzJw5s+BKAAAAABjpvv+LR/K/f/6HHLjnX+Wsz+yScrlUdEmFGYhcblTMzAQAAACAInzugLdlv90n5Re3P5MLr3u46HKGPWEmAAAAAGwmlXIpX5u/S3bfaUIu/dUfc9Utjxdd0rAmzAQAAACAzailuZLFR8/M5Le05JyrV+TW+54vuqRhS5gJAAAAAJvZpAljcv6xM9PSXM7i/29FuntG1TE2A0aYCQAAAACDYPJbtsjh+781Dz31Sq79v08WXc6wJMwEAAAAgEHymf3emq1bx+Rffv5IXunqKbqcYUeYCQAAAACDZNzYSg553/Z5ZtWruf+PLxVdzrAjzAQAAACAQTT5LS1Jkidf6Cq4kuGnqegCBkN7e3s6OjqSJG1tbWltbS24IgAAAABGq20nNidJnnh+TcGVDD+jIsysVqupVqtJks7OzoKrAQAAAGA0226rsUmSJ583M7NRlpkDAAAAwCDaZuKYlEqWmb8RwkwAAAAAGERNlXL+qnWMZeZvgDATAAAAAAbZthObLTN/A4SZAAAAADDItt1qbJ5e2ZXunlrRpQwrwkwAAAAAGGTbbdWc3lryzCqzMxshzAQAAACAQbbtxOYkyROWmjdEmAkAAAAAg2y7rcYmcaJ5o4SZAAAAADDI/jQz04nmjRBmAgAAAMAg65uZaZl5Q4SZAAAAADDItpk4JqWSmZmNEmYCAAAAwCBrqpTzV61jzMxsUFPRBQyG9vb2dHR0JEna2trS2tpacEUAAAAAjHZbjmvKi6/0FF3GsDIqwsxqtZpqtZok6ezsLLgaAAAAAEjKpVJe7e0tuoxhxTJzAAAAAChAU6WUnt5a0WUMK8JMAAAAAChAuZT01oSZjRBmAgAAAEABKuVSenqEmY0QZgIAAABAAcrlUmSZjRFmAgAAAEABmszMbJgwEwAAAAAKUC6X7JnZIGEmAAAAABSgUo7TzBskzAQAAACAAlTKpfT0Fl3F8CLMBAAAAIACrA0zzcxshDATAAAAAApQKZfSK8xsiDATAAAAAAqw9gCgpOYQoLoJMwEAAACgAJV1yZx9M+snzAQAAACAAlTKpSRONG+EMBMAAAAACiDMbJwwEwAAAAAKUC6tDTMdAlQ/YSYAAAAAFKBSWRtmdgsz69ZUdAGDob29PR0dHUmStra2tLa2FlwRAAAAAKPduiwzvQ4AqtuoCDOr1Wqq1WqSpLOzs+BqAAAAAOBPMzPtmVk/y8wBAAAAoAD2zGycMBMAAAAACrD+NHN7ZtZPmAkAAAAABaisS+Z6a8LMegkzAQAAAKAA62dm9vQUXMgwIswEAAAAgAKU14eZZmbWTZgJAAAAAAXom5lpz8y6CTMBAAAAoABNZaeZN0qYCQAAAAAFKK9L5szMrJ8wEwAAAAAK8Kdl5gUXMowIMwEAAACgAPbMbJwwEwAAAAAKIMxsnDATAAAAAApQdgBQw4SZAAAAAFCAigOAGibMBAAAAIACVEoOAGqUMBMAAAAAClCp2DOzUcJMAAAAAChAuWTPzEYJMwEAAACgAOtnZnYLM+smzAQAAACAAqzLMtNrz8y6CTMBAAAAoACVsj0zGzXkw8w77rgju+++ex5//PGiSwEAAACAAVMu2zOzUUM6zHzmmWfyT//0T3n11VeLLgUAAAAABtT6mZn2zKzfkA0zu7u7c/LJJ+fUU08tuhQAAAAAGHCVdcmcLLN+hYWZN998c2bNmrXBa8mSJUmSb37zm5kzZ07e9773FVUiAAAAAGw2fXtm9kgz69VU1Afvt99+uffeezc69rOf/SwPP/xwTj/99EGuCgAAAAAGhwOAGjckl5lfddVVefjhh/Oxj30sH/3oR5Mkn//85/Ob3/ym4MoAAAAAYGCsPwCopybMrFdhMzNfzw9+8IN+/z5jxoxccskl2X777QuqCAAAAAAGVpNl5g0bkjMzAQAAAGCkKzsAqGFvKszs7u7OYYcdlrPOOmuDsTvvvDNHHnlk9tprr8yZMydf+tKX8vTTT7+hz7nvvvvMygQAAABgRLFnZuPecJj50ksv5cQTT8ztt9++wVhnZ2eOPPLIlMvlLF68OKecckra29tz1FFHpaur600VXI+urq68+OKLG3319PSkt7d3s9cAAAAAAK+nLMxs2BvaM/Omm27K2Wefneeff36j4+eff34mTZqUiy++OM3NzUmSXXfdNZ/85Cdz9dVX57DDDnvjFdfh4osvzpIlSzY69tWvfjXbb799Zs2atVlrAAAAAIDX0yTMbFjDMzNXrlyZhQsXZubMmbnmmms2GO/q6sott9ySAw44oC/ITJLdd989U6ZMyY033vjmKq7DggULctttt230NXv27Gy77babvQYAAAAAeD19e2YKM+vW8MzMlpaWLFu2LNOmTdvo+COPPJI1a9Zk6tSpG4ztvPPOuf/++xuvskHNzc39gtQ/V6lUNvvnAwAAAMCm2DOzcQ3PzGxubn7NIDNJVq1alSRpbW3dYGz8+PFZvXp1ox8JAAAAACNOpbQ+zCy4kGHkDe2Z+XqG4uE67e3t6ejoSJK0tbVtNGgFAAAAgMFUqZiZ2agBDzMnTpyYJBudgbl69epsueWWA/2Rm1StVlOtVpOsPWkdAAAAAIpWXjcz056Z9Wt4mfmmTJ48OWPGjMmKFSs2GFuxYsXrLlEHAAAAgNFi/dEuZmbWb8DDzObm5sydOzc33HBDurq6+q7ffffdefDBBzNv3ryB/kgAAAAAGHbW75nZLcys24CHmUlywgkn5LHHHsvRRx+dG2+8MVdddVWOO+64vOMd78jBBx+8OT4SAAAAAIaV9aeZD8EjaIaszRJmzp49O5dcckm6u7tz0kkn5Vvf+lb23XffLF26NM3NzZvjIwEAAABgWCmXHQDUqDd9ANB999230etz5szJZZdd9mbffkA4zRwAAACAoeZPMzOFmfUa8NPMhyKnmQMAAAAw1FTWrZm2Z2b9NssycwAAAADg9ZVKpZRLiSyzfsJMAAAAAChIpVxKT480s17CTAAAAAAoSLlcSm9NmFmvUbFnpgOAAAAAABiKmsqldJuZWbdREWY6AAgAAACAoahctmdmIywzBwAAAICCVMql9Egz6ybMBAAAAICClIWZDRFmAgAAAEBBmoSZDRFmAgAAAEBByuUIMxsgzAQAAACAglTKpfT2Fl3F8DEqTjNvb29PR0dHkqStrS2tra0FVwQAAAAASblkmXkjRkWYWa1WU61WkySdnZ0FVwMAAAAAazVVhJmNsMwcAAAAAApSLtkzsxHCTAAAAAAoyNo9M4WZ9RJmAgAAAEBByuVSehwAVDdhJgAAAAAUpKlsz8xGCDMBAAAAoCAVYWZDhJkAAAAAUJByOemtCTPr1VR0AYOhvb09HR0dSZK2tra0trYWXBEAAAAArJuZ2SPMrNeoCDOr1Wqq1WqSpLOzs+BqAAAAAGCtSrkUWWb9LDMHAAAAgILYM7MxwkwAAAAAKEjZMvOGCDMBAAAAoCAVBwA1RJgJAAAAAAVZu8w8qQk06yLMBAAAAICCVMqlJIltM+sjzAQAAACAgpRLa8NMhwDVR5gJAAAAAAWpVNbNzBRm1kWYCQAAAAAFWZdlpluYWZemogsYDO3t7eno6EiStLW1pbW1teCKAAAAAODPZ2YWXMgwMSrCzGq1mmq1miTp7OwsuBoAAAAAWMuemY2xzBwAAAAACrL+NHNhZn2EmQAAAABQkMq6dE6YWR9hJgAAAAAUZP3MTHtm1keYCQAAAAAFscy8McJMAAAAAChIWZjZEGEmAAAAABSkSZjZEGEmAAAAABSk7ACghggzAQAAAKAgDgBqjDATAAAAAApiz8zGCDMBAAAAoCB9e2bWhJn1EGYCAAAAQEH6Zmb2CDPr0VR0AYOhvb09HR0dSZK2tra0trYWXBEAAAAAJJV1Uw17zcysy6gIM6vVaqrVapKks7Oz4GoAAAAAYK31MzO7ewouZJiwzBwAAAAACrJ+z0wzM+sjzAQAAACAgpRLTjNvhDATAAAAAApSqaybmSnMrIswEwAAAAAKsi7LTLcwsy7CTAAAAAAoSKW8fpl5wYUME8JMAAAAACjI+tPMLTOvjzATAAAAAAryp5mZwsx6CDMBAAAAoCDrDwASZtZHmAkAAAAABVl/AJAwsz7CTAAAAAAoSKVvz8yCCxkmhJkAAAAAUJCyPTMbIswEAAAAgII4AKgxwkwAAAAAKEhlXTonzKyPMBMAAAAACmLPzMYIMwEAAACgIPbMbIwwEwAAAAAK0rQuzOwWZtalqegCBkN7e3s6OjqSJG1tbWltbS24IgAAAABIxo5ZO9dwzavWmddjVISZ1Wo11Wo1SdLZ2VlwNQAAAACw1viWSpJk9Ss9BVcyPFhmDgAAAAAFGT92XZi5RphZD2EmAAAAABSkpbmccilZ/Up30aUMC8JMAAAAAChIqVTK+JaKZeZ1EmYCAAAAQIHGja3kJcvM6yLMBAAAAIACmZlZP2EmAAAAABRo/NiKA4DqJMwEAAAAgAKZmVk/YSYAAAAAFGh8S1Ne7upNT2+t6FKGPGEmAAAAABRo3Ni1EZ1DgDZNmAkAAAAABRrf0pQkeclS800SZgIAAABAgSaMrSRJXjQzc5OEmQAAAABQoPEta8NMhwBtmjATAAAAAAokzKyfMBMAAAAACjRu3TLz1ZaZb5IwEwAAAAAKtH5mpgOANk2YCQAAAAAFGm9mZt2EmQAAAABQoD/tmdldcCVDnzATAAAAAArkAKD6NRVdwGs5/fTTs3z58rS2tiZJdtppp1xwwQUFVwUAAAAAA8sBQPUbsmHmbbfdlosuuijTp08vuhQAAAAA2GzW75npAKBNG5Jh5tNPP50//vGPueCCC/LQQw9lypQp+fKXv5wdd9yx6NIAAAAAYECNaSpnbFPJzMw6FLZn5s0335xZs2Zt8FqyZEmefPLJ7Lvvvjn99NNz7bXXZo899sjChQvT0+M/KAAAAAAjz/iWprxoZuYmFTYzc7/99su99977muMXXXRR3z8fc8wxufDCC/Pggw9m2rRpg1EeAAAAAAya8S0VBwDVYUieZn777bfn+uuv73etVqulqWlIrooHAAAAgDdl3NiKZeZ1GJJhZldXV772ta/lySefTJL86Ec/yrRp0/L2t7+94MoAAAAAYOCNb6k4AKgOQ3Kq45w5c/KFL3whn/vc59LT05O3vvWt+fa3v51SqVR0aQAAAAAw4Mavm5lZq9VkYK/jTYWZ3d3dOfzwwzNr1qwsWrSo39idd96ZxYsX56677sqYMWOy//7759RTT81b3vKWut57/vz5mT9//pspDwAAAACGhfEtlXT31NLVXcvYMcLM1/KGl5m/9NJLOfHEE3P77bdvMNbZ2Zkjjzwy5XI5ixcvzimnnJL29vYcddRR6erqelMFAwAAAMBIM76lkiQOAdqENzQz86abbsrZZ5+d559/fqPj559/fiZNmpSLL744zc3NSZJdd901n/zkJ3P11VfnsMMOe+MV16Grq+s1Q9Oenh5TdQEAAAAYUsaNXRdmrunO1q1jCq5m6Gp4ZubKlSuzcOHCzJw5M9dcc80G411dXbnllltywAEH9AWZSbL77rtnypQpufHGG99cxXW4+OKL8+53v3ujr7vuuqvvYCEAAAAAGAr2n711zjhkaiaOE2S+noZnZra0tGTZsmWZNm3aRscfeeSRrFmzJlOnTt1gbOedd87999/feJUNWrBgQT73uc9tdOyhhx4yMxMAAACAIWX2Tq2ZvVNr0WUMeQ2Hmc3Nza8ZZCbJqlWrkiStrRv+5Y8fPz6rV69u9CMb1tzc3G9W6J+rVCqb/fMBAAAAgIH3hg8Aei29vb0D/ZYAAAAAAG/sAKDXM3HixCTZ6AzM1atXZ8sttxzoj9yk9vb2dHR0JEna2to2OmsUAAAAABjaBjzMnDx5csaMGZMVK1ZsMLZixYrXXaK+uVSr1VSr1SRJZ2f8yiIQAAARKElEQVTnoH8+AAAAAPDmDfgy8+bm5sydOzc33HBDurq6+q7ffffdefDBBzNv3ryB/kgAAAAAYBQY8DAzSU444YQ89thjOfroo3PjjTfmqquuynHHHZd3vOMdOfjggzfHRwIAAAAAI9xmCTNnz56dSy65JN3d3TnppJPyrW99K/vuu2+WLl36mqeMAwAAAAC8nlKtVqsVXcTmtrEDgNra2gquCgAAAABGj/Vn2cycOfMNv8eoCDP/3ED8pQEAAAAAjRmIXG6zLDMHAAAAABhowkwAAAAAYFgQZgIAAAAAw4IwEwAAAAAYFpqKLmAwbOw0cwAAAABgeHGaOQAAAACw2TnNHAAAAAAYNYSZAAAAAMCwIMwEAAAAAIYFYSYAAAAAMCwIMwEAAACAYaGp6AIGQ3t7ezo6OpIkbW1taW1tLbgiAAAAAKBRpVqtViu6iME0EEfAAwAAAACNGYhczjJzAAAAAGBYEGYCAAAAAMOCMBMAAAAAGBaEmQAAAADAsCDMBAAAAACGBWEmAAAAADAsNBVdwGBob29PR0dHkqStrS2tra0FVwQAAAAANKpUq9VqRRcxmDo7O5MkM2fOLLgSAAAAABg9BiKXs8wcAAAAABgWRsUy8z+3Zs2a9Pb29iXBAAAAAMDm9/LLL6dcfnNzK0fdzMxKpfKm/9KGut7e3jz++OPp7e0tuhTooy8ZavQkQ5G+ZKjRkwxF+pKhRk8yFA3VviyXy6lUKm/qPUbdnpmjwYsvvph3v/vdue222zJhwoSiy4Ek+pKhR08yFOlLhho9yVCkLxlq9CRD0Ujuy5E9RREAAAAAGDGEmQAAAADAsCDMBAAAAACGBWEmAAAAADAsCDMBAAAAgGFBmAkAAAAADAuVM88888yii2DgVSqVzJkzJ5VKpehSoI++ZKjRkwxF+pKhRk8yFOlLhho9yVA0UvuyVKvVakUXAQAAAACwKZaZAwAAAADDgjATAAAAABgWhJkAAAAAwLAgzAQAAAAAhgVhJgAAAAAwLAgzAQAAAIBhQZg5wtx555058sgjs9dee2XOnDn50pe+lKeffrroshjhuru7c9hhh+Wss87aYOzaa6/N3/7t32aPPfbI+9///lxwwQV59dVX+93z6quv5tvf/nY+8IEPZI899sjf/d3f5ac//elglc8Ict111+XQQw/N3nvvnblz5+aYY47JXXfd1e8ePclg++lPf5qPf/zjede73pV58+bln//5n7Nq1ap+9+hLinLZZZdlxowZWb58eb/repLBNnfu3MyYMWOD1xVXXNF3z9KlS/PhD384s2fPzoc//OFceumlG7zPiy++mLPOOivVajXvfOc786lPfSodHR2D+VUYIe6///4sXLgwe++9d/bee+8cccQRuf322/vdoycZLH/4wx82+jPyz1/rjYZneOXMM888s+giGBidnZ05/PDDs8MOO+S0007Lu971rlx++eX5+c9/noMPPjiVSqXoEhmBXnrppZx88sm55ZZbsscee2S//fbrG7viiity+umn56CDDsrxxx+frbfeOhdddFGeeOKJfOADH+i778tf/nKuvPLKLFiwIIcffniefvrpLFmyJG9/+9szc+bMIr4Ww9AVV1yR0047Le9973vz93//99l3331z66235sILL8x73vOe7LDDDnqSQXf55Zfn9NNPzwc/+MH8wz/8Q3bdddcsXbo07e3t+eQnP5lSqaQvKcwDDzyQL37xi+nu7s7HP/7xvO1tb0vi+c3ge/zxx/O9730vX/ziF3PyySfnkEMO6Xvtueee2WKLLXL++efnggsuyGc+85kcc8wxSZIlS5akqakp++yzT5KkVqvl85//fG699dacdNJJ+cQnPpH7778/F154YfbZZ5/suOOORX5NhpEHHngghx56aMaNG5cvf/nL+dCHPpTly5fnBz/4QQ488MBMmjRJTzKoWlpasv/++/f7+XjIIYdkl112SUdHRz772c9m3rx5o+cZXmPEWLBgQe39739/bc2aNX3X7rrrrtr06dNrP/nJTwqsjJHqP/7jP2oHHnhgra2trTZ9+vTaV7/61b6xV155pTZnzpzaySef3O/PXHLJJbUZM2bUfv/739dqtT/16OWXX97vvgULFtSq1Wqtp6dn838RRoR58+bVjj766H7XVq1aVWtra6stXLhQTzLoenp6au973/s26MsrrriiNn369NpvfvMbfUlh1qxZU/vYxz5W23///WvTp0+v3XrrrbVazfObYvzyl7+sTZ8+vXbfffdtdPzxxx+v7bbbbrVzzz233/Wzzjqrtscee9ReeOGFWq1Wq11//fW16dOn1zo6Ovru6e7urn30ox+tfepTn9p8X4AR59hjj60deOCBtZdffrnv2rPPPlubN29ebenSpXqSIWF9Tx5++OG17u7uUfUMt8x8hOjq6sott9ySAw44IM3NzX3Xd99990yZMiU33nhjgdUxEq1cuTILFy7MzJkzc80112wwfuedd+a5557LQQcd1O/6Rz7ykdRqtfzqV79Kktx0001Jkr/+67/e4L4nnngid9999+b5AowoL7/8cg488MB8+tOf7nd9woQJ2WGHHfLEE0/oSQZdqVTKpZdemr9cBDNmzJgka5/d+pKinHfeeVm1alVOOOGEftf1JEW4995709LSkmnTpm10/Ne//nVeffXVjfblK6+80rdk96abbspWW22VuXPn9t1TqVRy0EEH5be//W2eeeaZzfclGDFWrlyZjo6OHHrooWlpaem7PmnSpNx888058sgj9SRDwuLFi/P888/n61//eiqVyqh6hgszR4hHHnkka9asydSpUzcY23nnnfPAAw8UUBUjWUtLS5YtW5Zvf/vb2X777TcY//3vf58kG/Tktttum3HjxuV//ud/kqxdwrHNNttkyy237HfflClT+sZhU7bYYot85StfyQEHHNDv+gMPPJDf/e53mTlzpp5k0JVKpUybNi2TJ09OsnbPrJtuuimLFy/Orrvumn322UdfUohbbrklP/rRj3LOOedk3Lhx/cb0JEW45557stVWW+WUU07JnDlzsvvuu+ezn/1s7rzzziR/6sudd965359b329/3pdTpkxJqVTa6H36knp0dnamp6cnO+64Y772ta/lPe95T3bbbbfMnz+/L+TRkxTtnnvuyZVXXpljjz02O+20U5LR9QwXZo4Q6w8SaG1t3WBs/PjxWb169WCXxAjX3Nz8mr89T16/JydMmJAXX3wxydrffE6YMGGj9yTpuw8atWrVqpx66qlpamrKMcccoycp1GOPPZZ3v/vdWbBgQdasWZNFixalqalJXzLonn322Zx22mk59thjs+eee24wricpwj333JPnnnsu06ZNy3e/+9184xvfyPPPP5/58+fnzjvvzMqVK9Pc3JyxY8f2+3N/2W/6koGw/gDdr3/963nsscdyzjnn5Nxzz83KlSvz2c9+Ng888ICepHAXX3xxJk6cmKOOOqrv2mh6hjcVXQADo7e3t+gSoJ9N9eT6307WarW67oNGPPHEE1m4cGF+97vf5bzzzsvUqVP1JIUaN25cli5dmpdeeimXXnppjjjiiHznO9/Rlwy6f/zHf8wOO+yQ448/fqPjepIinHfeeRk3blx22223vmtz587NQQcdlPPPP3+Th6ToSwbS+lOft9tuuyxZsiTl8to5YO9617vy4Q9/OBdddFG/5ecboyfZnB599NH88pe/zPHHH98vlBxNz3AzM0eIiRMnJslGZ2CuXr16g+nDsLmt77mN9eSLL77Y99uiLbfc8jXvSTb+WyV4PXfccUcOPvjgPPTQQ/nud7+bD33oQ0n0JMWaOHFi3vve9+aDH/xgvv/972eHHXbId77zHX3JoLrsssvyn//5n/nGN76RJOnu7u77H5/e3t709PToSQqxzz779Asyk2TrrbfOXnvtlXvvvTdbbrllurq60tXV1e+ev+w3fclAWB8O7b///n1BZrI23Jw5c2buvvtuPUmhrrvuutRqtXz84x/vd300PcOFmSPE5MmTM2bMmKxYsWKDsRUrVrzucmDYHNb33IMPPtjv+hNPPJGXXnop73jHO/rue+qppzaYyr6+l9ffB/VYtmxZDj/88DQ1NeXHP/5x9ttvv74xPclgW7VqVa699toN9h1qbm7OzJkz88c//lFfMqiWLVuWV155JX/zN3+T3XbbLbvttltOOumkJMlRRx2VD33oQ3qSQffss8/miiuuyO9+97sNxrq6urL11lv39eVDDz3Ub/wv+23atGkb3LP+vvX7GMOmrN8H8y+DymTtL4G22GILPUmhbrjhhuy1114bzFofTc9wYeYI0dzcnLlz5+aGG27o90P37rvvzoMPPph58+YVWB2j0Z577pmJEydm2bJl/a4vW7YspVIp1Wo1SbLffvulVqvluuuu2+C+bbfdNjNnzhy0mhnefvGLX+SUU07J9OnTc8UVV2zQO3qSwVYqlXLGGWfku9/9br/rL7zwQv77v/87s2bN0pcMqq9+9au58sor+71OOeWUvrELL7xQTzLoSqVSFi1alO9973v9rj/66KO57bbbMnfu3FSr1VQqlY32ZUtLS/bZZ58ka/vy2Wefza9//eu+e3p6enL99ddn9uzZmTRp0ub/Qgx7U6dOzZQpU3Ldddf1+3/rhx9+OJ2dnZkzZ46epDBdXV25++67+3rsz42mZ3jlzDPPPLPoIhgYU6ZMydKlS7N8+fJMnDgxt99+e84444zsuOOOOeuss1KpVIoukRFsyZIl2WOPPfpmwlUqlTQ3N+f73/9+nnzyyYwZMyY/+9nPcsEFF+QTn/hEDjnkkCRrl2t0dnbmhz/8YZqamrJ69eosWbIkP//5z7No0aLMmjWryK/FMLFy5coceeSRaWpqyqJFi9LV1ZXHH3+87/X8889nu+2205MMqubm5vT09OTf/u3f8txzz2XMmDH57W9/m6985St59tlnc+655+pLBtWkSZOy3Xbb9Xs99dRTuf7663P00Ufnne98p+c3g26LLbbIyy+/nMsvvzzPPvtsmpub81//9V85/fTTM2bMmCxevDhvectb8sILL+SSSy7JmjVr+n62/uhHP8rxxx/fN3Fj6tSpufnmm3PZZZdlwoQJeeaZZ3L22WfnjjvuyDe+8Y287W1vK/jbMlxMnjw5l112WX7zm99k0qRJuffee3PGGWekVCrlnHPOyTbbbKMnKcR9992XH//4x/n0pz+d6dOn9xsbTc/wUm1TO38yrCxfvjznnXde7r333owfPz7VajWnnnpqttlmm6JLY4SbMWNG5s+fn0WLFvW7/uMf/zg//OEP84c//CHbbrttPvaxj+ULX/hCmpr+dP7YK6+8knPPPTf//u//npUrV2bKlCk57rjj8pGPfGSwvwbD1LJly3LyySe/5vguu+ySn/3sZ0n0JIOrVqvl6quvzr/+679mxYoVGTt2bObMmZMTTzyx39IyfUlRrr/++px44on54Q9/mDlz5vRd15MMpt7e3lx++eX5yU9+kocffjgtLS2pVqs5+eSTs8MOOyRZO5vtoosuylVXXZWnnnoqb33rWzN//vwcccQR/d7rueeeyze/+c386le/ypo1azJjxoyccMIJ2XfffYv4agxjy5cvz5IlS3LXXXelqakp733ve3Paaadl8uTJSfQkxbj55ptz3HHH5V/+5V9ecwXuaHiGCzMBAAAAgGHBnpkAAAAAwLAgzAQAAAAAhgVhJgAAAAAwLAgzAQAAAIBhQZgJAAAAAAwLwkwAAAAAYFgQZgIAAAAAw4IwEwAAAAAYFoSZAAAAAMCwIMwEAAAAAIYFYSYAAAAAMCwIMwEAAACAYeH/AXIxzw9Ry3cGAAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 1618.03x1000 with 1 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.plot(Lamb)\n",
"plt.yscale(\"log\")"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": true
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABLIAAAMsCAYAAABA14tEAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzs3X2UVXW9P/DPmYEjjAMICYISEqAgomnkEwpYGpWPKVCgqZfyOmaalVm2rFa07GG5rtduF3KNlqt8KE2vqEmZqVl6NTO0QElMjVEywAcIZng4MDO/P7ryEzkoM2cPe+85r9daZy3d3zP7++Y7Awyf+X72t9De3t4eAAAAAJBxNWkHAAAAAIAdoZAFAAAAQC4oZAEAAACQCwpZAAAAAOSCQhYAAAAAuaCQBQAAAEAuKGQBAAAAkAsKWQAAAADkgkIWAAAAALmgkAUAAABALihkAQAAAJALClkAAAAA5IJCFgAAAAC5oJAFAAAAQC70SDvAjnryySejtbU1dtlll7SjAAAAABGxcePGqK2tjXHjxqUdZadqamqK9evXpx2jrN69e8fee++ddowuk5tCVmtra2ze3BabN6edpDIbNqSdIBl1dWknSM7f/552gmS8/HLaCZKx335pJ0hGz55pJ0hGsZh2gmSsWJF2guT06ZN2gmR0l8/J7runnSAZ3eXnhN3l+6zu8vlob087AW/WXb5fHDgw7QS8UaHQlnaEVKxfvz7Wv/xy9H722bSjbGX9qFHd/jdJbgpZu+yyS2zeHFFTMybtKBVZtiztBMk48MC0EyTn5pvTTpCMG25IO0EyfvGLtBMkY889006QjMGD006QjNtvTztBco46Ku0Eybj++rQTJOO009JOkIzhw9NOkIzly9NOkIyhQ9NOkIy8/wD6jWq6yQNZ7rgj7QTJOPPMtBMko7t8XfXo8XS3KcB3VO9nn40xn/hE2jG28vS113b7QlY3+a0DAAAAQHeXmx1ZAAAAAJlRKGRva12hkHaCLpexFQcAAACA8hSyAAAAAMgFrYUAAAAAnZG11sIqYMUBAAAAyAWFLAAAAAByQWshAAAAQEc5tTAVGVtxAAAAAChPIQsAAACAXNBaCAAAANAZWWstrAJduuK33XZbjB49OhYtWtSV0wAAAABQBZQOAQAAAMgFrYUAAAAAnaG1cKez4gAAAADkgkIWAAAAALmQqdbCUqkUpVKp7Fhra2u0txd2ciIAAACAMgqF7LUWFrp/3SRThazGxsaYM2dO2bHZs2fHgAGDY+DAsTs5FQAAAABZkKlCVkNDQ8yaNavsWFNTU6xf3/0riwAAAACUl6lCVrFYjGKxWHastra2GnbIAQAAAHmRtdbCKmDFAQAAAMgFhSwAAAAAtvHLX/4yPvaxj8V73/vemDBhQpx99tmxaNGird5z5513xoknnhgHHnhgvO9974vvfe97sWnTpi7LpJAFAAAA0FGvn1qYpVeCz2S65ZZb4rOf/Wy8613viv/8z/+Mr3/967F27dqYOXNmPP7441vec/HFF8ehhx4ac+fOjalTp0ZjY2PMnj07sRxv1qXPyDr11FPj1FNP7copAAAAAEjYnDlz4qijjorvfOc7W65NmDAhjjnmmLjmmmviu9/9blxxxRVxwgknxFe/+tWIiJg4cWLU1dXF5ZdfHrNmzYqRI0cmnsuOLAAAAAC2WL9+fUyZMiVmzpy51fX6+voYMmRIrFixIhYuXBirVq2KD3/4w1u954QTToj29va4//77uyRbpk4tBAAAAMiNbnpqYe/evePSSy/d5vpzzz0Xf/3rX+Pkk0+OZ599NiIiRowYsdV7Bg0aFHV1dfH88893STaFLAAAAIBuoq2tLZqbm7c7XiwWo1gsdvi+a9eujYsvvjh69OgRZ599dtx7770REdGnT59t3ltfX/+WGSqhkAUAAADQTaxcuTJOOeWU7Y6ff/75ccEFF3TonitWrIhzzz03/vrXv8aVV14ZI0aMiLa2trf8mEKCD55/I4UsAAAAgI56/dTCLCkUYtCgQbFgwYLtvqWju7H+/Oc/x/nnnx8tLS0xd+7cmDx5ckRE9O3bNyIiWlpaYuDAgVt9THNzc9mdWklQyAIAAADoJmpqaqK+vj6Re82fPz8uueSS2H333eMnP/lJjBkzZsvY6ycSLl26NIYPH77l+ooVK2LdunUxatSoRDK8WcZKhwAAAACk7Z577okvfOELse+++8Ytt9yyVRErIuLggw+Ofv36xfz587e6Pn/+/CgUCjFx4sQuyWVHFgAAAEBnZK21MCFr1qyJSy+9NOrq6uIzn/lMLFu2LJYtW7ZlvFevXjFmzJj49Kc/Hd/61reiV69eMWXKlFi4cGF8//vfj6lTp3bZjiyFLAAAAAC2ePDBB2PNmjUREXHOOedsM77PPvvEXXfdFWeddVb07Nkzrrvuupg3b14MGjQoGhoa4rzzzuuybApZAAAAAGxx/PHHx/HHH79D7z3ttNPitNNO6+JE/59CFgAAAEBHZfTUwu4uYysOAAAAAOXlakdWz54RAwemnaIyxWLaCZJRKqWdIDlz5qSdIBnXz5j/9m/KgaeG7dj21az7wx/STpCMd//hmrQjJGLo0H9PO0JiRoxIO0EyvvGNtBMko1evtBMko7v8vX7ccWknSMb/PZIk99ra0k6QnCHxj7QjJGLMd4akHSER/X/WmHaERPzvuIa0I0Au5aqQBQAAAJAZWWstrAJWHAAAAIBcUMgCAAAAIBe0FgIAAAB0htbCnc6KAwAAAJALClkAAAAA5ILWQgAAAICOKhSy11pYKKSdoMtlbMUBAAAAoDyFLAAAAAByQWshAAAAQGdkrbWwClhxAAAAAHJBIQsAAACAXKiokPXJT34yxo0bF6+99tp23/Pzn/88Ro8eHb/61a8qmQoAAAAgO14/tTBLL6cWvrUZM2bEpk2b4uc///l233PrrbfGoEGD4phjjqlkKgAAAACqXEWFrPe9730xaNCguP3228uOv/jii/Hoo4/GtGnTokcPz5UHAAAAupG0d2C9+VUFKvpV9ujRI6ZPnx6LFy+OJUuWbDN+6623Rk1NTXz0ox+tZBoAAAAAqPxh79OnT4/a2tqYN2/eVtdbW1tj3rx5cfTRR8eQIUMqnQYAAACAKldxIWvIkCExadKk+PnPfx6bN2/ecv2hhx6KFStWxIwZM3b4XqVSKZqbm8u+Wltbo729rdK4AAAAAJXzsPdUJNJAOXPmzHjllVfid7/73ZZrt956a7zzne+MiRMn7vB9GhsbY/z48WVfixYtildeWZlEXAAAAAByKJEnsE+cODH22muvuP322+P9739/vPrqq/Gb3/wmLrzwwih0oBrY0NAQs2bNKjvW1NQUmzd3/8oiAAAAAOUlUsiqqamJ6dOnx9y5c2P16tVxxx13RETE1KlTO3SfYrEYxWKx7FhtbW20tlYcFQAAACAZVXJSYJYktuLTpk2L9vb2+PWvfx133nlnfPCDH4wBAwYkdXsAAAAAqlxihayBAwfGMcccE9dee2385S9/iZkzZyZ1awAAAABIrpAVETFjxox4/vnnY9999433vve9Sd4aAAAAIDucWpiKRJ6R9boJEybEkiVLkrwlAAAAAEREwjuyAAAAAKCrJLojCwAAAKBqOLVwp7PiAAAAAOSCQhYAAAAAuaC1EAAAAKAztBbudFYcAAAAgFxQyAIAAAAgF7QWAgAAAHRUoZC91sJCIe0EXS5jKw4AAAAA5SlkAQAAAJALWgsBAAAAOiNrrYVVwIoDAAAAkAu52pG1dm3EkiVpp6jMM8+knSAZhx6adoLk/OlPaSdIxvDhx6cdIREblqWdIBm9eqWdICEzzk47QSJe+EbaCZLz9NNpJ0jGs8+mnSAZgwalnSAZu++edoJkdJffH0OHpp0gGd1pk8LKmiFpR0jEH/6QdoJkTPtoQ9oREnHdJWknSMbJJ0f06ZN2CqpJrgpZAAAAAJng1MJUZGzFAQAAAKA8hSwAAAAAckFrIQAAAEBnZK21sApYcQAAAAByQSELAAAAgFzQWggAAADQUU4tTEXGVhwAAAAAylPIAgAAACAXtBYCAAAAdEbWWgurgBUHAAAAIBcSK2SdccYZ8f73vz+p2wEAAADAVrQWAgAAAHSUUwtTkbEVBwAAAIDyFLIAAAAAyAWthQAAAACdkbXWwiqQqUJWqVSKUqlUdqy1tTXa27t/rycAAAAA5WWqkNXY2Bhz5swpOzZ79uzo23dwRIzduaEAAAAAyIRMFbIaGhpi1qxZZceamppi1apCtLTs5FAAAAAA5Wgt3OkyVcgqFotRLBbLjtXW1lbDKZIAAAAAbIfSIQAAAAC5kOiOrObm5vjRj35Uduz000+Pnj17JjkdAAAAQDoKhey1FlZBK1uihax//vOf8e1vf7vs2PTp0xWyAAAAAOi0xApZ119/fVK3AgAAAIBtZOph7wAAAAC5kbXWwipgxQEAAADIBYUsAAAAAHJBayEAAABARzm1MBUZW3EAAAAAKE8hCwAAAIBc0FoIAAAA0BlZay2sAlYcAAAAgFxQyAIAAAAgF7QWAgAAAHSUUwtTkbEVBwAAAIDy7MgCAAAA6Iys7ciqAlYcAAAAgFzI1Y6sHj0idt897RSVee97006QjOXL006QnA99KO0EyVizJu0EyWhuTjtBMsaOTTtBQrrJT5hOXdiedoTElEppJ0jG4MFpJ0hGd/kzq1hMO0EyusufvUuXpp0gGd3l6yqi+/zZe+ihaSdIRv8N/0g7QiL+7d+GpB0hET1yVVWgO/AlBwAAANBRHvaeioytOAAAAACUp5AFAAAAQC5oLQQAAADojKy1FlYBKw4AAABALihkAQAAAJALWgsBAAAAOkNr4U5nxQEAAADIBYUsAAAAAHJBayEAAABARxUK2WstLBTSTtDlMrbiAAAAAFBeIjuyLrnkkpg3b952x/fff/+47bbbkpgKAAAAgCqVaGvhzTffXPZ6XV1dktMAAAAApC9rrYVVINFC1kEHHZTk7QAAAABgC6VDAAAAAHIh0R1Zmzdv3uZaoVCI2traJKcBAAAASFcVnVq4efPm+PjHPx5jx46Nr33ta1uuP/fcc3HccceV/Zh77rkn9t5778SzJFrI2n///be5ttdee8X999+/Qx9fKpWiVCqVHWttbY329u5/jCQAAABAVqxbty4uvvjieOKJJ2Ls2LFbjT355JMREdHY2Bi77bbbVmNDhgzpkjyJFrJuvfXWba4Vi8Ud/vjGxsaYM2dO2bHZs2fHbrsNjl12GVt2HAAAAIDkPPDAA/Htb387Vq9eXXb8qaeeiv79+8fRRx+90zIlWsg64IADKvr4hoaGmDVrVtmxpqamWLu2EOvXVzQFAAAAQDKy1lqYoDVr1sS5554bH/zgB+PLX/5yTJ48eZv3LF68eJtdWl0t0UJWpYrF4nZ3cNXW1nZVqycAAAAAb9CrV6+YP39+jBw5sux4e3t7LF68OPbbb78444wzYtGiRVFbWxtHH310fOlLX4pBgwZ1Sa5MFbIAAAAA6Ly2trZobm7e7vhbbSJ68/u2V8SKiFi6dGm0tLTEsmXL4vzzz48LL7wwFi9eHHPnzo0//elPMW/evOjbt2+nfg1vRSELAAAAoKMyemrhypUr45RTTtnuW84///y44IILKp5q4MCB8cMf/jBGjhy55cHu733ve2PfffeNs846K37yk5/EueeeW/E8b6aQBQAAANBNDBo0KBYsWLDd8Y4cyvdW6uvr46ijjtrm+uGHHx719fWxePHiROZ5s0RKh9/5zndiyZIlSdwKAAAAgE6qqamJ+vr67b6SKmQ988wz8dOf/jTWrl271fW2trbYtGlTDBgwIJF53syOLAAAAIDOyFpr4U70wgsvxNe//vWIiJg5c+aW6/fcc09s3LgxJkyY0CXzKmQBAAAA0CGTJ0+O8ePHx+WXXx4tLS2x//77x6JFi+Kqq66Ko446KqZMmdIl8ypkAQAAANAhPXv2jMbGxrjqqqvi5ptvjuXLl8fAgQPjzDPPjE996lNdNq9CFgAAAEBHZfTUwq5S7tnoffr0iS9+8YvxxS9+scvmfbOMrTgAAAAAlKeQBQAAAEAuaC0EAAAA6IystRZWASsOAAAAQC4oZAEAAACQC1oLAQAAADpDa+FOZ8UBAAAAyAWFLAAAAAByIVethYVC/nftPf542gmSMXhw2gmS89JLaSdIRn192gmSUSqlnSAZCxemnSAZa55sTztCItY1p50gOa+9lnaCZNTVpZ0gGevWpZ0gGQMGpJ0gGU8+mXaCZHSX3x8bNqSdIDm9eqWdIBltbWknSMY/YkjaERLRXT4fVS2LRYpCIe0EXS5jKw4AAAAA5SlkAQAAAJALuWotBAAAAMiMrLUWVgErDgAAAEAuKGQBAAAAkAtaCwEAAAA6yqmFqcjYigMAAABAeQpZAAAAAOSC1kIAAACAzshaa2EVsOIAAAAA5IJCFgAAAAC5oLUQAAAAoKOcWpiKxApZS5cujRtuuCEefPDBWL58eey6664xcuTImDFjRhx33HFRqILFBAAAAKDrJFLIuuuuu+IrX/lKvPOd74wzzzwzRowYES0tLfGrX/0qPv/5z8dDDz0U3/zmN6Mma5VKAAAAAHKj4kLW4sWL48tf/nIcfvjhMXfu3CgWi1vGjj322Nhrr73iqquuisMPPzxOPvnkSqcDAAAAyAYbdna6igtZV199dbS2tsbs2bO3KmK97txzz43Vq1dHv379Kp0KAAAAgCpWcSHrgQceiP322y/23HPPsuO9evWKr3/965VOAwAAAJAdHvaeiooKWa+99lqsX78+hg0blkiYUqkUpVKp7Fhra2u0t3f/TwgAAAAA5VVUyKqtrY2IfxWZktDY2Bhz5swpOzZ79uzo339w9Oo1NpG5AAAAAMiXigpZ/fr1iz59+sSyZcve8n3Lly+PQYMGve2phQ0NDTFr1qyyY01NTdHcXIgNGzodFwAAACA5WWstrAIVr/jkyZNj8eLF8dJLL5Ud37RpU5x88slx2mmnve29isVi1NfXl33V1tZGoeALBAAAAKBaVVwZOvvss6O2tjZmz55d9vlWc+bMidWrV8fUqVMrnQoAAACAKlbxqYX77bdfXHrppXHZZZfF9OnTY+bMmTF8+PB47bXX4q677or77rsvpk2bFtOmTUsiLwAAAEA2aC3c6SouZEVEnHbaabHffvvFDTfcEFdffXW88sor0adPnxg5cmR873vfiylTpkShCo6ABAAAAKDrJFLIiog4+OCD4+CDD07qdgAAAACwlcQKWQAAAABVo1DIXmthFXTDZWzFAQAAAKA8hSwAAAAAckFrIQAAAEBnZK21sApYcQAAAAByQSELAAAAgFzQWggAAADQUU4tTEXGVhwAAAAAylPIAgAAACAXtBYCAAAAdEbWWgurgBUHAAAAIBcUsgAAAADIhVy1FhYKEcVi2ikqM2BA2gmS0Z12Ty5dmnaCZIwYkXaCZOy+e9oJkrFmTdoJkjFsWNoJkrFwYdoJktOrV9oJktFdfo8MHZp2gmSsW5d2gmTk/fvE13WX77Pa2tJOkJxSKe0EyeiRq3/9bV93+T3SXT4fVXBI3vY5tTAVGVtxAAAAAChPIQsAAACAXOgmmxkBAAAAdrKstRZWASsOAAAAQC4oZAEAAACQC1oLAQAAADrKqYWpyNiKAwAAAEB5ClkAAAAA5ILWQgAAAIDOyFprYRWw4gAAAADkgkIWAAAAALmgtRAAAACgM7QW7nSdWvEzzjgjRo8eHRMnToy2tray73nqqadi9OjRMXr06Fi0aFFFIQEAAACg06XDmpqaWLlyZTz66KNlx++4445OhwIAAACAN+t0IWv48OExcODAmD9//jZjra2t8Ytf/CL233//isIBAAAAZFKh8K/Wwiy9CoW0V6XLdbqQVVtbG8cdd1zcc889USqVthp7+OGHY/Xq1XH88cdXHBAAAAAAIio8tfDEE0+Mf/7zn/Hggw9udf3OO++Mo446Kvr3719ROAAAAAB4XUWFrAMOOCCGDx8ed91115Zr69evj3vvvTdOPvnkDt+vVCpFc3Nz2Vdra2u0t5d/sDwAAADATpd2K+GbX1Wg4l/liSeeGL/5zW+ipaUlIiJ+/etfR48ePeKYY47p8L0aGxtj/PjxZV+LFi2KVatWVhoXAAAAgJzqUekNTjrppPjv//7vuO++++Kkk06KO++8Mz70oQ9FsVjs8L0aGhpi1qxZZceampqipaUQra2VJgYAAAAgjyouZA0bNiwOOuiguOuuu+LII4+MRx55JH784x936l7FYnG7BbDa2tpqePg+AAAAkAevn1qYJVVQOElkxU888cR4+OGH48Ybb4w99tgjxo8fn8RtAQAAAGCLRApZxx13XLS3t8fVV18dJ510UhSqoAIIAAAAwM6VSCFrwIABMWHChNi0aVOnTisEAAAAyJ20TymswlMLO/WMrOuvv36ba9dcc80210499dQ49dRTOzMFAAAAAGylOsp1AAAAAORexacWAgAAAFQdpxamImMrDgAAAADlKWQBAAAAkAtaCwEAAAA6I2uthVXAigMAAACQCwpZAAAAAOSC1kIAAACAjnJqYSoytuIAAAAAUJ5CFgAAAAC5oLUQAAAAoDOy1lpYBaw4AAAAALmQqx1Z7e0RpVLaKSrT3Jx2gmTU1aWdIDmvvZZ2gmT06pV2gmQMGJB2gmT07Zt2gmR0l6+rH/wg7QTJOeectBMko7v82btuXdoJknFk/Z/TjpCIRTXvTjtCIlavTjtBMvL+ffsbjRuXdoJk/P73aSdIxtixaSdIxrJlaSdIxuDBEfX1aadIkR1ZO50VBwAAACAXFLIAAAAAyIVctRYCAAAAZEKhkL3WwkIh7QRdLmMrDgAAAADlKWQBAAAAkAtaCwEAAAA6I2uthVXAigMAAACQCwpZAAAAAOSC1kIAAACAjnJqYSoytuIAAAAAUJ5CFgAAAADbtXnz5pgxY0Z84xvf2GbszjvvjBNPPDEOPPDAeN/73hff+973YtOmTV2WJfFC1o033hijR4+OadOmJX1rAAAAgOyoqcnWqwusW7cuLrzwwnjiiSe2Gbvlllvi4osvjkMPPTTmzp0bU6dOjcbGxpg9e3aXZInogmdk3XTTTTFmzJhYtGhR/PnPf453v/vdSU8BAAAAQBd74IEH4tvf/nasXr16m7GNGzfGFVdcESeccEJ89atfjYiIiRMnRl1dXVx++eUxa9asGDlyZOKZEi3XPfHEE/HMM8/ExRdfHAMHDozrrrsuydsDAAAAsBOsWbMmzj333BgzZkzccccd24wvXLgwVq1aFR/+8Ie3un7CCSdEe3t73H///V2SK9EdWT/72c9it912i8MOOyxOPvnk+PGPfxyXXHJJDBw4MMlpAAAAANLVzU8t7NWrV8yfP3+7u6qeffbZiIgYMWLEVtcHDRoUdXV18fzzzyeW5Y0SW/E1a9bEL37xizjppJOiZ8+e8dGPfjQ2b94cN998c1JTAAAAAPAW2traorm5ebuvUqm0Q/cpFotv2Rq4du3aiIjo06fPNmP19fXR3NzcuV/A20hsR9Ydd9wRGzZsiI997GMREbH33nvH4YcfHjfddFM0NDREz5493/YepVJpuwva2toa7e3JVRYBAAAAupuVK1fGKaecst3x888/Py644IKK52lra3vL8UKCu8PeKLFC1s9+9rMYN25cDBo0KNasWRMR/+qLvPTSS+Puu++OE0888W3v0djYGHPmzCk7Nnv27Ojff3D06jU2qcgAAAAAnZe11sL4V2vfggULtjteLBYTmadv374REdHS0rLNI6Wam5vL7tRKQiKFrMcffzyeeeaZiIg45JBDthm/4YYbdqiQ1dDQELNmzSo71tTUFM3NhdiwobKsAAAAAN1VTU1N1NfXd/k8r7cdLl26NIYPH77l+ooVK2LdunUxatSoLpk3kULWzTffHL169Yqrrroqamtrtxq77bbb4vbbb49FixbFAQcc8Jb3KRaL260M1tbWJvnMMgAAAAA66eCDD45+/frF/Pnz4+ijj95yff78+VEoFGLixIldMm/Fhaw1a9bE3XffHccee2xMmDBhm/EBAwbE7bffHtdff31cfvnllU4HAAAAkL5ufmrh2ykWi/HpT386vvWtb0WvXr1iypQpsXDhwvj+978fU6dOze6OrNtvvz02bNgQJ598ctnxffbZJw466KD45S9/GV/60pfiHe94R6VTAgAAAJCys846K3r27BnXXXddzJs3LwYNGhQNDQ1x3nnnddmcFReyfvazn8XAgQPjyCOP3O57pk+fHpdeemncdNNN8elPf7rSKQEAAADYiZYsWVL2+mmnnRannXbaTstRcSHrrrvuetv3TJs2LaZNm1bpVAAAAADZkbXWwipgxQEAAADIBYUsAAAAAHKh4tZCAAAAgKqktXCns+IAAAAA5IJCFgAAAAC5oLUQAAAAoKMKhey1FhYKaSfochlbcQAAAAAoTyELAAAAgFzQWggAAADQGVlrLawCVhwAAACAXFDIAgAAACAXtBYCAAAAdJRTC1ORsRUHAAAAgPJytSOrri5i5Mi0U1Rm2bK0EySjR66+ct7apElpJ0jG4sVpJ0hG1n6g0VmH3PvttCMkY+iZaSdIxBe/uFfaERIzeHDaCZJxxJ5NaUdIRFPsnXaERPx59bvTjpCId7f9Oe0Iifjfmu7x+aivTztBcl54Ie0EyejbN+0Eyegun48RI9JOkIy2trQTUG26UTkCAAAAYCfqLj+JzxErDgAAAEAuKGQBAAAAkAtaCwEAAAA6yqmFqcjYigMAAABAeQpZAAAAAOSC1kIAAACAzshaa2EVsOIAAAAA5IJCFgAAAAC5oLUQAAAAoKOcWpiKjK04AAAAAJRX8Y6sSy65JObNm7fVtZqamqirq4t99tknzjzzzDjuuOMqnQYAAACAKpdYa+HNN9+85b/b2tpi1apV8cMf/jA+97nPRalUio985CNJTQUAAACQvqy1FlaBxApZBx100DbXDjvssJg8eXL84Ac/UMgCAAAAoCJdWjqsr6+PESNGxNIgTWbOAAAgAElEQVSlS7tyGgAAAACqQJeeWlgqleLFF1+MPffcsyunAQAAANj5tBbudIkVsjZv3rzlv18vYM2dOzdWrVoV55133g7do1QqRalUKjvW2toabW3d/xhJAAAAAMpLrJC1//77b3NtwIABcdFFF8UZZ5yxQ/dobGyMOXPmlB2bPXt2DBw4OPbaa2xFOQEAAADIp8QKWbfeeuv/v2mPHtGvX78OtxQ2NDTErFmzyo41NTVFa6sdWQAAAEAGFArZay0sdP+6SWKFrAMOOKDiexSLxSgWi2XHamtro7294ikAAAAAyKkufdg7AAAAQLeVtR1ZVcCKAwAAAJALClkAAAAA5ELFhazvfOc7sWTJkiSyAAAAAOTD6w97z9KrCh72bkcWAAAAALmgkAUAAABALji1EAAAAKAznFq401lxAAAAAHJBIQsAAACAXNBaCAAAANBRr59amCVOLQQAAACAbFDIAgAAACAXtBYCAAAAdEbWWgurgBUHAAAAIBcUsgAAAADIBa2FAAAAAB1VKFTFKYFZk6tC1qZNEa+8knaKyrw7/px2hEQ82vzutCMk5oUX0k6QjLa2tBMko1evtBMk47Fjv5x2hESMG5B2gmT8/p60EyTnwAPTTpCMhx7aO+0IiZgyJe0Eydhtt7QTJON/l3WP70/q6tJOkIzly9NOkJy+fdNOkIy8/1vqdcOHp50gGYsXp50gGXvsEbHrrmmnoJpoLQQAAAAgF3K1IwsAAAAgM7J2amF3adV5CxlbcQAAAAAoTyELAAAAgFzQWggAAADQGVoLd7qMrTgAAAAAlKeQBQAAAEAuaC0EAAAA6KhCIXuthYVC2gm6XMZWHAAAAADKU8gCAAAAIBe0FgIAAAB0RtZaC6uAFQcAAAAgFxLZkbVixYq46aab4v7774+XXnopNm7cGHvssUccccQRMWvWrHjXu96VxDQAAAAAVLGKC1kPPfRQXHTRRbHLLrvEzJkz44ADDoiePXvGM888EzfccEPceeedcdVVV8URRxyRRF4AAACA9Dm1MBUVFbL+/ve/x2c/+9nYc88944Ybboi+fftuGTvssMNi6tSpMXPmzPjyl78c9913X9TW1lYcGAAAAIDqVFHp8Jprrom1a9fGt771ra2KWK+rq6uLiy66KMaPHx+rVq2qZCoAAAAAqlxFO7Luvvvu2GeffWLcuHHbfc+kSZNi0qRJlUwDAAAAkD1Zay2sAp0uZK1ZsyZWrVoVhx566DZjra2t0d7evtW12traKLxNr2apVIpSqVR27F/37P69ngAAAACU1+lCVltb23bHTj311Hj66ae3uvbFL34xPvnJT77lPRsbG2POnDllx2bPnh3veMfg2HXXsR0PCwAAAEDudbqQtdtuu0V9fX28+OKL24xdccUVsX79+oiIePnll+NTn/rUDt2zoaEhZs2aVXasqakpNm60IwsAAADIAKcWpqKiZ2RNmTIlbrvttnjuuedi5MiRW66PGjVqy38vW7Zsh+9XLBajWCyWHftXa2LnswIAAACQbxWVDhsaGqK+vj4uvvji7Z5KuGTJkkqmAAAAAICIqHBH1vDhw2POnDlx0UUXxfHHHx/Tp0+Pgw8+OHr37h0vvPBC3H333fHQQw/F3nvvHYccckhSmQEAAADSl7XWwipQUSErIuKII46Iu+66K2655Za4995746abboqWlpYYMGBAHHDAAXHFFVfElClTttsyCAAAAAA7ouJCVkTEgAEDoqGhIRoaGpK4HQAAAABsI5FCFgAAAEDV0Vq401lxAAAAAHJBIQsAAACAXNBaCAAAANBRhUL2WgsLhbQTdLmMrTgAAAAAlKeQBQAAAEAuaC0EAAAA6IystRZWASsOAAAAQC4oZAEAAACQC1oLAQAAADrKqYWpyNiKAwAAAEB5ClkAAAAA5EKuWgvXrYt45pm0U1TmtuffnXaERIwdm3aC5Nx9d9oJkvH+96edIBlPP512gmTU1aWdIBnLl6edIBl5/7vjjXrk6m/u7XvttbQTJOOee9JOkIwLP9KUdoRE/HH53mlHSESxmHaCZPTtm3aC5NTXp50gGStXpp0gGRs2pJ0gGT/5SdoJknHGGREDBqSdIkVZay2sAlYcAAAAgFzoJj/XBQAAANiJPOw9FRlbcQAAAAAoTyELAAAAgFzQWggAAADQGVlrLawCClkAAAAAbGPChAnx6quvbnP9sssui+nTp6eQSCELAAAAgDdZvnx5vPrqq/GZz3wmjjzyyK3Ghg0bllIqhSwAAACAjuvmpxY++eSTERHxgQ98IPbdd9/E7lupjK04AAAAAGlbvHhx9OrVK0aOHJl2lK0oZAEAAACwlaeeeip22223+MIXvhCHHXZYjBs3Ls4444xYuHBhqrm0FgIAAAB0RtZaCyOira0tmpubtzteLBajWCy+7X2eeuqpWLNmTYwcOTJOP/30WL58eTQ2Nsbpp58eN954Yxx44IFJxt5hClkAAAAA3cTKlSvjlFNO2e74+eefHxdccMHb3ufKK6+Murq62H///bdcmzBhQnz4wx+O7373u3HttdcmkrejKi5kXXLJJTFv3ry3fd91110Xhx12WKXTAQAAALAdgwYNigULFmx3fEd2Y0VEHHLIIdtcGzBgQLznPe+JJ554otP5KlVxIeu8886LGTNmbPn/W265JW699daYM2dODBw4cMv1UaNGVToVAAAAQHZksLWwpqYm6uvrK7rHa6+9Fvfdd18cdNBBsc8++2w1ViqVYsCAARXdvxIVF7KGDRsWw4YN2/L/Dz74YERE7LfffjF06NBKbw8AAADATlQoFOJrX/tafOhDH4orr7xyy/W///3vsWDBgpg2bVpq2TwjCwAAAIAt+vfvH5/4xCfiBz/4Qey2227xgQ98IJYvXx5z5syJvn37xnnnnZdaNoUsAAAAgI4qFLLXWlgoJHariy66KIYOHRo//elPY968edGrV6+YOHFifP7zn893a2GSSqVSlEqlsmOtra3R3p7cJwQAAACA8mpqamLmzJkxc+bMtKNsJVOFrMbGxpgzZ07ZsdmzZ0ffvoMjYuzODQUAAABAJmSqkNXQ0BCzZs0qO9bU1BSrVhVi7dqdHAoAAACgnKy1FlaBTBWyisViFIvFsmO1tbVJtnoCAAAAkDNKhwAAAADkQqZ2ZAEAAADkQjc/tTCrMrbiAAAAAFBe4oWsCy64IJYsWRJDhw5N+tYAAAAAVDGthQAAAACdkbXWwipgxQEAAADIBYUsAAAAAHJBayEAAABARzm1MBUZW3EAAAAAKE8hCwAAAIBc0FoIAAAA0BlZay2sAlYcAAAAgFxQyAIAAAAgF7QWAgAAAHSUUwtTkbEVBwAAAIDyFLIAAAAAyIVctRYWixFDh6adojJjx6adIBmrV6edIDlHH512gmR0l6+ttra0EyTjpZfSTpCMdw1qSTtCIsaM2TXtCIkZPjztBLxRd/mzd1XfvdOOkIg990w7QTI2bEg7QTLWrUs7QXLq69NOkIxRo9JOkIy6urQTJOO889JOkIzu8vnorPbo/q18WWNHFgAAAAC5oJAFAAAAQC7kqrUQAAAAIAva27P3aJT29u5/cKEdWQAAAADkgkIWAAAAALmgtRAAAACgE7LWWlgN7MgCAAAAIBcUsgAAAADIBa2FAAAAAB3k1MJ02JEFAAAAQC4oZAEAAACQC4m1FjY1NUVjY2M88sgj8fLLL0fv3r1jn332iY985CMxderUqK2tTWoqAAAAgNRlrbWwGiRSyHruuefiYx/7WAwfPjwuvPDCGDJkSDQ3N8dvf/vb+NrXvhZ//OMf4/LLL09iKgAAAACqVCKFrGuvvTYiIq6//vro3bv3luvHHHNM7LLLLnHdddfFJz7xiRgzZkwS0wEAAABQhRIpZL3yyitRKBSitbV1m7GPf/zjMXDgwKirq0tiKgAAAIDUZfXUwu4ukYe9H3PMMbFmzZqYNm1aXH311bFw4cLYtGlTRETsvffecc4558SwYcOSmAoAAACAKpXIjqyPfvSjsXr16rjqqqviiiuuiIiIXXbZJQ4++OA47rjj4tRTT42ePXu+7X1KpVKUSqWyY62trdHeXkgiLgAAAAA5lNipheecc058/OMfj4cffjgee+yxWLBgQTz22GPx+9//Pm666ab40Y9+FP369XvLezQ2NsacOXPKjs2ePTv69x8c9fVjk4oMAAAA0GlZay2sBokVsiIi6urq4thjj41jjz02IiJWrVoVc+fOjeuvvz6uueaa+MIXvvCWH9/Q0BCzZs0qO9bU1BQtLYX4v45FAAAAAKpMxc/IWrFiRUycODGuvvrqbcb69+8fX/nKV2KPPfaIZ5555m3vVSwWo76+vuyrtrY2CoVEHukFAAAAQA5VXBkaOHBgFIvFuOmmm2L16tXbjL/yyiuxZs2aGDNmTKVTAQAAAGTC66cWZulVDacWVtxaWFNTE5dddlk0NDTERz7ykTj99NNj//33j9ra2liyZEn8+Mc/jj322GO7LYMAAAAAsCMSeUbWEUccEfPmzYtrr702brnllpg7d260tbXFXnvtFccff3z8+7//e/Tp0yeJqQAAAAAywcPed77EHvY+cuTI+OY3v5nU7QAAAABgK56eDgAAAEAuJLYjCwAAAKCaaC3c+ezIAgAAACAXFLIAAAAAyAWthQAAAAAd1N6evdbC9va0E3Q9O7IAAAAAyAWFLAAAAAByQWshAAAAQCdkrbWwGtiRBQAAAEAuKGQBAAAAkAtaCwEAAAA6yKmF6bAjCwAAAIBcUMgCAAAAIBdy1VrY1haxYUPaKSrz8MNpJ0jG8OFpJ0jOs8+mnSAZzz+fdoJknHpq2gmSMXhw2gmScfNdu6YdIRHd5c/e7uTpp9NOkIzNm9NOkIy6urQTJOPqq9NOkIyzz047QTK6y9dVRESxmHaCZPz+92knSMZLL6WdIBnLlqWdIBlHHBHRr1/aKdKTtdbCamBHFgAAAAC5oJAFAAAAQC7kqrUQAAAAIAucWpgOO7IAAAAAyAWFLAAAAAByQWshAAAAQCdkrbWwGtiRBQAAAEAuKGQBAAAAkAtaCwEAAAA6yKmF6bAjCwAAAIBcUMgCAAAAIBd2uJB10UUXxdixY6O5uXmbsQ9+8IMxevTo+NGPfrTNWGNjY4wePTqefvrpioICAAAAZElbW7Ze1WCHC1kTJ06M1tbWePzxx7e63tTUFEuXLo3+/fvHb37zm20+7tFHH4099tgjxowZU3laAAAAAKrWDheyjjzyyCgUCvHHP/5xq+sPPPBA9O7dO/7t3/4tFixYsNWOrVKpFI8//nhMnDgxucQAAAAAVKUdLmQNHDgw9t1333jssce2uv7b3/42Dj300Dj22GNj06ZN8dBDD20ZW7hwYaxfvz4mTZqUXGIAAACADEi7lVBr4ds46qijYtGiRbFx48aIiGhpaYk//OEPMXny5Bg1alTstdde8cADD2x5/+9///vo0aNHHHnkkYmGBgAAAKD6dKiQNXHixNi0aVP86U9/ioiIRx55JDZt2hSTJ0/eMv673/0u2v6vDPjoo4/Ge97znqivr9+h+5dKpWhubi77am1tjfb2KikvAgAAALCNDhWyxo8fH717997SXvjAAw/EqFGjYujQoRERMXny5Hj11Vfjqaeeio0bN8af/vSnDj0fq7GxMcaPH1/2tWjRoli9emVH4gIAAAB0ifb29FsJ3/xqb097Vbpej468uVgsxiGHHLLlge+//e1v44QTTtgyfvjhh0exWIxHHnkkmpubo1QqbdmttSMaGhpi1qxZZceamppi7dpCtLR0JDEAAAAA3UWHClkR/3pO1n/913/FU089FStXroyjjz56y1hdXV0ccsgh8dhjj8WGDRtijz32iNGjR+/wvYvFYhSLxbJjtbW1USh0NC0AAAAA3UWHWgsj/lXIamlpiRtvvDHq6+tj/PjxW41PmjQp/vKXv8Rjjz3mtEIAAACg20q7ldCphTtg5MiRMWTIkLjzzjvjyCOPjB49tt7UNWnSpHj55ZfjiSee6FBbIQAAAAC8lQ4XsiL+tSvrjacVvtGIESNi2LBhERFxxBFHVJYOAAAAAP5Ph5+RFRFx2WWXxWWXXbbd8V//+tedDgQAAACQda+fWpgl1XBqYad2ZAEAAADAzqaQBQAAAEAudKq1EAAAAKDaZa21sBrYkQUAAABALihkAQAAAJALWgsBAAAAOsiphemwIwsAAACAXFDIAgAAACAXtBYCAAAAdELWWgurgR1ZAAAAAOSCQhYAAAAAuaC1EAAAAKATtBbufLkqZPXrF3HooWmnqMykSWkn4M3e8560EyRj5Au/STtCIlYNfV/aERJR0032ux7y0h1pR0jG+09OO0FiPnZCS9oREvG3lbumHSERgwennSAZvV/7e9oREnH11XulHSERGzaknSAZL7yQdoLk7D+ukHaERBzQXf7F/YMfpJ0gES+f++9pR0jE8uVpJ6DadJN/agEAAACQpIULF8ZZZ50V73nPe+Kwww6LL33pS/HKK6+kmilXO7IAAAAAsqC9/V+vLCkkuIH06aefjrPOOisOOuiguOKKK+KVV16JK6+8Mp566qm47bbbolgsJjdZByhkAQAAALCV7373u9G/f/9obGzcUrTab7/9YurUqXHbbbfFjBkzUsmltRAAAACALUqlUjz88MNx7LHHbrXzaty4cTF8+PC47777UstmRxYAAABAJ2TtDIXa2mTu8+KLL8bGjRtjxIgR24y9613vimeeeSaZiTpBIQsAAACgm2hra4vm5ubtjheLxbd9vtXatWsjIqJPnz7bjO26667R0pLeSdoKWQAAAAAd1N6evR1ZNTURK1eujFNOOWW77zn//PPjggsueMv7tGXtF/YGClkAAAAA3cSgQYNiwYIF2x3fkdMG+/XrFxFRdudVS0tL9O3bt/MBK6SQBQAAANBN1NTURH19fUX3eOc73xk9e/aMv/3tb9uM/e1vf4uRI0dWdP9KOLUQAAAAoBPa2rL1SkqxWIwJEybEvffeG6VSacv1J598MpYuXRqTJk1KbrIOUsgCAAAAYCsXXHBB/OMf/4hPfOITcd9998X//M//xDnnnBOjRo2KadOmpZZLIQsAAACArRxwwAHxwx/+MDZv3hyf+9zn4j/+4z/iqP/X3r3HaT3n/QN/T1MXJSKrkEMqioyNtq3QQXXjXnKIlpaQxezaZW+SatcpQsvtcCtLKYcc7tDPMcdlsXLIobWSlcXKYZ3JKGlqun5/uOshTWpmvjPf6zvzfD4e1+MxXZ+r7+f1fcxcM9f1vj7v72fPPeP6669fp+ts1ZYaXSPrjDPOiNtvvz3OPffcOOyww1YbX758eRxxxBExd+7cmD59euywww41mQ4AAACgIBTiroX5fLLH6969e0ybNi3Zg9ZQjVZkjR49OrbZZpsYN25cvPfee6uNT5kyJWbPnh0jR45UxAIAAACgRmpUyNpggw3ioosuiiVLlsTo0aMj/53S3z//+c+44oorol+/fnHEEUfUOCgAAAAADVuNr5G16667xgknnBDPPfdcTJ06NSIili1bFiNHjoyNN944LrjgghqHBAAAACg0ae9SWFu7FhayRC72/pvf/CY6d+4cl19+eXzwwQdx9dVXxz/+8Y+4+OKLY5NNNkliCgAAAAAauBpd7H2FJk2axMUXXxyDBg2KU089NebMmRPHH3989OjRo0rHKS8vj/Ly8krHKioqoqioKIm4AAAAAGRQIoWsiIj27dvHiBEj4rzzzotddtklTj755CofY+LEiTFhwoRKx8aMGROtW28eO+64U02jAgAAANRIQ9i1sBAlVsiKiOjbt2+cd9550bt372jcuOqHLi0tjWHDhlU6Nn/+fCuyAAAAABqwRAtZNZXL5SKXy1U6VlxcXMdpAAAAACgkBVXIAgAAAMiKQmstbAgS2bUQAAAAAGqbQhYAAAAAmZBoa+FWW20V8+bNS/KQAAAAAAVJa2HdsyILAAAAgExQyAIAAAAgE+xaCAAAAFBF+XzhtRbm82knqH1WZAEAAACQCQpZAAAAAGSC1kIAAACAaii01sKGwIosAAAAADJBIQsAAACATNBaCAAAAFBFdi1MhxVZAAAAAGSCQhYAAAAAmaC1EAAAAKAaCq21sCHIVCHrs88ipk9PO0XNrL9+2gmS0bZt2gmS88oraSdIRnmXvdKOkIiy19NOkIx//zvtBMno1+/AtCMkol09+bmKiLj3LxukHSERjerJmvBPP007QTK6PTI17QiJmN1vdNoRElFWlnaCZJSXp50gORu9Uz8uOjNzWtoJkvFN4+PTjpCI3erJ68VlyyKaNEk7BQ1JPXkZCQAAAEB9l6kVWQAAAACFwK6F6bAiCwAAAIBMUMgCAAAAIBO0FgIAAABUQ6G1FjYEVmQBAAAAkAkKWQAAAABkgtZCAAAAgCqya2E6rMgCAAAAIBMUsgAAAADIBK2FAAAAANVQaK2FDYEVWQAAAABkQo0KWaNGjYpdd911jePjx4+Pjh07xnvvvVeTaQAAAABAayEAAABAdWgtrHtaCwEAAADIBIUsAAAAADIhkdbCZcuWVXr/cmvsAAAAgHoony+81sJ8Pu0Eta/Ghayvv/46OnfunESWKC8vj/Ly8krHKioqIp8vSmQeAAAAALKnxoWs9ddfP2666aZKx2677ba47bbb1vlYEydOjAkTJlQ6NmbMmNhoo80jYqfqxAQAAAAg42pcyGrUqFGUlJRUOvb4449X6VilpaUxbNiwSsfmz58fX3xRFIsWVTUhAAAAQPIKrbWwIUjkGllJyeVykcvlKh0rLi6OIp2FAAAAAA2WXQsBAAAAyISCWpEFAAAAkAV2LUyHFVkAAAAAZEKNClnjxo2Lv/3tb2scP+mkk2LevHmx1VZb1WQaAAAAANBaCAAAAFAdhdZa2BBoLQQAAAAgE6zIAgAAAKgiF3tPhxVZAAAAAGSCQhYAAAAAmaC1EAAAAKAaCq21sCGwIgsAAACATFDIAgAAACATtBYCAAAAVJFdC9NhRRYAAAAAmaCQBQAAAEAmaC0EAAAAqIZCay1sCDJVyFp//YgOHdJOQUTEN9+knSA5zZunnSAZ5eVpJ0hG40z9VlqzLbdMO0Ey6ssf5vXXTztBcurLz9Zbb6WdIBn15Wfr+QGj046QjHryO6tdu7QTJOPTT9NOkJz6ci4tW6adIBlbbZV2gmS8807aCZKxySZpJ6Ch0VoIAAAAQCbUk7UPAAAAAHWrvnQwZIkVWQAAAABkgkIWAAAAAJmgtRAAAACgivL5wmstzOfTTlD7rMgCAAAAIBMUsgAAAADIBK2FAAAAANVQaK2FDYEVWQAAAABkgkIWAAAAAJmgtRAAAACgiuxamI4aF7JGjRoVd9555w8+5pxzzokhQ4bUdCoAAAAAGrDEVmTdeuutaxzbeuutk5oGAAAAgAYqsUJWly5dkjoUAAAAQMErtNbChsDF3gEAAADIhMRWZC1btqzS+4uKiqK4uDipaQAAAABooBIrZHXu3LnS+zfccMN44YUX1ukY5eXlUV5eXulYRUVF5PNF1c4HAAAAkBS7FqYjsULW9OnTK5+g8bpPMXHixJgwYUKlY2PGjImWLTePzTbbqVr5AAAAAMi2xApZJSUlNT5GaWlpDBs2rNKx+fPnx+LFVmQBAAAANFSJFbKSkMvlIpfLVTpWXFwcRepYAAAAQIEotNbChsCuhQAAAABkQmIrsl566aU1jrVo0SK22267pKYCAAAAoAFKrJB12GGHrXGsf//+8ac//SmpqQAAAABSZdfCdNS4kDVu3LgYN25cElkAAAAAYI1cIwsAAACATCioXQsBAAAAsqLQWgsbAiuyAAAAAMgEhSwAAAAAMkFrIQAAAEA1aC2se1ZkAQAAAJAJClkAAAAAZILWQgAAAIAqyucLr7Uwn6/7Of/rv/4rHnjggdXuHzhwYPz3f/934vMpZAEAAABQLXPnzo0BAwbE8ccfv8r9LVu2rJX5FLIAAAAAqLKvvvoq3n333Tj66KOjS5cudTKnQhYAAABANRRaa2Fdmzt3buTz+dhpp53qbE4XewcAAACgyubOnRsREffcc0/06dMndtppp9hvv/3irrvuqrU5rcgCAAAAqCeWL18eCxcuXON4LpeLXC73g8fI5/Mxbdq0H3xMv3794tVXX42IiMWLF8e4cePim2++ienTp8fIkSOjrKwsjjrqqKqfwFoU5fNpXNO+6l577bX4+uuI9dbrlHaUGqmla53VuddfTztBcjbaKO0EyagvS1ob15Py+lr+LmTGjh8+lnaERIz5615pR0jMAQeknSAZ//eaJ/Pqy++s9ddPO0Ey6svv3i23TDtBMpo1SzsB3/fvf6edIBl9Ft6XdoREFO2/X9oREnHtta9Fz54RnTpl+716Vb322mvx7rsRM2cW1nnvuedr0aTJh1FaWrrGx/z2t7+Nk0466QePs2zZsujcufMPPmbq1KnRsmXL+OSTT2L33XdfeX8+n4+jjjoq5s6dG88+++xai2ZVVU9efgEAAADQqlWrePHFF9c4vi6FpcaNG8e8efPWab7tt99+lX8XFRVF//7947nnnov58+evNl5TClkAAAAA9USjRo2iefPmtT5PPp+Pu+++OzbbbLPYY489VhlbsmRJRES0rIW2NIUsAAAAgGqoL5d4qY6ioqK47rrr4quvvooHHngg1ltvvYj4ti3x/vvvjx122CE23XTTxOe1ayEAAAAAVXbKKafEv//97zjhhBPisccei0ceeSSOPfbYePPNN+Oss86qlTkVsgAAAACosr59+8Z1110Xy5cvj5EjR8aIESOiUaNGccMNN0S3bt1qZU6thQAAAABVlM8XXmthPl/3c/bs2TN69uxZZ/NZkQUAAABAJliRBQAAAFANhbYiqyGwIqwP4d8AACAASURBVAsAAACATFDIAgAAACATtBYCAAAAVJGLvaejRoWsUaNGxZ133rnKfblcLjbddNP4yU9+EqWlpbH99tvXKCAAAAAARCS0IuvWW29d+fXixYvjrbfeiilTpsQhhxwSkyZNih49eiQxDQAAAAANWCKFrC5duqzy7549e8a+++4bgwYNihEjRsTDDz8cTZs2TWIqAAAAgIJQaK2FDUGtXex90003jeOPPz4+/vjjeOihh2prGgAAAAAaiFrdtbB3794REfHcc8/V5jQAAAAANAC1umvhZpttFhERn3zyyTo9vry8PMrLyysdq6ioiHy+KLFsAAAAADWhtbDu1Woha4WionUrQE2cODEmTJhQ6diYMWNi0003jy233CnJaAAAAABkRK0Wsj788MOIiNh8883X6fGlpaUxbNiwSsfmz58f33xjRRYAAABAQ1WrhaynnnoqIiJ69OixTo/P5XKRy+UqHSsuLo51XNgFAAAAUKvy+cJrLczn005Q+2rtYu8LFiyIKVOmRJs2bWLAgAG1NQ0AAAAADUQiK7JeeumllV8vXrw43njjjZg6dWosWLAgJk+evMZVVgAAAACwrhIpZB122GErv87lctG6devo2bNnHHfccbHtttsmMQUAAABAQSm01sKGoEaFrHHjxsW4ceOSygIAAAAAa1Rr18gCAAAAgCTV6q6FAAAAAPWRXQvTYUUWAAAAAJmgkAUAAABAJmgtBAAAAKiGQmstbAisyAIAAAAgExSyAAAAAMgErYUAAAAAVWTXwnRYkQUAAABAJihkAQAAAJAJWgsBAAAAqqHQWgsbAiuyAAAAAMiETK3IWrIk4oMP0k5RM7Nnp50gGVtumXaC5NxzT9oJknHAAWknSMY776SdIBkLF6adIBm5n+6VdoRE1KdPyl55Je0EyXj88bQTJGPffdNOkIyddko7QTL++te0EyTjm2/STpCMtm3TTpCc+vLa9+mn006QjC4H7Zd2hEQceWTaCZKx2WZpJ6ChyVQhCwAAAKAQ2LUwHVoLAQAAAMgEhSwAAAAAMkFrIQAAAEA1FFprYUNgRRYAAAAAmaCQBQAAAEAmaC0EAAAAqAathXXPiiwAAAAAMkEhCwAAAIBM0FoIAAAAUEX5fOG1FubzaSeofVZkAQAAAJAJClkAAAAAZILWQgAAAIBqKLTWwoYgkULWG2+8ETfffHM89dRT8dFHH0WzZs2iQ4cOceCBB8bBBx8cxcXFSUwDAAAAQANW40LW7bffHueee25st912ceyxx0a7du2irKwsHn/88Tj77LPjjjvuiAkTJkTLli2TyAsAAABAA1WjQtYLL7wQZ599duy9995x8cUXR5MmTVaODRgwIPbbb784/vjjY9SoUTFp0qQahwUAAAAoBHYtTEeNLvY+fvz4aNasWYwdO3aVItYKPXv2jKFDh8YTTzwRL7zwQk2mAgAAAKCBq3Yh68svv4xZs2bFHnvsEc2bN1/j4wYOHBgREQ899NBaj1leXh4LFy6s9FZRURH5fIGVOgEAAACoM9VuLXz//fcjn8/H1ltv/YOP23bbbSMi4r333lvrMSdOnBgTJkyodGzMmDHRosXmEbFTlbMCAAAAJK3QWgsbgkR2LfwhjRp9u+iroqJirY8tLS2NYcOGVTo2f/78+PLLovjii0TjAQAAAJAR1S5ktWnTJoqKiuKdd975wcfNnz8/IiK22mqrtR4zl8tFLperdKy4uDiKiqqeEwAAAID6odrXyGrRokX06NEjZs6cGWVlZauMzZkzJ/L/d6n8Bx54ICIi+vbtW/2UAAAAAAVkxa6FhXSza+FanHzyybFkyZIYPXp0LF26NCIiysrKYujQobHvvvvGjTfeGNddd11069YtevfunUhgAAAAABqmGhWydttttxg7dmw8+eSTMWjQoJg2bVrMmzcvzj333FiwYEGMHTs2Kioq4owzzkgqLwAAAAANVI0v9n7wwQfHLrvsEjfeeGNMmTIlPvroo2jWrFlsv/320b9//3j44YdjyJAhcdRRR8Upp5ySRGYAAACA1Nm1sO4lsmth+/bt45xzzql07JhjjolHH3003n///SSmAgAAAKCBSqSQ9UOKiopiwIABtT0NAAAAAPVcrReyAAAAAOqbFbsWFhK7FgIAAABAgbAiCwAAAKAaCm1FVkNgRRYAAAAAmaCQBQAAAEAmaC0EAAAAqAathXXPiiwAAAAAMkEhCwAAAIBM0FoIAAAAUEX5fOG1FubzaSeofVZkAQAAAJAJmVqRlctFbLll2ilqplE9KR3mcmknSM6ee6adIBllZWknSMbmm6edIBnrr592gmRss03aCZKx885pJ0hOfXmOHHBA2gmSUV++H+XlaSdIRn15rhfap/vV9fXXaSdIzltvpZ0gGVl/L7XC22+nnSAZv/992gmS8c03aSegoclUIQsAAACgUNSXDx+ypJ6sDwIAAACgvlPIAgAAACATtBYCAAAAVJFdC9NhRRYAAAAAmaCQBQAAAEAmaC0EAAAAqIZCay1sCKzIAgAAACATFLIAAAAAyASthQAAAABVZNfCdFiRBQAAAEAmKGQBAAAAkAk1KmSNGjUqOnbsGLfcckul4w8++GB07NgxZs2aVZNpAAAAAArO8uWFdWsIElmRddFFF8Vbb72VxKEAAAAAoFI1LmQ1btw4ioqKYsSIEbFs2bIkMgEAAADAampcyMrlcvH73/8+XnnllRg/fnwSmQAAAAAK2opdCwvpZtfCdTR48ODo379/XHPNNTF79uwkDgkAAAAAq0hs18KxY8fGJptsEqeffnosXLiwWscoLy+PhQsXVnqrqKiIfL6BXLkMAAAAgNUkVshq2bJlnH/++fHuu+/G+eefX61jTJw4Mbp27Vrpbc6cOfH55x8nFRcAAACgRtJuJWyIuxY2TvJgffv2jcMPPzymTZsWe+21V5X/f2lpaQwbNqzSsfnz58fixUU1jQgAAABARiW2ImuFUaNGRdu2bePMM8+MTz75pEr/N5fLRfPmzSu9FRcXR1FR4nEBAAAAyIjEK0NNmzaNiy++OBYuXBhXXHFF0ocHAAAAKAhptxI2xNbCWlnitMsuu8SJJ54YZWVltXF4AAAAABqgWuvV+9WvfhW77rprbR0eAAAAgAamRhd7HzduXIwbN67SseLi4pg2bVpNDg8AAABQkPL5wmvny+fTTlD7XD0dAAAAgExQyAIAAACgxi666KLYf//9Kx17+eWX4+ijj47ddtstunfvHiNHjoxPP/20ynMoZAEAAABUQ9q7FBbSroVXX311TJkypdKx1157LY4++uho1KhRXHLJJXHaaafFk08+Gcccc0yUl5dXaZ4aXSMLAAAAgIbr9ddfjz/+8Y/xzDPPxIYbbljpYy6//PLYZJNNYuLEiZHL5SIiYscdd4xDDjkk7rjjjjj88MPXeT4rsgAAAAColhEjRsSCBQvipptuih133HG18fLy8nj66adjwIABK4tYERE777xztG3bNh599NEqzWdFFgAAAEAV2bXwW3/84x+jU6dOaxx/9913Y8mSJdGuXbvVxrbbbrt4/fXXqzSfQhYAAABAPbF8+fJYuHDhGsdzudwqK6Mqk8/nY9q0aT/4mH79+kXr1q1/sIgVEfHVV19FRFTadrjBBhvEokWLfvD/f59CFgAAAEA98fHHH8fBBx+8xvHf/va3cdJJJ/3gMSoqKuKcc875wce0a9cuWrduvdY8yxNetqaQBQAAAFANhdZaGBHRqlWrePHFF9c4vrbVWBERjRs3jnnz5iWSp0WLFhERla68WrRoUWy00UZVOp5CFgAAAEA90ahRo2jevHnaMVbaeuuto0mTJvGvf/1rtbF//etf0b59+yodz66FAAAAANSKXC4Xu+++ezzyyCNRXl6+8v5XXnkl3n777ejdu3eVjmdFFgAAAEAV2bVw3Z100kkxZMiQOPbYY2PYsGGxYMGCuOSSS6JDhw5x6KGHVulYmSpkFRdHVHKR+0x56620E/B9n36adoJkDBiQdoJkfPhh2gmS8fbbaSdIxlo2IMmM+vL9iKg/35OZM9NOkIwD2/497QiJ+PuyH6cdIREff5x2gmQUUDdIjXz+edoJkrPbbmknSMYtt6SdIBkHHZR2gmS8/HLaCZKx1VYRTZumnYJCV1JSElOmTInLLrssTjnllNhggw2iV69eMWLEiHW6Ztd3ZaqQBQAAAEBhuvHGG9c41r1795g2bVqN51DIAgAAAKiGQmstbAhc7B0AAACATFDIAgAAACATtBYCAAAAVJFdC9NhRRYAAAAAmaCQBQAAAEAmaC0EAAAAqIZCay1sCKzIAgAAACATFLIAAAAAyASthQAAAADVoLWw7tV4RdbQoUOjX79+lY7dcMMN0alTpxg6dGgsXLiwplMBAAAA0IDV2oqsiRMnxqWXXhr9+/ePyy67LNZbb73amgoAAACgTuXzhbciK59PO0Htq5VrZF122WVx6aWXxsEHHxzjx49XxAIAAACgxhJfkXXBBRfEDTfcEMccc0yMGjUqioqKkp4CAAAAgAYosULW8uXL45xzzolbb701TjrppPjtb3+b1KEBAAAACk6htRY2BIkUsioqKmLkyJFx7733RkTEZ599Vq3jlJeXR3l5+RrnyOet7gIAAABoqBIpZH344YfxwAMPxOWXXx4PPfRQ3HLLLdG1a9fYf//9q3SciRMnxoQJEyodGzNmTPzoR5vHRhvtlERkAAAAADImkUJWkyZN4qqrropevXrFnnvuGXPmzIkzzzwzOnXqFB06dFjn45SWlsawYcMqHZs/f36Ul1uRBQAAAKTProXpSGTXwlatWkWvXr0iIqJ58+Zx2WWXxdKlS+Pkk0+ORYsWrfNxcrlcNG/evNJbcXFxFBXVyiaLAAAAAGRArVSGSkpK4tRTT40333wzzjzzzNqYAgAAAIAGJrFdC79v2LBh8eyzz8Z9990Xu+22Wxx55JG1NRUAAABAnSu01sKGoNZ69YqKimLcuHHRqlWrGDduXPz973+vrakAAAAAaABqvCLrxhtvXONYy5Yt48knn6zpFAAAAABQe62FAAAAAPWVXQvTYRtAAAAAADJBIQsAAACATNBaCAAAAFANhdZa2BBYkQUAAABAJihkAQAAAJAJWgsBAAAAqsiuhemwIgsAAACATFDIAgAAACATtBYCAAAAVEOhtRY2BFZkAQAAAJAJClkAAAAAZILWQgAAAIBq0FpY9zJVyFq6NOLjj9NOUTNduqSdIBllZWknSE59+cXz+edpJ+C7vvkm7QTJaJypvxJrtttuaSdITn35/duuXdoJkjFv/R+nHSERW/0o7QTJWLAg7QTJyOXSTpCMH9WTn6uIiLffTjtBMnbYIe0EyWjZMu0Eyagv34/68n6K7NBaCAAAAEAm1JPP2gEAAADqTj5feCvS8vm0E9Q+K7IAAAAAyASFLAAAAAAyQWshAAAAQDUUWmthQ2BFFgAAAACZoJAFAAAAQCZoLQQAAACoIrsWpsOKLAAAAAAyQSELAAAAgEzQWggAAABQDYXWWtgQ1KiQNWrUqLjzzjtXuz+Xy0XLli3jJz/5SZx66qnRpk2bmkwDAAAAAMmsyLr11ltX+XdZWVm8+OKLMWXKlJgzZ07MmDEjcrlcElMBAAAA0EAlUsjq0qXLavf17t07li1bFpMnT45nnnkm+vTpk8RUAAAAAKmza2E6avVi7y1atIiIiKKiotqcBgAAAIAGIJEVWcuWLVv5dT6fj6+++iqeffbZmDx5crRt2za6deuWxDQAAAAANGCJFLI6d+682n0bb7xx9O3bN4YPHx5NmzZdp+OUl5dHeXl5pWMVFRWRz1vZBQAAABSGQmstbAgSKWRNnz49Ir4tRN19990xffr0OPbYY6O0tLRKx5k4cWJMmDCh0rExY8bEJptsHhtttFON8wIAAACQPYkUskpKSlZ+3bVr18jlcnHppZdGRUVFnHjiiet8nNLS0hg2bFilY/Pnz49Fi4qioqLGcQEAAADIoEQKWd93+umnx9NPPx0TJkyInj17xq677rpO/y+Xy0Uul6t0rLi4OFwzHgAAACgEdi1MR63sWpjL5eK8886L5cuXx1lnnRVLly6tjWkAAAAAaEBqpZAV8W2L4cEHHxyvv/56XHfddbU1DQAAAAANRK0VsiIiRowYERtvvHFceeWV8e6779bmVAAAAAB1avnywro1BDUqZI0bNy7mzZu3xvGWLVvGrFmz4u9//3tsvfXWNZkKAAAAgAauVldkAQAAAEBSamXXQgAAAID6rqG08xUSK7IAAAAAyASFLAAAAAAyQWshAAAAQBXl84XXWpjPp52g9lmRBQAAAEAmWJEFAAAAUA2FtiKrIbAiCwAAAIBMUMgCAAAAIBO0FgIAAABUkYu9p8OKLAAAAAAyITMrspYsWRJFRcujcePX0o5SI199lXaCZBRa1bkmWrZMO0EylixJO0Ey6ssnCFtumXaCZMybl3aCZDRvnnaC5DSqJx9BbbVV2gmS8fXXaSdIxgcfpJ0gGU2bpp0gGUVFaSdIRnFx2gmS4/VJYfnkk7QTJKP+vKdaHEuW1JMXKFXUocPiuPbawqpRdOiwOCLqyR/ENchMIav4//4Srrde7c2xfPny+Pjjj6NVq1bRKMPvFJxH1WywQa0dOiJ8PwpNffm5ivA9qYoWLWrlsKvw/SgszqPw1MW5bLRRrRx2FfXle+I8CovzKDx1cS65XK0cdhV1cR5LljRa+X69IWnatGlstlnEZpulneT7mkbT+vLJzhoU5fP15fOFmlu4cGF07do1XnzxxWie4Y/vnUdhcR6Fpb6cR0T9ORfnUVicR2GpL+cRUX/OxXkUFudRWOrLeUTUn3OpL+cB35XtMjkAAAAADYZCFgAAAACZoJAFAAAAQCYoZAEAAACQCQpZAAAAAGSCQhYAAAAAmVB8zjnnnJN2iEJSXFwc3bt3j+Li4rSj1IjzKCzOo7DUl/OIqD/n4jwKi/MoLPXlPCLqz7k4j8LiPApLfTmPiPpzLvXlPGCFonw+n087BAAAAACsjdZCAAAAADJBIQsAAACATFDIAgAAACATFLIAAAAAyASFLAAAAAAyQSELAAAAgExo0IWsUaNGRceOHVe7lZSURJ8+fWL48OHx/vvvpx1zrYYOHRr9+vWrdOyGG26ITp06xdChQ2PhwoV1nKxqVnw/brnllkrHH3zwwejYsWPMmjWrjpM1TJU9P0pKSqJv375x2mmnxT//+c+0I66zNT3Xv3v73//937RjrtWoUaNi1113XeP4+PHjo2PHjvHee+/VYaqqOeOMM6Jjx45x6623Vjq+fPnyGDJkSOyyyy7x+uuv13G6tRs+fHjstNNOlf4+3WeffaJjx45x/fXXrzY2ceLE6NixY7z22mt1kLJ65s+fH7///e9jr732ip133jm6desWv/jFL+K2226LioqKtOOt1bo8z7P2N+Sjjz6K//mf/4kDDzwwunXrFrvsskv8x3/8R5x11lnxr3/9K+14a1XZ92THHXeMrl27xuGHHx73339/2hGr5eabb46OHTvGoYcemnaUdTZ06NDo2LFj9OrVK5YvX17pY+bOnbvy+zRnzpw6Tlg9b7/9dowdOzb22Wef+PGPfxy77757DB06NO67777I5/Npx1urtf3eGjRoUNoR19kPvR/Jgl/+8pex8847x+eff77Gx9x7773RsWPHeOihh+owWc3dcccdmXpew7ponHaAQvD9N1RlZWXx4osvxpQpU2LOnDkxY8aMyOVyKaWrvokTJ8all14a/fv3j8suuyzWW2+9tCOtk4suuih69OgR7dq1SztKjbzxxhtx8803x1NPPRUfffRRNGvWLDp06BAHHnhgHHzwwVFcXJx2xHXy3efH4sWL46233oopU6bEIYccEpMmTYoePXqkmK5q1lQ8iYjYeuut6zBJwzV69OiYNWtWjBs3LvbYY4/YaqutVhmfMmVKzJ49O84666zYYYcdUkq5Zr169YoZM2bE7Nmzo3fv3ivvnz9/frz99tuxySabxGOPPRbHHHPMKv9v1qxZ0bp16+jUqVMdJ143b775Zhx22GHRtm3b+N3vfhdbbLFFLFy4MJ544ok466yz4oUXXoiLLroo7Zg/6MQTT4zDDz985b9vv/32mD59ekyYMCE222yzlfd36NAhjXhVNnPmzBg+fHist956MWTIkCgpKYkmTZrE66+/HjfddFPcc889cdVVV0XPnj3TjrpW3/3du3z58vjiiy9iypQpccopp0R5eXkcdNBBKaarumnTpkWnTp1izpw58fe//z1+/OMfpx1pnTRq1Cg+/vjjmDVrVqU/N3fffXcKqapvxowZccYZZ8TWW28dRx11VLRr1y4WLVoUDz30UJx66qkxc+bMOP/886NRo8L/3H5Nr0+aNWtWx0karsMPPzxmzpwZ9957bxx99NGVPmb69OnRqlWr6N+/fx2nA75PISsiunTpstp9vXv3jmXLlsXkyZPjmWeeiT59+qSQrPouu+yyuPrqq+Pggw+O888/PzNFk8aNG0dRUVGMGDEibr311mjcOJs/orfffnuce+65sd1228Wxxx4b7dq1i7Kysnj88cfj7LPPjjvuuCMmTJgQLVu2TDvqWn3/+dGzZ8/Yd999Y9CgQTFixIh4+OGHo2nTpimlq5rKnuvUrQ022CAuuuiiOOKII2L06NExderUKCoqioiIf/7zn3HFFVdEv3794ogjjkg5aeX22GOPKCoqihdeeGGVQtbjjz8eTZs2jWOOOSYmTJgQCxcujObNm0dERHl5ecyePTv222+/tGKv1bXXXhsRETfeeOMqz+f+/fvHeuutF1OnTo1jjz22YAtxERHbbLNNbLPNNiv//eSTT0ZExI477rhawbTQvf/++/Ff//VfseWWW8ZNN90UG2200cqx7t27xyGHHBJDhgyJ0aNHx6OPPlrwf+Mr+93bvXv36NOnT0yePDlThay//e1v8frrr8eUKVNi1KhRMXXq1LjkkkvSjrVO2rZtG1999VXcd999qxWyKioq4v7774/OnTvH3LlzU0q47l599dUYPXp09OjRI6688spVPnAeMGBAtGnTJq666qro0aNHHHjggSkmXTden6Rvr732ilatWsVdd91VaSHr3XffjVmzZsWvf/3rzL4/gfqk8D+iSFGLFi0iIla+ycqKCy64IK6++uo45phj4sILLyz4F7jflcvl4ve//3288sorMX78+LTjVMsLL7wQZ599dvTv3z/+3//7f3H44YfHT3/60xgwYECMHTs2Jk+eHC+//HKMGjUq7ajVtummm8bxxx8fH3/8ceaWV5O+XXfdNU444YR47rnnYurUqRERsWzZshg5cmRsvPHGccEFF6SccM0222yz2GGHHeL5559f5f4nnnhi5fN86dKlMXPmzJVjL7/8cixevHiVwleh+fTTT6OoqKjSFsIjjzwyhg8fbmVAHbrmmmviq6++igsuuGCVItYKzZo1i+HDh0fXrl3jiy++SCFhzTVv3jzatWsXb7/9dtpRquS2226LjTfeOLp37x4HHnhgPPTQQ/HJJ5+kHWudFBcXx89+9rN4+OGHo7y8fJWxp59+OhYsWFDQBffvmjRpUlRUVMSYMWMq7Zr41a9+FUOGDFn5Wh7WpnHjxjF48OB49dVXY968eauNT58+PRo1ahQ///nPU0gHfJ9CVnz7BmrFbenSpfH555/H/fffH5MnT462bdtGt27d0o64TpYvXx5nnXVW3HDDDXHSSSfF6NGjM1eEi4gYPHhw9O/fP6655pqYPXt22nGqbPz48dGsWbMYO3ZsNGnSZLXxnj17xtChQ+OJJ56IF154IYWEyVjxpvy5555LOcm6++5z/bu3LFz/57vWdB5ruu5JIfrNb34TnTt3jssvvzw++OCDuPrqq+Mf//hHXHzxxbHJJpukHe8H7bnnnjFnzpxYsmRJREQsWrQonnvuuejTp0906NAh2rRpE48//vjKxz/77LPRuHHj2GOPPVJKvHb9+/ePsrKyOPTQQ2PSpEnx8ssvx9KlSyMiYtttt40TTjhhldVO1K4HH3wwtt9++9h5553X+JjevXvHJZdcEj/60Y/qMFlyysvL4913340tt9wy7SjrrKysLO6///444IADokmTJvHzn/88li1b9oNt64Vm4MCB8eWXX65csbjCPffcE3vuuWfB//5d4fHHH48dd9xxjT8/66+/fpxzzjnRt2/fug1WTfXhtUl9MHjw4CguLo4777xzlfsrKirizjvvjL59+8YWW2yRUjrgu6yLjIjOnTuvdt/GG28cffv2jeHDh2eibaqioiJGjhwZ9957b0REfPbZZyknqpmxY8fGwIED4/TTT4+77rprZYtOofvyyy9j1qxZsc8++/xg5oEDB8a1114bDz30UPzkJz+pw4TJWXHNmax8Eh1R+XM9ImLDDTfMTFHx66+/XuN5ZEmTJk3i4osvjkGDBsWpp54ac+bMieOPPz4T11zr1atXTJkyJV566aXo3r17PPPMM7F06dKVLei9evWKP//5z7F8+fJo1KhRzJo1K3bbbbeC/j3285//PBYsWBBXXXXVyjap9dZbL3bdddf42c9+FoMGDaq0ME/yysrK4osvvoif/vSnq41VVFSsdgHr4uLigv/QatmyZSu/XlHAuvLKK+OLL76IE088McVkVXP33XfHN998E4cddlhEfFvk7dGjR0ybNi1KS0sz8RwpKSmJtm3bxowZM1Ze52fx4sXxyCOPxAUXXBCLFy9OOeHaff7557F48eJ6VVyv7O96mzZt4i9/+UsKaRquLbbYInr37h333ntvnHbaaStbCGfOnBkfffRRjB07NuWEwAoKWfHtUtGIb19c3X333TF9+vQ49thjo7S0NOVk6+7DDz+MBx54IC6/tfUWpQAACX5JREFU/PJ46KGH4pZbbomuXbvG/vvvn3a0amnZsmWcf/75UVpaGueff35ceOGFaUdaJ++//37k8/m1Xjh82223jYgo6N3l1lWhv4H6rhXP9e/L0rUO1l9//bjpppsqHbvtttvitttuq+NE1de+ffsYMWJEnHfeebHLLrvEySefnHakddK1a9do2rRpPP/889G9e/d4/PHHo0OHDiuvw9SnT5+YNm1azJ07N3bYYYd46aWX4qSTTko59dqdcMIJceSRR8bTTz8dzz//fLz44ovx/PPPx7PPPhvTpk2L66+/XptOHfihlZWDBg1abefL008/PX75y1/WdqwaqexNesuWLWP48OExdOjQFBJVz2233RY777xztGrVKsrKyiIiYv/9948//OEP8eCDD8bAgQNTTrhuBg4cGJMnT45FixbFBhtsEH/+85+jcePG0b9//5gxY0ba8dZqxSUz6tOKpcpen2Rxo6n6YMiQIfHYY4/FX//615W7ME6fPj223nrr6NWrV8rpgBWy8+6tFpWUlKz8umvXrpHL5eLSSy+NioqKzHxS2KRJk7jqqquiV69eK9tezjzzzOjUqVNmdmj6vr59+8bhhx8e06ZNi7322ivtOIlasYNOll+EffjhhxERsfnmm6ecZN1997meVY0aNVrjeXy3nS0r+vbtG+edd1707t07MwXFXC4X3bp1W7mK74knnljlQ4MePXpELpeLZ555JhYuXBjl5eWZ2TCkWbNmMWDAgBgwYEBERHzxxRdx5ZVXxo033hjXXHNNnHbaaSknrP823njjaN68ebz77rurjV1yySUrV8x88skn8etf/7qu41XLd9+kN27cOFq0aJGplsKIiNmzZ8frr78eEVHpJSduuummzBSyDjjggBg/fnw8+uijccABB8Q999wT++67b2YKJy1atIgNN9xwrR8Gfvjhh9GqVatM7FpYH16f1Be9evWKNm3axF133RX9+vWLzz77LB577LH43e9+l6kPb6G+K/zf7Ck4/fTTo3379jFhwoT429/+lnacddKqVauVnxI0b948Lrvssli6dGmcfPLJsWjRopTTVd+oUaOibdu2ceaZZ2aiha1NmzZRVFQU77zzzg8+bv78+RERmdtJ67ueeuqpiIhMtIJB0vbcc894+eWXY+7cufHxxx+vch2WZs2aRbdu3eL555+P559/Plq3bh0dO3ZML+xafPTRR9GrV6+YNGnSamObbLJJnHHGGdG6deuVb+KpfXvvvXe8+uqr8eabb65yf4cOHaKkpCRKSkpihx12SCld1a3IXFJS8oPXNSpkt956a6y//vpx3XXXxdSpU1e5HXTQQfHSSy/FnDlz0o65TrbZZpvo0qVLzJgxIz777LN45plnMrGz33f16dMnXn311fj3v/9d6fjSpUvjwAMPjF/84hd1nIysa9SoUQwePDj+8pe/xIIFC+Luu++OiIhDDjkk5WTAdylkVSKXy8V555238uLpKy54myUlJSVx6qmnxptvvhlnnnlm2nGqrWnTpnHxxRfHwoUL44orrkg7zlq1aNEievToETNnzlzZdrDCnDlzVl7b5IEHHoiIyMxFSL9vwYIFMWXKlGjTps3KlRvQkOy5556xaNGiuPnmm6N58+bRtWvXVcZ79+4d//jHP+L5558v6N0KI7693l0ul4tp06bFggULVhv/9NNPo6ysLDp16pRCuoaptLQ0mjdvHiNGjFjjroSV7apF7SgrK4sHH3wwBgwYELvvvnt07959ldtxxx0XERE33nhjyknX3cCBA+Ppp5+Om2++OVq3br3a77BCd9xxx0VxcXGMGTNmtR0YIyImTJgQCxYsUHygWg499NDI5/Px5z//Oe65557YZ599omXLlmnHAr4jG30cKejatWscfPDBcccdd8R1110XJ5xwQtqRqmzYsGHx7LPPxn333Re77bZbHHnkkWlHqpZddtklTjzxxEwUsiIiTj755Bg6dGiMHj06Lr/88mjSpEmUlZXF0KFDo3Xr1nHkkUfGddddF926dSv4N7gRES+99NLKrxcvXhxvvPFGTJ06NRYsWBCTJ0/OTCtCxKrn8n0tWrSI7bbbrg7TkGXt27ePLbbYIu65557o16/fam2RvXv3jgsvvDAWLFgQRx11VEop102jRo1i7NixUVpaGgcddFAcccQR0blz5yguLo558+bFDTfcEK1bt45hw4alHbXBaNu2bUyYMCGGDx8e++23XwwePDh23XXXaNq0abzzzjvx4IMPxsyZM2PbbbfNzM7KWXbXXXfFN998s8ZVS9tvv3106dIlHnjggRg5cmRsuummdZyw6n72s5/FhRdeGJMmTYrjjjsucy1TO+64Y/zhD3+IsWPHxuDBg2PIkCHRtm3b+Pzzz2PGjBnx6KOPxqGHHhqHHnpo2lEblIULF8b1119f6dgRRxyRiQ0RIr79gKd///5x7bXXxltvvRVnnHFG2pGA71HI+gEjRoyIv/zlL3HllVfGf/7nf671At6FpqioKMaNGxcHHnhgjBs3LkpKSuLHP/5x2rGq5Ve/+lU8+eSTmWj13G233WLs2LFx9tlnx6BBg+KII46I9u3bx7nnnhvnn39+jB07Nho3bpyZP4ordmeK+Ha1YuvWraNnz55x3HHHrbxofVZ891y+r3///vGnP/2pDtOQdXvuuWfcfvvtlV7/ql27drHNNtvEBx98ED179kwhXdX07Nkz7rzzzrj22mvj9ttvjyuvvDKWL18ebdq0if322y+OP/742HDDDdOO2aD07NkzZsyYEbfffns88sgjMW3atFi0aFG0bNkySkpK4pJLLom99947Ux8mZNVtt90Wm222Weyxxx5rfMzgwYPjD3/4Q0ybNi1+85vf1GG66mnZsmXsvvvu8de//jVzbYUr/OIXv4gdd9wxbrrpppg0aVJ8+umnseGGG0b79u3jiiuuiL333jtzBbqs+/LLL9e4QdPgwYMzU8iKiDj88MNj2LBhscMOO2R2h3Goz4ry39/HGUjEm2++GTfeeGM89dRT8dFHH0WzZs2iQ4cO0b9//3j44Yfjtddei6OOOipOOeWUtKMCAABAJihkQQry+Xw8+uij8f7778fRRx+ddhwAAADIBIUsAAAAADLBroUAAAAAZIJCFgAAAACZoJAFAAAAQCYoZAEAAACQCQpZAAAAAGSCQhYAAAAAmaCQBQAAAEAmKGQBAAAAkAkKWQAAAABkgkIWAAAAAJnw/wF4CJfEW2Wt2gAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 1618.03x1000 with 2 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABLIAAAMsCAYAAABA14tEAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzs3Xuc1VW9P/73noGt4IjAERAvqIiCFzoSGaiBHvVh/TRviIaZFmpOpVamdvTo6cg51lHL6hQ+bDQ7JnYemB5vUdnFvJGXDDNRAxJz1LyACuEguGFmfn905BuxUWb2B9bnM/v5fDz246F77VnrNYurb9f7s0qdnZ2dAQAAAAA515A6AAAAAABsCIUsAAAAAApBIQsAAACAQlDIAgAAAKAQFLIAAAAAKASFLAAAAAAKQSELAAAAgEJQyAIAAACgEBSyAAAAACgEhSwAAAAACkEhCwAAAIBCUMgCAAAAoBAUsgAAAAAoBIUsAAAAAAqhV+oAG+qJJ56I9vb22GyzzVJHAQAAACLirbfeisbGxthrr71SR9mkWltbY8WKFaljVNWnT5/YcccdU8fYaApTyGpvb4+OSiUipz9RNtiyZakTZKOpKXWC7PSU76WhhxywfOut1Amy0VO+j87O1Amy8dJLqRNkZ7fdUifIxnPPpU6QjUGDUifIRk/5H4WVSuoE2dhyy9QJMtHeUUodITONlYL/N8jbGhtTJ+BvPflk6gSZ6Nhhhx7z+1ZXrFixIlYsXhx9nn46dZS1rBgxouf8/WQ9ClPI2myzzSJWrIhRf/lL6ii1ue++1Amy8f73p06QnZ5Sqe7bN3WCbDz7bOoE2XjlldQJstHRkTpBNq64InWC7NxyS+oE2fjqV1MnyMbJJ6dOkI3hw1MnyMYLL6ROkI0xY1InyMTySu/UETKzxXN/SB0hG/36pU7A3/rSl1InyMS8f//3HvP7Vlf1efrpGHXKKaljrGXe977X4wtZPeQIBwAAAAA9XWFOZAEAAADkRqmUv0e8lHpOW/f65GzHAQAAAKA6hSwAAAAACkFrIQAAAEB35K21sA7YcQAAAAAKQSELAAAAgELQWggAAADQVW4tTCJnOw4AAAAA1SlkAQAAAFAIWgsBAAAAuiNvrYV1YKPu+C233BIjR46MuXPnbsxlAAAAAKgDSocAAAAAFILWQgAAAIDu0Fq4ydlxAAAAAApBIQsAAACAQshVa2GlUolKpVJ1rL29PUqdnZs4EQAAAEAVpVL+WgtLpdQJNrpcFbJaWlpi+vTpVcemTZsW2/TvH3vUwQ8KAAAAAOvKVSGrubk5pk6dWnWstbU1SsuWRSxbtolTAQAAAJAHuSpklcvlKJfLVccaGxvr4ogcAAAAUBB5ay2sA3YcAAAAgEJQyAIAAACgEHLVWggAAABQCG4tTGKjFrImTZoUkyZN2phLAAAAAFAnclY6BAAAAIDqtBYCAAAAdEfeWgvrgB0HAAAAoBAUsgAAAAAoBK2FAAAAAF3l1sIkcrbjAAAAAFCdQhYAAAAAhaC1EAAAAKA78tZaWAfsOAAAAACFoJAFAAAAQCFoLQQAAADoKrcWJpGzHQcAAACA6op1IqtXr4j+/VOnqM0ll6ROkI1Fi1InyM6CBakTZOP111MnyMbEiakTZGPrrVMn4G/MvfrB1BEyM/rFOakjZOKly2ekjpCJoa/OTR0hE/e+sEvqCJk4YO+e8Xtve0Pv1BEy0bdv6gQZ6uhInSAb5XLqBNl46KHUCbJxzz2pE2TjtddSJ6DOFKuQBQAAAJAXeWstrAN2HAAAAIBCUMgCAAAAoBC0FgIAAAB0h9bCTc6OAwAAAFAIClkAAAAAFILWQgAAAICuKpXy11pYKmU63YIFC+LrX/96/Pa3v42IiD322CPOPvvsGDNmTKbrdEXOdhwAAACA1BYuXBhTpkyJJUuWxGWXXRaXXXZZrFy5Mk455ZR45plnkuVyIgsAAACAtVx22WUxaNCg+P73vx+bb755RES8973vjaOPPjruv//+GD58eJJcClkAAAAA3ZG31sKMLFu2LGbPnh3nnnvumiJWRMSAAQPi3nvvTZhMayEAAAAAf2PevHnR3t4e2223XfzHf/xHjB8/Pvbcc8848cQT44knnkiaTSELAAAAoIfo6OiItra29b4qlcq7zvHqq69GRMQll1wSL730Unz1q1+Nr3/967Fs2bI46aSTYuHChRv721ivmgpZp556auy1117x+uuvr/czP/rRj2LkyJHxs5/9rJalAAAAAPLj7VsL8/QqlWLRokUxduzY9b5aWlre9VtbtWpVREQMGTIkpk+fHhMmTIgPfvCD8d3vfjc6OzvjO9/5zsbe3fWq6RlZU6ZMidmzZ8ePfvSj+PjHP171MzfffHMMHjw4Dj744FqWAgAAAOBdDB48OObMmbPe8XK5/K5zNDU1RUTEgQceGA1/8xywIUOGxKhRo5K2F9ZUyPqnf/qnGDx4cNx2221VC1nPP/98PPzww/HpT386evXyXHkAAACgB8nhw94bGhrWFKK6a+edd46IqNqGuHr16ujTp09N89eiph3v1atXHHfccfHUU0/F/Pnz1xm/+eabo6GhIY4//vhalgEAAABgExk+fHjstNNO8dOf/nStYtZzzz0X8+bNi3HjxiXLVnPp8LjjjovGxsa49dZb13q/vb09br311jjwwANj6NChtS4DAAAAwCZywQUXxJ///Oc47bTT4p577omf/OQncdppp0W/fv3i1FNPTZar5kLW0KFDY+LEifGjH/0oVq9eveb92bNnxyuvvBJTpkzZ4Lkqlcp6n6rf3t4eHZ2dtcYFAAAAqF1OH/aelQMPPDD++7//Ozo7O+Pzn/98fOlLX4qRI0fGjTfeGFtvvXVm63RVJg+uOuGEE+Luu++O++67Lw466KCI+Gtb4Q477BATJkzY4HlaWlpi+vTpVcemTZsW2wwYEHv0759FZAAAAADewbhx45K2EVaTSSFrwoQJsd1228Vtt90WBx10ULz22mtx9913x+c+97kodaEa2NzcHFOnTq061traGqU334zo6MgiMgAAAAAFk0khq6GhIY477ri48sorY+nSpXH77bdHRMSxxx7bpXnK5fJ6r4FsbGzM9IgcAAAAQE1yeGthT5fZjk+ePDk6OzvjF7/4Rdxxxx3xwQ9+MAYOHJjV9AAAAADUucwKWYMGDYqDDz44vve978Uf/vCHOOGEE7KaGgAAAACyK2RFREyZMiWeeeaZ2G233eJ973tfllMDAAAA5EcPv7UwrzJ5Rtbb9ttvv5g/f36WUwIAAABARGR8IgsAAAAANpZMT2QBAAAA1A23Fm5ydhwAAACAQlDIAgAAAKAQtBYCAAAAdIfWwk3OjgMAAABQCApZAAAAABSC1kIAAACAriqV8tdaWCqlTrDR5WzHAQAAAKA6hSwAAAAACkFrIQAAAEB35K21sA7YcQAAAAAKoVgnslavjliyJHWK2jz3XOoE2XjmmdQJsnPLLakTZOPcc1MnyMbs2akTZGP77VMnyMarr6ZOkInRHU+ljpCdgQNTJ8jE0Dv/O3WEbAwfnjpBJg5o+3HqCNlYMDh1gkw0rl6dOkI2etIphfe+N3WCbHR0pE6QjfHjUyfIRqWSOgEUUrEKWQAAAAB54NbCJHK24wAAAABQnUIWAAAAAIWgtRAAAACgO/LWWlgH7DgAAAAAhaCQBQAAAEAhaC0EAAAA6Cq3FiaRsx0HAAAAgOoUsgAAAAAoBK2FAAAAAN2Rt9bCOmDHAQAAACiEzApZJ510Uhx00EFZTQcAAAAAa9FaCAAAANBVbi1MImc7DgAAAADVKWQBAAAAUAhaCwEAAAC6I2+thXUgV4WsSqUSlUql6lh7e3uUOjs3cSIAAAAA8iJXhayWlpaYPn161bFp06bFNlttFXts4kwAAAAA5EOuClnNzc0xderUqmOtra1RWrYsYunSTZwKAAAAoAqthZtcrgpZ5XI5yuVy1bHGxsa6uEYSAAAAgOqUDgEAAAAohExPZLW1tcV1111XdezEE0+M3r17Z7kcAAAAQBqlUv5aC+ugky3TQtZf/vKX+M///M+qY8cdd5xCFgAAAADdllkha8aMGVlNBQAAAADryNXD3gEAAAAKI2+thXXAjgMAAABQCApZAAAAABSC1kIAAACArnJrYRI523EAAAAAqE4hCwAAAIBC0FoIAAAA0B15ay2sA3YcAAAAgEJQyAIAAACgELQWAgAAAHSVWwuTyNmOAwAAAEB1TmQBAAAAdEfeTmTVATsOAAAAQCEU60TWqlURr76aOkVNXirvmDpCJoZuuzJ1hOxMmZI6QTZeeCF1gmz0kP+jMeOJMakjZOKkfrenjpCNRYtSJ8jO3nunTpCNfv1SJ8jGyh7y5+F++6VOkI2XX06dIBs95M/00vhxqSNkpvOBB1NHyMb73pc6QTZ6yp/rPeTvvdHenjoBdaZYhSwAAACAPPCw9yRytuMAAAAAUJ1CFgAAAACFoLUQAAAAoDvy1lpYB+w4AAAAAIWgkAUAAABAIWgtBAAAAOgOrYWbnB0HAAAAoBAUsgAAAAAoBK2FAAAAAF1VKuWvtbBUSp1go8vZjgMAAABAdZmcyDr//PPj1ltvXe/4nnvuGbfccksWSwEAAABQpzJtLbzxxhurvt+3b98slwEAAABIL2+thXUg00LW3nvvneV0AAAAALCG0iEAAAAAhZDpiazVq1ev816pVIrGxsYslwEAAABIy62FSWRayNpzzz3XeW+77baLX/3qVxv09ZVKJSqVStWx9vb2KHV21pQPAAAAgK6bOXNm/Nu//Vtcf/31MW7cuGQ5Mi1k3Xzzzeu8Vy6XN/jrW1paYvr06VXHpk2bFttsuWXs0e10AAAAAHTVwoUL49JLL00dIyIyLmSNHj26pq9vbm6OqVOnVh1rbW2N0muvRbz+ek1rAAAAAGQib62FG0GlUolzzz03BgwYECtWrEgdJ18Pey+Xy9HU1FT11djYGA110OsJAAAAkBff+MY34o033oizzjordZSIyPhEFgAAAAA9wwMPPBAzZsyIGTNmxCuvvJI6TkQoZAEAAAB0XU5vLezo6Ii2trb1fqRcLm/Q88xff/31+OIXvxif/OQnY8yYMXHnnXdmmbTbFLIAAAAAeohFixbFMcccs97xM888c4PaBC+66KIYOnRonHHGGVnGq1kmhaxLL700N0+vBwAAAKhXgwcPjjlz5qx3fENOY82cOTN+/etfxy233BIREatXr46Ojo6IiOjo6Ij29vZobGzMJnAXOZEFAAAA0B15ay2MiIaGhmhqaqppjh//+MexcuXKOOyww9YZ+8QnPhHbbbdd/OpXv6ppje5SyAIAAABgjWnTpsXy5cvXeu+hhx6Kr33tazFt2rQYM2ZMomQKWQAAAAD8jeHDh6/z3p///OeIiNh5551j5MiRmzrSGgpZAAAAAF2V01sLezqFLAAAAADe0Yc+9KGYP39+6hiRs9IhAAAAAFTnRBYAAABAd+SttbAO2HEAAAAACkEhCwAAAIBC0FoIAAAA0B1aCzc5Ow4AAABAIShkAQAAAFAIxWot7NcvYuLE1ClqMnTe3akjZGObbVInyM4HPpA6QTZWrkydIBvLlqVOkIkp/VMnyMjsfqkTZOL59x6VOkJmdlj2x9QRsjF4cOoE2SiXUyfIxle+kjpBNg49NHWCbPSQn1edT/0hdYTMlPbYN3WETHQ+9HDqCJnofP+41BEy8eabqRNko/3ZedGYOkQqpVL+WgtLpdQJNrqc7TgAAAAAVKeQBQAAAEAhFKu1EAAAACAv8tZaWAfsOAAAAACFoJAFAAAAQCFoLQQAAADoKrcWJpGzHQcAAACA6hSyAAAAACgErYUAAAAA3ZG31sI6YMcBAAAAKASFLAAAAAAKQWshAAAAQFe5tTCJzApZzz77bNxwww1x//33x8svvxxbbLFF7LLLLjFlypQ47LDDolQHmwkAAADAxpNJIWvWrFlx0UUXxQ477BAnn3xyDB8+PJYvXx4/+9nP4gtf+ELMnj07vvzlL0dD3iqVAAAAABRGzYWsp556Ki644IIYP358XHnllVEul9eMHXLIIbHddtvFVVddFePHj4+jjjqq1uUAAAAA8sGBnU2u5kLW1VdfHe3t7TFt2rS1ilhv+9SnPhVLly6NrbbaqtalAAAAAKhjNRey7rnnnth9991j2223rTq++eabx8UXX1zrMgAAAAD54WHvSdRUyHr99ddjxYoVMWzYsEzCVCqVqFQqVcfa29uj1NmZyToAAAAAFE9NhazGxsaI+GuRKQstLS0xffr0qmPTpk2LbbbeOvYYMCCTtQAAAAAolpoKWVtttVVsueWW8cILL7zj515++eUYPHjwu95a2NzcHFOnTq061traGqVVq7qdFQAAACBTeWstrAM17/gBBxwQTz31VLz44otVx1etWhVHHXVUfPSjH33XucrlcjQ1NVV9NTY2RkMd9HoCAAAAUF3NhazTTjstGhsbY9q0aVWfbzV9+vRYunRpHHvssbUuBQAAAEAdq/nWwt133z0uvPDCuOSSS+K4446LE044IXbaaad4/fXXY9asWXHXXXfF5MmTY/LkyVnkBQAAAMgHrYWbXM2FrIiIj370o7H77rvHDTfcEFdffXW8+uqrseWWW8Yuu+wS3/rWt+LQQw+NkrZAAAAAAGqQSSErImLMmDExZsyYrKYDAAAAgLVkVsgCAAAAqBulUv5aC+ugGy5nOw4AAAAA1SlkAQAAAFAIWgsBAAAAuiNvrYV1wI4DAAAAUAgKWQAAAAAUgtZCAAAAgK5ya2ESOdtxAAAAAKhOIQsAAACAQtBaCAAAANAdeWstrAN2HAAAAIBCUMgCAAAAoBCK1Vr41lsRzz2XOkVtNt88dYJslMupE2TnvvtSJ8jGyy+nTpCNYcNSJ8hE71/dlTpCNgYOTJ0gEzs88dPUEbIzfHjqBNl44onUCbLRv3/qBNk4+eTUCbKxdGnqBNl4+unUCbLRU36/iojOBx5MHSEbHakDZKOjh3wfW5RXpY6QicaGzojo+TflVeXWwiRytuMAAAAAUJ1CFgAAAACFUKzWQgAAAIC8yFtrYR2w4wAAAAAUgkIWAAAAAIWgtRAAAACgq9xamETOdhwAAAAAqlPIAgAAAKAQtBYCAAAAdEfeWgvrgB0HAAAAoBAUsgAAAAAoBK2FAAAAAN2htXCT69aOn3TSSTFy5MiYMGFCdHR0VP3Mk08+GSNHjoyRI0fG3LlzawoJAAAAAN0uHTY0NMSiRYvi4Ycfrjp+++23dzsUAAAAAPy9bheydtpppxg0aFD8+Mc/Xmesvb09fvKTn8See+5ZUzgAAACAXCqV/tpamKdXqZR6Vza6bheyGhsb47DDDouf//znUalU1hp74IEHYunSpXH44YfXHBAAAAAAImq8tfCII46Iv/zlL3H//fev9f4dd9wRH/jAB2LAgAE1hQMAAACAt9VUyBo9enTstNNOMWvWrDXvrVixIn75y1/GUUcd1eX5KpVKtLW1VX21t7dHR2dnLXEBAAAAspO6lfDvX3Wg5u/yiCOOiLvvvjuWL18eERG/+MUvolevXnHwwQd3ea6WlpYYO3Zs1dfcuXNj0dKltcYFAAAAoKB61TrBkUceGd/+9rfjrrvuiiOPPDLuuOOO+NCHPhTlcrnLczU3N8fUqVOrjrW2tkaprS3i757HBQAAAEB9qLmQNWzYsNh7771j1qxZsf/++8eDDz4Y3//+97s1V7lcXm8BrLGxsS6evg8AAAAUwNu3FuZJHdRNMtnxI444Ih544IH4wQ9+EEOGDImxY8dmMS0AAAAArJFJIeuwww6Lzs7OuPrqq+PII4+MUh1UAAEAAADYtDIpZA0cODD222+/WLVqVbduKwQAAAAonNS3FNbhrYXdekbWjBkz1nnvmmuuWee9SZMmxaRJk7qzBAAAAACspT7KdQAAAAAUXs23FgIAAADUHbcWJqGQBQAAAMA6fvrTn8Z1110XCxcujHK5HHvssUd87nOfi9GjRyfLlLPSIQAAAACp3XTTTfH5z38+dt555/j6178eF198cbzxxhtxwgknxKOPPposlxNZAAAAAN2Rt9bCDE2fPj0+8IEPxKWXXrrmvf322y8OPvjguOaaa+Kqq65KkkshCwAAAIA1VqxYEYceemiMGzdurfebmppi6NCh8corryRKppAFAAAA0GN0dHREW1vbesfL5XKUy+V3nKNPnz5x4YUXrvP+woUL449//GMcddRRNefsLoUsAAAAgK7K6a2FixYtimOOOWa9HznzzDPjrLPO6vLUb7zxRpx33nnRq1evOO2002pJWROFLAAAAIAeYvDgwTFnzpz1jr/baaxqXnnllfjUpz4Vf/zjH+Mb3/hGDB8+vJaINVHIAgAAAOghGhoaoqmpKbP5fv/738eZZ54Zy5cvjyuvvDIOOOCAzObuDoUsAAAAgO7IW2thxn784x/H+eefH1tvvXX8z//8T4waNSp1pOjZOw4AAABAl/385z+Pc889N3bbbbe46aabclHEiijaiayGhojNN0+dojY9pVq7dGnqBNnJ8MglGXj66dQJstFTfq1vs03qBNlYuTJ1guy8ww00hfL446kTZGO//VInyMajj6ZOkI1hw1InyMaIEakTZKMn/d67/fapE2Tj5ZdTJ8hEY9tfUkfIxmOPpU6QjT59Ivr1S50inZ7y9/6/s2zZsrjwwgujb9++8dnPfjZeeOGFeOGFF9aMb7755skKW8UqZAEAAACwUd1///2xbNmyiIg4/fTT1xnfddddY9asWZs6VkQoZAEAAADwNw4//PA4/PDDU8eoSiELAAAAoKtKpfy1FpZKqRNsdDnbcQAAAACoTiELAAAAgELQWggAAADQHXlrLawDdhwAAACAQlDIAgAAAKAQtBYCAAAAdJVbC5PI2Y4DAAAAQHUKWQAAAAAUQuaFrB/84AcxcuTImDx5ctZTAwAAAORHQ0O+XnUg8+9y5syZMWrUqJg7d278/ve/z3p6AAAAAOpUpoWs3/3ud7FgwYI477zzYtCgQXH99ddnOT0AAAAAdSzTQtYPf/jD6N+/f4wbNy6OOuqo+NnPfhaLFy/OcgkAAACA9N6+tTBPL7cWbrhly5bFT37ykzjyyCOjd+/ecfzxx8fq1avjxhtvzGoJAAAAAOpYZoWs22+/PVauXBkf+chHIiJixx13jPHjx8fMmTNj1apVGzRHpVKJtra2qq/29vbo6OzMKi4AAAAABZNZIeuHP/xh7LXXXjF48OBYtmxZLFu2LD784Q/H4sWL484779ygOVpaWmLs2LFVX3Pnzo1FS5ZkFRcAAACgNqlbCevw1sJeWUzy6KOPxoIFCyIiYp999lln/IYbbogjjjjiXedpbm6OqVOnVh1rbW2N0ptv1hYUAAAAgMLKpJB14403xuabbx5XXXVVNDY2rjV2yy23xG233RZz586N0aNHv+M85XI5yuVy1bHGxsa/PrRMeyEAAABAXaq5kLVs2bK4884745BDDon99ttvnfGBAwfGbbfdFjNmzIjLL7+81uUAAAAA0nv71sI8cWvhu7vtttti5cqVcdRRR1Ud33XXXWPvvfeOn/70p/Haa6/VuhwAAAAAdarmQtYPf/jDGDRoUOy///7r/cxxxx0XlUolZs6cWetyAAAAANSpmlsLZ82a9a6fmTx5ckyePLnWpQAAAADyI2+thXXAjgMAAABQCApZAAAAABRCza2FAAAAAHVJa+EmZ8cBAAAAKASFLAAAAAAKQWshAAAAQFeVSvlrLSyVUifY6HK24wAAAABQnUIWAAAAAIWgtRAAAACgO/LWWlgH7DgAAAAAhaCQBQAAAEAhaC0EAAAA6Cq3FiaRsx0HAAAAgOqKdSKrT5+InXZKnaImn/uXLVJHyMR/TXkwdYTs7LFH6gSZWN5rq9QRMrFFZUnqCNnYfvvUCbKxcmXqBNlYtix1guy8732pE2Rj1qzUCbLR1JQ6QTYmTkydIBv33Zc6QTbe+97UCbJx/fWpE2TnX/4ldYJsPP546gSZuPfNfVJHyMQBPeXvi2+8kToBdaZYhSwAAACAvMhba2EdsOMAAAAAFIJCFgAAAACFoLUQAAAAoKvcWphEznYcAAAAAKpTyAIAAACgELQWAgAAAHRH3loL64AdBwAAAKAQFLIAAAAAKASthQAAAABd5dbCJHK24wAAAABQXc0nss4///y49dZb13qvoaEh+vbtG7vuumucfPLJcdhhh9W6DAAAAAB1LrPWwhtvvHHNP3d0dMSSJUvi2muvjbPPPjsqlUocffTRWS0FAAAAkF7eWgvrQGaFrL333nud98aNGxcHHHBAfPe731XIAgAAAKAmG7V02NTUFMOHD49nn312Yy4DAAAAQB3YqLcWViqVeP7552PbbbfdmMsAAAAAbHpaCze5zApZq1evXvPPbxewrrzyyliyZEl85jOf2aA5KpVKVCqVqmPt7e1R6uzMJCsAAAAAxZNZIWvPPfdc572BAwfGOeecEyeddNIGzdHS0hLTp0+vOjZt2rTYZvDg2GPnnWvKCQAAAEAxZVbIuvnmm//fpL16xVZbbdXllsLm5uaYOnVq1bHW1lYnsgAAAIB8KJXy11pYKqVOsNFlVsgaPXp0zXOUy+Uol8tVxxobGyPa22teAwAAAIBi2qgPewcAAADosfJ2IqsO2HEAAAAACkEhCwAAAIBCqLmQdemll8b8+fOzyAIAAABQDG8/7D1Przp42LsTWQAAAAAUgkIWAAAAAIXg1kIAAACA7nBr4SZnxwEAAAAoBIUsAAAAAApBayEAAABAV719a2GeuLUQAAAAAPJBIQsAAACAQtBaCAAAANAdeWstrAN2HAAAAIBCUMgCAAAAoBC0FgIAAAB0ValUF7cE5k2xClkrV0Y8/XTqFDX5r63vSB0hG/0mpU6QnUoldYJMbPHs71NHyEZbW+oE2dh669QJMvHa1iNTR8jEP9x8c+oI2RkxInWCbGy/feoE2egpz8VYujR1gmwMH546QTZ6yp+F556bOkF2nnoqdYJsNDWlTpCJAwbOTR0hG89Dnph9AAAgAElEQVS8nDpBNvr1i9h889Qp2Egef/zxuOKKK2Lu3LnRu3fvOPDAA+O8886LrRP+904P+dsXAAAAAFmZN29efPzjH4+Ghoa44oor4txzz437778/PvGJT0Ql4YGQYp3IAgAAAMiLvJ3O7ujIbKpvfvObMWDAgGhpaYlyuRwREbvvvnsce+yxccstt8SUKVMyW6srcrbjAAAAAKRUqVTigQceiEMOOWRNESsiYq+99oqddtop7rrrrmTZFLIAAAAAWOP555+Pt956K4ZXef7kzjvvHAsXLkyQ6q+0FgIAAAB0Rw5bCzs6OqLtHS4OKZfLa52yquaNN96IiIgtt9xynbEtttgili9fXlvOGihkAQAAAPQQixYtimOOOWa942eeeWacddZZ7zhHR4bP2sqaQhYAAABADzF48OCYM2fOesff7TRWRMRWW20VEVH15NXy5cujX79+3Q9YI4UsAAAAgK4qlfLXWlgqRUNDQzQ1NdU0zQ477BC9e/eOP/3pT+uM/elPf4pddtmlpvlrkbMdBwAAACClcrkc++23X/zyl7+MSqWy5v0nnnginn322Zg4cWKybApZAAAAAKzlrLPOipdeeilOOeWUuOuuu+J///d/4/TTT48RI0bE5MmTk+XSWggAAADQHXlrLczQ6NGj49prr41vfOMbcfbZZ8cWW2wREyZMiPPOO2+DnrO1sShkAQAAALCOcePGxcyZM1PHWEsmhaxXXnklZs6cGb/61a/ixRdfjLfeeiuGDBkS++67b0ydOjV23nnnLJYBAAAAoI7VXMiaPXt2nHPOObHZZpvFCSecEKNHj47evXvHggUL4oYbbog77rgjrrrqqth3332zyAsAAACQXk5vLezpaipk/fnPf47Pf/7zse2228YNN9wQ/fr1WzM2bty4OPbYY+OEE06ICy64IO66665obGysOTAAAAAA9amm0uE111wTb7zxRnzlK19Zq4j1tr59+8Y555wTY8eOjSVLltSyFAAAAAB1rqYTWXfeeWfsuuuusddee633MxMnToyJEyfWsgwAAABA/uSttbAOdLuQtWzZsliyZEm8//3vX2esvb09Ojs713qvsbExSu/Sq1mpVKJSqVQda29vj9LfzQkAAABA/eh2Iaujo2O9Y5MmTYp58+at9d4Xv/jFOPXUU99xzpaWlpg+fXrVsWnTpsU2AwfGHkOGdD0sAAAAAIXX7UJW//79o6mpKZ5//vl1xq644opYsWJFREQsXrw4Pv3pT2/QnM3NzTF16tSqY62trVH6vzkBAAAAknJrYRI1PSPr0EMPjVtuuSUWLlwYu+yyy5r3R4wYseafX3jhhQ2er1wuR7lcrjrW2NhYFz8gAAAAAFRXU+mwubk5mpqa4rzzzlvvrYTz58+vZQkAAAAAiIgaT2TttNNOMX369DjnnHPi8MMPj+OOOy7GjBkTffr0ieeeey7uvPPOmD17duy4446xzz77ZJUZAAAAIL28tRbWgZoKWRER++67b8yaNStuuumm+OUvfxkzZ86M5cuXx8CBA2P06NFxxRVXxKGHHrrelkEAAAAA2BA1F7IiIgYOHBjNzc3R3NycxXQAAAAAsI5MClkAAAAAdUdr4SZnxwEAAAAoBIUsAAAAAApBayEAAABAV5VK+WstLJVSJ9jocrbjAAAAAFCdQhYAAAAAhaC1EAAAAKA78tZaWAfsOAAAAACFoJAFAAAAQCFoLQQAAADoKrcWJpGzHQcAAACA6hSyAAAAACiEYrUWtrdHtLWlTlGbQw5JnSAbjz+eOkF23nwzdYJsHHpo6gTZePrp1Amy0UN+Xv3D8OGpI2TjxRdTJ8jOAw+kTpCNzTdPnSAb99yTOkE2XnghdYJsbL116gTZeM97UifIRqWSOkF2esrvWc88kzpBJl7a7YDUETIx9PLLU0fIxkc+ErHVVqlTpJO31sI6YMcBAAAAKIRincgCAAAAyAMPe08iZzsOAAAAANUpZAEAAABQCFoLAQAAALojb62FdcCOAwAAAFAIClkAAAAAFILWQgAAAICucmthEjnbcQAAAACoTiELAAAAgELQWggAAADQHXlrLawDdhwAAACAQqj5RNb5558ft95667t+7vrrr49x48bVuhwAAAAAdarmQtZnPvOZmDJlypp/v+mmm+Lmm2+O6dOnx6BBg9a8P2LEiFqXAgAAAMgPrYWbXM2FrGHDhsWwYcPW/Pv9998fERG77757bL/99rVODwAAAAAR4RlZAAAAABSEWwsBAAAAuqpUyl9rYamUOsFGl6tCVqVSiUqlUnWsvb09Sp2dmzgRAAAAAHmRq0JWS0tLTJ8+verYtGnTYpsBA2KPzTffxKkAAAAAyINcFbKam5tj6tSpVcdaW1uj1NYWsXLlJk4FAAAAUEXeWgvrQK4KWeVyOcrlctWxxsbGuuj1BAAAAKA6pUMAAAAACiFXJ7IAAAAACsGthUnkbMcBAAAAoLrMC1lnnXVWzJ8/P7bffvuspwYAAACgjmktBAAAAOiOvLUW1gE7DgAAAEAhKGQBAAAAUAhaCwEAAAC6yq2FSeRsxwEAAACgOoUsAAAAAApBayEAAABAd+SttbAO2HEAAAAACkEhCwAAAIBC0FoIAAAA0FVuLUwiZzsOAAAAANUpZAEAAABQCMVqLWxsjOjfP3WK2rz5ZuoE2Rg1KnWC7FQqqRNko60tdYJs7LVX6gTZ6Cm/1l98MXWCbHzxi6kTZGfw4NQJsvHb36ZOkI0DD0ydIBtF//vV2559NnWCbDQ1pU6QjVdfTZ0gOz3l10gP+XvW0BfnpI6QjcsvT50gG4sXp06QVGf0/Fa+vHEiCwAAAIBCUMgCAAAAoBCK1VoIAAAAkAOdnREdHalTrK2zs+dfXOhEFgAAAACFoJAFAAAAQCFoLQQAAADohry1FtYDJ7IAAAAAKASFLAAAAAAKQWshAAAAQBe5tTANhSwAAAAAuuXJJ5+Mb3/72/HEE0/Em2++GcOHD49TTjklDjvssI2ynkIWAAAAAF22YMGC+OhHPxqjRo2Kf/3Xf42+ffvGrFmz4uyzz44XX3wxTjvttMzXzKyQ1draGi0tLfHggw/G4sWLo0+fPrHrrrvG0UcfHccee2w0NjZmtRQAAABAcnlrLdzUrrnmmujTp09ce+210dTUFBEREyZMiMWLF0dLS0uccsop0dCQ7ePZMylkLVy4MD7ykY/ETjvtFJ/73Odi6NCh0dbWFvfee2986Utfit/+9rdx+eWXZ7EUAAAAADkwatSo2G233dYUsd42YsSI+PWvfx0rVqyILbbYItM1Mylkfe9734uIiBkzZkSfPn3WvH/wwQfHZpttFtdff32ccsopMWrUqCyWAwAAACCxU089dZ33KpVK3H333bHDDjtkXsSKyKiQ9eqrr0apVIr29vZ1xj72sY/FoEGDom/fvlksBQAAAJBcXm8t7OjoiLa2tvV+plwuR7lcfpd5OmPmzJnv+JmDDjoohgwZss7X/fu//3s899xzcdlll2148C7IpJB18MEHxz333BOTJ0+OSZMmxfjx42P33XeP3r17x4477hinn356FssAAAAA8A4WLVoUxxxzzHrHzzzzzDjrrLPecY729va4+OKL3/Ezw4cPX6uQValU4qKLLorbb789TjnllDj66KO7lHtDZVLIOv7442Pp0qVx1VVXxRVXXBEREZtttlmMGTMmDjvssJg0aVL07t37XeepVCpRqVSqjrW3t0epszOLuAAAAAA90uDBg2POnDnrHX+301gREb169Yr58+dv8JqLFy+Os846Kx577LH47Gc/G2ecccYGf21XZXZr4emnnx4f+9jH4oEHHohHHnkk5syZE4888kg89NBDMXPmzLjuuutiq622esc5WlpaYvr06VXHpk2bFtsMHBh7/N2xNQAAAIAU8tZaGBHR0NCwzsPXN6b58+fH6aefHkuWLImvfe1r8eEPf3ijrpdZISsiom/fvnHIIYfEIYccEhERS5YsiSuvvDJmzJgR11xzTZx77rnv+PXNzc0xderUqmOtra1RWrEiy7gAAAAAdNNzzz0XJ598cpRKpZgxY0b84z/+40Zfs6HWCV555ZWYMGFCXH311euMDRgwIC666KIYMmRILFiw4F3nKpfL0dTUVPXV2NgYDaVSrXEBAAAAyMCFF14YS5cujTPOOCM6OzvjscceW+u1evXqzNes+UTWoEGDolwux8yZM+P444+P/v37rzX+6quvxrJly2LUqFG1LgUAAACQC3m9tXBTWbx4cfzmN7+JiIhLLrmk6mcefPDBGDhwYKbr1lzIamhoiEsuuSSam5vj6KOPjhNPPDH23HPPaGxsjPnz58f3v//9GDJkyHpbBgEAAAAolkGDBnXpgfBZyeQZWfvuu2/ceuut8b3vfS9uuummuPLKK6OjoyO22267OPzww+OTn/xkbLnlllksBQAAAJALeTuRVQ8ye9j7LrvsEl/+8pezmg4AAAAA1lLzw94BAAAAYFPI7EQWAAAAQD3RWrjpOZEFAAAAQCEoZAEAAABQCFoLAQAAALqoszN/rYWdnakTbHxOZAEAAABQCApZAAAAABSC1kIAAACAbshba2E9cCILAAAAgEJQyAIAAACgELQWAgAAAHSRWwvTcCILAAAAgEJQyAIAAACgEIrVWtjZGVGppE5Rmy9+MXWCbFxySeoE2XnssdQJsvGe96ROkI3HH0+dIBuDB6dOkIn7tz8hdYRMTLj4E6kjZOfii1MnyMbMmakTZOO++1InyMbkyakTZKNfv9QJsvHMM6kTZOL5vf6/1BEys8Md16SOkI1hw1InyMTcbT+YOkImRk/aN3WEbJxzTsRee6VOkUzeWgvrgRNZAAAAABSCQhYAAAAAhVCs1kIAAACAHHBrYRpOZAEAAABQCApZAAAAABSC1kIAAACAbshba2E9cCILAAAAgEJQyAIAAACgELQWAgAAAHSRWwvTcCILAAAAgEJQyAIAAACgEDa4kHXOOefEHnvsEW1tbeuMffCDH4yRI0fGddddt85YS0tLjBw5MubNm1dTUAAAAIA86ejI16sebHAha8KECdHe3h6PPvroWu+3trbGs88+GwMGDIi77757na97+OGHY8iQITFq1Kja0wIAAABQtza4kLX//vtHqVSK3/72t2u9f88990SfPn3iE5/4RMyZM2etE1uVSiUeffTRmDBhQnaJAQAAAKhLG1zIGjRoUOy2227xyCOPrPX+vffeG+9///vjkEMOiVWrVsXs2bPXjD3++OOxYsWKmDhxYnaJAQAAAHIgdSuh1sJ38YEPfCDmzp0bb731VkRELF++PH7zm9/EAQccECNGjIjtttsu7rnnnjWff+ihh6JXr16x//77ZxoaAAAAgPrTpULWhAkTYtWqVfHYY49FRMSDDz4Yq1atigMOOGDN+H333Rcd/1cGfPjhh+O9731vNDU1bdD8lUol2traqr7a29ujo7OzK3EBAAAA6EG6VMgaO3Zs9OnTZ0174T333BMjRoyI7bffPiIiDjjggHjttdfiySefjLfeeisee+yxLj0fq6WlJcaOHVv1NXfu3Fi0ZElX4gIAAABsFJ2d6VsJ//5VD+d/enXlw+VyOfbZZ581D3y/995748Mf/vCa8fHjx0e5XI4HH3ww2traolKprDmttSGam5tj6tSpVcdaW1uj9OabXYkLAAAAQA/SpUJWxF+fk/Vf//Vf8eSTT8aiRYviwAMPXDPWt2/f2GeffeKRRx6JlStXxpAhQ2LkyJEbPHe5XI5yuVx1rLGxMaJUqo/yIgAAAADr6FJrYcRfC1nLly+PH/zgB9HU1BRjx45da3zixInxhz/8IR555BG3FQIAAAA9VupWQrcWboBddtklhg4dGnfccUfsv//+0avX2oe6Jk6cGIsXL47f/e53XWorBAAAAIB30uVCVsRfT2X97W2Ff2v48OExbNiwiIjYd999a0sHAAAAAP+ny8/Iioi45JJL4pJLLlnv+C9+8YtuBwIAAADIu7dvLcyTeniseLdOZAEAAADApqaQBQAAAEAhdKu1EAAAAKDe5a21sB44kQUAAABAIShkAQAAAFAIWgsBAAAAusithWk4kQUAAABAIShkAQAAAFAIWgsBAAAAuiFvrYX1wIksAAAAAApBIQsAAACAQtBaCAAAANANWgs3vVJnZzEuZ5w3b17EqlUxapttUkepSeubg1JHyMSOlT+mjpCdpqbUCbLR1pY6QTa23TZ1Av7WvHmpE2Ti/jfHpo6QmQnDWlNHyEYP+bX+2rLeqSNk4h8alqSOkI2VK1MnyMbLL6dOkI2lS1MnyM6yZakTZKNv39QJsjFqVOoE2fjNb1InyMS8bbaJ+Id/iFE95cdlA82bNy+WL4+IyNv3PS+22CJ69I+H1kIAAAAACkFrIQAAAEAXdXb+9ZUnpVLqBBufE1kAAAAAFIJCFgAAAACFoLUQAAAAoBvydmthY2PqBBufE1kAAAAAFIITWQAAAABd1NmZvxNZDXVwXKkOvkUAAAAAegKFLAAAAAAKQWshAAAAQDfkrbWwHjiRBQAAAEAhKGQBAAAAUAg1FbIuuuiiGDlyZNx4441Vxzs6OuKEE06I97znPbFgwYJalgIAAADIjbdvLczTq7Mz9a5sfDUVsi644IIYNmxYXHrppfHCCy+sM37ttdfGo48+Gv/8z/8cu+22Wy1LAQAAAFDnaipkbbHFFnH55ZfHW2+9FRdccEF0/k3p749//GN861vfioMOOihOPPHEmoMCAAAAUN9qfkbWmDFj4vTTT4/f/OY3cf3110dExOrVq+Of//mfo3///vGVr3yl5pAAAAAAeZO6lfDvX/Ugk4e9n3HGGbHnnnvGN7/5zXjppZfiO9/5TvzhD3+Ir371qzFgwIAslgAAAACgzvXKYpLevXvHV7/61Zg0aVJ84QtfiLlz58YnP/nJGD9+fJfmqVQqUalUqo61t7dHqR6eWgYAAABAVZkUsiIidtlll/+/vTuPi7Lc/z/+HsBRCFMxQY+apCSaYpq5pSKJp/xWZq5piYlpdDpqJ5fEck00stROYqZJmVpfXHJJc6ksLcvMJZM2PS2SWm4pcXADhvn90Rd+moAs93DPPfN6Ph7zeNBc432972Bg5jPX5740ZswYTZ06Vc2aNdOIESNKfIz58+crKSmpwLEpU6aoZo0auqlWrbJGBQAAAAAAKJO8XQvdiTes/zGskCVJUVFRmjp1qiIjI+XnV/JDx8XFKTY2tsCxtLQ02RyOskYEAAAAAACARRlyjSyj2O12BQYGFnjz9fWVj81mdkQAAAAAAAAU4Pvvv1dERITmzJnjsjkMXZEFAAAAAADgLdyttdBMFy5c0KhRowq99rlR3GpFFgAAAAAAAKznueee07lz51w+D4UsAAAAAAAAlNqHH36oFStWaNq0aS6fy9DWwjp16ujAgQNGHhIAAAAAAMAtuWNrYW5urjIzMwsdt9vtstvths138uRJPf3003r88cfVqFEjw45bGK6RBQAAAAAA4CFOnDihHj16FDo+bNgwDR8+vMhjOJ1OpaSkFPmYzp07Kzg4WPHx8QoLC9PDDz+s9PT0UmUuCQpZAAAAAAAAHiI4OFh79uwpdLw4q7EcDocmT55c5GPq16+vjRs3av/+/Vq7dq18fMrn6lUUsgAAAAAAAErI6XS/1kKnU/Lx8VFgYGCZjuPn53fVS0d9//33mjlzpqZOnarg4GDl5OQo9//+h+Tm5ionJ0d+fsaXnbjYOwAAAAAAAErk/fffV1ZWlsaOHasmTZqoSZMmat++vSTp5ZdfVpMmTXTkyBHD52VFFgAAAAAAAEqkb9++ioqKuuy+zMxMDRo0SH379lXfvn0VHBxs+LwUsgAAAAAAAErB3VoLy1NISIhCQkIuu+/06dOS/rxOV0REhEvmpbUQAAAAAAAAlsCKLAAAAAAAAJRZUFDQVS8SX1YUsgAAAAAAAErIXXct9HS0FgIAAAAAAMASKGQBAAAAAADAEmgtBAAAAAAAKAV3ay30BtYqZDkcUnq62SnKpN5Pe82OgL9av97sBMaYPt3sBMb49luzExjDx0MWvDZqZHYCQ3R853/NjmCcQM/4nujgQbMTGKL69debHcEYnnIe+/aZncAYHvKuKDsy2uwIhklJMTuBMWKu/9LsCLiUp7xetNnMTgAv4yHPHAAAAAAAAHg6a63IAgAAAAAAcAPsWmgOVmQBAAAAAADAEihkAQAAAAAAwBJoLQQAAAAAACgFd2st9AasyAIAAAAAAIAlUMgCAAAAAACAJdBaCAAAAAAAUELsWmgOVmQBAAAAAADAEihkAQAAAAAAwBJoLQQAAAAAACgFd2st9AasyAIAAAAAAIAllKmQFR8frxYtWhQ6PmfOHIWHh+vIkSNlmQYAAAAAAACgtRAAAAAAAKA0aC0sf7QWAgAAAAAAwBIoZAEAAAAAAMASDGktzMnJKfD+XNbYAQAAAAAAD+R0ul9rodNpdgLXK3Mh69y5c2rSpIkRWZSVlaWsrKwCxxwOh2zu9hMCAAAAAACAclPmQlalSpW0dOnSAseWL1+u5cuXF/tY8+fPV1JSUoFjU6ZMUc3q1XVT5cqlygkAAAAAAABrK3Mhy8fHRxEREQWObd26tUTHiouLU2xsbIFjaWlpsl28WNJ4AAAAAAAALkHjWPkz5BpZRrHb7bLb7QWO+fr6Sj5cmx4AAAAAAMBbURkCAAAAAACAJbjViiwAAAAAAAArYNdCc7AiCwAAAAAAAJZQpkJWYmKivvzyy0LHhw8frgMHDqhOnTplmQYAAAAAAACgtRAAAAAAAKA03K210BvQWggAAAAAAABLYEUWAAAAAABACXGxd3OwIgsAAAAAAACWQCELAAAAAAAAlkBrIQAAAAAAQCm4W2uhN2BFFgAAAAAAACyBQhYAAAAAAAAsgdZCAAAAAACAEmLXQnOwIgsAAAAAAACWQCELAAAAAAAAlkBrIQAAAAAAQCm4W2uhN7BWIcvhkDIyzE5RNgEBZicwRp06ZicwzvjxZicwxokTZicwho+HLBTlL5p78ZTnhyTdcovZCYxh9b/neU6dMjuBMYKDzU5gDE95fRIWZnYCQ1Q4ddLsCIaJCfrC7AjGOOIhr09CQ81OYAxPOQ9e96Kcecg7RgAAAAAAAHg6a63IAgAAAAAAcBMsSCt/rMgCAAAAAACAJVDIAgAAAAAAgCXQWggAAAAAAFBCTqf7tRY6nWYncD1WZAEAAAAAAMASKGQBAAAAAADAEmgtBAAAAAAAKAV3ay30BqzIAgAAAAAAgCVQyAIAAAAAAIAl0FoIAAAAAABQQuxaaI4yF7Li4+O1evXqIh8zefJk9e/fv6xTAQAAAAAAwIsZtiJr2bJlhY7VrVvXqGkAAAAAAADgpQwrZDVv3tyoQwEAAAAAALg9d2st9AZc7B0AAAAAAACWYNiKrJycnALvt9ls8vX1NWoaAAAAAAAAeCnDCllNmjQp8P7KlStr9+7dxTpGVlaWsrKyChxzOByy5eZKPiwiAwAAAAAA5mLXQnMYVshauXJlwRP4FX+K+fPnKykpqcCxKVOmqGZQkG6qXr1U+QAAAAAAAGBthhWyIiIiynyMuLg4xcbGFjiWlpYm27lzZZ4DAAAAAAAA1mRYIcsIdrtddru9wDFfX1/aCgEAAAAAgNtwt9ZCb0BlCAAAAAAAAJZg2Iqsffv2FTpWpUoV3XDDDUZNBQAAAAAAAC9kWCHr/vvvL3QsOjpaL7/8slFTAQAAAAAAmIpdC81R5kJWYmKiEhMTjcgCAAAAAAAAFIprZAEAAAAAAMAS3GrXQgAAAAAAAKtwt9ZCb8CKLAAAAAAAAFgChSwAAAAAAABYAq2FAAAAAAAApUBrYfljRRYAAAAAAABK5cyZM5o0aZI6dOigm2++Wffee6/WrFnjsvlYkQUAAAAAAIASu3jxogYOHKgzZ85o5MiRCgkJ0bp16zR27FjZbDZ1797d8DkpZAEAAAAAAJSQ0+l+rYVOZ/nOt2TJEv38889as2aNwsLCJEnt27fXr7/+qq1bt1LIAgAAAAAAgHvYsGGDOnTokF/EyrN48WKXzck1sgAAAAAAAFAiOTk5OnjwoBo2bKhFixapS5cuuummm9S1a1etW7fOZfOyIgsAAAAAAKAU3K21UJJyc3OVmZlZ6Ljdbpfdbi/yGE6nUykpKUU+plOnTsrOztbq1at17bXXatSoUapcubJSUlI0evRoORwO3XfffaU6h6JQyAIAAAAAAPAQJ06cUI8ePQodHzZsmIYPH17kMRwOhyZPnlzkY2bMmCFJyszM1Ntvv63g4GBJ0m233aZevXpp9uzZFLIAAAAAAABQuODgYO3Zs6fQ8autxpIkPz8/HThwoMjH5K36atq0aX4RS5J8fHwUGRmpV155RadOndJ1111XzOTFY61ClsMhnT9vdoqyCQgwO4Ex/Kz1o1OkX34xO4ExPOVnq2pVsxMY45Jf5Jb2669mJzBGs2ZmJzCOO65fL43Wrc1OYIzTp81OYIiz9mpmRzDENfYMsyMYw1Nem9SsaXYC43jK65M6dcxOYIyPPzY7gTEiI81OYIyjR81OYBp33bXQx8dHgYGBLp8rMDBQNWrUUHZ29hVjefdVqlTJ8Hm52DsAAAAAAABKLCoqSvv379fPP/+cf19OTo4++ugjNWnSxCUFNQpZAAAAAAAAKLFhw4apSpUqGjJkiNauXatt27bp0Ucf1aFDhzR69GiXzOlB/WEAAAAAAADlx91aC8tbzZo1tXz5cs2ePVvTp0/XhQsX1LhxY7322mtq166dS+akkAUAAAAAAIBSqVu3rmbNmlVu89FaCAAAAAAAAEtgRRYAAAAAAEAJueuuhZ6OFVkAAAAAAACwBFZkAQAAAAAAlIK7rcjyBqzIAgAAAAAAgA8tw9wAACAASURBVCVQyAIAAAAAAIAl0FoIAAAAAABQQlzs3RxlKmTFx8dr9erVl91nt9tVvXp13XrrrYqLi9ONN95YpoAAAAAAAACAZNCKrGXLluV/ff78ef30009KTk5Wr169tGDBArVt29aIaQAAAAAAAODFDClkNW/e/LL/bteunbp27aqePXtqzJgxeu+99+Tv72/EVAAAAAAAAG7B3VoLvYHLLvZevXp1DR06VCdOnNDmzZtdNQ0AAAAAAAC8hEt3LYyMjJQkffHFF66cBgAAAAAAAF7ApbsW1qhRQ5J08uTJYj0+KytLWVlZBY45HA7ZvOHy+wAAAAAAwBJoLSx/Li1k5bHZbMV63Pz585WUlFTg2JQpU1SzWjXdVKmSkdEAAAAAAABgES4tZB07dkySVLNmzWI9Pi4uTrGxsQWOpaWlyZaZKV24YFg+AAAAAAAAWIdLC1mffvqpJKlt27bFerzdbpfdbi9wzNfXVyrmyi4AAAAAAABXcjrdr7XQG67I5LKLvaenpys5OVm1a9dWly5dXDUNAAAAAAAAvIQhK7L27duX//X58+f1ww8/aPHixUpPT9fChQsLXWUFAAAAAAAAFJchhaz7778//2u73a6QkBC1a9dOQ4YMUb169YyYAgAAAAAAwK24W2uhNyhTISsxMVGJiYlGZQEAAAAAAAAK5bJrZAEAAAAAAABGcumuhQAAAAAAAJ6IXQvNwYosAAAAAAAAWAKFLAAAAAAAAFgCrYUAAAAAAACl4G6thd6AFVkAAAAAAACwBApZAAAAAAAAsARaCwEAAAAAAEqIXQvNwYosAAAAAAAAWAKFLAAAAAAAAFgCrYUAAAAAAACl4G6thd6AFVkAAAAAAACwBGutyPLzk4KCzE5RNqdOmZ3AGL/+anYC46xZY3YCY/TsaXYCY1x3ndkJjPHUU2YnMIannMf+/WYnME5AgNkJjPHZZ2YnMMa995qdwBDX5PxhdgRjnD5tdgJjZGaancAYoaFmJzDO9u1mJzDGCy+YncAYffuancAY586ZncAYLElCObNWIQsAAAAAAMANsGuhOWgtBAAAAAAAgCVQyAIAAAAAAIAl0FoIAAAAAABQCu7WWugNWJEFAAAAAAAAS6CQBQAAAAAAAEugtRAAAAAAAKAUaC0sf6zIAgAAAAAAgCVQyAIAAAAAAIAl0FoIAAAAAABQQk6n+7UWOp1mJ3A9VmQBAAAAAADAEihkAQAAAAAAwBJoLQQAAAAAACgFd2st9AaGFLJ++OEHvfnmm/r00091/PhxBQQEKCwsTN27d1ePHj3k6+trxDQAAAAAAADwYmUuZK1YsULPPPOMbrjhBg0ePFj169dXRkaGtm7dqkmTJmnVqlVKSkpSUFCQEXkBAAAAAADgpcpUyNq9e7cmTZqkO+64Q88//7wqVKiQP9alSxfdfffdGjp0qOLj47VgwYIyhwUAAAAAAHAH7FpojjJd7H3OnDkKCAhQQkLCZUWsPO3atVNMTIy2bdum3bt3l2UqAAAAAAAAeLlSF7L++OMP7dy5U+3bt1dgYGChj+vWrZskafPmzVc9ZlZWljIzMwu8ORwO5XpDaREAAAAAAAAFKnVr4dGjR+V0OlW3bt0iH1evXj1J0pEjR656zPnz5yspKanAsSlTpqhm9eq6qWbNkocFAAAAAAAwmLu1FnoDQ3YtLIqPz5+LvhwOx1UfGxcXp9jY2ALH0tLSZLtwwdBsAAAAAAAAsI5SF7Jq164tm82mX375pcjHpaWlSZLq1Klz1WPa7XbZ7fYCx3x9fSWbreRBAQAAAAAA4BFKfY2sKlWqqG3bttq+fbsyMjIuG0tNTZXz/65ntXHjRklSVFRU6VMCAAAAAAC4kbxdC93p5g2XFi/TroUjRozQxYsXNW7cOGVnZ0uSMjIyFBMTo65du2rJkiV6/fXX1apVK0VGRhoSGAAAAAAAAN6pTIWsW265RQkJCfrkk0/Us2dPpaSk6MCBA3rmmWeUnp6uhIQEORwOjR8/3qi8AAAAAAAA8FJlvth7jx491KxZMy1ZskTJyck6fvy4AgICdOONNyo6Olrvvfee+vfvr4EDB+qJJ54wIjMAAAAAAIDp2LWw/Bmya2GDBg00efLkAscGDRqkLVu26OjRo0ZMBQAAAAAAAC9lSCGrKDabTV26dHH1NAAAAAAAAPBwLi9kAQAAAAAAeJq8XQvdCbsWAgAAAAAAAG6CFVkAAAAAAACl4G4rsrwBK7IAAAAAAABgCRSyAAAAAAAAYAm0FgIAAAAAAJQCrYXljxVZAAAAAAAAsAQKWQAAAAAAALAEWgsBAAAAAABKyOl0v9ZCp9PsBK7HiiwAAAAAAABYgrVWZPn4SJUqmZ2ibBo2NDuBMc6dMzuBce67z+wExqhZ0+wExvCUn6177jE7gTEyM81OYIzmzc1OYBy73ewExggIMDuBMU6cMDuBMTIyzE5gDE95fvztb2YnMMa335qdwDg+HvL5f8+eZicwhqe8p/r8c7MTGKNGDSkoyOwU8CLWKmQBAAAAAAC4CXdrLfQGHvLRAgAAAAAAADwdhSwAAAAAAACUyqFDhzRixAi1b99erVq10sCBA7V3716XzUchCwAAAAAAoITydi10p1t571p4+vRpDRgwQN99953GjRunF154QTabTQMHDtTXX3/tkjkpZAEAAAAAAKDEtmzZopMnT2rGjBm655571KlTJ82bN092u11vvfWWS+akkAUAAAAAAIASu3DhgiQpMDAw/z5/f3/5+/vrzJkzLpmTQhYAAAAAAEApmN1K+NdbebvrrrtUq1YtTZs2Tb/88otOnz6tGTNm6Pfff1ePHj1cMqefS44KAAAAAACAcpebm6vMzMxCx+12u+x2e5HHcDqdSklJKfIxnTt3VkhIiKZPn64RI0bo73//uyTJZrPp6aef1h133FHy8MVAIQsAAAAAAMBDnDhxosjVUMOGDdPw4cOLPIbD4dDkyZOLfEz9+vW1Z88ejR49Wq1bt9bAgQNVsWJFbdq0SdOmTZOvr68eeOCB0pxCkShkAQAAAAAAlFDeroXuxOmUgoODtWfPnkIfc7XVWJLk5+enAwcOXPVxXbt2VWhoqF599VVVqFBBktS+fXtlZWUpMTFRd911l6pWrVr8EygGrpEFAAAAAADgIXx8fBQYGFjorTiFrOI6cuSIbr755vwiVp7WrVvr4sWLSktLM2yuPBSyAAAAAAAAUGJhYWH68ssvlZ2dfdn9u3fvlo+Pj+rUqWP4nGUqZMXHxys8PFxvvfVWgeObNm1SeHi4du7cWZZpAAAAAAAA3I7ZuxSavWvhyJEj9csvv2jo0KH64IMP9Mknn2jixIlatWqVBg8erOrVqxs+pyErsmbMmKGffvrJiEMBAAAAAADAAiIjI7Vo0SJJ0pgxY/Svf/1L3333nV544QWNGTPGJXOW+WLvfn5+stlsGjNmjJYtWyY/P64fDwAAAAAA4A1at26t1q1bl9t8ZV6RZbfb9dRTT+nrr7/WnDlzjMgEAAAAAADg1vJ2LXSnm9Np9v8V1zOktbBPnz6Kjo7Wq6++qr179xpxSAAAAAAAAOAyhu1amJCQoGrVqunJJ59UZmZmqY6RlZWlzMzMAm8Oh0O5Zly5DAAAAAAAAG7BsEJWUFCQpk2bpsOHD2vatGmlOsb8+fPVsmXLAm+pqak68fvvRsUFAAAAAAAoE7NbCc3etdAMhl6ZPSoqSv369VNKSopuv/32Ev/7uLg4xcbGFjiWlpYm28WLZY0IAAAAAAAAizJsRVae+Ph4hYaGasKECTp58mSJ/q3dbldgYGCBN19fX/n4GB4XAAAAAAAAFmF4Zcjf31/PP/+8MjMz9dJLLxl9eAAAAAAAALdgdiuhN7YWumSJU7NmzfTYY48pIyPDFYcHAAAAAACAF3JZr96jjz6qFi1auOrwAAAAAAAA8DJluth7YmKiEhMTCxzz9fVVSkpKWQ4PAAAAAADglpxO92vnczrNTuB6XD0dAAAAAAAAlkAhCwAAAAAAAJZQptZCAAAAAAAAb+VurYXegBVZAAAAAAAAsAQKWQAAAAAAALAEWgsBAAAAAABKiF0LzcGKLAAAAAAAAFgChSwAAAAAAABYAq2FAAAAAAAApeBurYXegBVZAAAAAAAAsAQKWQAAAAAAALAEWgsBAAAAAABKiF0LzWGtQpY7/pSU1Ndfm53AGE2bmp3AOEeOmJ3AGMeOmZ3AGBcumJ0Al0iz32h2BEPUGz/Y7AjGmTHD7ATGCA01O4ExVq0yO4EhHj81wewIhvj3wD1mRzDGiRNmJzCGB/1N/63R7WZHMEStSpXMjmCM4GCzExjjiy/MTmCMTp2koCCzU8CL0FoIAAAAAAAAS7DWiiwAAAAAAAA3YfWmMStiRRYAAAAAAAAsgUIWAAAAAAAALIHWQgAAAAAAgBJyx/3ovGHXQlZkAQAAAAAAwBIoZAEAAAAAAMASaC0EAAAAAAAoBXdrLfQGrMgCAAAAAACAJVDIAgAAAAAAgCXQWggAAAAAAFAKtBaWvzKvyIqJiVHnzp0LHHvjjTfUqFEjxcTEKDMzs6xTAQAAAAAAwIu5bEXW/PnzNWvWLEVHR2v27NmqWLGiq6YCAAAAAAAoV06n+63IcjrNTuB6LrlG1uzZszVr1iz16NFDc+bMoYgFAAAAAACAMjN8Rdb06dP1xhtvaNCgQYqPj5fNZjN6CgAAAAAAAHghwwpZubm5mjx5spYtW6bhw4dr2LBhRh0aAAAAAADA7bhba6E3MKSQ5XA4NHbsWK1bt06S9Pvvv5fqOFlZWcrKyip0Dps3NHsCAAAAAACgQIYUso4dO6aNGzfqxRdf1ObNm/XWW2+pZcuWuueee0p0nPnz5yspKanAsSlTpqhm9eq66ZprjIgMAAAAAAAAizGkkFWhQgXNmzdPHTt2VIcOHZSamqoJEyaoUaNGCgsLK/Zx4uLiFBsbW+BYWlqabBcvGhEXAAAAAACgTNi10ByG7FoYHBysjh07SpICAwM1e/ZsZWdna8SIETp79myxj2O32xUYGFjgzdfXVz5cOB4AAAAAAMBrGVLI+quIiAiNHDlSP/74oyZMmOCKKQAAAAAAAOBlDNu18K9iY2P1+eef691339Utt9yiAQMGuGoqAAAAAACAcudurYXewCUrsiTJZrMpMTFRwcHBSkxM1FdffeWqqQAAAAAAAOAFyrwia8mSJYWOBQUF6ZNPPinrFAAAAAAAAIDrWgsBAAAAAAA8FbsWmsNlrYUAAAAAAACAkShkAQAAAAAAwBJoLQQAAAAAACgFd2st9AasyAIAAAAAAIAlUMgCAAAAAACAJdBaCAAAAAAAUELsWmgOVmQBAAAAAADAEihkAQAAAAAAwBJoLQQAAAAAACgFd2st9AasyAIAAAAAAIAlUMgCAAAAAACAJdBaCAAAAAAAUAq0FpY/axWycnOlc+fMTlE2oaFmJzCG1b8Pl7ruOrMTGOP0abMTGCMw0OwExqhZ0+wEhqgXcNLsCMaYNcvsBMax281OYIz0dLMTGOPee81OYIh/h501O4IxvvWQdxM5OWYnMEb9+mYnMEytD5aYHcEYnvK699gxsxMYIzLS7ATGuPZasxPAy9BaCAAAAAAAAEuw1oosAAAAAAAAN+B0ul9rodNpdgLXY0UWAAAAAAAALIFCFgAAAAAAACyB1kIAAAAAAIBScLfWQm/AiiwAAAAAAABYAoUsAAAAAAAAWAKthQAAAAAAACXEroXmYEUWAAAAAAAALIFCFgAAAAAAACyB1kIAAAAAAIBScLfWQm9QpkJWfHy8Vq9efcX9drtdQUFBuvXWWzVy5EjVrl27LNMAAAAAAAAAxqzIWrZs2WX/nZGRoT179ig5OVmpqalav3697Ha7EVMBAAAAAADADc2YMUMff/yx1q9ff8XY/v37NXPmTKWmpqpChQqKiorSmDFjdN1115VoDkMKWc2bN7/ivsjISOXk5GjhwoXasWOHOnXqZMRUAAAAAAAApmPXwsu98sorSk5O1o033njF2Pfff6+HHnpIzZs318yZM3Xq1CnNnj1b33zzjVatWlWixU8uvUZWlSpVJEk2m82V0wAAAAAAAMAEBw8e1HPPPacdO3aocuXKBT7mxRdfVLVq1TR//vz8olXjxo3Vq1cvrVq1Sv369Sv2fIbsWpiTk5N/y87O1unTp7VhwwYtXLhQoaGhatWqlRHTAAAAAAAAwI2MGTNG6enpWrp0qRo3bnzFeFZWlj777DN16dLlspVXTZs2VWhoqLZs2VKi+QxZkdWkSZMr7qtataqioqI0atQo+fv7F+s4WVlZysrKKnDM4XDIZuYaOQAAAAAAgEu4W2uhGZ577jk1atSo0PHDhw/r4sWLql+//hVjN9xwgw4ePFii+QwpZK1cuVLSn4WotWvXauXKlRo8eLDi4uJKdJz58+crKSmpwLEpU6aoZlCQbqpRo8x5AQAAAAAAPFFubq4yMzMLHbfb7Ve9JpXT6VRKSkqRj+ncubNCQkKKLGJJ0n//+19JKrDt8JprrtHZs2eL/Pd/ZUghKyIiIv/rli1bym63a9asWXI4HHrssceKfZy4uDjFxsYWOJaWlibb+fNlzgoAAAAAAOCpTpw4oR49ehQ6PmzYMA0fPrzIYzgcDk2ePLnIx9SvX18hISFXzZNr8LI1l1zs/cknn9Rnn32mpKQktWvXTi1atCjWvyuqKujr6ytx0XgAAAAAAOAG3HXXwuDgYO3Zs6fQxxRnh0A/Pz8dOHDAkEx5GwEWtPLq7Nmzuvbaa0t0PEMu9v5XdrtdU6dOVW5uriZOnKjs7GxXTAMAAAAAAIBL+Pj4KDAwsNBbcQpZRqpbt64qVKign3/++Yqxn3/+WQ0aNCjR8VxSyJL+bDHs0aOHDh48qNdff91V0wAAAAAAAMBN2e123Xbbbfrggw8u2+Dv66+/1qFDhxQZGVmi47mskCX9uQVj1apVNXfuXB0+fNiVUwEAAAAAAJSr3Fz3urmr4cOH67ffftPgwYO1ZcsWvf3223rkkUcUFham3r17l+hYZSpkJSYmFtkzGRQUpJ07d+qrr75S3bp1yzIVAAAAAAAALCgiIkLJycnKycnRE088oRdeeEEdOnTQokWLStzq6JKLvQMAAAAAAMC7LFmypNCxNm3aKCUlpcxzUMgCAAAAAAAoBXdu5/NULr1GFgAAAAAAAGAUClkAAAAAAACwBFoLAQAAAAAASsjpdL/WQqfT7ASux4osAAAAAAAAWAIrsgAAAAAAAErB3VZkeQNWZAEAAAAAAMASKGQBAAAAAADAEmgtBAAAAAAAKCEu9m4OVmQBAAAAAADAEiyzIuvixYvKlfS9u5U7S+rcObMTGMNmMzuBcaz+M5XH39/sBLjU2bNmJzDGhQtmJzCGJ/3OyskxO4ExPOV3lqd8Pw4dMjuBMTzluV6xotkJjJGebnYC44SGmp3AGBUqmJ3AGL6+ZicwRpUqZicwxHlfX/lcvGh2DFOEhZ3Xa699b3aMy4SFnZfkIa+zCmGZQpZv3i8rF/5hz83N1YkTJxQcHCwfH+suVuM83Avn4V485TwkzzmXcjmPcnjhzvfDvXAe7qdcziUw0DXHvYSnfE84jxKqUcN1xxbfD3fkKedSHufhc/Hi/3+/7kX8/f1Vo4bLfz2Ugr/8PeUDw0LYnE5v6KAsnszMTLVs2VJ79uxRYDm8EHIVzsO9cB7uxVPOQ/Kcc+E83Avn4V485TwkzzkXzsO9cB7uxVPOQ/Kcc/GU8wAuZd3SMgAAAAAAALwKhSwAAAAAAABYAoUsAAAAAAAAWAKFLAAAAAAAAFgChSwAAAAAAABYAoUsAAAAAAAAWILv5MmTJ5sdwp34+vqqTZs28vX1NTtKmXAe7oXzcC+ech6S55wL5+FeOA/34innIXnOuXAe7oXzcC+ech6S55yLp5wHkMfmdDqdZocAAAAAAAAArobWQgAAAAAAAFgChSwAAAAAAABYAoUsAAAAAAAAWAKFLAAAAAAAAFgChSwAAAAAAABYAoUsAAAAAAAAWIJXF7Li4+MVHh5+xS0iIkKdOnXSqFGjdPToUbNjXlVMTIw6d+5c4Ngbb7yhRo0aKSYmRpmZmeWcrGTyvh9vvfVWgeObNm1SeHi4du7cWc7JvFNBz4+IiAhFRUVp9OjR+s9//mN2xGIr7Ll+6e1///d/zY55VfHx8WrRokWh43PmzFF4eLiOHDlSjqlKZvz48QoPD9eyZcsKHM/NzVX//v3VrFkzHTx4sJzTXd2oUaN00003Ffj79M4771R4eLgWLVp0xdj8+fMVHh6u77//vhxSlk5aWpqeeuop3X777WratKlatWqlBx54QMuXL5fD4TA73lUV53lutb8hx48f17///W91795drVq1UrNmzfT3v/9dEydO1M8//2x2vKsq6HvSuHFjtWzZUv369dOGDRvMjlgqb775psLDw9W7d2+zoxRbTEyMwsPD1bFjR+Xm5hb4mG+++Sb/+5SamlrOCUvn0KFDSkhI0J133qmbb75Zt912m2JiYvTuu+/K6XSaHe+qrvZ7q2fPnmZHLLai3o9YwcMPP6ymTZvq9OnThT5m3bp1Cg8P1+bNm8sxWdmtWrXKUs9roDj8zA7gDv76hiojI0N79uxRcnKyUlNTtX79etntdpPSld78+fM1a9YsRUdHa/bs2apYsaLZkYplxowZatu2rerXr292lDL54Ycf9Oabb+rTTz/V8ePHFRAQoLCwMHXv3l09evSQr6+v2RGL5dLnx/nz5/XTTz8pOTlZvXr10oIFC9S2bVsT05VMYcUTSapbt245JvFe48aN086dO5WYmKj27durTp06l40nJydr7969mjhxoho2bGhSysJ17NhR69ev1969exUZGZl/f1pamg4dOqRq1arpo48+0qBBgy77dzt37lRISIgaNWpUzomL58cff9T999+v0NBQPf7446pVq5YyMzO1bds2TZw4Ubt379aMGTPMjlmkxx57TP369cv/7xUrVmjlypVKSkpSjRo18u8PCwszI16Jbd++XaNGjVLFihXVv39/RUREqEKFCjp48KCWLl2qd955R/PmzVO7du3MjnpVl/7uzc3N1ZkzZ5ScnKwnnnhCWVlZuu+++0xMV3IpKSlq1KiRUlNT9dVXX+nmm282O1Kx+Pj46MSJE9q5c2eBPzdr1641IVXprV+/XuPHj1fdunU1cOBA1a9fX2fPntXmzZs1cuRIbd++XdOmTZOPj/t/bl/Y65OAgIByTuK9+vXrp+3bt2vdunV66KGHCnzMypUrFRwcrOjo6HJOB+CvKGRJat68+RX3RUZGKicnRwsXLtSOHTvUqVMnE5KV3uzZs/XKK6+oR48emjZtmmWKJn5+frLZbBozZoyWLVsmPz9r/oiuWLFCzzzzjG644QYNHjxY9evXV0ZGhrZu3apJkyZp1apVSkpKUlBQkNlRr+qvz4927dqpa9eu6tmzp8aMGaP33ntP/v7+JqUrmYKe6yhf11xzjWbMmKEHH3xQ48aN0+LFi2Wz2SRJ//nPf/TSSy+pc+fOevDBB01OWrD27dvLZrNp9+7dlxWytm7dKn9/fw0aNEhJSUnKzMxUYGCgJCkrK0t79+7V3XffbVbsq3rttdckSUuWLLns+RwdHa2KFStq8eLFGjx4sNsW4iTp+uuv1/XXX5//35988okkqXHjxlcUTN3d0aNH9a9//Ut/+9vftHTpUl177bX5Y23atFGvXr3Uv39/jRs3Tlu2bHH7v/EF/e5t06aNOnXqpIULF1qqkPXll1/q4MGDSk5OVnx8vBYvXqyZM2eaHatYQkND9d///lfvvvvuFYUsh8OhDRs2qEmTJvrmm29MSlh83377rcaNG6e2bdtq7ty5l33g3KVLF9WuXVvz5s1T27Zt1b17dxOTFg+vT8x3++23Kzg4WGvWrCmwkHX48GHt3LlT//jHPyz7/gTwJO7/EYWJqlSpIkn5b7KsYvr06XrllVc0aNAgPfvss27/AvdSdrtdTz31lL7++mvNmTPH7Dilsnv3bk2aNEnR0dF6++231a9fP7Vu3VpdunRRQkKCFi5cqP379ys+Pt7sqKVWvXp1DR06VCdOnLDc8mqYr0WLFnrkkUf0xRdfaPHixZKknJwcjR07VlWrVtX06dNNTli4GjVqqGHDhtq1a9dl92/bti3/eZ6dna3t27fnj+3fv1/nz5+/rPDlbk6dOiWbzVZgC+GAAQM0atQoVgaUo1dffVX//e9/NX369MuKWHkCAgI0atQotWzZUmfOnDEhYdkFBgaqfv36OnTokNlRSmT58uWqWrWq2rRpo+7du2vz5s06efKk2bGKxdfXV3fddZfee+89ZWVlXTb22WefKT093a0L7pdasGCBHA6HpkyZUmDXxKOPPqr+/fvnv5YHrsbPz099+vTRt99+qwMHDlwxvnLlSvn4+Khv374mpAPwVxSy9OcbqLxbdna2Tp8+rQ0bNmjhwoUKDQ1Vq1atzI5YLLm5uZo4caLeeOMNDR8+XOPGjbNcEU6S+vTpo+joaL366qvau3ev2XFKbM6cOQoICFBCQoIqVKhwxXi7du0UExOjbdu2affu3SYkNEbem/IvvvjC5CTFd+lz/dKbFa7/c6nCzqOw6564o3/+859q0qSJXnzxRf3222965ZVX9N133+n5559XtWrVzI5XpA4dOig1NVUXL16UJJ09e1ZffPGFOnXqpLCwMNWuXVtbt27Nf/znn38uPz8/tW/f3qTEVxcdHa2MjAz17t1bCxYs0P79+5WdnS1Jqlevnh555JHLVjvBtTZt2qQbb7xRTZs2LfQxkZGRmjlzpq677rpyTGacrKwsHT58WH/729/MjlJsGRkZ2rBhg+69915VqFBBffv2VU5OTpFt6+6mW7du+uOPP/JX34NTvQAACwxJREFULOZ555131KFDB7f//Ztn69ataty4caE/P5UqVdLkyZMVFRVVvsFKyRNem3iCPn36yNfXV6tXr77sfofDodWrVysqKkq1atUyKR2AS7EuUlKTJk2uuK9q1aqKiorSqFGjLNE25XA4NHbsWK1bt06S9Pvvv5ucqGwSEhLUrVs3Pfnkk1qzZk1+i467++OPP7Rz507deeedRWbu1q2bXnvtNW3evFm33nprOSY0Tt41Z6zySbRU8HNdkipXrmyZouK5c+cKPQ8rqVChgp5//nn17NlTI0eOVGpqqoYOHWqJa6517NhRycnJ2rdvn9q0aaMdO3YoOzs7vwW9Y8eOev/995WbmysfHx/t3LlTt9xyi1v/Huvbt6/S09M1b968/DapihUrqkWLFrrrrrvUs2fPAgvzMF5GRobOnDmj1q1bXzHmcDiuuIC1r6+v239olZOTk/91XgFr7ty5OnPmjB577DETk5XM2rVrdeHCBd1///2S/izytm3bVikpKYqLi7PEcyQiIkKhoaFav359/nV+zp8/rw8++EDTp0/X+fPnTU54dadPn9b58+c9qrhe0N/12rVr68MPPzQhjfeqVauWIiMjtW7dOo0ePTq/hXD79u06fvy4EhISTE4IIA+FLP25VFT688XV2rVrtXLlSg0ePFhxcXEmJyu+Y8eOaePGjXrxxRe1efNmvfXWW2rZsqXuueces6OVSlBQkKZNm6a4uDhNmzZNzz77rNmRiuXo0aNyOp1XvXB4vXr1JMmtd5crLnd/A3WpvOf6X1npWgeVKlXS0qVLCxxbvny5li9fXs6JSq9BgwYaM2aMpk6dqmbNmmnEiBFmRyqWli1byt/fX7t27VKbNm20detWhYWF5V+HqVOnTkpJSdE333yjhg0bat++fRo+fLjJqa/ukUce0YABA/TZZ59p165d2rNnj3bt2qXPP/9cKSkpWrRoEW065aColZU9e/a8YufLJ598Ug8//LCrY5VJQW/Sg4KCNGrUKMXExJiQqHSWL1+upk2bKjg4WBkZGZKke+65R08//bQ2bdqkbt26mZyweLp166aFCxfq7Nmzuuaaa/T+++/Lz89P0dHRWr9+vdnxrirvkhmetGKpoNcnVtxoyhP0799fH330kT7++OP8XRhXrlypunXrqmPHjianA5DHOu/eXCgiIiL/65YtW8put2vWrFlyOByW+aSwQoUKmjdvnjp27Jjf9jJhwgQ1atTIMjs0/VVUVJT69eunlJQU3X777WbHMVTeDjpWfhF27NgxSVLNmjVNTlJ8lz7XrcrHx6fQ87i0nc0qoqKiNHXqVEVGRlqmoGi329WqVav8VXzbtm277EODtm3bym63a8eOHcrMzFRWVpZlNgwJCAhQly5d1KVLF0nSmTNnNHfuXC1ZskSvvvqqRo8ebXJCz1e1alUFBgbq8OHDV4zNnDkzf8XMyZMn9Y9//KO845XKpW/S/fz8VKVKFUu1FErS3r17dfDgQUkq8JITS5cutUwh695779WcOXO0ZcsW3XvvvXrnnXfUtWtXyxROqlSposqVK1/1w8Bjx44pODjYErsWesLrE0/RsWNH1a5dW2vWrFHnzp31+++/66OPPtLjjz9uqQ9vAU/n/r/ZTfDkk0+qQYMGSkpK0pdffml2nGIJDg7O/5QgMDBQs2fPVnZ2tkaMGKGzZ8+anK704uPjFRoaqgkTJliiha127dqy2Wz65ZdfinxcWlqaJFluJ61Lffrpp5JkiVYwwGgdOnTQ/v379c033+jEiROXXYclICBArVq10q5du7Rr1y6FhIQoPDzcvLBXcfz4cXXs2FELFiy4YqxatWoaP368QkJC8t/Ew/XuuOMOffvtt/rxxx8vuz8sLEwRERGKiIhQw4YNTUpXcnmZIyIiiryukTtbtmyZKlWqpNdff12LFy++7Hbfffdp3759Sk1NNTtmsVx//fVq3ry51q9fr99//107duywxM5+l+rUqZO+/fZb/frrrwWOZ2dnq3v37nrggQfKORmszsfHR3369NGHH36o9PR0rV27VpLUq1cvk5MBuBSFrALY7XZNnTo1/+LpeRe8tZKIiAiNHDlSP/74oyZMmGB2nFLz9/fX888/r8zMTL300ktmx7mqKlWqqG3bttq+fXt+20Ge1NTU/GubbNy4UZIscxHSv0pPT1dycrJq166dv3ID8CYdOnTQ2bNn9eabbyowMFAtW7a8bDwyMlLfffeddu3a5da7FUp/Xu/ObrcrJSVF6enpV4yfOnVKGRkZatSokQnpvFNcXJwCAwM1ZsyYQnclLGhXLbhGRkaGNm3apC5duui2225TmzZtLrsNGTJEkrRkyRKTkxZft27d9Nlnn+nNN99USEjIFb/D3N2QIUPk6+urKVOmXLEDoyQlJSUpPT2d4gNKpXfv3nI6nXr//ff1zjvv6M4771RQUJDZsQBcwhp9HCZo2bKlevTooVWrVun111/XI488YnakEouNjdXnn3+ud999V7fccosGDBhgdqRSadasmR577DFLFLIkacSIEYqJidG4ceP04osvqkKFCsrIyFBMTIxCQkI0YMAAvf7662rVqpXbv8GVpH379uV/ff78ef3www9avHix0tPTtXDhQsu0IkiXn8tfValSRTfccEM5poGVNWjQQLVq1dI777yjzp07X9EWGRkZqWeffVbp6ekaOHCgSSmLx8fHRwkJCYqLi9N9992nBx98UE2aNJGvr68OHDigN954QyEhIYqNjTU7qtcIDQ1VUlKSRo0apbvvvlt9+vRRixYt5O/vr19++UWbNm3S9u3bVa9ePcvsrGxla9as0YULFwpdtXTjjTeqefPm2rhxo8aOHavq1auXc8KSu+uuu/Tss89qwYIFGjJkiOVapho3bqynn35aCQkJ6tOnj/r376/Q0FCdPn1a69ev15YtW9S7d2/17t3b7KheJTMzU4sWLSpw7MEHH7TEhgjSnx/wREdH67XXXtNPP/2k8ePHmx0JwF9QyCrCmDFj9OGHH2ru3Ln6n//5n6tewNvd2Gw2JSYmqnv37kpMTFRERIRuvvlms2OVyqOPPqpPPvnEEq2et9xyixISEjRp0iT17NlTDz74oBo0aKBnnnlG06ZNU0JCgvz8/CzzRzFvdybpz9WKISEhateunYYMGZJ/0XqruPRc/io6Olovv/xyOaaB1XXo0EErVqwo8PpX9evX1/XXX6/ffvtN7dq1MyFdybRr106rV6/Wa6+9phUrVmju3LnKzc1V7dq1dffdd2vo0KGqXLmy2TG9Srt27bR+/XqtWLFCH3zwgVJSUnT27FkFBQUpIiJCM2fO1B133GGpDxOsavny5apRo4bat29f6GP69Omjp59+WikpKfrnP/9ZjulKJygoSLfddps+/vhjy7UV5nnggQfUuHFjLV26VAsWLNCpU6dUuXJlNWjQQC+99JLuuOMOyxXorO6PP/4odIOmPn36WKaQJUn9+vVTbGysGjZsaNkdxgFPZnP+dR9nAIb48ccftWTJEn366ac6fvy4AgICFBYWpujoaL333nv6/vvvNXDgQD3xxBNmRwUAAAAAwBIoZAEmcDqd2rJli44ePaqHHnrI7DgAAAAAAFgChSwAAAAAAABYArsWAgAAAAAAwBIoZAEAAAAAAMASKGQBAAAAAADAEihkAQAAAAAAwBIoZAEAAAAAAMASKGQBAAAAAADAEihkAQAAAAAAwBIoZAEAAAAAAMASKGQBAAAAAADAEihkAQAAAAAAwBL+H/DTj2cez1KTAAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 1618.03x1000 with 2 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABKgAAAMsCAYAAABwW5plAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzs3X+U1VW9P/7XYeAIOIqQ4A8MEVEQpaVyDfyFXOVrLc3fWHrNEjOnW1qZWnprteLm7VpmdQuXjl69JtrCNDXDslLT9Pojk0qsgKIcJVNUQBwCD8zM94+ufCQGZc7ZsN/nzOOx1llLzx72frJhfvhyv9671NXV1RUAAAAAkEmf3AEAAAAA6N0UqAAAAADISoEKAAAAgKwUqAAAAADISoEKAAAAgKwUqAAAAADISoEKAAAAgKwUqAAAAADISoEKAAAAgKwUqAAAAADISoEKAAAAgKwUqAAAAADISoEKAAAAgKwUqAAAAADIqm/uAJvqqaeeio6Ojthqq61yRwEAAAAi4rXXXoumpqbYZ599ckfZotra2mLVqlW5Y3RrwIABseuuu+aO0WN1U6Dq6OiISqUzVq7MnaQ2TU25E/CPXn01d4I0yuXcCdKo98/x1227be4EaTTK76O9PXeCdPo0yNnnrbfOnSCNv/0tdwLeqFF+znrttdwJ0uhbN/+l8dY6OnIn4I1Wr86dII3+/XMnSKNv386G+W+Rnli1alWsevHFGPDHP+aOsp5Vo0dHDB2aO0ZV6ubbxlZbbRUrV0a8+OLY3FFqMnBg7gRpNNIPHI88kjtBGjvvnDtBGr/+de4EaUyenDtBGqNH506QxjPP5E6QTqN8Hxlb39/O12mUr1mNYrvtcidIY/Hi3AnSaJQ/j4jG+R8dnZ25E6Txpz/lTpDGqFG5E6Sx/fbzY5ttcqfIY8Af/xhjzzwzd4z1zL/uurotUDXI/4cFAAAAoF410DkYAAAAgC2kVCre8xdKpdwJqlawnQQAAACgt1GgAgAAACArLX4AAAAA1Shai18ds5MAAAAAZKVABQAAAEBWWvwAAAAAesotfkkVbCcBAAAA6G0UqAAAAADISosfAAAAQDWK1uKX2MKFC+NrX/ta/PKXv4yIiHHjxsV5550X++23X/K1NutO3nbbbTFmzJiYN2/e5lwGAAAAgIQWLVoUp5xySixbtiy+/OUvx5e//OVYvXp1nHnmmfGnP/0p+XpOUAEAAACwni9/+csxdOjQ+Pa3vx39+/ePiIj9998/jj/++HjwwQdj1KhRSddToAIAAACoRoO2+K1YsSIeeuihuOCCC9YVpyIiBg8eHA888MBmWbMxdxIAAACAqsyfPz86Ojpi+PDh8cUvfjEmTZoUe++9d5x22mnx1FNPbZY1FagAAAAAGkRnZ2e0t7dv9FWpVN5yjpdeeikiIi655JL461//Gpdddll87WtfixUrVsTpp58eixYtSp67UC1+lUploxvV0dERXV2lLZwIAAAAoBulUvFa/EqlWLJkSZxwwgkb/ZBzzjknzj333DedZs2aNRERscMOO8TMmTOjz//9Pvfdd99417veFVdddVVcdtll6XJHwQpUra2tMXPmzG7HZsyYEYMG7RgR47ZsKAAAAIA6MWzYsHjiiSc2Ol4ul99yjubm5oiImDJlyrriVMTfC1Zjx47dLG1+hSpQtbS0xPTp07sda2tri+XLS/F/p8wAAAAA+Ad9+vRZV2Cq1m677RYR0W2X29q1a2PAgAE1zd+dQp1FK5fL0dzc3O2rqakpSqVCxQUAAAB6sz59ivVKZNSoUTFy5Mj40Y9+tF6R6plnnon58+fHxIkTk631OhUfAAAAANZz8cUXx1/+8pc466yz4v77748f/vCHcdZZZ8W2224bH/rQh5Kvp0AFAAAAwHqmTJkS//M//xNdXV3xyU9+Mj7/+c/HmDFj4uabb47tt98++XqFegYVAAAAQF0o6C1+KU2cOHGztPN1Z7MWqE488cQ48cQTN+cSAAAAANS5gpX6AAAAAOhttPgBAAAAVKNoLX51zE4CAAAAkJUCFQAAAABZafEDAAAA6KlecIvfllSwnQQAAACgt1GgAgAAACArLX4AAAAA1Shai18ds5MAAAAAZKVABQAAAEBWWvwAAAAAesotfkkVbCcBAAAA6G3q6gTV4MERBxyQO0Vt5s7NnYB/NHly7gRp7Lln7gRpjBiRO0EaTz+dO0EaS5fmTpBG//65E6RTLudOkMa0abkTpPGd7+ROkEaj/Hxy3325E6QxaVLuBGm0t+dOkM7RR3XljpDEj39Svycr3ugTx7fljpDEf92xa+4ISTQ3505Ao6irAhUAAABAYRStxa+O2UkAAAAAslKgAgAAACArLX4AAAAA1dDil4ydBAAAACArBSoAAAAAstLiBwAAANBTpVLxWvxKpdwJqlawnQQAAACgt1GgAgAAACArLX4AAAAA1Shai18ds5MAAAAAZKVABQAAAEBWNRWoPvShD8U+++wTS5cu3ejH/OAHP4gxY8bEj3/841qWAgAAACiO12/xK9Krt97id8opp8SaNWviBz/4wUY/5tZbb41hw4bFEUccUctSAAAAADSomgpU//zP/xzDhg2LO+64o9vxZ599Nh577LGYNm1a9O3reewAAABAA8l9YuofX3WspvR9+/aNk08+OX73u9/FggULNhi/9dZbo0+fPvHe9763lmUAAAAAaGA1l9dOPvnkaGpqittvv3299zs6OuL222+PKVOmxE477VTrMgAAAAA0qJoLVDvttFNMnjw5fvCDH8TatWvXvf/QQw/FCy+8EKeccsomz1WpVKK9vb3bV0dHR3R2dtYaFwAAAKB2HpKeVJIGxVNPPTVeeuml+PnPf77uvVtvvTXe/va3x6GHHrrJ87S2tsaECRO6fc2bNy+WLFmSIi4AAAAABZLkyeWHHnpoDB8+PO644444/PDD4+WXX46f/exn8YlPfCJKPajetbS0xPTp07sda2tri4j6rQQCAAAA0L0kBao+ffrEySefHFdccUUsX748vv/970dExEknndSjecrlcpTL5W7Hmpqaoqur5qgAAAAAadT5zXlFkmwnp02bFl1dXfHTn/407rzzznjXu94VQ4YMSTU9AAAAAA0qWYFq6NChccQRR8R1110Xv//97+PUU09NNTUAAAAADSzpWbRTTjkl/vSnP8Wee+4Z//RP/5RyagAAAIDicItfUkmeQfW6gw46KBYsWJBySgAAAAAanKd5AQAAAJBV0hNUAAAAAL2GW/ySsZMAAAAAZKVABQAAAEBWWvwAAAAAqqHFLxk7CQAAAEBWClQAAAAAZKXFDwAAAKCnSqXitfiVSrkTVK1gOwkAAABAb6NABQAAAEBWWvwAAAAAqlG0Fr86ZicBAAAAyKquTlB1dESsWJE7RW3+9KfcCdLYccfcCdL553e8nDtCEouWvy13hCSeeSZ3gjR+/vPcCdKYNi13gjQ6O3MnSKdRvv7+9NZXckdIYs3AQbkjJNHcnDtBGu94R+4EaaxenTtBGo10qODZxfX70OE3qlRyJ0jjx/N3zR0hiVGjcidIo3//3AloFHVVoAIAAAAoBLf4JVWwnQQAAACgt1GgAgAAACArLX4AAAAA1Shai18ds5MAAAAAZKVABQAAAEBWWvwAAAAAesotfkkVbCcBAAAA6G0UqAAAAADISosfAAAAQDWK1uJXx+wkAAAAAFklK1Cdfvrpcfjhh6eaDgAAAIBeQosfAAAAQE+5xS+pgu0kAAAAAL2NAhUAAAAAWWnxAwAAAKhG0Vr86lihClSVSiUqlUq3Yx0dHdHZWb+9lAAAAAB0r1AFqtbW1pg5c2a3YzNmzIihQ3eM4cPHbeFUAAAAAGxOhSpQtbS0xPTp07sda2tri44OJ6gAAACAgtDil0yhClTlcjnK5XK3Y01NTdHVtYUDAQAAALDZKfUBAAAAkFXSE1Tt7e1x/fXXdzt22mmnRb9+/VIuBwAAAJBHqVS8Fr9S/T4aKWmB6pVXXon//M//7Hbs5JNPVqACAAAAYAPJClSzZs1KNRUAAAAAvUihHpIOAAAAUDeK1uJXx+wkAAAAAFkpUAEAAACQlRY/AAAAgJ5yi19SBdtJAAAAAHobBSoAAAAAstLiBwAAAFCNorX41TE7CQAAAEBWClQAAAAAZKXFDwAAAKCn3OKXVMF2EgAAAIDexgkqAAAAgGoU7QRVHbOTAAAAAGRVVyeo+sbaeFu8nDtGTUaMeFvuCEn0rau/OW/uN4sb48+kf//cCdI444zcCdI466zcCdKYdfz3ckdIov2dJ+WOkMyTT+ZOkMa22w7KHSGJP/4xd4I0tt02d4I0Ro/OnSCN557LnSCNtWtzJ0inUT7X9903d4I03r5LV+4ISdz1w/p9VhBsDg1UZgAAAADYQjwkPamC7SQAAAAAvY0CFQAAAABZafEDAAAAqEbRWvzqmJ0EAAAAICsFKgAAAACy0uIHAAAAUA0tfsnYSQAAAACyUqACAAAAICstfgAAAAA9VSoVr8WvVMqdoGoF20kAAAAAepskJ6guuuiiuP322zc6vvfee8dtt92WYikAAAAAGkzSFr+bb7652/cHDhyYchkAAACA/IrW4lfHkhao9t1335TTAQAAANALKPUBAAAAkFXSE1Rr167d4L1SqRRNTU0plwEAAADIyy1+SSUtUO29994bvDd8+PC47777NunXVyqVqFQq3Y51dHREqbOzpnwAAAAAFE/SAtWtt966wXvlcnmTf31ra2vMnDmz27EZM2bEjkOHxrjhw6vOBwAAAEDxJC1QjR8/vqZf39LSEtOnT+92rK2tLUodHTXNDwAAAJBM0Vr86ljSAlWtyuXyRk9cNTU1RXR1beFEAAAAAGxuSn0AAAAAZFWoE1QAAAAAdcEtfkkVbCcBAAAA6G2SFKguvfTSWLBgQYqpAAAAAOhltPgBAAAAVKNoLX51zE4CAAAAkJUCFQAAAABZafEDAAAA6Cm3+CVVsJ0EAAAAoLdRoAIAAAAgKy1+AAAAANUoWotfHbOTAAAAAGSlQAUAAABAVlr8AAAAAKqhxS8ZOwkAAABAVgpUAAAAAGRVVy1+L7/SN275/dtyx6jJkCG5E6TR2Zk7QTrt7bkTpPG3v+VOkMZzz+VOkMbDD+dOkMZNfzopd4Qkhs3PnSCdRvn6u3Rp7gRprF6dO0Eaw4blTpDG4sW5E6Sxdm3uBGk0UtdLo/yZLFyYO0Ea8+eXckdIork5d4I0mppyJ8ioVCreF7tS/X5+FGwnAQAAAOhtFKgAAAAAyKquWvwAAAAACqNoLX51zE4CAAAAkJUCFQAAAABZafEDAAAA6Cm3+CVVsJ0EAAAAoLdRoAIAAAAgKy1+AAAAANUoWotfHbOTAAAAAGSlQAUAAABAVlr8AAAAAHrKLX5JJStQPf3003HjjTfGgw8+GM8//3xsvfXWsfvuu8cpp5wSRx11VJTqeJMAAAAA2HySlPrmzJkTxx9/fDz22GPxgQ98IK666qr493//99hxxx3jU5/6VPzbv/1bdHZ2plgKAAAAgC1s9uzZMWbMmHjsscc2y/w1n6D63e9+FxdffHFMmjQprrjiiiiXy+vGpk6dGsOHD48rr7wyJk2aFMcdd1ytywEAAAAUQ9Fa/DaTRYsWxaWXXrpZ16i5QHX11VdHR0dHzJgxY73i1Os+8pGPxPLly2PQoEG1LgUAAADAFlSpVOKCCy6IwYMHx6pVqzbbOjWX+u6///7Ya6+9Yuedd+52vH///vGFL3whpkyZUutSAAAAAMXw+kPSi/TaDM///vrXvx6vvvpqnHvuucnnfqOaTlAtXbo0Vq1aFSNGjEgSplKpRKVS6Xaso6Mjuro8aB0AAABgS3j44Ydj1qxZMWvWrHjhhRc261o1Faiampoi4u/FoxRaW1tj5syZ3Y7NmDEjtt12x4gYl2QtAAAAgEbT2dkZ7e3tGx0vl8vdPqLpHy1dujQ+/elPx4c//OHYb7/94u67704ZcwM1FagGDRoU22yzTSxevPhNP+7555+PYcOGRZ+3eHhYS0tLTJ8+vduxtra2WLasFCtXVh0XAAAAIJ0CPiR9yZIlccIJJ2x0/Jxzztmkdr3Pfe5zsdNOO8XHPvaxlPE2quaHpB922GFx1113xXPPPdftc6jWrFkTxx13XOy2224xe/bsN53rzap4TU1Nm6OVEgAAAKBhDBs2LJ544omNjm/K6anZs2fH//7v/8Ztt90WERFr166Nzs7OiPj7Ca2Ojo51XXWp1FygOuuss+Luu++OGTNmxLe+9a0NfqMzZ86M5cuXx0knnVTrUgAAAAC8iT59+kRzc3NNc9x1112xevXqOOqoozYYO+OMM2L48OFx33331bTGP6q5QLXXXnvFZz/72bjkkkvi5JNPjlNPPTVGjhwZS5cujTlz5sS9994b06ZNi2nTpqXICwAAAFAMBWzxS2HGjBmx8h+esfToo4/GV7/61ZgxY0bst99+ydesuUAVEfEv//Ivsddee8WNN94YV199dbz00kuxzTbbxO677x7f/OY348gjj4yS/jwAAACAwhs1atQG7/3lL3+JiIjddtstxowZk3zNJAWqiIj99ttvs1TQAAAAAGhsyQpUAAAAAL1GqVS8Fr/N2L327ne/OxYsWLDZ5i/YTgIAAADQ2yhQAQAAAJCVFj8AAACAahStxa+O2UkAAAAAslKgAgAAACArLX4AAAAAPdXLbvHb3Aq2kwAAAAD0NgpUAAAAAGSlxQ8AAACgGkVr8atjdhIAAACArBSoAAAAAMiqrlr8mpoimptzp6hNZ2fuBGmsXZs7QTrLl+dOkMb22+dOkEZ7e+4EaZTLuROksfPOuROkUankTpDO88/nTpDGLrvkTpBG//65E6TRKJ8jjfK1t1G6RRrl596Ixvm71Sh/JgMH5k6QxpIluROk0a9f7gQZucUvqYLtJAAAAAC9jQIVAAAAAFnVVYsfAAAAQGEUrcWvjtlJAAAAALJSoAIAAAAgKy1+AAAAAD3lFr+kCraTAAAAAPQ2ClQAAAAAZKXFDwAAAKAaRWvxq2N2EgAAAICsFKgAAAAAyEqLHwAAAEA1tPglU9VOnn766TFmzJg49NBDo7Ozs9uP+e1vfxtjxoyJMWPGxLx582oKCQAAAEDjqrrU16dPn1iyZEk89thj3Y5///vfrzoUAAAAAL1H1QWqkSNHxtChQ+Ouu+7aYKyjoyN++MMfxt57711TOAAAAIBCKpX+3uJXpFeplHtXqlZ1gaqpqSmOOuqo+MlPfhKVSmW9sYcffjiWL18eRx99dM0BAQAAAGhsNT3N65hjjolXXnklHnzwwfXev/POO+OQQw6JwYMH1xQOAAAAgMZXU4Fq/PjxMXLkyJgzZ86691atWhX33HNPHHfccT2er1KpRHt7e7evjo6O6Orq/oHsAAAAAFtc7pa+f3zVsZrTH3PMMfGzn/0sVq5cGRERP/3pT6Nv375xxBFH9Hiu1tbWmDBhQrevefPmxfLlS2qNCwAAAEDB9K11gmOPPTa+9a1vxb333hvHHnts3HnnnfHud787yuVyj+dqaWmJ6dOndzvW1tYWK1aUYvnyWhMDAAAAUCQ1F6hGjBgR++67b8yZMycOPvjgeOSRR+Lb3/52VXOVy+WNFraamprq+WH0AAAAQCN5/Ra/IqnjwkmSnTzmmGPi4Ycfjptuuil22GGHmDBhQoppAQAAAOgFkhSojjrqqOjq6oqrr746jj322CjVccUOAAAAgC0rSYFqyJAhcdBBB8WaNWuqur0PAAAAoO7kvrWvgW7xq+oZVLNmzdrgvWuuuWaD90488cQ48cQTq1kCAAAAgF6ivstrAAAAANS9mm/xAwAAAOh13OKXVMF2EgAAAIDeRoEKAAAAgKy0+AEAAABUo2gtfnXMTgIAAACQlQIVAAAAAFlp8QMAAADoKbf4JVWwnQQAAACgt1GgAgAAACArLX4AAAAA1Shai18ds5MAAAAAZFVXJ6j69YvYeefcKWrT3p47QRqNVCRubs6dII3nn8+dII0dd8ydIA1/HsXy0ku5E6RT798HXzdiRO4EaSxfnjtBGo3yub5iRe4EaaxdmztBGo3082KjfO195pncCdJ49NHcCdI4/PDcCdJolK9ZVWukL3aZ2UkAAAAAslKgAgAAACCrumrxAwAAACiEUql4LX6lUu4EVSvYTgIAAADQ2yhQAQAAAJCVFj8AAACAahStxa+O2UkAAAAAslKgAgAAACArLX4AAAAAPeUWv6QKtpMAAAAA9DYKVAAAAABklbxAddNNN8WYMWNi2rRpqacGAAAAKI4+fYr1qmPJ08+ePTvGjh0b8+bNi9/85jeppwcAAACgwSQtUP3qV7+KhQsXxoUXXhhDhw6NG264IeX0AAAAADSgpAWq7373u7HddtvFxIkT47jjjosf//jH8eKLL6ZcAgAAACC/12/xK9LLLX4RK1asiB/+8Idx7LHHRr9+/eK9731vrF27Nm6++eZUSwAAAADQgJIVqL7//e/H6tWr433ve19EROy6664xadKkmD17dqxZs2aT5qhUKtHe3t7tq6OjI7q6OlPFBQAAAKAgkhWovvvd78Y+++wTw4YNixUrVsSKFSviPe95T7z44otx9913b9Icra2tMWHChG5f8+bNi6VLl6SKCwAAAFCb3C19DXSLX98Uk8ydOzcWLlwYEREHHHDABuM33nhjHHPMMW85T0tLS0yfPr3bsba2tli1qn57KQEAAADoXpIC1c033xz9+/ePK6+8MpqamtYbu+222+KOO+6IefPmxfjx4990nnK5HOVyuduxpqamen7WFwAAAAAbUXOBasWKFXH33XfH1KlT46CDDtpgfMiQIXHHHXfErFmz4itf+UqtywEAAADk9/otfkVSxyd7at7JO+64I1avXh3HHXdct+N77LFH7LvvvvGjH/0oXn755VqXAwAAAKDB1Fyg+u53vxtDhw6Ngw8+eKMfc/LJJ0elUonZs2fXuhwAAAAADabmFr85c+a85cdMmzYtpk2bVutSAAAAAMVRtBa/OmYnAQAAAMhKgQoAAACArGpu8QMAAADolbT4JWMnAQAAAMhKgQoAAACArLT4AQAAAPRUqVS8Fr9SKXeCqhVsJwEAAADobRSoAAAAAMhKix8AAABANYrW4lfH7CQAAAAAWSlQAQAAAJCVFj8AAACAnnKLX1IF20kAAAAAepu6OkG1bFnEI4/kTlGbKVNyJ0jjb3/LnSCdhQtzJ0hjl11yJ0hj6dLcCdI46fBluSMk8cj8wbkjJLHnnrkTpLN6de4EaVQquROksc8+uROksXhx7gRpbL997gRpPP987gRplMu5E6Tzxz/mTpDGttvmTpDGuHG5E6SxfHnuBGkMGJA7AY2irgpUAAAAAIVRtBa/OmYnAQAAAMhKgQoAAACArLT4AQAAAPSUW/ySKthOAgAAANDbKFABAAAAkJUWPwAAAIBqFK3Fr47ZSQAAAACyUqACAAAAICstfgAAAAA95Ra/pAq2kwAAAAD0NjWfoLrooovi9ttvX++9Pn36xMCBA2OPPfaID3zgA3HUUUfVugwAAAAADSpZi9/NN9+87p87Oztj2bJlce2118Z5550XlUoljj/++FRLAQAAAORXtBa/OpasQLXvvvtu8N7EiRPjsMMOi//+7/9WoAIAAACgW5u11Nfc3ByjRo2Kp59+enMuAwAAAEAd26y3+FUqlXj22Wdj55133pzLAAAAAGx5WvySSVagWrt27bp/fr0wdcUVV8SyZcviox/96CbNUalUolKpdDvW0dERXV31e10iAAAAAN1LVqDae++9N3hvyJAhcf7558fpp5++SXO0trbGzJkzux2bMWNGDBy4Y0SMqyUmAAAAAAWTrEB16623/r9J+/aNQYMG9bi1r6WlJaZPn97tWFtbWzz3nBNUAAAAQAGUSsVr8SvVb90kWYFq/PjxNc9RLpejXC53O9bU1FTP+wwAAADARmzWh6QDAAAANKyinaCqY3YSAAAAgKwUqAAAAADIquYC1aWXXhoLFixIkQUAAACgPrz+kPQiver44d1OUAEAAACQlQIVAAAAAFm5xQ8AAACgGm7xS8ZOAgAAAJCVAhUAAAAAWWnxAwAAAOip12/xKxK3+AEAAABAdRSoAAAAAMhKix8AAABANYrW4lfH7CQAAAAAWSlQAQAAAJCVFj8AAACAniqV6vrWvKKpqwLVoEERhx+eO0Vt9tknd4I07rgjd4J0rr46d4I0/v3fcydIo3//3AnSmPHNwbkjJNG3rr5LbNyUKbkTpPPUU7kTpDF1au4EaVx1Ve4EaZx1Vu4EaTTK58fatbkTpLF6de4E6TTKzyeN8rV3+fLcCdL43e9yJ4Bi0eIHAAAAQFYN8v/GAQAAALawot3i19mZO0HVCraTAAAAAPQ2ClQAAAAAZKXFDwAAAKAaWvySKdhOAgAAANDbKFABAAAAkJUWPwAAAICeKpWK1+JXKuVOULWC7SQAAAAAvY0CFQAAAABZafEDAAAAqEbRWvzqmJ0EAAAAIKskJ6heeOGFmD17dtx3333x3HPPxWuvvRY77LBDHHjggTF9+vTYbbfdUiwDAAAAQAOquUD10EMPxfnnnx9bbbVVnHrqqTF+/Pjo169fLFy4MG688ca4884748orr4wDDzwwRV4AAACA/Nzil1RNBaq//OUv8clPfjJ23nnnuPHGG2PbbbddNzZx4sQ46aST4tRTT42LL7447r333mhqaqo5MAAAAACb349+9KO4/vrrY9GiRVEul2PcuHHxiU98IsaPH598rZpKfddcc028+uqr8aUvfWm94tTrBg4cGOeff35MmDAhli1bVstSAAAAAGwht9xyS3zyk5+M3XbbLb72ta/FF77whXj11Vfj1FNPjblz5yZfr6YTVHfffXfssccesc8++2z0YyZPnhyTJ0+uZRkAAACA4ilai19CM2fOjEMOOSQuvfTSde8ddNBBccQRR8Q111wTV155ZdL1qi5QrVixIpYtWxbvfOc7Nxjr6OiIrq6u9d5ramqK0lv0QlYqlahUKt2O/X3O+u2lBACBRedGAAAgAElEQVQAAKgHq1atiiOPPDImTpy43vvNzc2x0047xQsvvJB8zaoLVJ2dnRsdO/HEE2P+/PnrvffpT386PvShD73pnK2trTFz5sxux2bMmBGDB+8Yzc3jeh4WAAAAgE0yYMCA+OxnP7vB+4sWLYo//OEPcdxxxyVfs+oC1XbbbRfNzc3x7LPPbjB2+eWXx6pVqyIi4sUXX4x//dd/3aQ5W1paYvr06d2OtbW1xcqVpVizptrEAAAAAIkU9Ba/zs7OaG9v3+iHlMvlKJfLPZ761VdfjQsvvDD69u0bZ511Vi0pu1XTM6iOPPLIuO2222LRokWx++67r3t/9OjR6/558eLFmzzfm23S31sEq88KAAAA0OiWLFkSJ5xwwkbHzznnnDj33HN7NOcLL7wQH/nIR+IPf/hDfP3rX49Ro0bVGnMDNRWoWlpa4ic/+UlceOGFce2118bgwYM3+JgFCxbUsgQAAAAAm2jYsGHxxBNPbHS8p6enfvOb38Q555wTK1eujCuuuCIOO+ywWiN2q6YC1ciRI2PmzJlx/vnnx9FHHx0nn3xy7LfffjFgwIB45pln4u67746HHnoodt111zjggANSZQYAAADIr2gtfhHRp0+faG5uTjLXXXfdFRdddFFsv/328Z3vfCfGjh2bZN7u1FSgiog48MADY86cOXHLLbfEPffcE7Nnz46VK1fGkCFDYvz48XH55ZfHkUceWVV/IwAAAABb3k9+8pO44IILYty4cdHa2hrbb7/9Zl2v5gJVRMSQIUOipaUlWlpaUkwHAAAAQCYrVqyIz372szFw4MD4+Mc/HosXL17vGeP9+/dPfpoqSYEKAAAAoNcpYItfCg8++GCsWLEiIiLOPvvsDcb32GOPmDNnTtI1FagAAAAAWOfoo4+Oo48+eouu2ZilPgAAAADqhhNUAAAAAD1VKhWvxa9Uyp2gagXbSQAAAAB6GwUqAAAAALLS4gcAAABQjaK1+NUxOwkAAABAVgpUAAAAAGSlxQ8AAACgp9zil1TBdhIAAACA3kaBCgAAAICs6qrFr7MzYvXq3Clq8+STuROkMWlS7gTp/Obnr+SOkMRNcwbljpDEce/8a+4ISSxevFPuCEkU7cQyEfvvnztBGs89lztBGh/5SO4EadT7z1eve8c7cidI45lncidIo7Mzd4J0hgzJnSCNfn9rjJ97/+VfGuPn3ltvzZ0gjWefzZ0gMz8wJ2MnAQAAAMiqrk5QAQAAABSCh6QnVbCdBAAAAKC3UaACAAAAICstfgAAAADVKFqLXx2zkwAAAABkpUAFAAAAQFZa/AAAAAB6yi1+SRVsJwEAAADobRSoAAAAAMhKix8AAABANYrW4lfH7CQAAAAAWdV8guqiiy6K22+//S0/7oYbboiJEyfWuhwAAAAADabmAtVHP/rROOWUU9b9+y233BK33nprzJw5M4YOHbru/dGjR9e6FAAAAEBxaPFLpuYC1YgRI2LEiBHr/v3BBx+MiIi99tordtlll1qnBwAAAKDBKfUBAAAAkJVb/AAAAAB6qlQqXotfqZQ7QdUKVaCqVCpRqVS6Hevo6IiurvrdaAAAAAC6V6gCVWtra8ycObPbsRkzZsR22+0Y/fqN28KpAAAAANicClWgamlpienTp3c71tbWFq++WoqVK7dwKAAAAIDuFK3Fr44VqkBVLpejXC53O9bU1FTPrZQAAAAAbIRSHwAAAABZFeoEFQAAAEBdcItfUgXbSQAAAAB6m+QFqnPPPTcWLFgQu+yyS+qpAQAAAGhAWvwAAAAAqlG0Fr86ZicBAAAAyEqBCgAAAICstPgBAAAA9JRb/JIq2E4CAAAA0NsoUAEAAACQlRY/AAAAgGoUrcWvjtlJAAAAALJSoAIAAAAgKy1+AAAAAD3lFr+kCraTAAAAAPQ2ClQAAAAAZFVXLX5r10YsXZo7RW2mTs2dII1f/CJ3gnTuuWdQ7ghJ7LJL7gRp/M/dO+WOkMT22+dOkMbq1bkTpNG/f+4E6Tz3XO4Eaey4Y+4EadxzT+4Eaey7b+4EaaxYkTtBGj7Pi6dR/m69vLYxfu79whdyJ0hj7tzcCdIYODBiUGP81apKV9RvS13ROEEFAAAAQFYKVAAAAABkVVctfgAAAABF0NUV0dmZO8X6urrq9yI/J6gAAAAAyEqBCgAAAICstPgBAAAAVKFoLX71zAkqAAAAALJSoAIAAAAgKy1+AAAAAD3kFr+0nKACAAAAICsFKgAAAACyStbi19bWFq2trfHII4/Eiy++GAMGDIg99tgjjj/++DjppJOiqakp1VIAAAAA2RWtxa+eJSlQLVq0KN73vvfFyJEj4xOf+ETstNNO0d7eHg888EB8/vOfj1/+8pfxla98JcVSAAAAADSYJAWq6667LiIiZs2aFQMGDFj3/hFHHBFbbbVV3HDDDXHmmWfG2LFjUywHAAAAQANJUqB66aWXolQqRUdHxwZj73//+2Po0KExcODAFEsBAAAAZFfUW/zqVZKHpB9xxBGxYsWKmDZtWlx99dXx5JNPxpo1ayIiYtddd42zzz47RowYkWIpAAAAABpMkhNU733ve2P58uVx5ZVXxuWXXx4REVtttVXst99+cdRRR8WJJ54Y/fr1e8t5KpVKVCqVbsc6Ojqiq6uUIi4AAAAABZLsFr+zzz473v/+98fDDz8cjz/+eDzxxBPx+OOPx6OPPhqzZ8+O66+/PgYNGvSmc7S2tsbMmTO7HZsxY0Zsu+2OETEuVWQAAACAqhWtxa+eJStQRUQMHDgwpk6dGlOnTo2IiGXLlsUVV1wRs2bNimuuuSYuuOCCN/31LS0tMX369G7H2traYtmyUqxcmTIxAAAAALnV/AyqF154IQ499NC4+uqrNxgbPHhwfO5zn4sddtghFi5c+JZzlcvlaG5u7vbV1NQUpVKSR2YBAAAAUCA1V3yGDh0a5XI5Zs+eHcuXL99g/KWXXooVK1bE2LFja10KAAAAoBBev8WvSK96vsWv5ha/Pn36xCWXXBItLS1x/PHHx2mnnRZ77713NDU1xYIFC+Lb3/527LDDDhtt3QMAAACgd0vyDKoDDzwwbr/99rjuuuvilltuiSuuuCI6Oztj+PDhcfTRR8eHP/zh2GabbVIsBQAAAFAIHpKeTrKHpO++++7xH//xH6mmAwAAAKCX8NRxAAAAALJKdoIKAAAAoDfR4peOE1QAAAAAZKVABQAAAEBWWvwAAAAAeqirq3gtfl1duRNUzwkqAAAAALJSoAIAAAAgKy1+AAAAAFUoWotfPXOCCgAAAICsFKgAAAAAyEqLHwAAAEAPucUvLSeoAAAAAMhKgQoAAACArOqqxa9Pn4iBA3OnqM2vf507QRp96+pvTu9QLudOkMaee+ZOkMZ99+VOkMbq1bkTpLHzzrkTpNMov5dG+bu1zz65E6TRv3/uBGk880zuBGnsuGPuBGn0aaD/FT56dO4EaTz/fO4EaTTK95BG+X00yveQahWtxa+eNdC3DQAAAADqkQIVAAAAAFlp1AIAAADoIbf4peUEFQAAAABZKVABAAAAkJUWPwAAAIAqFK3Fr545QQUAAABAVgpUAAAAAGSlxQ8AAACgh9zil5YTVAAAAABkpUAFAAAAQFabXKA6//zzY9y4cdHe3r7B2Lve9a4YM2ZMXH/99RuMtba2xpgxY2L+/Pk1BQUAAAAoks7OYr3q2SYXqA499NDo6OiIuXPnrvd+W1tbPP300zF48OD42c9+tsGve+yxx2KHHXaIsWPH1p4WAAAAgIazyQWqgw8+OEqlUvzyl79c7/37778/BgwYEGeccUY88cQT652wqlQqMXfu3Dj00EPTJQYAAACgoWxygWro0KGx5557xuOPP77e+w888EC8853vjKlTp8aaNWvioYceWjf25JNPxqpVq2Ly5MnpEgMAAAAUQO6Wvl7Z4hcRccghh8S8efPitddei4iIlStXxi9+8Ys47LDDYvTo0TF8+PC4//771338o48+Gn379o2DDz44aWgAAAAAGkePClSHHnporFmzJn79619HRMQjjzwSa9asicMOO2zd+M9//vPo/L+y3WOPPRb7779/NDc3b9L8lUol2tvbu311dHREV1edlwMBAAAA2ECPClQTJkyIAQMGrGvzu//++2P06NGxyy67RETEYYcdFi+//HL89re/jddeey1+/etf9+j5U62trTFhwoRuX/PmzYtXXlnSk7gAAAAAm0VXV/6Wvn98dXXl3pXq9e3JB5fL5TjggAPWPSj9gQceiPe85z3rxidNmhTlcjkeeeSRaG9vj0qlsu501aZoaWmJ6dOndzvW1tYWr7xSimXLepIYAAAAgKLrUYEq4u/Pofqv//qv+O1vfxtLliyJKVOmrBsbOHBgHHDAAfH444/H6tWrY4cddogxY8Zs8tzlcjnK5XK3Y01NTVEq9TQtAAAAAEXXoxa/iL8XqFauXBk33XRTNDc3x4QJE9Ybnzx5cvz+97+Pxx9/3O19AAAAQMPK3dLXa2/xi4jYfffdY6eddoo777wzDj744Ojbd/1DWJMnT44XX3wxfvWrX/WovQ8AAACA3qnHBaqIv5+ieuPtfW80atSoGDFiREREHHjggbWlAwAAAKDh9fgZVBERl1xySVxyySUbHf/pT39adSAAAACAonv9Fr8iqedb/Ko6QQUAAAAAqShQAQAAAJBVVS1+AAAAAL1d0Vr86pkTVAAAAABkpUAFAAAAQFZa/AAAAAB6yC1+aTlBBQAAAEBWClQAAAAAZKXFDwAAAKAKRWvxq2dOUAEAAACQlQIVAAAAAFlp8QMAAACogha/dOqqQNXUFNHcnDtFbdauzZ0gjeefz50gnbPPzp0gjaefzp0gjT1G1/G9qG9QqZRyR0hi9OjcCdK46qrcCdJ5xztyJ0jjb3/LnSCN557LnSCNww/PnSCNnXfOnSCNSiV3gjQa5fMjIuL/W/G93BGSWHb4SbkjJNGnQfqAhgzJnSCNJUtyJ6BRNMinNgAAAAD1qq5OUAEAAAAUQVfX319FUqrjRg4nqAAAAADISoEKAAAAgKy0+AEAAABUoWi3+DU15U5QPSeoAAAAAMjKCSoAAACAHurqKt4Jqj51fAypjqMDAAAA0AgUqAAAAADISosfAAAAQBWK1uJXz5ygAgAAACArBSoAAAAAsqqpQPW5z30uxowZEzfffHO3452dnXHqqafGO97xjli4cGEtSwEAAAAUxuu3+BXp1dWVe1eqV1OB6uKLL44RI0bEpZdeGosXL95g/Nprr425c+fGZz7zmdhzzz1rWQoAAACABlVTgWrrrbeOr3zlK/Haa6/FxRdfHF1vKNX94Q9/iG9+85tx+OGHx2mnnVZzUAAAAAAaU83PoNpvv/3i7LPPjl/84hdxww03RETE2rVr4zOf+Uxst9128aUvfanmkAAAAABFk7ul7x9fqT355JPxwQ9+MPbff/+YOHFifOYzn4mXXnop/UKR6CHpH/vYx2LvvfeOb3zjG/HXv/41rrrqqvj9738fl112WQwePDjFEgAAAABsIfPnz48PfvCD0adPn7j88svjggsuiAcffDDOOOOMqFQqydfrm2KSfv36xWWXXRYnnnhifOpTn4p58+bFhz/84Zg0aVKP5qlUKhv9TXZ0dERXVylFXAAAAADexDe+8Y0YPHhwtLa2RrlcjoiIvfbaK0466aS47bbb4pRTTkm6XpITVBERu+++e1x44YUxd+7c2GuvveLjH/94j+dobW2NCRMmdPuaN29eLF++JFVcAAAAgKo18i1+lUolHn744Zg6deq64lRExD777BMjR46Me++9N81Cb5DkBNXrpkyZEl/84hdj8uTJ0bdvz6duaWmJ6dOndzvW1tYW7e2lWL261pQAAAAAbMyzzz4br732WowaNWqDsd122y0WLlyYfM2kBapalcvl9Spzb9TU1BQlHX4AAAAAG9XZ2Rnt7e0bHX+z2svrXn311YiI2GabbTYY23rrrWPlypW1hexGoQpUAAAAAPVic9ycV6slS5bECSecsNHxc845J84999w3naMzw29MgQoAAACgQQwbNiyeeOKJjY6/1empiIhBgwZFRHR7UmrlypWx7bbbVh9wIxSoAAAAABpEnz59orm5uaY53v72t0e/fv3iz3/+8wZjf/7zn2P33Xevaf7uJC1Q7bLLLrFgwYKUUwIAAAAUUhFb/FIol8tx0EEHxT333BPnnXfeulNXTz31VDz99NPxwQ9+MPmafZLPCAAAAEBdO/fcc+Ovf/1rnHnmmXHvvffG9773vTj77LNj9OjRMW3atOTrKVABAAAAsJ7x48fHtddeG2vXro3zzjsvvvrVr8YhhxwS119//SY9x6qnPIMKAAAAoIe6uorX4tfVlXa+iRMnxuzZs9NOuhFOUAEAAACQlQIVAAAAAFlp8QMAAACoQtFa/OqZE1QAAAAAZKVABQAAAEBWWvwAAAAAeqg33OK3JTlBBQAAAEBWClQAAAAAZKXFDwAAAKAKRWvxq2d1VaCqVCKeey53itocfnjuBGmMHJk7QTr9yqXcEZK4/+o6bjZ+g/vvb4w/j4MOyp0gjT/+MXeCNPr3z50gnUb5vbS3506Qxtq1uROkceDYZbkjJPG9+wbnjpDEjjvmTpDGqFG5E6RTOuik3BGSeP/7cydIY/Lk3AnS2G673AnS2HnniLe9LXcKGoEWPwAAAACyqqsTVAAAAABF4Ba/tJygAgAAACCr/7+9O4+SsjrzB/40DaUgCrYBNERFRMFouxEiREAURjPuoERRMUJUjIlmlKAYVxSU0XEZwRgQXHAZRMYVF0xUTHDBLShqolF/wSVBiYqdNjgNTf/+8MARaaSXt7lVxedzTp3T1K1+7/c9dHVXPXWf9ypQAQAAAJCUFj8AAACABsi3Fr9CZgUVAAAAAEkpUAEAAACQlBY/AAAAgHqyi1+2rKACAAAAICkFKgAAAACS0uIHAAAA0AD51uJXyKygAgAAACCpRhWoRo8eHXvsscdaxydMmBBdu3aN999/vzHTAAAAAFDEtPgBAAAANIAWv+xo8QMAAAAgKQUqAAAAAJLKpMVv+fLltd6/wlo3AAAAoAjV1ORfi19NTeoEDdfoAtW//vWv2HnnnbPIElVVVVFVVVXrWHV1ddTUlGQyDwAAAAD5o9EFqo033jhuu+22WsdmzJgRM2bMqPOxJk2aFBMnTqx1bMyYMbHZZltGxHcbEhMAAACAPNXoAlWzZs2ivLy81rE5c+bU61gjRoyIYcOG1Tq2cOHC+OSTkvjss/omBAAAAMhevrX4FbJMrkGVlVwuF7lcrtax0tLSKNHhBwAAAFB07OIHAAAAQFJ5tYIKAAAAoBDYxS9bVlABAAAAkFSjClTjx4+PP/7xj2sdP+200+KNN96I73znO42ZBgAAAIAipsUPAAAAoAHyrcWvkGnxAwAAACApK6gAAAAA6slF0rNlBRUAAAAASSlQAQAAAJCUFj8AAACABsi3Fr9CZgUVAAAAAEkpUAEAAACQlBY/AAAAgHqyi1+2rKACAAAAICkFKgAAAACS0uIHAAAA0AD51uJXyAqqQNWsWcTGG6dO0ThPP506QTbKylInyM6NvyrgJt2v6NcpdYJsVFWlTpCNYnmun3RicTw/crmS1BEy8+abqRNk4ycH/j11hEzMfmWr1BEycd/vN08dIRPt26dOkI1PPkmdIButW6dOkJ3ly1MnyMbNN6dOkI1ttkmdIBv33586QTYOPDBiiy1Sp6AYaPEDAAAAIKmCWkEFAAAAkC+0+GXHCioAAAAAklKgAgAAACApLX4AAAAA9VRTk38tfjUFvMeRFVQAAAAAJKVABQAAAEBSWvwAAAAAGiDfWvwKmRVUAAAAACSlQAUAAABAUlr8AAAAAOrJLn7ZanSBavTo0XHPPfd842MuuuiiGDJkSGOnAgAAAKAIZbaC6s4771zr2NZbb53VNAAAAAAUmcwKVLvvvntWhwIAAADIe/nW4lfIXCQdAAAAgKQyW0G1fPnyWu8vKSmJ0tLSrKYBAAAAoMhkVqDaeeeda71/0003jRdeeKFOx6iqqoqqqqpax6qrq6OmpqTB+QAAAACyYhe/bGVWoJo5c2btEzSv+xSTJk2KiRMn1jo2ZsyYaNNmy4j4bkPiAQAAAJCnMitQlZeXN/oYI0aMiGHDhtU6tnDhwliypCS++KLR0wAAAACQRzIrUGUhl8tFLperday0tDRKdPgBAAAAeSLfWvwKmV38AAAAAEgqsxVU8+fPX+tYmzZtYrvttstqKgAAAACKSGYFqqOOOmqtY/37949f//rXWU0FAAAAkJRd/LLV6ALV+PHjY/z48VlkAQAAAGAD5BpUAAAAACSVV7v4AQAAABSKfGvxK2RWUAEAAACQlAIVAAAAAElp8QMAAABoAC1+2bGCCgAAAICkFKgAAAAASEqLHwAAAEA91dTkX4tfTU3qBA1nBRUAAAAASSlQAQAAAJCUFj8AAACABsi3Fr9CZgUVAAAAAEkpUAEAAACQVEG1+JWWRrRunTpF4zQrkpLgF1+kTpCdvn1TJ8hGWVnqBNn45JPUCfiqv7xVkjpCJioqUifITrE8129/fKvUETJR6K9Lis2iRakTZKNt29QJslFZmTpBdt56K3WCbPTrlzpBNlq1Sp0gG+++mzpBNjbZJHWCdOzil60iKZcAAAAAUKgUqAAAAABIqqBa/AAAAADyRb61+BUyK6gAAAAASEqBCgAAAICktPgBAAAA1JNd/LJlBRUAAAAASVlBBQAAANAA+baCqpBZQQUAAABAUgpUAAAAACSlxQ8AAACgnlwkPVuNKlCNHj067rnnntXuy+VyscUWW8T3vve9GDFiROywww6NCggAAABAcctkBdWdd9656uulS5fGO++8E1OnTo0jjjgiJk+eHD179sxiGgAAAACKUCYFqt133321f/fq1St++MMfxqBBg2LUqFHx6KOPRsuWLbOYCgAAACAv5FuLXyFrsoukb7HFFnHSSSfFRx99FLNnz26qaQAAAAAocE26i1/fvn0jIuK5555rymkAAAAAKGBNuotfu3btIiJi8eLFdXp8VVVVVFVV1TpWXV0dK1aUZJYNAAAAoDG0+GWnSQtUK5WU1K2wNGnSpJg4cWKtY2PGjIm2bbeM0tLvZhkNAAAAgMSatEC1aNGiiIjYcsst6/T4ESNGxLBhw2odW7hwYVRUlERlZWbxAAAAAMgDTVqgeuqppyIiomfPnnV6fC6Xi1wuV+tYaWlpNGvSK2YBAAAA1E1NTf61+NXUpE7QcE1W8lmyZElMnTo1OnbsGAMGDGiqaQAAAAAocJmsoJo/f/6qr5cuXRpvvfVWTJs2LZYsWRJTpkxZ66ooAAAAAMikQHXUUUet+jqXy0WHDh2iV69eceKJJ8a2226bxRQAAAAAeSXfWvwKWaMKVOPHj4/x48dnlQUAAACADZDLjgMAAACQVJPu4gcAAABQjOzily0rqAAAAABISoEKAAAAgKS0+AEAAAA0QL61+BUyK6gAAAAASEqBCgAAAICktPgBAAAA1JNd/LJlBRUAAAAASSlQAQAAAJCUFj8AAACABsi3Fr9CZgUVAAAAAEkV1AqqRYsipk1LnaJx/uM/UifIxiefpE6QnWI6l2Lw+9+nTpCNcZeWpI6QiWVVBXyVxa949NHUCfi6nx33WeoImditb5vUETJx8smpE2Rj111TJ8jG+++nTpCN9u1TJ8jOF1+kTpCN3b7zceoImXjy1S1SR8jE3/6WOkE2tt02dQKKRUEVqAAAAADygV38sqXFDwAAAICkFKgAAAAASEqLHwAAAEAD5FuLXyGzggoAAACApBSoAAAAAEhKix8AAABAA2jxy44VVAAAAAAkpUAFAAAAQFJa/AAAAADqqaYm/1r8ampSJ2g4K6gAAAAASEqBCgAAAICktPgBAAAANEC+tfgVskwKVG+99Vbcfvvt8dRTT8WHH34YrVq1ii5dusRhhx0WAwcOjNLS0iymAQAAAKAINbpAddddd8XFF18c2223XQwfPjw6d+4cFRUVMWfOnLjwwgvj7rvvjokTJ0ZZWVkWeQEAAAAoMo0qUL3wwgtx4YUXxv777x9XXHFFtGjRYtXYgAED4qCDDoqTTjopRo8eHZMnT250WAAAAIB8YBe/bDXqIukTJkyIVq1axdixY1crTq3Uq1evGDp0aDz55JPxwgsvNGYqAAAAAIpUgwtUn332WcybNy/23nvvaN269Vofd8ghh0RExOzZs9d5zKqqqqisrKz1Vl1dHRF5VpoEAAAA2IC99tprccopp0Tv3r1jzz33jCOPPDIeeuiheh+nwS1+H3zwQdTU1MTWW2/9jY/bdtttIyLi/fffX+cxJ02aFBMnTqx1bMyYMdG8+ZYR8d16ZwUAAADIWr61+K1vb775ZhxzzDHRrVu3OP/886NVq1Yxa9asOOOMM+Jvf/tbnHjiiXU+Via7+H2TZs2+XKT15QqobzZixIgYNmxYrWMLFy6Mt94qyTQbAAAAAA1zww03RMuWLWPq1Kmruuv69OkTixcvjkmTJsXw4cNX1YXWpcEFqo4dO0ZJSUm8++673/i4hQsXRkTEd77znXUeM5fLRS6Xq3WstLS0/iEBAAAAaBLdunWLHXfccY1LP3Xp0iWeeuqpWLp0aWyyySZ1OlaDC1Rt2rSJnj17xty5c6OioiI222yzVWMLFiyIXXbZJUpKSuLhhx+OiIh+/fo1dCoAAACAvGIXv4if/OQna9xXVVUVTzzxRGy99dZ1Lk5FNLLF7/TTT4+hQ4fGOeecE9dcc020aNEiKioqYujQodGhQ4c47rjj4qabbooePXpE3759GzMVAAAAAOuwYsWKqKysXOv4N3WvrVRTUxPTp0//xsfst99+0aFDhzW+7+KLL45332N+VDEAACAASURBVH03/vM//7PuoaORBao999wzxo4dGxdeeGEMGjQojj322Nh+++3j4osvjnHjxsXYsWOjefPmcd555zVmGgAAAADq4KOPPoqBAweudfznP/95nHbaad94jOrq6rjooou+8TGdO3derUBVVVUV5513Xtx3330xfPjwOPzww+uVu9EXSR84cGDsuuuuceutt8bUqVPjww8/jFatWsUOO+wQ/fv3j0cffTSGDBkSxx9/fJxxxhmNnQ4AAAAgL+Rbi19ERPv27ePFF19c6/i6Vk9FRDRv3jzeeOONOs+5ePHiOO2002L+/Plx+umnx89+9rM6f++qOev9HbXYfvvt11pZO+GEE+Kxxx6LDz74IIupAAAAAFiLZs2arXHR8qb0xhtvxMknnxyffvpp/Nd//VccfPDBDTpOJgWqb1JSUhIDBgxo6mkAAAAAWI/efffdOP7446OkpCRuvfXW2G233Rp8rCYvUAEAAAAUG7v4RZx77rmxZMmSOO+886Kmpibmz5+/2vguu+wSzZvXrfSkQAUAAABAvSxevDiee+65iIgYO3ZsrY955plnoqysrE7HU6ACAAAAaIB8W0G1PrVr165eF1Jfl2aZHQkAAAAAGkCBCgAAAICktPgBAAAANMCG3OKXNSuoAAAAAEhKgQoAAACApLT4AQAAANRTTU3+tfjV1KRO0HBWUAEAAACQVEGtoGrXLuL441OnaJzly1MnyMa3vpU6AcVq//1TJ8jG28ML+KOLr3h2RuoE2ejWLXWC7BTL35E3FrVJHSETZ56ZOkE2vv3t1Amy0bygXtmuXdu2qRNkI99WFTTGF1+kTpCNJ17ZInWETLRqlTpBNnr3Tp0gG8Xy/0F6RfJnHAAAAGD9KqZifGpa/AAAAABISoEKAAAAgKS0+AEAAADUk138smUFFQAAAABJKVABAAAAkJQWPwAAAIAGyLcWv0JmBRUAAAAASSlQAQAAAJCUFj8AAACAerKLX7asoAIAAAAgKQUqAAAAAJJqVIFq9OjR0bVr17jjjjtqHX/kkUeia9euMW/evMZMAwAAAJB3VqzIr1shy2QF1eWXXx7vvPNOFocCAAAAYAPT6AJV8+bNo6SkJEaNGhXLly/PIhMAAAAAG5BGF6hyuVz86le/ildffTUmTJiQRSYAAACAvLZyF798um3wu/gNHjw4+vfvHzfccEO89NJLWRwSAAAAgA1EZrv4jR07NjbffPM466yzorKyskHHqKqqisrKylpv1dXVUVNT4Ff8AgAAAGANmRWoysrKYty4cfHee+/FuHHjGnSMSZMmRffu3Wu9LViwICoqPsoqLgAAAECjpG7pK6Zd/JpnebB+/frF0UcfHdOnT49999233t8/YsSIGDZsWK1jCxcujCVLSuIf/2hsSgAAAADySWYrqFYaPXp0dOrUKc4///xYvHhxvb43l8tF69ata72VlpZGSUnmcQEAAABILPOKT8uWLeOKK66IysrKuPbaa7M+PAAAAEBeSN3SV0wtfk2yJGnXXXeNU089NSoqKpri8AAAAAAUkSbrmTvllFNijz32aKrDAwAAAFAkGnWR9PHjx8f48eNrHSstLY3p06c35vAAAAAAeammJv/a6mpqUidoOFcdBwAAACApBSoAAAAAkmpUix8AAADAhirfWvwKmRVUAAAAACSlQAUAAABAUlr8AAAAAOrJLn7ZsoIKAAAAgKQUqAAAAABISosfAAAAQAPkW4tfIbOCCgAAAICkFKgAAAAASEqLHwAAAEA92cUvWwVVoGrWLGLjjVOnaJx8++FtqGZFtPZuyy1TJ8hGVVXqBNn45JPUCbLRrVvqBNkoludHMf3O+v73UyfIxquvpk6QjcMPT50gG6+8kjpBNorldVbzgnqFvnbF9Lt3+fLUCbKxaFHqBNno3Dl1gmwUy88VZKWI/mwAAAAAUIiK5PMZAAAAgPWrWFbv5gMrqAAAAABISoEKAAAAgKS0+AEAAADUk138smUFFQAAAABJKVABAAAAkJQWPwAAAIAGyLcWv0JmBRUAAAAASSlQAQAAAJCUFj8AAACABtDil51Gr6AaOnRo7LfffrWO3XLLLdGtW7cYOnRoVFZWNnYqAAAAAIpQk62gmjRpUlx11VXRv3//uPrqq2OjjTZqqqkAAAAA1quamvxbQVVTkzpBwzXJNaiuvvrquOqqq2LgwIExYcIExSkAAAAA1irzFVSXXnpp3HLLLXHCCSfE6NGjo6SkJOspAAAAACgimRWoVqxYERdddFHceeedcdppp8XPf/7zrA4NAAAAkHfyrcWvkGVSoKquro6zzz47HnjggYiI+Pjjjxt0nKqqqqiqqlrrHDU1VmMBAAAAFJtMClSLFi2Khx9+OK655pqYPXt23HHHHdG9e/c4+OCD63WcSZMmxcSJE2sdGzNmTLRtu2WUlHw3i8gAAAAA5IlMClQtWrSI66+/Pvr06RO9e/eOBQsWxPnnnx/dunWLLl261Pk4I0aMiGHDhtU6tnDhwqioKImKiiwSAwAAADScXfyylckufu3bt48+ffpERETr1q3j6quvjmXLlsXpp58en3/+eZ2Pk8vlonXr1rXeSktLo6SkSTYdBAAAACChJqn4lJeXx5lnnhlvv/12nH/++U0xBQAAAABFIrNd/L5u2LBh8eyzz8aDDz4Ye+65Zxx33HFNNRUAAADAepdvLX6FrMl65kpKSmL8+PHRvn37GD9+fLz88stNNRUAAAAABazRK6huvfXWtY6VlZXFH/7wh8ZOAQAAAEARa7IWPwAAAIBiZRe/bNkWDwAAAICkFKgAAAAASEqLHwAAAEAD5FuLXyGzggoAAACApBSoAAAAAEhKix8AAABAPdnFL1tWUAEAAACQlAIVAAAAAElp8QMAAABogHxr8StkVlABAAAAkJQCFQAAAABJafEDAAAAaAAtftkpqAJVdXVEZWXqFI3TunXqBNn44ovUCbIzbVrqBNk45ZTUCfiqxx9PnSAb3/526gTZKPS/HV/1u9+lTpCNsrLUCbLx6qupE2RjzpzUCbJx6KGpE2SjoiJ1gmwU0+/ewft9nDpCJrp12yJ1hExstlnqBNl46KHUCbKxySapE1AstPgBAAAAkFRBraACAAAAyAc1NfnX4ldTkzpBw1lBBQAAAEBSClQAAAAAJKXFDwAAAKAB8q3Fr5BZQQUAAABAUgpUAAAAACSlxQ8AAACgnuzily0rqAAAAABISoEKAAAAgKS0+AEAAAA0QL61+BWyRhWoRo8eHffcc88a9+dyuSgrK4vvfe97ceaZZ0bHjh0bMw0AAAAARSyTFVR33nnnav+uqKiIF198MaZOnRoLFiyIWbNmRS6Xy2IqAAAAAIpMJgWq3XfffY37+vbtG8uXL48pU6bEM888E/vss08WUwEAAAAkZxe/bDXpRdLbtGkTERElJSVNOQ0AAAAABSyTFVTLly9f9XVNTU3885//jGeffTamTJkSnTp1ih49emQxDQAAAABFKJMC1c4777zGfW3bto1+/frFyJEjo2XLlnU6TlVVVVRVVdU6Vl1dHRFWYgEAAAD5Id9a/ApZJgWqmTNnRsSXBab77rsvZs6cGcOHD48RI0bU6ziTJk2KiRMn1jo2ZsyY2GyzLSPiu42NCwAAAEAeyaRAVV5evurr7t27Ry6Xi6uuuiqqq6vj1FNPrfNxRowYEcOGDat1bOHChbFkSUksXdrouAAAAADkkUwKVF931llnxdNPPx0TJ06MXr16xR577FGn78vlcpHL5WodKy0tzTIiAAAAQIPZxS9bTbKLXy6Xi0suuSRWrFgRF1xwQSxbtqwppgEAAACgCDRJgSriy1a/gQMHxptvvhk33XRTU00DAAAAQIFrsgJVRMSoUaOibdu2cd1118V7773XlFMBAAAArFcrVuTXrZA1qkA1fvz4eOONN9Y6XlZWFvPmzYuXX345tt5668ZMBQAAAECRatIVVAAAAACwLk2yix8AAABAsSv0trp8YgUVAAAAAEkpUAEAAACQlBY/AAAAgHqqqcm/Fr+amtQJGs4KKgAAAACSsoIKAAAAoAHybQVVIbOCCgAAAICkFKgAAAAASEqLHwAAAEA9uUh6tqygAgAAACCpkpqawqivvfzyy1FVtSKqqlqmjtIopaWpE2Qj36rEjbF4ceoE2dhyy9QJslFdnTpBNorlOZLLpU6QjWL5uYoonp+t5kWyhrtZkXzU99lnqRNkY/PNUyfIxrJlqRNko5h+927RZnnqCJlYXiQNNMXynurTT1MnyEaLFksjl2sWu+22W+oo69Wf//znWLx4abz1Vn7VKLp0WRrt2rWMbt26pY5SbwXzG6q0tDRyuYhNN226OVasWBEfffRRtG/fPpoV8CtO51E/ZWVNduiI8P+Rb4rlPCKK51ycR35xHvllfZ1HU76+Wsn/SX5xHvXVtG+b1td5NPWbv2L5uYpYP+fS1O9DItbPefzf/zWL0mKpGtZDy5Yto127iHbtUif5upbRsmV+Fc3qqmBWUK0PlZWV0b1793jxxRejdevWqeM0mPPIL84jvxTLeUQUz7k4j/ziPPJLsZxHRPGci/PIL84jvxTLeUQUz7kUy3mwYSjssjYAAAAABU+BCgAAAICkFKgAAAAASEqBCgAAAICkFKgAAAAASEqBCgAAAICkSi+66KKLUofIJ6WlpbHXXntFaWlp6iiN4jzyi/PIL8VyHhHFcy7OI784j/xSLOcRUTzn4jzyi/PIL8VyHhHFcy7Fch4Uv5Kampqa1CEAAAAA2HBp8QMAAAAgKQUqAAAAAJJSoAIAAAAgKQUqAAAAAJJSoAIAAAAgKQUqAAAAAJLaoAtUo0ePjq5du65xKy8vj3322SdGjhwZH3zwQeqY6zR06NDYb7/9ah275ZZbolu3bjF06NCorKxcz8nqZ+X/xx133FHr+COPPBJdu3aNefPmredkG6banh/l5eXRr1+/+OUvfxl/+ctfUkess7U91796+5//+Z/UMddp9OjRsccee6x1fMKECdG1a9d4//3312Oq+jnvvPOia9euceedd9Y6vmLFihgyZEjsuuuu8eabb67ndOs2cuTI+O53v1vr79MDDjggunbtGjfffPMaY5MmTYquXbvGn//85/WQsmEWLlwYv/rVr2LfffeNXXbZJXr06BHHHHNMzJgxI6qrq1PHW6e6PM8L7W/Ihx9+GP/93/8dhx12WPTo0SN23XXX+Ld/+7e44IIL4v/9v/+XOt461fZ/stNOO0X37t3j6KOPjoceeih1xAa5/fbbo2vXrnHkkUemjlJnQ4cOja5du0afPn1ixYoVtT7mtddeW/X/tGDBgvWcsGH++te/xtixY+OAAw6I3XbbLX7wgx/E0KFD48EHH4yamprU8dZpXb+3Bg0alDpinX3T+5FC8JOf/CR22WWX+OSTT9b6mAceeCC6du0as2fPXo/JGu/uu+8uqOc1G7bmqQPkg6+/UaqoqIgXX3wxpk6dGgsWLIhZs2ZFLpdLlK7hJk2aFFdddVX0798/rr766thoo41SR6qTyy+/PHr27BmdO3dOHaVR3nrrrbj99tvjqaeeig8//DBatWoVXbp0icMOOywGDhwYpaWlqSPWyVefH0uXLo133nknpk6dGkcccURMnjw5evbsmTBd/aytKBIRsfXWW6/HJBuuc845J+bNmxfjx4+PvffeO77zne+sNj516tR46aWX4oILLogdd9wxUcq169OnT8yaNSteeuml6Nu376r7Fy5cGH/9619j8803jyeeeCJOOOGE1b5v3rx50aFDh+jWrdt6Tlw3b7/9dhx11FHRqVOn+MUvfhFbbbVVVFZWxpNPPhkXXHBBvPDCC3H55ZenjvmNTj311Dj66KNX/fuuu+6KmTNnxsSJE6Ndu3ar7u/SpUuKePU2d+7cGDlyZGy00UYxZMiQKC8vjxYtWsSbb74Zt912W9x///1x/fXXR69evVJHXaev/u5dsWJFfPrppzF16tQ444wzoqqqKg4//PCE6epv+vTp0a1bt1iwYEG8/PLLsdtuu6WOVCfNmjWLjz76KObNm1frz819992XIFXDzZo1K84777zYeuut4/jjj4/OnTvH559/HrNnz44zzzwz5s6dG+PGjYtmzfL/8/i1vT5p1arVek6y4Tr66KNj7ty58cADD8SPf/zjWh8zc+bMaN++ffTv3389p4MNhwJVROy+++5r3Ne3b99Yvnx5TJkyJZ555pnYZ599EiRruKuvvjp+85vfxMCBA2PcuHEFUwxp3rx5lJSUxKhRo+LOO++M5s0L80f0rrvuiosvvji22267GD58eHTu3DkqKipizpw5ceGFF8bdd98dEydOjLKystRR1+nrz49evXrFD3/4wxg0aFCMGjUqHn300WjZsmWidPVT23Od9WuTTTaJyy+/PI499tg455xzYtq0aVFSUhIREX/5y1/i2muvjf322y+OPfbYxElrt/fee0dJSUm88MILqxWo5syZEy1btowTTjghJk6cGJWVldG6deuIiKiqqoqXXnopDjrooFSx1+nGG2+MiIhbb711tedz//79Y6ONNopp06bF8OHD87bAFhGxzTbbxDbbbLPq33/4wx8iImKnnXZaoxCa7z744IP4j//4j/j2t78dt912W2y22Warxvbaa6844ogjYsiQIXHOOefEY489lvd/42v73bvXXnvFPvvsE1OmTCmoAtUf//jHePPNN2Pq1KkxevTomDZtWlx55ZWpY9VJp06d4p///Gc8+OCDaxSoqqur46GHHoqdd945XnvttUQJ6+7111+Pc845J3r27BnXXXfdah8kDxgwIDp27BjXX3999OzZMw477LCESevG65P09t1332jfvn3ce++9tRao3nvvvZg3b1789Kc/Ldj3J1AI8v8jhYTatGkTEbHqzVOhuPTSS+M3v/lNnHDCCXHZZZfl/QvXr8rlcvGrX/0qXn311ZgwYULqOA3ywgsvxIUXXhj9+/eP//3f/42jjz46vv/978eAAQNi7NixMWXKlHjllVdi9OjRqaM22BZbbBEnnXRSfPTRRwW3zJn09thjjzj55JPjueeei2nTpkVExPLly+Pss8+Otm3bxqWXXpo44dq1a9cudtxxx3j++edXu//JJ59c9TxftmxZzJ07d9XYK6+8EkuXLl2toJVv/vGPf0RJSUmtrXzHHXdcjBw50if569ENN9wQ//znP+PSSy9drTi1UqtWrWLkyJHRvXv3+PTTTxMkbLzWrVtH586d469//WvqKPUyY8aMaNu2bey1115x2GGHxezZs2Px4sWpY9VJaWlpHHjggfHoo49GVVXVamNPP/10LFmyJK8L6V81efLkqK6ujjFjxtTa5XDKKafEkCFDVr2Wh3Vp3rx5DB48OF5//fV444031hifOXNmNGvWLH70ox8lSAcbDgWq+PKN0crbsmXL4pNPPomHHnoopkyZEp06dYoePXqkjlgnK1asiAsuuCBuueWWOO200+Kcc84puOJaRMTgwYOjf//+ccMNN8RLL72UOk69TZgwIVq1ahVjx46NFi1arDHeq1evGDp0aDz55JPxwgsvJEiYjZVvtp977rnESeruq8/1r94K4fo6X7W281jbdUXy0c9+9rPYeeed45prrom///3v8Zvf/Cb+9Kc/xRVXXBGbb7556njfqHfv3rFgwYL4v//7v4iI+Pzzz+O5556LffbZJ7p06RIdO3aMOXPmrHr8s88+G82bN4+99947UeJ169+/f1RUVMSRRx4ZkydPjldeeSWWLVsWERHbbrttnHzyyautTqJpPfLII7HDDjvELrvsstbH9O3bN6688sr41re+tR6TZaeqqiree++9+Pa3v506Sp1VVFTEQw89FIceemi0aNEifvSjH8Xy5cu/sX083xxyyCHx2WefrVphuNL9998fvXv3zvvfvyvNmTMndtppp7X+/Gy88cZx0UUXRb9+/dZvsAYqhtcmxWDw4MFRWloa99xzz2r3V1dXxz333BP9+vWLrbbaKlE62DBYnxgRO++88xr3tW3bNvr16xcjR44siPal6urqOPvss+OBBx6IiIiPP/44caLGGTt2bBxyyCFx1llnxb333ruqVSbfffbZZzFv3rw44IADvjHzIYccEjfeeGPMnj07vve9763HhNlZeU2XQvnkOKL253pExKabblowxcJ//etfaz2PQtKiRYu44oorYtCgQXHmmWfGggUL4qSTTiqIa5r16dMnpk6dGvPnz4+99tornnnmmVi2bNmqVvA+ffrEb3/721ixYkU0a9Ys5s2bF3vuuWde/x770Y9+FEuWLInrr79+VbvSRhttFHvssUcceOCBMWjQoFoL7mSvoqIiPv300/j+97+/xlh1dfUaF34uLS3N+w+jli9fvurrlYWp6667Lj799NM49dRTEyarn/vuuy+++OKLOOqooyLiy+Jtz549Y/r06TFixIiCeI6Ul5dHp06dYtasWauuo7N06dL43e9+F5deemksXbo0ccJ1++STT2Lp0qVFVTSv7e96x44d4/HHH0+QZsO11VZbRd++feOBBx6IX/7yl6ta+ebOnRsffvhhjB07NnFCKH4KVPHlks2IL1803XfffTFz5swYPnx4jBgxInGyulu0aFE8/PDDcc0118Ts2bPjjjvuiO7du8fBBx+cOlqDlJWVxbhx42LEiBExbty4uOyyy1JHqpMPPvggampq1nnB7W233TYiIq93W6urfH9j9FUrn+tfV0jXEth4443jtttuq3VsxowZMWPGjPWcqOG23377GDVqVFxyySWx6667xumnn546Up107949WrZsGc8//3zstddeMWfOnOjSpcuq6xzts88+MX369Hjttddixx13jPnz58dpp52WOPW6nXzyyXHcccfF008/Hc8//3y8+OKL8fzzz8ezzz4b06dPj5tvvlm7zHrwTSshBw0atMZOkGeddVb85Cc/aepYjVLbm++ysrIYOXJkDB06NEGihpkxY0bssssu0b59+6ioqIiIiIMPPjjOPffceOSRR+KQQw5JnLBuDjnkkJgyZUp8/vnnsckmm8Rvf/vbaN68efTv3z9mzZqVOt46rbx0RTGtMKrt9UkhbtBUDIYMGRJPPPFE/P73v1+1K+HMmTNj6623jj59+iROB8WvcN6VNaHy8vJVX3fv3j1yuVxcddVVUV1dXTCf7LVo0SKuv/766NOnz6r2k/PPPz+6detWMDsWfV2/fv3i6KOPjunTp8e+++6bOk6mVu4oU8gvrhYtWhQREVtuuWXiJHX31ed6oWrWrNlaz+OrbWWFol+/fnHJJZdE3759C6ZQmMvlokePHqtW3T355JOrfRjQs2fPyOVy8cwzz0RlZWVUVVUVzEYbrVq1igEDBsSAAQMiIuLTTz+N6667Lm699da44YYb4pe//GXihMWvbdu20bp163jvvffWGLvyyitXrXBZvHhx/PSnP13f8Rrkq2++mzdvHm3atCmo1r6IiJdeeinefPPNiIhaL/1w2223FUyB6tBDD40JEybEY489Foceemjcf//98cMf/rBgCiJt2rSJTTfddJ0f8i1atCjat29fELv4FcPrk2LRp0+f6NixY9x7772x3377xccffxxPPPFE/OIXvyioD2WhUOX/b+wEzjrrrNh+++1j4sSJ8cc//jF1nDpp3779qqp+69at4+qrr45ly5bF6aefHp9//nnidA03evTo6NSpU5x//vkF0UrWsWPHKCkpiXffffcbH7dw4cKIiILbWeqrnnrqqYiIgmjJgqz17t07XnnllXjttdfio48+Wu06J61atYoePXrE888/H88//3x06NAhunbtmi7sOnz44YfRp0+fmDx58hpjm2++eZx33nnRoUOHVW/OaXr7779/vP766/H222+vdn+XLl2ivLw8ysvLY8cdd0yUrv5WZi4vL//G6wblszvvvDM23njjuOmmm2LatGmr3Q4//PCYP39+LFiwIHXMOtlmm21i9913j1mzZsXHH38czzzzTEHsdPdV++yzT7z++uvxt7/9rdbxZcuWxWGHHRbHHHPMek5GoWvWrFkMHjw4Hn/88ViyZEncd999ERFxxBFHJE4GGwYFqlrkcrm45JJLVl10fOWFYgtJeXl5nHnmmfH222/H+eefnzpOg7Vs2TKuuOKKqKysjGuvvTZ1nHVq06ZN9OzZM+bOnbtq+f9KCxYsWHXtkIcffjgiomAu3vl1S5YsialTp0bHjh1XrbSADUnv3r3j888/j9tvvz1at24d3bt3X228b9++8ac//Smef/75vN69L+LL68nlcrmYPn16LFmyZI3xf/zjH1FRURHdunVLkG7DNGLEiGjdunWMGjVqrbv01bbLFE2joqIiHnnkkRgwYED84Ac/iL322mu124knnhgREbfeemvipHV3yCGHxNNPPx233357dOjQYY3fYfnuxBNPjNLS0hgzZswaOxJGREycODGWLFmiqECDHHnkkVFTUxO//e1v4/77748DDjggysrKUseCDUJh9FMk0L179xg4cGDcfffdcdNNN8XJJ5+cOlK9DRs2LJ599tl48MEHY88994zjjjsudaQG2XXXXePUU08tiAJVRMTpp58eQ4cOjXPOOSeuueaaaNGiRVRUVMTQoUOjQ4cOcdxxx8VNN90UPXr0yPs3rhER8+fPX/X10qVL46233opp06bFkiVLYsqUKQXTEhCx+rl8XZs2bWK77bZbj2koZNtvv31stdVWcf/998d+++23Rnti375947LLLoslS5bE8ccfnyhl3TRr1izGjh0bI0aMiMMPPzyOPfbY2HnnnaO0tDTeeOONuOWWW6JDhw4xbNiw1FE3GJ06dYqJEyfGyJEj46CDDorBgwfHHnvsES1btox33303HnnkkZg7d25su+22luNT3QAAAtdJREFUBbPTcCG7995744svvljrKqMddtghdt9993j44Yfj7LPPji222GI9J6y/Aw88MC677LKYPHlynHjiiQXXurTTTjvFueeeG2PHjo3BgwfHkCFDolOnTvHJJ5/ErFmz4rHHHosjjzwyjjzyyNRRNyiVlZVx88031zp27LHHFsRGAhFffnDTv3//uPHGG+Odd96J8847L3Uk2GAoUH2DUaNGxeOPPx7XXXdd/Pu///s6L3ydb0pKSmL8+PFx2GGHxfjx46O8vDx222231LEa5JRTTok//OEPBdFyueeee8bYsWPjwgsvjEGDBsWxxx4b22+/fVx88cUxbty4GDt2bDRv3rxg/tit3K0o4svVhR06dIhevXrFiSeeuOpi74Xiq+fydf37949f//rX6zENha53795x11131Xp9qc6dO8c222wTf//736NXr14J0tVPr1694p577okbb7wx7rrrrrjuuutixYoV0bFjxzjooIPipJNOik033TR1zA1Kr169YtasWXHXXXfF7373u5g+fXp8/vnnUVZWFuXl5XHllVfG/vvvX1AfEhSqGTNmRLt27WLvvfde62MGDx4c5557bkyfPj1+9rOfrcd0DVNWVhY/+MEP4ve//33BtfetdMwxx8ROO+0Ut912W0yePDn+8Y9/xKabbhrbb799XHvttbH//vsXXOGt0H322Wdr3dho8ODBBVOgiog4+uijY9iwYbHjjjsW7I7bUIhKar6+XzGQibfffjtuvfXWeOqpp+LDDz+MVq1aRZcuXaJ///7x6KOPxp///Oc4/vjj44wzzkgdFQAAAJJSoIIEampq4rHHHosPPvggfvzjH6eOAwAAAEkpUAEAAACQlF38AAAAAEhKgQoAAACApBSoAAAAAEhKgQoAAACApBSoAAAAAEhKgQoAAACApBSoAAAAAEhKgQoAAACApBSoAAAAAEhKgQoAAACApP4/8tXOUK8zla8AAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 1618.03x1000 with 2 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"lamb, P = np.linalg.eig(B)\n",
"lamb, P = sort_eigenvalues_and_eigenvectors(lamb, P)\n",
"filtered_lamb = np.copy(lamb)\n",
"cutoff_mode = 400\n",
"filtered_B_inv, filtered_lamb, P = get_filtered_B_inv_lambda_and_P(filtered_lamb, \n",
" cutoff_mode, P)\n",
"filtered_gamma = np.dot(filtered_B_inv, A)\n",
"filtered_B = np.linalg.inv(filtered_B_inv)\n",
"plot_contact_well(filtered_gamma[:210], inferBound=True)\n",
"plot_contact_well(filtered_gamma[210:420], inferBound=True)\n",
"plot_contact_well(filtered_gamma[420:], inferBound=True)"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(1.5403101476740844e-05+0j)"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# maximum difference between loaded and computed is 1e-5.\n",
"max(lamb-Lamb)"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [],
"source": [
"save_gamma_pre = \"/Users/weilu/Research/server/sep_2019/saved_gammas/\"\n",
"np.savetxt(f\"{save_gamma_pre}/trial_2_cutoff400\", filtered_gamma)"
]
},
{
"cell_type": "code",
"execution_count": 107,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"'/Users/weilu/opt/notebook/Optimization'"
]
},
"execution_count": 107,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"os.chdir('/Users/weilu/opt/notebook/Optimization')"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"210\n",
"420\n",
"60\n",
"0 3.8340531662409814\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n"
]
},
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Protein</th>\n",
" <th>Z_scores</th>\n",
" <th>E_native</th>\n",
" <th>E_mgs</th>\n",
" <th>Std_mg</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1BD2_1</td>\n",
" <td>3.834053</td>\n",
" <td>-1091.522839</td>\n",
" <td>-9.338132</td>\n",
" <td>282.256051</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>6BJ8_1</td>\n",
" <td>4.115412</td>\n",
" <td>-2110.009245</td>\n",
" <td>-812.790146</td>\n",
" <td>315.210016</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>2JCC_1</td>\n",
" <td>3.745693</td>\n",
" <td>-922.515254</td>\n",
" <td>149.727164</td>\n",
" <td>286.260117</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>1AO7_1</td>\n",
" <td>3.806062</td>\n",
" <td>-1753.590663</td>\n",
" <td>-575.699559</td>\n",
" <td>309.477634</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>1LP9_1</td>\n",
" <td>3.944508</td>\n",
" <td>-920.931994</td>\n",
" <td>163.036214</td>\n",
" <td>274.804438</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>3QDJ_1</td>\n",
" <td>4.085536</td>\n",
" <td>-1782.495837</td>\n",
" <td>-490.495793</td>\n",
" <td>316.237590</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>3GSN_1</td>\n",
" <td>3.709800</td>\n",
" <td>-1900.434238</td>\n",
" <td>-753.721660</td>\n",
" <td>309.103604</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>1QRN_1</td>\n",
" <td>4.164756</td>\n",
" <td>-1712.503201</td>\n",
" <td>-527.714693</td>\n",
" <td>284.479679</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>3PWP_1</td>\n",
" <td>3.889196</td>\n",
" <td>-1460.943615</td>\n",
" <td>-319.651538</td>\n",
" <td>293.451918</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>5W1W_1</td>\n",
" <td>3.914030</td>\n",
" <td>-700.985851</td>\n",
" <td>428.268456</td>\n",
" <td>288.514471</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>1QSE_1</td>\n",
" <td>3.732709</td>\n",
" <td>-1716.888053</td>\n",
" <td>-616.997651</td>\n",
" <td>294.662787</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>4EUP_1</td>\n",
" <td>3.768051</td>\n",
" <td>-1483.163001</td>\n",
" <td>-360.029803</td>\n",
" <td>298.067414</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12</th>\n",
" <td>5TEZ_1</td>\n",
" <td>3.642150</td>\n",
" <td>-1519.094431</td>\n",
" <td>-585.955647</td>\n",
" <td>256.205452</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13</th>\n",
" <td>3D39_1</td>\n",
" <td>3.430565</td>\n",
" <td>-1648.903714</td>\n",
" <td>-582.649212</td>\n",
" <td>310.810205</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14</th>\n",
" <td>6EQA_1</td>\n",
" <td>3.060139</td>\n",
" <td>-1403.253274</td>\n",
" <td>-398.982295</td>\n",
" <td>328.178211</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15</th>\n",
" <td>2BNR_1</td>\n",
" <td>3.874194</td>\n",
" <td>-1704.803904</td>\n",
" <td>-577.879936</td>\n",
" <td>290.879614</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16</th>\n",
" <td>6BJ2_1</td>\n",
" <td>3.849727</td>\n",
" <td>-1664.218888</td>\n",
" <td>-458.193805</td>\n",
" <td>313.275509</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17</th>\n",
" <td>6BJ3_1</td>\n",
" <td>4.147049</td>\n",
" <td>-2014.495647</td>\n",
" <td>-825.600001</td>\n",
" <td>286.684707</td>\n",
" </tr>\n",
" <tr>\n",
" <th>18</th>\n",
" <td>5NME_1</td>\n",
" <td>3.448995</td>\n",
" <td>-1401.199554</td>\n",
" <td>-315.630916</td>\n",
" <td>314.749227</td>\n",
" </tr>\n",
" <tr>\n",
" <th>19</th>\n",
" <td>5MEN_1</td>\n",
" <td>3.883324</td>\n",
" <td>-1612.198812</td>\n",
" <td>-556.388894</td>\n",
" <td>271.883047</td>\n",
" </tr>\n",
" <tr>\n",
" <th>20</th>\n",
" <td>2VLJ_1</td>\n",
" <td>3.556692</td>\n",
" <td>-1174.475465</td>\n",
" <td>-143.948172</td>\n",
" <td>289.743225</td>\n",
" </tr>\n",
" <tr>\n",
" <th>21</th>\n",
" <td>2VLK_1</td>\n",
" <td>4.097878</td>\n",
" <td>-1391.214148</td>\n",
" <td>-203.154042</td>\n",
" <td>289.920829</td>\n",
" </tr>\n",
" <tr>\n",
" <th>22</th>\n",
" <td>2J8U_1</td>\n",
" <td>3.867065</td>\n",
" <td>-905.136654</td>\n",
" <td>164.735010</td>\n",
" <td>276.662461</td>\n",
" </tr>\n",
" <tr>\n",
" <th>23</th>\n",
" <td>2GJ6_1</td>\n",
" <td>3.879977</td>\n",
" <td>-1928.417980</td>\n",
" <td>-706.808902</td>\n",
" <td>314.849543</td>\n",
" </tr>\n",
" <tr>\n",
" <th>24</th>\n",
" <td>1OGA_1</td>\n",
" <td>4.578397</td>\n",
" <td>-1432.955561</td>\n",
" <td>-157.199781</td>\n",
" <td>278.646829</td>\n",
" </tr>\n",
" <tr>\n",
" <th>25</th>\n",
" <td>2F54_1</td>\n",
" <td>3.943001</td>\n",
" <td>-1797.814121</td>\n",
" <td>-683.673024</td>\n",
" <td>282.561697</td>\n",
" </tr>\n",
" <tr>\n",
" <th>26</th>\n",
" <td>5D2L_1</td>\n",
" <td>3.600108</td>\n",
" <td>-1346.186653</td>\n",
" <td>-264.050877</td>\n",
" <td>300.584287</td>\n",
" </tr>\n",
" <tr>\n",
" <th>27</th>\n",
" <td>2F53_1</td>\n",
" <td>3.459582</td>\n",
" <td>-1368.420767</td>\n",
" <td>-329.770020</td>\n",
" <td>300.224321</td>\n",
" </tr>\n",
" <tr>\n",
" <th>28</th>\n",
" <td>3QEQ_1</td>\n",
" <td>3.377197</td>\n",
" <td>-1726.197571</td>\n",
" <td>-613.399463</td>\n",
" <td>329.503471</td>\n",
" </tr>\n",
" <tr>\n",
" <th>29</th>\n",
" <td>1QSF_1</td>\n",
" <td>3.594095</td>\n",
" <td>-1594.671282</td>\n",
" <td>-517.028259</td>\n",
" <td>299.837071</td>\n",
" </tr>\n",
" <tr>\n",
" <th>30</th>\n",
" <td>2UWE_1</td>\n",
" <td>2.841172</td>\n",
" <td>-699.203977</td>\n",
" <td>91.916879</td>\n",
" <td>278.448733</td>\n",
" </tr>\n",
" <tr>\n",
" <th>31</th>\n",
" <td>5EUO_1</td>\n",
" <td>3.880985</td>\n",
" <td>-1474.338340</td>\n",
" <td>-296.470990</td>\n",
" <td>303.497025</td>\n",
" </tr>\n",
" <tr>\n",
" <th>32</th>\n",
" <td>3H9S_1</td>\n",
" <td>3.958820</td>\n",
" <td>-1884.030529</td>\n",
" <td>-679.597102</td>\n",
" <td>304.240492</td>\n",
" </tr>\n",
" <tr>\n",
" <th>33</th>\n",
" <td>3D3V_1</td>\n",
" <td>3.360240</td>\n",
" <td>-1713.535477</td>\n",
" <td>-624.402686</td>\n",
" <td>324.123553</td>\n",
" </tr>\n",
" <tr>\n",
" <th>34</th>\n",
" <td>2BNQ_1</td>\n",
" <td>5.651049</td>\n",
" <td>-3008.457623</td>\n",
" <td>-1266.073497</td>\n",
" <td>308.329333</td>\n",
" </tr>\n",
" <tr>\n",
" <th>35</th>\n",
" <td>4FTV_1</td>\n",
" <td>3.749797</td>\n",
" <td>-1490.902546</td>\n",
" <td>-412.216998</td>\n",
" <td>287.665028</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Protein Z_scores E_native E_mgs Std_mg\n",
"0 1BD2_1 3.834053 -1091.522839 -9.338132 282.256051\n",
"1 6BJ8_1 4.115412 -2110.009245 -812.790146 315.210016\n",
"2 2JCC_1 3.745693 -922.515254 149.727164 286.260117\n",
"3 1AO7_1 3.806062 -1753.590663 -575.699559 309.477634\n",
"4 1LP9_1 3.944508 -920.931994 163.036214 274.804438\n",
"5 3QDJ_1 4.085536 -1782.495837 -490.495793 316.237590\n",
"6 3GSN_1 3.709800 -1900.434238 -753.721660 309.103604\n",
"7 1QRN_1 4.164756 -1712.503201 -527.714693 284.479679\n",
"8 3PWP_1 3.889196 -1460.943615 -319.651538 293.451918\n",
"9 5W1W_1 3.914030 -700.985851 428.268456 288.514471\n",
"10 1QSE_1 3.732709 -1716.888053 -616.997651 294.662787\n",
"11 4EUP_1 3.768051 -1483.163001 -360.029803 298.067414\n",
"12 5TEZ_1 3.642150 -1519.094431 -585.955647 256.205452\n",
"13 3D39_1 3.430565 -1648.903714 -582.649212 310.810205\n",
"14 6EQA_1 3.060139 -1403.253274 -398.982295 328.178211\n",
"15 2BNR_1 3.874194 -1704.803904 -577.879936 290.879614\n",
"16 6BJ2_1 3.849727 -1664.218888 -458.193805 313.275509\n",
"17 6BJ3_1 4.147049 -2014.495647 -825.600001 286.684707\n",
"18 5NME_1 3.448995 -1401.199554 -315.630916 314.749227\n",
"19 5MEN_1 3.883324 -1612.198812 -556.388894 271.883047\n",
"20 2VLJ_1 3.556692 -1174.475465 -143.948172 289.743225\n",
"21 2VLK_1 4.097878 -1391.214148 -203.154042 289.920829\n",
"22 2J8U_1 3.867065 -905.136654 164.735010 276.662461\n",
"23 2GJ6_1 3.879977 -1928.417980 -706.808902 314.849543\n",
"24 1OGA_1 4.578397 -1432.955561 -157.199781 278.646829\n",
"25 2F54_1 3.943001 -1797.814121 -683.673024 282.561697\n",
"26 5D2L_1 3.600108 -1346.186653 -264.050877 300.584287\n",
"27 2F53_1 3.459582 -1368.420767 -329.770020 300.224321\n",
"28 3QEQ_1 3.377197 -1726.197571 -613.399463 329.503471\n",
"29 1QSF_1 3.594095 -1594.671282 -517.028259 299.837071\n",
"30 2UWE_1 2.841172 -699.203977 91.916879 278.448733\n",
"31 5EUO_1 3.880985 -1474.338340 -296.470990 303.497025\n",
"32 3H9S_1 3.958820 -1884.030529 -679.597102 304.240492\n",
"33 3D3V_1 3.360240 -1713.535477 -624.402686 324.123553\n",
"34 2BNQ_1 5.651049 -3008.457623 -1266.073497 308.329333\n",
"35 4FTV_1 3.749797 -1490.902546 -412.216998 287.665028"
]
},
"execution_count": 14,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"os.chdir(\"/Users/weilu/Research/server/sep_2019/peptide_optimization_trial_2/optimization/\")\n",
"# gamma_file_name = \"gamma_iter1_combined_mar06.dat\"\n",
"gamma_file_name = \"/Users/weilu/Research/server/sep_2019/peptide_optimization/saved_gammas/cutoff100\"\n",
"data = validate_hamiltonian_wei(\"phi_list.txt\", \"protein_list_small\", gamma_file_name, \"shuffle\", 1000, mode=0)\n",
"data\n"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"210\n",
"420\n",
"60\n",
"0 22.100828450470825\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n"
]
},
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Protein</th>\n",
" <th>Z_scores</th>\n",
" <th>E_native</th>\n",
" <th>E_mgs</th>\n",
" <th>Std_mg</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1BD2_1</td>\n",
" <td>22.100828</td>\n",
" <td>-425.944208</td>\n",
" <td>-19.039485</td>\n",
" <td>18.411288</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>6BJ8_1</td>\n",
" <td>18.234455</td>\n",
" <td>-583.705104</td>\n",
" <td>-187.090418</td>\n",
" <td>21.750838</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>2JCC_1</td>\n",
" <td>23.091225</td>\n",
" <td>-609.090184</td>\n",
" <td>-224.970073</td>\n",
" <td>16.634896</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>1AO7_1</td>\n",
" <td>21.665218</td>\n",
" <td>-552.214494</td>\n",
" <td>-167.905076</td>\n",
" <td>17.738544</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>1LP9_1</td>\n",
" <td>22.983383</td>\n",
" <td>-523.716471</td>\n",
" <td>-155.334523</td>\n",
" <td>16.028187</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>3QDJ_1</td>\n",
" <td>19.865607</td>\n",
" <td>-580.766858</td>\n",
" <td>-163.052759</td>\n",
" <td>21.026999</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>3GSN_1</td>\n",
" <td>22.184385</td>\n",
" <td>-410.258265</td>\n",
" <td>-61.283660</td>\n",
" <td>15.730641</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>1QRN_1</td>\n",
" <td>27.800921</td>\n",
" <td>-614.034462</td>\n",
" <td>-215.165011</td>\n",
" <td>14.347347</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>3PWP_1</td>\n",
" <td>27.572172</td>\n",
" <td>-611.500391</td>\n",
" <td>-211.485674</td>\n",
" <td>14.507915</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>5W1W_1</td>\n",
" <td>20.096043</td>\n",
" <td>-445.859601</td>\n",
" <td>-37.667697</td>\n",
" <td>20.312054</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>1QSE_1</td>\n",
" <td>23.340974</td>\n",
" <td>-603.070419</td>\n",
" <td>-186.338174</td>\n",
" <td>17.854107</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>4EUP_1</td>\n",
" <td>18.239404</td>\n",
" <td>-466.982175</td>\n",
" <td>-106.293743</td>\n",
" <td>19.775231</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12</th>\n",
" <td>5TEZ_1</td>\n",
" <td>11.864662</td>\n",
" <td>-252.121139</td>\n",
" <td>-68.540749</td>\n",
" <td>15.472872</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13</th>\n",
" <td>3D39_1</td>\n",
" <td>22.409665</td>\n",
" <td>-561.211537</td>\n",
" <td>-161.282695</td>\n",
" <td>17.846266</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14</th>\n",
" <td>6EQA_1</td>\n",
" <td>14.613196</td>\n",
" <td>-414.766125</td>\n",
" <td>-60.787924</td>\n",
" <td>24.223189</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15</th>\n",
" <td>2BNR_1</td>\n",
" <td>24.468354</td>\n",
" <td>-542.998945</td>\n",
" <td>-150.044647</td>\n",
" <td>16.059695</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16</th>\n",
" <td>6BJ2_1</td>\n",
" <td>30.525660</td>\n",
" <td>-526.321122</td>\n",
" <td>-114.284889</td>\n",
" <td>13.498029</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17</th>\n",
" <td>6BJ3_1</td>\n",
" <td>27.772542</td>\n",
" <td>-596.154343</td>\n",
" <td>-183.180723</td>\n",
" <td>14.869853</td>\n",
" </tr>\n",
" <tr>\n",
" <th>18</th>\n",
" <td>5NME_1</td>\n",
" <td>29.512753</td>\n",
" <td>-608.340154</td>\n",
" <td>-181.042832</td>\n",
" <td>14.478396</td>\n",
" </tr>\n",
" <tr>\n",
" <th>19</th>\n",
" <td>5MEN_1</td>\n",
" <td>27.623379</td>\n",
" <td>-505.243392</td>\n",
" <td>-146.431711</td>\n",
" <td>12.989421</td>\n",
" </tr>\n",
" <tr>\n",
" <th>20</th>\n",
" <td>2VLJ_1</td>\n",
" <td>20.092340</td>\n",
" <td>-487.017981</td>\n",
" <td>-112.575079</td>\n",
" <td>18.636102</td>\n",
" </tr>\n",
" <tr>\n",
" <th>21</th>\n",
" <td>2VLK_1</td>\n",
" <td>28.021486</td>\n",
" <td>-503.976124</td>\n",
" <td>-86.384478</td>\n",
" <td>14.902552</td>\n",
" </tr>\n",
" <tr>\n",
" <th>22</th>\n",
" <td>2J8U_1</td>\n",
" <td>22.794303</td>\n",
" <td>-505.975871</td>\n",
" <td>-148.746003</td>\n",
" <td>15.671893</td>\n",
" </tr>\n",
" <tr>\n",
" <th>23</th>\n",
" <td>2GJ6_1</td>\n",
" <td>23.066179</td>\n",
" <td>-646.109938</td>\n",
" <td>-217.962704</td>\n",
" <td>18.561689</td>\n",
" </tr>\n",
" <tr>\n",
" <th>24</th>\n",
" <td>1OGA_1</td>\n",
" <td>25.588701</td>\n",
" <td>-477.243840</td>\n",
" <td>-72.900548</td>\n",
" <td>15.801634</td>\n",
" </tr>\n",
" <tr>\n",
" <th>25</th>\n",
" <td>2F54_1</td>\n",
" <td>24.805781</td>\n",
" <td>-562.744899</td>\n",
" <td>-197.087611</td>\n",
" <td>14.740809</td>\n",
" </tr>\n",
" <tr>\n",
" <th>26</th>\n",
" <td>5D2L_1</td>\n",
" <td>19.102887</td>\n",
" <td>-403.100802</td>\n",
" <td>-28.129608</td>\n",
" <td>19.629032</td>\n",
" </tr>\n",
" <tr>\n",
" <th>27</th>\n",
" <td>2F53_1</td>\n",
" <td>21.095925</td>\n",
" <td>-508.036797</td>\n",
" <td>-119.429501</td>\n",
" <td>18.420965</td>\n",
" </tr>\n",
" <tr>\n",
" <th>28</th>\n",
" <td>3QEQ_1</td>\n",
" <td>20.391355</td>\n",
" <td>-463.013024</td>\n",
" <td>-32.820730</td>\n",
" <td>21.096797</td>\n",
" </tr>\n",
" <tr>\n",
" <th>29</th>\n",
" <td>1QSF_1</td>\n",
" <td>22.186445</td>\n",
" <td>-506.295432</td>\n",
" <td>-156.327369</td>\n",
" <td>15.773959</td>\n",
" </tr>\n",
" <tr>\n",
" <th>30</th>\n",
" <td>2UWE_1</td>\n",
" <td>19.715181</td>\n",
" <td>-445.946516</td>\n",
" <td>-128.822900</td>\n",
" <td>16.085250</td>\n",
" </tr>\n",
" <tr>\n",
" <th>31</th>\n",
" <td>5EUO_1</td>\n",
" <td>25.187256</td>\n",
" <td>-427.553686</td>\n",
" <td>0.675697</td>\n",
" <td>17.001827</td>\n",
" </tr>\n",
" <tr>\n",
" <th>32</th>\n",
" <td>3H9S_1</td>\n",
" <td>21.062154</td>\n",
" <td>-644.985289</td>\n",
" <td>-211.998716</td>\n",
" <td>20.557564</td>\n",
" </tr>\n",
" <tr>\n",
" <th>33</th>\n",
" <td>3D3V_1</td>\n",
" <td>24.753662</td>\n",
" <td>-767.277656</td>\n",
" <td>-293.136232</td>\n",
" <td>19.154395</td>\n",
" </tr>\n",
" <tr>\n",
" <th>34</th>\n",
" <td>2BNQ_1</td>\n",
" <td>8.525074</td>\n",
" <td>-378.045961</td>\n",
" <td>-223.890146</td>\n",
" <td>18.082637</td>\n",
" </tr>\n",
" <tr>\n",
" <th>35</th>\n",
" <td>4FTV_1</td>\n",
" <td>20.488735</td>\n",
" <td>-545.045406</td>\n",
" <td>-156.076909</td>\n",
" <td>18.984506</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Protein Z_scores E_native E_mgs Std_mg\n",
"0 1BD2_1 22.100828 -425.944208 -19.039485 18.411288\n",
"1 6BJ8_1 18.234455 -583.705104 -187.090418 21.750838\n",
"2 2JCC_1 23.091225 -609.090184 -224.970073 16.634896\n",
"3 1AO7_1 21.665218 -552.214494 -167.905076 17.738544\n",
"4 1LP9_1 22.983383 -523.716471 -155.334523 16.028187\n",
"5 3QDJ_1 19.865607 -580.766858 -163.052759 21.026999\n",
"6 3GSN_1 22.184385 -410.258265 -61.283660 15.730641\n",
"7 1QRN_1 27.800921 -614.034462 -215.165011 14.347347\n",
"8 3PWP_1 27.572172 -611.500391 -211.485674 14.507915\n",
"9 5W1W_1 20.096043 -445.859601 -37.667697 20.312054\n",
"10 1QSE_1 23.340974 -603.070419 -186.338174 17.854107\n",
"11 4EUP_1 18.239404 -466.982175 -106.293743 19.775231\n",
"12 5TEZ_1 11.864662 -252.121139 -68.540749 15.472872\n",
"13 3D39_1 22.409665 -561.211537 -161.282695 17.846266\n",
"14 6EQA_1 14.613196 -414.766125 -60.787924 24.223189\n",
"15 2BNR_1 24.468354 -542.998945 -150.044647 16.059695\n",
"16 6BJ2_1 30.525660 -526.321122 -114.284889 13.498029\n",
"17 6BJ3_1 27.772542 -596.154343 -183.180723 14.869853\n",
"18 5NME_1 29.512753 -608.340154 -181.042832 14.478396\n",
"19 5MEN_1 27.623379 -505.243392 -146.431711 12.989421\n",
"20 2VLJ_1 20.092340 -487.017981 -112.575079 18.636102\n",
"21 2VLK_1 28.021486 -503.976124 -86.384478 14.902552\n",
"22 2J8U_1 22.794303 -505.975871 -148.746003 15.671893\n",
"23 2GJ6_1 23.066179 -646.109938 -217.962704 18.561689\n",
"24 1OGA_1 25.588701 -477.243840 -72.900548 15.801634\n",
"25 2F54_1 24.805781 -562.744899 -197.087611 14.740809\n",
"26 5D2L_1 19.102887 -403.100802 -28.129608 19.629032\n",
"27 2F53_1 21.095925 -508.036797 -119.429501 18.420965\n",
"28 3QEQ_1 20.391355 -463.013024 -32.820730 21.096797\n",
"29 1QSF_1 22.186445 -506.295432 -156.327369 15.773959\n",
"30 2UWE_1 19.715181 -445.946516 -128.822900 16.085250\n",
"31 5EUO_1 25.187256 -427.553686 0.675697 17.001827\n",
"32 3H9S_1 21.062154 -644.985289 -211.998716 20.557564\n",
"33 3D3V_1 24.753662 -767.277656 -293.136232 19.154395\n",
"34 2BNQ_1 8.525074 -378.045961 -223.890146 18.082637\n",
"35 4FTV_1 20.488735 -545.045406 -156.076909 18.984506"
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"os.chdir(\"/Users/weilu/Research/server/sep_2019/peptide_optimization_trial_2/optimization/\")\n",
"# gamma_file_name = \"gamma_iter1_combined_mar06.dat\"\n",
"gamma_file_name = \"/Users/weilu/Research/server/sep_2019/saved_gammas/trial_2_cutoff400\"\n",
"data = validate_hamiltonian_wei(\"phi_list.txt\", \"protein_list_small\", gamma_file_name, \"shuffle\", 1000, mode=0)\n",
"data\n"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"210\n",
"420\n",
"60\n",
"0 0.9003155450024992\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n"
]
},
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Protein</th>\n",
" <th>Z_scores</th>\n",
" <th>E_native</th>\n",
" <th>E_mgs</th>\n",
" <th>Std_mg</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1BD2_1</td>\n",
" <td>0.900316</td>\n",
" <td>-565.363569</td>\n",
" <td>-558.334725</td>\n",
" <td>7.807089</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>6BJ8_1</td>\n",
" <td>0.340620</td>\n",
" <td>-559.377083</td>\n",
" <td>-556.341055</td>\n",
" <td>8.913235</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>2JCC_1</td>\n",
" <td>0.151485</td>\n",
" <td>-578.632012</td>\n",
" <td>-577.373781</td>\n",
" <td>8.305978</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>1AO7_1</td>\n",
" <td>0.549733</td>\n",
" <td>-554.882868</td>\n",
" <td>-549.744350</td>\n",
" <td>9.347298</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>1LP9_1</td>\n",
" <td>0.018086</td>\n",
" <td>-572.456799</td>\n",
" <td>-572.294553</td>\n",
" <td>8.970942</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>3QDJ_1</td>\n",
" <td>0.571400</td>\n",
" <td>-548.835394</td>\n",
" <td>-544.666126</td>\n",
" <td>7.296581</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>3GSN_1</td>\n",
" <td>0.721878</td>\n",
" <td>-546.292261</td>\n",
" <td>-539.487997</td>\n",
" <td>9.425782</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>1QRN_1</td>\n",
" <td>0.039428</td>\n",
" <td>-555.365484</td>\n",
" <td>-555.071793</td>\n",
" <td>7.448888</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>3PWP_1</td>\n",
" <td>0.253560</td>\n",
" <td>-570.922191</td>\n",
" <td>-568.716016</td>\n",
" <td>8.700786</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>5W1W_1</td>\n",
" <td>0.751747</td>\n",
" <td>-563.412353</td>\n",
" <td>-557.502728</td>\n",
" <td>7.861194</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>1QSE_1</td>\n",
" <td>0.578690</td>\n",
" <td>-559.544033</td>\n",
" <td>-554.102176</td>\n",
" <td>9.403750</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>4EUP_1</td>\n",
" <td>0.015861</td>\n",
" <td>-563.958000</td>\n",
" <td>-563.817637</td>\n",
" <td>8.849680</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12</th>\n",
" <td>5TEZ_1</td>\n",
" <td>0.454085</td>\n",
" <td>-579.688507</td>\n",
" <td>-576.275882</td>\n",
" <td>7.515384</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13</th>\n",
" <td>3D39_1</td>\n",
" <td>0.913302</td>\n",
" <td>-569.280411</td>\n",
" <td>-560.054925</td>\n",
" <td>10.101248</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14</th>\n",
" <td>6EQA_1</td>\n",
" <td>0.607607</td>\n",
" <td>-559.131031</td>\n",
" <td>-553.943662</td>\n",
" <td>8.537371</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15</th>\n",
" <td>2BNR_1</td>\n",
" <td>0.702593</td>\n",
" <td>-570.397373</td>\n",
" <td>-563.957349</td>\n",
" <td>9.166085</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16</th>\n",
" <td>6BJ2_1</td>\n",
" <td>0.468335</td>\n",
" <td>-556.645981</td>\n",
" <td>-552.711043</td>\n",
" <td>8.401973</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17</th>\n",
" <td>6BJ3_1</td>\n",
" <td>-0.096069</td>\n",
" <td>-563.400937</td>\n",
" <td>-564.108460</td>\n",
" <td>7.364763</td>\n",
" </tr>\n",
" <tr>\n",
" <th>18</th>\n",
" <td>5NME_1</td>\n",
" <td>0.644450</td>\n",
" <td>-558.065141</td>\n",
" <td>-552.460955</td>\n",
" <td>8.696081</td>\n",
" </tr>\n",
" <tr>\n",
" <th>19</th>\n",
" <td>5MEN_1</td>\n",
" <td>0.314084</td>\n",
" <td>-550.918059</td>\n",
" <td>-548.400112</td>\n",
" <td>8.016793</td>\n",
" </tr>\n",
" <tr>\n",
" <th>20</th>\n",
" <td>2VLJ_1</td>\n",
" <td>0.322381</td>\n",
" <td>-542.011146</td>\n",
" <td>-539.421195</td>\n",
" <td>8.033830</td>\n",
" </tr>\n",
" <tr>\n",
" <th>21</th>\n",
" <td>2VLK_1</td>\n",
" <td>0.350059</td>\n",
" <td>-542.555997</td>\n",
" <td>-539.493606</td>\n",
" <td>8.748207</td>\n",
" </tr>\n",
" <tr>\n",
" <th>22</th>\n",
" <td>2J8U_1</td>\n",
" <td>-0.288170</td>\n",
" <td>-574.485025</td>\n",
" <td>-576.761867</td>\n",
" <td>7.901027</td>\n",
" </tr>\n",
" <tr>\n",
" <th>23</th>\n",
" <td>2GJ6_1</td>\n",
" <td>0.356224</td>\n",
" <td>-570.758928</td>\n",
" <td>-567.118995</td>\n",
" <td>10.218105</td>\n",
" </tr>\n",
" <tr>\n",
" <th>24</th>\n",
" <td>1OGA_1</td>\n",
" <td>0.236676</td>\n",
" <td>-552.479891</td>\n",
" <td>-550.437823</td>\n",
" <td>8.628107</td>\n",
" </tr>\n",
" <tr>\n",
" <th>25</th>\n",
" <td>2F54_1</td>\n",
" <td>0.103204</td>\n",
" <td>-548.348960</td>\n",
" <td>-547.472613</td>\n",
" <td>8.491401</td>\n",
" </tr>\n",
" <tr>\n",
" <th>26</th>\n",
" <td>5D2L_1</td>\n",
" <td>0.565962</td>\n",
" <td>-558.635666</td>\n",
" <td>-553.753495</td>\n",
" <td>8.626318</td>\n",
" </tr>\n",
" <tr>\n",
" <th>27</th>\n",
" <td>2F53_1</td>\n",
" <td>0.606024</td>\n",
" <td>-562.123693</td>\n",
" <td>-556.408688</td>\n",
" <td>9.430324</td>\n",
" </tr>\n",
" <tr>\n",
" <th>28</th>\n",
" <td>3QEQ_1</td>\n",
" <td>0.621955</td>\n",
" <td>-551.620007</td>\n",
" <td>-545.238092</td>\n",
" <td>10.261056</td>\n",
" </tr>\n",
" <tr>\n",
" <th>29</th>\n",
" <td>1QSF_1</td>\n",
" <td>0.481709</td>\n",
" <td>-566.452834</td>\n",
" <td>-562.124111</td>\n",
" <td>8.986185</td>\n",
" </tr>\n",
" <tr>\n",
" <th>30</th>\n",
" <td>2UWE_1</td>\n",
" <td>0.876791</td>\n",
" <td>-586.309550</td>\n",
" <td>-579.238061</td>\n",
" <td>8.065195</td>\n",
" </tr>\n",
" <tr>\n",
" <th>31</th>\n",
" <td>5EUO_1</td>\n",
" <td>0.136994</td>\n",
" <td>-550.526436</td>\n",
" <td>-549.302675</td>\n",
" <td>8.932927</td>\n",
" </tr>\n",
" <tr>\n",
" <th>32</th>\n",
" <td>3H9S_1</td>\n",
" <td>0.546885</td>\n",
" <td>-555.893794</td>\n",
" <td>-551.095308</td>\n",
" <td>8.774218</td>\n",
" </tr>\n",
" <tr>\n",
" <th>33</th>\n",
" <td>3D3V_1</td>\n",
" <td>0.610284</td>\n",
" <td>-542.475441</td>\n",
" <td>-536.054752</td>\n",
" <td>10.520817</td>\n",
" </tr>\n",
" <tr>\n",
" <th>34</th>\n",
" <td>2BNQ_1</td>\n",
" <td>0.285020</td>\n",
" <td>-563.839068</td>\n",
" <td>-561.332622</td>\n",
" <td>8.793945</td>\n",
" </tr>\n",
" <tr>\n",
" <th>35</th>\n",
" <td>4FTV_1</td>\n",
" <td>-0.401177</td>\n",
" <td>-539.158902</td>\n",
" <td>-542.377129</td>\n",
" <td>8.021968</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Protein Z_scores E_native E_mgs Std_mg\n",
"0 1BD2_1 0.900316 -565.363569 -558.334725 7.807089\n",
"1 6BJ8_1 0.340620 -559.377083 -556.341055 8.913235\n",
"2 2JCC_1 0.151485 -578.632012 -577.373781 8.305978\n",
"3 1AO7_1 0.549733 -554.882868 -549.744350 9.347298\n",
"4 1LP9_1 0.018086 -572.456799 -572.294553 8.970942\n",
"5 3QDJ_1 0.571400 -548.835394 -544.666126 7.296581\n",
"6 3GSN_1 0.721878 -546.292261 -539.487997 9.425782\n",
"7 1QRN_1 0.039428 -555.365484 -555.071793 7.448888\n",
"8 3PWP_1 0.253560 -570.922191 -568.716016 8.700786\n",
"9 5W1W_1 0.751747 -563.412353 -557.502728 7.861194\n",
"10 1QSE_1 0.578690 -559.544033 -554.102176 9.403750\n",
"11 4EUP_1 0.015861 -563.958000 -563.817637 8.849680\n",
"12 5TEZ_1 0.454085 -579.688507 -576.275882 7.515384\n",
"13 3D39_1 0.913302 -569.280411 -560.054925 10.101248\n",
"14 6EQA_1 0.607607 -559.131031 -553.943662 8.537371\n",
"15 2BNR_1 0.702593 -570.397373 -563.957349 9.166085\n",
"16 6BJ2_1 0.468335 -556.645981 -552.711043 8.401973\n",
"17 6BJ3_1 -0.096069 -563.400937 -564.108460 7.364763\n",
"18 5NME_1 0.644450 -558.065141 -552.460955 8.696081\n",
"19 5MEN_1 0.314084 -550.918059 -548.400112 8.016793\n",
"20 2VLJ_1 0.322381 -542.011146 -539.421195 8.033830\n",
"21 2VLK_1 0.350059 -542.555997 -539.493606 8.748207\n",
"22 2J8U_1 -0.288170 -574.485025 -576.761867 7.901027\n",
"23 2GJ6_1 0.356224 -570.758928 -567.118995 10.218105\n",
"24 1OGA_1 0.236676 -552.479891 -550.437823 8.628107\n",
"25 2F54_1 0.103204 -548.348960 -547.472613 8.491401\n",
"26 5D2L_1 0.565962 -558.635666 -553.753495 8.626318\n",
"27 2F53_1 0.606024 -562.123693 -556.408688 9.430324\n",
"28 3QEQ_1 0.621955 -551.620007 -545.238092 10.261056\n",
"29 1QSF_1 0.481709 -566.452834 -562.124111 8.986185\n",
"30 2UWE_1 0.876791 -586.309550 -579.238061 8.065195\n",
"31 5EUO_1 0.136994 -550.526436 -549.302675 8.932927\n",
"32 3H9S_1 0.546885 -555.893794 -551.095308 8.774218\n",
"33 3D3V_1 0.610284 -542.475441 -536.054752 10.520817\n",
"34 2BNQ_1 0.285020 -563.839068 -561.332622 8.793945\n",
"35 4FTV_1 -0.401177 -539.158902 -542.377129 8.021968"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"os.chdir(\"/Users/weilu/Research/server/sep_2019/peptide_optimization_trial_2/optimization/\")\n",
"# gamma_file_name = \"gamma_iter1_combined_mar06.dat\"\n",
"# gamma_file_name = \"/Users/weilu/Research/server/sep_2019/peptide_optimization/saved_gammas/cutoff100\"\n",
"gamma_file_name = \"/Users/weilu/Research/server/sep_2019/saved_gammas/original_gamma\"\n",
"\n",
"data = validate_hamiltonian_wei(\"phi_list.txt\", \"protein_list_small\", gamma_file_name, \"shuffle\", 1000, mode=0)\n",
"data\n"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [],
"source": [
"gamma_file_name = \"/Users/weilu/Research/server/sep_2019/peptide_optimization/saved_gammas/original_gamma\"\n",
"original_gamma = np.loadtxt(gamma_file_name)"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"-559.5053481482374"
]
},
"execution_count": 18,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"np.dot(A_prime, original_gamma)"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [],
"source": [
"# we want to impose additional contraint so that A' * gamma = constnat.(-562.23)\n",
"c = np.dot(A_prime, original_gamma)\n",
"B_inv = filtered_B_inv\n",
"lambda_2 = (A_prime.dot(B_inv).dot(A) - c) / (A_prime.dot(B_inv).dot(A_prime) )\n",
"gamma_new = B_inv.dot(A-A_prime*lambda_2)"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"-559.5053481482375"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"np.dot(A_prime, gamma_new)"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"collapsed": true
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABLIAAAMsCAYAAABA14tEAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzs3X2UVXW9P/DPmYEjjAMICYISEqAgomnkEwpYGpWPKVCgqZfyOmaalVm2rFa07GG5rtduF3KNlqt8KE2vqEmZqVl6NTO0QElMjVEywAcIZng4MDO/P7ryEzkoM2cPe+85r9daZy3d3zP7++Y7Awyf+X72t9De3t4eAAAAAJBxNWkHAAAAAIAdoZAFAAAAQC4oZAEAAACQCwpZAAAAAOSCQhYAAAAAuaCQBQAAAEAuKGQBAAAAkAsKWQAAAADkgkIWAAAAALmgkAUAAABALihkAQAAAJALClkAAAAA5IJCFgAAAAC5oJAFAAAAQC70SDvAjnryySejtbU1dtlll7SjAAAAABGxcePGqK2tjXHjxqUdZadqamqK9evXpx2jrN69e8fee++ddowuk5tCVmtra2ze3BabN6edpDIbNqSdIBl1dWknSM7f/552gmS8/HLaCZKx335pJ0hGz55pJ0hGsZh2gmSsWJF2guT06ZN2gmR0l8/J7runnSAZ3eXnhN3l+6zu8vlob087AW/WXb5fHDgw7QS8UaHQlnaEVKxfvz7Wv/xy9H722bSjbGX9qFHd/jdJbgpZu+yyS2zeHFFTMybtKBVZtiztBMk48MC0EyTn5pvTTpCMG25IO0EyfvGLtBMkY889006QjMGD006QjNtvTztBco46Ku0Eybj++rQTJOO009JOkIzhw9NOkIzly9NOkIyhQ9NOkIy8/wD6jWq6yQNZ7rgj7QTJOPPMtBMko7t8XfXo8XS3KcB3VO9nn40xn/hE2jG28vS113b7QlY3+a0DAAAAQHeXmx1ZAAAAAJlRKGRva12hkHaCLpexFQcAAACA8hSyAAAAAMgFrYUAAAAAnZG11sIqYMUBAAAAyAWFLAAAAAByQWshAAAAQEc5tTAVGVtxAAAAAChPIQsAAACAXNBaCAAAANAZWWstrAJduuK33XZbjB49OhYtWtSV0wAAAABQBZQOAQAAAMgFrYUAAAAAnaG1cKez4gAAAADkgkIWAAAAALmQqdbCUqkUpVKp7Fhra2u0txd2ciIAAACAMgqF7LUWFrp/3SRThazGxsaYM2dO2bHZs2fHgAGDY+DAsTs5FQAAAABZkKlCVkNDQ8yaNavsWFNTU6xf3/0riwAAAACUl6lCVrFYjGKxWHastra2GnbIAQAAAHmRtdbCKmDFAQAAAMgFhSwAAAAAtvHLX/4yPvaxj8V73/vemDBhQpx99tmxaNGird5z5513xoknnhgHHnhgvO9974vvfe97sWnTpi7LpJAFAAAA0FGvn1qYpVeCz2S65ZZb4rOf/Wy8613viv/8z/+Mr3/967F27dqYOXNmPP7441vec/HFF8ehhx4ac+fOjalTp0ZjY2PMnj07sRxv1qXPyDr11FPj1FNP7copAAAAAEjYnDlz4qijjorvfOc7W65NmDAhjjnmmLjmmmviu9/9blxxxRVxwgknxFe/+tWIiJg4cWLU1dXF5ZdfHrNmzYqRI0cmnsuOLAAAAAC2WL9+fUyZMiVmzpy51fX6+voYMmRIrFixIhYuXBirVq2KD3/4w1u954QTToj29va4//77uyRbpk4tBAAAAMiNbnpqYe/evePSSy/d5vpzzz0Xf/3rX+Pkk0+OZ599NiIiRowYsdV7Bg0aFHV1dfH88893STaFLAAAAIBuoq2tLZqbm7c7XiwWo1gsdvi+a9eujYsvvjh69OgRZ599dtx7770REdGnT59t3ltfX/+WGSqhkAUAAADQTaxcuTJOOeWU7Y6ff/75ccEFF3TonitWrIhzzz03/vrXv8aVV14ZI0aMiLa2trf8mEKCD55/I4UsAAAAgI56/dTCLCkUYtCgQbFgwYLtvqWju7H+/Oc/x/nnnx8tLS0xd+7cmDx5ckRE9O3bNyIiWlpaYuDAgVt9THNzc9mdWklQyAIAAADoJmpqaqK+vj6Re82fPz8uueSS2H333eMnP/lJjBkzZsvY6ycSLl26NIYPH77l+ooVK2LdunUxatSoRDK8WcZKhwAAAACk7Z577okvfOELse+++8Ytt9yyVRErIuLggw+Ofv36xfz587e6Pn/+/CgUCjFx4sQuyWVHFgAAAEBnZK21MCFr1qyJSy+9NOrq6uIzn/lMLFu2LJYtW7ZlvFevXjFmzJj49Kc/Hd/61reiV69eMWXKlFi4cGF8//vfj6lTp3bZjiyFLAAAAAC2ePDBB2PNmjUREXHOOedsM77PPvvEXXfdFWeddVb07Nkzrrvuupg3b14MGjQoGhoa4rzzzuuybApZAAAAAGxx/PHHx/HHH79D7z3ttNPitNNO6+JE/59CFgAAAEBHZfTUwu4uYysOAAAAAOXlakdWz54RAwemnaIyxWLaCZJRKqWdIDlz5qSdIBnXz5j/9m/KgaeG7dj21az7wx/STpCMd//hmrQjJGLo0H9PO0JiRoxIO0EyvvGNtBMko1evtBMko7v8vX7ccWknSMb/PZIk99ra0k6QnCHxj7QjJGLMd4akHSER/X/WmHaERPzvuIa0I0Au5aqQBQAAAJAZWWstrAJWHAAAAIBcUMgCAAAAIBe0FgIAAAB0htbCnc6KAwAAAJALClkAAAAA5ILWQgAAAICOKhSy11pYKKSdoMtlbMUBAAAAoDyFLAAAAAByQWshAAAAQGdkrbWwClhxAAAAAHJBIQsAAACAXKiokPXJT34yxo0bF6+99tp23/Pzn/88Ro8eHb/61a8qmQoAAAAgO14/tTBLL6cWvrUZM2bEpk2b4uc///l233PrrbfGoEGD4phjjqlkKgAAAACqXEWFrPe9730xaNCguP3228uOv/jii/Hoo4/GtGnTokcPz5UHAAAAupG0d2C9+VUFKvpV9ujRI6ZPnx6LFy+OJUuWbDN+6623Rk1NTXz0ox+tZBoAAAAAqPxh79OnT4/a2tqYN2/eVtdbW1tj3rx5cfTRR8eQIUMqnQYAAACAKldxIWvIkCExadKk+PnPfx6bN2/ecv2hhx6KFStWxIwZM3b4XqVSKZqbm8u+Wltbo729rdK4AAAAAJXzsPdUJNJAOXPmzHjllVfid7/73ZZrt956a7zzne+MiRMn7vB9GhsbY/z48WVfixYtildeWZlEXAAAAAByKJEnsE+cODH22muvuP322+P9739/vPrqq/Gb3/wmLrzwwih0oBrY0NAQs2bNKjvW1NQUmzd3/8oiAAAAAOUlUsiqqamJ6dOnx9y5c2P16tVxxx13RETE1KlTO3SfYrEYxWKx7FhtbW20tlYcFQAAACAZVXJSYJYktuLTpk2L9vb2+PWvfx133nlnfPCDH4wBAwYkdXsAAAAAqlxihayBAwfGMcccE9dee2385S9/iZkzZyZ1awAAAABIrpAVETFjxox4/vnnY9999433vve9Sd4aAAAAIDucWpiKRJ6R9boJEybEkiVLkrwlAAAAAEREwjuyAAAAAKCrJLojCwAAAKBqOLVwp7PiAAAAAOSCQhYAAAAAuaC1EAAAAKAztBbudFYcAAAAgFxQyAIAAAAgF7QWAgAAAHRUoZC91sJCIe0EXS5jKw4AAAAA5SlkAQAAAJALWgsBAAAAOiNrrYVVwIoDAAAAkAu52pG1dm3EkiVpp6jMM8+knSAZhx6adoLk/OlPaSdIxvDhx6cdIREblqWdIBm9eqWdICEzzk47QSJe+EbaCZLz9NNpJ0jGs8+mnSAZgwalnSAZu++edoJkdJffH0OHpp0gGd1pk8LKmiFpR0jEH/6QdoJkTPtoQ9oREnHdJWknSMbJJ0f06ZN2CqpJrgpZAAAAAJng1MJUZGzFAQAAAKA8hSwAAAAAckFrIQAAAEBnZK21sApYcQAAAAByQSELAAAAgFzQWggAAADQUU4tTEXGVhwAAAAAylPIAgAAACAXtBYCAAAAdEbWWgurgBUHAAAAIBcSK2SdccYZ8f73vz+p2wEAAADAVrQWAgAAAHSUUwtTkbEVBwAAAIDyFLIAAAAAyAWthQAAAACdkbXWwiqQqUJWqVSKUqlUdqy1tTXa27t/rycAAAAA5WWqkNXY2Bhz5swpOzZ79uzo23dwRIzduaEAAAAAyIRMFbIaGhpi1qxZZceamppi1apCtLTs5FAAAAAA5Wgt3OkyVcgqFotRLBbLjtXW1lbDKZIAAAAAbIfSIQAAAAC5kOiOrObm5vjRj35Uduz000+Pnj17JjkdAAAAQDoKhey1FlZBK1uihax//vOf8e1vf7vs2PTp0xWyAAAAAOi0xApZ119/fVK3AgAAAIBtZOph7wAAAAC5kbXWwipgxQEAAADIBYUsAAAAAHJBayEAAABARzm1MBUZW3EAAAAAKE8hCwAAAIBc0FoIAAAA0BlZay2sAlYcAAAAgFxQyAIAAAAgF7QWAgAAAHSUUwtTkbEVBwAAAIDy7MgCAAAA6Iys7ciqAlYcAAAAgFzI1Y6sHj0idt897RSVee97006QjOXL006QnA99KO0EyVizJu0EyWhuTjtBMsaOTTtBQrrJT5hOXdiedoTElEppJ0jG4MFpJ0hGd/kzq1hMO0EyusufvUuXpp0gGd3l6yqi+/zZe+ihaSdIRv8N/0g7QiL+7d+GpB0hET1yVVWgO/AlBwAAANBRHvaeioytOAAAAACUp5AFAAAAQC5oLQQAAADojKy1FlYBKw4AAABALihkAQAAAJALWgsBAAAAOkNr4U5nxQEAAADIBYUsAAAAAHJBayEAAABARxUK2WstLBTSTtDlMrbiAAAAAFBeIjuyLrnkkpg3b952x/fff/+47bbbkpgKAAAAgCqVaGvhzTffXPZ6XV1dktMAAAAApC9rrYVVINFC1kEHHZTk7QAAAABgC6VDAAAAAHIh0R1Zmzdv3uZaoVCI2traJKcBAAAASFcVnVq4efPm+PjHPx5jx46Nr33ta1uuP/fcc3HccceV/Zh77rkn9t5778SzJFrI2n///be5ttdee8X999+/Qx9fKpWiVCqVHWttbY329u5/jCQAAABAVqxbty4uvvjieOKJJ2Ls2LFbjT355JMREdHY2Bi77bbbVmNDhgzpkjyJFrJuvfXWba4Vi8Ud/vjGxsaYM2dO2bHZs2fHbrsNjl12GVt2HAAAAIDkPPDAA/Htb387Vq9eXXb8qaeeiv79+8fRRx+90zIlWsg64IADKvr4hoaGmDVrVtmxpqamWLu2EOvXVzQFAAAAQDKy1lqYoDVr1sS5554bH/zgB+PLX/5yTJ48eZv3LF68eJtdWl0t0UJWpYrF4nZ3cNXW1nZVqycAAAAAb9CrV6+YP39+jBw5sux4e3t7LF68OPbbb78444wzYtGiRVFbWxtHH310fOlLX4pBgwZ1Sa5MFbIAAAAA6Ly2trZobm7e7vhbbSJ68/u2V8SKiFi6dGm0tLTEsmXL4vzzz48LL7wwFi9eHHPnzo0//elPMW/evOjbt2+nfg1vRSELAAAAoKMyemrhypUr45RTTtnuW84///y44IILKp5q4MCB8cMf/jBGjhy55cHu733ve2PfffeNs846K37yk5/EueeeW/E8b6aQBQAAANBNDBo0KBYsWLDd8Y4cyvdW6uvr46ijjtrm+uGHHx719fWxePHiROZ5s0RKh9/5zndiyZIlSdwKAAAAgE6qqamJ+vr67b6SKmQ988wz8dOf/jTWrl271fW2trbYtGlTDBgwIJF53syOLAAAAIDOyFpr4U70wgsvxNe//vWIiJg5c+aW6/fcc09s3LgxJkyY0CXzKmQBAAAA0CGTJ0+O8ePHx+WXXx4tLS2x//77x6JFi+Kqq66Ko446KqZMmdIl8ypkAQAAANAhPXv2jMbGxrjqqqvi5ptvjuXLl8fAgQPjzDPPjE996lNdNq9CFgAAAEBHZfTUwq5S7tnoffr0iS9+8YvxxS9+scvmfbOMrTgAAAAAlKeQBQAAAEAuaC0EAAAA6IystRZWASsOAAAAQC4oZAEAAACQC1oLAQAAADpDa+FOZ8UBAAAAyAWFLAAAAAByIVethYVC/nftPf542gmSMXhw2gmS89JLaSdIRn192gmSUSqlnSAZCxemnSAZa55sTztCItY1p50gOa+9lnaCZNTVpZ0gGevWpZ0gGQMGpJ0gGU8+mXaCZHSX3x8bNqSdIDm9eqWdIBltbWknSMY/YkjaERLRXT4fVS2LRYpCIe0EXS5jKw4AAAAA5SlkAQAAAJALuWotBAAAAMiMrLUWVgErDgAAAEAuKGQBAAAAkAtaCwEAAAA6yqmFqcjYigMAAABAeQpZAAAAAOSC1kIAAACAzshaa2EVsOIAAAAA5IJCFgAAAAC5oLUQAAAAoKOcWpiKxApZS5cujRtuuCEefPDBWL58eey6664xcuTImDFjRhx33HFRqILFBAAAAKDrJFLIuuuuu+IrX/lKvPOd74wzzzwzRowYES0tLfGrX/0qPv/5z8dDDz0U3/zmN6Mma5VKAAAAAHKj4kLW4sWL48tf/nIcfvjhMXfu3CgWi1vGjj322Nhrr73iqquuisMPPzxOPvnkSqcDAAAAyAYbdna6igtZV199dbS2tsbs2bO3KmK97txzz43Vq1dHv379Kp0KAAAAgCpWcSHrgQceiP322y/23HPPsuO9evWKr3/965VOAwAAAJAdHvaeiooKWa+99lqsX78+hg0blkiYUqkUpVKp7Fhra2u0t3f/TwgAAAAA5VVUyKqtrY2IfxWZktDY2Bhz5swpOzZ79uzo339w9Oo1NpG5AAAAAMiXigpZ/fr1iz59+sSyZcve8n3Lly+PQYMGve2phQ0NDTFr1qyyY01NTdHcXIgNGzodFwAAACA5WWstrAIVr/jkyZNj8eLF8dJLL5Ud37RpU5x88slx2mmnve29isVi1NfXl33V1tZGoeALBAAAAKBaVVwZOvvss6O2tjZmz55d9vlWc+bMidWrV8fUqVMrnQoAAACAKlbxqYX77bdfXHrppXHZZZfF9OnTY+bMmTF8+PB47bXX4q677or77rsvpk2bFtOmTUsiLwAAAEA2aC3c6SouZEVEnHbaabHffvvFDTfcEFdffXW88sor0adPnxg5cmR873vfiylTpkShCo6ABAAAAKDrJFLIiog4+OCD4+CDD07qdgAAAACwlcQKWQAAAABVo1DIXmthFXTDZWzFAQAAAKA8hSwAAAAAckFrIQAAAEBnZK21sApYcQAAAAByQSELAAAAgFzQWggAAADQUU4tTEXGVhwAAAAAylPIAgAAACAXtBYCAAAAdEbWWgurgBUHAAAAIBcUsgAAAADIhVy1FhYKEcVi2ikqM2BA2gmS0Z12Ty5dmnaCZIwYkXaCZOy+e9oJkrFmTdoJkjFsWNoJkrFwYdoJktOrV9oJktFdfo8MHZp2gmSsW5d2gmTk/fvE13WX77Pa2tJOkJxSKe0EyeiRq3/9bV93+T3SXT4fVXBI3vY5tTAVGVtxAAAAAChPIQsAAACAXOgmmxkBAAAAdrKstRZWASsOAAAAQC4oZAEAAACQC1oLAQAAADrKqYWpyNiKAwAAAEB5ClkAAAAA5ILWQgAAAIDOyFprYRWw4gAAAADkgkIWAAAAALmgtRAAAACgM7QW7nSdWvEzzjgjRo8eHRMnToy2tray73nqqadi9OjRMXr06Fi0aFFFIQEAAACg06XDmpqaWLlyZTz66KNlx++4445OhwIAAACAN+t0IWv48OExcODAmD9//jZjra2t8Ytf/CL233//isIBAAAAZFKh8K/Wwiy9CoW0V6XLdbqQVVtbG8cdd1zcc889USqVthp7+OGHY/Xq1XH88cdXHBAAAAAAIio8tfDEE0+Mf/7zn/Hggw9udf3OO++Mo446Kvr3719ROAAAAAB4XUWFrAMOOCCGDx8ed91115Zr69evj3vvvTdOPvnkDt+vVCpFc3Nz2Vdra2u0t5d/sDwAAADATpd2K+GbX1Wg4l/liSeeGL/5zW+ipaUlIiJ+/etfR48ePeKYY47p8L0aGxtj/PjxZV+LFi2KVatWVhoXAAAAgJzqUekNTjrppPjv//7vuO++++Kkk06KO++8Mz70oQ9FsVjs8L0aGhpi1qxZZceampqipaUQra2VJgYAAAAgjyouZA0bNiwOOuiguOuuu+LII4+MRx55JH784x936l7FYnG7BbDa2tpqePg+AAAAkAevn1qYJVVQOElkxU888cR4+OGH48Ybb4w99tgjxo8fn8RtAQAAAGCLRApZxx13XLS3t8fVV18dJ510UhSqoAIIAAAAwM6VSCFrwIABMWHChNi0aVOnTisEAAAAyJ20TymswlMLO/WMrOuvv36ba9dcc80210499dQ49dRTOzMFAAAAAGylOsp1AAAAAORexacWAgAAAFQdpxamImMrDgAAAADlKWQBAAAAkAtaCwEAAAA6I2uthVXAigMAAACQCwpZAAAAAOSC1kIAAACAjnJqYSoytuIAAAAAUJ5CFgAAAAC5oLUQAAAAoDOy1lpYBaw4AAAAALmQqx1Z7e0RpVLaKSrT3Jx2gmTU1aWdIDmvvZZ2gmT06pV2gmQMGJB2gmT07Zt2gmR0l6+rH/wg7QTJOeectBMko7v82btuXdoJknFk/Z/TjpCIRTXvTjtCIlavTjtBMvL+ffsbjRuXdoJk/P73aSdIxtixaSdIxrJlaSdIxuDBEfX1aadIkR1ZO50VBwAAACAXFLIAAAAAyIVctRYCAAAAZEKhkL3WwkIh7QRdLmMrDgAAAADlKWQBAAAAkAtaCwEAAAA6I2uthVXAigMAAACQCwpZAAAAAOSC1kIAAACAjnJqYSoytuIAAAAAUJ5CFgAAAADbtXnz5pgxY0Z84xvf2GbszjvvjBNPPDEOPPDAeN/73hff+973YtOmTV2WJfFC1o033hijR4+OadOmJX1rAAAAgOyoqcnWqwusW7cuLrzwwnjiiSe2Gbvlllvi4osvjkMPPTTmzp0bU6dOjcbGxpg9e3aXZInogmdk3XTTTTFmzJhYtGhR/PnPf453v/vdSU8BAAAAQBd74IEH4tvf/nasXr16m7GNGzfGFVdcESeccEJ89atfjYiIiRMnRl1dXVx++eUxa9asGDlyZOKZEi3XPfHEE/HMM8/ExRdfHAMHDozrrrsuydsDAAAAsBOsWbMmzj333BgzZkzccccd24wvXLgwVq1aFR/+8Ie3un7CCSdEe3t73H///V2SK9EdWT/72c9it912i8MOOyxOPvnk+PGPfxyXXHJJDBw4MMlpAAAAANLVzU8t7NWrV8yfP3+7u6qeffbZiIgYMWLEVtcHDRoUdXV18fzzzyeW5Y0SW/E1a9bEL37xizjppJOiZ8+e8dGPfjQ2b94cN998c1JTAAAAAPAW2traorm5ebuvUqm0Q/cpFotv2Rq4du3aiIjo06fPNmP19fXR3NzcuV/A20hsR9Ydd9wRGzZsiI997GMREbH33nvH4YcfHjfddFM0NDREz5493/YepVJpuwva2toa7e3JVRYBAAAAupuVK1fGKaecst3x888/Py644IKK52lra3vL8UKCu8PeKLFC1s9+9rMYN25cDBo0KNasWRMR/+qLvPTSS+Puu++OE0888W3v0djYGHPmzCk7Nnv27Ojff3D06jU2qcgAAAAAnZe11sL4V2vfggULtjteLBYTmadv374REdHS0rLNI6Wam5vL7tRKQiKFrMcffzyeeeaZiIg45JBDthm/4YYbdqiQ1dDQELNmzSo71tTUFM3NhdiwobKsAAAAAN1VTU1N1NfXd/k8r7cdLl26NIYPH77l+ooVK2LdunUxatSoLpk3kULWzTffHL169Yqrrroqamtrtxq77bbb4vbbb49FixbFAQcc8Jb3KRaL260M1tbWJvnMMgAAAAA66eCDD45+/frF/Pnz4+ijj95yff78+VEoFGLixIldMm/Fhaw1a9bE3XffHccee2xMmDBhm/EBAwbE7bffHtdff31cfvnllU4HAAAAkL5ufmrh2ykWi/HpT386vvWtb0WvXr1iypQpsXDhwvj+978fU6dOze6OrNtvvz02bNgQJ598ctnxffbZJw466KD45S9/GV/60pfiHe94R6VTAgAAAJCys846K3r27BnXXXddzJs3LwYNGhQNDQ1x3nnnddmcFReyfvazn8XAgQPjyCOP3O57pk+fHpdeemncdNNN8elPf7rSKQEAAADYiZYsWVL2+mmnnRannXbaTstRcSHrrrvuetv3TJs2LaZNm1bpVAAAAADZkbXWwipgxQEAAADIBYUsAAAAAHKh4tZCAAAAgKqktXCns+IAAAAA5IJCFgAAAAC5oLUQAAAAoKMKhey1FhYKaSfochlbcQAAAAAoTyELAAAAgFzQWggAAADQGVlrLawCVhwAAACAXFDIAgAAACAXtBYCAAAAdJRTC1ORsRUHAAAAgPJytSOrri5i5Mi0U1Rm2bK0EySjR66+ct7apElpJ0jG4sVpJ0hG1n6g0VmH3PvttCMkY+iZaSdIxBe/uFfaERIzeHDaCZJxxJ5NaUdIRFPsnXaERPx59bvTjpCId7f9Oe0Iifjfmu7x+aivTztBcl54Ie0EyejbN+0Eyegun48RI9JOkIy2trQTUG26UTkCAAAAYCfqLj+JzxErDgAAAEAuKGQBAAAAkAtaCwEAAAA6yqmFqcjYigMAAABAeQpZAAAAAOSC1kIAAACAzshaa2EVsOIAAAAA5IJCFgAAAAC5oLUQAAAAoKOcWpiKjK04AAAAAJRX8Y6sSy65JObNm7fVtZqamqirq4t99tknzjzzzDjuuOMqnQYAAACAKpdYa+HNN9+85b/b2tpi1apV8cMf/jA+97nPRalUio985CNJTQUAAACQvqy1FlaBxApZBx100DbXDjvssJg8eXL84Ac/UMgCAAAAoCJdWjqsr6+PESNGxNIgTWbOAAAgAElEQVSlS7tyGgAAAACqQJeeWlgqleLFF1+MPffcsyunAQAAANj5tBbudIkVsjZv3rzlv18vYM2dOzdWrVoV55133g7do1QqRalUKjvW2toabW3d/xhJAAAAAMpLrJC1//77b3NtwIABcdFFF8UZZ5yxQ/dobGyMOXPmlB2bPXt2DBw4OPbaa2xFOQEAAADIp8QKWbfeeuv/v2mPHtGvX78OtxQ2NDTErFmzyo41NTVFa6sdWQAAAEAGFArZay0sdP+6SWKFrAMOOKDiexSLxSgWi2XHamtro7294ikAAAAAyKkufdg7AAAAQLeVtR1ZVcCKAwAAAJALClkAAAAA5ELFhazvfOc7sWTJkiSyAAAAAOTD6w97z9KrCh72bkcWAAAAALmgkAUAAABALji1EAAAAKAznFq401lxAAAAAHJBIQsAAACAXNBaCAAAANBRr59amCVOLQQAAACAbFDIAgAAACAXtBYCAAAAdEbWWgurgBUHAAAAIBcUsgAAAADIBa2FAAAAAB1VKFTFKYFZk6tC1qZNEa+8knaKyrw7/px2hEQ82vzutCMk5oUX0k6QjLa2tBMko1evtBMk47Fjv5x2hESMG5B2gmT8/p60EyTnwAPTTpCMhx7aO+0IiZgyJe0Eydhtt7QTJON/l3WP70/q6tJOkIzly9NOkJy+fdNOkIy8/1vqdcOHp50gGYsXp50gGXvsEbHrrmmnoJpoLQQAAAAgF3K1IwsAAAAgM7J2amF3adV5CxlbcQAAAAAoTyELAAAAgFzQWggAAADQGVoLd7qMrTgAAAAAlKeQBQAAAEAuaC0EAAAA6KhCIXuthYVC2gm6XMZWHAAAAADKU8gCAAAAIBe0FgIAAAB0RtZaC6uAFQcAAAAgFxLZkbVixYq46aab4v7774+XXnopNm7cGHvssUccccQRMWvWrHjXu96VxDQAAAAAVLGKC1kPPfRQXHTRRbHLLrvEzJkz44ADDoiePXvGM888EzfccEPceeedcdVVV8URRxyRRF4AAACA9Dm1MBUVFbL+/ve/x2c/+9nYc88944Ybboi+fftuGTvssMNi6tSpMXPmzPjyl78c9913X9TW1lYcGAAAAIDqVFHp8Jprrom1a9fGt771ra2KWK+rq6uLiy66KMaPHx+rVq2qZCoAAAAAqlxFO7Luvvvu2GeffWLcuHHbfc+kSZNi0qRJlUwDAAAAkD1Zay2sAp0uZK1ZsyZWrVoVhx566DZjra2t0d7evtW12traKLxNr2apVIpSqVR27F/37P69ngAAAACU1+lCVltb23bHTj311Hj66ae3uvbFL34xPvnJT77lPRsbG2POnDllx2bPnh3veMfg2HXXsR0PCwAAAEDudbqQtdtuu0V9fX28+OKL24xdccUVsX79+oiIePnll+NTn/rUDt2zoaEhZs2aVXasqakpNm60IwsAAADIAKcWpqKiZ2RNmTIlbrvttnjuuedi5MiRW66PGjVqy38vW7Zsh+9XLBajWCyWHftXa2LnswIAAACQbxWVDhsaGqK+vj4uvvji7Z5KuGTJkkqmAAAAAICIqHBH1vDhw2POnDlx0UUXxfHHHx/Tp0+Pgw8+OHr37h0vvPBC3H333fHQQw/F3nvvHYccckhSmQEAAADSl7XWwipQUSErIuKII46Iu+66K2655Za4995746abboqWlpYYMGBAHHDAAXHFFVfElClTttsyCAAAAAA7ouJCVkTEgAEDoqGhIRoaGpK4HQAAAABsI5FCFgAAAEDV0Vq401lxAAAAAHJBIQsAAACAXNBaCAAAANBRhUL2WgsLhbQTdLmMrTgAAAAAlKeQBQAAAEAuaC0EAAAA6IystRZWASsOAAAAQC4oZAEAAACQC1oLAQAAADrKqYWpyNiKAwAAAEB5ClkAAAAA5EKuWgvXrYt45pm0U1TmtuffnXaERIwdm3aC5Nx9d9oJkvH+96edIBlPP512gmTU1aWdIBnLl6edIBl5/7vjjXrk6m/u7XvttbQTJOOee9JOkIwLP9KUdoRE/HH53mlHSESxmHaCZPTtm3aC5NTXp50gGStXpp0gGRs2pJ0gGT/5SdoJknHGGREDBqSdIkVZay2sAlYcAAAAgFzoJj/XBQAAANiJPOw9FRlbcQAAAAAoTyELAAAAgFzQWggAAADQGVlrLawCClkAAAAAbGPChAnx6quvbnP9sssui+nTp6eQSCELAAAAgDdZvnx5vPrqq/GZz3wmjjzyyK3Ghg0bllIqhSwAAACAjuvmpxY++eSTERHxgQ98IPbdd9/E7lupjK04AAAAAGlbvHhx9OrVK0aOHJl2lK0oZAEAAACwlaeeeip22223+MIXvhCHHXZYjBs3Ls4444xYuHBhqrm0FgIAAAB0RtZaCyOira0tmpubtzteLBajWCy+7X2eeuqpWLNmTYwcOTJOP/30WL58eTQ2Nsbpp58eN954Yxx44IFJxt5hClkAAAAA3cTKlSvjlFNO2e74+eefHxdccMHb3ufKK6+Murq62H///bdcmzBhQnz4wx+O7373u3HttdcmkrejKi5kXXLJJTFv3ry3fd91110Xhx12WKXTAQAAALAdgwYNigULFmx3fEd2Y0VEHHLIIdtcGzBgQLznPe+JJ554otP5KlVxIeu8886LGTNmbPn/W265JW699daYM2dODBw4cMv1UaNGVToVAAAAQHZksLWwpqYm6uvrK7rHa6+9Fvfdd18cdNBBsc8++2w1ViqVYsCAARXdvxIVF7KGDRsWw4YN2/L/Dz74YERE7LfffjF06NBKbw8AAADATlQoFOJrX/tafOhDH4orr7xyy/W///3vsWDBgpg2bVpq2TwjCwAAAIAt+vfvH5/4xCfiBz/4Qey2227xgQ98IJYvXx5z5syJvn37xnnnnZdaNoUsAAAAgI4qFLLXWlgoJHariy66KIYOHRo//elPY968edGrV6+YOHFifP7zn893a2GSSqVSlEqlsmOtra3R3p7cJwQAAACA8mpqamLmzJkxc+bMtKNsJVOFrMbGxpgzZ07ZsdmzZ0ffvoMjYuzODQUAAABAJmSqkNXQ0BCzZs0qO9bU1BSrVhVi7dqdHAoAAACgnKy1FlaBTBWyisViFIvFsmO1tbVJtnoCAAAAkDNKhwAAAADkQqZ2ZAEAAADkQjc/tTCrMrbiAAAAAFBe4oWsCy64IJYsWRJDhw5N+tYAAAAAVDGthQAAAACdkbXWwipgxQEAAADIBYUsAAAAAHJBayEAAABARzm1MBUZW3EAAAAAKE8hCwAAAIBc0FoIAAAA0BlZay2sAlYcAAAAgFxQyAIAAAAgF7QWAgAAAHSUUwtTkbEVBwAAAIDyFLIAAAAAyIVctRYWixFDh6adojJjx6adIBmrV6edIDlHH512gmR0l6+ttra0EyTjpZfSTpCMdw1qSTtCIsaM2TXtCIkZPjztBLxRd/mzd1XfvdOOkIg990w7QTI2bEg7QTLWrUs7QXLq69NOkIxRo9JOkIy6urQTJOO889JOkIzu8vnorPbo/q18WWNHFgAAAAC5oJAFAAAAQC7kqrUQAAAAIAva27P3aJT29u5/cKEdWQAAAADkgkIWAAAAALmgtRAAAACgE7LWWlgN7MgCAAAAIBcUsgAAAADIBa2FAAAAAB3k1MJ02JEFAAAAQC4oZAEAAACQC4m1FjY1NUVjY2M88sgj8fLLL0fv3r1jn332iY985CMxderUqK2tTWoqAAAAgNRlrbWwGiRSyHruuefiYx/7WAwfPjwuvPDCGDJkSDQ3N8dvf/vb+NrXvhZ//OMf4/LLL09iKgAAAACqVCKFrGuvvTYiIq6//vro3bv3luvHHHNM7LLLLnHdddfFJz7xiRgzZkwS0wEAAABQhRIpZL3yyitRKBSitbV1m7GPf/zjMXDgwKirq0tiKgAAAIDUZfXUwu4ukYe9H3PMMbFmzZqYNm1aXH311bFw4cLYtGlTRETsvffecc4558SwYcOSmAoAAACAKpXIjqyPfvSjsXr16rjqqqviiiuuiIiIXXbZJQ4++OA47rjj4tRTT42ePXu+7X1KpVKUSqWyY62trdHeXkgiLgAAAAA5lNipheecc058/OMfj4cffjgee+yxWLBgQTz22GPx+9//Pm666ab40Y9+FP369XvLezQ2NsacOXPKjs2ePTv69x8c9fVjk4oMAAAA0GlZay2sBokVsiIi6urq4thjj41jjz02IiJWrVoVc+fOjeuvvz6uueaa+MIXvvCWH9/Q0BCzZs0qO9bU1BQtLYX4v45FAAAAAKpMxc/IWrFiRUycODGuvvrqbcb69+8fX/nKV2KPPfaIZ5555m3vVSwWo76+vuyrtrY2CoVEHukFAAAAQA5VXBkaOHBgFIvFuOmmm2L16tXbjL/yyiuxZs2aGDNmTKVTAQAAAGTC66cWZulVDacWVtxaWFNTE5dddlk0NDTERz7ykTj99NNj//33j9ra2liyZEn8+Mc/jj322GO7LYMAAAAAsCMSeUbWEUccEfPmzYtrr702brnllpg7d260tbXFXnvtFccff3z8+7//e/Tp0yeJqQAAAAAywcPed77EHvY+cuTI+OY3v5nU7QAAAABgK56eDgAAAEAuJLYjCwAAAKCaaC3c+ezIAgAAACAXFLIAAAAAyAWthQAAAAAd1N6evdbC9va0E3Q9O7IAAAAAyAWFLAAAAAByQWshAAAAQCdkrbWwGtiRBQAAAEAuKGQBAAAAkAtaCwEAAAA6yKmF6bAjCwAAAIBcUMgCAAAAIBdy1VrY1haxYUPaKSrz8MNpJ0jG8OFpJ0jOs8+mnSAZzz+fdoJknHpq2gmSMXhw2gmScfNdu6YdIRHd5c/e7uTpp9NOkIzNm9NOkIy6urQTJOPqq9NOkIyzz047QTK6y9dVRESxmHaCZPz+92knSMZLL6WdIBnLlqWdIBlHHBHRr1/aKdKTtdbCamBHFgAAAAC5oJAFAAAAQC7kqrUQAAAAIAucWpgOO7IAAAAAyAWFLAAAAAByQWshAAAAQCdkrbWwGtiRBQAAAEAuKGQBAAAAkAtaCwEAAAA6yKmF6bAjCwAAAIBcUMgCAAAAIBd2uJB10UUXxdixY6O5uXmbsQ9+8IMxevTo+NGPfrTNWGNjY4wePTqefvrpioICAAAAZElbW7Ze1WCHC1kTJ06M1tbWePzxx7e63tTUFEuXLo3+/fvHb37zm20+7tFHH4099tgjxowZU3laAAAAAKrWDheyjjzyyCgUCvHHP/5xq+sPPPBA9O7dO/7t3/4tFixYsNWOrVKpFI8//nhMnDgxucQAAAAAVKUdLmQNHDgw9t1333jssce2uv7b3/42Dj300Dj22GNj06ZN8dBDD20ZW7hwYaxfvz4mTZqUXGIAAACADEi7lVBr4ds46qijYtGiRbFx48aIiGhpaYk//OEPMXny5Bg1alTstdde8cADD2x5/+9///vo0aNHHHnkkYmGBgAAAKD6dKiQNXHixNi0aVP86U9/ioiIRx55JDZt2hSTJ0/eMv673/0u2v6vDPjoo4/Ge97znqivr9+h+5dKpWhubi77am1tjfb2KikvAgAAALCNDhWyxo8fH717997SXvjAAw/EqFGjYujQoRERMXny5Hj11Vfjqaeeio0bN8af/vSnDj0fq7GxMcaPH1/2tWjRoli9emVH4gIAAAB0ifb29FsJ3/xqb097Vbpej468uVgsxiGHHLLlge+//e1v44QTTtgyfvjhh0exWIxHHnkkmpubo1QqbdmttSMaGhpi1qxZZceamppi7dpCtLR0JDEAAAAA3UWHClkR/3pO1n/913/FU089FStXroyjjz56y1hdXV0ccsgh8dhjj8WGDRtijz32iNGjR+/wvYvFYhSLxbJjtbW1USh0NC0AAAAA3UWHWgsj/lXIamlpiRtvvDHq6+tj/PjxW41PmjQp/vKXv8Rjjz3mtEIAAACg20q7ldCphTtg5MiRMWTIkLjzzjvjyCOPjB49tt7UNWnSpHj55ZfjiSee6FBbIQAAAAC8lQ4XsiL+tSvrjacVvtGIESNi2LBhERFxxBFHVJYOAAAAAP5Ph5+RFRFx2WWXxWWXXbbd8V//+tedDgQAAACQda+fWpgl1XBqYad2ZAEAAADAzqaQBQAAAEAudKq1EAAAAKDaZa21sBrYkQUAAABALihkAQAAAJALWgsBAAAAOsiphemwIwsAAACAXFDIAgAAACAXtBYCAAAAdELWWgurgR1ZAAAAAOSCQhYAAAAAuaC1EAAAAKATtBbufLkqZPXrF3HooWmnqMykSWkn4M3e8560EyRj5Au/STtCIlYNfV/aERJR0032ux7y0h1pR0jG+09OO0FiPnZCS9oREvG3lbumHSERgwennSAZvV/7e9oREnH11XulHSERGzaknSAZL7yQdoLk7D+ukHaERBzQXf7F/YMfpJ0gES+f++9pR0jE8uVpJ6DadJN/agEAAACQpIULF8ZZZ50V73nPe+Kwww6LL33pS/HKK6+kmilXO7IAAAAAsqC9/V+vLCkkuIH06aefjrPOOisOOuiguOKKK+KVV16JK6+8Mp566qm47bbbolgsJjdZByhkAQAAALCV7373u9G/f/9obGzcUrTab7/9YurUqXHbbbfFjBkzUsmltRAAAACALUqlUjz88MNx7LHHbrXzaty4cTF8+PC47777UstmRxYAAABAJ2TtDIXa2mTu8+KLL8bGjRtjxIgR24y9613vimeeeSaZiTpBIQsAAACgm2hra4vm5ubtjheLxbd9vtXatWsjIqJPnz7bjO26667R0pLeSdoKWQAAAAAd1N6evR1ZNTURK1eujFNOOWW77zn//PPjggsueMv7tGXtF/YGClkAAAAA3cSgQYNiwYIF2x3fkdMG+/XrFxFRdudVS0tL9O3bt/MBK6SQBQAAANBN1NTURH19fUX3eOc73xk9e/aMv/3tb9uM/e1vf4uRI0dWdP9KOLUQAAAAoBPa2rL1SkqxWIwJEybEvffeG6VSacv1J598MpYuXRqTJk1KbrIOUsgCAAAAYCsXXHBB/OMf/4hPfOITcd9998X//M//xDnnnBOjRo2KadOmpZZLIQsAAACArRxwwAHxwx/+MDZv3hyf+9zn4j/+4z/iqP/X3r3HaT3n/QN/T1MXJSKrkEMqioyNtq3QQXXjXnKIlpaQxezaZW+SatcpQsvtcCtLKYcc7tDPMcdlsXLIobWSlcXKYZ3JKGlqun5/uOshTWpmvjPf6zvzfD4e1+MxXZ+r7+f1fcxcM9f1vj7v72fPPeP6669fp+ts1ZYaXSPrjDPOiNtvvz3OPffcOOyww1YbX758eRxxxBExd+7cmD59euywww41mQ4AAACgIBTiroX5fLLH6969e0ybNi3Zg9ZQjVZkjR49OrbZZpsYN25cvPfee6uNT5kyJWbPnh0jR45UxAIAAACgRmpUyNpggw3ioosuiiVLlsTo0aMj/53S3z//+c+44oorol+/fnHEEUfUOCgAAAAADVuNr5G16667xgknnBDPPfdcTJ06NSIili1bFiNHjoyNN944LrjgghqHBAAAACg0ae9SWFu7FhayRC72/pvf/CY6d+4cl19+eXzwwQdx9dVXxz/+8Y+4+OKLY5NNNkliCgAAAAAauBpd7H2FJk2axMUXXxyDBg2KU089NebMmRPHH3989OjRo0rHKS8vj/Ly8krHKioqoqioKIm4AAAAAGRQIoWsiIj27dvHiBEj4rzzzotddtklTj755CofY+LEiTFhwoRKx8aMGROtW28eO+64U02jAgAAANRIQ9i1sBAlVsiKiOjbt2+cd9550bt372jcuOqHLi0tjWHDhlU6Nn/+fCuyAAAAABqwRAtZNZXL5SKXy1U6VlxcXMdpAAAAACgkBVXIAgAAAMiKQmstbAgS2bUQAAAAAGqbQhYAAAAAmZBoa+FWW20V8+bNS/KQAAAAAAVJa2HdsyILAAAAgExQyAIAAAAgE+xaCAAAAFBF+XzhtRbm82knqH1WZAEAAACQCQpZAAAAAGSC1kIAAACAaii01sKGwIosAAAAADJBIQsAAACATNBaCAAAAFBFdi1MhxVZAAAAAGSCQhYAAAAAmaC1EAAAAKAaCq21sCHIVCHrs88ipk9PO0XNrL9+2gmS0bZt2gmS88oraSdIRnmXvdKOkIiy19NOkIx//zvtBMno1+/AtCMkol09+bmKiLj3LxukHSERjerJmvBPP007QTK6PTI17QiJmN1vdNoRElFWlnaCZJSXp50gORu9Uz8uOjNzWtoJkvFN4+PTjpCI3erJ68VlyyKaNEk7BQ1JPXkZCQAAAEB9l6kVWQAAAACFwK6F6bAiCwAAAIBMUMgCAAAAIBO0FgIAAABUQ6G1FjYEVmQBAAAAkAkKWQAAAABkgtZCAAAAgCqya2E6rMgCAAAAIBMUsgAAAADIBK2FAAAAANVQaK2FDYEVWQAAAABkQo0KWaNGjYpdd911jePjx4+Pjh07xnvvvVeTaQAAAABAayEAAABAdWgtrHtaCwEAAADIBIUsAAAAADIhkdbCZcuWVXr/cmvsAAAAgHoony+81sJ8Pu0Eta/Ghayvv/46OnfunESWKC8vj/Ly8krHKioqIp8vSmQeAAAAALKnxoWs9ddfP2666aZKx2677ba47bbb1vlYEydOjAkTJlQ6NmbMmNhoo80jYqfqxAQAAAAg42pcyGrUqFGUlJRUOvb4449X6VilpaUxbNiwSsfmz58fX3xRFIsWVTUhAAAAQPIKrbWwIUjkGllJyeVykcvlKh0rLi6OIp2FAAAAAA2WXQsBAAAAyISCWpEFAAAAkAV2LUyHFVkAAAAAZEKNClnjxo2Lv/3tb2scP+mkk2LevHmx1VZb1WQaAAAAANBaCAAAAFAdhdZa2BBoLQQAAAAgE6zIAgAAAKgiF3tPhxVZAAAAAGSCQhYAAAAAmaC1EAAAAKAaCq21sCGwIgsAAACATFDIAgAAACATtBYCAAAAVJFdC9NhRRYAAAAAmaCQBQAAAEAmaC0EAAAAqIZCay1sCDJVyFp//YgOHdJOQUTEN9+knSA5zZunnSAZ5eVpJ0hG40z9VlqzLbdMO0Ey6ssf5vXXTztBcurLz9Zbb6WdIBn15Wfr+QGj046QjHryO6tdu7QTJOPTT9NOkJz6ci4tW6adIBlbbZV2gmS8807aCZKxySZpJ6Ch0VoIAAAAQCbUk7UPAAAAAHWrvnQwZIkVWQAAAABkgkIWAAAAAJmgtRAAAACgivL5wmstzOfTTlD7rMgCAAAAIBMUsgAAAADIBK2FAAAAANVQaK2FDYEVWQAAAABkgkIWAAAAAJmgtRAAAACgiuxamI4aF7JGjRoVd9555w8+5pxzzokhQ4bUdCoAAAAAGrDEVmTdeuutaxzbeuutk5oGAAAAgAYqsUJWly5dkjoUAAAAQMErtNbChsDF3gEAAADIhMRWZC1btqzS+4uKiqK4uDipaQAAAABooBIrZHXu3LnS+zfccMN44YUX1ukY5eXlUV5eXulYRUVF5PNF1c4HAAAAkBS7FqYjsULW9OnTK5+g8bpPMXHixJgwYUKlY2PGjImWLTePzTbbqVr5AAAAAMi2xApZJSUlNT5GaWlpDBs2rNKx+fPnx+LFVmQBAAAANFSJFbKSkMvlIpfLVTpWXFwcRepYAAAAQIEotNbChsCuhQAAAABkQmIrsl566aU1jrVo0SK22267pKYCAAAAoAFKrJB12GGHrXGsf//+8ac//SmpqQAAAABSZdfCdNS4kDVu3LgYN25cElkAAAAAYI1cIwsAAACATCioXQsBAAAAsqLQWgsbAiuyAAAAAMgEhSwAAAAAMkFrIQAAAEA1aC2se1ZkAQAAAJAJClkAAAAAZILWQgAAAIAqyucLr7Uwn6/7Of/rv/4rHnjggdXuHzhwYPz3f/934vMpZAEAAABQLXPnzo0BAwbE8ccfv8r9LVu2rJX5FLIAAAAAqLKvvvoq3n333Tj66KOjS5cudTKnQhYAAABANRRaa2Fdmzt3buTz+dhpp53qbE4XewcAAACgyubOnRsREffcc0/06dMndtppp9hvv/3irrvuqrU5rcgCAAAAqCeWL18eCxcuXON4LpeLXC73g8fI5/Mxbdq0H3xMv3794tVXX42IiMWLF8e4cePim2++ienTp8fIkSOjrKwsjjrqqKqfwFoU5fNpXNO+6l577bX4+uuI9dbrlHaUGqmla53VuddfTztBcjbaKO0EyagvS1ob15Py+lr+LmTGjh8+lnaERIz5615pR0jMAQeknSAZ//eaJ/Pqy++s9ddPO0Ey6svv3i23TDtBMpo1SzsB3/fvf6edIBl9Ft6XdoREFO2/X9oREnHtta9Fz54RnTpl+716Vb322mvx7rsRM2cW1nnvuedr0aTJh1FaWrrGx/z2t7+Nk0466QePs2zZsujcufMPPmbq1KnRsmXL+OSTT2L33XdfeX8+n4+jjjoq5s6dG88+++xai2ZVVU9efgEAAADQqlWrePHFF9c4vi6FpcaNG8e8efPWab7tt99+lX8XFRVF//7947nnnov58+evNl5TClkAAAAA9USjRo2iefPmtT5PPp+Pu+++OzbbbLPYY489VhlbsmRJRES0rIW2NIUsAAAAgGqoL5d4qY6ioqK47rrr4quvvooHHngg1ltvvYj4ti3x/vvvjx122CE23XTTxOe1ayEAAAAAVXbKKafEv//97zjhhBPisccei0ceeSSOPfbYePPNN+Oss86qlTkVsgAAAACosr59+8Z1110Xy5cvj5EjR8aIESOiUaNGccMNN0S3bt1qZU6thQAAAABVlM8XXmthPl/3c/bs2TN69uxZZ/NZkQUAAABAJliRBQAAAFANhbYiqyGwIqwP4d8AACAASURBVAsAAACATFDIAgAAACATtBYCAAAAVJGLvaejRoWsUaNGxZ133rnKfblcLjbddNP4yU9+EqWlpbH99tvXKCAAAAAARCS0IuvWW29d+fXixYvjrbfeiilTpsQhhxwSkyZNih49eiQxDQAAAAANWCKFrC5duqzy7549e8a+++4bgwYNihEjRsTDDz8cTZs2TWIqAAAAgIJQaK2FDUGtXex90003jeOPPz4+/vjjeOihh2prGgAAAAAaiFrdtbB3794REfHcc8/V5jQAAAAANAC1umvhZpttFhERn3zyyTo9vry8PMrLyysdq6ioiHy+KLFsAAAAADWhtbDu1Woha4WionUrQE2cODEmTJhQ6diYMWNi0003jy233CnJaAAAAABkRK0Wsj788MOIiNh8883X6fGlpaUxbNiwSsfmz58f33xjRRYAAABAQ1WrhaynnnoqIiJ69OixTo/P5XKRy+UqHSsuLo51XNgFAAAAUKvy+cJrLczn005Q+2rtYu8LFiyIKVOmRJs2bWLAgAG1NQ0AAAAADUQiK7JeeumllV8vXrw43njjjZg6dWosWLAgJk+evMZVVgAAAACwrhIpZB122GErv87lctG6devo2bNnHHfccbHtttsmMQUAAABAQSm01sKGoEaFrHHjxsW4ceOSygIAAAAAa1Rr18gCAAAAgCTV6q6FAAAAAPWRXQvTYUUWAAAAAJmgkAUAAABAJmgtBAAAAKiGQmstbAisyAIAAAAgExSyAAAAAMgErYUAAAAAVWTXwnRYkQUAAABAJihkAQAAAJAJWgsBAAAAqqHQWgsbAiuyAAAAAMiETK3IWrIk4oMP0k5RM7Nnp50gGVtumXaC5NxzT9oJknHAAWknSMY776SdIBkLF6adIBm5n+6VdoRE1KdPyl55Je0EyXj88bQTJGPffdNOkIyddko7QTL++te0EyTjm2/STpCMtm3TTpCc+vLa9+mn006QjC4H7Zd2hEQceWTaCZKx2WZpJ6ChyVQhCwAAAKAQ2LUwHVoLAQAAAMgEhSwAAAAAMkFrIQAAAEA1FFprYUNgRRYAAAAAmaCQBQAAAEAmaC0EAAAAqAathXXPiiwAAAAAMkEhCwAAAIBM0FoIAAAAUEX5fOG1FubzaSeofVZkAQAAAJAJClkAAAAAZILWQgAAAIBqKLTWwoYgkULWG2+8ETfffHM89dRT8dFHH0WzZs2iQ4cOceCBB8bBBx8cxcXFSUwDAAAAQANW40LW7bffHueee25st912ceyxx0a7du2irKwsHn/88Tj77LPjjjvuiAkTJkTLli2TyAsAAABAA1WjQtYLL7wQZ599duy9995x8cUXR5MmTVaODRgwIPbbb784/vjjY9SoUTFp0qQahwUAAAAoBHYtTEeNLvY+fvz4aNasWYwdO3aVItYKPXv2jKFDh8YTTzwRL7zwQk2mAgAAAKCBq3Yh68svv4xZs2bFHnvsEc2bN1/j4wYOHBgREQ899NBaj1leXh4LFy6s9FZRURH5fIGVOgEAAACoM9VuLXz//fcjn8/H1ltv/YOP23bbbSMi4r333lvrMSdOnBgTJkyodGzMmDHRosXmEbFTlbMCAAAAJK3QWgsbgkR2LfwhjRp9u+iroqJirY8tLS2NYcOGVTo2f/78+PLLovjii0TjAQAAAJAR1S5ktWnTJoqKiuKdd975wcfNnz8/IiK22mqrtR4zl8tFLperdKy4uDiKiqqeEwAAAID6odrXyGrRokX06NEjZs6cGWVlZauMzZkzJ/L/d6n8Bx54ICIi+vbtW/2UAAAAAAVkxa6FhXSza+FanHzyybFkyZIYPXp0LF26NCIiysrKYujQobHvvvvGjTfeGNddd11069YtevfunUhgAAAAABqmGhWydttttxg7dmw8+eSTMWjQoJg2bVrMmzcvzj333FiwYEGMHTs2Kioq4owzzkgqLwAAAAANVI0v9n7wwQfHLrvsEjfeeGNMmTIlPvroo2jWrFlsv/320b9//3j44YdjyJAhcdRRR8Upp5ySRGYAAACA1Nm1sO4lsmth+/bt45xzzql07JhjjolHH3003n///SSmAgAAAKCBSqSQ9UOKiopiwIABtT0NAAAAAPVcrReyAAAAAOqbFbsWFhK7FgIAAABAgbAiCwAAAKAaCm1FVkNgRRYAAAAAmaCQBQAAAEAmaC0EAAAAqAathXXPiiwAAAAAMkEhCwAAAIBM0FoIAAAAUEX5fOG1FubzaSeofVZkAQAAAJAJmVqRlctFbLll2ilqplE9KR3mcmknSM6ee6adIBllZWknSMbmm6edIBnrr592gmRss03aCZKx885pJ0hOfXmOHHBA2gmSUV++H+XlaSdIRn15rhfap/vV9fXXaSdIzltvpZ0gGVl/L7XC22+nnSAZv/992gmS8c03aSegoclUIQsAAACgUNSXDx+ypJ6sDwIAAACgvlPIAgAAACATtBYCAAAAVJFdC9NhRRYAAAAAmaCQBQAAAEAmaC0EAAAAqIZCay1sCKzIAgAAACATFLIAAAAAyASthQAAAABVZNfCdFiRBQAAAEAmKGQBAAAAkAk1KmSNGjUqOnbsGLfcckul4w8++GB07NgxZs2aVZNpAAAAAArO8uWFdWsIElmRddFFF8Vbb72VxKEAAAAAoFI1LmQ1btw4ioqKYsSIEbFs2bIkMgEAAADAampcyMrlcvH73/8+XnnllRg/fnwSmQAAAAAK2opdCwvpZtfCdTR48ODo379/XHPNNTF79uwkDgkAAAAAq0hs18KxY8fGJptsEqeffnosXLiwWscoLy+PhQsXVnqrqKiIfL6BXLkMAAAAgNUkVshq2bJlnH/++fHuu+/G+eefX61jTJw4Mbp27Vrpbc6cOfH55x8nFRcAAACgRtJuJWyIuxY2TvJgffv2jcMPPzymTZsWe+21V5X/f2lpaQwbNqzSsfnz58fixUU1jQgAAABARiW2ImuFUaNGRdu2bePMM8+MTz75pEr/N5fLRfPmzSu9FRcXR1FR4nEBAAAAyIjEK0NNmzaNiy++OBYuXBhXXHFF0ocHAAAAKAhptxI2xNbCWlnitMsuu8SJJ54YZWVltXF4AAAAABqgWuvV+9WvfhW77rprbR0eAAAAgAamRhd7HzduXIwbN67SseLi4pg2bVpNDg8AAABQkPL5wmvny+fTTlD7XD0dAAAAgExQyAIAAACgxi666KLYf//9Kx17+eWX4+ijj47ddtstunfvHiNHjoxPP/20ynMoZAEAAABUQ9q7FBbSroVXX311TJkypdKx1157LY4++uho1KhRXHLJJXHaaafFk08+Gcccc0yUl5dXaZ4aXSMLAAAAgIbr9ddfjz/+8Y/xzDPPxIYbbljpYy6//PLYZJNNYuLEiZHL5SIiYscdd4xDDjkk7rjjjjj88MPXeT4rsgAAAAColhEjRsSCBQvipptuih133HG18fLy8nj66adjwIABK4tYERE777xztG3bNh599NEqzWdFFgAAAEAV2bXwW3/84x+jU6dOaxx/9913Y8mSJdGuXbvVxrbbbrt4/fXXqzSfQhYAAABAPbF8+fJYuHDhGsdzudwqK6Mqk8/nY9q0aT/4mH79+kXr1q1/sIgVEfHVV19FRFTadrjBBhvEokWLfvD/f59CFgAAAEA98fHHH8fBBx+8xvHf/va3cdJJJ/3gMSoqKuKcc875wce0a9cuWrduvdY8yxNetqaQBQAAAFANhdZaGBHRqlWrePHFF9c4vrbVWBERjRs3jnnz5iWSp0WLFhERla68WrRoUWy00UZVOp5CFgAAAEA90ahRo2jevHnaMVbaeuuto0mTJvGvf/1rtbF//etf0b59+yodz66FAAAAANSKXC4Xu+++ezzyyCNRXl6+8v5XXnkl3n777ejdu3eVjmdFFgAAAEAV2bVw3Z100kkxZMiQOPbYY2PYsGGxYMGCuOSSS6JDhw5x6KGHVulYmSpkFRdHVHKR+0x56620E/B9n36adoJkDBiQdoJkfPhh2gmS8fbbaSdIxlo2IMmM+vL9iKg/35OZM9NOkIwD2/497QiJ+PuyH6cdIREff5x2gmQUUDdIjXz+edoJkrPbbmknSMYtt6SdIBkHHZR2gmS8/HLaCZKx1VYRTZumnYJCV1JSElOmTInLLrssTjnllNhggw2iV69eMWLEiHW6Ztd3ZaqQBQAAAEBhuvHGG9c41r1795g2bVqN51DIAgAAAKiGQmstbAhc7B0AAACATFDIAgAAACATtBYCAAAAVJFdC9NhRRYAAAAAmaCQBQAAAEAmaC0EAAAAqIZCay1sCKzIAgAAACATFLIAAAAAyASthQAAAADVoLWw7tV4RdbQoUOjX79+lY7dcMMN0alTpxg6dGgsXLiwplMBAAAA0IDV2oqsiRMnxqWXXhr9+/ePyy67LNZbb73amgoAAACgTuXzhbciK59PO0Htq5VrZF122WVx6aWXxsEHHxzjx49XxAIAAACgxhJfkXXBBRfEDTfcEMccc0yMGjUqioqKkp4CAAAAgAYosULW8uXL45xzzolbb701TjrppPjtb3+b1KEBAAAACk6htRY2BIkUsioqKmLkyJFx7733RkTEZ599Vq3jlJeXR3l5+RrnyOet7gIAAABoqBIpZH344YfxwAMPxOWXXx4PPfRQ3HLLLdG1a9fYf//9q3SciRMnxoQJEyodGzNmTPzoR5vHRhvtlERkAAAAADImkUJWkyZN4qqrropevXrFnnvuGXPmzIkzzzwzOnXqFB06dFjn45SWlsawYcMqHZs/f36Ul1uRBQAAAKTProXpSGTXwlatWkWvXr0iIqJ58+Zx2WWXxdKlS+Pkk0+ORYsWrfNxcrlcNG/evNJbcXFxFBXVyiaLAAAAAGRArVSGSkpK4tRTT40333wzzjzzzNqYAgAAAIAGJrFdC79v2LBh8eyzz8Z9990Xu+22Wxx55JG1NRUAAABAnSu01sKGoNZ69YqKimLcuHHRqlWrGDduXPz973+vrakAAAAAaABqvCLrxhtvXONYy5Yt48knn6zpFAAAAABQe62FAAAAAPWVXQvTYRtAAAAAADJBIQsAAACATNBaCAAAAFANhdZa2BBYkQUAAABAJihkAQAAAJAJWgsBAAAAqsiuhemwIgsAAACATFDIAgAAACATtBYCAAAAVEOhtRY2BFZkAQAAAJAJClkAAAAAZILWQgAAAIBq0FpY9zJVyFq6NOLjj9NOUTNduqSdIBllZWknSE59+cXz+edpJ+C7vvkm7QTJaJypvxJrtttuaSdITn35/duuXdoJkjFv/R+nHSERW/0o7QTJWLAg7QTJyOXSTpCMH9WTn6uIiLffTjtBMnbYIe0EyWjZMu0Eyagv34/68n6K7NBaCAAAAEAm1JPP2gEAAADqTj5feCvS8vm0E9Q+K7IAAAAAyASFLAAAAAAyQWshAAAAQDUUWmthQ2BFFgAAAACZoJAFAAAAQCZoLQQAAACoIrsWpsOKLAAAAAAyQSELAAAAgEzQWggAAABQDYXWWtgQ1KiQNWrUqLjzzjtXuz+Xy0XLli3jJz/5SZx66qnRpk2bmkwDAAAAAMmsyLr11ltX+XdZWVm8+OKLMWXKlJgzZ07MmDEjcrlcElMBAAAA0EAlUsjq0qXLavf17t07li1bFpMnT45nnnkm+vTpk8RUAAAAAKmza2E6avVi7y1atIiIiKKiotqcBgAAAIAGIJEVWcuWLVv5dT6fj6+++iqeffbZmDx5crRt2za6deuWxDQAAAAANGCJFLI6d+682n0bb7xx9O3bN4YPHx5NmzZdp+OUl5dHeXl5pWMVFRWRz1vZBQAAABSGQmstbAgSKWRNnz49Ir4tRN19990xffr0OPbYY6O0tLRKx5k4cWJMmDCh0rExY8bEJptsHhtttFON8wIAAACQPYkUskpKSlZ+3bVr18jlcnHppZdGRUVFnHjiiet8nNLS0hg2bFilY/Pnz49Fi4qioqLGcQEAAADIoEQKWd93+umnx9NPPx0TJkyInj17xq677rpO/y+Xy0Uul6t0rLi4OFwzHgAAACgEdi1MR63sWpjL5eK8886L5cuXx1lnnRVLly6tjWkAAAAAaEBqpZAV8W2L4cEHHxyvv/56XHfddbU1DQAAAAANRK0VsiIiRowYERtvvHFceeWV8e6779bmVAAAAAB1avnywro1BDUqZI0bNy7mzZu3xvGWLVvGrFmz4u9//3tsvfXWNZkKAAAAgAauVldkAQAAAEBSamXXQgAAAID6rqG08xUSK7IAAAAAyASFLAAAAAAyQWshAAAAQBXl84XXWpjPp52g9lmRBQAAAEAmWJEFAAAAUA2FtiKrIbAiCwAAAIBMUMgCAAAAIBO0FgIAAABUkYu9p8OKLAAAAAAyITMrspYsWRJFRcujcePX0o5SI199lXaCZBRa1bkmWrZMO0EylixJO0Ey6ssnCFtumXaCZMybl3aCZDRvnnaC5DSqJx9BbbVV2gmS8fXXaSdIxgcfpJ0gGU2bpp0gGUVFaSdIRnFx2gmS4/VJYfnkk7QTJKP+vKdaHEuW1JMXKFXUocPiuPbawqpRdOiwOCLqyR/ENchMIav4//4Srrde7c2xfPny+Pjjj6NVq1bRKMPvFJxH1WywQa0dOiJ8PwpNffm5ivA9qYoWLWrlsKvw/SgszqPw1MW5bLRRrRx2FfXle+I8CovzKDx1cS65XK0cdhV1cR5LljRa+X69IWnatGlstlnEZpulneT7mkbT+vLJzhoU5fP15fOFmlu4cGF07do1XnzxxWie4Y/vnUdhcR6Fpb6cR0T9ORfnUVicR2GpL+cRUX/OxXkUFudRWOrLeUTUn3OpL+cB35XtMjkAAAAADYZCFgAAAACZoJAFAAAAQCYoZAEAAACQCQpZAAAAAGSCQhYAAAAAmVB8zjnnnJN2iEJSXFwc3bt3j+Li4rSj1IjzKCzOo7DUl/OIqD/n4jwKi/MoLPXlPCLqz7k4j8LiPApLfTmPiPpzLvXlPGCFonw+n087BAAAAACsjdZCAAAAADJBIQsAAACATFDIAgAAACATFLIAAAAAyASFLAAAAAAyQSELAAAAgExo0IWsUaNGRceOHVe7lZSURJ8+fWL48OHx/vvvpx1zrYYOHRr9+vWrdOyGG26ITp06xdChQ2PhwoV1nKxqVnw/brnllkrHH3zwwejYsWPMmjWrjpM1TJU9P0pKSqJv375x2mmnxT//+c+0I66zNT3Xv3v73//937RjrtWoUaNi1113XeP4+PHjo2PHjvHee+/VYaqqOeOMM6Jjx45x6623Vjq+fPnyGDJkSOyyyy7x+uuv13G6tRs+fHjstNNOlf4+3WeffaJjx45x/fXXrzY2ceLE6NixY7z22mt1kLJ65s+fH7///e9jr732ip133jm6desWv/jFL+K2226LioqKtOOt1bo8z7P2N+Sjjz6K//mf/4kDDzwwunXrFrvsskv8x3/8R5x11lnxr3/9K+14a1XZ92THHXeMrl27xuGHHx73339/2hGr5eabb46OHTvGoYcemnaUdTZ06NDo2LFj9OrVK5YvX17pY+bOnbvy+zRnzpw6Tlg9b7/9dowdOzb22Wef+PGPfxy77757DB06NO67777I5/Npx1urtf3eGjRoUNoR19kPvR/Jgl/+8pex8847x+eff77Gx9x7773RsWPHeOihh+owWc3dcccdmXpew7ponHaAQvD9N1RlZWXx4osvxpQpU2LOnDkxY8aMyOVyKaWrvokTJ8all14a/fv3j8suuyzWW2+9tCOtk4suuih69OgR7dq1SztKjbzxxhtx8803x1NPPRUfffRRNGvWLDp06BAHHnhgHHzwwVFcXJx2xHXy3efH4sWL46233oopU6bEIYccEpMmTYoePXqkmK5q1lQ8iYjYeuut6zBJwzV69OiYNWtWjBs3LvbYY4/YaqutVhmfMmVKzJ49O84666zYYYcdUkq5Zr169YoZM2bE7Nmzo3fv3ivvnz9/frz99tuxySabxGOPPRbHHHPMKv9v1qxZ0bp16+jUqVMdJ143b775Zhx22GHRtm3b+N3vfhdbbLFFLFy4MJ544ok466yz4oUXXoiLLroo7Zg/6MQTT4zDDz985b9vv/32mD59ekyYMCE222yzlfd36NAhjXhVNnPmzBg+fHist956MWTIkCgpKYkmTZrE66+/HjfddFPcc889cdVVV0XPnj3TjrpW3/3du3z58vjiiy9iypQpccopp0R5eXkcdNBBKaarumnTpkWnTp1izpw58fe//z1+/OMfpx1pnTRq1Cg+/vjjmDVrVqU/N3fffXcKqapvxowZccYZZ8TWW28dRx11VLRr1y4WLVoUDz30UJx66qkxc+bMOP/886NRo8L/3H5Nr0+aNWtWx0karsMPPzxmzpwZ9957bxx99NGVPmb69OnRqlWr6N+/fx2nA75PISsiunTpstp9vXv3jmXLlsXkyZPjmWeeiT59+qSQrPouu+yyuPrqq+Pggw+O888/PzNFk8aNG0dRUVGMGDEibr311mjcOJs/orfffnuce+65sd1228Wxxx4b7dq1i7Kysnj88cfj7LPPjjvuuCMmTJgQLVu2TDvqWn3/+dGzZ8/Yd999Y9CgQTFixIh4+OGHo2nTpimlq5rKnuvUrQ022CAuuuiiOOKII2L06NExderUKCoqioiIf/7zn3HFFVdEv3794ogjjkg5aeX22GOPKCoqihdeeGGVQtbjjz8eTZs2jWOOOSYmTJgQCxcujObNm0dERHl5ecyePTv222+/tGKv1bXXXhsRETfeeOMqz+f+/fvHeuutF1OnTo1jjz22YAtxERHbbLNNbLPNNiv//eSTT0ZExI477rhawbTQvf/++/Ff//VfseWWW8ZNN90UG2200cqx7t27xyGHHBJDhgyJ0aNHx6OPPlrwf+Mr+93bvXv36NOnT0yePDlThay//e1v8frrr8eUKVNi1KhRMXXq1LjkkkvSjrVO2rZtG1999VXcd999qxWyKioq4v7774/OnTvH3LlzU0q47l599dUYPXp09OjRI6688spVPnAeMGBAtGnTJq666qro0aNHHHjggSkmXTden6Rvr732ilatWsVdd91VaSHr3XffjVmzZsWvf/3rzL4/gfqk8D+iSFGLFi0iIla+ycqKCy64IK6++uo45phj4sILLyz4F7jflcvl4ve//3288sorMX78+LTjVMsLL7wQZ599dvTv3z/+3//7f3H44YfHT3/60xgwYECMHTs2Jk+eHC+//HKMGjUq7ajVtummm8bxxx8fH3/8ceaWV5O+XXfdNU444YR47rnnYurUqRERsWzZshg5cmRsvPHGccEFF6SccM0222yz2GGHHeL5559f5f4nnnhi5fN86dKlMXPmzJVjL7/8cixevHiVwleh+fTTT6OoqKjSFsIjjzwyhg8fbmVAHbrmmmviq6++igsuuGCVItYKzZo1i+HDh0fXrl3jiy++SCFhzTVv3jzatWsXb7/9dtpRquS2226LjTfeOLp37x4HHnhgPPTQQ/HJJ5+kHWudFBcXx89+9rN4+OGHo7y8fJWxp59+OhYsWFDQBffvmjRpUlRUVMSYMWMq7Zr41a9+FUOGDFn5Wh7WpnHjxjF48OB49dVXY968eauNT58+PRo1ahQ///nPU0gHfJ9CVnz7BmrFbenSpfH555/H/fffH5MnT462bdtGt27d0o64TpYvXx5nnXVW3HDDDXHSSSfF6NGjM1eEi4gYPHhw9O/fP6655pqYPXt22nGqbPz48dGsWbMYO3ZsNGnSZLXxnj17xtChQ+OJJ56IF154IYWEyVjxpvy5555LOcm6++5z/bu3LFz/57vWdB5ruu5JIfrNb34TnTt3jssvvzw++OCDuPrqq+Mf//hHXHzxxbHJJpukHe8H7bnnnjFnzpxYsmRJREQsWrQonnvuuejTp0906NAh2rRpE48//vjKxz/77LPRuHHj2GOPPVJKvHb9+/ePsrKyOPTQQ2PSpEnx8ssvx9KlSyMiYtttt40TTjhhldVO1K4HH3wwtt9++9h5553X+JjevXvHJZdcEj/60Y/qMFlyysvL4913340tt9wy7SjrrKysLO6///444IADokmTJvHzn/88li1b9oNt64Vm4MCB8eWXX65csbjCPffcE3vuuWfB//5d4fHHH48dd9xxjT8/66+/fpxzzjnRt2/fug1WTfXhtUl9MHjw4CguLo4777xzlfsrKirizjvvjL59+8YWW2yRUjrgu6yLjIjOnTuvdt/GG28cffv2jeHDh2eibaqioiJGjhwZ9957b0REfPbZZyknqpmxY8fGwIED4/TTT4+77rprZYtOofvyyy9j1qxZsc8++/xg5oEDB8a1114bDz30UPzkJz+pw4TJWXHNmax8Eh1R+XM9ImLDDTfMTFHx66+/XuN5ZEmTJk3i4osvjkGDBsWpp54ac+bMieOPPz4T11zr1atXTJkyJV566aXo3r17PPPMM7F06dKVLei9evWKP//5z7F8+fJo1KhRzJo1K3bbbbeC/j3285//PBYsWBBXXXXVyjap9dZbL3bdddf42c9+FoMGDaq0ME/yysrK4osvvoif/vSnq41VVFSsdgHr4uLigv/QatmyZSu/XlHAuvLKK+OLL76IE088McVkVXP33XfHN998E4cddlhEfFvk7dGjR0ybNi1KS0sz8RwpKSmJtm3bxowZM1Ze52fx4sXxyCOPxAUXXBCLFy9OOeHaff7557F48eJ6VVyv7O96mzZt4i9/+UsKaRquLbbYInr37h333ntvnHbaaStbCGfOnBkfffRRjB07NuWEwAoKWfHtUtGIb19c3X333TF9+vQ49thjo7S0NOVk6+7DDz+MBx54IC6/tfUWpQAACX5JREFU/PJ46KGH4pZbbomuXbvG/vvvn3a0amnZsmWcf/75UVpaGueff35ceOGFaUdaJ++//37k8/m1Xjh82223jYgo6N3l1lWhv4H6rhXP9e/L0rUO1l9//bjpppsqHbvtttvitttuq+NE1de+ffsYMWJEnHfeebHLLrvEySefnHakddK1a9do2rRpPP/889G9e/d4/PHHo0OHDiuvw9SnT5+YNm1azJ07N3bYYYd46aWX4qSTTko59dqdcMIJceSRR8bTTz8dzz//fLz44ovx/PPPx7PPPhvTpk2L66+/XptOHfihlZWDBg1abefL008/PX75y1/WdqwaqexNesuWLWP48OExdOjQFBJVz2233RY777xztGrVKsrKyiIiYv/9948//OEP8eCDD8bAgQNTTrhuBg4cGJMnT45FixbFBhtsEH/+85+jcePG0b9//5gxY0ba8dZqxSUz6tOKpcpen2Rxo6n6YMiQIfHYY4/FX//615W7ME6fPj223nrr6NWrV8rpgBWy8+6tFpWUlKz8umvXrpHL5eLSSy+NioqKzHxS2KRJk7jqqquiV69eK9tezjzzzOjUqVNmdmj6vr59+8bhhx8e06ZNi7322ivtOIlasYNOll+EffjhhxERsfnmm6ecZN1997meVY0aNVrjeXy3nS0r+vbtG+edd1707t07MwXFXC4X3bp1W7mK74knnljlQ4MePXpELpeLZ555JhYuXBjl5eWZ2TCkWbNmMWDAgBgwYEBERHzxxRdx5ZVXxo033hjXXHNNnHbaaSknrP823njjaN68ebz77rurjV1yySUrV8x88skn8etf/7qu41XLd9+kN27cOFq0aJGplsKIiNmzZ8frr78eEVHpJSduuummzBSyDjjggBg/fnw8+uijccABB8Q999wT++67b2YKJy1atIgNN9xwrR8Gfvjhh9GqVatM7FpYH16f1Be9evWKNm3axF133RX9+vWLzz77LB577LH43e9+l6kPb6G+K/zf7Ck4/fTTo3379jFhwoT429/+lnacddKqVauVnxI0b948Lrvssli6dGmcfPLJsWjRopTTVd+oUaOibdu2ceaZZ2aiha1NmzZRVFQU77zzzg8+bv78+RERmdtJ67ueeuqpiIhMtIJB0vbcc894+eWXY+7cufHxxx+vch2WZs2aRbdu3eL555+P559/Plq3bh0dO3ZML+xafPTRR9GrV6+YNGnSamObbLJJnHHGGdG6deuVb+KpfXvvvXe8+uqr8eabb65yf4cOHaKkpCRKSkpihx12SCld1a3IXFJS8oPXNSpkt956a6y//vpx3XXXxdSpU1e5HXTQQfHSSy/FnDlz0o65TrbZZpvo0qVLzJgxIz777LN45plnMrGz33f16dMnXn311fj3v/9d6fjSpUvjwAMPjF/84hd1nIysa9SoUQwePDj+8pe/xIIFC+Luu++OiIhDDjkk5WTAdylkVSKXy8V555238uLpKy54myUlJSVx6qmnxptvvhlnnnlm2nGqrWnTpnHxxRfHwoUL44orrkg7zlq1aNEievToETNnzlzZdrDCnDlzVl7b5IEHHoiIyMxFSL9vwYIFMWXKlGjTps3KlRvQkOy5556xaNGiuPnmm6N58+bRtWvXVcZ79+4d//jHP+L5558v6N0KI7693l0ul4tp06bFggULVhv/9NNPo6ysLDp16pRCuoaptLQ0mjdvHiNGjFjjroSV7apF7SgrK4sHH3wwBgwYELvvvnt07959ldtxxx0XERE33nhjyknX3cCBA+Ppp5+Om2++OVq3br3a77BCd9xxx0VxcXGMGTNmtR0YIyImTJgQCxYsUHygWg499NDI5/Px5z//Oe65557YZ599omXLlmnHAr4jG30cKejatWscfPDBcccdd8R1110XJ5xwQtqRqmzYsGHx7LPPxn333Re77bZbHHnkkWlHqpZddtklTjzxxEwUsiIiTj755Bg6dGiMHj06Lr/88mjSpEmUlZXF0KFDo3Xr1nHkkUfGddddF926dSv4N7gRES+99NLKrxcvXhxvvPFGTJ06NRYsWBCTJ0/OTCtCxKrn8n0tWrSI7bbbrg7TkGXt27ePLbbYIu65557o16/fam2RvXv3jgsvvDAWLFgQRx11VEop102jRo1i7NixUVpaGgcddFAcccQR0blz5yguLo558+bFDTfcEK1bt45hw4alHbXBaNu2bUyYMCGGDx8e++23XwwePDh23XXXaNq0abzzzjvx4IMPxsyZM2PbbbfNzM7KWXbXXXfFN998s8ZVS9tvv3106dIlHnjggRg5cmRsuummdZyw6n72s5/FhRdeGJMmTYrjjjsucy1TO+64Y/zhD3+IsWPHxuDBg2PIkCHRtm3b+Pzzz2PGjBnx6KOPxqGHHhqHHnpo2lEblIULF8b1119f6dgRRxyRiQ0RIr79gKd///5x7bXXxltvvRVnnHFG2pGA71HI+gEjRoyIv/zlL3HllVfGf/7nf671At6FpqioKMaNGxcHHnhgjBs3LkpKSuLHP/5x2rGq5Ve/+lU8+eSTmWj13G233WLs2LFx9tlnx6BBg+KII46I9u3bx7nnnhvnn39+jB07Nho3bpyZP4ordmeK+Ha1YuvWraNnz55x3HHHrbxofVZ891y+r3///vGnP/2pDtOQdXvuuWfcfvvtlV7/ql27drHNNtvEBx98ED179kwhXdX07Nkz7rzzzrj22mvj9ttvjyuvvDKWL18ebdq0if322y+OP/742HDDDdOO2aD07NkzZsyYEbfffns88sgjMW3atFi0aFG0bNkySkpK4pJLLom99947Ux8mZNVtt90Wm222Weyxxx5rfMzgwYPjD3/4Q0ybNi1+85vf1GG66mnZsmXsvvvu8de//jVzbYUr/OIXv4gdd9wxbrrpppg0aVJ8+umnseGGG0b79u3jiiuuiL333jtzBbqs+/LLL9e4QdPgwYMzU8iKiDj88MNj2LBhscMOO2R2h3Goz4ry39/HGUjEm2++GTfeeGM89dRT8dFHH0WzZs2iQ4cO0b9//3j44Yfjtddei6OOOipOOeWUtKMCAABAJihkQQry+Xw8+uij8f7778fRRx+ddhwAAADIBIUsAAAAADLBroUAAAAAZIJCFgAAAACZoJAFAAAAQCYoZAEAAACQCQpZAAAAAGSCQhYAAAAAmaCQBQAAAEAmKGQBAAAAkAkKWQAAAABkgkIWAAAAAJnw/wF4CJfEW2Wt2gAAAABJRU5ErkJggg==\n",
"text/plain": [
"<Figure size 1618.03x1000 with 2 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABLIAAAMsCAYAAABA14tEAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzs3Xuc1VW9P/73noGt4IjAERAvqIiCFzoSGaiBHvVh/TRviIaZFmpOpVamdvTo6cg51lHL6hQ+bDQ7JnYemB5vUdnFvJGXDDNRAxJz1LyACuEguGFmfn905BuxUWb2B9bnM/v5fDz246F77VnrNYurb9f7s0qdnZ2dAQAAAAA515A6AAAAAABsCIUsAAAAAApBIQsAAACAQlDIAgAAAKAQFLIAAAAAKASFLAAAAAAKQSELAAAAgEJQyAIAAACgEBSyAAAAACgEhSwAAAAACkEhCwAAAIBCUMgCAAAAoBAUsgAAAAAoBIUsAAAAAAqhV+oAG+qJJ56I9vb22GyzzVJHAQAAACLirbfeisbGxthrr71SR9mkWltbY8WKFaljVNWnT5/YcccdU8fYaApTyGpvb4+OSiUipz9RNtiyZakTZKOpKXWC7PSU76WhhxywfOut1Amy0VO+j87O1Amy8dJLqRNkZ7fdUifIxnPPpU6QjUGDUifIRk/5H4WVSuoE2dhyy9QJMtHeUUodITONlYL/N8jbGhtTJ+BvPflk6gSZ6Nhhhx7z+1ZXrFixIlYsXhx9nn46dZS1rBgxouf8/WQ9ClPI2myzzSJWrIhRf/lL6ii1ue++1Amy8f73p06QnZ5Sqe7bN3WCbDz7bOoE2XjlldQJstHRkTpBNq64InWC7NxyS+oE2fjqV1MnyMbJJ6dOkI3hw1MnyMYLL6ROkI0xY1InyMTySu/UETKzxXN/SB0hG/36pU7A3/rSl1InyMS8f//3HvP7Vlf1efrpGHXKKaljrGXe977X4wtZPeQIBwAAAAA9XWFOZAEAAADkRqmUv0e8lHpOW/f65GzHAQAAAKA6hSwAAAAACkFrIQAAAEB35K21sA7YcQAAAAAKQSELAAAAgELQWggAAADQVW4tTCJnOw4AAAAA1SlkAQAAAFAIWgsBAAAAuiNvrYV1YKPu+C233BIjR46MuXPnbsxlAAAAAKgDSocAAAAAFILWQgAAAIDu0Fq4ydlxAAAAAApBIQsAAACAQshVa2GlUolKpVJ1rL29PUqdnZs4EQAAAEAVpVL+WgtLpdQJNrpcFbJaWlpi+vTpVcemTZsW2/TvH3vUwQ8KAAAAAOvKVSGrubk5pk6dWnWstbU1SsuWRSxbtolTAQAAAJAHuSpklcvlKJfLVccaGxvr4ogcAAAAUBB5ay2sA3YcAAAAgEJQyAIAAACgEHLVWggAAABQCG4tTGKjFrImTZoUkyZN2phLAAAAAFAnclY6BAAAAIDqtBYCAAAAdEfeWgvrgB0HAAAAoBAUsgAAAAAoBK2FAAAAAF3l1sIkcrbjAAAAAFCdQhYAAAAAhaC1EAAAAKA78tZaWAfsOAAAAACFoJAFAAAAQCFoLQQAAADoKrcWJpGzHQcAAACA6op1IqtXr4j+/VOnqM0ll6ROkI1Fi1InyM6CBakTZOP111MnyMbEiakTZGPrrVMn4G/MvfrB1BEyM/rFOakjZOKly2ekjpCJoa/OTR0hE/e+sEvqCJk4YO+e8Xtve0Pv1BEy0bdv6gQZ6uhInSAb5XLqBNl46KHUCbJxzz2pE2TjtddSJ6DOFKuQBQAAAJAXeWstrAN2HAAAAIBCUMgCAAAAoBC0FgIAAAB0h9bCTc6OAwAAAFAIClkAAAAAFILWQgAAAICuKpXy11pYKmU63YIFC+LrX/96/Pa3v42IiD322CPOPvvsGDNmTKbrdEXOdhwAAACA1BYuXBhTpkyJJUuWxGWXXRaXXXZZrFy5Mk455ZR45plnkuVyIgsAAACAtVx22WUxaNCg+P73vx+bb755RES8973vjaOPPjruv//+GD58eJJcClkAAAAA3ZG31sKMLFu2LGbPnh3nnnvumiJWRMSAAQPi3nvvTZhMayEAAAAAf2PevHnR3t4e2223XfzHf/xHjB8/Pvbcc8848cQT44knnkiaTSELAAAAoIfo6OiItra29b4qlcq7zvHqq69GRMQll1wSL730Unz1q1+Nr3/967Fs2bI46aSTYuHChRv721ivmgpZp556auy1117x+uuvr/czP/rRj2LkyJHxs5/9rJalAAAAAPLj7VsL8/QqlWLRokUxduzY9b5aWlre9VtbtWpVREQMGTIkpk+fHhMmTIgPfvCD8d3vfjc6OzvjO9/5zsbe3fWq6RlZU6ZMidmzZ8ePfvSj+PjHP171MzfffHMMHjw4Dj744FqWAgAAAOBdDB48OObMmbPe8XK5/K5zNDU1RUTEgQceGA1/8xywIUOGxKhRo5K2F9ZUyPqnf/qnGDx4cNx2221VC1nPP/98PPzww/HpT386evXyXHkAAACgB8nhw94bGhrWFKK6a+edd46IqNqGuHr16ujTp09N89eiph3v1atXHHfccfHUU0/F/Pnz1xm/+eabo6GhIY4//vhalgEAAABgExk+fHjstNNO8dOf/nStYtZzzz0X8+bNi3HjxiXLVnPp8LjjjovGxsa49dZb13q/vb09br311jjwwANj6NChtS4DAAAAwCZywQUXxJ///Oc47bTT4p577omf/OQncdppp0W/fv3i1FNPTZar5kLW0KFDY+LEifGjH/0oVq9eveb92bNnxyuvvBJTpkzZ4Lkqlcp6n6rf3t4eHZ2dtcYFAAAAqF1OH/aelQMPPDD++7//Ozo7O+Pzn/98fOlLX4qRI0fGjTfeGFtvvXVm63RVJg+uOuGEE+Luu++O++67Lw466KCI+Gtb4Q477BATJkzY4HlaWlpi+vTpVcemTZsW2wwYEHv0759FZAAAAADewbhx45K2EVaTSSFrwoQJsd1228Vtt90WBx10ULz22mtx9913x+c+97kodaEa2NzcHFOnTq061traGqU334zo6MgiMgAAAAAFk0khq6GhIY477ri48sorY+nSpXH77bdHRMSxxx7bpXnK5fJ6r4FsbGzM9IgcAAAAQE1yeGthT5fZjk+ePDk6OzvjF7/4Rdxxxx3xwQ9+MAYOHJjV9AAAAADUucwKWYMGDYqDDz44vve978Uf/vCHOOGEE7KaGgAAAACyK2RFREyZMiWeeeaZ2G233eJ973tfllMDAAAA5EcPv7UwrzJ5Rtbb9ttvv5g/f36WUwIAAABARGR8IgsAAAAANpZMT2QBAAAA1A23Fm5ydhwAAACAQlDIAgAAAKAQtBYCAAAAdIfWwk3OjgMAAABQCApZAAAAABSC1kIAAACAriqV8tdaWCqlTrDR5WzHAQAAAKA6hSwAAAAACkFrIQAAAEB35K21sA7YcQAAAAAKoVgnslavjliyJHWK2jz3XOoE2XjmmdQJsnPLLakTZOPcc1MnyMbs2akTZGP77VMnyMarr6ZOkInRHU+ljpCdgQNTJ8jE0Dv/O3WEbAwfnjpBJg5o+3HqCNlYMDh1gkw0rl6dOkI2etIphfe+N3WCbHR0pE6QjfHjUyfIRqWSOgEUUrEKWQAAAAB54NbCJHK24wAAAABQnUIWAAAAAIWgtRAAAACgO/LWWlgH7DgAAAAAhaCQBQAAAEAhaC0EAAAA6Cq3FiaRsx0HAAAAgOoUsgAAAAAoBK2FAAAAAN2Rt9bCOmDHAQAAACiEzApZJ510Uhx00EFZTQcAAAAAa9FaCAAAANBVbi1MImc7DgAAAADVKWQBAAAAUAhaCwEAAAC6I2+thXUgV4WsSqUSlUql6lh7e3uUOjs3cSIAAAAA8iJXhayWlpaYPn161bFp06bFNlttFXts4kwAAAAA5EOuClnNzc0xderUqmOtra1RWrYsYunSTZwKAAAAoAqthZtcrgpZ5XI5yuVy1bHGxsa6uEYSAAAAgOqUDgEAAAAohExPZLW1tcV1111XdezEE0+M3r17Z7kcAAAAQBqlUv5aC+ugky3TQtZf/vKX+M///M+qY8cdd5xCFgAAAADdllkha8aMGVlNBQAAAADryNXD3gEAAAAKI2+thXXAjgMAAABQCApZAAAAABSC1kIAAACArnJrYRI523EAAAAAqE4hCwAAAIBC0FoIAAAA0B15ay2sA3YcAAAAgEJQyAIAAACgELQWAgAAAHSVWwuTyNmOAwAAAEB1TmQBAAAAdEfeTmTVATsOAAAAQCEU60TWqlURr76aOkVNXirvmDpCJoZuuzJ1hOxMmZI6QTZeeCF1gmz0kP+jMeOJMakjZOKkfrenjpCNRYtSJ8jO3nunTpCNfv1SJ8jGyh7y5+F++6VOkI2XX06dIBs95M/00vhxqSNkpvOBB1NHyMb73pc6QTZ6yp/rPeTvvdHenjoBdaZYhSwAAACAPPCw9yRytuMAAAAAUJ1CFgAAAACFoLUQAAAAoDvy1lpYB+w4AAAAAIWgkAUAAABAIWgtBAAAAOgOrYWbnB0HAAAAoBAUsgAAAAAoBK2FAAAAAF1VKuWvtbBUSp1go8vZjgMAAABAdZmcyDr//PPj1ltvXe/4nnvuGbfccksWSwEAAABQpzJtLbzxxhurvt+3b98slwEAAABIL2+thXUg00LW3nvvneV0AAAAALCG0iEAAAAAhZDpiazVq1ev816pVIrGxsYslwEAAABIy62FSWRayNpzzz3XeW+77baLX/3qVxv09ZVKJSqVStWx9vb2KHV21pQPAAAAgK6bOXNm/Nu//Vtcf/31MW7cuGQ5Mi1k3Xzzzeu8Vy6XN/jrW1paYvr06VXHpk2bFttsuWXs0e10AAAAAHTVwoUL49JLL00dIyIyLmSNHj26pq9vbm6OqVOnVh1rbW2N0muvRbz+ek1rAAAAAGQib62FG0GlUolzzz03BgwYECtWrEgdJ18Pey+Xy9HU1FT11djYGA110OsJAAAAkBff+MY34o033oizzjordZSIyPhEFgAAAAA9wwMPPBAzZsyIGTNmxCuvvJI6TkQoZAEAAAB0XU5vLezo6Ii2trb1fqRcLm/Q88xff/31+OIXvxif/OQnY8yYMXHnnXdmmbTbFLIAAAAAeohFixbFMcccs97xM888c4PaBC+66KIYOnRonHHGGVnGq1kmhaxLL700N0+vBwAAAKhXgwcPjjlz5qx3fENOY82cOTN+/etfxy233BIREatXr46Ojo6IiOjo6Ij29vZobGzMJnAXOZEFAAAA0B15ay2MiIaGhmhqaqppjh//+MexcuXKOOyww9YZ+8QnPhHbbbdd/OpXv6ppje5SyAIAAABgjWnTpsXy5cvXeu+hhx6Kr33tazFt2rQYM2ZMomQKWQAAAAD8jeHDh6/z3p///OeIiNh5551j5MiRmzrSGgpZAAAAAF2V01sLezqFLAAAAADe0Yc+9KGYP39+6hiRs9IhAAAAAFTnRBYAAABAd+SttbAO2HEAAAAACkEhCwAAAIBC0FoIAAAA0B1aCzc5Ow4AAABAIShkAQAAAFAIxWot7NcvYuLE1ClqMnTe3akjZGObbVInyM4HPpA6QTZWrkydIBvLlqVOkIkp/VMnyMjsfqkTZOL59x6VOkJmdlj2x9QRsjF4cOoE2SiXUyfIxle+kjpBNg49NHWCbPSQn1edT/0hdYTMlPbYN3WETHQ+9HDqCJnofP+41BEy8eabqRNko/3ZedGYOkQqpVL+WgtLpdQJNrqc7TgAAAAAVKeQBQAAAEAhFKu1EAAAACAv8tZaWAfsOAAAAACFoJAFAAAAQCFoLQQAAADoKrcWJpGzHQcAAACA6hSyAAAAACgErYUAAAAA3ZG31sI6YMcBAAAAKASFLAAAAAAKQWshAAAAQFe5tTCJzApZzz77bNxwww1x//33x8svvxxbbLFF7LLLLjFlypQ47LDDolQHmwkAAADAxpNJIWvWrFlx0UUXxQ477BAnn3xyDB8+PJYvXx4/+9nP4gtf+ELMnj07vvzlL0dD3iqVAAAAABRGzYWsp556Ki644IIYP358XHnllVEul9eMHXLIIbHddtvFVVddFePHj4+jjjqq1uUAAAAA8sGBnU2u5kLW1VdfHe3t7TFt2rS1ilhv+9SnPhVLly6NrbbaqtalAAAAAKhjNRey7rnnnth9991j2223rTq++eabx8UXX1zrMgAAAAD54WHvSdRUyHr99ddjxYoVMWzYsEzCVCqVqFQqVcfa29uj1NmZyToAAAAAFE9NhazGxsaI+GuRKQstLS0xffr0qmPTpk2LbbbeOvYYMCCTtQAAAAAolpoKWVtttVVsueWW8cILL7zj515++eUYPHjwu95a2NzcHFOnTq061traGqVVq7qdFQAAACBTeWstrAM17/gBBxwQTz31VLz44otVx1etWhVHHXVUfPSjH33XucrlcjQ1NVV9NTY2RkMd9HoCAAAAUF3NhazTTjstGhsbY9q0aVWfbzV9+vRYunRpHHvssbUuBQAAAEAdq/nWwt133z0uvPDCuOSSS+K4446LE044IXbaaad4/fXXY9asWXHXXXfF5MmTY/LkyVnkBQAAAMgHrYWbXM2FrIiIj370o7H77rvHDTfcEFdffXW8+uqrseWWW8Yuu+wS3/rWt+LQQw+NkrZAAAAAAGqQSSErImLMmDExZsyYrKYDAAAAgLVkVsgCAAAAqBulUv5aC+ugGy5nOw4AAAAA1SlkAQAAAFAIWgsBAAAAuiNvrYV1wI4DAAAAUAgKWQAAAAAUgtZCAAAAgK5ya2ESOdtxAAAAAKhOIQsAAACAQtBaCAAAANAdeWstrAN2HAAAAIBCUMgCAAAAoBCK1Vr41lsRzz2XOkVtNt88dYJslMupE2TnvvtSJ8jGyy+nTpCNYcNSJ8hE71/dlTpCNgYOTJ0gEzs88dPUEbIzfHjqBNl44onUCbLRv3/qBNk4+eTUCbKxdGnqBNl4+unUCbLRU36/iojOBx5MHSEbHakDZKOjh3wfW5RXpY6QicaGzojo+TflVeXWwiRytuMAAAAAUJ1CFgAAAACFUKzWQgAAAIC8yFtrYR2w4wAAAAAUgkIWAAAAAIWgtRAAAACgq9xamETOdhwAAAAAqlPIAgAAAKAQtBYCAAAAdEfeWgvrgB0HAAAAoBAUsgAAAAAoBK2FAAAAAN2htXCT69aOn3TSSTFy5MiYMGFCdHR0VP3Mk08+GSNHjoyRI0fG3LlzawoJAAAAAN0uHTY0NMSiRYvi4Ycfrjp+++23dzsUAAAAAPy9bheydtpppxg0aFD8+Mc/Xmesvb09fvKTn8See+5ZUzgAAACAXCqV/tpamKdXqZR6Vza6bheyGhsb47DDDouf//znUalU1hp74IEHYunSpXH44YfXHBAAAAAAImq8tfCII46Iv/zlL3H//fev9f4dd9wRH/jAB2LAgAE1hQMAAACAt9VUyBo9enTstNNOMWvWrDXvrVixIn75y1/GUUcd1eX5KpVKtLW1VX21t7dHR2dnLXEBAAAAspO6lfDvX3Wg5u/yiCOOiLvvvjuWL18eERG/+MUvolevXnHwwQd3ea6WlpYYO3Zs1dfcuXNj0dKltcYFAAAAoKB61TrBkUceGd/+9rfjrrvuiiOPPDLuuOOO+NCHPhTlcrnLczU3N8fUqVOrjrW2tkaprS3i757HBQAAAEB9qLmQNWzYsNh7771j1qxZsf/++8eDDz4Y3//+97s1V7lcXm8BrLGxsS6evg8AAAAUwNu3FuZJHdRNMtnxI444Ih544IH4wQ9+EEOGDImxY8dmMS0AAAAArJFJIeuwww6Lzs7OuPrqq+PII4+MUh1UAAEAAADYtDIpZA0cODD222+/WLVqVbduKwQAAAAonNS3FNbhrYXdekbWjBkz1nnvmmuuWee9SZMmxaRJk7qzBAAAAACspT7KdQAAAAAUXs23FgIAAADUHbcWJqGQBQAAAMA6fvrTn8Z1110XCxcujHK5HHvssUd87nOfi9GjRyfLlLPSIQAAAACp3XTTTfH5z38+dt555/j6178eF198cbzxxhtxwgknxKOPPposlxNZAAAAAN2Rt9bCDE2fPj0+8IEPxKWXXrrmvf322y8OPvjguOaaa+Kqq65KkkshCwAAAIA1VqxYEYceemiMGzdurfebmppi6NCh8corryRKppAFAAAA0GN0dHREW1vbesfL5XKUy+V3nKNPnz5x4YUXrvP+woUL449//GMcddRRNefsLoUsAAAAgK7K6a2FixYtimOOOWa9HznzzDPjrLPO6vLUb7zxRpx33nnRq1evOO2002pJWROFLAAAAIAeYvDgwTFnzpz1jr/baaxqXnnllfjUpz4Vf/zjH+Mb3/hGDB8+vJaINVHIAgAAAOghGhoaoqmpKbP5fv/738eZZ54Zy5cvjyuvvDIOOOCAzObuDoUsAAAAgO7IW2thxn784x/H+eefH1tvvXX8z//8T4waNSp1pOjZOw4AAABAl/385z+Pc889N3bbbbe46aabclHEiijaiayGhojNN0+dojY9pVq7dGnqBNnJ8MglGXj66dQJstFTfq1vs03qBNlYuTJ1guy8ww00hfL446kTZGO//VInyMajj6ZOkI1hw1InyMaIEakTZKMn/d67/fapE2Tj5ZdTJ8hEY9tfUkfIxmOPpU6QjT59Ivr1S50inZ7y9/6/s2zZsrjwwgujb9++8dnPfjZeeOGFeOGFF9aMb7755skKW8UqZAEAAACwUd1///2xbNmyiIg4/fTT1xnfddddY9asWZs6VkQoZAEAAADwNw4//PA4/PDDU8eoSiELAAAAoKtKpfy1FpZKqRNsdDnbcQAAAACoTiELAAAAgELQWggAAADQHXlrLawDdhwAAACAQlDIAgAAAKAQtBYCAAAAdJVbC5PI2Y4DAAAAQHUKWQAAAAAUQuaFrB/84AcxcuTImDx5ctZTAwAAAORHQ0O+XnUg8+9y5syZMWrUqJg7d278/ve/z3p6AAAAAOpUpoWs3/3ud7FgwYI477zzYtCgQXH99ddnOT0AAAAAdSzTQtYPf/jD6N+/f4wbNy6OOuqo+NnPfhaLFy/OcgkAAACA9N6+tTBPL7cWbrhly5bFT37ykzjyyCOjd+/ecfzxx8fq1avjxhtvzGoJAAAAAOpYZoWs22+/PVauXBkf+chHIiJixx13jPHjx8fMmTNj1apVGzRHpVKJtra2qq/29vbo6OzMKi4AAAAABZNZIeuHP/xh7LXXXjF48OBYtmxZLFu2LD784Q/H4sWL484779ygOVpaWmLs2LFVX3Pnzo1FS5ZkFRcAAACgNqlbCevw1sJeWUzy6KOPxoIFCyIiYp999lln/IYbbogjjjjiXedpbm6OqVOnVh1rbW2N0ptv1hYUAAAAgMLKpJB14403xuabbx5XXXVVNDY2rjV2yy23xG233RZz586N0aNHv+M85XI5yuVy1bHGxsa/PrRMeyEAAABAXaq5kLVs2bK4884745BDDon99ttvnfGBAwfGbbfdFjNmzIjLL7+81uUAAAAA0nv71sI8cWvhu7vtttti5cqVcdRRR1Ud33XXXWPvvfeOn/70p/Haa6/VuhwAAAAAdarmQtYPf/jDGDRoUOy///7r/cxxxx0XlUolZs6cWetyAAAAANSpmlsLZ82a9a6fmTx5ckyePLnWpQAAAADyI2+thXXAjgMAAABQCApZAAAAABRCza2FAAAAAHVJa+EmZ8cBAAAAKASFLAAAAAAKQWshAAAAQFeVSvlrLSyVUifY6HK24wAAAABQnUIWAAAAAIWgtRAAAACgO/LWWlgH7DgAAAAAhaCQBQAAAEAhaC0EAAAA6Cq3FiaRsx0HAAAAgOqKdSKrT5+InXZKnaImn/uXLVJHyMR/TXkwdYTs7LFH6gSZWN5rq9QRMrFFZUnqCNnYfvvUCbKxcmXqBNlYtix1guy8732pE2Rj1qzUCbLR1JQ6QTYmTkydIBv33Zc6QTbe+97UCbJx/fWpE2TnX/4ldYJsPP546gSZuPfNfVJHyMQBPeXvi2+8kToBdaZYhSwAAACAvMhba2EdsOMAAAAAFIJCFgAAAACFoLUQAAAAoKvcWphEznYcAAAAAKpTyAIAAACgELQWAgAAAHRH3loL64AdBwAAAKAQFLIAAAAAKASthQAAAABd5dbCJHK24wAAAABQXc0nss4///y49dZb13qvoaEh+vbtG7vuumucfPLJcdhhh9W6DAAAAAB1LrPWwhtvvHHNP3d0dMSSJUvi2muvjbPPPjsqlUocffTRWS0FAAAAkF7eWgvrQGaFrL333nud98aNGxcHHHBAfPe731XIAgAAAKAmG7V02NTUFMOHD49nn312Yy4DAAAAQB3YqLcWViqVeP7552PbbbfdmMsAAAAAbHpaCze5zApZq1evXvPPbxewrrzyyliyZEl85jOf2aA5KpVKVCqVqmPt7e1R6uzMJCsAAAAAxZNZIWvPPfdc572BAwfGOeecEyeddNIGzdHS0hLTp0+vOjZt2rTYZvDg2GPnnWvKCQAAAEAxZVbIuvnmm//fpL16xVZbbdXllsLm5uaYOnVq1bHW1lYnsgAAAIB8KJXy11pYKqVOsNFlVsgaPXp0zXOUy+Uol8tVxxobGyPa22teAwAAAIBi2qgPewcAAADosfJ2IqsO2HEAAAAACkEhCwAAAIBCqLmQdemll8b8+fOzyAIAAABQDG8/7D1Przp42LsTWQAAAAAUgkIWAAAAAIXg1kIAAACA7nBr4SZnxwEAAAAoBIUsAAAAAApBayEAAABAV719a2GeuLUQAAAAAPJBIQsAAACAQtBaCAAAANAdeWstrAN2HAAAAIBCUMgCAAAAoBC0FgIAAAB0ValUF7cE5k2xClkrV0Y8/XTqFDX5r63vSB0hG/0mpU6QnUoldYJMbPHs71NHyEZbW+oE2dh669QJMvHa1iNTR8jEP9x8c+oI2RkxInWCbGy/feoE2egpz8VYujR1gmwMH546QTZ6yp+F556bOkF2nnoqdYJsNDWlTpCJAwbOTR0hG89Dnph9AAAgAElEQVS8nDpBNvr1i9h889Qp2Egef/zxuOKKK2Lu3LnRu3fvOPDAA+O8886LrRP+904P+dsXAAAAAFmZN29efPzjH4+Ghoa44oor4txzz437778/PvGJT0Ql4YGQYp3IAgAAAMiLvJ3O7ujIbKpvfvObMWDAgGhpaYlyuRwREbvvvnsce+yxccstt8SUKVMyW6srcrbjAAAAAKRUqVTigQceiEMOOWRNESsiYq+99oqddtop7rrrrmTZFLIAAAAAWOP555+Pt956K4ZXef7kzjvvHAsXLkyQ6q+0FgIAAAB0Rw5bCzs6OqLtHS4OKZfLa52yquaNN96IiIgtt9xynbEtttgili9fXlvOGihkAQAAAPQQixYtimOOOWa942eeeWacddZZ7zhHR4bP2sqaQhYAAABADzF48OCYM2fOesff7TRWRMRWW20VEVH15NXy5cujX79+3Q9YI4UsAAAAgK4qlfLXWlgqRUNDQzQ1NdU0zQ477BC9e/eOP/3pT+uM/elPf4pddtmlpvlrkbMdBwAAACClcrkc++23X/zyl7+MSqWy5v0nnnginn322Zg4cWKybApZAAAAAKzlrLPOipdeeilOOeWUuOuuu+J///d/4/TTT48RI0bE5MmTk+XSWggAAADQHXlrLczQ6NGj49prr41vfOMbcfbZZ8cWW2wREyZMiPPOO2+DnrO1sShkAQAAALCOcePGxcyZM1PHWEsmhaxXXnklZs6cGb/61a/ixRdfjLfeeiuGDBkS++67b0ydOjV23nnnLJYBAAAAoI7VXMiaPXt2nHPOObHZZpvFCSecEKNHj47evXvHggUL4oYbbog77rgjrrrqqth3332zyAsAAACQXk5vLezpaipk/fnPf47Pf/7zse2228YNN9wQ/fr1WzM2bty4OPbYY+OEE06ICy64IO66665obGysOTAAAAAA9amm0uE111wTb7zxRnzlK19Zq4j1tr59+8Y555wTY8eOjSVLltSyFAAAAAB1rqYTWXfeeWfsuuuusddee633MxMnToyJEyfWsgwAAABA/uSttbAOdLuQtWzZsliyZEm8//3vX2esvb09Ojs713qvsbExSu/Sq1mpVKJSqVQda29vj9LfzQkAAABA/eh2Iaujo2O9Y5MmTYp58+at9d4Xv/jFOPXUU99xzpaWlpg+fXrVsWnTpsU2AwfGHkOGdD0sAAAAAIXX7UJW//79o6mpKZ5//vl1xq644opYsWJFREQsXrw4Pv3pT2/QnM3NzTF16tSqY62trVH6vzkBAAAAknJrYRI1PSPr0EMPjVtuuSUWLlwYu+yyy5r3R4wYseafX3jhhQ2er1wuR7lcrjrW2NhYFz8gAAAAAFRXU+mwubk5mpqa4rzzzlvvrYTz58+vZQkAAAAAiIgaT2TttNNOMX369DjnnHPi8MMPj+OOOy7GjBkTffr0ieeeey7uvPPOmD17duy4446xzz77ZJUZAAAAIL28tRbWgZoKWRER++67b8yaNStuuumm+OUvfxkzZ86M5cuXx8CBA2P06NFxxRVXxKGHHrrelkEAAAAA2BA1F7IiIgYOHBjNzc3R3NycxXQAAAAAsI5MClkAAAAAdUdr4SZnxwEAAAAoBIUsAAAAAApBayEAAABAV5VK+WstLJVSJ9jocrbjAAAAAFCdQhYAAAAAhaC1EAAAAKA78tZaWAfsOAAAAACFoJAFAAAAQCFoLQQAAADoKrcWJpGzHQcAAACA6hSyAAAAACiEYrUWtrdHtLWlTlGbQw5JnSAbjz+eOkF23nwzdYJsHHpo6gTZePrp1Amy0UN+Xv3D8OGpI2TjxRdTJ8jOAw+kTpCNzTdPnSAb99yTOkE2XnghdYJsbL116gTZeM97UifIRqWSOkF2esrvWc88kzpBJl7a7YDUETIx9PLLU0fIxkc+ErHVVqlTpJO31sI6YMcBAAAAKIRincgCAAAAyAMPe08iZzsOAAAAANUpZAEAAABQCFoLAQAAALojb62FdcCOAwAAAFAIClkAAAAAFILWQgAAAICucmthEjnbcQAAAACoTiELAAAAgELQWggAAADQHXlrLawDdhwAAACAQqj5RNb5558ft95667t+7vrrr49x48bVuhwAAAAAdarmQtZnPvOZmDJlypp/v+mmm+Lmm2+O6dOnx6BBg9a8P2LEiFqXAgAAAMgPrYWbXM2FrGHDhsWwYcPW/Pv9998fERG77757bL/99rVODwAAAAAR4RlZAAAAABSEWwsBAAAAuqpUyl9rYamUOsFGl6tCVqVSiUqlUnWsvb09Sp2dmzgRAAAAAHmRq0JWS0tLTJ8+verYtGnTYpsBA2KPzTffxKkAAAAAyINcFbKam5tj6tSpVcdaW1uj1NYWsXLlJk4FAAAAUEXeWgvrQK4KWeVyOcrlctWxxsbGuuj1BAAAAKA6pUMAAAAACiFXJ7IAAAAACsGthUnkbMcBAAAAoLrMC1lnnXVWzJ8/P7bffvuspwYAAACgjmktBAAAAOiOvLUW1gE7DgAAAEAhKGQBAAAAUAhaCwEAAAC6yq2FSeRsxwEAAACgOoUsAAAAAApBayEAAABAd+SttbAO2HEAAAAACkEhCwAAAIBC0FoIAAAA0FVuLUwiZzsOAAAAANUpZAEAAABQCMVqLWxsjOjfP3WK2rz5ZuoE2Rg1KnWC7FQqqRNko60tdYJs7LVX6gTZ6Cm/1l98MXWCbHzxi6kTZGfw4NQJsvHb36ZOkI0DD0ydIBtF//vV2559NnWCbDQ1pU6QjVdfTZ0gOz3l10gP+XvW0BfnpI6QjcsvT50gG4sXp06QVGf0/Fa+vHEiCwAAAIBCUMgCAAAAoBCK1VoIAAAAkAOdnREdHalTrK2zs+dfXOhEFgAAAACFoJAFAAAAQCFoLQQAAADohry1FtYDJ7IAAAAAKASFLAAAAAAKQWshAAAAQBe5tTANhSwAAAAAuuXJJ5+Mb3/72/HEE0/Em2++GcOHD49TTjklDjvssI2ynkIWAAAAAF22YMGC+OhHPxqjRo2Kf/3Xf42+ffvGrFmz4uyzz44XX3wxTjvttMzXzKyQ1draGi0tLfHggw/G4sWLo0+fPrHrrrvG0UcfHccee2w0NjZmtRQAAABAcnlrLdzUrrnmmujTp09ce+210dTUFBEREyZMiMWLF0dLS0uccsop0dCQ7ePZMylkLVy4MD7ykY/ETjvtFJ/73Odi6NCh0dbWFvfee2986Utfit/+9rdx+eWXZ7EUAAAAADkwatSo2G233dYUsd42YsSI+PWvfx0rVqyILbbYItM1Mylkfe9734uIiBkzZkSfPn3WvH/wwQfHZpttFtdff32ccsopMWrUqCyWAwAAACCxU089dZ33KpVK3H333bHDDjtkXsSKyKiQ9eqrr0apVIr29vZ1xj72sY/FoEGDom/fvlksBQAAAJBcXm8t7OjoiLa2tvV+plwuR7lcfpd5OmPmzJnv+JmDDjoohgwZss7X/fu//3s899xzcdlll2148C7IpJB18MEHxz333BOTJ0+OSZMmxfjx42P33XeP3r17x4477hinn356FssAAAAA8A4WLVoUxxxzzHrHzzzzzDjrrLPecY729va4+OKL3/Ezw4cPX6uQValU4qKLLorbb789TjnllDj66KO7lHtDZVLIOv7442Pp0qVx1VVXxRVXXBEREZtttlmMGTMmDjvssJg0aVL07t37XeepVCpRqVSqjrW3t0epszOLuAAAAAA90uDBg2POnDnrHX+301gREb169Yr58+dv8JqLFy+Os846Kx577LH47Gc/G2ecccYGf21XZXZr4emnnx4f+9jH4oEHHohHHnkk5syZE4888kg89NBDMXPmzLjuuutiq622esc5WlpaYvr06VXHpk2bFtsMHBh7/N2xNQAAAIAU8tZaGBHR0NCwzsPXN6b58+fH6aefHkuWLImvfe1r8eEPf3ijrpdZISsiom/fvnHIIYfEIYccEhERS5YsiSuvvDJmzJgR11xzTZx77rnv+PXNzc0xderUqmOtra1RWrEiy7gAAAAAdNNzzz0XJ598cpRKpZgxY0b84z/+40Zfs6HWCV555ZWYMGFCXH311euMDRgwIC666KIYMmRILFiw4F3nKpfL0dTUVPXV2NgYDaVSrXEBAAAAyMCFF14YS5cujTPOOCM6OzvjscceW+u1evXqzNes+UTWoEGDolwux8yZM+P444+P/v37rzX+6quvxrJly2LUqFG1LgUAAACQC3m9tXBTWbx4cfzmN7+JiIhLLrmk6mcefPDBGDhwYKbr1lzIamhoiEsuuSSam5vj6KOPjhNPPDH23HPPaGxsjPnz58f3v//9GDJkyHpbBgEAAAAolkGDBnXpgfBZyeQZWfvuu2/ceuut8b3vfS9uuummuPLKK6OjoyO22267OPzww+OTn/xkbLnlllksBQAAAJALeTuRVQ8ye9j7LrvsEl/+8pezmg4AAAAA1lLzw94BAAAAYFPI7EQWAAAAQD3RWrjpOZEFAAAAQCEoZAEAAABQCFoLAQAAALqoszN/rYWdnakTbHxOZAEAAABQCApZAAAAABSC1kIAAACAbshba2E9cCILAAAAgEJQyAIAAACgELQWAgAAAHSRWwvTcCILAAAAgEJQyAIAAACgEIrVWtjZGVGppE5Rmy9+MXWCbFxySeoE2XnssdQJsvGe96ROkI3HH0+dIBuDB6dOkIn7tz8hdYRMTLj4E6kjZOfii1MnyMbMmakTZOO++1InyMbkyakTZKNfv9QJsvHMM6kTZOL5vf6/1BEys8Md16SOkI1hw1InyMTcbT+YOkImRk/aN3WEbJxzTsRee6VOkUzeWgvrgRNZAAAAABSCQhYAAAAAhVCs1kIAAACAHHBrYRpOZAEAAABQCApZAAAAABSC1kIAAACAbshba2E9cCILAAAAgEJQyAIAAACgELQWAgAAAHSRWwvTcCILAAAAgEJQyAIAAACgEDa4kHXOOefEHnvsEW1tbeuMffCDH4yRI0fGddddt85YS0tLjBw5MubNm1dTUAAAAIA86ejI16sebHAha8KECdHe3h6PPvroWu+3trbGs88+GwMGDIi77757na97+OGHY8iQITFq1Kja0wIAAABQtza4kLX//vtHqVSK3/72t2u9f88990SfPn3iE5/4RMyZM2etE1uVSiUeffTRmDBhQnaJAQAAAKhLG1zIGjRoUOy2227xyCOPrPX+vffeG+9///vjkEMOiVWrVsXs2bPXjD3++OOxYsWKmDhxYnaJAQAAAHIgdSuh1sJ38YEPfCDmzp0bb731VkRELF++PH7zm9/EAQccECNGjIjtttsu7rnnnjWff+ihh6JXr16x//77ZxoaAAAAgPrTpULWhAkTYtWqVfHYY49FRMSDDz4Yq1atigMOOGDN+H333Rcd/1cGfPjhh+O9731vNDU1bdD8lUol2traqr7a29ujo7OzK3EBAAAA6EG6VMgaO3Zs9OnTZ0174T333BMjRoyI7bffPiIiDjjggHjttdfiySefjLfeeisee+yxLj0fq6WlJcaOHVv1NXfu3Fi0ZElX4gIAAABsFJ2d6VsJ//5VD+d/enXlw+VyOfbZZ581D3y/995748Mf/vCa8fHjx0e5XI4HH3ww2traolKprDmttSGam5tj6tSpVcdaW1uj9OabXYkLAAAAQA/SpUJWxF+fk/Vf//Vf8eSTT8aiRYviwAMPXDPWt2/f2GeffeKRRx6JlStXxpAhQ2LkyJEbPHe5XI5yuVx1rLGxMaJUqo/yIgAAAADr6FJrYcRfC1nLly+PH/zgB9HU1BRjx45da3zixInxhz/8IR555BG3FQIAAAA9VupWQrcWboBddtklhg4dGnfccUfsv//+0avX2oe6Jk6cGIsXL47f/e53XWorBAAAAIB30uVCVsRfT2X97W2Ff2v48OExbNiwiIjYd999a0sHAAAAAP+ny8/Iioi45JJL4pJLLlnv+C9+8YtuBwIAAADIu7dvLcyTeniseLdOZAEAAADApqaQBQAAAEAhdKu1EAAAAKDe5a21sB44kQUAAABAIShkAQAAAFAIWgsBAAAAusithWk4kQUAAABAIShkAQAAAFAIWgsBAAAAuiFvrYX1wIksAAAAAApBIQsAAACAQtBaCAAAANANWgs3vVJnZzEuZ5w3b17EqlUxapttUkepSeubg1JHyMSOlT+mjpCdpqbUCbLR1pY6QTa23TZ1Av7WvHmpE2Ti/jfHpo6QmQnDWlNHyEYP+bX+2rLeqSNk4h8alqSOkI2VK1MnyMbLL6dOkI2lS1MnyM6yZakTZKNv39QJsjFqVOoE2fjNb1InyMS8bbaJ+Id/iFE95cdlA82bNy+WL4+IyNv3PS+22CJ69I+H1kIAAAAACkFrIQAAAEAXdXb+9ZUnpVLqBBufE1kAAAAAFIJCFgAAAACFoLUQAAAAoBvydmthY2PqBBufE1kAAAAAFIITWQAAAABd1NmZvxNZDXVwXKkOvkUAAAAAegKFLAAAAAAKQWshAAAAQDfkrbWwHjiRBQAAAEAhKGQBAAAAUAg1FbIuuuiiGDlyZNx4441Vxzs6OuKEE06I97znPbFgwYJalgIAAADIjbdvLczTq7Mz9a5sfDUVsi644IIYNmxYXHrppfHCCy+sM37ttdfGo48+Gv/8z/8cu+22Wy1LAQAAAFDnaipkbbHFFnH55ZfHW2+9FRdccEF0/k3p749//GN861vfioMOOihOPPHEmoMCAAAAUN9qfkbWmDFj4vTTT4/f/OY3cf3110dExOrVq+Of//mfo3///vGVr3yl5pAAAAAAeZO6lfDvX/Ugk4e9n3HGGbHnnnvGN7/5zXjppZfiO9/5TvzhD3+Ir371qzFgwIAslgAAAACgzvXKYpLevXvHV7/61Zg0aVJ84QtfiLlz58YnP/nJGD9+fJfmqVQqUalUqo61t7dHqR6eWgYAAABAVZkUsiIidtlll/+/vTuPi7Lc/z/+HsBRCFMxQY+apCSaYpq5pSKJp/xWZq5piYlpdDpqJ5fEck00stROYqZJmVpfXHJJc6ksLcvMJZM2PS2SWm4pcXADhvn90Rd+moAs93DPPfN6Ph7zeNBc432972Bg5jPX5740ZswYTZ06Vc2aNdOIESNKfIz58+crKSmpwLEpU6aoZo0auqlWrbJGBQAAAAAAKJO8XQvdiTes/zGskCVJUVFRmjp1qiIjI+XnV/JDx8XFKTY2tsCxtLQ02RyOskYEAAAAAACARRlyjSyj2O12BQYGFnjz9fWVj81mdkQAAAAAAAAU4Pvvv1dERITmzJnjsjkMXZEFAAAAAADgLdyttdBMFy5c0KhRowq99rlR3GpFFgAAAAAAAKznueee07lz51w+D4UsAAAAAAAAlNqHH36oFStWaNq0aS6fy9DWwjp16ujAgQNGHhIAAAAAAMAtuWNrYW5urjIzMwsdt9vtstvths138uRJPf3003r88cfVqFEjw45bGK6RBQAAAAAA4CFOnDihHj16FDo+bNgwDR8+vMhjOJ1OpaSkFPmYzp07Kzg4WPHx8QoLC9PDDz+s9PT0UmUuCQpZAAAAAAAAHiI4OFh79uwpdLw4q7EcDocmT55c5GPq16+vjRs3av/+/Vq7dq18fMrn6lUUsgAAAAAAAErI6XS/1kKnU/Lx8VFgYGCZjuPn53fVS0d9//33mjlzpqZOnarg4GDl5OQo9//+h+Tm5ionJ0d+fsaXnbjYOwAAAAAAAErk/fffV1ZWlsaOHasmTZqoSZMmat++vSTp5ZdfVpMmTXTkyBHD52VFFgAAAAAAAEqkb9++ioqKuuy+zMxMDRo0SH379lXfvn0VHBxs+LwUsgAAAAAAAErB3VoLy1NISIhCQkIuu+/06dOS/rxOV0REhEvmpbUQAAAAAAAAlsCKLAAAAAAAAJRZUFDQVS8SX1YUsgAAAAAAAErIXXct9HS0FgIAAAAAAMASKGQBAAAAAADAEmgtBAAAAAAAKAV3ay30BtYqZDkcUnq62SnKpN5Pe82OgL9av97sBMaYPt3sBMb49luzExjDx0MWvDZqZHYCQ3R853/NjmCcQM/4nujgQbMTGKL69debHcEYnnIe+/aZncAYHvKuKDsy2uwIhklJMTuBMWKu/9LsCLiUp7xetNnMTgAv4yHPHAAAAAAAAHg6a63IAgAAAAAAcAPsWmgOVmQBAAAAAADAEihkAQAAAAAAwBJoLQQAAAAAACgFd2st9AasyAIAAAAAAIAlUMgCAAAAAACAJdBaCAAAAAAAUELsWmgOVmQBAAAAAADAEihkAQAAAAAAwBJoLQQAAAAAACgFd2st9AasyAIAAAAAAIAllKmQFR8frxYtWhQ6PmfOHIWHh+vIkSNlmQYAAAAAAACgtRAAAAAAAKA0aC0sf7QWAgAAAAAAwBIoZAEAAAAAAMASDGktzMnJKfD+XNbYAQAAAAAAD+R0ul9rodNpdgLXK3Mh69y5c2rSpIkRWZSVlaWsrKwCxxwOh2zu9hMCAAAAAACAclPmQlalSpW0dOnSAseWL1+u5cuXF/tY8+fPV1JSUoFjU6ZMUc3q1XVT5cqlygkAAAAAAABrK3Mhy8fHRxEREQWObd26tUTHiouLU2xsbIFjaWlpsl28WNJ4AAAAAAAALkHjWPkz5BpZRrHb7bLb7QWO+fr6Sj5cmx4AAAAAAMBbURkCAAAAAACAJbjViiwAAAAAAAArYNdCc7AiCwAAAAAAAJZQpkJWYmKivvzyy0LHhw8frgMHDqhOnTplmQYAAAAAAACgtRAAAAAAAKA03K210BvQWggAAAAAAABLYEUWAAAAAABACXGxd3OwIgsAAAAAAACWQCELAAAAAAAAlkBrIQAAAAAAQCm4W2uhN2BFFgAAAAAAACyBQhYAAAAAAAAsgdZCAAAAAACAEmLXQnOwIgsAAAAAAACWQCELAAAAAAAAlkBrIQAAAAAAQCm4W2uhN7BWIcvhkDIyzE5RNgEBZicwRp06ZicwzvjxZicwxokTZicwho+HLBTlL5p78ZTnhyTdcovZCYxh9b/neU6dMjuBMYKDzU5gDE95fRIWZnYCQ1Q4ddLsCIaJCfrC7AjGOOIhr09CQ81OYAxPOQ9e96Kcecg7RgAAAAAAAHg6a63IAgAAAAAAcBMsSCt/rMgCAAAAAACAJVDIAgAAAAAAgCXQWggAAAAAAFBCTqf7tRY6nWYncD1WZAEAAAAAAMASKGQBAAAAAADAEmgtBAAAAAAAKAV3ay30BqzIAgAAAAAAgCVQyAIAAAAAAIAl0FoIAAAAAABQQuxaaI4yF7Li4+O1evXqIh8zefJk9e/fv6xTAQAAAAAAwIsZtiJr2bJlhY7VrVvXqGkAAAAAAADgpQwrZDVv3tyoQwEAAAAAALg9d2st9AZc7B0AAAAAAACWYNiKrJycnALvt9ls8vX1NWoaAAAAAAAAeCnDCllNmjQp8P7KlStr9+7dxTpGVlaWsrKyChxzOByy5eZKPiwiAwAAAAAA5mLXQnMYVshauXJlwRP4FX+K+fPnKykpqcCxKVOmqGZQkG6qXr1U+QAAAAAAAGBthhWyIiIiynyMuLg4xcbGFjiWlpYm27lzZZ4DAAAAAAAA1mRYIcsIdrtddru9wDFfX1/aCgEAAAAAgNtwt9ZCb0BlCAAAAAAAAJZg2Iqsffv2FTpWpUoV3XDDDUZNBQAAAAAAAC9kWCHr/vvvL3QsOjpaL7/8slFTAQAAAAAAmIpdC81R5kJWYmKiEhMTjcgCAAAAAAAAFIprZAEAAAAAAMAS3GrXQgAAAAAAAKtwt9ZCb8CKLAAAAAAAAFgChSwAAAAAAABYAq2FAAAAAAAApUBrYfljRRYAAAAAAABK5cyZM5o0aZI6dOigm2++Wffee6/WrFnjsvlYkQUAAAAAAIASu3jxogYOHKgzZ85o5MiRCgkJ0bp16zR27FjZbDZ1797d8DkpZAEAAAAAAJSQ0+l+rYVOZ/nOt2TJEv38889as2aNwsLCJEnt27fXr7/+qq1bt1LIAgAAAAAAgHvYsGGDOnTokF/EyrN48WKXzck1sgAAAAAAAFAiOTk5OnjwoBo2bKhFixapS5cuuummm9S1a1etW7fOZfOyIgsAAAAAAKAU3K21UJJyc3OVmZlZ6Ljdbpfdbi/yGE6nUykpKUU+plOnTsrOztbq1at17bXXatSoUapcubJSUlI0evRoORwO3XfffaU6h6JQyAIAAAAAAPAQJ06cUI8ePQodHzZsmIYPH17kMRwOhyZPnlzkY2bMmCFJyszM1Ntvv63g4GBJ0m233aZevXpp9uzZFLIAAAAAAABQuODgYO3Zs6fQ8autxpIkPz8/HThwoMjH5K36atq0aX4RS5J8fHwUGRmpV155RadOndJ1111XzOTFY61ClsMhnT9vdoqyCQgwO4Ex/Kz1o1OkX34xO4ExPOVnq2pVsxMY45Jf5Jb2669mJzBGs2ZmJzCOO65fL43Wrc1OYIzTp81OYIiz9mpmRzDENfYMsyMYw1Nem9SsaXYC43jK65M6dcxOYIyPPzY7gTEiI81OYIyjR81OYBp33bXQx8dHgYGBLp8rMDBQNWrUUHZ29hVjefdVqlTJ8Hm52DsAAAAAAABKLCoqSvv379fPP/+cf19OTo4++ugjNWnSxCUFNQpZAAAAAAAAKLFhw4apSpUqGjJkiNauXatt27bp0Ucf1aFDhzR69GiXzOlB/WEAAAAAAADlx91aC8tbzZo1tXz5cs2ePVvTp0/XhQsX1LhxY7322mtq166dS+akkAUAAAAAAIBSqVu3rmbNmlVu89FaCAAAAAAAAEtgRRYAAAAAAEAJueuuhZ6OFVkAAAAAAACwBFZkAQAAAAAAlIK7rcjyBqzIAgAAAAAAgA8tw9wAACAASURBVCVQyAIAAAAAAIAl0FoIAAAAAABQQlzs3RxlKmTFx8dr9erVl91nt9tVvXp13XrrrYqLi9ONN95YpoAAAAAAAACAZNCKrGXLluV/ff78ef30009KTk5Wr169tGDBArVt29aIaQAAAAAAAODFDClkNW/e/LL/bteunbp27aqePXtqzJgxeu+99+Tv72/EVAAAAAAAAG7B3VoLvYHLLvZevXp1DR06VCdOnNDmzZtdNQ0AAAAAAAC8hEt3LYyMjJQkffHFF66cBgAAAAAAAF7ApbsW1qhRQ5J08uTJYj0+KytLWVlZBY45HA7ZvOHy+wAAAAAAwBJoLSx/Li1k5bHZbMV63Pz585WUlFTg2JQpU1SzWjXdVKmSkdEAAAAAAABgES4tZB07dkySVLNmzWI9Pi4uTrGxsQWOpaWlyZaZKV24YFg+AAAAAAAAWIdLC1mffvqpJKlt27bFerzdbpfdbi9wzNfXVyrmyi4AAAAAAABXcjrdr7XQG67I5LKLvaenpys5OVm1a9dWly5dXDUNAAAAAAAAvIQhK7L27duX//X58+f1ww8/aPHixUpPT9fChQsLXWUFAAAAAAAAFJchhaz7778//2u73a6QkBC1a9dOQ4YMUb169YyYAgAAAAAAwK24W2uhNyhTISsxMVGJiYlGZQEAAAAAAAAK5bJrZAEAAAAAAABGcumuhQAAAAAAAJ6IXQvNwYosAAAAAAAAWAKFLAAAAAAAAFgCrYUAAAAAAACl4G6thd6AFVkAAAAAAACwBApZAAAAAAAAsARaCwEAAAAAAEqIXQvNwYosAAAAAAAAWAKFLAAAAAAAAFgCrYUAAAAAAACl4G6thd6AFVkAAAAAAACwBGutyPLzk4KCzE5RNqdOmZ3AGL/+anYC46xZY3YCY/TsaXYCY1x3ndkJjPHUU2YnMIannMf+/WYnME5AgNkJjPHZZ2YnMMa995qdwBDX5PxhdgRjnD5tdgJjZGaancAYoaFmJzDO9u1mJzDGCy+YncAYffuancAY586ZncAYLElCObNWIQsAAAAAAMANsGuhOWgtBAAAAAAAgCVQyAIAAAAAAIAl0FoIAAAAAABQCu7WWugNWJEFAAAAAAAAS6CQBQAAAAAAAEugtRAAAAAAAKAUaC0sf6zIAgAAAAAAgCVQyAIAAAAAAIAl0FoIAAAAAABQQk6n+7UWOp1mJ3A9VmQBAAAAAADAEihkAQAAAAAAwBJoLQQAAAAAACgFd2st9AaGFLJ++OEHvfnmm/r00091/PhxBQQEKCwsTN27d1ePHj3k6+trxDQAAAAAAADwYmUuZK1YsULPPPOMbrjhBg0ePFj169dXRkaGtm7dqkmTJmnVqlVKSkpSUFCQEXkBAAAAAADgpcpUyNq9e7cmTZqkO+64Q88//7wqVKiQP9alSxfdfffdGjp0qOLj47VgwYIyhwUAAAAAAHAH7FpojjJd7H3OnDkKCAhQQkLCZUWsPO3atVNMTIy2bdum3bt3l2UqAAAAAAAAeLlSF7L++OMP7dy5U+3bt1dgYGChj+vWrZskafPmzVc9ZlZWljIzMwu8ORwO5XpDaREAAAAAAAAFKnVr4dGjR+V0OlW3bt0iH1evXj1J0pEjR656zPnz5yspKanAsSlTpqhm9eq6qWbNkocFAAAAAAAwmLu1FnoDQ3YtLIqPz5+LvhwOx1UfGxcXp9jY2ALH0tLSZLtwwdBsAAAAAAAAsI5SF7Jq164tm82mX375pcjHpaWlSZLq1Klz1WPa7XbZ7fYCx3x9fSWbreRBAQAAAAAA4BFKfY2sKlWqqG3bttq+fbsyMjIuG0tNTZXz/65ntXHjRklSVFRU6VMCAAAAAAC4kbxdC93p5g2XFi/TroUjRozQxYsXNW7cOGVnZ0uSMjIyFBMTo65du2rJkiV6/fXX1apVK0VGRhoSGAAAAAAAAN6pTIWsW265RQkJCfrkk0/Us2dPpaSk6MCBA3rmmWeUnp6uhIQEORwOjR8/3qi8AAAAAAAA8FJlvth7jx491KxZMy1ZskTJyck6fvy4AgICdOONNyo6Olrvvfee+vfvr4EDB+qJJ54wIjMAAAAAAIDp2LWw/Bmya2GDBg00efLkAscGDRqkLVu26OjRo0ZMBQAAAAAAAC9lSCGrKDabTV26dHH1NAAAAAAAAPBwLi9kAQAAAAAAeJq8XQvdCbsWAgAAAAAAAG6CFVkAAAAAAACl4G4rsrwBK7IAAAAAAABgCRSyAAAAAAAAYAm0FgIAAAAAAJQCrYXljxVZAAAAAAAAsAQKWQAAAAAAALAEWgsBAAAAAABKyOl0v9ZCp9PsBK7HiiwAAAAAAABYgrVWZPn4SJUqmZ2ibBo2NDuBMc6dMzuBce67z+wExqhZ0+wExvCUn6177jE7gTEyM81OYIzmzc1OYBy73ewExggIMDuBMU6cMDuBMTIyzE5gDE95fvztb2YnMMa335qdwDg+HvL5f8+eZicwhqe8p/r8c7MTGKNGDSkoyOwU8CLWKmQBAAAAAAC4CXdrLfQGHvLRAgAAAAAAADwdhSwAAAAAAACUyqFDhzRixAi1b99erVq10sCBA7V3716XzUchCwAAAAAAoITydi10p1t571p4+vRpDRgwQN99953GjRunF154QTabTQMHDtTXX3/tkjkpZAEAAAAAAKDEtmzZopMnT2rGjBm655571KlTJ82bN092u11vvfWWS+akkAUAAAAAAIASu3DhgiQpMDAw/z5/f3/5+/vrzJkzLpmTQhYAAAAAAEApmN1K+NdbebvrrrtUq1YtTZs2Tb/88otOnz6tGTNm6Pfff1ePHj1cMqefS44KAAAAAACAcpebm6vMzMxCx+12u+x2e5HHcDqdSklJKfIxnTt3VkhIiKZPn64RI0bo73//uyTJZrPp6aef1h133FHy8MVAIQsAAAAAAMBDnDhxosjVUMOGDdPw4cOLPIbD4dDkyZOLfEz9+vW1Z88ejR49Wq1bt9bAgQNVsWJFbdq0SdOmTZOvr68eeOCB0pxCkShkAQAAAAAAlFDeroXuxOmUgoODtWfPnkIfc7XVWJLk5+enAwcOXPVxXbt2VWhoqF599VVVqFBBktS+fXtlZWUpMTFRd911l6pWrVr8EygGrpEFAAAAAADgIXx8fBQYGFjorTiFrOI6cuSIbr755vwiVp7WrVvr4sWLSktLM2yuPBSyAAAAAAAAUGJhYWH68ssvlZ2dfdn9u3fvlo+Pj+rUqWP4nGUqZMXHxys8PFxvvfVWgeObNm1SeHi4du7cWZZpAAAAAAAA3I7ZuxSavWvhyJEj9csvv2jo0KH64IMP9Mknn2jixIlatWqVBg8erOrVqxs+pyErsmbMmKGffvrJiEMBAAAAAADAAiIjI7Vo0SJJ0pgxY/Svf/1L3333nV544QWNGTPGJXOW+WLvfn5+stlsGjNmjJYtWyY/P64fDwAAAAAA4A1at26t1q1bl9t8ZV6RZbfb9dRTT+nrr7/WnDlzjMgEAAAAAADg1vJ2LXSnm9Np9v8V1zOktbBPnz6Kjo7Wq6++qr179xpxSAAAAAAAAOAyhu1amJCQoGrVqunJJ59UZmZmqY6RlZWlzMzMAm8Oh0O5Zly5DAAAAAAAAG7BsEJWUFCQpk2bpsOHD2vatGmlOsb8+fPVsmXLAm+pqak68fvvRsUFAAAAAAAoE7NbCc3etdAMhl6ZPSoqSv369VNKSopuv/32Ev/7uLg4xcbGFjiWlpYm28WLZY0IAAAAAAAAizJsRVae+Ph4hYaGasKECTp58mSJ/q3dbldgYGCBN19fX/n4GB4XAAAAAAAAFmF4Zcjf31/PP/+8MjMz9dJLLxl9eAAAAAAAALdgdiuhN7YWumSJU7NmzfTYY48pIyPDFYcHAAAAAACAF3JZr96jjz6qFi1auOrwAAAAAAAA8DJluth7YmKiEhMTCxzz9fVVSkpKWQ4PAAAAAADglpxO92vnczrNTuB6XD0dAAAAAAAAlkAhCwAAAAAAAJZQptZCAAAAAAAAb+VurYXegBVZAAAAAAAAsAQKWQAAAAAAALAEWgsBAAAAAABKiF0LzcGKLAAAAAAAAFgChSwAAAAAAABYAq2FAAAAAAAApeBurYXegBVZAAAAAAAAsAQKWQAAAAAAALAEWgsBAAAAAABKiF0LzWGtQpY7/pSU1Ndfm53AGE2bmp3AOEeOmJ3AGMeOmZ3AGBcumJ0Al0iz32h2BEPUGz/Y7AjGmTHD7ATGCA01O4ExVq0yO4EhHj81wewIhvj3wD1mRzDGiRNmJzCGB/1N/63R7WZHMEStSpXMjmCM4GCzExjjiy/MTmCMTp2koCCzU8CL0FoIAAAAAAAAS7DWiiwAAAAAAAA3YfWmMStiRRYAAAAAAAAsgUIWAAAAAAAALIHWQgAAAAAAgBJyx/3ovGHXQlZkAQAAAAAAwBIoZAEAAAAAAMASaC0EAAAAAAAoBXdrLfQGrMgCAAAAAACAJVDIAgAAAAAAgCXQWggAAAAAAFAKtBaWvzKvyIqJiVHnzp0LHHvjjTfUqFEjxcTEKDMzs6xTAQAAAAAAwIu5bEXW/PnzNWvWLEVHR2v27NmqWLGiq6YCAAAAAAAoV06n+63IcjrNTuB6LrlG1uzZszVr1iz16NFDc+bMoYgFAAAAAACAMjN8Rdb06dP1xhtvaNCgQYqPj5fNZjN6CgAAAAAAAHghwwpZubm5mjx5spYtW6bhw4dr2LBhRh0aAAAAAADA7bhba6E3MKSQ5XA4NHbsWK1bt06S9Pvvv5fqOFlZWcrKyip0Dps3NHsCAAAAAACgQIYUso4dO6aNGzfqxRdf1ObNm/XWW2+pZcuWuueee0p0nPnz5yspKanAsSlTpqhm9eq66ZprjIgMAAAAAAAAizGkkFWhQgXNmzdPHTt2VIcOHZSamqoJEyaoUaNGCgsLK/Zx4uLiFBsbW+BYWlqabBcvGhEXAAAAAACgTNi10ByG7FoYHBysjh07SpICAwM1e/ZsZWdna8SIETp79myxj2O32xUYGFjgzdfXVz5cOB4AAAAAAMBrGVLI+quIiAiNHDlSP/74oyZMmOCKKQAAAAAAAOBlDNu18K9iY2P1+eef691339Utt9yiAQMGuGoqAAAAAACAcudurYXewCUrsiTJZrMpMTFRwcHBSkxM1FdffeWqqQAAAAAAAOAFyrwia8mSJYWOBQUF6ZNPPinrFAAAAAAAAIDrWgsBAAAAAAA8FbsWmsNlrYUAAAAAAACAkShkAQAAAAAAwBJoLQQAAAAAACgFd2st9AasyAIAAAAAAIAlUMgCAAAAAACAJdBaCAAAAAAAUELsWmgOVmQBAAAAAADAEihkAQAAAAAAwBJoLQQAAAAAACgFd2st9AasyAIAAAAAAIAlUMgCAAAAAACAJdBaCAAAAAAAUAq0FpY/axWycnOlc+fMTlE2oaFmJzCG1b8Pl7ruOrMTGOP0abMTGCMw0OwExqhZ0+wEhqgXcNLsCMaYNcvsBMax281OYIz0dLMTGOPee81OYIh/h501O4IxvvWQdxM5OWYnMEb9+mYnMEytD5aYHcEYnvK699gxsxMYIzLS7ATGuPZasxPAy9BaCAAAAAAAAEuw1oosAAAAAAAAN+B0ul9rodNpdgLXY0UWAAAAAAAALIFCFgAAAAAAACyB1kIAAAAAAIBScLfWQm/AiiwAAAAAAABYAoUsAAAAAAAAWAKthQAAAAAAACXEroXmYEUWAAAAAAAALIFCFgAAAAAAACyB1kIAAAAAAIBScLfWQm9QpkJWfHy8Vq9efcX9drtdQUFBuvXWWzVy5EjVrl27LNMAAAAAAAAAxqzIWrZs2WX/nZGRoT179ig5OVmpqalav3697Ha7EVMBAAAAAADADc2YMUMff/yx1q9ff8XY/v37NXPmTKWmpqpChQqKiorSmDFjdN1115VoDkMKWc2bN7/ivsjISOXk5GjhwoXasWOHOnXqZMRUAAAAAAAApmPXwsu98sorSk5O1o033njF2Pfff6+HHnpIzZs318yZM3Xq1CnNnj1b33zzjVatWlWixU8uvUZWlSpVJEk2m82V0wAAAAAAAMAEBw8e1HPPPacdO3aocuXKBT7mxRdfVLVq1TR//vz8olXjxo3Vq1cvrVq1Sv369Sv2fIbsWpiTk5N/y87O1unTp7VhwwYtXLhQoaGhatWqlRHTAAAAAAAAwI2MGTNG6enpWrp0qRo3bnzFeFZWlj777DN16dLlspVXTZs2VWhoqLZs2VKi+QxZkdWkSZMr7qtataqioqI0atQo+fv7F+s4WVlZysrKKnDM4XDIZuYaOQAAAAAAgEu4W2uhGZ577jk1atSo0PHDhw/r4sWLql+//hVjN9xwgw4ePFii+QwpZK1cuVLSn4WotWvXauXKlRo8eLDi4uJKdJz58+crKSmpwLEpU6aoZlCQbqpRo8x5AQAAAAAAPFFubq4yMzMLHbfb7Ve9JpXT6VRKSkqRj+ncubNCQkKKLGJJ0n//+19JKrDt8JprrtHZs2eL/Pd/ZUghKyIiIv/rli1bym63a9asWXI4HHrssceKfZy4uDjFxsYWOJaWlibb+fNlzgoAAAAAAOCpTpw4oR49ehQ6PmzYMA0fPrzIYzgcDk2ePLnIx9SvX18hISFXzZNr8LI1l1zs/cknn9Rnn32mpKQktWvXTi1atCjWvyuqKujr6ytx0XgAAAAAAOAG3HXXwuDgYO3Zs6fQxxRnh0A/Pz8dOHDAkEx5GwEWtPLq7Nmzuvbaa0t0PEMu9v5XdrtdU6dOVW5uriZOnKjs7GxXTAMAAAAAAIBL+Pj4KDAwsNBbcQpZRqpbt64qVKign3/++Yqxn3/+WQ0aNCjR8VxSyJL+bDHs0aOHDh48qNdff91V0wAAAAAAAMBN2e123Xbbbfrggw8u2+Dv66+/1qFDhxQZGVmi47mskCX9uQVj1apVNXfuXB0+fNiVUwEAAAAAAJSr3Fz3urmr4cOH67ffftPgwYO1ZcsWvf3223rkkUcUFham3r17l+hYZSpkJSYmFtkzGRQUpJ07d+qrr75S3bp1yzIVAAAAAAAALCgiIkLJycnKycnRE088oRdeeEEdOnTQokWLStzq6JKLvQMAAAAAAMC7LFmypNCxNm3aKCUlpcxzUMgCAAAAAAAoBXdu5/NULr1GFgAAAAAAAGAUClkAAAAAAACwBFoLAQAAAAAASsjpdL/WQqfT7ASux4osAAAAAAAAWAIrsgAAAAAAAErB3VZkeQNWZAEAAAAAAMASKGQBAAAAAADAEmgtBAAAAAAAKCEu9m4OVmQBAAAAAADAEiyzIuvixYvKlfS9u5U7S+rcObMTGMNmMzuBcaz+M5XH39/sBLjU2bNmJzDGhQtmJzCGJ/3OyskxO4ExPOV3lqd8Pw4dMjuBMTzluV6xotkJjJGebnYC44SGmp3AGBUqmJ3AGL6+ZicwRpUqZicwxHlfX/lcvGh2DFOEhZ3Xa699b3aMy4SFnZfkIa+zCmGZQpZv3i8rF/5hz83N1YkTJxQcHCwfH+suVuM83Avn4V485TwkzzmXcjmPcnjhzvfDvXAe7qdcziUw0DXHvYSnfE84jxKqUcN1xxbfD3fkKedSHufhc/Hi/3+/7kX8/f1Vo4bLfz2Ugr/8PeUDw0LYnE5v6KAsnszMTLVs2VJ79uxRYDm8EHIVzsO9cB7uxVPOQ/Kcc+E83Avn4V485TwkzzkXzsO9cB7uxVPOQ/Kcc/GU8wAuZd3SMgAAAAAAALwKhSwAAAAAAABYAoUsAAAAAAAAWAKFLAAAAAAAAFgChSwAAAAAAABYAoUsAAAAAAAAWILv5MmTJ5sdwp34+vqqTZs28vX1NTtKmXAe7oXzcC+ech6S55wL5+FeOA/34innIXnOuXAe7oXzcC+ech6S55yLp5wHkMfmdDqdZocAAAAAAAAArobWQgAAAAAAAFgChSwAAAAAAABYAoUsAAAAAAAAWAKFLAAAAAAAAFgChSwAAAAAAABYAoUsAAAAAAAAWIJXF7Li4+MVHh5+xS0iIkKdOnXSqFGjdPToUbNjXlVMTIw6d+5c4Ngbb7yhRo0aKSYmRpmZmeWcrGTyvh9vvfVWgeObNm1SeHi4du7cWc7JvFNBz4+IiAhFRUVp9OjR+s9//mN2xGIr7Ll+6e1///d/zY55VfHx8WrRokWh43PmzFF4eLiOHDlSjqlKZvz48QoPD9eyZcsKHM/NzVX//v3VrFkzHTx4sJzTXd2oUaN00003Ffj79M4771R4eLgWLVp0xdj8+fMVHh6u77//vhxSlk5aWpqeeuop3X777WratKlatWqlBx54QMuXL5fD4TA73lUV53lutb8hx48f17///W91795drVq1UrNmzfT3v/9dEydO1M8//2x2vKsq6HvSuHFjtWzZUv369dOGDRvMjlgqb775psLDw9W7d2+zoxRbTEyMwsPD1bFjR+Xm5hb4mG+++Sb/+5SamlrOCUvn0KFDSkhI0J133qmbb75Zt912m2JiYvTuu+/K6XSaHe+qrvZ7q2fPnmZHLLai3o9YwcMPP6ymTZvq9OnThT5m3bp1Cg8P1+bNm8sxWdmtWrXKUs9roDj8zA7gDv76hiojI0N79uxRcnKyUlNTtX79etntdpPSld78+fM1a9YsRUdHa/bs2apYsaLZkYplxowZatu2rerXr292lDL54Ycf9Oabb+rTTz/V8ePHFRAQoLCwMHXv3l09evSQr6+v2RGL5dLnx/nz5/XTTz8pOTlZvXr10oIFC9S2bVsT05VMYcUTSapbt245JvFe48aN086dO5WYmKj27durTp06l40nJydr7969mjhxoho2bGhSysJ17NhR69ev1969exUZGZl/f1pamg4dOqRq1arpo48+0qBBgy77dzt37lRISIgaNWpUzomL58cff9T999+v0NBQPf7446pVq5YyMzO1bds2TZw4Ubt379aMGTPMjlmkxx57TP369cv/7xUrVmjlypVKSkpSjRo18u8PCwszI16Jbd++XaNGjVLFihXVv39/RUREqEKFCjp48KCWLl2qd955R/PmzVO7du3MjnpVl/7uzc3N1ZkzZ5ScnKwnnnhCWVlZuu+++0xMV3IpKSlq1KiRUlNT9dVXX+nmm282O1Kx+Pj46MSJE9q5c2eBPzdr1641IVXprV+/XuPHj1fdunU1cOBA1a9fX2fPntXmzZs1cuRIbd++XdOmTZOPj/t/bl/Y65OAgIByTuK9+vXrp+3bt2vdunV66KGHCnzMypUrFRwcrOjo6HJOB+CvKGRJat68+RX3RUZGKicnRwsXLtSOHTvUqVMnE5KV3uzZs/XKK6+oR48emjZtmmWKJn5+frLZbBozZoyWLVsmPz9r/oiuWLFCzzzzjG644QYNHjxY9evXV0ZGhrZu3apJkyZp1apVSkpKUlBQkNlRr+qvz4927dqpa9eu6tmzp8aMGaP33ntP/v7+JqUrmYKe6yhf11xzjWbMmKEHH3xQ48aN0+LFi2Wz2SRJ//nPf/TSSy+pc+fOevDBB01OWrD27dvLZrNp9+7dlxWytm7dKn9/fw0aNEhJSUnKzMxUYGCgJCkrK0t79+7V3XffbVbsq3rttdckSUuWLLns+RwdHa2KFStq8eLFGjx4sNsW4iTp+uuv1/XXX5//35988okkqXHjxlcUTN3d0aNH9a9//Ut/+9vftHTpUl177bX5Y23atFGvXr3Uv39/jRs3Tlu2bHH7v/EF/e5t06aNOnXqpIULF1qqkPXll1/q4MGDSk5OVnx8vBYvXqyZM2eaHatYQkND9d///lfvvvvuFYUsh8OhDRs2qEmTJvrmm29MSlh83377rcaNG6e2bdtq7ty5l33g3KVLF9WuXVvz5s1T27Zt1b17dxOTFg+vT8x3++23Kzg4WGvWrCmwkHX48GHt3LlT//jHPyz7/gTwJO7/EYWJqlSpIkn5b7KsYvr06XrllVc0aNAgPfvss27/AvdSdrtdTz31lL7++mvNmTPH7Dilsnv3bk2aNEnR0dF6++231a9fP7Vu3VpdunRRQkKCFi5cqP379ys+Pt7sqKVWvXp1DR06VCdOnLDc8mqYr0WLFnrkkUf0xRdfaPHixZKknJwcjR07VlWrVtX06dNNTli4GjVqqGHDhtq1a9dl92/bti3/eZ6dna3t27fnj+3fv1/nz5+/rPDlbk6dOiWbzVZgC+GAAQM0atQoVgaUo1dffVX//e9/NX369MuKWHkCAgI0atQotWzZUmfOnDEhYdkFBgaqfv36OnTokNlRSmT58uWqWrWq2rRpo+7du2vz5s06efKk2bGKxdfXV3fddZfee+89ZWVlXTb22WefKT093a0L7pdasGCBHA6HpkyZUmDXxKOPPqr+/fvnv5YHrsbPz099+vTRt99+qwMHDlwxvnLlSvn4+Khv374mpAPwVxSy9OcbqLxbdna2Tp8+rQ0bNmjhwoUKDQ1Vq1atzI5YLLm5uZo4caLeeOMNDR8+XOPGjbNcEU6S+vTpo+joaL366qvau3ev2XFKbM6cOQoICFBCQoIqVKhwxXi7du0UExOjbdu2affu3SYkNEbem/IvvvjC5CTFd+lz/dKbFa7/c6nCzqOw6564o3/+859q0qSJXnzxRf3222965ZVX9N133+n5559XtWrVzI5XpA4dOig1NVUXL16UJJ09e1ZffPGFOnXqpLCwMNWuXVtbt27Nf/znn38uPz8/tW/f3qTEVxcdHa2MjAz17t1bCxYs0P79+5WdnS1Jqlevnh555JHLVjvBtTZt2qQbb7xRTZs2LfQxkZGRmjlzpq677rpyTGacrKwsHT58WH/729/MjlJsGRkZ2rBhg+69915VqFBBffv2VU5OTpFt6+6mW7du+uOPP/JX34NTvQAACwxJREFULOZ555131KFDB7f//Ztn69ataty4caE/P5UqVdLkyZMVFRVVvsFKyRNem3iCPn36yNfXV6tXr77sfofDodWrVysqKkq1atUyKR2AS7EuUlKTJk2uuK9q1aqKiorSqFGjLNE25XA4NHbsWK1bt06S9Pvvv5ucqGwSEhLUrVs3Pfnkk1qzZk1+i467++OPP7Rz507deeedRWbu1q2bXnvtNW3evFm33nprOSY0Tt41Z6zySbRU8HNdkipXrmyZouK5c+cKPQ8rqVChgp5//nn17NlTI0eOVGpqqoYOHWqJa6517NhRycnJ2rdvn9q0aaMdO3YoOzs7vwW9Y8eOev/995WbmysfHx/t3LlTt9xyi1v/Huvbt6/S09M1b968/DapihUrqkWLFrrrrrvUs2fPAgvzMF5GRobOnDmj1q1bXzHmcDiuuIC1r6+v239olZOTk/91XgFr7ty5OnPmjB577DETk5XM2rVrdeHCBd1///2S/izytm3bVikpKYqLi7PEcyQiIkKhoaFav359/nV+zp8/rw8++EDTp0/X+fPnTU54dadPn9b58+c9qrhe0N/12rVr68MPPzQhjfeqVauWIiMjtW7dOo0ePTq/hXD79u06fvy4EhISTE4IIA+FLP25VFT688XV2rVrtXLlSg0ePFhxcXEmJyu+Y8eOaePGjXrxxRe1efNmvfXWW2rZsqXuueces6OVSlBQkKZNm6a4uDhNmzZNzz77rNmRiuXo0aNyOp1XvXB4vXr1JMmtd5crLnd/A3WpvOf6X1npWgeVKlXS0qVLCxxbvny5li9fXs6JSq9BgwYaM2aMpk6dqmbNmmnEiBFmRyqWli1byt/fX7t27VKbNm20detWhYWF5V+HqVOnTkpJSdE333yjhg0bat++fRo+fLjJqa/ukUce0YABA/TZZ59p165d2rNnj3bt2qXPP/9cKSkpWrRoEW065aColZU9e/a8YufLJ598Ug8//LCrY5VJQW/Sg4KCNGrUKMXExJiQqHSWL1+upk2bKjg4WBkZGZKke+65R08//bQ2bdqkbt26mZyweLp166aFCxfq7Nmzuuaaa/T+++/Lz89P0dHRWr9+vdnxrirvkhmetGKpoNcnVtxoyhP0799fH330kT7++OP8XRhXrlypunXrqmPHjianA5DHOu/eXCgiIiL/65YtW8put2vWrFlyOByW+aSwQoUKmjdvnjp27Jjf9jJhwgQ1atTIMjs0/VVUVJT69eunlJQU3X777WbHMVTeDjpWfhF27NgxSVLNmjVNTlJ8lz7XrcrHx6fQ87i0nc0qoqKiNHXqVEVGRlqmoGi329WqVav8VXzbtm277EODtm3bym63a8eOHcrMzFRWVpZlNgwJCAhQly5d1KVLF0nSmTNnNHfuXC1ZskSvvvqqRo8ebXJCz1e1alUFBgbq8OHDV4zNnDkzf8XMyZMn9Y9//KO845XKpW/S/fz8VKVKFUu1FErS3r17dfDgQUkq8JITS5cutUwh695779WcOXO0ZcsW3XvvvXrnnXfUtWtXyxROqlSposqVK1/1w8Bjx44pODjYErsWesLrE0/RsWNH1a5dW2vWrFHnzp31+++/66OPPtLjjz9uqQ9vAU/n/r/ZTfDkk0+qQYMGSkpK0pdffml2nGIJDg7O/5QgMDBQs2fPVnZ2tkaMGKGzZ8+anK704uPjFRoaqgkTJliiha127dqy2Wz65ZdfinxcWlqaJFluJ61Lffrpp5JkiVYwwGgdOnTQ/v379c033+jEiROXXYclICBArVq10q5du7Rr1y6FhIQoPDzcvLBXcfz4cXXs2FELFiy4YqxatWoaP368QkJC8t/Ew/XuuOMOffvtt/rxxx8vuz8sLEwRERGKiIhQw4YNTUpXcnmZIyIiiryukTtbtmyZKlWqpNdff12LFy++7Hbfffdp3759Sk1NNTtmsVx//fVq3ry51q9fr99//107duywxM5+l+rUqZO+/fZb/frrrwWOZ2dnq3v37nrggQfKORmszsfHR3369NGHH36o9PR0rV27VpLUq1cvk5MBuBSFrALY7XZNnTo1/+LpeRe8tZKIiAiNHDlSP/74oyZMmGB2nFLz9/fX888/r8zMTL300ktmx7mqKlWqqG3bttq+fXt+20Ge1NTU/GubbNy4UZIscxHSv0pPT1dycrJq166dv3ID8CYdOnTQ2bNn9eabbyowMFAtW7a8bDwyMlLfffeddu3a5da7FUp/Xu/ObrcrJSVF6enpV4yfOnVKGRkZatSokQnpvFNcXJwCAwM1ZsyYQnclLGhXLbhGRkaGNm3apC5duui2225TmzZtLrsNGTJEkrRkyRKTkxZft27d9Nlnn+nNN99USEjIFb/D3N2QIUPk6+urKVOmXLEDoyQlJSUpPT2d4gNKpXfv3nI6nXr//ff1zjvv6M4771RQUJDZsQBcwhp9HCZo2bKlevTooVWrVun111/XI488YnakEouNjdXnn3+ud999V7fccosGDBhgdqRSadasmR577DFLFLIkacSIEYqJidG4ceP04osvqkKFCsrIyFBMTIxCQkI0YMAAvf7662rVqpXbv8GVpH379uV/ff78ef3www9avHix0tPTtXDhQsu0IkiXn8tfValSRTfccEM5poGVNWjQQLVq1dI777yjzp07X9EWGRkZqWeffVbp6ekaOHCgSSmLx8fHRwkJCYqLi9N9992nBx98UE2aNJGvr68OHDigN954QyEhIYqNjTU7qtcIDQ1VUlKSRo0apbvvvlt9+vRRixYt5O/vr19++UWbNm3S9u3bVa9ePcvsrGxla9as0YULFwpdtXTjjTeqefPm2rhxo8aOHavq1auXc8KSu+uuu/Tss89qwYIFGjJkiOVapho3bqynn35aCQkJ6tOnj/r376/Q0FCdPn1a69ev15YtW9S7d2/17t3b7KheJTMzU4sWLSpw7MEHH7TEhgjSnx/wREdH67XXXtNPP/2k8ePHmx0JwF9QyCrCmDFj9OGHH2ru3Ln6n//5n6tewNvd2Gw2JSYmqnv37kpMTFRERIRuvvlms2OVyqOPPqpPPvnEEq2et9xyixISEjRp0iT17NlTDz74oBo0aKBnnnlG06ZNU0JCgvz8/CzzRzFvdybpz9WKISEhateunYYMGZJ/0XqruPRc/io6Olovv/xyOaaB1XXo0EErVqwo8PpX9evX1/XXX6/ffvtN7dq1MyFdybRr106rV6/Wa6+9phUrVmju3LnKzc1V7dq1dffdd2vo0KGqXLmy2TG9Srt27bR+/XqtWLFCH3zwgVJSUnT27FkFBQUpIiJCM2fO1B133GGpDxOsavny5apRo4bat29f6GP69Omjp59+WikpKfrnP/9ZjulKJygoSLfddps+/vhjy7UV5nnggQfUuHFjLV26VAsWLNCpU6dUuXJlNWjQQC+99JLuuOMOyxXorO6PP/4odIOmPn36WKaQJUn9+vVTbGysGjZsaNkdxgFPZnP+dR9nAIb48ccftWTJEn366ac6fvy4AgICFBYWpujoaL333nv6/vvvNXDgQD3xxBNmRwUAAAAAwBIoZAEmcDqd2rJli44ePaqHHnrI7DgAAAAAAFgChSwAAAAAAABYArsWAgAAAAAAwBIoZAEAAAAAAMASKGQBAAAAAADAEihkAQAAAAAAwBIoZAEAAAAAAMASKGQBAAAAAADAEihkAQAAAAAAwBIoZAEAAAAAAMASKGQBAAAAAADAEihkAQAAAAAAwBL+H/DTj2cez1KTAAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 1618.03x1000 with 2 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABKgAAAMsCAYAAABwW5plAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzs3X+U1VW9P/7XYeAIOIqQ4A8MEVEQpaVyDfyFXOVrLc3fWHrNEjOnW1qZWnprteLm7VpmdQuXjl69JtrCNDXDslLT9Pojk0qsgKIcJVNUQBwCD8zM94+ufCQGZc7ZsN/nzOOx1llLzx72frJhfvhyv9671NXV1RUAAAAAkEmf3AEAAAAA6N0UqAAAAADISoEKAAAAgKwUqAAAAADISoEKAAAAgKwUqAAAAADISoEKAAAAgKwUqAAAAADISoEKAAAAgKwUqAAAAADISoEKAAAAgKwUqAAAAADISoEKAAAAgKwUqAAAAADIqm/uAJvqqaeeio6Ojthqq61yRwEAAAAi4rXXXoumpqbYZ599ckfZotra2mLVqlW5Y3RrwIABseuuu+aO0WN1U6Dq6OiISqUzVq7MnaQ2TU25E/CPXn01d4I0yuXcCdKo98/x1227be4EaTTK76O9PXeCdPo0yNnnrbfOnSCNv/0tdwLeqFF+znrttdwJ0uhbN/+l8dY6OnIn4I1Wr86dII3+/XMnSKNv386G+W+Rnli1alWsevHFGPDHP+aOsp5Vo0dHDB2aO0ZV6ubbxlZbbRUrV0a8+OLY3FFqMnBg7gRpNNIPHI88kjtBGjvvnDtBGr/+de4EaUyenDtBGqNH506QxjPP5E6QTqN8Hxlb39/O12mUr1mNYrvtcidIY/Hi3AnSaJQ/j4jG+R8dnZ25E6Txpz/lTpDGqFG5E6Sx/fbzY5ttcqfIY8Af/xhjzzwzd4z1zL/uurotUDXI/4cFAAAAoF410DkYAAAAgC2kVCre8xdKpdwJqlawnQQAAACgt1GgAgAAACArLX4AAAAA1Shai18ds5MAAAAAZKVABQAAAEBWWvwAAAAAesotfkkVbCcBAAAA6G0UqAAAAADISosfAAAAQDWK1uKX2MKFC+NrX/ta/PKXv4yIiHHjxsV5550X++23X/K1NutO3nbbbTFmzJiYN2/e5lwGAAAAgIQWLVoUp5xySixbtiy+/OUvx5e//OVYvXp1nHnmmfGnP/0p+XpOUAEAAACwni9/+csxdOjQ+Pa3vx39+/ePiIj9998/jj/++HjwwQdj1KhRSddToAIAAACoRoO2+K1YsSIeeuihuOCCC9YVpyIiBg8eHA888MBmWbMxdxIAAACAqsyfPz86Ojpi+PDh8cUvfjEmTZoUe++9d5x22mnx1FNPbZY1FagAAAAAGkRnZ2e0t7dv9FWpVN5yjpdeeikiIi655JL461//Gpdddll87WtfixUrVsTpp58eixYtSp67UC1+lUploxvV0dERXV2lLZwIAAAAoBulUvFa/EqlWLJkSZxwwgkb/ZBzzjknzj333DedZs2aNRERscMOO8TMmTOjz//9Pvfdd99417veFVdddVVcdtll6XJHwQpUra2tMXPmzG7HZsyYEYMG7RgR47ZsKAAAAIA6MWzYsHjiiSc2Ol4ul99yjubm5oiImDJlyrriVMTfC1Zjx47dLG1+hSpQtbS0xPTp07sda2tri+XLS/F/p8wAAAAA+Ad9+vRZV2Cq1m677RYR0W2X29q1a2PAgAE1zd+dQp1FK5fL0dzc3O2rqakpSqVCxQUAAAB6sz59ivVKZNSoUTFy5Mj40Y9+tF6R6plnnon58+fHxIkTk631OhUfAAAAANZz8cUXx1/+8pc466yz4v77748f/vCHcdZZZ8W2224bH/rQh5Kvp0AFAAAAwHqmTJkS//M//xNdXV3xyU9+Mj7/+c/HmDFj4uabb47tt98++XqFegYVAAAAQF0o6C1+KU2cOHGztPN1Z7MWqE488cQ48cQTN+cSAAAAANS5gpX6AAAAAOhttPgBAAAAVKNoLX51zE4CAAAAkJUCFQAAAABZafEDAAAA6KlecIvfllSwnQQAAACgt1GgAgAAACArLX4AAAAA1Shai18ds5MAAAAAZKVABQAAAEBWWvwAAAAAesotfkkVbCcBAAAA6G3q6gTV4MERBxyQO0Vt5s7NnYB/NHly7gRp7Lln7gRpjBiRO0EaTz+dO0EaS5fmTpBG//65E6RTLudOkMa0abkTpPGd7+ROkEaj/Hxy3325E6QxaVLuBGm0t+dOkM7RR3XljpDEj39Svycr3ugTx7fljpDEf92xa+4ISTQ3505Ao6irAhUAAABAYRStxa+O2UkAAAAAslKgAgAAACArLX4AAAAA1dDil4ydBAAAACArBSoAAAAAstLiBwAAANBTpVLxWvxKpdwJqlawnQQAAACgt1GgAgAAACArLX4AAAAA1Shai18ds5MAAAAAZKVABQAAAEBWNRWoPvShD8U+++wTS5cu3ejH/OAHP4gxY8bEj3/841qWAgAAACiO12/xK9Krt97id8opp8SaNWviBz/4wUY/5tZbb41hw4bFEUccUctSAAAAADSomgpU//zP/xzDhg2LO+64o9vxZ599Nh577LGYNm1a9O3reewAAABAA8l9YuofX3WspvR9+/aNk08+OX73u9/FggULNhi/9dZbo0+fPvHe9763lmUAAAAAaGA1l9dOPvnkaGpqittvv3299zs6OuL222+PKVOmxE477VTrMgAAAAA0qJoLVDvttFNMnjw5fvCDH8TatWvXvf/QQw/FCy+8EKeccsomz1WpVKK9vb3bV0dHR3R2dtYaFwAAAKB2HpKeVJIGxVNPPTVeeuml+PnPf77uvVtvvTXe/va3x6GHHrrJ87S2tsaECRO6fc2bNy+WLFmSIi4AAAAABZLkyeWHHnpoDB8+PO644444/PDD4+WXX46f/exn8YlPfCJKPajetbS0xPTp07sda2tri4j6rQQCAAAA0L0kBao+ffrEySefHFdccUUsX748vv/970dExEknndSjecrlcpTL5W7Hmpqaoqur5qgAAAAAadT5zXlFkmwnp02bFl1dXfHTn/407rzzznjXu94VQ4YMSTU9AAAAAA0qWYFq6NChccQRR8R1110Xv//97+PUU09NNTUAAAAADSzpWbRTTjkl/vSnP8Wee+4Z//RP/5RyagAAAIDicItfUkmeQfW6gw46KBYsWJBySgAAAAAanKd5AQAAAJBV0hNUAAAAAL2GW/ySsZMAAAAAZKVABQAAAEBWWvwAAAAAqqHFLxk7CQAAAEBWClQAAAAAZKXFDwAAAKCnSqXitfiVSrkTVK1gOwkAAABAb6NABQAAAEBWWvwAAAAAqlG0Fr86ZicBAAAAyKquTlB1dESsWJE7RW3+9KfcCdLYccfcCdL553e8nDtCEouWvy13hCSeeSZ3gjR+/vPcCdKYNi13gjQ6O3MnSKdRvv7+9NZXckdIYs3AQbkjJNHcnDtBGu94R+4EaaxenTtBGo10qODZxfX70OE3qlRyJ0jjx/N3zR0hiVGjcidIo3//3AloFHVVoAIAAAAoBLf4JVWwnQQAAACgt1GgAgAAACArLX4AAAAA1Shai18ds5MAAAAAZKVABQAAAEBWWvwAAAAAesotfkkVbCcBAAAA6G0UqAAAAADISosfAAAAQDWK1uJXx+wkAAAAAFklK1Cdfvrpcfjhh6eaDgAAAIBeQosfAAAAQE+5xS+pgu0kAAAAAL2NAhUAAAAAWWnxAwAAAKhG0Vr86lihClSVSiUqlUq3Yx0dHdHZWb+9lAAAAAB0r1AFqtbW1pg5c2a3YzNmzIihQ3eM4cPHbeFUAAAAAGxOhSpQtbS0xPTp07sda2tri44OJ6gAAACAgtDil0yhClTlcjnK5XK3Y01NTdHVtYUDAQAAALDZKfUBAAAAkFXSE1Tt7e1x/fXXdzt22mmnRb9+/VIuBwAAAJBHqVS8Fr9S/T4aKWmB6pVXXon//M//7Hbs5JNPVqACAAAAYAPJClSzZs1KNRUAAAAAvUihHpIOAAAAUDeK1uJXx+wkAAAAAFkpUAEAAACQlRY/AAAAgJ5yi19SBdtJAAAAAHobBSoAAAAAstLiBwAAAFCNorX41TE7CQAAAEBWClQAAAAAZKXFDwAAAKCn3OKXVMF2EgAAAIDexgkqAAAAgGoU7QRVHbOTAAAAAGRVVyeo+sbaeFu8nDtGTUaMeFvuCEn0rau/OW/uN4sb48+kf//cCdI444zcCdI466zcCdKYdfz3ckdIov2dJ+WOkMyTT+ZOkMa22w7KHSGJP/4xd4I0tt02d4I0Ro/OnSCN557LnSCNtWtzJ0inUT7X9903d4I03r5LV+4ISdz1w/p9VhBsDg1UZgAAAADYQjwkPamC7SQAAAAAvY0CFQAAAABZafEDAAAAqEbRWvzqmJ0EAAAAICsFKgAAAACy0uIHAAAAUA0tfsnYSQAAAACyUqACAAAAICstfgAAAAA9VSoVr8WvVMqdoGoF20kAAAAAepskJ6guuuiiuP322zc6vvfee8dtt92WYikAAAAAGkzSFr+bb7652/cHDhyYchkAAACA/IrW4lfHkhao9t1335TTAQAAANALKPUBAAAAkFXSE1Rr167d4L1SqRRNTU0plwEAAADIyy1+SSUtUO29994bvDd8+PC47777NunXVyqVqFQq3Y51dHREqbOzpnwAAAAAFE/SAtWtt966wXvlcnmTf31ra2vMnDmz27EZM2bEjkOHxrjhw6vOBwAAAEDxJC1QjR8/vqZf39LSEtOnT+92rK2tLUodHTXNDwAAAJBM0Vr86ljSAlWtyuXyRk9cNTU1RXR1beFEAAAAAGxuSn0AAAAAZFWoE1QAAAAAdcEtfkkVbCcBAAAA6G2SFKguvfTSWLBgQYqpAAAAAOhltPgBAAAAVKNoLX51zE4CAAAAkJUCFQAAAABZafEDAAAA6Cm3+CVVsJ0EAAAAoLdRoAIAAAAgKy1+AAAAANUoWotfHbOTAAAAAGSlQAUAAABAVlr8AAAAAKqhxS8ZOwkAAABAVgpUAAAAAGRVVy1+L7/SN275/dtyx6jJkCG5E6TR2Zk7QTrt7bkTpPG3v+VOkMZzz+VOkMbDD+dOkMZNfzopd4Qkhs3PnSCdRvn6u3Rp7gRprF6dO0Eaw4blTpDG4sW5E6Sxdm3uBGk0UtdLo/yZLFyYO0Ea8+eXckdIork5d4I0mppyJ8ioVCreF7tS/X5+FGwnAQAAAOhtFKgAAAAAyKquWvwAAAAACqNoLX51zE4CAAAAkJUCFQAAAABZafEDAAAA6Cm3+CVVsJ0EAAAAoLdRoAIAAAAgKy1+AAAAANUoWotfHbOTAAAAAGSlQAUAAABAVlr8AAAAAHrKLX5JJStQPf3003HjjTfGgw8+GM8//3xsvfXWsfvuu8cpp5wSRx11VJTqeJMAAAAA2HySlPrmzJkTxx9/fDz22GPxgQ98IK666qr493//99hxxx3jU5/6VPzbv/1bdHZ2plgKAAAAgC1s9uzZMWbMmHjsscc2y/w1n6D63e9+FxdffHFMmjQprrjiiiiXy+vGpk6dGsOHD48rr7wyJk2aFMcdd1ytywEAAAAUQ9Fa/DaTRYsWxaWXXrpZ16i5QHX11VdHR0dHzJgxY73i1Os+8pGPxPLly2PQoEG1LgUAAADAFlSpVOKCCy6IwYMHx6pVqzbbOjWX+u6///7Ya6+9Yuedd+52vH///vGFL3whpkyZUutSAAAAAMXw+kPSi/TaDM///vrXvx6vvvpqnHvuucnnfqOaTlAtXbo0Vq1aFSNGjEgSplKpRKVS6Xaso6Mjuro8aB0AAABgS3j44Ydj1qxZMWvWrHjhhRc261o1Faiampoi4u/FoxRaW1tj5syZ3Y7NmDEjtt12x4gYl2QtAAAAgEbT2dkZ7e3tGx0vl8vdPqLpHy1dujQ+/elPx4c//OHYb7/94u67704ZcwM1FagGDRoU22yzTSxevPhNP+7555+PYcOGRZ+3eHhYS0tLTJ8+vduxtra2WLasFCtXVh0XAAAAIJ0CPiR9yZIlccIJJ2x0/Jxzztmkdr3Pfe5zsdNOO8XHPvaxlPE2quaHpB922GFx1113xXPPPdftc6jWrFkTxx13XOy2224xe/bsN53rzap4TU1Nm6OVEgAAAKBhDBs2LJ544omNjm/K6anZs2fH//7v/8Ztt90WERFr166Nzs7OiPj7Ca2Ojo51XXWp1FygOuuss+Luu++OGTNmxLe+9a0NfqMzZ86M5cuXx0knnVTrUgAAAAC8iT59+kRzc3NNc9x1112xevXqOOqoozYYO+OMM2L48OFx33331bTGP6q5QLXXXnvFZz/72bjkkkvi5JNPjlNPPTVGjhwZS5cujTlz5sS9994b06ZNi2nTpqXICwAAAFAMBWzxS2HGjBmx8h+esfToo4/GV7/61ZgxY0bst99+ydesuUAVEfEv//Ivsddee8WNN94YV199dbz00kuxzTbbxO677x7f/OY348gjj4yS/jwAAACAwhs1atQG7/3lL3+JiIjddtstxowZk3zNJAWqiIj99ttvs1TQAAAAAGhsyQpUAAAAAL1GqVS8Fr/N2L327ne/OxYsWLDZ5i/YTgIAAADQ2yhQAQAAAJCVFj8AAACAahStxa+O2UkAAAAAslKgAgAAACArLX4AAAAAPdXLbvHb3Aq2kwAAAAD0NgpUAAAAAGSlxQ8AAACgGkVr8atjdhIAAACArBSoAAAAAMiqrlr8mpoimptzp6hNZ2fuBGmsXZs7QTrLl+dOkMb22+dOkEZ7e+4EaZTLuROksfPOuROkUankTpDO88/nTpDGLrvkTpBG//65E6TRKJ8jjfK1t1G6RRrl596Ixvm71Sh/JgMH5k6QxpIluROk0a9f7gQZucUvqYLtJAAAAAC9jQIVAAAAAFnVVYsfAAAAQGEUrcWvjtlJAAAAALJSoAIAAAAgKy1+AAAAAD3lFr+kCraTAAAAAPQ2ClQAAAAAZKXFDwAAAKAaRWvxq2N2EgAAAICsFKgAAAAAyEqLHwAAAEA1tPglU9VOnn766TFmzJg49NBDo7Ozs9uP+e1vfxtjxoyJMWPGxLx582oKCQAAAEDjqrrU16dPn1iyZEk89thj3Y5///vfrzoUAAAAAL1H1QWqkSNHxtChQ+Ouu+7aYKyjoyN++MMfxt57711TOAAAAIBCKpX+3uJXpFeplHtXqlZ1gaqpqSmOOuqo+MlPfhKVSmW9sYcffjiWL18eRx99dM0BAQAAAGhsNT3N65hjjolXXnklHnzwwfXev/POO+OQQw6JwYMH1xQOAAAAgMZXU4Fq/PjxMXLkyJgzZ86691atWhX33HNPHHfccT2er1KpRHt7e7evjo6O6Orq/oHsAAAAAFtc7pa+f3zVsZrTH3PMMfGzn/0sVq5cGRERP/3pT6Nv375xxBFH9Hiu1tbWmDBhQrevefPmxfLlS2qNCwAAAEDB9K11gmOPPTa+9a1vxb333hvHHnts3HnnnfHud787yuVyj+dqaWmJ6dOndzvW1tYWK1aUYvnyWhMDAAAAUCQ1F6hGjBgR++67b8yZMycOPvjgeOSRR+Lb3/52VXOVy+WNFraamprq+WH0AAAAQCN5/Ra/IqnjwkmSnTzmmGPi4Ycfjptuuil22GGHmDBhQoppAQAAAOgFkhSojjrqqOjq6oqrr746jj322CjVccUOAAAAgC0rSYFqyJAhcdBBB8WaNWuqur0PAAAAoO7kvrWvgW7xq+oZVLNmzdrgvWuuuWaD90488cQ48cQTq1kCAAAAgF6ivstrAAAAANS9mm/xAwAAAOh13OKXVMF2EgAAAIDeRoEKAAAAgKy0+AEAAABUo2gtfnXMTgIAAACQlQIVAAAAAFlp8QMAAADoKbf4JVWwnQQAAACgt1GgAgAAACArLX4AAAAA1Shai18ds5MAAAAAZFVXJ6j69YvYeefcKWrT3p47QRqNVCRubs6dII3nn8+dII0dd8ydIA1/HsXy0ku5E6RT798HXzdiRO4EaSxfnjtBGo3yub5iRe4EaaxdmztBGo3082KjfO195pncCdJ49NHcCdI4/PDcCdJolK9ZVWukL3aZ2UkAAAAAslKgAgAAACCrumrxAwAAACiEUql4LX6lUu4EVSvYTgIAAADQ2yhQAQAAAJCVFj8AAACAahStxa+O2UkAAAAAslKgAgAAACArLX4AAAAAPeUWv6QKtpMAAAAA9DYKVAAAAABklbxAddNNN8WYMWNi2rRpqacGAAAAKI4+fYr1qmPJ08+ePTvGjh0b8+bNi9/85jeppwcAAACgwSQtUP3qV7+KhQsXxoUXXhhDhw6NG264IeX0AAAAADSgpAWq7373u7HddtvFxIkT47jjjosf//jH8eKLL6ZcAgAAACC/12/xK9LLLX4RK1asiB/+8Idx7LHHRr9+/eK9731vrF27Nm6++eZUSwAAAADQgJIVqL7//e/H6tWr433ve19EROy6664xadKkmD17dqxZs2aT5qhUKtHe3t7tq6OjI7q6OlPFBQAAAKAgkhWovvvd78Y+++wTw4YNixUrVsSKFSviPe95T7z44otx9913b9Icra2tMWHChG5f8+bNi6VLl6SKCwAAAFCb3C19DXSLX98Uk8ydOzcWLlwYEREHHHDABuM33nhjHHPMMW85T0tLS0yfPr3bsba2tli1qn57KQEAAADoXpIC1c033xz9+/ePK6+8MpqamtYbu+222+KOO+6IefPmxfjx4990nnK5HOVyuduxpqamen7WFwAAAAAbUXOBasWKFXH33XfH1KlT46CDDtpgfMiQIXHHHXfErFmz4itf+UqtywEAAADk9/otfkVSxyd7at7JO+64I1avXh3HHXdct+N77LFH7LvvvvGjH/0oXn755VqXAwAAAKDB1Fyg+u53vxtDhw6Ngw8+eKMfc/LJJ0elUonZs2fXuhwAAAAADabmFr85c+a85cdMmzYtpk2bVutSAAAAAMVRtBa/OmYnAQAAAMhKgQoAAACArGpu8QMAAADolbT4JWMnAQAAAMhKgQoAAACArLT4AQAAAPRUqVS8Fr9SKXeCqhVsJwEAAADobRSoAAAAAMhKix8AAABANYrW4lfH7CQAAAAAWSlQAQAAAJCVFj8AAACAnnKLX1IF20kAAAAAepu6OkG1bFnEI4/kTlGbKVNyJ0jjb3/LnSCdhQtzJ0hjl11yJ0hj6dLcCdI46fBluSMk8cj8wbkjJLHnnrkTpLN6de4EaVQquROksc8+uROksXhx7gRpbL997gRpPP987gRplMu5E6Tzxz/mTpDGttvmTpDGuHG5E6SxfHnuBGkMGJA7AY2irgpUAAAAAIVRtBa/OmYnAQAAAMhKgQoAAACArLT4AQAAAPSUW/ySKthOAgAAANDbKFABAAAAkJUWPwAAAIBqFK3Fr47ZSQAAAACyUqACAAAAICstfgAAAAA95Ra/pAq2kwAAAAD0NjWfoLrooovi9ttvX++9Pn36xMCBA2OPPfaID3zgA3HUUUfVugwAAAAADSpZi9/NN9+87p87Oztj2bJlce2118Z5550XlUoljj/++FRLAQAAAORXtBa/OpasQLXvvvtu8N7EiRPjsMMOi//+7/9WoAIAAACgW5u11Nfc3ByjRo2Kp59+enMuAwAAAEAd26y3+FUqlXj22Wdj55133pzLAAAAAGx5WvySSVagWrt27bp/fr0wdcUVV8SyZcviox/96CbNUalUolKpdDvW0dERXV31e10iAAAAAN1LVqDae++9N3hvyJAhcf7558fpp5++SXO0trbGzJkzux2bMWNGDBy4Y0SMqyUmAAAAAAWTrEB16623/r9J+/aNQYMG9bi1r6WlJaZPn97tWFtbWzz3nBNUAAAAQAGUSsVr8SvVb90kWYFq/PjxNc9RLpejXC53O9bU1FTP+wwAAADARmzWh6QDAAAANKyinaCqY3YSAAAAgKwUqAAAAADIquYC1aWXXhoLFixIkQUAAACgPrz+kPQiver44d1OUAEAAACQlQIVAAAAAFm5xQ8AAACgGm7xS8ZOAgAAAJCVAhUAAAAAWWnxAwAAAOip12/xKxK3+AEAAABAdRSoAAAAAMhKix8AAABANYrW4lfH7CQAAAAAWSlQAQAAAJCVFj8AAACAniqV6vrWvKKpqwLVoEERhx+eO0Vt9tknd4I07rgjd4J0rr46d4I0/v3fcydIo3//3AnSmPHNwbkjJNG3rr5LbNyUKbkTpPPUU7kTpDF1au4EaVx1Ve4EaZx1Vu4EaTTK58fatbkTpLF6de4E6TTKzyeN8rV3+fLcCdL43e9yJ4Bi0eIHAAAAQFYN8v/GAQAAALawot3i19mZO0HVCraTAAAAAPQ2ClQAAAAAZKXFDwAAAKAaWvySKdhOAgAAANDbKFABAAAAkJUWPwAAAICeKpWK1+JXKuVOULWC7SQAAAAAvY0CFQAAAABZafEDAAAAqEbRWvzqmJ0EAAAAIKskJ6heeOGFmD17dtx3333x3HPPxWuvvRY77LBDHHjggTF9+vTYbbfdUiwDAAAAQAOquUD10EMPxfnnnx9bbbVVnHrqqTF+/Pjo169fLFy4MG688ca4884748orr4wDDzwwRV4AAACA/Nzil1RNBaq//OUv8clPfjJ23nnnuPHGG2PbbbddNzZx4sQ46aST4tRTT42LL7447r333mhqaqo5MAAAAACb349+9KO4/vrrY9GiRVEul2PcuHHxiU98IsaPH598rZpKfddcc028+uqr8aUvfWm94tTrBg4cGOeff35MmDAhli1bVstSAAAAAGwht9xyS3zyk5+M3XbbLb72ta/FF77whXj11Vfj1FNPjblz5yZfr6YTVHfffXfssccesc8++2z0YyZPnhyTJ0+uZRkAAACA4ilai19CM2fOjEMOOSQuvfTSde8ddNBBccQRR8Q111wTV155ZdL1qi5QrVixIpYtWxbvfOc7Nxjr6OiIrq6u9d5ramqK0lv0QlYqlahUKt2O/X3O+u2lBACBRedGAAAgAElEQVQAAKgHq1atiiOPPDImTpy43vvNzc2x0047xQsvvJB8zaoLVJ2dnRsdO/HEE2P+/PnrvffpT386PvShD73pnK2trTFz5sxux2bMmBGDB+8Yzc3jeh4WAAAAgE0yYMCA+OxnP7vB+4sWLYo//OEPcdxxxyVfs+oC1XbbbRfNzc3x7LPPbjB2+eWXx6pVqyIi4sUXX4x//dd/3aQ5W1paYvr06d2OtbW1xcqVpVizptrEAAAAAIkU9Ba/zs7OaG9v3+iHlMvlKJfLPZ761VdfjQsvvDD69u0bZ511Vi0pu1XTM6iOPPLIuO2222LRokWx++67r3t/9OjR6/558eLFmzzfm23S31sEq88KAAAA0OiWLFkSJ5xwwkbHzznnnDj33HN7NOcLL7wQH/nIR+IPf/hDfP3rX49Ro0bVGnMDNRWoWlpa4ic/+UlceOGFce2118bgwYM3+JgFCxbUsgQAAAAAm2jYsGHxxBNPbHS8p6enfvOb38Q555wTK1eujCuuuCIOO+ywWiN2q6YC1ciRI2PmzJlx/vnnx9FHHx0nn3xy7LfffjFgwIB45pln4u67746HHnoodt111zjggANSZQYAAADIr2gtfhHRp0+faG5uTjLXXXfdFRdddFFsv/328Z3vfCfGjh2bZN7u1FSgiog48MADY86cOXHLLbfEPffcE7Nnz46VK1fGkCFDYvz48XH55ZfHkUceWVV/IwAAAABb3k9+8pO44IILYty4cdHa2hrbb7/9Zl2v5gJVRMSQIUOipaUlWlpaUkwHAAAAQCYrVqyIz372szFw4MD4+Mc/HosXL17vGeP9+/dPfpoqSYEKAAAAoNcpYItfCg8++GCsWLEiIiLOPvvsDcb32GOPmDNnTtI1FagAAAAAWOfoo4+Oo48+eouu2ZilPgAAAADqhhNUAAAAAD1VKhWvxa9Uyp2gagXbSQAAAAB6GwUqAAAAALLS4gcAAABQjaK1+NUxOwkAAABAVgpUAAAAAGSlxQ8AAACgp9zil1TBdhIAAACA3kaBCgAAAICs6qrFr7MzYvXq3Clq8+STuROkMWlS7gTp/Obnr+SOkMRNcwbljpDEce/8a+4ISSxevFPuCEkU7cQyEfvvnztBGs89lztBGh/5SO4EadT7z1eve8c7cidI45lncidIo7Mzd4J0hgzJnSCNfn9rjJ97/+VfGuPn3ltvzZ0gjWefzZ0gMz8wJ2MnAQAAAMiqrk5QAQAAABSCh6QnVbCdBAAAAKC3UaACAAAAICstfgAAAADVKFqLXx2zkwAAAABkpUAFAAAAQFZa/AAAAAB6yi1+SRVsJwEAAADobRSoAAAAAMhKix8AAABANYrW4lfH7CQAAAAAWdV8guqiiy6K22+//S0/7oYbboiJEyfWuhwAAAAADabmAtVHP/rROOWUU9b9+y233BK33nprzJw5M4YOHbru/dGjR9e6FAAAAEBxaPFLpuYC1YgRI2LEiBHr/v3BBx+MiIi99tordtlll1qnBwAAAKDBKfUBAAAAkJVb/AAAAAB6qlQqXotfqZQ7QdUKVaCqVCpRqVS6Hevo6IiurvrdaAAAAAC6V6gCVWtra8ycObPbsRkzZsR22+0Y/fqN28KpAAAAANicClWgamlpienTp3c71tbWFq++WoqVK7dwKAAAAIDuFK3Fr44VqkBVLpejXC53O9bU1FTPrZQAAAAAbIRSHwAAAABZFeoEFQAAAEBdcItfUgXbSQAAAAB6m+QFqnPPPTcWLFgQu+yyS+qpAQAAAGhAWvwAAAAAqlG0Fr86ZicBAAAAyEqBCgAAAICstPgBAAAA9JRb/JIq2E4CAAAA0NsoUAEAAACQlRY/AAAAgGoUrcWvjtlJAAAAALJSoAIAAAAgKy1+AAAAAD3lFr+kCraTAAAAAPQ2ClQAAAAAZFVXLX5r10YsXZo7RW2mTs2dII1f/CJ3gnTuuWdQ7ghJ7LJL7gRp/M/dO+WOkMT22+dOkMbq1bkTpNG/f+4E6Tz3XO4Eaey4Y+4EadxzT+4Eaey7b+4EaaxYkTtBGj7Pi6dR/m69vLYxfu79whdyJ0hj7tzcCdIYODBiUGP81apKV9RvS13ROEEFAAAAQFYKVAAAAABkVVctfgAAAABF0NUV0dmZO8X6urrq9yI/J6gAAAAAyEqBCgAAAICstPgBAAAAVKFoLX71zAkqAAAAALJSoAIAAAAgKy1+AAAAAD3kFr+0nKACAAAAICsFKgAAAACyStbi19bWFq2trfHII4/Eiy++GAMGDIg99tgjjj/++DjppJOiqakp1VIAAAAA2RWtxa+eJSlQLVq0KN73vvfFyJEj4xOf+ETstNNO0d7eHg888EB8/vOfj1/+8pfxla98JcVSAAAAADSYJAWq6667LiIiZs2aFQMGDFj3/hFHHBFbbbVV3HDDDXHmmWfG2LFjUywHAAAAQANJUqB66aWXolQqRUdHxwZj73//+2Po0KExcODAFEsBAAAAZFfUW/zqVZKHpB9xxBGxYsWKmDZtWlx99dXx5JNPxpo1ayIiYtddd42zzz47RowYkWIpAAAAABpMkhNU733ve2P58uVx5ZVXxuWXXx4REVtttVXst99+cdRRR8WJJ54Y/fr1e8t5KpVKVCqVbsc6Ojqiq6uUIi4AAAAABZLsFr+zzz473v/+98fDDz8cjz/+eDzxxBPx+OOPx6OPPhqzZ8+O66+/PgYNGvSmc7S2tsbMmTO7HZsxY0Zsu+2OETEuVWQAAACAqhWtxa+eJStQRUQMHDgwpk6dGlOnTo2IiGXLlsUVV1wRs2bNimuuuSYuuOCCN/31LS0tMX369G7H2traYtmyUqxcmTIxAAAAALnV/AyqF154IQ499NC4+uqrNxgbPHhwfO5zn4sddtghFi5c+JZzlcvlaG5u7vbV1NQUpVKSR2YBAAAAUCA1V3yGDh0a5XI5Zs+eHcuXL99g/KWXXooVK1bE2LFja10KAAAAoBBev8WvSK96vsWv5ha/Pn36xCWXXBItLS1x/PHHx2mnnRZ77713NDU1xYIFC+Lb3/527LDDDhtt3QMAAACgd0vyDKoDDzwwbr/99rjuuuvilltuiSuuuCI6Oztj+PDhcfTRR8eHP/zh2GabbVIsBQAAAFAIHpKeTrKHpO++++7xH//xH6mmAwAAAKCX8NRxAAAAALJKdoIKAAAAoDfR4peOE1QAAAAAZKVABQAAAEBWWvwAAAAAeqirq3gtfl1duRNUzwkqAAAAALJSoAIAAAAgKy1+AAAAAFUoWotfPXOCCgAAAICsFKgAAAAAyEqLHwAAAEAPucUvLSeoAAAAAMhKgQoAAACArOqqxa9Pn4iBA3OnqM2vf507QRp96+pvTu9QLudOkMaee+ZOkMZ99+VOkMbq1bkTpLHzzrkTpNMov5dG+bu1zz65E6TRv3/uBGk880zuBGnsuGPuBGn0aaD/FT56dO4EaTz/fO4EaTTK95BG+X00yveQahWtxa+eNdC3DQAAAADqkQIVAAAAAFlp1AIAAADoIbf4peUEFQAAAABZKVABAAAAkJUWPwAAAIAqFK3Fr545QQUAAABAVgpUAAAAAGSlxQ8AAACgh9zil5YTVAAAAABkpUAFAAAAQFabXKA6//zzY9y4cdHe3r7B2Lve9a4YM2ZMXH/99RuMtba2xpgxY2L+/Pk1BQUAAAAoks7OYr3q2SYXqA499NDo6OiIuXPnrvd+W1tbPP300zF48OD42c9+tsGve+yxx2KHHXaIsWPH1p4WAAAAgIazyQWqgw8+OEqlUvzyl79c7/37778/BgwYEGeccUY88cQT652wqlQqMXfu3Dj00EPTJQYAAACgoWxygWro0KGx5557xuOPP77e+w888EC8853vjKlTp8aaNWvioYceWjf25JNPxqpVq2Ly5MnpEgMAAAAUQO6Wvl7Z4hcRccghh8S8efPitddei4iIlStXxi9+8Ys47LDDYvTo0TF8+PC4//771338o48+Gn379o2DDz44aWgAAAAAGkePClSHHnporFmzJn79619HRMQjjzwSa9asicMOO2zd+M9//vPo/L+y3WOPPRb7779/NDc3b9L8lUol2tvbu311dHREV1edlwMBAAAA2ECPClQTJkyIAQMGrGvzu//++2P06NGxyy67RETEYYcdFi+//HL89re/jddeey1+/etf9+j5U62trTFhwoRuX/PmzYtXXlnSk7gAAAAAm0VXV/6Wvn98dXXl3pXq9e3JB5fL5TjggAPWPSj9gQceiPe85z3rxidNmhTlcjkeeeSRaG9vj0qlsu501aZoaWmJ6dOndzvW1tYWr7xSimXLepIYAAAAgKLrUYEq4u/Pofqv//qv+O1vfxtLliyJKVOmrBsbOHBgHHDAAfH444/H6tWrY4cddogxY8Zs8tzlcjnK5XK3Y01NTVEq9TQtAAAAAEXXoxa/iL8XqFauXBk33XRTNDc3x4QJE9Ybnzx5cvz+97+Pxx9/3O19AAAAQMPK3dLXa2/xi4jYfffdY6eddoo777wzDj744Ojbd/1DWJMnT44XX3wxfvWrX/WovQ8AAACA3qnHBaqIv5+ieuPtfW80atSoGDFiREREHHjggbWlAwAAAKDh9fgZVBERl1xySVxyySUbHf/pT39adSAAAACAonv9Fr8iqedb/Ko6QQUAAAAAqShQAQAAAJBVVS1+AAAAAL1d0Vr86pkTVAAAAABkpUAFAAAAQFZa/AAAAAB6yC1+aTlBBQAAAEBWClQAAAAAZKXFDwAAAKAKRWvxq2dOUAEAAACQlQIVAAAAAFlp8QMAAACogha/dOqqQNXUFNHcnDtFbdauzZ0gjeefz50gnbPPzp0gjaefzp0gjT1G1/G9qG9QqZRyR0hi9OjcCdK46qrcCdJ5xztyJ0jjb3/LnSCN557LnSCNww/PnSCNnXfOnSCNSiV3gjQa5fMjIuL/W/G93BGSWHb4SbkjJNGnQfqAhgzJnSCNJUtyJ6BRNMinNgAAAAD1qq5OUAEAAAAUQVfX319FUqrjRg4nqAAAAADISoEKAAAAgKy0+AEAAABUoWi3+DU15U5QPSeoAAAAAMjKCSoAAACAHurqKt4Jqj51fAypjqMDAAAA0AgUqAAAAADISosfAAAAQBWK1uJXz5ygAgAAACArBSoAAAAAsqqpQPW5z30uxowZEzfffHO3452dnXHqqafGO97xjli4cGEtSwEAAAAUxuu3+BXp1dWVe1eqV1OB6uKLL44RI0bEpZdeGosXL95g/Nprr425c+fGZz7zmdhzzz1rWQoAAACABlVTgWrrrbeOr3zlK/Haa6/FxRdfHF1vKNX94Q9/iG9+85tx+OGHx2mnnVZzUAAAAAAaU83PoNpvv/3i7LPPjl/84hdxww03RETE2rVr4zOf+Uxst9128aUvfanmkAAAAABFk7ul7x9fqT355JPxwQ9+MPbff/+YOHFifOYzn4mXXnop/UKR6CHpH/vYx2LvvfeOb3zjG/HXv/41rrrqqvj9738fl112WQwePDjFEgAAAABsIfPnz48PfvCD0adPn7j88svjggsuiAcffDDOOOOMqFQqydfrm2KSfv36xWWXXRYnnnhifOpTn4p58+bFhz/84Zg0aVKP5qlUKhv9TXZ0dERXVylFXAAAAADexDe+8Y0YPHhwtLa2RrlcjoiIvfbaK0466aS47bbb4pRTTkm6XpITVBERu+++e1x44YUxd+7c2GuvveLjH/94j+dobW2NCRMmdPuaN29eLF++JFVcAAAAgKo18i1+lUolHn744Zg6deq64lRExD777BMjR46Me++9N81Cb5DkBNXrpkyZEl/84hdj8uTJ0bdvz6duaWmJ6dOndzvW1tYW7e2lWL261pQAAAAAbMyzzz4br732WowaNWqDsd122y0WLlyYfM2kBapalcvl9Spzb9TU1BQlHX4AAAAAG9XZ2Rnt7e0bHX+z2svrXn311YiI2GabbTYY23rrrWPlypW1hexGoQpUAAAAAPVic9ycV6slS5bECSecsNHxc845J84999w3naMzw29MgQoAAACgQQwbNiyeeOKJjY6/1empiIhBgwZFRHR7UmrlypWx7bbbVh9wIxSoAAAAABpEnz59orm5uaY53v72t0e/fv3iz3/+8wZjf/7zn2P33Xevaf7uJC1Q7bLLLrFgwYKUUwIAAAAUUhFb/FIol8tx0EEHxT333BPnnXfeulNXTz31VDz99NPxwQ9+MPmafZLPCAAAAEBdO/fcc+Ovf/1rnHnmmXHvvffG9773vTj77LNj9OjRMW3atOTrKVABAAAAsJ7x48fHtddeG2vXro3zzjsvvvrVr8YhhxwS119//SY9x6qnPIMKAAAAoIe6uorX4tfVlXa+iRMnxuzZs9NOuhFOUAEAAACQlQIVAAAAAFlp8QMAAACoQtFa/OqZE1QAAAAAZKVABQAAAEBWWvwAAAAAeqg33OK3JTlBBQAAAEBWClQAAAAAZKXFDwAAAKAKRWvxq2d1VaCqVCKeey53itocfnjuBGmMHJk7QTr9yqXcEZK4/+o6bjZ+g/vvb4w/j4MOyp0gjT/+MXeCNPr3z50gnUb5vbS3506Qxtq1uROkceDYZbkjJPG9+wbnjpDEjjvmTpDGqFG5E6RTOuik3BGSeP/7cydIY/Lk3AnS2G673AnS2HnniLe9LXcKGoEWPwAAAACyqqsTVAAAAABF4Ba/tJygAgAAACCr/7+9O4+SsjrzB/40DaUgCrYBNERFRMFouxEiREAURjPuoERRMUJUjIlmlKAYVxSU0XEZwRgQXHAZRMYVF0xUTHDBLShqolF/wSVBiYqdNjgNTf/+8MARaaSXt7lVxedzTp3T1K1+7/c9dHVXPXWf9ypQAQAAAJCUFj8AAACABsi3Fr9CZgUVAAAAAEkpUAEAAACQlBY/AAAAgHqyi1+2rKACAAAAICkFKgAAAACS0uIHAAAA0AD51uJXyKygAgAAACCpRhWoRo8eHXvsscdaxydMmBBdu3aN999/vzHTAAAAAFDEtPgBAAAANIAWv+xo8QMAAAAgKQUqAAAAAJLKpMVv+fLltd6/wlo3AAAAoAjV1ORfi19NTeoEDdfoAtW//vWv2HnnnbPIElVVVVFVVVXrWHV1ddTUlGQyDwAAAAD5o9EFqo033jhuu+22WsdmzJgRM2bMqPOxJk2aFBMnTqx1bMyYMbHZZltGxHcbEhMAAACAPNXoAlWzZs2ivLy81rE5c+bU61gjRoyIYcOG1Tq2cOHC+OSTkvjss/omBAAAAMhevrX4FbJMrkGVlVwuF7lcrtax0tLSKNHhBwAAAFB07OIHAAAAQFJ5tYIKAAAAoBDYxS9bVlABAAAAkFSjClTjx4+PP/7xj2sdP+200+KNN96I73znO42ZBgAAAIAipsUPAAAAoAHyrcWvkGnxAwAAACApK6gAAAAA6slF0rNlBRUAAAAASSlQAQAAAJCUFj8AAACABsi3Fr9CZgUVAAAAAEkpUAEAAACQlBY/AAAAgHqyi1+2rKACAAAAICkFKgAAAACS0uIHAAAA0AD51uJXyAqqQNWsWcTGG6dO0ThPP506QTbKylInyM6NvyrgJt2v6NcpdYJsVFWlTpCNYnmun3RicTw/crmS1BEy8+abqRNk4ycH/j11hEzMfmWr1BEycd/vN08dIRPt26dOkI1PPkmdIButW6dOkJ3ly1MnyMbNN6dOkI1ttkmdIBv33586QTYOPDBiiy1Sp6AYaPEDAAAAIKmCWkEFAAAAkC+0+GXHCioAAAAAklKgAgAAACApLX4AAAAA9VRTk38tfjUFvMeRFVQAAAAAJKVABQAAAEBSWvwAAAAAGiDfWvwKmRVUAAAAACSlQAUAAABAUlr8AAAAAOrJLn7ZanSBavTo0XHPPfd842MuuuiiGDJkSGOnAgAAAKAIZbaC6s4771zr2NZbb53VNAAAAAAUmcwKVLvvvntWhwIAAADIe/nW4lfIXCQdAAAAgKQyW0G1fPnyWu8vKSmJ0tLSrKYBAAAAoMhkVqDaeeeda71/0003jRdeeKFOx6iqqoqqqqpax6qrq6OmpqTB+QAAAACyYhe/bGVWoJo5c2btEzSv+xSTJk2KiRMn1jo2ZsyYaNNmy4j4bkPiAQAAAJCnMitQlZeXN/oYI0aMiGHDhtU6tnDhwliypCS++KLR0wAAAACQRzIrUGUhl8tFLperday0tDRKdPgBAAAAeSLfWvwKmV38AAAAAEgqsxVU8+fPX+tYmzZtYrvttstqKgAAAACKSGYFqqOOOmqtY/37949f//rXWU0FAAAAkJRd/LLV6ALV+PHjY/z48VlkAQAAAGAD5BpUAAAAACSVV7v4AQAAABSKfGvxK2RWUAEAAACQlAIVAAAAAElp8QMAAABoAC1+2bGCCgAAAICkFKgAAAAASEqLHwAAAEA91dTkX4tfTU3qBA1nBRUAAAAASSlQAQAAAJCUFj8AAACABsi3Fr9CZgUVAAAAAEkpUAEAAACQVEG1+JWWRrRunTpF4zQrkpLgF1+kTpCdvn1TJ8hGWVnqBNn45JPUCfiqv7xVkjpCJioqUifITrE8129/fKvUETJR6K9Lis2iRakTZKNt29QJslFZmTpBdt56K3WCbPTrlzpBNlq1Sp0gG+++mzpBNjbZJHWCdOzil60iKZcAAAAAUKgUqAAAAABIqqBa/AAAAADyRb61+BUyK6gAAAAASEqBCgAAAICktPgBAAAA1JNd/LJlBRUAAAAASVlBBQAAANAA+baCqpBZQQUAAABAUgpUAAAAACSlxQ8AAACgnlwkPVuNKlCNHj067rnnntXuy+VyscUWW8T3vve9GDFiROywww6NCggAAABAcctkBdWdd9656uulS5fGO++8E1OnTo0jjjgiJk+eHD179sxiGgAAAACKUCYFqt133321f/fq1St++MMfxqBBg2LUqFHx6KOPRsuWLbOYCgAAACAv5FuLXyFrsoukb7HFFnHSSSfFRx99FLNnz26qaQAAAAAocE26i1/fvn0jIuK5555rymkAAAAAKGBNuotfu3btIiJi8eLFdXp8VVVVVFVV1TpWXV0dK1aUZJYNAAAAoDG0+GWnSQtUK5WU1K2wNGnSpJg4cWKtY2PGjIm2bbeM0tLvZhkNAAAAgMSatEC1aNGiiIjYcsst6/T4ESNGxLBhw2odW7hwYVRUlERlZWbxAAAAAMgDTVqgeuqppyIiomfPnnV6fC6Xi1wuV+tYaWlpNGvSK2YBAAAA1E1NTf61+NXUpE7QcE1W8lmyZElMnTo1OnbsGAMGDGiqaQAAAAAocJmsoJo/f/6qr5cuXRpvvfVWTJs2LZYsWRJTpkxZ66ooAAAAAMikQHXUUUet+jqXy0WHDh2iV69eceKJJ8a2226bxRQAAAAAeSXfWvwKWaMKVOPHj4/x48dnlQUAAACADZDLjgMAAACQVJPu4gcAAABQjOzily0rqAAAAABISoEKAAAAgKS0+AEAAAA0QL61+BUyK6gAAAAASEqBCgAAAICktPgBAAAA1JNd/LJlBRUAAAAASSlQAQAAAJCUFj8AAACABsi3Fr9CZgUVAAAAAEkV1AqqRYsipk1LnaJx/uM/UifIxiefpE6QnWI6l2Lw+9+nTpCNcZeWpI6QiWVVBXyVxa949NHUCfi6nx33WeoImditb5vUETJx8smpE2Rj111TJ8jG+++nTpCN9u1TJ8jOF1+kTpCN3b7zceoImXjy1S1SR8jE3/6WOkE2tt02dQKKRUEVqAAAAADygV38sqXFDwAAAICkFKgAAAAASEqLHwAAAEAD5FuLXyGzggoAAACApBSoAAAAAEhKix8AAABAA2jxy44VVAAAAAAkpUAFAAAAQFJa/AAAAADqqaYm/1r8ampSJ2g4K6gAAAAASEqBCgAAAICktPgBAAAANEC+tfgVskwKVG+99Vbcfvvt8dRTT8WHH34YrVq1ii5dusRhhx0WAwcOjNLS0iymAQAAAKAINbpAddddd8XFF18c2223XQwfPjw6d+4cFRUVMWfOnLjwwgvj7rvvjokTJ0ZZWVkWeQEAAAAoMo0qUL3wwgtx4YUXxv777x9XXHFFtGjRYtXYgAED4qCDDoqTTjopRo8eHZMnT250WAAAAIB8YBe/bDXqIukTJkyIVq1axdixY1crTq3Uq1evGDp0aDz55JPxwgsvNGYqAAAAAIpUgwtUn332WcybNy/23nvvaN269Vofd8ghh0RExOzZs9d5zKqqqqisrKz1Vl1dHRF5VpoEAAAA2IC99tprccopp0Tv3r1jzz33jCOPPDIeeuiheh+nwS1+H3zwQdTU1MTWW2/9jY/bdtttIyLi/fffX+cxJ02aFBMnTqx1bMyYMdG8+ZYR8d16ZwUAAADIWr61+K1vb775ZhxzzDHRrVu3OP/886NVq1Yxa9asOOOMM+Jvf/tbnHjiiXU+Via7+H2TZs2+XKT15QqobzZixIgYNmxYrWMLFy6Mt94qyTQbAAAAAA1zww03RMuWLWPq1Kmruuv69OkTixcvjkmTJsXw4cNX1YXWpcEFqo4dO0ZJSUm8++673/i4hQsXRkTEd77znXUeM5fLRS6Xq3WstLS0/iEBAAAAaBLdunWLHXfccY1LP3Xp0iWeeuqpWLp0aWyyySZ1OlaDC1Rt2rSJnj17xty5c6OioiI222yzVWMLFiyIXXbZJUpKSuLhhx+OiIh+/fo1dCoAAACAvGIXv4if/OQna9xXVVUVTzzxRGy99dZ1Lk5FNLLF7/TTT4+hQ4fGOeecE9dcc020aNEiKioqYujQodGhQ4c47rjj4qabbooePXpE3759GzMVAAAAAOuwYsWKqKysXOv4N3WvrVRTUxPTp0//xsfst99+0aFDhzW+7+KLL45332N+VDEAACAASURBVH03/vM//7PuoaORBao999wzxo4dGxdeeGEMGjQojj322Nh+++3j4osvjnHjxsXYsWOjefPmcd555zVmGgAAAADq4KOPPoqBAweudfznP/95nHbaad94jOrq6rjooou+8TGdO3derUBVVVUV5513Xtx3330xfPjwOPzww+uVu9EXSR84cGDsuuuuceutt8bUqVPjww8/jFatWsUOO+wQ/fv3j0cffTSGDBkSxx9/fJxxxhmNnQ4AAAAgL+Rbi19ERPv27ePFF19c6/i6Vk9FRDRv3jzeeOONOs+5ePHiOO2002L+/Plx+umnx89+9rM6f++qOev9HbXYfvvt11pZO+GEE+Kxxx6LDz74IIupAAAAAFiLZs2arXHR8qb0xhtvxMknnxyffvpp/Nd//VccfPDBDTpOJgWqb1JSUhIDBgxo6mkAAAAAWI/efffdOP7446OkpCRuvfXW2G233Rp8rCYvUAEAAAAUG7v4RZx77rmxZMmSOO+886Kmpibmz5+/2vguu+wSzZvXrfSkQAUAAABAvSxevDiee+65iIgYO3ZsrY955plnoqysrE7HU6ACAAAAaIB8W0G1PrVr165eF1Jfl2aZHQkAAAAAGkCBCgAAAICktPgBAAAANMCG3OKXNSuoAAAAAEhKgQoAAACApLT4AQAAANRTTU3+tfjV1KRO0HBWUAEAAACQVEGtoGrXLuL441OnaJzly1MnyMa3vpU6AcVq//1TJ8jG28ML+KOLr3h2RuoE2ejWLXWC7BTL35E3FrVJHSETZ56ZOkE2vv3t1Amy0bygXtmuXdu2qRNkI99WFTTGF1+kTpCNJ17ZInWETLRqlTpBNnr3Tp0gG8Xy/0F6RfJnHAAAAGD9KqZifGpa/AAAAABISoEKAAAAgKS0+AEAAADUk138smUFFQAAAABJKVABAAAAkJQWPwAAAIAGyLcWv0JmBRUAAAAASSlQAQAAAJCUFj8AAACAerKLX7asoAIAAAAgKQUqAAAAAJJqVIFq9OjR0bVr17jjjjtqHX/kkUeia9euMW/evMZMAwAAAJB3VqzIr1shy2QF1eWXXx7vvPNOFocCAAAAYAPT6AJV8+bNo6SkJEaNGhXLly/PIhMAAAAAG5BGF6hyuVz86le/ildffTUmTJiQRSYAAACAvLZyF798um3wu/gNHjw4+vfvHzfccEO89NJLWRwSAAAAgA1EZrv4jR07NjbffPM466yzorKyskHHqKqqisrKylpv1dXVUVNT4Ff8AgAAAGANmRWoysrKYty4cfHee+/FuHHjGnSMSZMmRffu3Wu9LViwICoqPsoqLgAAAECjpG7pK6Zd/JpnebB+/frF0UcfHdOnT49999233t8/YsSIGDZsWK1jCxcujCVLSuIf/2hsSgAAAADySWYrqFYaPXp0dOrUKc4///xYvHhxvb43l8tF69ata72VlpZGSUnmcQEAAABILPOKT8uWLeOKK66IysrKuPbaa7M+PAAAAEBeSN3SV0wtfk2yJGnXXXeNU089NSoqKpri8AAAAAAUkSbrmTvllFNijz32aKrDAwAAAFAkGnWR9PHjx8f48eNrHSstLY3p06c35vAAAAAAeammJv/a6mpqUidoOFcdBwAAACApBSoAAAAAkmpUix8AAADAhirfWvwKmRVUAAAAACSlQAUAAABAUlr8AAAAAOrJLn7ZsoIKAAAAgKQUqAAAAABISosfAAAAQAPkW4tfIbOCCgAAAICkFKgAAAAASEqLHwAAAEA92cUvWwVVoGrWLGLjjVOnaJx8++FtqGZFtPZuyy1TJ8hGVVXqBNn45JPUCbLRrVvqBNkoludHMf3O+v73UyfIxquvpk6QjcMPT50gG6+8kjpBNorldVbzgnqFvnbF9Lt3+fLUCbKxaFHqBNno3Dl1gmwUy88VZKWI/mwAAAAAUIiK5PMZAAAAgPWrWFbv5gMrqAAAAABISoEKAAAAgKS0+AEAAADUk138smUFFQAAAABJKVABAAAAkJQWPwAAAIAGyLcWv0JmBRUAAAAASSlQAQAAAJCUFj8AAACABtDil51Gr6AaOnRo7LfffrWO3XLLLdGtW7cYOnRoVFZWNnYqAAAAAIpQk62gmjRpUlx11VXRv3//uPrqq2OjjTZqqqkAAAAA1quamvxbQVVTkzpBwzXJNaiuvvrquOqqq2LgwIExYcIExSkAAAAA1irzFVSXXnpp3HLLLXHCCSfE6NGjo6SkJOspAAAAACgimRWoVqxYERdddFHceeedcdppp8XPf/7zrA4NAAAAkHfyrcWvkGVSoKquro6zzz47HnjggYiI+Pjjjxt0nKqqqqiqqlrrHDU1VmMBAAAAFJtMClSLFi2Khx9+OK655pqYPXt23HHHHdG9e/c4+OCD63WcSZMmxcSJE2sdGzNmTLRtu2WUlHw3i8gAAAAA5IlMClQtWrSI66+/Pvr06RO9e/eOBQsWxPnnnx/dunWLLl261Pk4I0aMiGHDhtU6tnDhwqioKImKiiwSAwAAADScXfyylckufu3bt48+ffpERETr1q3j6quvjmXLlsXpp58en3/+eZ2Pk8vlonXr1rXeSktLo6SkSTYdBAAAACChJqn4lJeXx5lnnhlvv/12nH/++U0xBQAAAABFIrNd/L5u2LBh8eyzz8aDDz4Ye+65Zxx33HFNNRUAAADAepdvLX6FrMl65kpKSmL8+PHRvn37GD9+fLz88stNNRUAAAAABazRK6huvfXWtY6VlZXFH/7wh8ZOAQAAAEARa7IWPwAAAIBiZRe/bNkWDwAAAICkFKgAAAAASEqLHwAAAEAD5FuLXyGzggoAAACApBSoAAAAAEhKix8AAABAPdnFL1tWUAEAAACQlAIVAAAAAElp8QMAAABogHxr8StkVlABAAAAkJQCFQAAAABJafEDAAAAaAAtftkpqAJVdXVEZWXqFI3TunXqBNn44ovUCbIzbVrqBNk45ZTUCfiqxx9PnSAb3/526gTZKPS/HV/1u9+lTpCNsrLUCbLx6qupE2RjzpzUCbJx6KGpE2SjoiJ1gmwU0+/ewft9nDpCJrp12yJ1hExstlnqBNl46KHUCbKxySapE1AstPgBAAAAkFRBraACAAAAyAc1NfnX4ldTkzpBw1lBBQAAAEBSClQAAAAAJKXFDwAAAKAB8q3Fr5BZQQUAAABAUgpUAAAAACSlxQ8AAACgnuzily0rqAAAAABISoEKAAAAgKS0+AEAAAA0QL61+BWyRhWoRo8eHffcc88a9+dyuSgrK4vvfe97ceaZZ0bHjh0bMw0AAAAARSyTFVR33nnnav+uqKiIF198MaZOnRoLFiyIWbNmRS6Xy2IqAAAAAIpMJgWq3XfffY37+vbtG8uXL48pU6bEM888E/vss08WUwEAAAAkZxe/bDXpRdLbtGkTERElJSVNOQ0AAAAABSyTFVTLly9f9XVNTU3885//jGeffTamTJkSnTp1ih49emQxDQAAAABFKJMC1c4777zGfW3bto1+/frFyJEjo2XLlnU6TlVVVVRVVdU6Vl1dHRFWYgEAAAD5Id9a/ApZJgWqmTNnRsSXBab77rsvZs6cGcOHD48RI0bU6ziTJk2KiRMn1jo2ZsyY2GyzLSPiu42NCwAAAEAeyaRAVV5evurr7t27Ry6Xi6uuuiqqq6vj1FNPrfNxRowYEcOGDat1bOHChbFkSUksXdrouAAAAADkkUwKVF931llnxdNPPx0TJ06MXr16xR577FGn78vlcpHL5WodKy0tzTIiAAAAQIPZxS9bTbKLXy6Xi0suuSRWrFgRF1xwQSxbtqwppgEAAACgCDRJgSriy1a/gQMHxptvvhk33XRTU00DAAAAQIFrsgJVRMSoUaOibdu2cd1118V7773XlFMBAAAArFcrVuTXrZA1qkA1fvz4eOONN9Y6XlZWFvPmzYuXX345tt5668ZMBQAAAECRatIVVAAAAACwLk2yix8AAABAsSv0trp8YgUVAAAAAEkpUAEAAACQlBY/AAAAgHqqqcm/Fr+amtQJGs4KKgAAAACSsoIKAAAAoAHybQVVIbOCCgAAAICkFKgAAAAASEqLHwAAAEA9uUh6tqygAgAAACCpkpqawqivvfzyy1FVtSKqqlqmjtIopaWpE2Qj36rEjbF4ceoE2dhyy9QJslFdnTpBNorlOZLLpU6QjWL5uYoonp+t5kWyhrtZkXzU99lnqRNkY/PNUyfIxrJlqRNko5h+927RZnnqCJlYXiQNNMXynurTT1MnyEaLFksjl2sWu+22W+oo69Wf//znWLx4abz1Vn7VKLp0WRrt2rWMbt26pY5SbwXzG6q0tDRyuYhNN226OVasWBEfffRRtG/fPpoV8CtO51E/ZWVNduiI8P+Rb4rlPCKK51ycR35xHvllfZ1HU76+Wsn/SX5xHvXVtG+b1td5NPWbv2L5uYpYP+fS1O9DItbPefzf/zWL0mKpGtZDy5Yto127iHbtUif5upbRsmV+Fc3qqmBWUK0PlZWV0b1793jxxRejdevWqeM0mPPIL84jvxTLeUQUz7k4j/ziPPJLsZxHRPGci/PIL84jvxTLeUQUz7kUy3mwYSjssjYAAAAABU+BCgAAAICkFKgAAAAASEqBCgAAAICkFKgAAAAASEqBCgAAAICkSi+66KKLUofIJ6WlpbHXXntFaWlp6iiN4jzyi/PIL8VyHhHFcy7OI784j/xSLOcRUTzn4jzyi/PIL8VyHhHFcy7Fch4Uv5Kampqa1CEAAAAA2HBp8QMAAAAgKQUqAAAAAJJSoAIAAAAgKQUqAAAAAJJSoAIAAAAgKQUqAAAAAJLaoAtUo0ePjq5du65xKy8vj3322SdGjhwZH3zwQeqY6zR06NDYb7/9ah275ZZbolu3bjF06NCorKxcz8nqZ+X/xx133FHr+COPPBJdu3aNefPmredkG6banh/l5eXRr1+/+OUvfxl/+ctfUkess7U91796+5//+Z/UMddp9OjRsccee6x1fMKECdG1a9d4//3312Oq+jnvvPOia9euceedd9Y6vmLFihgyZEjsuuuu8eabb67ndOs2cuTI+O53v1vr79MDDjggunbtGjfffPMaY5MmTYquXbvGn//85/WQsmEWLlwYv/rVr2LfffeNXXbZJXr06BHHHHNMzJgxI6qrq1PHW6e6PM8L7W/Ihx9+GP/93/8dhx12WPTo0SN23XXX+Ld/+7e44IIL4v/9v/+XOt461fZ/stNOO0X37t3j6KOPjoceeih1xAa5/fbbo2vXrnHkkUemjlJnQ4cOja5du0afPn1ixYoVtT7mtddeW/X/tGDBgvWcsGH++te/xtixY+OAAw6I3XbbLX7wgx/E0KFD48EHH4yamprU8dZpXb+3Bg0alDpinX3T+5FC8JOf/CR22WWX+OSTT9b6mAceeCC6du0as2fPXo/JGu/uu+8uqOc1G7bmqQPkg6+/UaqoqIgXX3wxpk6dGgsWLIhZs2ZFLpdLlK7hJk2aFFdddVX0798/rr766thoo41SR6qTyy+/PHr27BmdO3dOHaVR3nrrrbj99tvjqaeeig8//DBatWoVXbp0icMOOywGDhwYpaWlqSPWyVefH0uXLo133nknpk6dGkcccURMnjw5evbsmTBd/aytKBIRsfXWW6/HJBuuc845J+bNmxfjx4+PvffeO77zne+sNj516tR46aWX4oILLogdd9wxUcq169OnT8yaNSteeuml6Nu376r7Fy5cGH/9619j8803jyeeeCJOOOGE1b5v3rx50aFDh+jWrdt6Tlw3b7/9dhx11FHRqVOn+MUvfhFbbbVVVFZWxpNPPhkXXHBBvPDCC3H55ZenjvmNTj311Dj66KNX/fuuu+6KmTNnxsSJE6Ndu3ar7u/SpUuKePU2d+7cGDlyZGy00UYxZMiQKC8vjxYtWsSbb74Zt912W9x///1x/fXXR69evVJHXaev/u5dsWJFfPrppzF16tQ444wzoqqqKg4//PCE6epv+vTp0a1bt1iwYEG8/PLLsdtuu6WOVCfNmjWLjz76KObNm1frz819992XIFXDzZo1K84777zYeuut4/jjj4/OnTvH559/HrNnz44zzzwz5s6dG+PGjYtmzfL/8/i1vT5p1arVek6y4Tr66KNj7ty58cADD8SPf/zjWh8zc+bMaN++ffTv3389p4MNhwJVROy+++5r3Ne3b99Yvnx5TJkyJZ555pnYZ599EiRruKuvvjp+85vfxMCBA2PcuHEFUwxp3rx5lJSUxKhRo+LOO++M5s0L80f0rrvuiosvvji22267GD58eHTu3DkqKipizpw5ceGFF8bdd98dEydOjLKystRR1+nrz49evXrFD3/4wxg0aFCMGjUqHn300WjZsmWidPVT23Od9WuTTTaJyy+/PI499tg455xzYtq0aVFSUhIREX/5y1/i2muvjf322y+OPfbYxElrt/fee0dJSUm88MILqxWo5syZEy1btowTTjghJk6cGJWVldG6deuIiKiqqoqXXnopDjrooFSx1+nGG2+MiIhbb711tedz//79Y6ONNopp06bF8OHD87bAFhGxzTbbxDbbbLPq33/4wx8iImKnnXZaoxCa7z744IP4j//4j/j2t78dt912W2y22Warxvbaa6844ogjYsiQIXHOOefEY489lvd/42v73bvXXnvFPvvsE1OmTCmoAtUf//jHePPNN2Pq1KkxevTomDZtWlx55ZWpY9VJp06d4p///Gc8+OCDaxSoqqur46GHHoqdd945XnvttUQJ6+7111+Pc845J3r27BnXXXfdah8kDxgwIDp27BjXX3999OzZMw477LCESevG65P09t1332jfvn3ce++9tRao3nvvvZg3b1789Kc/Ldj3J1AI8v8jhYTatGkTEbHqzVOhuPTSS+M3v/lNnHDCCXHZZZfl/QvXr8rlcvGrX/0qXn311ZgwYULqOA3ywgsvxIUXXhj9+/eP//3f/42jjz46vv/978eAAQNi7NixMWXKlHjllVdi9OjRqaM22BZbbBEnnXRSfPTRRwW3zJn09thjjzj55JPjueeei2nTpkVExPLly+Pss8+Otm3bxqWXXpo44dq1a9cudtxxx3j++edXu//JJ59c9TxftmxZzJ07d9XYK6+8EkuXLl2toJVv/vGPf0RJSUmtrXzHHXdcjBw50if569ENN9wQ//znP+PSSy9drTi1UqtWrWLkyJHRvXv3+PTTTxMkbLzWrVtH586d469//WvqKPUyY8aMaNu2bey1115x2GGHxezZs2Px4sWpY9VJaWlpHHjggfHoo49GVVXVamNPP/10LFmyJK8L6V81efLkqK6ujjFjxtTa5XDKKafEkCFDVr2Wh3Vp3rx5DB48OF5//fV444031hifOXNmNGvWLH70ox8lSAcbDgWq+PKN0crbsmXL4pNPPomHHnoopkyZEp06dYoePXqkjlgnK1asiAsuuCBuueWWOO200+Kcc84puOJaRMTgwYOjf//+ccMNN8RLL72UOk69TZgwIVq1ahVjx46NFi1arDHeq1evGDp0aDz55JPxwgsvJEiYjZVvtp977rnESeruq8/1r94K4fo6X7W281jbdUXy0c9+9rPYeeed45prrom///3v8Zvf/Cb+9Kc/xRVXXBGbb7556njfqHfv3rFgwYL4v//7v4iI+Pzzz+O5556LffbZJ7p06RIdO3aMOXPmrHr8s88+G82bN4+99947UeJ169+/f1RUVMSRRx4ZkydPjldeeSWWLVsWERHbbrttnHzyyautTqJpPfLII7HDDjvELrvsstbH9O3bN6688sr41re+tR6TZaeqqiree++9+Pa3v506Sp1VVFTEQw89FIceemi0aNEifvSjH8Xy5cu/sX083xxyyCHx2WefrVphuNL9998fvXv3zvvfvyvNmTMndtppp7X+/Gy88cZx0UUXRb9+/dZvsAYqhtcmxWDw4MFRWloa99xzz2r3V1dXxz333BP9+vWLrbbaKlE62DBYnxgRO++88xr3tW3bNvr16xcjR44siPal6urqOPvss+OBBx6IiIiPP/44caLGGTt2bBxyyCFx1llnxb333ruqVSbfffbZZzFv3rw44IADvjHzIYccEjfeeGPMnj07vve9763HhNlZeU2XQvnkOKL253pExKabblowxcJ//etfaz2PQtKiRYu44oorYtCgQXHmmWfGggUL4qSTTiqIa5r16dMnpk6dGvPnz4+99tornnnmmVi2bNmqVvA+ffrEb3/721ixYkU0a9Ys5s2bF3vuuWde/x770Y9+FEuWLInrr79+VbvSRhttFHvssUcceOCBMWjQoFoL7mSvoqIiPv300/j+97+/xlh1dfUaF34uLS3N+w+jli9fvurrlYWp6667Lj799NM49dRTEyarn/vuuy+++OKLOOqooyLiy+Jtz549Y/r06TFixIiCeI6Ul5dHp06dYtasWauuo7N06dL43e9+F5deemksXbo0ccJ1++STT2Lp0qVFVTSv7e96x44d4/HHH0+QZsO11VZbRd++feOBBx6IX/7yl6ta+ebOnRsffvhhjB07NnFCKH4KVPHlks2IL1803XfffTFz5swYPnx4jBgxInGyulu0aFE8/PDDcc0118Ts2bPjjjvuiO7du8fBBx+cOlqDlJWVxbhx42LEiBExbty4uOyyy1JHqpMPPvggampq1nnB7W233TYiIq93W6urfH9j9FUrn+tfV0jXEth4443jtttuq3VsxowZMWPGjPWcqOG23377GDVqVFxyySWx6667xumnn546Up107949WrZsGc8//3zstddeMWfOnOjSpcuq6xzts88+MX369Hjttddixx13jPnz58dpp52WOPW6nXzyyXHcccfF008/Hc8//3y8+OKL8fzzz8ezzz4b06dPj5tvvlm7zHrwTSshBw0atMZOkGeddVb85Cc/aepYjVLbm++ysrIYOXJkDB06NEGihpkxY0bssssu0b59+6ioqIiIiIMPPjjOPffceOSRR+KQQw5JnLBuDjnkkJgyZUp8/vnnsckmm8Rvf/vbaN68efTv3z9mzZqVOt46rbx0RTGtMKrt9UkhbtBUDIYMGRJPPPFE/P73v1+1K+HMmTNj6623jj59+iROB8WvcN6VNaHy8vJVX3fv3j1yuVxcddVVUV1dXTCf7LVo0SKuv/766NOnz6r2k/PPPz+6detWMDsWfV2/fv3i6KOPjunTp8e+++6bOk6mVu4oU8gvrhYtWhQREVtuuWXiJHX31ed6oWrWrNlaz+OrbWWFol+/fnHJJZdE3759C6ZQmMvlokePHqtW3T355JOrfRjQs2fPyOVy8cwzz0RlZWVUVVUVzEYbrVq1igEDBsSAAQMiIuLTTz+N6667Lm699da44YYb4pe//GXihMWvbdu20bp163jvvffWGLvyyitXrXBZvHhx/PSnP13f8Rrkq2++mzdvHm3atCmo1r6IiJdeeinefPPNiIhaL/1w2223FUyB6tBDD40JEybEY489Foceemjcf//98cMf/rBgCiJt2rSJTTfddJ0f8i1atCjat29fELv4FcPrk2LRp0+f6NixY9x7772x3377xccffxxPPPFE/OIXvyioD2WhUOX/b+wEzjrrrNh+++1j4sSJ8cc//jF1nDpp3779qqp+69at4+qrr45ly5bF6aefHp9//nnidA03evTo6NSpU5x//vkF0UrWsWPHKCkpiXffffcbH7dw4cKIiILbWeqrnnrqqYiIgmjJgqz17t07XnnllXjttdfio48+Wu06J61atYoePXrE888/H88//3x06NAhunbtmi7sOnz44YfRp0+fmDx58hpjm2++eZx33nnRoUOHVW/OaXr7779/vP766/H222+vdn+XLl2ivLw8ysvLY8cdd0yUrv5WZi4vL//G6wblszvvvDM23njjuOmmm2LatGmr3Q4//PCYP39+LFiwIHXMOtlmm21i9913j1mzZsXHH38czzzzTEHsdPdV++yzT7z++uvxt7/9rdbxZcuWxWGHHRbHHHPMek5GoWvWrFkMHjw4Hn/88ViyZEncd999ERFxxBFHJE4GGwYFqlrkcrm45JJLVl10fOWFYgtJeXl5nHnmmfH222/H+eefnzpOg7Vs2TKuuOKKqKysjGuvvTZ1nHVq06ZN9OzZM+bOnbtq+f9KCxYsWHXtkIcffjgiomAu3vl1S5YsialTp0bHjh1XrbSADUnv3r3j888/j9tvvz1at24d3bt3X228b9++8ac//Smef/75vN69L+LL68nlcrmYPn16LFmyZI3xf/zjH1FRURHdunVLkG7DNGLEiGjdunWMGjVqrbv01bbLFE2joqIiHnnkkRgwYED84Ac/iL322mu124knnhgREbfeemvipHV3yCGHxNNPPx233357dOjQYY3fYfnuxBNPjNLS0hgzZswaOxJGREycODGWLFmiqECDHHnkkVFTUxO//e1v4/77748DDjggysrKUseCDUJh9FMk0L179xg4cGDcfffdcdNNN8XJJ5+cOlK9DRs2LJ599tl48MEHY88994zjjjsudaQG2XXXXePUU08tiAJVRMTpp58eQ4cOjXPOOSeuueaaaNGiRVRUVMTQoUOjQ4cOcdxxx8VNN90UPXr0yPs3rhER8+fPX/X10qVL46233opp06bFkiVLYsqUKQXTEhCx+rl8XZs2bWK77bZbj2koZNtvv31stdVWcf/998d+++23Rnti375947LLLoslS5bE8ccfnyhl3TRr1izGjh0bI0aMiMMPPzyOPfbY2HnnnaO0tDTeeOONuOWWW6JDhw4xbNiw1FE3GJ06dYqJEyfGyJEj46CDDorBgwfHHnvsES1btox33303HnnkkZg7d25su+22luNT3QAAAtdJREFUBbPTcCG7995744svvljrKqMddtghdt9993j44Yfj7LPPji222GI9J6y/Aw88MC677LKYPHlynHjiiQXXurTTTjvFueeeG2PHjo3BgwfHkCFDolOnTvHJJ5/ErFmz4rHHHosjjzwyjjzyyNRRNyiVlZVx88031zp27LHHFsRGAhFffnDTv3//uPHGG+Odd96J8847L3Uk2GAoUH2DUaNGxeOPPx7XXXdd/Pu///s6L3ydb0pKSmL8+PFx2GGHxfjx46O8vDx222231LEa5JRTTok//OEPBdFyueeee8bYsWPjwgsvjEGDBsWxxx4b22+/fVx88cUxbty4GDt2bDRv3rxg/tit3K0o4svVhR06dIhevXrFiSeeuOpi74Xiq+fydf37949f//rX6zENha53795x11131Xp9qc6dO8c222wTf//736NXr14J0tVPr1694p577okbb7wx7rrrrrjuuutixYoV0bFjxzjooIPipJNOik033TR1zA1Kr169YtasWXHXXXfF7373u5g+fXp8/vnnUVZWFuXl5XHllVfG/vvvX1AfEhSqGTNmRLt27WLvvfde62MGDx4c5557bkyfPj1+9rOfrcd0DVNWVhY/+MEP4ve//33BtfetdMwxx8ROO+0Ut912W0yePDn+8Y9/xKabbhrbb799XHvttbH//vsXXOGt0H322Wdr3dho8ODBBVOgiog4+uijY9iwYbHjjjsW7I7bUIhKar6+XzGQibfffjtuvfXWeOqpp+LDDz+MVq1aRZcuXaJ///7x6KOPxp///Oc4/vjj44wzzkgdFQAAAJJSoIIEampq4rHHHosPPvggfvzjH6eOAwAAAEkpUAEAAACQlF38AAAAAEhKgQoAAACApBSoAAAAAEhKgQoAAACApBSoAAAAAEhKgQoAAACApBSoAAAAAEhKgQoAAACApBSoAAAAAEhKgQoAAACApP4/8tXOUK8zla8AAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 1618.03x1000 with 2 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_contact_well(filtered_gamma[:210], inferBound=True)\n",
"plot_contact_well(filtered_gamma[210:420], inferBound=True)\n",
"plot_contact_well(filtered_gamma[420:], inferBound=True)"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [],
"source": [
"# impose A'gamma\n",
"save_gamma_pre = \"/Users/weilu/Research/server/sep_2019/saved_gammas/\"\n",
"np.savetxt(f\"{save_gamma_pre}/trial_2_cutoff400_impose_Aprime_constraint\", gamma_new)"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"collapsed": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"210\n",
"420\n",
"60\n",
"0 22.073925622758694\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n"
]
},
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Protein</th>\n",
" <th>Z_scores</th>\n",
" <th>E_native</th>\n",
" <th>E_mgs</th>\n",
" <th>Std_mg</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1BD2_1</td>\n",
" <td>22.073926</td>\n",
" <td>-846.030533</td>\n",
" <td>-438.667301</td>\n",
" <td>18.454499</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>6BJ8_1</td>\n",
" <td>18.269852</td>\n",
" <td>-1004.324453</td>\n",
" <td>-607.371078</td>\n",
" <td>21.727235</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>2JCC_1</td>\n",
" <td>23.133333</td>\n",
" <td>-1026.405787</td>\n",
" <td>-641.641369</td>\n",
" <td>16.632468</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>1AO7_1</td>\n",
" <td>21.629690</td>\n",
" <td>-971.717108</td>\n",
" <td>-586.869112</td>\n",
" <td>17.792580</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>1LP9_1</td>\n",
" <td>22.944863</td>\n",
" <td>-936.668865</td>\n",
" <td>-567.127738</td>\n",
" <td>16.105615</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>3QDJ_1</td>\n",
" <td>19.845226</td>\n",
" <td>-1007.446393</td>\n",
" <td>-588.950991</td>\n",
" <td>21.087964</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>3GSN_1</td>\n",
" <td>22.129463</td>\n",
" <td>-837.829729</td>\n",
" <td>-487.799204</td>\n",
" <td>15.817398</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>1QRN_1</td>\n",
" <td>27.795110</td>\n",
" <td>-1026.020277</td>\n",
" <td>-627.234270</td>\n",
" <td>14.347344</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>3PWP_1</td>\n",
" <td>27.632642</td>\n",
" <td>-1032.733486</td>\n",
" <td>-632.118083</td>\n",
" <td>14.497904</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>5W1W_1</td>\n",
" <td>20.072665</td>\n",
" <td>-856.575032</td>\n",
" <td>-448.143370</td>\n",
" <td>20.347655</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>1QSE_1</td>\n",
" <td>23.371117</td>\n",
" <td>-1018.295010</td>\n",
" <td>-600.899603</td>\n",
" <td>17.859455</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>4EUP_1</td>\n",
" <td>18.325557</td>\n",
" <td>-890.530313</td>\n",
" <td>-528.297996</td>\n",
" <td>19.766511</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12</th>\n",
" <td>5TEZ_1</td>\n",
" <td>11.855886</td>\n",
" <td>-687.641483</td>\n",
" <td>-503.628007</td>\n",
" <td>15.520855</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13</th>\n",
" <td>3D39_1</td>\n",
" <td>22.346258</td>\n",
" <td>-980.784498</td>\n",
" <td>-580.562575</td>\n",
" <td>17.910020</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14</th>\n",
" <td>6EQA_1</td>\n",
" <td>14.594050</td>\n",
" <td>-829.305617</td>\n",
" <td>-474.451029</td>\n",
" <td>24.315019</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15</th>\n",
" <td>2BNR_1</td>\n",
" <td>24.357313</td>\n",
" <td>-963.355060</td>\n",
" <td>-569.978428</td>\n",
" <td>16.150247</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16</th>\n",
" <td>6BJ2_1</td>\n",
" <td>30.537376</td>\n",
" <td>-946.093890</td>\n",
" <td>-534.483718</td>\n",
" <td>13.478898</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17</th>\n",
" <td>6BJ3_1</td>\n",
" <td>27.856648</td>\n",
" <td>-1006.868700</td>\n",
" <td>-593.676790</td>\n",
" <td>14.832794</td>\n",
" </tr>\n",
" <tr>\n",
" <th>18</th>\n",
" <td>5NME_1</td>\n",
" <td>29.386987</td>\n",
" <td>-1015.480976</td>\n",
" <td>-588.523592</td>\n",
" <td>14.528791</td>\n",
" </tr>\n",
" <tr>\n",
" <th>19</th>\n",
" <td>5MEN_1</td>\n",
" <td>27.623747</td>\n",
" <td>-913.184944</td>\n",
" <td>-554.009438</td>\n",
" <td>13.002418</td>\n",
" </tr>\n",
" <tr>\n",
" <th>20</th>\n",
" <td>2VLJ_1</td>\n",
" <td>20.065531</td>\n",
" <td>-910.995357</td>\n",
" <td>-537.330064</td>\n",
" <td>18.622248</td>\n",
" </tr>\n",
" <tr>\n",
" <th>21</th>\n",
" <td>2VLK_1</td>\n",
" <td>28.080716</td>\n",
" <td>-932.193789</td>\n",
" <td>-513.992499</td>\n",
" <td>14.892828</td>\n",
" </tr>\n",
" <tr>\n",
" <th>22</th>\n",
" <td>2J8U_1</td>\n",
" <td>22.787025</td>\n",
" <td>-915.677426</td>\n",
" <td>-558.047803</td>\n",
" <td>15.694441</td>\n",
" </tr>\n",
" <tr>\n",
" <th>23</th>\n",
" <td>2GJ6_1</td>\n",
" <td>23.161212</td>\n",
" <td>-1075.112165</td>\n",
" <td>-646.521563</td>\n",
" <td>18.504671</td>\n",
" </tr>\n",
" <tr>\n",
" <th>24</th>\n",
" <td>1OGA_1</td>\n",
" <td>25.406534</td>\n",
" <td>-905.543221</td>\n",
" <td>-501.006555</td>\n",
" <td>15.922544</td>\n",
" </tr>\n",
" <tr>\n",
" <th>25</th>\n",
" <td>2F54_1</td>\n",
" <td>24.858985</td>\n",
" <td>-986.202557</td>\n",
" <td>-619.818468</td>\n",
" <td>14.738497</td>\n",
" </tr>\n",
" <tr>\n",
" <th>26</th>\n",
" <td>5D2L_1</td>\n",
" <td>19.145154</td>\n",
" <td>-813.804751</td>\n",
" <td>-438.401893</td>\n",
" <td>19.608244</td>\n",
" </tr>\n",
" <tr>\n",
" <th>27</th>\n",
" <td>2F53_1</td>\n",
" <td>21.067683</td>\n",
" <td>-922.057320</td>\n",
" <td>-533.515113</td>\n",
" <td>18.442570</td>\n",
" </tr>\n",
" <tr>\n",
" <th>28</th>\n",
" <td>3QEQ_1</td>\n",
" <td>20.443343</td>\n",
" <td>-879.863290</td>\n",
" <td>-449.370077</td>\n",
" <td>21.057868</td>\n",
" </tr>\n",
" <tr>\n",
" <th>29</th>\n",
" <td>1QSF_1</td>\n",
" <td>22.192253</td>\n",
" <td>-925.050350</td>\n",
" <td>-575.433941</td>\n",
" <td>15.753985</td>\n",
" </tr>\n",
" <tr>\n",
" <th>30</th>\n",
" <td>2UWE_1</td>\n",
" <td>19.732309</td>\n",
" <td>-858.644498</td>\n",
" <td>-541.158389</td>\n",
" <td>16.089659</td>\n",
" </tr>\n",
" <tr>\n",
" <th>31</th>\n",
" <td>5EUO_1</td>\n",
" <td>25.208530</td>\n",
" <td>-858.235951</td>\n",
" <td>-429.634635</td>\n",
" <td>17.002234</td>\n",
" </tr>\n",
" <tr>\n",
" <th>32</th>\n",
" <td>3H9S_1</td>\n",
" <td>21.073720</td>\n",
" <td>-1067.144269</td>\n",
" <td>-634.043254</td>\n",
" <td>20.551712</td>\n",
" </tr>\n",
" <tr>\n",
" <th>33</th>\n",
" <td>3D3V_1</td>\n",
" <td>24.720721</td>\n",
" <td>-1191.861747</td>\n",
" <td>-717.461272</td>\n",
" <td>19.190398</td>\n",
" </tr>\n",
" <tr>\n",
" <th>34</th>\n",
" <td>2BNQ_1</td>\n",
" <td>8.570268</td>\n",
" <td>-819.975942</td>\n",
" <td>-664.848094</td>\n",
" <td>18.100699</td>\n",
" </tr>\n",
" <tr>\n",
" <th>35</th>\n",
" <td>4FTV_1</td>\n",
" <td>20.439400</td>\n",
" <td>-966.238074</td>\n",
" <td>-577.156020</td>\n",
" <td>19.035884</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Protein Z_scores E_native E_mgs Std_mg\n",
"0 1BD2_1 22.073926 -846.030533 -438.667301 18.454499\n",
"1 6BJ8_1 18.269852 -1004.324453 -607.371078 21.727235\n",
"2 2JCC_1 23.133333 -1026.405787 -641.641369 16.632468\n",
"3 1AO7_1 21.629690 -971.717108 -586.869112 17.792580\n",
"4 1LP9_1 22.944863 -936.668865 -567.127738 16.105615\n",
"5 3QDJ_1 19.845226 -1007.446393 -588.950991 21.087964\n",
"6 3GSN_1 22.129463 -837.829729 -487.799204 15.817398\n",
"7 1QRN_1 27.795110 -1026.020277 -627.234270 14.347344\n",
"8 3PWP_1 27.632642 -1032.733486 -632.118083 14.497904\n",
"9 5W1W_1 20.072665 -856.575032 -448.143370 20.347655\n",
"10 1QSE_1 23.371117 -1018.295010 -600.899603 17.859455\n",
"11 4EUP_1 18.325557 -890.530313 -528.297996 19.766511\n",
"12 5TEZ_1 11.855886 -687.641483 -503.628007 15.520855\n",
"13 3D39_1 22.346258 -980.784498 -580.562575 17.910020\n",
"14 6EQA_1 14.594050 -829.305617 -474.451029 24.315019\n",
"15 2BNR_1 24.357313 -963.355060 -569.978428 16.150247\n",
"16 6BJ2_1 30.537376 -946.093890 -534.483718 13.478898\n",
"17 6BJ3_1 27.856648 -1006.868700 -593.676790 14.832794\n",
"18 5NME_1 29.386987 -1015.480976 -588.523592 14.528791\n",
"19 5MEN_1 27.623747 -913.184944 -554.009438 13.002418\n",
"20 2VLJ_1 20.065531 -910.995357 -537.330064 18.622248\n",
"21 2VLK_1 28.080716 -932.193789 -513.992499 14.892828\n",
"22 2J8U_1 22.787025 -915.677426 -558.047803 15.694441\n",
"23 2GJ6_1 23.161212 -1075.112165 -646.521563 18.504671\n",
"24 1OGA_1 25.406534 -905.543221 -501.006555 15.922544\n",
"25 2F54_1 24.858985 -986.202557 -619.818468 14.738497\n",
"26 5D2L_1 19.145154 -813.804751 -438.401893 19.608244\n",
"27 2F53_1 21.067683 -922.057320 -533.515113 18.442570\n",
"28 3QEQ_1 20.443343 -879.863290 -449.370077 21.057868\n",
"29 1QSF_1 22.192253 -925.050350 -575.433941 15.753985\n",
"30 2UWE_1 19.732309 -858.644498 -541.158389 16.089659\n",
"31 5EUO_1 25.208530 -858.235951 -429.634635 17.002234\n",
"32 3H9S_1 21.073720 -1067.144269 -634.043254 20.551712\n",
"33 3D3V_1 24.720721 -1191.861747 -717.461272 19.190398\n",
"34 2BNQ_1 8.570268 -819.975942 -664.848094 18.100699\n",
"35 4FTV_1 20.439400 -966.238074 -577.156020 19.035884"
]
},
"execution_count": 23,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"os.chdir(\"/Users/weilu/Research/server/sep_2019/peptide_optimization_trial_2/optimization/\")\n",
"# gamma_file_name = \"gamma_iter1_combined_mar06.dat\"\n",
"# gamma_file_name = \"/Users/weilu/Research/server/sep_2019/peptide_optimization/saved_gammas/cutoff100\"\n",
"gamma_file_name = \"/Users/weilu/Research/server/sep_2019/saved_gammas/trial_2_cutoff400_impose_Aprime_constraint\"\n",
"\n",
"data = validate_hamiltonian_wei(\"phi_list.txt\", \"protein_list_small\", gamma_file_name, \"shuffle\", 1000, mode=0)\n",
"data\n"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {},
"outputs": [],
"source": [
"# mix gammas so that we don't overfitting too much.\n",
"gamma_file_name = \"/Users/weilu/Research/server/sep_2019/saved_gammas/original_gamma\"\n",
"original_gamma = np.loadtxt(gamma_file_name)\n",
"gamma_file_name = \"/Users/weilu/Research/server/sep_2019/saved_gammas/trial_2_cutoff400_impose_Aprime_constraint\"\n",
"gamma_new = np.loadtxt(gamma_file_name)\n",
"\n",
"alpha = 0.9\n",
"alpha_percent = int(alpha*100)\n",
"mixed_gamma = alpha*original_gamma + (1-alpha)*gamma_new\n",
"save_gamma_pre = \"/Users/weilu/Research/server/sep_2019/saved_gammas/\"\n",
"np.savetxt(f\"{save_gamma_pre}/trial_2_mixed_original_and_cutoff400_impose_Aprime_constraint_{alpha_percent}\", mixed_gamma)"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"210\n",
"420\n",
"60\n",
"0 3.61317979615153\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n"
]
},
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Protein</th>\n",
" <th>Z_scores</th>\n",
" <th>E_native</th>\n",
" <th>E_mgs</th>\n",
" <th>Std_mg</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1BD2_1</td>\n",
" <td>3.613180</td>\n",
" <td>-579.396917</td>\n",
" <td>-552.351354</td>\n",
" <td>7.485252</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>6BJ8_1</td>\n",
" <td>2.699095</td>\n",
" <td>-581.624451</td>\n",
" <td>-558.892556</td>\n",
" <td>8.422044</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>2JCC_1</td>\n",
" <td>2.582660</td>\n",
" <td>-601.020701</td>\n",
" <td>-580.587160</td>\n",
" <td>7.911820</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>1AO7_1</td>\n",
" <td>2.728040</td>\n",
" <td>-575.724580</td>\n",
" <td>-551.600588</td>\n",
" <td>8.842975</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>1LP9_1</td>\n",
" <td>2.213663</td>\n",
" <td>-590.667403</td>\n",
" <td>-572.036213</td>\n",
" <td>8.416452</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>3QDJ_1</td>\n",
" <td>3.590370</td>\n",
" <td>-571.765944</td>\n",
" <td>-546.880369</td>\n",
" <td>6.931201</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>3GSN_1</td>\n",
" <td>2.660365</td>\n",
" <td>-560.869135</td>\n",
" <td>-536.903557</td>\n",
" <td>9.008381</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>1QRN_1</td>\n",
" <td>2.839146</td>\n",
" <td>-578.898224</td>\n",
" <td>-558.679917</td>\n",
" <td>7.121263</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>3PWP_1</td>\n",
" <td>2.654854</td>\n",
" <td>-594.012756</td>\n",
" <td>-571.886119</td>\n",
" <td>8.334407</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>5W1W_1</td>\n",
" <td>3.460066</td>\n",
" <td>-578.070487</td>\n",
" <td>-552.034760</td>\n",
" <td>7.524634</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>1QSE_1</td>\n",
" <td>2.924239</td>\n",
" <td>-582.481582</td>\n",
" <td>-556.442048</td>\n",
" <td>8.904721</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>4EUP_1</td>\n",
" <td>2.148802</td>\n",
" <td>-580.286616</td>\n",
" <td>-562.041655</td>\n",
" <td>8.490758</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12</th>\n",
" <td>5TEZ_1</td>\n",
" <td>1.749300</td>\n",
" <td>-585.086156</td>\n",
" <td>-572.643489</td>\n",
" <td>7.112940</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13</th>\n",
" <td>3D39_1</td>\n",
" <td>2.981009</td>\n",
" <td>-589.855615</td>\n",
" <td>-561.080308</td>\n",
" <td>9.652874</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14</th>\n",
" <td>6EQA_1</td>\n",
" <td>2.772029</td>\n",
" <td>-572.639760</td>\n",
" <td>-549.969031</td>\n",
" <td>8.178387</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15</th>\n",
" <td>2BNR_1</td>\n",
" <td>2.898548</td>\n",
" <td>-590.045257</td>\n",
" <td>-564.258403</td>\n",
" <td>8.896472</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16</th>\n",
" <td>6BJ2_1</td>\n",
" <td>3.051761</td>\n",
" <td>-576.118376</td>\n",
" <td>-551.799677</td>\n",
" <td>7.968743</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17</th>\n",
" <td>6BJ3_1</td>\n",
" <td>2.817729</td>\n",
" <td>-585.574325</td>\n",
" <td>-565.586877</td>\n",
" <td>7.093460</td>\n",
" </tr>\n",
" <tr>\n",
" <th>18</th>\n",
" <td>5NME_1</td>\n",
" <td>3.195944</td>\n",
" <td>-580.935932</td>\n",
" <td>-554.264087</td>\n",
" <td>8.345530</td>\n",
" </tr>\n",
" <tr>\n",
" <th>19</th>\n",
" <td>5MEN_1</td>\n",
" <td>2.629798</td>\n",
" <td>-569.031403</td>\n",
" <td>-548.680578</td>\n",
" <td>7.738549</td>\n",
" </tr>\n",
" <tr>\n",
" <th>20</th>\n",
" <td>2VLJ_1</td>\n",
" <td>2.720131</td>\n",
" <td>-560.460357</td>\n",
" <td>-539.316638</td>\n",
" <td>7.773052</td>\n",
" </tr>\n",
" <tr>\n",
" <th>21</th>\n",
" <td>2VLK_1</td>\n",
" <td>2.829503</td>\n",
" <td>-562.037886</td>\n",
" <td>-538.218551</td>\n",
" <td>8.418204</td>\n",
" </tr>\n",
" <tr>\n",
" <th>22</th>\n",
" <td>2J8U_1</td>\n",
" <td>2.093933</td>\n",
" <td>-591.544645</td>\n",
" <td>-575.826164</td>\n",
" <td>7.506677</td>\n",
" </tr>\n",
" <tr>\n",
" <th>23</th>\n",
" <td>2GJ6_1</td>\n",
" <td>2.567402</td>\n",
" <td>-595.976589</td>\n",
" <td>-571.089123</td>\n",
" <td>9.693639</td>\n",
" </tr>\n",
" <tr>\n",
" <th>24</th>\n",
" <td>1OGA_1</td>\n",
" <td>2.678189</td>\n",
" <td>-570.133057</td>\n",
" <td>-547.966259</td>\n",
" <td>8.276785</td>\n",
" </tr>\n",
" <tr>\n",
" <th>25</th>\n",
" <td>2F54_1</td>\n",
" <td>2.359889</td>\n",
" <td>-570.241639</td>\n",
" <td>-551.089906</td>\n",
" <td>8.115524</td>\n",
" </tr>\n",
" <tr>\n",
" <th>26</th>\n",
" <td>5D2L_1</td>\n",
" <td>2.818430</td>\n",
" <td>-571.394120</td>\n",
" <td>-547.985915</td>\n",
" <td>8.305406</td>\n",
" </tr>\n",
" <tr>\n",
" <th>27</th>\n",
" <td>2F53_1</td>\n",
" <td>2.706106</td>\n",
" <td>-580.120374</td>\n",
" <td>-555.264009</td>\n",
" <td>9.185288</td>\n",
" </tr>\n",
" <tr>\n",
" <th>28</th>\n",
" <td>3QEQ_1</td>\n",
" <td>2.789457</td>\n",
" <td>-568.032172</td>\n",
" <td>-540.444691</td>\n",
" <td>9.889911</td>\n",
" </tr>\n",
" <tr>\n",
" <th>29</th>\n",
" <td>1QSF_1</td>\n",
" <td>2.525277</td>\n",
" <td>-584.382710</td>\n",
" <td>-562.789602</td>\n",
" <td>8.550789</td>\n",
" </tr>\n",
" <tr>\n",
" <th>30</th>\n",
" <td>2UWE_1</td>\n",
" <td>2.928198</td>\n",
" <td>-599.926297</td>\n",
" <td>-577.334078</td>\n",
" <td>7.715401</td>\n",
" </tr>\n",
" <tr>\n",
" <th>31</th>\n",
" <td>5EUO_1</td>\n",
" <td>2.611929</td>\n",
" <td>-565.911912</td>\n",
" <td>-543.319273</td>\n",
" <td>8.649790</td>\n",
" </tr>\n",
" <tr>\n",
" <th>32</th>\n",
" <td>3H9S_1</td>\n",
" <td>3.121284</td>\n",
" <td>-581.456318</td>\n",
" <td>-555.242705</td>\n",
" <td>8.398342</td>\n",
" </tr>\n",
" <tr>\n",
" <th>33</th>\n",
" <td>3D3V_1</td>\n",
" <td>2.983337</td>\n",
" <td>-574.944756</td>\n",
" <td>-545.125078</td>\n",
" <td>9.995410</td>\n",
" </tr>\n",
" <tr>\n",
" <th>34</th>\n",
" <td>2BNQ_1</td>\n",
" <td>1.183088</td>\n",
" <td>-576.645912</td>\n",
" <td>-566.508396</td>\n",
" <td>8.568690</td>\n",
" </tr>\n",
" <tr>\n",
" <th>35</th>\n",
" <td>4FTV_1</td>\n",
" <td>2.155122</td>\n",
" <td>-560.512860</td>\n",
" <td>-544.116074</td>\n",
" <td>7.608287</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Protein Z_scores E_native E_mgs Std_mg\n",
"0 1BD2_1 3.613180 -579.396917 -552.351354 7.485252\n",
"1 6BJ8_1 2.699095 -581.624451 -558.892556 8.422044\n",
"2 2JCC_1 2.582660 -601.020701 -580.587160 7.911820\n",
"3 1AO7_1 2.728040 -575.724580 -551.600588 8.842975\n",
"4 1LP9_1 2.213663 -590.667403 -572.036213 8.416452\n",
"5 3QDJ_1 3.590370 -571.765944 -546.880369 6.931201\n",
"6 3GSN_1 2.660365 -560.869135 -536.903557 9.008381\n",
"7 1QRN_1 2.839146 -578.898224 -558.679917 7.121263\n",
"8 3PWP_1 2.654854 -594.012756 -571.886119 8.334407\n",
"9 5W1W_1 3.460066 -578.070487 -552.034760 7.524634\n",
"10 1QSE_1 2.924239 -582.481582 -556.442048 8.904721\n",
"11 4EUP_1 2.148802 -580.286616 -562.041655 8.490758\n",
"12 5TEZ_1 1.749300 -585.086156 -572.643489 7.112940\n",
"13 3D39_1 2.981009 -589.855615 -561.080308 9.652874\n",
"14 6EQA_1 2.772029 -572.639760 -549.969031 8.178387\n",
"15 2BNR_1 2.898548 -590.045257 -564.258403 8.896472\n",
"16 6BJ2_1 3.051761 -576.118376 -551.799677 7.968743\n",
"17 6BJ3_1 2.817729 -585.574325 -565.586877 7.093460\n",
"18 5NME_1 3.195944 -580.935932 -554.264087 8.345530\n",
"19 5MEN_1 2.629798 -569.031403 -548.680578 7.738549\n",
"20 2VLJ_1 2.720131 -560.460357 -539.316638 7.773052\n",
"21 2VLK_1 2.829503 -562.037886 -538.218551 8.418204\n",
"22 2J8U_1 2.093933 -591.544645 -575.826164 7.506677\n",
"23 2GJ6_1 2.567402 -595.976589 -571.089123 9.693639\n",
"24 1OGA_1 2.678189 -570.133057 -547.966259 8.276785\n",
"25 2F54_1 2.359889 -570.241639 -551.089906 8.115524\n",
"26 5D2L_1 2.818430 -571.394120 -547.985915 8.305406\n",
"27 2F53_1 2.706106 -580.120374 -555.264009 9.185288\n",
"28 3QEQ_1 2.789457 -568.032172 -540.444691 9.889911\n",
"29 1QSF_1 2.525277 -584.382710 -562.789602 8.550789\n",
"30 2UWE_1 2.928198 -599.926297 -577.334078 7.715401\n",
"31 5EUO_1 2.611929 -565.911912 -543.319273 8.649790\n",
"32 3H9S_1 3.121284 -581.456318 -555.242705 8.398342\n",
"33 3D3V_1 2.983337 -574.944756 -545.125078 9.995410\n",
"34 2BNQ_1 1.183088 -576.645912 -566.508396 8.568690\n",
"35 4FTV_1 2.155122 -560.512860 -544.116074 7.608287"
]
},
"execution_count": 25,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"os.chdir(\"/Users/weilu/Research/server/sep_2019/peptide_optimization_trial_2/optimization/\")\n",
"# gamma_file_name = \"gamma_iter1_combined_mar06.dat\"\n",
"# gamma_file_name = \"/Users/weilu/Research/server/sep_2019/peptide_optimization/saved_gammas/cutoff100\"\n",
"gamma_file_name = \"/Users/weilu/Research/server/sep_2019/saved_gammas/trial_2_mixed_original_and_cutoff400_impose_Aprime_constraint_90\"\n",
"\n",
"data = validate_hamiltonian_wei(\"phi_list.txt\", \"protein_list_small\", gamma_file_name, \"shuffle\", 1000, mode=0)\n",
"data\n"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"210\n",
"420\n",
"60\n",
"0 6.4585874724654575\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n",
"210\n",
"420\n",
"60\n"
]
},
{
"data": {
"text/html": [
"<div>\n",
"<style scoped>\n",
" .dataframe tbody tr th:only-of-type {\n",
" vertical-align: middle;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: right;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Protein</th>\n",
" <th>Z_scores</th>\n",
" <th>E_native</th>\n",
" <th>E_mgs</th>\n",
" <th>Std_mg</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1BD2_1</td>\n",
" <td>6.458587</td>\n",
" <td>-593.430265</td>\n",
" <td>-546.367982</td>\n",
" <td>7.286776</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>6BJ8_1</td>\n",
" <td>5.247254</td>\n",
" <td>-603.871820</td>\n",
" <td>-561.444057</td>\n",
" <td>8.085708</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>2JCC_1</td>\n",
" <td>5.202229</td>\n",
" <td>-623.409390</td>\n",
" <td>-583.800540</td>\n",
" <td>7.613823</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>1AO7_1</td>\n",
" <td>5.109089</td>\n",
" <td>-596.566292</td>\n",
" <td>-553.456826</td>\n",
" <td>8.437798</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>1LP9_1</td>\n",
" <td>4.668548</td>\n",
" <td>-608.878006</td>\n",
" <td>-571.777872</td>\n",
" <td>7.946825</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>3QDJ_1</td>\n",
" <td>6.764150</td>\n",
" <td>-594.696494</td>\n",
" <td>-549.094613</td>\n",
" <td>6.741702</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>3GSN_1</td>\n",
" <td>4.745268</td>\n",
" <td>-575.446008</td>\n",
" <td>-534.319118</td>\n",
" <td>8.666926</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>1QRN_1</td>\n",
" <td>5.841006</td>\n",
" <td>-602.430963</td>\n",
" <td>-562.288040</td>\n",
" <td>6.872604</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>3PWP_1</td>\n",
" <td>5.231997</td>\n",
" <td>-617.103320</td>\n",
" <td>-575.056223</td>\n",
" <td>8.036529</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>5W1W_1</td>\n",
" <td>6.291112</td>\n",
" <td>-592.728621</td>\n",
" <td>-546.566792</td>\n",
" <td>7.337627</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>1QSE_1</td>\n",
" <td>5.483596</td>\n",
" <td>-605.419130</td>\n",
" <td>-558.781919</td>\n",
" <td>8.504859</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>4EUP_1</td>\n",
" <td>4.402582</td>\n",
" <td>-596.615231</td>\n",
" <td>-560.265673</td>\n",
" <td>8.256418</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12</th>\n",
" <td>5TEZ_1</td>\n",
" <td>3.155803</td>\n",
" <td>-590.483805</td>\n",
" <td>-569.011095</td>\n",
" <td>6.804199</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13</th>\n",
" <td>3D39_1</td>\n",
" <td>5.198826</td>\n",
" <td>-610.430820</td>\n",
" <td>-562.105690</td>\n",
" <td>9.295393</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14</th>\n",
" <td>6EQA_1</td>\n",
" <td>5.009679</td>\n",
" <td>-586.148490</td>\n",
" <td>-545.994399</td>\n",
" <td>8.015301</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15</th>\n",
" <td>2BNR_1</td>\n",
" <td>5.186734</td>\n",
" <td>-609.693141</td>\n",
" <td>-564.559457</td>\n",
" <td>8.701754</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16</th>\n",
" <td>6BJ2_1</td>\n",
" <td>5.882931</td>\n",
" <td>-595.590772</td>\n",
" <td>-550.888310</td>\n",
" <td>7.598672</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17</th>\n",
" <td>6BJ3_1</td>\n",
" <td>5.891674</td>\n",
" <td>-607.747713</td>\n",
" <td>-567.065293</td>\n",
" <td>6.905070</td>\n",
" </tr>\n",
" <tr>\n",
" <th>18</th>\n",
" <td>5NME_1</td>\n",
" <td>5.920641</td>\n",
" <td>-603.806724</td>\n",
" <td>-556.067219</td>\n",
" <td>8.063232</td>\n",
" </tr>\n",
" <tr>\n",
" <th>19</th>\n",
" <td>5MEN_1</td>\n",
" <td>5.079241</td>\n",
" <td>-587.144747</td>\n",
" <td>-548.961045</td>\n",
" <td>7.517600</td>\n",
" </tr>\n",
" <tr>\n",
" <th>20</th>\n",
" <td>2VLJ_1</td>\n",
" <td>5.202782</td>\n",
" <td>-578.909567</td>\n",
" <td>-539.212082</td>\n",
" <td>7.630050</td>\n",
" </tr>\n",
" <tr>\n",
" <th>21</th>\n",
" <td>2VLK_1</td>\n",
" <td>5.463745</td>\n",
" <td>-581.519776</td>\n",
" <td>-536.943496</td>\n",
" <td>8.158559</td>\n",
" </tr>\n",
" <tr>\n",
" <th>22</th>\n",
" <td>2J8U_1</td>\n",
" <td>4.680595</td>\n",
" <td>-608.604265</td>\n",
" <td>-574.890461</td>\n",
" <td>7.202888</td>\n",
" </tr>\n",
" <tr>\n",
" <th>23</th>\n",
" <td>2GJ6_1</td>\n",
" <td>4.978468</td>\n",
" <td>-621.194251</td>\n",
" <td>-575.059252</td>\n",
" <td>9.266908</td>\n",
" </tr>\n",
" <tr>\n",
" <th>24</th>\n",
" <td>1OGA_1</td>\n",
" <td>5.280923</td>\n",
" <td>-587.786224</td>\n",
" <td>-545.494696</td>\n",
" <td>8.008359</td>\n",
" </tr>\n",
" <tr>\n",
" <th>25</th>\n",
" <td>2F54_1</td>\n",
" <td>4.790465</td>\n",
" <td>-592.134319</td>\n",
" <td>-554.707199</td>\n",
" <td>7.812837</td>\n",
" </tr>\n",
" <tr>\n",
" <th>26</th>\n",
" <td>5D2L_1</td>\n",
" <td>5.171549</td>\n",
" <td>-584.152575</td>\n",
" <td>-542.218335</td>\n",
" <td>8.108643</td>\n",
" </tr>\n",
" <tr>\n",
" <th>27</th>\n",
" <td>2F53_1</td>\n",
" <td>4.870324</td>\n",
" <td>-598.117056</td>\n",
" <td>-554.119330</td>\n",
" <td>9.033840</td>\n",
" </tr>\n",
" <tr>\n",
" <th>28</th>\n",
" <td>3QEQ_1</td>\n",
" <td>5.062370</td>\n",
" <td>-584.444336</td>\n",
" <td>-535.651290</td>\n",
" <td>9.638381</td>\n",
" </tr>\n",
" <tr>\n",
" <th>29</th>\n",
" <td>1QSF_1</td>\n",
" <td>4.741348</td>\n",
" <td>-602.312586</td>\n",
" <td>-563.455094</td>\n",
" <td>8.195453</td>\n",
" </tr>\n",
" <tr>\n",
" <th>30</th>\n",
" <td>2UWE_1</td>\n",
" <td>5.110947</td>\n",
" <td>-613.543044</td>\n",
" <td>-575.430094</td>\n",
" <td>7.457122</td>\n",
" </tr>\n",
" <tr>\n",
" <th>31</th>\n",
" <td>5EUO_1</td>\n",
" <td>5.200232</td>\n",
" <td>-581.297388</td>\n",
" <td>-537.335871</td>\n",
" <td>8.453760</td>\n",
" </tr>\n",
" <tr>\n",
" <th>32</th>\n",
" <td>3H9S_1</td>\n",
" <td>5.837334</td>\n",
" <td>-607.018842</td>\n",
" <td>-559.390102</td>\n",
" <td>8.159331</td>\n",
" </tr>\n",
" <tr>\n",
" <th>33</th>\n",
" <td>3D3V_1</td>\n",
" <td>5.559947</td>\n",
" <td>-607.414072</td>\n",
" <td>-554.195404</td>\n",
" <td>9.571794</td>\n",
" </tr>\n",
" <tr>\n",
" <th>34</th>\n",
" <td>2BNQ_1</td>\n",
" <td>2.105181</td>\n",
" <td>-589.452756</td>\n",
" <td>-571.684169</td>\n",
" <td>8.440409</td>\n",
" </tr>\n",
" <tr>\n",
" <th>35</th>\n",
" <td>4FTV_1</td>\n",
" <td>4.915665</td>\n",
" <td>-581.866819</td>\n",
" <td>-545.855018</td>\n",
" <td>7.325927</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Protein Z_scores E_native E_mgs Std_mg\n",
"0 1BD2_1 6.458587 -593.430265 -546.367982 7.286776\n",
"1 6BJ8_1 5.247254 -603.871820 -561.444057 8.085708\n",
"2 2JCC_1 5.202229 -623.409390 -583.800540 7.613823\n",
"3 1AO7_1 5.109089 -596.566292 -553.456826 8.437798\n",
"4 1LP9_1 4.668548 -608.878006 -571.777872 7.946825\n",
"5 3QDJ_1 6.764150 -594.696494 -549.094613 6.741702\n",
"6 3GSN_1 4.745268 -575.446008 -534.319118 8.666926\n",
"7 1QRN_1 5.841006 -602.430963 -562.288040 6.872604\n",
"8 3PWP_1 5.231997 -617.103320 -575.056223 8.036529\n",
"9 5W1W_1 6.291112 -592.728621 -546.566792 7.337627\n",
"10 1QSE_1 5.483596 -605.419130 -558.781919 8.504859\n",
"11 4EUP_1 4.402582 -596.615231 -560.265673 8.256418\n",
"12 5TEZ_1 3.155803 -590.483805 -569.011095 6.804199\n",
"13 3D39_1 5.198826 -610.430820 -562.105690 9.295393\n",
"14 6EQA_1 5.009679 -586.148490 -545.994399 8.015301\n",
"15 2BNR_1 5.186734 -609.693141 -564.559457 8.701754\n",
"16 6BJ2_1 5.882931 -595.590772 -550.888310 7.598672\n",
"17 6BJ3_1 5.891674 -607.747713 -567.065293 6.905070\n",
"18 5NME_1 5.920641 -603.806724 -556.067219 8.063232\n",
"19 5MEN_1 5.079241 -587.144747 -548.961045 7.517600\n",
"20 2VLJ_1 5.202782 -578.909567 -539.212082 7.630050\n",
"21 2VLK_1 5.463745 -581.519776 -536.943496 8.158559\n",
"22 2J8U_1 4.680595 -608.604265 -574.890461 7.202888\n",
"23 2GJ6_1 4.978468 -621.194251 -575.059252 9.266908\n",
"24 1OGA_1 5.280923 -587.786224 -545.494696 8.008359\n",
"25 2F54_1 4.790465 -592.134319 -554.707199 7.812837\n",
"26 5D2L_1 5.171549 -584.152575 -542.218335 8.108643\n",
"27 2F53_1 4.870324 -598.117056 -554.119330 9.033840\n",
"28 3QEQ_1 5.062370 -584.444336 -535.651290 9.638381\n",
"29 1QSF_1 4.741348 -602.312586 -563.455094 8.195453\n",
"30 2UWE_1 5.110947 -613.543044 -575.430094 7.457122\n",
"31 5EUO_1 5.200232 -581.297388 -537.335871 8.453760\n",
"32 3H9S_1 5.837334 -607.018842 -559.390102 8.159331\n",
"33 3D3V_1 5.559947 -607.414072 -554.195404 9.571794\n",
"34 2BNQ_1 2.105181 -589.452756 -571.684169 8.440409\n",
"35 4FTV_1 4.915665 -581.866819 -545.855018 7.325927"
]
},
"execution_count": 27,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"os.chdir(\"/Users/weilu/Research/server/sep_2019/peptide_optimization_trial_2/optimization/\")\n",
"# gamma_file_name = \"gamma_iter1_combined_mar06.dat\"\n",
"# gamma_file_name = \"/Users/weilu/Research/server/sep_2019/peptide_optimization/saved_gammas/cutoff100\"\n",
"gamma_file_name = \"/Users/weilu/Research/server/sep_2019/saved_gammas/trial_2_mixed_original_and_cutoff400_impose_Aprime_constraint_90\"\n",
"\n",
"data = validate_hamiltonian_wei(\"phi_list.txt\", \"protein_list_small\", gamma_file_name, \"shuffle\", 1000, mode=0)\n",
"data\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.8"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
berkeley-dsc/purchasing | doc/pres/bids_presentation.ipynb | 2 | 7751920 | null | isc |
danielgreening/titanic-kaggle | notebooks/01-dan-titanic-notebook.ipynb | 1 | 1487 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Titanic: Machine Learning from Disaster | Kaggle \n",
"\n",
"This is a jupyter notebook exploring the [Kaggle Titanic competition](https://www.kaggle.com/c/titanic). My first proper attempt using this format so expect bad formatting :-). \n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Contents\n",
"- Environment \n",
"- Importing Data\n",
"- Exploring the Data\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"## The Environment\n",
"Nothing that special as it stands, everything you would expect in a python data project! Currently making use of the following libraries for analysis and plots:\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"import pandas as pd # for data manipulation\n",
"import matplotlib.pyplot as plt # for visulatisation "
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
johnnyliu27/openmc | examples/jupyter/mgxs-part-iii.ipynb | 1 | 73124 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This IPython Notebook illustrates the use of the **`openmc.mgxs.Library`** class. The `Library` class is designed to automate the calculation of multi-group cross sections for use cases with one or more domains, cross section types, and/or nuclides. In particular, this Notebook illustrates the following features:\n",
"\n",
"* Calculation of multi-group cross sections for a **fuel assembly**\n",
"* Automated creation, manipulation and storage of `MGXS` with **`openmc.mgxs.Library`**\n",
"* **Validation** of multi-group cross sections with **[OpenMOC](https://mit-crpg.github.io/OpenMOC/)**\n",
"* Steady-state pin-by-pin **fission rates comparison** between OpenMC and [OpenMOC](https://mit-crpg.github.io/OpenMOC/)\n",
"\n",
"**Note:** This Notebook was created using [OpenMOC](https://mit-crpg.github.io/OpenMOC/) to verify the multi-group cross-sections generated by OpenMC. You must install [OpenMOC](https://mit-crpg.github.io/OpenMOC/) on your system to run this Notebook in its entirety. In addition, this Notebook illustrates the use of [Pandas](http://pandas.pydata.org/) `DataFrames` to containerize multi-group cross section data."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Generate Input Files"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/home/nelsonag/python/openmc/lib/python3.6/site-packages/matplotlib/__init__.py:1405: UserWarning: \n",
"This call to matplotlib.use() has no effect because the backend has already\n",
"been chosen; matplotlib.use() must be called *before* pylab, matplotlib.pyplot,\n",
"or matplotlib.backends is imported for the first time.\n",
"\n",
" warnings.warn(_use_error_msg)\n"
]
}
],
"source": [
"import math\n",
"import pickle\n",
"\n",
"from IPython.display import Image\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"\n",
"import openmc\n",
"import openmc.mgxs\n",
"from openmc.openmoc_compatible import get_openmoc_geometry\n",
"import openmoc\n",
"import openmoc.process\n",
"from openmoc.materialize import load_openmc_mgxs_lib\n",
"\n",
"%matplotlib inline"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"First we need to define materials that will be used in the problem. We'll create three materials for the fuel, water, and cladding of the fuel pins."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"# 1.6 enriched fuel\n",
"fuel = openmc.Material(name='1.6% Fuel')\n",
"fuel.set_density('g/cm3', 10.31341)\n",
"fuel.add_nuclide('U235', 3.7503e-4)\n",
"fuel.add_nuclide('U238', 2.2625e-2)\n",
"fuel.add_nuclide('O16', 4.6007e-2)\n",
"\n",
"# borated water\n",
"water = openmc.Material(name='Borated Water')\n",
"water.set_density('g/cm3', 0.740582)\n",
"water.add_nuclide('H1', 4.9457e-2)\n",
"water.add_nuclide('O16', 2.4732e-2)\n",
"water.add_nuclide('B10', 8.0042e-6)\n",
"\n",
"# zircaloy\n",
"zircaloy = openmc.Material(name='Zircaloy')\n",
"zircaloy.set_density('g/cm3', 6.55)\n",
"zircaloy.add_nuclide('Zr90', 7.2758e-3)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"With our three materials, we can now create a `Materials` object that can be exported to an actual XML file."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [],
"source": [
"# Instantiate a Materials object\n",
"materials_file = openmc.Materials([fuel, water, zircaloy])\n",
"\n",
"# Export to \"materials.xml\"\n",
"materials_file.export_to_xml()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now let's move on to the geometry. This problem will be a square array of fuel pins and control rod guide tubes for which we can use OpenMC's lattice/universe feature. The basic universe will have three regions for the fuel, the clad, and the surrounding coolant. The first step is to create the bounding surfaces for fuel and clad, as well as the outer bounding surfaces of the problem."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [],
"source": [
"# Create cylinders for the fuel and clad\n",
"fuel_outer_radius = openmc.ZCylinder(x0=0.0, y0=0.0, R=0.39218)\n",
"clad_outer_radius = openmc.ZCylinder(x0=0.0, y0=0.0, R=0.45720)\n",
"\n",
"# Create boundary planes to surround the geometry\n",
"min_x = openmc.XPlane(x0=-10.71, boundary_type='reflective')\n",
"max_x = openmc.XPlane(x0=+10.71, boundary_type='reflective')\n",
"min_y = openmc.YPlane(y0=-10.71, boundary_type='reflective')\n",
"max_y = openmc.YPlane(y0=+10.71, boundary_type='reflective')\n",
"min_z = openmc.ZPlane(z0=-10., boundary_type='reflective')\n",
"max_z = openmc.ZPlane(z0=+10., boundary_type='reflective')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"With the surfaces defined, we can now construct a fuel pin cell from cells that are defined by intersections of half-spaces created by the surfaces."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [],
"source": [
"# Create a Universe to encapsulate a fuel pin\n",
"fuel_pin_universe = openmc.Universe(name='1.6% Fuel Pin')\n",
"\n",
"# Create fuel Cell\n",
"fuel_cell = openmc.Cell(name='1.6% Fuel')\n",
"fuel_cell.fill = fuel\n",
"fuel_cell.region = -fuel_outer_radius\n",
"fuel_pin_universe.add_cell(fuel_cell)\n",
"\n",
"# Create a clad Cell\n",
"clad_cell = openmc.Cell(name='1.6% Clad')\n",
"clad_cell.fill = zircaloy\n",
"clad_cell.region = +fuel_outer_radius & -clad_outer_radius\n",
"fuel_pin_universe.add_cell(clad_cell)\n",
"\n",
"# Create a moderator Cell\n",
"moderator_cell = openmc.Cell(name='1.6% Moderator')\n",
"moderator_cell.fill = water\n",
"moderator_cell.region = +clad_outer_radius\n",
"fuel_pin_universe.add_cell(moderator_cell)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Likewise, we can construct a control rod guide tube with the same surfaces."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [],
"source": [
"# Create a Universe to encapsulate a control rod guide tube\n",
"guide_tube_universe = openmc.Universe(name='Guide Tube')\n",
"\n",
"# Create guide tube Cell\n",
"guide_tube_cell = openmc.Cell(name='Guide Tube Water')\n",
"guide_tube_cell.fill = water\n",
"guide_tube_cell.region = -fuel_outer_radius\n",
"guide_tube_universe.add_cell(guide_tube_cell)\n",
"\n",
"# Create a clad Cell\n",
"clad_cell = openmc.Cell(name='Guide Clad')\n",
"clad_cell.fill = zircaloy\n",
"clad_cell.region = +fuel_outer_radius & -clad_outer_radius\n",
"guide_tube_universe.add_cell(clad_cell)\n",
"\n",
"# Create a moderator Cell\n",
"moderator_cell = openmc.Cell(name='Guide Tube Moderator')\n",
"moderator_cell.fill = water\n",
"moderator_cell.region = +clad_outer_radius\n",
"guide_tube_universe.add_cell(moderator_cell)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Using the pin cell universe, we can construct a 17x17 rectangular lattice with a 1.26 cm pitch."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [],
"source": [
"# Create fuel assembly Lattice\n",
"assembly = openmc.RectLattice(name='1.6% Fuel Assembly')\n",
"assembly.pitch = (1.26, 1.26)\n",
"assembly.lower_left = [-1.26 * 17. / 2.0] * 2"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Next, we create a NumPy array of fuel pin and guide tube universes for the lattice."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [],
"source": [
"# Create array indices for guide tube locations in lattice\n",
"template_x = np.array([5, 8, 11, 3, 13, 2, 5, 8, 11, 14, 2, 5, 8,\n",
" 11, 14, 2, 5, 8, 11, 14, 3, 13, 5, 8, 11])\n",
"template_y = np.array([2, 2, 2, 3, 3, 5, 5, 5, 5, 5, 8, 8, 8, 8,\n",
" 8, 11, 11, 11, 11, 11, 13, 13, 14, 14, 14])\n",
"\n",
"# Initialize an empty 17x17 array of the lattice universes\n",
"universes = np.empty((17, 17), dtype=openmc.Universe)\n",
"\n",
"# Fill the array with the fuel pin and guide tube universes\n",
"universes[:,:] = fuel_pin_universe\n",
"universes[template_x, template_y] = guide_tube_universe\n",
"\n",
"# Store the array of universes in the lattice\n",
"assembly.universes = universes"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"OpenMC requires that there is a \"root\" universe. Let us create a root cell that is filled by the assembly and then assign it to the root universe."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [],
"source": [
"# Create root Cell\n",
"root_cell = openmc.Cell(name='root cell')\n",
"root_cell.fill = assembly\n",
"\n",
"# Add boundary planes\n",
"root_cell.region = +min_x & -max_x & +min_y & -max_y & +min_z & -max_z\n",
"\n",
"# Create root Universe\n",
"root_universe = openmc.Universe(universe_id=0, name='root universe')\n",
"root_universe.add_cell(root_cell)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We now must create a geometry that is assigned a root universe and export it to XML."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [],
"source": [
"# Create Geometry and set root Universe\n",
"geometry = openmc.Geometry(root_universe)"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [],
"source": [
"# Export to \"geometry.xml\"\n",
"geometry.export_to_xml()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"With the geometry and materials finished, we now just need to define simulation parameters. In this case, we will use 10 inactive batches and 40 active batches each with 2500 particles."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [],
"source": [
"# OpenMC simulation parameters\n",
"batches = 50\n",
"inactive = 10\n",
"particles = 10000\n",
"\n",
"# Instantiate a Settings object\n",
"settings_file = openmc.Settings()\n",
"settings_file.batches = batches\n",
"settings_file.inactive = inactive\n",
"settings_file.particles = particles\n",
"settings_file.output = {'tallies': False}\n",
"\n",
"# Create an initial uniform spatial source distribution over fissionable zones\n",
"bounds = [-10.71, -10.71, -10, 10.71, 10.71, 10.]\n",
"uniform_dist = openmc.stats.Box(bounds[:3], bounds[3:], only_fissionable=True)\n",
"settings_file.source = openmc.source.Source(space=uniform_dist)\n",
"\n",
"# Export to \"settings.xml\"\n",
"settings_file.export_to_xml()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let us also create a `Plots` file that we can use to verify that our fuel assembly geometry was created successfully."
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [],
"source": [
"# Instantiate a Plot\n",
"plot = openmc.Plot(plot_id=1)\n",
"plot.filename = 'materials-xy'\n",
"plot.origin = [0, 0, 0]\n",
"plot.pixels = [250, 250]\n",
"plot.width = [-10.71*2, -10.71*2]\n",
"plot.color_by = 'material'\n",
"\n",
"# Instantiate a Plots object, add Plot, and export to \"plots.xml\"\n",
"plot_file = openmc.Plots([plot])\n",
"plot_file.export_to_xml()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"With the plots.xml file, we can now generate and view the plot. OpenMC outputs plots in .ppm format, which can be converted into a compressed format like .png with the convert utility."
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [],
"source": [
"# Run openmc in plotting mode\n",
"openmc.plot_geometry(output=False)"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAPoAAAD6AgMAAAD1grKuAAAABGdBTUEAALGPC/xhBQAAACBjSFJNAAB6JgAAgIQAAPoAAACA6AAAdTAAAOpgAAA6mAAAF3CculE8AAAADFBMVEX///9yEhLpgJFNv8TqQYT7AAAAAWJLR0QAiAUdSAAAAAd0SU1FB+IEGA8UMPReaV0AAAWFSURBVGje7Zs7cttADIZ9CSvXcrP0iCxUqbBc8Ag6xR6BhV2EvYvwFD4CCx1ABT1jMdgndpegRQnOrCbjpPlGESISC4A/gd27e8H583CX3b4+iKJrRHkS4vkghMPBonRYWGwtfgD2YN+dRDUOoh6lACw0Noi9w2fESuEoAR/uVuMolX039oXGT7F3eFL2iEfhUX1f4cPdL/ishs+68ai+udE4xPhexbjX2FfjGNoPj/DPNX4Tsd+EODr8FvsVdf1Hd9P2VvCi4+s/aXvrf+upAD+1/9GV1mkOH5X9vV6THtfvACslcaUCbESL61drBPtdI8SrFMWrELsXCkuFDYW75gbiP7d9Cf7bAYI/aCwUShrBvh30+lWQkzVgZ/HD4OixNCgcQpJ3BxU/Ln91elKoM5VEE38QtJ+Yv6cQ9xjKNYayyl8TypP8DfJnQ2H/b/N3ye9P83cT33SQv/sQh9gV7zZ/0dNj5HQaC5vVzv9+/WFN2w8KVaZ2BwL1+pv4g0x1QRfjq0dB4Q3kT277oP6VNL6gKxNU9a8zK+WLbi/WwpdihbboKqyxFOulHMj6v4W/AXbmUeAxrv9J/CqEBXaRKsXaodD4nsYvkT/G6H1D4SR/iPy1Roj9JsQ5e18/7EUHv1+Fvx/Xj5V9Ugb5K8TW4TZEEdcvoz/up0VTe9qsVIppKVX6a7D6y9ZvwEKjrtQxPtv6fXII9vCxKOGaIeAIfEF8IvAG8ie3vRK9rRQl+PPpSctbhfpTUCpviH+kxsZgpT91+snoX1l49KK3iUQvICRy5aUw6l8leoVwoo3Uv1rKreF/UFLY6d9QP4L9Wf2r7EP9GOSfcsjZ56f60kz+XmVPXv+RuP49ff0T/53Rv6n/7m2lvXT9Wqd/VUz8hvh5M/ED6ILmt4mfHYZSaePnTWpsf/SvqV9O6dLYYClLEetnoH/LBLFoBvrX189uTv8++kot5vTvQD4/9jP690g9P/4z/bvo/XVG/xYoZZx+8fr3MxAtsf7tUOkG2JqsTtCIpgCt/qX1226KqZS7gfzJbe+c9jLrtIZ8lXD+s4umlW6AKIVrlML2/cXjgPFjlJqIRC+Fj0bVJe+vSh56pSdR6YkQ1ygF10Wqf0FeLta/iKn9Mv1L24ti2e+7W4n1b3T/W+L+t9H9T/SvVboUmqJJon1/hZq8LnzRDlDrX1u0xRT1+6vEpomMmyYkqi95vIH8yW1PN+122KkLcNLKi/WTF01z/cNASrWE/l3ev6T17zX909z9X27/euK/Rf3zWP+Waf9eEv37KkWJ+rfDl6ZglNDa+cEBhwYDvkoNP/rX69814NaI3imq0l7OYDy/qSdDGwr7r+Y3VbzoKZr6XX2lfxfOb87qXzr+b1j/Xlp/nP6dn98McdH7cn7zjPObKsYWS3Eb9w8n85smHtqQuPuZ30T2dlIT6F9xFl+n8xslegL9a4c2KRr9W4rp/GYqumiM9Nec/j2v/yj9u1h//hv9e93vc++f63/u+rPjL3f+5Lbn1j9m/eXWf+7zh/v8+2b9e/Hzn6s/uPqHrb8g71n6L3f+5Lbnvn8w33+4718/+5d47//c/gO7/5E7/nPbc/tv3P4fs//I7X9y+6/fqH+v6j9z+9/c/ju3/8+eP+TOn9z23PkXc/7Gnf9x5483q38Xzn+582fu/Js9fy8kb/6fO39y23P3n3S8/S/c/Tfc/T83uX/pgv1XE/9duP+Lu/+Mvf8td/znti8kb/8ld/9nx9t/Sjw/Ltr/yt1/+337f6/bf0zoB3nJ/ucVc/81d/83e/957vzJbc89/8A8f8E9/5HE78XnT/4H/cs5f8Q9/8Q9f8U+/5U7f3Lbc88fdrzzjyvm+cuf/Uu887/c88fs88954/8vO4SjPC+2QRIAAAAldEVYdGRhdGU6Y3JlYXRlADIwMTgtMDQtMjRUMTk6MjA6NDgtMDQ6MDCGN87lAAAAJXRFWHRkYXRlOm1vZGlmeQAyMDE4LTA0LTI0VDE5OjIwOjQ4LTA0OjAw92p2WQAAAABJRU5ErkJggg==\n",
"text/plain": [
"<IPython.core.display.Image object>"
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Convert OpenMC's funky ppm to png\n",
"!convert materials-xy.ppm materials-xy.png\n",
"\n",
"# Display the materials plot inline\n",
"Image(filename='materials-xy.png')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"As we can see from the plot, we have a nice array of fuel and guide tube pin cells with fuel, cladding, and water!"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Create an MGXS Library"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now we are ready to generate multi-group cross sections! First, let's define a 2-group structure using the built-in `EnergyGroups` class."
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [],
"source": [
"# Instantiate a 2-group EnergyGroups object\n",
"groups = openmc.mgxs.EnergyGroups()\n",
"groups.group_edges = np.array([0., 0.625, 20.0e6])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Next, we will instantiate an `openmc.mgxs.Library` for the energy groups with the fuel assembly geometry."
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [],
"source": [
"# Initialize a 2-group MGXS Library for OpenMOC\n",
"mgxs_lib = openmc.mgxs.Library(geometry)\n",
"mgxs_lib.energy_groups = groups"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now, we must specify to the `Library` which types of cross sections to compute. In particular, the following are the multi-group cross section `MGXS` subclasses that are mapped to string codes accepted by the `Library` class:\n",
"\n",
"* `TotalXS` (`\"total\"`)\n",
"* `TransportXS` (`\"transport\"` or `\"nu-transport` with `nu` set to `True`)\n",
"* `AbsorptionXS` (`\"absorption\"`)\n",
"* `CaptureXS` (`\"capture\"`)\n",
"* `FissionXS` (`\"fission\"` or `\"nu-fission\"` with `nu` set to `True`)\n",
"* `KappaFissionXS` (`\"kappa-fission\"`)\n",
"* `ScatterXS` (`\"scatter\"` or `\"nu-scatter\"` with `nu` set to `True`)\n",
"* `ScatterMatrixXS` (`\"scatter matrix\"` or `\"nu-scatter matrix\"` with `nu` set to `True`)\n",
"* `Chi` (`\"chi\"`)\n",
"* `ChiPrompt` (`\"chi prompt\"`)\n",
"* `InverseVelocity` (`\"inverse-velocity\"`)\n",
"* `PromptNuFissionXS` (`\"prompt-nu-fission\"`)\n",
"* `DelayedNuFissionXS` (`\"delayed-nu-fission\"`)\n",
"* `ChiDelayed` (`\"chi-delayed\"`)\n",
"* `Beta` (`\"beta\"`)\n",
"\n",
"In this case, let's create the multi-group cross sections needed to run an OpenMOC simulation to verify the accuracy of our cross sections. In particular, we will define `\"nu-transport\"`, `\"nu-fission\"`, `'\"fission\"`, `\"nu-scatter matrix\"` and `\"chi\"` cross sections for our `Library`.\n",
"\n",
"**Note**: A variety of different approximate transport-corrected total multi-group cross sections (and corresponding scattering matrices) can be found in the literature. At the present time, the `openmc.mgxs` module only supports the `\"P0\"` transport correction. This correction can be turned on and off through the boolean `Library.correction` property which may take values of `\"P0\"` (default) or `None`."
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [],
"source": [
"# Specify multi-group cross section types to compute\n",
"mgxs_lib.mgxs_types = ['nu-transport', 'nu-fission', 'fission', 'nu-scatter matrix', 'chi']"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now we must specify the type of domain over which we would like the `Library` to compute multi-group cross sections. The domain type corresponds to the type of tally filter to be used in the tallies created to compute multi-group cross sections. At the present time, the `Library` supports `\"material\"`, `\"cell\"`, `\"universe\"`, and `\"mesh\"` domain types. We will use a `\"cell\"` domain type here to compute cross sections in each of the cells in the fuel assembly geometry.\n",
"\n",
"**Note:** By default, the `Library` class will instantiate `MGXS` objects for each and every domain (material, cell or universe) in the geometry of interest. However, one may specify a subset of these domains to the `Library.domains` property. In our case, we wish to compute multi-group cross sections in each and every cell since they will be needed in our downstream OpenMOC calculation on the identical combinatorial geometry mesh."
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [],
"source": [
"# Specify a \"cell\" domain type for the cross section tally filters\n",
"mgxs_lib.domain_type = 'cell'\n",
"\n",
"# Specify the cell domains over which to compute multi-group cross sections\n",
"mgxs_lib.domains = geometry.get_all_material_cells().values()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can easily instruct the `Library` to compute multi-group cross sections on a nuclide-by-nuclide basis with the boolean `Library.by_nuclide` property. By default, `by_nuclide` is set to `False`, but we will set it to `True` here."
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {},
"outputs": [],
"source": [
"# Compute cross sections on a nuclide-by-nuclide basis\n",
"mgxs_lib.by_nuclide = True"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Lastly, we use the `Library` to construct the tallies needed to compute all of the requested multi-group cross sections in each domain and nuclide."
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {},
"outputs": [],
"source": [
"# Construct all tallies needed for the multi-group cross section library\n",
"mgxs_lib.build_library()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The tallies can now be export to a \"tallies.xml\" input file for OpenMC. \n",
"\n",
"**NOTE**: At this point the `Library` has constructed nearly 100 distinct `Tally` objects. The overhead to tally in OpenMC scales as $O(N)$ for $N$ tallies, which can become a bottleneck for large tally datasets. To compensate for this, the Python API's `Tally`, `Filter` and `Tallies` classes allow for the smart *merging* of tallies when possible. The `Library` class supports this runtime optimization with the use of the optional `merge` paramter (`False` by default) for the `Library.add_to_tallies_file(...)` method, as shown below."
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [],
"source": [
"# Create a \"tallies.xml\" file for the MGXS Library\n",
"tallies_file = openmc.Tallies()\n",
"mgxs_lib.add_to_tallies_file(tallies_file, merge=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In addition, we instantiate a fission rate mesh tally to compare with OpenMOC."
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {},
"outputs": [],
"source": [
"# Instantiate a tally Mesh\n",
"mesh = openmc.Mesh(mesh_id=1)\n",
"mesh.type = 'regular'\n",
"mesh.dimension = [17, 17]\n",
"mesh.lower_left = [-10.71, -10.71]\n",
"mesh.upper_right = [+10.71, +10.71]\n",
"\n",
"# Instantiate tally Filter\n",
"mesh_filter = openmc.MeshFilter(mesh)\n",
"\n",
"# Instantiate the Tally\n",
"tally = openmc.Tally(name='mesh tally')\n",
"tally.filters = [mesh_filter]\n",
"tally.scores = ['fission', 'nu-fission']\n",
"\n",
"# Add tally to collection\n",
"tallies_file.append(tally)"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/home/nelsonag/git/openmc/openmc/mixin.py:71: IDWarning: Another Filter instance already exists with id=126.\n",
" warn(msg, IDWarning)\n",
"/home/nelsonag/git/openmc/openmc/mixin.py:71: IDWarning: Another Filter instance already exists with id=21.\n",
" warn(msg, IDWarning)\n",
"/home/nelsonag/git/openmc/openmc/mixin.py:71: IDWarning: Another Filter instance already exists with id=2.\n",
" warn(msg, IDWarning)\n",
"/home/nelsonag/git/openmc/openmc/mixin.py:71: IDWarning: Another Filter instance already exists with id=3.\n",
" warn(msg, IDWarning)\n",
"/home/nelsonag/git/openmc/openmc/mixin.py:71: IDWarning: Another Filter instance already exists with id=4.\n",
" warn(msg, IDWarning)\n",
"/home/nelsonag/git/openmc/openmc/mixin.py:71: IDWarning: Another Filter instance already exists with id=96.\n",
" warn(msg, IDWarning)\n",
"/home/nelsonag/git/openmc/openmc/mixin.py:71: IDWarning: Another Filter instance already exists with id=15.\n",
" warn(msg, IDWarning)\n",
"/home/nelsonag/git/openmc/openmc/mixin.py:71: IDWarning: Another Filter instance already exists with id=114.\n",
" warn(msg, IDWarning)\n"
]
}
],
"source": [
"# Export all tallies to a \"tallies.xml\" file\n",
"tallies_file.export_to_xml()"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n",
" %%%%%%%%%%%%%%%\n",
" %%%%%%%%%%%%%%%%%%%%%%%%\n",
" %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%\n",
" %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%\n",
" %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%\n",
" %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%\n",
" %%%%%%%%%%%%%%%%%%%%%%%%\n",
" %%%%%%%%%%%%%%%%%%%%%%%%\n",
" ############### %%%%%%%%%%%%%%%%%%%%%%%%\n",
" ################## %%%%%%%%%%%%%%%%%%%%%%%\n",
" ################### %%%%%%%%%%%%%%%%%%%%%%%\n",
" #################### %%%%%%%%%%%%%%%%%%%%%%\n",
" ##################### %%%%%%%%%%%%%%%%%%%%%\n",
" ###################### %%%%%%%%%%%%%%%%%%%%\n",
" ####################### %%%%%%%%%%%%%%%%%%\n",
" ####################### %%%%%%%%%%%%%%%%%\n",
" ###################### %%%%%%%%%%%%%%%%%\n",
" #################### %%%%%%%%%%%%%%%%%\n",
" ################# %%%%%%%%%%%%%%%%%\n",
" ############### %%%%%%%%%%%%%%%%\n",
" ############ %%%%%%%%%%%%%%%\n",
" ######## %%%%%%%%%%%%%%\n",
" %%%%%%%%%%%\n",
"\n",
" | The OpenMC Monte Carlo Code\n",
" Copyright | 2011-2018 Massachusetts Institute of Technology\n",
" License | http://openmc.readthedocs.io/en/latest/license.html\n",
" Version | 0.10.0\n",
" Git SHA1 | 6c2d82a4d7dfe10312329d5969568fc03a698416\n",
" Date/Time | 2018-04-24 19:20:48\n",
" OpenMP Threads | 8\n",
"\n",
" Reading settings XML file...\n",
" Reading cross sections XML file...\n",
" Reading materials XML file...\n",
" Reading geometry XML file...\n",
" Building neighboring cells lists for each surface...\n",
" Reading U235 from /opt/xsdata/nndc/U235.h5\n",
" Reading U238 from /opt/xsdata/nndc/U238.h5\n",
" Reading O16 from /opt/xsdata/nndc/O16.h5\n",
" Reading H1 from /opt/xsdata/nndc/H1.h5\n",
" Reading B10 from /opt/xsdata/nndc/B10.h5\n",
" Reading Zr90 from /opt/xsdata/nndc/Zr90.h5\n",
" Maximum neutron transport energy: 2.00000E+07 eV for U235\n",
" Reading tallies XML file...\n",
" Writing summary.h5 file...\n",
" Initializing source particles...\n",
"\n",
" ====================> K EIGENVALUE SIMULATION <====================\n",
"\n",
" Bat./Gen. k Average k \n",
" ========= ======== ==================== \n",
" 1/1 1.03784 \n",
" 2/1 1.02297 \n",
" 3/1 1.02244 \n",
" 4/1 1.02344 \n",
" 5/1 1.02057 \n",
" 6/1 1.04077 \n",
" 7/1 1.00795 \n",
" 8/1 1.02418 \n",
" 9/1 1.02241 \n",
" 10/1 1.03731 \n",
" 11/1 1.01477 \n",
" 12/1 1.05315 1.03396 +/- 0.01919\n",
" 13/1 1.02824 1.03205 +/- 0.01124\n",
" 14/1 1.02858 1.03118 +/- 0.00800\n",
" 15/1 1.02176 1.02930 +/- 0.00647\n",
" 16/1 1.06046 1.03449 +/- 0.00741\n",
" 17/1 1.02066 1.03252 +/- 0.00657\n",
" 18/1 1.03088 1.03231 +/- 0.00569\n",
" 19/1 1.02021 1.03097 +/- 0.00520\n",
" 20/1 1.02717 1.03059 +/- 0.00466\n",
" 21/1 1.03455 1.03095 +/- 0.00423\n",
" 22/1 1.02917 1.03080 +/- 0.00387\n",
" 23/1 1.02800 1.03058 +/- 0.00356\n",
" 24/1 1.02935 1.03050 +/- 0.00330\n",
" 25/1 1.01612 1.02954 +/- 0.00322\n",
" 26/1 1.00549 1.02803 +/- 0.00336\n",
" 27/1 1.02824 1.02805 +/- 0.00316\n",
" 28/1 1.01487 1.02731 +/- 0.00307\n",
" 29/1 1.05544 1.02879 +/- 0.00326\n",
" 30/1 1.00467 1.02759 +/- 0.00332\n",
" 31/1 1.03942 1.02815 +/- 0.00321\n",
" 32/1 1.02587 1.02805 +/- 0.00306\n",
" 33/1 1.02938 1.02811 +/- 0.00292\n",
" 34/1 1.02838 1.02812 +/- 0.00280\n",
" 35/1 1.00052 1.02701 +/- 0.00290\n",
" 36/1 1.01722 1.02664 +/- 0.00281\n",
" 37/1 1.01881 1.02635 +/- 0.00272\n",
" 38/1 1.03928 1.02681 +/- 0.00266\n",
" 39/1 1.03802 1.02720 +/- 0.00260\n",
" 40/1 1.00710 1.02653 +/- 0.00260\n",
" 41/1 1.02558 1.02650 +/- 0.00251\n",
" 42/1 1.03499 1.02676 +/- 0.00245\n",
" 43/1 1.01128 1.02629 +/- 0.00242\n",
" 44/1 1.00442 1.02565 +/- 0.00243\n",
" 45/1 1.03444 1.02590 +/- 0.00238\n",
" 46/1 1.01799 1.02568 +/- 0.00232\n",
" 47/1 1.00814 1.02521 +/- 0.00231\n",
" 48/1 1.00500 1.02467 +/- 0.00231\n",
" 49/1 1.01960 1.02454 +/- 0.00225\n",
" 50/1 1.02431 1.02454 +/- 0.00219\n",
" Creating state point statepoint.50.h5...\n",
"\n",
" =======================> TIMING STATISTICS <=======================\n",
"\n",
" Total time for initialization = 2.8179E-01 seconds\n",
" Reading cross sections = 2.5741E-01 seconds\n",
" Total time in simulation = 2.5787E+01 seconds\n",
" Time in transport only = 2.5724E+01 seconds\n",
" Time in inactive batches = 1.7591E+00 seconds\n",
" Time in active batches = 2.4028E+01 seconds\n",
" Time synchronizing fission bank = 1.3217E-02 seconds\n",
" Sampling source sites = 1.0464E-02 seconds\n",
" SEND/RECV source sites = 2.6486E-03 seconds\n",
" Time accumulating tallies = 2.7351E-04 seconds\n",
" Total time for finalization = 5.5454E-05 seconds\n",
" Total time elapsed = 2.6109E+01 seconds\n",
" Calculation Rate (inactive) = 56847.1 neutrons/second\n",
" Calculation Rate (active) = 16647.3 neutrons/second\n",
"\n",
" ============================> RESULTS <============================\n",
"\n",
" k-effective (Collision) = 1.02204 +/- 0.00176\n",
" k-effective (Track-length) = 1.02454 +/- 0.00219\n",
" k-effective (Absorption) = 1.02370 +/- 0.00186\n",
" Combined k-effective = 1.02329 +/- 0.00157\n",
" Leakage Fraction = 0.00000 +/- 0.00000\n",
"\n"
]
}
],
"source": [
"# Run OpenMC\n",
"openmc.run()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Tally Data Processing"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Our simulation ran successfully and created statepoint and summary output files. We begin our analysis by instantiating a `StatePoint` object. "
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {},
"outputs": [],
"source": [
"# Load the last statepoint file\n",
"sp = openmc.StatePoint('statepoint.50.h5')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The statepoint is now ready to be analyzed by the `Library`. We simply have to load the tallies from the statepoint into the `Library` and our `MGXS` objects will compute the cross sections for us under-the-hood."
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {},
"outputs": [],
"source": [
"# Initialize MGXS Library with OpenMC statepoint data\n",
"mgxs_lib.load_from_statepoint(sp)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Voila! Our multi-group cross sections are now ready to rock 'n roll!"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Extracting and Storing MGXS Data"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The `Library` supports a rich API to automate a variety of tasks, including multi-group cross section data retrieval and storage. We will highlight a few of these features here. First, the `Library.get_mgxs(...)` method allows one to extract an `MGXS` object from the `Library` for a particular domain and cross section type. The following cell illustrates how one may extract the `NuFissionXS` object for the fuel cell.\n",
"\n",
"**Note:** The `MGXS.get_mgxs(...)` method will accept either the domain *or* the integer domain ID of interest."
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {},
"outputs": [],
"source": [
"# Retrieve the NuFissionXS object for the fuel cell from the library\n",
"fuel_mgxs = mgxs_lib.get_mgxs(fuel_cell, 'nu-fission')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The `NuFissionXS` object supports all of the methods described previously in the `openmc.mgxs` tutorials, such as [Pandas](http://pandas.pydata.org/) `DataFrames`:\n",
"Note that since so few histories were simulated, we should expect a few division-by-error errors as some tallies have not yet scored any results."
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style>\n",
" .dataframe thead tr:only-child th {\n",
" text-align: right;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: left;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>cell</th>\n",
" <th>group in</th>\n",
" <th>nuclide</th>\n",
" <th>mean</th>\n",
" <th>std. dev.</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>1</td>\n",
" <td>1</td>\n",
" <td>U235</td>\n",
" <td>8.093482e-03</td>\n",
" <td>1.597406e-05</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>1</td>\n",
" <td>1</td>\n",
" <td>U238</td>\n",
" <td>7.347745e-03</td>\n",
" <td>2.082526e-05</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>1</td>\n",
" <td>1</td>\n",
" <td>O16</td>\n",
" <td>0.000000e+00</td>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1</td>\n",
" <td>2</td>\n",
" <td>U235</td>\n",
" <td>3.615911e-01</td>\n",
" <td>1.206052e-03</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>1</td>\n",
" <td>2</td>\n",
" <td>U238</td>\n",
" <td>6.743056e-07</td>\n",
" <td>2.229534e-09</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>1</td>\n",
" <td>2</td>\n",
" <td>O16</td>\n",
" <td>0.000000e+00</td>\n",
" <td>0.000000e+00</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" cell group in nuclide mean std. dev.\n",
"3 1 1 U235 8.093482e-03 1.597406e-05\n",
"4 1 1 U238 7.347745e-03 2.082526e-05\n",
"5 1 1 O16 0.000000e+00 0.000000e+00\n",
"0 1 2 U235 3.615911e-01 1.206052e-03\n",
"1 1 2 U238 6.743056e-07 2.229534e-09\n",
"2 1 2 O16 0.000000e+00 0.000000e+00"
]
},
"execution_count": 29,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df = fuel_mgxs.get_pandas_dataframe()\n",
"df"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Similarly, we can use the `MGXS.print_xs(...)` method to view a string representation of the multi-group cross section data."
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Multi-Group XS\n",
"\tReaction Type =\tnu-fission\n",
"\tDomain Type =\tcell\n",
"\tDomain ID =\t1\n",
"\tNuclide =\tU235\n",
"\tCross Sections [cm^-1]:\n",
" Group 1 [0.625 - 20000000.0eV]:\t8.09e-03 +/- 1.97e-01%\n",
" Group 2 [0.0 - 0.625 eV]:\t3.62e-01 +/- 3.34e-01%\n",
"\n",
"\tNuclide =\tU238\n",
"\tCross Sections [cm^-1]:\n",
" Group 1 [0.625 - 20000000.0eV]:\t7.35e-03 +/- 2.83e-01%\n",
" Group 2 [0.0 - 0.625 eV]:\t6.74e-07 +/- 3.31e-01%\n",
"\n",
"\tNuclide =\tO16\n",
"\tCross Sections [cm^-1]:\n",
" Group 1 [0.625 - 20000000.0eV]:\t0.00e+00 +/- 0.00e+00%\n",
" Group 2 [0.0 - 0.625 eV]:\t0.00e+00 +/- 0.00e+00%\n",
"\n",
"\n",
"\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"/home/nelsonag/git/openmc/openmc/tallies.py:1269: RuntimeWarning: invalid value encountered in true_divide\n",
" data = self.std_dev[indices] / self.mean[indices]\n"
]
}
],
"source": [
"fuel_mgxs.print_xs()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"One can export the entire `Library` to HDF5 with the `Library.build_hdf5_store(...)` method as follows:"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {},
"outputs": [],
"source": [
"# Store the cross section data in an \"mgxs/mgxs.h5\" HDF5 binary file\n",
"mgxs_lib.build_hdf5_store(filename='mgxs.h5', directory='mgxs')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The HDF5 store will contain the numerical multi-group cross section data indexed by domain, nuclide and cross section type. Some data workflows may be optimized by storing and retrieving binary representations of the `MGXS` objects in the `Library`. This feature is supported through the `Library.dump_to_file(...)` and `Library.load_from_file(...)` routines which use Python's [`pickle`](https://docs.python.org/2/library/pickle.html) module. This is illustrated as follows."
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {},
"outputs": [],
"source": [
"# Store a Library and its MGXS objects in a pickled binary file \"mgxs/mgxs.pkl\"\n",
"mgxs_lib.dump_to_file(filename='mgxs', directory='mgxs')"
]
},
{
"cell_type": "code",
"execution_count": 33,
"metadata": {},
"outputs": [],
"source": [
"# Instantiate a new MGXS Library from the pickled binary file \"mgxs/mgxs.pkl\"\n",
"mgxs_lib = openmc.mgxs.Library.load_from_file(filename='mgxs', directory='mgxs')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The `Library` class may be used to leverage the energy condensation features supported by the `MGXS` class. In particular, one can use the `Library.get_condensed_library(...)` with a coarse group structure which is a subset of the original \"fine\" group structure as shown below."
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {},
"outputs": [],
"source": [
"# Create a 1-group structure\n",
"coarse_groups = openmc.mgxs.EnergyGroups(group_edges=[0., 20.0e6])\n",
"\n",
"# Create a new MGXS Library on the coarse 1-group structure\n",
"coarse_mgxs_lib = mgxs_lib.get_condensed_library(coarse_groups)"
]
},
{
"cell_type": "code",
"execution_count": 35,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style>\n",
" .dataframe thead tr:only-child th {\n",
" text-align: right;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: left;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>cell</th>\n",
" <th>group in</th>\n",
" <th>nuclide</th>\n",
" <th>mean</th>\n",
" <th>std. dev.</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>1</td>\n",
" <td>1</td>\n",
" <td>U235</td>\n",
" <td>0.074672</td>\n",
" <td>0.000179</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>1</td>\n",
" <td>1</td>\n",
" <td>U238</td>\n",
" <td>0.005964</td>\n",
" <td>0.000017</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>1</td>\n",
" <td>1</td>\n",
" <td>O16</td>\n",
" <td>0.000000</td>\n",
" <td>0.000000</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" cell group in nuclide mean std. dev.\n",
"0 1 1 U235 0.074672 0.000179\n",
"1 1 1 U238 0.005964 0.000017\n",
"2 1 1 O16 0.000000 0.000000"
]
},
"execution_count": 35,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Retrieve the NuFissionXS object for the fuel cell from the 1-group library\n",
"coarse_fuel_mgxs = coarse_mgxs_lib.get_mgxs(fuel_cell, 'nu-fission')\n",
"\n",
"# Show the Pandas DataFrame for the 1-group MGXS\n",
"coarse_fuel_mgxs.get_pandas_dataframe()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Verification with OpenMOC"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Of course it is always a good idea to verify that one's cross sections are accurate. We can easily do so here with the deterministic transport code [OpenMOC](https://mit-crpg.github.io/OpenMOC/). We first construct an equivalent OpenMOC geometry."
]
},
{
"cell_type": "code",
"execution_count": 36,
"metadata": {},
"outputs": [],
"source": [
"# Create an OpenMOC Geometry from the OpenMC Geometry\n",
"openmoc_geometry = get_openmoc_geometry(mgxs_lib.geometry)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now, we can inject the multi-group cross sections into the equivalent fuel assembly OpenMOC geometry. The `openmoc.materialize` module supports the loading of `Library` objects from OpenMC as illustrated below."
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {},
"outputs": [],
"source": [
"# Load the library into the OpenMOC geometry\n",
"materials = load_openmc_mgxs_lib(mgxs_lib, openmoc_geometry)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We are now ready to run OpenMOC to verify our cross-sections from OpenMC."
]
},
{
"cell_type": "code",
"execution_count": 38,
"metadata": {
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[ NORMAL ] Importing ray tracing data from file...\n",
"[ NORMAL ] Computing the eigenvalue...\n",
"[ NORMAL ] Iteration 0:\tk_eff = 0.823436\tres = 0.000E+00\n",
"[ NORMAL ] Iteration 1:\tk_eff = 0.780042\tres = 1.941E-01\n",
"[ NORMAL ] Iteration 2:\tk_eff = 0.739063\tres = 6.559E-02\n",
"[ NORMAL ] Iteration 3:\tk_eff = 0.710328\tres = 5.301E-02\n",
"[ NORMAL ] Iteration 4:\tk_eff = 0.689038\tres = 3.942E-02\n",
"[ NORMAL ] Iteration 5:\tk_eff = 0.674339\tres = 3.021E-02\n",
"[ NORMAL ] Iteration 6:\tk_eff = 0.665075\tres = 2.149E-02\n",
"[ NORMAL ] Iteration 7:\tk_eff = 0.660373\tres = 1.387E-02\n",
"[ NORMAL ] Iteration 8:\tk_eff = 0.659460\tres = 7.242E-03\n",
"[ NORMAL ] Iteration 9:\tk_eff = 0.661679\tres = 1.995E-03\n",
"[ NORMAL ] Iteration 10:\tk_eff = 0.666463\tres = 3.649E-03\n",
"[ NORMAL ] Iteration 11:\tk_eff = 0.673324\tres = 7.367E-03\n",
"[ NORMAL ] Iteration 12:\tk_eff = 0.681842\tres = 1.039E-02\n",
"[ NORMAL ] Iteration 13:\tk_eff = 0.691660\tres = 1.273E-02\n",
"[ NORMAL ] Iteration 14:\tk_eff = 0.702469\tres = 1.447E-02\n",
"[ NORMAL ] Iteration 15:\tk_eff = 0.714008\tres = 1.569E-02\n",
"[ NORMAL ] Iteration 16:\tk_eff = 0.726057\tres = 1.649E-02\n",
"[ NORMAL ] Iteration 17:\tk_eff = 0.738428\tres = 1.693E-02\n",
"[ NORMAL ] Iteration 18:\tk_eff = 0.750965\tres = 1.709E-02\n",
"[ NORMAL ] Iteration 19:\tk_eff = 0.763536\tres = 1.703E-02\n",
"[ NORMAL ] Iteration 20:\tk_eff = 0.776034\tres = 1.679E-02\n",
"[ NORMAL ] Iteration 21:\tk_eff = 0.788369\tres = 1.641E-02\n",
"[ NORMAL ] Iteration 22:\tk_eff = 0.800470\tres = 1.594E-02\n",
"[ NORMAL ] Iteration 23:\tk_eff = 0.812280\tres = 1.539E-02\n",
"[ NORMAL ] Iteration 24:\tk_eff = 0.823753\tres = 1.479E-02\n",
"[ NORMAL ] Iteration 25:\tk_eff = 0.834854\tres = 1.416E-02\n",
"[ NORMAL ] Iteration 26:\tk_eff = 0.845560\tres = 1.351E-02\n",
"[ NORMAL ] Iteration 27:\tk_eff = 0.855851\tres = 1.286E-02\n",
"[ NORMAL ] Iteration 28:\tk_eff = 0.865717\tres = 1.220E-02\n",
"[ NORMAL ] Iteration 29:\tk_eff = 0.875152\tres = 1.156E-02\n",
"[ NORMAL ] Iteration 30:\tk_eff = 0.884153\tres = 1.093E-02\n",
"[ NORMAL ] Iteration 31:\tk_eff = 0.892725\tres = 1.031E-02\n",
"[ NORMAL ] Iteration 32:\tk_eff = 0.900872\tres = 9.722E-03\n",
"[ NORMAL ] Iteration 33:\tk_eff = 0.908602\tres = 9.152E-03\n",
"[ NORMAL ] Iteration 34:\tk_eff = 0.915926\tres = 8.605E-03\n",
"[ NORMAL ] Iteration 35:\tk_eff = 0.922853\tres = 8.083E-03\n",
"[ NORMAL ] Iteration 36:\tk_eff = 0.929399\tres = 7.586E-03\n",
"[ NORMAL ] Iteration 37:\tk_eff = 0.935576\tres = 7.114E-03\n",
"[ NORMAL ] Iteration 38:\tk_eff = 0.941398\tres = 6.666E-03\n",
"[ NORMAL ] Iteration 39:\tk_eff = 0.946880\tres = 6.242E-03\n",
"[ NORMAL ] Iteration 40:\tk_eff = 0.952037\tres = 5.841E-03\n",
"[ NORMAL ] Iteration 41:\tk_eff = 0.956883\tres = 5.463E-03\n",
"[ NORMAL ] Iteration 42:\tk_eff = 0.961434\tres = 5.107E-03\n",
"[ NORMAL ] Iteration 43:\tk_eff = 0.965705\tres = 4.771E-03\n",
"[ NORMAL ] Iteration 44:\tk_eff = 0.969708\tres = 4.456E-03\n",
"[ NORMAL ] Iteration 45:\tk_eff = 0.973460\tres = 4.159E-03\n",
"[ NORMAL ] Iteration 46:\tk_eff = 0.976972\tres = 3.881E-03\n",
"[ NORMAL ] Iteration 47:\tk_eff = 0.980259\tres = 3.620E-03\n",
"[ NORMAL ] Iteration 48:\tk_eff = 0.983333\tres = 3.375E-03\n",
"[ NORMAL ] Iteration 49:\tk_eff = 0.986206\tres = 3.146E-03\n",
"[ NORMAL ] Iteration 50:\tk_eff = 0.988890\tres = 2.932E-03\n",
"[ NORMAL ] Iteration 51:\tk_eff = 0.991396\tres = 2.731E-03\n",
"[ NORMAL ] Iteration 52:\tk_eff = 0.993735\tres = 2.543E-03\n",
"[ NORMAL ] Iteration 53:\tk_eff = 0.995917\tres = 2.368E-03\n",
"[ NORMAL ] Iteration 54:\tk_eff = 0.997952\tres = 2.204E-03\n",
"[ NORMAL ] Iteration 55:\tk_eff = 0.999848\tres = 2.050E-03\n",
"[ NORMAL ] Iteration 56:\tk_eff = 1.001616\tres = 1.907E-03\n",
"[ NORMAL ] Iteration 57:\tk_eff = 1.003262\tres = 1.774E-03\n",
"[ NORMAL ] Iteration 58:\tk_eff = 1.004795\tres = 1.650E-03\n",
"[ NORMAL ] Iteration 59:\tk_eff = 1.006222\tres = 1.534E-03\n",
"[ NORMAL ] Iteration 60:\tk_eff = 1.007550\tres = 1.425E-03\n",
"[ NORMAL ] Iteration 61:\tk_eff = 1.008785\tres = 1.325E-03\n",
"[ NORMAL ] Iteration 62:\tk_eff = 1.009934\tres = 1.231E-03\n",
"[ NORMAL ] Iteration 63:\tk_eff = 1.011002\tres = 1.143E-03\n",
"[ NORMAL ] Iteration 64:\tk_eff = 1.011995\tres = 1.062E-03\n",
"[ NORMAL ] Iteration 65:\tk_eff = 1.012918\tres = 9.859E-04\n",
"[ NORMAL ] Iteration 66:\tk_eff = 1.013775\tres = 9.153E-04\n",
"[ NORMAL ] Iteration 67:\tk_eff = 1.014571\tres = 8.497E-04\n",
"[ NORMAL ] Iteration 68:\tk_eff = 1.015311\tres = 7.886E-04\n",
"[ NORMAL ] Iteration 69:\tk_eff = 1.015997\tres = 7.318E-04\n",
"[ NORMAL ] Iteration 70:\tk_eff = 1.016635\tres = 6.790E-04\n",
"[ NORMAL ] Iteration 71:\tk_eff = 1.017226\tres = 6.300E-04\n",
"[ NORMAL ] Iteration 72:\tk_eff = 1.017775\tres = 5.844E-04\n",
"[ NORMAL ] Iteration 73:\tk_eff = 1.018285\tres = 5.420E-04\n",
"[ NORMAL ] Iteration 74:\tk_eff = 1.018757\tres = 5.026E-04\n",
"[ NORMAL ] Iteration 75:\tk_eff = 1.019195\tres = 4.660E-04\n",
"[ NORMAL ] Iteration 76:\tk_eff = 1.019602\tres = 4.321E-04\n",
"[ NORMAL ] Iteration 77:\tk_eff = 1.019979\tres = 4.005E-04\n",
"[ NORMAL ] Iteration 78:\tk_eff = 1.020328\tres = 3.713E-04\n",
"[ NORMAL ] Iteration 79:\tk_eff = 1.020652\tres = 3.441E-04\n",
"[ NORMAL ] Iteration 80:\tk_eff = 1.020952\tres = 3.189E-04\n",
"[ NORMAL ] Iteration 81:\tk_eff = 1.021230\tres = 2.955E-04\n",
"[ NORMAL ] Iteration 82:\tk_eff = 1.021488\tres = 2.738E-04\n",
"[ NORMAL ] Iteration 83:\tk_eff = 1.021727\tres = 2.536E-04\n",
"[ NORMAL ] Iteration 84:\tk_eff = 1.021948\tres = 2.350E-04\n",
"[ NORMAL ] Iteration 85:\tk_eff = 1.022153\tres = 2.177E-04\n",
"[ NORMAL ] Iteration 86:\tk_eff = 1.022344\tres = 2.016E-04\n",
"[ NORMAL ] Iteration 87:\tk_eff = 1.022520\tres = 1.867E-04\n",
"[ NORMAL ] Iteration 88:\tk_eff = 1.022683\tres = 1.729E-04\n",
"[ NORMAL ] Iteration 89:\tk_eff = 1.022833\tres = 1.601E-04\n",
"[ NORMAL ] Iteration 90:\tk_eff = 1.022973\tres = 1.482E-04\n",
"[ NORMAL ] Iteration 91:\tk_eff = 1.023102\tres = 1.372E-04\n",
"[ NORMAL ] Iteration 92:\tk_eff = 1.023222\tres = 1.271E-04\n",
"[ NORMAL ] Iteration 93:\tk_eff = 1.023333\tres = 1.176E-04\n",
"[ NORMAL ] Iteration 94:\tk_eff = 1.023436\tres = 1.089E-04\n",
"[ NORMAL ] Iteration 95:\tk_eff = 1.023531\tres = 1.008E-04\n",
"[ NORMAL ] Iteration 96:\tk_eff = 1.023619\tres = 9.327E-05\n",
"[ NORMAL ] Iteration 97:\tk_eff = 1.023700\tres = 8.632E-05\n",
"[ NORMAL ] Iteration 98:\tk_eff = 1.023775\tres = 7.988E-05\n",
"[ NORMAL ] Iteration 99:\tk_eff = 1.023845\tres = 7.391E-05\n",
"[ NORMAL ] Iteration 100:\tk_eff = 1.023910\tres = 6.838E-05\n",
"[ NORMAL ] Iteration 101:\tk_eff = 1.023969\tres = 6.329E-05\n",
"[ NORMAL ] Iteration 102:\tk_eff = 1.024024\tres = 5.855E-05\n",
"[ NORMAL ] Iteration 103:\tk_eff = 1.024076\tres = 5.415E-05\n",
"[ NORMAL ] Iteration 104:\tk_eff = 1.024123\tres = 5.011E-05\n",
"[ NORMAL ] Iteration 105:\tk_eff = 1.024166\tres = 4.634E-05\n",
"[ NORMAL ] Iteration 106:\tk_eff = 1.024207\tres = 4.290E-05\n",
"[ NORMAL ] Iteration 107:\tk_eff = 1.024244\tres = 3.966E-05\n",
"[ NORMAL ] Iteration 108:\tk_eff = 1.024279\tres = 3.669E-05\n",
"[ NORMAL ] Iteration 109:\tk_eff = 1.024311\tres = 3.392E-05\n",
"[ NORMAL ] Iteration 110:\tk_eff = 1.024341\tres = 3.137E-05\n",
"[ NORMAL ] Iteration 111:\tk_eff = 1.024368\tres = 2.904E-05\n",
"[ NORMAL ] Iteration 112:\tk_eff = 1.024393\tres = 2.686E-05\n",
"[ NORMAL ] Iteration 113:\tk_eff = 1.024417\tres = 2.481E-05\n",
"[ NORMAL ] Iteration 114:\tk_eff = 1.024438\tres = 2.296E-05\n",
"[ NORMAL ] Iteration 115:\tk_eff = 1.024458\tres = 2.121E-05\n",
"[ NORMAL ] Iteration 116:\tk_eff = 1.024477\tres = 1.961E-05\n",
"[ NORMAL ] Iteration 117:\tk_eff = 1.024494\tres = 1.815E-05\n",
"[ NORMAL ] Iteration 118:\tk_eff = 1.024510\tres = 1.679E-05\n",
"[ NORMAL ] Iteration 119:\tk_eff = 1.024524\tres = 1.551E-05\n",
"[ NORMAL ] Iteration 120:\tk_eff = 1.024538\tres = 1.435E-05\n",
"[ NORMAL ] Iteration 121:\tk_eff = 1.024550\tres = 1.326E-05\n",
"[ NORMAL ] Iteration 122:\tk_eff = 1.024561\tres = 1.226E-05\n",
"[ NORMAL ] Iteration 123:\tk_eff = 1.024572\tres = 1.133E-05\n",
"[ NORMAL ] Iteration 124:\tk_eff = 1.024582\tres = 1.047E-05\n"
]
}
],
"source": [
"# Generate tracks for OpenMOC\n",
"track_generator = openmoc.TrackGenerator(openmoc_geometry, num_azim=32, azim_spacing=0.1)\n",
"track_generator.generateTracks()\n",
"\n",
"# Run OpenMOC\n",
"solver = openmoc.CPUSolver(track_generator)\n",
"solver.computeEigenvalue()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We report the eigenvalues computed by OpenMC and OpenMOC here together to summarize our results."
]
},
{
"cell_type": "code",
"execution_count": 39,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"openmc keff = 1.023293\n",
"openmoc keff = 1.024582\n",
"bias [pcm]: 128.8\n"
]
}
],
"source": [
"# Print report of keff and bias with OpenMC\n",
"openmoc_keff = solver.getKeff()\n",
"openmc_keff = sp.k_combined.nominal_value\n",
"bias = (openmoc_keff - openmc_keff) * 1e5\n",
"\n",
"print('openmc keff = {0:1.6f}'.format(openmc_keff))\n",
"print('openmoc keff = {0:1.6f}'.format(openmoc_keff))\n",
"print('bias [pcm]: {0:1.1f}'.format(bias))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"There is a non-trivial bias between the eigenvalues computed by OpenMC and OpenMOC. One can show that these biases do not converge to <100 pcm with more particle histories. For heterogeneous geometries, additional measures must be taken to address the following three sources of bias:\n",
"\n",
"* Appropriate transport-corrected cross sections\n",
"* Spatial discretization of OpenMOC's mesh\n",
"* Constant-in-angle multi-group cross sections"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Flux and Pin Power Visualizations"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We will conclude this tutorial by illustrating how to visualize the fission rates computed by OpenMOC and OpenMC. First, we extract volume-integrated fission rates from OpenMC's mesh fission rate tally for each pin cell in the fuel assembly."
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {},
"outputs": [],
"source": [
"# Get the OpenMC fission rate mesh tally data\n",
"mesh_tally = sp.get_tally(name='mesh tally')\n",
"openmc_fission_rates = mesh_tally.get_values(scores=['nu-fission'])\n",
"\n",
"# Reshape array to 2D for plotting\n",
"openmc_fission_rates.shape = (17,17)\n",
"\n",
"# Normalize to the average pin power\n",
"openmc_fission_rates /= np.mean(openmc_fission_rates[openmc_fission_rates > 0.])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Next, we extract OpenMOC's volume-averaged fission rates into a 2D 17x17 NumPy array."
]
},
{
"cell_type": "code",
"execution_count": 41,
"metadata": {},
"outputs": [],
"source": [
"# Create OpenMOC Mesh on which to tally fission rates\n",
"openmoc_mesh = openmoc.process.Mesh()\n",
"openmoc_mesh.dimension = np.array(mesh.dimension)\n",
"openmoc_mesh.lower_left = np.array(mesh.lower_left)\n",
"openmoc_mesh.upper_right = np.array(mesh.upper_right)\n",
"openmoc_mesh.width = openmoc_mesh.upper_right - openmoc_mesh.lower_left\n",
"openmoc_mesh.width /= openmoc_mesh.dimension\n",
"\n",
"# Tally OpenMOC fission rates on the Mesh\n",
"openmoc_fission_rates = openmoc_mesh.tally_fission_rates(solver)\n",
"openmoc_fission_rates = np.squeeze(openmoc_fission_rates)\n",
"openmoc_fission_rates = np.fliplr(openmoc_fission_rates)\n",
"\n",
"# Normalize to the average pin fission rate\n",
"openmoc_fission_rates /= np.mean(openmoc_fission_rates[openmoc_fission_rates > 0.])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now we can easily use Matplotlib to visualize the fission rates from OpenMC and OpenMOC side-by-side."
]
},
{
"cell_type": "code",
"execution_count": 42,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.text.Text at 0x7f6dafba74a8>"
]
},
"execution_count": 42,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX4AAADHCAYAAAAeaDj1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XuYHFW19/Hvj0ASCCGQEBIChFsQzYGTRIaLiocIAgHUiAISRYM30AOPcF4QEC9EPSpyOApyNSBvEBQENIKvqEQQJEogAyQSlEsI0dyDQK4kAcJ6/6ga7On09NqZ7pnpmVqf55lneqpWV+2qWr2murp3bZkZIYQQimOLrm5ACCGEzhWFP4QQCiYKfwghFEwU/hBCKJgo/CGEUDBR+EMIoWCi8Hczkq6V9NUann+hpOvr2aYQOoKkd0t6uobnD5e0RlKverarJ+j2hV/SqZKekPSKpKWSrpG0fSete76kVyXtWDb9cUkmaY+SaQdJulvSCkkvSXpE0ifbWO6pkjbmSdvycyWAmX3OzL7Z3jab2bfN7DPtfX5bytq8StJsSe/bjOdPkfTf9W5Xd9GN8vidku6TtFrSSkm/kjSy7HnbSbpM0j/yfHgu/7vV8kviTdLaklxfAWBmD5rZvu3dLjP7h5lta2Yb27uMtpS1eZGk76X+g5E0VtLCerdpc3Trwi/pHOC7wBeBAcAhwO7ANEm9O6kZzwMTStq0P7BNWTvfAdwHPACMAAYBnweOqbLch/Kkbfk5s+4tr7+HzGxbYHvgauDWzipe3Vk3y+N7gDuBYcCewGzgT5L2ymN6A/cC/waMA7YD3gG8CBxUZf2jSnK9u+TMqDzfDwM+Anyqi9uTzsy65Q9ZQq0BTiqbvi3wAvCp/O9JwB3Az4DVwGNkB6wlfhjw8/w5zwNfKJk3CbgN+HH+3CeBppL584GvADNLpl0KfBkwYI982nTgqs3YtlOB6W3MmwL8d/54R+D/ASuAl4AHgS3yeecDi/J2Pw0cUbJNN5cs7wP5dq0A7gfeVrZ95wJ/AVbm+7BvSpvJioYBB5ZMux1Ymi/rj8C/5dNPA14DXs2P6a8Sjs1BQDOwClgGfK+rc7IAefwgcHWFbfgN8OP88Wfy47HtZuwDA0ZUmD4WWFjyd1s5XTEXgD3yZW9Zso/uInutzAU+m7qPvDbnz72q5O9PAn/LlzUPOD2f3g9YB7yRH/c1ebu2AC4AniP7J3kbMDB/Tl/g5nz6CmAmMKSmvOvqxK/hBTMOeL3loJbNuxG4peSAvgacAGxFVsiezx9vATwKfA3oDeyVH6SjS567HjgW6AV8B5hR9oJ5b56Eb8tjFpKdrVmeeNsAG4H3bMa2nUpa4f8OcG2+LVsB7wYE7AssAIaVvAD2Ltmmm/PHbwHWAkfmzz8vf0H0Ltm+R/LEHJgn8ue8Nuf74QyyQr5TScyngP5AH+AyYFal7cr/9o7NQ8DH88fbAod0dU4WNY/JityS/PGtwI2buQ/cwu/kdMVcYNPC/0eyd6J9gdFk/yQPT9lH1doMvBVYAvxXyfzjgL3JXo+HAa8Aby/frpL4s4AZwK5kr48flhz704Ff5cegF3AAsF0tededL/XsCPzTzF6vMG9JPr/Fo2Z2h5m9BnyP7MAfAhwIDDazb5jZq2Y2D7gOOLnkudPN7G7LrhPeBIyqsL6bgE+QFdC/kZ2VtNiB7IW5ZDO375D884CWn0MqxLwG7AzsbmavWXZN1MheoH2AkZK2MrP5ZvZched/BPi1mU3L982lwNbAO0tifmBmi83sJbLkG+21mewFdClwipktb5lpZjeY2Woz20D2QhslaUAby/KOzWvACEk7mtkaM5tRpV2NrLvk8UDazuPSdg5qI8bzWEmu/6DC/Go57eaCpN2AdwHnm9l6M5sFXE+2vS1S9lF5m9eS7av7yf6pAGBmvzaz5yzzANklsndXWdbngC+b2cKS18cJkrbMt28Q2T+ajWb2qJmtctpWVXcu/P8Edsx3TLmd8/ktFrQ8MLM3yM5mhpGd0QwrLbDAhcCQkucuLXn8CtC3wjpvAj5Kdtb747J5L5O9rds5cbtazDCz7Ut+KhW2/yE7Q79H0jxJF+TbOBc4myx5lku6VdKwCs8fBvy95Y983ywAdimJKd/+bb02k/2zu4uSRJfUS9LF+Qd9q8jOMqF1YSvlHZtPk71jeUrSzM35ILnB9IQ8Lm3ni23EeN5ekutfKJ/p5HRKLgwDXjKz1SXT/k71XK+0j1q1mez18BHgYLLLOABIOkbSjPyLHCvI3km0leuQHcOpJcfvb2T/7IaQHZffkX1mtljSJZK2qrIsV3cu/A8BG4APlU6UtC3Zh6b3lkzerWT+FmRvpxaTvZCeLyuw/c3s2M1piJn9next97HAL8rmvZK39cObs8zE9a42s3PMbC+ya/X/R9IR+byfmtmh/Ovt+ncrLGJxPh8ASSLbV4sqxG5Ou9aQfXj9cUlj8skfBcaTXVIYQPY2HLK3wuRtLFX12JjZs2Y2Adgp37Y7JPWj++kuebw2b+uJFZ56Ukk7fw8c3RHHoq2cTsyFxcBASf1Lpg2n9lw3M7uNbN98DUBSH7LPWy4luxa/PXA3bec6ZMfwmLJj2NfMFuXv5r9uZiPJ3o2/j9bvVDZbty38ZrYS+DpwhaRxkrbKv3Z2G9mZ0E0l4QdI+lD+3/tsshfaDLLr16slnS9p6/ysdD9JB7ajSZ8mu164tsK884BTJX1R0iAASaMk3dqO9bxJ0vskjcgL9kqyM4Q3JO0r6fA8Adfzrw+Tyt0GHCfpiPwM4hyyffPnWtoFkF8aup78xUB2bX8D2RnhNsC3y56yjOzadIuqx0bSKZIG52e+K/LnVNrGhtbN8vgCYKKkL0jqL2kHZV/BfUe+DeTtXQD8XNJbJW0haZCy/iOb9Y+oVLWcTskFM1tAltffkdRX0r/n23pze9tU5mLgs5KGkn3O0ofsM4TXJR0DHFUSuwwYVHaZ81rgW5J2z7dpsKTx+eP3SNpf2ddFV5Fd+qkp17tt4Qcws0vI3tJeSrZDHiZLuiPy62Qt7iR7O/Yy8HHgQ/l/0Y1k/z1Hk53p/JOsWLV13blaW54zs+Y25v0ZODz/mSfpJWAy2VlALfYhO8NaQ3bGcbWZ/YEs6S4m256lZGdCX6rQrqeBU4Ar8tj3A+83s1drbFeLy4Bj8xfZj8neWi8C/kpWsEr9iOz67QpJv0w4NuOAJyWtAS4HTjazdXVqd6fqRnk8HTia7N3JErLjOQY41MyezWM2kL2rewqYlm/PI2SXOR7e3PaUqJbTqbkwgeyd5mJgKnCRmf2+hja9ycyeIPvw+Iv55aQvkP3zfpns3e5dJbFPAbeQ1YIV+SWry/OYeyStJnt9HJw/ZSjZN7pWkV0CeoDWJwSbTWaV3nX0HJImkX0ockpXtyWE9oo8DvXUrc/4QwghbL4o/CGEUDA9/lJPCCGE1uKMP4QQCiYKfwghFEy1XmldRtrOYHD1oD13cJezzcDVbswrj/V3Y0a+fY4bs4rt3JhX8W+02B+/zWuqdp7NrGNrN2Zoq46KlS1q1bGxsrXL/X3IDgmXFJ+UH5NyqvLaYidgBWavJKysvqRBlvW5quYFf0H9KnXCLjPUD+m7faWv6re2YWMfN8Ze9ctI3639da1f5/f5qtdy1LvSHTJa69NrgxuzfkVCPzX/ZQZrvZwFtyayELMXk/K6psIvaRzZ9097Adeb2cVl8/uQfX/7ALKOOx8xs/n+kgezaf+eMt/8iLuU/T72gBvzyNaHuTE/bX6LG3Mv73VjFvyr42WbxnK/G/Ng1Vt+ZP7KSDfmXC51Y76Cf4v8h6463I3hg+v9mP36+jH+/zxYOMkJmOwuomNye1eyW7ZUc43bNvaf5Mdc4IeMGD/TjZm7cm83Zv38gf66RvnrmjPb729Wr+X02eMlf10DKt3eqmxddyb0kbvYD2HGpISgzzvzj3Lm/0u7L/XkvciuIutWPhKYoLIBGch6xr1sZiOA71P5tgEhNJTI7dDT1XKN/yBgrpnNy3t63kp2L5ZS48luLQtZz7Mj8tsLhNDIIrdDj1ZL4d+FkrsFkt1XpPyC8Jsxlt12diXZ7UU3Iek0Sc2SmrOeySF0mbrlduu89i8vhNAZGuZbPWY22cyazKyJhA9KQ+gOWue1fy08hM5QS+FfBK0+rdyVTW9x+mZMfkfBAWQfhIXQyCK3Q49WS+GfCewjaU9lAyyfTMkd6HJ3ARPzxycA91l0FQ6NL3I79Gg13bIhv7/2ZWRfebvBzL4l6RtAs5ndJakv2e1Dx5Bd4DzZsmHhqi93lybjPyveGfZf7vDbt9fjT7oxI/mrG/Ory0/yV3a9H7Jqlj9ozsd6/cSN+ToXuTHf4KtuzL4848Z8gUqj4LW269P+ie6Uff2v357665+5MYOP+4cb88KXhjuNacKWNFf9ILYjclsaZtm48tX4Xwtm9KFuyNDH3ZcZY5jlxtz45v+2tt2RMMbQavy+HsfzSzdmKh90Y1L6wpzAz92YiW9+dt+2x6uORJpZOmYvN4ZZ0/0YvDtIT8Zsccd/j9/M7qbsnvJm9rWSx+upPGJPCA0tcjv0ZA3z4W4IIYTOEYU/hBAKJgp/CCEUTBT+EEIomCj8IYRQMFH4QwihYKLwhxBCwTTkmLt7Ng20Sc1HVo05a8Pl7nI+2ef/ujHNNLkxDx6XcJ/rXyfsx6sS+lb4QwjAbQnrOtdf16JL/XvH7JJyF4JLErbLH8+D9591mxuzgu3dmOmDq+cOK5qw16p34OoI2rbJ2N/pmJgwbEFCHyZsXMLmpYz9cbyfa7Pxx6sY1fysv66mhLxOOGyzm/bx25PQeZGpCfswYUwc/TZhu/y+a+ANV/FEE7YmLa/jjD+EEAomCn8IIRRMFP4QQiiYKPwhhFAwUfhDCKFgahlsfTdJf5D0V0lPSjqrQsxYSSslzcp/vlZpWSE0ksjt0NPVclvm14FzzOwxSf2BRyVNM7PyG9w/aGbvq2E9IXS2yO3Qo7X7jN/MlpjZY/nj1cDf2HRA6hC6ncjt0NPVNBBLC0l7kI1E9HCF2e+QNJusu8i5ZlZxWCxJp5EPT9R7+BCu5j+rrnNmnwPdds1nDzfm+3zJjUkZI/s+3unG7H3GYDdm1hlj3JjxZ/p9NH5x5TFuzIdm/caN4biE/iD+IERJHdxuSBil6UimuTFve+GxqvOfb3rFXUaLWnO7NK8ZPBwuqL6+oeP9kbOWPLy3G8PB/v5e1dc/ttvt78esmznKjVnaNMCNGfqUv66U5axjGzeGA/11rXrCX8x26/39bPjr2vmi59yYpXc6I3md4y7iTTV/uCtpW+DnwNlmtqps9mPA7mY2CriCKv3TzGyymTWZWdOWg/2DG0JHq0dul+Y12/n/+EPoDDUVfklbkb0wfmJmvyifb2arzGxN/vhuYCtJO9ayzhA6Q+R26Mlq+VaPgB8BfzOz77URMzSPQ9JB+foSbv4SQteJ3A49XS3X+N8FfBx4QtKsfNqFwHAAM7sWOAH4vKTXgXXAydaId4ULobXI7dCjtbvwm9l0qP6phZldCVzZ3nWE0BUit0NPFz13QwihYKLwhxBCwUThDyGEgqlLB656E9CLjVVjXmSQu5yxK6e7MY9u73euOCChI8fhNz/kByXYYcIf/CB/0DD2J6HRKUc/pXNWQnsmyd/Pk5b5y3n3Tn90Y6488bzqAfMSOvh0gL7br2XE+JlVY3Zjgb+ghJGzUjpnrdvgL6e/35+Mt/C0GzPw9oShxab4IUNPXenG9D7Rb48lbFfK/iGlE9wt/mLGMMuNWTC++pfG5n5zrb+iXJzxhxBCwUThDyGEgonCH0IIBROFP4QQCiYKfwghFEwU/hBCKJgo/CGEUDBR+EMIoWAasgPXFrzB1lQfJWnnhF4sWw3wb5Z4wP0JI0x9wA9hXsKNGQ/117XslCFuzHan+p189jk7YbtSJIycxfUJnbM2Ga68gp38dV2x3F/XyNvLh8Zt7eKm+QmNqb8NG/swd2X10bPuG3C4v6Dj/f2UMnJWSucsveiva+C5CbnW7Idwf0KujfXXNfDhhM5iCdu10yB/XXIGxQKSjteNCaPPDV/596rzN2zsk9CYTD1G4Jov6QlJsyRtcniV+YGkuZL+Iuntta4zhI4WeR16snqd8b/HzP7ZxrxjgH3yn4OBa/LfITS6yOvQI3XGNf7xwI8tMwPYXtLOnbDeEDpS5HXotupR+A24R9Kjkk6rMH8XaHXnqYX5tBAaWeR16LHqcannUDNbJGknYJqkp8zMv4VimfzFdRpAn+GD69CsEGpS97xmt13r3MQQ2qfmM34zW5T/Xg5MBQ4qC1kE7Fby9675tPLlTDazJjNr6j14QK3NCqEmHZHXGuTfSjyEzlBT4ZfUT1L/lsfAUcCcsrC7gE/k34I4BFhpZktqWW8IHSnyOvR0tV7qGQJMVTbIxpbAT83st5I+B2Bm1wJ3A8cCc4FXgE/WuM4QOlrkdejRair8ZjYPGFVh+rUljw04Y3OWu3rVAO773fuqxjxz9L7ucnb/uN8B486bjnJjvjvvfDfmz+f767pl+ng3ZgjL3Zh9vp2wXZf52zX+/HvcGD6a0Dkn5egelhAzxV/X3qeWn3hv6mAerjp/DfdXnd9ReW2vbsn6+QOrxtwx6sPuct7JW9yYdTM3af4mkkbOSuic9cCl5VfBNtUHfzirQ8b465rxuL9dG/A7Mh2WsF0vv9jXjXkGvw5tnXC8/ox/3L3c4dX0ch63bAghhIKJwh9CCAUThT+EEAomCn8IIRRMFP4QQiiYKPwhhFAwUfhDCKFgovCHEELBNOQIXLxKdq/DKv7KSHcxRx493Y15N/59t8bfnNDR6Wg/ZMJTd/pB5/ghfN0PeZGE+8L4fcVa342mLX/zQ25810luzEeG3ebGjOFxN+aWd3yqesBTV7vL6Ah9t17LiFEzq8asThiJaVTzs27M0ib/flcDb08YqSph5Kykzlkfn+3GTJrlr2tSwnJm3OR38krZrpT9s8eJ892Yoc0r3ZjfNfkFZD8nd+ZuvdZdRos44w8hhIKJwh9CCAUThT+EEAomCn8IIRRMFP4QQiiYdhd+SftKmlXys0rS2WUxYyWtLIn5Wu1NDqFjRW6Hnq7dX+c0s6eB0QCSepENOze1QuiDZlb95vohNJDI7dDT1etSzxHAc2b29zotL4RGEbkdepx6deA6GbiljXnvkDQbWAyca2ZPVgqSdBpwGsCA4dvxX5+uPurVwxzst+qUH7ohA69KGGFqih/CTPNjbqnTaFZN/ro+9WV/Xeuv9FfVt1/CdiWM0jVxjt85i8v8dS1jmr+c/Zz5c/1FlKgpt0vzmp2HM2f2gVVXdvyoD/ktSjj+Q5+qU17f768rZeSspM5Z5q9rkhLWNcfv5MXjCXl9nL+uofv7nbNSjtfxCT0lz599RfWAdf38tuRqPuOX1Bv4AHB7hdmPAbub2SjgCuCXbS3HzCabWZOZNW0zeOtamxVCzeqR26V5zQ6DO66xIWyGelzqOQZ4zMyWlc8ws1VmtiZ/fDewlaQd67DOEDpD5HbokepR+CfQxlthSUOl7L2ZpIPy9b1Yh3WG0Bkit0OPVNM1fkn9gCOB00umfQ7AzK4FTgA+L+l1YB1wslnChbwQuljkdujJair8ZrYWWt8GMn9RtDy+Ekj4CDGExhK5HXqy6LkbQggFE4U/hBAKJgp/CCEUTEOOwLVk3q5MmvDdqjFbXbnKXc6Vg/z+AD8842w35oIJl7kxr2zo5cbsOcHv/PkLjndjDl3gdyy57lunuDGf/fbNbgwf8Nd140/90bW2Z4Ub08yFfnt4jxvxtuseqzr/+cdfSVhP/aWMwDWVD7rLOa/ZPyYpI3ANPTWh89FYf10zHvdHvEoZOSupc5af1kkjcB2SsF0pnSmXvjVhPyccr6lNZ7oxMQJXCCGEdovCH0IIBROFP4QQCiYKfwghFEwU/hBCKJgo/CGEUDBR+EMIoWCi8IcQQsE0ZAcu1gNPVQ/pv/1qdzGPJIzS9Ql+7MbcOnC8G/MfPOjGjEgY+ukZ9nVjDl1fvYMSwKCEOwQfceGv3Jh7z32/GzPxxITRtfwBhhh//j1uzH033e+3hxurzt+I39muI6xf188dgav/qKvc5cxu2seNWcc2bkzvE592YwY+vN6N2UAfNyalU1XKyFkpy0lpD01+yEsn9nVj5rOHG7Osye8w2B+/nnm5U/cRuCTdIGm5pDkl0wZKmibp2fz3Dm08d2Ie86ykicktC6GDRV6Hokq91DMFGFc27QLgXjPbB7g3/7sVSQOBi4CDgYOAi9p6IYXQBaYQeR0KKKnwm9kfgZfKJo+HN99T3wgVbzJyNDDNzF4ys5eBaWz6QguhS0Reh6Kq5cPdIWa2JH+8FBhSIWYXYEHJ3wvzaSE0qsjr0OPV5Vs9+ZBzNQ07J+k0Sc2Smnn9hXo0K4Sa1D2vX468Do2hlsK/TNLOAPnv5RViFtH6+xy75tM2YWaTzazJzJrYcnANzQqhJh2X1ztEXofGUEvhvwto+TbDRODOCjG/A46StEP+4ddR+bQQGlXkdejxUr/OeQvwELCvpIWSPg1cDBwp6VngvfnfSGqSdD2Amb0EfBOYmf98I58WQpeLvA5FpewyZmMZ2jTMJjafXjXm62snucvp28/fttdW+qPj/GV7N4QDUvbjt/11XX7haW7MWfzQjbmZE9yYUxb/3I1hWMJ2nZQwmtG7/BDO8tc1j53dmFmMqTr/vKY/Mbc54cDX2RZjRluf+++rGvOPAbu7yxmc0NmHA/3Ns3n+YvRiwvE/N2FXNvsh3J+wrpSRsxI6Z3Gpvy4b5K9LeyWsa6a/rhfo78YMX1l9BL8NYw/njcdnJeV13LIhhBAKJgp/CCEUTBT+EEIomCj8IYRQMFH4QwihYKLwhxBCwUThDyGEgonCH0IIBdOQI3AtWzqMS757UdWYjef7oyjtzaluzOdv9ttzwHl+DH/y+03ccqE/ktfpayf763rejzl6v23dmN8OO8yNGXdJQn8Qf7AvXjzHjxm0wV/Xl86b4sbcdq8zLsrqlB4+9den1wZGDHiuaow3ehjA3VP9/bTqCb896zb4MTsldGJ6+UV/pKqBt/sjeXFcQq6d4YekjJy1Q8J2LU/oi731Wj9mu4TjNfF4vzOllztzeyUc0Fyc8YcQQsFE4Q8hhIKJwh9CCAUThT+EEAomCn8IIRSMW/gl3SBpuaQ5JdP+R9JTkv4iaaqkijculjRf0hOSZklKuTFrCJ0mcjsUVcoZ/xRgXNm0acB+ZvbvwDPAl6o8/z1mNtrMuuY7dCG0bQqR26GA3MJvZn8EXiqbdo+ZvZ7/OYNszNEQupXI7VBU9ejA9SngZ23MM+AeSQb80Mza7Hkk6TQgG35qh+Fuy97Ng27Djl15jxvDGf7oOAvld8DYNWFP7vauBW5Mn5Q+GCv9kMG3r3Fjxr3rATdm9nn7uDGjPvCsGzPorfUZoexhDnZjfnPE2Krzv9D/ab8tmZpzu1VeDx7OnDsPrLrCf44f5LdqmB+y3fqE/d23PiNMPcO+bsweJ853Y4bu7yf20rcOcGPms4cbc8hes92YpM5ZKfv5YX8/P85oN2bpnc7BWNHPb0uupsIv6cvA68BP2gg51MwWSdoJmCbpqfwsaxP5C2cygHZrarzxIEOh1Cu3W+X1iMjr0Bja/a0eSacC7wM+Zm0M3Gtmi/Lfy4GpwEHtXV8InSVyO/R07Sr8ksYB5wEfMLNX2ojpJ6l/y2PgKGBOpdgQGkXkdiiClK9z3gI8BOwraaGkTwNXAv3J3uLOknRtHjtM0t35U4cA0yXNBh4Bfm1mv+2QrQihHSK3Q1G51/jNbEKFyT9qI3YxcGz+eB4wqqbWhdCBIrdDUUXP3RBCKJgo/CGEUDBR+EMIoWDUxrfVutSWTaNswMN3V43ZplfFL1y0smDxW9yYB4b538I77OxH3BguS9iPNyeM0nWKP0rXBH7pr+uTCaMZDfdD+HrCdn00YV2H+yEPfMY/Focvu8+NeWPNNtUDPngg9kRzQqPrS9s2Gfs7t/VJGKiKD/ohNi5h8xYnrOt4//jPxn+djWr2O/mR0s0h4bDNbkrodMgz/roSRs5K6Uyn3yZsV8JLGm9gsSeasDVpeR1n/CGEUDBR+EMIoWCi8IcQQsFE4Q8hhIKJwh9CCAUThT+EEAomCn8IIRRMFP4QQiiYhuzA1a9pX9uvuc3BugDozavucoYl9FDZSC83ZjSz3JiUEcHO4nI3ZgUVx/ZuZdnKndyYdw74sxtz36L3ujGP7vJ2N+YbfNWN6Y8/ItjNP/msGzP0Y/PcmKWznZGKPtqEPdkFHbg0zFoG42qbf0wYfagbMvRxfz+NScjrG5noxtzBh92Y1fR3Y45P6MU0NaH3Wn9WuzEn8HM3ZiI3ujFJI2eNSRjGbNZ0P4bfO/MnY7a4Ph24JN0gabmkOSXTJklalN+2dpakY9t47jhJT0uaK+mClAaF0Fkit0NRpVzqmQKMqzD9+2Y2Ov/Z5P4KknoBVwHHACOBCZJG1tLYEOpsCpHboYDcwp+PI/pSO5Z9EDDXzOaZ2avArYB/I5oQOknkdiiqWj7cPVPSX/K3yztUmL8LsKDk74X5tIoknSapWVLz6y+srKFZIdSsbrldmtfg31gwhM7Q3sJ/DbA3MBpYAvxvrQ0xs8lm1mRmTVsOHlDr4kJor7rmdmleg3PX0BA6SbsKv5ktM7ONZvYGcB3ZW99yi4DdSv7eNZ8WQsOK3A5F0K7CL2nnkj+PB+ZUCJsJ7CNpT0m9gZOBu9qzvhA6S+R2KAJ3sHVJtwBjgR0lLQQuAsZKGg0YMB84PY8dBlxvZsea2euSzgR+B/QCbjCzJztkK0Joh8jtUFQN2YFL2tvgkupBX/E7jSSNZrTCD7ntuve7MSdd9St/QTsmtGdhQow3Eg+Q0A+MXT/mj4q08LkRbsyhe3sdS2D6/kf6DZrih3BpQsyt33ICrsZsURd04BplcI8TdY2/oEMm+TEJPQv2Gz/TjZm7cm83Zv38gf66RvnrmjP7wE5bTt89/C9zjRjwnL+uO/3xlwfzAAADEUlEQVR1cbEfwoxJCUGfd+YfhdnsGIErhBDCpqLwhxBCwUThDyGEgonCH0IIBROFP4QQCiYKfwghFEwU/hBCKJgo/CGEUDAN2oFLLwB/L5m0I/DPLmpOe0WbO15727u7mQ2ud2M8FfIairPPu1JR2pyc1w1Z+MtJas7ubth9RJs7XndrbyXdbRu6W3sh2lxJXOoJIYSCicIfQggF010K/+SubkA7RJs7XndrbyXdbRu6W3sh2ryJbnGNP4QQQv10lzP+EEIIddLwhV/SOElPS5orKeEu411L0nxJT0ialQ2w3XjyQcSXS5pTMm2gpGmSns1/VxpkvMu00eZJkhbl+3qWpGO7so2bo7vlNURud5SuyO2GLvySegFXAccAI4EJkkZ2bauSvMfMRjfwV8imAOPKpl0A3Gtm+wD3kjSUR6eawqZtBvh+vq9Hm9ndndymdunGeQ2R2x1hCp2c2w1d+MkGup5rZvPM7FXgVmB8F7ep2zOzPwLlQxCNB27MH98IfLBTG+Voo83dVeR1B4ncTtPohX8XYEHJ3wvzaY3MgHskPSrptK5uzGYYYmZL8sdLgSFd2ZjNcKakv+RvlxvqLXwV3TGvIXK7s3VYbjd64e+ODjWzt5O9jT9D0n90dYM2l2Vf9eoOX/e6BtgbGA0sAf63a5vT40Vud54Oze1GL/yLgN1K/t41n9awzGxR/ns5MJXsbX13sEzSzgD57+Vd3B6XmS0zs41m9gZwHd1nX3e7vIbI7c7U0bnd6IV/JrCPpD0l9QZOBu7q4ja1SVI/Sf1bHgNHAXOqP6th3AVMzB9PBO7swrYkaXkx546n++zrbpXXELnd2To6t7es58Lqzcxel3Qm8DugF3CDmT3Zxc2qZggwVRJk+/anZvbbrm3SpiTdAowFdpS0ELgIuBi4TdKnye4geVLXtXBTbbR5rKTRZG/d5wOnd1kDN0M3zGuI3O4wXZHb0XM3hBAKptEv9YQQQqizKPwhhFAwUfhDCKFgovCHEELBROEPIYSCicIfQggFE4U/hBAKJgp/CCEUzP8H1wj1HqNkQuMAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f6dafd978d0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Ignore zero fission rates in guide tubes with Matplotlib color scheme\n",
"openmc_fission_rates[openmc_fission_rates == 0] = np.nan\n",
"openmoc_fission_rates[openmoc_fission_rates == 0] = np.nan\n",
"\n",
"# Plot OpenMC's fission rates in the left subplot\n",
"fig = plt.subplot(121)\n",
"plt.imshow(openmc_fission_rates, interpolation='none', cmap='jet')\n",
"plt.title('OpenMC Fission Rates')\n",
"\n",
"# Plot OpenMOC's fission rates in the right subplot\n",
"fig2 = plt.subplot(122)\n",
"plt.imshow(openmoc_fission_rates, interpolation='none', cmap='jet')\n",
"plt.title('OpenMOC Fission Rates')"
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "openmc",
"language": "python",
"name": "openmc"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.5"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| mit |
Radcliffe/project-euler | Euler 021 - Amicable numbers.ipynb | 1 | 1766 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Euler Problem 21 - Amicable numbers\n",
"\n",
"Let d(n) be defined as the sum of proper divisors of n (numbers less than n which divide evenly into n).\n",
"If d(a) = b and d(b) = a, where a ≠ b, then a and b are an amicable pair and each of a and b are called amicable numbers.\n",
"\n",
"For example, the proper divisors of 220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110; therefore d(220) = 284. The proper divisors of 284 are 1, 2, 4, 71 and 142; so d(284) = 220.\n",
"\n",
"Evaluate the sum of all the amicable numbers under 10000."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"31626\n"
]
}
],
"source": [
"d = [0]*50000\n",
"s = 0\n",
"for i in range(1,50000):\n",
" for j in range(2*i, 50000, i):\n",
" d[j] += i\n",
"for i in range(1,10000):\n",
" j = d[i]\n",
" if j >= 49999:\n",
" print('FAIL')\n",
" elif d[j]==i and j != i:\n",
" s += i\n",
"print(s)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.2"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| mit |
mssalvador/Fifa2018 | Teknisk Tirsdag Tutorial (Supervised Learning).ipynb | 1 | 412004 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Teknisk Tirsdag: Supervised Learning\n",
"\n",
"I denne opgave skal vi bruge Logistisk Regression til at forudsige hvilke danske fodboldspillere der egentlig kunne spille for en storklub."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"variables": {
"len(df)": "<p><strong>NameError</strong>: name 'df' is not defined</p>\n"
}
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/usr/local/lib/python3.5/dist-packages/IPython/core/interactiveshell.py:2850: DtypeWarning: Columns (23,35) have mixed types. Specify dtype option on import or set low_memory=False.\n",
" if self.run_code(code, result):\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Kolonnenavn: Name antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Age antal fyldte felter: 17981 datatype: int64\n",
"Kolonnenavn: Nationality antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Overall antal fyldte felter: 17981 datatype: int64\n",
"Kolonnenavn: Potential antal fyldte felter: 17981 datatype: int64\n",
"Kolonnenavn: Club antal fyldte felter: 17733 datatype: object\n",
"Kolonnenavn: Value antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Wage antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Special antal fyldte felter: 17981 datatype: int64\n",
"Kolonnenavn: Acceleration antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Aggression antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Agility antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Balance antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Ball control antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Composure antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Crossing antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Curve antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Dribbling antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Finishing antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Free kick accuracy antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: GK diving antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: GK handling antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: GK kicking antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: GK positioning antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: GK reflexes antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Heading accuracy antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Interceptions antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Jumping antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Long passing antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Long shots antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Marking antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Penalties antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Positioning antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Reactions antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Short passing antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Shot power antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Sliding tackle antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Sprint speed antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Stamina antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Standing tackle antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Strength antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Vision antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: Volleys antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: CAM antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: CB antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: CDM antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: CF antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: CM antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: ID antal fyldte felter: 17981 datatype: int64\n",
"Kolonnenavn: LAM antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: LB antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: LCB antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: LCM antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: LDM antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: LF antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: LM antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: LS antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: LW antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: LWB antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: Preferred Positions antal fyldte felter: 17981 datatype: object\n",
"Kolonnenavn: RAM antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: RB antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: RCB antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: RCM antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: RDM antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: RF antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: RM antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: RS antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: RW antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: RWB antal fyldte felter: 15952 datatype: float64\n",
"Kolonnenavn: ST antal fyldte felter: 15952 datatype: float64\n",
"('GK kicking', ['73-1', '68-2', '67+4', '65+1', '61-3', '63-7', '59-1', '60+2', '62+2', '60-1', '61+2', '60+1', '54-1', '65+4', '55+2', '68+8', '57+2', '55-1', '56+4'])\n",
"('GK diving', ['81-2', '76+1', '76-1', '75+1', '78+3', '72-1', '75+4', '70-2', '73+2', '71-2', '65+2', '68-1', '67+2', '63+2', '62-1', '66+1', '63+1', '64-3', '62+1', '64+5', '54-3', '56+2', '55+5', '55+4'])\n",
"('GK positioning', ['71-2', '69+1', '66-2', '69+2', '64+1', '65+4', '60+3', '66-1', '65+1', '63-1', '70+2', '62-1', '64+2', '62+4', '61-1', '60+1', '58+2', '58+4', '59+2', '51+3', '45-1'])\n",
"('GK handling', ['78-2', '72-1', '78-1', '67-1', '69+1', '75-1', '73+1', '66+3', '65+1', '63+2', '64+3', '66+2', '63-1', '65+3', '59+3', '58-1', '60+2', '60-1', '57+2', '52+2', '56+4', '53-1', '47-1', '52+3', '55+2'])\n",
"('GK reflexes', ['86-2', '83-1', '85-1', '79+1', '74+1', '81-1', '83+3', '78+2', '73-1', '75+2', '70+1', '70-1', '69+2', '67+2', '62+3', '68+2', '65+1', '65-3', '65-1', '61-3', '67+8', '60+1', '55+5', '56-4', '53+3', '55+3', '57+5'])\n",
"('Penalties', ['81+7', '65+2', '70-5', '64+6', '70+4', '67+11', '55+1', '70+2', '70+3', '36-10', '53+2', '67+15', '69+2', '61+5', '51+1', '58+13', '51+5', '56+7', '66+2', '58-4', '69-1', '40-1', '49-1', '61-6', '52-2', '60-7', '60-3', '58+5', '46-1', '61-1'])\n",
"('Volleys', ['70+1', '69+3', '72+1', '71+1', '69+4', '66+1', '68+2', '64+1', '69+1', '61+5', '62-4', '49+2', '39+4', '59+1', '60+2', '71+8', '51+1', '49+6', '63+5', '32-1', '52+8', '65-2', '53-1', '62+4', '59+2', '40-12', '57+1', '55-4', '57+2', '29-1', '54+10', '51-1', '56+6', '51+7', '33-1', '52-1', '15+8'])\n",
"('Free kick accuracy', ['81+1', '66-5', '73+1', '57+5', '60-4', '56+4', '60+8', '53+11', '63-7', '77-3', '58+2', '69+1', '52+10', '62-3', '69-2', '65+1', '70+5', '39+2', '58+6', '62-4', '65+5', '61+10', '71+4', '56+11', '64+1', '39+10', '55+21', '64+8', '70+3', '68+4', '70+17', '69+12', '65+24', '52+9', '70+21', '39-9', '66+30', '64-3', '70+4', '67-1', '39-6', '65+29', '56-2', '64-2', '36+4', '53+1', '32-1', '45-1'])\n",
"('Balance', ['90+2', '71+2', '85+2', '89+2', '65+7', '85+1', '47-3', '70+3', '72+6', '80+6', '64+1', '64+4', '52-2', '61-1', '73+4', '70+7', '66+6', '33+4', '53+1', '66+2', '63+2', '82+2', '66+4', '69+3', '80-6', '56-7', '67-2', '49+2', '64+2', '86-3', '62+1', '73-1', '72-2', '63+5', '81-1', '53-13', '50-5', '70+1', '55-3', '70+2', '73+5', '81+1', '65+1', '79-1', '75+1', '77+2', '63-2', '60+3', '68-4', '73-3', '58-1', '71+1'])\n",
"('Aggression', ['58-10', '65+10', '57+5', '66+7', '77+5', '68+1', '68+3', '87+1', '82+1', '76+3', '72+3', '80+3', '65-2', '72+5', '42+7', '78-3', '74+7', '82+2', '81+2', '70-1', '75+1', '76+7', '67+4', '66+3', '78+3', '60+12', '71+1', '65-1', '69+10', '74-6', '23+3', '57+1', '67+6', '67+39', '67-2', '53+14', '33+2', '51+2', '56+1', '65+2', '72-2', '66-2', '82+10', '78+17', '72+14', '59+1', '64+3', '58-1', '53+4', '49+4', '67-3', '65+4', '59-7', '61+1', '68-3', '85-2', '53+5', '51+1', '58+7', '48+2', '57+9', '40+2', '30-1', '61+2', '60+8', '46+1'])\n",
"('Jumping', ['74+1', '76-4', '67+2', '65+2', '73-8', '59+1', '77-4', '78+1', '86+1', '59+2', '80-2', '68+1', '76+4', '68-1', '81+2', '76-5', '72+4', '63+2', '67-2', '75-6', '73-3', '70+14', '70-3', '66-1', '64+4', '82+6', '75-4', '74+4', '73-4', '78-2', '72-1', '68+7', '60+1', '77-2', '79+2', '64+2', '67+8', '74+7', '65+1', '68+6', '64-4', '59-1', '76-3', '66-3', '69+7', '63+1', '77+2', '57+4', '62+1', '70-2', '71+2', '67+16', '71+9', '87+2', '66+2', '76-2', '46+2', '70+1', '68+2', '39-2', '60+3', '73+5', '66+5', '63+7', '52-2', '60-2'])\n",
"('Agility', ['60+6', '78+1', '58-2', '71+1', '70+1', '69+1', '68+2', '74+4', '64-1', '75-1', '64-2', '43-3', '84+1', '58+4', '68-2', '77-8', '76-3', '50-8', '58-4', '70+14', '70-2', '70+3', '81-2', '63-2', '65+4', '55-4', '65+1', '66+3', '48-3', '46+13', '67+8', '83+6', '68+1', '62-3', '83+3', '85+2', '82-8', '82+3', '61-3', '72-1', '83+1', '66-3', '62+1', '67+2', '79+2', '55+1', '71-4', '72+1', '59+4', '67-2', '60+7', '36+2', '62+3', '48+3', '35-2', '68+10', '53+2', '49+1', '63+3', '75+1', '50-1', '77+2', '46+1'])\n",
"('Curve', ['81+2', '77+2', '78+1', '60+7', '75-2', '74+2', '71+1', '76+1', '68+4', '39+7', '67+3', '79+1', '73-2', '75+10', '61+2', '67+4', '59+24', '70+1', '58+10', '72-3', '69+7', '65+3', '64+1', '61+5', '52-6', '66+3', '73+2', '73+1', '52+4', '39+8', '53+1', '64+2', '59+1', '68+2', '72+2', '58+3', '62+4', '66+5', '63+11', '71+3', '62+1', '63-2', '69+15', '55+22', '57+4', '58+21', '69+8', '68-3', '50-3', '63+19', '43+3', '45+5', '57-1', '64+9', '34+3', '37-1', '42-3', '28+5', '36+6', '56+2', '53+10', '46+12', '31-1', '56+1', '45-1', '41+5', '27+2'])\n",
"('Shot power', ['81+1', '73+3', '85+6', '83+3', '77+3', '78-1', '75+4', '74-1', '70+28', '73+2', '70+13', '75+3', '73+1', '68-1', '58+9', '66+1', '80+6', '63+2', '73-5', '56+2', '63-3', '64+29', '79-3', '67+2', '76+1', '74-2', '70+1', '54+1', '71-6', '71+4', '68+2', '62-1', '71+1', '64+10', '63+1', '67+1', '69+2', '58+5', '75+1', '60+5', '65+2', '69+4', '57+3', '81-4', '74+2', '65+3', '55+1', '64-1', '55-4', '43-4', '66-2', '56-1', '61+3', '57-1', '60-2', '58-3', '52+3', '67+10', '50+4', '54+2', '43+10', '45-1', '36+13', '56-2', '21+1'])\n",
"('Heading accuracy', ['85-1', '73+1', '76+2', '74+1', '72+3', '78+1', '78-1', '75+2', '75-1', '65+2', '68-7', '42-7', '69+2', '70+2', '56+2', '46+8', '74+2', '64+4', '72-2', '72+2', '60+2', '64-1', '55+7', '59+2', '68-4', '43+3', '69-1', '74-2', '61+1', '61+2', '63+4', '57+5', '71-1', '59-5', '65-1', '59-1', '62-1', '72+1', '62+3', '64-3', '63-3', '56-6', '53+6', '64+1', '60+4', '62+4', '65+1', '60-5', '50-10', '54+3', '48-2', '69-3', '63+1', '64+2', '52+5', '57+2', '37+2', '57-1', '60-1', '70+4', '48+1', '43-1', '60+6', '52-11', '47+7', '43+2', '41+2'])\n",
"('Long shots', ['80+3', '73+2', '72+2', '79+3', '62+2', '74+1', '73+1', '78+2', '64+2', '73-1', '66+2', '60+6', '70+5', '77-2', '68-2', '65+1', '69+1', '70-4', '67-1', '68-4', '55+5', '64+3', '55+25', '75+1', '52-3', '63+3', '68+1', '75+6', '66+4', '43+1', '53-14', '52+1', '72+5', '63+1', '59+2', '59-1', '69+4', '66+1', '53+9', '64-1', '59+1', '61+3', '54+8', '71+2', '62-1', '62+1', '60+7', '61+1', '41-4', '58+3', '66-2', '43-1', '60+4', '38+10', '59+20', '60-2', '63+10', '27+3', '42+20', '56+5', '57+1', '23-1', '50+1', '39-1', '35+5', '47+3', '17+10'])\n",
"('Acceleration', ['70+9', '80+1', '49-1', '67+2', '79-2', '65-2', '91-2', '74-3', '75+1', '41-6', '74+1', '70+3', '75+5', '74+2', '71+2', '68+1', '71+4', '89-2', '58-10', '78+1', '86+1', '66-1', '66+1', '74+4', '71-3', '80+2', '64-2', '57-4', '78+3', '73+9', '82-3', '68+3', '68+2', '55-8', '55-1', '43-2', '77+3', '82+10', '49-10', '72+1', '61+1', '79+8', '70-2', '60-2', '86+7', '81+4', '69+3', '65-10', '64-3', '73+4', '75-6', '64+5', '33+10', '92+2', '76-1', '62+2', '65+7', '58+8', '44-2', '77+1', '82+3', '68-1', '61+3', '73+3', '59+1', '64+12', '85-1', '78+14', '59-1', '75+4', '73+10', '71+6', '77+13', '62+1', '64-5'])\n",
"('Composure', ['79+1', '74+2', '70-1', '75+1', '75+2', '66+4', '74+1', '65-8', '68-3', '82+18', '72+6', '67-1', '70+3', '78+10', '72-2', '66+2', '64+4', '74-5', '65+2', '72-1', '68+2', '67+1', '68+3', '65+5', '64-3', '60-3', '69+2', '61+2', '69+1', '58-1', '61+3', '57-3', '59+2', '55-3', '61-1', '68-2', '68-1', '28+4', '63-1', '50+4', '60-1', '62+3', '59-2', '64+24', '62+1', '63+2', '63+3', '58+5', '62-2', '56+2', '52-3', '62-1', '70+5', '55+4', '52+1', '65-1', '64-1', '58-2', '54-4', '58+2', '55+3', '65-2', '56-1', '51+5', '51+3', '51-4', '56+7', '44+1', '56+1', '52-2', '43+1', '42+1', '40+1', '45+2', '44+5', '35+2'])\n",
"('Positioning', ['80+1', '80+3', '76-2', '76+1', '80+2', '72+2', '72+4', '73-2', '75+1', '68+2', '58-1', '74+1', '74+3', '56+4', '71-3', '57+2', '70+3', '68-1', '77+1', '72+8', '66+2', '66-2', '62-3', '69+2', '65+2', '63-3', '65+1', '74+2', '70+1', '58+10', '66+1', '68+6', '70-2', '63+4', '66-8', '61+2', '62-2', '64+1', '70+2', '70+9', '69-1', '68+4', '66+5', '67+4', '10-3', '62-1', '67+3', '67+1', '51+2', '55+3', '60+2', '67+2', '56+29', '69+3', '54+1', '51-4', '61+1', '46+4', '52-7', '40+14', '58+2', '56+3', '39+2', '60-2', '50+2', '30-1', '56-4', '53+1', '52+1', '50+7', '51-1', '47+6', '47+1', '56+7', '17+10', '27+3', '42+1', '52-1'])\n",
"('Sliding tackle', ['71+4', '82-1', '77-1', '31+8', '73+1', '79-2', '70+3', '78-1', '77+1', '58+37', '77+3', '78+1', '66+2', '72+1', '73+2', '70+1', '34+14', '65-1', '74+2', '73+3', '42+9', '32-4', '70+2', '80+5', '58+2', '66-3', '67-2', '65-2', '16+4', '68-1', '68+1', '69-1', '67-1', '68+3', '70-1', '69+2', '71-3', '18+3', '20+2', '29-9', '66-1', '52+12', '67-3', '48+6', '55+1', '65+1', '62+3', '44+26', '62-2', '63+5', '61+2', '64+1', '53-3', '59+2', '60+1', '61+5', '63+14', '62-4', '64+4', '60-2', '60-4', '65-3', '21+10', '67+2', '63+1', '31+10', '61-2', '23-2', '59+3', '51+3', '68-5', '34-1', '52+2', '66+1', '54+1', '52+1', '57+4', '56+2', '41+1', '54+3', '50-1'])\n",
"('Crossing', ['79+2', '85+1', '63+2', '79+4', '70+2', '74-5', '80+2', '68-8', '72+1', '74+2', '61+1', '71+2', '70-3', '65-3', '72+4', '66-3', '72-8', '79+3', '73+3', '56-3', '61-4', '67+1', '66-2', '60+2', '61-3', '67-2', '41+5', '62+1', '65-1', '66+2', '65+2', '64+2', '37-6', '66+1', '57-10', '66+7', '68+4', '36+10', '63+5', '67-1', '50+1', '62-3', '69-1', '60-1', '46+1', '71+1', '64-1', '58+2', '67+9', '53+1', '68+2', '59+2', '65+3', '54+10', '73-1', '64-5', '53+2', '54+2', '50+8', '58+1', '51+8', '60+8', '50+3', '65+6', '51-3', '54+7', '55+3', '61+29', '60+5', '48-7', '59+9', '55-2', '42+3', '58+11', '56-1', '38-9', '52-6', '56+3', '32-1', '45+9', '55+1', '65+1', '63-1', '36+6', '64+37', '48+7', '45+1', '33+3', '32+2'])\n",
"('Interceptions', ['37+1', '43+4', '81+2', '76+2', '64+13', '76+1', '69+1', '71+3', '73+1', '75-1', '74+1', '64+1', '72+1', '49+13', '49+17', '48-11', '36-10', '75-2', '57-2', '21-11', '66+1', '69-4', '67-2', '68-3', '67+1', '68+2', '66+2', '68+1', '68-1', '68-4', '67+3', '66-2', '61+1', '74+7', '17+1', '67-4', '62-1', '68+4', '64-1', '60+10', '67-1', '10-11', '45+6', '65+1', '64+12', '69+5', '59+4', '64+2', '36+24', '63+29', '39+10', '49+15', '59+2', '54+2', '64+4', '48+2', '56+4', '62+5', '23+10', '58+4', '58-6', '55+2', '63+2', '55+5', '57+3', '58-3', '18-6', '60+2', '58-4', '63-2', '48+1', '59+1', '57+1', '44+3', '56+1', '48+24', '24-1', '57-1', '50+5', '15-11', '34+5', '27+20', '49+2', '52+2', '31+1'])\n",
"('Strength', ['70+1', '79+1', '66+1', '34+3', '65-2', '76+2', '71+3', '68+1', '47+3', '52-5', '80+1', '68+6', '85-1', '75+5', '87-4', '75+2', '83+5', '77-1', '56-5', '85+1', '68+4', '76+1', '78+2', '65-1', '83-1', '54+5', '84+6', '60+2', '74+1', '81-3', '51-7', '68+2', '75+1', '57-3', '78-6', '69-3', '69+1', '65+3', '85-5', '78-2', '73-1', '70-1', '67-5', '74+2', '78+1', '72-2', '83+4', '74-1', '57-10', '84-4', '73+3', '48-2', '80-1', '66+5', '57+1', '40+10', '68-1', '55-6', '69+11', '79-1', '71-1', '54-7', '54+2', '82-5', '50+3', '73-2', '59-19', '57+4', '68+3', '74+4', '33+2', '87-3', '58+10', '70+3', '37+5', '71-4', '32+2', '55-1', '69+8', '74+8', '66+6', '65+2', '70+6', '45-10', '67+7', '47+9', '48+12', '72+3', '70+15'])\n",
"('Vision', ['72+2', '79+1', '77+1', '77-4', '73-2', '57-1', '73+1', '78+3', '78+1', '78+2', '66+6', '74+2', '67-3', '74+1', '71-2', '62+8', '67-1', '70+2', '66-2', '38-10', '70-4', '73-3', '68+3', '66+1', '68-3', '62+1', '63-4', '69+10', '36-10', '74-2', '69+1', '72+1', '52+5', '68+1', '61+2', '48+2', '58+5', '67+3', '57-4', '69+2', '54-4', '70-2', '66+10', '72+4', '60-5', '70-1', '52-1', '67+1', '65+2', '42-5', '65+1', '65+5', '63+2', '71+4', '53+1', '64+1', '29+15', '71+1', '71-1', '66+2', '57+8', '62+11', '60-3', '52+4', '60+8', '61+11', '55-2', '56+3', '54+1', '63+7', '66-5', '45+24', '52+1', '49+14', '60+4', '59+5', '52+3', '49+1', '61-1', '44+1', '31+3', '37+1', '58+3', '55+8', '51-2', '44+3', '30+1', '47+1', '50+1'])\n",
"('Stamina', ['68+2', '82+1', '85+2', '73+3', '75+1', '77+2', '84+7', '75+19', '58-2', '70+2', '74+2', '66+4', '79+2', '41+20', '72-3', '72+2', '72+1', '78-2', '84-3', '56+3', '86-3', '78-1', '80+2', '60+2', '69-1', '85+1', '62-4', '70-1', '63+2', '64+7', '76+3', '68-2', '66-8', '87+3', '85+3', '62-1', '60-4', '81-4', '78+3', '74+9', '74+1', '65-4', '72-1', '76+6', '67+2', '43-2', '73-2', '67-1', '65-1', '72-10', '65+4', '29-11', '59+3', '79-3', '72-2', '69+3', '65+1', '74+4', '64-3', '79+8', '68-1', '64-2', '64+2', '69+1', '73+10', '58-10', '67-2', '66+9', '80-2', '52+7', '61-22', '66+2', '75+20', '70-3', '51-8', '67+1', '74-1', '90+7', '61+30', '54+12', '60+4', '62+1', '73+22', '44-3', '48-1', '63+4', '40+1', '70+6', '69-7', '78+38', '29-9', '62+3', '58+2', '61+6', '53+2', '60-2'])\n",
"('Marking', ['84-1', '65+1', '77-2', '78-2', '73+2', '68+2', '78+1', '64+22', '63+1', '62+4', '25+4', '70-1', '74+1', '70+1', '42+21', '73-1', '72+1', '57+1', '79+4', '72+3', '41+7', '75-3', '70+2', '24-7', '67-4', '57+2', '68-1', '59+2', '71-2', '69-2', '74-4', '70-2', '65+2', '62-1', '69+1', '66+2', '59-3', '65+4', '66-2', '61+2', '68-3', '20+3', '70+4', '24+4', '64-3', '66+1', '34-3', '67-6', '55+16', '65-1', '72-1', '43+3', '60-2', '66+9', '60+1', '63+2', '62+6', '64+1', '68+4', '61+1', '56-5', '52+3', '63+4', '64+6', '31-1', '50-4', '62-3', '54+4', '60+2', '60-1', '57+5', '63-1', '64-4', '59+4', '58-2', '57-6', '61+3', '62-4', '22-2', '14-19', '55-1', '54+3', '59-2', '57+3', '40+6', '56-1', '23-1', '25-1', '56+1', '54+6', '15+10', '46+2', '50+1', '45+1', '47+3'])\n",
"('Finishing', ['52+2', '81+1', '79+1', '60+2', '79+3', '70+1', '69+4', '74+1', '72-1', '78+1', '69+1', '74+2', '64-3', '45+1', '73+1', '71+1', '80-3', '74+3', '75+1', '65-1', '71-1', '73-1', '77+1', '77-1', '67+3', '70-1', '73+2', '58-2', '58-1', '65+2', '57-3', '71-2', '47+10', '59+2', '65+3', '69+2', '68+2', '62+6', '52+1', '53+4', '69+5', '65-2', '70+2', '44+4', '66+3', '63-1', '58+3', '59+1', '66+1', '50+2', '36-12', '64-2', '68+4', '45+2', '52-3', '58+7', '53-2', '63-3', '33+3', '65+1', '58-4', '58+6', '55+3', '42+3', '64+2', '62-1', '61+1', '61+2', '40-1', '67+2', '38-1', '69-2', '61+3', '62+2', '57-5', '64+5', '51-1', '37+4', '68-3', '63-2', '32-8', '35+3', '49+2', '38+10', '46+1', '26-1', '53-4', '69+3', '54-1', '57-2', '49+1', '48+3', '13+7', '29+13', '56-1'])\n",
"('Sprint speed', ['73+7', '83+1', '53-1', '69+1', '84+1', '69+2', '89+1', '58+3', '80-3', '77-4', '73+1', '90+1', '67+3', '89+3', '70-9', '74+1', '38-3', '70+1', '49+8', '82-3', '71+1', '76+5', '78+2', '64+1', '69+3', '75-3', '85-4', '77+2', '63+4', '68+2', '88-2', '64+3', '55-9', '68-1', '77+4', '71-2', '85+1', '68+1', '72-2', '66+4', '80+2', '80-2', '65-3', '67-2', '80+3', '69+6', '79-2', '78+5', '47-2', '83-2', '57+1', '52-14', '73+6', '37-10', '86-1', '58+4', '54+11', '84+5', '77+3', '66+5', '76+1', '55-10', '69-1', '83+11', '68-4', '77+7', '68+6', '71+5', '70-2', '80-5', '68+7', '85+5', '74+4', '73+2', '71-5', '66-10', '90-2', '60-2', '70-10', '67+12', '55+17', '32-1', '87-2', '72-1', '66+6', '64+2', '81+2', '70+5', '66+8', '46-3', '75+3', '70+15', '71+3', '65+3', '71+39', '70+3', '74+2', '61+1', '68+4', '95+2', '65+2', '75+8', '58-2', '73-3', '72+12', '79+17', '60+1', '63-11'])\n",
"('Reactions', ['79+2', '78+2', '73+1', '74-2', '76-1', '74+6', '74+4', '77+2', '76+3', '71-2', '72+1', '79+4', '77+1', '75-2', '71+1', '73+3', '71-1', '69-1', '70-1', '72+4', '73+7', '63-2', '66-1', '76+1', '68+1', '66-3', '67+1', '59+4', '61+2', '68+3', '62-3', '75+1', '66+2', '64+3', '76+2', '56+4', '62-2', '69-2', '61-2', '60-2', '65+1', '69+6', '62+1', '55-1', '66+13', '62+2', '58-2', '61+1', '63+4', '53-1', '65-1', '59-3', '64+5', '59+2', '65-2', '67+2', '58-1', '60-5', '62+6', '68+2', '57-2', '63-9', '62+9', '63-1', '59+1', '52-1', '57-1', '59-1', '59+10', '55+2', '56+1', '61-1', '56-1', '54+6', '56-2', '56+3', '57+3', '51+1', '52+7', '49+1', '51+2', '57+5', '55-3', '43-7', '54-2', '48+1', '45+1', '49+5', '52+1', '39-6', '54+3'])\n",
"('Long passing', ['80+1', '70+3', '72+2', '81+1', '70+1', '76+1', '82-1', '65+10', '55+24', '77+1', '73-1', '74+2', '61+1', '75-2', '76-1', '74+6', '62+13', '62+4', '72+4', '55-2', '66+6', '71+3', '52+10', '60-2', '62+2', '56-10', '70-2', '53-3', '65+6', '66+2', '70-1', '66+1', '53+3', '61+2', '59-1', '56-2', '74+4', '65+4', '67+5', '71+1', '74-5', '65-2', '61-1', '67+1', '65+1', '44+5', '54+5', '65+3', '59+8', '47+3', '67-1', '53-2', '57+6', '64-3', '75+1', '57+1', '52+3', '60-1', '69+2', '47+4', '43+3', '67+4', '62+1', '65+2', '55-3', '58+4', '57+2', '65+8', '57+21', '54+10', '44+4', '47-4', '48+8', '64+2', '57-1', '56+2', '46-6', '63-3', '45-10', '55+11', '51-3', '51+2', '38+3', '60-3', '40+12', '48+2', '61+4', '50+6', '38+1', '26+16', '26+4', '58+2', '34-1', '62+20', '49-5', '49-1', '38+6', '36+1', '48+10', '59+6', '34+10', '30+6', '25+4'])\n",
"('Standing tackle', ['82-1', '72-5', '83-1', '34+8', '76-2', '80-2', '69+3', '80+2', '64+35', '76+2', '46+10', '72+1', '71+2', '39+5', '77+3', '75-2', '75+1', '73+2', '35+6', '71-1', '74+1', '66-3', '72-1', '76+3', '41+10', '70+3', '73+1', '34-5', '68-1', '67-1', '59+2', '69-2', '40+10', '70-1', '65+3', '71-2', '72-4', '67+2', '66-2', '71+1', '60-3', '66+3', '44+10', '64-1', '72-2', '63+4', '73-2', '60+5', '17+2', '27+4', '65-2', '37-3', '67+1', '67-2', '58+10', '69-3', '70+1', '49+4', '69-1', '64+1', '69+4', '67+4', '66+4', '63+1', '51-9', '65+1', '68+1', '68+2', '62+1', '60+2', '62+2', '48+4', '45+2', '68+15', '65-3', '63-2', '63+2', '57-4', '63-1', '13-2', '61-1', '60-2', '37+10', '20-1', '30-2', '64+2', '59+7', '60+1', '55+2', '33+2', '73+5', '26-1', '52+4', '57+1', '54+7', '60+4', '54+4', '58+2', '47+1'])\n",
"('Dribbling', ['78+3', '87+1', '84+1', '68+3', '77+1', '80+1', '76+1', '76-2', '74+2', '71-3', '73+2', '71+2', '77+3', '74+4', '76-1', '75-2', '75+1', '72+4', '73-2', '69-5', '72-1', '72+3', '72+2', '74+1', '70+1', '74-1', '78-1', '67-1', '72+1', '38+2', '66-2', '59-2', '64-1', '71+4', '67+2', '56+1', '73+1', '60-1', '66-1', '68+1', '79+1', '66+2', '67+1', '48+15', '69-1', '71+1', '58+4', '42+2', '72-2', '64+3', '63-2', '65+1', '68+2', '36+2', '66+1', '64+1', '66+4', '65-2', '59+10', '63-1', '60-2', '54+8', '62-2', '66+3', '65-1', '57-1', '54-4', '54+10', '62-1', '65+2', '55-2', '59+5', '60+5', '34+3', '58-10', '64+4', '54+1', '49+1', '64-2', '47-2', '65+3', '63+2', '35+7', '49+3', '52+4', '37-1', '58-1', '59-1', '37+7', '31+2', '47+4', '62+5', '50+6', '53+2', '11+6', '36+4', '55-1', '59+1', '41+1', '53+1', '43-1'])\n",
"('Ball control', ['83+2', '77+1', '79+1', '85+1', '80+1', '70+1', '76+1', '82+6', '68+6', '74+1', '66+1', '74+5', '63-3', '75-2', '71-2', '74+3', '72-2', '74+2', '59-3', '70-1', '71-1', '68+1', '75+1', '38+3', '67+2', '48+3', '56-2', '70-3', '72+3', '62+2', '61-2', '67+1', '64+1', '72-1', '72-3', '56+2', '55-2', '72+2', '66-1', '63-1', '71+2', '63+1', '58-2', '65-1', '65+5', '59-2', '62-1', '66+3', '67-1', '68+4', '55-4', '71+1', '63+3', '61-3', '63-2', '65+2', '60-1', '61+2', '66+2', '68-1', '67+3', '72+1', '60+2', '69+1', '65+1', '67+6', '61-1', '56+14', '48+5', '50+4', '60-4', '61+4', '60-2', '58+1', '61+1', '57+1', '43+6', '51+2', '64+3', '55+2', '50+2', '58+4', '39-1', '60+5', '64+4', '64-1', '43+7', '48+1', '56+5', '47+6', '30+19', '41+11', '40+1', '48+4', '14-2', '38+1'])\n",
"('Short passing', ['79+2', '73+3', '84+1', '82+1', '78+2', '80+1', '81+3', '67-5', '76+3', '67+1', '78+1', '75+1', '72-2', '77-2', '77-1', '68-2', '65+2', '59-6', '74-2', '71+1', '66+1', '69-3', '79-1', '68+1', '67+6', '58+1', '64-2', '70+1', '74+3', '74+2', '55-10', '70-2', '67+7', '67-1', '72+2', '56-1', '64+4', '73+1', '72+3', '69+4', '65+5', '64-1', '73+2', '63-1', '69+1', '66+4', '67+2', '61+4', '62+1', '70-3', '73+4', '67-2', '66+2', '68-1', '64+3', '65+6', '57+1', '60-3', '67+3', '63+2', '54+5', '75+4', '66-1', '65-1', '59-2', '54-1', '65+1', '59+4', '69-1', '61+6', '62-2', '70+3', '62-5', '64+1', '63+4', '74+5', '67+13', '69+3', '62+4', '62+2', '63-2', '63+3', '60+13', '68+15', '60+6', '66-3', '65+9', '60+4', '68+2', '54+1', '61+3', '45+4', '64+2', '58-2', '54+6', '65-3', '50-10', '59+8', '62+7', '54-2', '60+1', '49+1', '46+10', '54+2', '53+6', '49+4', '18+11', '42+1', '37-1', '58+12', '61+2', '52-6', '62-1', '45+5', '60+3', '58+8', '58+4', '40+10', '44+3', '38+8', '46+1', '33+3', '38+1', '56+1', '31+3', '42-2'])\n",
"('Club', ['Real Madrid CF', 'FC Barcelona', 'Paris Saint-Germain', 'FC Bayern Munich', 'Manchester United', 'Chelsea', 'Juventus', 'Manchester City', 'Arsenal', 'Atlético Madrid', 'Borussia Dortmund', 'Milan', 'Tottenham Hotspur', 'Napoli', 'Inter', 'Liverpool', 'Roma', 'Beşiktaş JK', 'AS Monaco', 'Bayer 04 Leverkusen', 'AS Saint-Étienne', 'Athletic Club de Bilbao', '1. FC Köln', 'Villarreal CF', 'FC Schalke 04', 'Olympique de Marseille', 'Atalanta', 'RB Leipzig', 'Real Sociedad', 'Torino', 'Sporting CP', 'Leicester City', 'Southampton', 'FC Porto', 'UD Las Palmas', 'Olympique Lyonnais', 'Lazio', 'Genoa', 'Everton', 'RC Celta de Vigo', 'Valencia CF', nan, 'Sevilla FC', 'Toronto FC', 'Borussia Mönchengladbach', 'SL Benfica', 'RCD Espanyol', 'OGC Nice', 'Spartak Moscow', 'Swansea City', 'Sassuolo', 'TSG 1899 Hoffenheim', 'Stoke City', 'Shakhtar Donetsk', 'West Ham United', 'SV Werder Bremen', 'Watford', 'Galatasaray SK', 'Lokomotiv Moscow', 'Zenit St. Petersburg', 'Bournemouth', 'Sampdoria', 'Antalyaspor', 'Girondins de Bordeaux', 'VfL Wolfsburg', 'New York City Football Club', 'Hertha BSC Berlin', 'SD Eibar', 'Ajax', 'RC Deportivo de La Coruña', 'Crystal Palace', 'West Bromwich Albion', 'CSKA Moscow', 'Eintracht Frankfurt', 'Real Betis Balompié', 'Fenerbahçe SK', 'Fiorentina', 'Burnley', 'Tigres U.A.N.L.', 'San Lorenzo de Almagro', 'Chicago Fire Soccer Club', 'Feyenoord', 'FC Krasnodar', 'Angers SCO', 'U.N.A.M.', 'Montreal Impact', 'Chievo Verona', 'LA Galaxy', 'Vissel Kobe', 'Bologna', 'LOSC Lille', 'Orlando City Soccer Club', 'Atlanta United FC', 'Independiente', 'Club Atlético Lanús', 'RSC Anderlecht', 'İstanbul Başakşehir FK', 'Hannover 96', 'Newcastle United', 'Málaga CF', 'Trabzonspor', 'PSV', 'FC Augsburg', 'Club Tijuana', 'VfB Stuttgart', 'Hamburger SV', 'CD Leganés', 'Getafe CF', 'Deportivo Alavés', 'Portland Timbers', 'Kayserispor', 'Udinese', 'Standard de Liège', 'Alanyaspor', '1. FSV Mainz 05', 'Sparta Praha', 'FC Nantes', 'Al Ahli', 'SC Braga', 'Brighton & Hove Albion', 'Levante UD', 'Boca Juniors', 'Columbus Crew SC', 'Querétaro', 'Dijon FCO', 'Olympiakos CFP', 'KRC Genk', 'FC Basel', 'Club América', 'Montpellier Hérault SC', 'Monterrey', 'Seattle Sounders FC', 'River Plate', 'CPD Junior Barranquilla', 'Racing Club de Avellaneda', 'En Avant de Guingamp', 'Rangers', 'Colorado Rapids', 'Necaxa', 'Aston Villa', 'KV Oostende', 'Akhisar Belediyespor', 'Rubin Kazan', 'Rosario Central', 'Ferrara (SPAL)', 'Wolverhampton Wanderers', 'Stade Rennais FC', 'Pachuca', 'Granada CF', 'Colo-Colo', 'KAA Gent', 'Middlesbrough', 'Toulouse FC', 'BSC Young Boys', 'FC St. Gallen', 'Santos Futebol Clube', 'Cagliari', 'Rio Ave FC', 'Norwich City', 'Grêmio Foot-Ball Porto Alegrense', 'Estudiantes de La Plata', 'Cruzeiro', 'Universidad de Chile', 'Atletico Nacional Medellin', 'FC Ufa', 'Girona CF', 'SM Caen', 'Independiente Medellín', 'Djurgårdens IF', 'Vitória Guimarães', 'São Paulo Futebol Clube', 'Royal Antwerp FC', 'Kaizer Chiefs', 'Fulham', 'Sunderland', 'Huddersfield Town', 'PAOK Thessaloniki', 'Fluminense Football Club', 'Leeds United', 'Derby County', 'AC Ajaccio', 'Club León', 'Sociedade Esportiva Palmeiras', 'Hellas Verona', 'Rayo Vallecano', 'Club Brugge KV', 'Real Sporting de Gijón', 'Celtic', 'Hull City', 'Universidad Católica', \"CD O'Higgins\", 'Club Atlas', 'SC Freiburg', 'Melbourne City', 'Grupo Desportivo de Chaves', 'Al Hilal', 'CA Osasuna', 'Perth Glory', 'Panathinaikos FC', 'FC Utrecht', 'Club Atlético Huracán', 'Birmingham City', 'Botafogo de Futebol e Regatas', 'Deportivo Toluca', 'Amiens SC Football', 'Clube Atlético Paranaense', 'Göztepe', 'FC Groningen', 'FC Ingolstadt 04', 'New England Revolution', 'FC Red Bull Salzburg', 'Clube Atlético Mineiro', 'Crotone', 'Banfield', 'Grasshopper Club Zürich', 'Vitesse', 'AZ Alkmaar', 'SV Darmstadt 98', 'Avaí Futebol Clube', 'Coritiba Foot Ball Club', 'Legia Warszawa', 'RC Strasbourg', 'Brescia', 'Vancouver Whitecaps FC', 'Western Sydney Wanderers', 'Guadalajara', 'Cerezo Osaka', 'CS Marítimo', 'Osmanlıspor', 'Santos Laguna', 'Dinamo Moscow', 'Monarcas Morelia', 'Frosinone', 'Cruz Azul', 'Real Zaragoza', 'Deportes Iquique', 'Sydney FC', 'Brisbane Roar', 'AEK Athens', 'Colon de Santa Fe', 'Atiker Konyaspor', 'Unión Española', 'Reading', 'Asociacion Deportivo Cali', 'Palermo', 'FC Metz', 'Sporting Kansas City', 'FC Seoul', 'Bursaspor', 'Benevento Calcio', 'FC Rostov', 'Associação Atlética Ponte Preta', 'Al Nassr', 'San Jose Earthquakes', 'Nîmes Olympique', 'Al Ittihad', 'Godoy Cruz', 'Gimnàstic de Tarragona', 'Philadelphia Union', 'Sport Club do Recife', 'CD Universidad de Concepción', 'FC Paços de Ferreira', 'New York Red Bulls', 'Club Atlético Tigre', 'FC Lorient', 'Belgrano de Córdoba', 'Sheffield Wednesday', 'CD Tenerife', 'SC Heerenveen', 'Independiente Santa Fe', 'Puebla', 'Vitória Setúbal', 'FC København', 'Kalmar FF', 'CD Aves', \"Newell's Old Boys\", 'Terek Grozny', '1. FC Union Berlin', 'Real Valladolid', 'ADO Den Haag', 'Santiago Wanderers', 'Bari', 'Ulsan Hyundai Horang-i', '1. FC Heidenheim', 'Argentinos Juniors', 'Brentford', 'Gençlerbirliği SK', 'FC St. Pauli', 'Melbourne Victory', 'VfL Bochum', 'Córdoba CF', 'Atlético Clube Goianiense', 'Kardemir Karabükspor', 'AJ Auxerre', 'Real Oviedo', 'Vitória ', 'Arsenal Tula', 'RC Lens', 'CF Os Belenenses', 'SK Rapid Wien', 'Everton de Viña del Mar', 'CD Los Millionarios Bogota', 'GwangJu FC', 'Sangju Sangmu FC', 'Jeonbuk Hyundai Motors', 'FC Dallas', 'ES Troyes AC', 'F.B.C. Unione Venezia', 'Al Qadisiyah', 'Fortuna Düsseldorf', 'Boavista FC', 'D.C. United', 'Medicana Sivasspor', 'CD Once Caldas Manizales', 'FC Ural', 'Kashiwa Reysol', 'Malmö FF', 'Cádiz C.F.', 'Portimonense SC', 'Urawa Red Diamonds', 'UD Almería', 'AIK Solna', 'CD Huachipato', 'Estoril Praia', '1. FC Nürnberg', 'Pescara', 'Stade de Reims', 'Moreirense FC', 'Empoli', 'Orlando Pirates', 'FC Anzhi Makhachkala', 'Heracles Almelo', 'Eintracht Braunschweig', 'Cremonese', 'CD Antofagasta', 'AS Nancy Lorraine', 'Lobos de la BUAP', 'Suwon Samsung Bluewings', 'Defensa y Justicia', 'Ipswich Town', 'Rosenborg BK', 'KAS Eupen', 'FC Sion', 'Adelaide United', 'Real Salt Lake', 'FC Midtjylland', 'Minnesota Thunder', 'AD Alcorcón', 'Al Faisaly', 'FC Tosno', 'FC Twente', 'F.C. Tokyo', 'IF Elfsborg', 'Carpi', 'Parma', 'IFK Norrköping', 'Unión de Santa Fe', 'Corporación Club Deportivo Tuluá', 'Kawasaki Frontale', 'Associação Chapecoense de Futebol', '1. FC Kaiserslautern', 'Preston North End', 'Molde FK', 'Bristol City', 'Brøndby IF', 'Albacete Balompié', 'GFC Ajaccio', 'KV Kortrijk', 'Kashima Antlers', 'CD Feirense', 'Oxford United', 'Talleres de Cordoba', 'FC Lugano', 'SV Zulte-Waregem', 'Deportes Tolima', 'Amkar Perm', 'Kasimpaşa SK', 'Gimnasia y Esgrima La Plata', 'Queens Park Rangers', 'Shimizu S-Pulse', 'Aalborg BK', 'Águilas Doradas', 'FC Lausanne-Sports', 'Tiburones Rojos de Veracruz', 'Perugia', 'La Spezia', 'Pohang Steelers', 'FC Barcelona B', 'Evkur Yeni Malatyaspor', 'Willem II', 'Novara', 'Sporting Charleroi', 'FK Austria Wien', 'Gamba Osaka', 'DSC Arminia Bielefeld', 'Nottingham Forest', 'Salernitana', 'Vercelli', 'Śląsk Wrocław', 'Sagan Tosu', 'CD Numancia', 'Strømsgodset IF', 'Yokohama F. Marinos', 'Cardiff City', 'FC Sochaux-Montbéliard', 'Jeju United FC', 'Lechia Gdańsk', 'Piast Gliwice', 'SD Huesca', 'FC Zürich', 'Heart of Midlothian', 'Atlético Tucumán', 'BK Häcken', 'Audax Italiano', 'Club de Deportes Temuco', 'San Luis de Quillota', 'Al Taawoun', 'Lech Poznań', 'FC Luzern', 'Cesena', 'Chacarita Juniors', 'Aberdeen', 'Excelsior', 'SpVgg Greuther Fürth', 'San Martín de San Juan', 'Wisła Kraków', 'Hammarby IF', 'Virtus Entella', 'Vegalta Sendai', 'Alianza Petrolera', 'CD Palestino', 'KV Mechelen', 'Central Coast Mariners', 'La Equidad', 'Avellino', 'Omiya Ardija', 'Cracovia', 'Curicó Unido', 'CF Reus Deportiu', 'SK Brann', 'C.D. Leonesa S.A.D.', 'US Quevilly-Rouen', 'Sporting Lokeren', 'Houston Dynamo', 'Termalica Bruk-Bet Nieciecza', 'Tondela', 'SV Sandhausen', 'Al Fayha', 'Jeonnam Dragons', 'Sandefjord Fotball', 'Pogoń Szczecin', 'Östersunds FK', 'Burton Albion', 'Al Raed', 'Jagiellonia Białystok', 'Bahía Blanca', 'Ventforet Kofu', 'Stade Brestois 29', 'CD Lugo', 'Korona Kielce', 'PEC Zwolle', 'MSV Duisburg', 'AFC Eskilstuna', 'Waasland-Beveren', 'Club Atlético Patronato', 'La Berrichonne de Châteauroux', 'SK Sturm Graz', 'Royal Excel Mouscron', 'Júbilo Iwata', 'SønderjyskE', 'Al Shabab', 'US Orléans Loiret Football', 'Bourg en Bresse Péronnas 01', 'FC Nordsjælland', 'FC Thun', 'CD America de Cali', 'VVV-Venlo', 'Charlton Athletic', 'Sevilla Atlético', 'Ternana', 'Gangwon FC', 'IFK Göteborg', 'Odense Boldklub', 'Arsenal de Sarandí', 'SG Dynamo Dresden', 'Bolton Wanderers', 'Plymouth Argyle', 'Southend United', 'Vélez Sarsfield', 'Daegu FC', 'Sanfrecce Hiroshima', 'Odds BK', 'Aarhus GF', 'Blackburn Rovers', 'Lyngby BK', 'FC Erzgebirge Aue', 'Sint-Truidense VV', 'Karlsruher SC', 'Jaguares Fútbol Club', 'Sarpsborg 08 FF', 'Temperley', ' SSV Jahn Regensburg', 'Patriotas Boyacá FC', 'Barnsley', 'Sandecja Nowy Sącz', 'Górnik Zabrze', 'VfL Osnabrück', 'Valenciennes FC', 'Tours FC', 'Lorca Deportiva CF', 'Albirex Niigata', 'Cittadella', 'Aalesunds FK', 'Deportivo Pasto', 'Roda JC Kerkrade', 'Motherwell', 'Holstein Kiel', 'Scunthorpe United', 'Atlético Huila', 'Wisła Płock', 'Atlético Bucaramanga', 'Sparta Rotterdam', 'Stabæk Fotball', 'Würzburger FV', 'VfR Aalen', 'Clermont Foot 63', 'Randers FC', 'Vålerenga Fotball', 'Incheon United FC', 'Hibernian', 'SCR Altach', 'Sheffield United', 'Le Havre AC', 'Walsall', 'Chamois Niortais FC', 'Sportfreunde Lotte', 'Millwall', 'SpVgg Unterhaching', 'FC SKA-Energiya Khabarovsk', 'Hansa Rostock', 'Wellington Phoenix', 'Hobro IK', 'Wigan Athletic', 'Peterborough United', 'Chemnitzer FC', 'Grimsby Town', 'Ascoli', 'Al Fateh', 'Foggia', 'Bristol Rovers', '1. FC Magdeburg', 'SG Sonnenhof Großaspach', 'Bury', 'Lillestrøm SK', 'Arka Gdynia', 'Ross County FC', 'Paris FC', 'Bradford City', 'Hamilton Academical FC', 'Luton Town', 'NAC Breda', 'Portsmouth', 'Zagłębie Lubin', 'Kilmarnock', 'Hokkaido Consadole Sapporo', 'Örebro SK', 'SV Wehen Wiesbaden', 'Coventry City', 'Milton Keynes Dons', 'Rochdale', 'FK Haugesund', 'Dundee FC', 'Oldham Athletic', 'Ohod Club', 'Rotherham United', 'HJK Helsinki', 'LASK Linz', 'AC Horsens', 'SC Fortuna Köln', 'St. Johnstone FC', 'Sogndal', 'Envigado FC', 'Blackpool', 'SC Preußen Münster', 'Hallescher FC', 'Ettifaq FC', 'Crawley Town', 'Exeter City', 'AFC Wimbledon', 'Doncaster Rovers', 'IK Sirius', 'Jönköpings Södra IF', 'Rot-Weiß Erfurt', 'Notts County', 'SV Mattersburg', 'Viking FK', 'Cambridge United', 'Tigres FC', 'Mansfield Town', 'SV Meppen', 'Tromsø IL', 'Swindon Town', 'Werder Bremen II', 'FC Admira Wacker Mödling', 'SC Paderborn 07', 'Partick Thistle F.C.', 'Silkeborg IF', 'Al Batin', 'Colchester United', 'FSV Zwickau', 'Crewe Alexandra', 'Northampton Town', 'Kristiansund BK', 'Lincoln City', 'Dundalk', 'Wycombe Wanderers', 'Yeovil Town', 'GIF Sundsvall', 'FC Carl Zeiss Jena', \"St. Patrick's Athletic\", 'Fleetwood Town', 'Wolfsberger AC', 'Cork City', 'Gillingham', 'SKN St. Pölten', 'Carlisle United', 'Chesterfield', 'Newcastle Jets', 'Morecambe', 'Port Vale', 'Newport County', 'Shrewsbury', 'Accrington Stanley', 'Forest Green', 'Bohemian FC', 'Cheltenham Town', 'Barnet', 'Halmstads BK', 'Shamrock Rovers', 'Derry City', 'Stevenage', 'Finn Harps', 'FC Helsingør', 'Sligo Rovers', 'Bray Wanderers', 'Limerick FC', 'Galway United', 'Drogheda United'])\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"Teknisk Tirsdag - Data Cleaning.ipynb:4: SettingWithCopyWarning: \n",
"A value is trying to be set on a copy of a slice from a DataFrame.\n",
"Try using .loc[row_indexer,col_indexer] = value instead\n",
"\n",
"See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy\n",
" \"cell_type\": \"markdown\",\n",
"Teknisk Tirsdag - Data Cleaning.ipynb:1: SettingWithCopyWarning: \n",
"A value is trying to be set on a copy of a slice from a DataFrame.\n",
"Try using .loc[row_indexer,col_indexer] = value instead\n",
"\n",
"See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy\n",
" {\n",
"Teknisk Tirsdag - Data Cleaning.ipynb:2: SettingWithCopyWarning: \n",
"A value is trying to be set on a copy of a slice from a DataFrame.\n",
"Try using .loc[row_indexer,col_indexer] = value instead\n",
"\n",
"See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy\n",
" \"cells\": [\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Variablenavn: Name Variabletype: object\n",
"Variablenavn: Age Variabletype: int64\n",
"Variablenavn: Nationality Variabletype: object\n",
"Variablenavn: Overall Variabletype: int64\n",
"Variablenavn: Potential Variabletype: int64\n",
"Variablenavn: Club Variabletype: object\n",
"Variablenavn: Value Variabletype: float64\n",
"Variablenavn: Wage Variabletype: float64\n",
"Variablenavn: Special Variabletype: int64\n",
"Variablenavn: Acceleration Variabletype: float64\n",
"Variablenavn: Aggression Variabletype: float64\n",
"Variablenavn: Agility Variabletype: float64\n",
"Variablenavn: Balance Variabletype: float64\n",
"Variablenavn: Ball control Variabletype: float64\n",
"Variablenavn: Composure Variabletype: float64\n",
"Variablenavn: Crossing Variabletype: float64\n",
"Variablenavn: Curve Variabletype: float64\n",
"Variablenavn: Dribbling Variabletype: float64\n",
"Variablenavn: Finishing Variabletype: float64\n",
"Variablenavn: Free kick accuracy Variabletype: float64\n",
"Variablenavn: GK diving Variabletype: float64\n",
"Variablenavn: GK handling Variabletype: float64\n",
"Variablenavn: GK kicking Variabletype: float64\n",
"Variablenavn: GK positioning Variabletype: float64\n",
"Variablenavn: GK reflexes Variabletype: float64\n",
"Variablenavn: Heading accuracy Variabletype: float64\n",
"Variablenavn: Interceptions Variabletype: float64\n",
"Variablenavn: Jumping Variabletype: float64\n",
"Variablenavn: Long passing Variabletype: float64\n",
"Variablenavn: Long shots Variabletype: float64\n",
"Variablenavn: Marking Variabletype: float64\n",
"Variablenavn: Penalties Variabletype: float64\n",
"Variablenavn: Positioning Variabletype: float64\n",
"Variablenavn: Reactions Variabletype: float64\n",
"Variablenavn: Short passing Variabletype: float64\n",
"Variablenavn: Shot power Variabletype: float64\n",
"Variablenavn: Sliding tackle Variabletype: float64\n",
"Variablenavn: Sprint speed Variabletype: float64\n",
"Variablenavn: Stamina Variabletype: float64\n",
"Variablenavn: Standing tackle Variabletype: float64\n",
"Variablenavn: Strength Variabletype: float64\n",
"Variablenavn: Vision Variabletype: float64\n",
"Variablenavn: Volleys Variabletype: float64\n",
"Variablenavn: CAM Variabletype: float64\n",
"Variablenavn: CB Variabletype: float64\n",
"Variablenavn: CDM Variabletype: float64\n",
"Variablenavn: CF Variabletype: float64\n",
"Variablenavn: CM Variabletype: float64\n",
"Variablenavn: ID Variabletype: int64\n",
"Variablenavn: LAM Variabletype: float64\n",
"Variablenavn: LB Variabletype: float64\n",
"Variablenavn: LCB Variabletype: float64\n",
"Variablenavn: LCM Variabletype: float64\n",
"Variablenavn: LDM Variabletype: float64\n",
"Variablenavn: LF Variabletype: float64\n",
"Variablenavn: LM Variabletype: float64\n",
"Variablenavn: LS Variabletype: float64\n",
"Variablenavn: LW Variabletype: float64\n",
"Variablenavn: LWB Variabletype: float64\n",
"Variablenavn: Preferred Positions Variabletype: object\n",
"Variablenavn: RAM Variabletype: float64\n",
"Variablenavn: RB Variabletype: float64\n",
"Variablenavn: RCB Variabletype: float64\n",
"Variablenavn: RCM Variabletype: float64\n",
"Variablenavn: RDM Variabletype: float64\n",
"Variablenavn: RF Variabletype: float64\n",
"Variablenavn: RM Variabletype: float64\n",
"Variablenavn: RS Variabletype: float64\n",
"Variablenavn: RW Variabletype: float64\n",
"Variablenavn: RWB Variabletype: float64\n",
"Variablenavn: ST Variabletype: float64\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAe0AAAFYCAYAAAB+s6Q9AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XtcVHX+x/H3CBIiGIgDpqZu/tQo72Y/sWzFS166qOUG\nEriVa2p529zAVUGNzVvlupiladpuVj8Ku/izDH/Z6vYzpNW2UrOH2U93EZWA0EW5yOX8/nCdFWUY\nvJwZzvB6/sWcM+d8P/OdM/Pme+ZcbIZhGAIAAPVeI08XAAAA6obQBgDAIghtAAAsgtAGAMAiCG0A\nACyC0AYAwCJ8PV1AbfLyijxdgiQpJCRAhYXFni6j3qJ/nKNvnKNvnKNvnGsIfWO3Bzmdx0i7Dnx9\nfTxdQr1G/zhH3zhH3zhH3zjX0PuG0AYAwCJMDe3S0lINHjxY7777ro4fP674+HjFxsZq+vTpOnv2\nrJlNAwDgdUwN7ZdfflnXX3+9JCk1NVWxsbF688031a5dO6Wnp5vZNAAAXse00P7hhx906NAhDRgw\nQJKUlZWlQYMGSZKioqKUmZlpVtMAAHgl00J7yZIlmjVrluNxSUmJ/Pz8JEmhoaHKy8szq2kAALyS\nKad8vf/+++rRo4duvPHGGufX9cZiISEB9eZIwdoOwQf9Uxv6xjn6xjn6xrmG3DemhPb27duVnZ2t\n7du368SJE/Lz81NAQIBKS0vl7++v3NxchYWFuVxPfTkXz24PqjfnjNdH9I9z9I1z9I1z9I1zDaFv\navunxJTQXr58uePvFStWqHXr1vrb3/6mjIwMjRw5Ulu3blX//v3NaBoAAK/ltvO0p06dqvfff1+x\nsbE6efKkRo0a5a6mAQDwCqZfxnTq1KmOv9evX292cwAAeC2uiAYAgEUQ2gAAWES9vssX0FBt/yqn\n1vkDerR2UyUA6hNG2gAAWAShDQCARRDaAABYBKENAIBFENoAAFgEoQ0AgEUQ2gAAWAShDQCARRDa\nAABYBKENAIBFENoAAFgEoQ0AgEUQ2gAAWAShDQCARRDaAABYBKENAIBFENoAAFgEoQ0AgEUQ2gAA\nWAShDQCARRDaAABYBKENAIBFENoAAFgEoQ0AgEUQ2gAAWISvWSsuKSnRrFmzVFBQoLKyMj3xxBPK\nyMjQ/v37FRwcLEkaP368BgwYYFYJAAB4FdNC+89//rO6dOmiCRMmKCcnR4899ph69uypp556SlFR\nUWY1CwCA1zIttEeMGOH4+/jx4woPDzerKQAAGgSbYRiGmQ3ExMToxIkTWrVqlV577TXl5eWpvLxc\noaGhSkpKUvPmzZ0uW1FRKV9fHzPLA+qljzOPXNXywyLbX4syANQzpoe2JB04cEAJCQmaPXu2goOD\nFRERoVdeeUUnTpxQcnKy0+Xy8orMLq1O7PagelNLfUT/OHelfbP9q5yrandAj9ZXtbw7sN04R984\n1xD6xm4PcjrPtKPH9+3bp+PHj0uSIiIiVFlZqU6dOikiIkKSNHDgQB08eNCs5gEA8Dqmhfbu3bu1\nbt06SVJ+fr6Ki4uVnJys7OxsSVJWVpY6duxoVvMAAHgd0w5Ei4mJ0Zw5cxQbG6vS0lIlJycrICBA\nM2bMUJMmTRQQEKBFixaZ1TwAAF7HtND29/fXCy+8cMn0jRs3mtUkAABejSuiAQBgEYQ2AAAWYdru\nccBT6nK6lBVOiQKAizHSBgDAIghtAAAsgtAGAMAiCG0AACyC0AYAwCIIbQAALILQBgDAIghtAAAs\ngtAGAMAiCG0AACyC0AYAwCIIbQAALILQBgDAIrjLF+CFuNMZ4J0YaQMAYBGENgAAFkFoAwBgEYQ2\nAAAWQWgDAGARhDYAABZBaAMAYBGENgAAFkFoAwBgEYQ2AAAWYdplTEtKSjRr1iwVFBSorKxMTzzx\nhG6++WYlJCSosrJSdrtdzz33nPz8/MwqAQAAr2JaaP/5z39Wly5dNGHCBOXk5Oixxx5Tr169FBsb\nq+HDh2vZsmVKT09XbGysWSUAAOBVTNs9PmLECE2YMEGSdPz4cYWHhysrK0uDBg2SJEVFRSkzM9Os\n5gEA8Dqm3+UrJiZGJ06c0KpVq/Too486doeHhoYqLy/P7OYBAPAapof2f/3Xf+nAgQN6+umnZRiG\nY/qFfzsTEhIgX18fM8urM7s9yNMl1Gv1qX+CAv1dPsdVvR9nHql1/rDI9nVb/lDBFS1fl9dwterD\ne1Yfaqiv6BvnGnLfmBba+/btU2hoqG644QZFRESosrJSTZs2VWlpqfz9/ZWbm6uwsLBa11FYWGxW\neZfFbg9SXl6Rp8uot+pb/xSdLnX5HFf1ulpHXZcPCvSvcV1X2/614On3rL5tN/UJfeNcQ+ib2v4p\nMe037d27d2vdunWSpPz8fBUXF6tfv37KyMiQJG3dulX9+/c3q3kAALyOaSPtmJgYzZkzR7GxsSot\nLVVycrK6dOmixMREpaWlqVWrVho1apRZzQMA4HVMC21/f3+98MILl0xfv369WU0CAODVuCIaAAAW\nQWgDAGARpp/yBXij7V/leLoEAA0QI20AACyC0AYAwCIIbQAALILQBgDAIghtAAAsgtAGAMAiOOUL\nDRKnbLnmqo8G9GjtpkoAnMdIGwAAiyC0AQCwCEIbAACLILQBALAIQhsAAIsgtAEAsAhCGwAAi+A8\nbcADOE8cwJVgpA0AgEUQ2gAAWAShDQCARRDaAABYBKENAIBFENoAAFgEoQ0AgEUQ2gAAWAShDQCA\nRRDaAABYhKmXMV26dKn27NmjiooKTZw4UZ9++qn279+v4OBgSdL48eM1YMAAM0sAAMBrmBbau3bt\n0vfff6+0tDQVFhZq9OjR6tu3r5566ilFRUWZ1SwAAF7LtNDu06ePunXrJklq1qyZSkpKVFlZaVZz\nAAB4PZthGIbZjaSlpWn37t3y8fFRXl6eysvLFRoaqqSkJDVv3tzpchUVlfL19TG7PFjMx5lHPF2C\nVxgW2b7W+a762dXyAK4902/N+cknnyg9PV3r1q3Tvn37FBwcrIiICL3yyit68cUXlZyc7HTZwsJi\ns8urE7s9SHl5RZ4uo95yd/8UnS51W1tXKyjQv97W6+o9c1X31b7nfK6co2+cawh9Y7cHOZ3n8ujx\nb7/99oob/uyzz7Rq1SqtWbNGQUFBioyMVEREhCRp4MCBOnjw4BWvGwCAhsZlaC9evPiKVlxUVKSl\nS5dq9erVjqPFp06dquzsbElSVlaWOnbseEXrBgCgIXK5e7xVq1aKj49X9+7d1bhxY8f06dOn17rc\nRx99pMLCQs2YMcMx7YEHHtCMGTPUpEkTBQQEaNGiRVdROgAADYvL0G7Tpo3atGlz2SuOjo5WdHT0\nJdNHjx592esCAAB1CO0pU6aosLBQR48eVdeuXVVVVaVGjbiQGgAA7uYyfT/88ENFR0frt7/9rSQp\nJSVF6enpphcGAACqcznSXrdunT744AM9/vjjkqTExETFx8drzJgxphcH77T9q5xa5w/o0dpNlQCA\ntbgcaQcFBalJkyaOx/7+/tUOSAMAAO7hcqQdEhKi9957T2VlZdq/f78++uijWq9iBgAAzOFypL1g\nwQLt3btXZ86c0dy5c1VWVqbf/e537qgNAABcwOVIu1mzZkpOTtZPP/0kSYyyAQDwEJeh/dFHH+nZ\nZ5+VzWaTYRjy8fFRUlKShgwZ4o76AADAv7gM7ZdffllvvfWW2rZtK0k6fPiwpk2bRmgDAOBmLn/T\nDgsLcwS2JP3sZz/TjTfeaGpRAADgUk5H2pmZmZKkm266SSkpKerXr58aNWqkzMxMtWvXzm0FAgCA\nc5yG9ksvvVTt8YW30bTZbOZVBAAAauQ0tF9//XV31gEAAFxw+Zv2X//6Vz344IPq0aOHevbsqejo\naH355ZfuqA0AAFzA5dHjzzzzjGbPnq1evXrJMAzt2bNH8+fP16ZNm9xRHwAA+BeXoR0aGqrIyEjH\n4zvuuEOtWrUytSgAAHApp6GdnZ0tSeratavWrVtX7ejxW265xW0FouFxdRcwAGionIb2L3/5S8dV\n0CRpw4YNjnk2m03Tpk0zvzoAAODgNLQ//fRTd9YBAABccPmbdkJCQo3Tly5des2LAQAAzrkM7QsP\nQisvL1dWVpbatGljalEAAOBSLkN79OjR1R4/9NBDmjhxomkFAQCAmrkM7aqqqmqPjx8/riNHjphV\nDwAAcMJlaN9yyy3VjiIPCgrShAkTTC8M1sUpW6iLjzOPqOh0qdP5A3q0dl8xgEW4DO3vvvvOHXUA\nAAAXnIb2H/7wh1oXnD59+jUvBgAAOOc0tH18fNxZBwAAcMFpaE+ZMkWSlJmZWe20L0lau3ZtnVa+\ndOlS7dmzRxUVFZo4caK6du2qhIQEVVZWym6367nnnpOfn99VlA8AQMPh8tacL7zwgjIyMiRJBQUF\nGj9+vPbu3etyxbt27dL333+vtLQ0rV27VgsXLlRqaqpiY2P15ptvql27dkpPT7/6VwAAQAPhMrRf\ne+01vf3221q8eLGio6M1bNgwl793S1KfPn0cz2vWrJlKSkqUlZWlQYMGSZKioqKUmZl5leUDANBw\nOA3tqqoqVVVVKSAgQC+99JIKCgo0bNgwPfjgg5ecu10THx8fBQQESJLS09N11113qaSkxLE7PDQ0\nVHl5edfoZQAA4P2c/qZ9/vzs886fp7127VrZbDYdOHCgTg188sknSk9P17p163T33Xdfsr7ahIQE\nyNe3fhwQZ7cHebqEeu3C/gkK9PdgJfVPfe2PPYcKap3vqm5Xn4mPM4+4rKG2Nq52/cMi27tsvz7j\nO8e5htw3TkP7Wpyf/dlnn2nVqlVau3atgoKCFBAQoNLSUvn7+ys3N1dhYWG1Ll9YWHzVNVwLdnuQ\n8vKKPF1GvXVx/9R2wYyGJijQ32v7w9VnwtXrdtU3V7t+K39m+c5xriH0TW3/lLj8TftKFRUVaenS\npVq9erWCg4MlSf369XMc1LZ161b179/frOYBAPA6Lq+IdqU++ugjFRYWasaMGY5pixcv1ty5c5WW\nlqZWrVpp1KhRZjUPAIDXMS20o6OjFR0dfcn09evXm9UkAABejcuYAgBgEVzGFAAAi3B5GdOaLFmy\nxJRiAACAcy5/0965c6eWLVumkydPSpLOnj2r4OBgJSYmml4cAAD4N5enfC1fvlxJSUkKDQ3VqlWr\nNGbMGM2aNcsdtQEAgAu4DO3AwED16NFDjRs3VseOHTV9+nSOAAcAwANc7h6vqKjQ7t271axZM733\n3nvq0KGDjh496o7aAADABVyG9oIFC5Sfn6+EhASlpKSooKBAkyZNckdtAADgAi5D+8CBA7rnnnsk\nSevWrZMkvfXWW+ZWBQAALuE0tL/99lvt379f69atU0lJiWN6RUWFVq5cqbFjx7qlQAAAcI7T0L7u\nuutUUFCgoqIi7dmzxzHdZrMpISHBLcUBAIB/cxraHTp0UIcOHdS3b1/16NHDnTUBAIAauPxNu7S0\nVE8++aROnTolwzAc09944w1TCwMAANW5DO158+Zp8uTJatWqlTvqAQAATrgM7TZt2nDfawAA6gGX\nod2/f3+lpaXp9ttvl6/vv59+4403mloYAACozmVo/+lPf5IkrV692jHNZrNp27Zt5lUFAAAu4TK0\nP/3000um5eTkmFIMAABwzmVon1dWVqaMjAy9++67OnTokP73f//XzLoAAMBFXIb2V199pY0bN2rL\nli2qqqrSM888o6FDh7qjNgAAcAGnt+Zcs2aNRowYoV//+tcKDQ3Vxo0b1bZtW917771q3LixO2sE\nAACqZaS9fPly/cd//IeSk5PVt29fSecOQAMAAJ7hNLS3b9+u9957T/PmzVNVVZVGjx6t8vJyd9YG\nAAAu4HT3uN1u1+OPP66MjAwtXLhQ//jHP5STk6NJkyZpx44d7qwRAACojkeP9+nTR3369NHcuXO1\nefNmrVy5Uj//+c/Nrg311Pavqp/yFxTor6LTpR6qBgAaDqcj7ZoEBgYqJiZGb7/9tln1AAAAJy4r\ntAEAgOcQ2gAAWISpoX3w4EENHjxYGzZskCTNmjVL9913n+Lj4xUfH6/t27eb2TwAAF6lzpcxvVzF\nxcVKSUlRZGRktelPPfWUoqKizGoWAACvZdpI28/PT2vWrFFYWJhZTQAA0KCYNtL29fWtdv/t8zZs\n2KD169crNDRUSUlJat68udN1hIQEyNfXx6wSL4vdHuTpEuqNoED/Ok3DOd7aN64+E3V53bU952rX\nv+dQQa3zh0W2r3W+p/Gd41xD7hvTQrsmI0eOVHBwsCIiIvTKK6/oxRdfVHJystPnFxYWu7E65+z2\nIOXlFXm6jHrj4nOyOU/bOW/uG1efCVev21XfXO36XanPn2m+c5xrCH1T2z8lbj16PDIyUhEREZKk\ngQMH6uDBg+5sHgAAS3NraE+dOlXZ2dmSpKysLHXs2NGdzQMAYGmm7R7ft2+flixZopycHPn6+ioj\nI0NxcXGaMWOGmjRpooCAAC1atMis5gEA8DqmhXaXLl30+uuvXzJ96NChZjUJAIBX44poAABYBKEN\nAIBFuPWULwDe4+JbtFpt/YAVMdIGAMAiCG0AACyC0AYAwCIIbQAALILQBgDAIghtAAAsglO+ADRI\n1+KUsgE9Wl+DSoC6Y6QNAIBFENoAAFgEoQ0AgEUQ2gAAWAShDQCARRDaAABYBKENAIBFENoAAFgE\noQ0AgEUQ2gAAWAShDQCARRDaAABYBKENAIBFENoAAFgEoQ0AgEUQ2gAAWAShDQCARZga2gcPHtTg\nwYO1YcMGSdLx48cVHx+v2NhYTZ8+XWfPnjWzeQAAvIppoV1cXKyUlBRFRkY6pqWmpio2NlZvvvmm\n2rVrp/T0dLOaBwDA65gW2n5+flqzZo3CwsIc07KysjRo0CBJUlRUlDIzM81qHgAAr+Nr2op9feXr\nW331JSUl8vPzkySFhoYqLy/PrOYBAPA6poW2K4ZhuHxOSEiAfH193FCNa3Z7kKdLuGY+zjxS6/xh\nke1rnR8U6F+naTiHvnHO6n1j5veCN33nXGsNuW/cGtoBAQEqLS2Vv7+/cnNzq+06r0lhYbGbKqud\n3R6kvLwiT5dxzRSdLq11vqvXevHyQYH+LtfZUNE3znlD35j1veBt3znXUkPom9r+KXHrKV/9+vVT\nRkaGJGnr1q3q37+/O5sHAMDSTBtp79u3T0uWLFFOTo58fX2VkZGh559/XrNmzVJaWppatWqlUaNG\nmdU8AABex7TQ7tKli15//fVLpq9fv96sJgEA8GpcEQ0AAIsgtAEAsAiPnfKF+mv7VzmeLgEAUANG\n2gAAWAShDQCARRDaAABYBKENAIBFENoAAFgEoQ0AgEUQ2gAAWAShDQCARRDaAABYBKENAIBFENoA\nAFgEoQ0AgEUQ2gAAWAShDQCARXBrTgC4Qq5uYzugR2s3VYKGgpE2AAAWQWgDAGARhDYAABZBaAMA\nYBGENgAAFkFoAwBgEZzyBQAe4uyUsaBAfxWdLuWUMVyCkTYAABZBaAMAYBGENgAAFuHW37SzsrI0\nffp0dezYUZLUqVMnJSUlubMEAAAsy+0Hot1+++1KTU11d7MAAFgeu8cBALAIt4+0Dx06pEmTJunU\nqVOaMmWK7rjjDqfPDQkJkK+vjxurc85uD/J0CXX2ceaRWucHBfpf8zbNWKe3oG+c8/a+cfW9Udvr\nDwr0155DBVfV/rDI9le1fH1lpe/ja82tod2+fXtNmTJFw4cPV3Z2tsaNG6etW7fKz8+vxucXFha7\nszyn7PYg5eUVebqMOis6XerW9s6fU4pL0TfONYS+cfW94ez1X6u+sdL3Vl1Z7fv4StT2T4lbd4+H\nh4drxIgRstlsatu2rVq0aKHc3Fx3lgAAgGW5NbQ3bdqkV199VZKUl5engoIChYeHu7MEAAAsy627\nxwcOHKjf/OY32rZtm8rLyzV//nynu8YBAEB1bg3twMBArVq1yp1NAgDgNTjlCwAAiyC0AQCwCG7N\neY05u9VeXXErPsB7XO33AXAxRtoAAFgEoQ0AgEUQ2gAAWAShDQCARRDaAABYBKENAIBFcMoXAMAp\nV6etcZqqezHSBgDAIghtAAAsgtAGAMAiCG0AACyC0AYAwCIIbQAALIJTvi6T2Xft4a5AAK4Vvk+8\nDyNtAAAsgtAGAMAiCG0AACyC0AYAwCIIbQAALILQBgDAIhrcKV9XcgpEUKC/ik6XmlANADRsZt9F\nzB2nvbnzTmeMtAEAsAhCGwAAiyC0AQCwCLf/pr1w4UJ9/fXXstlsmj17trp16+buEgAAsCS3hvYX\nX3yhv//970pLS9MPP/yg2bNnKy0tzZ0lAABgWW7dPZ6ZmanBgwdLkjp06KBTp07p9OnT7iwBAADL\ncmto5+fnKyQkxPG4efPmysvLc2cJAABYlkfP0zYMo9b5dnvQNW/zF0NuvubrBABcmSv5Tr6cbPC2\n73y3jrTDwsKUn5/vePzjjz/Kbre7swQAACzLraF9xx13KCMjQ5K0f/9+hYWFKTAw0J0lAABgWW7d\nPd6rVy/deuutiomJkc1m07x589zZPAAAlmYzXP2wDAAA6gWuiAYAgEUQ2gAAWESDuzWnK1lZWZo+\nfbo6duwoSerUqZPOnDmj/fv3Kzg4WJI0fvx4DRgwwINVes6mTZu0du1a+fr6atq0aercubMSEhJU\nWVkpu92u5557Tn5+fp4u02Mu7p+PP/6YbUfSO++8o02bNjke79u3T2+99Zbmz58vSercubMWLFjg\noeo8q6a+6dKli4qLixUQECBJSkxMVJcuXTxVosecOXNGiYmJOnXqlMrLy/Xkk0/Kbrc36O2G37Qv\nkpWVpTfeeEOpqamOabNmzdLQoUMVFRXlwco8r7CwUDExMdq4caOKi4u1YsUKVVRU6K677tLw4cO1\nbNkytWzZUrGxsZ4u1SNq6p/y8nK2nYt88cUX2rJliw4dOqSnn35a3bp108yZM3X//ffr5z//uafL\n86gL+yYpKUmdOnXydEketWHDBuXm5mrmzJnKzc3VL3/5S9nt9ga93bB7HHWWmZmpyMhIBQYGKiws\nTCkpKcrKytKgQYMkSVFRUcrMzPRwlZ5TU//gUitXrtSECROUk5PjuGFQQ992zlu5cqWeeOIJT5dR\nb4SEhOjkyZOSpH/+858KDg5u8NsNoV2DQ4cOadKkSRo7dqx27twp6dx/fOPGjdOvf/1r/fTTTx6u\n0DOOHj2q0tJSTZo0SbGxscrMzFRJSYljd3hoaGiDvixtTf0jse1c6JtvvtENN9wgHx8fNWvWzDG9\noW870r/75vwFp1JTU/Xwww8rOTlZpaWlHq7OM+655x4dO3ZMQ4YMUVxcnBISEhr8dsNv2hdp3769\npkyZouHDhys7O1vjxo1TSkqKWrRooYiICL3yyit68cUXlZyc7OlSPeLkyZN68cUXdezYMY0bN67a\npWj5peXS/lm0aJGCg4PZdv4lPT1do0ePvmQ62071vhk3bpw6d+6stm3bat68eXrjjTc0fvx4D1fo\nfh988IFatWqlV199Vd99952efPJJBQX9+xKmDXG7YaR9kfDwcI0YMUI2m01t27ZVixYt1L59e0VE\nREiSBg4cqIMHD3q4Ss8IDQ1Vz5495evrq7Zt26pp06Zq2rSpYxSQm5ursLAwD1fpOTX1T6dOndh2\nLpCVlaWePXuqefPmjt2eEtuO9O++kaQhQ4aobdu2khr2dvPll1/qzjvvlCTdfPPNKisrU2FhoWN+\nQ9xuCO2LbNq0Sa+++qokKS8vTwUFBVq8eLGys7MlnftgnT+yvKG58847tWvXLlVVVamwsFDFxcXq\n16+f49K0W7duVf/+/T1cpefU1D/JyclsO/+Sm5urpk2bys/PT40bN9ZNN92k3bt3S2LbubBvDMPQ\nI488on/+85+SGvZ2065dO3399deSpJycHDVt2lQdOnRo0NsNu8cvMnDgQP3mN7/Rtm3bVF5ervnz\n5+u6667TjBkz1KRJEwUEBGjRokWeLtMjwsPDNXToUD300EOSpLlz56pr165KTExUWlqaWrVqpVGj\nRnm4Ss+pqX+aNm3KtvMveXl5at68uePx7NmzlZycrKqqKnXv3l39+vXzYHWedWHf2Gw2PfTQQ3rk\nkUfUpEkThYeHa+rUqR6u0DOio6M1e/ZsxcXFqaKiQvPnz5fdbm/Q2w2nfAEAYBHsHgcAwCIIbQAA\nLILQBgDAIghtAAAsgtAGAMAiCG14hby8PCUmJmrkyJGKjY3VyJEj9cc//tHTZV2VAwcOOK5ffujQ\nIe3fv1/SuRvYvPPOO8rLy9O0adM8WWKt4uPj9fnnnysrK0tjx4695uv/8ssvNWjQIL300kvXfN1A\nfcV52rA8wzD0xBNP6IEHHtCSJUskSfn5+XrkkUfUsmVLDR061MMVXpmIiAglJSVJkv7nf/5HLVq0\n0K233uqYb7fbq92NrqHJzMzUsGHDuMEGGhRCG5aXmZkpHx+faqO5Fi1a6N1333XczOTUqVOaN2+e\nfvrpJ50+fVqPPvqo7rvvPq1YsUInT57UiRMn9Pe//13/+Z//qaSkJL377rv6/PPPVVVVpcOHD6t1\n69ZasWKFbDabXn/9dW3ZskWVlZW66aabNG/ePOXn52vixIm64447tHv3boWEhOj+++/XBx98oJyc\nHP3hD3/QzTffrOeff167du2Sn5+fwsPDtWTJEm3evLnGtr744gstX75cCQkJ2rBhgwIDA+Xv7+94\njUePHlVsbKz+8pe/KDs7W08//bRsNpu6deumHTt2aPXq1WrXrp3j+ZWVlVq4cKFjxN63b1/NmDFD\nDz74oObMmaNevXpJkh555BE9+uij6tixoxYsWKCSkhIVFxfrqaeeUr9+/TRr1iz5+fnp8OHDev75\n5/XNN99o7dq18vPzU2VlpZYuXao2bdq4fN/i4+N1yy236Pvvv1deXp4mTpyoe++9t9b36ujRozp2\n7JimTp2qjRs3yjAMNWnSRDExMZozZ46Ki4t19uxZ/epXv9KQIUOqLZOYmKglS5botttu0zfffKMj\nR45o9uzCFT1qAAAHSUlEQVTZev/993Xw4EGNGjVKkydPVn5+vhISElRRUaHTp09r3LhxGjVqVK3b\nxEsvvaRt27apUaNGGjlypOLi4nTs2LEa+w+4KgZgca+99pqRkpJS63Pmz59vpKenG4ZhGGfOnDEG\nDx5sFBQUGKmpqUZMTIxRUVFhlJSUGD169DBOnjxpbNy40Rg4cKBRUlJiVFVVGYMGDTL2799vfP31\n10Z8fLxRVVVlGIZhPPvss8af/vQnIzs724iIiDD+7//+zzAMw4iKijJWrFhhGIZhpKamGr/73e+M\nkydPGj169DAqKioMwzCMDz/80MjJyXHa1q5du4yYmBjDMAwjMTHRePvtt6v9nZ2dbfTv398wDMOY\nOXOm8cc//tEwDMPYsWOH0blzZ+PIkSPV+uC///u/jccff9yoqqoyKioqjDFjxhhZWVnG+vXrjYUL\nFxqGYRj5+fnGnXfeaVRUVBgTJkwwMjMzDcMwjB9//NGIiooyysvLjcTERGPmzJmO9aanpxs5OTmG\nYRjGqlWrjMWLFxuGYRhxcXHGzp07q72OC8XFxRnPPPOMYRiGceTIESMyMtKorKys9b2KjY119H1q\naqqxbNkywzAMIykpyVizZo3jNfTr188oKiq6ZJm4uDjj97//vWP5YcOGGWVlZUZ2drbRu3dvwzAM\nY//+/cYnn3xiGIZh5ObmGrfffrthGIbT9+mvf/2r8Ytf/MKoqKgwzp49a0ycONE4deqU0/4DrgYj\nbViej4+PKisrHY/T0tK0efNmlZWVqWXLlkpNTVVWVpb27t2r999/X5Lk6+uro0ePSpJ69+4tHx8f\n+fj4KCQkRKdOnZIkdevWzTGyveGGG3Tq1Cnt27dP//jHPzRu3DhJUnFxsXx9z32MQkJC9LOf/UzS\nuUuanh+5tmzZUseOHdP111+v/v37Ky4uTkOGDNGIESPUsmVLp201alT3Q06+++47/epXv5Ik3XXX\nXQoICLjkOV9//bUiIyNls9nk4+Oj2267TXv37tX999+vsWPH6re//a0+/vhjDRs2TD4+PsrKytKZ\nM2e0cuVKR58VFBRIkuPGFtK5vRqJiYkyDEN5eXnV5rly/mYQ7dq1k81mU0FBQa3vVffu3WWz2Wp8\nbef3tISGhio8PFyHDx+ucZkL35dbb71Vfn5+atmypYqKiiRJYWFhWrt2rdauXSsfH59qNzap6X36\n9ttvq21Dq1atkiSn/RceHl7n/gEuRmjD8jp37qyNGzc6HkdHRys6OlpZWVlavny5JMnPz0/z5s1T\n165dqy27Y8cO+fj4VJtm/OvKvjVN9/Pz08CBAy+5vebRo0cvef6Fj8+vMzU1VT/88IN27NihuLg4\nrVixwmlbl6OqqqpayNcU+BeHnWEYstlsstvtuvHGG/XNN99oy5YtmjVrlqRzfbZixYpq1ws/7/zP\nDuXl5ZoxY4bee+89tW/fXhs2bNC+ffsuq+6L66ntvWrcuHGN66kpyM9Pu3iZ8/9kXfz3ecuXL1e7\ndu20bNkynTlzxhHyUs3vk81mq/H9qq3/gCvF0eOwvD59+ig4OFirV692TCsvL9fOnTsdo6LevXtr\ny5YtkqTS0lLNnz9fFRUVl91Wr1699Je//EVnzpyRJL3xxhv629/+Vqdls7Oz9dprr6lDhw567LHH\nNGTIEH333Xd1WtZms6m8vNzp/JtuuslRx86dOx31XahHjx76/PPPZRiGKioq9MUXX6h79+6SpPvu\nu0/p6ek6deqUunTpIql6n/3000969tlnL1nnmTNn1KhRI7Vu3VplZWXatm2bzp49W6fXJEm7du2S\nJB0+fFiNGjVS8+bNr+i96t69uz777DNJ5+6Y9eOPPzr2elyu/Px8x121Nm/erEaNGtX6mnr27KnM\nzEyVl5eroqJC8fHx+vHHH+vUf8DlYqQNr/Dyyy9r2bJlGjlypAIDA1VSUqLevXvrhRdekCRNmTJF\nc+fO1dixY3X27FlFR0fXOMpypWvXrnr44YcVHx+v6667TmFhYXrggQccu41rEx4erm+//VZjxoxR\n06ZNdf3112vKlCmOW5vWpm/fvlq6dKnTEfjUqVP19NNPa/PmzerZs6datmx5yahw2LBh+vLLLzV2\n7FhVVVVp8ODB6t27tyTp7rvvVkpKiiZOnOh4/pw5c5ScnKwPP/xQZ8+e1eTJky9pNzg4WPfee6/G\njBmjVq1aafz48UpISHCElSsVFRWaPHmyjh49qqSkJDVq1OiK3qtp06Zpzpw5io+PV1lZmVJSUtS0\nadM61XCxuLg4paSk6J133tGDDz6oyMhIzZw5U1FRUTU+v2fPnrr77rv18MMPS5LuuecehYWF1an/\ngMvFXb4AL7B3716VlZXptttuU35+voYPH67PP//c6e7k+iA+Pl6TJ0/miGrgMjDSBrxAQECAY/dr\neXm5FixYUK8DG8CVYaQNAIBFcCAaAAAWQWgDAGARhDYAABZBaAMAYBGENgAAFkFoAwBgEf8PcSW0\niIpD8+gAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f79d78003c8>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Træningsæt størrelse: 1272\n"
]
}
],
"source": [
"# Run the datacleaning notebook to get all the variables\n",
"%run 'Teknisk Tirsdag - Data Cleaning.ipynb'"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Efter at have hentet vores rensede data, hvor vi minder os selv om at vi har: <br>\n",
"* dansker_set\n",
"* topklub_set\n",
"* ikke_topklub_set\n",
"* overall_set "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Det første, vi gerne vil kigge lidt på, er, om vi var grundige nok i vores foranalyse. Derfor laver vi et heatmap, der skal fortælle os hvor stor sammenhængen er (korrelation) mellem kolonnerne i forhold til hinanden."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABEwAAAPOCAYAAAAV3o3nAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xl4Tdfi//H3yUliiDEqxlBSrbliiqEoquarppqSalWr\nP2Ppt1VDKKmxytUq1YoilNJyEdM13RpKSAU1RImhpK0igpDIIL8/zpUrpe1Zp+Rk+Lyex9OTnfXZ\ne+191t7nZHXvtSypqampiIiIiIiIiIhIGhdnV0BEREREREREJLNRh4mIiIiIiIiIyO+ow0RERERE\nRERE5HfUYSIiIiIiIiIi8jvqMBERERERERER+R11mIiIiIiIiIiI/I6rsysgYLFYnF0FERERERGR\nHC01NdXZVXik3rA87uwq2O3T1LPOrgKgDpNMox9ljcrP5RxX544wyhTuN4lfYuOMMiUK5SP5p8NG\nGdcy1UkKDzXKuNVuR9LBTWaZGi05d+WGUaZskfwkHdhgtp2arblx85ZRJr9HXi4aHutihfJx+9J5\nu8vnKuoNwK3VM+3O5O0wBICkn3+0O+NW8kkAo3bgWqY6AAk3Yu3O5M5fCIDbV6LtzuQqUgrAqO24\n1WgJQOKvp+3OuBcvb8v8csr+TIknbJmLZ+zPFCsHOPb+OFK3pOhI+7dTqiIAKSd22Z2xPvWMLXNy\nj/2ZCvVJidpvd3kAq08dx65T548YZdy8qzp0/Uj87ZxRxt2rLLHzRhllCvWdYNRuwNZ2ks9EGGVc\ny/k6tJ3zhtdq7yL5jc4dsJ0/SReOGWXcSlcmftM8o0yeln2N2jTY2rUjbTTh2hWjTO6CRYyuBWC7\nHphcD8F2TXSkbibXd7Bd458a/C+jzImPXsiwujlyrB3aTga9PwnXr5plChTmduwlo0yuQkWNvhuA\n7fuBI8dN7SD7tIO/8x3RpG65ChW1u6zkHHokR0RERERERETkd9RhYiA0NJQqVaoQExPj7KqIiIiI\niIiIyCOkDhMDoaGheHt7s2mT2aMjIiIiIiIiIs5ktWSdf5mFxjCxU2xsLIcPH2bixInMmzePHj16\n8N133zFx4kQee+wxypUrh6enJ4MGDWLGjBmEh4eTkpKCv78/7dq1c3b1RURERERERMSA7jCx08aN\nG3n22Wdp1KgRZ8+e5eLFi0ybNo2pU6cSHBzM8ePHAQgPDyc6OpolS5awaNEi5syZQ0JCgpNrLyIi\nIiIiIiImdIeJnUJDQ+nfvz9Wq5VWrVqxfv16oqOjqVy5MgCNGzcmJSWFAwcOcOjQIQICAgC4c+cO\nly5dwtvb25nVFxERERERkRzMaslEz7pkEeowscOvv/7KoUOHmDx5MhaLhYSEBPLnz5+ujOW/jc/d\n3Z0uXbrQr18/Z1RVRERERERERB4CPZJjh9DQUHr16sWaNWtYvXo1Gzdu5Nq1a8THxxMVFUVKSgq7\nd+8GoHr16mzfvp07d+5w+/ZtgoKCnFx7ERERERERETGlO0zssG7dOqZMmZL2s8Vi4YUXXsDFxYVB\ngwZRunRpypcvj4uLCzVr1sTPz49u3bqRmppKz549nVhzEREREREREXGEOkzssGrVqvuWDRgwgF27\ndtG+fXtKly7NmDFjKFOmDABDhw5l6NChGV1NERERERERkQfKTNP1ZhWW1NTUVGdXIqvauXMnH374\nIR4eHhQpUoRp06bh7u5uvB6LBt8RERERERFxquz+p/FQ13LOroLdZiSfcXYVAHWYZArqMBERERER\nEXGu7P6nsTpMzOmRnEzi6twRRuUL95tEP8oaZeZyjhVelY0yXX87xubKtY0yLY6F823d+kaZJvv2\nsL91M6NMnQ3buL1jqVEmV+MeDh3r+E3zjDJ5WvYl+exBo4zr4zW48N7rdpcv/d5nAEbvT4tj4QDE\nzB5ud8azv238nkszh9mdKTpkOgCx80bZnSnUdwIAt1ZNtzuTt6OtTj+N6mN3psyE+QBcv3nL7kwB\nj7wA3DDI5P9vJjNvx5FjfXP5lL8o+T8eL9ra2a21s+zfTvuBRL3Zw+7yAD7/XGrUpsHWrhP33v+4\n5Z9xr9eRc+++bJQpO3kBcV+aDf6dr2cg7+d5wigzOv4UpwZ3M8o88dFXXPxgsFGm2Nsfcfu7r40y\nuRp0cega6si1OmHrQqNM7ua9ufn1B0YZjy5vE/laR6NMxc9XObQ/N5dNNMp4dB9J/Ia5Rpk8rfs5\ntB2TawHYrgfXF441yhToPY5R648ZZSa0qezQ/phcD8F2TXTkWDtyDDLq/XEo48D5k2EZtYNs0w48\nurwNkGGZ7EzTCpvTLDkiIiIiIiIiIr+T4zpMfvrpJ9544w06d+5Mx44dCQoKIiEh4aFuIywsjMGD\nbf/Xzs/P76GuW0REREREREQevRzVYXLnzh0GDRpE7969+eabb1i1ahWlSpUiMDDQ2VUTERERERER\neWSslqzzL7PIUWOY7Nq1i8cff5z69f83vsYrr7xCy5Ytad68OVu3bgVs0whHRkbSp08fRo0aRVJS\nElarlffff5+SJUvy/PPPU7lyZRo2bEipUqWYOXMmbm5uFChQgH/+85/O2j0REREREREReUhy1B0m\np0+fpnLl9IOeWiwWnnzySUqWLMnJkycB2Lp1Ky1btmTmzJn06dOHhQsX0rt3b2bPng3A+fPnGTBg\nAF27duXatWtMmzaNxYsXky9fPnbt2pXh+yUiIiIiIiIiD1eOusPEYrGQkpJy3/LU1FQaNGjA9u3b\nKVOmDCdPnsTX15dRo0Zx5swZ5syZQ0pKCp6engDkyZOHChUqAODp6cno0aNJSUnh/Pnz1KtXDw8P\njwzdLxERERERERF5uHJUh0n58uVZujT9NLSpqamcOnWKMWPG8Oabb1KhQgUaNWqExWLBzc2NmTNn\n4uXllS7j5uaW9nrkyJF89tln+Pj4MH78+AzZDxERERERERETmlbYXI56JKdhw4ZcuHCBb7/9Nm3Z\nggULqFWrFsWKFcNisRAaGkrLli0BePrpp9myZQsAe/bsYe3atfetMy4ujhIlSnD9+nXCwsJISkrK\nmJ0RERERERERkUcmR3WYuLi4EBwczFdffUWnTp3o2LEjp0+fZvTo0QA0a9aM/fv3U6tWLQAGDhzI\n1q1b6dWrF5988gk1atS4b509e/akR48eBAYG0rdvX+bOnculS5cydL9ERERERERE5OHKUY/kABQt\nWjRt8Nbf69u3L3379k37uVixYgQHB99XLiwsLO31kCFDGDJkSNrPHTt2BKBdu3b3lRURERERERFx\nhsw0XW9WYUlNTU11diVyOoueJRMREREREXGq7P6ncWBuH2dXwW5BCVHOrgKQwx7JERERERERERGx\nR457JCez+iU2zqh8iUL5WOFV2SjT9bdj9KOsUWYu59jV8BmjzDO7d3GwayujTI0VGznzzktGmXJT\nFxG/Ya5RJk/rftzesfSvC94jV+MexG+aZ7adln1JidpvlLH61OHSzGF2ly86ZDoAka91tDtT8fNV\nANxaNd3uTN6OtjrdXD7F7ozHi8MBuLF4nN2Z/P5jAUjYutDuTO7mvR3ezpXrN+3OFCng4XDmskHm\nsb+xHUcyt3d9ZXcm1zPdAEjct9rujHvdDgAk/7DF7oxrteeMzgOwnQu31s4yyuRtP5CUU2aPTFqf\n8DNqa2Brb45cp7bXqmeUafr9XqKD3jDKlAr81Oi8Btu5nXx8h1HGtVJjbq2eaZTJ22GIQ8fNpK2B\nrb050g5+ntjfKFNy5GyHjoEj7drkHAXbeZqweb5RJneLPsSve/DjzX8kT9v+Dh2DqEvXjTI+RQs4\ndNwSti82yuRu6u/QsXbkGGTU++NQxoHvR45sx5FjoHaQfdpBnra2a67JMcjdog+AUd3ytOz714Uk\nx1GHiYiIiIiIiEg2p2mFzWW7R3IuXLiAr68vAQEB+Pv78+KLL7J58+Y/LL9x40aHtnM3d/z4cT76\n6KM/LPfxxx+zeLFZb7WIiIiIiIiIOFe2vMOkXLlyhISEABAbG0vHjh1p1KgRuXPnvq/sZ599RqtW\nZo+P3JurVKkSlSpV+tt1FhEREREREZHMI1t2mNyrUKFCFC1alCNHjjB79mySkpKwWCxMmDCBTZs2\nceLECQYOHMisWbOYMWMG4eHhpKSk4O/vT7t27Xj33Xfx8vLi6NGj/Pzzz0ybNo09e/ak5QICAliy\nZAkfffQR8+fPZ9OmTdy5c4cmTZowcOBAZ+++iIiIiIiISPZ7vCQDZPtjduHCBWJjY/nmm2/o0qUL\nISEh9OzZk1mzZtG3b1/y5cvHrFmzCA8PJzo6miVLlrBo0SLmzJlDQkICAImJiQQHB/PSSy/xr3/9\nK13u97788kuWL1/OypUriYszG8hVRERERERERDKHbHmHyZkzZwgICCA1NZVcuXIxZcoUxowZw1tv\nvQWAn58fn3zySbrMgQMHOHToEAEBAQDcuXOHS5cuAVC7dm0AihcvzuHDh/9wu7lz58bf3x9XV1eu\nXr1KbGzso9g9EREREREREXnEsmWHyb1jmNxlsVhITU0FICkpCReX9DfXuLu706VLF/r163ff+qxW\na9rru+v4vejoaBYsWMCqVavw8PCgXbt2f3c3RERERERERB4KzZJjLts/knNXtWrVCAsLA2D//v1U\nrVoV+F8HSPXq1dm+fTt37tzh9u3bBAUF/en6ft9xcvXqVTw9PfHw8ODo0aNER0eTlJT0CPZERERE\nRERERB61HNNhMnjwYP71r3/x0ksvsXLlSgYPHgxApUqV6NKlCzVr1sTPz49u3brRq1cvqlSp8qfr\nu5u792cPDw+6d+/O+vXr6d69O+PGjXuk+yQiIiIiIiIij0a2eySndOnSrFy58r7lxYoVY968efct\nX7hwYdrroUOHMnTo0HS/nzx5ctrrpk2b0rRp0/tyfn5+AAQHB/+9youIiIiIiIhIpmBJ/aNBOSTD\nWPQsmYiIiIiIiFNl9z+NJ3tUcHYV7PbuzZPOrgKQDe8wyaqSf/rj2XcexLVMdTZXrm2UaXEsnF0N\nnzHKPLN7F/0oa5SZyzlmF3zKKNP/2gmig94wypQK/JTbu74yyuR6phtJBzYYZdxqtiZh68K/LniP\n3M17k3z6e6OMa/laXJsfaHf5gn1s4+ycHNDV7kyFT1YAEL9utt2ZPG37A3Bz2US7Mx7dR9oyX39g\nf6bL2wDcWjXd7kzejsMcrtvl6zftzjxWwMPhzBWDTJG/sR1HMon7Vtudca/bAYCUqP12Z6w+dQBI\nPrrd7oxrlaZG5wHYzoWby6cYZTxeHE7ib+eMMu5eZY3aJ9jaqCOZvc89a5Spt+U/xMwebpTx7D/F\nobol/nLKKONe4glu71hqlMnVuAcJm+cbZXK36EPShWNGGbfSlUk5FWaUsT7h59Dn1fWFY40yBXqP\nM7pWg+16nXJyj1HGWqG+0bUAbNcDR+rmSCb8p6tGmdplCju0HUe+GzhyrB2pW4a9P5vuvxP7TzMt\n+xK/Ya5ZpnU/hzIZdQzUDjJnO8jT2jYphyPfWxzZjsi9cswYJiIiIiIiIiIi9tIdJiIiIiIiIiLZ\nnKYVNqc7TIBu3bpx5MiRdMs+/PBD5s+//3bgsLCwtBl2RERERERERCR7UocJ0K5dOzZsSP/M4r//\n/W/atm3rpBqJiIiIiIiIiDOpwwRo06YNmzdvTvv5yJEjeHl5ERUVRbdu3fD396d///4kJiamy92d\nThhg8ODBhIWFERcXx+DBg+nduzf+/v5ERkZm2H6IiIiIiIiIyMOhDhOgSJEieHt7c/iwbaaaDRs2\n0L59e65du8a0adNYvHgx+fLlY9euXX+5roULF9KoUSMWLlzIe++9x5QpZjM3iIiIiIiIiDxsVkvW\n+ZdZaNDX/2rXrh3r16+nevXqbNu2jWXLlhEZGcno0aNJSUnh/Pnz1KtXDw8Pjz9dT0REBDExMaxZ\nswaA+Pj4jKi+iIiIiIiIiDxE6jD5rxYtWvDpp5/Stm1bHn/8cQoWLMjIkSP57LPP8PHxYfz48X+a\nT0pKAsDNzY3AwEB8fX0zotoiIiIiIiIi8gjokZz/ypcvH0899RRz586lffv2AMTFxVGiRAmuX79O\nWFhYWqfIXRaLhfj4eOLj4zl+/DgATz/9NFu2bAHg1KlTfPHFFxm7IyIiIiIiIiK/Y7VYssy/zEId\nJvdo3749u3fvplmzZgD07NmTHj16EBgYSN++fZk7dy6XLl1KK9+jRw9efPFFRowYQZUqVQDw9/fn\np59+omfPnowePZratWs7ZV9ERERERERExHF6JOceLVq0ICIiIu3nIUOGMGTIkLSfO3bsCNjGO3nQ\n7+/6+OOPH3FNRURERERERORRsqSmpqY6uxI5nSUT3XIkIiIiIiKSE2X3P41nFXzK2VWw28BrJ5xd\nBUB3mGQaSeGhRuXdarfj27r1jTJN9u3hYNdWRpkaKzYy2/DE6n/tBP0oa5SZyzl+ntjfKFNy5GyS\nDmwwyrjVbE3ivtVGGfe6HUjcu8osU68jyWci/rrgPVzL+RL3ZZDd5fP1DATgzDsv2Z0pN3URAPHr\nZtudydPW9r7cWjXd7kzejsMc3k78pnn2Z1r2dbhul6/ftDvzWAHb7FhXDDJF/kbGkbo5kjFp1+71\nbHfYJR/dbnfGtUpTW+aHLfZnqj3HjcXj7C4PkN9/LLfWzjLK5G0/kKTzR4wybt5VubV6ptl2Ogwx\natNga9cRnZ43yviu/Dex80YZZQr1neDQ/jhybXPkMy5h+2KjTO6m/qRE7TfKWH3qkHJil1nmqWe4\nNHOYUabokOncXD7FKOPx4nASNs83yuRu0cfoHAXbeerIZ5wjdXPkXFh68IJRpkeN0g7VzZE26six\nduQYZNT7k7B1oVmmee8My2TUMVA7yJztIHfz3oBj31sc2Y7IvTSGiYiIiIiIiIjI76jDRERERERE\nRETkd3J8h0n79u356aef0n5u06YN3377bdrPAwYMYOfOnc6omoiIiIiIiMhD4eypgjWtcBbk5+fH\n/v22Z55jYmKIj49P+xng0KFD1KpVy1nVExEREREREREnyPGDvvr5+bFt2zY6d+7MgQMH+Mc//sH3\n338PQFRUFKVLl2bLli0sXrwYFxcXKlSoQFBQEDdu3GDw4MEkJCTQpEkTli9fzrZt2wgPD2f69Om4\nurpSokQJgoKCcHd3d/JeioiIiIiIiIiJHH+HSZ06ddI6SMLDw2nQoAEpKSkkJCSwf/9+/Pz8iI+P\nZ968eSxbtozTp09z4sQJ/vWvf+Hj48PSpUvJnz9/2vref/99Zs+ezaJFiyhSpAgbN2501q6JiIiI\niIiIAGC1ZJ1/mUWOv8OkUKFC5M2bl4sXL3Lo0CHefPNNqlevzsGDBwkPD6dz585cu3aN/v1tU55G\nRUURGxtLVFQUdevWBaB58+YEBwdz+fJlzp07x6BBgwC4desWhQsXdtq+iYiIiIiIiIhjcnyHCdge\ny9m5cycWi4XcuXNTq1YtIiIi+OGHHxg7diwtW7Zk9erVFC1alH79+gGQmpqKi4vtBh3LfwelcXNz\nw8vLi5CQEKfti4iIiIiIiIj8fTn+kRywdZh89dVX1KhRA4BatWrxn//8h6JFi5KcnIzVaqVo0aL8\n8ssvHDlyhKSkJMqUKcORI0cA2LFjBwAFCxYE4NSpUwCEhIQQGRnphD0SERERERERkb9DHSbYxjE5\nevRo2mw4RYoUITY2Fj8/PwoXLkzDhg3p3Lkzs2bNom/fvkyaNImOHTsSHh5OQEAAly9fTrvbZMKE\nCYwYMYKePXvy/fffU758eWfumoiIiIiIiIjTxyXRGCZZVP78+Tl27Fi6ZZs2bUp7PXny5HS/e+WV\nV4iOjmbAgAE0atSIiIiItKmIa9euzYoVKx59pUVERERERETkkbGkpqamOrsSWdH169cZOnQoN2/e\nBGDUqFFUq1bNoXXdHQNFREREREREnCO7/2kc7FnR2VWw26sxmWNoC3WYZAIWi4Wkg5v+uuA93Gq0\nZH/rZkaZOhu2ceadl4wy5aYuIjroDaNMqcBP+Xlif6NMyZGz6UdZo8xczrH3uWeNMvW2/IfdjRsZ\nZRru2OlQ5tjL7Y0ylRes5f08T9hdfnS8bayceYWfsjvT9+oJAP6Z/0m7M2/e+BGAuYXs306/WNt2\nPi5g/3YGXbdtZ2u1OnZnmv9gu7NrZbHKdmc6XbTdTdZg0la7M9+NaA5Aw8nb7M7sfrdZhmYc2R+T\n86felv8AcDSgnd2ZKiGhACRsXWh3Jnfz3kbtE2xt9AvDLwCvxETy06g+RpkyE+azvmx1o0ybc4dZ\nVMSsbi9diSSsZVOjjN+m7YzN7WOUGZcQxeyC9p/XAP2vneD0W/5GmfIfLnZof5Y8Vsko0+vycSJf\n62iUqfj5KpKP7zDKuFZqzNoSVY0y7X854lBmqkcFo8w7N0/y74o1jTLPRx5w6Pz5MJ9Z3d6KO2n0\nGQe2z7k9Z68YZeo/XsSh4+bIeerIsXbkGGTU++PIcTP5nAfbZ70jdXPkWqV2kH3awVtxJwGM2kH/\na459F83ufxovKGL22epML1857uwqABrDRERERERERETkPuowERERERERERH5nRzVYbJkyRJefPFF\n/P396dKlC999993fXudnn31GRETEH/6+WbNmaeOciIiIiIiIiDiDs2e+0Sw5mdiFCxdYvnw5X3/9\nNW5ubpw9e5bRo0fToEGDv7Xe119//SHVUEREREREREQyixzTYRIXF8ft27dJSkrCzc2Nxx9/nMWL\nFxMQEEDVqlU5cuQIt2/fZsaMGZQqVYoZM2YQHh5OSkoK/v7+tGvXjujoaN59911SUlIoWbIkU6ZM\nYdSoUbRs2ZI6derw1ltvcevWLRISEggMDKR6dbPBAUVEREREREQkc8gxj+RUrFiR6tWr07x5c959\n913Wr19PcnIyAIULFyYkJIT27duzcOFCwsPDiY6OZsmSJSxatIg5c+aQkJDAjBkzePnll/nyyy/x\n8vLiyJEjaeu/dOkSXbt2JSQkhGHDhvH55587a1dFRERERERE5G/KMXeYAEydOpWoqCh27tzJvHnz\nWLp0KampqdSvXx+AGjVqsGPHDg4cOMChQ4cICAgA4M6dO1y6dIljx44xatQoAN555x0Ali5dCsBj\njz3G7NmzCQ4OJjExkbx58zphD0VERERERETuZ7VkosFBsogc02GSmppKYmIiPj4++Pj4EBAQQOvW\nrUlOTk6bbzs1NRWLxYK7uztdunShX79+6dZhtVr/cG7uhQsXUqxYMT744AN++OEHpk6d+sj3SURE\nREREREQejRzzSM7XX39NYGBgWofHjRs3uHPnDkWKFCE8PByAgwcP4uPjQ/Xq1dm+fTt37tzh9u3b\nBAUFAVC1alX27t0LwMyZM9PNsnP16lXKlCkDwJYtW0hKSsrI3RMRERERERGRhyjHdJh06tSJIkWK\n0LVrV1566SX69+/P6NGjyZ07Nz///DOvvvoqoaGhvPzyy9SsWRM/Pz+6detGr169qFKlCgCDBw9m\n+fLl+Pv7c+HCBfz8/NLW36FDB7744gv69OlD9erVuXTpEt98842zdldEREREREQkjbOnCta0wpmY\n1Wpl+PDh9y0PDg7mxRdf5Mknn0y3fOjQoQwdOjTdshIlSrBgwYJ0yyZPnpz2esOGDWmvmzdvDkDn\nzp3/btVFREREREREJINZUv9oUI4cIiAggMDAwPs6TDKSRYPviIiIiIiIOFV2/9P4K6/Kzq6C3br9\ndszZVQBy0B0mfyQkJMTZVQDg3JUbRuXLFsnP7R1LjTK5GvcgfsNco0ye1v24vesrs+08042kAxv+\nuuA93Gq2Zu9zzxpl6m35D/0oa5SZyzmHjtuSxyoZZXpdPs7WanWMMs1/2M/2WvXsLt/0e9t4OtFB\nb9idKRX4KQA76jWwO9N4r22snv2tm9mdqbNhGwDry1a3O9Pm3GGHt3P6LX+7M+U/XAzA85/ssjvz\n7wHPZPpM84932p3ZOqgRADeXT7E74/Gi7Q695DMRdmdcy/kCkHIqzO6M9Qk/ozYNtnYd0el5o4zv\nyn+TFB1plHErVZFTg7sZZZ746Cuj8xps53bC1oVGmdzNe3O4e2ujTPVlG/ihZxujTLUv15N89qBR\nxvXxGozL7WOUGZsQxYEOLYwyNVdvNmqfYGujkRevGWUqFivIT6P6GGXKTJjPwa6tjDI1Vmx06HPk\n+sKxRpkCvcc5tD//rljTKPN85AGHPucTL54xyrgXK+fQcXPk3HbkWDtyDDLq/dlYwdco0+pkBNtq\n1DXKNDu4jw3laxhlWp8+yNGAdkaZKiGhagfZqB20Pm373DFpB1VCQgGM6tbs4D67y0rOkeM7TERE\nRERERESyO00rbC7HDPoqIiIiIiIiImKvTNlhEhoaSpUqVYiJifnb67pw4QKdOnX6W+uIi4tj1y7b\nLfKfffYZERFmt/yKiIiIiIiISNaSaTtMvL292bRpk7OrAsDRo0fZvXs3AK+//jq+vmbP9omIiIiI\niIg4k7OnCta0wg9BbGwshw8fZuLEicybN48ePXpw7Ngxxo0bh8ViwdfXl+HDhz9w2alTpxg/fjwW\niwUPD490U/4ChIeHM336dFxdXSlRogRBQUFEREQwf/58bt26xfDhw9m3bx+bNm3izp07NGnShIED\nBzJ+/Hji4uJ4/PHHiYiIoGXLljzzzDOMGTOG8+fPk5iYyODBg3nmmWdo0aIF3bp1Y/v27SQmJvLF\nF1+QL18+Jx1NERERERERkexn4sSJHDp0CIvFwsiRI6le/X8TTixZsoQ1a9bg4uJC1apVGTVqlEPb\nyHR3mGzcuJFnn32WRo0acfbsWS5evMj777/PuHHjWLZsGVeuXCE6OvqBy4KCghg/fjwLFy6kYcOG\nLFmyJN2633//fWbPns2iRYsoUqQIGzduBODHH38kODiYqlWrAvDll1+yfPlyVq5cSVxcHK+++ipt\n2rShW7f/jZy9bt063N3dWbx4MR9//DFBQUEApKSkUL58eZYsWULp0qXZu3dvBh05ERERERERkexv\n3759nDvOTdEEAAAgAElEQVR3jq+++ooJEyYwYcKEtN/FxcURHBzMkiVLWLp0KVFRURw8aDbL312Z\n7g6T0NBQ+vfvj9VqpVWrVqxfv54zZ85QsWJFAKZOnQrwwGWHDx8mMDAQgMTERKpVq5a23suXL3Pu\n3DkGDRoEwK1btyhcuDDFihXjqaeewt3dHYDcuXPj7++Pq6srV69eJTY29oH1PHLkCH5+fgAUK1YM\nd3f3tLK1a9cGoHjx4ty4YTZdsIiIiIiIiMjDlp1mydmzZw/PPfccAD4+Ply7do24uDjy5cuHm5sb\nbm5u3Lp1i7x58xIfH0/BggUd2k6m6jD59ddfOXToEJMnT8ZisZCQkED+/Plxcbn/RpgHLcuTJw+L\nFi3Cck9DuHDhAgBubm54eXkREhKSLhMWFpbWWRIdHc2CBQtYtWoVHh4etGv353N9p6ampr1OTExM\nq5PVan1gGRERERERERH5ey5fvkyVKlXSfvb09OTSpUvky5ePXLlyMWDAAJ577jly5cpF27ZtKVeu\nnEPbyVSP5ISGhtKrVy/WrFnD6tWr2bhxI9euXaN8+fIcOnQIgJEjRxIVFYWPj899yypWrMiOHTsA\n2yMze/bsSVv33R6lU6dOARASEkJkZGS67V+9ehVPT088PDw4evQo0dHRJCUl4eLiQnJycrqy1apV\nIywsDIBffvkFFxcXChQo8AiOioiIiIiIiIj8kXtvVIiLi2Pu3Lls3LiRrVu3cujQofv+9rdXprrD\nZN26dUyZMiXtZ4vFwgsvvEBqamraAK41atTAx8eHUaNG8d577923LDAwkM8//5xcuXLx4YcfEhcX\nl7a+CRMmMGLEiLS7Tbp165ZuiuBKlSrh4eFB9+7dqVWrFt27d2fcuHGMHDmSadOmUbx48bSybdu2\nZd++fQQEBJCUlMT48eMf8dERERERERERES8vLy5fvpz282+//UbRokUBiIqKwtvbG09PT8A2ZMaR\nI0fShvQwkak6TFatWnXfsgEDBgAwcODAdMufeuopli5dmm6Zj48PX375ZbplhQoVYuXKlYDtQK1Y\nsSLd7/38/NLGIrFarQQHBz+wbrt27bpv2b0Dy9y1bdu2tNfDhw9/4LpEREREREREMpJLNhrDpGHD\nhnz88cd0796do0eP4uXllTY7balSpYiKiiIhIYHcuXNz5MgRmjRp4tB2LKkaZMPpLNmo4YqIiIiI\niGRF2f1P49CS1f66UCbR7ucf/rLMtGnTCA8Px2KxMHbsWI4dO0b+/Plp0aIFy5YtY+XKlVitVnx9\nfXnnnXccqoc6TDIBi8VC0oENRhm3mq25OneEUaZwv0nc3rH0rwveI1fjHg7VLXHfaqOMe90O7G7c\nyCjTcMdOh/anH2WNMnM5R9LBTUYZtxotSTm5568L3sNaoT4/vtHZ7vJPfvoNAAe7trI7U2OFbSrt\n82P62p3xHj8PgNh59s9dXqiv7e6rX6cM/IuS/1N8+CwAbu/6yu5Mrme6OVy31nN2253Z8P8aZmim\n3dzv7M6E9mvg8Ha21ahrd6bZwX0ArC9b/S9K/k+bc4cBiPsyyO5Mvp6BHO7e2u7yANWXbTBqA2Br\nB5sr1zbKtDgWzvWFY40yBXqPcyjjyP4c6NDCKFNz9Wajaw7Yrjv/rljTKPN85AHi1802yuRp25+9\nzz1rlKm35T+Eljb7Itjuwg9G10OwXRPjN80zyuRp2Zdbq6YbZfJ2HEbkax2NMhU/X8UXnma3G78S\nE8kKr8pGma6/HXOo7Tjynh75+ZpRpmrJgg4dt9XFq/x1wXt0+PWoQ8fakWOQUe/PsZfbG2UqL1jr\nUObkgK5GmQqfrDD67AHb54/aQfZpBxU+sT0h4Mh3EJO6VV6wVh0mmYg9HSYZIVM9kiMiIiIiIiIi\nD5/FqicbTGWqWXJERERERERERDKDLNVhEhoaSpUqVYiJiXFqPYYOHUpCQoJT6yAiIiIiIiIij06W\n6zDx9vZm0yaz8SQethkzZpA7d26n1kFEREREREREHp0sM4ZJbGwshw8fZuLEicybN48ePXrw3Xff\nMXHiRB577DHKlSuHp6cnb7zxBm+//TY///wzvr6+bNiwgR07dhAQEECFChUAGDZsGCNHjuTatWuk\npKQwevRoKlasyGeffcbmzZtxcXGhadOmvPHGGw9c1qxZM9auXcuNGzcYOXIkSUlJWCwWJkyYgMVi\n4d1338Xb25sTJ05QqVKlB04/LCIiIiIiIpJRXDSGibEsc4fJxo0befbZZ2nUqBFnz57l4sWLTJs2\njalTpxIcHMzx48cB2LlzJ7dv32b58uXUq1eP3377LW0dFSpUYMyYMSxcuJBGjRqxcOFC3nvvPaZM\nmQLA/PnzWbp0KcuWLaNAgQJ/uOyumTNn0qVLF0JCQujZsyezZtlm+Th69CjDhg3j66+/5ttvv+X6\n9esZcYhERERERERE5CHJMneYhIaG0r9/f6xWK61atWL9+vVER0dTubJtiq3GjRuTkpJCVFQUNWva\npjxs0qQJrq7/28Xq1W1TUUVERBATE8OaNWsAiI+PB6Bly5a88sortGvXjn/84x9/uOyuI0eO8NZb\nbwHg5+fHJ598AkCZMmUoWrQoAF5eXty4ceO+zhYRERERERERybyyRIfJr7/+yqFDh5g8eTIWi4WE\nhATy58+frozFYru9KDU1FavVmm7ZXW5ubmn/DQwMxNfXN93vx40bR1RUFBs2bCAgIIAVK1Y8cNm9\n27w7V3dSUhIuLrYbdu5u/67sPp+3iIiIiIiIZG4Wa5Z5wCTTyBJHLDQ0lF69erFmzRpWr17Nxo0b\nuXbtGvHx8URFRZGSksLu3bsB290dR44cAWDXrl2kpKTct76nn36aLVu2AHDq1Cm++OILbty4waxZ\ns/Dx8WHgwIEULFiQixcv3rcsLi4ubT3VqlUjLCwMgP3791O1atVHfShEREREREREJANkiTtM1q1b\nlzbOCNju7HjhhRdwcXFh0KBBlC5dmvLly6cNzPrNN9/Qo0cP6tatS6FChe5bn7+/PyNGjKBnz57c\nuXOHUaNGkT9/fq5evUqXLl3Imzcvvr6+lCpV6r5l965v8ODBjBo1iuXLl+Pm5sbEiRNJSkrKkGMi\nIiIiIiIiIo9OlugwWbVq1X3LBgwYwK5du2jfvj2lS5dmzJgxlClThvj4eLp06ULLli25ePFi2hTE\nISEhadl8+fLx8ccf37fOwMBAu5Zt27YNAA8PD+bNm3ff71euXPnA1yIiIiIiIiLOYNEsOcYsqVl4\ngI2dO3fy4Ycf4uHhQZEiRZg2bRoWiyVtWuE7d+4waNAgmjRp4uyq/qnfj7UiIiIiIiIiGSsL/2ls\nl01P1nR2FezW8scDzq4CkMU7TLILi8XCjZu3jDL5PfISv+n+u1v+TJ6WfR3KJGxdaJTJ3bw3iXvv\nvyvoz7jX68juxo2MMg137GTJY5WMMr0uHyfp4CajjFuNlvSjrFFmLudYVtSsbt0vHWdbjbp2l292\ncB8AP43qY3emzIT5AGyvVc/uTNPv9wLwbd36dmea7NsDQGjpanZn2l34AYDvmja2O9Ng+w4Ajga0\nsztTJSQUgNe+irA783k33wzN9Flq/wfE/B41Hc6YnKfu9ToCkHThmN0Zt9K2WcySz9h/DFzL+XJq\ncDe7ywM88dFXRu0GbG3ndswvRplcniU4/moHo0yl4NVsrlzbKNPiWDjx62YbZfK07c+BDi2MMjVX\nbzY6d8B2/iRePGOUcS9Wjo0VfP+64D1anYwg8rWORpmKn68i8ZdTRhn3Ek+wMfKiUaZVxWJEdHre\nKOO78t/sb93MKFNnwzajzwSwfS440nYufjDYKFPs7Y8cqltYy6ZGGb9N27lu+P2ogEdeh+oWHfSG\nUaZU4KcOHWtHjkFGvT9bq9UxyjT/Yb9D393+XdHsD7bnIw8Q9WYPo4zPP5eqHWSjdvB8pO07jkk7\n8PnnUgCjujXcsVMdJplIZukwyRKDvoqIiIiIiIiIZKQsMYaJiIiIiIiIiDjORWOYGNMdJv8VGhpK\nlSpViImJ+cMyx48f56OPPgLAz88PgAkTJnD+/Hni4uLYtWtXhtRVRERERERERB4tdZj8V2hoKN7e\n3mmz6jxIpUqVGDw4/fODo0aNwtvbm6NHj7J79+5HXU0RERERERERyQB6JAeIjY3l8OHDTJw4kXnz\n5tGjRw++++47Jk6cyGOPPUa5cuXw9PSkbt26LFmyJO0uE4CAgAACAwMZP348cXFxeHp68vXXX7Nx\n40YsFgtr1qzh6NGjjBgxwol7KCIiIiIiIjmZxUX3S5jSEQM2btzIs88+S6NGjTh79iwXL15k2rRp\nTJ06leDgYI4fP/6X63j11Vdp06YNr732Gk899RQREbZZIbZu3Uq7dmazEIiIiIiIiIiIc6nDBNvj\nOO3atcNqtdKqVSvWr19PdHQ0lStXxmq10rix2XSVHTp0YP369SQmJnLhwgWqVbN/alURERERERER\ncb4c/0jOr7/+yqFDh5g8eTIWi4WEhATy58+frozFYjaacOPGjZk5cyZ79+6laVOzedZFRERERERE\nxPlyfIdJaGgovXr14t133wUgNTWV559/nvj4eKKionj88cfZvXt32qw4f8TFxYXk5GQA3NzcqFOn\nDh999BEffvjhI98HERERERERkT+jaYXN5fgOk3Xr1jFlypS0ny0WCy+88AIuLi4MGjSI0qVLU758\neVz+YoCcypUrM23aNIoXL86rr75K69atOXz4MGXLln3UuyAiIiIiIiIiD1mO7zBZtWrVfcsGDBjA\nrl27aN++PaVLl2bMmDGUKVMGPz+/tDtNwsLCAAgJCUnL7dq1K+31d999R/fu3R9x7UVERERERETk\nUbCkpqamOrsSmdHOnTv58MMP8fDwoEiRIkybNg13d3e7sq+//jq5c+dmxowZWK3WvyxvOkaKiIiI\niIiIPFzZ/U/j7b5/PsxEZtI0IszZVQDUYZIpWCwWLsbGGWWKFcpH8tmDRhnXx2uQErXfKGP1qUPy\n6e/NtlO+FslnIswy5Xw59nJ7o0zlBWvZWq2OUab5D/tJObnHKGOtUJ9lRSsZZbpfOk4/zB7Hmss5\nDnRoYXf5mqs3A3B94Vi7MwV6jwMgrKX9gxH7bdoOQHi75+zO1A7dAsCuhs/YnXlmt+0OrcjXOtqd\nqfi57Q6xc+++bHem7OQFAPRZesDuzPweNR3OvPaV/efC5918Hd5O7yX2n6cLe9UCMDoXrBXqA5D8\n02G7M65lqgOQFB1pd8atVEUuvPe63eUBSr/3Gcdf7WCUqRS8msRfTxtl3IuX59cpA40yxYfPMjp3\nwHb+pJzY9dcF72F96hl+fKOzUebJT7/h/Ji+Rhnv8fNIOn/EKOPmXdXo2ga261t00BtGmVKBnzpU\ntw93nDLKvNX4Cc6885JRptzURQ69PybXarBdr+M3zDXK5Gndj0szhxllig6Zzv7WzYwydTZs44ee\nbYwy1b5cT8KNWKNM7vyFHDpujpzbjhxrR45BRr0/jhw3R/bnu6Zms0822L7D6HMebJ/1agfZpx00\n2L4DcOz7nkndqn25Xh0mmUhm6TDRtMIiIiIiIiIiIr+T48cwEREREREREcnuLFbdL2EqWx+xCxcu\n4OvrS0BAAAEBAXTr1o3w8PA/LNupU6cMrqGIiIiIiIiIZEbZ/g6TcuXKpc1ks3//fubMmUNwcLCT\nayUiIiIiIiIimVm27zC51+XLl/Hy8iIyMpJx48bh6uqKi4sLM2fOTFduzZo1LF68GBcXFypUqEBQ\nUBArV67k+++/JyYmhjNnzvDqq6/StWtXdu/ezfTp07FarbRp04aXX36Z8PBwpk+fjqurKyVKlCAo\nKMjuGXZERERERERExPmyfYfJmTNnCAgI4Pbt21y8eJHg4GAuXrxIYGAglStXZubMmaxdu5amTf83\nInR8fDzz5s2jQIEC9OrVixMnTgDw448/smzZMs6ePcuwYcPo0qUL48aNY9myZRQsWJD+/fvTvXt3\n3n//fRYsWEChQoWYOnUqGzdu5B//+IezDoGIiIiIiIjkcC5Wi7OrkOVk+w6Tex/JiYqK4s033+SD\nDz5g2rRpJCQk8Ntvv9G+ffrpbO92ftzNxMbaprSrUaMGVquV4sWLc+PGDWJiYsiVKxeenp4AzJ07\nl8uXL3Pu3DkGDRoEwK1btyhcuHBG7a6IiIiIiIiIPATZvsPkXj4+PuTKlYsJEybw2muv0bhxY4KD\ng7l161ZamcTERMaPH8/q1aspWrQo/fr1S/udq2v6w+Xi4sKdO3fSLXNzc8PLyyutk0ZERERERERE\nsp5sPUvO78XGxnLp0iUuX75MmTJlSExM5NtvvyUpKSmtzM2bN7FarRQtWpRffvmFI0eOpPv9vQoX\nLkxKSgoXL14kNTWVfv36YbHYbnM6deoUACEhIURGRj76nRMRERERERH5AxYXS5b5l1lk+ztM7o5h\nAnD79m0CAwO5cuUKAwYMwNvbm4CAAMaPH0+bNm0AWydIw4YN6dy5MxUrVqRv375MmjSJ3r17P3D9\nY8eOZfDgwQC0bt2aAgUKMGHCBEaMGJF2t0m3bt0yZmdFRERERERE5KHI1h0mpUuXJiIi4oG/u7cT\no0WLFgCsXLkSgMmTJ6cr+8orr6T72cPDg23btgFQv3596tevn+73tWvXZsWKFX+v8iIiIiIiIiLi\nNJbU1NRUZ1cip7v7GI+IiIiIiIg4R3b/03hn/YbOroLdGu3Z7ewqANn8DpOs5Pal80blcxX15sJ7\nrxtlSr/3GZdmDjPKFB0ynWvzA40yBfsEEfdlkFEmX89A3s/zhFFmdPwptteqZ5Rp+v1efnyjs1Hm\nyU+/YVuNukaZZgf3caBDC6NMzdWb6UdZu8vP5RwAq4tXsTvT4dejAHxc4Em7M4Ou/wjA7IJP2Z3p\nf802Ffc7buXszkxNOgPACq/Kdme6/nYMgPVlq9udaXPuMABP9F9pd+bU7E4APDlwld2ZH2d1dDjj\nSN0cyex97lm7M/W2/AfA6BpSdMh0AJLPPPhOvwdxLefLkscq2V0eoNfl48wtZH/7BOgXe4Kby6cY\nZTxeHG7U1sDW3v6Z3/7zDeDNGz9yfkxfo4z3+HmMze1jlBmXEOXQcbuxeJxRJr//WHY1fMYo88zu\nXQ4d68sf/59R5rFB07h9Jdook6tIKTZW8DXKtDoZ4VC7fsvV/msowIfJZ9hRr4FRpvHe71hW1Kxu\n3S85VjeTzwSwfS6cv3LDKONdJL9DdTP57AHb548jx9qRY5BR748jmRHu5Y0ykxJPO7SdeYXNrlV9\nr55QO8hG7eDDZNt3RJN20Peq7buoSd0mJZ62u2xW5WLNUUOYPhQ6YiIiIiIiIiIiv6MOExERERER\nERGR38kSHSYXLlzA19eXgIAAAgIC6NatG+Hh4X9avlMn2y3nzZo14+bNmw+1Pvv37+fKlSt2lQ0L\nC0ubRUdERERERETEGSxWS5b5l1lkiQ4TgHLlyhESEkJISAj/93//x5w5c5xWl2+++cbuDhMRERER\nERERyXqy5KCvly9fxsvLC4DIyEjGjRuHq6srLi4uzJw58y/zu3fvZvr06VitVtq0acPLL79MWFgY\nM2bMwNXVlWLFijFp0iRCQ0P5/vvviYmJ4cyZM7z66quULFmSLVu2cPLkST7++GNefvllKleuTMOG\nDalevTrjx4/HxcUFDw+P+6YnFhEREREREZGsIct0mJw5c4aAgABu377NxYsXCQ4OBuDKlSsEBgZS\nuXJlZs6cydq1a2natOkfric1NZVx48axbNkyChYsSP/+/enevTtjx47liy++oESJEowfP561a9di\nsVj48ccfWbZsGWfPnmXYsGGsXr2aSpUqERgYSMmSJTl//jyffPIJFSpU4KWXXuKdd97h6aefJjg4\nmEWLFuHn55dRh0hERERERETkgTLToy5ZRZZ7JGf58uXMnz+foUOHkpycTJEiRZg+fTr+/v6sW7eO\n2NjYP11PTEwMuXLlwtPTE6vVyty5c0lISMBisVCiRAkA/Pz8OH78OAA1atTAarVSvHhxbty4f2q7\nPHnyUKFCBQCioqJ4+umn09Zx7Nixh3kIRERERERERCSDZJk7TO7l4+NDrly5+OWXX5gwYQKvvfYa\njRs3Jjg4mFu3bv1p1sXFhTt37qRbZrFYSE1NTfs5KSkJi8XW++bq+ueHyM3N7YHLk5KScHHJMv1R\nIiIiIiIiInKPLPkXfWxsLJcuXaJYsWLExsZSpkwZEhMT+fbbb0lKSvrTbOHChUlJSeHixYukpqbS\nr18/LBYLFouFn3/+GYB9+/ZRtWrVP1yHxWIhJSXlvuUVKlQgIiICsM2k82frEBEREREREZHMK8vc\nYXJ3DBOA27dvExgYiLu7O/7+/gwYMABvb28CAgIYP348bdq0+dN1jR07Nm2q39atW1OgQAGCgoJ4\n6623cHV1xdvbm7Zt27JmzZoH5uvWrcvgwYOZPXt2uuWjR49m3LhxWCwWChYsyKRJkzh69OhD2HsR\nERERERERx7lYs+T9Ek6VJTpMSpcunXbnxu9169aNbt26pf3cokULAFauXAnAtm3b7svUr1+f+vXr\np1tWu3Ztli5dmm5Zp06d0l57eHikrWvgwIEMHDgQgLCwsLQyTzzxBCEhIenW4efnp4FfRURERERE\nRLIYS+q9g3eIU9wdL0VEREREREScI7v/aRzW4o9nk81s/DZvd3YVgCxyh0lOcGv1TKPyeTsMYXPl\n2kaZFsfCiXyto1Gm4uerODmgq1GmwicrOPPOS0aZclMXMa/wU0aZvldPEB30hlGmVOCnHOzayihT\nY8VGfhrVxyhTZsJ8ri8ca5Qp0Hscq4tXsbt8h19tj3v1o6zdmbmcA2B340Z2Zxru2AnAjnoN7M40\n3vsdAFur1bE70/yH/QBG70+NFRsB+K5pY7szDbbvAOC1rx5819qDfN7NF4A3Vhy0O/Np1xoObyej\nMgc6tLA7U3P1ZgCjc6HMhPkAJGxdaHcmd/PebChfw+7yAK1PH2RXw2eMMs/s3sXVuSOMMoX7TTI6\nd8B2/pi0T7C10W016hplmh3cxwqvykaZrr8dc+hzJGb2cKOMZ/8pnB/T1yjjPX4eYS3NvtT5bdrO\nr1MGGmWKD59FwvbFRpncTf2NrodguyY60nb+XbGmUeb5yANG5zXYzu1v69b/64L3aLJvj0NtZ33Z\n6kaZNucOE7z/nFHm1TplHTpujrw/jhxrR45BRr0/GZUx+W4Atu8HjhwDtYPs0w7ufkc0OQZN9u0B\nMKpbi2PhdpfNqjStsDk9xCQiIiIiIiIi8juZ/g6Ts2fPMnHiRGJiYrhz5w6+vr4MHz4cd3d3Z1dN\nRERERERERLKpTH2HSUpKCoMGDaJv3758/fXXfPPNNwB88sknTq6ZiIiIiIiIiGRnmfoOk927d1O+\nfHnq1rU9y22xWHj77bdxcXFh4cKFrF+/HoDmzZvz+uuv8+677+Lp6cnRo0eJiYnhtddeY+XKlVy9\nepXFixezefNmdu7cSVxcHL/++isvv/wynTt3JiwsjBkzZuDq6kqxYsWYNGkSly9fTttWSkoKH3zw\nAWFhYZw8eZLhw4dz8+ZN2rdvz7Zt23j++edp3LgxRYoUoVOnTowaNYqkpCSsVivvv/8+JUuWdOZh\nFBERERERkRzOxUVjmJjK1B0mp0+fplKlSumW5c6dm/Pnz7Nq1Sq+/vprALp27UqrVraBIl1dXVm4\ncCFvvfUWERERLFiwgLfffjtt+t9Tp06xatUqrl+/TocOHejYsSNjx47liy++oESJEowfP561a9dy\n/fp1GjRowIABAzh69CiXLl36w3omJyfTuHFjGjduzMiRI+nTpw8NGjTg22+/Zfbs2bz//vuP6AiJ\niIiIiIiIyKOQqTtMLBYLKSkp9y0/fvw4Tz/9NK6uturXrFmTyMhIAKpXt4067eXlRfny5QF47LHH\nuHHjBgB16tTB1dUVT09PChYsyNWrV7FYLJQoUQIAPz8/9u/fz4svvsjAgQO5ceMGLVu2xNfXl9On\nT/9hXe9uNyIigjNnzjBnzhxSUlLw9PR8SEdDRERERERERDJKpu4wKV++PEuWLEm3LDExkZMnT6ab\nIzspKQkXF9twLFarNW35va/vlr9z5066ZRaL5b51WSwWnnzySVavXs3u3buZPn06nTt3xmL53y1M\nycnJ6erl5uaW9t+ZM2fi5eXl8H6LiIiIiIiIPEwWa6YewjRTytRHrGHDhkRHR7Nt2zbA1tnxwQcf\ncPbsWQ4ePEhycjLJyckcOnTovkd3/sjBgwdJSUkhJiaGmzdvUqhQISwWCz///DMA+/bto2rVqqxb\nt46TJ0/y3HPPMWTIEI4cOUK+fPn47bffAPj+++8fuP6nn36aLVu2ALBnzx7Wrl37dw+DiIiIiIiI\niGSwTH2HiYuLC8HBwYwZM4ZZs2bh7u5OgwYNGDFiBEuXLsXf35/U1FS6du1KqVKl7FpnqVKlGDJk\nCOfOnePNN9/ExcWFoKAg3nrrLVxdXfH29qZt27acOHGCsWPHkjdvXqxWK6NHj6ZYsWLMmTOHgIAA\nmjRpku6Ok7sGDhzIyJEjWbduHRaLhUmTJj3swyIiIiIiIiIij1im7jAB21gkn3766X3Le/XqRa9e\nvdItmzx5ctrr4cOH3/d65cqVlClTJt3vAGrXrs3SpUvTLatSpUraoLL3WrlyZdrrvn37AqTdAQNQ\nrFgxgoOD/3K/RERERERERDKKi1Wz5JjK1I/kiIiIiIiIiIg4gyX13hFPxSke9GiPiIiIiIiIZJzs\n/qdxxAvPO7sKdvP917+dXQUgCzySk1Mk/fyjUXm3kk8SM3v4Xxe8h2f/KdxaNd0ok7fjMOLXzTbK\n5Gnb36HMP/M/aZR588aP7KjXwCjTeO93nB/T1yjjPX4e22vVM8o0/X4vYS2bGmX8Nm3n4wL2H4NB\n1x80A+MAACAASURBVG1tZnfjRnZnGu7YCUA/ytqdmcs5AIfqZvKevnnDltlWo67dmWYH9wGwvmx1\nuzNtzh0GoPZ7m+zOhL/XEoC64+y/cO8b+7zDGUfq5kjmp1F97M6UmTAfwOi649l/CgCJv5yyO+Ne\n4gnWlqhqd3mA9r8cYYVXZaNM19+OcfPrD4wyHl3eduias6hIRaPMS1ciuTRzmFGm6JDpfOFptp1X\nYiJZXbyKUabDr0e5vnCsUaZA73Hsfe5Zo0y9Lf8xuhaA7Xpwde4Io0zhfpO4cfOWUSa/R16H6rax\ngq9RptXJCIc+FyM6mX0Z/v/s3Xl4Tdfi//H3ORkaiZhiHmIMMZcqWr5aamy52lSIEqVNCRKhrqEx\nq1BzDalSWm1qDCl1W7RXlEtVe9Ei5iCCxhQkgmaQ3x/5OVck9OxTTSI+r+fJ05x11mfvtdfZ2ZLV\nvddqEPEd33k2NJRpe2SvoX8TIOPfhY8K1zCUGXD9KKcvJxrKVCrualO/2fL52NLXtvRBTn0+Mwt6\nGMoMvXHcpuuOLfuJKGXsGu914ZDOg3x0Hgy9cRzA0HngdeEQgKG29Yk/YnVdeXJowEREREREREQk\nnzNpDhPD8uWAyenTp5k8eTLx8fHcuXOHBg0aMGLECBwdHR/J9rdv387Zs2d54403Hsn2RERERERE\nRCRvyXeTvqalpREYGIifnx9r1qxh7dq1AISGhj6yfbRo0UKDJSIiIiIiIiL5WL67w2Tnzp1UqVKF\nxo0zni82mUwMGzaM8+fP0717d5ydnenZsyfOzs7Mnj0be3t7SpUqxZQpU7h8+TLDhg3DbDaTlpbG\n9OnTLfl7y3bv3s3x48fp0aMHI0eOpEKFChw9epSaNWsSEhLCkSNHGDlyJK6urtSpU4erV69mWvJY\nREREREREJCeZ7PLd/RJ/u3w3YHLy5Elq1qyZqczJyQlHR0cOHz7M1q1bKVq0KO3bt+ezzz6jTJky\nTJw4kQ0bNpCQkMDzzz/PwIEDiYqK4tKlS+zbty9L2b2ioqKYPXs2bm5utGjRgoSEBEJDQxk4cCBt\n2rQhKCiIAgUK5GQXiIiIiIiIiMhflO+GmEwmE2lpadm+V6FCBYoWLcq1a9cwmUyUKVMGgCZNmnD4\n8GGaNWvG+vXr+eCDD0hOTubpp5/Otuxe7u7ulChRArPZTMmSJUlMTCQ6OpqGDTNmsm7VqtXfe8Ai\nIiIiIiIi8sjluwGTKlWqcODAgUxlycnJ3Lx5EwcHByBjUOXeNbZTUlIwmUxUr16d9evX06hRI2bN\nmsW6deuyLbuXnZ1dptfp6emkp6djMpks+xIRERERERHJTWY702PzlVfku0dymjVrxrRp04iMjKRV\nq1bcuXOH6dOnc+3aNUudwoULYzKZOH/+PGXLluXnn3/mmWee4ZtvvqFChQq0bt2aIkWKsGnTJhwc\nHLKU1ar18DXA3d3dOXjwIC1atGD79u3Y2+e7bhYRERERERHJ1/LdX/Jms5klS5YwduxY5s+fj6Oj\nI88//zy9evUiKCjIUu/9999n6NCh2NvbU6FCBV555RWOHj3KuHHjcHZ2xs7OjtGjR3P79u0sZb/9\n9ttD29C/f39Gjx7N559/TrVq1UhMTPy7D1tEREREREREHqF8N2ACULJkST7++OMs5REREZbvGzVq\nxIoVKzK9X7t2bdasWZMld39Z1apVs93m3e8vX77MjBkz8PT0ZOHChRQtWtS2AxERERERERGRXJEv\nB0xym6OjI6NGjcLJyQknJydmzpyZ200SERERERGRJ5jJnHfmBnlcmNLvnf1UcoUmhhUREREREcld\n+f1P44M9XsntJlitzrJvcrsJgO4wyTNSz+w3VN/evR6X5rxrKFMiaBZJq6cayrh0HUHSysnGMj7B\n3PxqlqGM82vvsrBIDUOZfteO8ksHY8s2P7sxkmuLRxnKFPELYVvj5wxlXvh5F//t2NpQptG//s1H\nha3vgwHXjwKwvenzVmda/PQjAPMKVbc6E5hwDIB+VLQ6s5AYm/cTUerhkyrfy+vCIQC+cPO0OtPr\nyhEAmk+LtDqzY3jGedZixlarM9v/2RKAF2b9YHVm27sv5mjbzk8eYHWmbPBHANz+/lOrM05t3gLg\njyvnrM485VaOTR4NrK4P0P74PkM/O5Dx85MaZX2fAdjXbpljbbswfZChTKlhc1lZoqahjM+lwzZl\nUv77L0MZh0YdOfDGy4YydZd/y+52LQ1lmmzeyh/bV/x5xXs81aI7VxKSDGXcCrnwbcV6hjIvx+zn\ns2LWX6cA+sQfsenciRnZ21Cm4gdLbfq31JZ/s41cqyHjen3kwnVDGc9ShW3qN1v+zbalr23pg5z6\nfGzJ5NR5beR3Hcj4fUfnQf45D/7K77xG2tYn/ojVdeXJoQETERERERERkXzObGfO7SY8djRgApw+\nfZrJkycTHx/PnTt3aNCgASNGjMDR0TG3myYiIiIiIiIiueCJH2JKS0sjMDAQPz8/1qxZw9q1awEI\nDQ3N5ZaJiIiIiIiISG554gdMdu7cSZUqVWjcuDGQMQHrsGHD6Ny5M15eXpZ6Xl5enD17lpEjRzJm\nzBgCAwN57bXXOH/+PADnzp3Dy8uLtLQ0goOD8fX1pXv37uzatStXjktEREREREREbPfED5icPHmS\nmjUzT3rn5OT00MdxChcuzLx582jdujVbt2ZMGrhlyxbatm3Lhg0bKFGiBGFhYYSGhjJ5srEJU0VE\nREREREQeNZOd6bH5yiue+AETk8lEWlqaoUy9ehmz47dt25bIyIzVLLZs2UK7du3Yt28fW7ZswdfX\nl6CgIP744w+Sk5MfebtFRERERERE5O/zxE/6WqVKFZYtW5apLDk52fKozV2pqamW7x0cHADw8PDg\n4sWL/P777yQmJlK5cmUcHBzw9/enY8eOf3/jRURERERERORv8cTfYdKsWTPOnTtnuVPkzp07TJ8+\nnc2bN3PlyhXS09O5dOkSsbGx2eZffPFFZs+eTatWGWuj169fny1btgBw5coVZs2alTMHIiIiIiIi\nIvIAJjvzY/OVVzzxd5iYzWaWLFnC2LFjmT9/Po6Ojjz//PMEBARw8+ZNXn/9dTw9PbPMc3JXmzZt\n8PHx4euvvwagQ4cO/PTTT/j4+JCWlkZAQEBOHo6IiIiIiIiIPAJP/IAJQMmSJfn444+zlE+ZMiVL\n2QcffJDpdb169Th06JDltb29PSEhIY++kSIiIiIiIiKSYzRgIiIiIiIiIpLPmcx551GXx4UpPT09\nPbcb8aQzmfLOskkiIiIiIiJPovz+p/HRvl653QSr1VgUkdtNAHSHSZ5xO/GaofpOrkW4tniUoUwR\nvxASv5xgKOPacxxJa6Ybyrh0Gcatbz4ylCnwygDmFapuKBOYcIxvK9YzlHk5Zj9xU43NK1N6xHz+\nVb6uoUzHswfY0ay5oUzznTsY7lDZ6vrTUk4BsKXus1ZnXjrwCwAfulrf14MTjwEY+nwCEzIy/aho\ndWYhMQAsLlrD6ozf1aMAbPJoYHWm/fF9ANQYtM7qzNG5r9qc8Ry83urMkQ8752jbDr/d2epMzSUZ\nx2HkZ7vAKwMASDl/zOqMQ9nqbKzytNX1ATqc/NWm60fyT18Zyjg2fc3QuQYZ59ukAtUMZUbfOkH8\nRyMMZYoNmGpTH3xWzNNQpk/8EW5v/dJQxqllT76v1chQps2h/xq6tkHG9e3WxoWGMgU69CMh6aah\nTCEXZ5vOA1v6eqi99f8mAMxMPcWBN142lKm7/FubPh9b2jbBqaqhzLjb0VxJSDKUcSvkYlPbbOkD\nW/ralj7Iqc/HyO8gkPF7yOinqhjKTPrjpE1tW1+6tqFM57gonQf56DyYmZrxO6+R86BzXBSAobZN\n+uOk1XXlyaF7ckRERERERERE7pPvBkzOnj1LgwYN8PX1pWfPnrz55pvs2rUrS70hQ4Zw+/ZtRo4c\nydatW7Nsw8sr6+1Kd+tu376d5cuX/23HICIiIiIiIvIome3Mj81XXpEvH8mpXLkyYWFhAJw5cwZ/\nf39mzZqFp+f/boedPXu2zdtv0aLFX26jiIiIiIiIiORd+XLA5F7u7u74+/szffp0bt68ibOzMz17\n9uT9999nw4YNAGzdupXPP/+c+Ph4pkyZQuHChUlNTeWf//wnp0+fplatWkycONGyzYiICI4fP06P\nHj0YOXIkFSpU4OjRo9SsWZOQkBCOHDnCyJEjcXV1pU6dOly9ejXLcsQiIiIiIiIiknflnXtd/kZ1\n6tThxIkTHD58mBkzZtCyZcssdZYuXcqQIUP4+OOPAYiOjmbo0KGEh4cTFRXF0aNHs912VFQU7777\nLmvWrGHbtm0kJCQQGhrKwIEDCQsL4/z583/rsYmIiIiIiIj8GZOd+bH5yivyTkv+RklJSdjZ2VGh\nQgWKFi2a5f2mTZsCUK9ePU6dypiF2d3dnTJlymAymahbt66l/H7u7u6UKFECs9lMyZIlSUxMJDo6\nmoYNGwLQqlWrv+moREREREREROTv8kQMmBw8eJCaNWvi4ODwp3VNJlOm/95ffj87O7tMr9PT00lP\nT3/gdkREREREREQk78v3AyZnzpxh6dKl9O7d+4F19uzZA8Cvv/5KlSpVLLmLFy9y584dDhw4QNWq\n1q+X7u7uzsGDBwHYvn277Y0XERERERERkVyRLyd9PXXqFL6+viQnJ5OWlsbYsWMpU6bMQzP+/v78\n/vvvTJs2DQBPT09mz57NiRMnaNCgAdWqVbN6//3792f06NF8/vnnVKtWjcTExL90PCIiIiIiIiJ/\nRV6aG+Rxke8GTMqXL8++ffuyfS8iIsLyfWRkJMADV69Zs2ZNlrLs6t67zbvfX758mRkzZuDp6cnC\nhQuznTdFRERERERERPKufDdgkhc4OjoyatQonJyccHJyYubMmbndJBERERERERExwJSenp6e2414\n0mliWBERERERkdyV3/80PjnkjdxugtWqzF6e200AdIdJnvHHlXOG6j/lVo6bX80ylHF+7V1ub/nc\nUMbppTdt2s+tzYsNZQq082NL3WcNZV468Au/dDC2bPOzGyP5Y8cqQ5mnmnfjx5YtDGWe37qdI++8\nZijj+clXhJesZXV974uHAPjVu73VmafDNwEQ+XRjqzOtfv0ZgIhS1rfN60JG2xYXrWF1xu/qUQD6\nUdHqzEJiANjW+DmrMy/8vAuAF2dvszrzw5AXAGg1x/pJnCODWticsaVttmTOve9vdabcmI8BuH39\nitUZp8JuAPxx9YLVmaeKluLw252trg9Qc8l6PnStbigzOPEYVxOTDGWKurqwscrThjIdTv7KpALW\nz4EFMPrWCZJWTjaUcfEJNvRzABk/C0auOZBx3UlMumko4+rizH6fDoYy9VZutOkaejvxmqGMk2sR\nrt0wdjxFCjrb9O/VNBcPQ5nhScf5rJinoUyf+CPcXD/HUMa5c5ChawFkXA8WFrH++g7Q79pRNnk0\nMJRpf3wfv1+7YShTpkhBm/rt/OQBhjJlgz+yqa9t6YOc+nxWlqhpKONz6bBN+zHyuwFk/H4QPbi7\noUzVD1foPMhH58Hd3xGNnAdVP1wBYKht/a4dtbquPDk064uIiIiIiIiIyH3y1R0mZ8+epVOnTtSp\nU8dS5urqiqenJ4MGDco2ExERgaurK23atMl2e4MGDco0sSvAokWLePbZZ2nQwNjosIiIiIiIiEhu\nMNnZ5XYTHjv5asAEoHLlyoSFhVld38vLy/A++vbtazgjIiIiIiIiIo+PfDdgcr/du3ezbNky5s6d\nS5s2bWjdujV79+7F1dWVRYsWERoaStGiRencuTODBw8mOTmZ5ORkxo4dS+HChUlPT2fcuHEcOHCA\n2rVr8/777zNy5EjatWvH1atX2bNnD/Hx8Zw6dYq3334bb29v1q1bx5IlSyhdujRFixaladOmNg3M\niIiIiIiIiEjuyPcDJveKjY2lc+fOjBgxgq5du3L06P8m9tm1axelSpVi8uTJxMbGcurUKQoXLszp\n06dZtGgRbm5uvPjiiyQkJGTa5rFjx1i5ciWnT5/m3Xff5fXXX2fWrFlERETg7OxMx44dadq0aU4f\nqoiIiIiIiIj8BfluwOTUqVP4+vpaXj///POW7wsWLIinZ8aM2aVLlyYxMdHy3tNPP82HH37I2LFj\nadu2LS1atODs2bO4u7tTokQJAIoXL54pczdnZ2dn2d7Vq1cpWLAgxYsXB+C554ytWiAiIiIiIiLy\nqJnstOaLUfluwOT+OUx2797N4cOHAbC7b5Kbe9fZLlmyJOvXr2f37t2sWLGCX3/9lVdfffWhGQB7\ne/ss75vN/zsRTSbTXzsgEREREREREclxGmL6/3788Ud+/PFHmjdvzpgxYzh48KBN2ylSpAjXrl3j\n+vXr3L59m59//vkRt1RERERERERE/m757g4TW7m7uzNs2DAWL16MyWR64DLEf8be3p7+/fvTo0cP\nKlasSJ06dTLdcSIiIiIiIiKS0/R3qXH5asCkfPnyREREZCpr0qQJTZo0ATIez7lr7ty5lvfvWrFi\nRZZt3ru9u99/8MEHWeq5uLgQGRkJgJubG19++SVFihTh7bffxt3d3dZDEhEREREREZFckK8GTPKK\n27dv8+abb1KgQAFq1qxJw4YNc7tJIiIiIiIiImKAKf3+WUwlx2liWBERERERkdyV3/80PvNen9xu\ngtXcp3yW200AdIdJnpHy62ZD9R2ebseZUW8ZyriHfErilxMMZVx7jiNp5WRDGRefYG5+NctQxvm1\nd4koVctQxuvCIU4O7WkoU2Xml1xbPMpQpohfCFG+HQ1laof9i5iRvQ1lKn6wlG8r1rO6/ssx+wH4\nsWULqzPPb90OYNN+vnDztDrT68oRADZ5NLA60/74PgC2NbZ+Ke4Xft4FQD8qWp1ZSAwAb63Ya3Xm\n0+4Zd4m9s2qf1ZlPujWwOZNTbbs8759WZ4oHzgDg1ubFVmcKtPMD4I/4363OPFWsDJFPN7a6PkCr\nX3+26fqRGrXVUMa+dksWF61hKON39SjfeRq7y7Dtkb02Xd+N/LxBxs+ckWsBZFwPUvZuNJRxaNiB\nc+/7G8qUG/Mxh9/ubChTc8l6/tixylDmqebduH39iqGMU2E3m85RWz4fWzJxUwMMZUqPmM+h3p0M\nZWot3WBT276v1chQps2h//LfM1cNZRq5F7WpbUfeec1QxvOTr2zqa1v6IKc+H1uuVbYcjy1t+9W7\nvaHM0+GbdB7ko/Pg7u+IRs6Dp8M3ARhqW5tD/7W67uNKywobpx4TEREREREREbnPQwdMzp49S4MG\nDfD19bV8hYSEPLKd3zvh6l39+/d/YH1fX1+OHTv2yPYvIiIiIiIiIpKdP30kp3LlyoSFheVEWwBY\nsGBBju1LRERERERE5EmgR3KMs6nHdu/eTb9+/fD19eXgwYN89913+Pj40LNnT8uSu2lpaQQHB+Pr\n60v37t3ZtWvXA7d3+PBhfHx8SEpKstx1cujQIbp164aPjw9Tp07NVP/GjRt4e3tz/PjxTOWffvop\n3bp1w9vbm/nz5wOQkJBA3759eeONN+jXrx9JSUnZls2bN48vv/wSgGPHjuHr6wtA27ZtGTx4MOHh\n4fz4449069aNnj17MmDAAJKTkwGYNGkSXbt2pXv37hw7dozBgwdbjjc5OZnWrVuTmppqS1eLiIiI\niIiISC6wedLXY8eOsXnzZlJSUhgzZgyrVq3C0dGRoKAg9uzZQ2xsLCVKlGDy5MnEx8fz5ptvsmHD\nhizbiY+PZ9y4cXz44Ye4uLhYyidNmsSECRPw9PRk+PDhnDt3DsiYuXjEiBEEBATg4eGRZXvLly/H\nbDbz0ksv0bt3b5YsWULz5s3p1asXS5cuZdeuXRw4cCBL2YPExsYSGhqKh4cHGzduZMaMGVSoUIHh\nw4ezY8cOnJyciIuLY/Xq1fzyyy98++23dO7cmW+//ZbnnnuOXbt20aJFC+ztNb+uiIiIiIiIyOPi\nT/+KP3XqlOVuC4Dnn3+ehg0bUqNGDRwdHTl8+DDnz5/n7bffBiAxMZHz58+zb98+9uzZw969Gas9\n/PHHHyQnJ+Po6GjZVnp6OkOGDMHPz4+yZctm2a+nZ8aqHNOmTbOUh4aGUqZMGV544YUsbXVycqJn\nz57Y29tz9epVrl27xqFDhwgKCgKgd+/eAKxatSpL2eHDh7M9/gIFClgGZooVK8bo0aNJS0sjNjaW\npk2bcuXKFRo2zJhN+tlnn+XZZ58lNTWV6dOnk5KSwpYtW3jtNWMzbouIiIiIiIg8SiazHskxyqY5\nTHbv3m0Z+HBwcKBOnTosWbIkU53ffvsNf39/OnZ88HKsN27coEaNGqxcuZK2bdtmes/8gA+zUKFC\n7Ny5k6tXr1K0aFFL+blz51i6dClfffUVLi4ulv3a2dlx586dTNvIrsxkMlm+v/fxGQcHB8v3wcHB\nLFq0iKpVqzJx4sQHbsve3p5mzZqxa9cujh8/ToMGxpb0EhEREREREZHc9ZeHmCpXrkx0dDRXrlwB\nYO7cuVy4cIH69euzZcsWAK5cucKsWbOyZF1dXQkODqZEiRKsXr0603tVq1blt99+AzIGKqKjowHo\n1asXfn5+TJo0KVP9q1evUqxYMVxcXIiKiuLcuXOkpKRQp04dfvrpJwBWrlzJV199lW1ZwYIFuXTp\nEgB79uzJ9lhv3LhBmTJlSEhIYPfu3aSkpFC3bl12794NZMy7MmHCBAA6d+7M3Llzady4scEeFRER\nEREREZHc9pcn1ihQoADBwcG88847ODo6UqtWLUqWLEmHDh346aef8PHxIS0tjYCAgAduIzg4mG7d\nuvF///d/lrJRo0Yxfvx4AJ5++mmqVq1qee/1119n48aNbNmyhZdeegmAmjVr4uLigo+PD8888ww+\nPj5MmDCBefPmMXz4cHx9fXFxcWHGjBmkp6dnKbt+/Tr9+vVj//79NGrUKNt2vvHGG3Tv3p1KlSrh\n5+fHvHnzWLlyJVWrVuWNN94AYNy4cQDUqVOH69ev06lTp7/UvyIiIiIiIiKS8x46YFK+fHkiIiKy\nlDdp0sSymg1krCRz/yM19vb2hISEPHTnd+/MKFy4MJs2bcpUVqNGDVasWJGp/r2PBi1evDjTe3Z2\ndlkeC7oru6WK7y8rWLAg//rXvyyvBw4cmKk9AEFBQZa5TwDL3CQjR47Msv1Tp05Rrlw5qlWrlm2b\nRERERERERHKKlhU2Tku3/A1WrFjB6tWrLUssi4iIiIiIiMjjxZSenp6e24140t074ayIiIiIiIjk\nvPz+p/H5Sf1zuwlWKzs661MiuUF3mOQRyXEnDdV3LF2FhKSbhjKFXJy5kpBkKONWyIXLBjPFbcw8\nP2WLocyP771E29AdhjLfDWxOhwU7DWU29m/GO6v2Gcp80q0Bb63YayjzafeGVBuQ9RG4BznxkReA\nobZ90i1jxaZG4zdbnfnv+HYANJ8WaXVmx/BWANQYtM7qzNG5rwLw4uxtVmd+GJKxvLiRvv60e8Yy\n4P2oaHVmITEADLarZHXmw7TTAAy1r2x1ZmbqKZv3E2i2PjPvTkbGls9nUMR+qzNzveoBEHMl0epM\nRTdXQ+cAZJwHRs5PyDhHjRwLZBzPm8uynxT8QT7v8QzPjN1kKLNnYnubrqH1RnxjKLN/6is0HL3R\nUGbvpA74h/9qKPOx99M2XattaZstn8+FazcMZUoVKchHu04Zygx4rrJN53XpLvMMZeLWBFLpnXBD\nmdOfeFPujcV/XvEe55b72dS2Eq/ONJS5tG4oJy8lGMpUKVHIpraV6fqRoczvqwfY1Ne29EFe/nxs\nydjStlJeHxrKXIgYrPMgH50HcWsCAQydBxciBgMYatuldUOtrvu40iM5xqnHRERERERERETu89gP\nmMTExODv74+3tzfe3t4EBQURHx8PQEREBFOnTrXUnTJlSqbX2fHy8uLs2bMsWrSIffuy/z/327dv\nZ/ny5Y/uIEREREREREQkT3msH8lJS0sjMDCQsWPHWpYCXrRoESEhIcycmfn2q7Vr1xIbG8v8+fOt\n2nbfvn0f+F6LFi1sb7SIiIiIiIiI5HmP9YDJzp078fDwsAyWAPj5+WWZrGfv3r2sXr2azz77DLM5\n6001kyZNYt++fVSuXJmUlBQgY6ngdu3aMXfuXEJDQylbtiznzp0jMDCQnj17cvz4cXr06MHIkSOp\nUKECR48epWbNmoSEhHDkyBFGjhyJq6srderU4erVq1oxR0RERERERHKNWXOYGPZY99jJkyepUaNG\npjKz2YydnZ3l9fnz5wkICGDkyJE4Oztn2caJEyfYu3cv4eHhDB06lFOnMk/k1rp1a7Zu3QrAli1b\naNu2bab3o6KiePfdd1mzZg3btm0jISGB0NBQBg4cSFhYGOfPn39UhysiIiIiIiIiOeSxHjAxm82k\npqZaXvfv3x9fX1/atGnDrVu3ANi/fz99+/Zl2rRpmeredeLECerXr4/ZbKZMmTJUqFAh0/tt27Yl\nMjJj9YUtW7bQrl27TO+7u7tTokQJzGYzJUuWJDExkejoaBo2zFiJo1WrVo/0mEVERERERETk7/dY\nD5h4eHhw4MABy+sFCxYQFhZGWload+7cAaB9+/b07t2bmjVrMm9e1uWr0tPTMz2mczd37z4uXrzI\n77//TmJiIpUrZ14i9N67We5uLz09HZPJBGD5r4iIiIiIiEhuMZnNj81XXpF3WmKDpk2bEhcXZ7kD\nBDIekUlKSsoykDF8+HAiIyPZtWtXpvLKlSsTFRVFeno6586d49y5c1n28+KLLzJ79myr7xZxd3fn\n4MGDQMaKOiIiIiIiIiLyeHmsJ301mUwsXryYiRMnEhoaioODA87OzixYsAAnJ6dMdZ2cnJg+fToD\nBgwgPDwcNzc3ADw9PalevTrdunWjUqVKeHp6ZtlPmzZt8PHx4euvv7aqXf3792f06NF8/vnnCHXv\nVgAAIABJREFUVKtWjcTExL9+sCIiIiIiIiKSYx7rARMANzc35syZk+17Xl5emV57enpmuhvlrokT\nJ2Ypu3dVm3r16nHo0KFstxsREZHl+8uXLzNjxgw8PT1ZuHAhRYsWtfJoRERERERERB49k1bJMeyx\nHzDJixwdHRk1ahROTk44OTkxc+bM3G6SiIiIiIiIiBhgSk9PT8/tRjzpNDGsiIiIiIhI7srvfxpf\nmj0kt5tgtRJDZud2EwDdYZJnJP9+wlB9xzLVSEy6aSjj6uLMlYQkQxm3Qi5cNpgpXsjFpv00+yDr\n41IPs3NkK9qG7jCU+W5gczos2Gkos7F/M95Ztc9Q5pNuDXhrxV5DmU+7N6R6wFdW1z82/zUA/MN/\ntTrzsffTADSe8J3VmZ/HtQWgxYytVme2/7MlADUGrbM6c3TuqwC0mmP9RMmRQS0ADH0+n3RrAMBg\nu0pWZz5MOw1APypanVlIDABD7Sv/Sc3/mZl6yua22ZLxHLze6syRDzsDMChiv9WZuV71AIi5Yv08\nThXdXA2dA5BxHjSfZuz6sWN4Kwau+c1QJrRLfZt+rhuN32wo89/x7Wy67tYb8Y2hzP6pr9Bw9EZD\nmb2TOhi65kDGdceW664tbXtz2R5Dmc97PMPv124YypQpUpCPfzptKOPftBIvzt5mKPPDkBco3SXr\n6n4PE7cmkErvhBvKnP7Em3JvLDaUObfcz6a2lfL60FDmQsRgjl9MMJTxKFnIpraV9VloKHN+ZT+b\n+tqWPsjLn48tmTJdPzKU+X31AJuOR+dB/jkPfl89AMDQ8cStCQQw1LYLEYOtritPDg2YiIiIiIiI\niORzmsPEuDzXYzExMfj7++Pt7Y23tzdBQUHEx8cDGZOqTp061VJ3ypQpmV7f1aRJk0fWnmPHjuHr\n65tpuyEhIcTGxj6yfYiIiIiIiIhI3pKnBkzS0tIIDAzEz8+P8PBwwsPDqV27NiEhIVnqrl27ltjY\nWIYNG5bj7Rw1ahQVKlTI8f2KiIiIiIiISM7IU4/k7Ny5Ew8PDxo1amQp8/PzyzL5zt69e1m9ejWf\nffYZZnP2Yz5z5sxh586dFClShI8//piLFy9aBldSU1OZOnUq7u7utGnThtatW7N3715cXV1ZtGgR\nFy9eJCgoCEdHR2rUqJFl276+vowZM4bNmzeTmJjIqVOnOHPmDMHBwbzwwgssWrSIb775hgoVKpCa\nmkqfPn0e6V0vIiIiIiIiIkaYHvC3szxYnuqxkydPZhmgMJvN2NnZWV6fP3+egIAARo4cibOzc7bb\nuX79Ou3atWP16tVcv36do0ePcvHiRQYOHEhYWBivv/46y5cvByA2NpbOnTuzatUqEhISOHr0KF98\n8QUvv/wyYWFhlCxZ8qFtjouL45NPPmHUqFGsWrWKa9eusWzZMlatWsX48eP5+eef/2KviIiIiIiI\niEhOy1MDJmazmdTUVMvr/v374+vrS5s2bbh16xYA+/fvp2/fvkybNi1T3XsVLFgQT09PAEqVKkVi\nYiIlSpQgLCyMHj168Pnnn3Pt2rUsdUuXLk1iYiLR0dE0aJCxksaf3RnSsGHDTNkzZ85QvXp1nJyc\nKF68OPXq1fsLPSIiIiIiIiIiuSFPDZh4eHhw4MABy+sFCxYQFhZGWload+7cAaB9+/b07t2bmjVr\nMm9e9ktL3XtHCmSspz137lyaN2/OsmXLGDhw4EPrpqenWx71ubvfB7G3z/xU071ZAJPJ9NC8iIiI\niIiIiOQ9eWrApGnTpsTFxREZGWkpi4qKIikpKcvAxvDhw4mMjGTXrl1Wbfvq1au4u7uTnp7Oli1b\nSElJeWDdypUrc/DgQQB2795t6BjKlSvH8ePHSUlJIT4+3rIdERERERERkdxitrN7bL7yijw16avJ\nZGLx4sVMnDiR0NBQHBwccHZ2ZsGCBTg5OWWq6+TkxPTp0xkwYADh4eG4ubk9dNvdunXj/fffp1y5\ncpZJW3fs2JFt3V69ejF48GC+//57qlevbugYihcvTseOHfH29qZq1arUq1cvy2CPiIiIiIiIiORt\neWrABMDNzY05c+Zk+56Xl1em156enpnuRrnr3rtC5s6da/m+ZcuWlu//85//PLRueHj4A7cbFhYG\nkGkwpXr16pbySpUqERAQgL29PZ06daJ8+fLZHo+IiIiIiIiI5E15bsAkP7h8+TJdu3bF0dGRTp06\nUbp06dxukoiIiIiIiDzBTHZ5akaOx4IpPT09Pbcb8aTTxLAiIiIiIiK5K7//aXxtUXBuN8FqRfpO\nzu0mALrDJM9IvnDKUH3HUpVJSLppKFPIxZnLCUmGMsULuXDFYMbNxkyzD7I+XvUwO0e2om1o9vPQ\nPMh3A5vTYcFOQ5mN/Zvxzqp9hjKfdGtgU6Z6wFdW1z82/zUAQ/v5pFvGctmNJ3xndebncW0BeGHW\nD1Zntr37IgCeg9dbnTnyYWcAWs3ZbnUmMqgFYFsfDLWvbHVmZuopmzP9qGh1ZiExOdq2WkO+tjpz\naPY/ABiy7sCf1Pyf2a/WBSDmSqLVmYpurrw07z9W1wfYEvh/NJ9m7PqxY3grBkXsN5SZ61XPpp/r\nRuM3G8r8d3w7m67V9d/7xlDmtymv8MzYTYYyeya2Z+Ca3wxlQrvUt+m6a0u/vblsj6HM5z2e4cK1\nG4YypYoU5OOfThvK+DetZOjaBhnXtzJdPzKU+X31AKr0W2Moc3JhF8q9sdhQ5txyP5vaVsrrQ0OZ\nCxGDOX3Z+usHQKXirja1razPQkOZ8yv72dTXtvRBTn0+pbtkv/rkg8StCbTpeHKqbToP8s958Pvq\nAQCG2ha3JhDAUNsuRAy2uq48OTRgIiIiIiIiIpLP6ZEc4x67HouJicHf3x9vb2+8vb0JCgoiPj4e\ngIiICKZOnWqpO2XKlEyvAc6ePZtl8thLly4xduzYB+6zVatWJCVl/r99Q4YM4fbt23/1cERERERE\nREQkD3qsBkzS0tIIDAzEz8+P8PBwwsPDqV27NiEhIVnqrl27ltjYWIYNG/an2y1RogQTJ0401JbZ\ns2dnWepYRERERERERPKHx2rAZOfOnXh4eNCoUSNLmZ+fH9OmTctUb+/evaxevZoZM2ZgNj/4ELdt\n28Y777zDmTNnLHed7Ny5k9dff52uXbuydOnSTPV///13vLy8uHjxouWuk5EjRzJr1izefvttOnTo\nQFRUFACTJk3Cy8uLESNG0LVrV86ePfuIekFERERERERE/m6P1RwmJ0+epEaNGpnK7h8QOX/+PAEB\nAYSGhuLs7PzAbcXExLBgwQI++eQTrl+/DmTMijxhwgRWrlxJ4cKFGTBgAD4+PgD88ccfDB8+nEmT\nJlGyZMlM20pOTmbJkiWsWLGCdevWYW9vz549e1i7di3Hjx/ntddeexSHLyIiIiIiImIT00NuJpDs\nPVY9ZjabSU1Ntbzu378/vr6+tGnThlu3bgGwf/9++vbty7Rp0zLVvdetW7cYOHAgY8aMwdXV1VIe\nHx/PU089RbFixbCzs2PhwoWWx27Gjx9Pq1atqFWrVpbt3b3jpXTp0ty4cYPo6Gjq16+P2WymRo0a\nlCtX7pH1gYiIiIiIiIj8/R6rARMPDw8OHPjfkpYLFiwgLCyMtLQ07ty5A0D79u3p3bs3NWvWZN68\n7JeeiouL45lnnmH58uWZys1ms2U79ytVqhTr168nOTk5y3t2dnaW7++u3X3vnS8mk8nKIxQRERER\nERGRvOCxGjBp2rQpcXFxREZGWsqioqJISkrKNGgBMHz4cCIjI9m1a1eW7VSuXJnx48dz5swZduzY\nYSkvWrQoaWlpXLhwgfT0dPr160dCQgIAgwcPplWrVoSGhv5pOytUqEBUVBTp6elER0dz/vx5Ww9Z\nRERERERE5C8z2Zkfm6+84rGaw8RkMrF48WImTpxIaGgoDg4OODs7s2DBgiwr1jg5OTF9+nQGDBhA\neHg4bm5uWbYVEhKCv78/s2fPtpSPGzeOQYMGAdChQwcKFSpkec/f359u3brRpk2bh7azbt26VKpU\nCW9vb2rVqkXVqlWzDOiIiIiIiIiISN71WA2YALi5uTFnzpxs37u70s1dnp6eme5GAShfvjwREREA\nuLu78+233wJYyp577jmee+65TJl7t/HVV19lKvvggw8s77Vs2ZKWLVuSnJzMc889x9SpU7l58yYd\nOnSgRIkSho9VRERERERERLKaPHkyv/32GyaTieDgYOrVq5elzsyZM/n1118JCwuzaR+P3YDJ48DR\n0ZEDBw7wxRdfYDabCQoKwt5eXS0iIiIiIiLyV/3888/ExMSwatUqoqOjCQ4OZtWqVZnqnDhxgl9+\n+QUHBweb92NKvztLqeQaTQorIiIiIiKSu/L7n8Y3lk3M7SZYrWCPsQ99f86cOZQtWxZvb28gY/GX\nNWvWULBgQUsdPz8/3nnnHebPn687TB53KeePGarvULY6iUk3DWVcXZy5kpBkKONWyIXLBjPFbcw0\n+yDyzyveY+fIVrQN3fHnFe/x3cDmdFz4o6HMv/o9z1sr9hrKfNq9oU2ZagMirK5/4qOMR9DeWbXP\n6swn3RoA0Gj8Zqsz/x3fDoDm06z/fHYMbwVAjUHrrM4cnfsqAC/O3mZ15ochLwAY6utPuzcEYLBd\nJaszH6adtjkz1L6y1ZmZqacA6EdFqzMLibG5bbWGfG115tDsfwAwZN2BP6n5P7NfrQvA2fgbVmfK\nFyto6ByAjPPAyPkJGefooIj9hjJzverx5rI9hjKf93jG0M8bZPzM2XINrTfiG0OZ/VNfoeHojYYy\neyd1YOCa3wxlQrvUp8OCnYYyG/s345mxmwxl9kxsb9N198I1689PgFJFCvLRrlOGMgOeq2zTeV26\nS/ar/T1I3JpAqvRbYyhzcmEXyr2x2FDm3HI/m9pWyutDQ5kLEYOJvpRgKFO1RCGb2lbWZ6GhzPmV\n/Wzqa1v6IC9/PrZkbGlbTmV0HuTN8yBuTSCATRkjbbsQMdjqupL7Ll++TO3atS2vixUrxqVLlywD\nJhERETRu3Jhy5cr9pf3knelnRUREREREREQMuvfuoGvXrhEREUGfPn3+8nZzbMAkJiYGf39/vL29\n8fb2JigoiPj4eCBj9Gfq1KmWulOmTMn0+lG4dOkSY8dm3Nbzyy+/cOXKFQD69+9veFshISHExsY+\n0vaJiIiIiIiI/F1MZvNj8/VnSpYsyeXLly2vL168aFlo5aeffiI+Pp4ePXoQEBBAVFQUkydPtqnP\ncmTAJC0tjcDAQPz8/AgPDyc8PJzatWsTEhKSpe7atWuJjY1l2LBhj7QNJUqUYOLEiZZ93B0wWbBg\ngeFtjRo1igoVKjzS9omIiIiIiIjIn2vWrBmbN2c89hwVFUXJkiUtj+O0b9+eb7/9ltWrVzN//nxq\n165NcHCwTfvJkTlMdu7ciYeHB40aNbKU+fn5ZZlUZ+/evaxevZrPPvsM832jSmfPniUoKIhKlSpx\n+vRp6taty/jx44mLiyM4OJiUlBRMJhMhISGULl2aYcOGcenSJZKTkwkMDKRKlSoMGjSIoUOH8u9/\n/5vjx48zb948XnvtNXbv3s3Ro0eZOHEiZrMZFxcXPvjgA44ePcqyZcswmUycPHmSdu3aERAQgK+v\nL2PGjGHz5s0kJiZy6tQpzpw5Q3BwMC+88AKLFi3im2++oUKFCqSmptKnTx+aNGmSE10tIiIiIiIi\nkq81bNiQ2rVr4+Pjg8lkYty4cURERODq6kqbNm0e2X5yZMDk5MmT1KhRI1PZ/QMi58+fJyAggNDQ\nUJydnbPdztGjR5k/fz6lS5emS5cuHDlyhM8//5wuXbrw8ssvs2nTJubPn0+vXr24evUqy5YtIyEh\ngW3b/jfRWrNmzahZsyZjxoyhbNmylvKQkBCGDx9O/fr1WbJkCV988QVNmjRh//79bNy4kTt37tCq\nVSsCAgIytSkuLo5PPvmE7du3s3LlSurXr8+yZcvYvHkzN27coG3bto/k2SkRERERERERW5nMdrnd\nhEfqn//8Z6bXnp6eWeqUL1/e5hVyIIceyTGbzaSmplpe9+/fH19fX9q0acOtW7cA2L9/P3379mXa\ntGmZ6t6rUqVKlClTBpPJRP369Tl58iQHDx6kcePGADRp0oRDhw5RpUoVkpKSGDZsGD/99BOvvPLK\nn7YxOjqa+vXrZ9oOQK1atShQoAAuLi7Z5ho2zFhxo3Tp0iQmJnLmzBmqV6+Ok5MTxYsXp169elb2\nkoiIiIiIiIjkFTkyYOLh4cGBA/9binLBggWEhYWRlpbGnTt3gIznjHr37k3NmjWZNy/7JaPu1oWM\nWXBNJhMmk8nyaE9KSgpms5kCBQqwevVqunXrxrZt2xg1apSh9t7dDoC9/cNvwrn//fT09Ex3z5hM\nJkP7FhEREREREZHclyMDJk2bNiUuLo7IyEhLWVRUFElJSdjZZb4taPjw4URGRrJr164s2zlz5gwX\nL17kzp07/Pbbb1SrVo26deuye/duIGP1mzp16hAVFcWGDRto1KgR48ePJzo6OtN2TCYTaWlpmco8\nPDzYt29fpu3Yoly5chw/fpyUlBTi4+M5ePCgTdsRERERERERkdyTI3OYmEwmFi9ezMSJEwkNDcXB\nwQFnZ2cWLFiAk5NTprpOTk5Mnz6dAQMGEB4ejpubm+W9ypUrM3v2bE6cOEHDhg3x8PBg0KBBjBo1\nitWrV+Pg4MDkyZNxcnJi1qxZrFq1Cjs7O95+++1M+2jcuDGDBg3io48+spSNHj2aCRMmYDKZKFy4\nMFOmTCEqKsrwsRYvXpyOHTvi7e1N1apVqVevXpZBIREREREREZEclc/mMMkJOTJgAuDm5sacOXOy\nfc/LyyvTa09Pz0x3o9zl4ODAlClTMpWVKlWKxYsXZ6m7ZMmSLGUREREABAQEWCZvvXt3SrVq1bJM\nBtOkSZNMq9vcrXu3XvXq1S3vVa9e3VJeqVIlAgICsLe3p1OnTpQvXz67wxYRERERERGRPCrHBkye\nJJcvX6Zr1644OjrSqVMnSpcundtNEhEREREREREDTOl3Z0yVXKOJYUVERERERHJXfv/T+ObaGbnd\nBKs5v/7PP6+UA3SHSR6R/PsJQ/Udy1QjIemmoUwhF2euJCQZyrgVcuGywUxxGzPPT9liKPPjey/x\n0rz/GMpsCfw/OizYaSizsX8z3lqx11Dm0+4NeXPZHkOZz3s8Q7UBEVbXP/FRxqNs76zaZ3Xmk24N\nAGg0frPVmf+ObwdAixlbrc5s/2dLAGoMWmd15ujcVwF4cfY2qzM/DHkBsK0PAs2VrM7Mu3MagMF2\n1mc+TMvIDLWvbHVmZuopm/fTj4pWZxYSA4Dn4PVWZ4582BmAIesO/EnN/5n9al0AYq4kWp2p6OZq\n6ByAjPOg+bSsj3E+zI7hrRgUsd9QZq5XPZt+rp8Zu8lQZs/E9jZdQ+uN+MZQZv/UV2g4eqOhzN5J\nHfAP/9VQ5mPvp2kbusNQ5ruBzW3qN1s+nwvXbhjKlCpSkI92nTKUGfBcZZvO69Jdsl818EHi1gRS\npd8aQ5mTC7tQ7o2sjzY/zLnlfja1rZTXh4YyFyIGE30pwVCmaolCNrWtrM9CQ5nzK/vZ1Ne29EFe\n/nxKvDrTUObSuqE2tS2nMjoP8uZ5ELcmEMCmjJG2XVo31Oq68uTIkVVyREREREREREQeJ3n6DpOY\nmBimTJnClStXAChbtizjxo2jWLFiREREcPz4cUaMGAHAlClTMJvNltdG+Pv7c/PmTV599dVM2xQR\nERERERGRJ1OevcMkLS2NwMBA/Pz8CA8PJzw8nNq1axMSEpKl7tq1a4mNjWXYsGE27WvPnj188cUX\nf7XJIiIiIiIiInmSyc7usfnKK/LsHSY7d+7Ew8ODRo0aWcr8/PyyTMSzd+9eVq9ezWeffYbZnHn8\n5+zZswwbNgxnZ2d69uyJq6srs2bNwt7enjJlyvD+++8za9Ysbt68iZ+fHy+//LIlu2zZMjZs2IDZ\nbKZ169a89dZbBAcH06JFC9q3b8+oUaN4/vnneeGFFwgODub69eukpaUxevRoPD09WbRoEd9//z1m\ns5mWLVvi7+//93aYiIiIiIiIiDwyeXbA5OTJk9SoUSNT2f0DIufPnycgIIDQ0FCcnZ2z3c7hw4fZ\nunUrRYsW5dVXX2Xp0qUUKVKEadOmsWnTJkaOHMlXX33F4sWLiYjImHAzNjaWTZs2sWLFCgC6d+9O\n+/btGTZsGH379qVs2bJcuHCBV155hdDQUP7v//4Pb29vTpw4QUhICJ999hmffvopO3bswM7OzrId\nEREREREREXk85NkBE7PZTGpqquV1//79uXHjBnFxcXz99dcA7N+/n759+zJt2jTCwsKwt896OBUq\nVKBo0aJcvnyZmJgYAgMzZky+efMmRYsWzXbfBw4cICYmhl69egGQlJTEuXPnePbZZ+natSv+/v6W\nQZB9+/YRHx9vadOtW7cAaNeuHX369KFjx4784x//eES9IiIiIiIiImIDc9551OVxkWcHTDw8PDLN\nK7JgwQIAWrVqxZ07dwBo3749vXv35syZM8ybN48hQ4Zk2Y6Dg4PlvyVLliQsLOxP9+3g4MCLL77I\nxIkTs7x3+fJlnJ2duXLlChUrVsTBwYExY8bQoEGDTPUmTJhAdHQ0GzduxNfXl/Dw8GwHdERERERE\nREQk78mzk742bdqUuLg4IiMjLWVRUVEkJSVhd98kMMOHDycyMpJdu3Y9cHuFCxcG4MSJEwCEhYVx\n5MiRbOvWrl2b3bt3c+vWLdLT05k0aRK3b98mNjaWnTt3snTpUqZMmUJqair169fn3//+t2Xbn332\nGYmJicyfP5+qVasSEBBA4cKFuXHjxl/qDxERERERERHJOXn2lgeTycTixYuZOHEioaGhODg44Ozs\nzIIFC3BycspU18nJienTpzNgwADCw8Nxc3PLdpshISG89957lrtNunXrlm29smXL0qtXL3r06IGd\nnR2tW7fGycmJSZMm8e6771K+fHmaN2/O0qVL6dmzJ++99x5vvPEGd+7cYdSoUbi6unL16lW6dOmC\ns7MzDRo0oEiRIo+8j0RERERERESsokdyDMuzAyYAbm5uzJkzJ9v3vLy8Mr329PTMdDcKQPny5S0T\nuQI0atSI8PDwLNvavXt3lm326NGDHj16ZKq3cOFCy/dBQUGW7+fNm5dlm2PGjMm23SIiIiIiIiKS\n9+XZR3JERERERERERHKLKT09PT23G/GkM5lMud0EERERERGRJ1p+/9P41r9Cc7sJVivQcWBuNwHI\n44/kPElSzmU/Ae2DOJTz5OZXswxlnF97lz92rDKUeap5N5J/Xm8o49i4M8k/fWUs0/Q1fmr9oqFM\n03//QNLqqYYyLl1HEPl0Y0OZVr/+bNPxpB1/8CTE2bHzeM5QHzT99w8A7O3cxupMw/XfA3Bm1FtW\nZ9xDPgXg/OQBVmfKBn8EwOG3O1udqbkk4zw7976/1ZlyYz4G4PK8f1qdKR44A4Aag9ZZnTk691UA\nPAdb/7Nw5MOMY6815GurM4dm/8PmjC1t60dFqzMLicnYX+9OVmdqLd0AQNLKyVZnXHyCOeb/utX1\nAap/vJZTw3sZylSe9oWhY4GM44kZ2dtQpuIHSzk5tKehTJWZX3JzffaPoz6Ic+cgm66hu9u1NJRp\nsnmroZ9ryPjZjv9ohKFMsQFTbWrbfp8OhjL1Vm40dM2BjOvOrc2LDWUKtPOz6TzY3vR5Q5kWP/3I\nsuI1DWV6XD5MRKlahjJeFw6xrfFzhjIv/LyL7zwbGsq0PbKX81eNTZpftmhBm/ptfenahjKd46Js\n6mtb+iCnPh9bMhurPG0o0+Hkr+xs8X+GMs22/4cNZeoYynT6/aDOg3x0HjTb/h8AQ+dBp98PAhhq\nW4eTv1pd93FlMusBE6PUYyIiIiIiIiIi9zE0YHL27Nksk63OmzePL7/88i81YtCgQezevZuIiAi+\n//77v7QtEREREREREZG/Kk89knP/YIyIiIiIiIiIPAJaVtiwRzpgsmzZMjZs2IDZbKZ169a89dZb\nxMXFMWzYMABSU1OZOnUq7u7ufPLJJ3zzzTeULVuWGzcynk+dN28eRYsWxcPDg2XLlmEymTh58iTt\n2rUjICCAH3/8kcmTJ1O8eHEqV65MsWLFCAwMtOz/Qftat24dYWFhmM1m+vTpw8svv5xtWZMmTSxL\nDA8aNIgePXrw888/Exsby9mzZ1m6dCnvvfceFy5c4ObNmwQGBtKyZUsOHTrEhAkTMJlMNGjQgC5d\nujBmzBiWL18OwIIFC3BxcaFXL2PP2IuIiIiIiIhI7jA8YHLq1Cl8fX0tr8+dO8dbb71FbGwsmzZt\nYsWKFQB0796d9u3bc/nyZQYOHEjTpk1Zs2YNy5cvZ8CAAaxYsYKNGzeSkpJCmzZZJ63cv38/Gzdu\n5M6dO7Rq1YqAgABmzJjBtGnTqFGjBj169KBZs2aZMhcvXsyyr4CAAD766CO+/vprkpOTGTFiBC1a\ntMhS9vLLLz/wmFNSUli+fDlXrlyhefPmvPbaa8TGxhIUFETLli2ZNGkSEyZMwNPTk+HDh+Pk5ERy\ncjJxcXGULl2aH374gdDQx2dGYhEREREREZEnneEBk8qVKxMWFmZ5PW/ePAAOHDhATEyM5S6KpKQk\nzp07R/ny5Zk0aRLz5s0jISGB2rVrExMTQ7Vq1Xjqqad46qmnqF0764zUtWrVokCBApnKzp07R61a\nGTNEt2jRgrS0tEzvlyhRIsu+Tp48SZUqVXBycsLJyYkFCxawf//+LGUPU69ePQAKFSrEgQMHWLVq\nFWazmWvXrgEZg0ienp4ATJs2DYB//OMfbNy4kZdffpmCBQtSvHhx6zpYRERERERERHLdI3skx8HB\ngRdffJGJEydmKn/vvfdo3rw53bt3Z9OmTfzwww+kp6djvmdJo+zWu7a3f3jTTCZTlrIBbTwdAAAg\nAElEQVS5c+dm2ZfZbObOnTuZ6mVXdr+UlJRMxwbwr3/9i+vXr7N8+XKuXbtGly5dLNu7X8eOHQkM\nDKRAgQJ07NjxofsSERERERER+VtpDhPDHtmywrVr12b37t3cunWL9PR0Jk2axO3bt7l69Sru7u6k\np6ezZcsWUlJScHd3Jzo6muTkZG7cuMHBgwet2keJEiWIjo4mLS2NnTt3Znk/u31VqVKFU6dOkZSU\nxB9//EGfPn2yLUtPT8dkMnHr1i1u3brF4cOHs91++fLlMZvNfP/99yQnJwNQtWpVfvvtNwCCg4OJ\njo6mWLFiFC5cmPXr12f7yJGIiIiIiIiI5F2P7A6TsmXL0qtXL3r06IGdnR2tW7fGycmJbt268f77\n71OuXDl8fX0ZM2YMBw8e5NVXX8XHx4fy5ctTt25dq/YxePBgAgMDKV++PFWqVMlyZ0d2+9q7dy+D\nBg2iT58+APTu3RtnZ+csZSaTie7du9O1a1eqVq2a7WNCbdu2pX///vz666+8/vrrlC5dmvnz5zNq\n1CjGjx8PwNNPP03VqlUBaNeuHVu3bqVgwYK2dquIiIiIiIiI5AJDAybly5cnIiIiU9m9q9T06NGD\nHj16ZHq/ZcuWtGzZ0vL6P//5DwDNmzdn4MCBmeo2adIk2+/vrlzj5OTEokWLKF++PGPHjsXd3d2q\nfQF06tQpU91OnTplKQsKCiIoKOiBbSpfvjwbNmywvP7HP/5h+f7uZLf3+vHHH/Hx8clSLiIiIiIi\nIpKTTNlMJSEP90iXFf67paenExAQgIuLC25ubrRr1y63m5StP/74A19fX+rWrUvTpk1zuzkiIiIi\nIiIi8v/Yu/O4qOrF/+OvYRNFRFHEElfcF1AzueYWadqidV1wSbBcbnYTzZtf06vivt9SS7My6aqA\noinmdc/MrpWKmZq5oSGpuJuiSAozML8/+DlXgnLOZGy9n48Hj8dw5vM+53M+c+bM8OGcz8cgkzWv\nEVclX+U1gK2IiIiIiIjkn+L+p3H6Z/8u6CrYrUSH/gVdBaCIXWFSnGUmfGWovHPd1qStmmUo49Fz\nFBl71xnKuLV4nszEbwxlnP0fxXJkh6GMS8NgjoQZm02oYdQGLEkHjG2nRlM2VQswlHnm9CHMyUcN\nZVz9GmA5c8hQxqVqAFfeft3u8j6vzQHgzNgBdmeqTvsIgGsLR9md8X41+zi7s+0juzPuT2bX6fbG\nhXZnSj77avZ2bvxk/3a8ymdvZ+ti+7fTaRAAw+Lsf33e6RbgcOYfn3xvd2buXxvna+boS13uU/J/\nGizJvh1xMNXsznzAaQDu7Ii2O+MeHMrBkKfsLg/Q5OMtmPdtMJRxbd6ZcSVqGspMTT+F+eBWY9tp\n0smh86Ej5/fjf+tqKFPvw7Wkrf6Xse30GOlQu2We3G0o41y7JccGPm8oUz9yHW+41jCUmW1OIjV6\nkqGMZ+gEx44DBz4Trs7/P0OZCkPfZJ5nHUOZ4akniPWpbyjT+8oxbnwUYSjjNWCKQ6/pycs3DWVq\nVyzjULt9XLGBoUzI5aMOtbUjbZBfr8/lOcMNZSq+Po+UxWMNZcoOmuZQ3Rz57qbjoPgcB14DpgAY\nOg6eOZ19zjVSt7KDptldtsjSLDmG6SYmEREREREREZFfKDQdJsnJyXTr1u1Xn9+yZUs+1uZ/29u5\ncyfLly/P122LiIiIiIiISMEqNB0m97No0aJ821ZGRgZLliwBoG3btrzwwgv5tm0RERERERERKXiF\nbgyT0aNHU7FiRY4cOcL58+d588032b17NwkJCYSHh7NgwQLmzp3Lvn37yMzMJDQ0lM6dOzN69Ghc\nXV1JSUlhzpw5jB49mnPnzlGiRAlmz55NhQoViIiI4OzZs1gsFoYNG0bLli0JCwujUaNGHD58mPT0\ndObOncvixYtJSEhg4sSJBAQEcPLkSUaNGsXSpUvZtGkTAO3bt+fll1/Os7516tRh5MiRXLlyhYyM\nDIYOHUrbtm0LuGVFRERERETkT0tjmBhWKK8wycjIIDIykn79+vHJJ58waNAgSpcuzYIFC9i3bx/n\nzp0jJiaGZcuW8d5773Hnzh0AvLy8mD9/Pp988gkVKlQgNjaWnj17sn37dtavX4+Pjw9RUVG8++67\nTJ8+3ba9cuXKERUVRZcuXVi6dCkDBw6kRo0aTJw40Vbm7NmzrF27lpiYGGJiYti8eTNnzpzJs74n\nTpzg+vXrxMTEEBkZyY0bN/K1/URERERERETk9yl0V5gANG/eHIBKlSpx6FDOUeX379/Pd999R1hY\nGABZWVlcuXIFgICA7JGTjxw5QsuWLQF49tlnAZgwYQLffvst+/fvByA9PZ2MjAwAW9kmTZqwc+fO\nPOt07NgxAgMDcXHJbrJmzZpx/PjxPOtbs2ZN0tLSGDlyJE8++aStDiIiIiIiIiJSNBTKDhNn5/9d\nKvTLubDd3Nzo0aMHgwcPzpVzdXW15bOysnI998orr9C5c+6pa+9uw2q1YjKZ8qyTyWTKURez2YyT\nk1Oe9S1ZsiSrVq1i//79rF27lh07djBjxozf3GcRERERERGRP4rJWbfkGFUob8nJy93OioCAAHbs\n2EFWVhbp6elMmTIlV9nGjRuzZ88eAHbs2MH7779PYGAg27dvB+Cnn35izpw5tvL79u0D4ODBg/j7\n++Pk5ERmZmaOddavX5+DBw9isViwWCx899131K+f93zoR44cYf369TRv3pyJEyeSmJj4+xtARERE\nRERERPJNobzCJC/169enR48erF69mqCgIHr16oXVas1zBptnnnmGXbt2ERoaiouLC7NmzaJ8+fLs\n2bOH3r17k5mZSXh4uK38+fPnGThwIKmpqcyfPx9vb2/MZjPDhg3j8ccfB8DPz49evXoRGhqK1Wol\nJCSEypUr51lXPz8/5syZw8qVK3F2dmbgwIF/SJuIiIiIiIiIyB+j0HSY+Pn5ERcXl2NZcHAwwcHB\nACxdutS2/B//+Af/+Mc/cpSdOXOm7bGbmxuzZ8/OtY1p06blue2ePXtSp06dHMvuzoZzr759+9K3\nb99f3e699Y2MjMxzWyIiIiIiIiJS+BWaDhMRERERERER+YM4FZkROQoNk/WXo6pKvvu1gWZFRERE\nREQkfxT3P40zvl5V0FWwm1urngVdBUBXmBQamSd3GyrvXLslP69fYChTqks4lu8/M5RxadwBy5Ed\nxjINgx3azp3tS+9f8B7u7V8k84d4QxnnWkHcWp57oODfUvqFCCxJBwxlXGo0xXzuuKGMa+V6hrbj\nUqMpgKF2c2//IgAZF36wO+P2UC0A0n86Z3emRPns8X3M50/YnXF9OPu2uPTrl+zfTjnf7My1C/Zn\nvB8C4PRPqXZnqpX3zNdM8rVbdmf8vEs7vJ202Ol2Zzx6jwHgzo5ouzPuwaEADKaa3ZkPOI3lx4N2\nlwdwqd6EjEtJhjJuvjVI/2qloUyJ1r2wnDl0/4L3cKka4FDdbm9dbChTstMgh86HmYnfGMv4P+pQ\nu5n3bTCUcW3emfSdK4xtp20f0netNpZ5rAe3N39gKFPy6cGGzjmQfd7JuHjKUMatUk2Hjrc72z4y\nlHF/cgAZe9cZyri1eN6h96kjx9vh8zcMZRo97OXY+3TPWkMZt790daitHWmD/Hp98us1deT1ceQc\nouOg+BwHLlUDAAwdB67Ns2dGNVI3Z/9H7S4rfx7qMBEREREREREp7pw0rbBRxfompkGDBtGqVSt2\n7DB2hcRvuXLlCuPHj39g6xMRERERERGRwqdYd5gsXryYNm3aPNB1+vj4MHny5Ae6ThEREREREREp\nXP4Ut+ScO3eOWbNmMWrUKNLS0ujSpQuff/45HTp0oGfPnmzZsoVq1arRsGFD2+O33nqL0aNHU6pU\nKU6dOsX169eZMWMGZcqUYdiwYcTFxfHkk0/Sq1cvduzYQUZGBv/+97+xWq0MGzaMO3fu0K5dO1at\nWsXnn39e0E0gIiIiIiIif2Im3ZJjWLG+wuR+srKyaNCgAWvWrGH//v1UrlyZ1atX8+2333Lz5k0A\nLBYLS5Ys4bXXXuPdd9/Nkc/MzKRmzZrExMTg5+fHnj17+OSTT/D392fFihV4enoWxG6JiIiIiIiI\nyO/0p+4wAQgICMBkMlG+fHkaNGgAgLe3N6mp2TNOPPbYYwA0adKEpKTcMx00b94cgEqVKpGamkpi\nYiLNmjUDoH379vmxCyIiIiIiIiLygBXLDpObN2+SkZEBZF9F4uHhYXvOYrHkKOvs7Jzn47tzcGdl\nZdmWmUymXNv6ZcZqteLk5PSr5UVERERERESk8CuWHSaTJk3is88+w2q1curUKW7cuMHly5cB+Pbb\nbw2t6275AwcO4O/vf9/yVatW5fDhwwDs3LnTYM1FRERERERE/gBOTkXnp5AoPDV5gIYOHcrSpUvp\n06cP7dq1o0ePHiQlJREWFsapU6cMXfmRnp7O4MGDefvttxkyZMh9y3ft2pV9+/YRFhbG1atXbVeb\niIiIiIiIiEjRUSxnyalevTorV67MsSwuLs72eNCgQQA5Zq+59/l7H7dv357g4OA813VvftSoUUD2\njDxDhgyhTZs2HDhwgG+++eb37o6IiIiIiIiI5LNi2WFSkDw9PVmyZIltRp2xY8cWcI1ERERERETk\nz07TChtnst4d3VQKjAaHFRERERERKVjF/U9jy7cbC7oKdnN55NmCrgKgK0wKjcxEY7fuOPs/SuLw\nPoYy/vNWcOXt1w1lfF6bw42PIgxlvAZMITV6kqGMZ+gE5nnWMZQZnnqCc1NeMZSpHPE+h3o/bSgT\nELuZH4b1MpSp9c5Kkie+bCjjN3ERMRXq212+79VjAGyu2cTuzNOnDgKw/qFGdme6XMgexHhL7aZ2\nZ546ecDhuh0b+LzdmfqR6wD4vEkLuzNPHNwLwONz/2t35ot/tMvOvm3/QM6fv9YWgPbzv7Q7s31o\nG4fr5kjmxCvd7c7UeX8NAAdDnrI70+TjLQBYfjxod8alehMGU83u8gAfcJrtjR81lGn//TcOnUMP\ndOtoKNM07lN2Bbc1lHlsx06H6ja1ZC1DmXG3f+DTes0MZToe32/ouIHsY+fSv4YZyviOfIevWrU2\nlGn99Vd8/8IzhjKNl2/CcuaQoYxL1QCHjrd9nTsYyjTf8Blxvg0MZbpdOmrofAjZ58RYH/s/ewB6\nXznGBr/GhjKdk7/ng7J1DWUGpyRw6HyKoUzAw2Udajcjn4uQ/dnoSFs70gb59fqsq9TQUOb5i0cM\nfTeA7O8HjtTt44rGXtOQy0d1HBSj46Bz8vcAho6DkMtHAce+v4rcSyOSioiIiIiIiIj8QoF2mCQn\nJ9OtW7eCrIJD4uLi2LZtW0FXQ0RERERERMQ+Ts5F56eQ0C05DiiKnTwiIiIiIiIiYr9C2WGSkJDA\n5MmTcXJywsPDg5kzZ5KQkEBMTAwmk4lTp07RqVMnwsPD2bVrF9OnT6dChQrUqFEDb29vhg4dalvX\n/PnzuXjxIhcuXODKlSuMHDmStm3b8tFHH7F161aysrJo164d4eHhHD16lEmTJuHm5oabmxtz584l\nOTk517KlS5dSrlw5ateu7VCdRERERERERKRwK5QdJtOmTeONN94gMDCQyMhIli1bRlBQEIcOHWLz\n5s1kZWXxxBNPEB4ezptvvsns2bOpW7cuffv2pVWrVrnWd+nSJT766CMSEhIYNWoUbdtmD8C3fPly\nnJycaN++PS+99BJxcXH06dOHv/71r+zevZsrV67kuexejtZJREREREREJN84aQhTowpliyUmJhIY\nGAhAUFAQR49mj3LcoEEDSpYsiYeHh63suXPnaNCgAc7OzraOkF9q2bIlAHXr1uXSpUsAuLu7Exoa\nSr9+/bh+/TopKSm0b9+e9957j3nz5lG+fHn8/f3zXHYvR+skIiIiIiIiIoVXoewwuZfZbMbp//eE\nubj89gUxJpMpz+VZWVk5fj937hxLlixh8eLFREVFUblyZSC7Y2X16tXUrFmT0aNHs2fPnjyX3cvR\nOomIiIiIiIhI4VUoO0xq167NgQPZ82B/8803NGr063Oi+/j4kJiYSGZmJl9//XWeZb799lsAjh8/\nzsMPP8z169fx9vbGw8ODI0eOcO7cOcxmM9HR0aSkpPDcc8/x4osvcuzYsTyX3Y89dRIRERERERHJ\nLyZn5yLzU1gU+BgmSUlJhIWF2X4fOXIk48aNY9KkSZhMJry8vJgxYwZHjhzJMz98+HCGDh2Kn58f\nNWvWtF2Ncq/SpUvzyiuvcO7cOcaMGUP9+vXx8PCgd+/ePPLII/Tu3ZtJkyYxYMAAXnvtNTw9PXFz\nc2PGjBkcPXo017IVK1b85j7ZUycRERERERERKbwKtMPEz8/PdiXJL0VFReX4PSgoiKCgINvv8fHx\nQPZYJIsWLcLPz4/x48dTtWrVXOtq0qQJoaGhOZZFRkbmud1fjjnStm3bXMvunfHG0TqJiIiIiIiI\nSOFV4FeY/F5Wq5Xw8HA8PDwoX748nTp1KugqFco6iYiIiIiIiIj9TFar1VrQlfiz08CwIiIiIiIi\nBau4/2mcefSLgq6C3ZwbPF7QVQCKwRUmxYXlzCFD5V2qBnBt4ShDGe9XZ/Hz+gWGMqW6hJO2apah\njEfPUQ5t59/e9Qxl+l87zoFuHQ1lmsZ9SsrisYYyZQdNY1ewsemhH9uxk2MDnzeUqR+5jg/K1rW7\n/OCUBAC+atXa7kzrr78C4OOKDezOhFzOntZ7oZf9dXv1Rnbd5pepY3dm6M0TAMzztD8zPDU7E+dr\n//50u5S9P61nf2535qs3niiWmaQ3+tmdqTF7GQDmfRvszrg27wxAxqUkuzNuvjXY3vhRu8sDtP/+\nGwZTzVDmA05jScr7ltBf41KjKRv8GhvKdE7+nrdK1zaUGXHrJJfnDDeUqfj6PEPvA8h+LzhSt8wf\n4g1lnGsFcfSlLoYyDZasJ75TsKFM0NYdmA9uNZRxbdKJOzevG8q4lynn0HFg5NwG2ec3I+dQyD6P\nJk982VDGb+Iihz5LHdmfZeWNfc73++k4Jy7dNJSp41vGoXY71PtpQ5mA2M0OtbUjbZBfr4+R7yCQ\n/T3EkbZ2JLOnw+OGMn/57AsdB8XoOLj7HdHIcfCXz74AHPsuKnIvjUYqIiIiIiIiIvILRaLDJDk5\nmW7duuX7duPi4pg1y/6rK7ZuNfafLREREREREZF84eRcdH4KiSLRYVIUJCcns3HjxoKuhoiIiIiI\niIg8AEV6DJOEhAQmT56Mk5MTHh4ezJw5k4SEBGJiYjCZTJw6dYpOnToRHh7Orl27mD59OhUqVKBG\njRp4e3vnmB746NGjTJo0CTc3N9zc3Jg7dy4Aly9fZujQofzwww8MHDiQHj16EB8fz9y5c3FxccHX\n15cZM2YwefJkDh06xIIFC3jiiSdyratMmTIF1UwiIiIiIiIiYlCRvsJk2rRpvPHGG0RFRfHoo4+y\nbFn2oISHDh1i5syZxMbGEhUVBcCbb77J7NmziYyM5NixY7nWFRcXR58+fYiKimLQoEFcuXIFgLNn\nzzJv3jzeffdd27omTJjA3LlziY6OxsvLi/Xr1zNw4EBatGhBeHj4r65LRERERERERIqGIt1hkpiY\nSGBgIABBQUEcPZo9+0WDBg0oWbIkHh4etrLnzp2jQYMGODs707Zt7hlP2rdvz3vvvce8efMoX748\n/v7+AAQGBuLs7Iyvry+pqamkpKRgMpl46KGHbNv9ZQfMr61LREREREREpCCYnJyKzE9hUXhq8juZ\nzWac/n/Durj89p1GJpMp17KWLVuyevVqatasyejRo9mzZ0+e6zKZTDnm5zabzbnW92vrEhERERER\nEZGioUh3mNSuXZsDBw4A8M0339CoUaNfLevj40NiYiKZmZl8/fXXuZ6Pjo4mJSWF5557jhdffDHP\n23YAvLy8MJlMnD9/HoC9e/fSqFEjnJycsFgshtYlIiIiIiIiIoVTkRn0NSkpibCwMNvvI0eOZNy4\ncUyaNAmTyYSXlxczZszgyJEjeeaHDx/O0KFD8fPzo2bNmrarUe6qWrUqr732Gp6enri5uTFjxgx2\n7tyZ57qmTJnCiBEjcHFxoUqVKjz77LPcvHmTo0ePMn36dFq3bp1rXSIiIiIiIiIFphBN11tUFIkO\nEz8/P9uVJL90dyDWu4KCgggKCrL9Hh8fD4C7uzuLFi3Cz8+P8ePHU7Vq1Ry5tm3b5hrbpFu3brbH\nHh4efP755wA0b96cFStW5Cjr7e3NF198kWN9IiIiIiIiIlI0FYkOkwfBarUSHh6Oh4cH5cuXp1On\nTgVdJREREREREREppEzWe0cwlQKR1yC0IiIiIiIikn+K+5/GWYl7C7oKdnPyb1HQVQD+RFeYFHbm\ns4cNlXet0oiMPWsNZdz+0pXMH+INZZxrBZFx+bSx7VSs5tD+nBk7wFCm6rSPMJ87bmw7leuxrUFz\nQ5knj+4j/doFQ5kS3g+RcfGUoYxbpZqkrZpld3mPnqMAuP7BP+3OlBucPZ5O2up/2b+dHiMBsBzZ\nYXfGpWEwgKFj1O0vXQG4nppmd6acp4fDdRsWd8juzDvdAgAYsvo7uzPv9gh0eDv5lTn6Uhe7Mw2W\nrAdgXImadmempme/B9K/Wml3pkTrXiQO72N3eQD/eSuwJOV92+avcanRlMFUM5T5gNNYztjfzgAu\nVQMcOk9l7F1nKOPW4nnOTXnFUKZyxPvc2b7UUMa9/YsMd65uKDMv80eHXp9TI0INZWq+Fc0IlxqG\nMm9Zkri5dIKhTJkXJ5Fx4QdDGbeHapF+/ZKhTIlyvqTFTjeU8eg9hvll6hjKDL15gnWVGhrKPH/x\nCD+ve9tQptTzr5H0Rj9DmRqzl3Eh5ZahzENlSzvUbo60gSNt7Ugb5Nfr48h7wcj3Ccj+TvHz2jmG\nMqW6vs6n9ZoZynQ8vl/HQTE6Dkp1fR3A0HHQ8fh+wLHvvCL3KtKz5IiIiIiIiIiI/BGKfYdJcnIy\ndevW5eDBgzmWd+/endGjR9uVv3fwV4ArV64wfvz4B1pPERERERERESk8in2HCUCVKlXYsGGD7ffT\np09z8+ZNh9fn4+PD5MmTH0TVRERERERERP54Jqei81NIFJ6a/IECAwPZtWsXmZmZAGzcuJFWrVoB\n8J///IeePXvSu3dvIiIiAIiLi2P48OG88MILXLr0v3uO//vf//K3v/2NM2fO2K46efLJJ1m8eDF9\n+/YlJCSEW7dukZqaSv/+/enTpw/vv/8+TzzxRD7vsYiIiIiIiIj8Hn+KDhNXV1cCAwOJj88e8HT7\n9u20a9cOgNu3b7N48WJiY2M5deoUCQkJAFy4cIGYmBh8fX2B7KtS3nvvPebMmYOT0/+aLTMzk5o1\naxITE4Ofnx979uzhk08+wd/fnxUrVuDp6ZnPeysiIiIiIiIiv9efZpacp556ig0bNlChQgV8fX0p\nVaoUAF5eXrz66qsAJCYmkpKSAkDjxo1t0/3evn2bIUOGMGvWLDw9Pblx40aOdTdvnj3rSqVKlUhN\nTSUxMZEWLbKnQWrfvj2RkZH5so8iIiIiIiIiebEWoltdioo/TYu1bNmS+Ph4Nm7cSKdOnQAwm81M\nnjyZuXPnEh0dTWBgoK28q6ur7fHFixd55JFHWL58eZ7rdnZ2tj22Wq1YrVbbVSh3O11ERERERERE\npOj403SYuLm58eijj7JmzRrbmCJpaWk4Ozvj4+PDhQsXOHz4MGazOVe2Ro0aTJw4kTNnzvDVV1/d\nd1tVq1bl8OHDAOzcufPB7oiIiIiIiIiI/OH+NB0mkH1bToMGDWzjipQtW5ZWrVrRvXt3FixYwKBB\ng5gxYwYWiyVX1mQyMW3aNKZPn05aWtpvbqdr167s27ePsLAwrl69mmPMExEREREREREp/Ir9GCZ+\nfn7MnDkTgMcff5zHH38cgKCgIIKCgnKV79+/f658XFwckH3lyKZNmwBsyz7//HNb2VGjRgFw7tw5\nhgwZQps2bThw4ADffPPNg90pERERERERESM0holhxb7DpCB4enqyZMkS3n33XQDGjh1bwDUSERER\nERERESNMVqvVWtCV+LPTwLAiIiIiIiIFq7j/aZz548GCroLdnKs3KegqALrCpNAw799sqLxrs6c5\nPfolQ5lqM5eQGj3JUMYzdAI/r51jKFOq6+v8vO5tY5nnX2NTtQBDmWdOH+KHYb0MZWq9s5KbSycY\nypR5cRLHBj5vKFM/ch0XZ4UbylQatcBQGzxz+hAAX7dtY3em1c4vAdj5l8fszrTdswuALbWb2p15\n6uQBhzOba9p/cnz6VPZJf3G5unZnBl1PAODFmG/tzizt+wgAA1bstzvzUZ9mAPxt5QG7Mx/2aupw\n3RzJGDmHVJu5BADzwa12Z1ybZM9IZjlzyO6MS9UADnTraHd5gKZxn7LBr7GhTOfk7w3VC7LrNphq\nhjIfcNrQMQ3Zx/WZsQMMZapO+4gdj/zFUCb42z0OnXctSfYf0wAuNZqS9EY/Q5kas5c5dN61HDM2\n0LpL/baYz58wlHF9uA67gtsayjy2YyfrH2pkKNPlwmE+rdfMUKbj8f1cnf9/hjIVhr7p0GepkfM7\nZJ/jHTlG956+ZijTopq3Q+12akSooUzNt6IdamtH2iC/Xp9tDZobyjx5dJ9D23Hk9XHkfKDjoPgc\nBx2PZ3//MnIc1I9cBzj2XbRY0z/qDdNNTCIiIiIiIiIiv1BsOkySk5Np2rQpYWFhhIaG0rNnT7Zt\n2/ZA1n13cNjjx4+TlJQEwD/+8Q/u3LnzQNYvIiIiIiIiIoVLsbolp0aNGkRFRQGQkpJC165dadOm\nDe7u7g9k/du2baNRo0bUqFGDuXPnPpB1ioiIiIiIiPzhnIrN9RL5plh1mNyrbNmy+Pj4cOTIEd57\n7z3MZjPOzs5MnTqVhx9+mCeffJIOHTqwf/9+PD09WbRoEZcvX2bkyJEAWCwWZtOv4jYAACAASURB\nVM2aRdWqVQFISEggNjYWb29vypcvz/Dhw1m/fj23bt1i7NixudY/depUDh8+TGZmJn369KFbt24F\n2RwiIiIiIiIiYkCx7WJKTk4mJSWFNWvWMGDAAJYuXcqLL77IwoULATh79izPP/88K1eu5ObNmyQk\nJHD58mWGDBlCVFQU3bt3Z/ny5bb11a1blzZt2vD6668TEPC/QfLefvvtXOtPSUnhiy++IDY2luXL\nl2OxWPJ9/0VERERERETEccXqCpOkpCTCwsKwWq2UKFGCWbNmMWbMGJKSknjvvffIzMzE29sbgNKl\nS1OvXj0AKlWqRGpqKlWqVGHq1KnMnz+fmzdv0rBhw/tu88CBA7nWX7ZsWapXr87f//53nnrqKf76\n17/+ofstIiIiIiIiIg9WseowuXcMk7tcXV15++23qVixYo7lzs7OOX63Wq288847tG7dmj59+rBl\nyxa++OKL+27z19a/ePFijhw5woYNG1i3bh0fffSRYzslIiIiIiIi8jtZTcX2BpM/TLFvscDAQD77\n7DMAdu/ezfr163+17PXr16latSpWq5Xt27djNptzPG8ymcjMzLzv+pOTk1m2bBkNGzZk1KhRpKSk\nPOC9EhEREREREZE/UrG6wiQv4eHhjBkzho0bN2IymZgxY8avlu3VqxdTpkyhcuXKhIWFERERwVdf\nfWV7vnnz5kydOhUPD4/fXH/FihU5cOAAmzZtwtXVle7du/+h+ygiIiIiIiIiD1ax6TDx8/MjLi4u\n13JfX18iIyNzLY+Pj7c9fuedd2yPg4ODbY+//PLLHGW7d+9u6/z4/PPPAfDw8Mhz/Zp2WERERERE\nRAoN3ZJjmFpMREREREREROQXTFar1VrQlfizM5lMBV0FERERERGRP7Xi/qex5dyxgq6C3Vwq1y/o\nKgDF6Jacoi7j8mlD5d0qVuPW8imGMqVfiOD25g8MZUo+PZif184xlCnV9XVub11sbDudBrGsfD1D\nmX4/HWfHI38xlAn+dg83l04wlCnz4iS2NWhuKPPk0X3s69zBUKb5hs+Y51nH7vLDU08AsCu4rd2Z\nx3bsBDDU1v1+Og7AQq+6dmdevZEAwNSStezOjLv9g8OZT+s1szvT8fh+AB4Zv8XuzLeTnwKg+cSt\ndmf2TeyUrxlH9ufUiFC7MzXfigbAcmSH3RmXhtm3OGZcSrI74+Zbw9AxDdnH9VulaxvKjLh1EvO5\n44YyrpXrsblmE0OZp08dZDDVDGU+4DTXFo4ylPF+dRZxvg0MZbpdOurQedfy40FDGZfqTRx6Tb9q\n1dpQpvXXX5F5crehjHPtlqSm/Wwo4+lRik3VAgxlnjl9iPll7D+/Awy9ecLQ+RCyz4nnprxiKFM5\n4n0OdOtoKNM07lMmufsbyky4k8jicvZ/jgAMup7AhZRbhjIPlS3tULs50gaOtLUjbZBfr8+MUsba\n7Z8//+BQWzuS+bptG0OZVju/1HFQjI6Du9/3jBwHrXZmD63gyHZE7qUOExEREREREZHiTmOYGFZk\nWiw5OZmmTZsSFhZGaGgoPXv2ZNu2bXbnr1y5wvjx4wH45ptv+OmnnwD4+9//brgu06ZN4+zZs4Zz\nIiIiIiIiIlI0FKkrTGrUqEFUVBQAKSkpdO3alTZt2uDu7n7frI+PD5MnTwZgzZo1DBgwgPLly/Pe\ne+8ZrsfYsWMNZ0RERERERESk6ChSHSb3Klu2LD4+Phw+fJiFCxdiNpsxmUxMmzaNSpUqMXLkSK5c\nuUJGRgZDhw6lZs2aDBs2jBEjRvDZZ59x8uRJ5s+fT9euXYmPjychIYHJkyfj5OSEh4cHM2fOJCEh\ngZiYGEwmE6dOnaJTp06Eh4cTFhZGREQEW7duJTU1laSkJM6cOcOYMWNo164dixYtYuPGjVSpUgWL\nxUL//v0JCgoq6CYTERERERGRPyvdkmNYke0wSU5OJiUlhTVr1tCjRw+eeeYZtmzZwoIFC+jXrx/X\nr18nJiaGmzdv8t///teWa9WqFfXr1yciIoKHH37YtnzatGm88cYbBAYGEhkZybJlywgKCuLQoUNs\n3ryZrKwsnnjiCcLDw3PU4+LFi3z44Yfs3LmT2NhYAgMDiYmJYevWrdy6dYuOHTvSv3//fGsXERER\nEREREfn9ilQXU1JSkm0MkwkTJjBr1iwOHz5MixYtAAgKCuLo0aPUrFmTtLQ0Ro4cyZ49e3j22Wfv\nu+7ExEQCAwNzrAegQYMGlCxZEg8PjzxzzZplz85RqVIlUlNTOXPmDHXq1MHd3Z0KFSoQEGBsJH0R\nERERERERKXhF6gqTe8cwuctkMtnmyzabzTg5OVGyZElWrVrF/v37Wbt2LTt27GDIkCF2b+fuegBc\nXH67iX75vNVqtWXv1k9ERERERESkIFl1S45hRb7FGjduTHx8PJA9+02jRo04cuQI69evp3nz5kyc\nOJHExMQcGZPJRGZmZo5ltWvX5sCBAznW44jKlStz8uRJzGYz165d4/Dhww6tR0REREREREQKTpG6\nwiQvw4YNY+zYsaxatQpXV1emT5+Ou7s7c+bMYeXKlTg7OzNw4MAcmRYtWjBs2DAWLlxoWzZu3Dgm\nTZqEyWTCy8uLGTNmcOTIEcP1qVChAp07dyYkJAR/f38CAgJwdnb+3fspIiIiIiIiIvmnyHSY+Pn5\nERcXl2u5r68vixcvzrU8MjIy17K7+fDwcNvgrXevTqlVq1au232CgoJyzG5zt+zdcnXq1LE9V6dO\nHdvy6tWrEx4ejouLC126dMHPz8/+HRURERERERGRAldkOkyKkqtXr9KzZ0/c3Nzo0qULlSpVKugq\niYiIiIiIyJ+ZxjAxzGS9O2KqFBgNDCsiIiIiIlKwivufxuZLSQVdBbu5+tYo6CoAusKk0EhZPNZQ\n+bKDpjG1ZC1DmXG3f2DHI38xlAn+dg97OjxuKPOXz77gQLeOhjJN4z4lvlOwoUzQ1h3c2b7UUMa9\n/YsOtfXtjQvvX/AeJZ99lcyErwxlnOu25uz4QXaXrzI5+1a0z5u0sDvzxMG9AFx5+3W7Mz6vzQHg\n0r+G2Z3xHfkOANcWjrI74/3qLADSYqfbnfHoPQaAM2MH2J2pOu0jAK7eTLM7U6GMR7HM/Lzubbsz\npZ5/DYC0VbPsznj0zH79b2/NfdvkrynZaRCJw/vYXR7Af94KLs8ZbihT8fV5ZOxdZyjj1uJ5Q8ca\nZB9vRt4HkP1eGEw1Q5kPOM3JISGGMrXf/ZiLs8INZSqNWuBQuxk5BiD7ODBynoLsc9WdHdGGMu7B\nodzZ9pGxzJMDOBLW2VCmYdQGh47RGx9FGMp4DZji0OfVreVTDGVKvxDBzaUTDGXKvDiJ6x/801Cm\n3OAZTP0swVBmXIe6DrVb2up/Gcp49BjpUFs70gb59fqkRk8ylPEMnZBvGSPfDSD7+4GOg+JzHHiG\nZu+HI98RHdmOyL3UYSIiIiIiIiJS3OnOBsOK9E1MycnJNG3alLCwMMLCwujVqxcRERG5pgx2xPbt\n28nIyODKlSuMHz/+AdRWRERERERERIqKIt1hAlCjRg2ioqKIiopi5cqVmM1m1q9f/7vXu2TJEsxm\nMz4+PkyePPkB1FREREREREREiopid0tOQEAAp0+fJiYmhvXr1+Pk5ESHDh0YMGAAFy9eZOTIkQBY\nLBZmzZpF1apV+eSTT4iKisLJyYn+/fuTkZHBwYMH+dvf/sa0adMYMWIEcXFxxMfHM3fuXFxcXPD1\n9WXGjBls2LCBb7/9lmvXrpGUlMTAgQMJCQlh0aJFbNu2DScnJ4KDg3nllVcKuGVERERERERExF5F\n/gqTe5nNZrZv346XlxdbtmxhxYoVxMTE8Omnn3L+/HkuX77MkCFDiIqKonv37ixfvpxbt26xcOFC\nYmJiiIyMZP369fz1r3/Fx8eHDz/8EFdXV9v6J0yYwNy5c4mOjsbLy8t2JcuJEydYsGAB7777LtHR\n2QPOffTRR6xYsYLY2FjKlClTIO0hIiIiIiIiAmRPK1xUfgqJIn+FSVJSEmFhYQAkJCQwaNAgKlas\nyOnTp+nXrx8AaWlpnDt3Dj8/P6ZOncr8+fO5efMmDRs25NSpU9SsWRN3d3fc3d1577338txOSkoK\nJpOJhx56CICgoCC++eYbGjRoQJMmTXB2dqZSpUqkpqYC0KlTJ/r370/nzp157rnn8qElRERERERE\nRORBKfIdJnfHMAEYNmwYNWpkz9f8+OOP5xp75J///CetW7emT58+bNmyhS+++AInJyeysrLuux2T\nyZRjXm6z2Yzp/48y7OKSuxknTZpEYmIimzdvJiwsjI8//jjPciIiIiIiIiJS+BSea10egJEjR/Lm\nm2/SsGFD4uPjuX37NlarlalTp3Lnzh2uX79O1apVsVqtbN++HbPZTM2aNUlKSiItLY309HT69++P\n1WrFZDLlmG3Hy8sLk8nE+fPnAdi7dy+NGjXKsx6pqaksWLAAf39/wsPD8fLy4tatW/nSBiIiIiIi\nIiK/ZDU5FZmfwqJYXfJQpUoVOnXqRGxsLP369aNv3744OzvToUMH3N3d6dWrF1OmTKFy5cqEhYUR\nERHB/v37GTZsGP379wfgpZdewmQy0aJFC1544QVmzJhhW/+UKVMYMWIELi4uVKlShWeffZb//Oc/\nuerh6enJ9evX6dGjB6VKlaJp06aULVs239pBRERERERERH6fIt1h4ufnR1xcXI5lr7/+uu1x3759\nczwXHBxMcHCw7fcvv/zS9rhLly45yt7bUXJ3G82bN2fFihU5ynXr1s322MPDg88//xyAiIgIQ/si\nIiIiIiIiIoVHke4wERERERERERE7OBWeW12KCpP13pFMpUDcHTxWRERERERECkZx/9M449r5gq6C\n3dy8Hy7oKgC6wqTQMJ8/Yai868N1+GFYL0OZWu+s5NyUVwxlKke8z7WFowxlvF+dRcrisYYyZQdN\nY4K7v6HMpDuJHOr9tKFMQOxm9j//pKFMs3XbHMqceKW7oUyd99cYaoNJdxIB+LhiA7szIZePAvBv\n73p2Z/pfOw5ArE99uzO9rxwDYH6ZOnZnht7Mfg/8t0VLuzPt9u4GYEvtpnZnnjp5AICAURvtzhya\n9azDmcB/2p/5bobj23Eks6fD43Zn/vLZFwAc/1tXuzP1PlwLQOYP8XZnnGsFMbVkLbvLA4y7/QNx\nvva/DwC6XTrq0PlwxyN/MZQJ/naPQ3U7OSTEUKb2ux8zmGqGMh9w2tD7GrLf26dHv2QoU23mEo6+\n1OX+Be/RYMl6NlULMJR55vQhh9rNfPawoYxrlUaGzjmQfd75tF4zQ5mOx/c79F5wpG4flK1rKDM4\nJYHZHrUNZd5IO8m4EjUNZaamn+Lk5ZuGMrUrlnGo3Yx8LkL2Z6Mjbe1IG+TX6zOjlLF2++fPPzDP\n0/7PeYDhqSccqpuR7xOQ/Z1Cx0HxOQ7eSDsJOPa90kjdhqca+3tM/hx0TY6IiIiIiIiIyC8UWIdJ\nTEwMPXv2JDQ0lB49erBr1y4ARo8ezY4dOxxa59atWx9kFX/VtGnTOHv2bL5sS0REREREROR3MzkV\nnZ9CokBuyUlOTmbVqlWsXr0aV1dXfvzxR8aNG8djjz32u9a5ceNGOnXq9ABrmrexY43dbiIiIiIi\nIiIiRUuBdJjcunWL9PR0zGYzrq6uVK9enejoaNvz8fHxREdHc+HCBd58800aNGjA0qVL2bRpEwDt\n27fn5ZdfZvTo0bi6upKSkkJ6ejqHDh1iwYIFhIeH29YVFhZGo0aNOHz4MOnp6cydOxdfX19GjRrF\npUuX+Pnnnxk6dCjBwcF88sknREdH4+rqSr169ZgwYUKey8LCwoiIiGDr1q2kpqaSlJTEmTNnGDNm\nDO3atWPRokVs3LiRKlWqYLFY6N+/P0FBQfneziIiIiIiIiLimALpMKlXrx4BAQG0b9+edu3a0bZt\nWzp27IiLS3Z1TCYTkZGRxMbGsnbtWjw9PVm7di2rV68GICQkhKeeegoALy8vpkyZQnx8PDExMTk6\nS+4qV64cUVFRREVFsXTpUgYPHkzr1q3p2rUrZ8+e5bXXXiM4OJjIyEgWLVrEQw89xJo1a7hz506e\ny+518eJFPvzwQ3bu3ElsbCyBgYHExMSwdetWbt26RceOHenfv/8f3KIiIiIiIiIiv6EQ3epSVBTY\nLDmzZ88mMTGRL7/8ksWLF7NixQqWLVsGwCOPPAKAr68v3333HceOHSMwMNDWodKsWTOOH8+euSMg\n4P6j6LdsmT3rRpMmTdi5cydlypTh+++/Z+XKlTg5OZGSkgJA586dGTJkCM899xydO3fG3d09z2X3\natYse9T7SpUqkZqaypkzZ6hTpw7u7u64u7vbVT8RERERERERKVwKpIvJarWSnp6Ov78/L730Eh9/\n/DGXLl3i/PnseaGdnZ1zlDWZTDnmxDabzTg5ZVfd1dXVru3du64NGzZw48YNli9fzoIFC2zlBg8e\nzIIFC7Barbz44otcv349z2X3utuJc++27tYNsq+WEREREREREZGipUA6TFavXk1ERIStIyM1NZWs\nrCzKly+fZ/n69etz8OBBLBYLFouF7777jvr16+co4+TkhMViyTO/b98+AA4ePIi/vz/Xr1/Hz88P\nJycntm3bRkZGBllZWcydOxcfHx/69+9PkyZNOH/+fJ7LfkvlypU5efIkZrOZa9eucfjwYaPNIyIi\nIiIiIiIFrEBuyenWrRunTp0iJCSEUqVKYbFYGDduXK7bXe7y8/OjV69ehIaGYrVaCQkJoXLlyjnK\n+Pv7c/ToUaZPn86YMWNyPHf+/HkGDhxIamoq8+fPx2w28/e//52DBw/SvXt3KlWqxMKFC/Hw8KBX\nr154enpSpUoV6tevz9dff51r2W+pUKECnTt3JiQkBH9/fwICAnJcMSMiIiIiIiKS7zSGiWEF0mHi\n7OzMqFGj8nxu5syZtsfBwcEEBwcD0LdvX/r27furZb29vfniiy/yXGfPnj2pU6dOjmXr16+3PX7u\nuedsj19++eUc5V5++eVcy6KiogByrLNOnTq25dWrVyc8PBwXFxe6dOmCn59fnvUSERERERERkcKp\nwAZ9Lc6uXr1Kz549cXNzo0uXLlSqVKmgqyQiIiIiIiIiBpis946mKgVCA8OKiIiIiIgUrOL+p3H6\nzWsFXQW7lSjjXdBVAHSFSaFhSTpgqLxLjaZc+tcwQxnfke+QtmqWoYxHz1H8vHaOoUyprq/z87q3\njWWef42FXnUNZV69kcD3LzxjKNN4+SZOvNLdUKbO+2s4EtbZUKZh1AbOjh9kKFNl8mI+KGt/GwxO\nSQBgW4PmdmeePJo9APK6Sg3tzjx/8QgAsT6/PX7PvXpfOQbAv73r2Z3pfy17qvCPKzawOxNy+SgA\nm6rZP333M6cPAdBs3Ga7M/unPu1w5pHxW+zOfDv5qXytW3ynYLszQVt3AJC2+l92Zzx6jAQgM/Eb\nuzPO/o/yab1mdpcH6Hh8P2+Vrm0oM+LWSe5sX2oo497+RUPHGmQfb8vK2/8+AOj303Euzgo3lKk0\naoGh9yhkv08HU81Q5gNOc3vrYkOZkp0GOXSu/m+LloYy7fbudujzKvOHeEMZ51pBfNWqtaFM66+/\ncug4mF+mzv0L3mPozRMcDHnKUKbJx1v4vEkLQ5knDu5lnqexug1PPWHoMw6yP+eOX7phKFPP18uh\ndnPkeHOkrR1pg/x6fRz5Hjbbw9i59420kw69Po58Lug4KD7HwdCbJwAMHQcdj+8HMFS3N9JO2l1W\n/jw06ouIiIiIiIiIyC8UiStMYmJiWLduHW5ubty5c4fXX3+dxx57jNGjR9OpUyfbwLC/5fz581y9\nepWAAGP/HRQREREREREp8jRLjmGFvsMkOTmZVatWsXr1alxdXfnxxx8ZN24cjz32mKH17Nmzh59/\n/lkdJiIiIiIiIiJyX4W+w+TWrVukp6djNptxdXWlevXqREdH256Pj48nOjqaCxcu8Oabb9KgQQOW\nLl3Kpk2bAGjfvj09evRgwYIFuLi48NBDD9G+fXtbvk2bNnTq1Invv/8eX19f3nzzTdLT0xk9ejQ3\nb97EYrEwbtw4Pv30U+rWrcszzzzD+PHjcXFxYfz48WzYsIEff/yRp556ismTJ2MymfDw8GDmzJnc\nvHmTkSNHUqpUKUJDQ+26EkZERERERERECl6h7zCpV68eAQEBtG/fnnbt2tG2bVs6duyIi0t21U0m\nE5GRkcTGxrJ27Vo8PT1Zu3Ytq1evBiAkJISnnnqKrl27Uq5cuRydJQCXL1+mc+fOjBs3jqFDh7Jz\n506OHz9OYGAgL7/8Mt9//z0zZszg73//O//973955plnuHr1qm0E5f379/P0008zZcoUJk+eTPXq\n1YmJiSEmJoYuXbpw7NgxduzYQbly5fK34URERERERETEYUXiJqbZs2cTHR1NvXr1WLx4Mf3797d1\nWDzyyCMA+Pr6cuvWLY4dO0ZgYCAuLi64uLjQrFkzjh8//qvrLlWqFE2aNAGgSZMmJCUlcfjwYYKC\nggBo3Lgxp0+fpmnTphw9epQbN25QunRpSpYsye3btzl69CiBgYEcOnSIiIgIwsLC+M9//sNPP/0E\nQJUqVdRZIiIiIiIiIgXLZCo6P4VEob/CxGq1kpGRgb+/P/7+/oSFhfH0009z/vx5AJydnXOUNZlM\nOebPNpvNODn9er9QVlZWrvwv15GVlUWpUqVwcnJi7969BAYGcufOHXbv3k2pUqVwc3OjZMmSLFu2\nDNM9L25ycjKurq4PpB1EREREREREJP8U+itMVq9eTUREhK0DIzU1laysLMqXL59n+fr163Pw4EEs\nFgsWi4XvvvuO+vXrYzKZsFgsucrfuXOHw4cPA3Dw4EFq1apF48aNiY+Pty2rXTt7/u7AwEBiYmJo\n2rQpgYGBREdH07x5cyD71qGdO3cCsHHjRnbv3v1gG0JERERERERE8k2hv8KkW7dunDp1ipCQEEqV\nKmUbhNXd3T3P8n5+fvTq1YvQ0FCsVishISFUrlyZpk2bMmrUKLy9vXnuueds5cuWLct//vMfpk+f\njo+PD61bt6Z58+aMGTOGfv36YbVaGT9+PACPPvoo0dHR1K1bF7PZzN69e3n11VcBGDt2LBEREXz4\n4YeUKFGCt956i1u3bv3xDSQiIiIiIiJyP5pW2LBC32Hi7OzMqFGj8nxu5syZtsfBwcG2WWj69u1L\n3759c5Rt1aoVX331VZ7rGTNmTI7fS5cuzTvvvJOrXNu2bTlw4ICtXnevTAHw9/dn+fLlOcqXLVuW\nuLi4X9s1ERERERERESmk1MUkIiIiIiIiIvILJuu9o5tKgTAVolGARURERERE/oyK+5/Gd35OK+gq\n2M29lEdBVwEoArfk/FmYz58wVN714Tqk71ptKFPisR5Yju00lHGp35aMCz8Yyrg9VAtL0gFj26nR\nlFMjQg1lar4VjeXHg8a2U70Jn9ZrZijT8fh+Mi4lGcq4+dbAfPbw/Qvew7VKI1KjJ9ld3jN0AgDX\nFuZ9y1pevF+dBcDNpRPszpR5MbtO5n0b7M64Nu8MwJ0d0XZn3IOzX//UtJ/tznh6lMqu2/7N9tet\n2dMAvPKx/cfO+yFNHM4MWf2d3Zl3ewQ6nHGkbscGPm93pn7kOgDGlahpd2Zq+ikA0r9aaXemROte\nnHilu93lAeq8v4bMH+INZZxrBTHcubqhzLzMHx06tzlynsrYu85Qxq3F85we/ZKhTLWZS7i9dbGh\nTMlOgxhMNUOZDzhN5kljA6E7127JD8N6GcrUemclQ52qG8rMz/qRtNX/MpTx6DHSofN7+pWzhjIl\nfKoYOldD9vl6nmcdQ5nhqSeI821gKNPt0lHSVs0ylPHoOYrE4X0MZfznreBSirHx4HzLlnao3T6u\naKwNQi4fdaitHWmD/Hp9rn/wT0OZcoNnkBY73dh2eo9xKLO5ZhNDmadPHdRxUIyOA4/e2cMnGDkO\nnj6V/dnryHZE7qVbckREREREREREfqHAO0xiYmLo2bMnoaGh9OjRg127dgEQFhbGiRMniIuLY9u2\nbblyQUFBAEybNo2zZ4391+Zex48fJynJ2NUDcXFxzJo1677LREREREREROTBmz59Or169aJ3794c\nOnQox3O7du2iR48e9OrVi3fffdfhbRToLTnJycmsWrWK1atX4+rqyo8//si4ceN47LHHbGW6dev2\nm+sYO3bs76rDtm3baNSoETVq1Phd6xEREREREREptIrRtMJ79+7l9OnTrFy5ksTERMaMGcPKlf+7\nDXzq1KlERkbi6+tLaGgonTp1olatWoa3U6AdJrdu3SI9PR2z2YyrqyvVq1cnOjrnmAfz58+nXLly\n9O7dmxEjRnDx4kUaN25sez4sLIyIiAi2bt1KamoqSUlJnDlzhjFjxtCuXTsWLVrExo0bqVKlChaL\nhf79+9uuTklISCA2NhZvb2/Kly/Pjz/+SHR0NE5OTtSuXZspU6ZgNpsZPXo0586do0SJEsyePTtH\n/d566y1KlixJpUqVbMtiYmJYv349Tk5OdOjQgQEDBvyBrSgiIiIiIiLy57F79246dOgAgL+/Pzdu\n3ODWrVuULl2as2fP4uXlxUMPPQRAu3bt2L17t0MdJgXaxVSvXj0CAgJo3749o0ePZtOmTVgsljzL\nfv3111gsFlauXEmXLl1ISUnJVebixYt8+OGHjB07lpUrV5KSkkJMTAwrV65k4sSJ7N27N0f5unXr\n0qZNG15//XUCAgK4ffs2ixcvJjY2llOnTpGQkMAnn3xChQoViI2NpWfPnmzfvt2W37x5MxcuXODV\nV1+1LTt79ixbtmxhxYoVxMTE8Omnn3L+/PkH1GIiIiIiIiIif25Xr16lXLlytt+9vb25cuUKAFeu\nXMHb2zvP54wq8FlyZs+eTWJiIl9++SWLFy9mxYoVLFu2LFe5H374gaZNhbc1pQAAIABJREFUmwIQ\nGBiIu7t7rjLNmmXPflKpUiVSU1M5c+YMderUwd3dHXd3dwICAn6zLl5eXrbOj8TERFJSUjhy5Agt\nW7YE4NlnnwWyxys5efIkn376KZs2bcqxju+//57Tp0/Tr18/ANLS0jh37hwPP/ywkWYRERERERER\neWCsJlNBV+EP80dNCV2gHSZWq5WMjAz8/f3x9/cnLCyMp59+Os8rMqxWK05O/7sgJisrK1cZF5ec\nu/PLjOk3DpCMjAwmT57MunXr8PHxYfDgwQA4Ozvnua1z585Ru3ZttmzZwvPP/29qTldXVx5//HEm\nT578G3suIiIiIiIiIo6oWLEiV69etf1++fJlfHx88nzu0qVLVKxY0aHtFOgtOatXryYiIsLWG5Sa\nmkpWVhbly5fPVbZGjRocPnwYgP3795ORkXHf9VeuXJmTJ09iNpu5du2aLX8vk8lEZmYmaWlpODs7\n4+Pjw4ULFzh8+DBms5nGjRuzZ88eAHbs2MH7778PwOOPP8706dNZuHBhjhejYcOGxMfHc/v2baxW\nK1OnTuXOnTvGG0dEREREREREcmnVqhVbt24F4MiRI1SsWJHSpUsD4Ofnx61bt0hOTsZisbBjxw5a\ntWrl0HYK9AqTbt26cerUKUJCQihVqhQWi4Vx48blebtN27ZtWbNmDaGhodSrVw9fX9/7rr9ChQp0\n7tyZkJAQ/P39CQgIwNnZOUeZ5s2bM3XqVGbMmEGrVq3o3r079erVY9CgQcyYMYO1a9eya9cuQkND\ncXFxYdasWXz99ddA9r1Qw4YNY+LEiTzxxBMAPPzww/Tr14++ffvi7OxMhw4d8twfERERERERETGu\nWbNmNGzYkN69e2MymZgwYQJxcXF4enry5JNPMnHiREaMGAHAM8884/CsuAXaYeLs7MyoUaPyfC4q\nKgqAOnXq2JYtXLjQ9njcuHG/Wq5OnTq25dWrVyc8PBwXFxe6dOmCn59fju10796d7t27A9jGKrmr\nf//+ALlmxrl3quNnn33WNrbJXX379qVv37557peIiIiIiIhIfvuDhvkoMP/3f/+X4/d69erZHj/6\n6KM5phl2VIEP+vpHu3r1Kj179sTNzY0uXbrkmP5XRERERERERCQvJusfNZys2O23BqMVERERERGR\nP15x/9P459tFZ2zNUiULx7AWxf4Kk6Li7E+phspXKe/J7a3/j737Do+qSvw//p6EhEDoIYReEkpA\nQEEIUl16/7IGkKVLE2UBXRRhlVgARUBdkRopUsVFDBuB0IOidAXXRKQlBKWIQAIJoaTN74/5mTWA\nes9IMkn4vJ4nD8m95zP33DNn7swc7rl3kVGmUMfhXA+fZZQp3OMZbu1abZQp2KovqV9tMMp4NOrG\n/o6tjTJNtuzkNa8Ao8wrN2O4sXHeHxf8lUJdR7G5RgOjTKcThznUo71RpmH4Nr5s3sJy+Ra7vwTg\nx5eHW85UmuzoM/va/cVy5pHtnwEQ1a+L5Uy9Dx23295Wp5HlTPsjXwHw7d86W87U/2gTAGenPGU5\nUyHEceHmDnO/tJzZ+nfH89J5/m7LmU1PN8/RjDP7Ez/v7lMi76bUqOkApJ/YaznjXsMxzdHkeODR\nqBsXZo61XB7Ab/x7HHmiu1GmztL1pJ06bJQpUK0Bp14YZJSpNmM5e1q3Mso027nLqeO7M21g8roG\nx2vbpA+Aox+MpIpRJpTTfNWtnVGm0YbtpB+z/joAcK/VgoSkZKNMyaLeOdZHPw9q+scFf+XRA3uN\nXtfgeG2fnviEUabKm0uJfCjIKNPmmwMc7NzGKNN4UyQpP582yniWqeJUux1/qqdRpuaCT5xqa2fa\nIKeenx31Ghtl2kYdZOfDjxhlWn+9z+izATg+HzhzrFI/yD/94JfPiM58FjWpW+uv91kum1dl5PMB\noezg0rvkiIiIiIiIiIjkRrlqwGTVqlU8/vjjDBgwgF69erFnzx7L2aeffvp312/evPnPVs8p06dP\nJywszCXbFhERERERERHn5JopOWfOnGHNmjWsXbsWDw8P4uLimDRpEs2aNbOUnz9//m+uS0lJYenS\npXTq1OleVVdEREREREQkz9CEHHO5ZsDk2rVr3Lp1i9TUVDw8PKhatSorV64EYODAgdStW5fo6Ghu\n3brFv/71L86cOcOSJUu4fv06EyZMYNiwYezfv5+BAwfSrFkz9u3bR0JCAgsWLGDhwoUcO3aMV199\nlVdffTVzm19++SXvvvsuXl5e+Pj48NZbbxESEkLhwoWJjY0lISGBadOmUadOHVatWsX69etxc3Oj\nXbt2DB06lGvXrvHiiy9y9epV0tPTmTRpEoGBgYSHh7No0SL8/Pzw8vKiRo0aLmpVEREREREREXFG\nrhkwCQwMpH79+rRt25ZHH32UVq1a0aFDBwoUcFSxZMmSrFixghUrVrBs2TLatm3L8ePH2bJlC56e\nnlkeq0iRIixbtoy33nqLrVu3MmzYMP773/9mGSwBWLlyJRMnTqRRo0Zs3bqVK1euAJCWlsbSpUuJ\njIxk7ty5TJw4kc2bN7N6tePip3379qVTp06sW7eOli1b0rt3b06ePMnrr7/OkiVL+Ne//sUnn3xC\nsWLFCA4Ozv7GExEREREREZF7KtcMmADMmDGDmJgYvvjiCxYtWsTq1atZvnw5AE2bOq50/dBDD7Fr\n1y4AatWqdcdgCUCjRo6rLpctWzZzEORuOnXqxCuvvEL37t3p2rUrvr6+AJnTgB566CHeeustoqKi\nOH36NIMGOe6OkJyczNmzZzl8+DDx8fF8+umnANy4cYOEhAS8vb3x8fEBoGHDhn+6XUREREREREQk\nZ+WaARO73U5KSgoBAQEEBAQwcOBAOnfuzLlz5zLX//KvzWYDuOtgCYC7u3uWx/0tf/3rX2nZsiXb\nt2/n6aefZtYsxy13MzIyMsvYbDY8PDz4y1/+wuTJk7PklyxZQkhICA0a/O+Ws/Hx8bi5/e9auvn9\nXt4iIiIiIiKS+2Xoq6mxXHOXnLVr1xISEpI5wJCUlERGRkbmmRpffeW4//Y333xDQECA0WO7ubmR\nnp5+x/K5c+dSoEAB+vTpQ5cuXYiJiQHg66+/BuDw4cMEBATwwAMPsH//fm7cuIHdbmfq1KncvHmT\nBx98kO3btwNw8uRJPvjgA0qUKEFSUhKJiYmkpqZy6NAh5xpERERERERERFwm15xhEhwcTGxsLL17\n96Zw4cKkpaUxadIkvLy8ADh37hzDhg0jKSmJ2bNnExcXZ/mxfX19SU1NZezYsbz33nuZy8uXL8+Q\nIUMoVqwYxYoVY8iQIURGRnLr1i1GjhzJ+fPnmTlzJuXLl2fQoEH0798fd3d32rVrh5eXFwMGDOCf\n//wn/fr1IyMjg5deegk3NzdGjx7NgAEDqFChgi74KiIiIiIiIpIH5ZoBE3d3dyZMmPCb6x9//HFq\n1qyZ+befnx9NmjTJ/Hv//v0ArFixInPZgAEDMn+PiIi44zEfe+wxHnvssTuWt23bltatW2dZ1r9/\nf/r3759lWZEiRZg9e/Yd+V69etGrV6/f3BcRERERERGRnKTLRZjLNVNyRERERERERERyC5tdw0wu\n98tFbEVERERERMQ18vtX4yvXrru6CpaVKFLY1VUActGUnPtdyoVTRuU9/aqREPpPo0zJkdO4sSnU\nKFOo80hubltilPFqP5SbO1eaZVoPYFXp2kaZ/pe+51CP9kaZhuHb2NfuL0aZR7Z/xtERd07d+j2B\nC9dxdspTRpkKIQuIqFLfcvkup78FYH/H1n9Q8n+abNkJQORDQZYzbb454PR2dtRrbDnTNuoggFFb\nBy5cB8D3w3pYztReHA5Aw0mbLGcOTe3sdKbRq1ssZ756tSMAD7+82XLm68mdnM4485w609a3dq22\nnCnYqi9fNm9huTxAi91fGu0LOPYn9rkBf1zwV/zfXmm0/+BoA2f25+KscUYZ32feMTp+gOMY8nlQ\nU6PMowf2cnJsH6NM9ff+zVfd2hllGm3YzkiqGGVCOe3U85P61QajjEejbk61wXcDuxllHlixgfXl\n6hplup+PZnONBn9c8Fc6nTjMx2XqGGV6/3zEqbo58z6fkJRslClZ1DvH6uZMWzuznZx6fnJqO85k\nPigVaJQZEn9U/SAf9YPu56MBjPrBkPijAE5tR+TXNGAiIiIiIiIiks/ptsLm8vWAyapVqwgPD8fT\n05ObN28ybtw4SpUqRcGCBalWrZpTj3nx4kVmz57N5MmT73FtRURERERERCS3yLcDJmfOnGHNmjWs\nXbsWDw8P4uLimDRpEk2aNKFu3bpOD5j4+vpqsEREREREREQkn8u3AybXrl3j1q1bpKam4uHhQdWq\nVQkJCWHo0KGUKlUKHx8f4uLiWLlyJW5ubtSoUYMpU6YQFhbGwYMHSUhI4MSJE/zjH/9gw4YNxMTE\n8NZbb+Hj48PYsWMJCwujffv29OnTh507d5KSksIHH3wAwHPPPcf169e5efMmISEh1K9vNq9cRERE\nRERE5F7SjBxz+fa2woGBgdSvX5+2bdsyceJEIiIiCAgIoGXLlowbN4769etz48YNFi1axEcffURs\nbCzHjh0DIC4ujvnz5zNy5EhCQ0OZO3cuTz75JBs2ZL0wXHp6Ov7+/qxatYqKFSuyb98+Ll68SO/e\nvVmxYgXjxo1j4cKFrth9EREREREREfkT8u0ZJgAzZswgJiaGL774gkWLFrF69WrKly+fub548eKM\nGjUKgJiYGK5cuQJA3bp1sdls+Pr6UqtWLdzd3SldujSHDh26YxuNGjUCoGzZsiQlJVG6dGnmzZvH\n4sWLSUlJoXDh3HE7JBERERERERGxLt8OmNjtdlJSUggICCAgIICBAwfSuXPnzPUpKSlMnjyZ8PBw\nfH19GTlyZOa6AgUK3PX3u92X293dPcv6ZcuW4efnx8yZM4mKimLGjBn3etdEREREREREjOguOeby\n7ZSctWvXEhISkjnIkZSUREZGBhUrViQ9PZ3k5GTc3d3x9fXl/PnzREdHk5qa+qe3m5CQQOXKlQHY\nvn37PXlMEREREREREclZ+XbAJDg4GB8fH3r37s2gQYMYNWoUkyZNolGjRkydOpWjR4/SvHlzevbs\nyZw5cxg+fDjTpk0jLS3tT223R48efPDBBwwdOpT69etz8eJFPvnkk3u0VyIiIiIiIiKSE/LtlBx3\nd3cmTJhw13U9e/YEoGnTplmWDxkyJMvfrVu3pnXr1nf8HhYWBkBkZGRm2V9va9OmTZm/t23b1tld\nEBEREREREREXybcDJiIiIiIiIiLicLdrcsrvs9nVai5ns9lcXQUREREREZH7Wn7/avzz1WRXV8Gy\nMsW9XV0FQGeY5BqpZ44YlfeoWIebO5YZZbzaDiYtartRpkC9dk7VLT3moFHGPaAxR0c8ZpQJXLiO\ntFOHjTIFqjVgQ8V6RpluZ6JIOX/SKONZrjqpP0YbZTwq1eXS7Octly895i0Afpo+2nKm7IQ5ACSE\n/tNypuTIaQDc2rXacqZgq74A3NgUajlTqLPjTlU3k65YzngVLeGo25f/tl63Fn0AGLzqa8uZZf0f\nztHM0NV33sL8tyzp29Dp7Xz7t85/UPJ/6n/kmGr4gkc1y5kZqacAuLVnreVMwWa9iOrXxXJ5gHof\nRpD6zRajjMdDHXmugPV9AXg77RRp3+8yyhSo3Yr0E3uNMu41mnJz50qjjFfrAZz4e2+jTI25H3N9\n3TtGmcKPjWOMW1WjzOyMONKPfWmUca/Vgu+H9TDK1F4czkiqGGVCOU3SyteMMkUHvEL6yf1GGffq\nTUg9e9Qo41Eh0Og9ARzvC9MKVzfK/PP6SZb7BBplBl0+ypVFLxllSgx/nSNPdDfK1Fm6nnMJ14wy\n5UsWcardnGkDZ9ramTbIqefnwsyxRhm/8e85tR1nMuvL1TXKdD8frX6Qj/pBieGvAxj1g+7nHZ/D\nndmOyK9pwEREREREREQkn8twdQXyoGy9S86qVat4/PHHGTBgAL169WLPnj0AHD16lFOnTv2px54+\nfTphYWHs2rWLDz/88E891pYtZv8zCdCkSRNLy0REREREREQk78m2M0zOnDnDmjVrWLt2LR4eHsTF\nxTFp0iSaNWvGtm3bqFu3LtWqmZ0OfTetWrX60/XcuHEjHTt2/NN1EREREREREZH8IdsGTK5du8at\nW7dITU3Fw8ODqlWrsnLlSo4dO8ZHH31EqVKl8PHxIS4ujpUrV+Lm5kaNGjWYMmUKYWFhfP3118TH\nx3Pq1CmGDRtG7969CQ8PZ9GiRfj5+eHl5UWNGjUICwvjxIkT9O/fn4kTJ1KpUiWOHTtG7dq1ef31\n1zl69CgTJ06kaNGi1K1bl4SEBN58883Mek6ePJlvv/2WOXPm0KtXL8aPHw9AWloa06dPp3Llyvzn\nP/9hxYoVuLm5MWTIELp0+d/8+u+//57XXnuNxYsXZy47efIkkydPxmaz4e3tzZtvvkmxYsWyq6lF\nRERERERE5B7Ltik5gYGB1K9fn7Zt2zJx4kQiIiJIS0ujVq1atGzZknHjxlG/fn1u3LjBokWL+Oij\nj4iNjeXYsWMAHD9+nDlz5jB37lxWrlyJ3W7nX//6F0uXLmX+/PmcPn36jm1+9913jBs3jrVr1/L5\n55+TmJjI3Llz+fvf/86KFSs4d+7cHZlhw4YRFBTE6NGj+fnnnzPL9uzZkw8//JBr164xb948Vq1a\nxeLFi1m/fn1mNj4+nldeeYV33nkHb+//XcV3ypQpTJ48mWXLltG8eXNWrVqVDS0sIiIiIiIiYo3d\nnnd+cotsvejrjBkziImJ4YsvvmDRokWsXr2a5cuXZylTvHhxRo0aBUBMTAxXrjjukPHQQw/h7u5O\n2bJlSUpKIiEhAW9vb3x8fABo2LDhHdurXLkyvr6+AJQpU4akpCRiYmIyy7Zp04a9e3/7bgW+vr5M\nnTqV2bNnk5iYyAMPPEBsbCz+/v54eXnh5eXF/PnzAcctp/7xj38wfPhwypcvn+Vxvv32W0JCQgBI\nSUmhXj2zu7KIiIiIiIiIiGtl24CJ3W4nJSWFgIAAAgICGDhwIJ07d85ylkdKSgqTJ08mPDwcX19f\nRo4c+b+KFbizam5u/zsh5m73yHZ3d7+jDna7HZvNBpD572957733aNGiBX379mXz5s189tlnuLm5\nkZFx5/WEr127Rq1atfjoo4/o0KFDlnWFChVi+fLlf7g9EREREREREcmdsm1Kztq1awkJCckc2EhK\nSiIjIwMfHx9sNhvp6ekkJyfj7u6Or68v58+fJzo6mtTU1Ls+XokSJUhKSiIxMZHU1FQOHTpkqR6V\nK1cmOtpxH+5du3bdsd7NzY20tDQAEhISqFy5Mna7nR07dpCamoq/vz+nTp0iOTmZW7duMWTIEOx2\nO0WLFuXFF1/E19eXNWvWZHnMwMDAzG1t3Ljxd89qEREREREREcluGfa885NbZNsZJsHBwcTGxtK7\nd28KFy5MWloakyZNwsvLi0aNGjF16lSmTZtG8+bN6dmzJ4GBgQwfPpxp06YxePDgOx7Pzc2N0aNH\nM2DAACpUqECNGjUs1ePpp59m0qRJLFu2jOrVq5OUlJRlfUBAAEeOHOGNN96gT58+TJkyhQoVKjBw\n4EBCQkI4dOgQY8eOZciQIQA88cQTWc4cefHFF+nTpw8tW7bMXPbSSy8REhLCwoULKViwIG+//bYz\nTSgiIiIiIiIiLpJtAybu7u5MmDDhrut69uxJz549AWjatGmWdb8MTPzC29ubyMhIAHr16kWvXr1+\nc5thYWF3/H7p0iXeeustAgMDCQ0NpWTJklkypUqV4rPPPsv8u3Xr1pm/f/HFF5m/d+/ePUtu//79\ngOMaLJs3b86yLCAggA8//PA36ykiIiIiIiIiuVu2XvQ1N/D09OSll17KvGirzvYQERERERGR+83d\nrgMqv89mV6u5nC4OKyIiIiIi4lr5/avxmfhrrq6CZRVLFXF1FYD74AyTvOLGlkVG5Qt1HE7y2plG\nGe9e40k/ud8o4169iXOZY1+aZWq1IO37Oy/K+3sK1G7F0QtXjTKBfsX58eXhRplKkxex+egFo0yn\nQD/e3nXSKPNcq+rcunzWcvmCPhUAuLlzpeWMV+sBACQlX7ecKepdGIDLicmWMz7FvAFINNhOsf+/\nnSvXrGdKFHFkbl69bDnjVdxxa/ILV6y/YfiVcBywzxtkyv3/jDPbyanM2SlPWc5UCFkAQNLK1yxn\nig54BYAbm0ItZwp1HknaD99aLg9QoHJ9biYmGGW8ipUkcdkrRplig18j9dxxo4xH+ZpGrzdwvOZu\nbltilPFqP5TUH6ONMh6V6jp1fHfmvSchyfrxA6BkUW9Sv9pglPFo1M2of4Kjj46kilEmlNNOPac3\nks0+pBbyLsKtBLP3noIl/bj24RSjTJF+IUbvI+B4L7kVf94oU7BUOVLPHDHKeFSsw66YS0aZVgGl\nnWq3lH3rjDKejzzmVFs70wY59fw4026pZ48aZTwqBDp1vE6L2m6UKVCvnfpBPuoHXsUcl1Qw6QcF\n6rUDMKqbR4VAy2Xl/pFtd8kREREREREREcmr8u0ZJqtWrSI8PBxPT09u3rzJuHHjKFWqFAULFqRa\ntWr3fHs7duygZcuWeHp60qRJk8wLwIqIiIiIiIi4WoarK5AH5csBkzNnzrBmzRrWrl2Lh4cHcXFx\nTJo0iSZNmlC3bt1sGTBZunQpjzzyCJ6envf8sUVEREREREQkZ+XLAZNr165x69YtUlNT8fDwoGrV\nqoSEhDB06FBKlSqFj48Pzz//PK1atcLHx4fg4GBeeuklUlNTcXd3Z+rUqZQvX5727dvTrl07Dh06\nRNGiRXn//ff5+eefeeaZZ/Dw8KBRo0Z8/fXX9OzZk2+++YYRI0awdOlSAGbNmsXu3bspUaIECxYs\nwM1Ns59ERERERERE8op8+S0+MDCQ+vXr07ZtWyZOnEhERAQBAQG0bNmScePGUb9+fdLS0mjVqhVP\nP/00s2bNYujQoSxbtozBgwczb948AH788Ud69OjBv//9bxITEzl27BhLly6lc+fOrFy5kpSUFAD+\n+te/4uvry8KFC/H09OTq1at07NiRNWvWcPXqVY4dO+bK5hAREREREZH7nN2ed35yi3x5hgnAjBkz\niImJ4YsvvmDRokWsXr2a8uXLZylTv359AA4fPsypU6eYP38+6enplCpVCoAiRYoQGOi4WnLZsmVJ\nSkoiJiaGLl26ANCmTRuioqLu2Pavc35+fiQlJWXbfoqIiIiIiIjIvZcvB0zsdjspKSkEBAQQEBDA\nwIED6dy58x3lPDw8Mv+dNWsWZcqUybLe3d39jse12+3YbDaAzH9vd7eciIiIiIiIiOQd+XJKztq1\nawkJCckcqEhKSiIjI4OKFSuSnp5+R/kHH3yQ7dsd9/Xeu3cv69ev/83Hrly5MtHR0QDs2rUrc7nN\nZrvrY4uIiIiIiIhI3pMvzzAJDg4mNjaW3r17U7hwYdLS0pg0aRKXL19m6tSpeHt7Zyk/evRoXnzx\nRTZu3IjNZmPatGm/+diDBg3i2WefZcuWLTz44IOZF3MNCgqiX79+LF++PFv3TURERERERMRUhmY+\nGMuXAybu7u5MmDDhrut69uwJQGRkZOYyPz8/Fi9efEfZ/fv3Z/7+3nvvAXDixAlCQkJ4+OGH2bBh\nA/Hx8QBZBlnulhMRERERERGRvCNfDphkJ29vb15++WVsNhtubm6/ezaKiIiIiIiIiORNNruuSOpy\nv3XxWBEREREREckZ+f2rceylvHP3Vv/SRV1dBUBnmOQa6Sf2GpV3r9GUoyMeM8oELlzHuTdGGWXK\nvziPs1OeMspUCFnAxVnjjDK+z7zD+nJ1jTLdz0fzw0tDjTKVX1/CjS2LjDKFOg7ncHAHo0yDsK2c\nemGQUabajOVsrtHAcvlOJw4DsOuRZpYzrfbtASDyoSDLmTbfHAAgokp9y5kup78FcGp/dtRrbDnT\nNuog4Nz+zNt7ynJmVNNqACzYF2c589QjVZ3OOFM3ZzImr4VCHYcDkPrNFssZj4c6AnAr/rzlTMFS\n5Yz6ADj6wYaK9Ywy3c5EkXL+pFHGs1x19rRuZZRptnOX0WsHHK+f7wZ2M8o8sGKD0esNHK+5L5u3\nMMq02P0lqT9GG2U8KtXlwsyxRhm/8e9xcmwfo0z19/5N+sn9f1zwV9yrNyEp+bpRpqh3YUZSxSgT\nymm21WlklGl/5CunXgvXw2cZZQr3eIYfXx5ulKk0eRE7H37EKNP6631G71fgeM/aG3fZKNO0qo9T\n7fbT9NFGmbIT5jjV1s60QW5+fpw5JjpTN2c+U6kf5J9+0PrrfQBG/aDaDMd1JU3q1mznrj8uJPed\nfHmXHBERERERERGRP+O+HjDp06dP5i2Cf/H222/ToEEDfvzxx7tmwsLC2LZtW05UT0REREREROSe\nyLDnnZ/c4r6ektOtWzc2bdpE3br/mwqydetWNm/ejJ+f310zwcHBOVU9EREREREREXGR+/oMky5d\numQ5WyQ6OpoyZcrw/PPPc/z4cY4cOUKfPn0YOHAgw4YNIzExkdmzZ7Ny5UoAZsyYwd/+9jd69+7N\nf/7zHwAGDhzI/PnzGTx4MP/3f//HuXPnXLJvIiIiIiIiIuK8+3rAxMfHh0qVKvHtt44LVG7atInu\n3btnrg8LC6Nv376sWLGC4cOHc/Hixcx1Bw8e5MSJE3z00UcsW7aMOXPmcO3aNQCKFCnCsmXLaNWq\nFVu3bs3ZnRIRERERERGRP+2+HjABx7SciIgIACIjI+nYsWPmurZt2zJ//nzeffddfHx8CAgIyFwX\nHR1N48aOq28XLlyY6tWrc/r0aQAaNXJcCb9s2bKZgygiIiIiIiIirmK3552f3OK+HzBp3749O3fu\nJCoqiqpVq1K8ePHMdU2bNmXt2rX4+/szceJE9u3bl7nOZrNleZxRP3DEAAAgAElEQVTU1FTc3BzN\n6e7unrk8v9/LW0RERERERCQ/uu8HTIoUKUKtWrUIDQ3NMh0HYOXKlVy5coX/+7//Y/DgwXz//feZ\n6+rWrcv+/fsBSE5O5ocffqBKlSo5WncRERERERERyR739V1yftG9e3deeOEF3nrrrSzLK1euzDPP\nPEPRokXx9PRk2rRprF69GnBMu6lbty79+/cnLS2N5557jsKFC7ui+iIiIiIiIiK/KwPNfjClARMc\n03IOHz6c+feKFSsAqFmzJq1atcpSdsyYMZm//+Mf/7jjsX7JAgwYMOBeV1VEREREREREcsB9PyVH\nREREREREROR2NruuSupyt19AVkRERERERHJWfv9qfOznRFdXwbJaZYq5ugqApuTkGmk/fGtUvkDl\n+iSE/tMoU3LkNK6HzzLKFO7xDInLXjHKFBv8GslrphtlvB+fwPpydY0y3c9H803vTkaZhz7ezPV1\n7xhlCj82joOd2xhlGm+K5PhTPY0yNRd8wqrStS2X73/JcRHi3a1aWs403/UFAJtrNLCc6XTCMV3t\ng1KBljND4o86nZnhXcNy5oXkE4Bz+/OXf31uOfPZPx51OtNm1i7LmchnWuVo3WKfsz5t0P/tlYDZ\nsapA5foApPwUaznjWdafr7q1s1weoNGG7bxbtKZR5tmk49xKuGCUKVjSz6nj1OxiZnUbk3icn995\n1ihTZty7bA1saJTpcPQQy32sv0YBBl0+yq2LPxplCvpW4sgT3f+44K/UWbqe7wZ2M8o8sGIDqWeP\nGmU8KgRyI/maUaaQdxG21WlklGl/5CtGYnZh+FBOGx1DwXEcvbLoJaNMieGvc3JsH6NM9ff+zaKS\ntYwywxOOsaFiPaNMtzNRHL9g9uG+pl8xp9ot5tm+RpmAd1c71dbOtEFOPT8f+Vr/DALwt4vfO7Ud\nZ54fZ44H6gf5px/88hnRpB88sGIDgFHdhiccs1w2r8rn40HZQlNyRERERERERERuc98MmPTp04fo\n6Ogsy95++22WLFlyR9n9+/czduxYAJo0aZIj9RMRERERERGR3OO+GTDp1q0bmzZtyrJs69atdO3a\n1UU1EhEREREREckZGfa885Nb3DcDJl26dGHbtm2Zf0dHR1OmTBmuXLlC//79GThwIE899RRXrly5\na/7kyZMMGjSIwYMHM2rUKBITE5k5cyYff/xxlm1cunSJZ599lv79+9O7d2927bJ+/QIRERERERER\nyR3umwETHx8fKlWqxLffOi5YuGnTJrp3787rr7/OCy+8wIoVK2jcuDHLly+/a37KlClMnjyZZcuW\n0bx5c1atWkWPHj0yz1o5efIklSpV4sKFCyQkJLBq1SoWL17M1atXc2wfRUREREREROTeuG8GTMAx\nLSciIgKAyMhIOnbsSExMDA8++CDguF7JkSNH7pr99ttvCQkJYeDAgXz66adcvnyZmjVrkpiYSHx8\nPDt27KB79+74+/uTnJzM+PHj2bdvn6b8iIiIiIiIiMvZ7XnnJ7e4r24r3L59exYsWEDXrl2pWrUq\nxYsXz7I+NTUVN7e7jyEVKlSI5cuXY7PZsizv1q0bW7duZe/evcyfP59ChQqxZs0aDh06xLp169i5\ncyfTpk3Ltn0SERERERERkXvvvjrDpEiRItSqVYvQ0FC6d+8OQI0aNTh8+DAABw8epG7dunfNBgYG\nZl6PZOPGjezduxdwDJiEhYXh6+tLoUKF+O6771i/fj2NGjXi1VdfJSYmJgf2TERERERERETupftq\nwASge/fu7N69mzZt2gAwadIk3nnnHQYNGkRUVBSDBg26a+6ll14iNDSUAQMGEBYWRu3atQEoXbo0\nhQsXplu3bgBUrFiRTz/9lH79+jF06FCGDRuWMzsmIiIiIiIiIvfMfTUlBxzTcn45owSgevXqrFix\nIkuZJk2a0KRJEwD2798PQEBAAB9++OEdjxcfH09iYiItW7YEoHjx4ixevDi7qi8iIiIiIiJiLINc\ndHGQPOK+O8PkXtq+fTtPPPEE48eP/81rn4iIiIiIiIhI3mOz23PTNWjvT7dfSFZERERERERyVn7/\nahx1/qqrq2BZvXLF/7hQDrjvpuTkVjevXjYq71Xch+SP3jDKeP/tRa6vn2OUKdx9NDc2zjPKFOo6\nipvblhhlvNoPZYZ3DaPMC8kn2FGvsVGmbdRBjo54zCgTuHAdkQ8FGWXafHOA/R1bG2WabNnJcwWq\nWS7/dtopALYGNrSc6XD0EADvFq1pOfNs0nEA5hWvZTkz6uoxAKf254NSgZYzQ+KPArC5RgPLmU4n\nHFPyyvaabTnz09oxTmfKPW799XN+zagcrduuR5pZzrTatweAS7Oft5wpPeYtANJ++NZypkDl+oT5\n1bFcHiD4whFmF7PepwHGJB536hhq8noDx2tuaqHqRplJN05ydUmIUab40ClObceZdktc9opRptjg\n1/g8qKlR5tEDe1lf7u4XYf8t3c9HG/VPcPTRWwkXjDIFS/o59d5jcmwDx/FtJFWMMqGcztV1G+NW\n1SgzOyOOhKRko0zJot5O1c2ZNnCmrZ1pg5x6fpzJjLKZZebZnduOyecWcHx2UT/IP/0glNOAc59f\nTeo2z37actm8Kp+PB2ULzSMREREREREREbmNBkzuIi4ujieffJJevXoRHBzMlClTSElJAeDChQvU\nrl2b7du3Z5bfv38/tWvX5sKF//0vVXp6Os2bN2f2bOv/6ysiIiIiIiIiuYMGTG6Tnp7OmDFjGD58\nOGvXruWTTz4BYO7cuQBs3LiRKlWqsHHjxiy5ChUqsGnTpsy/9+/fT6FChXKu4iIiIiIiIiJyz2jA\n5Da7d+/G39+foCDHNStsNhvjx4/n73//OwAbNmzg5ZdfZs+ePVy/fj0z16JFCyIiIjL/3rhxIy1a\ntMjZyouIiIiIiIjcRYbdnmd+cgsNmNwmNjaW2rVrZ1nm5eWFp6cnsbGxJCUl0axZM5o0aUJkZGRm\nGR8fHwoWLMjp06dJTU0lKiqKevXq5XT1RUREREREROQe0IDJbWw2G+np6Xddt2HDBrp06QJAt27d\n2LBhQ5b1nTp1YsOGDXz55Zc0adJEtwsWERERERERyaN0W+Hb+Pv7s2rVqizLUlJSiIuLY+PGjdhs\nNj777DMyMjL48ccfSUxMzCzXoUMHhg8fzg8//EDv3r354Ycfcrr6IiIiIiIiIndIz3B1DfIenWFy\nm+bNm3P27NnM6TYZGRnMnDmTGTNm4O3tzebNmwkPD2f9+vV07tyZLVu2ZGZ9fX0pVqwY0dHRNGzY\n0FW7ICIiIiIiIiJ/kgZMbuPm5sbixYtZs2YNwcHB9OvXj6JFi+Lv709wcHCWsj179sxyoVdwTMsJ\nCgrCzU1NKyIiIiIiIpJXaUrOXZQpU4YFCxb8YblGjRrxwQcfANCkSRMA+vfvn7n+9gEWERERERER\nEVfITXefySt0GoSIiIiIiIiIyG1sdruGmVxNd9MRERERERFxrfz+1fjgDwmuroJljSuXdHUVAE3J\nyTVSzp80Ku9Zrjo3NoUaZQp1HknKgXCz7QT1IP3EXqOMe42mpH230yhT4IHWbA00u1Buh6OHSFz2\nilGm2ODX+KBUoFFmSPxRbmycZ5Qp1HWUU8/PrkeaWS7fat8eAA71aG850zB8GwCHgztYzjQI2wrA\n6YlPWM5UeXMpAFH9uljO1PvQcT2g6+GzLGcK93gGgJ+mj7acKTthDgBVR3xsORO3sLfTGf+Ray1n\nYkN75WhmVenaljP9L30PwLtFa1rOPJt0HICb25ZYzni1H0rkQ0GWywO0+eYAZ1590ihT8dX3mV3M\n+r4AjEk8zqXZzxtlSo95i7NTnjLKVAhZ4NQxZ3ONBkaZTicO803vTkaZhz7ebNQHwNEP4udNMMqU\nGjXdqf2ZVri6Ueaf109y7cMpRpki/UKMjlPgOFZdWfSSUabE8NfZUa+xUaZt1EFGUsUoE8ppxrhV\nNcrMzohj58OPGGVaf73P6JgDjuPOz1eTjTJlins71W7Pulc1yrybHudUWzvTBjn1/DjzOcyZtv48\nqKlR5tEDe3nBo5pRZkbqKfWDfNQPHj3g+C5i0g9mpJ4CMKpb26iDlsvK/UMDJiIiIiIiIiL5XHo+\nP4MmO2jAxElxcXG88cYbxMfHk5GRQYMGDZgwYQKdOnWibNmyuLu7c/36dXr16kXfvn1dXV0RERER\nERERMaABEyekp6czZswYQkJCCAoKwm63M3XqVObOnQvAwoUL8fb25vr167Rr147HH38cd3d3F9da\nRERERERERKzSgIkTdu/ejb+/P0FBjnn2NpuN8ePH4+bmxvr16zPLXb16lZIlS2qwRERERERERFxK\ntxU2pwETJ8TGxlK7dtaLNXl5eWX+PmLECGw2GzExMYSEhOR09URERERERETkT9KAiRNsNhvp6em/\nuf6XKTnXrl3jiSeeIDAwkICAgBysoYiIiIiIiIj8GW6urkBe5O/vT1RUVJZlKSkpHD9+PMuyIkWK\nEBQUxDfffJOT1RMRERERERGRP0kDJk5o3rw5Z8+eJTIyEoCMjAxmzpxJRERElnJ2u52oqCiqVTO7\nd7yIiIiIiIjIvZSekXd+cgtNyXGCm5sbixcv5uWXX2bOnDl4enrSrFkzRo8ezaeffsqIESNwd3fn\n5s2bPProozRs2NDVVRYRERERERERAxowcVKZMmVYsGDBHct/OetERERERERERPIuDZiIiIiIiIiI\n5HO6rbA5m92uVnM1m83m6iqIiIiIiIjc1/L7V+PPYy65ugqWPRpQ2tVVAHSGSa6R8lOsUXnPsv4k\nf/SGUcb7by9yc9sSo4xX+6GkHAg3yngG9SBl3zqzzCOP8UGpQKPMkPij/PDSUKNM5deX8HGZOkaZ\n3j8f4cLMsUYZv/HvcXHWOKOM7zPv8JFvbcvl/3bxewA+D2pqOfPogb0AbA20fl2dDkcPAXCwcxvL\nmcabHFPTttVpZDnT/shXAJyd8pTlTIUQx7S4I090t5yps3S9I9tvkeXM2Q+H58tMmJ/110LwhSMA\nTvVRk2OIZ1APo238sp3DwR2MMg3CthJe9gGjTI+fvuPk2D5Gmerv/dupul37cIpRpki/EEJL1DLK\njLxyjMiHgowybb45YNRvwNF3Tk98wihT5c2lTh2rl/uYvY8MunyUmztXGmW8Wg/gx5eHG2UqTV7k\nVN9x5n1xjFtVo8zsjDhGUsUoE8ppVpU2e532v/Q9r3kFGGVeuRnDhSvXjDJ+JYo41W7OtIEzbe1M\nG+TU8+PMMcSZ15wzdRtlM2uDefbT6gf5qB/0v+T4PGHSD+bZTwMY1W3Q5aOWy8r9QwMmIiIiIiIi\nIvlcej4/gyY7aMDkLuLi4njjjTeIj48nIyODBg0aMGHCBDp16kTZsmVxc3MjPT2drl27MmDAAAAm\nTpzIxYsXWbx4cebj7Ny5k6eeeoodO3ZQsWJFV+2OiIiIiIiIiBjSgMlt0tPTGTNmDCEhIQQFBWG3\n25k6dSpz584FYOHChXh7e3Pt2jWef/553N3d6du3LwBnzpwhPj6eUqVKARAREUGlSpVcti8iIiIi\nIiIi4hw3V1cgt9m9ezf+/v4EBTnmddtsNsaPH8/f//73LOWKFCnCq6++yrJlyzKXtWjRgk2bNgFw\n8+ZN4uLiKFeuXM5VXkRERERERETuCQ2Y3CY2NpbatbNehMjLywtPT887ypYtW5Zr166RlpYGQIcO\nHdi4cSMAn332Gc2aNcv+CouIiIiIiIj8gQx73vnJLTRgchubzUZ6errl8tevX8fNzdGMFSpUIDU1\nlXPnzhEREUGnTp2yq5oiIiIiIiIiko00YHIbf39/oqKisixLSUnh+PHjd5SNiYmhcuXKmQMmAB07\ndmTdunWcOnXqjjNVRERERERERCRv0IDJbZo3b87Zs2eJjIwEICMjg5kzZxIREZGlXHJyMq+//joj\nR47Msrxjx44sX76cVq1a5VidRURERERERH5PeoY9z/zkFrpLzm3c3NxYvHgxL7/8MnPmzMHT05Nm\nzZoxevRoPv30U0aMGAFAUlISPXv2pHPnzlnylSpVomLFinTs2NEV1RcRERERERGRe0ADJndRpkwZ\nFixYcMfyX846uZs333wz8/dPPvkk8/cVK1bc28qJiIiIiIiISLaz2e323HO+y33KZrO5ugoiIiIi\nIiL3tfz+1XjLsZ9dXQXLOtYq4+oqADrDRERERERERCTfy8jnA0LZQQMmucTNq5eNynsV9yF5zXSj\njPfjE7ixcZ5RplDXUU5lbm5bYpTxaj+Ut4vUMMo8d+0EWwMbGmU6HD3E8ad6GmVqLviEyIeCjDJt\nvjnAwc5tjDKNN0XyXIFqlsu/nXYKgG11GlnOtD/yFQCzi9W0nBmT6LhDVGiJWpYzI68cA3Bqf5zZ\nzuYaDSxnOp04DEDZXrMtZ35aO8bpTLnHrb9+zq8ZlaN1+zyoqeXMowf2AnB1SYjlTPGhUwBIi/vG\ncqZA1YfYULGe5fIA3c5E8W5R630a4Nmk41wPn2WUKdzjGaO+Bo7+9ppXgFHmlZsxJC57xShTbPBr\nzPA2O4a+kHzCqXZz5r3HmWPo+nJ1jTLdz0dzZdFLRpkSw1/nVvx5o0zBUuXY+fAjRpnWX+9jUUnr\nxzaA4QnHGEkVo0wop52q26rSZnf163/pe6fq9qx7VaPMu+lxJCQlG2VKFvV2qm7OtIEzbe1MG+TU\n85ObM/OKm71+Rl117vWjfpA7+0EopwGM+sGoq47PiM5sR+TXdJccEREREREREZHb6AwTJ8XFxfHG\nG28QHx9PRkYGDRo0YMKECXTq1ImyZcvi7u6eWVYXfhURERERERFXSteMHGMaMHFCeno6Y8aMISQk\nhKCgIOx2O1OnTmXu3LkALFy4EG9vbxfXUkREREREREScpQETJ+zevRt/f3+Cghxzsm02G+PHj8fN\nzY3169e7uHYiIiIiIiIi8mdpwMQJsbGx1K6d9cJLXl5eLqqNiIiIiIiIyO/TXXLMacDECTabjfT0\n9N9cP2LEiMxrmJQsWZL33nsvp6omIiIiIiIiIveABkyc4O/vz6pVq7IsS0lJIS4uDtA1TERERERE\nRETyOt1W2AnNmzfn7NmzREZGApCRkcHMmTOJiIhwcc1ERERERERE5F7QgIkT3NzcWLx4MWvWrCE4\nOJh+/fpRtGhRxo4d6+qqiYiIiIiIiNwhPcOeZ35yC03JcVKZMmVYsGDBHct/OetERERERERERPIu\nm92uS+W6ms1mc3UVRERERERE7mv5/avxuujzrq6CZY/VLefqKgA6w0REREREREQk39Nthc1pwCSX\nuHX5rFH5gj4VSFz2ilGm2ODXuB4+yyhTuMcz3Ng4zyhTqOsobmxZZJbpOJyphaobZSbdOMm+dn8x\nyjyy/TOnMvs7tjbKNNmyk6h+XYwy9T6M4AWPapbLz0g9BUBElfqWM11OfwvAvOK1LGdGXT0GwHKf\nQMuZQZePAvCaV4DlzCs3YwDYXKOB5UynE4cB2FankeVM+yNfAeD717ctZy7+5zkA/ILftZy5EPZs\nrs9sDWxoOdPh6CEAvh/Ww3Km9uJwANJjDlrOuAc0JrSE9f4JMPLKMaP+CY4+euqFQUaZajOWs/Ph\nR4wyrb/ex6KSZvszPOEYCaH/NMqUHDmNSQX9jTJTb8U61dYxz/Y1ygS8u5qDndsYZRpvimRV6dpG\nmf6XvufIE92NMnWWrif1zBGjjEfFOux6pJlRptW+PWyoWM8o0+1MFGPcqhplZmfEOdVuJsdqcByv\nn3WvapR5Nz2OkVQxyoRymp+vJhtlyhT3dqrdnPkM4kxbO9MGOfX8ONNuzxWw/rkF4O20U07V7Z+e\nZse3aSmx6gf5qB+8mx4HYNQPpqXEAhjV7e20U5bLyv1DF30VEREREREREbmNBkwMxcXF8eSTT9Kr\nVy+Cg4OZMmUKKSkptGnThvfffz9L2enTp9Omjdn/qomIiIiIiIiI62nAxEB6ejpjxoxh+PDhrF27\nlk8++QSAuXPn4uvry44dOzLL2u12oqOjXVVVERERERERkUzp9rzzk1voGiYGdu/ejb+/P0FBQYDj\n7jbjx4/Hzc2NQ4cO4e3tzcmTJ6levTpff/01AQEBnD1rdm0SEREREREREXE9nWFiIDY2ltq1s17Y\nycvLC09PTwA6duzI+vXrAYiIiKBDhw45XkcRERERERER+fM0YGLAZrORnp7+m+vbtm3Ltm3bSE9P\n58CBA5lnooiIiIiIiIi4Uobdnmd+cgsNmBjw9/cnKioqy7KUlBSOHz8OQLFixahYsSJLly7lwQcf\npEABzXgSERERERERyYs0YGKgefPmnD17lsjISAAyMjKYOXMmERERmWU6derE+++/r+k4IiIiIiIi\nInmYBkwMuLm5sXjxYtasWUNwcDD9+vWjaNGijB07NrNMu3btcHd3p1mzZi6sqYiIiIiIiMj/ZGTY\n88xPbqE5I4bKlCnDggUL7li+YsUKwDEtZ8+ePZnLfzkbRURERERERETyDpvdnouuqHKfstlsrq6C\niIiIiIjIfS2/fzX+8PAZV1fBsn4NKrq6CoCm5IiIiIiIiIiI3EFTcnKJWmP/Y1T+2Ht/5aWII0aZ\n17vUIeZiolEmwLcYX/2QYJRpVLkkq78xG73s+1BF9sZdNso0repDyoVTRhlPv2pEn7tqlKlbvjiJ\nydeNMsW8C3Mz6YpRxqtoCX68nGS5fCWfogAsPnjacmZY4yoAxF2yvp2qpR3bOXrBersF+hUH4HJi\nsuWMTzFvAM5fuWY5U65EEQCjPtqockkAYg1eC/6+xQA48bP1TI0yjowzbW3yOg34/3VzJnMuwXpb\nly/paGtn2sDkNVe3fHG+PWf22qlfvgTHL5gd22r6FTPqa+DobwdOxxtlgqqUcmo7U7cfM8pMalfL\n6LkBx/Nj8roGx2v7guH++JUoQsrP1o9TAJ5lqpCQZP34AVCyqLdRnwZHv94Vc8ko0yqgtFPvV870\nUWfa4OerZpkyxb2dek5zqm4jqWKUCeW0U3XLqf3Jzc/PlWtmn3VKFCls9D4Pjvd6Z7aTU8+p+kHu\n7AclihQGMNqfkkUdnyud+Syan6Xn7xNosoXOMBERERERERERuY3OMLkHzpw5w9ixYxkwYACzZs2i\ncuXKZGRkULJkSSZMmEClSpVcXUURERERERERMaABk3usS5cuTJgwAYAvv/yS4cOH8+mnn1KwYEEX\n10xERERERETuVxn5/KK22UFTcrJRixYtaNy4Mdu2bXN1VURERERERETEgAZMslndunU5efKkq6sh\nIiIiIiIiIgY0YJLNkpOTcXd3d3U1RERERERERMSArmGSzaKjo+nataurqyEiIiIiIiL3sXRdw8SY\nzjDJRp9//jmxsbG0adPG1VUREREREREREQM6w+Qei4iIIDo6muTkZEqVKsXs2bNxc9O4lIiIiIiI\niEheogGTe6BixYqEhYUBEBwc7OLaiIiIiIiIiGSVkaEpOaZsdrsmMrmazWZzdRVERERERETua/n9\nq/GiA6ddXQXLhgdVcXUVAF3DRERERERERETkDpqSk0vcvHrZqLxXcR+SP3rDKOP9txe5vn6OUaZw\n99Hc2DjPKFOo6yhubltilPFqP5QZ3jWMMi8kn2BHvcZGmbZRBzk64jGjTODCdUQ+FGSUafPNAfZ3\nbG2UabJlJ88VqGa5/NtppwDYGtjQcqbD0UMAvFu0puXMs0nHAZhXvJblzKirxwCc2p8PSgVazgyJ\nPwrA5hoNLGc6nTgMQNlesy1nflo7xulMucetv37OrxmVo3Xb9Ugzy5lW+/YAcGn285Yzpce8BUDa\nD99azhSoXJ8wvzqWywMEXzjC7GLW+zTAmMTjTh1DTV5v4HjNTS1U3Sgz6cZJri4JMcoUHzrFqe04\n026Jy14xyhQb/BqfBzU1yjx6YC/ry9U1ynQ/H23UP8HRR28lXDDKFCzp59R7j8mxDRzHt5GY/e9a\nKKdzdd3GuFU1yszOiCMhKdkoU7Kot1N1c6YNnGlrZ9ogp54fZzKjbGaZeXbntmPyuQUcn13UD/JP\nPwjFcVaEM59fTeo2z553zr5wVnr+PoEmW+gMExERERERERGR22jA5DecOXPmNy/gOmzYMEaNGpVl\nWZs2bXj//fezLJs+fbpuKSwiIiIiIiKSB2nAxNDly5eJiYnh0KFDJCUlZS739fVlx44dmX/b7Xai\no6NdUUURERERERER+ZM0YGIoIiKC1q1b07x5c7Zu3Zq53NPTk5IlS3Ly5EkAvv76awICAlxVTRER\nEREREZFMGXZ7nvnJLTRgYmjDhg107dqVbt26ERERkWVdx44dWb9+PeAYWOnQoYMrqigiIiIiIiIi\nf5IGTAz8+OOPXLhwgYcffpgWLVpw9OhR4uPjM9e3bduWbdu2kZ6ezoEDBwgKMruzioiIiIiIiIjk\nDrqtsIENGzZw69Yt/vrXvwKQlpbGpk2b6N+/PwDFihWjYsWKLF26lAcffJACBdS8IiIiIiIi4nrp\nuWiqS3ZITU1l4sSJnDt3Dnd3d6ZNm0alSpXuWnbcuHF4enry5ptv/u5j6gwTAxs3bmTp0qWEh4cT\nHh7OnDlz2LhxY5YynTp14v3339d0HBEREREREZEcsmHDBooVK8bq1at56qmnePvtt+9abvfu3fzw\nww+WHlMDJr/j1KlTDBw4kIEDB9K4cWNOnjxJrVq1Mtc3atSIy5cvc/78+cxl7dq1w93dnWbNmrmi\nyiIiIiIiIiL3nb1799K+fXsAmjVrxqFDh+4ok5KSwvz583n66actPabmjPyGihUrcvjw4d8tY7PZ\n2LJlCwArVqwAHNNy9uzZk1kmMjIy+yopIiIiIiIiIly6dIlSpUoB4Obmhs1mIyUlBU9Pz8wyoaGh\n9O3blyJFilh6TJvdns8nMuUBNpvN1VUQERERERG5r+X3r4SGAM0AACAASURBVMazdse6ugqWPdPc\n/3fXf/zxx3z88cdZlv33v/8lPDycwMBAAFq1asX27dszB0zi4uKYNm0aoaGh7N+/n3Xr1v3hNUx0\nhomIiIiIiIiI5Bm9e/emd+/eWZZNnDiRixcvEhgYSGpqKna7PcvZJZ999hnnzp3j8ccf59q1a8TH\nx7Nw4UJGjBjxm9vRgEkucevyWaPyBX0qcH3dO0aZwo+N4+bOlUYZr9YDSD20ySjj0bAzqV9tMMs0\n6sZyn0CjzKDLRzk5to9Rpvp7/ya87ANGmR4/fcfZKU8ZZSqELOCn6aONMmUnzOHjMnUsl+/98xEA\ndrdqaTnTfNcXAGyu0cByptMJx9S0r7q1s5xptGE7ANvqNLKcaX/kKwDOvTHKcqb8i/MAODriMcuZ\nwIXrACj3+DzLmfNrHHUq/7dQy5lzH43M9RmT10KPn74DcKqPpuxbZznj+chjrC9X13J5gO7no/n2\nb52NMvU/2uTUsSD2uQFGGf+3V3I42Owi4A3CtpK8dqZRxrvXeD4oZXYMHRJ/lM+DmhplHj2w16gP\ngKMfHH+qp1Gm5oJPWFW6tlGm/6XvnXofMemf4OijzhzfY57ta5QJeHe1U8/ps+5VjTLvpscxkipG\nmVBOO/X8TC1U3Sgz6cZJEpKSjTIli3o71W7OtIEzbe1MG+TU8xNaotYfF/yVkVeOObUdZzLOtIH6\nQf7pB/0vfe/YlkEbhHIawKntSN7VvHlzNm/eTMuWLdm5cydNmjTJsv6JJ57giSeeAMg8w+T3BktA\nAyYiIiIiIiIi+V56Rv6ectSlSxf27NlD3759s9wy+P3336dx48Y0aGD9P41/oQGTP+HMmTOMHTuW\nsLCwzGWzZ89m/fr1+Pn5kZaWhq+vL9OnT6dQoUIurKmIiIiIiIhI/uXu7s60adPuWP7kk0/esaxJ\nkyZ3nIFyN7qtcDYYNGgQK1asYPXq1Xh7e7Njxw5XV0lEREREREREDOgMk2yUnp5OQkICfn5+rq6K\niIiIiIiI3Mfy+5Sc7KABk2ywfPlytmzZwk8//UTNmjVp2LChq6skIiIiIiIiIgY0JScb/DIlZ9u2\nbdSpU4fZs2e7ukoiIiIiIiIiYkADJtmsY8eOfPXVV66uhoiIiIiIiIgY0JScbPbf//6XatWquboa\nIiIiIiIich/TNUzMacDkTzp16hQDBw7M/NvLy4vTp0+zZcsWAAoWLHjXWxuJiIiIiIiISO6lAZM/\noWLFihw+fNjV1RARERERERGRe8xmt9t1Xo6L2Ww2V1dBRERERETkvpbfvxq/vuO4q6tg2Utta7q6\nCoAu+ioiIiIiIiIicgdNycklUs6fNCrvWa46NzaFGmUKdR5JyoFws+0E9SD9xF6jjHuNpqR9t9Mo\nU+CB1mwNbGiU6XD0EInLXjHKFBv8Gh+UCjTKDIk/yo2N84wyhbqOcur52fVIM8vlW+3bA8ChHu0t\nZxqGbwPgcHAHy5kGYVsBOD3xCcuZKm8uBSCqXxfLmXofRgBwPXyW5UzhHs8A8NP00ZYzZSfMAaDq\niI8tZ+IW9nY64z9yreVMbGivHM2sKl3bcqb/pe//H3v3Hhdlmf9//D1iCqKomakrZHhEVFJTITVd\nj6DFw5XV1jLMWlz7squZLmanzdbKQ7pfi764lFsqWXaifOBZyQ675QE8YQSecFpKzfMBQRDm98f8\ndjbU6r5ujUF4PR8PHjoz19v5zDXX3MDlfV23JGl+Peuz/ZPOuv8Xo2j965YzvoMe0sede1huL0n9\nd2xR/vQ/GGUCp7+qxACz/7mYcGaPjiX+2Shz04S5+nbGw0aZ5k//3dYxZ02bLkaZqL3btWNklFGm\n83trjMaA5B4HJ5IeM8rcGD/b1uuZWae1Uebx8/t07q0ZRpm69z1tdJyS3MeqUwufNMo0iHte6Z26\nG2UGZG3VeLUwyiTLqQk1bjXKJJYd1MbbI4wy/TI3GR1zJPdx5/vTBUaZm+v72+q3ST63GmXmlx60\n1dd2+qCi3h87P4fZ6etPe9xhlOm75UtNvcHsAgpzSvIYB1VoHPTd4v5dxGQczCnJkySj2gZkbbXc\nFtUHZ5gAAAAAAABcgjNMfkZ+fr4mTpyo1NTUcvd/9NFHWrJkiWrVqqWLFy8qLi5OUVFR2rx5sx55\n5BG1adNGklRaWqoZM2aoVatW3igfAAAAAAAuK2wDEyY2ZGZmaunSpVq0aJECAgJ0/PhxjRo1Sm3b\nuk9T7tGjh15++WVJ7omVxYsX669//as3SwYAAAAAAAZYkmPDm2++qT/96U8KCAiQJDVq1EgffPCB\nWrZseVnbY8eO6eabb67oEgEAAAAAwFXgDBMbDhw4oJCQ8huH/mfyRJK2bNmi2NhYFRQU6Pz580pJ\nSanoEgEAAAAA8GBJjjkmTGxwOBwqKyv70cd/uCRn69atmjRpkpYuXVpR5QEAAAAAgKvEkhwbWrZs\nqV27dpW7b//+/SoouPzSd927d9fBgwdVWlpaUeUBAAAAAICrxISJDWPGjNErr7yi48ePS5KOHj2q\nSZMm6dChQ5e1/eabb1SvXj35+PhUdJkAAAAAAEhyL8m5Xr4qC5bkWJCXl6fY2FjP7YSEBD366KP6\n/e9/Lz8/P9WsWVNPPvmkWrdurePHj3v2MJGkkpISPf/8894qHQAAAAAA2MCEyc8IDAzU9u3br/hY\n//79L7svPDxcmzZt+qXLAgAAAAAAvyCHy+WqPOe7VFMOh8PbJQAAAABAtVbVfzV+avXX3i7BsueG\ntPd2CZI4wwQAAAAAgCqvMu0Ncr1gwqSSuHD8W6P2tRs115nFzxhlAh54VueXv2SUqTPsERWuTDLK\n+N0Vr8K1C80ykXF6zq+1Ueapwn3aNPDXRpmIDZ/YymyO7GeUCV+7UVn3DTXKdHprlabeEGy5/ZyS\nPEnSqhZhljNDne6rOyXVb2c5E386V5K0pFGI5cyY4zmSpGd9W1nOPFO0X5K0pk0Xy5move7lcutD\nu1nODMrOkCQ1/s08y5mjH02RJDWJmW85cyR1UqXPrAvpajkzOGebJOnr3w+znGn/j+WSpNL9Wy1n\nfFp1V3ID6+NTksafyjUan5J7jOZNHWOUCZ6zRBtvjzDK9MvcpIUNzV5P3MlcnUx+3CjTcPxMPVW7\npVHmuQsHbPX1/kn3GmVazX9bW4dcvoT1p3Rf/bGW3mT2P0ujj32t7LHRRpnQRWkqyc82ytwQGKrP\nInoaZfps+kIrAjsZZe7Oz9KEGrcaZRLLDtrqN5NjteQ+Xk/yudUoM7/0oMarhVEmWU59f/ryKxD+\nlJvr+9vqNzs/g9jpazt9UFHvj51+m1LT+s8tkjTvYp6t2h6vZXZ8m1l8gHFQhcbB/NKDkmQ0DmYW\nH5Ako9rmXcyz3BbVB1fJAQAAAAAAuAQTJj8iPz9fMTExl93/0UcfKSYmRqNGjdKIESO0Zs0aSdLm\nzZvVvn17HTlyxNO2tLRUvXr1UmJiYoXVDQAAAADApbx9qWAuK1zFZWZmaunSpVq0aJECAgJ0/Phx\njRo1Sm3btpUkNW/eXKtXr9bYsWMluSdR/Pz8vFgxAAAAAACwgzNMDLz55pv605/+pICAAElSo0aN\n9MEHH6hlS/d6ut69e2vVqlWe9itXrlTv3r29UisAAAAAALCPCRMDBw4cUEhI+Y0F/zN5IrknUGrX\nri2n06mSkhJlZWWpUyezTd4AAAAAAID3sSTHgMPhUFlZ2U+2iYqK0ooVKxQaGqrw8HA5HI4Kqg4A\nAAAAgCu7WIn2BrlecIaJgZYtW2rXrl3l7tu/f78KCv57ybvBgwdr3bp1WrNmjSIjIyu6RAAAAAAA\ncA0wYWJgzJgxeuWVV3T8+HFJ0tGjRzVp0iQdOnTI06Zx48YKCAjQ7t271bVrV2+VCgAAAAAArgJL\ncn5CXl6eYmNjPbcTEhL06KOP6ve//738/PxUs2ZNPfnkk2rdurVnEkVyL8vZt2+fatRgPgoAAAAA\n4H2V6XK91wsmTH5EYGCgtm/ffsXH+vfvf9l94eHhCg8PlySNHj3ac39MTMwvUyAAAAAAAPjFOFwu\nF9NMXsbGsAAAAADgXVX9V+NHPszydgmWvTS8clxtljNMAAAAAACo4liSY44Jk0qi+PABo/a1mrZU\nwbIXjDL+o55Q0frXjTK+gx5S8ZblRplaPYapeNOHZpmI4XrjxhCjzIMncvTNkw8ZZW55/nW9d3Oo\nUWbk99k68uJEo0yThJd19KXJRpnGj/xNyxq3t9x+1NGvJUmf9rjDcqbvli8lSetCrG9IPDhnmyRp\n65DLl6L9mO6rP5YkrQ/tZjkzKDtDkvTtjIctZ5o//XdJUvbYaMuZ0EVp7ux9Cy1nvn0rrkpmUptY\n/yzEHMmWJFtj1OQYUqvHMKPn+M/zbI8ZbJTpkrpOy5t2MMoMO/yV9k38nVGm9cvv2Krt3FszjDJ1\n73tayQ3aGWXGn8rVx517GGX679hiNG4k99hxThtrlGkxa5GtY/WSRmbfR8Ycz1HRxjeNMr797te/\n/xJnlAn660JbY8fO98UJNW41yiSWHdR4tTDKJMuppTeZfU5HH/taz/q2Mso8U7RfR06dM8o0aVDX\nVr/Z6QM7fW2nDyrq/bFzDLHzmbNTW7zDrA+SXE7GQRUaB6OPuX+eMBkHSS6nJBnVNuZ4juW2qD7Y\nlRQAAAAAAOASTJj8iPz8/Ms2bE1MTNTgwYMVGxure++9V1OnTtWJEyckSZs3b1b79u115MgRT/vS\n0lL16tVLiYmJFVo7AAAAAAC4OkyYGBozZoxSUlL09ttvKyIiQvHx8Z7HmjdvrtWrV3tub968WX5+\nft4oEwAAAAAAj1KX67r5qiyYMLkKMTEx8vPz81x+uHfv3lq1apXn8ZUrV6p3797eKg8AAAAAANjE\nhMlV6tixo/bt2ydJatSokWrXri2n06mSkhJlZWWpU6fKcTkkAAAAAABgHVfJuUoFBQXy8fHx3I6K\nitKKFSsUGhqq8PBwORwOL1YHAAAAAACXFbaDM0yu0u7duxUa+t9LHw4ePFjr1q3TmjVrFBkZ6cXK\nAAAAAACAXUyYXIV33nlHDRo0UEjIf6/v3bhxYwUEBGj37t3q2rWrF6sDAAAAAAB2sSTnJ+Tl5Sk2\nNtZz29fXV06nU2vXrtXZs2fVokULzZo167JcVFSU9u3bpxo1mI8CAAAAAOB6xITJjwgMDPRc/caK\n8PBwhYeHS5JGjx7tuT8mJuaa1wYAAAAAgAn2MDHncLkq0UWOqyk2hgUAAAAA76rqvxr/fpn1EwK8\n7R+juni7BEnsYQIAAAAAAHAZluRUEkWnjxu1963fSAXvzjbK+N/zmApXJhll/O6Kt5UpWv+6UcZ3\n0EOaV7eNUWbKub1aF2K2se7gnG3a8/BvjTJt//6BPu7cwyjTf8cWbR3S3yjTffXHmlIz2HL7eRfz\nJEnrQ7tZzgzKzpAkJQa0tZyZcGaPJCm5QTvLmfGnciXJ1uux8zxr2lifgY7a655Zbzoi0XLm8PsT\nbGea3WP983Po3fgKre3THndYzvTd8qUk6fTrT1vO1H9ohiTp4sEdljM1b+2sFYGdLLeXpLvzszS/\nnvUxLUmTzu7R+eUvGWXqDHvEaKxJ7vH2rG8ro8wzRft1ZvEzRpmAB57VHH+zY+jUgr22+s3O9x47\nx9C0Zh2NMtGHduvUwieNMg3inteFE4eMMrVvbKaNt0cYZfplbtLChtaPbZIUdzJX49XCKJMsp63a\nlt7U3igz+tjXtmqb5HOrUWZ+6UGdPFtglGlYz99WbXb6wE5f2+mDinp/KnMmqb7Z5yf+tL3PD+Og\nco6DZDklyWgcxJ92/4xo53mqMpbkmOMMEwAAAAAAgEtwhslVyM/P18SJE5Wamuq5LzExUWlpaWrS\npInnvnHjxqlPnz7eKBEAAAAAANjAhMkvYMyYMbr//vu9XQYAAAAAAJKk0rIyb5dw3WFJDgAAAAAA\nwCWYMAEAAAAAALgES3J+AUuWLNHatWs9tx977DF17Gi22z8AAAAAAPAeJkx+AexhAgAAAACoTLis\nsDmW5AAAAAAAAFyCM0yuUl5enmJjYz23fX191bdvXy9WBAAAAAAArhYTJlchMDBQ27dv93YZAAAA\nAAD8JJbkmHO4XC56zcscDoe3SwAAAACAaq2q/2r8u0VbvF2CZe+M7eHtEiSxhwkAAAAAAMBlWJJT\nSRSdOWnU3jegoQrenW2U8b/nMRWuTDLK+N0Vr8K1C80ykXEqSl9slPEd8IDm+Lcxykwt2Ks1bboY\nZaL2blf22GijTOiiNKV36m6UGZC1VZsj+xllwtdu1JSawZbbz7uYJ0laH9rNcmZQdoY7W9d6X085\nt1eSlNygneXM+FO5kqSpN1h/PXNK3K9nWeP2ljOjjn4tSVoX0tVyZnDONklS49/Ms5w5+tEUSVKT\nmPmWM0dSJ0mSmo5ItJw5/P4E289jJ/NpjzssZ/pu+VKS9P3fJlnO3DzZXdPFgzssZ2re2lnLm3aw\n3F6Shh3+ymh8Su4xembxM0aZgAeeNfq8Se7P3Mw6rY0yj5/fp7NvPmuUqXf/M7aeJ6m+Wb/Fn87V\nyeTHjTINx8+0dQx97+ZQo8zI77N15MWJRpkmCS/rwskjRpnaDZvos4ieRpk+m74wOrZJ7uPbeLUw\nyiTLaXQ8lNzHRDufHzu1Tahxq1EmseygTp07b5RpULeOrdrs9IGdvrbTBxX1/tjJxDvMMkkue89j\n52dExkHVGQfJckqS0TiYWuD++dWktiSX03JbVB9MmAAAAAAAUMVdZA8TYyzJsSE/P18xMTHl7ktM\nTFRUVFS5+/bs2aN27dpp8+bNFVkeAAAAAAC4SkyYXEMXL15Udna25/bKlSsVFBTkxYoAAAAAAIAd\nLMm5hvr27au0tDSFhrrXXX/++ee67bbbvFwVAAAAAKC647LC5jjD5Brq06ePPvnkE7lcLmVlZall\ny5a64YYbvF0WAAAAAAAwxITJNeTr66u2bdsqMzNTq1atumxPEwAAAAAAcH1gwuQai4qK0urVq/X5\n55/rzjvv9HY5AAAAAACotMx13XxVFkyYXGO//vWvtWHDBrVu3Vq1a9f2djkAAAAAAMAGNn21KS8v\nT7GxsZ7bvr6+6tGjh/z8/HTbbbcpMjLSi9UBAAAAAICrwYSJDYGBgdq+ffuPPv7yyy97/j5r1qyK\nKAkAAAAAAFxDDpfLVXkWCFVTDofD2yUAAAAAQLVW1X81Hvr3L7xdgmWrHu7p7RIksYcJAAAAAADA\nZViSU0lcOHXUqH3tBo1V8P6LRhn/EQkqXLvQKOMXGafC1clmmSHjVZS+2CjjO+ABJQa0NcpMOLNH\nH3fuYZTpv2OLssdGG2VCF6XpX33MrnjU67PPlXXfUKNMp7dW6fFaLS23n1l8QJK0PrSb5cyg7AxJ\n0hs3hljOPHgix3bmqdrWX89zF9yvJ7lBO8uZ8adyJdnrg8a/mWc5c/SjKZKkJjHzLWeOpE6q0Iyd\n17O6ZWfLmSEHdkiSTi180nKmQdzzkqTS/VstZ3xaddeaNl0st5ekqL3bbR0/7BxD7dT2nF9ro8xT\nhft09s1njTL17n9G8+uZ9cGks3s0x7+NUWZqwV4VLHvBKOM/6gltvD3CKNMvc5PSmnU0ykQf2m00\nPiX3GC35Nscoc0PzEH3Rr49RpufGz7SwofVjmyTFncxVvKOFUSbJ5VR6p+5GmQFZW7WkkfXjuySN\nOZ6j8TKrLVlOTakZbJSZdzFPx88UGGUaBfjb6relN7U3yow+9rWtvrbTBxX1/tjpt4p6nqT6Zp+f\n+NP2Pj+Mg8o5DpJcTvefBuMg/rT7Z0ST2pLltNwW1QcTJgAAAAAAVHGV6XK91wsmTK5Cfn6+Jk6c\nqNTUVM99586d0xNPPKHjx4+rtLRUDRs21OzZsxUQEODFSgEAAAAAgAn2MLnGFi1apLCwMC1dulTL\nli1Tp06dlJaW5u2yAAAAAACAAc4wucbOnDmjkpISz+34+HgvVgMAAAAAAOxgwuQaGz16tB566CF9\n9tln6t27t+666y6FhJht0gQAAAAAwLXEHibmWJJzjbVo0UJr1qzRlClTVFJSogceeEDvv/++t8sC\nAAAAAAAGmDC5xoqKinTDDTeod+/emjZtmhITE7V8+XJvlwUAAAAAAAwwYXKNPfjgg/riiy88tw8f\nPqygoCAvVgQAAAAAqO5cZa7r5quyYA+Tq5SXl6fY2FjP7WnTpumll17S//3f/8nHx0cBAQGaPn26\n9woEAAAAAADGmDC5CoGBgdq+fftl97/++uteqAYAAAAAAFwrDpfLVXnOd6mmHA6Ht0sAAAAAgGqt\nqv9q3G/+Z94uwbKNk/p4uwRJ7GECAAAAAABwGZbkVBJFZ08Ztfet10AF779olPEfkaDClUlGGb+7\n4lW4OtksM2S8itIXG2V8BzygeXXbGGWmnNur1S07G2WGHNihvX8caZRp83/vaV1IV6PM4Jxt+qKf\n2axoz42faUrNYMvt513MkySld+puOTMga6s7a9DXU87tlSQl1W9nORN/OtedtfF6Fja0/jxxJ93P\ns6ZNF8uZqL3uZXRNRyRazhx+f4Ikqdk91j8/h96Nt52xU5udzL/63Gk50+uzzyVJp19/2nKm/kMz\nJEkXv9llOVPzljCtCOxkub0k3Z2fpcSAtkaZCWf26PyHfzPK1Bk+2dax4Dm/1kaZpwr36eybzxpl\n6t3/jOb4mx1DpxbstdVvBcteMMr4j3pC60O7GWUGZWcorVlHo0z0od06tfBJo0yDuOdVdOakUcY3\noKE23h5hlOmXuUlv3BhilHnwRI7Gq4VRJllOfdrjDqNM3y1faulN7Y0yo499bau2ST63GmXmlx7U\nqXPnjTIN6taxVZudPrDT13b6oKLeHzuZeIdZJsll73nsHKsYB1VnHCTLKUlG42DCmT2SZFRbkstp\nuS2qD84wAQAAAAAAuAQTJoby8/MVExPjub17927dd999ntu7du1Sz549PbfPnDmjPn0qx/orAAAA\nAED15HK5rpuvyoIJk6sUGhoqp9OpCxcuSJIyMjJUq1Yt7d+/X5KUmZmp7t2tL5kAAAAAAADex4TJ\nVapRo4bCwsK0c+dOSe4JkxEjRigjI8NzOzw83JslAgAAAAAAQ0yYXAPh4eHaunWrXC6XDh8+rKio\nKG3d6t5ckwkTAAAAAIC3ucpc181XZcGEyTUQERGhjIwM7d+/X61atVKrVq20f/9+FRUV6fjx42rR\nwmznaAAAAAAA4F1MmFwD7dq1k9Pp1ObNm3X77bfL4XCoSZMmWrt2rbp2NbsEJQAAAAAA8D4mTK4B\nh8OhDh066KOPPlK3bt0kSbfffrveeustluMAAAAAALyurMx13XxVFkyY2JCXl6fY2FjP165duxQe\nHq5vvvlGrVq1kuSeMNmxYwcTJgAAAAAAXIdqeruA601gYKC2b99+2f1hYWG6//77Pbe7du2q3Nzc\niiwNAAAAAABcIw6Xy1V5znepphwOh7dLAAAAAIBqrar/anznixu9XYJlnyf083YJkjjDBAAAAACA\nKs9V5u0Krj9MmFQSF45/a9S+dqPmKnj/RaOM/4gEFa1/3SjjO+ghFW9ZbpSp1WOYijd9aJaJGK6k\n+u2MMvGnc/VV7N1GmQ4pK7SqRZhRZqhzl/ZPutco02r+23JOG2uUaTFrkRY2tN4HcSfdS74+7XGH\n5UzfLV9KklKbhFrOxBzJliR9FtHTcqbPpi8kScubdrCcGXb4K0ky6utW89+WJO0YGWU50/m9NZKk\nJjHzLWeOpE6SJDUdkWg5c/j9CZU+k9aso+VM9KHdkmT0+Rnq3CVJKslYYTlzQ7e79d7N1senJI38\nPlubBv7aKBOx4ROtCzG7itngnG36+vfDjDLt/7Fc/+pzp1Gm12efq2DZC0YZ/1FPKDGgrVFmwpk9\ntvpgdcvORpkhB3Yo676hRplOb63SGzeGGGUePJFjNKYl97i+mLXBKFOz00DlTR1jlAmes8TW96v5\n9cze00ln92jqDcFGmTkleYp3tDDKJLmctr5nP16rpVFmZvEBnTxbYJRpWM/fVr+Nl1kfJMtpq6/t\n9EFFvT9z/NsYZaYW7LX1PHaOVXbeH8ZB1RkHE87skSSj9ydZTkkyqi3+NNsp4HJs+goAAAAAAHAJ\nJkyuID8/XzExMZ7bu3fv1n333ee5vWvXLvXs+d//bT9z5oz69OkjSerQoYPn6jkjRozQ+vXrK65w\nAAAAAACuwOVyXTdflQVLciwIDQ2V0+nUhQsXVLt2bWVkZKhWrVrav3+/WrVqpczMTHXv3l2SVLdu\nXaWkpEiSvvvuOz344IMaNGiQN8sHAAAAAACGOMPEgho1aigsLEw7d+6UJGVkZGjEiBHKyMjw3A4P\nD78sd+zYMTVp0qRCawUAAAAAAFePCROLwsPDtXXrVrlcLh0+fFhRUVHaunWrpPITJufOnVNsbKxG\njRqlhx9+WH/84x+9WTYAAAAAALCBJTkWRUREaPbs2Z5lOK1atdL+/ftVVFSk48ePq0UL967NP1yS\nc/ToUY0dO1ZLly5VgwYNvFk+AAAAAKAaKyurPHuDXC84w8Sidu3ayel0avPmzbr99tvlcDjUpEkT\nrV27Vl27XvmyjI0bN1br1q2Vk5NTwdUCAAAAAICrwYSJRQ6HQx06dNBHH32kbt26SZJuv/12vfXW\nW1fcv0SSiouLtWfPHs/ZJwAAAAAA4PrAkpwfkZeXp9jYWM/thIQEhYeHKzExUa1atZLknjCZO3eu\n5s2b52n3nz1MJKmwsFBjx45Vs2bNKrZ4AAAAAAB+wMWSHGNMmFxBYGCgtm/fftn9YWFhuv/++z23\nu3btqtzc3HJtvvrqq1+8PgAAAAAA8MtyuFwuppm8zOFweLsEAAAAAKjWqvqvxhHPbfB2CZZtemqg\nt0uQxBkmAAAAAABUeSzJMceESSVRdPq4UXvf+o1UDHlIRgAAIABJREFUsOwFo4z/qCd0Pu0Vo0yd\n6D+pcGWSUcbvrngVrX/dKOM76CHN8W9jlJlasFfpnbobZQZkbVXOuOFGmZDXPtTHnXsYZfrv2KLN\nkf2MMuFrN2pKzWDL7eddzJMkrQu58lWarmRwzjZJ0vx6bS1nJp3dI0lKqt/Ocib+tHupmp3X88aN\nIZYzD55wX4FqTZsuljNRe93L7ZqOSLScOfz+BNuZZvdY//wceje+Qmv7LKKn5UyfTV9Iko4l/tly\n5qYJcyVJF7/ZZTlT85YwpTYJtdxekmKOZCsxwPqYlqQJZ/bYOoaafN4k92fuOb/WRpmnCvfp9OtP\nG2XqPzTD1vPY6bczi58xygQ88Kw+7XGHUabvli+V1qyjUSb60G6j8Sm5x+iFk0eMMrUbNrH1vcfk\n2Ca5j2/jZbZpfLKclbq2CTVuNcoklh3UybMFRpmG9fxt1WanD+z0tZ0+qKj3x04m3mGWSXLZex6T\nn1sk988ujIOqMw6S5ZRk7+dXk9qSXE7LbVF9cJUcAAAAAACASzBhcgX5+fnq0qWLYmNjFRsbq9/9\n7nd6+umnVVpaKkk6cuSI2rdvrw0b/rsGbPPmzWrfvr2OHPnv/1SVlpaqV69eSky0/j+/AAAAAADA\n+5gw+RHBwcFKSUlRSkqK3nnnHZWUlCgtLU2StHLlSrVo0UIrV64sl2nevLlWr17tub1582b5+flV\naN0AAAAAAFyqzOW6br4qCyZMLAoLC5PT6V7XtmLFCv3lL3/RF198ofPnz3va9O7dW6tWrfLcXrly\npXr37l3htQIAAAAAgKvDhIkFJSUlSk9PV4cOHXTgwAGdPXtWPXv2VHh4uD7++GNPu0aNGql27dpy\nOp0qKSlRVlaWOnXq5MXKAQAAAACAHVwl50fk5eUpNjZWkpSbm6u4uDgNHDhQL7/8soYOHSpJuvvu\nu5Wamqq7777bk4uKitKKFSsUGhqq8PBwORwOr9QPAAAAAMB/cFlhc0yY/Ij/7GEiSRMnTlRwsPvy\nqCtXrpTD4dAnn3yisrIy/fvf/9aZM2c8ucGDBysuLk7ffPONRo4cqW+++cYr9QMAAAAAAPuYMLEg\nISFBcXFxql+/vvz9/ZWamup57PHHH9fatWt1yy23SJIaN26sgIAA7d69WzNnzmTCBAAAAACA6xB7\nmFgQFBSkyMhIbdiwQTExMeUe++1vf1tuo1fJvSynR48eqlGD7gUAAAAA4HrEGSZXEBgYWO4sEkma\nPHnyFdt269ZNb7zxhiQpPDxckjR69GjP45dOsAAAAAAAUNHYw8Scw+WqRBc5rqbYGBYAAAAAvKuq\n/2p8+9NrvF2CZZkzorxdgiTOMKk0Lhz/1qh97UbNdf7Dvxll6gyfrKKNbxplfPvdr5Jtq40yN3Qd\nopKMFWaZbndrSaMQo8yY4znaN/F3RpnWL7+j5U07GGWGHf5K38542CjT/Om/6/DsPxllmj72it67\nOdRy+5HfZ0uS/tXnTsuZXp99Lkla06aL5UzU3u2SpIy7B1rOdFuxQZK0PrSb5cyg7AxJ0ncvxFvO\n/OqJJElSzrjhljMhr30oSWp2T5LlzKF33TX9alSy5cx3y8ZX+ozJZ2HY4a8kydYYLd70oeVMrYjh\nSmvW0XJ7SYo+tFu7Rg0xyoQtW23rWHBgyv1GmZbz3tT2mMFGmS6p61Tw/otGGf8RCXrjRrNj6IMn\ncvRpjzuMMn23fGk0BiT3ONjz8G+NMm3//oGW3tTeKDP62Ne2vo+YjE/JPUbtHN/3T7rXKNNq/tu2\n3tNJPrcaZeaXHtR4tTDKJMtp6/15zq+1Ueapwn06ebbAKNOwnr+tfrPTB3b62k4fVNT7k9ygnVFm\n/KlcW89jJ2OnDxgHVWccjD72tfu5DPogWU5JsvU8wA8xYQIAAAAAQBVXxpIcY+xKCgAAAAAAcAnO\nMLEhPz9f0dHR6tjRfdp4cXGx2rZtq+nTp2vQoEFq2rSpfHx8dP78eY0YMUL33mt2Gi4AAAAAAPAu\nJkxsCg4OVkpKiuf2tGnTlJaWJkl67bXX5O/vr/Pnz2vgwIG655575OPj461SAQAAAADVXFXf1PaX\nwJKcayQsLExOp7PcfadPn1bDhg2ZLAEAAAAA4DrDhMk1UFJSovT0dHXo4L7iwrhx4zR69GgNHz5c\n8fHWr/gBAAAAAAAqB5bk2JSXl6fY2FhJUm5uruLi4jRw4EC98MILniU5586d09ixYxUSEqJWrVp5\nuWIAAAAAAGAVEyY2/XAPk4kTJyo4OPiyNnXr1lWPHj20Y8cOJkwAAAAAAF7jKvN2BdcfluRcAwkJ\nCZo7d64KCwvL3e9yuZSVlXXFyRQAAAAAAFB5cYbJNRAUFKTIyEgtWLBAknsPEx8fHxUVFalv377q\n2rWrlysEAAAAAAAmmDCxITAwUKmpqeXumzx5crk/AQAAAACoLMrKuKywKYeLizF7ncPh8HYJAAAA\nAFCtVfVfjTtNXentEizLmnOXt0uQxBkmlUbxoX1G7Ws1a63C1clGGb8h41W8ZbnZ8/QYptK9Xxpl\nfNrcoYtfbTTK1OzQT+tCzJYuDc7ZpjOLnzHKBDzwrN64McQo8+CJHBWuTDLK+N0Vb+v9+Syip+X2\nfTZ9IUnaNmyQ5UzX5eslSdtjBlvOdEldJ0lyThtrOdNi1iJJUtZ9Qy1nOr21SpJ0fvlLljN1hj0i\nSTo8+0+WM00fe0WSdOu49yxnDr420nam5fj3LWcOJI+o0MzSm9pbzow+9rUkaX69tpYzk87ukSQV\nrX/dcsZ30EP6uHMPy+0lqf+OLcqf/gejTOD0V5UYYP21SNKEM3t0LPHPRpmbJszVtzMeNso0f/rv\nto45a9p0McpE7d2uHSOjjDKd31tjNAYk9zg4kfSYUebG+Nm2Xs/MOq2NMo+f36dzb80wytS972mj\n45TkPladWvikUaZB3PNK79TdKDMga6vGq4VRJllOTahxq1EmseygNt4eYZTpl7nJ6JgjuY87358u\nMMrcXN/fVr9N8rnVKDO/9KCtvrbTBxX1/tj5OcxOX3/a4w6jTN8tX2rqDWb7Ac4pyWMcVKFx0HeL\n+3cRk3EwpyRPkoxqG5C11XJbVB9s+goAAAAAAHAJzjABAAAAAKCKc7GHiTEmTH5Efn6+oqOj1bFj\nR0lScXGx2rZtq+nTp+vChQuaOXOmdu/erdq1a6t+/fqaPn26mjVrpmnTpumrr75SgwYNdOHCBYWE\nhGj69OmqUYOTeQAAAAAAuF4wYfITgoODlZKS4rk9bdo0paWlKTMzU82bN9eMGe51z6tXr9ajjz6q\nZcuWSXJfKadfv36SpAceeEA7d+5Uly5ma7EBAAAAAID3MGFiICwsTNnZ2frnP/+pDRs2eO4fMmSI\nevXqdVn74uJinT9/XjfddFNFlgkAAAAAQDksyTHHOhGLSkpKlJ6erl/96lcKDg6Wj49PuccDAgI8\nf//b3/6m2NhYDRo0SLfddpuCgoIqulwAAAAAAHAVmDD5CXl5eYqNjVVsbKx69eql8PBwRUREqLS0\n9CdzkydPVkpKijZu3KgLFy7ovfesX4oUAAAAAAB4HxMmP+E/e5ikpKQoIiJCwcHBCgwM1IEDB1Rc\nXFyubVZW1mX5GjVqaODAgcrIyKiokgEAAAAAuEyZy3XdfFUWTJhYlJCQoLlz58rHx0cDBgzQ/Pnz\nPY+tXbtWs2fPlusKb+zOnTsVHBxckaUCAAAAAICrxKavFgUFBSkyMlILFizQE088oRdffFHR0dEK\nCAhQ06ZN9corr8jhcEhy72Hy+uuvq7S0VI0bN9bMmTO9XD0AAAAAADDBhMmPCAwMVGpqarn7Jk+e\n7Pn7k08+ecXcrFmzftG6AAAAAADAL8/hutI6ElSo/5yZAgAAAADwjqr+q3HII8u9XYJlOS8N83YJ\nkjjDpNK4cPxbo/a1GzXXmcXPGGUCHnhW55e/ZJSpM+wRFa5MMsr43RWvwrULzTKRcXrOr7VR5qnC\nfdo08NdGmYgNn9jKbI7sZ5QJX7tRWfcNNcp0emuVpt5gfb+bOSV5kqRVLcIsZ4Y6d0mSkuq3s5yJ\nP50rSVrSKMRyZszxHEnSs76tLGeeKdovSVrTpovlTNTe7ZKk9aHdLGcGZbs3YW78m3mWM0c/miJJ\nahIz/2da/teR1EmVPrMupKvlzOCcbZKkr39v/ZtX+3+4vymX7t9qOePTqruSG1gfn5I0/lSu0fiU\n3GM0b+oYo0zwnCXaeHuEUaZf5iYtbGj2euJO5upk8uNGmYbjZ+qp2i2NMs9dOGCrr/dPutco02r+\n29o6pL9Rpvvqj7X0pvZGmdHHvlb22GijTOiiNJXkZxtlbggM1WcRPY0yfTZ9oRWBnYwyd+dnaUKN\nW40yiWUHbfWbybFach+vJ/ncapSZX3pQ49XCKJMsp74/XWCUubm+v61+s/MziJ2+ttMHFfX+2Om3\nKTXN9umbdzHPVm2P1zI7vs0sPsA4qELjYH7pQUkyGgcziw9IklFt8y7mWW6L6oNNXwEAAAAAAC7B\nGSYAAAAAAFRxrrKqveTol8CEySXy8/MVHR2tjh07SpKKi4vVtm1bTZ8+XRcuXNDMmTO1e/du1a5d\nW/Xr19f06dPVrFkzTZs2TUePHtU//vEPz7+1ceNGPfzww0pPT1dgYKC3XhIAAAAAADDEhMkVBAcH\nKyUlxXN72rRpSktLU2Zmppo3b64ZM2ZIklavXq1HH31Uy5Ytk+SebDlx4oRuvPFGSdKqVasUFBRU\n8S8AAAAAAABcFfYwsSAsLEzZ2dn65z//qXHjxnnuHzJkiF599VXP7d69e2v16tWSpKKiIh08eFDN\nmjWr8HoBAAAAAMDVYcLkZ5SUlCg9PV2/+tWvFBwcLB8fn3KPBwQEeP4+ePBgrVy5UpL0ySefqGdP\ns130AQAAAAD4JZSVua6br8qCCZMryMvLU2xsrGJjY9WrVy+Fh4crIiJCpaWlP5lr3ry5SkpK9N13\n32nVqlWKioqqoIoBAAAAAMC1xITJFfxnD5OUlBRFREQoODhYgYGBOnDggIqLi8u1zcrKKnc7MjJS\nH374ofLy8tS+vdl12QEAAAAAQOXAhMnPSEhI0Ny5c+Xj46MBAwZo/vz5nsfWrl2r2bNny+X67ylD\nkZGRWrJkifr06eONcgEAAAAAuIzL5bpuvioLrpLzM4KCghQZGakFCxboiSee0Isvvqjo6GgFBASo\nadOmeuWVV+RwOMq1DwwMVGRkpBerBgAAAAAAV4MJk0sEBgYqNTW13H2TJ0/2/P3JJ5+8Ym7WrFme\nv3/wwQeev//w8sQAAAAAAOD64HBVpvNdqqkfnqECAAAAAKh4Vf1X41YPf/DzjSqJ/X//rbdLkMQZ\nJpVG8eEDRu1rNW2pgmUvGGX8Rz2hovWvG2V8Bz2k4i3LjTK1egxT8aYPzTIRw/XGjSFGmQdP5Oib\nJx8yytzy/Ot67+ZQo8zI77N15MWJRpkmCS/r6EuTf77hDzR+5G9a1tj6RsGjjn4tSfq0xx2WM323\nfClJWhfS1XJmcM42SdLWIf0tZ7qv/liStD60m+XMoOwMSdK3Mx62nGn+9N8lSdljoy1nQhelubP3\nLbSc+fatuCqZSW1i/bMQcyRbkmyNUZNjSK0ew4ye4z/Psz1msFGmS+o6LW/awSgz7PBX2jfxd0aZ\n1i+/Y6u2c2/NMMrUve9pJTdoZ5QZfypXH3fuYZTpv2OL0biR3GPHOW2sUabFrEW2jtVLGpl9Hxlz\nPEdFG980yvj2u1///kucUSborwttjR073xcn1LjVKJNYdlDj1cIokyynlt5k9jkdfexrPevbyijz\nTNF+HTl1zijTpEFdW/1mpw/s9LWdPqio98fOMcTOZ85ObfEOsz5IcjkZB1VoHIw+5v55wmQcJLmc\nkmRU25jjOZbbonIqKSnRtGnT9N1338nHx0czZ85UUFBQuTb/+7//q82bN8vlcmngwIEaN27cT/6b\nbPoKAAAAAACuaytWrFBAQIDefvttPfzww5o3b165x/fs2aPNmzdr2bJlevvtt5WamqqjR4/+5L/J\nhAkAAAAAALiuffnllxo0aJAkqWfPntq2bVu5x+vVq6cLFy6ouLhYFy5cUI0aNeTn5/eT/yZLci6R\nn5+v6OhodezYUZJUXFystm3bavr06Ro0aJCaNm2qGjVqqLS0VHfddZfuv/9+SdK0adN09OhR/eMf\n//D8Wxs3btTDDz+s9PR0BQYGeuX1AAAAAABQVla192g5duyYbrzxRklSjRo15HA4VFxcrFq1akmS\nmjVrpqioKPXr10+lpaX64x//qLp16/7kv8mEyRUEBweXu7rNtGnTlJbm3vfgtddek7+/v86dO6c/\n//nP8vHx0b333ivJPdly4sQJz5u0atWqy9ZMAQAAAAAA+9577z2999575e7buXNnuduXbuL773//\nW+vXr9eGDRt08eJFjRo1SkOHDlWjRo1+9HlYkmNBWFiYnE5nufvq1q2r6dOna/HixZ77evfurdWr\nV0uSioqKdPDgQTVr1qxCawUAAAAAoCobOXKk3n333XJfw4cP9+xJUlJSIpfL5Tm7RJKysrJ02223\nyc/PT/Xq1VO7du20Z8+en3weJkx+RklJidLT09Whw+VXU2jatKnOnTunixcvSpIGDx6slStXSpI+\n+eQT9ezZs0JrBQAAAADgSlxlpdfNlx29evXSmjVrJLm3xwgPDy/3+C233KLdu3errKxMJSUl2rNn\nz8+uCGHC5Ary8vIUGxur2NhY9erVS+Hh4Ro4cOAV254/f141ari7sXnz5iopKdF3332nVatWKSoq\nqiLLBgAAAACgWho6dKjKysp07733aunSpZoyZYok6dVXX9X27dvVsWNH9erVS/fdd59iY2M1YsSI\nn91rlD1MruCHe5hMnDhRwcHBV2y3f/9+3XLLLZ4JE0mKjIzUhx9+qLy8PLVvb3btcwAAAAAAYM7H\nx0czZ8687P4//OEPnr9PnDhREydOtPxvcobJz0hISNDcuXNVWFhY7v6CggI9//zzGj9+fLn7IyMj\ntWTJEvXp06ciywQAAAAAANcQZ5j8jKCgIEVGRmrBggWSpHHjxkmSzp49q9/+9rcaMmTIZe0DAwMV\nGRlZ4bUCAAAAAHAldvcGqc6YMLlEYGCgUlNTy903efLkcn9eyaxZszx//+CDDzx//+HliQEAAAAA\nwPXB4br04sSocA6Hw9slAAAAAEC1VtV/NW7x0FveLsEy5+v3ebsESZxhUmkUnT5u1N63fiMVvDvb\nKON/z2MqXJlklPG7K95Wpmj960YZ30EPaV7dNkaZKef2al1IV6PM4Jxt2vPwb40ybf/+gT7u3MMo\n03/HFm0d0t8o0331x5pS88obDF/JvIt5kqT1od0sZwZlZ0iSEgPaWs5MOOO+Nnlyg3aWM+NP5UqS\nrddj53nWtOliORO1d7skqemIRMuZw+9PsJ1pdo/1z8+hd+MrtLZPe9xhOdN3y5eSpNOvP205U/+h\nGZKkiwd3WM7UvLWzVgR2stxeku7Oz9L8etbHtCRNOrtH55e/ZJSpM+wRo7Emucfbs76tjDLPFO3X\nmcXPGGUCHnhWc/zNjqFTC/ba6jc733vsHEPTmnU0ykQf2q1TC580yjSIe14XThwyytS+sZk23h5h\nlOmXuUkLG1o/tklS3MlcjVcLo0yynLZqW3qT2Sb1o499bau2ST63GmXmlx7UybMFRpmG9fxt1Wan\nD+z0tZ0+qKj3pzJnkuqbfX7iT9v7/DAOKuc4SJZTkozGQfxp98+Idp6nKmNJjjk2fQUAAAAAALgE\nEyYAAAAAAACXYEmOTfn5+YqOjlbHju5ThouLi9W2bVtNnz5dgwYNUtOmTeXj4+Npz+avAAAAAABv\ncZWyJMcUEyZXITg4uNxEyLRp05SWliZJeu211+Tv7++t0gAAAAAAwFVgSc41FBYWJqez6m8WBAAA\nAABAVceEyTVSUlKi9PR0dejQwdulAAAAAACAq8SSnKuQl5en2NhYSVJubq7i4uI0cOBAvfDCCxo3\nbpxnD5OGDRvq5Zdf9mapAAAAAIBqjMsKm2PC5Cr8cA+TiRMnKjg42PMYe5gAAAAAAHD9YknONZKQ\nkKC5c+eqsLDQ26UAAAAAAICrxBkm10hQUJAiIyO1YMECb5cCAAAAAEA5LMkxx4SJTYGBgUpNTS13\n3+TJk8v9CQAAAAAArk8Ol8vl8nYR1Z3D4fB2CQAAAABQrVX1X42b3/uqt0uw7Nu3/+DtEiRxhkml\nUXTmpFF734CGKnh3tlHG/57HVLgyySjjd1e8CtcuNMtExqkofbFRxnfAA5rj38YoM7Vgr9a06WKU\nidq7Xdljo40yoYvSlN6pu1FmQNZWbY7sZ5QJX7tRU2oG/3zD/2/exTxJ0vrQbpYzg7Iz3Nm61vt6\nyrm9kqTkBu0sZ8afypUkTb3B+uuZU+J+Pcsat7ecGXX0a0nSupCuljODc7ZJkhr/Zp7lzNGPpkiS\nmsTMt5w5kjpJktR0RKLlzOH3J9h+HjuZT3vcYTnTd8uXkqTv/zbJcubmye6aLh7cYTlT89bOWt7U\n7PLsww5/ZTQ+JfcYPbP4GaNMwAPPGn3eJPdnbmad1kaZx8/v09k3nzXK1Lv/GVvPk1TfrN/iT+fq\nZPLjRpmG42faOoa+d3OoUWbk99k68uJEo0yThJd14eQRo0zthk30WURPo0yfTV8YHdsk9/FtvFoY\nZZLlNDoeSu5jop3Pj53aJtS41SiTWHZQp86dN8o0qFvHVm12+sBOX9vpg4p6f+xk4h1mmSSXveex\n8zMi46DqjINkOSXJaBxMLXD//GpSW5LLabktqg8mTAAAAAAAqOLYw8QcV8kBAAAAAAC4BBMmBvLz\n89WlSxfFxsYqNjZWv/vd7/T000+rtLRU/fv316uvll8TNnv2bPXv399L1QIAAAAAALtYkmMoODhY\nKSkpntvTpk1TWlqaGjdurPT0dP3hD+7NaVwul3bv3u2tMgEAAAAA8GBJjjnOMLlKYWFhcjqdqlWr\nlho2bKh9+/ZJkjIzM9WqVSsvVwcAAAAAAOxgwuQqlJSUKD09XR06uK/oEBkZqbS0NEnSqlWrNHjw\nYG+WBwAAAAAAbGLCxFBeXp5nD5NevXopPDxcAwcOlCQNGDBA69evV2lpqbZs2aIePXp4uVoAAAAA\nANxLcq6Xr8qCPUwM/XAPk4kTJyo4ONjzWEBAgAIDA7Vo0SLddtttqlmT7gUAAAAA4HrEGSZXISEh\nQXPnzlVhYaHnvqioKL366qssxwEAAAAA4DrGhMlVCAoKUmRkpBYsWOC5b+DAgfLx8VHPnj29WBkA\nAAAAALgarBkxEBgYqNTU1HL3TZ48udztgIAAffHFF57bH3/8cYXUBgAAAADAjymrRHuDXC8cLpfL\n5e0iqjuHw+HtEgAAAACgWqvqvxrfPPxv3i7Bsu8/nPzzjSoAZ5hUEhdOHTVqX7tBYxW8/6JRxn9E\nggrXLjTK+EXGqXB1sllmyHgVpS82yvgOeECJAW2NMhPO7NHHnc2uRNR/xxZlj402yoQuStO/+txp\nlOn12efKum+oUabTW6v0eK2WltvPLD4gSVof2s1yZlB2hiTpjRtDLGcePJFjO/NUbeuv57kL7teT\n3KCd5cz4U7mS7PVB49/Ms5w5+tEUSVKTmPmWM0dSJ1Voxs7rWd2ys+XMkAM7JEmnFj5pOdMg7nlJ\nUun+rZYzPq26a02bLpbbS1LU3u22jh92jqF2anvOr7VR5qnCfTr75rNGmXr3P6P59cz6YNLZPZrj\n38YoM7VgrwqWvWCU8R/1hDbeHmGU6Ze5SWnNOhplog/tNhqfknuMlnybY5S5oXmIvujXxyjTc+Nn\nWtjQ+rFNkuJO5ire0cIok+RyKr1Td6PMgKytWtLI+vFdksYcz9F4mdWWLKem1Az++YY/MO9ino6f\nKTDKNArwt9VvS29qb5QZfexrW31tpw8q6v2x028V9TxJ9c0+P/Gn7X1+GAeVcxwkuZzuPw3GQfxp\n98+IJrUly2m5LaoPJkwAAAAAAKjiKtPleq8XbPoKAAAAAABwCc4wsSE/P1/R0dHq2NF9unBxcbHa\ntm2r6dOnKyMjQy+99JJq1KihgoICDRs2TGPHjvVuwQAAAAAAwAgTJjYFBwcrJSXFc3vatGlKS0vT\nggULtGTJEjVp0kRFRUUaO3ashg4dqptvvtmL1QIAAAAAABNMmFwjYWFhcjqdOnXqlM6fPy9J8vX1\n1bJly7xcGQAAAACgumMPE3PsYXINlJSUKD09XR06dNAjjzyiESNG6H/+53+0dOlSnT592tvlAQAA\nAAAAQ5xhYlNeXp5iY2MlSbm5uYqLi9PAgQMlSYMGDdI///lPbdiwQQsWLFBqaipLcgAAAAAAuI4w\nYWLTD/cwmThxooKD3ddTLyoqUuPGjTV8+HANHz5cjz/+uP71r39p+PDh3iwXAAAAAFCNuUpZkmOK\nJTnXQEJCgubOnaucnBzFxMSooKBAklRWVqbvv/9eQUFBXq4QAAAAAACY4AyTayAoKEiRkZFatWqV\nxo0bp7Fjx8rX11clJSXq37+/unXr5u0SAQAAAACAASZMbAgMDFRqamq5+yZPnuz5O8tvAAAAAACV\nCVfJMedwuVwubxdR3TkcDm+XAAAAAADVWlX/1fjGqL96uwTLTqz5i7dLkMQZJpVG0dlTRu196zVQ\nwfsvGmX8RySocGWSUcbvrngVrk42ywwZr6L0xUYZ3wEPaF7dNkaZKef2anXLzkaZIQd2aO8fRxpl\n2vzfe1oX0tUoMzhnm77o18co03PjZ5pSM9hy+3kX8yRJ6Z26W84MyNrqzhr09ZRzeyVJSfXbWc7E\nn851Z228noUNrT9P3En386xp08VyJmrvdklS0xGJljOH358gSWp2j/XPz6F3421n7NRmJ/OvPnda\nzvT67HNJ0unXn7acqf/QDEnSxW92Wc7UvCUVmMzmAAAgAElEQVRMKwI7WW4vSXfnZykxoK1RZsKZ\nPTr/4d+MMnWGT7Z1LHjOr7VR5qnCfTr75rNGmXr3P6M5/mbH0KkFe231W8GyF4wy/qOe0PpQs6Wp\ng7IzlNaso1Em+tBunVr4pFGmQdzzKjpz0ijjG9BQG2+PMMr0y9ykN24MMco8eCJH49XCKJMspz7t\ncYdRpu+WL7X0pvZGmdHHvrZV2ySfW40y80sP6tS580aZBnXr2KrNTh/Y6Ws7fVBR74+dTLzDLJPk\nsvc8do5VjIOqMw6S5ZQko3Ew4cweSTKqLcnltNwW1QebvgIAAAAAAFyCM0wAAAAAAKji2MPEHBMm\nFuXn5ys6OlodO7pPES4uLlbbtm1Vq1YthYSEaORI9zKP6dOnq06dOpo6daokafHixTp27JimTJni\ntdoBAAAAAIAZluQYCA4OVkpKilJSUvTOO++opKREHTt2VEZGhqfN/v379dVXX3luZ2ZmKjw83Bvl\nAgAAAAAAmzjD5CqEhYVp9+7dyszMlCSdOnVKtWrVUnFxsQoLC+Xn56edO3dq1qxZXq4UAAAAAFCd\nsSTHHGeY2FRSUqL09HTdcccd8vf31+HDh7Vt2zZ17txZnTp10vbt23XgwAH96le/Up06dbxdLgAA\nAAAAMMAZJgby8vIUGxsrScrNzVVcXJwGDhyoLVu2aMuWLcrJydGdd96p8+fPKyMjQ82aNWM5DgAA\nAAAA1yHOMDHwwz1MIiIiFBwcLEkKDw/Xtm3btGPHDt12223q2rWrdu7cqYyMDCZMAAAAAAC4DjFh\nYlNCQoLmzp2rwsJCde/eXTt27FCNGjVUp04dNWzYUAUFBcrNzVXXrl29XSoAAAAAoJpzlZVdN1+V\nBRMmNgUFBSkyMlILFixQQECAatSooQ4dOngeb9OmjerVq6fatWt7sUoAAAAAAGAHe5hYFBgYqNTU\n1HL3TZ482fP3Sx+bMWNGhdQFAAAAAACuPYfL5XJ5u4jqzuFweLsEAAAAAKjWqvqvxgG/fszbJVh2\n5pPZ3i5BEmeYVBoXjn9r1L52o+YqeP9Fo4z/iAQVrX/dKOM76CEVb1lulKnVY5iKN31olokYrqT6\n7Ywy8adz9VXs3UaZDikrtKpFmFFmqHOX9k+61yjTav7bck4ba5RpMWuRFja03gdxJ3MlSZ/2uMNy\npu+WLyVJqU1CLWdijmRLkj6L6Gk502fTF5Kk5U07/EzL/xp2+CtJMurrVvPfliTtGBllOdP5vTWS\npCYx8y1njqROkiQ1HZFoOXP4/QmVPpPWrKPlTPSh3ZJk9PkZ6twlSSrJWGE5c0O3u/XezdbHpySN\n/D5bmwb+2igTseETrQsx22NqcM42ff37YUaZ9v9Yrn/1udMo0+uzz1Ww7AWjjP+oJ5QY0NYoM+HM\nHlt9sLplZ6PMkAM7lHXfUKNMp7dW6Y0bQ4wyD57IMRrTkntcX8zaYJSp2Wmg8qaOMcoEz1li6/vV\n/Hpm7+mks3s09YZgo8yckjzFO1oYZZJcTlvfsx+v1dIoM7P4gE6eLTDKNKznb6vfxsusD5LltNXX\ndvqgot6fOf5tjDJTC/baeh47xyo77w/joOqMgwln9kiS0fuTLKckGdUWfzrXcltUH+xhAgAAAAAA\ncAnOMLlEfn6+oqOj1bGj+3+piouL1bZtW9WqVUshISEaOXKkJGn69OmqU6eOpk6dKklavHixjh07\npuDgYL300ku65ZZb5HK5VKtWLc2ZM0c33XST114TAAAAAKB6c5WVeruE6w5nmFxBcHCwUlJSlJKS\nonfeeUclJSXq2LGjMjIyPG3279+vr776ynM7MzNT4eHhkqShQ4cqJSVFb775prp27aoPPvigwl8D\nAAAAAACwjwkTC8LCwrR7925lZmZKkk6dOqVatWqprKxMhYWFkqSdO3eqa9fL14IfP35cTZo0qdB6\nAQAAAADA1WFJzs8oKSlRenq67r33XmVkZOjw4cPKzs5W587/j70zj6sp///46942ZDd2oTKWpBJK\nlmkso6gwGYokJINmrIOKlLGGQck6lrIbIrRSTNkqGVuStSItok1J99a9vz96nPPt3nvOufcefvjO\n9/N8POYx7u187ufs53xen/f79TZDZWUlbt++jTZt2qBdu3Zo0KABACAqKgppaWkoLi6Grq4unbZD\nIBAIBAKBQCAQCAQC4b8DIpgwkJmZCVdXVwDAo0ePMGPGDAwfPhwpKSlISUlBRkYGBg8ejPfv3yM1\nNRVt27al03GA2pScpUtrSzaFh4djxYoV2LhRvYo2BAKBQCAQCAQCgUAgfCokxMNEbUhKDgN1PUz6\n9+8Pff3acmGWlpb4559/cOfOHZiamsLc3Bx3795FamqqjGBSFxsbGxnvEwKBQCAQCAQCgUAgEAhf\nP0QwUcLixYuxadMmVFZWol+/frhz5w6EQiEaNGiAZs2aoaKiAo8ePWL0LwFqvU0owYVAIBAIBAKB\nQCAQCATCfwckJUcJenp6sLGxwc6dO7Fw4UIIhUL07NmT/vu3336LrKws6Ojo0N9RHiYU/v7+n3OV\nCQQCgUAgEAgEAoFAkEFaQ1Jy1IUIJnJ06NABp0+flvlu4cKF9L/l/7Zq1SqZz46OjnB0dPz/W0EC\ngUAgEAgEAoFAIBAI/++QlBwCgUAgEAgEAoFAIBAIBDkEUqlU+qVX4n8dgUDwpVeBQCAQCAQCgUAg\nEP6n+bcPjRtYzf3Sq6Ay728EfelVAEBScr4aqkoK1Vpep2lLVJxSr1Sx7k+LURm7V6029W1moDJ6\nt3ptRv6MD/GharWpN8wN2xp3VavNr2WPccnMQq02Q++kIH2qg1ptjELO49p3g9VqMzDxCu5PGqVW\nm15Ho+CtbaDy8utEzwEAF436qtzmh/Taik0HmndXuc20ogzebZbrqL49q6tqt2d3024qt/m55BEA\nfvug5dg/VG5TGL4IANDacavKbQpOz/+sbfhsT7SBmcptRj6/AwAo2btM5TZNZ6wBANQ8u6lyGw3D\nfoj5trfKywOA7ZPbvO4ffO6hfNZtdf0uarVZXvkU7w6vVKtNo8l+2NpIvX0w/91jbND9Vq02Syqe\noOL4WrXa6Dr74HKf/mq1GXIrCefbGqvVxiEvTa3zE6g9R8WvMtRqo9W+O64P+U6tNgMuJ2JvM9Xv\nbQAwo/gR5gg6qdVmhzQb8b36qdVm2P2bONhC9fs7AEx5m4Gfod667UY2FmmqZ4L/R3Um3pZVqNWm\nRWNdXvvtyDc91Grj8uYhr33NZx98ruPDZ799rn52NFHv+plTyu/6IefB13ke7JBm1/5fjfNgTmnt\nO6I667Yb2Sov+9+KlJQVVhuSkkMgEAgEAoFAIBAIBAKBIAeJMPkIjhw5grNnz0JbWxsfPnyAu7s7\njh49CgB4+PAhOnXqhAYNGsDe3h5OTk5feG0JBAKBQCAQCAQCgUAgqAoRTHiSk5ODv/76C6dOnYKW\nlhaysrKwfPlyHD58GADg6uoKX19fdO2qXog0gUAgEAgEAoFAIBAInxqSkqM+JCWHJ+Xl5aiqqoJY\nLAYAdO7cmRZLCAQCgUAgEAgEAoFAIPx3QwQTnnTv3h0mJiYYNmwYvLy8EBUVherq6i+9WgQCgUAg\nEAgEAoFAIBA+ASQl5yPYsGEDnj17hitXrmDv3r04duwYDh48SMoEEwgEAoFAIBAIBALhq4Kk5KgP\niTDhiVQqRVVVFQwNDTF16lScPHkSBQUFyM3N/dKrRiAQCAQCgUAgEAgEAuEjIYIJT06dOgVfX19I\npVIAwLt37yCRSNCiRYsvvGYEAoFAIBAIBAKBQCAQPhaSksMTR0dHPH/+HOPHj0eDBg1QXV2N5cuX\no169el961QgEAoFAIBAIBAKBQCB8JEQw4YmGhgaWLl3K+vdDhw59xrUhEAgEAoFAIBAIBAKBHeJh\noj4kJYdAIBAIBAKBQCAQCAQCQQ6BlDLhIHwxSFUdAoFAIBAIBAKBQPiy/NuHxtq9p3/pVVAZ0e39\nX3oVABDBhEAgEAgEAoFAIBAIBAJBAZKSQyAQCAQCgUAgEAgEAoEgBxFMCAQCgUAgEAgEAoFAIBDk\nIIIJgUAgEAgEAoFAIBAIBIIcRDAhEAgEAoFAIBAIBAKBQJCDCCYEAoFAIBAIBAKBQCAQCHIQwYRA\nIBAIBAKBQCAQCAQCQQ4imBAIhH8NEonkS6/CV4NEIkFZWdmXXg3CfwkJCQlfehUIBAKBQCAQvjo0\nv/QKEAiE/zB37lwIBALWvwcGBn7Gtfnvw8bGBtbW1nBwcICpqalKbby9vRW+09DQQMeOHeHs7IzG\njRvL/O3mzZsKywuFQnTo0AGtW7dm7CM3N5exj5YtW0IoZNat+fSzZ88eNG7cGPb29pgyZQqaNm0K\nU1NTzJs3j3F5ADh8+DBGjRqF5s2bsy7zpQgODlb4jjo2NjY20NRUfISVl5ejsLAQ+vr6SElJQXp6\nOkaPHv1Vbh8fJBIJysvLFc7LuvA5dw4fPozevXtz/i4T+fn5yMnJQd++fSESiaCtrc24XHh4OOfv\njB07Vq1+AeDMmTP48ccfGf9WXl6Ow4cP4+3bt1i2bBmSkpJgZGSk9vYRCAQCgUD434YIJl8hIpEI\nr1+/RocOHf5ffv/IkSOcf3dxcWH8/vHjx1i/fj0qKipw4sQJhISEoF+/fujZsyfrb1VXVyMmJgYF\nBQVwd3fH48ePoa+vDy0tLYVlKysrOderfv36rH97//49bty4gXfv3sl8r+wlvLy8HO/evYNUKqW/\na9euHevyAQEBsLe359xmJlTdD5MnT1brd+uSn5+P7du3o7S0FEFBQYiMjISZmRnat2/P2kZdsUB+\nm5gGrJ+qH6YBllAoRMeOHWFmZsbYT2RkJG7cuIGwsDBs2LABFhYWsLe3h6GhIeu6NWvWDLm5uRg6\ndCgEAgESExPRtGlTAMCiRYvw559/yiy/b98+3Lx5kxZk0tLSYGJigvz8fIwePRozZ85U6GPBggV4\n8OABfSxyc3PRpUsXlJSUYN68eYznKZ9+Ll26hOPHj+Ovv/7CsGHD4OnpialTp7JuO1B7DcyZMweN\nGjWCnZ0dRowYgQYNGnC2AYCrV6+itLQUdnZ28PHxwfPnz+Hu7o4ffviBtc2wYcMUvtPQ0ICenh4W\nLlyocF0VFRUhPT0d1tbWEAgEuHbtGgwNDZGXl4eLFy9i69atCr83f/58eHh4oLq6GgEBAXBzc4O3\ntzd2797NuT3qrhtQe46KxWKMGTMGs2fPRklJCcaNG4dJkyax9vM5hDA+5055eTmsra3RsWNHaGlp\nQSqVQiAQ4NSpU6zbEhISgpiYGLx//x7nzp3Dxo0b0bJlS8bff/ToEQAgJycH2dnZMDc3h0Qiwe3b\nt9G1a1el9+r79+/jzz//RElJCQBALBbjzZs3rIKJl5cXBgwYgL///htA7bnEdD0zkZGRgfLycpnn\nQr9+/RiXzc/Px4ULFxSeI7/88gvr76t77TAJh3Vh64s6hgCQmZmJO3fuQF9fn/X+ySTs1oXp2Thl\nyhQcPHiQ/jx//nzG6/JTIBKJEBcXh6dPn0IoFMLIyAhDhw79pH1UVVUhPj4erVq1Qp8+fRAUFITU\n1FTo6+tj3rx5aNGihUq/U3ffM8HnmPJpc/XqVQwaNIj+nJ6eDiMjI87fYbpH1YXpWigvL8e5c+fo\ne9/p06dx9uxZ+v7JJFhbW1ujX79+sLS0RP/+/aGnp8fZLxNlZWXIyMhAp06dWO+fn+v6AYC7d++i\nRYsW6NChA8LCwuhzZ8qUKahXr57C8nyuua/9On3z5g2++eYb+t9Xr16Fnp4e+vTpw7j8li1bYGlp\nCXNzc8Z9JE9RURFOnTqF1q1bw9bWFr6+vvR+Xr58OfT19RXanDx5EuPHj/+4DSP8T0MEk6+MyMhI\n7Ny5EwAQERGB1atXw9jYmPFlsn///hAIBDIvaRQCgQA3btxg7KO4uJjXuq1atQr+/v7w9/cHAAwa\nNAi+vr44duwYaxtfX180b94cKSkpcHd3R0pKCnbt2oXNmzcrLGtnZ8e5PfHx8az9TJs2De3bt5d5\nYHK9rADA8uXLkZCQgNatW9N9KhsgGBkZ4c8//8SrV6/w/fffY/To0So95FXdDxYWFgBqXwJCQ0Px\n8OFDCIVCGBsbw9XVlbOPZcuWYcqUKfSAoHnz5vDy8sKhQ4dY26grFgBAUlIS1q5dC5FIhJiYGGzZ\nsgV9+/bF4MGDP2k/N27cQGpqKqysrCAQCJCSkgJjY2OUlJSgc+fO8PX1VWijra0Na2trDBo0CNev\nX6eFow4dOsDb2xvffvutQpsHDx4gNDSU/uzg4IAZM2Zg7969SExMVFheS0sLFy5coF+ci4qKsHbt\nWvz555+YOHEi42BRX18fq1atQteuXQEAz549w8GDB+Hl5QU3NzfG65tPPxKJBBKJBOfPn8fvv/8O\nAKioqFBYri6zZs3CrFmz8Pr1a1y+fBkeHh5o3bo1nJ2d6fORiW3btmHfvn24ePEiNDQ0cPjwYUyf\nPp1TMJkwYQIaNWpEixOJiYkoKiqCpaUlVq9erXAvycrKwrFjx+hr2cPDA56enti1axeruCgSiWBp\naYmgoCBMnToVDg4OOH36NOc+4LNuAHDs2DEcOXIEUVFR6NatG5YsWQI3NzdOweRzCGF8zp1NmzZx\n7h8m4uLicPz4cfre5OPjA2dnZ8bfX7p0KQBg5syZOH36NC22isVizJ8/X2lfq1evxoIFC7Bp0yb4\n+/vj4sWLnAOXiooKTJo0CdHR0QCAUaNGcT6rKGbNmoWSkhK0atWK/k4gELAKJrNmzcLgwYPRpk0b\npb9Noe61c/z4cTRo0ACDBg1Cr169VOrj+PHj2LZtG5o3b47Zs2fjwIEDsLCwwJkzZ2BpaQlPT0+F\nNkOHDkXHjh3pban7LBYIBDIDLgr55/Xbt2+Vrhv1HGD6DbZnfU5ODmbMmAELCwv07NkTFRUViIiI\nwLZt2xAUFMT4HObTz5IlS6Crq4vi4mKEhoaiR48e8Pf3x927d+Ht7Y09e/YotMnMzERISAhat24N\nJycnzJs3D1lZWWjcuDHWrFmD3r17K7The0zVbbNnzx4ZwWT9+vWMx7Eurq6u6NixI0xNTRknRZiu\nhaVLl9LrlJGRgY0bNyIoKAj5+fnw9/dHUFCQQpuIiAjcunULqampCAsLQ1FREczNzWFpaQlLS0vG\ngX9cXBw2bdqENm3awNPTEytXrkSXLl3w5MkTTJ06lXFQ/LmuH39/f2RlZaGyshImJiaoqqqCra0t\n7t27B29vb2zZskWhDZ9r7mu+TkNCQnDhwgUcPXoUZWVl+PHHHzFo0CCcP38eVlZWmDFjhkKbFi1a\n4Pjx4/Dx8UH79u3p49+7d2/GiMXFixfD3Nwcd+/exbFjxzBx4kT8/vvvuHPnDvz9/WXe5yjOnz9P\nBBPCR0EEk6+MI0eO4PTp03B3dwdQe2NwdXVlHFAlJSXx6qOuml5RUYHS0lIAtQMNapDFhKampsxM\nfZcuXVjTCSjy8vKwbt06+oV68uTJiImJYVz20qVLrL+jbMCjpaXFKMJwkZ6ejsTERKXCSl0cHBzg\n4OAAsViMpKQkLFy4EEKhEM7Ozhg7dizrb6mzH4Dalw8LCwt4enpCLBYjJSUF3t7ejC8dFBKJBNbW\n1ti7dy8AwMrKCtu3b+fcHnXFAqD2ZT80NBRz584FUDtzMWfOHE7BhE8/JSUliIiIoCOLPnz4gMWL\nF2Pfvn2sA9KkpCRERUXhn3/+wcCBA+Hv74+ePXsiMzMTixYtYjyPysrKEB8fj969e0MoFCItLQ0F\nBQV4/PgxPnz4oLD8y5cv0ahRI/pzkyZN8Pz5c9TU1KCqqopxvZ4+fUqLJQBgaGiIhw8fon79+qip\nqWFsw6ef4cOHY+DAgbC1tYW+vj62b9+uUmpSQUEBoqOjERcXh6ZNm+L777/H6dOncfHiRSxbtoyx\njba2Nho2bIi4uDg4OTlBU1OTdVsoEhMTZSLcxo8fjylTpuDnn39mXL6wsBCPHj1C9+7dAQAvXrzA\ny5cvkZubyyoEiUQinDt3DpGRkQgLC0NOTo5C5NmnWDegNjJEU1MTsbGx9H2V7dhQfA4hjM+506RJ\nE8YUFi6o403d96qqqlBdXc3ZJi8vD+/evUOzZs3oNjk5OZxtAKBevXro378/tLW1YWxsDGNjY7i7\nu2PIkCGMy0skErx48YJet8TERJU8joqLi3HixAmly1E0bdoUixYtUnl5QP1rJzExEcnJyYiMjERI\nSAj69+8PGxsbmJubs7YJCwtDXFwcHfV08eJF6OrqQiqVwtnZmXHAt3PnTkRHRyMrKwsDBw6EjY0N\nfe2xIf/MU+V5amNjgwcPHsDQ0BAjRoyApaWl0neJDRs2wNfXFwMHDpT5PiEhAatWrWIUMvj0U1hY\niMDAQNTU1GDkyJHYtm0bgNp79pkzZxjb+Pr64qeffsLbt2/h6uqK33//HX379sWLFy/g5eWFo0eP\nKrThc0z5tJEfKDNNSMlD3T+vXr0KQ0ND2NjYYPDgwazpdkDtfWzWrFkAgKioKIwdO5YWVtgmoRo1\naoTvv/8e33//PYDae0FsbCyOHj0KHx8fPHz4UKHNnj17cODAARQWFmLOnDkIDw/HN998A5FIhMmT\nJzMOij/X9fPw4UOcOHECIpEINjY2uHz5MoDaSBq2yG0+19zXfJ2eO3cOx48fB1ArUpiammLdunWQ\nSCRwcXFhFEymTJmCKVOmAKgVH1NTUxEeHo6AgAA0atRIQQARiUT0/ndwcMCYMWMA1E4is73zVlZW\n4tmzZ6znf5cuXTi3i0AggslXhoaGBrS1tembGdcD6mP9LrZv347Tp0+jpKQE7dq1Q25uLpycnFiX\nb9SoEU6dOoXKykrcvXsXFy9eVBqeKhaLUVZWRq/ns2fPIBKJONuwhV47OjqythkyZAgSEhLQp08f\naGho0N9zpfF0794dxcXFansb3LlzB5GRkUhJSUG/fv0wcuRIXL9+HfPnz2fd5+ruh4qKCkybNo3+\nbGZmpjS1QlNTEzdu3IBEIsGbN29w8eJF6OjocLZRVyyg+mnWrBm9LS1atFD68OXTT25uLiorK+lj\nKBaLkZWVhbKyMrx//56xzYkTJzB27Fj4+fnJnAf6+vqYMGECY5v169dj+/bt2Lx5M6RSKTp27IjV\nq1ejsrISq1atUlh+1KhRGDFiBLp16waBQIAnT57A3t4e58+fx8iRIxn7MDMzg6OjI8zMzCAQCPDg\nwQMYGBggPDyccfaRbz8zZ86UGXC7ubmhYcOGjMtSuLi4QCwWY/To0QgKCqKvh9GjR3PeD7755htM\nnToV79+/h7m5Oc6dO8d5vQGAjo4O1q5dC3NzcwiFQty/fx9isRjXrl1jTAPy9vaGj48PHYLcsmVL\nLFiwgBbAmPDz80NYWBj8/f3RsGFDnD17FgsWLOBcLz7rBgA9e/bEDz/8AH19ffTo0QOHDh3iTOkD\nPo8Qxufc4ZPCQqUIZWdnw8/PD8nJyXBzc+Pc/hkzZsDR0ZE+LysqKjjTVyjq16+P+Ph4dOjQAZs3\nb4aenh7y8vJYl/f19cWKFSuQlpaGgQMHonv37pwTAhSDBg3CkydPGKPRmOjfvz+OHDmCPn36yMzG\nc72Aq3vtCIVCWFlZwcrKCtXV1bh69SpOnjwJPz8/WFhYMEbb1a9fn/7PwMAAurq6AGoHSmzvFUOG\nDMGQIUNQVVWFv//+Gzt27EB2djasra1hY2PDmJYmkUjw4cMHeiAi/5lpu6hoo1u3biEqKgpr166F\nmZkZbGxsYGVlJXPvpigqKlIQS4DawSjbc5dPP9Qx1NDQUIgaYnvOCQQCelIrMjISffv2BQB07NiR\nsQ+A3zHl04bPQLlr167o2rUrFixYgLS0NERGRmLr1q3o2rUrbGxsMGLECIU2dc/9q1ev4rfffqM/\ncwmV1AA5JSUFz549Q5s2bTB8+HD62Mmjo6ODtm3bom3bttDT06NTP7S1tVnfdz7X9UP1r62trZBS\nz3Ye8LnmvubrVFdXl94/169fp6PmhEIh53gGqBXM8vPzkZ+fj9evX0NbWxudOnVSWK7uOUwJ70x/\nq0tWVhZWrlzJGsGuLOqKQCCCyVeGubk5Fi9ejIKCAuzZsweXLl2ClZUV47Jcfhdv3rxR2ldiYiLi\n4+Ph6uqKQ4cO4cGDB5xRD+vWrUNoaCiaNWuGPXv20MoxFwsWLICbmxuysrJga2sLgUCA1atXc7ZR\nN/QaqB0oy89sKkvjefnyJYYPH45OnTpBQ0NDpZx9SskfM2YMli5dSr8k9OnTh3Mmuu5+oAYsXPtB\nIpHg/v37dPjo3bt3lc6OrlmzBoGBgSguLsaMGTNgYmKi9PioKxYAQIcOHeh+oqKiEBcXp3Rwwacf\nd3d3/Pjjj2jUqBEEAgFKSkowe/Zs3Lhxg1U8mjNnDqKjo2FtbQ2gNo3M2dkZ3377LZydnRnbdOvW\nDWvXrkVZWZlMzjLbwHfmzJlwcnJCdnY2AKB9+/ZKhcPly5fj8ePHePbsGQDA0dERPXv2hEgkYvVu\n4NOPvM/QqVOnlPoM/f7776hfvz69vc+fP4eBgQEAcKZzbdy4EY8fP6ajzr799lvGkOO6BAUFITw8\nHMnJyZBKpejUqRN27NiByspKxnzqAQMGqJROU5fLly9j+fLl9GcXFxesX79eJiz9U6wbUHtcf/31\nVzRp0gRAbQgz23lG8TmEMD7nDp8UFhcXF1hbW+PevXvQ1tbGrFmz0LZtW842Y8aMwZgxY1BcXAyp\nVCojvnKxadMmvHnzBitWrEBISAgePXqEDRs2sC7fpUsXhISEKP1diroprjt27ECjRo1kngtsKa7X\nrl0DAJlnp7IXcF9fX+Tn59PXWZcuXVSOkMzLy0N6ejoePnyIZs2a0b8hDzUgop4b1OCI+o8LHR0d\n2NjYwMTEBGfOnEFoaChu3LiBkydPKh34+NIAACAASURBVCybm5sLOzs7AP+JXqA+A+B8Bvfp0wd9\n+vSBRCJBSEgIFi1aBC0tLVy9elVhWa6ZbWWisDr9FBQU0JFmdf9NfWai7vkrvy6qnNuqHlM+bZi2\noe5ntsgHCmNjY3z48AFisRhxcXGoqalhFEyaN2+O/fv3o6ysDGVlZbC0tARQm1rLNlAeOHAgdHR0\nMG7cOMyaNYvTa4yi7v6U94D7lPua7foB2KN0iouLkZCQAKlUitLSUrrymFQqpScA2VDnmuPTpu51\nSq3TqFGjACh/V1bn+qEm7MrLy5GcnEyL1O/fv2f1Kdy4cSPS09NRU1MDExMT9OnTB66urnTatjwv\nXrzAhg0bIJVK6X9T2/Ty5UvGNt27dyeiCOGjEEhVic8jfFZSU1Nx+/ZtaGtrw8TEhHUGmoJSzOtG\nZOzevRtxcXGc7ZydnXHs2DG4uLhg//79qFevHiZNmsQYPgqwG4Gx5XbX5e3bt9DW1paZWWXDzc0N\noaGhMuvi7u6Offv2KW1bWloKoVCoUj+vXr1i/J7LJHXv3r0KIYUHDhyQiQZho6qqCuXl5dDS0oJA\nIOBcx8ePH2PNmjX0ALtr165YtmwZ5wvF7t27OUUbNsrLy1UWC4Dah9K5c+dw+/ZtaGlpwdTUFCNH\njmSdQeHbD9UX5bnTpEkTpX24uLhgwYIF9Axfeno61q5di8OHD7O2Wb58ORITE2nPAmXC2ZUrV3Di\nxAkFk0euh/HDhw8RHh6u0IZL0OLTj6urK+0zdOjQITx9+lSpz9DGjRvx9u1brF+/HkCtF06TJk2w\nZMkS1jZ8t0ldc+bg4GBGk2qmweuFCxcQERGB1NRUmXtSdXU1Hj58yJnyx2fdAH5Gy0DtfUodMSMs\nLAyHDx+m9zV1jrK95PI5d9zc3LBq1SosX74cBw8eRGJiInbv3s24/wMCAjgHJ1znDh/zcEDx+FD7\nQP741BU+5PPvuYQPCrFYrDAQKy4uVpjJrEtFRQWys7MhFArRuXNnpcaFdnZ20NPTw+jRozFs2DCl\nkYCFhYWIiopCdHQ0dHR0YGtrixEjRnCeN3X9B+p6dFGwnTuUEB4VFYXq6mo6ooDNhF4kEmH79u3w\n9PSkB8aPHz9GdHS00ijYZ8+e4fz584iLi0P79u1ha2uL4cOHMz4bv//+e3qAVxepVIqYmBg6/eFj\n++EyCL1//z6jebSVlRUsLCwglUpx8+ZN2vtJKpUiNTUV169fV2jD55jyacNne4BaH5Jz584hISEB\nXbt2ha2tLaytrVnP7fLycoSEhODdu3dwcXFBx44dUVVVhWnTpsHLywsmJiYKbe7du0d7mOTn56NL\nly704JztXadnz55o3LgxpFIpysvL6WNIfU5LS1No86muHwq2ey+TuX1d2J6N6l5zfNpQKZ3Z2dno\n2bMn7dX14cMH7Ny5kzMKU53rJzk5GStWrEBZWRnmzZsHZ2dnVFVVwdHRER4eHozP05UrV+Lp06fQ\n0dGBmZkZ+vbtCzMzM9ZzjS01joLJCJyaGK5LXl4eWrRooTTyhUAAiGDy1cGnjOYvv/wCXV1dpKSk\nYOjQoUhOTsaMGTOUVh04cOAABAIBdHR0EBISghYtWqB+/fqswgTlWQH8ZxBibGxM5/gywafyxKxZ\nszB+/HjExsaiTZs20NPTw4EDBxAVFcXaz/Xr17Fy5Uro6OhALBZDKBTi999/Z3XlBmoFk23btskY\nq/76668yZn8U165dw9WrVxETEyMzC1xdXY3o6GhcuXKFtR8AtPK/a9cuehsHDBhA523KExYWhnHj\nxnH+pjxr166FtbU1evXqJfPCzxXqra5YANRGR9ja2sLGxoYxXPJT9SM/SKTgmglxcnJS8B9wcXHh\nrAzl6OiIsLAwlb1sRo4cCR8fH4Vwba4oGzs7O7i6uiq0oXK3P1U/06ZNw4EDB2ReDpRtP5NIqqwN\nwG+bnJyc0KFDBwVDTbYB9ujRo2nDPlXIycnBqlWrMGPGDPqcEQqFMDAwUJp6p+66AbVCLmW0fPjw\nYdy4cQM7duzgjMzhI2aMGjUKwcHBCvuabb/wOXeePXuGVatW4d69e2jQoAG6desGHx8fxoEL1wsr\nk4hRFz6iHlB7fJiMvdmOz/v37xX2T35+Pqs5a3V1NcRiMTw8PLB371762NTU1GDixIk4f/48Y7tz\n584hODgYhoaGEIlEyMnJwW+//cZpfgzU7u/4+HgkJSWhZcuWsLe3Z/WBMjIyQocOHTBw4EDGQR5T\nShOXkMFWXWnGjBl49eoV7YvQrl07mfsik8BNRUouWbKE7kckEmHTpk1o3Lgx47r9+eefiI+PR7Nm\nzWBjY4Phw4crjRI5c+YM5z2a6Zzj0w8X8pVGKFJSUjjbMZln8zmmfNpwwbY9I0eORE1NDb777jsM\nHjwY9evXl9n3qkySqdKPPM+ePUNSUhLOnj2Lly9fKhU3VYXPfvsYgUEd+FxzfNqsWLECYrEYJiYm\niI+Ph5WVFTp16oQ//vgDI0aMYNwePtcPNaEmv98yMjIQHR3Nud9KS0vxzz//IDU1FXfv3oVAIICx\nsbFCetbmzZvRv39/lavqALURgEeOHMGhQ4dQU1OD6dOnIz8/H1KpFMuWLaOjkgkENkhKzlcGnzKa\npaWlCA4OhqurK3x9fVFWVgY/Pz+lgkndqAhra2sUFxdzmvzJG45WVlayGkJS8Kk8wRR6HRAQwNlP\nUFAQDh06RA928vLysGjRItZoGaB2Jn3ixInw8vKijVWXLVvGmLNPucVfuXJFZtAhEAhUct6Ojo6W\nWZedO3di4sSJrILJtWvXYGZmplKIKkVCQoJCVJGyUMv09HQkJCSoZXwbHByM+Ph4+Pn54d27dxg2\nbBhsbGw415VPP/v27WMcJHJhYmKCuXPn0iVLk5OTGWe26qKul42enh6nwS0Tbdq0UZqq8Sn64eMz\nJJFIZDwb7t27p5IxIJ9t0tLSwh9//KHy8gYGBiqXrgZq08W2bduGyMhIpKen00Iol7kf33UD+Bkt\nr127llHM4KJz584qhelT8Dl3YmJi8Msvv8DU1JSx7HtdqBm8Xbt20UaPQG0k4cqVKzmfPXzMwwH1\njb3d3d2xdetWWmA5efIkp/CemJiIAwcO4N69ezKRDEKhkLNa1JEjR3D27FlamK6oqFBaXhuoNRFt\n3rw5mjRpgtOnT2P//v0IDAzE4sWL6XQGCq7UIrZ7KlO6UufOnVFRUYHg4GDGQWLLli3RsmVLVFRU\nMKbCMc2Q3759G2FhYTLfaWtrw8vLCy4uLoz9HD9+HC1btkR5eTnCwsIU+mIaXB8+fJizih7TOcfW\nDyXYqxuiz3ZftLCwQFZWFjp37kx/9/79e+Tl5bE+F9VJF/uYNnyom7px//59mb/dv39fbcGE63ki\nEolw79493Lx5Ezdv3kRWVhaMjY1pI095+JQi5nP9+Pv70wLDsWPHkJWVJSMwMJGfn4+FCxdiz549\ntLCQlpaGgIAAOs1PHj7XHJ82jx8/ps1Yf/rpJwwaNAj9+/fHn3/+yRqVwuf68fPzk9lvmZmZ6Ny5\nMzZt2gQbGxvGfiiaNGkCIyMjlJeX4/3797hz5w5jZPs333yjVlUdANi/fz9dCe7ChQsoLy9HdHQ0\nysrK8MsvvxDBhKAUIph8ZfApoykWi/Hq1StoaGggMzMTbdu2RWZmJmsf1MsSW7isMrNYCqFQiKdP\nn3Iuo07libt378LU1BS3bt0CAGRnZ6NXr16QSqUoKiri7EdLS0tmZrht27ZKB1o1NTUyN3A7Ozv8\n9ddfjMuWlpbC0tISW7ZsUWvQT1FdXY2ysjI6J7OwsJBz+bS0NDg4OKBBgwbQ0tJSKZw8NjZW7fXi\nY3zbrl07uLq6wtXVFfn5+diyZQvGjBnDGAr7Mf2oO0gEakWwGzdu4MGDB9DQ0ICHh4fMSywT6nrZ\n6OvrY968eQoGw1y54MbGxggICEDfvn1lzkuuhzSffur6DO3evRumpqZ0qg0bfn5+8Pf3R2ZmJoRC\nIbp06YKVK1dytuG7TeqaM0skEtja2sLIyEhmea57FJVSZGFhQQuhycnJSr2T+BhH8zFa5iNmNG/e\nHE5OTjAzM5NZN7boCj7nTufOnREdHY0//vgDDRo0QL9+/WBhYcEpNr1//x5LlizB6tWrERMTg507\nd+LXX3/l3BY+oh6g/vFZsWIF5s6dCw8PDxw7dgytWrWiBwxMDB06FEOHDsXZs2dZB2tMCIVCmXXQ\n1dVV+uw5deoUoqOj8e7dO9jb22PHjh1o0aIFioqKMH36dISHh8sszyTYlJeXIyYmBtHR0YwDWD5C\nRt2BlkQiUUnI4jI1FYvFjH+Ljo5WO/qFq0IcG1yTBWx+JFywPftjY2OxefNmhIWF0QPl/Px8zJ8/\nHytWrGA8PnxEFuo8uHv3Lp4+fQoNDQ306NED3bp1U3tbuOCKVKEq/akD235zcXFBdnY2TE1NYWFh\ngSVLltDVXuSFGgo+pYj5XD98BAZ/f39MmTJFJgrD2NgYkydPxu+//46NGzcqtFHmM8cEn+u0rgiu\npaWFrl27Kn3Xv3jxImeUDRNs+23v3r2s++3UqVNITU3FP//8A11dXVhaWmLw4MFYuHAho8jEVVWn\nYcOGjEKOjo4OOnbsCKB2XDJmzBgIhUI0bdpUaao3gQAQweSrg6mMZk5ODmcZzXnz5iEtLQ1z5syB\nh4cHysvLOV+Mhw8fDoDZNJZLDKibGw6ALqfLhTqVJ5KTk2FqaspqPMs1EOvQoQNWrlxJ5xEnJSXR\nN0c2tLW1ER0dDUtLS7oNmzodGhoKHx8fxioLqsxULViwAE5OTtDR0aFLhK5YsYJ1+dDQUAXzRGXi\nVN2cWwoNDQ1cuHCBtQ0f49v8/HxcunQJly9fxuvXr2Ftba00nJ5PP+oOEoFaYaqqqop2zs/MzISX\nlxenn48yQUGeRo0aoVGjRigrK1O5zevXrwFAYT24zmk+/SQkJGDOnDn055qaGoSGhmL69OmsbXr0\n6KGQfrNjxw6lRr58tkldc2YuY2s28vPzZV5M7ezsWCO5PmbdAFmjZXd3d5WMsPmIGVRev6rwOXfs\n7OxgZ2eHDx8+4MaNGzh8+DB27NiBe/fusbZZuHAhYmJiYGdnhy5duuDo0aOcXh8As6inyqBB3ePT\no0cP7Nq1CwsXLkS3bt3g5eWltA+g9uVdXmig0khnzpyp8NJvbm6On3/+Gf369YNUKkVKSorSY5WV\nlQVvb2+FSjrNmzfnHKx++PABly5dwvnz55GUlIRRo0Zh9uzZjMvyETIA0L4yFRUVeP/+PTp27IhZ\ns2axzqo3a9YMqamptG8Uxd9//03fh+XhE/2izBdIFYqLixETE4OIiAi8ffuW8V1j3LhxjO9BUqkU\nWVlZjL+7b98+HDt2TGagbGBggP3792PRokWM7wd8RJbi4mLMnj0burq66NmzJyoqKnDs2DE0a9YM\n69atY7z2+GwPF2zviHz68fHxgZGREWO7jRs3Mu43PqWIKdS5fvgIDKWlpbC1tVX43sbGhtVHjU9U\nCqD+dcqnWhKfKBs++y0jIwP9+/dHw4YNYWVlRQszVVVV2LJlC2saD1NVHbYJMpFIBIlEgqqqKiQk\nJMDDw4P+G1vVRQKhLsTD5Cvj+vXr2LRpE10usbKyErNnz4axsTGkUiljpQc+fhdArSeJ/KzNhAkT\nWKMs+FBeXo7w8HC6/nnHjh3x448/orKykn6pl0cikSAtLY1Opbhx4wYt1rBRXV2NiIgIpKWlQSAQ\nwMTEBKNGjeJUjgsKChAYGCjThs3D5FNRVFQEDQ0NuqoG09/fvn0LHx8frF+/nhanqqurMW/ePM4o\nkro3/erqaqSmpiIzMxPu7u6sbfgY3zo6OuKHH37ADz/8oHLtej79sPkkMBl6Uajj53P8+HE4Ozuz\nGljKCzOvXr1C+/btWYUrpn0hEomgra3N6g7PNDvOpx+K5cuX4/Xr1/D19cXbt2+xdu1aDB48mHPW\nPyEhAYGBgSgtLQVQG7HWpk0ble4DL1++REZGBoRCIYyMjJRWSFGVuLg4DB8+nNVHhUtccHZ2RmBg\nIJ2KQb2QcqXnqQuf40rBZsLINVAWiUSIiIhAeno6NDQ0YGxsDDs7O4WZxY85d1avXo28vDzUq1cP\nxsbGMDExgbGxMWPEjPw18+TJE7x69YoexCgzDM7Pz0dOTg769u1L78tPhbzpq0Qioc0hVTF9DQwM\nhEgkogXoxMREALX+L8ePH2f0p0lNTaWfI8bGxkoFk3fv3uHIkSMoKiqCj48PkpKSYGRkhMaNGzMu\nHx8fj6ioKFy/fh0WFhawt7dHUFAQq68KAPz888/w8PBgFDKOHz9O+2nV5ciRI7h69Sr8/f3p6+fZ\ns2e0PxaT8JidnY1ff/0VhoaG6NGjB2pqanD37l3k5eVh3759jKLJuHHjFEQpoPbZ7+LiolSAV4fy\n8nJcvHgRERERePToEWpqarBt2zaF/ULB9qyiYHpmcZnls/lBTZgwAbt27VKIuiwsLGQVWby8vGBp\naanwDDxx4gSSkpIYq5Tx2R4u2PxIPnU/TCadFEyliM3NzdGnTx/GIgl8rh/57VTFh8XR0ZG1qpuD\ngwNjf7NmzcLYsWMVhJbY2FjExcUxRqXwuU7Nzc3piF2pVIrMzEwYGBhwTl45OzvT0SJisZiOFlm8\neDFrtAif/cbmr0Kl8cgLJkxVdXr37s1aVYfaZydPnoRIJEKvXr0QEBAAkUgEX19fNG/enLWMNYFA\nQSJMvjIGDBiAnTt3Ijo6GpGRkSgtLYVEIsHAgQNZ26jrdxEbG4s9e/bg0aNHsLKykimV1qNHD4Xl\nlTndc6nHDRs2hKWlJR0yKhKJMGXKFM4HlZeXF1q1akULJjdv3qTD7eSh0niuXbuGZs2ayYS6X716\nlXG2m3pBb9y4MXx9fRkrCMjDJtioWnlBVQPT58+fIywsDFlZWfD396e/FwqFcHBw4OxDPmJn6NCh\nmDJlCqNgQokFVF64PFwDng4dOrDOynyKfqhjqk76DoU6fj7UC1zXrl1V+m0qyogpXYUtysjb2xt/\n/PEH7OzsGCt2MM2OHzx4EN7e3mr1Q7F69Wrcu3cPzs7O0NXVRUhIiNJKRNu2bUNgYCC8vLwQHByM\nCxcuQFdXl7MNUFsxKioqCubm5hCJRAgODsb48eMxadIkhWX9/PywcuVK1llI+Zc1qhIKVSFJHRYs\nWICpU6dCKBTS4cpMkWF81w3gd1wpMYNpBlIZqqYZ1T135P0elJ07VNSBpqYm6tWrB11dXVYhQ/6a\nURaNVJeQkBDExMSgsrISZ8+excaNG9GyZUuZssl1Uff4JCUlqbwuTKSmpsoM1MzNzTF9+nTMnz9f\nZlAsL+pRM6sZGRnIyMjgFPW8vb0xYMAA/P333wBqhfJFixYx+mcBwK+//orOnTtj8+bNsLKyAlAb\nBcaFj48Pp5DBRFRUFPbs2SNz/RsaGiIoKIjVc6tTp04IDw/HtWvX8Pz5cwgEAkyePBkDBw5kfaby\njX5RF09PT9y+fRsDBw7ElClTMGDAAIwfP55VLAH4RbJQFfDkDTGLiopYZ681NTUZn3EtW7ZETU0N\nY5sXL14wRkQ6OTmxppvx2R4+0SKfIgKoLmznDp9SxHyun7S0NPz0008A/iMw/PTTT5wCg7GxMfbs\n2QMPDw96/cViMQIDA+l+5eETlcLnOuV652aDT7QIn/2mbhrP+/fvUV1dDR0dHdSrVw/169dXav7q\n4uKC77//Hu/evaMj+LW1tdG3b19eE86E/z2IYPKVUFJSgtjYWERERCA7OxsjRozAu3fvONMpKCi/\ni/r160NbW1vpIN7GxgY2NjbYt28fZ/QBBVdY/Js3bzjbrlixAs+fP8fz589hYmKCtLQ0hbK88uTm\n5sqE7M6dO5c1b5ZPGg+fwc7HvoSramDat29f9O3bFw4ODhgwYIBafcjP+r5+/Zo1jUtdsaAuTZs2\nxebNm2FiYiLzQGXa13z6+ZjULHX8fChx7dChQypV/fHx8aGXVxXKRPTEiRNo2bKlzN8ePHjA2IYq\nTahOPxQXLlzAvn37sGDBAhQWFmLp0qX47bffYGpqytqmfv360NPTg0QiQbNmzeDk5IRp06bB3t6e\ns6+4uDicPHmSHvxUV1dj8uTJjIIJFeGiqg8BNYPq5uaGwsJCGBgYIDk5GQ8fPsTo0aM521paWiI6\nOlrlEuPUum3dulUhYoNtsEMd161btyqYCrPddz9GCFM1zajuuVNVVQUdHR2UlJQgNzeXUQyvC7Ve\n7969Q3JyMgICAuiyn/JQx6egoACXL1+mUzN3797NGQEG1J43x48fp+/pPj4+cHZ2ZhVM1D13KKKj\noxEREUGb8E6fPh0TJkxQKliJxWKEhobKpJEWFxfj9u3bMgLUx4h6FRUVmDRpEqKjowHUVkHiiqq4\nfPkyIiMjsXHjRlRUVGDUqFGoqqri7IOPkCEUChnFUl1dXc7rSCgUYvDgwSp78/BJ4+HDhw8foKOj\ng8aNG6Nhw4bQ0tLi5UGmDFdXV7i7u8PT0xM9evSARCLB3bt3ERwcjIULFzK24SuysKHsPqcOfPxi\n+MBHmNm5cyftYXLp0iWVShFfvnwZUVFRal0/fAQGb29vrFu3DsOGDYO+vj5qamqQmZmJYcOG0e8P\n8nCtR0lJCeP3fK5TPoIWnzSezyHM+Pn5AfhPVZ0rV64gODiYtaoOBdM+UKVoA4EAEMHkq2HQoEHo\n2LEjli5disGDB0MoFCqtckOhiqjChJWVFdatW6cQ9SCfT04ZZlVXV+Pq1av0TVwsFmP37t0yFQXk\nefr0KY4ePQpXV1fs2rULeXl5SpV9gUCAv//+G71794ZEIkFSUhLriwL1km1ubq5w4ztw4ABjG2qw\nc+nSJfq7mpoalJeXs6bKfKxRrroGprm5ufjxxx/VKqlbV5QQCAQwNzdH//79GZelXmz79++PwsJC\nmJiYIDw8HA8ePMDEiRM5100sFqOwsFBhXZiEDIlEgoSEBLWiRahjum7dOpSXlyvsAy7U9fMBmKv+\n2NraKhyvj4kymj17NlavXo3u3bujuroa27Ztw5UrV1jDdwFg+/btjDNMXP0kJCRg9+7ddGiqvb09\n1qxZwxh+T9G6dWuEh4fDyMgIv/32Gzp06IC3b9+yLl+XugKDUChkfaGiBkHv3r1DcHAwsrKyIBAI\nYGhoCE9PT9bfX7BgATw8PFBTU4MNGzbAzc0N3t7e2L17N2ub06dP49ChQypfO9S6rV69Gps3b6Zf\nRK9du4Z169YhIiJCoU12djYyMzOxefNmLFq0iP6+uroaa9askbm3UHyMECYWi1FQUCCTZiTv51GX\nVatWwdjYGNbW1nBzc4OZmRkEAgFnpE10dDTu3r2LBw8eQCgUwtTUlNP7BqiNBqx736W8Qvbv38/a\nhpo9p86Vqqoqzm2hjs/bt28RGRmp9HlFERISQlcvAmoHWm5ubkoFk8DAQISEhGDbtm2QSqXo1KkT\ntm7dCrFYLFNF6WNEPYlEghcvXtD7IDExERKJhHX51q1bY/r06Zg+fToyMzMRERGBmpoajBs3Do6O\njqz3OHWFDKlUig8fPijcb6l73KeCT/QLH/bt24eioiJ6sFxQUACRSISnT5+qnE6qCmPHjoWenh6O\nHDmCzZs3QyAQwMDAAKtWrWI15OQjshQUFLCmKfIxsWXjU0eLsMFHmDExMYGJiQld5ZEqRezt7c1a\nirh169aYNm0apk2bpvL1w2cf1KtXD3369EH9+vXRvn17WFhYQE9PDxoaGti2bRujFwefqBS26xRQ\nTdRQFT7RIp9LmAFUr6pDIHwKiIfJV0JERATtwTFkyBCMGjUKAQEBCm75TOTn52P79u0oLS1FUFAQ\nIiMjYWZmpvTGZWdnB1dXV4WoByoPXR51/CEonJycsG/fPsyePRuBgYFo3rw5xo8fj5MnT7K2yc3N\nxZYtW+h8/V69euHXX39ljM64du0arl69ipiYGIwcOZL+vqamBlFRUbhy5QprP3v27EHjxo3h4OAA\nV1dXNG3aFGZmZpg7d67CshkZGejevTtSUlIYf4ur7CRQ6y3x5MkTlQ1MR40axRiRIp92U5e8vDxG\n8YNLqJk8eTKWLVuGqqoqbN68GfPmzcOOHTs4X1pzc3MZv2dK/aAGiWxwmT2uWLECiYmJ9IBJFaNY\nvn4+FFTVn8jISM6qP+qSl5eHJUuWYNiwYTh37hyGDh2Kn3/+mbN8q4ODA06cOMF5zJlQ1x9CLBbj\n3bt3aNy4MSIiIlBcXIwRI0YovX+EhoYiPDwcZmZm9Mv+hAkTGCNMKH788UfMnTsXZmZmkEqluH37\nNrZt28Z6n6Pyn4OCgqCvrw8HBwdMnTqVs0yknZ0dgoODaXGBQtl+TEhIwK5du7BixQocOXIEL1++\nxOrVqxnLVj569AgXL17E8ePHZQajAoEAffv2haOjI2s/fISw5ORk+Pv7K6QZsXllUL4JoaGhkEql\nmDp1KqZNm8YqIgO10TJUaUZl4c0UEydOVIiM4PIeAGpzyWNjY5GdnY3vv/8eSUlJmDp1qlKh1sbG\nBh4eHgoRCGzPq59++glHjx6lz//KykpMnToVJ06cULpdGRkZtDBDvbyzlVKdMWMGPDw80Lx5c3h5\necHNzQ2RkZGcot7Tp0/p9Ln69euje/fu8PHxYZ0hF4lE2LFjBzw9Pel7xpMnT7BhwwYYGhqqbGir\njLrG4UypqlyCvbpIJBKZ6BcDAwPO6JdPQU5ODiIiIhAZGYnnz5+zRvl9Srg8HG7duoUjR47I7IMp\nU6ZAKBSiV69eCsuz+R8BtVVluM65fxNspYgtLS0ZxQ+pVEpXezEyMqJNRW/evIn4+PhPdv3Ie3H0\n799fpqQuk2BSWVmJdevW4erVq4xRKUyThfIG//Kpl5/qOv3UvjRsqOuvwlRVx8LCAv369fukkVYE\nQl1IhMlXgr29Pezt7VFaWoqYEhpcxAAAIABJREFUmBjs2LEDz58/R0BAAMaNG8c5G7Js2TJMmTKF\nzn+mXtyUzWS2adNGaZWbuqjjD3Ht2jX06dMHkydPRnR0NCZPngwHBwdoamoqTTVp164d1qxZg4KC\nAsbBSl1MTU2hqamJK1euyOTRCwQCpaF2ly5dwvHjx/HXX39h2LBh8PT0xNSpUxmXpXIemQQTDQ0N\nFBYWwsbGhjUShqnKBdesKp+SuosXL8ayZctw584dnD59GvPmzcOaNWs4xQ+qLGFAQADc3NzQp08f\nzvUCakPk686EvHz5Ej179mQ83+oKIo8fP6ZL1xoYGCjNPU5LS8Ply5fVeoFW188HUL3qj6urK+e6\nML0UU6agTZs2RVBQEPz8/NCvXz+4u7ujurqaUzAxNDRUWp5UHsof4v379zh37hw2btyIVq1ayTjC\nyzNt2jR6AK9qVBtQO7M+bNgwPHz4EAKBADNnzlT6AtW0aVMMGTKE/jxs2DBO8VQkEuHcuXOIjIxE\nWFgYcnJy6FQINgwNDaGvr6/ydlBYW1tDX18fnp6e6Nu3L0JDQ1mX7datG7p16wYbGxu1/DsAICYm\nBvHx8WoJYXXTjAQCAas5KIVIJEJBQQHOnTuH7du302XNuRgxYgTWrVuHFy9eoKamBl27dsWyZcs4\nr6V27dohICAA5ubmdDSgMs8cFxcXWFtb4969e9DW1sasWbNUMgs2MDBgDeFngnrmGBgYQCKRICsr\ni1EMl2fmzJkoKytD69atZUQDNsFEJBLB0tISQUFBmDp1KhwcHDgjx4Ba810u0U8eKkW17sCoU6dO\n0NfXV0jp+BhiYmLULvfLF3WjXz4FHTp0wKxZszBr1iylkxyfCq45SbbqV2wiC5cxtCqVwP4N8ClF\n7Ofnx1jthRIyPhV8SuryiUqJi4tTu9wvHz5XpJG6aTx8q+oQCB8DEUy+Mpo0aQInJyc4OTmhoKAA\nERERWLJkCecLmEQigbW1NR1+bGVlRedtc2FsbIyAgAD07dtXZmDG5hGhjj/EsWPH4OXlBT09PVha\nWkJPTw+xsbGorq7mdLIGgMjISPqmHxERgdWrV8PY2JhxMEeZykZERKCiooKu9CESifD7779zhoZT\n5X3Pnz9Ph6qzeX5QFBUVIT09HdbW1hAIBLh27RoMDQ2Rl5eHixcvYuvWrYztfvzxRzx58oROZxKJ\nRFi/fj2rqMOnpC4f8aOmpgY7d+7EpUuXMH/+fNy7d09piTX56gaFhYVKU5L8/PyQnp6OXr16QSqV\nYvfu3TA3N2fN6wVqxbDi4mK10nnq+vlQYoSydJk5c+bghx9+wNKlSzmFSaoM9F9//YVWrVrB0tIS\nEokEycnJrINRyieHmimRSqVIS0vDxYsXlc4ESSQS2NrawsjISKYUM9e+ZvOH4BJM2rdvj0WLFqFX\nr14yAg5bmD9bdaF//vkHAPc5amBgAH9/fwwYMAASiQSpqalo1aoVEhISACjee/z8/BAWFgZ/f380\nbNgQZ8+exfz58xl/m1ofLS0tODs7w9TUVKVrR34QXlNTg7Nnz9Iv30wRTR+TnqWOEMbHkBaoPXYe\nHh6wt7dHmzZtsGXLFqUDgzVr1sDb2xvGxsYAgDt37mDlypWc3ioBAQE4c+YMrl+/Dg0NDZiamsLO\nzo6zn4yMDAQHByMzMxMCgQBdunSBp6enUuHJ3t4eY8eORbdu3WSOK1uU2tixY/HDDz/g2bNn0NTU\nhL6+Pm7fvs3ZBwCUlZWxGmgyoY6oJ1/Bh0LZeXP79m2F+662tja8vLzg4uLCOZBWBz7lfv9boYzo\n/7/hEzHDJ/D7fyVYnE8pYj5CBh/4mKTWFXPi4+MhEolkolKY4FPu92tGXWFGJBIhOTn5/10AIxDq\nQgSTr5jWrVvD3d1dqTGrpqYmbty4AYlEgjdv3uDixYuMpSDlef36NYDaQVZd5ActISEhGDVqlFr+\nEFTo6LNnz5CamkoPelq2bIn+/ftz+hYcOXIEp0+fprd78eLFcHV15Zz93r59O06fPo2SkhK0a9cO\nubm5cHJy4tz+4cOHY+DAgbC1tYW+vj62b9/OaY4JAFlZWTh27Bj9sPbw8ICnpyd27drFaY6rrvkt\n28wTF3zEj40bNyI2NhbBwcHQ0dFBTk4OoyklFy1btkRGRgbnMunp6TKRBBKJhDW6iRocSiQSDBs2\nDJ07d5YRDLhSctTx86Gq8VC+NK9evZIJQZW/DqgB3aNHj7Bs2TL6ezMzM9ZjWdfLgjLhBGq9PJSF\njnKdT2yo6w8BgI7iKi8vV6kPLiNfZYMD6ny8fPmyzPeUwa/8PtfT08OkSZNgYGCAlJQUiMVi9OzZ\nk/G3qfVRN+KDyqOv6xGiDC4T6GvXrnG2VUcIowxP//jjD4VoJC6z0bFjx2LkyJHQ0dGhqzAoM32l\nyhVTUL4nXGhqasLMzAydO3cGUPsi6+joyDlj6O3trZCWtXjxYqXpp1u3bsXMmTMVzJPZePnyJY4e\nPSrjuXXz5k1anGPD3NwcT548Ufk8UkfU42se/rmqynwuYeZr4FOm/vAxL+WCz7r9f6YyfU2w3f8B\ndtGIj5DBBz5eHHzEHLY2f/755ycVgL5WPpcARiDUhQgm/wLWrFmDwMBAFBcXw93dHaamppzeEBTr\n1q2DSCTC69evOW8yRUVFtNeJvb09BgwYoCCysGFoaAg9PT107twZhoaG+PvvvxEREcEpmGhoaEBb\nW5t+2CjzYABqTfPi4+Pp/PkHDx6wVlmhmDlzJm0wKpFI4OjoqDQ0vLCwEI8ePaJDQF+8eIGcnBzk\n5uZyRqeoa35rZ2eHiIgI2sfF2NhY6cwtJX5s375dLfHD3Nwc3377Lc6ePYu0tDR629iQfzl8+/Yt\nq7kshb6+vsyAtKioiHVA8jEO/WxpM0yzTlQ1ntjYWMbfYou0EolEOHToEHr37k1X0VCW7nDw4EFc\nv36dNl9dvHgxBgwYwBlG3b17d4SGhuLhw4cQCoUwNjZmrRZFYW9vjylTpiA7Oxt+fn5ITk6Gm5sb\nZxtLS0vOv8tDhdDfv3+fjrqhmD9/PqewyWbky5bGMX/+fNr0lYqcYjN9pUw4y8vLUVhYCH19faSk\npCA9PZ3ThJMSgJYuXcpaxpENPoNydYSwpk2b4v3791i+fDn27t1L77OamhrMmjWLVZigTF+/++47\nuLm5oXfv3kpNXxs3boy9e/fSqQpJSUmsJtgUfKqgqZuWRWFoaKhWRQMvLy84OjoiNDQUnp6eiI+P\n59x+iri4OBw4cAANGzaEpqYma/QHVSaaimgCau/zXNcTm2k4Bdsg7nNVlflcwszn4lMLGWzweWbx\nWbfPtT3/rbBdW3xNRdWFj0kqHzHncwlAXyv/69tP+DIQweRfwIEDBzB+/HisWbNGrXZRUVH0oJ0r\n9WXhwoVYuHAhHjx4gOjoaDg5OUFfXx/29vYYNmwYo6CRmJiI1NRU3L59GxKJBCYmJjA3N8eECROU\npliYm5tj8eLFyM/Px549e3Dp0iWlvidUmHNNTQ0+fPiAnj17Kt0f6pi+Unh7e8PHxwd5eXkAaj0q\nZs+ejczMTJlqGfJQVXiAWrGgbdu2nFEZy5YtQ5MmTWBhYQGxWIyUlBQkJydj9erVrG2++eYbNG7c\nGCdOnKAH2MrEj7q+J2FhYZy+J5Tx4KZNm+hj/urVK1y4cAHLly9n/H3qBU8sFmPYsGF02d4XL16w\nznhTA9iHDx/i7du3GDRoEHbs2IG0tDS4u7tzhm/WHcBXV1fj1q1brOHx9vb2yM3NpWfxVSUwMBAH\nDx5EcHAwpFIpDAwMWFOxKKKionD06FH6886dOzFx4kROwWTp0qXo168fPD096XPA29ub8+Wcjz9E\nXe+Z6upqPHz4EMbGxqyeDbGxsThw4ACePHmCe/fuybRVFs2yePFi3Lp1i74HKIsa4uMPQYks1dXV\nSkWWurRs2RLOzs4KqUlcKUZ8BuXqCGGJiYk4cOAA7t27J1ONTCgUcnowZGRkwNfXF6Ghofjpp59o\n01cu1q9fj9DQUOzatQsCgQC9evVSKrzzqYKmbloWRbNmzeDi4gJjY2OVUq00NTUxbtw4nDlzBjY2\nNrRpLFdZckD1KLXRo0cjOjoaK1eupJ8/FGxlovlEjQGfr6rM5xJmPhefqzwuH68HPuv2ubbna4aP\naMRHyOADn5K6fMSczyUAfa38r28/4ctABJN/Ad26dcO+ffvw9OlTDBo0CDY2NgovPEwcPnxYrdSX\nnj17omfPnvjtt9+QlpaG3bt3Y/ny5bh165bCsgEBAaisrMTo0aMxcOBAmJqaqhQpAtSWEk1NTUXX\nrl2hra2NpUuXonfv3pxtbGxsEBoaCgcHB4wZMwYtWrRA/fr1OduoY/pKMWDAAOzcuRPR0dGIjIxE\naWkpJBIJBg4cyNlOXfPb/Px8bNy4kf5sZ2en1NTNx8dHbZFFHd8TKr+9ffv29LFs2bIl4uLiWPPb\nP+YFb+XKldi0aROuXbuGhw8fws/PD0uXLuU0S5SPWunRowdrShtlXisWi5GZmQk9PT3U1NTg1atX\nMDIyYq2m0bp1azg4OMhU0Xj16hWn2SVlukn59xQWFirZ+lo/nbplXc3MzFjPT3k/EQpVfEXkj1Fl\nZaVMypE8NjY2GDJkCNavX48ZM2bQA0WhUKg0XSIrK4ux5C4bfExf+YgsAPDdd98pfKdMAOIzKFdH\nCBs6dCiGDh2Ks2fPYsyYMUq3gYKP6Wu9evXQvXt36Ojo0N4iyu6h6grBgPppWRQWFhYKIhHX8ZFK\npUhJSUHTpk1x4sQJdOzYETk5OZzrBqhedW7SpElwdXWl7we2trZK0+yo9S8rK1MreqxTp04IDw+X\nqSozefLkT15V5nMJM5+Lz2VayQc+6/Y1b8/ngs87BR8hgw98jg8fMedzCUBfK//r20/4MhDB5F/A\n2LFjMXbsWIhEIly/fh3Hjx/Hb7/9hr///puzHZ/Ul/v37yMqKgqXL19Gt27dEBAQwLhcZGQkiouL\ncevWLVy6dAlbtmyBUCiEmZkZ+vbty1oKEgBtoEqZAr5+/Rrt27dHq1atWNtYWlrCyMgIQO0Ld3Fx\nsdKcfXVMX0tKShAbG4uIiAhkZ2djxIgRePfuncqzkQ4ODvS/hw4dioqKCk7zW7FYLJPCkp+fr3Tw\nxkdkUcf3hE9+e91okZ07d9LH1NDQEHPmzOFcN21tbXTo0AF79+7FxIkT0bp1a0gkEs42R44ckfn8\n+vVr2qtHHmpbFi9ejN27d9MlnF+9esX5UqZuFQ2gVgR0cnKCjo4Ofd7Jp7PII5FIcP/+fbq85N27\nd1m3n8lPhC9CoRBPnz7lXEZbWxszZszAwYMHZY6pm5sb53Vqa2uLCxcuoEePHjJRAmxiE5M/hDIH\nfD4iC6C+MTPAb1CujhBGoaWlBU9PT9rMe/r06ZgwYQJsbW0Zl2cyfWVblmLRokWQSqW0t8ipU6cQ\nHh6OLVu2sLbhUwVt1apVKCkpwTfffEOn8wwePFip75a6x2fjxo14/fo1li9fjsDAQFy+fFml8qGq\nVp1btGgRFi1apFbkJcXSpUthYWGhVvTY56gq87mEGQKBL/82oYmPmPO5BKCvlf/17Sd8GYhg8i/h\n2bNndGlUgUCg1OsA+E/qS0FBAfbs2YPLly/DyspKYbn09HRERUXh4sWL0NPTg729PX755Rfo6upy\n/n6zZs0wfPhwDB8+HAUFBbh69SpOnDiBkJAQpKWlsbZbsGAB7O3t4eDgAKlUijt37mDu3LmclQvW\nr1+P/fv3Q1NTE+3atVNa2hJQz/R10KBB6NixI5YuXYrBgwdDKBSqVIJVWRlMNiV8wYIFmDp1KoRC\nISQSCYRCodJQfz4iizq+Jx+T3+7t7Y358+fDxMQEQK34smTJEpw5c4a1jZaWFpYvX447d+7A19cX\niYmJSrdH3gizefPmSlMxsrKyaLEEqH25ys7OZl1e3SoaADBw4EDExsaiqKgIQqFQaaUoAPD19cXa\ntWvx7NkzALWiiJ+fH+OyZ8+eRUhICGbOnIk9e/aotW51K75IpVIIhUKVyo0vXLiQLoeu6nX64MED\nHDp0CC1atKC/45oR6tGjBxYsWIDS0lLk5ubi/9q777Cm7v0P4O+EodeJeinUgYqKAoKKOGr14qq4\nrVAFB+DCShFXtSIoTpQlFIujVqxUXJcqVFAccBVbiqKVqrhQAQVBtDJFJZDk9wdPzi+B5GQQiODn\n9Tz3eW5CDufLCPV8zvfz/nz++efYsmULhg8fLvMcyoRwilMlj6PmRfnly5flXpQrUwgTiYiIYKag\nAdUtXS4uLjKLIKIiusiKFSvkjpssKCio9bOTFeot0q1bN+brEBWC5e0wWbNmDSZNmoQ+ffpg+fLl\nmDhxIuLi4uS2tSn78zl58iRTlBW1Fvn5+cltyVF26pwyOy9FysvLJVqkFCmaNRRNjPsl5GPV1ApA\nDeFj//qJZlDBpAn44osv0LFjRwwbNgyhoaEKTxEQb33R0dHBd999J7X1ZcuWLZgyZQqOHTum8IjX\nnJwc3LhxA9evX8dff/2Fli1bYsiQIXBzc2O9Ew9U370W7/W2sLCQO9mgRYsWGDduHPr06SORP8AW\nBCUe+goALi4uaNWqldTX+vn5IS4uDt7e3hg1apREngAbtjuGbFNJhgwZgpiYGLx//x4cDgccDkfu\ndm9ViizK5J7Upb+9Xbt2EruKFAl6DA0NRUpKCpYvXw4tLS3o6OhI7KCRZsGCBUhJScGYMWMAADEx\nMXKLE/369cNXX32Ffv36gcPh4O7du6wjJ5WZoqHqWFigutUuIiJC7jmA6naKwYMH4+3btxJFT0XG\n3Ko6uUOV9+nTp0/l7nwTFxYWhujoaKWmX5mamkpk6si76BdRJY/DwMAARUVFyM3NhZ2dXa1xsdIo\nUwgT4fP5EjswBAIB6xjRpKQkhIaGMmPWKysrYWhoyLqry8LCArdv32aKmqIx4NI8ffoUWVlZCA4O\nlshuqqqqgq+vL2vb1T///IOxY8di//79cHJywsyZM+XmqwCK/3wuXLiAuLg43LhxAw8fPmSe5/P5\nuHfvntyClipT5xTdeSmiStGMEEIIIZpBBZNGrKKiAhs2bACXy0WbNm1w584dREdHY9CgQfD29kbz\n5s1Zj1+2bBl27dolcQE8c+ZM/Pe//5V4nbJ30wHgm2++wdChQzF69GisXbtW7rQFcX379sVPP/3E\nhAL+9ddfMDY2ZtoEevbsWesY8S3uisrIyICfnx/Ky8tx4sQJ/Prrrxg0aJDUsXWiO+klJSU4d+4c\n9uzZg8zMTPj7+8Pe3l7qmoD/r4SXlpYiNjaW2QFRWVmJmJgYmReYERERSElJYaaqLFmyRO5UlSFD\nhuDs2bPMORQpbimTe6JKf7vo6+vSpQs2bdqEIUOGgMPh4MaNGzInMyUkJGDs2LH47bffAEiGMGZm\nZrJeAK9atUqiYFBRUYFvv/2W9e76+vXr8eTJEzx+/BhCoRAzZsxgLZiIT9EQ7bqRVZQQBcp+//33\n4HK5Eh+T1fokar0Q3/kBsBc/RL8n/v7+WLt2rcy1SxMfH4+4uDiF2z1EVHmf2traIiUlBRYWFhI7\nlmRlZfz+++9KT79SlbQ8jvv377MeI2rPEm9DkteepUwhTETU8mJsbAyBQIDs7GzWcOoffvgBoaGh\n8PT0RFhYGC5cuCB3R+D58+dx+PBhtGjRAgKBAO/fv4eenh5iYmJq/d69f/8e6enpKCwslPh5cDgc\nuaNn379/j7/++gunT5/GL7/8gtLSUqaww0bRvJRx48bBzMwMW7dulfhbweVyYWxsLPc84lPnFi1a\nBEtLS6nht6rsvDx06BAmTpwIHx8f+Pr6KlU0I4QQQohmcIRst6nIB23btm3o1KlTrbtzhw4dQmZm\npszdBefPn8f+/fvx8OFDtG7dmrlTKRQKYWpqyhqq2RDE24ny8/PRoUMHph9c1vSBqqoqnDt3DgUF\nBVi4cCEyMjLQvXt3id0m0s6zadMmbNq0CYcPH8bjx4+xYcMGHDt2TKF1FhQUIC4uDmfOnJEbKjl/\n/nwMGDAAZ86cgYODA5KSkuDk5ISxY8dKfb2joyOOHj3KXGQLhULMmjWLtXh16tQphIaGok2bNgCq\nt32vXLlSIj+lJtGFqDhnZ2ep32Og+s6oeH+7sbExa3/7unXrZJ4bgNQLkejoaEyfPh1hYWFSj2G7\nIJszZ06tHBNpX6O6JScnswb/fv311wgODmYuppKTk7Fjxw7ExcXJPCY/P7/WhJvHjx/LLM4B1YW4\n8+fPK/U+cHBwwIEDB5gdTBUVFXBxcZFbKGVr+5P1Pv3iiy/A5/NrvTYxMVHq53F0dMSxY8cwZ84c\nHDx4EM2bN8fs2bMlJg6pS2xsLN6/f482bdpgy5YtTB4H26QYR0dHhQvKqhTCxJWXl+PJkyfQ1tZG\n9+7dkZaWJjMvRPQ7P2vWLObv2fz58/Hzzz8rtFZFZWRkKJ2fk5ycjMjISEyYMAFTp07Fnj170LFj\nR7ktjqr8fFTx448/4uuvv5b7OkdHR0yZMgUTJkxQeOdlcHAwzp8/D0NDQ0yePFmhoFhCCCGEaBbt\nMGnEbt68KXWc67x582BnZyfzONE0h/DwcJkTRDQhJSUFe/bsweHDh8Hn8zF//nxoaWmhsLAQ69ev\nZ+0937BhA9q3b4/U1FQsXLgQqamp2LdvH4KDg2Ueo62tjR49ejCPe/bsWWsXABsDAwMsXLhQoe+h\nQCDAsmXLcP36dSxYsABz587FihUrZBZMVJmqEhERgZiYGLRr1w5A9V3Y+fPnsxZMlM09Uba/ffPm\nzdDV1cW7d+8Uej1QHe4IVF9gPnz4EG/evGFtPxDXqlUrREZGwsrKCgKBACkpKWq/IMnJycHRo0eZ\n8MnKykpcv36dtR1l9uzZWLRoEXx8fHDkyBHk5OTI3PVSWFiI169fw8vLC35+fszXXlVVheXLl+P8\n+fMyz+Pj46P0+0DZdg8RURGqsrKStSAj7uLFiwq9TkSV6VfSCm1aWlowMjKCra0ttLUl/7Mnrag3\ndOhQmQHQ4pRpzxLt4ImOjpZaCGOj7O+cgYEBYmJiYGZmhtWrV6Nz5854/fq13DUqS5Ww4c8//1yi\nuCgv/FlElbwUVbx+/RrJycm1xkvX/L1TZeflqlWrsGrVKpWCYgkhhBCiGVQwacRkhXACUOjC39bW\nFuvWrcO9e/eY/AoPDw/WKRf1KSQkBEFBQQCq2zDevn2Lc+fOoaSkBEuXLmUtmOTn52PHjh3MXe+5\nc+fK3brfunVr/Prrr3j37h1u3bqFixcvSoRRqlNlZSUePHiA5s2bIzk5GV26dMGzZ89kvl7aVBV5\nW7YNDAwk8jratWsHIyMj1mNWrVpVK/dk69atyn1xLNatW4edO3di0qRJUu+qy9pZAFTvylC23SEo\nKAjh4eFMC4ylpSUzDlkZhYWFMu8ae3p6ws7ODhEREXB3d0diYqLcrBgbGxt0794d7u7usLa2Zm3J\nyMzMxMmTJ5GdnY1NmzYxz3O5XNbiF6Da+0DZdg+Ra9euwdfXFzweD+fOnUNISAgGDRrEGsg6evTo\nWruRtLS0ZE6bEt89Z2Njg+LiYpkZOyKFhYW4d+8ebGxswOFwkJycjB49ejDTt2qGi2ZkZKCsrAzD\nhw+HjY0NWrRooXCBTrw9S1tbm3W3SF0KYcr+zvn7+6OkpARTpkxBbGwsiouL5Ya+fqhk5aVUVlZi\n+/btSo2pVkRSUhISEhIknpP3t0pZqgTFEkIIIUQzqGDSiHXo0AHXrl3DkCFDJJ6/cuUKs2OAzfr1\n6zFr1iysXbuWya/w9vZmxik2tGbNmjEX+FeuXMHUqVPB4XCgp6fHWhwCqv/xXFpaylyMPXnyBDwe\nj/WYHTt2ICIiAu3atcOPP/6Ifv36qX17t4iPjw8KCwuxevVq+Pr64vXr16xTEVSZqtKqVStMmzYN\ngwcPhkAgwN9//41OnToxBYPvvvuu1jHv3r1DfHw8SkpKwOFwmHYeddm5cyeA6q+fbZS0NKpMo9HW\n1oaFhQUzFSUmJkZm8TAwMBBr1qyp9XxKSgo2bNhQ66JJ/Bz29vaIjo5mdmu5urpKLejVDHvl8/n4\n7bffcOfOHQDSQ1+tra1hbW2NKVOmyB3RWpMq74Mvv/wSX3zxBZ48eQItLS0YGxvL3cUBVAcaR0RE\nMMUVZ2dnfPPNN6wFE/EWpKqqKty4cQNZWVkyX//HH39g586dzGjojh07YvXq1bX+5onLzs7GsWPH\nmO+Bq6sr3N3dsW/fPomQWpGTJ0/i2bNnOHPmDH744QcYGhrC1tYWo0aNkhkCLaLoWHGgboUwZX7n\ngOpx2ocOHUJ2djYz8lneLqBLly5h1KhREs/FxcVh8uTJMo+5fv16ree4XC46d+6s0H+DFCEtLyUv\nLw+dOnVibc+TtnNItNPI0dFR5t+6wMBAJvhWRF67lCqUDYolhBBCiGZQwaQR8/b2hoeHB7p37w5T\nU1Mmef/58+cyQzjF8fl82NraMo8nTZpUK/C1IfF4PAgEAlRUVCApKQmurq7Mx2QFZIqsXLkSLi4u\nyM7Oxvjx48HhcKQGl4oLCQmR2tKkTjdv3sTu3bthaGiIBQsWYMWKFWjevDnKy8sV2s2iaG88gFqt\nMrImXIiLjIzEgAEDlArlVcWRI0dgZWWlVEFGmXYHkZUrVyoc+srn87F06VIEBQWhefPmEAgECA0N\nxaVLl2TmpwDVu2NSU1Ohp6eHEydOwMjICLm5uVJfyzYlSRbRZJ2dO3dKbaVhm6wj/j6YMGECgOoQ\nSzZnz57FmTNnlA591dbWRrt27ZjCRIcOHeROiGnRooXE49GjR8PZ2VlmW1tAQACCgoKY1o8HDx7g\nu+++w+nTp2We49WrV3j48CGzE+XZs2fIyclBXl6ezDYbIyMjuLm5wc3NDY8ePcKZM2cQEBAAc3Nz\nJlBXmhcvXmD37t0oKSkmO9c+AAAgAElEQVTBrl27cObMGfTv31/q2MO6FMKU+Z0DlBvNfvv2bdy5\ncwe//PIL8vLymOerqqoQHh7OWjAJDw/H9evXmXHs6enpsLS0xIsXLzB16lSJKWQiW7ZsgY+Pj8Rz\nK1askDlWuLCwENeuXcPPP/8MY2NjzJ8/HwUFBcjLy5P471dN7dq1Q15eHrOr6cqVK0zh+dtvv611\nY6Auk38UpUpQLCGEEEI0iwomjViXLl0QHR2NP/74gwnhnDVrFmsIpzhdXV3Ex8djyJAhEAqFuHr1\nqkZ7qKdOnQo7OzvweDyMGDECxsbG4PF42LBhQ61RtjVZW1sjOjoar1+/ho6OjkIX5kKhECdOnICl\npaXE3Ve2UE1lBQQEYPXq1Xj16hUWLVqE8PBwGBsbo7i4GEuWLMHo0aPVdq4vvvgC165dQ1lZmcTz\nbGGKb968gY2NDYyMjCS+B2wX5aooLy+XOI+odYHtPMpMoxEpKyuDi4sL89jBwUFmsKqnpydOnjyJ\nefPmYd26dfD394eZmRmioqJYx4gGBgbi5cuXWL9+PUJDQ3H58mWZo0qlXTjLI5qso0qxpby8XOn3\nQUREBA4cOMA83rt3L1xcXOQWTDp37sxMEzl79iwSEhLkvnf8/f0l/ja9fPmSNStEX19fIiejT58+\ncr+n69atg5eXF3Pxr6+vj5UrVyIrK0viQrgm0d/AuLg4XLt2DcOHD5f7PfD29oazszNz8d2+fXt4\nenpKDRmuSyGs5u/cpUuXWKchKTPyWV9fHy1atEBlZSUzYQuofq/5+fnJPAcA6Ojo4MKFC0zxt7Cw\nENu3b8dPP/2EWbNmSRRMzp8/j59//hmPHj3C7du3meerqqpQWVkp8xyiVk0jIyPEx8cr3Kp59+5d\nida3KVOmYNGiRThw4ACuXLlS6/Wq7mRRxpYtWzBlyhQcO3ZMqWI4IYQQQjSHCiaNHIfDUSqEU4TH\n48HNzQ3R0dHYu3cvuFwuLCws5N6Nrk9z5szByJEjUVZWxtwd1tXVhbW1Nezt7aUeU7PloSa2i5CM\njAxkZGRIXFDLmu6hKtH6gerpRaKxlnp6elK3yMsLR2VrlXBycoKJiYnEP8RlfW94PB727NmD7du3\nM0Wy8vJyHDhwQKH8CmVkZGTgX//6F9q2bYuysjKYm5vDxcWlVvBlTcq0O4jUDH29evUqa+irvb09\njI2N4e7uDldXV4liiywGBgYoKipCbm4u7OzsmOKPuvz73/8GAGRlZaGkpASTJk2Cl5cXMjMzsWjR\nItaCgWjHkDJZPKqGvm7duhWxsbEYOHAg0tLSMGbMGJkFBtHFuvgo6ZYtW8LAwACbN2+WeY5PP/0U\nixcvxmeffcaMLm7dujUzCUnaiOlhw4bJnVol7vbt24iLi8Off/4JS0tLjB8/Hps2bVIoyFYgEMDG\nxoYpOH322WfMTp2a6lIIMzAwgFAoRG5uLnbs2IGKigrWop4yI58//fRTTJ8+HTY2NkyQKpfLhZmZ\nmdz3aE5OjsT7q23btsjMzASfz0dFRYXEa0VtTn5+fhI7irhcLvT19WWeQ9VWzdLSUiQmJmLAgAHg\ncrlIT09HQUEBMjIy8P79+1qvV3UnizJUCYolhBBCiGZRweQjlJCQgO3bt0NfXx/FxcUICAhgtlRr\nmrSLwRkzZsh8vSoXHyL1PWq2ppoXONIusidNmiTzeHnBg3p6egr3wYtyTTp16sQUTHg8HvT09BAT\nE6O2O6opKSnYtm0b3NzcYG5ujvLycqSnp2P9+vXYuHGj1J93WFgYli5dimXLlkn9HoWGhso8nzKh\nr+K7HURBrAUFBczHpWW+AMCSJUtQXFysVBitNGzBsgDwww8/IDw8HBcvXoSWlhYiIyOxYMECmZOV\ngNo7hhTZyaNq6Os///yDd+/eMXkc+/fvx+vXr6WGRnt7e9cq6goEAmRmZuLNmzdwd3eXeg5DQ0MY\nGhoyu1DMzMwAQGInRE1hYWG1RksDsnMoZs6cCSMjI1haWkIoFCI+Ph7x8fHMx9lyjbS1tZGSkgKB\nQIB//vkHFy9elFnIqEsh7NChQzh37hzevn2L06dPIygoCPr6+lJbXgAwGTk1d1Js3rxZZlH41KlT\nOHv2LKysrMDj8RAWFoYZM2Zg9uzZMtc1ceJEjBs3Dr179waHw8GjR48wefJkxMbGMi1h4nR1deHq\n6oqLFy+irKxMojAn62+Oqq2afn5+2L17N4KDgyEUCmFkZIRt27bh3bt3UoOtVd3JQgghhJCmjQom\nH6EDBw4gOjoabdu2RW5uLjZt2iSxJb8xEV1kvHnzBpGRkXj9+jW8vb1x9epV5uJKFhsbG7x69Qpa\nWlrgcDjg8/nQ09ND27Zt4eXlxRpeqaj09HR89dVXEAqFyMrKwldffQWgevt/dnZ2rdfXpU/ezs4O\nW7duhampqcToVGktOWlpaTh58qTEc7q6uvD09MScOXPUVjDZv38/9u3bhy5dujDP9e3bF8OGDcPq\n1asl8kZERKNCRS0FN2/ehJWVlULna926NVxdXVFSUgKg+mJr2bJlOHjwYK3Xird69OrVS+ELoqKi\nIpw4cUKh16oaLAtU/zxatWqFhIQEODg4QFtbG3w+n/V8oilTyhAPfdXW1kb37t2RlpYm97i1a9dK\nFDNNTEzg6ekp9XttamoqtfAgFAoxe/ZsmQUTVX4PL1y4gMTExFp5KbKoOv1EtEvv1KlTKCoqwqJF\ni2BpaSk3OFqVQlhCQgKOHz/OTD/y8vKCo6OjzIKJKsXghIQEREVFMbs2qqqqMHfuXNaCyeLFi+Hg\n4ICnT58CqP57LG93k5ubG0aMGAFDQ0OF1qVqq2bv3r2xfft2lJaWSuwC69ixo9TX1yV0nBBCCCFN\nFxVMPkI6OjpMyGfnzp1rbZ1ujDw9PTFs2DBcvnwZQPXde2nBfuImTJiAoUOHMhfKf/zxB27evAlH\nR0d4eHiopWASGxur1Ovr0mL0008/wcTEBE+ePGGek/W5ZF0AcLlc1jwBZVVVVUkUS0SMjIxkTq8p\nLS0FAAwePBhA9Y6BJUuWKHS+sLAwREdHo7i4GB07dkReXh4cHBykvnb69OkSjysqKiAQCKClpcWa\n5TN8+HCFw2hVDZYFqnckzJs3D2/fvoWVlRVOnz4td3qNKpkpOTk5OHr0KIqLiwFUT9q5fv26zMwL\nkffv32PixInM45EjR8oMm5b2PqyqqsLFixcVHuGrKGNjY4mCoTyqfM/qsktPlUKY6OOi93NFRQWq\nqqqUXrc84u9JLpcrt9Xs999/x4kTJ2rtFmFra9TT02PNkqlJlVZNoHoK3JUrV5gdT/J2W9UldJwQ\nQgghTRcVTD5CNf8RrM78BU0pLy/H7Nmzma30EydOxLFjx1iP+fvvvyXCOkeMGIF9+/Zh+fLlavue\nKHsxxtZi9ObNG9Zj27dvr/AOg3bt2uHGjRu17tBevnyZaR1QB7bvo6yiRM0LaGUuqH///XckJibC\nyckJhw8fxt27d5kAx5qKiorg6+uLwMBAcDgcTJ06FVVVVSgvL2fGTIsbOnQoOBwOhEIh9uzZg9at\nW0NLS4u5EJPW8qFqsCxQvTslIyMDPXr0AFC9C0ZaWGhdeXp6ws7ODhEREXB3d0diYiK2bNki97iO\nHTvC399fIi9G1t17ad69e4fExES1j1MVCAQYP348zMzMJH4+bK1cyqrLLj1VCmGTJ0+Gs7Mznj59\nio0bN+Lq1ausY8lVMWHCBNjZ2aF///4QCAS4desWazskAGzfvh1eXl4K7xYBqt9HR44cwcCBAyUK\nW2yBwcq2agLVE2mSkpIU/ltel9BxQgghhDRdVDD5CInaRABItIooknfwoRIIBHj27Bnzj+MrV65A\nIBCwHmNoaAh3d3dYWVmBy+Xizp07aNmyJS5cuKDUhZ86iS4MSktLERsby2Q1VFZWIiYmhvWuv7m5\nOUJCQmBpaSlxISKt1cTLywseHh7o0aMHTE1NwefzcevWLeTn5ys0klpR4r9r4mS1JAF1K+iJChp8\nPh/v37+Hubm5zCDjLVu2wMzMjPn8n3zyCVNkCQ4OrvV9uHr1qsLrEKdKsCwAFBQU4JdffsH9+/fB\n5XLRt29feHh4KDWaGZCflaKtrQ17e3tER0fD1tYWtra2cHV1ldui5O/vj+joaPz555/Q0tJCv379\nWDN4amrdurXcAp+0XThaWlowMjKCra2t1J0k4tNh6ktddukpUwgTCoWIjY1FYWEhxowZA319fejq\n6mLJkiWsAaJ79uzBN998I/Gcn5+fzGlOAODi4oIxY8bg/v374HA4WLx4sdyCb5cuXZQOHE9OTgYA\niUKmusO2geqJSkVFRQpPo1F1JwshhBBCmjYqmHyElG0TaQx8fHzg4+OD9PR0DB8+HL1795Z7lzwo\nKAi///47njx5Aj6fj/Hjx2PkyJF49+6dWsf9qmL58uUYMGAAzpw5AwcHByQlJWHDhg2sxxQWFgJA\nrVwMaRe+Xbt2RUxMDJKTk5mR1HPnzlV4JLWiVPldq0tBz9bWFhEREZgyZQqmTZuGDh06yLx7n5eX\nh5CQEOaxaNqHubm53GlFilI1WBaoDkqdNWsWPD09UVlZidTUVHh7e0ttb6lLVopQKERqair09PRw\n4sQJGBkZITc3V+7XtmrVqjqFLiuisLAQ9+7dg42NDTgcDpKTk9GjRw/k5+fj4sWL+P7772sd06dP\nH0REREgUmkTZH+pSl6KeMoWwjRs3orKyEpaWlkhMTMTQoUPRrVs3zJ8/X+rklgsXLiAuLg43btzA\nw4cPmeerqqpw//591oLJgwcPEB0dzbTXiLJd2DJZunfvjuXLl2PgwIESbX7SpheJNFTYdk5ODsaO\nHYuuXbtK7DRi+/uhyk4WQgghhDRtHKG6G8gJ0ZC8vDxmZ8iTJ0+YO7iyqHL3uqG4uLggIiKCaS3h\n8XhYsWIF9uzZw3pcTk6OUmNBP0TPnz9n/biibU55eXkoKiqCqamp1LwUBwcHmeGtM2bMQFRUlELn\nYRMdHc368Zo5KuJEP3txot+Lmvz8/JCbmys1KyUgIIC5Yy5NQUEBXr58CX19fYSGhqK4uBgODg4Y\nOXIk69p9fHygp6cHS0tLiRG86pwmsmDBAoSHhzMFCT6fD3d3d+zbtw9z585FZGRkrWPc3NwwaNAg\nDBkyhCk0paenq7W4Y2VlxYwIFxX1jI2NFboonzdvHmbNmiWxvpiYGKmFMEdHR2YnSWVlJYYPH46h\nQ4dizZo1EiOaxeXm5mLr1q21RvcaGxuz7raYPHkynJycYGBgIPE82++BrBweaWG97u7u2L17N9Pa\nVpOsKUaqkvV3RJXMGkIIIYR8vGiHCWkSAgICUFhYCD8/PwDAwYMH0bZtW9Y7+KrcvW4olZWVePDg\nAZo3b47k5GR06dIFz549Yz3mwIEDSo8F/RCp64KmY8eOrK1V7du3R1paGgYMGCDx/OXLl5Veg6y2\nF1WDZYHqdoD4+HgMGTIEQqEQV69elXlMXbJSDAwMmItkeRNexFVWVuLVq1e1psyos2Dy6tUrPHz4\nkCn4PHv2DDk5OcjLy2NGDddUXl6OBQsWMI/79++v9ryPuuzS4/P5ErtDJk2ahP/+979SXyteiNLR\n0YGJiYncLJbOnTujWbNmTGiyogwNDWUGJNf0/PlzdOrUCePHj1f48+/evRsAEB4eDnNzc6XWpozj\nx4/D0dERkZGRUgszbP9NIIQQQgipiQompEn4+++/cfToUeaxr68v67ZwAMjOzsaxY8eYf1S7urpK\n3L3WJB8fHxQWFmL16tXw9fVFcXExnJ2dWY9RZSzox2zdunXw8PCAiYkJTExMwOfzcfv2bbx48UJq\ngKcqbS/KBsuK2759O0JDQ7Fv3z5wOBxYWFjIzGMBVM9KUdWOHTvA4/Hw8uVLmbsd6mrdunXw8vJC\nXl4eAEBfXx8rV65EVlaWzEkrAoEAd+7cgYWFBQDg1q1bcvOMlFWXop4yhTBVW3/09PQQHBys0O4f\nUS5Sr169EBAQUCuMVdoxERER8PLywubNm6WumS2PxN/fHwcPHqy3HXyin4342HDxtRFCCCGEKIMK\nJqRJEAgEEqNeb9++LXe6irS717m5uax3rxuKaE0CgQA7duyAgYGBQhcYyo4FbWqktWJdunQJo0aN\nqvVaIyMjREdHMzkuXC4XTk5O+Oyzz6R+blVGBCsbLCvOwMAAzs7OyMrKAofDQa9evZgRqTXVJStF\nVWfPnmVaxOLi4rBt2zb07dsXX375pdrOMWzYMJw6dUqpY3x8fODr68uM1zYxMcHGjRvVtqa64PF4\ncHNzQ3R0NPbu3Qsul8taCFM1z0eZ3T81p0gpkoHk5eUFQLU8khYtWmDcuHHo06cPdHR01D7F6PXr\n14iJifno/vYRQgghpH5QhglpEu7duwdfX19kZ2eDw+GgZ8+e8PLyknqXUeTPP/9EUFAQ8vPzAVSP\nOXVzc0Pfvn0hFAoxfPjwhlo+4+bNm9i9ezcMDQ2xYMECrFixAv/617/w6tUr+Pj4SL3wF4mIiMBv\nv/2Gfv36QSgU4u+//8bMmTM/qh0mM2fOxLJlyzB8+HCUlJRg69atKC0txf79+9Xy+U+ePImoqCiJ\ntpc1a9bIbHupmZPyzTffMEWG2bNnS+yKqmnz5s1IT09Hv379mDGvAwcOZC5WxdUlK0XVLJ/Zs2fj\n0KFDWLhwIQ4fPoyKigo4OTnJbC9RRVhYGI4cOVLreWXzLsR3nGhKQkICtm/fDn19fRQXFyMgIIB1\nhxFQtzyfuuQZ5efno0OHDjJ3vojnkBQXFzMFRB6PB0NDQ1y6dEnm505NTZX6vLItRLKIxlTn5ubi\n6dOnzNjrtLQ0mJiYYOfOnWo5DyGEEEI+DrTDhDQJZmZmCAwMVCr0ddiwYdi7dy/i4+Nx5swZlJSU\nQCAQ4PPPP2+IJUsVEBCA1atX49WrV1i0aBHCw8NhbGyM4uJiLFmyRGrBhMfjYc+ePXB3d2fGgj56\n9Ai9e/f+qIolQHV2jaenJ5KSkvDnn39i0aJFrMUCZdW17UU8tLeyspL1tXfu3JHYQSAQCODo6Cj1\ntXXJSlE1y0f0uUUXzvLOo4oLFy4gMTERLVq0qNPnCQwMVPvYWmUdOHAA0dHRaNu2LXJzc7Fp0yap\nrV/iVG39USbPKCUlBXv27MHhw4fB5/OxYMECvHjxAkKhEOvXr8d//vOfWseIRmxv27YNU6dOhaWl\nJYDqgu/Zs2dZ19alSxccOnSIKW736NFDre1ja9euBQAsXrwYp06dYgp+lZWVWLFihdrOQwghhJCP\nAxVMSJMQGBiI169fKxT6WlxcjPPnzyMuLg5Pnz7FuHHjUFZWhgsXLjT0smvR1dWFtbU1AODQoUPM\nJA49PT2JLAJxAQEBAKq37Hfu3BmdO3eGjY0NgoKCEBYWJnViRVPz+PFj5v8vW7YMYWFhGDhwICws\nLPD48WP07NmzzudQpe2lLsGy3bp1Q0FBARPIWlhYKPPrqEtWiqpZPlZWVlizZg0KCgqwf/9+XLp0\nSWY7k6qMjY3VknXxIWyk1NHRQdu2bQFUB7NWVFTU27mUyTMKCQlBYGAggOoC1Zs3bxAfH4/S0lIs\nXbpUasFEJD09HevXr2ceW1lZSYzqlmblypWYPHkypkyZwuyEW7ZsGTMNSF3y8/NRVlaGdu3aAagu\nIioyLpsQQgghRBwVTEiTkJaWpnDo6/Dhw2FkZIS1a9dixIgR4HK5as1dUJeabR6yevLT0tJw8uRJ\nied0dXXh6emJOXPmfBQFE/HwSQ6HA6FQiKKiImzevFluCKWixNu7evXqpdA0GGWDZcVlZ2dj7Nix\n6NatGwQCAXJyctCtWzfY29vXyq+oS1aKKpNogOoL3xs3bsDExAQ6Ojr47rvvahWG6kogEGD8+PEw\nMzODlpaWynkXH0KehaoBrqpSNM+oWbNm6Nq1KwDgypUrmDZtGrhcLvT09JiCiywGBgbw8PDAgAED\nwOVycefOHbRp04b1GF1dXYlCnIWFBRM8q06LFi2CnZ0dWrVqBaB6epK7u7vaz0MIIYSQpo0KJqRJ\nUCb01c/PD3FxcfD29saoUaMwceLEhlwqK1HIo3jAI1B9hzw7O1vqMbIuarhcrty2j6ZCPHwyLy9P\nqdYsRanS9qJssKw4ZYoCeXl5Enf2W7duDQAwNzfHu3fvWI9VZRINUL2TZ9euXcyOKKA6Q0adGSbK\nTKsSFZJqYnvvNCRVA1xVMWHCBNjZ2aF///5M/s2MGTOkvpbH40EgEKCiogJJSUlwdXVlPvb27VvW\n8wQHB+OPP/7AkydPwOfzMWnSJNYdKQDQt29f/PTTTxg2bBgEAgH++usvGBsbM7vE1LEbDACmTZuG\nadOmoaioCED1Lr0PoXBGCCGEkMaFQl9Jk1Az9LVHjx4YPHgw6x3FkpISnDt3DnFxcbh16xbmzJkD\ne3t7tf2DXRWqhDx+/fXXcHV1lbhwBarbPo4fP459+/apdY0fspqtWd7e3tDT05M6DlhZNdtebG1t\nFW57qW81w2XFzZgxA1FRUWo71/nz57F//348fPiQKcwA1UVLU1NTHDp0SG3nKi0tRUREBO7fvw8u\nl4u+ffvCyckJLVu2rPXaugSkNoSGXl9ubi7u378PDocDU1NTmZ//yJEjiIqKAo/Hg4WFBfz9/cHj\n8bBhwwa0b9+eyQQRl5CQgLFjx0oN5AXAOtLdyclJ5sfUtRsMqA5ojoyMRFlZmUTxvObkIEIIIYQQ\nNlQwIU1GQUGBRIDr9OnT4ebmpvCxcXFxOHPmjNJjTDXt6dOn8PDwQI8ePWBqago+n49bt24hPz8f\n4eHh+Pe//63pJTYYaZNn5syZI/PCThkrV66EmZkZcwfeyclJ4baX+ubm5obFixdLzUqJiYmRGdwK\nqD6JJjw8HAsXLlRtwQpyc3PDoEGDMGTIEFRWViI1NRXp6enYtWtXvZ63sXvw4AGio6NrFQt27Ngh\n9fXPnz9HWVkZ05YFAFFRUbC3t5do7RGJjo7G9OnTZY7TVrQNUN40nrqYOHEiwsLCYGhoKPF8XQOE\nCSGEEPJxoZYc0qipK8DVwMAACxcurPcLwPrQtWtXxMTEMG0fHA4Hc+fOxeeff/7RbUFXpjVLWXVp\ne1GXwsJCtG/fvtbzdclKUXUSzWeffYYdO3YofFGuivLycixYsIB53L9/f8ybN09tn7+pWr16NZyc\nnJjAYHmk7T6R1cIDgAlTHj9+vMJrUmUaT11069aNCc0mhBBCCFEVFUxIo9ZYAlzrG5fLxYgRIzBi\nxAhNL0WjfHx8sGnTJmRlZYHL5aJnz57YtGlTvZxLmRHByggMDJTaQpSSkoINGzYgISGh1sfqkpWi\n6iSaNWvWwMnJqdYdfHUSCAS4c+cOLCwsAAC3bt2CQCCot/M1FYaGhnBwcKi3zy8eslyTrLaakJAQ\nBAUFAVB+Go8q2rdvDwcHB/Tv318i50naNCtCCCGEEFmoYEIatQ85wJU0PDMzM7W030hTlxHByuDz\n+Vi6dCmCgoLQvHlzCAQChIaG4tKlSzJbIADVi2Y1J9GIyAudNTQ0hKOjo1LnUpaPjw98fX3x5MkT\nANWTijZu3Fiv52zMRNNmevXqhYCAAAwcOFCiGKbIZCdFiIcsi8hrr2nWrBmMjIwAKD+NRxUDBw7E\nwIEDJZ6rqqpS+3kIIYQQ0rRRhglpEj7EAFfScNzd3bF7924MHTpUog1JNIFEXh6HIp49e8ba9iKt\nVUZVJ0+eRFRUFNatWwd/f3+YmZlhzZo1tUZNq0NqaqrU5wcPHsx6XEhICHg8HqytrevlolwW8R0n\nRNK6detYP66udilV2mscHBxw7NgxVFRUYMyYMYiMjGRaZtQdTCzy6NEjFBcXA6ieBuTn54fY2Fi1\nn4cQQgghTRcVTEiT05gDXEndvH37tlYWx4sXL9TWNiIQCCTaXnr27KlQ24sq0tLS4OHhAVdXV7i4\nuKj989dl0gkg++JcnRkm0jg7O6ttksrHoD6CVWfOnInAwEB07doV8fHxOHDgAKKiopj2msjIyFrH\nqDKNpy58fHyQmZmJzMxMWFpaIj09HYsWLaIMHEIIIYQohVpySJPTmANcSd0sXLgQ33//PRN2GRUV\nhZ9//hlnz55Vy+dviKwYf39/ZpeMtbU1IiIiUFBQwHxcXRkMZWVlAKrHJSvD3t4eHA5HaphuQ4QM\nU41ftoYKVm3WrBm6du0KQPH2mjlz5mDkyJES03h0dXVhbW0Ne3t7taxL3OPHj3H06FE4OTlh3759\nyM/Pl8gdIoQQQghRBBVMCCFNho+PD5YtWwZXV1ccO3YMn3zyCY4fP67pZSnFxMSE+f+9evWqtxaX\nzp074/r16xgyZIhSx2l6pO/HNvlJGSEhIQgMDARQv8GqPB4PAoEAFRUVSEpKYkZtA9W7vGRRdhpP\nXfD5fLx58wZA9XSpTz/9FA8ePKiXcxFCCCGk6aKCCSGkyTA1NcW+ffuwatUq9O7dG56enppektKm\nT58u8biiogICgQBaWlpqbasQBXeWlpYiIyMDffv2BZ/Px927d2FpaYlBgwZJPU6dAbeyiHax1CQU\nCpGdnV3v52+sVNn5oYqpU6fCzs4OPB4PI0aMgLGxMdNeY21trbbz1MXcuXMRHx+PuXPnYsqUKdDW\n1sawYcM0vSxCCCGENDJUMCGENHo1w14FAgFSU1Px22+/AYBaQl8bSlFREXx9fREYGAgOh4OpU6ei\nqqoK5eXl+PHHH9GvXz+1nEe0U8Td3R0XL15Ey5YtAQBv3rzB+vXr1XIOVWl6F0tjperOD2U1dHuN\nKrp168aEA48ePRrl5eW0w4QQQgghSqOCCSGk0bt69aqml6A2W7ZsgZmZGVMA+uSTT3D48GHcvXsX\nwcHBCA8PV+v58vLyJHauNG/eHM+ePVPrOZTVELtYmqKG3PnRkO01ynj69CmysrIQHByMb7/9lnm+\nqqoKvr6++N///nkB6fcAAAWWSURBVKfB1RFCCCGksaGCCSGEfEDy8vIQEhLCPG7dujUAwNzcHO/e\nvVP7+SZOnAhbW1smOyUrKwtffvml2s9D6l9j2PlR396/f4/09HQUFhbi3LlzzPMcDgdLly7V4MoI\nIYQQ0hjRWGFCCPmAODg44MSJE1I/NmPGDERFRan9nGVlZXj69CkAoEuXLrh79y7lPZBGLSMjgykC\n1sdoZUIIIYR8HGiHCSGkyamqqoK2duP889a+fXukpaVhwIABEs9fvny5XlpVcnJycPToURQXFwMA\nKisrcf36dSQlJan9XITUt4YarUwIIYSQj0PjvKIghBAprl69iu3bt4PH4+HcuXMICQmBtbU1RowY\noemlKWzdunXw8PCAiYkJTExMwOfzcfv2bbx48QIHDhxQ+/k8PT1hZ2eHiIgIuLu7IzExEVu2bFH7\neQhpCCEhIQgKCgJQv6OVCSGEEPJx4Gp6AYQQoi4//PADIiIioK+vDwBwdnZGWFiYhlelHCMjI0RH\nR2Pq1KnQ1dVFy5Yt4eTkhFOnTqF9+/ZqP5+2tjbs7e3Rpk0b2NraIiAgAJGRkWo/DyENoVmzZjAy\nMgJQv6OVCSGEEPJxoB0mhJAmQ1tbG+3atWMmzHTo0EFi3HBjweVyMWLEiAbZGSMUCpGamgo9PT2c\nOHECRkZGyM3NrffzElIfGmq0MiGEEEI+DlQwIYQ0GZ07d0ZoaCiKiopw9uxZJCQkoFevXppe1gct\nMDAQL1++xPr16xEaGopLly5h7dq1ml4WISppyNHKhBBCCGn6aEoOIaTJEAgEiI2NRVpaGnR0dNCv\nXz9MmDCBtuLL8eLFC+Tm5sLa2hoVFRVo1qyZppdEiMqeP38uMVoZAKKiomBvbw8ulzqRCSGEEKI4\nKpgQQpqUtLQ05OXlYdKkSXj58iU++eQTTS/pg3bo0CGcO3cOb9++xenTp+Hr6wt9fX0sXrxY00sj\nhBBCCCFEo+hWCyGkyfD390dERATCw8MBACdOnMC2bds0vKoPW0JCAo4fP462bdsCALy8vJCYmKjh\nVRFCCCGEEKJ5VDAhhDQZ6enp+P7779GyZUsAgIeHB+7du6fhVX3Y+Hw+ADDhuBUVFaiqqtLkkggh\nhBBCCPkgUOgrIaTJqKqqQmVlJXPxX1hYiIqKCg2v6sM2efJkODs74+nTp9i4cSOuXbsGFxcXTS+L\nEEIIIYQQjaMME0JIk3Hx4kXs3bsXeXl56Nu3LzIzM+Hl5YWxY8dqemkftNzcXNy+fRu6urowNzfH\np59+quklEUIIIYQQonFUMCGENBn37t1Dt27d8PjxY+jo6KB79+5o3ry5ppf1QTpy5Ajrx+fMmdNA\nKyGEEEIIIeTDRBkmhJAmw8/PD7q6urC0tISpqSkVS1gUFRUx/zt48KDE46KiIk0vjxBCCCGEEI2j\nHSaEkCZjyZIlyMjIQJ8+faCjo8M8HxoaqsFVfficnJxw+PBhTS+DEEIIIYSQDwqFvhJCmowFCxZo\negmNkigklxBCCCGEEPL/qCWHENLo7dixAwAwePBgDB48GGlpacz/Hzx4sIZXRwghhBBCCGmMaIcJ\nIaTRu3//vsTj5ORkfP311xpaTeNgb28PDocDoVCIrKwsfPXVVwAAoVAIDoeDX3/9VcMrJIQQQggh\nRLOoYEIIafRqRjFRNJN8u3bt0vQSCCGEEEII+aBRwYQQ0ujVzOCgTA75OnXqpOklEEIIIYQQ8kGj\nKTmEkEbPysoKxsbGAMC0mBgbG1N7CSGEEEIIIURlVDAhhDR6z58/Z/047aYghBBCCCGEKIsKJoQQ\nQgghhBBCCCE10FhhQgghhBBCCCGEkBqoYEIIIYQQQgghhBBSAxVMCCGEEEIIIYQQQmqgggkhhBBC\nCCGEEEJIDVQwIYQQQgghhBBCCKnh/wDiJwx+M615oAAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f79d77c4550>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"corr = overall_set.corr()\n",
"\n",
"fig = plt.figure(figsize=(20, 16))\n",
"ax = sb.heatmap(corr, xticklabels=corr.columns.values,\n",
" yticklabels=corr.columns.values,\n",
" linewidths=0.25, vmax=1.0, square=True,\n",
" linecolor='black', annot=False\n",
" )\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Hvad vi ser her, er en korrelationsmatrix. Jo mørkere farver, des højere korrelation, rød for positiv- og blå for negativ-korrelation. <br>\n",
"Vi ser altså at der er høj korrelation, i vores nedre højre hjørne; Dette er spilpositionerne. Vi ser også et stort blåt kryds, som er målmandsdata. Disse har meget negativ korrelation med resten af vores datasæt. (Dobbeltklik evt. på plottet, hvis det er meget svært at læse teksten)<br>\n",
"Derudover kan vi se, at ID kolonnen slet ikke korrelere. Man kan derfor vælge at tage den ud."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Vi tilføjer nu vores \"kendte\" labels til vores data. (Hvis man spiller for en af vores topklubber, får man et 1-tal, og ellers får man et 0) <br>\n",
"Vi deler også vores træningssæt op i en *X* matrix med alle vores numeriske features, og en *y* vektor med alle vores labels."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"overall_set['label'] = overall_set['Club'].isin(topklub_set.Club).astype(int)\n",
"y = overall_set['label']\n",
"X = overall_set.iloc[:,0:-1].select_dtypes(include=['float64', 'int64'])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Vi kan kigge lidt overordnet på tallene mellem de 2 klasser."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Age</th>\n",
" <th>Overall</th>\n",
" <th>Potential</th>\n",
" <th>Value</th>\n",
" <th>Wage</th>\n",
" <th>Special</th>\n",
" <th>Acceleration</th>\n",
" <th>Aggression</th>\n",
" <th>Agility</th>\n",
" <th>Balance</th>\n",
" <th>...</th>\n",
" <th>RB</th>\n",
" <th>RCB</th>\n",
" <th>RCM</th>\n",
" <th>RDM</th>\n",
" <th>RF</th>\n",
" <th>RM</th>\n",
" <th>RS</th>\n",
" <th>RW</th>\n",
" <th>RWB</th>\n",
" <th>ST</th>\n",
" </tr>\n",
" <tr>\n",
" <th>label</th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>25.026730</td>\n",
" <td>65.619497</td>\n",
" <td>70.600629</td>\n",
" <td>1.655747e+06</td>\n",
" <td>9361.635220</td>\n",
" <td>1571.663522</td>\n",
" <td>63.682390</td>\n",
" <td>54.246855</td>\n",
" <td>62.617925</td>\n",
" <td>62.869497</td>\n",
" <td>...</td>\n",
" <td>49.207547</td>\n",
" <td>47.996855</td>\n",
" <td>50.830189</td>\n",
" <td>49.125786</td>\n",
" <td>51.566038</td>\n",
" <td>52.295597</td>\n",
" <td>51.045597</td>\n",
" <td>51.738994</td>\n",
" <td>49.856918</td>\n",
" <td>51.045597</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>25.166667</td>\n",
" <td>77.099057</td>\n",
" <td>81.856918</td>\n",
" <td>1.630118e+07</td>\n",
" <td>71496.855346</td>\n",
" <td>1817.268868</td>\n",
" <td>69.382075</td>\n",
" <td>62.413522</td>\n",
" <td>68.784591</td>\n",
" <td>66.122642</td>\n",
" <td>...</td>\n",
" <td>58.400943</td>\n",
" <td>56.378931</td>\n",
" <td>61.515723</td>\n",
" <td>58.900943</td>\n",
" <td>61.589623</td>\n",
" <td>62.281447</td>\n",
" <td>60.044025</td>\n",
" <td>61.707547</td>\n",
" <td>59.371069</td>\n",
" <td>60.044025</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>2 rows × 67 columns</p>\n",
"</div>"
],
"text/plain": [
" Age Overall Potential Value Wage \\\n",
"label \n",
"0 25.026730 65.619497 70.600629 1.655747e+06 9361.635220 \n",
"1 25.166667 77.099057 81.856918 1.630118e+07 71496.855346 \n",
"\n",
" Special Acceleration Aggression Agility Balance ... \\\n",
"label ... \n",
"0 1571.663522 63.682390 54.246855 62.617925 62.869497 ... \n",
"1 1817.268868 69.382075 62.413522 68.784591 66.122642 ... \n",
"\n",
" RB RCB RCM RDM RF RM \\\n",
"label \n",
"0 49.207547 47.996855 50.830189 49.125786 51.566038 52.295597 \n",
"1 58.400943 56.378931 61.515723 58.900943 61.589623 62.281447 \n",
"\n",
" RS RW RWB ST \n",
"label \n",
"0 51.045597 51.738994 49.856918 51.045597 \n",
"1 60.044025 61.707547 59.371069 60.044025 \n",
"\n",
"[2 rows x 67 columns]"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"overall_set.groupby('label').mean()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Observationer\n",
"* Alderen siger ikke rigtig noget om, hvorvidt du spiller for en topklub eller ej\n",
"* Topklubsspillere er i gennemsnittet en faktor 10 mere værd end ikke-topklub spillere\n",
"* Topklubsspillere er i gennemsnittet generelt ca. 10+ på alt i forhold til ikke-topklub spillere"
]
},
{
"cell_type": "markdown",
"metadata": {
"variables": {
"y.where(y==0).count()": "636",
"y.where(y==1).count()": "636"
}
},
"source": [
"Vi er nu klar til at gå i gang med vores første Machine Learning algoritme.\n",
"På forhånd ved vi, at der i vores træningssæt er {{y.where(y==1).count()}} som spiller i topklubber, og {{y.where(y==0).count()}} der ikke gør. <br>\n",
"Der er en 50/50 chance for at ramme rigtigt, hvis man bare gætte tilfældigt. Vi håber derfor, at algoritmen kan slå den 50% svarrate."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Logistisk regression"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# hent nødvendige pakker fra Scikit Learn biblioteket (generelt super hvis man vil lave data science)\n",
"from sklearn.linear_model import LogisticRegression\n",
"from sklearn.model_selection import train_test_split"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Vi fitter nu en logistic regression classifier til vores data, og fitter en model, så den kan genkende om man spiller for en topklub eller ej, og evaluere resultatet:"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"0.83411949685534592"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"model = LogisticRegression()\n",
"model = model.fit(X,y)\n",
"\n",
"model.score(X,y)"
]
},
{
"cell_type": "markdown",
"metadata": {
"variables": {
"'{:.0f}'.format(100*model.score(X, y))": "83"
}
},
"source": [
"Altså har vores model ret i \n",
"{{'{:.0f}'.format(100*model.score(X, y))}}% af tiden i træningssættet. <br>\n",
"\n",
"Pretty good!! Den har altså fundet nogle mønstre der kan mappe data til labels, og gætter ikke bare."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Men vi kan ikke vide, om den har overfittet, og derved har tilpasset sig for godt til sit kendte data, så nyt data vil blive fejlmappet. <br>\n",
"Hvad vi kan prøve, er at splitte vores træningssæt op i et trænings- og testsæt. På den måde kan vi først fitte og derefter evaluere på \"nyt\" kendt data, om den stadig performer som forventet. "
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Træningsæt størrelse: 1017 - Testsæt størrelse: 255\n"
]
}
],
"source": [
"X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)\n",
"print('Træningsæt størrelse: {} - Testsæt størrelse: {}'.format(len(X_train), len(X_test)))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Og vi er nu klar til at prøve igen!"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Logistisk regression 2.0\n",
"Igen fitter vi en logistisk regression til vores træningsdata, og danner en model, men denne gang uden at bruge testdatasættet."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"0.82595870206489674"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"model2 = LogisticRegression()\n",
"model2 = model2.fit(X_train, y_train)\n",
"model2.score(X_train, y_train)"
]
},
{
"cell_type": "markdown",
"metadata": {
"variables": {
"'{:.0f}'.format(100*model2.score(X, y))": "83"
}
},
"source": [
"Modellen matcher nu \n",
"{{'{:.0f}'.format(100*model2.score(X, y))}}% af tiden i træningssættet. <br> \n",
"Men har den overfittet?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Evaluering af modellen\n",
"Vi genererer derfor vores *y* forudsigelse og også sandsynlighederne for vores testsæt, da disse bruges til at evaluere modellen."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"y_pred = model2.predict(X_test)\n",
"y_probs = model2.predict_proba(X_test)"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Nøjagtigheden af vores logistiske regressions models prediction på testsættet er 84% \n",
"\n",
"Arealet under vores ROC AUC kurve er 90%\n"
]
}
],
"source": [
"# Evalueringsmålinger\n",
"from sklearn import metrics\n",
"print('Nøjagtigheden af vores logistiske regressions models prediction på testsættet er {:.0f}'.format(100*metrics.accuracy_score(y_test, y_pred))+'%', '\\n')\n",
"print('Arealet under vores ROC AUC kurve er {:.0f}'.format(100*metrics.roc_auc_score(y_test, y_probs[:, 1]))+'%')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Det ser jo ret fornuftigt ud.<br>\n",
"\n",
"For at sige noget om vores nye model, kan vi også lave en \"confusion_matrix\""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<img src='http://revolution-computing.typepad.com/.a/6a010534b1db25970b01bb08c97955970d-pi',\n",
" align=\"center\"\n",
" width=\"40%\"\n",
" alt=\"confusion matrix\">\n",
" \n",
"T og F står for henholdsvist True og False<br>\n",
"P og N står for henholdsvist Positive og Negative"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[[112 9]\n",
" [ 32 102]]\n"
]
}
],
"source": [
"confusion_matrix = metrics.confusion_matrix(y_test, y_pred)\n",
"print(confusion_matrix)"
]
},
{
"cell_type": "markdown",
"metadata": {
"variables": {
"confusion_matrix[0,0]": "112",
"confusion_matrix[0,0]+confusion_matrix[1,1]": "214",
"confusion_matrix[0,1]": "9",
"confusion_matrix[0,1]+confusion_matrix[1,0]": "41",
"confusion_matrix[1,0]": "32",
"confusion_matrix[1,1]": "102"
}
},
"source": [
"Resultatet fortæller os, at vi har {{confusion_matrix[0,0]}}+{{confusion_matrix[1,1]}} = {{confusion_matrix[0,0]+confusion_matrix[1,1]}} korrekte forudsigelser og {{confusion_matrix[0,1]}}+{{confusion_matrix[1,0]}} = {{confusion_matrix[0,1]+confusion_matrix[1,0]}} ukorrekte"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Man kan også bede classifieren om en rapport:"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" precision recall f1-score support\n",
"\n",
" 0 0.78 0.93 0.85 121\n",
" 1 0.92 0.76 0.83 134\n",
"\n",
"avg / total 0.85 0.84 0.84 255\n",
"\n"
]
}
],
"source": [
"print(metrics.classification_report(y_test, y_pred))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Logistisk regression med krydsvalidering\n",
"\n",
"Vi er egentlig meget tilfredse med vores model, men ofte kan det være en god idé at teste på flere små testsæt, og holde dem op mod hinanden. <br>\n",
"\n",
"Her laver vi en 10-folds krydsvalidering og får altså 10 scorer ud:"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[ 0.9296875 0.9453125 0.9140625 0.921875 0.9765625 0.9375\n",
" 0.94444444 0.74603175 0.46825397 0.44444444] \n",
"\n",
"0.822817460317\n"
]
}
],
"source": [
"# 10-folds cross-validation\n",
"from sklearn.model_selection import cross_val_score\n",
"scores = cross_val_score(LogisticRegression(), X, y, scoring='accuracy', cv=10)\n",
"print(scores,'\\n')\n",
"print(scores.mean())"
]
},
{
"cell_type": "markdown",
"metadata": {
"variables": {
"'{:.0f}'.format(100*scores.mean())": "82"
}
},
"source": [
"Her preformer modellen altså i gennemsnit \n",
"{{'{:.0f}'.format(100*scores.mean())}}%. \n",
"\n",
"Det lyder meget lovende, men vi holder os til vores *__model2__* og kan nu prøve modellen af på det rigtige datasæt"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Danskersættet \n",
"Vi skal nu prøve vores model på vores danske spillere<br>\n",
"\n",
"### Opgave:\n",
"Vi skal lave prediction og probability på vores danske spillere, ligesom vi gjorde tidligere for testsættet. (Lige under __Evaluering af modellen__)<br>\n",
"\n",
"Husk din dataframe kun må indeholder numeriske værdier, når vi bruger modellen.<br>\n",
"Fx. \"__df.select_dtypes(include=['float64', 'int64'])__\""
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"dansker_pred = None ### Fjern NONE og UDFYLD MIG ###\n",
"dansker_probs = None ### Fjern NONE og UDFYLD MIG ###"
]
},
{
"cell_type": "markdown",
"metadata": {
"variables": {
"np.bincount(dansker_pred)[0]": "319",
"np.bincount(dansker_pred)[1]": "27"
}
},
"source": [
"Modellen har fundet {{np.bincount(dansker_pred)[0]}} nuller og {{np.bincount(dansker_pred)[1]}} ét-taller"
]
},
{
"cell_type": "markdown",
"metadata": {
"variables": {
"top_klub_ratio": "75"
}
},
"source": [
"Hvis du satte *top_klub_ratio* til 75 i __Opgave 1__ i __Data Cleaning__, skulle der være omkring 27-28 ét-taller. <br>\n",
"*top_klub_ratio* blev sat til: {{top_klub_ratio}}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Vi tilføjer disse kolonner til vores dataframe."
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": true,
"scrolled": false
},
"outputs": [],
"source": [
"dansker_set_df = dansker_set.copy()\n",
"dansker_set_df[['prob1','prob2']] = pd.DataFrame(dansker_probs, index=dansker_set.index)\n",
"dansker_set_df['Probabilities [0,1]'] = dansker_set_df[['prob1','prob2']].values.tolist()\n",
"dansker_set_df['Prediction'] = pd.Series(dansker_pred, index=dansker_set.index)\n",
"del dansker_set_df['prob1'], dansker_set_df['prob2'] \n",
"# dansker_set_df.head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Og sortere listen, så de bedste danske spillere står øvers, og tilføjer et index, så vi kan få et bedre overblik"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"scrolled": true
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Name</th>\n",
" <th>Club</th>\n",
" <th>Overall</th>\n",
" <th>Potential</th>\n",
" <th>Probabilities [0,1]</th>\n",
" <th>Prediction</th>\n",
" </tr>\n",
" <tr>\n",
" <th>in</th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>C. Eriksen</td>\n",
" <td>Tottenham Hotspur</td>\n",
" <td>87</td>\n",
" <td>91</td>\n",
" <td>[1.2361997292487104e-07, 0.9999998763800271]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>A. Christensen</td>\n",
" <td>Chelsea</td>\n",
" <td>81</td>\n",
" <td>89</td>\n",
" <td>[0.00595764605638005, 0.99404235394362]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>K. Schmeichel</td>\n",
" <td>Leicester City</td>\n",
" <td>83</td>\n",
" <td>84</td>\n",
" <td>[0.014948898649614573, 0.9850511013503854]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>S. Kjær</td>\n",
" <td>Sevilla FC</td>\n",
" <td>81</td>\n",
" <td>82</td>\n",
" <td>[0.0792499037714689, 0.9207500962285311]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>D. Wass</td>\n",
" <td>RC Celta de Vigo</td>\n",
" <td>80</td>\n",
" <td>80</td>\n",
" <td>[0.08093367436833954, 0.9190663256316605]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6</th>\n",
" <td>J. Vestergaard</td>\n",
" <td>Borussia Mönchengladbach</td>\n",
" <td>79</td>\n",
" <td>84</td>\n",
" <td>[0.09443758718579498, 0.905562412814205]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>N. Jørgensen</td>\n",
" <td>Feyenoord</td>\n",
" <td>79</td>\n",
" <td>81</td>\n",
" <td>[0.09662360026251093, 0.9033763997374891]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>Y. Poulsen</td>\n",
" <td>RB Leipzig</td>\n",
" <td>76</td>\n",
" <td>83</td>\n",
" <td>[0.11856360569546154, 0.8814363943045385]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>K. Dolberg</td>\n",
" <td>Ajax</td>\n",
" <td>78</td>\n",
" <td>88</td>\n",
" <td>[0.1340973698375778, 0.8659026301624222]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>P. Højbjerg</td>\n",
" <td>Southampton</td>\n",
" <td>75</td>\n",
" <td>81</td>\n",
" <td>[0.19744945518739987, 0.8025505448126001]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>M. Braithwaite</td>\n",
" <td>Middlesbrough</td>\n",
" <td>77</td>\n",
" <td>80</td>\n",
" <td>[0.20992890568457212, 0.7900710943154279]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12</th>\n",
" <td>L. Andersen</td>\n",
" <td>Grasshopper Club Zürich</td>\n",
" <td>76</td>\n",
" <td>83</td>\n",
" <td>[0.23658486733875572, 0.7634151326612443]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13</th>\n",
" <td>F. Sørensen</td>\n",
" <td>1. FC Köln</td>\n",
" <td>77</td>\n",
" <td>81</td>\n",
" <td>[0.2387127042826872, 0.7612872957173128]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14</th>\n",
" <td>L. Lerager</td>\n",
" <td>Girondins de Bordeaux</td>\n",
" <td>75</td>\n",
" <td>80</td>\n",
" <td>[0.28360075282343045, 0.7163992471765696]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15</th>\n",
" <td>V. Fischer</td>\n",
" <td>1. FSV Mainz 05</td>\n",
" <td>75</td>\n",
" <td>82</td>\n",
" <td>[0.28803632021595915, 0.7119636797840408]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16</th>\n",
" <td>M. Jørgensen</td>\n",
" <td>Huddersfield Town</td>\n",
" <td>75</td>\n",
" <td>78</td>\n",
" <td>[0.30175956933231884, 0.6982404306676812]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17</th>\n",
" <td>M. Krohn-Dehli</td>\n",
" <td>Sevilla FC</td>\n",
" <td>79</td>\n",
" <td>79</td>\n",
" <td>[0.34163848506912053, 0.6583615149308795]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>18</th>\n",
" <td>P. Sisto</td>\n",
" <td>RC Celta de Vigo</td>\n",
" <td>74</td>\n",
" <td>83</td>\n",
" <td>[0.35254475144372266, 0.6474552485562773]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>19</th>\n",
" <td>L. Schøne</td>\n",
" <td>Ajax</td>\n",
" <td>77</td>\n",
" <td>77</td>\n",
" <td>[0.3653813781431249, 0.6346186218568751]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>20</th>\n",
" <td>J. Poulsen</td>\n",
" <td>FC Midtjylland</td>\n",
" <td>71</td>\n",
" <td>71</td>\n",
" <td>[0.41554897703083404, 0.584451022969166]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>21</th>\n",
" <td>R. Falk Jensen</td>\n",
" <td>FC København</td>\n",
" <td>74</td>\n",
" <td>77</td>\n",
" <td>[0.41712565782872424, 0.5828743421712758]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>22</th>\n",
" <td>J. Lössl</td>\n",
" <td>Huddersfield Town</td>\n",
" <td>75</td>\n",
" <td>76</td>\n",
" <td>[0.4321175862344081, 0.5678824137655919]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>23</th>\n",
" <td>E. Sviatchenko</td>\n",
" <td>Celtic</td>\n",
" <td>73</td>\n",
" <td>75</td>\n",
" <td>[0.4361724537479308, 0.5638275462520692]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>24</th>\n",
" <td>A. Bjelland</td>\n",
" <td>Brentford</td>\n",
" <td>73</td>\n",
" <td>73</td>\n",
" <td>[0.4629540156936526, 0.5370459843063474]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>25</th>\n",
" <td>A. Cornelius</td>\n",
" <td>Atalanta</td>\n",
" <td>73</td>\n",
" <td>78</td>\n",
" <td>[0.4666099871886722, 0.5333900128113278]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>26</th>\n",
" <td>P. Mtiliga</td>\n",
" <td>FC Nordsjælland</td>\n",
" <td>69</td>\n",
" <td>69</td>\n",
" <td>[0.4794912216897943, 0.5205087783102057]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>27</th>\n",
" <td>M. Rasmussen</td>\n",
" <td>Aarhus GF</td>\n",
" <td>69</td>\n",
" <td>69</td>\n",
" <td>[0.48675749765285403, 0.513242502347146]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>28</th>\n",
" <td>M. Jensen</td>\n",
" <td>Rosenborg BK</td>\n",
" <td>74</td>\n",
" <td>74</td>\n",
" <td>[0.5020672719966166, 0.49793272800338345]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>29</th>\n",
" <td>A. Scholz</td>\n",
" <td>Standard de Liège</td>\n",
" <td>74</td>\n",
" <td>79</td>\n",
" <td>[0.5049879774285326, 0.4950120225714674]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>30</th>\n",
" <td>A. Christiansen</td>\n",
" <td>Malmö FF</td>\n",
" <td>74</td>\n",
" <td>75</td>\n",
" <td>[0.5096762833242563, 0.4903237166757437]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>...</th>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" </tr>\n",
" <tr>\n",
" <th>317</th>\n",
" <td>M. Roerslev</td>\n",
" <td>FC København</td>\n",
" <td>52</td>\n",
" <td>68</td>\n",
" <td>[0.8631321739682192, 0.1368678260317808]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>318</th>\n",
" <td>K. Tshiembe</td>\n",
" <td>Lyngby BK</td>\n",
" <td>52</td>\n",
" <td>68</td>\n",
" <td>[0.8634039506795222, 0.13659604932047775]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>319</th>\n",
" <td>O. Albayrak</td>\n",
" <td>Hobro IK</td>\n",
" <td>56</td>\n",
" <td>64</td>\n",
" <td>[0.8636862223098634, 0.13631377769013664]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>320</th>\n",
" <td>O. Snorre</td>\n",
" <td>Lyngby BK</td>\n",
" <td>52</td>\n",
" <td>73</td>\n",
" <td>[0.8637484895953144, 0.13625151040468567]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>321</th>\n",
" <td>T. Damsgaard</td>\n",
" <td>Randers FC</td>\n",
" <td>51</td>\n",
" <td>66</td>\n",
" <td>[0.8637660405380061, 0.13623395946199385]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>322</th>\n",
" <td>J. Eskesen</td>\n",
" <td>Odense Boldklub</td>\n",
" <td>52</td>\n",
" <td>68</td>\n",
" <td>[0.8638436078001344, 0.1361563921998657]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>323</th>\n",
" <td>N. Lyngø</td>\n",
" <td>Aalborg BK</td>\n",
" <td>54</td>\n",
" <td>65</td>\n",
" <td>[0.8638480408791316, 0.13615195912086842]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>324</th>\n",
" <td>O. Ottesen</td>\n",
" <td>FC Midtjylland</td>\n",
" <td>57</td>\n",
" <td>67</td>\n",
" <td>[0.863986086521014, 0.1360139134789859]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>325</th>\n",
" <td>D. Thøgersen</td>\n",
" <td>Aarhus GF</td>\n",
" <td>52</td>\n",
" <td>70</td>\n",
" <td>[0.863995687351485, 0.13600431264851498]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>326</th>\n",
" <td>M. Warming</td>\n",
" <td>Brøndby IF</td>\n",
" <td>51</td>\n",
" <td>66</td>\n",
" <td>[0.864179921766968, 0.135820078233032]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>327</th>\n",
" <td>M. Mattsson</td>\n",
" <td>Silkeborg IF</td>\n",
" <td>54</td>\n",
" <td>76</td>\n",
" <td>[0.8642832619995633, 0.13571673800043674]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>328</th>\n",
" <td>E. Simonsen</td>\n",
" <td>Lyngby BK</td>\n",
" <td>53</td>\n",
" <td>77</td>\n",
" <td>[0.8643983530602066, 0.13560164693979332]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>329</th>\n",
" <td>G. Marcussen</td>\n",
" <td>Lyngby BK</td>\n",
" <td>50</td>\n",
" <td>69</td>\n",
" <td>[0.8644066756136866, 0.13559332438631339]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>330</th>\n",
" <td>M. Andersen</td>\n",
" <td>Aalborg BK</td>\n",
" <td>52</td>\n",
" <td>66</td>\n",
" <td>[0.8644086683355966, 0.13559133166440343]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>331</th>\n",
" <td>F. Roepstorff</td>\n",
" <td>FC Helsingør</td>\n",
" <td>51</td>\n",
" <td>70</td>\n",
" <td>[0.8644360366151669, 0.1355639633848331]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>332</th>\n",
" <td>M. Haarup</td>\n",
" <td>Hobro IK</td>\n",
" <td>54</td>\n",
" <td>66</td>\n",
" <td>[0.8644842744974983, 0.13551572550250168]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>333</th>\n",
" <td>A. Vaporakis</td>\n",
" <td>FC Helsingør</td>\n",
" <td>53</td>\n",
" <td>63</td>\n",
" <td>[0.8644874549734057, 0.13551254502659427]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>334</th>\n",
" <td>M. Hegaard</td>\n",
" <td>FC Helsingør</td>\n",
" <td>51</td>\n",
" <td>69</td>\n",
" <td>[0.864535621341468, 0.13546437865853198]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>335</th>\n",
" <td>A. Kappenberger</td>\n",
" <td>FC Helsingør</td>\n",
" <td>52</td>\n",
" <td>66</td>\n",
" <td>[0.8645552105643415, 0.13544478943565855]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>336</th>\n",
" <td>M. Johannsen</td>\n",
" <td>FC Helsingør</td>\n",
" <td>54</td>\n",
" <td>58</td>\n",
" <td>[0.8645567173499312, 0.13544328265006875]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>337</th>\n",
" <td>G. Arndal-Lauritzen</td>\n",
" <td>Brøndby IF</td>\n",
" <td>50</td>\n",
" <td>67</td>\n",
" <td>[0.864584838948699, 0.135415161051301]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>338</th>\n",
" <td>A. Skov Olsen</td>\n",
" <td>FC Nordsjælland</td>\n",
" <td>53</td>\n",
" <td>66</td>\n",
" <td>[0.8646176815512268, 0.13538231844877324]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>339</th>\n",
" <td>T. Arndal</td>\n",
" <td>AC Horsens</td>\n",
" <td>52</td>\n",
" <td>65</td>\n",
" <td>[0.864647326784709, 0.135352673215291]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>340</th>\n",
" <td>C. Enemark</td>\n",
" <td>Brøndby IF</td>\n",
" <td>50</td>\n",
" <td>69</td>\n",
" <td>[0.8646551987933163, 0.13534480120668368]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>341</th>\n",
" <td>A. Ammitzbøl</td>\n",
" <td>Aarhus GF</td>\n",
" <td>55</td>\n",
" <td>64</td>\n",
" <td>[0.8649192100937313, 0.13508078990626865]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>342</th>\n",
" <td>I. Esen</td>\n",
" <td>FC Helsingør</td>\n",
" <td>50</td>\n",
" <td>69</td>\n",
" <td>[0.8649298106428374, 0.13507018935716258]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>343</th>\n",
" <td>A. Junge</td>\n",
" <td>FC Helsingør</td>\n",
" <td>50</td>\n",
" <td>56</td>\n",
" <td>[0.865287155002264, 0.13471284499773598]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>344</th>\n",
" <td>M. Iversen</td>\n",
" <td>Aalborg BK</td>\n",
" <td>50</td>\n",
" <td>62</td>\n",
" <td>[0.8666456075747598, 0.13335439242524016]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>345</th>\n",
" <td>O. Drost</td>\n",
" <td>AC Horsens</td>\n",
" <td>51</td>\n",
" <td>58</td>\n",
" <td>[0.8668261929640377, 0.13317380703596227]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>346</th>\n",
" <td>F. Nørgaard</td>\n",
" <td>AC Horsens</td>\n",
" <td>50</td>\n",
" <td>62</td>\n",
" <td>[0.8669208380435555, 0.13307916195644454]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>346 rows × 6 columns</p>\n",
"</div>"
],
"text/plain": [
" Name Club Overall Potential \\\n",
"in \n",
"1 C. Eriksen Tottenham Hotspur 87 91 \n",
"2 A. Christensen Chelsea 81 89 \n",
"3 K. Schmeichel Leicester City 83 84 \n",
"4 S. Kjær Sevilla FC 81 82 \n",
"5 D. Wass RC Celta de Vigo 80 80 \n",
"6 J. Vestergaard Borussia Mönchengladbach 79 84 \n",
"7 N. Jørgensen Feyenoord 79 81 \n",
"8 Y. Poulsen RB Leipzig 76 83 \n",
"9 K. Dolberg Ajax 78 88 \n",
"10 P. Højbjerg Southampton 75 81 \n",
"11 M. Braithwaite Middlesbrough 77 80 \n",
"12 L. Andersen Grasshopper Club Zürich 76 83 \n",
"13 F. Sørensen 1. FC Köln 77 81 \n",
"14 L. Lerager Girondins de Bordeaux 75 80 \n",
"15 V. Fischer 1. FSV Mainz 05 75 82 \n",
"16 M. Jørgensen Huddersfield Town 75 78 \n",
"17 M. Krohn-Dehli Sevilla FC 79 79 \n",
"18 P. Sisto RC Celta de Vigo 74 83 \n",
"19 L. Schøne Ajax 77 77 \n",
"20 J. Poulsen FC Midtjylland 71 71 \n",
"21 R. Falk Jensen FC København 74 77 \n",
"22 J. Lössl Huddersfield Town 75 76 \n",
"23 E. Sviatchenko Celtic 73 75 \n",
"24 A. Bjelland Brentford 73 73 \n",
"25 A. Cornelius Atalanta 73 78 \n",
"26 P. Mtiliga FC Nordsjælland 69 69 \n",
"27 M. Rasmussen Aarhus GF 69 69 \n",
"28 M. Jensen Rosenborg BK 74 74 \n",
"29 A. Scholz Standard de Liège 74 79 \n",
"30 A. Christiansen Malmö FF 74 75 \n",
".. ... ... ... ... \n",
"317 M. Roerslev FC København 52 68 \n",
"318 K. Tshiembe Lyngby BK 52 68 \n",
"319 O. Albayrak Hobro IK 56 64 \n",
"320 O. Snorre Lyngby BK 52 73 \n",
"321 T. Damsgaard Randers FC 51 66 \n",
"322 J. Eskesen Odense Boldklub 52 68 \n",
"323 N. Lyngø Aalborg BK 54 65 \n",
"324 O. Ottesen FC Midtjylland 57 67 \n",
"325 D. Thøgersen Aarhus GF 52 70 \n",
"326 M. Warming Brøndby IF 51 66 \n",
"327 M. Mattsson Silkeborg IF 54 76 \n",
"328 E. Simonsen Lyngby BK 53 77 \n",
"329 G. Marcussen Lyngby BK 50 69 \n",
"330 M. Andersen Aalborg BK 52 66 \n",
"331 F. Roepstorff FC Helsingør 51 70 \n",
"332 M. Haarup Hobro IK 54 66 \n",
"333 A. Vaporakis FC Helsingør 53 63 \n",
"334 M. Hegaard FC Helsingør 51 69 \n",
"335 A. Kappenberger FC Helsingør 52 66 \n",
"336 M. Johannsen FC Helsingør 54 58 \n",
"337 G. Arndal-Lauritzen Brøndby IF 50 67 \n",
"338 A. Skov Olsen FC Nordsjælland 53 66 \n",
"339 T. Arndal AC Horsens 52 65 \n",
"340 C. Enemark Brøndby IF 50 69 \n",
"341 A. Ammitzbøl Aarhus GF 55 64 \n",
"342 I. Esen FC Helsingør 50 69 \n",
"343 A. Junge FC Helsingør 50 56 \n",
"344 M. Iversen Aalborg BK 50 62 \n",
"345 O. Drost AC Horsens 51 58 \n",
"346 F. Nørgaard AC Horsens 50 62 \n",
"\n",
" Probabilities [0,1] Prediction \n",
"in \n",
"1 [1.2361997292487104e-07, 0.9999998763800271] 1 \n",
"2 [0.00595764605638005, 0.99404235394362] 1 \n",
"3 [0.014948898649614573, 0.9850511013503854] 1 \n",
"4 [0.0792499037714689, 0.9207500962285311] 1 \n",
"5 [0.08093367436833954, 0.9190663256316605] 1 \n",
"6 [0.09443758718579498, 0.905562412814205] 1 \n",
"7 [0.09662360026251093, 0.9033763997374891] 1 \n",
"8 [0.11856360569546154, 0.8814363943045385] 1 \n",
"9 [0.1340973698375778, 0.8659026301624222] 1 \n",
"10 [0.19744945518739987, 0.8025505448126001] 1 \n",
"11 [0.20992890568457212, 0.7900710943154279] 1 \n",
"12 [0.23658486733875572, 0.7634151326612443] 1 \n",
"13 [0.2387127042826872, 0.7612872957173128] 1 \n",
"14 [0.28360075282343045, 0.7163992471765696] 1 \n",
"15 [0.28803632021595915, 0.7119636797840408] 1 \n",
"16 [0.30175956933231884, 0.6982404306676812] 1 \n",
"17 [0.34163848506912053, 0.6583615149308795] 1 \n",
"18 [0.35254475144372266, 0.6474552485562773] 1 \n",
"19 [0.3653813781431249, 0.6346186218568751] 1 \n",
"20 [0.41554897703083404, 0.584451022969166] 1 \n",
"21 [0.41712565782872424, 0.5828743421712758] 1 \n",
"22 [0.4321175862344081, 0.5678824137655919] 1 \n",
"23 [0.4361724537479308, 0.5638275462520692] 1 \n",
"24 [0.4629540156936526, 0.5370459843063474] 1 \n",
"25 [0.4666099871886722, 0.5333900128113278] 1 \n",
"26 [0.4794912216897943, 0.5205087783102057] 1 \n",
"27 [0.48675749765285403, 0.513242502347146] 1 \n",
"28 [0.5020672719966166, 0.49793272800338345] 0 \n",
"29 [0.5049879774285326, 0.4950120225714674] 0 \n",
"30 [0.5096762833242563, 0.4903237166757437] 0 \n",
".. ... ... \n",
"317 [0.8631321739682192, 0.1368678260317808] 0 \n",
"318 [0.8634039506795222, 0.13659604932047775] 0 \n",
"319 [0.8636862223098634, 0.13631377769013664] 0 \n",
"320 [0.8637484895953144, 0.13625151040468567] 0 \n",
"321 [0.8637660405380061, 0.13623395946199385] 0 \n",
"322 [0.8638436078001344, 0.1361563921998657] 0 \n",
"323 [0.8638480408791316, 0.13615195912086842] 0 \n",
"324 [0.863986086521014, 0.1360139134789859] 0 \n",
"325 [0.863995687351485, 0.13600431264851498] 0 \n",
"326 [0.864179921766968, 0.135820078233032] 0 \n",
"327 [0.8642832619995633, 0.13571673800043674] 0 \n",
"328 [0.8643983530602066, 0.13560164693979332] 0 \n",
"329 [0.8644066756136866, 0.13559332438631339] 0 \n",
"330 [0.8644086683355966, 0.13559133166440343] 0 \n",
"331 [0.8644360366151669, 0.1355639633848331] 0 \n",
"332 [0.8644842744974983, 0.13551572550250168] 0 \n",
"333 [0.8644874549734057, 0.13551254502659427] 0 \n",
"334 [0.864535621341468, 0.13546437865853198] 0 \n",
"335 [0.8645552105643415, 0.13544478943565855] 0 \n",
"336 [0.8645567173499312, 0.13544328265006875] 0 \n",
"337 [0.864584838948699, 0.135415161051301] 0 \n",
"338 [0.8646176815512268, 0.13538231844877324] 0 \n",
"339 [0.864647326784709, 0.135352673215291] 0 \n",
"340 [0.8646551987933163, 0.13534480120668368] 0 \n",
"341 [0.8649192100937313, 0.13508078990626865] 0 \n",
"342 [0.8649298106428374, 0.13507018935716258] 0 \n",
"343 [0.865287155002264, 0.13471284499773598] 0 \n",
"344 [0.8666456075747598, 0.13335439242524016] 0 \n",
"345 [0.8668261929640377, 0.13317380703596227] 0 \n",
"346 [0.8669208380435555, 0.13307916195644454] 0 \n",
"\n",
"[346 rows x 6 columns]"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"dansker_set_df.loc[:,'pred=1'] = dansker_set_df['Probabilities [0,1]'].map(lambda x: x[1]).sort_values(ascending=False)\n",
"dansker_sorted = dansker_set_df.sort_values('pred=1', ascending=False)\n",
"dansker_sorted = dansker_sorted[['Name', 'Club', 'Overall', 'Potential', 'Probabilities [0,1]', 'Prediction']]\n",
"dansker_sorted.loc[:,'in'] = np.arange(1, len(dansker_set_df)+1)\n",
"dansker_sorted.set_index('in')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Efter flot hattrick mod Irland, kan man vidst ikke være i tvivl om Kong Christian tager pladsen på tronen\n",
"<img src='kongen.png',\n",
" align=\"center\"\n",
" width=\"40%\"\n",
" alt=\"kongen\">"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Men hvilke danske spillere spiller egentlig for topklubber, og hvordan er de rangeret i forhold til vores model?"
]
},
{
"cell_type": "code",
"execution_count": 39,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Name</th>\n",
" <th>Club</th>\n",
" <th>Overall</th>\n",
" <th>Potential</th>\n",
" <th>Probabilities [0,1]</th>\n",
" <th>Prediction</th>\n",
" </tr>\n",
" <tr>\n",
" <th>in</th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>A. Christensen</td>\n",
" <td>Chelsea</td>\n",
" <td>81</td>\n",
" <td>89</td>\n",
" <td>[0.00469680685795848, 0.9953031931420415]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7</th>\n",
" <td>S. Kjær</td>\n",
" <td>Sevilla FC</td>\n",
" <td>81</td>\n",
" <td>82</td>\n",
" <td>[0.10268761388443448, 0.8973123861155655]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>17</th>\n",
" <td>M. Krohn-Dehli</td>\n",
" <td>Sevilla FC</td>\n",
" <td>79</td>\n",
" <td>79</td>\n",
" <td>[0.32668814694969617, 0.6733118530503038]</td>\n",
" <td>1</td>\n",
" </tr>\n",
" <tr>\n",
" <th>198</th>\n",
" <td>J. Larsen</td>\n",
" <td>Borussia Dortmund</td>\n",
" <td>62</td>\n",
" <td>79</td>\n",
" <td>[0.8181799678362287, 0.18182003216377135]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>224</th>\n",
" <td>R. Corlu</td>\n",
" <td>Roma</td>\n",
" <td>58</td>\n",
" <td>69</td>\n",
" <td>[0.8314270782764579, 0.16857292172354213]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Name Club Overall Potential \\\n",
"in \n",
"2 A. Christensen Chelsea 81 89 \n",
"7 S. Kjær Sevilla FC 81 82 \n",
"17 M. Krohn-Dehli Sevilla FC 79 79 \n",
"198 J. Larsen Borussia Dortmund 62 79 \n",
"224 R. Corlu Roma 58 69 \n",
"\n",
" Probabilities [0,1] Prediction \n",
"in \n",
"2 [0.00469680685795848, 0.9953031931420415] 1 \n",
"7 [0.10268761388443448, 0.8973123861155655] 1 \n",
"17 [0.32668814694969617, 0.6733118530503038] 1 \n",
"198 [0.8181799678362287, 0.18182003216377135] 0 \n",
"224 [0.8314270782764579, 0.16857292172354213] 0 "
]
},
"execution_count": 39,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"dansker_sorted[dansker_sorted['Club'].isin(top_clubs)].set_index('in')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Man kan undre sig over hvad Jacob Larsen laver hos stopklubben Borussia Dortmund, men en hurtig googling viser, at han simpelthen blev headhuntet til klubben som 16-årig."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Og så er der jo nok nogen, der vil spørger - Hvad med Bendtner?\n",
"Så han skal da også lige have en plads i vores analyse:"
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {
"scrolled": true
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Name</th>\n",
" <th>Club</th>\n",
" <th>Overall</th>\n",
" <th>Potential</th>\n",
" <th>Probabilities [0,1]</th>\n",
" <th>Prediction</th>\n",
" </tr>\n",
" <tr>\n",
" <th>in</th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" <th></th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>42</th>\n",
" <td>N. Bendtner</td>\n",
" <td>Rosenborg BK</td>\n",
" <td>73</td>\n",
" <td>73</td>\n",
" <td>[0.568000951323095, 0.43199904867690503]</td>\n",
" <td>0</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Name Club Overall Potential \\\n",
"in \n",
"42 N. Bendtner Rosenborg BK 73 73 \n",
"\n",
" Probabilities [0,1] Prediction \n",
"in \n",
"42 [0.568000951323095, 0.43199904867690503] 0 "
]
},
"execution_count": 40,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"dansker_sorted.loc[dansker_sorted.Name == 'N. Bendtner'].set_index('in')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Opgave:\n",
"Vi kan også kigge på ham i det store billede. Prøv evt. at lege lidt rundt med forskellige spillere eller andre features.<br>\n",
"Er der noget specielt, der kunne være sjovt at kigge på?"
]
},
{
"cell_type": "code",
"execution_count": 41,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Name</th>\n",
" <th>Age</th>\n",
" <th>Nationality</th>\n",
" <th>Overall</th>\n",
" <th>Potential</th>\n",
" <th>Club</th>\n",
" <th>Value</th>\n",
" <th>Wage</th>\n",
" <th>Special</th>\n",
" <th>Acceleration</th>\n",
" <th>...</th>\n",
" <th>RB</th>\n",
" <th>RCB</th>\n",
" <th>RCM</th>\n",
" <th>RDM</th>\n",
" <th>RF</th>\n",
" <th>RM</th>\n",
" <th>RS</th>\n",
" <th>RW</th>\n",
" <th>RWB</th>\n",
" <th>ST</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>2697</th>\n",
" <td>N. Bendtner</td>\n",
" <td>29</td>\n",
" <td>Denmark</td>\n",
" <td>73</td>\n",
" <td>73</td>\n",
" <td>Rosenborg BK</td>\n",
" <td>4000000.0</td>\n",
" <td>10000.0</td>\n",
" <td>1790</td>\n",
" <td>70.0</td>\n",
" <td>...</td>\n",
" <td>51.0</td>\n",
" <td>51.0</td>\n",
" <td>65.0</td>\n",
" <td>54.0</td>\n",
" <td>70.0</td>\n",
" <td>69.0</td>\n",
" <td>72.0</td>\n",
" <td>69.0</td>\n",
" <td>53.0</td>\n",
" <td>72.0</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>1 rows × 71 columns</p>\n",
"</div>"
],
"text/plain": [
" Name Age Nationality Overall Potential Club \\\n",
"2697 N. Bendtner 29 Denmark 73 73 Rosenborg BK \n",
"\n",
" Value Wage Special Acceleration ... RB RCB RCM RDM \\\n",
"2697 4000000.0 10000.0 1790 70.0 ... 51.0 51.0 65.0 54.0 \n",
"\n",
" RF RM RS RW RWB ST \n",
"2697 70.0 69.0 72.0 69.0 53.0 72.0 \n",
"\n",
"[1 rows x 71 columns]"
]
},
"execution_count": 41,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df.loc[df.Name == 'N. Bendtner']"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Ekstra lege/analyse opgaver\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Danske Rezan Corlu som ellers ligger ret lavt selv på potentiale har alligevel sikret sig en plads hos A.S. Roma i en alder af 20 år.\n",
"Men hvordan var det egentlig med de topklub spillere? Hvor langt ned kan man gå i potentiale, og stadig spille for en topklub?"
]
},
{
"cell_type": "code",
"execution_count": 42,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Name</th>\n",
" <th>Age</th>\n",
" <th>Nationality</th>\n",
" <th>Overall</th>\n",
" <th>Potential</th>\n",
" <th>Club</th>\n",
" <th>Value</th>\n",
" <th>Wage</th>\n",
" <th>Special</th>\n",
" <th>Acceleration</th>\n",
" <th>...</th>\n",
" <th>RB</th>\n",
" <th>RCB</th>\n",
" <th>RCM</th>\n",
" <th>RDM</th>\n",
" <th>RF</th>\n",
" <th>RM</th>\n",
" <th>RS</th>\n",
" <th>RW</th>\n",
" <th>RWB</th>\n",
" <th>ST</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>17331</th>\n",
" <td>A. Zerbin</td>\n",
" <td>18</td>\n",
" <td>Italy</td>\n",
" <td>53</td>\n",
" <td>73</td>\n",
" <td>Napoli</td>\n",
" <td>120000.0</td>\n",
" <td>4000.0</td>\n",
" <td>1324</td>\n",
" <td>42.0</td>\n",
" <td>...</td>\n",
" <td>39.0</td>\n",
" <td>37.0</td>\n",
" <td>49.0</td>\n",
" <td>41.0</td>\n",
" <td>52.0</td>\n",
" <td>51.0</td>\n",
" <td>51.0</td>\n",
" <td>53.0</td>\n",
" <td>41.0</td>\n",
" <td>51.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16714</th>\n",
" <td>P. Fritsch</td>\n",
" <td>18</td>\n",
" <td>Germany</td>\n",
" <td>55</td>\n",
" <td>71</td>\n",
" <td>Borussia Dortmund</td>\n",
" <td>160000.0</td>\n",
" <td>3000.0</td>\n",
" <td>1349</td>\n",
" <td>52.0</td>\n",
" <td>...</td>\n",
" <td>49.0</td>\n",
" <td>54.0</td>\n",
" <td>44.0</td>\n",
" <td>50.0</td>\n",
" <td>41.0</td>\n",
" <td>42.0</td>\n",
" <td>42.0</td>\n",
" <td>42.0</td>\n",
" <td>48.0</td>\n",
" <td>42.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16406</th>\n",
" <td>D. Sauerland</td>\n",
" <td>20</td>\n",
" <td>Germany</td>\n",
" <td>56</td>\n",
" <td>68</td>\n",
" <td>Borussia Dortmund</td>\n",
" <td>160000.0</td>\n",
" <td>5000.0</td>\n",
" <td>1526</td>\n",
" <td>55.0</td>\n",
" <td>...</td>\n",
" <td>46.0</td>\n",
" <td>41.0</td>\n",
" <td>55.0</td>\n",
" <td>47.0</td>\n",
" <td>57.0</td>\n",
" <td>56.0</td>\n",
" <td>53.0</td>\n",
" <td>58.0</td>\n",
" <td>49.0</td>\n",
" <td>53.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15718</th>\n",
" <td>J. Maddox</td>\n",
" <td>18</td>\n",
" <td>England</td>\n",
" <td>58</td>\n",
" <td>74</td>\n",
" <td>Chelsea</td>\n",
" <td>260000.0</td>\n",
" <td>7000.0</td>\n",
" <td>1402</td>\n",
" <td>71.0</td>\n",
" <td>...</td>\n",
" <td>42.0</td>\n",
" <td>34.0</td>\n",
" <td>51.0</td>\n",
" <td>41.0</td>\n",
" <td>56.0</td>\n",
" <td>57.0</td>\n",
" <td>52.0</td>\n",
" <td>57.0</td>\n",
" <td>45.0</td>\n",
" <td>52.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15549</th>\n",
" <td>R. Corlu</td>\n",
" <td>19</td>\n",
" <td>Denmark</td>\n",
" <td>58</td>\n",
" <td>69</td>\n",
" <td>Roma</td>\n",
" <td>210000.0</td>\n",
" <td>4000.0</td>\n",
" <td>1473</td>\n",
" <td>73.0</td>\n",
" <td>...</td>\n",
" <td>43.0</td>\n",
" <td>34.0</td>\n",
" <td>51.0</td>\n",
" <td>40.0</td>\n",
" <td>56.0</td>\n",
" <td>57.0</td>\n",
" <td>53.0</td>\n",
" <td>58.0</td>\n",
" <td>45.0</td>\n",
" <td>53.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15479</th>\n",
" <td>T. Bola</td>\n",
" <td>18</td>\n",
" <td>England</td>\n",
" <td>59</td>\n",
" <td>72</td>\n",
" <td>Arsenal</td>\n",
" <td>250000.0</td>\n",
" <td>6000.0</td>\n",
" <td>1344</td>\n",
" <td>59.0</td>\n",
" <td>...</td>\n",
" <td>54.0</td>\n",
" <td>58.0</td>\n",
" <td>41.0</td>\n",
" <td>50.0</td>\n",
" <td>40.0</td>\n",
" <td>40.0</td>\n",
" <td>42.0</td>\n",
" <td>40.0</td>\n",
" <td>51.0</td>\n",
" <td>42.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15409</th>\n",
" <td>E. Nketiah</td>\n",
" <td>18</td>\n",
" <td>England</td>\n",
" <td>59</td>\n",
" <td>80</td>\n",
" <td>Arsenal</td>\n",
" <td>350000.0</td>\n",
" <td>8000.0</td>\n",
" <td>1404</td>\n",
" <td>77.0</td>\n",
" <td>...</td>\n",
" <td>37.0</td>\n",
" <td>33.0</td>\n",
" <td>50.0</td>\n",
" <td>37.0</td>\n",
" <td>59.0</td>\n",
" <td>56.0</td>\n",
" <td>58.0</td>\n",
" <td>58.0</td>\n",
" <td>39.0</td>\n",
" <td>58.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15389</th>\n",
" <td>Obama</td>\n",
" <td>17</td>\n",
" <td>Spain</td>\n",
" <td>59</td>\n",
" <td>76</td>\n",
" <td>Atlético Madrid</td>\n",
" <td>300000.0</td>\n",
" <td>4000.0</td>\n",
" <td>1408</td>\n",
" <td>66.0</td>\n",
" <td>...</td>\n",
" <td>37.0</td>\n",
" <td>29.0</td>\n",
" <td>48.0</td>\n",
" <td>34.0</td>\n",
" <td>58.0</td>\n",
" <td>56.0</td>\n",
" <td>58.0</td>\n",
" <td>58.0</td>\n",
" <td>40.0</td>\n",
" <td>58.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15341</th>\n",
" <td>A. Guarnone</td>\n",
" <td>18</td>\n",
" <td>Italy</td>\n",
" <td>59</td>\n",
" <td>74</td>\n",
" <td>Milan</td>\n",
" <td>260000.0</td>\n",
" <td>3000.0</td>\n",
" <td>997</td>\n",
" <td>54.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15180</th>\n",
" <td>J. Beste</td>\n",
" <td>18</td>\n",
" <td>Germany</td>\n",
" <td>59</td>\n",
" <td>78</td>\n",
" <td>Borussia Dortmund</td>\n",
" <td>290000.0</td>\n",
" <td>3000.0</td>\n",
" <td>1510</td>\n",
" <td>69.0</td>\n",
" <td>...</td>\n",
" <td>58.0</td>\n",
" <td>53.0</td>\n",
" <td>52.0</td>\n",
" <td>54.0</td>\n",
" <td>50.0</td>\n",
" <td>55.0</td>\n",
" <td>47.0</td>\n",
" <td>54.0</td>\n",
" <td>59.0</td>\n",
" <td>47.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15103</th>\n",
" <td>R. Nelson</td>\n",
" <td>17</td>\n",
" <td>England</td>\n",
" <td>59</td>\n",
" <td>83</td>\n",
" <td>Arsenal</td>\n",
" <td>350000.0</td>\n",
" <td>7000.0</td>\n",
" <td>1471</td>\n",
" <td>84.0</td>\n",
" <td>...</td>\n",
" <td>42.0</td>\n",
" <td>36.0</td>\n",
" <td>48.0</td>\n",
" <td>39.0</td>\n",
" <td>59.0</td>\n",
" <td>58.0</td>\n",
" <td>56.0</td>\n",
" <td>61.0</td>\n",
" <td>44.0</td>\n",
" <td>56.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15063</th>\n",
" <td>G. McEachran</td>\n",
" <td>16</td>\n",
" <td>England</td>\n",
" <td>59</td>\n",
" <td>79</td>\n",
" <td>Chelsea</td>\n",
" <td>300000.0</td>\n",
" <td>4000.0</td>\n",
" <td>1521</td>\n",
" <td>64.0</td>\n",
" <td>...</td>\n",
" <td>52.0</td>\n",
" <td>47.0</td>\n",
" <td>57.0</td>\n",
" <td>52.0</td>\n",
" <td>55.0</td>\n",
" <td>58.0</td>\n",
" <td>49.0</td>\n",
" <td>56.0</td>\n",
" <td>53.0</td>\n",
" <td>49.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14374</th>\n",
" <td>T. Chalobah</td>\n",
" <td>17</td>\n",
" <td>England</td>\n",
" <td>60</td>\n",
" <td>77</td>\n",
" <td>Chelsea</td>\n",
" <td>375000.0</td>\n",
" <td>6000.0</td>\n",
" <td>1491</td>\n",
" <td>71.0</td>\n",
" <td>...</td>\n",
" <td>58.0</td>\n",
" <td>59.0</td>\n",
" <td>48.0</td>\n",
" <td>55.0</td>\n",
" <td>47.0</td>\n",
" <td>50.0</td>\n",
" <td>49.0</td>\n",
" <td>49.0</td>\n",
" <td>56.0</td>\n",
" <td>49.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14511</th>\n",
" <td>K. Scott</td>\n",
" <td>19</td>\n",
" <td>United States</td>\n",
" <td>60</td>\n",
" <td>75</td>\n",
" <td>Chelsea</td>\n",
" <td>450000.0</td>\n",
" <td>7000.0</td>\n",
" <td>1553</td>\n",
" <td>61.0</td>\n",
" <td>...</td>\n",
" <td>53.0</td>\n",
" <td>46.0</td>\n",
" <td>59.0</td>\n",
" <td>53.0</td>\n",
" <td>57.0</td>\n",
" <td>59.0</td>\n",
" <td>52.0</td>\n",
" <td>59.0</td>\n",
" <td>55.0</td>\n",
" <td>52.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15044</th>\n",
" <td>D. Reimann</td>\n",
" <td>20</td>\n",
" <td>Germany</td>\n",
" <td>60</td>\n",
" <td>74</td>\n",
" <td>Borussia Dortmund</td>\n",
" <td>375000.0</td>\n",
" <td>4000.0</td>\n",
" <td>989</td>\n",
" <td>44.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>15034</th>\n",
" <td>Javi Díaz</td>\n",
" <td>20</td>\n",
" <td>Spain</td>\n",
" <td>60</td>\n",
" <td>72</td>\n",
" <td>Sevilla FC</td>\n",
" <td>290000.0</td>\n",
" <td>1000.0</td>\n",
" <td>1125</td>\n",
" <td>58.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14655</th>\n",
" <td>Tachi</td>\n",
" <td>19</td>\n",
" <td>Spain</td>\n",
" <td>60</td>\n",
" <td>77</td>\n",
" <td>Atlético Madrid</td>\n",
" <td>400000.0</td>\n",
" <td>3000.0</td>\n",
" <td>1369</td>\n",
" <td>63.0</td>\n",
" <td>...</td>\n",
" <td>57.0</td>\n",
" <td>59.0</td>\n",
" <td>46.0</td>\n",
" <td>54.0</td>\n",
" <td>42.0</td>\n",
" <td>45.0</td>\n",
" <td>44.0</td>\n",
" <td>43.0</td>\n",
" <td>54.0</td>\n",
" <td>44.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13783</th>\n",
" <td>A. Bernede</td>\n",
" <td>18</td>\n",
" <td>France</td>\n",
" <td>61</td>\n",
" <td>73</td>\n",
" <td>Paris Saint-Germain</td>\n",
" <td>425000.0</td>\n",
" <td>7000.0</td>\n",
" <td>1565</td>\n",
" <td>65.0</td>\n",
" <td>...</td>\n",
" <td>50.0</td>\n",
" <td>46.0</td>\n",
" <td>57.0</td>\n",
" <td>51.0</td>\n",
" <td>58.0</td>\n",
" <td>59.0</td>\n",
" <td>55.0</td>\n",
" <td>59.0</td>\n",
" <td>51.0</td>\n",
" <td>55.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13738</th>\n",
" <td>S. Schreck</td>\n",
" <td>18</td>\n",
" <td>Germany</td>\n",
" <td>61</td>\n",
" <td>78</td>\n",
" <td>Bayer 04 Leverkusen</td>\n",
" <td>525000.0</td>\n",
" <td>5000.0</td>\n",
" <td>1457</td>\n",
" <td>67.0</td>\n",
" <td>...</td>\n",
" <td>46.0</td>\n",
" <td>40.0</td>\n",
" <td>56.0</td>\n",
" <td>47.0</td>\n",
" <td>57.0</td>\n",
" <td>59.0</td>\n",
" <td>51.0</td>\n",
" <td>58.0</td>\n",
" <td>48.0</td>\n",
" <td>51.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13771</th>\n",
" <td>H. Wilson</td>\n",
" <td>20</td>\n",
" <td>Wales</td>\n",
" <td>61</td>\n",
" <td>79</td>\n",
" <td>Liverpool</td>\n",
" <td>550000.0</td>\n",
" <td>13000.0</td>\n",
" <td>1556</td>\n",
" <td>77.0</td>\n",
" <td>...</td>\n",
" <td>47.0</td>\n",
" <td>40.0</td>\n",
" <td>53.0</td>\n",
" <td>44.0</td>\n",
" <td>60.0</td>\n",
" <td>60.0</td>\n",
" <td>58.0</td>\n",
" <td>61.0</td>\n",
" <td>48.0</td>\n",
" <td>58.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13831</th>\n",
" <td>N. Dorsch</td>\n",
" <td>19</td>\n",
" <td>Germany</td>\n",
" <td>61</td>\n",
" <td>78</td>\n",
" <td>FC Bayern Munich</td>\n",
" <td>500000.0</td>\n",
" <td>7000.0</td>\n",
" <td>1607</td>\n",
" <td>68.0</td>\n",
" <td>...</td>\n",
" <td>59.0</td>\n",
" <td>59.0</td>\n",
" <td>58.0</td>\n",
" <td>60.0</td>\n",
" <td>56.0</td>\n",
" <td>58.0</td>\n",
" <td>53.0</td>\n",
" <td>57.0</td>\n",
" <td>59.0</td>\n",
" <td>53.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14172</th>\n",
" <td>M. Pantović</td>\n",
" <td>20</td>\n",
" <td>Serbia</td>\n",
" <td>61</td>\n",
" <td>69</td>\n",
" <td>FC Bayern Munich</td>\n",
" <td>375000.0</td>\n",
" <td>12000.0</td>\n",
" <td>1497</td>\n",
" <td>67.0</td>\n",
" <td>...</td>\n",
" <td>45.0</td>\n",
" <td>39.0</td>\n",
" <td>54.0</td>\n",
" <td>43.0</td>\n",
" <td>60.0</td>\n",
" <td>60.0</td>\n",
" <td>59.0</td>\n",
" <td>61.0</td>\n",
" <td>47.0</td>\n",
" <td>59.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13928</th>\n",
" <td>Juan Moreno</td>\n",
" <td>20</td>\n",
" <td>Spain</td>\n",
" <td>61</td>\n",
" <td>70</td>\n",
" <td>Atlético Madrid</td>\n",
" <td>400000.0</td>\n",
" <td>7000.0</td>\n",
" <td>1543</td>\n",
" <td>62.0</td>\n",
" <td>...</td>\n",
" <td>50.0</td>\n",
" <td>45.0</td>\n",
" <td>57.0</td>\n",
" <td>49.0</td>\n",
" <td>59.0</td>\n",
" <td>60.0</td>\n",
" <td>54.0</td>\n",
" <td>61.0</td>\n",
" <td>52.0</td>\n",
" <td>54.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14061</th>\n",
" <td>Olabe</td>\n",
" <td>21</td>\n",
" <td>Spain</td>\n",
" <td>61</td>\n",
" <td>70</td>\n",
" <td>Atlético Madrid</td>\n",
" <td>400000.0</td>\n",
" <td>7000.0</td>\n",
" <td>1500</td>\n",
" <td>62.0</td>\n",
" <td>...</td>\n",
" <td>50.0</td>\n",
" <td>46.0</td>\n",
" <td>58.0</td>\n",
" <td>51.0</td>\n",
" <td>60.0</td>\n",
" <td>60.0</td>\n",
" <td>57.0</td>\n",
" <td>60.0</td>\n",
" <td>52.0</td>\n",
" <td>57.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>14073</th>\n",
" <td>M. Gabbia</td>\n",
" <td>17</td>\n",
" <td>Italy</td>\n",
" <td>61</td>\n",
" <td>76</td>\n",
" <td>Milan</td>\n",
" <td>450000.0</td>\n",
" <td>7000.0</td>\n",
" <td>1386</td>\n",
" <td>62.0</td>\n",
" <td>...</td>\n",
" <td>55.0</td>\n",
" <td>60.0</td>\n",
" <td>41.0</td>\n",
" <td>51.0</td>\n",
" <td>41.0</td>\n",
" <td>42.0</td>\n",
" <td>43.0</td>\n",
" <td>42.0</td>\n",
" <td>52.0</td>\n",
" <td>43.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13834</th>\n",
" <td>F. Benko</td>\n",
" <td>19</td>\n",
" <td>Germany</td>\n",
" <td>61</td>\n",
" <td>78</td>\n",
" <td>FC Bayern Munich</td>\n",
" <td>550000.0</td>\n",
" <td>8000.0</td>\n",
" <td>1643</td>\n",
" <td>65.0</td>\n",
" <td>...</td>\n",
" <td>54.0</td>\n",
" <td>53.0</td>\n",
" <td>60.0</td>\n",
" <td>56.0</td>\n",
" <td>59.0</td>\n",
" <td>59.0</td>\n",
" <td>56.0</td>\n",
" <td>59.0</td>\n",
" <td>55.0</td>\n",
" <td>56.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12876</th>\n",
" <td>L. Jones</td>\n",
" <td>21</td>\n",
" <td>England</td>\n",
" <td>62</td>\n",
" <td>70</td>\n",
" <td>Liverpool</td>\n",
" <td>400000.0</td>\n",
" <td>11000.0</td>\n",
" <td>1328</td>\n",
" <td>46.0</td>\n",
" <td>...</td>\n",
" <td>52.0</td>\n",
" <td>61.0</td>\n",
" <td>43.0</td>\n",
" <td>54.0</td>\n",
" <td>38.0</td>\n",
" <td>39.0</td>\n",
" <td>41.0</td>\n",
" <td>38.0</td>\n",
" <td>50.0</td>\n",
" <td>41.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12985</th>\n",
" <td>N. Schiappacasse</td>\n",
" <td>18</td>\n",
" <td>Uruguay</td>\n",
" <td>62</td>\n",
" <td>78</td>\n",
" <td>Atlético Madrid</td>\n",
" <td>625000.0</td>\n",
" <td>5000.0</td>\n",
" <td>1453</td>\n",
" <td>64.0</td>\n",
" <td>...</td>\n",
" <td>42.0</td>\n",
" <td>35.0</td>\n",
" <td>52.0</td>\n",
" <td>39.0</td>\n",
" <td>62.0</td>\n",
" <td>59.0</td>\n",
" <td>61.0</td>\n",
" <td>62.0</td>\n",
" <td>44.0</td>\n",
" <td>61.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13274</th>\n",
" <td>K. Bare</td>\n",
" <td>19</td>\n",
" <td>Albania</td>\n",
" <td>62</td>\n",
" <td>75</td>\n",
" <td>Atlético Madrid</td>\n",
" <td>575000.0</td>\n",
" <td>5000.0</td>\n",
" <td>1629</td>\n",
" <td>69.0</td>\n",
" <td>...</td>\n",
" <td>56.0</td>\n",
" <td>55.0</td>\n",
" <td>62.0</td>\n",
" <td>59.0</td>\n",
" <td>60.0</td>\n",
" <td>60.0</td>\n",
" <td>58.0</td>\n",
" <td>58.0</td>\n",
" <td>57.0</td>\n",
" <td>58.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>13074</th>\n",
" <td>A. Pinamonti</td>\n",
" <td>18</td>\n",
" <td>Italy</td>\n",
" <td>62</td>\n",
" <td>80</td>\n",
" <td>Inter</td>\n",
" <td>625000.0</td>\n",
" <td>6000.0</td>\n",
" <td>1446</td>\n",
" <td>55.0</td>\n",
" <td>...</td>\n",
" <td>37.0</td>\n",
" <td>36.0</td>\n",
" <td>50.0</td>\n",
" <td>37.0</td>\n",
" <td>60.0</td>\n",
" <td>55.0</td>\n",
" <td>61.0</td>\n",
" <td>58.0</td>\n",
" <td>39.0</td>\n",
" <td>61.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>...</th>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8967</th>\n",
" <td>João Costa</td>\n",
" <td>21</td>\n",
" <td>Portugal</td>\n",
" <td>66</td>\n",
" <td>76</td>\n",
" <td>FC Porto</td>\n",
" <td>800000.0</td>\n",
" <td>2000.0</td>\n",
" <td>935</td>\n",
" <td>18.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9512</th>\n",
" <td>Moreto Cassamá</td>\n",
" <td>19</td>\n",
" <td>Portugal</td>\n",
" <td>66</td>\n",
" <td>81</td>\n",
" <td>FC Porto</td>\n",
" <td>1400000.0</td>\n",
" <td>2000.0</td>\n",
" <td>1803</td>\n",
" <td>74.0</td>\n",
" <td>...</td>\n",
" <td>58.0</td>\n",
" <td>53.0</td>\n",
" <td>65.0</td>\n",
" <td>58.0</td>\n",
" <td>67.0</td>\n",
" <td>67.0</td>\n",
" <td>64.0</td>\n",
" <td>67.0</td>\n",
" <td>59.0</td>\n",
" <td>64.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9418</th>\n",
" <td>J. Riley</td>\n",
" <td>20</td>\n",
" <td>England</td>\n",
" <td>66</td>\n",
" <td>78</td>\n",
" <td>Manchester United</td>\n",
" <td>1000000.0</td>\n",
" <td>18000.0</td>\n",
" <td>1719</td>\n",
" <td>78.0</td>\n",
" <td>...</td>\n",
" <td>65.0</td>\n",
" <td>62.0</td>\n",
" <td>59.0</td>\n",
" <td>62.0</td>\n",
" <td>58.0</td>\n",
" <td>63.0</td>\n",
" <td>56.0</td>\n",
" <td>60.0</td>\n",
" <td>65.0</td>\n",
" <td>56.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9580</th>\n",
" <td>N. Lomb</td>\n",
" <td>23</td>\n",
" <td>Germany</td>\n",
" <td>66</td>\n",
" <td>71</td>\n",
" <td>Bayer 04 Leverkusen</td>\n",
" <td>625000.0</td>\n",
" <td>8000.0</td>\n",
" <td>1073</td>\n",
" <td>38.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9690</th>\n",
" <td>O. Ejaria</td>\n",
" <td>19</td>\n",
" <td>England</td>\n",
" <td>66</td>\n",
" <td>81</td>\n",
" <td>Liverpool</td>\n",
" <td>1400000.0</td>\n",
" <td>13000.0</td>\n",
" <td>1703</td>\n",
" <td>71.0</td>\n",
" <td>...</td>\n",
" <td>56.0</td>\n",
" <td>53.0</td>\n",
" <td>63.0</td>\n",
" <td>57.0</td>\n",
" <td>64.0</td>\n",
" <td>65.0</td>\n",
" <td>63.0</td>\n",
" <td>64.0</td>\n",
" <td>58.0</td>\n",
" <td>63.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9711</th>\n",
" <td>A. Donnarumma</td>\n",
" <td>26</td>\n",
" <td>Italy</td>\n",
" <td>66</td>\n",
" <td>70</td>\n",
" <td>Milan</td>\n",
" <td>575000.0</td>\n",
" <td>16000.0</td>\n",
" <td>930</td>\n",
" <td>13.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9514</th>\n",
" <td>Álvaro Tejero</td>\n",
" <td>20</td>\n",
" <td>Spain</td>\n",
" <td>66</td>\n",
" <td>78</td>\n",
" <td>Real Madrid CF</td>\n",
" <td>1000000.0</td>\n",
" <td>22000.0</td>\n",
" <td>1758</td>\n",
" <td>76.0</td>\n",
" <td>...</td>\n",
" <td>65.0</td>\n",
" <td>62.0</td>\n",
" <td>56.0</td>\n",
" <td>60.0</td>\n",
" <td>58.0</td>\n",
" <td>59.0</td>\n",
" <td>56.0</td>\n",
" <td>59.0</td>\n",
" <td>65.0</td>\n",
" <td>56.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8741</th>\n",
" <td>C. Willock</td>\n",
" <td>19</td>\n",
" <td>England</td>\n",
" <td>67</td>\n",
" <td>82</td>\n",
" <td>SL Benfica</td>\n",
" <td>1600000.0</td>\n",
" <td>4000.0</td>\n",
" <td>1502</td>\n",
" <td>83.0</td>\n",
" <td>...</td>\n",
" <td>43.0</td>\n",
" <td>33.0</td>\n",
" <td>56.0</td>\n",
" <td>41.0</td>\n",
" <td>65.0</td>\n",
" <td>66.0</td>\n",
" <td>60.0</td>\n",
" <td>66.0</td>\n",
" <td>48.0</td>\n",
" <td>60.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8737</th>\n",
" <td>Caio Henrique</td>\n",
" <td>19</td>\n",
" <td>Brazil</td>\n",
" <td>67</td>\n",
" <td>81</td>\n",
" <td>Atlético Madrid</td>\n",
" <td>1600000.0</td>\n",
" <td>15000.0</td>\n",
" <td>1603</td>\n",
" <td>67.0</td>\n",
" <td>...</td>\n",
" <td>49.0</td>\n",
" <td>42.0</td>\n",
" <td>64.0</td>\n",
" <td>52.0</td>\n",
" <td>63.0</td>\n",
" <td>63.0</td>\n",
" <td>57.0</td>\n",
" <td>63.0</td>\n",
" <td>51.0</td>\n",
" <td>57.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8581</th>\n",
" <td>Unai Simón</td>\n",
" <td>20</td>\n",
" <td>Spain</td>\n",
" <td>67</td>\n",
" <td>80</td>\n",
" <td>Athletic Club de Bilbao</td>\n",
" <td>1200000.0</td>\n",
" <td>7000.0</td>\n",
" <td>1095</td>\n",
" <td>46.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7995</th>\n",
" <td>R. Habran</td>\n",
" <td>23</td>\n",
" <td>France</td>\n",
" <td>67</td>\n",
" <td>72</td>\n",
" <td>Paris Saint-Germain</td>\n",
" <td>1000000.0</td>\n",
" <td>32000.0</td>\n",
" <td>1779</td>\n",
" <td>87.0</td>\n",
" <td>...</td>\n",
" <td>55.0</td>\n",
" <td>51.0</td>\n",
" <td>59.0</td>\n",
" <td>53.0</td>\n",
" <td>65.0</td>\n",
" <td>66.0</td>\n",
" <td>64.0</td>\n",
" <td>67.0</td>\n",
" <td>56.0</td>\n",
" <td>64.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7871</th>\n",
" <td>Gerson</td>\n",
" <td>20</td>\n",
" <td>Brazil</td>\n",
" <td>67</td>\n",
" <td>80</td>\n",
" <td>Roma</td>\n",
" <td>1500000.0</td>\n",
" <td>24000.0</td>\n",
" <td>1701</td>\n",
" <td>71.0</td>\n",
" <td>...</td>\n",
" <td>52.0</td>\n",
" <td>45.0</td>\n",
" <td>66.0</td>\n",
" <td>55.0</td>\n",
" <td>66.0</td>\n",
" <td>68.0</td>\n",
" <td>62.0</td>\n",
" <td>67.0</td>\n",
" <td>56.0</td>\n",
" <td>62.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7789</th>\n",
" <td>Paulo Lopes</td>\n",
" <td>39</td>\n",
" <td>Portugal</td>\n",
" <td>67</td>\n",
" <td>67</td>\n",
" <td>SL Benfica</td>\n",
" <td>50000.0</td>\n",
" <td>3000.0</td>\n",
" <td>1120</td>\n",
" <td>38.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7759</th>\n",
" <td>V. Yurchenko</td>\n",
" <td>23</td>\n",
" <td>Ukraine</td>\n",
" <td>67</td>\n",
" <td>73</td>\n",
" <td>Bayer 04 Leverkusen</td>\n",
" <td>1000000.0</td>\n",
" <td>23000.0</td>\n",
" <td>1769</td>\n",
" <td>67.0</td>\n",
" <td>...</td>\n",
" <td>59.0</td>\n",
" <td>55.0</td>\n",
" <td>66.0</td>\n",
" <td>61.0</td>\n",
" <td>66.0</td>\n",
" <td>67.0</td>\n",
" <td>63.0</td>\n",
" <td>67.0</td>\n",
" <td>61.0</td>\n",
" <td>63.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6678</th>\n",
" <td>A. Isak</td>\n",
" <td>17</td>\n",
" <td>Sweden</td>\n",
" <td>68</td>\n",
" <td>84</td>\n",
" <td>Borussia Dortmund</td>\n",
" <td>1800000.0</td>\n",
" <td>18000.0</td>\n",
" <td>1574</td>\n",
" <td>80.0</td>\n",
" <td>...</td>\n",
" <td>44.0</td>\n",
" <td>38.0</td>\n",
" <td>56.0</td>\n",
" <td>42.0</td>\n",
" <td>66.0</td>\n",
" <td>64.0</td>\n",
" <td>67.0</td>\n",
" <td>66.0</td>\n",
" <td>47.0</td>\n",
" <td>67.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6987</th>\n",
" <td>Diogo Dalot</td>\n",
" <td>18</td>\n",
" <td>Portugal</td>\n",
" <td>68</td>\n",
" <td>83</td>\n",
" <td>FC Porto</td>\n",
" <td>1600000.0</td>\n",
" <td>4000.0</td>\n",
" <td>1686</td>\n",
" <td>71.0</td>\n",
" <td>...</td>\n",
" <td>67.0</td>\n",
" <td>67.0</td>\n",
" <td>58.0</td>\n",
" <td>63.0</td>\n",
" <td>61.0</td>\n",
" <td>63.0</td>\n",
" <td>61.0</td>\n",
" <td>62.0</td>\n",
" <td>67.0</td>\n",
" <td>61.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7093</th>\n",
" <td>M. Chrien</td>\n",
" <td>21</td>\n",
" <td>Slovakia</td>\n",
" <td>68</td>\n",
" <td>77</td>\n",
" <td>SL Benfica</td>\n",
" <td>1400000.0</td>\n",
" <td>6000.0</td>\n",
" <td>1744</td>\n",
" <td>67.0</td>\n",
" <td>...</td>\n",
" <td>61.0</td>\n",
" <td>59.0</td>\n",
" <td>67.0</td>\n",
" <td>62.0</td>\n",
" <td>66.0</td>\n",
" <td>68.0</td>\n",
" <td>64.0</td>\n",
" <td>66.0</td>\n",
" <td>62.0</td>\n",
" <td>64.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7164</th>\n",
" <td>Galeno</td>\n",
" <td>19</td>\n",
" <td>Brazil</td>\n",
" <td>68</td>\n",
" <td>79</td>\n",
" <td>FC Porto</td>\n",
" <td>1500000.0</td>\n",
" <td>5000.0</td>\n",
" <td>1695</td>\n",
" <td>79.0</td>\n",
" <td>...</td>\n",
" <td>52.0</td>\n",
" <td>45.0</td>\n",
" <td>60.0</td>\n",
" <td>51.0</td>\n",
" <td>68.0</td>\n",
" <td>67.0</td>\n",
" <td>66.0</td>\n",
" <td>68.0</td>\n",
" <td>55.0</td>\n",
" <td>66.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7506</th>\n",
" <td>Rúben Dias</td>\n",
" <td>20</td>\n",
" <td>Portugal</td>\n",
" <td>68</td>\n",
" <td>78</td>\n",
" <td>SL Benfica</td>\n",
" <td>1300000.0</td>\n",
" <td>5000.0</td>\n",
" <td>1458</td>\n",
" <td>62.0</td>\n",
" <td>...</td>\n",
" <td>62.0</td>\n",
" <td>67.0</td>\n",
" <td>48.0</td>\n",
" <td>60.0</td>\n",
" <td>47.0</td>\n",
" <td>48.0</td>\n",
" <td>48.0</td>\n",
" <td>46.0</td>\n",
" <td>59.0</td>\n",
" <td>48.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7604</th>\n",
" <td>Óscar</td>\n",
" <td>19</td>\n",
" <td>Spain</td>\n",
" <td>68</td>\n",
" <td>81</td>\n",
" <td>Real Madrid CF</td>\n",
" <td>1700000.0</td>\n",
" <td>37000.0</td>\n",
" <td>1667</td>\n",
" <td>64.0</td>\n",
" <td>...</td>\n",
" <td>51.0</td>\n",
" <td>48.0</td>\n",
" <td>63.0</td>\n",
" <td>55.0</td>\n",
" <td>65.0</td>\n",
" <td>63.0</td>\n",
" <td>61.0</td>\n",
" <td>65.0</td>\n",
" <td>53.0</td>\n",
" <td>61.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>7500</th>\n",
" <td>Wallyson Mallmann</td>\n",
" <td>23</td>\n",
" <td>Brazil</td>\n",
" <td>68</td>\n",
" <td>75</td>\n",
" <td>Sporting CP</td>\n",
" <td>1300000.0</td>\n",
" <td>8000.0</td>\n",
" <td>1890</td>\n",
" <td>70.0</td>\n",
" <td>...</td>\n",
" <td>61.0</td>\n",
" <td>60.0</td>\n",
" <td>66.0</td>\n",
" <td>62.0</td>\n",
" <td>67.0</td>\n",
" <td>66.0</td>\n",
" <td>67.0</td>\n",
" <td>67.0</td>\n",
" <td>62.0</td>\n",
" <td>67.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6545</th>\n",
" <td>Wallace Oliveira</td>\n",
" <td>23</td>\n",
" <td>Brazil</td>\n",
" <td>69</td>\n",
" <td>78</td>\n",
" <td>Chelsea</td>\n",
" <td>1400000.0</td>\n",
" <td>40000.0</td>\n",
" <td>1888</td>\n",
" <td>76.0</td>\n",
" <td>...</td>\n",
" <td>68.0</td>\n",
" <td>66.0</td>\n",
" <td>67.0</td>\n",
" <td>68.0</td>\n",
" <td>67.0</td>\n",
" <td>69.0</td>\n",
" <td>64.0</td>\n",
" <td>68.0</td>\n",
" <td>70.0</td>\n",
" <td>64.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6486</th>\n",
" <td>R. Bentancur</td>\n",
" <td>20</td>\n",
" <td>Uruguay</td>\n",
" <td>69</td>\n",
" <td>83</td>\n",
" <td>Juventus</td>\n",
" <td>2300000.0</td>\n",
" <td>37000.0</td>\n",
" <td>1760</td>\n",
" <td>62.0</td>\n",
" <td>...</td>\n",
" <td>62.0</td>\n",
" <td>59.0</td>\n",
" <td>68.0</td>\n",
" <td>64.0</td>\n",
" <td>65.0</td>\n",
" <td>66.0</td>\n",
" <td>61.0</td>\n",
" <td>65.0</td>\n",
" <td>63.0</td>\n",
" <td>61.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6369</th>\n",
" <td>A. Werner</td>\n",
" <td>21</td>\n",
" <td>Argentina</td>\n",
" <td>69</td>\n",
" <td>81</td>\n",
" <td>Atlético Madrid</td>\n",
" <td>1500000.0</td>\n",
" <td>14000.0</td>\n",
" <td>1135</td>\n",
" <td>41.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6358</th>\n",
" <td>Pedro Pereira</td>\n",
" <td>19</td>\n",
" <td>Portugal</td>\n",
" <td>69</td>\n",
" <td>82</td>\n",
" <td>SL Benfica</td>\n",
" <td>1700000.0</td>\n",
" <td>4000.0</td>\n",
" <td>1723</td>\n",
" <td>75.0</td>\n",
" <td>...</td>\n",
" <td>68.0</td>\n",
" <td>66.0</td>\n",
" <td>62.0</td>\n",
" <td>65.0</td>\n",
" <td>60.0</td>\n",
" <td>64.0</td>\n",
" <td>56.0</td>\n",
" <td>62.0</td>\n",
" <td>68.0</td>\n",
" <td>56.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6322</th>\n",
" <td>C. Pinsoglio</td>\n",
" <td>27</td>\n",
" <td>Italy</td>\n",
" <td>69</td>\n",
" <td>69</td>\n",
" <td>Juventus</td>\n",
" <td>700000.0</td>\n",
" <td>34000.0</td>\n",
" <td>1062</td>\n",
" <td>43.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6253</th>\n",
" <td>J. Wilson</td>\n",
" <td>21</td>\n",
" <td>England</td>\n",
" <td>69</td>\n",
" <td>76</td>\n",
" <td>Manchester United</td>\n",
" <td>1500000.0</td>\n",
" <td>48000.0</td>\n",
" <td>1632</td>\n",
" <td>74.0</td>\n",
" <td>...</td>\n",
" <td>45.0</td>\n",
" <td>40.0</td>\n",
" <td>59.0</td>\n",
" <td>45.0</td>\n",
" <td>67.0</td>\n",
" <td>65.0</td>\n",
" <td>68.0</td>\n",
" <td>66.0</td>\n",
" <td>48.0</td>\n",
" <td>68.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>6160</th>\n",
" <td>T. Alexander-Arnold</td>\n",
" <td>18</td>\n",
" <td>England</td>\n",
" <td>69</td>\n",
" <td>85</td>\n",
" <td>Liverpool</td>\n",
" <td>1900000.0</td>\n",
" <td>23000.0</td>\n",
" <td>1904</td>\n",
" <td>81.0</td>\n",
" <td>...</td>\n",
" <td>68.0</td>\n",
" <td>64.0</td>\n",
" <td>66.0</td>\n",
" <td>66.0</td>\n",
" <td>65.0</td>\n",
" <td>68.0</td>\n",
" <td>62.0</td>\n",
" <td>67.0</td>\n",
" <td>69.0</td>\n",
" <td>62.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5876</th>\n",
" <td>M. Delač</td>\n",
" <td>24</td>\n",
" <td>Croatia</td>\n",
" <td>69</td>\n",
" <td>72</td>\n",
" <td>Chelsea</td>\n",
" <td>950000.0</td>\n",
" <td>31000.0</td>\n",
" <td>1008</td>\n",
" <td>31.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5808</th>\n",
" <td>C. Brannagan</td>\n",
" <td>21</td>\n",
" <td>England</td>\n",
" <td>69</td>\n",
" <td>79</td>\n",
" <td>Liverpool</td>\n",
" <td>1700000.0</td>\n",
" <td>38000.0</td>\n",
" <td>1881</td>\n",
" <td>64.0</td>\n",
" <td>...</td>\n",
" <td>65.0</td>\n",
" <td>64.0</td>\n",
" <td>68.0</td>\n",
" <td>67.0</td>\n",
" <td>65.0</td>\n",
" <td>66.0</td>\n",
" <td>63.0</td>\n",
" <td>65.0</td>\n",
" <td>66.0</td>\n",
" <td>63.0</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>106 rows × 71 columns</p>\n",
"</div>"
],
"text/plain": [
" Name Age Nationality Overall Potential \\\n",
"17331 A. Zerbin 18 Italy 53 73 \n",
"16714 P. Fritsch 18 Germany 55 71 \n",
"16406 D. Sauerland 20 Germany 56 68 \n",
"15718 J. Maddox 18 England 58 74 \n",
"15549 R. Corlu 19 Denmark 58 69 \n",
"15479 T. Bola 18 England 59 72 \n",
"15409 E. Nketiah 18 England 59 80 \n",
"15389 Obama 17 Spain 59 76 \n",
"15341 A. Guarnone 18 Italy 59 74 \n",
"15180 J. Beste 18 Germany 59 78 \n",
"15103 R. Nelson 17 England 59 83 \n",
"15063 G. McEachran 16 England 59 79 \n",
"14374 T. Chalobah 17 England 60 77 \n",
"14511 K. Scott 19 United States 60 75 \n",
"15044 D. Reimann 20 Germany 60 74 \n",
"15034 Javi Díaz 20 Spain 60 72 \n",
"14655 Tachi 19 Spain 60 77 \n",
"13783 A. Bernede 18 France 61 73 \n",
"13738 S. Schreck 18 Germany 61 78 \n",
"13771 H. Wilson 20 Wales 61 79 \n",
"13831 N. Dorsch 19 Germany 61 78 \n",
"14172 M. Pantović 20 Serbia 61 69 \n",
"13928 Juan Moreno 20 Spain 61 70 \n",
"14061 Olabe 21 Spain 61 70 \n",
"14073 M. Gabbia 17 Italy 61 76 \n",
"13834 F. Benko 19 Germany 61 78 \n",
"12876 L. Jones 21 England 62 70 \n",
"12985 N. Schiappacasse 18 Uruguay 62 78 \n",
"13274 K. Bare 19 Albania 62 75 \n",
"13074 A. Pinamonti 18 Italy 62 80 \n",
"... ... ... ... ... ... \n",
"8967 João Costa 21 Portugal 66 76 \n",
"9512 Moreto Cassamá 19 Portugal 66 81 \n",
"9418 J. Riley 20 England 66 78 \n",
"9580 N. Lomb 23 Germany 66 71 \n",
"9690 O. Ejaria 19 England 66 81 \n",
"9711 A. Donnarumma 26 Italy 66 70 \n",
"9514 Álvaro Tejero 20 Spain 66 78 \n",
"8741 C. Willock 19 England 67 82 \n",
"8737 Caio Henrique 19 Brazil 67 81 \n",
"8581 Unai Simón 20 Spain 67 80 \n",
"7995 R. Habran 23 France 67 72 \n",
"7871 Gerson 20 Brazil 67 80 \n",
"7789 Paulo Lopes 39 Portugal 67 67 \n",
"7759 V. Yurchenko 23 Ukraine 67 73 \n",
"6678 A. Isak 17 Sweden 68 84 \n",
"6987 Diogo Dalot 18 Portugal 68 83 \n",
"7093 M. Chrien 21 Slovakia 68 77 \n",
"7164 Galeno 19 Brazil 68 79 \n",
"7506 Rúben Dias 20 Portugal 68 78 \n",
"7604 Óscar 19 Spain 68 81 \n",
"7500 Wallyson Mallmann 23 Brazil 68 75 \n",
"6545 Wallace Oliveira 23 Brazil 69 78 \n",
"6486 R. Bentancur 20 Uruguay 69 83 \n",
"6369 A. Werner 21 Argentina 69 81 \n",
"6358 Pedro Pereira 19 Portugal 69 82 \n",
"6322 C. Pinsoglio 27 Italy 69 69 \n",
"6253 J. Wilson 21 England 69 76 \n",
"6160 T. Alexander-Arnold 18 England 69 85 \n",
"5876 M. Delač 24 Croatia 69 72 \n",
"5808 C. Brannagan 21 England 69 79 \n",
"\n",
" Club Value Wage Special Acceleration \\\n",
"17331 Napoli 120000.0 4000.0 1324 42.0 \n",
"16714 Borussia Dortmund 160000.0 3000.0 1349 52.0 \n",
"16406 Borussia Dortmund 160000.0 5000.0 1526 55.0 \n",
"15718 Chelsea 260000.0 7000.0 1402 71.0 \n",
"15549 Roma 210000.0 4000.0 1473 73.0 \n",
"15479 Arsenal 250000.0 6000.0 1344 59.0 \n",
"15409 Arsenal 350000.0 8000.0 1404 77.0 \n",
"15389 Atlético Madrid 300000.0 4000.0 1408 66.0 \n",
"15341 Milan 260000.0 3000.0 997 54.0 \n",
"15180 Borussia Dortmund 290000.0 3000.0 1510 69.0 \n",
"15103 Arsenal 350000.0 7000.0 1471 84.0 \n",
"15063 Chelsea 300000.0 4000.0 1521 64.0 \n",
"14374 Chelsea 375000.0 6000.0 1491 71.0 \n",
"14511 Chelsea 450000.0 7000.0 1553 61.0 \n",
"15044 Borussia Dortmund 375000.0 4000.0 989 44.0 \n",
"15034 Sevilla FC 290000.0 1000.0 1125 58.0 \n",
"14655 Atlético Madrid 400000.0 3000.0 1369 63.0 \n",
"13783 Paris Saint-Germain 425000.0 7000.0 1565 65.0 \n",
"13738 Bayer 04 Leverkusen 525000.0 5000.0 1457 67.0 \n",
"13771 Liverpool 550000.0 13000.0 1556 77.0 \n",
"13831 FC Bayern Munich 500000.0 7000.0 1607 68.0 \n",
"14172 FC Bayern Munich 375000.0 12000.0 1497 67.0 \n",
"13928 Atlético Madrid 400000.0 7000.0 1543 62.0 \n",
"14061 Atlético Madrid 400000.0 7000.0 1500 62.0 \n",
"14073 Milan 450000.0 7000.0 1386 62.0 \n",
"13834 FC Bayern Munich 550000.0 8000.0 1643 65.0 \n",
"12876 Liverpool 400000.0 11000.0 1328 46.0 \n",
"12985 Atlético Madrid 625000.0 5000.0 1453 64.0 \n",
"13274 Atlético Madrid 575000.0 5000.0 1629 69.0 \n",
"13074 Inter 625000.0 6000.0 1446 55.0 \n",
"... ... ... ... ... ... \n",
"8967 FC Porto 800000.0 2000.0 935 18.0 \n",
"9512 FC Porto 1400000.0 2000.0 1803 74.0 \n",
"9418 Manchester United 1000000.0 18000.0 1719 78.0 \n",
"9580 Bayer 04 Leverkusen 625000.0 8000.0 1073 38.0 \n",
"9690 Liverpool 1400000.0 13000.0 1703 71.0 \n",
"9711 Milan 575000.0 16000.0 930 13.0 \n",
"9514 Real Madrid CF 1000000.0 22000.0 1758 76.0 \n",
"8741 SL Benfica 1600000.0 4000.0 1502 83.0 \n",
"8737 Atlético Madrid 1600000.0 15000.0 1603 67.0 \n",
"8581 Athletic Club de Bilbao 1200000.0 7000.0 1095 46.0 \n",
"7995 Paris Saint-Germain 1000000.0 32000.0 1779 87.0 \n",
"7871 Roma 1500000.0 24000.0 1701 71.0 \n",
"7789 SL Benfica 50000.0 3000.0 1120 38.0 \n",
"7759 Bayer 04 Leverkusen 1000000.0 23000.0 1769 67.0 \n",
"6678 Borussia Dortmund 1800000.0 18000.0 1574 80.0 \n",
"6987 FC Porto 1600000.0 4000.0 1686 71.0 \n",
"7093 SL Benfica 1400000.0 6000.0 1744 67.0 \n",
"7164 FC Porto 1500000.0 5000.0 1695 79.0 \n",
"7506 SL Benfica 1300000.0 5000.0 1458 62.0 \n",
"7604 Real Madrid CF 1700000.0 37000.0 1667 64.0 \n",
"7500 Sporting CP 1300000.0 8000.0 1890 70.0 \n",
"6545 Chelsea 1400000.0 40000.0 1888 76.0 \n",
"6486 Juventus 2300000.0 37000.0 1760 62.0 \n",
"6369 Atlético Madrid 1500000.0 14000.0 1135 41.0 \n",
"6358 SL Benfica 1700000.0 4000.0 1723 75.0 \n",
"6322 Juventus 700000.0 34000.0 1062 43.0 \n",
"6253 Manchester United 1500000.0 48000.0 1632 74.0 \n",
"6160 Liverpool 1900000.0 23000.0 1904 81.0 \n",
"5876 Chelsea 950000.0 31000.0 1008 31.0 \n",
"5808 Liverpool 1700000.0 38000.0 1881 64.0 \n",
"\n",
" ... RB RCB RCM RDM RF RM RS RW RWB ST \n",
"17331 ... 39.0 37.0 49.0 41.0 52.0 51.0 51.0 53.0 41.0 51.0 \n",
"16714 ... 49.0 54.0 44.0 50.0 41.0 42.0 42.0 42.0 48.0 42.0 \n",
"16406 ... 46.0 41.0 55.0 47.0 57.0 56.0 53.0 58.0 49.0 53.0 \n",
"15718 ... 42.0 34.0 51.0 41.0 56.0 57.0 52.0 57.0 45.0 52.0 \n",
"15549 ... 43.0 34.0 51.0 40.0 56.0 57.0 53.0 58.0 45.0 53.0 \n",
"15479 ... 54.0 58.0 41.0 50.0 40.0 40.0 42.0 40.0 51.0 42.0 \n",
"15409 ... 37.0 33.0 50.0 37.0 59.0 56.0 58.0 58.0 39.0 58.0 \n",
"15389 ... 37.0 29.0 48.0 34.0 58.0 56.0 58.0 58.0 40.0 58.0 \n",
"15341 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"15180 ... 58.0 53.0 52.0 54.0 50.0 55.0 47.0 54.0 59.0 47.0 \n",
"15103 ... 42.0 36.0 48.0 39.0 59.0 58.0 56.0 61.0 44.0 56.0 \n",
"15063 ... 52.0 47.0 57.0 52.0 55.0 58.0 49.0 56.0 53.0 49.0 \n",
"14374 ... 58.0 59.0 48.0 55.0 47.0 50.0 49.0 49.0 56.0 49.0 \n",
"14511 ... 53.0 46.0 59.0 53.0 57.0 59.0 52.0 59.0 55.0 52.0 \n",
"15044 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"15034 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"14655 ... 57.0 59.0 46.0 54.0 42.0 45.0 44.0 43.0 54.0 44.0 \n",
"13783 ... 50.0 46.0 57.0 51.0 58.0 59.0 55.0 59.0 51.0 55.0 \n",
"13738 ... 46.0 40.0 56.0 47.0 57.0 59.0 51.0 58.0 48.0 51.0 \n",
"13771 ... 47.0 40.0 53.0 44.0 60.0 60.0 58.0 61.0 48.0 58.0 \n",
"13831 ... 59.0 59.0 58.0 60.0 56.0 58.0 53.0 57.0 59.0 53.0 \n",
"14172 ... 45.0 39.0 54.0 43.0 60.0 60.0 59.0 61.0 47.0 59.0 \n",
"13928 ... 50.0 45.0 57.0 49.0 59.0 60.0 54.0 61.0 52.0 54.0 \n",
"14061 ... 50.0 46.0 58.0 51.0 60.0 60.0 57.0 60.0 52.0 57.0 \n",
"14073 ... 55.0 60.0 41.0 51.0 41.0 42.0 43.0 42.0 52.0 43.0 \n",
"13834 ... 54.0 53.0 60.0 56.0 59.0 59.0 56.0 59.0 55.0 56.0 \n",
"12876 ... 52.0 61.0 43.0 54.0 38.0 39.0 41.0 38.0 50.0 41.0 \n",
"12985 ... 42.0 35.0 52.0 39.0 62.0 59.0 61.0 62.0 44.0 61.0 \n",
"13274 ... 56.0 55.0 62.0 59.0 60.0 60.0 58.0 58.0 57.0 58.0 \n",
"13074 ... 37.0 36.0 50.0 37.0 60.0 55.0 61.0 58.0 39.0 61.0 \n",
"... ... ... ... ... ... ... ... ... ... ... ... \n",
"8967 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"9512 ... 58.0 53.0 65.0 58.0 67.0 67.0 64.0 67.0 59.0 64.0 \n",
"9418 ... 65.0 62.0 59.0 62.0 58.0 63.0 56.0 60.0 65.0 56.0 \n",
"9580 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"9690 ... 56.0 53.0 63.0 57.0 64.0 65.0 63.0 64.0 58.0 63.0 \n",
"9711 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"9514 ... 65.0 62.0 56.0 60.0 58.0 59.0 56.0 59.0 65.0 56.0 \n",
"8741 ... 43.0 33.0 56.0 41.0 65.0 66.0 60.0 66.0 48.0 60.0 \n",
"8737 ... 49.0 42.0 64.0 52.0 63.0 63.0 57.0 63.0 51.0 57.0 \n",
"8581 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"7995 ... 55.0 51.0 59.0 53.0 65.0 66.0 64.0 67.0 56.0 64.0 \n",
"7871 ... 52.0 45.0 66.0 55.0 66.0 68.0 62.0 67.0 56.0 62.0 \n",
"7789 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"7759 ... 59.0 55.0 66.0 61.0 66.0 67.0 63.0 67.0 61.0 63.0 \n",
"6678 ... 44.0 38.0 56.0 42.0 66.0 64.0 67.0 66.0 47.0 67.0 \n",
"6987 ... 67.0 67.0 58.0 63.0 61.0 63.0 61.0 62.0 67.0 61.0 \n",
"7093 ... 61.0 59.0 67.0 62.0 66.0 68.0 64.0 66.0 62.0 64.0 \n",
"7164 ... 52.0 45.0 60.0 51.0 68.0 67.0 66.0 68.0 55.0 66.0 \n",
"7506 ... 62.0 67.0 48.0 60.0 47.0 48.0 48.0 46.0 59.0 48.0 \n",
"7604 ... 51.0 48.0 63.0 55.0 65.0 63.0 61.0 65.0 53.0 61.0 \n",
"7500 ... 61.0 60.0 66.0 62.0 67.0 66.0 67.0 67.0 62.0 67.0 \n",
"6545 ... 68.0 66.0 67.0 68.0 67.0 69.0 64.0 68.0 70.0 64.0 \n",
"6486 ... 62.0 59.0 68.0 64.0 65.0 66.0 61.0 65.0 63.0 61.0 \n",
"6369 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"6358 ... 68.0 66.0 62.0 65.0 60.0 64.0 56.0 62.0 68.0 56.0 \n",
"6322 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"6253 ... 45.0 40.0 59.0 45.0 67.0 65.0 68.0 66.0 48.0 68.0 \n",
"6160 ... 68.0 64.0 66.0 66.0 65.0 68.0 62.0 67.0 69.0 62.0 \n",
"5876 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"5808 ... 65.0 64.0 68.0 67.0 65.0 66.0 63.0 65.0 66.0 63.0 \n",
"\n",
"[106 rows x 71 columns]"
]
},
"execution_count": 42,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"top_df = df[df.Club.isin(top_clubs)]\n",
"top_df[top_df.Overall < 70].sort_values('Overall', ascending=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Vi kan altså se, at der bliver satset på ungdommen, hvor deres kommende potentiale nok taler for deres plads i en storklub.<br>\n",
"\n",
"Men hvad så med ikke-topklubsspillere og deres performance?"
]
},
{
"cell_type": "code",
"execution_count": 43,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Name</th>\n",
" <th>Age</th>\n",
" <th>Nationality</th>\n",
" <th>Overall</th>\n",
" <th>Potential</th>\n",
" <th>Club</th>\n",
" <th>Value</th>\n",
" <th>Wage</th>\n",
" <th>Special</th>\n",
" <th>Acceleration</th>\n",
" <th>...</th>\n",
" <th>RB</th>\n",
" <th>RCB</th>\n",
" <th>RCM</th>\n",
" <th>RDM</th>\n",
" <th>RF</th>\n",
" <th>RM</th>\n",
" <th>RS</th>\n",
" <th>RW</th>\n",
" <th>RWB</th>\n",
" <th>ST</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>11</th>\n",
" <td>K. De Bruyne</td>\n",
" <td>26</td>\n",
" <td>Belgium</td>\n",
" <td>89</td>\n",
" <td>92</td>\n",
" <td>Manchester City</td>\n",
" <td>83000000.0</td>\n",
" <td>285000.0</td>\n",
" <td>2162</td>\n",
" <td>76.0</td>\n",
" <td>...</td>\n",
" <td>66.0</td>\n",
" <td>57.0</td>\n",
" <td>84.0</td>\n",
" <td>70.0</td>\n",
" <td>85.0</td>\n",
" <td>85.0</td>\n",
" <td>81.0</td>\n",
" <td>85.0</td>\n",
" <td>71.0</td>\n",
" <td>81.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>16</th>\n",
" <td>S. Agüero</td>\n",
" <td>29</td>\n",
" <td>Argentina</td>\n",
" <td>89</td>\n",
" <td>89</td>\n",
" <td>Manchester City</td>\n",
" <td>66500000.0</td>\n",
" <td>325000.0</td>\n",
" <td>2074</td>\n",
" <td>90.0</td>\n",
" <td>...</td>\n",
" <td>52.0</td>\n",
" <td>44.0</td>\n",
" <td>75.0</td>\n",
" <td>54.0</td>\n",
" <td>87.0</td>\n",
" <td>84.0</td>\n",
" <td>86.0</td>\n",
" <td>86.0</td>\n",
" <td>57.0</td>\n",
" <td>86.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>29</th>\n",
" <td>H. Lloris</td>\n",
" <td>30</td>\n",
" <td>France</td>\n",
" <td>88</td>\n",
" <td>88</td>\n",
" <td>Tottenham Hotspur</td>\n",
" <td>38000000.0</td>\n",
" <td>165000.0</td>\n",
" <td>1318</td>\n",
" <td>65.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>36</th>\n",
" <td>C. Eriksen</td>\n",
" <td>25</td>\n",
" <td>Denmark</td>\n",
" <td>87</td>\n",
" <td>91</td>\n",
" <td>Tottenham Hotspur</td>\n",
" <td>65000000.0</td>\n",
" <td>165000.0</td>\n",
" <td>2064</td>\n",
" <td>77.0</td>\n",
" <td>...</td>\n",
" <td>64.0</td>\n",
" <td>53.0</td>\n",
" <td>83.0</td>\n",
" <td>68.0</td>\n",
" <td>82.0</td>\n",
" <td>84.0</td>\n",
" <td>77.0</td>\n",
" <td>83.0</td>\n",
" <td>69.0</td>\n",
" <td>77.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>42</th>\n",
" <td>David Silva</td>\n",
" <td>31</td>\n",
" <td>Spain</td>\n",
" <td>87</td>\n",
" <td>87</td>\n",
" <td>Manchester City</td>\n",
" <td>44000000.0</td>\n",
" <td>220000.0</td>\n",
" <td>1977</td>\n",
" <td>72.0</td>\n",
" <td>...</td>\n",
" <td>59.0</td>\n",
" <td>50.0</td>\n",
" <td>81.0</td>\n",
" <td>64.0</td>\n",
" <td>81.0</td>\n",
" <td>82.0</td>\n",
" <td>75.0</td>\n",
" <td>82.0</td>\n",
" <td>65.0</td>\n",
" <td>75.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>46</th>\n",
" <td>H. Kane</td>\n",
" <td>23</td>\n",
" <td>England</td>\n",
" <td>86</td>\n",
" <td>90</td>\n",
" <td>Tottenham Hotspur</td>\n",
" <td>59000000.0</td>\n",
" <td>165000.0</td>\n",
" <td>2057</td>\n",
" <td>68.0</td>\n",
" <td>...</td>\n",
" <td>60.0</td>\n",
" <td>57.0</td>\n",
" <td>74.0</td>\n",
" <td>62.0</td>\n",
" <td>82.0</td>\n",
" <td>78.0</td>\n",
" <td>84.0</td>\n",
" <td>79.0</td>\n",
" <td>62.0</td>\n",
" <td>84.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>56</th>\n",
" <td>T. Alderweireld</td>\n",
" <td>28</td>\n",
" <td>Belgium</td>\n",
" <td>86</td>\n",
" <td>87</td>\n",
" <td>Tottenham Hotspur</td>\n",
" <td>40500000.0</td>\n",
" <td>165000.0</td>\n",
" <td>2047</td>\n",
" <td>62.0</td>\n",
" <td>...</td>\n",
" <td>79.0</td>\n",
" <td>84.0</td>\n",
" <td>74.0</td>\n",
" <td>81.0</td>\n",
" <td>67.0</td>\n",
" <td>67.0</td>\n",
" <td>67.0</td>\n",
" <td>65.0</td>\n",
" <td>77.0</td>\n",
" <td>67.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>76</th>\n",
" <td>D. Subašić</td>\n",
" <td>32</td>\n",
" <td>Croatia</td>\n",
" <td>85</td>\n",
" <td>85</td>\n",
" <td>AS Monaco</td>\n",
" <td>22000000.0</td>\n",
" <td>46000.0</td>\n",
" <td>1305</td>\n",
" <td>51.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>79</th>\n",
" <td>K. Glik</td>\n",
" <td>29</td>\n",
" <td>Poland</td>\n",
" <td>85</td>\n",
" <td>85</td>\n",
" <td>AS Monaco</td>\n",
" <td>30000000.0</td>\n",
" <td>60000.0</td>\n",
" <td>1612</td>\n",
" <td>53.0</td>\n",
" <td>...</td>\n",
" <td>72.0</td>\n",
" <td>83.0</td>\n",
" <td>55.0</td>\n",
" <td>74.0</td>\n",
" <td>48.0</td>\n",
" <td>50.0</td>\n",
" <td>52.0</td>\n",
" <td>45.0</td>\n",
" <td>68.0</td>\n",
" <td>52.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>81</th>\n",
" <td>I. Gündoğan</td>\n",
" <td>26</td>\n",
" <td>Germany</td>\n",
" <td>85</td>\n",
" <td>87</td>\n",
" <td>Manchester City</td>\n",
" <td>46000000.0</td>\n",
" <td>190000.0</td>\n",
" <td>2148</td>\n",
" <td>73.0</td>\n",
" <td>...</td>\n",
" <td>73.0</td>\n",
" <td>69.0</td>\n",
" <td>83.0</td>\n",
" <td>77.0</td>\n",
" <td>81.0</td>\n",
" <td>81.0</td>\n",
" <td>76.0</td>\n",
" <td>81.0</td>\n",
" <td>75.0</td>\n",
" <td>76.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>86</th>\n",
" <td>J. Vertonghen</td>\n",
" <td>30</td>\n",
" <td>Belgium</td>\n",
" <td>85</td>\n",
" <td>85</td>\n",
" <td>Tottenham Hotspur</td>\n",
" <td>28500000.0</td>\n",
" <td>130000.0</td>\n",
" <td>2079</td>\n",
" <td>68.0</td>\n",
" <td>...</td>\n",
" <td>80.0</td>\n",
" <td>83.0</td>\n",
" <td>74.0</td>\n",
" <td>81.0</td>\n",
" <td>70.0</td>\n",
" <td>70.0</td>\n",
" <td>70.0</td>\n",
" <td>69.0</td>\n",
" <td>78.0</td>\n",
" <td>70.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>88</th>\n",
" <td>S. Ruffier</td>\n",
" <td>30</td>\n",
" <td>France</td>\n",
" <td>85</td>\n",
" <td>85</td>\n",
" <td>AS Saint-Étienne</td>\n",
" <td>24500000.0</td>\n",
" <td>49000.0</td>\n",
" <td>1257</td>\n",
" <td>45.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>90</th>\n",
" <td>V. Kompany</td>\n",
" <td>31</td>\n",
" <td>Belgium</td>\n",
" <td>85</td>\n",
" <td>85</td>\n",
" <td>Manchester City</td>\n",
" <td>26000000.0</td>\n",
" <td>170000.0</td>\n",
" <td>1913</td>\n",
" <td>61.0</td>\n",
" <td>...</td>\n",
" <td>76.0</td>\n",
" <td>82.0</td>\n",
" <td>67.0</td>\n",
" <td>77.0</td>\n",
" <td>62.0</td>\n",
" <td>63.0</td>\n",
" <td>63.0</td>\n",
" <td>61.0</td>\n",
" <td>74.0</td>\n",
" <td>63.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>94</th>\n",
" <td>Bernardo Silva</td>\n",
" <td>22</td>\n",
" <td>Portugal</td>\n",
" <td>84</td>\n",
" <td>91</td>\n",
" <td>Manchester City</td>\n",
" <td>43500000.0</td>\n",
" <td>165000.0</td>\n",
" <td>2012</td>\n",
" <td>85.0</td>\n",
" <td>...</td>\n",
" <td>63.0</td>\n",
" <td>53.0</td>\n",
" <td>79.0</td>\n",
" <td>66.0</td>\n",
" <td>82.0</td>\n",
" <td>83.0</td>\n",
" <td>75.0</td>\n",
" <td>83.0</td>\n",
" <td>68.0</td>\n",
" <td>75.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>96</th>\n",
" <td>D. Alli</td>\n",
" <td>21</td>\n",
" <td>England</td>\n",
" <td>84</td>\n",
" <td>90</td>\n",
" <td>Tottenham Hotspur</td>\n",
" <td>43000000.0</td>\n",
" <td>115000.0</td>\n",
" <td>2122</td>\n",
" <td>77.0</td>\n",
" <td>...</td>\n",
" <td>72.0</td>\n",
" <td>69.0</td>\n",
" <td>81.0</td>\n",
" <td>75.0</td>\n",
" <td>83.0</td>\n",
" <td>81.0</td>\n",
" <td>81.0</td>\n",
" <td>81.0</td>\n",
" <td>73.0</td>\n",
" <td>81.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>103</th>\n",
" <td>T. Horn</td>\n",
" <td>24</td>\n",
" <td>Germany</td>\n",
" <td>84</td>\n",
" <td>90</td>\n",
" <td>1. FC Köln</td>\n",
" <td>31000000.0</td>\n",
" <td>39000.0</td>\n",
" <td>1260</td>\n",
" <td>45.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>111</th>\n",
" <td>Bruno</td>\n",
" <td>33</td>\n",
" <td>Spain</td>\n",
" <td>84</td>\n",
" <td>84</td>\n",
" <td>Villarreal CF</td>\n",
" <td>18500000.0</td>\n",
" <td>59000.0</td>\n",
" <td>2059</td>\n",
" <td>42.0</td>\n",
" <td>...</td>\n",
" <td>74.0</td>\n",
" <td>78.0</td>\n",
" <td>82.0</td>\n",
" <td>82.0</td>\n",
" <td>74.0</td>\n",
" <td>72.0</td>\n",
" <td>71.0</td>\n",
" <td>71.0</td>\n",
" <td>75.0</td>\n",
" <td>71.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>116</th>\n",
" <td>R. Fährmann</td>\n",
" <td>28</td>\n",
" <td>Germany</td>\n",
" <td>84</td>\n",
" <td>85</td>\n",
" <td>FC Schalke 04</td>\n",
" <td>25000000.0</td>\n",
" <td>54000.0</td>\n",
" <td>1190</td>\n",
" <td>38.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>117</th>\n",
" <td>Sergio Asenjo</td>\n",
" <td>28</td>\n",
" <td>Spain</td>\n",
" <td>84</td>\n",
" <td>85</td>\n",
" <td>Villarreal CF</td>\n",
" <td>25000000.0</td>\n",
" <td>46000.0</td>\n",
" <td>1341</td>\n",
" <td>59.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>120</th>\n",
" <td>D. Payet</td>\n",
" <td>30</td>\n",
" <td>France</td>\n",
" <td>84</td>\n",
" <td>84</td>\n",
" <td>Olympique de Marseille</td>\n",
" <td>29500000.0</td>\n",
" <td>60000.0</td>\n",
" <td>2076</td>\n",
" <td>79.0</td>\n",
" <td>...</td>\n",
" <td>60.0</td>\n",
" <td>51.0</td>\n",
" <td>79.0</td>\n",
" <td>63.0</td>\n",
" <td>82.0</td>\n",
" <td>83.0</td>\n",
" <td>78.0</td>\n",
" <td>83.0</td>\n",
" <td>64.0</td>\n",
" <td>78.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>121</th>\n",
" <td>Falcao</td>\n",
" <td>31</td>\n",
" <td>Colombia</td>\n",
" <td>84</td>\n",
" <td>84</td>\n",
" <td>AS Monaco</td>\n",
" <td>28000000.0</td>\n",
" <td>68000.0</td>\n",
" <td>2010</td>\n",
" <td>73.0</td>\n",
" <td>...</td>\n",
" <td>54.0</td>\n",
" <td>54.0</td>\n",
" <td>71.0</td>\n",
" <td>57.0</td>\n",
" <td>79.0</td>\n",
" <td>74.0</td>\n",
" <td>82.0</td>\n",
" <td>76.0</td>\n",
" <td>56.0</td>\n",
" <td>82.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>125</th>\n",
" <td>A. Gómez</td>\n",
" <td>29</td>\n",
" <td>Argentina</td>\n",
" <td>84</td>\n",
" <td>84</td>\n",
" <td>Atalanta</td>\n",
" <td>31000000.0</td>\n",
" <td>60000.0</td>\n",
" <td>2013</td>\n",
" <td>94.0</td>\n",
" <td>...</td>\n",
" <td>59.0</td>\n",
" <td>45.0</td>\n",
" <td>77.0</td>\n",
" <td>59.0</td>\n",
" <td>83.0</td>\n",
" <td>84.0</td>\n",
" <td>76.0</td>\n",
" <td>85.0</td>\n",
" <td>65.0</td>\n",
" <td>76.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>129</th>\n",
" <td>N. Keïta</td>\n",
" <td>22</td>\n",
" <td>Guinea</td>\n",
" <td>83</td>\n",
" <td>88</td>\n",
" <td>RB Leipzig</td>\n",
" <td>34000000.0</td>\n",
" <td>68000.0</td>\n",
" <td>2055</td>\n",
" <td>82.0</td>\n",
" <td>...</td>\n",
" <td>71.0</td>\n",
" <td>65.0</td>\n",
" <td>82.0</td>\n",
" <td>76.0</td>\n",
" <td>80.0</td>\n",
" <td>81.0</td>\n",
" <td>74.0</td>\n",
" <td>80.0</td>\n",
" <td>75.0</td>\n",
" <td>74.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>131</th>\n",
" <td>G. Rulli</td>\n",
" <td>25</td>\n",
" <td>Argentina</td>\n",
" <td>83</td>\n",
" <td>89</td>\n",
" <td>Real Sociedad</td>\n",
" <td>25500000.0</td>\n",
" <td>28000.0</td>\n",
" <td>1284</td>\n",
" <td>54.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>132</th>\n",
" <td>T. Lemar</td>\n",
" <td>21</td>\n",
" <td>France</td>\n",
" <td>83</td>\n",
" <td>91</td>\n",
" <td>AS Monaco</td>\n",
" <td>38500000.0</td>\n",
" <td>37000.0</td>\n",
" <td>2171</td>\n",
" <td>86.0</td>\n",
" <td>...</td>\n",
" <td>72.0</td>\n",
" <td>66.0</td>\n",
" <td>78.0</td>\n",
" <td>72.0</td>\n",
" <td>81.0</td>\n",
" <td>82.0</td>\n",
" <td>77.0</td>\n",
" <td>82.0</td>\n",
" <td>75.0</td>\n",
" <td>77.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>135</th>\n",
" <td>Ederson</td>\n",
" <td>23</td>\n",
" <td>Brazil</td>\n",
" <td>83</td>\n",
" <td>89</td>\n",
" <td>Manchester City</td>\n",
" <td>26000000.0</td>\n",
" <td>87000.0</td>\n",
" <td>1320</td>\n",
" <td>64.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>136</th>\n",
" <td>Fabinho</td>\n",
" <td>23</td>\n",
" <td>Brazil</td>\n",
" <td>83</td>\n",
" <td>88</td>\n",
" <td>AS Monaco</td>\n",
" <td>29500000.0</td>\n",
" <td>37000.0</td>\n",
" <td>2114</td>\n",
" <td>73.0</td>\n",
" <td>...</td>\n",
" <td>82.0</td>\n",
" <td>82.0</td>\n",
" <td>77.0</td>\n",
" <td>82.0</td>\n",
" <td>74.0</td>\n",
" <td>76.0</td>\n",
" <td>72.0</td>\n",
" <td>74.0</td>\n",
" <td>82.0</td>\n",
" <td>72.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>138</th>\n",
" <td>A. Belotti</td>\n",
" <td>23</td>\n",
" <td>Italy</td>\n",
" <td>83</td>\n",
" <td>90</td>\n",
" <td>Torino</td>\n",
" <td>37000000.0</td>\n",
" <td>58000.0</td>\n",
" <td>1935</td>\n",
" <td>80.0</td>\n",
" <td>...</td>\n",
" <td>52.0</td>\n",
" <td>51.0</td>\n",
" <td>65.0</td>\n",
" <td>52.0</td>\n",
" <td>78.0</td>\n",
" <td>72.0</td>\n",
" <td>82.0</td>\n",
" <td>75.0</td>\n",
" <td>54.0</td>\n",
" <td>82.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>139</th>\n",
" <td>E. Forsberg</td>\n",
" <td>25</td>\n",
" <td>Sweden</td>\n",
" <td>83</td>\n",
" <td>85</td>\n",
" <td>RB Leipzig</td>\n",
" <td>31500000.0</td>\n",
" <td>75000.0</td>\n",
" <td>1949</td>\n",
" <td>78.0</td>\n",
" <td>...</td>\n",
" <td>55.0</td>\n",
" <td>45.0</td>\n",
" <td>76.0</td>\n",
" <td>59.0</td>\n",
" <td>79.0</td>\n",
" <td>81.0</td>\n",
" <td>74.0</td>\n",
" <td>81.0</td>\n",
" <td>61.0</td>\n",
" <td>74.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>143</th>\n",
" <td>R. Mahrez</td>\n",
" <td>26</td>\n",
" <td>Algeria</td>\n",
" <td>83</td>\n",
" <td>84</td>\n",
" <td>Leicester City</td>\n",
" <td>30500000.0</td>\n",
" <td>88000.0</td>\n",
" <td>1935</td>\n",
" <td>85.0</td>\n",
" <td>...</td>\n",
" <td>54.0</td>\n",
" <td>41.0</td>\n",
" <td>74.0</td>\n",
" <td>55.0</td>\n",
" <td>80.0</td>\n",
" <td>81.0</td>\n",
" <td>74.0</td>\n",
" <td>82.0</td>\n",
" <td>60.0</td>\n",
" <td>74.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>...</th>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" <td>...</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4822</th>\n",
" <td>Jair</td>\n",
" <td>28</td>\n",
" <td>Brazil</td>\n",
" <td>71</td>\n",
" <td>71</td>\n",
" <td>Jeonnam Dragons</td>\n",
" <td>2400000.0</td>\n",
" <td>7000.0</td>\n",
" <td>1828</td>\n",
" <td>76.0</td>\n",
" <td>...</td>\n",
" <td>55.0</td>\n",
" <td>49.0</td>\n",
" <td>66.0</td>\n",
" <td>56.0</td>\n",
" <td>70.0</td>\n",
" <td>70.0</td>\n",
" <td>70.0</td>\n",
" <td>71.0</td>\n",
" <td>58.0</td>\n",
" <td>70.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4823</th>\n",
" <td>K. Vandendriessche</td>\n",
" <td>27</td>\n",
" <td>France</td>\n",
" <td>71</td>\n",
" <td>71</td>\n",
" <td>KV Oostende</td>\n",
" <td>2400000.0</td>\n",
" <td>12000.0</td>\n",
" <td>1924</td>\n",
" <td>71.0</td>\n",
" <td>...</td>\n",
" <td>69.0</td>\n",
" <td>70.0</td>\n",
" <td>70.0</td>\n",
" <td>70.0</td>\n",
" <td>68.0</td>\n",
" <td>68.0</td>\n",
" <td>70.0</td>\n",
" <td>66.0</td>\n",
" <td>69.0</td>\n",
" <td>70.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4824</th>\n",
" <td>C. Fai</td>\n",
" <td>24</td>\n",
" <td>Cameroon</td>\n",
" <td>71</td>\n",
" <td>74</td>\n",
" <td>Standard de Liège</td>\n",
" <td>2500000.0</td>\n",
" <td>9000.0</td>\n",
" <td>1740</td>\n",
" <td>88.0</td>\n",
" <td>...</td>\n",
" <td>70.0</td>\n",
" <td>67.0</td>\n",
" <td>62.0</td>\n",
" <td>67.0</td>\n",
" <td>59.0</td>\n",
" <td>65.0</td>\n",
" <td>53.0</td>\n",
" <td>62.0</td>\n",
" <td>70.0</td>\n",
" <td>53.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4825</th>\n",
" <td>S. Hagen</td>\n",
" <td>31</td>\n",
" <td>Norway</td>\n",
" <td>71</td>\n",
" <td>71</td>\n",
" <td>Odds BK</td>\n",
" <td>1600000.0</td>\n",
" <td>4000.0</td>\n",
" <td>1530</td>\n",
" <td>56.0</td>\n",
" <td>...</td>\n",
" <td>66.0</td>\n",
" <td>70.0</td>\n",
" <td>58.0</td>\n",
" <td>68.0</td>\n",
" <td>48.0</td>\n",
" <td>51.0</td>\n",
" <td>49.0</td>\n",
" <td>47.0</td>\n",
" <td>64.0</td>\n",
" <td>49.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4826</th>\n",
" <td>M. Rygaard</td>\n",
" <td>26</td>\n",
" <td>Denmark</td>\n",
" <td>71</td>\n",
" <td>73</td>\n",
" <td>Lyngby BK</td>\n",
" <td>2900000.0</td>\n",
" <td>9000.0</td>\n",
" <td>1818</td>\n",
" <td>78.0</td>\n",
" <td>...</td>\n",
" <td>54.0</td>\n",
" <td>50.0</td>\n",
" <td>66.0</td>\n",
" <td>57.0</td>\n",
" <td>68.0</td>\n",
" <td>69.0</td>\n",
" <td>64.0</td>\n",
" <td>69.0</td>\n",
" <td>57.0</td>\n",
" <td>64.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4827</th>\n",
" <td>M. Männel</td>\n",
" <td>29</td>\n",
" <td>Germany</td>\n",
" <td>71</td>\n",
" <td>71</td>\n",
" <td>FC Erzgebirge Aue</td>\n",
" <td>1600000.0</td>\n",
" <td>5000.0</td>\n",
" <td>1184</td>\n",
" <td>52.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4828</th>\n",
" <td>Cristian López</td>\n",
" <td>28</td>\n",
" <td>Spain</td>\n",
" <td>71</td>\n",
" <td>71</td>\n",
" <td>RC Lens</td>\n",
" <td>2400000.0</td>\n",
" <td>8000.0</td>\n",
" <td>1705</td>\n",
" <td>80.0</td>\n",
" <td>...</td>\n",
" <td>49.0</td>\n",
" <td>48.0</td>\n",
" <td>58.0</td>\n",
" <td>49.0</td>\n",
" <td>69.0</td>\n",
" <td>64.0</td>\n",
" <td>70.0</td>\n",
" <td>66.0</td>\n",
" <td>51.0</td>\n",
" <td>70.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4829</th>\n",
" <td>Eduardo Fonseira</td>\n",
" <td>29</td>\n",
" <td>Brazil</td>\n",
" <td>71</td>\n",
" <td>71</td>\n",
" <td>Clube Atlético Mineiro</td>\n",
" <td>1600000.0</td>\n",
" <td>18000.0</td>\n",
" <td>963</td>\n",
" <td>32.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4830</th>\n",
" <td>L. Rosić</td>\n",
" <td>24</td>\n",
" <td>Serbia</td>\n",
" <td>71</td>\n",
" <td>77</td>\n",
" <td>SC Braga</td>\n",
" <td>2800000.0</td>\n",
" <td>7000.0</td>\n",
" <td>1442</td>\n",
" <td>58.0</td>\n",
" <td>...</td>\n",
" <td>60.0</td>\n",
" <td>70.0</td>\n",
" <td>47.0</td>\n",
" <td>61.0</td>\n",
" <td>43.0</td>\n",
" <td>44.0</td>\n",
" <td>46.0</td>\n",
" <td>42.0</td>\n",
" <td>57.0</td>\n",
" <td>46.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4831</th>\n",
" <td>R. Beerens</td>\n",
" <td>29</td>\n",
" <td>Netherlands</td>\n",
" <td>71</td>\n",
" <td>71</td>\n",
" <td>Reading</td>\n",
" <td>2300000.0</td>\n",
" <td>27000.0</td>\n",
" <td>1760</td>\n",
" <td>80.0</td>\n",
" <td>...</td>\n",
" <td>49.0</td>\n",
" <td>39.0</td>\n",
" <td>64.0</td>\n",
" <td>49.0</td>\n",
" <td>69.0</td>\n",
" <td>71.0</td>\n",
" <td>64.0</td>\n",
" <td>71.0</td>\n",
" <td>54.0</td>\n",
" <td>64.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4832</th>\n",
" <td>B. Douglas</td>\n",
" <td>27</td>\n",
" <td>Scotland</td>\n",
" <td>71</td>\n",
" <td>71</td>\n",
" <td>Wolverhampton Wanderers</td>\n",
" <td>2000000.0</td>\n",
" <td>31000.0</td>\n",
" <td>1956</td>\n",
" <td>76.0</td>\n",
" <td>...</td>\n",
" <td>70.0</td>\n",
" <td>67.0</td>\n",
" <td>66.0</td>\n",
" <td>67.0</td>\n",
" <td>64.0</td>\n",
" <td>68.0</td>\n",
" <td>62.0</td>\n",
" <td>66.0</td>\n",
" <td>71.0</td>\n",
" <td>62.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4833</th>\n",
" <td>S. Johnstone</td>\n",
" <td>24</td>\n",
" <td>England</td>\n",
" <td>71</td>\n",
" <td>79</td>\n",
" <td>Aston Villa</td>\n",
" <td>2600000.0</td>\n",
" <td>40000.0</td>\n",
" <td>1162</td>\n",
" <td>45.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4834</th>\n",
" <td>R. Elliot</td>\n",
" <td>31</td>\n",
" <td>Republic of Ireland</td>\n",
" <td>71</td>\n",
" <td>71</td>\n",
" <td>Newcastle United</td>\n",
" <td>1400000.0</td>\n",
" <td>30000.0</td>\n",
" <td>1128</td>\n",
" <td>47.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4835</th>\n",
" <td>D. Capelli</td>\n",
" <td>31</td>\n",
" <td>Italy</td>\n",
" <td>71</td>\n",
" <td>71</td>\n",
" <td>La Spezia</td>\n",
" <td>1600000.0</td>\n",
" <td>4000.0</td>\n",
" <td>1457</td>\n",
" <td>34.0</td>\n",
" <td>...</td>\n",
" <td>60.0</td>\n",
" <td>70.0</td>\n",
" <td>49.0</td>\n",
" <td>63.0</td>\n",
" <td>41.0</td>\n",
" <td>43.0</td>\n",
" <td>45.0</td>\n",
" <td>40.0</td>\n",
" <td>58.0</td>\n",
" <td>45.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4836</th>\n",
" <td>K. Ziani</td>\n",
" <td>34</td>\n",
" <td>France</td>\n",
" <td>71</td>\n",
" <td>71</td>\n",
" <td>US Orléans Loiret Football</td>\n",
" <td>1200000.0</td>\n",
" <td>5000.0</td>\n",
" <td>1836</td>\n",
" <td>75.0</td>\n",
" <td>...</td>\n",
" <td>50.0</td>\n",
" <td>42.0</td>\n",
" <td>65.0</td>\n",
" <td>51.0</td>\n",
" <td>68.0</td>\n",
" <td>69.0</td>\n",
" <td>64.0</td>\n",
" <td>69.0</td>\n",
" <td>53.0</td>\n",
" <td>64.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4837</th>\n",
" <td>A. Kozlov</td>\n",
" <td>30</td>\n",
" <td>Russia</td>\n",
" <td>71</td>\n",
" <td>71</td>\n",
" <td>Dinamo Moscow</td>\n",
" <td>1700000.0</td>\n",
" <td>21000.0</td>\n",
" <td>1801</td>\n",
" <td>71.0</td>\n",
" <td>...</td>\n",
" <td>70.0</td>\n",
" <td>70.0</td>\n",
" <td>63.0</td>\n",
" <td>69.0</td>\n",
" <td>58.0</td>\n",
" <td>62.0</td>\n",
" <td>59.0</td>\n",
" <td>60.0</td>\n",
" <td>69.0</td>\n",
" <td>59.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4838</th>\n",
" <td>S. Berge</td>\n",
" <td>19</td>\n",
" <td>Norway</td>\n",
" <td>71</td>\n",
" <td>82</td>\n",
" <td>KRC Genk</td>\n",
" <td>3500000.0</td>\n",
" <td>6000.0</td>\n",
" <td>1851</td>\n",
" <td>75.0</td>\n",
" <td>...</td>\n",
" <td>68.0</td>\n",
" <td>69.0</td>\n",
" <td>69.0</td>\n",
" <td>70.0</td>\n",
" <td>66.0</td>\n",
" <td>67.0</td>\n",
" <td>64.0</td>\n",
" <td>65.0</td>\n",
" <td>68.0</td>\n",
" <td>64.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4839</th>\n",
" <td>O. Pérez</td>\n",
" <td>44</td>\n",
" <td>Mexico</td>\n",
" <td>71</td>\n",
" <td>71</td>\n",
" <td>Pachuca</td>\n",
" <td>160000.0</td>\n",
" <td>9000.0</td>\n",
" <td>1244</td>\n",
" <td>60.0</td>\n",
" <td>...</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" <td>0.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4840</th>\n",
" <td>C. Pasquato</td>\n",
" <td>27</td>\n",
" <td>Italy</td>\n",
" <td>71</td>\n",
" <td>71</td>\n",
" <td>Legia Warszawa</td>\n",
" <td>2500000.0</td>\n",
" <td>8000.0</td>\n",
" <td>1707</td>\n",
" <td>90.0</td>\n",
" <td>...</td>\n",
" <td>44.0</td>\n",
" <td>33.0</td>\n",
" <td>62.0</td>\n",
" <td>44.0</td>\n",
" <td>68.0</td>\n",
" <td>70.0</td>\n",
" <td>64.0</td>\n",
" <td>71.0</td>\n",
" <td>49.0</td>\n",
" <td>64.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4841</th>\n",
" <td>A. Kolomeytsev</td>\n",
" <td>28</td>\n",
" <td>Russia</td>\n",
" <td>71</td>\n",
" <td>72</td>\n",
" <td>Lokomotiv Moscow</td>\n",
" <td>2200000.0</td>\n",
" <td>26000.0</td>\n",
" <td>1904</td>\n",
" <td>58.0</td>\n",
" <td>...</td>\n",
" <td>68.0</td>\n",
" <td>68.0</td>\n",
" <td>72.0</td>\n",
" <td>70.0</td>\n",
" <td>69.0</td>\n",
" <td>69.0</td>\n",
" <td>69.0</td>\n",
" <td>68.0</td>\n",
" <td>69.0</td>\n",
" <td>69.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4842</th>\n",
" <td>S. Kitsiou</td>\n",
" <td>23</td>\n",
" <td>Greece</td>\n",
" <td>71</td>\n",
" <td>75</td>\n",
" <td>Sint-Truidense VV</td>\n",
" <td>2600000.0</td>\n",
" <td>8000.0</td>\n",
" <td>1878</td>\n",
" <td>78.0</td>\n",
" <td>...</td>\n",
" <td>70.0</td>\n",
" <td>67.0</td>\n",
" <td>68.0</td>\n",
" <td>69.0</td>\n",
" <td>67.0</td>\n",
" <td>68.0</td>\n",
" <td>65.0</td>\n",
" <td>68.0</td>\n",
" <td>70.0</td>\n",
" <td>65.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4843</th>\n",
" <td>Y. Yotún</td>\n",
" <td>27</td>\n",
" <td>Peru</td>\n",
" <td>71</td>\n",
" <td>72</td>\n",
" <td>Orlando City Soccer Club</td>\n",
" <td>2700000.0</td>\n",
" <td>7000.0</td>\n",
" <td>1937</td>\n",
" <td>71.0</td>\n",
" <td>...</td>\n",
" <td>67.0</td>\n",
" <td>63.0</td>\n",
" <td>70.0</td>\n",
" <td>68.0</td>\n",
" <td>66.0</td>\n",
" <td>69.0</td>\n",
" <td>61.0</td>\n",
" <td>67.0</td>\n",
" <td>69.0</td>\n",
" <td>61.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4844</th>\n",
" <td>G. Zardes</td>\n",
" <td>25</td>\n",
" <td>United States</td>\n",
" <td>71</td>\n",
" <td>72</td>\n",
" <td>LA Galaxy</td>\n",
" <td>2900000.0</td>\n",
" <td>7000.0</td>\n",
" <td>1812</td>\n",
" <td>85.0</td>\n",
" <td>...</td>\n",
" <td>56.0</td>\n",
" <td>54.0</td>\n",
" <td>62.0</td>\n",
" <td>54.0</td>\n",
" <td>70.0</td>\n",
" <td>69.0</td>\n",
" <td>70.0</td>\n",
" <td>70.0</td>\n",
" <td>58.0</td>\n",
" <td>70.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4845</th>\n",
" <td>C. Menéndez</td>\n",
" <td>29</td>\n",
" <td>Argentina</td>\n",
" <td>71</td>\n",
" <td>71</td>\n",
" <td>Tiburones Rojos de Veracruz</td>\n",
" <td>2400000.0</td>\n",
" <td>8000.0</td>\n",
" <td>1670</td>\n",
" <td>66.0</td>\n",
" <td>...</td>\n",
" <td>45.0</td>\n",
" <td>45.0</td>\n",
" <td>61.0</td>\n",
" <td>47.0</td>\n",
" <td>69.0</td>\n",
" <td>64.0</td>\n",
" <td>70.0</td>\n",
" <td>65.0</td>\n",
" <td>47.0</td>\n",
" <td>70.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4846</th>\n",
" <td>T. Zentena</td>\n",
" <td>25</td>\n",
" <td>Chile</td>\n",
" <td>71</td>\n",
" <td>71</td>\n",
" <td>Everton de Viña del Mar</td>\n",
" <td>2600000.0</td>\n",
" <td>4000.0</td>\n",
" <td>1744</td>\n",
" <td>81.0</td>\n",
" <td>...</td>\n",
" <td>48.0</td>\n",
" <td>42.0</td>\n",
" <td>60.0</td>\n",
" <td>47.0</td>\n",
" <td>71.0</td>\n",
" <td>70.0</td>\n",
" <td>71.0</td>\n",
" <td>72.0</td>\n",
" <td>52.0</td>\n",
" <td>71.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4847</th>\n",
" <td>Vágner Corraldo</td>\n",
" <td>29</td>\n",
" <td>Brazil</td>\n",
" <td>71</td>\n",
" <td>71</td>\n",
" <td>Santos Futebol Clube</td>\n",
" <td>1800000.0</td>\n",
" <td>13000.0</td>\n",
" <td>1915</td>\n",
" <td>78.0</td>\n",
" <td>...</td>\n",
" <td>70.0</td>\n",
" <td>67.0</td>\n",
" <td>65.0</td>\n",
" <td>67.0</td>\n",
" <td>65.0</td>\n",
" <td>67.0</td>\n",
" <td>63.0</td>\n",
" <td>67.0</td>\n",
" <td>71.0</td>\n",
" <td>63.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4848</th>\n",
" <td>D. Sjölund</td>\n",
" <td>34</td>\n",
" <td>Finland</td>\n",
" <td>71</td>\n",
" <td>71</td>\n",
" <td>IFK Norrköping</td>\n",
" <td>1200000.0</td>\n",
" <td>5000.0</td>\n",
" <td>1839</td>\n",
" <td>46.0</td>\n",
" <td>...</td>\n",
" <td>60.0</td>\n",
" <td>61.0</td>\n",
" <td>70.0</td>\n",
" <td>68.0</td>\n",
" <td>63.0</td>\n",
" <td>64.0</td>\n",
" <td>60.0</td>\n",
" <td>63.0</td>\n",
" <td>63.0</td>\n",
" <td>60.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4849</th>\n",
" <td>C. Mavinga</td>\n",
" <td>26</td>\n",
" <td>DR Congo</td>\n",
" <td>71</td>\n",
" <td>72</td>\n",
" <td>Toronto FC</td>\n",
" <td>2300000.0</td>\n",
" <td>6000.0</td>\n",
" <td>1736</td>\n",
" <td>77.0</td>\n",
" <td>...</td>\n",
" <td>70.0</td>\n",
" <td>70.0</td>\n",
" <td>64.0</td>\n",
" <td>69.0</td>\n",
" <td>60.0</td>\n",
" <td>66.0</td>\n",
" <td>58.0</td>\n",
" <td>63.0</td>\n",
" <td>70.0</td>\n",
" <td>58.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4850</th>\n",
" <td>E. Conferio</td>\n",
" <td>33</td>\n",
" <td>Chile</td>\n",
" <td>71</td>\n",
" <td>71</td>\n",
" <td>CD Antofagasta</td>\n",
" <td>1500000.0</td>\n",
" <td>4000.0</td>\n",
" <td>1763</td>\n",
" <td>86.0</td>\n",
" <td>...</td>\n",
" <td>50.0</td>\n",
" <td>40.0</td>\n",
" <td>62.0</td>\n",
" <td>47.0</td>\n",
" <td>72.0</td>\n",
" <td>69.0</td>\n",
" <td>70.0</td>\n",
" <td>71.0</td>\n",
" <td>52.0</td>\n",
" <td>70.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4851</th>\n",
" <td>F. Ben Khalfallah</td>\n",
" <td>34</td>\n",
" <td>Tunisia</td>\n",
" <td>71</td>\n",
" <td>71</td>\n",
" <td>Brisbane Roar</td>\n",
" <td>1200000.0</td>\n",
" <td>6000.0</td>\n",
" <td>1808</td>\n",
" <td>75.0</td>\n",
" <td>...</td>\n",
" <td>53.0</td>\n",
" <td>48.0</td>\n",
" <td>67.0</td>\n",
" <td>56.0</td>\n",
" <td>70.0</td>\n",
" <td>71.0</td>\n",
" <td>67.0</td>\n",
" <td>71.0</td>\n",
" <td>57.0</td>\n",
" <td>67.0</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"<p>4336 rows × 71 columns</p>\n",
"</div>"
],
"text/plain": [
" Name Age Nationality Overall Potential \\\n",
"11 K. De Bruyne 26 Belgium 89 92 \n",
"16 S. Agüero 29 Argentina 89 89 \n",
"29 H. Lloris 30 France 88 88 \n",
"36 C. Eriksen 25 Denmark 87 91 \n",
"42 David Silva 31 Spain 87 87 \n",
"46 H. Kane 23 England 86 90 \n",
"56 T. Alderweireld 28 Belgium 86 87 \n",
"76 D. Subašić 32 Croatia 85 85 \n",
"79 K. Glik 29 Poland 85 85 \n",
"81 I. Gündoğan 26 Germany 85 87 \n",
"86 J. Vertonghen 30 Belgium 85 85 \n",
"88 S. Ruffier 30 France 85 85 \n",
"90 V. Kompany 31 Belgium 85 85 \n",
"94 Bernardo Silva 22 Portugal 84 91 \n",
"96 D. Alli 21 England 84 90 \n",
"103 T. Horn 24 Germany 84 90 \n",
"111 Bruno 33 Spain 84 84 \n",
"116 R. Fährmann 28 Germany 84 85 \n",
"117 Sergio Asenjo 28 Spain 84 85 \n",
"120 D. Payet 30 France 84 84 \n",
"121 Falcao 31 Colombia 84 84 \n",
"125 A. Gómez 29 Argentina 84 84 \n",
"129 N. Keïta 22 Guinea 83 88 \n",
"131 G. Rulli 25 Argentina 83 89 \n",
"132 T. Lemar 21 France 83 91 \n",
"135 Ederson 23 Brazil 83 89 \n",
"136 Fabinho 23 Brazil 83 88 \n",
"138 A. Belotti 23 Italy 83 90 \n",
"139 E. Forsberg 25 Sweden 83 85 \n",
"143 R. Mahrez 26 Algeria 83 84 \n",
"... ... ... ... ... ... \n",
"4822 Jair 28 Brazil 71 71 \n",
"4823 K. Vandendriessche 27 France 71 71 \n",
"4824 C. Fai 24 Cameroon 71 74 \n",
"4825 S. Hagen 31 Norway 71 71 \n",
"4826 M. Rygaard 26 Denmark 71 73 \n",
"4827 M. Männel 29 Germany 71 71 \n",
"4828 Cristian López 28 Spain 71 71 \n",
"4829 Eduardo Fonseira 29 Brazil 71 71 \n",
"4830 L. Rosić 24 Serbia 71 77 \n",
"4831 R. Beerens 29 Netherlands 71 71 \n",
"4832 B. Douglas 27 Scotland 71 71 \n",
"4833 S. Johnstone 24 England 71 79 \n",
"4834 R. Elliot 31 Republic of Ireland 71 71 \n",
"4835 D. Capelli 31 Italy 71 71 \n",
"4836 K. Ziani 34 France 71 71 \n",
"4837 A. Kozlov 30 Russia 71 71 \n",
"4838 S. Berge 19 Norway 71 82 \n",
"4839 O. Pérez 44 Mexico 71 71 \n",
"4840 C. Pasquato 27 Italy 71 71 \n",
"4841 A. Kolomeytsev 28 Russia 71 72 \n",
"4842 S. Kitsiou 23 Greece 71 75 \n",
"4843 Y. Yotún 27 Peru 71 72 \n",
"4844 G. Zardes 25 United States 71 72 \n",
"4845 C. Menéndez 29 Argentina 71 71 \n",
"4846 T. Zentena 25 Chile 71 71 \n",
"4847 Vágner Corraldo 29 Brazil 71 71 \n",
"4848 D. Sjölund 34 Finland 71 71 \n",
"4849 C. Mavinga 26 DR Congo 71 72 \n",
"4850 E. Conferio 33 Chile 71 71 \n",
"4851 F. Ben Khalfallah 34 Tunisia 71 71 \n",
"\n",
" Club Value Wage Special \\\n",
"11 Manchester City 83000000.0 285000.0 2162 \n",
"16 Manchester City 66500000.0 325000.0 2074 \n",
"29 Tottenham Hotspur 38000000.0 165000.0 1318 \n",
"36 Tottenham Hotspur 65000000.0 165000.0 2064 \n",
"42 Manchester City 44000000.0 220000.0 1977 \n",
"46 Tottenham Hotspur 59000000.0 165000.0 2057 \n",
"56 Tottenham Hotspur 40500000.0 165000.0 2047 \n",
"76 AS Monaco 22000000.0 46000.0 1305 \n",
"79 AS Monaco 30000000.0 60000.0 1612 \n",
"81 Manchester City 46000000.0 190000.0 2148 \n",
"86 Tottenham Hotspur 28500000.0 130000.0 2079 \n",
"88 AS Saint-Étienne 24500000.0 49000.0 1257 \n",
"90 Manchester City 26000000.0 170000.0 1913 \n",
"94 Manchester City 43500000.0 165000.0 2012 \n",
"96 Tottenham Hotspur 43000000.0 115000.0 2122 \n",
"103 1. FC Köln 31000000.0 39000.0 1260 \n",
"111 Villarreal CF 18500000.0 59000.0 2059 \n",
"116 FC Schalke 04 25000000.0 54000.0 1190 \n",
"117 Villarreal CF 25000000.0 46000.0 1341 \n",
"120 Olympique de Marseille 29500000.0 60000.0 2076 \n",
"121 AS Monaco 28000000.0 68000.0 2010 \n",
"125 Atalanta 31000000.0 60000.0 2013 \n",
"129 RB Leipzig 34000000.0 68000.0 2055 \n",
"131 Real Sociedad 25500000.0 28000.0 1284 \n",
"132 AS Monaco 38500000.0 37000.0 2171 \n",
"135 Manchester City 26000000.0 87000.0 1320 \n",
"136 AS Monaco 29500000.0 37000.0 2114 \n",
"138 Torino 37000000.0 58000.0 1935 \n",
"139 RB Leipzig 31500000.0 75000.0 1949 \n",
"143 Leicester City 30500000.0 88000.0 1935 \n",
"... ... ... ... ... \n",
"4822 Jeonnam Dragons 2400000.0 7000.0 1828 \n",
"4823 KV Oostende 2400000.0 12000.0 1924 \n",
"4824 Standard de Liège 2500000.0 9000.0 1740 \n",
"4825 Odds BK 1600000.0 4000.0 1530 \n",
"4826 Lyngby BK 2900000.0 9000.0 1818 \n",
"4827 FC Erzgebirge Aue 1600000.0 5000.0 1184 \n",
"4828 RC Lens 2400000.0 8000.0 1705 \n",
"4829 Clube Atlético Mineiro 1600000.0 18000.0 963 \n",
"4830 SC Braga 2800000.0 7000.0 1442 \n",
"4831 Reading 2300000.0 27000.0 1760 \n",
"4832 Wolverhampton Wanderers 2000000.0 31000.0 1956 \n",
"4833 Aston Villa 2600000.0 40000.0 1162 \n",
"4834 Newcastle United 1400000.0 30000.0 1128 \n",
"4835 La Spezia 1600000.0 4000.0 1457 \n",
"4836 US Orléans Loiret Football 1200000.0 5000.0 1836 \n",
"4837 Dinamo Moscow 1700000.0 21000.0 1801 \n",
"4838 KRC Genk 3500000.0 6000.0 1851 \n",
"4839 Pachuca 160000.0 9000.0 1244 \n",
"4840 Legia Warszawa 2500000.0 8000.0 1707 \n",
"4841 Lokomotiv Moscow 2200000.0 26000.0 1904 \n",
"4842 Sint-Truidense VV 2600000.0 8000.0 1878 \n",
"4843 Orlando City Soccer Club 2700000.0 7000.0 1937 \n",
"4844 LA Galaxy 2900000.0 7000.0 1812 \n",
"4845 Tiburones Rojos de Veracruz 2400000.0 8000.0 1670 \n",
"4846 Everton de Viña del Mar 2600000.0 4000.0 1744 \n",
"4847 Santos Futebol Clube 1800000.0 13000.0 1915 \n",
"4848 IFK Norrköping 1200000.0 5000.0 1839 \n",
"4849 Toronto FC 2300000.0 6000.0 1736 \n",
"4850 CD Antofagasta 1500000.0 4000.0 1763 \n",
"4851 Brisbane Roar 1200000.0 6000.0 1808 \n",
"\n",
" Acceleration ... RB RCB RCM RDM RF RM RS RW \\\n",
"11 76.0 ... 66.0 57.0 84.0 70.0 85.0 85.0 81.0 85.0 \n",
"16 90.0 ... 52.0 44.0 75.0 54.0 87.0 84.0 86.0 86.0 \n",
"29 65.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"36 77.0 ... 64.0 53.0 83.0 68.0 82.0 84.0 77.0 83.0 \n",
"42 72.0 ... 59.0 50.0 81.0 64.0 81.0 82.0 75.0 82.0 \n",
"46 68.0 ... 60.0 57.0 74.0 62.0 82.0 78.0 84.0 79.0 \n",
"56 62.0 ... 79.0 84.0 74.0 81.0 67.0 67.0 67.0 65.0 \n",
"76 51.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"79 53.0 ... 72.0 83.0 55.0 74.0 48.0 50.0 52.0 45.0 \n",
"81 73.0 ... 73.0 69.0 83.0 77.0 81.0 81.0 76.0 81.0 \n",
"86 68.0 ... 80.0 83.0 74.0 81.0 70.0 70.0 70.0 69.0 \n",
"88 45.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"90 61.0 ... 76.0 82.0 67.0 77.0 62.0 63.0 63.0 61.0 \n",
"94 85.0 ... 63.0 53.0 79.0 66.0 82.0 83.0 75.0 83.0 \n",
"96 77.0 ... 72.0 69.0 81.0 75.0 83.0 81.0 81.0 81.0 \n",
"103 45.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"111 42.0 ... 74.0 78.0 82.0 82.0 74.0 72.0 71.0 71.0 \n",
"116 38.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"117 59.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"120 79.0 ... 60.0 51.0 79.0 63.0 82.0 83.0 78.0 83.0 \n",
"121 73.0 ... 54.0 54.0 71.0 57.0 79.0 74.0 82.0 76.0 \n",
"125 94.0 ... 59.0 45.0 77.0 59.0 83.0 84.0 76.0 85.0 \n",
"129 82.0 ... 71.0 65.0 82.0 76.0 80.0 81.0 74.0 80.0 \n",
"131 54.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"132 86.0 ... 72.0 66.0 78.0 72.0 81.0 82.0 77.0 82.0 \n",
"135 64.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"136 73.0 ... 82.0 82.0 77.0 82.0 74.0 76.0 72.0 74.0 \n",
"138 80.0 ... 52.0 51.0 65.0 52.0 78.0 72.0 82.0 75.0 \n",
"139 78.0 ... 55.0 45.0 76.0 59.0 79.0 81.0 74.0 81.0 \n",
"143 85.0 ... 54.0 41.0 74.0 55.0 80.0 81.0 74.0 82.0 \n",
"... ... ... ... ... ... ... ... ... ... ... \n",
"4822 76.0 ... 55.0 49.0 66.0 56.0 70.0 70.0 70.0 71.0 \n",
"4823 71.0 ... 69.0 70.0 70.0 70.0 68.0 68.0 70.0 66.0 \n",
"4824 88.0 ... 70.0 67.0 62.0 67.0 59.0 65.0 53.0 62.0 \n",
"4825 56.0 ... 66.0 70.0 58.0 68.0 48.0 51.0 49.0 47.0 \n",
"4826 78.0 ... 54.0 50.0 66.0 57.0 68.0 69.0 64.0 69.0 \n",
"4827 52.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"4828 80.0 ... 49.0 48.0 58.0 49.0 69.0 64.0 70.0 66.0 \n",
"4829 32.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"4830 58.0 ... 60.0 70.0 47.0 61.0 43.0 44.0 46.0 42.0 \n",
"4831 80.0 ... 49.0 39.0 64.0 49.0 69.0 71.0 64.0 71.0 \n",
"4832 76.0 ... 70.0 67.0 66.0 67.0 64.0 68.0 62.0 66.0 \n",
"4833 45.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"4834 47.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"4835 34.0 ... 60.0 70.0 49.0 63.0 41.0 43.0 45.0 40.0 \n",
"4836 75.0 ... 50.0 42.0 65.0 51.0 68.0 69.0 64.0 69.0 \n",
"4837 71.0 ... 70.0 70.0 63.0 69.0 58.0 62.0 59.0 60.0 \n",
"4838 75.0 ... 68.0 69.0 69.0 70.0 66.0 67.0 64.0 65.0 \n",
"4839 60.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 \n",
"4840 90.0 ... 44.0 33.0 62.0 44.0 68.0 70.0 64.0 71.0 \n",
"4841 58.0 ... 68.0 68.0 72.0 70.0 69.0 69.0 69.0 68.0 \n",
"4842 78.0 ... 70.0 67.0 68.0 69.0 67.0 68.0 65.0 68.0 \n",
"4843 71.0 ... 67.0 63.0 70.0 68.0 66.0 69.0 61.0 67.0 \n",
"4844 85.0 ... 56.0 54.0 62.0 54.0 70.0 69.0 70.0 70.0 \n",
"4845 66.0 ... 45.0 45.0 61.0 47.0 69.0 64.0 70.0 65.0 \n",
"4846 81.0 ... 48.0 42.0 60.0 47.0 71.0 70.0 71.0 72.0 \n",
"4847 78.0 ... 70.0 67.0 65.0 67.0 65.0 67.0 63.0 67.0 \n",
"4848 46.0 ... 60.0 61.0 70.0 68.0 63.0 64.0 60.0 63.0 \n",
"4849 77.0 ... 70.0 70.0 64.0 69.0 60.0 66.0 58.0 63.0 \n",
"4850 86.0 ... 50.0 40.0 62.0 47.0 72.0 69.0 70.0 71.0 \n",
"4851 75.0 ... 53.0 48.0 67.0 56.0 70.0 71.0 67.0 71.0 \n",
"\n",
" RWB ST \n",
"11 71.0 81.0 \n",
"16 57.0 86.0 \n",
"29 0.0 0.0 \n",
"36 69.0 77.0 \n",
"42 65.0 75.0 \n",
"46 62.0 84.0 \n",
"56 77.0 67.0 \n",
"76 0.0 0.0 \n",
"79 68.0 52.0 \n",
"81 75.0 76.0 \n",
"86 78.0 70.0 \n",
"88 0.0 0.0 \n",
"90 74.0 63.0 \n",
"94 68.0 75.0 \n",
"96 73.0 81.0 \n",
"103 0.0 0.0 \n",
"111 75.0 71.0 \n",
"116 0.0 0.0 \n",
"117 0.0 0.0 \n",
"120 64.0 78.0 \n",
"121 56.0 82.0 \n",
"125 65.0 76.0 \n",
"129 75.0 74.0 \n",
"131 0.0 0.0 \n",
"132 75.0 77.0 \n",
"135 0.0 0.0 \n",
"136 82.0 72.0 \n",
"138 54.0 82.0 \n",
"139 61.0 74.0 \n",
"143 60.0 74.0 \n",
"... ... ... \n",
"4822 58.0 70.0 \n",
"4823 69.0 70.0 \n",
"4824 70.0 53.0 \n",
"4825 64.0 49.0 \n",
"4826 57.0 64.0 \n",
"4827 0.0 0.0 \n",
"4828 51.0 70.0 \n",
"4829 0.0 0.0 \n",
"4830 57.0 46.0 \n",
"4831 54.0 64.0 \n",
"4832 71.0 62.0 \n",
"4833 0.0 0.0 \n",
"4834 0.0 0.0 \n",
"4835 58.0 45.0 \n",
"4836 53.0 64.0 \n",
"4837 69.0 59.0 \n",
"4838 68.0 64.0 \n",
"4839 0.0 0.0 \n",
"4840 49.0 64.0 \n",
"4841 69.0 69.0 \n",
"4842 70.0 65.0 \n",
"4843 69.0 61.0 \n",
"4844 58.0 70.0 \n",
"4845 47.0 70.0 \n",
"4846 52.0 71.0 \n",
"4847 71.0 63.0 \n",
"4848 63.0 60.0 \n",
"4849 70.0 58.0 \n",
"4850 52.0 70.0 \n",
"4851 57.0 67.0 \n",
"\n",
"[4336 rows x 71 columns]"
]
},
"execution_count": 43,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"bund_df = df[~df.Club.isin(top_clubs)]\n",
"bund_df[bund_df.Overall > 70]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Måske er de 22 klubber, vi har udvalgt ikke helt nok til at beskrive topklubber"
]
},
{
"cell_type": "code",
"execution_count": 44,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"220 FC Barcelona\n",
"331 Juventus\n",
"467 Real Madrid CF\n",
"223 FC Bayern Munich\n",
"433 Paris Saint-Germain\n",
"378 Manchester United\n",
"398 Napoli\n",
"478 Roma\n",
"530 Sevilla FC\n",
"324 Inter\n",
"143 Chelsea\n",
"551 Sporting CP\n",
"241 FC Porto\n",
"369 Liverpool\n",
"68 Atlético Madrid\n",
"52 Arsenal\n",
"92 Borussia Dortmund\n",
"61 Athletic Club de Bilbao\n",
"83 Beşiktaş JK\n",
"502 SL Benfica\n",
"384 Milan\n",
"80 Bayer 04 Leverkusen\n",
"Name: Club, dtype: object"
]
},
"execution_count": 44,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"top_clubs"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Du kan evt. gå tilbage til __Data Cleaning__ notebooken, og prøve at ændre tallet for *top_klub_ratio*"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| apache-2.0 |
fang-lei/MachineLearningCourse-Python | Exercise01.ipynb | 1 | 469884 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"Exercise 01"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Q1: distribution P(x,y)"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import numpy\n",
"import matplotlib\n",
"import math\n",
"%matplotlib inline\n",
"from matplotlib import pyplot as plt\n",
"from mpl_toolkits.mplot3d import Axes3D\n",
"R = numpy.arange(-4,4+1e-9,0.1)\n",
"x,y = numpy.meshgrid(R,R)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Define the probability function (discrete)"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/plain": [
"<mpl_toolkits.mplot3d.art3d.Path3DCollection at 0x10c33a2e8>"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAxoAAAHkCAYAAAC5R1kSAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3XmYFOW5N/5v79tMT88wzAz7NizDIhAEAVEU0FEhbiQu\nnBOjAaOSuCf6qokn+ia/E837xtcFkmOiBhPhKB4VExYFIsguOyj7DsKMs3X3TO9V3b8/SJXVNb1P\ndXc93ffnurzAoaf7mZruqueu577vRxOJREAIIYQQQgghStLmewCEEEIIIYSQwkOBBiGEEEIIIURx\nFGgQQgghhBBCFEeBBiGEEEIIIURxFGgQQgghhBBCFEeBBiGEEEIIIURxFGgQQgghhBBCFEeBBiGE\nEEIIIURx+jQeSzv7EUIIIYQQQgBAk+wBtKJBCCGEEEIIURwFGoQQQgghhBDFUaBBCCGEEEIIURwF\nGoQQQgghhBDFUaBBCCGEEEIIURwFGoQQQgghhBDFUaBBCCGEEEIIURwFGoQQQgghhBDFUaBBCCGE\nEEIIURwFGoQQQgghhBDFUaBBCCGEEEIIURwFGoQQQgghhBDFUaBBCCGEEEIIURwFGoQQQgghhBDF\nUaBBCCGEEEIIURwFGoQQQgghhBDFUaBBCCGEEEIIURwFGoQQQgghhBDFUaBBCCGEEEIIURwFGoQQ\nQgghhBDFUaBBCCGEEEIIURwFGoQQQgghhBDFUaBBCCGEEEIIURwFGoQQQgghhBDFUaBBCCGEEEII\nURwFGoQQQgghhBDFUaBBCCGEEEIIURwFGoQQQgghhBDFUaBBCCFJhMNh8DyPSCSS76EQQgghzNDn\newCEEKJGkUhEDDCCwSCCwSC0Wi20Wi10Oh10Op34/1qtFhqNBhqNJt/DJoQQQlSDAg1CCJGIRCLg\neR48zyMcDourGFrtxQVg4d+ErwsBhkajEYMP4U+NRkNBCCGEkKJFgQYhhOBielQ4HAbHcVFBhBBg\nSP8uEB4XiUQQiUQQCoWivlf6fdIARL4SQgghhBQiCjQIIUVLCBA4jhNXKaQrFMlIg4lYzy38KaRg\nhUIh8WvSVZB4AQgFIYQQQlimSaO4kaogCSEFQZj8cxwnpkfFCzA4joPP50M4HFZsNUIIcKT/CRKl\nYtEqCCGEEBVJejGiQIMQUjSE+gshPSoSiUSlRkkfFwqF4Pf7wXGcOPGPFRRIazG6uhohT8WKF4TI\nC9Klr09BCCGEkByhQIMQQoTUpVhF3FKRSASBQAB+vx/hcBg6nQ5msxlarRYcx0Gn04mrIcJ/0v+X\nihWAKLUKIv1/6c8iBE4Gg4FSsQghhGQbBRqEkOIkrY1IVn/B8zwCgQACgQAikQgMBgPMZjP0ej00\nGg04jkMoFIJOp0v4etKgQ/53KXkQoNQqiN/vBwAYDIao50qlHoQQQghJU9KLBxWDE0IKSqz2tPEm\n8hzHwe/3IxgMQqPRwGQywWQyJQwo4pGmNcUaU6wAhOO4Ts8hDwCSBSHSgnTh7waDQXxd4U8hHSxe\nQXq8WhAKQgghhGSKAg1CSEFI1p5WEIlEEAwG4ff7wfM8tFotrFYrTCZT0sl8pqSrCfKxyFdC5D+D\nIFYAIl+NENKn5OOO1xVL2nVL+Jrw+ERBSDqduQghhBQvCjQIIcxKpz1tOBwW06PC4TD0ej1KSko6\npRnlknSc8YIQaQAipILFKkjXarVinUg4HE4aCMT793T2BqGCdEIIIYlQjQYhhDnCBDwYDMLn88Fo\nNEKn08Wtv/D7/QgEAgAAo9Eo1l+kSghSMkmpyoZYAYjwNalsFaRL/x5rFSTR5oQUhBBCSMGgGg1C\nSOGQt6flOA6BQABGozEqRUr4N7/fj1AoBI1GA4vFApPJFLOGIhVqmiDHS8Xy+XyIRCIwGo1RAYg8\nFUsaEKQTCKS6CiIUzwupXPJULCpIJ4SQ4kCBBiFE9aTdo6RpQbHSjYT0KJ7nodPpYLPZYDQai2Ii\nK0zsY63WZFqQnkpNRqo7pEsL0uUrIVSQTgghhYcCDUKIKsVrTyu9+y38yfM8QqFQVHtaq9Uqtqcl\nyQvSYwUgydryyn8f8V5X+mes1063ID2VblyEEELyjwINQoiqpNueFgC8Xi8AwGQywWw2q6aWggXJ\n2vLGqgdJtAoi/3u2C9IT1YMQQgjJLwo0CCGqkE572lAoBL/fL054jUYjrFZrxvUXJLZU9wZJZRUk\n1h4hiV5X+qf8daWvz/O8uA+K9HsS1YJQEEIIIblBgQYhJG/SaU8r1F/4/X6xPa3NZoPH44HBYKAg\nI8dSScWS1oTEasubaUG69M9Yrx2rIJ3jOOh0Ouj1+oT1IIQQQpRDgQYhJOeEiSjHceJENF6+f6L2\ntJFIBB6PJx8/AokjnVUQ6ftA/hzyAER4vkxTsQKBALRabadULPmY5SshqdShEEIIiY0CDUJIzsjb\n08arv4jVntZsNsNsNsedwBL1y3dBuhBIxHptaSpWsoL0dOpQCCGkmFGgQQjJunjtaWPVXwSDQfj9\nfvA8D61WC6vVCpPJFHMyRxO8aKwej1RWQeSrIclWQVLtTEUF6YQQkj0UaBBCsiKV9rQCYedtv98v\ntqe1WCwwGAw0WStysfZLATqvRCRbBQG+7VKWjYL0UCgkfi2VzQnpfU0IKQYUaBBCFJVue1phgz0g\ns/a0QrEvKS7S91MqBenSoFf6HPE6YilZkC4fc7INCgkhpFBQoEEIUUSm7Wk1Gg0sFgtMJhN1jiKK\nkKdiCZN+k8kEvV6fUkF6rAAklUAgk1Qs+ZilKyHyehBCCGEJBRqEkIx1pT2tTqeDzWaD0Wjs0gSK\nVjSi0bFILNW2vNIAJFlBupKrIIkK0hPVglAQQghRIwo0CCFpS7c9rZAeJdRf2Gw26PV6mhwR1Ui1\nLa+8K5b8ObJZkC7dG0T+vYnqQQghJF8o0CCEpCzV9rQAxPa0wq7NJpMJJpMprfoLNaEJW/FKtgqS\nakF6rF3SlShIF1Kx5J2xktWC0HuaEJJtFGgQQpLKVntaJeQqdUre2pSQTAvS5bUZ8QIQpQrSha9J\nxxwrCEl1BYYQQlJFgQYhJKZM2tMGAgGEw2Ho9XqUlJRQe1pStFJNxZIGIOFwOOpxuSpIFwISvV4f\nFXzINyekVCxCSLoo0CCEREmnPS3P8/D7/WJ7WqPRCLPZDL0+d6cWKgYnqVLLJLmrBenSIEaJgnRh\nJVL4N+nKi/R7qCCdEJIuCjQIIQC+bU8bDAbh8XhgNpthMBhipkcJ9RdCYSq1pyWk67JRkC4NAuIF\nAkIQIzw+1r/HKkiXd5mjgnRCiBwFGoQUsVjtaaV53dIJgtCeNhAIgOd5xdrTsoCVu7UsjJFkJpVV\nEHkAkmpBeiqv3ZWCdPneILQKQkjxoECDkCKUqD2t9DHAxZUOIT1KaE9rtVpV056WUqdIMUu2ChKr\nHiTWKggAhEIhhMNhxQvSpXVe0jFTQTohhY8CDUKKSCrtaYXJAM/z6OjoEHO3TSYTzGYzs+1pSfEq\n1kA01VQs4Zwg/F0q1gpItnZIlwYuwutQKhYhbKNAg5AikE572lAoBADw+/3QarWqr78QilcJIamT\n11RwHAez2QytVttpFUS4QZHNgnQgOggRzlnC+SjeuCkVixB1o0CDkAKVTntaof7C7/eLk3aj0Qib\nzUYXbsYU6917oox02vJKUzDlz5FuQbrwfdI/5a8tL0iXjznZBoWEkNyjQIOQAqNEe9r29naxhz4h\npDikkg6lZEG6vCYj2Wunm4ol/b5YBempvjYhJHMUaBBSIGJd3OOlR8nb05rNZjFtQvg+Vu6MszRW\nQtSoq5+fVFZB5KshyVZBUi0KT3UVRL4re6xVEErFIkR5FGgQwrBY7WnjpSgIm3L5/X7wPA+tVgur\n1QqTyUQXU0JIVggTeTlpVzt5ABJvFSTbBenSx9LeIIQogwINQhiUqD2t/AIYDofF+guhPa3FYoHB\nYIh7sWRplSBXY2XpmBCidsK5J5Ud0qU1IfK0qHgBiBIF6dK9QYCL7X+1Wi30ej0VpBOSIgo0CGFI\nKu1pBRzHiRvsAdSelhCaACamluOTrYL0VFdBpH9KBQIBcUwcx3VKU01WkB7veQkpZBRoEMKAdNvT\n+v1+cBwHjUaTUXtauntPSPFg6bOeSkG6PABRqiBdWDmO9drSMSTaG0S6EiINhigAIYWKAg1CVKor\n7Wl1Oh1sNhuMRmNGFzCWAg2WxpptNFkhxSrbBenSx8R67Xj/Jk33SlSQnmhzQvpcE5ZRoEGIyqTb\nnlZIjxLqL2w2G/R6PV2cCPkXCkSLW6KC9Fj1IPFWQQCIwYnSBenC3iBUkE4KDQUahKhEqu1pAYjt\naYPBIDQaDUwmE0wmk2L1FxoNO7tt04oGIV0jT/MpFtIgINWCdOEmkPQ5clWQLl8JSbQ5YbH9Lol6\nUaBBSB5Re1q2yFtgqhUr4yREreSpWMJNIKGhhjwAiZWKFSsA6WpBunyHdOFr0jHHCkJS3ZeEEKVR\noEFIHmTSnjYQCCAcDkOv16OkpCRhe9quYmmVQDgGNLkmhGSbPJ1JqisF6akGAenuDSJ8j/Cn8FqU\nikVyhQINQnIonfa0PM/D7/eL7WmNRiPMZjP0evrY5prwe5OuOBFSSOg9nVgqN15Sbcsr/XsqbXnj\nrXLLv0/6Z6yxSxuMCGm30u+hvUFINtCMhZAcSKc9rVB/IRQGZtKetqtYWtHIJnk3L0GmkwFC1Ig+\n69mXyiqIPABJtAqSTmvcdFKxhOuOPI03UT0IIYlQoEFIlggXjWAwiEAgAIPBEPfkLExoA4EAeJ7v\ncnvarmIp0MhG6lSs3dSNRmNUm0qlUyIIIeqVrYL5ZKsgsQrSE62CyP+ejVQs+bhjrYTQOY8IKNAg\nRGHy9rTBYBA+nw9Go7HTxSQcDovpUcKE1mq1UnvaPJGnqwm7qWu1WoRCIYTD4ZirUKlMBjItDCXK\noWMdHx0b9Uk1FUvaEUveLTDbBemx9gYR/k1YidfpdGkHQKRwUKBBiELitaeN1XJW2p4W+HZCq1R7\n2q5idUUjUxzHwefziWkDZrNZDDDkrxPr9eOlwaVSGNqVu5GEKIGVz3o+qa0FcKoF6cK5J9Z5J1EK\naLLXTrQKEgwGEQqFoNVqO600U0F68aFAg5AuSKU9rfCncOfH7/eD4zhotdq81F+ko5A7OQnpANLf\nh5LtgtO9G6lEGlah/q4IIalJ57wjvfkhf46uFKQLf5c2LolVkB4KhcSvybt5Ufpp4aBAg5AMpNOe\nVjjBdnR0IBKJ5KQ9bVepdVxKkBd45+P3kc7dyFQnAmoNVgkpBGpb0ciE0gXp8v055K8V6/9TLUiX\nfh8VpLONAg1C0tCV9rQ6nU6sv1A7lk7cqaZOxSrwttlsMBgMuRhmSpKlYcmDkFgTAQAIBAJ0N1CC\nUoOSK+b3R7FLZRUk1rlH/hzC+UZY3Zd2WEzl9WO9tvBnOgXp6XTkItmn/hkPIXkmnOQybU9rMpkQ\nCASY3AOjEFKn4hV4q6UeJhXSC3Gsu5HSi7/wHo1VjJ5Ja0xS+CgQS64QzoWZiFdnKO/AF+vmh9fr\nBYCY551sF6TLgxBKxcoftmY9hOSQ9AQmrb+Ilx4VDAbh9/vB83xUvj8AsasUK5QosM6VeGOVF3ir\nvR4mU9J0CI1GA57nYTabxYL+WJ1p4hWjUzoCISQV0hsf8kDE6/VCo9HAYDB0qgnJVUF6rL1B5N+b\nqB6EKIcCDUJk5KsXidKjYqXjWCyWqHx/FibrhSLbBd4syUcxOmEX/U4TK9YVjUzJi8EFXSlIV2IV\nRPhTuFZI07EefvhhTJ48GQ888EBGPzOJjQINQv4lXnvaWBM1juPEDfaAxOk4LAYcLI45GAzC4/Hk\nrcCbJYmKQlPJx6Y9QQoLTaKJkhK9n1JthBGvHTiQekF6rNeW/il//aamJlit1nR+VJICCjRIUUul\nPa30sdK75emk4whpLERZwooSAHH39WwVeBfDRCxRPnaqvfnjTQCK4fiRwkbv4dRkErgqXZCe7vlH\no9HA6XSioqIirXGT5CjQIEUp3fa00naoOp0ONpsNRqMx5ZMpa4GG2lc05AXeAGC1WmE2m/M4qsJF\naVik2Kn1XFgMkt0ASaUbX7KC9EgkQoFGllCgQYpKuu1phfQoaTtUvV6f0eSIpQuVWgONWAXeRqMR\nLpcr6xNWmhDHlmoqRLp7gmTjeNPvMD46NsnRMUoul/uNJOvGF+v8Iy1I37ZtG+bPn49BgwahtrYW\nFosF+/fvR48ePdCvXz+mOhOqWWG1XyEkBuFkEwqFEAgEEAwGxRUMoVOP9KTIcRw6OjrgcrkQCARg\nMplQVlaG0tLSjHP+6QKVOaGjl9vthtvtBs/zsFqtcDgcsFgsBddFqlAIAYRer4fRaITZbIbVaoXN\nZhNXn0wmk1gwKtQ9+Xw+eDweeDwe+Hw++P1+BIPBqNVHoiw6psnRMUqNWjY2THT+sdlssFgs6NWr\nF26//XY4HA5s3boV+/fvxwMPPIBBgwbBZrNh5MiRmD17Np5++mmsXbtWfO4FCxZgwIABsFgsmDhx\nIrZv355wLOvWrcO4ceNgNpsxZMgQLFq0qNNjli5dirq6OlgsFowePRorV66M+vf//M//xIQJE2C3\n21FdXY1bbrkFR44c6fQ8zz77LHr27Amr1YprrrkGx44dy/AIKoeu0KRgCasXQoAhrGLEumMqpEe5\nXC643W5wHCdOZq1Wa5fvbFDqVPoikQj8fj9cLhc6OjoAACUlJSgrKxPbt+Z6PCz9DtVKOgEwGAww\nmUywWCxREwAhANFoNAiHw2LraK/XC4/HA6/XGxWAyFv2EpIN+Z48E2UINxmHDRuG559/HosXL8a6\ndevA8zwOHTqEVatW4cUXX8RVV10Ft9uNv/3tb1i+fDkA4N1338Xjjz+O5557Drt378bo0aNRX1+P\n5ubmmK916tQpzJo1C9OnT8fevXvx8MMPY968eVi9erX4mM2bN2POnDm49957sWfPHtx00024+eab\nceDAAfExGzZswIMPPoht27ZhzZo1CIVCuPbaa+Hz+cTHvPDCC3jttdfw+uuv44svvoDNZkN9fT2C\nwWCWjmRqNGmcnOksTpgQrz0t0PlCIRQTBwIBsVuR2WxWvFtRe3s7AKC0tFSx58ymSCSCtrY22Gw2\ncS+QXInVMlj4ncTT2tqa9RoNoR+7mpfTeZ6Hz+eD1WotqJWeeGkQ4XA46nHx0rCE1RKbzUaTxRg8\nHg8MBgOMRmO+h6JaHo8Her0+5+dD1gjnIIvFoupzpdz58+dx6aWXwuVyxa1F02g0mDhxIi677DK8\n/PLL4tf79OmDhx56CE888USn73vyySexcuVK7Nu3T/zanXfeCZfLhRUrVgAA7rjjDni9Xnz88cfi\nYyZNmoSxY8di4cKFMcfb3NyMqqoqfP7555gyZQoAoGfPnvj5z3+ORx99FADgdrtRXV2NRYsW4bbb\nbsvwyCSV9IRaOFciUvSE/O9AIIBQKCTu4B0rPYrneXg8HjidTvh8Puj1etjtdtjt9rSKvNPB0h3X\nfKxoyH8nRqMxKmWNFK94aRAlJSWdVkGAzmlY0s5klIbVGR2H1FCQmpxaUqfS1drairKysoRteUOh\nEHbu3Inp06dHfX3GjBnYsmVLzO/bunUrZsyYEfW1+vr6qMdv2bIl6WPknE4nNBqNWLx+8uRJNDQ0\nRI3NbrfjsssuS/g8uUDF4IRp6ban5TgOfr8/57tFs5Y6lUtCy+Cu/E7o+BavZHuCCDcghBXOWHuC\nJOpGQwhAwVi6WPv8OJ1OlJeXJ3xMc3MzeJ5HdXV11Nerq6tx+PDhmN/T0NAQ8/Fut1usAY33mIaG\nhpjPGYlE8Mgjj2DKlCkYPny4+DoajSat58kVCjQIkzJpTxsIBMDzfEbtabuKxYlwNsdMO3hnF2vv\ntWyQByA8z8NisQCIvTuxvM4j3oaE1JK3+LB6lz4fWD33CIEGC7/j+fPn48CBA9i0aVO+h5ISCjQI\nU9JpTxsOh8W9FoRcf6vVmnF72q6gQOMi+Z4kLO3grfbxkdTQniCxsTx2oh6sBmVOpxMOhyPhYyor\nK6HT6dDY2Bj19cbGRtTU1MT8npqampiPt9vtYr1PvMfEes6f/vSnWLFiBTZs2IAePXpEvU4kEkFj\nY2PUqkZjYyPGjh2b8OfKNqrRIKonbU/rdrvh9XpTak/rdDrh9/s75frn6wTIWqChpHA4DJ/PB6fT\nCa/XC51Op2hNDIuBHFEf4ZwSqxuW0GzAaDRCq9XG7IYltOQV6sRY6Ial9vGpCWuT53xh8TilEmgY\nDAaMGzcuqtVtJBLB2rVrMXny5JjfM2nSpKjHA8Cnn36KSZMmJXzM6tWrox4DXAwyli1bhs8++wx9\n+/aN+rcBAwagpqYm6nncbje2bdsWd2y5QisaRLWEAEPoIAVADBzknT9ipeLkqv4iFSyeeJWYvMt3\n8DaZTDCbzUx1IxGw+Dskyoi3CiLthiWvCYmXhiX/O72v1I+CsdSxeqxSqdEAgMceewx33303xo0b\nhwkTJuCll16C1+vF3XffDQB46qmncP78eXGvjPvvvx8LFizAk08+iR/96EdYu3Yt3n//fbHjFAA8\n/PDDuOqqq/D73/8eM2fOxJIlS7Bz50786U9/Eh8zf/58LFmyBB9//DFsNpu4AiK0eweARx55BL/+\n9a9RW1uL/v3745e//CV69+6Nm266SanDlBEKNIjqJGtPKz2RsZKKU2x33JUo8E5Hro6vmt5TJH1K\n//7STcMSzmlSaknDovd2cnSMkhOyDVjjdDqjUpHiue2229Dc3Ixnn30WjY2NGDNmDD755BN0794d\nwMWi7LNnz4qP79+/P5YvX45HH30Ur7zyCnr37o033ngjqsvUpEmTsHjxYjzzzDN45plnMHjwYCxb\ntkws9AaAP/7xj9BoNLjqqquixvPWW2/hrrvuAgA88cQT8Hq9uO++++B0OnHFFVdg5cqVeW9bTfto\nENWIdTdQfsF1u93iaoX0TrnQ8lJob6k2gUAAHo+HmWIz4NtjXVJSktLjY60qCbs/Z/tndrlc0Ov1\nsNlsWXsNIVVGDStk8bDawz7bhE07U30vZ1NX9wRR+rMUDofh9XpVff7MN/pcpU7Y/0hovMCKuXPn\nYsqUKXjooYfyPRTWJD0h0VmF5FW67WmFyWwwGIRGo4HZbIbZbFb15A+I3peClUADSG0ZnJVVJULU\nIFkaljwIiZWGlagjFskeOr7Jsbpy73K5UkqdIumjQIPkRbrtaYWiS6FWg1qhZl+yYxurq1dJSUle\n7ooWW2paPPR5YJc0UEi0J4i8FkRKHnjQniDKoHNL6qSpzixJtUaDpI8CDZJT6banFe6UCxNZrVYL\nnufF4idW5GOn7a7SaDSd0jmAwirwJsWBpc9dLIk2JYxXC5JsTxD5ZJCCkeToGKWGteMUiUTgdDrF\nXbaJsijQIFknXAylBd6Jiig5jhM32AOiJ7Iej0dc1WAJi4GGXK4LvNNBKxqkGCm1Jwhw8fOd6MZP\nMaNzS+pYPVYulytpe1uSGQo0SNbEak8LIG56lLSQON5EltWLH4uBhrCiIaSt0Q7ehLAj0SqINAVL\nODdzHBeViiVPv6I0LJIK1uoQAVrRyDYKNIjikrWnlT9WWkis0+lgs9nibuJGd65zQ/gdhsNhdHR0\nMFHgTe+Lb9GxIPEIAYhA2lFJuLkgDUQS7QkiDUYKeRWE1d2uc43V4+T1ehEIBKhGI0so0CCKidee\nNtayPs/zYnqUUH9hs9mg1+sTnqSEQIO1uyasrGjIC7wBwG63q77tJQWghGRGfq7uahoWdcMirHE6\nnSgtLYXBYMj3UAqSumcPRPXSaU8LXFye9/v9Yntak8kEk8mUciExqxcstQcasQq8ASAYDKo+yCCE\nZFe6xejybli52hMkW1i7sZUvrK5otLW1weFwMDduVtAMgmSkK+1pu5Lnz+p+FAK1BRqJCrx9Pl++\nh5cyWtEgJPeU2BMkVi0IrYKwjbXfndPppELwLKJAg6RF3p4WQNwVDKE9bSAQUGwjN7WvDMSjphNv\nrB28YwV+NHknhURNn0E1UvL4pLoniLwWRCrW6ke+VkFYvbGVa6xeL4RAg37H2UGBBkkqUXvaWB9M\neRqO0WiE2WxWJAWH1UADyP/EPdMdvFm5yLL4niAk33L9uSn2NKxCxmrqFG3Wl10UaJC40m1PK9Rf\nZHOfBQo00icv8E418GPpYsHSWAkhnSm1J0g2itFZudmSbywHGpQ6lT0UaJBOMmlPGwgEwPN80va0\nXUWBRupoB2/lqf0Cqvbx5QuL5wvyrVT3BIm3CiJPv6JVECLV1tZGKxpZRIEGEUlXL5K1p5XfJTcY\nDLBarUnb03YVy4FGLii5ssRS4X2ugjhW79gREg/L72n5niCCWGlYwg20TPcEYfH45Bqr7yWXy4Xe\nvXvnexgFiwKNIteV9rRA/u6SsxhoZHMyLBR4+3w+sbNXV1eWKKgjhLBI6TSscDgMrVbLxE2XfGL1\n+LS1tWHUqFH5HkbBokCjSKXbnlbepSgb9RepEC4gLE5+szHuTAu8Cw2r7wlCSG5lWozO8zw8Hg8V\noyfB4nFwuVyUOpVFFGgUmXTa06p1EsvqpFKj0SAcDivyXJkWeKeDVjTYRb8zkg4WJ4dKS7QniMfj\ngU6ng16vT7oniLwWpJj2BGH1vENdp7KLAo0iIE2PCofDcLvdMBgMsFgsOW9PqwRWAw0lUIF3Ytla\nuhc2nQwEAnQnkxSUYj2XpkoIFHQ6HQwGQ9S/xVoBEZqoSKlpT5BsYjF1KhKJwOl0oqKiIt9DKVjq\nmDmSrIjXnlYIPKQnhFhFxGazGWazOefpUcmwGmhkOu5ctQ6WY2lFI1sXN/mqnlarTXgnkwIQQgpP\nvHMg7QnSGYtjpxWN7KJAowAla08rFLUJjw0Gg/D7/WIRcaxdotWkWAKNbBR4p4OlQENpwq72fr9f\nTE0zmUxRdyqTFZRKUzGU7utP0kfHPD46NvFl0kmpq8XorJ47WF7RoEAjeyjQKCCptqcVagV8Pp84\nkRJSqfLyo2AQAAAgAElEQVRdf5EKJWsdcinVQEOttTFqplQrXqH2xe/3A4hOTROCcuH1lOjrz9Ik\nghSmYryRkE/Jzh3y8wdLe4KwGGh4PB6EQiEKNLKIAg3GZdKeVljp4DiO2Rz/Qrw45qLAOx3FtKIh\nrX3pStpgOn39KQAhhB3Z/gymm4YlfF36/fHOHbk8f7B2rnI6nbDb7aqpQS1EdGQZ1ZX2tMDFk0FZ\nWZnq6i9SwdqJTCCsaMjv+lCBd/5wHAefzxdV+2I2mxV/jyXqaFOsudyEsCDfN1qU3hMkmzcw8n2s\nMtHW1gaHw0Hn0iyiQIMxXWlPq9PpYLPZwHEcQqEQk0EGwHaNhiBfBd7pYGlFI52xCsfe5/OJ+8Lk\nqy4plQBEnkaR7C4m6YyF93A+0SQrOTUeo64Wo8dKwcr0Bgaru4I7nU44HI58D6OgUaDBAHl72nA4\nnHBJlOd5BAIBMQXHYDDAZrNBr9eL9Q0s1jgIWA80hN8Nz/Ni8JerAu9iJi+uV/Ox7+pdzEAgIAZR\ntAJCEmHxXJpLLB6fVFdQpZkRSu0Jwto5xuVy0YpGllGgoWLx2tPGmzAId8iDwSA0Gg1MJhNMJlOn\nux3CyYfFwi0gfgqSmkkLib1eLzMF3qwEdYlWNIRj7/P5xOL60tJSMfBO93XyfTySFZP6fD7x3/KZ\nRkFIISmEz0e6NzBS2RNEOH/k+7yYqdbWVioEzzIKNFQoWXta+WPTbU+rVIeefGFpzPICbwCw2Www\nmUx5HllqWL6ARCIRsYOUsLJXUlJSsEV/0kJ0vV4vbi5GnbBIMvQ7jo/V81+6upqGJbyHhJsbrKyi\nUmvb7CvMKy6jUm1PKzxWSMFJtwUqS7n3sbAQKMUq8DYYDOjo6KAi7yyL1b3LYrEU1XGXp0FQJywS\nj5rPo2pSrMcoWRqWNP1KmL9IzyHS71fjOYQCjeyjQCPP0m1PK5/AZtICtZACDTVJVuAtpL+pbdyJ\nsLKiIbwnhA5SAHXvSoY6YRGSHAvnv3yQzlF0Oh00Gg14nofFYomqBZXXgkjJzxv5OIe4XC707ds3\nZ69XjCjQyDOe5xEKhZK2p1WyQ5FaJ+qpUtv40y0yVsu4C4XQQQoAQqGQ6rp3sSYbnbAoACGksMm7\nYKaThiXN4hCeI9Y5RPg3JTmdTowePVrR5yTRKNDIM+nqRbL6C6W65Khtop4utYw/3R28WZxoqXlF\nQ9gbRgi+AbbqX1jT1U5Y+Q5AWPz85Qodm/hYbduqRl09hwDKp3JS6lT2UaCRZ7E+IPIcc4PBAKvV\nmlGXnHivKbwOi/IdaGS6g3e+x10I5JtParVasXWzy+XKyWSActo7S9YJSy0bipHO6HxElNDVgCzZ\nOSSVZhbxakESaWtro0AjyyjQyDPph0DanhbIXo65cAFn9QKTrwm7Ujt4s3Tc1fI+ibW6J109YjVo\nLnRKTB4oACH5RDcWUpOt45RqM4tU9gTRarUIBoNwuVyoqamBRqOB0+lERUWF4uMm36JAI8+kEyjh\nDm0ucszVMoHsilyMX8n6GBYDvHxP4uXpafFW92i1iC257oRF74vEaCJNuirXAVmmaVhbt27Frbfe\nitLSUtTW1kKv12Pp0qVoaGjAsGHDMGjQILE1OFEGVUvmWTgcRkdHBwCgpKQEZWVlsFgsWS9kZW3C\nK5WLCbswwXW73Whvb0c4HIbNZoPD4cjJ76fYCRvPOZ1OcYNDu92O0tJS1W9ymG8sHxth4qDX68WU\nRKvVCpvNBqvVCrPZDKPRCK1Wi3A4LN6k8Xq98Hg88Hg88Pl8CAQCCIVCnYpMSWd0fBKjFQ32CDcy\nDAYDTCYTLBYLbDYbbDYbxo4di7/97W949NFHMXToULS0tODPf/4zbrnlFtTV1cFqtWLYsGG4+eab\n8f777wMAFixYgAEDBsBisWDixInYvn17wtdft24dxo0bB7PZjCFDhmDRokWdHrN06VLU1dXBYrFg\n9OjRWLlyZdS/b9iwATfeeCN69eoFrVaLjz/+uNNz3HPPPZ1uuNxwww1dOHLZQSsaeabX61FWVpbz\nFpwsBxpA9safboF3ulg77rker7z+JdX0NFrRKGyp9vJPVAcCAIFAgDphEZIFLARkGo0G3bp1w403\n3ggAcLvd6NOnD/x+P1pbW3Ho0KGo/1pbW/Huu+/i8ccfx+uvv44JEybgpZdeQn19PY4cOYLKyspO\nr3Hq1CnMmjUL8+fPx+LFi7FmzRrMmzcPPXv2xDXXXAMA2Lx5M+bMmYMXXngBM2fOxDvvvIObb74Z\nu3fvxvDhwwEAHo8HY8aMwdy5c3HrrbfG/Zmuv/56/OUvfxHPd2pshqJJ48JMV/AsCQaDOZ8gtbe3\nAwBKS0tz+rpKcblc0Ov1sNlsijxfpgXe6VJ63Nnm8XjAcRzKysqy+jry+hez2Qyz2ZzWylFra6t4\n1zsbhEL0cDis6hUtj8cDg8EAo9GY76HklTT4EM6x8sA5352w1KCjowNGo7Ho3y/xCK2zLRZLnkei\nbl6vF1qtNmvn32w4c+YMLr/8crS2tsY9p0+cOBGXXXYZXn75ZQAXzyt9+vTBQw89hCeeeKLT4598\n8kmsXLkS+/btE7925513wuVyYcWKFQCAO+64A16vN2qVYtKkSRg7diwWLlzY6Tm1Wi0++ugjMUAS\n3HPPPXC5XPjggw/S/+GVk/Rkqd6rJckq1u6syyk1fp7n4fF44HQ64ff7YTQaUVZWhpKSEsWDDIC9\n457t8XIch46ODrhcLgSDQVgsFjgcDlit1owm89kcK0tFyCy9x7JFmj6h1WrF9uA2m02ssxI+4xzH\nIRAIwOfzwePxoKOjA16vV2zOwXGcWHBaiFh5XxN1Y+191NbWBofDEXfcoVAIO3fuxPTp08WvaTQa\nzJgxA1u2bIn5PVu3bsWMGTOivlZfXx/1+C1btiR9TKrWrVuH6upqDBs2DPPnz0dra2vaz5FtlDql\nAvmYfLI24ZXryviV3gCx0Cn9PpEff61WC6vVCpPJpMj+MIQkku5mYoXcCYvla0CuRCIRui6kgMX3\nktPphMPhiPvvzc3N4Hke1dXVUV+vrq7G4cOHY35PQ0NDzMe73W4EAgGYTKa4j2loaEhr/Ndffz1m\nz56NAQMG4Pjx43jqqadwww03YMuWLao6H1GgUaSEYkqWpXtiy9YGiOlgLcBT8riku4M6IbmUyo7o\nxRKAEJIuFmo05ITN+lgbt+C2224T/z5ixAiMGjUKgwYNwrp163D11VfncWTRKNBQgXy8yVmb8Mql\n03Y12wXe6ch3u9h0KfE+kQd42Tr+rL+niTp1NQBhoQ5ETWNRIzo+ibG6e3qyzfoqKyuh0+nQ2NgY\n9fXGxkbU1NTE/J6ampqYj7fb7WKhdrzHxHvOVA0YMACVlZU4duyYqgINWg8sUqx36UnlhBYOh+H1\neju1SLXb7Xm7i87qZDiTMUciEfj9frhcLng8Hmi1WpSWlub1+JPipfT7LV4r3pKSkpTqQNTQipfF\nc1Gu0TEqXMlSpwwGA8aNG4e1a9eKX4tEIli7di0mT54c83smTZoU9XgA+PTTTzFp0qSEj1m9enXU\nYzJx7tw5tLS0oEePHl16HqXRioYK5GvCC7C53AkknrDzPA+fzyfusG42m2EymXLeQrgQZPLeCIfD\n4gpSNjt4ybEaxJHCk2xH9ESteGOtgAirKiyeqwsBHffEWF3REFKnEnnsscdw9913Y9y4cWJ7W6/X\ni7vvvhsA8NRTT+H8+fPiXhn3338/FixYgCeffBI/+tGPsHbtWrz//vtixykAePjhh3HVVVfh97//\nPWbOnIklS5Zg586d+NOf/iQ+xuPx4NixY+KxPXHiBPbu3YuKigr06dMHHo8Hzz33HGbPno2amhoc\nO3YMTz75JIYMGYL6+nqFj1TXUKBRpAphRUM6dlYKvAt5Mixssie0qE11DwxCikVXAhCA6kDyoVDP\n19nA2vvQ5XKhf//+CR9z2223obm5Gc8++ywaGxsxZswYfPLJJ+jevTuAi8XfZ8+eFR/fv39/LF++\nHI8++iheeeUV9O7dG2+88UZUl6lJkyZh8eLFeOaZZ/DMM89g8ODBWLZsmbiHBgDs2LEDV199tfj5\nfvzxxwEAP/zhD/Hmm29Cp9Nh3759ePvtt+F0OtGzZ0/U19fj+eefV93O5rSPhgqEw2GEQqGcvibH\ncXC73bDb7Vm/05wNwm7ADocDoVAoqsBb2D1YjSc9n88Hv9+f9C6KWgSDQXR0dMDhcMQN2KQrSBqN\nRgwwch3g5WKPEiHFRU3Bq5zX64VOp1Plxk35wmKPfyB+HYi8zivTAERIL7VYLHRDIIZIJAKPxwOT\nyaS6yZuaCNcA1t5H99xzD66++mr85Cc/yfdQWJZ0osXeDJMogvUVDYHb7c57gXc6WFvRSPQ+4TgO\nPp8vagXJbDbn7fjn4tiq+b1FCo/SnbCE5yqU8z9RB1ZTp5IVgxNlUKBRpIQLF0sdkIBvd/D2+/0A\nAJ1Ol7XN9bKJ1doYIUXN5/OB4zjF9sAghUuYFKt5FYg1SnXCEj6zwm739BmOjY5Lalg7TqnUaJCu\nY2t2VqDy+eFk5Y6WUH8hFHgbDAaEQiFYrVamlmpZOxFLJyLC8riQoqa2FSRa0civw4cP48yZMwiF\nQti+/RC6dzejT58+OHz4NDyeAH784zmq64ZSaOIFIED8OhAACAQCCAQCTLTizSVWro/5xuJxikQi\ncLlc6NatW76HUvAo0ChSwgVJzSeIRAXeQl2LmscfC2vdvoTj6/F4xBS10tJS6PV6JsZfrHL1ufD7\n/dBqtdizZw/efvtjNDWVwmA4jbNnK+Hx7IRGo0e3bhUoLx+M3/zmBZjNDtTW9sCoUSMxefJkeg/l\nUKxCdOH8KtTzpNoJS7oiUgy/w2L4GbuC1dQpWtHIDQo0VKCQc9ozkcoO3sK41Tj+RFjJjRb2wBBS\n1LRaLZMpakoTUlMIsHnzZrz//jpcuHAQX39thcnkRFlZGTjOhT59gmhoMOLChd4YPjyCHj3asXz5\n1wgEWtGjxzns3/8NGhoaUFVVhSlTpjA3QSk0Op0uZhpWsXfCos966lj7fUciETidTlRUVOR7KAWv\nuGcNKpKPSb/aAo1YO3jHu3vOyoSdNUINTCAQQCQSEVPUcrEPRlextus6q3w+H86ePYtDh47iwAEO\nX399HqFQDYYPN8Dr1ePs2TAmTOiJ//W/7sDGjbtgs2ng8XhQVWWGxeJHjx4VcLuPY+lSHuXlF9Or\nkrWYJLmXqBVvJoXoLAcgLI45l1i8Dre3tyMcDsNut+d7KAVP3TMHklVqCTTkk9tUNnhjNdBQ67h5\nnhd/B8DFTQ6FVqBOpzOfQyMq0traisWLl2LNmv2orbVi7tzxOHnSCrfbj4kTx+Cjj3ZCp/Nh2rQ6\nTJ06FceOncVf//o5gkE9Jk7sjV/84hG8+uoibNliAM9vh8nUF7/73X/h+usvx6xZs7I6dposxpfO\nscl2Jyw1Udt5Wq1YSQWWamtrQ1lZGVM1nqyiQEMlinFFQ17gnckO3qxdCNQWaEh/B7E2OWQpRS3f\n7+dCd+rUKbz22n9j167tuHBBizNnDLBYTJg8eTLq6uqwceNmXHfdCIwceTvef38lXnxxAYYM6Y0e\nPfTwePQYOLAvunfvjpqacng8u2Ew9IbH04GtW5uxa9dBrF69DTfccAXq66/N949aNJT8vCjVCUuN\nhehqGIPasXaMnE4nHA4Hc+NmEQUaRUyj0YDn+Zy+plI7eLNQzB6LWgINYZPDUChELWpJQqFQCLt3\n70ZDQwO++caPvn2HwG7/GidOtOKDD/Zj924ekybtwhdf6FFbG8aAAQNw8KAbHk8HrrvuCvzpTy/C\n7XajsrISH330d/j9Adx44xg0NfEYOLAUHR170dHhw759fjgc+ynQKDCZdMJKVIieywAk3+dpVrB4\nnCjQyB0KNFQiH292rVbb6a5StqRS4J0uFgONfIpEImKAwXFcSr8DtQRGalGMF6WtW7fijTc24fz5\nL1FSYsWNN07GNdf8FAsXLsLu3fvRv78BQ4cOxddfb8PYsd/BqFGjYLP9BU1Nfhw+fAzjxo1DeXk5\nDh06hAULliAQsOHpp2fDZDLhiy8O4N57r4fVakVDQzNqa/tjxYoV6NevH0aMGJHvH51kWaI6kHQD\nkGLrhKUmLO6TQx2ncocCjSKWi4l6OgXe6WIx0MjHxD1WkKe2PTCUwOL7Qe04jvvXBM6FtrYGWCwT\nUVbmQK9evfDcc08gFAohFArhtdfegt/fDZWV5TAajRg9ejQikWa0trZg27ZtuPTSS3Hq1CkEg71h\nMjVj0KBBeP/9Vdi0yQ+Hw4nvfKc3Tp06hZdeegXHj1fgiiuq8Pvf/xJGo1GRn4PeF7GptS1pVwIQ\nQLlCdLUeHzVi7RjRruC5Q4FGERMmZtko5MqkwDtdLE4scxloyIM8g8EAq9WadpDH4nHOFhYupkqN\n0efz4bnnXoDTGYZW60X37pdh4EAf2tvdOHz4MIYOHQqtVoumpiYxBVN47R/96N+wZ88eLF78GXbt\n+ie++OILmEwW3HRTf9TWXokhQ4bguus6UF6+B4MG9cHChcuwY8cReDyAXn8cZ8448ZvfvIJ///eb\nMHjwYEV+HsI+6oSlTixeH4TUKZJ9FGioRD5OdNl4TSUKvNPB4gku2xP3cDgsBhhKBXksHOdcBUTF\nMCk5ffo0li1bhlWrvoRGU4ErryxD//6lcLla8dvfbkb//qvw7rv/hfXrN2D58n0YMaICs2dPEYMC\ni8WC4cOHo7x8E/z+VmzZ0gaNpgIPPXQ1LrvsMgDA4MGDsX//IZw7dwFVVVbU1OhQWmrFpZeOw9df\n+7Frlx/jxh2kQIMkla1OWCx2U8oHFo8TpU7lDgUaRUypXaqVKvBOF8t32rMxbmEVSdhkz2QywWw2\ndznIY+0CQrqmpaUFr766BIcOnUf37mZYLE6MGjURU6ZMxqefrsbOnRsQiRixZs0anDnzNdraAK83\niLq6Ojz//G+wadMB/OQnt+Omm27Cz39+H9xuNz78cAXcbi8GDBgAAHC5XNi7dy9Wrz4LiyWCH/5w\nKp588n6UlpbCZDJh8eLFWLJkNVavdsHtbsfVV1+FXr165fnIFKZC/nynG4DwPB/z3BwIBFTXCUst\nWE0vczqdGDRoUL6HURQo0FCJfK5oZDrpzUaBdzpYDTSUPjbSPTA0Go24B4ZSQR6rx1lpHMfB5/OB\n4zjVtuEUdOX3pdfrYTTq0K9fDaZMmYT16w9j1aom9Ot3Fvfffx+GDh2Cr776Cu+9dxh9+/K4//7L\nUVdXB6/Xi7Vr9+HUqe5YvXo9brrpJpSWlqK0tBQ//em94vMfP34cf/zjUuj1YYwdW4pz587gnXc+\nx5VXXsCcObcBAKqrq2G1DsWOHbtx9KgNWq0Oc+bc0eXjQqIV6+c61U5YwWBQvJGmlk5YasXaz04r\nGrlDgUYRE04M4XA47b0rslXgnQ5WJ8BKjTvZHhjFJlvvh1AoFBVg6HS6gp18HD16FJFIBPPn34mD\nBw9i+PDh8Ho5nDnTiNraWhiNRtTX18NsNuP48c3o2bMSU6dOFX/Gu+6qx5YtOzBnzvcAABcuXIBG\no8H69Rtx+nQD5sy5GSdOnMDOnWdRUaHDgw/ejRUr1uCTTy6goaEFPM/jnXfew549B3HlldXYu9eB\nYNCJoUMpfYrkhrQOhOd5hMNhWK1W6oQVB4vXYOBioFFRUZHvYRQFCjRUIl/tbYHUTxS5KPBORzEG\nGsIEVzrxzfYeGKwe566QH2dhtU6v14t7jwiPU/M+AOk4efIkfvWrBdi//zBKSoIoKxuOMWN24uqr\nv4NLLhmG/v37i4+98sqLBd3l5eU4f/48SktLYbfbMW/eXMybN1d8vlde+W9wnB8+XwRtbTaMGXPg\nX4XjERiNF9P7brllJgYO3Iu6ujo4nU784x/bsG+fF0OGHIDVOg4ORxDbtu3Ajh278IMf/BusVmt+\nDlCBUtv7UE2kacXpdMLieR6hUCjqcYVaiM5y6hStaOQGBRpFLNXUKfmdcyH3P993zlmeAKc7bmEP\nDJ/Pl5c0NRYoUXMU6zhLWwGHw+FOr6nUPgD5DECCwSAuXLiAtrZGtLRUwe0+AcCN5mYd/vrX7Sgt\n1aCtrQ2jRo1Cjx490NraijNnzuDo0aN4771NqKoy4ec/fwAWiwXAxYv4li1b4HR6UFJixRVX9EEo\nFMHYsWPR0dGBK674Cv36VcPhcECn02HatGlwOp3YvXs3Bg+2oaGhGVVVveFwhNHYeAp//vN2BIPl\n8PsDePjhn2b0M9LnpDNWz59qQp2wLmJpvJFIBC6XiwKNHKFAQyXy+SGNdbGRF3hrtVpYLBaYzWbV\nnFCy2Z43m9IZq1AH4/P5xDS1XO+BwXJAlyp5vVFX0wGVCkB0Ol1U+kW2LF36IdatO4lJk0Zh/Hge\nVutwjB49GhUVFfif//kMzc3n8dJL76F794+wcOGL+Nvf3se2bW0YONAHj8eCtjYvmpqa0LdvXwDA\nRx8tx6pVZ9Gvnx5z534PQ4YMEV+re/fu+NWvHu/08yxfvgrLlp3GiBEO/O53N6Jnz544e/YsFi4M\nwec7B5tNg6+/voC1a9di6tSpeVtJJcWjKxvRKdkJS3pOUNu1jtVrA6VO5Q6dqVUk1xM64UQofc18\nF3inQ23jSVWsO+NysfbAsNlsMBgMORrlt1IZL6tiBXKlpaVZO87pBiDS9Its3vlsbm6F282jqqon\n7rvvHnR0dOC1196CxxPAvHm3Ytu2bXjxxZVoaQnh8OHDKCmxoqTk4grHtddW4aOPPsX/+3/v4IEH\nvofBgwejvNyO8nKgrm6wGGSEQiEcOXIEPXv2RHl5OcLhMLZt2watVosJEybAajWB447DYhkutsD1\ner2orDRh1qypGDt2IFavPoZ33tmO7t2745JLLunyz01IrnW1E5aaVkKFcQvjYkU4HKZAI4co0Chy\n0lUBof6iK5u75ZJS7XlzLVFAGasOxmKxZG0fkkKSzvshViBXUlKS13qjVAOQUCgU9f6RTzjSuVnh\ncrmwZcsWHDlyHmVl7bjhhrsAAM3NzTh1ygOv9+Kdv+uuuw7btx+G0WhC7969MXLkSEybdh59+vRB\na2sreH4TXK6LrXEHDx6MWbNuwKWXfgdVVVXia61evQZ//esmdO8ewgsv/AonTpzAm2+uB8f5cfz4\ncfh8AfB8b3g8F3++trY2AMCTT94Nq9WKcDiM48f/Ao7jUVNTk9bxZfWuay6wdO7Mh1yuHKfSCYuF\nVEy1c7vdAIDS0tI8j6Q4UKChIvlKUQmFQqop8E5HV9vz5pN8zNIWtYBye2AooZBSp4QAw+fzMfF+\nTzUA4Xm+U+qF1+tNuAISiUTw+ut/xcaNZ+DzNaGqqgIrVqzA7bffjr59+2LOnMnw+Xy45JJLYDKZ\n8OKLv0AkEsGRI0dw6NAhTJo0CXq9HlVVVbj11slYvHgZNm7cgcGDB2Pnzp2oqKiI2vuC53kcP34Y\nx4/b8dlnn2Hs2LGorNRi797jeO+9MAYPDqFPHzt69eoOjuOwYMEinD4dwJw5EzBt2jQEg0GMGVOL\ngwdPYfv27aitrcWQIUNoItUFhfK5zha1HB+lUjHlf1fis8PiiobT6URZWZkqrq/FQJ1XV5J1Qv2F\nkBKj9N4LucBqoCE9IfM8D5/PJxbas/h7UItE7wdhxU66WzrLK0WJJh5CEKXVahPmfms0GgQCAbS2\nnkNlJYejR5uwc+fXOHDgEK69dgYuv/xyOBwO8ftMJhOamprwxhvL4XRqYDAYMHnyZAAXdwL3eKpw\n9GgH1q5di2XLTqBbtwj69esHjUaDsrIyXHPNDKxb9wVaWvQwmUzo0aMHnn76Abz//kfYvv1rTJw4\nDFde+e1rXpw4AV9++SW+/PIYQiEvPvxwC1yuaphMKzFy5Hg8+uitGD16dJaPNilmap5Ap9sJS54C\nq0Q6JmsZBcC3HadYGzerKNAoIrEKvIUTFIstI1kONMLhMNrb28Wd1LPdorYrWF7RCIfDYopUJBJR\n1UpRNgh3LCORCMxms/h1+aQjHA6jqakJ3/lOHb74ohFarQ5G4yHodBF8+eV5nDu3D5FIBDNnzox6\nT9psNlRVWaDX+1BZWSl+feTIkZg9+wJsNgv69u2LHTtOoHv3Uuzfvx8ffrgNw4Z1x/z5c/Ef//Ez\nfPPNN+IO4aWlpfjBD+7Eddc1oaqqKur38uMfz8GpU6fw8cefY8eOFrS3b4XXq4PF0gSnU4fjx08U\n7O8xl9R4zlELVs97ue6Exdp7yOl0wuFwMDduVlGgoSLZetMnKvD2er2dTjKsYC3QEAI9IT2K53nV\nFtqzTLiQCisYwMW78RaLpWhXioTJgmD37t1YsGApunUrwbXXDoLJZML48bfjwoULOHToJE6fbkFD\nQwN+/ev/g+7dSzF16lQMGjQIp06dwqhRAzF69Gj069dPfD6r1YpbbrlJ/P9f/eohGI1G/P3v/0Bj\noxYOhxPhcBh2ux12ux3AxdSupqYm9OnTBz169IgaL8/zeO+9j3HyZCuGD6+E3+/EkSOjUVMTxrRp\n/bBzZyP69zejra0Np0+fjhoLSR2Ld6NzhcWUoGSU6oQlTcFisVFIW1tb1GotyS4KNApYKgXeLN+t\nZiXQkAd6wknebrczMfFl5T0ivB+EPV8ANlMClZDo9xUMBvHnP/8NW7ZcQFlZAI88cju+//3vQ6PR\nYMyYMRg27CQ4jsNbb32ATz/9BlrtLpw+3Yaf/ezHeOutD3HsGHDHHT44nU7s27cPo0ePxvDhw6Pu\negorpNOnT4PT2Ybz55vw5ZdfimlOkUgE//Vfi3D4sAvf+96lGDduHMLhMLp164ZIJIKGhgacOdOM\nhgYd6ut74wc/+HesWvUJjEYjZsyYjsbGRuzcuROvvfY5+vUDfvObJ/LSkY2QQpBuACJ8Xcrn8zFT\niFw0CrMAACAASURBVE6b9eUWBRoqotSHMp0dvFmZRCai1vHLOxsJrVN5nofX61XtSViOhfeIUOsC\nXJxIZzPAYOX3FgvHcdi7dy80GjPKygCO02PjxuO45pqLF97jx4/jlVfeg04HXH75ULhcLXC7a9C/\nfw0cDgcGDqxBINCI7t27Y+HCJdiw4RvU1q7Bb3/7JPr27Quv14slSz5AJBLBD35wG8rKyuB2B7Fp\nUwQGwwYx0Li4QWAj3G4TLlxowIsv/gnBII8HH7wTJ0+exOLF61BVpcfcuRMwceJEGI1G3HLLzeLP\nYbfbcerUKZw+vRUtLXYcO3YMdXV1eTqqpJCx/HnvqlQ6YQmrxgCY6YQlpE6R3KBAo4BksoM3q5ve\nAbH3AVEDeeGxvHWqMF4Wj7nayIvpAaCkpARGozFrr8lySsXGjRvx9ttbUVKixc9+9j0cPHgagwb1\nRllZGQD8q2j04mMnTBiPW2+9BcuXL8dnn+3DmjVr8eMf342Ojg6UlJRg/fptsFpPwGqtFs81J06c\nwK5dLeA44LLLjmDUqFEYO7YOra3bMH78CPj9fmi1WixatBiNjTwmTLBi/PhLsW3bhwiFNP8qNl+M\n3bvDuPzySkydOhXLlv0DO3cexe23X4uxY8cCuLi53+efd0Cr1aFbtzps2LABNptN3DAwFhZ/X7lA\nxyU2tV1X1EaoAxGCCaEmTA2dsJJpa2ujFY0cokBDRTL5gAl5/z6fDxzHQavVplVYzPpFRk2Bhnwl\nKV7hMSspXwI17lciD6qFlEC3262aMaqRwWCAwRCBw1GKCRMmoLS0FBcuNOJ3v1uI2bOvQ21tLR5+\n+HvQ6XTo06cPAOD06QYcPqxDTc1R1NdfKwYlzzzzOG6++SvY7XaxfmP16g3o1SuAESNG4JJLLoHF\nYsHkyZMxceJEtLa2wu/3Q6/X48KFFng8Ztjt5ejTpw/uuedacByH3r17o6ysF/r1u4D6+gnQ6/XY\nufMovvoKOHLkqBhoVFaWo0cPAy65ZDzsdjM2bGjEyZP/jV/+8qdMNrbIF1bOQflE55PE5NcFNXTC\nSsblcmHw4MGKPR9JjAINRim1g7caJ5HpUEOgId8DI1naDmuBhpoIQbXQNU0aVAsXLDqu8Y0fPx47\nduzG0aPNWLDgTzh82IyGhs/hdJagre08fvvb/6/TBfiGG6ajqmoHxowZE/V1o9EoTvwBYM+ePVi/\nvgO1tRbMnn2TeIdTq9Viz549WLRoJXr1suOhh+7FvHl34siRiyseOp0OdXV14u9v3ryb4HQ6MW7c\nOASDQcyePQ2jR5/AlCmXw+fz4Q9/+C/4fD707q1HKKRHnz59sHfvXlitJdSFiiiGziOpS/WmZi47\nYSVCu4LnFgUaKpLKB0bpHbyFyXA4HGa2YDZfFwT5XXWLxQKTycTscYxHDcFoKBSKastM3brS09HR\ngU8++QSffLIOhw5dgMk0EqNG+dCzpxkGQzl8viq4XMD+/ftRVVWF6upq8XsHDBiAAQMGgOM4HD16\nFDU1NVE76u7atQv79x/EoEH9MH16I+rqBkS11gWApqYmNDZqoNO58cEHH6GpyYXvf/+7US1yhVqm\nUaNGRU046urqxPqL1atX4803dyIU4jFokBlW60CcObMJ4bAZ48fXwWQydfrZacKYGH2GEqPjk1hX\nP1/Z6ISVrA6EisFziwINRqRT4J0O1u+u52NFQz7pTXcPDFaPea7HK08LzHTVTkmsTjqWL1+BX/96\nCdraePTta8LYsW2455556NGjB/x+P9av34BAwIdXX12O7t11ePrp+bDZbFHPsXbtWixduhtDh5bg\nZz/7iXgsPvhgLXbvDuP224GHH75PfHx7ezsaGxsxaNAgXH755dDpdLBYLFi8eB3On9di6NB9qKmp\nAQC0tLTg1Vf/Ap6P4MEH70JVVZX4PJFIBG63G++99yHcbidqavwIh4FZs66AwWDEvn0BHDx4FH/8\n439jx44d+O53v4sRI0aoouhU7Vg7B+USHZvkslmvlk4AEolEwPN83DoQnudx4MABDB06FKWlpRRo\n5BgFGioS68OaSYF3Jq/J6kk1VxOJSCQiBhhdnfSydsxzPVkTjrXP5xPTAktKSmAwGBKOJVfHVe2T\n11jjs9tLUVqqh9FowPDhZWhpqcTHH6/FU089BK1Wi3/7tzuxdetWbNv2DQDgwIED2L59HyZPHofR\no0fjk08+xapVq9HRYUcwyEWtbk2ePBIazVcYNWq4+HodHR24664Hce5cBx588EbcddddmDZtGiKR\nCBobm3D2bCMuueQS8fEtLS04fz6E9nY3tm3bhlmzZgEAzpw5A4fDgaNHj2L9+gaYTMCLLz6Ffv36\noaKiAu3t7bBYPsaZMxfw1VcB7N69Hjt2nMKCBc+JtSTCuZLjOHHykauiU8I+ep8kl8tjlEonLPkK\nyKFDhzBt2jQAQK9evWC1WvGXv/wFp0+fxvDhw1FXV0epVFlUWDkeBUC4Qx8KheB2u+F2u8FxHKxW\nKxwOB6xWq6KpOaxNeuWyvaIhtKh1u93o6OgAcLGrkd1uz3gnb9aOea7GK9QdCcdao9GgtLQUdrud\n0qQyFIlEsHr1GrjdHXj55SfwzjvPY/bsW2E2G2AwfHufyePx4JtvvsHUqX0xd+5svPrqn/Hmmxuw\ncuV6tLa24h//2IUzZ8px9dXVuOee27Bhwwbs2LEDkUgEN9xwPf73//5ZVL1Ge3s7mppCcLlsOHv2\na/HrGo0GN998Ix588F7U1NSgpaUFmzZtQrdu3XDjjSMBtGP58v3Yu3cvvvjiC7zwwhK8/PIb6NOn\nDyZP7o6xY8tRV1eHbt26QaPRYM2atVi+/ByqquwYOTKAsjI7HA4r7HY7zGYzjEajeL4Uaqm8Xi88\nHg+8Xq94E4fjOPHOKCEAO+fnfFLbMRLqQAwGg7hJq81mw4gRI/DPf/4TCxYswOzZs+H3+7F582bc\nf//9mDJlCrp164aamhpMmzYN77zzDgBgwYIFGDBgACwWCyZOnIjt27cnfO1169Zh3LhxMJvNGDJk\nCBYtWtTpMUuXLkVdXR0sFgtGjx6NlStXRv37hg0bcOONN6JXr17QarX4+OOPY77Ws88+i549e8Jq\nteKaa67BsWPHMjxiuUErGioiTGqld3KznSrC2qRXLluBhnwPDKEWhjYFU54QYPh8vqj9RjI91qy+\nl7OhoaEBH364A62twPz51Rg/fjxqa2tRW1uL6upqcRK+e/duLFlyABUVEZSXl6OlxQGDoRFDhvSG\nw+HAxIkDcO5cE2bOnImzZ8/irbe2oKQkgp49e6Jnz56dXrempgbPPvtDHD58GHfeeWfc8S1Z8iE2\nbWrGtGnHMHv2d/H551/B4wlDp9PB5/OhudmDr77aBbvdArvdhl27vsHGjZtwzTUzAOBfgQUwfPgw\nzJ37a3z11Vf/Cq5WY9KkSejRo4eYgmc0GqHX63NadMqCQv25SPax0urbbDbj0ksvxaWXXgqO4/Dq\nq6+ipaUFFosFR44cwcGDB3HgwAEcPHgQ4XAY7777Lh5//HG8/vrrmDBhAl566SXU19fjyJEjUXVl\nglOnTmHWrFmYP38+Fi9ejDVr1mDevHno2bMnrrnmGgDA5s2bMWfOHLzwwguYOXMm3nnnHdx8883Y\nvXs3hg+/uBrs8XgwZswYzJ07F7feemvMn+WFF17Aa6+9hrfffhv9+/fHL37xC9TX1+PgwYNZbeve\nFRRoqIzQZ74rBd7pUkPnpkwpPfZwOCwGGErWwkixFtxla7yxgjnpfiPpUvvFLh8ikQjMZhf69bNi\n0KBBaGpqgk6nw+DBg3H27FmcOHECo0aNQt++fVFbq0dFhQ1jxozBddedg9U6EjNnzoROp8O///sd\n4nOeP38ejY37EA6XoqSkBOFwGN988w1KSkpw/vx59O3bF2azGddeey2uvfbaqPH4fD6sX78e5eXl\nmDBhAsrLS2G3N6OsrAQVFRV47LEfwuPxYODAgeA4DkeOHME//sHj2DEnysra0NCgQ0PDxfQunudx\n5ZVXYtiwYaisrITJZML48ePxq1/9X+zaxaGjw4e77vo38bWlOdvyY5TrrjdqwMr5J19YmUTnE4vH\nyO12Q6vVorS0FHq9HpdccklUGicATJw4Effddx/uuusuAMAf//hHLF++HG+++SaeeOKJTs/5hz/8\nAQMHDsSLL74IABg6dCg2btyIl156SQw0XnnlFVx//fV47LHHAADPP/88Vq9ejddeew0LFy4EAFx3\n3XW47rrrAMT/fL788sv45S9/KaaXvv3226iursZHH32E2267rauHJyso0FARjUaDsrKynF8ApK1B\nWaNUoCEU2wu7nMbbA0MpLAd3XSVductWMFfshMnz3//+CY4dM6CtbQOams7BYukBq9WEAQMqsGrV\nJpSX1+LHP/bg8ssvx3/8xyPiBPrBB+8FABw9ehQcx2HYsGHiZKK1tRUGwwiUll4swFy58hMsX74X\nHHceHNcTV13VF3fdNafTmI4cOYLNmzdj9eoGVFREMGDAAEyfPhXHjp1Ee7sHwWBQLA4HLu75cccd\nd6Cyci0qK7uhf//+OHLkCMaOHQu3242FCxchGAzhgQd+IHab6ujoQGWlBSbTDgSD3VL6jCnV9aZQ\nAhDyLfodFh5hV/B4KeihUAg7d+7E008/LX5No9FgxowZ2LJlS8zv2bp1K2bMmBH1tfr6ejz66KPi\n/2/ZsgWPP/54p8csW7Ys5bGfPHkSDQ0NmD59uvg1u92Oyy67DFu2bKFAg6QmHxNQlie9Xd3ZXLoH\nhkajSboHhlJYOuZKrWjId0w3Go2wWCyKBnMsHdds6ujowB/+8Bfs2rUb7e1OnDpVjm++OYu6OgvK\nygw4fbodZ8/qAZzCuXPnwPN8p0Dv7NmzeO2198FxwIMP3oJhw4YBAEaNGoVp006hb98ecDgcaG5u\nRUuLBpFIO0wmIBjkOo3n/PnzWLDgf9Dc7ITVGkG/fv1gt9uxe/duHDoEfP31ecyYcQH9+vUTv8fv\n96O0tBS33nqL+DVh5++jR4/i+HEP/P4w1qxZg6FDh2LFinX48ssDaGvTIBAAdu9uwoULF9CjR4+M\njmGxBCBqG49a0HkkORZXNIRAI96Ym5ubwfN8VItvAKiursbhw4djfk9DQ0PMx7vdbgQCAZhMpriP\naWhoSHnsDQ0N0Gg0XX6eXKNAQ2Xy8YHVarXMnlQzPV7Sjd+EPTDMZnNOjz8rx7yrgYY8HS3bq0UE\nuHDhAjZuPIQTJ1y49NJKVFbysNsrMXv2taiursauXV9i5MgynDnTjNWrT6BPn22YPHly1HMYDAYY\njRpoNJGoeplevXrhkUfuF///xhtvQP/++9Cz561ob2+P2vAvHA5j6dIPcPjwKXBcB7p3d2DevO9i\n2LBh0Ov1GD58OOrrT6CkxIpevXqJ37dnzx68884qDBvWEz/60Q86fS4HDhyI22+/FF988QVWrDiB\nVavWw+3uhZMnv4bHUwaL5QK8XgtefXURbrllOoYPH67YZ7tQAhBWzj9EvQox0CDKo0CDMJ86BaS2\nmZx8X4ZM9sBQSjGc5GKlo1kslqyuFuViRYOFVZMBAwZgzJhuaGkxoFu3Sixc+Bj++c/PsHLlHkya\nNAj33nuxFuI///MPaGm5OBFub2+P2oivpqYGP/vZPeA4LioIkCsvL8fUqVPF/9+2bRvOnj2Hq6++\nChqNBhs3HsX581r8/+ydd3iUVdr/P9NLkknvPSEJLYQEQu8IShFRRMUG7LoWfHV1Xdu76tb3t8Vd\nXd21rA0bIKuydAQE6UVaKAkkJCGNJJMymcxkevv9MWaWkNAkJDMwn+viusLMMzNnzjzPee7vOef+\n3vfem8eoUaM6rDAEBwezYMF9nd6zpKSEoiIjAkGtZzJAJBJ5zp3y8nLKyqoJDw9HqWxBJApArz9D\nTk4sRqOC6Og+1NbWUFioIT6+wJNseS25XgSIHze9WaDUl/C1PtJoNISEhFzw+YiICEQiEWq1usPj\narW6w9bOc4mJieny+HZ3yosdc6H3vNDnuC3C1R1WNdRqdQfXP2/DLzS8jN64aH0hcLoQlzPb3lVd\nBm8o/OZrfX657XU6nZhMJiwWC0CPbUfz40aj0XDkyBHuvvtuRoyoJDXVXam7rq6RujohNTXuZOqA\ngACefnohGo2Gbdt28+WX27nttpHExcWRmpr6w4qG+xppampCr9eTkpLiuWb0ej3r1m0gKCiIW26Z\nikgkoq2tjeXLt1JRIUSpVDBt2jSmTRvM2bMNjB07tkMhvnPR6/WcOnWKPn36IJfLKSgoQyJRM2LE\nzVRXV/Phh18TExPMo48uRCqVsmvXPlavbiAvT8jzz9/Fnj17WL78LJGRTh566PYftn2tJyCglszM\nKT3W913hFyB+rld87R4Gl64KLpFIGDJkCFu2bGHWrFmA+3tu2bKFJ598ssvXjBw5spNV7aZNmxg5\ncmSHY85/j3Z3vMslNTWVmJgYtmzZ4klg1+nctYcef/zxy36fnsYvNPz4ZNDbzsWExoVsU3vKzeti\n+FKfX25f9Va+i5+OLFmynPXrz5KUtI7/+7//9axGzJo1jaSkAvr16+c5NiwsDI1Gw6lT1VRVSVm6\n9CscjgRmzuzHuHFj+OtfP0SnM+JyWREIgnjwwUnk5+cjFAo5fvw4q1aVExwMgwYNJDExEaVSSVZW\nNDrdcSIjJyEQCJg+fdol27xixWo2bapm+PAj3H//nZjNEBycSlRUFFVVVZSXO2lr06DT6di3bz97\n9hwjKcnJhAkzSEtLQy6X43R+R2ZmOn379iU6OpoJE0qx21NISUlBq9Ve0cxhT+AtAqS3x0Jvxb+i\ncWl8sY9aW1svuqIB8Itf/IIFCxYwZMgQj72t0WhkwYIFALz44ovU1tZ6amU8+uijvPXWWzz//PP8\n5Cc/YcuWLXz11VesX7/e854///nPmTBhAq+99hozZsxg2bJlHDp0iPfff99zjMFgoLS01BMblJeX\nc/ToUcLCwkhMTATgqaee4g9/+AN9+vQhJSWFl19+mYSEBG677bbu7KZuxS80vAz/isaV0ZXQOD/p\n+GptU68VvtTnFztHHA4HJpPJU72+N/Jd2vHlc7k7OH36NDt3HqWsrIaWllA2btzKT37yAACRkZEe\nq8V29u7dy2ef7UAmM7FgwWAKCoScOmXBarVhNpsxGBwYDCAUWjEYdLz99ucMG3acRx5ZQHp6Ojk5\nhwgNDfSsVAiFQkJDVVgsUezYcYD8/Pwu21lZWcmrr/6d2Ngonn/+WRQKOQoFKJVyZDIZDz98OxqN\nhqFDh2K1WjEYDERERLBnz37+9rdPsFpTmT+/H5Mnu6uNx8bGdrCyDQ0N5dZbp/D665+ycOFzxMaG\n8sorT3eysfRGekqA3MjXiZ/uw9eERktLy0VXNADuuusumpqaeOWVV1Cr1QwePJiNGzcSGRkJuJOy\nq6urPcenpKSwbt06nn76ad58800SEhL48MMPOzhRjRw5kqVLl/KrX/2KX/3qV2RkZLBq1aoO2zoP\nHjzIxIkTPddru0vV/Pnz+eijjwB47rnnMBqNPPLII2i1WsaOHcuGDRu8toYG+IWGH67euak3OVdo\ntOcEWCyWa+Zq1F34YkB8fnvtdrunsrJAIOi1fBc//8VsNhMdnU5mppW4uEi2bt3GwYMHeeaZJ3E6\nnSQlJXlMECIjI38Q5BAWFsqUKVNoazNy+vT3qFSBxMfH89hjszGZTISHh7Nx40Y2bdJQWtqI0Wgk\nOjqaF154olMbpFIpUqkAqdSdQN7a2opIJCIwMNBzzMqVK9mwoZWgoEZmzizk9ttnMWRIFadPl/LS\nS28yenRf7rzzds/7tXvGv/baO4jFiaSmapkyZTxGo5H33/8Mo9HCQw/NIzIyEpfLxdKl/2br1u+p\nrW2jttZAQ4OMFSvW+oTQuBDdLUD8XByXy+Xvp0vga/cwcI9H7Q56F2PRokUsWrSoy+cWL17c6bFx\n48Zx6NChi77nnDlzmDNnzgWfHz9+/GXly/7mN7/hN7/5zSWP8xb8QsPL6C3XKfDNZdD29prNZs+N\n1RdcjXxNaJx7Xpzr2NWbCfVd4Wv92p1s3LiJLVsOMXJkPImJYsrK6igoqMdqTcBg+BMSSTpDh0ZS\nVlaPzSbg8cfnMnbsWEJDQ4mOjkYul1NV1YhWG0VlZR1Ah21W99xzD3FxO4iNjfVY037/fQHjx4/s\ncOOeMWMa/fv3JT4+nurqav7xj6VIpSIWLJiNzWYjIyODMWPGsHHjfmJjw8jIyEAikZCens62bbs5\nc0ZIVFR1p+8HMGfOdPr0OUpeXh4JCQmUl5dTWNiC0eiuzhsZGYnVauXIkXIaGiKZMCGKjAwllZUu\nMjLSru0P0EtcrQCxWCz+HBA/PwpfFGOXytHw0/34hYYfn6tU3U77jHr73wqFAplM5hMDn68FxAKB\nAIfDgV6v9wiM3k6o7028UZQfOVLCwYMabLYWLJYAWlqiycioA4RER0dSWwsnTpxg//4aVCoZbW1t\nSCSSDm4ld945jays4wwdOrTT+6tUKhITE6murqalpYUNG3aya5cJp3OPZ0tBeHg4EomEzMxMwL3H\nuKXFhVhs4Z13PkOrVXDvvflMnjyZdeuWdOrDGTOmEh19sJNLlF6vp66ujrS0tA61NpKTk7n99hyM\nRjMDBgwAwGq1Mm3aMGJjjzJ37p1ER0dTUlLCsWMn+PTTpdxxx6wOqyvXK5cSIDabzePo5U9C74w3\nXuPeiK/1kV9o9Dx+oeHH54TG+TPq4HY2UigUvdyyK8MX+rvdEtjhcHiNY5efrhk3Lo9duwqorY1i\n4sRoJk2KZMKEhz1Wja2trRQWnqSkJJDkZCOpqanY7fYOuUvp6emkp6djsVgoKioiMTHRY3lrMpn4\n7LP1nDnjDjjHjs3F6TxMSkosf/zj+wiFAp5++sEO9rX9+/fnpz81IBQK+eabXbS0WC/qvR8TE+PZ\nJtWOy+XiX//6lFOn9MyZk8O0af9NLheJRB3+/9FHH7F8+XbkcishIYMwm5dgs8lIT49k27ZqLBYh\n/fuf6lJI3Si0iwWRSITNZvNMzvhdsPxcKb5wDzsXl8vlFxq9gF9oeBm9lUAL3j1otM/AtW+ROndG\nvbW1tbebd8V4+035fEtgwOPa5c1t97WVou5Co9FQWHiKkBA5wcFyhg0bRl5eHgCffbaMPXsqufnm\n/syaNZOYmO9xuVz8/vfvkJwcxqJFP+1klLB69TrWry8hLy+cJ574GeDekpiREYNAoCYxMZFBgwYx\nduxYiouLWbPmKDpdC/v27ePWW29FLBbjcrloamoiNzcXmUxGeno6arXas9rRFQ6Hg7NnzxIdHY1U\nKmXFilVUVtbT1NSMyQS7d+9FqVQybty4Dueh0WikpaWFdet2cOqUjMhINcHBDkpL66mvT6Sl5Thi\nsRGlUtapqq4fN9ciCd0XVpcvhjePdd6AL676+IVGz+MXGl5ITwdL3iw02i1qzWazZ0Y9MDAQiUTi\nabcvBpfe2ubzBYZYLCYwMBCTyeSZufTjXRw+fJhf//ovVFVZCA6WkZ4u8tQwAWhubqWlBTSaViIi\nIpg+fTobN26kpkYIaDCbzZ22EjmdTlyujmOCUCjkZz+bj9VqRS6Xex7PzMzkrrtG8OGHK1mz5hTx\n8fEMGzaM3bt3s2zZTjIzw3jiiZ8RHh5OeHh4l9/BbrfT2NjIoUOHWbPmOIMHR3HPPbezfftJamqE\nzJvXj759DWzYUEtLyx4yMzMxm80cPXqU7Oxs/v3vddTWGhg+fAChoRVMn/4wffv2xWq1sm7dRjZs\nKKe6upnw8AQ2bNjCww8v6NbfwJe51DXd3QJEJBL5xDjijeOzN+GLVcHBLTTCwsJ6uxk3FH6h4ccr\nhYbL5cJisWA2m3E6nUgkEpRK5QVrYHhT2y+HK6lo3hNcquZIu5OXt+PLVe5/DE6nk/ffX0ZRkQix\nGEJDDTQ2RlFRUeEpBHXffXMYMuSUJ4cBYNSoUQDExsZSWVnpSepPTExEKBQyefIEUlOTOrmzCIXC\nDiID3H2el5fH1q0H0elsqFQqwG0jqdEIaGrS43Q6EQqFVFdXs23bTgYM6EteXh5Go5EVK1axZ89+\nHI4IQkJM6PVBtLYaCAkJYerUHKqr6xk7dixWq5Xy8n8TERFEWFgY//znh2zfrmfChFpaWoxotQJm\nz87jueee9bStvr6e1NREAgLKkUhakcncwuzrr4OYNm0aSqXymvwuvsDVXs9XI0DO3b51/hYsb8BX\ng2g/F8fhcKDT6S444eHn2uAXGl7Ijbyi4XQ6PQKj3aJWLpdftAaGL94MvEVodCXoLlRzxBvODz8d\nEQgE5OT0Q61uZsyYIYwbN46ysjIiIyOpr68nJiaGyMhIT7J2OzKZjPj4eDQaDUuW7Kak5DjJyeks\nWDCZrKws3nzzM0QiIWlpabS1tSGVSjusIlZWVnL69Gny8vIICwtDpVLxy18+jNls9tTUmDhxIiEh\nISQlJXnOpx07drF8eTWDBtWQm5tLaWkpmzdXUlKiJzRUTG5uP2bP7k96ejoCgYDk5ESkUrfoDQgI\n4Ne/ftoTkGZlpXD48CbsdgEPPDCDdes2UFVVi16vJygoCIfDwbvvLqG01MrNN2cxePDdfP/99yxZ\nUkBBwSbi4+MZMWJEz/5gNwBXIkAcDgc2m63Day+UA+LHu/BFMabT6TpZbfu59viFhh+g92eCz6+B\ncSUWtd66DcmbOV9gXErQ+VIfX8t2elPSq9Fo5Ntvt9CnTxJz576Kw+HAbrfz9ddrOHiwjPBwBQ88\nMJtp06Z1Cvo2b/6Wr746RkiIDpEoAKfTjskkxGQyodFoaGpyIhI52blzJytW7KK5uY758+/g7rvv\nBOCTT77m+HEbd9zRzLx5dwNuV6r6+nrq6+vJzs7GaDSSm5vb4aY+cGB/EhIOIRQqaGhoIDU1H+uM\nKgAAIABJREFUlZEjo8nOVpKdnUV+fr5nW4Ner2fx4rXU1bn7fMqUKR3Gg9zcHNauPcTx404yMkop\nL3dy7NhZ+vcvYvjw4QgEAgICZCiVVrKyshg/fjxqdQMKxWFUqlaSkpKu9U/k5xwuR4A4HA5cLpfX\nCBBvuda9GV/qI61WS0hIiE+1+XrALzS8kN6qpdEbgaTD4fAIDHC7R8nl8itKIuxtkfRj6K1VpPOr\npl9uUUNfERo30g3k+PHjLF9eSFAQtLW1sWXLSaCJkyfFVFc3oVaH8+WXBz3Jj6GhoUilUvLy8n4I\n+iA6Ooa7776VtrZZtLa2kp2dTWBgIAsXuovs1dXVUVbmoKXFysGDJcyd694ClZAQSWNjDdHRUZ72\nnD17lrfe+hqLRcDUqaVs315MeLiMX/7yUc8WpUGDBhEWFsWxYy62bt3GvHl38+ijC7v8fgqFgsTE\nEAQCbQcnq3ZCQkJITg5Gp3Nb2zY16dDpDPTp0wdwC5Wf/ex+mpubPSs6s2bdSkpKMsnJyYjFYqxW\nq1dX1L2WeMuM9LkC5NyJjgttvzp3HLpWAsQXxrrexhf7SKPR+IVGL+AXGn6Ang8kz68qfTU1MHwl\nCD6XnhYa529J84Wihn4uTkBAACJRJTU1ao4etdDYKCM6WsnUqVHo9UoMBhcikZNvvy1Dq7UgkegJ\nD4/j6aeDmDLlJlJTU4iNjSUkJITm5ma+/noTmzfv44knFnhyOLRaLSaTifr6FCZOnIBQKGTz5m9p\nadEzf/4UhgwZ4mmP+5wSIhC4A8LWVgEikQWLxeIRGgKBgEGDUrFaS0lPT73o9xOLxTzxxM8wmUwe\ni9127HY7MpmMX/7yMU8NnXPdrA4dOsTnn28iLS2cRx9d6JnIkMlkyGQy/vSnN6ivNzB69ECefPIR\nf+DhhbTncJw/RvWkAPGfFxfGW4TqleBf0egd/ELDC+kti9trHfS212Qwm83dWlXaLzQuTPuWtPbC\nhj9WYPhKH/tKO68Ws9nMv//9DcePV9HYGIVOd4yXXnqEPn36kJiYiMViQSZzF+V7//0lqNVNHD9e\nS0NDHTrdTUgkkg5VvxsaGqipcW9VaWxsJCIiAnCvGsybN89znN1uZ+PGA5w6JSQp6UyHehQRERE8\n99xDWK1WIiIiSEo6RHh4OAaDgU8+WU5KShy33XYrd999J3fcYbvkSoLBYEChUBAUFERhYSE1NTWM\nGjUKq9XKH/7wOlKpmOeee6LLxM76+nrOnhUikWiwWCwUFxej1Wr57ruDHDt2nJqaMFpajtHU1MDt\nt0/3b6PyIXpCgNwIY0h34UtBe0tLCyEhIb3djBsOv9DwA1zb7Ufn18Do7qJvN0pweSU4nU5MJtNV\nbUnz05FzrX9dLlcHu86eTFg1m81s3ryZ06eLCAoKxGI5S0BAIFVVdR2qfB85coQTJ4q5887pBAQE\n8Mor76JWi7qsO5OZmckDD4z0/H0+VquVI0eOEB4ezrRpw0lMPM2QIUOw2+00NDQQHR2NSCTqEPS3\nJ1pv2LCB7dtbOXOmhYkTxxMcHOwRGeXl5VRVVTF06NAOuRx79+5l+fLvGDw4mblzZ/Pxx2uoqhJ4\nVua2bClHJLIya9YpBg8eTHl5OWlpaQQEBAAwbtw4nE4nJ06c4oMPPqKoSENDQx3l5QacTiO5uXLO\nnk1AperD2bNnb1ih4UtB4qXoTgHii7P1PY0v3nNbW1v9NTR6Ab/Q8EKulxWN82tgtNdkONe9pjto\nb3tvOzhdCddqRePcnBeBQNBtAsOXxNy1OI/PrS3SXgegK8vOnkhY3bt3L3/84zJ0OiH33JPLrbdO\n41//WsX69fUkJBxi8uTJuFwuVqz4jhMnQCbbz7333sNdd42loaGRwMBA1q9fz4gRIzyJ1yKRiPHj\nxwPu1Q2j0UhycrKn7fv27eOjj/YQGQkvvfQYkydPAuDTT5fyxRe7GDgwhN///tfIZLJO7c3JyWHy\n5BpiY8M7bIGy2Wx88MFXlJc7uesuDS0tBmw2O3PmzOS99z7m0CEhYOG++6QkJYXhcDQTFxeH0+kk\nLS0cmcxBRkYGX3yxgh07zjJhQgILF97vqf4bFBREUZEDu12NwVCJXt9GWJgAuTyCxMR4ZLIm8vPj\nsVgs1NTUkJCQ0K2/k7fjK9fz1XI1AqS9fpDfBaszvijG/MX6ege/0PADdG8geaEaGBKJpFve/3x8\naaBrp7uFhsPhwGQydUvOS1f4itDoznOhq+KF7YGyw+HwzHye65jTEwmrERERBAa6cDikJCYmkp2d\nzZgxxVRW1nu2QwkEAsaOHYRCcZKcnGwEAgGTJ0/CZrPx8suvUVLiXqWYPXt2h/fWaDT87W+LMRic\nPPbYLE/tDZVKhUrlQqWSd9jyVFJSTlmZFb2+gpKSErKzswEoLCxEq9WSn59PXFwcqakJbN5cgFy+\nkRkzpgFucRMVFYRer8VqtbJ791nsdkhJOYTLFU1kZA2jRg1AIpHw2GM/8eRquFwuXn31SQICAoiK\nikIoFCAU/vccXbJkCV9/vY2UlASGDo1GoYjmwAE7ZnMAU6cqycjI4JtvTqDTJaLVavngg32kph7k\nlVd+fs3GKD/ex8UEiM1mw2q1IhaLezQJ3ZfwpYm9dlpaWvxCoxfwCw0/QPdsnfoxNTC6A2+pSfFj\nuNrg/fyk+u7IebnRuZDAaA9Cz7fdvFrHnHOLll3KPtdkMhESEsKHH/6FpqYmj7C4/fZbkclkVFZW\n0tbWhkQiYfr0WzxBfTtisZg+fWKxWs8SHx/f6f3d7XRitws6fM/Bgwfzv/8bQ2BgIAqFwvP4Qw/d\nj073TyIjszzbj5qbm3n//dVote7vMmrUKMrKqqmoEFJWVu157bp131BdrWH69DwmTJiA3b4Ku93B\n6NGjkUgktLUZmDLlJk+7ZTIZW7duJTAwkPz8fE8/3X33HQwbdobU1FRqampYvbqA4mI7AQGNvPTS\nEwQHB6NUfsnJk9VMnz6dfv36oVQGoFY3cvDgIcrK6klKyrohtxX6x4nOnHsNnru9tzddsPx0D62t\nrV2Oe36uLX6h4YX0lr0t/LhgvbsSjn8s3lRw8HK52t/YbrdjMpm6Nan+YviKmLualZdLCYxzP+Ny\n2nG52zWsVmuHYy4WqLz33qfs31/BqFHxzJw5k9LSUnbu3E9ZWQMORzO7dp1h8OB4Fi1aSL9+/TpV\n8QaYO/c2RCIRZ86c4emnn0WlCuXRRxeiUqnYuXMXQ4emkJ2d3aGSOEBMTEyn90pJSeHNN//a4TG5\nXE54uByh0OzZmnXHHdNJSysgJyfHc1xBQQnFxWL6929EoVBw//33eJ6bPHlyp886cuQIn3zyPUFB\nLuLj4z0Bg1KpZMCAAdTX17Ny5XqCgqyMGRPJggW3ExYWhlqtZtq0qdx7b6hnnJsy5SbWrFnDrl1n\n0OkaUatD0Gg0nQobXs/40njpDXiDC5Y34e33gq7wr2j0Dn6h4Qf4cYHk+dt1eivh2BeFBvy4oLg9\nqb5dYHRnUv2NyuUKjO7gQsHK+YHK+fkfAE1NTWzbtofCQitVVaWsXLmD0NBkFAo7RmMMOl0Fzc1R\nFBQU8vrrq5g4sZCFC+/v8B7ffruFtWsPMGZMFkePFrN2rYGQkLOMHn2cwMBA/v3vU4SEwNixY6mq\nqmL//v0MHz6c5ORkACwWCzt27CAgIICRI0d2Ou/q6urYvHkrY8YMJicnxyM0EhISiIiIYO/evWg0\nGnJycrjzzpvp2/cEw4cPv6y+i46OJiZGgEolJzg4uNPzR44cYetWLQkJ0bz88s+Iiopi//79fPbZ\nFhISlDzzzOMIhULMZjObNm1m8+bvEAqTEIt1NDaGs3r1aubNm+ex4vVz43Il+Qc3qgDxRaHhTwbv\nHfxCwwvprWRwuLxg/dzZ9PZ8ALlc3muDzvUuNNptgU0m0zVx7bocfGlFAy6vnT9WYFyL798eYJzf\nvnODlQMHDtDSEo7Nto2mJiVWq5LwcCFPPjkDlUpFSMgI9u7dS1tbDKdPi6isrOK1194hMNCd6J2V\nlUVlZS1VVULKy2sZO3YoxcUVpKamMmjQIJxOJ3377iU0NBCVSsVPf/oUx48bmD69gNde+38AHD16\nlM8+O0RgICQmJpKYmAhAWVkZu3btQ6ttYssWMxkZVZ5aHO0cOHCADz/cT0SEi5dfTqBfv34dLHYv\nhFarJTAwkJSUFObPv5X6+npPXzU2NiKVSgkODmbAgAGMHFlGWlq8Z2VCo9HQ3CxAJmvDbrcjkUg4\nceIEX35ZiMMRwPz5MQgEWfznPxt4441CCgqK+fvf/+ivL+Pnqq/zG1WAeCvtJhF+odHz+IWGl9LT\nybeXCtbPD3Z7YrvO5XK9Co2u3I6uhWvXjUZXbmjXagXjajg3/0OtVv+QXyHE6RyCTKYkJMRAXl5f\nZs6ciVQqxeVyMWTIEPR6PcXFxRQXl7BkSSVtbac4dqyBF19cyMyZU4mLO0z//v1JSUlh6tSbMBqN\nlJSUkJqayssvP41AIKCtrQ2BQI5Y7CI42J2Tcfz4ccrKyoiJcRIaGtjhhr1ly05WrVLTp4+e3NwQ\nBg7M6FQnIyoqipgYiIgIxG63U1tbS1xcnOd5i8XC5s3fYrfbmThxAsHBwezfv59ly7aSlRXNwoX3\n8vnna6mocOeC9enTh7ff/gqpFKZMyScrK4s5c6aRmJjouT7GjRuHTCYjMjISmUyG0+kkKiqKrCw5\nCoWKBQvmIxKJ2LXrEFVVdjSaNo+YvxHwjyNdcy3vJdeLAGm3+PYl/EKjd/ALDT/AhYN1Xwh2fVVo\nXIiuZtp7u8+vhz4+X2D8WDe09pWGnsJsNvPaax9x5EgxY8dmcPPNI3E6nYwZM4qlS//Dq6++z8MP\n30VycjJOpxORSERubi6RkZGcOVPL0aMyiouPsW7dN9x7791MnDgRoVDomTD4z3/WsGlTBfn5YTzx\nxMMABAUF8bvfPcmZM2cYP348ra2tLF68lro6AQ8+mMtNN93Uod9ycwdQVdXE+PETPAnc4K7QXV9f\nz9ixY8nKyuKVVxbhcDh4442PaG628tBD0z15G8XFxSxbdoDTpwvZsGEvL730OPX19dTUCDCbS2hq\naiI8PBCdzr39Qa/X09YmQK0+Q1lZGyLREoKCMhk/PoUHHnAXGQwICGDcuHEeg4rFi5dw4kQVw4al\nMWXKFPR6PcHBwfzud8+zfft2xo8f36VF7/WIL1/LPUFPj7W+JkC8fXW7K7RabZcFPv1cW/xCw0vp\n7RWN9qDMZDLhdDo9s75isdhrBxdfu3Ge/xt7c5/7itDoautUVwIjICDgmruhdRcCgQCttpGaGgEH\nDzZz772DSU9Pp76+nspKPRqNgJqaGlJSUhAKhXzxxdcUFVWyYMFs/vSn37Bs2TKWLi3l6NF6Zs1q\nIzg4GLvd7nGVcjodCATufBCr1eoJUrKysujbty/gzg2Kjw9GIGglKSmpkzjLz88nPz+/w2M6nY7P\nP9/0Q4VuCVOnTkWlUtHS0kJbmw2DQYDBYKC+vp7CwkISExNJSBBQVaXAaAygsbGRCRMmUF5ezv79\nDt577wt+8YuHsFgsREVF4XQ6eeQRJ0ePHuX77xtpbRViMgkwGt2iYseOHRgMBsaOHYtAIKC0tJS1\na7dRXa2gsPA0O3ceRCSKJDExgOnTJ5KZmcnSpV/gcMi4//7ZZGRk9MCv68cb8aZxzpsFSG/fl64E\nu92OTqfz5I356Tl8407r55rTPmC0V5RunwGUSCQEBgZ6dVDWvsXEm24Ol0N7m7uqO+Ltfe4LnC/c\nfE1gtCORSHjggTtQKDaQmBhHbGws4E6Ovu++CWi1WvLy8gD36sexY5WUlgooKytjwIABTJgwAY3G\nQEJCNC0tLVitVpKSkjyByh133EZu7hliY2O7dMDau3cvp06VM3PmZGJiYlCpVOj1et58800UCgX/\n8z//02mbFLjdoMzmRurqajAaszyPh4aG8thjc9FoNOTm5vLWWx+ya5eWyZOr+OMfX+b777/HYrGQ\nnZ2NRCJh6NChFBXtxuVyO1qFhIQA7jocQ4cOJS8vj8mTq5DL5VRVVZGVlUVNTQ1ffLEXvR4CAwOJ\njY3lu+9209oaSnh4MVFRedjtGnQ6AaWl21iy5DscDi0CQRwSiZGoKOUNITR8KVD005HeFiC+dr/V\n6XSee4CfnsW37rg3ED19A2gfNIxGI+D2D1coFD6zV9kXhQa4nbtaW1u9XmD42oqGxWLBYrF4fb9e\niqamJv7v/17l5Mk6AgIEqFShqNVqqqurCQsLw2AwEBYWhkQiwW63o1AouOuuSZSWljFy5EgAYmNj\nefzxhzh27Bj/+McqFAoXL7zwEJGRkZ6tkNnZ2dTW1rJ+/UYyM9MZOnSox3p3zZo9FBeLCA4+wOzZ\nszEYDKxYsYLPPjuFWOwiO3s7N910EwKBALvdzpkzZ4iJcdfcCAmJJigoHIPB5PlOTqcTvV5PaGgo\nYrGY2NgIoqI0xMZGIBQKGTFiRIc+GDVqFOHh4URGRnaw67XZbFRVVZGQkEBKSgrwXwteiURCWlog\ner2Zo0cLWbx4K0FBLQwcGMQttyyiT590goOD2bp1K2vWnOT0aSlicQOBgY1YLGGcPKnGbDZ3aQ98\nveCLW196Cl/um54QIL5YFbylpYWQkBCfavP1gu/def10Kw6HA7PZjMViAdyzhEFBQT6X5AXeHwS3\n43K5PBa14Huizltpz20Bd2E7XxYY4F7q//vf/8G6dWdxOAwEBbVRX2+htvYUen0KUmk9DkcMTqeG\nlpa/kZAQx1/+8jL5+flkZ2d3mrkTi8UIha4fKml3vr53797Dl1/W0K9fNUOHDkUqlSKVSpk6dSjR\n0aXk5+cjl8txOp1kZ2cTF7cGqVRMcnIyBoMBgUDA5s3fsmrVCfr2DeKZZxYxZ85k+vYtZuzY0Z7P\nKSgo4N13NxEQ4OLFF3/KnXfezsSJzRfcOy0Siejfv3+nx1esWMW335YyenQiCxbc1+E5pVLJL37x\nGE6nk7ff/ojy8iocDgmTJiUydeoUj/vUrl1VBATEs3ChEpUqm/Xri9BomomLC6atre26Fhp+biy6\nU4C0B+u+FLT7hUbv4Zt3YD9XzfkVpRUKBRaL5YdgxPdEhi8MHudXTm/v58DAwF5u2aXx5hWN87dI\ngTsJ+Fol9fbUudbQ0EBNjQOl0khqqoj4+L5s2WJl9+4y4uKsDB+egcMh5uTJWk6flqJWN/LWW+8j\nlwcyd+4MlEplh7b269ePZ55xW1EXFBRgMpmYPn06QqEQg8FAVlYmubkVDB6c0SEYmT59GtOnd2xb\nXl4e69d/jkAgQCwWewIUh8OO1erCZLJgMpno27cv/fr1QygUYrFYEAqFSKVS5HIXCoUYiUSCUCi8\nZKE8k8nEkSNHiI+PJzk5mb1797J163Y0GhVtbUaOHz+OQqGgT58+ntfs2rWbw4eLyM8fiM2m58SJ\nNuTy/xoqSCQSRCIXoaEqHnnkpzQ2NlJRYSAoKAW73cErr7zD/PlTL7vOh5/rB190VPqxXI0AsVgs\nnppOve2CdSm0Wq1faPQSfqHhpVyri+H8gm/nWtTabDavDCQvB2/eOnWhyukWi6XTnnhvxRuFRlc5\nGAqFAoPB4POrQ+3fbcqUgYhEGgyGGCIjxQweXIlGk8LkyQN58slHcblclJaW8vbbHxIWFkBNjZPW\nVj1ZWcdwuVykpqYiEAg4ffo0BQVHyc8fytmzZ3nhhQ/5YfGHtLQ0PvpoFfHxIbz88s8Ri8VYrdZO\nQk2v11NdXU16errnHG7nyJEjrFy5jVGj+vPsszNJSEhAqVT+ID4crFmzjlOnKpk9ewqpqak88cSd\nKJVKFAoF9fX1rFq1nsjIMGbNmukRLps2beLkyZPMmTOHwsJCPv/8KCkpIl544VG++mob1dUxTJok\nIyenL2+9tQ6FwsXzzy9ELBZz4sQJVq78jtOnlYSGnuHhhx+msbGRyMhIxGIxp06doqKigocfnklk\nZKTn38svx1JSUsKTT/4RiyWKiROrrmuh4Q+6/FyIiwkQu92OxWJBJBJ5/t/bLliXon1Fw0/P4xca\nNwDtW0rMZvNFC755c7B+Kbyx7e2J9e3b0s6vnO6NbfYFuhIY7Vukzq+mfS3oiZvlnj17+OSTrQQH\n2xgzZiQ7d54lPj6O55//BaWlpcTHxyMSiZBIJGRnZ/POO3/H4XCwbt0GGhqa2L37KF9/fZD77x/L\n1KlTWblyE9u3t9HQoGXSpNFIJG6BK5PJqK2tpaZGgNOpxWQy8fXX/+Hzz9cxceJgfvWrFz3f9+OP\nv+Dw4WamTcvgrrvmAO6tl1u2bGHt2m84fTocqbSYV1757/KHSCTC4XCwd28JpaVCgoK2MGrUKI+l\nrcPhoKCggE2b6lCpKpDJJAwbNgytVsvf/76S8nILJSVV3HvvHYSEuAgNdYuTESOyCAwsZ+bMmQgE\nAqRSF1Kp291q+fKVbNvWREKClZtuimXo0FxcLhdpaWkIBAKsViuLF6+irAwefNBKdnY24F7lbWpq\n4pNPvkSvNxEQUIJUOuOa/9a9hX/suTC+nKNxrWkXEeDe9tv+tze4YF2M1tZWv+NUL+EXGl5Kd1x4\n59t6XqoGhkAg8Gw98TW8qe3n5r0IBIJOAuNcfO1m35vtvZjAaKenVl6u9Y2xra2N48cLMRoFZGdn\n8uyzt5GcnIxcLic5OZl//nMxJpOVRYvu9yRAi0QiZs2aiV6v58knX6GgoBlooE+fPgwcmI5afYQB\nAzLo168f//rXrzEYDCQlJdHU1MSCBYOJjY1FpVKxa9f3lJaGIhSe5vHHtcjlcs9qp8vVsW8rKyv5\n6qvDNDUFMGIE3HbbJM9z7ZMacrmcW28dyb59hygoUHPy5FaeeELJwIEDAcjNzWXMmApOnSpi2bIC\nKivruOuu2cTFiWhqaiUsLI2cnBzi4+MJDQ1Fq9WSkZHGzJnTUCjcxQSfe+4B5HI54eHh6HTN6PXl\nDBgwinnz5vL22x/R0tLG448/SFxcHGKxmJSUSKxWtcfBC9w5H2vXFqBWqwkMjEMgELJu3X7y8vI8\nFdD9+PHT9fja2y5Yl6J965SfnscvNK5DurJLVSqVl6zH4Msz7N7QdofDgclk6pD3IpPJLrjXt6ua\nD95Kb7bvcgTG9YTVaqWpqQWbrR6TKY6dO/cyffotKJVKwO1EVVFhxGyGs2fPeoSG3W7HarWiUCiY\nNm0kGs0O6usb+X//7zPuvXcsf/rTs54+y87Oprm5mT//+QMMBiePPDKDQYMGAfDQQ/cjky1nxIix\niEQiXn31HfR6Kw88MJ2JEwUdbF+jo6PJzAwiKUnGww/fR1RUFACFhYV89tla+vZNYP78e5k4cQLZ\n2QP5298+wm53olKpsNls7Nq1C7lczlNPPcJnny3ju++qkMlkRERE8O67r3scrORyOXFxcTidTt58\n832OH9dzyy1F3HHHbZ4cD6FQiF6vp67OhkAQSWRkKI2NjZSU6GhtdVJdXU1cXBxCoZCHH56P0Wgk\nKCiI5uZmTp06RUlJGRoNDByYSL9+aezZU8SBA/uYN6+Yv/712U5uWNcD3j7u9Ba+MCb3JlfiOuUt\nAqSlpcVfFbyXuD7v1NcBP+ZCOj/Z2J10Kb/sgMybVgWulN4UGucn1p+b93IxfO1G1tN9fL0KDI1G\ng0ajIT09vctzYMOGDSxZshmBIJHQUBNnzjTyu9/9g3nzbiEhIYGqqipmzcrGaDQyYMAAwJ179c9/\nfkBtbSvz589k6tSppKamsmTJaurq5Gg0LV32m/tm3/F3HTlypMcat7a2lsZGC21tAsxmM8OGDevw\n+oCAAJ55ZlGn5Nndu3ezb18LJpOVu+82o1AoiIiI4IUXHsHhcBAWFsbhw4f59NP9yOVuW9q5c29n\n6NAzHqtaqVRKVlYW56NQyJFKjcjlMk8+x7kByoABsUildSQlJREVFcUdd+Sh0+kZOHAgJ0+eZOnS\ndQwYkExKSiJqtZpvvtnJ3r2ViER6oqPjyMoaQUpKCklJSRw9WkVzcwSlpaXXndDo7YkZPzc2PS1A\ntFqtf2Wyl/DtO7Yf4MLJxleaECsUCn325tMbQsNut2MymbpMrL8cfGlFoye5GoHhjUnr7Wi1WtRq\nNcuWraW+3saDD44jOTmZ7dt30r9/XwYPHsymTZv4wx8+QqdTMXq0krS0LPbvL+XAgeM0NloJCrKg\n00WRmNiKyaRCKNxATo7byrayUotaLaC2tpaUlBSGDBlCTEwM5eXlyOVyFi/+jFGjhnmC9/DwcJ56\n6gEMBgN9+vTpdB6q1Wo+/fRrQkIc3H77KHJzc7HZbCxdupTCwkrmzLmZ4cOHewpmtmM0Gjlx4ixQ\nS1bWCM/2JnAXFKysrCQ7O5vo6GhiY4UoFBLCwsJQKBRd2tiei9PpZPLk0YwaZSInJ4eWlhZqamoY\nOHAgUqkUs9nMAw/M63D8mDFjAPc5cezYMQ4dMlNbewCp9CTNzUIsllrsdikgJigolh07Cti8uYU5\nc1J47LFbMJut3Hzzzd1wBvjxBXyxRkRPcy37qDsFSFlZGSkpKcjlcrRarX9Fo5fwCw0v5XIu4CvJ\nBbiSz/TFwPfcKtvXuu3nO3d1lVh/JXhjUNwV11rMXa8rGK2trTQ2NvL556uorTVit7dgNgfx7bff\nIpcr2bHDwYABZ4iMjOS995ajVmuJinIyZsxE1q/fh8MRRFCQgerqRtLThYSFRWE2O6irE7By5VrW\nri0kLy+KBx+8mYaGhg4z74mJiSQmJvLqq2/x3Xdt6PXbO6wSxMfH43A4WLx4CZWVaubPv5309HQA\nSktLOXrUQEiImMzMTCQSCTt27OBf/1pPc3MEwcF7PY5Mdrud5cu/prm5lTvvnElCQiQg77AC4nQ6\nee+9pRQXW5g7t57bbpvFyy8/gVAovKAVscvlYvfu3eh0OiZMmMChQ4dYsmQ3SUkKBg7lPthmAAAg\nAElEQVQcyDvvfE55uY27766noaGRlSu3MXhwP5599nEUCgVNTU2oVCocDgdSqZQBAwYgl6/FYFAQ\nEaEEjOTlTUQmk5GYmEhAQAD79x+huLiZ9es30txsIT09it/85s8MHNifn/zkvmtmm+zHj6/QGzHC\nlQoQs9nMiBEjEAgEpKSkEBwczMaNG1GpVPTv35+srCykUmmPfocblRvDKNpHudCFbLfbaWtro7W1\n1bMnOzg4GKVSeVXe3948G3wprvWg1+7cpdPp0Ov1OJ1OAgICCA4OvqJVjHPxVTHX3bTnFLW2tnqs\naVUqFUFBQVcsMrzpHNbr9Zw5c4a///1D/vKXJVRV1aLX24mKkhIba+T77yWUlNSQlmagurqc3/72\nb1itgSQnpxEc7GLx4lWcOuUANCQkhNPQUIvFYuPFF+/jkUceJCFBTXW1nuLiampqzrJy5VaamrSe\nXI5zGT58EEOHihg2bBAmk6lD/+j1eo4dq6Gw0EFpaann8ezsbG69NZWZM3OIi4sD3IXwUlJiycpq\nZerU/xbha2hoYNeuM+ze3UJpaSlPPvkQL7/8EEOGDOkw+xkYKCcgAJRKBSaTiUOHDlFbW9uhratX\nr2bevJ/x1VdfUVdXx7JlO/n882MUFBT8sHILJpM7OV2hkCKXu+tsrF9/iKIiAceO1dHc3MyKFav4\n7W8Xs3r1OsBdN0OlUhEb2x+lMo1Zs6YQEhLMzp2NhIeHM3z4cPr378/MmVMZNCiCoiIdR4+aWL++\nko0bT7B69TZOnz7dbeeHN+BrY1BP4u+bi+Mt/dMuQCQSCTKZDIVCQUBAACqVinXr1vHqq68yadIk\ndDod27Zt45577mHQoEEolUr69evHnXfeyfLlywF46623SE1N/cHZbgQHDhy46Gdv27aNIUOGIJfL\nyczM5JNPPul0zJdffkm/fv1QKBTk5OSwYcOGTsdc6nMXLlzYaZvY9POLG3kxvj1VeAPR7lV9oRoY\n3YE3BWlXyrVajWkXGCaT6bKcu64EX+7v7uB6XcFoa2tDo9GwePFX1NfrsFjaMJkCSE2VYTYbOXEi\njNhYNSkpJjSaNpRKOQJBLN9/fxqB4CxBQXLOnk1AKq0gPT2B4GAxLpcdpTIRs1lKeXk5mzfv5+RJ\nM1JpCH36iNDrW/j++xZ0Oiv9+x9DoVB0WLkYN24s48aNZefOnfzqV39n5Mgs5s69A4Dg4GDmzh1L\nbW0d+fn5nteoVCruvfduAM9M4ZAhQ/jLX2JQqVSoVCrAPfERHR3NTTf1RaNp/WHVwL26Wl5ezief\nrCAlJYYHH5zHI4/Mp6GhgaSkJDZu3Mjnnx8lKUnIs88+hEKhQKFQ8MUXa9i9W4jRuJoZM2aQnh6M\nRmOgtLSMxkYdc+dmk5eXh1KpZNGiBTQ2NpKQkIBebyI8/ADTpk0kKSmJtWs309QkoKHBnRPz1FMv\nYLXauO++OwgICGDIkCFs334QhcJEYGAgSqUSl8vFxx8vY9s2NZGRQmJj5bS2tlJerqamJp6ioiJS\nU1O9rkbAlXKjjjmXg79vLo0v9JFEImH06NGMHj0al8vFwIED2bx5M8nJyRQVFVFYWEhhYSFFRUXU\n1NSwfPlynnnmGd577z2GDRvG66+/zs0330xJSQkRERGd3r+iooKZM2eyaNEili5dyrfffstDDz1E\nXFwcU6ZMAdw25ffeey9//vOfmTFjBkuWLGH27NkcOXLEs030cj932rRpfPzxx56+96WVVcEVnDDe\nf2ZdZ9hsNhwOR6dAVy6XX9VWnQtht9vR6XSoVCqfC/ZsNht6vZ7g4OBuKdZ2vsAQi8XI5fJuERjt\nOBwOWltbCQoKQiKRdMt7Xkt0Oh1CofCqK5l35YqmUCi65ZxzuVy0tLRc08rgTqcTq9XaafXQaDSi\n0Wj46KN/U1fXitlswmxWkppqxWi0UlYWTlxcA2JxEC0ttURERKDVKnE4HMTFGVmxYjPNzQlIpcWE\nhqYTHy8kN3cAlZVhKJU6UlMVlJWdRSaLx+VqwWBQEBysITo6mv37Jcjlp5k4cTD//vduhEIX77//\ne6RSKbt27WLq1KlERETw9NMvcPAg3HxzLM899xiHDh0iKSmJ1NRUwL1dqqKigmHDhnmERHNzM+++\n+xkSiZjHHptPUFAQ4Ha/eu+996isbOW++2Ywbty4Tn21ceNG3nvvCHJ5E089dXcHIbNv3z4+//w7\nwsPBahUikYj4+c8XsmrVar78cie33JLHz3/+PzidTvR6Pb/5zduUlwv56U/7MWvWrEv+To2NjZw4\ncYKsrCz279/PSy99jcMh5be/vZm773YLqNbWVpqamjzf/+TJk3z77TaKivRMmJDGnDmzefXVt1i1\n6gARERIWLZpLbm4uYWFhOJ1Or6kRcKW4XC4MBgMymcwnxp6exOl0YjQaUSgUPl/481phMpkAOuRf\neTMul4uEhASOHz9OcnJyl8eMGDGC4cOH88Ybb3hek5iYyJNPPslzzz3X6fjnn3+eDRs2cOzYMc9j\n8+bNo7W1lfXr1wNwzz33YDQaWb16teeYkSNHkpuby9tvv33Zn7tw4UJaW1tZsWJFN/RGt3PJAc63\noskbDLPZjNFoxOl0IhaLu20m/UL48gx7d7X9/Fl2sVjs2cLT3f3uy/39YzhfYFypK9rl0Bt9ajKZ\n0Gq1vP/+Murr3U5LZrOC9HQpbW1tnDgRRnx8IwkJZvT6NsLDZQgESTQ3O8jMdFFV1ciePS5sNgFC\nYRt2uwiLpQWtNpe6Ohf9+9spL9dQWRlFRUUdNpuJUaMiCQuzcfJkCg5HPdnZodTVydiz5wRarQuR\nSMSKFSvYteso5eWhHD5cxNy5t7J3bxlWaxs5OaP55JNPWL26mNzcOH7/+2eoqanhd797k7a2aAwG\nA7fddhsA1dXVlJSYkUigvr7eIzTWr9/Il19WY7M1M3hwqUdotLS0oNVqSUlJIT8/n6NHj7NnTxuf\nfrqZuLg44uPj0ev1BAUF8dxz99HY2Mg772xGLLaj0WhYuHABc+bc4RE6QqEQlUrF1Km5nD5dxeDB\ngzv0f1NTEw6Hg+jo6A6PR0ZGMnHiRKxWK/n5+Ywbtx2Lxc748eM5deoUy5evZ/DgDG677VYADh8+\nzL/+tYmAACeLFs1gwIABiMVi5s+fS37+AOrq6nj33TWkpOzn97//BaGhoVecoCoSiTziwxsEiDe0\nwdu4Ucbjq+F8lzlvp30i8kIF+2w2G4cOHeJ///d/PY8JBAJuuukm9u7d2+Vr9u3bx0033dThsZtv\nvpmnn37a8/+9e/fyzDPPdDpm1apVV/y527ZtIzo6mtDQUCZNmsQf/vAHnylA6BcaXozNZvNU8e6J\nWaf2gcMXLW6vNsDsapa9p/rdV/ixORo9ITB6g/a8knff/Ry1WoPJ5MRkkpKRIUOr1XPiRDixsQbi\n4izo9W1ERkrR6ZJoarKRmemisrKBkpJELBYdzc0apFIxaWkmHI7xiER1mEyHOHJERFVVKjKZDaPR\nhEZzFplMx+HDCfTpYyQjw0RDgwGFQoFUGoNOp0OpPInTCUuWBGI2n0YiSeLkyXpWrhQgFseiULRR\nUlLCsmXb0Wol9OkjpK6ujqeffpnSUjVpaRZUqlE0NzcTHh5Ov379mDv3LBKJ2DPzDxAbG82gQSEE\nByuZNs1dqM9kMvHGGx/R0GBjwYJJDBs2jDvumE1d3ZfIZO7VWIAPPvic48dbufXWfsyaNZMFC0yI\nxWKP5W9wcHCHvhYIBEyaNJExY6wEBQWh1+vZt28fCoWC1at3o1armTAhm9mzZxMaGkpTUxMSiQST\nycR77y0lMFDG66//yfP5u3fv5uBBG3r9CWbMmIZYLEYikSCRuJBKxSQlJXnOT4FAgEql4m9/e5uT\nJ01YLHrPGHmlCao2m81zzIVWP3oi+PcH05fGL8KuH1pbW5FKpV3mr8GFJyuio6MpLi7u8jX19fVd\nHq/T6bBYLMhksgseU19ff0WfO23aNObMmUNqaiplZWW8+OKLTJ8+nb179/rEeerbd/rrnKCgoF4J\n+n3xJvRjhUZXAqOn8gR8cUXjStraWwLjWrtj2Ww2Ghsbee+9pTQ0NNPWBmazmIwMJxpNKydORBId\nrSMqyoLBYCQyUo5Ol0xjo5XMTCcVFQ2cPp2IUilFr9dRWHgSrRak0n4kJAQgkRgoLdXQ2KhCKNRg\nNjsIDKzF6RSj1w/A4ShEqSxEowlCLpciEERTX+9g4EAhzc01aDR9USiKEAq1BAQEkpkpA7JpaLAy\nY0Y85eW1fPddNVarnZAQFQqFjKVLl1JVFYpEYmTmzCFs2fI9f/3rZ0ybNpRZs2YiEgnp27cvRqMR\nh8NBSEgIN900mSFD8ggJCfFMUriLVtqxWNyFBwH69OnD888vpKGh4ZzJDBdOp/scEYlEHgva8/u5\noqKC+Ph4AN544wM0GiMPPzyH0tJSPv74GKGhOlwuMUVFVdTXBxAaup0BAwbwzjtfoVRKGD8+h+PH\n9Tgc5UyfXkHfvn0BGD58ODqdib590xGLxRQUFFBTU8NPf3oLarWauro6jh49islkYuPGw5w+XYFa\nHYFQWIRMlkBFRQXh4eEXPEcuJUAcDkcHAXIuvSlA/PjWeNxb+JozZXtVcF9ahTmXu+66y/P3gAED\nyM7OJj09nW3btjFx4sRebNnl4RcaXkxv2Md5Q4XtH8OVBu0ul8tTe6S9uGFv7cn1lf6+3HPjel3B\nsNvtaLVa/vGPxTQ0NKDTiTGZxPTtCw0NWoqKooiK0hMWZsVkMhMZqUCvT0KttpCV5eTMmUbKyxOQ\nyWTYbDYUCjEBARaOHctBJDpJTEwtDQ1iGhoCkEplqFQhhIaaCAhoQafLRSwuISCgBb1eQVubmTNn\npJw+XUVwcD0mE5hMo4iOjiIz04ZcnkxoaAB1dRnU1FSgUh1AKo2gsrIPYrGUsDAVkZExqFRBHDsm\nIyLiLJMmhXPmTCtHjlRx+PAJKipsVFV9QUVFNWVlIQwceBSDwUpBwQlGjszh2WcfRyAQsG/fPmw2\nG6mpqWzevB2x2MZ9943qYLNbX1/PBx9sIDRUwvPPP8pDD91HVVUVmZmZnmOcTieNjY2oVCoUCgVr\n1qxj/fpTDBkSxZw5M6mrM6DVCmhoaCAmJoa4uAJSUpKYPHk0X38tp7WVH5LC9eh0Aux2G2lpaYSH\nr6W0VMCePQfo27cvVquViIgIFi68HwCDwcD77/+HggItQ4a40OvjsFrXUFdnpKmpHpfLglwextCh\n8TQ3Z2AyRfL66//gJz95kEmTJl3ROdSVAGm35e5qBeRczt165c35H9cL/r69ML4mNFpaWggJCbng\n8xEREYhEItRqdYfH1Wo1MTExXb4mJiamy+NVKpUnP/BCx7S/54/5XIDU1FQiItyFRP1Cw89V0RsX\nsq8KjXYu1fbzq6f/2OKG3YGvCbtLtbUrgXE9iDen04lGo+Gttz6hubmR5ma3wOjfX0RtbRNFRdFE\nRgpQqSyYzRYiIixUViZRX28kK8tJebmaiookJBIZRqONiAgp4eEWjh0LxmwuJCtLyJkzoNXKCQpy\nV5bPzBQTERHNoUNxtLYWkZJiR6lMISIijOJiAyaTBZutksZGM9XVIQiFNURGNiORyBg0KIiysiQc\nDhNZWWa+/bYevT6WwEAHQqGdxEQ5kZE2iooGoNcXo9EU0NSkQ6UaQVBQPFqtFKXSiESixWhMp7Gx\nhehoGYcPn6C+vg2jMYITJ7Rs376dkpJqvvmmBJtNS05OPEVFVdjtUqZOHYvNZkOtVhMXF/eDqBdg\nNtux2+2EhISQnZ3doZ/ffvtfLF26hczMBF599VdYLFbMZhcHDhwB4Pbb3cJl6NChyGQy0tLSCAgI\nQCwW079/f0wmEwEBATgcDn72MxsNDQ0EBgaSmzsYg+EsYrGI1tZW3nzzI8xmO48/fh8xMTGcPXsW\nh0NLS0stFRUK4uMjCAkJ5exZNSZTAiqVmqSkOBISYkhMjOHQocPs2SOmsfETcnJyLrqycTm0jwPn\nz7Z2JUDazUH+P3tvGmvZedb5/vZea+15Hs8+86k6o2t2OYNDQiADgQ7K7XsjAVdAywLU4iq60NC0\n0lHUiEFIzYcONA2dRhABaRNE8DWYTE4cJ7ZjO5V4qOlUnTrzuOd5WPN0P1SdouLEsZ3UdEz9pJLq\nw9p7vedda7/v83+f6cbP/jAJ6AfJWLxdHJT1+E5xEOdnv1nfq73vkiRx+vRpnnzyyeuFJlzX5ckn\nn+TXfu3XvudnHnzwwe8qVfuVr3yFBx988DuueeV3PPHEE9ev+UHuC7C3t0ez2aRQKLyOv/7Oc09o\n3OM7OEiG7428ltG+3z1d1/U7LjDebNxNAgNunvHkui7NZpNPfvLTtFp1qlUfliUyP+9le7vG5csF\nUikvoZCJaVrkciYbG2PYtszCgsP6ep29vTF8vhCKYpHN+shmDRYXU2QyTURxh8XFFWzbQRD8uK7I\n0FCPEydm2dvL4Lp1JKlEu22haQ3C4RPU6y5zcxqLiyVgmunpEltbHhQlRChUp1Y7iaJozMwYFIsN\nZHmEqalhVDVFJNLFspZYXDxCLtfm8GGdy5e76LqDKCZpNv3MzzsMBj263bdy4sQSudwhXLdFp7PB\nxoYfUfTyzncG8XhUHnlkEb+/gii6tNsldnYULGsMSerj8Xj4pV/6NTY2BvyH//AhfvInf5JTp15i\nenqanZ0d/vRP/5q3ve0ok5MTLC4u8sADD3DlyhaNRoBwWKPZbPKhD32QVOpZPvtZja9/vc599x3m\n3e9+9/Xn4/V6MQwDURSvN84EEAQBy7L453++xJkzV/jIR36eBx4oc+TIEUqlEsWijq5f9bKcP3+e\nT33qcYaHfXzoQyeZn5/k5MkjfP7zX+M97znN0FAWn0/ENE2+8Y0Goujh2LE5arUVxsdztzSH6/sJ\nkDfaIfmVAuQgrvH3uLs4SCL1tTwaAL/5m7/JQw89xOnTp6+XmVUUhYceegiAj33sY5RKpeu9Mn71\nV3+VP/uzP+OjH/0ov/RLv8STTz7JI488cr3iFMCv//qv82M/9mN84hOf4IMf/CB/93d/x0svvcRf\n/MVfvO77yrLM7/7u7/LhD3+YoaEh1tbW+OhHP8rs7Cwf+MAHbu5E3SLuCY27mHsejTfOK8e+LzA0\nTQP4obun32wO0ny/cqx3m8C4mVzNwXiYTqfB7q4P1/WysOBhY6PG8vIokYiIz3f1ZHl42GRlpYCu\nD1hYsFlbq1IqjeL3h5Flm8nJAKCxuJggl2syPe1nc7PC5mYZwxBw3WGCwWW83gF7ew8Qje4wOppA\nVVWOHcuztpYlHI4xM+Oyu1vjW9/SaDQ0UqkBx45NEQzusrIyS7ncw+P5FtGoiCQdR5JCyLKX48cn\nUVWVL33JD9Q5cWIXXXdwnBBDQwt4PAZzcya9XpHz54fI5TTGxuIYRg6oc+WKBXgIBBr4fAaadhRZ\nXkZVRQ4fFrj//hCLi28jErGZnw9QLit8+tNPsLS0Q7db4Ctf+Qq9Xo+nnx6wufkyk5Mp/uEfvsWT\nTz7PAw/cx6VLIi+/fJF/9+8+zNTUN1hYWGB2dhav18v73vc+Op0+9Xrnet15TdNYX1/nb/7m8/j9\nHt7znrcwMzPD6OgojUaDUqmE4zh4veD1XvUQzc3NEQgEmJqa4hd/8V1omkY+n+cf//GfWFzs0u9r\nfO5zf4DP5+Opp57i4kWTdNrDv//3P83Q0BCKomBZf8vq6hWefnoLSZIpFEJ86Utf4t3vfvf3DXO4\n2bzRBPQbf7P7gmOfq/N0LwTrRm5sMHmP7+Ygzs++R+P78TM/8zM0Gg1++7d/m2q1ysmTJ/nyl79M\nNpsFrh5M7O7uXr9+cnKSL3zhC/zGb/wGf/Inf8Lo6Cif+tSnvqMS1YMPPshnPvMZPv7xj/Pxj3+c\nmZkZHnvssetr2eu5ryAIXLhwgU9/+tN0Oh2Gh4f5wAc+wO/93u8dmGI19/po3MU4jvMdbvLbQb/f\nB7hewvIg0el0rleLsm37ugfD4/Fc92DcLQJjn263iyiK109j72YURcEwDOLx+F0tMH6YOa1Wq/zV\nX/09nU6djQ0JQdCYnw+wtraLZY0SDjfo92MkEm0ikSDLy1Hi8T6jo2E2NraJxUYxjB6yHOPwYQPb\ndrh0KUouVycaTVCt7pDNDrG11eHKlSaOs4TH4yeVuh/XXabbTZDJ9BkaSqMoo6hqjxMnwpTLTXy+\naUKhJru7Xjqdi8zMjKAoc0QiCkNDPp588mm63QT5vE04PMuRI1efzZUrEeLxCtvbVVqtKidPHkXT\ngrhugtlZDVnWuHLFQ7H4IqKYZ2EhwtjYELu7PlZWNhgMKiSTFun0UaLRPrpeYGvrORzHQzZ7P0ND\nfnI5gWJxj8HAiyjaiOIModAyjUYTOEYupxGJJCiX19nbq9HpOIyMnODIEYP19RqOM8KP/ug4//E/\n/ir/9E+fQ1E0PvzhDxEKhVheXqZUKrGwsEAymeSP//gvuHJlG0XxYttdRLHA7GyUj33s/+GP/ugv\n2NjQ+dmfPUkikeBLX3qGXC7Jz/3c/0UymaTdbpNKpXjiiSd47LGXkKQmOzseTpzI8tu//Z9otVps\nbm6yuLhENpvhp37qA3i9XkqlEp/4xKd5+eXzbG4K2PYOodAh/P4WP/dz7+JjH/tPN/9Fvkl8r/Cr\nVxYZuZeA/i8YhoFpmgdiTb4THMQ+I3/4h39Iq9W63rviHjeVe300DjJ3yqNh2/Ztv+/NwOPx4DgO\ng8EAwzDweDwEg0H8fv9dJzD2OUgeDbi6yXQ6nTueQH+zqVQqPPzw/0e322BpyYvPZ3HffRKrq1XW\n18eRpACGYRCJiGQyNufO5UinuywsOGxsNGg2JQKBFO02zMyErnUAj5PP15ic9NNs9onFQvh8Y1y6\n1GRn5zl03WF4+O2MjytYVpDdXRDFKuvrCdbXNQqF5+j1AtRqcRSlgt8vc/SowORkhlrtPXi9Aw4f\nttndrdLvj3Lo0BzVqkQkskmx+AL1+iwnTgQZGQmwvV1jcjLH8PBhLl6sIwiXmZkZYW1tjmi0QygU\nwHVdgsE2hjHNzo7E5KSJomiUSlnyeYdAIEsuJ+LzGZw9m0TXW0xMlHGcCJpWoNWSWVmJUijs8K53\n5Th/Pk2xWCYUWiEcjpLNRlFVP7XaCJnMNjMzA5rNIbJZHUFIsbGxxp/+6Sc5f75Ludyl0SgzOjrO\npz71VRRF59/8m5McPXqIc+eWkKRx3ve+FKIo8tJLdcJhH6IoIgheLEu//rtaXXUolWq89711vva1\np3nmmWU+8IETdDpd6nUvJ06M8JGP/DSFQgFN0/jv//2vqFYtHnro3dfjqJ955ht86UtPUy43GR09\nxNGjGt1ugOefX6RWC3PmzDKtVuuurWn/vTwgpmleL8F5oxD5fhWwbuwB8mbmIK3Hd4KDOD/7Vafu\ncWe4JzTu8R14vd7v2mwOApZlXT+t2xcYgUDgTb8p3g5uDJECrnfyvpsFxuvdDEulEv/wD5+j261x\n9qyHcFjh6NEoV65U2Noax+8PMxiYTEwEyGYtLlxIkc02WViQ2N5u0O36CAYztNsis7MeBgOZxcUE\n+fyAkRGTXk8mFgsjimNUKh7m513K5U263XFEsUggYLG+XsTjqdLr5TFNDUFYxXG8SNJ9xONNFEVC\nVXUM4wIvvPAjpFK7zM7q1Gp9YrEjBAJJajWJw4fjTE3BU0+NUq+fRZJW2NwMMTY2yuamw9ragPe8\nx0XXL1CvF3CcLY4fX8BxHKamvFjWWxEEL5FIlW5XplabI5sdwu/PEYnsIMuLrK6OkU4L5HI6tZqN\npkEkIlEs+hkZCTMYbGHb41SrKuGwjWUZtNu7yHKeRiPPqVMxRHETRZnGMDz4fBJer0gm02dx8WrD\nvmSyRqWywl/91TZHjlzAsjLo+g47O2tsbGi4bpyf/MkxotE4zz57ife9b5b3v//9rK+vMzwcZ2lp\nh+XlLR566P/mQx/aJRDwUygU+OIXv872ts3zz3+bX/zFn+Xb3z6LpiVJp9NEIpFrpXtdbJvvOGx5\n8slvc/68xDvfWeDf/tufZmFhgeXlZf7Lf/kkKytFRkbSlMtlYrHYgamstr8u7ouHfV5PBayD1AH9\nB+XN9LfcbA5q6NSrdQS/x61H+J3f+Z3Xe+3rvvAeN4/b7V2wrKtVYYLB4G297w+KZVnIsoyqqsBV\noZRIJG5pB/WbyX6vgf1yeHcT+wJjMBhcbx7pui7xePyu9RAB171ZPp/vVa/Z29vj4Yc/y5kzz/Ps\nswMUpc/cnI9arYiuhxEED7IsMjoqkEjYXLgQw+vtMzIi0WxW8PkCuG6UXs/H4cMCojhgbS2Cz9cj\nFPKhqi3S6SD9fopeT2B21oOu19neFun399A0B8OoYNstdH0Kx/Fx6lSQUEgnnZ5mZCROPn+MkydT\nHDoUoVyOEYtJRKMGhtGgXofBwELTkoyOGrhuma9/vUe7vc3MzBTV6jq6btLpRGi1JKLROpLUQZKm\nMc06ihJCknoEg32WlixWVnrMzICuN7h4UabTaSIIwwwNOQwPezhzpsPKSg+fr0k8LpDN5vD5YG8v\njiwvMzMjIcvDpNNhxsdHkOUWhw7lcJwAzWYar7fJyIiGZQ0TjQqEw+NAj4mJAM2mj29/u0azuYkg\nNIhERun1SqhqlmTS4MEHR7GsJI4TJhLRAIV2W2V5eZ2NjTCBQAvbNvn0p5/hxRcvYBhJOp1tarUG\nP/7j7+T06dPUajWmpydYX3+ezU0v7fYWtVqQVsvDwkKGRCLB5cuXOX36CG9/+yynTp261gn807iu\nyn33xXnnO9/GqVOn8Hg8RKNRRFHl+PFRLl68wD//83kiEZv77lu4be/5D8O+eHjlOnljArogCDc0\nMrz6b19QuK6LbdvX9wvTNDFN83pY1o3G6EFYh29kP6/loMS/32723x2fz3dgngiFmoEAACAASURB\nVO1nPvMZTp48yf3333+nh/Jm5Hdf64KDcfzyr5R7yeCvjmmaaJqGaZrXK84YhnHg6nvvh3vdTewL\nDFVVvyNEal/UHbQ5vpHd3V2+8pWv0WhUeOYZi0ymybFjKZaXa1QqPoLBJN2uw+xsGFU1OH8+xshI\ng9nZANVqh0gkSDA4Sq0GCwvQaHS4fDlNJmORTJpomkGhYLO9PUaxaDM7C9vbVdbXCwiCzfnzl+l2\n9/B4FHT9BNVqm7GxPcbGhojHDxMOd+j1UgwN1ZDlLdbWxkmn+/zETxymWpVIJrNUKj2Wl3VE8RLl\n8jMUi9Nks00MI0a73edtb/MyPf029vY6eDwlwuEysdgc8fgASYowMzPD1JTMyy+Pcu6cQDC4hm2H\nqNcjxGJBNM1DJKKxsKCztxeh3dYYHfUiyx2SyXF8vgj1epb5eRgMLtFoZFlZqZDPR7maytfk8uUa\nS0si739/nFSqQ6k0QSzmxXWDuK5APt/miSeqnDunksu16HRKSFIWv19gMEhy6NAUW1s7rK5GgBaF\nQhBF6dPtmrTbTTY24mSzewSDO1y+PML58//E3l6LQMDmyJEQ6+st/vqvl9D1Pu94x9v58z9/jOHh\nGEePHmFv7wKdjsF733s/Pp+PmZkZvvCFL/HYYyscORLmP//n/xfLsnjhhRf4whe2MM0S733vHA8/\n/BQvvPAi29slbFuj2Uyxvf0iGxs6sMOZM3E+/OH/886+4G+QN1IG94epgPW9+n8c1DXkXzsHwT54\nJZ1O564NbfzXwD2hcZdzuw3/G8sf3m0bgeu6WJaFqqpYloUgCITD4esnK/unaweJu0nYvZrA2A+R\nOihz+73mdGdnh2eeeZZSqcjXvmYwNFTn+PH0tQ7cfkKhHJ0OzM2F6PUUzp1LMDoqMzmp0273iMVC\nSNI41arLwoKX3d0qS0t50mkIh6+e6ObzFpubI+ztGczNedjcrLC1NYokSaiqS72+i6Iso2mzBIMN\nxscrdLsaMISq2pTLFocPQzTa5MknBxjGHrOzLpomkEiECAQK1GohjhyRSCbLPP30GLK8Qjzep9+X\nSSR6ZLMn2drys7AQYnjYpdnMYhjbrK3JJBJF3v/+cdbXhxAEmJ9fY3u7RDY7j2G0cd0RvN4totEi\nijLE889vEA77SacjTEyMEgpFKJUSNJtnyeW6tFpDDA2NEI1KFIvrDAbnGB+fZWvLh+PIBINrlMv3\nEwr5yOVGkOUVBOEchjHK+fMOtt3HcTqUyxJeb5RodJrxcYHxcZsLFyLIcgzbrtHtwuTkAru7Vc6f\nj+G6qwwPN1la8mNZMDs7wDAGDAYyqmqyspKh2z2PLPf48peLnDlzjsuXLXy+Hh/5yP+BKOq8+KLA\n/fc7nDhxjP/6Xz9Jv1/H50tgmipnz57l0Uc/x4UL67huA8cZZm1tD8OYYmXlCdbXo3i9DXy+EOGw\nSjIZQtc9dLsCzWbzh+6rcTu4WWvOG6mAte+93eduTUC/G/e+u4mDFjrluu7rqjp1j1vHvdCpu5zb\nHTq1vyHcTfkNrutimiaKoqBpGh6Ph3A4TCgUQhTF6+O0LAvbtgkEAnd4xK8f0zRxHOeOjvmVIVI+\nn49IJPJdVbruxnfje3FjONr29jZPPPEE3/jG8zz2WAPbrjA25qPRqCIIPiBGvy8wO+vHdXusrEQI\nhxVCIQFZbpFKhej30wwGsLAgoShVyuUYwaCK4/iQJJWhIT/FYhJVtZmeFmm3iyhKDEEwGQwC5PM2\n8bjJ2bNeTNMmEOiSSEi85S1vw+uVqFb9VCrLmOY6KysRdnfXkOUmg0GDWMyLrkfo95NMTOgYxi7V\nahyvV6bbdZEkmSNHkpRKMVQ1w+SkiuO00PUkkmRi23mgga7X0fUcmiaQShlYVpdMZoxCIcPKipfB\noEI+P0DT8rTbXSTJoNvtYRgukuSh2Rxmasqk31/iwgWBTqfC2NhhRNFifDzCuXO7NJs5Jic1JibC\nuG6AfD4IjCMICjMzQR5//BxLSwFgncOHc/j9AsPDERxnjnRa5kd/dJTNzS4XL5avNS4UUBQNWTbo\ndMbw+WpoWhnTdInF4kSjcbxem7e+dQzDsCiXk0xNmczMJOn1FLxehWRyAcsyqdeX6XS67OyE6PdX\nqFS6bGxcZnd3h3PnLCxL4ad+6ijf/OZF/v7vv8nLL7/E3l6ATEbnwQcP89BDP8fW1kvUag6CUCUe\nDxAIFDh9eoSTJ4cJhWKsrFziK1/5GjMzE4yMjNzBX8Brs5/PdqvCX75X+JXPt5+w/y95IfsekBvD\nr/bX8VeGYN0u9g9U7oVOfW/2n833C0292/hv/+2/8cu//Mu3tQz1vyLuhU4ddO6kR+NOsy8wVFXF\ntm1EUSQSibxq/sXd5B14vdzJMb+WB+Og4vF42NraYn19ncXFVb7xDZ2pqSaHDwdpNHoEAn4CgTEa\nDYujRwPs7dU5dy7L8DCk0zqDgcLwcIhud4xy2eS++wRWV4ssL48SDkt4PBaC4GF83GJpKYuiqMzN\nOWxulqlWx/D7I3S7LocOBcjnDc6dC7O19QydjkwgYHD06DFaLZWlJRVd7+C6e1jWAoNBkWCwj6pq\nhEI+HGeKra0Qkcgu8fgGjzwSQRAaDA/7OHzYx0/8RIr19TFEMcD8/BVarTpLSyFct0Mul2Nuzsvc\nnM7y8gwjIz0EocPlyxcol2McOTLO3l6QQ4cUhoeLrK0labVgclLC5yswNJTh/Pk1SqUExeJl0ukW\n5fIpPJ4QqZRNMplgeNhmezvI2lqMdNrDYNCg3x8jnbZIJGZxnHXq9WdR1SCynCIQUBCEAY4TJxLx\n0mweIRjcY3R0j1rtatWter1KqWQSCPQ5fHiCjY0YsdgyDzxgUqsN4/fH8fkSiKKXubkYxWKby5dT\nmOYSHo9Ds+kwNqaQz59gdFRlZibM2prCysoMgcAmPl8dr9dPJDJA14+zs6MyGFygXNbRdR+bm8v0\n+wkiEYV4fA/bfjeqGqTZbLK4uEGt5uPnf/69vPvd7+Kxxz6HppmcPx9maKhHv+9SraZ48smnectb\n3nKnfwZ3Ja/s4wF3XwK667p3dQ7aneag7bFwteT5vdCpO8c9j8Zdzo2nOreDfePT5/PdMYPTdV0M\nw0CWZXRdvx4iFQwGv8OD8Ups28Y0zQOTyA53Jvn+9XowXsm+R+NuLhe8tbXFc889x+OPP80Xv9jA\n52sQCtn0ek0SiRCqmkGWXY4cCSLLdXZ3I0QiOh6PF1DI5/1Uq2kUxWJhwU+rtUenE8PvN9E0H+m0\nTTbrZXU1imFoTE1JNJtFIIrH46HTCTA+DqmUxdJSCMvqEYu5LC9fot8H1/WjqkkUpYnHs42uT5BO\nexgdzWFZbcbGQmSzCwQCI8zOmng8DTQthaa16HbTGMYOrtvE4xnDNOOMjbkYRpNodIxkMsDuroQk\ntYnF2mxseLAskXxewrJ6eDw+Go0emjZONtsjn9dpNCIEgwHy+TiDQZNSqYrjwGAwxYkTfnR9m/V1\nm16vQzY7QTQq8Y53TFKv63zjG30EYYuxsTCiGCOTcfF6Z1CUBnNzATY3W2xshPB6G+RyAUZGRsjl\nBFz3FIPBNidPRtjaanLx4gBZHhCN+sjl/FhWG8s6ST5vceJEEkkKoao2th0gEIgyPOyyvb3B6mqa\nbFalVltlb6+E1+vi9RbY22uQSDQJhUTOnrXodlcYGsqQy3nJ58PY9jzZbJy3vjVJu12lVJJQ1Qau\n68Pvb9Hv7xIOv535+TGOHImxvHyeRx99CVVVGRqa4NChCN1ul29+06RUWqHR2OLKlYu02zLR6C7v\netfbMQzjutf1bsS2bWzbviuKULxWAvq+B+R2JaCbponH4zkwFcRuNwfN42MYBn/wB3/A7//+7x8o\nL8wB4jU9GveExl3O/mnP7UTTtDsiNPYFxn4fjP2ma6FQCEEQXnPz2Bcad3toz43cTnHkui6apr1h\ngXHj5/dr799tQmNra4uzZ8/yyCNf4otfLOP3N/D7XWS5TSYTpNPJoaoWR48GabVKVCpRIhEdyxLw\n+zVyOT/b2wkMw2BhIUCttouiRJEkG1mWKBQgm/Vy6VIE0+wzMiLSaBQRhBDgo932MznpJR7XWF4O\n47o9UqkAzWaJra1Vmk0Bw4hg29VrYmGEfF5kfv4omYyPSMRiczNCvx/ibW+LEYlYGEYOVW3g8w0x\nNuYnn9dQlByqmsXn26Vc3sQ0/aRSYRqNGOm0zvx8CE3LsLvbQ5ZVvN42oVAYUfTRag0zP+8wNKTy\n8ssqxWKFQiGL62ocOpRlY6NKqTRMJlPl8OEgzaaE3+/S6Qj4/S7HjiXodh3W1iREcZd6vYZpCoyM\nRDHNCSIRaLcvs7zc5tKlHoFAn3TaSy531YNRqYySywnI8iXW1jR6PYtMJk6/3yWTgYmJLOXyJNPT\nQUZGYG1tB9v2YttBLl3aQtN2SCb9vPCCQKm0jSi2CYVEdnYqaNo4hUKKqSmLjY06zWaWfN5lY6NE\npdImn3cwjDmWl4sIwjbpdIBGI0ivVyEaLWAYZTRNRVUnMU0/mcyAbDaEqgrU62263RjZbJ8HHhjl\nyhU/6+sX2d3dplzeRNf99PsupjmO4/R56aVFPve5JRqNbX78x3+EL37xcb75zW8zMTFGIBCg0Wjc\n0YMc+BehcTcbXq8UIPvhV5IkXQ/Bej0VsF75na+FYRjXBc89vpuDJjRarRZ//ud/zu/8zu8cGLvg\ngHFPaBx0brdHA64Kjf3F/Hawb8DKsnxdYEQikTccxnNQcghuZH9jvJVjfqXA8Pv9b0hg7OM4zl0n\nNLa2tlhcXORv//ZzPP74Dj5fE8cxMIw+hUKUSiWDrhucOBGiXi/SakUJBAx03Usi4ZDNiqyuJrBt\nhbm5ILXaLoYRxuv10O9LTEyIJJM2i4sRbLtDLuelXt/D7w/hOEFaLR8TEy6BwIDV1RDQIRoNIssN\nUqkQ585VWV52sKyVa2VYZ5CkPj5fEkFQOX68wM6OF02L4PGsEIsZeL3D+HwmpRIUi9uIYo9IZI54\nfITxcQGo4zghWi2LbjeKYWySy+n0+xk0zSYeF5HlGrGYSLPZZWUlRjZ71ctQq4UwDJ1eT8d1ZRIJ\n6HZN6vUhpqctYrEuqhphZWUVw4iQTPo5dSqDxxPm4kWbjY1vMhjUiEbT5PMgivM0GlsUChqmGWBn\nx4Ou1zBNHUnycPLkFLu7Q6yvX8TnKxIIxOl0PNi2RiwW4dChFIVClHZ7lkZjEUGosbNTZnl5m3o9\ngK7rzM4G2NjYpFQaIxy+6h2R5Sb5fIRgcA7XFRgf75PPRxkMJgkE6uTzWRIJgd3dy3S7eYLBMJOT\nFnt7exhGlkxGYnW1Q622SzzewzDmMM0eExMikYjB2NhhTBPOnu3iumXm5yUCgROYpky7XWF9fQXL\nMhGENPH4FAsLFoFAFUVJ0G5vo6pxLKuILPd56qlVLl1SSKV09vb2+F//63Ps7q7xwAOnOHfuHMvL\nyxQKhdtq2B4EofFqvFr+x/cTIN8v/2P/O/fZr2R4T2h8b0zTBA6O0CgWizz66KP81m/91oGxCw4Y\n94TGQWc/dvV2cruExisNYEmSrodI/SCG7EEI7XklN3o0bvYi+GoC4wedn7shrG6f7e1tlpeX+Zu/\neYyvfnUTQWhi2xaSZJFOi2xvp3EcnRMnIlQqRXq9MJLkoKoehoYEUikPi4sxXHfA9HSIanUPuOqd\n6HZFDh2SiER0FhfDeL0dkkmBZrNEJBLCcVJ0u35mZgR8vj7b2xFEsU8gEETTWmQyAbrdOLu7Ks3m\nJXq9TeAohw6FmJycw+froyhNWq0k5fKAwaBIu30FVR3GsloUi376/TUikT7tdphwOMr0dBRFaRKP\n50kmoyjKCJlMg3C4ycpKlFarSTBos7R0kWazSyaTQdMOUam8jGnWsKw4a2srlMsDvF6N+++fxLZF\nLlwIYpobjI46mGaaeFykVvNSr3dIJvtIUoJWK0cqNaBYXKff9yMIfUKho+TzIcLhGpcuDahWJcbG\nfMRiPlKpMK7bpNudJRDoMzKisbPTxzDCFApxYrE4hw7FKJXWOHNGIhBok0ppLC1VaDQ0+n0JXYdE\noksuF6DTmQe2GQwGaFqP0dEM2exxvN4IjrOM4wzw+U7T72+iKAZjYzGSSZGlJZBlm2hUIxrVgQni\ncYdEYpLRUQFF2WJzM06/P2BmJkSzWUdRfAwP5zDNMRKJBv3+Jt3uMLGYRD6fotHYpVqt0ulECAQm\nefvbwywsJLHtYRKJALrup9Op4/crpNOj7O0FKRQUgkGNxcUii4tnabXiKEoZ0xzwyCPP8a1vlRgd\n9dPpdPizP/vf9Pst5uZmKZfLVCoVUqnUTV8bDmJC72vx/QTIG0lAt237eiWte4bpd3PQhNja2hpf\n//rX+chHPnLved4a7gmNg87tFhoejwdN064v1LcCx3Fuygn7K7mbQ3tejVvhhbnZAuPG792f3zsl\nNHZ3d1lbW+Mv//JRnnpqBdtuYRgWsZhANiuytBTHcXosLISo1aqoqh9RFJBlmJwMEIlYXLgQQRCu\nNour18uIoh/XjdLtepmZ8ePzDbhyJYTP1ycU8tBuV0gkQhhGhsHAz/y8iOM02NmJEAgoeL0hHKfP\n8HCQTidFvy+Sy/W4cuVb9HphYjGbYDBDIqFjWU3q9cK1DtQysryBxzN0zctSwDDWUNU2g0GKdtuD\nz6dcEyUagYBIsRhmZMRgdBR0fZRWq0mn08SyWvR6Ap3OAFmeIJOpMjwMtVqEUMhAEGLs7bUxjDZe\nrx/bnqbTOUu3u4EgZFDVBo2GiN9vMTMTxLK8KMoQ1epldL1MMjlGLGYhSYdxnBaCUMPrjWAYQ9h2\nkWDQQVFUJEnFNI/Ram3jul1EUSAWmyIW8xIKBSiVtlCUGq3WHOvrZ1HVPratUChMoOsOfn+AeLxN\nIuEhFnsPwWCTanUbSXIRBIN+P0GzaTE9bVIqrfPCC2FqtSv4fBKVSpFOp4vrjtBoKNRq63i9XYaH\nj9JslqlUBIaGDEZHfXzrWxqW5SKKLcAmFksxGMgYxgj33Sei6xu89JKF3+8yPz9GJCLS61V54YUi\nnU6GSGSNYHBApeJlZWWJZtNmc3MT0yxi23EcZ5x2+zy63iQWyyIIOu12Fr/f4MiRMOWyzPnzXUSx\njSCYrK9vcP78WS5eDNDp7JDLRfnLv3yUp59eYng4jOM4PPbY5zEMjZGREQzDQFGUHzjHwrKsN53Q\neDVeT/4H/IsA2f//vgA56A0IbzYHTWgsLi5y9uxZfuVXfuVOD+XNyj2h8Wbgdns09hOwb7bQcBwH\nVVWRZfmmGsD73E0n7q+Xm+mFuVUC40buVP5OqVRiY2ODT37yH3jmmUuYZh9VNSkU/MRiHi5ejCJJ\nfRYWIpRKJQxDwOeLMBjA9HQISdK5cCFMOKyQTntot+uEQgEsK0mv52F+PoDrdlhbCxEMyoiil36/\nTioVQFVzyLLE/LyAYdQplSL4fAq27cfj6TM05KNeT9DruRw6BP1+mdVVhZWVTVQ1RyLRJRDQaDYn\nME2LUEghkbCwLAGvN0QyOcHp03nGxmz29lIYhsXEhAQMiEQC6LpIr5dDUZbR9SKLiwpra6tMTAzT\n6dTweERCoQiWNU48vovrtun3s0SjXrLZYVKpIKmUB1UFxxkBKkhSjXY7gSA45POHqderKEodXffQ\n7+eZmIDBoEizGUAUu6hqHo+nz333hdnaUuj18ohimVJpi0AgTjIJKyt5er0tjh/34zhB/P44rjtg\nfX0bj0clGLRYXx/HMMrMzAjIso4oehgaGqbR6DE1FSIa9bC2NoLjVBgbC7K7W6LRMPH5soyNHcZx\ntnCcAZa1QCDQpdXqAPK1JPNJvN6rz8myOvT7ceJxh0xmhm53E6+3h8czTaejUKlso+sdDh+eR9c7\nVKtpZmZsTp1K0WgkKBYrKIpDIKAzNZXnuefOsboawrKudi+XpDF0XaPXE2m3e3Q662haCF2fIBis\nYhh9VNVBUdr4/XPE4z6OHg3SbA4oFgMEAgMkyUM47CUQsFhbSwJ9TpwIUas1eOGFHfr9JrZ9tZP8\nuXPnePzxHtXqOidPzvE//+ff8PjjzzE1lcfv93PmzBlc1yWRSLyu39Ob0aPxRni1BHRRFDFNE1EU\nrxvS38sD8mbogP6DYhjGgRIaL774Ipubm/zCL/zCnR7Km5V7QuOgcydCp3Rdx+v13rRNaF9gDAYD\nLMsiEAjcdAN4nztlCP+g3AyhcTsExo33uZ3zW61W2dra4k/+5O949tmz6LqGohgcOhRFFE3On48Q\nj6uMjUnUajVc14PjRBkMHI4ciWPbfS5fjpBMaoRC7rXqU2FUNU2v57Kw4EfTGmxtRYhEVGyba+FP\nEt1uHl0XWFjw0e+XaDbj+P0amubD57tq3JZKCWTZZGzMpdstousJFKXF6mqfwWAF2y7T7x9CVRV8\nvjaFQoiZmXlyuSyGkSObbXHsWJrd3SiBgEQwqOP1DpieniaXK+C6hykUOsRiLVqtArrepts1kGUF\ny2ri8cQIhWa5//4QExMCljWJprXxeHxUKkU0rU00mscwxjh2zIeul+j383g8TXQ9ht/f59ixIVot\nk1YrRr+/gqo28XgypNMCweA4ptmk0dhjMBCw7SESiT6BgEK1atFsttD1EaJRDb9/F48nzs6OjWm2\nyOWSlMst6vUmzeY4Hk+JkREVUYxQLmsIgsDc3Cz1+jbVaptOZ4potEe/X8RxPITDfiQpgygK5HID\nut0KXu9pCgWLVqtFt9tkYSGPKE7QaDjk813GxxMsLXnY2VlCFJMUCgKNxgoez2Hy+QLJpEKrVaLd\ntnCcAen0/RjGFprWBAq4rsDGxhqa1mNqKoHjeFheDtJsLuE4PRKJNMPDaYaHDyHLLaCL6zo4zjFi\nsV2CQRNRDJJMWijKMJIUolBoIAh+6vUEPl8fSRIJhyEYtNjcTOG6KvPzEoNBj04ngGmqOE6IsTGB\nUMjg5Zf9DAZlxsd9tNtlnn/+Int7bbpdP1Dj8uXL/P3fL7O9fYUf+ZHTfPazj/LlLz/F5OQo4XCY\njY0NRFH8Du+Hbdu4rntg4uxvJ/thvPt9P/a9H28kAf3NLED28ygPyh777LPP0ul0+PCHP3ynh/Jm\n5Z7QOOjcCaFhGAYej+eHFhq2bV/3YOw30otEIresSRTc/kT2H5YfJtzrdgmMG7ld89tsNtnY2OCP\n//gzPPfct9A0F1k2WFhIousyFy6EyedNEomrxq7fL2BZGWTZYmEhQr9fY3MzTjqtI4rOtepTITqd\nq9ccORKg2y1TLkcJh3V0HRynSzYrUqvlsCwPc3MS7XaRXi+Oz2ciyxKRiMbQkHCtQpXF+LiXVmsP\nx0kiii6ViofFxa/TbO7guvchSV4kScHr7eE4MXw+KJUC9HqXsawSlcowq6uL9Ho96vVNFMUlGo1R\nLAZJpVoEgy2WlwO0Wi2GhqIkEn5ggCCEUZQRVHUXQdhmYyOCJMnEYhlEUSeTEel2/ShKmsFgkcFg\nB8MYJxazSCaH6PdrKIqMIEQpl31EozVct4tpjhAMynS7Pra3V0mldERxCFmOIAg71OslNC3F8LCP\nbjeBadYIBEqoapp0ehafr0Ot1sA0Q3g8TRxnGsfZwra30LQ00egQkmRSrXaxbQdBaCPL84jiHqFQ\nk2rVJJvNEIsl2NpqIsslxsYibG+PUa1uIEkDQqEglUodVc0RCkXweLZpNFro+iFiMZW9vQGdTgvH\naWEYBapVEa93j3w+wMqKQb3ewHEK+P0dNG0Nyxojl0uQywVptyt0uwa27WIY01Qq55HlDSQpQTQq\ncOLE2/H7PbTbW/R6AyzrfubmLBYWcmSzQ/T7TWQ5i6rKBAIlXLfP7m6OVmuN8fER4nEvgYDB7m4G\n29aZmRFQlC79fhjDULCsMKOjHqJRkytXIhhGn+FhAdMcIAhBFAW63RhTUxbJpMm5cwa7u6tEo2Fk\nucKlS1d48cVtNjYgEumxt7fHpz71NVZWFnnwwQd44YUXePHFF8lms/j9fhzHuWX9KA4q+0LjxjX0\nB0lA3xcgrycB/aCw39vqIAmNr371qwB88IMfvMMjedNyT2i8Gbjd3cH3u1X/oPG/tm2jKAqKouA4\nDsFgkHA4fEsFxj4HVWi8ES/BnRAY+9zq+e31eqysrPCJTzzMmTPfZDCQUFWd48czdLttLl8OMTZm\nI0kqnU6HZDLAYJBB0wyOHYvRalXZ3g6RSOh4vWCaMvl8kEolg6bpHD8eptks0mhECAQMVNVFFAdk\nswJ7e1kcx2Z+Pki9voumxRBFh15PIJOxyGRc1tbimKbC6KhIs7mHICQRRZFOJ8DwsEW1epHV1QyW\nZRAOW4yNhQiFwoCIouTo91ex7SqyPI9ttzFNjV6vjWl6kKQQg0EBy7rMYNChWIxSrVYYDFr0ek38\nfpdMZpJQaJqjRyW83iqaNommNVAUH83mFo1GA0mKo2lpcrkWsZhKszmJaVbo9XSq1SrhsIkkZfH5\nsni9O7RaDVR1AkFokkxmCYcF6vVNZDlJq+VB03ZIpy1gDkUpYxg+qtU9fL422ewsihJHUUqo6h6D\nQYFgsIHXm6NeL2NZReLxaWw7hsfTRlEayHKEYLCJIMxQr29h27vkcrO029DryZjmANe1UZQKun6U\nVusctl3B74/i94vU6waC4CUe79Ltlmm15slk2vj9XorFEsGgTCQyheOISFKRQEAhGj2KrlcYDHyI\nYod8XsFxxun1Qni9rWsVyvrU62283inC4SLBYJ1GQ8I0w4yODnHkyAyO02R7e5tSaY5YrMb8fIx0\nuoBtq2xsuPT7PVy3iyy3UdUjWFYL27Zw3S4TEzE6nXFs22JiwkbXuwwGMQxjgK7HGBlxiMct1tYi\nqKpMLufBtvuIYhhZtmg2E0xNmWSzFru7frrdFuFwCEEwyOfDtFoO6+s+lAQYEgAAIABJREFUJiYU\nUimLixfrXLp0Dl2PomlNZLnJY4+d4cyZLpmMjmEY/I//8besra1w//0nKJfLLC8vk8lkDsz6ebO5\n0ZB+PWvp6xUgr7cD+v533s0cNKHx+c9/nmQyyXvf+947PZQ3K/eExpuBOyU0AoHAG/qcZVnfJTC+\nXyfvm43H40FV1VuayH4reL3hSHdSYMC/zO+tEBqapnHx4kU+8YmHeemlM7RaAXRd5fjxFI1Gi42N\nAIWCAyjIskw2G6JWy2IYCqdOJahUKlQqIaJRC9O0EASD0dEwm5spTFPh2LEw1ere9epTg4FLNGqQ\nTLpsbmYBnbm5ENXqLo4Twev10u0KDA3ZJJM2S0tXK1QVCiL1eolAIIHH46fdlhgeNolGVZ57zmB7\n+xKSpCKKCj5fAEmK0OvliUbbiGIVRbmPcFhmbi5PJCKSyUSBMNFogePHg8RiHVT1Pvr9NbxeA8sy\n8fsdbLtwrV/DOoqyQbk8jiC0yecTOI5OMiliWSH6/SiqeoV+v0q3O41h7BIMOoiigGEY2LafVgv6\n/T08njKadhJJKuI4CoOBgK53GAw8mKaE69Zw3SqmeZp+f/laXw4L11VRVR+y7GUwqGAYuwjCMXq9\nFfp9G1XtY1l9TFPCMHwMBlVMs4rXex+KsoGihNH1DoZRwTCiWFaQZnPrWmhUGtsu0+2OIggNTHOD\nbjeDaQYJh216vR6KImEYO7Tb06jqDq7bIxCIMhh06fWieL0ikUgXWW6iKKdJp3tomkOxWMNxKmSz\npxgMPGhakVBIIZudR1Gq1GpRHKdGJFKkWs1Rq6mEwxK5nMTISIJOp3mtC/keudyAoaFJIpEga2sy\nm5slTLOM4xiI4jzxeIdQyItldXHdNh7PAzQaFbLZHpGIiKKkMc0euh4jn7dIJAy2tmIoikoq5Vyr\npBVCUUyq1SSTkwb5vEWxKNHrdfH5AoiiychIhFbLYGMjwtiYTDbr0mq5KEoPXU8gSQ5HjsSo1fq8\n9JJBPN4mHHZYXd3g5ZdfYm8vgqI0icUEPvOZL/DVr24SjxvEYjEefvizFIt7zM7OYBgG9XqdSCRy\n1xvCPwz7QuOVHo03yhtNQH81AbL/XXfLnN+s+bmdPPLII0xNTfGOd7zjTg/lzco9oXHQ8Xg8t11o\n7C90r1doWJaFLMuoqorrurddYNyIpmm3JJH9VvJaXoI7LTBeOdabKeQcx+GFF17gj/7of7O4+BJ7\ne35sW+bUqQzlcotSyU8qZWFZMq5rkc+H2NpKY9t9Tp9OUCpVaTb9hEIummaRSnlJJr0sLSVw3QFH\nj0Ypl/dQ1SCi6KXbtcnlbKJRk5WVND6fwtRUiHq9hMcTxOsN0G57GB2FcFhjaSmBIPTIZiWazTLB\nYBRBiNJqeRkZsa71z0hhWVVWVi7TaPTRdRW/P4FpFgiFqhQKFrq+wMREENft4/XaKIqK60ZotTzE\nYk1EsU+xOI7X20BV2yiKjSh6mZiYwudLEwhUiUQG9HrHMc0tFEWm39fodmU0zUXXPcCAYLCBaZ7C\nMIoYRol+P3Qtr8XCNA28XhdN20TX55DlIrJcRtd96LqAZfXQdQ1dF7GsXRxnHtft4jhlVDWErlvo\nuomm6dh2ENsuYxijWFYfw6hjWQlc18C2RQzDxHH2r5nEsjoYRgvTjOK6/Wv3dK+Vdy6j63M4ThnL\n8mAYHkyzgqaFMQwfrtvBcRooyii6vovrxlHVOoZRw3XjCIKfbreNqhpIkoNpluh0juO6m0hSD1m+\nanhbVhBN89BuL2MYDeAUkUgbRfFTLhcRhBqJxCymGaTf38Lr1YhGc4yNxdnZydBsXsHj2SIUyjMx\nMY6miayu7jAYrOK6Aj7fUaamPExPj5BMhggELLrdHF6vD9ddZDDQaLUS5PMSjpMikdCIx3VKpTiy\nbBKPG7iujChG0HWdSiXNyIjG6KhDqSTS6fTx+QJ4vRajoxE6HYXV1RijozK5nJdu10RVZTQtgSB4\nuO++MO12n5WVELFYl0jEi9frIIoWpVICj8fl1KkQnU6LM2eayPIeohik09nh/PnzPPusQqVSZXo6\nx2c/+888+ugZwmGLkZERnn76aer1OsPDw3eNEXwz2Df8b4Uh/Xo7oN84jrst/+NWzs+t4uGHH+b0\n6dOcOnXqTg/lzcprCg3PG2gGd3u7xt3jOoZh3NamfaqqomkayWTy+15nmiaapl0vdxcMBm9LeNT3\no9PpXO/HcRBwXZd2u004HP6uULV9gaFpGq7r4vf7CQQCd9Rl3W63CQQCN6WT+bPPPss//uNTSJLC\nxYshstk6x46N89JL24hikkhEpd02yOcDBAICZ8+GGB5uMDdX4Ny5DSKRDKDR73s4dMiPaVqcPx9h\ndLRGOh1ne7tIOj2Erlv0ei5TUy6DgcbaWoapqQ7BYIRSaZdcroAsexgMXA4fduj1VLa20oyONoEQ\njUaJfH4IWRaRZZepKYNeT2Vvb4hCoYKm+XjxxW9Qq7X/f/bePEqOuzz3/9TW1fsy3T37PtKMRvtm\nWxgbDMEYhyUQsyQxXIxDMNm5wWThJHc55yY53CQ3AWI2E2L4YQfjgFnMYhuwbMCysWxptIxGM5p9\n7Z7et+raf3+MppFkGRuvEvFzTh8d9XRX1dRUfet93vd9nhddDwAJZHkcWRYRhEvo6lqkXI5g26s4\nTpRKpYJtBwmFVpDlAIaxGTiEbStIkgdZVtF1DddVCQQ0wEQQduI4h/B4PDhOGNu20fU8liXjuiqW\ntYRtb0JRpnEcE9tuAgSgiuvqOE43gjAJdAFFRFHHdZtwXfP054oIQj+CMI8gBAHx9HtNQBXLUnHd\nVVS1D0lKIwg+JElBEKpIUhTTLCCKISwrhaL0IMtZLEtFFF0EwUQUoxhGHtf1UastA+14vXkEIQFo\nOE4Ny4rguiUghCAUcd1WHGcWGACWcRwBQfACdRzHh+NUkCQvrpvDdYcQhDFctx3XXUEUXSQpgSCI\nOE4FQXDweALU60u47uX4fIfw+ZqxbR3HkRGEAKLoUKutVSX8/suIxWbwerdRKj2OplUQxUGSSZVw\nWCWVWqFaLWAYApK0jUjkKIHAmkbDNB0qlSiCICOK05imRK3Wg+McxesdYNs2hYGBHkqlNkRRx++v\nY1l1fL4ktVqWfL6Lnp4VAgGV5WUJx9HwePw4jkZ7e5hUqsDSUisDAysoSohSqQZYaFoMVdUZGAiw\nsJAjnU4Sjy8iinEUpYIsiywuRvD76/T2yqRSeWq1ZgRhEUFop6WliixLTEz4UNUqHR0q5XIBx4mf\nJqSd7N4t0tLSwg9/uEw47PLRj76XI0eO8tBDI7ztba/hkksuaYjPu7u7n/Ma8WJjXVfo9/tf8kDa\ndd2G5sNxnMbr3DYrURSf9HqhnsHr5+eXHab7UuINb3gDN998M29729te6kP5VcXTXmwvE42LAC82\n0ajX69RqNWKx2JMWLNd1sSwLTdOwLAtJkvB6vS85wVhHsVhEluWLhmgA5HI5/H5/o4J0PoLxbIcY\nPt8oFAp4PB78fv+z3sYDDzzAD3/4GKZZ5vBhlb6+PL29SQ4fXiIQCCHLNoVCjQ0bYtRqOseOhdi4\nMU8yGWNsbJ5IJIplQbVqsXlzmGy2zIkTETZtKqIofmZn5wiHwzhOkGrVYMMGiXS6yPx8K4ODBUxT\nJZdbobW1mVJJpVYz2LhRJJ1eC+C6uzPouo9icYWWlgSlkh9Nq9Pf77K6WiKd7qK9fen0Z1LMzc1y\n6pSD47gEArOAB8vajSA8jmk2oygVIpE4Pl+Ier2Opi3iugJe72WEw6PoukA+L2IYOsGghOuu6TV0\nfRnbHsZ1T+E4VRynF6jgOHUcp4ptDyAIYwhCB45TBWpAE2AACpBHkvpwnBRgoygRFKWCIISAAuFw\nOx5PCVluIhKREEULny9IMOhDlmUSiTCSFMDrdZmZWcBxHHbt2kZvby+yLGMYBpFIBMMwaG9vp1Kp\noCgKuq7j9XpRVbXRylgul2lqamJubo6vfe0+DEPnN37j1wgGg2iahiAIZLNZZFmmVjNPC6TLmKZA\nNpuhWtVxHJdKxaRUWsKy4phmGk0LYhh5HAcsa20iu+tGkOUKrhvDdRdx3WFgHGgFMriujSBEAAHX\n1ZAkC0XxYVkZTPNSJOkgoVA3klTCskQcJ3aaXOdwXRdNi6FpM7juHkTxERTFQ70ewLJ0HCcKGIhi\nGo9HRpZ34PWOU6slqNenAD+um6SlJcSll3bgODYeTxuGkaJS6aG5eYFw2MfKigxYyLIEmMTjPkql\nCgsLbfT2LuPxBCmXawgCp7VENr29EqurZVKpZiKRORSlBVku4PEoLC2F8HgsenuhWKyQz0dx3TlE\nsZeWlhI+n8rEhAdR1GhtFanXq0CMajVNudzOhg1lgkEfExM2jlMjEJAQBINEIkk6vcrCQpLXvS7A\nJZfs5M47f4wsw803/zeq1SqPPvoYl166l6Ghocaa9nwkKl4IWJZFvV6/IIjGU2HdIObc17kEZL1C\ncib5eK7P6Ivh/JwJ13V5xStewS233MJVV131Uh/OrypeJhq/CljXTLxY0HWdarV6FtFY782s1+sN\nguHz+V6S9qhfhFKphCiKBIPBl/pQnjHWqwRer/eCJRjreC5E7v777+fQoZMsLa0wOupl69YKkYif\nEyeyhEIewEOpVGL79nbm5zNMTjaxfXsZSfIwN7dKNBpA1/1oWpWdO5NMTq4wN5dg69Yy1apAPp8l\nmYySz3up1Ups3hxkZiZFNtvJ4GCJclmmUlmltTVONhvEMCoMDanMzKQoFrvo7s5SKnmo1VZJJqMU\ni1F0vcTAgMT8fJZSqZe2tkUqFRVdLxGN+jl1qsbJkyfQ9UUcR0FVL6Wp6TjVagiPR6RUygIRvF4L\nn88PVKlWtyBJj+C6fkSxBdOso+sr2LaEorQCCzhOEihj2zlctwvHKbO2VNeAfmAJsBDFBLJcwHG8\nCEKZSKQVr1dD02yiUT/9/W1kswU0TWZ4uJnLL9/Hd77zKKoa4R3veAWvfOUrAfB6vfj9/kbC4Mz7\nfj2QWc+sptNp7rnnXtrakrz+9Vc3ApozAxuA//zPu5mZWea3fustdHV1Na6DcrmM67qEw+Ff6vpx\nXZdyuYzP5yOdTjeCnmq1Sj6fPy3SXmJlJYfrmqyulimXK6yuZshm69i2DkQwzQK2HcM0FxCEIRxn\nAtdtA9KsVXK8iKKE46wZCsiygyhWEYTLcJzHse0eYApZdrDtdkDEcTSgjqJ4UJQSjnM5cADbbkIQ\nyqiqjGUlqFQ0XHetWrFv31vw+XJY1gDB4DSBgEou5wdEZLmOIIDfL2GadRYWOunsXMTvD1EuVxFF\niXrdjywLdHY6FIsaS0tJwuE5VLUNQcji9XpYWQkgigI9PQa1Wp1iMYbrLmAYHSSTBaLRAFNTIra9\n1lJoWTqCEKJez5PJtNHfXyAeDzE5qWGaNqpqI0mQTIbJ54tMTcUZHMzT0tLE1FQGy3JwXQ+KInLp\npT3MzKQ4fFjhNa8J8d73voNPfer/wzBs/vAPrycYDDIyMsKGDRtoa2v7pdeTFwLr11QgELignmvP\nBOcjIOe2XT9V9eOZ/q6maaLr+kVzflzXZXh4mO9+97vs2LHjpT6cX1W8TDR+FfBiEw3DMKhUKkSj\nUQRBwDRNNE3Dtm1kWcbr9V5wBGMd5XIZgFAo9BIfyTNHPp9HkqSGt/2FSDDW8csSDdd1uffe+5ie\nnmdkZIrpaT9799axbZiZqRCJiJhmmFotwyWX9HHs2ALLywn27NHI503y+QrxuI9iMYxl5dm1q41j\nx+bJ5VoYHq6wumpgGFVaWqKsrARwnAIbN/oZH1+kVuthYKBELidhmnlaWiIsL0dx3RyDg35OnVqh\nXu+hszNDLidhGAXi8QD5fBLLWqW/X2V2Nket1kdLyxylkoxlWUSjErreytTUE0xOjlGruUjSEF7v\nCK4bIRxuxTRziGKYWq2AZflwnBUEYQuqOoFl1XGcfgwjhSDoAKeD10kEwYfrRhGELK4bBAwkKYAo\nlnEcCUlSSCZtQqFmVNWit7eHrVs30t3dTTQaJRAI0NbWRltbW2PomKZpzM/P09PTQ7lc5l/+5Tbq\ndZs/+IN3UKlUuP327zMw0MwHPnDDMxL533///XzmM4/T0uLwN3/zPmKxWCOwWUepVOJv//YLLC5K\nvP/927j22mt/qZaOYrHIzMwMGzduPKt6lk6nyefzbNy48RndH9Vqle9///t8/vOPkEw6vOUtr0DX\ndWZmZlhdLTI1NcP4+By5XAVB8J8W4EexrAVgEMeZQBD6cd1pXNcLWAiCius6iKIfUSwgSS6K0o+q\nziNJ27Hto+i6gG37MAwAGccRkKRlXFfEcTYgy1N4PN1s2AB9fd3oehOOoyLLq0iSjKJ4cJwqq6v9\nNDfPEgoFKZfrCIIXy5IQBIW2Np1azWBhoYVweBafrwPXTaOqKtmsH8eR6eqqYRgmxWIUx1nEtnto\nasoSiXiZnnaxLIlEoo7jOAiCF9sus7zcRk9Pjvb2GKdOFTFNCVnWkSSZ1tYAlUqZsbEmenrSdHa2\nMjeXwrIkLEtAUbwMDKgUChVGR8O0tCwSi7VQq2URBJViUUKSfFxzTT/FYoX9+7Ns3+7jL/7ij/jq\nV7/O6mqe3/7tt5FIJJifnycej7+o1emLLZB+Oqy3X52vAnImziUf625Z5+JiOz+u69Le3s6JEyfO\nSna8jOcVLxONXwWsi7NfzP2VSiV8Pt9pp5o1guHzrbVUXMgLTKVSwXGcXzpb+lLAcRx0XUfTNIAL\nmmCs45lWjBzH4b777md5eYUDByZZXvawe7dFLlclm7VpaoJiMYZtp9izp4+RkUVKpSaGh+usrJQx\nTYdk0svSUgRFybBjRwcjI7PU6y10d1dIpw0EQae1NczkZBBFWWVoKMLo6CK23U4ikadSURDFGs3N\nIaano3g8KTZuDHPy5ArQTTyeIZcTgBrxuJdUqhnXnae/P8T0dAHT7KapaZ5SCRxHIRKx0fU2crlx\nFEVnZGSKfL4F1z0MqAhCD5KURlH8SJIFhBGENJoWx7ZLCMIqorgJ101j2y5gAm0IQoW12RidSFL+\ntBbHxjQdBEFix442rrrqKorFIk1NTbzrXe8kHo+jqiq2bTeqjKIo4vV6n/IeXQ8uCoUChmHQ1NTE\nPffcwxe/OEpPj83/+l9/jKIoFAoFEonEWdnOM6/JpaUl/uM/vkFHR5J3vvO6xs/OrX7cd9/9zM4u\n8cY3Xk1zczPw5IDGNE3Gxsbo6uoikUg09vHJT97KwYNZ3vCGfn77t98JrJGGv/u7T5HJ2Nx442u4\n7LLLGp+fnZ1FlmU6Ojqe9HsfP36c2277Bj09zdx00w1PMjK4557vcPfdB2htlbj88ksZHR1lfn6F\nyclpFheLlMslNE2hVlubhQIpoA+YALYhiqMIQhLIIQhhBAEUpQWYR5JkJMmDpi3jOJecvlaCWFYV\nUAiHW9i79woUZRZYq2g5TgpN20QwOEk06qdQsBDFCK5bRxB8xGJVLMtkYaGTUGiKUKgDw0jh8fgo\nl31YlpeOjgK27VIsRnCcBRynn3A4TWtrlKkpg0pFJB4vI4oKsuzBcSrMzbXR3p5mYKCFiYkMhrFW\nJVOUIO3tKvV6lWPHorS2rtDT087y8jKO40PTTEQxxMDAWpLq2LEAkcgCsVgrpplHVQOsrtqYZoBN\nm9aSZpOTKoIwi9/fg89XpKOjnePHc2ian3e/ezM+n4+vfe0gvb0BPvzh3+f48eMsLCzwyle+kmg0\nim3bL4gW4WILpJ8tngkBOZ/+Y12cfrF0DOi6TjKZpFKpXFTt1BcZXiYavwp4MYnGuj5gPfhVFKVR\nwbgYUK1WsSyLSCTyUh/KU2KdYKy3SAmCgKIoF8Xi/XREw7IsHnjgAVKpFA88MEWxKDA8bLO0lMM0\nPSQSAvPzEXy+FXbs6OOJJ5aw7QidnWsEQ5Yl2tr8HDvmJxZbZfv2Lp54YhZRTBCLVclkdPx+SCb9\nHDkSIBZbYWCgiaNHF/F624hEamSzFrKs0d4eYXQ0Qji8yMBAE2NjaVS1k2Awd/ozNvG4zPx8C5I0\nTW9vmLk5DcdpJRCYp1RyEMUwkUiVarWNbPYEzc0hCgWHxx9PU6sdY02ovQ2YZn29dd0EkrSMIIRx\n3RCOM4XrdrDW9qQgCM7ph7gPjydDItFJc7NKW1sbkmSye/dufv3Xf5277/4e8/Mav/M7r+LKK688\n6zyvicH1hhGDqqrPqspYKBR46KGH6OzsZNu2bdx66xcZGVnmrW/d+6Se5nXScWarhSiKVKtVZmZm\nGBgYOK9T3XpAc66oFeDee+/l618/wcCAh7/8yz9quNl87nO38dhjq1xzzQbe9a63A2tJhL//+0+z\numpz441XsW/fPgAmJib45Cf/E1mGj3zkhie14dTrdXRdJxQKnUWY6vU6s7OzdHV1UavViEajZ1V0\n1o0aPv7xT3Pw4ASRiEk6XaBer1MoOJTLFWo1B8sSsG0RsAAdUBHFDLAVURxHFAdOV0SCp9u3krhu\nDvAjy8uEw14GBt5EOJwG+pCkWfx+mXrdh+vGkaQUshxBUUoIgkUqNUAoNEUg0IRh5FDVMLWahGmG\naW9fxXUFCoUorrsI9OHzpWhrizI7W6daDRCP57BtCVEUkGWdubkOmpvTDA42MzmZRtfXNDyKEqW9\nHUxT5/jxKPH4Cp2dLWQyKwhCmEqlhus2sWHDGnkYG/Pi9S4RDjfjugWCwSjLyzUqlTBbtmhIksT0\ntIjjLOHxdJ4mGElOnsxTKIQYGqogyyqZjIlhZNH1Tpqaavzar+3lhz88zPKyjxtv3MaWLVv4whfu\nIpmM8IEPvJdqtcrs7CxDQ0PPWfthGAaGYVwUa/ELgXMJyPnmfABP0n9cqEMfU6kU27dvp1KpXNAJ\nvIscT/uH/685ledlPAnrg+Pq9XojCPD5fBesaO+psD6d9ULEuQRjvYJRqVRe6kN7xniq82sYBj/+\n8Y/JZDJ897sTWJZFTw9o2jLLy1FiMT/j40G83iyXXqryxBNeRkZKJBIeUqllKpUgbW0hjh71I8tZ\nrrgiwqFDLsePF4lE/GSzq0CAjg4fR44EsawVdu+WOXZMY2pKJ5GIkc8XcRyFtjaJY8c6gGV27FA4\nedJhbk6kqSnI6uoSINPcLDI724phTNDXJzE/72d2NoDPV6ZQOIXrthKJZCmX/czNzdPUZBAMNjM7\nqzM9/RNqtQKwFziJJE0jij4MIwSsAMvYdh8wy1p+pgVZXhNoezwlenoG2bdvkP7+Xi6//HI6Ojro\n7Ozknnvu4fOfP8bcXJ3u7m5uvvmPyOfzjWoArF1D605vgiA8Z51UNBrlLW95C7C2BqTTBbJZiUKh\nhKqqjaBjPQBZ//+Z+NKXvsIjj6R53et6uP7633rSA32dmIyNjeH3+9mwYUNjW36/H1UV8Xo9Z80O\nuO66N3PZZQv09/ej6zqiKOL3+/njP34PhUKBwcHBxvbXjgkc5+yZQ7quc/z4ceLxOMlk8knH9dWv\nfp39++d41au6uOGG6897foLBIJLkIxLZxNvfPsRv/ubbqFarFAoFRkZGmJqa4uDBY5w6NU467aFU\nmkXXQzhODdfN4TgSUAUEBCGIIBSAZVw3AMxjWXvI5cawrJ+yeXMnfv8SpumjUGhHFE8gijqy7Dlt\n2bsZv3+WZHIRw3BwHBHT9FOvx2huXkIQamQyCWAJWU6gKCrNzVWWlmSOHvWQTOZRVRdQcN0yS0td\nJJM59u2zmZ11GB01cF0DWRZpawvhODpHj0YIhysMD5uUSi75fP30nBUfg4MgigYTE2vDI+PxOIKg\nEovJzM/LzM8rbN8uI8sW8/NgWasIQguBQIShoQDHjhX56U9thoYsWlstikUXy8pQqTQTDEbZsSPA\nyZNFvvzlMRKJHG1tTfzoRw/zwx8+xNxcmHg8xcGDB3nooccYHdV4y1umeOMbr+Vb3/oOiiLzpjf9\nOoqikMvliMVizzjQvBAD5hcL56tgws+TBesdDrCWVHoqB6x1IvJSzwApFAqNFvCX8dLhZaJxEeCF\nvEnOdTjyeDx4vd5G5vpiw4VINNaDQ13Xz6vBuBCP+ZlC13V+9rOfkUql+MY3xlAUjURCYmFhiUql\nlWQyzvi4n1CozL59IiMjEidO5GhqUlldXUFV20gmI5w8GWTTpiKXX+5y7JjD+HiOSCRALpejuTmB\nLDuMjYUYGMiwbZvL5KSO61aJxxPk82Xi8TAej8P4eBMdHQts2eIyM+MwN2cQiQRYXV0gGg3S3Kww\nO9uMZU3S22uzsBBjYcGDz5cjm83gOD2Ew8uUyy6LiyVCoTqBQBvpdBVBWGJm5gjl8mZgFDgCNGFZ\nHqAOLLDWUpNjrW0mQCQCQ0N9bNzYwqlTRcLhXj70oWu58sorcV2XAwcOcPToUeLxOIODg2zdOsrg\nYDd+vx9BEGhpaQF+TlINw0AQhBfE6U0QBG688Z1MTEywZ88eTNPk61//JqZpcd11v0EgEGgQgXXy\nsZb5XLfhXPPYP3N766+RkRE++9n78Ptd/vIvb6SlpQVBEHj961/Phg0baGlpIRQKNbapqiqRSIR1\n3/71+yMYDBIOhzEMoxHUDAwM8Cd/ch2KotDZ2dnY/49+9CO+8pURurtF/vzPf/9Jv69p2lgWmKb1\npJ+5rsttt93O2Ngi1157GVdfrbJt2zYAAoEAgUDgrDat9YGTx44d4wc/+CFHj1pkMnnq9RC2vYzr\nduO6M7juBmCSNVcwGZgBDMrlCMePj9PTcymBwCKCsEIwuAnHWaJabUaWNSKRUxiGQ73egesuUK97\nCQRWEYQqq6tdiOIyXq+D6ypEImuEcXQ0QHNznkQij+t6cJwyuVwnfr/Fzp11UimD8XEX1zUQRWhr\nCwE1Tp6M4Pfn6OvT0DQLTXOp1aBS8TI8bOHxmExOyjhOlkAgiiTR2GKLAAAgAElEQVR5aWvzMzNT\n5oknRLZuFenpsVlacjDNDI7ThNcbZng4xMmTZX7wgzr9/TaDgzr1ukCtViCfjxIIyOze7WVxscrD\nD9cIBiskk0EikTBgMTPjQ1VNdu8WKRQq3Hrrg9j2HLLczfHjx1heXuLRR4t4PBIDA33MzS1w771H\neNWrBnnnO6/jyJEjVKtVLrnkkvPqkS7WdfiFxrqL1TqZWE9Anq/9ar29ah3PVYD+XJDL5YhGoy/4\nfl7GL8bLROO/KM6XXT93RsPFuOheSEH70xGMixGCIOA4DpqmcfTo0dN2pWMEAkViMT+p1AodHf2E\nQjFOnvRyySU6l1xiMDbmUC5nicUC5HIp+vv7qdfrjIzI7NolsHu3xtSUSb1eIBKJUiissm1bJ6ZZ\n59AhhS1bHAYHcywsaMRiNk1NLeTzqwwNteI4GqOjQTZsSDE0lGV+XsS2IR6Psri4SEtLlGjUw+Ji\nlGRyivb2KisrTRiGjd9fJp0uEg4PEQ7PUipVqVR0VHUeVW0mlcri9+eoVGaZmQmi6xLwKNAC+AGJ\nNWIRRVWT+Hwpuru7kCSL5uZOPvKR32fXrl14PB4eeugharUal1xyCbBW1r/99v1ks2vmBVdeeSX/\n5//8+VkP4PVKo66vicZFUSSfz9Pe3o7rujzwwAPU63Ve+9rXUqlU2L//QXp7e9i7dy+1Wo10Ok13\nd/czvua6u7sb8w/Gxsa4775TmCZs2zbOrl27Gts5c3s33ng9r371JAMDA8iyfN7qx9pQMhtFWct0\n2rbdCDY2btx41vUlSdKTPPrPN0/gTFLT3t6OKIqN6ocoing8HlQVVPX8FZ93vett7N49wYYNG570\ns3q9zrFj80xNiVxxRfkXWmOurq6SzWb59rcfZGUlhyB00dPTTXd3hlQqR6UiUijk0HUBy8qxRjK8\np/8NACVcd5py2c/U1E/p738tfn+ebHYORanj96eo13Xq9S0oylEkKYMs61jWGLncMIqSRpKyCIKF\nIJTRNJtMJk57+wx+/yq27cV1q1Sr7fh8Ips311hc1Dh1qglFMRFFl0TCjyhWmJ4Ooygl2tsrp4fE\nKdRqDsWih02b/Pj9BjMzMpZVwOMJIMsqXV1B5uaqHDjgMDws0dFhk0o52HYGw4jg9UYYHAywuKiz\nf79OS4tOf7+OIEjYtkY2G0BVXXbsUMjn6xw6ZKIoBaLRENFoFK/X5dQpFXDZtMlB102mpjyn3cPC\ndHQkTg/phBMnMnR0WAgCfP7z36BeXyWX6+Lo0ZNEIvfy7W8/Tq0mIssy0WiUr3/9XjZv7ufNb/51\nSqUSKysr59X5vIw1rLf6ruPZ3q/w4hCQlysaFwZengx+keD5cp1aDxKr1eovnDL9fE+AfrGwNmnY\nxOv1vmSLy5nn2LIsvF5v4xw/lZPHOhG50FEqlThx4gSPPfYYt932GEtLJ/F6VUqlFBs2tFMui0xP\nKwwPK8RiVaanLVxXQ5YjVKtZtmzpIJ+3mJhQGBwUCQSqLC2ZiKKJIDRRqeQZHk5QKNQZH/fR02Oh\nKAVWVnRk2cbjaaFcLjAwEKVa1ZmcDNHRoeH3V0ilQJZdAoEYy8uLxGI+PB6FlZUEkUiOeLzC6moS\n07TwemtkMitAF6papFw2qVQsII0gxMnlSoCNrqdIpyXm5tKY5iQQBnyskQwN0JAklVhM4Nprd3Lr\nrZ/kT/7kJt73vv+Gz6fwzW8+Sr2eZ+vWLfT29tLV1cX4+HjjmpiYGMXjMXntay9/kp30uvvb0aNH\ncRyHtrY27rzza3z5yz/GNLMEAj4+/env88QTK/T3BxkdHeW228ZYXDzFq151CZ/+9G3cffdj+P06\n/f39nDp1ikKhQFNT0zP6W/v9fnK5WdrbfVx11RV4vd5GJeHM69jj8dDa2orH40EURY4cOcLk5CTd\n3d14PB4kSSKZTLJtWx9XXrn3LJeqc/vAdV0nn883Kjqwdj/9+Mc/Znx8nN7e3oZmTFEU8vl8o4Vs\nPbhZn6jc3t7Opk0tXHnlvrPWt8OHD3PffT8imYwzPDz8pPtudnaWubk5Nm/upb/fwxVXXHHeuTFr\nrWZp/uEfvsD+/Y+Ry9VwnCC9vTJ9fXGuumo7e/YMsW/fHjZv3kg0GsXjcTBNDctKn7YwXgV6gCLg\nxzSLrK7mcd0sorgJQUhhGK247jKmuYLP14ptlzCM9tNC8+XT91crhlGiUukmEskQClUxzRCGUcc0\n1wavdnUZ6HqVpaUErpvB4wkTi1n4/TpLS1GqVZt4vI6iGAhCEE2rsLwco6vLordXZGnJIZOpIoqg\nqhK9vSE0TWNkxEdzc43eXh+lUo1yWUPTfEiSn6EhFdA5etSDIKRJJPyoqo2qiqTTXmo1L5s3C/j9\nJlNTMpXKCqoaJR4XaWlRmZ11WVkR6e+3iEZdMhmBQiFDrRYlmRQZGgoxO6szN+cQjVYJhwUEQUbX\nyywsRIlEbC65JM7cXI6DB1dw3Sxer0gqtcjjjx/kscegWFxk48YOvvCFr/K97x0mEnFpbW3l/vvv\nJ51O09XV1XBfvFiG1L1QsCwLQRCe1p3uuUxAtyzrLF3IcyEfBw8eZGZmhuuvP39r5Mt4XvC0k8Ff\nrmj8F8F6dr1erwM05jY8VabzQqoM/DI4M1B7sYnGuRWMpzvH67gYzrWmaSwtLXHvvT/iwQcXaG2t\nnBahamzd2sGRI208/rjGjh0+vN4MJ096SSZNZDlGpbLEjh1+Dh2K8cgjNYaHvUhSiqkplWQSoIlC\nYZEdO1SOHAnw2GMm/f0qljXH5KRCMimgqq2Uywts3Spy8mSAkRGRvj4ZUVxkdtZLIuESjcZZXh6n\nu1ukqSnB3FyAjo4i3d3zzM+3EAikiMWKrK4WiEQ2EovVqVTSOE4IWEYQ2ikUishyHk3LUij4yOcF\nqtWDQASIAiKC4BAK5dm3by/XXHMVCwurTEzMoutJHnzwEW66aRMA6XSehQWRmZnlxnn85jfv4Tvf\nGWf37iY+9KEP8t//+wexbRuPxwP8XICcTqdpbW3l+PHj/Pu/7ycSEfjoR2+iUKhQLEKpVCaZTLJh\nQ5BqVaezsxOfz8emTaMMD68F+OVyjWoVqtUaU1NT/Mu/3IUguNx88/X09vaiadovJOR+v5+bbnpf\n4/+HDx/my1/+LsPDndx443vO+72VlRX+7d++T7m8tsasC7YlSaKvrw/4edLkTFH4OuH4zGduY2Ii\nxzvf+Uouv/xyBEFgbm6OO+54GE2DRCLB3r17ARgdHeVzn/sWTU0qN998U8NV5sx2jo0bNzaI/Pra\n99Wv3svhwy71us773tdxVja1XC5zyy1fIZNxufHGK55ymnCxWOTWW79MsVigUrGQpBC/+ZubaWlp\nYe/evecNSDOZDKurq+zf/zAjIyc5fnyU2VmDWi192gZ3rcrhujJLSyuEwwdIJJJ4PNPIcjM+n0A2\nu4qquijKHPW6jiDsRZaPYts2qmqhKMfRtHbWbHgdZNlDJJJD0wxOnuwjFCoQDhu4rowsp0mlkgiC\nRTSaQxAcbDtGvV4hn1fp6fHS16czOyuyurpOMDx0dQUoFEr89KcC3d0mO3bYFIsO2WyRSkVFkrxs\n2iRQq2kcPuzB58vS0hJAUfwEAg5zcz5M08PQkInrmkxPK9j2GuFqaorR2enh+HGZ6WmH/n4TcCkU\nHEwzTz7fSXNzmF27/Bw/XuJnP6sSiZRJJIIEAn4sq8apU0GSSY3XvtbHxAQcPFhAEMr4fF46O+NY\nlsmhQy7hsMErXhEmk8nxD/9wB9VqCtdt5dChQ0xNTbF/f45YzGVgYIDHHnuCBx8c4a1vvZIrrriC\niYkJHMdhcHDwv1S2/Lk8V3+R/uPcFqz1hOGZ3302E9DXKxov46XFy0TjIsBzWcjW7S91XW/0dj/T\n4PfFnN3xfOFMovFi4ZclcefiQiYa9XqdUqnEV75yN4cPr+LzZbCsAIZhsXmzj8cfb2ZkpMLQkI9T\np2aZnk4Qjaqk0wE0TWPHDpUnnohy6FCV7m6VmZl5FhejNDX5mZwM4fEss3NngsOHg4yM1GltVZid\nnWZ+PkAi4WNxsYlyeZFNm1xOnIhw9KhLR4eIZc2wsBCluVnBMCIsLo7T2ysRiXQwP6/Q0bGKKBaY\nne0gEpknGs2Qy2mIYhfBYI1sdhpJiiAIszhOK5qmAnnq9Qr1eolqNUK5fOK0mDcEOICD15th+/Zt\nfPCD7+Oqq64iGo0iiiK3334n9903Ry5XIJ/PE4vF+I3feAM9PYfZsmVL43yKooAg/Pw6XW87WB+I\nWS6X+fjHP8/Kis4NN7yOQCCAxyOgKGvZweuvv449e8bYsmULwWCQm2/+Q1zXRZZl2tra+Lu/29To\npb7ppuuZm5tj+/btpFIpJMlFENb2eeDAAe6880fs2dPPe97z28/oWpiZmWF8XAAWME2zQY7ORCgU\norlZxetds5U8H0RRZGxsjAcfPMCll+5k165dwJqhQDZbIZORKBQKiKKI67rEYjG6u31omkEymWwI\n4fP5PMUiSJLeGLIGa4ToW996gCuu2Mmv/dprG+uY1+vFtm1e+cptwFG2bh3CWIvwG1ir8gqoqtUQ\nw5+7/i4uLjI9Pc3oaBnXlXjHO3bR09PD5s2bf+FanUgkSCQSbNq0CdM0ufvubzE6Osn4+ApjYxOs\nrIxQrUZZs89tp1RKU626RKM2Ph/U6zlkeQ+uewrD2IzHcxLLOkQopOC68whCG4IgYNsreDwKsqxi\nWRVmZoaJRseJRjMIgoRlpahWY0iSTFNTDtcF245jGMuUy15aWlR27KixsCCSzxsIgomiqLS1eajV\najz6qExra52tWy3KZZdSqUq5rOK6QTZutLAsg+PHvchyhljMj6qGaWqC6WkvCwsKQ0MWomixtAS2\nncYwuohGo2zY4OP48TI//alOZ6dGNMrpeSQlUqlmmposXv3qIGNjBQ4cKBMIVIjFPCQSMSxLZ3zc\nTyRiccUVCsvLMDJSwTQryHKE3t61a3F0VMLj0diyxUHTBJaWdEqlCroeY9OmJIoCR47UgCyxmITH\n4/CJT9xGJpNmebmFn/3sMK7rctddP8G24UMfejuyLPPDHz7E9u3DXHrppei6Tq1WIxaLPf1NdZHh\nhUjgPZ0A/dz2q6cSoJ9JPta3VSgUfiX/DhcbXra3vQiw3kbxy+B8BOPc9qhfhItx8B38fAZIOBx+\nRsPHngueK8FYR61WwzCMCyrzsj6k8VOfuo25uRKCUCSVCtDZWSYcDnD0KESjNp2dAU6enCCR6ESW\nTWZm/GzYUCWZjPLEEyWCQZGmJom5uUWSyRYUxeHUqQC9vXna2+McPlwgEFCJRl2mp+cJh2MEgyIz\nM1Ha2tJ0dsY5flxDVb00NWnMz6fw+dqIx02WloI4zjRdXXFSKS+1mkNnZ/n0rI4eksk5dF2mXDaI\nRuPYdoFMpoKirNnZ6noSXa9hmnUMo0K1qmEYrVSrE+i6xlqG2QAMFMWhra0PVY2hqq1EIjqvetUW\nfvd3r8fv91OtVnnkkUe4//6DeL1+/vRP301XVxfVapVbb/0yjuPwe7/3bnw+H6dOnaK7u7shfp6e\nnuZ737ufwcF+du3axf/9v7eytOTy3vdewute9zpmZ2cJBAJPGbg/U8zPzyOKIh0dHdxxx1f4ylem\n2bpV5G//9s8bVZSNGzc+ZXtIJpPhxz/+Mb29vQ1ycD6su2L9orXjU5/6N771rTRXXOHjr//6Q433\np6ammJ2dZe/evY3vn9leIctygziYpskTTzxBLBZj48aNjYDl3//9y9x9d4rLLlP4n//zzxpW3edz\n0Dszm3r8+HGKxSJ9fX1Uq1U6OjrOCoJEUWR2dpZbbvlPJMll585uwuEI1157zbNue7Rtm9tvv5Px\n8VlmZ7OMj08yN3eYalUCbKAbmMTjGSQSyaIobQSDNooSRpa9qGocx1nF6w1hWRlUVcTj2YzjTOE4\nm/H5xvF4vKwZBfmxbRlBCOD3LyJJEvV6O7Y9h20PEAot0dISZnFRxzD8KEoJWQ4Qj4NlaZw82Uwi\nsUgikaRazSJJIYpFA8uKsHHj2ho4M6MCC6hqJ15vkdbWOJOTRXK5MJs2lU/b1xpYVgFNayccLjM8\n3Mbo6CKrq1Gam1MoSgRFcXAcnfn5KNGoxtatcWZnV8hkIsjyAorSRkuLiSSJnDjhweutsWFDgFKp\nRLkcolabx3G66e+v4/OpnDjhYNsara0igmBj214qlQzZbDtDQ2vr1YkTJapVDZ/PIhDwEo9HyGYz\nnDoVZ+PGAv39rYyNrVCvCziOgc8XYPv2VjKZHI8+KrN9O/zFX9zE5z73ZZaXy9x445sYHBzkscce\nIx5fa9O72FGtVlEU5bxJhhcLTzX/Yz2Wve6668jn8wwPDzdigL//+7+nr6/votZHXsB4Wub5skbj\nIsBaluqZzdGwLItarUatVsNxHHw+H8Fg8Je2wLyYdANnYr3Pe703/IXAugajUqmcpcF4ti5A60HU\nhWAl7DgOlUqFf/qnz/Cd7+wnlcqyuirS3++huRmOHpUwjCKdnUHS6VnC4SjgYX7eS18ftLfDxISL\nplWIxXxks4s0NydwXZHp6SCdnRadnS4zMy6aViccVkml5vD712xal5biJJN1+vpE5udF6nWXeFxi\nZWUKWY7R1OQlm/ViWWlaW6FcTlIs2rS21qlUUmQyXUQiJRynQrks4PN5UBSRlZVlXDeJx5PBMERq\nNQ+12iqGUaZSKaBpSarVItXqNKYpsxbkaShKjX37LuPGG9/Fm998FXv3bkBRitRqYU6dOs78fJqd\nOzeRTCZxHIeHHz6Fptls3dpJKBTi5MmTfOMbIywv6wwNxWlvb6e5ufl0kFfHMAy+973v8bWvrVAs\nLvHmN7+OoaEehocT7Nu3ryFafT6GTUUikcYgy5aWZpqbDV7zmsuJRqP80z99lu9+9xiRiN1ocToX\nfr+f4eHhxpyKb3/7O9xxx7dJJsNnWfDKstxYNzRN4yc/+Qmapp1FlETRRdMWePWr99Db29N4PxaL\n0dfXd9a6sy44Xe/vlmW5Ifbu6uo6basqNCqDwaAfrzfLlVfupbm5uRGEfP/793H33ffS2hpv6FTW\nv5dOp/nkJ+/isccWGB5uYdu2bciy3KgOua7L0tISCwsLPPHEDK7r8I53XMuePbsblZf17Z0JwzA4\nfPgwmUyGe+/9AadOneKhhx5hdnaamZlpKpUKu3bt4Mor95FKLREKBQmHm6jXNUwzj2VlgDZsO0+9\nruC6nO5nN3BdC8taRhTbcZxFLGsbgpA9TSoqCEIWCGKazVhWBUkKo6pZVLVALteNaWaR5TiKotHc\nbFEuC6ysBFCUEl6vQjgMslxjcjKBbZfo7lZw3TqO46FUWps23t9vkUg4zM0p5HKrqGoAn8+lvz/M\n8nKN8XEfXV01mpslSiWLSqVIqRTB65XYtStGPl9idFRGVXOEwyrhsIKiOMzN+bFtgZ07vUCdqSmR\nWi2NLEfo7PSQSMiMj0vk8xYDA+D3W+TzIqVSllIpSk+PQn+/j6kpk6UlnUhEIxQCRfFSr1eZmgrT\n0uKwa1eMhYUyCws6UMXrVejqiiAIJocOqfh8FS67LEGhUGZxUade1/B4wgwOBvH5HB5+2KZWSzE0\nFMIwCtx//0Hm5laoVIJ4PAUmJia4886jjI2NcemlW3n00Z9xxx3fIhLx0dLSQjqdplKpXDRzOwzD\nOK/4+8XE+fQfHo8HRVEaiQhZlpmenubAgQMcOnSIT3ziE/zjP/4j3/jGNzhw4ACTk5O4rkt3dze3\n3HIL73rXu/irv/or7rnnHnbs2PELDQH279/Pddddx5/+6Z/ypS99iXA4zM6dO8/6zF133cXb3/52\nPvKRj3DXXXfR29t7lukF8Iz2+z/+x//g+uuv52/+5m/Yv38/l19++TPW2L2IeFmj8auCp2uvsSwL\nTdMaA7zW/OnPLz5+PvZ3oeKFbJ16vioY5+JCOde5XI5bbrmNarVMOm1RKons3dtELFbg8GGVjo4q\nHR1eVlezbNjQTijUzfg47N0bIhYrc+KETDK5lh3M5VL09iapVFo4etRlzx4/kUiZyUmBpqYKTU1h\nUqkpBgd7CIWiTE4G2LEDEokKExMKmlanvd3P1NQEXm8vLS0tLC8rtLZm6e01mZrqRNeLtLdXmZlJ\nMz+/kWi0iuMskE57CIctFMXH4uISkUgXoZCNpuWo1+MYxjy2LWAYOqbZTK1mYZrHqNc9OI4M1JAk\ni1hMZceOfezatZmdO7exZ88eYrEYmqZx//3387WvKSwu6jzyyCNce+21bNu2jT/6I5tsNkulUkHX\ndYaHh3nLW2awLLtR4ahUKnz2s1+mVjP4vd97Jzt27GB6OsOuXYPIskxvby+9vb0v6N+6ubm5MT9j\nzV3IwXV/rp/IZrPIsvyUgy8dx+Ghh0Y4flxg06ZjbN269byfe/jhh/n85x+ltdXlf//vzgbR2bNn\nD3v27HnWx+84TiPQOPf94eFhhoaGGn3ejuNgmiY/+tEIp06JDAwcoqen5yz7XZ/PRySiIIomkUjk\nSW46Y2NjfPrTdxMIiNx44+uIRCJ0dXU9yU1nPQhaXl7mvvv2U63mOXLExLImqVT6kaQJLGsAWf4p\n0IvfnyYQiNPS4mXnzo1s3z7Igw8eIpns4uTJxzlxYhrbXsYwVBwnjqbNYxjDBAJLWNYGfL4Sup7C\n663j9Z46PXHej+NUkaQeHGcMQajh9frQ9WkqlW14PDMoSg6PR0QUV9A0iVwuSjQ6RzgsIcsKrptj\nZqabcDhDf38ZTXOo1QQqFRdd9zEwoOPxaMzPe7CsDB5PHK83SF+fl4mJAg89ZDM46BKPG2iagG0X\nKBZj+P0yu3erLC9XeeSRNROHeDxENBpBlh2mplQkyWbrVpdq1WZiwsI089h2iM7OJLGYxOiohK6b\ntLdbiCKUyyK6XiadDtHbG2HHDi+joxXm58v4/WsJj6amMJpWYnRUobNT4g1vCHLiRJ5Dh3I4ThWv\nt+n0elXm8ccF4nGdV75SIZNRmJjIU61qQIRNm9ZMB44ccZGkIr29IEk+6nWLTKZOsRhl504Bn0/k\nwIEldD2HzxfAcVy++MX/4OTJWWZnm4jFHkWWZb7whW/hOC4f+tD1eL1eDhw4wNDQEJs2bWpk7i8U\nAfpTkekLBev37A033MANN9wAwDve8Q5e//rXs3XrVo4dO9Z4ffWrX+VNb3oTCwsLfPjDH+Zzn/sc\nl156Kf/8z//MNddcw/j4OIlE4kn7mJmZ4U1vehN/8Ad/wB133MEPfvAD3v/+99Pe3s7VV18NrK15\nv/M7v8PHPvYx3vjGN3L77bfz1re+lUOHDrF582YA7rzzzqfd78c+9jH+9V//lS996Uv09vby13/9\n11xzzTWcOHHiJa0oPRu83Dp1kcAwjPMGo6ZpNloV1v2tnw9//QuxneeZYF1MGwgEnrdqzAtFMNah\n6zrVavUs16EXE8vLy3zxi3dhGBVOnrSwbYvLLosxPj5DNhujs7NGLucDUgwMdHPkSAVQ2bvXy8zM\nIvl8mJaWOvl8CMdZYtu2DRw7VqRW87B9O6ysZMnnfTQ3mxQKYarVaYaGupicrFKrhdm+3SSfr7Cy\n4qO5uY5tR1hcPEl/fw/lskU67WVgoIjruoyPNxGJrLnXzMysEA5vRFWXyGQsHMdLNKphmlGWl2dI\nJNoxzTSVigfD8GFZp7BtFduGej2IYRQxjGV0XTpdwQPQ8Xr9hEIh/P4OJCmEJOmoqs7evdt5z3uu\nbQTIjzzyCHff/W2WlwNcfXUf733vmrPJxz/+WX7ykyxXX93OBz5wA7DWIrO0tEQ4HGZubo7/9/++\nRr0u8sEPvvqsbNiZw67WA93zua5kMhlgre/fdV1yuRyRSORZtwuurq6ysrLC8PAwCwsLfOITd6Cq\nEh/+8O+e94EL8Oijj3Ls2BhXX/2ahiXuuRgZGeELX7iHtrYQf/ZnH3zKB+Q6GTjzns3n83z+87ej\nKDLvf/+7G1nf0dFRvvjFbzI42MH73vfuxn1Yr9eZn5+nq6ur0W4qCAKqqiLLMg88sJ+xsSmuvfa1\njcyh67pkMplG9dc0TRKJxJP6xg8ePMhnPvMDQiGXj370/WdVZ85svxofH+fee/dTLKb52c88BAJT\nBINdRCJ1QqEYiYQfXQdVhYWFMoaRJZeLYxhTWFYv0WiJeDxAPO5nerrA6mqZ2dmjzM5mEYQchtGE\nJPnweErIci+quoqiDKKqi8j/P3tvGiVHfZ/7f7q6q3rfe/aenn00+2i0Cy1IQoDtf4yxwQSDbWzH\niXPDCce5PnFiHydxTnKSk+vl3tg4dnwNMbHBDoTV7AhjEEgaxIAkRrNoNGtPT0/3TPf03l3VS/1f\ntKaDLMDEZjG+PC9rauuaWn7P7/t9nkfnQ6cLotGYsdkMlEoZjMY+NJplSqVq9PooOl2BUqmIqlZT\nKMQoFFrxeKYRBDOqKlIoJEmnfZhMMaqqtKRSKYrFOrLZAIWCj6amKJIksrQkks/H0Ott6HQyjY1O\nAoEICwseWlvL7U+Kkj73Prag10Nnp0QslmJx0YIk+RHFRlyuFAaDgbNny6GLbW0q+XyBWExCUZbJ\nZhvxelPU1bkYH4+TSgl4PBm0WhGdTiSfTzA7W01DQ5T+/iZOn14kkdAjimvo9Xbq643IcoqXX7bi\n8UTp7W3A718ilTIjyyvodLW0t5fvv1OntIjiCl6vk2IxQz5vJhYLk8nU09+fx2DQMz6uUCzGsFgM\n6PUlHA43gcASgUA1AwMpqqtdTE5GyWazCIKIyaSltdVNMLjK2JiN9vZVGhoaCARCZDJFFEWLwWBi\n9+4mVlejPPOMTF+fwFe/+mf827/dzuxsiE9/+sO0tbUxMTGBzWY7Lyvm7YSqqqTTaQwGw1velvxm\n4fLLL+eLX/wiV1555XnL1yv3l112Gdu3b+ef//mfgfJvbK/NxDIAACAASURBVGxs5KabbuKLX/zi\nBfv7i7/4Cx555BFOnTpVWfaxj32MeDzOww8/DMC1115LJpPhgQceqKyzc+dOhoaG+Jd/+RcAduzY\n8SuPW19fz5//+Z/zZ3/2Z0DZ8bGmpobbbruNa6655s26RG8G3ksG/13BK2e9VVWtVDAKhQJarfac\naPTNC/D6bZll/3XxZpz7W00w3mnMz89z332Pks+nOH48i8WSY9u2akZGRjlxQovTqUerLQ8Au7pc\nvPBCHRMTWXp6jMzMLDA+XofTaaRUElGUJL29BkZGqjl1Kk1np5GzZxeYnvbgduspFo1EoxFaWkyc\nPl3F5KSGri4zgcAyU1NOamt1mEx6gkE/7e0m0ulm5uYEOjvziGKEiYkq6utXaGoqz1QajR5qatwE\ng3NIkpWqqhLxuBm/P0hNjYjHYyUSWaPsFDWDqppRVSeFQnlwUiicRZZ1lEoiUEKvNyJJJTyeNurr\nHTQ3u6mp8SCKIgsLKywshDl9OsjXvnYbV1+9wDXXXMVFF13E6OgU4XCgMtAUBAG3247LFcHlKlcD\nisUiP/3pnTz55CR79rRx3XXX8KlP7SebzbJjxw4kqZyKvW7zWiwWkWWZs2fP4nK5qKqq4oknDvH8\n8xNcddVBamtr+ed//jEA//N/3sDU1BR33XWEwcEysRkeHmZhwc+BA/txu91v6F6oqqqqDJ7j8TiJ\nBOj1RdLp9GsSje3bt7N9+3ag/KwMDw+jqio7duyoPCODg4N89avlAMLXIhn5fJ7vfOcWlpbW+Oxn\nr6qkfs/NzXHqVAKdDhYXF+nqKrt5TU9PMzEBiuInl8tVrGdvv/1Onnlmnr17G/noRz9yQajhwYOX\ncPDgJZXjlkollpaW+OY3b6NYVLnppo/h9XrPM8FYXl7m7rsfor7ewx/+4X4cDscF11Sj0RCNRjlx\n4gTj45McOpSkoSHFRRd56en5Pfr7e3E6nZjN5vNaYMuDUYHR0VEymY38/OcnyGRkpqacLC4uoNVq\n8XhUoBuzeY1odJ7l5SJ6fQhZbkSjWSSfrwbm0emq0WhW0Wq9SFKGXM6AXq8hkTiD0QiSpCOXS6Kq\ng0jSGBqNhMWSP1dhqaVQSKCqdiRJQ1NTlGQyRzjspViMoNEIVFcb0evXCIWM5PMZJKmEyaSntlYk\nEslw9GjZgaqzM0c+r0VRMqytmdDptHR3QyYjMzYmIQgRjEYLLpcDux3OnJHI5aClpVwVikYF8vk1\nYjEvtbU2hobMjI4mWVxMYbMlcbvN2GwWFCXFmTMWqqp0XHqpiampNY4fj6KqSYxGEz5fFcVigZMn\nwWIpsnWrllhMw9mzCVKpNMWi45z4W2BsrASkqKsTUVUt+TwkEjlWVhz09blwuyUmJrLkcin0eg1m\nsx6v10kotMrwcIGODolLLzVy9mycUChEsVjCYLDS2WkhHk/y1FMK1dUpLrrIw9qalvn5FZLJAoLg\npKennCnz8MMBRDGAz1dDoSDz1a9+Hb8/Sirl5vnnn2dmZoZ77nkJmw2+9KU/YmlpiePHX2LXru10\ndnaSy+UoFotvSovla+HdNh5QVfU17bzXJ2VHRkb48pe/XFmu0Wg4ePAgR48efdV9Hjt2jIMHD563\n7PLLL6+QAYCjR4/yhS984YJ17r//fqD8vvtVx52dnWV5eZlLLvmv95XNZmP79u0cPXr0t41o/Eq8\nRzTeRVh3psnlchWC8evoL94I1onGO2ET+5vgzWidersJxtttyTs9Pc3hw0eIxSI89liahoYku3bV\n8/zzM4yPi5jNdlZXC3i9In19eo4d05LJJBgcdHLy5CiBQB1Wq4NgUEtVFWzcKPLCCzZyuQQbNpgZ\nHz9DMNiI0+lgfl7CbE7Q0aFjdNTF9HSR7m4LZ87Msrjoxem0kkqJRCJhGhv1TE83MztboqNDZXEx\nyMSEj6amPDU1ccLhFF6vDa+3gdnZOZxOJ16vgVDIxPz8Eh5PkZqaOpaWIphMdozGRXI5FVmuQZYz\nQIpsdoVCwYKq2hGENBqNAZ2uhE6XOydELyBJJaqr69i1azNbt27FZrNx8uRJbr/9Ls6cMfDUU8/i\ndjvYt28f119/NRs2vMCjjz7H//pfN3PjjZ/m2muv5sCBMFqtluXlZYxGI+HwGrGYSDKZQa/Xc/HF\nF5/3P9HpdPj9fqLRKIODg5w4cYIf/vBpPB6BL37xcwwPj3HiBLS0nGTbNh2xmAJoWF1dxe8PsLSk\n4nSGSCaT/OQnh5idFTCZjFx00UXceed9WCwmrrnmI28oF6e/v5/PfU5BkiR8Ph/z8/M888yzDAz0\nMTg4+KrbTE1NceutT6Gq4HA4Ki0CwHmuL/F4nNnZWTo7OysEIZlMMj0dYXm5bGW7TjTKbWcz6HQ6\n2traKvu46KKLkGWFpqYygVmvXsRiCTKZEoVCCavVWnHOu//+nxEIhLnqqt+jtra2sh9BEFAUBVkW\nKJXKhNBgMJyXej4+Ps7hw3Fqa6Ps3bsbt9tdaZV6ZevVgw8+yoMPLuLzJdm3r46hoS3nkZp1vLL6\nIUkSpVKJrVu3UiqV2LZtG4lEgkOHfsHKisrJkyqKMks+L1JVJSBJ7ZjNaySTOqJRAaMxj6JICEKY\nTMaF0RihVLKi0YSB7nMajU2USmPIsgtJilIojKLViuRyM0ALgqAgCEkMBi16/RqFgsLMTCsm01kk\nqYTDYUKnWyESsVAoFDCZsuj1Wux2Hel0mhdekGhoUNiwIYeiaFGUHLGYAY3GQEdHnkJB5uxZE6q6\ngihacDpdVFcLTE5qmZkp0dQkIwg60mn1nLtUHTU1VvbutTA2FuPYsThGYwqHQ6S62kWhIDM+LuJ0\natmzR8/SksCpU0kUJYlGY6etrRqtVuDllzWIokxHh5ZCQcPKikwymSWRcNLT48FuFxkfV5DlBGZz\nCb1ei9NpZXm53LrZ02NiYMDIxESCpaVVII/ZbKK11Uo8Hufw4QJ1dTIHDpgIBGKMj6+QychIkpue\nnnKF9OjRAiZTlO7uGjQaM9FoktXVPLLsoL+/gCTpGB/PUyiEcDicmM12qqosnDkTIxy2MjRkwOHQ\n8eyzk2Qyz6PR2MjlNDz00EOcOjXN6dNG0umncbvdfOc7t5FO57nxxo/h8Xh46aWXaGhoeFNbMH/b\nW6deDa9nb7u6ukqxWKSmpua85TU1NUxOTr7qNsvLy6+6fiKRQJZl9Hr9a66zvLz8ho+7vLyMRqN5\n3f28m/Ae0XiXQFEU0uk0xWIRnU73lhGMdbyTeRS/KX7d832nKhhvlyXv5OQkY2NjTE7O8vOfZ+np\nybB1q5XJyTALCxIWSy3RaJ6NG514PFlefFGPzxejq8vG7GyAeFyPzVZDMKhl2zYjHk+Rkyclamqi\ntLTYmJ09i8vVittdg9+vo7dXZsOGNKOjRjIZmc5OK1NTZ4lGW6mursbvFzAaM7S3axkbq2N2Vqa9\nXc/4uJ+pqTa8Xgf5fJyFhRiNjR70+hamp6epr3fR1GQnEDCRSCzjducwGNpYXJzD5dLidCpks0US\nCTfF4io6XRFByFIouBFFB4KwRrGoRZIcCIKCKKoYDB4EQUuhkGVhIcvS0gxHjpxh48bDfOITVzM4\nOEh9fT333nsvhw5l+MlPhvH5fHR0dGCxWPD7YWUlxcrKCs3NzaRSKb71rTuQJIEvfOEP+PjHP8rQ\n0OnzBuD5fJ65uTkaGhpQFIWbb/4J0Sh89rO5c/dEuXXHYDBw7bUfoKfnNPv27cHr9fInf1IOp2tt\nbcXpdGKzWWhtbaVQKNDRUYVOF8br9XL69GmeeiqIxQK7dgUQRZGRkRH6+/tfU/QtCEIlvRzgySef\n5q67AkxNBV+TaDidTqqrdZRK6uuKFX/4w59y/HiE979/guuvvxYAl8vFJz95GeFwuJK7AeXn76Mf\nveqCfbjdbq6++qoKwcjlcqiqyvXXX82ePQt0d3dXnqloNMoTT4yytKSho+PUeUQDoKWlhRtv/FAl\nE2H996uqSiQSoa+vj0svDVBX56lsu04UVFVleHiYhx9+DrtdQ1VVgZ6eTj75yY9VDDx+2bZznZis\nu+Opqsri4iIej4dQKITP5+Pii3fhdDo5fvw4i4senn02jCxnUVUJh0OLVtuAyZRElhuAAqJopVgs\np67n8zLFYolicQlRVFDVUxgMBlQ1gKo2IIrSuZl5OxqNH1HUodFUkcuFWF3twW4/g8Oxhk4nUSwu\nEom4KRYFLJY4ZrP+HHlLMzrqpbY2Rm+vQiajI5uVSSYlSiUrbW1ZVDXL3JyRUimIVtuMxeKgqUnH\nxISG2dkijY0ydruGYlGLoqRYWqrC7S5w8cXl6sTwcBydriySbmjwUCqpjI1pMRpVhoY0JJMwPZ0h\nm02Qz9vp6KjBZNIyNlakWExTXa1Bq4V8HtJpmaUlO11ddjZuNHL6dIr5+TVEUcZm0+P1uojF1jh+\nXKWuDi6/3MTMTJxTp1ZQlCwGg5OOjrI267nnijgcabZvd5BM6pmbi5BIyJRKdnp7yyGTp0+XgAh1\ndTb0eitms56FhQgrK3Y2b7ZhtYqcOZMjm40gimacTjstLR5mZ5d45hmFri6Rnh4DCwtJlpaC5PMS\nJpOLri47kUiCO+9coro6wqZNjfj9c/zN33zjnM2zlWPHjpHL5Xj00SWamwW++tXPv+n9/O+m8UA8\nHv9tFE//P4f3iMa7BOve8VarFZ1O95Y/7Osfx3dbuRT++21f73SL1FtNNCYmJggEAhw6NMypUypD\nQwrt7XnC4TB6vRajsYlQKM+2bVXMzgYYHpZob8/j9UI8HqW21o3F0sLcnMqmTQ6MxiAnTzppaMhS\nV2cmGo3Q0ODB4Wji7FkNAwMSBsMap0/rqavL0dJiZ3FxhqoqK1VVDfj90NVVoqsrx6lTTqqrM3R1\nSYyNBQgEOvB6a1lcjOP3r1FX50CrbWNq6gytrUVqa+0Eg2as1jkaGnKEw+3Mz5+ltnaF6mqRWExL\noWBBqw1gsZjIZHQUClUoioxGE6ZUyiCKOiSpiCjqsNtN1NfX0trqo6+vD6vVysLCIi+/PM7CAhw7\nNkYi8QCf/azM5s2bufLKKwkE/p1kMs4LL7yA1Wqlr6+P664LVVyKEokEkUiETEZLsSiQz+dpaGhg\n37595/1fHnzwYX72s9Ns2lTFpz99HSaTSC6Xx2QyMTg4iMvlwuVyYTKZ2LRpE5s2baps+0ohtcVi\nwev1VlqvPvWp6yvvi1gsxvbtdiwWEw6Hg3//9//g8cdX2bVrlr/8y5sqbZivNxgZGOjhzJkltm/v\nfc11qqur+fKXbwR43fYNUdSh03FBj/cric0bwXpld91hxmAwYLfbLyASLpeL/fu7CQTC9Pf3V5an\nUinuv/9BjEYDV1zxexecz/DwMD/+8c9paXHw+c9/7lUFuYqi8NJL47z0ksrevUb+5m8+WZk9/eUM\novVnfGRkhNnZOWZnAwQCOQqFKNmsB41mkWLRi9FYdpGqq8tTLBrZvr2L3bvBYmnlqaemyOUKpFIG\nLJYUxaIZhyNFqeRBp8tRKpnRalVKJSOiaKZUAlF0kM3GEEUzmcw8Op0Go7GGbHYOjWYbhcI4omhD\nr49SX+8nnzeQzyuk0yY0Git2ewidTqJQsJDLhVldbcftzjI4KBOL6YjHFdJpDaWShZaWFIKQwe83\nUCwuotM1YrPZaWmRmJiAZ5/N4/VmaWzUIggiqpplcdGJw6Gya5eeQABefDGNqqaQJDs+XxWCoDI+\nrkWrzdLZKaAoKuFwgUwmRSJhZ8OGKlwuifFxmVwuca4iqcXhsJJIRBkfF2lrk7jsMgtjY3FeemkV\nVU1jNNpoa3OQTqc4cqRIdbXMvn1G/H4t4+OrZDJZtNoaenrMlEolRkYK6PVx2trsaLUGkkmZlZUs\n8biDTZu0GI06JiayKEoMg8GA0Wiivt7FwsISY2NF+vrKFZIzZxLMzy+jqjosFhsbNrgIhSIcOpTB\n65XZvVtPJCIwPR0ilSohik76+yUUReHIERm9PkR7ex0Gg5NCQWF5uUAm42TjxjLRfOyxKWQ5gMVS\ng8vleVOF5O+2sUAulyOTybwm0fB4ytcnFAqdtzwUCl3wHllHbW3tq65vs9kq+rLXWmd9n2/kuLW1\ntaiqSigUOq+qEQqFXtda/LcV7xGNdwnMZvPbGqD3TgTfvVl4o0TjnSYYv4w3+1pPTk4SiUS4666f\nEwhAe7tMVVWOYDBLc3Mdq6vNLC1l2bGjhpGR0wwPS3i9Ouz2cohVa2sjJ082MTmZZcsWOxMT05w6\n5cLtFjCby4O1rq4qUqkmRkdz9PeLwCIvv+zE64XqagPxeIje3mpSqWamplQGB/UYjXFOn7bS2Jii\nvV1kZmYJk6mdhgYvwWCcYjFNS4uFqalW5uen6ezUks87mZsz0dAQpqlphdnZFhKJaRobNUiSi1BI\ng9GYx2ZbRparSCSs5PMGJCmJKM6g01mQJAfZrBmdzkU+X6JUShON6onFdPj9M4yO+tm/fyfXXXcV\nn/60lSNHjnDPPb9gZuYsN9+c4Lrrolx22WX81V99nr/9229yxx1z5PNP8olPXMcll1zC//2/P+TO\nO49w5ZVbed/7Lq/YLTY1le1bk8kkt956B6qq8pnPXIcsK8gyZLMyZrOZL3zhD0mlUpX8hjfqu//L\nwuX1D17Z6tXCjTf+YUX70dRUS2PjEj5fDZFIhFtvvYNwOMEf/MFVdHR0VPIiXoktW7awefPmSivS\n7bf/B9PTAT7xiQ+f19L0SoIxOjrKT37yEBs3dnD11R+uvE9uuOFa9u9foLW19TV/j6qqTE1NYbVa\nK1a6AGfOnOHhh39Of39HJX3bbDYzPz/P1NQU27Ztu2BQIQgCV199Ybr32NgYDz00g9EIg4P95/0O\nKFdCVlbAYklU2lRfiYceeoQnn3yRwcFGrrmmgW3bNlFfX1/5+3rFo1gsUigUuP32/2BiYoFwOMbK\nih2TaYFSqRmLJYtOV0IURYpFlXy+RD5fYnR0kVyumYmJ+1DVdmpqJtDpjAwOdlMqzWCztTI5aUQQ\nJojHRQQhQaFQjSjGKRZr0WpXUdV6IIRG044g+CmV+hHFGWTZiijGgUn0eg3F4iy5nJ502oMohjEY\n7Hg8y6hqimy2jnR6AUWpwmo1MzCQYnVVYHlZRZYLCIIJn6+AIKQJBIwUCkEkqRaTqUwwpqZUnn46\nT2OjjM8nI4oGSqUcgYAdi0XHli1aotESo6MyxWIcsOHzeTCZNExMaCkUFOrry+ngqVQJWc4QDNro\n6LAzOGhkbCzJwkIMvT6DzWakvt5FKhVnZATq61Xe9z4LU1NrnDgRRlEyiGIV7e0mCoUCx44VsFpT\nbNpkIpORWFxMEI3mUBQ3GzcaEEUdp08rlEpruN1G9Ho9DoeZxcUkgYCWwUE7Q0MGxsdTZLNJBEHA\nZjPT1uYmGFzh6adztLSoXHKJiYWFGGNjQXK5IgaDnQ0bjGSzWZ56KofdvsbAgIli0Ug4HCMazZPP\nuxgYKN+/p0/nKZWW8Xg8WCwuXC4zExNrrK6a2LLFiM0mMTWVIJ0OodU68Pma+cxnPoLX631LiMa7\npaIRi8UwmUwYDIZX/bsoimzevJknn3yy4sCnqipPPvkkN91006tus3PnTh555JHzlj3++OPs3Lnz\nvHV+eR9PPPFEZZ3XO+6f/umfAuVKa21tLU8++SQDAwNAWQw+PDzMjTfe+OtcjncU7+VovIvwdhKN\ntyOP4q3CutvM6zncvJk5GL8p1q+1Xq//ja+1qqrMzMwwMzPD97//AMeOTWMwZMjlUhiNWhob7YyP\nWygUkuzaVcf8/DQrKyJmM2QyJRyOEj6fnTNnjGQyGTZudLC8PM3amgGTCeJxHQZDio4ON3NzBtbW\nFLq7jYRCU6yu6nE6dciyGUjS3u5mddVCOFygq0tEloPMz5twu0Gr1RAKBfB4HIiii1Aog8ejYrWW\nmJurpVgM096uZW1NRzRqor5eplSK4PfXodPFqK0tkM0aWV0V0evjOBwK6bSHRCKDVqvgcGiAJKpa\nTS5nJJ8HjUbCbBbweAoMDNSyaVMbnZ1uLJYihYKWUGiN6WmZZ589hMdj5cCBA2zZ0sv8/Bx+vwGN\nZoW2thYcDgfhcJBMZpW+vmacTieqqnLo0HMsLGhoaTGxcWO51UqSJEZHR7Hb7SwsLPCf//kSwWCW\nnp5qdu7cQUeHnQMH9mI0GjEYDNhstjfV0OGVfvOSJNHV1cW+fVsZHOwnmUxy333P4fdraGqSqK+v\nJxqNVhzuisXieYMLjUZDMpnkxz9+jIkJleZm3QXe8Ot4+ulnePTRCLK8yiWXXFQhL5IkUVVVVakg\nZLNZcrnceW5TJ06c4NvffoAXXzzJtm39Fd3EPffcz333hUgk/Lz//fsxGAxoNBr+9/++hUceWcJs\njldS2FVV5fDhw4yPj+P1ei+oWBgMBsLhaZqaHOzdu6vy91KphN/vp6WlBZ9Pz/79O181KPHeex9l\nZCRPc7OBz33uMxf0Uq9Pdvzbv93OPfc8xvh4gMVFI15vnro6M1deuY8dO5q46qor2Lq1jSuueD8b\nNzZx6aUX09XlZtOmbhoawGIxUirJJJNpIhEHweAMhUITorhGqRSlvt5JsejC6dSSy7kxGpOUShKi\nGKdQUBGEFPl8FkHIoKppNJosIFEqKZRK7ahqCkFoQacLnktDV8nnl0kkWpDlBKJowWAoUVdXIJcr\nEA7byeejCIKLhoYSNluOpSULa2tRJEmPyaSjtdVMNJpidNSIwxHH49EjSaDRlEM283ktPT1aJEkm\nEBBJpULk8w4aG0V8PgOzs0WCwTwORw6LBXQ6PYqSYWbGhstVYPt2D0tLcRYWFEqlsmtVa6sDvb7I\nyIgOVU2xebOLfD7N0lKBVCpJoeCgu9uCy6VhdLQ8CK2r02I2Q6GgIxqNs7Rko6NDS0eHmenpHMFg\nDL2+gMUi4fO5SSbTnDghUV+fZ9MmF0tLcQKBFIqSx2g009vrRqvNc+QICEKUwUEPxWKWcDhLPC5T\nLDrp7TXjdAqcOFFkbS1Eba0eu11ErzeytBQjGHTQ36+jqcnA9HSOpaUVRFHAbjfQ0VHN8nKMEydE\nmpvz9Pe7WF5OsrgYRZYFHA4Xn/rUpXzwg5e+6j3/m2LdsOKd+k7+d+H3+7n//vv5whe+8Jrna7PZ\n+Ou//msaGxvR6/V85Stf4eTJk/zgBz/AbDbzpS99iR/96Ed8+MPlyYr29nb+4R/+gXg8js/n4847\n7+Sb3/wmN998c2XypKGhga985SuYzWZcLhc333wzd911F7fcckvlXfJax73lllsqEzbFYpF//Md/\npKenB0VRuOmmm5BlmW9961u/bWOyX5mj8R7ReJdgvS/47UQul3vXEg2AX7a3fSXBWBd+vpME45X4\nTa/1eq/31NQU3/nOfYyMnEIQCiSTCVpbqzCZtLz4ogGTKc3AgIOFhQWSSRBFPYlEgdZWK263wMiI\nHlVN0N3tYHFxmmLRiE4nEokI+Hw66upEXn5ZJJ/P0NpqZmFhAlnWY7HoicdNuN0FmprMzMwYSCRy\ndHWZCIWmWVuz4vHoyGYhmQzR2Ggnl6tmdTVLR4ceRUly9qwbhyNNfX2B5WUVRTFSXy8QDs8Ti9VR\nU1NEq00SjQoUiwbq6yGdXiUSaSSfD+HxKFgsDlZXk6TTNUhSAYslgc/nwGzWUCio5HJ2YjEFvz9F\nJiNQX2/mE5/4fa64Yh9VVWaCwTOEQjWcOTNMsagwNLSRzs4WisUFTp1a4dSpcTZv7mFwsB+Px8i9\n9z7D6Ohpdu/eTk9PO62tRi6+eE8lfPG73/0hd989RqEQYu/e3ZRKUTo63OzatROj0Uh9ff3rBjWm\nUqmKLS6U2+CSySROp7NimWs0Gv9b9836fWaxWPB49GzYYOPiiy8mGAzy7W/fwejoKENDfQhCue2r\nLJiWyefz6HQ6jMYSDQ0Ce/fuwWw2v+qz43Q6sFhi7N27hcbGxlc9j3g8zte//j0OHTrGhg2+SttR\nMBhkZOQser2GXbs2odFoyGaziKIWVQ1z4MBW2tvbK8edmZkmm42zY0dvpXrk9/v5znce5IUXgrS0\nmM8LwkqlUphMJvbs2cHWrUPnDcgee+wx/vVfHyMUmueaaz5yQYXk2Wef5e67H2ZgoIPeXiv79u25\nQGy6Pjv59NOHOX58jsVFie3bnezY0cQNN3ycK664jA0bNtDW1obT6aSqqgqTyYTL5cJms9HQ0IDP\n56O/v5dt2zazc2c/fX1tNDeLSJKOQiFLJpNHlstZMsWihE5XbjmyWgVKJTNmM4hiEwZDHlHsQBRT\n6HQtCEIcQXAiijEggSSpKIofrbYZRYmTzdah02nQ65NYLFpAIZuVWVysRa9fxWSy4HarGAwpgkE7\niUQWg6GEyaSlrs5IKpVhdNSCwxGnqkqPTldCoymwvGwim5Xo7ASzOU8wKJFIhMhmHdTV6WhvN7Ow\noOD3FzCb01gsAjabCY1GZmzMgsmUZdeuaiKRBAsLeXK5OJJkpb3dgtWq4cUXNWQyCbq7zeh0Mmtr\nKrFYnETCQU+Pgfp6iYmJPOFwHJutiNWqxeWyE4slmZoy09oqMDBgZ3Y2RjCYplRSMJuNdHa6KRZl\nhoe1GI0Jtm6tJplMsrSUIZ2W0Wod9PRYsVrh+HGVdDpMU5MRs1kgnS6xspIkFnPR3/9f5xAKrWCx\nCNjtEg0NHpaX1xgfN9LZCX19NhYWkgQCaxQKKlarmd7eKnK5DEeOgN2eYGDATTqdYXk5SSJRQpJc\nfPjDQ3zwg/sZGBiomCy82VgnGu+WEN+pqSmefvpp/uRP/uQ1v++9vWVHuL//+7/nG9/4BhqNhjvu\nuKMygXL77bezsLDADTfcAJSNLnbv3s13v/td/u7v/o6xsTG++c1vVogIQGNjIz09PXzta1/jn/7p\nnwiHw9x6663nVT1+1XEBdu3aRTab5W//9m+5+eabgjYYUAAAIABJREFUqa+v54477njViY93GL+S\naLyXo/EuwbrP/NuFtyKP4u1CKpWiVCpVBmfrBEOW5Yqv/m+TTe1vcq3XMxTOnDnDbbc9iSgmkWUT\nqVSUvXu7OXVqhulpOzt3lshkSvj9S9TVeYjHRTIZme3ba/D7Q0xMmOnuzpLPawmF/DQ3N7O6WiAe\n17B5s4lEIsnLL4t4vUk0Gj2Li7O0tLSSSChEoybWoyBGRlTq6nJ4PDbGxsaoqWlDp8udC9tL4PE4\nOXVKi9GYpq/PzqlTM2QyTXR3pwmHM0QiBerqrEiSxNjYBHV1XVRXy8zOZshk0ni95ayRyclZjMZO\nGhpCFIsagkEbsdg8DQ21OBw50ukSq6smEokwkmSjpkaivd2K1+tldTXNqVMTxOM6cjmR6uocH/rQ\nJXzsY1eztLTEnXfeydGjUdxuO3/0R5ewY8cOTp48yfe+9zBGY4lPf/oKmpqaGBkZ4dZbj+F0wl/9\n1WepqalhbW2Nu+66H4fDykc+8iFuueXHPP/8Eu9/f/ertvBA+X5VFAWXy8Xc3Bz33vsoXV3NXHbZ\npXzta99hZibFtdfuoLq6mptvfgBJUvnSlz7D0aPDPProGBdd5OOGG67nySefZHU1yvved9mvlX9z\n+PBhvve9w7hcKn/9139EVVVVpbLxSuvdV1q0RiIRfvzje7DbzXz609djMpkq2R+vRCaTYWVlhcbG\nxspz5/f7+Yd/+BHZLPzpn15e0Z2oqsrk5CSSJFWsZPV6/WsGkBaLRZLJZCVoDyCdTvPtb99CKpXj\nf/yP6ytEY3Jyku9//26qqix8/vN/dEFbxV133c3dd0/S22vgK1/5swuO9+Uv/xMvvVTi93/fy6c+\n9YkLziWZTOL3+/n2t+9jZUVl714rtbV1XHrpwfPct34Z8XgcjUZT8ef3+wOASjKZRasVEAQNBoOE\n0WioVJZisRiLi6uEwxlkWSGTMVAoJMhmtYhiGlkuoteXUJQCer2EosgYjU4UJYVG40GrzSEIVkQx\nS6GQwWzWotWWAw4VxYcsz6IoXdTUzKLV2hDF4rnMnxo0GhmbLY9er0UUJdLpJH5/LT5fEKPRSamU\nolQSiEYNgEhbW55iUWVlRSKfL7eF1dYmaW6uZmwsTDKpx2KJIYpl8qsoacbG7Hg8Ufr6vCwsBMhk\nyjoRjaaOzs6yScnLL4NOt0ZVlQmNRkGjsbC2tsLqai2DgzJOp42xsRiynEWSNBgMOnw+D6HQCmNj\nNjo6YrS1eZmaWiST0ZDLZTGbnXR1WchkMhw/LuJ2L9Pc3EgisYKi6InFEpRK1fT3l6t8o6NFIIzd\nbsdgKGC3u5md9RMO17B5cw6n08H4eJRsNoVOZ8Bs1tLWVoXfH+L0aSudnVGamxuZn18inS6iKBoM\nBgtdXWZSqTQjIyIOxyL19V5UNXkuYDFDoeDissvq6OvrY9OmTW/590yWZQqFwltqoftm4uGHH+Zb\n3/oWzz333Dt9Kr/reC9H4z38evhd0Gj8MsF4pzUYvwr/nWu9bnX89NNPc++9w1gsaZJJM1ptjj17\n2jlyJMHjj68yOGhBlqPMzORoaqpCo2kkHE6xZ4+P558f5fBhE52dAjU1aVZXY7S3+4hEWpmby7Nz\np4czZ2Y5flygpaWIx1O25tuwoZVYrAW/X8f27TbC4VVOnDDi82Xx+YwEAgEcDhNVVT5CoRJ9fRIO\nh8rIiIdMJs6WLTWMjMwwMWHB56thdnaZ6WkVn8+GIBiZnh6js7OFrq5WZmdTpFJRmpo8RKNOJidP\n09HRRV+fj/n5AFNTDuz2KN3dEIk0MDcXIxy24HYn2LjRTKnUydjYWcJhN8vLQVyuMAcObOMf//Ev\nGR0d5dFHjzE/L3P//aOEw0Guu+5a/viP/xiT6U6Gh49z662HyGaz7Nmzh899TuXeex/mu9+9j49/\n/BJ2796NRqPBYrFU7rnTp09z6NASDgfs3Bnkhhuu5eDBwHmBdrlcjrm5OZqamlAUha9//fukUgo3\n3vj7vPzyyzz55Brz8xH27NlNOi2TTpe3KWs+VESx3BK1tpYgFoNoNEk4HOaee54nHIbqag8bNmzg\nxz++h/p6D9ddd80bqnhs27aNfD5fmWU/cuQIjz9+lPe9b9d5blDrFq3FYpGTJ08yOprFZEpz4MB8\n5Xeuaz3WSce3v/0DpqeTXHvtTg4cOACA1+vlM5+5lGw2W+lDXneSqq+vR1VVJElCr9e/7jOr1Wov\nIFZms5k///MbK60e61heXiYYBEVJkkqlKkRDVVWSySTvf//leL31tLS0nEcywuEwgUCAgwe34nSO\ns337lgvOIx6P87WvfZ94PEtdnURNjY6PfOQjrxmwJssyzz33HMlkkqefPk06HSaVcqIoIfJ5NxCh\nVHKh0URRVSeCEAPs6HQJRNGKTpdFkgwYDCqSpMFqTVEoqOTzMtmsisUioSh5TCYLspzB4XAiyyms\nVj2yHMRs1iPLKUSxhFbbRDa7QCbTg8UygV6vPWdtGyCVMpPL5ZBlC6Jowm6PoNeLKIqJVCpCKNRE\nY2OS/n6FbFYil8uSSEioqomWlhyCkGd5WURR/MhyCx6Pg6EhE2NjcYaHE5hMaRwOkZoaD4VClpdf\n1uJwqGzfXrbxLesPMuTzDnp6qpEkLWNjeVQ1jtstIYoiFouZSCTL7KyW/n4rg4MmxsYSLCyEgCIm\nk4HOThfRaIxf/EKmoSHHgQN1BAJrjI8vk04rCIKLnp5yhW54WMZgiNDR4UIQzGQyMqurMvG4g61b\nJQwGifHx9DnxtxGTyYzP52F2NsDp08o58beJqakkCwsBSiUBk8lGV5eDaDTOE09kqK1NsWdPNbGY\njunpEIlEOVujv1+kWCxy/HgOnS50TrPiQJIE5uZyxGJV7NvnpLe3l927d79uRfTNxLvNgfL1rG3f\nw9uL91qn3kV45Uzi24FcLodWq31D3vu/Tcjn8+e50hiNxjc90PDNxH+1hohvuK/2vvse4Ac/uJel\npVmmp7Xo9Rm2b29kbi7G4mKeqioBWV4DwOdzcuaMlVKpTDAWFuZZXNTgdArIsoIk5Wlp8XD2rIlM\nJsf27VWEwzMsLYnY7ZzzuF+jqcnJ8rKVSERh61Y3mUyA+XkJm61IsSiQSoVpbq4inbYRCpXo6TGj\n1cY5fdqE1ZqnpkYgEAigqkYcjnKgnqJkaWtzsrLiIBJZoK3NgapaWFrSYLdnqa3VEgrVEA7P0txs\nxWp1MTu7iqKodHa60GrzRKMKq6siNluB3t5aFEUmEoGFhbIY8JJLNtLT4yaXy7O8HGVmJs9LLx1h\n9+5tfPazH0cQckxNnWRqyk4uN8PQ0CD79u3m5ZenCARUzOYkXq+XmpoafvGLEQIBLZ2dVnp7y606\n//mfD3LPPc9htwt0dXURj8+zYUMNO3ZsQ6/X43K5CIfD5HI5zGYzd9xxJz/60VESiUWamhp54okR\nkkkNAwMNtLe3I8uL7NjRQ29vD93drfT0VLFjxw5qa2vp62tm794t1NbW0traREuLkQMH9uJyuQgG\nZzEaZQ4e3MvExAT33z/H2toa27d3MzU1xQMPPILFYnrNAD6dTkdLS0tFgP3Tnz7A4cMZJCnGzp3/\n5Qq1rtfQarW43W602jUGBpq46KKdFZ3RunC8UCggyzKHDj1LMFiktdVCS0tLpQ3U6/XS3NyMIAgU\nCgUymQz5fB5RFCvP7NmzZ3nssccxGAyVCoeqqjzwwIM88shTNDbWVqqXUG6ZWFtbq7i7vBI1NTW4\n3UV27Ro8TwD+6KOP8a//eh/FYorLLru0kkIOUCgU+MY3/pVHHpmku7uKG2647oL2hampKaampnjp\npVlSKS3XX38p11139XnntY5oNMpPf/qfPPXUUzz66BwnTpwgkRDRaFTMZqiutuPzmWlrq6G11U5b\nWw01NQbq622YzWVdgSAYKRaT5HJ2EokVYjEPyWSURKIWRVkjn6+nUFhFVWvJ54MIQgP5fABVbUNR\nAihKH4VCkEKhD1hFkjxYLDJWaxqz2YCiRM/t24hGU8BkclJbm8ViUUil3CQSS0SjNVgsWdrby/a2\niUSReLyILDtoacnjdpcIhSSi0SC5nAObTWBgwMHqaoqpKdBq1zCbTTQ0mDCZVE6fFslmZTZs0KPT\nKcTjWmKxKLGYgw0b9DQ3G5ieVlheTmIwyJjNIvX1LnK5LCdPSlRXK2zZ4mZ5Oc7iYhpFUZAkCz09\nToxGlSNHVAqFKL29DgRBJhYrsLaWIZNx0NdnpqpKy+honkhkFZdLxGbTUlXlJBhcY3raTHe3jt5e\nG9PTcZaW1s6ZLRjo6akmm81x9Cg4nRk2bfIQjydZWkqSyRQQRTt9fQ7MZpXh4RKZTIjmZhNWq5Z0\nukg4nCYed1baq8bHZYLBZaxWLU6ngcbGahYXI0xMGOntFTl4cANXXHEF/f39b+u3uVAooKrqu2Y8\ncPjwYeLxOFdddaFF9nt4U/GeRuN3CW830VAUBUEQ3nQf7rcKpVKJTCaDLMsAv/UE45XI5XLodLrX\nfYmrqspPf3oX9977GBMTM0xM6KivV+nutjAzkyQSSWOzSSSTUbxeN1arnhMnDJjNGbZscTM7GyAa\nLWAwiKTTCk1NFqqr9YyMGCiVypWG+fkzpFISkqQlFgOnU6GuzsCZM2by+TxDQ24WFydIJo3YbCKJ\nhIAkpWhtdRIImInFFIaG7MRiCywsmKipEVDVPOFwWfit1bpYXU3R0KDHYtEyM+NGo4nQ3W1mZUVH\nOCzQ0aEDopw9W4Ven6CzUyQWMxAKlaitLVJVpWdlxcTi4hw+X905keQcoVA1icQCQ0PtDAw0Eout\nsLQE09MBDAaBT3ziCjZs8LK4OE4w6OHUqcMoSo5PfvJjOBwWAoExZmdXOHNmhq1b++no8KEofkZG\nlpmenmL//l10dvrw+UQEoZzo63A4eOihX+D3q3R2WhkaGmL79s309/dWdDdnz57lG9/4McPDL7Fx\n4wbGx88wM5OgsdHM/v178XodDAw0sHnzZlwuFzt3bqGjox0Aq9VKQ0NDhYDa7fbKINhgMODz+TCb\nzQiCwObNG7n44p3Y7XZsNhuqGmJoqI2NGwe55Zb/4LHHYkhShK1bN7G0tEQ4HMbpdL6OUNKI2Rxn\n//6LqK6u5uzZs8zNzVFdXX2euLuvr5cNGzoRBIHp6Wl+9rNH0OtFfD4fkiRhMBjYsKGZri4X27Zt\nq2g/8vk8sixXNCDT09Pceut/EItFGRzsrxzjttvu5N57lykWg+zcWa4kJJNJfvCDn3HypIzXSyUD\nY3p6mv/zf+7k2LFRursbK+1KxWKx0o7V19d3npsVwKFDzzAyksFqVdi1a9sFz92xYy8Qj+cZGGi8\nwKFqcXGRb37zDk6e9PO+9/Wzb18/mzdvvqAKs7q6yl133cOzzz7DU0+tsbq6gs0Gra11XHnldg4c\n2M5HP/r/cfDgXi69dB+7du1g585t7NixlT17drB37y727t3G5ZcfYGCghcsv34/Xa2Dv3q04nXkG\nBloRhBQ+nwuNpoDLZUCrlbDZtGg0Ena7FlUt4nTqEIQYtbUWdLowJpPxXB6FRDptJZuV0WhqMRii\n2O0iFosGjSZOMFhHKhVEq/Vgt8OGDRLpdJ5oVCSdTlMquWhqKuJyFQgERMLhJfJ5GyaTQG+vlWg0\nzdSUFkFYxWy24PUaMZlKTExIJJMyra1aTKYC6bSWRCLO8rKN1laJri4zs7NplpYyCIKMySTS2uqh\nVMpx/LgOozHJtm01xONxlpezpFIyGo2dnh4bdjuMjBRJJFbxeiUsFlBVkXA4xfKyjYEBPc3NRqam\ncgSDq4hiCYfDQHt7NdFoipERHT5fgY0bnSwtxVlcjKEoJQwGC319bnS6IocPl4AVentdgEwkkmVt\nTUFRHPT3W3C7tZw8mScSCeF263C5RBwOO35/hIUFG729Ojo7LZw9myIQWEUQNNhsRrq7a4jHkwwP\na6itldm9u4kPfegD7Nmz+y3TYbwe1i2z3y1E4/HHH0en0/GBD3zgnT6V33W8RzR+V7AeAPV24le5\nN/22YJ1glD92ZavIdY3GbzvBWIcsy69ZPcrn89x55908/fRzDA9PMzFRorfXSG2twtRUGllOI0kW\nkskoW7d2EI+X3VFaWwXq68HvX0GW82g0NlIpmY0b64HyR9puV/B6RZaXF9FoRFTVRCRSorXVgMWi\ncPKkAUnK0t5uJxCYQRBMgI5IRMTrFairkzh9Wo8sZxkYcOH3T5JImHE6RVKpEoqyRmurm7U1F2tr\naQYHnSSTUSYnHTQ0FGloKLCwUEBRdHR0WAkEzhCJuGhpMSGKCUKhPKWSge5uG6HQPH5/DU5nko4O\nC/m8k4mJKXQ6Kzt2tGEyxQmFbExMTGAy2fjgB3djtyusrGiYmjqL359kaKiVK654P7ncNH6/loWF\nKIXCCpdddiler4fR0QjJ5CparUJnZyelUomTJ1cwGFQuvngbtbW1zM3NcdttLzI1Nc6ePVvo6mqh\ns9PGrl27kCQJVVX54Q9v5447Hsdu1yEIAkePnkFVVXbu7GfLliE2bHBx8cW70ev11NTUnKdd+E2w\nfr+bTCaGhgbp7Ow4V12QKRRC7N+/HZ1Ox9e+divPPHOalhY31dXVr7qvmpoatmwZorq6mtXVVb7+\n9ds4fHiahgbjeeLqV+Kuu+7nnnuWyWb9XHzxzkr1w+Fw0NTUhMlkQpIkJiYmiEajuN3uSsvgsWPH\neOihZdbWltm8uQsoE4RsNkUiscju3RtpbS2HDJZTtVO4XEX2799TqRwkk0mOHTuFIMDu3UPY7XYA\nfvGLX/C97x1icvJldu3aekGlw+utpb6+xIEDeyrbqKrKM888w5Ejx/jABw5y0UXd5/XCr9vwLi8v\nMzk5h0aj8sEPHqC/v/+8/2U56O05jh07xs9+tkQyGaOjw8SWLRu48cZPnSOwndTV1WEwGCrvgHw+\nTyAQIBqN8txzz3H27FkefPDnjI6e4NFHjzM+foKXXlpifn4Sv18hFlsmndajqilkWUQUZXI5LaKo\nIMsi+XwKRbGQy6UpFBpIJhOk0w3k83G0Wi+iGMVmM+LxlNDrkxSLHlKpIOFwA8ViAqdTj9utx+2G\nRCLP4qKRYnENvd5FS4uI01kkGDSztraKIJix2SR6euwkEinGx0UghNFoorZWwmQqMTmpZW1Nwest\nYbGUkGUt6XSShQUbjY0CGzc68PsTLC5mKBazGAxGurs96HQFjh7VAGsMDHgoFtNEIjKxWJZcrlyd\nqK7WMTqaZ3V1BYdDi/X/Z+89g+M6zyz/X+cc0Y1GIwNEzjkRIEWKpGwlZ+84jvO/dmYdqrbWU1s1\nVVu169nacvaMZ23PSA6SLFmmLFvBShQpkiKYwAASRE4NNNABnXPu/n8A2WNa1szUlC1LWp0vKJLo\n2/c273v7Oe/znHM0QiwWEw6Hn5WVW90JDWtrYba3/QAoFFJaW01kMmkmJ0Gni9LbayIcjuB2x4hG\nswiFOjo7dTfF3zkiERdVVQq0WhGFggiXK4rXq6erS05VlZyFhQQOhxuFQoReL6OuzoLbHeLaNQn1\n9Xl6eoxsbYXY2gqQThdQqdR0dpqBLKdP5xCL/fT0WLj//kO85z33Fjt6fw5kMhmEQuEf3c3qT4Vn\nnnkGk8nEgQMH/tyn8nbHO0Tj7YQ32nXq9dyb3iz4fYJxq4MhEAjIZDJF+8u3AlKp1Gu6R/F4nKef\nfoapqUscP77GykqMnh4dAsEOm5tp5PIc8biGbDbE6GgTDkeEGzeytLUpEImCuFxBVCoxkYieVCrJ\n3r117Oy4mJ0VUlFRQChMEA57MZm0hMM6/P4MnZ16UqkdFhelGI151GohoZCb0tISUikVTmeBpiYZ\nKlWCa9dECARRrFYpDocNsViJTKbE6y1gsRQoL1ewvKwlmYwyOFjC9vYmW1tqmppUZLMeXK44CoUU\nnU7D2toiYrGW6uoSfL4oLpebmhoLGo2W5eV5cjkjXV3lpNNONjakpNNJBgcrKBTAbk/icLhpba1l\nYKCcQCCJzRZmdXWDkZFuDh7sIhCIs7i4yNJSCLNZwkc/+hHy+QCLizPMz4vQamOMjIxgNMLMzBLX\nrsUpLxdxxx13UF2tIhTycOrUFDU15QgEApaWlikr0zAxMUJJSQlyuZzHHnsSh2OLpqZGnnzyRZaX\nobpazIEDB6ip0TM21kV9fT1SqRSr1fqvrqtUKkU4HC7OXwcCu2Nw/9HdxNraWu64Y4zy8nKi0Siv\nvnqFbFbAwEATCoWC48ePE4/HXzeoKpvNcvHiVfL5HKOjna9LTgqFLJHIJvv3975u8vj8/Dzf/e6v\nuXRpgeZmK1arFaVSebOIcjEy0lZM987n81RUlDMxMVhMUM9ms+RyORobGxge7r9tQ0Gv19PZWc/4\neO9t2oi1tTWuX99GqxWyb99wkWhcvnyZX//6OazWUsbGxookA3Z967///Sc4dy5EXZ2E4eHh2wjE\nbvfkKDMz63z840e4++59RderW0gmk5w+fZoHH7yI17tNQ4Oavr4GvvjFL9Db241cLr+tcMtkMiwt\nLfHSSy9z4sRJfvWryxw//gKTk0muXj3F4qKGzc2ruN2leL1LBAJmgsF1wmEToZDt5s8N4nEL0eg2\n6XQZiYSLfN6MSBRGpSpDq02j06mwWAQYjQLMZiUyWRCRyEws5sLrLSca9VMoaFGpBFRU7D4H0mnw\n+SJsbBhRq/1otWrKy+UoFAk2N5X4fAGkUhFarZymJi2xWJzZWTkikRe9XovVqkCvF7C2Jsbvz2G1\nZlCr82QyImKxMGtrWkpKMgwMGHC5QmxuJkin40ilalpbDSiVec6fh2TSS329EpksTyJRwOeL4/Pp\n6OyUU1UlY2kphdPpQS4XolZLaGgow+eLcPWqiNraPF1du90JpzNEKgVyuYrOThMiUZozZwoIBD5a\nWvQIhWmCwRR+f5pEQkdXlxqzWcz16ym8Xhd6vQSdTkJZmRG73cfqqor2dhEtLbcIjI9CQYBGo6Cr\ny0o0GuPs2QJGY5y+PjPBYBSHI0wslkMs1tPVZUClgvPns8RiLmpqlBw+PMrnPveJ19X5vJF4qxGN\no0eP0tDQcJvb0zv4k+AdovF2whvd0chkMhQKhTcd0Xg9gnFrRGrXNSX9liUaoVCIEydOcPXqVZ58\ncpntbT9tbVr8/jVCIdBqpTidChSKBEND1aytRdjcTFJRISaZ9JBMZqms1LGyokYgiDExUcvGhp2N\njQIlJZDJpBAI0tTXm1lfVxGNJhgYKMHpXMVul2I2C8nlhBQKERobrbhcSjyeNP39RpJJBzabDJ0u\nh1gsIBRyU15eQjKpwunM0dAgRa1OMT0tRyyO09KiYWNjnXhcicmkIBwOEAqFqK8vJRrVsrNjp7Gx\nHKFQzvY2qFRRGhqMeL1GHI51mprK0Gi0bG2F8Xh26OlpQCYrYLPZCQQ09PSYKS2V4HLJmZu7hkpl\n5IMfvINIZBunU8XMzHnkcgVf+MJfEAz6cDpTzM5eJhgM89nPfhyfz8fOjoPl5UXi8RiHD9/J2pqN\nTCaJ0bhLCEpLS3niiTMsLuaoqREzMTHB0FA7paUGFhcXKSsr4+LFi/zyl6t4PDuMjnbQ1FRDXZ2U\niYlxVCoVFovlNm1EoVDg+vXrOJ1OysrKmJmZ4Yc/fIREIkxNTTXf+c6PeOaZSaxWLcFgkG996yGu\nXp1mcLCbCxcu8JOfPIFaLaG8vBybzYbT6cRkMv277ne1Wk17ex0DA020trbyyiuv8OCD11hfX2Ri\nov8PdjBlMhn9/e2MjHSwZ88evF4vv/jFE7jdTvbs2VN834qKCg4e3FskGTabjeXl5eK4VSqVwu/3\nMz09i0Ih5siRcfR6PQKBAI1Gw8BAHw0NDcUxwlticKlUili82x2KRCL4/X4kEslt1ruhUIhsNovB\nYCh2OG6dV3V1NU1NJRw8OH6bbuLBBx/n5ZfDyOV+Bgf7brtmqVSKx2NHKo1z550Tt7lGhUIhQqEQ\nV67MIxTCkSN7X1MMXr16le985yGczk1EIiG1tWa++tX/Ql9fz22EJZvN4vF4OHHiJA888CRnzkzy\n6qtpvN55Uikjen0Kg0FBf38d9fVK7rxzhPZ2LXfdtZ+ODj3vfvdBWlu1vOtdB2lr0zExMURdnZTO\nzibM5ix79lRiMuUwmUoRCsMIBGpiMR+xmB6/38POjo5oNEYuJ0eplGIwZKiuNqLTFcjlMvh8Rvx+\nB+FwORUVSSwWMQqFlGw2jN2uIhhMoVKl0WqlVFSoicdjXL0qRyr1UFKixmyWoVaDzSbE4ylQXp7F\naBQhEMjI5eKsrRnQ6TKMjZnw+cJsbaWIRiMIhRoaG1Wo1XmuXi0QCnkoK9vN/FEq1TfJiIaODglN\nTSpWV6M4HD5AgEolo7OzjFgsztmzBUpK4nR2GgmFIuzsRIlGCwgEWjo6NGi1Ai5cyBCNurBYpOj1\nEqRSGQ5HFLdbS0+PnOpqGYuLcZxONzKZGK1WSktLGTs7Ya5cEVFXl6er61a2RoBUChQKDV1dJoTC\nDKdPZwEPra0GhML0zfGqFKmUnu5uNSaTiGvXUng8ToxGCb29jfzN3/wX2tr+faGdbwRujVK/VYjG\nI488wsDAAD23LBHfwZ8K7xCNtxP+HEQjn8+/brLmG40/RDDUajUSieS2AusW0fi33GreTEin0wSD\nQaanp5mamuKRR+bx+baprFTg8awjl2sRCMRsbiqorhbS1KRmeTmOzxfGYJATiexQVmZCo5EzM6NA\np0sxNGRmddWB15tGoRATjyeprFRjsSi5fFlGNhuit9fI2toioZAElUpKIiGitFRITY2e+Xkp0WiM\n3l4jTucSHo8EnU5ELCZCLI7S0mLF5VLj8+VukhA3a2sK9PocEkkat3v7JtlT4vPFKC0VYzIpWVnR\nk8nsMDBQjsuVY2tLQHu7EoUiytyclkIhyOBkzx/bAAAgAElEQVRgKS5XCrtdSEODBLNZytaWjq2t\nBfr6WigpMbC6usj2NtTXmxgYKMfnE7C25sBu3+C97z1CScluINiubeQOH/zg/UilYVZWJHg8TqTS\nNIcPHySbDXLpkoB0OsTBg8Ps3TtEPL7D889vsLp6g0OH9iGXZygrE9DQUI9Wq0UoFPLd7z7C6dPb\nlJTk6OzsJBbbpKurlr6+HkwmUzFpG7g5PnWOxx9/Bo1GTjQa5e///tdMTa3Q0GDm6tVrPP+8n2TS\nzehoL889dwa3W0BLi4FMJsOrr25QKGQYHe3i179+icnJJEplmOrqCr7xjZ8xOblAba0BhULBK6+8\nQjKZfN2uA+xqPUpKSopGBDbbIvX1ZkZHh1heXmZychK9Xn+bKFoul6PRaIDdPIlHH13E4XAyPNz2\nB2fGI5EI3/zmjzlxYhW9PovZbCab3f05MtLFHXcM/avnePXqVY4dO4HRqMdgMCASiUgkEnznOw9y\n6tQ1mprKsVqtiMViNjY2+O53H2Jq6jJtbbte9KlUikAgwLlz5xCLxezZs6foEHYLQmEW8HLgwEhR\nt5HNZnnkkV9w/PgZPvCBe7nvviO3kYyNjQ2+8Y0HWVhY5VOfup9Dh0ZvIxmpVIqZmRlmZ2eZnIyg\n1Qr56lc/zYEDE7eRuFwuRzAY5PHHn+TRR09y48Y0GxtaLJYkVquc9773IPv3N/PhD3+AI0fGmJgY\nZ2xskObmZjo62ikUCmg0Gra3HUXSs7CwzpUrS9y4scLsrJP19R1WVuLY7X62trIEg3FiMQECgQip\ntIDRqMFqFVBba8JgAKm0cNPMYYvNTQsCgQuFwkhdnYzqaiHRqJhIJILHoyKTkVJWlsJk2rULT6fj\nXL+uQi73UVamQKsVI5HksdvB5RJQUZFGrxcCEjKZCEtLWlSqFKOjZqLRKNvbWeLxGGCgo0NHSYmQ\n+Xnw+30YDEJUKiFmsx6XK8j8vIz6+jxtbWo2NkI4HH4yGSFyuYLu7lIKhRRnzuSQSHw0NGgQCDKE\nwyn8/hyJhJauLhUlJcKb41VO9HoZWq0Iq9XA9naYpSUF7e1CWlrUrK2FcTi85PNi1GoFXV1lxONx\nzpzJYzRG6OgoIRKJ4HZHiEQKgIauLj1qdYGpqQzhsIuKCgV6vQSRSIrDEWFnR0dPj4LqajmLi3Ec\nDhdSqYj6eiv/7b99nvHx0TddQZ9OpxGLxW+ZXK1//ud/5vDhw7S0tPy5T+Xtjn+TaLy57uR38K/i\nloXm2/X9Xg+/b1N7K0X59XZv32rWvD6fj8XFRc6fv8LkZJC6ugRWq5hQyEtDQxlqdSVzczn27SvB\nZIqwsJDCbI5iMKgJh90MDPSQSCSZnMyyf7+YvXsLLC4GSKezqNUlRCJx9u6tZXPTzauvQk9PnL4+\nKUtLDtbXBRgMFYTD0NxsxmpNcfZsntpaH729RmZmVllbE6LTmXC7obJSTG+vmslJIalUkKEhM1NT\n15iZEWA2a4lG8wSDYVpa6rl+XYPDEWdkxMLSkp2pKTldXXFGRkRcvZrl8uUd2tuNXLu2wKVLVjo7\ndbS0xLHZgiwu6tm7t56zZ69w8WIl/f0yDh1Scvp0KWfObHHHHVaOHBng3DkXJ09OMTDQw2c+c4iH\nHnoSm03H008/x3vecw8VFRU89tjznDwZQ6U6zn333YdCcZKnnjrFo49eQ6FQ8O53v5tc7gVu3Jjj\n61//IV/4wl9gNpuRy9eRy3cLw8OHD3PixAl+8IPnaWyc5Etf+jxWq5ZcLozZbMZqtfLlL/9/JBIJ\n3G43ZWVlrK+v88MfPo7JpOaLX/wcL754lvPn06jVU7z3vXejVgvI53eLxfHxMZLJDN3dbWi1Wj73\nuffhdrsZHt4d88nlckXb2Xe/ex9G41X27Ru5mfotIJfbdY06ffo0P/nJDHV1V/ja1xpwuVysrq4y\nMDBw21jQ76Krq4uvfa2h6Bj1yCNPMz2dJRyO8YlPfPQPvqatrY3BwXkqK0tfNx9iN9xPjEwWK3Yo\nbpH/3928cDqdvPrqGVpamos2twBHj77E9HSeQuE0f/mXHwd29Q7hcJpIREA0Gi0WY+FwGL9fTDq9\na2utVCrJ5XI8/fSzPPnkKq2tl/jqV/+qmJbu9/txOBz09PQwNjZ224bEzs4Ok5M2/H4YGFh4Teq3\nz+fD5wOFIoNaraa8vPy2f3/xxZc4enSG6mr49Kfbqaure83vAPz0pz/n6tUtUqkdAoFShoZqueee\nGoaHh6msrHzN821xcZFQKMT581fxeLx4PCmi0TjJpIhMJgsUyOVAKs0gk8mRyQpotRpUKjFKpQ6z\nWYdcLieXSyGRSNje9pHJxHE6ZWxtrRII1KNQrCGRNFNRoaeuLodSWU80GsHlkhCLhSkUhKjVRtra\nCohEYnw+GYGAm+3tSqqqgvT3CykUjKRSGba3BSSTEmprd8MWk0kRyWSQjY0yLBYRd94px24XMjvr\nJx6Pk8/raG+3IJFImJtLkcv5UauVyOVqamvLWF93cu5cjtZWGU1NCuz2MD6f42ZuiJq2NhWxWJzj\nx8PodC7q68uRyVSIRAI8ngLhsIKhISVisZjFxQTp9A5SaQlqtY7W1jKmp1c5eTJFb6+MlhbFzeC8\nLdJpOTKZns5OI35/iBdfDGMy+ensrEAgkOP1BvB6C2QyWnp7d7tu168nyOWcGI1mNBo9FouB+fkN\nnE4Vg4NqSkpUzM/vEI/vIBAoKS0t4zOfeQ9VVVW3kfs3C259l75VJgQKhQLBYPA1gZvv4M+Ddzoa\nbyHk8/k3tHjOZrNkMpk3zKf797ErBE38mx2M30ehUCCVSr3pU80DgQAej4cHHniMZ5+do1DwkMsJ\nEQgitLVVs70tYXs7xeCgiUxmm42NHEpljmhUST4fZnS0ia2tOLOzaTo7NYjFfra3wyiVQiIRHalU\nnPHxBnZ23Fy/DhUVeQqFMD6fG51OSTJZQiwmYGSkgmzWz/XrQlSqJCpVAb/fSUmJkXRawc6OkM5O\nPQZDhulpIfl8hKoqJS7XGoWCEplMhtcrxGIpUFurY3FRSTQaY2ysDIdjnY0NBU1NKgSCEDs7IWQy\nOWq1BqfTRj4vprzciNebZWfHRl2dFVCysWEjnc7S2lpNIBBiY2MDlUpPX18NKyszLC+r2LNHTl9f\nDU6nmLW1dVKpGPfccwe53Bqzs2K2tuzcdddeysqMOBw3WFgIYrev8aEPvZetLSfxeJh43I/VamFg\noI9XXlnEbs/T1LSblN3YaGJ5eZXjx8/S1FSL3W7n8mU3anWegwf3MjTUy+hoZ3GcQCgU8r3v/RNP\nP32BkhIJoVCI48c3SKfTDA+3UVKiQSoNcPDgGPX19QwMtDM+3kdZWRkGg4H+/p6iyNpsNlNbW4tE\nIkEkElFTU1MseK1WKwMDvZjNZlQqFd3djQwPt7Fnzx7i8Tjr60vU15cyNNTPd77zIM8/v4lCEaK9\nvQ2fz0cymXzNmpZIJMVi2+3eJh73MT7eQ1VVFfPz8zidTkpLS4vrTqvVMjExUnSHOn78OA8++AQq\nlYiKigqy2SzpdJqOjkaGh1vp7u5GJpORTCYBbluXTz/9LI88sobXu8rBg3uL7xGPh8hmPRw8OFrs\nNqhUKurqSunsLL/N2am0tJSSkgIjI220tLTcJGBidnbcbG66aGwsZWxsl7QVCgX+4R9+zG9/u4hQ\n6KempqYYRpbNZlEoFOTzISoqZNxxx7+kvIdCIZ588jdksxlGRhoZGWmjubm5eL6BQIDz58/j9XrZ\n3AxRWanhM5/5xGt0L88++xyPP/4sKys2HA45Y2OV3H13D3ff/W76+/uLwYO53G5A3pNPPsXLL5/g\n2WenOHnyKmtrQXZ2cuTzEVQqHVarmPJyLSMj9fT21nD//fvZu7eT0dFu+vpa0Ghk6HRK5udduN12\n5uYELC1dYW2thEBgmULBhMUCFRUK2tsrsVggGgWvN8zWVg6fT4hEEsVg0NHcrEWtzmG3S3C7bXi9\nJvT6LL29BgqFPLFYGpcrg8+npqGhQEWFnHi8QCIRYnNTj1SaZ2hITyaTwOEoEAr5iEZ1tLYqqKiQ\nsLKSxuHwIhYXUKsltLVZiUbjnDsHJSUx2tsNxGIxAoE4kYiQQkFHT48Oo1HItWs5wmEHRqMKrVZA\naakOmy3EyoqElpYC9fVy1tbCOJ075PMyVCopfX0VhEJRzpzJYTRGqK9X3xzvixIKCQE13d06tFq4\ncCFFNOrAYtk1u1CrVWxuRnE6VXR3y6ipkbO0FMPhcCEWS9Hp5HR2luNyBZmaElBTk6WrqwS3O8TW\nlp9EQoBSqedjH7uD++47RF1d3ZvaeCWTybylOhrf+ta3+PznP/+ajYJ38EfHO8ngbyfcEkG+UdhN\ngY39qxaYfwrkcrmbAVG3B+39e88hn88TDAZRq9Vvygd3NBolGo3yve/9lGAwg1QaZ3sb9uzJU15e\nziuvhCgpydLebubq1euo1VY0mjwrKzJqa+M0NdVw+vQmUqmMqiohm5tuVCoV5eUaLlwQYLUGGRtr\n58SJq4CJ0tIE29sJtNos1dVlXLqUQ6tNs29fHWfPXiGZtFBZmcThEKBQhGhurufy5Qi5XJ69e0tY\nWbHhdKqpqckQCkmIRLbp6WlnZSWI1ytgbGx3J3FqCmprk1RXW5iauorJVIdKlWV7O41Gk2DPnipu\n3EiTTrs4eLCD6Wkb6+tKBgbS6PU6Xn01ilwe4+DBBi5cWGBjQ0t3d5SammrOn/cTCtkZHW1GoZBx\n4cIymUyW7u49DA938POfv0AgYOLAAQV79+7lN785ztzcAhUVLXzmM0ew2+0cPTqDTOblgx+8i4mJ\nCR577HGeftpPT4+A//2//4ZTp05x48YsyWSBiYlBKisr+Z//82cEg/ClL+2nr6+P69evo1ar0Wg0\nVFVVcerUKR599Cx1dSq+9KXP8b/+1z+wsZHnL/+yj/3793Pq1CkMBgNDQ0Nv2BqKRqMoFAqEQiE/\n+tFPmJlx8aEPjdHU1MS3v/1TQMB//a+feo3F6y0UCoUiGdnY2ODrX/852Sx8+cvvpa2t7Q++5mtf\n+y6TkwnuuaeET33qo+RyOUQi0W1i5/X1dX7wg19gMCj58pc/Xxy3mpqa4vHHjzE0tDsm9MdEoVDA\n5XJRUlJSfBYUCgW++c1/ZGEhzAc+0Mvhw4fI5/NEIhEeeuhx4vEkH//4B4rPPZFIhEgk4syZM/zw\nhxcxmQr8j//xmdd8fg8//ChPPWWju1vGhz98L1ar9TY9yPr6Ojabjd/85jTLy1Le/W4Nzc1NDAwM\n3LbzmkgkCAaD/PjHj+N2u/F6JaTTOVSqOBqNkc7OMnQ6PX193eRyuSKRcblc5HI5JienSCTCzM3F\nSKVs+P21CIWz5HIdqNXLqNUNlJXtJliXlqrJZDK43UE8nhCBQJZotIBQGEehMFFZmUOhUCORCAmH\n/SwvqxAIlhGLGygtjbFnjxWbzU04LCQSCZPJmOnoyCCXK3E4IqRSQTweC0ZjnM5OCy6Xl0BATjy+\nRSJRRWdnFrVaxdxckGQyhkgkQqEQ09JSisvlY3paQVWVC7O5glQqQC4nxufLkcmo6e3dva92w/sc\nyGRlqNVJmpuruXRpHYdDT09PFKVSx9aWn1QqRjKpRaEo0NFhwuXyMz8vx2x2oNWWIRLFyOfFeDwF\ncjkVvb0SCoVC8fhy+a6Qvrq6nGvXbLhcBgYGkuh0BlZWvCQSEfJ5LUoldHZa2draYXpaRk2Nm7Ky\nKiIRP4lEnnC4gFCo4Z57Gmlvb6elpeVN3ym4Nbb8++YFb1YUCgUsFgurq6t/sJv4Dv6o+Ddv3nc6\nGm8hvNEdjTdaVP0f7WD8IfxLkvKb56GYzWbZ3t7m61//Z86cOU84vBsa1d5uQqPJcemSCIEgRHW1\nCrd7HZlMTT4vYWtLRlOTnNpaGQsLyZstYTmhkIvy8lKkUimzswpKSnIMDJSwsuLG40mgUIgJhcJY\nLArMZjkzMxpEoijj49XYbEv4fCCTCYhEdkXidXVG5uclRCIJhoctuFzL7OyI0WqFRKMixOII7e2V\nbG3JcLl2Oy3ZrJPFRQEaTQaZDLzeLXQ6PYWCAq83R329EqtVyfXrSjKZAPv312GzuVlaEjA4aEKl\n8jE7W0AiyTM0ZGVlZQmnU8bevbXI5R7m5kQUCmkOH27FZnOzvCympkZIZ2c9Nlseu30JhULK4GAL\nPt8Cc3M5YjEvX/nKZ5md3cDlCuPzrTEw0E9jo4HZWQ8zMwEaG/XU1FQTCKwhFu/O8h88eIC5uWWe\nfdZHPL7FffcdQaXKUFurxGotw2g0YjQa+b//91FOnLhGVZWeQCDA5ctOVKoCd945TlNTNS0tRkZH\nR1EoFDQ0NLxmDMZutxOPx9FoNLjdbiYnJ1EoFGg0Gs6ePcuNGzeKXYHJyUlSqRQmk4l0Oo3b7S46\nq70epFIpQqEQgUBAd3cHIyPttLW14XK5OHVqjnQa+vsbyGQyvPjii+Ryudt2/X7XKz+ZTDI1NY1I\nVGBioh+9Xk88Hi+G8t2CTqdAowkxMrJbNMtkMiQSyW0uWfPz8xw/biOVyjA83FrUe+wKyEfp6Gh/\n3evKZrO8+OJLLCwsUFtbU1zXm5ubfP/7P2Fz00ZHR1vx9TabjZdffrmYNfK7u7C7n0sbvb01DAwM\nIBaLEYvFbG9v8+STV3A6c3R0lBYth2+Rld0OyQrV1Xr6+3soFHbHtAKBAFeuXCEej+HxBGhutnL4\n8J23mWik02m+/e0HOXZsk5YWOT09Fu655y76+/uLHZPdgt/Nt7/9AC+8cAK7PUMiIWXPHjFtbRV8\n/vN/wZ13DrN//z4aG/eQzWZJJBIcO3aCqamLPPnkdU6deo6rV6VsbV0nmy1BqUxhsSgZGmpj375q\n9u4doqGhBLFYgsfjZ37ewdxcgK0tD+GwGrU6gsVioLe3kooKBW53Gr9/m9lZJdGoE4NBTVWVkfZ2\nA35/jJWVNMGgh0ymhM5OJfX1Cra2ErjdTvx+LTKZhOFhA0Jhho2NPH6/i0hER3OzmuZmDWtrMba2\nQkAOlUpJT085QmGayckC+bybmho1CgUIhQIcjjQej4qODgkVFWKWlxO4XNsIhUo0Ggn9/VU4nUHO\nn89TUZGgrk5NLJYkFIoQiSiQSNT09RlRKgtcvpwllXJgMmnQ64VoNAo2N1O43bvajPJyMUtLcVwu\nB0KhEp1OSm9vFVtbPqamoKYmQ1OTDp8vgsvlJxaTIpWq6O01IRbnmJxMk8k4qarSoFaLyGYLuFwp\nQiENd9xRwV13DXDo0CEsFsubnmTAbuF+K0jzraB7TCQS/J//83/4u7/7uzdVDfA2xTti8LcTbn2x\nvVF4o0TVf0yCcQtvNqKxsLDAN7/5ANeuXcbhgGg0zfh4PdGomxs3BGi1SUSiLKlUkLq6CgIBGdvb\n0N9fglodZn4+TT4fRSJREY97GRhoxutNcuOGkI4OBWVlOdbXvSQSSQQCFaFQmM5OK9lsgulpBWVl\nUFMjxencJp2GfF5OIFCgtdWA0ShgakpEPh+iqUmHw7FKNiu9WYxIqKwUUV+v48YNAaFQjL4+E273\nCh6PEL1eTDQqRCAI0dFRjculYGcny/BwGblcgOlpMXp9nqYmBevrm4RCUF6uJhTaxuWKYrUayGaF\nbG+votFo0Gh0eL0+3G4XTU11ZLNpNjaWyWQk9PfXEwqtsrKSQ6MRcOhQB4uLXtbW8tTVyWlra2Zj\nYwe7fQmnc4d7792H12vj8mUpmYybj3zk/aytLZFIeIlEgjQ3N9LX185vf7vI7KyXxkY9VVXlpNMO\nmpsrUCoV9Pf3s7CwxMMPn8PtXqOtrYmTJy8Rj0Nvby3Dw8PU1am5885d9ySDwUBFRQVLS0vk83nU\najXPP/8CR4/+FrN5l5h861uPcvHiNN3djTz11PP84hfLhMM26uqq+P73f8P58y6qqqSsrq7ywAMX\nWF6eZ2yslx//+OccPTqJXJ6ipqaGY8eOsbq6WkzW/kMQiURFYmI0Gqms1DA42ERbWxvPPvscDz20\ngtu9zMGDY39wranVavr6Wtm7d9cu9vLly3z3u4+wublWLLaTySQajYbOznbKy8spFAp8//sP8tJL\nZ2hpqSsSCrPZjMGwSzJ+d+QIKBKjQqHAo4/+kqNHn6ey0lzMDVhaWuKf/ukEN264aWw0FHfxz507\nxzPP2AmH/YyOdhaL9ocfPsrRo1skk/ZiAF8+n+fhhx/jV796gT17qmhoaLjtc9u1yQ1RX69l375x\nFAoFYrGYGzdu8IMf/BqXy8FXv/rXDA31IxKJyOfzZDIZHnnkcX7xi1nU6gyf//wHGBrqv+3aHn/8\nCZ5++hj5fAqhUMDdd0/wvvfdj16vL/6Ox+PhG9/4IS+/fBK3O08+r2T//gomJtr41Kc+wdjYUFEL\nc/nyZa5cucJDD73IuXMnOX9eiMMxg1BYQkmJmJYWA4cOjXL4cCdHjhxkaKiDTCbD+vo258/f4OJF\nO/Pz6zidcsRiHwZDCePjdXR0lFJWZkIsTnPtWpy1tTm8XgMyWYa2Nj3V1SYqKjRsbQWYmcmSSrmQ\nSo10dZVQUyNnfT2O3b5NNKpEpVLQ329AKs2xuprF798mEtHR1KSmrU3P2loYuz1EJpNCqVTR2VmK\nXJ5ncjJDMumkokKNwSDFYNBgtyfY3JTT3S2lrk6OzRbD7XaTyShRq2X09VkJBiOcO5dGpQpgsciQ\nSARkMilcLhHptIreXjU6HVy/niYQ2EKl0mI2y2hoKGV9PcbqqpSWljw1NXIcjgQ7Ox6SSQVKpYSe\nnlICgQiTk2k0mgBVVUoKhSyhUBS/X0Q+r6G3V4dOJ2BqKkEoZKekRI3JJKe01MD6egibTc7QkJqD\nB9u47777XnPvvdmRz+fJZrNvGaLh8Xj4yU9+wt/+7d++JYjcWxzviMHfwX8cf2pR9e+PSP1bIu9/\nL95MD5bLly/z7LOnUCiyLC7mMZmSHDrUxssvn+f0aQdlZVJUqhTxeILW1nIuX1YzPR1kdNTCtWuz\nXLmSwWotIBLJice9jIw0c+pUimPHXAwOGhGL3dy4kaOiQk2hYMLn8zE21sT58z5OnozS36+iri6G\nwxGmvr4SsbgKhyPNxEQlS0s2zp5N0NiYprZWSDjsQyQyo9FUYbPB3r0mSktjXLmSpbzcRVOTFptt\nFadTisFgZnNTSEUFDA8bOXVKQCrlZe9eK+fPX+bsWairU2CxJLHZ3LS0NGI2V+HzRdizp5zOzjrO\nns3gcATYv7+bY8fgxo0kR46Uo9fLOHUqg0KxxT33TPD002LW1xNUVcXZt2+YEydszMwsUFJi5F3v\n6ubkybMcP55lYqKGj3xkLw89JGB6OkRLi4P9+8cIBE5js23zox/9lE9/+j/xs589zrFjMQqFV/jP\n//lTdHbqCQbDOJ1ORkZG+PjH38c3vvEQr766wle+8uGbKdaQSmUwmUx88YsfIRwOF2eqBwYGeOml\nlzh+/CT33vturl+/zs9+NonVKua///e/4vjxK8zNCaivv0ZnZwfZrAChsEAul6O8vJTycmdRVF1X\np0Wvj1FVVYXP58NkKlBaqkUqleL1hvD7IRAIsbCwwGOPXUYgoNgxeeqplxkcbOPQoUN/8F4UCAT0\n9vYW/9zYuIeWllW6u3ftaX/zm6eZn7fx4Q/fc1v69e/a8trtdtbXhYjFLiKRSPHZIJfLi/bSLpeL\nlZUwkchux+HW6IJcLufIkSPFYy0tLXHu3EWGhvppbd218UwkEkxNrbC2JmRwcKGY+F1eXk5zs5ps\nNkdVVVXxGP39/dx/v4eKCsttovS2tnrW1nbo6PiX64jFYly6tM7GhpDFxUUaGnbT1yORCI88chSx\nWMTHPvah1zho7Yq/BUilMXK5XJHMpFIp3G73TVcsHyaTAYvFUjSviMfjeDweTp6cZWtLzCc/2cTY\n2BhWq5VCoYBAICAcDvPYY7/C63Vjs2URizW86111VFdXMzo6WuzEeL1eLly4gM1mY3LSB9iIxxsw\nm2X09Yno6rqPxsY9VFZWYjabuXr1Kpubmzz33CkcjjiRSIh4vAStdgeVqoqBARM6nZHy8iFSqRST\nk3NEIi6czlIkEjtKpYWqqlo6OqqIRAy4XFHW11243WYslgAWi4rm5t0xurm5MNGoHYFAh0ZTwvBw\nKT5fkGvXYmQyW6TTNTQ1VVBebuDGDQcbGw7y+SQKhZ62Nt1NB6cYcvk2lZVWVCojZWV6Zma2mJlJ\nMTAgpbVVgd3uI532EosZUavN9PZasdvdnDgRQqcLUl0tR6/XIZVKWFrKkslI6OkRUygUmJ2Nkss5\nEAorMRpNtLeXMTW1xuxsiI6OPNXVYrzeLG63s3j8gQEzOzsBTp2KotOFqK+Xo1JpEIlyrK/nSaeV\n9PbuEuTp6TC5nAOFohy9voTmZguXL69x7VqMgQEZ4+OV3H334besXuCtJgYPBAJFrdM7+PPjnY7G\nWwxvZEfjTyWq/lN0MH4fyWSy6HTz58CZM2d4/vmXuXr1BmfOpNFokoyOWlld3cDrTSOXS4hEslRV\nqaioUHP5sohEIsjAgJXt7UWiUSFyuZSdHQlmM7S3m1leTuNyRaislBKLOclkBJSWqllaUiAUhhkZ\nqWR93YnDARaLlFwujlhcoL7ezOKinEQiwfh4JQ7HGhsbQvT6POk0CAQRWlt3R6Lc7hQjIxayWSfL\ny3kUihRCoZREwktbWy2BgAi7fTe112zOMj2dJZMJU1mpwulcJZ0Wo1Ip8PsFaLUpWlsrWVuTEQ4n\nOXiwCa/XzeXLYvbskdHYKGNxMYzHk2B8vBq3e5GFhQK1tWqqqwusrvpxOMLcdVcHbvcy09Miyssl\nTEw0Mzsbw26PMT7ehE6nY3k5TDhso76+hvp6Izs7S8zPR6irK+GOO4Y4c2YHtztJa2sper2aSGQD\niSRNIpHgAx94D3NzCzz9tI1EYpumpqSEkH0AACAASURBVD2cO3eNQoGbSd79NDUZqKurIhwOs2fP\nHpaXl/nHfzyKz+fAarXwox/9litXglRW7oqQr1/fRKsVcccdo2g0YvT6JAcOTNDY2EhDg5m9e7up\nqamhqamRkZF2+vv7kEgkjIz0s3//MCUlJVit1psjL2PIZDKammppbNQwMTGOUqlkZWUWo1HMwYMT\nnDr1Ks8+6yUWc3DnnXt58smneOaZY1RWWm7bOf9dlJeXc+DACF1dnSSTSR588CmuXctSWZl/XUvI\n0tJSDIY4w8NdmEwmNjY2mJubo7S0tFig73amcsURMolEQjKZLHYtbuGRR57gN79xk05vF7sOEokE\ntVpIebmA/fsnig48MpmMvXuHmJgYRqVSFY+hUqno7e2+LcsDoL6+noMHR2hpaS7+nUwmQ6WCykoR\n+/dPFI8zPz/P449fZXs7Qnt7GWazGdglJufPn6eyspKWFiN33DF0my7jpz/9OY89do6GBhOf+MQ9\njI+PIZfLkclkNwXnP+Hkyet0dpbS1KRlfHwMg8FAOp0mHo9z/vx5pqameOklO8FgjoMHq5iY6OCe\ne+4pdql2dnY4duwYL798gqeesuN0ziOTmWhoMHP//d3cd98RPvSh+6mrq0UsFvPyyyf5xS+e4sSJ\ny5w75ycU2qRQKKG5WUFzs4lPfvL99PfvIZPJEA4HOHFinStXLrKzo0IozFJVJaGjo46RkUZSqQTX\nr/tYWlrGZtNRXp6gslJFa2sVer2Q69cj2Gxu8vksBoOOwcEKJJIs168n8fk2SKf11NVp6e01s7kZ\nYHU1TDIZQy7X0t1tQasVcPFiEr9/G71eSUmJjMbGMtbX/Vy9Co2NWerr1QQCcQKBIIGAArFYyeBg\nCWJxlitXkiQSDrRaLWVlCioqdCwvJ7HbRbS3i6iokGG3x/F63SQSGrRaKUNDlTgcPi5eTGMwBDGb\nJYhEkEjEcTolCAQqBgcNKBR5rlxJEolsoddrsVgUlJfrWV9PsrUlo6tLTE2NgrW1OG63i1xOgVYr\npafHissVYHIyS2lphNbWEt7//nu5884Dr7FWfivhVkfj1mbCmx3Ly8ucPn2av/qrv3pLnO9bHO+M\nTr2d8EaPTsFuwf7HIhpvBMG4hVQqhUgkekOJRqFQ4PTp00xPT/Pss2eZnIzT1CSmtDSL3e4hlcpQ\nKKgJh1P091chEiW4dEmIUhnHZBLg8djRavWk01KcTjHt7bse9zdupIhGAxiNSoJBF3V1FeTzQmZn\npVgsWRobpayv+wgEkmi1KhKJOA0NJRiNcqamRECQkZFy1tcX8ftBoRATDgsoL5dQV2dgZkZIJBJj\nYMCM273Czg5oNCKCQTEyWYKenhpsNtjcTDI8bCKXc7KykkEmSyMSyYhEdmhtrSMSEbG1JaKzU0tZ\nmehmNkWYiYlq1tbm2NwsUF2tJJsN4HC4UCqViEQSPJ4tpFIpJSUGvN4UsZiThoZ6YrE8Ho8TobBA\ndXUFwaAPu30FmUxJS0spm5s3uH7dT3NzKXV1KmZmkmxu+vnIR97Fzk6Q9fUMEkmQwcF+1Oo0yaST\nGzc2GBzsoq1tD888s8rysovW1jJ2dnZwuwPU1xvp6emitbUai0XF8vIyarUarVbLP/7jrzh3bp7G\nRguzswucPRtGIonyrncdxOPZRKXKcOjQvpsCTwsHDoyh1WqpqalhcLCvGExnNpuL4l+BQIBSqSze\n/0Kh8La1plQqi+N/Go2GmpoaZDIZSqWS8fEhJiZGUKlUqNUqhMId9u/f1Uj8+MfPMjOToapKQGVl\nJc899zxbW3Zqa2tvW2u3tBa74XhZTKYcBw7sI51O8/d//wCXL0/T1dWGWCwuBnjW1tZitVqRy+V8\n//sP8+KLTtTqMO3tbcVrqquro6mpCYlEwuzsLN/+9k9ZXl6kv/9fwuqy2SThsJ19+/qoq6stnlN1\ndTXd3Z2o1WoKhQKrq6vE4/HbdijX19d5+OGjRKNB6uvri689ffo0jz32NFqt4jYR6OzsLMvLy4yM\njNDb230bWdFoNKRSLvbsMTI+Plb8vF944QUeeOASm5uLfPKT/6lIQG7h1VcvsL6eoLZWzf79E8X/\nN4/Hw+bmJmfPzhIIiHjXu/r54Affj8FgKOpnZmZmeOCBk2xsOGluVtHaauH++++lpqaGXC6Hz+dj\ncnKSF198mV//eotIZIOSEj2Dg618/ONHOHLkIB0dHaTTaZaWlnjkkV/z1FNnmJlZYXtbhdEYprRU\nw4c+dIh9+9oYHh6kqsrKE0+8xIUL5zl/PsbGhg2RSExZWQl3391GS0sV1dUWbDYnZ8542NpaJBYz\n0tmpZWDAgk6nRSzOc+VKhI2NAFJpErNZy9BQPWJxjosXo3i9a8BuZ66/38rGhp/l5TCJRBiZTEdv\nbxkGg4hLl+Ls7Gyh1coxGuV0dlayuenl4sUClZUJampUZDIZotEobrecfF7BwIAepTLHzEySUGgL\niURHebmSxsYSlpcjLCzkqa/PUV4uIxBIEgj4CAa1qFQyxseriESiXLmSQSLxYTAoMJkUyOVi1tcL\nRCJiurvl6PUF5ufT+HybSCQ6LBY5LS0WlpYCzM4KaGjIUVOjwO3e7VbF4yrUajljY9Ukk0kuXMgg\nlweoqFDxvvcd5v3vvxedTld0cMxkMuRyudd8j7/Zi+FcLkcul3vLEI2ZmRlmZmb47Gc/++c+lf8X\n8A7ReLvhjQ7t+2NoHd5IgnELv5u0/adGLpfj7NmzzM/P88tfnmNqykNzs4JCwYvTGcRoVOH1qkkm\n4xw82IrDYWd+HiyWPJAmlQpSW1uGyyXH58szOlqOUOhhYSGDRJIAFKRSfgYHW3C5UszO5mhrk6NW\nh1hf91Mo5BCJDCSTScbGmojFwly8KMBszmCxCHG7HeTzQvJ5FaEQdHaaMRjyTE0VyOUC1Naq2dlZ\nB+QIhRKcTil1dVLq6zXMzWXx+SI0NmoIBm0Egzl0OjkejxSZLM7g4B7W13PYbCn27rUCLhYWsshk\nabRaIR7PJhKJHJFIjt+fo7RUSHNzNYuLYlKpKPfeO4zdHmB+Xkx3t5aGBgNXrxYIBsN87GMHWFnZ\nZGZGTEeHmoGBFq5cSREIhDlwoJtgMM72dh6x2M/Q0CDhsIdweJvNTQcHDoyg0yW4cmWHublFPv3p\nD3PhwizT02A2pxgY6Gd9fQ6dTkhlpYU77zxAQ4OJc+euce3aDfbuHeKZZ47z1FNu0ukt6uuruXDh\nOoVCnsHBVtraWigry3Lw4Dhms5ne3m727RulUCgglUoxm834/X6Wl5cxm80kk0mOHTuGx+OhqqqK\nGzdu8PzzL6HRqNHpdLz00kvMz+8KnVOpFFNTU4hEIrRabXH9/P69LBQKi0W70WhkaKiP6urqmyna\nSczmAgcO7GNpaYkHH7zAyso2PT21KBQK1tbWUKlUt63ruro6BgZ60Wq1zM3N8dRT8/h8CTo7K24G\nsqURiUQolcqibmt9fZVkMsTYWBdVVVVFw4rfXddXrlzh+HEXuVyUiYm+oki6urqaQ4fGiyTDZrOx\nvr5eTBGH3W7D9773Ky5cmKanp6nY4Xj55Zd54oltAgE7Bw/+y4jRj3/8BJOTCbTaKP39u4nAHo+H\nb3/750xOblBeLi2OXoVCIX75y1+xvb3Nhz70fnp6um77PHZ2dlhb26SqSs/o6GDxmp577gUefvg3\njI/3sndvI/v2jRevKRgM8vWv/zNnzy5y6FAHExMtDA8PIxaLEQgEbG9v893vPsjq6iqFQgGTScNX\nvvIFRkeHkclkpNNplpeXeeGFlzl6dJlIZAODYVfM/elPv4/R0d2QQ7vdzrVr1/j5z5/l2LEF3G47\nmYyB/n4jAwOVfPazn+Tw4b0EAgGcTiePPXaaV145wfa2nHw+R0WFkJ6eBj784UOUlmpZWLBz/foC\nr7wSJR5fQyYzMDa2h7GxWvz+KFtbTubmEmxvxzEak1itWgYGGhEIMrz6aoidnWXkcgO1tQYGBipZ\nX/cyPx8ilQogl+vo67NiMkm4fDmKy2VHqZRhMMjp66vF4djtAJhMUcrL5SgUEnK5LJubAhIJGYOD\nGvT6AgsLSXy+LXK5XQLQ21vB8rKfmZksFksMk0lyM4AyytaWEplMyuhoKblckunpBOm0G5VKQ1WV\nmrIyNUtLGVwuAS0tAkwmAZubKQKBHVIpDSUlMvr6KrDZfFy6lMViiVBWJiObzREKBfF6FUgkSoaG\nTIjFWS5ejJNMOigp0XLXXSP89V9/ujhaeev78xapLxQKRSvlW+TjlqPk7xq+vJkK+ltE43cNDt7M\nmJqawm6389GP/uEcoHfwR8U7ROPthjeSaPz/7J1XdFuHneZ/AIhGdIKdYO+9N7FLsuQWx3bs9DrJ\nTLLZZOZkZuecnd3Zsw8zL5vkpHiyjh3HjuM4tuMi27ItWZYliyqkRIoiKfbeCwCiEb3vA0VE8npm\nkkwSxxl/5+gFJC8uKeDi/93/VwQCAT6f73feDLwfBGMfgUAAgUDwByUagUCA0dFRJicn+fnPLzE9\nvUpyshCXaxuRSExqqprJyXjEYhc9PYXMzy+xvh5EoxHg9wdQqaIUFKQyMRHH7q6bhoZELJZFtrcF\nKBTgcEiQSn00NOSyuBhgft5NSYkMn2+DrS0nCQnxWK06wMfBg2WsrW0yMREiI0NANOrE7XaQkqJh\nZ0eF0xnmwIFMfD4zExNRFAofEokAr9dCXp4Bm03MxoaA+vpE9Ho/Y2M+AgEHWq0cu32L9PRUgkFY\nWpKTkxNHcbGG6WkfJpOToiIVdvsKJpOfhAQ5NpsIcNDUVMrGhoDNzQgHDmQil/vp7weRyMXBg3lM\nT8+xsOChqioJMDIzY0csjpKZGc/a2gzLy3aqq7MIh7eZmdkmHA5SW5vC3NwY4+M2ursrSEqKcO2a\nh/X1db71rS9y9eosIyNR8vJElJeXMzq6TCTiIy1NS3l5AXK5FbPZgtfr5Stf+SwDA9d48815ZDI3\narWKkyfncTqDNDcX3dj8bNHZWUtNTQ0VFblUVeXh9/vRarXk5ubS33+Za9eGMRgyGBwc5Ec/eoG1\ntUXKyor5znce4+2359HpwhiNRn7600EWFlaory/imWeO8+abVsTiHXQ6NY8+eoaxMSMFBVqGhq7x\nxBNXWV6epL29iUce+RkvvXSGlBQVSUlJXL58GYvF8q8m1ggEAvLz82loqEWlUiESiVhamiAjQ01X\n1wFeeeU1fv7zC9hsq9TV1bzna3tv+2KhsDCR8vJyZmdneeGFNxCLIScnJ/Y8tbVVtLfXUlBQgM1m\n4/vf/wmXLl2hoqI45mXY2+D4aG+vIycnh2g0itvtvuW9abPZ+O53f0Zv7zxpadJY07bZbGZgYBqR\nCNrb626RUvn9G7S2VlBcXBQ7Tny8iPj4XQ4ebLvFWzI8PAyEaG+vjW0mhoaGePrpUVZXTdTW5sYK\nDRcXFzl27DiZmRl85CNddHYeuOX698QTL3LtWpjMTLjzzjtiw5fJZGJra4uhoWm8Xjh4sI6Wlhbi\n4uKIRCJMTU0xNjbGO+8YiUQE/Nf/eh933nkotukKh8M8//wxnnlmAKdzjfh4Jc3NpXz965+hvr4W\nmUzGzMwMQ0ND/PKXb3Lu3DIezxZSqYY77qjh4MFK7r33XkpKiuntPU9f3yWOH5/h+vVRAgExOp2K\nw4fzaW+v4siRLpzOXY4f72d4eISxMQkq1Z734siRZpqa8hkfX+L69WlWVkLs7saRlycgNzeBsrJc\nAgEvZ844sFjmUKm05OUl0dCQzeKiievX7fj9O8jlWurqMkhOljI0tMv6+hpSqRidTk5jYx47O7tc\nvOhDqbSRkiJDr5cjk4mZnw9htQqpqZGTlCRicdHNzs4mLpeGpCQJra3ZrK5aGRnxolTa0ekk6PVK\n4uIizM2JCIcFtLQkIBYHmZz04nRuIRCoyc5WkpurZXrazfx8kOzsADodWK1+XC47drsWnU5KV1ce\nRqOV4eEgcrmNxEQZWq0cgSDCyoqQQEBCXZ0SpTLC6KgHm20VqVRNY2MR3/jGZ6mpqb7FML1fErnf\n7bKfxrbfkbP/vfvypPfaftxMPt4PArJ/Hn+KcfHvhfPnz+N0Orn//vvf71P5z4APzeAf4j+G36Ud\nfJ9g7A/7vy+T92+DP2Srud/vZ21t7Ya2exSt1oVGE8/OjpHU1Co8niCjo2I6OqIcPapkcHCbgYFZ\nVCoddruLioo09Hovvb1hCgq2aG9PZ3BwiLm5KApFAhsbQnJyZLS2qrl4MYjXu0RGhpjl5WWMxhTS\n0hIZHhaTlOTjzjsNvP22hbNn51GrZfh8NoLBeCoq0njnHTfRqJvDh/Pp7b1CX5+IpKQ4pNIwoVCQ\n6moDFy6IGBy00dGRytTULFevBkhPD6NQyHG77bS3F+Nyhejrc3LoUDKJiXampjwkJ7tISZGzs7OJ\nTJZIUlIKU1NxpKdDT08Kb78d5Ny5FQ4cSGdoaJTe3j2JV05OgO3tLVZWlCQlpWA2O3G74ygtzePs\nWQsbGzs88MARjEY3W1sRyssjHDhQwwsvzLGwsElTUxUZGXlsbERYWVmhvLycmRk7Ho+F3t7zHDpU\ni1o9yvnzw3g8Ab75zY/y+OO/4rHHzvHZzzZTVlbEww8PsLExSVtbC1KphLg4L2JxHBUVFXziE1uE\nQkFsNhudnZ00NDTw0kuvsbX1Eh//+P386lcv8c47y3R2ZtLW1syJE1O43ZCZOcba2jrLyxHE4nVc\nLhdisQCpNIxYLCYjI4PcXCFJSSq0Wi2trZV4vUPU1paTmppKcbESvz+EwWC4YWQEnU55Iy3IzOqq\nkI2NDSKRCI89do74ePgf/yOJ3d1dLl68QnNz3S2t2jcjLS2N//2//y42pPh8fnw+8HoDRKNRent7\nMZt3OHLkNjQaTUzWcfvtR2It3tevT3LunBuP5wodHR2xYwuFwlhXxMbGBnNzHgA2Nzdj5myNRsPd\nd98d+5nnnnuB/v457r+/je7ubmCvRVwmi0MmC91y17S0tJS//VsJMpnsluK7goIC/tt/K7jlPWm3\n22lqaqK5ufmWx4VCIX//9/8Fn88XS7ECKCwspLFxBK1Wecuxe3sv8uKLmywtmfjnf/772OOLi4us\nrKxwxx0HKCxcpqOjLfY1k8nEt7/9OH5/hI99rA29Xk95eXns61euXOHxx99BrQ7x0Y8WkJqaQlnZ\nXhxvKBTi9OnTnDx5BYnEB6goLS3nwQfvITExEbFYzOrqKmtra7z44jm2t8PExztITEzknnvuIT09\nnezsbBwOB4899iQWi4nxcQEikQWVKp7s7GzuuGPP7xIIBBgcHOG55wbw+VZxOLIpL9dQWamjrKwO\nuVzO66/3YTKZ8fsliMUamppUKJVKhEIRZrORX/1qDbV6mbS0TAyGohvbvmlee20esdiMQpFOdXUp\nQqGQwUErgYAJqVSNTqenpiaXmZlVXn55i9RUK7m5ySQnJ994jTnx+6NUVUkRCIRsbHgIhayYzamk\npenp7DQwPDzHW2+to1DYSUxMJitrzzMzMhIkLi5MY6MKr9fN5KSDUGgbrzedvLw0cnOTGRxcY2LC\nSmqqE6VSSjAoIBx2YzTqSEoSc+RIKktLG5w+vYFUaicpSY7BkIZMJr1hbBdRWyslGo0wN+chENgk\nGjVQUFDAJz5xD2lpaUilUoLBYOy9djMxeDf52CcgNyMajcYk0vvDfSgUuuWz7Gbisr/V/EMTkD9m\nrP7vA3a7/ZZwiA/x/uLDjcYHCPt3vf6Y+G0kSOFwGI/Hg8fjIRKJEB8f/0fbYLwb+3ry3+eqNxAI\n4HA4ePHFV/jFLy7hcKzi8QgJBKwcOFDOxoaPiYkAdXU65HIHKys2hMIIfr8aj8dDV1cpDscO165B\nUlIYpTKIw2FCo1HjcskwGiM0Nqai0/m5fj1IIGBFoZBgtW5QUJCJxxNlfl5JaWk8hYVS5ud3sNmc\niMUSnE4XZWVpKJUiLl+OQyJxUleXzMrKPA5HBLFYgt0uICdHTk6OhuHhCA6Hg4qKBMzmBWy2CEql\nFKNRglIZoqEhm/l5P8vLHior1YRCRtbW3CgUQlwuOcGgg87OKjY3PYyNhWloSCA1NXgjgcZJYqIM\nu30dgUBMfHw829tClEo/zc3lzM5GMJsD3HFHJX6/g0uXoiQmQmdnHhMTW0xPWzl8uIRgcJOBASfg\noq0ti9nZdWZm7HzkI00IhTb6+tx4PDt8+cv3cuXKPFevOmhtzSE5Wc/Zs3Z8Phv33HOI4eEJdnfD\nGAzxVFRU4PNtotMJiUYjHDlyEIMhnr6+EVZWVnjggft47bUzvPbaFGLxLpFImGefHWF93U5VlYGF\nhRUWFpwYDEo6OlrZ3FxArxdy9OhBSkqKSUuL0NPTSmpqKpWVxVRVZVNYWIhCoaClpYampjqEQiG5\nubkcOtSOwWBAKpVy4EAjnZ0tKJVKcnJyqKvLp7PzAHL5ngk1P19Oe3s70WiUsbFxNBox3d2tHDt2\nguPHTYRCW7S2NnDs2Kv09vaTm5t5S3rSzYNIfn4uRUVaeno6cDqdPPzwq1y5YiEjQ0haWlrs/SuT\nyZDL5TdK1KQIhSa6uxvJzMzkypUrXL16ldTUVGQyGQA6nQ653EtFRRqNjY2EQiHGxsYQi8W3nMux\nY28yPR0hPV1ATc0eOZJKpdTWltLUVBKLvt3e3kYgEJCamhojMyMjIzzxxK+IRALk5GQDe3eC/+//\nfZxjx/rQaARkZ+89brfb+e53H+Hs2ctUVxfHEn8cDgdvvHGCQMDPJz5xP/X1NTHp1d5AFWV3d4W2\ntqpYMlUwGOS73/0pp0+vUVys4ZOf/HjMZO90OjGbzfT3TxAICOjurqGysjKWKnX27Fk2NjZYXXWg\nVov5y7/8HCUlJUSjURYXF7lw4QIDA9cZG4ujtFTH5z9/Gz09HSQmJuJ2u1ldXeXhh3/FhQvzRKN2\nVCoFX/jCPdx332FqavbO/dlnj3Hp0gUGBnw3unOilJRk8uUvP0BxcS5Go5Fz5/p55ZUp1tYm8Pm0\nVFencPvtJZSUFKHXazhx4ip9fRPY7S6k0gQOHcqjtDQZny+C2bzJmTNenM51DIZ4ioszaGgoZHp6\ngytXrITDJhQKNU1NuWRkKBgasrK8vIpIJCAhQUFLSwFer4fz552Ew5vo9UoMBjXp6RomJ10sLYXI\nz4+SmirB4fDjdFpZXVWhVAo4dCgXu93G2JibQMCMRKKisFBLSko8w8M+TCYfRUViEhIEmEw+nE4r\n29sqUlMlHDiQxeKimclJDxKJHYVCiF6vQCKB+fk9QtPWlohIFGRiwhPbfuTlqcnKUjM56WZpKUhh\noYDUVAlGoxeLxYTDoSYjQ8tf/uUd3H77IQwGQ8y/cHNaYyQSif27eTvxr8mjbiYg+9uP31V+9fsk\nH6FQCOB9C1f5bXH8+HGSkpLo6el5v0/lPwM+lE79ueGPbQb/TSRIf0oEYx/BYDA2LP1Hsd8n8i//\n8lNefvkCTqcZk2mvpK6ubm8gX1lxUlysxOvdZGfHQ1qamuVlOQKBh9tuK2dxcZm5uRApKQJCIS/R\nqIfCQgPLy1JsNj/t7Qbs9iWWl0GhCOLxiAgErNTU5GE0RllYiNLSkkx8vIOlJTsQxOdT4vG46Ooq\nY2fHwrVrAjIyQKMJYbEYkUgk+HxKbLYo9fVpqFR+hobChEJWkpPl2Gzr6PV6fD4BKysyiotl5Ocr\nmJrysLNjIzVVitO5RVycFLU6noUFKWp1kPb2AubnbczNuSgpURKJmFlbc6BQxOF2S/H77XR11bK9\n7WFyUkRdnZacHDmjoy5MJiutrQaMxjnm5lykp8uJRp1YLFuIRHsZ7Xsxu3sFXiaTj0jERllZEVar\nF5fLg0Kx14ZsNNoIh23o9RpEogh+vxmv10l2diYGgwi7fZvr1+f42MduRybzcO7cAtvbq3zlK5/l\ntdcu0du7SWrq3uvzjTfW2d3dpaWljPHxaSwWPxUV6dTW1uJyrVNQoKetrZXS0iKKinQ0Nzcgk8lo\nb2+hubmO7e1tEhISKCsrw+VysbGxQV5eHhqNhtHR0ZgJ3Gg0Mjk5iUKhIBqNsrq6yu7uLjKZ7Jbh\nQ6PRxPwCKSkpFBYWIpPJbrSMV9DV1XKjnyKE17tBV1c9UqmUn/3sNBMTLrKzJWi1Wl599TV2dsxk\nZ2fH3otSqZT09PRYJO3a2jxxcR5aW+uw2+08+ugzrKys3DKAJyUl0dLSQGbmXvLWD3/4HBcuWEhJ\nCceGcZFIRGFhIYWFhYhEIk6cOMnjj1+6IQFrjj1/ZmYKWVnCWKqU2+3G5/Oh1Wpjhu/R0VF++MNf\nMTIyQlNTTWzAefXVk5w6ZSMUMtLdfQDYu/68/vo7rK9HKSpSU1y8lzS1ubnJyZOjOBxRKirSYolR\n58+f58knx1heXqK1tSIm8Tp//jwPP/wsBkMif/EXn4n9Xvt3laenp/H5vDQ3l8V8Htvb23znO48x\nMjLNgw/20N5eSUVFRex3feedd3j88WFcLhtf+cqdHDnSiVarxe/3s7u7y5NPPs8bb2ySmSmipyeH\nw4e7qKioQCaT4XK5+M53HuXtt6/i9+8ikSj43Ofu4L77bqOkpASPx8NTT/2KCxd6uXzZi9frpbRU\nSVNTCX/7t18nNzeTmZkZzpy5xMmTGzgcCwiFe2Tg6NFq9HotDoeDEyeGuXJlHp9vF7Vax/33t1BS\nksrS0jZra0tcvBjC7zeTn6+gvDyb2toixsaWuXRph3B4G5VKTVNTPtnZWq5cMbK4uIpQCAkJKtrb\niwkGffT22vH51tFoVOTk6MjLS2RszMbMjJ+MDD/JyRJEojh8Pidzc3IkEgEHDxrw+91MTrpwOk1E\no2pKSnRkZ6u5ft3N2pqTlJQQWq0QgSAOr9fJ3JyChIQohw7lsbW1w+Skm0jEilQqIztbhUoVx8SE\nEI8nTH29mvj4PX+ZzbaNx6MiwufgngAAIABJREFUN1dJZWUK09NWZmb8JCV5SEqSEImA2+1gbU2B\nWi3lk59s5o47eigrK0Mul9+yZdiXSO2Thf2Nw3754/5rap98vFse9W6P0/414f2UX33QiMbzzz9P\nYWEhLS0t7/ep/GfAh0Tjzw1/7I1GIBAAeM/NwJ8iwdjH/t2d/yjRcDgcfO97j/L22xfY3LSwvS2k\nuFhFZqaUsTE/DoeV5OS9u/eJiYnIZFKmpuQkJkZoakplbm6TrS03SqUYt9tDRoYSg0HL1asi/H4H\nbW2ZrK5OY7FEkUjAZhOjUPgpLU1mcTGC0RigtFSD17uJxeIlKUnB0pIcodBDT08Jy8ubzM4GSU8X\nEYm4CQY9ZGensLIix+UK0tGRze7uOtPTEZTKANGoiHDYTmVlAVtbApaWwjQ1JaHTuZic9BAMOpFI\n5Hg8VurrS7Db/YyPiykqklJSomRmxoLZbEejkeDxWNFoFCQkKJmakiKT+Th6tJrZWRPj407q6hKQ\nSm3MzloRCvckRC6XkfT0FPz+KJubIlJThTQ3VzA87Mfh8PPgg+2sr2/S3x+muFhFV1cZ165ZmZ+3\n8NnPHsRu36a3101CQpS7726lv3+NsTETH/94FwJBmDfesOP3G/nkJz/KqVPjLC4GqajQIxKJGBw0\nIZOF6Ok5wPT0FKGQj4qKXCorK5FIbOTl7f3/9fS0U1KSjN1ux+fzcc89d2GzWXnppZOkpCSQkpLC\nQw/9nEuXBqmqKubEiVM8+eQFLJZlcnOz+O53n+TChXnS0+XMzs7y05/2Mzc3RWdnE4888jSnTy+j\n0QSIj5fz0EPPMTg4Rnl5HqOjozz88DN4vXYyMtIZGxtjYmKClJSU2J3MfSniPvE3GAz09BwgOzub\n+Ph4PB4TiYlCDh7sZHh4mKeemmBtbY2WlnI8Hg/Xr19HrVbHIljD4TClpUUcOFBPcnIy09PTnDq1\nhsvlprm5FIVCgc1mu0X6GBcXx9raAiKRh56eVvR6PZOTk3g8nluidBcWFpmZ2SYlRU5b26+JRkJC\nAkVFe8Zuq9XKd77zKGfPXqG0NCfmk5ibm6O/fxWhMER7e12MDCiVcsRiCz09zWRkZAB7kpT8fANF\nRWra2tpifxutVoteL6KyMp3GxsZbZCqrq1MUFCRz4EBz7PFXXnmTvj4vMtluLG43FArx4x8/wSuv\nnOXeew9z112dsY1LNBplfX2dd96ZwuOJcvBgHeXle+3mm5ubvPTSK3g8brxeB7m5Sdx99+1IJBI8\nHg+vvvoazzzzJjJZBJFIQHt7FQ88cD96vR6/38/jj/+CkyfPYjQ6CQTkPPhgOx/9aA+VlZUEAgFe\nfvlVLl26yPnzDjweD9XVWpqbS/nqV7+EXq9jYGCA48ff5sSJbYLBNdRqDUePNvGJTxxCJpOytbXF\nqVOTXL++TTTqQKtV86lPHSIvL5G+vuvMzEwyNCQkHHZQWamjvDyLqqoirl6dpbfXjECwjVqtpq2t\nhJycBC5f3mRubhmBIIpOt/e+DYd9nDtnwelcRaVSk5uro6QklYkJC9evu0hMdJOYKEGv1wB+rl8X\nEo2G6OxMRSTyMT/vwW4343KpKC/XUVycwOSknaWlXRQKD2q1mNRUPdGol2vXxMhkfo4e3dt+TE+7\n8XotRKMKCgqUJCZKGRsLYbUGKCgQo9MJsVgC7O5a2d5WYjDIaGnJZH7ezNSUB5nMgUYjJSVFi0AQ\nZHp6jzDceWc+R4920N7e/q/GRu/j5u3EuwnIze/n99qAvNf2490E5N3HfzcBubkEMxwO/38EZP+5\n3i3Lei8Eg0Hgg0M0fvGLX9DY2EhNzXt70D7E7xUfEo0/N7z7wvCHxntJkP6UCcY+9i+q+wPKb4vN\nzU0effQphoeHmJx0YjaHaG/PQiCwMDERJC7OQ1ycBLfbTGNjKTs7ASYmoKpKRUpKgIUFC16vB6FQ\nicvlprExn2jUT3+/AI3GT3a2jK2tZUBMJCJla0tAYWE8qakiJicjeL1O0tIUOByb6PV6JBIJU1NS\nkpLC1NcnMz9vZHvbhUolwet1k5amJCNDy7VrYoJBJ11d2aysTGM0Qny8AKdTiEYTprw8g5mZKOvr\nLhoaEvF6N1hf96FQCLDZZAgELjo7K1hZcTI66qOuTotS6WJxcYdIJEgkEo/H46StrQy328/gIOTk\nxFFTo2V2dpPNzT1zptdrQyQSkJSkZmFBhEjk4a67Wm+kxPjp6ckhMTHI0NAuVquZpqZ01tYmGR83\nkpenQyx2sbNjQigUIhZH8XpN+P0+9HoNTqcdcKDRqPH73QSDNgSCAGlpKfj9RqTSAOFwmKKiFGSy\nXba2LOTn51BXl4HRuE1//zCf/ORH0eulvPLKFba31/jMZz7OSy+9xenTM6SkiPH7/TzxxBDz84s0\nNZXyzDNv0N/vR6t1odWqOX16Grc7TG1tLqure5Ku1FQp9fXVXLlyjXA4SktLGUKhkJmZJVJSFLS3\nNzM8fB2Hw09NTTYKhYL+/jkEAgGdnXVcvnyNixe9SCS7VFYW88MfPkdf3xoJCXsN1P/yL08wOztN\ncXEhwWCQ7e1tFApFbFAWCoVUVJTT3FyPQqFAJBKxsTFNUVEara1NPProUxw7NkU4bKKsrASXy4XP\n57vRL6FAIpGQkJCARGKnoaGQiooKXnrpFX72szeJRJwx07VQKKS+vobu7haSk5MZGRnhRz96naGh\n69TVlcSiY3NzcykvT6OnpwOpVMr58+d5++1zpKYmx9rCjUYjp0+P4nRCVZUh5pVIT08nI0NGZ2cD\nBoOBSCSC1WolMzOTpqb6GMkYGhpiZGSE0tJSioqKYoP8Cy8cY2ZmloMHe2ItzDabjTNnzqBUKvn4\nxz9KY2MdIpGIYDCIyWQiMzONhAQ3PT2/NpI7nU5efPEdVlYEFBUpqa6uRiAQYDab+eEPH2N5eY2j\nR+tpaiqiqqoqdv07ffo0Tz+9RCjk4H/9r6/T0tKA3+/HZDKxtLTEpUujTEwIaWxM4+tf/wzV1XsS\nssHBQQYGBjh/fomtLQF33lnMkSP1tLW1IZPJuHDhAv39/Rw/voHDYaeiQk1TUwlf+coX0OsTGBwc\n5JVXTvP665vAJjqdkrvuauPTn74Ln8/L5OQkJ06MMz6+g0zmJCVFx9e//ilKS7M4ffoKMzMTTExI\nEYl8NDQkUlSURk5OOpcvT/H229sIhduo1Qra2srIz0/m4sVlpqeXgDBarZqDBysRiUKcPWvEbl9G\nLteQl6ejpiab8XEj1687USp3SUiQkpubjFQKg4NBvF4vDQ0JyOVh1tc9WK0WjEYlpaVqamqSmZ42\ns7joQCj0oFRKKS1NRyKJcOlSiEjETWdnOuGwh8VFFw6HDbdbSUmJAoMhnqkpH0ajh8TEEBqNCJks\nHo/HwdRUPImJe9uP9XUzk5MuolEb8fEKCgv1qFRxXLsWxOUK0tqqp6urhnvvvfeWLpXfBe9FPvZl\nUTcTEPiPya9uJh/vJb96r+3HzfKrm48VDAZjG5oPAh577DGOHDkS225+iD8oPiQaf254P4jGvgTp\ng0Aw9hEOhwkGg7810VhYWODYseNMTU3wzjtWXC43Bw/msbExxdpaFLUaHA4REomHxsZCFheDzM25\nqKlJIBIxsra2i1otxWKJJxTycPhwFevrG4yNhcnMFAJuvF47KSkJWCzxmM1B6uuTiUZNTE9HkUr9\nyOXxeL071NeXYjYHmJiIUlmpIDU1yMKCFY/Hg0ikwO320NiYh0AQpL9fgFrto6BAwebmMj6fgGhU\ngsUipKREQ2amnGvXgjgcVnJzVdjtq4TDcchkUpaXpSQlRWlqymRuzsHyshODQUwwuIPb7ScxUcnK\nigyBwMftt9ewtLTJ6KiPwkIJ8fEeNjeNCAQQCMTj8XhpbS0mEolw+TKkpEB7ezZTU+vMz1vJz1cS\nCplZXTWh1cbjdIbxencoKspiZyeAySShtFRLbW0ply458Xh8fO1rH2N8fJH+/iA1NXpaWso5e3ab\n5eUdvvrVe1lf3+KttxwkJUW4774jvPHGDBMTJu68swmLxc7rr1sIBLY5fLiT48evsbwcpLRUh9Pp\npK/PTFycj46ORvr7h3C7w9TU5JCRkcHCwiQGg4aOjlZUKgkKhYuennaKi4tJSIDa2lyqq6spLMyn\nqEhHT08HGo2G2toyWlrKKCgowGAwUF9fSFfXXplbdXU59fV51NXVkZycTE6OjtbWCvLz89HrtWg0\ne4lJGRkZjI+PIRCE6elpYn19nRMn1nE6d2loKOb551/m2WcvEAjskJWVydraGjs7O7EBXiAQoNPp\n6O4+EOuumJiYxGRyUFiYSFJSIo888nMuXbpGVVVxzAMhk8moqCgnLy8PgUDAm2+eY3zcT2JilMbG\nOlwuF06n80YHyp6symq1cu3aDDKZkM7ORuRyOS6XC5lMRmJiIlKpFJ/Px49+9ByXLrlITvbHmsA1\nGg1paQqqqzOpq6sjGo0yNzeHWCymsLAwZt5+4YVjPPnkqVsIj91u5wc/eJYLF4ykpERibebj4+M8\n9dQAi4s7lJenxkjDW2+9xRNPTLC2NkNPT2tsaPr5z5/hmWd6SUyU8uCDH4t9/+joKCsrK1RV5VNU\npKSjoyN2w2Vqaorjx6ex2XzcddeBmCdjfn6eX/7yJSQSIVKph7q6QkpKimIG4ccff5YTJ2YpKVHT\n1pbJwYNdpKamEggEWFxc5Mc/fp2JiR1qajTU1hq4++47ycnJYWlpif7+fp56agSTaZ3sbDk1Nbl8\n4xt/RUZGOlNTU7zwwhu89toqsIVWG89dd3Xw+c/fi8vlYmRkhNdeu874+A5KpYu0NA3f/OYXKCrK\n5IUXTnH9+jUmJyVIJEF6erKoqMglN3fP5N3ba0UiMaPTKWlvr6CgIIVz5+YYH58nGAygUik4eLAS\nsTjC2bObmEwLSCQa8vISaWkpYHJyi+FhOxKJHY1GTnm5AZVKTF+fB7vdSUmJHK1WiNMZwWq1sbio\noKgontbWdObnjSws2AiFPMhk8dTUGFAohJw/78XlslBerkGhiGA2+7BYbBiNKkpL5RQWqpiZ2WVz\n041cHkClkpCbmwL4GRgQ3Ni+5mK325mddeLxWBEKVVRUJJGcLOfqVTcmk5vCQjH19QV86Uufj22y\n/lD4TeRXNz//e8mv9vH7ll+9e+Z4v9KvfhNEo1EeeughPvWpT5GVlfV+n85/BnxINP7ccPOdjD8G\n9i82+yTjT51g7GOfaPymaVdTU1NcvnyZvr5BXn11h7i4XaqqEllZmcHtBpFIzM6OkOxsKQUFOsbG\nAuzs2MjJUWC3rxGNxqHTKZmZkaJS+ensLGB2dp2VFQ86nQi/341CISA/P5Xx8ThcLjctLalsbs6w\nsSEgISEOh2PvA7CpqZjFxQCzs26qqzWAmbW1XZTKOKxWJeGwl0OHKtnY2GRkJEJmZhSRyHOj1E+F\n3a7Aao3S0pKBROJkdDQIOFEqxXg8ZoqLc7HZQszNSaiqUpKbK2Z62o7VakOhkOLxWMnNTUWhkHPt\nWhxabZCurlxmZ1dZWXGh1QoJBj1IpWAwJDIzIyYUCnD33bWsrq4yNOQjJ2fv5zY3twgEQkQiYjwe\nD6WlGSiVCq5eFSCTebnzzgYmJoxMTXk4erQEhWKXq1dtuN0WmpoMbGzMMza2QlFRCiKRnZ0dMyKR\nELE4QDhsIxDwkpCgwuPZQSYLolAoCAR2iYtzI5UKychIQyCwkpAgRSqVkpOTQEJCiEgkRHFxMSUl\nWlQqMVtbW9x9923k5upYWlpBJpPy6U/fh8/n4ty5Phob66ipqeD48VMsLi5y++1H2djY4Nlnj6PT\nKSgrK+OFF15hYOAaNTUVeDweXnrpVUKhACUlJUxOTjIyMkJWVhbJycksLCwQDAbJz8+PDbY6nY7q\n6ipSUlIQi8U0NtbQ1lZDdnY2Op2OuDgLzc0l1NbWcu5cP8vLIbKzFaSmJvO97/2CixfHyMrSER8f\nz8zMDLDnm9gfSPLzcygvz6CurvaGIfo6ZnOU8vJkdDodV65cIRKJ3CIJyc7OIDNTSHf3XtLUd77z\nKKdPXyEvLzVGApKSkqioyKazs5GkpCTeeustHnnkZbxeK2VlJbHzcLutSCRODh5sR6/XY7PZCAaD\n5ObmkpmZiVAo5Ny5czzyyGlmZsZpa/u13OnNN88xMeEnJUVAQ0Nt7Jjz89MIhV66u5tjsbVyuRyT\naYHMTBVdXb+WUnk8HlZX5ygqSqepqT52XTh1qpeFhQCZmZKYOd1oNPKDH+xtlBobczh8+DBSqZTd\n3V1eeeU4fr+PggIdVVWZ1NfXx87zjTdOcuzYFtGonf/5P79BXt5eQeLs7CxDQ0NsbZlxOqMcOFDC\nfffdi1qtviEfe4T+/mEkkghKpZgvfOFBOjr2zv3SpUs8/PBJlpamUamk5OWl8A//8NdUVJSxtbXF\n00+/xMsvTxIMbqJQKLjzzgN88Yv3EwwGGBkZ4dixISYmzKhUbjIyNPz1X/8FxcXZPPvs6wwPDzIx\nIUYiCXL4cC4VFbmkp6dy4cIop09vIxabSUhQcvhwA9XVeZw9O8Xk5CLRaBStVsMdd9Qjl8PZs2ts\nbMwAKrKyNBw4UMj09BpXr+4QjVpQKuOprs5Cr5dz8aIDk8mCwSBEr5egUKjY2bExNiYhJ0dEV1cm\na2tGFhctuN0+RCIl9fXp6PUSLl1yYrEYSU8Xo9WKiY9XsrVlZW4unuJiCVVVOubmdtjYcCIQhJDL\nZVRVGZBKo5w75ycUctDWlk406mV52YXdbsPtVlFTk0B2torR0V3W1hwkJgYpLEzlb/7mqzQ1Nfxe\nCmt/F7yXPOrfkl/9R8zn7yYg795+3CzB+te6P97rOd4PfPe73+WrX/0qycnJ7/ep/GfAh0Tjzw1/\nzI1GOBzG5/PF1rcfBIKxj30D979HNCYmJlhYWOCZZ05w6pSRjIwwMpkHi8WESqXA7VZisURobjYg\nl7u5fj1ENOpEpZLgcGxRWpqPwxFkelpMaamc/Hwxs7MWrFYHUqkcp9NJZaUBpTKOvj4QCu2Ul2tZ\nXp7B4xEik8mx26VkZ8vIylIwPR3GbLaTnR2Pw7G3ddDpFMzOylEoAnR3FzI3t8bSkhe9fn/gj5Kf\nn8r0tBiPx093dw5m8wJLSxFUqjAej4i4ODcNDUWsrISYnfXS3JyMTGZjfn4X8BMMxuP3O+npqWF7\n28bgIBQWisnMFLKysoXT6UUgkOLxBKiszECnk3LxYhSh0Mnhw/ksLMyxvOxCoxHd+LuHyMvLYGZG\ngNcb4t57m9je3qKvz0dy8l7U7fLyJkbjLomJcgIBG9FoCI1GycZGEIHARVtbPbOzFtbWBDQ2Gigs\nzOatt6x4PLt861tf4PLlSS5ccNPYmExTUzknTiyzuLjJN77xSWZnFzl50kRycpSjR7t4+eURRkdX\nueuuVjY2jLz44gou1xq33dbFL35xjoEBI8XFWsxmM08/vcDW1iIHDtTw2GOvcuWKm9TUvZbi55+f\nYnvbSkNDAceOvcWFCx6Uyl10OjW//OVllpedlJToGRoa5le/WmNnZ4nm5mq+//2n6e3dJikpxO7u\nLj/60XGGh0dpaqrk0qVL/OQnz6NQiDAYDExM7PkqDAZDLK0pPj6e6uoq8vPzEQgEFBRkU1CgpLu7\n80Zh5HWi0Tja2iqYnp7m8cfPsrAwRUNDNYFAAKvVSnx8PFqtFrFYjFqtRqUKU1qqp6Wlhd7eXh57\n7DLz8xN0dDTe0kZeUFCASqXCZrPx1luD7O4KqKhIw2AwYDabEQqFJCYm3lSmd57BQQ8qlT/mdRAI\nBJSVldDVtefpWFtb49vffpz+/iGqq4tjcqu5uTmuX99EpRLQ2dkSG/Cys9PJyhLR3b1nIHc4HLhc\nLrq72+nqaiItLY1AIMCFCxfwer3cd99HaGqqQyKRsL29zdmzZ8nIyODee4/Q3NyAUChke3ubyclJ\nmppqKSpS09XVgVwujw1qY2NjCIVBuroaY6RqYGCAJ58cZn3dxOc+9xHq6/dSxCYnJ3n22ZfRahUo\nlV4aG0vIzs5GJpMhEol46KGnOXPGSnd3Fg8+eJDGxr0CwL6+PkZHRxkdNeN2i/jiF4/y4IN3k5SU\ndKOs8GfMz09js8WRkqLm7//+y3R3tyEUCnnssad4/vnLOJ0bQDxHjtTzhS98lPh4OVNTUzzzzHmu\nX98kPt5NSoqav/mbL1FeXsCLL55gaGiAkZE9wn7bbXnU1BRiMKRz7tw13nprnbg4ExqNgqNHm6mv\nL+bkyWtcuzZJMBhBrVZzzz3NqNVxnD27zNbWApGIjvx8PUeOVDM/v8Hw8A6BgAWJREF1dQZJSXL6\n+iysrW2h04XRasXk5WVgte7S1xchOTlIR0cmVquN5WUrdnuAYFBNc3MqKSlSBgcdbG9voFaL0GrF\nFBVlsrVl4+pVATk5UFenY3V1h40NB6EQiMUq6urS0Gji6O11s7trorBQiVotYHc3hMlkY2tLRXW1\nmoqKRCYmLKys2JFKfaSl6fi7v/srjh49+CdbUPebyq/+PfP5v0VAbiYfgUAAiWQvZvp3lV/9MfFP\n//RP/MM//ENsw/sh/qD4kGj8uWF/6P9D4maJ1D72B5Q/dYKxj32isd9gfDP25Rmrq6s8+uhx+vsX\nSUyMEgjYiUYDFBSkMzcnwe32cehQIUbjPAsLETSaCF6vENilqamUlZUws7MeWlpSEYt3WFiwExcX\nxutV4vO5OHSoGpPJxNBQlNTUMFKph52dbRSKeIJBDXa7kKamDNRqP8PDAfz+HdRqKbu72xQV5eB2\nh5maklJQEEdZmZK5OSNm8y4ymRS320NxcQp6vYz+fiGRiI2WFgOrqzPY7VHEYiFWaxxpaXGUliYz\nMRFka8tBcbHqhrHch1YrZXVVhkTi4/DhShYWjIyPu8nNlSAQOLDbHWi18ZjN8fh8QQ4dKsfhMDM4\nGEKvD5KUJMBq3SIcFuD3x+FwQHV1GmlpCs6fD+L32zhypIjl5WlmZhxoNOD3ewAXaWkpGI0ifL4I\nd9zRQCgU5tw5HykpQu64o4aRkRXGx7fp7MxHLrczNLRJNOqlsFCN07nNwsI66elaolEr4Ecul7O7\na0Ei8aNQSBAIorhcdlJSZCQnJ7O6uoxMFiE/34BYHIfJtEFRUQpFRQWsry8il4dpaqpGr9djNs9T\nU5NHTU01weAucrmHgwc7yMzMxO1ep7w8g8bGBlQqKTKZg56eA+Tl5eF2b5KVpaSrqx2pVILDsURb\nWxWlpSXMzEwRjXrp7GwgFApx9eoCUil0dDTwyiunGRgIolZ7SEtL4gc/eIHLlxfIydHgdrv56U+f\nwW63UFS0582w2+0kJSWRk5ODTCZDrVZTUpJJY2MxJSUlzM3NMTJiRKmM0txcw1NPPcfx4/0kJcnJ\nzMyM3ZnMyMggOzubcDiMyWRifn6ZlBQFra0NXLhwgZdffpOEBHVs46JUKsnKSojF146OjvKDHzzH\n2Nh1mptrY+QkIyOV9PQwBw/uSclOnjzF+fN9ZGVlxIjT6uoqvb2zBINRGhuLY5n3WVlZFBToOHSo\nHbVazfz8PAMDA2RnZ1NZWRkjGd/+9qOcOTNIfn5qzNcxMDDAT35ygcnJOerqft0ifuzYqzz99Dxm\n8xxHjnTFYsK/972f8MYbcyQnCzh69Chy+d6NgR/84CdcvDjIF7/4AEePdpCRkUEgEGBoaAihUIjT\nuUlubiLt7b9uJH/xxeMcP25CJHLwrW/9FUVFRcTHx/P66yc4ceIdNBoxUmmAQ4cOUFFRgUgkYmpq\nih//+BQLCxYOHsylo6OM5uZmfD4fvb29DA8Pc/GiF4UCvvzlI9x2WwepqakcO/YqTz11nK2tTex2\nGT09JXz600fJz89jc3OTn/zkONeuLSISuUlIUPHNb36OuroyTp06x+DgZfr6QohEXg4ezKG+vpiC\ngnzOnBng5MklwIhKpeKOO1poba3k9dcvMzh4Hb8/ikKh5r77WkhIkHDmzOyNba+a7GwN99zTyOLi\nBlevbuHxWImL03DgQD75+YkMDJhZXzcSHx9Bq5VRU5OHw7HLmTNe5HIb5eU6IhE/RqMDk8mP3a6g\nuTmRnBwlIyMW1tfXkUjEaDRSGhrysVqdnDvnIynJS1mZBrvdjsnkwu2GaFRDQ0MyyclSLl/eZWdn\ni6Skve1HcnIim5sWpqdllJfLaWxMYXbWyNKSlXDYj1qt5utf/wT33HOUhISED8xn3c34t+RX72U+\nv7mzIxwOv6f5PBqNEgwGYwTjT7180OPx8H/+z//hn//5nz8wnpIPOD4kGn9u+EMSjffyYEgkkt9K\ngvSngmg0it/vv4VoRCIRNjc3mZ6e5kc/Os716+NIJOB02snPT0KvV3D5sgihcJf29izm5yexWMJI\npXHYbEJSU0WUlKQwMRFie9tOWZkGh2MVm82LXq9kaUmGROLl8OFy5ufXmZvzkpwMXq+dYNBFfn4a\nq6sKvN4IBw8WYLevMDsbQqEI4vcLiUZ3qasrZH09yMSEj+pqNQqFg8VFG+Gwn0BAhc/noaurnN1d\nGwMDURITg+j1UWy2beLiJPh8MsxmAbW1ySQnw/CwH7fbSmKiDKdzi+TkJKJREdPTUgwGEQ0NqczO\nGllft6PR7MVLJibGYzDoGR6OA7wcPVrK0tIcc3N+dLoo4XCIuDgv+fkZLC3FYbOFOXSoiHDYytWr\nXiQSN3q9EKfTiEgkY3c3hNkMRUVqysoyuXw5iMfj5d57a1ldnWVoyEZ6ehxKpR+73UwwGMLvD+P3\ne8jMTEAsljI2FkAm8/HAA3dy8eIis7NBbr+9gqysZI4d28RuN/J3f/clLl8e49y5LZqbs6irK+Lk\nySlmZub55jc/y+bmOm+8MUFOjpaPfKSbt966wuXLo3zlK59ALhfyzDNnkUjCfPWrn6e39zInT/Zy\n992HKS0t4Je/fBW73cK7OAmNAAAgAElEQVSXvvRZTCYTJ06cpba2kq6uNkZGRtjc3OSjH/0IeXk5\nTExMkJuby513HiY9PQ23201n5wE6O/fiYdPS0igsTIrJfXQ6JXq9l56edlQqFUNDwwiFETo76xkZ\nGeGVV7ZwODbp7m7iscee4sUXe9Hp4sjM3PNmeDweMjMzY4QgJSWFjAwJHR1N6HQ6Tp68yMqKkIIC\nBXl5uTz33EvMzMxRWVkeu+Oenp5OVVUuzc11ADz66PP09XlRqx2UlZXidrsJBAIYDAaysrIQCoVM\nTU3R17eBSBSko6OBuLg4LBYLycnJFBcXo9Vq2dnZ4Sc/eYORESeZmSLy8vKAPblVWpqMpqY9crSX\ngnQKoVBIZWVlLP73+99/nJMnN5HL7VRU7BXg2Ww23n57CJdLQHV1Junp6cBe58/U1AR6vZzu7gMx\nydTuroOtrWVqavKorNw7hkAgYGhohN3dPWP+vr9jfX2d48eHMZnC1NRkkJubC8CFCxd49NFeVleX\n+e///b/Q3r63bRkbG+PYsddQq+UoFB66uxsoLi4mLi4Om83Gk0+e4Pr1ILfdVszXvvYFMjIysFgs\nPPTQT5mYmEIgCKHRSPj0p++PRSO//fYZnnxynEDAwm23FdDV1UBLSwszMzOcPXuOvr4xZmcltLen\nc++9LXR07PWrfO97T3Lp0jDhcBCFIp6vfe3jtLZWMzIyysDAAKdOOQiHd2lrS6e5uZy6uhrefruf\n11+fJhjcQi5X8ZGPHKC7u44TJ/rp77+GywUymYoHHmglOVnO2bOTrKzMYrEoMRhUPPBAC+vrWwwM\nrGC3mwmFVLS351JUlMTly+vMz68QFwcajZz29nLC4QCnTzsRi63k5anR6fZibZeXXWxuyqmpkZOX\nF8/4uJG1tXWCQQkKhZTW1jw8Hg9nzzqRy61kZMiIiwvh9QbZ2YnidKppbtaTkSFjZMTB5uYa8fES\ntFop1dW5bG/b6O8Pk50dpbk5lfX1HVZXrXg8QcRiDZ/5zEHuu+828vPzPzDt178pbjaH/1vbj31S\n8V7yq3A4/P8Z1d99/H9PfvVe6Vd/CPmV2Wzm5z//Of/4j//4gZpZPsD4kGj8OeL3TTRuJhjRaBS5\nXB6TSEWj0X91M/CnjH2iIZFIEAqF+Hw+zp59h0ceeYOVlSk8HhEej52enhrMZiuDgwKys4Xo9RG2\ntzcRCIQEgwoslgj19enodGGuXt0r0UtJkWO1rpGWlkYoBLOzMnJy4qiqSmB21sT2tgOFQozDYSct\nTUFamprhYTkCgZuurjyWlycxm8NIpSKsViF6PVRVZTAzE2J7201pqRq/34jV6iUxMZ7lZRnRqIvu\n7hIWF1eZnPSRkhIlEvEQDrvIzU1jbU2KzRamoyOLUMjI1FQQicQDiAkG7TQ3l7O15Wd8PEJtrYb0\n9DBzczu43U4EAjler4eGhnyEwgiXLkVRq33U1OhZXV3CYvEhEsXhckFuroq8vEQGBsLs7jrp7MzG\nZJpnedmHQgFerwCp1Et9fSkzMz6Wlrz09OShVHoZGfERCNjIzFSwu7tJIADhMNhs/D/2zju+zfu8\n9l/sQYKbAPfeU1wSl0iJkkzJluQhz9iOHce1HNttYjfXaUavk0/S9mY0tRuvOB6Kh+QlW3svapIS\nKVIU994kQAIgAGKv+wclXsU3q2mSJq3PX/yQAH4vAL7v+5zf85xziI6WUFSUQ1OTGaPRwSOPrEer\nnaKhwUR0tJiqqgR6ekZobx+ipCQOmczM4OAkCoUEWECh8CAUwsLCAk6nE7Vajkqlort7ApkMSkpy\n6OjoY3TUQVKSitjYaE6e7MLh8FNSkkpXVx8XLy6gUNjJyUnnk0/OMz7uIzMzmMnJSfbunWJhQU9l\nZQG/+MUnNDbaiYx04Ha7ee21c/T2TlJQEM/evYfZseMqZvMYWVnpS5qGtLQYPB4Pv/zlB+j1s1RU\nlONwOOjp6SErK4vS0mLCwsJQKpWUluZRVVVEXFwcAQEBeL3TVFXlk5yczO7dxxkbg7S0AMRiMT/9\n6XYuXGilsDAdWAy0k8vlpKamolarkclkJCZqSE2Vs3JlNYODg+zYcZmxMRP5+TEolUra2toICAgg\nISFhyX1KIvGiUFioqanA5XLxr//6OidPNpKSEoNMJsPrXcwyiYkRs2rVcmJiYnj33fd5990TCIU2\n0tMXMyjkcjnz81MEBXlYs6YGhUJBY2MjCwsLFBUVER0djUAg4JNPdvPee8Po9YPU1f2/xO2RkUHs\ndhMVFfkkJCTg9/uvhRpGUFAQR3FxMW63m0uXLqFSqbj55lXU1JSjVCrp6+vjwIFDZGSkc8cd9RQV\nLTpGnT59mnPnLrBhwxpWrsynqKgIv9+/dFyZmWpyciJZsWIFIpEIrVaL2Wymt3eE0FAZNTXliMVi\nvF4vb765gwMHDEREePmHf/g70tLS8Hg8vPTSGxw6dJbc3GiSk5XU1dUQHBzM2NgYHR0dHDkygsXi\nY+vWTdx223pCQkI4c+YML774MfPzU0ilQnJzE3jkkS8il8vp7e1l+/aDnDplZtmyQGprk6mvX4dG\no+HFF9/ixIkzzM97EYsDrgX+laHT6bh06RIffTSBw6EjPz+cysp81q9fy7Fj59i9uxWLZRKhUMXG\njStYt66Mo0cbOXfuIgYDiESB3HFHKXFxQZw+3cHY2CDj4wFERyu4995K5uZmuXRpkNlZPRbL4jHl\n50fT1DRCf/8IXq+AwEAlq1fnAW6OHJnFbp9EowkgKiqQhAQNXV16+vqElJQEkJUVwtjYPDrdLFar\nEoVCQUVFAl6vndOnTTidk4SFyQkOXtTDjYzYmJ6WU1YWRFpaIF1deqampvD7ZahUMlasSMVstnH8\nuJWwMCs5OWE4nXZ0OjNGowe3W8XmzYXccksVy5cv/x83ZvO7xOdCoXCJGFx//HWy8IeMX/069yv4\n9d2P6wTkD+l+jI2NsWfPHp555pnPicafB58Tjf9u+GN2NH4dwQgICPiVEalf1xn4a4HD4UAqlbJ9\n+4e8884BjMYpRkZALLaydm0B/f1aenutJCcr8HgM2GxWEhIiGR2VY7O5WbMmE4NhlJ4eD0FBHrxe\nAR7PPMXFWUxP++jtdbFihZrgYAv9/SbcbjterxKz2UhpaSpWq4XWVhkxMQJiYyXodBP4fCJcLimz\ns0Ly8kKJihLR1ubCYplDo1FgMk2hVkcikUjp6VEQEyOkoiKOwcEZZmZsqFQSHA47kZEyYmKCuXxZ\nhMUyT0VFDFNTvUxNuVEqBczPSwgIcFNWlkZ/v4O+PjP5+UEIhXOMj88TECBmbk6Jz+fkppuWMTk5\nTUuLh4QEAQqFA5NJj1Ipx2SSMz/vp7IyicBAFxcuOHG79SQkKJmfn0AolOB2C5ielpKeriQ3N5rm\nZhMjI1oKCkJxu3WMj1sJChJhNosQiazU1pbR12emv99DfX0marWAxkYDs7PTLF8eh9E4Rk/PJCEh\nMhwOJzKZA41GzeCgGbvdT01NPm63h+PHrSiVDp544n4OH27n4kUdGzcWEx0dyOHDQxgMMzz66K0M\nDQ1x7FgbNTUF5Odr6OwcQK83UF9fSni4iNHRcXJzs8jOVqFWh+B2u8nKiiE1NQC1Wk18fDxKpYnl\ny3NISkpEJHKjVFpZvbqaiIgIBgc70WiUrF5dzejoKFNTBjIy1MTHx3L0aDNms4D8/BgGBgb46KNR\n9PopVq4s4sUX32L//l7k8gWioqJ44413aW1tp6SkkICAAIaHh4mKiqKqagUpKSmIRCKSkqJISwug\nurqa+fl5Llzowe/3UViYytGjJ9ixo5n5+QlWrqzEZDIxMzNDSkoKaWlpyOWL5MtimSA5OYSVKyvZ\nt+8A27ZdZnKyh5qaCmDxnE9LS6O6esW1YEQtJ0/2YLcLKCpazLro7OxEKBSSkpJCYGAgbrebQ4ca\n6OtzEx0tZNmyAhwOBy6Xi7KyEqqrVxAUFERTUxOvvdZAR0cPpaXZS9oMh8PG7OwwpaWZ5ORkY7FY\n0Gq11NRUU129jIyMDEwmEy+88BpnzjSxenX1km1tQ0MDr712lp6eTurqKpbGs95++yN27dLidk9R\nW1vJ9aTuF1/8iAsXTCQkCJe0El1dXbz88iGuXBlhw4YKyssXycT58+d56aVdLCwY2Lr1LurqqlEo\nFLS0tHDw4GEiIoJQKBysW1dBYmIiVquVqakp9u+/yMQErF2byz33bEGlUtHV1cXzz3/E0NAYFRXx\nFBcnU1lZgdFo5NSpU3R19dDe7kajkfOtb22lsnIFXq+Xf/3Xn3PwYA+RkW7Uaim33lpPRUUFhw8f\n5cyZc3R1LWC3S7nttmXU1ZUQHBxMS0sLb799FaNxnNhYJcuXZ/P44w9z8uQ5du48y9zcJE5nADff\nXER9fRkXL16hsbGZyUkfPp+SW27JISUljPb2IcbGhunulhMeLuTuu0uw2620tQ0yMTHH7KyK2tp4\nSkvjaWkZpr9/GLtdhEIRwJo1Ochkfo4fn8ZoHCEoKIjYWBWFhSm0t8/Q3OwgPd1HYmIAZrMdg8HA\nzIwMiURBTU08crmX5mYLVus0SqUKjUZOWpqa3l4Tvb2QmSkgMVHO6KiRiYlJLBY5crmMiopEPB4n\np05ZEAp1REcrUKnEgIDxcTt6vZLVq+O46aZi1qxZs0R2P8evFvQulwu3241IJEKhUCzVBb9t/Op3\nZX9cX+NPOX7V19fHmTNneOKJJz7/Xv88+Jxo/HfDH4No/D4E48b1rncG/qucN/4QLIZevU1DQyP9\n/RP094tISVm0Tu3rm2dmxkBoqAyLxUBUVDBRUcFcuiQGTKxbl8HAQBczMx4CAkSYzRAa6qegIJGu\nLg8TEyaKiiKw28eZmrIRFiZjYkKG12uitjab0dFp+vv9pKUp8fstOBwWYmLCmZqSYzC4qa1Nwe2e\noavLg0zmQCgU43QaKCvLQat1cfWqj2XLgoiJ8TIwMIvNZkUgCMBmc7B8eSpSqY/GRiGBgXYyMoLQ\nakfweMR4vSJmZiSkpMhISFDQ0WFnZmaWqCgpNpsWiURKcHAAXV1yVCo3a9Zk0d8/ysCAlbAwAR6P\nA6nUQ1paLD09QiwWF+vWpWM0jtHV5USpdAICwEJhYSYTEx6GhnxUV8ehVnu4fFmPwaAjKEiEy2Uk\nISEWj0dAX5+ExEQZVVUZtLfP0d2tY9myMMRiI93dk8jlAmw28PkWKCvLZ3BQT3+/iKqqePLzEzl1\nSsvU1Bx33LEco3GcCxcm0GhkJCVJsdmMTE/rkEh8gI3QUAUikYjBQQOBgVBeXszZs1eYmIC8vAiC\ngoLYt28Yo9HC5s21HD/exMGDBoKDbSxfXsK2bSdpaRlmzZpijEYTb799HoNhgkcf/SJ79hxh795T\nrFlTQXl5Cfv3H8NsNvHoow+QkhJPR0cHFRUrqKjIIj8/F4VCQWqqhoKCWEpLSwkICMDhmGD58ixy\nc3O4dKmV+XknhYXxuFwuPvjgCtPTFvLzYzl37gJvvHESrXaYsrLipfC+nJwcMjMzkclkhIaGEh8f\nRElJJklJSQwODjE4aCI6WklhYS4//vGrHD58BbVaRlxcHFarFalUyvLlJRQVFSKRSBgfH2d4eJqk\npDBKS5fx1lvv8PHHh4mLi1gaxQoLCyMyUsKyZYmUlpbS0NDAtm0XGB8foK6uemn+OyEhivh4EeXl\ny7FarfzkJz/nyJFzpKREo1Kp8Pv9WK1WOju7CQuTsWpVJX6/n6GhIbKysli3rpq8vBzcbjc//enP\n2b//MhERiza3AENDQ+ze3c7cnJu8vGg0Gg0Aer2enp4hIiIUvyIgd7ttmEzj1NQUk5ychMu1mK9i\nNuuQSKysWbOSsLAwbDYbHo+Hzs5OAgOFrF5duUSArl69yoULWmQyNxs3rkUkEmGz2fjFL97n+PEF\nMjIC+frXnyQ+Ph6LxcKPf/wqDQ2trFyZQWlpLFVVVfh8Pk6cOMHw8DBDQ0YkEiFf/vI9FBcX4XK5\n2LlzDzt2DKBUOtiypZg1a6qJiorinXd28PHHh7BaLbjdUjZtquSRR+5nenr6WiBfP1qtk5qaaKqq\nsqiurqazs4tf/OIU09N9BAQoyc1N5BvfeIKOji527NjP6OgkBoOSdesyqa8vZnR0ivb2q3R22nE4\nJNTVJZCZqUavtzA2NkJTk5+AABe3356HTCZkbGyW3t4pRkeVVFerKSuLoadnnIGBEQwGMWKxkptu\nykKlgjNnptHphhCJgkhICKGyMpOurmkuXDCjVttQqyUEBirwel309wtwucTU1kYREODlypV5jMZJ\nPJ5AoqJkFBTE0t9vpKPDR1KSh7g4JV6vH4vFgk6nQCJRUFERhVDo5MIFMwsL46hUSiIjZcTGhtPX\nZ2JwUEhZmYra2kw2bdpERkbGX9U97c+B6xMMN9YG18cr/xzZH3/o+NWRI0fYs2cPJpMJnU5HX18f\njzzyyJ/98/sfit9JND5XyvyV4T/D0D0ez9Iuo1AoRKlUIpPJfutr3ri78NeA+fl5du/ej8fjpLl5\nGrtdwoYNCQQHj9PevkB8vIWgIBUWyyw1NZW43Z2cPOmirk7GypVSenrGuHp1EKVSjcHgJidHjUbj\n5PRpC0bjAJmZwQwNDWI0KggJCaetTUhYmJtVqyI5c0bH6dMDaDQhzMxY8PtDWbYsnkOH5nG79dx0\nUzonT57n3DkBkZGLI11ut4OqqnSOHPFy+PAoy5eHIZVO0tZmJDExGK83HKPRwoYNhZw8eYlDh7Qs\nW+YnOdmB2WwmOjoMmSyRsTEBa9emMT09Q0eHi6ioBTQaOWazloSERMxmO42NPlau9LBuXQDNzVOc\nPt2OUqnEbLYRFaUhOlrAwYMWTKZJ6utTOXfuIufPg0Ihw+sFoVBEdXUSR47A0aMjVFSoGRgY4ty5\nBTQaIQKBFJfLzKZNVRw+fJlDhwxs2hSBRuOktXUCvd58zcbXhFSqITIygvZ2K2FhPh58sJa33z7M\n9u2XWb06jujoWRoaFu1ao6MFuFwWTCYTYrESo9GFx+OjsrKEl146ztiYjqef3kBzcxuffDJMcXEA\nTz65ng8+2MdPf/ouGzaUoNfraWvrJTU1jk2bkllYMNPe3k5eXjILC93Exkbi8XgICxPh8fgIDQ29\ndkNbJOZWq5XRUSMzMwImJycZGxvj6FEt0dEzVFVVsG3bR1y54uD227WsWbOKH/3oNQC+9rWHUalU\nvPPOdgoL83j66ccxmUyMj4/z+OMPodPpSEpKwuFwcNNNXUilEpKSkmhubsVuB5vNwfz8PG+8sQet\ndvE8XbZsGbt37yM4WMXatWtQKBSIxWJuv/1W8vL6lwTeDocHh2Oxszc4OMgrr3xAaKiSp59+bGnX\nv77+JvLyclGr1deSwycYHRUyODhIeno6ly9fRqFQUFlZuXSOLRYEIBYvFgX9/f0MDw9TXl5Oeno6\nfr+f4eFh9HovNpuAmZkZNBoNZrMZjUbD00/fvxQo+N57H3DmzDirViXz0ENfABavNQsLTqxWsFqt\nS+ump6dz552F+Hw+MjMzMZlMXLp0ieTkZL7znS8RFBSEVCrl6NGjnD3bzm231fHDH/4DAoEAu93O\n88+/hl5vZevWu/jiFxfXGh0d5eWXd6BSyXjmmS8RGBhIQEAAV65cYefOoxQWpvLEE1VER0fjdDrp\n7OxkbGyM/PxkfL4RCgtzgEU73OnpafR6JxaLkMTERFasWAHA6dOn2batZen/PD4+HrVazbFjx9i3\nrwm1WkRioo+CggzWr19PZ2cnhw4dorl5iPFxCfffX0BhYSFRUVG0tbXx6quHAQdpaUoiIiK59957\nuXLlCs899xIikQmPJ4SYmEQeffQ+WltbeeWVN+nqGmNyUsXGjWmkpKRgNpu5cuUK584ZEAi8lJeH\noVKpCAhQMjw8ysmTbhISLNx6axYCQTgm0wJXrkwwORnIqlURVFZGMD2tZ2aml/FxEVKpig0bUpif\nN3Hq1ACgw+nUkJwcy/LleTQ0tPHRR12EhZmIiwshIWFRV9PYaEEs9lBZGY7NZuPKlRl8vjnMZg0J\nCaFUVsbS1NTLkSPTaDROkpJkBAcH4/N56O9fdO1bvVqDyWShudmISKQjMDCamJg4UlJiuXBhiLY2\nA/n5PvLzQ9i0qR6NRoNIJMJuty8VytdzKv4nw+PxYLfb8fl8Sw5Tv+szuV4f3EjYrtcKN5KL6z9/\nto64kWDc+Ho3/v36d3QjPttFaW1t5aWXXlq6XshkMmpra8nPz6egoID8/Hzy8vJ+7Xic0Wjkqaee\nYt++fQiFQrZs2cILL7ywtNnwm/C///f/5vXXX2d+fp6qqipeeeUV0tLSlv7udDp55pln+OCDD3A6\nndTX1/Pyyy//iuXu77P2r/tMduzYwd133/1bj+8vCZ8Tjf8B+EMIxmfx58zu+EMwMzNDU1MTVquV\nvXuHCQ72UVamoa2tk4sX3cTFyfF6F3UT69YtY9++ZnbtGqCoKAibTcfgoJuMjHj8/ngmJ13cfHMO\nTU2tnD5tIDPTR3T0oqg7KSkDrdZOc7OD1asDWb58np4eEw6Hi/DwCCwWMzk5eSiVU5w+7aO42EB1\ntYqrV0e4elWGUhnOzAxkZgYRG6vg1CkvFksfKSkBjI6Oo9MJiIwMo7/fS3Cwg82bczl0qJFDh3qI\niJBjtdpwOEQsWxbP8eNzdHSYqa1NoKWljQsXPMTE+JDJpDidVmprl3H8uJ/jx/XU1EShUhkYGdGj\n0TgQicIxGm2sXp1Jd/cQhw/Pk5fnJi9PyuzsLJOTKqTSMKanhaxapSEhAc6enWNuro+UFBWTk5NM\nTYmQSuXMzCxqW7ZsKWD//kvs3NlOdnYAQqGBzs4F4uJC8fmCMZtt3HNPDUePXuDTT2dZu1bJHXdE\ncvFiN7t3nyQkRIrPt6ixCA8Po7HRi0Lh4Mkn7+NnP9vO9u39bNmSQHKyj7Nn+5iZMVJRoWZ6epqz\nZy8ik4kIDwehcDFDxW4XYTIJUKlUuFwumprGmJ0d4LvffYJ/+ZdXOXbMwEMP5fLFL27m5Zc/5ezZ\nTp588gtcvdrBz372DjfdtJxnntnA5OQkFy9e5P771zI3N4darUahUFBdPUhcnJqwsDCiosKZmpok\nMjKM+fl5DAYffv8i8W1svMSHH07S3z9NTk4O//Zvv0CrdfHww2vIzs5m585PCQ8PXSp+rVYrmzff\nQkZGDykpKSgUCqKiVPj9FoKDgzl//jy7d4+gVguorKygt7eXM2eaWbOmksLCwqVz4m//9gHm5ubI\nz8+nqamJ6enFESWz2UxXVxfHj19gzZoKSktLgcWb8333rWF8fILy8nLa29t59dWjKBR+vvWtsCXR\n9dq1a0lMTCQ6Ohqv18tbb31KX58fh8PBbbfdhkAgICUlhUcfrcdut1NZWUl7ezvbth0gPj6Er3zl\nYWDxRmw2L7Cw4Fmyq73edXj88XvR6XQsW7YMnU7HG2/sQKVS8uUvP7AUwrlv3362b+8mI6OF73//\n60vFyJkzV7h0yU1CQjtFRYuZG2azmcnJBQyGReJzvUui1WqZmvIRGGjH7XYv3eDb2zu4dMmNw9HN\nP/7j3y4VSJ98cpKeHgEPPpjG//k/iyRGq9Xyox+9gcvlZ/36QkJCQiguLmZiYoIPPtiDTCYgNlaA\nWh1MWVkZVquVc+fO0draxcCAkJiYQP7pnx5CLpej0+l4/fVdzMwIqKgIoapKQ11dHVarlR/84GXc\n7gUkEjEqlZInn/wyBoOBbdt2oNdrGR4WkZsbyt///QYWFhZoamri8OFWxsZkrFoVxurVCYSGLro0\n7d07ALjIyJATHh5JenoS/f2DfPzxFLGxc1RVxRMZGUF0dASHD7cwOiqnrExGZmYQEsliSGNXlwOx\nWMSqVYuBg5cuDeL3m5idDSM1NYKNGws5c+YyO3e2I5PpCQ6OJCdnUWzd0DALOMjKUgICpqbMuN0m\nxseDSU5WccstcVy61M3Ro2MEBi5q1VJSYhEIBDQ1WRGLPZSXh2K322lvn8Xn0+FwRJOQoKawMIXz\n57vZv19LcrKH6OgQvvjF+0hJSfkVhyW3243L5Vo6X27csf9sTsV/Z/h8PhwOx9KYVGBg4H+q0/Ob\nSMONZOM6Abmx+3EdN45nXf/sfxcB+c53vsM3v/lNRkdH2bZtGw0NDURFRXHixAleffVVvF4vACtW\nrKCxsfFXXusLX/gCWq2W48eP43K5ePjhh9m6dSvvvvvub3yPP/zhD3nxxRd5++23SUpK4jvf+Q71\n9fV0d3cvmQl87Wtf4+DBg+zcuZOgoCCefPJJtmzZwpkzZ/7Da//yl79k/fr1S3XYjVlHfw34fHTq\nrwzXrRl/H3g8nt97ROq3redwOJZamX+p+PjjT3n33X6cTi3JySpmZgYQCGSAmIkJBUlJUnJzI+jp\nMTE5qScyUsbCwhyhoUoSEyNpaRHj91tYvz6HgYFOxsbcBAeLsFh8BAZ6KCpKo7fXy8iIiWXLwrDb\nRxkbsxIaKmN+XoXPZ2PDhjJGR6e4fNlJYqIIodCC2awnLCwEo1GBweCjujoJmcxCW5sDn8+EUinB\nap1l2bIsjEYnHR1iMjPlZGcr6eubRq+3IBZLsVqdZGdrUKvlnD3rx+3WU1ISw9RUP2azH4lEjFYr\nQa0WUlKSQHe3hdFRE/HxUlyuWRwODxqNioEBBSKRm40bixgfH6O314NaDT6fB4HASnJyDGNjQqan\n3ZSXRyOVGmlvX8DjmUcikeF0zlNSksnkpJn2diF5eYFLIvipKT1KpRSnc4Hk5EjCw1U0NvqRSBzc\nccdy+vr6uXJFj0YjQiCw4vPZCQwMZHJSgN3uY9OmFXi9Do4eNaNSOamrS2VwcIgrV4YID5fi99tQ\nKhcD2fr6bPj9Hu677xauXh3m5MkFsrODWL9+BQ0NvVy9OsymTWUEB7s5ffoqwcEK4uOlhIWJsdls\nOJ02vF476ekxCPW3RtwAACAASURBVAQCmptHEQh8rF69nKNHz9HY6CQoyE5hYS5vvHGcy5enqazM\nwOl08uabp9Dpxnj66cfp6+tn796j3HxzHevWrcDlciGRSMjLi6O4OJnc3FyEQpifH6GqqoCEhHiO\nHbuAyQR5edFMT0+zbVsbIyOTlJSkc+zYCd54Yy9KpY+amhpmZ2fR6XTU1a2kpCSL6OhoAgIC0OtH\nyMyMorJyBe+++ynHj1uQSg0UFxewffuHnDt3kZKSQpKTkxEKhWg0GsLCvJSX55Kens777+/m2DEL\nIpGeysoyWltb6enpYfny5RQUFKBUKrFarVy50kFgoJja2nK6urp47bUdCAQeysrKkMvlCIVCBgf7\ncTotVFYWEhYWxocf7qSrq4dVq2pJTU1FKBTS1tbGmTNaRCIna9ZUIJPJsFgslJQsIzMzlJUrK3G7\n3Tz//OscOnSezMx4MjIylvIs9u7tR6+3UlSURGhoKAKBAL1ez8jICCkpkSxfXoLVamVycpKEBA1h\nYQ5Wr64mNDSUxsZGpqenKS3NJDc3koqKCiwWC7t27UEggOLiBMrKMsnOzmZwcJD9+w+i0USi0Xio\nqCgkJiaGoaEhOjs7kUjA77dQU1NKTEzMkk12e/sobreA+vpySktLMZvNXLp0iV27xnC5bDz77MOs\nXbsKqVTK66+/y8cfdxMVJWTdunTq6lYSGhrKCy+8xqFD55BKPchkQu64o56yslIOHDhMS0sLAwNO\nRCIpW7feSkVFEf39/TQ0nOPQIRPBwW7uvLOIoqIchEIhH354nNOndSQn+0lPD6GysgyFQs7771+k\nv3+c8HAf8fHBrF+/CpPJxPvv92A2jxEVpSQ7O56KiiJOn75KQ8McUVF2oqPlJCdHI5UKOXdOj07n\nYNmyQGJi5MzPO9HrZ+nqkqNWi7njjmKmp2dobZ1mYUGP3x9IaWk8ycnhXLgwy8jIHJGRHkJDxYSG\nhmC3m2ltlaBSLYYGarWz9PZa8HgsiEQq8vM1xMYGcfGimampBdLSxISHi5ibs7OwYGRyMoDISAlr\n12YxNqaludmMTGYkLEzJgw/exv3330l4ePivjOVIpVJkssUQz8/mQlzXA7hcriWdwo3Wr/9dyMdv\nGpP6U2kxf9/sj+vH9h8dvxIKhYSGhnL27FliY2N54403ePLJJ3n22WfZsmULlZWL1tLXN1YAenp6\neOaZZ9i/fz8lJSXExy9ed771rW/x2GOPLVlkfxZ333033/zmN3nooYdQq9XcfPPNPPfcc2RnZ5Ob\nm4vZbOYLX/gCr7/+OuvXryc6Oprq6mq+8Y1vsGHDBmJjY+nu7v691v7e977Hww8/THFxMQEBAUvd\n4L8gfK7R+O+I3zXG9McgGDfC6XQiEon+oonGooXlKMuXZ7F583rOnRtlfNzDunWZKJVGurqseDwW\nxGIFCwt6KirysFqdXLwoIC4O0tLkjI2NYTY7EQjkzM/7yMoKIy5OycWLbubndSQmKtFqB/B6RQQF\nBTI2FkB4OFRXp9LbO83QkImwMCFOpxmp1E96eixdXWLsdidr1qQxM9PH0JAHlcqH1SpCJFqgsjKP\nkRE7HR1WSkvDUShMDA/PIRL5sVoDcDic1NXlYbHouXTJS0iIi6AgHwsLswQHB2GxiJicFFFcHEFc\nnJirVxcwGmcJCZFjtc6RmhqLTCajpUVEaKiHmpoE+vuHmZhYQKEQYbf7iI1VkJERTVubH7PZRnV1\nPCbTCJOTLpRKHwaDBKnUTkVFFgMD87S2WigsDCIoyMb4uAHwYLMpcLudrF1bhN1u5dQpB+HhbvLy\ngpmcHEOrtQBCrFY/aWlhpKfHcuaMHavVyq23LmNqaoDW1jmCg70IhW7EYjvh4aGMjtoxGuGmmwpR\nqwPZu3cOt9vI3XdXMjIywPnzfSQnBxMY6EQodOH1epiamsfv91JSkoVWa+DcOTuBgU4eeuguPvmk\nkcbGGTZuLCEjI5bdu1vQ62e49941SKUempuvkpeXSmKiiNhYNRKJBJ1uksBAWLWqgomJSa5c0aJS\nQWlpAW+9tY+rVz0kJgrx+Xy88soxrl7tZtOmOsbHx3n11Q9JSFDz5S/fj8vlZGpqilWrVlBQEEtZ\nWdk1nUQ3KSmRVFeXc+DASdrb3dcKwWh++MM3aWjoID4+mIiICJqamggMDOTOOzdTUrIMkUiETCZA\nJNJTV1eB2+3mnXfO0NdnJS1NhVgsZseOnZjNRtauXUts7OKusEIhRio1sHp1OUKhkOef/4ALFyaI\njZWSkJCAVqslPDyciooCamtXEBISwp49hzh2zAzMUVtbgU6nY3JykjVrVlFTU0xqaiqdnZ28885F\nhoYM5OZGERkZidvtJiYmBrXat+RQ9eab7/D++w0EBwuoqakhICAAq9XKkSPNzM+LKSiIJjk5GavV\nSnBwMAKBnuzsKHJzc+np6eGjj3YRGxvNrbeuoapqBQKBgOeff409ey6Tnh7BnXfeTlhYGCMjI7z4\n4l5aWiaoqsqiqqoKsVjMuXPnePvtTiYnp7j33lvIyMhAIBCwfftOPv54Er9/lq1bH1qyt33++Xc4\neVJLTU0Kjz32IAkJCQwNDfH88x/R2TnGli2V1NWVkJOTQ3NzMy+88D5ms5G8vHBKSzMoLi6isbGR\nDz7Yi8OxgN3uo7g4hS1b7mBgYIDm5mYuXx5HpxNx110V3HffZmw2G5cvX+bjj/swmx3ccksWK1cu\nEp+jR0+xY0cXIpGRnJwwamtLKSsr4+23d3HsWC8ymYWQEBl33FFPXl4mb711iLa2DiQSP+HhKr78\n5bvwel28995FtNp+FIpAsrJiufPOes6da+fYsWFkMiMhIQpKSzOJi4vkyJFRRkcNJCWJ0GgUhIeH\nYjQaOX/eh1Lp5Pbb8zCb5+nsnEKvN2KxBFJREUdOjoampimGh6eRy90EBYkpKEjG63Vy8qQTsdjC\nqlXxWCwGhodNWK1W7PYgSkujSE0No7lZz+iogbAwNyEhYkJDg3E4LLS3ywgK8nLzzZnodHquXJnH\n5ZpDLlexZcsqvvjFLSQlJf3W+8b14vdGVySZTIZUKl1yX7quC7hOQJxO55I24Hrxe/2++tdCQK7X\nCG63G6lUSkBAwJLW6s+N3+V+9Vli9+vCB6/D7/ezb98+IiMjWbVqFQBisZjo6GgKCwt/hWQA7N27\nlzNnzvBv//ZvS79LTk7mn/7pn6iqqiIrK+v/O97h4WH++Z//mR/96EdLOjGZTMaxY8fweDysX7+e\nc+fO8ctf/pKf//znS6GPERERvPXWW8TFxVFeXs6+fft+r7W/973vcebMGf7lX/6FnTt3IhaLlzq1\nfyH4XKPxPwnXZyzdbjdCoXDJqvI/e/G4MWH0LxU1NTWUlpaiUCjw+/3ccUcJ09MzrFu3jsbGJnp6\nrhIYqOCBB9bxwgsfsHv3CBUVgTgcc/T1zZCRkYBIFIdW62LDhhza2jo5fdpEVpaP6GgPZvM02dnR\nBAfH0tcnY/36YCIj3bS0TGG39xAcHIDBYKSoKI2goAUaGty4XDrWrYvlwoWLtLQIUSqD0esFyGQy\nVq6M5MQJD8eP95OSEsDw8ARDQ040mkB6euQoFDY2bizmwIEzHDw4SGKiiIgIBwsLTrKz0zl9WkR7\n+wJr1iTR3z/AxYsuYmL8BATIcDj01NYWcfLkFQ4enGfdOgXV1TA0NIHP50UuD8NsXiQd0dEmzpxx\nkpQ0SlFRBEND/YyPK1AqQxkYkJKaKqG+PoKjR3s5dqyXqCgJQqEBnc5LaKiSri4JAoGN9etLOXLk\nPB991EFWFiQmupifdxEeHoTPp2Fy0sfmzXmMj09w6pSRxEQtZWVhTEyMcPXqACKRAotFQGBgIBs2\nJLN9exszMyNs3JhDR0cXu3e3kJwsJzXVi1i8qFvweGTMzgqIjIwgIyOdV19tIiJimL/5mw0cOXKK\nN988xYoVGu69Nw6tVseBA0eIjlYglVqx2+04nU5MJggMdJKRkcH27Yfo7hai0YRQWlrEz362B6n0\nCl//+gP09/fz/PNvs2pVAU8/Xc/8/DyXL19mw4YSxsamyc3NxeFwoFL5CQqSIJfLaW3tpbtbSEJC\nL5mZGbzyyi7sdgFPPrme4OBgfvzjl8nKSuS55/4em83G5OQkd911C9nZHRQUFFzbKPAhFgsJDg7m\n0qVLvPXWVZKT2/jBD1K5evUqXV29rFmziv/1v54EwO12U1eXisViIysri3PnzrFv3zRJSZOUl5cz\nPj5Od3c3lZWVfPWrW4HFgKuoKCUymR21Wk1raytvvHEAtVrBs88+gVwuB2D16iqEwvOUlS3DarXy\nwgvb0Ok8PPLIaioqFh2rUlJSKCuLQCwWkZCQwKVLl/jgg6OUlWVwzz13Lp2vU1Nz6HQwO6sHFkeY\nfD4fjz66kfn5ecrLyxkcHOT11z9Fo1Hxd3/3N0il0msp6M3s3atHqz3Ns88ufu4ejweTaQGLxYvF\nYsHtdi+J36OjpTgcHtRqNS6Xi/b2doKCgsjLExMXpyYkJISJiQna2trQaELIyZlmxYpiVCoVbW1t\n6HQ6YmOD8fnmiYuLQywW09jYiNFoRCTyIxBAWloaarWatrY2+vv7mZ4WIJd7ePbZB/H7/YyPj3P4\n8AUuXnRz221qHnhgHZGRkYyMjLBt2zFMJj9r1sQSExNDZWUlHR0d/OIXx5BKreTkhBATE8PmzZvZ\ns2c/b711gqAgC5GRKgoL87jvvrv493//BXv3nsPlsiIWB3PrreuJiYnhl7/chdVqxG5XEBAQzOOP\n305fXx8vvvgJQqEerzecxMRkbrttPR98sJcXXtiFUGggMDCClStXEBAQwK5dV/B4FggJEaJUKigq\nymJkZJxdu3QkJJi4+eZ0rFYRnZ0jjI/PMzsbSn19GiEhIZw/34fDMQxICAiQU16ehk43y86dM0RF\nzVFREYvdLmV4WIvB4MZgCGLVqnBCQkJobBzB5ZpGIvETECAlNzceo9HAqVM24uNd3H13GgMDw5w5\nM4jDYcTt1rBhw0pWrFhOfHz8H7wzf6Nu4MbNteuE48Yi1+Vy/cq98bOjV9d36v9S8Mcek/pT4T86\nfnV9ysPr9dLc3ExdXd3vtc7MzMyvaCZg8TsMCwtjZmbmNz5HIBAskYzr0Gg0S8/RarVIpVKCgoJ+\n42N+37W///3vU1dXh1Kp5MiRIzzxxBNYrVaeeuqp3+s9/iXgc6LxV4jPFv5/KoLxm9b7S8V1gatA\nIODmmzdgNpsRCoWsX19PQkI88fHxBAUFkZ0dw8zMPJs3b752Q+8kIMDOPfeU8vHHBzh2bICYGAky\nmZP5eQvLluVw+rSIpiYjdXVJdHf309KyQGKiApEoGJPJyM03l3Pq1GUOHjRQVSUhN9eF0ajDYAhE\nJotlctJPXV08UVHzNDdbiY4eIiYmgLm5aUJC8lGrNbS0QEgIbN6soaGhnRMn2lGpVMzN2VGpgikt\nDeTQIQMLC5NUV8fR0tJGc7ObsDApdrsYt9vO2rXpHD7sYNeuXvLygvD79QwOzpOQEInTqWF21kV9\nfS5NTa0cO6YlI8NDfLwQl8uCRpPK+LiGq1fd1NdHExVlobV1jrGxWUJCZNhsVjIy8lCp9Jw+7aGs\nTMA99yRz8uQlTpzoQKGQY7U6EAjkFBbGcviwDqNRy7p1GTQ3t3H4cDdxcRASIsLrdZGdncjoqIVL\nl2zcdVcmaWkmGhunGRmZJS0tEINhlpmZWUQiOXNzbhITRTzwwAZeffUQH3/cze23Z1+bb+0gNlZJ\ndrYEt9vK2NgYbrePhYVFAXt+fh7Hjx/E7x/na19bT29vP++/30puroonnqilpaWN1157h7KyVNTq\nWeRyGUajEZnMj0wmRKFQ0NMzTFeXgMjIYUpLS3nrrUOYTAKeeGI1cXGxvPTS+6SkqPnmNx9Bp9Nx\n8eJF6urKiY8foKSk+FqCtxiRyINKpaKjo4Pz563MzHRQX7+OV1/9Jb29JrZsKaampobGxkakUinf\n+MaX8Xq9JCYm4nQ6iY+/QlKSGrFYzIcfHqWzU4BMdo7Nmzfx0UefIhQKueuu25fIQV5eHpWVQ6Sm\nxhEYGMj27ftobfViszl54IH7aG9vx+v18vWvfwWXy0VQUBCnTp3CZBIgky3qujo6OmhsbKWurorH\nHvsSsKgj8fn8+P2LBZjJZGLfvoOEhATz1FOPLhUIfX0DdHcLkEgGuPtuP2azmbm5OR566E4GBwcp\nKipiZmaGH//4TdxuP1/72n1LOpOZmRkmJ8HtNmOz2ZBIJOj1esrLi5mba6C2tgSVSsXx48eZmJjm\nrrvWX8vByGRwcJBXX/0QkQi2br2X8PDwpce+914rSUli/vEfv4pUKr2Wb/IhFy4sUF+v4Sc/+TYi\nkQiDwcBbbx1ApxPw6KPL2bq1goCAAFpbW3nttRPI5fDww+uIi4sjJiaG3bv38PHHHSQlCXnssTIS\nEhKQSqW88MLP6eoykJsbQH19IDU1FYSEhPCTn7yC2WxFpfITECBh9erVCAQCfvKTV/D77QgEi/qi\nZ57ZSl9fH//+768zPz+HwSAmOzuRe+65lfPnG3nppV/Q2zuNyaTgnntWEBsbS0vLVc6fb2R01Edg\noIovfKGchYUFPvjgIE7n4rhRYaGGL31pHUeONPDKKx9gs1lwOMLYtKmc4OBg9uy5hNNpRiSSEBqq\nZM2aIkZGxnnnnT40mlmKiqIICopELhdx9aqJqalA1q6NITQ0lCtXhnE6R7DZ5MjlKqqrUzAYjOza\nNUpwsJa0tHDkcgUBARJGR11MTwdQVxdDREQ4LS1DOJ3TeL0iZDIZZWUJmEwm9u6dQ6PRU1ubiNXq\noqNjnPl5E0ZjJOvXF1BaWkxOTs7SDvIfGwKB4P9Lmr6x0L1OQK53Om583mcJyJ9bfH59TMrhcFzr\naCr+4AmH/0r8OvE5LBKQ5uZmnnnmGQwGA729vb+VaAoEArq7u/+kx/rHwre//e2lnwsLC7Farfz4\nxz/+nGh8jj8P/tQE4zr+WojGZ3H9uOVyOcXFxUu/f/rpx/F4PMhkMgIDA7FYrKSkJFFcXExDwxUm\nJlwUFeUTE6PlwIFpPJ5Jiooi6ezsoavLQ3BwMH19XkJCHNx8cz4HDlxi//5uEhKU2GwWDAYR6enx\nnDwpob/fyk03ZdDUdJmzZ30kJfmvZWGYqKpaxvHjLo4c0XPTTcFIpfMMDU1js9lQKCIwmx2sWZPB\n6Ogkp0+7yM6eoaBAycTEBHp9EDJZKKOjUlJSFKxdG8jp06OcPNlBRIQUnU6PUBhLVlYMhw5Z8fvN\n3H57AYcPn+b48T5CQyXIZF78fh/Llydz7JiQhoYpampi6OsboLHRjFotRCBQ4HItsHlzGUePXuLT\nT7XU1kpZsULAzMw0IpEPqTSchQUBq1enYzKZOXVqgbi4cVasiGRgoJ/2dgl+vwS93k9cnIhVq5I5\ncKCHTz9tp7Q0nKkpLWfPdhAXp7rmXGVj3boKPvnkFPv2Gbj99kjuuEPB6dMdbN9+gJgYKUajhfn5\n+WujTTJUKjdPP/0IP/zhG7z9djd33ZVEVpb4WtCYlqKiUMxmM/39/SwsLCz9L8THx/Peew1otQK+\n8pWMa2M9Z1GrBfzt395Nc/NlXnzxbZYvz+LBB4NQqQIYHx9HrVYgkzmIjIykr6+PkREBPp+WwMBA\nXnrpHbq7vdx7bzrr1q3llVfeRiIR8cQT9+Pz+ZibmyMtLY2NGw2kpyde0yvYMJu9zM/P09PTw/vv\nX0IiEfLss/H4fD5efvkNysoK+MEPvrpkN1lVlYdM1ktubg79/f0cOzaKUAjFxYNIJBL27z9BSUkO\n//APf7f0fgsKUrHZekhPT2F4eJhXX92P1wtf+5qcrKwsRkZGKCws5CtfkRIZGUlQUBAHDpzh/HkH\nItEFcnJyGBoawmaz8dWvPoTBYFjqnOzePURoKCxbVkBUVBQ6nY7a2pXIZBIyMzPxer387GdvMjpq\n5/77K5d2HcfGxnA6/Xg8i3owh8NBa2srcXFxPPJIKZGRkYSFhV1zqBpk/fo8vvvdvwcWXVt2777I\n5KSQmBgN9fX1+P3+ayF7QoRC/9Lo58DAAG63G4nEhUgkxuFwMDY2xvDwMJGRwSQk2EhJWUw9v3Dh\nAgaDgaioACQSG7GxscDiqIXD4SAkBJRKMenp6dhsNj755BPm5vRIJBAUFMjatWvp7Oxk//796HR6\nzGYBcXHx3H77bTQ1NdHV1cX4uB2HQ8QTT9SRlpZGV1cXQ0NDtLa6iImBxx6rRy6X09bWxsmTFzl/\n3k1NjZInnyxFKBTS0tLCkSOdzM2JqK+PX8qD6Ojo4NQpHSqVh5tvTkUsFjM1NcPQ0ChNTQIKC2U8\n/ngxg4Mj7Nt3gtHROebnVdx22zLCwsI4fvwydrsJh0NJQEAQGzeWMTY2wXvvXUGlmiE+XkNUVBT5\n+VkcPtzCmTMeyssV5OQEMTtrYGpKz9ycGIkkiLq6REwmM4cPjyCTzRAeriYoKIjc3ETOnu3iyhUL\nVVVBFBWFMjw8xcjILAsLEqRSFdXVsVgsFg4dmiEwUEdGRgQKhQqxWIROZ2NsLIS1axPJz8+hrKzs\nv0Qg+1nXpOu40RXpOgn5dd2PzwrQ/xT6iD/ETeqvCfPz83z3u9/lo48+4rnnnuOpp57CZDKh1+t/\n6/NSUlKWrlM3wuv1Xjv3o37t86KiopauMTd2NbRa7dJIU1TUokGC2Wz+la6GVqtdet0/ZG2A5cuX\n8/3vf//atewvd5z9RnxONP4K4fV6WVhY+JMTjOv4jwjQ/5JwXdz3WdzoVhEVFcWDD96P37/omvPw\nw7ctud1MTk4yMPAp8fHhbN36EN/+9r/S1QVbtkRy000OLlwY4ezZDkJDA9HrzUREJBAaquLwYSt2\n+zQbNqTS0HCeCxdAoVDidAoRCGD16iQOH3Zz8GAf2dlBCARTdHdbSEwMY2Ehgrk5G7fcsozDh89w\n8OA42dk+oqO92Gxm0tMTmJpy09Zmp74+iaioGdra9Gg0BoKDFdhsBgoLS7h6dYgTJ1xUV3tZt07F\n1atTNDf3IpOFYDB4yckJJyFBwokTc8zODpCTE8bg4BA9PW7kcjmzsyLCwz3ccUc+Bw5c5NNPr5KQ\nIMPpNKPXS4iL0zAw4GNiwseGDbm0tFzh+PFJUlK8xMWJ8PvtxMZGMjZmpqdHyKZNKWRkuLhwYYLZ\n2Q7UailGox63OwilUklLixuFwsm995azc+cJ3nyzgexsBULhAmNjU2g04Xg8gSwseLn99iqamq7w\n6aezVFXJeOihXE6caOKnP32LiAgZPp8Vi2XRoclolOH3e9i69Va2bfuId98dYsOGCB57rJY9e07y\nyivbKS+PR683Mzs7i1QqRaEAuVxMREQEV6+O0NrqIzV1nsrKFfz0px8hEMCTT96KyWTivff2sGxZ\nKo88UoBcLmd0dJTY2HDm52eIitIwPj5Ob68dsXixC9DaeoW9ewcoLg7hmWe+wtGjx9i27R02blzF\n6tXWpREsjUaMWCwiNDSUXbv2sXfvLNPTDZSUlPDmm+8yOqrlS1/awm23bV5KQ6+sjEIoFJKUlMQn\nn+ziyBEjMzPnqK6u5vjx4wwNTbBx403cdtsmpFIpWq0WlUqA1+tHpVJx8uRJ3n+/ifR0FV//+pMI\nBAI8Hg91dWVIJJcpLy9mZmaGF17YcW0E7BYKCxftZtPS0igqukxYWDCRkZF8+ukejh3rprY2jfvu\nW7RhdLlcOJ0enM7/FwbW0NCAVCrlqae24PF4yM7O5tChQ7zzTivJyWKee+5rSy4uWq2BuTnQ6QwA\nTExMYDabKS1NIjJyhszMTPR6/f9l7z2j4jzvde/f9M7QGTqIDhKiiV7UO5Il9ypbTrLd4uzkTVsp\ne+2cs1ZyTpKdk9iOYie2IxfJlq3Ilm1ZslURaoAAgei9w9CmMr28HxA6jnfazk6c2MfXN1gw8zyz\nnnXfc93/q3Do0NtoNEr27l2NTCZj+fLlnDx5ksOHG8jICOJb37qLgIAA/H4/+/cfpqvLzfbt8Xzr\nW/cTEhLCwMAA+/efwmoV8sgjleTm5qJWqzl//jyvvnqdkBB48sndxMQsTomOHHmHI0cmWLVKzLe/\nfRs6nQ6Hw8H+/e/Q3y9g585oqqvTyMzMpKenhxdfPIvX62fNmjh0Oh3p6elcunSJl1++RliYne3b\nk4iLi2HZsmW88MJB6uvNZGZ62LgxlKKibEJDQ9m373cYjX6Sk4WkpWlZvnw5c3NzHDzYilK5QF5e\nKEFBAURHR1NXd41z5+xkZdm57bYkRCI/U1N6rl2bYHpazsaNsQQFBdHdPYLT2cv0tBilMpDbbstl\nfHyCN99sRCLRo1BEEBMTS3FxDu+/f4X9+9tITfWQnS1AJlPicNgYGhIgFstYuzYGi8XChQsjCAR6\nBIIItNpg8vKSuHixjcOHx1m+XExUlASXy8nk5DQzM0IEAg0VFRE4HA7OnZtALJ4iNDScgIBAli9P\npK6uk6tXTZSWBrB69TLKy8uIiYn5JLaT/xL+WCzrH/IXuN3u//R/Hycgf83e/mmRSf218Pl8HDp0\niO9+97tUVVVx/fr1m89CSEgIISEhf/Y1SkpKMBqNNDc33yQJp0+fxu/334yn/jgSExPR6XScPn2a\n7OxsYDHVrq6ujscfX5Sw5ufnIxaLOX36NLt27QKgu7ubkZGRmzLTv+a9AZqbmwkKCvrUkAz43Az+\nqYTFYsHj8aBUKj8RE5fH48Hr9d6UY3xa4Ha78fl8f/K6lwoJl4hbSEgISUlJKBSKG4ayIkpKViEU\nCgkIkBAZ6WXDhvVotVpaWsaRy8U8/vjddHZ2UlfnJSLCS2gozM2NIxLJsNslTE+LyMkJIypKTEuL\nDYNhhtBQBRaLHp0uHKVSTnOzGK3Ww+rVy+jrG2BkxIpaLcJu9xIWJiYtLZqWFh/T0xZKS6OwWocZ\nHrah0QiYGmt98QAAIABJREFUnpYhFtvYsCGPwcFpmppsJCVJkckWMBrnUasVzM0pMJm8VFYmIRZb\naGx04PMZ0Wgk2O2zJCTEMDtro6tLejNJqrtbz+TkPHL5Yht5cnI4UVFBXLjgxe02s2FDCqOj3QwP\n21EoBJjNQoKC/BQWZtDebqOnx0RpaSRyuZGurhnAid0uB5xUV1ei1xu5fNlDcrKMFSsCGBgYZWRE\nDwhwOJwkJASh0wVz7twCLpeN228vZnS0n7q6CQIDvYjFLhQKDwEBGvr6rBgMAnbuLCI0VMU774xh\nt8+xe/cq5ubGuXChlaAgKeAgLEyOSqWiqWkKs9nPrl2VOBx2Dh0axOOZ54kn7qC/v58TJy5RUJBM\nYqIUjUaJ0+lkcHAMiUTA2rXF1Nc38sEHBny+ee6//w7273+bM2e62LAhl40bS2lqasXhcLB8eQRZ\nWToSEhKYmJikv3+WmBg1MTGR7Nv3No2NZjIytCQlJfHMM68yNDTME0/soagoh5mZGUJCgvB4Jqmo\nyCUkJJjXXz/NwAAkJkpvSG1epK2tg0cffZDCwjzm5uYIDl78n8rKPMLDw/jVr47Q0LBAVNSiDOvo\n0XeZnZ3ljjuqqawsQKfT0dnZSVOTHrXaT0VFEa+99iYHDx4jPz+L22/fSWRkJA6HgytXmvH7/ZSU\nLMdgMPCzn73A3JyeJ574IqtW5SISiaipuUx7u5WwMCGFhXlcvnyZ69evs3FjFbm5sRQVFdHW1sav\nf11DR8cIlZXZpKen4/P5mJqaoqdnhMhIFWVlRTQ1NfHhh6cpKsolOzuM1asrsNls/OQnL1Jb20V1\ndRl33bWbwMBAmpqaOHSoA73eyM6dlaSnp2M2m2lr6+DatXlUKg8bNlQxNzfH4OAgBoORhQUXeXmJ\nZGZm3iBkAywsmJFKvZSW5mG329m//3WMxnkEAgexsYFs3Lj2hoTqEAqFH4HATlFRBiUlxbz66hu8\n/fYpNBohMpmXjRvLSUhI4Omnf0tT03UkEh8BARLuvnsXbrebp59+Db1+BIFARHx8CI88speLF69w\n4MApPB4TAoGEysqV7Nq1nZdffpuamiZEIidKpZR77tmBThfK/v1n6evrISBARHR0ILt3b6W/f5g3\n3+xGLJ5Dp5OTlRVPTEwUZ8500thoJSNDQnp6EEKhkPn5eVpbXbhcQrZtSyMoSMjly/3MzIxhMCiI\njw+gurqIjo5hLlwYRyo1oNXKWLYsnNBQDXV1JmZmXBQVBREaKqS7ewaDQc/MjJLgYAlVVSmMjEzR\n0GAhIGCB4GAZ4eFqlEopnZ0ODAYRZWVhRESIaWmZY2pqGFARHCynvDyT0dFZzpyxEhvrYvnyMHbu\n3MKaNWv+kwb+nx1/zHy+VEy3ZD5fKqNbJOfO/9SK/afM5590mtQnDb/fT3d3N3v27OHEiRM899xz\nfPvb30ar1f6XX2spYOP1118nNzeXoaEhHnnkETZv3swDDzxw8+/S09OJjY29adD2er386Ec/IjMz\nE5fLxZNPPonT6eSpp566EdAhY3Jykl/+8pfk5OQwNzfHI488Qnx8PN///vf/4vdeMowvpfQdOnSI\nf/u3f+NrX/saVVVVf4NP82+Cz1OnPotYepA/qZSIpRbOpfz6Twv+FEH6OMGQSqWo1erf6xdZWtCX\nxuAxMTGsXJlNQEAAOt1iIkplZQGJiYkYjXMsLMywaVMZOTmZXLw4jcnkpbp6JVbrEB0dDqRSB16v\nBKfTQEVFLhMTFpqavCxfriImRsDg4AQLC3a8XgUWi4e8vFhCQ0VcvOjB4ZglNTWQ+flhfD4pQqGE\noSEp0dFiVq2Kpbt7lsFBIyEhItxuMyqVhISECFpahLhcTjZtSmdqqo/eXhcqlQeHQ4RUaic/P5W+\nPhvt7TaKi8MJCXHS3z+P1+vA6VThdDpYvXoFLtcCFy64UCoXSEhQMj8/gcsFDoeQ6Wkxy5cHkZwc\nSHOzhfFxPfHxSlyuWbxeUKlkdHVJUKs97NpVQmfnII2Nc8TEiJBIbHg8DtRqFVNTYpxOEdXVBQgE\ndi5csODzGUhJ0WC1TmEw2DCb7czOikhJCaCgIJMzZ6YYGZln8+YMRCIjV64MIBDY8Pk8KBReUlKW\nce3aKL29QtatS6GgIINjx7oZGhpn69ZsVConV692IZcLcDqtREVpiImJ5Pz5NkZHBZSUJBAbG83B\ng00MD4/xL/+yC4XCz1tvnSUxMYL4eClpabF4PB46Owew2XwUFCQxOzvLwYMdTE3NcO+92+no6OHA\ngbMkJ4ezbVsxSqUMvV6PUglarZ9Nm9bcKAEcwel0UFmZw5Ejx3j99Qa0Wj+PPfYwJpOR8fFx0tNj\nSEyUU1FRwfDwMGfPDuHxeCgszOD48Q/Zv/80KpWPL33pQYKCArFarYjFblQqB2vXVjA0NMRvf9tA\nf/8URUWLaUvnzp0jKSmJvLxY1q0rR6VSceDAe3R2CoiNFZCUtIy33jrKyMgot922lbKybJKSkqir\nq+PEiSmcThMVFYvdEZcvXyY3N5usrGDWrFkkBU8/fYTLl6dJTQ2gpKQEs9l8oxW8i6AgKWvXltPS\n0sJTT71CaKiGu+/eQlVVGVKplKeeepmzZ81ERnrZsaMagUCAxWKhrq4VjwdWrUpFoVBw4sQJALRa\nH5mZkRQVreLDD0/y3HNHCQ1VUlmZQmVlMQEBAezbd4DTp4eoqEjhrrs2k5+fz9DQEC+8UENvr4k9\nezZw++3VBAQEUFdXx5EjwywsmHjyyXvIz1/J6OgoH35Yy8WLDmJipHznO48TEKChs7OT06dbGRgQ\nsH17Nnv23M7ExAStra3U1c1gtwv40peqKS3No7m5mba2Nhob3QQGivjmNx9CrZZx7lwtra19jIxI\nqKhI5J57tnL9eic1NZcYH7ficsm47771ZGcnc+jQh7S3t7KwICE4WMXXv/4wev0Uhw7VYbWOIxYr\nyM6Op7p6He+/X8/ly+MEBdkJC5OSnp6AWCzg1KlpDAYbJSVhRERImZgwMTOjp6dHRmyskttuK6Kv\nb4T6+lGcznnEYiX5+fEkJoZz/rye4WEDy5aJCQ0V43L5sVqNdHXJCAwUsHFjGpOTeq5dMyEQmJHL\n1aSkhBATE0xTk5nRUQcrVyqJiJAwOGhgfn4ag0FJYKCMdesymZkxcO6cAbXaiE6nYNeuTdx5527C\nwsI+0b3k74mPN2L/d6J3vV7vP02a1N8DNpuNH/7whzz55JPceeedHDhwgIyMjP/W/W3bto36+nq+\n973v8dprr7FlyxZ++ctf/t7E4Ctf+QqbN2++6R8rKyvDbrfzgx/8gGeeeYaoqCgOHjz4e8/l+vXr\nGRoa4t/+7d944YUXyM3N5aWXXvq9Mr4/996Dg4P86Ec/4qc//SnPPvssQ0NDfP/73+erX/3qX32/\nfwf8WaIh+C9o7z99Iv3PKJYMZ58UHA4HNpuN4ODgT+w9/xaw2+04HA6CgoJu/m7ptOejmlWFQvF7\nI+WPN5l+vDzoD2FJeqVQKHA4HBw7dhyxWMzWrZt5+eWDnDkzTllZBDk5GfzmNx/i8UjIzVUxOKjH\n6/WSmBhOS4sLudzBtm25XLjQwNiYiowMH7OzfjyeWQoKcmlsHGVyUsyWLSHY7Xaam/UEB4vx+SSY\nTBYqKzOYnjZQU+NixQoPKSkxXL7cQFBQNH6/g4kJGTk5i7KgkyeHkcshJUXN+Pg0crmayEgV9fUe\nwsNtbN1azPHjtRiNWtLTfUxMuFEo7KSlpVBfP43dLmDz5hgmJydpa7MTHu7G41Fit8+zZk0Bra2D\nNDcLWLdOgU4XQk1NC0plABKJF6PRT07Oogfg6NEJwsO9bN2aTU3NJSwWDdHRPiYmhAQHOykuzuf9\n99uYmxNw++2LX+Lr6iYJDPQhlcpYWDCTk5PG5OQ8DQ0eysvVbN26hueeewe7XcTq1Yta77ExA5GR\ngfT3m5FIvNxxxybOnq3j3LkFtmwJZvv29Tz99Gu4XELWrEnBbrdjNtsICtLQ0DBEQICEhx66nYMH\n3+HCBRvbt4exe/c2/tf/ehGXS8C991bi9Xrp7h4gPDyIrq4RwsK0VFdv4be/PcSVK2bWrg1h7doK\nnnrqd7jdIp58chvBwcG8++6HJCREAotlTNnZ2bzyyhtcuqRnw4Z41q9fzQ9/+BI2GzzxxCbi4+M5\nffoMOl0EHs+ibyg/P59f/epFzp7Vs3p1OPfffwf/+38/i8nk5pFHdpKVlcXY2Bgul4vXXnsHjUbJ\nl770AK+8coh3352kpETJd77zFXp7e5mZmUEikTA0NExlZQVTU1P89KfHEIngm9+8hdjYWJqbmwkO\nDqajo5PY2BhKSkr4wQ/+g6YmF7t3x7Jnz33Mz89js9k4fPg99HojX/ziHTidTp577gjBwQq+/OXF\nNm6JRML+/a/wxhtjFBRI+B//4+sMDw8zMTHBxMQUzc193H77RqKjo/nFL36L1+vjrru2oFQqSUpK\n4uTJkzz3XCNRUT7+5/98HK1Wy8LCAvv3H+TECT3FxUq+9rVHGRkZYWZmhpqaBkZHHdx7bzl5eXkc\nPvw2Ho+bqSkDfj88+ugDjI6O8sor7xMZqUYikREfH0l19TZ+85uXqK+fICtLhUKhoqAgh8jISH7y\nkxcxmwUUFoYSFBTM2rVrGB0dZd++k8jlXsrKEgkPDyczM5MzZ2o4fHiElBQnVVV5BAUF3WiQf4/O\nThFbtmhITk5CIBBgNps5frwXp1PAzp1JaDQaJidnMBhmuHzZTVSUl3vvXU9fXz8tLcP4fFbGx9VU\nVoZRVVXKq6++y/y8E5HIhlAYwPr1WQiFQt58sw2p1EpkpBqFQkJsrI7BwVEuXxawfLmT8vIcrl3r\nwGDwYLNZsNuDWLMmApVKxenT/Xi9NgIChEilElJSopmbm+X8eR8JCRZKSzNpbe3EaJTg8xlwOiMo\nKFATFBTI+fMjOBweYmL8iMVSRCIxHo+Vzk4FkZFOqqqyaGvrZXBQgFo9jUAQzrZtuWzevPEzJf35\na/BRQvFRA/rHJcJLpOUPdVR8GuH3+zlx4gRf//rXSUlJ4ZlnniE1NfUffVmfYxF/9sH6fKLxKcTS\nF+BPCksZ4p82E9nSdS9F3rpcrpvtwxKJBLVa/Xsj5T/UVLpk0Ptz9y0QCG6eQojFYjIzM0hPT0Mk\nEpGSkkRqahBr1lQQHh5Ob28HajXs3XsPLpeN2lonSqWL6upcuro6GBxc3MDtdh8ajZeVK5Po6vIy\nMmKhpCQK0DMwYEYm82E0yvH5bGzeXMj4uJ76ehcxMX4CAtyYzbPIZHIsFikzMwIKC6MJDvbQ0GDB\naJwmJESB220kMTEGkUhCc7OI8HABlZUJ9PQMMTRkQqEQ4HR6iYiQkZoaTWOjm7k5K5WVcdhsowwM\nLCCXezEYJEgkDjZtKqKvb4a6OisrVqgJDnYzOqq/McqX4XD4qKzMQKHwcfasFZdrhhUrwjAax7BY\n3LjdPvR6MUlJGgoLU7h6dZa+vhlycoKRyy0MDk4jkwmYnRUhl/u4666t9PRMUFtrY8UKNcuXa+ns\nHKSrqx/w4PU6iYsLRSwWU1NjQyBw8q//ejdtbR2cPTtIcrKaxEQ5bred+fk5JiZMeL1QVrYCl8vF\nm2+O43Qa+OY3H6Kzs5vjx5tYvjyS9HQ1arUMk8nE4OAUfr+fNWtWMTQ0xOuvD2O1TvO9732ZK1ca\n+d3vzpObm0Beno7Q0CB8Ph/j41NIJH6qqlbdkPuMYDRO8sUv3sPp07UcOnSS8vJs1q5dQVxcDC6X\ni/7+AcRiL5WViwV7L73UxeTkMHv23Mbw8DBvvXWCoqKV5OVFsWbNIuk5fboeq1XAypWxTE1N8fTT\nb9HX18s3vvEohYV56PV6vF4Xs7Pj5OUlExMTzX/8x35qaobIyopg69atjI+PIxaLMZsniYpSsnp1\nOR988CG//W0zMzODPPbYFwgODkav12OxmG721KhUKn7yk+eprW3mvvt2sGvXFkJDQ280mY/g97up\nrMxjfHyc48c/IDExjqQkKWvWlKDRaPjJT57n1KlBCgsT+OIXHyAsLIyxsTFOnmzHYvFTWpqOTqfj\n3LlzAFgsepKSwiktLeTw4bf4zW+OkpgYQnFxDBs3rkEmk/Gzn71Mbe0Imzdns3v3WrKysmhvb+fA\ngSYmJqx88YvVbNu2kbGxMdra2rhwwYxM5uLb334cmUxKQ0MD/f2jTEz4ycmJ4cEH7+PSpTquXm3B\nZLLi8wnZuLGYhIR4fvWrA3R3d+H1etBqpdx33+0MDAzywgsncThmUKmE5OensmPHdl5++QgnTnSh\n0/nQ6aSUluYTEBDAq69epKdnhsxMFWlpIURF6ZicnOTttyfxeKxs356OTqdmZmae69f7aW8Xk5MT\nQnV1AV1dg1y50oLRaMPjUVBdvYqUFB3vvddGd3c3arWIoCA5lZX5zMwYOHZsHo1mgaKiKMRiL1NT\nRkZHjej1SlavjmPFCh2XLw/Q1zeCUOhDqZRQUpKJQODh2DEjXu8chYUR+HwLjIyYMJmsGAwaVq2K\nZOXKKJqaJujtnUGpdKDRiElMjEAg8FBf70MkcrNlSzJOp4XWVgM22ww+n4q1a7N56KHd5OSs/MxI\nf/47WCIMHy28A24ePC5JsP6Q/Gppwr+0t31ayMfo6CiPPPIIL7zwAj/+8Y/50Y9+RGho6D/6sj7H\n/8XnPRqfRXzSi8PHpUSfFixdq9PpvDnBWCIYH40p/DjBWBpl/63uVaPRkJ+ff/Pnb3/7yzenKVVV\nFXi9PpYvzyAlJYVz51qZm/Ozfn0lIyMjHD06ytxcL9nZofT09NHXB2q1hu5uCAlxs2NHOseOXeHt\nt68TEyPDZrNiNgtJSYnj7FkR3d0LbNyYQlNTC+fOOYmO9qDVKvD7bZSXL+fMmVZOnDCwaZOaNWvc\n9PSM4nQ6kckCsVo9FBQkYjZbOHPGSnz8IAUFYQwM9NHfL0EqVdHfLyYmRkR1dSInTrTy1lvNREdL\n8fmMzM56CQ8PpKPDj8/nobo6l9raOo4d6ycpyceib89JaGgA3d3BtLS42bUrieRkG1euTDA6Okd4\nuAyLxYxSGYVWq6Wx0Y5a7Wfv3nIOHTrBCy+cIiFBQnLyAna7BI1Gjd0ehMfj58EHq6ira+Lo0WHS\n0vxs2BDGxMQYb775Lna7E7dbjFwuJy0tnl//+jJK5Sh7966hra2DV189R2qqmqIiGRqNiM7OTubm\nrMzMCAgMXOw1+MUvTqBQDPPwwxsYHx/n5ZePkpqqo7hYTlxcKH19fQwN6RkfX3zG4uLi2LfvBDIZ\nPP74LVgsFo4fP010dBhVVRrS0xNwu930908yNCRkft5AbGwsP//5IUQieOKJOxCLxfT396NWq8nK\nEpKaGotcLufYsUtcvw6hoX3ccssOnn/+VXw+Hw88sAW/309WVhZ1dXUsLIBKtSi3OHjwTerqxtm6\nNYsf/vBfcbvdmM1mtFo5TqedwMBArl27xrPPHkejEfCd7/wLWq2WyclJNBo1wcEQGqq9kSb1AoOD\nVu65p4wdO7aiUi2mcy0s+HA6BdhsNkZHRzl06D2WLYviC18oIzg4mNDQUPbvf4PTp01s3Gjhq199\nhMnJSfr7+wkIkKPV2tBoNExNTfHss6+iUEi5664iJBIJGRkZvPvuu7z0UicpKfDv//4VhEIh4+Pj\ndHQMMDIiJDvby549u7h8+TJtbW1oNBJcLhc6nQ6RSMQPfvB/UKnErFoVhFqtJCEhgRMnPuTtt9tI\nSpKwd28WCQkJiEQi9u8/Qnu7j23bwtmwIetmb8apU71YrfDggyUkJCSg1+tpampiaEhIcLCYxx7b\ngdls5o03jqDXT6PXQ1SUim9/+36OHHmX733vJzidNoRCNWVlJaSmpvLzn7+K02lDpRIhlyvZtGkd\nAwMDvPhiAyEhZvLyQomIiEWn03Hs2AVaWwWUlcm4555YTCYLjY2tDA1Zsdmk3HprFgAnT17D7zfj\n8wWg1QZSXV1Gc3M7zz/fREyMkczMQHS6YNRqKa2tC0xPy9mwYdHw3tw8iMdjw+FQolBoWL06namp\nad58c5DQ0BmyskKQSOR4PB5mZlxMTKjYsCGesLBQLl/upq1tAoHAj1IpJy8vEavVyocfmggNNbF+\nfTxGo5eGhkGcTgPz8yGsW7ecyspSkpKS/m5xtZ92/Lk0qU9L9O4fg9vtZt++ffz4xz/m/vvv5+WX\nX/6rfBif4x+Pzycan0J80hONpWg+mUz2qTlVWppgLJ3qiMVi1Go1CoXiD04wllK1/tIJxn8HSws6\ngFarJScnm6ioKGQyGRkZCWRnx1BYWHhDutJDUlIEjz32MBcvttLeLqSwMIyUFAUdHZNMTxuQySTY\n7Q5SUyOIigrgwgUfTuc85eUJjI11MTa2gFQKc3NSwsPFlJdn0tNjoqPDQEqKCoHAgMFgIShIyfi4\nDLfbw6ZN2VgsU1y9akeptCGXg9drIiUlgclJN729QlatCmPZMhltbTPMzMwik0lwOq1kZcURGKjk\n/HkPQqGFzZvTGRrqYXjYgkTix2IREhEhJj8/lZYWK/39RoqLdTdM49MIBC5MJglCoZMdOyoZHZ2m\npsbGsmViMjM1jI6OMTY2g9sNDgdkZ8eybFkkH3wwj9VqpLo6G5NpjObmMeRyLy6XgJAQMXl5K7h6\nVU9vr4vNmzOIipJRWzvIyMggkZEyZDIHcrmY6WkDXV0eoqMVPPzwXRw9eoUrV8ZZvz6djIwgWlr6\nmJ+fveEtEbJiRRotLV3U1toIDvbx2GN7OHz4JGfPtlFZmUZ+fhQej4eFhQUmJ6dRqcRs2FDBmTMX\nOHp0GrHYzDe+8SjHj5/h/fdrWbMmh9zcMKKiIrFYLLS2DiMQQFVVPrW1l3jllQ6czhn+/d//PxYW\nLFy+XEdSUhRarYu1a8sxGo0cOXKNqSknZWVp+P1+fvGLV5BKYfv2IqqqClGpVFy8eJWBAQdxcUqS\nkhL5yU9+TU1NM/fcs5WtWyvQarXMzc1x7doAMpmAiooCjh07wW9/e4bQUDl79+6ipGQVDoeDs2fr\nmJ72kZERSnh4OD/72XN0dvZwyy1VFBenkZ2dzYULFzh6dByrdZYHHrgVu93O5cuX0WpVuN2zVFXl\no9Vq+fGPn6e2tpsdO0rYsWM1ycnJdHV1cfx4H2azix07KoiIiODs2bN4vV6MxhlSUiLIyVnBvn3P\nc+TIJfLy4ikvT2Dt2irMZjPPPPMOTU3T7N5dxK23bkQikdDR0cHp0+M4nR4ee+wuEhPjOX/+PFNT\nU4yO2omKUvHQQ/dz6tQ53njjfVQqIWKxlzVrFn1Zv/jFqzQ19ZCaGkB8fADr1lXR19fH889fwWCY\nYePGVHJzkwgMDOTs2St88IGZhAQZt95aSGiolu7ubi5d6mNoSMj69UmUl2fS0HCdurp6pqc9CIVS\n/uVfdhMUJOfAgfOMj/ciEsmIjQ3hgQdu5cKFZo4dGyQszE5kpJzExAhkMhm1tWMMDbkoKwsnNVVL\nT88YExNjTExIUSpl3HVXBQ6HhQ8+6GNhYQK5XEliYhAFBZnU149y9aqVzEwxy5ZpmJ83MzMzx+Sk\nCKFQzoYNaTemkZOYTCOoVHICA8WsWLGMri49LS0CcnNV5OaG0t8/yfCwHpsNRCIlpaXLCA6WcerU\nLAbDFAkJCgIDRfj9UvT6efr7FeTlhbJ7dxFr164mLi7uP/VWfI7F/XhJFvynUic/Pv2QSCQ3vR8S\nieQmqfhz5vOPvt4nAb/fz+XLl7nzzjsZGBjg0KFD7N2791MXRvP/ED43g39W8UnGzS4Zp6VS6T+9\nRtbv999sBV6KDVSpVCiVyn84wfhLoNVq0ekWY0rDw8OpqMintLTwRsuoBJ3Ow6ZNG28k7IwhkQh5\n9NE7GBnp5+JFFwEBDiIiRBgME4AYq9XP1JSMnJxQ0tICuX7dxOTkNEFBUhwOAzpdIGFhWurrBYjF\nNrZvz6avr4uBARsqlR+7XUBAgJe8vFQ6O53091soLtYhkxno7Z1HIHBitSrweh1s2VLI/LyBCxfs\nhIW5iIqSYDZP43KB1SpgdlZMfr6OxEQNDQ0mJicniY1V4HbPIRbLkMlEtLeL0Wp97NpVQnt7P01N\nM0RGCpFI7IhEbrRaDf39fiwWPzt25CMSWamtncNunyYiQgqY0WgCmJgwMTgoITc3gvLyLC5fHqGz\nc5zs7FA0Gicm0wJCoY/RUS8KBezdeztNTV2cOjVPaqqCggIdPT2DNDVdRyDwIhC4SUmJwufzcfLk\nLC6XjW9840H6+vo5dqyN+Hg1WVkByOUCRkdHGRycxu2WsH59Pn6/n1dfbWd2dponn7wLodDNkSOn\niIkJJiDARW5uMgKBgJMnm5mYEFBUlEBwcDDPP3+KoaFhHnxwK+npsYyOjuJ2u5mdnSctTUdKyjKe\nfvoNLl0yUlQUzfbtm3jrreNMT0+TlaUjPT2MoqJC6usbOH16HjBz3323cvjwO7zxxikqK1dSWZlK\nfn4uZrOZmprrLCwIKChIwmg08otfvMH8/Ax79myjsnIVEomEq1db6OiwEh4upqKihGeeeYHjxy+y\nbVsZpaUpFBUVMTAwwLFjXZhMbjZsyEcqlXLo0NsEBqqJjBRSUpJFWloaP//5ixw/PkVqqpqvfvUR\nAMbHx2lr68fphOLidCQSCT/72QvMzMxQVraMvLxEcnNz+d3vjnLgQD9isYVvfOMLREVFMDQ0RGNj\nJ+PjYnJzdWzevImjR4/R1taJUOhBrYZNm6oYGxvj6aePotdPsm5dCoWFaWRkZPDaa0d4440RwsIE\nPPjgJjIyUhgcHOTEiQZ6egRs2pTOvffeQnt7J62t1xkZseD1irj//u1ER0fw7LNvMDk5gkAgICpK\ny8MPP8CpU7W8+WYTGo0DnU5KUVEW0dHRHDp0nqYmE4WFwRQWLk4NJicnuXBhjoUFH9u3ZxEVpaam\nppFX0dEoAAAgAElEQVTBwV5GRkRERCh47LHb6ejo4d13r+LxzCOVyikoSCE/P4v332+no2OGhAQh\n0dEK1GolFouZ+no3QqGf3btz8PlsXLrUj8EwxcKCgvT0MFavXkl9/SBXr+oJDrYTEiImNDQAv99D\na6sbl0vAxo3LUKu91NdPMT8/jtutJCRESnFxGr29ei5dspOSAvHxKhwOJwaDCb1egMejoLIyjtBQ\nCbW108zMjKDVyggKkpCVtYzR0VkaGvykp8vYvDmNTZs2sGLFik9d8Mgngb9VmtQfM59LpdKbBAT4\ng+bzJfnVkrf3by2/mp2d5etf/zo//OEP+da3vsW+ffuIjo7+h+/Ln+NP4nOi8VnFJ91r4XA4/qmJ\nxtKpzMLCAg6HA5FIhFwuv+nRWDq5+Ws9GP8oSCSSmxtJbGwsOTkrCQgIICIigoQELeXluaSmpmI0\nzmMw6KmoyKG4OJfa2jH0ei9bt2ahUBhoa7PgdpsRCBa7MCoqcjCbbVy65CUy0k9GhoaxsRHm5234\n/WKMRiEZGSEkJgZy9aoNvX6apCQ1Tqf+hndERne39Ia3pICengFaW02EhfkBJ2Kxk/h4HQMDAmZm\nvKxfn4JMZqKpyYTLZUQsluD1WigtXcn0tJX6eu+NL/hh9PaOMDg4jUQixOn0kpQUQmKijvPnbVit\nFjZuTMVsHqWtbRaJxIXFIkSt9rJhQyktLdM0NVmprIwhMVFCc/Mgev3UjQZrF3l5aXg8Xk6eXECt\ndnH33ZX09vZx6VIPoaESpFIP4eFKtFotTU0mzGYf9923DoHAwbFjfdjtM6xcGYpC4WZmZo7x8Wmm\np/2kp4eQmZnG737XQn+/gTvvLCM+PoBz55rweOyAA51ORUZGCidPXqax0UtKioq7797Fa699QF1d\nB+vXryAzMxiBQIDBYKC3dwaFQsjOnRt5660PeOutYaKjJTzyyJ3o9VNcu3YdrVaGUuli7doyhoeH\nOXy4k5kZM/fcsxm328Wzz75BZGQQBQXhlJXlo1AoePfdGgYGBGRmasnKyuKpp16mtbWbW24pp6go\nhcjISPr7+7lyRY9Y7GLXrs28++5xDhw4TXZ2HGvWpFNevtg0fexYPVNTkJ8fQ0JCAs88s5+5uVmK\nihLIyYkjPz+f9947zltvTeF2z/Ktby2WaTU0NCAU+nC7rZSUrEAsFvPTn75CY2M/t99eybp1+eh0\nOjo6Ojh5chy328mePbvw+/0cPXocmUyIw2EkMzOWpKRE9u17lZqafioqUli9OpW8vLwbfplGRkdt\n3H//OjZurKKlpYXR0VF6e80olQK++MX76O3t59e/PoxaDSKRi+LiLPLycnnqqVc4f76f3NxQ8vN1\nZGSkMzIywsGDzYyPW7n11nxWrUplcnKSjo4O6uocaDQCvvnNh3C57LzxxnEMhlnMZhFFRcns2XMH\nBw++T23tddRqD1qthMrKVchkUl5/vZWZmXny80NJSgpBrVYyPDzOxYseQkLgzjuLMZsN1NQ0otdP\nYzBIqaxMpqQkkw8/vEZTUzdyuZuAAAmFhVmIxfDuu9PY7QYqK2PRaGBkZA69fpahIRnZ2SFs3LiS\npqY+mpvHEAqtKBRSVqyIJywsgHPn5jEYbBQWhhAY6Ke3dxazeZ6pKTnh4VLWrEmnv3+Cq1ctaLUL\nBAVJCAtTo1RK6Ox0YTKJqKyMJCxMRFPTDHr9CELhYppUeXkW4+NznD5tISbGQ25uBNu2baCqqupT\nF1f7ScHj8fzd06T+0ujdJe/jx6cfSwTkT0Xv/jF4vV5eeeUV7r77bpKTk3n77bdZs2bNp0ZB8f84\nPican0X8Iwr0HA7HzQXnnw1LEwyHw4FAIPg9idTSJGYpHvCjRrh/ZoLx5yAQCNDpdDeTwFJSkiko\nSCcpaRkBAQFIJAukpARzyy07MBpNXL9uJCpKxZ4927l6tZOmJgtJSTKk0gXMZiMajZLpaRkmk4+q\nqhRksgWuXl3A5ZpDo5HhdM6TlZWMyeSkpUVESoqcgoJwenvHGBmZRyYTYbd7SEjQsmxZOFeuuDEa\nzZSXx2KxjDAwYEEu9zM7K0ahcLFlSzHd3Xrq641kZakIDHQzMaHH5/NjNEpwOPysXZuFQuGhpsaM\n0zlDUlIANts0QqEcq9XF0JCE9HQtZWWpNDVN0t4+Tny8HKnUisvlQSYT0dvrRyj088ADmxkfH+PM\nmWlCQjzExS0W+y0sONDrbRgMIqqq0snIiOf994eZmppm/fpkZDIb3d3jgIu5OR9hYVI2b17LqVNt\nXLliorw8hqysMOrquhgaGkatFqJUQnJyLFNT05w5Y0EqtfP97z/BxYsNnDjRyvLl4WRmBqBUSpme\nnqarS4/LJWDLlhJMJhMvvdSK3T7HF76wHZVKRF1dM1KpAIfDSl5eEsHBQezff46ODjO33FJISUke\nL730FlariZSUQDIydCxblkhNzRUuX7YTGOjm/vvv4sCBtzh+/BJr1mRTUBBJcnIyer2e2tpB7HYf\nmzYVMTU1xXPPvY9Y7GHbtlxKSnIQCoWcOXOF3l4fSUkqKirK+eUvX+LKlRY2bMglNzeKnJwcOjs7\nOXZsCKvVxn33VeN2u3n11bcID9cSEOCisjIXnU7Hz372MufOzVJZuYyHHroDg8HA2NgYvb3jAKxb\nV4TRaOTppw9jsRhYty6VoqIMli1bxsGDb/P++3OEhfl4/PH78Hhc9Pf3MzY2w8IClJamk5yczFNP\nvUJnZy/p6SEkJQWzenUFtbW1vPjidVwuI3v2rGflylSmpqY4f/4qLS1+li8P4V//9WFaW9uprb2C\nyWTB4xGydWsZ8fFxPPvs2/T29hMZKSMuTkt5eTFtbR288ko3fr+JnTtXkJiow2g0cupUAy0tUFoa\nxc6dpfT2DnLhwhX0eitut4wHHthMWlocBw+ep7e3G5VKRFiYkg0bKhkcHOXIkTFUKivFxVGEh6tx\nOFxcvz7B8LCM9esTKSlZRn19N21tXdjtPkQiMRs25KFWi3nrrQFmZ0eIjpYRFqZApwujp2eCpiZY\nvlzN2rVJ9PSM0N4+jN3uBBSUlaUQExPEqVMTjI9PEh8vJTBQiESiwGw2cf26hIgIIRs3pjM0NMb1\n6wYEAgtyuYr09HBiY0OprzcyNmYnL09DWJiQgYF5DIbFuNqgIBkbNqxgdnaes2fnUatN6HRydu5c\nz2233UJ4ePg/bjH9J8ZfKpP6e+Gvjd79qPl86YDvD00//H4/7e3t3HfffZw/f579+/fz1a9+FY1G\n84nc3+f4m+BzovFZxSfp0YB/TqLh8XiwWq03CcaSRGpp8VuSfH10gfu0E4yPw+v14nA4cDgcyGQy\nFAoFKpWK5cuzyM5ejkQiISEhnmXLVKxfX0lMTAw9Pd2Agzvu2E5kZDBnzhhwOp1s374Cvb6Xnh47\nSqUbm02ERLLY6TA4aKGxcYHc3EDCwlwMDk7hcrlwOBTY7R7KylJRKLzU1trxeGZZtkyD1TqJWKzA\n6fQxNCQhOVlFYWE8HR3T9PbqCQ0V4vNZUakkhIcHcv06eDxuqqtzmJsbobnZjFxux+8XIJU6yMvL\npL/fSkeHi8rKWBISxFy7NoZeP4VYLMbjcbByZRJKpYzTp21IJAvs2pXP0FAv166NIZN5cbshNFRC\nVlYKV67MMTJiY/v2FQQEOLl0aRiDYQqxGGQyD9nZ6fT1TVFX5yEzM5Dt2wu5erWbq1d7iI6WIZXa\nCQxcTDS7dm1RzvDoo7cxPj7Oe+/1oFA4yMsLRaHwMzo6xuDgFCaTkLKyNOLjY3nttSZGRqa5/fZS\nIiLkNDS04/U6sFhsxMQEUFZWxIEDJ7hwYYHS0ih2797ABx9c4Pr1TuLjtURESEhNXUZfXx8nT87g\n8dj4ylce4tq1Ng4dOk9SUjD5+eFkZCRjNpuprW1nZkZAaWkyERERPPvsYi9GdXUBK1fGI5FI6Osb\n4No1E2q1l/vuu4OXXnqTd96pp7g4mdLSeNLT09Dr9Zw714PJ5Gf9+lw0Gg1PP/0aNpuZwsIY8vKS\nSU5O5vDh9zl92kJYmI+vf/0xWlvbuHSpAYVCiETipKqqEIPBwL59H9DbO8G9966lsnJRxtXf309T\nkxG53MuXvvQADQ1N7N//DjqdErXaSUVFHsHBwTz33Ls0NMywdesKNm1ahdfrpbe3l8bGRQ/P3r27\nCAhQ8atfvY7bbcXvd5GWFsmOHdt44YXXeffdXtLS1JSVxZKcnMjk5CRHjzbT1+dk1648qqpWcv16\nJz09XYyOuhCLhXzta3txOGy89NJpbLZp5HIhWVmxrF27mjffPMnJk2NkZSnJzQ0nKCiA+fl5amvH\nmJz0sXNnNpmZOmpqrtLX183srAiNRsaTT97L9PQ0hw+34PVOo9FISE6OID09mXPnumhosJKfr2H5\n8hAMBgtTU1OMjfkBJbfdVkxwsJSTJ/uZnh5CJpMTEiKjsjKf9vZhTp0yERfnZvnyICwWMxMTs0xP\nu1hYULB+fSoxMWrOnx9jZGQYjUZEQICElSuTMZmsnDvnICjIxdq1cUxN6entncXpdODxqCkoiCE5\nOYzLl6cZHJwnJgaCg4X4fEKcTivd3VI0GhHbty/HYJjn0qVZ/P5ZVColmzeX8OijDxIXF/ePXUD/\nSfHPXrr3x6YfUqn05vQD/m/yo9vtxul08vDDD/PGG2/Q2dnJ5OQk+/bt47vf/S4PP/wwL730EsnJ\nyZ+Zvfn/IXxOND6r+CQnGgKBAIfDcXNR+UdjSSJlt9t/j2AsjZI/KpFyu914PJ6b+tKl1I2/dsT7\nz4KPnnQtbUQKheIPjtMlEgkxMYs6cJFIRGFhLhUV+cTGxhIQEIDfP0V+fgrbt2+jqamD0VEPpaXJ\nFBQk0tiop69vjoQEOT7fPA6Hm+BgFb29Enw+N9u356LXD9PcbEOjcSIU+hEKF8jKSmZkxEF3t5fS\n0khiY4W0temZm5tFKJTgdNrJz09Go5Fx5owTgcDImjXJjI/3MTZmRSQCg0FEVJSMwsJUWlpMdHXN\nkp0diFxuYWRkFrHYz/S0BPCwe3cls7MznDtnIjDQSVycHKfTiNPpZW7OyeysmOLieNLTdVy8qGd4\neJzMzGDEYgsmkw2/30Nfn5+AAD9f+MKtNDV1UVMzSUaGmvh4KUajEaPRyNSUA7vdz5o1KwkLC+C9\n96ZwOo3s2LESv9/C9esD+HwuTCZISNBSXFzAe+9dp6XFwPr1qSQmaqipaWFiYgyBwINaLSAnJ5P2\n9j5OnjQTEuLny1++m4aGFj78sI6UlBBCQwXExITf8FGMYjZ72bNnK2KxgFdeqcXvX6C8PJ6kpAgc\nDgdNTR0MDvrIyAhh9epKnn/+KI2NfWzcmE1OThQikYiJiQna2uYQiXzcddcOLl1q4LXXGgkLk7B1\n60qSk+OYmpri2rVepqdh1ap4UlJS+OUvD9PZOcDGjSvIzY1Dq9XS09PDhQsGRCInjz32IFevNvPq\nq8dZtiyEuDgpFRWrcLvd7N9/mrY2K9u357Bz50YuXrzC5OQUJpMJtVpMdfUGrlypZ//+BgSCBW67\nrZiVK9MwmUx88MEl2tr8ZGUF8oUv3MepU7VcvXoNmQwUCtiyZTXz8/P8+tc1TE7qqa7OYeXKBFwu\nF42N17hwwU5QEHz/+48zPj7O229/iMtlx+USUF6eRX5+Pr/+9VFaWoZITw8gOTmQxMQ4RkdH+d3v\nhrDZ7Nx1VwlxcSE0NrbS3z9Ifz8kJQXxta/tpba2nmPH6pBIHEilIoqLlxMfH8ubbzbS2zvLypUB\nJCYGIJGImJyc5NIlB1Kpn/vvr8LrtXHsWB1m8zQWi5Tly6PZtWsdp09f48qVUUJDXYSEiImJCQN8\nXLpkxGz2snFjEsHBAq5c6Wd+fgKjUY5Op+L229fQ1zfG2bN6QkJshIRICAlRIpGIaG+3MjUloLxc\nR3S0lPr6EcbGhvB6pajVUtaty8VqXeDYsTmUShNpaQH4fDbm5mwYDE4MBjVlZdFkZIRRXz/BwMAE\nKpUXlUpEamoU4OHCBQ9isZMdOzJYWDDQ0jKHzTaLx6Nk3bqVn8fV/hm43e5PZeneX2I+b2trY2Bg\ngBMnTnDo0CFaWloQiUQYjUaampoYGRnB6XSi1Wo/N39/evA50fisYunL8icFp9OJSCT6hxKNjxIM\nAKVS+UcJhtfrRSAQIJVKb3pL/li76t/b4Pa3hM/nw+FwYLfb8fv9yOXy3/sM/hIsNcvDolE+Ly+H\n1NQUBAIBqakJpKVpqaysICQkhPb2djQaMY899iBms4mzZ21oNIupTf393QwNWZHJYGFBQFiYiJyc\nJK5ft9PfbyQ/PxSp1EB//xwSiZ+5ORl+v5vq6hJmZqa5eHGBkBAnISECHA4TUqmM+Xkfk5NiCgsj\nSUxU09g4z+TkBKGhErxeE2FhWhQKKVevClAoXNx6axG9vb1cuzaLRuPB7/eh0fhISYnn+nUbo6NO\ntmzJRKt1UF8/icmkvzGVc7BqVRZzcxZqa10kJMjYsCGD7u4Bmpr6kMv9gI/o6AAiI8OpqZlldnaB\nHTtyABNXrozh81kQi/0EBAjIyEiloaGflhYfVVVxlJWlc+lSF+3t/URHK1CpvERFheJ0Orl8eQGh\n0M2TT95NT08v773XQWion7g4KcHBckwmE62tE8zOCtmyJY/U1ARee62O0dEx1q9PIzpagdFoZGJi\nkt5eO6GhEvbuvZcDB45x6tQAxcVxlJYm4vG4GBkZYWRkHp9PwNatFRgMBl588SoLC3Pce+8aoqOD\n6O/vR6+fZWrKSUpKCJWVZTz33BEuXRpiw4YsyspS8Hg8jI2N0d09B/i57bbNDA4Os3//RYRCO1u2\nZJKVtQybzUZNzVW6uwVkZ4dy++238PLLR6irayU5OYioKDmrVuXQ19fHwYMdGAxmnnjiNhISdJw7\ndxGLxcTsrIP4+CB27armN795nffea2PFimBKSqJJTk5icnKSDz/sZXLS8/+zd97Rcd3nmX5m7tzp\nDb13EIUAAQIECQLsBSTYKUoyZVs+iuOm+MSxk6PNZr3H3o29m+M4m2Tj7jje2LEUW5VNJMEGdhIE\nSAIkAAJE72UADGYwvd27f1BQYFqukSiK4nMO/+OZuQPgfnfe3/d+78ezz26ksrKE1147zsTEKD5f\niJgYLR//+NOcO3eVl1++jdkcYe3adPLzM3A6nRw92kR7u8SWLYvYsWMVTU2tNDe34HD4USoFnnvu\nCVQqBT/5ySWmpkbIyTGTnR1NVlYGly+3UFc3S1aWmr17lxEI+Lhx4zb9/TbsdpE9e5azenUpr79+\nkdbWDrRaGYtFZM2aCvx+Ly+/PEQwaGfjxiyio0Wmp+fo6Rmhq0ukoiKRXbsqaWxs58qVNmTZhyiq\nqa5eTHp6AkeO9DMxMUNJiYW4OBVzcwGcTjvt7Sri49V89KNr6O0d4NKlQWR5Fo1GS35+Ivn56Vy7\nNs3gYIDycjNpaVoGB+04HDNMTWnR6VRs3lyE2z3HyZPjSNI4FosKq1VJVJSZvj4Xg4MaVq9OoKgo\nhubmIQYHx5Bl0GhUVFUVoNUqOHrUQThsp6oqGZUqSH//LE6nk+lpLatXZ/PMM5tYtaoKi8Xy0NbX\n9xNJkvB6vQQCgffFJvVesdB+lZGRwdmzZ3E6nXz729/m+eefZ/HixYTDYW7evMmLL77Ij3/8YyYm\nJti7d+/7femP+d14vBn8USUUCj1Q+5TT6USlUmEwGB7Ye84TiUTw+XwEg0GUSiU6ne6XCvC8wFi4\n0fs32aPu3666cJBtnvls8YX54u9nwZ+3gQUCAYC3T4re62vyeDzAPUHS2dnJ6dMXWb68hLy8PP76\nr7+H3a7g2WcrGB8f5/jxIaKjgyQkmJmYGCc5OQVRlLh0KUxBQYhNm5Zz+PA5gkELyckhJidlkpIg\nJyebM2dGkCTYti2TwcFBursDxMdHmJvTIklzbNtWTVNTBzduyKxZIxIbG0Vzcztmcyx+v5/ZWTXV\n1bGYzWaOHOnHZJJYujSe4eFRAoF7X8RaWiSSk0M8/fQWXn75JCMjItXVWtxuCa93jri4WHp6nPh8\nSp54ohi3283hwwPExHjJyopnaspGTEwCgYCX27clKioM7Ny5iR/+8ABOp0BVVRQeT5BAIITVqqel\nZRaVCj772e3cutXOkSPDFBRIlJXlMzAwhFZrYmxskoEBBTU1qSxZUsR3vnOUcBi2bMnC7/czMeHA\nbFbT3u4iKkrJn/7pJ/jFLw5z4YKLTZvMLF9eSktLG8GghN3uYGYGnnqqEr1ez3e+cxa9Hv7oj9bh\ncDhobe3DYlHR2jpLVpaZP/mTP+J//+/v0NYm8+STKSxZUsTt2+2EQmH6+iZwu2U+97ndzMzM8M//\nfIXYWImPfGQ9Xq8Xh8PJ1NQ0DQ2zlJZa+MIXPs3Xv/5PjIyE2bAhBavVisFgIBgMcuBAC6EQfOlL\n2wmHw/zbv50gJkaFKGqJi7NQW7uJV145wqlTTjZsMLJvXy03b7YwOTlNf/8YdrvIJz5RTVpaGv/0\nT6+jVEYoL09DrVaTlZVBf38/r7wyTFaWxBe/+FHa2tq4caMbtTpMX1+Edesy2bVrG//rf30fux3K\nykxoNAbS0hLx+Xy88cZd1Gp47rlqfD4fV660odGE6O2FjAw1/+W//Anf//5PaGlxkpcnEYnoyMu7\nNx918OBNZmYU7NmThsFgoL29n0jEx/Aw6HQKPvOZndy508Hx433ExMwhCGbi43VUVJRy5MglOjtF\nNm/WkJqaQmfnAMFgCJstQDisY+/eIsLhMMeO3UWlcmIwGNBqlZSV5dPTM8j58yGKiwOsWlVKc3M7\nc3MygcAcLlcU69bFER0dTV1dJ+FwiIQEUCoFYmOtBIMerl2TSU4OsmXLUtrbu+jtDaHTTeHxRJGR\noSQrK41z57qYmlKzYoUSjUbP6OgMshxibk6PViuwdm0Os7MOzp93Eh09g9Uai04XxmqNo7t7kP5+\nM1u3GiktXcLSpUuxWq3vaa36oLKwtisUCrRaLaIofuAFxkICgQD/+I//yLe+9S0++9nP8tWvfhWj\n0fgr/y8UCnH37l1UKhUFBQXvw5U+5g/g8WbwR5UH3dEIBoNvdwgeFJFIBK/X+0s+1YVt5PnPPz/k\nLUnS75QidX+L99fF+93vL70/W/xBdD4WenXD4TBqtRq9Xv/AHkTzHSGA2NhYVqxYRmpqKjqdjuzs\nRIqKEli1ahWCINDV1U1KipUXXvg816610tQUoaBAT2mpld7eEUZG7CiVCnw+mby8GLKz47h82cv0\n9CzLlsUTCEwwNOREr1cyMqLCYIiwa1c13d0jNDbOkpEhoNMFCQTcaLVqJiaUOBywcWM+VmuEK1dm\ncTrHiYnRIElO0tIScbtD3LqlJD1dy5YtRXR09HH79ihGYwSFIkxcnI7U1ASamjzY7QH27i1Dlme4\nenUMr/fecLpaHWTVqmX09Ni4fj3CsmUxVFam0dbWS2trN6Ioo1CEyc1Nwmo1c+rUDD6fj2eeqcbj\nsVFf34lC4UKSZOLiNBQVFXDpUg/NzT62bFlEWVkqV6920N3dh8mkQqeTKSrKwefzUVfnADx8+tM7\nGBoa4OjRRgyGMCpVkNRUK1FRVk6d6qK3N8CTT66gqCiVI0euMjo6hMUiEBMjkp+fQ1tbFydPOrFa\nI3zpSx+no+Mub755gdhYDWp1iOLibERR5I037i16+9jH1lJQkMqRI+dxOKYIh4MkJBjZtGktdXUX\nOXRogowMDR/96Hp8Pg9NTTeZnZ0jEFCwbl0pSUlJ/PjHZ+nrG6empoDCwng8Hg99fX00N3vQ62X+\n+3//Ai0trbzyymXi45VERytYujQXpVLJK69c4c4dP3v2lLJ+fSktLZ309HRht/sRRSXPPfcUNpuN\nn/70OoHADFVVaeTkxKNQKKivv86NGxHKy+PYv38zzc3tnDt39a0aJrB1axWJifH87GcNDA2NsWxZ\nAhkZZtRqkb6+AS5c8GEyyXz+83uw2SY4ePAcPp8Tv19FRUU2NTVreOONqzQ3j7FokYbUVD0Wi4G5\nuTmuXJkjHIb9+ysxGCSOH7/JzMwoXq+a1FQzH/vYLq5ebef06RHS0yVSUnSYTFqCwSDt7S5mZpTs\n2LGYtDQD58/fZWioF0nSYDKJ7NixCodjjsOHJzEYXCxZEoNGI2G3exkZcTA+rmPdunRKS5O5erWP\n7u5hNJoIOp2SsrJc1Golp0+7iEQ8bN2aSyTioq3NhsdjZ3ZWQ1aWifLyDNrbbbS3u0lJkYiLExFF\nkUDAz8CAgCSJrF6dik4X5sKFSWZmBtHrdURHi5SVLaKzc4KmpgglJTo2bMihtnYLJSUlj20wv4Z5\nm9R8bf+g2KR+V2RZ5ty5czz99NNMT0/z2muv8fGPf/zXLmEUBIH4+PjHm78/WDzuaDyqzNt9HhRu\ntxtJkh5I/OD8gPP8CY9Op/ul0/v5v9mFiRbv1YD3ws7HvCVr4c994WbV+X/vhgCZFxiBQABZlt8W\nQw+zr3lmZuatU1ctFy9epKmpje3bN6BQKPj7v38dgE9+cgMNDY1cvuwmPd2PXm9iZmacxYsLGRmZ\npLVVxfr1WrKyUjl58gaiaMRkCmO3h8nPtxIbG8uxY2NYLDJbt+bT0nIbm00kKUlidFTEaHRTW7uW\nY8ca6esT2brViCwruXt3EIvFjMMRwu8X2LAhi0gkwpEj4yQm+liyJIP+/j6UShOiGKS1FQoKYMuW\nNbz22gUcDpGKCj1OZ5BIJEh0tJk7d1zAvS+Vg4PDnDw5Tnp6gKSkBJzOKZKS0hgeHufOHSVbtsSx\nfPlS/vVfjxMMKikqMuFyBTCbdWi1IpcuzWAyyXzxi09RX3+RixdtFBYKmEwWZNlHSkoKV692MDCg\nYv/+HLKzs/nRj44hyxEWL47F7w+SkBBNMBikvn6GpCT4n//z87z44qvcuDFDSYkeQdBisWiIjycG\neXUAACAASURBVI+nru4m4+MCn/50OUlJSfzLv7yJWh0hNTUGWZYpKSlgZGSEV18dJz9f4r/9t8/y\n6quH6OiYJDNTz+iol6qqfLKzs/jnfz6B3Q5/9Ef3opfPnWtErVYwOupFp1PxJ3/yDBcuXOHAgUEK\nC2XWr6/A4XAACpqbu+jpUfDEEzmsWrWS//N//pVAQCInxwKIlJcX4nK5+PnPO4mOhk99ajPj4+M0\nNt7FZJLp7o5QWGjmM5/5BH/3dz+kpydMVZUBnc6MyaRFEAROnuzG61XwqU9VIssyx45dQ6MJ4nKp\nMJtFnn12NxcuXKWuzkZhYYj8/CzC4QBarZ6Ghk4GB3V89KMZZGRkcODAOYLBAPdubzXbtlXg8Xj4\nxS/uEh3to6wsg2DQB6iZmZmmuVlJZaWW2tq1vP56HTMzoNe7CQSMVFQkYbVaOXSoE0mSWLEiCkmS\nmJx0IQgBeno0JCRE2Lt3DQ0NLdy+7SUpyUkoZCYlRU1aWgrnz3czOalm61Yrer2emzf7kKQAfr8G\nURTYuHEx09PTnDgxS3y8nfT0FCIRN4JgxGaz0ddnpLpaJC0tiUuX7hAIqDEafYCewsI4ZFnmwgUn\nen2YdevSmZmZoafHh1I5zdxcLImJIZYvL+L8+RZ6e3WUlHgwm+PZsWMDBQUFv9QVflS+PL8bzM/Y\nhcNhBEFAp9M9tNHxfygTExN8+ctfpr6+nr/927/lueeee6ifX4/5g/mtN/ZjofEB5UELDY/HQzgc\nxmKxvGfvMV98F7aQtVrtLz2g5r/4v9cC4zexcA5koQhZOOOx0HL1+zxo5xcOzg95i6L4UKWN/CHI\nssz169cBqKio4NSpU7zxxnWWLk3kqad28z/+xw8YHRXYuTMOr9dLa+so0dF63G7w+yOsW5eLx+Ph\n2DEHWVk+CgrS6ezsQK+PRaUK09kpUFoqUFZWxOHDjQSDGvLyRCYnXRiNKhISomlqcqHRSOzZU8qd\nO3e5fTtAWlqQUEhDJOKksrKMhoY7dHSI1NaaSE5O5OzZW4iiFoNBgdMZprw8Fa1Wy6FDo8TFSezZ\nU05T003GxiApSWJsTCA2NkxNzVreeOMS/f0C+/YlolaraWzsRKdT4/dLBIOwZUspXq+Xn/98kMzM\nEDt2rKC5+RY2W4iYGIG+PpniYhMbNqzmRz86ztQU7NmTjkKhoK2tH5NJw9iYH4UCnnlmI11d3bz6\n6giLFgVYt66M7u5efD6ZQMDH4KCCDRtSqa6u5NvfPojPp2Dz5jRkWcbh8CCKcOOGHYMB/ut//SQn\nT9Zz/PgQhYVKcnPTCQb9REVFcelSK/39Ih/96CKWL6/g//7fl4hEJLKyrIRCMkVF2bhcLl57bYCE\nBJkvfOEJbt5soaGhj6QkFWNjYRYvjqemZj3f/e4r9PUp2bcviejoaO7e7SMSCdPf7wLU/Omf7sZm\ns/Gzn10jKipAVlYyarWCzMx0mps7uHDBz9q1Op54opZDh+qw2TyoVCHm5tTU1haRmJjID394BlmW\nqK5ORBAEJEnG63Vz6ZKbpCSZP/uzZzh16iw3btiIj/fjdGooLIyhvLyUf//3ekZGlGzZYsVkMjE6\nOk0kEqSvL4BCIfDcc2uZnJzkzTfvYjLNIYomzGYVlZWlXL16m2vXIlRXK1myJI/btzvxeiXm5jx4\nvUa2bcvGaDRy4MAtlMoAsbEiSqWCjIxE3O456usDZGUF2LWrmqamZoaHI2i1DpxOK0VFegoKcjl6\ntIXpaQVLlyoRBC0u170FlIODSnQ6BTU1+UxM2Lh61YHZPI1aHYPZLLF48SKuXr1DV5eOdeuUxMfH\ncvNmN+GwElmWUCiMrFiRBMDJk5MYDD4KCmIIBv04HGEEwUtvr5HcXIk1a8o4e/YGIyMqkpMdyLKZ\nj3xkE2VlZe9oR11YD+dr4ge5rv0hfBhsUuFwmB//+Md8/etf58knn+Qb3/gGMTEx7/dlPea947HQ\neFSJRCKEw+EH9n5er5dgMPie+GznB5znY2p/V4EBD09i1O8z97HwgbuwSxMOh/H7/UiShEqlQqvV\nPnKnXMBbp7aTxMTEIIoir79+kMHBcZ55Zg8DAwN8//vniYqS+eQnt3Hw4HE6O6GgQMLtVhIOz1JS\nUkxLywCDgxp27YpBo9Fw8WIXOp0KjUaJ0xmgoiIDlUrFoUM2UlNDbNlSwuXL1/B4jMTFhRkcFElJ\nCbFmTSUHDzYyPq5g3ToDgUCY0VE70dFGbDaZSERix45SJidt1NXNkJHhIzc3jeHhAczmWDweN11d\nAitXGli+fCm/+MU5/H4VhYVaHA4/RqMGs1lLY+McOt29lKGWllauXp0lMzOMIOhQKv0UFuZz7VoH\nXV1qnn46laysDF5++SygICFBg8sVYPHiNBQKBUePjhEXB5/+dC2XLl3l9m0nmZkwMyOTmKhl+fIy\nDhy4RF+fwEc+kkp0dDQnTzahVMooFBAOK9i4cSkej4dXXhkiPV3imWfW09Z2h+7uaWJjBfr7JZYs\niWLr1o1897uvMTqqZPfuZIxGI319o6hU0N3tRKEQ+NzndjI4OMhLL7WSmnrPhhUI+IiJiaa9vY8b\nNyJs3hzDvn3b+f73X2J2NkxSkpK5OYmSknREUeTgwW60WiUf//gKnE4n1651YbHA0BAkJop85jPP\n8LOfvcH1615WrFARFxdPJBJAq9XR0NDH1JTIJz+5FLPZzMsvn0OpDKJW37NBbt68gtHRUV55ZYzs\nbD9bty5naGiImZkAHo+T/n4169fHs25dNf/yLwdwOiE5OUIopKKgIBmFQkFd3Sharczu3YuZmZmh\ntXUCnc7L5KSR5GQFTz+9jYMHT3H7dpglS0KIohmdTkar1dPSMo7DoWbfvixUKhXnznUAXkCDKCrY\nsKGM0dEx3nzTQVaWi2XLChgbG8XjUeDxOBkfN7FmjYWcnEyOHbvxVvBCgEhETWZmFLIsceWKB5NJ\noqZmEaOj43R0eNDp7Hg8MSQmSlRXl3Hq1HW6u9VUVoZQq41MTtoAFXNzIEl61q9PIRwOc/78BGq1\nE6vViCjKJCUlMD09xfXrKpYsCbNqVSmXL99kelpEq7UTDsewf/9KVq1a9SuWmPtr4vwBzTwLO8Lz\ndfFR7X7MHyBJkoRarf6VZ9wHHVmWaW5u5otf/CKRSITvfe97VFVVPVKf8THvyGOh8ajyoIXGfJRq\nVFTUu/aa9wsMjUbzK6f3CwXGPA9zKtT9zM+O3P+wnWf+oTrfEZnfaP4w7St5kNxLZbqK1Wpl6dKl\n/PSnL3Hp0iA1NfksXbqEv/3bV/F4FNTUJGCzTdPf7yAuTsP0tIgs+9i2bRldXf1cuhSguDhETEwM\nQ0N9xMYm43A4GRzUsnatidTUZI4du4UkKUhKUjA76yU5OZqoKCPnz88RExNh375KrlxporcXMjND\nOJ0iWq2XlSuXUV/fxsCAyJNPJqLRaLhwoR2d7t7JpNcbobo6F4DXXx8lNTVEbW0Z1683MzOjJC5O\nZmBAICtLSU3NOl56qZ7xcSW1tbEoFAru3BnCbNZhs4WRJNi3r5KZmRlefnmAzEw/K1YUMjAwAOgI\nBDx0dkJ1dRRbtqzne997nbk5JRUVZoJBGYVCQqtV09RkRxThc5+r5fbtNk6eHCQ5OYDJZEEQQuTm\nZnP9eift7SK7dsVTVVXBSy8dIxCQiY0V8HhkKipyEQSBV1/twmyGZ59dxcDAADduDBMbq2B8XEFK\nipqPfGQ3/+//vUFrq0xtrZnk5ET6+4dRKAT6+2fweESefroMQRB48cVrmM1hcnLikWWJtLRExscn\nOXHCzZIl8KlPPcnrrx9lZMRHVFSI2VmRiopkcnKyefHFS8zNwdatSYiiyMDAJIIQpqcnjF4Pn/3s\nbm7evMXJk0MkJ/vQas1YrSry8xdx+vQN7t5Vs2dPNFlZmZw920ggECEcjhAOa9m6tQiVSsW///tt\nTKYAixcnEAz6EQQtPp+Ta9egqAieemoLBw+eZGxMJirKhc9npLDQSnJyEseOdeBywfr197a99/TY\nEIQgNpsWg0Fi9+6V3L3by4ULsyQnz6HXW9HrJZKSkrl5s5uBASPbt1tITk7k3LlbBIMSSmUE0LJi\nRTqSJHHs2ARWa4CysmSczllsthCi6GNw0EheHqxaVcaZM00MD6vIzHTj84lYrfdqzN27PsJhkZqa\nZILBIE1NNgRhFqXSglYbYeXKorfuJYniYh8lJXl0dvbgdisJBObweqN56ql70cApKSm/c01e2BFe\nWBvvP5S5vwPyQan59/NhsEk5HA6+9rWv8fLLL/OVr3yFL3zhCw9FFP5jHgiPh8EfZR5k6tT8YPS7\ncQozX3jn7VharRaj0fgrSVILLUnz4uKDdtp1/2KjhVtV5ze8L/w9znc2HpV9H78vKpWKzMxMEhMT\nASgqKqS8PJsVK5ZjNpuZmRkiNlZg//4nCYdDXLniwGhU8slPbuPu3Q4aG51YLEFEMYJaHSA9PZmB\ngQD9/TLr1mWQni7S3DzOyMgogqAgEvFTXp5HVJSR+no/CoWLnTuLGB/vp7NzGpUqgtMpkJSkYc2a\npbS0TNPSMkN5eTRxcffSmfx+L7OzKiIR2LmzEoUiyMmT04TD0+TlWZHlOSIRgelpFwMDIiUlsaxf\nX0xTUz/NzYMkJirRaAIYDGpUKoFbt4KEwzKf+MQGfL4Z6usHCQan0ekUmEwK8vKyuXVriJYWierq\nJKqqsrhxo4ubNzsQRQmlUmLx4gzMZgN1dTbcbg979y5FqfRw4UI74bALl0sgKcnA00/v5NKlO1y8\n6KCszEJpaRQjI5P09PRjs/nw+RRs3bqMlJQY3nijE5ttlKVLE7BaZYLBEOPj07S2yqSn63n++ado\naLjFmTN3iImRMBplUlLuzQ5cvDjO6GiQ7dsXk5Agcu5cG+Pjw4AKo1HFzp0bGR6e4MCBMazWIJs2\nZQFBenqGGR62YbOJbNxYwLp15Rw/3szt270kJCixWBQkJ99LHrtwYQ5JirB//0pk2cOJE7fweGz4\nfCrS0szs3VvDpUt3OHvWRnGxjvx8E263h+lpO0NDAbxekX37KklONnLsWCeDgz1YLCJms0BxcS42\nm4MzZzzExkrs2lWEzTbJjRvdeDxuPB4NlZWZlJcv4vz5fjo6JklPF4iJufdlORDw0t4OoqjkySeX\nEwzOcfbsEH7/BKKoJTFRR2XlElpaRrl2zcuyZSaWLImir2+c4eFx3G6QZS3r1xcQH6/n5MlxpqZG\nSU/XYTaDKGpxOudobxfJzNSxc2cp3d2DNDfbACcqlUBqqomUlBhaW33YbBJVVbEkJgq0tU0yPT2B\nz6fDaBTZvHkpLpeb48en0evnWLTIglodweEIMDnpwmbTUVtbwK5dVaxatYqoqKjfqzb9um3Tvy2M\nYz6KfP7wZv61Hta6OG+TeliX7r0bSJLEK6+8wv79+4mLi+PgwYPU1tY+ckLqMb+Rx8Pgjyrz+yAe\nFIFAAI/H83s/VBYiy/LbHYz5HRDv1MGY/4ItSdLbD5KH9WHyhzA/7B4Oh1EqlW9bpN5p8Hzh3Mc7\neZwfpZ/L78u9lJ8rpKamUlRUxD/8w/fo6HDy1FP3tkZ/+9unUCph9eoERkfHmZjwExurYmBAiU7n\nY8+e1TQ1tXLrFpSVySgUWmZnJ0hJSWdgwMb4uJatW2MxmUycPt2FWi0TEyPicHjIyUlErRY4dWqO\n1NQIe/eu5OzZy4yNqUhLCzE1JRITE6KychnHj99ibExg794kZFmmqakHg0HE71cQCkls2lSM1+vl\ntdfGyMjws2ZNEXfudODxqNDrJXp6hLdSfKr52c9OMTOjpKrKiM93T7AbjVru3vW+Na9RxcjICMeP\nj5CU5CM2NoZAwE12dgbd3SM0N0NNTRTV1eX8/Od1+HwCcXESLpdMUVESRqORN9/sRxRlnnqqlKGh\nIVpabJjNAZxODWazxI4d6zl1qoGbN2XWr9eQk5POnTs9yLKK2Vk3c3Nadu3KJzY2lp/85DJqdYi8\nPCsejxeDQY8sh7hyJUhmpszzzz/NG28c4+5dLxkZYWZnBbKzzeTmZvPmm81MTAg88UQKOp2Oa9c6\nEYQILte9e+GJJ6qZmprilVf6SUnxsHhxFh6PA1G8Zwtqb1exbp2ZNWtW8Itf1DE3pyQ6OoDfL1Jc\nnIjBYODYsQEEQaa2Nhun00lHxxRarZ+pKQPR0RGeeqqG+vqrNDX5KSoKotdbUSj86PVmOjrGmJrS\ns2dPCkajkVOnWpHlAGr1vc3IK1bk4XK5ePNNOykpPtavX0xf3wATE2HUag9jYyZKSjSUlRVz9Og1\nJicFCgrChMMa9HolgqDkzh0fgiCwdeu962tomEartSMIVvT6yFvipIvGRqislCkszKK5uQO/XyAQ\ncOPzmVm2zIxer+fChXGUygg5OTpkGUIhUCr9dHSoSUoKs3nzUm7f7uTOnTDx8bNIkpWEBCWJiYlc\nuzaAzaaltjaKzMxMqqurH0gwyAe1+/FhsEl1dXXxF3/xF4yMjPCtb32L2traR+ozPuZ35rF16lFl\nPpXoQREMBnG73Vit1t/7ROZ+gaHRaNDpdB9KgTEfk6tUKt/emPpu7Pt4p7mPDxsej4eJiQkyMzNx\nuVz86EcvolQq+PSnn+XAgcO8/PIAhYUR9u7dyGuv1eFyGUlPDzM5CQkJMnl5uZw9O4DbrWDXroy3\nvPgzWK0SPp+aSMTP5s3lDA6OceqUmyVLQixZkktz8y1UKivgZ2REQ0WFgfz8XA4caCYUUlBaamB2\n1kM4LBEdraO1NYjBEGHfvpXcutXO9etesrKCyLIWhcJNfn4+LS29dHdr2LMnjpSUJI4ebQBUmM0K\n3O4IpaWpqNVqjhwZJSZGZs+eMtra7tDXFyAhIcz4uEhcnMTOnZt49dV67t5Vsn27GbPZTGtrD2q1\nBocjgN+vZvv2QlQqFT//eRtWa4AlS1JwOh0olVokycf16xIFBQo+9rFd/Nu/HWBkBBYtijA7K5GU\npCMmJoZLl0bweAT27y8kEAhw6VIvOl2IcFgFhFi/vpzh4XHq6lwsWRJm/fpyWlpamZuTkSQf4+Na\n1q6Np6SkmJ/+9AxeLxQXawmFFGi1KgRBprHRg8kEn/jEOtra7tDQMEVsrIdgUI/VCqtWLefEiWvc\nuaNiyxYD6ekpNDa2IUlKvN4AgYCOmppctFotr73Wjk4XYNGiaAIBP1qtnlDIQ0ODTG5uhKee2kRd\n3TmGhmTi4jx4PHqysnRkZqZz8mQndruSLVtiUSqVtLYOIwghXC4tajVs3bqU8fFJ6uqmSU52kpKS\nRCjkRq+3Mj4+SXe3jvXrDRQW5lJXdw2vV4XR6CUc1lFUFIcoipw5Y0OjkdiwIQ273U53txuNZo7Z\n2Sji48Ns3LiCCxdu0tqqoLQ0gF4fhd/vRKnUMDo6x9ycnnXrohBFkStXRhGEIEajCkFQkpeXgsvl\n5Ny5EOnpPmpqyrh9u4PRUdBq7bjd0eTnq8nKSqe+vhObTcWKFQJxcYns3FlLQkLC+3yn/3ZL6v1p\ngL9L7Pm7dV2Puk3K6/Xyd3/3d/zgBz/gi1/8In/1V3+FXq9/vy/rMe8fj4XGo8qDFhqhUAiXy4XZ\nbP6d5wfmW8fzW6znZzAWFt4Pg8CYn0UJhULvStLIO4mP++c+3mnA8sPGwohgm83GzZs3KS4uJjc3\nl7/5m28xPBzk2WerkGWZH/3oKnq9zLJlcYyOjuNySSQk6LhzRyY6OsATT6zj5MnL9PQILF0KLhfI\nspv09Aza28ex2TTs2pWEIAicP9+HVhtBrxfxePyUlmYQiUQ4etRBdnaIHTsqOXv2MrOzGuLjQ4yP\ni6SmQnX1cg4ebGJyUsmWLdFEIhKdnaMYjWpmZ3lroWEJDoeDQ4fGSU31UliYwfj4CBqNhWDQS3u7\nkhUrdKxevZyXXz7N3JyKRYuUzM6GSUjQY7GYuHx5CoVCwTPPlDM8PMzVqzaio71Ikh6VKsTatRXc\nuNHBlSth1q3TUFqaz/nzjYRCIgpFgLk5LVVViaSlpfHSS9cBicrKGNxuD1NTXrTaCN3dSqKiwuzf\nv4lLl5poaQmQlxdCEIzo9RIpKSlcu9bN8LCW/fvTsVqtHD/eBEio1UrCYQVVVXmEQiEOHBglMTHE\npk2L6e8fZHTUh8kUor//XrrY9u0b+PnPTzA0pGDZMoFwWEQQImi1GtranASDAk8+uRi32825c4No\ntS5E0YBKJbFyZTF9fcOcOeOjpCTMqlUlNDXdwu1WIsseZmdNrFwZRUZGOocOteD3yxQUiG91A5QI\nQoS2NgmzWWLnzqX09g5w/focsbFOwmEzVqtEeXkx9fXN9PToqKnRkZSUQGNjB5GIgmAwhCTpWbUq\nDaVSybFjw+j1fvLyoggEfPj9SlQqH21tWnJywtTUVHL2bCODg0pSUlwEAgZSUtRYrVbubb4X2bDB\ngizL3Lo1gSAEAD2iqGDNmsWMj09w4oSHjAwnZWX5jI+P4HQqCYXmsNksVFYaychIob6+HYdDSVpa\nEI3GxB//8UfIyMh4n+/o38z9aYD3d4XhvTuY+TCkScmyzIkTJ3jhhRfIycnhO9/5Dnl5eY/UZ3zM\nH8RjofGo8qCFRiQSwel0YjKZfuuQ13zRXdg6vv9kZ+Em70dZYMx7i+eH3RfOobybvFPk7oPY9/Ew\ncn9E8DvtILHb7dhsNhYtWoTNZuOHP3wJg0HL5z//SV588RUOHZpgxQoVa9aUc+DAaUIhEzExAaan\nVWRmqsjJyaaurpdgEGpr07DZbHR1OYmKAodDg1LpZ/v2Sjo6ejl71ktZWYSUlER6e3vQ6aLxeFyM\njupYs8ZCZmY6hw+3IEkKsrPVzM56sVr1mEwaGho8WCwS+/atoLm5lbY2P2lpQTweNXp9gMrKcs6e\nvUV3t5rdu6OJjY3h3LkWVCoRhULC6xWoqkrHYDDwyivdREVFWLs2m5GRYcbHg8TEKOjqEkhJkXj6\n6VpeffUk3d0KKisFZFmD3+/CYrFy9+4Mc3Mi+/blIcsydXVdaDQ+rFYdoVCI4uIsnM45jh93kZPj\nZ8eOKi5caGBqSiAqysfUlIZFizQUFy/m0KGbzM6q2LjRikKhpL/fhlarxGZTolIp2Lt3ORMTE7z5\n5ihJSR4SE+MJh93ExiYwMjLBrVsCGzYYWbasmCNHLuB2C1gsAbxeNcXFsVgslrctUZs3p+N0Orl7\n145OF2B62oDVGmbPnnVcvtzMtWs+liwJYjRGEww60eut9PZOYLMZ2LkzEavVysmTrUhSCINBQSSi\noKQknUAgwKlTTuLjQ2zZUkRXVw9DQ2GMRjc2m4nsbIHq6nKOHm1gYEBFZSUoFDrcbhdKpZKxsRDh\nsJotWzIJBoOcPTuKVjuH0WhEpYqQm5vO5KSNy5dlSkrCrF1bzsWLTczOiqjVDnw+K8XFRhIS4jlz\npg+3G8rL1QSDESYm5hDFCHa7EaNRZuPGIoaHx7h40U1Skh2zORaNJojZHEdPzxADAyZqaoykpSVz\n9uwtAgEBjcaHSmXi+eefJD8//wNdJ97JenX/wcw7Wa9+18/8qNukAEZGRvjLv/xLGhsb+fu//3v2\n79//oTy8esw78lhoPMoEAoEH9l6SJOFwON4e2n4n5sWPz+f7UAuMhadbwNsD4O/nvo/f5G9+VOY+\n/jMRwZFI5O05mIGBAa5ebaC0tIT09HS+/vXvMDUl8dxzq3C5XLz00i3M5ggFBdFMTEyiUGiJilJx\n/XqE5OQg+/Zt4M036xkZ0bB4scT0tIzRGCIrK4vr14eZmhLZuzeVSCTClSv96HQySqVAIBCiqiof\nv9/PwYPTZGcH2Ly5jIaGJlwuLVZrmKEhNbm5SqqrKzhwoAGbTcnq1Qb8fompqVksFj3DwyEkScGu\nXUuYnp7m5MkJEhK8xMRE4fe7SE1NZXrazrVrEqtWaamuXsrhw+fweNTExARxOlXk5ZlISEigrq6f\nSAR27MhidnaWtrYpjMYwc3NaNJogu3atoaWlg/p6F8XFQVJT4xkbG0WtNuN0uhgf11NTE09aWioH\nDjQRCkkkJyvwekPExZlRqeDqVR8WS5i9e5fR2dnFnTs+4uK8eL0moqIirFu3kuPHG7h7V6SmRk9c\nXAwtLV0oFCo8niCBgI4NGzLQaDQcOtSNXh8gJ8eKz+dDFO/FB1+7BtnZYfbuXcepUxcZHFSQnOzF\n7daRmiqSlZXBmTNdzMyo2LYtDkEQuHGjH0EIEwioUSoVbNpUjN1u58iRaVJS5igszGR21kY4rCUY\ndNPdrWXFCi2lpQWcONHI7KyKhAQfgYCatDQjOp2OhgY7ALW1mTidTm7dsiOKDsJhK3p9iHXrymlt\n7eby5RClpUGys9MZHBzE71fh9bpwOi2sXRtNVFQUp093EwqFSUiQCQYjmM0GVKowt28LxMZG2Lx5\nMf39Q7S2+rBY7ITD0cTHyyxZUkB9/S36+3Vs2qQhPj6Omze7CYXuvY5SaeSP/3gzixYteldTBh8m\nftsuJOBX6uL93Y8Pg00qFArxve99j29+85s8++yzfP3rX39PIu4f84HmsdB4lAkGg/wev7//FLIs\nMzs7i8FgeMes9IUCQxRFdDrdL1msPiwC42Hf5v1Ocx8LU1zg4Ryu/G1EIhF8Ph+RSORdjwgeGxtj\nenqaoqIihoeH+cEPfoHVqufP/uzT/OhHP+P4cTvV1WqWLSvg+PELyLIZgyHAzIyawkItGRkZHD3a\nTTgss359AtPTdoaH54iOFhkfVyGKAXbvruL27btcueKjqCiExRLFzMw4sbHJjI3ZGBzUsXmz9a1Y\n3puAithYcLlCZGZGYzTqOX16GotFYs+epbS3d9DVFSQ+3o/DocNkClBTs5oTJ67R3i6wZYuemJgo\nbt68i1qtw+sN4PFoWL8+DYPBwMGDXeh0IYqKYpiddSLLKnQ6mZs3JVJTIzz11Ebq6s7T19cc2wAA\nIABJREFU2wtZWX5mZyEqCnJzs7l2bZDJSTX79qUiCAKXLt1FFCUkSYksK1izphCfz8cbb4yTkuJn\n9ep8enp6mJ6W0GqD9PdryM8XWL16GYcPX2FqSs2SJTLBoIhaLWM06rlzx0UoJLBnTz4ul4sLF0Yx\nGNyoVAYEIcTy5YsZGBjl7NkApaURVq8u5fLl63g8IoJwzxK1bJmJ9PQ0jh5tw+tVsHSplmBQxu32\nodFAX58Sg0Fm+/ZS+vuHuHrVSXy8E1G0oNOFycvLobm5m44ODZs368nKSuPChRaCQSVKZYBQSE9F\nxb3447q6EdTqMMuXx+F2u5iY8KPVBhgaMhAfH2Lr1koaGm7R2iqRl+dBkgzo9RFMpig6OyeYntaz\nbVvsWwle3UhSEFFUIEkyS5ak4vf7OXfOT1KSnw0bFtPb28/oqIRGM8fMjIXcXIHy8iJOnrzB0JCa\niooIgmDE5ZoDYGIigixreOaZZWRlZbFo0aKH/p5/t7m/Ni48pJlnvvsx//8AtFrte9apfr+QZZmG\nhgb+/M//HJ1Ox3e/+12WLVv2SH3Gx7xrPBYajzIPUmjAPbuJXq9Hq9UC/2FRmf+C91hgPLwC47fx\nQZ37uH/Afl5gvJd/X36/H5VKhUqloqOjg0uXrrFy5TLS0tL42te+h90On/hEJQ6HgwMHOjEag6Sl\nmbHbZ7FYrBgMCi5cCJKVFWL37tXU1Z1jYkJLZmaQmRkVMTERCgvzOH++B5tNxd69KW/tORjAYFAS\nCikJBiXWrSvA5/Nx8KCN9HQfK1bk0dXVhd+vQa+P0N2torBQYO3aFbzxxgWmp0VKSgRcLglRjGCx\nmGhvdxEKKdm9Ow+Hw8HFixNYLF7UagOS5KeiopDh4QnOng1QXi6zdm059fWX8Xq1aDQebDY1ixfr\nyMvL5dixTrxeWLMmGq/Xz9iYA4NBYGxMQKOJsGvXcvr6Bjl71k5amgerNZpw2EViYir9/SNvfWE3\nkZ+fzfHjV/H7RQwGH16vioKCKAwGA6dPT6BWy2zcmMbMzAy9vV5MJj+zsybM5hA7d67h8uVmGhtD\nlJeHMZujcTqn0GhMjI7amZ42UFubgNVq5cSJO0AEqxVCIZmcnARkOcLZs24SEsLU1pbQ0XGXnp4Q\nFosLp9NMcrLMqlUVHD3aQG+vmg0bRLRaI4ODYygUAg5HmHBYy/r19zavnz49glbrISHBRCQSJDo6\nmmDQxdWrCvLy7gmMCxcaGR0ViImZw+s1kZWlJi0tlbNne7DbBTZutKJSqWhrGwUC+HwaFAqJ6uoc\nnE4nZ864SU52kZubisczSzCoIRCYo7fXwPLlakpK8jl16jp2u0hCgptwWEdKihG1WuT6dSegYPv2\nbNLS0qiqqnrkTuX/syzsfoRCoXfcX/Xbuh8fJGZmZvjqV7/K4cOH+drXvsbzzz//+G/iMb+Jx0Lj\nUSYUCj3QXRqzs7NvR9IuFBgqlQq9Xv9rBcbCiNYPavF9J+6fBRBF8ZHKSf995z4eVLIL/Or8y8My\nfNnb24vdbqesrIze3l5+8IPXiIrS8cILz/PDH/4bdXWzVFUpWbIkl/PnG1EoTKhUAaantZSVGUhL\nS+PIkU4iEVixwsrs7Bx2u4/oaA19fQp0uhC7d6+gra2TxkYf2dkBBEFPODxHdnYunZ0DdHdrqa21\nkJ6eQl1dI6DFZArjcikoLo7DZDJx7NgIBoPMli25DA4O0t8fICoqiM2mw2wOsnPnWurrG2lulqmq\nUmAyWRkbG0WrNTI15WJqSs369TFYrVbOnOlDpZJITBTxegMkJ8cgCDLnz3tJTo6we/cKGhub6e2N\nkJDgxenUExcnsXJlOcePX6evT2T79nsRrLdu9aJSqfB6I4RCGtavzwLgyJFBzGY/ubkxzM05iERE\nVKoALS0CmZlBtm2r5vTpK4yNacjI8OLx6EhMVJGSkszVq8PY7QK7dqUgSRJNTQOoVCHCYRGlUsHa\ntYtxOBwcPjxDWpqbZcsWMTo6jNOpQBQD9PfrWLpUw7JlxRw92sDUlIpFi8L4/QJmswqdTktrqwtJ\nEqitzcTj8XD16iRa7RyCYEQUw1RWFtHfP8q5cwGKiwNUVS3hxo1WXC4VcM8SVVFhJikpgVOn7uJ2\nQ3GxSCRyLzFLFCX6+5XodBHWrMlmfHyCGzcCxMQ40Omi0elC5ORk0dbWx507Gtav15Cbm8Hly7fw\nelUolW4kyczSpbHodDpOnRpFqYywYkUMSUlJ7Ny5/Vc61Y/5D+63Sc3X+d/W/XinwfP3u0b9OiRJ\n4sUXX+QrX/kKtbW1fPOb3yQpKen9vqzHPPw8FhqPMu+H0FCpVG8XVZVKhU6n+6Xh8A+LwPhDZwE+\n6CzsTv22yN33Yu7j/vmXh9224HA43hbnzc3N1NdfZf36SrKysvjrv/4+MzMKPv7xMubm5jh2rAu9\nPkhMjA6Xy0NmZhJKZYTTp71kZYXYtauK+vpL2GwakpICTE2pSUiIUFGxlLq624yNCWzfHoMsy9y+\nPYher8bjgVBIycaNi/D7/Rw9Ok5cnJf8/GRstkkEwYAohmlpUbB4MWzeXMWhQ2eZmtKQkxNidlZB\nfLxAQkIiDQ1jOJ2wbVsyPp+PW7em0OvDyLIGSQqxenURdvssb77pICfHy+rVS7h9uw2PR41GE2Rk\nREtJiZbS0sUcOdKE3a6kpESFzwcQwmDQ0tnpR6FQsH17Pna7nUuXpjCb59BozCiVAUpL8+nrG+HK\nFYkVK5QsX76Yc+eu4fWqUancOJ0Giov1JCUlcupULz4fLF9uJBSKMDXlRqdTMDGhRqeT2LatjP7+\nIS5edJKcPIfRGIVC4SMpKZXe3mE6O7Vs3mwgJyeDM2eu4/er0et9BINaiopiMBgMnDw5hihKrFuX\njNPppKfHhU7nxW43Y7WGqKlZwfXr7TQ2higu9mOxxOL12hEEAxMTdqamjNTUxBAVFUV9fSfhsITF\nEiESUZKTE48khbl40UNUVIg1a7IYGhqmpyeMxeLC640mIUFi5cqlnD59na4uDWvWKIiKiqWvbwhJ\nEpibCxAKGVm79t729JMnB1Gp/KSm6omJieZTn/o4RqPx/b5NHlp+3zSphYtmf93hzMO2D0mWZe7c\nucOXvvQl7HY73/3ud9mwYcNDW1N/Hd/4xjf48pe/zJe+9CX+4R/+4f2+nA8Tj4XGo0w4HP6lIvZe\nMh9vC7wtMBZaVD5MAiMQCLwttOa3fH/YeadYyV9nvfpD5j4eBXva/bS1tTEzM8PKlSvp6enhBz84\niMWi5oUXPsNPfvIL6upmWbZMoqAgk+bmVpRKM5LkY2JCx/LlBrKzM3nzzVaCQQWLF2twOv2AjMWi\no60tiF4vsXNnKT09fTQ1uUlO9gIGFAovS5cWcft2L7duCWzapCcnJ41z564jSTpEMYDbraG0NIr4\n+HgOH+4BwixfbmV21snUVJCoKCUjIxpMpiC7dlVz40YbjY0BCgsDaDRmgkEHcXHJ9PaOMjioZ8eO\nGOLj4zhxohlZVmE2R/D5YPHiBNRqNSdP2jCbJbZuzae/f4De3gAWixe73UhUVIitW1dx5kwjt24p\nqK4GszmK0dFRVCo9dvs9gbFpUwJGo5ETJ7pQKsPExSnx+YLEx0ehUIS4ciVEQkKIrVtLaG/vpLdX\nJjbWjddrJiFBpqKilFOnmunrU7Nlix6z2cytW70oFAI+X4RwWMvatekoFAqOHx/GYPCTnW3F7/ch\nSSrU6iDNzSoyM0Ns21bFhQtN9PZCaqobv99AQoKCpKRkGhoGmJrSsGNHHGq1moaGHhSKCJKkRKEQ\nqK7OxefzcfToNHFxbkpLU5mcnMBuB70+wPCwmfx8gaqqUk6damRoSEVhYYBQSIteD6Koobvbhd8v\nsmXLvS7O5cujCIILtVpHdLSRv/iLz2CxWN7nO+Dh5t1Kk/pd5uLeyZr6IJ6fbrebv/mbv+EnP/kJ\nL7zwAi+88MLb1ugPEk1NTezfvx+LxcKGDRseC40Hy2Oh8SjzIITGvEVq3pcqCAJms/lDJTCAtzsY\n78Ww8aPK7zr3cf9D9v7XWNg9etTsaQsZHx9Hr9djsVi4du0ax45dYtOm5ZSUlPDVr36X8XEFH/1o\nAYFAgNOnu9BowhiNIl5vkOLiNGRZ4vhxB2lpIWpry2hsvInNpvr/7d15eJTlufjx70xmMks2ICEL\nWSCBhGxkYRdRFlEExFqv1l89niq1Pe2px3pABaHluHsUi4oCHpf22Pa01eJWBdkFFAUBk0wIJAHC\nEggJgSxknX3e3x90pkmIQCDJTCb357q81CToMzNvZp77fe6FwYNtVFbqiIlxMGXKRNat28OJExpu\nusmIyxXAyZOVBAUFUVNjw2IJZMaMobhcLjZtOoXR2MLgwUZaWpqIjIxEq3Wyc6eT5GQHt912PVu2\n7KSqSktsrIX6eh0xMZCamsLnn5dSXa1hzpzBqFQq8vOPExiowmpV43SqmTo1BbPZzNq11URFtZCZ\nGc+5c9WYzRr0egfFxRrS0lRMmzaBdet2cuaMluRkO42NasLDAwgPDycv7yxNTQHMnZuAzWZjz54K\nAgMtgA5wMGlSOvX19axb10BSUgs33JBFUdFB6usD0OlaOX3aSGpqAJmZKWzZUkhNzYWic6czEEWx\nodfrOH7chqJomDkziebmZnburMZobMRgCCYgwEF6ehJVVdV8+aWTrCwHU6eOYefOPZw/r0Ovb6Sx\nMZSMDAPx8XFs3nyIhgYV111nRFECqKioRaNxUlOjQ6eDm25Ko7a2lq1ba4mIaGDAgDBcrlYGDBhE\nXd15iosNXHedlpycVLZt20dDQyAhIY3Y7cGkpIQSFhbG9u2nsdvhppuisVqtHDx4DrW6GYsllIED\nNTz00I8JDw/HYDB4+3L3Wb3VTaqzwvPOUlM7vj9219yPtWvXsmjRIrKysnjttddISkq65v+uNzQ3\nNzNmzBj+53/+h2eeeYbc3FwJNHqXBBr+zOl0dlqY1h0cDgdmsxm73e55s3XfTQ4NDfUEGG2DDG8f\nAfcEp9OJxWLB4XD0WrGxP+tK3Qf8Mz2wP6WndSYvL4/q6mpuvPFGTpw4weuvf4rRqGLBgnv59NP1\nrF1bQ3q6hREjhnL06GG02gE4HBaOHw9k4sQgUlNHsG7dPsxmLYmJcP68nfBwPWFhIezdex6NRsWc\nOSlUVVWRl9dAWFgzNpsOlcrMDTfkcvToaXbutDNhAmRlJbN7dz4OhxG12kxtbRCjRwcxdGgCn31W\njMUCublGmptttLRYCAnRUlamYDAozJo1ivLyU+za1Uh0dBOBgaGoVK2MHDmCw4dP/WNGhp7U1OFs\n27YXq1WPXn+h5iIrayARERGsX38MRVGYPHkwzc3NnDjRgNHo5Nw5A0ajnVmzxlFSUsZXX7WSnNxK\nWFg4Vut5QkIiqKg4Q3l5EDNmhDJ0aDwbN36LzaYhNNSCxRJAYmIYgYFavvrqPDqdwrRp8dTU1HD4\nsJng4GZaWwcQGupg+vRx5OUdZPduJ2PGOIiNHcKpUydxOnU0NzdRWxvCtGnhhIeHs3lz6T/a+oLd\nDgMHBhMQ4CQ/305YmItbbknj1KnTFBQ0ERZWj90eRnCwldGjM9i79xAlJTqmTNEybFgseXnFWK0B\nOBwWbLYQJk6MJCgoiI0bj6NSOUlLC8LhcNLcbEertVFWpiMqysW9984mJiZGcu4vwReG7l1Jauq1\nNuY4fvw4Cxcu5MCBA6xYsYLvf//7ffrz7L777mPw4MEsX76cadOmSaDR+yTQ8Gc9EWi0DTDUajUG\ng8GTA9/S0oLD4SA0NNTzZujPAUbbbkY6nc4nio39UcfUgs5O6vxp3se1UhSFEydOoNfriYmJYdeu\nXXz44XZuvDGLGTOm85vfrODYMTU/+EEsOp2ObduK0GoD0GrBbFYYOzYBjUbD2rVVhIc7mDJlOMeO\nHePMGYWBA20cO6YlIsLCrbdOZtu2fRw5EsiECSoURUdzcz0hIQM5daqe+no9M2fGoNPp+Pzzo2g0\ndgYM0GC1OhgxIgpQ2Lq1iSFDHMyalYPJVER5ucLgwWZqaoxERjq44YbxrF+/h6NHA5kxQ49eH8Th\nw+VotTqamuxYLHqmTIlFq9WyceMJDAYbCQkhtLS0YDQGo9Xa2btXIT7ezpw5E9m9O4+yMoXY2Baa\nm40MHqyQmprMF1+UcOqUjjlzLnSv2rfvMKDC4XDhdAYyadKFqdfr1p1mwAAbo0ZFUl9fR12dA6PR\nxqFDeuLibNx00zi+/DKPY8c0pKRYsNn0hIWpGDQogoMHz3DunJ7bbotCr9ezc+dhXC4bOp0GRVEz\ndmwiZrOZjRvriYqyMmVKCuXlJ6mocGI0NlNVFUxsrJ2JE7PZsaOA48f1jB+vEBAQTGtrIwEBWk6f\nbsFsNnDzzbGo1Wp27DiJStXCgAE61GoYNiwKs7mFL76wkZBgY+7cicTHx5Oenu7Va9bX+frQvas5\n/XCfALtZrVZeffVVVqxYwb/927/x+OOPExIS4o2H023ee+89nn/+eb799lu0Wq0EGt4hgYY/c7lc\n2O32bvlvuecQ2Gy2iwIMuPBGZzabsVqtntx4X2lx2p1cLhcWiwW73e5T3Yz6g7bPvTu4U6lUl5zo\ney11H/7E4XB4Uvl2797NiRMnmTFjOrW1tbz66kcEBCg88MD32bNnL59+WkV8fAtxcVHU1VUTEhKB\n2dyEyaQiJ0fFuHGZbNmyj5YWI0OGWGloCCAuTkd0dBRffHEaq1XFnDlDaWxspLDwLAaDDZtND9iY\nPj2Hqqpq1q9vIDm5lZycCy13bTY9Go2NEyd05ObqyclJZ+3aPdTXa0hLg6YmhaAgNcHBRg4ebMbh\nUDN7dhJNTU3s2lVNcHALAQFGVCob48alcfp0NZ9/biEjw86UKTns3p1HU5MOna6FmpogMjN1JCcP\nZ+PGA9TWqpgwQY/DoaK2tgG9XkNlJajVKmbOTKWuro7t288xcGATYWGhKIqVuLhYamtr2bMHxoxR\nMXlyLlu27KK+XktoaBNNTUaGDw8kOjqaHTtO0NioZsqUMEDFkSPn0GgctLYa0GhgxoxMampq2LCh\njiFDGklMjKWlpR5FMWC1NlFaqiM7W0V29ki2b8+jrs5AXJwZi0VPfHwQwcHB7NlTjcUSwKxZcdjt\ndr79tgK1uhWXy0hgoIvJkzM5c6aaDRuaSExsYty4NEaMSGTy5MlevS59XV8eunep04+amhrGjh1L\nSkoKGRkZREVF8dFHHxEbG8tbb73FqFGj+vx7ZUVFBWPHjmXr1q1kZmYCSKDhHRJo+LPuCDSuJMBw\n/1zbVq5u/nKnuWO7VJ1O59PdjPyJoihYLJYreu47K6pse2fP3WK3Y/DRX19HRVEoKSlBo9GQkpLC\n7t27effdbWRmxvLTn/6YxYuXsX+/ws03Gxg0aADffnsYjcaAWu2gpSWQsWMjCQ0NZe3a4+j1TsaO\nHUxtbT21tVYGDgygrCyAgQNtzJ17PXv3FlJQYGPkSDtOpw6NxkxsbALFxeUcP27gttsGMXhwBFu3\nmlAUDUbjhRaxo0ZFYTQa2bDhNEaji5tuSqSyspLjxy2Ehlo4dy6I0NALLWx37y5k714Ho0c7GDgw\nnJqaKrTaUGprz1NdHcSMGeFERESwZctB7HaIjHRhsUBc3AC0WjW7djUTEuJi1qx0ystPUlTUQlhY\nI1ZrGMHBNm64YQzffHOAvDy4/no1w4bFUlR0CLs9EJutlaamEK6/PpxBgwaxceNhHA4XI0ZosFpd\nuFwKGo2D0lIVISEObrrpQkpUfr6ZiIgGAgLCCA52kpGRisl0hKIiLTfeqCEhIYY9ew5gt+vRaC6k\nRI0ZE0FoaCgbNx7H5XIxbtwAbDY7FRWNBAbaqK42Ehbm4uabcygrO8FXXzUTF9dAWFgEY8aM5Hvf\nm+vtS8+n+UKaVE9xBxrvvfceJpOJwsJCjhw54sl+iI2NJTs7m+zsbLKysrjhhhuIjY318qq77pNP\nPuHOO+8kICCg3T7Ffbrjfm1Fj5NAw59dS6DRNsBQqVQYDAbPHWQ396bOndriPr24ksnSfSX46Ngu\nVafTXfQ8iJ7h7iRlsViAq3/uu1L30fYkrr++xo2NjRiNRpxOJzt27ODAgcPMnj0Dg8HAiy/+FasV\n5s27gfLycjZsKCcsrIVBg0KxWJqJixuCzdbKjh120tMdzJo1iU2bvqCmRk9UlJm6Oj0JCWrS0kay\neXMxZ88GMHPmIFQqFUVFJ9Hp1LS0qHG51EyZMgKr1cpnn1UREdFKSkoM58/X4nLpCAy0YzIFkJzs\nZNasyaxf/wUVFVqSkiw0NQUSEaEiJiaGffsqqKnRcvvtQ1CpVOzaVYZW6wICcDph4sTh2O121q49\nS1SUhYkTk6ioqODcOYXgYCsnThgYNkxhxozr2LDha44e1ZCbe2GGh0plISgolLKyOhoadMyefSGF\na/v2o6jVFoKDtTidChkZ8VitFrZubSImxsbMmdkUFx/i+HEbwcEN1NWFEhPjYsKEbLZs+ZajR/VM\nmqRgNIZSWVmNWq2lsdGB1RrETTfF/aML1zECAqxERQWiKAoDBoTiclnYs8dFbKyDW2/N5eDBQxQX\nX5ilYbEMYMKEodx33z3evrx8nq+nSXUHp9PJ73//e55++mnuvPNOnnvuOerr6yksLKSwsJD9+/dT\nWFhIRUUFK1eu5MEHH/T2kruspaWF8vLydl+bN28eaWlpLF68mLS0NC+trN+RQMOfuTdqXeE+KnZH\n+5cLMADP9y71ZtyVydK+kObij+1S+4qOgw574rnvrKVkb8778FWX6uKlKAomkwm73c7YsWPJz8/n\nD3/YTEyMkUcf/SWvvPImO3a0MGmSmuHD48nLO4BKFYTT2UpNTRATJ4YRGzuE9euLsdkgPV1HS8uF\nYv6gIA0lJQ4MBoU5c7I4efIUu3adZ/DgJrTaUNRqC5mZKZSVnWLvXpg8OZDs7BS2bduD1WpAr2+l\nsdFIVlYIQ4YMYcOGw7S2Kv+YQm6loqIegwHOntUSGOjilltGUVVVzeef1zNkSCORkZFYLA0MGBBB\nXV0dRUVarrsukDFjMti0aTcNDYFERLTS0qJn+PAgIiIi2LHjFGaziltvjcVsNlNUdAaNxorVakCj\ncTJ9ejbV1WdZt66eYcOaGDVqONXVlTQ3B6BWWzh2TE9u7oVBfxs27KG6OoDERAvNzSoGDtRiNOo5\ncKARi0XDLbcMwel0sndvJVqtGY3GgFYLEyZc6ES1fn0TiYmtTJuWTUnJYaqrFXS6Js6eDeWGG4bw\n/e/PYdCgQX0m7ccb+nKa1JVy/w7/53/+J3a7ndWrV3P99dd/5/tabW0tGo3Gb1odS+qUV0ig4c+6\nEmh0DDDcQ8QudYLhTjm52s2XLwYfEmB4T2ebXJ1O16sf9p3lNHv7muwtbTuoXclGS1EUqqurCQ29\nMLX766+/5vPP9zJr1mSSkpJ48sk3OHtWxd13p2O329m0qQSt1k5w8IWC8PT0OBTFxaZN5xkyxM6s\nWbkUFhZx8qRCeLiZs2eNREbauemm61m/fjelpRqmTw9Erw+mvPwUWq2B+nozzc1Gpk2L/kd3pTI0\nGgexsYFYLHbCwoLRahW++cZKVJSL2bNzOXCglOJiK5GRzZjNQYSFOZgwIZft2wsoLQ3kllsMREdH\nsXfvAVyuQJxOK2ZzENddF/WPqelHUamcjBoVisVioaHBhsGgcPSohgEDHMyePZbS0jK++aaZuLgm\nNJpQDAY7cXEJFBcf59AhPTffHOwZ9Ge1atHpWjCb9aSmhhIaGsqOHWdQqVTceGMkra1mDh+uQaMx\nc/58MEajnenTszl6tJwvvzQzbFgjsbFDsFob0WhCqK+v4/jxIGbOjGDSpPEMHz5chu5dgj+nSbXV\n0NDA008/zXvvvcfSpUt56KGH2hWD9wfTp08nJydHAo3eJYGGv3On/HwXd4GtxWK5ZIDh7iDlcrmu\nOcC4lK6kuXzXbIWr/f+2vYvuz/MYfJEvzyG50o4ufbXuo2ORfXe1aM7Ly+PcuXOelrurV/8dg0HF\nww/fx6ZNW3j//UqSk1vJyEiivPw4druegAAbZWWBjBmjY8yYLNau/Zq6ukCSk100NioMHHjh7qrJ\nVIfFombu3CRaW1vZtes0BoOZgAADimJnwoRUzp9vYN268yQlmbnpplxMpiJqatSEhFiorDSSkqJh\n7Ngs1q/fS0WFluuu02C3a2hpaUSn01NRYcZiCWTWrEQcDgfbtp1Ep2slLMyA02knMTEGu93C55+b\nGTbMzuzZ48jLK+T4cRfh4c2cPx9MXJyKMWOy2LhxH8eO6bj5ZgPBwaGUlJxApQqgudmOxaLjuusi\n0Wg0bNtWiV7vICkp5B+tw7Wo1VZMJhVDhji59dax7N9fQmGhhejoBmy2YAYNcpGYOIzdu0s4cSKI\nW24xkpSUyOjRo4mOju6T12Rv6Q9pUi6Xiw8++IAlS5Zw/fXX8/LLL5OQkODtZYn+QwINf2ez2ejs\nNWwbYACeAKPtxro3A4xLuZrg40rX2fEuen+fx9Db+uocks6uyY5DKXtqmFZ36XgntycbHCiKwsmT\nJ9HpdERHR/Ptt9/yt79tZsKENL7//dtZvHgZxcUq7rhjMJGRg9m8eR+KokWnc2A2a8jJiSI0NJR1\n604QGKgwbVoc587VcPx4MyEhDs6d0xMcbGfOnEkUFpawc2craWlWwsMjaGyswWgcyLlzNZw4YWTq\n1FCSkxNZv34PZnMgkZE2WlvVDB0aSnBwEF99dQ6A2bOHU19fj8lUg17fgt0eRGCgg6lTczl+/BSb\nNzeTmmomNzeVI0cO09KiRa02c/q0kbFjg0hPT2H9+n2cOxdAerqC1apBr1eh02kpLW3BblcxY0Y8\nLS0t7N174f9hMAQREOAkO3sENTW1bNliZvhwM7feOoG8vEKqqsBobKKuLoTUVB2gRBQMAAAgAElE\nQVRZWel89tk+Tp3SMnmyhuDgQdx88xRiY2M912d/TwfsTH9Jkzpy5AiPPPII5eXlvPbaa8yaNatf\nvt7CqyTQ8HcdAw13Bx/3nXtfDjAu5XI59iqV6qI0l7Yfqu4Aw2q14nQ60Wg06HQ6n7mL7u86dvHy\nh3SFrtZ9uK9PbwTuHWtgvHEn1316BZCfn09p6WGmTZuCoii88MI7WK0q/u3fbuHkyZOsWVPKgAFm\nEhPDaWpqJDAwCK3Wzp49CiNGOJkz53q2bdvF8eMqhg4109SkJyICkpOHs3NnKadO6bj99giCg4P5\n+utiVCo14MJu1zJxYgJarZZPPy0nONjBuHHRnD9/nupqC8HBLo4fDyQy0sGsWdexb18ReXlWRo60\noFIFERhoY9CgSA4dOkl5eRBz5oQTExPFli352O0BGI1W7PZAMjIi0ev1bN1aRUCAiylTYqirq+PI\nkSaCgqy0tIQSFGTn5pvHU1JSxueft5CWZiYxMZ66umpstkBaWho5dcrIjTcOIDk5kc8+20tjo4a4\nOBuKYuC+++4gNTX1ote6sxO5S6UDujuz+aP+kiZlNptZvnw5r7/+Or/61a/49a9/jdFo9PayRP8k\ngYa/c09O7hhg6HQ6DAbDRQFG297bvhhgXE5nJx8dN3oqlcrzdXfLXgkwekdv3kX3FV2t++jJjZ57\n4GbHQm9fU1ZWhsViISMjg5KSEt5++2NiYkKZP/8XvPHGH1i/vpbx41WMG5fBzp17aW3Vo9ebqa01\nMmqUkREjkvjss/2cP69m0qQgbDaorq7FYNBy5gzAhRkZTU1NbN5cycCBFzpnOZ0WoqKiaG1t5Ouv\nXaSnO5k1axJbt35FVZWGqKhWGhoMJCRoSE1NYcuWA1RWarj11oHo9XpMpmOo1SpaW50oip6pU4fj\ncrlYu7ackBALI0YMoKmpEbNZRXAwFBdriY93MmfOJHbvzqeoyE5iYgtWq5HwcBVxcXHs3XuE8nIj\nt98+iMGDB7Njhwm7XYVW60BRjPzsZ7cxatSoLr2OXU0HdF+Tffn3tD+kSSmKwpYtW3jkkUcYNmwY\nq1atIjU11e8ep+hTJNDwdzabDbPZjNls9usA41Lcj8tut2O32y9KJeuY4uJPBb6+omORfX9vE+ze\n6HUMQNy6u+6jY6G3L9XAXImmpibP3eeioiK2b9/N5MljSUtL44knVnDypMKPfpSO0Wjkgw/2oCgK\nUVEqzGYnsbED0WrVfP11EyEhLm67bRTl5ScxmRoZOLAZiyWYoCA7N9wwhvz8UnbvdjBhAqSlJWEy\nFWOxaAEztbVBTJgwgKFD4/nss/00NcGoUYHYbOBw2AkMVHP0qIOAABWzZ6dx/vx5tm+vIiSkCb3e\niKJYSE5OoK7uPF9/rZCZ6eTmm8ezc+eFjlNhYc3U1wczcqSe1NRkNmwwUVWlYepUIzqdgbKy06hU\nKhoaXICeefOmkpSURHR0dLc8x23TAdtel752ItdV/SFNCi4MqFu8eDG7d+/mpZde4kc/+pFP3kQQ\n/Y4EGv6utrYWm81GYGDgRW+w/h5guDmdTqxWa7uJ0hqNpt92F+pN7jQdq9Xq83fRva1j3UfHHPvL\npQN2xh9T1DoqKyvj9OnTjBs3joaGBl566R0UBRYsuJeCggJ+97sDDBli4frrUygvP0l1tZOwMDvH\njulISHAxc+ZkNm78ikOHAhgzxoXTqQfMGI1hHD16ltpaA3PmDCEkJIStWw/icrkIDVWw21Wkpsag\nVqvYurWG0FAXs2enc/LkSUpKWggJaaahIYigIAs33jia/fuPsGePkzFjXAwbFsfJk+VYrYGYzU2c\nPRvMlCnhxMfHsn59Ac3NahITXdjtAYSG6tBq1ezf34pareKHP8whNjaWrKysXnkdOws+vuu9su0c\nGm/rL2lSdrudN954gxdeeIF77rmHZ599lgEDBnh7WUK4SaDh79xHxZ0FGO5NjL8GGG276VzJB83l\n7jK3/RDtzo5X/qptJykpsr86Xan7aHtdAu2GHer1er9PUXOrra0FIDw8nGPHjvGXv3zCiBGx/OhH\nP2TFijf5/PN6pk4N5rrrRvPhh5tpaNAxeLCZpiYdw4cbiY6OZtu2YzQ2qpkzJxan00l+fjkajROb\nTQOomD49g6amJj799AxRUa1kZydQV1dDfb2LoCAHxcVahg2zM336eLZv38vx4xrS0uyYzYEMHKhm\n0KBwTKZTnDlj4HvfiyY0NJRt2/bjdCro9QoOh4bRo+NRq9Vs2FBJUJCTadOGERUVxfTp071+GtWV\nEzlvDMHsL2lSe/bsYf78+eh0Ol5//XXGjh3rd49T9HkSaPg7h8Ph+QBoe4LR9i6pv70xdbyLey11\nAD3Z8cpf9fU0nb7gcjNo3AICAggMDESj0UhQDJSXl1NQUMDo0aOJjIzkuedWUllp58c/noROp+PN\nN7ehKArZ2SFYLDaamqwYDCqOHlURFOTitttGU15+ii++qCUqqhGDYQBarY1hwxI4caKSfftUTJig\nIidnJF98sY/mZgMDBphpagoiPT2YoUOHsn79QerrVdx00yDU6gBKSioICFBoalKjUmm4+eY0zGYz\na9eeZMCAFpKSIomOjuDuu39IYGCgt5/C79T2dPxSQXFPpqn2lzSp2tpannjiCf7+97/z9NNP8+//\n/u/yHit8lQQa/s7pdHrqEvw9wGh7VA70WB3A5XKZvX03z1t6ah6DuDJt7+K6f7/bBh8SFF/s3Llz\n1NTUMHLkSOrr61m16g+oVPAf/zGPPXv28OabhcTH25k7dwImUxFlZTYGDWqhvj6I6GiFG2+cwKZN\n33DgQAA33qgmLCyMI0dOoFYbsVisNDYGMW1aNOHh4Xz22QFsNoURIzTYbKDTadBooKjIitEIc+Zk\ncvbsWXbuPEtYWCNabSixsQP41a/+zacDjMu5kmYInQUfXbku+0ualMvl4s9//jOPP/44t9xyC7/9\n7W+JiYnx9rKEuBQJNPzdV199RWhoKMOGDfPkePvbm68vTPPuamtTfwo++kMdgC/rGOC17aLW1QJf\nf7our4bD4QBAo9Fw9uxZNmzYTHx8LNOnT+PNN99h27YqJk+O4NZbp/E///MelZUBpKY6aG4Go1Eh\nJCSUw4cbaGwM5I47ElGr1WzffhiVyoJer0VRYPToJKxWKxs21DB4sIMZM1KpqKjgyJFWQkJaOHcu\nmKQkAw899FOMRqNf3qm+kpPiK61H6i9pUiUlJcyfP5+amhpWr17N9OnT/e5xCr8kgYa/u//++/n4\n44//kQ6QTXZ2Njk5OeTm5jJixIg+vanwhQDjcjor7m17N68vb/J66wRJdM7dsrqrAV5nQbH7rrOb\ndGK7WH19PcXFxaSlpREWFsbLL/8PR4/WctddNxAWFsZrr23E4YAZM4ZgtVopLj6DTuegsVGHVuti\n5szRnD17lrVrzxIb20RycjwtLQ3YbAGAhaIiDbm5gfzwh3OIjo7udwW9V3Kzpu01qVKpsNlsnnks\n/pom1dzczPPPP88777zDI488wsKFC9Hr9d5elhBXSgINf+e+c3TixAny8vLIy8ujoKCAgoICLBYL\nWVlZ5OTkkJ2dTW5uLikpKT6f7tJx4Fhf62R0ufx6X+941dnAN18L8PxZT7UK7sp16UvdhXqb+/lv\naGigubmZIUOG4HK5+Mtf3sdud/Cv//pD8vLyePPN3Qwe7OLee2eyZ88+vvnmPJGRTShKMKGhCunp\nKRQWHiE/X82UKTrGjMkkLS2N+Ph4bz9En3K569JfUwIVRWHdunUsWrSIzMxMXnvtNYYPH+7tZQnR\nVRJo9Fcul4tTp06Rl5dHfn6+J/g4f/48o0aN8px85OTkkJ6e7hOpMO5p3u5jcn/qZNTZHebOOl55\nc3pvx+e/rwV4fZ03nn9phvBPHZ//SwXYra2tfPXVVwwePJjc3Fw+/PBj1q0rYezYSObNu5unnnqV\ngwdVTJmiITQ0nBtvnEh6eroXHlXf0jZNSqPRoNVqO20FDX37tPjEiRMsXLiQoqIiXnnlFe68884+\ns3YhOpBAQ/yToihUVlaSn5/v+ctkMlFdXU16enq7k4+MjIxey4V1f8BbrVZPq1T3LAx/djWbvJ6c\nKC2tar3H6XRiNpt94vm/0u5CfXWT15mOndS6mqZjt9s5duwY8fHxGI1G3nvvffLyjnD33bcyevTo\nHly5f7iSblIdU686S1X1hRs2l2K1Wnnttdd45ZVX+OlPf8qTTz5JSEiIt5d1Wc8//zwff/wxpaWl\nGAwGJk2axLJly0hJSfH20oT3SaAhLk1RFM6dO0d+fr4n7cpkMnHy5ElSU1M9wUdOTg5ZWVkYjcZu\n3VC03eBKq9TOg4+O3cR6aqJ0x0Jj0fP6Uievy9Uj+XpKYGfa1sF05/Pv3hDL79Kldewm5X7/6WpH\nqo7X5aVu2LiDj968NhVFYefOnSxYsIDw8HBWrVpFdna2z/9+uM2ePZu7776bsWPH4nA4WLJkCQcO\nHKCkpASDweDt5QnvkkBDdJ2iKNTV1VFQUOBJu8rPz+f48eOMGDGiXdF5dnY2oaGhXX7D7LjB9eUN\nlrf1RMerrg47FN2r4wbrWmbBeNOV1n342hDMnqqDEVeubZpUdz//Xe3G5r4+e+L1r66uZunSpWze\nvJnnn3+e+++/3yd+B65FTU0NkZGRfPnll0yePNnbyxHeJYGG6B6KotDY2IjJZPKkXRUUFHD48GGG\nDh3qSblyn3wMGjSo0zft0tJSwsLCMBqNqNVqdDqdbHCvUmdpV5cLPgC/2OD2VR0L7f1xg9vVlMDe\nvsPscDgwm81Sh+Ql3hy611nw0VOBsdPp5J133uGpp57ie9/7HsuWLWPw4MHd9VC8qqysjJEjR1JU\nVCS1R0ICDdFzFEWhtbWVwsJCT9G5yWSiuLiYIUOGtDv1iIyM5I033uDdd99l4cKFPPbYYxJg9IDL\nDc9y02g0nonS8hr0jrZ3cPvbBtcX6j7anuJJmmbv6440qZ5aV8fgo7PAuGPw8V3rVhSFwsJC5s+f\nj8Vi4fXXX+f666/3+uPsLoqiMHfuXJqamvjiiy+8vRzhfRJoiN7l/jDZv38/+fn57Nq1i02bNnHu\n3DkGDBjAjTfe6Ck8Hz16NDExMX7zBuyL3CkiFosFwLOx7eu59X1Jx0Jj2eD+05XeYb6Wa7O/TJX2\nZT2ZJtUTrjRddd++fZSUlJCVlUVWVhYAzzzzDH/961/5zW9+w3/+53+i1Wq99TB6xC9/+Us2bdrE\n119/LVPLBVxBoCGfdqJbuT/IU1JSWLt2LR999BEBAQE8/vjjzJgxg0OHDpGXl8eKFSvYv38/wcHB\n7Vrt5uTkEB8f32/u9PaUy7UK7iy9xW63e/68O52lNzpe+au2E9XVarVnCrQvb7B6W2ddgTprBX01\n12Z/SFPzdW3TpDQaDUajsU90s3M32FCr1e0ChY6ncrt37+bFF1/0XJ/BwcGEhoby05/+lNTUVM6c\nOUNcXJzfXHMPPvgg69evZ+fOnRJkiCsmJxqiR9x5551s3LiRhx56iEWLFjFo0KB233dvhN2Bh7vm\no7CwEK1W267gPCcnh6SkJL/t39/drraTl8xU6B7+UujtS7pybbatRXIH2QaDQQLlXuSraVLdTVEU\nSkpKePbZZ2lqaiIsLIzz589jMpmor68HYNCgQeTk5PC///u/DB061MsrvnoPPvggn3zyCV988QVJ\nSUneXo7wHZI6JbzjyJEjBAcHd+muh/tOZllZ2UWzPlwuF1lZWZ7gIzc3l+Tk5D7fv787OZ1OrFZr\nt7ZKvVxufVfzl/2ZTFTvXVeS3qJWq9FoNP3+2uxNfS1N6mqZzWZeeuklVq9ezYMPPsivf/1rgoKC\ngAvX5qlTpzCZTBQWFlJQUMAf//jHPjEzozMPPPAA7777Lp9++mm72RlhYWHo9Xovrkz4AAk0RN/m\n3uiWl5eTl5fnmfVRUFCA2Wxm1KhR7QYNjhw50i/vnF1K2xSd3shB74l2u32dDDz0ro61SFqtFrVa\n7TfzPvqCjmlS/vo7oCgKW7du5ZFHHiEhIYFVq1aRlpbm19fQd71/v/POO9x7771eWJHwIRJoCP/k\ncrmoqKhol3ZVUFBAfX09mZmZ7dKu0tPT/TJ1pW16AoBer/fq47xcYW9v9a3vTVLo7V0da5G+6xSp\nq0PdJC3wyvWXNCmA06dPs3jxYr7++muWL1/Ov/zLv8iJpejvJNAQ/YeiKFRVVV2UdlVVVUVGRka7\n4CMzMxO9Xt8nPww7Dhvz5RSdKx3o1tfuLvf2KZK4WNsg72ruoHdW9+FyuSQtsAv6S5qU3W7nzTff\n5Pnnn+fuu+/mueeeY+DAgd5elhC+QAIN0b8pikJNTQ35+fnt0q5OnjzJyJEjPWlX7kGDQUFBPvtB\n2fHubV+dxXC5u8uddRTylcfYMUXHnzdXvkpRFCwWi6ebV3fUIrX9b3clLdBfTua6qj+lSe3bt8/T\npvb1119n3Lhx/e71FuISJNAQoiNFUaivr6egoMCTdpWfn8+xY8cYPny4p+NVbm4uWVlZhIWFef2D\nxd9rAHy949WVpuiIntPxJK83UwUvNwizr57MdVV/SpOqq6vjySef5KOPPuKpp57il7/8paRFCnEx\nCTSEuBKKotDU1ITJZPKcfphMJg4dOkRCQoIn8HAHIeHh4b3y4dqfawA6Bh/uf+6Y2tLTwYe/B3l9\ngcPhwGw2+9RJXn+r+7Db7ZjNZr+fSeJyufjrX//K0qVLmTFjBsuXL2fIkCHeXpYQvkoCDSGulqIo\nmM1mCgsLPUXnJpOJgwcPEh0d7an3cAchkZGR3fbB63K5sFgs3dqq1h/0Zserjq+B++6t6D1tU3T6\nQqB9JcFxZ6mBvvx73Z/SpEpKSnj44Yeprq5m1apVzJgxw6dfGyF8gAQaQnQnd+pAUVFRu7SroqIi\nwsPD2w0azM3NJSYmpkt3XjsWGcuwtyvTWVrLd3W8utzmrmN6iBR69z5/eg26Ehy3DUK8/Vj7U5pU\nS0sLL7zwAr///e955JFHWLhwocyHEOLKSKAhRE9zD2orLi5uV3S+f/9+goKC2nW7ysnJISEh4aIU\nitbWVtauXcutt94KSJFxd+hqxyu1Wo3dbvfUAMhr0Ps6Dj3059fgaq7P3koX6y9pUoqi8Nlnn7Fw\n4ULS09NZuXIlI0aM8PayhOhLJNAQwhvcxcOHDx9uN+ujsLCQgIAAz8lHVlYWVVVVrF69mrNnz/LN\nN98wcuRIr+ef+6vLbe7gQnpLYGCgZ6K0P26wfFHHWhiDwdDvfg/c12fHEzq3nq776C9pUgDl5eUs\nWrSIgoICVqxYwZ133tnvrjchuoEEGkL4Cnf+dllZGXl5eXzwwQds3ryZlpYWxo0bR3h4OCNGjPCc\nfCQnJ8tGt4c5nU5aW1txuVyoVCo0Go1nk+fW2eZONiTdR2phLq1t3UfbAKQ76z76U5qUzWZj5cqV\nvPTSS9x///08+eSThIaGentZQvRVEmgI4Wt2797NY489xs6dO5k2bRr//d//TVRUFHl5ee1mfbS0\ntDBq1Kh2Beepqal+uwHoTZcrtvf1drv+oO1MEqlH6prO6j46q0vqGIB09tz2pzSpr776igULFjBw\n4EBWr15Ndna2Xz5WIXqRBBpC+BKLxUJCQgIxMTEsW7aMmTNndvpBpygKFRUV7dKuCgoKqK2tJTMz\ns13dR0ZGhmzQrlDHO7dd2dxerqi3L3YU8gaZSdJzulL3oVKpsNls/aJt89mzZ1m6dCkbN27kv//7\nv/npT3/qt49ViF4mgYYQvubQoUMkJyd3eWOlKApnzpwhPz/f85fJZKKyspL09PR2wUdmZiYGg0E2\nuf/Qscg4MDAQvV5/zc9Pb7bb9Qdt58L4++bWV/Tn0zmn08kf/vAHnnzySW6//XaWLVtGZGSkt5cl\nhD+RQEMIf6YoCrW1tZ5uV+7go7y8nJSUFE/aVU5ODllZWQQHB/vFBqIrvDHs7XKTpH2xnWlPUhQF\ni8WCzWaTuTBe1DZNSqvVtqtJ8qcAWVEU9u/fz/z582ltbWX16tXccMMNfWb9QvQhEmgI0d8oisL5\n8+c9Mz7cfz969ChJSUnt5nyMGjWKAQMG+OUHsK9NVe9qO1N/CD7cdRjulsF6vV7S/LzgSk+SOhs2\n2Neu0cbGRp599ln+8pe/sGTJEhYsWIBWq/X2srpk9erVLF++nDNnzpCdnc3KlSsZN26ct5clRGck\n0BC9y2azMX78ePbv34/JZCIrK8vbSxJc2PA1NTVRWFjoOf0wmUyUlpYSHx/vKTZ3t92NiIjwuQ3E\nleo49NCXO+hcrp1p242d+5/7Si2DN06SRHvd0U3qSgPkjtdqb3O5XHz88ccsXryY8ePHs2LFCoYO\nHdrr67hWf/vb37jvvvt46623GD9+PK+88grvv/8+hw8fJiIiwtvLE6IjCTRE75o/fz5lZWVs2LCB\ngoICCTR8mKIomM1m9u/f3y7t6uDBg0RFRXlOPrKzsxk9ejSRkZE+uVl3a9vFCOizd8/7ek5921kM\nvnCS1F/1ZDeprl6j7mGDPXWNlpWV8cgjj3D06FFeffVVbrvtNp/5feiqiRMnMmHCBF599VXgwnMd\nHx/PQw89xKJFi7y8OiEuctlfNHn3F91mw4YNbNmyhQ8//JD169d7ezniMlQqFUajkYkTJzJx4kTg\nn3dADxw44Ck4f/HFFykqKmLgwIGeE4/c3FxycnIYMmSI1+9Sd1bo3Ze7GLXdpLl1NkvBZrO163jV\nmxu7znR291yr1fbZDV9f1RsF95e6RtsGIG2vUej+ug+LxcLLL7/MqlWreOCBB/j73/9OUFDQNT02\nb7Lb7eTl5fHrX//a8zWVSsWMGTPYvXu3F1cmxNWTQEN0i+rqan7+85/z6aefYjAYvL0ccZVUKhV6\nvZ6xY8cyduxY4J8b+ZKSEk/a1auvvsr+/fsxGAztul3l5OQwdOjQXrvD3nGatL92MfqujV3HtJae\n3th1pmOg58+zGHxZx0DPaDT2aspg22u0bU1Ex7oPh8OBzWbzfP9q6j4URWHbtm08/PDDxMXF8fXX\nX5Oent7nr7mamhqcTidRUVHtvh4VFcWhQ4e8tCohro0EGqJb/OQnP+GBBx4gNzeX8vJyby9HdCOV\nSkVgYKDnNOMnP/mJZ4N76NAhz8nH22+/TWFhISqVyvOz7uBj+PDh3brJbXvXVq1WExQU1O/Sc9zB\nnFqt/s6NndPpvGhj153BR8dAz2Aw9NmTpL7KPZfEV4fuuU/X2l6jnQ0btNvtF/2ZgIAAvvzySzIz\nMxkyZAgAlZWVLFmyhJ07d/Lb3/6We+65R645IXxY//pkFl2yZMkSli1b9p3fV6lUlJSUsHHjRpqb\nm3nssccA6ELdj+ijVCoVGo2GjIwMMjIy+PGPf+xJnTh27Jin5uPPf/4zjz76KHa7naysrHbBR0pK\nSpe71rRtkyrpOZ27ko3dtd5V7jhZvT8Ger6gr84lcb9/tL1mOqv7qKys5Pvf/z4AgwcPJjExkcLC\nQm644QbWrl3LmDFj/CrIiIiIICAggOrq6nZfr66uJjo62kurEuLaSDG4+E61tbXU1tZe8mcSExO5\n6667WLduXbuvu+9w3nPPPbzzzjs9uUzh41wuFydPniQvL4+8vDwKCgowmUw0NjYyatSodmlXqamp\nnQYOVquVvXv3kp2d7ZN3bfuiq2m3C3gK7rs6WV10n+7oJtUXuFwujh8/zqZNm9i0aROnTp2irq6O\nc+fOARAcHOy5eTFjxgzuuOMOL6/42nVWDJ6QkMBDDz3EwoULvbw6IS4iXadEz6uoqKCxsdHz75WV\nlcycOZMPP/yQ8ePHe468hXBTFIXTp097Tj4KCgooKCigpqaGjIyMdoMGjx07xlNPPUV1dTVFRUVE\nRkb61V1MX3K5bkJuAQEBBAYGotFo5LXoRb6eJtXd6uvreeKJJ/joo4948skneeCBB9BoNJw7dw6T\nyYTJZPK8d0ycONEvbmqtWbOGefPm8cYbb3ja237wwQeUlpYyePBgby9PiI4k0BC9r7y8nMTERJmj\nIbpEURSqq6s9NR+ff/4533zzDRaLxTPjIysri5ycHEaNGoXBYPDbDZYvaVuH4a4J6Uvtdv1FX02T\nuhoul4t3332XpUuXMn36dJYvX05sbOwl/4yiKH5zzb3++uu8+OKLVFdXk5OTw8qVKz3NOYTwMRJo\niN5XXl5OUlKSzNEQV+XUqVP8+te/5s9//jMZGRn813/9F4MGDWo36+PEiROkpKS0KzrPzs4mODjY\nbzYb3tZ28KFarfbMw1CpVJ12vHI6ne3a7XZMvertdrv+or+kScGFx1paWsqCBQs4c+YMq1at4uab\nb/bLxyqEn5BAQwjRd7S0tBAfH49Wq+WZZ57h/vvvv6jIWFEUGhoaKCgo8KRd5efnU1ZWRmJioifw\nyM3NZdSoUQwcOFA2Kl3gHnxotVpRFKVLgw87S7vq7Xa7/qK/pUm1tLSwbNkyfve737FgwQIWLVok\nrdKF8H0SaAgh+pbNmzdz3XXXERIScsV/RlEUWlpaMJlMnlkfJpOJkpIS4uLiPEMG3UFIRESE327Y\nroV7Y+tyudBqtej1+muuweg4xK1j0bk74OjKHAV/15/SpBRFYf369SxcuJDU1FRWrlxJcnKyt5cl\nhLgyEmgIIfondyvc/fv3e7pdFRQUcODAASIjI9ulXI0ePZqoqKh+u8F1uVyYzWYcDgcBAQGeNKme\ncjUdr/rDa9Of0qQATp48ycKFCykoKODll1/mBz/4gTQXEKJvkUBDCCHc3GlBBw4c8BSdFxQUsH//\nfgYMGOCp+cjNzSUnJ4fY2Fi/3vh03Njq9XqvzSW5XMcrd/DRNgjxl9emv6VJ2Ww2Vq9ezW9/+1vm\nzZvH008/TWhoqLeXJYToOgk0hPCW8vJynnnmGbZt28aZM2eIjY3lnnvu4Yo4fN4AABDKSURBVDe/\n+U27YWrCu9ybvJKSEk/alTv40Ol07YYM5uTkMGzYsD7fVUlRFOx2OxaLxac3tpcLPvyh41V/S5Pa\ntWsX8+fPJzQ0lNWrV5Obm9unXi8hRDsSaAjhLZs2bWLNmjX8y7/8C8OHD+fAgQP87Gc/49577+XF\nF1/09vLEJbhTew4fPtzu5KOwsBBFUdp1u8rNzWX48OF9prC5bbva7qrD6E3u4KNjANK241XbEw9f\nLTrvb2lS586dY+nSpWzYsIHnnnuOn/3sZ34bUAnRj0igIYQvWb58OW+88QZlZWXeXoroIvcG9/jx\n455Wu+4AxGazkZWV1S74SElJ8anaApfLhcViwW63o1arPRtbf3C5drvgOx2v+lualNPp5E9/+hNP\nPPEEt912G8uWLSMqKsrbyxJCdA8JNITwJUuXLmXz5s3s3bvX20sR3cTlcnHq1Cny8vI8aVcmk4mG\nhgYyMzPbpV2lpaX1eg2EL9Vh9La2px7uf+7Y8arj6UdPPi/9LU2qqKiI+fPn09zczOrVq7nxxhv7\nxXUnRD8igYYQvqKsrIyxY8fy8ssvc//993t7OaIHKYpCZWWl5+TD3fHq7NmzZGRkeLpd5ebmkpGR\n0SN3tN13zi0WCy6Xi8DAQPR6fb/f6Hmj41V/S5NqbGzkueee489//jOLFy9mwYIFBAYGentZQoju\nJ4GGEN1tyZIlLFu27Du/r1KpKCkpISUlxfO106dPM3XqVKZPn86bb77ZG8sUPkZRFM6ePetJuXJP\nOa+oqCA1NbVd0fmoUaMwGo1XvRF1Op2YzWacTqff3znvDh2DD/fph1tnU86vpK6lv6VJuVwu/v73\nv7N48WLGjh3LihUrGDZsmLeXJYToORJoCNHdamtrqa2tveTPJCUlefLfKysrmTZtGpMmTeKdd97p\njSWKPkJRFOrq6igoKPCcfphMJo4fP05ycnK7ovPs7GxCQkIuuUm12Ww4nU5sNhtqtdozD8NfN7Y9\n6Vo7XvWnNCmAo0eP8uijj3L48GFeffVV5s6dK9edEP5PAg0hvOn06dNMnz6dcePG8X//93/ywSsu\nS1EUGhoaPFPOCwoKyM/P58iRIwwbNqxdwXlWVhYDBw7E4XDw5ptvsnLlStatW0dCQgKBgYFyvXWz\nzoIPl8t1Uccr9wkJgMFg8OuaGIvFwiuvvMLKlSv593//d5YuXUpwcLC3lyWE6B0SaAjhLZWVlUyZ\nMoXExET+8Ic/tLubKV1XRFcoikJLSwuFhYWeWR8mk4mSkhIGDhxIQEAAVVVV3HHHHSxdupSRI0f6\n7cbW17g7XjkcDux2Ow6H46Kf8ZWOV91JURS2b9/Oww8/TExMDKtXryYjI6PPPy4hRJdIoCGEt/zx\nj3+8qOhbURRUKlW7FAwhrkZZWRkPP/wwa9euJTk5malTp1JQUMCBAwcYPHiwJ+0qOzub0aNHEx0d\nLZvAHtJZmpT799zX2+1ejaqqKpYsWcIXX3zBiy++yI9//OM+NYulIxmuKsRVu+ybln80URfCB913\n333cd9993l6G8EPPPPMMzz77LJGRkbz77rv8v//3/1CpVCiKgs1m4+DBg56C85dffpn9+/cTGhrq\nCTxyc3PJyckhLi6uT28Qva1jNymj0diuJkatVrfbqHYsOnc4HNhsNs/3e6LjVXdyOBy8/fbbPPvs\ns9x1112UlJQwaNAgby/rmpWWlqIoCm+//Xa74aqtra0yXFWIayQnGkII0ce88MILWCwWFi1ahNFo\nvOTPutN6SktL27XbLSwsJDAwsF23q5ycHBITE9sVNYuLdWc3KW+0272aNebl5TF//nwAVq9ezcSJ\nE/36GpHhqkJcEUmdEkII0Z57c3vkyJF2E85NJhOKolw05XzEiBF9KrWnJ/VGN6nLdbxyt9ftmHrV\nE+rr63nqqad4//33eeKJJ3jwwQf9ZqL8pchwVSGuiAQaQgghLs+9uT1x4oTn5MMdgFgslouCj5SU\nlH7VOtfbQ/eutd1uV7lcLv72t7/xm9/8hqlTp/LSSy8RGxvbXQ/Hp8lwVSGumAQaQgghrp7L5aKi\nooJvv/223clHfX09mZmZ7dKu0tPT/a6Vqy8P3XN3vPquonN38NH29ONyJ1OKonDo0CEWLFhAVVUV\nK1eu5JZbbvGJx9tVMlxViB4ngYYQwnesXr2a5cuXc+bMGbKzs1m5ciXjxo3z9rJEFymKQlVVVbua\nj4KCAqqrq0lPT/cMGMzNzSUjI8PThamv6YtD9y4XfMA/O17t2rWLiIgI0tLSCAwM9BQ/v/XWW8yf\nP5/HHnsMg8HgxUdzbWS4qhA9TgINIYRv+Nvf/sZ9993HW2+9xfjx43nllVd4//33OXz4MBEREd5e\nnrhGiqJw7tw5T8qVe8r5yZMnSU1N9QQfOTk5ZGVlYTQafTb48HaaVE9wp121Tb+aOHEiJ06cQKfT\nkZycTEVFBTExMTz99NPMmTOnTwcZXSXDVYW4KhJoCCF8w8SJE5kwYQKvvvoqcGEzFx8fz0MPPcSi\nRYu8vDrRExRFob6+vl29R0FBAceOHWPEiBGedrvuICQ0NNSrGzxfTpPqCQ0NDezYsYM1a9ZQWVnJ\nmTNnOH36NE6nk4CAANLS0hg9ejSjR4/mF7/4BXq93ttL7hEyXFWIqyaBhhDC++x2O0ajkQ8//JDb\nb7/d8/V58+bR0NDAxx9/7MXVid6kKAqNjY2YTKZ2Acjhw4cZOnRou4LzrKwsBg0a1Csb/b6YJnUt\nbDYbr7/+Or/97W+59957efrppwkLC8NisVBUVERBQYHn9Tl+/DjV1dV+O3NFhqsKcdUk0BBCeF9V\nVRWxsbHs3r2bCRMmeL7+2GOP8eWXX7J7924vrk54m6IotLa2UlhYSH5+Pnl5eZhMJoqLi4mJifEU\nm7uDkMjIyG4LPjpLk/LnadCKorB7927mz59PcHAwq1evZvTo0Zd8Pl0ul98GGUKIayKTwYUQQvg2\nlUpFUFAQkyZNYtKkScA/A4CioiLy8vIoKChg/fr1FBUVERER4Um7ys7OZvTo0cTExHQp+OhvaVIA\nNTU1LF26lM8++4xnn32Wn//851d0aiNBhhDiakmgIYTocREREQQEBFBdXd3u69XV1URHR3tpVcKX\nqVQq9Ho948aN83QmUxQFu93OwYMHPWk9K1asYP/+/QQHB3sCj9zcXHJycoiPj+90k1xaWordbich\nIaFfpEk5nU7+7//+j8cff5zZs2dTXFwstQdCiF4hqVNCiF7RWTF4QkICDz30EAsXLvTy6kRf5T6Z\nOHToULt2u4WFhWg0Gk+6VU5ODikpKaxZs4ZVq1Zxxx138Pbbb/t9mtSBAweYP38+jY2NrF69milT\npvj1qY0QoldJjYYQwjesWbOGefPm8cYbb3ja237wwQeUlpYyePBgby9P+BH3HImysjJPzcfmzZsp\nLi5Go9Ewffp0RowY4Sk6T05Ovuwgu76mqamJ5557jj/96U889thjPPzww+h0Om8vSwjhX6RGQwjh\nG+666y5qamp4/PHHqa6uJicnh02bNkmQIbqdSqVCo9GQmpqKWq3mj3/8IwcOHGD27Nk8+uij1NTU\nkJ+fz5o1a1iyZAlms5lRo0a163g1cuTIPjk7w+Vy8emnn7Jo0SLGjBlDQUEBiYmJ3l6WEKKfkhMN\nIYQQfunAgQOMHj2a2NhYXnvtNebOnXvRz7hcLk6fPs23337rSbsymUzU1dWRmZnZLvUqPT2dwMBA\nnw0+jh07xqOPPkppaSkrVqzge9/7ns+uVQjhFyR1SgghRP+kKArvvPMOd999d5emXCuKQlVV1UWD\nBs+cOUN6enq74CMzMxO9Xu/VDb3VauWVV17htdde4xe/+AX/9V//RXBwsNfWI4ToNyTQEEIIIa6V\noiielKu2AcjJkycZOXJkuzkfWVlZBAUF9XjwoSgKO3bs4OGHHyY6OppVq1aRmZkppxhCiN4igYYQ\nQgjRExRF4fz58xedfBw9epThw4e3a7eblZVFWFhYtwUBZ86cYcmSJezYsYNly5Zx7733yrwLIURv\nk0BDCCH6iueff56PP/6Y0tJSDAYDkyZNYtmyZaSkpHh7aeIKKYpCU1MTJpOpXQBy6NAhEhIS2qVd\nZWdnEx4e3qXgw+Fw8Lvf/Y5nn32WH/zgBzz//POEh4f34CMSQojvJIGGEEL0FbNnz+buu+9m7Nix\nOBwOlixZwoEDBygpKelSjYHwLYqiYDabKSws9LTbNZlMHDx4kOjo6HaBR25uLpGRkRcFH4qikJ+f\nz/z583G5XKxevZrrrrtO0qSEEN4kgYYQQvRVNTU1REZG8uWXXzJ58mRvL0d0I0VRsFqtFBUVtUu7\nKioqYtCgQZ60q5ycHEaMGMGbb77JmjVrePzxx/nVr36FRiPd6YUQXieBhhBC9FVlZWWMHDmSoqIi\n0tPTvb0c0cMURcFut1NcXNyu6Hzv3r1MnDiR9957j7i4OG8vUwgh3CTQEEKIvkhRFObOnUtTUxNf\nfPGFt5cjvMRdcB4cHIxWq/X2coQQoq3LBhrSokIIIXzQAw88QHFxMe+99563lyK8SKVSMXDgQL8I\nMmw2Gzk5OajVavbv3+/t5QgheoEEGkII4WMefPBB1q9fz44dO4iJifH2coToFosWLSIuLk4K2IXo\nRyTQEEIIH/Lggw/yySefsH37dhISEry9HCG6xYYNG9iyZQvLly+nCynbQog+TtpWCCGEj3jggQd4\n9913+fTTTwkKCqK6uhqAsLAw9Hq9l1cnxNWprq7m5z//OZ9++qm0aRain5ETDSGE8BFvvPEGjY2N\nTJ06lSFDhnj+WrNmjbeXJsRV+8lPfsIDDzxAbm6ut5cihOhlcqIhhBA+wuVyeXsJQlyRJUuWsGzZ\nsu/8vkqloqSkhI0bN9Lc3Mxjjz0GIGlTQvQz0t5WCCGEEF1SW1tLbW3tJX8mMTGRu+66i3Xr1rX7\nutPpRKPRcM899/DOO+/05DKFED1L5mgIIYQQwjsqKipobGz0/HtlZSUzZ87kww8/ZPz48QwZMsSL\nqxNCXKPLBhqSOiWEEEKIHtFxknlQUBCKopCUlCRBhhD9gBSDCyGEEKLXyBwNIfoPCTSEEEL0aS+8\n8AJqtZqHH37Y20sRlzF06FCcTidZWVneXooQohdIoCGEEKLP2rdvH2+99RbZ2dneXooQQogOJNAQ\nQgjRJzU3N/Ov//qv/O53v2PAgAHeXo4QQogOJNAQQgjRJ/3Hf/wHc+fOZfr06d5eihBCiE5I1ykh\nhBB9znvvvYfJZOLbb7/19lKEEEJ8Bwk0hBBC9CkVFRXMnz+frVu3otVqvb0cIYQQ30EG9gkhhOhT\nPvnkE+68804CAgJwf4Y5nU5UKhUBAQFYrVZpoSqEED1PJoMLIYTwLy0tLZSXl7f72rx580hLS2Px\n4sWkpaV5aWVCCNGvyGRwIYQQ/iUoKIj09PSLvhYeHi5BhhBC+BDpOiWEEKLPk1QpIYTwPZI6JYQQ\nQgghhOiqy97hkRMNIYQQQgghRLeTQEMIIYQQQgjR7STQEEIIIYQQQnQ7CTSEEEIIIYQQ3U4CDSGE\nEEIIIUS3k0BDCCGEEEII0e26MrBPmpQLIYQQQgghroicaAghhBBCCCG6nQQaQgghhBBCiG4ngYYQ\nQgghhBCi20mgIYQQQgghhOh2EmgIIYQQQgghup0EGkIIIYQQQohuJ4GGEEIIIYQQottJoCGEEEII\nIYTodhJoCCGEEEIIIbrd/wfU1cwtnH2KlwAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x10c335a90>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"z = sum(sum(math.e**(-0.5*(x**2+y**2))))\n",
"F = 1/z*math.e**(-0.5*(x**2+y**2))\n",
"fig = plt.figure(figsize=(10,6))\n",
"ax = plt.axes(projection='3d')\n",
"ax.scatter(X,Y,F,s=1,alpha=0.5)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Q2: conditional distribution"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false,
"scrolled": true
},
"outputs": [
{
"data": {
"text/plain": [
"<mpl_toolkits.mplot3d.art3d.Path3DCollection at 0x105918b00>"
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAxoAAAHkCAYAAAC5R1kSAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAAPYQAAD2EBqD+naQAAIABJREFUeJzs3Xt4FPXZN/Dvnk/JJgRCEggESAIJZ+QYsIiIUoEqiqVa\nq6LSanksnqrU2vZ56tv3eq72fZ762qpPX61nCx7baqt4QhBFzoqgnERUCOGUw+4me97Zff9IZ5yd\nzO7ObmZ357d7f67LK5hsdiazuzO/e373ff90sVgMhBBCCCGEEKImfb53gBBCCCGEEFJ4KNAghBBC\nCCGEqI4CDUIIIYQQQojqKNAghBBCCCGEqI4CDUIIIYQQQojqKNAghBBCCCGEqI4CDUIIIYQQQojq\nKNAghBBCCCGEqM6YxmNpZT9CCCGEEEIIAOhSPYBmNAghhBBCCCGqo0CDEEIIIYQQojoKNAghhBBC\nCCGqo0CDEEIIIYQQojoKNAghhBBCCCGqo0CDEEIIIYQQojoKNAghhBBCCCGqo0CDEEIIIYQQojoK\nNAghhBBCCCGqo0CDEEIIIYQQojoKNAghhBBCCCGqo0CDEEIIIYQQojoKNAghhBBCCCGqo0CDEEII\nIYQQojoKNAghhBBCCCGqo0CDEEIIIYQQojoKNAghhBBCCCGqo0CDEEIIIYQQojoKNAghhBBCCCGq\no0CDEEIIIYQQojoKNAghhBBCCCGqo0CDEEIIIYQQojoKNAghhBBCCCGqo0CDEEIIIYQQojoKNAgh\nhBBCCCGqo0CDEEIIIYQQojoKNAghhBBCCCGqo0CDEEIIIYQQojoKNAghJIVoNAqO4xCLxfK9K4QQ\nQggzjPneAUII0aJYLCYEGKFQCKFQCHq9Hnq9HgaDAQaDQfh/vV4PnU4HnU6X790mhBBCNIMCDUII\nEYnFYuA4DhzHIRqNCrMYen3vBDD/M/77fICh0+mE4IP/qtPpKAghhBBStCjQIIQQ9KZHRaNRRCKR\nuCCCDzDE/+bxj4vFYojFYgiHw3G/K/49cQAinQkhhBBCChEFGoSQosUHCJFIRJilEM9QpCIOJuSe\nm//Kp2CFw2Hhe+JZkEQBCAUhhBBCWKZLo7iRqiAJIQWBH/xHIhEhPSpRgBGJROD3+xGNRlWbjeAD\nHPF/vGSpWDQLQgghRENSXowo0CCEFA2+/oJPj4rFYnGpUeLHhcNhBAIBRCIRYeAvFxSIazH6Oxsh\nTcVKFIRIC9LF26cghBBCSI5QoEEIIXzqklwRt1gsFkMwGEQgEEA0GoXBYIDVaoVer0ckEoHBYBBm\nQ/j/xP8vJheAqDULIv5/8d/CB04mk4lSsQghhGQbBRqEkOIkro1IVX/BcRyCwSCCwSBisRhMJhOs\nViuMRiN0Oh0ikQjC4TAMBkPS7YmDDum/xaRBgFqzIIFAAABgMpninktJPQghhBCSppQXDyoGJ4QU\nFLn2tIkG8pFIBIFAAKFQCDqdDhaLBRaLJWlAkYg4rUlun+QCkEgk0uc5pAFAqiBEXJDO/9tkMgnb\n5b/y6WCJCtIT1YJQEEIIISRTFGgQQgpCqva0vFgshlAohEAgAI7joNfrYbfbYbFYUg7mMyWeTZDu\ni3QmRPo38OQCEOlsBJ8+Jd3vRF2xxF23+O/xj08WhKTTmYsQQkjxokCDEMKsdNrTRqNRIT0qGo3C\naDSipKSkT5pRLon3M1EQIg5A+FQwuYJ0vV4v1IlEo9GUgUCin6ezNggVpBNCCEmGajQIIczhB+Ch\nUAh+vx9msxkGgyFh/UUgEEAwGAQAmM1mof5CKT5IySSlKhvkAhD+e2LZKkgX/1tuFiTZ4oQUhBBC\nSMGgGg1CSOGQtqeNRCIIBoMwm81xKVL8zwKBAMLhMHQ6HWw2GywWi2wNhRJaGiAnSsXy+/2IxWIw\nm81xAYg0FUscEKQTCCidBeGL5/lULmkqFhWkE0JIcaBAgxCieeLuUeK0ILl0Iz49iuM4GAwGOBwO\nmM3mohjI8gN7udmaTAvSldRkKF0hXVyQLp0JoYJ0QggpPBRoEEI0KVF7WvHdb/4rx3EIh8Nx7Wnt\ndrvQnpakLkiXC0BSteWVvh6Jtiv+KrftdAvSlXTjIoQQkn8UaBBCNCXd9rQA4PP5AAAWiwVWq1Uz\ntRQsSNWWV64eJNksiPTf2S5IT1YPQgghJL8o0CCEaEI67WnD4TACgYAw4DWbzbDb7RnXXxB5StcG\nUTILIrdGSLLtir9KtyvePsdxwjoo4t9JVgtCQQghhOQGBRqEkLxJpz0tX38RCASE9rQOhwNerxcm\nk4mCjBxTkoolrgmRa8ubaUG6+KvctuUK0iORCAwGA4xGY9J6EEIIIeqhQIMQknP8QDQSiQgD0UT5\n/sna08ZiMXi93nz8CSSBdGZBxO8D6XNIAxD++TJNxQoGg9Dr9X1SsaT7LJ0JUVKHQgghRB4FGoSQ\nnJG2p01UfyHXntZqtcJqtSYcwBLty3dBOh9IyG1bnIqVqiA9nToUQggpZhRoEEKyLlF7Wrn6i1Ao\nhEAgAI7joNfrYbfbYbFYZAdzNMCLx+rxUDILIp0NSTULorQzFRWkE0JI9lCgQQjJCiXtaXn8ytuB\nQEBoT2uz2WAymWiwVuTk1ksB+s5EpJoFAb7pUpaNgvRwOCx8T8nihPS+JoQUAwo0CCGqSrc9Lb/A\nHpBZe1q+2JcUF/H7SUlBujjoFT9Hoo5YahakS/c51QKFhBBSKCjQIISoItP2tDqdDjabDRaLhTpH\nEVVIU7H4Qb/FYoHRaFRUkC4XgCgJBDJJxZLus3gmRFoPQgghLKFAgxCSsf60pzUYDHA4HDCbzf0a\nQNGMRjw6FskpbcsrDkBSFaSrOQuSrCA9WS0IBSGEEC2iQIMQkrZ029Py6VF8/YXD4YDRaKTBEdEM\npW15pV2xpM+RzYJ08dog0t9NVg9CCCH5QoEGIUQxpe1pAQjtaflVmy0WCywWS1r1F1pCA7bilWoW\nRGlButwq6WoUpPOpWNLOWKlqQeg9TQjJNgo0CCEpZas9rRpylTolbW1KSKYF6dLajEQBiFoF6fz3\nxPssF4QonYEhhBClKNAghMjKpD1tMBhENBqF0WhESUkJtaclRUtpKpY4AIlGo3GPy1VBOh+QGI3G\nuOBDujghpWIRQtJFgQYhJE467Wk5jkMgEBDa05rNZlitVhiNuTu1UDE4UUorg+T+FqSLgxg1CtL5\nmUj+Z+KZF/HvUEE6ISRdFGgQQgB80542FArB6/XCarXCZDLJpkfx9Rd8YSq1pyWk/7JRkC4OAhIF\nAnwQwz9e7udyBenSLnNUkE4IkaJAg5AiJteeVpzXLR4g8O1pg8EgOI5TrT0tC1i5W8vCPpLMKJkF\nkQYgSgvSlWy7PwXp0rVBaBaEkOJBgQYhRShZe1rxY4DemQ4+PYpvT2u32zXTnpZSp0gxSzULIlcP\nIjcLAgDhcBjRaFT1gnRxnZd4n6kgnZDCR4EGIUVESXtafjDAcRx6enqE3G2LxQKr1cpse1pSvIo1\nEFWaisWfE/h/i8nNgGRrhXRx4MJvh1KxCGEbBRqEFIF02tOGw2EAQCAQgF6v13z9BV+8SghRTlpT\nEYlEYLVaodfr+8yC8DcoslmQDsQHIfw5iz8fJdpvSsUiRNso0CCkQKXTnpavvwgEAsKg3Ww2w+Fw\n0IWbMcV6956oI522vOIUTOlzpFuQzv+e+Kt029KCdOk+p1qgkBCSexRoEFJg1GhP293dLfTQJ4QU\nByXpUGoWpEtrMlJtO91ULPHvyRWkK902ISRzFGgQUiDkLu6J0qOk7WmtVquQNsH/Hit3xlnaV0K0\nqL+fHyWzINLZkFSzIEqLwpXOgkhXZZebBaFULELUR4EGIQyTa0+bKEWBX5QrEAiA4zjo9XrY7XZY\nLBa6mBJCsoIfyEuJu9pJA5BEsyDZLkgXP5bWBiFEHRRoEMKgZO1ppRfAaDQq1F/w7WltNhtMJlPC\niyVLswS52leWjgkhWsefe5SskC6uCZGmRSUKQNQoSBevDQL0tv/V6/UwGo1UkE6IQhRoEMIQJe1p\neZFIRFhgD6D2tITQADA5rRyfbBWkK50FEX8VCwaDwj5FIpE+aaqpCtITPS8hhYwCDUIYkG572kAg\ngEgkAp1Ol1F7Wrp7T0jxYOmzrqQgXRqAqFWQzs8cy21bvA/J1gYRz4SIgyEKQEihokCDEI3qT3ta\ng8EAh8MBs9mc0QWMpUCDpX3NNhqskGKV7YJ08WPktp3oZ+J0r2QF6ckWJ6TPNWEZBRqEaEy67Wn5\n9Ci+/sLhcMBoNNLFiZB/oUC0uCUrSJerB0k0CwJACE7ULkjn1wahgnRSaCjQIEQjlLanBSC0pw2F\nQtDpdLBYLLBYLKrVX+h07Ky2TTMahPSPNM2nWIiDAKUF6fxNIPFz5KogXToTkmxxwmJ7LYl2UaBB\nSB5Re1q2SFtgahUr+0mIVklTsfibQHxDDWkAIpeKJReA9LcgXbpCOv898T7LBSFK1yUhRG0UaBCS\nB5m0pw0Gg4hGozAajSgpKUnanra/WJol4I8BDa4JIdkmTWcS609ButIgIN21Qfjf4b/y26JULJIr\nFGgQkkPptKflOA6BQEBoT2s2m2G1WmE00sc21/jXTTzjREghofd0ckpuvChtyyv+t5K2vIlmuaW/\nJ/4qt+/iBiN82q34d2htEJINNGIhJAfSaU/L11/whYGZtKftL5ZmNLJJ2s2Ll+lggBAtos969imZ\nBZEGIMlmQdJpjZtOKhZ/3ZGm8SarByEkGQo0CMkS/qIRCoUQDAZhMpkSnpz5AW0wGATHcf1uT9tf\nLAUa2UidkltN3Ww2x7WpVDslghCiXdkqmE81CyJXkJ5sFkT672ykYkn3W24mhM55hEeBBiEqk7an\nDYVC8Pv9MJvNfS4m0WhUSI/iB7R2u53a0+aJNF2NX01dr9cjHA4jGo3KzkIpGQxkWhhK1EPHOjE6\nNtqjNBVL3BFL2i0w2wXpcmuD8D/jZ+INBkPaARApHBRoEKKSRO1p5VrOitvTAt8MaNVqT9tfrM5o\nZCoSicDv9wtpA1arVQgwpNuR236iNDglhaH9uRtJiBpY+aznk9ZaACstSOfPPXLnnWQpoKm2nWwW\nJBQKIRwOQ6/X95lppoL04kOBBiH9oKQ9Lf+Vv/MTCAQQiUSg1+vzUn+RjkLu5MSnA4hfDzXbBad7\nN1KNNKxCfa0IIcqkc94R3/yQPkd/CtL5f4sbl8gVpIfDYeF70m5elH5aOCjQICQD6bSn5U+wPT09\niMViOWlP219a3S81SAu88/F6pHM3UulAQKvBKiGFQGszGplQuyBduj6HdFty/6+0IF38e1SQzjYK\nNAhJQ3/a0xoMBqH+QutYOnErTZ2SK/B2OBwwmUy52E1FUqVhSYMQuYEAAASDQbobKEKpQakV8/uj\n2CmZBZE790ifgz/f8LP74g6LSrYvt23+azoF6el05CLZp/0RDyF5xp/kMm1Pa7FYEAwGmVwDoxBS\npxIVeGulHkYJ8YVY7m6k+OLPv0flitEzaY1JCh8FYqkVwrkwE4nqDKUd+ORufvh8PgCQPe9kuyBd\nGoRQKlb+sDXqISSHxCcwcf1FovSoUCiEQCAAjuPi8v0BCF2lWKFGgXWuJNpXaYG31uthMiVOh9Dp\ndOA4DlarVSjol+tMk6gYndIRCCFKiG98SAMRn88HnU4Hk8nUpyYkVwXpcmuDSH83WT0IUQ8FGoRI\nSGcvkqVHyaXj2Gy2uHx/FgbrhSLbBd4syUcxOmEXvabJFeuMRqakxeC8/hSkqzELwn/lrxXidKxb\nb70Vs2fPxo9//OOM/mYijwINQv4lUXtauYFaJBIRFtgDkqfjsBhwsLjPoVAIXq83bwXeLElWFKok\nH5vWBCksNIgmakr2flLaCCNRO3BAeUG63LbFX6XbP3v2LOx2ezp/KlGAAg1S1JS0pxU/Vny3PJ10\nHD6NhaiLn1ECIKy+nq0C72IYiCXLx1bamz/RAKAYjh8pbPQeViaTwFXtgvR0zz86nQ4ulwsVFRVp\n7TdJjQINUpTSbU8rbodqMBjgcDhgNpsVn0xZCzS0PqMhLfAGALvdDqvVmse9KlyUhkWKnVbPhcUg\n1Q0QJd34UhWkx2IxCjSyhAINUlTSbU/Lp0eJ26EajcaMBkcsXai0GmjIFXibzWa43e6sD1hpQCxP\naSpEumuCZON402uYGB2b1OgYpZbL9UZSdeOTO/+IC9K3b9+OVatWob6+Hg0NDbDZbNi3bx9qampQ\nV1fHVGdCLSus9iuEyOBPNuFwGMFgEKFQSJjB4Dv1iE+KkUgEPT09cLvdCAaDsFgsKCsrQ2lpacY5\n/3SByhzf0cvj8cDj8YDjONjtdpSXl8NmsxVcF6lCwQcQRqMRZrMZVqsVdrsdDodDmH2yWCxCwShf\n9+T3++H1euH1euH3+xEIBBAKheJmH4m66JimRsdIGa0sbJjs/ONwOGCz2TB06FB873vfQ3l5ObZt\n24Z9+/bhxz/+Merr6+FwODB+/HgsW7YMP//5z7FhwwbhuR966CGMHDkSNpsNs2bNws6dO5Puy6ZN\nmzB16lRYrVaMHj0aTz31VJ/HvPjii2hubobNZsOkSZOwfv36uJ//53/+J2bMmAGn04mqqipcdtll\nOHz4cJ/n+dWvfoUhQ4bAbrfjwgsvxJEjRzI8guqhKzQpWPzsBR9g8LMYcndM+fQot9sNj8eDSCQi\nDGbtdnu/72xQ6lT6YrEYAoEA3G43enp6AAAlJSUoKysT2rfmen9Yeg21SjwAMJlMsFgssNlscQMA\nPgDR6XSIRqNC62ifzwev1wufzxcXgEhb9hKSDfkePBN18DcZm5qacN9992Ht2rXYtGkTOI7DwYMH\n8cYbb+B3v/sd5s2bB4/Hg2effRavvfYaAOD555/HnXfeiV//+tf4+OOPMWnSJCxcuBDt7e2y2/rq\nq6+wZMkSXHDBBfjkk09w6623YuXKlXj77beFx3z44Yf4/ve/jx/+8IfYs2cPLr30UixduhT79+8X\nHvP+++/jJz/5CbZv34533nkH4XAYF110Efx+v/CY3/72t3jwwQfxyCOPYMeOHXA4HFi4cCFCoVCW\njqQyujROznQWJ0xI1J4W6Huh4IuJg8Gg0K3IarWq3q2ou7sbAFBaWqrac2ZTLBZDV1cXHA6HsBZI\nrsi1DOZfk0Q6OzuzXqPB92PX8nQ6x3Hw+/2w2+0FNdOTKA0iGo3GPS5RGhY/W+JwOGiwKMPr9cJk\nMsFsNud7VzTL6/XCaDTm/HzIGv4cZLPZNH2ulGpra8O0adPgdrsT1qLpdDrMmjULM2fOxAMPPCB8\nf9iwYVi9ejXuvvvuPr+3Zs0arF+/Hnv37hW+d9VVV8HtduP1118HAFx55ZXw+Xx49dVXhce0tLRg\nypQpePjhh2X3t729HYMHD8bmzZtx7rnnAgCGDBmCu+66C7fffjsAwOPxoKqqCk899RSWL1+e4ZFJ\nKeUJtXCuRKTo8fnfwWAQ4XBYWMFbLj2K4zh4vV64XC74/X4YjUY4nU44nc60irzTwdId13zMaEhf\nE7PZHJeyRopXojSIkpKSPrMgQN80LHFnMkrD6ouOgzIUpKamldSpdHV2dqKsrCxpW95wOIzdu3fj\nggsuiPv+ggULsHXrVtnf27ZtGxYsWBD3vYULF8Y9fuvWrSkfI+VyuaDT6YTi9S+//BKnTp2K2zen\n04mZM2cmfZ5coGJwwrR029NGIhEEAoGcrxbNWupULvEtg/vzmtDxLV6p1gThb0DwM5xya4Ik60ZD\nCEDBWLpY+/y4XC4MGDAg6WPa29vBcRyqqqrivl9VVYVDhw7J/s6pU6dkH+/xeIQa0ESPOXXqlOxz\nxmIx3HbbbTj33HMxduxYYTs6nS6t58kVCjQIkzJpTxsMBsFxXEbtafuLxYFwNveZVvDOLtbea9kg\nDUA4joPNZgMgvzqxtM4j0YKE1JK3+LB6lz4fWD338IEGC6/xqlWrsH//fmzZsiXfu6IIBRqEKem0\np41Go8JaC3yuv91uz7g9bX9QoNFLuiYJSyt4a33/iDK0Jog8lvedaAerQZnL5UJ5eXnSxwwaNAgG\ngwGnT5+O+/7p06dRXV0t+zvV1dWyj3c6nUK9T6LHyD3nLbfcgtdffx3vv/8+ampq4rYTi8Vw+vTp\nuFmN06dPY8qUKUn/rmyjGg2ieeL2tB6PBz6fT1F7WpfLhUAg0CfXP18nQNYCDTVFo1H4/X64XC74\nfD4YDAZVa2JYDOSI9vDnFLluWHyzAbPZDL1eL9sNi2/Jy9eJsdANS+v7pyWsDZ7zhcXjpCTQMJlM\nmDp1alyr21gshg0bNmD27Nmyv9PS0hL3eAB466230NLSkvQxb7/9dtxjgN4g45VXXsHGjRsxfPjw\nuJ+NHDkS1dXVcc/j8Xiwffv2hPuWKzSjQTSLDzD4DlIAhMBB2vlDLhUnV/UXSrB44lVj8C5dwdti\nscBqtTLVjYTH4mtI1JFoFkTcDUtaE5IoDUv6b3pfaR8FY8qxeqyU1GgAwB133IEVK1Zg6tSpmDFj\nBu6//374fD6sWLECAHDPPfegra1NWCvj5ptvxkMPPYQ1a9bghhtuwIYNG/DSSy8JHacA4NZbb8W8\nefPw+9//HosXL8a6deuwe/duPProo8JjVq1ahXXr1uHVV1+Fw+EQZkD4du8AcNttt+E3v/kNGhoa\nMGLECPzyl79EbW0tLr30UrUOU0Yo0CCak6o9rfhExkoqTrHdcVejwDsduTq+WnpPkfSp/fqlm4bF\nn9PEtJKGRe/t1OgYpcZnG7DG5XLFpSIlsnz5crS3t+NXv/oVTp8+jcmTJ+PNN99EZWUlgN6i7OPH\njwuPHzFiBF577TXcfvvt+MMf/oDa2lo89thjcV2mWlpasHbtWtx7772499570djYiFdeeUUo9AaA\nP/3pT9DpdJg3b17c/jzxxBO49tprAQB33303fD4fbrrpJrhcLnzrW9/C+vXr8962mtbRIJohdzdQ\nesH1eDzCbIX4Tjnf8pJvb6k1wWAQXq+XmWIz4JtjXVJSoujxcrNK/OrP2f6b3W43jEYjHA5H1rbB\np8poYYYsEVZ72Gcbv2in0vdyNvV3TRC1P0vRaBQ+n0/T5898o8+Vcvz6R3zjBVbceOONOPfcc7F6\n9ep87wprUp6Q6KxC8ird9rT8YDYUCkGn08FqtcJqtWp68AfEr0vBSqABKJsGZ2VWiRAtSJWGJQ1C\n5NKwknXEItlDxzc1Vmfu3W63otQpkj4KNEhepNueli+65Gs1qBVq9qU6tnJdvUpKSvJyV7TYUtMS\noc8Du8SBQrI1QaS1IGLSwIPWBFEHnVuUE6c6s0RpjQZJHwUaJKfSbU/L3ynnB7J6vR4cxwnFT6zI\nx0rb/aXT6fqkcwCFVeBNigNLnzs5yRYlTFQLkmpNEOlgkIKR1OgYKcPacYrFYnC5XMIq20RdFGiQ\nrOMvhuIC72RFlJFIRFhgD4gfyHq9XmFWgyUsBhpSuS7wTgfNaJBipNaaIEDv5zvZjZ9iRucW5Vg9\nVm63O2V7W5IZCjRI1si1pwWQMD1KXEicaCDL6sWPxUCDn9Hg09ZoBW9C2JFsFkScgsWfmyORSFwq\nljT9itKwiBKs1SECNKORbRRoENWlak8rfay4kNhgMMDhcCRcxI3uXOcG/xpGo1H09PQwUeBN74tv\n0LEgifABCE/cUYm/uSAORJKtCSIORgp5FoTV1a5zjdXj5PP5EAwGqUYjSyjQIKpJ1J5Wblqf4zgh\nPYqvv3A4HDAajUlPUnygwdpdE1ZmNKQF3gDgdDo13/aSAlBCMiM9V/c3DYu6YRHWuFwulJaWwmQy\n5XtXCpK2Rw9E89JpTwv0Ts8HAgGhPa3FYoHFYlFcSMzqBUvrgYZcgTcAhEIhzQcZhJDsSrcYXdoN\nK1drgmQLaze28oXVGY2uri6Ul5czt9+soBEEyUh/2tP2J8+f1fUoeFoLNJIVePv9/nzvnmI0o0FI\n7qmxJohcLQjNgrCNtdfO5XJRIXgWUaBB0iJtTwsg4QwG3542GAyqtpCb1mcGEtHSiVduBW+5wI8G\n76SQaOkzqEVqHh+la4JIa0HE5GY/8jULwuqNrVxj9XrBBxr0GmcHBRokpWTtaeU+mNI0HLPZDKvV\nqkoKDquBBpD/gXumK3izcpFl8T1BSL7l+nNT7GlYhYzV1ClarC+7KNAgCaXbnpavv8jmOgsUaKRP\nWuCtNPBj6WLB0r4SQvpSa02QbBSjs3KzJd9YDjQodSp7KNAgfWTSnjYYDILjuJTtafuLAg3laAVv\n9Wn9Aqr1/csXFs8X5BtK1wRJNAsiTb+iWRAi1tXVRTMaWUSBBhGIZy9StaeV3iU3mUyw2+0p29P2\nF8uBRi6oObPEUuF9roI4Vu/YEZIIy+9p6ZogPLk0LP4GWqZrgrB4fHKN1feS2+1GbW1tvnejYFGg\nUeT6054WyN9dchYDjWwOhvkCb7/fL3T26u/MEgV1hBAWqZ2GFY1Godfrmbjpkk+sHp+uri5MmDAh\n37tRsCjQKFLptqeVdinKRv2FEvwFhMXBbzb2O9MC70LD6nuCEJJbmRajcxwHr9dLxegpsHgc3G43\npU5lEQUaRSad9rRaHcSyOqjU6XSIRqOqPFemBd7poBkNdtFrRtLB4uBQbcnWBPF6vTAYDDAajSnX\nBJHWghTTmiCsnneo61R2UaBRBMTpUdFoFB6PByaTCTabLeftadXAaqChBirwTi5bU/f8opPBYJDu\nZJKCUqznUqX4QMFgMMBkMsX9TG4GhG+iIqalNUGyicXUqVgsBpfLhYqKinzvSsHSxsiRZEWi9rR8\n4CE+IcgVEVutVlit1pynR6XCaqCR6X7nqnWwFEszGtm6uEln9fR6fdI7mRSAEFJ4Ep0DaU2Qvljc\nd5rRyC4KNApQqva0fFEb/9hQKIRAICAUEcutEq0lxRJoZKPAOx0sBRpq41e1DwQCQmqaxWKJu1OZ\nqqBUnIqhdl9/kj465onRsUksk05K/S1GZ/XcwfKMBgUa2UOBRgFR2p6WrxXw+/3CQIpPpcp3/YUS\natY65JI247mDAAAgAElEQVTSQEOrtTFaplYrXr72JRAIAIhPTeODcn57avT1Z2kQQQpTMd5IyKdU\n5w7p+YOlNUFYDDS8Xi/C4TAFGllEgQbjMmlPy890RCIRZnP8C/HimIsC73QU04yGuPalP2mD6fT1\npwCEEHZk+zOYbhoW/33x7yc6d+Ty/MHaucrlcsHpdGqmBrUQ0ZFlVH/a0wK9J4OysjLN1V8owdqJ\njMfPaEjv+lCBd/5EIhH4/f642her1ar6eyxZR5tizeUmhAX5vtGi9pog2byBke9jlYmuri6Ul5fT\nuTSLKNBgTH/a0xoMBjgcDkQiEYTDYSaDDIDtGg1evgq808HSjEY6+8ofe7/fL6wLk6+6JCUBiDSN\nItVdTNIXC+/hfKJBVmpaPEb9LUaXS8HK9AYGq6uCu1wulJeX53s3ChoFGgyQtqeNRqNJp0Q5jkMw\nGBRScEwmExwOB4xGo1DfwGKNA4/1QIN/bTiOE4K/XBV4FzNpcb2Wj31/72IGg0EhiKIZEJIMi+fS\nXGLx+CidQRVnRqi1Jghr5xi3200zGllGgYaGJWpPm2jAwN8hD4VC0Ol0sFgssFgsfe528CcfFgu3\ngMQpSFomLiT2+XzMFHizEtQlm9Hgj73f7xeK60tLS4XAO93t5Pt4pCom9fv9ws/ymUZBSCEphM9H\nujcwlKwJwp8/8n1ezFRnZycVgmcZBRoalKo9rfSx6banVatDT76wtM/SAm8AcDgcsFgsed4zZVi+\ngMRiMaGDFD+zV1JSUrBFf+JCdKPRKCwuRp2wSCr0GifG6vkvXf1Nw+LfQ/zNDVZmUam1bfYV5hWX\nUUrb0/KP5VNw0m2BylLuvRwWAiW5Am+TyYSenh4q8s4yue5dNputqI67NA2COmGRRLR8HtWSYj1G\nqdKwxOlX/PhFfA4R/74WzyEUaGQfBRp5lm57WukANpMWqIUUaGhJqgJvPv1Na/udDCszGvx7gu8g\nBVD3rlSoExYhqbFw/ssH8RjFYDBAp9OB4zjYbLa4WlBpLYiY9LyRj3OI2+3G8OHDc7a9YkSBRp5x\nHIdwOJyyPa2aHYq0OlBXSmv7n26RsVb2u1DwHaQAIBwOa657F2uy0QmLAhBCCpu0C2Y6aVjiLA7+\nOeTOIfzP1ORyuTBp0iRVn5PEo0Ajz8SzF6nqL9TqkqO1gXq6tLL/6a7gzeJAS8szGvzaMHzwDbBV\n/8Ka/nbCyncAwuLnL1fo2CTGattWLervOQRQP5WTUqeyjwKNPJP7gEhzzE0mE+x2e0ZdchJtk98O\ni/IdaGS6gne+97sQSBef1Ov1Qutmt9udk8EA5bT3laoTllYWFCN90fmIqKG/AVmqc4iSZhaJakGS\n6erqokAjyyjQyDPxh0DcnhbIXo45fwFn9QKTrwG7Wit4s3TctfI+kZvdE88esRo0Fzo1Bg8UgJB8\nohsLymTrOCltZqFkTRC9Xo9QKAS3243q6mrodDq4XC5UVFSovt/kGxRo5Jl4AMXfoc1FjrlWBpD9\nkYv9V7M+hsUAL9+DeGl6WqLZPZotYkuuO2HR+yI5GkiT/sp1QJZpGta2bdtw+eWXo7S0FA0NDTAa\njXjxxRdx6tQpNDU1ob6+XmgNTtRB1ZJ5Fo1G0dPTAwAoKSlBWVkZbDZb1gtZWRvwiuViwM4PcD0e\nD7q7uxGNRuFwOFBeXp6T16fY8QvPuVwuYYFDp9OJ0tJSzS9ymG8sHxt+4GA0GoWURLvdDofDAbvd\nDqvVCrPZDL1ej2g0Ktyk8fl88Hq98Hq98Pv9CAaDCIfDfYpMSV90fJKjGQ328DcyTCYTLBYLbDYb\nHA4HHA4HpkyZgmeffRa33347xowZg46ODvz5z3/GZZddhubmZtjtdjQ1NWHp0qV46aWXAAAPPfQQ\nRo4cCZvNhlmzZmHnzp1Jt79p0yZMnToVVqsVo0ePxlNPPdXnMS+++CKam5ths9kwadIkrF+/Pu7n\n77//Pi655BIMHToUer0er776ap/nuP766/vccFm0aFE/jlx20IxGnhmNRpSVleW8BSfLgQaQvf1P\nt8A7Xawd91zvr7T+RWl6Gs1oFDalvfyT1YEAQDAYpE5YhGQBCwGZTqfDwIEDcckllwAAPB4Phg0b\nhkAggM7OThw8eDDuv87OTjz//PO488478cgjj2DGjBm4//77sXDhQhw+fBiDBg3qs42vvvoKS5Ys\nwapVq7B27Vq88847WLlyJYYMGYILL7wQAPDhhx/i+9//Pn77299i8eLF+Mtf/oKlS5fi448/xtix\nYwEAXq8XkydPxo033ojLL7884d908cUX48knnxTOd1pshqJL48JMV/AsCYVCOR8gdXd3AwBKS0tz\nul21uN1uGI1GOBwOVZ4v0wLvdKm939nm9XoRiURQVlaW1e1I61+sViusVmtaM0ednZ3CXe9s4AvR\no9Gopme0vF4vTCYTzGZzTrYXi8Wwb98+4e6dVoiDD/4cKw2c890JSwt6enpgNptz9n5hDd8622az\n5XlPtM3n80Gv12ft/JsNx44dw5w5c9DZ2ZnwnD5r1izMnDkTDzzwAIDe88qwYcOwevVq3H333X0e\nv2bNGqxfvx579+4VvnfVVVfB7Xbj9ddfBwBceeWV8Pl8cbMULS0tmDJlCh5++OE+z6nX6/H3v/9d\nCJB4119/PdxuN/7617+m/8erJ+XJUrtXS5JVrN1Zl1Jr/zmOg9frhcvlQiAQgNlsRllZGUpKSlQP\nMgD2jnu29zcSiaCnpwdutxuhUAg2mw3l5eWw2+0ZDeazua8sFSH39zh8+eWXeOutt9DZ2ZnysZ9+\n+ikefvh1PPTQy2hra+vXdtUkTp/Q6/VCe3CHwyHUWfGf8UgkgmAwCL/fD6/Xi56eHvh8PqE5RyQS\nEQpOCxEr72uibay9j7q6ulBeXp5wv8PhMHbv3o0LLrhA+J5Op8OCBQuwdetW2d/Ztm0bFixYEPe9\nhQsXxj1+69atKR+j1KZNm1BVVYWmpiasWrVK0Tk71yh1SgPyMfhkbcAr1Z/9V3sBxEKn9vtEevz1\nej3sdjssFosq68OQ/onFYnjyyZfx2WccOjtduPLK5Ukf3zv7FIPFolf9rvjOnTuxbdseLFhwLkaN\nGoWnn34ObncPrrtuOSorKzN6znQXEyvkTlgsXwNyJRaL0XVBARbfSy6XC+Xl5Ql/3t7eDo7jUFVV\nFff9qqoqHDp0SPZ3Tp06Jft4j8eDYDAIi8WS8DGnTp1Ka/8vvvhiLFu2DCNHjsQXX3yBe+65B4sW\nLcLWrVs1dT6iQKNI8cWULEv3xJatBRDTwVqAp+ZxSXcFdZIfOp0OdXVV6OpqRU1NVcrHNzY2Ys2a\nFTCbzRg4cGC/th2NRvHFF1+goqICAwcOxBtvbMHWrUGYzdtgt9uxa9dJeDzAnDlHYLVa8cEHH6Cq\nqgrnnHNOv7YLKFsRvVgCEELSxUKNhhS/WB9r+81bvvybm0Djxo3DhAkTUF9fj02bNuH888/P457F\no0BDA/LxJmdtwCuVTtvVbBd4pyPf7WLTpcb7RBrgZev4s/6e1pLrrvs+li51K17Iqqamps/3zpw5\ng40bN6G+fhSmTZum6Hm2bduGp57ajKoqI37+81swf/50mM0fY9asc1BbW4vFi8fD4+nGuHHjsG3b\nNjz55F4MGRJFfX191uqI+huAsFAHoqV90SI6Psmxunp6qsX6Bg0aBIPBgNOnT8d9//Tp06iurpb9\nnerqatnHO51OoVA70WMSPadSI0eOxKBBg3DkyBEKNEj+ibv0sHZyAJSd0HJV4J0OVgfDmbxPEq2B\nQT3Ktc9gMPR7EasPP/wQa9d+idGjj2LixImK0qo4jgPHARzXO4ifM2cO5syZI/z8kkuWCP8eNmwY\n6up2o7a2QlFzBbXPc5n28Rf/fr4DEBbPRblGx6hwpUqdMplMmDp1KjZs2CAUYsdiMWzYsAGrV6+W\n/Z2WlpY+rWrfeusttLS0xD1G+hxvv/123GMy0draio6ODtkbP/lEgYYG5GtGA2A70Eh0AeA4Dn6/\nX1hh3Wq1wmKx5LyFcCHI5L0RjUaFACOXAR6rQZya3ntvMz744CMsXjwPkydPTvn4PXv24OWX30FL\nyzgsWnSxqvvS0NCAceMOY9y4EUmDy3379sHn82HatGmYPXs2BgwYgEGDBqXs8tPU1IRf//pWmM1m\nGAwGbNy4CZs3f4TFi+cqnkHJllQroqcbgPBBDYvn6kJAxz05Vmc0+NSpZO644w6sWLECU6dOFdrb\n+nw+rFixAgBwzz33oK2tTVgr4+abb8ZDDz2ENWvW4IYbbsCGDRvw0ksvCR2nAODWW2/FvHnz8Pvf\n/x6LFy/GunXrsHv3bjz66KPCY7xeL44cOSIc26NHj+KTTz5BRUUFhg0bBq/Xi1//+tdYtmwZqqur\nceTIEaxZswajR4/GwoULVT5S/UOBRpFifd0B6aCSlQLvQh4M84vs8S1qla6BQdTz9ts7sGtXCNHo\na/jgg12YNWty0kH33r2f4aOPOESjn6oeaIwfPx6/+c3YpJ+/trY2PProP+H16mA0GjF16lSMHz9e\n8TbEwciHH36C7dvDqK7elzLQaG9vRywWy7igPFP9CUAAqgPJh0I9X2cDa+9Dt9uNESNGJH3M8uXL\n0d7ejl/96lc4ffo0Jk+ejDfffFM4d5w6dQrHjx8XHj9ixAi89tpruP322/GHP/wBtbW1eOyxx+K6\nTLW0tGDt2rW49957ce+996KxsRGvvPKKsIYGAOzatQvnn3++8Pm+8847AQDXXXcdHn/8cRgMBuzd\nuxdPP/00XC4XhgwZgoULF+K+++7TXNYABRoakO8ZDRbxA/ZoNIpwOJzXAu90sBZoKJn5Es8g6XS6\njNbAIOmLRCL4xz9eQ0+PF5deugROpxOLF8/BgAEfweNx4fXXO+B2b0k66D7vvHMRi32ACROa09p2\nKBRCd3c3Kioqkn7OUr0H7HY7ystNMJnCSVMYlFi8+DxUVX2C886b3edn4vdvW1sb7r//acRiwG23\n/QC1tbX92q4a8t0JS4vnSi1g9U59rrF0TRNTMqMBAKtWrcKqVatkf/bEE0/0+d7cuXOxe/fupM+5\nbNkyLFu2LOHPzzvvvKT1nFarFW+88UbSbWgFBRpFivVAg+fxePJe4J0OlgMNqUgkAr/fHzeDZLVa\n83b8c3FstfTeam1txfr1B9DTAzQ27sesWbPQ0tKCSZMm4dNPP4XNtgMzZ47Dzp07MWTIEAwdOrTP\nc9TV1eG66+oSbuPzzz/H9u07MW3aOWhqagLQG1g+/PDjOHq0C1dfPR8zZ87M+G8oLy/HXXfdhHA4\n3O+akMmTJytKF/P5fPD5YojFdPD5fP3aZrap3QmLf65COf8TbWA1IEtVDE7UQYFGkeIvXCx1QAK+\nKfAOBAIAeotWs7W4XjaxWhvDp6j5/X5EIhHV1sAg6aupqcGMGUPQ3e1FY2Nj3M8mTZqEGTNm4K23\n3sIf/7gBdXVG/PKXq9Ne5+KNNzbhjTc60dbWKQQakUgEp065cfasDh0dHXGPVzLgOHv2LA4fPoxx\n48ahvLwcpaWlae2TEsFgEM888zx6eny45prvCilWn3zyCfbvP4hly2aisrKyz3FjhVqdsPjXiV/t\nnj7D8ui4KMPacVI6o0H6h63RWYHK54eTlTtafP0FX+BtMpkQDodht9uZqgFg7UQsHojwKVJ8iprW\nZpCKZUYjHA5j06ZNMBgMuP76q5O+/202GxwOwG43Z5TKds45Y9HWtgXTpo0TvmexWLBy5TK0trZi\n+vTpwve7u7vx//7fUwiFONx00w8Srqnx9NMvYudODy6++Ctcd93Vae+TEm1tbdixow09PUBLyxFM\nmDABsVgML7zwFj75JIqrropi/vz5iEajeOaZdTh27AyuueYy1NUlnt1hQSadsIDewCwYDGqiE5aW\nsHJ9zDcWj1MsFoPb7e732j8kNQo0ihR/QdLyCSJZgTdfm6Hl/ZfDWrcv/vh6vV4hRa20tBRGo5GJ\n/S9EBw4cwNq1u2E09rZ4lbsrz79u5557LoYPH46BAwcmnfVzuVzYtGkTqqurMWvWLOH7c+bMwezZ\ns/u81g0NDWhoaIj73smTJ3HwYA/CYeD48eMJL+ADB5ahvNyD8nKn4r85XcOGDcPFFzejp8crFFjq\ndDpMnz4GHHcATU2jAfQWg+7a9TVOnNBj+vSDzAcaycjVgfDnV76/v9JOWOIZkWI4DxTD39gfrKZO\n0YxGblCgoQGFnNOeCSUrePP7rcX9T4aV3OhYLBaXoqbX65lMUVMbn5qSTzU1NairM8FkMqTsmtS7\nyncdOjs78ac/PYHy8hJcccVlfV7HHTt24NlnD2Ho0ANoamqKK8xWen4aNWoUli2bhHA4gubmxMXl\nV1+9HAsWnM5qr3ej0YjLLrtU+H++FmPp0ktwySVLhDv+5eXluPTSmWhrO5X3lrj5ZDAYZNOwir0T\nVr4/6yxh7fWOxWJwuVz9rg0jqRX3qEFD8jHo11qgIbeCd6K756wM2FkjXeSQT1HL90KHSrC26nqm\nKisrce+9q6HT6RS/JgcPHsR7752G03kas2e3Yfjw4XE/HzlyJEaP3oPhw6syrpkwGo24+OLULXJN\nJlNeOz2JB9Q6nQ4XXDA/b/uiZfnuhKUlLO5zLrF4He7u7kY0GoXTmb2ZVdJL2yMHklVaCTQyWcGb\n1UBDq/vNcZzwGgAQWtQCvdPLRBu6urpgtVpTLmYn1dTUhLlzD6K8vARDhgzp8/PGxkbcd98dMBgM\nqg+qOI7DgQMHMHDgwIxnMbZt24ZNm3biwgtnY+LEiXj22efR0eHGtdd+F4MHD075+52dnfjwww8x\ncuTIuLoS0iud1zzbnbC0RGvnaa1iJRVYrKurC2VlZUzVeLKKAg2NKMYZDWmBdyYreLN2IdBaoCF+\nDeQWOWQpRS3f7+dsW79+PZ5++g2MGTMcd911MxwOh+LfraiowI9/fEPSx2Rrxmrbtm144on3UVmp\nxy9+8W+K9tvn8+G9997DoEGDMH36dGzevBubN/vgcOxGVVUVtm9vhcsFzJp1GGazGe++uxHV1VVo\naWmRHfDs2LEDa9d+gVGjvsC4ceNgt9tlt2k2mzU/c6cmNT8vanXC0mIhuhb2QetYO0Yulwvl5eXM\n7TeLiueMSvrQ6XTgOC6n21RrBW8WitnlaCXQ4Bc5DIfD1KKWAR0dHXj66X9gzx4vYjHA7/enFWiI\ndXd3g+O4tBbIi0ajOHbsGCorK9PertFohNEIGI3KB407duzA009/gsrKGEaNGoULL5wNh2M3zjtv\nFmpqarB48QS4XG6MHz8eO3fuxLp1h1FTcxDNzc2yxZ11dXVobDyIMWNqhZk63rFjx/Dccy9i//5j\nmDSpCbfcslJzK+uyLJNOWMkK0XMZgOT7PM0KFo8TBRq5Q4GGRuTjza7X6/vcVcoWJQXe6WIx0Min\nWCwmBBiRSETRa6CVwEgr8nVRstlsGDNmJKLRo7jqqvkYNGhQRs/T3t6O++9/AuFwFKtXX624VmLj\nxo144YWdaGwsxR13/FgYNJ46dQqff/45Jk6ciLKyMtnfnTFjBioqKlBRUSE7k8Dz+/0IBAIYMGAA\nhg4diuHDdaiqcqKkpARTpkzBlClThMd+5zuLhX+PGjUKY8bswbBhg1FaWopwOIwzZ86gurpamB1t\nbm7Gf/xHE06cOIFDhw7h6NGv0N7euwbI7t0fYccOA/z+4ygpqYDX6+33KuVEmWR1IOkGIMXWCUtL\nYrFYRu2z84k6TuUOBRpFLBcD9XQKvNPFYqCRj4G7XJCntTUw1MDi+0Epu92Ou+5aBb/fLwQZgUAA\ner0ee/bsQVlZGcaMGZPyeTweD7q6OEQivRdaaaARDoexefNmWK3WuLa2fr8fXi/g8wXjjvGTT76I\nPXu8+M53TuDqq6+U3aZOp0u5MJ7P58Pvf/8IOjv9+NGPLkNTUxP+4z9Ww2QypUxlqq+vx69/fYcw\nyHzyyb9g+/bjuPji8bjkkiUAej8DbW1tePDBl+HxeBAO69DV5YfH0w2Oi6Cx0YauLj16ejw4efJk\n0QQaWm1L2p8ABFCvEF2rx0eLWDtGtCp47lCgUcT4gVk2CrkyKfBOF4sDy1wGGtIgz2QywW63px3k\nsXicsyWfF1OHwyGkLe3duxfPPPM6zGY/Tp60oqQkivPOa0JpaSlmzZqVcAXwkSNHYuXKixAOh4X1\nJcT27duHZ57ZCZsNGDJkCEaOHAkAuOCCCzB48GAMHz48bvA3aFAZBgzworxcfjZDKb/fj/Z2P7q6\ndOjs7ASAtArexfvU0eFGVxfQ1eUG0LsY3YYNGxAMBmE0AqWlDtTUWOF2+/Dhh8cQDpuwaNFC7Njx\nFdra9GhtbU3anpfkD3XC0iYWrw986hTJPgo0NCIfJ7psbFONAu90sHiCy/bAPRqNCgGGWkEeC8c5\nVwFRrj+rwWAQe/bsQXV1NQYPHoxDhw79K/1HhwEDemC3m8Bx3Xj11f0wGEyoqKjA+PHjE+77Oeec\nk3Bb1dXVGDrUAJvNFNdf3mazYcaMGX0ef+21V+Lii8/26SZ14sQJeDwejBkzRlFKxcCBA7Fy5Xfg\ncrn6vZ7FNddcgZkzDwvHYO/evXj++b1wOHT44Q8vwpAhQ2C323Hs2DGMGDEUbW1daGpqgs1mg9Fo\njFuwkLAhW52wWOymlA8sHidKncodCjSKmFqrVKtV4J0ulu+0Z2O/+VkkfpE9i8UCq9Xa7yCPtQtI\nodm8eTOefno3amv1GDu2Fm+/fQzNzWZcf/04DBv2bdTU1CAQCODpp/8KjuNw8uRJtLa24sILL0y7\ncHvIkCH45S9/Ar1en3BWRMxsNmPo0KFx3+vq6sIDDzwLjyeGH/7wQkydOlX2d48fP46PP/4YkyZN\nQl1dXcLgKF2DBw8WWt7GYjGcPXsWOt1x1NY2oLm5GQ6HA7/97YM4dMiLyy8fjxtu+AF+97uHcexY\nEN///syM1xFhVSF/vtMNQDiOkz03B4NBzXXC0gpW08tcLhfq6+vzvRtFgQINjcjnjEamg95sFHin\ng9VAIxvrFPBpajqdTlgDQ60gj9XjrLZIJAK/349IJJLTLjilpaVwOmNwOEwwm00wGgGn04klS5Yg\nFovhn/98HcePn8KKFVfAaDTivvv+jPZ2PQYMGIDzzjuvz/O1t7fjb397DV6vG2PGNGLu3LlxAYm0\nK1O6etNbdNDrkxeI/v3vb+Cddzoxb14bbr/9ZtnHtLW1wW63Z5TiEA6HsX79erz88nYAQ7FgwRyU\nlJT868YKoNN9cyeb46LguN4g6fHHn0FV1SAsWvRt5gZP6SrWz7XSTlihUEi4kaaVTlhaxdrfTjMa\nuUOBRhHjTwzRaDTttSuyVeCdDlYHwGrtd6o1MIpNtt4P4XA4LsAwGAw5HXxMmTIF+/btwzvv7ERd\n3WCsWXOZUMTd1dWFt97ai7Y2PerrP8O8efMwYkQZHI7uuELvM2fOwOv1YsSIEdizZw/++c8v0dq6\nHyNGuGCxWDB//jerY+/btw+nT59GS0tLRi10y8vLcfvtK+DxePrcMWxra4PX60VDQwMaG4fj6NF2\njB5dJ/s8+/btw6OP/hPl5SbcdddNac80bNmyBc899xFOnDiMiRPHCrMcOp0ON910Ddra2tDY2AiT\nyYR/+7drcerUKbS1tWHt2s9RXd2KmTOnZ9zdi7BLXAfCcRyi0Sjsdjt1wkqAxWsw0BtoiNNDSfZQ\noKER+WpvCyg/UeSiwDsdxRho8ANc8cA322tgsHqc+0N6nPnZOqPRKKw9wj8um+sAeDwe/OEPj+PF\nF1+Fy1ULn+8fmDlzutAmtry8HPPmNaO19TQmTJgAi8WCVauuRyQSQWdnJ959913U19fj4Yefg9cb\nxc03fwfjxo3DnDkH8NlngzB4sCku9cnj8eCJJ/6Jkyd7923BggUZHT9x+hKvo6MD99//NHy+GG6+\neQkWLrwIc+d+K2HRt8/ng9erg9EYFmq+0uFwODBggAUNDdNw441Xorq6WvhZeXl53CxJZWUlKisr\n0draCpvtSzQ3Tymau52FOgBWgzitOJ1OWBzHIRwOxz2uUAvRWU6dKpbPeL5RoFHElKZOSe+c87n/\n+b5zzvIAON395tfA8Pv9eUlTY4EaNUdyx1ncCjgajfbZplrrAMgFIF1dXWhrC8BmGwSrNYxAIIwH\nHngZt9yyFM3NzdDr9Vi2bGnctvl9efzxl3H4cBRLlrSC42KIRHSIRCKoqanB3Xf/BJFIBKFQKG5t\nC5vNhqFDy6DTueMG5jyO4/Dpp59i4MCBitfgEAuFgohEDMJrlGxdjWnTpsFoNKK8vBwDBw5Me1vT\npk1DTU0NysrKFAV2kUgE77zzEbq6RmDw4IFZa2ChJayeP7WEOmH1Yml/Y7EY3G43BRo5QoGGRuTz\nQyp3sZEWeOv1ethsNlitVs2cULLZnjeb0tlXvg7G7/cLaWq5XgOD5YBOKWm9UX/TAdUKQIYMGYKr\nrpqD73xnEgYMGIAXXngXkQhSDoI7OjoQDLowYIAZ9fX1mDdvHrxeL5qamoTH9K7YHX8JMJlMWL36\nh+jq6sJzz/0NL7+8Hk6nDYMGDcTy5Zdj165dePzx9zFokA6/+MWqtNKZXC4XwuEwHA5OaJubjMFg\n6FNI7vf7cfDgQbhcLjQ0NMBut8Pn86G2trbP66TT6YRgyOv1AgBaW1vx2mtvo7FxBObPPz/u8Tt3\n7sQXX3yJcLgTLtdA+Hy+pIEQKXz9WYhOzU5Y4nOC1q51rF4bKHUqdyjQ0JBcD+j4E6F4m/ku8E6H\n1vZHKbk741Jya2A4HA6YTKYc7eU3lOwvq+QCudLS0qwd53QCkBMnTuCddzagrMyJhQsXwmw2o7q6\nGuFwGCNHjkQ0Gk145/P551/F11/bMXfuoLiF95QwmUzo7u7Gvn1daGvrAuBDdfVQzJp1DGazGRYL\nYLNEBd4AACAASURBVLHE/w3Hjh3DRx99hIkTJ2LUqFGyz9ve3g6vtwQGQwxer1dRkBKLxXDixAnY\n7XZUVFTg+ef/inXrtqGnpwvnntsEvd6Enp4ofvSjJZgwYQJ6enrw+eef45VX3sX06WOxePHFcc+3\na9cuvPbaGTQ0nMLs2S1C4bvP58Nnnx1CMDgSXq8L777bgfr6bXG1K4Soob+dsLRWiM5i6lQ0GqVA\nI4co0Chy4lkBvv6iP4u75ZJa7XlzLVlAKVcHY7PZiiKNo7/SeT/IBXIlJSV5rTeSBiBbt27HH//4\nNsxmC+x2Oy666CJUVVUhGo2is7MTNptNdtARi8VQXl6Cigovamtr0NnZiQMHDqC5uVk2Bcnj6V0N\nu76+Xvj7R4wYgaVLJ6KzswtutxdOZwmGDx+OhoYGDBo0CGVlZXF3+//xj7fw5psdmDu3DT/96Srs\n2LEDbW1tmDdvnlALMWXKFNxwQwClpaWoqqpSdFw+/fRTPPLIP1FWZsLdd/8IkQgHvd4Mmy2G0lIr\nOjtDCAT0CAQC2L9/Px577BWcPfs12tuHIxDYK3SO4j9vEyZMwJw5rWhuHgGLxQIAOHnyJB588Fn4\n/V5cccUwHDo0FhwXyyhdi0UsnTvzIZczx0o6YWWjFqzYeDweACi6Vtb5QoGGhuQrRSUcDmumwDsd\n/W3Pm0/SfRa3qAXUWwNDDYWUOsUHGH6/X/Pv99GjGzBoUAx6vRNGo1EYGG/ZsgUvvbQZ06ePwne/\ne7lw11OcevHd7y7F+ee3Y8iQIXjssWexZUsn5s07jJtvvj5u4BGLxfCnPz2NQ4d6sGzZJCxa1DsD\nYDAYsHjxItn9kkt7GjNmJL744iyam0eiu7sb69ZtwLFjelitVnz7298G0Lvmhly7XalAIACv14uB\nAwfC7/cjENDBYokgHA7jyisvx9SpE+BwODB8+HCcPHkSHo8HEyZMwMaNG9HWpkNJyUAsWVKJadMm\n9Rlk1dfXY82aW+K+197ejtOnORiNVsydOxfXXjsCjz76GP793/8bixd/CytXrizYwVqhfK6zRSvH\nR61UTOm/1Xhfszij4XK5UFZWponrazHQ3tWV5ARff8GnxKi99kIusBpoiE/IHMfB7/cLhfYsvg5a\nkez9wM/YiVdL1/pM0fTp0/H88w/h1KlTaG5uFr5/9OjX+PJLPcrKWoUUr0gkgn379qGiogKVlZUw\nm80YNmwYotEoSkttKCmJwG43w+v19rnbGYlwiESgKD3u+PHjeOutjRg7thEtLS3C9xcsuADnnjsH\nVqsVHMehqakaFssZRbUYYsFgEPff/whOn/bihhsWY+rUqTCbzXA6ncIMw5QpU4THi59/1qxZiEaj\nqKqqwsSJE7F161b8/vf/g29/+zwMHz484TbHjh2L665zwWg0or6+HjqdDh9++DH27LEgFNqByy+/\nvGhmN0hfWh5Ap9sJS/oZV6MQnbWMAuCbjlOs7TerKNAoInIF3vwJisWiR5YDjWg0iu7ubmEl9Wy3\nqO0Plmc0otGokCIVi8U0NVOkhFyb2ClTJuLs2VNxrWe3bduGxx//AJWVOtx1141wOBxC/cE113wf\nF1zQhsGDB0Ov1/cpPr3mmstx4sQJjBkzBoFAIOmgY9u2bfjb307i0KE2TJ8+PW4miN+ewWDAj360\nAuFwGO+8swHvvrsFS5dejJqampR/byAQQHu7Fx0dOnR2dsJgMGDy5MmKjpXD4cCFF14o/P+bb27F\njh1hOJ07EwYa/PtjxowZcXVo1167DJHIS5g6dRzKysoUbZ9VWjznaAWr571cd8Ji7T3kcrlQXl7O\n3H6zigINDcnWmz5ZgbfP5+tzkmEFa4EGH+jx6VEcx2m20J5l/IWUn8EAelPRbDYbMzNF4XAYgUBA\nyCHmOA7PPvscjh07Dbfbg5MnrdDpNmLjxq2YO3fGv/6+GGw2U5+/0Wg0yg60+UGH1WoVaj9SDTqa\nmpowY0YrJk9uTJpuptPp4Pf78eabe3DsmB4jRuxJGGjEYjF4PB44nU6UlZVh5cqlOHToUNzMhRIc\nx+HMmTMYPHgwDAYDFi5sgdO5B7NnT5d9/JkzZ/C///f/wfHjHpSWWjBnzjlYtGgBysrKcNFFF2HB\nggVMthlNB4t3o3OFxZSgVNTqhCVOwWKxUUhXV1fcOjokuyjQKGBKCrxZvlvNSqAhDfT4k7zT6WRi\n4MvKe4R/P/BrvgBspgSGw2H8938/jPfe+xhTptRh+vTJqKysxK5dx9DWpkNVlQclJVYcPvw1vvqq\nCpHIVvzgB8tw++3fxaBBg2C1WmUv/h0dHdi+fTsaGhowevTojAYdI0eOxB13/BBAb6emZHc9nU4n\nzj9/HI4ePYHx48f32Z+uri688cZbOH78OFpbw5g9uwFXXvldtLe34+23D+Crr05h9eofKX7tXnrp\nb3jvvSOYP38MrrjiMrS0tAjpXd3d3fjoo48A9KakGQwGvPnmW3j77S8RDFpRXR0A8BH27GlFTY0D\nd931Y2GGhpBCl+65gP++mN/vZ6YQnRbryy0KNDRErQ9lOit4szKITEar+y/tbMS3TuU4Dj6fT7Mn\nYSkW3iN8rQsAhEKhrAYY2X7deteKaMXRowYcP74df/3rLtTWDsYPfjAPM2eaMW/eDxCJRNDe3o6N\nG7ejtNSI//W/HkdzcyVWrbpRmDGTevfdjVi79guMG/cZ7rvvzoTHRjzo6J1JeR7Hj5/Btddejrq6\nOiHf+8CBAzCbzX1mS8QDjSVLFiUccOzZswd/+9tX6OraC7O5CTU1JwH0DgI6O3Xo6OhBNBqN209+\nRlbOmTNd6OjQob3d1ednX3/9NZ54YgOiUQOOHj2KI0dOo7ragenTh8PpjGL27Jnw+/3YvPkMPJ4g\nWltbMXjwYPj9fnz11VcYP348HA6H/AtGChor5+lsUNIJi581BsBMJyw+dYrkBgUaBSSTFbxZXfQO\nkF8HRAukhcfS1qn8/rJ4zLVGWkwPACUlJTCbzVnbZrZTKg4cOAC9PoSpU4MAqvHZZ90wGIyYMWM6\nxo4dKzyutLQUlZWV2L17N86e7cLAga6kn4Vhw2oxYsTnaGjou7gdAJw9exafffYZxo8fj0GDBgHo\nvSB//HErTp7U48iRIxg5ciT0ej0OHjyIRx55AxznxZIlMzB37lw4HI608r7r6+sxceInKCmZjYaG\nOmHWY/78+SgvL8fw4cPjbo5s3LgJr722FQsXTseFFy6A1JVXLsXEiftlZ09KS0sxcKARHAccOXIc\n27YB8+db8D//8xuhTXA4HMb48R+jq6sLv/vdkwgGOxAMBhCNjsDy5SdwxRWXJ3/hGEXnIHlau65o\nDV8HwgcT/AygFjphpdLV1UUzGjlEgYaGZPIB4/P+/X4/IpEI9Hp9WoXFrF9ktBRoSGeSEhUes5Ly\nxdPieiXSoJpPCfR4PJrZx0zt2bMfJ09WobY2hquuWgq9Xo+zZ8/C6/UKr0F3dzfuv/8JuFxhXHXV\nXKxaNRA1NTV47733UFpaGheQ8GbNmoXx48fDbrfLHqMXXngF773XgXnzvsCqVTcCACoqKnDZZbNw\n+vSZuFW6zWYzjMYYDhz4HE88Afj9QSxffkXc8/E3MILBIDZu3Ai9Xo85c+ZAp9Ohq6sLJpMJt922\nMi74iEQisNlsOPfcc/vs46effo6DB/WoqTksG2hUVlYmbJ87cOBA3HXXj2AwGNDa2orq6h2YPXta\nXBMMk8mEGTNm4P77H8CWLQcRCp1FaekYDB16Ag7HjCSvGLtYOQflE+vnk2yTXhe00AkrFbfbjcbG\nRtWejyRHgQaj1FrBW4uDyHRoIdCQroGRKm2HtUBDS/igmu+aJg6q+QsW68d1wYK56Oh4Ebt2OfD8\n8zuwfPl0vPvuF4jFvkBpaSmampr+1VQggmBQB6PRiDlz5uC9997DY49tx4ABEfzsZzV9Osm53W5s\n2bIFtbW1mDhxIj7//HPs378fM2bMQE1NDQYPrsCgQe2orPzmTp9Op8P8+ef32cfRo0fjpz+9GuvW\nWfHll0E4nSUAgEOHDuHVV9/BtGnjcP7586DT6XD48GG8+OJeGI2961iYTCY8+OA6mEx6rF59LQYM\nGKBoBmTRovmoqvoIU6Yo60Il9cEHW7Bjx0FcfvkFWLnyWhw7dgw+n6/PcSopKUN1dQPMZgNqa0sQ\nCARx9GgrIpGIJtdbIdnB+nkkl5Te1MxlJ6xkaFXw3KKzpoYo+cCovYI3PxiW5kKzJF8XBOlddZvN\nBovFwuxxTEQLwSjfhYkPMAq5W1d9fT1uuGEF/P5nYTYbMHz4cJSV7UYsFoPT6QQADBgwALfcchVc\nLpeQKtTbCjeGigoHbDYbAODYsWMIh8MYNWoUtmzZgscf34cRIz7Bz342BOvWvYrduyPo6PDghhuu\nwfTp56CmZjBmzZqlaD+HDx+O225bhTNnzmDo0KEAgJ07d2PTph50dGzHvHnnQafTYciQIairM8Fs\nNqKyshLHjx+Hx6ODyRQV6mmA1AOOqqoqLFp0MfR6Pbq6unDs2DGMHDkSJSUl6O7uRigUQmVlZZ/9\n5M8PW7d+hk8+ARob96OzsxMvvLATY8Y4cdttNwuzKTt27EBDQx1+9rOhKC0txf/9v4/h4EE9SktP\noru7uyDTLQrxM6QmOj7J9ff6m41OWKnqQKgYPLco0GBEOgXe6WD97no+ZjSkg95018Bg9Zjnen+l\naYGZztqpKZvbDYVCeOaZ59HR4caKFcvxi1/8BDqdDmazGffccxNisVhcAWNdXR3q6uqE/29ubsa/\n//sQAL3ni6+++goPPLAOkQjwk58sQ21tLUaM+AQlJTH89rePor29FSNG1KChoQ4dHR148MHn4PX2\n1rgoXbvCYrFg2LBhwv/PnDkdnZ09OOecscKxqqysxL33roZO1zv74nQ6sXKlHxaLJa6QPNmAIxKJ\nYNeuXSgpKUFjYyNeeunv2Lz5BGbPrsb8+d/Cf/3XIzCZnLjppqVobm6G1+uF3W6Pq9VZuvR8jBnz\nOc4771x88sleeL1AT09AeF/v27cPjz22GVZrDGvWXI1Tp07BYBiK2tov8e1vTy7IgQlr56BcomOT\nWjbr1dIJQGKxGDiOS1gHwnEc9u/fjzFjxqC0tJQCjRyjQEND5D6smRR4Z7JNVk+quRpwxmIxIcDo\n76CXtWOe60E9f6z9fr+QFlhSUgKTyZR0X3J1XLN1PM6cOYP33z+MgwePIBLpwZo1dwlpBkoXjSsr\nK8OxY8fw8MN/AceFEQxGYDD0zm5MnDgR993XgK1bt+LPf96JqqparFmzAjU1Nf9aHE8HvT7ar8UM\nGxsbZXOf+RXMgd47kDNmKK950Ol02LNnD/785/dQWhrDz39+I4xGE3Q6I4xGI5588gVs334MNTXV\ncLvd+Pjjj/GXv7yJIUPKcNNN18JisQAAJkyYgHPOOQd6vR6VlZWoqhqMuro64e+tqKhARQVgs5ng\ndDpRXV2NlSu9cDgW4ZxzzkFnZyetJlyE6PVOLZfHSEknLOkMyMGDBzF//nwAwNChQ2G32/Hkk0/i\n66+/xtixY9Hc3EypVFlUWDkeBYC/Qx8Oh+HxeODxeBCJRGC321FeXg673a5qag5rg16pbM9o8MWs\nHo8HPT09AHrv+DqdzoxX8mbtmOdqf/m6I/5Y63Q6lJaWwul0FmyalFhNTQ3GjCmBXl+Jo0dDOHv2\nbNzPOY7D8ePHEQ6HEz7Hu+9uxH/910M4eLALbrcZV165ALfdtlwY/NvtdsyaNQsrVkzBtdcuFBbR\nq6iowB13rMCdd34P48ePx5kzZ/DHPz6KF154GRzHKf4bxAtSin3++ed455134Ha7FT/XBx98gOee\newEdHR1wOp1wOmNwOk2wWq1Yvvwy/PSni/C9712O0lInRo8ejsWLGzF79mx4PB6cOWPG6dO97XE3\nbtyIRx99Em1tbQgEAvD5fIj+f/bOOzyqKv//r6mZySSTSSOkkZ6QQjqB0EEgIChFhV1xwYbY6/7Y\nXXVdd/e77fvsd4uKZVdXkRVFxQVBemclIL2GmpBGJr1NMpOpvz/iXDMpECAkMzqv5+F5yMwt5565\n957zPp9mtTJs2DA0Gg1GoxGz2Ux4eDgvvfQoP/vZY2g0GuRyORMnTiQnJ4f33lvBr371Nnv37u11\n+924Nq7yfh5InK2P7HEgMplMKNKqUqlITk5mx44dLFu2jLvuuguDwcC+fft49NFHGTNmDP7+/gwe\nPJhJkybx0UcfAbBs2TKioqJQKpWMHDmSgwcPXvXcu3btIisrC4VCQXx8PMuXL++yzWeffUZiYiJK\npZK0tDQ2btzo8P3evXu58847CQ0NRSwW8+WXX3Z7rldeeYWQkBA8PT2ZMmUKFy9evMEe6x/cFg0n\nwj6p7biSe6tdRVxt0tuZWyU0OtfAsMfCdFyZddM32AWGXq93qDdyo33tqveyRCLh4YcfxNPzCwYN\n8u0Sb7Bu3Vds2nSGkSPDuf/+Bd0eY9u2g5w/r2bYsCbuvHM0o0eP7rIwoVKpyMvL67JvUFAQAG1t\nbaxfv57t28sJCall3LhqBg8ezK5duzlz5iK3334bkZGRXfbX6XS88cb7NDcbeOyxHxMWFga0i4/3\n3/8PFy7YaGlpYdasWdfsi6amJj7/fC8lJWJ8fL5h+vTpvPjiw3h4eAhxKqmpqQA89thCKioqiItr\nr1Y+atQooF24yeVy3nprFRcutGIytfLTn/602xVPu4uet7c3IpEIg8EguF1otVpWrdpIfb0/2dnF\njBt3zea7FN93Ae/m1uEq1dMVCgXZ2dlkZ2djNpt5/fXXqa2tRalUcv78eQoKCjhz5gwFBQVYrVZW\nrVrFCy+8wD/+8Y9vM9H9lby8PM6fPy+k/u7I5cuXmTlzJo8//jgrV65k27ZtPPzww4SEhDBlyhQA\n9u3bx7333suf/vQnZsyYwUcffcTs2bM5evSokCWwpaWF9PR0HnroIebO7T6d9p/+9CfeeOMNPvzw\nQyIjI3n55ZfJy8sT6ho5I26h4WTYB7ibCfC+Xpwhc9ON0tdtt1qtgsDoy1iYjriauLtV7e1OzHWs\nN3K9OPtgdy2qqqr4+uuvKS+vpKXFgE6nE1ymbDYb9fVNNDZCQ0Nzj8e4446xBAUdZ9KkOxk2bNgN\ntWPTpi1s3VqKRFLMpEl3EhgYiNlsZv36fZw9KyYw8JAgNGw2G2fPnsVisaBWqykpaUGng/LyckFo\nSCQSwsL8aWmpEsRMd9TU1HDw4EGysrIICAggI2MIanWFYI3pLtAb2gPjO/pbq1QqYXC32WyoVArk\nci8kErkgHjpiNptZtuw9CgtrWLBgCqmpqQ5Bp0VFRXh7h6NU1pOYmIDRaOz3vP+3Ald5/wwUrjKJ\nHkhcsY+ampoQi8V4e3sjlUpJTU0VFi3sjBw5kiVLlrBw4UIA3n77bb766iv+9a9/sXTp0i7HfOut\nt4iOjuZ///d/AUhISOC///0vf/3rX4V30Wuvvcb06dN5/vnnAfjNb37D1q1beeONN3jzzTcBmDZt\nGtOmTQN6fj7//ve/88tf/pKZM2cC8OGHHxIUFMSaNWuYN2/ezXbPLcEtNJwIkUiEj49Pvw8AHVOD\nuhp9JTTswfb2Kqc91cDoK1xZ3N0sHS13t0rMuSIffriKLVvKaW0tJi4uid27dzNo0CAUCgVffrkD\npVLCqFEqoqLCBIun1Wrl0qVL+Pv74+fnR25uLpmZmZjNZoxGIytXfkZjo4777rsbf3//LufU6/WI\nxWIhjgFAIhGjVHqQlZXNXXfNFu7VnJw4AgO1pKenCdtevnyZZcvWYLWKePrp2SxYMBadTucQTC4S\niXjkkUU0NzdftRrvH//4FzZuvER29pcsX/4WixYtwGazceTIET766GMmTBgnZLfqLSKRiF//+nmO\nHz8uWDpMJpNw39n/LiurR6uVUltb26XwmMFgICPDm4yMcSQmJmI0Gh3O0R95/90MDO7f8PuHvSp4\nTy7oJpOJw4cP8+KLLwqfiUQiJk+eTH5+frf77N+/n8mTHWv75OXl8dxzzwl/5+fn88ILL3TZZu3a\ntb1ue1FREVqtlttuu034TK1WM2LECPLz891Cw03vGIgJqCtPem+2snnHGhgikeiaNTD6Clfq876y\naHSumC6Xy1EqlX0q5lypXzty4sQJ9uw5jtHYzIQJQ2lpaebNN9dhNMqJjBTT0hKMRFKLWKzixIkW\n/P39CQ8Pp7CwkH//ex9hYXJ+/vMnHUznWq2W/PxSmpogJ+c8ubm5Due8cuUKy5Z9hIeHhKefflAQ\nAXl5U4mNjSEkJET47Tds2MSePRcYMybWIdhboVCgVIqwWGwolUpGjx7d7fVJpVLB6nD58mU2bNhO\nSkoc4zr4IZnNRsxmH/T672JQbDYbn322jdOnQSr9mvnzr38gTUhIICwsDA8PD2pra1m2bDlWq40n\nn1xEQEAASqWSBx64k7KyMoc+0uv1fPPNN3z+eT5arYXi4q3U1TWzcOGPhcWZ/sr7fytxtvY4C674\nHulvXNGiYRcaPbW5pqYGi8XSxfoaFBTEuXPnut1Hq9V2u31TUxNtbW14eHj0uI1Wq+1127VaLSKR\n6KaP09+4hYaTMRAPrFgsdtmX6o32V8fCb/YaGAqFol/731X6/GaFRmd3tFttLXI19Ho97723nCtX\nZKSnRzJ79h386U9votM1oFINIixsCMnJ0UgkCRw7dgmTycTnn2/FaJSRnj4IiwVMJmuX3yckJISp\nU4fS1KQjMTGxy3mrqqqoqLDg4WGhrq5OEBoymYyhQ4c6bHvlShVarZjycscA9eDgYJYufQir1eow\n+JnNZs6fP09QUFAXS8rBgwfZsKGGwsIqRo0aJViyXnxxKTk528jOzha2bc9QNRSJ5DyJiY5tuho2\nm40TJ07Q0tLC8OHDgfb7uKqqipISIzZb+/Xb/a2TkpKIjIyktbWVM2fOUFJSSkVFNfn5VUAJKpUc\nrdaXgwcvMWNGLYMGDbrpvP8DLUBc5f3jxnn5PgoNN32PW2i4cXnXKehdMbnOdRlupAZGX/FDeMl1\n546mVCpvqbWoPywafX2OsrIy6uvV+Po2MHVqFqdOnaWpKZaUlEaeeeZ+QkJChFiNmTMN1NXV8Ze/\nfIhe316hOzk5mejoaAf3J2i3Itx11+wez5uSksLChQ3I5XKioqKu2sbZs28nMvKYELTYke5iJ3bv\n3s3KlQeJiJDzi1885RDYn56eTlFRJYmJkaxdu+7b67qdQYMGce+993Y51ty5s5gzp+vzffToUerq\n6hg9erTg7mRHq9Xy7rsbaGkRIZPJBKEVHx/PggUjsNlsxMfHC9sbDAb+9rd/cuVKIzpdE/X1AbS1\n7efKFR9mzozi6acf5T//WcPu3Uf47W//yq9+9UKXoNC+Kjw20ALETTsDWaDUlXC1Puq4qNIdAQEB\nSCQSKisrHT6vrKxk8ODB3e4zePDgbre3Z6e82jY9HbOn89hsNiorKx0WdiorK8nIyOj1cfobt9Bw\nMgbioXVVdxPo3Wp7d3UZnKHwm6v1eW/ba7Va0ev1QprT/nJHc1UiIiKYOTOF5uZIoqOjkclkNDa2\nkJ09HrPZzJUrV1Cr1YJrX0hICE88MZ/6+nr27z/ChQvVLFggZdCgQT2ew37/2zM2QbsQmTBhQq/a\nGBgYKAQ19oarPVdxcXEsXRrHqVOn+L//Ww/A0KHtgqm3x6utreWDDzZRW9te0HDs2LEO36tUKvz9\n5Xh4mBwCxSUSCRMnThT+NpvNbNmyBbPZTFWVjsZGGRER3qjVOhobw7BY5ISFBVFcXExq6jBWrNhB\nQUErGzdu5Cc/+Umv+8ItQNx8H3G1MQyuXRVcJpORlZXF9u3bufPOO4H269y+fTtPP/10t/vk5uZ2\nSVW7ZcsWB1fM3NzcLsfYunVrF5fWqxEVFcXgwYPZvn27EMDe1NTEgQMHeOKJJ3p9nP5G8uqrr/Z2\n215v6ObGsQ88/YnZbMZisXRZFXQF7IHFHh4e3Q7kRqMRnU5HW1ubIDCUSmW/ZfTqCXtAaedVaGdE\nJBKh1+uRyWRXDdi2WCzo9XpaWlqwWq0oFAq8vLz6VdAZDAYhj/qtwv589tU1SSQSkpOTOHz4OF98\ncQKl0siSJQ/Q2trKsmXrOHz4LElJ4Wg0GiwWC+vWfcWFC5fIyspg48Z9XL4sIjpaQUJCAtD+O1it\nViFew2Kx8MYb77JmzR4GD/a+rhW0lpYWJBJJl2ertraWsrKyHgvYhYeHExwsR6drpLGxkejoqC7b\nKRQKKiouMHiwggkTxlzXsyAWizlz5hRisZGsrEQGDx7scHwPDw+GD09j9OgMgoODMZlMSKXSLtex\ncuXH/Pa3X3Do0El+9KPxTJiQTFpaCkePFiOTibjnnhEUFWnZsKGIgAAbbW2tiMUaRo2KF/r7Ruko\nQCQSCVKpFJlMJvzr2O8d0/CaTCZMJpPw3rZXRu543N5gX4CRyWTuRYBusLvVulOa94xdFLtSH+3c\nuROTySSIiO5Qq9W88sorhIeH4+Hhwcsvv8zx48d59913UalU/OIXv2DFihXMmTMHgNjYWH7/+9/T\n2NjIkCFD+PTTT/nLX/7CG2+8QXR0NNBeKPDll19GpVLh5+fHG2+8wWeffcZ7770nWIVbWlooKChA\nq9XyzjvvkJOTg1KpxGQyCVZti8XCH/7wB5KSkjAajTz99NO0tbXx2muvDZQ78q+vtYHbouFkuC0a\n10d3Fo3OQcc3mzb1VuFKfX61e8QuMOzV6wci3sWOq93LOp2OEydOEBkZ+e0iw3f3RbslyIZEIhIW\nAcrLy9mw4TRNTRATc4H777+Ty5cvM3z4cLRabbdWjba2NsrLG6ioEFFRUeGQEepqnDp1ivffX0dE\nhB+PP/6Q8PwcP36c//mfvyCTDebRR2c4BHTbkUqltLS0sG1bLUFB1aSnp3VxsVKr1Tz77KPXVj6P\nswAAIABJREFU1V9Wq5Xjx4/j5eXFc88t4csv17F8+WbKyyvIy5vCRx99Sl1dEwsX3kNgYCAqleqq\nCzcWixWRSIlE0khmZiaRkZEcPHgQvb49/eX48eOpqmqkoqIKjUbD7373C0pKSq5qfblZ+ssC4krP\niRvnxdUsa/X19Ve1aADMmzePmpoaXnnlFSorK0lPT2fz5s3CO0yr1VJaWipsHxkZyVdffcVzzz3H\na6+9RlhYGO+9955DJqrc3FxWrlzJSy+9xEsvvURcXBxr1651cEc9dOgQEydOFJ5Xe5aqRYsW8a9/\n/QuApUuX0traypIlS2hoaGDs2LFs3LjRaWtogFtouOHmMzcNJB2Fhj0moK2t7ZZlNeorXG1CDF0n\nJmazGYPBIAiMgYp3cWW2bNnKZ5+dIzFxP88++zC5ucXExMQA7YPXz372IBKJRIgHGDx4MDk5oTQ0\nNBMfH09AQACJiYmsWPEx+fnFTJuWwrRpUx3O4enpyYMPzuqSVcmO0Wjkiy/Wote3cddddwruVeXl\n5ZSViYE6DAYDXl5eAKxZs43Tp70ICCi96iQ+Pj6etLSThIYGCAP7oUOHOH78DJMmjb1mXIgd+7tJ\nLBZz9OhR3n57K15eNn7xi4eoqKijuFhMUVE5lZWVHDhQRmMjjBx5Hr1ez2efrSc6OpTJkyc5HFOv\n1/Of/3yJzQZ/+tM8oqOjhdogmZmZPP64BG9vbwICAnjggXvRarVUVlaycuUXTJ58fdaXvqKvBYib\nq2O/59z0jKuNYQCNjY1dkl10x+OPP87jjz/e7Xfvv/9+l8/GjRvH4cOHr3rMu+66i7vuuqvH78eP\nH98rj5ZXX32V6/BGGnDcQsPJGKisU+CawW/29hoMBmFgdYWsRq4mNDreFx0zdg1kQH13uFq/+vio\nqas7w7Zt9UyZkttFCHROYyiXy3nooa6xAdXVDdTUiKipqe/yXWlpKfn5h0hKisPLy4sjR45w4cJF\nxo0bS3BwMKWlpWzbdgm9HpKTz5KTkwPAqFGjsNlshISECCIDYMSIFGprGxk5cjRjxowB2i0N27Zt\no6lJx7RpU/Hy8iI8PJyXX37WoS3/+c9Ojh2zIpPt65XQsFqtfPjhx1y8eIWf/OROVCoVnp42PD3b\n3YzmzJlOTMwJUlNTCQ4OZvr0ZC5fLiUoKIiTJ0+yd28zJSWnyc0dgUKhEGK0Lly4wObNRUgk8P/+\nXzaxsbHCOSUSCZmZmcLfCoWCyMhI/v3vtezbZ0As/i9XrlxBqVQyatSoAb/vb1aAtLW1uWNA3NwQ\nrijGrhWj4abvcQsNNy5XqdqOfUXd/n+lUtltrIYz4moTYpFIhMViobm5WRAYAx1QP5D0lSgfNmwY\nzc0NlJaG8vLLv+HBB+9n3ry51+3zvGDBXLKyzpKSkoLRaGTjxk0olUry8qayf/9+vvjiCmfPlpOZ\nmcmqVVs4c0aEWCzi7rvvprq6mtBQM4MGDXbIxOTt7S1Uqe3ItGl55OVNdbj+8vJyvvjiCE1NEBoa\n3GOA47hxacjlp0hP713Vcr1ez/HjJVy+LObixYvMmDGDn//8fjw8PISK4PYK5ACpqSns2nWKt9/+\nnPvum8bUqVqiokJRqVSsXr2GY8cKmT9/KjExMQwfHoBEImbIkCHC/gcOHKCqqorx48c7BM5brVY0\nGgkaTQFHjihYv/4wUVFRhIWFERER0atr6W+uJUDssR72rIPuIHRHXHHhbSBwtT5yC43+xy003Lic\n0Oi8og72wmHKAW7Z9eEK/W1PCWyxWJwmY9f3hbKyMv7+938jkdgIDCxCr/dl9+4iRo8uF9x4oN3U\nf+7cOeLj43tMyxgUFCQUbVqxYgU7dxbj7x9EdHQUycnJ5OSUkZERz44du7h8uZBBgzyJj59GYWEh\nH364C7NZyrx5uVdN+9iRzr99YGAgKSn+NDTormqpyMubSl6eo2uXPbB86NCheHh4UFRUxIYN22lq\nqsHHJ5CpU9PR6VoYOXIk0F67oyeMRiNGI0gkNnx9fXn88fYaHzqdjqNHL3LmjJhz5y6Qnp7Ok08+\n7LBvfX09K1fuoKJCjFKpdPCvLi4u5uRJHZWValpaDBiNFQwbFoyfn1+v+suZsIsFiUSCyWQSFmfc\nWbDcXC+uMIZ1xGazuYXGAOAWGk7GQAXQgnO/NOwrcHYXqY4r6o2NjQPdvOvG2QflzimBoT3A19vb\n26nb7kqWIp1Oh04HKSm53H33CM6fL0atVuHp6UlLSwtarZYhQ4awYsUq9u2rZdy40zz66APdHuvc\nuXMUFhZSVFTK5s3NmM1XGDMmhtDQUHx8fHjllfaAw1de+TM6XQzTpgWTlpZGdXU1Go0Es9mKj4+P\nkKPdx8en18LdHqA9YkQ6WVlZDivoNpuNkpISfHx8uhUxNpuNf/zjI86ebeXuu0u5446ZHDjwDV9+\nqaW+/ijh4cN57LEI7rnnbmEfk6m9cnh3Vp/4+HiefHI2EonEwdIgFouZN28qhw8f5ujRAurq/sWU\nKeNQKpWCRcTb25u4uACUyjqHfY8cOcLevQdQq1tISfGhsLCawsIWTp4spqCgQHA1c3VuRRC6K1iX\nr4Yzv+ucAVe0+riFRv/jFhpOSH9PlpxZaNhT1BoMBmFF3cvLC5lMJrTblSaXdpy1zZ0FhlQqxcvL\nC71eL6xcurl5bDYbtbW1DBumJjMzkxEjRnDbbSL+53/+wOLFmwgJ0WA2BzFkiIX9+wuxWGzIZCFY\nrdYukzeLxcLy5Ws5e9ZGdraVhAQxGRl3sHDhgi6/16xZE4mMPMP48aOBdkvEz3++5FvXIA0HDhxg\nxYodDBnizfPPP9qrTG0FBQW8995OJBLw9fV1iHc4dOgQH3ywjcBAOT/72ePdihepVIxE8p2vd2Zm\nBpcvV9HamkpgoD/Dhn3nZlVXV8cbb3yA1WrjyScXdVs0r7sq6ABpaWm0trayY0cd5eXnOHLkMmq1\nJy+8sJDQ0FCkUimPP/4QZrPZIYPLxo17+fprAzNnRvDII/fz9tvv8957m2lq8u5SgMsVudYz3dcC\nRCKRuMR7xBnfz86EK1YFh3ah4YqWSFfGLTTcOKXQsNfHMBgMWK1WZDIZnp6ePda/cKa294brqWje\nH9gFnV6vx2q1CtYLe3/bM3k5O65S5X79+vX89rfLkctDiYqKoq2tjYaGBrZsOU5pqZrm5ouEhARR\nWlqJWBzL4MFlnDxZxvLlK7n/fkcBIRaLiY4ejF5fzm23TSIxMbFHV5asrCyysrIcPusYi3DhwgWK\niyvx9ESoPVFbW8uqVWvw9fXmnnvmdhEfGo0GX18RUqm4i9XCYDCg14vQ681cunSJgoIC0tPTiYuL\nA9p/rwUL5vL66+9y/PgFRo6sJT4+np//PJ7uqKqqoqTEiNXanmKys9C4GiKRiLS0NObOraS1Vceh\nQxUO6YTtfdk5TeT48VnAYUaOzEQqlXL//T8mMrLdfau71L6uws0+zzcjQDq6b3V2wXIGXHUS7ebq\nWCwWmpqa8Pf3H+im/KBwCw0n5Ids0bBarYLAsKeoVSgUV11ZdcXBwFmERneCrqeaI85wf3xfqKys\nw2KRIpVWo9Fo+POf36a+vpWcnGiCgxtYtOgxAgMD0Wg0nD17lvJyPzZvbsDDo4yzZ8+iUCgoKSkh\nPDyc6OhoHnzwPlpbW/Hy8sJoNFJXV8e+ffsICwvrdc2H5uZmjh4tRiyWkJMTJ1gfCgoK2LOnGo2m\nmrFjtYKr0alTp9i5cx+jRmXx0kuPIRKJ8Pb2djhmbm4uKpWKgIAA1qzZxJYt9ZSW1vD883HCNjqd\njqoqOeXlekpLS686CYiLi2PBghFYrdZepajsjFqtZt68u7HZbIwefRGZTOYQTN4Rs9nMyZMnGTJk\nCC+9NEb43MvLi5kzZ6LX69m0aRPBwcGMGDHCJd9Dt4LrESAWi0VwhbPv21MMiBvnwhXFWFNTk+AV\n4ab/cAsNN8DArwR3roFxPSlqndUNyZnpLDCuJehcqY9vZTv7Kuh11qzbCQkJJDo6Go1GQ1XVLhob\nxSxZMpPMzEyhQB+0T65ra2sJC8untbWVv/99LQ0NlzGbg4mPV/Lqq88il8sdBs/8/Hw++eQ84eFH\n+PWvI1GpVA7nr6+v5/Tp0wwdOlSwCrQH+nsQGhooxCgcOHCAvXu/YehQK4mJ8Q5VxXfv3s/GjfW0\ntOzrYiWxI5VKhVSxw4bFU1KSz7BhcQ7bREdHM3duKkaj6ZriQSKRMHHixG6/q66uxtPTs8u1Qvs9\nUVNTg0ajEVIx260qAIcPH+arr/YwblwmEyaMF679vff2EhAg4uWXH3Ow/AD87W+vs3LlGaKiVLz1\nVjihoaFXbfsPnd4IEIvFgs1mcxoB4kqT6IHClfqooaEBjUbjUm3+PuAWGk7IQNXSGIiJpMViEQQG\n2KshK64riHCgRdKNMFBWpM5V03tb1NBVhIarDCCBgYFMmjSJ1avXYrVa+fGPJ2A0GsnOzkYmk3Hq\n1CkUCoUQ7+Dv78/MmTM5cOAANlshHh4KNBobgwapuxWHgwcPJjT0LEOG+DmIFjurV69j27Yr5Oae\n5plnlgDthf2effZBGhsbhaxXW7bkk59vYtasYObPv9vhGKNGZdHSso9x4xxFRllZGXV1dSQnJzvc\nVxMnTmDcuLFIJBKKi4s5c+YMmZmZBAUFMWPG7dfdh2VlZSiVSvz9/Vm7di1vvbWKoUMj+cMffsml\nS5doaWkhOzsbaBcSq1fvIzJSw7PPLulyvx86dIL9+42IxceYMKG9aFZVVRVtbQ2cPFnKxx9/RnJy\nAt7e3qSmpiISiWhtNWKztSCTifDx8bnu9g80zrIi3VGAdLyXe3K/6vgeulUCxBXedQONK/ZRXV2d\nW2gMAG6h4Qbo/4lk56rSN1MDw1UmwR3pb6HR2SXNFYoafl85ffo0VVVVeHp6sn59AXK5grS0ZKH2\nxKlTp1i2bD0eHjaWLl1ESEiIsO/w4cNRq9WIRCI+/XQdNpsNvV7fZRV/2LBhpKSk9CgifX3VaDRX\n8PNzXKX38/NzCJScPHkESuVRRo3K7nKMjIwMMjIyHD5rbm7m9dc/orbWxoMP6hg1apTD9/a2fPLJ\nOvbvb2HGjGoefnhhb7oNs9lMa2srarWagoIC3nprDSqVhKVLF7Nt2z7On/fFbL7E5cuX+cc/1tHa\nKkIqlRIXF8fXX39NcXEDKlV7StfOfTJx4mhEon0MH54GtFuENm48i9lcgVwew/btx9m9uwR/fwVL\nlkiQyWQMGRLEo4+OZ86cOW5XjFuAPYaj82/VnwLEPSHtGWcRqteD26IxMLiFhhMyUClub/Wk116T\nwWAw9GlVabfQ6Bm7S5q9sOGNCgxX6WNnb2dtbS1///snHD5chkqlRSz2JiMj2qH2hIeHB3K5Dblc\nLKRwtdlsfPPNNxgMBkaPHs3Jkye5eNGCTNZIeXm5Q6E9+71lj5doaGhALpfj6ekpbDN79h2MGJHt\n4ArVHbm5XauVXw2JREJraxNnz5Zy8KBnF6FhJyoqmCtXzhMR0XNNjI5YLBbefvt9Cgtr+MlPpn3r\n+idCIrFgNpuZMyePlpb1TJ06h+DgYHx8ZEilJnx8fNi9ezeHD1tQq/UsWnRntxae+Ph44uPjKS8v\n58MPP6K1tRmLRUR4eCzx8aFIJHDmTCUGQwPPPPMbGhqq8fUdzaBBdYhECubMud1BELq5dfSHAHHm\nd4iz4UqT9vr6+l7XCnLTd7iFhhvg1rofda6B0ddF35x9cjkQWK1W9Hr9TbmkuXGkY+pfm83mkK6z\nt6ulcrkcg6GWxsZCdDorsbHDCAzUcOXKFRISEoD2mIylSxcil8sJDAwE2gvGLV++E4OhXUAkJiYy\nc2YhcrmMyMjIbtPeAly8eJG33/4ctVrOc88tFsSHRCLpMQjafq1ms7lLrYqzZ8/S2NhIVlZWty5b\nnp6eZGfHU1BgoaREh8lk6rbexT33zCUvr6lL3ENHzOb2TFVBQUF4eHhQXFxLWZmYiooKpk2bxhNP\nSFGpVIIb2qRJk4R9ly5dgtFoxN/fn8rKSoKCRMTGJhEfH8/27TsoKCjkjjumdKnqvW/fPj79tASJ\npICUlFjuu+8eIV1ufX09W7duZffuCozGQCIiymhstLBpUxVi8VoeeOCBbkWMM+NKk8Rr0ZcCxBVX\n6/sbVxxzGxsb3TU0BgC30HBCvi8Wjc41MOw1GTrWwOgL7G0f6AxO18Otsmh0jHkRiUR9JjBcSczd\nivu4Y20Rex2A7lJ2Xmu1dMOGzTQ1mVGpwggO9mbUKB8KCtp4++0veOmlxUJgdufAYo1Gw+DBcvR6\nM4GBgSiVSubNu4vW1laWLXuP5mY9jzxybxcLRW1tLbW1YDS2odPpumSF6ul6V6z4mFOnSliwYDpp\nae3uRCUlJTz//P/Q1ibm1VcXM3bs2G73nzhxIgaDlaSkWEFkNDQ0sH79Rvz8NEyblodYLO42rsFq\ntXLgwAHMZjMtLS189tkxYmM9+dnPnmThwhlUVFQwcuRIxGIxqampPV5Dx+scMWIEoaGhDBo0CIvF\nwoYNBzh/XkxIyGFBaFitVqqrq0lISCAu7iTnzqm4eNGD6upqQWiUlZVhNpuZNSsCqVSOySShpKQI\nna6Ar75SI5V+xOLFD12zf50FV3meb5abESD2+kHuLFhdcUUx5i7WNzC4hYYboG8nkj3VwOhuZbMv\ncKUXnZ2+FhoWiwW9Xt8nMS/d4SpCoy/vhe6KF9onsBaLRVj57Jgx51qrpVptLRZLIBERbYwdm8Jt\nt42iunozPj5yPDw8emyLRqNh6dLHsVgsDvEY1dXVnDvXSHNzu9Wjo9Cw2WxkZmby8MNmvLy8CA7u\n6qZ09uxZVq/eTHp6PDNmTAfa62ecOlXC+fMiioqKBKFRVlZGZaUcs9lEc3OzcAyz2UxRURHBwcF4\neXkxZMgQlixxrGB+4sQJ1q0rwd+/mIyMdIKDg7FYLLS1tTm4dF26dIkPPtiFxSIiO1uDxQIWi5XS\n0lI+/3wz/v7ejB8/vle/H7RbIY4dO0Z4eDgeHh5IJBJuuy2dwYMLSUtLw2q1cvLkSQ4cOMixYzXk\n5kbw5z//itWr11BT0yCkBrbZbKxatYnjx6386EdJpKam8Ne/foVCEYNaXcHevVVs3LiPefPudsnA\n8B8iVxMgJpMJo9GIVCrt1yB0V8KVFvbs1NfXu4XGAOAWGm6AvnGdupEaGH2Bs9SkuBFudvLeOai+\nL2Jefuj0JDDsQrlz2s3ryZgza1YeCQlniYuLY9CgQUilUn7600F4enpy8eJFIX6mra2NlJQUh9+x\nO7ec8PBw7r47m5aWVocK2tCeM/706dPExsYSFBREbW0t1dXVxMXFCZOrkydPkp9voLHxONOmTUUi\nkSCXy7n33mkUFRUxZsx39SNSUlK4775sbDYbEyZMED7ftGkLa9acIDnZh2effbTbey8uLo6MjOME\nBmoICAjAZDLxxhvvcuVKIw8/PIeEhARaW1v5/PP1FBUdIyUlkenTpzNqVCOhoaEUFBRw/rwZX996\n6urquhVN3fHVV5v48stiUlKO8NJLzwJw++3Tuf3bJFfHjx/nzTc3Ulx8Hrk8hMrKOiQSCfPm3eVw\nHJFIRHp6LEbjOeLjYxk6dCg/+lEFEokEs9lMZeU2hgzxwWKx9KpdzoL7PdGVjimsO7r3DmQWLDd9\nQ2NjozsN9QDgFhpOyEClt4Ubm6z3VcDxjeJMBQd7y83+xmazGb1e36dB9VfDVcTczVheriUwOp6j\nN+3ouFpqMplYvvzf7Nt3iLy8CYSHh2Oz2aitrWXz5u0cOXKQb76pJzRUhUbjh0zmxaBBn3DpkpZH\nHlnAxIkTuz2vWCxm8uTJAHzzzTds27aN1NRUxo0bx/r1m1i/voi0tMM899wjvPTS76mqMvHUU3OY\nOHEitbW1JCYmMmtWK8nJcQ7Pa3p6Ounp6Q7nUqvVPPfc413aYDIZMRrBYDB1+c5OcHAwP//5U8Lf\n9fX1FBc3UFkpory8nISEBCoqKigsbMPfP5W5c8c7xE+kp6czf34tGo2Pg9WmtbVVKKrXnfjw89Pg\n719EYKBPt/2nVCpRKGwkJkYycWI6OTk5Xbax2WxUVFRw++15zJ59hyAop06dSlVVFX/72wcEBNhY\nuHCGQ8YuZ8eV3pfOgDNkwXImnH0s6A63RWNgcAsNN8CNTSQ7u+sMVMCxKwoNuLFJsT2o3i4w+jKo\n/odKbwXGzVBaWsqaNfkUFNjQ6fKZMGEcTU1NnDlzho0bK7h4sRidTkZAgAVPz0EYjS1s2XKeykpf\nlMpVKJVKEhMTheer4z+wp5X9hAMHmoiLu0RkZCQ+Pt74+ICfnzcXL17k2LFKWlra3ZBKSkp47bWV\nyGRiXnjhQSE25Hr7raysjBEjcoiIGEJERITDfXjy5EnKysoYNWpUF3ciX19fFi7MQ6vVEhsbi81m\nIzIykjlz0tDrDUKRPzteXl7Mnj2rSxu2bdvOqlWniY+X8ctfPtfl3TNtWh5paakO7lkdsVqtJCX5\nkZOTQ0ZGBk1NTRw6dIj4+HghUH3//v38+9+7CA/34qc/fcxh/3YrkRWRKACFQkFtbS1+fn7u59HF\nuZ74gx+qAHFFoeEOBh8Y3ELDCRmoYHDo3WS942q6PR5AoVAM2Evn+y407BmA9Hr9Lcna1RtcyaIB\nvWvnjQqMG7n+sLAwJk9OxcPjMJMnJ3Ps2DE+++woAQFtpKWpSUrKQaPRcNtt4wgNDUWv1/Puux9y\n+PBZwIe33trJnDmV5OVNFQLQbTYbW7Zs49KlcmbOnERCQjCXL5cSExONv78/iYmJpKUNIygoiLq6\nOkaOjEOna2HixIk0NTXR3AxSqQWdTkdAQABNTU14eXn1eqHg5MmT/OMfX6HRyFi69BGHDFKtra0s\nX76e4mIx5eXlhISEkJOT4yBoMjMz+fzz//C///sRU6akMGvWHdx++/Tr6leVyhNPTwteXt6IRCJ0\nOh2FhYXExsbi6emJ1WrFz8+vR5emL77Ywr59euAYGRkZfPLJF+zZo2X8+NMsXrwIaBdxTU0iGhvb\nn7+OLnIymYxBgwyoVHL+/e+Pqa+XMWfOSKZMmXJd1+HG+bjZ99wPVYA4KzabzR0MPkC4hYaT0t/B\nt9earHee7PaHu05v+b4Kje6yHd2KrF0/NLrLhtbXFozOyOVyHntsMampSQDfPkegUql58cWnu3Uz\n/PWvX8JisfDnP7/J+fMtmExGjh49ytChQ/H19aWlpYU9e85w6ZKYiIiTPPXUIzz44AI8PT2RSqUY\njUYGDRqESCQiMDCQX/3qaUQiERqNBqvVyiOPGJDJZERERLB3717++c8vyMqK5ZlnnhDacODAAb75\n5gRTp44T0u8CGI1GGhsbaWsTYTCYHbJvQbv7ZHR0IDZbNYcOFVBZWUtjYzM//vF8h+3Ky6uoqBBT\nXl7V6740Go00Nzfj7+9PTEwMSuUujMb252Tlys/5+mstt902hNmzZ/LGG+/T0mLggQfuIioqirq6\nOtTq76qpZ2TE09BwjJSU9jokSqUHCgUoFHLhfOPGjUOtVhMcHCzEyZjNZvLz89m8eTvffCPFYDhK\nXZ0MpVLM8OGRvb6Wgcb9HumeWzmWfF8EiD3FtyvhFhoDg1touAF6nqy7wmTXVYVGT3S30j7Qff59\n6OPOAuNGs6HZM01dz/br169n27a9HD58mfp6IyNHBrFw4XxSU1OvGsskkUh49NGFaLVaNm3axerV\nhWRlHeSpp5bg7e3N7bcP5/z5YnJzc1Gr1Xh5efHVVxs5ePAMs2ffxtChQ4W22u8fe8rOtLQ0YaKw\ne/ce9u+vobi4nIceWiRUut6w4b8cPGhGqdwvCI3GxkZee+1f6PVG5s/PJiYmpktsgkQiYcmSBzAY\nDKxevZajR4sZMqRr3Y558+4kMfGkkNnqWlgsFpYte4/LlxtYsOA2LBYLdXUqLBY99fX130682u/X\n4uJiiotb0etBq9Wi1Wr59NO9JCYG8eijDyASiZg+fRpTp04RfoN58+YycmQJQ4YMEc6pUCgYOXKk\nQztOnz7NBx98TXOzjoQEKdXVntTUVNPS0khVVWWPdU2cCVd+lvuD/n7XupoAcXbrdnc0NDTg7+8/\n0M34weEWGk7KQFs07JMyvV6P1WoVVn2lUqnTvlxcbeDs/Bs7c5+7itDoznWqO4GhUqlueTY0O19/\n/TW///0q6utbUSiqaWwM4Ztvapkxo8HBlchgMLBr1y68vLwYPXq00H4fHx98fHw4ePAoBsMZdu5s\nxGZ7h5/+9Cny8qaSl/fducRiMV9/fZLjx20MHXqerKwsh4mK2Wxmy5atNDQ0MXXqbUK63pSUZGJj\nrxAZqcZmswmpZydPzkGlOsGIEd/FTNTW1lJe3kZbG/j7+wtVza3W9viPgIAAVCqV4OJ3330/Yu7c\nVry8vKipqeH99z9BrVZx//33EhwcfM0MUlqtlu3bdxIbG01aWhpabRNVVSJqa2uZMGECCxY0oFar\nCQkJ4d5772bUqMscO3aCf/5zHQkJShITh5KUlMSuXbupqBCjVtdSU1NDfn4+UqmUsWPHCv3g4eFB\nXFwc0B4PtXr1GlpbDdx99yzBNcxkMiGRSAgMFBEeHswzzzyITqfjpz99hTNnwrlwoZn6+nr3hMaF\ncab3nDMLkIEel64Hs9lMU1OTSyVs+L7gFhpugO9eGPaK0vYUtTKZDC8vr36blN0I9nSEzjQ49IaO\nhQY71x1x9j53BToLt/4WGPBdATqbTUZAgIkXXnieAwcO0twsYvDgwbS1tQn1M44fP85HHx3D2xsi\nIiIIDw93ONb8+XdhMLSwatU3rF+/n+DgQSxceK/DNiKRiDvvHEd4+Clyc0cIn9knKpWVlWzadIaG\nBoiJuURubi4Wi4WpU6cSFRWFRqMB4N13P+D06XLmzZvE008/hFgsFlwmIyIiuO++MRgq0eYGAAAg\nAElEQVSNRlJSUoRz7927l08+yScqyosXXnhMmBiJxWLBQnLp0iWOHtXh5aUjL6+CyMjIa/Zhfn4+\nq1aVEB9/mYyMDB5+eC5lZWXk5OSgVCqZPv27uA5PT0+SkpJYt24HpaUS0tL8mTJlCgaDgYkTJ6BW\nezNkyBDefPMD1qw5gEYT8a1lo2tsSElJCdu3X6K1FeLjTxAbG8vp02d4880PsVo9ycgYzI9+NAdf\nX198fX354x9fYc2aTURFhbqMe4YrTRTdODLQAsTVxtumpiZhDHDTv7hnMk5Kfw8A9pdGa2sr0O5T\nrlQq+y1F7c3iikID2l1BGhsbnV5guJpFo62tjba2tgHv1wsXLnDmjB6zuZKAgHiMRgt/+MPvOH36\nNP/61zr27DnMs88uRqFQEBoaSkSEBLVa2e2qm0wm4957f8yVK1r277dQWFjR7TlHjBhBWloaKpVK\ncHe0M2jQINLTg6itbSI2NlaYqMjlctLS0oRYrMLCKoqLZZSWlpGZmdklBiMzM1M4rr14YVNTExUV\nzWg07ROd7t4dSUlJzJx5GS8vVRch1dTUhFwuRyKRsGbNOnS6Vm67bRxVVVWEhtaTkzMcmUxGXFyc\nYHXoifnzZzJs2BmysrKEz3x8fJg8efK37ZXg6SklIKCVkJAQzGYzR48eRaPRCMcOCwtj9OhwWlr0\n7NlzgJUr99DcfIUzZ3QYjW1otQak0rXExUWSlZVFdHQ0zzyzhNWrV/O3v/2NH//4x72u9zEQuKLr\nS3/hyn3THwLEFauC19fXo9FoXKrN3xecb0bjpl+xWCwYDAba2tqAdt9qb29vp/cv7g5nnwTbsdls\nQopacD1R56zYY1ugPdjaGYRbQEAA4eFKtFpflEpfDIY2RCIRdXV1VFWJsNl0tLa2olAoCAsL45VX\nnnGYJBgMBlatWo3JZGH+/Dl4e3vz+ONLyM7+hpiYGM6dO0dAQEC3bjo7d+5k48YDTJ8+kkmTJgLt\n91rnqt0dEYlESKVSFi68k8LCQkaNGoWnp6dDBXT7P4vF4lC8sLKyBrO5HrW6fTXfLkC0Wi0lJSWk\npqbi7e3NvffO73LewsJC3nrrU9RqD+bOncrWrefR6aC29lP277cQFeXDrFkzhUmC2WymoqKC4ODg\nbn/fyMhIwVrSWSRJJBKeeOJ+Zs2aTHh4OL6+vhw4cIB33tmJj4+Nl19+BH9/fzw8PBg6NIbS0jKK\niiqor5eRmRlBVFQwra0NGI0qtNpa9u2zotU28NRT0Zw7d44//3kV9fWBwCqef/7Zq9wdbtz0H30p\nQOzPoStN2t1CY+BwC40fKJ0rSiuVStra2pBKpS4pMlzh5dG5crq9n+1uJc6MM1s0OrtIAahUKsEl\nqa/p7b1mXxVduvQxmpubKSsrEwKqc3JyqKyspLq6mosXL1JQcIGUlKH4+PgQEBAguDAVFxeze3cp\nZjNkZV0kIyODgIAAbr/9dvbs2cOKFfsIDZXxi1882eV6jx07R0GBmLCw84LQ6Ny+zpljtFot7777\nMb6+3jz88E+EY+7Zs4cdO77h9tvHMWLECIdj2CcnEokUH59QlEqVsHBhsVh4443lFBZamDfvCjNn\nzux2lfTSpUucOXOZ4OBAVCoVo0eH09TUyrBhcVy5kk9MTJBD0P7q1WvYufMi48ZFc++983r1e3TE\nz8/PwWrk7e2Nt7cNb28Zcnl7xqmGhgY+/ngn5eViZs+OYtQoT2pq6hk3LoURI0ZgNpvZuXMnmzcf\nwmbT8+yzrxATE4inpxGxuJqkpK51P9y4Bq6YUelGuRkB0tbWJtR0GugsWNeioaHBLTQGCLfQcFJu\n1cPQueBbxxS1JpPJKSeSvcGZXad6qpze1taG0Wgc4Nb1DmcUGt3FYCiVSlpaWpzCOrR3716WLfsE\nhcLGq68uFdx4du3azYkT56iqqub0aSkHD/6Lqqoodu7Mx8MjjNBQOfPnz0Cj0RAREcH48eGYTBZi\nY2Mdjt8uFMBq7f43ueOOyYSFHe1S/A7a78kPPviIwkItixbNFtyFCgsLOX26DR+fNqqrqwkLC6Om\npoY//OEdiop8sdksgtCwWCysW/cV9fVNzJ49g3nz5pKRcYHo6GhUKpUwMVGrPVGpmvDw8KC5uZm1\na9djMBi56647UavViMVizp0rwmDwxt+/PQZk0aJIoa3Dhw/vUgi0vr6ZhgZoaGjusf87u42JRCKa\nm5tpaWlxqC4O7S5dL77oj1KpxNvbm61bt5KffwQ/PxsqlYgRI0Zw7NgxvvyyhosXd5KdnY1UKmXK\nlClMnDiRxYufZteuGry9v2bYsDHk5gY6xK84K+5Jl5ueuJoAMZvNtLW1IZFIhL8HOgvWtbBbNNz0\nP26h8QPA7lJiMBiuWvDNmSfr18IZ224PrLev7naunO6MbXYFuhMYdhepzm4yt4LeDpbl5RWcOlWJ\nxTKI/fsPIJFIqKioYP36/1JQICUxsQmzuYGqqjqGDNEQERHO+fM2ysuv8Le/fY5aLeVnP1vMokUL\nuj3+mDFjCAgIIDAwEK1Wi0qlcshiFRMTIwiIzulWW1paOHGijJISMRcvXhS2S01NZe7cCnx8vAkJ\nCQHsK4GDGTy4goyMycIxtFotmzefob4eYmNPMXbsWNLT04Xv7ZOUp556mOrqasLDw7l06RJ795bT\n1gbp6ZdIS0vDbDaj0XgTHa1m6NBIIf2u/Z9SqezS5/PmzSI+/hghISHYbDbq6ur49NO1+Pp6M23a\nFPLz97N9+1Fmzx7L8OHD2bVrF1arlcOHz1Jfb+Ghh27vklI3KCgIaJ+Q/O53/6S8PJAFC0L4zW+e\nF+qSZGeXkJmZIEy+mpqa2LBhE2azkcBAf+TyVsrKCtiwoY7y8o946aUnnNZi6X739Iwrx2jcauwi\nAtpdMe3/d4YsWFejsbHRnXFqgJC8+uqrvd221xu66RvsbiA3in1C1tLSQltbu2+4SqUSCnp1frjt\nFo1b5XJyK3GmtlssFvR6PS0tLVitVhQKBV5eXl2EndlsxmQyoVQqB7C1vcdgaC/wNlAxD/b7WafT\nYTQahfoiSqXSYbBra2sTgopvVTusVus1B8eQkGDy8zfR3KylsrKYL7/cy6lTzcTFKYmK8uSee2Zx\n6VIJDQ1DuOuuYTzwwP3ExGhoa2tm167TSCRmamoqOXWqgISEWMGlx45YLGbQoEEUFRXx+uurOXz4\nOFlZSXh4eGA2m4W6GYcOHeK111bQ3FxLYuJQoN2q5uMjJSJCypgxY/D09ATaJw7JyUnExMQI1+fr\n60tkpD+TJ49g0qRJwudKpZKGhnJ8fWHSpLFCNpeqqio+/fQ/1NZWExUVhVwuF1wWVCoVzc1X8POD\niooqCguLGDYsmWHDUsjMjCEnJxuxWCxMUuzPiMlkwmw2o9PpEIlEeHh4sGbNZrZuPY6/v/zbGhln\n2b37AEePHqOoqJgLF5RoNG34+Kj45z93cPy4Fp2uiro6M1eunMPbW0VYWNfaHq2trezdux+TqYaZ\nM8eQmpoKtAfST5gwioSEeGHbgwcPsmLFceRyTx56aBRqtRcXLzaj1+uoqSmnpKSMzMxhQqE/Z8Ju\n1XbG5BMDjbtvro79+exY28kuIiQSCVKpFJms3Q3RPmZIJBJhcc1isXR5vi0WC1ar1SHQvC8FyI4d\nO7BYLMycObPPjukGgF9fawP3U/Q9pLt0qT2Ji4648gq7M7TdLjA6xr14eHj06OvbXc0HZ2Ug23c1\nC4azUltbyzvv/Bu9XoyHRzCXLtWgUBjw8qpn9Oi7BPejBQt0nDt3kdzcXGQyGWlpaaxduwPwIyBA\nzJEjDUADw4dfYtiwYd3+DkajkYaGVqxWMRaLhUOHDrF+/W6mTs1l7NixrF27jp07dVgsJubO/S5u\nIDc3t1fXIhKJGD58eJfPZTJZl/S6AIcPH2bdunLCw0sZPjwbHx8f4TuFQsH99y/g8OHD/PWvW/Hw\naCA3t5S4uDiHInnwXQyJfXX0yJEjfPzxVuLiBjF//lwqKuqpqhJRWVlJdnY2I0eeZNcuM9XV3uTl\n+TN2rB/Dhw9HrVYTGalAJJIwffo0Nm3awv79Umy2XeTk5KDVaqmtrSUxMRGj0YhSqeRPf/oFOp2O\nxMREzGYzu3btwmazMXHiROG+q6urQyaTMWyYkoCAwcycOROpdAuVlRY0mjZ27jzH+vUHycxMYPbs\n2b3q6/7G2d87A4UrvJMHkuvJOjXQaXjt1NfXu0za6e8bzjtS/8C5kQepc7CxXC5HoVD0ekImEolu\n2ooyUAyk0OgcWN8x7uVquNpA1t997IoCw866devYvPkQ3t4afHyaaGsbhEbTjFzennHq4sWLxMTE\nMGLECIfgaoDJk0egUBxl/PhsCgouYjKZ2L79v6xZs42HHppPaGiow/ZyuRybTQcosFgs5Ocf4eBB\nCyrVcZKTkykvNyKTVZOQMBS9Xs+uXbvw9vYWigLW1tZSVlbG0KFDBYtgS0sLn322BolEzD33zBFW\n5A0GA6dOnaK2tpa4uDiio6O7XHtiYiLZ2Rdoba1j9eovueOOaQQGBjpsExcXx/jxp1Ao5F0ERkeO\nHTuGTqcjNzeXyspKSkvleHjU4e3tzZIl8ygrKyMtLQ2FQsHixQsZOzaH0tJSRo4ciUajQSwWY7PZ\neO65R1Aqlcjlcjw9PRGJtjF8eCKtra289toKamqszJ1bSn7+aSwWG08/vVBo14ULF/j440PYbBAS\nEkJycjIGg4HXXnufykoTixZNECqH33HHDEaPzqWmpoavv/4FVmsEZrPl+m6efmKgF2bc/LDpbwHS\n0NDQJaW2m/7B+UdsN9ekp2Dj63UdsQ/KrshACA2z2Yxer+82sL43uJJFoz+5GYHhDEHrly9fZu3a\nfFpbNYwe7Y3NFkFTkwm9voqaGgsff7weT89wFi4cR0REBLt37yUpaSjp6eno9XrS09MZNWoU0F4T\no7y8nN/9bgX19e3HDgkJYePGTRQXVzB79nSMRiOenkHYbC383//9g9bWViZODCQvbww+Pj7k5g4l\nPLy9cN3hw4dZseIYGo2IqKgoQkJCeOedf3PunJ677y7ljjva3QouXLjAjh2lSKWQnV1EYmIiAOvX\nb+Cf/9xNfb2WSZMyefXVZ1AoFII7hFQqJTIykieeWMQrr7zJ+vVXCA4+xPTp0/nyy/UcOFDAPfdM\nIT09ncWLF121HysqKnj//c00N4tQKBSMHTsWqVRKREQECoWC+Ph44uO/c2Oy2WxkZGSQlpbWZYIi\nkUgwGo2YTCZiY2P52c/iEYvFGAwGJBIREgnodDquXGmjpuYKR48eZdq0aUB77EZUVPs12oPI2xd1\nLBiNOKT4FYlE+Pv78/HH/0EiiWLYsDYmTpzQZ/eWm1uPK9aI6G9uZR/1pQC5dOkSkZGRKBQKGhoa\n3BaNAcItNJyU3jzAHWtgiESiLsHGN3pOV5z4dqyyfavb3jlzV3eB9deDq4i7Wy3mXNmC0ZGtW3dT\nXq7DZCpHrb6DWbNup76+ns8/30x9fT0ikZTGxla2bduGQuHJnj0WwsOP88QTUj79dJOwom42mzl3\n7hxpaWnMnTuchoYG6uvref31dzhxooTaWh8iI4+Rl5fHk09Kqaio4NNPjwJqpkwZT1paGmKxmIcf\nXgjA2bNnWbVqMy0txaSnZ+Pr6/ttWtnTGAz+SKXfDewxMTGMGTNYEA52xGIxHh5yVCrw91cJAfj/\n+MdyyspqefDBucTGxuLt7c2IETEEBVWQmJiIzWZj//4znDhhIympwCFovCNFRUUcPHiQ9PR0/P39\nCQxUoFC0ERAQgJ+fHzNmzOix33uaoLS1tXHy5ElsNhvDhg0T7jM7ixfPo6mpiejoaLRaLRs31rFl\nyxFyc3Px8fHBz8+Pn//8SQDhXrRarTz55AJqa2tJSkoSjmW1WqmtraWmpgJPzxpycsZTXl6OTqcj\nIiKidzeQGzdOzkDMEa5XgBgMBkaOHIlIJCIyMhIfHx82b96MWq0mKSmJhISELnFvbm4NrjWC/8Do\naWLXXQ2Mq8UCXM/5wHWFxq3EnsJPr9dfNXPX9eCKfXwrhEZfCgxnsGiEhw8mISGI0lIVBw9WUVq6\nHJNJidmsw2KRU1h4DE9PBfn5uYSGlqHRmNmz5wRHjx4nOjoDkUjKxo0bKS6u4dQpC3fcUUFaWgrL\nl39GSUkVPj7DiYlpIyBAT1JSEmKxmNTUVJKTk5HJZNhsNodUuPY+KSwspKzMi6ioBB577AE8PT3Z\nvn0v1dVhJCcbmTJlirCPt7c3jzxyf5drmzFjOgkJcSgUCkJCQpBKpdTV1XHuXBVXroi5fPkysbGx\niMXiLvUt7r57MklJZxk3bkyPfbdx4w42bKhhx44DqFQB5OYmMHXqZNRqNQCnTp3i/PnzjB49WsgS\ndS3Ky8t5992NgJSnnvIkOTkZQJiUBAcHI5PJaGlpISsrizNn6vHykmIymWhubkan0+Hn54dEIsFq\ntbJ79x7Wrs0nNzeO+fPvdjjXypWfsnXrcWpqqjGZfPn88z289946cnKyePHFxb1uc3/hau+g/sTd\nN1fHWfqnJwEil8v56quvKCgooKCggJ07d7Jr1y5Wr14NtGfFi4uLIzk5mXvuuYf58+ezbNky/vzn\nP6PVaklLS+P111/vNj7Nzq5du3jhhRc4ffo0Q4YM4aWXXmLRIkdL7WeffcYrr7zC5cuXiY+P549/\n/CPTp0932OZa533ggQdYvny5wz7Tpk1jw4YNN9Rn/Y1baLgI9oluTzUw+gJnmKTdKLdKJNlTA+v1\neiEvv5eXl0O2jRvFlfu7L/i+WDA60traSlJSIs8848/vfreMhoYrqFT+mEweDBki5fz5/Vy4EIZC\ncYbAwHwaG02YTGZMpgAaG0WEhZmor29kwwYF/v5avLzU7NmTz3/+s4ajR33w8GglMbGK1lYp5eUG\nCgsLEYlE7Nixh+TkBCZNmkR9fT1r1qxFIpFx550zhEn6yJEj0esNhIeH4e3tDUB6ehLFxdVMnDgK\nqVQqxGh1XLSwZ4KRSCR4eHgIE3U7vr6+/OhHE6iqqnIYHMvLy1mx4guCg/1YsGA+mZmZXWp6aLVa\n3nnnnwQHB7F48WJSUxO4fLkao1HChQtiAgPL+f/svWeUHGed7//pUJ1z98z05Bw0oyzZxgEnDMZg\n0rIRDAt3WWDZu/u/LHv2HAMHuJy9ey97AXOMScYmGPBeMLAYbJyxbCvYlsajOKPJsXPO1RW6/i/k\nGSRZthxkacY7n1fSTHXVM09VP/X7Pr/0p3/qWhnH3Xf/nqNHNSRJ4S//8oSQqVQq5PN56uvrKZfL\nPPHEE3g8Hi699FLGx8d58smnqNUK2O1eSqUS0WiUYDB4SnjFt7/9C2w2gX/6p7/hC1/oxGazYbFY\n+MEPfsqRI2He856LufzyywEYH59mZkbD4ZjCZPpPBEGgUhGZnZ0hFEqTzTrxepMIgsyhQzVisQhG\n4zPI8kfO4ZP22vivuua8HNbn5uyshTkSBIHLL7+cyy+/HE3T2LhxI4888gjt7e2Mjo5y7Ngxjh07\nxujoKEtLS/z85z/nM5/5DLfffjsXX3wxt9xyC9dffz0TExOnlA1fZm5ujhtvvJFPfepT3H333Tz6\n6KN87GMfo6mpaWXTZu/evXzgAx/gK1/5Cu985zv52c9+xnvf+15GRkZWPKEv97o33HADP/rRj1bm\nfjVU2Hy5rN03+n8BlpOzTzd0X+tO+ktdD9bGInI653rspwuM5VKq50JgLLPW5vtceTTOVBVtrQsM\nOFFp6n/9r1t4+OGn8HgCBAI+AoFWAoEizz33NIcPt1Or6bBYIoCOcrlKPu9Als14vVNUKmaefbaF\nzk4Fq7WMLKsEAhKzs81UqyItLSH0ej2y7GVs7FlSKTu3334nmzZtZO9eHUePzlNfX89Xv/p99uwZ\npa1tAJfrRIf0bdu2UV9fz/vf/ycrjevMZjOXXHIJF198MTqdjgceeIhvfetu6utd3HzzP9Lb20uh\nUODb3/4R1arMJz95E/X19cCJsM25uTkaGhqwWCx0dnZyySWXnCJQxsfHGR4uU19f5B3vyLwgIRzg\nN7/5DT/96QRO5xiXXHIJV1xxBZdeeimRSIT9+/ef0vTuhOemE1GcQKfTSKVSuN1uvvnNO9m/f4rL\nLmtn48aN/OQnh/H7Nbq7u7nnngd5+mmRq69u4q1vvZq77noAgE9/+iY8Hg+jo6OUSiWyWR2SJFMu\nl1eS7TVNIxrNEI+byGbz2Gw2arUaF120ld27v008buY//kNCluOkUlkiET0OR5KNGxv57Gf/maam\nJr74xX/l/vsjiGIDx44dO2M53XVWJ6tlx341shajHrLZLD6fD5/PxxVXXMEVV5zqWX3Tm97EJz7x\nCT784ROhpt/97ne5//77+cEPfsC//Mu/vOB83/nOd+jq6uLf//3fAejv72f37t3ccsstK0Lj1ltv\n5YYbbuCf/umfAPjyl7/MI488wm233ca3v/1tAG655ZaXdV2z2XzGNXQtsLbf7G9wRFGkXC5Tq9Ve\nF0P3dNaa4Xsy52rsp++yG41GnE7nWUsDvxrW8ny/Gk4XGK+0KtrL4ULMaaVSIZvNcuutP+C++3YT\njyuEQnmCwSWczmNMTm5BFBX0+ihWa42GBgdG4wY0TSYYLDM3F6dQGAIWyWYXGBnJ0NoaI5Vqw2wO\ncdllVubnDTQ0XIROV0QUFez2GuVygunp7dhsUfr7vYTDIb7yle+Qz+sxmeyYTAvs3WtmctLC298e\n5cYb38add/4cRamQz6vYbHre+963sWXLFgRB4OmnDzMxYScWS6008YvFYkxPl6hWYWlpaUVo/OEP\nf+Cee4bp7XXg87kYHg5z441beMc7/hgSsHXrVt71rggNDYFTduYkSSIej9PU1MTmzZtpbv4DPp9z\nxcA3GAy0tLScYpQXCgWq1Sp/8Rd/itv9IPfcc4iJibv49Kf/lsXFOKOjOdLpE4Z8Z6eeQMCB2+1m\n69ZeMpmDbN++CYfDwXJqhiRJ/O53v+e++2bZts3Bxz9+zUpzwGV0Oh0f+cj7mZqaYufOnUiSxL33\n3ksikUBRepHlIh0dYDIFCYVURDGMpllQ1RYef/xxmpqa+NSn/hZR/A6S5MBms6Eoykp1nNVgqK2G\nMaw2/qusx68FTdNec6j2+WQ5DPLFGvbJsszw8DCf/exnV36m0+m47rrr2Ldv3xk/8/TTT3Pddded\n8rPrr7+eT3/60yv/37dvH5/5zGdecMy99977iq+7a9cuGhoa8Hq9XHvttfzrv/7rmmlAuC40VjGy\nLK94MARBeN2vt7xwrMUSt6/VwDzTLvv5mve1wqv1aJwPgXEhqFar5HI5vvvdnxKLpYnHcxgMXiyW\nI9RqOtLpLcTj09hsx2hpMREM2rFYdqLXK7S2SkxMLFCrDbFpk59UyoyqVikU8kxO9qKqi1QqT1Or\naQQCAZxOB6Koo73djCSJpFKX0t09jc0mcvz4JB0dnZhMQXI5Hd3dGhaLi0ymmcXFaVTVzJ49c0xP\nTzE7a6NcDiGKVUqlNLOzMh/5SOb5/I4ab36zzI4db2bTpk2kUik6Ozv5i7+4CEmSTgmZqlYlRBFE\nUSaRyJJK6Ugm0zz88MNMTy/x7ndfT3NzMx/+8Imu5sVikd/85ndYLBaSyQwHD8a58cbN3HjjO7j/\n/i0rZaHPRD6f56tfvZ1CQebv/u79CIKAXg8Gwwlh8KlP/RV6/Q+wWr1cfPHFvOc971mJ2X7Xu97J\nddddi6qq2O12/uEf/gSArq4ujh4dxeEAt9vBxo0b+frXbyeTeZSPf/x9DAycaGzY2dlJZ2cnAD/+\n8Y/5v//3QaxWiZtuuprBwR1cdNFFfOMbd+J2t/KNb3yIRCJJLBZj3744mpajra2N//N/vsjY2Bi7\ndu0im81y9dVXv2R5zvNh/K8b02dnXYS9ccjlciulrc9EMplEVdUX5FA1NDQwPj5+xs9Eo9EzHp/P\n56lWq5jN5hc9JhqNvqLr3nDDDbz//e+ns7OT6elpbr75Zt7xjnewb9++NfGcru03/Rscp9N5QYz+\ntfgSerVC40KG8axFj8YrGeuFEhivd3UsWZZJJBLcfvvdxOMpikUQRSP5/DSyXMHpvASvdwlZLhON\nKlgsRVpa3oXZrNHbqzEzE+PhhytUq1Gam90EAha6u/WMj28mEIhTX59nakoimfRiseSp1SwEg3qq\n1QpHjnhpaIjS12cllRJYXFwkHPYgSSXe+U490WiGsbEGXC4Nu73IkSPT1GpG/P7NqKrG4KDy/Lkt\nBIN2dLoaf/jDEzz33HPs3w/t7W287W1v5Y47fk42W+Wyy3rw+XzPhxFFaW9vR9M03vKWa2lsDNLa\n2oqqqlx66QTd3d189as/YW5OT2vryCn9PsbGxnjggXlsNvD7JXI5E7lcHmClo/jJTE1NsXv30+zY\nsYX6+npyOZliUUcul+Oaa66htbWV+vp6DAYDGzZs4JZbvoKqqi/YGMhmswArHsn+/v6V31199ZXk\n81kGBk70F0mlRLLZE31OKpUKIyMjNDY20tbWxuzsLCaTCbO5ht1u4r3vfTft7e0kk0myWYl8/oRQ\neM973k02myWZ/DHVapWHH34Ek8nM4cOj7N4t0tk5wfbt26mrqzulQs7JXEgBss7aWo8vFGstdCqb\nza701VmL/Pmf/7GwxtDQEJs2baK7u5tdu3ZxzTXXXMCRvTzWhcYq5kKUj1sNHbZfDa/UaNc0baX3\nyHJzQ6vV+op7j5wL1sp8v9xn443qwVAUhWw2yze/+UPi8Tj5vJFKxcjAAIyNTTM+7kSnCxEIeEgm\noaFBYvPmt5HPx8jlhnG5vMzMDCAIZnS6IkajRl1dnsXFNjyeLN3dFY4fj9DU1ENLi0C1WqSpyUAk\nsp+ZmQG2b9fT0WElmy3jcFgxGFqwWKx0dU3hcrk4fFhPXZ2Gw1GlVqvh90tAD2BIgIAAACAASURB\nVKqaobdXRBTLzM+3IghWfD4vjY0WMpkl9u9vpKUlTn+/m1BokZtv/irz83FMJi/Dw/vR6cBm20JX\n1+Ncc83FjI8vYjKZ+PjHb0LTNJaWlrjooouwWq1ce+0mJicX2LRp08q85fN5Dh06issVYevWrbz9\n7deytLR0Sv4F/LEfhSAIPPbYU/z2t3FCoRSf+9z/xyc+8R4KhQLbtm3DYDCcIhjgj8b5yczNzfGt\nb/0/zGY9f/d3H8ThcJzy+/379/P734d47rklvvSlT/G3f3tCJOzcuZPHH3+cn/xkhNZWPVdeuYlf\n//oQXV02vvvdf8bn89He3o4kSeRyOf7bf3sn5XKZnTt3AuDxeHjXu67lV7/6FT/5yRFEsYTdbgQy\nNDQM4fV6TymreXoH9JcSIAaD4TV3SF7n5bE+ty/OWhMamUwGj8fzor8PBAIYDAZisdgpP4/FYiu9\nc04nGAye8XiXy7WSqP1ixyyf89VcF054WgOBAFNTU+tCY53XxoX4Iq9VobHM2cZ+evf0V9vc8Fyw\n1oTd2cZ6JoHxRhBvtVqNdDrNt771Y1KpBKnUCYExOGggHE5y8KCPqakJKhUPDoeB7m4bkuTFYoHt\n263cd98i8Xgz/f0iZrNMIGDmyivrOXKkE0EQGRhQmJ9P8eyzOZJJkUIhyZVX1tPW5uTAgSCp1CHs\n9jCZjP35Dt0tJJMafX1gtWrkclcgioeZnj5GPl9i27YhpqebUZQKb397I1NTMqIYoFIJYTQqtLZa\n0OlE9u83EYuFsdni5PNubDYrghBgaipGoVDE48mQy3Vjs83S3JzjqaeeY8+eozQ1DRAI+Ni1axeH\nDo3z+OOLvOUtTfz3//53pFJZurtP5FeIokg2m2VycpJHH43h9TZy441vo7m5+QU9JVKpFN/61ony\njX//93/Ntm1DLC6meNObTgiWk3tVvBiiKFIoFAgEAqiqyt69e1lYyOD3uwiHw6RSKfr6+la6nDc1\nNdHcrNHU5MZms50SGuZ2u/F4NLxeG6qqks8XWVhIMDj4NysemF/84tfs2jXHVVe186EP/dXKZ0ul\nEnff/XsOHFARhAyCIODztSHLUF/fxtLS0imNBpfXgdOF0pkEiKqqL2gQ+Eo7JJ/MWjIWzxdrZT2+\nUKzF+Vlu1vdiz7sgCOzYsYPHHnuMd7/73cCJv/Oxxx7jH//xH8/4mUsvvZQHHnjglJ89/PDDXHrp\npaccc/o5HnnkkZVjXs114US+XCqVorGx8WX89Rcew5e+9KWXe+zLPnCdc8PyS+Z8Uq1W0ev1a66R\njU6nQxRFjEbjGfMqarUalUqFUqmELMuYzWYcDsc56T/yWnipMa82ZFmmVqutGGrLLAuMUqmEJEkr\n4WevpXnka6FarWIwGF7znGraicpGX//693j44UeZn1fI53X09empVBKEQi5stgqyrJFMRlCUMLK8\nEahx4439qGoRUfRhNIoYDDaCwRp1dXoOHbJSqxXo73eRTscwGKxompVIRMJgyFBXp5JMtmEyFfD5\nbNRqKRoabExP6wiFCuzc6UBVs0QiLszmMppmJpudJ5vNkc8HcTqddHRAPp9AkrwIgsbRo3EymXn8\n/irhcBu1WgGPRyYUmkMQzNTVtVOpOOjoqGEyFcnlAjQ3m+npacXrNVJX5yASEajVLOzcaUenK3D4\ncIWJiWeZnVVZXDxCoZBiz54C4+Mz6HQ5fvWr3/PggyO0tLiQ5RSKkqCnp4vGxsaVZyYWi2G325mf\nn+eBB0bJ5VS2bGll69atXHvtZXR1dZ5yP042FDKZDLt27UJRFDweD7fe+n1+97unqa+3sri4yD33\nHATyfPCD1/Hkk/u5777j6PVZGhuDfPe7P2JhIcTHP/5XXHXV5StVuJbP39zczOBgC36/i76+Pvbv\n30sm48TnU1d6lDzzzDBTU0Wamizs3LkNgEOHDnHrrT8jmVykrc3Hxz/+ft73vrdy8OAwkYhIqWRH\nlhfp6+s7Y8jYyZwsQAwGw8o6IQgCRqMRg8GwIv5VVUVRFBRFQZZlZFlGVdWV0sQnnw9Y8ZicyHdZ\nm+EkrxfLgu71qOz4RkGW5ZVncC1w4MABZmZmuOmmm170GJfLxRe+8AVaW1sxm818/vOf59ChQ9xx\nxx3Y7XZuvvlmfvKTn/C+970PgJ6eHv7t3/6NXO5ELtYvfvELvv71r3PbbbfR1dUFnFhHPv/5z2O3\n2/H5fNx2223cc8893HnnnSsVpM523VKpxOc//3lcLheqqjI8PMzHPvYxXC4XX/va11bDPfifZztg\n3aOxiln3aLxyTh97rVZbCZECXnP39HPNWprv08e6mjwY55pEIsH3vvdTcrkki4smNE3Phg06Zmbi\njI+34HAYMZlO7Cx3dOjJZq/AbB5FVXNomkw4rKLXmwiFUpRKSSyWGnv3dmK3j2AyuYlG08zPe9A0\nO6WSn+5uiR07HExP76ChoYBef6K0ckODjUrlEjKZFGbzGKIoMjbWhs9XQ1UrzM7O4PXGMZt3YDIN\nU6stcvz4LNXqdiKRCOWyxGWXOXA4wiwudpFOFxkYkIjH8wQCQTZuvJhq1UZ3t0axmGV83IvbbWX7\n9gYkKYzDUSaZbCeR0Lj22iamp+eIxZzY7RmgRiDgoVxeQpb7GR8v0dCgsGvXPp58cg9WK7S2bqe5\n+QiNjX5GRzXuvvshurq6+NnPfsmjj+7F4ajn3e++iPb21ufFmUo0GqWxsXEl1EFVVX7847uZm4vS\n1VWHxWLjne+8gSeffJK77jpOT89hPvvZT5JIlEilTuRY1NfX43Do8Hpb2LZtG88+ewS9/kT40dzc\nHM89l8VohOuuy7B//zAPPniQK6/s58/+7E9WnvFnnx3mvvum2LzZQUdHG5pWWhHZqqryZ3/2HrZs\nmTgljGthYYHpaR3d3a187nOfxOPxEAqFaG/vxmy2Ui4v8B//MU8olOCWW77yqtahV9oh+eTv7Okh\nZrVabT0E6zROFmbrvJC1OD/LHo2X4s///M9JJpN84QtfIBaLsXXrVh566KEVQRCNRllcXFw5vqOj\ng/vvv59Pf/rT3HrrrbS0tHDnnXeeUonq0ksv5e677+Zzn/scn/vc5+jt7eXee+89xUN7tusaDAYO\nHz7MXXfdRTabpampieuvv54vf/nLa2KDEkD3CoyctWENvYFY7qFxPikUCgArDb3WEtlsdqValKqq\niKJItVpFp9OthEitFoGxTC6Xw2g0nnV3czVQLpeRJAm3272qBcZrmdNYLMYPf/hzstkEMzMCBoNI\nf7+Z6eklFKUFuz1JoeDC48ngcFgZHtaxuHgATUtQq5kwGt00NbkQRS+qOoNOV2VxcRCzeYRy2YJe\nnyIQaEOWBapVJ4Iwi06nomlDDA5WEYQmLJYSDQ1+Fhct6HQKvb16FhbCxGIWisXjRCJWPJ4M7e31\nHDjgwG7PcN11/TzzzDCRiA5VreBwtGK3R5BlPV7vdjyeOAsLMUwmlcHBDSiKA1G00d9fJZXK8vTT\nZUymefr6LkUQ0tTVeXnuuSyhUJqeHpmGhgZmZlTC4XF0ujo6O6sMDPSwsODBYilTX28kHo8hCH6G\nh4eJxx24XHG2bm2mVhvCZkvhdHqJRmcIBhspFAwcPpzEYsmwaVMd5XIrg4MnwpQefPAgmzZ5+Pd/\n/9fnmw/+hv3758hkrOj1Bez2Jv7hH65ElmW+/OXvU1dn5nvf+zrxeJxoNMrOnTuxWCyEw2EcDgdW\nq5V0Ok0mk6G7u5tiscj3vncHwWADH/zgX/HDH/6Mhx+Oc/nlLj71qY9yxx0/IZ8v09joYffuCNu2\n+fnrv/5LEokEHR0dhMNhvv/9/4fX6+CTn/wIFosFURT52c/uIZVK09bWwODgIJs3b155rkKhEJIk\n8cUvfpmnnlLZssXJnXd+Gb/ffy4f/TNypvCr0z3l6wnof0SSJGRZXhNr8oWgVqtRLpdX1Zp/Nr7y\nla+QTqdXelesc0456yKx7tFYxVwoj4aqquf9uueC5QaHxWIRSZLQ6XRYrdYLHh71UqwljwaceMlk\ns9kLnkB/rolGo/z0p78il0syNqbHZFIYHBSYnIwxM9OGIFiQJAmHw4jfr3DoUD1+fw6fL8GBA0so\nig+LpYxOp6NYHMftNpHPb6OxcZ7BwTL5vIt0uobJtIHm5i4GB+HZZ59jZqYJTZvE6cwzMRHBYkni\n822kWtXo61NZXIwxP9+CIJixWp0sLuYoFKJUq0P4/WY6OzNIUoVq1UR39wC1moiqTuFwxFGUTXg8\nS/T0mJmeziCKelIphVQqy44dcdxuDxMTTWhalmpVQRQVrNYkxWIjCws8f44EkUgT9fUGVFWHXq8g\nihOMjW1GUbIMDlpJJFLk834ikTSq6uaKK040+guHWxEEFZerRj5foVKpMT6eY2xM4MorTbS3J8hm\nA5RKImZzjZmZKQqFHMlkmcOHbezdu5d7732ARx5J0N5e5Kab3s/+/SMoSoSOjg4ymQzBYA9Go5nF\nxUU2btxIb2/vyj1drnp14r45VpIrd+/ew+hoDUVJYzQaee9730FHx0E2btxILBbjyJEUhQJcddVO\nduzYRjKZJJ/Pr4RDzM/PMzmp4PFkSaVSNDc3s7S0xL59IUQRrr225xSRUa1WOXbsGGNjY8zO5vF4\nSlx11c6z7rCeK87kAZFleaUE58lC5KUqYC0nor/RxcdaWo8vBGtxfparTq1zYVjP0VjlnG+jX1EU\nVFV9QRz+akdRFKrV6spundVqfd0bHJ4Llj0uqzknZjlEqlKpAGAymS5oDsbZeCVzGg6H+cEP7mbv\n3qd49lmRUqnEwICZRGKRYtGFIKiUywKNjTq8Xo3RUTe1WoG2NoFodIHFxTSFQhmdzktbm4iipCkU\ntmAwhGlstNDc7KO/vx1B6MBk8nDJJR7sdpl43I/DoVAsnqgStX17E5GID1E0YjYvsLAwiyR5qNVK\nTE5mcbtLdHY6mJlxYjCIbNhgJZEIUauZaW1tp1Ty0t2tp73dQrHYhssFoligVivS2dmEqvqRJCs2\nWwhVLRCPWwiHF9DrzdTXW/D7ZXS6ZgyGBtrbFWQ5hV7fjM0m4nL1Ulen0tVlo1JpRK834HQW8HgM\nOBwBVBXGx1USiVn0+gg6XS9ms4Fg0Eu1msFi0SHLdhYXBRRlFpMpSyxmZn4+hsHgIBi009pqIZEw\nUSjYEcUJJCnN4mKRTCZEPm8nGNQxNNTL5KSKTudkx45OxscnOXDgABs3ernxxncyNjZGsVjEbDaz\nZ88eVFXF5/MRiUSo1WrY7XY0TWN2doapqRiNjXYuu+wiHA4HPT09uFwunE4n8/OHSSQm2LlzG5FI\nhLvuOsjc3ChXXnmi87nf78dmK7JjRzebNm2iXC6TTCaRpCQGQ4bu7k7279+P0Wjk0Ucf45e//A2P\nPDLLM8+MEo9bEYQUfr+fQiFNY2PjKU0CzxeapqEoCmazGaPReEr+hyAIK6IC/pjP8XLzP9Y6qqqi\nadqaCUs53yw/D2sph+VXv/oVHR0dXH755Rd6KG9E1nM01nllrLUddkVRqFQqKyFmer0et9u9ZhbA\n1TzfJwsMTdMwGAyoqvqCMqGrjZdz75eWlvjtbx8km03wzDMqbneBTZucjI8nWFoyY7W6KRYVurtt\nBAIShw65aGxM0d9vZmkpg81mQlEcxOMVmpp86HR5RHETnZ1RYrEUxaKdWk1EELYQDusZGNBht6sk\nEg04nUkEoYbT6eW66/TMz29A01Suu67K9PQcoZCHSiVDOFygVjtGLmfh0KE+jEaVq69uIhyWcToD\nzM+XKJe99PeXaGjIMzFhx+VK0N5ez+RklmRSQqdzMDmpZ+NGI3V1FiKRq1CUGZaWjCSTFVpawoji\nDnS6BrZvlzhwYD+hkI+uLgeSZKenpxVNy/P00wX8fj19fU0kk1683g3kchkmJ2HzZiMWS4G9exsw\nGArU1QmUShIuFxw8mCGZ1Nixo8SmTc1MTg5itWYoFHwUiyGam8tEo1ZGRuYYGgKXy8jSkhedLkOx\n6KCtrZnNmx3MzcHDD0/gdisUi0Vuu+2nVCoFZLmXQqHIF77wRaanFVpafJRKEZ58cpT6ejv/43/8\nNbt2jWM2V7n55n/kscd2ceDAJDfeOMRVV13Fnj17MJvN7Ny5c2XnXxR1RKOdPPvsYTZv7sPtBo/H\njk6n48CBA0QiEa6++ircbjcA//t/f519+8IEAhVgA7fd9iNyuQ4E4efMzMjodEFaW9Ns2BCkv99I\nLGbk97+fY9euCYrFCh/96Idf3y/EK+BsFbCWBcaZ8j9eawWs1cJqXY9XG2vpvuZyufPmQVznhawL\njVXMejL4iyPLMqIoIssyer0eu92OJElrrr73crjXauJ0gbEcIqUoCqVSac3N8cksLi7y0EOPkUrF\nePJJhUAgxaZNPsbHE0SjJqxWL7mcSl+fnUpF4uBBF83NCfr6LMRiWZxOK1ZrC4uLIqHQCKpaRZaH\nEIRFFKWIIJi49toO9u8v4XQa2bDBwOJilJmZZiwWA7JcpVwu0tbmZHy8DrtdZGBAz/x8CFFsob6+\nmWxWoqGhSKm0wNTUADbbFN3dNSqVFB6PFZstSDbrYOfOAMVikbExN6OjB+jt3YkkSdTVyXg8vRQK\nedrbC+h0s4yONlBfr2Cx2LFa6xHFaeLxFpJJG0NDMocPH2NhwUw6XUEUTbS0FOnvrzAx4SSRmCKT\nyVGpFOnubsRkcjA7ayGReI58XkJRttHSYubii/sRxThWa5lCwcrx4yYEIYfRmCYWa8VuL+PztWA0\nQjBYw2jsx2hsolLZRz4vs7DgY2goSGNjE15vmIEBgclJG8UiWK0VEokkTmcDRqOexx/P4nAc55JL\n4MCBNLOzKTweM2azyNTUFPm8gqrWs2/fM8zOlonF4phMt6MoNYaH0xgM+/B4PPzoR3sxm1Xq6uoo\nFArs3XuAjo563vpWPVdddQlbtmyht7cXv99PsVjkZz97hKWlE1X5LrvsMuLxOMPDY8zOmjAY0nR3\nazQ2tnLo0CQzMyCKGdzuIlbrJi66aBMf/egH+f737+Qb37iTSMTBI488yYc+9IEL1mPmlZTBfTEB\ncrYE9GUBt57/8cZgLdgHp5PNZvH5fBd6GP9lWRcaq5zzbfif3Phutb0Ilt39lUoFRVEwGAzY7fYV\nF+6ye38tsZqE3YsJjOXY7rUyt2ea04WFBZ544ikikTB/+INEMJhg82Y/U1NpkkkzNlsdmYzGwICN\nfL7MyIiHtrYSHR1VMpkCTqcNo7GVaBSGhgyEQs8xP1+Pph3Hbs/Q3OzDbjeiKIOkUjJXX23j0Uef\n5O67F2lsrJHPl2htzTE1NU+5PEBb2xRbt3aQSCTI5Vowm10kk3r8/jLV6hSxWAuNjRmamwvUagKL\nizGcTh+KYmZgQKVSyRAKdWCzhalWcxQKCj09EaCT2VmBzs4qfr+ZWMzOzMwhajU9TqdAV1eViQkv\npVIDfn8Yq1UkHm8kGi2Sz/tpbo4RCGSQpD5mZ0sEAnZEEZqajFgsQebm7GzYUMXrTTIyYkWSZNzu\nFKpaT12djtHRGs88k6ahYY6NGzdSrbajaQfJ53XIMvT2KgwP19i3r4jDEaK3t0ZdXQcGwzxGYx+1\nWpFLLzUyORnguefSWCwVzGYL4XCcubkEMzNudu6UcLlmyGSszM2d2KnMZtP09jqwWk1YrRezc+cR\nWlo8JJMKBkOaxsZ2YrEcGzYEsNtTHD3aTW/vJEZjiuPH5/nNb7xIUo2HHoqwY4eO//k/P8cf/vA4\ns7Pz3HDD9VgsFkwmE7299ZhMSVpbW/nmN+/g6aeP097uobHRxIc//BH6+vooFAr4fI8iCGl8vjyD\ngz3s25dhbm6e22//Mb29XezYsZVjxyQCgeaVUqHnk3O15rySCliSJJ1yzGpNQF+N777VxFqrOqVp\n2suqOrXO68d6jsYq53znaCy/ECwWy6pZSDRNQ5ZlyuUyoiii0+mw2+3YbDaMRuPKONdifsmL9aY4\nnywLjGKxiCzLL5qDsRqfjTOxbNCYzWbm5+d55JFHePLJPfz2tykUJUprq4lkMorBYEbTXBQKevr6\nLECBiQkHdnsZu11PsZjG67VRLPopFmFgQKBSiRMOOxGEArmciCznMJsFzOY+7HYfjY1VDh58htHR\nErFYlEKhHkmaRtN0hMNOMhmNWm2OQqFIoVBBFFUSCTMbNljweiUmJmzkciFsNh3BoIMtW3pJJCAa\ndeL1RjCb089fX0QQ3ECRYFBPreYjnTZRKIxit5cRRT9Go0Sh4KBUWsTtLqPTdZDNagSDNQwGkfr6\nFkwmGB2tYbVGaWqS8Hq34XC4CYVmmJ+fpaHBg9nsRFH6aG0VSSQOEwoZMJn01Gp6arUc27a1UamY\niEY92GxLpFIhqlU7fr9APu98vgpYhHQaMhkXXm+JRGIRnc5MS4ubcrmDpiYTGzZYmJnJkc8LaFqe\nsbEJstk8gYCFubk6VDVKS4uIxVKPIAh4PG48HjcDAwGcTjvJZBfBYInGRgGDwY5eX0OS/FgsJgYH\n7Swuhtmzp0QwKOL324hEIhiNCpLUTbmcAzIcPPgspZILkynPr389zAMP7KZWy7Bp0yaGh4cZHOzj\nbW97MwD/+Z/3MTIi4nAYuO22L7Nhwwbi8Ti33vpLEoky73//Nj784b9i+/YtdHc7SCRS/PrXkyST\nU1x//RW8+c09NDZ6mJqaoq2tbaWb8Png9e4Vcab+HyaTaaX3wkvlfyyv46fngJwvljdU1nM0zszy\nvVnNeYWn87WvfY2/+Zu/eclu2+u8atZzNNY6F9KjcaFZFhiVSgVVVTEajS+Z4L2avAMvlws55rN5\nMNYqOp2Oubk5pqenOXp0kqeeqtLVlaK720oymcNqNWOxtJFMKmzcaCEUSnDwYB1NTeD3VykWyzQ2\nWsnl2ohEJAYH9UxNxZmYaMZuN5JKRYnFJjAaK2haH7lcFJ9vjGPHyoyO+lFVPbLsoKHBiKrOY7Fc\nhdUaxeczMT1dxWYLUiiYSaVsCEISnW6eX/yinWCwwNDQpdhsTTQ3B8lmLSwsmLnoonrq6paIRJo5\nenQeh8OC3++krU1iZqYeVTVwySUVHn10H7lcHVZrEUUxYrfr2LrVgMFwMZomEokco1IpY7NdhN3u\nIJEIUKlMUK2K6HTNDAw0Y7OZCYcjxOMJqlUjx49beNObFAKBDMPDEgsLEg5HiYYGI9dc08vcXJCR\nkTIGwzHa21MYja309iooSjeVSowtWwzo9a3MzYkoShKb7TiNjX1s395OPN6OJIXYsCHH0pLA44/P\nk04nCAQS9PW1YjYrZDK9lEp53vKWBo4fb8flcmEwWLHboavLwdxcjCeecDE0BMFglCNH5vD5nFgs\nPczNTWCzzeFw+HnmGStzc4cpFNwIgkBvr4m5OTfNzQZ27tSYmEjw4IN5ymU9slzg4MGj5HLHKRSa\nGRkJoao/4Ec/ehybzcTWrS2Uy2acTgP9/Rrbt/djs9moVCqk02n0eg2j0cDmzZtXytdaLBZSqQjV\naoLdu8Ps2pXB5VogkahiNrdTLpf56Ec/eoG/Oa8/p/fxgDN3QD+9Atb5zP/QNG1VFrlYLay1dyyc\nyNFYD526cKwLjXVO4eTOsRfK4NQ0DUmSEEVxRWA4nc5TvBdnYl1ovDxercBYTSL0xZibm2NkZIRn\nnz3C4cMGursztLYKZDJZGhoEjMYOEgmJzZstTE4ucfhwkLo6A05nFVGUaGiwMTXVSihUYdMmAxMT\nUaam2jCZzBQKCoKgIxTax+xsM3r9Im73POVyicnJKoJgxGazsWOHBYtFTybzXgKBDE6nh2i0SjDY\nhNfbSqFgoaEhSqlUZmSkmVwuQrFYRBSj6PVPI0l+NM1Of79MNhsnFvMRCDQgigLl8ixeb4LnnlMZ\nH69y+eVBUqks6XQDnZ3NRCJuFGWGaPRJCoUByuUaLS0G5ueTiKIJTZOZnzfR359jcLDA4cPdBALz\neL025uen6OhoQZJqlEo9OBwj1NVNceCAg5YWMw0NQSqVKB0dAuWyxvAw9PSoWCzTZLNOJElElj04\nnWUcjixPPhnj+HGFiy92YDBUyWTsNDW5icd9+P0iAwMZHntskWPHUgwNBZHlHAZDDbNZIRRqpLs7\ny8zMBBMTBmo1Kz5fkGw2QzY7SjxeZGRkKxbLGLXaIktLPiqVErOzNtLpAtdfX+LIkTAzM10MDaWB\nGqJow2hMYzZfw5EjcyhKCLPZzMiImdnZSUTRRn29SktLjYMHDQSDnWza5CEajXH//WFKpRI6nZ2x\nsTGi0Qya1seb39zEJz7xIb7//bt46KGn8PmaedvbNhIIBLBarciyzOHDh/nhD3/P7GyN5mY7S0um\n50PmNBTFhaqOE49vPuuzfS5ZTeEvZ0tAP7n/xxs1AX0tsdZCyyRJolgsrguNC8h66NQqZ3mxPZ+I\noojJZDrvQmNZYCz3wVhuumaz2TAYDGdd3FRVRZblVR/aczLLYz4fJS41TUMUxbOGSL3U55dr76+2\nHb/Z2VlGRkb45S8f4Pe/j2A2JzGbNUqlDH6/hWy2gUpFZWjIQjYbIRJx4HBIKIoOs1mkocHEwoKX\nalViw4YT5W1LJScGQ41SyUhjow6/H55+WiUSmUeWIwhClZaWFmTZjiwHsNvz9PcLaNp2nE6NQMBC\nODzL/PwC1aodSfLT3V3DYik8X95WpbGxFVFMAUkcjnYyGQ96fZhqdZ65OR1erwFV9SAIJXp6nGha\nG6JoJpeLoigxZNkGiFQq9TQ2agwMuDh8WCKZ1OHxFJHlPHa7F6vVTKXSREdHlXx+kokJDb1eIxgM\nYDJpSFKBmZky0aiLDRt0yPICRmMLiUSSdNqGwZBncLAOk8lPKOQkEjlMtbqEzdaE32/EbG6jWAxT\nqUxhMPiJRq0UCovo9SV8vgB1dTZqtSGy2WkKhXFk2UQ+byGdTqEoMqVS65HGqQAAIABJREFUkmq1\niCBspbXVgMORoVyGeLxMJlOhWBTp73eytDTP2Fgr1eoUdvuJMqs6nR6XqwNNM6Iox3E6DVSrA1it\naex2qKtz4HbrKZUaaGqq47LLAkSjC4higEDAiCybyGRi2GxV6uquIhwOkcstIcspHI4m0uksmlZH\nMJjD51Mol7tJpcKADr0+xdjYHFNTaSYmqhSLUfT6Es8+W2BubpRoNMRXv/pTZmaOMDjYyYc+9Hau\nvHIn/f11bN7cRrE4i9G4g0DAwjXXvOm8rbmqqq6ETq1WThYgBoNhJfxKEISVEKzljZplEXKmEryn\nn/NsSJK0EvK1zgtZa6Fl6XSa733ve3zpS19aM3bBGuOsoVPrQmOVc3Kc6vlCFMWVxfx8sGzAlkql\nFYGx3NH3lbx410oOwcksvxhfzzGfLjDMZvOr6oNRq9VWndCYm5vjyJEj3H33fTz00CJmc5parUq1\nWqCpyUE0GqBaldiyxUYiESaVcmKxyFSretxulbo6A1NTXhSlxMCAlVhsEUlyYDDoKBSMtLYa8Plq\nHDnioFbLEYuNks2W8PudmM1BFMXP0JAel6uITjeITpfD4RAoFOJYrXrm5irMzuoxmRapr1dJJuvQ\n64uUSjVkOUNLix2droO6uh62b/ciiovodPXk83nyeSeyPIfRmEEUmymV9ASDCoqSw2CwYjarzM3Z\nyecn8Xiy5HINSBK43QqqmgDMhMN5EgkXPT062togFnMSiSTRNAOQx2LRYTTaiccDCMI0Xm+RVMqO\nz2emo2MjuVwEp7OMweBietpEQ0OJWi1BMilgMlUQhA50uhJ1dVWeeSZEOFyP1RqiudmNw+Gkrs7I\n1JSNfH6WzZvtjI7Gicdd2Gwl/H43LpeeQMDI5KQfUTxRaWppKcfUVBGdDnw+D4qSRq+vUSj0EQhU\n0OuTuFwW2toaqK/fgMvloqtLx8LCJLFYHyZTDLvdhNMp0NrqJRp1k89XeNOb/BiNCouLZnw+I3V1\nbTQ1CXi9NXK5ID6fg74+K+HwLJWKA7vdQLXqIxo9TD4/z9KSj1gsQzBoxGSScDj0+HztLC0JpFL7\n8XiKmM1taFoJo9HJ8eMHGB4+wOIiCEILH/jAxVgsFn73uxHq650YDGaeeSaBpk1SqaR54ond7Nix\nFZfL9bp/b9aC0HgxXiz/46UEyEvlfyyfc5nlSobrQuPMLJeSXytCIxQK8etf/5p//ud/XjN2wRpj\nXWisdZZdx+eT8yU0TjeABUHAbrdjtVpflSG7LDRWkyF8Nk72aJzrRfDFBMarnZ9lQXghvF2nMz8/\nz/Hjx/nxj+/l0UdnMRrTKIqM0Sjj8xlZWPBTq1XZvNlOLBYil7NjMqlUKtDQYMDv13H0qAso0Ntr\nJx4PoapWDAYz+byBzk4TNluVY8cc6HRZvF4d+/fvIRTKAXa83g7s9gJWax6bbSdut0KlUmJ8fIZE\nYpZ8PsDMTBFVXUCSIlQqDeRyCXK5KlNTR0km5wiHTRgMXjo6NKrVJKLoo77eiiA0IwgJvN4CoVCA\naFRDEOaJxeZwuVqpVLLMzAjAEnZ7nmjUydxcilIphMWiEgplqVQUqtVmIILNFmJ+3oooFgkG61DV\n/PM9NcrMzrqor0/Q2mpEELqR5RwLCzry+TDt7XYcjkayWT8zM3vI51Po9T6amhxYra3odEUSiWmS\nSQVop1g8DqTxepupVGLodIOIYoRMZo5i0YROV48gFJHlBFarhWIxRrW6EUFIkc/Poqpm6utbUBSF\nYlEmEFBpaHBTrQ7R1FTBYilSLst0dbWjaV7m59MEAnmsVj179tTI5eYwmRRUtUgqlSWTcWO1OonF\nholG41SrQUQxyvR0gXJ5nt5eNwcOyAwPjwJhvF4jxaIJi8WA3d7J0JANm63A5KSVWk3E6axRqcQp\nlWRsNg9e7046O6uUyzMcP25DknL09GzAZJIxGjMcPJgnk6ljaEiip8fL9HSWI0eeIxo1c+TIPiYn\nDzE/n0OSXIRC88zPCwwP78Zk0jE4OEAoFCIUCuH3+8/52rAWE3rPxksJkFeSgK6q6kolrXXD9IWs\nNSE2NTXF448/zt///d+v38/Xh3WhsdY530JDp9MhiuLKQv16UKvVzskO++ms5tCeF+P18MKca4Fx\n8nmX5/dCCY2FhQUmJye5447/5IknJqnVMkiSjNOpp65OYGzMQ62WZ2jIRiIRo1w2YzQaKJehrc2M\nw6Fy+LADgyFPR4eFeDyCXm8G7OTzBrq7TQhCibExO2ZzEZsN0ukYJpOOyUmZbFaPXp/E4Sjh91+E\nxyNRqchMTEwjy3FKpTZ0Oic+Xw5Ny6JpbTgcEjqdh1oth6alyGY7KBREFCWLJC2ytKRhMlUplZw4\nHCWCQahUOnC7AwhCDFGMsbSkkk6Lz1dkmqdaTSLLXfT0tKBpabLZLIJgQ5YlolEXJlOMDRtMiGIz\n4XCIdFpFFBPYbAJWq4dqtQ1JGkWnS5LJ+IjHF/B6G6hUTozRaHQxNSUgSWOoapx02o/RmMJkamBu\nboL6+hqy7CQed2I0LqHTZfH5ehkcrGdhwUIkEsHjiWE2NyNJLmy2LKlUlGg0hyiqZDJBcrk4Xm8E\ni6WRUsmAxaIBNcxmaG62Eot1srR0EI+njNHoYHY2STZrRBCMiOIc8XiebLaTQKBCOh1H01S6u32Y\nzX0UCir19SlcLiOzs1bK5RAeTx2CUKJQiKEoXVgsDhKJo6RSBRTFg8FQYX7egiTNMDTkYnLSTCgU\nxu/X43LpGRwcoFSSSCbb8HpDDA25OXw4TzabwO32Uldnpr/fx+homLExIybTDE6niCD4KJeTZDIe\npqaOkM8fJxyGSMSK0ShSqaQQRQVNm0EQLkZRUni9Vn74w9/y5JPjNDXZUFWVX/3qt1SrFVpaWla+\n36+2Wp2iKG84ofFinEmAvFQH9OV/LwuQN2oH9FfLWhMaR48eZWRkhI997GMXeihvVNaFxhuB8+3R\nqFarKzGx55JarUalUqFUKp1TA3iZ1bTj/nI5l16Y10tgnMyFyt9ZWlpiZmaGb3/7HnbvHkVRClQq\nEg0NJtxuPUeOODEYcgwOOgmHw0iSAaPRTqmk0d1tw2gUOXzYid1eJhCAdDqJxWKmVvNQKOjo7TWh\naTkmJx3YbCUEAbLZGB6PiWq1gXRaxWSaIZ9fRBQ7kKQYiqIRicTRtBiS1I3J5GLbNiNWq4TT2UdP\njw+Pp43WVgv9/W40rRuXy0NzcxlVzWIyNQFFkskA5fIYxWKEcNhFoVBEVSNMTR2nrq6LlpZ6lpY0\ndLoFTKYkicQAVmuZQECHpkl0d294PgSqjUplEb0+gU7XjaaJWK06UqkMRqOE0+lmZsZCOv0Mfn8Z\no3E7Ho9KKlUhlcoBWXQ6B273EFbrIqlUiEqlFb0+jc3mprHRRT4fpVj0UqnYMRoXcbsljMZuotFF\nSiUHipJEEJKAh3LZTTJ5HIejhsPR/nxYWht6/SJebxqTKYiquonFZnG7zfh8AZaW5kgmO3G7c4ji\nLJmMHb3eiMFgolgsIgg5BEEkn9+A1xvH6VRJJnN4vWbq6gZIp0vodPM0NtpQlI2EQkcolyUURQUi\nSFIXgYCPjg5Ip0OYzR04HGW83m7q6iREcQlF6cJutxMKTRAOp8lkcpRKCktLdtzuKJ2dNez2AXK5\nNPPzBfL5Ihs3erFa65ictBIOP0OhkEdVdaiqSDLpJRyeJxodIZNRKJXaMJkWaW52EwxaEcUkotiH\nXm/EZltAlhXGxjKUy2lU1UA6Pc/Bgwd55JES8fgMmzb18J3v3MUDD+yjo6Mek8nEnj170DTtZfcK\neCN6NF4Jp+d/LAsQo9G40tdk2ZA+kwfkTOV3/6sIEEmS1pTQOHDgALOzs9x0000XeihvVNaFxlrn\nQoROVatV9Hr9OXsJLQuMYrGIoihYLJZzbgAvc6EM4VfLuRAa50NgnHyd8zm/0WiUmZkZvvnNn7N7\n9wiSJFIqVenocGA0qhw54sTlKtPaKhCPJ6jVdICTQkFlcNCNohQZHXXg84nY7Sq5XBKXy0a1GqBQ\nqDEwYKZSSTI358LpFNG0GsViAq9XoFQKUq3q8XpTPPbYQywsuNHr84CJarWMKC4hSb14PD4uvtiN\nzaZiNvcQCs2SSBhxucp0ddmJxRpYWooAYcxmjfr6jTQ1eTGbgwSDNWy2JJVKL8WiBCwRjaaJRivk\nchVyOSMtLTra2nSYTDsxGmX0+iyimCebdaFpJVIpI16vSEuLjlSqHUHII0ll0uk8RqOAyWSkuXkL\nJlOCRGKUfH6QVGqRWq1IraZgtRoxm82k01bS6TlglmJxI1ZrCkGAVKqCpsnUakY0zY/dHqFcXiKR\n2ICqzqMoemQ5j8GQI5u1IIpu3O4chcIS5fIGFGWabNaMwZDD4cgjyw3IcgC3u0AmE6VSaUFVFymV\nGhDFJUymMLmcA1m24HZLiGKFZLKKwyFitV5GNHoUUYxRV9dKsVj5/9l78yC5zvLe/3OWPr3v0z3T\ns2hmNDOaGUkjWYtlIy/EJoQYgkPYQuoScsPvhgR+lYQkXH7curm3yM1N1a1UUSHgkFwCXAIJEAhw\nbTC24wVv2JYsWdtsmn3v6X093X36bL8/RjPIkmzLxosE+lZNTVWf06fffvs973m+z/N8n4f1dRHT\n1PF6VZLJNXK5Xfh8GVS1SCpVQ5bL+P0DqKpEo7GC369TqSRYWpqn2XSxY0eQYnGGtbUYsViY7m4n\n6fQSouhDEOoYxnZkeRHDyFCptNLS4kcUFdbWFnE6VWRZwTB2Y9tnmZ8fpVAwEMUSstyHKBrI8gKq\nqqFpe1CUFZxOAZfLRzDYpF4fYmiok46OKoVChlTKSSaTIhKJ09Pjxu3WOHXKQ62WpqdHoVBI8pOf\njLK2lqdScWKa64yNjfFv/zbH4uIkN998kG9+8zvcd9+j9PR04PV6mZ2dRZKk50U/TNPEtu2rJs/+\n9cRmGu9m34/N6MfLEaD/PBOQTR3l1fKMffLJJykWi7znPe95o4fy84prRONqxxtBNJrNJoIg/MxE\nwzTNrQjGZiM9n8/3mjWJgtdfyP6z4mdJ93q9CMb5eL3mN5PJMDc3x2c/+02eeuoommZTq2kMD0do\nNmucOeOjra1JOGySzebPNZBrQVV1hoa8VCpZ5uaCxGIbuo1KpUA06qZcjlOrGQwPOymVUqyuBvD7\nm+i6iabliUYlCoV2DMNmaEghn1/lzJkqmcwShhHE4ciSSEg0GjuRZYmWlgIul4kkdVIup8hkTJLJ\nSSxrjUymi/X1VSqVWRYWZkinXdh2GU3zYZpJEgmBTKabSMRNPG6RTM4hilGcThnL8mAYRRQlQzLZ\nST6/QjCoYdsm27YNY5pNGg2ZZnONUilNPt9FMjlDINDA5XJhWW4EoUG5rFCvl2k0zlIu70aWc9h2\nGkFwY5oy+XyFSsVClps0m7OY5h7K5WUqlSyaZqBpEqap0mzaqGqNWm2acnmQanUB286jqibVqolp\n6tTrDprNPPX6LIXCIJXKHJZVodHY0K/ouoiqKmhaEk1boVQaQNMWEEWJWq1EtZoGQpimn3J5lXo9\nj2kmqFbn0PUEjcYKlcoUuh5GklwUi2kqlQput4Rt50in+xDFeTyeKqoqUqupeDwhPB4fmraELFdQ\nlIPAKqVSA9Ms43JVMM1uMpkahpHC49HR9RgLCys0m63s3u1BUdapVhO43TLhsBO/X2FtbZm1NQ1R\nHObAAR/1+iKnT69RqTQRxRai0QDXXeemVqtRKOzC6y3Q2eliYKALn8+iVusilytRrU6Sza5QKETQ\ntCz1uhNBqNPf7yST6UHXVRIJMAwVy3JTr5uoapDubpNQSOfkSYPV1VmCQTfV6jonToxy8uQKCwsC\nHk+RpaUlvvKVx5iaGuXw4YMcOXKEI0eOEo/HcDqdGIZxyd4Wv8jYJBrnz8krEaBvEpDLEaBfLdjs\nbXU1EY2HHnoIgHe84x1v8Eh+bvGSREN4GRWNrtzi+T/H2Cz5+nqiWq1iWdYrrn6ySTA2CYvL5Xpd\ndBO2bVMoFPB4PFdNd3DTNCmVSvj9/sv2Lm4SjEajgW3bOJ1OXC7Xa77xvx7zWyxuGEf/+I/3oOsF\nGg0/mlZm//4EY2NLpFKt7N5dJZ83qNcrxOMhUikvglBhz54o4+OLlMtttLVlUFUPUKKtLcTsrA+X\nq8KuXUHGxxewrC4CgRz5vILbXSQU8jA3F8bvr9LX52NqahGns5tqdYajRzOY5hK2rWKat9LbWyIW\nc7C6uk4qJaJpVTyeGLKs4nKVKBQO4HCM4XQGaTYzSFIvmrZEsxnD40nhdApo2l4U5SxOpwOHQ8S2\nQ+d0Bj56eiRCIYXp6ThwhmZTwDBMRDGOKOaQZR+yrOP36xSLg9TrzyGKJrVaAFn2Igg5RNGBw+Gl\n0ZjDNEcwzSlsGwTBhW1HgCSWBc1mEFhAFHchSSuIIpimF9t2IghlbNtEENqBBWy7C0HIYRgaEESS\nZEADaghCJ7a9iCBs2zrHtr2AgCyDbasIQiu2vYwg9COKK5gmCIIHQbCwLBHbrp8bXwbL2o0gjCOK\nEcBAknQMw4tl6YhiHVk2sKwBRHESUezDMOYQRQmHI44syzSbZUQR/P4gjcY6mnYIr/c4Hk8Lqmqw\n4btxYZo1RLGBy2XT2vpmVPUY1WoLtr0AGHi9I9TreRoNjURCprNzkKmpUer1PrzeUTo7OzCMMDMz\nU5RKbtzuIvv2dQEupqb8WNYpJMlFJOKiv38bhUIb9foCpdIiS0vrNJsD2PYUgtCPosxiGCayvJOu\nLpPBwS5k2cbtbqNSKdBotLJ9exFRFFlc9CDLaTyeGLqeJRaLkkyqlEoRduwoIAgy2ayEaWawrE68\n3hJvetNunnpqlkzGw2//9iAdHR18+9sP090d5aMf/TBra2usra2xd+/eq2b/fLVhWRa1Wg2Xy/Uz\nOVMubEB4qVK7L9T/40omILZto6oqTqfzqomGfepTnyIUCvFXf/VXb/RQfl7xkgv2GtG4wvFGEA1V\nVTEMg2Aw+LLeZxgGjUbjeQTj9S41m8/ncbvdr0tfilcDlmVRLBa3Ij0vhjeKYJyPfD7/mhCNWq3G\nxMQEX/3qfdh2gUIhhG3n2LevgzNnlqlU4vT1VUmnm9h2nba2IHNzPlyuAnv2xDl9eh7TbCcSKZDL\nCTidVdrbI4yNeQkGSwwNhRkdnUNRtuF0FsjnZYLBKl6vg6mpFlpaCnR3B5maWsTv3waUSKUszp59\nhEymiiheR0+PSrNZQ1EkLCuMqqqUShqWVaK9XUBVDxKPr+HxyGiaiSRFcLkMikVwOgtoWpVyeRem\neRpBsKlUTCwrjCznMc0glpVFFHXc7uuxrDEiERe67sW2/WjaPLWahGV5sKxVTHMQmAMMRDGIaXqx\nrOS5lJgebPssgtCFbZfY4PcuQMK2DQShBOwAFrEsF7Yt4nA0kSQv0EAU/TgcWUSxB0lax7IUJEnA\n4RAQRTfVahpJ8uF0qng8vbhcNTTNQpZFwMayJECj0QDbLhAI9CNJZep1kGUwDB3DkBFFE0FwU6ms\n4HBskBhN86BpBapVFQjidDYBP5ZVwDRb0PUloA9ZTgES4MIwKliWH0GoIkkuLCsHDCOKE+fIURJB\nMIEWNp6JtXPERcGyCjgcN+LxnEaWY2haBVF04vHEKBbz6HoRrxfi8YNI0gqVSiv1+jhOp0Rf32HS\n6XmWlrLYdhW/30NHRwumuYdS6RHqdVAUP729IbzeXVQqy5TL06RSBrrejtOZxOGIo6qTiKKIbQ9i\nmimaTWg204RCXRw61I9h9NLTk0WSJFZXvec0M2F0PU8sFmF9vUwuF2dwMIskuchmbWy7iGkmcDqL\n9PW1MD2dJZeL0tmZAdw0mxqCoJHLtROL1Xnve9/Mgw8eZXVV4IMf3Me+ffv4t3/7AW1tLbzrXe+k\n2WySy+VIJBI/19GPTaLxckurXw5eqAP6ixGQTbH6lUI+Xi0i9nriD/7gD9i3bx+f+MQn3uih/Lzi\nJRfn1bFSfoHxRmwwL7dbtWEY1Ov1rWoUHo8Hp9N5VYz9jcbldNu+EgjGJl7t+TUMg2PHjvHNbz6E\nJJVYXw/ichlcd52LkydNjh9v0NrqwjSzFAoW7e0+RkejQIZDh8KcPKkyNtbA5/NQKpURRZGuLoET\nJxLYdpGDB/2MjhaYm/Pg9QYpFsu43TqJhMHkZILW1jTXXWcxPV1kfd2D3x+hWFRpa7MRxUVyuREM\n4ziKskStJiPLMapVHdtuoCh19u3zs7Q0jKadJJFYxradOJ1t5HKzZLOLKEqN7dtbSKX68fmmiEZn\nMYwE4KFaPYWmpXE6AzgcSXR9CMOYpVZ7Al3vpFoF01wF6sAwtn0a6MA0FWAW23YBbsBCEJYQhAFE\ncR1ByCCKXQhCDVkOIQhl3O4wDkceRYkTCMRRFFCUQbxeN4oi0d3dgW1LrK+v0tYWZ+/evQC0tLTg\n8/m2Uilt2yYej5PP52lvb6dWqyFJ0vNIsixvaD7S6TSJRIJisbiVctJoNBAEYauqz9/8zf/GMK7j\n137tZhKJBJZlkc/n+f7376XZ1Ljjjl9G0zRqtRqpVIqlpTUMw0AQdmAYJqlUgZWVafJ58dx3imJZ\nEpqWodFoo9nMIAhxoIJpOrDtJIIwjK5PYVkBBKGOaZ6kUglj2zUAHA4VTWug6wVs+yC2PUqptE69\nnsa2S/h8nXi9TubmjlMsFtD1dtzuConEbajqY5RK96PrcQIBi23bBrEslfX1x0ildGq1bXi9i7S0\nSMRiCaLRMJnMnRQKi+RyizQaNQTBh2WJVCphLKtIT0+W9XUfglDB69UxDPB6LbJZgdFRNwMDZeLx\nKvm8jGmWMM0YiuJlYEBkbs7i6aehs9OgvV3FNAVEsUY2G8Hnq3DwoMDCQoWvfOUIirKG0xnjiSee\n5siRZzl9WiYeTzE42M9DDz3B5GSR973vEDfddBNPPPEEfr+fQ4cObe0JV4ox/LPgtXx2XG4H9M2/\nzQpYm++9EjqgX0kd5S8XxWLxWlfwNxjXiMZVgNfbeL7cz9N1nUajsUUwvF7va6q/uBxcbUTjxXAl\nEYzXAo8//jjf//7jOJ01Zmc9tLQ0ueEGF8eP25w5oxIKucnlMhiGk64uDydOeLGsNDfdFODkyQZn\nz1bx+fyUyyXicQWfz+L06QDt7Sn27XOyuFhledl7jjyU6egAWdaZno6zbVuakZEmS0t1stkGgUCM\nQqFOe7uNLDc5ccLP+vosolhDFAWaTZ1k0sThyBAMWgwMJFha2kM+P069/gyFgoNcroTP52ZxMU2j\noWAYi1jWYTTtJLadplAIYJpeBOEspunCMOJY1iyVih9JUjDNU9h2BNMMY9t5oIppDiGKiwjCHILQ\ngSjWkGU/slzF6QzjdpeQpCCRSByv10E4vJeOjjYURaS3t4doNEpPTw+GYdDa2rqV8iBJEk6n83lG\nzv3338/Xvqbg8Vi85S1vwe/3v6BR09HRAUAkEmF2dhZRFGlra3ve79vd3Q1APB7feu38KOn6+jrN\nppdSScDv9zMyMrJ17LbbbrusNbTZeG5ycpK2tjZUVaVYLJLNZvnsZ79ENtvB4KCfQMBJoaCjqu1k\nMlmKxTZ0XUPXO2g0cpimgmlmgWF0ffJcJKQBTFKtBqhWs4ADWdYpl5cpFlWazREUJUcgoOBwyKyu\n3othJJDlCMFgE7/fTSYzTT6fQdMOIMtHiUTydHR0oCgyxWKUlZU0mnacZtNBuexHEOoIQhhJWsLn\nO8P09F40rU40KmLbOrJs0GxaTE566e0t0dJSpFCQsO0KlhVGkmwGBmBlReeZZ0QSiQ2CYVkigqCS\ny0VxuzVGRgxSKY3RUQtJ0nA6LVpa/Mhyk6kpL06nyo4dTsrlInfd9X9R1TV0vZOjR59lcXGRRx5J\nEQjYdHV1cfLkKR5//DS/8Ru/xKFDh5idnUWWZXp6el7GbnBl4fV8hr0UAdlMu9okHxfqPK4EAnIl\no1gsXnY1tmt4bXCNaFzDRdg01i/lpbJteyuCYRgGkiRdEQRjE1fCGF4OLhXRuBTBeKVNDF9tvBpE\n7uGHH+ahh57FNKtMTLjo7m5w880BTp6E8fECwaCbQiFLW1sEh0NkbMxPf3+Bw4c9jI01mZ0t4vMF\nqVQq7NgRwOWqcfKkj4GBPHv3Npmbq2HbIj5fnHxepbtbxrIajI0l6O/PMTSksr7eQJY1/P428vkq\nHR0Stl1jcrKDjo5lMpmHSaVEbNuFokgIwoYxBxqFwgiTk2eQpBSVSghBCOFyVZEkDVEM4PUWgXYs\nKw0cRZL60DQVTVtD0zRsexhRHMO2m9h2FNPMYtvuc3oFB5KURxQjuFx+FCWJ19tJICASj7fQ2uql\ns3M727a14fP56OjoIBaLbUURN1MGm83mVrWcy1k3tm0zMjLCnj1z9Pe34/F4LjJqLmXQnDlzhi9+\n8Ud4vSKf+tTvvaDnsFKpsL6+zvbt27eIcmtrKx/60Fsol8vs27fvFa2lzcZqe/bsed7rlmWxsLDG\n7Ow6H/jA29ixYwcejwdVVbEsi1KpRKlUYn5+nmKxyMLCEqlUjrm5ORYX4xhGFcPooFbLYhhuDGMN\nGMQwJmk2+7HtaWCael3ENFNYlgNR9CHLq0iSSKPRR6EwjWHsRxQXcLvPEI/34HC4WFvTqFbzGMZZ\nLKuObV+HwzGFz+cCbCqVaWy7n1JJolQap1hU+KVf+mUsy2BxMUxHR4XBwSyFgoNqVcO2PYiiRFeX\nQS6ncexYhHhcP1dGWUAQVPL5EA6HyeBgk2JRZXo6giDUURSIRv0oSp35eS+SpLFtWx1Na1AsuqnV\nNGo1iZ6eAD6fzsSEzdjYWfx+CcvSuOuufyKbzZ2r2HUETdP4znd+giTBJz7x26iqyjPPHOOGGw4w\nNDREo9HAsiw8Hs8r+r1fa1xJTqoXIyCXin5cSEA2065eTf3H1RZ2pMqHAAAgAElEQVTRsG37GtG4\nAnCNaFwFeCMiGhdis9pEo9HYIhg+nw+Hw3FFbTpXY0TjfGJ3pRKMTfws83vffQ9w8uRZ1tdTTEy4\n2bVL501vcjA2ZmGaefx+H6VSkV272gGTEyecjIxo7NvXYHGxjmmCz9dCuVxmZKSFxUWNI0cUdu+u\nMzhYIZ1WsSwBr7eNUqnAjh0mjUaNU6c6GBpq0ttbJJdrEIlI+P0dZDIZurstGo0aExPb6O6ukkis\nMTq6RrncQBBMBEHC6RSJxVyk07swzUcxjOcolbqIx8GycsiyjCi2YlkL1GobhoFpnsYwOjHNIqa5\nim1XsawhYB6YAXqQpPK5yIKC1xsiHBYIh/309l5PX18nnZ0dDAwMEAgE6O7uJpfL8dRTT9PdvY3r\nr7+exx9/nCNHTvH2t99OS0sLo6OjmKbJwMAA8FOnwCYuNDYurKozODjI//yfn9x6bW1tjampKUZG\nRggEAlue1fOvqaoqzaaJolhb5T0v9Kjats0//MM/MTVV5X3v28+v/MqvbH3moUOHXtFaeimIosh/\n+k8fel7Fn83Xv/vduwF473vfxa5du543zieffJLPf/5hvN4Gd955A5IkMTFxluXlJDMzc6RSnahq\nCVVNoKplIIiuZxGETixrFl3fR71+GkFYRxSbOBzPIcsxbDvE0tISpilgGAqimEUUD+P3n8btLuJ2\nB3E6QdP2IIp5ms0ZqlUD04xSq6msrDjp7CzR27tKseiiVhMRRRAEiWhUo1ZrcOpUJ7FYjkSigmGA\nZVWoVMKIIvT21qlWGywsxBCENJIUJhj0EgjUWFryYlkmbW01DKNJrRag0WhSKjno6fHT328wN+cg\nmWzgdluIok0o5KZU0jh5UmRgQOTwYZvJyVXOnFkGHDgcAvfeey+LiylOnXKSyZSIRCJ84QtfR9NM\n/vAPP4jX6+XUqVP09/fT3t7+mqyDV4or6Zl2ITZJxIWR7UsRkAv1nT+rAP1qIxpwLaJxJeAa0biG\ni3Chl13Xder1OqZpIsvyFUkwNnE1Eg34aRralUowXils2+bee+9jfn6Z0dEFFha8HDgA+/fXWVho\noqpN/P4QlUqGffu6mZio8vTTNvv2ORgaKrO2phIO67hccYrFDPv2RZmYKPLUUyK7dzuw7Txraw2i\nURcuVweZzDo7djio1zVOnIgzNNRAkrKk0yaRiIjH00EyuURvr0CtZjAxEaSrq0QstkQm40JVl1lc\nzKCqTTwegWDQQ7nch6qexus9Qa22B0FYxjRTFAoCgjCAaZ7BNC2aTRe2fQZIIAgKtl1GFGtAGEkK\n4nBM43DE8HgabN/ewrZt/ezevYfBwX4SiQSdnZ1EIpGtai6qqvJ3f/cVKpUGH/3of+D48eN8/etT\nbN8+yfDwMD/4wZOMjgrEYsewLIsvfOEeLMvmj/7oN+jo6ODZZ5+lu7ub7u7u56VInY9NI+NS3tOv\nfe27nDhR453vTPLBD/7W1rjOv9aBAwfw+Xy43W68Xi/1en3ruueXTW00dDQNNO31K2whCAIOhwPT\nNLdem5ub45FHlgDYt2/2eelagiDQ0dHB9u1uWlpi3HHHHbhcLu6886d74dNPP813vnMvfr+E3+9n\ncnKJ5eVF1tdrlEqt1OtLGEbsnKEXpNHQqNerwCIwDEwiCP1IUhM4jqbZCEIZQdAQRR1JWj6XsrUX\nOIEgBIACi4vfw7L2E4vFEYQCsqwgSTqCYHD2bC/R6DxtbTkMQ8Aw6tTrIcBBZ2cVTdNZXIwhSTlk\nOY7H48blKpNMeslkHMTjlXNODi+6Xiafj9HR4aavz2BuTiSdbqAoDTweBy0tXlS1zMmTDrq74aab\nBBYXbWZnixgGOBxetm9XKJVUfvCDIolEjp0748zPz/AXf/E3lMsSkuTm0UcfpVSq8NhjBfbsOcEn\nP/n/8u1vf49MpsBv/dZvEIvFWFpaIhqN4vP5Xp8Fw5UV0Xi5uBQBuRz9B1xMQDbL9f48oFQqXdNo\nvMG4RjSuArzeN/ymcaBpGs1mc4tg+P1+ZFm+ojegTaHp1QDLss6l0mx4nq8GgnG5RM6yLH70o/tJ\nJtd59tkFkkmF666TUZQS8/MW4bCFokSoVJLs3+/l9OkKTz/dZOdOHw5HlsVFm2h0I1JQKKTYu1dh\ndFTkyBGDvj43lpVkZQViMSfVaoJUapmBAYXpaYPTpxU6OhzIcpJUSiEalbCsOMnkLN3dArWawvS0\nn9bWAoIwTyoVIhCooCgOjh1bPGcsC2haN83mPIryLNXqCIqyiGmuYFkmmpZA06YRxdNY1jYEYQHb\nDgBhBEHE4XDhcjURhCguV5VDh/Zwxx0fIZFIcP311yMIAqFQ6KJ5+8lPfsKDDx7hjjtuoq2tjZmZ\nCtUqLC8vs337doaGRtmxowuPx8Pb3naIaHSc4eEhLMvC5QJRlIhEIjz22ON861uTDA4+x1/8xZ8h\nCAKqquL1ercMjwv/X/g7t7QEiEQqRCKhi45tEglZlrfSll4speNDH3o3Kysr7Ny5k0aj8bI8qrlc\njhMnTjA4OEhXV9fW62tra8zPz7Nnzx78fv9LrkmAnp4ebropAUBvb+9Fx7dv386nP/3Hz+sMvfmd\nAebnF5maCjAyAp/4xCcQBIFKpUKlUuHUqVOsra3xzDOnmZ4eJ5VSyGQm0PVubFsFCoAH265gGBtr\nBdaALILgxLaTyPINyPJpRHEZWXZgmqs0Gm00Gm5qtecIhRRcrgCGkaNQ2IXPN00ikUTTBAxDpNn0\nAj5isTymabK0lECS5nG744iik0CgRCrlIZl0EIsVkGUHuu7GMPLk8zFisSoHD5rMzgpMTjZxOOq4\nXG5iMR+aVuPkSYW2NoPDh0VWVy0WFkpoGkiSl74+G01rcuSIi3C4xMCAG12X0PUGlYoLXfcxPGxg\nmk3uvXcBSVoiFNpGOr3GZz5zFxMTeep1L729z+B2u/ne947T3e3lE5/4KKOjo6ysrHDzzTcTCoUu\nGTm7hovxagvQN/eJq2Xem80mqqpeIxpvMK6Vt70KsBn+fz2wmb6z6Zl0OBy4XK6rpmb2Ky3N+3pi\nk2BsRjA2Pa+vp+fulaJc3qjs9EJjNQyDBx98kEwmw2OPLVAsCuzcaZJM5mg0XLS0WKythVGUNfbs\n6eHUqQy6HqC3t8HqagFRdBGLSczPB3G7k+za1cGZM2lsO0Jbm8r6ehlZdhKPy8zNhVCURXp7I0xN\nlYAYra0lMpkqluWivV0mlWpB06bYti3C+rpNvR4kFlujXG6iaW0EAll0PUIyOc36eor19fK5UqlJ\nbLsJ7MfhmGajgp/jnFA7c65C0QCQQpLEcylQNuFwkJ07W7juuv3s3TvCv/7rIzSbUT72sZsvKXC2\nLIvx8XF8Ph89PT389V/fxSOPVLjjjgh/+Ie/x6OPPkq9Xuf222/H7XZvpS1urqHNQgxOp5NCoYAg\nCMTjcR577DG+/e2fMDwc42Mf+3/40pe+xvj4Kh/84Ns4ePDgRWM4n3Rs/um6TjabJR6PP48QvFD6\nFWyUPx4dHWVoaGhLBL557fNFrZcq6anrOsePHycej7Nr166tz/j617/B3Xcvc+CAm//yX/5o65p/\n+Zd/w8REk/e+dwfvec+7t661tLREtVpleHgYQRAuSxdg2zbZbBa/3/+ipZvn5uZ48MHH2Lt3mBtv\nvPEFz3vggX/nRz96lGx2jbNncxhGHlVtUKs5qdczWFYXtj2Hbe8CJoB2YBXwARqyvB1JWgVa0LSN\n9ed07mL7dp2WlsO4XMvnyiiLSFICy8oiSRG83gxgks324HIt4na3Y1kpPB43pZJMvR4kHk9hWQKG\n4QEKlEo9hEIpenujzM8XaDQCKEoeWQ4QiYBp1jl7NkZLS4rOzhYymTS2HaBWqyAILWzfvtGU7uxZ\nH273KqFQHNPM4/GESKfrqGqQnTvrSJLE/LyIZSVRlHZcrjIdHS1MTxfJ5/0MD1eRJCeZjI5h5Gk0\n2olE6tx2234eeeQ06+tuPvzhEXbt2sWXv/wd4vEgH/nI76CqKgsLCwwNDf3MZc2bzSbNZvOq2Itf\nC1xIQC7VaBC4SP9xpZK+VCrFnj17qFarV7QD7yrHtfK213B52OxQvflQBq6qfhSbuJJTpy4kGJsR\njGq1+kYP7bLxQvOraRqPP/446XSaBx6YxzRNensFGo0VVlfDhEIeslk/Llea/ftlTp70cuaMSlub\nk5WVFbJZP21tQSYnvUhSigMHQpw+rTAxodHS4iSZXKFU8pFI+Dh7NoBpLjEwIDA1pTA3JxKLOUmn\nVyiXI8TjPhYXAywvz9HZabO21sLiopNIJEOzmSWd7sbvX8EwGiSTFcJhG1VtkkqZWJYNLGHbO9nQ\nU5xE14Ns9KGwgCUEoRNF8eJwrOLz+Rka6uC2227httveTFtbG21tbciyjG3btLa2ksvlXlCLcOrU\nKb7whfvwem3+63/9CL/6q7cSCh3n5ptvQBRFbr/99uedL4riVilpQRBwu91baYytra1b5916660M\nDw8TDocxTZOZmSQLCyLLy8scPHgQVVURBAGPx7P1AL4w51tRFDwez9a6/da3/o1qtc5v/ua7nheN\nOZ98fO97P+DBB9e54YYx/vRPP7p1/HJSOp5++mn+6Z+O0dJi8alPhQmFQoiiSDQaIh6fJ5GIPK9A\nRTQaIBTKPq+xaC6X4/Of/waVCnzkIw3279//Eit6A0ePHuWf//kRursDfPzjv39Rj4C1tTWee+45\nRkZG+P3f/90XvI5hGJRKJZ5+epTp6SC/+qtd/PEfH2DHjh24XC5+8pOfcPbsWR5++CnOnq2Rz+ep\n1z2Ypgh42CAadQxjDsPwIAgLCMI+bHsKTUszOVkkkdAYGNiBpvUgimM4HAqy3MAw5kind+J0ruD1\nZjFNC9su02g4KRZbaG1dwe/X0TQ/zWYaTYvh9zfYvbvO0pLN6Ci43U08HotAwI1t15iaihEI1Nm9\nu0mxaJHJ6KiqjWm66e8H224wNeVClvPE4zK27cDnE1hbk1lZcbJ7dxNF0VleFtH1NJLUisfjp6/P\nzcREmaeeshgasmhtNSgWbQwji6rG8fkCXH+9l6mpMv/yL1PEYnkSiQgPP/wTHnrocZaXA6TTKZ59\n9lmeeOIY4+N17rxznne84w7uuedeZFnine98Bw6Hg3w+TzgcvmxD80o0mF8vvJQAfTPDAXjRCljn\n9/94I+ezWCwSCoV+oX/TKwHXiMZVgNfyJrlQgKwoCi6Xa8tzfbXhSiQalmXRaDS20qQuTJG6Esd8\nuajX6zzzzDOk02nuuWcaRWnQ2iqxuLhCodBGNBpmdtaLz1fm4EE4fdrF2bNlYjGFZHKVZjNGPB5i\nasqPy5Xn4EEnY2MOZmZUYjEPa2ureDwhWlsDTE8HgTUGBw1mZlysrEA8vkFCXK42EokgS0s+Go0Z\n2tpqpFKtLCyYhMMlstkq6XQ/fv8i1WqBTMbA7c7jdgcZHZ0nmcximkmgDzCBs0CIDePPC+QQRYVo\ntJ3ubi+HDt2CLEucPGlxww0t/Of//GcAHD9+nL/9269x4407ec973sUNN9xw0ZzNzMywvLzMoUOH\nkGUZRQGn86fVky6soAQ/JannN8N8sUpvm5GNTfzO79zJwsICb3rTm0gmk3zuc19DFAU+/vHfJRaL\nXfIa5xOQ5eVlnn56DVWFG25Y4Prrr78oCmJZFuFwgFBohXDYv0WGLjRebNvm9OnT2LbN3r17t4z6\nzs5OWltPEI/7CQQCyLKMZVnceuut7Nq1i1AohKqqW8bMhz70m+TzG+ViNwnIxjEBSbIuIgszMzN4\nvV4SicRF37VQ2Gj06PFUMQzjovfefff9PPBAhltuWeLP/uxjl5wv27b5ylf+mTNnkuzb10pXl8yb\n33yY/v7+rXPe8pa38Ja3vIWPfexjLC8vMzk5yY9+9BAnT55gaSlBqbRIs9nLBsl1Y9sFYJmNXio9\n2HaBdNpNNLqI05kjGOxF17NoWi+KksblmsU0DSyrBcOoUyy2EInM4fc3qdUimGYWQQgjCE56e8uk\n0zpnzrgIBrP4/ToulwKUmJ+P4/OV6OtTqVSaFApQrRroupO+Pi+yXGd+XgFyBAICoqgQiThZXoal\nJQcjIw56ew1WVkDXs0AUlyvA4KCPqakqP/6xTl/fRhWset3GNAuUSmE8Hon9+12srKg89VQDv79K\na6sPvz+AIBgsLHhwOnUOHBDJ56t86UuPY5qLyHI3o6OjrK2tcvRoGUWR6O/fztLSCg88cJpbb93B\n+9//Hk6fPo2qqlx//fWXbDh3te7DrzU2nQWb99imA/KF0q90Xd967xvZAT2fz18yRfUaXl9cIxq/\noLiUd/3CHg1X46Z7JRntL0UwrkZsamBqtRqnTp1iaWmJ739/Gp+vREuLl9XVFVpb+wgGo8zOuti3\nr86BAzrj4wKqWqSlxUMqtUp7ew+1WoipKS979lQ4cKDG1JRAo1ElEvGQSq0RiXQSDvuZnw8yMJBm\naCjD7KwDTbNoa3OzvLyC272N1tYwa2sudD1Fe3uN1dVO0ukKoVCJZDJPJjOI212mUlkhlRJwOFJI\nUoD19TyNRpn19UlMM85G+soKEAQ2PMyKUsfjKePz+YlEtnHo0A7++q//EqfTycMPP0yl8gw9PT/t\nHzExcZaxMQFZnuTd7764PLSmaXzxi99hcdGmXq9zxx138MlPBnC73ZfMI96MNGqaBoDT6XxFzTB3\n7dq1VWFpbGyMdNpEkjYM7BciGuejq6uLt751gGq1xs6dOy8y0jYJx6//+js5dOjg1jUvpf2YnZ3l\nH/7hXmxb4OMfdzE0NATA7t27+e//vf2Snee9Xu9FqVeCIBCNRmk0GsCGQePxePijP/og9Xqd7du3\nb71/bGyMr371ITwegU996veIRqPPu/6tt96K1+ulvb39kqlTfX2d9PSk6O/vuujYJmzbZmUly/q6\nSCAQ5L3vfc9LzunGvL6VZrPJsWPHOHLkCPff/yQzMwEKBftcepMbUIAlwIthLDI2lqCrS0PXUzid\nTZzOhXNEdD+CcBrT1HE6VWR5nEplO4JQRBSbyLIDn69APt9gbKydWKxEOFxFkkQgSzKZwOWq0d1d\nodFoUC4HUdUsuu5g2zYPbrfK0pIT06zg8ZiIokQs5mR9XeX4cZHhYZmeHoO1NRPDyGGaARQlwI4d\nHlZW6jz2mE57e5P+/iaWJdFsquTzHpxOgT17HOTzDZ57TkdRioTDfkKhIE6nxcyMgiDA8LBFo2Ew\nO2uh6wVMM0BnZ4xQSGRiAiYnc3R2moDFl770f2k0MhQKXZw+PUkgcD8//OFz1Gob2qJQKMT3vvcA\nO3du553vfDvlcplkMklnZ+eL/m6/yLiw5P2LVcC68H59KQH6a0FArkU0rgxcIxpXAV7Nm+RSxu+l\nmsBdSQb7y8H5FbPeqM3lwjl2uVy4XK4XJBhXk4C9Vqtx9uxZlpaWueeeOcLhHOFwkFwux7ZtLZTL\nCcbG4MABD+FwhZkZkUikTCQSplBYZs+eKKoa5eRJuO46J35/kfl5gXBYIxwOk80uMDjYTb0eYmxM\nZmjIprd3jfl5J9GoTiKxkRLl9XbT2hpndVUiHq/Q2VlnaamTajVFNJpnfb1EqdRPMKhSqaxSLofY\n0FOEyeebOBxNcrkl0ukmtt0JpNkw6DyAQDjsY2Qkylvf+st84AMf4MiRZ7n77jE6OwM4nU4Abr/9\ndvbt2/c8j9ltt70ZWX6S4eGhrfWn6zoTExMkEgkikQitrUFqtQLRaBRBELYa250P27ZpNptba0hR\nFJxO56tCUoeGhvjwh4uIokh/fz+rq6v8+MePMTw8yIEDBy75HofDwQc+8L4XvOb50Y+e8xq1XUr/\n4fF48Ho5J2B3bUVpBEEgGAxe8r4VBOEicnOpfPJNfVYwGKRWq21da6Oxn41tX9qB4vF4uOWWWy75\n3Wzb5q1vfSuHDx/G6/Ve8vh3vvM9JiYWue22A9x6q3mRDualoCgKhw8f5vDhw/zJn/wJ4+PjPPHE\nE3zta3czMzNJvZ4A1oFWYBXLqrG8PIcgvB2fbwFN24Ysn8WyjhEK+TCMZSyrG1nWsKxlZHnjt9G0\nGrncDkKhIuFwElFU0PUClUorDkeT9vYCzWaTUilBs5nHMETa2rx4PGVWV12YZhO3W0cUBSIRJ6VS\ng2PHZAYGBK6/3iSZ5Fy3dBcOh4vBQSf5fIWnnrKIRCp0d/sQBAeiqJHNegCZ4WGbRkNjfNyBIOTw\neHyEwyGCQZvpaSeaJtLXt2GkJpMSmpZD03y0tUXo7FQYH68xN9cgFlMJhxVMU6LZrLC6GqC93cub\n3+xhfDzJv/zLERSlgMsV4P77H0HTVE6d8rK+/hw7dw7yrW/9kMXFKu9//w0cPnyYRx99lGAwyOHD\nhxEEAV3Xrxqt4muJy3muXs79+mIE5FI9QF4JNonGNbyxuCYGvwpgWdbzQpGv9BqbKVLASxq/xWJx\nK0f7akKz2aRarW7ld7+eeLkEYxNXg4BdVVVWV1d58MEf8+ijayQSFSqVALq+xs6dfUxMVKnVHOzd\nK5BMZikUPMTjGoVCCMNYZmSkj/HxEqrqZudOnUymRKnkJhZrUi6HUdV5du3qYW6uRrnsob+/TD5f\nJp32E4/XgSjJ5DS9vV2oKmSzMu3tOcBmfr4Nr3cRv99JJqPi8WxDEBYpFm0EIYIoLmKaUSqVEqLo\nplJZIZ+vUC77gSQgsbG9WUiSQCQSZmgozn/8jx/kHe94+7m+GCZnz57lyJHj2LbIb//2+wmFQlva\nhVpN47d+692XfKj9+7//O9/4xjG6ux38+Z9/HMuyKJfLtLS0XPQAfS0Jxgvhm9/8Fl//+jy7d8P/\n+l//32V91tLSEt/85t309rbzvve9+wUNgdnZWdLpNAcOHEBRFGDjPsnn81iWtTVfm0T7wufRhWlX\nl9t88HxDRtd1bNveSp1qb2/fMmBUVeXMmTP09/fT0dFx0fd44IF/57HHTvLrv/7mS6bBwQb5/vM/\n/1vm5kQ+/OFh7rzzzpcc4+bYjh07RrlcJp8vUS6rtLQEMU2Lffv2Yts2/f39jI6O8j/+x1/y5JNn\nqNWUcxWs4mxUrAoSDEq0tLTjdodwOl3YtorT6cA0VVwucDj2YNsz2PYgXu80kqSg6wobTSh9yLJA\nMFim2TSo1bqw7XlEsY9AYB2v10kqpaDrNl5vA0kS8fmcNBoq8/OtdHWtE4tFyWaLGIaIpknIsove\nXgFV1ZiZ8eP3L+L3dyEIOVwuL8kk6LqLoSEd0zRYWXFhmstIUjehUIn29ijj4xUqFSe9vTVEUaZS\nsTGMHMViF7FYkcHBdsbGkpRKHkKhPA6HH49HwjBUZmYixGIFRkbamZlZo1z2IQhpnM4YHR0ihtFk\ndNRDIFBkYCBKLpelVvOhqilsu429e50Eg0EefTRPOGzz3/7b7/Lss8/x2GOneNe7buHmm29menoa\ny7LYsWPHL5S3vFarIYriixZMeLl4IQJyvvPtUhWwLoeA/P3f/z0nT57kG9/4xqs23mu4CNfE4D8P\n+Fk2MtM0t4zfzdzuyzF+ryYv+/m4sAfI64GXS+IuxJUcParVahSLRf71X+/m1Kkcfn8O23ajaTqD\ngy5OnEgwOlpneNjNzMwiMzMxIhEFy3JRq1UYHpY5dSrOmTMNtm93sri4wuJilJYWhWLRQ7GYp68v\nyORkgvFxm+5uG12fZ2amhbY2hUDATTq9Sk+Pi5aW7Swvm3R2lolGG8zNdRKNLhGLrZPPgywH8Pka\n5HIziGI7sjyLpknU6y5Ms4KmlSiVlimVwhhGBqiyQTIaxGI+br75OqLROCsrRbLZEPff/ywdHe3s\n3bsXAFmWOXJknUZDYM+eUxw6dIiFhQUefXSeRkPkwIGpLdH3pgd/M61AkkCWN3KcnU7nRelK5zfE\ntG17q9qbKIrYtk0ulyMYDCLLMs1mk0qlQiQSeVWMnJ07h7nuukWuv37ostfs2NgYTz1VZXl5kre9\nrXxJklypVPj7v/9XUin48IcbW1W3RFGkpaXlovMvVXK3Uqng9XqftxdNTEyQSqW48cYb8fl85/Xq\n+On9d346x+Z7r7vuuovSOX74wx/xgx8ssXPnUT75yY9d5Ek9enScU6dsensnL0k0UqkUhUKBd73r\nJhYWll+QjGxC0zSq1Spf/vI3SafT5PMClUoTy2pimk4kqY4gBLjnnsfx+drYuzdCLBbjH//xi6ys\nrPCZz3yO++47Sq22BHSwUTXKT6MxRzCYwOtt4HDsQteXEMX9CMIYzeYyitJEFMep12OIog9dX8fj\nCeB0ZgGDlZUduFzTuN0msqzgdK5TLHrIZBz4/UVcLgeyLGGaKpOTUVpbK+zfr5PJCKyv19A0AVH0\ns327ga5rnDkTwOVK0tbmQRQ9+P0bhKJed7NjRw1RbLKyImKaGUxzG4FAiO3bnYyPizz1lE5Pj0Y4\nDJomYJol0ulWotEAt9ziZXKywNNPV/B6q0QiTqLREIbRZGrKTTCoc+utCqurAqdOqRhGFVkO0t3d\ngiDA2JiI02mwc6dJoyGQTDapVKo0GmGGhmI4HHD6dA3IEQ5LKIrF5z73VbLZNMlkK0ePnjwXwXoS\n04SPf/y9yLLMww8/zp49wxw6dAhN06jVaj+XTeJei0yBlxKgv1QH9EuRj81rXWvWd2VA+vSnP325\n5172idfw6uPllrc1TZN6vY6qqliWtdVQ68UEpOdjM4KymSZytWAzp/219gLDhgFTr9epVjcEpC6X\nC5/Pd9lzvInNjsqvppfoZ8WmQXTXXV/hnnuOUCwmKRQkQqEmHR1O5uc9VKsa/f1u0uk5dN2LxyOT\nybgIhTR6etzMz8uUywbbtjnIZOYxTT+BgEwm48HpLNPT42JtzUOpZNHZCZnMHJVKgGhUpNHwoKpp\nEgkHut5OLqeTSDTQtCwrK514PAUUpUq5LOFwuFEUg1RqDZKTJyYAACAASURBVNNsR1FSNJsWqupE\nVUs0myWKxQylUpBisYRlJdnIeVeJREQ+/ek/5f/8n//N+9//fu64423ceON1NBprzM8vc/Zshb6+\nCN3d3YTDYXQ9S1eXl1tuOYwkSSiKgqqu09oqc8MNB5EkiVqtxl13fZn773+MgYFuRkZGGB5u47bb\nbr4o9Wazh0qtVkPX9XPicIVHHvkx4+MT9Pb2cOTIEe6667ssLs5w4MBe/u7vvsz3vvcE0ahCNBrl\n7rt/wOzsHH1921/Rmm9ra+P2229ieHhDK/GDH9zLd797H21t0Yu0DJvw+/3YdopDhwbZuXPnC673\nY8dOYBgGN9646yW7P28aCJsk4e67f8jXvnY/imKwY8cAgiBQrVb57Gf/hccfXyca1enp6cE0TVKp\nFJ/5zD/y+ONH2LmzD4/HszWmzdQMh8OxdX1ZlnE4HKRSKZaX1+nra+H66/dv5ZYbhnEuyugiGq1x\n0003PK+6FWxE+T7zmS/z8MMTHDzYxzve8fYXLYuaz+f5zGe+yH33PczyskaxKBIM1onHg+ze3UZ3\nd4iOjgA+n4Vty6hqg+npLOPjVc6efZr19Ty/9mtvZffuAUxTY2npDLZtAWFMM0OtFsG2sxgGCEIN\nqCEIMoIQwjQNBKENw1jEsirIsh/DSFGt7sSysrjdBrKsY1ka9bqbcjmM250+p8NwY5olksl2FEVl\nYEA+p99wUKs1sO0Q3d02Pl+TmRkPlUqaSMSLy2UQCrnJZk2Wl7309mq0tgqk0xalUhZNC+L1SoyM\nhEmlKkxMOIhEyoTDEqIIpqmRTAaQZZGDBwOoqsr0tHBuvD7a2px4vQLT0wr1usnOnQqS1GBtTaJc\nzmCaIbZvd9HaKjM1JZDJaLS3m/h8No2GRKVSIp0O0tsrMzDgYX5eY21NxeWq4/crxGIbnzk+7qG1\n1eDAgRBTU0mefXaGRmND16KqaZ555igPPVSjUFjg4MHdfOELX+Xee5+ioyNEKBTimWeeQVXVy9JC\nXenQdf2SmozXAufvB5v3q6IoOBwOZFneEqdfeM/eeeedfP7zn+fJJ5+kWCxSq9XYv3//Na3Ga4e/\neKkTrkU0rgK8nJvDMAwajcZW3rPb7cblcr3sG+xaROOF8bNGMC7ElRTRME3znDH3JXK5CvV6jVzO\nxe7dHmIxgaNHvbS0lNmxo4WZmQWKxR5CoThraxIjIzJ79picPu2iWq3Q2+tlZmaGUGg7LS1xVldl\nduyos2tXkzNnNromb9vmYHJyGlHsIRaLkE5LlMsqXV0yi4t9LC8X6O6uMDeXYXKyj/b2Kpq2SC7n\nIhAAv99mbW2ZQKCXwP/P3ntHOXLVaf8fqRRKWWqp1TnH6ek4PTnYHntsYxZ7DSwYAwYWfiwLLH5f\n8EtawPAedpfd84LZ9Ro4sDZgzBocMNg4jHFOkz09Mz0dp6M6SWpJrSxVSaX6/dHTvZMcAKfh+Dln\nzplTfVX31q1w7zc9jz1COh0kHneTy82f3MBnkOVikskMsjzCsoGhIghhqqpKWLfuAoLBEE899TQ7\nd16E0WikpqaGT33qY8RiPyEalfD5fDQ2NmK32/nQhz7A2NgYu3f/gd7eHtra2vj4xz9ysgZg2Vse\nCAQYGgoRi2kZHBzE6XRSVVWFIAjk8/lVr1s+n0eSJBRFYd++/Rw4MMiVV16EyWTi3nuPkM9DbW01\ngUCQhQUtdnsYWZbx+6MEAhpCoRCDg4P89rfDiCKsWdNCNptl9+5n2bKli23btr3q+77y3siyzJNP\nHmF0VEtLyzGamprO2b60tJS/+7uPvew5jUYjX/jC35FIJCgtLX3JdsFgkOeee46Ghga6u7tXj4+N\nzTA1pWVqam51c2O326mpcaPVRqmsrESv16+mYvn9eVR1+XwrhfWLi4s8/PAfqKws47LLLj3Lc3rp\npbvo7OzA7XavpnbB/5Bl9PT00NXVdU42nUwmc9LD+j96A+f6BmQyGX73u98TCASYnc1SKNi44IJi\nysvL2bFjBzqd7jQacVVVWVhYIBwO88wz+5iamsHng9HREAsLj+LxlLBjxwXY7V2Mjj7EwMA4UIyq\nBolGNRiNWfL5DKIoIcsZBCGB0+lFkkbQ6boRhGnSaQOiqMdsHj55vWZkOQeUYrdPodGkURQP2WyA\nTMaL1Zph7doYoZDK7KyAouQQBANVVSKFQozxcSeCsIDLJQIiLpfK3JyG6WkdbW0qlZXL0Y9cbhFZ\nLsFsdtLRYWZsLMazz2YpLs5QUWFCFE2AzMyMFbNZx/r1AuGwwpEjGVQ1isFgo7y8CFHUMDSkR6PJ\n0diokMup+P15Mpk46bSdujoPbreOoSGJbDaN05lDr9ciCCLpdJTpaTsNDRY6OpZpdufmouh0aaxW\nIxUVdjKZNAcOQHm5wq5dJqamlujvDyHLEkZjEQ0NdiRJ4rHH4tjti6xbV0YmE+Ub3/h3otE4hYKX\nAwcO0N/fz+7dPjwelW98o5SjR4+xZ89R3vWui+js7CQYDK7SYJ8PeCusUy9XgF4oFLj22mvp6+tj\naGiIgYEBEokE99xzD2azmba2Ntrb22lvb2fz5s1s27aNH/zgB3z3u9/F7/fT1dXFf/7nf7Jhw4aX\n7P/pp5/mhhtuYGBggOrqar72ta/x0Y9+9LQ299xzDzfeeCNTU1M0Nzfzr//6r1xxxRWntXk1/d54\n443ceuutRKNRtm3bxo9+9KPTWOzOF7wd0ThP8Eqb/nw+TyqVIpPJoKoqJpMJq9W6yrH/xyKXy60W\na55vyGazGAyG19zr8lpFMM6Eoijkcrk3XbMkHA7z//7fj3jiiWfw+zOEQrB2rQ2TKcXAgAG9PoXN\npiUUmqWkpJh83sLCgkBrqxGHI8PQkA6NJoXDIRIIzOD1FgFm5uZ01NSouN0SIyNGIENxsQGfbwyD\nwYbZLBKJ6LHbM5SWwtxcCel0nOpqCIUWicVKKSrKIklh4nEzNpuCXi8yP7+A0ehBFJOkUlkSCQfZ\nrI9cLoEsK2QydtJphUxmGlmWUFUNkMZo1FNSUofB0EwgkGNy0s/+/QMcPXqMpqYq3G43JpOJdeva\nCAaneOwxH+HwJBs3LhdK/+pX93HffQtks7Ps2LEZrVZLNBrl4MGDq8J7Dgc0NTnYtm0rBoNhtVYg\nl8shyzLBYJDf/e4B/H4/TU1N/PrXD7J3r4TNlmTr1k1MTw9TVCRwySUX0NjYSFmZyiWXbMPr9VJb\nW0pzs41t27ZhtVqZnR2mosLGhRdu45FHHuehh0Jks/Ps3LmV4eFh+vv7KS0tfVWFrIIgIIoF3O4c\nO3de8KrrhoaHh3nqqaew2+2n/cZgMGCz2V72/di9ezc/+9koCwsnuPjiLaub9aqqUqqqYOfOC1aV\nvwVBYMOGHrZv76G2tnbV41lcXIzbraW7u4Z169YhCAKqqvL0009z110TBAJzbN7cjl6vP0uEzGq1\nnla4qqoqv/zlr7nrrj9QUmJfNWgMBsOqJ3V6eppgMMgFF2yko6OK1tbWVUPk1POn02kGBwe5887D\nBIMyF19czY4da7nqqqtoaWnBaDSedV80Gg02m42SkhI2bFjHJZdcgFabxGzOMDWVY3pawmiM4XYL\nOBxlhMM6jMYF0mkJ8AAzyHIpEERVSxGENJmMHpCQ5SVUNY1OJ1IoSORya1DVBTQaCwbDElrtIrlc\nLZKUQFVt6HQKZWUymYzE4qKHQiGCTueguDiPKKaZnXWQTKaw2cBkApvNSCyWYWLCSXV1hspKPdFo\njlgsQSZjxWAwsnathWw2zeCgAUEI43KZsdu1GAwwNyeSyQisWaPFaJSYmdETjwcAJ+XlOioqjIyP\na1hYyFNZmcNuV0mlNCSTURYXnZSWamhvd+LzpZmZyWE0JrBadbjdVhQlw9CQFYsly7ZtXoLBKD5f\nHllOIIpWGhrs6PUyR44YKBSSdHc7KRSyBAJ5EokEiuKitdWM0wn9/Rqi0Qjl5TqsVg35vI5QKM7i\noou2Nh2VlQaOHo0yPDyOyQQ6ncz09DTPPHOI/n49JlMEi8XELbf8muef72PNmhokSeLxxx8HwOPx\nrG6c3yoshSvpnSvvwFsNK06E7u5urrjiCq677jr27dvHZz7zGW644Qba29vRaDQMDAxw9913s7S0\nRKFQ4NOf/jQ33XQT3/72t5mcnOSrX/0qn/jEJ85Znzo1NcX27du55ppr+MlPfoLX6+Uzn/kMW7Zs\noaGhAYA9e/Zw5ZVX8uUvf5mbbroJWZb53Oc+x3vf+97VqNZdd931iv3+27/9G9///vf56U9/yhe/\n+EWef/55vve97/HpT3/6rTb/rxjReLsY/DyBLMvn9Cas5HWvKASbTKY/e+MLy7n5siyfd4wNqqqy\ntLSExWJ5zdK+XusIxpmQJIlUKoXL5XpTQrtzc3P89Kd3kc+nGB9XyedzbNzo4sSJaRYXi6ipSRGJ\nGMnnAzQ0VDE4mEFV9fT2mvD55llcdFJeniYet5BO+1izpoGJCYlkUktHB4TDS8zM2KmqyiJJJmZn\nR6itrSaRgGhUoLFRIp8vMDzswuPx4/U6GBtbwG6vwWgM4fcnEQQnbneaVMpBIDCJ11tKPp8gEslT\nKFhR1QkkyYCi6Mhk9EhSAkmaJ5vVks/n0GiW00nc7kYaGz3U1pbQ2FiLKOo5cWKekZEpNJpaGhsl\nPvCB97B9+3YAfvWru9m9e4xNm0r4zGc+ASwvJA888CyXXrqBSy65BICf//yX/P73M2zYYOErX7n+\nnPMcDofx+/1UVFTw3HPPcdttR/B4FL7ylQ8zMzPD4cPHueiirauK1ispA38M5ePg4CC7dz/D5s1d\ndHZ28s1v3sz8PHz84xu49NJL/+hnQ5IkHnnkUTQaDe985zte0lj59re/z969Wa6+uuwlIx2qqjIy\nMoLFYqGq6n9oYvv6+rjzzkfo6Kjluuuu/bPfgVM1R3w+H/feu5uGhgquvfZ9q+OYnJzk6NGjdHV1\nUV1dvfpbjUaDoijceOO/MzICH/1oM+95z3tOO//i4iLf+c6tpFIa/v7vL6e7u3t1U3hqDcjMzAy3\n3vobtNo8DocVq9XCRz5yDTab7U+i8lQUhYceeoSJiUmOHIkiSVo8ngCJRJ6lpQgHDpxAVQNIkg3w\nYDQuIAhtWCzzCEIHFss0gtCBwTCKRrOcYqiqBpzOEmQ5gSA0oNPFUNUsRqOKVqsjn5dJJBpwucYx\nGMowGpdQFJVYrAStNonFomAwqGi1JlKpOIFABU1Ni1gsdkKhFPl8Dlm2YjRqqK83sLSUxOdzYjZP\nYTJVYrUmMRgMTE1pUVUtjY3LkaNQSCSXm0OWqykrS1JeXsTAQIxUSktxcRqdTo9GoyOXi+PzlVBR\nEWHt2moGBmZJJET0+iWMRgfl5SLZbIrjx214PBHa2sqZnV0gmbQgSYvodKU0Ni4/M8eOCej1i1RV\nucjnM+RyZqLRIOl0OR0dOUTRyNCQjKJEsVpFDIYCLpebubl55ua8dHYm8XqLGBmJkMlk0Gr1mM0C\n9fVuFhZCDA7aaWwMUVFRwdxcgHRaQZYFTCYz27bVEApFePZZifZ2Ld/61uf52c/+m8nJAH/7t++m\noaGB4eFh7Hb7m0a/q6oqqVQKURTPqUHyVsTll1/Ol770Ja6++urTjhcKBZLJJJdddhmbNm3iP/7j\nP4Dla6yqquL666/nS1/60lnn+/KXv8wjjzzCsWPHVo9de+21xGIxHn74YQA+8IEPkE6neeCBB1bb\nbNmyhZ6eHn74wx8CsHnz5lfst7y8nC9+8Yt8/vOfByAej1NSUsLtt9/O+9///tdqil4LvF0M/peC\nU9NrVvK6V0L3giD8UfUXf2x/5yNei7G/3gbGm43JyUnuu+8R8vkUR45IWCxZNmzw8uKLA/T16XG7\njRgMOdLpLE1NLg4frmRkJEtbm8j4+AzHj5fj8RjR6SCRSFNf7+T48WqGh2XWrjUyPu5jaKiU8nIj\nNpvK7OwC1dWl2Gz1zM0VWLtWQBRjDA56qakJU1sbZ34+iyi6KC31MD09gd1eTGUlBIMiU1PzlJRw\nktY2jNHowGCYRpIUJMlDLpcjn48hyyEkSUc+b0SrzSGKFkymHDU1TaxZU8aWLVvYsGEDra2tq57v\nAwcOcNdd99Dfv1yIu3HjRgwGA+9+91WsXTvK+Pg4jzzyCLt27WLr1q1s2bIF+J/iyOJiN16vj7Ky\ns2saFEUhHo/z3e/+mGAwx8c+djFdXV10d49QVuamurqa2tpatm7durpZPbUm68zahZX/n+tdb2tr\no62tDVh2QpSU2MjllhmuYrEY9933ADablauvvvJVbRZGRka4777jaLXQ1NSweu4z0dXVxNLSUdra\nXjqsf/ToUX70o4exWOCrX/3kqnevp6eH9vb2VaPqT8WpmiMrxBft7e10dHSc1fbhh5/i8ccjXHJJ\nmM997v9bZb5RVRWtVss111zK5OQkmzdvPqfwoMEgkMspq5omK8dX5jSTyRCNRgmFtIiink9+8ioq\nKytXyTlWcGYh65n3NZvNrvYhCAJXXfUuZFnmvvvuZ2pqmsHBYhRFgyimaGtbi6K4GRyMIQhzFApe\nCgU/sqxHq53CYDCiKOPodEVoNGny+QrMZh2JRBJRNFAojKKqIAhNZDI+crl6XK5Riopm0emMSFKQ\nRKIEnU7Bbg8hCBpU1UE6vcjiopfa2jTd3RlCIQ3xeJxczoDBYKa5WUMymeHoUROiGMHttmMy2bFY\nFKanjUiSjvr65XsWDArkcmFSqWqKi+00NpoYGEgwM5OiqCiJxWLBbLaQyyUZG7Pi9WbZtcvMiRNL\nHDy4BCQxmczU1BSTz+c5elSD1aqwYYOWaFTL2FiCVCqJojhPFn9rGRwsoKpJysr0qKqALEM8nmFx\n0UF7exFut4Hh4SzZbBijUYPFYqSy0kUgEGL//jxNTQYuvdTE2FiMQCCAohQQRRstLTai0ThPPSXj\n9SbZutXD0pLA9PQiiUQerdZFW9syo93DD8+h189RXV1CPi/xrW99l5mZCMmkmwMHDjAxMcF99/Vh\nt8NXv/p3zM/Pc/BgH9u2baK5uZlsNouiKOekX36tcL7tB1RVJRqNnlOfaMUp++KLL/KP//iPq8c1\nGg27du1i79695zznvn372LVr12nHLr/88lVjAGDv3r3ccMMNZ7W5//77geXv8iv1Ozk5id/vX3Vk\nAdjtdjZt2sTevXvfaobGK+JtQ+M8wqnMNCsGxp+THvVyWDE03kw9ij8Fr0WNxhttYLzR2h+jo6M8\n++we4vEIjz+eoaIiwfbtFezfP8nAgAGr1UkoJGEyCaxZY+TAAQ+SFKe3182LL44xNVWBzeYgECig\n1Sq0tel58UUv+Xya9nY7/f3DjI/X4nA4SKUUQqEIXq+LRKKWuTmJ9nYjIyMz9PfX0NCQxeMJMz+f\noLzcQ1lZORMTk5SWeqmrK2J21sDU1CxebwZRrGN6eoqiIhdOZ5ZMxkQsVkw+H0GjyZLNJlAUC4ri\nQaOJodWCXm8+mXtdQTRq4tChEMeOPc7vftfHunVurrzySnp6eti0abnY9557HmZqapJvf/s/+Oxn\nr6O0tBSdTscDDwxRKCyrV3d0dJBIJPjxj3+BohT41Keu453vfAfr1687rXg6HA7z/PPPU11dTVlZ\nGfk85PN68vk81dXVfPObN5x2v89M31kpclzxkufzeWRZXm1z6ub0VLaklXPq9Xr+1//6O1KpFEVF\nRezdu5fdu2ew22HDhnXn1O84E1VVVbS1WdFqNS/rSb3qqndxxRWXv2x61gr7llZ7NsPMn6NPcCYl\n8KsRNWxtrWV6OsyaNXVn9V0oFOjt7aWnp+c0A2SFBUtVVa6//sNIkkRVVRWKopxW+zE+Ps5PfnIv\nTqfItdcuF6E2Njae9k09F5tOPB7n8OHDaDQa9u8fxG4XmJ/P4HbryOV01NV5cbkc1NXVsWvXTnQ6\nHXfe+RtmZmaYmqrB5UqTSklUVdnQavXMzAgYDEEUpQpBiJDN6tHrE2SzGjSaJBaLhkwmgtHYiSyP\nA72o6nF0uiyiqGIyDVEoOMnndUiSFr3eiNsdAkCSykinp8lkyiguNtDdnSAYFJibk8nnVQwGG/X1\nCpKUob/fidE4h9ttw2h0YrPlmZnR4/PpqK9PIggqsZiGXC5ELFaFx+Ogu9vCwECUPXsS2O0JPB4d\nLpeDfD7L6KgZl0vPjh0G5ufhyJEE+XwSrdZOfb0XjUbD8eMa9HqZlhYduZyWxcVldqlEwklbWzF2\nu57BQRlZjmO1qhgMAi6XDb8/yYkTetasMdHVZWZoKM78fAhVzWGxmKivdxCLxXjuuTxlZRIXX2xm\nbi7K0NAi6bSEweCmrU0gl8uxZ08OsznCmjUlaDQWIpEEoVAOSXLS0ZHHYNAxNJQjnw/gdLqwWBwU\nF1sZHY0SDNro6RFxOnU8//wI6fQBNBo72ayGhx56iGPHxhkYMJFKPYPb7eYHP7idVCrHZz97LR6P\nh76+PioqKk7TtPlzsbKmnk/7gZfT0QiFQiiKclZ9TElJCSMjI+f8jd/vP2f7eDy+SkLzUm38fv+r\n7tfv96PRaF72POcT3jY0zhPIskwqlUJRFHQ63etmYKzgrSB896fiTx3vmxXBeKMoeVeK40ZGpnjm\nGYm2tjRbtjg4fjzIxIQeu72EaFSiq8tBUZHEwYMidXUJurpcDA2N4fcbcDpLCQRUqqpMuN1w6JCD\niooE7e1OBgbGmJ9voKjIi98vY7Fkqa4ucPx4Kblcmu5uI/39s4yM2CkrczMzE2JqKkV5uR2droaJ\niVFqajxUVXmYmxMRxUnKyuyEQk1MTIxSWgrFxTricRVJsqOqsyc3iQUkyYVWWwxEUNUcBoMHQVjO\nnxZFEZfLwXImXY5oNMXSUoZHH51kdPTnXHddkJ07d7JmzRquvVbHv/3bPfh8ORYWFigtLaW8vJzG\nRjOFQmGVOWlubo7BwTiKsqwp4XK5VheFldSdBx98iHvvnaatbYB/+Zcvc/3117G4uLjqYX+55/RU\nL/mpG+FTU3RW/p2ZVnlm5GOF3rGpqYnNm49it5spKyvD5/Nx4MABOjs7aW5uPuc4XC4XX/7y51bH\nVCgU8Pl8eL3es3KYTx1nMBhc3YivoL29nRtuMGM2m1+SzerU6zx1fnK5HL/+9b3E4ymuvfY9FBUV\noarqybS/X+N0WvjIR67FbrevUgL7/X6KiopOK/JewRVXvIOdOy86rQatUChw992/wecL8MEPXn2a\nYVUoFAgGg9x0009RFJV/+IcPUllZuXo/TsXs7CyzswVSqRQf+1gnZWVlq387F5Xn8PAwv//9E6TT\nEfr7dcAg6fQa9PojKMoadLp+JKmVw4d3o6pt2O0PY7dXUl9vo6Ojhc2be9i9+zkCARmfr4KSkijp\ntEpxsYJeXyAS0SKKKrJsQqOJk8/bMBhipNM6zGZIJmcxm3Ooah+iuEwFnU470GqdwCwWixOdLgHk\nCIUa0WhOYDQKmM0mqqqW8Pu1TE5q0WhkRNFKZaUGWU4yOOjGaFykuNiGINhwOPLMzCwXiDc0pCgt\nzZFIaMnlIsRiZTidTrZsERkfXzYwzOYURUUWiovdFAoKo6N6zOYcvb0aYjGVEydWnAtOGhqKsVh0\nDAyoKEqGkhINggDZbIF0Os38vJ3WVhfd3SYGBpJMTS2h10vY7SKVlXaWlpY4eFClrAwuu8zM5GSM\no0eDyHIGUXTR2Ogkm83ywgt5nM4kmzY5SCSMTE2FicclCgUHa9eaT9YAFIAwZWV2jEYbFosRny/M\n4qKD3l47Npue0dEsmUwYvd5y0nj0MDk5z7PPyrS26mlrE/H5EszPL5DLGTCbi2htdRAOx7n77nm8\n3jDr1lUxMzPFN7/5PWIxEAQb+/btO0kIMU9trZZvfet/n/P5/3NwPu0HYrHYOSMab+ONxduGxnmC\nlfC9zWb7s1MMXg1WFsLzLVwKf3za15udIvV6GxqDg4PMzc3x+OMHOHYMNmzI0dqaJxAIotNpsFiq\nWVyU2bjRw9TUAvv2KbS2KtTXFwiHF3E6LTgcdczNFejutmMwBOnrK6K+PkNjo5bZ2XnsdhNudzV+\nf57mZg1GY5r+fgeVlTHWr3fS3+9jdtZBWVkJc3OLzM1lqKy0Mz1dxeTkOC0tApLkweczU1oaoK4u\ny/h4I+Pjo1RVFRAEN8GgisGQx2xeQK93kUi4yGaNFAopllWTZbRaLUajitFYwGIRKC0tZc2aRrq6\nOtmwYQNer5dwOMzevXt57LEXGRub4o47DmEymbjgggtoaGjgwx/eytjYGAcO9GE0Gmlra+OrX72e\npaUlxsfH0el0NDY28u53d6IoCq2ty7Sw+Xyehx56mEQiya5dF1NdXUVt7QwNDcsCcVVVVadtvP8U\nnItx5dTox6kK2WcKXplMJj796Y+tGiAPP/w4DzwQYPv2Of7xH89taKz8dgWPP/4499xziNZWJ1/4\nwqfP+R1aJhW4jUxG5TOfuXo13Uqj0awWTL4UVFXl3nt/S1/fCa699p2rRtn8/DzPPDNJIgE9PcNs\n2LCBbDbL4OAgR49mKCqSSCQSq97LJ598knvv3U9HRwmf/vTHzznOM4kuotEozz9/grk5DZ2dx08z\nNLRaLYlEglgMCgUNmUwGURRP0/wIhULs3v0YbreTD32oC6fTSVFR0WnK56fWZRw/fpwHH3yaVCrM\nkSNm3O4FSkurqKzsxustprx8HZIkYTZvYmZmHkUp4fjx5VSoYFCD33+I559P4PWGKC+voLd3LRrN\nCTKZAjMzZnS6EOl0ES6Xil5fBOjQ6Qzkclo0GhOKYgQsaLWlqKofQahBkiYwGnVotYtoNCGMxkrS\n6TlkuR2TaRJRjGIwmNHp/KRSWkIhKzbbAhaLDbtdJJeLMDRUisk0j9crodWasVrzLCyoTE0ZaG5O\nUl6eIxYTyOfDxGJe7HbYuNHIzEycQ4eyGAwJbDY74QwGRQAAIABJREFUpaVuNJoCo6M6dLrlb1I2\nW2B+fpldKpVy0NRUjMulP8kulcBuz6HXC9hsVhKJCGNjdurrRS67zMrgYIzDh0NoNClMJjv19Q5S\nqSR79hTwemUuusiEzycwPBwim82i0XhZs2bZmD58WMFojNHQ4EAQRBIJicXFDLGYk95eHaKoY3g4\ngyxHEUURk8lMeXkRPt88g4MK7e1mOjtNjI7GmZ72o6o6rFY7LS1FBAJhHn88TWWlxPbtRsJhLePj\nAZLJAnq9i44OA7Iss2ePhNEYoLGxDFF0kc/L+P150mkX3d0Ker3Ao4+eQJLmsFpLKCryvKZFw+fb\nXiCbzZJOp1/S0PB4lucnEAicdjwQCLwkS15paek529vt9tWa0Jdqs3LOV9NvaWkpqqoSCAROi2oE\nAgF6enpe6dLfcnjb0DhPcKZo1euNN0P47rXCqzU03mwD40y81nM9NDREOBzm3nufZnYWWltzlJQk\nmZ7OUFdXRiBQQyCQYvPmMg4dGmTvXhN1dXqKijKEQlEaGqqIRuuYns6xcWMRQ0PjHD7sobxci8cj\nEwgs0txcSyzWiM+Xo73dAATp63PR1JSntVVhdjZ6ctNQSSAQxuuF2loDAwNu8vlpmpv1nDjh4cQJ\nHXV1WQTBj89XTlGRj/r6EPPzHqanweGIUlJSIBLxEA5LaLVJTKYcev0SiuJCUaoxGDLk82ZUVU+h\nkCKRKJBM6hkb8/HMM8PU1j7H5Zdv5K/+6q943/vex8UXX8wtt/ycoaEJbr/9AWKxBFde+VdcdNFF\nHDw4wBNPxEmnn6WtrQ2tVstdd/2O554LcPHFQ3zykx/lqqvetXrfJEliZGSE3/zmMJIk0NTUwM6d\nO1m3bh1Wq/VVOwbGxsYQBIG6ujoCgQAHDx6ktbWVxsZGRkdHCQQCbNiwAVEUVzntzxSpOvV5OrVA\n+czoR01NGfX1PlpaWldrG9Lp9MtS0abTGVKp5Zqcl4p2LjNrFZBlzWmpXudqNzMzQ0VFxeoirSgK\n+/cPMzSkobt7eNXQqKioYNeuJqLRBLW1taTTaQRBYP369QQCIRwO+2k6HZHIEqEQBAKR0/o8cuQI\nAwNDXHjhjrNSwVwuF+985zpmZ/3nXMwbGxv55Ccvo1AorBqXK3MuCAJHjx7lgQfmqKiY4f/+37/H\n6XSuGiKnpkzNz8/T19fH8PA4zz2Xp7FR5rLLyunp2cLatWtXhRnPhZXv1eHDh1lcbOT558dIpbLs\n359jYOApbLZqyssdpNMhNBo7fr8Xo3GeZLKAyZTFaCxHlpPo9SKCEAQ0qOoJtFo7udwAFksDshxA\nEFrQ6ebJZMBstmO3T6MoBVRVTyymkMtVUlQ0idsdRaczIssBpqaqEUUFrzeGTmdEq1VYWsoxOWmk\npUVDeblMNCoQi4VJpdyYzVq6u5fpa/v6cuh0MUwmOyUlbgyGAidO6FDVHDU1y0bz0pKKJCUIh+3U\n17vo6hIZHEwyNRXDZErjdJooKXGRTEbp69NQXq5y+eVWxsai9PWFyOUyGAxuGhtLyOVy7N+vYLOl\nWLfOQiqlZ2YmztJSFll209VlRK8XGBzMUSgs4XabMBqNOBwW5ucTzM4KdHU56OkRGRpKksnEEQQt\ndruFhgY3CwuLPPNMlro6lUsuMTMzE2NwcIFsVkEUHbS0mMhkMjz1VBaHY4nOTjOKYiIYjBKJ5Mjl\niujsXH6+BgZyFAp+PB4PVmsRRUXLooWhkJn1603Y7QZOnIiTSgUQBCfV1bV8/OPvobKy8nUxNM6X\niEY0GsVsNr8kc6Zer6e3t5cnnniCq666Cli+xieeeILrrz83oceWLVt45JFHTjv2hz/8YbVmb6XN\nmed47LHHVtu8XL+f+9xy9Liuro7S0lKeeOIJOjs7geVi8P379/PZz372T5mONxVv09ueR3gjDY2V\nzdPrQRP7emPFg/hSIePXi6b2T8WpIoN/7lyrqsrY2Bjj4+P81389yP79E5jNWbLZOHo9VFY6GB21\noyhxtm0rZ2pqkmBQh92uIZPJnSyadjI+biWVSrN+vRu/f4JAQMThUMlkCihKjLo6N8Ggi1hMor3d\nQiAwycyMlbIyLRpNgXA4SEmJC/AQDMaprhYBifFxDxZLlLo6CAQEUikDFRUq0egsi4uluN0yFkuG\nSERPJqOnpCRHPh8lHC5HlqNYLAnsdgvZrEQq5SWb1QNxdLoMDodATY2eri4v69fX09lZRWWliNGY\nR1V1+Hx+RkbyTE3tp7jYQ11dHVu29LKwMMuxY1pEMcHWrRtOpt7IZLMLXHTR+tUoxMDAIAsLMVpa\nvHR0tKOqKgMDA/z2t79HEDRUV1fj90/icmnZtetCLBbLKxquL7zwAg8+uOwFD4fD/Pu/382+ff2s\nXVvDE088zR13nGBx8QS9vR1873s/5+mnfXg8BXQ6Hd/97n9x9Ogx1q3rRKPR4Pf7MZvNq/2dKXhl\nMBgwGo2role1tbVceOEGmpoaSSaTfP/7P+HBB/fidOrweDwoinLa5kKj0VBTU0N9vZVLLtmxSjl7\nJqxWKy0tlaxbV09HR8dLvlO/+c3v+NnPniES8bFu3bJ+hlarxek0Ul5e4MILLzitj4aGetraWk56\njJf1gcxmM11dHbS0NJ82z1VVlVRV6di163SK3ptvvp3HHlvCao3S1dV52ng0Gg1NTY309nafJryX\nyWR46KGHmZ6eYtu2bVRVVZ11TfF4HFEUCQZPsHZtJZs2bThFFX55/rXa5cLfe+65n3vv9WG1pli/\nvpTLL9/BVVe9k8rKSoxG46pBcir5x0p/Op0OURSpq6tj7dq1bN3aSW9vN6K4hMWiY37eQCg0jiRV\nY7NlkaQlPB4jilKFKKbJ5TQIQoJ8XkAQCgiCFaNRT6FgwGg0kMulEUVQlBCimEejEclmYySTzajq\nIoJQissVxW5PUyg4yGaTxOOekxTDaUymAqpqJxZbwu8vpqpKorpaRyxWIB5PkEpZEAQTLS0COl2O\nsTEDmcwCBoOTsjIdXq+OyUkNfn+BsjIJmw1kWUsmE2duzonbrbJ+vZv5+QTT0zKQwGQSqatzotPJ\n9PUtC3Fu2OBGllPMzeVJJuMUCg5aWsy4XBr6+2FpKUp5uRaLBfJ5HUtLcRYW7DQ1aWlstDAxIbGw\nEMNozGO1Gqiq8pBMJjl61EBpqUxvbxELC3FmZxPIcg6TyUJbmxtByLFnD2i1Ebq6PChKhmAwQywm\noSgu2tutOJ0ajhxRWFoKUFpqxOHQYzSamJ+PsrDgpKNDR02NyPh4lvn5RfR6LQ6HSFOTF78/ypEj\nemprc3R0FOH3J5idjSBJWpzOIj72sUu58spLqaysfM2ZoVZSNd+sdfKPxczMDPfffz833HDDS47X\nbrdz4403UlVVhdFo5Otf/zpHjx7l1ltvxWKx8NWvfpU77riDd7/73cCys+Ff/uVfiMViVFdXc/fd\nd3PTTTdxyy23UF9fDyw7Rb7+9a9jsVgoKirilltu4Z577uG2225bJcB4qX5vu+221YJ+RVH4zne+\nQ1tbG7Isc/311yNJEjfffPNbbU/2tmDf2/jT8JcY0Tg1grHCSvNWYJF6LeZaVVV8Ph+BQICf/vQP\nFAoZDAYNkpSgqKgUk8nAgQM61qxJsXNnMYcO+Th2bAGHo4ilpRR1dRbcbnjhBS2pVJStW8s5dGiC\nkREDdnsRi4tZjEYta9aIvPBCKaqaZN06D/v3D3PsWC0eTxGLizKLizFqakoZGWliejpCd7eH/v4M\nhw4V0dlppKUlwuysQKEAtbVmBgdPAGuorS1hZibE9HSekhIT1dUaxsbmSCYbKC5O0dISwe8vx+/3\nYbfrsdu1lJZGkSQbmUwRS0sZ0mknwWCGsbFxqquztLdXcs0176WtrY2xsTEefPBR9uw5xp49HuLx\nu/k//8dBTU0Nf/M3V+JyPUFf3wjf+c7N/MM//C3bt2+nra2N2267k0OHjvOJT3yIa699Hzt2zFJZ\nWYksy2SzWR588AmefDJBPJ5lw4YNfOELnzntnp6JiYkJfvGL+6ivL+dDH7qG++9/lv5+sNv3sW3b\nFjQaFa12ecNdW1tFXd0UTU3Li5HbbUaWlwu7fT4fExMKS0sxlpaWePbZF3jyyVF27mziAx9432kM\nSmdipWhcp9OtRhIKhQKplEIyqSeVSgGcs/hcEAQ6OzsRBIFCocDo6ChTU1Ns3rz5tKLLlUX35ZBO\nZ0inIZXKnnZ848aNbNy4cXVcK1S1K+lfr6Y2zW63c9FFF511fOPGNSjKAG1travHVFVl7969JJNJ\nLrzwwrNosQcGBrjnngFMJmhubj7r2g4ePMgvf/kHmptL+MY3Pv+S35Pdu//AY4+9SGmpnoYG2L59\nI1dffdVp6VdnRj9OdS6lUini8Th6vZ5IJEJJSQnR6LJw4fvffzUajYZjx44xOVnBvn1zJJN5crkO\ncrkh9Pol7HY94bAJUSwQj1djNE6SyZSiKGOoahW53BgaTReyPIKqdiNJ/eh0LszmJRRlErPZQDY7\nSixWgaJk0Os1iKKD0tIY2WyeRKIUSZpAlkuoqDBRX58iGNQRicTJ5w2IoovWVg2plMTgoBFBWMRk\nslJU5MHpVDlxQiCVUigrS6PTGVBVPblcjKmpZea6XbuWPfmHDkXQaJKIoofaWi/5fI4XX1xWJu/t\nFUgkdExPx0kkMmQyTjo7vRgMOgYHJRQljstlwGAw4HRa8fsDTE8LdHba6Ow0cfz4EvPzi2g0Klar\niYYGJ+HwEs8+K1FZKbNrl5WZmSiDgwEyGQm9voj2dv3J4m8ZszlCa6sXrdZKJJIkFMqSTpfQ02PC\nYNAzOCiRz4ew222YzXbKylwnGfwK9PRY6OkROXEiSSoVQ1UN2O1OWlrczM8v8uijSWpqZC64QGRx\nUcuJEwukUiqi6OHqq9eydu3aV0xNfC1wPhgZ8PKF4Ct4//vfTygU4sYbbyQQCNDd3c2jjz66ahD4\n/X5mZmZW29fW1vLQQw/x+c9/nptvvpnKykpuu+2205iotmzZwp133snXvvY1vva1r9HU1MT9999/\nGmPfK/UL8KUvfYl0Os2nPvUpotEoO3bs4JFHHnnNa27eCLyto3GeYEXw643C66FH8UYhmUxSKBSw\n2+3A/0QwVmgvjUbjW8LAWMGfM9eqqhIOhxkZGeEXv3gKvT6OLFtIJMJccMEa+vsnGR93sGVLAUlS\nT1LEFpFM6kkmM2zaVMbs7CLHj5vp6pIAA1NTE1RUVJJMFohGVdats5FIpDh0yEhdXQyHw8LQ0Che\nbzUaTZ6lJYGaGhWbzczBg3qKiiK0t3s5eHAMqKShQWJ6OowkGaisNCFJImNjgzQ2NmM0FhgfT6LV\npqmrcxCPmxgbG6S6uhWbLcHMTJilpWJ0Oh+1tctUnjMzEVIpD0ZjGItFoKbGQ3m5C61WYGIiTCgU\nZXExDZTg8US48MLNfOITH8Tj8bB//35uv/33zMz4qKtr5X//7w/Q0NDA0aNHuemmhxAE+NKX3kNr\nayuHDx/me9/bjdEIX/nK39DU1EQqleKhhx5Gq9Vy2WWXcvToUR5+eA+XX76ZnTsvOuv+KIrCb37z\nO/z+MNdc89ccPnyYH//4CFVVBf7pn/6BAwcOcPDgIFdffSltbW1MT0+v1nPA8rNssVjQaJbrAhKJ\nBF6vl3Q6zZNPPondbmfHjh386Ec/5amnAlx0kZdPfvIj/OQntxMMRvnkJz/wqutCTpw4QTAYZP36\n9ej1eo4dO7YqQHgq81UqlcJkMpHL5fjnf/4h4+MaPvzhFq6++upzUrQuLCxw330PYbeb6O3tobW1\ndbXmYWhoiMbGxrPyqE+lqgVeFZPUq8WZKV+zs7P88z//gkQCPve5S9i0adNp7QOBAD/+8S+xWET+\n/u8/dhaF6AMPPMDttw/Q0AD/9E83nLURWNaFCHHHHb/h6afjXH65m0984kOYzeaXvZ6ZmRkWFxc5\ndmyQycl54vE48biGfD5GoeACQmi1HkymOILgpKrKjFYr0tXVTDwex+l08sILfSSTcXw+E9nsKIlE\nGWbzOKmUDqs1w9KSBperQCymx+nMk0gIOByQyahYrWay2QJGoxtF0aLRCCe92SGsVjMajYqiZIlE\n6jAYRjAam3E6F7HZRAIBhUxGC0iYTHYqKgrIco7JSRs63QQmUz12exy328HYWJJYzER5eRRBMCEI\noCgppqaKKS6O0t5extSUn1jMgqIEEIQyGhqWtyP9/VoMhjjl5WYUJYOiWIjFFolEyujszOJ02hka\niiFJWYxGMBoFKivdLC6GGBx00NQUpaGhgrGxeVIpyGbTWCxFtLRYSKfTHDpkwO32U1tbRTy+iCwb\nV5W/29uXU+b6+/NAEIfDgSjmcTjcTE7OEAyW0NubxeVyMjQUIZNJotOJWCwCDQ3FzMwEGBiw0dwc\noba2iunpeVIpBVnWIIpWWlrMpFJpXnxRj9M5S3l5JaqaIJMRiETS5PNFXHZZGe3t7axbt+51X88k\nSSKfz7+uFLqvJR5++GFuvvlmXnjhhTd7KH/peMWP8tupU+cJzsVu8npiZWOj1+vPG3GeFayomhsM\nBtLpNKlUalXl/M1MkXo5ZLPZP2quVyg9n3zyKX74w/uZmDhOJGJAluNs3lyP3x9lYECludmIRhNl\ncTGGw2EkHneSyWTZvLmaUMjP0JCOigrQatMsLS0zxKRSLuLxPN3dHiQpwvHjBjweBVGUCAbnT6bn\nOInHobXVjtmscOyYFb0+QUuLiM83TyZjprhYJBIJkMko1Na6SCSs+P2TVFY6MRgczM3J6HRxamrM\nRCIefL4TVFRYKS4uYXJyjnTaRFWViMtVIJs1MjeXRa8XaW62UVsrAiKLi1H8fgOBQByNJstf//Uu\nrrvuPVRV2ZEkP0tLVgYGjjM8PEVTUwVdXV2sXVvP0NA8yWQGiFNRUUF1dTVWq0RJiZ5MJoPT6aS8\nvByNJsLataX09PQgyzJ9fX3cccchJifDdHfX0Nvby65d26mrq129N6FQiGeffRa9Xo8kSfz8548z\nOJihttZAT08PBkOYjRvbaG1toaGhgR07Nq96spxO51nK2qfS1a4s8nq9nubmZmpqatBoNNTVVVNX\nJ3LRRTtIpVLce+8LzMwUaG62U1FRQV9f3ysKcLrdy5oeOp2Ovr4+fvCDR+jrO86GDW04HA70ej2P\nPfYEt9/+MKJYoKWlhX37XiCZDLJjRy/FxcXkcrmTqQe/JpmMUF1dzaOPPsqddx7lueeeZ3g4TGmp\nEbPZzCOPPIrFYqa1tXXVGaDT6ZBlmXQ6TT6fR6/XMz4+ztLSEl6vd3UuJiYm+M///Bmzsz46Otau\nHh8fH+fRR/+A0Wh4SWarM999QRAYGurHaFS4+OKtp82/LMvYbDYuuGALW7duPM2IUBSF2dlZamtr\nKS+HnTu3nEVHCXD77Xdy551P09BQxNatFezcuYPi4uJzfoNWNF3279/P3Xc/xuOPDzA4OM7srIFM\nJoiiONBokmg0ZlQ1jaIYSSYTRKN6pqcXmJjIc/jwiwwNpRgePkI+b8DtNmAypaivL0NRYtjtZlS1\nBK22gE7XglabQ6OpRatV0WprTqbJVVEoSIhiKYqyiNksIIqJk4J+FSST84RCdWg0IVwuIw6HgMmU\nIRbTsbBgOCnmZ6WyUo/BkGF01E4yOY/DYcfhECgtFfH7JcbGDHg8cVyu5fQyVc0wPW1Hqy3Q22sj\nn0/j82lIpcIUCg6am80UFwsMD6uEQimKixWsVhWdzkwikWRiwkpdnZauLidTU3Hm5lKoqoTZLNLc\n7EFVZfbvFzAa42zY4CWRiLOwkCGRyKLROGhpseByCRw+XCAeD1FVZcBi0SLLGhYXEwSDTjo7Raqr\nRU6ckFhYCCGKKg6HkZoaL+FwjKNH9dTWqnR3u5idjTM7GyWXK2A2W1m71g3keP55FZ0uQne3l1wu\nTTCYJhrNoaouOjpsOJ0a+vryRKN+SkoMuFwGjEaR2dkYfr+TLVtcXHZZN+985ztXvwGvN/L5PPDn\nUVG/kTh48CDT09N86EMferOH8peOV0ydetvQOI9wqojXG4FsNosgCOfNh2UFuVxuVW+kUChgMple\nc0HD1xJ/ilH329/ez623/o6FhUkmJgSMxhSbNlUzPR1lZiZHaamWbDZCLpenqsrF2JgNVU2yfXs1\n09OzzMyAx6NFlrMUClnq6z34fHbS6SwbN3rx+334fEa8XpCkLNGon/JyF/F4EbGYTG9vMZlMhOFh\nM+XlYDZn8fsDCIKIxWJncTGE3W6gpMSGz2cnlwvQ3GwjGrUQDBZoaBAQhCRTUyXAIg0NemTZxcxM\nCpMpS319EeFwgfn5CCaThTVrnAiCRCikYXY2RTqdpKengR07OhGEJeJxLTMzUV58cYLJyVHe9a5L\nueaa9+BwyAQCMYJBhf7+/bhcVrq6umhtrWR4uJ+9e7Pk8342buylsbGR++9/ggcfnEOrXWTjxvW0\ntjaTyWR45plnsNuXN+0zM6OUlpq5+OIdqxGodDqNLMsYDAbuuec+/vu/RwgGT3DFFZcgSWFKSrRc\ndNEOvF4vXV0d1NXVvabPotlspra2FovFgtVqxWTK0dhoY/v2bbz44ov8+MdPcvx4P5s3d62OeYWp\n6lRPaC6X48CBA4RCISYnF7BYBC64YONJJfN7GRk5wfi4CASwWIzs2zeJIIi84x1bSSaT3H//Ixw5\ncoS9ewvEYj6am6u5++7d+HxTWCxgNheRySwwMjLCAw8sMDc3zZYtnfziF7/mF7/4PdlshIqKCoaH\nhykUCsRiMW655QFefHGUNWsqViMfe/fu5fe/nyORCLN9e/fqNd1xxz3cd98CkjTHtm0bV6/rySef\n5Mknn6WsrOSs2hKDwcDmzb1ceOGm04yTiYkJvvvdWzl+/Djr13ef9W4++ugf+MlPHiUcnuWDH3w/\nHo/ntL+vOAMef/x5xsZk1qwp4tprrzmnsaeqKvv27WPPnj389rf7OXAgSC63iMnkZMOGcrq6Snnv\ne9/Bxo31vPe972Ljxmbe9a5L6e2t58ILN7B2rZempjJKSgREUY+qSsgyRCI5ZmfjBIMCwWAEVTUj\nyxkggdUqIAghrFYtOl0MiwV0uhiiqKDTRTAazeRyfozGBjKZBZLJZvL5JQTBhcWSx+tdXh8kqUAk\nkiccdmGxRHA49DgcBrTaBOPjLtLpMG63EYdDh9NpOJneaMbrTeB269HptOTzaWZn7agqdHaKaLUS\n8/MC8XgQWXbS0CBSUWFgbCyP35/GZpOw2bQUFdnJZNIMDprwenNs2uRhfj7G7GwaWZYwGi2sWeNC\nFBX27gVFCdPe7kKjkYhEciwtpclkXLS3WyguFhgYyBEOhykq0mGzaSkuLmJhYYmJCSutrTra2+1M\nTMSZnY2gqgWsVpG2Ni+ZTIa9e8HpTNHT4yEWSzI/nyCdzqPXO2hvd2KxqOzfXyCdDlBXZ8Fq1ZJK\nKSwupojFXHR0iJSXGxgaklhY8GOzCbhcIlVVXmZnwwwPm1i7Vs+uXS1cddVVdHR0vKFrcz6fR1XV\n82Y/8NxzzxGLxXjve9/7Zg/lLx1vGxp/SXijDQ1Zlk+q4J4fOYGFwjJn+kq6xVvdwDgV2WwWnU73\nsh9xVVX51a/u5r77HmV0dJKRER1lZf8/e+8VJNd5nvn/Tuec0+SMyRETMABmCIAEKYqkKFnB9tra\n2mDtll2++ru21he+c7nKJYlea+2VVKJlyhIlcS3JFoNEiQITcpgBJgGTY+ecczj/iwFQhimtvV6J\nIll87rr6dNdX3adPf7/zvu/z1Ojt1bOzkyUazWAwKEmnI7hcFoxGNcvLajSaHJOTNnZ2fMRiVbRa\nOdlsHpdLjculYWFBTa2WZHq6nt3dLeJxBTqdQCZTQqHIU1+vZW/v0E7x2DEnbvcWfr+O+noZxWKG\nSCSEy2WkXLYRiyUYHLRTKBTZ2jJhs+VobZWwvy8ll4PeXg3h8B4ej42mJgkmUw6PR0KhIKG3V0Mq\nFcHnc1Cteunrc6JQ6Nna2iWRMNPUJGVkpIFKRSQYTLC9XSAej/Lww1M89tgECkUVn8+N36/n+vVz\nSKXwW7/1GTo763G7b7OxYSKV2mFg4AjNzc1EoxFisSgOhwKn04HRaMTt3ieVijEx0Y3L5aJYLPK1\nr73AuXMpdLo0MzMnmJk5xokTk/c3t+FwmC984Wu8/fZ1BgY6KRRy+Hwe+vsbGRkZoq+vl4mJsXet\n5UAQBNrb2+nr60WpVBIOh1le3sZoVDA7O0UoFOLixYv88Ic/5sc/Pk9LixOj0cjKygo3btzgW9+6\njs/n57/8l6fRamW8/vplLl+e5/r18t07tSbW1kIsLq4DVarVMoVCjGvXbvLd7+6TTu9w6lQboVCA\n+fkNCoUqen0909PNmM1w7VqNWMxLQ4OcZNLL1avLrK3tcuVKjJWVy1QqGV59dYOlpdsMDrbz5ptv\n4XbvMjbWS0tLC6lUCo1Gg1abYmqqn+7u7vu/73w+QyLhZmZm+P4sRSaT4X/9r+9z7VqGuroK3d3d\n9z+rYDBINpvFYDC8AyQWFxd57bUDisUCx471veP7m5+/xeJiDIOhxuzsNP9czz//As8//yOOHevj\nxIl2ZmdnUKvV7zju4OCA5eVlvv3tt7h5M4LRmMFu1/Gf/tNv8MgjE3zkI48xNjZCfX09jY2N6PV6\nbDYber0ep9OJ0+mkvb2dgYF+jh2bZGZmijNnjjE83MHQUCMulxazWUAqldxtL1JRqUAup6NUkpDL\nGalUauTzNiqVMqVSHbVamVrNgUIhIggSzGYlBkMOi0VNpZKjXBaJxx0Ui3GgHqczg90uUq0qyeej\n+HxWyuU8NlsZg+GwWhGNZtjZMVBfn8XlkiOKAuVyDr9fR60mo79fjkJRxu+XkUwGyeVMtLWpaGtT\ns7dXxOvNo1Tm0WplNDRYKJfz3LqlRKfLcex2LoCDAAAgAElEQVSYg0QihdebJ5fLI5EY6eszYDAI\nzM3VSKcPqxMajUClIiUcThMMGhkcVNHaqmZjo4DfH0Emq2IyqejocBKLpbl5U0Zzc5WxMQtebxKP\nJ0GxWEOl0jEwYEUmq3DhQg1RDDMwYEUUi0SjeWKxIuWymcFBHVarlMXFMtFoEKtVhsUix2Qy4HZH\nOTgwMDAgo6tLx9ZWBq83gkQiYDCo6e11kkymuXZNwOUqcvJkC08//VFmZk6+I8Pm3dA9i/33C2i8\n9tpryGQyPvrRj/66l/JB14eg8UGRIAi/FtD4P7k3vVd0DzDutUjJ5fL7MxrvdcC4p2Kx+AurR6VS\niRde+B5vv32J69d3WF8X6e9X43KV2djIUSikUSh0pNNRjh7tJJHIsbSkoL1doKkJ9vfDFAplpFId\n6XSOwUEXglBmbk6B2Vyio0OFx+OmUACZTEM8XqSpSYVOV2NpSY9cnmNiwsXe3jbptAK1WiCbLSGX\nF2luNuJ2mykUkhw96iQYjLC5qaG7W45aneDgoIZMJlBXp2N3d5VKxUp7u5lkMkwwmMVuN+Nw6NjZ\n2SCbtdPdrUOvT3FwYCYQ8NDbW0dbWx0ezw77+1oSCR9nzowxMdGH17tOMKjn9u1bFIsl/vN//m0m\nJweJRlfweCysr98km00yM3OCzs42stkttrcDLC5uMjzcxdTUBHo9vPbaOvPzS4yN9TA+PkZvbyOr\nq+sEAn6OHDlCPp8inw8xO3v0vuPQ/v4+Fy9eRK/Xk0gk+NnPbpPJiIyMNDM1NcXx44NMTo7/m8+/\nYrH4S2tZrKurY3i4jVOnplGpVPzX//r/8Z3vXMDtDpLPO9DpUgQCAb7+9fNsba2iUinI52PUamUu\nX77N/HyNUmmNcNiD3x9DKlUgiipqNZGRkXqq1SIXL1YpFvcIBLxEIlFUKhlgIpNRMjRkwmiscuuW\nSLkcx2SSkUz6aGysI5EQcbvVHDkiIRJZJxhUEov50Gp1FApJoEQ0miIabcRmK+JyOXjmmb/l1q07\n/O7vfpK6OhdXr15FrVaj1+tpa2vlkUdOPDAUK5fLyWTCqNU5zpyZuR9g6PF4+MIXnuPixZsMDLTf\nn+m6J5vNhsGQY2qq7wGYuZeZ0dvbTVubhocfnn3ApereMf/7f/+YtTWBnh4dTz755M+FjFAoxBe+\n8BzXr2+j0RSw2dT8/u9/lo9//CM0NzdjsVh+4TkUCoUolUrMzc0RCoW4fPkK29tbXLkyx97eLltb\nB1SrJUQRmptd6PVyurubMZkk9Pc3YzCU6ey0o1LlaGoyoFBkqKvTolKlsNlU1GpJtFqBalVBPp8g\nnW4mmfSSy7Wh1cYxGjXU1SnQaNJks2YSiRi5nBmVSkFzs4heL1CpaInForjdVhoacjQ0yCkWq+Ry\nGcJhDZWKgu5uAa22is8nJZkMks2aaGyU09OjZ38/h9tdvNuKpaSlxYJEUuTGDTlSaZqJCTvFYpZg\nsEgymaNSMdLXd1idWFmpEo2GsVqlGAxSrFYTgcBhdaK3V0p/v4Ht7SRe76EFslqtoKfnELYuXRIx\nGjOMjtpIpdL4/RkymQoSiZHBQSM6ncj161XS6QBNTWoMBim1mpRAIEMkYmJ4WEVTk4q1tTw+XxC1\nWorJpKStzUkweNhe1d5eY2TEgtudxOOJUyqJaLU6BgftQIXz56t326ucfOxjj/D000/+i0GXv0qV\ny+X7JhLvB7388svYbDZOnz79617KB10fgsYHSe/mjAZw33HmvToM/s8B414FQxAEyuUyKpXqfQUa\n/7x6lM1meemll7lxY44339xjZyfPyIgBQQiyv19GqaxSKOgpl5NMT3fh82VZWakwOKhFJkvg8yVQ\nqaTkcmby+RzHj7ffvbsto7VVglyeJRIJo9WqKRZNJBJF+vvNlEoJlpfVuFzgdEoJBn2AHKlUSyxW\npKlJidEosLSkB+JMTBwG/UWjSlpatKRSHiKRCg6HFlHU4HZv43JZ0evNBAI5isUYvb11pNN6dnbW\ncLnsNDW5ODg4IByu0dRkob1dTSiUw+2uotEUOHt2knQ6SChUYWMjjFxe5t//+0+h0SSIROTcuXOb\njQ0/4+PdPPHER6lWD9jby3FwUEIuTzA1NUVDg4vFRQ+lUhGrVUVTUxP5fJ75+Q0UCoGJiX4kEgkr\nKyu88MJt3O4Qk5PdTE5OcObM9P3cBUEQ+OpXv8kPf+gBgpw9ewa7XcboaAujo6NIJBLUavU7zr17\nFUJBEO5XD+x2O+l0mi996VkWFpYYGurj/PnzfPnLf0+1mqWjo50f/OCHnD9/hba2JlQqFRsbG4ii\n+K+ukAiCgEaj4ZVXXuX1199iYSFAIqFmZERFd7eOCxcOWF6+gUplRiIpMjraTCCQYW6uQk+PFLu9\nxvZ2kFQqg1rtxGQyMTHRQKGQYW5OxGDIYDQKiGKBWi2HINhQqxs4etSMVltgeblKsRhBp9MhleYI\nBt0sL2c4OBCYmjLR0CDg9VbR6WQYjXYcDjOTk61Eo2muXKnQ3FzG5ZKyvb3HlSvXiUS4W23Lcfny\nHD/4wTax2C4TEyN885vf5fz5K3R2tqJSqTg4OEChUDAyMszs7LH7kAHcrezcoVoVmJjovt+WVavV\n2NvbQ61WMzQ09A472xdffJmvf/0nlMsJHn/8sXdAxtzcHFeuXOXo0X66uzXMzJx8xzGFQoG/+7vv\ncOXKdZLJPIIg5/d+7xN8+tNP4XA4fu5mLp/Pk0gkePnlH3Ht2lX+/u/P86MfvcTlyxHOnz/HrVtl\nFhaucucO3Lkzz+qqhJWV6yws1Lh58zy3b8tZW7vG3p6J7e2bBIMOPJ47JBKNhMNbpNNtRKM7xOOd\nxON7pNNdFIs+arVGNJoUWq2S+no5NlsO0JDNxohGTSSTJaRSEYNBS0uLgFxeIRLRE4/7SSTstLRA\nV5eKTKZGOp0nmVRSrWrp7BTR6Sr4fFKiUR+ZjAmHQ6Cvz4DXm2F3t4QgpNFo1LS3m1EqK8zNSSmX\nkwwOGpFIisTjVeLxDMmkkYEBNfX1CtbXSwSDEdRq0OlktLY6iURSLCzIaWk5rMh5PEm83vjdwWst\nAwNWpNIKFy+KCEKUnh4zglAikSgQi5UpFIwMDh4CzPJymUgkgNksw2iU43JZcbujbG9r6e+X0tOj\nv9teFQUE9Ho1Q0N1ZDJZLl8WsVhyjI3ZSSQy+HwpstkqMpmJoSEzWi1cvVohmw3Q0qLh7Nlpfu/3\nPvuOzJdfh95voPG9732Pzs7OBzIuPtSvRB+CxgdJ73ZFo1wuI4riew40fhFg3GuRqtVqlEql9y1o\nJJNJXn/9dRYWFvjHf9zE54vT328kGt0hkRAwGBQEAmrU6jzj403s7mZxuws0NckpFIJkMmXq6/Xs\n7uqADDMzbezv+9jdreFySalUMhSLOVpbHbjdOnK5HOPjDvz+PXZ2VDQ1yRCEEqlUhLo6C5mMiXi8\nyNiYg0IhzsqKFperhtMp4vUGyecFtFoV4XAIQajS1GTB59OQy/kZGqojlVLh9dbo7JSj11fZ3rZR\nKAQYHXWSyShxuwuYzRW6ulxEoxK2ttaw2VxMTx/B7V5jf99KLLbO44/P0thoYnt7g4MDPV7vTc6e\nPcPERAd+fwyvN8XNm/OYzVo+/elPUSrF2dtbZnU1jyjGOXVqls5OB6urK1y+HEIuT3PixHE6Ox1U\nq1muXbtFfb2TxsZG3O41mpvNzMxMI5PJCAQCPPPMs9y8ucDo6ACRSIhUKszUVC+dnZ00NTXR3Nz8\nwPkWjUZJJBLo9XoWFxf5H//j7/B49ujr6+Yv/uIbvP56CIslT7lc5qWXNojFcoyNtXH58jzXruXR\nanO0tzfx3HPnuHMnQ1ubCr/fz5e//CorK0scOzZKOBzmxo0bGI1GBEHA7/ej1+vvr6NcLvPqqz/h\n0qVLvPnmHnt7JU6ccOB01iiVzGQyERYW4oRCASYmXGSzEpaXq7S0iGi1JZLJLHK5SLncgM2m54kn\nBshkEiwslJFIQuj1KmSyEi6XkUBAg0ZTx8MPN6FW59jYqFKpxBEEPSpVib4+F3t7JVZXSyiVEZqb\nRapVA6VSlnzeiEYj4/TpHsLhJIuLUF9fwmAQKZdLqFRSYjEDlYqMjg4JEkmOK1dSpNO7KJUK4vF9\nLly4wPJygv39Eg6HyP7+Pl/96k/Y3r7D9PQ7q0tms5n2dhsTE90PVCwuXLjAl7/8Y9bWlpmeHn+H\nZ/2bb15iaSmLxSIyPT3+wHP5fJ6//MvneeutGL29Op5++ul3QEY2m2VjY4PvfW8er7fMpz89yVNP\nPURPT887NnGiKOL1etnY2OCv/urbnDv3E65eLbC5uUI+r0UiKaDXK7HbdbhcSjo762hq0tDT04jd\nLqWtzYHJBJ2ddRiNEpqaLKjVEux2FWq1AotFjkajxG5XodMpaGkxoNGU6eurx2ot0NLiQqmMI5Xq\nyeWSxONqwuEK+TzI5fq7bV5q9Hop1WqG7W0zmYwbQbDQ0CCjs1NBNFohGMyRy4lIpUaOHJFhsYDH\noyQe91Eq2bDbpYyMWPD70+zuVqlW46hUalpbdSiVFW7dkpLNxunoUKFS1cjnBaLRNIGAkYEBFe3t\nara3c3crbiI6nZK+Pie5XJ6rV8FmyzE8bCWRSBEIZMhmD9fyYHXCT13dYa6FXK7A788QChkZGVHR\n2Ki4214VQKmUYTAo6OmpIxRKcfOmhLa2GkNDZvz+NF5vnGIR1GodQ0M2JJIy589XgDC9vWYkkhLR\naJ54vEixaGJ4WIfNJmVxsUg47MdikTM62sV//+9/SF9f77/9T+WXrHs3St4voPH8888zPj7OyMjI\nr3spH3R9CBofJP06QOOeW9N7QT8PMHQ63Tt89e+BhlKpfM9Y2P5LKpVKJBIJFhYW7vryrxGLeWlq\nUhMK7aJU6hAEGW63iqYmCUeO6NjYyBONprFYlKRSQWw2M3q9htu31RgMh0PdOztBIpESOp2MXC6D\nzaamocHAwoKacjnG1JSD7e0twmEpFouCUqmGUlmmo8PB1tahxePUlBOfb4/dXSWNjVJEMUs0GsFq\nNQJWkskMg4MuRLHG5qYRgyFDV5eavb0a4XCV/n4t8fge29t6Ghvl1NVVODgokMnIOHrUTiLhYXvb\ngk6XYmSkjlxOx8bGLsViiY985Djlsoe9PQVbW7uMjLRy8uQ4odAdtrb0rK8vMjzcxRNPnCEY3GJ/\n34jfv4zJpOUTn3iaQCCEz5enXA5gNhsZGBhgcfE2kUiR5mYtjY0NaLVaXnjhNebnq7hcZaanp5md\nPUZzcz3r6+tYrVY2NjZ49dVtstkiExNdHDs2xczMoVXrvXOvUCiwubmJTqcjnU7z+c8/y5tv3qS9\n3cHW1hbnzkUQxRRnzkzjdu9RqaSYnR2nt7cXqTTO4GAT4+NHqa934HKVOH36JA0NDeRyQex2KadP\nzxCJRLh1ax+NRmB2dpKvfe15XnppFwhx9eo8X//6T4nFdhkaGuTtt9/m2rVrvPzyOru7Sbq65ECc\neLyKRiMQDOpQqQpAlHRaJJ83U1cnQSYrIpUKmM0Ktre1CEKVEyfqyGTi7O5KkEqT3LmzRzDopr3d\nSChkJRotMzSkAeJ4vVCrpQkGRQ4O7tDYKCeT0bK2VqSxsYzdLsFg0NPc7CAUMqJQVDl5splAIMKd\nO1WMxhwKBWQyMXQ6GcGgiWJRYHLSws7OMm+9FSWdPsDlasViEWhvt3Du3B4LC2lcrjgNDUrm5vZZ\nXb3F8nKMjY0FjEYFra2tD1wrBEHAbrc/4GYFsL6+zvy8D60WZmen3rGxamlpoKlJypkzDwYKHiai\nl4hE/ECKU6eO4XA4HnhtMBjk85//GktLG/T32zhyxMpHPnIWl8v1wBpEUSQQCHDz5k2+8pVXuHLl\nLYJBAxJJieZmFePjvTz55AQf/egZnnjiFB/5yMM89tgpTpyY5tixowwM9DM5Ocrx49OcOXOSqakJ\nurubmZwcx+nUMTw8iF4PLS3NCEIJnU5LLpelWKyRz4v4/cm7xgspolEFhUIemcyCwVCgrs5MU5MC\nvb5GNmskHvewv+9CFIPY7Ubq6lTY7RAMVnC7yxQKaVQqM52dCozGGru7MsJhN7WaCatVzvCwhXA4\nw9aWCCTQ6Qx0dZnQ62FlRUY6naG+XkCrFQEFkUic3V09nZ0CfX06dnZS+HwJqlVQq1UMDjoQxTIX\nLtRQKGL09pqpVgskEgXi8QrFooHBQS1Wq4SlpTLRqP++c5bTacbjSbK5qWZg4LA6sb2dxOeLUKtJ\n0es1DA25yOXyXLxYxWJJMzBgJZ3OEAymSadFQM/goBGDQeD69RKpVICGBjUmkxyZTIHXm74LMGqa\nm1Wsr+fw+QIoFFLa2+v4b//tc5w8Of2e29CXSiVkMtl7LSzuF+rZZ5/l7Nmz9PT0/MsHf6j/F30I\nGh8k/dO02HdDlUqFarX6aweNfy1g3NM/Tdp+P4BGNBpldXWVn/70Tb7//Q2KRT8qFaRSQVpb60ml\n5BwcSBgZMWKzFVhbK1Aup1GptKTTEcbGukgk8iwvy+nqktLUBLu7UXK5AnK5lnQ6w/BwI4JQYW5O\njtFYoK1NzsGBm1xORK3Wk83W6Ow0YrfLmZ9XUq0mmJhwsrOzQTwux2RSkM0WkUqLtLfbcbsN5PNZ\njh1rIBgMcfu2isFBDSZTjoODIhKJlMZGPW73OoWCjuZmI+l0Crfbi8lkwmDQsLl5m3RaxdhYM8Wi\nn/39CqVSlTNneohEYhwcqIjHNzhz5gQ6XZXdXTdbWwJ2e5WnnnqcZHL/bstCjsZGNY8//ijF4hZr\na3m2tyP09tZx8uQ0lUqA69eTrK9vc/ToEcbGBlEqM1y4sMLW1hazs9MolVXU6iynT5/EarVSq9V4\n5pmv8eMfb6PRZDhx4gR6fZ6xsQ6Ghobu57EEAgGKxSIajYbvfOfvef75q6RSbjo62njzzXnyeYHR\n0VYGBwexWHLMzk7Q1NTE2NgwDz00QXNzMwqFgv7+Po4c6UIikWA0Gunt7cVisSCRSBgc7Gdq6iha\nrZaGhga6umycPj2NxWJhc3OTRCLF6GgHi4trnD/vZm3tJsVigldf3WFnx4/LBdVqAlGUo1RK2NrS\nYrXW7maoJJHLbTQ0qDEYNCiVZdbXb7O6qkGrlTIzU08w6MHnA0EoUCopcToFwmE3gYATEBgfd1Au\nR0gkAMqEQhocDhCEELduFfH7C3R2alEqS6jVGiwWJfv7NtTqCrOzjfj9Qba3K8jlWaRSGQ6Hikol\nzuuv5zg4CHDmTCPVagKPRyAcPiAUUmEw5Dh9up/t7SoeTxlBcFMsJlAqddjtOgIBIzJZjkwmiN9f\nZGsrg9MpweVy4ff7+cpXvsHy8m16e4/cz/24dy1pamqivV3PmTMnHmi1euONN/jGN/6BujoLJ0+e\nfAAySqUSX/rS13jppfN87GOn+c3f/Bgul+uB33ksFmN/f58LF7YoFODf/bvHePTRh99RMb4XIPjX\nf/1Dlpauk8nosFo1PPlkP489NsNnP/sZJibGaGlpwWq1otFokMvlVCoVAoEA6+vreDwerl27wdWr\n1/n+91/n9dfP8frrG7z22k+4di3KhQtvs7BQZmnpFtvbMjyeXcJhPblcmGrViEKRxWg00dyspLnZ\nRGurAZtNQj4vI5MJsrNjIRrdoVy2YzaL9PTosNn0VKtFwuEq+/ty5PIEBoOezk4DGk2JzU05oZAb\nqVSH2axgcNBCOJxidVUAwmg0Bjo69BgMsLIC8XgWl0vEZJKi0xlIp3NsbOhoaxMYGTHi9Sbx+VIU\nCjXkcjW9vUbk8hKXL1cpFPw0N2tQqwVEUUIwWCAaNTA8rKa+Xs76eoFAwI9KpcRkUtDbW4/bHWNx\nUUZXl0hfnxG/P4XPF6NQkKFUahkasiKRVLh4sQwEaW83IJfXyGRKRCJlcjkDw8NanE45KytFgkEf\nRqMKi0VOQ4Od/f0oGxtq+vul9Pcb2d5O4PGEqdUE7HYLf/AHn+Kxx05jMpnec/9boihSLpffN6Ah\niiJ//dd/zWc+8xlaWlp+3cv5oOtD0Pgg6dcBGuVy+ecOMb4bqlar5PP5fzVg3NM90FAoFO/pi2I8\nHiccDvPss9/hlVdWgcjdYKw0fX3NeDxyfL4ik5M2KhUvu7tVNJoquZyGajXF1FQXPl+BO3dKDA8b\nkMnieDwplErI5UwUChlmZo4QCoVYXJTQ2goSSQq/P4hSKaNatZLL1ZiYaKRaTTM/L8NiqeB0Cvj9\nHkRRhlSqJZEo09Ghx25XcOvWoUPViRP17OzsEQjIaGpSk8+HCAZTWK06ajUdwaCbjo4G5HINgYCA\nwZCnv7+JSMRIJOJjdLQNhUKNz1cmHj9geLiLUqnKxsYdkkkJDz88BPhYW9Pjdm/w5JOzWCwGdnaW\n2NqqIQgZfv/3/wN+v5/t7TtsbCSwWOQ8/vhHODjYJhjc5s6dfZqbHXR0dLC+voog5JDLD4ej4/E4\nFy9GqNVKnDw5wsDAAE1NLr797RfZ29thcLCfhYVlstkCY2PtHDlyhCNHjtDU1EQqlUKpVLKzs8Mz\nz3yLq1dvMTLSzdraJtvbKZqadJw6NUNnZx0jIy0MDw+j1Wrp7e2lrq4O4N/s3iKRSHA4HPfbcQYH\n+5mc7GZgoJ98PsmdO5eIRnUUCjmk0iwrKwsIQhW73c6dOyoaG0XGxsxsb4cIBrNIpSCRSBkcbECv\nl3DuXIFAIITVWsBg4G5AXJV0WkVXl5bGRjUrK6DRKOjsPGy9EQTl3bkGLU1NUgYHzWxuJkkmRRSK\nBA6Hlr6+NvR6OTdvKpDLs5w61YTX6+XgoMCdOyv4/UkGBuw0NRm5eVMkmUwCYQQhgVpdB1SIxTT0\n9Jjo7JQhivVEIhWs1goyWR6Xqx6XS00q1Y7BUOXUqRb8/gTptByTqUhDQx2lUhxBEEilkrz44hZ+\nf5jBwSbUajXFYpFkMsn8/DwKhYLOzs4HWtAAvvnNf+Tq1RJGY5bx8dEHvpd0Os1LL13A7xfo7jbR\n2dn5wPP7+/t88YvPsb6+y0c/Osr0dA/Dw8PvuI6trKzwpS99g/X1FQIBBXa7jt/5nVkee+whpqen\nqaure+A1+Xyeg4MDLl++wve//wqvv/42b7/t4eLFC9y6JWF/f4lg0Eax6KFataBUplGrjTgch9ap\nAwP1NDXpeOihQQYGbAwPd9DVZcHptKDRVIlERMLhA7a3NXi9GyQSNmSyHE6nmrY2G+3tKorFKsFg\nDa83SiRiweHI4nCoaWy0IJcXWF9XEo+H0GqVWK1q+vqshMNJVlYkQPBuKKQOvb7G6iqEQllstgoG\ngwSz2UQmk2F5WUVdXZmjR61Eo4ftT/k8yGRGhobMGI0C8/OHw9mHrVwSTCYdBwcpdndV9PUJtLUp\n2dpK4/cHAQU6nZLR0Qbi8QyXLlWx2TJ0durI5wtEImmSSQmCoGd42IheD9evl0infTidWsxmOXq9\nloODDH6/lpGRw2yNjY0sPl8AmUyB0ahiYKCOYDDJjRsCra0VhoYsBINJPJ4Y+byARmPid37nFE89\n9QhtbW3vaeOV9xNoADzzzDN87nOf+7nZNh/ql6oPQeODJFEU31XQuJdG/m7POvxbAeOfqlAovGdB\nI5PJEIvF+Iu/+Drnzt2kVEqSTFaxWkW6uuysrEhJJtOMjNgIBDZIJCTodApCISV6fYnR0Qa2twt4\nPFmamxXkcn5SqRIul569PQ0SSY6HHupkby/Azk4Zp1NCsRgjk0nT2GgmEDBTq1WZnW3D7z9gY0OC\n0ykiinlSqTBOp5l02kgyWWZysoFSKc6tWwqs1ioNDVK8Xg/FohSNRksikUKvl9HSYmN7W0u5HOXY\nsTYCgQo7OyLDwwaMxgK3bqmpVlPMzrawtxdjd1fK6KgFu11kfd1EKuXjiSemyOfB40ni9+9x9OgQ\nCkWK/f0wGxtpZma6aW9vuvv4Nj5fmD/8w/9AJBLB7a4Sj2/idNr5rd/6BDdurLK+LsduLzA1NUVf\nXytXrixx+XIEpxMeeughrNYyLS1WstksDoeDubk5XnnFTTqd4PjxQY4fn2B8vOt+BQPguee+xXe/\n+zo63aGb0eXLG9RqIseODTAxMUZ3t4WHHjqJUqnEarW+Y2P4q1AsFmN+fp4f/GARnU6gocGJVitB\nra5y506KQMDG6Kie1lYJt2/vkcmUgUOL06EhF3J5hUuXQC5P0tmpJ58PUF/vQqGwEA5LsdvztLRo\nWFmpkkweZiLIZEWOHOkinS6wvCwlFlvCZEqSySjw++MIgohcLuHUqSGsVgNXrgio1RnGxqyEwyEi\nkRLlskgsViWdDlKtlohGrVQqOZqb1chkBZxOF2azmUjETGenkp4ePVtbeUolOUajBEEo0dBgRSoV\nWVpS43RKmZ2tx+MJ4fHkgRJ6vYXJyTbsdhVzc4cA/eSTp7hx42dEoynGxo7Q3t6OVCrl5Zd/xLe+\ndYv9/TuMjw9RKpUolUpUKpW7LnZKTKbc/arXPbndbmKxGIOD7XR3Gzlx4sQDEFkqlXC73Vy4sEml\nIvL006cZHBx84LxIJBJcvHiRhYUFzp/Po9OJ/O7vnuTRR2cZHh5+R/aG2+3m5s2bvPDCD/mHf7jB\ntWvX2N42UKt5kckstLdrcLmUPProJEeP2vmN33iC8fFmfvM3P8n0dC8zM8eZmhpELpdisehZXt7F\n43GzvBxnZWWRO3fg4GCXdFqDVFrGYlHQ3u5icNCI02mmWCwTCMTZ2JCTTnsRRSvd3Qo6OjRUKgKF\nQorNTRXpdAaLRcRu19HZaSUWy7CwIEOhCGOxGGhtNWIySVhfFwmFSpjNBUwmORaLgUIhy82bCgyG\nLEeP2kilUvj9GdLpKtWqkcFBPRbLvfYnHybTYbWso6MOtzvO2pqavj6BI0f0+HxpAoEohYIChULJ\n4KCVUinPpUtlpNIwjY1qFIoqhUKZSJU778gAACAASURBVEQgl9MzMqLFbpexvFwgHPai12uwWhW0\ntjrZ3Y2ytqagv1+gu1vP3l4Sny9MpaJAq1UxNlZPPp/j/PkKen2C3l4LxWKBcDhNPC4iikaefLKf\nJ5+c5ejRo+/Idnmv6V5FQy6Xv+eqLb9If/qnf8of//Efv+c/2w+APgSND5Le7YrGuz1U/csAjHv6\nv03afjdUqVTwer18/vPPcuHCVVKpIolEhb4+K3p9hfl5GYKQorVVRzC4i0KhoVaT4/UqOXJESUuL\nktXVAolEEptNRTIZwOGwo1IpWF3VYLNVGBuzsrMTJhTKodPJSKXimM0KnE4dt2/rkUpzPPxwO1tb\nmwQChxaU+XwZlapMe7udrS0NuVyBkycb8fl22NmR4nJJqdXyJBJBHA4L+byBRCLP6GgdUGJhQYXZ\nXGR42MTubpJwuMbwsJVYbJuDA3A6NWg0RTweN8WinK4uB4HABh7PocNUQwPs7UXx+ys8/vgIxWKM\nrS0z+bybj33sEQqFIru7a2xtxentbaSvr+5ucFeUcjnC2bOnqFS83LpVZn/fy/T0AK2tLiqVXebm\ndtje3uTEiSk2N7eoVMr09DTcH+D+5jdf4Y039rFYKoyNjSGVRpiY6Kavrw+5XE4ymeR//s+/ZWtr\nk6Ghfl588XW2tkRaWhScPn2KlhYT09ODdHR0oFAoqKur+z+aJyQSCQKBAEajkVqtxsLCAoVCAbPZ\nTCqVYnV1FYPBgFwup1wuU6lUfu45LIoi8XicK1eu8JWvvMrm5hK1mhq5vMrMTB8+X4qdHQNdXTk6\nO3VksxXm5hbY2QFRrPDwwz1UKhnm5mqo1WlMJgnVagaLxYQo2igULIyNGdnZuc7lywUSiQMaGxuA\nHIODrQQCWZaWBAYGlMjlQebnI0QiacxmGzKZnImJFgShyuXLYDBkaW1Vc/PmDRYWtpBK9VQqJoaG\nTDidMvb35RgMRbq76xGEPHV1TmKxPAcHRkZHdXR1qdncTBEOJ5DJpAhChf7+Rmq1Cpcu1ZDLoxw7\nVkcwGCIcLlAuQzYr0NmpxeVSc/VqlXw+SmurhkIhzOLiNoVChXy+nrY2JUNDg8hkMjweD7u7Idra\nzJw8eQyZTIZEImF9fZ1r167R1dXFxMQYOp2OcrlMtVolEonwxS8+x/nza4yPd3Hy5MkHIOPg4IAv\nfvFZ3G4PTz11jOPHBx4YPL+nl19+hW98Y5lKJc7Zs52cOTPFyZMn3wEYq6urXLlyhRde+BE/+ckB\n4fAmtZqNkRELAwM2fvu3P87sbB+f/OQnePTRh+jv76evr+/+9fDNNy+wuLjIiy9e4qc//RnXrkWY\nn1/A65WQTCYQBCkGg4qWFjWDg+2Mj9fT3d2MWi0nHk+wvl5ha2sdr9eCThfDZjMwNFRPQ4Mcn6+E\n1+slENBSqwm0t8twuTQYjXri8SRzczLU6ggOh5bGRiNGo5T19QqBQBmbrYjFosDhsFCp5Lh5U4lK\nlWFy0kmplCUUyhOPF8jnjfT1qXA6ZayuFggEfCgUSoxGBYODjXi9cebmoKWlRGennmQyRySSJJNR\nIZfrGR+3oVLVmJurUCj4cTj0GAwS9Ho1BwdFQiEN/f0SGhrkbG7mCQS8SCQajEY5IyONuN2xu+9f\nprvbSCSSJhCIkc3KUSh0jI3ZkcmqXLpUpFz209SkR6eTUqmI+P0Fkkk9p0838Nhj4zzyyCM4nc73\nhWHJ+w008vk8f/7nf86f/dmfvaf2AB9QfQgaHySJoviuWty+W0PVv0zAuKf3Gmisra3xhS88y8LC\nHH7/oT3nzEwHqVSQlRUBo7GITFahWIzT0lJPPK7C6xUZH7eh16e5c6dErZZGqdSQyYQZHT1CNFrk\n9m0J/f0q6uoq7O7GyefzCIKGZDJBX5+LarXE4qIGl0vkyBEtbreHTKaKVKoimSzR0WHAbldw44YC\nQUgxNVXP3t4asZgUnU5GNltDqy3R2elia0tNNptndrYFv9/N6qqUri41anX2fq+xTqclFPIgCBLq\n6myEQpDPBxgd7SaTUREKJWhq0tLYWI/XWyUS2aGv7wgSiZy9vU08njhTU31oNHF2drK43XE+97mP\nk05ncLshmdxidHSYgQEXd+6ssLIiweGoMDU1xcHBBvH4AVtb+wwN9SGKItevJ5FKS5w9e4LjxydR\nKIq88so829trTE0dZWFhkUqlzLFj/XR1dTE0NMju7i5vvXWR+noXq6urvPLKAel0iunpfvr6Omhr\nUzA7O4NGo8HpdD6QCC2KIuvr6wSDQex2O0tLS3zlK9+mUEjR1NTI5z//FX7600UcDiUej4evfOUc\ny8srTE4O8Pzz3+N731ukXA7R2trMF7/4Vd544wq9vW0AXLx4kWq1itVq5dy5c3z1qy+xu3ubWEyF\nSlXm2LE2PJ4kS0tFmppENJoyarUWm81AKKQnHI6j05UxmWp4PHry+QOq1Qp6vYTmZhtut5RgEEZH\ndej1OTY2SoRCB2SzKkwmkbNnx/B4siwsVOjtlWO1VvF6E4hilVxOgcmk5vHHhymX88zPi+j1WUym\nw9RnlUrOwkKMSMRAf79IZ6eJlZUy2WwYp9OB2axgYKANny/H7dsCg4NKWlvlbG0liMeTxOOHVYHB\nQQcKhZxLl6qYTFmCwVU2NnYplYpIpRbyeRWdnQqWlq5z9WoRSNHQoEcQ8hiNBlZWdtnZUTExYeLU\nqU4efvjM/fCz9vZ2hoeb71ek7s1u/NVffZM33ohisxUZGhq6XyWt1Wqk02muXLlFsVhlcLAFs9lM\ntVq9f0NodXWV117bpVAo8/TTpzly5MgD17Rbt27x1a9+h2IxRaVSob+/if/4H99pZ7q5ucnc3Bzf\n/e6r/OxnIQTBj9Fo4OMfP8ljj43y8Y8/zczMYWuVw+Egm82SSqX44Q9f5q233uLFF6/x05++zu3b\nOXZ2vHddoxSYTCKtrQ5mZto5cWKYmZlBBgY60WjkxGJxbt6MsLR0i+VlFYXCLnK5leFhK0NDVpxO\nGwpFmY2NAru7XnI5CVqtnuFhA06nmmSyRiwWYWlJhcGQpLlZi9OpR60W2Noq4/FUcDoLWCwKrFYj\n1WqO+Xk5EkmKqak6BKFIPF4iEsmTTJoYHdXR3KxkayuP3x9AIlGi0ykYHq6/2/5UwWxO0NysoVqt\nkMnkiERkVKs6RkZ0GAwiCwtF4nEPBoMBu11Fa6uNvb0s29sKenpEWlvVeL15AoEgxaIajUbOyIiT\nRCLNxYtljMbD96/VKiSTGWIxKbWantFRI0ajwI0beVIpDxaLFrtdhd1uZnc3yd6eislJPWfO9PHU\nU0/R2dn5vtiw31OtVqNSqbxvQCMcDvPcc8/xJ3/yJ+8LkHuf60PQ+CDp3QaNX/VQ9a8CMOCw/z2f\nz78nQGNubo5nn32BnZ1VFhaq1Gp5zpzpYn9/i91dEYsFisUKUmmOjg4nbreWSKTAsWMu0uk9Dg5E\ndDqRdFqBIKSZmOjE7S6xsVFkeNiIRBLB7U6jVgukUocWlFNTrfj9EVZX5fT0qFEoDl2i1GoFuZyB\nVKrExEQjlUqSW7ekmExlbDYIhXwIghxR1BCPi3R3G3E45Fy/LqNWSzE9Xc/OzgahkIDNpiCfz5LL\nJWhpcRKNakmnkxw/foREIs/GhobWVoGuLiOrqxCJZHj00R683gMWF1V0dSno6TGzuioSDCZ54omj\n5PNFdnbkiKKPmZlp4vEUe3vrbG56eOyxaZTKOIuL4PX6+cxnHiefzxOL+QkGfZhMBj71qSe4eHGD\njQ2RpiYJ09PTGI05IhEfly7doqWlDr/fz9WrEeTyAqdPHzr0HDlSx+7u7v2h7i9/+R+4fj1DfX2N\nyclJZLIoExNH6O/vx2Kx0NnZeX+zKZFIuHnzJi+++Cp6vYZ0Os1f/uX3uHZtna4uJzdvLvCTn8Qo\nFILMzEzwxhtXSSZFBgfr0el0LC9votfLeeihKZaXV/H5MnR1WbFazfz4xwvEYjUGBlwsLy/z9a/f\nZG9vjdnZSb71re/y9tsBTCaRhx7qZHc3xs5OEaOxhFRaQq2WY7Op2djQIIplZmYaKJdTSCROGht1\npFIVtrZWKRQyFAoOEgkYHtYhkcTxequIYo5kUkdDg46TJ5upVg2srpaQSNyUSkFEUYpcXsPn0yKV\nCjzxxABS6WGPvSgGSSZjKJVlWltduN1SYjEJQ0MK9Po4lUoTopimVtOhVJYZHW3B48mztFShublA\nLLaBxxNHKoV8Xo8gQKUSYH09zs6OjJYWKSaThHI5QyAQJJEwIpWamJlpwGCoMDeXwevdRyKR43Qq\nGBnpwuc7tMONRvdQqcJUKhoKhTIzM5NEo1HOnz+PRqO570x1T4IgsLu7Q6mU5MSJEZqbm5HJZMhk\nMm7fvk0ymeTxx08xNdVzP3G8Wq0SCoX4/vf/kWKxyMCAndHRjvvPC4KAKIrEYjHeeOM8584lsVgE\n/viPf4/jx6ceaPeMRqNsbW3x3HP/yE9/6kalimCxaPjsZz/GJz95lomJCRobG5HL5YiiyPLyMqur\nq/zN3/wDr7zyKouLGfb2AlSrFXQ6HV1deoaG2nn66eOcOTPJpz71JD09HXeNGnz87Gd3uHbtCleu\nVAmFblMuW2lultLermd2doyODhM+X4rdXTcbG0X8/gxSaQ6Hw8rkZCMGg4StrQI+3x77+2YcjjIj\nI3a0Wjm1WoWdnSJer0BDQwmnU4VOp6NazXLrlhxRTDM+bkehqBKPlwgEkgSDRoaH1XeTs1P4fEFq\nNRV6vZqjRxsoFotcvVpBoYjgcqnR6WRIpRI8niqplJrhYSU2m8DaWpFw2I1UqsdiUTA83MjOTpSF\nBejoKNPaqiUSyRCNRslmdajVGiYmnAhClevXywhCCKdTi14vRSoVcLvLJBIahoYU2GwSbt/OEwgc\noFJp70JzA9vbEZaWJPT0wLFjrXzyk59gbGzsPT2H8Yt0DzTuWci/13VwcMCLL77IH/3RH70v1vs+\n14eg8UHTrwM0ftmzDr8qwPinKhQKyGSyf9PA7S9DFy9e5NVXz7GwsMLFiyX0+gLT03Vsbe0RjZZQ\nqeRkMhWamjQ0NOiYn5eSzyeYmKjH41kjk5GiUskJh+XYbCL9/XY2N0sEAhmam5VkMj7y+Rp2u56t\nLTUyWYqJiUb29kJ4vSL19Qqq1Qy1WonW1sOWqFKpwOxsGx7PLltbEhwOkVqtRKGQoK2tjnBYQyJR\nZXq6kXI5ytKSgF5fwmQSCYc9CIIcqVRDIlGhtVVLQ4OBW7eUVCopHnmkm+1tNxsbNcbHHSiVETY2\ncghCldZWA3t7q4TDNXp6nORyPvb2wiiVcrq6LGxvr7C7W+TkySNoNDGWlg5bUv7gDz7D+rqH/X05\nCkWYkydPEo978Hg2uXPngE9+8lG0WpELF4pEIh5mZsbQaGpIJBH29kIolVKmp4/xk58ssb8v0t6u\nZnJyEputgtWqxe1243IdJkv/3d+t4XZvcPbsSXK5KBpNnocfnqWuro6hoUEcDgfBYBCDwcDBwQHP\nPPM3LC4uMTY2xN/+7fc4dy6JShWjv7+H69cXkEhEZmbGaG5uQq2Ocfr0FK2trfT2tjI4WM/4+Pjd\n927j1KljGI1G+vqOMDhYz/Hjh45SZrNAf7+TqakpkskkOzs7tLRYmZgY5TvfeRmPx0eplCeVgmBw\nj0QiTn9/I1arihs3pIhihpMn6/H7DwiFRKTSGrWakdZWFU6nnIWFIsVijclJOxJJmv39ODIZBAIG\nrFaYmmrg4CBJKCTHZCpTKMRYW9u/G5DmRKEQmJ1tIJGIsLsLMlkWUVQQCm3i8aQIBBSAjqEhLRJJ\nknRai8WiIpczotPV6OuzcnCQZn29SmNj9a4z0R7r62FiMT12u5H/n733/I78LNP8P5VzrlIu5VDK\nasUOUkvqZLdt3E47JgzsYGbgLJwZ9sW+2LP/wgBnB3YHGJsBEwzYYBoHHNp2J3dUaLVyKuVQOee4\nL2TpZ/t45jcBbAy+zqlXkqqec+ro+T6f577u6z5+vIJgcC+BTCLZwWq1YDLJKS7WsbUlQSy20NOj\noLZWz+Jihnjcg1RqxGjMc/hwJem0hsnJLE1NYjSaBNvbLuRyIRpNNclkApUqz8WL13n++S2i0Q2O\nHu05+B+ORqN4PB4GBo4yMND5nmnjq6urfOc75xkdXaW9vfzAaieVSpHJZIyOjvLMMwu43R4+85n7\nqaurOwjXSKVSvPjiSzz55Muo1dDSYmBwsJe6urr37LOpVIpvfON7vPzyFOBFrZbz+c8/yOc//wh1\ndXUHzerpdJpLly5x/fp1nnvuNjdujBIMChCLFVRXS2ltreKznz3LyZOHeeihB2hsrCMQCLC5uck/\n//MLXL16iYsXI6ytjROJWDCbkxQXK7n//n76++swGg1IJHlu3lxlcnIVpzNJNqvEahVQXW2mvb0K\nsTjDyEiIzc15IhETpaVSBgZKSaXSeDxBNjYSOBxSamrylJWpkEikJBIhpqYk5HIxurpMKBR5gsEM\nTmeAjQ0N7e0Kmpt1rK4G2N52kUxKUShUdHcXASlu3UqSyexisWiwWOSYTBrW1lLs7kpob5dSWipl\ndTWO2+0glVKj00np6SljZ8fPzZspTKYQRUVS8vkckUgEl0sKqOjpMaBU5hkfTxCJbKPXaykokFNS\nomd1NcHWlpy2NjEVFQpWVqI4nQ5yOQVqtYSOjmJ2d31cv56hoCBMY6OJRx99gJMnh1Gr1R/bQ+/H\nDTSWlpa4cuUKX/3qVz8W6/2Y6xPQ+FPSh13RgN9vU/WHARj7SiaTiESiDxU08vk8V65cYWJigpde\nus61azHq68UUFGTY3HSTSKQADaFQgu7ucoTCBCMjQlSqGGbzXnSnWq0jnZayuyumpUVLcbGQ6ekk\nkUgAo1FOILCD1VpCPi9kbk5OYWGG+noZKys+/P4EOp2SeDxCRYURs1nF6KgECDIwYMVuX8blyqFS\niYjHsxiNAqqqzMzNyYhEYgwOWtnZWWJ9XYDRCKlUjkwmQH29FZdLgc+X5fDhUnK5IGNjQrTaNA0N\nKtbW1vH7M5hMSkIhD+FwhLIyCz6fmHB4l64uG7GYAIcjS2GhgNbWOux2CAYdHDvWRjwOTmecTMZF\na2sLwaCfra1ltrbcnD7dTSq1yp07SQIBB3/7t3/F2NgqOzsC1OoIbW1tpFJbuN0bzM6u89BDZ4nF\nIrzxRohYbJdz586gVGYwGjOIRELMZjNVVVX85CdvMjLipKxMislkYmtridraApqbG6mvr6Ora89C\ntT9H5n//7yd56aUx9HoBoVCI115bI5FI0ttrQ6WSksu5OXHiMPX19XR01HPsWAdlZWXo9Xo6Ozso\nLS0FQKvVUlxcfDAhXKfTHaS6SaVSLBYLYrEYgUBARUUFNTU1iEQiSktLOXy4mf7+w+zs7PCb37xJ\nIhGguLiESCSOy+UjFouwsWFGJApiMsUJh70kEiLS6TyBgJzGRg1lZTLu3k0Ri8Wor9djMAgpKChm\nbW2dmzcFZDLrnDvXht3uYWsrgkyWI59PU1FhRKMRMjEhQSQK86lPNRCNBnG7heRycRIJOVVVSsrK\n1ExNZYhE4jQ2SjGZxAQCOYTCLNvbSsxm6OkpZWZmh1dfnScQWKW4WI1Op0arlbKyoiGXC9Lbq0Ol\nkrC8nEUoDKFU6unosGKzlbC4CG53mrY2FSpVnGBQRTYbIRxWo9VCT085bneWrS0lVmsWtTpNOJxA\nqZQgFFZRXFxIf7+VSCTA1atehEIParWU7u56bLa9qkMqleKb3/weL788SmGhgurq6vf8r2cyGe7c\nuYtUCsPDfWi1WmDvQLa0tIRCoSAU2sRmK2Fg4ChyufzAjuXxeBgdnWRyMkFRkZgvfekvMZvNJJPJ\nAxB5+uln+NWvXsHn85FKSXnsseN84QuPYLPZDm7Ek8kkr7/+OleuXOHFFxeZn19HKExhsZg4d66b\noaFOPve5x+nt7cJsNuPz+XjhhZe5cOEiL7ywxMTEdXZ3zSgUfgoK1Jw4cYgTJxo4duwwzc3VjI7O\ncvPmBOPjTubnfWSzYfR6IydP1mGzFaBQqAiHfVy6FMHhmEMiMVJVZeT48SpCoShLSy52d8N4vVpa\nW6VUV2uIx7NEIn7m56Xkcim6uoyo1QL8/jQOh5e1NQ0tLTLa2/VsbATZ3HQRi0mQSNR0de1VO0ZG\n4oTDG+j1egoK5JSXG1hcjGC3Q0MDWK0KHI4YXq+bcFiDViujv7+CYDDM6GgamcyD2azAYJAjlYpY\nW4NoVEJ7uwK9Ps/cXAqPZx2JREthoRybrZClpQAzMwLq6rJUVChwOmO4XG7icRUqlZwjR8pJJhPc\nupVGLvdRWqri4YdP88gjD6DT6Q4gc7+35/3P8T/2w3A2myWbzX5sQGNqaoqpqSm+9KUvfdRL+XPQ\nJ6Dxp6YPe2jf76PX4cMEjH29e9L2H1rZbJbr168zNzfHs8/eYGTETUODgnzeg8MRwGhU4fGoSaUS\nDA/b2N3dZHY2T1FRHkiSSASorCzC4ZDj9eY5cqQEodDN/HwGsTiGQCAnkfDR02PD5UozO5ujqUmO\nVhtidTVALpdGIjEQj8c4cqSeaDTKyIiQoqIcZWUitre3SSSyCARKQqEczc0WjEYBN26IgCDt7WY2\nNxcJh4VIpWICASEFBQLq6izMzAgJBuMMDlpxOBZZWQGLRUQ+nyQQcGKxGEgklAQCSVpbi1Cr5UxM\nSFEqYwwP21hYCLK0FOfUqTryeTejoyCRxDh1qoG5uR3m5iJ86lOHEAoD3LwpIpPx8Td/8yhTU853\nmsUl1NfXs77uJhzeQSwW0NfXhNc7y8iIj3jcy6OPPsCNGxs4nWCzGWhqakQodCKRZHA4nJw8eYKl\nJTu/+MUqLtciJ070MzMzhVic4dSpo7S3tzM83IdYLGR5eZnS0lKuXr3KD35wnfn5Sdrbbbz11g1c\nrr1ZI93d3Wi18YOm8erqKoaGjhxE16rV6t970olAIECpVCIS7X2fMzNOTCYTAwN15HJxFhcl6PVh\n2tpKWF6eYWbGSyiURiQqpaNDj8WSZ3IyQTjsRaORkc9HaWysJhrNMj0txmDwk0q5SSRyCARSQEwq\nlaajowyZLM/lyxlEoiD9/RWoVHmyWSXBYIy5OR8FBSlaW4u5ezeF3++nulqH0SikoqKGXC7L3JwM\nozHJ0aOl2O1eNjejpNMBnE4vCoWIpqYipqdVQIRTp6oQidIIBEUHAFNZqaCiQsvUVAa3O0ZtrYxo\ndIeNjQAKhYidHRVGI3R1FXH9+iyTk36Ki4UoFHkUCglyOYyNpYAsJ09WEQp5mJ9PIxQGEYtVnDhx\niC9/+TO0trYc7EfJZJLXXruGxwONjeYD0MhkMrz99tsEg0Eefvgsx493v2co35UrV/jud19ja2uV\n//k//5bu7s4D26lAIODZZ3/NT396icpKA6dONXDmzAnMZjMSiQSRSMT6+jqTk5O8+eYUq6tCTp+u\n5YEHjnDo0CHkcvlB39yVK1e4du0a588vsb7uQKfLUFFRwH/7b5/m9Ol+Dh06RHFxMU6nk7GxMf7v\n//051669zdWrGUKhJRQKIy0tJZw8Wc2jj57jwQdPEo/HcTgcvPzyTS5enGBz00cspqK4OE11dQHn\nzg1SUWFibMzO6uoiN28KCIXWKSjQYLNZOXy4GofDx+Skk91dN9Goge5uHU1NBlyuCB6Pk9VVBblc\njt5eE1qtAK83hdPpZXVVjc0mpafHwva2n81NN6GQGJFIQ1eXCY0Gxsdj+HzrKBQ6ioqUNDUVsbjo\nZ3o6T0VFipISOdFoimDQj8ulQiaTceRIIZlMkrGxGJmME41GQ2mpEotFzdJSGqdTSFOTEJNJwPp6\nEr/fSTKpxWyW09VVyuqql9HRDIWFYUpK5CSTaYLBIG63HKlURXe3CbE4y+3bMRKJHcxmLffcc4Sv\nfe2LB3G1+8/P/Z6ffD5PJpN5D3zsz6x6d+DLH9OBfh80/rWgiz8mjYyMsLm5yWc/+9mPeil/DvoE\nNP7U9GGChkAgIJFI/IcrAx8FYOwrlUohEAj+oKCRSqWYmJhgdnaWH/3oGgsLGxQUCIlEHIhEEoqK\ntMzOKpFIIgwP17G8vMrWVhqtVkAymUKtzlFbW8TsrJhQKEZ3txmvd4XdXQFqNQSDEmSyBJ2dVayt\npVlejmKzKUgkdtjdjbxT4TAACU6caGFjw8HUVIbKyj2A8Pu9GAwagkEN0WiWo0crSSQ83L2bR6dL\no1JlCYWc6HQ6EgkZLhd0dFgwm/OMjubJZAI0NOjZ3l4mHAaFQkogIECvz9DYWMbiophQKMGZMzYc\njnXu3hVQWSmlrAxWVhz4/TGsVg0+3xpbW0HKy80kkzFcrg2kUgUqlRSfb5vtbRf19RVkMl52d9fZ\n3fUxMNCIz7fI1FQUrVbEqVOHGBlxMj3tpbu7ApFIwspKDJksTmdnG1arlmx2l9u3l7BY1HR2dnD+\n/CTT0x5qarQolXJ2dtZparJy6FA7R492U1Zm5PLlG+TzGeRyOd/5zq+4dctBRYUCqVTK/Pw2hYUq\nTp06TmNjFY2NJrq6uhCLxVRWVlJUVPSeW8qNjQ0SiQRqtRqHw8G1a9eQy/d86BcuXGBs7A7l5VbC\n4TC//e2LhEJBysvLWVtbY2xsDJPJhFwuJxgMkk6n/8WHusViobxcx+LiLHfupNHrkxQXGykp0VJe\nXsDKShqPR4jNJqSpycjvfrfI9PQddDozCkWenp5atrbCjI/naGmRUlIiJBzOotNJMZmqEQjEZDI7\nLC7amZuToVJFKCras7jIZAoiETEejxSt1sfKyhZra3kkkgx6vRyIU1tbTjSaZmpKTEVFHo9nkjt3\nNgmH4ygUSvJ56OqqRKvN43Zb0WhydHcX4vM5CARyJJMZAgE5TU0apNIQly87CAajlJZKEQqj5HIi\nRkYmWVjQYLEkOXWqjtVVDxMTAZMzhQAAIABJREFU29jta0QiUZqaLBQV6RgfF7GxsUwo5CQQWCOT\nMZPJhEmnVVRUKNFoRAwMHMZqtb5nT5JIJNTWltHUZOHw4cMHFy1TU1N873tvMjm5xqFDVZSUlLzn\nu7Hb7UxMbKPRCN8zVTyXyxEKhXj77RHm5+NUVal5/PHH0Gq1B8MCA4EA3/zmj7h5c4uODj29veWc\nPXsvlZWVCIVCMpkM09PT3Lp1i5///A6rq1vo9Rmqqgr4+tef4NSp4xQWFiKRSLDb7bz11iV+9KM3\nGR+/wdqaHp0uSlWVhnPnTvDgg/0MDvZjtVq5cOESL730OpcvLzIx4SGd9qHRmBgaqqavr5rOzjbU\naikvvjjB3bu3WV/XI5XGaW420N5eS2trJUtL24yMuPB6t8jlTBw5UkJLi5m1NR8bG+tsbSkRCIQc\nPmzBaBThcMRwuTwsL6uprRXT11eIw7E3wM7vF5LPa+nqMmAyibh7N4rLtYZIpKOgQE5XVzl2u5ex\nsTQFBWEsFgkymYR0OsH6uhShUEpfnxGpNMPUVJxweBuJREd5uZrKSj3z8zFWVjJUVqYxmcDtThAO\n+wmF9BgMMo4fr8Ll8jM2lkKl8mMyydHp5ECWjQ0RqZSUzk41KlWWyck4Pt8GCoWW7u56vva1v6Sj\no/09PY0CgQChUIhIJDqw8+6/RCLRwe/u25M+qPrxbvj4KABkfx0fl/6SK1euEA6HeeSRRz7qpfw5\n6BPQ+FPTh13R+I9YkLLZLLFYjFgs9qEDxr5SqRTAH+QGJplMsrq6yq1bt3jqqbdZX19AqRQTCjmw\n2apIpbJMTUmxWgU0Namw2534/VEkEgXhcJzGxgKMRvE7FQU/7e2FbGwsEI+LkErluN1Syssl1Nbq\nmJlJ4fUGKCyU4POtkc+LMJk0rKxo0euz9PdXsrzsYGMjisEgJJEIIpVCVVUBc3NystkEw8PVbGws\nsbYGen2edDqHUBjBZrOyvi7F601z7FgpqZSD2dksCkUKqVRAJOLEai0mHBazuyukvd1EYaGI0dEc\niUSA3t5S1tbm2N3NYrEoSCZjRKM+SkoK8PslhEJhenvryWZFLCxIMJvT9Pe3MTubxu1O8OCDPaRS\nae7cEaHTxXnoodNMTPjxeFK0tpag0ehYWYmQTruorq4glQoSiWyxs+Pm2LFuamu13LmzwejoAvfd\nd5zV1V1u3EgilQY5efI4m5uLqFQZSkos9PT00N1t49Klm1y+fJPW1gYuXbrK8887CIU2OH16gNnZ\nKUSiNENDfXR0dNDaWsbwcD8qlQqDwUBxcTHz8/OIRCIsFgsXLrzB88+/htmsw+fz8Q//8Etu3Bin\nvt7K88+/zLPP2gkGV7Fai/j+91/lzh0fFRVy7HY7Tz89z/b2KseOdfB//s+PeeWVDRSKIAaDnr//\n+6d4++0RWlvriMViXLx4EYFAcDC7QSAQUFRUxMbGJi6XH50uT2WliaUlIU5nmsHBUnS6GEJhCZlM\niLm5COFwjO5uE8mkkhs3/JSV7R2yvN4wQmEOv1+LTKbg+PEqIhEvly8HCYe9FBSIsFhUWK2FOBwi\nnE4RnZ1aTKY0dnueRGIbk8mCxaKit7ee7e0QY2M5GhvFVFZKWVtzYrfvkEio0WhUHD9ej1ic5vr1\nLFptmtpaPZlMmFQqx8qKC69XTWenAatVytRUjFu3xnC7E0ilIbq6Wkkk0kxMiBAIdjAak4jFUgKB\nDJAHRMhkIYxGIS5XJZlMmK6uAhwOOy5XGpkMpNIKTp608cgjx5mYWGZkBLTaCJ2dHcDe3vXcc89z\n5coNOjvbaGhoeE81N5/PMzMzhU4nYXj46IHtbWNjg+eeO09hoZmhoVaGh4++J5r2mWee5cc/fpX2\n9goGB+sZGho4SLtKJpP8+tfPc+PGbcLhCCKRhEcfPcM995xBpVIhFovJ5XLMzs7y5JMXWF1dRa0W\nUlZm4r//9y9x7FgvMpmMWCzG/Pw8v/vda/zsZzdYXLxDIKCjqkrNmTO1nDt3P48//hAajYZgMMjT\nT/+a8+ffYG7OhdMpwWyOYrUa+eIXH6anp4FMJsPOzg7nzy8wOXmLREKP2azg7NlaamvLKC42MTq6\nyNtve4nHt5DJDAwM1NLSUsjMzA5LS3ZcLgVisZzjx4sxGsVsbIRwOl0sL6upqhLR31+K1xtkY8ON\nzweplIbubj2FhRJmZiLs7q6RzWoxm5UcOVLJ5qaH0dEkarUfo1GKxaJBKhWwsACxmIDeXi1qdY7F\nxQR+/w7ptJbycjXNzQUsLvqZm0thsUTQavNks3lSqSgOhx6VSsrgYBnxeIzx8SjZrAutVk1ZmRaT\nScHiYgafT0RHh4LCQjF2ewKPZ5tsVkd9fSFf+crDHD3ah1KpJJfLHcDBPiDk8/n3PPv2geFfA5D9\n6kc2m/1AAHn/XK0/5LN1f5bMxwU0Xn/9dcRiMWfPnv2ol/LnoE9A409JAoHgIwGNf6sF6f2AoVQq\nP3TA2Fc6nSafz/9eQSOVShEMBvnVr87zk59cIxBYJx4Xkkr5OHq0me3tBDMzKTo7DSgUQdbX/QiF\nOZJJLbFYjMHBRoJBD2NjAgoKsqhUaYJBNzqdhkhEjtOZo7e3GL0+yeRkmnTaj0olwefbprbWSjwO\ny8tqGhsV1NXJWF724vOFkEqlRCJhbLZi1GopIyNiZLIofX1FrKws4/OlkcmkRCJ5ysrkVFUZmZgQ\nEg6HOXKkBIdj8Z2ZGiLCYRFyeZyOjmpWVwVsbyfp7y8ll3MwM5NCJkuhUAgIBncxGAykUmLcbgF1\ndWqqqsyMjgpIJqM89FA3S0t2JiZSdHWZKSxMMjMTwO/3c+RIBZubM8zOhmhqKsBgiLG4uMvurofT\np1vY2ppjYiJEY6OF2lodIyMuFha2+eu/foTdXS+3b+fQaKIMDBxhdHSObDZDaame9vZmNJoAiUQU\nl8vD5z//OCsrq5w/P0sksk1xcSEvvzyF15ulubmQ0tJiYrFNjh/voL6+nsOHu+jtbcXtdiOXyyks\nLOSXv/w1L7/8FjU1Vu7cucM//dMV5uamOXLkED/+8YtMTOQpK8tTXFzM7dtLCIVCjh5te2cNDhob\nS2hqsrG9vYxCkeb48cMoFAqcziWamsro7u5keXmJaDRCT08DIpGIixfnSSbzdHXVcvny2/z0p4s4\nnYsMDR3lxRdf5rXXLlFWVvROQlGYK1d8eL0xGhtVZLMevN4sKpUEh0OJxSKipUVHJJIikylEKvWx\nsDDH7q6T2tpC1te1QJbBwXI8nh1mZ1MIhUFkMgUlJTmOHm1lY0PC+PgmZnOQ0lIp6+spUqkQ2ayR\nigoj99/fw9ZWgAsXnITDsxQXi4nH0+RyGcJhLWq1lqNHLRQUaBgfTyMSBdFqpYjFCUpKLOzu5hgb\n8+D3byOXO0gkjAQCHiQSBZlMGJNJgMlkYXpaQWVlnsZGLdlsHp1Oi1JpJpOR0tFRiNEoZmenmOJi\nBTU1GrLZILmcmHxeRi5XyuOPd/GpT/Vw4sQwVqsViSSPWOxnePjIwfRgh8PBj370JnNzUaqq5FRW\nVgJ7++DFixdJJpM89tgDDA4efo897tVXX+UXv9jA51vnc5975KBnY1+//e0F5uezVFUpePjhcwcH\n0lgsxurqKj/5yWWWllI89lgPjz12z3ticPcm0P+AqalJ0mkRBoOa//E/vsQ99wxjMBiQSCT4fD5e\nffUNnn12lO3teRIJLTabhfvvb+PkyUEOHerA7/dz9+5dnn76Bd544w5Op5ds1sChQ1q6u8v5ylee\noK2tgStXbjIxMc4rr7jZ3FxAoVBRU1PE44/3U1iox+sNc+vWLJcvhxGJdjEY9Jw40UZTUzGjo2vM\nzi4QCMiQy9UMDVkxmyUsLXlxOBzY7RqsVhHDw+X4/SE2N924XBliMQ29vQasVgXz8yF2dzeIxzUY\njXL6+6twuXyMjEQRibzodEoqK/Xo9TKmp9N4vRna25UYDAI2NuL4/U78fg0lJTL6+sqx293MziaQ\nywNoNCJ0OhlicZ6VFQUCgZj+fjNCYZLp6RiRyA4ikZbqah3l5TpmZyOsrWVoaBBQWCh5p/fDRSik\npbRUz1//9VnuvfckpaWlB/0L+9/bfk/l/uvd1Yl/yR71bgDZh4//qP3q91n9yGQyAB9ZuMq/Vy+8\n8AIWi4Xh4eGPeil/DvoENP7U9GE3g/9bLEh/TICxr3Q6fdDI+5/Vvi/6299+kvPnrxIOu3E6BWi1\naQ4dKmd5OcX6epiGBjXx+A4eT4ziYi1rawoEgiinT7ewsrLG0lKGwkIBmUycfD5GXV0Z6+sy/P4k\n/f1lBAKrrKyASpUmkRCRTHpob6/C6cxjt+fp6ytApQqyshIgn0+TSqmJxcIcP96M1+tjbEyA1Qom\nUw6ncxeBQEg6rSIYzNPZWYxKleb27Ty5nJ/KShVO5xogBaQ4HGJqauTU1OjembQbpK3NhNe7gsuV\nRquVEgiIkEii9PY2sraWZ3MzzdBQFWJxgLGxFCJRFJtNx8bGMi5XHJNJSSwWIhYLUlhowevNE4l4\naW2tIRzOsrubR6dL0NLSxOJilFgsTEdHHdFomu3tBPm8m7q6WlwuN7lcBIkkh81Wg1jsZnfXQTgc\n4dOfvo+VlQUuX97AZBJis9Xzm9/Ms7rqpbW1lM3NbTY2QlRX6xkaOo5anaamRoder6ehoYFjx3q4\nfv02t26NY7PV8eabF/nhD2+yuTmPzVbDz352keXlDFVVMtRqNbOzq5hMcgYHj6DTSTEakwwPD1Bb\nW0tNjZn+/g5qamqw2Wz097fT29uDQqGgt7eL/v5eVCoVOp2OY8e6aWqykU6naW620dvbSENDAyaT\niaIiGd3ddbS0tBAMBtjdXaetrZLKynKefPJFJiYSlJWByWTipZcusLu7RGdnLX/3d19hbm6Fu3dz\nlJeLOHTIwvKyh1hMQnGxBqEwi1YrwuVy4/FY0emE9PeXMDMzzuZmFoEgSSIhw2qV0dpahsOhx+vN\nYDSGmZmZZXMzgV4vIBg0o9HkGBioYW3Nw+xsApMpxcrKLDs7KXS6NIlEFdksHDtWTC4XYWdHjUQS\nIpUCu30KqTRFMlnA2lqGjg4V2ewuW1tJFIosOl0VUmmOo0friMdzhEIVNDXJsVhEhEIh0uk00agG\nUNPTU4hcnuTiRR/xuIOiIt07AFPI1laEqakkR49aeOCBDu69915sNhtCoZBgMPjOd9R3ABkASqWS\nWMxFYaGY4eHjB1WH27dv8+ST11lYWKGvrwmDwQDsHSbdbjcqlYpQaJ0jR5oPGsoBXn75FX75y5fo\n62vm0KEChob23jOZTOLxePje955mfHyWqioDxcUy7rnnJCUlJQgEAqLRKG+99RZ3795lbCyCRCLh\niSfOcPbsEMXFxYjFYjKZDL/61W/40Y8usru7RDyuobOzis9+dpizZ0/T3NyMw+FgcnKSn//8Ateu\nLRMOe5BItAwP13HsWD1nz55Fr9fxgx/8kqtXL3HzZppQyEVRkZTOThtPPHEOsTjPyMgMt27NMDqa\nRa/3U1Sk4syZw9hspVy+PMfdu7NEImKUSh2nTtVgNkuZmXGys7PJyoqW0lIhp0/vRemurblxOJIE\nAmr6+gxUV6tZWPCys7NJKKRGq5UzNFRNKBRibCxCOu1AqdRSU6OnuFjN3bsxtrYSVFcLMJvFBAIp\nwmEfGxtqTCYhJ07UsL3tYXo6CvhQKGQHw/NmZ4XE43l6enSoVFns9gSBgIN4XENlpZrmZgtzcwHm\n5xMUFsaxWKSk03kikQBbWyq0Whmf/nQfZ8+eoLGxEYVC8Z7qxH6FYh8W9oMfhELhAWC8Gz7eb496\nf/UDPnr71ccNNJ599lnq6uo4fPjwR72UPwd9Ahp/avqwKxr/mgXpjxEw9rV/u/OfBY1gMMi3vvV9\n3njjKjs7PhwOIQ0NmnesHXuNhwUFcgKBLczmPY/93JwCszlHb28RS0u77O5GUaslRKMxSkrUWK16\nRkdF72Tzl7OxMYfXC1Ip+P0SVKoEjY2F2O15XK4UTU16ksldXK4YZrOS9XU5QmGUoSEba2s7LCyk\nsVr3Zl0kkzFKSgxsbamIxTIMDdUQDG4xO5tDq00hFudJJn3U1FjxesVsb0NvbyF6fYKJiQTJZACT\nSUEgsPNOEk6e9XU51dUSmpoKmJqK43AEOXTITCCwyvp6HL1eQiIB6bSPhoYq3G5wu3P09FgpLFRx\n7VoOgSDC448fZ3JyjTt3wpw8WYden+T27SihkJdHHz3M7Owco6NeurvLMJvzjI/H8HjcfP3rf8n4\n+BxXrkSw2VQ0NdVz4cIuPl+Ikye7mZ9fYWcnidWqpKurE693DYNBgF6vZmDgGDU1Ouz2dRYWFrn/\n/rPcvDnGs8+OE43uoNGo+NnPbrKyEsZmMxKJ7KXllJaqOHlyEIkkTlmZhMHBPZhob69iePgYSqWS\n8vJyursPodfrEQgEWCwWjEYjsPcwf/8B5N3xpzKZ7OCGUigUIpfLD24lLRYLZrOZbDZLWVkZx451\n0NW11wycyYQwGDKcOHGc5eVlXnxxDb3eyFe/+hd4vV4WFuawWKJsbUVxu4MIhWKy2SwtLSUolSLG\nxxWUlgoYHKwgmQxy+/YiCws+AgE4dqycmhod09MZvN4gRUVC8vkQMpmaYNBNNFpGU5OR/v4KpqfX\nWF+Po1JlEQpzFBer0evF7O5qMJv1nDlTRSCww/p6DoiQSOxZTmSyKLduJXE48nR369DpsrhcMQwG\nBfl8KVVVZgYHa9nedjMxkcRsTqJU7kXzKpUirl1zsbkZYHjYikyWZGoqyfb2HHa7l1Bol+Hhdra2\n0szPZxEKV/D5/FRUFPE3f/NFFAoF+Xye733vhzz33CWMRunBYLx8Ps/ExARbW1ucPn2Kvr6uA8jY\n308WFmawWJQMDR07OHC98spr/NM/vYxQmODrX/8KDQ31B3+TzWZ56qlfMT6epb5ewUMPPYREIiEW\nixGNRnE6nbz22gwuF/yX/zLAX/zFw6jVamCvgnLt2jWeemqUQMDHfffZGBjooK+v7+B3Xn31Nb73\nvefY2lrD5ZLR0VHGZz4zxMmTQ1RVVbGxscHk5CTPPPMGIyOb5HJB9Hojn/3sKU6f7qGnp4d0Os0/\n/uPPefvti8zPS8lkotTXKzhypIXPf/5RvF43589fYnx8hrk5OeXlKWpr9QwPH6a+3sprr91lbGya\neBw0GgP33ttEUZGSsbENtrfXWV3VUlIi4r779kIq9uK3Y3i9Kvr6DNTVabDbfWxtbeH3a1CrZQwN\nVZJOxxgfDxGN7lUYGhqMVFbqmZ4Os7oapaAgickkQSaTk0yGmJtTolbnOH26Cp8vwMxMhETCi1Co\npLZWi8kkZXo6i8+XoqFBisEgwOlMEgx6cbk0lJUpOHy4jOVlN3NzcRSKAAaDDItFC6RZWNgDhvvv\nr+Wee/o/cGr7+/V+e9S7AWS/MvEvVUA+qPrx77Vf7QPOv2S/erfF693v+UFKp9PAxwc0fvKTn9DT\n00NHR8dHvZQ/B30CGn9qev/G8IfWB1mQ/pgBY1/7m+q+h/rfq52dHb7//R9z584Ys7Nh3O4M/f3l\nCAReZmbSiMVxxGIp0aibnp5GPJ4UMzMC2to0FBamsNu9xOMxhEI1kUiUnp4a8vkUN2+CVpugslLB\n7u4auZyYXE6GwwG1tUpKSsTMzuaIx8OUlqoJBrcxGIxIJFLm5mQUFOTo6irAbnexsxNFp5MQi0Uo\nKFBgtZoYHxeTyUQ5ebKatbUFtrdzqFQQjQrQaNI0N5ezuCjA4Yhz7FgxsdgGKyspFIoMqZSMXC5I\nX18TOztp5uczHDlSiNmcYHo6TCwWRK+XvwMhRnI5ERsbEoqLhXR1VTE9nWBjI8zZs42EQhtMTMTQ\naLKUlIjZ3d3A6Qy9U+XwEI9HKSgw4vfHSSQ8FBWZCARiBINRFIoUVVV7dolMJoROp0Aul5BMehAI\n4hQWFlJYKCKd9mC3b3HmzHGKikRcvz6H3b7M1772BFevjvDKK6soFBGMRgPPPTfDzk6Q9nYrq6ub\nrK2FqazUMjBwlFhsF6tVxeBgP42NNpqbizl8uBuAxsZGbLYGlpeXEYvFFBcXMzMzw9jYGIWFhUSj\nUX72s+fY3Nygvr6Oq1ev8tOfnkejkaHX63n66We4eXOMhoZa3G4358+/SDqdorS0lK2tLZaXlykp\nKTlIlHr3IWHfHrE/KyGVSlFdXUV3dwdqtRqtVksqtUtrq5Xe3h6eeeZ53ngjgk6XIJvVkkikOHmy\nlUwmwdtvJ1EqQxQXS8nn48jlSvx+cDgEKJVhqqsl+HxGNjbsZDIR5PIcNTVW4vE0MzNyjh4t4dSp\natbWPIyOLrC4uEkkEmFgwIbRKOXatRwKRZ7TpxtIJHw4nSkmJ6dYXd0D5T3ffoxgMI9G48dkymGx\nFCOTwcKCEo0mw5kzDWxuOllcTLC5OcX2toPiYjnV1YXMzQnZ3Q0SiWwSDnsIh+XIZCmSSRVicYRM\nJkY0KsPn09LQIKauzkhDQw2JhIqGhkK6uw8d7Avnz7/J+rqA2lolNpsNgLW1Nb797d8wMrJCVZX+\noMoRiUR48803EYlEPPbYAxw/fvg9lxfXr99kfDyERpNmYOD/uz29c+cOo6Oj1NdbKSrK099/GKlU\nSjqdJhwO893v/pTJyUWOHq2mra2YY8eOHhziZmZm+OY3f8jOziYKBVRUmPmrv/ocFRUVCAQCpqam\nePXVC4yOTjMzI6a52cBjj/Vx6tQQNTU1eDweZmdn+cEPXuLmzRUghFar5otffJD77z9OXV0dXq+X\n73znGW7fvsb2tgaFQsjgYDmDg1089ND976S07c0BWlvTUFsLbW1mDh1qpaTEzEsvjTMyMkMqlUar\n1XPuXDdFRSpu3FhmbW2JjQ0tBQVCzp1rJpGIY7c73unPUNHXp6Ox0cDqqo+dnR2cTiUKhZyhIStC\nYZq7d4MEAluk01psNhONjRZmZ30sL4dRqaLo9RLKyszk80nGxgQIhSlOnbKSTEZZWooSCrlJJtU0\nNKgpKVEwO5vE6YxTWJjFYBAhFEqJRkMsLqqwWAScOFHN1pab2dkI+bwflUpJba0JtVrMnTtpIpE0\nR4+aGRzs4Ny5cwfpcv9RfRB87F86vBtA4D9nv3o3fHyQ/eqDqh/vtl+9+73S6fRBhebjoCeffJIz\nZ84cDMn8RH9QfQIaf2r6KEBj34L0cQCMfWWzWdLp9L8bNOx2O88//wJzczNcvOgjEoly4kQ129tz\nbG7m0WohFBIhlcbo6aljZSXN0lKEjg4juZyTzc0QWq0Mr1dJJhPj1Kk2tra2mZrKYrUKgAjxeJCi\nIiMejxK3O01XVwH5vJu5uRwyWQKFQkki4eXQIRtud4qZGWhrU1NcnGZ52U8sFkUoVBGNRunqqgYy\n3LwpRKtN0NCgYWtrjUhkL6bU74e6Oi1Wq4qxsSyhkI/mZiNut51wOIdCIcPhkGA05unpqWJ+Ps7q\napjWVh3ZrJONjRAqlYhQSEYuF2J4uJPNzShTU1kOHy6guDjP5GSAQMBPWZmSYHCTYDCJVqvE58sh\nlUbp7GxieTmN35/lzJl2pFIhly+n0GgyPPJIPzdvrnP3ro+HHupGpcpy5UqCbDbAF7/4ILduLTAy\n4uXMmVZKSvS88IITl2uDJ574C15//Q7j40mqqyUYDAauXNkmk0ly5Egri4t2AoE4bW1WDh06RCy2\nQ1WVDqu1lL6+bhobLchkEkKhEPfeewahMM/586+iUEiwWq18+9v/zJtv3sRmq+Dates89dQ1VlZm\n6Oho5h/+4RkuX3ZTUJDB6/Xy85/PsrPjoru7jl//+nWuXUug1UbQ6zU888xt1tej2Gwm7tyZ4Gc/\nW8PtXuHYsS6+8Y2neOONFfT6NHK5nG9+80nu3p2kq6udZDLJ7OwsRqMRnU53cECAvT0gnU4jEolo\nbm6ktrb6nUNDgnB4k3vuGaCrq4aJiWlWVlKUlyuAFMPD3dx77xBvvbXM7i4MDpZRViYhGtVhMikQ\nCKTMzEwTj+cQCvMsLKhpaBBRU6Ngc9OF3x8lnZbh9YbJZtNoNCm2tgrIZn1UValIpfzk82LC4Qyr\nqwJisW0EgiSxmIxQKIFGI0AkStHd3YLRqGd8XIxQ6MFg8OP3h3E4ckCSVEqAx7NBNJrH79eRzwto\nb9cDAYLBHCpVDqm0mrIyOR0dRTgcWTIZDc3NGiorjXzpS5/j3ntP0dbWSlublYGBowcHJJFIRHl5\nAbW1SgYGBg4uULLZLHfuTCCR5Bka6kWn0wFw6dIlfvCDcVZWlhgc7D6ocjidTm7dukVzcxMNDRpO\nnjx+0JcRj8f51rd+zMWLHtrajDz00KdQKBQHN8wOh4M335wjFMpz7lw/g4ODSCQSUqkUk5OTTE9P\nc/16ELkc/tf/+jLDwwOIxWJCoRCLi4v8+tev8dprfmpqxJw+Xcs995ykvb2dXC7H1tYW3/72z7h2\nbY5sNoxareaJJ87xqU8NU11dzebmJt/61o+5efNtdndVqNVi7ruvgZMnDzM8PMidO5P8/OdvMj+/\ngMNhoLNTz+BgFS0tTWi1Kl5+eYLR0TmSyRharZZPfaqHoiI1ly7NYLfPHwDGww+3kculsdt3WFnx\ns72tpLdXS0uLia0tHw6Hg60tGWKxlBMnypFKM0xPB/B6dwiHNTQ0GOjuLmN21snCQgCRKIJaLaOx\nsQSZLM/bb6dIpSL09RUgkaTZ3Izh83nxetXYbGqqq9XMz4fY2YmhVqfQaiVYrRbS6ThjY2IUigT3\n3luN3+9nfj5MNOpFJNLS3GymoEDJ+HgcpzNGQ4OE7u5avvjFL7ynb+YPoX+L/erdn/9B9qt9/b7t\nV+8/c3xU6Vf/FuXzeb797W/zmc98hvLy8o96OX8O+gQ0/tT0/qSJP7T2N5t9yPhjB4x97YOGXC7/\nN61xbm6Omzdvcv36CL91wGe/AAAgAElEQVT9rQexOERbm5n19QWiURCJJHg8QioqZNTWGpiaSuHx\n7PU6BAKb5PNiDAY1CwsyNJokx4/Xsri4xfp6DINBRDIZRaUSUFNTxPS0mEgkwpEjxWxvz7O1JcBo\nFBMMClAo0vT21mO3p1hcjLxzwHKysRFGpRISCKjJZGKcPNnG9vYuExM5KisFSCQxAgEvOp2aYFBF\nIJDj8GErEkmEO3cyCIVh9HoxoZCTkpJiwuEcq6syWls1VFUpmJ6O4PV6sVhkRCJOFIq9QVRLSzL0\n+iyDg/XMz3tZWAjS1KRBIPCxtuZBoRATi0lJpYIMDnaysxNmbk5Md7eJ+noTY2Mhdne9nD5dj8u1\nzOSkn6IiOTpdiu3tNTyeAHq9lGw2QDqdxGIxEg4HyOeDaLVqEok4qVQYqTRDQUEBweAucnkaiUSI\n1WpCKg2Qy+1VCJqaTECUubkVHnjgFFVVBt58c4S1tTWeeOIvefvt25w/P4ZGk0WlUvHUU5eYnLTT\n0lLO7353kVdfDQAuamrKefXVCYLBPK2tJSQScRYWdikqUnL8+BFWV5cQCKIMDvZSXl6O379KU1MJ\nfX09aLUyVKoww8PHqKqqIpFwUlmpYWDgGCKRCL9/z+NvszUwOnqHZDJNT089oVCIV16xE4kk6emp\n5ze/+R2/+MUk4fAmPT2HuHTpElNT01RXV6NWq5HJZO85IOTzeYqKihgY6KG0tASVSsXk5ALpdJZz\n54Y4cqSVCxeusbu7Q0dHOQ0NRh577FEymQzz837k8ixHjtRx964dj8dAW5uckhI5i4srxOMRkkkz\n2ayYvr4SVCrweDRUVu7NI3C5VolGQyQSKra3FXR366mqkrK1FUehyFJSUoZIlKO5uYRUKsv161ks\nljQdHUauXr3F3bthUqkEOl0Jra1miorkLC/LUKliHDpUilgcJ5eTkE5niURKOXOmkYGBaiYmtpid\ndaBUZigpMfL1r3+Jhx++j1AoxLVr19DpdJSXlx9AxuTkJFNTUzQ3N2Oz2Q4gw+l0IhQKGRo6zMBA\nF0VFRQf7wl7C3Dzl5UaOHes7gL0f/vDnPPfcEvm85yCmFsDj8eBwOAiFfGSzAXp6WigoKEChULwT\nX/sUs7NLnD7dRk9PDd3d3QcHvAsXLvDkk1eJRLzcf38Tg4Pd1NbWHvz8H//xn/n1r++i1cYoKJBy\n331D3HPPPej1egKBAH//99/nzTdvEo/HkUpVfOEL9/LggydoaGhgY2ODb33rh9y+fYOdnb0p1g89\n1MqpU0c5evQoV6/e4Kc/fZ2FhXmcTi3d3SZOnarHZqtHLBbxwgtjTEzYyeeTmM1G/ut/vY+SEh1v\nvTXJ8vIc6+saDAa4/34b+XwGu32HhQUn6+tyOjuVtLSY8ftjOJ0uVlcl5PNiTp4sQ6PJMzfnw+PZ\nxePRUFenYWCgmqUlB3NzXnK5MAqFko4OK1qtmCtXogSDXurrVWi1QmIxcLt9rK+rsNnktLQYWFhw\nsbUVRSRKo1IpaGkpRSzOcuVKmnw+zPHjpeRyMez2CIGAn1hMQ0eHiYoKLXfvhtjcDGIypaivL+bv\n/u7L9PZ2/14G1v5H9EH2qH/NfvWfaT5/P4C8v/rxbgvWvzT744M+46PQN77xDb7yla+8Z8bNJ/qD\n6RPQ+FPTh1nRyGazJBKJg/LtxwEw9rXfwP3/BxozMzPY7XaeeeZ3vPaak9LSLHL5XrKIRqMiGlXj\n9ebo6ytDoYgyOZkhnw+j0UgJBndpbKwhGEwzPy+hsVFBba2UxUUvPt9eck84HKa1tQy1Wsz16yAU\nBmhu1rO+vkAkAnK5gkBARkWFnPJyFfPzWdxuPxUVe5OFMxkhRqOa5WU5SmWCoaF6lpa2WFmJYzYL\nSaejSCQ5qquLWFiQEI+nGB6uwuWys7ycQ6PJkEoJEImidHTUsrkJKytJjhwpQq32MzcXJZuNIhIp\nSCT8HDvWhssVZnJSRFOTkoYGBQsLblwuP1qtlFjMh9msQadTMz0tQaFI8uCDvczObnP3bpDu7gI0\nmhCzs06y2SRSqZBo1I3ZbCCVgp2dPDpdira2BiYm4kSjeb7whXvx+0NcuhSnuFjIQw8NcfnyBrOz\nbj7zmWFyuTi/+52XXM7Hl7/8ad54Y5rbtx0MDzejVEr55S83cblWeeyx+3n++euMj8eoqNg7GLz+\n+jaJRJTDh5u5fn2M7e0MdXU6amtrmZycRKsVMzR0BJ1OCbgYHu6jsbGRggIZLS3F9PT0UFNTQ3Nz\nCcPD/SgUCrq7DzE42EtJSQlqtZqjR3toa2tBKBRSUlJCb28nZrMZsVhMW1sLHR1tSKVSioqKOHHi\nGDbbXrpUZ2cLvb17Q/9MJhNqdZTOzhra2tpYXFxke9tPfX0BFouJ7373ZUZHPZSXS5HL5TzzzK9w\nu100NNS/p/dj3yKhUCho+3/svWd8nPWV9v+drpnRNGmkUe+9WbKam2Rb7jYGjMGEkkIJECAJu9ks\nu88m+Wye5Nlsng3Z5dlAiHEAGzA4NNuAu2xZLpJtyZaLrGrVURmVadL09n8he9bOsgnZTfYPWa5X\n+szMPb/RPXP/7nOdc53rlORSVpZJeno6bW1tHDgwwuzsDPfdt4HCwnwGBwcpLCwkMVHGxYt9dHW5\nyclRkZ6u4xvf+Cpe7yzvvTeIyWTlS18qx+Waor3di1g8i1KpQ6cTkpVl4NChXjo6xOTkuCkoiKK3\n14bDYSMiIh69XkNNTR49PX28++4IbncvpaUJOBw2vF4/NpsIp1PA4sVxZGdH09Liwm6fIClJR1VV\nAX/3d3/BiRMXaGgwEx/v5u67q1izZhUpKSns2XOIri4jOTmxfP/7z4SbqH/1q9f54IMhAoGxsGTK\narXy85+/wYkTo8TGhsID+AYGBvjZz7bT1HSBqqpi9Ho9AJOTkxw8eBCVSsU999zG4sXVt8hGBgcH\nmJycorg4hYKCfAAcDgf/9E9bOXjwErW1hWzZspH09HTkcjl+v5+BgQHq67txuULcfnst5eXlCIVC\nTCYThw4dwmQyMTbmwGBQ8sgjXw5Pkz9y5Ai7dn2E2TzN7KyI2toivvWtr5OUlITL5WLbttc5cqSB\nkREHPp+cLVsWsX79EubNm8fExAS/+MVrtLaeobtbQmSkiDvumCMYtbW1HD3ayI4d++jp6WF8XEVl\nZSxr1841tIdCId59t4nz53sIBp3odBoeeeR2kpJ0fPxxMz097QwOqoiJkXDPPWUolRJGRy10dZno\n74+guFhMXp4Wt9vHxMQEHR1BXK4gCxfqiY4W0tMzzdTUBENDSjIylKxYkUVf3ygdHZO4XDNIJCrK\ny5OIiZFz8qSVyUkTBoOIqCgp0dFRjI+buXJFSmamiIoKPX19cxXlud68SMrKElGphDQ0OJmdnSIv\nT4VKBdPTHiYnrZhMKubNU1NQEE17+zQDA1ZkMhcJCVF85zuPsXr18s/sgLpPK7/6fc3nv4uA3Ew+\nvF4vUunc3vOflV/9d+JHP/oRf/u3f/tHH5z6BT4RXxCNPzfcCPr/lLhZInUDWq32c0EwbuAG0ZDJ\nZLcMT4K5c9jT08PQ0BC/+tVempr60OtDeL1WQiEvWVkJ9PRIcTjcrFiRjcnUy7VrQTSaIC6XELBT\nVZXP4GCA7m4nCxbEIRZP0tdnQywO4HJF4nbPsmLFPCYnJ2hpCREfH0AmczA9bUKpVOD1arBaRVRV\nJaJWe7hwwYvHM4VaHYHdPk52dhoOh5/OzggyMyUUFETS0zPJ5KQNuVyGw+EgJ8eAXi+nqUlIMGhl\n8eIUBgY6mJoKIJWKsNlEGAxCCgriuXLFz9iYnZISHQ6HkfFxFyqVlIkJGWKxg7q6eVy7ZqatbZaS\nEg0KxQyDg5MIhSHcbjkul4Ply+cxM+Pg9OkgaWliSku19PQMMzw8jVYrw+2em9QcFaWmq0uASOTi\nnntW0tExTmuri8WLE4iJCdLWZsVsNlNXl83kZB9tbcNkZEQhlc5it0/j9XoRi/0EAjaEQj8qlQq7\nfRqlMoBGo8JmmyYUchIVJUev12OxDBMbKyc6WodGMzeVXK/XkJmZicEQIjFRjdfrZenSRWRnqwkE\n/IjFYu68cw16vYq2tjYKCgpYtmwxTU1n6e7uZunSWhwOB2+9tRuxOER+fj7vvPMBR4+eIisrFYvF\nwtatbzA5OU5ubg4NDcfZt+8IsbFRyOVyDh8+zNDQEGlpaTgcDi5fvoxCoQhPd77RP3RjYJtEIiE3\nN5f09HQEAgF5ebmUlqaycGE1crmcwcFuFAo/K1fWXHcQ6sFkGmXRomI6Ozs5cOAwGo2KqKiocIAg\nlUpRKBThRnWJxExZWSaFhQW89tpOdu06j9M5yuLFC7l6tYNQyM9Xv7qJ++67MxzkXrx4muRkFX/5\nl0/T32+ko8PE4sV5rFw5n1OnRujvdxMTY0cgmCAyMoaICCHDw1KUSiGPPrqOjo4uWltd+HyDTEzM\nkJYWwxNP3M/JkyNYrXMSm5QUGSMjcmZnJ7DbXURE+PnBD77N8uU1SCQSJiaGuHChBak0ii99aT0p\nKSlERkYSDM4yPu4jMTGKVatqw1nnsbERrNYJKitzyc7OAkAoFHL16hXAQ01NeTjTOTIywqlTXQQC\nUF1dEG7wPXToEK++2sXoaA+rVi0J9080NBznrbf2snDhfG67rZaKivnhgG6un+M0MzNB5s9Pp7Cw\nELFYzMjICD/72cv09Q2xZs08qqtzKSkpCe+lH3+8j+3bexAKHXzzm3ezYkUtcrkci8XCtWvXePfd\nelpa/CxaFM+9965g4cIFCIVCTp06xZkzZzhxYgiTCdauzWbFilJqamrw+/28995uzp07w5kzfsRi\nPxs35lFXt4AVK1Zw+vQZXn31Azo7ezAaI6mqimHt2iJKSooRCATs3HmM1tYugkEXWq2axx67i9RU\nPXv3nqC7+zI9PXN2sps3z0OrlWMyWblwYZDOTjFFRRKKi/XI5XKcTidXrvhxOEJUVGiJjZUxNeVi\nYsJEZ6ccgwFWrEhnZGScjg4TNtsswaCK6upEEhOVnDljZmTEiFotRKeTUVCQytSUjVOn/MTHz1ln\nm0xTGI023G4QCDRUVsYTHS3l9Gk7U1NjxMVJ0ekkaLVaRken6O5WUFQkp7Iyju7uCQYGLAQCbjQa\nFU8++SVuv30NOp3uc3Ovuxm/S371Sc3nN+KJGwTkk5rPQ6EQPp/vFvOKz/LwQafTyU9/+lN+/OMf\nf256Sj7n+IJo/LnhT0k0PqkH40YD46eVIH1WEAqF8Hg8txCNYDDI6OgonZ2d/OIXe7l06QpSKczM\nWMnMjCE6Wklzswih0M6SJSn09l5lejqATCbGYhESFyciL89Ae7uf8XErBQUabLYhLBYXen0k/f0R\nSKUuVq4spLfXSE+Pi9hYAW63Bb/fQUZGPMPDSlyuIHV1WVgsg/T0+FEqfXg8QoJBG2VlWRiNPq5e\ndTNvnprISBvXrs3dCH0+FW63k6VLC7HbbZw5EyImxo/BIGR6egShUIzHE8H0tJDS0lgMBiGtrV6c\nzmni4+VYrSOoVFoEAhG9vREkJYkoL4+nu9vM0JANg0GCx2NGIIDYWDVdXTJEIjcbNszn2rVBLl50\nkJYmQSabc4OSSCTMzkbgdHqprS0EAjQ2+tHrQyxblkFn5wAdHSaSkiLw+yeZmjKj06mYmQkRCMxS\nXl7I4KCF/n4heXlqKiqKqa83MTU1y9NPb6GnZ4DDh+2kpclYu3YhR49e48qVYb7ylXW43TN8/PEQ\nQuEsDz98D/v3n+P06WusWVNJRISIt9++gtHYw4MP3sNbbx2koWGIlJS5Jt7XXmulu7uHpUvLee21\n99m/fwqFwoJIJGD79jNcuzZFYWEcDQ1N7N9vxu8fJzs79fqsAxdZWUoGBwf54AMjVquJxYvnsXXr\nezQ1uYiJceP3+9i69SSdnSMUFydx4MAR3nijFbN5gNLSIv7f/3uZffuOk5mZhFQq5fjx4zidzlvK\n/CKRCJ1OF76hV1eXX6+8aJDJZFitfZSUpFJeXsavfvUWhw5ZUSgslJaWcOrUKTo6OsKSHaVSiVqt\npqxsHrm5OUilUi5cuIzR6CQrK4rKynL8fifR0TLKysoQCoV4PB6io6NZtqya225bjVar5erVdrq7\njaSmRrN27Sr6+zvQaoV8//vfxWCI4uzZABKJE6/XhEQiYtOmdYyPm3A4nGzZspqVK+dx++1rKCws\nJBicQqsNcu+9W5idddLRMUV8vBKPx4fdriEzUxWuOsTExDAxMYHBoKaubkm4GTs7O5vcXD11dYvD\nPRWhUIiCgjwWL55HYWFh2CbW4/FQW7uIJUvmk5ycDMz1Uuj1etLTdSxYUEhWVlZ4j/N4PIyO9lBU\nlML8+aXhx1955V1On3aj1TqorV0cfv9f/GIrR4+e5q67VrJ8+TwqKyvDkrbOzk4OH76Gx+PnrrtW\nUFRUhEAgoL29ne3b30EoDAAO5s3LYPnypchkMoLBID//+a/4+ON2srLkFBREsWrVcvLy8pidnaWj\no4Nt2+rp7p6mpERFWVkyd955BwaDgaamJpqamti924TPZ6O2NomlS8vZuPE2Ojo6eOedfbS2ttPb\nK6eiQseaNflhG+ZXX91Hc/MV/H4PKpWKRx+9g6ysBPbvP0lX1xXa22WoVEHuvLOIuDgtdruDM2d6\naWsLkpcH+fnRREdr8HjcNDfbmZ52U1ioIClJCUixWMy0tUmJjQ2xYUMeNpuNvr4ppqZmcThUVFTo\nSUlR0tIywcDAICKRELVaRkVFFjMzTurrnajVdnJz1Xg8TqanZ7FaQ7jdGqqrY0hIiKC11crY2AiR\nkZIwORkft3LmzJzMdNGiOIaHp+jvn8Ll8iKVanjwwRXceecqMjIyPjfOSp8WNzeH/67qxw1S8Uny\nq0Ag8O8a1X/7/X+f/OqT3K/+FPKryclJtm/fzve+973PVczyOcbvJRpf0L3PGf4UF04gEMDlcuH1\nehEKhSgUCmQyWdhtAvhv7Qv5Y+C3szZut5vjxxt5//1zREd7CYWk2O0zrF+/gJMnL3HwoJNlyyRU\nVMDQkImBARmRkYlMTARYtiyR2FgbZ864SUkZIjMzkuHhAQSCaHQ6PVeviklMFLF2rYaTJ80cP96O\nVqtkfHwKmSyKoqJYGhr8gJX167M5duwUzc0CIiIUeDwAAhYvTuDo0SBNTSYKCnT09g7R1eUgIUHB\nzIwMicRGXV0+R46cY+/eXrKzwWCwMTXlJSsrncHBFPr7fdTVpXP1ajenT0+TkuInJkaK222nsjIP\ns9nD2bNu1qyJRq93cvnyFBbLLGq1nJkZG+np+URESDlxIkBlpZe77kqivr6FgwcvoNEo8HodBIOR\nFBUlc+DAFKGQizvvrGTfvmN88EE3ZWUyiop8jI9PIJUKkUgisdkclJfHo9Go+PBDKzKZg0cfXc22\nbXt4/fUW1q1LJzFxgqamPozGSZYujaWv7xpvv72HhAQdWVlG7PY53Xt0tAi328Xw8DCRkQrUahAI\nAjgcDuRyMcHgnNRvbhI9REZGIBKJiI5W4nbPotVqUSqVJCSAwaBGqVQyb14WbncnublZpKenM3++\nDqlUTHJyMkuWVOJynaKmppz4+HjWri3AYrFRVFSE0+nEaJwkKysZtVrNypXlGAw9lJWVolKpyMiQ\nIJdLiYmJQSaTIpVCRIT0epbayvT03DTp3t5etm07S1xciP/9v1M4efI0J09eZPPmlZSXlzM9PU0w\nGCQmJib8m05OTubZZ78Z/q0vXFiE33+RwsJc2tvbeeWVI/j9QgwGA6WlpRiNRqKiolAqleFjHnzw\nHhYt6gs7EH34YRt2O2Rl9VFVVRXOcBoMhnACIhAIIpdH4fcHEIvFPPbYl/F4PMTExLB0aS0ikRCh\nUMiBAx2IRHOB/OOPf43p6Wni4uJu2buMxikuXrSSkFDPhg3rSE9PJS4ujh073mFyciZcUQGIj4/n\n+9//NkKhEIlkroH/4sWLZGVlUV5eHn7d++/voaWlky1b1oRtLW02G8899zKzs16eeupeMjMzgbkh\neC+9tAudTsEzzzwWNo24du0aR4+eoKysiJ/85LvhTLDD4WBiYoK1axcRG9tOTc2CsLR0cHCQK1em\nmZ2dm2tRXFwMwPDwMNu2vU10tIr77y9FrVaHSU4wGOTMmRbq6+1UVIj5h3/4q3CAe/r0aa5d68fh\ncBAKCSkoKGDt2rUAjI2N8fOfv4bH40KlEhIRIee+++7FYDAwMjLC2bNn2bWrC53OQllZLIWF5WzZ\nspm2tjbefPMtTp9up69PSW2tjmXL0qmsrEAgEPDCC29jt1sJBsUolSoefHAFwWCQxsZzWCxjtLbK\nSUsT8MAD6QgEc3vqqVOdDA0pKS0VkJamICkpEY/Hw/HjE4RCHrKypCiVGqKjtYyOjtHUJCQjw8um\nTRlMTpq4cqWPsTEHdruO5csNKJVKzp0bxO22AGrUah0VFekMDIzwzjtDxMWNk50dQ2SkjGDQy8RE\niNlZJTU1c5XCS5em8HqnEQp1REZqKC/PpLt7iPfeM5Gb66GuLgaz2Ul7+xA2m59gUM2dd+aRl5dH\nfn7+/7ig9EYC7ub+kxtJzBuB/w0ycOOxG38DtxCUG0TjZtxMbm7GJ9n43vy+Nz7bDeJy4+9P+/1Y\nLBY0Gs3/uO/zs4wvKhqfM/wxKxo3VzBCoVA4+3mzROqTKgOfF7jdbqRSKTt3/obXX9+HxTLKwACI\nxQ5Wriyhp8dEV5eD9HQ5fr8Zp9NBSkoMg4MROJ0+VqzIxWwepLPTj1rtJxAQ4PdbmT8/j7GxIF1d\nXqqrY9FoZujpseHzuQgEFNjtFioqMnE4ZrhwQUZCgoCkJAkm0zDBoAivV8rkpJDi4iji40W0tXmZ\nmZnCYJBjt48SE6NHIpHR2SknPl7IokXJXLs2ztiYA5VKgtvtQq+XkZSk4/x5EbOzNpYsSWRkpAuj\n0YdSCTabGKXSR0VFFj09Xnp6Zpg/PwqhcJKBARsyGdhscgIBJ2vWVGA0mjh71kdGhhi9PsDY2Bge\njx+fL4LZ2QBVVemoVCIaGnyAlSVLUhga6sFonEEuF+F0htDpIC8vnfPnPVitLm6/fT4WyzitrW5i\nYkJkZckZGxthdHQSmUyM1+tAp5OiUqm4etWNSOThnnvWc+bMNS5dClBTk8q8edl8+OEQo6MTPP30\nFnp7r1FfP0JOjo7ly0tpbGzn4sUuHnroDsDJ/v0XiYlRcNddy7lypZOGhrM8+OCdpKREsW/fSYTC\nIA8/fC9m8yQHDzayevUyamsrOXHiDJOTE3z1q/ejUMhoaGgkOzuLtWtX0NfXx8DAAGvWrCY3Nzvs\nBrV8eS16vZ7JyUnKy+ezZEk1Op2OyMhIamurWbKkmoiICHJysikpSWTJkoVotVq0WiG5uRoWLVqE\n1+ulp6eLxEQNNTULePPNvZw/H0CvdxMfb+Cf/unXNDa2kp+filwu58qVK4jF4ltmPKSmprJgQRl6\nvR6hUEhnZwcKhZC6uoVcvHiRF1/8iO7udhYu/LfGY5lMRlxcXFjy0Nl5BZkswIoVi3G73ezc+R5m\n8xSFhQXh3o+cnCxyc6NYsmQhfr+f55/fxr59TURHR5CYmEh2djbZ2dkkJamorp4bQDgyMsKhQ0cJ\nBHy3kIeTJ88wNuYhJyeKkpJi4uLiiIyMpLp6PkuXVhMbG4vdbufDDz/CZDKRmZkZDljeffcDduy4\niMnUE7aUDQaDvPbabi5dCpGQEKC4uAgAs9nMoUOt2GxQXJwQ/gxXr16lvn4An89HVVV+WMu9Z89H\nvPvuKHb7EKtW1YR16M8/v5U9e1rJzY1ly5bNREZG4nA4OH36NFarlby8OLKyNNTULAnr+i9cuMC+\nfYM4nS7uu289BQUFCAQCGhsbeeGFnej1CpKTpSxbVkF6ejqhUAiLxcKLL77DqVN2VqxIZ9Om2vC8\niz17PqSlpZWBAQfBoITHHruDTZvWo9PpOHr0KL/85T6Mxl7k8ghycxN59tlvotWqaWtrY9euQxw7\nNkNuroDi4ljuvHMD+fn5vPTSTo4ePYndHkQiUXH//UspK8uiq6uXy5cv09DgRiRysHJlOrm5yWg0\nao4du0hDg43ERBfJyZEUFWWj0Sg4fHiI/v4p4uKCxMcrKSrKwmq1cuCAHYFgmvJyAzqdDI8nSE/P\nNAMDESxYoKOkRE9HxxhDQ8M4HDIUCiXLluUgEvk5ccKG1ztOdHQkMTERJCbq6emx09srorhYTHq6\ngu7uSYaHjbhcMuRyKQsXpuHzeTh61I5YPEVSkoLISBF+f5CRETdms5IVK1JYs6acurq6f0eC/yfj\n5oqF1+sNu9vJ5fJwXPC75Fe/b/bHjTX+lPKr7u5uTpw4wZNPPvnF9/rfgy+kU39u+GMQjU9DMG5e\nz+PxIJVK/39z3vjPwOPx8Otf7+D48WZ6eoz09IjIyJCSn6+lu9vK+LgZnU7GzIyZuDgNcXEazp0T\nAzZWrcqht/cq4+P+69auoNOFKClJ5epVP0bj3MA6l2uY0VEnUVEyjEYZgYCNpUvzGRwco6cnRFaW\nglBoBrd7hoSEaMbG5JjNPpYuzcDnG6e93Y9M5r4uebJQUVGAyeTlypUQpaVqEhOD9PZOMjMzi0ik\nwOl0U1WVhVQapLlZeH2wn5bx8f7r0isRJpOY9HQZKSkKLl92YTJNkZQkY3Z2jGBQhEajoLtbhkrl\nZ+XKArq7h+nsnCE+XkQoNEMg4CEhIZq+Pikej581a4owm0e5cMGNRuNFofDj8VhRqVRYLAKmpoRU\nVycTFyejsXEWs3mMqqo4pqYGMBpn0WhkuFxB5HIPubmZXL3qwmoNcvfdiwkEXBw5YkehcLN+fQmd\nnddobb1GWVkikZEOhobGEQiCBINOJBI3kZEyZmYc2GxuDAYpcXEGzp8fJBgMsWhRMb29g1y44ECn\nCzBvXiEffXSe8Z8avl0AACAASURBVPEgxcUGRkdH2b9/CpdrgpqacnbsOMClS16Sk+ey3jdb1L7x\nxm727zcjk00TGangl788RFubkezsaE6ebGL79laMxk6qqsr42c9e4uDBCxgMcw2/P//5Nrq6Opk/\nfx79/f00Njai0+lIS0tjdnYWh8NBXl4eOTlzEiaDwcDChfPCcxZ0OgUxMR6WLavB5/PR0HAZjwfm\nz8/g/PnzvPzyCfr62qmpqWZ8fJzLly+Hr12FQoFWq2XhwvnU1lah1+u5evUqLS3jKJVBli5dwKlT\np9i79xB6vTY8XFAqlbJwYQW1tVVER0dz6tQpdu26xsTEGIsWFYez/RERc4QiMjISr9fLgQNnMJtF\nFBbGkJaWFpZBREdHo9Vq8Xq9fPTRPn7zmxEmJ6+xfPnCcGYyPz+b/PwYFi1aiEgk4tixY3R1dZGW\nlhYO1Juamnj11TYGBoxUVuaGB9UNDw8zNDRORkYMFRVzlQuBQEBUlIL4eD/Llv2b1WxkZCSJiWqK\nixPCDk9ut5u4uDiiovwsWFBAbm5uWNohEMDs7BC1taVh6VYwGOTIkROMjwfJylKTmJhIIBBgdHSU\nV145yqVL46xeXc7KlSuQyWQYjUa2bXuTQMBHSUkMFRXZ4SrHzMwMhw4d5/TpOVnlX/3VU6SkpOD3\n+3nxxV/z0UeNxMfL0Wph7drlFBQUMD09zcWLF3nzzfOMjTm57bYCVqwop7S0lJ6eHl5+eScDAz2M\njAhJSFDx3e8+TEVFKSaTiZdf3sXBg4NERzsxGGRs3ryB5ctr2LnzA+rrjzIyEiAQkLNpUxnV1XnM\nzMxw6dJlPvzQTCBgpqoqjrKybDIz06mvb+XIkXE0GisGg4JFi+aRlhbPvn2ddHePoFb7MBiULF5c\nisfjZvfucbzeMTIz1SQna9HrtbS1jV6365aSn69jbMzC6Og4k5MSxGIly5alERER5PTpKazWIWQy\nFbGxEeTnJ9DZaaG9PURuLmRkqLHZ3JjNFqxWBTKZgoULExAKvZw6ZcPhGEKjkaPXS4iN1dHdbWNg\nQERVlZrly/O57bbbyM7O/lzd0/47EAqF8Hq9t8QGERERt/Rm/Clnf/xn5VeHDh1i79692Gw2JiYm\n6O7u5uGHH/5vP3//Q/GFdOrPDf8Vhu73+3G73Z8okfqPcHN24fMAq9XKnj0f4/d7aGkZw+WSsG5d\nChrNMJcuzZKcPINarWJmZpLa2kX4fO0cO+alrk5GTY2Uzs4hLl++hkIRi9nso6AgFoPBQ2PjDBZL\nL7m5Gvr6rmGxyNFqo2lrExIV5WPZshhOnJigsbEXg0HL+PgMoZCO0tJkDhyw4vdPs3r1nGzq1CkB\nMTHS61p4N4sWZXH4cJADBwapro5CKh3h4kULKSkagsFobLYZ1q8v5ejRs+zbN05ZGWRkuLDb7cTF\naZHJUhkehpUrszCZJrh82UNc3Czx8RFYrePExSVhNjtpbYWlS0OsXKnk7Nlxjh5tIzJSjs02S1RU\nHDExOvbvn8HlmmLTpkIOHz5BfX0nWq0UmcyP3x+kqiqH/fsHuHDBxoYN+Vy6dIX6+gESEwPExQmv\ne/criYiIZWhITGlpPNnZMvbu7WNqqp1163I5d+4877zTSEZGJMnJfrzeuUnJQmEkMzMhoqOjkMsj\n2LGjH6dzlL/5m0f5yU+2sn37RR58sIisrGQ++ugS/f3TPPzwSk6dauaXv3yHVavKeOihaK5dG+T4\n8VNs3lyByWRidHSU1NRUtmxxo1YrGR0dZe3acgYGjCQnJ6PT6Vi4sIPYWB16vZ6qqkKczguUlOQT\nExNDYqKEUAhiY2NRq4dRq0GnU+H3+3E4fDidcw2I165do6PDh9lswmKx8PbbH3HmjJvpaTu3376O\n5557BZ8vyLe//QAymYzjxxvJycmmrKyMYDCI0+mkrKyMsrI5p6RQKMQ3vrERv99Pfn4+Q0NDiEQg\nEgmx2+38y7+8wtBQgAceMLNhwwaGhoaQSCQkJCSEr4fly5cTFRVFYmIiIpGIDz88SXu7AL3+HJmZ\nmRiNRgCSkpLCjZPFxcXU1PSRmhqPVqtl//4DHD/exqZNy6murgbmzCEee+xOJicnWbBgAdPT02zd\nupPoaDVf//pXEIvnJpIXFxfS0zPG/PnZOJ1OzGYzk5OTYbmKSCS67vrWhMcjIDY2lvnz5wOQkZFB\nXt454uJ0YVIEsG7dGkpLS4iJiQHgypUrjI6OsmjRorCUym638+tfv0kwGOLRRx8I93C0t7fz6qt7\nSE3V8+STj4QDzblm/tOsW7eQv//774TXOn36NEbjCHffvZbp6Wny8/ORSqWYzWYkEglJSRF4vYHw\ngD+Ay5cvc/y4leRkMz/+8VPhBvP339/DsWNXKCtL5MtfTqesbI4kjY2NYTQa6emZZHRUwKpVhaxe\nvRqBQMC1a9f41399G4HAR2amHK1WzerVq/H7/Rw/fpwrV65y4oSTvDz45jeXkZaWhl6v57nnXqS3\n105EhJWoKB3r1q2mqqqKDz/cR0NDI21tMwiFMlatSiEuLg6FQkF7ewcffzxJbOwEZWVxFBTMZ/78\nUt58cy+7d3ej1U6SmBjDihVLUavV7Np1GrfbjkwmICpKxYoV5QwODvP661fQaMbIyIgjISGF3NxM\nDh48z7FjbsrKhKSnRxAK+ZmcnGRwUEBERCQrVyZis9k5eXIYGCcYjEOvjyU/P4nTp7vo7DSRnu4n\nOjqIRCLH7Z7FaJSgUKhZvjwOu91Oc/M0ItEYGk0C8fFJpKcncvr0NS5csDJvnoCysig2bFhNbGws\nQqEQl8sVDpT/EGnOnyv8fj8ul4tgMBh2mPp95+TTyK9uEI9PSpL+tuzqD5Vf3SAxFy5c4IUXXsDh\ncABzFdulS5dSXFxMSUkJxcXFFBUVfaILlcVi4emnn+ajjz5CKBSyefNmnn/++Vukpp+EH/zgB2zb\ntg2r1crixYv55S9/SVZWVvh5j8fDX/7lX7Jr1y48Hg9r1qzhxRdfvKUX79Os/Unn5K233mLLli2/\n8/N9lvAF0fgfgP8MwfhtfNZ7NMbHxzlz5gwOh4MPP+xHowlSWWmgra2ds2d9JCVFEAhIsNmsrFpV\nykcftbB7dy9lZWqczgmuXfORk5NMKJTMyIiX9esLOHPmAo2NZnJzg8THg8tlJS0tB5PJRUuLm+XL\nI6mqstLZacPl8hAdrWdmxk5BQREKxSiNjUHmzzezZImKy5cHuHxZhkKhZ3wccnPVJCbKaWgIMDvb\nTXq6ksHBYSYnhcTERNHTE0Ct9rBxYwH79zezf38Hen0EDocTt1vEvHnJ1NdP0d4+w7JlqbS0tNHU\nFCQxMUhEhBSvd5Zly8qor4ejR60sXx6PVjtNT48Jg0GJRKLDZnNQV5dPR0cfBw7YKS0NUFmpYHBw\ngsuX5chkOqangxQW6klNFXP48CRTU91UVcXR0dHJyZMeIiO5Xk0JsH59BXv2XOLgQSO33ZbF0NAQ\nJ070k5AgISFBiMtlJxgMIRarGRkRkp8v56675vHqq82Mj/dwzz0VnD9/kd27L1FUpGLduihGR428\n885eYmOV+Hx2zGYzOp2OQECI2+0nLi4Os9lDT4+QsjILxcUF/OY3V5BIZnj22TL6+oy8+24nixeP\n8NBD9/IP/7CV/fs7+MY31qHVqtm69WMyMrR8+9uP8c477/PDH/4zDzywke99bzH79x/EbLbwv/7X\nNzGbzfT09FBVVUlRUeF116MgTz99P1NTU5SUlOB0Orn3XjN6fTQxMTEUFKQzPd1OdnYaTqeTmZkg\nPt9cVvvMmbPs2HGNgoJeCgsLeeWVN+jqGuMrX1lPaWkpvb29REREhDPhAHV1dcTHxxMVFUUoFCIy\nUo5S6UIul9Pb28vzz/8GsRieffbh6+fFjFarDZMDgNWrK9Hru5g/v4yhoSGee+51QiH4znceJDU1\nFYDExES+850nw8ecPXuVixdDZGZ2UF1djdfrJRAIUFhYGH5NX18fHR0+oqKmsVgsJCQkIJFIqKqq\noqqqKtwn9eqr7zAw4GHLlglqamoAkMvlJCSI8fkCREVFhTOqCQkJ/PCH3wkHI8eONXDwYDMbNiwO\nH+twOHjllT0YjXMSpxu9DENDQ7S1WQiFYHBwkJKSEmCuGjIwAH7/JE6nMxx4nD9/lcuXwWC4yvLl\ny4A5srJz51EGB0N89asC1q1bR0REBMPDw/zzP7+JSCTg299+gLi4OGQyGaOjoxw6VE9UlIbVq2NI\nTU1Ao9Hg8/mYmpqir8/I0JCQ/PwADz/8pfAa//Iv27FYgtTUpFwnvQtxuVzU19djMpmu22BLeOyx\nB0lMTGR2dpYPP9zP3r39pKQ42bgxndLSfBYuXMiuXe/S3t7H9LSF2Vk1GzYsoaKigqGhIfbs2cPH\nH/cjEPipqooiISGBkpIiWlvPs3fvOVQqE2lpsRQWlnDnnRvYtm0n9fXvI5FMEhkZy9q1dcTGxrJz\n5xEcDhtCoRSNJpKNGxcyPGzkjTdakclG0evjSUlJo7y8mH37mmlqaicjw01hoRS9PoZgMMC5c17E\nYqit1eNyublwwUgwaMZqjSE1NZra2lSamzvYt2+QqCgniYkRJCbOzTc5d86JRAJLluhwOh1cuDBB\nMGjC748nPj6OkpIMTp7soL3dRFZWiJQUJQ88cD/p6em3OCz5fD68Xm/4N3xzxv6351T8OSMYDOJ2\nu8MyqcjIyP9Spec/Ig03k40bBOTm6scN/Hbvxye9128TkO9973v87d/+LYODg7z22mscP36cuLg4\njh49yksvvUQgEACgurqa5ubmW97r/vvvx2QyUV9fj9fr5Wtf+xqPP/44b7zxxn/4P/70pz/lF7/4\nBTt27CAtLY3vfe97rFmzho6ODqRSKQDPPPMM+/fv57333kOtVvPUU0+xefNmTpw48QevvX37dtau\nXRuOw24kLz4v+IJofM7wh2x6fwyC8dt+3J9VHDhwmHffHSInx0NpqZaOjquMjoJSqWNwUEZ6uoQV\nK3QcOzbL4cOXiItTMDw8idcbR3FxCvv22RGJLNxxRwn79h3j6NEe9Ho5EkkAn8/PwoU5HDwo5OjR\nISorowmFujh/XkpGhgqxOIbZWSu33VbCgQPN7N07QlWViMxMOxMTNjQaBVJpMsPDflauTGdoaISz\nZ2dITrYQHy/DZpskLS0Li8VFSwusWiVl3Tox585N0NR0lchIFXa7k6SkBAwGH4cOObFajSxblsrZ\nsy20tYFMpmJ0VERKiojly5Oor/dy8GA3GRlywERvr5OkJA1dXRLsdgebNs1n//6THDkyRna2mMRE\nFzabg4wMNT5fLF1dLlatSsZoHOH48QmSk/2kpMix281IJEkIBEq6usSsXq0kJyeKY8f62L//PJmZ\nKoaHx+jsFKDVSpmdDeFwuLnnnrW88cYR3nmnnzvuSCIpaYaLF42Mjk6Tni7BarUwMjKGVBqB0xnA\n7Q6wdGkFL744TX//JN/61jL6+wfYu3eArCwTTzyxit27D/Dcc6+zbFkBWVl2Jiam6e7uZcGCWNxu\nJ0ajkZgYHSkpY8THR+FyuRCLhYjFIcRiMRaLhakpUKnsOJ1Ozp7tobdXSEVFF1arlfff70athsLC\nAj788BCNjRPU1XVz772b+PnPt+F0enn66fsxGAy88sob5OSkc889dzM5OcmlS5fYuHE9GzasJSIi\nglAoxBNP3Ibf76egoAC/309hYS9lZVkEAgF6e8cZGBBiNBqRSqW88MIepNIQf/M3jyAUCmlpaSEj\nIyMsLZLJZHz7248yMTFBRkYG3d3dBIMCgsHQdanPEXbvPkdVVSpf/eoD4etk1apVrFq1CoD+/n7m\n7r8CAoEARqORI0eOUVCQS1VVVfiYu+5aRUbGJZYsWXQ9ML7xvz9IUlISAGVlZdx77yRarYb4+Hgu\nXLjAkSOnWbasisrKSgQCwS2DxiIiIlCr1fh8PmQyGX/910/h9/sRiUQ0Nzfz9tv1pKdH89hjX0Ui\nkSAUCjl79hJtbUEMhithoiGTyUhOjiIYNN8yaC87O5vbb88nFAqRmzs3E2J8fJzy8nICgQAJCQmo\nVCqcTuf1CtdSYmIuUFVVAcwRALPZTE5ONBERUxQWFqJUKgmFQteNMwSIRHMJmBtSr+bmZt5910h2\n9hD/+I9/FX58+/adtLSMsHhxMo8/nk5ZWRmhUIimpiZMJtP1IEhAXl4elZWVuFwuzp07x5tvXkaj\nCXH33eUkJyeTmJhIfX09e/Y0o1Z70etl5OVl8/Wvf5W2tjb27NlDY2M7w8My7rorl/z8fAwGA729\nvezYcYpQyE1qqpTYWAP337+Zs2fP8X//77tIJHPWxPn5eTzyyAP8+tdv8sMf/gqfz4Lfr2fjxqUk\nJCTw3ntHmZk5iccTgUKh5a67FjI2Ns7bb59BIBhFIkkgJSWV2tpK9u8/zauvniMqykpychQ5ORmI\nxWKOHRsHfBQVKREIwGi04/NZGRhQk5ERyZ13pnHuXDuHDl1DKp1Bq1WQl5eOVCrl1Ckz4KWoSAmI\n6eubJhCwMTERTVpaNCtXZtPc3M6ePX1ER8+Qlibj/vu3hCuEMJd5v9lV6oYU52Z3pRsGKPDv7WJv\nJiCfd9yQSbndbgQCwS19GH8KfFL1A343AbkZv6/5XCQShV3DampqeP7554G5Xs2Ojg4uX76My+W6\n5ZjOzk4OHjxIa2tr+Hfyr//6r2zYsIGf/exnt+wpN+P555/n+9//PrfddhsAO3bswGAwsHv3brZs\n2YLdbueVV17h7bffZunSpQC8+uqr5Ofnc/bsWaqqqujo6PjUa2s0mnAF9/OIL4jG5xC/L/D/YxCM\nP2S9zwIyMlLJyBikoqKQmppF/PCH2+nq8rF5cwGxsf1cvmwjKWmWqCgldvskS5ZU4feHOHEiSF2d\nhxUrlLS1DXPuXCdKpZ7paR+FhdHExQmor7dgtXaTk6Oio6OLgQEf0dF6RkfFeL0BNmxI58CB83z8\n8WWio2U4nRZsNjlFRUkcOaKgt3eWFSuyaGxs5sQJSE4OEhEhwu2eZcmSIg4fDrBvn5Hlyw3I5eO0\nt0+TmKhBItFjszlZu3Yera1XOXzYRmlpiIKCIBbLNDMz0UREGBgYEFBXF0NCgo9z58xMTfVgMEQw\nNTWJWp1HUpKAU6f8KJUeNm1K48iRcxw8eBGlMgKXy0NEhJwFC5I4eHACn8/B2rXZNDe30NwMsbF+\npFIJLpeTRYvyOXLEy8GDY6xalUhCgoUrVyaIjbWhVktxuWxkZxfi84U4fdpHXZ2Y++7L4OOPm3nz\nzXri42WAleFhIdHRalwuJXa7h8cfv4Pt2/fy3nvj3H13HJs3J3DkyEXeeusAlZUGRkbGOXWqBZ1O\ngU4HYnEAgUCA0ynEZBKgVCpRqVTs3TtKX18Pf//3j7J165ts3XqWTZsyefrpu9m27T2uXh3ma1+7\nHaPRyIEDjZSX5/Pkk4txuVxcvHiRTZtqGBoaISsri8jISIqK5Gi1kcTGxqLRRKJWT6DRRDIzM8PU\nlBeXC6anpxkcHGTv3nFyckapqqrkhRe209/v5b77xqiurmbr1h0oFDIefPBeYK4ROTs7m5/8pDgs\n2fjKV25jaGiIxYsXMzY2hkAAQuGc69vu3R9z+PAECxZ08+yz36SlpYWpqSmWLl0aLtXn5ubyzDN3\nI5FIrgekDYyNCRgamiAUCvH++3sYGBhly5aNYeej9PR0nnnm3uvXTwa7dv2G3/zGSGHhMOXl5YRC\noesDJ4vDlZXBwUFGR904nXNVxMTERMbGxtBoNGzefFf4ejx+/AxHjtgJBs9QWVkJgEQi4ZvffAiT\nyUROTg6Tk5O8+OIOpFIxTz/9cDhLZ7fbGR+XEhFhD2c7fT4fdXUL0WjaqKycz+zsLEajkdnZWZ54\n4mt4vV40Gg1TU1Ps2PEOKpWCr3zlS+Fgv6GhgV27TpOXF823vvVYeC989dWdtLZOsHFjIV/+8gOE\nQiEmJyd57rmXsdm8PP74nRQXFyMSiRgbG+Pll3eiVit57LF1yOVy0tLSGBsbo6mpCZlMRnm5hOLi\nTKRSKQ6HA5PJxPi4melpEAjErF+/Hpib3/H66w3Y7fDAA2VkZmaSk5NDT08PW7e+i0wWIC1NSEyM\njmXLljE1NcXevXu5erWHgQEh1dVafvCDLyGVSunq6uK11z7GaBSwYEEkVVUG1q5dxczMDP/8zzvx\nemeQy+eqD3/xFw/T3d3N//k/v0IgsOJ06sjPT+bBB++isfEU//iPLzA5acZq1XHHHfNJSkrixIkW\nTp1qYXJSilSqYcuWciwWCx980EQwOIHDYSArK5nVqxdz4MBJXnvtJDLZFGp1DGVlBcjlco4cGSQQ\ncJGQICIiQopCocRqneLCBQlpaQK+9KVULlxo5+jRLoLBGSCOefOyUSqVnDw5ht/vxmAAqVRCKCTC\n5bLQ1aUkI0PBli2ZnD/fwccfdyORmNFq49i8eSMLFiy4xTThk3CDAN88b+FGoHuDgNzoCfjt6sfN\nBOTzVv34z8ik/lT4ffKrT0NAbpa+2Ww24uPjw89HRETcIkm9GU1NTeh0ulueW7lyJQKBgDNnznDH\nHXf8u2P6+/sZHx9nxYoV4cfUajXV1dU0NTWxZcsWWlpa8Pv9t7wmNzeXlJQUmpqaqKqqorm5+VOv\n/dRTT/HII4+QkZHBE088wUMPPfR7zupnC18QjT8j3Ng8fD4fQqEQpVKJVCr9L28gnweiUVtbS0VF\nBXK5nFAoxF13lTM2Ns6qVatobj5DZ+dlIiPlPPjgKp5/fhd79gywcGEkbvcU3d3j5OSkIBIlYTJ5\nWbeugLa2dhobbeTlBYmP92O3j5GfH49Gk0h3t4y1azXExPhobR3F5epEo1FiNlsoK8tCrZ7l+HEf\nXu8Eq1Yl0tR0ltZWIQqFBrNZgEwmo6Ymhvp6P0eOdJORoaSvz0hvr4e4uEg6OyOIiHCwYUM5+/ad\nYN++XlJThej1bmZnPeTlZdPYKOLy5VlWrEijp6eXs2e9JCaGiIyU4XZPs3RpKQ0NXg4csLJ6tYKl\nSwV0dw9fHxSnY2bGR1lZCnb7DMeOucjIGKC6Oo6Ojg46OiTI5VrGx6VkZSlZvTqOAwe6OHy4m8xM\nOaOjk3R0uIiNVWC3KxCLZ9m4sZx9+06zc2cXNTUKFi0S0t8/hNvtQiaLxO32kZeXh15vYe/eaUpK\nLHzta1V88MFhXnrpQ9LS5Ph8VsbGxhEI4giFFDgcPsrKipmZ8XDkiJ3Vq8U8/vg6fv3rvWzbdoj1\n64sxmUwcPnyW3NxEFixQEwp5uHDhAipVBDqdC7FYhMPhwGIBkSiAVCqlv3+E+no7TmcbTz75ZX70\no61YLAKeeGIpeXnZvPTSHhITI3n22ac5deo0W7fuYPXqWmpqFmI2m5mZmeHRR9fidDopKipCo9Gw\nePEwhYUZyGQyxGLR9V4KET09PTQ1TaFQwPLlIzQ3n+PQoT4WLIjjiSceoqGhgelpM6tXr6KkpIRg\nMIhareZb39oMzN3AEhIMJCZOk5oaj9Vq5fXXjzAxMZeBrK6upqGhgaioKBYsWBC+1jdsWEtcXCt5\neXnY7XYaGtqvy3YuExcXR1NTEyqVitLSf5sRUVhYQHn5IOXluQiFQl588dd0dpp44IEVLFgw5+6U\nkpLCV76yDJfLRUlJCWfOnGHHjqMkJSn47nefCmeLly1bQDDYxNKlc7Kp/fsPMjk5xcaNc+5LMBds\nX7vmRSr1YjKZwg3ctbW1iMXicP/MhQsXaG/voKZmMY888jUCgQCTk5O88MIubLYQDz00w/z585mZ\nmeHKlSs0N08TGTlNXZ0xbGdrscxZCk9NzZGXG0GN0+nG7Z7Leno8HjweDzMzM8zO+nE6pWEdP8xN\nEb961YNa7eGuu6JJSUkBoL7+GG+/PUhpqYgf//ivgblg9cUXX6Wra849asmSeEpLS687er2D3T5L\nbKwYjSZIUVERBoOB5uZmBgYGGB4OERMj4O/+7mH0ej02m40PPtjHoUPTlJcL+PrXiygqKkKr1fLT\nn77A+LgblcpDaqqcNWvWEBMTw8sv78ThsOFwiFAoVDz11GacTic7d77P9LSJnh4xRUVannlmJSMj\noxw8WM/58/2MjUWyfn0GSUlJjIyYaGo6S2enF7FYztq1mQQCAU6cuIjPZ8VoVJOTE8t999XS0NDE\nm2824PNNEQrFUl1dgkaj4dChTjweB0plCIVCTnFxOuPjJg4dmkv83HZbFkajk9OnO3E6HczMxFJb\nm41Wq+XUqQHc7nEUigAyWQRZWfFYLNOcPOklOTnAffel0NnZS0NDL16vmWAwjnXrllNVVUliYuJ/\nKbF2I3j9pOrHzfIrr9d7y73xtysfn7Xqxx9bJvWnwh8qv7ohjQoEArS0tFBXV/ep1hkfH7+lZwLm\nvsOoqCjGx8f/w2MEAsEtfVkABoMhfIzJZEIqlYb3tE96zadd+0c/+hF1dXUoFAoOHTrEk08+icPh\n4Omnn/5U/+NnAV8Qjc8hfjvw/1MRjP9ovc8qbmSvBAIB69evw263IxQKWbt2DSkpySQnz808yM9P\nYHzcyu23386VK1d4+eV2lEoX995bwbvv7uPIkV4SEiTIZB6s1hlKSwtobBRx5oyFuro0Ojt7aW2d\nJTVVjkikwWazsH79AhoazrN/v5nFiyUUFfmwWCYwmyORyRIZGQlRV5dMXJyVlhYH8fF9JCYqmZoa\nQ6stxmCIpbVVgE4Ht99uoLHxEkePXkKlUjE15UKl0lBREcmBA2ZmZ0dYsiSZ1tY2zp3zEx0txeMR\n4/W6WLkyh/37L7F7dxfFxSrATHe3hdTUWHw+A9PTHtatK6Gp6TyHD5vIzw+QlgYezwyRkWlIJP8f\ne+8dHYV1b/t/phfNjMqMeu8SEuqAhAqIJqptsDHggq97jX1tx0ne9Ut7N2/53uTGSdxuwDW2wQZj\ng2mSANGRERPw6gAAIABJREFUAAkhCdQl1Hub0YxmNP39IdCzc53yy312TH7ea2mprNGcM0s6c84+\n3/3d25/GRhcrVwYRFDTFxYsjdHePotPJMZkm8fMLQSiUcPasHR8fAVu2xHD4cDkHD17Gy0vC9PQk\nExN2/Px01NZ6YrNZuPPOHI4fP8eePc2kpkrIzBQyNTVGfX0rIpEHBoOLkJBAoqLCef/9FsLC+ti6\ndTEHDhzh7bfLSE31JCdHjMWi58qVq0gkM43GcrkcpdKD+noRMMD//J9P8rOfvcalS5fYujWVlJQE\n9u49R1NTF1u35tHV1cXJk+cIDw9kxQorERH+DA8Po9MpEAotaLVauru7GR8XIJfPhLwdOnSO+noB\nvr41pKam8PvfFyORwAsv3I3FYuHFF3/N4sVp/Mu/PEN9fT3l5eU88sjdTExMEBUVhcVioaioBYVC\nTlhYGOXlF3G5Zg4tw8PDfPJJBSMjoNNpCQ8P5803d+Hnp+HeezchEokwGAzceus6Cgry8PHxwel0\nEh3tg1KpJzQ0lKqqKt5/vxZfX4iOjsZut3PlyhXS0tJYsWIFMDPWypUZdHX1k56eTk1NDW+/fRaV\nCl580Z+AgABGR0dJTEzkX/91xhbWbrfT0zNKf7+QoaEhXC4X1dXViEQicnJyZt9bJicnMRhApbJc\nb46foquri4SEhNksi6GhIQ4cqGZkBEJDa2YPAUlJSdx11yASiWRW/lVScpLMzKTZXgu3280nnxyh\npmbmYHHvvXcjkUjQaDSoVHKcTgdeXl7I5XLMZjMxMTEsWdKGSjXjwNXb20tTUxMJCfE89piGyMjI\nWSlaa2s7a9cuJT/fQEREBEajkZKSIzidbu6/fw02m42srCwmJiYoLi5Fo1Fx++1xaDRqQkJCGBgY\nuE5qPYiLc5GcPFNdGh4eZmBgAJPJgsUCHh4qFi+eIWcz1ps9WK3wzDNLSU1NRS6XU1ZWxrvvXkCn\nc7BlSyrBwcEEBASwe/ennDrVjK+vk8hIIZmZaaxevZI9e/bS3d3P8LAei0XJnXcWkpKSwvnz5zl7\n9iwNDdN4eEi5884sNBoNXV1dXLnSyLFjFubMcfDQQ3ORSqWMjIxw9Ggtvb1S8vO9yMnxR6mUMTg4\nyJkzI4hEDnJzfZHJZExMTDEyMsDly2JiYsQ8/HAq9fVN7N17EoNhgslJLUVFc9FqtRw7VofF0oxI\nJMLTU0ZubiLDw8Ps3t2Lv/8oCxYE4XQqGBqaYHDQzPCwjuXLtWi1WsrLW7DZehEIhHh4SMnMjMZg\nMHDo0DgBARMsXx6FXm+nuroDo9GAXq9j5cp0srIyZpv1vw7cqH58EV886N4gIA6H47/0HPwxAfmm\nm8+/aZnU14U/J7+qqqriueeeY3x8nObm5j9rxy8QCGhsbPxa5/r/Ci+++OLs16mpqUxNTfGrX/3q\nO6LxHb4ZfN0E4wZuFqLxx7gxb7lcPutkA/Dss4/hcDiQyWSoVCqMximioiLIyMjg1KlaenttpKfP\nJShoiMOHB3A4+khP96W+vomGBgeenhqam514eU2zevVcDh+u5NChRsLClJjNRsbHRcTEhHLihJjW\n1ilWrIjjwoVqzp51ERHhvp6FYSA3N42yMhtHjoyxYoUXUqmetrZ+zGYLcrmOyclpli6No6urj9On\nbSQmDpGaqqSnp5fRUQ0ymRddXRKioxUsXari9OkuTpy4ip+flKGhMSCE2NhASkunEAgm2bAhjeLi\nUxw50oRWK0ahcOBwOJk/P5YjR0ScOzfE0qVhNDW1UF5uws/PjVQqx263smpVFseOXeLAgTGWL1ey\ndKmI5uZu7HY7CoUGs9nJnDnRREZaOHBggujoEdavj+PMmQt8/nkFKpULsdiG2WwjKSmRAwdsjIyM\nsWVLJlevNlBS0k5kpJC0NClTU5O0tLTjdksxGsHDw4M5c+awfXsFnZ09PPLIcs6ereDjj6tIS/Ni\n06YQ+vv72b17LzqdAodjCpvNhkAgYHxciEAwTVJSEmVllVy8aOP22wXcfvtq/uM/PuT48UaeeGI9\no6Oj7Nx5kMzMOB5/PJ/p6Wlqa2tZsiQdP79rpKamIJPJkMvdSCQzVan6+lYaGgR4ejazcGE227fv\nY2xMwCOPzLg4/fznvyEkRMdDD22dDZlbtWo5qan9REZGIpfLSUryY3BwgvDwcOrr66mvtzE2NoLT\n6WTfvkNcvNjLmjUp3HLLjLTKZrPxve89jNPpRCaTIRKJiIwU4uurwdPTk9dff4fTp/WsWNHHE088\nSFtbG0ajkVWrimY33plEbFCrpahUKg4ePExJSR25udHcffeMlEoikfDAAxvo7OwkOzubpqYmtm07\nglgM3/++ZrZSsGjRItRqNYGBgSgUCt54411qavTccksbGzfOVGW0Wi3Z2eEMDIyRkJDAxMQEBw8W\no9X6sHLl/51XefkFiovHGBg4S25u7uwaXrBgDi5XPUlJMz0XtbW1OJ1OnnvuASwWC6GhobS2tvLW\nW58SGOjFE088gFgsxuVy8dln+ykp6SUjw4OnnnoQ4Lq86hCtrSJcLgdr165FJBLR19fH8eOdTE9D\nUlI8OTk5AFy6dIlPP+0gIMDNz3728KxWev/+Eg4fHiQ3V81LL30fqVSKzWbj1Vf/QG+vnTVr4li3\nLoLk5GSGh4f53e/ew+l0MH++L1KpjDlz5jA4OMhnnxUjFNrw9HSj06lZtWrVbPN2Q0Mb/f0CkpKC\neOGFzdfneJzjx5sZGxOwYcOcWalfRUUFO3ZcQaWysWRJKIGB/oSHh3Py5DlKS4eJiJhk0aJAkpKS\niYgI5733DtDbCzExDvz91cyZE4/dbuezzxoQCKaJi1Oi0WgJDAygvb2TsrJpoqLMbNqUxOSknvr6\na7S2jjAwoGH16hj8/f05e/YqFkszVqsMuVzFkiWJjI6OsWdPG56ew0RF+aBSqfDzU3Pp0hB9fTIW\nLw6goMCX2tprNDX1Y7WKkUhU5OSEYjKZOHx4EE/PUZKSdMhkaqxWB4ODRnp7fVi2LIK0tLlkZGTM\nOot9k/hT/QJfdEW6QUK+qvrxx/0fX0dW1bdJJvV1QK/X87Of/YxPPvmEn/70pzz11FMYDAbGxsb+\n7O9FRUUREBDA8PDwl37udDoZHx//k/0ZAQEBuN1uhoaGvlTVGBoampVBBQQEYLPZmJyc/FJVY2ho\naPZ5/5axAebPn8+//uu/Yrfbb5oU+++Ixk0Ip9OJyWT62gnGDQgEgtnS5M2EG2Fbf4wvulUEBATM\narOnp6f5p3+6jeHhYdLS0ujr66OtbS+hoVoeffQ+Xnzx1zQ0wO23+7JixTQVFZ2cPXsVb28VY2OT\n6HRheHurKS2dwmIZYNWqaE6dKqeiAhQKJVarEIEACgsjKC21U1zcQmKiBoFggIYGIxERPpjNvoyO\nmlmzZh6lpWcoLu4hMdFNUJADs9lIbOyMK1ZtrYUVK8Lx9x+kpmYcf/8xPD0VmM3j5OdnUVd3jRMn\nrOTnOykq0lBb28eFC43I5Z6MjztIStISFibl6NFRxsbaSEvT0dLSSk2NFaVSzPi4GJ3OwYYNaRw4\ncIE9e66QmKjE4dDT02MiJMSP6WlfRkbsrFuXTmVlLYcO9ZGUBMnJguuEy4RE4sPIiIx588JJShJS\nXNzN6GgDWVl+dHR0cPToRby8xExPu5iedrB6dR4ffniaw4f72Lw5gbg4PefOddHS0kdKigcGwwSN\njc04HG6mp8HlgvT0VE6f7qGurp/vfW8xAwMDfP55I5GREh56aCF1dVd5552PiYsLxO3uR62W09fX\nx43lolAo6OjoprLSjsPRyI9+9Dg///lrDA3Bgw/mcPvtq9i+fTcBAV58//tbmZiYoK6ujnnzUvH0\nVJCcnIxUKsXXVwmY0Wq1161unej1AxgMBt5992Oqqw2sXRvNHXesZ//+g9jtDrZu3YRAIMBoNJKS\nksLmzSaCggLx9fVlfHySiQnQ6w3XE6E/wGYT8L3vrScqKorKykqCg4P5X//rudn/6bCwAEJCJggN\nndnEXn11F1NTAh5/3EVGRgZ9fX34+vry058+hUQiQaFQMDg4ytCQgMHBMdxuN2VlZQwOjrB6dRFx\ncXHAjITL03PGWlelUtHU1MSBA2VkZiZ+SaYgEgkRiWZuHt1uN5WVlVitVu6+e9PsbfDJkyfZv78T\nrbaT9PTUWT31/PmZDA0ZmD9/pqpy5swZOjq6KSpaxi23rEUgENDR0cG2bYdxOOCZZ24hOXnmsb29\nvXR2urFYxjGZTGi1WkQiEb6+WrTaAQICdGg0GsbHx5mYmCA1NRyxuIuoqCjcbjeXL1/G4XCQmuqN\nzeYgLCwMvV7PxYsXEYvFpKRICQnR4e3tTV9fH1euXEGjURAW5iIyMgiZTEZrayv9/f2AG6EQdDod\nmZmZtLS00NPTw+CgA4EA/umf8omLi6O3t5eLFy9y/Lie6Ggnzz9/FzqdDrPZzI4d+6mqsrJ4sZLH\nHksgJSUFo9HI669/gtEI8fEyUlO9WbZsGV1dXfzud/sQiYyEhioJCPDlrrs2s3//IX75y8/w9NQT\nFORFRkYKa9eu5OWX3+Lzz2tRKicJCPBk2bJC5HI57713EqfTiLe3BE9PDwoK5tPU1Mp77zURFDTG\nwoXBeHtrkEhE1NcP0dOjZMkSHQsX6mhr66W9vY+xMQkSiYaVK+PQ6/XX+yYG8Pb2x9vbi9TUWE6d\nqqO6epQFC5QkJmoYHR1jZKSN8XERYrEn+fmB1123+pDJhgkI0KLReBIfH0pVVTMXL5rIy/Nh+fJY\nFi5c+CU7528L/pQt6xezJW4QkD9uPv8qAvK37O03i0zqb4XL5WLXrl28+OKLLFq0iCtXrsyaU2i1\nM9Wxv4ScnBz0ej2XL1+eJQllZWW43e4vufV9EZGRkQQEBFBWVjbrZjc5OcmFCxd48sknAcjMzEQs\nFlNWVsb69esBaG5upru7e/YC428ZG2aCQL29vW8akgHfBfbdlDAajTgcDpRKJR4eHojF4q/1huJG\nEJdcLv/axvg6YLfbcblcf3beNwIJbxA3rVZLdHQ0CoUCX19fFi9eQE7OPIRCIRqNhMBAJ8uXL8PT\n05Pa2j7kcjFPPrmFxsZGLlxw4u/vRKeDsbE+RCIZFouE4WERaWm+BAWJqa01MzExgk6nwGgcJCDA\nD6VSTk2NGE9PB4WF0bS2ttPdbUKlEmGxOPH1FZOQEEJtrZPhYSO5ucGYTF10d5tRq4WMjEgRiSys\nWJHJtWtDVFdPERMjQy43Mz4+hoeHnPFxJQaDk4KCaCSSKSorp3G7J/DykjA1NUxISBCjo2ZaWuQk\nJ2tITdXR3DxCT88IHh4zKd5hYT4EBvpQUeECpli3LoWOjiZaWkx4eLiw2UClspORkUhDwzTd3RaK\nihKQySaoqRnHZjMglYpxu6fIzExiYMBEQ4OE1FQtCxZEcPlyD1evdhIerkAoNGA0GgEXnZ0OJBIb\nW7eup6qqlVOnjGRn+5OZGUpVVRtNTdeIi/NBqbTics3IA7q6THh5iVi+fDEHDlygrs5Gbm4YmZnJ\n7N5dRXt7J/ffvxYPDzh27DyRkYFEREiIiQnC6XTS09OPy2UnJ2emD+TIkZ7r0rQFfPzxAfbv78bT\nc5pbblnLhx9+xtmzldx//0by8tIZHh7G398ff38XCxbMBMLV1NQxMjLFnDmBSCRi3n33DPX1I4SG\nyunv72f79s8wmSbYuvVuvLy86OnpYd68NGJj1RQU5OFwODh37jIu18wNf01NDW++eY7W1qssWpTN\n6Ogo9fX15OYupKAgndTUFOx2OxcvXsblcrFw4Vw6Ozt59dW9XL1ay6JFC5HL5TgcDiIiQgkLE7Nk\nSQFWq5X//M/9VFUZCAkREhkZSUdHB3K5nMLC7NlQv+LiUvbvH8Zo7GPZsjzMZjODg4Pk5Mxj7twg\ncnKy6e3t5dVXP6eqqpvISM0soZBKpQwNtRIX509OzgLq6ur46KN9hIYGcscdtxIZGcHU1BSvvrqL\n8vJJAgLsxMfHz67p6uoaJBI3ixbNQy6XU1NTg7+/P6GhEhYuTCEmJoYzZ87w7rt7SEtLZO3aPBYu\nzMZut/PLX/4nJSWXWbQolfvu20R4eDjXrl3j978vpr6+m82bV7B06SJEIhFHjx7lnXdqGBzs4gc/\neJSsrAyEQiHbt3/Ivn1dhITIeOaZfyI9PY3JyUn+4z/e4+zZHoqKklm3Lpf09HSampp45ZW9tLZ2\ns3JlMgsXJpKWlkZZWRm//30JZvMYyclacnKSmDdvHh9+uIuPPjqGSuVALnezdOl8srOzeeutHRw/\nXo7dbkMiEXP33beQmBjHtm0f0dBwFZNJiEaj4Ec/egy3287bb3/G4GAP4+NSUlNDeeKJLVRUXGL/\n/pNMThpwOhVs3FjAggXJ7N59kpqaOtxuAZ6eSu65Zw1Op5Xdu+uZnOxCq1UQHe1PVlYy5eVNnD1r\nJDbWTWysJ0IhGAyTtLQ4sFqlFBVF4+Mj5MKFPoaGOrFaPdBqZeTnJ9LePkB5uYmAgGkCA+WoVDIc\nDgfXrjkwmaQUFATi6yumqmqEwcFORCIPfHzkLFw4h+7uUU6cmCI83Elamj+33LKSgoKCr8xF+Dbj\nRvXjRiCdVCpFJpPNBtPdIOg3wuhsNhtWq/W/pGLf2O+/at//U6F7X0e15O8Bt9tNc3Mz9913HyUl\nJWzbto0f/ehHf1NFS6fTceHCBT7++GPS09Pp7OzkscceY+XKlWzdunX2cQkJCYSGhpKQkADMXPa+\n9NJLzJkzB5vNxtNPP43VauWVV15BJBIhk8kYGBjg9ddfJy0tjbGxMR577DHCw8P58Y9//FePffDg\nQc6cOYNMJsNoNLJr1y5+8pOf8Nxzz826WX0L8F1g3z8iPDw8UCgU31j582aXTn0VbhAMi8WC2+1G\nKpWiUCi+dOPjds/YoN4og8+fP58FCxYgEAgIDAzkmWfkqNVqwsPDmTdvLnZ7E3l5uajVal5+uZj2\ndivr12dQXn6B8vJhIiLA01OC2axn0aI0TpywUlZmZNUqNUuWCGlo6MLtdiKX+zA5aSMtLZTAQBMn\nTliIiOggI0NHa2sLnZ1SlEovurpEhIYKWbUqhLKyBg4fvoJOJ8fhMGA2a4iLC+DoUTlut4VVq+Zw\n4kQ5x493ERbmRK0WYbfbyMpK4MiRaY4dG2LFilACAydoaBjC39+ATKbCYpmioCD9etbGFFlZLgoL\nPWlububixQYkEjUjI26Sk32IjdVQXNzD8HAjaWk6Ojo6qahowNdXjtksxWq1smFDHrt2nWDnzkaW\nLNHi62uhoaGT8XE9Hh4e2GzTpKQk0t7eQ3GxnsxMC/fck8GBAyf59a93Eh6uICLCyODgIA6HA5NJ\ngtPpYsmSfI4cOcOuXf0UFqp5/PGlfPppKS+//B4ZGSGEhs6U0mdS7kEsFqDT6Th06CTnz9vw9R3h\n1ltX8u///gdstkYefnjF9WTrkyQkhLF164xDVH9/P8HBOvr6uggM9GVwcJC2tins9hlJTldXN7t2\n1RMbK+EnP3mW0tKj/Pa321i9upCiIhFKpRK73U5ysgar1U5cXBxnzpyhq0uCXN6PzWbjtdfepaPD\nwpYt81myZAmXLl1CIpHw/PNbsdvtREZGMjQ0hFIJHh4zrkrbtu2gudnGnXcOctttt9LU1ATA888/\niNVqJTg4mBMnTmAygdFow+FwUFp6lFOnarn99sJZdxSn00lmZii9vSPExcVRU1PD9u3FaDRC/sf/\neGx2M8/Ons/4uIn09EScTievvPIWnZ1T3H13HgUFBcANS0YJVqsDnU5Hf38/Bw6UEh0dyr/8yzOz\n6+z48QqOHDHgclXMWr/KZDLmz4/B07Ob+Ph4TCYTe/ceQC6X8f3vz1j+arVaSkpK2LGjmogICT/5\nyT/P3vKdPXuZ8+dtaLVXWLBgAXa7HYPBgNE4jdU6s8YVCgV9fX24XC48PUUIhQJ8fX0RCoVUV1ej\nVCoJCYGQEB9EIhENDQ20tbWhUAjx9bXi6+uFVCrl5MmTTExMoFKJsNkchISEEBYWRklJCQaDAaHQ\njUQiIjs7G7fbzcGDB+nt7cNohKAgGd/73sM0NTVx6NAhGhs76e2VkJMTybPPruXy5cvs37+flhYD\nFouIBx/MJSQkhNbWVrq7u2locBAQIOGBB5bgdDo5evQYV6+2UV8vJD9fxx135NLS0saOHZ/Q1DSE\nwaBg48YstFotJ09WYbFMYjDIUKk0PPBAEU1NLWzbVopEMoJCMZP4vnhxDnv2HOPChfMEB1uIixMT\nFDRDGk+dGkEodJKb64vD4aCqqh2BYJKREW/CwrxZujSB8vIaPv20Ea12ipCQmTwMlUrFmTND2O2Q\nk+ON0+mktrYft1uPxaLD11dHXl4ily41snNnG+HhRlJSfLjttrVfsl7+R8AXqx//XevdG5X5f1SZ\nlNls5pe//CXbt2/nmWee4Uc/+hEKheK/9Zw7d+7kqaeeYtmyZQiFQu64445Za9wbaG1txWAwzH7/\ngx/8ALPZzKOPPoperyc/P5/i4uIv9Qf95je/QSQScccdd2C1Wlm5ciWvv/76/6exJRIJr7/+Os89\n9xxut5uYmBh++9vf8tBDD/23XvM3je+Ixk0IkUj0jR78/5GIxo3bni9qVr+KYHzR3eKP7fNgRhpy\nQ7YBsHHjBtatm0ahUDA9Pc1tt3UiFotZtWolIyMT9PT0ERjoz6pVibz55hH27WsiPd0LgWCQhoYJ\nIiP9cDj8GR2dZs2adM6ereTYsWESE12Eh7ux2QzodFF0dflTV+dg9Wp//P1nwqrGxqbQaOQYDAZi\nYuag0Yxz4oSNlJRRVq0K4fz5KsrLhcjlHoyNgVwuY+FCX44csVJa2kxioobe3iFaWhwEBakwGj2R\nyaa49dZsDh48xd69bSQnQ2TkNEbjNH5+Pjid/nR0uFizJp6BgQHOn5/A33+IkBAlRuMYKlUYCoUn\nNTVCQkKU3HFHECUll9i16xRarQSXy4jJJEWjUTEy4olA4GDr1uXs3VvCxx9fJT1dRna2BJttks7O\nHsRiNRaLgMTEOGJjHXz4YQvBwR3cfvt8zpw5zyuv7CY2Vk1UlBWBQHI96EyE2SwgMTEBb+9B3n23\ngehoF08/fTsHD5byq1+9x4IFUfj4mFGpZDQ2NiKTCREIZpyfamtrqaiYZmKiif/9v5/jpZde45NP\natm8OYPnn8/h+PEz6PVGNm7MwG63o9FoUCoVqNXg5eWB1WrlyJFq2tuFREY2kpCQwC9+sQ2lUszz\nzz+EWCzm6tWrJCUl8dBDMqKiohCJRDgcThyOmUri1atX2bbtKFIp/PCHd6NQKNi/fz8JCQn8y7/M\nSG0kkhmpi1ptw8NDeT1Nei8CATz33CbCwsKor68nKSmJp57ywN/fHw8PDy5fbqGxUUhDQyvz58/n\n4MHDTE9Ps2nThtlk2pGRketzcc02XB49Ws6SJQt45plHAbDZbJhMVkymmYOAzWajrKwMsVjMD37w\nGMB1++H9HDw4SFRUPzk5OSgUCiYnJ1m0aD5O53kKC2fCALdte4+hIT0PP7xptmekqqqK4uIO5HJI\nS5tLbGwswPW+GVAoZrI2enp6aGtrIz8/Ax+fVhYuzGJ8fJz33/8Yg8HMPfesRigUkpKSQkNDA2+8\nsRcPDxFPPLEJb++ZBPJPP/2M3bubSEyU8otfPI1KpUIsFrN37zFqa+3cdlswP//5o6jVarq6uvjw\nw1MYDAK2bk0nOTmZgICA625cNXh7u7n//uWEhoai1WrZseNjPv20l9RUePrpQkJDQ5mcnOS99z6n\ntRWKivxYtiyChISE6/kXZ7Db3eTlBeDv709ISAj19fV8+GETfn5T3HJLPDqdD3K5nIMHT3D+vI35\n8wXce28kSuUMkTp9up3xcRHLlgXj4+ODwWCiq6ub5mYHGo2cjRvTGR8f56OPShEIjOj1GlJTQykq\nKmDv3qNs23YEqXQCHx8fUlISUSqVHDjQCliJi1MgkUiZmnJgMo3R3CwjOlrBli3xXLhQw8GDV5FI\nJvHw8CchIRpvby+OH+/Eap0kNlaMSCRmcHASp9PE4KCawEAv1q9PoK6uhc8+a8bTc5SgID9WrVo2\nm5b+/xf8Nda7Lpfrv1jvArNuVzeyaW4m692vgtvtpqSkhO9///vExsZy8eLFWVnnfxdeXl5/NpwP\n+Erp+M9+9jP+nCJIJpPx6quv8uqrr/7NYxcVFVFUVPRn53Yz4Dvp1E2Ir/KS/jpx4yblZrsduTHv\nG5a3MwciEzabDYlEgkql+lJJ+auSSm806P2l1y0QCGZvo8RiMXPmJJKQEI9IJCI2Npq4OG8KC/Px\n8/OjtbUBlQoeeOAubDYLZ85YUSptrFuXTlNTAx0dZjQaIRaLC7XaSUpKNE1NTrq7jeTkBCEQDNHW\nZkAudzE5KcfpNLNq1QL6+wc5f95GaCh4ejowGEaQyeQYjVJGRwXMmxeMTueisnKSiYkhdDoFdvsE\nYWHBCIViampE+PnBokVRtLR00d4+jkolxGZz4OsrJT4+lOpqO3q9haVLozGZumhpMSGT2TGZxEgk\nFpYunce1a3qqqsxkZfkQEuKmpaUPg2ESh0OC1Wpj4cI5KJUSjh41IxabKCqKp7u7jaamQWQymJ4G\nPz8Jc+fGU1ExweCghQ0bshAI9JSXD+ByTaLRCJHLbQQG+tPZOUZPj5jMzEByclIpLm6jpaWf5csT\nUCjMnD17FZHIjtttQaeTERISyIULzXR2Cpk3L4jExDg+/ria9vZ+7r9/NSqVkAMHzuDnpyEqSkl0\ntD8Oh4O2tm6MRifp6eFYrVY++qiO3t5xNmwopKurlw8+OIWPj5StW9eiUsm5du0aoaFavLxsLFiQ\nyejoKBcudCEUCsnLS+PAgVI++qgBq3WIrVu3cOnSZc6fv8jq1UvIyopg3rx52O12amqu4OEhYtGi\nBRxOZNs/AAAgAElEQVQ6VMrOndeYmLjGLbes5Pz581RUXGD16uXk588lLS3tevhgLSIRFBRkcu5c\nOW+9dYru7mY2bdqAVCplcHCQmJgwgoKcLF6cz/j4OG+/fYL6+nFiYjRotVouXLiATqcjKyuGRYvm\nExAQwK5d+zl2bBKhcJTc3Pm0t7fT2dlJQcECkpL8yM7OpqGhge3bz9DY2E9aWjgBAQHo9XpUKhVT\nU91kZMSSkpLM++/vZMeOo0RF+XPPPZsICgpidHSUPXvO0d3tIjZ2plrY1dWFTCZjamqAiAgv8vMX\nUldXx2uvfYC/vze3376EwsI8ZDIZL7+8ncOHuwgOFrNx43rUajXDw8N8/vklenvdZGWFkJ2djcFg\noK+vj8rKToRCF0uXZiORSLh06RKTk0b6+8eIiPCmoGAhly9f5uzZc4ATp9NMXl4qMTExfPLJXpqb\n25FKXajVAlauLMRut/Paa+8xMNCHRGLH39+DpUsLqK6+zBtv7EYonEYkcpCZGceKFct4//1d7N17\nEqXShUIBRUUz/RuvvbaD6uqrKBQuvL1l3HvvRkwmE9u2lTIw0IGXl4S4uCC2bNnI0aNn+OyzqygU\nRrRaCdnZyURHR7FnzzkuXx4mMlJIRIQnERHBTE1NcfhwP0ajhcWLgwkO9mBkZJKurl6uXBETFqZg\n8+aFdHR0U17eyOSkAYdDSWFhIomJwZSVtdPS0o2XlxMvLzHx8WFYLFOcODGNRGJm1apoJifHaGwc\nZmrKiNmsZv78EJKTg7h4sZ/W1hE0GiteXmL8/LxxOqe5fFmIRDJzaWGxGKiuHsNsHgJULF2axkMP\nbSQ5Ofmm2nu+LtwgDCKR6EskxOFwAMxKsL5KfnVDAn1jb7tZyEdPTw+PPfYYb7/9Nr/85S956aWX\n0Ol0f+9pfYf/i78onfqOaNyk+CaJxg3HjJuVaAiFwlmCIRaL/yzBuHFz8dcSjL8GMpmMoKCg2UTn\nhQvnUVCwAC8vL7y9vfDwmGDp0oWkp6dz8WIjJhOsX5+Hj4+AM2dM6PUjJCR4MznZi8XixsNDTnu7\nFC8vJ0uXJtHc3ENjowF/fzEulxmx2EFkZCAtLUL0ehtLl8ZgNvdQV2dCJDLhcskRCi0UFmbR2zvJ\npUt2UlJUhIYKuXZtgMnJKZxOGWazk8zMcHx8xJw6ZWV6epi5c30ZG+vCaHQiFIro7RUTHCxh4cJY\n6uvHaGoaJSxMhlBowGy2otEouHZNjNvtZMOGhQwO9lFRYcDTcxqNxoXTaUQmUzA8bGd4WEReXiQR\nEZ6cPTvKwEAvc+f64nKNMTY2Bbjo6XGj1Qq5885VlJd3UFk5RmFhFBERUmpqOhkbG0UsBonETkJC\nJAMD41RWzvTNbN16K2Vl1Zw7105OTjjR0Qo6OgYwmfSYzVN4eAhISUmgtraZ8+en0WrdbNmynp07\nj1Jefo116+aTnh5BXV0zdrsVrVZIRIQ3UVHhXLnSSFPTFP7+EubOTeSNNz6noqKPBQsiSUmZw65d\nB3G7XaxaNZ+srHhkMhkGg56BgRESE4Pw9/dl+/bDXL5sID5+pp/hd797l+HhIR5+eDP5+fOuW2fa\nGB6eOawHBwfx+uufUlGhJzRUOHv41ev13HHHKvLzMwgODqalpZX6+iF0Oik5OVn87nfb2b+/kuho\nHatXr0YqlSKRSBgd7UanE1FYmE9FRQVvvllBW1sjGzasRqVSMTg4iL+/DzLZBIWF2cjlcn71q3c5\nffoacXFacnJycDqdiMVirl2rx89PTmFhHhUVFbz++mfYbEa+972HSUxMQCAQsG/fEVpb3YSGipk7\nN5mamhpGR0eJjw8kNlZNXl4uDQ0NvPLKXhobm3j66QdZuHABEomEI0fKOHbMgMs1xu23r8FqtdLf\n38/AwAAGwyTJyaEEBQVRWnqM3t4+kpNDiInRkJ+fR3NzMy+/vIORkUE2bSpk0aIswsLC+OijT9ix\now4PDwdPPbWZ/PyFOJ1OfvvbDzhxYoKCgnAefvguwsPDaW1t5aOPLtLZaeaee5awadNtmEwm6uvr\nKSsbBVz88IcPkJ6eTHNzM1VVdVy65CAoSMozz9yH3W6lsrKSyso2+vvFrFmTyubNt1Bbe4Wqqku0\nt0/hcIh59NH1JCVFs3v3ITo72xgYEODn58GLLz5JZ2cnO3eWYjKNYrNJWbQomS1bbmXXriOcO3cV\nqXQatVrGihW5eHur2L37Cn19vURFKQgN1RAWFkx7ey9lZVP4+jpZuTIWm81CW1sPPT0TjI0pWLEi\nnpSUYE6fbqapqR2hcCarZ/HidMDB55+P4HCMkJbmi0xmZ3TUwtDQJAMDahYuDCQrK5RLlzppaelH\nKLSiVErIyIhGJhNw4sQUdruRgoIQRCIrzc3jTE6Oodcryc2N4d57V5KTk41arb6p9p1vCg6HA7PZ\njN1uRyqVzprC3Oj9uPEhFotnK/Y39kS73Y7VasVms83a8X7bCMgMaX+N+++/n4KCAj799FOysrK+\nFXP7Dl/Cdz0a3+G/jxsL+2aST30xxGdqamq2gvFVZegbb7JfJZH6OvDFOYSGhnLffffMfv/00/cw\nNjbG3LlzaWxspK6uj7Cw4FnXq7o6IRs2+BIQ4OLcuVZOnapFrVai15vw9Q3G39+Hw4cNGAx9rFgR\nw7lz5zl92oZKJcJulyAWi1i5MpHi4nr27m0kJUWNUDhGc7OBsDAdVquOsTEbq1encvFiDaWlA8TH\nO4mKEuBwmFCrFYhEWurr3axZE0BYmJMLF/oYGanDy0vM5KQBP79Y1GolxcVGbLZJ7rorncOHT7Bv\nXyVeXgI8PBy43SIWLEhg//4WRkfHWLduDm1tbZw40UZgoABvbxFut5X4+Eh6esY4d87Krbfq2LzZ\nl+Lii7zzzuf4+UkRi6cwmUyIxWL6+5UIhXaee+4e3nprJx9+WEdBgTebNnnR2zvA0aOnkMvFOBwu\nVCoVFouFs2f7CQ018OyzW9iz5yAvv7yX3NxgNm8OwW63cfbsWeRyEQ6HC09PT/r7+ykrGycsbJRf\n/OIpPvhgN//2bx+xYkU8Tz4Zg9Fo5MqVK/j6ShCLzfj7+1/PMHAxMdHN+vXr2LFjDzU1w6xdO5ef\n/vR+uru7uXbtGllZIQwPT5CQkHA9ONHO+Pggd9wh5PDhI5w7d43Vq1N56aXn0Ov1jI2NkZYWipfX\nTNL2lStXOHiwEy8vyMhIY3x8nM8/LyYrK4UXXriF4OBg3G43k5MWJifBZDIxMDDAK6+8j0Qi5J//\n+UF8fHxwu914enri5QXe3krEYjFvvvk+NTWD3HZbBk8//cjsulKrZdjtNjw8PLh27Rrbt+/G11fN\nCy88jlwuRyQS0d8/SF+fEK12JoTq8uXLdHd3c+utS8nOHiIrK4uuri62by/GZoNnnlnL4sWLcblc\n1w9DYLPNSEXa29upqrpEVFQ4mzcLSElJwm6389vfvkVX1xTr16ezcuUSgoOD6ejooLS0Fbsdnn9+\nFWlpaYyOjjI0NMTYmACh0EJcXBxTU1McPXoUcOHpCT4+GoKCgvj88wN0dQ0QGemNRGIgNjYWs9nM\nv//7f+JyOcjK0iIWy0hISODChQt8+OE5fH3d3HprOCEhgQQFBfHKK9upqBgjI0POww8nkpiYiNVq\nZffuUwwNweLFASxZ4odOp6O8vJxPPqlHLnezenU83t7eDAwM0NLSypkzU8TFOXjqqSJGRkbYs2cf\ntbWtdHQoue22ONLSUigtPU1l5e/R6x2AkjvvXMH09DQff1yOQDCORqNBq/Vm7dpCzpyp5O23rxIT\nYyQ31w8fHw0Wi4XmZj2jo3KKisJRq9VcvnwNm82E2axEoVCzcmUafX0DfPRRA97ew8TEaFGrVXh7\nK2hvt9DbK2XFimAWL/alurqNxsY+bDYhYrGC3NyZJv+DB/vx9BwnLc0fodCD4eFJRkeNdHRoWLw4\ngnvuySIpKenvYld7M+CvdZP6a6x3b3z+Y+vdP049/7qsd78KbrebiooKnn32WTw8PDh27BgZGRnf\nEYybGN8RjZsQ3/SCuzHeFxN1v61wu93Y7XYsFsss0fDw8EAmk33pMX8PgvHXIDR0JlgQIDk5mV/8\nIhqpVHq9qWwJzc1tLF++hOHhYSorR3G73Tz++O3s3LmXI0eMZGS4SU8XMTAwSleXBwKBhv5+McuW\n+RIXJ+f06R70+iv4+8sYGRlHIAglOjqA0tIphEITGzfOkIKSkgZ8fYUolU7cbifZ2QmUll7j5MkB\nliwJRafrprKyC39/CRKJkulpI+vWzefcuRr27RslN1fE4sUedHS0U1nZgEikZmLCRWpqILGxUkpK\neunvv0JGxsxBvLq6DbVaiMEgQat1smXLYnbsOMIf/lDNwoWeaDRmWlq6mJw0IhAosVicrF2bSXt7\nFwcOjJCS4uLee5MoL6/i97//CInEjVo9484SHBzIiRMDiMUTPPLIMhoamjh4sJGYGBnLl+uwWmfI\ngdFoYWpqhghGR0fx+uvHEIl6eeihxQwPD/P++4dJSPBl0SIvPD3ltLW1MTpqQK8Hp9ONTqfj3XdP\n43I5efzxItxuN599dpSEhBDWrw9Dp/PGZDJhMExhNM7kWZjNZt59twyHA/75n2/By8uL4uKjhIYG\nsmlTHL6+Onx8fBgYGGN4WMDw8Cgmk4lf//pdLBZ48snbuOeeaK5evYparSYzU42PjwY/Pz8+/fQQ\nxcXjGAzneeGFJzh8uISRkTE2b16NyWQiLS2N5uZmBgedSCQz/u0dHR188slRcnKS+PGP78fLywux\nWMzY2MzrNBgmmZqa4s03P2B62sYDD9yBVColKCiIU6dO0dHhwmg0MDU1RX9/P5WVVcTFxfDoo97E\nx8djsVj44IPDXLsm5KGHRKxdu/Z6H4gDb28RVqsTLy8vGhsbef/9z4mNDeLpp9fg7e2Nl5cX77zz\nEceO6Vm+fJxnn31sdhyDwYTZPPP3DggIoLi4BJfLRVqaD06nm8jISM6fP8+OHScIC1Px8MML8fPz\nw9PTk7fe2sG5cwaWL/fjxz++F61Wy+DgIMeOXaW3V8Cjj6bx+OPLaWlpoba2lr4+ByIR3HffYry8\nvCgrK2NkZASrFYRCCVu23MnZs2d56aVXcLmmUakgIiKc1atX8ZvfbGdszIRa7UYmE7NkyRLsdjtv\nvLEfodBCTIwCLy81ycnJlJdf4NChPkJDTSxfHkFQkBabzcaxY9W0tkpZsULHokWhmExTXLhwkZYW\nI3a7lI0bZ6wy9+07BRixWFT4+flw771rOXWqnFdfPYZWO0FIiBeRkaFERUWwf/8lhof1zJunJDlZ\nzeiokYGBEQYGBHh4qFm3LomBgUH27r2CTDaMp6cvOp0PKSnxHD9eS3X1CDk5aubM8WJkZIT+/nEm\nJoQIhSoWLw7DbDZTWtqNQjFKUJA3KpWaiAh/rlxpo6FBRG6uJ8uWzSErK+tbaVf7bcD/q9C9b4P1\n7p/C6OgoP/7xjzl48CC/+MUveOSRR771Z47v8JfxnXTqJsU3nWsxPT09e+D9NuKGJnVqaorp6WlE\nIhFyuXy2R+OGI8ff2oPx94JEIpm9SQoNDSUtLRWNRoO/vz+RkV7k5aUTFxeHXj/OxMQQ+flpZGen\nc/p0L0NDTlavTkKp1HP1qhG73YBAIMNmmyQ/PxWDwUx5uZPgYJgzR01vbw/j4xbcbhEGg5DERB+i\noryprLQwNDRCXJwnVusQk5N21GoZra0SPDwcrF07j+bmTmpq9AQEgFBoQSCYJiBAS2enkPFxFytW\nJCCTGamqMjA9PYZSKcbhMJCUFMPw8BR1dULmzFGTnR3G1atdNDX1oNGIcDotBASo0Wq9uHjRht1u\n4667ChgY6KS8fAClchqp1IlC4UCn86GlRU9vr4A1a1KIjPTm+PEeent7SEsLQCYzMzFhxGyeorvb\nga+vhM2bb6WkpIaLF8dZsSKBuXP9uXSpnaGhATw8BKhULoKD/ejo6OH8eQty+TQPP3wX+/ad5MSJ\nVvLyYpg3L4y+vkGGhgYxmQx4ekpYtCibmporlJSM43brefrph/jss1IOH65i0aJk8vPjkMmkGI1G\n+vr6kcmgsDCb8vIKPvqoC4Ohj6eeepCLFy/x8ceHyM9PIysriPT0VGw2GxUVV7DbBWRmxtDY2Mj2\n7afp6bnGD3/4BMHBAdTU1ODr643bPcrixVnIZDLefLOYmppJ5szxJjk5mX37Dlx3HosiMzOa1NRU\njh49zvHjM5KkW24p4ujRMoqLj7NkSQ4ZGcHk5eUyMDDAp59eor/fRnp6MF5eXnz++QFUKg+SknRk\nZ88hLi6OP/xhN3v3DiIWj3PvvVswmUz09vZisUwCJgoK5mGxWPjVr96jtraJRx65k5UrC/D39+f8\n+fOUlAxjsxm48841mEwmLly4gIeHDLN5mPz8VHQ6Hf/2b69x9Gglq1YtYOnSVHJzc6mvr+ftt8/T\n0THKAw+so6hoKf39/bS1tXHx4hhyuYOtW+9kcHCQsrITOBx2LBYzGRnRzJ2bzCuvvMXJk5UkJvoR\nGqpg6dJFdHR08NprB7h2rYeVK5PIyUkgPj6e0tKj/OEPrQiFUzz4YBEZGUkMDw+zd+8JKivtzJ/v\nz9ata7Fap6murubKlUEmJkRs2bKIwsJsPv/8KA0NV5mYAA8PKT/4waNMT1vYufMUZvMQEomUpKRQ\nbrttNfv2neDYsWvXHa/ExMSEIhAIKC5uo6tripwcX+LjfZiYMNHf30tdnRulUsR99xViNk9y5Egd\nev0AVqucuXODWbZsPqdPN1JZOYCPjwWdTkJgoBaXy05VlQWLxU1RURRqtYuqql7GxwcwGhUEBCgo\nKJhDU1MvFRUGAgJs+PlJZ5Pa29pm3OAWLQrBz0/CxYtDDA52IpEo8faWkZc3l56eUY4fnyIszMX8\n+UGsXr2cvLy8m86u9pvCV8mk/l/b2v+11rs35Fd/bL3rdDr/ovXun4LT6eSDDz5gy5YtxMTEsG/f\nPgoLC/9hLHn/wfFdj8Y/Iv4eAXrT09OzbzjfNtjt9lmCIRAIUKlUs+Rixs5UOhve90Ud6reZYPwl\nCAQC/P398fHxASA2NoasrASio6PQaDRIJFPExflw6623oNcbuHJFT3Cwiq1b11JZ2UR1tZHYWBky\nmRmDQY9arWRkRIbB4GLx4jjk8ikqK6ew2cbx9JRitY4RFxeJwWDlyhUx0dFy5s0LoLm5h46OURQK\nETabnbAwT2JigqiosGE0GlmyJJrJyU5aW43I5Q4mJsTI5VaKirJpbh6jsnKS9HQvAgJctLf3YzJN\nMT0txWp1snjxXJRKMaWlBtzucfLywhkd7aa7exyXy8n4uIiICA/y89M5e3aAlpZxFi+OwMvLQnV1\nBzabiakpNxKJg6KifBoaujl1ykxysoYlS+Zw5UoblZX1aLVSpFIbfn6a62V7PW63ixdeeICOji5K\nSzsJD1eSmxuCQGCnq6ubsTEDVquL1NQIXC4Xe/a0MTqq58knN+J2W/nkk9P4+6uIj1cTGxuExWLh\n8uVWRkfdZGSEolKpePvt07S1dfP443cQFRXI6dPn8fT0QCyeZN68BCIjI/jww0M0NEBiogepqam8\n9tpO6uqa2LKliAULEhAKhUxOTtLa2o+Pj4yCgmxeffVdDh3qJCxMzhNPPEhvby8DAwN4eAjx8nKz\nbNlMuNWHH16lr2+IjRuLEAgElJQcISwshPBwEYWF2Wg0GrZt28ulS9PExsrJy8vj6NEy9Ho9MTE6\n4uJ8yM1dyOnTp3n//RaGh7t56KG7kEqlVFdXo1IpsFiGyM9Px9vbm1/96h1On25h9eoF3H33BjQa\nDX19fZSXt+N0usnPT2V8fJx33vkYb281yckzRDoyMpLf/vYtDh3qIzZWxdNPP4hSqaSnp4fy8gaM\nRim5uXHEx8fzySd7mZiYQCy2EhSkorAwjyNHjvHWW8cRiazcdlsWhYU56HQ6XnnlDxw9qiczU8cj\nj2zC01NDS0sLZ8+2MDwMa9ZksWzZYkpLj9Hd3cXQkAmFQsTdd29gYGCQN97Yg8tlQqFwkpYWzfLl\nS9m2bQeHDjUQG6skMdGbefPSsNvtvPvuSRoaJigsDGfBgigEAgGNjY2UlY3icrm4995FhIZqOXny\nPNeuXaOjQ0hsrJann76Hqqo6Skou4HJZEInkLF8+j6ysuezZc5Hm5l78/NxotRLCw4MYHx/n0KFx\nnE4ja9bE4eEBTU299PUN0tMjIzMziFWrMjl/voHKynZgCoVCyrx5cfj7e1FSMvB/2Dvv6CjPM+3/\npndp1HtBHSSBEAiQEFWmWWC6sWMnbonjZHdjJ8fJt19yku8k2bMtm2qv48RrG8fYGGzAmN6b6EJC\nvXehOqPRaDR93vf9/pDFwcTZZLMxtjG/c/gLHc37jmae572e+76uG6t1jPz8EEJD5fT32xkdtdHW\npiYmRsPy5dNoa+ulosKKWu3AaNSRlhZBTEwIV6/aGRz0MW9eKFFRChobh7BYBhgb02E2q1m+fAaD\ng1aOH7cSHOwgNlbHunXLWLduzc1p6/f4KKIo4na78Xg8d2Q47+3cGqGrVCpvig+NRnPT+zG5t056\nP243n08e8H2c90OSJOrq6nj00Uc5e/YsW7du5dvf/vY9wfn54p7QuFu5k2Zw+GwKjYk5CuM3BYbB\nYECv199c/CZnZdy6wH3eBcbtCIKAx+PB4/Gg0WjQ6XQYDAZycrLJzc1BpVKRnJxESspE+s1EBn8z\n4GHLljVER4dw8qQNn89HaWkOg4MtNDa60esDuFwK1Go3ixbl09o6RmWli1mzQomI8NHWNoDb7cbr\n1eLxBCguzkKrlTh92oXfP0Rmphm7vY9AQIHfL9HdrWTKFD1z5iRTV2ehqWmQ2FglMIZcPhEH29Ag\nQ5IENm0qZGCgm8uXbRgMbjQaAYXCQ1xcNJ2dLjo7ZSxdmkpKionLl/vp7OwiIkKFXD5OWFgQfr/I\ntWsSwcESTz21huvXGzh3rospU7QEBweQyXwIgkBHhxu3GzZvXoxer2DPnk68XiurVk0jEBilpqYV\nj8fF2JhISoqZnJxs9u2rp6VlnE2b5hITo+fo0eu4XKPExGiIjNQQFGSksrKB2lqBmBg5paXLeOut\nY1y61MayZbnk5cUxPGxhfNzB8LAVs1nDffct4MCBE+zbN4zR6OF73/smJ06UceTIOYqKppGVZSQz\nM4ORkRHOn+/A6xUpKZlNfX0jr79eBrh4+ukNpKTE09HRwdiYnfHxiRN6gJdeOsj16zfYsGEBixfP\n5+LFiyiVSkRx9ObQvDfeeJcPPhjCZHLxta89TkNDA7W1dSQmhhEaKrJ06UI6Ozt57bVLtLYOsmnT\nUjIy0rlw4QJarRaXa4Dp05PJz8/jV796hf37O0lLM/Hcc0+jVqsZGhqirq4Vv19izpxMXC4XP//5\nVm7c6GXDhgXMnz+d9PR0Dh06yv79FgIBK88++3XsdjvXrl0jEPDhdo+Tl5eCWq3mV796g8rKFh54\noJDCwnTmzJlDeXk5b71Vh8UyynPPPcqsWdOprq6mt/cGLS0OIiLUPPLIgxw5cpydOw8RE2NCq/Wy\ndGkhWq2Wn/98G9evd7FoUSpz504hKyuLyspK3nqrgbGxcb72tVXMmjWNtrY2qqvrqajwEx2t5kc/\nepbOzk4OHjyJ3W7H5ZKzZMl0Fi9ewCuv7OLatTqCg2WEhWlYtWopdrudrVvLsVoHmDs3loyMSIKD\ng7h48TrHj4+TnKxm/fpZBAJeKivraG7ux2LRsGZNHvPn53DgwCWqqmoACArSsWHDfajVcnbt6sDp\nHCQjI4jISB16vY7r1zuoqJDIydGzcOEUmpo6qa5uZXzciyTpKCnJISEhlCNHOunu7iY6WkloqJKY\nmAgsllEuX5aIiJBYtSqL7u4e6uqG8PudyGRGZs1KICUlgvPnh+jstJGSoiQsTMn4uB+nc5T2di1B\nQSpWr57OyMgIZWXDyGRWjEYdq1YV8swzj9+c5HyPj/JZH7r3p6ofk+bzyeu83Xz+1FNPsXPnThoa\nGujv7+ell17iBz/4AU899RRvvPEGaWlpd83e/AXintC4W7mTFQ2ZTIbH47m5qHzaTLZIud3ujwiM\nyVLyrS1Sfr//Zs54IBC4mbDx15Z4PyvcetI1uRHpdLqPLaerVCri4+NvmgYLCmayYMEs4uPjCQ4O\nRhQHmTUrndWrS6moqKe3N0BRUSoFBSlcvTpIS8swKSk6JMmK0+kjJMRAW5sKCLBmzWwGB7u5ds1J\nUJAXpVJCoXCRnp5Mb6+X1laJoqJYEhMV1NQMY7EMo1ar8PmcTJ+egtGo5fRpL0rlOKWl2XR1tdDc\nbEWlEnE65URGqigomEZFhZ3m5lGKi+MIChqnpuYGfr8Tp1OJXO5jzZrFDAzYOH7cQWKigqKiGLq6\nemhq6kIQRHw+GZmZkaSnJ3H48AAjIw7WrZtJIDBCWVkLMI7fL2I2TxiML15sp7raR0lJKrNnT+HM\nmXqamtqIj9ej1XrQ6yfanq5f92MywQ9+8C1OnbrMyZPdzJoVw5w5sXi9Hvr6+hgcHEUURebNy8Fq\ntbJtWyujo0N861sP43aP8d57x0hMDMVg8DJzZjqiKHLoUCXd3SILFqQTHx/HK68cpLe3m3XrCpk6\nNRafz8fg4BBtbXaiojQsWbKAX//6D5w40cnChRls2rQMi8WCxWJhdNSKwSBj6dIiLly4wOuvN2Cz\n3eCHP/wWSqWcc+fKCAsLQhRHWLRoFmq1mpde2k95uYWSkmmUli7n4sWLH7Zu2ImLM7B4cTH79h1k\n27Zm/H4LP/7x85hMBurq6hgdHcXlcjNrVioGg4Gf/WwrV640sWXLUu67bw6hoaG0tbVx7twNBMHP\n+vXLGBwc5NVXdxIbG0pMjJzFi2cTGRnJL36xlRMnBigsTGDTphWAxODgILW1fXi9ckpK8jGbzRAO\nYfsAACAASURBVLzwwhu4XGNERqrJyoqmsHAub731Lu+8U094uJyHHlpEfn4uw8PD7N1bRkODxJIl\nqTz11CNcvXrtwwefUWQyGevXL0OhUPDii+8xNNRHTIyarKwYSkqW8N57+3nvvVYiImDVqiymTk1l\nYGCADz64TG2tnxUrMli1ag4dHd1cv15JV5cLQVDyta+tIz4+gtdfP0hvbztKpZK4ODNf+tJGzp+/\nxp49LYSGeklLCyIlJRqFQsHJk800NHhZtCiOWbPiaG7upqWlhb4+CYVCw+OPr0Crldi9u4qhoXYM\nBh0JCSEsW1ZMRUUrp0+PM3WqkmnTQj78vFjp7vYyNqZi6dIU4uL0nD7dRmdnGyqVkuBgNQsXzsRm\nG+PQITvBwS4KCiJxOkfp6rIwNubD4TBSXJzE1KlRXLjQS0fHIEFBAYKCFMTHRyJJPi5dEtFoAjzw\nQDbj4zYqKoZxuy2Iop6lS/N46qlN5Obmfi7X3TuB3+//xNukPgluj95VqVQ3qx8qlQqFQkFtbS3t\n7e0cPnyYHTt2UFVVhUKhYHR0lIqKCrq7u/F6vQQHB6PVaj/tW7rHX8Y9oXG3MvmwfKfwer1/NLn0\nTnOrwADQ6/V/UmAIgoBMJrsZ8fenSryTAmSyxAufnXi/j2MycWRyorlWq/3Ie/CXoFAobprj9Xo9\n+fkzSE+fOEnKzJxCZqaZhQsXEBoaSkNDHSaTkm9+83HsdjunTrkJCvKzatU0WloaaW93oNFIuN0y\nwsPlzJyZRnW1i/Z2O3PnRqFSjdDaakWhCDA6qga8rF5dyODgEOfOuYiI8BETo8TpHMHnk7DbRYaH\nlcydG09qqpkrV0bo6blBQoIeSRpFoVChVMqprVUQFCTy0ENLaGho5eLFAaKjJTQaLypVAL3eQHu7\nD5tNxtq1swkKEjl9eoCRkV4SE43I5ePo9TosFgeNjTLS04PZuHEpZWUNlJd3k5MTQkQEOBwOnM5x\nOjo8CIKfzZuXY7HYOHRogJAQifvvz8bptHPtWi0ejxuvF7KzY4mNjWXPnkZ6ex088cQyIiP1HD5c\njkLhR68PEBcXRFRUBMeOXaa6GtLT9axfv4rt249w9Wo9CxdmMHVqyM1qQG2tBZVKYsuWNRw/XsZ7\n79UTF6dly5Yl6HQq2trasFptBAIChYXZHxq2y2hvH+CZZzaSk5PGuXMXUChkuFxWpk2LIz8/j1//\n+g2OH7eRmxvMN77xBNevV9PW1o5aLWA0itx33wKqq6t57bVKBgYGeP75J0lOjufChQsA2O1WcnOT\nyMhI4z/+41VOnOhi8eIMHnrofgD6+vqoq+tGEGQsXpyP1WrlxRf3MDY2QmnpTIqKphMVFcXevUc5\nc8ZJWJjIc899nfr6ei5evAr4EQQXc+dOzFF45ZVDNDX1sH79PIqLszGbzVy/fp2jR4cRRRf/+I/P\nIJfD/v1H8flcOBxecnLiWbBgPi+++CanTtUxc2Y0ublhzJw5g46ODt588yo9PQ6+9KUFFBbm0NnZ\nSUtLC9XVLgwGGT/84bfo6+vjtdfeR6HwIAgSBQXpLF68iFde2cX58x1kZhrIyDAzZUoiIyMj7NnT\nxNCQhwceyCUzM5qGhlZaW5upr5cIC9Pw/POP09nZxa5dZfj9I4Ca/PwUFi8uZM+ei1RUDJCSoiQx\nUU9YWDAOh4Pz5+14PCJr1+YSEqLg5MkqLJY+RkbUxMebeOSRVVRWNnP0aAdms4vQUCVxcaGYTHoq\nK+0MDclYsiSe5GQD1dW99Pf34HTqMBiULF8+E5tthAMH+lAoLERFqTCZZMjlCrq7nfT16Vm0KI6c\nnAjKy7toa+tFJpPQapXMnZuJRgOHDtkJBGwsXJiIQuGhpcWK3T7KyIiOBQvSePjhZRQV3Yur/VOI\noojL5cLr9X4qbVKfFLe2XyUlJXHq1CnsdjsvvPACzzzzDNOmTSMQCFBRUcG2bdt49dVXGRgYYN26\ndZ/2pd/jL+PPCg3Z/+Bh9fOTbfoFwO/339H2KbvdjlKpvDkx+E4iCAJutxufz4dcLken031kAZ4U\nGLdO9P7v2qNun656q5Ftktuj/SaFyqfFZBuY1+sFuHlS9Elfk9PpRCaTodfraWpq4vjxcxQUTLS5\n/OQnLzEyIuPRRwvo7+/n4MFuwsK8REdPxMDGxMSgUsGFCwGysvyUlMxh795TeL3BJCQIDAwEiIqS\nMWVKEqdP9yMIsGZNKp2dnTQ2eoiKEnA6NQjCGMuXF1Je3kh5ucTSpTri4iI4f/46Wm0wMpkfm01B\nQUEEERER7NzZ/KEXIZ2GhiaGhiRiY5W0tUF4uI8NG1byzjvHaW1VsHZtOBqNhoqKZvR6HW63gMcj\nsXz5dDweD2+/3UF8vJc1a+Zy8eJVbDY5cXEaenr8pKcbyc/P4+23yxgZkfHkkzMRBIHDh68THCzD\nYNATCPiZO3cGLS0dHD5so6BAzfPPP8M///N/MjQUoLAwGpCjUEyI4pMnmxAE+OY3V9Pc3MKuXS2k\npckpLV3I0NAQbrcPi2WEuroxli/PpKhoLv/0T39gbAyefroIs9nMhQvXMBjUNDb2YTCo+da3nmL7\n9l28//4ARUVavvvdb3Do0BG6uwfQ6RS0tg7z0EMr0Gg0/OxnexFF+M537sdsNnPw4AmCg3XU1fUQ\nExPCM888wS9/+TvOnHGwcmUYX/nKFq5fv87o6ESrWX+/l698pQS9Xs8LL+xDo5F45JESDAYDPp+P\ntrY2du9uJTlZzo9//G127tzN1avt5OfH4fVKzJuXT0REBD/5yWsMDEg88cR0pk+faIFyu92cP9+G\nQgHf+94T1NTU8N5710hKUpGcHE9cXDQ5OTm88MIbXLniZ8OGaFatuo/6+npstlEuX25mdFTBV7+6\niMjISH7723dRqQIYjXoMBj1btqzl3Lkytm9vJyMjwIoVhTfXhBMnrlJdLWPDhhiWLVvCrl0HsNns\nOBwevF4NTz65DLlczu9+dwSVyk1srBm9XkdBwXRqaxvYu9dCVpaXVauK6O/vZ3TUQ0dHDz09Btat\nS2TGjFzefHM/TqcHlUoCNCxfPhOv18uOHY0EBbnJyYkBBJRKLUNDg5SXK8jPV3D//Qs4ePAUFouE\nUmnH6w1m7txowsPD2bu3Dr8/wLRpOuRyBT6fhCg6qalREhMjcP/9s6mqaqC+3kNQkAWv10x8vJyk\npHjOnGnFYlFTVKRCq9XT3j6IKPpwOvVotQoWL87EYrFy6tQY4eEWwsIi0Wj8GAwhdHb20tERxIoV\nQcycOfE3vBdX+/HcurbLZDK0Wu1flSb1Wcbr9fLLX/6S3/zmNzz99NP86Ec/wmg0/tHP+f1+mpqa\nUCqVZGVlfQpXeo+/gj/7Qb1X0ficcqcrGj6f72aF4E4hCAIul+sjfaq3lpEn73/S5C2K4l+UInV7\niffW/tLJEu/k69/aXzqZrnEnBxvd2qsbCARQq9Xo9fo7thFNvicA4eHhzJkzMQROp9ORmhpDdnY0\nRUVFKJVKmpubiYsL4bvf/TsuX67h6lWBqVMNzJwZRnNzN93dVpRKBR6PSHp6OKmpUZSVORkZGaWw\nMBavt5/2dhtarYz+fgUGg8ADDxTT0NDLpUs2MjI0mM0CNtsIkiRhtSoYH4eSkmxCQmScPj2CzXaD\nKVOCEIQRFAoNLpefpiY5yckGSksLqKhop7y8m8TECSO8XC6gUilpbPTj98OXvrQUv9/B0aO9+HzD\nxMSoUKs96HR6entH6epSUVSUyJIlszh5sona2i5mzIggNFTC6XTicjlpanKj0cCzzz5BTU0T+/d3\nEh+vZMGCRPx+N42NLQwM2HC75cyfP5WYmGjeeaeGgQEbDz20gKgoLdeuNSKKHsbG3ERF6Skunsf2\n7Uc5fdpOQUEEK1bMoby8hurqOnQ6MBph9uwcent7effdDsbHR/nudx9HELxs27afyEg9Go2bgoIs\nTCYj27adoLraQ0lJJmvXrmDHjv10dXUTHq4mJkbH3LmzuHz5Mjt39uD32/jxj5/D6Rzj/fePYjZr\nkaRx5s+fjtls5j//8wOuXh1m7drZrFw5n9bWNgYHB+jvH0GrlbN6dQnXrlWydetl5HInmzYVkpOT\nhs1mo6yskuZmyMkJY/Pm9WzbtpuzZ68QHa0jLEzOsmWL6e3t5bXXrjE0ZOPJJ1cyY0Yazc3N9PT0\n0tzsIjxcxTe/+RT79h1j9+4yEhL0hIfLKCqaiVwu57XXTlJTY2PNmunMn5+F1WqlubmZ+noHMpmM\n5557DEny8+qrB/H5bKjVElOnxrNkyUK2bz/IkSM3mD49iAULEjEaJ0zoly7dYHAQNm+eS15eCvv3\nn6WpqQG3W4bJpOXppx9mYGCQd96pRpJGSEqamDAfGhrC6dM1lJf7mD8/iuLiFFpauqmursdq9SMI\nGjZuLCYhIYzdu6vp6molNFRFRISW3NwMursHOXbMQVSUxKpVGYyO2qipaWdkZIyxMS2LF6czY0YS\np0610djYTXCwQHCwnOTkGATBR1mZF7ncx/r1uXg8o1y71ofTOYTLpWXKlCBmzpxCbe0QNTVOUlIg\nNlZLICB+mBimRJJULFyYjEYT4PTpAazWTkwmLaGhKmbMSKOxsY9r1yRmzDBQUpLGihXLyMnJudcG\n8yeYbJOaXNs/L21SfymSJHH69Gk2b96MxWLhvffe45FHHvlI3PytKBQKIiMj703+/nxxr6JxtzLZ\n7nOnGB8fRxRFgoKCPvHXmjQ4T57w6HS6j5zeT35mb020+KQM3rdWPm7NGJ/k1kzyyX9/CwEyKTC8\nXi+SJN0UQ58VM+DHYbPZ0Ov1aDQazp8/T3l5LStXLgbgF7/YBcCTT5Zw8eJlysocJCV5MBqDGB7u\nIyMjk4EBCzU1ChYt0pKWlsShQ1dRKAyEhAhYrT7S00MIDQ3hyJFBgoNF1qyZTnl5Jb29ChISBAYH\nlej1TpYvX8jBg1dpa1Oydm0YKpWKy5ebCAoy4PMJuFwSixZlALBzZzfx8X6WLZv4XWNjKkJCRNra\nJJKSYNmyRezYcZ7hYRkPPBBPIBCgqqoTs1mLzSYgSSIPPFBEd/cNdu3qJztb4IEHFnHqVBljYxLB\nwXJ6ewVmzYpk6tQsXn/9HB4PfOUr+TidTs6erSc8XI3DIaLTySktXcLZs1c4dszBkiUGHnxwNW+9\ntZuRES8JCUYGB50UFGSg0Wh4660KFAr4h39YQX9/P4cOVZOYqEGp1BMWZmTu3Nns3n2MK1d8bNgQ\ny6ZNa/nFL/4Lp9NLZmYUbrfArFnZOBwO3nijkqAg+OEPv0xjYyP79l0hIyMEhyNARkY8c+fO4Ze/\nfIOGBjlf/vIUli27jzfffBev14cgBHA6Azz55Ea6urr47W8vEx0N3/jGWsbGxmhtbcfhcHD16gh5\neWF84xtP8NOf/prubj8lJfGEhoZiMplwOp3s2HEFr1fGc8+twGQy8cYbHxASomZszE94uIknn/wS\n27fv5vDhIebO1VBSUsTY2Bher5czZ67T1aXg0UezmTdvHr/61Vb8fj9GowpJkrNp00p6enp47bXr\nREcHKC0tIBAI4PV6aWvr5uJFL/PmGXjmma/wyitv0tNjx2QSsNuVlJZOVFp+97ujBAIi8+ZFotFo\n0Go12Gw2jh8fJTpa4KtfLaW6uoby8h5MJi8DA1ry8kIpLV3Gb3+7gxs3ICdHhkJhICLCgCRJnD07\nCMhYv34qLpeLy5c7UCrHGRszERYGmzYt58SJC1y54iIz041OF4LBAAaDkYqKXiwWLWvXxqLX6zlz\nph5RdCOKKtRqJUuWTGd4eJgPPrASH28nOzuFsTErHo+SsbERurtNzJunISkpjjNnanG5lJjNXkBL\nRkY4oihSVubAYBBYsiSZ4eFhmppcKJUWHI4woqMDFBTkcOpUJe3tOmbOdGEyRXL//UvIzMz8xOYt\nfN6Z9NgFAgEUCgU6ne4zGx3/1zIwMMD3v/99Tp48yb/927/x2GOPfab3r3v81fzZL/Y9ofE55U4L\nDafTSSAQ+ETL35OL760lZK1W+5ENavLB/5MWGP8dt/pAbhUht3o8/trBRpMDBydN3iqV6jOVNvLX\nIEkSFRUVAOTn53P8+HF2777KzJmxbNr0AD/60W/p7ZWzZk0kLpeLqqpezGYtHo8cjyfAokUZjI87\n2b/fRmqqm7y8NKqqqlCpQtFqRVpaFOTkKCgomMGePVdwu5Xk5ekYHh5HFANERARTV+dBpRLYsKGA\n+vomLl1ykpYWQK3W43RaSU/PoL6+g+ZmFStWmJkyJYkDByqQy5XEx6sZGXGRmBiGTqfh+HELkZES\nX/vaag4fPkltrZusLAUulwydLkBWVgZnztTT26vi8cenERQUxI4dF1CpAkyZEsr4uJuUlFhcLheH\nD1tJSZH4/vef4aWXttLc7CE/3wio0OnkhIeHc+pUAzabnK9/vRi1Ws1//ddJTCaBvLxk3G43YWEh\n9PUNcPr0KFlZCr7zna/xH//xe3p7AxQWhqHV6tFq1eh0Oo4fb8DtlvOtb61kfHycP/yhjPBwkdzc\nVGQyiI2NobKynlOn7Myfb+S5557m3/7tPxka8jB9egQej0h2dhoKhYKtWy8givDtb68iEAiwY8cx\nIiO1jI76iYoK5sEH1/Lmm7s4dcrBsmXB3H//UqqraxkdddDZ2c/QEDzySCGhoaH85jd7kMtFFi5M\nx2Aw3JzCvnt3L0lJIv/v/32TY8dOcuFC44eta16KizMpKprHv//7G/T3y1izJp7IyEjGx8dxOp2c\nO9f7YcViLRaLhZ07z2M2+/H5VMTEBLNmzXJ27TrE2bNOFi7UkJubycjICIGASHl5OxaLhsceyyM2\nNpY33jiAJPlQKhUoFCpWry7mxo0bbN/eQUKCm/nzp+F0jhMIyOnuvkFtrZL77gtlyZIitm/fx+ho\nAI3Gi9+vZ8GCNPR6PTt31qBQBCgoiEAURZxOAUFwUFEhJzlZZMuWZRw/fo6WFi+hoXbc7iAyMkwk\nJydy6FAtFouMhQuNaLU62toGAB/Dwxp0OhmrVs2gr6+fkycthIZaMRrDMRpFkpISqahopqVFz5Il\namJiIrl4sZ5AQI5MFkAmMzJ3bjySJHHkyAAGg4ecnAi8XhcWix+53Elnp4nUVJGFC/M5daqc7m4l\ncXGjQDAPPlhCXl7ex7ajfprTpj8rfBHapAKBAK+++io//elP2bhxI//6r/9KWFjYp31Z9/jkuCc0\n7lYEQSAQCNyx13O5XPh8Psxm89/8d08anCdjav9SgQGfncSo/4nv49YN99YqTSAQwOPxIIoiSqUS\nrVZ7151ywcS9Dg4OEhYWhlKp5P33P6C7e4DNm9fQ0dHByy+fwWyW+OpXV7N798QciWnTRJxOGX7/\nKFOnZlFb2013t5Y1a8LR6XScOtWEVivDaFRit3uYMSMBhULB/v1WEhMDrFkzhxMnzjI6qic2VuDG\nDQXR0QJFRQW8/345/f2wcmUYgiBQX99PcLDmw9cLsGrVLCwWK7t2DZKR4WPp0plcvlyO16tBr5fo\n6pIzY4aRwsICXn/9FOPjsGpVAk6nk9bWIUJDNfT0BFCpBB55ZAXXrtVw4MAws2bJmTMnm6qqOgRB\nhcfjoq9PztKlCUybNpWXXjqKKEJpaToul4vOziGCg9U0NDgxm2U888xD7Np1kDNnxliwQE9e3lSa\nmloRBBl9fRaGh2WsXZtDeHg4L798AqVSZOXKqXg8Hmy2cZRKifJyO3FxKn7wg7/nhRde5dq1cRYu\nNJOUFM/4+DhqtZqysgasVgVPPllIWFgYL720H61WIC8vCZlMRmxsNL29vezZM0BGhsSPf/wsb765\ng5qaAdLS9AwMuJk/P5vExERefvkgFgs89lguZrOZc+euAgF6elzodCqef/4JLly4yM6dTaSkCMyZ\nk40oihiNRsrKrlNVJbF2bQyrV6/k5Ze3Ybe7MRrluFwyHnhgPoIg8F//dQmDQaK0NBtBEBgZGcPp\ntHPhgou0NAX/9/9+k1deeZP6+lESE0VsNhkFBSkkJiawbdsZrFYZq1fHYTQa6ezsJxDw0NzsRauV\n8Xd/t476+kYOHGgkNHQcmcxIVJSeuXPzOXCgjOpqGSUlWlJSkmhoaMfrDTA0NI7Ho2fDhhzUajW7\ndlUgl48THKxFpVIwY0Y6fX0DHDniJD3dzcqVE8Meh4YCSJIDqzWIoqJQ0tNTef/9K4yNSUyZIiFJ\nKsxmHYLgp6LCR1CQxKpV0+jp6aWqyoFeb8XnCyMqSqKwMJ/Dhy/T0qJh/nwRvT6Irq4+QIbDIUOS\n9CxenIAgCJw40YdWO0ZoqBGVSiIiIgKrdZhr11Tk5gosWJDH2bPlWK0qtNoRBCGMLVsKKS4u/qOw\nkNvXxMkDmklurQhProt3a/Vj8gBJFEXUavUf7XGfdyRJorKykmeffRZBEHjppZcoLCy8q+7xHh/L\nPaFxt3KnhcZklGpISMjf7HfeLjAmWhE+enp/q8CY5LOcCnU7k96R2zfbSSY31cmKyORE88/SvJI7\nic/n4/LlywQHBzN9+nTefHM75851sHz5VPLycvmXf9mB0ylj5cpYhoaGaWsbJTRUhc2mRBTdrF49\nl6amDk6fdjF9eoCEhBiamhoxGiPweJz09mqZPz+IpKQE3n//OqIokp6uZWRkHINBT1iYgStXXJjN\nAg8/vJgzZy5SVxcgM1PC7ZajVHrIzEznypVWeno0PPhgIiaTiQMHrqNSiYSGahgf95CdnYggCBw4\nYCUxUeBrX3uA998/RFeXQGqqjKEhkZgYNdOmZXHwYBWDgwq+/OUslEolhw9XotNJaDRq/P4A8+dP\nx2KxsGvXEJmZAl//+ib27DlAb6+X+Hgl/f1+srMjycxM5+23z2OzyXj88RnI5XKOHbuG0SjH7ZZQ\nKmWUli6kpqaePXuGyM4W2Lx5GefOXWJw0IHBIKevT2Lx4lRycqbx0ksHcblkbNo0FYVCQWtrLyqV\nSF2dHYNBxvPPP8Hhw8c5eLCH7GwFM2Zk4Ha70ev1XLhQQ1ubki1b0iguns/Pf74Vn08gOTkYn09i\n6tQkxsbG2L27i6goOd/4Rint7R2cP19PRISSzk6BrKwQHn54A7/85es0N0ssXx5CREQETqcLURS5\ndKkbl0vBN76xBIBt206h1XpQq7UYDBNtVZWVNezbZ2XGDJEVK4poaWllZMSNxWLlxg0N69alM2vW\nTF54YQcej0hsrBJBkJObm4LH4+GDD3oICZFYt24mQ0NDVFX1YjT66erSkJ6u4UtfWsdrr71Ha6tA\nbq5IIKAjKkqPVqujrKwXp1POpk0Z+P1+Ll5sRS534vHo0etlrF49n/r6Zo4etZGaOk5SUgJerwOl\n0kB7ey+9vSZKS8OJj4/j0KEr+HwTsbGgJT8/kUAgwOHDQ5jNPoqLp2CxDNPd7UGjcdLbayI9XU5x\n8YTA6OlRkJ7uxudTodNNtGK2tvoQBBXLl8fj8/m4dGkApdKGXB6EXi9RUDCV5uYuzp8XyM31kJeX\nSW1tM06nAq/XjtsdyqZNOcyePZuYmJi/eE2+tSJ869p4+6HM7RWQz8uafztfhDap0dFRfvKTn7Bj\nxw5++MMf8g//8A+fiSj8e9wR7gmNu5XJmNY7hcfjweVyERIS8r9e8CcFxqT/YLKC8acExq1TRT+v\nm82tTN7bpNH89u/gJ+X7+DwSCAQYHBwkOjqaQCDAW2/txOFw8eijm7h06RJbt1aRmCjx+OMPsHXr\nTvr6dOTkSAwOCuh0XtLT07h6tRerVcG6dYl4vV7On+9Cp/Mjlytxu90UFU3D4/Gyb98oWVl+Vq6c\ny9GjZ/B6jYSEBOjrU5CaqiQ/fwa7dl3D4ZgQOg6Hg6amQUJCNFgsMmQyP+vXF9PS0smBAxZycwNM\nn55OfX0DCoURr9dNd7eShQvDmTEjl9deO4nfD4WF4YyPexgf9xIUpKG62onRKPL002s5c+YiZ85Y\nyMmRExkZgcMxQlhYJHV1HfT0qNm8OZ20tFReeeUQIDF1aggul4+oqBACAT/Hjw8TFSXxf/7P47z/\n/kGuXh0mM1OJz6ckMlJPcnISBw5cobNTySOPpBAbG8vOnSeRyQSMRhWBABQXz2BsbIz33ushIUHk\nySfvp6qqhpqaG0RGToiCGTPCWbZsCS++uJOeHjlr18ZiNpvp7OxDLhdpaBhBEOR89avL6e3tZefO\nGiIj/WRlJSGXS8TFxVBd3UxZmZdFi4w8+OBqtm3bzfCwm+BgCbtdzuLFUwkNDf2wZUuitDQNSZLo\n6bEAHmprfYSHw3e/+yR79hzk/PkBUlMFJElHXJyJpKQk9u+/QleXis2b44iMjOTcuQoCAT/j4yKg\nZvPm+TgcDt56q4bQUBcZGbGIoo/Q0FC6uvq4fFmisFDD/fcv4v33j2K1imi1TlwuA3PnxhIdHc3O\nnZUEAiJz5oQgSTAy4kQu99HYKCcsTODBBxdz7Vo15eV2oqIcBAJGYmLUZGamcexYFd3dGlatCiI4\nOJjKytYPQzFALtdQUjIx7PDAgRuYzQ4SEyMQRQ9qtZGxMRs1NWry8xUUFk7n+PFLjIyoMBhG8fkM\npKUZMBgMXLxoRRRlLFwYgc/no6lpBLncgcNhJjg4wNKl+dTUNHPpkp+MjHFCQyPw+8cBDX19I4yM\nmNiwIZmpU6eSnZ39NwsI+XOHMp+36scXoU1KFEXeffddvv/971NcXMwvfvELEhISPu3Lused5Z7Q\nuFu500LD6/XidDr/V0JDkqSbFYz/TmBMnu6LonhXCYxJJs3ugUAAuVx+s0Xq44znt/o+Pq7H+W56\nX/6nOBwOLl68SEJCAllZWfzqVy9TX29j8+bZhIWF8etfHwEkliyJ5caNPm7c8BASIqO3V45G42b9\n+kVcvlxDRYVIQYEMvd5EX183YWHRDAzYGBrSsmxZ5Icxrw2o1RIJCTpGRsaIiAhBr1dy41aZZwAA\nIABJREFU5oyT2NgAX/rSfRw8eJLOThkZGRJWq0RwsEB29lROn26iv1/Jww+nIpPJOHFiIilKpVLi\n9fqZNy8Ll8vF7t1DpKYGePDBJZw4cZahIYiKkrhxA9LS9BQUzLxpTN+wIRmA8vIWDAYFo6MTD2Tr\n1xfT39/P2293k5HhY9myAhoamhgbE5DJfLS1QVFRBCUli/jNb97Fbp944JQk2YfRqnKuX7ehVEp8\n85sPUF1dy759bcTFeYiMjAB8JCUlUFHRTG2tgtLSSJYsmc8f/vABTmeA8HAl4+Mi8+ZlolQq2bGj\nHr0eNm7Mo7+/n8rKLsLDlfT1KYiNVfHEE1vYuvU9Kit9FBdriYuLwWYbRalUUVXVg82m5oknCjCZ\nTPzhDydRKDyYzTrkchmzZ2czNDTE7t1DpKX5efDBEiorq2hvt6HXB+jtVTFnTjhLly7kt7/dhcUi\nIz9fi0ymQatVABKXLo2gVMp48smF9PT0cOpUByaTA5/PiNksZ/nyYk6evMKlSz6KiuSkpSXR3t6N\n3w9DQ2PY7XrWrEkhJCSE3bvLkSQPISETD5NTpyYyNjbGsWPjxMf7WLNmDtXVdXR3+9BqHVitJrKz\n9cycmcPevZcYGJCTlydDLtfh83mQySTa2wMoFHJWrcrEbrdz9uwAev0IarUZvV4kLy+L6upWysvl\nFBbKyMlJ48qVGlwuOYGAE4/HxMyZQRgMBk6f7kMul8jI0CKKEl6vCHhoadESHe1n2bJ8qqoaqKsL\nEBVlQxTNREXJiYqK4sqVToaGdKxaFUpycjJFRUWYTKZP/Dv+ea1+fBHapJqbm/nOd75Db28vv/nN\nb1i5cuVddY/3+Iu5JzTuViZTie4UPp+P8fFxzGbz/9jAd7vA0Gg06HS6L6TAmIzJlcvlNyem/i3m\nfXyc7+OLhtvtZmhoiISEBBwOB6+/vh2ZTMYTTzzM7t17effdDqZOhY0bl7F9+37sdgMpKQJDQyLh\n4ZCSkszZs704nTLWr0/FarVy7doQZrOA369GEDwsWTKTnp4BjhxxkJcnMm9eNmfPXkaSjGg0fvr7\nVcyYYSAnZxrvvHMVrxcWL47EZhujv3+M0FANXV0SGk2Ahx5aSkVFLadPj5KTIxIREYHF0k9oaBRd\nXf309GgoLY0lJWUK27efQxQhNVXH2JiH6GgzarWSkyethIVJPP10KWfOnKeiwk5ysoDLpSAkRMH0\n6dkcPXqN1lY1Dz8cT0xMDPv3XwAkNBoZHg8sWDANURTZsaONyEiRdetm09raRkvLCBERMtrbZaSk\naNi4sZTf//49WltllJQYMRqN9PQMolYraW+34/OpefTRQgRB4O23rxEc7CMpKRyv10VcXBSDg1bO\nnfOTn6/gscc2sH37+/T1+YiMFBgZkZOXF0NCQjw7d17F6ZSxdm0KkiRRXd2BVivS1ydDq5V46qkH\nqKio4sCBHqZM8RIXFwt4iYiI5OrVRpqbNWzYEMO0aZm8994JPB4BrVbA71cxf34GSqWSnTubMJkE\nlixJwW63091tR6fz09ioJCVFzsMPr2bnzoM0NwfIzPTj8UzE/oaEhHL+fBc2m4ING6Ygl8s5d64R\nhcKLz6dGpZKxcmUBfX39vP/+EElJDnJz07DZhvH5VNjtI3R2Gli40MS0aRkcOHARh0NBaKibQEBN\nWlo4SqWCM2dG0GhEVqxIZXh4mIYGBxrNKA6HmfBwgZKSeZw9W0FlpcSsWX6CgsIYGxtBFBUMDjoZ\nH9ezYEEIKpWK8+dvoFT6CApSIZfLSE2NYXx8jDNnAiQleVi+PJ+qqnp6eiR0uhGczlAyMjRMmZLA\nyZONDA0pmTdPSXh4NKtXryQyMvLT/qr/j6oftxrPP+m18YvQJuVyufjZz37Gyy+/zLPPPss//uM/\notfrP+3Lusenxz2hcbdyp4WG3+/H4XAQFBT0F/sHJkvHk1OsJz0Yty68XwSBMdkq5vf7/yYl9I8T\nH7f7Pj6uxeCLxq0RwRaLhevXr5OdnU1KSgr//M+/obfXy6OPzgfgd787j1YrUlQUQ3f3DUZGAkRH\na2lqgpAQDxs3lnDkSBmNjXJmz5bj8ylwu21ERcXQ2jqMxaKhtDQOjUbD0aMtaLV+wsJ0OBxO0tPj\nkCSBI0ccpKQIbNq0iMOHTzIwoCIxUWBwUE50tIy8vBwOHapmcFDBhg0JiKLI5cut6PVyfD45fr/A\nihX5jI6OsnNnHykpHkpKZlJTU4fdDgaDRHv7hDG9pGQBr756AKtVzoIFZnw+CYfDiU6noqlpYgjj\nl7+8kBs3brB3bzsxMW6ioyMJBFwkJibQ2trD1asiJSXBLF1axFtv7WN8XE5EhMTYmMT06XGYTCb2\n7m1BLpfYsCGb4eFhrl3rwWTyMzKiJihIYv36+zh16jIXL3opLFSQkZFMV9cNZDL1h4Z1LRs2ZBAX\nF8fWrScBgaQkPX6/SHJyFG63m6NHbcTECDz22HIuXbpKXZ2d8HAPVquWlBQdCxbM4513TtDRoWDF\niiCCgoJoaelBoZDT1+dBEFRs3JiPx+Nhz54GTCYn4eHByOUCKSkJ9PYOcPasn/x8KC1dxKFDp7Ba\nQasdx+EwMmtWOElJiezaVYHLBYWFwQiCxNDQGGq1SHu7HJNJYt26uTQ3t1FWNkJ09BgKRRBBQZCe\nnsKFC/W0tuq4/34TcXGxnDtXhd8PouhHFPUUFSUil8vZt68bo9FLbm4EbreL0dEASqWb5mYdU6aI\nLF8+j5MnL9PeLiM5ecJkHh2tJjg4mPLyAcbGVCxdGvKhMbcfhcID6FGpYP78qQwNDXP48DjJyWPk\n52dx40YPo6MyAoExhoaCmTPHQHJyPKdO1WGzyUlM9KHRBPHEE5tJSkr6VL/Pf47b0wBvrwrDJ3cw\n80Vok5pIIjvC888/T2pqKi+++CIZGRl31T3e46/intC4W7nTQkMQBOx2OyaT6c+avCYX3VtLx7ef\n7Nw6yftuFhher/fmsMPJoYCf1LyP20/47sS8j88it0cEf9wMktHRUSwWCykpKQwPD/P737+F0ajj\n619/jDff3MHevQPMnati6dK57Nx5GI/HQHR0gOFhSEpSkZSUxLFjnfh8sHZtGn19fdTXj2I2izid\nGsDNqlXzaGzs4MSJcfLzRbKykqmqqkWpDMLvdzMwoKWw0Exq6hR27aogEIC8PBN2u4tAQCI4WENV\nlQeTacKYfvXqda5ccZCWFkCStMjlbjIy0igvb6G1VcOGDdHEx8fywQcXkCQ5wcEyxsdF8vISUKvV\nN43NGzbMoqGhkZYWJxERAfr7VURFwZo197Fjx1EaGxWsXGkiNDSEuro2VCoNVqsLt1vDmjXT0Gg0\nvP12JQaDl6lTo3A6nRiNRnw+F+fOeUlJ8fPII6Xs3n2I7m5ISvIzOiojMVFPXFwcJ040Y7Op2Lgx\nGblczuXLLajVIh6PAoVCxurVhfT3D7BzZy8pKW7mzZvGjRs9uN0K3G4Hra0q5s83U1w8h7feOszo\nqIykJBG3W05SUihqtYozZ4ZQKGDjxlyGh4e5erUfvX4cl8uIySSyZs1izp4t5/x5DwUFEsnJ8XR3\n9yBJaoaHR7FaDZSWJhAWFsYHH1QiCH7Cw+UIAqSmRuPzeTl5cpyYGD+rV8+mrq6R1lYPJtMYNlsQ\nyckKiopms3fveTo7VSxYoESjMdDfP4xcLmdwMIAoalixIhWPx8Px473o9Q7MZiNyuUBSUhzDw8Nc\nuADTpwssXjyLs2evYLEo0elGcbvNZGcbiYmJ5ujRVpxOmD1bi98v0NtrR6kMYLcbMRgk7rsvl66u\nG5w75yAmxobZHIFK5cFkCqetrZuuriDuu89AQkIcp09X43bL0WhcqNVBfP3rGz/3E5o/rvXq9oOZ\nj2u9+kvXxru9TQqgt7eX733ve1y5coWf//znbNmy5Qt5eHWPj+We0Lib8Xq9d+y1RFFkdHQUo9H4\nJ81/k+LH7XZ/oQXGradbABqN5iMDB+/kdfwl/c13i+/jfxMRfKsXpru7mytXrpCbm0t8fDz/9E8v\nMjws8NhjCxgfH+eNNyoIChKYPj2Svr5+fD4l4eEqKitFYmP9bNxYwgcfnKCzU0VengybTUSj8REf\nn8D16zewWFRs2JCMKIqcPt2GThdAq1XjdnuZNSsVr9fLvn02UlP9rFlTyOnT57HZ1ISF+ejvV5GU\nJKe4eB7vvnuBwUE5K1aEIYoSjY29GI0arFYRUZSxenUedrudPXt6iItzkZmZiMUyiFYbjMvloLpa\nxty5Ou67r5ht2w4yOqogLU3O6KhAXJyR4OAgzp7tRxBkPPJIPgMDA1y40EtQkAe/X4tGI7B06Vyq\nqpo4edLJrFkiM2akU1FRSyCgQZI8WK16Fi6MJi0tlW3byvD5JKZPN+Dx+PF6BdRqgZoageBgkS1b\nFlJVVUd5uZ34eA+CoMdsljN9+jROnqykpUXDmjWhJCTEcepUOYIgQxQD+P0aFi5MRavVsmNHAyZT\ngNmzYxgbG2N01I9W66emRkFyssSDD65g797jtLaKpKV5cbnUREdriIiI4MKFLqxWFRs2TFQXysqa\nkMv9CIIShULGkiXTGRkZYe/eYeLjx5k9O4P+/j7sdgmZzENHh5bZs/XMmpXDvn0XsFoVJCZ68XpV\nREfr0WjUlJePAXD//anY7XbKy4fRaOyIYjB6/UR0bE1NC2VlfmbO9JGRMYXW1nY8HhVutwO7PYiF\nC8MICQnh+PEWfD6BmBgBv19Cr9egUAjU1ioJDxdYtiyb9vYuqqvdhISMEAiEEhEhkZubxcmTVXR0\n6LjvPi0REeFUVLTg90v4fAEUChNPPrmM9PT0TyTO/LPAn5uFBPzRunh79eOL0Cbl9/t56aWX+Pd/\n/3ceffRRfvrTn961n4l7/NXcExp3Mz6f748Siz4pJEnCZrNhMBjQaDR/9H+3CgyVSoVOp/tIi9UX\nRWB81qd5f5zvY/JvMsln0Vz55xAEAbfbjSAIf/OI4IGBAUZGRsjKyqK3t5eXX95OSIiBv//7p/j9\n7//A4cMjzJ+voaAgm/37TxMIGAkK8jIyoiIzU0dycjL79zcTCEgsWxaPxWKhtdVOaKic4WEVKpWH\ntWsXUFXVyJkzTmbMEIiOjqS3twuTKRyr1UZvr5alS8NITIzngw8qEAQZSUkTM0OiooLQ6zWcO2fH\nbJbYvHliDkN1tZO4OB/j42oMBj/FxQUcP36NxkYVq1ebiY6OpKzsOqBCkgK4XCqKi5MICgrinXfq\nMZkECgsTsFiGGR72YjbLqK+XERsr8vDD97NnzzEaGgSyswP4fEpUKh+RkdHU1g5gsajZvHni4f/Q\noWoUCh86nfLDNKZMnE4nH3xgITHRx6pVs6isrKavL4DR6KavT0t6uor58wvYvfscfX0qiorUKBR6\n7HY7Wq2azk4PgqBk3bocnE4nhw61YzKNExRkQpL85OSk0tMz0RI1c6bEsmWFHDt2DrtdiVY7jt1u\nYMaMYJKTk9i7txqnE4qKggkERG7csKHVwo0bCnQ6iTVrZtPR0cXp0yPExIyh15tRq/0kJiZSW9tO\nU5OW5cv/P3vvHR5XfeX/v6ZX9V4tyZKsXmy5F1xxJ8Cz2Q1hFwhJ9pfwzRI7YAKEJQRCiAkhpphA\ndrNkd0nChm4bdxsbV9lWdZFtNatYlmSN2kiaPvf3h5mJJIRtGUkzGt3X8/jBSLL9mbmfufe8P+d9\nzvEjKSme/fuLMJulKJVmbDYt+fkRaDQaduxoQKl0MHt2JEZjN/X1vajVJq5c8SMszMaKFbM5erSU\n8nIHU6b0IZXqUans6HT+XLjQgsGgY+XKMHQ6HQcPXsTptKJSSXA4BLKyYjCbzRw4YCYqysLixRlU\nV1+iocGORtNNW1sAKSky8vMz2bWriIYGJQUFDuRyPd3d14RPS4sDp1PFPfcUkJiYSHJystd/5kea\nwffG/oc0LlzZD9fPAajV6lHLVHsKQRA4fvw469evR6PRsHnzZqZNm+ZTr1FkxBCFhi8zlkIDoL29\nHa1Wi1qtBv5uUXEFeKLA8F6BcSPGa93H4AJ7l8AYzf1ltVrd78WFCxc4duwEM2ZMIzo6mueee4P2\ndrj//jl0dnby3ntn0eutTJ4cRFtbOzqdH1otHD1qJyHBxl13LWTbtv00NSlJSXHQ1gbBwU5SUpI5\nfLiGq1fl3HlnLHa7nePHa9FoQBBkWK125s9Px2Kx8MEHzSQkWFi4MIuysjN0d8sJCHBQU6NgyhQF\nt902k/feO0hLi4xZs9SYzdDb24O/v46qqj7sdinf+EbmFx2SGggK6sPPzw+73cSUKYm0tBj4/HMr\nBQVSli2bzbZt++juVuLv30dbm5yUFA3JyZPZseMiJpOE5cujMZlMnD/fglYr0N6uQC53cNddc6ms\nrGXXrjaSknqZNCmOzs6raLVBtLRcpapKxZIlQaSnJ/PJJ4fp7ZUSEmKlrw+SkoJQq9UcONCGUimw\nenUqLS0tnDvXjb+/CaPRj4AAOytXzufIkWKOHbMxY4ZAVFQEjY2XEQQlHR1G2tt1LF8eTVBQENu2\nnQYchIdLsdkEYmNDcDptHDpkIjzcztq10zhzpoILFywEBXVjNPoTFQWzZk1l+/ZCqquVLFmiws8v\ngAsX6rg2/M6B3a5h0aJr9Qw7d9aj0fQSE+OP3W7Fzy8Am81IYaGU1FQ7K1fO5sCB4zQ0SAkLM9LX\np2fSJAVxcbEcOFBNe7uMpUuDkclklJc3IJFcK0wHJ3PmXMuK7N3bQ0yMkdTUeHp62jGbFdhsPVRX\na5k+XUV2dip79xZhMMiJiOjBbtcQE6NDqVRSVNSFIEhYtSqJ+Ph4Zs2a5XOn8l+X/tkPm8025Pyq\nG2U/xhMGg4Gnn36aLVu28Oyzz/KDH/xA3BMi10MUGr6MzWYbEAyONh0dHe6WtP0FhlwuR6vVfqXA\n6G9LGa8336EYXAugUCi+1K53PDPcuo+x6uwCX65/8Zbiy0uXLtHe3k5OTs4XU87fIzhYy/r1/8qb\nb/43u3Z1MneunJycFPbvP/5FtyoLBoOK3Fw/EhIm8fHHZ3E4YO7cUNrbu2huNhIcrKS+XoZabeUb\n35jN6dPnOXasj+RkCzpdACZTOzEx8VRXN1JVpWb58iASE+PYtq0QQVAQFOTEaHSSlnbtVHzXrivo\ndAJ33JFFVVUVFy6YCAmx0N6uwc/Pwpo1i9iz5zjFxQILFigIDw/l4sVqZDINXV29GAwqbrstjODg\nYHburEQud5KQoKGvz4Kfnx6l0smxY2YiIhx885sLOHr0FBUVFmJjTRiNakJCBKZOzWH37hJqa5Xc\ncUcw/v7+HD9egVQqxWp1YLcrue22ychkMt5/v5qgIAvZ2RG0t7fT0yOgVFo5e1ZBQoKNVavms3Pn\nYRoaFKSkWOjtVRARofyiE9Vl2tvl3HlnPIIgcPRoNTKZDbgmSOfOTaO7u5stWwzEx/cyZ04GtbW1\nGAwCKpWZujotublKCgpy2br1GC0tMtLTr3Wx0mgkKJXXprU7HDJWr56M0Wjk6NEWNJpuZDIdSqWT\n6dPTqa1t5MABK9nZVubMyeHEiTKMRjlSqZGurgCmTfMjOjqK3bvP09MD2dlKHI5rbYflcid1dTLU\nagfz5yfR0tLKyZMmQkM7UauD0WptJCYmcPZsLefOqVi4UEVKSgKHD5fS1ydHJuvB4fAnLy8UjUbD\nnj2XkUodzJgRQlRUFGvWrPpSplrk7wy2Sbnu8zfKfgxVeO7pe9RX4XQ6eeedd/j3f/93VqxYwYsv\nvkhUVJSnlyXi/YhCw5fxhNCQy+Xum6pcLkej0QwoDp8oAuNWawHGO/2zUzdquTsadR+D61+83bZg\nNBrdGa6ysjIOHDjOggUzmDRpEs8++3sMBgn//M/T6O7uZtu2C2i1VsLDdXR3dxMXF4lEYmf/fjOJ\niTbuvHMee/Z8TnOzkthYK21tCsLCHF8E7GdoapKxZk0YEomE4uIaNBo5JhPY7VIWLZqC1Wrl448v\nExFhIjc3nitXLmO1qlCrHZw5I2HKFAkrVsznww/30dysID1doLPTSVCQjJCQEE6daqG7W8Lq1XFY\nLBZOnmxGp7MikagQBDtz5mTS1mZg27YuUlPNLFkyjRMnSujulqPVWmhqUpOVpWbq1Bw++ug4bW1S\npk9XYbVK6O3tRatVUlNzrTPbmjWZGAwG9u9vJiioB53OHzCTnj6Z+vpmjh51MGuWjNmzc9mz5whG\noxyVqgejUUdGho7o6Ch27qzEbIY5cwKxWm1cvtyNWi3Q1qZGo3GyenUB1dW1HDjQTWxsN4GBIUAf\nwcERXLp0mYsXNSxb5kdKSiI7dxZisSjQ6UxYrWoyM0PRarXs3t2EQuFk8eI4Ojo6qKzsRq3uo7PT\nn4AAK8uXz+bEiXIKC+1kZ1sIDg6jp8eARKKhpaWDtjY9y5aFEhwczN69FdhsDoKCnDidUhISQnE6\n7Rw+3EdQkJ0FCxKpr2+kstJKQICRvr5gIiKczJ6dz549J7l4UcX8+RKCg8Oorq7D4ZBhNFqw2fQs\nWBCFUqlk165LKBQWYmI0hIaG8OCD30av13v6Y+K1DLeblCszPPj+6MIb5yEJgsC5c+dYt24d7e3t\nbN68mUWLFnntPfWr+PWvf82TTz7JunXrePnllz29nImEKDR8GbvdPuAmNpq42tsCboHR36IykQSG\nxWJxCy2VSjVitQDjmaHaSn6V9epW6j58wZ42mHPnztHe3s6MGTOoqqrizTc/IjBQxaOP/itvv/1X\nduxop6BAICtrMoWFJUilfoCZlhYN06ZpmTw5iS1byrFaJeTkaOnuNmO12ggMVFNRYUetdnLHHflU\nVdVw7Fg3sbEmpFId0Et2djpnztRSXi5j2TI9ycmT2Lu3ELtdjUZjoadHRU5OMGFhYWzZUgXYmTs3\njPb2DvfgwytXVOj1Vu64Yx6nTp3m2DEzWVk29PpAensNBASE0dDQQkODlpUrQ4iMjGTHjmIcDilB\nQU5MJoHU1HCUSgV797YRECCwenUmVVU1XLxoIjCwl85OPYGBVm6/fR779p2krAzmzZMSEhJKTc0l\npFI1XV19dHfrWLIkCr1ez44dF5BK7URFKTCZLAQG6pFIbBQWOoiMtLF8eR6nT1dQVSUQHm7EZPIn\nLEygoCCX3buLqalRsWKFzj2ZWyKRYTbbsdvVzJ8fj0wmY9u2OnQ6C6mpQZhMfdhsUpRKK2Vl1zIs\nK1fO4eDBE1RVQXx8L2azlvBwCZGRURQW1nH1qorVq8NQqVQcO1YJ2AEZEomMOXNSvpj+3UZYWA95\neXE0N1/BYACdzkpDgx9paTJmzcplz54T1NfLSU+3fnHtBBQKFZWVRsxmBcuXx+J0Ojl8uBGZzIhK\npSE4WM/69d8nICDAo/vf2xmpblI3Uxc3lDV1LJ6fPT09/OpXv+JPf/oTjz76KI8++qjbGj2eOHny\nJP/0T/9EQEAAixYtEoXG2CIKDV9mLISGyyLl8qXKZDL8/f0nlMAA3BmM0Sg29lVutu5j8EN28N/R\nP3vka/a0/rS2tqLRaPDz8+PkyZNs336IJUtmkJWVxdNPb6a5WcI996RjtVrZs+cCSqUNvV5BX5+F\nrKw4BEFg585O4uJsrFpVwPHjp2hulhEWZqG5WU1kpJ3bbpvFtm2F1NbKuf12PRKJnOrqBjQaLR0d\nNsxmBUuWJCAIAjt21KPX9xEVpcdo7CY4OBSFwsGRIw6Sk+3cccd8du48SFOTgvh4C52dSiIiIDU1\nmc8+u0hrq5y1ayMBOHWqBqUSLBYpTqeEhQvTMJlMfPJJM1FRfeTnJ9LU1EhPjwyt1k5FhYL0dCmL\nF89iy5Zr/0Z6uoPubglBQTICAwMpLW2jp0fG2rWTsNlsHD1aj1JpRipVAQ7mzMnAYGjn00+7SEzs\nY9GiXEpLz9DRIUOl6qGpSceUKTKys6ewe3cZbW0KcnJAEFTYbOYvis6vWayWL59MT08PBw82o9N1\no9X6IZPZSEtLpLm5lc8/d5CX52DBgql8/vkJOjuVqNVd9PT4k5GhJT4+jt27L9DZCbNn6wAZjY0G\nZDIHBoMSpRKWLs2gra2NvXsNhIZ2ERQUiMPRg79/MF1dXZw9q2H2bAV5eWl89tkpOjoU+Pt3Y7Pp\nSU31JyAggM8+u4zNBkuWRGK1WjlzphWZrBeTyY+gIDk//vF9hISEjMtgcqwYq25SQxWeD2VNHXx/\nHKm5H1u3buWxxx4jJyeHV199laSkpK/993qCnp4epk2bxu9//3uee+458vPzRaExtohCw5dxOBxD\nFqaNBHa7HZPJhM1mc99sXafJ/v7+boHRX2R4OgU8GjgcDsxmM3a7fcyKjX2Z4dR9wN/tgRPJnjYU\nJSUltLS0MH/+fC5dusQbb3yCVith/fr72bJlO1u2XCUz00JKSgJVVReRSv1wOs3U1qqYNUtHenoK\nW7eeoK9PQXKylI4OC0FBagIC9Jw61YVMJmHt2jSampo4ebKTwEAjNpsaicTE3Ll51NQ0ceiQjVmz\nJOTmpnL0aBFWqwa53ER7u46pU/XExcWxbds5LBaYOlVHX5+Vrq4+/PwU1NSAWu1k1apc6usbOXSo\nk6goIxpNANBHUlIi1dWNlJXJWbxYS0ZGMnv2HMdsVqHR9GEyacjMDCQsLIzt22sQBIHbbovAaOyh\nuroDrdaBwaBBq7WxcuUMKioq+fzzPlJS+ggNDaevz4BOF0JTUwt1dTqWLAlg0qRYdu4swmKRERho\nwWSSkpAQgEql4PDhTlQqgSVLJtHW1sb5873odD2YTIH4+dlYunQmp06d49gxG1On2omPj6G+vh67\nXYnRaKSjw4+FC0MIDQ1l164KrFYnsbFgs0FgoB6ZzEFxsY2AACe3355OY+NliouNBAR0YLcHoNNZ\nyM/P4OTJi1RUqLjtNgUJCTEUFZ3DYpFht5uxWv2YNSv8iyxODRKJg4wMHXa7E6OUmozDAAAgAElE\nQVTRikJhpapKRUSEk/vuW0V0dDSRkZGe3speizcM3bsZa+rXbcxRW1vLhg0bOHPmDJs2beKuu+4a\n18+z+++/n7CwMF566SUWLVokCo2xRxQavsxoCI3+AkMqlaLRaNwe+N7eXux2O/7+/u6boS8LjP7d\njFQqlVcUG/sig60FQ2XqfGnex9dFEATq6urQaDRERERw7NgxPvzwMxYsyGXx4oX87GebqK2V8s1v\nxqFQKNi//wxyuQSVSkpfn5OCgngUCgVbtjQRGmpn4cJkKiuraW4WCA62UlOjICzMzIoV89m79ySV\nlQpmz5YAGrq6DPj5BdLY2EFnp4bly6NRq9Xs3VuJXG4jKEiB2WwjMTECqVRg3z4jUVF21qyZRlFR\nKZcuCYSH92Ew6AgPtzNv3gx3B6dlyzRotXoqKi6hUCgxGm2YzWoWLYpDLpezfXstWq2VhAR/ent7\nUal0KBQ2Tp4UiI+3s2bNbI4cOUllpUBsbC+9vVpCQwVSU5M5dOg8DQ0q1qwJRqfTcfz4BaRSsNsF\nnE4lc+YkALB1ayOBgVZycyNpbzdgMNjQam1cvKgiJsbK0qUzOHjwFDU1cqZMsWC1qgkIgMDAEM6d\na+HqVTVr10aiVqs5ePACYEOplCEIEqZNS8RisbBjRzuRkVYWLEihrq6exkYHWm0PV67oiYmxMWtW\nLgcOlFBTo2bmTAG5XE9vbzdSqZympmuia9myGGQyGZ99VodE0ktgoAqpFBISIujr6+Hzz23Ex1tZ\nu3YWcXFxZGRkeG7DjgO8fejerWQ/XBlgFxaLhVdeeYVNmzbx/e9/n6effho/Pz9PvJwR49133+WF\nF17g1KlTKBQKUWh4BlFo+DJOpxObzTYif5drDoHVav2SwIBrNzqTyYTFYnF7472lxelI4nQ6MZvN\n2Gw2r+pmNBHo/967xJ1EIrnuRN+vU/fhS7gsfQDHjx+nrq6eJUsWYzAY2LTpA+RygYceupvCwkI+\n/vgK8fE9xMVF0d7egk4XjMXSS0kJ5OVJmDEjmz17TtDToyUmxkJnp4y4OBXh4eEcOtSE2SxhzZoE\nurq6KC1tRaO5Vh8gCFYWL86jqamZHTu6SUkxMW3aFM6fv4DFokKhsHLpkor8fDW5uRls21aIwSAn\nM1NCby+o1aDTaTl3rgeHQ8rq1cl0dXVx5EgLen0vCoUOsFBQkEZTUwv79lnIyrKxcOFUDh8+idGo\nQqPppa1NR2amiilTUti+vZz2dimzZmmw2aCtrRO1Ws6VK9eCs+XL0+jo6GD//qsEBXUTGBiAIJiJ\niYnBYGijsFDCtGlS5s3LY+/eo7S3K/D3N2I0apk8WUlUVBSffVaL0ShjwQJ/QEJl5VXkcjt9fRrk\ncli6NAuDwcD27QaiorpISoqlr68Tp1ONxWLk/HkVubkScnOn8NlnRbS3a4iNNWE2q4mN1eLn50dh\nYQtms4yVK2Ox2WycOtWIVNqH06lFqXQyf342V640s2OHkcREI9Onp5OcnMi8efM8ui+9nfE8dO96\n2Y+2tjYKCgpITU0lMzOTiIgIPvzwQ2JiYvjDH/5Adnb2uL9XNjY2UlBQwN69e8nKygIQhYZnEIWG\nLzMSQuNmBIbr5/q3cnXhKyfNg9ulqlQqr+5m5EsIgoDZbL6p936oosr+J3uuFruDxcdEvY6CIHD+\n/HnkcjkpKSkcO3aMd9/dT1ZWLA8++M88/vhGyssFbr9dS3BwICdOXECh0CCV2untVTJ9egR+fn5s\n3VqLWu1k+vQwDIZ22tosBAXJqKqSERR0rSC8sLCU4mIbaWkWBEGDVNpHVFQcFRV1XLqkZc2aYMLD\nw9izpwRBUKDX2+nrk5KVFY5Wq2Xnzia0WifLlk3m8uXL1NSY0OvNGAw6/P0trFw5l2PHyjhxws7U\nqXaCgkJpa7uCQqHHYOiipUXHsmWhhIWFsXPnaex2CA8XsFgEoqMDUCplHD3ag5+fk1WrMqmrq6O8\nvJfAQCNmsz9+flbmzZvG8eNnKCqCuXOlJCTEcvr0BWw2BTabie5uPXPnhnzR1vcidruTlBQFFosD\nh0NAJrNz4YIEPz87S5ak09BwmeJiE6GhXchkAej1DjIz0ygtreT0aQULFsiZNCma48dPY7Opkcuv\nWaKmTQvF39+fnTtrcTqdTJ9+rXNWY2M3SqWVlhYtAQFOli3Lo6rqEocP9xAb20VAQCjTpk3hG99Y\n6+mt59V4g01qtHAJjXfffZfS0lLKysqorKx0ux9iYmLIzc0lNzeXnJwc5s+fT0xMjIdXPXw++eQT\n7r77bmQy2YA4xZXdcV1bkVFHFBq+zNcRGv0FhkQiQaPRuE+QXbiCOpe1xZW9uJnJ0uNFfAxul6pS\nqb70PoiMDq5OUmazGbj19344dR/9M3ET9RobjUa0Wi12u50DBw5w9mwlq1YtRa1W8+KLf8Fqhfvv\nn099fT2ffnqJwMA+QkL8MJl6iIuLwWzu5eBBGxkZdlatmsvOnQdpa1MRGWmivV1NXJyU9PQp7N59\njtZWGStWhABQXl6HWi2ntxecThkLF6ZgsVjYtq2J0NA+pkyJpqOjDYdDiUplp6xMRkqKkxUr5rJ9\n+0EaGxVMnmyhu1tBWJiUyMhITp5spK1NwR13RCORSDh6tAqFwgnIcDhg9uxkbDYbW7a0EBFhZs6c\nyTQ0NNLa6kSvt3DpkoaEBIGlS2ezY8cRqqvl5Oc7sNvVgAmt1o+amg46O1WsXh2LXC7nwIFqJBIz\ner0Ch0MgMzMOi8XM3r1GoqKs3H57DhUVF6mttaLXd9He7k9UlJOZM3PZs+cU1dVq5s4FjcaPpqYW\npFIF3d12LBYdS5des7vt3l2DTGYhIkKJIAgEBvrjdJopLHQSE2Nn5cqpnD17gbNnzYSEdGI2BzJz\n5iTuv/9ej+6t8YC326RGAofDwR//+EeeffZZ7r77bp5//nk6OjooKyujrKyM8vJyysrKaGxs5LXX\nXuNHP/qRp5c8bHp7e6mrqxvwtQceeID09HQef/xx0tPTPbSyCYcoNHwZV6A2HFypYpfav5HAANzf\nu97NeDiTpb3B5uKL7VLHC4MHHY7Gez9US8mxnPfhrVyvi5cgCJSVlWG1WikoKKCkpIS3395JVJSO\nRx/9IS+//BYHD/YyZ46UyZPjKC4+A+hwOK7VXMycGUBMTDSffnoOmw0yMlT09tpwOBzo9QoqKuxo\nNAKrV+dQX9/A0aOdhIf3IJf7IZOZycxMpbKygZMnYf58JTk5qezfX4jFokGt7qO7W0tOjh/R0dHs\n2HGRvj6B+fODMZst1Nd3oNFAa6sCpdLJihW5NDU1s3dvO9HR3YSHh2GxdOPvH0pHRzunTyuYPVtJ\nQUEWu3Ydo6NDQVhYH729aiZP1hESEsLBg42YTBJWrozFZDJRXn4FudyCxaJBLneweHEuLS2tbNvW\nQUKCkezsybS2XsFolCKVmqmpUTN1qoqpU7PYsaOQlhYZiYlmenokBAUp0GrVnDnTjdks5/bbo3E4\nHJw40YRCYUIu16BQwMyZ6V/YrozuzlkVFRdpaRFQqYy0tvozf340d921muDg4HFj+/EE49kmdbMI\ngkBpaSk//vGPsdlsbN68mblz537lfc1gMCCXy32m1bFonfIIotDwZYYjNAYLDNeE7+tlMFyWk1sN\nvrxRfIgCw3MMFeSqVKoxfdgP5Wn29J4cK/p3ULuZQEsQBFpbW/Hz80Or1XL06FH27StkxYp5JCUl\n8cwzb3L1qoRvfSsDq9XK7t3nUShs+PkpsFjsZGTE4nQ62LWrk+hoGytX5lNWdpr6eoGQEBOtrVoi\nImwsXjyX7duPcf68nMWLlWi1ftTW1qNQaOjoMNHTo2XRosgvuitVIpfbiY1VYTJZCQjQo1AIFBZa\nCA93smpVPmfPnufsWQvh4b2YTFoCAuzMnJnPZ5+VcP68kttv1xIVFUFh4RmcTiUOhxmTScesWeH4\n+/uzfXs1EomDnJwATCYzXV0WNBqB6mo5gYF2Vq0q4Pz5Ko4f7yE21ohc7o9GYyM2Np5z52q5cEHN\nsmV6Jk+exL59p7BYFKhUvZhMatLS/PH39+fAgWYkEgkLFoRjMpm4cKENudxEZ6cerdbG4sW5VFfX\n8fnnJhISuomJicZi6UYu96Ojo51Ll3Tcfnsoc+bMIDk5GZ1ON4Y7aXzhyzap/nR1dfHss8/y7rvv\n8tRTT/Hwww8PKAafCCxevJi8vDxRaIwtotDwdVyWn6/CVWBrNpuvKzBcHaScTufXFhjXYzg2l6+a\nrXCr/27/U3RfnsfgjXjzHJKb7egyXus+BhfZj1SL5qKiIq5evcqCBQu4dOkSmzd/jEYj4Sc/uZ9d\nu/bw3ntNpKT0kZmZRF1dLTabGpnMSlWVkmnT1Eybls3WrUdob1eSkuKku1sgKEhOQIA/JSUdWCxS\n1q5Nore3l+PHm1CrXTMy7MyalU5HRyfbtnWSlGRiyZJ8SkpOYzBI8fMz09SkJTVVzvTpuXz6aSGN\njQpmz5Zjs8np7e1GpVLT2GjCbFayYkUCTqeTffvqUKn6CAjQ4HDYSEyMwmYzs2+fiYQEG6tWTaeo\nqIzaWichIT10duqJjZUwbVoOO3eepKZGxbJlGvR6fyoqLiGRyOjpsWGxqJg1KxyFQsG+fZdRq+0k\nJfl90TpcgVRqobRUQnS0gxUrCigvr6CszExkZBdWq57gYCeJiQkcO1bxhcC4NqwxPz+fyMjIcbkn\nx4qJYJNyOp28//77PPHEE8ydO5eXX36Z+Ph4Ty9LZOIgCg1fx2q1MtQ17C8wALfA6B9Yj6XAuB63\nIj5udp2DT9En+jyGsWa8ziEZak8OHko5WsO0RorBJ7mj2eBAEATq6+tRqVRERkZy6tQp/u//djNz\nZjp33XUHjz++kXPnJNx5Zxjh4WHs3n0SQVCgUl0bEpiTE05AQADbtl1CpRJYuDCWq1fbqK3twc/P\nztWravR6G6tXz6GsrIJDh/pIT7cQEhKK0diGRhPE1attXLqkZeFCf1JSEvn000JMJiXh4RZMJhmT\nJgWg12s5fPgqAKtWTaajo4PS0jbU6l5sNh1KpZ1Fi6ZSU1PP7t09pKWZmDo1jcrKSnp65EilJi5f\n1lJQoCMjI5Xt209y9aqMjAwBi0WOWi1BpVJw/nwvNpuEpUvj6O3t5cSJa/+GRqNDJnOQm5tMW5uB\nPXtMTJ5sYsWKmRQVlXHlCmi1Rtrb/UhLU5GTk8Gnn56koUHBvHly9Ppgli27jZiYGPf+nOh2wKGY\nKDapyspKHnnkEerq6nj11VdZuXLlhLzeIh5FFBq+zmCh4erg4zq592aBcT1u5LGXSCRfsrn0f6i6\nBIbFYsHhcCCXy1GpVF5ziu7rDO7i5Qt2heHWfbj2pyeE++AaGE+c5PZvuVtcXMz58xdZtOg2BEHg\n179+G4tFwve/fzv19fX87W/nCQw0kZgYgtHYjVJ5bUZGYaFAcrKD1avnsn//UWprJUyaZMZoVBEa\nKpCS8vcZGXfcEYper+fIkXNIJFLAic2mYNYs19yQOvR6OzNmRNHR0UFLixm93kltrZLwcDsrV87m\nxIlyioutTJliRirVI5ebCQmJ4MKFeurqdKxeHUJUVAR79hRjs8nQai3YbEoyM8O/mCdyBZnMyW23\nRdHe3k5lpRGdzkJvrz86nY1ly2ZQUVHFvn29pKebSEyMo729BatVSW9vNw0NWhYsCPxCKJ2gu1tO\nbKwVQdBw//13kpaW9qVrPVRG7np2QFdnNl9kotikTCYTL730Em+88Qb/9m//xpNPPolWq/X0skQm\nJqLQ8HVck5MHCwyVSoVGo/mSwOjfe9sbBcaNGCrzMTjQk0gk7q+7WvaKAmNsGMtTdG9huHUfoxno\nuQZuDi709jaqqqowm81kZmZSUVHBf/zHR0RF+bNu3f/Hm2/+ie3bDcyYIWH69EwOHTpBX58atdqE\nwaAlO1tLcnISn35aTmenlDlzdNhsEpqb29BoFDQ3A1ybkWE0Gtm9u4mgoF6Cg/1xOMxERETQ19fN\nkSNOMjIcrFw5h717D3PlipyIiD66ujTEx8tJS0tlz54zNDXJWbEiCLVaTWlpDVKphL4+B4KgZuHC\nyTidTrZurcPPz0xyciBGYzdmswSdDs6dUxAX52D16jkcO1bM6dM2EhN7sVi0hIRIiI2N5cSJSurq\ntNxxRzBhYWEcOFCKzSZBLrcBOr73vTVkZ2cP6zoO1w7o2pPj+XM6EWxSgiCwZ88eHnnkERISEnj9\n9ddJS0vzudcpMq4QhYavY7VaMZlMmEwmnxYY18P1umw2Gzab7UtWssEWF18q8PUWBhfZT/Q2wa5A\nb7AAcTHSdR+DC729qQbmZjAaje7T59OnT/PZZ8eYN6+A9PR0fv7zTdTXC3zrWxlotVref78QQRCI\niJBgMjmIiQlCoZBy5IgRPz8na9fmcOlSHaWl3QQF9WCxXCuwnj9/GsXF5zl2zM7MmZCenkRp6TnM\nZgVg+qJzViCTJsXx6aflGI2Qna3EagW73YZSKaW62o5MJmHVqnQ6Ozv57LMr+PkZUau1CIKZlJR4\n2ts7OXJEICvLwbJlMzh06FrHqYCAHjo69EyZoiYtLYUdO0q5ckXOwoVaVCoNVVWXkUgkdHU5ATUP\nPLCQpKQkIiMjR+Q97m8H7L8vvS0jN1wmgk0Krg2oe/zxxzl27Bi//e1v+da3vuWVhwgiEw5RaPg6\nBoMBq9WKUqn80g3W1wWGC4fDgcViGTBRWi6XT9juQmOJy6ZjsVi8/hTd0wyu+xjssb+RHXAofNGi\nNpiqqiouX77M9OnT6erq4re/fRtBgPXr76OkpIT//M8zREebmTs3lbq6elpaHAQE2KipUREf72T5\n8nns3HmYCxdkTJvmxOFwzcgIoLq6FYNBw+rV0fj5+bF371mcTif+/gI2m4S0tCikUgl797bh7+9k\n1aoM6uvrqajoxc+vh64uHTqdmQULplJeXklhoYNp05wkJMRSX1+HxaLEZDLS2qrntttCiIuLYfv2\nEnp6pCQmOrHZZPj7q1AopJSX9yGVSvjmN/OIiYkhJydnTK7jUOLjq+6V/efQeJqJYpOy2Wy8+eab\n/PrXv+bee+/ll7/8JYGBgZ5eloiIC1Fo+DquVPFQAsMVxPiqwOjfTedmHjQ3OmXu/xAdyY5Xvkr/\nTlJikf2tMZy6j/77Ehgw7FCtVvu8Rc2FwWAAICQkhJqaGv78509ITo7hW9/6Jps2vcW+fR0sXKhn\n9uypfPDBbrq6VISFmTAaVUyerCUyMpL9+2vo7payenUMDoeD4uI65HIHVqsckLB4cSZGo5EtW5qJ\niOgjNzee9vY2Ojqc6HR2zp1TkJBgY/HiGXz22Qlqa+Wkp9swmZQEBUkJDg6htLSB5mYN3/hGJP7+\n/uzfX47DIaBWC9jtcqZOjUMqlbJjRxM6nYNFixKIiIhg8eLFHs9GDScj54khmBPFJlVYWMi6detQ\nqVS88cYbFBQU+NzrFBn3iELD17Hb7e4HQP8MRv9TUl+7MQ0+xf06dQCj2fHKVxnvNp3xwI1m0LiQ\nyWQolUrkcrkoioG6ujpKSkqYOnUq4eHhPP/8azQ12fiXf5mDSqXirbf2IwgCubl+mM1WjEYLGo2E\n6moJOp2TNWumUlfXwMGDBiIiutFoAlEorCQkxHPpUhMnT0qYOVNCXt4UDh48SU+PhsBAE0ajjowM\nPZMmTWL79rN0dEhYsiQYqVRGRUUjMpmA0ShFIpGzbFk6JpOJrVvrCQzsJSkpnMjIUO6555solUpP\nv4VfSf/s+PVE8WjaVCeKTcpgMPDzn/+cjz/+mGeffZYf/OAH4j1WxFsRhYav43A43HUJvi4w+qfK\ngVGrA7iRl9nTp3meYrTmMYjcHP1PcV2f7/7iQxTFX+bq1au0tbUxZcoUOjo6eP31PyGRwP/7fw9Q\nWFjIW2+VERdnY+3amZSWnqaqykpwcC8dHToiIwUWLJjJrl3HOXNGxoIFUgICAqisvIRUqsVsttDd\nrWPRokhCQkL49NMzWK0CyclyrFZQqeTI5XD6tAWtFlavzqK1tZVDh1oJCOhGofAnJiaQf/u373u1\nwLgRN9MMYSjxMZx9OVFsUk6nk3feeYenn36a22+/nd/85jdERUV5elkiItdDFBq+zuHDh/H39ych\nIcHt8fa1m683TPMebmtTXxIfE6EOwJsZLPD6d1EbboGvL+3LW8FutwMgl8tpbW1lx47dxMXFsHjx\nIt56623277/CvHmhrFixiN///l2ammSkpdnp6QGtVsDPz5+LF7vo7lZy552JSKVSPvvsIhKJGbVa\ngSDA1KlJWCwWduxoIyzMztKlaTQ2NlJZ2YefXy9Xr+pJStLw8MPfRavV+uRJ9c1kim+2Hmmi2KQq\nKipYt24dbW1tbN68mcWLF/vc6xTxSUSh4es8+OCDfPTRR1/YAXLJzc0lLy+P/Px8kpOTx3VQ4Q0C\n40YMVdzb/zRvPAd5Y5VBEhkaV8vq4Qq8oUSx69TZhdiJ7ct0dHRw7tw50tPTCQgI4OWXf091tYF/\n/Mf5BAQE8OqrO7HbYenSaCwWC+fONaNS2enuVqFQOFm+fCqtra1s3dpKTIyRlJQ4enu7sFplgJnT\np+Xk5yv55jdXExkZOeEKem/msKb/npRIJFitVvc8Fl+1SfX09PDCCy/w9ttv88gjj7BhwwbUarWn\nlyUicrOIQsPXcZ0cXbp0iaKiIoqKiigpKaGkpASz2UxOTg55eXnk5uaSn59Pamqq19tdBg8cG2+d\njG7kr/f2jldDDXzzNoHny4xWq+Dh7Etv6i401rje/66uLnp6eoiOjsbpdPLnP7+HzWbnn//5mxQV\nFfHWW8cIC3Ny333LKSw8yfHjnYSHGxEEPf7+AhkZqZSVVVJcLOW221RMm5ZFeno6cXFxnn6JXsWN\n9qWvWgIFQWDbtm089thjZGVl8eqrrzJ58mRPL0tEZLiIQmOi4nQ6aWhooKioiOLiYrf46OzsJDs7\n2535yMvLIyMjwyusMK5p3q40uS91MhrqhHmojleenN47+P0fbwJvvOOJ919shvB3Br//1xPYfX19\nHD58mLCwMPLz8/ngg4/Ytq2CgoJwHnjgHn7xi1c4e1bCbbfJ8fcPYcGCWWRkZHjgVY0v+tuk5HI5\nCoViyFbQML6zxZcuXWLDhg2cPn2a3/3ud9x9993jZu0iIoMQhYbI3xEEgaamJoqLi92/SktLaWlp\nISMjY0DmIzMzc8y8sK4HvMVicbdKdc3C8GVuJcgbzYnSYqtaz+FwODCZTF7x/t9sd6HxGuQNxeBO\nasO16dhsNmpqaoiLi0Or1fLuu+9RVFTJPfesYOrUqaO4ct/gZrpJDbZeDWVV9YYDm+thsVh49dVX\n+d3vfsd3v/tdnnnmGfz8/Dy9rBvywgsv8NFHH3H+/Hk0Gg1z5sxh48aNpKamenppIp5HFBoi10cQ\nBK5evUpxcbHbdlVaWkp9fT1paWlu8ZGXl0dOTg5arXZEA4r+Aa7YKnVo8TG4m9hoTZQeXGgsMvqM\np05eN6pH8nZL4FD0r4MZyfffFRCLn6XrM7iblOv+M9yOVIP35fUObFziYyz3piAIHDp0iPXr1xMS\nEsLrr79Obm6u138+XKxatYp77rmHgoIC7HY7TzzxBGfOnKGiogKNRuPp5Yl4FlFoiAwfQRBob2+n\npKTEbbsqLi6mtraW5OTkAUXnubm5+Pv7D/uGOTjA9eYAy9OMRser4Q47FBlZBgdYX2cWjCe52boP\nbxuCOVp1MCI3T3+b1Ei//8Ptxuban6Nx/VtaWnjqqafYvXs3L7zwAg8++KBXfAa+Dm1tbYSHh/P5\n558zb948Ty9HxLOIQkNkZBAEge7ubkpLS922q5KSEi5evMikSZPclitX5iM4OHjIm/b58+cJCAhA\nq9UilUpRqVRigHuLDGW7upH4AHwiwB2vDC6098UAd7iWwLE+Ybbb7ZhMJrEOyUN4cujeUOJjtISx\nw+Hg7bff5he/+AXf+MY32LhxI2FhYSP1UjxKVVUVU6ZM4fTp02LtkYgoNERGD0EQ6Ovro6yszF10\nXlpayrlz54iOjh6Q9QgPD+fNN9/kr3/9Kxs2bOCnP/2pKDBGgRsNz3Ihl8vdE6XFazA29D/BnWgB\nrjfUffTP4ok2zbFnJGxSo7WuweJjKGE8WHx81boFQaCsrIx169ZhNpt54403mDt3rsdf50ghCAJr\n167FaDRy8OBBTy9HxPOIQkNkbHE9TMrLyykuLubo0aPs2rWLq1evEhgYyIIFC9yF51OnTiUqKspn\nbsDeiMsiYjabAdyB7Xj31o8nBhcaiwHu37nZE+avszcnylRpb2Y0bVKjwc3aVU+ePElFRQU5OTnk\n5OQA8Nxzz/GXv/yFn/3sZ/z4xz9GoVB46mWMCj/84Q/ZtWsXR44cEaeWi8BNCA3xaScyorge5Kmp\nqWzdupUPP/wQmUzG008/zdKlS7lw4QJFRUVs2rSJ8vJy9Hr9gFa7eXl5xMXFTZiT3tHiRq2Ch7K3\n2Gw295932VnGouOVr9J/orpUKnVPgfbmAGusGaor0FCtoG9lb04Em5q3098mJZfL0Wq146KbnavB\nhlQqHSAUBmfljh07xosvvujen3q9Hn9/f7773e+SlpZGc3MzsbGxPrPnfvSjH7F9+3YOHTokigyR\nm0bMaIiMCnfffTc7d+7k4Ycf5rHHHiM4OHjA912BsEt4uGo+ysrKUCgUAwrO8/LySEpK8tn+/SPN\nrXbyEmcqjAy+UujtTQxnb/avRXKJbI1GIwrlMcRbbVIjjSAIVFRU8Mtf/hKj0UhAQACdnZ2UlpbS\n0dEBQHBwMHl5efzXf/0XkyZN8vCKb50f/ehHfPLJJxw8eJCkpCRPL0fEexCtUyKeobKyEr1eP6xT\nD9dJZlVV1ZdmfTidTnJyctziIz8/n5SUlHHfv38kcTgcWCyWEW2VeiNv/dl8d1sAAB/VSURBVHD9\ny76MOFF9bLkZe4tUKkUul0/4vTmWjDeb1K1iMpn47W9/y+bNm/nRj37Ek08+iU6nA67tzYaGBkpL\nSykrK6OkpIT//u//HhczM4bioYce4q9//StbtmwZMDsjICAAtVrtwZWJeAGi0BAZ37gC3bq6OoqK\nityzPkpKSjCZTGRnZw8YNDhlyhSfPDm7Hv0tOmPhQR+NdrvjHXHgoWcZXIukUCiQSqU+M+9jPDDY\nJuWrnwFBENi7dy+PPPII8fHxvP7666Snp/v0Hvqq+/fbb7/Nfffd54EViXgRotAQ8U2cTieNjY0D\nbFclJSV0dHSQlZU1wHaVkZHhk9aV/vYEALVa7dHXeaPC3rHqWz+WiIXenmVwLdJXZZGGO9RNtAXe\nPBPFJgVw+fJlHn/8cY4cOcJLL73Et7/9bTFjKTLREYWGyMRBEASuXLnyJdvVlStXyMzMHCA+srKy\nUKvV4/JhOHjYmDdbdG52oNt4O10e6yySyJfpL/Ju5QR9qLoPp9Mp2gKHwUSxSdlsNt566y1eeOEF\n7rnnHp5//nmCgoI8vSwREW9AFBoiExtBEGhra6O4uHiA7aq+vp4pU6a4bVeuQYM6nc5rH5SDT2/H\n6yyGG50uD9VRyFte42CLji8HV96KIAiYzWZ3N6+RqEXq/3cPxxboK5m54TKRbFInT550t6l94403\nmD59+oS73iIi10EUGiIigxEEgY6ODkpKSty2q+LiYmpqapg8ebK741V+fj45OTkEBAR4/MHi6zUA\n3t7x6mYtOiKjx+BM3lhaBW80CHO8ZuaGy0SySbW3t/PMM8/w4Ycf8otf/IIf/vCHoi1SROTLiEJD\nRORmEAQBo9FIaWmpO/tRWlrKhQsXiI+PdwsPlwgJCQkZk4frRK4BGCw+XL8fbG0ZbfHh6yJvPGC3\n2zGZTF6VyZtodR82mw2TyeTzM0mcTid/+ctfeOqpp1i6dCkvvfQS0dHRnl6WiIi3IgoNEZFbRRAE\nTCYTZWVl7qLz0tJSzp49S2RkpLvewyVCwsPDR+zB63Q6MZvNI9qq1hcYy45Xg6+B6/RWZOzob9EZ\nD0L7ZsTxUNZAb/5cTySbVEVFBT/5yU9oaWnh9ddfZ+nSpV59bUREvABRaIiIjCQu68Dp06cH2K5O\nnz5NSEjIgEGD+fn5REVFDevkdXCRsTjs7eYYytbyVR2vbhTcDbaHiIXeY48vXYPhiOP+IsTTr3Ui\n2aR6e3v59a9/zR//+EceeeQRNmzYIM6HEBG5OUShISIy2rgGtZ07d25A0Xl5eTk6nW5At6u8vDzi\n4+O/ZKHo6+tj69atrFixAhCLjEeC4Xa8kkql2Gw2dw2AeA3GnsFDD335GtzK/hwru9hEsUkJgsCn\nn37Khg0byMjI4LXXXiM5OdnTyxIRGU+IQkNExBO4iocvXrw4YNZHWVkZMpnMnfnIycnhypUrbN68\nmdbWVo4fP86UKVM87j/3VW4U3ME1e4tSqXRPlPbFAMsbGVwLo9FoJtznwLU/B2foXIx23cdEsUkB\n1NXV8dhjj1FSUsKmTZu4++67J9x+ExEZAUShISLiLbj821VVVRQVFfH++++ze/duent7mT59OiEh\nISQnJ7szHykpKWKgO8o4HA76+vpwOp1IJBLkcrk7yHMxVHAnBiQjh1gLc3361330FyAjWfcxkWxS\nVquV1157jd/+9rc8+OCDPPPMM/j7+3t6WSIi4xVRaIiIeBvHjh3jpz/9KYcOHWLRokX86le/IiIi\ngqKiogGzPnp7e8nOzh5QcJ6WluazAcBYcqNie29vt+sL9J9JItYjDY+h6j6GqksaLECGem8nkk3q\n8OHDrF+/nqCgIDZv3kxubq5PvlYRkTFEFBoiIt6E2WwmPj6eqKgoNm7cyPLly4d80AmCQGNj4wDb\nVUlJCQaDgaysrAF1H5mZmWKAdpMMPrkdTnB7o6Le8dhRyBOIM0lGj+HUfUgkEqxW64Ro29za2spT\nTz3Fzp07+dWvfsV3v/tdn32tIiJjjCg0RES8jQsXLpCSkjLswEoQBJqbmykuLnb/Ki0tpampiYyM\njAHiIysrC41GIwa5XzC4yFipVKJWq7/2+zOW7XZ9gf5zYXw9uPUWJnJ2zuFw8Kc//YlnnnmGO+64\ng40bNxIeHu7pZYmI+BKi0BAR8WUEQcBgMLi7XbnER11dHampqW7bVV5eHjk5Oej1ep8IIIaDJ4a9\n3WiStDe2Mx1NBEHAbDZjtVrFuTAepL9NSqFQDKhJ8iWBLAgC5eXlrFu3jr6+PjZv3sz8+fPHzfpF\nRMYRotAQEZloCIJAZ2ene8aH67/V1dUkJSUNmPORnZ1NYGCgTz6AvW2q+nDbmfqC+HDVYbhaBqvV\natHm5wFuNpM01LDB8bZHu7u7+eUvf8mf//xnnnjiCdavX49CofD0sobF5s2beemll2hubiY3N5fX\nXnuN6dOne3pZIiJDIQoNkbHFarUyY8YMysvLKS0tJScnx9NLEuFawGc0GikrK3NnP0pLSzl//jxx\ncXHuYnNX293Q0FCvCyBulsFDD725g86N2pn2D+xcvx8vtQyeyCSJDGQkukndrEAevFfHGqfTyUcf\nfcTjjz/OjBkz2LRpE5MmTRrzdXxd/u///o/777+fP/zhD8yYMYPf/e53vPfee1y8eJHQ0FBPL09E\nZDCi0BAZW9atW0dVVRU7duygpKREFBpejCAImEwmysvLB9iuzp49S0REhDvzkZuby9SpUwkPD/fK\nYN1F/y5GwLg9PR/vnvr+sxi8IZM0URnNblLD3aOuYYOjtUerqqp45JFHqK6u5pVXXmHNmjVe83kY\nLrNmzWLmzJm88sorwLX3Oi4ujocffpjHHnvMw6sTEfkSN/ygiXd/kRFjx44d7Nmzhw8++IDt27d7\nejkiN0AikaDVapk1axazZs0C/n4CeubMGXfB+Ysvvsjp06cJCgpyZzzy8/PJy8sjOjra46fUQxV6\nj+cuRv2DNBdDzVKwWq0DOl6NZWA3FEOdnisUinEb8I1XxqLg/np7tL8A6b9HYeTrPsxmMy+//DKv\nv/46Dz30EB9//DE6ne5rvTZPYrPZKCoq4sknn3R/TSKRsHTpUo4dO+bBlYmI3Dqi0BAZEVpaWvjX\nf/1XtmzZgkaj8fRyRG4RiUSCWq2moKCAgoIC4O+BfEVFhdt29corr1BeXo5GoxnQ7SovL49JkyaN\n2Qn74GnSvtrF6KsCu8G2ltEO7IZisNDz5VkM3sxgoafVasfUMth/j/aviRhc92G327Fare7v30rd\nhyAI7N+/n5/85CfExsZy5MgRMjIyxv2ea2trw+FwEBERMeDrERERXLhwwUOrEhH5eohCQ2RE+M53\nvsNDDz1Efn4+dXV1nl6OyAgikUhQKpXubMZ3vvMdd4B74cIFd+bjP/7jPygrK0Mikbh/1iU+Jk+e\nPKJBbv9TW6lUik6nm3D2HJeYk0qlXxnYORyOLwV2Iyk+Bgs9jUYzbjNJ4xXXXBJvHbrnyq7136ND\nDRu02Wxf+jMymYzPP/+crKwsoqOjAWhqauKJJ57g0KFD/OY3v+Hee+8V95yIiBczsZ7MIsPiiSee\nYOPGjV/5fYlEQkVFBTt37qSnp4ef/vSnAAyj7kdknCKRSJDL5WRmZpKZmcm//Mu/uK0TNTU17pqP\nd955h0cffRSbzUZOTs4A8ZGamjrsrjX926SK9pyhuZnA7uueKg+erD4RhZ43MF7nkrjuH/33zFB1\nH01NTdx1110AhIWFkZiYSFlZGfPnz2fr1q1MmzbNp0RGaGgoMpmMlpaWAV9vaWkhMjLSQ6sSEfl6\niMXgIl+JwWDAYDBc92cSExP5x3/8R7Zt2zbg664TznvvvZe33357NJcp4uU4nU7q6+spKiqiqKiI\nkpISSktL6e7uJjs7e4DtKi0tbUjhYLFYOHHiBLm5uV55ajseuZV2u4C74H64k9VFRo6R6CY1HnA6\nndTW1rJr1y527dpFQ0MD7e3tXL16FQC9Xu8+vFi6dCl33nmnh1f89RmqGDw+Pp6HH36YDRs2eHh1\nIiJfQuw6JTL6NDY20t3d7f7/pqYmli9fzgcffMCMGTPcKW8REReCIHD58mV35qOkpISSkhLa2trI\nzMwcMGiwpqaGX/ziF7S0tHD69GnCw8N96hTTm7hRNyEXMpkMpVKJXC4Xr8UY4u02qZGmo6ODn//8\n53z44Yc888wzPPTQQ8jlcq5evUppaSmlpaXue8esWbN84lDrb3/7Gw888ABvvvmmu73t+++/z/nz\n5wkLC/P08kREBiMKDZGxp66ujsTERHGOhsiwEASBlpYWd83Hvn37OH78OGaz2T3jIycnh7y8PLKz\ns9FoND4bYHkT/eswXDUh46ndrq8wXm1St4LT6eSvf/0rTz31FIsXL+all14iJibmun9GEASf2XNv\nvPEGL774Ii0tLeTl5fHaa6+5m3OIiHgZotAQGXvq6upISkoS52iI3BINDQ08+eSTvPPOO2RmZvLv\n//7vBAcHD5j1cenSJVJTUwcUnefm5qLX630m2PA0/QcfSqVS9zwMiUQyZMcrh8MxoN3uYOvVWLfb\n9RUmik0Krr3W8+fPs379epqbm3n99ddZtmyZT75WEREfQRQaIiIi44fe3l7i4uJQKBQ899xzPPjg\ng18qMhYEga6uLkpKSty2q+LiYqqqqkhMTHQLj/z8fLKzswkKChIDlWHgGnxosVgQBGFYgw+Hsl2N\ndbtdX2Gi2aR6e3vZuHEj//mf/8n69et57LHHxFbpIiLejyg0RERExhe7d+9m9uzZ+Pn53fSfEQSB\n3t5eSktL3bM+SktLqaioIDY21j1k0CVCQkNDfTZg+zq4Alun04lCoUCtVn/tGozBQ9wGF527BMdw\n5ij4OhPJJiUIAtu3b2fDhg2kpaXx2muvkZKS4ulliYiI3Byi0BAREZmYuFrhlpeXu7tdlZSUcObM\nGcLDwwdYrqZOnUpERMSEDXCdTicmkwm73Y5MJnPbpEaLW+l4NRGuzUSySQHU19ezYcMGSkpKePnl\nl/mHf/gHsbmAiMj4QhQaIiIiIi5ctqAzZ864i85LSkooLy8nMDDQXfORn59PXl4eMTExPh34DA5s\n1Wq1x+aS3KjjlUt89BchvnJtJppNymq1snnzZn7zm9/wwAMP8Oyzz+Lv7+/pZYmIiAwfUWiIiHiK\nuro6nnvuOfbv309zczMxMTHce++9/OxnPxswTE3Es7iCvIqKCrftyiU+VCrVgCGDeXl5JCQkjPuu\nSoIgYLPZMJvNXh3Y3kh8+ELHq4lmkzp69Cjr1q3D39+fzZs3k5+fP66ul4iIyABEoSEi4il27drF\n3/72N7797W8zefJkzpw5w/e+9z3uu+8+XnzxRU8vT+Q6uKw9Fy9eHJD5KCsrQxCEAd2u8vPzmTx5\n8rgpbO7frnak6jDGEpf4GCxA+ne86p/x8Nai84lmk7p69SpPPfUUO3bs4Pnnn+d73/uezwoqEZEJ\nhCg0RES8iZdeeok333yTqqoqTy9FZJi4Atza2lp3q12XALFareTk5AwQH6mpqV5VW+B0OjGbzdhs\nNqRSqTuw9QVu1G4XvKfj1USzSTkcDv7nf/6Hn//856xZs4aNGzcSERHh6WWJiIiMDKLQEBHxJp56\n6il2797NiRMnPL0UkRHC6XTS0NBAUVGR23ZVWlpKV1cXWVlZA2xX6enpY14D4U11GGNN/6yH6/eD\nO14Nzn6M5vsy0WxSp0+fZt26dfT09LB582YWLFgwIfadiMgEQhQaIiLeQlVVFQUFBbz88ss8+OCD\nnl6OyCgiCAJNTU3uzIer41VrayuZmZnublf5+flkZmaOyom26+TcbDbjdDpRKpWo1eoJH+h5ouPV\nRLNJdXd38/zzz/POO+/w+OOPs379epRKpaeXJSIiMvKIQkNEZKR54okn2Lhx41d+XyKRUFFRQWpq\nqvtrly9fZuHChSxevJi33nprLJYp4mUIgkBra6vbcuWact7Y2EhaWtqAovPs7Gy0Wu0tB6IOhwOT\nyYTD4fD5k/ORYLD4cGU/XAw15fxm6lommk3K6XTy8ccf8/jjj1NQUMCmTZtISEjw9LJERERGD1Fo\niIiMNAaDAYPBcN2fSUpKcvvfm5qaWLRoEXPmzOHtt98eiyWKjBMEQaC9vZ2SkhJ39qO0tJTa2lpS\nUlIGFJ3n5ubi5+d33SDVarXicDiwWq1IpVL3PAxfDWxHk6/b8Woi2aQAqqurefTRR7l48SKvvPIK\na9euFfediIjvIwoNERFPcvnyZRYvXsz06dP53//9X/HBK3JDBEGgq6vLPeW8pKSE4uJiKisrSUhI\nGFBwnpOTQ1BQEHa7nbfeeovXXnuNbdu2ER///7d3fzFV138cx18HEBGYpiID/+AoEEGCA6WSa9N5\nUZvNcq3RXKV2o83METOIZbaMppalqTRTN7MuVMw5rezvJnqRW6kcBAHNzBwKZ2Em/kP+nM/v4rdz\n6oiG4Dl8zzk8H5sXHs7F+/j3++Lz/rzfSYqMjOTPm4/dLny4XK4uE6/cJySSNGjQoJC+E9Pa2qo1\na9Zo/fr1eumll7R06VLFxsZaXRaAvkHQAKxy4cIFTZ06VcnJyfr000+9vpvJ1BX0hDFG165dU1VV\nlWfXh8PhUF1dnYYOHarw8HA1NjZq1qxZWrp0qdLS0kL2wTbQuCdedXR0qL29XR0dHV3eEygTr3zJ\nGKMDBw6osLBQiYmJKisr04QJE4L+cwHoEYIGYJVt27Z1ufRtjJHNZvNqwQB64/Tp0yosLNSXX36p\n1NRUTZs2TZWVlaqpqdGIESM8bVfZ2dnKzc1VQkICD4F+crs2Kfff80Aft9sbjY2NKikp0cGDB/Xe\ne+/phRdeCKpdLLdiuSrQa93+oxUaQ9SBADR37lzNnTvX6jIQgt555x2VlpYqPj5e27dv17PPPiub\nzSZjjNra2nTixAnPhfMPP/xQx48f1+DBgz3BIycnR3a7XaNHjw7qB0Sr3TpNKjo62utOTFhYmNeD\n6q2Xzjs6OtTW1ub5uj8mXvlSR0eHNm/erNLSUuXn56uurk7Dhg2zuqx7Vl9fL2OMNm/e7LVc9fr1\n6yxXBe4RJxoAEGRWrlyp1tZWFRUVKTo6+j/f627rqa+v9xq3W1VVpcjISK9pV3a7XcnJyV6XmtGV\nL6dJWTFutzc1Hj16VAUFBZKksrIy5eXlhfSfEZarAneF1ikAgDf3w+2vv/7qteHc4XDIGNNly3lK\nSkpQtfb4U19Mk+pu4pV7vO6trVf+cOnSJb399tvatWuX3nrrLS1atChkNsr/F5arAneFoAEA6J77\n4fbs2bOekw93AGltbe0SPsaNG9evRudavXTvXsft9pTL5dLOnTv1xhtvaNq0afrggw80atQoX32c\ngMZyVeCuETQAAL3ncrnU0NCgI0eOeJ18XLp0SZmZmV5tVxkZGSE3yjWQl+65J17d6dK5O3z8+/Sj\nu5MpY4xOnjypV199VY2NjVq/fr0ee+yxgPi8PcVyVcDvCBoAAkdZWZlWr16tpqYmZWdna/369Zo4\ncaLVZaGHjDFqbGz0uvNRWVkpp9OpjIwMz4LBnJwcTZgwwTOFKdgE49K97sKH9M/Eq59++klxcXFK\nT09XZGSk5/Lzpk2bVFBQoOLiYg0aNMjCT3NvWK4K+B1BA0Bg2Llzp+bOnatNmzZp0qRJWrNmjXbt\n2qVTp04pLi7O6vJwj4wx+vPPPz0tV+4t5+fOndP48eM94cNutysrK0vR0dEBGz6sbpPyB3fb1b/b\nr/Ly8nT27FkNHDhQqampamhoUGJiopYvX64nnngiqENGT7FcFegVggaAwJCXl6fJkyfro48+kvT/\nh7kxY8Zo8eLFKioqsrg6+IMxRpcuXfK671FZWakzZ84oJSXFM27XHUIGDx5s6QNeILdJ+cPly5dV\nUVGh8vJyXbhwQU1NTTp//rw6OzsVHh6u9PR05ebmKjc3VwsWLFBUVJTVJfsFy1WBXiNoALBee3u7\noqOjtXv3bj355JOe1+fNm6fLly9rz549FlaHvmSMUUtLixwOh1cAOXXqlMaOHet14TwrK0vDhg3r\nkwf9YGyTuhdtbW36+OOP9f7772vOnDlavny5hgwZotbWVlVXV6uystLz+/P777/L6XSG7M4VlqsC\nvUbQAGC9xsZGjRo1SocPH9bkyZM9rxcXF+vQoUM6fPiwhdXBasYYXb9+XVVVVTp27JiOHj0qh8Oh\n2tpaJSYmei6bu0NIfHy8z8LH7dqkQnkbtDFGhw8fVkFBgWJjY1VWVqbc3Nz//PV0uVwhGzIA3BM2\ngwMAApvNZlNMTIymTJmiKVOmSPonAFRXV+vo0aOqrKzU/v37VV1drbi4OE/bVXZ2tnJzc5WYmNij\n8NHf2qQkqbm5WUuXLtXXX3+t0tJSzZ8//65ObQgZAHqLoAHA7+Li4hQeHi6n0+n1utPpVEJCgkVV\nIZDZbDZFRUVp4sSJnslkxhi1t7frxIkTnraetWvX6vjx44qNjfUEj5ycHNntdo0ZM+a2D8n19fVq\nb29XUlJSv2iT6uzs1Oeff65ly5ZpxowZqq2t5e4BgD5B6xSAPnG7y+BJSUlavHixXnvtNYurQ7By\nn0ycPHnSa9xuVVWVIiIiPO1Wdrtd48aNU3l5uTZs2KBZs2Zp8+bNId8mVVNTo4KCArW0tKisrExT\np04N6VMbAH2KOxoAAkN5ebnmzZunjRs3esbbfvHFF6qvr9eIESOsLg8hxL1H4vTp0547H99//71q\na2sVERGh6dOnKyUlxXPpPDU1tdtFdsHmypUrevfdd/XZZ5+puLhYhYWFGjhwoNVlAQgt3NEAEBjy\n8/PV3NysZcuWyel0ym6367vvviNkwOdsNpsiIiI0fvx4hYWFadu2baqpqdGMGTO0ZMkSNTc369ix\nYyovL1dJSYlu3LihBx980GviVVpaWlDuznC5XNq3b5+Kior00EMPqbKyUsnJyVaXBaCf4kQDABCS\nampqlJubq1GjRmndunWaOXNml/e4XC6dP39eR44c8bRdORwO/fXXX8rMzPRqvcrIyFBkZGTAho8z\nZ85oyZIlqq+v19q1a/XUU08FbK0AQgKtUwCA/skYo61bt2r27Nk92nJtjFFjY2OXRYNNTU3KyMjw\nCh+ZmZmKioqy9IH+5s2bWrNmjdatW6cFCxbozTffVGxsrGX1AOg3CBoAANwrY4yn5erfAeTcuXNK\nS0vz2vORlZWlmJgYv4cPY4wqKipUWFiohIQEbdiwQZmZmZxiAOgrBA0AAPzBGKO///67y8nHb7/9\npgceeMBr3G5WVpaGDBnisxDQ1NSkkpISVVRUaNWqVZozZw77LgD0NYIGAASLFStWaM+ePaqvr9eg\nQYM0ZcoUrVq1SuPGjbO6NNwlY4yuXLkih8PhFUBOnjyppKQkr7ar7OxsDR8+vEfho6OjQ1u2bFFp\naameeeYZrVixQsOHD/fjJwKAOyJoAECwmDFjhmbPnq2HH35YHR0dKikpUU1Njerq6np0xwCBxRij\nGzduqKqqyjNu1+Fw6MSJE0pISPAKHjk5OYqPj+8SPowxOnbsmAoKCuRyuVRWVqZHHnmENikAViJo\nAECwam5uVnx8vA4dOqRHH33U6nLgQ8YY3bx5U9XV1V5tV9XV1Ro2bJin7cputyslJUWffPKJysvL\ntWzZMr3yyiuKiGA6PQDLETQAIFidPn1aaWlpqq6uVkZGhtXlwM+MMWpvb1dtba3XpfOff/5ZeXl5\n2rFjh0aPHm11mQDgRtAAgGBkjNHMmTN15coVHTx40OpyYBH3hfPY2FgNGDDA6nIA4N+6DRqMqACA\nALRw4ULV1tZqx44dVpcCC9lsNg0dOjQkQkZbW5vsdrvCwsJ0/Phxq8sB0AcIGgAQYBYtWqT9+/er\noqJCiYmJVpcD+ERRUZFGjx7NBXagHyFoAEAAWbRokfbu3asDBw4oKSnJ6nIAn/jmm2/0ww8/aPXq\n1epByzaAIMfYCgAIEAsXLtT27du1b98+xcTEyOl0SpKGDBmiqKgoi6sDesfpdGr+/Pnat28fY5qB\nfoYTDQAIEBs3blRLS4umTZumkSNHen6Ul5dbXRrQay+++KIWLlyonJwcq0sB0Mc40QCAAOFyuawu\nAbgrJSUlWrVq1R2/brPZVFdXp2+//VZXr15VcXGxJNE2BfQzjLcFAAA9cvHiRV28ePE/35OcnKz8\n/Hx99dVXXq93dnYqIiJCzz33nLZu3erPMgH4F3s0AACANRoaGtTS0uL5+YULF/T4449r9+7dmjRp\nkkaOHGlhdQDuUbdBg9YpAADgF7duMo+JiZExRvfffz8hA+gHuAwOAAD6DHs0gP6DoAEACGorV65U\nWFiYCgsLrS4F3Rg7dqw6OzuVlZVldSkA+gBBAwAQtH755Rdt2rRJ2dnZVpcCALgFQQMAEJSuXr2q\n559/Xlu2bNF9991ndTkAgFsQNAAAQenll1/WzJkzNX36dKtLAQDcBlOnAABBZ8eOHXI4HDpy5IjV\npQAA7oCgAQAIKg0NDSooKNCPP/6oAQMGWF0OAOAOWNgHAAgqe/fu1dNPP63w8HC5/w/r7OyUzWZT\neHi4bt68yQhVAPA/NoMDAELLtWvX9Mcff3i9Nm/ePKWnp+v1119Xenq6RZUBQL/CZnAAQGiJiYlR\nRkZGl9eGDx9OyACAAMLUKQBA0KNVCgACD61TAAAAAHqq2+/wcKIBAAAAwOcIGgAAAAB8jqABAAAA\nwOcIGgAAAAB8jqABAAAAwOcIGgAAAAB8ricL+xhSDgAAAOCucKIBAAAAwOcIGgAAAAB8jqABAAAA\nwOcIGgAAAAB8jqABAAAAwOcIGgAAAAB8jqABAAAAwOcIGgAAAAB8jqABAAAAwOf+B0gztMsG0pz5\nAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x10ee1c518>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"z = sum(sum(math.e**(-0.5*(x**2+y**2))))\n",
"F = 1/z*math.e**(-0.5*(x**2+y**2))\n",
"Fcon = F*((x**2+y**2)**0.5>=1)\n",
"Fcon1 = Fcon/Fcon.sum()\n",
"fig = plt.figure(figsize=(10,6))\n",
"ax = plt.axes(projection='3d')\n",
"ax.scatter(X,Y,Fcon1,s=1,alpha=0.5)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Q3: Marginal distribution"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python [default]",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| gpl-3.0 |
brycepg/fto-scraper | fto_graph.ipynb | 1 | 424400 | {
"cells": [
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from collections import OrderedDict\n",
"import math\n",
"import datetime\n",
"import time\n",
"\n",
"import matplotlib.pyplot as plt\n",
"import pandas as pd\n",
"from IPython.core.display import HTML, display\n",
"\n",
"import bokeh.io\n",
"import bokeh.plotting\n",
"import bokeh.models\n",
"import bokeh.palettes\n",
"\n",
"import fto\n",
"from fto import stats\n"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"\n",
" <div class=\"bk-root\">\n",
" <a href=\"http://bokeh.pydata.org\" target=\"_blank\" class=\"bk-logo bk-logo-small bk-logo-notebook\"></a>\n",
" <span id=\"a269d98a-8594-4972-9a92-a217fbdc0391\">Loading BokehJS ...</span>\n",
" </div>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"application/javascript": [
"\n",
"(function(global) {\n",
" function now() {\n",
" return new Date();\n",
" }\n",
"\n",
" var force = \"1\";\n",
"\n",
" if (typeof (window._bokeh_onload_callbacks) === \"undefined\" || force !== \"\") {\n",
" window._bokeh_onload_callbacks = [];\n",
" window._bokeh_is_loading = undefined;\n",
" }\n",
"\n",
"\n",
" \n",
" if (typeof (window._bokeh_timeout) === \"undefined\" || force !== \"\") {\n",
" window._bokeh_timeout = Date.now() + 5000;\n",
" window._bokeh_failed_load = false;\n",
" }\n",
"\n",
" var NB_LOAD_WARNING = {'data': {'text/html':\n",
" \"<div style='background-color: #fdd'>\\n\"+\n",
" \"<p>\\n\"+\n",
" \"BokehJS does not appear to have successfully loaded. If loading BokehJS from CDN, this \\n\"+\n",
" \"may be due to a slow or bad network connection. Possible fixes:\\n\"+\n",
" \"</p>\\n\"+\n",
" \"<ul>\\n\"+\n",
" \"<li>re-rerun `output_notebook()` to attempt to load from CDN again, or</li>\\n\"+\n",
" \"<li>use INLINE resources instead, as so:</li>\\n\"+\n",
" \"</ul>\\n\"+\n",
" \"<code>\\n\"+\n",
" \"from bokeh.resources import INLINE\\n\"+\n",
" \"output_notebook(resources=INLINE)\\n\"+\n",
" \"</code>\\n\"+\n",
" \"</div>\"}};\n",
"\n",
" function display_loaded() {\n",
" if (window.Bokeh !== undefined) {\n",
" Bokeh.$(\"#a269d98a-8594-4972-9a92-a217fbdc0391\").text(\"BokehJS successfully loaded.\");\n",
" } else if (Date.now() < window._bokeh_timeout) {\n",
" setTimeout(display_loaded, 100)\n",
" }\n",
" }\n",
"\n",
" function run_callbacks() {\n",
" window._bokeh_onload_callbacks.forEach(function(callback) { callback() });\n",
" delete window._bokeh_onload_callbacks\n",
" console.info(\"Bokeh: all callbacks have finished\");\n",
" }\n",
"\n",
" function load_libs(js_urls, callback) {\n",
" window._bokeh_onload_callbacks.push(callback);\n",
" if (window._bokeh_is_loading > 0) {\n",
" console.log(\"Bokeh: BokehJS is being loaded, scheduling callback at\", now());\n",
" return null;\n",
" }\n",
" if (js_urls == null || js_urls.length === 0) {\n",
" run_callbacks();\n",
" return null;\n",
" }\n",
" console.log(\"Bokeh: BokehJS not loaded, scheduling load and callback at\", now());\n",
" window._bokeh_is_loading = js_urls.length;\n",
" for (var i = 0; i < js_urls.length; i++) {\n",
" var url = js_urls[i];\n",
" var s = document.createElement('script');\n",
" s.src = url;\n",
" s.async = false;\n",
" s.onreadystatechange = s.onload = function() {\n",
" window._bokeh_is_loading--;\n",
" if (window._bokeh_is_loading === 0) {\n",
" console.log(\"Bokeh: all BokehJS libraries loaded\");\n",
" run_callbacks()\n",
" }\n",
" };\n",
" s.onerror = function() {\n",
" console.warn(\"failed to load library \" + url);\n",
" };\n",
" console.log(\"Bokeh: injecting script tag for BokehJS library: \", url);\n",
" document.getElementsByTagName(\"head\")[0].appendChild(s);\n",
" }\n",
" };var element = document.getElementById(\"a269d98a-8594-4972-9a92-a217fbdc0391\");\n",
" if (element == null) {\n",
" console.log(\"Bokeh: ERROR: autoload.js configured with elementid 'a269d98a-8594-4972-9a92-a217fbdc0391' but no matching script tag was found. \")\n",
" return false;\n",
" }\n",
"\n",
" var js_urls = ['https://cdn.pydata.org/bokeh/release/bokeh-0.12.3.min.js', 'https://cdn.pydata.org/bokeh/release/bokeh-widgets-0.12.3.min.js'];\n",
"\n",
" var inline_js = [\n",
" function(Bokeh) {\n",
" Bokeh.set_log_level(\"info\");\n",
" },\n",
" \n",
" function(Bokeh) {\n",
" \n",
" Bokeh.$(\"#a269d98a-8594-4972-9a92-a217fbdc0391\").text(\"BokehJS is loading...\");\n",
" },\n",
" function(Bokeh) {\n",
" console.log(\"Bokeh: injecting CSS: https://cdn.pydata.org/bokeh/release/bokeh-0.12.3.min.css\");\n",
" Bokeh.embed.inject_css(\"https://cdn.pydata.org/bokeh/release/bokeh-0.12.3.min.css\");\n",
" console.log(\"Bokeh: injecting CSS: https://cdn.pydata.org/bokeh/release/bokeh-widgets-0.12.3.min.css\");\n",
" Bokeh.embed.inject_css(\"https://cdn.pydata.org/bokeh/release/bokeh-widgets-0.12.3.min.css\");\n",
" }\n",
" ];\n",
"\n",
" function run_inline_js() {\n",
" \n",
" if ((window.Bokeh !== undefined) || (force === \"1\")) {\n",
" for (var i = 0; i < inline_js.length; i++) {\n",
" inline_js[i](window.Bokeh);\n",
" }if (force === \"1\") {\n",
" display_loaded();\n",
" }} else if (Date.now() < window._bokeh_timeout) {\n",
" setTimeout(run_inline_js, 100);\n",
" } else if (!window._bokeh_failed_load) {\n",
" console.log(\"Bokeh: BokehJS failed to load within specified timeout.\");\n",
" window._bokeh_failed_load = true;\n",
" } else if (!force) {\n",
" var cell = $(\"#a269d98a-8594-4972-9a92-a217fbdc0391\").parents('.cell').data().cell;\n",
" cell.output_area.append_execute_result(NB_LOAD_WARNING)\n",
" }\n",
"\n",
" }\n",
"\n",
" if (window._bokeh_is_loading === 0) {\n",
" console.log(\"Bokeh: BokehJS loaded, going straight to plotting\");\n",
" run_inline_js();\n",
" } else {\n",
" load_libs(js_urls, function() {\n",
" console.log(\"Bokeh: BokehJS plotting callback run at\", now());\n",
" run_inline_js();\n",
" });\n",
" }\n",
"}(this));"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%load_ext autoreload\n",
"%autoreload 2\n",
"bokeh.io.output_notebook()"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"class HTMLDict(OrderedDict):\n",
" def _repr_html_(self):\n",
" output_string_list = [\"<table><tbody>\"]\n",
" for key, val in self.items():\n",
" output_string_list.append('<tr><th>%s</th><td>%s</td></tr>' % (key, val))\n",
" output_string_list.append(\"</tbody></table>\")\n",
" return ''.join(output_string_list)\n",
" "
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"df = fto.load_dataframe(\"/home/hugh/data/fto-stats.csv\")\n",
"monthly_df = fto.stats.generate_monthly_dataframe(df)"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th>Month</th>\n",
" <th>Births</th>\n",
" <th>Deaths</th>\n",
" <th>Pregnancies</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <td>March 2016</td>\n",
" <td>54</td>\n",
" <td>63</td>\n",
" <td>21</td>\n",
" </tr>\n",
" <tr>\n",
" <td>April 2016</td>\n",
" <td>68</td>\n",
" <td>44</td>\n",
" <td>29</td>\n",
" </tr>\n",
" <tr>\n",
" <td>May 2016</td>\n",
" <td>45</td>\n",
" <td>43</td>\n",
" <td>18</td>\n",
" </tr>\n",
" <tr>\n",
" <td>June 2016</td>\n",
" <td>58</td>\n",
" <td>68</td>\n",
" <td>28</td>\n",
" </tr>\n",
" <tr>\n",
" <td>July 2016</td>\n",
" <td>79</td>\n",
" <td>59</td>\n",
" <td>28</td>\n",
" </tr>\n",
" <tr>\n",
" <td>August 2016</td>\n",
" <td>37</td>\n",
" <td>67</td>\n",
" <td>16</td>\n",
" </tr>\n",
" <tr>\n",
" <td>September 2016</td>\n",
" <td>37</td>\n",
" <td>49</td>\n",
" <td>19</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"display(HTML(monthly_df.to_html(index=False)))"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
" <div class=\"bk-root\">\n",
" <div class=\"plotdiv\" id=\"d2002eb8-56f3-464c-a475-80e3c10e93b0\"></div>\n",
" </div>\n",
"<script type=\"text/javascript\">\n",
" \n",
" (function(global) {\n",
" function now() {\n",
" return new Date();\n",
" }\n",
" \n",
" var force = \"\";\n",
" \n",
" if (typeof (window._bokeh_onload_callbacks) === \"undefined\" || force !== \"\") {\n",
" window._bokeh_onload_callbacks = [];\n",
" window._bokeh_is_loading = undefined;\n",
" }\n",
" \n",
" \n",
" \n",
" if (typeof (window._bokeh_timeout) === \"undefined\" || force !== \"\") {\n",
" window._bokeh_timeout = Date.now() + 0;\n",
" window._bokeh_failed_load = false;\n",
" }\n",
" \n",
" var NB_LOAD_WARNING = {'data': {'text/html':\n",
" \"<div style='background-color: #fdd'>\\n\"+\n",
" \"<p>\\n\"+\n",
" \"BokehJS does not appear to have successfully loaded. If loading BokehJS from CDN, this \\n\"+\n",
" \"may be due to a slow or bad network connection. Possible fixes:\\n\"+\n",
" \"</p>\\n\"+\n",
" \"<ul>\\n\"+\n",
" \"<li>re-rerun `output_notebook()` to attempt to load from CDN again, or</li>\\n\"+\n",
" \"<li>use INLINE resources instead, as so:</li>\\n\"+\n",
" \"</ul>\\n\"+\n",
" \"<code>\\n\"+\n",
" \"from bokeh.resources import INLINE\\n\"+\n",
" \"output_notebook(resources=INLINE)\\n\"+\n",
" \"</code>\\n\"+\n",
" \"</div>\"}};\n",
" \n",
" function display_loaded() {\n",
" if (window.Bokeh !== undefined) {\n",
" Bokeh.$(\"#d2002eb8-56f3-464c-a475-80e3c10e93b0\").text(\"BokehJS successfully loaded.\");\n",
" } else if (Date.now() < window._bokeh_timeout) {\n",
" setTimeout(display_loaded, 100)\n",
" }\n",
" }\n",
" \n",
" function run_callbacks() {\n",
" window._bokeh_onload_callbacks.forEach(function(callback) { callback() });\n",
" delete window._bokeh_onload_callbacks\n",
" console.info(\"Bokeh: all callbacks have finished\");\n",
" }\n",
" \n",
" function load_libs(js_urls, callback) {\n",
" window._bokeh_onload_callbacks.push(callback);\n",
" if (window._bokeh_is_loading > 0) {\n",
" console.log(\"Bokeh: BokehJS is being loaded, scheduling callback at\", now());\n",
" return null;\n",
" }\n",
" if (js_urls == null || js_urls.length === 0) {\n",
" run_callbacks();\n",
" return null;\n",
" }\n",
" console.log(\"Bokeh: BokehJS not loaded, scheduling load and callback at\", now());\n",
" window._bokeh_is_loading = js_urls.length;\n",
" for (var i = 0; i < js_urls.length; i++) {\n",
" var url = js_urls[i];\n",
" var s = document.createElement('script');\n",
" s.src = url;\n",
" s.async = false;\n",
" s.onreadystatechange = s.onload = function() {\n",
" window._bokeh_is_loading--;\n",
" if (window._bokeh_is_loading === 0) {\n",
" console.log(\"Bokeh: all BokehJS libraries loaded\");\n",
" run_callbacks()\n",
" }\n",
" };\n",
" s.onerror = function() {\n",
" console.warn(\"failed to load library \" + url);\n",
" };\n",
" console.log(\"Bokeh: injecting script tag for BokehJS library: \", url);\n",
" document.getElementsByTagName(\"head\")[0].appendChild(s);\n",
" }\n",
" };var element = document.getElementById(\"d2002eb8-56f3-464c-a475-80e3c10e93b0\");\n",
" if (element == null) {\n",
" console.log(\"Bokeh: ERROR: autoload.js configured with elementid 'd2002eb8-56f3-464c-a475-80e3c10e93b0' but no matching script tag was found. \")\n",
" return false;\n",
" }\n",
" \n",
" var js_urls = [];\n",
" \n",
" var inline_js = [\n",
" function(Bokeh) {\n",
" Bokeh.$(function() {\n",
" var docs_json = {\"ebe91c11-cd15-4858-9f1b-ae4cfccfe83d\":{\"roots\":{\"references\":[{\"attributes\":{\"days\":[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]},\"id\":\"045146a8-3cc3-48ba-920d-96932f859e48\",\"type\":\"DaysTicker\"},{\"attributes\":{\"dimension\":1,\"plot\":{\"id\":\"6e9abb9f-1d46-46c2-ac41-eab1a719eacf\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"ticker\":{\"id\":\"72ae4a97-f062-4462-a356-3f3ddfd667ce\",\"type\":\"BasicTicker\"}},\"id\":\"d2132af7-8002-4950-867a-3c2b900f8d17\",\"type\":\"Grid\"},{\"attributes\":{},\"id\":\"0fb47630-a166-49fd-a11b-74d11fe1e4e6\",\"type\":\"BasicTickFormatter\"},{\"attributes\":{\"data_source\":{\"id\":\"d863f707-0ceb-4259-a306-49ef0317b139\",\"type\":\"ColumnDataSource\"},\"glyph\":{\"id\":\"b7fef780-a04b-4d7c-9ed3-17fabdbee376\",\"type\":\"Line\"},\"hover_glyph\":null,\"nonselection_glyph\":{\"id\":\"4049d8fe-6f88-4dc6-98f4-415e28473edb\",\"type\":\"Line\"},\"selection_glyph\":null},\"id\":\"79dc9554-6b53-4de3-98f1-0e622fa038d4\",\"type\":\"GlyphRenderer\"},{\"attributes\":{\"active_drag\":\"auto\",\"active_scroll\":\"auto\",\"active_tap\":\"auto\",\"logo\":null,\"tools\":[{\"id\":\"2fd92d1a-a272-436e-a478-658ae068b54e\",\"type\":\"PanTool\"},{\"id\":\"72dd9200-840f-4652-8cf4-b10f2435f0fd\",\"type\":\"WheelZoomTool\"},{\"id\":\"f0bb5820-40b9-48ac-8fdd-8c381b5988be\",\"type\":\"BoxZoomTool\"},{\"id\":\"54818f2e-db80-48a1-95f4-f198ea1814b2\",\"type\":\"SaveTool\"},{\"id\":\"e147c89f-4340-4e6e-a7a5-8b82dc8c6d30\",\"type\":\"ResetTool\"},{\"id\":\"286527f3-e16b-416b-b795-5efbef532e1c\",\"type\":\"HelpTool\"}]},\"id\":\"b7de74d0-0a0f-4074-a3d2-0f5ace96b2ca\",\"type\":\"Toolbar\"},{\"attributes\":{\"base\":60,\"mantissas\":[1,2,5,10,15,20,30],\"max_interval\":1800000.0,\"min_interval\":1000.0,\"num_minor_ticks\":0},\"id\":\"81b42395-9101-46e7-a02e-be548f0c6302\",\"type\":\"AdaptiveTicker\"},{\"attributes\":{\"line_alpha\":{\"value\":0.1},\"line_cap\":\"round\",\"line_color\":{\"value\":\"#1f77b4\"},\"line_width\":{\"value\":5},\"x\":{\"field\":\"TS\"},\"y\":{\"field\":\"Births\"}},\"id\":\"5832a3a5-4b98-4285-8503-4d8f2a72e2a6\",\"type\":\"Line\"},{\"attributes\":{\"line_cap\":\"round\",\"line_color\":{\"value\":\"#fc8d62\"},\"line_width\":{\"value\":5},\"x\":{\"field\":\"TS\"},\"y\":{\"field\":\"Deaths\"}},\"id\":\"f7dbe8e2-d7df-412f-bfb3-fe298cccd1e7\",\"type\":\"Line\"},{\"attributes\":{\"months\":[0,2,4,6,8,10]},\"id\":\"a741042e-74d6-4893-b8c4-01583365c363\",\"type\":\"MonthsTicker\"},{\"attributes\":{},\"id\":\"72ae4a97-f062-4462-a356-3f3ddfd667ce\",\"type\":\"BasicTicker\"},{\"attributes\":{\"label\":{\"field\":\"Deaths\"},\"renderers\":[{\"id\":\"12160f16-8c70-4612-9668-afedbf3553f7\",\"type\":\"GlyphRenderer\"}]},\"id\":\"edbe1443-4db0-46c4-8eb7-71534e2f5347\",\"type\":\"LegendItem\"},{\"attributes\":{\"plot\":{\"id\":\"6e9abb9f-1d46-46c2-ac41-eab1a719eacf\",\"subtype\":\"Figure\",\"type\":\"Plot\"}},\"id\":\"286527f3-e16b-416b-b795-5efbef532e1c\",\"type\":\"HelpTool\"},{\"attributes\":{\"plot\":null,\"text\":null},\"id\":\"87e6aacc-0a37-4e5f-b9e6-b3865e695097\",\"type\":\"Title\"},{\"attributes\":{\"plot\":{\"id\":\"6e9abb9f-1d46-46c2-ac41-eab1a719eacf\",\"subtype\":\"Figure\",\"type\":\"Plot\"}},\"id\":\"54818f2e-db80-48a1-95f4-f198ea1814b2\",\"type\":\"SaveTool\"},{\"attributes\":{\"plot\":{\"id\":\"6e9abb9f-1d46-46c2-ac41-eab1a719eacf\",\"subtype\":\"Figure\",\"type\":\"Plot\"}},\"id\":\"2fd92d1a-a272-436e-a478-658ae068b54e\",\"type\":\"PanTool\"},{\"attributes\":{\"line_alpha\":{\"value\":0.1},\"line_cap\":\"round\",\"line_color\":{\"value\":\"#1f77b4\"},\"line_width\":{\"value\":5},\"x\":{\"field\":\"TS\"},\"y\":{\"field\":\"Deaths\"}},\"id\":\"c4888092-a8c0-406d-ada4-afce6f7f10d2\",\"type\":\"Line\"},{\"attributes\":{\"months\":[0,1,2,3,4,5,6,7,8,9,10,11]},\"id\":\"655d1de6-6186-4768-b698-a5b97f06abd6\",\"type\":\"MonthsTicker\"},{\"attributes\":{\"plot\":{\"id\":\"6e9abb9f-1d46-46c2-ac41-eab1a719eacf\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"ticker\":{\"id\":\"e329acf6-4dba-4d98-9511-7c74d0574d58\",\"type\":\"DatetimeTicker\"}},\"id\":\"1051e188-9ac0-495d-8441-b7235bcc87bb\",\"type\":\"Grid\"},{\"attributes\":{\"background_fill_alpha\":{\"value\":0},\"border_line_alpha\":{\"value\":0},\"items\":[{\"id\":\"331ce033-230c-4c48-9dd0-d9ae81ae5ae2\",\"type\":\"LegendItem\"},{\"id\":\"edbe1443-4db0-46c4-8eb7-71534e2f5347\",\"type\":\"LegendItem\"},{\"id\":\"3d5d727a-caea-43f7-8690-e400e7ba30a1\",\"type\":\"LegendItem\"}],\"margin\":0,\"padding\":5,\"plot\":{\"id\":\"6e9abb9f-1d46-46c2-ac41-eab1a719eacf\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"spacing\":0},\"id\":\"be540950-e98f-476d-be43-31707b1c0085\",\"type\":\"Legend\"},{\"attributes\":{\"days\":[1,15]},\"id\":\"ddecaac1-cf6e-4049-8548-422305441e99\",\"type\":\"DaysTicker\"},{\"attributes\":{\"num_minor_ticks\":5},\"id\":\"e329acf6-4dba-4d98-9511-7c74d0574d58\",\"type\":\"DatetimeTicker\"},{\"attributes\":{\"overlay\":{\"id\":\"313b3539-77cf-4f00-9553-46727fe48572\",\"type\":\"BoxAnnotation\"},\"plot\":{\"id\":\"6e9abb9f-1d46-46c2-ac41-eab1a719eacf\",\"subtype\":\"Figure\",\"type\":\"Plot\"}},\"id\":\"f0bb5820-40b9-48ac-8fdd-8c381b5988be\",\"type\":\"BoxZoomTool\"},{\"attributes\":{\"base\":24,\"mantissas\":[1,2,4,6,8,12],\"max_interval\":43200000.0,\"min_interval\":3600000.0,\"num_minor_ticks\":0},\"id\":\"fc1b90c9-13e1-4be2-99a7-ac3e5130c076\",\"type\":\"AdaptiveTicker\"},{\"attributes\":{\"days\":[1,4,7,10,13,16,19,22,25,28]},\"id\":\"214e50e4-337d-4fd6-9e67-6cc4f52cc337\",\"type\":\"DaysTicker\"},{\"attributes\":{},\"id\":\"019117d2-4507-4804-bfee-93db831564e5\",\"type\":\"ToolEvents\"},{\"attributes\":{\"line_cap\":\"round\",\"line_color\":{\"value\":\"#66c2a5\"},\"line_width\":{\"value\":5},\"x\":{\"field\":\"TS\"},\"y\":{\"field\":\"Births\"}},\"id\":\"2a0318b8-6aef-47bb-b11c-07ad53eb8c91\",\"type\":\"Line\"},{\"attributes\":{\"line_cap\":\"round\",\"line_color\":{\"value\":\"#8da0cb\"},\"line_width\":{\"value\":5},\"x\":{\"field\":\"TS\"},\"y\":{\"field\":\"Pregnancies\"}},\"id\":\"b7fef780-a04b-4d7c-9ed3-17fabdbee376\",\"type\":\"Line\"},{\"attributes\":{\"formatter\":{\"id\":\"0fb47630-a166-49fd-a11b-74d11fe1e4e6\",\"type\":\"BasicTickFormatter\"},\"minor_tick_line_alpha\":{\"value\":0},\"plot\":{\"id\":\"6e9abb9f-1d46-46c2-ac41-eab1a719eacf\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"ticker\":{\"id\":\"72ae4a97-f062-4462-a356-3f3ddfd667ce\",\"type\":\"BasicTicker\"}},\"id\":\"767ba32f-f2bc-4355-8edf-793709658548\",\"type\":\"LinearAxis\"},{\"attributes\":{},\"id\":\"9b4fb645-9190-4bbf-b23b-74f7506d92f5\",\"type\":\"YearsTicker\"},{\"attributes\":{\"data_source\":{\"id\":\"d863f707-0ceb-4259-a306-49ef0317b139\",\"type\":\"ColumnDataSource\"},\"glyph\":{\"id\":\"2a0318b8-6aef-47bb-b11c-07ad53eb8c91\",\"type\":\"Line\"},\"hover_glyph\":null,\"nonselection_glyph\":{\"id\":\"5832a3a5-4b98-4285-8503-4d8f2a72e2a6\",\"type\":\"Line\"},\"selection_glyph\":null},\"id\":\"95e35bc3-2282-41e1-b437-3074014c9e38\",\"type\":\"GlyphRenderer\"},{\"attributes\":{\"line_alpha\":{\"value\":0.1},\"line_cap\":\"round\",\"line_color\":{\"value\":\"#1f77b4\"},\"line_width\":{\"value\":5},\"x\":{\"field\":\"TS\"},\"y\":{\"field\":\"Pregnancies\"}},\"id\":\"4049d8fe-6f88-4dc6-98f4-415e28473edb\",\"type\":\"Line\"},{\"attributes\":{\"plot\":{\"id\":\"6e9abb9f-1d46-46c2-ac41-eab1a719eacf\",\"subtype\":\"Figure\",\"type\":\"Plot\"}},\"id\":\"72dd9200-840f-4652-8cf4-b10f2435f0fd\",\"type\":\"WheelZoomTool\"},{\"attributes\":{\"label\":{\"field\":\"Pregnancies\"},\"renderers\":[{\"id\":\"79dc9554-6b53-4de3-98f1-0e622fa038d4\",\"type\":\"GlyphRenderer\"}]},\"id\":\"3d5d727a-caea-43f7-8690-e400e7ba30a1\",\"type\":\"LegendItem\"},{\"attributes\":{\"plot\":{\"id\":\"6e9abb9f-1d46-46c2-ac41-eab1a719eacf\",\"subtype\":\"Figure\",\"type\":\"Plot\"}},\"id\":\"e147c89f-4340-4e6e-a7a5-8b82dc8c6d30\",\"type\":\"ResetTool\"},{\"attributes\":{\"months\":[0,4,8]},\"id\":\"ce7b4eab-78b5-4eed-a115-63cdbcf1c680\",\"type\":\"MonthsTicker\"},{\"attributes\":{\"bounds\":\"auto\",\"callback\":null,\"end\":80},\"id\":\"911b37d4-212a-4ca2-9642-8da70bab9a13\",\"type\":\"Range1d\"},{\"attributes\":{\"max_interval\":500.0,\"num_minor_ticks\":0},\"id\":\"bd17ee7b-8738-469e-84a2-98334c3a22b1\",\"type\":\"AdaptiveTicker\"},{\"attributes\":{\"formatter\":{\"id\":\"192345dd-a940-4e4e-954c-eeab9753aad1\",\"type\":\"DatetimeTickFormatter\"},\"plot\":{\"id\":\"6e9abb9f-1d46-46c2-ac41-eab1a719eacf\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"ticker\":{\"id\":\"e329acf6-4dba-4d98-9511-7c74d0574d58\",\"type\":\"DatetimeTicker\"}},\"id\":\"0eec81a9-74a8-4c39-b553-670b5c71e9ea\",\"type\":\"DatetimeAxis\"},{\"attributes\":{},\"id\":\"192345dd-a940-4e4e-954c-eeab9753aad1\",\"type\":\"DatetimeTickFormatter\"},{\"attributes\":{\"below\":[{\"id\":\"0eec81a9-74a8-4c39-b553-670b5c71e9ea\",\"type\":\"DatetimeAxis\"}],\"left\":[{\"id\":\"767ba32f-f2bc-4355-8edf-793709658548\",\"type\":\"LinearAxis\"}],\"plot_width\":800,\"renderers\":[{\"id\":\"0eec81a9-74a8-4c39-b553-670b5c71e9ea\",\"type\":\"DatetimeAxis\"},{\"id\":\"1051e188-9ac0-495d-8441-b7235bcc87bb\",\"type\":\"Grid\"},{\"id\":\"767ba32f-f2bc-4355-8edf-793709658548\",\"type\":\"LinearAxis\"},{\"id\":\"d2132af7-8002-4950-867a-3c2b900f8d17\",\"type\":\"Grid\"},{\"id\":\"313b3539-77cf-4f00-9553-46727fe48572\",\"type\":\"BoxAnnotation\"},{\"id\":\"be540950-e98f-476d-be43-31707b1c0085\",\"type\":\"Legend\"},{\"id\":\"95e35bc3-2282-41e1-b437-3074014c9e38\",\"type\":\"GlyphRenderer\"},{\"id\":\"12160f16-8c70-4612-9668-afedbf3553f7\",\"type\":\"GlyphRenderer\"},{\"id\":\"79dc9554-6b53-4de3-98f1-0e622fa038d4\",\"type\":\"GlyphRenderer\"}],\"title\":{\"id\":\"87e6aacc-0a37-4e5f-b9e6-b3865e695097\",\"type\":\"Title\"},\"tool_events\":{\"id\":\"019117d2-4507-4804-bfee-93db831564e5\",\"type\":\"ToolEvents\"},\"toolbar\":{\"id\":\"b7de74d0-0a0f-4074-a3d2-0f5ace96b2ca\",\"type\":\"Toolbar\"},\"x_range\":{\"id\":\"38403e47-d99a-46ea-bb54-fa560fa78146\",\"type\":\"Range1d\"},\"y_range\":{\"id\":\"911b37d4-212a-4ca2-9642-8da70bab9a13\",\"type\":\"Range1d\"}},\"id\":\"6e9abb9f-1d46-46c2-ac41-eab1a719eacf\",\"subtype\":\"Figure\",\"type\":\"Plot\"},{\"attributes\":{\"bounds\":\"auto\",\"callback\":null,\"end\":1472688000000.0,\"start\":1456790400000.0},\"id\":\"38403e47-d99a-46ea-bb54-fa560fa78146\",\"type\":\"Range1d\"},{\"attributes\":{\"callback\":null,\"column_names\":[\"TS\",\"Pregnancies\",\"Deaths\",\"Births\",\"Month\"],\"data\":{\"Births\":[54,68,45,58,79,37,37],\"Deaths\":[63,44,43,68,59,67,49],\"Month\":[\"March 2016\",\"April 2016\",\"May 2016\",\"June 2016\",\"July 2016\",\"August 2016\",\"September 2016\"],\"Pregnancies\":[21,29,18,28,28,16,19],\"TS\":[1456790400000.0,1459468800000.0,1462060800000.0,1464739200000.0,1467331200000.0,1470009600000.0,1472688000000.0]}},\"id\":\"d863f707-0ceb-4259-a306-49ef0317b139\",\"type\":\"ColumnDataSource\"},{\"attributes\":{\"days\":[1,8,15,22]},\"id\":\"ee2e9e68-ec21-4718-9d0e-30e1a4c54e16\",\"type\":\"DaysTicker\"},{\"attributes\":{\"bottom_units\":\"screen\",\"fill_alpha\":{\"value\":0.5},\"fill_color\":{\"value\":\"lightgrey\"},\"left_units\":\"screen\",\"level\":\"overlay\",\"line_alpha\":{\"value\":1.0},\"line_color\":{\"value\":\"black\"},\"line_dash\":[4,4],\"line_width\":{\"value\":2},\"plot\":null,\"render_mode\":\"css\",\"right_units\":\"screen\",\"top_units\":\"screen\"},\"id\":\"313b3539-77cf-4f00-9553-46727fe48572\",\"type\":\"BoxAnnotation\"},{\"attributes\":{\"data_source\":{\"id\":\"d863f707-0ceb-4259-a306-49ef0317b139\",\"type\":\"ColumnDataSource\"},\"glyph\":{\"id\":\"f7dbe8e2-d7df-412f-bfb3-fe298cccd1e7\",\"type\":\"Line\"},\"hover_glyph\":null,\"nonselection_glyph\":{\"id\":\"c4888092-a8c0-406d-ada4-afce6f7f10d2\",\"type\":\"Line\"},\"selection_glyph\":null},\"id\":\"12160f16-8c70-4612-9668-afedbf3553f7\",\"type\":\"GlyphRenderer\"},{\"attributes\":{\"months\":[0,6]},\"id\":\"7b1d91f2-d0a5-4ee6-8e16-ef250f0a7cd7\",\"type\":\"MonthsTicker\"},{\"attributes\":{\"label\":{\"field\":\"Births\"},\"renderers\":[{\"id\":\"95e35bc3-2282-41e1-b437-3074014c9e38\",\"type\":\"GlyphRenderer\"}]},\"id\":\"331ce033-230c-4c48-9dd0-d9ae81ae5ae2\",\"type\":\"LegendItem\"}],\"root_ids\":[\"6e9abb9f-1d46-46c2-ac41-eab1a719eacf\"]},\"title\":\"Bokeh Application\",\"version\":\"0.12.3\"}};\n",
" var render_items = [{\"docid\":\"ebe91c11-cd15-4858-9f1b-ae4cfccfe83d\",\"elementid\":\"d2002eb8-56f3-464c-a475-80e3c10e93b0\",\"modelid\":\"6e9abb9f-1d46-46c2-ac41-eab1a719eacf\"}];\n",
" \n",
" Bokeh.embed.embed_items(docs_json, render_items);\n",
" });\n",
" },\n",
" function(Bokeh) {\n",
" }\n",
" ];\n",
" \n",
" function run_inline_js() {\n",
" \n",
" if ((window.Bokeh !== undefined) || (force === \"1\")) {\n",
" for (var i = 0; i < inline_js.length; i++) {\n",
" inline_js[i](window.Bokeh);\n",
" }if (force === \"1\") {\n",
" display_loaded();\n",
" }} else if (Date.now() < window._bokeh_timeout) {\n",
" setTimeout(run_inline_js, 100);\n",
" } else if (!window._bokeh_failed_load) {\n",
" console.log(\"Bokeh: BokehJS failed to load within specified timeout.\");\n",
" window._bokeh_failed_load = true;\n",
" } else if (!force) {\n",
" var cell = $(\"#d2002eb8-56f3-464c-a475-80e3c10e93b0\").parents('.cell').data().cell;\n",
" cell.output_area.append_execute_result(NB_LOAD_WARNING)\n",
" }\n",
" \n",
" }\n",
" \n",
" if (window._bokeh_is_loading === 0) {\n",
" console.log(\"Bokeh: BokehJS loaded, going straight to plotting\");\n",
" run_inline_js();\n",
" } else {\n",
" load_libs(js_urls, function() {\n",
" console.log(\"Bokeh: BokehJS plotting callback run at\", now());\n",
" run_inline_js();\n",
" });\n",
" }\n",
" }(this));\n",
"</script>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"def generate_montly_figure(monthly_df):\n",
" monthly_df.index = month_to_timestamp(monthly_df.Month)\n",
" monthly_df.index.name = \"TS\"\n",
" max_val = find_maximum_value(monthly_df)\n",
" palette = bokeh.palettes.Set2_3\n",
" source = bokeh.models.ColumnDataSource(monthly_df)\n",
" fig = bokeh.plotting.figure(x_axis_type=\"datetime\", width=800)\n",
" x_axis = monthly_df.index.to_series()\n",
" PROPS = {'line_width': 5, 'line_cap': 'round', 'source': source}\n",
" #fig.line(\"TS\", \"Births\", source=source)\n",
" fig.line(\"TS\", \"Births\", color=palette[0], legend=\"Births\", **PROPS)\n",
" fig.line(\"TS\", \"Deaths\", color=palette[1], legend=\"Deaths\", **PROPS)\n",
" fig.line(\"TS\", \"Pregnancies\", color=palette[2], legend=\"Pregnancies\", **PROPS)\n",
" fig.y_range = bokeh.models.Range1d(0, max_val, bounds=\"auto\")\n",
" fig.x_range = bokeh.models.Range1d(monthly_df.index.min(), monthly_df.index.max(), bounds=\"auto\")\n",
" fig.toolbar.logo = None\n",
" configure_legend(fig.legend) \n",
" fig.yaxis.minor_tick_line_alpha = 0\n",
" return fig\n",
"\n",
"\n",
"def find_maximum_value(monthly_df):\n",
" max_series = monthly_df.max()\n",
" max_val = max_series[max_series.apply(lambda val: not isinstance(val, str))].max()\n",
" max_val_roundup = math.ceil(max_val/10) * 10\n",
" return max_val_roundup\n",
"\n",
"def month_to_timestamp(month_series):\n",
" return month_series.apply(lambda val: pd.Timestamp.strptime(val, \"%B %Y\"))\n",
"\n",
"def configure_legend(legend):\n",
" legend.background_fill_alpha = 0\n",
" legend.border_line_alpha = 0\n",
" legend.spacing = 0\n",
" legend.margin = 0\n",
" legend.padding = 5\n",
"\n",
"monthly_df = stats.generate_monthly_dataframe(df)\n",
"fig = generate_montly_figure(monthly_df)\n",
"bokeh.io.show(fig)"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import bokeh.charts"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<table><tbody><tr><th>Average Birth Queue Time</th><td>3.8 months</td></tr><tr><th>Projected Birth Queue Time Entering Now</th><td>4.9 months</td></tr><tr><th>Average Number of Babies per Pregnancy</th><td>2.4 babies</td></tr></tbody></table>"
],
"text/plain": [
"HTMLDict([('Average Birth Queue Time', '3.8 months'),\n",
" ('Projected Birth Queue Time Entering Now', '4.9 months'),\n",
" ('Average Number of Babies per Pregnancy', '2.4 babies')])"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"records = stats.average_stats(df, monthly_df)\n",
"record_list = stats.RecordFormatList(records)\n",
"HTMLDict(record_list)"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from fto import fto_web"
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
" <div class=\"bk-root\">\n",
" <div class=\"plotdiv\" id=\"e596e404-014c-44f7-b48a-c9e9f1aede8f\"></div>\n",
" </div>\n",
"<script type=\"text/javascript\">\n",
" \n",
" (function(global) {\n",
" function now() {\n",
" return new Date();\n",
" }\n",
" \n",
" var force = \"\";\n",
" \n",
" if (typeof (window._bokeh_onload_callbacks) === \"undefined\" || force !== \"\") {\n",
" window._bokeh_onload_callbacks = [];\n",
" window._bokeh_is_loading = undefined;\n",
" }\n",
" \n",
" \n",
" \n",
" if (typeof (window._bokeh_timeout) === \"undefined\" || force !== \"\") {\n",
" window._bokeh_timeout = Date.now() + 0;\n",
" window._bokeh_failed_load = false;\n",
" }\n",
" \n",
" var NB_LOAD_WARNING = {'data': {'text/html':\n",
" \"<div style='background-color: #fdd'>\\n\"+\n",
" \"<p>\\n\"+\n",
" \"BokehJS does not appear to have successfully loaded. If loading BokehJS from CDN, this \\n\"+\n",
" \"may be due to a slow or bad network connection. Possible fixes:\\n\"+\n",
" \"</p>\\n\"+\n",
" \"<ul>\\n\"+\n",
" \"<li>re-rerun `output_notebook()` to attempt to load from CDN again, or</li>\\n\"+\n",
" \"<li>use INLINE resources instead, as so:</li>\\n\"+\n",
" \"</ul>\\n\"+\n",
" \"<code>\\n\"+\n",
" \"from bokeh.resources import INLINE\\n\"+\n",
" \"output_notebook(resources=INLINE)\\n\"+\n",
" \"</code>\\n\"+\n",
" \"</div>\"}};\n",
" \n",
" function display_loaded() {\n",
" if (window.Bokeh !== undefined) {\n",
" Bokeh.$(\"#e596e404-014c-44f7-b48a-c9e9f1aede8f\").text(\"BokehJS successfully loaded.\");\n",
" } else if (Date.now() < window._bokeh_timeout) {\n",
" setTimeout(display_loaded, 100)\n",
" }\n",
" }\n",
" \n",
" function run_callbacks() {\n",
" window._bokeh_onload_callbacks.forEach(function(callback) { callback() });\n",
" delete window._bokeh_onload_callbacks\n",
" console.info(\"Bokeh: all callbacks have finished\");\n",
" }\n",
" \n",
" function load_libs(js_urls, callback) {\n",
" window._bokeh_onload_callbacks.push(callback);\n",
" if (window._bokeh_is_loading > 0) {\n",
" console.log(\"Bokeh: BokehJS is being loaded, scheduling callback at\", now());\n",
" return null;\n",
" }\n",
" if (js_urls == null || js_urls.length === 0) {\n",
" run_callbacks();\n",
" return null;\n",
" }\n",
" console.log(\"Bokeh: BokehJS not loaded, scheduling load and callback at\", now());\n",
" window._bokeh_is_loading = js_urls.length;\n",
" for (var i = 0; i < js_urls.length; i++) {\n",
" var url = js_urls[i];\n",
" var s = document.createElement('script');\n",
" s.src = url;\n",
" s.async = false;\n",
" s.onreadystatechange = s.onload = function() {\n",
" window._bokeh_is_loading--;\n",
" if (window._bokeh_is_loading === 0) {\n",
" console.log(\"Bokeh: all BokehJS libraries loaded\");\n",
" run_callbacks()\n",
" }\n",
" };\n",
" s.onerror = function() {\n",
" console.warn(\"failed to load library \" + url);\n",
" };\n",
" console.log(\"Bokeh: injecting script tag for BokehJS library: \", url);\n",
" document.getElementsByTagName(\"head\")[0].appendChild(s);\n",
" }\n",
" };var element = document.getElementById(\"e596e404-014c-44f7-b48a-c9e9f1aede8f\");\n",
" if (element == null) {\n",
" console.log(\"Bokeh: ERROR: autoload.js configured with elementid 'e596e404-014c-44f7-b48a-c9e9f1aede8f' but no matching script tag was found. \")\n",
" return false;\n",
" }\n",
" \n",
" var js_urls = [];\n",
" \n",
" var inline_js = [\n",
" function(Bokeh) {\n",
" Bokeh.$(function() {\n",
" var docs_json = {\"f97c0641-77f2-4404-bca1-1e54284d3ad0\":{\"roots\":{\"references\":[{\"attributes\":{\"max_interval\":500.0,\"num_minor_ticks\":0},\"id\":\"e70bec11-1c3c-4af6-a9ce-b69642afc38a\",\"type\":\"AdaptiveTicker\"},{\"attributes\":{\"text\":\"<h1>FTO Hourly Statistics</h1>\"},\"id\":\"0265ae34-c338-4ee4-8a2c-469e0264c815\",\"type\":\"Div\"},{\"attributes\":{},\"id\":\"e6eb8c18-587d-4d32-9be7-584919a82473\",\"type\":\"BasicTicker\"},{\"attributes\":{},\"id\":\"6edb720f-299e-467d-a729-26251383602a\",\"type\":\"ToolEvents\"},{\"attributes\":{\"children\":[{\"id\":\"11951298-d00a-4b0e-952b-6bf811b0b0d7\",\"type\":\"WidgetBox\"},{\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"},{\"id\":\"2ebbe383-aed7-471a-9394-cb067527920a\",\"subtype\":\"Figure\",\"type\":\"Plot\"}],\"sizing_mode\":\"scale_width\"},\"id\":\"751c511a-332d-4afb-8439-cad2e55a6a32\",\"type\":\"Column\"},{\"attributes\":{\"axis_label\":\"Population\",\"axis_label_text_color\":{\"value\":\"#e41a1c\"},\"axis_label_text_font_size\":{\"value\":\"16pt\"},\"axis_label_text_font_style\":\"bold\",\"formatter\":{\"id\":\"38a20ffc-1f08-4022-bfc5-2cc808ffbd3f\",\"type\":\"BasicTickFormatter\"},\"plot\":{\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"ticker\":{\"id\":\"e6eb8c18-587d-4d32-9be7-584919a82473\",\"type\":\"BasicTicker\"},\"y_range_name\":\"population\"},\"id\":\"52f786d5-f3ef-4f34-9c61-7e4e3513973e\",\"type\":\"LinearAxis\"},{\"attributes\":{\"active_drag\":{\"id\":\"b202de9c-41fe-4a52-be91-04d9a76cf394\",\"type\":\"BoxZoomTool\"},\"active_scroll\":\"auto\",\"active_tap\":\"auto\",\"logo\":null,\"tools\":[{\"id\":\"b54047eb-194f-4e19-aef9-4a66ed72384f\",\"type\":\"PanTool\"},{\"id\":\"b202de9c-41fe-4a52-be91-04d9a76cf394\",\"type\":\"BoxZoomTool\"},{\"id\":\"1cc2d776-7f8e-42b5-b316-4167f890ce28\",\"type\":\"ResetTool\"},{\"id\":\"177fb635-9940-4675-8981-e0a591e4071a\",\"type\":\"CrosshairTool\"},{\"id\":\"500c318f-6a52-4711-b05b-fd95fa09e41b\",\"type\":\"HoverTool\"}]},\"id\":\"87eae3c0-c7f2-40d4-a449-328e6c1f6a28\",\"type\":\"Toolbar\"},{\"attributes\":{\"bounds\":\"auto\",\"callback\":null,\"end\":382,\"start\":123},\"id\":\"cb3f450e-4079-436f-9c2c-5c2b44dbff10\",\"type\":\"Range1d\"},{\"attributes\":{\"days\":[1,4,7,10,13,16,19,22,25,28]},\"id\":\"d8ae6b2c-f11b-41f3-afc4-97839406854e\",\"type\":\"DaysTicker\"},{\"attributes\":{\"bounds\":\"auto\",\"callback\":null,\"end\":342,\"start\":276},\"id\":\"f503788e-792c-4197-9e36-d3ae5356f850\",\"type\":\"Range1d\"},{\"attributes\":{\"base\":60,\"mantissas\":[1,2,5,10,15,20,30],\"max_interval\":1800000.0,\"min_interval\":1000.0,\"num_minor_ticks\":0},\"id\":\"dff20f88-68d2-4925-8664-9b16d415de61\",\"type\":\"AdaptiveTicker\"},{\"attributes\":{\"base\":60,\"mantissas\":[1,2,5,10,15,20,30],\"max_interval\":1800000.0,\"min_interval\":1000.0,\"num_minor_ticks\":0},\"id\":\"4358dd5e-694a-4b5b-9791-d4fdefdbe764\",\"type\":\"AdaptiveTicker\"},{\"attributes\":{\"days\":[1,8,15,22]},\"id\":\"963150ce-b92a-4946-811d-2b0252b5ed54\",\"type\":\"DaysTicker\"},{\"attributes\":{\"days\":[1,15]},\"id\":\"a8e51fd6-6cdf-4304-b657-cf4eb924ac6e\",\"type\":\"DaysTicker\"},{\"attributes\":{\"months\":[0,1,2,3,4,5,6,7,8,9,10,11]},\"id\":\"9ec79f7f-157a-40d1-aa7e-0c169b9a2a9c\",\"type\":\"MonthsTicker\"},{\"attributes\":{\"axis_label\":\"Birth Queue\",\"axis_label_text_color\":{\"value\":\"#377eb8\"},\"axis_label_text_font_size\":{\"value\":\"16pt\"},\"axis_label_text_font_style\":\"bold\",\"formatter\":{\"id\":\"ab66c96d-2fd9-4733-b6d7-81e7643686fb\",\"type\":\"BasicTickFormatter\"},\"plot\":{\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"ticker\":{\"id\":\"fa1bd8cd-712b-42f8-8353-cc666a86ddab\",\"type\":\"BasicTicker\"}},\"id\":\"2a437546-87c2-4e96-a14f-0ab9c0e84542\",\"type\":\"LinearAxis\"},{\"attributes\":{\"dimensions\":\"width\",\"overlay\":{\"id\":\"76b5b429-a514-4516-bc79-50f3e8543a73\",\"type\":\"BoxAnnotation\"},\"plot\":{\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"}},\"id\":\"b202de9c-41fe-4a52-be91-04d9a76cf394\",\"type\":\"BoxZoomTool\"},{\"attributes\":{\"line_alpha\":{\"value\":0.1},\"line_cap\":\"round\",\"line_color\":{\"value\":\"#1f77b4\"},\"line_width\":{\"value\":3},\"x\":{\"field\":\"Date\"},\"y\":{\"field\":\"Population\"}},\"id\":\"3786a2e6-c89e-4077-aaed-c4ffba956e22\",\"type\":\"Line\"},{\"attributes\":{\"formatter\":{\"id\":\"9aadacf5-84fd-46ba-80ee-633d6946a9a4\",\"type\":\"DatetimeTickFormatter\"},\"plot\":{\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"ticker\":{\"id\":\"a7f91300-a887-47cf-b18b-4be7c4c9bb33\",\"type\":\"DatetimeTicker\"},\"visible\":false},\"id\":\"07941450-49a3-47c1-8c84-5bc2f6b4cfd4\",\"type\":\"DatetimeAxis\"},{\"attributes\":{\"num_minor_ticks\":5},\"id\":\"0ca5882b-d581-49f2-93f3-a07dfb3856d8\",\"type\":\"DatetimeTicker\"},{\"attributes\":{\"base\":24,\"mantissas\":[1,2,4,6,8,12],\"max_interval\":43200000.0,\"min_interval\":3600000.0,\"num_minor_ticks\":0},\"id\":\"2e76e280-63fb-437e-9ce4-164f3096d1ac\",\"type\":\"AdaptiveTicker\"},{\"attributes\":{\"base\":24,\"mantissas\":[1,2,4,6,8,12],\"max_interval\":43200000.0,\"min_interval\":3600000.0,\"num_minor_ticks\":0},\"id\":\"9b94b31e-25c4-402a-8ee1-907d2a681e2c\",\"type\":\"AdaptiveTicker\"},{\"attributes\":{\"days\":[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]},\"id\":\"7e20ebd2-9d90-4e80-9619-fdf0b36d9bc9\",\"type\":\"DaysTicker\"},{\"attributes\":{},\"id\":\"fa1bd8cd-712b-42f8-8353-cc666a86ddab\",\"type\":\"BasicTicker\"},{\"attributes\":{\"months\":[0,6]},\"id\":\"ed3f7a2a-4f1f-48c5-b304-012e38ee4267\",\"type\":\"MonthsTicker\"},{\"attributes\":{\"bottom_units\":\"screen\",\"fill_alpha\":{\"value\":0.5},\"fill_color\":{\"value\":\"lightgrey\"},\"left_units\":\"screen\",\"level\":\"overlay\",\"line_alpha\":{\"value\":1.0},\"line_color\":{\"value\":\"black\"},\"line_dash\":[4,4],\"line_width\":{\"value\":2},\"plot\":null,\"render_mode\":\"css\",\"right_units\":\"screen\",\"top_units\":\"screen\"},\"id\":\"76b5b429-a514-4516-bc79-50f3e8543a73\",\"type\":\"BoxAnnotation\"},{\"attributes\":{\"line_alpha\":{\"value\":0.1},\"line_cap\":\"round\",\"line_color\":{\"value\":\"#1f77b4\"},\"line_width\":{\"value\":3},\"x\":{\"field\":\"Date\"},\"y\":{\"field\":\"Birth Queue\"}},\"id\":\"bc3728dd-1043-45bf-b35f-fd74d5b56e93\",\"type\":\"Line\"},{\"attributes\":{\"months\":[0,2,4,6,8,10]},\"id\":\"9371833f-faa4-4087-bfd0-626a102b2f2d\",\"type\":\"MonthsTicker\"},{\"attributes\":{\"children\":[{\"id\":\"0265ae34-c338-4ee4-8a2c-469e0264c815\",\"type\":\"Div\"}],\"sizing_mode\":\"scale_width\"},\"id\":\"11951298-d00a-4b0e-952b-6bf811b0b0d7\",\"type\":\"WidgetBox\"},{\"attributes\":{\"data_source\":{\"id\":\"09751f14-363e-4096-be27-e3bf1ce4fc78\",\"type\":\"ColumnDataSource\"},\"glyph\":{\"id\":\"c4a3d9f6-cbd9-4639-b213-48d109ba8956\",\"type\":\"Line\"},\"hover_glyph\":null,\"nonselection_glyph\":{\"id\":\"3786a2e6-c89e-4077-aaed-c4ffba956e22\",\"type\":\"Line\"},\"selection_glyph\":null,\"y_range_name\":\"population\"},\"id\":\"613fc096-c059-408d-9dc3-b04b1da93f85\",\"type\":\"GlyphRenderer\"},{\"attributes\":{\"code\":\"\\n var arr = document.getElementsByClassName(\\\"bk-canvas-wrapper\\\");\\n for(var i = 0, len = arr.length; i < len; i++) {\\n arr[i].style.cursor = \\\"none\\\";\\n }\\n var elem = document.getElementById(\\\"static-tooltip\\\");\\n if (elem == null) {\\n return;\\n }\\n var tooltip = elem.parentNode.parentNode.parentNode;\\n tooltip.style.top = \\\"\\\"; // unset what bokeh.js sets\\n tooltip.style.left = \\\"\\\";\\n tooltip.style.top = \\\"4px\\\";\\n tooltip.style.left = \\\"122px\\\";\\n\\n \"},\"id\":\"b3ad4d7e-6ad8-4a3b-a356-2913b4b01ce9\",\"type\":\"CustomJS\"},{\"attributes\":{},\"id\":\"c69fc03b-d1ab-4060-aeca-49432993d1f9\",\"type\":\"BasicTicker\"},{\"attributes\":{\"dimensions\":\"height\",\"plot\":{\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"}},\"id\":\"177fb635-9940-4675-8981-e0a591e4071a\",\"type\":\"CrosshairTool\"},{\"attributes\":{\"active_drag\":\"auto\",\"active_scroll\":\"auto\",\"active_tap\":\"auto\"},\"id\":\"786f34ed-2e4e-4811-83cd-395a04be5b23\",\"type\":\"Toolbar\"},{\"attributes\":{},\"id\":\"c1f9e013-f556-4a5f-ba52-03eab53f89b2\",\"type\":\"BasicTickFormatter\"},{\"attributes\":{},\"id\":\"38a20ffc-1f08-4022-bfc5-2cc808ffbd3f\",\"type\":\"BasicTickFormatter\"},{\"attributes\":{\"callback\":{\"id\":\"b3ad4d7e-6ad8-4a3b-a356-2913b4b01ce9\",\"type\":\"CustomJS\"},\"line_policy\":\"nearest\",\"mode\":\"vline\",\"plot\":{\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"renderers\":[{\"id\":\"613fc096-c059-408d-9dc3-b04b1da93f85\",\"type\":\"GlyphRenderer\"}],\"show_arrow\":false,\"tooltips\":\"\\n <div id=\\\"static-tooltip\\\">\\n <span>Population: @Population</span><br />\\n <span>Birth Queue: @{Birth Queue}</span><br />\\n <span>Pregnant Mothers: @{Pregnant Mothers}</span><br />\\n <span>Date: @{Date Formatted}</span><br />\\n </div>\"},\"id\":\"500c318f-6a52-4711-b05b-fd95fa09e41b\",\"type\":\"HoverTool\"},{\"attributes\":{},\"id\":\"6e832d89-20c9-49e0-bf14-8baff8b05598\",\"type\":\"YearsTicker\"},{\"attributes\":{\"bounds\":\"auto\",\"callback\":null,\"end\":1475046000000.0,\"start\":1455534000000.0},\"id\":\"c9ab1709-3456-4d4a-afcf-e5b6953c7bee\",\"type\":\"Range1d\"},{\"attributes\":{\"formatter\":{\"id\":\"c1f9e013-f556-4a5f-ba52-03eab53f89b2\",\"type\":\"BasicTickFormatter\"},\"minor_tick_line_color\":{\"value\":null},\"plot\":{\"id\":\"2ebbe383-aed7-471a-9394-cb067527920a\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"ticker\":{\"id\":\"c69fc03b-d1ab-4060-aeca-49432993d1f9\",\"type\":\"BasicTicker\"}},\"id\":\"b963823d-46bf-4c7b-a0d3-380e7c5566cf\",\"type\":\"LinearAxis\"},{\"attributes\":{\"bounds\":\"auto\",\"callback\":null,\"end\":5},\"id\":\"3295f0c8-47e6-4945-912f-55a042a57270\",\"type\":\"Range1d\"},{\"attributes\":{},\"id\":\"68ab0725-1236-418b-87df-9175b935e5a1\",\"type\":\"ToolEvents\"},{\"attributes\":{\"months\":[0,2,4,6,8,10]},\"id\":\"ed66f1c7-2881-4b65-82cf-1a27f581edac\",\"type\":\"MonthsTicker\"},{\"attributes\":{\"plot\":{\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"ticker\":{\"id\":\"a7f91300-a887-47cf-b18b-4be7c4c9bb33\",\"type\":\"DatetimeTicker\"}},\"id\":\"f4c91080-a7aa-4eda-9366-58c04b46b9da\",\"type\":\"Grid\"},{\"attributes\":{\"months\":[0,4,8]},\"id\":\"f774701a-d5fa-4fc9-a248-1781d24e63ce\",\"type\":\"MonthsTicker\"},{\"attributes\":{\"months\":[0,6]},\"id\":\"068847f5-0386-474c-9fa1-8983928ff3c1\",\"type\":\"MonthsTicker\"},{\"attributes\":{},\"id\":\"ab66c96d-2fd9-4733-b6d7-81e7643686fb\",\"type\":\"BasicTickFormatter\"},{\"attributes\":{\"days\":[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]},\"id\":\"ba73d819-6d15-47f6-97e8-9fa3aeff0f2a\",\"type\":\"DaysTicker\"},{\"attributes\":{\"days\":[1,4,7,10,13,16,19,22,25,28]},\"id\":\"334b2244-3342-4ee3-b1ba-2165160be67f\",\"type\":\"DaysTicker\"},{\"attributes\":{\"axis_label\":\"Pregnant Mothers\",\"axis_label_text_font_size\":{\"value\":\"14pt\"},\"formatter\":{\"id\":\"8be3bc82-2e46-40aa-a62b-9524f689454e\",\"type\":\"DatetimeTickFormatter\"},\"plot\":{\"id\":\"2ebbe383-aed7-471a-9394-cb067527920a\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"ticker\":{\"id\":\"0ca5882b-d581-49f2-93f3-a07dfb3856d8\",\"type\":\"DatetimeTicker\"}},\"id\":\"d05c05d6-0807-4df8-aa9a-87b29190f0c0\",\"type\":\"DatetimeAxis\"},{\"attributes\":{\"plot\":null,\"text\":null},\"id\":\"21872c55-2d33-40d2-ba04-ebf3db5a63e9\",\"type\":\"Title\"},{\"attributes\":{\"data_source\":{\"id\":\"09751f14-363e-4096-be27-e3bf1ce4fc78\",\"type\":\"ColumnDataSource\"},\"glyph\":{\"id\":\"1bd45d2a-313c-4808-a0c5-ccbe13b70f6b\",\"type\":\"Line\"},\"hover_glyph\":null,\"nonselection_glyph\":{\"id\":\"bc3728dd-1043-45bf-b35f-fd74d5b56e93\",\"type\":\"Line\"},\"selection_glyph\":null},\"id\":\"f8fa2936-8b07-4eac-afa6-22d8545d216a\",\"type\":\"GlyphRenderer\"},{\"attributes\":{\"below\":[{\"id\":\"07941450-49a3-47c1-8c84-5bc2f6b4cfd4\",\"type\":\"DatetimeAxis\"}],\"extra_y_ranges\":{\"population\":{\"id\":\"f503788e-792c-4197-9e36-d3ae5356f850\",\"type\":\"Range1d\"}},\"left\":[{\"id\":\"2a437546-87c2-4e96-a14f-0ab9c0e84542\",\"type\":\"LinearAxis\"},{\"id\":\"52f786d5-f3ef-4f34-9c61-7e4e3513973e\",\"type\":\"LinearAxis\"}],\"plot_width\":1600,\"renderers\":[{\"id\":\"07941450-49a3-47c1-8c84-5bc2f6b4cfd4\",\"type\":\"DatetimeAxis\"},{\"id\":\"f4c91080-a7aa-4eda-9366-58c04b46b9da\",\"type\":\"Grid\"},{\"id\":\"2a437546-87c2-4e96-a14f-0ab9c0e84542\",\"type\":\"LinearAxis\"},{\"id\":\"3be810a6-48e7-4732-a3c7-278a26ae0dfa\",\"type\":\"Grid\"},{\"id\":\"76b5b429-a514-4516-bc79-50f3e8543a73\",\"type\":\"BoxAnnotation\"},{\"id\":\"f8fa2936-8b07-4eac-afa6-22d8545d216a\",\"type\":\"GlyphRenderer\"},{\"id\":\"613fc096-c059-408d-9dc3-b04b1da93f85\",\"type\":\"GlyphRenderer\"},{\"id\":\"52f786d5-f3ef-4f34-9c61-7e4e3513973e\",\"type\":\"LinearAxis\"}],\"sizing_mode\":\"scale_width\",\"title\":{\"id\":\"eb3c4083-1eaf-4dc4-93d3-814e8b844c1b\",\"type\":\"Title\"},\"tool_events\":{\"id\":\"68ab0725-1236-418b-87df-9175b935e5a1\",\"type\":\"ToolEvents\"},\"toolbar\":{\"id\":\"87eae3c0-c7f2-40d4-a449-328e6c1f6a28\",\"type\":\"Toolbar\"},\"x_range\":{\"id\":\"c9ab1709-3456-4d4a-afcf-e5b6953c7bee\",\"type\":\"Range1d\"},\"y_range\":{\"id\":\"cb3f450e-4079-436f-9c2c-5c2b44dbff10\",\"type\":\"Range1d\"}},\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"},{\"attributes\":{\"months\":[0,4,8]},\"id\":\"9e154ee8-a33b-46fc-9cdc-f0bd3ad7bdac\",\"type\":\"MonthsTicker\"},{\"attributes\":{},\"id\":\"9e8a62bd-811a-42dc-906e-b779f09f4e68\",\"type\":\"YearsTicker\"},{\"attributes\":{\"line_cap\":\"round\",\"line_color\":{\"value\":\"#e41a1c\"},\"line_width\":{\"value\":3},\"x\":{\"field\":\"Date\"},\"y\":{\"field\":\"Population\"}},\"id\":\"c4a3d9f6-cbd9-4639-b213-48d109ba8956\",\"type\":\"Line\"},{\"attributes\":{\"line_color\":{\"value\":\"#4daf4a\"},\"line_width\":{\"value\":2},\"x\":{\"field\":\"Date\"},\"y\":{\"field\":\"Pregnant Mothers\"}},\"id\":\"91379bec-9b6a-4676-aefb-25650069eb2d\",\"type\":\"Line\"},{\"attributes\":{\"dimension\":1,\"plot\":{\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"ticker\":{\"id\":\"fa1bd8cd-712b-42f8-8353-cc666a86ddab\",\"type\":\"BasicTicker\"}},\"id\":\"3be810a6-48e7-4732-a3c7-278a26ae0dfa\",\"type\":\"Grid\"},{\"attributes\":{\"line_alpha\":{\"value\":0.1},\"line_color\":{\"value\":\"#1f77b4\"},\"line_width\":{\"value\":2},\"x\":{\"field\":\"Date\"},\"y\":{\"field\":\"Pregnant Mothers\"}},\"id\":\"d3d666a4-9525-408f-ae1c-0d5d99a0a3cb\",\"type\":\"Line\"},{\"attributes\":{\"line_cap\":\"round\",\"line_color\":{\"value\":\"#377eb8\"},\"line_width\":{\"value\":3},\"x\":{\"field\":\"Date\"},\"y\":{\"field\":\"Birth Queue\"}},\"id\":\"1bd45d2a-313c-4808-a0c5-ccbe13b70f6b\",\"type\":\"Line\"},{\"attributes\":{\"dimension\":1,\"plot\":{\"id\":\"2ebbe383-aed7-471a-9394-cb067527920a\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"ticker\":{\"id\":\"c69fc03b-d1ab-4060-aeca-49432993d1f9\",\"type\":\"BasicTicker\"}},\"id\":\"9f271225-28ff-4d64-8a82-2488ad65a90c\",\"type\":\"Grid\"},{\"attributes\":{},\"id\":\"9aadacf5-84fd-46ba-80ee-633d6946a9a4\",\"type\":\"DatetimeTickFormatter\"},{\"attributes\":{\"callback\":null,\"column_names\":[\"Birth Queue\",\"Date\",\"Date Formatted\",\"Pregnant Mothers\",\"Population\"],\"data\":{\"Birth Queue\":[146,147,148,149,150,150,150,149,149,150,150,151,151,151,154,154,154,153,153,153,152,152,152,152,152,152,152,152,152,153,153,153,153,153,152,151,151,151,151,152,152,152,152,152,153,152,152,151,152,152,153,154,154,155,155,155,156,157,157,157,158,157,156,156,156,157,157,157,157,157,157,156,155,154,154,155,155,154,154,154,154,152,152,154,154,154,155,157,157,157,157,158,157,159,161,162,163,163,163,163,164,164,164,163,164,162,166,166,166,165,164,164,164,164,164,164,164,163,164,165,163,163,162,163,163,162,162,162,162,162,162,163,163,163,163,163,164,164,164,166,166,166,166,166,165,165,164,164,164,164,164,164,164,165,165,165,164,164,163,160,160,159,159,162,164,163,163,164,165,165,165,163,163,163,163,163,161,160,158,160,160,160,160,160,160,161,160,160,159,160,160,159,160,160,159,159,159,159,159,159,159,159,160,160,160,162,164,163,160,161,161,161,161,161,161,159,159,159,160,160,159,159,159,159,159,159,158,158,158,158,158,159,156,156,154,153,152,151,151,151,151,151,152,153,153,153,152,152,151,150,150,150,150,151,148,147,148,148,149,150,149,149,151,151,153,153,153,153,154,150,150,153,150,150,150,150,150,150,150,151,151,151,151,151,151,151,151,153,153,153,150,150,152,152,154,155,155,154,154,154,154,154,155,156,156,156,156,149,150,151,151,149,150,150,150,149,149,149,150,150,151,150,150,150,150,150,150,148,147,147,146,146,147,147,148,148,148,148,149,150,148,148,148,149,151,151,151,151,151,150,151,151,151,150,149,149,149,149,150,150,151,151,152,152,152,154,154,153,152,152,152,153,153,153,153,152,153,155,157,158,158,159,159,159,159,159,159,159,159,160,159,159,159,159,159,158,158,155,155,155,154,153,153,153,154,155,155,155,155,155,155,155,155,155,155,155,156,156,156,155,153,153,153,153,153,153,153,153,152,150,149,149,149,149,149,149,149,148,148,149,149,149,149,149,149,149,149,147,147,147,149,148,148,148,147,147,147,147,147,147,147,149,149,149,148,148,150,151,151,151,150,149,148,148,148,148,145,145,145,145,149,149,149,149,149,150,150,150,150,151,150,149,149,149,149,150,149,149,149,147,148,148,148,147,146,146,146,145,145,145,144,143,142,141,141,140,140,139,139,139,139,139,139,139,139,139,138,139,139,138,139,139,141,142,142,141,141,140,140,142,143,143,143,143,145,145,145,144,144,144,145,145,145,143,143,143,143,142,142,142,141,143,143,143,143,143,143,143,143,143,142,142,142,142,144,144,148,148,148,147,148,148,148,148,148,147,147,146,141,141,145,145,145,145,145,144,144,144,144,146,146,146,146,146,146,144,144,144,144,144,144,143,143,143,143,144,144,145,146,146,146,145,144,143,143,143,143,143,143,143,143,143,143,143,143,140,139,139,139,139,139,140,140,141,140,143,143,144,146,146,146,148,146,147,147,147,148,148,147,147,147,147,149,149,149,149,149,149,150,150,150,150,151,151,152,152,152,151,151,150,150,150,150,150,150,149,148,148,148,148,148,148,148,149,149,150,151,150,150,150,150,149,149,149,149,149,148,149,149,148,148,148,147,147,147,146,147,147,148,147,147,147,145,145,146,145,146,146,146,147,149,151,151,151,150,150,150,150,149,150,148,149,149,149,148,148,148,147,147,148,148,148,150,149,149,149,151,152,152,155,155,155,155,155,155,155,155,155,155,155,155,154,153,153,152,152,152,151,151,152,153,154,155,155,155,155,156,154,155,155,157,156,154,154,154,153,154,154,154,154,154,154,154,153,155,150,150,151,152,152,152,152,153,153,152,152,153,153,154,153,152,155,155,156,155,156,156,156,156,157,153,149,149,151,152,152,151,151,151,150,150,150,147,148,150,152,151,152,152,152,152,152,154,154,149,149,149,149,150,151,151,151,149,149,149,149,149,149,148,148,148,148,149,149,150,150,149,149,149,149,149,148,148,148,148,148,148,147,146,146,150,151,151,151,152,152,152,153,153,154,156,156,156,156,156,157,157,156,155,154,152,152,150,150,150,149,150,150,149,148,147,146,146,147,147,147,147,148,148,149,149,149,149,149,148,147,147,147,147,148,148,148,148,148,146,146,146,146,145,145,145,144,144,144,145,145,145,142,143,142,143,146,143,141,141,141,140,139,139,139,139,139,139,139,136,137,140,140,140,139,139,139,139,134,133,136,137,137,137,143,142,142,145,145,145,143,143,143,145,144,145,145,144,143,146,146,146,146,146,145,145,145,143,142,139,138,138,137,137,138,138,140,140,139,141,141,141,144,144,144,144,145,145,145,145,146,148,148,148,149,150,150,150,149,149,150,150,150,150,150,149,149,149,149,149,149,149,149,149,149,151,151,152,152,152,152,152,152,152,152,153,160,161,171,172,173,179,183,182,183,182,182,182,181,181,181,179,178,179,179,180,183,183,183,183,183,183,183,182,182,189,189,189,189,189,189,191,191,191,191,191,191,191,191,191,191,191,191,188,189,186,186,187,187,178,175,176,176,176,175,175,175,175,175,175,174,173,175,175,174,169,168,168,168,168,168,168,168,167,167,164,164,165,168,169,170,171,169,169,169,169,174,174,174,174,174,175,176,176,176,178,173,172,171,171,170,170,170,169,169,168,169,169,168,168,169,169,170,171,171,170,169,166,161,158,158,156,156,157,158,156,155,155,155,155,155,156,156,156,156,156,156,156,157,157,158,158,162,162,161,161,161,162,162,165,164,164,164,164,164,165,164,164,164,164,164,164,155,156,158,159,155,154,154,154,154,154,154,156,156,156,156,155,155,157,157,156,156,156,156,153,153,153,152,152,152,152,152,152,151,151,151,152,153,153,154,155,153,153,153,153,154,154,154,154,154,154,153,153,155,155,154,154,154,155,154,154,152,152,152,149,148,147,147,147,146,146,147,147,147,148,148,148,148,147,147,147,142,141,141,141,141,141,140,140,140,144,144,144,144,145,146,146,146,147,148,150,150,150,150,150,150,150,150,149,148,149,149,149,149,149,147,149,148,147,148,149,149,149,149,149,148,148,148,148,149,149,148,151,153,153,152,152,152,152,152,149,148,151,152,152,151,151,151,151,151,151,151,151,152,152,151,150,150,149,151,149,149,149,148,148,144,145,145,145,145,145,146,145,145,145,145,145,144,144,144,145,145,145,145,145,148,146,147,146,145,145,137,136,136,136,136,135,135,135,133,132,134,136,135,135,135,135,135,137,142,142,142,140,138,137,135,135,135,136,140,140,140,140,140,140,140,140,143,143,143,143,143,143,142,142,139,140,141,138,143,143,141,141,143,143,142,142,140,140,141,141,141,141,142,140,141,141,141,141,142,142,142,142,142,142,142,142,142,142,144,144,147,147,149,148,148,148,140,139,139,139,139,139,138,138,138,138,138,138,138,138,138,138,137,137,137,134,135,135,134,134,134,132,133,133,132,132,131,130,130,130,130,130,131,131,131,131,131,131,130,130,130,130,129,129,129,132,132,132,132,132,131,134,135,135,135,137,136,137,133,129,130,133,133,133,135,135,128,128,128,129,128,128,127,130,130,131,131,131,131,129,131,131,132,131,131,131,131,131,131,131,131,131,131,131,131,131,132,132,132,131,131,131,131,131,131,130,131,133,133,132,132,132,133,133,133,133,131,131,131,132,132,132,131,131,131,131,131,131,126,126,127,126,127,129,129,129,130,130,128,128,128,130,130,130,130,130,128,128,128,127,126,126,126,127,127,127,128,128,128,126,127,127,128,128,131,131,129,125,125,125,125,126,125,123,125,125,123,125,125,125,125,125,125,125,125,125,125,125,126,126,127,125,125,129,131,131,131,127,127,129,128,128,128,128,128,128,128,128,128,128,128,128,128,127,127,127,127,127,127,127,127,127,127,126,126,126,126,125,125,126,128,128,128,128,128,128,127,127,126,126,126,126,126,126,126,126,127,127,127,127,128,129,129,129,130,130,129,129,129,129,129,129,129,129,129,129,130,127,127,126,126,126,126,126,125,127,136,141,142,143,146,150,152,154,153,153,153,152,152,152,150,148,150,150,150,150,150,149,151,152,152,150,151,152,152,151,152,152,153,153,155,155,153,154,154,155,155,155,155,155,155,152,153,154,155,156,155,156,159,159,159,159,159,159,160,163,164,165,167,167,171,182,215,234,257,263,271,272,278,279,279,279,281,281,284,285,287,289,290,290,292,292,293,294,295,295,298,299,301,305,306,312,312,312,313,317,317,319,319,321,322,323,325,327,327,327,326,329,331,331,336,338,337,338,338,338,338,338,339,340,340,342,342,342,341,342,341,340,340,340,342,342,341,341,341,343,344,340,339,337,337,336,338,338,338,340,340,340,341,342,342,346,347,354,356,357,359,359,358,361,364,367,368,368,369,369,366,365,365,365,363,362,363,364,366,366,366,369,370,367,368,367,368,368,370,370,371,375,375,374,373,373,372,373,373,374,373,373,375,376,376,376,376,377,376,377,378,378,378,378,378,381,381,382,382,382,381,381,381,377,377,377,377,376,376,377,376,376,376,318,318,315,314,314,315,314,315,315,313,314,315,316,316,315,315,314,313,312,313,312,312,312,313,313,313,313,314,314,312,310,310,310,308,308,307,303,303,300,299,297,295,296,293,291,291,292,292,293,295,295,295,294,294,294,293,291,289,288,288,289,287,286,289,290,290,289,288,287,287,287,288,288,288,288,289,289,287,287,285,285,285,282,280,280,280,279,277,276,275,268,267,264,264,264,264,264,264,264,264,264,264,263,264,263,263,263,263,264,264,265,265,265,264,261,261,262,262,262,262,271,270,270,270,270,270,269,268,270,271,271,272,271,270,268,268,267,268,268,267,267,266,265,265,265,265,265,265,264,263,262,262,261,262,262,260,260,260,260,259,259,258,258,258,257,258,257,259,259,259,258,258,257,258,257,256,256,257,255,255,254,253,252,252,253,254,254,254,255,254,253,253,254,254,254,254,253,250,250,251,251,251,252,252,251,251,251,252,253,254,254,254,254,253,253,252,251,251,251,251,251,251,250,252,249,249,249,249,243,248,247,247,248,249,249,253,255,256,257,256,256,256,256,253,254,257,257,257,258,260,259,259,260,260,260,260,260,260,260,260,260,260,260,260,260,261,261,261,260,260,259,259,259,258,258,258,258,258,258,257,257,257,257,257,258,256,255,255,255,255,255,255,255,254,254,254,254,254,254,255,254,255,253,253,253,251,252,253,252,253,254,254,254,254,254,255,255,255,255,254,253,252,254,254,255,255,255,256,257,257,257,259,257,258,258,258,257,256,257,257,256,256,257,256,257,256,258,259,258,257,256,256,256,257,257,256,258,259,259,258,256,249,249,249,246,246,246,246,246,246,242,243,242,242,242,241,241,240,240,239,239,239,239,238,238,238,239,238,238,238,239,239,239,237,237,239,239,238,237,236,237,237,237,238,237,237,238,239,240,243,245,245,249,249,250,250,252,251,251,251,252,253,253,254,253,253,253,254,254,254,255,255,256,255,255,255,247,246,247,253,252,252,251,250,251,251,251,252,252,252,252,253,253,254,254,255,256,255,255,256,255,255,254,254,254,254,254,255,252,252,251,252,253,253,254,256,258,257,258,258,259,259,260,260,260,260,262,262,262,263,264,263,256,258,259,257,260,259,259,259,261,262,262,262,262,262,264,264,265,265,265,263,264,264,264,264,263,263,264,265,264,264,262,262,262,261,259,259,259,258,261,261,260,260,260,261,260,260,260,260,260,258,258,258,258,258,257,256,256,256,256,257,257,256,255,255,255,257,257,257,257,259,259,259,257,256,256,257,257,256,257,257,257,258,259,258,256,253,253,253,252,250,250,251,250,249,248,248,248,248,247,247,249,251,252,253,253,253,253,253,253,253,253,253,253,252,252,252,250,248,249,249,250,250,250,250,250,250,249,249,247,246,247,247,246,245,246,246,247,247,247,244,244,245,246,245,245,247,247,247,247,247,248,247,248,248,247,247,248,248,247,246,247,246,246,245,245,242,241,241,241,242,243,241,242,241,243,243,243,243,243,241,241,242,242,242,243,243,243,243,244,243,244,245,244,244,244,244,244,244,244,245,246,246,247,247,247,247,247,247,247,246,246,246,246,246,246,246,246,245,247,247,246,245,246,246,246,244,244,244,243,243,244,244,244,244,244,244,244,240,240,240,239,239,239,239,241,241,241,243,243,243,243,242,242,242,242,242,243,243,242,242,242,242,244,244,244,245,246,241,241,241,240,243,243,243,245,245,245,245,245,246,246,246,246,246,246,247,249,250,249,249,248,248,249,249,249,250,250,250,250,250,250,251,251,248,249,248,248,248,248,248,248,252,253,252,254,256,256,256,254,254,257,259,259,259,261,261,261,261,263,263,263,263,264,260,261,265,265,266,267,265,265,266,265,266,267,267,267,267,266,266,267,268,269,269,267,266,267,267,266,266,266,266,266,266,266,266,267,267,266,267,267,266,266,266,266,266,267,267,268,265,265,265,265,264,264,264,263,263,264,264,265,266,265,266,266,266,266,266,266,266,266,266,266,266,265,265,264,264,264,264,264,264,264,262,261,260,259,259,259,261,261,248,247,249,249,246,245,244,250,250,250,250,249,248,247,246,246,246,246,246,246,246,248,248,248,248,248,249,249,250,252,253,253,253,253,254,254,254,254,255,255,255,254,254,254,253,253,251,251,250,250,248,248,248,249,249,250,251,250,250,250,250,249,249,249,249,252,252,253,254,254,254,254,254,254,254,254,253,255,255,255,255,256,257,257,259,259,259,257,257,258,258,258,258,258,257,257,257,257,257,257,257,258,258,258,258,258,259,259,259,259,259,260,261,262,262,262,262,262,262,262,262,261,260,260,257,257,257,256,254,255,255,256,256,256,256,255,255,254,255,255,256,256,257,256,256,256,256,256,257,257,259,259,258,257,257,257,255,254,254,254,254,254,252,251,250,249,250,250,243,243,243,244,245,246,246,247,246,246,244,243,243,243,241,241,241,241,241,241,241,241,239,239,239,238,238,237,240,239,237,236,238,238,237,236,236,236,236,235,235,234,234,233,233,235,234,234,233,234,234,233,232,233,233,233,233,233,234,234,233,232,231,232,232,232,232,232,232,233,233,233,233,233,232,233,233,233,231,231,232,232,232,231,230,227,228,228,228,228,225,227,227,226,227,227,227,227,227,226,227,228,228,229,222,221,221,220,219,220,220,217,217,218,217,217,217,218,218,219,219,220,219,219,219,220,219,219,220,219,219,219,218,217,215,215,214,215,213,210,210,209,209,210,210,210,209,209,208,208,208,208,209,209,209,209,209,209,210,211,211,211,211,211,209,209,210,210,210,207,211,211,212,212,213,213,212,212,212,212,211,213,214,215,215,215,215,215,215,214,215,212,211,209,209,211,211,211,211,209,209,209,209,209,209,209,210,211,213,213,212,212,212,212,211,211,210,210,210,196,196,196,196,197,198,199,198,196,195,195,191,192,193,193,193,193,193,194,196,197,196,198,198,195,195,195,197,196,196,197,196,195,195,209,209,208,209,207,207,207,207,206,205,204,203,202,202,203,203,202,203,203,203,203,203,204,203,203,203,203,202,201,201,203,203,203,204,204,201,201,201,201,201,200,200,200,199,199,198,198,198,200,201,201,201,201,201,201,201,201,201,203,203,203,202,202,202,202,202,202,202,202,202,202,202,202,203,204,204,204,205,205,206,206,204,203,203,205,206,204,204,204,202,204,204,204,203,203,203,202,202,202,201,201,201,200,200,199,199,200,200,201,201,198,197,197,196,199,199,199,199,199,200,201,201,200,200,201,201,201,202,203,203,200,200,202,202,202,202,202,202,203,204,204,204,204,205,206,207,207,207,206,206,206,206,206,206,205,204,205,205,203,204,205,205,203,202,201,201,202,202,202,202,203,203,201,200,200,201,201,201,202,202,201,201,200,200,200,200,200,200,200,200,200,200,200,200,199,201,200,199,199,198,199,200,200,200,200,200,202,202,202,201,202,203,203,203,203,230,231,230,230,231,231,231,232,231,232,232,231,231,231,232,232,231,232,236,236,238,239,239,239,239,240,240,240,239,239,239,239,240,240,240,240,240,239,239,238,238,238,237,236,237,237,237,237,237,236,237,237,237,237,237,238,238,238,238,238,237,237,237,236,236,236,236,236,235,235,235,235,235,234,236,232,233,232,232,232,232,235,235,236,236,236,235,235,235,237,237,238,238,238,239,238,238,238,237,237,237,237,236,239,239,238,238,240,240,240,241,241,241,241,241,243,243,243,245,245,245,245,245,247,246,246,246,247,247,247,247,246,246,247,248,249,249,248,248,248,249,249,249,249,249,249,249,248,248,251,254,254,254,254,253,253,253,254,254,254,254,254,253,255,255,255,255,255,254,257,257,257,258,258,258,258,259,259,258,258,257,257,257,256,256,258,256,253,253,254,255,255,255,254,253,254,254,254,253,253,252,253,253,253,253,253,252,251,251,252,252,252,253,253,255,255,255,262,263,265,266,266,267,267,267,267,267,268,268,267,268,268,268,268,267,267,267,267,267,267,266,266,266,265,264,265,264,264,264,265,265,265,265,267,267,267,268,268,267,267,267,267,267,267,266,264,265,264,264,265,265,264,263,263,264,263,263,262,262,264,262,262,262,262,261,261,261,260,259,259,260,260,256,256,256,257,257,258,259,259,259,260,259,259,259,259,259,259,258,256,255,255,255,254,253,254,254,251,247,249,250,250,250,249,249,250,248,249,249,250,253,254,198,198,199,199,197,196,196,197,197,197,196,196,196,196,196,194,194,193,193,194,194,194,196,197,197,196,196,196,195,196,196,195,195,196,196,196,198,200,201,200,198,199,199,201,201,201,201,201,201,201,200,200,200,201,200,201,201,201,205,236,241,246,247,248,248,248,248,249,251,252,256,256,258,258,259,260,262,263,263,263,262,264,265,265,263,263,263,264,264,264,264,267,265,265,265,263,263,263,263,263,261,261,262,261,261,261,258,258,259,259,259,259,259,260,263,259,260,261,261,261,262,263],\"Date\":[1455534000000.0,1455537600000.0,1455541200000.0,1455544800000.0,1455548400000.0,1455552000000.0,1455588000000.0,1455591600000.0,1455598800000.0,1455602400000.0,1455606000000.0,1455609600000.0,1455613200000.0,1455616800000.0,1455652800000.0,1455721200000.0,1455724800000.0,1455760800000.0,1455764400000.0,1455768000000.0,1455771600000.0,1455775200000.0,1455778800000.0,1455782400000.0,1455786000000.0,1455789600000.0,1455793200000.0,1455796800000.0,1455800400000.0,1455804000000.0,1455807600000.0,1455811200000.0,1455822000000.0,1455829200000.0,1455836400000.0,1455840000000.0,1455847200000.0,1455850800000.0,1455850800000.0,1455912000000.0,1455912000000.0,1455915600000.0,1455919200000.0,1455922800000.0,1455926400000.0,1455930000000.0,1455933600000.0,1455937200000.0,1455940800000.0,1455944400000.0,1455948000000.0,1455951600000.0,1455955200000.0,1455958800000.0,1455962400000.0,1455966000000.0,1455969600000.0,1455973200000.0,1455976800000.0,1455980400000.0,1455984000000.0,1455987600000.0,1455991200000.0,1455994800000.0,1455998400000.0,1456002000000.0,1456005600000.0,1456009200000.0,1456012800000.0,1456016400000.0,1456020000000.0,1456023600000.0,1456027200000.0,1456030800000.0,1456034400000.0,1456038000000.0,1456041600000.0,1456045200000.0,1456048800000.0,1456052400000.0,1456056000000.0,1456059600000.0,1456063200000.0,1456066800000.0,1456070400000.0,1456074000000.0,1456077600000.0,1456081200000.0,1456084800000.0,1456088400000.0,1456092000000.0,1456095600000.0,1456099200000.0,1456102800000.0,1456106400000.0,1456110000000.0,1456113600000.0,1456117200000.0,1456120800000.0,1456124400000.0,1456128000000.0,1456131600000.0,1456135200000.0,1456138800000.0,1456164000000.0,1456167600000.0,1456200000000.0,1456203600000.0,1456207200000.0,1456210800000.0,1456214400000.0,1456218000000.0,1456221600000.0,1456225200000.0,1456228800000.0,1456232400000.0,1456236000000.0,1456239600000.0,1456243200000.0,1456246800000.0,1456275600000.0,1456279200000.0,1456282800000.0,1456286400000.0,1456290000000.0,1456293600000.0,1456297200000.0,1456300800000.0,1456304400000.0,1456308000000.0,1456311600000.0,1456315200000.0,1456318800000.0,1456322400000.0,1456326000000.0,1456329600000.0,1456369200000.0,1456372800000.0,1456376400000.0,1456380000000.0,1456383600000.0,1456387200000.0,1456390800000.0,1456394400000.0,1456398000000.0,1456401600000.0,1456405200000.0,1456408800000.0,1456412400000.0,1456416000000.0,1456423200000.0,1456430400000.0,1456434000000.0,1456441200000.0,1456444800000.0,1456448400000.0,1456459200000.0,1456462800000.0,1456466400000.0,1456513200000.0,1456516800000.0,1456520400000.0,1456524000000.0,1456527600000.0,1456531200000.0,1456534800000.0,1456538400000.0,1456542000000.0,1456545600000.0,1456549200000.0,1456552800000.0,1456556400000.0,1456560000000.0,1456563600000.0,1456567200000.0,1456570800000.0,1456574400000.0,1456578000000.0,1456581600000.0,1456585200000.0,1456588800000.0,1456592400000.0,1456596000000.0,1456599600000.0,1456603200000.0,1456606800000.0,1456610400000.0,1456614000000.0,1456617600000.0,1456621200000.0,1456624800000.0,1456628400000.0,1456632000000.0,1456635600000.0,1456639200000.0,1456642800000.0,1456646400000.0,1456650000000.0,1456653600000.0,1456657200000.0,1456660800000.0,1456664400000.0,1456668000000.0,1456671600000.0,1456675200000.0,1456678800000.0,1456682400000.0,1456686000000.0,1456689600000.0,1456693200000.0,1456696800000.0,1456700400000.0,1456704000000.0,1456707600000.0,1456711200000.0,1456714800000.0,1456718400000.0,1456722000000.0,1456725600000.0,1456729200000.0,1456732800000.0,1456736400000.0,1456740000000.0,1456743600000.0,1456747200000.0,1456750800000.0,1456754400000.0,1456758000000.0,1456761600000.0,1456772400000.0,1456776000000.0,1456779600000.0,1456786800000.0,1456790400000.0,1456801200000.0,1456804800000.0,1456808400000.0,1456812000000.0,1456815600000.0,1456819200000.0,1456822800000.0,1456826400000.0,1456830000000.0,1456833600000.0,1456837200000.0,1456840800000.0,1456844400000.0,1456848000000.0,1456851600000.0,1456858800000.0,1456862400000.0,1456866000000.0,1456869600000.0,1456873200000.0,1456880400000.0,1456884000000.0,1456887600000.0,1456891200000.0,1456894800000.0,1456898400000.0,1456902000000.0,1456905600000.0,1456909200000.0,1456912800000.0,1456916400000.0,1456920000000.0,1456923600000.0,1456927200000.0,1456930800000.0,1456945200000.0,1456948800000.0,1456952400000.0,1456970400000.0,1456974000000.0,1456977600000.0,1456981200000.0,1456984800000.0,1456988400000.0,1456992000000.0,1456995600000.0,1456999200000.0,1457002800000.0,1457006400000.0,1457010000000.0,1457013600000.0,1457017200000.0,1457020800000.0,1457024400000.0,1457035200000.0,1457038800000.0,1457046000000.0,1457049600000.0,1457056800000.0,1457060400000.0,1457064000000.0,1457067600000.0,1457071200000.0,1457074800000.0,1457078400000.0,1457082000000.0,1457085600000.0,1457089200000.0,1457092800000.0,1457096400000.0,1457100000000.0,1457103600000.0,1457107200000.0,1457110800000.0,1457114400000.0,1457118000000.0,1457121600000.0,1457125200000.0,1457128800000.0,1457132400000.0,1457139600000.0,1457143200000.0,1457146800000.0,1457150400000.0,1457154000000.0,1457157600000.0,1457161200000.0,1457164800000.0,1457168400000.0,1457172000000.0,1457175600000.0,1457179200000.0,1457182800000.0,1457186400000.0,1457190000000.0,1457193600000.0,1457197200000.0,1457200800000.0,1457204400000.0,1457208000000.0,1457211600000.0,1457215200000.0,1457218800000.0,1457222400000.0,1457226000000.0,1457229600000.0,1457233200000.0,1457236800000.0,1457240400000.0,1457244000000.0,1457247600000.0,1457251200000.0,1457254800000.0,1457258400000.0,1457262000000.0,1457265600000.0,1457269200000.0,1457272800000.0,1457276400000.0,1457280000000.0,1457283600000.0,1457287200000.0,1457290800000.0,1457294400000.0,1457298000000.0,1457301600000.0,1457305200000.0,1457308800000.0,1457312400000.0,1457316000000.0,1457319600000.0,1457323200000.0,1457326800000.0,1457330400000.0,1457334000000.0,1457337600000.0,1457341200000.0,1457344800000.0,1457348400000.0,1457352000000.0,1457355600000.0,1457359200000.0,1457362800000.0,1457366400000.0,1457377200000.0,1457380800000.0,1457384400000.0,1457406000000.0,1457409600000.0,1457413200000.0,1457416800000.0,1457420400000.0,1457424000000.0,1457427600000.0,1457431200000.0,1457434800000.0,1457438400000.0,1457442000000.0,1457445600000.0,1457449200000.0,1457452800000.0,1457467200000.0,1457470800000.0,1457510400000.0,1457514000000.0,1457517600000.0,1457539200000.0,1457550000000.0,1457553600000.0,1457557200000.0,1457571600000.0,1457578800000.0,1457582400000.0,1457586000000.0,1457589600000.0,1457593200000.0,1457596800000.0,1457600400000.0,1457604000000.0,1457607600000.0,1457611200000.0,1457614800000.0,1457618400000.0,1457622000000.0,1457625600000.0,1457629200000.0,1457632800000.0,1457636400000.0,1457640000000.0,1457643600000.0,1457650800000.0,1457661600000.0,1457665200000.0,1457668800000.0,1457672400000.0,1457676000000.0,1457679600000.0,1457683200000.0,1457686800000.0,1457690400000.0,1457694000000.0,1457697600000.0,1457701200000.0,1457704800000.0,1457708400000.0,1457712000000.0,1457715600000.0,1457719200000.0,1457722800000.0,1457726400000.0,1457730000000.0,1457733600000.0,1457737200000.0,1457740800000.0,1457744400000.0,1457748000000.0,1457755200000.0,1457758800000.0,1457762400000.0,1457766000000.0,1457769600000.0,1457773200000.0,1457776800000.0,1457780400000.0,1457784000000.0,1457787600000.0,1457791200000.0,1457794800000.0,1457798400000.0,1457802000000.0,1457805600000.0,1457809200000.0,1457812800000.0,1457816400000.0,1457820000000.0,1457823600000.0,1457827200000.0,1457830800000.0,1457834400000.0,1457838000000.0,1457841600000.0,1457845200000.0,1457848800000.0,1457852400000.0,1457856000000.0,1457859600000.0,1457863200000.0,1457866800000.0,1457870400000.0,1457874000000.0,1457877600000.0,1457881200000.0,1457884800000.0,1457888400000.0,1457892000000.0,1457895600000.0,1457899200000.0,1457902800000.0,1457906400000.0,1457910000000.0,1457913600000.0,1457917200000.0,1457920800000.0,1457924400000.0,1457928000000.0,1457931600000.0,1457935200000.0,1457938800000.0,1457942400000.0,1457946000000.0,1457949600000.0,1457953200000.0,1457956800000.0,1457960400000.0,1457964000000.0,1457967600000.0,1457974800000.0,1457978400000.0,1457982000000.0,1457985600000.0,1457989200000.0,1457992800000.0,1457996400000.0,1458007200000.0,1458010800000.0,1458014400000.0,1458018000000.0,1458021600000.0,1458025200000.0,1458028800000.0,1458032400000.0,1458036000000.0,1458039600000.0,1458043200000.0,1458046800000.0,1458050400000.0,1458054000000.0,1458057600000.0,1458064800000.0,1458068400000.0,1458072000000.0,1458086400000.0,1458090000000.0,1458093600000.0,1458097200000.0,1458100800000.0,1458104400000.0,1458108000000.0,1458111600000.0,1458115200000.0,1458118800000.0,1458122400000.0,1458126000000.0,1458129600000.0,1458133200000.0,1458136800000.0,1458140400000.0,1458147600000.0,1458151200000.0,1458154800000.0,1458162000000.0,1458165600000.0,1458176400000.0,1458180000000.0,1458183600000.0,1458187200000.0,1458190800000.0,1458194400000.0,1458198000000.0,1458201600000.0,1458205200000.0,1458208800000.0,1458212400000.0,1458216000000.0,1458219600000.0,1458223200000.0,1458226800000.0,1458230400000.0,1458241200000.0,1458244800000.0,1458248400000.0,1458252000000.0,1458259200000.0,1458262800000.0,1458266400000.0,1458270000000.0,1458273600000.0,1458277200000.0,1458280800000.0,1458284400000.0,1458288000000.0,1458291600000.0,1458295200000.0,1458298800000.0,1458302400000.0,1458306000000.0,1458309600000.0,1458313200000.0,1458316800000.0,1458320400000.0,1458324000000.0,1458327600000.0,1458331200000.0,1458334800000.0,1458338400000.0,1458342000000.0,1458345600000.0,1458349200000.0,1458352800000.0,1458356400000.0,1458360000000.0,1458363600000.0,1458367200000.0,1458370800000.0,1458374400000.0,1458378000000.0,1458381600000.0,1458385200000.0,1458388800000.0,1458392400000.0,1458396000000.0,1458399600000.0,1458403200000.0,1458406800000.0,1458410400000.0,1458414000000.0,1458417600000.0,1458421200000.0,1458424800000.0,1458428400000.0,1458432000000.0,1458435600000.0,1458439200000.0,1458442800000.0,1458446400000.0,1458450000000.0,1458453600000.0,1458457200000.0,1458460800000.0,1458464400000.0,1458468000000.0,1458471600000.0,1458475200000.0,1458478800000.0,1458482400000.0,1458486000000.0,1458489600000.0,1458493200000.0,1458496800000.0,1458500400000.0,1458504000000.0,1458507600000.0,1458511200000.0,1458514800000.0,1458518400000.0,1458522000000.0,1458525600000.0,1458529200000.0,1458532800000.0,1458536400000.0,1458540000000.0,1458543600000.0,1458547200000.0,1458550800000.0,1458554400000.0,1458558000000.0,1458561600000.0,1458565200000.0,1458568800000.0,1458572400000.0,1458576000000.0,1458579600000.0,1458583200000.0,1458586800000.0,1458590400000.0,1458594000000.0,1458597600000.0,1458601200000.0,1458604800000.0,1458608400000.0,1458612000000.0,1458615600000.0,1458619200000.0,1458622800000.0,1458626400000.0,1458630000000.0,1458633600000.0,1458637200000.0,1458640800000.0,1458644400000.0,1458648000000.0,1458651600000.0,1458655200000.0,1458658800000.0,1458662400000.0,1458666000000.0,1458669600000.0,1458673200000.0,1458676800000.0,1458680400000.0,1458684000000.0,1458687600000.0,1458691200000.0,1458694800000.0,1458698400000.0,1458702000000.0,1458705600000.0,1458709200000.0,1458712800000.0,1458716400000.0,1458720000000.0,1458723600000.0,1458727200000.0,1458730800000.0,1458734400000.0,1458756000000.0,1458759600000.0,1458763200000.0,1458766800000.0,1458770400000.0,1458774000000.0,1458777600000.0,1458781200000.0,1458784800000.0,1458788400000.0,1458792000000.0,1458795600000.0,1458799200000.0,1458802800000.0,1458806400000.0,1458810000000.0,1458813600000.0,1458817200000.0,1458820800000.0,1458824400000.0,1458828000000.0,1458831600000.0,1458835200000.0,1458838800000.0,1458842400000.0,1458846000000.0,1458849600000.0,1458853200000.0,1458856800000.0,1458860400000.0,1458864000000.0,1458867600000.0,1458871200000.0,1458874800000.0,1458878400000.0,1458882000000.0,1458885600000.0,1458889200000.0,1458892800000.0,1458896400000.0,1458928800000.0,1458932400000.0,1458936000000.0,1458939600000.0,1458943200000.0,1458946800000.0,1458950400000.0,1458954000000.0,1458957600000.0,1458961200000.0,1458964800000.0,1458968400000.0,1458972000000.0,1458975600000.0,1458979200000.0,1458982800000.0,1458986400000.0,1458990000000.0,1458993600000.0,1458997200000.0,1459000800000.0,1459004400000.0,1459008000000.0,1459011600000.0,1459015200000.0,1459018800000.0,1459022400000.0,1459026000000.0,1459029600000.0,1459033200000.0,1459036800000.0,1459040400000.0,1459044000000.0,1459047600000.0,1459051200000.0,1459054800000.0,1459058400000.0,1459062000000.0,1459098000000.0,1459101600000.0,1459105200000.0,1459108800000.0,1459112400000.0,1459116000000.0,1459119600000.0,1459123200000.0,1459126800000.0,1459130400000.0,1459134000000.0,1459137600000.0,1459141200000.0,1459144800000.0,1459148400000.0,1459152000000.0,1459155600000.0,1459188000000.0,1459191600000.0,1459216800000.0,1459220400000.0,1459224000000.0,1459227600000.0,1459231200000.0,1459234800000.0,1459238400000.0,1459242000000.0,1459245600000.0,1459249200000.0,1459252800000.0,1459256400000.0,1459260000000.0,1459263600000.0,1459267200000.0,1459278000000.0,1459281600000.0,1459296000000.0,1459299600000.0,1459350000000.0,1459353600000.0,1459357200000.0,1459360800000.0,1459364400000.0,1459386000000.0,1459389600000.0,1459393200000.0,1459396800000.0,1459400400000.0,1459404000000.0,1459407600000.0,1459411200000.0,1459414800000.0,1459418400000.0,1459422000000.0,1459425600000.0,1459443600000.0,1459458000000.0,1459465200000.0,1459468800000.0,1459472400000.0,1459476000000.0,1459479600000.0,1459483200000.0,1459486800000.0,1459490400000.0,1459530000000.0,1459540800000.0,1459544400000.0,1459548000000.0,1459551600000.0,1459555200000.0,1459558800000.0,1459562400000.0,1459566000000.0,1459569600000.0,1459573200000.0,1459576800000.0,1459580400000.0,1459584000000.0,1459587600000.0,1459591200000.0,1459594800000.0,1459623600000.0,1459627200000.0,1459630800000.0,1459634400000.0,1459638000000.0,1459641600000.0,1459645200000.0,1459648800000.0,1459652400000.0,1459656000000.0,1459659600000.0,1459663200000.0,1459666800000.0,1459670400000.0,1459674000000.0,1459677600000.0,1459706400000.0,1459710000000.0,1459713600000.0,1459717200000.0,1459728000000.0,1459731600000.0,1459735200000.0,1459738800000.0,1459742400000.0,1459746000000.0,1459749600000.0,1459753200000.0,1459756800000.0,1459760400000.0,1459764000000.0,1459792800000.0,1459796400000.0,1459800000000.0,1459807200000.0,1459810800000.0,1459821600000.0,1459825200000.0,1459828800000.0,1459832400000.0,1459836000000.0,1459868400000.0,1459872000000.0,1459882800000.0,1459886400000.0,1459890000000.0,1459893600000.0,1460044800000.0,1460055600000.0,1460062800000.0,1460070000000.0,1460073600000.0,1460077200000.0,1460080800000.0,1460084400000.0,1460088000000.0,1460091600000.0,1460095200000.0,1460098800000.0,1460102400000.0,1460106000000.0,1460109600000.0,1460113200000.0,1460116800000.0,1460120400000.0,1460142000000.0,1460145600000.0,1460149200000.0,1460152800000.0,1460156400000.0,1460160000000.0,1460163600000.0,1460167200000.0,1460170800000.0,1460174400000.0,1460178000000.0,1460181600000.0,1460185200000.0,1460188800000.0,1460192400000.0,1460196000000.0,1460199600000.0,1460228400000.0,1460232000000.0,1460235600000.0,1460239200000.0,1460242800000.0,1460246400000.0,1460250000000.0,1460253600000.0,1460257200000.0,1460268000000.0,1460336400000.0,1460340000000.0,1460343600000.0,1460347200000.0,1460350800000.0,1460354400000.0,1460358000000.0,1460361600000.0,1460365200000.0,1460397600000.0,1460401200000.0,1460404800000.0,1460408400000.0,1460422800000.0,1460426400000.0,1460444400000.0,1460448000000.0,1460451600000.0,1460458800000.0,1460462400000.0,1460466000000.0,1460469600000.0,1460487600000.0,1460491200000.0,1460498400000.0,1460502000000.0,1460505600000.0,1460509200000.0,1460520000000.0,1460538000000.0,1460545200000.0,1460566800000.0,1460570400000.0,1460574000000.0,1460595600000.0,1460599200000.0,1460602800000.0,1460660400000.0,1460664000000.0,1460674800000.0,1460678400000.0,1460685600000.0,1460700000000.0,1460736000000.0,1460739600000.0,1460743200000.0,1460746800000.0,1460750400000.0,1460754000000.0,1460757600000.0,1460761200000.0,1460764800000.0,1460768400000.0,1460782800000.0,1460786400000.0,1460790000000.0,1460793600000.0,1460797200000.0,1460800800000.0,1460836800000.0,1460840400000.0,1460844000000.0,1460847600000.0,1460851200000.0,1460854800000.0,1460858400000.0,1460862000000.0,1460865600000.0,1460869200000.0,1460872800000.0,1460876400000.0,1460880000000.0,1460883600000.0,1460887200000.0,1460890800000.0,1460894400000.0,1460898000000.0,1460901600000.0,1460905200000.0,1460908800000.0,1460916000000.0,1460919600000.0,1460923200000.0,1460926800000.0,1460930400000.0,1460934000000.0,1460937600000.0,1460941200000.0,1460944800000.0,1460948400000.0,1460952000000.0,1460955600000.0,1460959200000.0,1460962800000.0,1460966400000.0,1460970000000.0,1460973600000.0,1460977200000.0,1460980800000.0,1460998800000.0,1461013200000.0,1461027600000.0,1461031200000.0,1461034800000.0,1461038400000.0,1461042000000.0,1461045600000.0,1461049200000.0,1461052800000.0,1461056400000.0,1461060000000.0,1461063600000.0,1461096000000.0,1461099600000.0,1461110400000.0,1461121200000.0,1461135600000.0,1461139200000.0,1461142800000.0,1461146400000.0,1461150000000.0,1461153600000.0,1461157200000.0,1461160800000.0,1461164400000.0,1461175200000.0,1461178800000.0,1461182400000.0,1461204000000.0,1461207600000.0,1461229200000.0,1461232800000.0,1461236400000.0,1461240000000.0,1461243600000.0,1461247200000.0,1461250800000.0,1461258000000.0,1461261600000.0,1461319200000.0,1461322800000.0,1461326400000.0,1461330000000.0,1461333600000.0,1461337200000.0,1461340800000.0,1461344400000.0,1461348000000.0,1461351600000.0,1461355200000.0,1461358800000.0,1461362400000.0,1461366000000.0,1461369600000.0,1461373200000.0,1461376800000.0,1461380400000.0,1461434400000.0,1461438000000.0,1461448800000.0,1461452400000.0,1461456000000.0,1461459600000.0,1461463200000.0,1461466800000.0,1461474000000.0,1461477600000.0,1461481200000.0,1461484800000.0,1461488400000.0,1461513600000.0,1461517200000.0,1461520800000.0,1461524400000.0,1461528000000.0,1461531600000.0,1461535200000.0,1461538800000.0,1461542400000.0,1461556800000.0,1461560400000.0,1461564000000.0,1461567600000.0,1461571200000.0,1461574800000.0,1461578400000.0,1461582000000.0,1461585600000.0,1461589200000.0,1461592800000.0,1461596400000.0,1461603600000.0,1461607200000.0,1461610800000.0,1461614400000.0,1461618000000.0,1461628800000.0,1461639600000.0,1461643200000.0,1461646800000.0,1461661200000.0,1461664800000.0,1461668400000.0,1461672000000.0,1461675600000.0,1461679200000.0,1461682800000.0,1461686400000.0,1461697200000.0,1461700800000.0,1461736800000.0,1461740400000.0,1461744000000.0,1461747600000.0,1461751200000.0,1461754800000.0,1461758400000.0,1461762000000.0,1461765600000.0,1461772800000.0,1461780000000.0,1461783600000.0,1461787200000.0,1461805200000.0,1461808800000.0,1461812400000.0,1461816000000.0,1461819600000.0,1461826800000.0,1461852000000.0,1461855600000.0,1461862800000.0,1461870000000.0,1461873600000.0,1461877200000.0,1461888000000.0,1461906000000.0,1461909600000.0,1461913200000.0,1461916800000.0,1461920400000.0,1461924000000.0,1461927600000.0,1461931200000.0,1461934800000.0,1461963600000.0,1461967200000.0,1461970800000.0,1461974400000.0,1461978000000.0,1461981600000.0,1461985200000.0,1461988800000.0,1461992400000.0,1461996000000.0,1461999600000.0,1462028400000.0,1462032000000.0,1462035600000.0,1462039200000.0,1462042800000.0,1462046400000.0,1462050000000.0,1462053600000.0,1462057200000.0,1462060800000.0,1462064400000.0,1462068000000.0,1462071600000.0,1462075200000.0,1462078800000.0,1462082400000.0,1462086000000.0,1462089600000.0,1462093200000.0,1462096800000.0,1462143600000.0,1462147200000.0,1462150800000.0,1462154400000.0,1462158000000.0,1462161600000.0,1462165200000.0,1462168800000.0,1462172400000.0,1462176000000.0,1462179600000.0,1462237200000.0,1462240800000.0,1462244400000.0,1462248000000.0,1462284000000.0,1462287600000.0,1462291200000.0,1462294800000.0,1462298400000.0,1462302000000.0,1462305600000.0,1462309200000.0,1462323600000.0,1462327200000.0,1462330800000.0,1462334400000.0,1462338000000.0,1462341600000.0,1462345200000.0,1462348800000.0,1462352400000.0,1462356000000.0,1462359600000.0,1462363200000.0,1462366800000.0,1462370400000.0,1462374000000.0,1462384800000.0,1462406400000.0,1462449600000.0,1462453200000.0,1462456800000.0,1462460400000.0,1462464000000.0,1462471200000.0,1462474800000.0,1462489200000.0,1462492800000.0,1462496400000.0,1462503600000.0,1462507200000.0,1462510800000.0,1462514400000.0,1462518000000.0,1462521600000.0,1462525200000.0,1462528800000.0,1462532400000.0,1462536000000.0,1462539600000.0,1462543200000.0,1462546800000.0,1462550400000.0,1462554000000.0,1462557600000.0,1462561200000.0,1462564800000.0,1462568400000.0,1462572000000.0,1462579200000.0,1462582800000.0,1462586400000.0,1462590000000.0,1462593600000.0,1462597200000.0,1462600800000.0,1462604400000.0,1462611600000.0,1462615200000.0,1462640400000.0,1462644000000.0,1462647600000.0,1462651200000.0,1462654800000.0,1462658400000.0,1462662000000.0,1462665600000.0,1462669200000.0,1462672800000.0,1462676400000.0,1462680000000.0,1462683600000.0,1462687200000.0,1462690800000.0,1462694400000.0,1462698000000.0,1462723200000.0,1462726800000.0,1462730400000.0,1462734000000.0,1462737600000.0,1462741200000.0,1462744800000.0,1462748400000.0,1462752000000.0,1462755600000.0,1462759200000.0,1462762800000.0,1462766400000.0,1462770000000.0,1462773600000.0,1462777200000.0,1462780800000.0,1462802400000.0,1462813200000.0,1462820400000.0,1462824000000.0,1462827600000.0,1462831200000.0,1462834800000.0,1462838400000.0,1462842000000.0,1462845600000.0,1462849200000.0,1462852800000.0,1462856400000.0,1462860000000.0,1462863600000.0,1462867200000.0,1462870800000.0,1462906800000.0,1462910400000.0,1462914000000.0,1462935600000.0,1462939200000.0,1462942800000.0,1462946400000.0,1462950000000.0,1462996800000.0,1463000400000.0,1463014800000.0,1463018400000.0,1463022000000.0,1463025600000.0,1463029200000.0,1463036400000.0,1463040000000.0,1463043600000.0,1463047200000.0,1463050800000.0,1463054400000.0,1463058000000.0,1463061600000.0,1463065200000.0,1463076000000.0,1463079600000.0,1463086800000.0,1463090400000.0,1463104800000.0,1463108400000.0,1463112000000.0,1463115600000.0,1463122800000.0,1463151600000.0,1463155200000.0,1463158800000.0,1463162400000.0,1463166000000.0,1463169600000.0,1463173200000.0,1463176800000.0,1463180400000.0,1463184000000.0,1463187600000.0,1463191200000.0,1463194800000.0,1463198400000.0,1463202000000.0,1463205600000.0,1463209200000.0,1463212800000.0,1463216400000.0,1463220000000.0,1463245200000.0,1463252400000.0,1463256000000.0,1463270400000.0,1463274000000.0,1463277600000.0,1463281200000.0,1463284800000.0,1463292000000.0,1463295600000.0,1463299200000.0,1463328000000.0,1463331600000.0,1463335200000.0,1463338800000.0,1463342400000.0,1463346000000.0,1463349600000.0,1463353200000.0,1463356800000.0,1463360400000.0,1463364000000.0,1463367600000.0,1463378400000.0,1463382000000.0,1463385600000.0,1463389200000.0,1463392800000.0,1463443200000.0,1463446800000.0,1463475600000.0,1463479200000.0,1463486400000.0,1463490000000.0,1463529600000.0,1463533200000.0,1463536800000.0,1463540400000.0,1463544000000.0,1463547600000.0,1463551200000.0,1463558400000.0,1463630400000.0,1463634000000.0,1463637600000.0,1463641200000.0,1463644800000.0,1463648400000.0,1463659200000.0,1463662800000.0,1463698800000.0,1463702400000.0,1463720400000.0,1463788800000.0,1463846400000.0,1463850000000.0,1463871600000.0,1463875200000.0,1463889600000.0,1463893200000.0,1463929200000.0,1463932800000.0,1463936400000.0,1463940000000.0,1463943600000.0,1463947200000.0,1463950800000.0,1463954400000.0,1463961600000.0,1463965200000.0,1463968800000.0,1463972400000.0,1463976000000.0,1464048000000.0,1464062400000.0,1464066000000.0,1464069600000.0,1464073200000.0,1464076800000.0,1464080400000.0,1464084000000.0,1464087600000.0,1464091200000.0,1464094800000.0,1464141600000.0,1464145200000.0,1464148800000.0,1464152400000.0,1464156000000.0,1464177600000.0,1464181200000.0,1464184800000.0,1464217200000.0,1464220800000.0,1464224400000.0,1464228000000.0,1464231600000.0,1464235200000.0,1464307200000.0,1464310800000.0,1464314400000.0,1464325200000.0,1464328800000.0,1464393600000.0,1464397200000.0,1464400800000.0,1464404400000.0,1464408000000.0,1464411600000.0,1464415200000.0,1464418800000.0,1464454800000.0,1464458400000.0,1464462000000.0,1464465600000.0,1464469200000.0,1464476400000.0,1464483600000.0,1464487200000.0,1464490800000.0,1464494400000.0,1464498000000.0,1464501600000.0,1464505200000.0,1464534000000.0,1464537600000.0,1464544800000.0,1464548400000.0,1464552000000.0,1464555600000.0,1464559200000.0,1464562800000.0,1464566400000.0,1464570000000.0,1464580800000.0,1464584400000.0,1464588000000.0,1464591600000.0,1464620400000.0,1464624000000.0,1464627600000.0,1464631200000.0,1464634800000.0,1464638400000.0,1464642000000.0,1464645600000.0,1464649200000.0,1464667200000.0,1464670800000.0,1464674400000.0,1464678000000.0,1464742800000.0,1464746400000.0,1464753600000.0,1464757200000.0,1464825600000.0,1464829200000.0,1464843600000.0,1464847200000.0,1464854400000.0,1464858000000.0,1464861600000.0,1464919200000.0,1464922800000.0,1464926400000.0,1464930000000.0,1464933600000.0,1464937200000.0,1464998400000.0,1465002000000.0,1465005600000.0,1465009200000.0,1465012800000.0,1465016400000.0,1465020000000.0,1465023600000.0,1465027200000.0,1465030800000.0,1465034400000.0,1465038000000.0,1465041600000.0,1465045200000.0,1465048800000.0,1465052400000.0,1465056000000.0,1465059600000.0,1465063200000.0,1465066800000.0,1465070400000.0,1465074000000.0,1465077600000.0,1465081200000.0,1465084800000.0,1465088400000.0,1465092000000.0,1465095600000.0,1465099200000.0,1465102800000.0,1465106400000.0,1465110000000.0,1465113600000.0,1465117200000.0,1465120800000.0,1465124400000.0,1465128000000.0,1465131600000.0,1465135200000.0,1465138800000.0,1465142400000.0,1465146000000.0,1465149600000.0,1465153200000.0,1465156800000.0,1465160400000.0,1465164000000.0,1465167600000.0,1465171200000.0,1465174800000.0,1465178400000.0,1465182000000.0,1465185600000.0,1465189200000.0,1465192800000.0,1465196400000.0,1465261200000.0,1465264800000.0,1465268400000.0,1465279200000.0,1465304400000.0,1465351200000.0,1465354800000.0,1465358400000.0,1465362000000.0,1465365600000.0,1465369200000.0,1465372800000.0,1465376400000.0,1465380000000.0,1465383600000.0,1465387200000.0,1465390800000.0,1465394400000.0,1465398000000.0,1465401600000.0,1465405200000.0,1465408800000.0,1465412400000.0,1465416000000.0,1465419600000.0,1465423200000.0,1465426800000.0,1465430400000.0,1465434000000.0,1465437600000.0,1465441200000.0,1465444800000.0,1465520400000.0,1465524000000.0,1465527600000.0,1465531200000.0,1465560000000.0,1465563600000.0,1465606800000.0,1465610400000.0,1465617600000.0,1465621200000.0,1465624800000.0,1465628400000.0,1465632000000.0,1465635600000.0,1465639200000.0,1465642800000.0,1465646400000.0,1465650000000.0,1465653600000.0,1465657200000.0,1465660800000.0,1465664400000.0,1465668000000.0,1465671600000.0,1465675200000.0,1465678800000.0,1465682400000.0,1465686000000.0,1465689600000.0,1465693200000.0,1465696800000.0,1465700400000.0,1465704000000.0,1465707600000.0,1465743600000.0,1465747200000.0,1465750800000.0,1465754400000.0,1465758000000.0,1465761600000.0,1465765200000.0,1465768800000.0,1465772400000.0,1465776000000.0,1465779600000.0,1465783200000.0,1465786800000.0,1465790400000.0,1465794000000.0,1465797600000.0,1465801200000.0,1465804800000.0,1465808400000.0,1465812000000.0,1465815600000.0,1465819200000.0,1465822800000.0,1465826400000.0,1465830000000.0,1465833600000.0,1465837200000.0,1465840800000.0,1465844400000.0,1465848000000.0,1465851600000.0,1465855200000.0,1465858800000.0,1465862400000.0,1465866000000.0,1465869600000.0,1465873200000.0,1465876800000.0,1465880400000.0,1465884000000.0,1465887600000.0,1465891200000.0,1465894800000.0,1465898400000.0,1465902000000.0,1465905600000.0,1465909200000.0,1465912800000.0,1465916400000.0,1465920000000.0,1465923600000.0,1465927200000.0,1465930800000.0,1465934400000.0,1465938000000.0,1465941600000.0,1465945200000.0,1465948800000.0,1465952400000.0,1465956000000.0,1465959600000.0,1465963200000.0,1465966800000.0,1465970400000.0,1465974000000.0,1465977600000.0,1465981200000.0,1465984800000.0,1465988400000.0,1465992000000.0,1465995600000.0,1465999200000.0,1466002800000.0,1466006400000.0,1466010000000.0,1466013600000.0,1466017200000.0,1466020800000.0,1466024400000.0,1466028000000.0,1466031600000.0,1466035200000.0,1466038800000.0,1466042400000.0,1466046000000.0,1466049600000.0,1466053200000.0,1466056800000.0,1466060400000.0,1466064000000.0,1466067600000.0,1466071200000.0,1466074800000.0,1466078400000.0,1466082000000.0,1466085600000.0,1466089200000.0,1466092800000.0,1466096400000.0,1466100000000.0,1466103600000.0,1466107200000.0,1466110800000.0,1466114400000.0,1466118000000.0,1466121600000.0,1466125200000.0,1466128800000.0,1466132400000.0,1466136000000.0,1466139600000.0,1466143200000.0,1466146800000.0,1466150400000.0,1466154000000.0,1466157600000.0,1466161200000.0,1466164800000.0,1466168400000.0,1466172000000.0,1466175600000.0,1466179200000.0,1466182800000.0,1466186400000.0,1466190000000.0,1466193600000.0,1466197200000.0,1466200800000.0,1466204400000.0,1466208000000.0,1466211600000.0,1466215200000.0,1466218800000.0,1466222400000.0,1466226000000.0,1466229600000.0,1466233200000.0,1466236800000.0,1466240400000.0,1466244000000.0,1466247600000.0,1466251200000.0,1466254800000.0,1466258400000.0,1466262000000.0,1466265600000.0,1466269200000.0,1466272800000.0,1466276400000.0,1466280000000.0,1466283600000.0,1466287200000.0,1466290800000.0,1466294400000.0,1466298000000.0,1466301600000.0,1466305200000.0,1466308800000.0,1466312400000.0,1466316000000.0,1466319600000.0,1466323200000.0,1466326800000.0,1466330400000.0,1466334000000.0,1466337600000.0,1466341200000.0,1466344800000.0,1466348400000.0,1466352000000.0,1466355600000.0,1466359200000.0,1466362800000.0,1466366400000.0,1466370000000.0,1466373600000.0,1466377200000.0,1466380800000.0,1466384400000.0,1466388000000.0,1466391600000.0,1466395200000.0,1466398800000.0,1466402400000.0,1466406000000.0,1466409600000.0,1466413200000.0,1466416800000.0,1466420400000.0,1466424000000.0,1466427600000.0,1466431200000.0,1466434800000.0,1466438400000.0,1466442000000.0,1466445600000.0,1466449200000.0,1466452800000.0,1466456400000.0,1466460000000.0,1466463600000.0,1466467200000.0,1466470800000.0,1466474400000.0,1466478000000.0,1466481600000.0,1466485200000.0,1466488800000.0,1466492400000.0,1466496000000.0,1466499600000.0,1466503200000.0,1466506800000.0,1466510400000.0,1466514000000.0,1466517600000.0,1466521200000.0,1466524800000.0,1466528400000.0,1466532000000.0,1466535600000.0,1466539200000.0,1466542800000.0,1466546400000.0,1466550000000.0,1466553600000.0,1466557200000.0,1466560800000.0,1466564400000.0,1466568000000.0,1466571600000.0,1466575200000.0,1466578800000.0,1466582400000.0,1466586000000.0,1466589600000.0,1466593200000.0,1466596800000.0,1466600400000.0,1466604000000.0,1466607600000.0,1466611200000.0,1466614800000.0,1466618400000.0,1466622000000.0,1466625600000.0,1466629200000.0,1466632800000.0,1466636400000.0,1466640000000.0,1466643600000.0,1466647200000.0,1466650800000.0,1466654400000.0,1466658000000.0,1466661600000.0,1466665200000.0,1466668800000.0,1466672400000.0,1466676000000.0,1466679600000.0,1466683200000.0,1466686800000.0,1466690400000.0,1466694000000.0,1466697600000.0,1466701200000.0,1466704800000.0,1466708400000.0,1466712000000.0,1466715600000.0,1466719200000.0,1466722800000.0,1466726400000.0,1466730000000.0,1466733600000.0,1466737200000.0,1466740800000.0,1466744400000.0,1466748000000.0,1466751600000.0,1466755200000.0,1466758800000.0,1466762400000.0,1466766000000.0,1466769600000.0,1466773200000.0,1466776800000.0,1466780400000.0,1466784000000.0,1466787600000.0,1466791200000.0,1466794800000.0,1466798400000.0,1466802000000.0,1466805600000.0,1466809200000.0,1466812800000.0,1466816400000.0,1466820000000.0,1466823600000.0,1466827200000.0,1466830800000.0,1466834400000.0,1466838000000.0,1466841600000.0,1466845200000.0,1466848800000.0,1466852400000.0,1466856000000.0,1466859600000.0,1466863200000.0,1466866800000.0,1466870400000.0,1466874000000.0,1467079200000.0,1467082800000.0,1467086400000.0,1467090000000.0,1467093600000.0,1467097200000.0,1467100800000.0,1467104400000.0,1467108000000.0,1467111600000.0,1467115200000.0,1467118800000.0,1467122400000.0,1467126000000.0,1467129600000.0,1467133200000.0,1467136800000.0,1467140400000.0,1467144000000.0,1467147600000.0,1467151200000.0,1467154800000.0,1467158400000.0,1467162000000.0,1467165600000.0,1467169200000.0,1467172800000.0,1467176400000.0,1467180000000.0,1467183600000.0,1467187200000.0,1467190800000.0,1467194400000.0,1467198000000.0,1467201600000.0,1467205200000.0,1467208800000.0,1467212400000.0,1467216000000.0,1467219600000.0,1467223200000.0,1467226800000.0,1467230400000.0,1467234000000.0,1467237600000.0,1467241200000.0,1467244800000.0,1467248400000.0,1467252000000.0,1467255600000.0,1467259200000.0,1467262800000.0,1467266400000.0,1467270000000.0,1467273600000.0,1467277200000.0,1467280800000.0,1467284400000.0,1467288000000.0,1467291600000.0,1467295200000.0,1467298800000.0,1467302400000.0,1467306000000.0,1467309600000.0,1467313200000.0,1467316800000.0,1467320400000.0,1467324000000.0,1467327600000.0,1467331200000.0,1467334800000.0,1467338400000.0,1467342000000.0,1467345600000.0,1467349200000.0,1467352800000.0,1467356400000.0,1467360000000.0,1467363600000.0,1467367200000.0,1467370800000.0,1467374400000.0,1467378000000.0,1467381600000.0,1467385200000.0,1467388800000.0,1467392400000.0,1467396000000.0,1467399600000.0,1467403200000.0,1467406800000.0,1467424800000.0,1467428400000.0,1467435600000.0,1467442800000.0,1467446400000.0,1467450000000.0,1467453600000.0,1467457200000.0,1467460800000.0,1467464400000.0,1467468000000.0,1467471600000.0,1467475200000.0,1467478800000.0,1467482400000.0,1467486000000.0,1467489600000.0,1467493200000.0,1467496800000.0,1467500400000.0,1467504000000.0,1467507600000.0,1467511200000.0,1467514800000.0,1467518400000.0,1467522000000.0,1467525600000.0,1467529200000.0,1467532800000.0,1467536400000.0,1467540000000.0,1467543600000.0,1467547200000.0,1467550800000.0,1467554400000.0,1467558000000.0,1467561600000.0,1467565200000.0,1467568800000.0,1467572400000.0,1467576000000.0,1467579600000.0,1467583200000.0,1467586800000.0,1467590400000.0,1467594000000.0,1467597600000.0,1467601200000.0,1467604800000.0,1467608400000.0,1467612000000.0,1467615600000.0,1467619200000.0,1467622800000.0,1467626400000.0,1467630000000.0,1467633600000.0,1467637200000.0,1467640800000.0,1467644400000.0,1467648000000.0,1467651600000.0,1467655200000.0,1467658800000.0,1467662400000.0,1467666000000.0,1467669600000.0,1467673200000.0,1467676800000.0,1467680400000.0,1467684000000.0,1467687600000.0,1467691200000.0,1467694800000.0,1467698400000.0,1467702000000.0,1467705600000.0,1467709200000.0,1467712800000.0,1467716400000.0,1467720000000.0,1467723600000.0,1467727200000.0,1467730800000.0,1467734400000.0,1467738000000.0,1467741600000.0,1467745200000.0,1467748800000.0,1467752400000.0,1467756000000.0,1467759600000.0,1467763200000.0,1467766800000.0,1467766800000.0,1467770400000.0,1467774000000.0,1467777600000.0,1467781200000.0,1467784800000.0,1467788400000.0,1467792000000.0,1467795600000.0,1467799200000.0,1467802800000.0,1467806400000.0,1467810000000.0,1467813600000.0,1467817200000.0,1467820800000.0,1467824400000.0,1467828000000.0,1467831600000.0,1467835200000.0,1467838800000.0,1467842400000.0,1467846000000.0,1467849600000.0,1467853200000.0,1467856800000.0,1467860400000.0,1467864000000.0,1467867600000.0,1467871200000.0,1467874800000.0,1467878400000.0,1467882000000.0,1467885600000.0,1467889200000.0,1467892800000.0,1467896400000.0,1467900000000.0,1467903600000.0,1467907200000.0,1467910800000.0,1467914400000.0,1467918000000.0,1467921600000.0,1467925200000.0,1467928800000.0,1467932400000.0,1467936000000.0,1467939600000.0,1467943200000.0,1467946800000.0,1467950400000.0,1467954000000.0,1467957600000.0,1467961200000.0,1467964800000.0,1467968400000.0,1467972000000.0,1467975600000.0,1467979200000.0,1467982800000.0,1467986400000.0,1467990000000.0,1467993600000.0,1467997200000.0,1468000800000.0,1468004400000.0,1468008000000.0,1468011600000.0,1468015200000.0,1468018800000.0,1468022400000.0,1468026000000.0,1468029600000.0,1468033200000.0,1468036800000.0,1468040400000.0,1468044000000.0,1468047600000.0,1468051200000.0,1468054800000.0,1468058400000.0,1468062000000.0,1468065600000.0,1468069200000.0,1468072800000.0,1468076400000.0,1468080000000.0,1468083600000.0,1468087200000.0,1468090800000.0,1468094400000.0,1468098000000.0,1468101600000.0,1468105200000.0,1468108800000.0,1468112400000.0,1468116000000.0,1468119600000.0,1468123200000.0,1468126800000.0,1468130400000.0,1468134000000.0,1468137600000.0,1468141200000.0,1468144800000.0,1468148400000.0,1468152000000.0,1468155600000.0,1468159200000.0,1468162800000.0,1468166400000.0,1468170000000.0,1468173600000.0,1468177200000.0,1468180800000.0,1468184400000.0,1468188000000.0,1468191600000.0,1468195200000.0,1468198800000.0,1468202400000.0,1468206000000.0,1468209600000.0,1468213200000.0,1468216800000.0,1468220400000.0,1468224000000.0,1468227600000.0,1468231200000.0,1468234800000.0,1468238400000.0,1468242000000.0,1468245600000.0,1468249200000.0,1468252800000.0,1468256400000.0,1468260000000.0,1468263600000.0,1468267200000.0,1468270800000.0,1468274400000.0,1468278000000.0,1468281600000.0,1468285200000.0,1468288800000.0,1468292400000.0,1468296000000.0,1468299600000.0,1468303200000.0,1468306800000.0,1468310400000.0,1468314000000.0,1468317600000.0,1468321200000.0,1468324800000.0,1468328400000.0,1468332000000.0,1468335600000.0,1468339200000.0,1468342800000.0,1468346400000.0,1468350000000.0,1468353600000.0,1468357200000.0,1468360800000.0,1468364400000.0,1468368000000.0,1468371600000.0,1468375200000.0,1468378800000.0,1468382400000.0,1468386000000.0,1468389600000.0,1468393200000.0,1468396800000.0,1468400400000.0,1468404000000.0,1468407600000.0,1468411200000.0,1468414800000.0,1468418400000.0,1468422000000.0,1468425600000.0,1468429200000.0,1468432800000.0,1468436400000.0,1468440000000.0,1468443600000.0,1468447200000.0,1468450800000.0,1468454400000.0,1468458000000.0,1468461600000.0,1468465200000.0,1468468800000.0,1468472400000.0,1468476000000.0,1468479600000.0,1468483200000.0,1468486800000.0,1468490400000.0,1468494000000.0,1468497600000.0,1468501200000.0,1468504800000.0,1468508400000.0,1468512000000.0,1468515600000.0,1468519200000.0,1468522800000.0,1468526400000.0,1468530000000.0,1468533600000.0,1468537200000.0,1468540800000.0,1468544400000.0,1468548000000.0,1468551600000.0,1468555200000.0,1468558800000.0,1468562400000.0,1468566000000.0,1468569600000.0,1468573200000.0,1468576800000.0,1468580400000.0,1468584000000.0,1468587600000.0,1468591200000.0,1468594800000.0,1468598400000.0,1468602000000.0,1468605600000.0,1468609200000.0,1468612800000.0,1468616400000.0,1468620000000.0,1468623600000.0,1468627200000.0,1468630800000.0,1468634400000.0,1468638000000.0,1468641600000.0,1468645200000.0,1468648800000.0,1468652400000.0,1468656000000.0,1468659600000.0,1468663200000.0,1468666800000.0,1468670400000.0,1468674000000.0,1468677600000.0,1468681200000.0,1468684800000.0,1468688400000.0,1468692000000.0,1468695600000.0,1468699200000.0,1468702800000.0,1468706400000.0,1468710000000.0,1468713600000.0,1468717200000.0,1468720800000.0,1468724400000.0,1468728000000.0,1468731600000.0,1468735200000.0,1468738800000.0,1468742400000.0,1468746000000.0,1468749600000.0,1468753200000.0,1468756800000.0,1468760400000.0,1468764000000.0,1468767600000.0,1468771200000.0,1468774800000.0,1468778400000.0,1468782000000.0,1468785600000.0,1468789200000.0,1468792800000.0,1468796400000.0,1468800000000.0,1468803600000.0,1468807200000.0,1468810800000.0,1468814400000.0,1468818000000.0,1468821600000.0,1468825200000.0,1468828800000.0,1468832400000.0,1468836000000.0,1468839600000.0,1468843200000.0,1468846800000.0,1468850400000.0,1468854000000.0,1468857600000.0,1468861200000.0,1468864800000.0,1468868400000.0,1468872000000.0,1468875600000.0,1468879200000.0,1468882800000.0,1468886400000.0,1468890000000.0,1468893600000.0,1468897200000.0,1468900800000.0,1468904400000.0,1468908000000.0,1468911600000.0,1468915200000.0,1468918800000.0,1468922400000.0,1468926000000.0,1468929600000.0,1468933200000.0,1468936800000.0,1468940400000.0,1468944000000.0,1468947600000.0,1468951200000.0,1468954800000.0,1468958400000.0,1468962000000.0,1468965600000.0,1468969200000.0,1468972800000.0,1468976400000.0,1468980000000.0,1468983600000.0,1468987200000.0,1468990800000.0,1468994400000.0,1468998000000.0,1469001600000.0,1469005200000.0,1469008800000.0,1469012400000.0,1469016000000.0,1469019600000.0,1469023200000.0,1469026800000.0,1469030400000.0,1469034000000.0,1469037600000.0,1469041200000.0,1469044800000.0,1469048400000.0,1469052000000.0,1469055600000.0,1469059200000.0,1469062800000.0,1469066400000.0,1469070000000.0,1469073600000.0,1469077200000.0,1469080800000.0,1469084400000.0,1469088000000.0,1469091600000.0,1469095200000.0,1469098800000.0,1469102400000.0,1469106000000.0,1469109600000.0,1469113200000.0,1469116800000.0,1469120400000.0,1469124000000.0,1469127600000.0,1469131200000.0,1469134800000.0,1469138400000.0,1469142000000.0,1469145600000.0,1469149200000.0,1469152800000.0,1469156400000.0,1469160000000.0,1469163600000.0,1469167200000.0,1469170800000.0,1469174400000.0,1469178000000.0,1469181600000.0,1469185200000.0,1469188800000.0,1469192400000.0,1469196000000.0,1469199600000.0,1469203200000.0,1469206800000.0,1469210400000.0,1469214000000.0,1469217600000.0,1469221200000.0,1469224800000.0,1469228400000.0,1469232000000.0,1469235600000.0,1469239200000.0,1469242800000.0,1469246400000.0,1469250000000.0,1469253600000.0,1469257200000.0,1469260800000.0,1469264400000.0,1469268000000.0,1469271600000.0,1469275200000.0,1469278800000.0,1469282400000.0,1469286000000.0,1469289600000.0,1469293200000.0,1469296800000.0,1469300400000.0,1469304000000.0,1469307600000.0,1469311200000.0,1469314800000.0,1469318400000.0,1469322000000.0,1469325600000.0,1469329200000.0,1469332800000.0,1469336400000.0,1469340000000.0,1469343600000.0,1469347200000.0,1469350800000.0,1469354400000.0,1469358000000.0,1469361600000.0,1469365200000.0,1469368800000.0,1469372400000.0,1469376000000.0,1469379600000.0,1469383200000.0,1469386800000.0,1469390400000.0,1469394000000.0,1469397600000.0,1469401200000.0,1469404800000.0,1469408400000.0,1469412000000.0,1469415600000.0,1469419200000.0,1469422800000.0,1469426400000.0,1469430000000.0,1469433600000.0,1469437200000.0,1469440800000.0,1469444400000.0,1469448000000.0,1469451600000.0,1469455200000.0,1469458800000.0,1469462400000.0,1469466000000.0,1469469600000.0,1469473200000.0,1469476800000.0,1469480400000.0,1469484000000.0,1469487600000.0,1469491200000.0,1469494800000.0,1469498400000.0,1469502000000.0,1469505600000.0,1469509200000.0,1469512800000.0,1469516400000.0,1469520000000.0,1469523600000.0,1469527200000.0,1469530800000.0,1469534400000.0,1469538000000.0,1469541600000.0,1469545200000.0,1469548800000.0,1469552400000.0,1469556000000.0,1469559600000.0,1469563200000.0,1469566800000.0,1469570400000.0,1469574000000.0,1469577600000.0,1469581200000.0,1469584800000.0,1469588400000.0,1469592000000.0,1469595600000.0,1469599200000.0,1469602800000.0,1469606400000.0,1469610000000.0,1469613600000.0,1469617200000.0,1469620800000.0,1469624400000.0,1469628000000.0,1469631600000.0,1469635200000.0,1469638800000.0,1469642400000.0,1469646000000.0,1469649600000.0,1469653200000.0,1469656800000.0,1469660400000.0,1469664000000.0,1469667600000.0,1469671200000.0,1469674800000.0,1469678400000.0,1469682000000.0,1469685600000.0,1469689200000.0,1469692800000.0,1469696400000.0,1469700000000.0,1469703600000.0,1469707200000.0,1469710800000.0,1469714400000.0,1469718000000.0,1469721600000.0,1469725200000.0,1469728800000.0,1469732400000.0,1469736000000.0,1469739600000.0,1469743200000.0,1469746800000.0,1469750400000.0,1469754000000.0,1469757600000.0,1469761200000.0,1469764800000.0,1469768400000.0,1469772000000.0,1469775600000.0,1469779200000.0,1469782800000.0,1469786400000.0,1469790000000.0,1469793600000.0,1469797200000.0,1469800800000.0,1469804400000.0,1469808000000.0,1469811600000.0,1469815200000.0,1469818800000.0,1469822400000.0,1469826000000.0,1469829600000.0,1469833200000.0,1469836800000.0,1469840400000.0,1469844000000.0,1469847600000.0,1469851200000.0,1469854800000.0,1469858400000.0,1469862000000.0,1469865600000.0,1469869200000.0,1469872800000.0,1469876400000.0,1469880000000.0,1469883600000.0,1469887200000.0,1469890800000.0,1469894400000.0,1469898000000.0,1469901600000.0,1469905200000.0,1469908800000.0,1469912400000.0,1469916000000.0,1469919600000.0,1469923200000.0,1469926800000.0,1469930400000.0,1469934000000.0,1469937600000.0,1469941200000.0,1469944800000.0,1469948400000.0,1469952000000.0,1469955600000.0,1469959200000.0,1469962800000.0,1469966400000.0,1469970000000.0,1469973600000.0,1469977200000.0,1469980800000.0,1469984400000.0,1469988000000.0,1469991600000.0,1469995200000.0,1469998800000.0,1470002400000.0,1470006000000.0,1470009600000.0,1470013200000.0,1470016800000.0,1470020400000.0,1470024000000.0,1470027600000.0,1470031200000.0,1470034800000.0,1470038400000.0,1470042000000.0,1470045600000.0,1470049200000.0,1470052800000.0,1470056400000.0,1470060000000.0,1470063600000.0,1470067200000.0,1470070800000.0,1470074400000.0,1470078000000.0,1470081600000.0,1470085200000.0,1470088800000.0,1470092400000.0,1470096000000.0,1470099600000.0,1470103200000.0,1470106800000.0,1470110400000.0,1470114000000.0,1470117600000.0,1470121200000.0,1470124800000.0,1470128400000.0,1470132000000.0,1470135600000.0,1470139200000.0,1470142800000.0,1470146400000.0,1470150000000.0,1470153600000.0,1470157200000.0,1470160800000.0,1470164400000.0,1470168000000.0,1470171600000.0,1470175200000.0,1470178800000.0,1470182400000.0,1470186000000.0,1470189600000.0,1470193200000.0,1470196800000.0,1470200400000.0,1470204000000.0,1470207600000.0,1470211200000.0,1470214800000.0,1470218400000.0,1470222000000.0,1470225600000.0,1470229200000.0,1470232800000.0,1470236400000.0,1470240000000.0,1470243600000.0,1470247200000.0,1470250800000.0,1470254400000.0,1470258000000.0,1470261600000.0,1470265200000.0,1470268800000.0,1470272400000.0,1470276000000.0,1470279600000.0,1470283200000.0,1470286800000.0,1470290400000.0,1470294000000.0,1470297600000.0,1470301200000.0,1470304800000.0,1470308400000.0,1470312000000.0,1470315600000.0,1470319200000.0,1470322800000.0,1470326400000.0,1470330000000.0,1470333600000.0,1470337200000.0,1470340800000.0,1470344400000.0,1470348000000.0,1470351600000.0,1470355200000.0,1470358800000.0,1470362400000.0,1470366000000.0,1470369600000.0,1470373200000.0,1470376800000.0,1470380400000.0,1470384000000.0,1470387600000.0,1470391200000.0,1470394800000.0,1470398400000.0,1470402000000.0,1470405600000.0,1470873600000.0,1470873600000.0,1470873600000.0,1470873600000.0,1470877200000.0,1470880800000.0,1470884400000.0,1470888000000.0,1470891600000.0,1470895200000.0,1470898800000.0,1470902400000.0,1470906000000.0,1470909600000.0,1470913200000.0,1470916800000.0,1470920400000.0,1470924000000.0,1470927600000.0,1470931200000.0,1470934800000.0,1470938400000.0,1470942000000.0,1470945600000.0,1470949200000.0,1470952800000.0,1470956400000.0,1470960000000.0,1470963600000.0,1470967200000.0,1470970800000.0,1470974400000.0,1470978000000.0,1470981600000.0,1470985200000.0,1470988800000.0,1470992400000.0,1470996000000.0,1470999600000.0,1471003200000.0,1471006800000.0,1471010400000.0,1471014000000.0,1471017600000.0,1471021200000.0,1471024800000.0,1471028400000.0,1471032000000.0,1471035600000.0,1471039200000.0,1471042800000.0,1471046400000.0,1471050000000.0,1471053600000.0,1471057200000.0,1471060800000.0,1471064400000.0,1471068000000.0,1471071600000.0,1471075200000.0,1471078800000.0,1471082400000.0,1471086000000.0,1471089600000.0,1471093200000.0,1471096800000.0,1471100400000.0,1471104000000.0,1471107600000.0,1471111200000.0,1471114800000.0,1471118400000.0,1471122000000.0,1471125600000.0,1471129200000.0,1471132800000.0,1471136400000.0,1471140000000.0,1471143600000.0,1471147200000.0,1471150800000.0,1471154400000.0,1471158000000.0,1471161600000.0,1471165200000.0,1471168800000.0,1471172400000.0,1471176000000.0,1471179600000.0,1471183200000.0,1471186800000.0,1471190400000.0,1471194000000.0,1471197600000.0,1471201200000.0,1471204800000.0,1471208400000.0,1471212000000.0,1471215600000.0,1471219200000.0,1471222800000.0,1471226400000.0,1471230000000.0,1471233600000.0,1471237200000.0,1471240800000.0,1471244400000.0,1471248000000.0,1471251600000.0,1471255200000.0,1471258800000.0,1471262400000.0,1471266000000.0,1471269600000.0,1471273200000.0,1471276800000.0,1471280400000.0,1471284000000.0,1471287600000.0,1471291200000.0,1471294800000.0,1471298400000.0,1471302000000.0,1471305600000.0,1471309200000.0,1471312800000.0,1471316400000.0,1471320000000.0,1471323600000.0,1471327200000.0,1471330800000.0,1471334400000.0,1471338000000.0,1471341600000.0,1471345200000.0,1471348800000.0,1471352400000.0,1471356000000.0,1471359600000.0,1471363200000.0,1471366800000.0,1471370400000.0,1471374000000.0,1471377600000.0,1471381200000.0,1471384800000.0,1471388400000.0,1471392000000.0,1471395600000.0,1471399200000.0,1471402800000.0,1471406400000.0,1471410000000.0,1471413600000.0,1471417200000.0,1471420800000.0,1471424400000.0,1471428000000.0,1471431600000.0,1471435200000.0,1471438800000.0,1471442400000.0,1471446000000.0,1471449600000.0,1471453200000.0,1471456800000.0,1471460400000.0,1471464000000.0,1471467600000.0,1471471200000.0,1471474800000.0,1471478400000.0,1471482000000.0,1471485600000.0,1471489200000.0,1471492800000.0,1471496400000.0,1471500000000.0,1471503600000.0,1471507200000.0,1471510800000.0,1471514400000.0,1471518000000.0,1471521600000.0,1471525200000.0,1471528800000.0,1471532400000.0,1471536000000.0,1471539600000.0,1471543200000.0,1471546800000.0,1471550400000.0,1471554000000.0,1471557600000.0,1471561200000.0,1471564800000.0,1471568400000.0,1471572000000.0,1471575600000.0,1471579200000.0,1471582800000.0,1471586400000.0,1471590000000.0,1471593600000.0,1471597200000.0,1471600800000.0,1471604400000.0,1471608000000.0,1471611600000.0,1471615200000.0,1471618800000.0,1471622400000.0,1471626000000.0,1471629600000.0,1471633200000.0,1471636800000.0,1471640400000.0,1471644000000.0,1471647600000.0,1471651200000.0,1471654800000.0,1471658400000.0,1471662000000.0,1471665600000.0,1471669200000.0,1471672800000.0,1471676400000.0,1471680000000.0,1471683600000.0,1471687200000.0,1471690800000.0,1471694400000.0,1471698000000.0,1471701600000.0,1471705200000.0,1471708800000.0,1471712400000.0,1471716000000.0,1471719600000.0,1471723200000.0,1471726800000.0,1471730400000.0,1471734000000.0,1471737600000.0,1471741200000.0,1471744800000.0,1471748400000.0,1471752000000.0,1471755600000.0,1471759200000.0,1471762800000.0,1471766400000.0,1471770000000.0,1471773600000.0,1471777200000.0,1471780800000.0,1471784400000.0,1471788000000.0,1471791600000.0,1471795200000.0,1471798800000.0,1471802400000.0,1471806000000.0,1471809600000.0,1471813200000.0,1471816800000.0,1471820400000.0,1471824000000.0,1471827600000.0,1471831200000.0,1471834800000.0,1471838400000.0,1471842000000.0,1471845600000.0,1471849200000.0,1471852800000.0,1471856400000.0,1471860000000.0,1471863600000.0,1471867200000.0,1471870800000.0,1471874400000.0,1471878000000.0,1471881600000.0,1471885200000.0,1471888800000.0,1471892400000.0,1471896000000.0,1471899600000.0,1471903200000.0,1471906800000.0,1471910400000.0,1471914000000.0,1471917600000.0,1471921200000.0,1471924800000.0,1471928400000.0,1471932000000.0,1471935600000.0,1471939200000.0,1471971600000.0,1471975200000.0,1471978800000.0,1471982400000.0,1471986000000.0,1471989600000.0,1471993200000.0,1471996800000.0,1472000400000.0,1472004000000.0,1472007600000.0,1472011200000.0,1472014800000.0,1472018400000.0,1472022000000.0,1472025600000.0,1472029200000.0,1472032800000.0,1472036400000.0,1472040000000.0,1472043600000.0,1472047200000.0,1472050800000.0,1472054400000.0,1472058000000.0,1472061600000.0,1472065200000.0,1472068800000.0,1472072400000.0,1472076000000.0,1472079600000.0,1472083200000.0,1472086800000.0,1472090400000.0,1472094000000.0,1472097600000.0,1472101200000.0,1472104800000.0,1472108400000.0,1472112000000.0,1472115600000.0,1472119200000.0,1472122800000.0,1472126400000.0,1472130000000.0,1472133600000.0,1472137200000.0,1472140800000.0,1472144400000.0,1472148000000.0,1472151600000.0,1472155200000.0,1472158800000.0,1472162400000.0,1472166000000.0,1472169600000.0,1472173200000.0,1472176800000.0,1472180400000.0,1472184000000.0,1472187600000.0,1472191200000.0,1472194800000.0,1472198400000.0,1472202000000.0,1472205600000.0,1472209200000.0,1472212800000.0,1472216400000.0,1472220000000.0,1472223600000.0,1472227200000.0,1472230800000.0,1472234400000.0,1472238000000.0,1472241600000.0,1472245200000.0,1472248800000.0,1472252400000.0,1472256000000.0,1472259600000.0,1472263200000.0,1472266800000.0,1472270400000.0,1472274000000.0,1472277600000.0,1472281200000.0,1472284800000.0,1472288400000.0,1472292000000.0,1472295600000.0,1472299200000.0,1472302800000.0,1472306400000.0,1472310000000.0,1472313600000.0,1472317200000.0,1472320800000.0,1472324400000.0,1472328000000.0,1472331600000.0,1472335200000.0,1472338800000.0,1472342400000.0,1472346000000.0,1472349600000.0,1472353200000.0,1472356800000.0,1472360400000.0,1472364000000.0,1472367600000.0,1472371200000.0,1472374800000.0,1472378400000.0,1472382000000.0,1472385600000.0,1472389200000.0,1472392800000.0,1472396400000.0,1472400000000.0,1472403600000.0,1472407200000.0,1472410800000.0,1472414400000.0,1472418000000.0,1472421600000.0,1472425200000.0,1472428800000.0,1472432400000.0,1472436000000.0,1472439600000.0,1472443200000.0,1472446800000.0,1472450400000.0,1472454000000.0,1472457600000.0,1472461200000.0,1472464800000.0,1472468400000.0,1472472000000.0,1472475600000.0,1472479200000.0,1472482800000.0,1472486400000.0,1472490000000.0,1472493600000.0,1472497200000.0,1472500800000.0,1472504400000.0,1472508000000.0,1472511600000.0,1472515200000.0,1472518800000.0,1472522400000.0,1472526000000.0,1472529600000.0,1472533200000.0,1472536800000.0,1472540400000.0,1472544000000.0,1472547600000.0,1472551200000.0,1472554800000.0,1472558400000.0,1472562000000.0,1472565600000.0,1472569200000.0,1472572800000.0,1472576400000.0,1472580000000.0,1472583600000.0,1472587200000.0,1472590800000.0,1472594400000.0,1472598000000.0,1472601600000.0,1472605200000.0,1472608800000.0,1472612400000.0,1472616000000.0,1472619600000.0,1472623200000.0,1472626800000.0,1472630400000.0,1472634000000.0,1472637600000.0,1472641200000.0,1472644800000.0,1472648400000.0,1472652000000.0,1472655600000.0,1472659200000.0,1472662800000.0,1472666400000.0,1472670000000.0,1472673600000.0,1472677200000.0,1472680800000.0,1472684400000.0,1472688000000.0,1472691600000.0,1472695200000.0,1472698800000.0,1472702400000.0,1472706000000.0,1472709600000.0,1472713200000.0,1472716800000.0,1472720400000.0,1472724000000.0,1472727600000.0,1472731200000.0,1472734800000.0,1472738400000.0,1472742000000.0,1472745600000.0,1472749200000.0,1472752800000.0,1472756400000.0,1472760000000.0,1472763600000.0,1472767200000.0,1472770800000.0,1472774400000.0,1472778000000.0,1472781600000.0,1472785200000.0,1472788800000.0,1472792400000.0,1472796000000.0,1472799600000.0,1472803200000.0,1472806800000.0,1472810400000.0,1472814000000.0,1472817600000.0,1472821200000.0,1472824800000.0,1472828400000.0,1472832000000.0,1472835600000.0,1472839200000.0,1472842800000.0,1472846400000.0,1472850000000.0,1472853600000.0,1472857200000.0,1472860800000.0,1472864400000.0,1472868000000.0,1472871600000.0,1472875200000.0,1472878800000.0,1472882400000.0,1472886000000.0,1472889600000.0,1472893200000.0,1472896800000.0,1472900400000.0,1472904000000.0,1472907600000.0,1472911200000.0,1472914800000.0,1472918400000.0,1472922000000.0,1472925600000.0,1472929200000.0,1472932800000.0,1472936400000.0,1472940000000.0,1472943600000.0,1472947200000.0,1472950800000.0,1472954400000.0,1472958000000.0,1472961600000.0,1472965200000.0,1472968800000.0,1472972400000.0,1472976000000.0,1472979600000.0,1472983200000.0,1472986800000.0,1472990400000.0,1472994000000.0,1472997600000.0,1473001200000.0,1473004800000.0,1473008400000.0,1473012000000.0,1473015600000.0,1473019200000.0,1473022800000.0,1473026400000.0,1473030000000.0,1473033600000.0,1473037200000.0,1473040800000.0,1473044400000.0,1473048000000.0,1473051600000.0,1473055200000.0,1473058800000.0,1473062400000.0,1473066000000.0,1473069600000.0,1473073200000.0,1473076800000.0,1473080400000.0,1473084000000.0,1473087600000.0,1473091200000.0,1473094800000.0,1473098400000.0,1473102000000.0,1473105600000.0,1473109200000.0,1473112800000.0,1473116400000.0,1473120000000.0,1473123600000.0,1473127200000.0,1473130800000.0,1473134400000.0,1473138000000.0,1473141600000.0,1473145200000.0,1473148800000.0,1473152400000.0,1473156000000.0,1473159600000.0,1473163200000.0,1473166800000.0,1473170400000.0,1473174000000.0,1473177600000.0,1473181200000.0,1473184800000.0,1473188400000.0,1473192000000.0,1473195600000.0,1473199200000.0,1473202800000.0,1473206400000.0,1473210000000.0,1473213600000.0,1473217200000.0,1473220800000.0,1473224400000.0,1473228000000.0,1473231600000.0,1473235200000.0,1473238800000.0,1473242400000.0,1473246000000.0,1473249600000.0,1473253200000.0,1473256800000.0,1473260400000.0,1473264000000.0,1473267600000.0,1473271200000.0,1473274800000.0,1473278400000.0,1473282000000.0,1473285600000.0,1473289200000.0,1473292800000.0,1473296400000.0,1473300000000.0,1473303600000.0,1473307200000.0,1473310800000.0,1473314400000.0,1473318000000.0,1473321600000.0,1473325200000.0,1473328800000.0,1473332400000.0,1473336000000.0,1473339600000.0,1473343200000.0,1473346800000.0,1473350400000.0,1473354000000.0,1473357600000.0,1473361200000.0,1473364800000.0,1473368400000.0,1473372000000.0,1473375600000.0,1473379200000.0,1473382800000.0,1473386400000.0,1473390000000.0,1473393600000.0,1473397200000.0,1473400800000.0,1473404400000.0,1473408000000.0,1473411600000.0,1473415200000.0,1473418800000.0,1473422400000.0,1473426000000.0,1473429600000.0,1473433200000.0,1473436800000.0,1473440400000.0,1473444000000.0,1473447600000.0,1473451200000.0,1473454800000.0,1473458400000.0,1473462000000.0,1473465600000.0,1473469200000.0,1473472800000.0,1473476400000.0,1473480000000.0,1473483600000.0,1473487200000.0,1473490800000.0,1473494400000.0,1473498000000.0,1473501600000.0,1473505200000.0,1473508800000.0,1473512400000.0,1473516000000.0,1473519600000.0,1473523200000.0,1473526800000.0,1473530400000.0,1473534000000.0,1473537600000.0,1473541200000.0,1473544800000.0,1473548400000.0,1473552000000.0,1473555600000.0,1473559200000.0,1473562800000.0,1473566400000.0,1473570000000.0,1473573600000.0,1473577200000.0,1473580800000.0,1473584400000.0,1473588000000.0,1473591600000.0,1473595200000.0,1473598800000.0,1473602400000.0,1473606000000.0,1473609600000.0,1473613200000.0,1473616800000.0,1473620400000.0,1473624000000.0,1473627600000.0,1473631200000.0,1473634800000.0,1473638400000.0,1473642000000.0,1473645600000.0,1473649200000.0,1473652800000.0,1473656400000.0,1473660000000.0,1473663600000.0,1473667200000.0,1473670800000.0,1473674400000.0,1473678000000.0,1473681600000.0,1473685200000.0,1473688800000.0,1473692400000.0,1473696000000.0,1473699600000.0,1473703200000.0,1473706800000.0,1473710400000.0,1473714000000.0,1473717600000.0,1473721200000.0,1473724800000.0,1473728400000.0,1473732000000.0,1473735600000.0,1473739200000.0,1473742800000.0,1473746400000.0,1473750000000.0,1473753600000.0,1473757200000.0,1473760800000.0,1473764400000.0,1473768000000.0,1473771600000.0,1473775200000.0,1473778800000.0,1473782400000.0,1473786000000.0,1473789600000.0,1473793200000.0,1473796800000.0,1473800400000.0,1473804000000.0,1473807600000.0,1473811200000.0,1473814800000.0,1473818400000.0,1473822000000.0,1473825600000.0,1473829200000.0,1473832800000.0,1473836400000.0,1473840000000.0,1473843600000.0,1473847200000.0,1473850800000.0,1473854400000.0,1473858000000.0,1473861600000.0,1473865200000.0,1473868800000.0,1473872400000.0,1473876000000.0,1473879600000.0,1473883200000.0,1473886800000.0,1473890400000.0,1473894000000.0,1473897600000.0,1473901200000.0,1473904800000.0,1473908400000.0,1473912000000.0,1473915600000.0,1473919200000.0,1473922800000.0,1473926400000.0,1473930000000.0,1473933600000.0,1473937200000.0,1473940800000.0,1473944400000.0,1473948000000.0,1473951600000.0,1473955200000.0,1473958800000.0,1473962400000.0,1473966000000.0,1473969600000.0,1473973200000.0,1473976800000.0,1473980400000.0,1473984000000.0,1473987600000.0,1473991200000.0,1473994800000.0,1473998400000.0,1474002000000.0,1474005600000.0,1474009200000.0,1474012800000.0,1474016400000.0,1474020000000.0,1474023600000.0,1474027200000.0,1474030800000.0,1474034400000.0,1474038000000.0,1474041600000.0,1474045200000.0,1474048800000.0,1474052400000.0,1474056000000.0,1474059600000.0,1474063200000.0,1474066800000.0,1474070400000.0,1474074000000.0,1474077600000.0,1474081200000.0,1474084800000.0,1474088400000.0,1474092000000.0,1474095600000.0,1474099200000.0,1474102800000.0,1474106400000.0,1474110000000.0,1474113600000.0,1474117200000.0,1474120800000.0,1474124400000.0,1474128000000.0,1474131600000.0,1474135200000.0,1474138800000.0,1474142400000.0,1474146000000.0,1474149600000.0,1474153200000.0,1474156800000.0,1474160400000.0,1474164000000.0,1474167600000.0,1474171200000.0,1474174800000.0,1474178400000.0,1474182000000.0,1474185600000.0,1474189200000.0,1474192800000.0,1474196400000.0,1474200000000.0,1474203600000.0,1474207200000.0,1474210800000.0,1474214400000.0,1474218000000.0,1474221600000.0,1474225200000.0,1474228800000.0,1474232400000.0,1474236000000.0,1474239600000.0,1474243200000.0,1474246800000.0,1474250400000.0,1474254000000.0,1474257600000.0,1474261200000.0,1474264800000.0,1474268400000.0,1474272000000.0,1474275600000.0,1474279200000.0,1474282800000.0,1474286400000.0,1474290000000.0,1474293600000.0,1474297200000.0,1474300800000.0,1474304400000.0,1474308000000.0,1474311600000.0,1474315200000.0,1474318800000.0,1474322400000.0,1474326000000.0,1474329600000.0,1474333200000.0,1474336800000.0,1474340400000.0,1474344000000.0,1474347600000.0,1474614000000.0,1474614000000.0,1474617600000.0,1474621200000.0,1474624800000.0,1474628400000.0,1474632000000.0,1474635600000.0,1474639200000.0,1474642800000.0,1474646400000.0,1474650000000.0,1474653600000.0,1474657200000.0,1474660800000.0,1474664400000.0,1474668000000.0,1474671600000.0,1474675200000.0,1474678800000.0,1474682400000.0,1474686000000.0,1474689600000.0,1474693200000.0,1474696800000.0,1474700400000.0,1474704000000.0,1474707600000.0,1474711200000.0,1474714800000.0,1474718400000.0,1474722000000.0,1474725600000.0,1474729200000.0,1474732800000.0,1474736400000.0,1474740000000.0,1474743600000.0,1474747200000.0,1474750800000.0,1474754400000.0,1474758000000.0,1474761600000.0,1474765200000.0,1474768800000.0,1474772400000.0,1474776000000.0,1474779600000.0,1474783200000.0,1474786800000.0,1474790400000.0,1474794000000.0,1474797600000.0,1474801200000.0,1474804800000.0,1474808400000.0,1474812000000.0,1474815600000.0,1474819200000.0,1474822800000.0,1474826400000.0,1474830000000.0,1474833600000.0,1474837200000.0,1474840800000.0,1474844400000.0,1474848000000.0,1474851600000.0,1474855200000.0,1474858800000.0,1474862400000.0,1474866000000.0,1474869600000.0,1474873200000.0,1474876800000.0,1474880400000.0,1474884000000.0,1474887600000.0,1474891200000.0,1474894800000.0,1474898400000.0,1474902000000.0,1474905600000.0,1474909200000.0,1474912800000.0,1474916400000.0,1474920000000.0,1474923600000.0,1474927200000.0,1474930800000.0,1474934400000.0,1474938000000.0,1474941600000.0,1474945200000.0,1474948800000.0,1474952400000.0,1474956000000.0,1474959600000.0,1474963200000.0,1474966800000.0,1474970400000.0,1474974000000.0,1474977600000.0,1474981200000.0,1474984800000.0,1474988400000.0,1474992000000.0,1474995600000.0,1474999200000.0,1475002800000.0,1475006400000.0,1475010000000.0,1475013600000.0,1475017200000.0,1475020800000.0,1475024400000.0,1475028000000.0,1475031600000.0,1475035200000.0,1475038800000.0,1475042400000.0,1475046000000.0],\"Date Formatted\":[\"02/15/16-11\",\"02/15/16-12\",\"02/15/16-13\",\"02/15/16-14\",\"02/15/16-15\",\"02/15/16-16\",\"02/16/16-02\",\"02/16/16-03\",\"02/16/16-05\",\"02/16/16-06\",\"02/16/16-07\",\"02/16/16-08\",\"02/16/16-09\",\"02/16/16-10\",\"02/16/16-20\",\"02/17/16-15\",\"02/17/16-16\",\"02/18/16-02\",\"02/18/16-03\",\"02/18/16-04\",\"02/18/16-05\",\"02/18/16-06\",\"02/18/16-07\",\"02/18/16-08\",\"02/18/16-09\",\"02/18/16-10\",\"02/18/16-11\",\"02/18/16-12\",\"02/18/16-13\",\"02/18/16-14\",\"02/18/16-15\",\"02/18/16-16\",\"02/18/16-19\",\"02/18/16-21\",\"02/18/16-23\",\"02/19/16-00\",\"02/19/16-02\",\"02/19/16-03\",\"02/19/16-03\",\"02/19/16-20\",\"02/19/16-20\",\"02/19/16-21\",\"02/19/16-22\",\"02/19/16-23\",\"02/20/16-00\",\"02/20/16-01\",\"02/20/16-02\",\"02/20/16-03\",\"02/20/16-04\",\"02/20/16-05\",\"02/20/16-06\",\"02/20/16-07\",\"02/20/16-08\",\"02/20/16-09\",\"02/20/16-10\",\"02/20/16-11\",\"02/20/16-12\",\"02/20/16-13\",\"02/20/16-14\",\"02/20/16-15\",\"02/20/16-16\",\"02/20/16-17\",\"02/20/16-18\",\"02/20/16-19\",\"02/20/16-20\",\"02/20/16-21\",\"02/20/16-22\",\"02/20/16-23\",\"02/21/16-00\",\"02/21/16-01\",\"02/21/16-02\",\"02/21/16-03\",\"02/21/16-04\",\"02/21/16-05\",\"02/21/16-06\",\"02/21/16-07\",\"02/21/16-08\",\"02/21/16-09\",\"02/21/16-10\",\"02/21/16-11\",\"02/21/16-12\",\"02/21/16-13\",\"02/21/16-14\",\"02/21/16-15\",\"02/21/16-16\",\"02/21/16-17\",\"02/21/16-18\",\"02/21/16-19\",\"02/21/16-20\",\"02/21/16-21\",\"02/21/16-22\",\"02/21/16-23\",\"02/22/16-00\",\"02/22/16-01\",\"02/22/16-02\",\"02/22/16-03\",\"02/22/16-04\",\"02/22/16-05\",\"02/22/16-06\",\"02/22/16-07\",\"02/22/16-08\",\"02/22/16-09\",\"02/22/16-10\",\"02/22/16-11\",\"02/22/16-18\",\"02/22/16-19\",\"02/23/16-04\",\"02/23/16-05\",\"02/23/16-06\",\"02/23/16-07\",\"02/23/16-08\",\"02/23/16-09\",\"02/23/16-10\",\"02/23/16-11\",\"02/23/16-12\",\"02/23/16-13\",\"02/23/16-14\",\"02/23/16-15\",\"02/23/16-16\",\"02/23/16-17\",\"02/24/16-01\",\"02/24/16-02\",\"02/24/16-03\",\"02/24/16-04\",\"02/24/16-05\",\"02/24/16-06\",\"02/24/16-07\",\"02/24/16-08\",\"02/24/16-09\",\"02/24/16-10\",\"02/24/16-11\",\"02/24/16-12\",\"02/24/16-13\",\"02/24/16-14\",\"02/24/16-15\",\"02/24/16-16\",\"02/25/16-03\",\"02/25/16-04\",\"02/25/16-05\",\"02/25/16-06\",\"02/25/16-07\",\"02/25/16-08\",\"02/25/16-09\",\"02/25/16-10\",\"02/25/16-11\",\"02/25/16-12\",\"02/25/16-13\",\"02/25/16-14\",\"02/25/16-15\",\"02/25/16-16\",\"02/25/16-18\",\"02/25/16-20\",\"02/25/16-21\",\"02/25/16-23\",\"02/26/16-00\",\"02/26/16-01\",\"02/26/16-04\",\"02/26/16-05\",\"02/26/16-06\",\"02/26/16-19\",\"02/26/16-20\",\"02/26/16-21\",\"02/26/16-22\",\"02/26/16-23\",\"02/27/16-00\",\"02/27/16-01\",\"02/27/16-02\",\"02/27/16-03\",\"02/27/16-04\",\"02/27/16-05\",\"02/27/16-06\",\"02/27/16-07\",\"02/27/16-08\",\"02/27/16-09\",\"02/27/16-10\",\"02/27/16-11\",\"02/27/16-12\",\"02/27/16-13\",\"02/27/16-14\",\"02/27/16-15\",\"02/27/16-16\",\"02/27/16-17\",\"02/27/16-18\",\"02/27/16-19\",\"02/27/16-20\",\"02/27/16-21\",\"02/27/16-22\",\"02/27/16-23\",\"02/28/16-00\",\"02/28/16-01\",\"02/28/16-02\",\"02/28/16-03\",\"02/28/16-04\",\"02/28/16-05\",\"02/28/16-06\",\"02/28/16-07\",\"02/28/16-08\",\"02/28/16-09\",\"02/28/16-10\",\"02/28/16-11\",\"02/28/16-12\",\"02/28/16-13\",\"02/28/16-14\",\"02/28/16-15\",\"02/28/16-16\",\"02/28/16-17\",\"02/28/16-18\",\"02/28/16-19\",\"02/28/16-20\",\"02/28/16-21\",\"02/28/16-22\",\"02/28/16-23\",\"02/29/16-00\",\"02/29/16-01\",\"02/29/16-02\",\"02/29/16-03\",\"02/29/16-04\",\"02/29/16-05\",\"02/29/16-06\",\"02/29/16-07\",\"02/29/16-08\",\"02/29/16-09\",\"02/29/16-10\",\"02/29/16-11\",\"02/29/16-12\",\"02/29/16-13\",\"02/29/16-14\",\"02/29/16-15\",\"02/29/16-16\",\"02/29/16-19\",\"02/29/16-20\",\"02/29/16-21\",\"02/29/16-23\",\"03/01/16-00\",\"03/01/16-03\",\"03/01/16-04\",\"03/01/16-05\",\"03/01/16-06\",\"03/01/16-07\",\"03/01/16-08\",\"03/01/16-09\",\"03/01/16-10\",\"03/01/16-11\",\"03/01/16-12\",\"03/01/16-13\",\"03/01/16-14\",\"03/01/16-15\",\"03/01/16-16\",\"03/01/16-17\",\"03/01/16-19\",\"03/01/16-20\",\"03/01/16-21\",\"03/01/16-22\",\"03/01/16-23\",\"03/02/16-01\",\"03/02/16-02\",\"03/02/16-03\",\"03/02/16-04\",\"03/02/16-05\",\"03/02/16-06\",\"03/02/16-07\",\"03/02/16-08\",\"03/02/16-09\",\"03/02/16-10\",\"03/02/16-11\",\"03/02/16-12\",\"03/02/16-13\",\"03/02/16-14\",\"03/02/16-15\",\"03/02/16-19\",\"03/02/16-20\",\"03/02/16-21\",\"03/03/16-02\",\"03/03/16-03\",\"03/03/16-04\",\"03/03/16-05\",\"03/03/16-06\",\"03/03/16-07\",\"03/03/16-08\",\"03/03/16-09\",\"03/03/16-10\",\"03/03/16-11\",\"03/03/16-12\",\"03/03/16-13\",\"03/03/16-14\",\"03/03/16-15\",\"03/03/16-16\",\"03/03/16-17\",\"03/03/16-20\",\"03/03/16-21\",\"03/03/16-23\",\"03/04/16-00\",\"03/04/16-02\",\"03/04/16-03\",\"03/04/16-04\",\"03/04/16-05\",\"03/04/16-06\",\"03/04/16-07\",\"03/04/16-08\",\"03/04/16-09\",\"03/04/16-10\",\"03/04/16-11\",\"03/04/16-12\",\"03/04/16-13\",\"03/04/16-14\",\"03/04/16-15\",\"03/04/16-16\",\"03/04/16-17\",\"03/04/16-18\",\"03/04/16-19\",\"03/04/16-20\",\"03/04/16-21\",\"03/04/16-22\",\"03/04/16-23\",\"03/05/16-01\",\"03/05/16-02\",\"03/05/16-03\",\"03/05/16-04\",\"03/05/16-05\",\"03/05/16-06\",\"03/05/16-07\",\"03/05/16-08\",\"03/05/16-09\",\"03/05/16-10\",\"03/05/16-11\",\"03/05/16-12\",\"03/05/16-13\",\"03/05/16-14\",\"03/05/16-15\",\"03/05/16-16\",\"03/05/16-17\",\"03/05/16-18\",\"03/05/16-19\",\"03/05/16-20\",\"03/05/16-21\",\"03/05/16-22\",\"03/05/16-23\",\"03/06/16-00\",\"03/06/16-01\",\"03/06/16-02\",\"03/06/16-03\",\"03/06/16-04\",\"03/06/16-05\",\"03/06/16-06\",\"03/06/16-07\",\"03/06/16-08\",\"03/06/16-09\",\"03/06/16-10\",\"03/06/16-11\",\"03/06/16-12\",\"03/06/16-13\",\"03/06/16-14\",\"03/06/16-15\",\"03/06/16-16\",\"03/06/16-17\",\"03/06/16-18\",\"03/06/16-19\",\"03/06/16-20\",\"03/06/16-21\",\"03/06/16-22\",\"03/06/16-23\",\"03/07/16-00\",\"03/07/16-01\",\"03/07/16-02\",\"03/07/16-03\",\"03/07/16-04\",\"03/07/16-05\",\"03/07/16-06\",\"03/07/16-07\",\"03/07/16-08\",\"03/07/16-09\",\"03/07/16-10\",\"03/07/16-11\",\"03/07/16-12\",\"03/07/16-13\",\"03/07/16-14\",\"03/07/16-15\",\"03/07/16-16\",\"03/07/16-19\",\"03/07/16-20\",\"03/07/16-21\",\"03/08/16-03\",\"03/08/16-04\",\"03/08/16-05\",\"03/08/16-06\",\"03/08/16-07\",\"03/08/16-08\",\"03/08/16-09\",\"03/08/16-10\",\"03/08/16-11\",\"03/08/16-12\",\"03/08/16-13\",\"03/08/16-14\",\"03/08/16-15\",\"03/08/16-16\",\"03/08/16-20\",\"03/08/16-21\",\"03/09/16-08\",\"03/09/16-09\",\"03/09/16-10\",\"03/09/16-16\",\"03/09/16-19\",\"03/09/16-20\",\"03/09/16-21\",\"03/10/16-01\",\"03/10/16-03\",\"03/10/16-04\",\"03/10/16-05\",\"03/10/16-06\",\"03/10/16-07\",\"03/10/16-08\",\"03/10/16-09\",\"03/10/16-10\",\"03/10/16-11\",\"03/10/16-12\",\"03/10/16-13\",\"03/10/16-14\",\"03/10/16-15\",\"03/10/16-16\",\"03/10/16-17\",\"03/10/16-18\",\"03/10/16-19\",\"03/10/16-20\",\"03/10/16-21\",\"03/10/16-23\",\"03/11/16-02\",\"03/11/16-03\",\"03/11/16-04\",\"03/11/16-05\",\"03/11/16-06\",\"03/11/16-07\",\"03/11/16-08\",\"03/11/16-09\",\"03/11/16-10\",\"03/11/16-11\",\"03/11/16-12\",\"03/11/16-13\",\"03/11/16-14\",\"03/11/16-15\",\"03/11/16-16\",\"03/11/16-17\",\"03/11/16-18\",\"03/11/16-19\",\"03/11/16-20\",\"03/11/16-21\",\"03/11/16-22\",\"03/11/16-23\",\"03/12/16-00\",\"03/12/16-01\",\"03/12/16-02\",\"03/12/16-04\",\"03/12/16-05\",\"03/12/16-06\",\"03/12/16-07\",\"03/12/16-08\",\"03/12/16-09\",\"03/12/16-10\",\"03/12/16-11\",\"03/12/16-12\",\"03/12/16-13\",\"03/12/16-14\",\"03/12/16-15\",\"03/12/16-16\",\"03/12/16-17\",\"03/12/16-18\",\"03/12/16-19\",\"03/12/16-20\",\"03/12/16-21\",\"03/12/16-22\",\"03/12/16-23\",\"03/13/16-00\",\"03/13/16-01\",\"03/13/16-02\",\"03/13/16-03\",\"03/13/16-04\",\"03/13/16-05\",\"03/13/16-06\",\"03/13/16-07\",\"03/13/16-08\",\"03/13/16-09\",\"03/13/16-10\",\"03/13/16-11\",\"03/13/16-12\",\"03/13/16-13\",\"03/13/16-14\",\"03/13/16-15\",\"03/13/16-16\",\"03/13/16-17\",\"03/13/16-18\",\"03/13/16-19\",\"03/13/16-20\",\"03/13/16-21\",\"03/13/16-22\",\"03/13/16-23\",\"03/14/16-00\",\"03/14/16-01\",\"03/14/16-02\",\"03/14/16-03\",\"03/14/16-04\",\"03/14/16-05\",\"03/14/16-06\",\"03/14/16-07\",\"03/14/16-08\",\"03/14/16-09\",\"03/14/16-10\",\"03/14/16-11\",\"03/14/16-12\",\"03/14/16-13\",\"03/14/16-14\",\"03/14/16-15\",\"03/14/16-17\",\"03/14/16-18\",\"03/14/16-19\",\"03/14/16-20\",\"03/14/16-21\",\"03/14/16-22\",\"03/14/16-23\",\"03/15/16-02\",\"03/15/16-03\",\"03/15/16-04\",\"03/15/16-05\",\"03/15/16-06\",\"03/15/16-07\",\"03/15/16-08\",\"03/15/16-09\",\"03/15/16-10\",\"03/15/16-11\",\"03/15/16-12\",\"03/15/16-13\",\"03/15/16-14\",\"03/15/16-15\",\"03/15/16-16\",\"03/15/16-18\",\"03/15/16-19\",\"03/15/16-20\",\"03/16/16-00\",\"03/16/16-01\",\"03/16/16-02\",\"03/16/16-03\",\"03/16/16-04\",\"03/16/16-05\",\"03/16/16-06\",\"03/16/16-07\",\"03/16/16-08\",\"03/16/16-09\",\"03/16/16-10\",\"03/16/16-11\",\"03/16/16-12\",\"03/16/16-13\",\"03/16/16-14\",\"03/16/16-15\",\"03/16/16-17\",\"03/16/16-18\",\"03/16/16-19\",\"03/16/16-21\",\"03/16/16-22\",\"03/17/16-01\",\"03/17/16-02\",\"03/17/16-03\",\"03/17/16-04\",\"03/17/16-05\",\"03/17/16-06\",\"03/17/16-07\",\"03/17/16-08\",\"03/17/16-09\",\"03/17/16-10\",\"03/17/16-11\",\"03/17/16-12\",\"03/17/16-13\",\"03/17/16-14\",\"03/17/16-15\",\"03/17/16-16\",\"03/17/16-19\",\"03/17/16-20\",\"03/17/16-21\",\"03/17/16-22\",\"03/18/16-00\",\"03/18/16-01\",\"03/18/16-02\",\"03/18/16-03\",\"03/18/16-04\",\"03/18/16-05\",\"03/18/16-06\",\"03/18/16-07\",\"03/18/16-08\",\"03/18/16-09\",\"03/18/16-10\",\"03/18/16-11\",\"03/18/16-12\",\"03/18/16-13\",\"03/18/16-14\",\"03/18/16-15\",\"03/18/16-16\",\"03/18/16-17\",\"03/18/16-18\",\"03/18/16-19\",\"03/18/16-20\",\"03/18/16-21\",\"03/18/16-22\",\"03/18/16-23\",\"03/19/16-00\",\"03/19/16-01\",\"03/19/16-02\",\"03/19/16-03\",\"03/19/16-04\",\"03/19/16-05\",\"03/19/16-06\",\"03/19/16-07\",\"03/19/16-08\",\"03/19/16-09\",\"03/19/16-10\",\"03/19/16-11\",\"03/19/16-12\",\"03/19/16-13\",\"03/19/16-14\",\"03/19/16-15\",\"03/19/16-16\",\"03/19/16-17\",\"03/19/16-18\",\"03/19/16-19\",\"03/19/16-20\",\"03/19/16-21\",\"03/19/16-22\",\"03/19/16-23\",\"03/20/16-00\",\"03/20/16-01\",\"03/20/16-02\",\"03/20/16-03\",\"03/20/16-04\",\"03/20/16-05\",\"03/20/16-06\",\"03/20/16-07\",\"03/20/16-08\",\"03/20/16-09\",\"03/20/16-10\",\"03/20/16-11\",\"03/20/16-12\",\"03/20/16-13\",\"03/20/16-14\",\"03/20/16-15\",\"03/20/16-16\",\"03/20/16-17\",\"03/20/16-18\",\"03/20/16-19\",\"03/20/16-20\",\"03/20/16-21\",\"03/20/16-22\",\"03/20/16-23\",\"03/21/16-00\",\"03/21/16-01\",\"03/21/16-02\",\"03/21/16-03\",\"03/21/16-04\",\"03/21/16-05\",\"03/21/16-06\",\"03/21/16-07\",\"03/21/16-08\",\"03/21/16-09\",\"03/21/16-10\",\"03/21/16-11\",\"03/21/16-12\",\"03/21/16-13\",\"03/21/16-14\",\"03/21/16-15\",\"03/21/16-16\",\"03/21/16-17\",\"03/21/16-18\",\"03/21/16-19\",\"03/21/16-20\",\"03/21/16-21\",\"03/21/16-22\",\"03/21/16-23\",\"03/22/16-00\",\"03/22/16-01\",\"03/22/16-02\",\"03/22/16-03\",\"03/22/16-04\",\"03/22/16-05\",\"03/22/16-06\",\"03/22/16-07\",\"03/22/16-08\",\"03/22/16-09\",\"03/22/16-10\",\"03/22/16-11\",\"03/22/16-12\",\"03/22/16-13\",\"03/22/16-14\",\"03/22/16-15\",\"03/22/16-16\",\"03/22/16-17\",\"03/22/16-18\",\"03/22/16-19\",\"03/22/16-20\",\"03/22/16-21\",\"03/22/16-22\",\"03/22/16-23\",\"03/23/16-00\",\"03/23/16-01\",\"03/23/16-02\",\"03/23/16-03\",\"03/23/16-04\",\"03/23/16-05\",\"03/23/16-06\",\"03/23/16-07\",\"03/23/16-08\",\"03/23/16-09\",\"03/23/16-10\",\"03/23/16-11\",\"03/23/16-12\",\"03/23/16-18\",\"03/23/16-19\",\"03/23/16-20\",\"03/23/16-21\",\"03/23/16-22\",\"03/23/16-23\",\"03/24/16-00\",\"03/24/16-01\",\"03/24/16-02\",\"03/24/16-03\",\"03/24/16-04\",\"03/24/16-05\",\"03/24/16-06\",\"03/24/16-07\",\"03/24/16-08\",\"03/24/16-09\",\"03/24/16-10\",\"03/24/16-11\",\"03/24/16-12\",\"03/24/16-13\",\"03/24/16-14\",\"03/24/16-15\",\"03/24/16-16\",\"03/24/16-17\",\"03/24/16-18\",\"03/24/16-19\",\"03/24/16-20\",\"03/24/16-21\",\"03/24/16-22\",\"03/24/16-23\",\"03/25/16-00\",\"03/25/16-01\",\"03/25/16-02\",\"03/25/16-03\",\"03/25/16-04\",\"03/25/16-05\",\"03/25/16-06\",\"03/25/16-07\",\"03/25/16-08\",\"03/25/16-09\",\"03/25/16-18\",\"03/25/16-19\",\"03/25/16-20\",\"03/25/16-21\",\"03/25/16-22\",\"03/25/16-23\",\"03/26/16-00\",\"03/26/16-01\",\"03/26/16-02\",\"03/26/16-03\",\"03/26/16-04\",\"03/26/16-05\",\"03/26/16-06\",\"03/26/16-07\",\"03/26/16-08\",\"03/26/16-09\",\"03/26/16-10\",\"03/26/16-11\",\"03/26/16-12\",\"03/26/16-13\",\"03/26/16-14\",\"03/26/16-15\",\"03/26/16-16\",\"03/26/16-17\",\"03/26/16-18\",\"03/26/16-19\",\"03/26/16-20\",\"03/26/16-21\",\"03/26/16-22\",\"03/26/16-23\",\"03/27/16-00\",\"03/27/16-01\",\"03/27/16-02\",\"03/27/16-03\",\"03/27/16-04\",\"03/27/16-05\",\"03/27/16-06\",\"03/27/16-07\",\"03/27/16-17\",\"03/27/16-18\",\"03/27/16-19\",\"03/27/16-20\",\"03/27/16-21\",\"03/27/16-22\",\"03/27/16-23\",\"03/28/16-00\",\"03/28/16-01\",\"03/28/16-02\",\"03/28/16-03\",\"03/28/16-04\",\"03/28/16-05\",\"03/28/16-06\",\"03/28/16-07\",\"03/28/16-08\",\"03/28/16-09\",\"03/28/16-18\",\"03/28/16-19\",\"03/29/16-02\",\"03/29/16-03\",\"03/29/16-04\",\"03/29/16-05\",\"03/29/16-06\",\"03/29/16-07\",\"03/29/16-08\",\"03/29/16-09\",\"03/29/16-10\",\"03/29/16-11\",\"03/29/16-12\",\"03/29/16-13\",\"03/29/16-14\",\"03/29/16-15\",\"03/29/16-16\",\"03/29/16-19\",\"03/29/16-20\",\"03/30/16-00\",\"03/30/16-01\",\"03/30/16-15\",\"03/30/16-16\",\"03/30/16-17\",\"03/30/16-18\",\"03/30/16-19\",\"03/31/16-01\",\"03/31/16-02\",\"03/31/16-03\",\"03/31/16-04\",\"03/31/16-05\",\"03/31/16-06\",\"03/31/16-07\",\"03/31/16-08\",\"03/31/16-09\",\"03/31/16-10\",\"03/31/16-11\",\"03/31/16-12\",\"03/31/16-17\",\"03/31/16-21\",\"03/31/16-23\",\"04/01/16-00\",\"04/01/16-01\",\"04/01/16-02\",\"04/01/16-03\",\"04/01/16-04\",\"04/01/16-05\",\"04/01/16-06\",\"04/01/16-17\",\"04/01/16-20\",\"04/01/16-21\",\"04/01/16-22\",\"04/01/16-23\",\"04/02/16-00\",\"04/02/16-01\",\"04/02/16-02\",\"04/02/16-03\",\"04/02/16-04\",\"04/02/16-05\",\"04/02/16-06\",\"04/02/16-07\",\"04/02/16-08\",\"04/02/16-09\",\"04/02/16-10\",\"04/02/16-11\",\"04/02/16-19\",\"04/02/16-20\",\"04/02/16-21\",\"04/02/16-22\",\"04/02/16-23\",\"04/03/16-00\",\"04/03/16-01\",\"04/03/16-02\",\"04/03/16-03\",\"04/03/16-04\",\"04/03/16-05\",\"04/03/16-06\",\"04/03/16-07\",\"04/03/16-08\",\"04/03/16-09\",\"04/03/16-10\",\"04/03/16-18\",\"04/03/16-19\",\"04/03/16-20\",\"04/03/16-21\",\"04/04/16-00\",\"04/04/16-01\",\"04/04/16-02\",\"04/04/16-03\",\"04/04/16-04\",\"04/04/16-05\",\"04/04/16-06\",\"04/04/16-07\",\"04/04/16-08\",\"04/04/16-09\",\"04/04/16-10\",\"04/04/16-18\",\"04/04/16-19\",\"04/04/16-20\",\"04/04/16-22\",\"04/04/16-23\",\"04/05/16-02\",\"04/05/16-03\",\"04/05/16-04\",\"04/05/16-05\",\"04/05/16-06\",\"04/05/16-15\",\"04/05/16-16\",\"04/05/16-19\",\"04/05/16-20\",\"04/05/16-21\",\"04/05/16-22\",\"04/07/16-16\",\"04/07/16-19\",\"04/07/16-21\",\"04/07/16-23\",\"04/08/16-00\",\"04/08/16-01\",\"04/08/16-02\",\"04/08/16-03\",\"04/08/16-04\",\"04/08/16-05\",\"04/08/16-06\",\"04/08/16-07\",\"04/08/16-08\",\"04/08/16-09\",\"04/08/16-10\",\"04/08/16-11\",\"04/08/16-12\",\"04/08/16-13\",\"04/08/16-19\",\"04/08/16-20\",\"04/08/16-21\",\"04/08/16-22\",\"04/08/16-23\",\"04/09/16-00\",\"04/09/16-01\",\"04/09/16-02\",\"04/09/16-03\",\"04/09/16-04\",\"04/09/16-05\",\"04/09/16-06\",\"04/09/16-07\",\"04/09/16-08\",\"04/09/16-09\",\"04/09/16-10\",\"04/09/16-11\",\"04/09/16-19\",\"04/09/16-20\",\"04/09/16-21\",\"04/09/16-22\",\"04/09/16-23\",\"04/10/16-00\",\"04/10/16-01\",\"04/10/16-02\",\"04/10/16-03\",\"04/10/16-06\",\"04/11/16-01\",\"04/11/16-02\",\"04/11/16-03\",\"04/11/16-04\",\"04/11/16-05\",\"04/11/16-06\",\"04/11/16-07\",\"04/11/16-08\",\"04/11/16-09\",\"04/11/16-18\",\"04/11/16-19\",\"04/11/16-20\",\"04/11/16-21\",\"04/12/16-01\",\"04/12/16-02\",\"04/12/16-07\",\"04/12/16-08\",\"04/12/16-09\",\"04/12/16-11\",\"04/12/16-12\",\"04/12/16-13\",\"04/12/16-14\",\"04/12/16-19\",\"04/12/16-20\",\"04/12/16-22\",\"04/12/16-23\",\"04/13/16-00\",\"04/13/16-01\",\"04/13/16-04\",\"04/13/16-09\",\"04/13/16-11\",\"04/13/16-17\",\"04/13/16-18\",\"04/13/16-19\",\"04/14/16-01\",\"04/14/16-02\",\"04/14/16-03\",\"04/14/16-19\",\"04/14/16-20\",\"04/14/16-23\",\"04/15/16-00\",\"04/15/16-02\",\"04/15/16-06\",\"04/15/16-16\",\"04/15/16-17\",\"04/15/16-18\",\"04/15/16-19\",\"04/15/16-20\",\"04/15/16-21\",\"04/15/16-22\",\"04/15/16-23\",\"04/16/16-00\",\"04/16/16-01\",\"04/16/16-05\",\"04/16/16-06\",\"04/16/16-07\",\"04/16/16-08\",\"04/16/16-09\",\"04/16/16-10\",\"04/16/16-20\",\"04/16/16-21\",\"04/16/16-22\",\"04/16/16-23\",\"04/17/16-00\",\"04/17/16-01\",\"04/17/16-02\",\"04/17/16-03\",\"04/17/16-04\",\"04/17/16-05\",\"04/17/16-06\",\"04/17/16-07\",\"04/17/16-08\",\"04/17/16-09\",\"04/17/16-10\",\"04/17/16-11\",\"04/17/16-12\",\"04/17/16-13\",\"04/17/16-14\",\"04/17/16-15\",\"04/17/16-16\",\"04/17/16-18\",\"04/17/16-19\",\"04/17/16-20\",\"04/17/16-21\",\"04/17/16-22\",\"04/17/16-23\",\"04/18/16-00\",\"04/18/16-01\",\"04/18/16-02\",\"04/18/16-03\",\"04/18/16-04\",\"04/18/16-05\",\"04/18/16-06\",\"04/18/16-07\",\"04/18/16-08\",\"04/18/16-09\",\"04/18/16-10\",\"04/18/16-11\",\"04/18/16-12\",\"04/18/16-17\",\"04/18/16-21\",\"04/19/16-01\",\"04/19/16-02\",\"04/19/16-03\",\"04/19/16-04\",\"04/19/16-05\",\"04/19/16-06\",\"04/19/16-07\",\"04/19/16-08\",\"04/19/16-09\",\"04/19/16-10\",\"04/19/16-11\",\"04/19/16-20\",\"04/19/16-21\",\"04/20/16-00\",\"04/20/16-03\",\"04/20/16-07\",\"04/20/16-08\",\"04/20/16-09\",\"04/20/16-10\",\"04/20/16-11\",\"04/20/16-12\",\"04/20/16-13\",\"04/20/16-14\",\"04/20/16-15\",\"04/20/16-18\",\"04/20/16-19\",\"04/20/16-20\",\"04/21/16-02\",\"04/21/16-03\",\"04/21/16-09\",\"04/21/16-10\",\"04/21/16-11\",\"04/21/16-12\",\"04/21/16-13\",\"04/21/16-14\",\"04/21/16-15\",\"04/21/16-17\",\"04/21/16-18\",\"04/22/16-10\",\"04/22/16-11\",\"04/22/16-12\",\"04/22/16-13\",\"04/22/16-14\",\"04/22/16-15\",\"04/22/16-16\",\"04/22/16-17\",\"04/22/16-18\",\"04/22/16-19\",\"04/22/16-20\",\"04/22/16-21\",\"04/22/16-22\",\"04/22/16-23\",\"04/23/16-00\",\"04/23/16-01\",\"04/23/16-02\",\"04/23/16-03\",\"04/23/16-18\",\"04/23/16-19\",\"04/23/16-22\",\"04/23/16-23\",\"04/24/16-00\",\"04/24/16-01\",\"04/24/16-02\",\"04/24/16-03\",\"04/24/16-05\",\"04/24/16-06\",\"04/24/16-07\",\"04/24/16-08\",\"04/24/16-09\",\"04/24/16-16\",\"04/24/16-17\",\"04/24/16-18\",\"04/24/16-19\",\"04/24/16-20\",\"04/24/16-21\",\"04/24/16-22\",\"04/24/16-23\",\"04/25/16-00\",\"04/25/16-04\",\"04/25/16-05\",\"04/25/16-06\",\"04/25/16-07\",\"04/25/16-08\",\"04/25/16-09\",\"04/25/16-10\",\"04/25/16-11\",\"04/25/16-12\",\"04/25/16-13\",\"04/25/16-14\",\"04/25/16-15\",\"04/25/16-17\",\"04/25/16-18\",\"04/25/16-19\",\"04/25/16-20\",\"04/25/16-21\",\"04/26/16-00\",\"04/26/16-03\",\"04/26/16-04\",\"04/26/16-05\",\"04/26/16-09\",\"04/26/16-10\",\"04/26/16-11\",\"04/26/16-12\",\"04/26/16-13\",\"04/26/16-14\",\"04/26/16-15\",\"04/26/16-16\",\"04/26/16-19\",\"04/26/16-20\",\"04/27/16-06\",\"04/27/16-07\",\"04/27/16-08\",\"04/27/16-09\",\"04/27/16-10\",\"04/27/16-11\",\"04/27/16-12\",\"04/27/16-13\",\"04/27/16-14\",\"04/27/16-16\",\"04/27/16-18\",\"04/27/16-19\",\"04/27/16-20\",\"04/28/16-01\",\"04/28/16-02\",\"04/28/16-03\",\"04/28/16-04\",\"04/28/16-05\",\"04/28/16-07\",\"04/28/16-14\",\"04/28/16-15\",\"04/28/16-17\",\"04/28/16-19\",\"04/28/16-20\",\"04/28/16-21\",\"04/29/16-00\",\"04/29/16-05\",\"04/29/16-06\",\"04/29/16-07\",\"04/29/16-08\",\"04/29/16-09\",\"04/29/16-10\",\"04/29/16-11\",\"04/29/16-12\",\"04/29/16-13\",\"04/29/16-21\",\"04/29/16-22\",\"04/29/16-23\",\"04/30/16-00\",\"04/30/16-01\",\"04/30/16-02\",\"04/30/16-03\",\"04/30/16-04\",\"04/30/16-05\",\"04/30/16-06\",\"04/30/16-07\",\"04/30/16-15\",\"04/30/16-16\",\"04/30/16-17\",\"04/30/16-18\",\"04/30/16-19\",\"04/30/16-20\",\"04/30/16-21\",\"04/30/16-22\",\"04/30/16-23\",\"05/01/16-00\",\"05/01/16-01\",\"05/01/16-02\",\"05/01/16-03\",\"05/01/16-04\",\"05/01/16-05\",\"05/01/16-06\",\"05/01/16-07\",\"05/01/16-08\",\"05/01/16-09\",\"05/01/16-10\",\"05/01/16-23\",\"05/02/16-00\",\"05/02/16-01\",\"05/02/16-02\",\"05/02/16-03\",\"05/02/16-04\",\"05/02/16-05\",\"05/02/16-06\",\"05/02/16-07\",\"05/02/16-08\",\"05/02/16-09\",\"05/03/16-01\",\"05/03/16-02\",\"05/03/16-03\",\"05/03/16-04\",\"05/03/16-14\",\"05/03/16-15\",\"05/03/16-16\",\"05/03/16-17\",\"05/03/16-18\",\"05/03/16-19\",\"05/03/16-20\",\"05/03/16-21\",\"05/04/16-01\",\"05/04/16-02\",\"05/04/16-03\",\"05/04/16-04\",\"05/04/16-05\",\"05/04/16-06\",\"05/04/16-07\",\"05/04/16-08\",\"05/04/16-09\",\"05/04/16-10\",\"05/04/16-11\",\"05/04/16-12\",\"05/04/16-13\",\"05/04/16-14\",\"05/04/16-15\",\"05/04/16-18\",\"05/05/16-00\",\"05/05/16-12\",\"05/05/16-13\",\"05/05/16-14\",\"05/05/16-15\",\"05/05/16-16\",\"05/05/16-18\",\"05/05/16-19\",\"05/05/16-23\",\"05/06/16-00\",\"05/06/16-01\",\"05/06/16-03\",\"05/06/16-04\",\"05/06/16-05\",\"05/06/16-06\",\"05/06/16-07\",\"05/06/16-08\",\"05/06/16-09\",\"05/06/16-10\",\"05/06/16-11\",\"05/06/16-12\",\"05/06/16-13\",\"05/06/16-14\",\"05/06/16-15\",\"05/06/16-16\",\"05/06/16-17\",\"05/06/16-18\",\"05/06/16-19\",\"05/06/16-20\",\"05/06/16-21\",\"05/06/16-22\",\"05/07/16-00\",\"05/07/16-01\",\"05/07/16-02\",\"05/07/16-03\",\"05/07/16-04\",\"05/07/16-05\",\"05/07/16-06\",\"05/07/16-07\",\"05/07/16-09\",\"05/07/16-10\",\"05/07/16-17\",\"05/07/16-18\",\"05/07/16-19\",\"05/07/16-20\",\"05/07/16-21\",\"05/07/16-22\",\"05/07/16-23\",\"05/08/16-00\",\"05/08/16-01\",\"05/08/16-02\",\"05/08/16-03\",\"05/08/16-04\",\"05/08/16-05\",\"05/08/16-06\",\"05/08/16-07\",\"05/08/16-08\",\"05/08/16-09\",\"05/08/16-16\",\"05/08/16-17\",\"05/08/16-18\",\"05/08/16-19\",\"05/08/16-20\",\"05/08/16-21\",\"05/08/16-22\",\"05/08/16-23\",\"05/09/16-00\",\"05/09/16-01\",\"05/09/16-02\",\"05/09/16-03\",\"05/09/16-04\",\"05/09/16-05\",\"05/09/16-06\",\"05/09/16-07\",\"05/09/16-08\",\"05/09/16-14\",\"05/09/16-17\",\"05/09/16-19\",\"05/09/16-20\",\"05/09/16-21\",\"05/09/16-22\",\"05/09/16-23\",\"05/10/16-00\",\"05/10/16-01\",\"05/10/16-02\",\"05/10/16-03\",\"05/10/16-04\",\"05/10/16-05\",\"05/10/16-06\",\"05/10/16-07\",\"05/10/16-08\",\"05/10/16-09\",\"05/10/16-19\",\"05/10/16-20\",\"05/10/16-21\",\"05/11/16-03\",\"05/11/16-04\",\"05/11/16-05\",\"05/11/16-06\",\"05/11/16-07\",\"05/11/16-20\",\"05/11/16-21\",\"05/12/16-01\",\"05/12/16-02\",\"05/12/16-03\",\"05/12/16-04\",\"05/12/16-05\",\"05/12/16-07\",\"05/12/16-08\",\"05/12/16-09\",\"05/12/16-10\",\"05/12/16-11\",\"05/12/16-12\",\"05/12/16-13\",\"05/12/16-14\",\"05/12/16-15\",\"05/12/16-18\",\"05/12/16-19\",\"05/12/16-21\",\"05/12/16-22\",\"05/13/16-02\",\"05/13/16-03\",\"05/13/16-04\",\"05/13/16-05\",\"05/13/16-07\",\"05/13/16-15\",\"05/13/16-16\",\"05/13/16-17\",\"05/13/16-18\",\"05/13/16-19\",\"05/13/16-20\",\"05/13/16-21\",\"05/13/16-22\",\"05/13/16-23\",\"05/14/16-00\",\"05/14/16-01\",\"05/14/16-02\",\"05/14/16-03\",\"05/14/16-04\",\"05/14/16-05\",\"05/14/16-06\",\"05/14/16-07\",\"05/14/16-08\",\"05/14/16-09\",\"05/14/16-10\",\"05/14/16-17\",\"05/14/16-19\",\"05/14/16-20\",\"05/15/16-00\",\"05/15/16-01\",\"05/15/16-02\",\"05/15/16-03\",\"05/15/16-04\",\"05/15/16-06\",\"05/15/16-07\",\"05/15/16-08\",\"05/15/16-16\",\"05/15/16-17\",\"05/15/16-18\",\"05/15/16-19\",\"05/15/16-20\",\"05/15/16-21\",\"05/15/16-22\",\"05/15/16-23\",\"05/16/16-00\",\"05/16/16-01\",\"05/16/16-02\",\"05/16/16-03\",\"05/16/16-06\",\"05/16/16-07\",\"05/16/16-08\",\"05/16/16-09\",\"05/16/16-10\",\"05/17/16-00\",\"05/17/16-01\",\"05/17/16-09\",\"05/17/16-10\",\"05/17/16-12\",\"05/17/16-13\",\"05/18/16-00\",\"05/18/16-01\",\"05/18/16-02\",\"05/18/16-03\",\"05/18/16-04\",\"05/18/16-05\",\"05/18/16-06\",\"05/18/16-08\",\"05/19/16-04\",\"05/19/16-05\",\"05/19/16-06\",\"05/19/16-07\",\"05/19/16-08\",\"05/19/16-09\",\"05/19/16-12\",\"05/19/16-13\",\"05/19/16-23\",\"05/20/16-00\",\"05/20/16-05\",\"05/21/16-00\",\"05/21/16-16\",\"05/21/16-17\",\"05/21/16-23\",\"05/22/16-00\",\"05/22/16-04\",\"05/22/16-05\",\"05/22/16-15\",\"05/22/16-16\",\"05/22/16-17\",\"05/22/16-18\",\"05/22/16-19\",\"05/22/16-20\",\"05/22/16-21\",\"05/22/16-22\",\"05/23/16-00\",\"05/23/16-01\",\"05/23/16-02\",\"05/23/16-03\",\"05/23/16-04\",\"05/24/16-00\",\"05/24/16-04\",\"05/24/16-05\",\"05/24/16-06\",\"05/24/16-07\",\"05/24/16-08\",\"05/24/16-09\",\"05/24/16-10\",\"05/24/16-11\",\"05/24/16-12\",\"05/24/16-13\",\"05/25/16-02\",\"05/25/16-03\",\"05/25/16-04\",\"05/25/16-05\",\"05/25/16-06\",\"05/25/16-12\",\"05/25/16-13\",\"05/25/16-14\",\"05/25/16-23\",\"05/26/16-00\",\"05/26/16-01\",\"05/26/16-02\",\"05/26/16-03\",\"05/26/16-04\",\"05/27/16-00\",\"05/27/16-01\",\"05/27/16-02\",\"05/27/16-05\",\"05/27/16-06\",\"05/28/16-00\",\"05/28/16-01\",\"05/28/16-02\",\"05/28/16-03\",\"05/28/16-04\",\"05/28/16-05\",\"05/28/16-06\",\"05/28/16-07\",\"05/28/16-17\",\"05/28/16-18\",\"05/28/16-19\",\"05/28/16-20\",\"05/28/16-21\",\"05/28/16-23\",\"05/29/16-01\",\"05/29/16-02\",\"05/29/16-03\",\"05/29/16-04\",\"05/29/16-05\",\"05/29/16-06\",\"05/29/16-07\",\"05/29/16-15\",\"05/29/16-16\",\"05/29/16-18\",\"05/29/16-19\",\"05/29/16-20\",\"05/29/16-21\",\"05/29/16-22\",\"05/29/16-23\",\"05/30/16-00\",\"05/30/16-01\",\"05/30/16-04\",\"05/30/16-05\",\"05/30/16-06\",\"05/30/16-07\",\"05/30/16-15\",\"05/30/16-16\",\"05/30/16-17\",\"05/30/16-18\",\"05/30/16-19\",\"05/30/16-20\",\"05/30/16-21\",\"05/30/16-22\",\"05/30/16-23\",\"05/31/16-04\",\"05/31/16-05\",\"05/31/16-06\",\"05/31/16-07\",\"06/01/16-01\",\"06/01/16-02\",\"06/01/16-04\",\"06/01/16-05\",\"06/02/16-00\",\"06/02/16-01\",\"06/02/16-05\",\"06/02/16-06\",\"06/02/16-08\",\"06/02/16-09\",\"06/02/16-10\",\"06/03/16-02\",\"06/03/16-03\",\"06/03/16-04\",\"06/03/16-05\",\"06/03/16-06\",\"06/03/16-07\",\"06/04/16-00\",\"06/04/16-01\",\"06/04/16-02\",\"06/04/16-03\",\"06/04/16-04\",\"06/04/16-05\",\"06/04/16-06\",\"06/04/16-07\",\"06/04/16-08\",\"06/04/16-09\",\"06/04/16-10\",\"06/04/16-11\",\"06/04/16-12\",\"06/04/16-13\",\"06/04/16-14\",\"06/04/16-15\",\"06/04/16-16\",\"06/04/16-17\",\"06/04/16-18\",\"06/04/16-19\",\"06/04/16-20\",\"06/04/16-21\",\"06/04/16-22\",\"06/04/16-23\",\"06/05/16-00\",\"06/05/16-01\",\"06/05/16-02\",\"06/05/16-03\",\"06/05/16-04\",\"06/05/16-05\",\"06/05/16-06\",\"06/05/16-07\",\"06/05/16-08\",\"06/05/16-09\",\"06/05/16-10\",\"06/05/16-11\",\"06/05/16-12\",\"06/05/16-13\",\"06/05/16-14\",\"06/05/16-15\",\"06/05/16-16\",\"06/05/16-17\",\"06/05/16-18\",\"06/05/16-19\",\"06/05/16-20\",\"06/05/16-21\",\"06/05/16-22\",\"06/05/16-23\",\"06/06/16-00\",\"06/06/16-01\",\"06/06/16-02\",\"06/06/16-03\",\"06/06/16-04\",\"06/06/16-05\",\"06/06/16-06\",\"06/06/16-07\",\"06/07/16-01\",\"06/07/16-02\",\"06/07/16-03\",\"06/07/16-06\",\"06/07/16-13\",\"06/08/16-02\",\"06/08/16-03\",\"06/08/16-04\",\"06/08/16-05\",\"06/08/16-06\",\"06/08/16-07\",\"06/08/16-08\",\"06/08/16-09\",\"06/08/16-10\",\"06/08/16-11\",\"06/08/16-12\",\"06/08/16-13\",\"06/08/16-14\",\"06/08/16-15\",\"06/08/16-16\",\"06/08/16-17\",\"06/08/16-18\",\"06/08/16-19\",\"06/08/16-20\",\"06/08/16-21\",\"06/08/16-22\",\"06/08/16-23\",\"06/09/16-00\",\"06/09/16-01\",\"06/09/16-02\",\"06/09/16-03\",\"06/09/16-04\",\"06/10/16-01\",\"06/10/16-02\",\"06/10/16-03\",\"06/10/16-04\",\"06/10/16-12\",\"06/10/16-13\",\"06/11/16-01\",\"06/11/16-02\",\"06/11/16-04\",\"06/11/16-05\",\"06/11/16-06\",\"06/11/16-07\",\"06/11/16-08\",\"06/11/16-09\",\"06/11/16-10\",\"06/11/16-11\",\"06/11/16-12\",\"06/11/16-13\",\"06/11/16-14\",\"06/11/16-15\",\"06/11/16-16\",\"06/11/16-17\",\"06/11/16-18\",\"06/11/16-19\",\"06/11/16-20\",\"06/11/16-21\",\"06/11/16-22\",\"06/11/16-23\",\"06/12/16-00\",\"06/12/16-01\",\"06/12/16-02\",\"06/12/16-03\",\"06/12/16-04\",\"06/12/16-05\",\"06/12/16-15\",\"06/12/16-16\",\"06/12/16-17\",\"06/12/16-18\",\"06/12/16-19\",\"06/12/16-20\",\"06/12/16-21\",\"06/12/16-22\",\"06/12/16-23\",\"06/13/16-00\",\"06/13/16-01\",\"06/13/16-02\",\"06/13/16-03\",\"06/13/16-04\",\"06/13/16-05\",\"06/13/16-06\",\"06/13/16-07\",\"06/13/16-08\",\"06/13/16-09\",\"06/13/16-10\",\"06/13/16-11\",\"06/13/16-12\",\"06/13/16-13\",\"06/13/16-14\",\"06/13/16-15\",\"06/13/16-16\",\"06/13/16-17\",\"06/13/16-18\",\"06/13/16-19\",\"06/13/16-20\",\"06/13/16-21\",\"06/13/16-22\",\"06/13/16-23\",\"06/14/16-00\",\"06/14/16-01\",\"06/14/16-02\",\"06/14/16-03\",\"06/14/16-04\",\"06/14/16-05\",\"06/14/16-06\",\"06/14/16-07\",\"06/14/16-08\",\"06/14/16-09\",\"06/14/16-10\",\"06/14/16-11\",\"06/14/16-12\",\"06/14/16-13\",\"06/14/16-14\",\"06/14/16-15\",\"06/14/16-16\",\"06/14/16-17\",\"06/14/16-18\",\"06/14/16-19\",\"06/14/16-20\",\"06/14/16-21\",\"06/14/16-22\",\"06/14/16-23\",\"06/15/16-00\",\"06/15/16-01\",\"06/15/16-02\",\"06/15/16-03\",\"06/15/16-04\",\"06/15/16-05\",\"06/15/16-06\",\"06/15/16-07\",\"06/15/16-08\",\"06/15/16-09\",\"06/15/16-10\",\"06/15/16-11\",\"06/15/16-12\",\"06/15/16-13\",\"06/15/16-14\",\"06/15/16-15\",\"06/15/16-16\",\"06/15/16-17\",\"06/15/16-18\",\"06/15/16-19\",\"06/15/16-20\",\"06/15/16-21\",\"06/15/16-22\",\"06/15/16-23\",\"06/16/16-00\",\"06/16/16-01\",\"06/16/16-02\",\"06/16/16-03\",\"06/16/16-04\",\"06/16/16-05\",\"06/16/16-06\",\"06/16/16-07\",\"06/16/16-08\",\"06/16/16-09\",\"06/16/16-10\",\"06/16/16-11\",\"06/16/16-12\",\"06/16/16-13\",\"06/16/16-14\",\"06/16/16-15\",\"06/16/16-16\",\"06/16/16-17\",\"06/16/16-18\",\"06/16/16-19\",\"06/16/16-20\",\"06/16/16-21\",\"06/16/16-22\",\"06/16/16-23\",\"06/17/16-00\",\"06/17/16-01\",\"06/17/16-02\",\"06/17/16-03\",\"06/17/16-04\",\"06/17/16-05\",\"06/17/16-06\",\"06/17/16-07\",\"06/17/16-08\",\"06/17/16-09\",\"06/17/16-10\",\"06/17/16-11\",\"06/17/16-12\",\"06/17/16-13\",\"06/17/16-14\",\"06/17/16-15\",\"06/17/16-16\",\"06/17/16-17\",\"06/17/16-18\",\"06/17/16-19\",\"06/17/16-20\",\"06/17/16-21\",\"06/17/16-22\",\"06/17/16-23\",\"06/18/16-00\",\"06/18/16-01\",\"06/18/16-02\",\"06/18/16-03\",\"06/18/16-04\",\"06/18/16-05\",\"06/18/16-06\",\"06/18/16-07\",\"06/18/16-08\",\"06/18/16-09\",\"06/18/16-10\",\"06/18/16-11\",\"06/18/16-12\",\"06/18/16-13\",\"06/18/16-14\",\"06/18/16-15\",\"06/18/16-16\",\"06/18/16-17\",\"06/18/16-18\",\"06/18/16-19\",\"06/18/16-20\",\"06/18/16-21\",\"06/18/16-22\",\"06/18/16-23\",\"06/19/16-00\",\"06/19/16-01\",\"06/19/16-02\",\"06/19/16-03\",\"06/19/16-04\",\"06/19/16-05\",\"06/19/16-06\",\"06/19/16-07\",\"06/19/16-08\",\"06/19/16-09\",\"06/19/16-10\",\"06/19/16-11\",\"06/19/16-12\",\"06/19/16-13\",\"06/19/16-14\",\"06/19/16-15\",\"06/19/16-16\",\"06/19/16-17\",\"06/19/16-18\",\"06/19/16-19\",\"06/19/16-20\",\"06/19/16-21\",\"06/19/16-22\",\"06/19/16-23\",\"06/20/16-00\",\"06/20/16-01\",\"06/20/16-02\",\"06/20/16-03\",\"06/20/16-04\",\"06/20/16-05\",\"06/20/16-06\",\"06/20/16-07\",\"06/20/16-08\",\"06/20/16-09\",\"06/20/16-10\",\"06/20/16-11\",\"06/20/16-12\",\"06/20/16-13\",\"06/20/16-14\",\"06/20/16-15\",\"06/20/16-16\",\"06/20/16-17\",\"06/20/16-18\",\"06/20/16-19\",\"06/20/16-20\",\"06/20/16-21\",\"06/20/16-22\",\"06/20/16-23\",\"06/21/16-00\",\"06/21/16-01\",\"06/21/16-02\",\"06/21/16-03\",\"06/21/16-04\",\"06/21/16-05\",\"06/21/16-06\",\"06/21/16-07\",\"06/21/16-08\",\"06/21/16-09\",\"06/21/16-10\",\"06/21/16-11\",\"06/21/16-12\",\"06/21/16-13\",\"06/21/16-14\",\"06/21/16-15\",\"06/21/16-16\",\"06/21/16-17\",\"06/21/16-18\",\"06/21/16-19\",\"06/21/16-20\",\"06/21/16-21\",\"06/21/16-22\",\"06/21/16-23\",\"06/22/16-00\",\"06/22/16-01\",\"06/22/16-02\",\"06/22/16-03\",\"06/22/16-04\",\"06/22/16-05\",\"06/22/16-06\",\"06/22/16-07\",\"06/22/16-08\",\"06/22/16-09\",\"06/22/16-10\",\"06/22/16-11\",\"06/22/16-12\",\"06/22/16-13\",\"06/22/16-14\",\"06/22/16-15\",\"06/22/16-16\",\"06/22/16-17\",\"06/22/16-18\",\"06/22/16-19\",\"06/22/16-20\",\"06/22/16-21\",\"06/22/16-22\",\"06/22/16-23\",\"06/23/16-00\",\"06/23/16-01\",\"06/23/16-02\",\"06/23/16-03\",\"06/23/16-04\",\"06/23/16-05\",\"06/23/16-06\",\"06/23/16-07\",\"06/23/16-08\",\"06/23/16-09\",\"06/23/16-10\",\"06/23/16-11\",\"06/23/16-12\",\"06/23/16-13\",\"06/23/16-14\",\"06/23/16-15\",\"06/23/16-16\",\"06/23/16-17\",\"06/23/16-18\",\"06/23/16-19\",\"06/23/16-20\",\"06/23/16-21\",\"06/23/16-22\",\"06/23/16-23\",\"06/24/16-00\",\"06/24/16-01\",\"06/24/16-02\",\"06/24/16-03\",\"06/24/16-04\",\"06/24/16-05\",\"06/24/16-06\",\"06/24/16-07\",\"06/24/16-08\",\"06/24/16-09\",\"06/24/16-10\",\"06/24/16-11\",\"06/24/16-12\",\"06/24/16-13\",\"06/24/16-14\",\"06/24/16-15\",\"06/24/16-16\",\"06/24/16-17\",\"06/24/16-18\",\"06/24/16-19\",\"06/24/16-20\",\"06/24/16-21\",\"06/24/16-22\",\"06/24/16-23\",\"06/25/16-00\",\"06/25/16-01\",\"06/25/16-02\",\"06/25/16-03\",\"06/25/16-04\",\"06/25/16-05\",\"06/25/16-06\",\"06/25/16-07\",\"06/25/16-08\",\"06/25/16-09\",\"06/25/16-10\",\"06/25/16-11\",\"06/25/16-12\",\"06/25/16-13\",\"06/25/16-14\",\"06/25/16-15\",\"06/25/16-16\",\"06/25/16-17\",\"06/28/16-02\",\"06/28/16-03\",\"06/28/16-04\",\"06/28/16-05\",\"06/28/16-06\",\"06/28/16-07\",\"06/28/16-08\",\"06/28/16-09\",\"06/28/16-10\",\"06/28/16-11\",\"06/28/16-12\",\"06/28/16-13\",\"06/28/16-14\",\"06/28/16-15\",\"06/28/16-16\",\"06/28/16-17\",\"06/28/16-18\",\"06/28/16-19\",\"06/28/16-20\",\"06/28/16-21\",\"06/28/16-22\",\"06/28/16-23\",\"06/29/16-00\",\"06/29/16-01\",\"06/29/16-02\",\"06/29/16-03\",\"06/29/16-04\",\"06/29/16-05\",\"06/29/16-06\",\"06/29/16-07\",\"06/29/16-08\",\"06/29/16-09\",\"06/29/16-10\",\"06/29/16-11\",\"06/29/16-12\",\"06/29/16-13\",\"06/29/16-14\",\"06/29/16-15\",\"06/29/16-16\",\"06/29/16-17\",\"06/29/16-18\",\"06/29/16-19\",\"06/29/16-20\",\"06/29/16-21\",\"06/29/16-22\",\"06/29/16-23\",\"06/30/16-00\",\"06/30/16-01\",\"06/30/16-02\",\"06/30/16-03\",\"06/30/16-04\",\"06/30/16-05\",\"06/30/16-06\",\"06/30/16-07\",\"06/30/16-08\",\"06/30/16-09\",\"06/30/16-10\",\"06/30/16-11\",\"06/30/16-12\",\"06/30/16-13\",\"06/30/16-14\",\"06/30/16-15\",\"06/30/16-16\",\"06/30/16-17\",\"06/30/16-18\",\"06/30/16-19\",\"06/30/16-20\",\"06/30/16-21\",\"06/30/16-22\",\"06/30/16-23\",\"07/01/16-00\",\"07/01/16-01\",\"07/01/16-02\",\"07/01/16-03\",\"07/01/16-04\",\"07/01/16-05\",\"07/01/16-06\",\"07/01/16-07\",\"07/01/16-08\",\"07/01/16-09\",\"07/01/16-10\",\"07/01/16-11\",\"07/01/16-12\",\"07/01/16-13\",\"07/01/16-14\",\"07/01/16-15\",\"07/01/16-16\",\"07/01/16-17\",\"07/01/16-18\",\"07/01/16-19\",\"07/01/16-20\",\"07/01/16-21\",\"07/02/16-02\",\"07/02/16-03\",\"07/02/16-05\",\"07/02/16-07\",\"07/02/16-08\",\"07/02/16-09\",\"07/02/16-10\",\"07/02/16-11\",\"07/02/16-12\",\"07/02/16-13\",\"07/02/16-14\",\"07/02/16-15\",\"07/02/16-16\",\"07/02/16-17\",\"07/02/16-18\",\"07/02/16-19\",\"07/02/16-20\",\"07/02/16-21\",\"07/02/16-22\",\"07/02/16-23\",\"07/03/16-00\",\"07/03/16-01\",\"07/03/16-02\",\"07/03/16-03\",\"07/03/16-04\",\"07/03/16-05\",\"07/03/16-06\",\"07/03/16-07\",\"07/03/16-08\",\"07/03/16-09\",\"07/03/16-10\",\"07/03/16-11\",\"07/03/16-12\",\"07/03/16-13\",\"07/03/16-14\",\"07/03/16-15\",\"07/03/16-16\",\"07/03/16-17\",\"07/03/16-18\",\"07/03/16-19\",\"07/03/16-20\",\"07/03/16-21\",\"07/03/16-22\",\"07/03/16-23\",\"07/04/16-00\",\"07/04/16-01\",\"07/04/16-02\",\"07/04/16-03\",\"07/04/16-04\",\"07/04/16-05\",\"07/04/16-06\",\"07/04/16-07\",\"07/04/16-08\",\"07/04/16-09\",\"07/04/16-10\",\"07/04/16-11\",\"07/04/16-12\",\"07/04/16-13\",\"07/04/16-14\",\"07/04/16-15\",\"07/04/16-16\",\"07/04/16-17\",\"07/04/16-18\",\"07/04/16-19\",\"07/04/16-20\",\"07/04/16-21\",\"07/04/16-22\",\"07/04/16-23\",\"07/05/16-00\",\"07/05/16-01\",\"07/05/16-02\",\"07/05/16-03\",\"07/05/16-04\",\"07/05/16-05\",\"07/05/16-06\",\"07/05/16-07\",\"07/05/16-08\",\"07/05/16-09\",\"07/05/16-10\",\"07/05/16-11\",\"07/05/16-12\",\"07/05/16-13\",\"07/05/16-14\",\"07/05/16-15\",\"07/05/16-16\",\"07/05/16-17\",\"07/05/16-18\",\"07/05/16-19\",\"07/05/16-20\",\"07/05/16-21\",\"07/05/16-22\",\"07/05/16-23\",\"07/06/16-00\",\"07/06/16-01\",\"07/06/16-01\",\"07/06/16-02\",\"07/06/16-03\",\"07/06/16-04\",\"07/06/16-05\",\"07/06/16-06\",\"07/06/16-07\",\"07/06/16-08\",\"07/06/16-09\",\"07/06/16-10\",\"07/06/16-11\",\"07/06/16-12\",\"07/06/16-13\",\"07/06/16-14\",\"07/06/16-15\",\"07/06/16-16\",\"07/06/16-17\",\"07/06/16-18\",\"07/06/16-19\",\"07/06/16-20\",\"07/06/16-21\",\"07/06/16-22\",\"07/06/16-23\",\"07/07/16-00\",\"07/07/16-01\",\"07/07/16-02\",\"07/07/16-03\",\"07/07/16-04\",\"07/07/16-05\",\"07/07/16-06\",\"07/07/16-07\",\"07/07/16-08\",\"07/07/16-09\",\"07/07/16-10\",\"07/07/16-11\",\"07/07/16-12\",\"07/07/16-13\",\"07/07/16-14\",\"07/07/16-15\",\"07/07/16-16\",\"07/07/16-17\",\"07/07/16-18\",\"07/07/16-19\",\"07/07/16-20\",\"07/07/16-21\",\"07/07/16-22\",\"07/07/16-23\",\"07/08/16-00\",\"07/08/16-01\",\"07/08/16-02\",\"07/08/16-03\",\"07/08/16-04\",\"07/08/16-05\",\"07/08/16-06\",\"07/08/16-07\",\"07/08/16-08\",\"07/08/16-09\",\"07/08/16-10\",\"07/08/16-11\",\"07/08/16-12\",\"07/08/16-13\",\"07/08/16-14\",\"07/08/16-15\",\"07/08/16-16\",\"07/08/16-17\",\"07/08/16-18\",\"07/08/16-19\",\"07/08/16-20\",\"07/08/16-21\",\"07/08/16-22\",\"07/08/16-23\",\"07/09/16-00\",\"07/09/16-01\",\"07/09/16-02\",\"07/09/16-03\",\"07/09/16-04\",\"07/09/16-05\",\"07/09/16-06\",\"07/09/16-07\",\"07/09/16-08\",\"07/09/16-09\",\"07/09/16-10\",\"07/09/16-11\",\"07/09/16-12\",\"07/09/16-13\",\"07/09/16-14\",\"07/09/16-15\",\"07/09/16-16\",\"07/09/16-17\",\"07/09/16-18\",\"07/09/16-19\",\"07/09/16-20\",\"07/09/16-21\",\"07/09/16-22\",\"07/09/16-23\",\"07/10/16-00\",\"07/10/16-01\",\"07/10/16-02\",\"07/10/16-03\",\"07/10/16-04\",\"07/10/16-05\",\"07/10/16-06\",\"07/10/16-07\",\"07/10/16-08\",\"07/10/16-09\",\"07/10/16-10\",\"07/10/16-11\",\"07/10/16-12\",\"07/10/16-13\",\"07/10/16-14\",\"07/10/16-15\",\"07/10/16-16\",\"07/10/16-17\",\"07/10/16-18\",\"07/10/16-19\",\"07/10/16-20\",\"07/10/16-21\",\"07/10/16-22\",\"07/10/16-23\",\"07/11/16-00\",\"07/11/16-01\",\"07/11/16-02\",\"07/11/16-03\",\"07/11/16-04\",\"07/11/16-05\",\"07/11/16-06\",\"07/11/16-07\",\"07/11/16-08\",\"07/11/16-09\",\"07/11/16-10\",\"07/11/16-11\",\"07/11/16-12\",\"07/11/16-13\",\"07/11/16-14\",\"07/11/16-15\",\"07/11/16-16\",\"07/11/16-17\",\"07/11/16-18\",\"07/11/16-19\",\"07/11/16-20\",\"07/11/16-21\",\"07/11/16-22\",\"07/11/16-23\",\"07/12/16-00\",\"07/12/16-01\",\"07/12/16-02\",\"07/12/16-03\",\"07/12/16-04\",\"07/12/16-05\",\"07/12/16-06\",\"07/12/16-07\",\"07/12/16-08\",\"07/12/16-09\",\"07/12/16-10\",\"07/12/16-11\",\"07/12/16-12\",\"07/12/16-13\",\"07/12/16-14\",\"07/12/16-15\",\"07/12/16-16\",\"07/12/16-17\",\"07/12/16-18\",\"07/12/16-19\",\"07/12/16-20\",\"07/12/16-21\",\"07/12/16-22\",\"07/12/16-23\",\"07/13/16-00\",\"07/13/16-01\",\"07/13/16-02\",\"07/13/16-03\",\"07/13/16-04\",\"07/13/16-05\",\"07/13/16-06\",\"07/13/16-07\",\"07/13/16-08\",\"07/13/16-09\",\"07/13/16-10\",\"07/13/16-11\",\"07/13/16-12\",\"07/13/16-13\",\"07/13/16-14\",\"07/13/16-15\",\"07/13/16-16\",\"07/13/16-17\",\"07/13/16-18\",\"07/13/16-19\",\"07/13/16-20\",\"07/13/16-21\",\"07/13/16-22\",\"07/13/16-23\",\"07/14/16-00\",\"07/14/16-01\",\"07/14/16-02\",\"07/14/16-03\",\"07/14/16-04\",\"07/14/16-05\",\"07/14/16-06\",\"07/14/16-07\",\"07/14/16-08\",\"07/14/16-09\",\"07/14/16-10\",\"07/14/16-11\",\"07/14/16-12\",\"07/14/16-13\",\"07/14/16-14\",\"07/14/16-15\",\"07/14/16-16\",\"07/14/16-17\",\"07/14/16-18\",\"07/14/16-19\",\"07/14/16-20\",\"07/14/16-21\",\"07/14/16-22\",\"07/14/16-23\",\"07/15/16-00\",\"07/15/16-01\",\"07/15/16-02\",\"07/15/16-03\",\"07/15/16-04\",\"07/15/16-05\",\"07/15/16-06\",\"07/15/16-07\",\"07/15/16-08\",\"07/15/16-09\",\"07/15/16-10\",\"07/15/16-11\",\"07/15/16-12\",\"07/15/16-13\",\"07/15/16-14\",\"07/15/16-15\",\"07/15/16-16\",\"07/15/16-17\",\"07/15/16-18\",\"07/15/16-19\",\"07/15/16-20\",\"07/15/16-21\",\"07/15/16-22\",\"07/15/16-23\",\"07/16/16-00\",\"07/16/16-01\",\"07/16/16-02\",\"07/16/16-03\",\"07/16/16-04\",\"07/16/16-05\",\"07/16/16-06\",\"07/16/16-07\",\"07/16/16-08\",\"07/16/16-09\",\"07/16/16-10\",\"07/16/16-11\",\"07/16/16-12\",\"07/16/16-13\",\"07/16/16-14\",\"07/16/16-15\",\"07/16/16-16\",\"07/16/16-17\",\"07/16/16-18\",\"07/16/16-19\",\"07/16/16-20\",\"07/16/16-21\",\"07/16/16-22\",\"07/16/16-23\",\"07/17/16-00\",\"07/17/16-01\",\"07/17/16-02\",\"07/17/16-03\",\"07/17/16-04\",\"07/17/16-05\",\"07/17/16-06\",\"07/17/16-07\",\"07/17/16-08\",\"07/17/16-09\",\"07/17/16-10\",\"07/17/16-11\",\"07/17/16-12\",\"07/17/16-13\",\"07/17/16-14\",\"07/17/16-15\",\"07/17/16-16\",\"07/17/16-17\",\"07/17/16-18\",\"07/17/16-19\",\"07/17/16-20\",\"07/17/16-21\",\"07/17/16-22\",\"07/17/16-23\",\"07/18/16-00\",\"07/18/16-01\",\"07/18/16-02\",\"07/18/16-03\",\"07/18/16-04\",\"07/18/16-05\",\"07/18/16-06\",\"07/18/16-07\",\"07/18/16-08\",\"07/18/16-09\",\"07/18/16-10\",\"07/18/16-11\",\"07/18/16-12\",\"07/18/16-13\",\"07/18/16-14\",\"07/18/16-15\",\"07/18/16-16\",\"07/18/16-17\",\"07/18/16-18\",\"07/18/16-19\",\"07/18/16-20\",\"07/18/16-21\",\"07/18/16-22\",\"07/18/16-23\",\"07/19/16-00\",\"07/19/16-01\",\"07/19/16-02\",\"07/19/16-03\",\"07/19/16-04\",\"07/19/16-05\",\"07/19/16-06\",\"07/19/16-07\",\"07/19/16-08\",\"07/19/16-09\",\"07/19/16-10\",\"07/19/16-11\",\"07/19/16-12\",\"07/19/16-13\",\"07/19/16-14\",\"07/19/16-15\",\"07/19/16-16\",\"07/19/16-17\",\"07/19/16-18\",\"07/19/16-19\",\"07/19/16-20\",\"07/19/16-21\",\"07/19/16-22\",\"07/19/16-23\",\"07/20/16-00\",\"07/20/16-01\",\"07/20/16-02\",\"07/20/16-03\",\"07/20/16-04\",\"07/20/16-05\",\"07/20/16-06\",\"07/20/16-07\",\"07/20/16-08\",\"07/20/16-09\",\"07/20/16-10\",\"07/20/16-11\",\"07/20/16-12\",\"07/20/16-13\",\"07/20/16-14\",\"07/20/16-15\",\"07/20/16-16\",\"07/20/16-17\",\"07/20/16-18\",\"07/20/16-19\",\"07/20/16-20\",\"07/20/16-21\",\"07/20/16-22\",\"07/20/16-23\",\"07/21/16-00\",\"07/21/16-01\",\"07/21/16-02\",\"07/21/16-03\",\"07/21/16-04\",\"07/21/16-05\",\"07/21/16-06\",\"07/21/16-07\",\"07/21/16-08\",\"07/21/16-09\",\"07/21/16-10\",\"07/21/16-11\",\"07/21/16-12\",\"07/21/16-13\",\"07/21/16-14\",\"07/21/16-15\",\"07/21/16-16\",\"07/21/16-17\",\"07/21/16-18\",\"07/21/16-19\",\"07/21/16-20\",\"07/21/16-21\",\"07/21/16-22\",\"07/21/16-23\",\"07/22/16-00\",\"07/22/16-01\",\"07/22/16-02\",\"07/22/16-03\",\"07/22/16-04\",\"07/22/16-05\",\"07/22/16-06\",\"07/22/16-07\",\"07/22/16-08\",\"07/22/16-09\",\"07/22/16-10\",\"07/22/16-11\",\"07/22/16-12\",\"07/22/16-13\",\"07/22/16-14\",\"07/22/16-15\",\"07/22/16-16\",\"07/22/16-17\",\"07/22/16-18\",\"07/22/16-19\",\"07/22/16-20\",\"07/22/16-21\",\"07/22/16-22\",\"07/22/16-23\",\"07/23/16-00\",\"07/23/16-01\",\"07/23/16-02\",\"07/23/16-03\",\"07/23/16-04\",\"07/23/16-05\",\"07/23/16-06\",\"07/23/16-07\",\"07/23/16-08\",\"07/23/16-09\",\"07/23/16-10\",\"07/23/16-11\",\"07/23/16-12\",\"07/23/16-13\",\"07/23/16-14\",\"07/23/16-15\",\"07/23/16-16\",\"07/23/16-17\",\"07/23/16-18\",\"07/23/16-19\",\"07/23/16-20\",\"07/23/16-21\",\"07/23/16-22\",\"07/23/16-23\",\"07/24/16-00\",\"07/24/16-01\",\"07/24/16-02\",\"07/24/16-03\",\"07/24/16-04\",\"07/24/16-05\",\"07/24/16-06\",\"07/24/16-07\",\"07/24/16-08\",\"07/24/16-09\",\"07/24/16-10\",\"07/24/16-11\",\"07/24/16-12\",\"07/24/16-13\",\"07/24/16-14\",\"07/24/16-15\",\"07/24/16-16\",\"07/24/16-17\",\"07/24/16-18\",\"07/24/16-19\",\"07/24/16-20\",\"07/24/16-21\",\"07/24/16-22\",\"07/24/16-23\",\"07/25/16-00\",\"07/25/16-01\",\"07/25/16-02\",\"07/25/16-03\",\"07/25/16-04\",\"07/25/16-05\",\"07/25/16-06\",\"07/25/16-07\",\"07/25/16-08\",\"07/25/16-09\",\"07/25/16-10\",\"07/25/16-11\",\"07/25/16-12\",\"07/25/16-13\",\"07/25/16-14\",\"07/25/16-15\",\"07/25/16-16\",\"07/25/16-17\",\"07/25/16-18\",\"07/25/16-19\",\"07/25/16-20\",\"07/25/16-21\",\"07/25/16-22\",\"07/25/16-23\",\"07/26/16-00\",\"07/26/16-01\",\"07/26/16-02\",\"07/26/16-03\",\"07/26/16-04\",\"07/26/16-05\",\"07/26/16-06\",\"07/26/16-07\",\"07/26/16-08\",\"07/26/16-09\",\"07/26/16-10\",\"07/26/16-11\",\"07/26/16-12\",\"07/26/16-13\",\"07/26/16-14\",\"07/26/16-15\",\"07/26/16-16\",\"07/26/16-17\",\"07/26/16-18\",\"07/26/16-19\",\"07/26/16-20\",\"07/26/16-21\",\"07/26/16-22\",\"07/26/16-23\",\"07/27/16-00\",\"07/27/16-01\",\"07/27/16-02\",\"07/27/16-03\",\"07/27/16-04\",\"07/27/16-05\",\"07/27/16-06\",\"07/27/16-07\",\"07/27/16-08\",\"07/27/16-09\",\"07/27/16-10\",\"07/27/16-11\",\"07/27/16-12\",\"07/27/16-13\",\"07/27/16-14\",\"07/27/16-15\",\"07/27/16-16\",\"07/27/16-17\",\"07/27/16-18\",\"07/27/16-19\",\"07/27/16-20\",\"07/27/16-21\",\"07/27/16-22\",\"07/27/16-23\",\"07/28/16-00\",\"07/28/16-01\",\"07/28/16-02\",\"07/28/16-03\",\"07/28/16-04\",\"07/28/16-05\",\"07/28/16-06\",\"07/28/16-07\",\"07/28/16-08\",\"07/28/16-09\",\"07/28/16-10\",\"07/28/16-11\",\"07/28/16-12\",\"07/28/16-13\",\"07/28/16-14\",\"07/28/16-15\",\"07/28/16-16\",\"07/28/16-17\",\"07/28/16-18\",\"07/28/16-19\",\"07/28/16-20\",\"07/28/16-21\",\"07/28/16-22\",\"07/28/16-23\",\"07/29/16-00\",\"07/29/16-01\",\"07/29/16-02\",\"07/29/16-03\",\"07/29/16-04\",\"07/29/16-05\",\"07/29/16-06\",\"07/29/16-07\",\"07/29/16-08\",\"07/29/16-09\",\"07/29/16-10\",\"07/29/16-11\",\"07/29/16-12\",\"07/29/16-13\",\"07/29/16-14\",\"07/29/16-15\",\"07/29/16-16\",\"07/29/16-17\",\"07/29/16-18\",\"07/29/16-19\",\"07/29/16-20\",\"07/29/16-21\",\"07/29/16-22\",\"07/29/16-23\",\"07/30/16-00\",\"07/30/16-01\",\"07/30/16-02\",\"07/30/16-03\",\"07/30/16-04\",\"07/30/16-05\",\"07/30/16-06\",\"07/30/16-07\",\"07/30/16-08\",\"07/30/16-09\",\"07/30/16-10\",\"07/30/16-11\",\"07/30/16-12\",\"07/30/16-13\",\"07/30/16-14\",\"07/30/16-15\",\"07/30/16-16\",\"07/30/16-17\",\"07/30/16-18\",\"07/30/16-19\",\"07/30/16-20\",\"07/30/16-21\",\"07/30/16-22\",\"07/30/16-23\",\"07/31/16-00\",\"07/31/16-01\",\"07/31/16-02\",\"07/31/16-03\",\"07/31/16-04\",\"07/31/16-05\",\"07/31/16-06\",\"07/31/16-07\",\"07/31/16-08\",\"07/31/16-09\",\"07/31/16-10\",\"07/31/16-11\",\"07/31/16-12\",\"07/31/16-13\",\"07/31/16-14\",\"07/31/16-15\",\"07/31/16-16\",\"07/31/16-17\",\"07/31/16-18\",\"07/31/16-19\",\"07/31/16-20\",\"07/31/16-21\",\"07/31/16-22\",\"07/31/16-23\",\"08/01/16-00\",\"08/01/16-01\",\"08/01/16-02\",\"08/01/16-03\",\"08/01/16-04\",\"08/01/16-05\",\"08/01/16-06\",\"08/01/16-07\",\"08/01/16-08\",\"08/01/16-09\",\"08/01/16-10\",\"08/01/16-11\",\"08/01/16-12\",\"08/01/16-13\",\"08/01/16-14\",\"08/01/16-15\",\"08/01/16-16\",\"08/01/16-17\",\"08/01/16-18\",\"08/01/16-19\",\"08/01/16-20\",\"08/01/16-21\",\"08/01/16-22\",\"08/01/16-23\",\"08/02/16-00\",\"08/02/16-01\",\"08/02/16-02\",\"08/02/16-03\",\"08/02/16-04\",\"08/02/16-05\",\"08/02/16-06\",\"08/02/16-07\",\"08/02/16-08\",\"08/02/16-09\",\"08/02/16-10\",\"08/02/16-11\",\"08/02/16-12\",\"08/02/16-13\",\"08/02/16-14\",\"08/02/16-15\",\"08/02/16-16\",\"08/02/16-17\",\"08/02/16-18\",\"08/02/16-19\",\"08/02/16-20\",\"08/02/16-21\",\"08/02/16-22\",\"08/02/16-23\",\"08/03/16-00\",\"08/03/16-01\",\"08/03/16-02\",\"08/03/16-03\",\"08/03/16-04\",\"08/03/16-05\",\"08/03/16-06\",\"08/03/16-07\",\"08/03/16-08\",\"08/03/16-09\",\"08/03/16-10\",\"08/03/16-11\",\"08/03/16-12\",\"08/03/16-13\",\"08/03/16-14\",\"08/03/16-15\",\"08/03/16-16\",\"08/03/16-17\",\"08/03/16-18\",\"08/03/16-19\",\"08/03/16-20\",\"08/03/16-21\",\"08/03/16-22\",\"08/03/16-23\",\"08/04/16-00\",\"08/04/16-01\",\"08/04/16-02\",\"08/04/16-03\",\"08/04/16-04\",\"08/04/16-05\",\"08/04/16-06\",\"08/04/16-07\",\"08/04/16-08\",\"08/04/16-09\",\"08/04/16-10\",\"08/04/16-11\",\"08/04/16-12\",\"08/04/16-13\",\"08/04/16-14\",\"08/04/16-15\",\"08/04/16-16\",\"08/04/16-17\",\"08/04/16-18\",\"08/04/16-19\",\"08/04/16-20\",\"08/04/16-21\",\"08/04/16-22\",\"08/04/16-23\",\"08/05/16-00\",\"08/05/16-01\",\"08/05/16-02\",\"08/05/16-03\",\"08/05/16-04\",\"08/05/16-05\",\"08/05/16-06\",\"08/05/16-07\",\"08/05/16-08\",\"08/05/16-09\",\"08/05/16-10\",\"08/05/16-11\",\"08/05/16-12\",\"08/05/16-13\",\"08/05/16-14\",\"08/11/16-00\",\"08/11/16-00\",\"08/11/16-00\",\"08/11/16-00\",\"08/11/16-01\",\"08/11/16-02\",\"08/11/16-03\",\"08/11/16-04\",\"08/11/16-05\",\"08/11/16-06\",\"08/11/16-07\",\"08/11/16-08\",\"08/11/16-09\",\"08/11/16-10\",\"08/11/16-11\",\"08/11/16-12\",\"08/11/16-13\",\"08/11/16-14\",\"08/11/16-15\",\"08/11/16-16\",\"08/11/16-17\",\"08/11/16-18\",\"08/11/16-19\",\"08/11/16-20\",\"08/11/16-21\",\"08/11/16-22\",\"08/11/16-23\",\"08/12/16-00\",\"08/12/16-01\",\"08/12/16-02\",\"08/12/16-03\",\"08/12/16-04\",\"08/12/16-05\",\"08/12/16-06\",\"08/12/16-07\",\"08/12/16-08\",\"08/12/16-09\",\"08/12/16-10\",\"08/12/16-11\",\"08/12/16-12\",\"08/12/16-13\",\"08/12/16-14\",\"08/12/16-15\",\"08/12/16-16\",\"08/12/16-17\",\"08/12/16-18\",\"08/12/16-19\",\"08/12/16-20\",\"08/12/16-21\",\"08/12/16-22\",\"08/12/16-23\",\"08/13/16-00\",\"08/13/16-01\",\"08/13/16-02\",\"08/13/16-03\",\"08/13/16-04\",\"08/13/16-05\",\"08/13/16-06\",\"08/13/16-07\",\"08/13/16-08\",\"08/13/16-09\",\"08/13/16-10\",\"08/13/16-11\",\"08/13/16-12\",\"08/13/16-13\",\"08/13/16-14\",\"08/13/16-15\",\"08/13/16-16\",\"08/13/16-17\",\"08/13/16-18\",\"08/13/16-19\",\"08/13/16-20\",\"08/13/16-21\",\"08/13/16-22\",\"08/13/16-23\",\"08/14/16-00\",\"08/14/16-01\",\"08/14/16-02\",\"08/14/16-03\",\"08/14/16-04\",\"08/14/16-05\",\"08/14/16-06\",\"08/14/16-07\",\"08/14/16-08\",\"08/14/16-09\",\"08/14/16-10\",\"08/14/16-11\",\"08/14/16-12\",\"08/14/16-13\",\"08/14/16-14\",\"08/14/16-15\",\"08/14/16-16\",\"08/14/16-17\",\"08/14/16-18\",\"08/14/16-19\",\"08/14/16-20\",\"08/14/16-21\",\"08/14/16-22\",\"08/14/16-23\",\"08/15/16-00\",\"08/15/16-01\",\"08/15/16-02\",\"08/15/16-03\",\"08/15/16-04\",\"08/15/16-05\",\"08/15/16-06\",\"08/15/16-07\",\"08/15/16-08\",\"08/15/16-09\",\"08/15/16-10\",\"08/15/16-11\",\"08/15/16-12\",\"08/15/16-13\",\"08/15/16-14\",\"08/15/16-15\",\"08/15/16-16\",\"08/15/16-17\",\"08/15/16-18\",\"08/15/16-19\",\"08/15/16-20\",\"08/15/16-21\",\"08/15/16-22\",\"08/15/16-23\",\"08/16/16-00\",\"08/16/16-01\",\"08/16/16-02\",\"08/16/16-03\",\"08/16/16-04\",\"08/16/16-05\",\"08/16/16-06\",\"08/16/16-07\",\"08/16/16-08\",\"08/16/16-09\",\"08/16/16-10\",\"08/16/16-11\",\"08/16/16-12\",\"08/16/16-13\",\"08/16/16-14\",\"08/16/16-15\",\"08/16/16-16\",\"08/16/16-17\",\"08/16/16-18\",\"08/16/16-19\",\"08/16/16-20\",\"08/16/16-21\",\"08/16/16-22\",\"08/16/16-23\",\"08/17/16-00\",\"08/17/16-01\",\"08/17/16-02\",\"08/17/16-03\",\"08/17/16-04\",\"08/17/16-05\",\"08/17/16-06\",\"08/17/16-07\",\"08/17/16-08\",\"08/17/16-09\",\"08/17/16-10\",\"08/17/16-11\",\"08/17/16-12\",\"08/17/16-13\",\"08/17/16-14\",\"08/17/16-15\",\"08/17/16-16\",\"08/17/16-17\",\"08/17/16-18\",\"08/17/16-19\",\"08/17/16-20\",\"08/17/16-21\",\"08/17/16-22\",\"08/17/16-23\",\"08/18/16-00\",\"08/18/16-01\",\"08/18/16-02\",\"08/18/16-03\",\"08/18/16-04\",\"08/18/16-05\",\"08/18/16-06\",\"08/18/16-07\",\"08/18/16-08\",\"08/18/16-09\",\"08/18/16-10\",\"08/18/16-11\",\"08/18/16-12\",\"08/18/16-13\",\"08/18/16-14\",\"08/18/16-15\",\"08/18/16-16\",\"08/18/16-17\",\"08/18/16-18\",\"08/18/16-19\",\"08/18/16-20\",\"08/18/16-21\",\"08/18/16-22\",\"08/18/16-23\",\"08/19/16-00\",\"08/19/16-01\",\"08/19/16-02\",\"08/19/16-03\",\"08/19/16-04\",\"08/19/16-05\",\"08/19/16-06\",\"08/19/16-07\",\"08/19/16-08\",\"08/19/16-09\",\"08/19/16-10\",\"08/19/16-11\",\"08/19/16-12\",\"08/19/16-13\",\"08/19/16-14\",\"08/19/16-15\",\"08/19/16-16\",\"08/19/16-17\",\"08/19/16-18\",\"08/19/16-19\",\"08/19/16-20\",\"08/19/16-21\",\"08/19/16-22\",\"08/19/16-23\",\"08/20/16-00\",\"08/20/16-01\",\"08/20/16-02\",\"08/20/16-03\",\"08/20/16-04\",\"08/20/16-05\",\"08/20/16-06\",\"08/20/16-07\",\"08/20/16-08\",\"08/20/16-09\",\"08/20/16-10\",\"08/20/16-11\",\"08/20/16-12\",\"08/20/16-13\",\"08/20/16-14\",\"08/20/16-15\",\"08/20/16-16\",\"08/20/16-17\",\"08/20/16-18\",\"08/20/16-19\",\"08/20/16-20\",\"08/20/16-21\",\"08/20/16-22\",\"08/20/16-23\",\"08/21/16-00\",\"08/21/16-01\",\"08/21/16-02\",\"08/21/16-03\",\"08/21/16-04\",\"08/21/16-05\",\"08/21/16-06\",\"08/21/16-07\",\"08/21/16-08\",\"08/21/16-09\",\"08/21/16-10\",\"08/21/16-11\",\"08/21/16-12\",\"08/21/16-13\",\"08/21/16-14\",\"08/21/16-15\",\"08/21/16-16\",\"08/21/16-17\",\"08/21/16-18\",\"08/21/16-19\",\"08/21/16-20\",\"08/21/16-21\",\"08/21/16-22\",\"08/21/16-23\",\"08/22/16-00\",\"08/22/16-01\",\"08/22/16-02\",\"08/22/16-03\",\"08/22/16-04\",\"08/22/16-05\",\"08/22/16-06\",\"08/22/16-07\",\"08/22/16-08\",\"08/22/16-09\",\"08/22/16-10\",\"08/22/16-11\",\"08/22/16-12\",\"08/22/16-13\",\"08/22/16-14\",\"08/22/16-15\",\"08/22/16-16\",\"08/22/16-17\",\"08/22/16-18\",\"08/22/16-19\",\"08/22/16-20\",\"08/22/16-21\",\"08/22/16-22\",\"08/22/16-23\",\"08/23/16-00\",\"08/23/16-01\",\"08/23/16-02\",\"08/23/16-03\",\"08/23/16-04\",\"08/23/16-05\",\"08/23/16-06\",\"08/23/16-07\",\"08/23/16-08\",\"08/23/16-17\",\"08/23/16-18\",\"08/23/16-19\",\"08/23/16-20\",\"08/23/16-21\",\"08/23/16-22\",\"08/23/16-23\",\"08/24/16-00\",\"08/24/16-01\",\"08/24/16-02\",\"08/24/16-03\",\"08/24/16-04\",\"08/24/16-05\",\"08/24/16-06\",\"08/24/16-07\",\"08/24/16-08\",\"08/24/16-09\",\"08/24/16-10\",\"08/24/16-11\",\"08/24/16-12\",\"08/24/16-13\",\"08/24/16-14\",\"08/24/16-15\",\"08/24/16-16\",\"08/24/16-17\",\"08/24/16-18\",\"08/24/16-19\",\"08/24/16-20\",\"08/24/16-21\",\"08/24/16-22\",\"08/24/16-23\",\"08/25/16-00\",\"08/25/16-01\",\"08/25/16-02\",\"08/25/16-03\",\"08/25/16-04\",\"08/25/16-05\",\"08/25/16-06\",\"08/25/16-07\",\"08/25/16-08\",\"08/25/16-09\",\"08/25/16-10\",\"08/25/16-11\",\"08/25/16-12\",\"08/25/16-13\",\"08/25/16-14\",\"08/25/16-15\",\"08/25/16-16\",\"08/25/16-17\",\"08/25/16-18\",\"08/25/16-19\",\"08/25/16-20\",\"08/25/16-21\",\"08/25/16-22\",\"08/25/16-23\",\"08/26/16-00\",\"08/26/16-01\",\"08/26/16-02\",\"08/26/16-03\",\"08/26/16-04\",\"08/26/16-05\",\"08/26/16-06\",\"08/26/16-07\",\"08/26/16-08\",\"08/26/16-09\",\"08/26/16-10\",\"08/26/16-11\",\"08/26/16-12\",\"08/26/16-13\",\"08/26/16-14\",\"08/26/16-15\",\"08/26/16-16\",\"08/26/16-17\",\"08/26/16-18\",\"08/26/16-19\",\"08/26/16-20\",\"08/26/16-21\",\"08/26/16-22\",\"08/26/16-23\",\"08/27/16-00\",\"08/27/16-01\",\"08/27/16-02\",\"08/27/16-03\",\"08/27/16-04\",\"08/27/16-05\",\"08/27/16-06\",\"08/27/16-07\",\"08/27/16-08\",\"08/27/16-09\",\"08/27/16-10\",\"08/27/16-11\",\"08/27/16-12\",\"08/27/16-13\",\"08/27/16-14\",\"08/27/16-15\",\"08/27/16-16\",\"08/27/16-17\",\"08/27/16-18\",\"08/27/16-19\",\"08/27/16-20\",\"08/27/16-21\",\"08/27/16-22\",\"08/27/16-23\",\"08/28/16-00\",\"08/28/16-01\",\"08/28/16-02\",\"08/28/16-03\",\"08/28/16-04\",\"08/28/16-05\",\"08/28/16-06\",\"08/28/16-07\",\"08/28/16-08\",\"08/28/16-09\",\"08/28/16-10\",\"08/28/16-11\",\"08/28/16-12\",\"08/28/16-13\",\"08/28/16-14\",\"08/28/16-15\",\"08/28/16-16\",\"08/28/16-17\",\"08/28/16-18\",\"08/28/16-19\",\"08/28/16-20\",\"08/28/16-21\",\"08/28/16-22\",\"08/28/16-23\",\"08/29/16-00\",\"08/29/16-01\",\"08/29/16-02\",\"08/29/16-03\",\"08/29/16-04\",\"08/29/16-05\",\"08/29/16-06\",\"08/29/16-07\",\"08/29/16-08\",\"08/29/16-09\",\"08/29/16-10\",\"08/29/16-11\",\"08/29/16-12\",\"08/29/16-13\",\"08/29/16-14\",\"08/29/16-15\",\"08/29/16-16\",\"08/29/16-17\",\"08/29/16-18\",\"08/29/16-19\",\"08/29/16-20\",\"08/29/16-21\",\"08/29/16-22\",\"08/29/16-23\",\"08/30/16-00\",\"08/30/16-01\",\"08/30/16-02\",\"08/30/16-03\",\"08/30/16-04\",\"08/30/16-05\",\"08/30/16-06\",\"08/30/16-07\",\"08/30/16-08\",\"08/30/16-09\",\"08/30/16-10\",\"08/30/16-11\",\"08/30/16-12\",\"08/30/16-13\",\"08/30/16-14\",\"08/30/16-15\",\"08/30/16-16\",\"08/30/16-17\",\"08/30/16-18\",\"08/30/16-19\",\"08/30/16-20\",\"08/30/16-21\",\"08/30/16-22\",\"08/30/16-23\",\"08/31/16-00\",\"08/31/16-01\",\"08/31/16-02\",\"08/31/16-03\",\"08/31/16-04\",\"08/31/16-05\",\"08/31/16-06\",\"08/31/16-07\",\"08/31/16-08\",\"08/31/16-09\",\"08/31/16-10\",\"08/31/16-11\",\"08/31/16-12\",\"08/31/16-13\",\"08/31/16-14\",\"08/31/16-15\",\"08/31/16-16\",\"08/31/16-17\",\"08/31/16-18\",\"08/31/16-19\",\"08/31/16-20\",\"08/31/16-21\",\"08/31/16-22\",\"08/31/16-23\",\"09/01/16-00\",\"09/01/16-01\",\"09/01/16-02\",\"09/01/16-03\",\"09/01/16-04\",\"09/01/16-05\",\"09/01/16-06\",\"09/01/16-07\",\"09/01/16-08\",\"09/01/16-09\",\"09/01/16-10\",\"09/01/16-11\",\"09/01/16-12\",\"09/01/16-13\",\"09/01/16-14\",\"09/01/16-15\",\"09/01/16-16\",\"09/01/16-17\",\"09/01/16-18\",\"09/01/16-19\",\"09/01/16-20\",\"09/01/16-21\",\"09/01/16-22\",\"09/01/16-23\",\"09/02/16-00\",\"09/02/16-01\",\"09/02/16-02\",\"09/02/16-03\",\"09/02/16-04\",\"09/02/16-05\",\"09/02/16-06\",\"09/02/16-07\",\"09/02/16-08\",\"09/02/16-09\",\"09/02/16-10\",\"09/02/16-11\",\"09/02/16-12\",\"09/02/16-13\",\"09/02/16-14\",\"09/02/16-15\",\"09/02/16-16\",\"09/02/16-17\",\"09/02/16-18\",\"09/02/16-19\",\"09/02/16-20\",\"09/02/16-21\",\"09/02/16-22\",\"09/02/16-23\",\"09/03/16-00\",\"09/03/16-01\",\"09/03/16-02\",\"09/03/16-03\",\"09/03/16-04\",\"09/03/16-05\",\"09/03/16-06\",\"09/03/16-07\",\"09/03/16-08\",\"09/03/16-09\",\"09/03/16-10\",\"09/03/16-11\",\"09/03/16-12\",\"09/03/16-13\",\"09/03/16-14\",\"09/03/16-15\",\"09/03/16-16\",\"09/03/16-17\",\"09/03/16-18\",\"09/03/16-19\",\"09/03/16-20\",\"09/03/16-21\",\"09/03/16-22\",\"09/03/16-23\",\"09/04/16-00\",\"09/04/16-01\",\"09/04/16-02\",\"09/04/16-03\",\"09/04/16-04\",\"09/04/16-05\",\"09/04/16-06\",\"09/04/16-07\",\"09/04/16-08\",\"09/04/16-09\",\"09/04/16-10\",\"09/04/16-11\",\"09/04/16-12\",\"09/04/16-13\",\"09/04/16-14\",\"09/04/16-15\",\"09/04/16-16\",\"09/04/16-17\",\"09/04/16-18\",\"09/04/16-19\",\"09/04/16-20\",\"09/04/16-21\",\"09/04/16-22\",\"09/04/16-23\",\"09/05/16-00\",\"09/05/16-01\",\"09/05/16-02\",\"09/05/16-03\",\"09/05/16-04\",\"09/05/16-05\",\"09/05/16-06\",\"09/05/16-07\",\"09/05/16-08\",\"09/05/16-09\",\"09/05/16-10\",\"09/05/16-11\",\"09/05/16-12\",\"09/05/16-13\",\"09/05/16-14\",\"09/05/16-15\",\"09/05/16-16\",\"09/05/16-17\",\"09/05/16-18\",\"09/05/16-19\",\"09/05/16-20\",\"09/05/16-21\",\"09/05/16-22\",\"09/05/16-23\",\"09/06/16-00\",\"09/06/16-01\",\"09/06/16-02\",\"09/06/16-03\",\"09/06/16-04\",\"09/06/16-05\",\"09/06/16-06\",\"09/06/16-07\",\"09/06/16-08\",\"09/06/16-09\",\"09/06/16-10\",\"09/06/16-11\",\"09/06/16-12\",\"09/06/16-13\",\"09/06/16-14\",\"09/06/16-15\",\"09/06/16-16\",\"09/06/16-17\",\"09/06/16-18\",\"09/06/16-19\",\"09/06/16-20\",\"09/06/16-21\",\"09/06/16-22\",\"09/06/16-23\",\"09/07/16-00\",\"09/07/16-01\",\"09/07/16-02\",\"09/07/16-03\",\"09/07/16-04\",\"09/07/16-05\",\"09/07/16-06\",\"09/07/16-07\",\"09/07/16-08\",\"09/07/16-09\",\"09/07/16-10\",\"09/07/16-11\",\"09/07/16-12\",\"09/07/16-13\",\"09/07/16-14\",\"09/07/16-15\",\"09/07/16-16\",\"09/07/16-17\",\"09/07/16-18\",\"09/07/16-19\",\"09/07/16-20\",\"09/07/16-21\",\"09/07/16-22\",\"09/07/16-23\",\"09/08/16-00\",\"09/08/16-01\",\"09/08/16-02\",\"09/08/16-03\",\"09/08/16-04\",\"09/08/16-05\",\"09/08/16-06\",\"09/08/16-07\",\"09/08/16-08\",\"09/08/16-09\",\"09/08/16-10\",\"09/08/16-11\",\"09/08/16-12\",\"09/08/16-13\",\"09/08/16-14\",\"09/08/16-15\",\"09/08/16-16\",\"09/08/16-17\",\"09/08/16-18\",\"09/08/16-19\",\"09/08/16-20\",\"09/08/16-21\",\"09/08/16-22\",\"09/08/16-23\",\"09/09/16-00\",\"09/09/16-01\",\"09/09/16-02\",\"09/09/16-03\",\"09/09/16-04\",\"09/09/16-05\",\"09/09/16-06\",\"09/09/16-07\",\"09/09/16-08\",\"09/09/16-09\",\"09/09/16-10\",\"09/09/16-11\",\"09/09/16-12\",\"09/09/16-13\",\"09/09/16-14\",\"09/09/16-15\",\"09/09/16-16\",\"09/09/16-17\",\"09/09/16-18\",\"09/09/16-19\",\"09/09/16-20\",\"09/09/16-21\",\"09/09/16-22\",\"09/09/16-23\",\"09/10/16-00\",\"09/10/16-01\",\"09/10/16-02\",\"09/10/16-03\",\"09/10/16-04\",\"09/10/16-05\",\"09/10/16-06\",\"09/10/16-07\",\"09/10/16-08\",\"09/10/16-09\",\"09/10/16-10\",\"09/10/16-11\",\"09/10/16-12\",\"09/10/16-13\",\"09/10/16-14\",\"09/10/16-15\",\"09/10/16-16\",\"09/10/16-17\",\"09/10/16-18\",\"09/10/16-19\",\"09/10/16-20\",\"09/10/16-21\",\"09/10/16-22\",\"09/10/16-23\",\"09/11/16-00\",\"09/11/16-01\",\"09/11/16-02\",\"09/11/16-03\",\"09/11/16-04\",\"09/11/16-05\",\"09/11/16-06\",\"09/11/16-07\",\"09/11/16-08\",\"09/11/16-09\",\"09/11/16-10\",\"09/11/16-11\",\"09/11/16-12\",\"09/11/16-13\",\"09/11/16-14\",\"09/11/16-15\",\"09/11/16-16\",\"09/11/16-17\",\"09/11/16-18\",\"09/11/16-19\",\"09/11/16-20\",\"09/11/16-21\",\"09/11/16-22\",\"09/11/16-23\",\"09/12/16-00\",\"09/12/16-01\",\"09/12/16-02\",\"09/12/16-03\",\"09/12/16-04\",\"09/12/16-05\",\"09/12/16-06\",\"09/12/16-07\",\"09/12/16-08\",\"09/12/16-09\",\"09/12/16-10\",\"09/12/16-11\",\"09/12/16-12\",\"09/12/16-13\",\"09/12/16-14\",\"09/12/16-15\",\"09/12/16-16\",\"09/12/16-17\",\"09/12/16-18\",\"09/12/16-19\",\"09/12/16-20\",\"09/12/16-21\",\"09/12/16-22\",\"09/12/16-23\",\"09/13/16-00\",\"09/13/16-01\",\"09/13/16-02\",\"09/13/16-03\",\"09/13/16-04\",\"09/13/16-05\",\"09/13/16-06\",\"09/13/16-07\",\"09/13/16-08\",\"09/13/16-09\",\"09/13/16-10\",\"09/13/16-11\",\"09/13/16-12\",\"09/13/16-13\",\"09/13/16-14\",\"09/13/16-15\",\"09/13/16-16\",\"09/13/16-17\",\"09/13/16-18\",\"09/13/16-19\",\"09/13/16-20\",\"09/13/16-21\",\"09/13/16-22\",\"09/13/16-23\",\"09/14/16-00\",\"09/14/16-01\",\"09/14/16-02\",\"09/14/16-03\",\"09/14/16-04\",\"09/14/16-05\",\"09/14/16-06\",\"09/14/16-07\",\"09/14/16-08\",\"09/14/16-09\",\"09/14/16-10\",\"09/14/16-11\",\"09/14/16-12\",\"09/14/16-13\",\"09/14/16-14\",\"09/14/16-15\",\"09/14/16-16\",\"09/14/16-17\",\"09/14/16-18\",\"09/14/16-19\",\"09/14/16-20\",\"09/14/16-21\",\"09/14/16-22\",\"09/14/16-23\",\"09/15/16-00\",\"09/15/16-01\",\"09/15/16-02\",\"09/15/16-03\",\"09/15/16-04\",\"09/15/16-05\",\"09/15/16-06\",\"09/15/16-07\",\"09/15/16-08\",\"09/15/16-09\",\"09/15/16-10\",\"09/15/16-11\",\"09/15/16-12\",\"09/15/16-13\",\"09/15/16-14\",\"09/15/16-15\",\"09/15/16-16\",\"09/15/16-17\",\"09/15/16-18\",\"09/15/16-19\",\"09/15/16-20\",\"09/15/16-21\",\"09/15/16-22\",\"09/15/16-23\",\"09/16/16-00\",\"09/16/16-01\",\"09/16/16-02\",\"09/16/16-03\",\"09/16/16-04\",\"09/16/16-05\",\"09/16/16-06\",\"09/16/16-07\",\"09/16/16-08\",\"09/16/16-09\",\"09/16/16-10\",\"09/16/16-11\",\"09/16/16-12\",\"09/16/16-13\",\"09/16/16-14\",\"09/16/16-15\",\"09/16/16-16\",\"09/16/16-17\",\"09/16/16-18\",\"09/16/16-19\",\"09/16/16-20\",\"09/16/16-21\",\"09/16/16-22\",\"09/16/16-23\",\"09/17/16-00\",\"09/17/16-01\",\"09/17/16-02\",\"09/17/16-03\",\"09/17/16-04\",\"09/17/16-05\",\"09/17/16-06\",\"09/17/16-07\",\"09/17/16-08\",\"09/17/16-09\",\"09/17/16-10\",\"09/17/16-11\",\"09/17/16-12\",\"09/17/16-13\",\"09/17/16-14\",\"09/17/16-15\",\"09/17/16-16\",\"09/17/16-17\",\"09/17/16-18\",\"09/17/16-19\",\"09/17/16-20\",\"09/17/16-21\",\"09/17/16-22\",\"09/17/16-23\",\"09/18/16-00\",\"09/18/16-01\",\"09/18/16-02\",\"09/18/16-03\",\"09/18/16-04\",\"09/18/16-05\",\"09/18/16-06\",\"09/18/16-07\",\"09/18/16-08\",\"09/18/16-09\",\"09/18/16-10\",\"09/18/16-11\",\"09/18/16-12\",\"09/18/16-13\",\"09/18/16-14\",\"09/18/16-15\",\"09/18/16-16\",\"09/18/16-17\",\"09/18/16-18\",\"09/18/16-19\",\"09/18/16-20\",\"09/18/16-21\",\"09/18/16-22\",\"09/18/16-23\",\"09/19/16-00\",\"09/19/16-01\",\"09/19/16-02\",\"09/19/16-03\",\"09/19/16-04\",\"09/19/16-05\",\"09/19/16-06\",\"09/19/16-07\",\"09/19/16-08\",\"09/19/16-09\",\"09/19/16-10\",\"09/19/16-11\",\"09/19/16-12\",\"09/19/16-13\",\"09/19/16-14\",\"09/19/16-15\",\"09/19/16-16\",\"09/19/16-17\",\"09/19/16-18\",\"09/19/16-19\",\"09/19/16-20\",\"09/19/16-21\",\"09/19/16-22\",\"09/19/16-23\",\"09/20/16-00\",\"09/20/16-01\",\"09/20/16-02\",\"09/20/16-03\",\"09/20/16-04\",\"09/20/16-05\",\"09/23/16-07\",\"09/23/16-07\",\"09/23/16-08\",\"09/23/16-09\",\"09/23/16-10\",\"09/23/16-11\",\"09/23/16-12\",\"09/23/16-13\",\"09/23/16-14\",\"09/23/16-15\",\"09/23/16-16\",\"09/23/16-17\",\"09/23/16-18\",\"09/23/16-19\",\"09/23/16-20\",\"09/23/16-21\",\"09/23/16-22\",\"09/23/16-23\",\"09/24/16-00\",\"09/24/16-01\",\"09/24/16-02\",\"09/24/16-03\",\"09/24/16-04\",\"09/24/16-05\",\"09/24/16-06\",\"09/24/16-07\",\"09/24/16-08\",\"09/24/16-09\",\"09/24/16-10\",\"09/24/16-11\",\"09/24/16-12\",\"09/24/16-13\",\"09/24/16-14\",\"09/24/16-15\",\"09/24/16-16\",\"09/24/16-17\",\"09/24/16-18\",\"09/24/16-19\",\"09/24/16-20\",\"09/24/16-21\",\"09/24/16-22\",\"09/24/16-23\",\"09/25/16-00\",\"09/25/16-01\",\"09/25/16-02\",\"09/25/16-03\",\"09/25/16-04\",\"09/25/16-05\",\"09/25/16-06\",\"09/25/16-07\",\"09/25/16-08\",\"09/25/16-09\",\"09/25/16-10\",\"09/25/16-11\",\"09/25/16-12\",\"09/25/16-13\",\"09/25/16-14\",\"09/25/16-15\",\"09/25/16-16\",\"09/25/16-17\",\"09/25/16-18\",\"09/25/16-19\",\"09/25/16-20\",\"09/25/16-21\",\"09/25/16-22\",\"09/25/16-23\",\"09/26/16-00\",\"09/26/16-01\",\"09/26/16-02\",\"09/26/16-03\",\"09/26/16-04\",\"09/26/16-05\",\"09/26/16-06\",\"09/26/16-07\",\"09/26/16-08\",\"09/26/16-09\",\"09/26/16-10\",\"09/26/16-11\",\"09/26/16-12\",\"09/26/16-13\",\"09/26/16-14\",\"09/26/16-15\",\"09/26/16-16\",\"09/26/16-17\",\"09/26/16-18\",\"09/26/16-19\",\"09/26/16-20\",\"09/26/16-21\",\"09/26/16-22\",\"09/26/16-23\",\"09/27/16-00\",\"09/27/16-01\",\"09/27/16-02\",\"09/27/16-03\",\"09/27/16-04\",\"09/27/16-05\",\"09/27/16-06\",\"09/27/16-07\",\"09/27/16-08\",\"09/27/16-09\",\"09/27/16-10\",\"09/27/16-11\",\"09/27/16-12\",\"09/27/16-13\",\"09/27/16-14\",\"09/27/16-15\",\"09/27/16-16\",\"09/27/16-17\",\"09/27/16-18\",\"09/27/16-19\",\"09/27/16-20\",\"09/27/16-21\",\"09/27/16-22\",\"09/27/16-23\",\"09/28/16-00\",\"09/28/16-01\",\"09/28/16-02\",\"09/28/16-03\",\"09/28/16-04\",\"09/28/16-05\",\"09/28/16-06\",\"09/28/16-07\"],\"Population\":[316,316,316,316,316,315,316,316,315,314,314,314,314,314,312,310,310,311,311,311,311,311,310,310,310,310,310,310,310,310,310,309,308,308,307,307,307,307,307,308,308,308,307,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,305,305,305,305,305,305,306,306,306,306,306,306,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,304,306,306,306,306,306,306,306,305,305,305,305,305,304,304,303,303,303,305,305,305,305,305,305,305,305,305,305,305,305,305,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,303,303,303,303,303,303,303,303,303,302,302,302,301,301,301,301,301,301,301,301,301,301,301,301,301,301,300,300,301,300,300,300,300,300,300,300,300,300,300,300,300,299,299,299,299,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,297,297,297,297,297,297,298,297,297,297,297,297,297,297,297,297,297,297,297,297,297,297,297,297,297,297,301,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,299,302,301,301,301,300,300,300,300,300,300,300,300,300,300,300,300,300,309,309,308,307,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,312,312,312,312,312,312,312,312,312,312,312,312,312,311,311,311,310,310,310,310,310,310,310,309,309,309,309,309,309,309,308,308,308,306,306,305,305,305,305,305,305,304,304,304,304,304,304,303,302,302,302,302,302,300,299,299,299,298,299,299,299,300,300,300,300,300,300,300,300,300,300,300,300,299,299,299,299,299,299,299,299,299,299,299,299,299,299,299,299,299,299,299,298,298,298,298,298,297,297,297,297,297,297,297,297,297,297,297,297,297,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,297,297,297,297,296,296,296,295,295,295,295,295,294,294,294,294,294,294,294,294,295,295,295,295,295,295,295,295,295,295,295,294,293,292,292,292,292,292,292,292,292,292,292,292,292,293,293,293,293,293,293,293,293,293,293,293,293,293,293,293,293,293,292,292,292,292,292,291,291,291,291,291,291,291,291,291,290,290,290,290,290,290,290,290,290,290,290,289,289,289,289,289,289,289,289,289,289,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,293,293,293,293,293,293,293,293,293,293,293,292,292,291,291,290,290,290,290,290,290,290,290,289,289,289,288,288,288,288,288,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,286,286,286,287,287,287,287,287,287,287,287,287,287,287,289,289,289,289,289,288,288,288,288,287,287,287,286,286,286,285,285,285,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,283,285,285,285,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,285,285,285,285,285,285,285,285,285,285,287,287,287,287,287,287,287,287,287,286,286,286,286,287,287,287,287,287,286,286,286,286,286,286,286,286,285,285,285,285,285,285,285,285,285,285,285,286,286,286,286,285,285,285,285,285,285,289,289,289,288,288,288,288,288,288,288,288,288,288,288,288,288,288,287,292,291,290,290,290,290,290,289,289,289,289,289,289,289,289,289,289,289,289,289,288,288,288,288,287,289,289,289,289,289,289,289,289,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,293,293,293,293,293,293,293,293,293,293,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,293,293,293,293,293,293,293,293,293,293,292,292,292,292,292,291,291,291,291,291,291,291,291,291,291,294,294,293,293,293,293,292,293,294,294,294,294,294,294,294,294,294,294,294,294,294,294,294,294,294,294,294,294,294,294,294,294,293,293,293,293,293,293,293,293,293,293,293,293,293,293,293,293,293,293,292,295,295,295,295,295,295,295,295,295,295,295,295,295,297,297,296,296,296,296,296,296,296,299,299,298,298,298,298,297,297,297,296,296,296,296,296,296,294,292,291,291,291,291,290,290,290,290,290,289,289,289,289,289,288,288,288,288,288,288,288,287,287,287,287,287,287,287,287,286,286,286,286,286,286,285,284,284,284,284,284,284,284,285,285,285,285,285,284,284,284,284,284,284,284,282,282,282,282,282,282,282,282,282,282,282,282,282,282,282,282,282,282,285,285,287,286,286,286,286,286,286,286,286,286,285,285,286,286,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,284,284,284,288,288,288,288,288,289,289,289,289,292,291,291,291,291,291,291,290,290,290,290,290,289,289,289,290,298,298,297,297,297,297,297,297,297,297,300,299,296,295,295,295,295,299,300,300,300,300,300,300,300,300,300,298,298,298,298,297,297,297,297,297,297,297,298,298,298,298,298,298,299,299,299,299,299,298,298,298,301,306,311,311,311,311,311,311,311,311,311,311,310,310,310,310,310,310,310,310,310,311,312,312,312,312,312,312,312,312,312,312,312,312,312,312,312,311,311,311,311,311,311,311,311,317,317,317,317,317,317,317,316,316,316,316,318,318,318,318,320,320,320,320,320,320,320,320,320,320,320,320,320,320,319,319,319,319,319,319,319,319,319,319,319,318,318,317,317,317,317,317,317,317,317,317,317,317,317,317,316,316,316,316,316,316,316,316,319,319,319,319,319,320,320,320,320,320,320,320,320,320,320,320,320,318,318,318,318,318,318,318,318,318,318,318,317,317,317,317,316,316,316,316,316,316,316,316,316,316,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,313,313,313,313,313,313,317,318,318,318,318,318,318,318,318,318,318,318,318,318,318,318,319,319,320,320,320,320,320,319,319,319,319,319,319,319,319,319,319,319,319,319,319,319,318,318,318,318,318,318,318,317,317,317,315,315,315,315,314,314,314,314,316,316,316,315,315,315,315,315,315,315,314,314,314,314,314,314,314,317,317,316,316,316,316,317,317,317,317,317,317,317,317,319,319,319,318,318,318,317,317,320,320,320,317,318,318,318,318,318,317,313,313,315,315,315,315,315,314,314,317,317,317,317,317,317,317,317,317,317,317,317,317,317,317,317,317,317,317,317,316,316,316,321,321,321,321,321,321,320,320,320,320,319,321,321,321,321,321,321,321,321,320,320,320,320,320,320,320,320,320,320,320,320,320,320,320,320,320,320,320,320,319,319,319,319,319,319,317,316,316,315,314,314,314,314,314,314,314,314,314,314,314,313,313,313,309,309,309,308,307,307,307,314,314,314,314,315,315,314,314,314,314,314,313,313,315,315,315,315,315,315,315,314,314,314,314,313,313,313,313,313,313,313,313,313,313,313,313,313,313,313,313,313,313,313,314,314,314,314,313,313,313,316,316,315,315,315,315,316,316,316,316,315,315,311,311,310,310,309,308,308,308,308,308,309,309,308,308,308,308,308,308,308,308,308,308,308,308,308,308,307,307,307,307,307,307,303,303,303,303,303,303,300,300,300,300,300,300,300,300,300,300,302,302,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,300,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,303,303,303,303,303,303,303,303,303,303,303,302,302,302,302,302,302,302,302,302,301,301,301,301,301,301,301,300,298,298,298,298,298,298,297,297,297,296,296,296,295,295,295,295,295,295,295,295,295,295,295,295,295,295,300,300,300,300,300,300,300,300,300,300,300,300,300,299,299,299,299,299,299,299,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,299,299,299,301,301,301,301,301,301,301,301,301,306,306,306,306,305,305,305,305,305,305,305,305,305,305,305,305,305,305,304,304,304,304,304,304,303,303,303,303,303,303,303,303,303,302,302,302,302,302,302,302,302,302,302,302,302,302,301,301,301,301,301,301,300,300,300,300,300,300,300,300,300,300,300,300,300,299,299,299,299,299,299,299,299,299,299,299,299,299,299,299,299,299,299,299,299,300,300,300,300,300,300,300,300,299,299,299,298,298,298,298,297,297,297,297,296,296,296,296,296,296,295,295,295,295,295,295,295,295,295,295,295,295,295,295,295,295,295,295,295,295,295,295,295,295,295,294,294,294,297,297,297,297,296,296,296,296,296,296,296,296,296,295,295,294,294,294,292,292,292,291,291,291,291,291,291,291,288,288,288,289,289,289,289,289,289,289,289,289,293,293,293,293,293,293,293,293,293,293,297,297,297,298,298,299,299,299,299,299,299,299,299,299,299,299,299,300,301,301,301,301,301,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,304,304,304,304,303,303,303,303,303,303,303,303,303,303,304,304,304,305,305,305,305,305,305,305,305,305,305,305,304,304,304,304,304,304,304,304,303,303,303,303,303,303,303,303,302,302,302,302,302,302,302,302,307,307,307,307,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,305,305,305,305,305,305,305,305,305,305,305,305,305,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,306,306,306,306,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,304,304,304,304,304,304,304,304,304,305,305,305,305,305,305,305,305,307,306,306,306,306,306,306,306,306,305,305,305,305,305,305,305,305,304,304,304,304,304,304,304,303,303,303,305,304,304,304,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,313,313,313,313,313,313,313,312,312,312,311,311,311,311,311,311,311,311,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,311,311,311,312,312,312,313,313,313,314,314,314,314,314,314,314,314,313,312,312,312,319,319,319,319,319,319,319,319,319,323,322,323,324,324,324,324,324,324,324,324,324,323,322,323,323,323,323,323,323,323,323,324,324,324,324,325,325,325,325,325,325,325,325,325,325,325,325,325,325,325,325,325,325,325,325,325,324,324,324,325,325,325,325,325,325,325,325,325,325,325,325,325,325,324,324,332,332,332,332,331,330,330,330,330,330,330,330,330,330,330,330,330,330,330,330,330,330,330,330,331,331,331,332,333,333,333,333,334,334,334,334,334,334,333,334,334,334,334,334,334,333,333,333,333,333,333,333,333,333,333,333,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,342,342,342,342,342,342,341,341,340,340,340,340,340,339,339,341,341,341,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,338,336,336,336,336,336,336,336,336,336,335,334,334,334,334,334,334,334,334,333,333,333,333,333,333,333,333,333,333,333,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,331,330,330,330,330,330,330,330,330,330,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,331,331,331,330,330,330,330,328,328,328,328,328,328,328,328,328,328,328,328,328,328,328,328,328,328,328,327,327,327,327,327,327,327,327,327,327,327,327,327,327,327,327,327,327,327,327,327,327,326,326,326,326,326,326,326,327,327,327,327,327,327,327,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,325,328,328,328,328,328,328,328,328,328,328,328,327,327,327,327,327,326,325,325,323,323,323,323,323,323,323,323,323,323,323,330,329,329,329,329,329,328,328,328,328,328,328,328,327,327,327,327,327,327,327,327,327,327,327,327,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,325,325,325,324,324,324,324,324,324,323,324,324,324,324,324,324,324,324,324,324,324,327,327,327,326,323,322,322,321,321,321,321,321,321,321,321,320,320,320,320,320,320,320,320,320,320,320,320,320,320,320,320,320,320,319,319,319,319,319,319,319,318,317,316,316,315,315,317,317,317,317,317,317,317,317,317,317,316,316,316,316,316,316,316,315,315,314,314,314,314,314,314,314,313,313,313,313,313,313,313,313,313,313,314,314,314,314,314,314,314,314,314,313,315,315,315,311,311,311,311,311,311,310,310,310,310,310,310,311,311,311,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,307,307,307,307,307,307,306,306,306,306,306,306,306,306,306,306,305,305,305,305,305,305,305,304,304,304,304,304,304,304,304,303,303,303,303,303,303,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,301,301,301,301,301,301,301,301,301,301,301,301,301,300,300,300,300,300,300,300,300,300,300,300,300,301,301,301,301,301,308,308,307,307,307,307,307,307,307,306,306,306,306,306,309,309,309,309,309,309,309,309,309,309,309,309,309,309,309,309,309,309,309,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,307,307,307,307,307,307,307,307,307,307,307,307,307,307,307,307,307,306,305,305,305,305,305,305,305,305,305,305,305,305,305,308,308,308,308,307,307,307,307,307,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,307,307,307,307,307,307,306,306,306,306,305,305,305,305,305,305,305,305,304,304,304,304,304,304,304,304,304,304,304,304,304,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,300,300,300,299,299,299,297,297,297,297,296,296,296,296,296,296,294,294,294,294,294,294,294,296,296,296,296,296,296,296,296,298,298,298,298,298,298,298,297,297,297,297,297,297,297,297,297,297,297,297,297,296,296,296,297,297,297,297,297,297,297,297,299,299,299,299,299,299,299,299,299,299,298,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,294,297,297,297,297,297,297,297,297,297,297,297,297,297,297,297,295,295,295,295,295,295,295,295,295,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,295,294,294,294,294,294,294,294,294,294,293,293,293,293,293,293,293,294,294,294,294,294,294,294,294,294,294,294,293,293,293,293,293,293,293,293,293,293,293,293,292,292,292,292,292,292,292,292,292,292,292,292,292,291,291,290,290,290,290,290,290,290,290,290,290,290,290,290,290,290,290,290,294,294,294,293,293,293,293,293,293,293,293,293,293,293,293,293,293,292,292,292,292,292,292,292,292,293,293,293,295,295,295,294,294,294,294,294,294,294,294,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,291,291,291,291,291,291,291,291,291,291,291,291,291,292,291,291,291,291,291,291,291,291,291,291,291,290,290,290,290,290,290,290,290,291,290,290,290,290,290,290,290,290,290,289,289,289,289,289,289,289,289,289,288,288,288,288,288,287,287,287,287,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,285,285,285,285,285,285,285,285,285,285,285,287,291,291,291,291,291,291,291,291,291,290,290,290,290,290,290,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,288,288,288,289,289,289,288,288,288,288,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,285,285,285,285,285,285,285,285,285,286,286,286,286,286,286,285,285,285,285,285,285,285,285,285,285,285,284,284,284,284,284,284,284,284,284,284,284,284,283,283,282,282,282,282,282,282,283,283,283,283,283,283,283,283,282,282,282,282,282,282,282,282,282,282,282,282,282,282,282,282,282,282,282,281,281,281,281,281,281,281,281,281,281,281,281,280,280,280,279,279,279,279,279,279,279,278,278,278,278,278,278,277,277,277,277,277,277,277,277,277,277,277,277,277,277,276,276,276,276,276,276,276,276,277,280,280,280,280,280,280,280,280,280,280,280,280,280,280,290,290,290,290,289,289,289,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,287,287,287,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,284,283,283,283,282,280,280,280,280,280,280,280,280,280,280,280,280,280,280,280,280,280,280,280,280,281,281,281,281,280,279,279,279,279,279,279,279,279,279,279,279,279,279,279,279,279,279,279,279,279,283,283,283,283,283,283,282],\"Pregnant Mothers\":[1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,0,0,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,2,2,2,2,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,3,3,3,3,3,3,3,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,2,2,2,2,2,2,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,2,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,2,3,3,3,3,3,3,3,3,3,3,3,2,2,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,3,3,3,3,2,2,3,3,2,3,4,4,4,4,4,4,4,4,4,4,4,4,5,4,3,3,3,3,3,3,3,3,3,3,2,2,2,2,2,2,2,1,0,0,0,0,0,0,0,1,1,1,1,1,1,2,2,2,2,2,2,2,1,1,1,2,3,5,4,4,4,4,4,4,4,4,3,1,0,0,0,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,0,0,0,2,2,3,3,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,2,2,3,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,2,2,2,2,2,2,2,2,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,2,1,2,1,1,2,2,2,2,1,2,2,2,2,2,2,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,2,2,2,2,2,2,1,1,1,1,2,2,2,3,3,3,3,1,1,1,1,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,1,1,1,1,1,1,1,2,2,2,2,2,2,3,3,3,3,3,3,3,3,3,3,3,2,2,2,2,2,2,2,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,2,2,1,1,2,2,2,2,2,2,2,2,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,5,5,5,4,4,3,3,3,3,3,3,3,3,3,3,4,4,3,2,2,2,2,2,1,1,1,1,1,2,2,2,3,3,3,3,3,3,3,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,1,1,1,2,2,2,3,3,3,3,4,4,4,4,4,4,4,4,4,4,4,4,5,5,4,4,4,3,3,3,3,3,4,4,4,4,4,4,4,4,4,4,4,4,5,4,4,4,4,4,4,4,5,5,4,4,4,3,3,3,3,3,3,3,3,3,3,3,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,2,2,2,3,4,4,4,4,4,4,4,4,4,4,4,5,5,5,5,5,5,5,5,5,4,4,4,3,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,3,3,3,3,3,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,2,2,2,2,2,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,2,2,1,1,1,1,1,2,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,0,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,3,3,3,2,2,2,2,2,2,2,2,3,3,3,4,4,4,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0]}},\"id\":\"09751f14-363e-4096-be27-e3bf1ce4fc78\",\"type\":\"ColumnDataSource\"},{\"attributes\":{\"days\":[1,8,15,22]},\"id\":\"759a8935-595e-482f-9b64-ed7ae793b1f3\",\"type\":\"DaysTicker\"},{\"attributes\":{\"below\":[{\"id\":\"d05c05d6-0807-4df8-aa9a-87b29190f0c0\",\"type\":\"DatetimeAxis\"}],\"left\":[{\"id\":\"b963823d-46bf-4c7b-a0d3-380e7c5566cf\",\"type\":\"LinearAxis\"}],\"plot_height\":150,\"plot_width\":1600,\"renderers\":[{\"id\":\"d05c05d6-0807-4df8-aa9a-87b29190f0c0\",\"type\":\"DatetimeAxis\"},{\"id\":\"36fcaefc-7e4c-47d4-bc8b-c7010f224007\",\"type\":\"Grid\"},{\"id\":\"b963823d-46bf-4c7b-a0d3-380e7c5566cf\",\"type\":\"LinearAxis\"},{\"id\":\"9f271225-28ff-4d64-8a82-2488ad65a90c\",\"type\":\"Grid\"},{\"id\":\"178d7500-8294-4489-970a-a5e47d438de0\",\"type\":\"GlyphRenderer\"}],\"sizing_mode\":\"scale_width\",\"title\":{\"id\":\"21872c55-2d33-40d2-ba04-ebf3db5a63e9\",\"type\":\"Title\"},\"tool_events\":{\"id\":\"6edb720f-299e-467d-a729-26251383602a\",\"type\":\"ToolEvents\"},\"toolbar\":{\"id\":\"786f34ed-2e4e-4811-83cd-395a04be5b23\",\"type\":\"Toolbar\"},\"x_range\":{\"id\":\"c9ab1709-3456-4d4a-afcf-e5b6953c7bee\",\"type\":\"Range1d\"},\"y_range\":{\"id\":\"3295f0c8-47e6-4945-912f-55a042a57270\",\"type\":\"Range1d\"}},\"id\":\"2ebbe383-aed7-471a-9394-cb067527920a\",\"subtype\":\"Figure\",\"type\":\"Plot\"},{\"attributes\":{\"data_source\":{\"id\":\"09751f14-363e-4096-be27-e3bf1ce4fc78\",\"type\":\"ColumnDataSource\"},\"glyph\":{\"id\":\"91379bec-9b6a-4676-aefb-25650069eb2d\",\"type\":\"Line\"},\"hover_glyph\":null,\"nonselection_glyph\":{\"id\":\"d3d666a4-9525-408f-ae1c-0d5d99a0a3cb\",\"type\":\"Line\"},\"selection_glyph\":null},\"id\":\"178d7500-8294-4489-970a-a5e47d438de0\",\"type\":\"GlyphRenderer\"},{\"attributes\":{\"max_interval\":500.0,\"num_minor_ticks\":0},\"id\":\"a1e78381-0e1a-474b-ad39-85b213ab9095\",\"type\":\"AdaptiveTicker\"},{\"attributes\":{\"plot\":{\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"}},\"id\":\"1cc2d776-7f8e-42b5-b316-4167f890ce28\",\"type\":\"ResetTool\"},{\"attributes\":{\"num_minor_ticks\":5},\"id\":\"a7f91300-a887-47cf-b18b-4be7c4c9bb33\",\"type\":\"DatetimeTicker\"},{\"attributes\":{\"plot\":null,\"text\":null},\"id\":\"eb3c4083-1eaf-4dc4-93d3-814e8b844c1b\",\"type\":\"Title\"},{\"attributes\":{\"days\":[1,15]},\"id\":\"8aea957f-368f-402f-a308-b0bf7d765c1e\",\"type\":\"DaysTicker\"},{\"attributes\":{\"plot\":{\"id\":\"2ebbe383-aed7-471a-9394-cb067527920a\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"ticker\":{\"id\":\"0ca5882b-d581-49f2-93f3-a07dfb3856d8\",\"type\":\"DatetimeTicker\"}},\"id\":\"36fcaefc-7e4c-47d4-bc8b-c7010f224007\",\"type\":\"Grid\"},{\"attributes\":{\"months\":[0,1,2,3,4,5,6,7,8,9,10,11]},\"id\":\"fe18b668-5507-48ed-8e58-b6976e7d7243\",\"type\":\"MonthsTicker\"},{\"attributes\":{\"plot\":{\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"}},\"id\":\"b54047eb-194f-4e19-aef9-4a66ed72384f\",\"type\":\"PanTool\"},{\"attributes\":{},\"id\":\"8be3bc82-2e46-40aa-a62b-9524f689454e\",\"type\":\"DatetimeTickFormatter\"}],\"root_ids\":[\"751c511a-332d-4afb-8439-cad2e55a6a32\"]},\"title\":\"Bokeh Application\",\"version\":\"0.12.3\"}};\n",
" var render_items = [{\"docid\":\"f97c0641-77f2-4404-bca1-1e54284d3ad0\",\"elementid\":\"e596e404-014c-44f7-b48a-c9e9f1aede8f\",\"modelid\":\"751c511a-332d-4afb-8439-cad2e55a6a32\"}];\n",
" \n",
" Bokeh.embed.embed_items(docs_json, render_items);\n",
" });\n",
" },\n",
" function(Bokeh) {\n",
" }\n",
" ];\n",
" \n",
" function run_inline_js() {\n",
" \n",
" if ((window.Bokeh !== undefined) || (force === \"1\")) {\n",
" for (var i = 0; i < inline_js.length; i++) {\n",
" inline_js[i](window.Bokeh);\n",
" }if (force === \"1\") {\n",
" display_loaded();\n",
" }} else if (Date.now() < window._bokeh_timeout) {\n",
" setTimeout(run_inline_js, 100);\n",
" } else if (!window._bokeh_failed_load) {\n",
" console.log(\"Bokeh: BokehJS failed to load within specified timeout.\");\n",
" window._bokeh_failed_load = true;\n",
" } else if (!force) {\n",
" var cell = $(\"#e596e404-014c-44f7-b48a-c9e9f1aede8f\").parents('.cell').data().cell;\n",
" cell.output_area.append_execute_result(NB_LOAD_WARNING)\n",
" }\n",
" \n",
" }\n",
" \n",
" if (window._bokeh_is_loading === 0) {\n",
" console.log(\"Bokeh: BokehJS loaded, going straight to plotting\");\n",
" run_inline_js();\n",
" } else {\n",
" load_libs(js_urls, function() {\n",
" console.log(\"Bokeh: BokehJS plotting callback run at\", now());\n",
" run_inline_js();\n",
" });\n",
" }\n",
" }(this));\n",
"</script>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"layout = fto_web.run(df)\n",
"bokeh.io.show(layout)"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import bokeh.themes\n",
"import yaml\n",
"m = layout.children[1]"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"m"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"layout.apply_theme?"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from bokeh.themes import Theme"
]
},
{
"cell_type": "code",
"execution_count": 68,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
" <div class=\"bk-root\">\n",
" <div class=\"plotdiv\" id=\"3b840391-5260-4ada-9846-98fddc974d12\"></div>\n",
" </div>\n",
"<script type=\"text/javascript\">\n",
" \n",
" (function(global) {\n",
" function now() {\n",
" return new Date();\n",
" }\n",
" \n",
" var force = \"\";\n",
" \n",
" if (typeof (window._bokeh_onload_callbacks) === \"undefined\" || force !== \"\") {\n",
" window._bokeh_onload_callbacks = [];\n",
" window._bokeh_is_loading = undefined;\n",
" }\n",
" \n",
" \n",
" \n",
" if (typeof (window._bokeh_timeout) === \"undefined\" || force !== \"\") {\n",
" window._bokeh_timeout = Date.now() + 0;\n",
" window._bokeh_failed_load = false;\n",
" }\n",
" \n",
" var NB_LOAD_WARNING = {'data': {'text/html':\n",
" \"<div style='background-color: #fdd'>\\n\"+\n",
" \"<p>\\n\"+\n",
" \"BokehJS does not appear to have successfully loaded. If loading BokehJS from CDN, this \\n\"+\n",
" \"may be due to a slow or bad network connection. Possible fixes:\\n\"+\n",
" \"</p>\\n\"+\n",
" \"<ul>\\n\"+\n",
" \"<li>re-rerun `output_notebook()` to attempt to load from CDN again, or</li>\\n\"+\n",
" \"<li>use INLINE resources instead, as so:</li>\\n\"+\n",
" \"</ul>\\n\"+\n",
" \"<code>\\n\"+\n",
" \"from bokeh.resources import INLINE\\n\"+\n",
" \"output_notebook(resources=INLINE)\\n\"+\n",
" \"</code>\\n\"+\n",
" \"</div>\"}};\n",
" \n",
" function display_loaded() {\n",
" if (window.Bokeh !== undefined) {\n",
" Bokeh.$(\"#3b840391-5260-4ada-9846-98fddc974d12\").text(\"BokehJS successfully loaded.\");\n",
" } else if (Date.now() < window._bokeh_timeout) {\n",
" setTimeout(display_loaded, 100)\n",
" }\n",
" }\n",
" \n",
" function run_callbacks() {\n",
" window._bokeh_onload_callbacks.forEach(function(callback) { callback() });\n",
" delete window._bokeh_onload_callbacks\n",
" console.info(\"Bokeh: all callbacks have finished\");\n",
" }\n",
" \n",
" function load_libs(js_urls, callback) {\n",
" window._bokeh_onload_callbacks.push(callback);\n",
" if (window._bokeh_is_loading > 0) {\n",
" console.log(\"Bokeh: BokehJS is being loaded, scheduling callback at\", now());\n",
" return null;\n",
" }\n",
" if (js_urls == null || js_urls.length === 0) {\n",
" run_callbacks();\n",
" return null;\n",
" }\n",
" console.log(\"Bokeh: BokehJS not loaded, scheduling load and callback at\", now());\n",
" window._bokeh_is_loading = js_urls.length;\n",
" for (var i = 0; i < js_urls.length; i++) {\n",
" var url = js_urls[i];\n",
" var s = document.createElement('script');\n",
" s.src = url;\n",
" s.async = false;\n",
" s.onreadystatechange = s.onload = function() {\n",
" window._bokeh_is_loading--;\n",
" if (window._bokeh_is_loading === 0) {\n",
" console.log(\"Bokeh: all BokehJS libraries loaded\");\n",
" run_callbacks()\n",
" }\n",
" };\n",
" s.onerror = function() {\n",
" console.warn(\"failed to load library \" + url);\n",
" };\n",
" console.log(\"Bokeh: injecting script tag for BokehJS library: \", url);\n",
" document.getElementsByTagName(\"head\")[0].appendChild(s);\n",
" }\n",
" };var element = document.getElementById(\"3b840391-5260-4ada-9846-98fddc974d12\");\n",
" if (element == null) {\n",
" console.log(\"Bokeh: ERROR: autoload.js configured with elementid '3b840391-5260-4ada-9846-98fddc974d12' but no matching script tag was found. \")\n",
" return false;\n",
" }\n",
" \n",
" var js_urls = [];\n",
" \n",
" var inline_js = [\n",
" function(Bokeh) {\n",
" Bokeh.$(function() {\n",
" var docs_json = {\"99b5593e-368d-4de1-9ad5-3bf6e525c34d\":{\"roots\":{\"references\":[{\"attributes\":{\"max_interval\":500.0,\"num_minor_ticks\":0},\"id\":\"e70bec11-1c3c-4af6-a9ce-b69642afc38a\",\"type\":\"AdaptiveTicker\"},{\"attributes\":{\"text\":\"<h1>FTO Hourly Statistics</h1>\"},\"id\":\"0265ae34-c338-4ee4-8a2c-469e0264c815\",\"type\":\"Div\"},{\"attributes\":{},\"id\":\"e6eb8c18-587d-4d32-9be7-584919a82473\",\"type\":\"BasicTicker\"},{\"attributes\":{},\"id\":\"6edb720f-299e-467d-a729-26251383602a\",\"type\":\"ToolEvents\"},{\"attributes\":{\"children\":[{\"id\":\"11951298-d00a-4b0e-952b-6bf811b0b0d7\",\"type\":\"WidgetBox\"},{\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"},{\"id\":\"2ebbe383-aed7-471a-9394-cb067527920a\",\"subtype\":\"Figure\",\"type\":\"Plot\"}],\"sizing_mode\":\"scale_width\"},\"id\":\"751c511a-332d-4afb-8439-cad2e55a6a32\",\"type\":\"Column\"},{\"attributes\":{\"axis_label\":\"Population\",\"axis_label_text_color\":{\"value\":\"#e41a1c\"},\"axis_label_text_font_size\":{\"value\":\"16pt\"},\"axis_label_text_font_style\":\"bold\",\"formatter\":{\"id\":\"38a20ffc-1f08-4022-bfc5-2cc808ffbd3f\",\"type\":\"BasicTickFormatter\"},\"plot\":{\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"ticker\":{\"id\":\"e6eb8c18-587d-4d32-9be7-584919a82473\",\"type\":\"BasicTicker\"},\"y_range_name\":\"population\"},\"id\":\"52f786d5-f3ef-4f34-9c61-7e4e3513973e\",\"type\":\"LinearAxis\"},{\"attributes\":{\"active_drag\":{\"id\":\"b202de9c-41fe-4a52-be91-04d9a76cf394\",\"type\":\"BoxZoomTool\"},\"active_scroll\":\"auto\",\"active_tap\":\"auto\",\"logo\":null,\"tools\":[{\"id\":\"b54047eb-194f-4e19-aef9-4a66ed72384f\",\"type\":\"PanTool\"},{\"id\":\"b202de9c-41fe-4a52-be91-04d9a76cf394\",\"type\":\"BoxZoomTool\"},{\"id\":\"1cc2d776-7f8e-42b5-b316-4167f890ce28\",\"type\":\"ResetTool\"},{\"id\":\"177fb635-9940-4675-8981-e0a591e4071a\",\"type\":\"CrosshairTool\"},{\"id\":\"500c318f-6a52-4711-b05b-fd95fa09e41b\",\"type\":\"HoverTool\"}]},\"id\":\"87eae3c0-c7f2-40d4-a449-328e6c1f6a28\",\"type\":\"Toolbar\"},{\"attributes\":{\"bounds\":\"auto\",\"callback\":null,\"end\":382,\"start\":123},\"id\":\"cb3f450e-4079-436f-9c2c-5c2b44dbff10\",\"type\":\"Range1d\"},{\"attributes\":{\"days\":[1,4,7,10,13,16,19,22,25,28]},\"id\":\"d8ae6b2c-f11b-41f3-afc4-97839406854e\",\"type\":\"DaysTicker\"},{\"attributes\":{\"bounds\":\"auto\",\"callback\":null,\"end\":342,\"start\":276},\"id\":\"f503788e-792c-4197-9e36-d3ae5356f850\",\"type\":\"Range1d\"},{\"attributes\":{\"base\":60,\"mantissas\":[1,2,5,10,15,20,30],\"max_interval\":1800000.0,\"min_interval\":1000.0,\"num_minor_ticks\":0},\"id\":\"dff20f88-68d2-4925-8664-9b16d415de61\",\"type\":\"AdaptiveTicker\"},{\"attributes\":{\"base\":60,\"mantissas\":[1,2,5,10,15,20,30],\"max_interval\":1800000.0,\"min_interval\":1000.0,\"num_minor_ticks\":0},\"id\":\"4358dd5e-694a-4b5b-9791-d4fdefdbe764\",\"type\":\"AdaptiveTicker\"},{\"attributes\":{\"days\":[1,8,15,22]},\"id\":\"963150ce-b92a-4946-811d-2b0252b5ed54\",\"type\":\"DaysTicker\"},{\"attributes\":{\"days\":[1,15]},\"id\":\"a8e51fd6-6cdf-4304-b657-cf4eb924ac6e\",\"type\":\"DaysTicker\"},{\"attributes\":{\"months\":[0,1,2,3,4,5,6,7,8,9,10,11]},\"id\":\"9ec79f7f-157a-40d1-aa7e-0c169b9a2a9c\",\"type\":\"MonthsTicker\"},{\"attributes\":{\"axis_label\":\"Birth Queue\",\"axis_label_text_color\":{\"value\":\"#377eb8\"},\"axis_label_text_font_size\":{\"value\":\"16pt\"},\"axis_label_text_font_style\":\"bold\",\"formatter\":{\"id\":\"ab66c96d-2fd9-4733-b6d7-81e7643686fb\",\"type\":\"BasicTickFormatter\"},\"plot\":{\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"ticker\":{\"id\":\"fa1bd8cd-712b-42f8-8353-cc666a86ddab\",\"type\":\"BasicTicker\"}},\"id\":\"2a437546-87c2-4e96-a14f-0ab9c0e84542\",\"type\":\"LinearAxis\"},{\"attributes\":{\"dimensions\":\"width\",\"overlay\":{\"id\":\"76b5b429-a514-4516-bc79-50f3e8543a73\",\"type\":\"BoxAnnotation\"},\"plot\":{\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"}},\"id\":\"b202de9c-41fe-4a52-be91-04d9a76cf394\",\"type\":\"BoxZoomTool\"},{\"attributes\":{\"line_alpha\":{\"value\":0.1},\"line_cap\":\"round\",\"line_color\":{\"value\":\"#1f77b4\"},\"line_width\":{\"value\":3},\"x\":{\"field\":\"Date\"},\"y\":{\"field\":\"Population\"}},\"id\":\"3786a2e6-c89e-4077-aaed-c4ffba956e22\",\"type\":\"Line\"},{\"attributes\":{\"formatter\":{\"id\":\"9aadacf5-84fd-46ba-80ee-633d6946a9a4\",\"type\":\"DatetimeTickFormatter\"},\"plot\":{\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"ticker\":{\"id\":\"a7f91300-a887-47cf-b18b-4be7c4c9bb33\",\"type\":\"DatetimeTicker\"},\"visible\":false},\"id\":\"07941450-49a3-47c1-8c84-5bc2f6b4cfd4\",\"type\":\"DatetimeAxis\"},{\"attributes\":{\"num_minor_ticks\":5},\"id\":\"0ca5882b-d581-49f2-93f3-a07dfb3856d8\",\"type\":\"DatetimeTicker\"},{\"attributes\":{\"base\":24,\"mantissas\":[1,2,4,6,8,12],\"max_interval\":43200000.0,\"min_interval\":3600000.0,\"num_minor_ticks\":0},\"id\":\"2e76e280-63fb-437e-9ce4-164f3096d1ac\",\"type\":\"AdaptiveTicker\"},{\"attributes\":{\"base\":24,\"mantissas\":[1,2,4,6,8,12],\"max_interval\":43200000.0,\"min_interval\":3600000.0,\"num_minor_ticks\":0},\"id\":\"9b94b31e-25c4-402a-8ee1-907d2a681e2c\",\"type\":\"AdaptiveTicker\"},{\"attributes\":{\"days\":[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]},\"id\":\"7e20ebd2-9d90-4e80-9619-fdf0b36d9bc9\",\"type\":\"DaysTicker\"},{\"attributes\":{},\"id\":\"fa1bd8cd-712b-42f8-8353-cc666a86ddab\",\"type\":\"BasicTicker\"},{\"attributes\":{\"months\":[0,6]},\"id\":\"ed3f7a2a-4f1f-48c5-b304-012e38ee4267\",\"type\":\"MonthsTicker\"},{\"attributes\":{\"bottom_units\":\"screen\",\"fill_alpha\":{\"value\":0.5},\"fill_color\":{\"value\":\"lightgrey\"},\"left_units\":\"screen\",\"level\":\"overlay\",\"line_alpha\":{\"value\":1.0},\"line_color\":{\"value\":\"black\"},\"line_dash\":[4,4],\"line_width\":{\"value\":2},\"plot\":null,\"render_mode\":\"css\",\"right_units\":\"screen\",\"top_units\":\"screen\"},\"id\":\"76b5b429-a514-4516-bc79-50f3e8543a73\",\"type\":\"BoxAnnotation\"},{\"attributes\":{\"line_alpha\":{\"value\":0.1},\"line_cap\":\"round\",\"line_color\":{\"value\":\"#1f77b4\"},\"line_width\":{\"value\":3},\"x\":{\"field\":\"Date\"},\"y\":{\"field\":\"Birth Queue\"}},\"id\":\"bc3728dd-1043-45bf-b35f-fd74d5b56e93\",\"type\":\"Line\"},{\"attributes\":{\"months\":[0,2,4,6,8,10]},\"id\":\"9371833f-faa4-4087-bfd0-626a102b2f2d\",\"type\":\"MonthsTicker\"},{\"attributes\":{\"children\":[{\"id\":\"0265ae34-c338-4ee4-8a2c-469e0264c815\",\"type\":\"Div\"}],\"sizing_mode\":\"scale_width\"},\"id\":\"11951298-d00a-4b0e-952b-6bf811b0b0d7\",\"type\":\"WidgetBox\"},{\"attributes\":{\"data_source\":{\"id\":\"09751f14-363e-4096-be27-e3bf1ce4fc78\",\"type\":\"ColumnDataSource\"},\"glyph\":{\"id\":\"c4a3d9f6-cbd9-4639-b213-48d109ba8956\",\"type\":\"Line\"},\"hover_glyph\":null,\"nonselection_glyph\":{\"id\":\"3786a2e6-c89e-4077-aaed-c4ffba956e22\",\"type\":\"Line\"},\"selection_glyph\":null,\"y_range_name\":\"population\"},\"id\":\"613fc096-c059-408d-9dc3-b04b1da93f85\",\"type\":\"GlyphRenderer\"},{\"attributes\":{\"code\":\"\\n var arr = document.getElementsByClassName(\\\"bk-canvas-wrapper\\\");\\n for(var i = 0, len = arr.length; i < len; i++) {\\n arr[i].style.cursor = \\\"none\\\";\\n }\\n var elem = document.getElementById(\\\"static-tooltip\\\");\\n if (elem == null) {\\n return;\\n }\\n var tooltip = elem.parentNode.parentNode.parentNode;\\n tooltip.style.top = \\\"\\\"; // unset what bokeh.js sets\\n tooltip.style.left = \\\"\\\";\\n tooltip.style.top = \\\"4px\\\";\\n tooltip.style.left = \\\"122px\\\";\\n\\n \"},\"id\":\"b3ad4d7e-6ad8-4a3b-a356-2913b4b01ce9\",\"type\":\"CustomJS\"},{\"attributes\":{},\"id\":\"c69fc03b-d1ab-4060-aeca-49432993d1f9\",\"type\":\"BasicTicker\"},{\"attributes\":{\"dimensions\":\"height\",\"plot\":{\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"}},\"id\":\"177fb635-9940-4675-8981-e0a591e4071a\",\"type\":\"CrosshairTool\"},{\"attributes\":{\"active_drag\":\"auto\",\"active_scroll\":\"auto\",\"active_tap\":\"auto\"},\"id\":\"786f34ed-2e4e-4811-83cd-395a04be5b23\",\"type\":\"Toolbar\"},{\"attributes\":{},\"id\":\"c1f9e013-f556-4a5f-ba52-03eab53f89b2\",\"type\":\"BasicTickFormatter\"},{\"attributes\":{},\"id\":\"38a20ffc-1f08-4022-bfc5-2cc808ffbd3f\",\"type\":\"BasicTickFormatter\"},{\"attributes\":{\"callback\":{\"id\":\"b3ad4d7e-6ad8-4a3b-a356-2913b4b01ce9\",\"type\":\"CustomJS\"},\"line_policy\":\"nearest\",\"mode\":\"vline\",\"plot\":{\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"renderers\":[{\"id\":\"613fc096-c059-408d-9dc3-b04b1da93f85\",\"type\":\"GlyphRenderer\"}],\"show_arrow\":false,\"tooltips\":\"\\n <div id=\\\"static-tooltip\\\">\\n <span>Population: @Population</span><br />\\n <span>Birth Queue: @{Birth Queue}</span><br />\\n <span>Pregnant Mothers: @{Pregnant Mothers}</span><br />\\n <span>Date: @{Date Formatted}</span><br />\\n </div>\"},\"id\":\"500c318f-6a52-4711-b05b-fd95fa09e41b\",\"type\":\"HoverTool\"},{\"attributes\":{},\"id\":\"6e832d89-20c9-49e0-bf14-8baff8b05598\",\"type\":\"YearsTicker\"},{\"attributes\":{\"bounds\":\"auto\",\"callback\":null,\"end\":1475046000000.0,\"start\":1455534000000.0},\"id\":\"c9ab1709-3456-4d4a-afcf-e5b6953c7bee\",\"type\":\"Range1d\"},{\"attributes\":{\"formatter\":{\"id\":\"c1f9e013-f556-4a5f-ba52-03eab53f89b2\",\"type\":\"BasicTickFormatter\"},\"minor_tick_line_color\":{\"value\":null},\"plot\":{\"id\":\"2ebbe383-aed7-471a-9394-cb067527920a\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"ticker\":{\"id\":\"c69fc03b-d1ab-4060-aeca-49432993d1f9\",\"type\":\"BasicTicker\"}},\"id\":\"b963823d-46bf-4c7b-a0d3-380e7c5566cf\",\"type\":\"LinearAxis\"},{\"attributes\":{\"bounds\":\"auto\",\"callback\":null,\"end\":5},\"id\":\"3295f0c8-47e6-4945-912f-55a042a57270\",\"type\":\"Range1d\"},{\"attributes\":{},\"id\":\"68ab0725-1236-418b-87df-9175b935e5a1\",\"type\":\"ToolEvents\"},{\"attributes\":{\"months\":[0,2,4,6,8,10]},\"id\":\"ed66f1c7-2881-4b65-82cf-1a27f581edac\",\"type\":\"MonthsTicker\"},{\"attributes\":{\"plot\":{\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"ticker\":{\"id\":\"a7f91300-a887-47cf-b18b-4be7c4c9bb33\",\"type\":\"DatetimeTicker\"}},\"id\":\"f4c91080-a7aa-4eda-9366-58c04b46b9da\",\"type\":\"Grid\"},{\"attributes\":{\"months\":[0,4,8]},\"id\":\"f774701a-d5fa-4fc9-a248-1781d24e63ce\",\"type\":\"MonthsTicker\"},{\"attributes\":{\"months\":[0,6]},\"id\":\"068847f5-0386-474c-9fa1-8983928ff3c1\",\"type\":\"MonthsTicker\"},{\"attributes\":{},\"id\":\"ab66c96d-2fd9-4733-b6d7-81e7643686fb\",\"type\":\"BasicTickFormatter\"},{\"attributes\":{\"days\":[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]},\"id\":\"ba73d819-6d15-47f6-97e8-9fa3aeff0f2a\",\"type\":\"DaysTicker\"},{\"attributes\":{\"days\":[1,4,7,10,13,16,19,22,25,28]},\"id\":\"334b2244-3342-4ee3-b1ba-2165160be67f\",\"type\":\"DaysTicker\"},{\"attributes\":{\"axis_label\":\"Pregnant Mothers\",\"axis_label_text_font_size\":{\"value\":\"14pt\"},\"formatter\":{\"id\":\"8be3bc82-2e46-40aa-a62b-9524f689454e\",\"type\":\"DatetimeTickFormatter\"},\"plot\":{\"id\":\"2ebbe383-aed7-471a-9394-cb067527920a\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"ticker\":{\"id\":\"0ca5882b-d581-49f2-93f3-a07dfb3856d8\",\"type\":\"DatetimeTicker\"}},\"id\":\"d05c05d6-0807-4df8-aa9a-87b29190f0c0\",\"type\":\"DatetimeAxis\"},{\"attributes\":{\"plot\":null,\"text\":null},\"id\":\"21872c55-2d33-40d2-ba04-ebf3db5a63e9\",\"type\":\"Title\"},{\"attributes\":{\"data_source\":{\"id\":\"09751f14-363e-4096-be27-e3bf1ce4fc78\",\"type\":\"ColumnDataSource\"},\"glyph\":{\"id\":\"1bd45d2a-313c-4808-a0c5-ccbe13b70f6b\",\"type\":\"Line\"},\"hover_glyph\":null,\"nonselection_glyph\":{\"id\":\"bc3728dd-1043-45bf-b35f-fd74d5b56e93\",\"type\":\"Line\"},\"selection_glyph\":null},\"id\":\"f8fa2936-8b07-4eac-afa6-22d8545d216a\",\"type\":\"GlyphRenderer\"},{\"attributes\":{\"below\":[{\"id\":\"07941450-49a3-47c1-8c84-5bc2f6b4cfd4\",\"type\":\"DatetimeAxis\"}],\"extra_y_ranges\":{\"population\":{\"id\":\"f503788e-792c-4197-9e36-d3ae5356f850\",\"type\":\"Range1d\"}},\"left\":[{\"id\":\"2a437546-87c2-4e96-a14f-0ab9c0e84542\",\"type\":\"LinearAxis\"},{\"id\":\"52f786d5-f3ef-4f34-9c61-7e4e3513973e\",\"type\":\"LinearAxis\"}],\"plot_width\":1600,\"renderers\":[{\"id\":\"07941450-49a3-47c1-8c84-5bc2f6b4cfd4\",\"type\":\"DatetimeAxis\"},{\"id\":\"f4c91080-a7aa-4eda-9366-58c04b46b9da\",\"type\":\"Grid\"},{\"id\":\"2a437546-87c2-4e96-a14f-0ab9c0e84542\",\"type\":\"LinearAxis\"},{\"id\":\"3be810a6-48e7-4732-a3c7-278a26ae0dfa\",\"type\":\"Grid\"},{\"id\":\"76b5b429-a514-4516-bc79-50f3e8543a73\",\"type\":\"BoxAnnotation\"},{\"id\":\"f8fa2936-8b07-4eac-afa6-22d8545d216a\",\"type\":\"GlyphRenderer\"},{\"id\":\"613fc096-c059-408d-9dc3-b04b1da93f85\",\"type\":\"GlyphRenderer\"},{\"id\":\"52f786d5-f3ef-4f34-9c61-7e4e3513973e\",\"type\":\"LinearAxis\"}],\"sizing_mode\":\"scale_width\",\"title\":{\"id\":\"eb3c4083-1eaf-4dc4-93d3-814e8b844c1b\",\"type\":\"Title\"},\"tool_events\":{\"id\":\"68ab0725-1236-418b-87df-9175b935e5a1\",\"type\":\"ToolEvents\"},\"toolbar\":{\"id\":\"87eae3c0-c7f2-40d4-a449-328e6c1f6a28\",\"type\":\"Toolbar\"},\"x_range\":{\"id\":\"c9ab1709-3456-4d4a-afcf-e5b6953c7bee\",\"type\":\"Range1d\"},\"y_range\":{\"id\":\"cb3f450e-4079-436f-9c2c-5c2b44dbff10\",\"type\":\"Range1d\"}},\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"},{\"attributes\":{\"months\":[0,4,8]},\"id\":\"9e154ee8-a33b-46fc-9cdc-f0bd3ad7bdac\",\"type\":\"MonthsTicker\"},{\"attributes\":{},\"id\":\"9e8a62bd-811a-42dc-906e-b779f09f4e68\",\"type\":\"YearsTicker\"},{\"attributes\":{\"line_cap\":\"round\",\"line_color\":{\"value\":\"#e41a1c\"},\"line_width\":{\"value\":3},\"x\":{\"field\":\"Date\"},\"y\":{\"field\":\"Population\"}},\"id\":\"c4a3d9f6-cbd9-4639-b213-48d109ba8956\",\"type\":\"Line\"},{\"attributes\":{\"line_color\":{\"value\":\"#4daf4a\"},\"line_width\":{\"value\":2},\"x\":{\"field\":\"Date\"},\"y\":{\"field\":\"Pregnant Mothers\"}},\"id\":\"91379bec-9b6a-4676-aefb-25650069eb2d\",\"type\":\"Line\"},{\"attributes\":{\"dimension\":1,\"plot\":{\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"ticker\":{\"id\":\"fa1bd8cd-712b-42f8-8353-cc666a86ddab\",\"type\":\"BasicTicker\"}},\"id\":\"3be810a6-48e7-4732-a3c7-278a26ae0dfa\",\"type\":\"Grid\"},{\"attributes\":{\"line_alpha\":{\"value\":0.1},\"line_color\":{\"value\":\"#1f77b4\"},\"line_width\":{\"value\":2},\"x\":{\"field\":\"Date\"},\"y\":{\"field\":\"Pregnant Mothers\"}},\"id\":\"d3d666a4-9525-408f-ae1c-0d5d99a0a3cb\",\"type\":\"Line\"},{\"attributes\":{\"line_cap\":\"round\",\"line_color\":{\"value\":\"#377eb8\"},\"line_width\":{\"value\":3},\"x\":{\"field\":\"Date\"},\"y\":{\"field\":\"Birth Queue\"}},\"id\":\"1bd45d2a-313c-4808-a0c5-ccbe13b70f6b\",\"type\":\"Line\"},{\"attributes\":{\"dimension\":1,\"plot\":{\"id\":\"2ebbe383-aed7-471a-9394-cb067527920a\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"ticker\":{\"id\":\"c69fc03b-d1ab-4060-aeca-49432993d1f9\",\"type\":\"BasicTicker\"}},\"id\":\"9f271225-28ff-4d64-8a82-2488ad65a90c\",\"type\":\"Grid\"},{\"attributes\":{},\"id\":\"9aadacf5-84fd-46ba-80ee-633d6946a9a4\",\"type\":\"DatetimeTickFormatter\"},{\"attributes\":{\"callback\":null,\"column_names\":[\"Birth Queue\",\"Date\",\"Date Formatted\",\"Pregnant Mothers\",\"Population\"],\"data\":{\"Birth Queue\":[146,147,148,149,150,150,150,149,149,150,150,151,151,151,154,154,154,153,153,153,152,152,152,152,152,152,152,152,152,153,153,153,153,153,152,151,151,151,151,152,152,152,152,152,153,152,152,151,152,152,153,154,154,155,155,155,156,157,157,157,158,157,156,156,156,157,157,157,157,157,157,156,155,154,154,155,155,154,154,154,154,152,152,154,154,154,155,157,157,157,157,158,157,159,161,162,163,163,163,163,164,164,164,163,164,162,166,166,166,165,164,164,164,164,164,164,164,163,164,165,163,163,162,163,163,162,162,162,162,162,162,163,163,163,163,163,164,164,164,166,166,166,166,166,165,165,164,164,164,164,164,164,164,165,165,165,164,164,163,160,160,159,159,162,164,163,163,164,165,165,165,163,163,163,163,163,161,160,158,160,160,160,160,160,160,161,160,160,159,160,160,159,160,160,159,159,159,159,159,159,159,159,160,160,160,162,164,163,160,161,161,161,161,161,161,159,159,159,160,160,159,159,159,159,159,159,158,158,158,158,158,159,156,156,154,153,152,151,151,151,151,151,152,153,153,153,152,152,151,150,150,150,150,151,148,147,148,148,149,150,149,149,151,151,153,153,153,153,154,150,150,153,150,150,150,150,150,150,150,151,151,151,151,151,151,151,151,153,153,153,150,150,152,152,154,155,155,154,154,154,154,154,155,156,156,156,156,149,150,151,151,149,150,150,150,149,149,149,150,150,151,150,150,150,150,150,150,148,147,147,146,146,147,147,148,148,148,148,149,150,148,148,148,149,151,151,151,151,151,150,151,151,151,150,149,149,149,149,150,150,151,151,152,152,152,154,154,153,152,152,152,153,153,153,153,152,153,155,157,158,158,159,159,159,159,159,159,159,159,160,159,159,159,159,159,158,158,155,155,155,154,153,153,153,154,155,155,155,155,155,155,155,155,155,155,155,156,156,156,155,153,153,153,153,153,153,153,153,152,150,149,149,149,149,149,149,149,148,148,149,149,149,149,149,149,149,149,147,147,147,149,148,148,148,147,147,147,147,147,147,147,149,149,149,148,148,150,151,151,151,150,149,148,148,148,148,145,145,145,145,149,149,149,149,149,150,150,150,150,151,150,149,149,149,149,150,149,149,149,147,148,148,148,147,146,146,146,145,145,145,144,143,142,141,141,140,140,139,139,139,139,139,139,139,139,139,138,139,139,138,139,139,141,142,142,141,141,140,140,142,143,143,143,143,145,145,145,144,144,144,145,145,145,143,143,143,143,142,142,142,141,143,143,143,143,143,143,143,143,143,142,142,142,142,144,144,148,148,148,147,148,148,148,148,148,147,147,146,141,141,145,145,145,145,145,144,144,144,144,146,146,146,146,146,146,144,144,144,144,144,144,143,143,143,143,144,144,145,146,146,146,145,144,143,143,143,143,143,143,143,143,143,143,143,143,140,139,139,139,139,139,140,140,141,140,143,143,144,146,146,146,148,146,147,147,147,148,148,147,147,147,147,149,149,149,149,149,149,150,150,150,150,151,151,152,152,152,151,151,150,150,150,150,150,150,149,148,148,148,148,148,148,148,149,149,150,151,150,150,150,150,149,149,149,149,149,148,149,149,148,148,148,147,147,147,146,147,147,148,147,147,147,145,145,146,145,146,146,146,147,149,151,151,151,150,150,150,150,149,150,148,149,149,149,148,148,148,147,147,148,148,148,150,149,149,149,151,152,152,155,155,155,155,155,155,155,155,155,155,155,155,154,153,153,152,152,152,151,151,152,153,154,155,155,155,155,156,154,155,155,157,156,154,154,154,153,154,154,154,154,154,154,154,153,155,150,150,151,152,152,152,152,153,153,152,152,153,153,154,153,152,155,155,156,155,156,156,156,156,157,153,149,149,151,152,152,151,151,151,150,150,150,147,148,150,152,151,152,152,152,152,152,154,154,149,149,149,149,150,151,151,151,149,149,149,149,149,149,148,148,148,148,149,149,150,150,149,149,149,149,149,148,148,148,148,148,148,147,146,146,150,151,151,151,152,152,152,153,153,154,156,156,156,156,156,157,157,156,155,154,152,152,150,150,150,149,150,150,149,148,147,146,146,147,147,147,147,148,148,149,149,149,149,149,148,147,147,147,147,148,148,148,148,148,146,146,146,146,145,145,145,144,144,144,145,145,145,142,143,142,143,146,143,141,141,141,140,139,139,139,139,139,139,139,136,137,140,140,140,139,139,139,139,134,133,136,137,137,137,143,142,142,145,145,145,143,143,143,145,144,145,145,144,143,146,146,146,146,146,145,145,145,143,142,139,138,138,137,137,138,138,140,140,139,141,141,141,144,144,144,144,145,145,145,145,146,148,148,148,149,150,150,150,149,149,150,150,150,150,150,149,149,149,149,149,149,149,149,149,149,151,151,152,152,152,152,152,152,152,152,153,160,161,171,172,173,179,183,182,183,182,182,182,181,181,181,179,178,179,179,180,183,183,183,183,183,183,183,182,182,189,189,189,189,189,189,191,191,191,191,191,191,191,191,191,191,191,191,188,189,186,186,187,187,178,175,176,176,176,175,175,175,175,175,175,174,173,175,175,174,169,168,168,168,168,168,168,168,167,167,164,164,165,168,169,170,171,169,169,169,169,174,174,174,174,174,175,176,176,176,178,173,172,171,171,170,170,170,169,169,168,169,169,168,168,169,169,170,171,171,170,169,166,161,158,158,156,156,157,158,156,155,155,155,155,155,156,156,156,156,156,156,156,157,157,158,158,162,162,161,161,161,162,162,165,164,164,164,164,164,165,164,164,164,164,164,164,155,156,158,159,155,154,154,154,154,154,154,156,156,156,156,155,155,157,157,156,156,156,156,153,153,153,152,152,152,152,152,152,151,151,151,152,153,153,154,155,153,153,153,153,154,154,154,154,154,154,153,153,155,155,154,154,154,155,154,154,152,152,152,149,148,147,147,147,146,146,147,147,147,148,148,148,148,147,147,147,142,141,141,141,141,141,140,140,140,144,144,144,144,145,146,146,146,147,148,150,150,150,150,150,150,150,150,149,148,149,149,149,149,149,147,149,148,147,148,149,149,149,149,149,148,148,148,148,149,149,148,151,153,153,152,152,152,152,152,149,148,151,152,152,151,151,151,151,151,151,151,151,152,152,151,150,150,149,151,149,149,149,148,148,144,145,145,145,145,145,146,145,145,145,145,145,144,144,144,145,145,145,145,145,148,146,147,146,145,145,137,136,136,136,136,135,135,135,133,132,134,136,135,135,135,135,135,137,142,142,142,140,138,137,135,135,135,136,140,140,140,140,140,140,140,140,143,143,143,143,143,143,142,142,139,140,141,138,143,143,141,141,143,143,142,142,140,140,141,141,141,141,142,140,141,141,141,141,142,142,142,142,142,142,142,142,142,142,144,144,147,147,149,148,148,148,140,139,139,139,139,139,138,138,138,138,138,138,138,138,138,138,137,137,137,134,135,135,134,134,134,132,133,133,132,132,131,130,130,130,130,130,131,131,131,131,131,131,130,130,130,130,129,129,129,132,132,132,132,132,131,134,135,135,135,137,136,137,133,129,130,133,133,133,135,135,128,128,128,129,128,128,127,130,130,131,131,131,131,129,131,131,132,131,131,131,131,131,131,131,131,131,131,131,131,131,132,132,132,131,131,131,131,131,131,130,131,133,133,132,132,132,133,133,133,133,131,131,131,132,132,132,131,131,131,131,131,131,126,126,127,126,127,129,129,129,130,130,128,128,128,130,130,130,130,130,128,128,128,127,126,126,126,127,127,127,128,128,128,126,127,127,128,128,131,131,129,125,125,125,125,126,125,123,125,125,123,125,125,125,125,125,125,125,125,125,125,125,126,126,127,125,125,129,131,131,131,127,127,129,128,128,128,128,128,128,128,128,128,128,128,128,128,127,127,127,127,127,127,127,127,127,127,126,126,126,126,125,125,126,128,128,128,128,128,128,127,127,126,126,126,126,126,126,126,126,127,127,127,127,128,129,129,129,130,130,129,129,129,129,129,129,129,129,129,129,130,127,127,126,126,126,126,126,125,127,136,141,142,143,146,150,152,154,153,153,153,152,152,152,150,148,150,150,150,150,150,149,151,152,152,150,151,152,152,151,152,152,153,153,155,155,153,154,154,155,155,155,155,155,155,152,153,154,155,156,155,156,159,159,159,159,159,159,160,163,164,165,167,167,171,182,215,234,257,263,271,272,278,279,279,279,281,281,284,285,287,289,290,290,292,292,293,294,295,295,298,299,301,305,306,312,312,312,313,317,317,319,319,321,322,323,325,327,327,327,326,329,331,331,336,338,337,338,338,338,338,338,339,340,340,342,342,342,341,342,341,340,340,340,342,342,341,341,341,343,344,340,339,337,337,336,338,338,338,340,340,340,341,342,342,346,347,354,356,357,359,359,358,361,364,367,368,368,369,369,366,365,365,365,363,362,363,364,366,366,366,369,370,367,368,367,368,368,370,370,371,375,375,374,373,373,372,373,373,374,373,373,375,376,376,376,376,377,376,377,378,378,378,378,378,381,381,382,382,382,381,381,381,377,377,377,377,376,376,377,376,376,376,318,318,315,314,314,315,314,315,315,313,314,315,316,316,315,315,314,313,312,313,312,312,312,313,313,313,313,314,314,312,310,310,310,308,308,307,303,303,300,299,297,295,296,293,291,291,292,292,293,295,295,295,294,294,294,293,291,289,288,288,289,287,286,289,290,290,289,288,287,287,287,288,288,288,288,289,289,287,287,285,285,285,282,280,280,280,279,277,276,275,268,267,264,264,264,264,264,264,264,264,264,264,263,264,263,263,263,263,264,264,265,265,265,264,261,261,262,262,262,262,271,270,270,270,270,270,269,268,270,271,271,272,271,270,268,268,267,268,268,267,267,266,265,265,265,265,265,265,264,263,262,262,261,262,262,260,260,260,260,259,259,258,258,258,257,258,257,259,259,259,258,258,257,258,257,256,256,257,255,255,254,253,252,252,253,254,254,254,255,254,253,253,254,254,254,254,253,250,250,251,251,251,252,252,251,251,251,252,253,254,254,254,254,253,253,252,251,251,251,251,251,251,250,252,249,249,249,249,243,248,247,247,248,249,249,253,255,256,257,256,256,256,256,253,254,257,257,257,258,260,259,259,260,260,260,260,260,260,260,260,260,260,260,260,260,261,261,261,260,260,259,259,259,258,258,258,258,258,258,257,257,257,257,257,258,256,255,255,255,255,255,255,255,254,254,254,254,254,254,255,254,255,253,253,253,251,252,253,252,253,254,254,254,254,254,255,255,255,255,254,253,252,254,254,255,255,255,256,257,257,257,259,257,258,258,258,257,256,257,257,256,256,257,256,257,256,258,259,258,257,256,256,256,257,257,256,258,259,259,258,256,249,249,249,246,246,246,246,246,246,242,243,242,242,242,241,241,240,240,239,239,239,239,238,238,238,239,238,238,238,239,239,239,237,237,239,239,238,237,236,237,237,237,238,237,237,238,239,240,243,245,245,249,249,250,250,252,251,251,251,252,253,253,254,253,253,253,254,254,254,255,255,256,255,255,255,247,246,247,253,252,252,251,250,251,251,251,252,252,252,252,253,253,254,254,255,256,255,255,256,255,255,254,254,254,254,254,255,252,252,251,252,253,253,254,256,258,257,258,258,259,259,260,260,260,260,262,262,262,263,264,263,256,258,259,257,260,259,259,259,261,262,262,262,262,262,264,264,265,265,265,263,264,264,264,264,263,263,264,265,264,264,262,262,262,261,259,259,259,258,261,261,260,260,260,261,260,260,260,260,260,258,258,258,258,258,257,256,256,256,256,257,257,256,255,255,255,257,257,257,257,259,259,259,257,256,256,257,257,256,257,257,257,258,259,258,256,253,253,253,252,250,250,251,250,249,248,248,248,248,247,247,249,251,252,253,253,253,253,253,253,253,253,253,253,252,252,252,250,248,249,249,250,250,250,250,250,250,249,249,247,246,247,247,246,245,246,246,247,247,247,244,244,245,246,245,245,247,247,247,247,247,248,247,248,248,247,247,248,248,247,246,247,246,246,245,245,242,241,241,241,242,243,241,242,241,243,243,243,243,243,241,241,242,242,242,243,243,243,243,244,243,244,245,244,244,244,244,244,244,244,245,246,246,247,247,247,247,247,247,247,246,246,246,246,246,246,246,246,245,247,247,246,245,246,246,246,244,244,244,243,243,244,244,244,244,244,244,244,240,240,240,239,239,239,239,241,241,241,243,243,243,243,242,242,242,242,242,243,243,242,242,242,242,244,244,244,245,246,241,241,241,240,243,243,243,245,245,245,245,245,246,246,246,246,246,246,247,249,250,249,249,248,248,249,249,249,250,250,250,250,250,250,251,251,248,249,248,248,248,248,248,248,252,253,252,254,256,256,256,254,254,257,259,259,259,261,261,261,261,263,263,263,263,264,260,261,265,265,266,267,265,265,266,265,266,267,267,267,267,266,266,267,268,269,269,267,266,267,267,266,266,266,266,266,266,266,266,267,267,266,267,267,266,266,266,266,266,267,267,268,265,265,265,265,264,264,264,263,263,264,264,265,266,265,266,266,266,266,266,266,266,266,266,266,266,265,265,264,264,264,264,264,264,264,262,261,260,259,259,259,261,261,248,247,249,249,246,245,244,250,250,250,250,249,248,247,246,246,246,246,246,246,246,248,248,248,248,248,249,249,250,252,253,253,253,253,254,254,254,254,255,255,255,254,254,254,253,253,251,251,250,250,248,248,248,249,249,250,251,250,250,250,250,249,249,249,249,252,252,253,254,254,254,254,254,254,254,254,253,255,255,255,255,256,257,257,259,259,259,257,257,258,258,258,258,258,257,257,257,257,257,257,257,258,258,258,258,258,259,259,259,259,259,260,261,262,262,262,262,262,262,262,262,261,260,260,257,257,257,256,254,255,255,256,256,256,256,255,255,254,255,255,256,256,257,256,256,256,256,256,257,257,259,259,258,257,257,257,255,254,254,254,254,254,252,251,250,249,250,250,243,243,243,244,245,246,246,247,246,246,244,243,243,243,241,241,241,241,241,241,241,241,239,239,239,238,238,237,240,239,237,236,238,238,237,236,236,236,236,235,235,234,234,233,233,235,234,234,233,234,234,233,232,233,233,233,233,233,234,234,233,232,231,232,232,232,232,232,232,233,233,233,233,233,232,233,233,233,231,231,232,232,232,231,230,227,228,228,228,228,225,227,227,226,227,227,227,227,227,226,227,228,228,229,222,221,221,220,219,220,220,217,217,218,217,217,217,218,218,219,219,220,219,219,219,220,219,219,220,219,219,219,218,217,215,215,214,215,213,210,210,209,209,210,210,210,209,209,208,208,208,208,209,209,209,209,209,209,210,211,211,211,211,211,209,209,210,210,210,207,211,211,212,212,213,213,212,212,212,212,211,213,214,215,215,215,215,215,215,214,215,212,211,209,209,211,211,211,211,209,209,209,209,209,209,209,210,211,213,213,212,212,212,212,211,211,210,210,210,196,196,196,196,197,198,199,198,196,195,195,191,192,193,193,193,193,193,194,196,197,196,198,198,195,195,195,197,196,196,197,196,195,195,209,209,208,209,207,207,207,207,206,205,204,203,202,202,203,203,202,203,203,203,203,203,204,203,203,203,203,202,201,201,203,203,203,204,204,201,201,201,201,201,200,200,200,199,199,198,198,198,200,201,201,201,201,201,201,201,201,201,203,203,203,202,202,202,202,202,202,202,202,202,202,202,202,203,204,204,204,205,205,206,206,204,203,203,205,206,204,204,204,202,204,204,204,203,203,203,202,202,202,201,201,201,200,200,199,199,200,200,201,201,198,197,197,196,199,199,199,199,199,200,201,201,200,200,201,201,201,202,203,203,200,200,202,202,202,202,202,202,203,204,204,204,204,205,206,207,207,207,206,206,206,206,206,206,205,204,205,205,203,204,205,205,203,202,201,201,202,202,202,202,203,203,201,200,200,201,201,201,202,202,201,201,200,200,200,200,200,200,200,200,200,200,200,200,199,201,200,199,199,198,199,200,200,200,200,200,202,202,202,201,202,203,203,203,203,230,231,230,230,231,231,231,232,231,232,232,231,231,231,232,232,231,232,236,236,238,239,239,239,239,240,240,240,239,239,239,239,240,240,240,240,240,239,239,238,238,238,237,236,237,237,237,237,237,236,237,237,237,237,237,238,238,238,238,238,237,237,237,236,236,236,236,236,235,235,235,235,235,234,236,232,233,232,232,232,232,235,235,236,236,236,235,235,235,237,237,238,238,238,239,238,238,238,237,237,237,237,236,239,239,238,238,240,240,240,241,241,241,241,241,243,243,243,245,245,245,245,245,247,246,246,246,247,247,247,247,246,246,247,248,249,249,248,248,248,249,249,249,249,249,249,249,248,248,251,254,254,254,254,253,253,253,254,254,254,254,254,253,255,255,255,255,255,254,257,257,257,258,258,258,258,259,259,258,258,257,257,257,256,256,258,256,253,253,254,255,255,255,254,253,254,254,254,253,253,252,253,253,253,253,253,252,251,251,252,252,252,253,253,255,255,255,262,263,265,266,266,267,267,267,267,267,268,268,267,268,268,268,268,267,267,267,267,267,267,266,266,266,265,264,265,264,264,264,265,265,265,265,267,267,267,268,268,267,267,267,267,267,267,266,264,265,264,264,265,265,264,263,263,264,263,263,262,262,264,262,262,262,262,261,261,261,260,259,259,260,260,256,256,256,257,257,258,259,259,259,260,259,259,259,259,259,259,258,256,255,255,255,254,253,254,254,251,247,249,250,250,250,249,249,250,248,249,249,250,253,254,198,198,199,199,197,196,196,197,197,197,196,196,196,196,196,194,194,193,193,194,194,194,196,197,197,196,196,196,195,196,196,195,195,196,196,196,198,200,201,200,198,199,199,201,201,201,201,201,201,201,200,200,200,201,200,201,201,201,205,236,241,246,247,248,248,248,248,249,251,252,256,256,258,258,259,260,262,263,263,263,262,264,265,265,263,263,263,264,264,264,264,267,265,265,265,263,263,263,263,263,261,261,262,261,261,261,258,258,259,259,259,259,259,260,263,259,260,261,261,261,262,263],\"Date\":[1455534000000.0,1455537600000.0,1455541200000.0,1455544800000.0,1455548400000.0,1455552000000.0,1455588000000.0,1455591600000.0,1455598800000.0,1455602400000.0,1455606000000.0,1455609600000.0,1455613200000.0,1455616800000.0,1455652800000.0,1455721200000.0,1455724800000.0,1455760800000.0,1455764400000.0,1455768000000.0,1455771600000.0,1455775200000.0,1455778800000.0,1455782400000.0,1455786000000.0,1455789600000.0,1455793200000.0,1455796800000.0,1455800400000.0,1455804000000.0,1455807600000.0,1455811200000.0,1455822000000.0,1455829200000.0,1455836400000.0,1455840000000.0,1455847200000.0,1455850800000.0,1455850800000.0,1455912000000.0,1455912000000.0,1455915600000.0,1455919200000.0,1455922800000.0,1455926400000.0,1455930000000.0,1455933600000.0,1455937200000.0,1455940800000.0,1455944400000.0,1455948000000.0,1455951600000.0,1455955200000.0,1455958800000.0,1455962400000.0,1455966000000.0,1455969600000.0,1455973200000.0,1455976800000.0,1455980400000.0,1455984000000.0,1455987600000.0,1455991200000.0,1455994800000.0,1455998400000.0,1456002000000.0,1456005600000.0,1456009200000.0,1456012800000.0,1456016400000.0,1456020000000.0,1456023600000.0,1456027200000.0,1456030800000.0,1456034400000.0,1456038000000.0,1456041600000.0,1456045200000.0,1456048800000.0,1456052400000.0,1456056000000.0,1456059600000.0,1456063200000.0,1456066800000.0,1456070400000.0,1456074000000.0,1456077600000.0,1456081200000.0,1456084800000.0,1456088400000.0,1456092000000.0,1456095600000.0,1456099200000.0,1456102800000.0,1456106400000.0,1456110000000.0,1456113600000.0,1456117200000.0,1456120800000.0,1456124400000.0,1456128000000.0,1456131600000.0,1456135200000.0,1456138800000.0,1456164000000.0,1456167600000.0,1456200000000.0,1456203600000.0,1456207200000.0,1456210800000.0,1456214400000.0,1456218000000.0,1456221600000.0,1456225200000.0,1456228800000.0,1456232400000.0,1456236000000.0,1456239600000.0,1456243200000.0,1456246800000.0,1456275600000.0,1456279200000.0,1456282800000.0,1456286400000.0,1456290000000.0,1456293600000.0,1456297200000.0,1456300800000.0,1456304400000.0,1456308000000.0,1456311600000.0,1456315200000.0,1456318800000.0,1456322400000.0,1456326000000.0,1456329600000.0,1456369200000.0,1456372800000.0,1456376400000.0,1456380000000.0,1456383600000.0,1456387200000.0,1456390800000.0,1456394400000.0,1456398000000.0,1456401600000.0,1456405200000.0,1456408800000.0,1456412400000.0,1456416000000.0,1456423200000.0,1456430400000.0,1456434000000.0,1456441200000.0,1456444800000.0,1456448400000.0,1456459200000.0,1456462800000.0,1456466400000.0,1456513200000.0,1456516800000.0,1456520400000.0,1456524000000.0,1456527600000.0,1456531200000.0,1456534800000.0,1456538400000.0,1456542000000.0,1456545600000.0,1456549200000.0,1456552800000.0,1456556400000.0,1456560000000.0,1456563600000.0,1456567200000.0,1456570800000.0,1456574400000.0,1456578000000.0,1456581600000.0,1456585200000.0,1456588800000.0,1456592400000.0,1456596000000.0,1456599600000.0,1456603200000.0,1456606800000.0,1456610400000.0,1456614000000.0,1456617600000.0,1456621200000.0,1456624800000.0,1456628400000.0,1456632000000.0,1456635600000.0,1456639200000.0,1456642800000.0,1456646400000.0,1456650000000.0,1456653600000.0,1456657200000.0,1456660800000.0,1456664400000.0,1456668000000.0,1456671600000.0,1456675200000.0,1456678800000.0,1456682400000.0,1456686000000.0,1456689600000.0,1456693200000.0,1456696800000.0,1456700400000.0,1456704000000.0,1456707600000.0,1456711200000.0,1456714800000.0,1456718400000.0,1456722000000.0,1456725600000.0,1456729200000.0,1456732800000.0,1456736400000.0,1456740000000.0,1456743600000.0,1456747200000.0,1456750800000.0,1456754400000.0,1456758000000.0,1456761600000.0,1456772400000.0,1456776000000.0,1456779600000.0,1456786800000.0,1456790400000.0,1456801200000.0,1456804800000.0,1456808400000.0,1456812000000.0,1456815600000.0,1456819200000.0,1456822800000.0,1456826400000.0,1456830000000.0,1456833600000.0,1456837200000.0,1456840800000.0,1456844400000.0,1456848000000.0,1456851600000.0,1456858800000.0,1456862400000.0,1456866000000.0,1456869600000.0,1456873200000.0,1456880400000.0,1456884000000.0,1456887600000.0,1456891200000.0,1456894800000.0,1456898400000.0,1456902000000.0,1456905600000.0,1456909200000.0,1456912800000.0,1456916400000.0,1456920000000.0,1456923600000.0,1456927200000.0,1456930800000.0,1456945200000.0,1456948800000.0,1456952400000.0,1456970400000.0,1456974000000.0,1456977600000.0,1456981200000.0,1456984800000.0,1456988400000.0,1456992000000.0,1456995600000.0,1456999200000.0,1457002800000.0,1457006400000.0,1457010000000.0,1457013600000.0,1457017200000.0,1457020800000.0,1457024400000.0,1457035200000.0,1457038800000.0,1457046000000.0,1457049600000.0,1457056800000.0,1457060400000.0,1457064000000.0,1457067600000.0,1457071200000.0,1457074800000.0,1457078400000.0,1457082000000.0,1457085600000.0,1457089200000.0,1457092800000.0,1457096400000.0,1457100000000.0,1457103600000.0,1457107200000.0,1457110800000.0,1457114400000.0,1457118000000.0,1457121600000.0,1457125200000.0,1457128800000.0,1457132400000.0,1457139600000.0,1457143200000.0,1457146800000.0,1457150400000.0,1457154000000.0,1457157600000.0,1457161200000.0,1457164800000.0,1457168400000.0,1457172000000.0,1457175600000.0,1457179200000.0,1457182800000.0,1457186400000.0,1457190000000.0,1457193600000.0,1457197200000.0,1457200800000.0,1457204400000.0,1457208000000.0,1457211600000.0,1457215200000.0,1457218800000.0,1457222400000.0,1457226000000.0,1457229600000.0,1457233200000.0,1457236800000.0,1457240400000.0,1457244000000.0,1457247600000.0,1457251200000.0,1457254800000.0,1457258400000.0,1457262000000.0,1457265600000.0,1457269200000.0,1457272800000.0,1457276400000.0,1457280000000.0,1457283600000.0,1457287200000.0,1457290800000.0,1457294400000.0,1457298000000.0,1457301600000.0,1457305200000.0,1457308800000.0,1457312400000.0,1457316000000.0,1457319600000.0,1457323200000.0,1457326800000.0,1457330400000.0,1457334000000.0,1457337600000.0,1457341200000.0,1457344800000.0,1457348400000.0,1457352000000.0,1457355600000.0,1457359200000.0,1457362800000.0,1457366400000.0,1457377200000.0,1457380800000.0,1457384400000.0,1457406000000.0,1457409600000.0,1457413200000.0,1457416800000.0,1457420400000.0,1457424000000.0,1457427600000.0,1457431200000.0,1457434800000.0,1457438400000.0,1457442000000.0,1457445600000.0,1457449200000.0,1457452800000.0,1457467200000.0,1457470800000.0,1457510400000.0,1457514000000.0,1457517600000.0,1457539200000.0,1457550000000.0,1457553600000.0,1457557200000.0,1457571600000.0,1457578800000.0,1457582400000.0,1457586000000.0,1457589600000.0,1457593200000.0,1457596800000.0,1457600400000.0,1457604000000.0,1457607600000.0,1457611200000.0,1457614800000.0,1457618400000.0,1457622000000.0,1457625600000.0,1457629200000.0,1457632800000.0,1457636400000.0,1457640000000.0,1457643600000.0,1457650800000.0,1457661600000.0,1457665200000.0,1457668800000.0,1457672400000.0,1457676000000.0,1457679600000.0,1457683200000.0,1457686800000.0,1457690400000.0,1457694000000.0,1457697600000.0,1457701200000.0,1457704800000.0,1457708400000.0,1457712000000.0,1457715600000.0,1457719200000.0,1457722800000.0,1457726400000.0,1457730000000.0,1457733600000.0,1457737200000.0,1457740800000.0,1457744400000.0,1457748000000.0,1457755200000.0,1457758800000.0,1457762400000.0,1457766000000.0,1457769600000.0,1457773200000.0,1457776800000.0,1457780400000.0,1457784000000.0,1457787600000.0,1457791200000.0,1457794800000.0,1457798400000.0,1457802000000.0,1457805600000.0,1457809200000.0,1457812800000.0,1457816400000.0,1457820000000.0,1457823600000.0,1457827200000.0,1457830800000.0,1457834400000.0,1457838000000.0,1457841600000.0,1457845200000.0,1457848800000.0,1457852400000.0,1457856000000.0,1457859600000.0,1457863200000.0,1457866800000.0,1457870400000.0,1457874000000.0,1457877600000.0,1457881200000.0,1457884800000.0,1457888400000.0,1457892000000.0,1457895600000.0,1457899200000.0,1457902800000.0,1457906400000.0,1457910000000.0,1457913600000.0,1457917200000.0,1457920800000.0,1457924400000.0,1457928000000.0,1457931600000.0,1457935200000.0,1457938800000.0,1457942400000.0,1457946000000.0,1457949600000.0,1457953200000.0,1457956800000.0,1457960400000.0,1457964000000.0,1457967600000.0,1457974800000.0,1457978400000.0,1457982000000.0,1457985600000.0,1457989200000.0,1457992800000.0,1457996400000.0,1458007200000.0,1458010800000.0,1458014400000.0,1458018000000.0,1458021600000.0,1458025200000.0,1458028800000.0,1458032400000.0,1458036000000.0,1458039600000.0,1458043200000.0,1458046800000.0,1458050400000.0,1458054000000.0,1458057600000.0,1458064800000.0,1458068400000.0,1458072000000.0,1458086400000.0,1458090000000.0,1458093600000.0,1458097200000.0,1458100800000.0,1458104400000.0,1458108000000.0,1458111600000.0,1458115200000.0,1458118800000.0,1458122400000.0,1458126000000.0,1458129600000.0,1458133200000.0,1458136800000.0,1458140400000.0,1458147600000.0,1458151200000.0,1458154800000.0,1458162000000.0,1458165600000.0,1458176400000.0,1458180000000.0,1458183600000.0,1458187200000.0,1458190800000.0,1458194400000.0,1458198000000.0,1458201600000.0,1458205200000.0,1458208800000.0,1458212400000.0,1458216000000.0,1458219600000.0,1458223200000.0,1458226800000.0,1458230400000.0,1458241200000.0,1458244800000.0,1458248400000.0,1458252000000.0,1458259200000.0,1458262800000.0,1458266400000.0,1458270000000.0,1458273600000.0,1458277200000.0,1458280800000.0,1458284400000.0,1458288000000.0,1458291600000.0,1458295200000.0,1458298800000.0,1458302400000.0,1458306000000.0,1458309600000.0,1458313200000.0,1458316800000.0,1458320400000.0,1458324000000.0,1458327600000.0,1458331200000.0,1458334800000.0,1458338400000.0,1458342000000.0,1458345600000.0,1458349200000.0,1458352800000.0,1458356400000.0,1458360000000.0,1458363600000.0,1458367200000.0,1458370800000.0,1458374400000.0,1458378000000.0,1458381600000.0,1458385200000.0,1458388800000.0,1458392400000.0,1458396000000.0,1458399600000.0,1458403200000.0,1458406800000.0,1458410400000.0,1458414000000.0,1458417600000.0,1458421200000.0,1458424800000.0,1458428400000.0,1458432000000.0,1458435600000.0,1458439200000.0,1458442800000.0,1458446400000.0,1458450000000.0,1458453600000.0,1458457200000.0,1458460800000.0,1458464400000.0,1458468000000.0,1458471600000.0,1458475200000.0,1458478800000.0,1458482400000.0,1458486000000.0,1458489600000.0,1458493200000.0,1458496800000.0,1458500400000.0,1458504000000.0,1458507600000.0,1458511200000.0,1458514800000.0,1458518400000.0,1458522000000.0,1458525600000.0,1458529200000.0,1458532800000.0,1458536400000.0,1458540000000.0,1458543600000.0,1458547200000.0,1458550800000.0,1458554400000.0,1458558000000.0,1458561600000.0,1458565200000.0,1458568800000.0,1458572400000.0,1458576000000.0,1458579600000.0,1458583200000.0,1458586800000.0,1458590400000.0,1458594000000.0,1458597600000.0,1458601200000.0,1458604800000.0,1458608400000.0,1458612000000.0,1458615600000.0,1458619200000.0,1458622800000.0,1458626400000.0,1458630000000.0,1458633600000.0,1458637200000.0,1458640800000.0,1458644400000.0,1458648000000.0,1458651600000.0,1458655200000.0,1458658800000.0,1458662400000.0,1458666000000.0,1458669600000.0,1458673200000.0,1458676800000.0,1458680400000.0,1458684000000.0,1458687600000.0,1458691200000.0,1458694800000.0,1458698400000.0,1458702000000.0,1458705600000.0,1458709200000.0,1458712800000.0,1458716400000.0,1458720000000.0,1458723600000.0,1458727200000.0,1458730800000.0,1458734400000.0,1458756000000.0,1458759600000.0,1458763200000.0,1458766800000.0,1458770400000.0,1458774000000.0,1458777600000.0,1458781200000.0,1458784800000.0,1458788400000.0,1458792000000.0,1458795600000.0,1458799200000.0,1458802800000.0,1458806400000.0,1458810000000.0,1458813600000.0,1458817200000.0,1458820800000.0,1458824400000.0,1458828000000.0,1458831600000.0,1458835200000.0,1458838800000.0,1458842400000.0,1458846000000.0,1458849600000.0,1458853200000.0,1458856800000.0,1458860400000.0,1458864000000.0,1458867600000.0,1458871200000.0,1458874800000.0,1458878400000.0,1458882000000.0,1458885600000.0,1458889200000.0,1458892800000.0,1458896400000.0,1458928800000.0,1458932400000.0,1458936000000.0,1458939600000.0,1458943200000.0,1458946800000.0,1458950400000.0,1458954000000.0,1458957600000.0,1458961200000.0,1458964800000.0,1458968400000.0,1458972000000.0,1458975600000.0,1458979200000.0,1458982800000.0,1458986400000.0,1458990000000.0,1458993600000.0,1458997200000.0,1459000800000.0,1459004400000.0,1459008000000.0,1459011600000.0,1459015200000.0,1459018800000.0,1459022400000.0,1459026000000.0,1459029600000.0,1459033200000.0,1459036800000.0,1459040400000.0,1459044000000.0,1459047600000.0,1459051200000.0,1459054800000.0,1459058400000.0,1459062000000.0,1459098000000.0,1459101600000.0,1459105200000.0,1459108800000.0,1459112400000.0,1459116000000.0,1459119600000.0,1459123200000.0,1459126800000.0,1459130400000.0,1459134000000.0,1459137600000.0,1459141200000.0,1459144800000.0,1459148400000.0,1459152000000.0,1459155600000.0,1459188000000.0,1459191600000.0,1459216800000.0,1459220400000.0,1459224000000.0,1459227600000.0,1459231200000.0,1459234800000.0,1459238400000.0,1459242000000.0,1459245600000.0,1459249200000.0,1459252800000.0,1459256400000.0,1459260000000.0,1459263600000.0,1459267200000.0,1459278000000.0,1459281600000.0,1459296000000.0,1459299600000.0,1459350000000.0,1459353600000.0,1459357200000.0,1459360800000.0,1459364400000.0,1459386000000.0,1459389600000.0,1459393200000.0,1459396800000.0,1459400400000.0,1459404000000.0,1459407600000.0,1459411200000.0,1459414800000.0,1459418400000.0,1459422000000.0,1459425600000.0,1459443600000.0,1459458000000.0,1459465200000.0,1459468800000.0,1459472400000.0,1459476000000.0,1459479600000.0,1459483200000.0,1459486800000.0,1459490400000.0,1459530000000.0,1459540800000.0,1459544400000.0,1459548000000.0,1459551600000.0,1459555200000.0,1459558800000.0,1459562400000.0,1459566000000.0,1459569600000.0,1459573200000.0,1459576800000.0,1459580400000.0,1459584000000.0,1459587600000.0,1459591200000.0,1459594800000.0,1459623600000.0,1459627200000.0,1459630800000.0,1459634400000.0,1459638000000.0,1459641600000.0,1459645200000.0,1459648800000.0,1459652400000.0,1459656000000.0,1459659600000.0,1459663200000.0,1459666800000.0,1459670400000.0,1459674000000.0,1459677600000.0,1459706400000.0,1459710000000.0,1459713600000.0,1459717200000.0,1459728000000.0,1459731600000.0,1459735200000.0,1459738800000.0,1459742400000.0,1459746000000.0,1459749600000.0,1459753200000.0,1459756800000.0,1459760400000.0,1459764000000.0,1459792800000.0,1459796400000.0,1459800000000.0,1459807200000.0,1459810800000.0,1459821600000.0,1459825200000.0,1459828800000.0,1459832400000.0,1459836000000.0,1459868400000.0,1459872000000.0,1459882800000.0,1459886400000.0,1459890000000.0,1459893600000.0,1460044800000.0,1460055600000.0,1460062800000.0,1460070000000.0,1460073600000.0,1460077200000.0,1460080800000.0,1460084400000.0,1460088000000.0,1460091600000.0,1460095200000.0,1460098800000.0,1460102400000.0,1460106000000.0,1460109600000.0,1460113200000.0,1460116800000.0,1460120400000.0,1460142000000.0,1460145600000.0,1460149200000.0,1460152800000.0,1460156400000.0,1460160000000.0,1460163600000.0,1460167200000.0,1460170800000.0,1460174400000.0,1460178000000.0,1460181600000.0,1460185200000.0,1460188800000.0,1460192400000.0,1460196000000.0,1460199600000.0,1460228400000.0,1460232000000.0,1460235600000.0,1460239200000.0,1460242800000.0,1460246400000.0,1460250000000.0,1460253600000.0,1460257200000.0,1460268000000.0,1460336400000.0,1460340000000.0,1460343600000.0,1460347200000.0,1460350800000.0,1460354400000.0,1460358000000.0,1460361600000.0,1460365200000.0,1460397600000.0,1460401200000.0,1460404800000.0,1460408400000.0,1460422800000.0,1460426400000.0,1460444400000.0,1460448000000.0,1460451600000.0,1460458800000.0,1460462400000.0,1460466000000.0,1460469600000.0,1460487600000.0,1460491200000.0,1460498400000.0,1460502000000.0,1460505600000.0,1460509200000.0,1460520000000.0,1460538000000.0,1460545200000.0,1460566800000.0,1460570400000.0,1460574000000.0,1460595600000.0,1460599200000.0,1460602800000.0,1460660400000.0,1460664000000.0,1460674800000.0,1460678400000.0,1460685600000.0,1460700000000.0,1460736000000.0,1460739600000.0,1460743200000.0,1460746800000.0,1460750400000.0,1460754000000.0,1460757600000.0,1460761200000.0,1460764800000.0,1460768400000.0,1460782800000.0,1460786400000.0,1460790000000.0,1460793600000.0,1460797200000.0,1460800800000.0,1460836800000.0,1460840400000.0,1460844000000.0,1460847600000.0,1460851200000.0,1460854800000.0,1460858400000.0,1460862000000.0,1460865600000.0,1460869200000.0,1460872800000.0,1460876400000.0,1460880000000.0,1460883600000.0,1460887200000.0,1460890800000.0,1460894400000.0,1460898000000.0,1460901600000.0,1460905200000.0,1460908800000.0,1460916000000.0,1460919600000.0,1460923200000.0,1460926800000.0,1460930400000.0,1460934000000.0,1460937600000.0,1460941200000.0,1460944800000.0,1460948400000.0,1460952000000.0,1460955600000.0,1460959200000.0,1460962800000.0,1460966400000.0,1460970000000.0,1460973600000.0,1460977200000.0,1460980800000.0,1460998800000.0,1461013200000.0,1461027600000.0,1461031200000.0,1461034800000.0,1461038400000.0,1461042000000.0,1461045600000.0,1461049200000.0,1461052800000.0,1461056400000.0,1461060000000.0,1461063600000.0,1461096000000.0,1461099600000.0,1461110400000.0,1461121200000.0,1461135600000.0,1461139200000.0,1461142800000.0,1461146400000.0,1461150000000.0,1461153600000.0,1461157200000.0,1461160800000.0,1461164400000.0,1461175200000.0,1461178800000.0,1461182400000.0,1461204000000.0,1461207600000.0,1461229200000.0,1461232800000.0,1461236400000.0,1461240000000.0,1461243600000.0,1461247200000.0,1461250800000.0,1461258000000.0,1461261600000.0,1461319200000.0,1461322800000.0,1461326400000.0,1461330000000.0,1461333600000.0,1461337200000.0,1461340800000.0,1461344400000.0,1461348000000.0,1461351600000.0,1461355200000.0,1461358800000.0,1461362400000.0,1461366000000.0,1461369600000.0,1461373200000.0,1461376800000.0,1461380400000.0,1461434400000.0,1461438000000.0,1461448800000.0,1461452400000.0,1461456000000.0,1461459600000.0,1461463200000.0,1461466800000.0,1461474000000.0,1461477600000.0,1461481200000.0,1461484800000.0,1461488400000.0,1461513600000.0,1461517200000.0,1461520800000.0,1461524400000.0,1461528000000.0,1461531600000.0,1461535200000.0,1461538800000.0,1461542400000.0,1461556800000.0,1461560400000.0,1461564000000.0,1461567600000.0,1461571200000.0,1461574800000.0,1461578400000.0,1461582000000.0,1461585600000.0,1461589200000.0,1461592800000.0,1461596400000.0,1461603600000.0,1461607200000.0,1461610800000.0,1461614400000.0,1461618000000.0,1461628800000.0,1461639600000.0,1461643200000.0,1461646800000.0,1461661200000.0,1461664800000.0,1461668400000.0,1461672000000.0,1461675600000.0,1461679200000.0,1461682800000.0,1461686400000.0,1461697200000.0,1461700800000.0,1461736800000.0,1461740400000.0,1461744000000.0,1461747600000.0,1461751200000.0,1461754800000.0,1461758400000.0,1461762000000.0,1461765600000.0,1461772800000.0,1461780000000.0,1461783600000.0,1461787200000.0,1461805200000.0,1461808800000.0,1461812400000.0,1461816000000.0,1461819600000.0,1461826800000.0,1461852000000.0,1461855600000.0,1461862800000.0,1461870000000.0,1461873600000.0,1461877200000.0,1461888000000.0,1461906000000.0,1461909600000.0,1461913200000.0,1461916800000.0,1461920400000.0,1461924000000.0,1461927600000.0,1461931200000.0,1461934800000.0,1461963600000.0,1461967200000.0,1461970800000.0,1461974400000.0,1461978000000.0,1461981600000.0,1461985200000.0,1461988800000.0,1461992400000.0,1461996000000.0,1461999600000.0,1462028400000.0,1462032000000.0,1462035600000.0,1462039200000.0,1462042800000.0,1462046400000.0,1462050000000.0,1462053600000.0,1462057200000.0,1462060800000.0,1462064400000.0,1462068000000.0,1462071600000.0,1462075200000.0,1462078800000.0,1462082400000.0,1462086000000.0,1462089600000.0,1462093200000.0,1462096800000.0,1462143600000.0,1462147200000.0,1462150800000.0,1462154400000.0,1462158000000.0,1462161600000.0,1462165200000.0,1462168800000.0,1462172400000.0,1462176000000.0,1462179600000.0,1462237200000.0,1462240800000.0,1462244400000.0,1462248000000.0,1462284000000.0,1462287600000.0,1462291200000.0,1462294800000.0,1462298400000.0,1462302000000.0,1462305600000.0,1462309200000.0,1462323600000.0,1462327200000.0,1462330800000.0,1462334400000.0,1462338000000.0,1462341600000.0,1462345200000.0,1462348800000.0,1462352400000.0,1462356000000.0,1462359600000.0,1462363200000.0,1462366800000.0,1462370400000.0,1462374000000.0,1462384800000.0,1462406400000.0,1462449600000.0,1462453200000.0,1462456800000.0,1462460400000.0,1462464000000.0,1462471200000.0,1462474800000.0,1462489200000.0,1462492800000.0,1462496400000.0,1462503600000.0,1462507200000.0,1462510800000.0,1462514400000.0,1462518000000.0,1462521600000.0,1462525200000.0,1462528800000.0,1462532400000.0,1462536000000.0,1462539600000.0,1462543200000.0,1462546800000.0,1462550400000.0,1462554000000.0,1462557600000.0,1462561200000.0,1462564800000.0,1462568400000.0,1462572000000.0,1462579200000.0,1462582800000.0,1462586400000.0,1462590000000.0,1462593600000.0,1462597200000.0,1462600800000.0,1462604400000.0,1462611600000.0,1462615200000.0,1462640400000.0,1462644000000.0,1462647600000.0,1462651200000.0,1462654800000.0,1462658400000.0,1462662000000.0,1462665600000.0,1462669200000.0,1462672800000.0,1462676400000.0,1462680000000.0,1462683600000.0,1462687200000.0,1462690800000.0,1462694400000.0,1462698000000.0,1462723200000.0,1462726800000.0,1462730400000.0,1462734000000.0,1462737600000.0,1462741200000.0,1462744800000.0,1462748400000.0,1462752000000.0,1462755600000.0,1462759200000.0,1462762800000.0,1462766400000.0,1462770000000.0,1462773600000.0,1462777200000.0,1462780800000.0,1462802400000.0,1462813200000.0,1462820400000.0,1462824000000.0,1462827600000.0,1462831200000.0,1462834800000.0,1462838400000.0,1462842000000.0,1462845600000.0,1462849200000.0,1462852800000.0,1462856400000.0,1462860000000.0,1462863600000.0,1462867200000.0,1462870800000.0,1462906800000.0,1462910400000.0,1462914000000.0,1462935600000.0,1462939200000.0,1462942800000.0,1462946400000.0,1462950000000.0,1462996800000.0,1463000400000.0,1463014800000.0,1463018400000.0,1463022000000.0,1463025600000.0,1463029200000.0,1463036400000.0,1463040000000.0,1463043600000.0,1463047200000.0,1463050800000.0,1463054400000.0,1463058000000.0,1463061600000.0,1463065200000.0,1463076000000.0,1463079600000.0,1463086800000.0,1463090400000.0,1463104800000.0,1463108400000.0,1463112000000.0,1463115600000.0,1463122800000.0,1463151600000.0,1463155200000.0,1463158800000.0,1463162400000.0,1463166000000.0,1463169600000.0,1463173200000.0,1463176800000.0,1463180400000.0,1463184000000.0,1463187600000.0,1463191200000.0,1463194800000.0,1463198400000.0,1463202000000.0,1463205600000.0,1463209200000.0,1463212800000.0,1463216400000.0,1463220000000.0,1463245200000.0,1463252400000.0,1463256000000.0,1463270400000.0,1463274000000.0,1463277600000.0,1463281200000.0,1463284800000.0,1463292000000.0,1463295600000.0,1463299200000.0,1463328000000.0,1463331600000.0,1463335200000.0,1463338800000.0,1463342400000.0,1463346000000.0,1463349600000.0,1463353200000.0,1463356800000.0,1463360400000.0,1463364000000.0,1463367600000.0,1463378400000.0,1463382000000.0,1463385600000.0,1463389200000.0,1463392800000.0,1463443200000.0,1463446800000.0,1463475600000.0,1463479200000.0,1463486400000.0,1463490000000.0,1463529600000.0,1463533200000.0,1463536800000.0,1463540400000.0,1463544000000.0,1463547600000.0,1463551200000.0,1463558400000.0,1463630400000.0,1463634000000.0,1463637600000.0,1463641200000.0,1463644800000.0,1463648400000.0,1463659200000.0,1463662800000.0,1463698800000.0,1463702400000.0,1463720400000.0,1463788800000.0,1463846400000.0,1463850000000.0,1463871600000.0,1463875200000.0,1463889600000.0,1463893200000.0,1463929200000.0,1463932800000.0,1463936400000.0,1463940000000.0,1463943600000.0,1463947200000.0,1463950800000.0,1463954400000.0,1463961600000.0,1463965200000.0,1463968800000.0,1463972400000.0,1463976000000.0,1464048000000.0,1464062400000.0,1464066000000.0,1464069600000.0,1464073200000.0,1464076800000.0,1464080400000.0,1464084000000.0,1464087600000.0,1464091200000.0,1464094800000.0,1464141600000.0,1464145200000.0,1464148800000.0,1464152400000.0,1464156000000.0,1464177600000.0,1464181200000.0,1464184800000.0,1464217200000.0,1464220800000.0,1464224400000.0,1464228000000.0,1464231600000.0,1464235200000.0,1464307200000.0,1464310800000.0,1464314400000.0,1464325200000.0,1464328800000.0,1464393600000.0,1464397200000.0,1464400800000.0,1464404400000.0,1464408000000.0,1464411600000.0,1464415200000.0,1464418800000.0,1464454800000.0,1464458400000.0,1464462000000.0,1464465600000.0,1464469200000.0,1464476400000.0,1464483600000.0,1464487200000.0,1464490800000.0,1464494400000.0,1464498000000.0,1464501600000.0,1464505200000.0,1464534000000.0,1464537600000.0,1464544800000.0,1464548400000.0,1464552000000.0,1464555600000.0,1464559200000.0,1464562800000.0,1464566400000.0,1464570000000.0,1464580800000.0,1464584400000.0,1464588000000.0,1464591600000.0,1464620400000.0,1464624000000.0,1464627600000.0,1464631200000.0,1464634800000.0,1464638400000.0,1464642000000.0,1464645600000.0,1464649200000.0,1464667200000.0,1464670800000.0,1464674400000.0,1464678000000.0,1464742800000.0,1464746400000.0,1464753600000.0,1464757200000.0,1464825600000.0,1464829200000.0,1464843600000.0,1464847200000.0,1464854400000.0,1464858000000.0,1464861600000.0,1464919200000.0,1464922800000.0,1464926400000.0,1464930000000.0,1464933600000.0,1464937200000.0,1464998400000.0,1465002000000.0,1465005600000.0,1465009200000.0,1465012800000.0,1465016400000.0,1465020000000.0,1465023600000.0,1465027200000.0,1465030800000.0,1465034400000.0,1465038000000.0,1465041600000.0,1465045200000.0,1465048800000.0,1465052400000.0,1465056000000.0,1465059600000.0,1465063200000.0,1465066800000.0,1465070400000.0,1465074000000.0,1465077600000.0,1465081200000.0,1465084800000.0,1465088400000.0,1465092000000.0,1465095600000.0,1465099200000.0,1465102800000.0,1465106400000.0,1465110000000.0,1465113600000.0,1465117200000.0,1465120800000.0,1465124400000.0,1465128000000.0,1465131600000.0,1465135200000.0,1465138800000.0,1465142400000.0,1465146000000.0,1465149600000.0,1465153200000.0,1465156800000.0,1465160400000.0,1465164000000.0,1465167600000.0,1465171200000.0,1465174800000.0,1465178400000.0,1465182000000.0,1465185600000.0,1465189200000.0,1465192800000.0,1465196400000.0,1465261200000.0,1465264800000.0,1465268400000.0,1465279200000.0,1465304400000.0,1465351200000.0,1465354800000.0,1465358400000.0,1465362000000.0,1465365600000.0,1465369200000.0,1465372800000.0,1465376400000.0,1465380000000.0,1465383600000.0,1465387200000.0,1465390800000.0,1465394400000.0,1465398000000.0,1465401600000.0,1465405200000.0,1465408800000.0,1465412400000.0,1465416000000.0,1465419600000.0,1465423200000.0,1465426800000.0,1465430400000.0,1465434000000.0,1465437600000.0,1465441200000.0,1465444800000.0,1465520400000.0,1465524000000.0,1465527600000.0,1465531200000.0,1465560000000.0,1465563600000.0,1465606800000.0,1465610400000.0,1465617600000.0,1465621200000.0,1465624800000.0,1465628400000.0,1465632000000.0,1465635600000.0,1465639200000.0,1465642800000.0,1465646400000.0,1465650000000.0,1465653600000.0,1465657200000.0,1465660800000.0,1465664400000.0,1465668000000.0,1465671600000.0,1465675200000.0,1465678800000.0,1465682400000.0,1465686000000.0,1465689600000.0,1465693200000.0,1465696800000.0,1465700400000.0,1465704000000.0,1465707600000.0,1465743600000.0,1465747200000.0,1465750800000.0,1465754400000.0,1465758000000.0,1465761600000.0,1465765200000.0,1465768800000.0,1465772400000.0,1465776000000.0,1465779600000.0,1465783200000.0,1465786800000.0,1465790400000.0,1465794000000.0,1465797600000.0,1465801200000.0,1465804800000.0,1465808400000.0,1465812000000.0,1465815600000.0,1465819200000.0,1465822800000.0,1465826400000.0,1465830000000.0,1465833600000.0,1465837200000.0,1465840800000.0,1465844400000.0,1465848000000.0,1465851600000.0,1465855200000.0,1465858800000.0,1465862400000.0,1465866000000.0,1465869600000.0,1465873200000.0,1465876800000.0,1465880400000.0,1465884000000.0,1465887600000.0,1465891200000.0,1465894800000.0,1465898400000.0,1465902000000.0,1465905600000.0,1465909200000.0,1465912800000.0,1465916400000.0,1465920000000.0,1465923600000.0,1465927200000.0,1465930800000.0,1465934400000.0,1465938000000.0,1465941600000.0,1465945200000.0,1465948800000.0,1465952400000.0,1465956000000.0,1465959600000.0,1465963200000.0,1465966800000.0,1465970400000.0,1465974000000.0,1465977600000.0,1465981200000.0,1465984800000.0,1465988400000.0,1465992000000.0,1465995600000.0,1465999200000.0,1466002800000.0,1466006400000.0,1466010000000.0,1466013600000.0,1466017200000.0,1466020800000.0,1466024400000.0,1466028000000.0,1466031600000.0,1466035200000.0,1466038800000.0,1466042400000.0,1466046000000.0,1466049600000.0,1466053200000.0,1466056800000.0,1466060400000.0,1466064000000.0,1466067600000.0,1466071200000.0,1466074800000.0,1466078400000.0,1466082000000.0,1466085600000.0,1466089200000.0,1466092800000.0,1466096400000.0,1466100000000.0,1466103600000.0,1466107200000.0,1466110800000.0,1466114400000.0,1466118000000.0,1466121600000.0,1466125200000.0,1466128800000.0,1466132400000.0,1466136000000.0,1466139600000.0,1466143200000.0,1466146800000.0,1466150400000.0,1466154000000.0,1466157600000.0,1466161200000.0,1466164800000.0,1466168400000.0,1466172000000.0,1466175600000.0,1466179200000.0,1466182800000.0,1466186400000.0,1466190000000.0,1466193600000.0,1466197200000.0,1466200800000.0,1466204400000.0,1466208000000.0,1466211600000.0,1466215200000.0,1466218800000.0,1466222400000.0,1466226000000.0,1466229600000.0,1466233200000.0,1466236800000.0,1466240400000.0,1466244000000.0,1466247600000.0,1466251200000.0,1466254800000.0,1466258400000.0,1466262000000.0,1466265600000.0,1466269200000.0,1466272800000.0,1466276400000.0,1466280000000.0,1466283600000.0,1466287200000.0,1466290800000.0,1466294400000.0,1466298000000.0,1466301600000.0,1466305200000.0,1466308800000.0,1466312400000.0,1466316000000.0,1466319600000.0,1466323200000.0,1466326800000.0,1466330400000.0,1466334000000.0,1466337600000.0,1466341200000.0,1466344800000.0,1466348400000.0,1466352000000.0,1466355600000.0,1466359200000.0,1466362800000.0,1466366400000.0,1466370000000.0,1466373600000.0,1466377200000.0,1466380800000.0,1466384400000.0,1466388000000.0,1466391600000.0,1466395200000.0,1466398800000.0,1466402400000.0,1466406000000.0,1466409600000.0,1466413200000.0,1466416800000.0,1466420400000.0,1466424000000.0,1466427600000.0,1466431200000.0,1466434800000.0,1466438400000.0,1466442000000.0,1466445600000.0,1466449200000.0,1466452800000.0,1466456400000.0,1466460000000.0,1466463600000.0,1466467200000.0,1466470800000.0,1466474400000.0,1466478000000.0,1466481600000.0,1466485200000.0,1466488800000.0,1466492400000.0,1466496000000.0,1466499600000.0,1466503200000.0,1466506800000.0,1466510400000.0,1466514000000.0,1466517600000.0,1466521200000.0,1466524800000.0,1466528400000.0,1466532000000.0,1466535600000.0,1466539200000.0,1466542800000.0,1466546400000.0,1466550000000.0,1466553600000.0,1466557200000.0,1466560800000.0,1466564400000.0,1466568000000.0,1466571600000.0,1466575200000.0,1466578800000.0,1466582400000.0,1466586000000.0,1466589600000.0,1466593200000.0,1466596800000.0,1466600400000.0,1466604000000.0,1466607600000.0,1466611200000.0,1466614800000.0,1466618400000.0,1466622000000.0,1466625600000.0,1466629200000.0,1466632800000.0,1466636400000.0,1466640000000.0,1466643600000.0,1466647200000.0,1466650800000.0,1466654400000.0,1466658000000.0,1466661600000.0,1466665200000.0,1466668800000.0,1466672400000.0,1466676000000.0,1466679600000.0,1466683200000.0,1466686800000.0,1466690400000.0,1466694000000.0,1466697600000.0,1466701200000.0,1466704800000.0,1466708400000.0,1466712000000.0,1466715600000.0,1466719200000.0,1466722800000.0,1466726400000.0,1466730000000.0,1466733600000.0,1466737200000.0,1466740800000.0,1466744400000.0,1466748000000.0,1466751600000.0,1466755200000.0,1466758800000.0,1466762400000.0,1466766000000.0,1466769600000.0,1466773200000.0,1466776800000.0,1466780400000.0,1466784000000.0,1466787600000.0,1466791200000.0,1466794800000.0,1466798400000.0,1466802000000.0,1466805600000.0,1466809200000.0,1466812800000.0,1466816400000.0,1466820000000.0,1466823600000.0,1466827200000.0,1466830800000.0,1466834400000.0,1466838000000.0,1466841600000.0,1466845200000.0,1466848800000.0,1466852400000.0,1466856000000.0,1466859600000.0,1466863200000.0,1466866800000.0,1466870400000.0,1466874000000.0,1467079200000.0,1467082800000.0,1467086400000.0,1467090000000.0,1467093600000.0,1467097200000.0,1467100800000.0,1467104400000.0,1467108000000.0,1467111600000.0,1467115200000.0,1467118800000.0,1467122400000.0,1467126000000.0,1467129600000.0,1467133200000.0,1467136800000.0,1467140400000.0,1467144000000.0,1467147600000.0,1467151200000.0,1467154800000.0,1467158400000.0,1467162000000.0,1467165600000.0,1467169200000.0,1467172800000.0,1467176400000.0,1467180000000.0,1467183600000.0,1467187200000.0,1467190800000.0,1467194400000.0,1467198000000.0,1467201600000.0,1467205200000.0,1467208800000.0,1467212400000.0,1467216000000.0,1467219600000.0,1467223200000.0,1467226800000.0,1467230400000.0,1467234000000.0,1467237600000.0,1467241200000.0,1467244800000.0,1467248400000.0,1467252000000.0,1467255600000.0,1467259200000.0,1467262800000.0,1467266400000.0,1467270000000.0,1467273600000.0,1467277200000.0,1467280800000.0,1467284400000.0,1467288000000.0,1467291600000.0,1467295200000.0,1467298800000.0,1467302400000.0,1467306000000.0,1467309600000.0,1467313200000.0,1467316800000.0,1467320400000.0,1467324000000.0,1467327600000.0,1467331200000.0,1467334800000.0,1467338400000.0,1467342000000.0,1467345600000.0,1467349200000.0,1467352800000.0,1467356400000.0,1467360000000.0,1467363600000.0,1467367200000.0,1467370800000.0,1467374400000.0,1467378000000.0,1467381600000.0,1467385200000.0,1467388800000.0,1467392400000.0,1467396000000.0,1467399600000.0,1467403200000.0,1467406800000.0,1467424800000.0,1467428400000.0,1467435600000.0,1467442800000.0,1467446400000.0,1467450000000.0,1467453600000.0,1467457200000.0,1467460800000.0,1467464400000.0,1467468000000.0,1467471600000.0,1467475200000.0,1467478800000.0,1467482400000.0,1467486000000.0,1467489600000.0,1467493200000.0,1467496800000.0,1467500400000.0,1467504000000.0,1467507600000.0,1467511200000.0,1467514800000.0,1467518400000.0,1467522000000.0,1467525600000.0,1467529200000.0,1467532800000.0,1467536400000.0,1467540000000.0,1467543600000.0,1467547200000.0,1467550800000.0,1467554400000.0,1467558000000.0,1467561600000.0,1467565200000.0,1467568800000.0,1467572400000.0,1467576000000.0,1467579600000.0,1467583200000.0,1467586800000.0,1467590400000.0,1467594000000.0,1467597600000.0,1467601200000.0,1467604800000.0,1467608400000.0,1467612000000.0,1467615600000.0,1467619200000.0,1467622800000.0,1467626400000.0,1467630000000.0,1467633600000.0,1467637200000.0,1467640800000.0,1467644400000.0,1467648000000.0,1467651600000.0,1467655200000.0,1467658800000.0,1467662400000.0,1467666000000.0,1467669600000.0,1467673200000.0,1467676800000.0,1467680400000.0,1467684000000.0,1467687600000.0,1467691200000.0,1467694800000.0,1467698400000.0,1467702000000.0,1467705600000.0,1467709200000.0,1467712800000.0,1467716400000.0,1467720000000.0,1467723600000.0,1467727200000.0,1467730800000.0,1467734400000.0,1467738000000.0,1467741600000.0,1467745200000.0,1467748800000.0,1467752400000.0,1467756000000.0,1467759600000.0,1467763200000.0,1467766800000.0,1467766800000.0,1467770400000.0,1467774000000.0,1467777600000.0,1467781200000.0,1467784800000.0,1467788400000.0,1467792000000.0,1467795600000.0,1467799200000.0,1467802800000.0,1467806400000.0,1467810000000.0,1467813600000.0,1467817200000.0,1467820800000.0,1467824400000.0,1467828000000.0,1467831600000.0,1467835200000.0,1467838800000.0,1467842400000.0,1467846000000.0,1467849600000.0,1467853200000.0,1467856800000.0,1467860400000.0,1467864000000.0,1467867600000.0,1467871200000.0,1467874800000.0,1467878400000.0,1467882000000.0,1467885600000.0,1467889200000.0,1467892800000.0,1467896400000.0,1467900000000.0,1467903600000.0,1467907200000.0,1467910800000.0,1467914400000.0,1467918000000.0,1467921600000.0,1467925200000.0,1467928800000.0,1467932400000.0,1467936000000.0,1467939600000.0,1467943200000.0,1467946800000.0,1467950400000.0,1467954000000.0,1467957600000.0,1467961200000.0,1467964800000.0,1467968400000.0,1467972000000.0,1467975600000.0,1467979200000.0,1467982800000.0,1467986400000.0,1467990000000.0,1467993600000.0,1467997200000.0,1468000800000.0,1468004400000.0,1468008000000.0,1468011600000.0,1468015200000.0,1468018800000.0,1468022400000.0,1468026000000.0,1468029600000.0,1468033200000.0,1468036800000.0,1468040400000.0,1468044000000.0,1468047600000.0,1468051200000.0,1468054800000.0,1468058400000.0,1468062000000.0,1468065600000.0,1468069200000.0,1468072800000.0,1468076400000.0,1468080000000.0,1468083600000.0,1468087200000.0,1468090800000.0,1468094400000.0,1468098000000.0,1468101600000.0,1468105200000.0,1468108800000.0,1468112400000.0,1468116000000.0,1468119600000.0,1468123200000.0,1468126800000.0,1468130400000.0,1468134000000.0,1468137600000.0,1468141200000.0,1468144800000.0,1468148400000.0,1468152000000.0,1468155600000.0,1468159200000.0,1468162800000.0,1468166400000.0,1468170000000.0,1468173600000.0,1468177200000.0,1468180800000.0,1468184400000.0,1468188000000.0,1468191600000.0,1468195200000.0,1468198800000.0,1468202400000.0,1468206000000.0,1468209600000.0,1468213200000.0,1468216800000.0,1468220400000.0,1468224000000.0,1468227600000.0,1468231200000.0,1468234800000.0,1468238400000.0,1468242000000.0,1468245600000.0,1468249200000.0,1468252800000.0,1468256400000.0,1468260000000.0,1468263600000.0,1468267200000.0,1468270800000.0,1468274400000.0,1468278000000.0,1468281600000.0,1468285200000.0,1468288800000.0,1468292400000.0,1468296000000.0,1468299600000.0,1468303200000.0,1468306800000.0,1468310400000.0,1468314000000.0,1468317600000.0,1468321200000.0,1468324800000.0,1468328400000.0,1468332000000.0,1468335600000.0,1468339200000.0,1468342800000.0,1468346400000.0,1468350000000.0,1468353600000.0,1468357200000.0,1468360800000.0,1468364400000.0,1468368000000.0,1468371600000.0,1468375200000.0,1468378800000.0,1468382400000.0,1468386000000.0,1468389600000.0,1468393200000.0,1468396800000.0,1468400400000.0,1468404000000.0,1468407600000.0,1468411200000.0,1468414800000.0,1468418400000.0,1468422000000.0,1468425600000.0,1468429200000.0,1468432800000.0,1468436400000.0,1468440000000.0,1468443600000.0,1468447200000.0,1468450800000.0,1468454400000.0,1468458000000.0,1468461600000.0,1468465200000.0,1468468800000.0,1468472400000.0,1468476000000.0,1468479600000.0,1468483200000.0,1468486800000.0,1468490400000.0,1468494000000.0,1468497600000.0,1468501200000.0,1468504800000.0,1468508400000.0,1468512000000.0,1468515600000.0,1468519200000.0,1468522800000.0,1468526400000.0,1468530000000.0,1468533600000.0,1468537200000.0,1468540800000.0,1468544400000.0,1468548000000.0,1468551600000.0,1468555200000.0,1468558800000.0,1468562400000.0,1468566000000.0,1468569600000.0,1468573200000.0,1468576800000.0,1468580400000.0,1468584000000.0,1468587600000.0,1468591200000.0,1468594800000.0,1468598400000.0,1468602000000.0,1468605600000.0,1468609200000.0,1468612800000.0,1468616400000.0,1468620000000.0,1468623600000.0,1468627200000.0,1468630800000.0,1468634400000.0,1468638000000.0,1468641600000.0,1468645200000.0,1468648800000.0,1468652400000.0,1468656000000.0,1468659600000.0,1468663200000.0,1468666800000.0,1468670400000.0,1468674000000.0,1468677600000.0,1468681200000.0,1468684800000.0,1468688400000.0,1468692000000.0,1468695600000.0,1468699200000.0,1468702800000.0,1468706400000.0,1468710000000.0,1468713600000.0,1468717200000.0,1468720800000.0,1468724400000.0,1468728000000.0,1468731600000.0,1468735200000.0,1468738800000.0,1468742400000.0,1468746000000.0,1468749600000.0,1468753200000.0,1468756800000.0,1468760400000.0,1468764000000.0,1468767600000.0,1468771200000.0,1468774800000.0,1468778400000.0,1468782000000.0,1468785600000.0,1468789200000.0,1468792800000.0,1468796400000.0,1468800000000.0,1468803600000.0,1468807200000.0,1468810800000.0,1468814400000.0,1468818000000.0,1468821600000.0,1468825200000.0,1468828800000.0,1468832400000.0,1468836000000.0,1468839600000.0,1468843200000.0,1468846800000.0,1468850400000.0,1468854000000.0,1468857600000.0,1468861200000.0,1468864800000.0,1468868400000.0,1468872000000.0,1468875600000.0,1468879200000.0,1468882800000.0,1468886400000.0,1468890000000.0,1468893600000.0,1468897200000.0,1468900800000.0,1468904400000.0,1468908000000.0,1468911600000.0,1468915200000.0,1468918800000.0,1468922400000.0,1468926000000.0,1468929600000.0,1468933200000.0,1468936800000.0,1468940400000.0,1468944000000.0,1468947600000.0,1468951200000.0,1468954800000.0,1468958400000.0,1468962000000.0,1468965600000.0,1468969200000.0,1468972800000.0,1468976400000.0,1468980000000.0,1468983600000.0,1468987200000.0,1468990800000.0,1468994400000.0,1468998000000.0,1469001600000.0,1469005200000.0,1469008800000.0,1469012400000.0,1469016000000.0,1469019600000.0,1469023200000.0,1469026800000.0,1469030400000.0,1469034000000.0,1469037600000.0,1469041200000.0,1469044800000.0,1469048400000.0,1469052000000.0,1469055600000.0,1469059200000.0,1469062800000.0,1469066400000.0,1469070000000.0,1469073600000.0,1469077200000.0,1469080800000.0,1469084400000.0,1469088000000.0,1469091600000.0,1469095200000.0,1469098800000.0,1469102400000.0,1469106000000.0,1469109600000.0,1469113200000.0,1469116800000.0,1469120400000.0,1469124000000.0,1469127600000.0,1469131200000.0,1469134800000.0,1469138400000.0,1469142000000.0,1469145600000.0,1469149200000.0,1469152800000.0,1469156400000.0,1469160000000.0,1469163600000.0,1469167200000.0,1469170800000.0,1469174400000.0,1469178000000.0,1469181600000.0,1469185200000.0,1469188800000.0,1469192400000.0,1469196000000.0,1469199600000.0,1469203200000.0,1469206800000.0,1469210400000.0,1469214000000.0,1469217600000.0,1469221200000.0,1469224800000.0,1469228400000.0,1469232000000.0,1469235600000.0,1469239200000.0,1469242800000.0,1469246400000.0,1469250000000.0,1469253600000.0,1469257200000.0,1469260800000.0,1469264400000.0,1469268000000.0,1469271600000.0,1469275200000.0,1469278800000.0,1469282400000.0,1469286000000.0,1469289600000.0,1469293200000.0,1469296800000.0,1469300400000.0,1469304000000.0,1469307600000.0,1469311200000.0,1469314800000.0,1469318400000.0,1469322000000.0,1469325600000.0,1469329200000.0,1469332800000.0,1469336400000.0,1469340000000.0,1469343600000.0,1469347200000.0,1469350800000.0,1469354400000.0,1469358000000.0,1469361600000.0,1469365200000.0,1469368800000.0,1469372400000.0,1469376000000.0,1469379600000.0,1469383200000.0,1469386800000.0,1469390400000.0,1469394000000.0,1469397600000.0,1469401200000.0,1469404800000.0,1469408400000.0,1469412000000.0,1469415600000.0,1469419200000.0,1469422800000.0,1469426400000.0,1469430000000.0,1469433600000.0,1469437200000.0,1469440800000.0,1469444400000.0,1469448000000.0,1469451600000.0,1469455200000.0,1469458800000.0,1469462400000.0,1469466000000.0,1469469600000.0,1469473200000.0,1469476800000.0,1469480400000.0,1469484000000.0,1469487600000.0,1469491200000.0,1469494800000.0,1469498400000.0,1469502000000.0,1469505600000.0,1469509200000.0,1469512800000.0,1469516400000.0,1469520000000.0,1469523600000.0,1469527200000.0,1469530800000.0,1469534400000.0,1469538000000.0,1469541600000.0,1469545200000.0,1469548800000.0,1469552400000.0,1469556000000.0,1469559600000.0,1469563200000.0,1469566800000.0,1469570400000.0,1469574000000.0,1469577600000.0,1469581200000.0,1469584800000.0,1469588400000.0,1469592000000.0,1469595600000.0,1469599200000.0,1469602800000.0,1469606400000.0,1469610000000.0,1469613600000.0,1469617200000.0,1469620800000.0,1469624400000.0,1469628000000.0,1469631600000.0,1469635200000.0,1469638800000.0,1469642400000.0,1469646000000.0,1469649600000.0,1469653200000.0,1469656800000.0,1469660400000.0,1469664000000.0,1469667600000.0,1469671200000.0,1469674800000.0,1469678400000.0,1469682000000.0,1469685600000.0,1469689200000.0,1469692800000.0,1469696400000.0,1469700000000.0,1469703600000.0,1469707200000.0,1469710800000.0,1469714400000.0,1469718000000.0,1469721600000.0,1469725200000.0,1469728800000.0,1469732400000.0,1469736000000.0,1469739600000.0,1469743200000.0,1469746800000.0,1469750400000.0,1469754000000.0,1469757600000.0,1469761200000.0,1469764800000.0,1469768400000.0,1469772000000.0,1469775600000.0,1469779200000.0,1469782800000.0,1469786400000.0,1469790000000.0,1469793600000.0,1469797200000.0,1469800800000.0,1469804400000.0,1469808000000.0,1469811600000.0,1469815200000.0,1469818800000.0,1469822400000.0,1469826000000.0,1469829600000.0,1469833200000.0,1469836800000.0,1469840400000.0,1469844000000.0,1469847600000.0,1469851200000.0,1469854800000.0,1469858400000.0,1469862000000.0,1469865600000.0,1469869200000.0,1469872800000.0,1469876400000.0,1469880000000.0,1469883600000.0,1469887200000.0,1469890800000.0,1469894400000.0,1469898000000.0,1469901600000.0,1469905200000.0,1469908800000.0,1469912400000.0,1469916000000.0,1469919600000.0,1469923200000.0,1469926800000.0,1469930400000.0,1469934000000.0,1469937600000.0,1469941200000.0,1469944800000.0,1469948400000.0,1469952000000.0,1469955600000.0,1469959200000.0,1469962800000.0,1469966400000.0,1469970000000.0,1469973600000.0,1469977200000.0,1469980800000.0,1469984400000.0,1469988000000.0,1469991600000.0,1469995200000.0,1469998800000.0,1470002400000.0,1470006000000.0,1470009600000.0,1470013200000.0,1470016800000.0,1470020400000.0,1470024000000.0,1470027600000.0,1470031200000.0,1470034800000.0,1470038400000.0,1470042000000.0,1470045600000.0,1470049200000.0,1470052800000.0,1470056400000.0,1470060000000.0,1470063600000.0,1470067200000.0,1470070800000.0,1470074400000.0,1470078000000.0,1470081600000.0,1470085200000.0,1470088800000.0,1470092400000.0,1470096000000.0,1470099600000.0,1470103200000.0,1470106800000.0,1470110400000.0,1470114000000.0,1470117600000.0,1470121200000.0,1470124800000.0,1470128400000.0,1470132000000.0,1470135600000.0,1470139200000.0,1470142800000.0,1470146400000.0,1470150000000.0,1470153600000.0,1470157200000.0,1470160800000.0,1470164400000.0,1470168000000.0,1470171600000.0,1470175200000.0,1470178800000.0,1470182400000.0,1470186000000.0,1470189600000.0,1470193200000.0,1470196800000.0,1470200400000.0,1470204000000.0,1470207600000.0,1470211200000.0,1470214800000.0,1470218400000.0,1470222000000.0,1470225600000.0,1470229200000.0,1470232800000.0,1470236400000.0,1470240000000.0,1470243600000.0,1470247200000.0,1470250800000.0,1470254400000.0,1470258000000.0,1470261600000.0,1470265200000.0,1470268800000.0,1470272400000.0,1470276000000.0,1470279600000.0,1470283200000.0,1470286800000.0,1470290400000.0,1470294000000.0,1470297600000.0,1470301200000.0,1470304800000.0,1470308400000.0,1470312000000.0,1470315600000.0,1470319200000.0,1470322800000.0,1470326400000.0,1470330000000.0,1470333600000.0,1470337200000.0,1470340800000.0,1470344400000.0,1470348000000.0,1470351600000.0,1470355200000.0,1470358800000.0,1470362400000.0,1470366000000.0,1470369600000.0,1470373200000.0,1470376800000.0,1470380400000.0,1470384000000.0,1470387600000.0,1470391200000.0,1470394800000.0,1470398400000.0,1470402000000.0,1470405600000.0,1470873600000.0,1470873600000.0,1470873600000.0,1470873600000.0,1470877200000.0,1470880800000.0,1470884400000.0,1470888000000.0,1470891600000.0,1470895200000.0,1470898800000.0,1470902400000.0,1470906000000.0,1470909600000.0,1470913200000.0,1470916800000.0,1470920400000.0,1470924000000.0,1470927600000.0,1470931200000.0,1470934800000.0,1470938400000.0,1470942000000.0,1470945600000.0,1470949200000.0,1470952800000.0,1470956400000.0,1470960000000.0,1470963600000.0,1470967200000.0,1470970800000.0,1470974400000.0,1470978000000.0,1470981600000.0,1470985200000.0,1470988800000.0,1470992400000.0,1470996000000.0,1470999600000.0,1471003200000.0,1471006800000.0,1471010400000.0,1471014000000.0,1471017600000.0,1471021200000.0,1471024800000.0,1471028400000.0,1471032000000.0,1471035600000.0,1471039200000.0,1471042800000.0,1471046400000.0,1471050000000.0,1471053600000.0,1471057200000.0,1471060800000.0,1471064400000.0,1471068000000.0,1471071600000.0,1471075200000.0,1471078800000.0,1471082400000.0,1471086000000.0,1471089600000.0,1471093200000.0,1471096800000.0,1471100400000.0,1471104000000.0,1471107600000.0,1471111200000.0,1471114800000.0,1471118400000.0,1471122000000.0,1471125600000.0,1471129200000.0,1471132800000.0,1471136400000.0,1471140000000.0,1471143600000.0,1471147200000.0,1471150800000.0,1471154400000.0,1471158000000.0,1471161600000.0,1471165200000.0,1471168800000.0,1471172400000.0,1471176000000.0,1471179600000.0,1471183200000.0,1471186800000.0,1471190400000.0,1471194000000.0,1471197600000.0,1471201200000.0,1471204800000.0,1471208400000.0,1471212000000.0,1471215600000.0,1471219200000.0,1471222800000.0,1471226400000.0,1471230000000.0,1471233600000.0,1471237200000.0,1471240800000.0,1471244400000.0,1471248000000.0,1471251600000.0,1471255200000.0,1471258800000.0,1471262400000.0,1471266000000.0,1471269600000.0,1471273200000.0,1471276800000.0,1471280400000.0,1471284000000.0,1471287600000.0,1471291200000.0,1471294800000.0,1471298400000.0,1471302000000.0,1471305600000.0,1471309200000.0,1471312800000.0,1471316400000.0,1471320000000.0,1471323600000.0,1471327200000.0,1471330800000.0,1471334400000.0,1471338000000.0,1471341600000.0,1471345200000.0,1471348800000.0,1471352400000.0,1471356000000.0,1471359600000.0,1471363200000.0,1471366800000.0,1471370400000.0,1471374000000.0,1471377600000.0,1471381200000.0,1471384800000.0,1471388400000.0,1471392000000.0,1471395600000.0,1471399200000.0,1471402800000.0,1471406400000.0,1471410000000.0,1471413600000.0,1471417200000.0,1471420800000.0,1471424400000.0,1471428000000.0,1471431600000.0,1471435200000.0,1471438800000.0,1471442400000.0,1471446000000.0,1471449600000.0,1471453200000.0,1471456800000.0,1471460400000.0,1471464000000.0,1471467600000.0,1471471200000.0,1471474800000.0,1471478400000.0,1471482000000.0,1471485600000.0,1471489200000.0,1471492800000.0,1471496400000.0,1471500000000.0,1471503600000.0,1471507200000.0,1471510800000.0,1471514400000.0,1471518000000.0,1471521600000.0,1471525200000.0,1471528800000.0,1471532400000.0,1471536000000.0,1471539600000.0,1471543200000.0,1471546800000.0,1471550400000.0,1471554000000.0,1471557600000.0,1471561200000.0,1471564800000.0,1471568400000.0,1471572000000.0,1471575600000.0,1471579200000.0,1471582800000.0,1471586400000.0,1471590000000.0,1471593600000.0,1471597200000.0,1471600800000.0,1471604400000.0,1471608000000.0,1471611600000.0,1471615200000.0,1471618800000.0,1471622400000.0,1471626000000.0,1471629600000.0,1471633200000.0,1471636800000.0,1471640400000.0,1471644000000.0,1471647600000.0,1471651200000.0,1471654800000.0,1471658400000.0,1471662000000.0,1471665600000.0,1471669200000.0,1471672800000.0,1471676400000.0,1471680000000.0,1471683600000.0,1471687200000.0,1471690800000.0,1471694400000.0,1471698000000.0,1471701600000.0,1471705200000.0,1471708800000.0,1471712400000.0,1471716000000.0,1471719600000.0,1471723200000.0,1471726800000.0,1471730400000.0,1471734000000.0,1471737600000.0,1471741200000.0,1471744800000.0,1471748400000.0,1471752000000.0,1471755600000.0,1471759200000.0,1471762800000.0,1471766400000.0,1471770000000.0,1471773600000.0,1471777200000.0,1471780800000.0,1471784400000.0,1471788000000.0,1471791600000.0,1471795200000.0,1471798800000.0,1471802400000.0,1471806000000.0,1471809600000.0,1471813200000.0,1471816800000.0,1471820400000.0,1471824000000.0,1471827600000.0,1471831200000.0,1471834800000.0,1471838400000.0,1471842000000.0,1471845600000.0,1471849200000.0,1471852800000.0,1471856400000.0,1471860000000.0,1471863600000.0,1471867200000.0,1471870800000.0,1471874400000.0,1471878000000.0,1471881600000.0,1471885200000.0,1471888800000.0,1471892400000.0,1471896000000.0,1471899600000.0,1471903200000.0,1471906800000.0,1471910400000.0,1471914000000.0,1471917600000.0,1471921200000.0,1471924800000.0,1471928400000.0,1471932000000.0,1471935600000.0,1471939200000.0,1471971600000.0,1471975200000.0,1471978800000.0,1471982400000.0,1471986000000.0,1471989600000.0,1471993200000.0,1471996800000.0,1472000400000.0,1472004000000.0,1472007600000.0,1472011200000.0,1472014800000.0,1472018400000.0,1472022000000.0,1472025600000.0,1472029200000.0,1472032800000.0,1472036400000.0,1472040000000.0,1472043600000.0,1472047200000.0,1472050800000.0,1472054400000.0,1472058000000.0,1472061600000.0,1472065200000.0,1472068800000.0,1472072400000.0,1472076000000.0,1472079600000.0,1472083200000.0,1472086800000.0,1472090400000.0,1472094000000.0,1472097600000.0,1472101200000.0,1472104800000.0,1472108400000.0,1472112000000.0,1472115600000.0,1472119200000.0,1472122800000.0,1472126400000.0,1472130000000.0,1472133600000.0,1472137200000.0,1472140800000.0,1472144400000.0,1472148000000.0,1472151600000.0,1472155200000.0,1472158800000.0,1472162400000.0,1472166000000.0,1472169600000.0,1472173200000.0,1472176800000.0,1472180400000.0,1472184000000.0,1472187600000.0,1472191200000.0,1472194800000.0,1472198400000.0,1472202000000.0,1472205600000.0,1472209200000.0,1472212800000.0,1472216400000.0,1472220000000.0,1472223600000.0,1472227200000.0,1472230800000.0,1472234400000.0,1472238000000.0,1472241600000.0,1472245200000.0,1472248800000.0,1472252400000.0,1472256000000.0,1472259600000.0,1472263200000.0,1472266800000.0,1472270400000.0,1472274000000.0,1472277600000.0,1472281200000.0,1472284800000.0,1472288400000.0,1472292000000.0,1472295600000.0,1472299200000.0,1472302800000.0,1472306400000.0,1472310000000.0,1472313600000.0,1472317200000.0,1472320800000.0,1472324400000.0,1472328000000.0,1472331600000.0,1472335200000.0,1472338800000.0,1472342400000.0,1472346000000.0,1472349600000.0,1472353200000.0,1472356800000.0,1472360400000.0,1472364000000.0,1472367600000.0,1472371200000.0,1472374800000.0,1472378400000.0,1472382000000.0,1472385600000.0,1472389200000.0,1472392800000.0,1472396400000.0,1472400000000.0,1472403600000.0,1472407200000.0,1472410800000.0,1472414400000.0,1472418000000.0,1472421600000.0,1472425200000.0,1472428800000.0,1472432400000.0,1472436000000.0,1472439600000.0,1472443200000.0,1472446800000.0,1472450400000.0,1472454000000.0,1472457600000.0,1472461200000.0,1472464800000.0,1472468400000.0,1472472000000.0,1472475600000.0,1472479200000.0,1472482800000.0,1472486400000.0,1472490000000.0,1472493600000.0,1472497200000.0,1472500800000.0,1472504400000.0,1472508000000.0,1472511600000.0,1472515200000.0,1472518800000.0,1472522400000.0,1472526000000.0,1472529600000.0,1472533200000.0,1472536800000.0,1472540400000.0,1472544000000.0,1472547600000.0,1472551200000.0,1472554800000.0,1472558400000.0,1472562000000.0,1472565600000.0,1472569200000.0,1472572800000.0,1472576400000.0,1472580000000.0,1472583600000.0,1472587200000.0,1472590800000.0,1472594400000.0,1472598000000.0,1472601600000.0,1472605200000.0,1472608800000.0,1472612400000.0,1472616000000.0,1472619600000.0,1472623200000.0,1472626800000.0,1472630400000.0,1472634000000.0,1472637600000.0,1472641200000.0,1472644800000.0,1472648400000.0,1472652000000.0,1472655600000.0,1472659200000.0,1472662800000.0,1472666400000.0,1472670000000.0,1472673600000.0,1472677200000.0,1472680800000.0,1472684400000.0,1472688000000.0,1472691600000.0,1472695200000.0,1472698800000.0,1472702400000.0,1472706000000.0,1472709600000.0,1472713200000.0,1472716800000.0,1472720400000.0,1472724000000.0,1472727600000.0,1472731200000.0,1472734800000.0,1472738400000.0,1472742000000.0,1472745600000.0,1472749200000.0,1472752800000.0,1472756400000.0,1472760000000.0,1472763600000.0,1472767200000.0,1472770800000.0,1472774400000.0,1472778000000.0,1472781600000.0,1472785200000.0,1472788800000.0,1472792400000.0,1472796000000.0,1472799600000.0,1472803200000.0,1472806800000.0,1472810400000.0,1472814000000.0,1472817600000.0,1472821200000.0,1472824800000.0,1472828400000.0,1472832000000.0,1472835600000.0,1472839200000.0,1472842800000.0,1472846400000.0,1472850000000.0,1472853600000.0,1472857200000.0,1472860800000.0,1472864400000.0,1472868000000.0,1472871600000.0,1472875200000.0,1472878800000.0,1472882400000.0,1472886000000.0,1472889600000.0,1472893200000.0,1472896800000.0,1472900400000.0,1472904000000.0,1472907600000.0,1472911200000.0,1472914800000.0,1472918400000.0,1472922000000.0,1472925600000.0,1472929200000.0,1472932800000.0,1472936400000.0,1472940000000.0,1472943600000.0,1472947200000.0,1472950800000.0,1472954400000.0,1472958000000.0,1472961600000.0,1472965200000.0,1472968800000.0,1472972400000.0,1472976000000.0,1472979600000.0,1472983200000.0,1472986800000.0,1472990400000.0,1472994000000.0,1472997600000.0,1473001200000.0,1473004800000.0,1473008400000.0,1473012000000.0,1473015600000.0,1473019200000.0,1473022800000.0,1473026400000.0,1473030000000.0,1473033600000.0,1473037200000.0,1473040800000.0,1473044400000.0,1473048000000.0,1473051600000.0,1473055200000.0,1473058800000.0,1473062400000.0,1473066000000.0,1473069600000.0,1473073200000.0,1473076800000.0,1473080400000.0,1473084000000.0,1473087600000.0,1473091200000.0,1473094800000.0,1473098400000.0,1473102000000.0,1473105600000.0,1473109200000.0,1473112800000.0,1473116400000.0,1473120000000.0,1473123600000.0,1473127200000.0,1473130800000.0,1473134400000.0,1473138000000.0,1473141600000.0,1473145200000.0,1473148800000.0,1473152400000.0,1473156000000.0,1473159600000.0,1473163200000.0,1473166800000.0,1473170400000.0,1473174000000.0,1473177600000.0,1473181200000.0,1473184800000.0,1473188400000.0,1473192000000.0,1473195600000.0,1473199200000.0,1473202800000.0,1473206400000.0,1473210000000.0,1473213600000.0,1473217200000.0,1473220800000.0,1473224400000.0,1473228000000.0,1473231600000.0,1473235200000.0,1473238800000.0,1473242400000.0,1473246000000.0,1473249600000.0,1473253200000.0,1473256800000.0,1473260400000.0,1473264000000.0,1473267600000.0,1473271200000.0,1473274800000.0,1473278400000.0,1473282000000.0,1473285600000.0,1473289200000.0,1473292800000.0,1473296400000.0,1473300000000.0,1473303600000.0,1473307200000.0,1473310800000.0,1473314400000.0,1473318000000.0,1473321600000.0,1473325200000.0,1473328800000.0,1473332400000.0,1473336000000.0,1473339600000.0,1473343200000.0,1473346800000.0,1473350400000.0,1473354000000.0,1473357600000.0,1473361200000.0,1473364800000.0,1473368400000.0,1473372000000.0,1473375600000.0,1473379200000.0,1473382800000.0,1473386400000.0,1473390000000.0,1473393600000.0,1473397200000.0,1473400800000.0,1473404400000.0,1473408000000.0,1473411600000.0,1473415200000.0,1473418800000.0,1473422400000.0,1473426000000.0,1473429600000.0,1473433200000.0,1473436800000.0,1473440400000.0,1473444000000.0,1473447600000.0,1473451200000.0,1473454800000.0,1473458400000.0,1473462000000.0,1473465600000.0,1473469200000.0,1473472800000.0,1473476400000.0,1473480000000.0,1473483600000.0,1473487200000.0,1473490800000.0,1473494400000.0,1473498000000.0,1473501600000.0,1473505200000.0,1473508800000.0,1473512400000.0,1473516000000.0,1473519600000.0,1473523200000.0,1473526800000.0,1473530400000.0,1473534000000.0,1473537600000.0,1473541200000.0,1473544800000.0,1473548400000.0,1473552000000.0,1473555600000.0,1473559200000.0,1473562800000.0,1473566400000.0,1473570000000.0,1473573600000.0,1473577200000.0,1473580800000.0,1473584400000.0,1473588000000.0,1473591600000.0,1473595200000.0,1473598800000.0,1473602400000.0,1473606000000.0,1473609600000.0,1473613200000.0,1473616800000.0,1473620400000.0,1473624000000.0,1473627600000.0,1473631200000.0,1473634800000.0,1473638400000.0,1473642000000.0,1473645600000.0,1473649200000.0,1473652800000.0,1473656400000.0,1473660000000.0,1473663600000.0,1473667200000.0,1473670800000.0,1473674400000.0,1473678000000.0,1473681600000.0,1473685200000.0,1473688800000.0,1473692400000.0,1473696000000.0,1473699600000.0,1473703200000.0,1473706800000.0,1473710400000.0,1473714000000.0,1473717600000.0,1473721200000.0,1473724800000.0,1473728400000.0,1473732000000.0,1473735600000.0,1473739200000.0,1473742800000.0,1473746400000.0,1473750000000.0,1473753600000.0,1473757200000.0,1473760800000.0,1473764400000.0,1473768000000.0,1473771600000.0,1473775200000.0,1473778800000.0,1473782400000.0,1473786000000.0,1473789600000.0,1473793200000.0,1473796800000.0,1473800400000.0,1473804000000.0,1473807600000.0,1473811200000.0,1473814800000.0,1473818400000.0,1473822000000.0,1473825600000.0,1473829200000.0,1473832800000.0,1473836400000.0,1473840000000.0,1473843600000.0,1473847200000.0,1473850800000.0,1473854400000.0,1473858000000.0,1473861600000.0,1473865200000.0,1473868800000.0,1473872400000.0,1473876000000.0,1473879600000.0,1473883200000.0,1473886800000.0,1473890400000.0,1473894000000.0,1473897600000.0,1473901200000.0,1473904800000.0,1473908400000.0,1473912000000.0,1473915600000.0,1473919200000.0,1473922800000.0,1473926400000.0,1473930000000.0,1473933600000.0,1473937200000.0,1473940800000.0,1473944400000.0,1473948000000.0,1473951600000.0,1473955200000.0,1473958800000.0,1473962400000.0,1473966000000.0,1473969600000.0,1473973200000.0,1473976800000.0,1473980400000.0,1473984000000.0,1473987600000.0,1473991200000.0,1473994800000.0,1473998400000.0,1474002000000.0,1474005600000.0,1474009200000.0,1474012800000.0,1474016400000.0,1474020000000.0,1474023600000.0,1474027200000.0,1474030800000.0,1474034400000.0,1474038000000.0,1474041600000.0,1474045200000.0,1474048800000.0,1474052400000.0,1474056000000.0,1474059600000.0,1474063200000.0,1474066800000.0,1474070400000.0,1474074000000.0,1474077600000.0,1474081200000.0,1474084800000.0,1474088400000.0,1474092000000.0,1474095600000.0,1474099200000.0,1474102800000.0,1474106400000.0,1474110000000.0,1474113600000.0,1474117200000.0,1474120800000.0,1474124400000.0,1474128000000.0,1474131600000.0,1474135200000.0,1474138800000.0,1474142400000.0,1474146000000.0,1474149600000.0,1474153200000.0,1474156800000.0,1474160400000.0,1474164000000.0,1474167600000.0,1474171200000.0,1474174800000.0,1474178400000.0,1474182000000.0,1474185600000.0,1474189200000.0,1474192800000.0,1474196400000.0,1474200000000.0,1474203600000.0,1474207200000.0,1474210800000.0,1474214400000.0,1474218000000.0,1474221600000.0,1474225200000.0,1474228800000.0,1474232400000.0,1474236000000.0,1474239600000.0,1474243200000.0,1474246800000.0,1474250400000.0,1474254000000.0,1474257600000.0,1474261200000.0,1474264800000.0,1474268400000.0,1474272000000.0,1474275600000.0,1474279200000.0,1474282800000.0,1474286400000.0,1474290000000.0,1474293600000.0,1474297200000.0,1474300800000.0,1474304400000.0,1474308000000.0,1474311600000.0,1474315200000.0,1474318800000.0,1474322400000.0,1474326000000.0,1474329600000.0,1474333200000.0,1474336800000.0,1474340400000.0,1474344000000.0,1474347600000.0,1474614000000.0,1474614000000.0,1474617600000.0,1474621200000.0,1474624800000.0,1474628400000.0,1474632000000.0,1474635600000.0,1474639200000.0,1474642800000.0,1474646400000.0,1474650000000.0,1474653600000.0,1474657200000.0,1474660800000.0,1474664400000.0,1474668000000.0,1474671600000.0,1474675200000.0,1474678800000.0,1474682400000.0,1474686000000.0,1474689600000.0,1474693200000.0,1474696800000.0,1474700400000.0,1474704000000.0,1474707600000.0,1474711200000.0,1474714800000.0,1474718400000.0,1474722000000.0,1474725600000.0,1474729200000.0,1474732800000.0,1474736400000.0,1474740000000.0,1474743600000.0,1474747200000.0,1474750800000.0,1474754400000.0,1474758000000.0,1474761600000.0,1474765200000.0,1474768800000.0,1474772400000.0,1474776000000.0,1474779600000.0,1474783200000.0,1474786800000.0,1474790400000.0,1474794000000.0,1474797600000.0,1474801200000.0,1474804800000.0,1474808400000.0,1474812000000.0,1474815600000.0,1474819200000.0,1474822800000.0,1474826400000.0,1474830000000.0,1474833600000.0,1474837200000.0,1474840800000.0,1474844400000.0,1474848000000.0,1474851600000.0,1474855200000.0,1474858800000.0,1474862400000.0,1474866000000.0,1474869600000.0,1474873200000.0,1474876800000.0,1474880400000.0,1474884000000.0,1474887600000.0,1474891200000.0,1474894800000.0,1474898400000.0,1474902000000.0,1474905600000.0,1474909200000.0,1474912800000.0,1474916400000.0,1474920000000.0,1474923600000.0,1474927200000.0,1474930800000.0,1474934400000.0,1474938000000.0,1474941600000.0,1474945200000.0,1474948800000.0,1474952400000.0,1474956000000.0,1474959600000.0,1474963200000.0,1474966800000.0,1474970400000.0,1474974000000.0,1474977600000.0,1474981200000.0,1474984800000.0,1474988400000.0,1474992000000.0,1474995600000.0,1474999200000.0,1475002800000.0,1475006400000.0,1475010000000.0,1475013600000.0,1475017200000.0,1475020800000.0,1475024400000.0,1475028000000.0,1475031600000.0,1475035200000.0,1475038800000.0,1475042400000.0,1475046000000.0],\"Date Formatted\":[\"02/15/16-11\",\"02/15/16-12\",\"02/15/16-13\",\"02/15/16-14\",\"02/15/16-15\",\"02/15/16-16\",\"02/16/16-02\",\"02/16/16-03\",\"02/16/16-05\",\"02/16/16-06\",\"02/16/16-07\",\"02/16/16-08\",\"02/16/16-09\",\"02/16/16-10\",\"02/16/16-20\",\"02/17/16-15\",\"02/17/16-16\",\"02/18/16-02\",\"02/18/16-03\",\"02/18/16-04\",\"02/18/16-05\",\"02/18/16-06\",\"02/18/16-07\",\"02/18/16-08\",\"02/18/16-09\",\"02/18/16-10\",\"02/18/16-11\",\"02/18/16-12\",\"02/18/16-13\",\"02/18/16-14\",\"02/18/16-15\",\"02/18/16-16\",\"02/18/16-19\",\"02/18/16-21\",\"02/18/16-23\",\"02/19/16-00\",\"02/19/16-02\",\"02/19/16-03\",\"02/19/16-03\",\"02/19/16-20\",\"02/19/16-20\",\"02/19/16-21\",\"02/19/16-22\",\"02/19/16-23\",\"02/20/16-00\",\"02/20/16-01\",\"02/20/16-02\",\"02/20/16-03\",\"02/20/16-04\",\"02/20/16-05\",\"02/20/16-06\",\"02/20/16-07\",\"02/20/16-08\",\"02/20/16-09\",\"02/20/16-10\",\"02/20/16-11\",\"02/20/16-12\",\"02/20/16-13\",\"02/20/16-14\",\"02/20/16-15\",\"02/20/16-16\",\"02/20/16-17\",\"02/20/16-18\",\"02/20/16-19\",\"02/20/16-20\",\"02/20/16-21\",\"02/20/16-22\",\"02/20/16-23\",\"02/21/16-00\",\"02/21/16-01\",\"02/21/16-02\",\"02/21/16-03\",\"02/21/16-04\",\"02/21/16-05\",\"02/21/16-06\",\"02/21/16-07\",\"02/21/16-08\",\"02/21/16-09\",\"02/21/16-10\",\"02/21/16-11\",\"02/21/16-12\",\"02/21/16-13\",\"02/21/16-14\",\"02/21/16-15\",\"02/21/16-16\",\"02/21/16-17\",\"02/21/16-18\",\"02/21/16-19\",\"02/21/16-20\",\"02/21/16-21\",\"02/21/16-22\",\"02/21/16-23\",\"02/22/16-00\",\"02/22/16-01\",\"02/22/16-02\",\"02/22/16-03\",\"02/22/16-04\",\"02/22/16-05\",\"02/22/16-06\",\"02/22/16-07\",\"02/22/16-08\",\"02/22/16-09\",\"02/22/16-10\",\"02/22/16-11\",\"02/22/16-18\",\"02/22/16-19\",\"02/23/16-04\",\"02/23/16-05\",\"02/23/16-06\",\"02/23/16-07\",\"02/23/16-08\",\"02/23/16-09\",\"02/23/16-10\",\"02/23/16-11\",\"02/23/16-12\",\"02/23/16-13\",\"02/23/16-14\",\"02/23/16-15\",\"02/23/16-16\",\"02/23/16-17\",\"02/24/16-01\",\"02/24/16-02\",\"02/24/16-03\",\"02/24/16-04\",\"02/24/16-05\",\"02/24/16-06\",\"02/24/16-07\",\"02/24/16-08\",\"02/24/16-09\",\"02/24/16-10\",\"02/24/16-11\",\"02/24/16-12\",\"02/24/16-13\",\"02/24/16-14\",\"02/24/16-15\",\"02/24/16-16\",\"02/25/16-03\",\"02/25/16-04\",\"02/25/16-05\",\"02/25/16-06\",\"02/25/16-07\",\"02/25/16-08\",\"02/25/16-09\",\"02/25/16-10\",\"02/25/16-11\",\"02/25/16-12\",\"02/25/16-13\",\"02/25/16-14\",\"02/25/16-15\",\"02/25/16-16\",\"02/25/16-18\",\"02/25/16-20\",\"02/25/16-21\",\"02/25/16-23\",\"02/26/16-00\",\"02/26/16-01\",\"02/26/16-04\",\"02/26/16-05\",\"02/26/16-06\",\"02/26/16-19\",\"02/26/16-20\",\"02/26/16-21\",\"02/26/16-22\",\"02/26/16-23\",\"02/27/16-00\",\"02/27/16-01\",\"02/27/16-02\",\"02/27/16-03\",\"02/27/16-04\",\"02/27/16-05\",\"02/27/16-06\",\"02/27/16-07\",\"02/27/16-08\",\"02/27/16-09\",\"02/27/16-10\",\"02/27/16-11\",\"02/27/16-12\",\"02/27/16-13\",\"02/27/16-14\",\"02/27/16-15\",\"02/27/16-16\",\"02/27/16-17\",\"02/27/16-18\",\"02/27/16-19\",\"02/27/16-20\",\"02/27/16-21\",\"02/27/16-22\",\"02/27/16-23\",\"02/28/16-00\",\"02/28/16-01\",\"02/28/16-02\",\"02/28/16-03\",\"02/28/16-04\",\"02/28/16-05\",\"02/28/16-06\",\"02/28/16-07\",\"02/28/16-08\",\"02/28/16-09\",\"02/28/16-10\",\"02/28/16-11\",\"02/28/16-12\",\"02/28/16-13\",\"02/28/16-14\",\"02/28/16-15\",\"02/28/16-16\",\"02/28/16-17\",\"02/28/16-18\",\"02/28/16-19\",\"02/28/16-20\",\"02/28/16-21\",\"02/28/16-22\",\"02/28/16-23\",\"02/29/16-00\",\"02/29/16-01\",\"02/29/16-02\",\"02/29/16-03\",\"02/29/16-04\",\"02/29/16-05\",\"02/29/16-06\",\"02/29/16-07\",\"02/29/16-08\",\"02/29/16-09\",\"02/29/16-10\",\"02/29/16-11\",\"02/29/16-12\",\"02/29/16-13\",\"02/29/16-14\",\"02/29/16-15\",\"02/29/16-16\",\"02/29/16-19\",\"02/29/16-20\",\"02/29/16-21\",\"02/29/16-23\",\"03/01/16-00\",\"03/01/16-03\",\"03/01/16-04\",\"03/01/16-05\",\"03/01/16-06\",\"03/01/16-07\",\"03/01/16-08\",\"03/01/16-09\",\"03/01/16-10\",\"03/01/16-11\",\"03/01/16-12\",\"03/01/16-13\",\"03/01/16-14\",\"03/01/16-15\",\"03/01/16-16\",\"03/01/16-17\",\"03/01/16-19\",\"03/01/16-20\",\"03/01/16-21\",\"03/01/16-22\",\"03/01/16-23\",\"03/02/16-01\",\"03/02/16-02\",\"03/02/16-03\",\"03/02/16-04\",\"03/02/16-05\",\"03/02/16-06\",\"03/02/16-07\",\"03/02/16-08\",\"03/02/16-09\",\"03/02/16-10\",\"03/02/16-11\",\"03/02/16-12\",\"03/02/16-13\",\"03/02/16-14\",\"03/02/16-15\",\"03/02/16-19\",\"03/02/16-20\",\"03/02/16-21\",\"03/03/16-02\",\"03/03/16-03\",\"03/03/16-04\",\"03/03/16-05\",\"03/03/16-06\",\"03/03/16-07\",\"03/03/16-08\",\"03/03/16-09\",\"03/03/16-10\",\"03/03/16-11\",\"03/03/16-12\",\"03/03/16-13\",\"03/03/16-14\",\"03/03/16-15\",\"03/03/16-16\",\"03/03/16-17\",\"03/03/16-20\",\"03/03/16-21\",\"03/03/16-23\",\"03/04/16-00\",\"03/04/16-02\",\"03/04/16-03\",\"03/04/16-04\",\"03/04/16-05\",\"03/04/16-06\",\"03/04/16-07\",\"03/04/16-08\",\"03/04/16-09\",\"03/04/16-10\",\"03/04/16-11\",\"03/04/16-12\",\"03/04/16-13\",\"03/04/16-14\",\"03/04/16-15\",\"03/04/16-16\",\"03/04/16-17\",\"03/04/16-18\",\"03/04/16-19\",\"03/04/16-20\",\"03/04/16-21\",\"03/04/16-22\",\"03/04/16-23\",\"03/05/16-01\",\"03/05/16-02\",\"03/05/16-03\",\"03/05/16-04\",\"03/05/16-05\",\"03/05/16-06\",\"03/05/16-07\",\"03/05/16-08\",\"03/05/16-09\",\"03/05/16-10\",\"03/05/16-11\",\"03/05/16-12\",\"03/05/16-13\",\"03/05/16-14\",\"03/05/16-15\",\"03/05/16-16\",\"03/05/16-17\",\"03/05/16-18\",\"03/05/16-19\",\"03/05/16-20\",\"03/05/16-21\",\"03/05/16-22\",\"03/05/16-23\",\"03/06/16-00\",\"03/06/16-01\",\"03/06/16-02\",\"03/06/16-03\",\"03/06/16-04\",\"03/06/16-05\",\"03/06/16-06\",\"03/06/16-07\",\"03/06/16-08\",\"03/06/16-09\",\"03/06/16-10\",\"03/06/16-11\",\"03/06/16-12\",\"03/06/16-13\",\"03/06/16-14\",\"03/06/16-15\",\"03/06/16-16\",\"03/06/16-17\",\"03/06/16-18\",\"03/06/16-19\",\"03/06/16-20\",\"03/06/16-21\",\"03/06/16-22\",\"03/06/16-23\",\"03/07/16-00\",\"03/07/16-01\",\"03/07/16-02\",\"03/07/16-03\",\"03/07/16-04\",\"03/07/16-05\",\"03/07/16-06\",\"03/07/16-07\",\"03/07/16-08\",\"03/07/16-09\",\"03/07/16-10\",\"03/07/16-11\",\"03/07/16-12\",\"03/07/16-13\",\"03/07/16-14\",\"03/07/16-15\",\"03/07/16-16\",\"03/07/16-19\",\"03/07/16-20\",\"03/07/16-21\",\"03/08/16-03\",\"03/08/16-04\",\"03/08/16-05\",\"03/08/16-06\",\"03/08/16-07\",\"03/08/16-08\",\"03/08/16-09\",\"03/08/16-10\",\"03/08/16-11\",\"03/08/16-12\",\"03/08/16-13\",\"03/08/16-14\",\"03/08/16-15\",\"03/08/16-16\",\"03/08/16-20\",\"03/08/16-21\",\"03/09/16-08\",\"03/09/16-09\",\"03/09/16-10\",\"03/09/16-16\",\"03/09/16-19\",\"03/09/16-20\",\"03/09/16-21\",\"03/10/16-01\",\"03/10/16-03\",\"03/10/16-04\",\"03/10/16-05\",\"03/10/16-06\",\"03/10/16-07\",\"03/10/16-08\",\"03/10/16-09\",\"03/10/16-10\",\"03/10/16-11\",\"03/10/16-12\",\"03/10/16-13\",\"03/10/16-14\",\"03/10/16-15\",\"03/10/16-16\",\"03/10/16-17\",\"03/10/16-18\",\"03/10/16-19\",\"03/10/16-20\",\"03/10/16-21\",\"03/10/16-23\",\"03/11/16-02\",\"03/11/16-03\",\"03/11/16-04\",\"03/11/16-05\",\"03/11/16-06\",\"03/11/16-07\",\"03/11/16-08\",\"03/11/16-09\",\"03/11/16-10\",\"03/11/16-11\",\"03/11/16-12\",\"03/11/16-13\",\"03/11/16-14\",\"03/11/16-15\",\"03/11/16-16\",\"03/11/16-17\",\"03/11/16-18\",\"03/11/16-19\",\"03/11/16-20\",\"03/11/16-21\",\"03/11/16-22\",\"03/11/16-23\",\"03/12/16-00\",\"03/12/16-01\",\"03/12/16-02\",\"03/12/16-04\",\"03/12/16-05\",\"03/12/16-06\",\"03/12/16-07\",\"03/12/16-08\",\"03/12/16-09\",\"03/12/16-10\",\"03/12/16-11\",\"03/12/16-12\",\"03/12/16-13\",\"03/12/16-14\",\"03/12/16-15\",\"03/12/16-16\",\"03/12/16-17\",\"03/12/16-18\",\"03/12/16-19\",\"03/12/16-20\",\"03/12/16-21\",\"03/12/16-22\",\"03/12/16-23\",\"03/13/16-00\",\"03/13/16-01\",\"03/13/16-02\",\"03/13/16-03\",\"03/13/16-04\",\"03/13/16-05\",\"03/13/16-06\",\"03/13/16-07\",\"03/13/16-08\",\"03/13/16-09\",\"03/13/16-10\",\"03/13/16-11\",\"03/13/16-12\",\"03/13/16-13\",\"03/13/16-14\",\"03/13/16-15\",\"03/13/16-16\",\"03/13/16-17\",\"03/13/16-18\",\"03/13/16-19\",\"03/13/16-20\",\"03/13/16-21\",\"03/13/16-22\",\"03/13/16-23\",\"03/14/16-00\",\"03/14/16-01\",\"03/14/16-02\",\"03/14/16-03\",\"03/14/16-04\",\"03/14/16-05\",\"03/14/16-06\",\"03/14/16-07\",\"03/14/16-08\",\"03/14/16-09\",\"03/14/16-10\",\"03/14/16-11\",\"03/14/16-12\",\"03/14/16-13\",\"03/14/16-14\",\"03/14/16-15\",\"03/14/16-17\",\"03/14/16-18\",\"03/14/16-19\",\"03/14/16-20\",\"03/14/16-21\",\"03/14/16-22\",\"03/14/16-23\",\"03/15/16-02\",\"03/15/16-03\",\"03/15/16-04\",\"03/15/16-05\",\"03/15/16-06\",\"03/15/16-07\",\"03/15/16-08\",\"03/15/16-09\",\"03/15/16-10\",\"03/15/16-11\",\"03/15/16-12\",\"03/15/16-13\",\"03/15/16-14\",\"03/15/16-15\",\"03/15/16-16\",\"03/15/16-18\",\"03/15/16-19\",\"03/15/16-20\",\"03/16/16-00\",\"03/16/16-01\",\"03/16/16-02\",\"03/16/16-03\",\"03/16/16-04\",\"03/16/16-05\",\"03/16/16-06\",\"03/16/16-07\",\"03/16/16-08\",\"03/16/16-09\",\"03/16/16-10\",\"03/16/16-11\",\"03/16/16-12\",\"03/16/16-13\",\"03/16/16-14\",\"03/16/16-15\",\"03/16/16-17\",\"03/16/16-18\",\"03/16/16-19\",\"03/16/16-21\",\"03/16/16-22\",\"03/17/16-01\",\"03/17/16-02\",\"03/17/16-03\",\"03/17/16-04\",\"03/17/16-05\",\"03/17/16-06\",\"03/17/16-07\",\"03/17/16-08\",\"03/17/16-09\",\"03/17/16-10\",\"03/17/16-11\",\"03/17/16-12\",\"03/17/16-13\",\"03/17/16-14\",\"03/17/16-15\",\"03/17/16-16\",\"03/17/16-19\",\"03/17/16-20\",\"03/17/16-21\",\"03/17/16-22\",\"03/18/16-00\",\"03/18/16-01\",\"03/18/16-02\",\"03/18/16-03\",\"03/18/16-04\",\"03/18/16-05\",\"03/18/16-06\",\"03/18/16-07\",\"03/18/16-08\",\"03/18/16-09\",\"03/18/16-10\",\"03/18/16-11\",\"03/18/16-12\",\"03/18/16-13\",\"03/18/16-14\",\"03/18/16-15\",\"03/18/16-16\",\"03/18/16-17\",\"03/18/16-18\",\"03/18/16-19\",\"03/18/16-20\",\"03/18/16-21\",\"03/18/16-22\",\"03/18/16-23\",\"03/19/16-00\",\"03/19/16-01\",\"03/19/16-02\",\"03/19/16-03\",\"03/19/16-04\",\"03/19/16-05\",\"03/19/16-06\",\"03/19/16-07\",\"03/19/16-08\",\"03/19/16-09\",\"03/19/16-10\",\"03/19/16-11\",\"03/19/16-12\",\"03/19/16-13\",\"03/19/16-14\",\"03/19/16-15\",\"03/19/16-16\",\"03/19/16-17\",\"03/19/16-18\",\"03/19/16-19\",\"03/19/16-20\",\"03/19/16-21\",\"03/19/16-22\",\"03/19/16-23\",\"03/20/16-00\",\"03/20/16-01\",\"03/20/16-02\",\"03/20/16-03\",\"03/20/16-04\",\"03/20/16-05\",\"03/20/16-06\",\"03/20/16-07\",\"03/20/16-08\",\"03/20/16-09\",\"03/20/16-10\",\"03/20/16-11\",\"03/20/16-12\",\"03/20/16-13\",\"03/20/16-14\",\"03/20/16-15\",\"03/20/16-16\",\"03/20/16-17\",\"03/20/16-18\",\"03/20/16-19\",\"03/20/16-20\",\"03/20/16-21\",\"03/20/16-22\",\"03/20/16-23\",\"03/21/16-00\",\"03/21/16-01\",\"03/21/16-02\",\"03/21/16-03\",\"03/21/16-04\",\"03/21/16-05\",\"03/21/16-06\",\"03/21/16-07\",\"03/21/16-08\",\"03/21/16-09\",\"03/21/16-10\",\"03/21/16-11\",\"03/21/16-12\",\"03/21/16-13\",\"03/21/16-14\",\"03/21/16-15\",\"03/21/16-16\",\"03/21/16-17\",\"03/21/16-18\",\"03/21/16-19\",\"03/21/16-20\",\"03/21/16-21\",\"03/21/16-22\",\"03/21/16-23\",\"03/22/16-00\",\"03/22/16-01\",\"03/22/16-02\",\"03/22/16-03\",\"03/22/16-04\",\"03/22/16-05\",\"03/22/16-06\",\"03/22/16-07\",\"03/22/16-08\",\"03/22/16-09\",\"03/22/16-10\",\"03/22/16-11\",\"03/22/16-12\",\"03/22/16-13\",\"03/22/16-14\",\"03/22/16-15\",\"03/22/16-16\",\"03/22/16-17\",\"03/22/16-18\",\"03/22/16-19\",\"03/22/16-20\",\"03/22/16-21\",\"03/22/16-22\",\"03/22/16-23\",\"03/23/16-00\",\"03/23/16-01\",\"03/23/16-02\",\"03/23/16-03\",\"03/23/16-04\",\"03/23/16-05\",\"03/23/16-06\",\"03/23/16-07\",\"03/23/16-08\",\"03/23/16-09\",\"03/23/16-10\",\"03/23/16-11\",\"03/23/16-12\",\"03/23/16-18\",\"03/23/16-19\",\"03/23/16-20\",\"03/23/16-21\",\"03/23/16-22\",\"03/23/16-23\",\"03/24/16-00\",\"03/24/16-01\",\"03/24/16-02\",\"03/24/16-03\",\"03/24/16-04\",\"03/24/16-05\",\"03/24/16-06\",\"03/24/16-07\",\"03/24/16-08\",\"03/24/16-09\",\"03/24/16-10\",\"03/24/16-11\",\"03/24/16-12\",\"03/24/16-13\",\"03/24/16-14\",\"03/24/16-15\",\"03/24/16-16\",\"03/24/16-17\",\"03/24/16-18\",\"03/24/16-19\",\"03/24/16-20\",\"03/24/16-21\",\"03/24/16-22\",\"03/24/16-23\",\"03/25/16-00\",\"03/25/16-01\",\"03/25/16-02\",\"03/25/16-03\",\"03/25/16-04\",\"03/25/16-05\",\"03/25/16-06\",\"03/25/16-07\",\"03/25/16-08\",\"03/25/16-09\",\"03/25/16-18\",\"03/25/16-19\",\"03/25/16-20\",\"03/25/16-21\",\"03/25/16-22\",\"03/25/16-23\",\"03/26/16-00\",\"03/26/16-01\",\"03/26/16-02\",\"03/26/16-03\",\"03/26/16-04\",\"03/26/16-05\",\"03/26/16-06\",\"03/26/16-07\",\"03/26/16-08\",\"03/26/16-09\",\"03/26/16-10\",\"03/26/16-11\",\"03/26/16-12\",\"03/26/16-13\",\"03/26/16-14\",\"03/26/16-15\",\"03/26/16-16\",\"03/26/16-17\",\"03/26/16-18\",\"03/26/16-19\",\"03/26/16-20\",\"03/26/16-21\",\"03/26/16-22\",\"03/26/16-23\",\"03/27/16-00\",\"03/27/16-01\",\"03/27/16-02\",\"03/27/16-03\",\"03/27/16-04\",\"03/27/16-05\",\"03/27/16-06\",\"03/27/16-07\",\"03/27/16-17\",\"03/27/16-18\",\"03/27/16-19\",\"03/27/16-20\",\"03/27/16-21\",\"03/27/16-22\",\"03/27/16-23\",\"03/28/16-00\",\"03/28/16-01\",\"03/28/16-02\",\"03/28/16-03\",\"03/28/16-04\",\"03/28/16-05\",\"03/28/16-06\",\"03/28/16-07\",\"03/28/16-08\",\"03/28/16-09\",\"03/28/16-18\",\"03/28/16-19\",\"03/29/16-02\",\"03/29/16-03\",\"03/29/16-04\",\"03/29/16-05\",\"03/29/16-06\",\"03/29/16-07\",\"03/29/16-08\",\"03/29/16-09\",\"03/29/16-10\",\"03/29/16-11\",\"03/29/16-12\",\"03/29/16-13\",\"03/29/16-14\",\"03/29/16-15\",\"03/29/16-16\",\"03/29/16-19\",\"03/29/16-20\",\"03/30/16-00\",\"03/30/16-01\",\"03/30/16-15\",\"03/30/16-16\",\"03/30/16-17\",\"03/30/16-18\",\"03/30/16-19\",\"03/31/16-01\",\"03/31/16-02\",\"03/31/16-03\",\"03/31/16-04\",\"03/31/16-05\",\"03/31/16-06\",\"03/31/16-07\",\"03/31/16-08\",\"03/31/16-09\",\"03/31/16-10\",\"03/31/16-11\",\"03/31/16-12\",\"03/31/16-17\",\"03/31/16-21\",\"03/31/16-23\",\"04/01/16-00\",\"04/01/16-01\",\"04/01/16-02\",\"04/01/16-03\",\"04/01/16-04\",\"04/01/16-05\",\"04/01/16-06\",\"04/01/16-17\",\"04/01/16-20\",\"04/01/16-21\",\"04/01/16-22\",\"04/01/16-23\",\"04/02/16-00\",\"04/02/16-01\",\"04/02/16-02\",\"04/02/16-03\",\"04/02/16-04\",\"04/02/16-05\",\"04/02/16-06\",\"04/02/16-07\",\"04/02/16-08\",\"04/02/16-09\",\"04/02/16-10\",\"04/02/16-11\",\"04/02/16-19\",\"04/02/16-20\",\"04/02/16-21\",\"04/02/16-22\",\"04/02/16-23\",\"04/03/16-00\",\"04/03/16-01\",\"04/03/16-02\",\"04/03/16-03\",\"04/03/16-04\",\"04/03/16-05\",\"04/03/16-06\",\"04/03/16-07\",\"04/03/16-08\",\"04/03/16-09\",\"04/03/16-10\",\"04/03/16-18\",\"04/03/16-19\",\"04/03/16-20\",\"04/03/16-21\",\"04/04/16-00\",\"04/04/16-01\",\"04/04/16-02\",\"04/04/16-03\",\"04/04/16-04\",\"04/04/16-05\",\"04/04/16-06\",\"04/04/16-07\",\"04/04/16-08\",\"04/04/16-09\",\"04/04/16-10\",\"04/04/16-18\",\"04/04/16-19\",\"04/04/16-20\",\"04/04/16-22\",\"04/04/16-23\",\"04/05/16-02\",\"04/05/16-03\",\"04/05/16-04\",\"04/05/16-05\",\"04/05/16-06\",\"04/05/16-15\",\"04/05/16-16\",\"04/05/16-19\",\"04/05/16-20\",\"04/05/16-21\",\"04/05/16-22\",\"04/07/16-16\",\"04/07/16-19\",\"04/07/16-21\",\"04/07/16-23\",\"04/08/16-00\",\"04/08/16-01\",\"04/08/16-02\",\"04/08/16-03\",\"04/08/16-04\",\"04/08/16-05\",\"04/08/16-06\",\"04/08/16-07\",\"04/08/16-08\",\"04/08/16-09\",\"04/08/16-10\",\"04/08/16-11\",\"04/08/16-12\",\"04/08/16-13\",\"04/08/16-19\",\"04/08/16-20\",\"04/08/16-21\",\"04/08/16-22\",\"04/08/16-23\",\"04/09/16-00\",\"04/09/16-01\",\"04/09/16-02\",\"04/09/16-03\",\"04/09/16-04\",\"04/09/16-05\",\"04/09/16-06\",\"04/09/16-07\",\"04/09/16-08\",\"04/09/16-09\",\"04/09/16-10\",\"04/09/16-11\",\"04/09/16-19\",\"04/09/16-20\",\"04/09/16-21\",\"04/09/16-22\",\"04/09/16-23\",\"04/10/16-00\",\"04/10/16-01\",\"04/10/16-02\",\"04/10/16-03\",\"04/10/16-06\",\"04/11/16-01\",\"04/11/16-02\",\"04/11/16-03\",\"04/11/16-04\",\"04/11/16-05\",\"04/11/16-06\",\"04/11/16-07\",\"04/11/16-08\",\"04/11/16-09\",\"04/11/16-18\",\"04/11/16-19\",\"04/11/16-20\",\"04/11/16-21\",\"04/12/16-01\",\"04/12/16-02\",\"04/12/16-07\",\"04/12/16-08\",\"04/12/16-09\",\"04/12/16-11\",\"04/12/16-12\",\"04/12/16-13\",\"04/12/16-14\",\"04/12/16-19\",\"04/12/16-20\",\"04/12/16-22\",\"04/12/16-23\",\"04/13/16-00\",\"04/13/16-01\",\"04/13/16-04\",\"04/13/16-09\",\"04/13/16-11\",\"04/13/16-17\",\"04/13/16-18\",\"04/13/16-19\",\"04/14/16-01\",\"04/14/16-02\",\"04/14/16-03\",\"04/14/16-19\",\"04/14/16-20\",\"04/14/16-23\",\"04/15/16-00\",\"04/15/16-02\",\"04/15/16-06\",\"04/15/16-16\",\"04/15/16-17\",\"04/15/16-18\",\"04/15/16-19\",\"04/15/16-20\",\"04/15/16-21\",\"04/15/16-22\",\"04/15/16-23\",\"04/16/16-00\",\"04/16/16-01\",\"04/16/16-05\",\"04/16/16-06\",\"04/16/16-07\",\"04/16/16-08\",\"04/16/16-09\",\"04/16/16-10\",\"04/16/16-20\",\"04/16/16-21\",\"04/16/16-22\",\"04/16/16-23\",\"04/17/16-00\",\"04/17/16-01\",\"04/17/16-02\",\"04/17/16-03\",\"04/17/16-04\",\"04/17/16-05\",\"04/17/16-06\",\"04/17/16-07\",\"04/17/16-08\",\"04/17/16-09\",\"04/17/16-10\",\"04/17/16-11\",\"04/17/16-12\",\"04/17/16-13\",\"04/17/16-14\",\"04/17/16-15\",\"04/17/16-16\",\"04/17/16-18\",\"04/17/16-19\",\"04/17/16-20\",\"04/17/16-21\",\"04/17/16-22\",\"04/17/16-23\",\"04/18/16-00\",\"04/18/16-01\",\"04/18/16-02\",\"04/18/16-03\",\"04/18/16-04\",\"04/18/16-05\",\"04/18/16-06\",\"04/18/16-07\",\"04/18/16-08\",\"04/18/16-09\",\"04/18/16-10\",\"04/18/16-11\",\"04/18/16-12\",\"04/18/16-17\",\"04/18/16-21\",\"04/19/16-01\",\"04/19/16-02\",\"04/19/16-03\",\"04/19/16-04\",\"04/19/16-05\",\"04/19/16-06\",\"04/19/16-07\",\"04/19/16-08\",\"04/19/16-09\",\"04/19/16-10\",\"04/19/16-11\",\"04/19/16-20\",\"04/19/16-21\",\"04/20/16-00\",\"04/20/16-03\",\"04/20/16-07\",\"04/20/16-08\",\"04/20/16-09\",\"04/20/16-10\",\"04/20/16-11\",\"04/20/16-12\",\"04/20/16-13\",\"04/20/16-14\",\"04/20/16-15\",\"04/20/16-18\",\"04/20/16-19\",\"04/20/16-20\",\"04/21/16-02\",\"04/21/16-03\",\"04/21/16-09\",\"04/21/16-10\",\"04/21/16-11\",\"04/21/16-12\",\"04/21/16-13\",\"04/21/16-14\",\"04/21/16-15\",\"04/21/16-17\",\"04/21/16-18\",\"04/22/16-10\",\"04/22/16-11\",\"04/22/16-12\",\"04/22/16-13\",\"04/22/16-14\",\"04/22/16-15\",\"04/22/16-16\",\"04/22/16-17\",\"04/22/16-18\",\"04/22/16-19\",\"04/22/16-20\",\"04/22/16-21\",\"04/22/16-22\",\"04/22/16-23\",\"04/23/16-00\",\"04/23/16-01\",\"04/23/16-02\",\"04/23/16-03\",\"04/23/16-18\",\"04/23/16-19\",\"04/23/16-22\",\"04/23/16-23\",\"04/24/16-00\",\"04/24/16-01\",\"04/24/16-02\",\"04/24/16-03\",\"04/24/16-05\",\"04/24/16-06\",\"04/24/16-07\",\"04/24/16-08\",\"04/24/16-09\",\"04/24/16-16\",\"04/24/16-17\",\"04/24/16-18\",\"04/24/16-19\",\"04/24/16-20\",\"04/24/16-21\",\"04/24/16-22\",\"04/24/16-23\",\"04/25/16-00\",\"04/25/16-04\",\"04/25/16-05\",\"04/25/16-06\",\"04/25/16-07\",\"04/25/16-08\",\"04/25/16-09\",\"04/25/16-10\",\"04/25/16-11\",\"04/25/16-12\",\"04/25/16-13\",\"04/25/16-14\",\"04/25/16-15\",\"04/25/16-17\",\"04/25/16-18\",\"04/25/16-19\",\"04/25/16-20\",\"04/25/16-21\",\"04/26/16-00\",\"04/26/16-03\",\"04/26/16-04\",\"04/26/16-05\",\"04/26/16-09\",\"04/26/16-10\",\"04/26/16-11\",\"04/26/16-12\",\"04/26/16-13\",\"04/26/16-14\",\"04/26/16-15\",\"04/26/16-16\",\"04/26/16-19\",\"04/26/16-20\",\"04/27/16-06\",\"04/27/16-07\",\"04/27/16-08\",\"04/27/16-09\",\"04/27/16-10\",\"04/27/16-11\",\"04/27/16-12\",\"04/27/16-13\",\"04/27/16-14\",\"04/27/16-16\",\"04/27/16-18\",\"04/27/16-19\",\"04/27/16-20\",\"04/28/16-01\",\"04/28/16-02\",\"04/28/16-03\",\"04/28/16-04\",\"04/28/16-05\",\"04/28/16-07\",\"04/28/16-14\",\"04/28/16-15\",\"04/28/16-17\",\"04/28/16-19\",\"04/28/16-20\",\"04/28/16-21\",\"04/29/16-00\",\"04/29/16-05\",\"04/29/16-06\",\"04/29/16-07\",\"04/29/16-08\",\"04/29/16-09\",\"04/29/16-10\",\"04/29/16-11\",\"04/29/16-12\",\"04/29/16-13\",\"04/29/16-21\",\"04/29/16-22\",\"04/29/16-23\",\"04/30/16-00\",\"04/30/16-01\",\"04/30/16-02\",\"04/30/16-03\",\"04/30/16-04\",\"04/30/16-05\",\"04/30/16-06\",\"04/30/16-07\",\"04/30/16-15\",\"04/30/16-16\",\"04/30/16-17\",\"04/30/16-18\",\"04/30/16-19\",\"04/30/16-20\",\"04/30/16-21\",\"04/30/16-22\",\"04/30/16-23\",\"05/01/16-00\",\"05/01/16-01\",\"05/01/16-02\",\"05/01/16-03\",\"05/01/16-04\",\"05/01/16-05\",\"05/01/16-06\",\"05/01/16-07\",\"05/01/16-08\",\"05/01/16-09\",\"05/01/16-10\",\"05/01/16-23\",\"05/02/16-00\",\"05/02/16-01\",\"05/02/16-02\",\"05/02/16-03\",\"05/02/16-04\",\"05/02/16-05\",\"05/02/16-06\",\"05/02/16-07\",\"05/02/16-08\",\"05/02/16-09\",\"05/03/16-01\",\"05/03/16-02\",\"05/03/16-03\",\"05/03/16-04\",\"05/03/16-14\",\"05/03/16-15\",\"05/03/16-16\",\"05/03/16-17\",\"05/03/16-18\",\"05/03/16-19\",\"05/03/16-20\",\"05/03/16-21\",\"05/04/16-01\",\"05/04/16-02\",\"05/04/16-03\",\"05/04/16-04\",\"05/04/16-05\",\"05/04/16-06\",\"05/04/16-07\",\"05/04/16-08\",\"05/04/16-09\",\"05/04/16-10\",\"05/04/16-11\",\"05/04/16-12\",\"05/04/16-13\",\"05/04/16-14\",\"05/04/16-15\",\"05/04/16-18\",\"05/05/16-00\",\"05/05/16-12\",\"05/05/16-13\",\"05/05/16-14\",\"05/05/16-15\",\"05/05/16-16\",\"05/05/16-18\",\"05/05/16-19\",\"05/05/16-23\",\"05/06/16-00\",\"05/06/16-01\",\"05/06/16-03\",\"05/06/16-04\",\"05/06/16-05\",\"05/06/16-06\",\"05/06/16-07\",\"05/06/16-08\",\"05/06/16-09\",\"05/06/16-10\",\"05/06/16-11\",\"05/06/16-12\",\"05/06/16-13\",\"05/06/16-14\",\"05/06/16-15\",\"05/06/16-16\",\"05/06/16-17\",\"05/06/16-18\",\"05/06/16-19\",\"05/06/16-20\",\"05/06/16-21\",\"05/06/16-22\",\"05/07/16-00\",\"05/07/16-01\",\"05/07/16-02\",\"05/07/16-03\",\"05/07/16-04\",\"05/07/16-05\",\"05/07/16-06\",\"05/07/16-07\",\"05/07/16-09\",\"05/07/16-10\",\"05/07/16-17\",\"05/07/16-18\",\"05/07/16-19\",\"05/07/16-20\",\"05/07/16-21\",\"05/07/16-22\",\"05/07/16-23\",\"05/08/16-00\",\"05/08/16-01\",\"05/08/16-02\",\"05/08/16-03\",\"05/08/16-04\",\"05/08/16-05\",\"05/08/16-06\",\"05/08/16-07\",\"05/08/16-08\",\"05/08/16-09\",\"05/08/16-16\",\"05/08/16-17\",\"05/08/16-18\",\"05/08/16-19\",\"05/08/16-20\",\"05/08/16-21\",\"05/08/16-22\",\"05/08/16-23\",\"05/09/16-00\",\"05/09/16-01\",\"05/09/16-02\",\"05/09/16-03\",\"05/09/16-04\",\"05/09/16-05\",\"05/09/16-06\",\"05/09/16-07\",\"05/09/16-08\",\"05/09/16-14\",\"05/09/16-17\",\"05/09/16-19\",\"05/09/16-20\",\"05/09/16-21\",\"05/09/16-22\",\"05/09/16-23\",\"05/10/16-00\",\"05/10/16-01\",\"05/10/16-02\",\"05/10/16-03\",\"05/10/16-04\",\"05/10/16-05\",\"05/10/16-06\",\"05/10/16-07\",\"05/10/16-08\",\"05/10/16-09\",\"05/10/16-19\",\"05/10/16-20\",\"05/10/16-21\",\"05/11/16-03\",\"05/11/16-04\",\"05/11/16-05\",\"05/11/16-06\",\"05/11/16-07\",\"05/11/16-20\",\"05/11/16-21\",\"05/12/16-01\",\"05/12/16-02\",\"05/12/16-03\",\"05/12/16-04\",\"05/12/16-05\",\"05/12/16-07\",\"05/12/16-08\",\"05/12/16-09\",\"05/12/16-10\",\"05/12/16-11\",\"05/12/16-12\",\"05/12/16-13\",\"05/12/16-14\",\"05/12/16-15\",\"05/12/16-18\",\"05/12/16-19\",\"05/12/16-21\",\"05/12/16-22\",\"05/13/16-02\",\"05/13/16-03\",\"05/13/16-04\",\"05/13/16-05\",\"05/13/16-07\",\"05/13/16-15\",\"05/13/16-16\",\"05/13/16-17\",\"05/13/16-18\",\"05/13/16-19\",\"05/13/16-20\",\"05/13/16-21\",\"05/13/16-22\",\"05/13/16-23\",\"05/14/16-00\",\"05/14/16-01\",\"05/14/16-02\",\"05/14/16-03\",\"05/14/16-04\",\"05/14/16-05\",\"05/14/16-06\",\"05/14/16-07\",\"05/14/16-08\",\"05/14/16-09\",\"05/14/16-10\",\"05/14/16-17\",\"05/14/16-19\",\"05/14/16-20\",\"05/15/16-00\",\"05/15/16-01\",\"05/15/16-02\",\"05/15/16-03\",\"05/15/16-04\",\"05/15/16-06\",\"05/15/16-07\",\"05/15/16-08\",\"05/15/16-16\",\"05/15/16-17\",\"05/15/16-18\",\"05/15/16-19\",\"05/15/16-20\",\"05/15/16-21\",\"05/15/16-22\",\"05/15/16-23\",\"05/16/16-00\",\"05/16/16-01\",\"05/16/16-02\",\"05/16/16-03\",\"05/16/16-06\",\"05/16/16-07\",\"05/16/16-08\",\"05/16/16-09\",\"05/16/16-10\",\"05/17/16-00\",\"05/17/16-01\",\"05/17/16-09\",\"05/17/16-10\",\"05/17/16-12\",\"05/17/16-13\",\"05/18/16-00\",\"05/18/16-01\",\"05/18/16-02\",\"05/18/16-03\",\"05/18/16-04\",\"05/18/16-05\",\"05/18/16-06\",\"05/18/16-08\",\"05/19/16-04\",\"05/19/16-05\",\"05/19/16-06\",\"05/19/16-07\",\"05/19/16-08\",\"05/19/16-09\",\"05/19/16-12\",\"05/19/16-13\",\"05/19/16-23\",\"05/20/16-00\",\"05/20/16-05\",\"05/21/16-00\",\"05/21/16-16\",\"05/21/16-17\",\"05/21/16-23\",\"05/22/16-00\",\"05/22/16-04\",\"05/22/16-05\",\"05/22/16-15\",\"05/22/16-16\",\"05/22/16-17\",\"05/22/16-18\",\"05/22/16-19\",\"05/22/16-20\",\"05/22/16-21\",\"05/22/16-22\",\"05/23/16-00\",\"05/23/16-01\",\"05/23/16-02\",\"05/23/16-03\",\"05/23/16-04\",\"05/24/16-00\",\"05/24/16-04\",\"05/24/16-05\",\"05/24/16-06\",\"05/24/16-07\",\"05/24/16-08\",\"05/24/16-09\",\"05/24/16-10\",\"05/24/16-11\",\"05/24/16-12\",\"05/24/16-13\",\"05/25/16-02\",\"05/25/16-03\",\"05/25/16-04\",\"05/25/16-05\",\"05/25/16-06\",\"05/25/16-12\",\"05/25/16-13\",\"05/25/16-14\",\"05/25/16-23\",\"05/26/16-00\",\"05/26/16-01\",\"05/26/16-02\",\"05/26/16-03\",\"05/26/16-04\",\"05/27/16-00\",\"05/27/16-01\",\"05/27/16-02\",\"05/27/16-05\",\"05/27/16-06\",\"05/28/16-00\",\"05/28/16-01\",\"05/28/16-02\",\"05/28/16-03\",\"05/28/16-04\",\"05/28/16-05\",\"05/28/16-06\",\"05/28/16-07\",\"05/28/16-17\",\"05/28/16-18\",\"05/28/16-19\",\"05/28/16-20\",\"05/28/16-21\",\"05/28/16-23\",\"05/29/16-01\",\"05/29/16-02\",\"05/29/16-03\",\"05/29/16-04\",\"05/29/16-05\",\"05/29/16-06\",\"05/29/16-07\",\"05/29/16-15\",\"05/29/16-16\",\"05/29/16-18\",\"05/29/16-19\",\"05/29/16-20\",\"05/29/16-21\",\"05/29/16-22\",\"05/29/16-23\",\"05/30/16-00\",\"05/30/16-01\",\"05/30/16-04\",\"05/30/16-05\",\"05/30/16-06\",\"05/30/16-07\",\"05/30/16-15\",\"05/30/16-16\",\"05/30/16-17\",\"05/30/16-18\",\"05/30/16-19\",\"05/30/16-20\",\"05/30/16-21\",\"05/30/16-22\",\"05/30/16-23\",\"05/31/16-04\",\"05/31/16-05\",\"05/31/16-06\",\"05/31/16-07\",\"06/01/16-01\",\"06/01/16-02\",\"06/01/16-04\",\"06/01/16-05\",\"06/02/16-00\",\"06/02/16-01\",\"06/02/16-05\",\"06/02/16-06\",\"06/02/16-08\",\"06/02/16-09\",\"06/02/16-10\",\"06/03/16-02\",\"06/03/16-03\",\"06/03/16-04\",\"06/03/16-05\",\"06/03/16-06\",\"06/03/16-07\",\"06/04/16-00\",\"06/04/16-01\",\"06/04/16-02\",\"06/04/16-03\",\"06/04/16-04\",\"06/04/16-05\",\"06/04/16-06\",\"06/04/16-07\",\"06/04/16-08\",\"06/04/16-09\",\"06/04/16-10\",\"06/04/16-11\",\"06/04/16-12\",\"06/04/16-13\",\"06/04/16-14\",\"06/04/16-15\",\"06/04/16-16\",\"06/04/16-17\",\"06/04/16-18\",\"06/04/16-19\",\"06/04/16-20\",\"06/04/16-21\",\"06/04/16-22\",\"06/04/16-23\",\"06/05/16-00\",\"06/05/16-01\",\"06/05/16-02\",\"06/05/16-03\",\"06/05/16-04\",\"06/05/16-05\",\"06/05/16-06\",\"06/05/16-07\",\"06/05/16-08\",\"06/05/16-09\",\"06/05/16-10\",\"06/05/16-11\",\"06/05/16-12\",\"06/05/16-13\",\"06/05/16-14\",\"06/05/16-15\",\"06/05/16-16\",\"06/05/16-17\",\"06/05/16-18\",\"06/05/16-19\",\"06/05/16-20\",\"06/05/16-21\",\"06/05/16-22\",\"06/05/16-23\",\"06/06/16-00\",\"06/06/16-01\",\"06/06/16-02\",\"06/06/16-03\",\"06/06/16-04\",\"06/06/16-05\",\"06/06/16-06\",\"06/06/16-07\",\"06/07/16-01\",\"06/07/16-02\",\"06/07/16-03\",\"06/07/16-06\",\"06/07/16-13\",\"06/08/16-02\",\"06/08/16-03\",\"06/08/16-04\",\"06/08/16-05\",\"06/08/16-06\",\"06/08/16-07\",\"06/08/16-08\",\"06/08/16-09\",\"06/08/16-10\",\"06/08/16-11\",\"06/08/16-12\",\"06/08/16-13\",\"06/08/16-14\",\"06/08/16-15\",\"06/08/16-16\",\"06/08/16-17\",\"06/08/16-18\",\"06/08/16-19\",\"06/08/16-20\",\"06/08/16-21\",\"06/08/16-22\",\"06/08/16-23\",\"06/09/16-00\",\"06/09/16-01\",\"06/09/16-02\",\"06/09/16-03\",\"06/09/16-04\",\"06/10/16-01\",\"06/10/16-02\",\"06/10/16-03\",\"06/10/16-04\",\"06/10/16-12\",\"06/10/16-13\",\"06/11/16-01\",\"06/11/16-02\",\"06/11/16-04\",\"06/11/16-05\",\"06/11/16-06\",\"06/11/16-07\",\"06/11/16-08\",\"06/11/16-09\",\"06/11/16-10\",\"06/11/16-11\",\"06/11/16-12\",\"06/11/16-13\",\"06/11/16-14\",\"06/11/16-15\",\"06/11/16-16\",\"06/11/16-17\",\"06/11/16-18\",\"06/11/16-19\",\"06/11/16-20\",\"06/11/16-21\",\"06/11/16-22\",\"06/11/16-23\",\"06/12/16-00\",\"06/12/16-01\",\"06/12/16-02\",\"06/12/16-03\",\"06/12/16-04\",\"06/12/16-05\",\"06/12/16-15\",\"06/12/16-16\",\"06/12/16-17\",\"06/12/16-18\",\"06/12/16-19\",\"06/12/16-20\",\"06/12/16-21\",\"06/12/16-22\",\"06/12/16-23\",\"06/13/16-00\",\"06/13/16-01\",\"06/13/16-02\",\"06/13/16-03\",\"06/13/16-04\",\"06/13/16-05\",\"06/13/16-06\",\"06/13/16-07\",\"06/13/16-08\",\"06/13/16-09\",\"06/13/16-10\",\"06/13/16-11\",\"06/13/16-12\",\"06/13/16-13\",\"06/13/16-14\",\"06/13/16-15\",\"06/13/16-16\",\"06/13/16-17\",\"06/13/16-18\",\"06/13/16-19\",\"06/13/16-20\",\"06/13/16-21\",\"06/13/16-22\",\"06/13/16-23\",\"06/14/16-00\",\"06/14/16-01\",\"06/14/16-02\",\"06/14/16-03\",\"06/14/16-04\",\"06/14/16-05\",\"06/14/16-06\",\"06/14/16-07\",\"06/14/16-08\",\"06/14/16-09\",\"06/14/16-10\",\"06/14/16-11\",\"06/14/16-12\",\"06/14/16-13\",\"06/14/16-14\",\"06/14/16-15\",\"06/14/16-16\",\"06/14/16-17\",\"06/14/16-18\",\"06/14/16-19\",\"06/14/16-20\",\"06/14/16-21\",\"06/14/16-22\",\"06/14/16-23\",\"06/15/16-00\",\"06/15/16-01\",\"06/15/16-02\",\"06/15/16-03\",\"06/15/16-04\",\"06/15/16-05\",\"06/15/16-06\",\"06/15/16-07\",\"06/15/16-08\",\"06/15/16-09\",\"06/15/16-10\",\"06/15/16-11\",\"06/15/16-12\",\"06/15/16-13\",\"06/15/16-14\",\"06/15/16-15\",\"06/15/16-16\",\"06/15/16-17\",\"06/15/16-18\",\"06/15/16-19\",\"06/15/16-20\",\"06/15/16-21\",\"06/15/16-22\",\"06/15/16-23\",\"06/16/16-00\",\"06/16/16-01\",\"06/16/16-02\",\"06/16/16-03\",\"06/16/16-04\",\"06/16/16-05\",\"06/16/16-06\",\"06/16/16-07\",\"06/16/16-08\",\"06/16/16-09\",\"06/16/16-10\",\"06/16/16-11\",\"06/16/16-12\",\"06/16/16-13\",\"06/16/16-14\",\"06/16/16-15\",\"06/16/16-16\",\"06/16/16-17\",\"06/16/16-18\",\"06/16/16-19\",\"06/16/16-20\",\"06/16/16-21\",\"06/16/16-22\",\"06/16/16-23\",\"06/17/16-00\",\"06/17/16-01\",\"06/17/16-02\",\"06/17/16-03\",\"06/17/16-04\",\"06/17/16-05\",\"06/17/16-06\",\"06/17/16-07\",\"06/17/16-08\",\"06/17/16-09\",\"06/17/16-10\",\"06/17/16-11\",\"06/17/16-12\",\"06/17/16-13\",\"06/17/16-14\",\"06/17/16-15\",\"06/17/16-16\",\"06/17/16-17\",\"06/17/16-18\",\"06/17/16-19\",\"06/17/16-20\",\"06/17/16-21\",\"06/17/16-22\",\"06/17/16-23\",\"06/18/16-00\",\"06/18/16-01\",\"06/18/16-02\",\"06/18/16-03\",\"06/18/16-04\",\"06/18/16-05\",\"06/18/16-06\",\"06/18/16-07\",\"06/18/16-08\",\"06/18/16-09\",\"06/18/16-10\",\"06/18/16-11\",\"06/18/16-12\",\"06/18/16-13\",\"06/18/16-14\",\"06/18/16-15\",\"06/18/16-16\",\"06/18/16-17\",\"06/18/16-18\",\"06/18/16-19\",\"06/18/16-20\",\"06/18/16-21\",\"06/18/16-22\",\"06/18/16-23\",\"06/19/16-00\",\"06/19/16-01\",\"06/19/16-02\",\"06/19/16-03\",\"06/19/16-04\",\"06/19/16-05\",\"06/19/16-06\",\"06/19/16-07\",\"06/19/16-08\",\"06/19/16-09\",\"06/19/16-10\",\"06/19/16-11\",\"06/19/16-12\",\"06/19/16-13\",\"06/19/16-14\",\"06/19/16-15\",\"06/19/16-16\",\"06/19/16-17\",\"06/19/16-18\",\"06/19/16-19\",\"06/19/16-20\",\"06/19/16-21\",\"06/19/16-22\",\"06/19/16-23\",\"06/20/16-00\",\"06/20/16-01\",\"06/20/16-02\",\"06/20/16-03\",\"06/20/16-04\",\"06/20/16-05\",\"06/20/16-06\",\"06/20/16-07\",\"06/20/16-08\",\"06/20/16-09\",\"06/20/16-10\",\"06/20/16-11\",\"06/20/16-12\",\"06/20/16-13\",\"06/20/16-14\",\"06/20/16-15\",\"06/20/16-16\",\"06/20/16-17\",\"06/20/16-18\",\"06/20/16-19\",\"06/20/16-20\",\"06/20/16-21\",\"06/20/16-22\",\"06/20/16-23\",\"06/21/16-00\",\"06/21/16-01\",\"06/21/16-02\",\"06/21/16-03\",\"06/21/16-04\",\"06/21/16-05\",\"06/21/16-06\",\"06/21/16-07\",\"06/21/16-08\",\"06/21/16-09\",\"06/21/16-10\",\"06/21/16-11\",\"06/21/16-12\",\"06/21/16-13\",\"06/21/16-14\",\"06/21/16-15\",\"06/21/16-16\",\"06/21/16-17\",\"06/21/16-18\",\"06/21/16-19\",\"06/21/16-20\",\"06/21/16-21\",\"06/21/16-22\",\"06/21/16-23\",\"06/22/16-00\",\"06/22/16-01\",\"06/22/16-02\",\"06/22/16-03\",\"06/22/16-04\",\"06/22/16-05\",\"06/22/16-06\",\"06/22/16-07\",\"06/22/16-08\",\"06/22/16-09\",\"06/22/16-10\",\"06/22/16-11\",\"06/22/16-12\",\"06/22/16-13\",\"06/22/16-14\",\"06/22/16-15\",\"06/22/16-16\",\"06/22/16-17\",\"06/22/16-18\",\"06/22/16-19\",\"06/22/16-20\",\"06/22/16-21\",\"06/22/16-22\",\"06/22/16-23\",\"06/23/16-00\",\"06/23/16-01\",\"06/23/16-02\",\"06/23/16-03\",\"06/23/16-04\",\"06/23/16-05\",\"06/23/16-06\",\"06/23/16-07\",\"06/23/16-08\",\"06/23/16-09\",\"06/23/16-10\",\"06/23/16-11\",\"06/23/16-12\",\"06/23/16-13\",\"06/23/16-14\",\"06/23/16-15\",\"06/23/16-16\",\"06/23/16-17\",\"06/23/16-18\",\"06/23/16-19\",\"06/23/16-20\",\"06/23/16-21\",\"06/23/16-22\",\"06/23/16-23\",\"06/24/16-00\",\"06/24/16-01\",\"06/24/16-02\",\"06/24/16-03\",\"06/24/16-04\",\"06/24/16-05\",\"06/24/16-06\",\"06/24/16-07\",\"06/24/16-08\",\"06/24/16-09\",\"06/24/16-10\",\"06/24/16-11\",\"06/24/16-12\",\"06/24/16-13\",\"06/24/16-14\",\"06/24/16-15\",\"06/24/16-16\",\"06/24/16-17\",\"06/24/16-18\",\"06/24/16-19\",\"06/24/16-20\",\"06/24/16-21\",\"06/24/16-22\",\"06/24/16-23\",\"06/25/16-00\",\"06/25/16-01\",\"06/25/16-02\",\"06/25/16-03\",\"06/25/16-04\",\"06/25/16-05\",\"06/25/16-06\",\"06/25/16-07\",\"06/25/16-08\",\"06/25/16-09\",\"06/25/16-10\",\"06/25/16-11\",\"06/25/16-12\",\"06/25/16-13\",\"06/25/16-14\",\"06/25/16-15\",\"06/25/16-16\",\"06/25/16-17\",\"06/28/16-02\",\"06/28/16-03\",\"06/28/16-04\",\"06/28/16-05\",\"06/28/16-06\",\"06/28/16-07\",\"06/28/16-08\",\"06/28/16-09\",\"06/28/16-10\",\"06/28/16-11\",\"06/28/16-12\",\"06/28/16-13\",\"06/28/16-14\",\"06/28/16-15\",\"06/28/16-16\",\"06/28/16-17\",\"06/28/16-18\",\"06/28/16-19\",\"06/28/16-20\",\"06/28/16-21\",\"06/28/16-22\",\"06/28/16-23\",\"06/29/16-00\",\"06/29/16-01\",\"06/29/16-02\",\"06/29/16-03\",\"06/29/16-04\",\"06/29/16-05\",\"06/29/16-06\",\"06/29/16-07\",\"06/29/16-08\",\"06/29/16-09\",\"06/29/16-10\",\"06/29/16-11\",\"06/29/16-12\",\"06/29/16-13\",\"06/29/16-14\",\"06/29/16-15\",\"06/29/16-16\",\"06/29/16-17\",\"06/29/16-18\",\"06/29/16-19\",\"06/29/16-20\",\"06/29/16-21\",\"06/29/16-22\",\"06/29/16-23\",\"06/30/16-00\",\"06/30/16-01\",\"06/30/16-02\",\"06/30/16-03\",\"06/30/16-04\",\"06/30/16-05\",\"06/30/16-06\",\"06/30/16-07\",\"06/30/16-08\",\"06/30/16-09\",\"06/30/16-10\",\"06/30/16-11\",\"06/30/16-12\",\"06/30/16-13\",\"06/30/16-14\",\"06/30/16-15\",\"06/30/16-16\",\"06/30/16-17\",\"06/30/16-18\",\"06/30/16-19\",\"06/30/16-20\",\"06/30/16-21\",\"06/30/16-22\",\"06/30/16-23\",\"07/01/16-00\",\"07/01/16-01\",\"07/01/16-02\",\"07/01/16-03\",\"07/01/16-04\",\"07/01/16-05\",\"07/01/16-06\",\"07/01/16-07\",\"07/01/16-08\",\"07/01/16-09\",\"07/01/16-10\",\"07/01/16-11\",\"07/01/16-12\",\"07/01/16-13\",\"07/01/16-14\",\"07/01/16-15\",\"07/01/16-16\",\"07/01/16-17\",\"07/01/16-18\",\"07/01/16-19\",\"07/01/16-20\",\"07/01/16-21\",\"07/02/16-02\",\"07/02/16-03\",\"07/02/16-05\",\"07/02/16-07\",\"07/02/16-08\",\"07/02/16-09\",\"07/02/16-10\",\"07/02/16-11\",\"07/02/16-12\",\"07/02/16-13\",\"07/02/16-14\",\"07/02/16-15\",\"07/02/16-16\",\"07/02/16-17\",\"07/02/16-18\",\"07/02/16-19\",\"07/02/16-20\",\"07/02/16-21\",\"07/02/16-22\",\"07/02/16-23\",\"07/03/16-00\",\"07/03/16-01\",\"07/03/16-02\",\"07/03/16-03\",\"07/03/16-04\",\"07/03/16-05\",\"07/03/16-06\",\"07/03/16-07\",\"07/03/16-08\",\"07/03/16-09\",\"07/03/16-10\",\"07/03/16-11\",\"07/03/16-12\",\"07/03/16-13\",\"07/03/16-14\",\"07/03/16-15\",\"07/03/16-16\",\"07/03/16-17\",\"07/03/16-18\",\"07/03/16-19\",\"07/03/16-20\",\"07/03/16-21\",\"07/03/16-22\",\"07/03/16-23\",\"07/04/16-00\",\"07/04/16-01\",\"07/04/16-02\",\"07/04/16-03\",\"07/04/16-04\",\"07/04/16-05\",\"07/04/16-06\",\"07/04/16-07\",\"07/04/16-08\",\"07/04/16-09\",\"07/04/16-10\",\"07/04/16-11\",\"07/04/16-12\",\"07/04/16-13\",\"07/04/16-14\",\"07/04/16-15\",\"07/04/16-16\",\"07/04/16-17\",\"07/04/16-18\",\"07/04/16-19\",\"07/04/16-20\",\"07/04/16-21\",\"07/04/16-22\",\"07/04/16-23\",\"07/05/16-00\",\"07/05/16-01\",\"07/05/16-02\",\"07/05/16-03\",\"07/05/16-04\",\"07/05/16-05\",\"07/05/16-06\",\"07/05/16-07\",\"07/05/16-08\",\"07/05/16-09\",\"07/05/16-10\",\"07/05/16-11\",\"07/05/16-12\",\"07/05/16-13\",\"07/05/16-14\",\"07/05/16-15\",\"07/05/16-16\",\"07/05/16-17\",\"07/05/16-18\",\"07/05/16-19\",\"07/05/16-20\",\"07/05/16-21\",\"07/05/16-22\",\"07/05/16-23\",\"07/06/16-00\",\"07/06/16-01\",\"07/06/16-01\",\"07/06/16-02\",\"07/06/16-03\",\"07/06/16-04\",\"07/06/16-05\",\"07/06/16-06\",\"07/06/16-07\",\"07/06/16-08\",\"07/06/16-09\",\"07/06/16-10\",\"07/06/16-11\",\"07/06/16-12\",\"07/06/16-13\",\"07/06/16-14\",\"07/06/16-15\",\"07/06/16-16\",\"07/06/16-17\",\"07/06/16-18\",\"07/06/16-19\",\"07/06/16-20\",\"07/06/16-21\",\"07/06/16-22\",\"07/06/16-23\",\"07/07/16-00\",\"07/07/16-01\",\"07/07/16-02\",\"07/07/16-03\",\"07/07/16-04\",\"07/07/16-05\",\"07/07/16-06\",\"07/07/16-07\",\"07/07/16-08\",\"07/07/16-09\",\"07/07/16-10\",\"07/07/16-11\",\"07/07/16-12\",\"07/07/16-13\",\"07/07/16-14\",\"07/07/16-15\",\"07/07/16-16\",\"07/07/16-17\",\"07/07/16-18\",\"07/07/16-19\",\"07/07/16-20\",\"07/07/16-21\",\"07/07/16-22\",\"07/07/16-23\",\"07/08/16-00\",\"07/08/16-01\",\"07/08/16-02\",\"07/08/16-03\",\"07/08/16-04\",\"07/08/16-05\",\"07/08/16-06\",\"07/08/16-07\",\"07/08/16-08\",\"07/08/16-09\",\"07/08/16-10\",\"07/08/16-11\",\"07/08/16-12\",\"07/08/16-13\",\"07/08/16-14\",\"07/08/16-15\",\"07/08/16-16\",\"07/08/16-17\",\"07/08/16-18\",\"07/08/16-19\",\"07/08/16-20\",\"07/08/16-21\",\"07/08/16-22\",\"07/08/16-23\",\"07/09/16-00\",\"07/09/16-01\",\"07/09/16-02\",\"07/09/16-03\",\"07/09/16-04\",\"07/09/16-05\",\"07/09/16-06\",\"07/09/16-07\",\"07/09/16-08\",\"07/09/16-09\",\"07/09/16-10\",\"07/09/16-11\",\"07/09/16-12\",\"07/09/16-13\",\"07/09/16-14\",\"07/09/16-15\",\"07/09/16-16\",\"07/09/16-17\",\"07/09/16-18\",\"07/09/16-19\",\"07/09/16-20\",\"07/09/16-21\",\"07/09/16-22\",\"07/09/16-23\",\"07/10/16-00\",\"07/10/16-01\",\"07/10/16-02\",\"07/10/16-03\",\"07/10/16-04\",\"07/10/16-05\",\"07/10/16-06\",\"07/10/16-07\",\"07/10/16-08\",\"07/10/16-09\",\"07/10/16-10\",\"07/10/16-11\",\"07/10/16-12\",\"07/10/16-13\",\"07/10/16-14\",\"07/10/16-15\",\"07/10/16-16\",\"07/10/16-17\",\"07/10/16-18\",\"07/10/16-19\",\"07/10/16-20\",\"07/10/16-21\",\"07/10/16-22\",\"07/10/16-23\",\"07/11/16-00\",\"07/11/16-01\",\"07/11/16-02\",\"07/11/16-03\",\"07/11/16-04\",\"07/11/16-05\",\"07/11/16-06\",\"07/11/16-07\",\"07/11/16-08\",\"07/11/16-09\",\"07/11/16-10\",\"07/11/16-11\",\"07/11/16-12\",\"07/11/16-13\",\"07/11/16-14\",\"07/11/16-15\",\"07/11/16-16\",\"07/11/16-17\",\"07/11/16-18\",\"07/11/16-19\",\"07/11/16-20\",\"07/11/16-21\",\"07/11/16-22\",\"07/11/16-23\",\"07/12/16-00\",\"07/12/16-01\",\"07/12/16-02\",\"07/12/16-03\",\"07/12/16-04\",\"07/12/16-05\",\"07/12/16-06\",\"07/12/16-07\",\"07/12/16-08\",\"07/12/16-09\",\"07/12/16-10\",\"07/12/16-11\",\"07/12/16-12\",\"07/12/16-13\",\"07/12/16-14\",\"07/12/16-15\",\"07/12/16-16\",\"07/12/16-17\",\"07/12/16-18\",\"07/12/16-19\",\"07/12/16-20\",\"07/12/16-21\",\"07/12/16-22\",\"07/12/16-23\",\"07/13/16-00\",\"07/13/16-01\",\"07/13/16-02\",\"07/13/16-03\",\"07/13/16-04\",\"07/13/16-05\",\"07/13/16-06\",\"07/13/16-07\",\"07/13/16-08\",\"07/13/16-09\",\"07/13/16-10\",\"07/13/16-11\",\"07/13/16-12\",\"07/13/16-13\",\"07/13/16-14\",\"07/13/16-15\",\"07/13/16-16\",\"07/13/16-17\",\"07/13/16-18\",\"07/13/16-19\",\"07/13/16-20\",\"07/13/16-21\",\"07/13/16-22\",\"07/13/16-23\",\"07/14/16-00\",\"07/14/16-01\",\"07/14/16-02\",\"07/14/16-03\",\"07/14/16-04\",\"07/14/16-05\",\"07/14/16-06\",\"07/14/16-07\",\"07/14/16-08\",\"07/14/16-09\",\"07/14/16-10\",\"07/14/16-11\",\"07/14/16-12\",\"07/14/16-13\",\"07/14/16-14\",\"07/14/16-15\",\"07/14/16-16\",\"07/14/16-17\",\"07/14/16-18\",\"07/14/16-19\",\"07/14/16-20\",\"07/14/16-21\",\"07/14/16-22\",\"07/14/16-23\",\"07/15/16-00\",\"07/15/16-01\",\"07/15/16-02\",\"07/15/16-03\",\"07/15/16-04\",\"07/15/16-05\",\"07/15/16-06\",\"07/15/16-07\",\"07/15/16-08\",\"07/15/16-09\",\"07/15/16-10\",\"07/15/16-11\",\"07/15/16-12\",\"07/15/16-13\",\"07/15/16-14\",\"07/15/16-15\",\"07/15/16-16\",\"07/15/16-17\",\"07/15/16-18\",\"07/15/16-19\",\"07/15/16-20\",\"07/15/16-21\",\"07/15/16-22\",\"07/15/16-23\",\"07/16/16-00\",\"07/16/16-01\",\"07/16/16-02\",\"07/16/16-03\",\"07/16/16-04\",\"07/16/16-05\",\"07/16/16-06\",\"07/16/16-07\",\"07/16/16-08\",\"07/16/16-09\",\"07/16/16-10\",\"07/16/16-11\",\"07/16/16-12\",\"07/16/16-13\",\"07/16/16-14\",\"07/16/16-15\",\"07/16/16-16\",\"07/16/16-17\",\"07/16/16-18\",\"07/16/16-19\",\"07/16/16-20\",\"07/16/16-21\",\"07/16/16-22\",\"07/16/16-23\",\"07/17/16-00\",\"07/17/16-01\",\"07/17/16-02\",\"07/17/16-03\",\"07/17/16-04\",\"07/17/16-05\",\"07/17/16-06\",\"07/17/16-07\",\"07/17/16-08\",\"07/17/16-09\",\"07/17/16-10\",\"07/17/16-11\",\"07/17/16-12\",\"07/17/16-13\",\"07/17/16-14\",\"07/17/16-15\",\"07/17/16-16\",\"07/17/16-17\",\"07/17/16-18\",\"07/17/16-19\",\"07/17/16-20\",\"07/17/16-21\",\"07/17/16-22\",\"07/17/16-23\",\"07/18/16-00\",\"07/18/16-01\",\"07/18/16-02\",\"07/18/16-03\",\"07/18/16-04\",\"07/18/16-05\",\"07/18/16-06\",\"07/18/16-07\",\"07/18/16-08\",\"07/18/16-09\",\"07/18/16-10\",\"07/18/16-11\",\"07/18/16-12\",\"07/18/16-13\",\"07/18/16-14\",\"07/18/16-15\",\"07/18/16-16\",\"07/18/16-17\",\"07/18/16-18\",\"07/18/16-19\",\"07/18/16-20\",\"07/18/16-21\",\"07/18/16-22\",\"07/18/16-23\",\"07/19/16-00\",\"07/19/16-01\",\"07/19/16-02\",\"07/19/16-03\",\"07/19/16-04\",\"07/19/16-05\",\"07/19/16-06\",\"07/19/16-07\",\"07/19/16-08\",\"07/19/16-09\",\"07/19/16-10\",\"07/19/16-11\",\"07/19/16-12\",\"07/19/16-13\",\"07/19/16-14\",\"07/19/16-15\",\"07/19/16-16\",\"07/19/16-17\",\"07/19/16-18\",\"07/19/16-19\",\"07/19/16-20\",\"07/19/16-21\",\"07/19/16-22\",\"07/19/16-23\",\"07/20/16-00\",\"07/20/16-01\",\"07/20/16-02\",\"07/20/16-03\",\"07/20/16-04\",\"07/20/16-05\",\"07/20/16-06\",\"07/20/16-07\",\"07/20/16-08\",\"07/20/16-09\",\"07/20/16-10\",\"07/20/16-11\",\"07/20/16-12\",\"07/20/16-13\",\"07/20/16-14\",\"07/20/16-15\",\"07/20/16-16\",\"07/20/16-17\",\"07/20/16-18\",\"07/20/16-19\",\"07/20/16-20\",\"07/20/16-21\",\"07/20/16-22\",\"07/20/16-23\",\"07/21/16-00\",\"07/21/16-01\",\"07/21/16-02\",\"07/21/16-03\",\"07/21/16-04\",\"07/21/16-05\",\"07/21/16-06\",\"07/21/16-07\",\"07/21/16-08\",\"07/21/16-09\",\"07/21/16-10\",\"07/21/16-11\",\"07/21/16-12\",\"07/21/16-13\",\"07/21/16-14\",\"07/21/16-15\",\"07/21/16-16\",\"07/21/16-17\",\"07/21/16-18\",\"07/21/16-19\",\"07/21/16-20\",\"07/21/16-21\",\"07/21/16-22\",\"07/21/16-23\",\"07/22/16-00\",\"07/22/16-01\",\"07/22/16-02\",\"07/22/16-03\",\"07/22/16-04\",\"07/22/16-05\",\"07/22/16-06\",\"07/22/16-07\",\"07/22/16-08\",\"07/22/16-09\",\"07/22/16-10\",\"07/22/16-11\",\"07/22/16-12\",\"07/22/16-13\",\"07/22/16-14\",\"07/22/16-15\",\"07/22/16-16\",\"07/22/16-17\",\"07/22/16-18\",\"07/22/16-19\",\"07/22/16-20\",\"07/22/16-21\",\"07/22/16-22\",\"07/22/16-23\",\"07/23/16-00\",\"07/23/16-01\",\"07/23/16-02\",\"07/23/16-03\",\"07/23/16-04\",\"07/23/16-05\",\"07/23/16-06\",\"07/23/16-07\",\"07/23/16-08\",\"07/23/16-09\",\"07/23/16-10\",\"07/23/16-11\",\"07/23/16-12\",\"07/23/16-13\",\"07/23/16-14\",\"07/23/16-15\",\"07/23/16-16\",\"07/23/16-17\",\"07/23/16-18\",\"07/23/16-19\",\"07/23/16-20\",\"07/23/16-21\",\"07/23/16-22\",\"07/23/16-23\",\"07/24/16-00\",\"07/24/16-01\",\"07/24/16-02\",\"07/24/16-03\",\"07/24/16-04\",\"07/24/16-05\",\"07/24/16-06\",\"07/24/16-07\",\"07/24/16-08\",\"07/24/16-09\",\"07/24/16-10\",\"07/24/16-11\",\"07/24/16-12\",\"07/24/16-13\",\"07/24/16-14\",\"07/24/16-15\",\"07/24/16-16\",\"07/24/16-17\",\"07/24/16-18\",\"07/24/16-19\",\"07/24/16-20\",\"07/24/16-21\",\"07/24/16-22\",\"07/24/16-23\",\"07/25/16-00\",\"07/25/16-01\",\"07/25/16-02\",\"07/25/16-03\",\"07/25/16-04\",\"07/25/16-05\",\"07/25/16-06\",\"07/25/16-07\",\"07/25/16-08\",\"07/25/16-09\",\"07/25/16-10\",\"07/25/16-11\",\"07/25/16-12\",\"07/25/16-13\",\"07/25/16-14\",\"07/25/16-15\",\"07/25/16-16\",\"07/25/16-17\",\"07/25/16-18\",\"07/25/16-19\",\"07/25/16-20\",\"07/25/16-21\",\"07/25/16-22\",\"07/25/16-23\",\"07/26/16-00\",\"07/26/16-01\",\"07/26/16-02\",\"07/26/16-03\",\"07/26/16-04\",\"07/26/16-05\",\"07/26/16-06\",\"07/26/16-07\",\"07/26/16-08\",\"07/26/16-09\",\"07/26/16-10\",\"07/26/16-11\",\"07/26/16-12\",\"07/26/16-13\",\"07/26/16-14\",\"07/26/16-15\",\"07/26/16-16\",\"07/26/16-17\",\"07/26/16-18\",\"07/26/16-19\",\"07/26/16-20\",\"07/26/16-21\",\"07/26/16-22\",\"07/26/16-23\",\"07/27/16-00\",\"07/27/16-01\",\"07/27/16-02\",\"07/27/16-03\",\"07/27/16-04\",\"07/27/16-05\",\"07/27/16-06\",\"07/27/16-07\",\"07/27/16-08\",\"07/27/16-09\",\"07/27/16-10\",\"07/27/16-11\",\"07/27/16-12\",\"07/27/16-13\",\"07/27/16-14\",\"07/27/16-15\",\"07/27/16-16\",\"07/27/16-17\",\"07/27/16-18\",\"07/27/16-19\",\"07/27/16-20\",\"07/27/16-21\",\"07/27/16-22\",\"07/27/16-23\",\"07/28/16-00\",\"07/28/16-01\",\"07/28/16-02\",\"07/28/16-03\",\"07/28/16-04\",\"07/28/16-05\",\"07/28/16-06\",\"07/28/16-07\",\"07/28/16-08\",\"07/28/16-09\",\"07/28/16-10\",\"07/28/16-11\",\"07/28/16-12\",\"07/28/16-13\",\"07/28/16-14\",\"07/28/16-15\",\"07/28/16-16\",\"07/28/16-17\",\"07/28/16-18\",\"07/28/16-19\",\"07/28/16-20\",\"07/28/16-21\",\"07/28/16-22\",\"07/28/16-23\",\"07/29/16-00\",\"07/29/16-01\",\"07/29/16-02\",\"07/29/16-03\",\"07/29/16-04\",\"07/29/16-05\",\"07/29/16-06\",\"07/29/16-07\",\"07/29/16-08\",\"07/29/16-09\",\"07/29/16-10\",\"07/29/16-11\",\"07/29/16-12\",\"07/29/16-13\",\"07/29/16-14\",\"07/29/16-15\",\"07/29/16-16\",\"07/29/16-17\",\"07/29/16-18\",\"07/29/16-19\",\"07/29/16-20\",\"07/29/16-21\",\"07/29/16-22\",\"07/29/16-23\",\"07/30/16-00\",\"07/30/16-01\",\"07/30/16-02\",\"07/30/16-03\",\"07/30/16-04\",\"07/30/16-05\",\"07/30/16-06\",\"07/30/16-07\",\"07/30/16-08\",\"07/30/16-09\",\"07/30/16-10\",\"07/30/16-11\",\"07/30/16-12\",\"07/30/16-13\",\"07/30/16-14\",\"07/30/16-15\",\"07/30/16-16\",\"07/30/16-17\",\"07/30/16-18\",\"07/30/16-19\",\"07/30/16-20\",\"07/30/16-21\",\"07/30/16-22\",\"07/30/16-23\",\"07/31/16-00\",\"07/31/16-01\",\"07/31/16-02\",\"07/31/16-03\",\"07/31/16-04\",\"07/31/16-05\",\"07/31/16-06\",\"07/31/16-07\",\"07/31/16-08\",\"07/31/16-09\",\"07/31/16-10\",\"07/31/16-11\",\"07/31/16-12\",\"07/31/16-13\",\"07/31/16-14\",\"07/31/16-15\",\"07/31/16-16\",\"07/31/16-17\",\"07/31/16-18\",\"07/31/16-19\",\"07/31/16-20\",\"07/31/16-21\",\"07/31/16-22\",\"07/31/16-23\",\"08/01/16-00\",\"08/01/16-01\",\"08/01/16-02\",\"08/01/16-03\",\"08/01/16-04\",\"08/01/16-05\",\"08/01/16-06\",\"08/01/16-07\",\"08/01/16-08\",\"08/01/16-09\",\"08/01/16-10\",\"08/01/16-11\",\"08/01/16-12\",\"08/01/16-13\",\"08/01/16-14\",\"08/01/16-15\",\"08/01/16-16\",\"08/01/16-17\",\"08/01/16-18\",\"08/01/16-19\",\"08/01/16-20\",\"08/01/16-21\",\"08/01/16-22\",\"08/01/16-23\",\"08/02/16-00\",\"08/02/16-01\",\"08/02/16-02\",\"08/02/16-03\",\"08/02/16-04\",\"08/02/16-05\",\"08/02/16-06\",\"08/02/16-07\",\"08/02/16-08\",\"08/02/16-09\",\"08/02/16-10\",\"08/02/16-11\",\"08/02/16-12\",\"08/02/16-13\",\"08/02/16-14\",\"08/02/16-15\",\"08/02/16-16\",\"08/02/16-17\",\"08/02/16-18\",\"08/02/16-19\",\"08/02/16-20\",\"08/02/16-21\",\"08/02/16-22\",\"08/02/16-23\",\"08/03/16-00\",\"08/03/16-01\",\"08/03/16-02\",\"08/03/16-03\",\"08/03/16-04\",\"08/03/16-05\",\"08/03/16-06\",\"08/03/16-07\",\"08/03/16-08\",\"08/03/16-09\",\"08/03/16-10\",\"08/03/16-11\",\"08/03/16-12\",\"08/03/16-13\",\"08/03/16-14\",\"08/03/16-15\",\"08/03/16-16\",\"08/03/16-17\",\"08/03/16-18\",\"08/03/16-19\",\"08/03/16-20\",\"08/03/16-21\",\"08/03/16-22\",\"08/03/16-23\",\"08/04/16-00\",\"08/04/16-01\",\"08/04/16-02\",\"08/04/16-03\",\"08/04/16-04\",\"08/04/16-05\",\"08/04/16-06\",\"08/04/16-07\",\"08/04/16-08\",\"08/04/16-09\",\"08/04/16-10\",\"08/04/16-11\",\"08/04/16-12\",\"08/04/16-13\",\"08/04/16-14\",\"08/04/16-15\",\"08/04/16-16\",\"08/04/16-17\",\"08/04/16-18\",\"08/04/16-19\",\"08/04/16-20\",\"08/04/16-21\",\"08/04/16-22\",\"08/04/16-23\",\"08/05/16-00\",\"08/05/16-01\",\"08/05/16-02\",\"08/05/16-03\",\"08/05/16-04\",\"08/05/16-05\",\"08/05/16-06\",\"08/05/16-07\",\"08/05/16-08\",\"08/05/16-09\",\"08/05/16-10\",\"08/05/16-11\",\"08/05/16-12\",\"08/05/16-13\",\"08/05/16-14\",\"08/11/16-00\",\"08/11/16-00\",\"08/11/16-00\",\"08/11/16-00\",\"08/11/16-01\",\"08/11/16-02\",\"08/11/16-03\",\"08/11/16-04\",\"08/11/16-05\",\"08/11/16-06\",\"08/11/16-07\",\"08/11/16-08\",\"08/11/16-09\",\"08/11/16-10\",\"08/11/16-11\",\"08/11/16-12\",\"08/11/16-13\",\"08/11/16-14\",\"08/11/16-15\",\"08/11/16-16\",\"08/11/16-17\",\"08/11/16-18\",\"08/11/16-19\",\"08/11/16-20\",\"08/11/16-21\",\"08/11/16-22\",\"08/11/16-23\",\"08/12/16-00\",\"08/12/16-01\",\"08/12/16-02\",\"08/12/16-03\",\"08/12/16-04\",\"08/12/16-05\",\"08/12/16-06\",\"08/12/16-07\",\"08/12/16-08\",\"08/12/16-09\",\"08/12/16-10\",\"08/12/16-11\",\"08/12/16-12\",\"08/12/16-13\",\"08/12/16-14\",\"08/12/16-15\",\"08/12/16-16\",\"08/12/16-17\",\"08/12/16-18\",\"08/12/16-19\",\"08/12/16-20\",\"08/12/16-21\",\"08/12/16-22\",\"08/12/16-23\",\"08/13/16-00\",\"08/13/16-01\",\"08/13/16-02\",\"08/13/16-03\",\"08/13/16-04\",\"08/13/16-05\",\"08/13/16-06\",\"08/13/16-07\",\"08/13/16-08\",\"08/13/16-09\",\"08/13/16-10\",\"08/13/16-11\",\"08/13/16-12\",\"08/13/16-13\",\"08/13/16-14\",\"08/13/16-15\",\"08/13/16-16\",\"08/13/16-17\",\"08/13/16-18\",\"08/13/16-19\",\"08/13/16-20\",\"08/13/16-21\",\"08/13/16-22\",\"08/13/16-23\",\"08/14/16-00\",\"08/14/16-01\",\"08/14/16-02\",\"08/14/16-03\",\"08/14/16-04\",\"08/14/16-05\",\"08/14/16-06\",\"08/14/16-07\",\"08/14/16-08\",\"08/14/16-09\",\"08/14/16-10\",\"08/14/16-11\",\"08/14/16-12\",\"08/14/16-13\",\"08/14/16-14\",\"08/14/16-15\",\"08/14/16-16\",\"08/14/16-17\",\"08/14/16-18\",\"08/14/16-19\",\"08/14/16-20\",\"08/14/16-21\",\"08/14/16-22\",\"08/14/16-23\",\"08/15/16-00\",\"08/15/16-01\",\"08/15/16-02\",\"08/15/16-03\",\"08/15/16-04\",\"08/15/16-05\",\"08/15/16-06\",\"08/15/16-07\",\"08/15/16-08\",\"08/15/16-09\",\"08/15/16-10\",\"08/15/16-11\",\"08/15/16-12\",\"08/15/16-13\",\"08/15/16-14\",\"08/15/16-15\",\"08/15/16-16\",\"08/15/16-17\",\"08/15/16-18\",\"08/15/16-19\",\"08/15/16-20\",\"08/15/16-21\",\"08/15/16-22\",\"08/15/16-23\",\"08/16/16-00\",\"08/16/16-01\",\"08/16/16-02\",\"08/16/16-03\",\"08/16/16-04\",\"08/16/16-05\",\"08/16/16-06\",\"08/16/16-07\",\"08/16/16-08\",\"08/16/16-09\",\"08/16/16-10\",\"08/16/16-11\",\"08/16/16-12\",\"08/16/16-13\",\"08/16/16-14\",\"08/16/16-15\",\"08/16/16-16\",\"08/16/16-17\",\"08/16/16-18\",\"08/16/16-19\",\"08/16/16-20\",\"08/16/16-21\",\"08/16/16-22\",\"08/16/16-23\",\"08/17/16-00\",\"08/17/16-01\",\"08/17/16-02\",\"08/17/16-03\",\"08/17/16-04\",\"08/17/16-05\",\"08/17/16-06\",\"08/17/16-07\",\"08/17/16-08\",\"08/17/16-09\",\"08/17/16-10\",\"08/17/16-11\",\"08/17/16-12\",\"08/17/16-13\",\"08/17/16-14\",\"08/17/16-15\",\"08/17/16-16\",\"08/17/16-17\",\"08/17/16-18\",\"08/17/16-19\",\"08/17/16-20\",\"08/17/16-21\",\"08/17/16-22\",\"08/17/16-23\",\"08/18/16-00\",\"08/18/16-01\",\"08/18/16-02\",\"08/18/16-03\",\"08/18/16-04\",\"08/18/16-05\",\"08/18/16-06\",\"08/18/16-07\",\"08/18/16-08\",\"08/18/16-09\",\"08/18/16-10\",\"08/18/16-11\",\"08/18/16-12\",\"08/18/16-13\",\"08/18/16-14\",\"08/18/16-15\",\"08/18/16-16\",\"08/18/16-17\",\"08/18/16-18\",\"08/18/16-19\",\"08/18/16-20\",\"08/18/16-21\",\"08/18/16-22\",\"08/18/16-23\",\"08/19/16-00\",\"08/19/16-01\",\"08/19/16-02\",\"08/19/16-03\",\"08/19/16-04\",\"08/19/16-05\",\"08/19/16-06\",\"08/19/16-07\",\"08/19/16-08\",\"08/19/16-09\",\"08/19/16-10\",\"08/19/16-11\",\"08/19/16-12\",\"08/19/16-13\",\"08/19/16-14\",\"08/19/16-15\",\"08/19/16-16\",\"08/19/16-17\",\"08/19/16-18\",\"08/19/16-19\",\"08/19/16-20\",\"08/19/16-21\",\"08/19/16-22\",\"08/19/16-23\",\"08/20/16-00\",\"08/20/16-01\",\"08/20/16-02\",\"08/20/16-03\",\"08/20/16-04\",\"08/20/16-05\",\"08/20/16-06\",\"08/20/16-07\",\"08/20/16-08\",\"08/20/16-09\",\"08/20/16-10\",\"08/20/16-11\",\"08/20/16-12\",\"08/20/16-13\",\"08/20/16-14\",\"08/20/16-15\",\"08/20/16-16\",\"08/20/16-17\",\"08/20/16-18\",\"08/20/16-19\",\"08/20/16-20\",\"08/20/16-21\",\"08/20/16-22\",\"08/20/16-23\",\"08/21/16-00\",\"08/21/16-01\",\"08/21/16-02\",\"08/21/16-03\",\"08/21/16-04\",\"08/21/16-05\",\"08/21/16-06\",\"08/21/16-07\",\"08/21/16-08\",\"08/21/16-09\",\"08/21/16-10\",\"08/21/16-11\",\"08/21/16-12\",\"08/21/16-13\",\"08/21/16-14\",\"08/21/16-15\",\"08/21/16-16\",\"08/21/16-17\",\"08/21/16-18\",\"08/21/16-19\",\"08/21/16-20\",\"08/21/16-21\",\"08/21/16-22\",\"08/21/16-23\",\"08/22/16-00\",\"08/22/16-01\",\"08/22/16-02\",\"08/22/16-03\",\"08/22/16-04\",\"08/22/16-05\",\"08/22/16-06\",\"08/22/16-07\",\"08/22/16-08\",\"08/22/16-09\",\"08/22/16-10\",\"08/22/16-11\",\"08/22/16-12\",\"08/22/16-13\",\"08/22/16-14\",\"08/22/16-15\",\"08/22/16-16\",\"08/22/16-17\",\"08/22/16-18\",\"08/22/16-19\",\"08/22/16-20\",\"08/22/16-21\",\"08/22/16-22\",\"08/22/16-23\",\"08/23/16-00\",\"08/23/16-01\",\"08/23/16-02\",\"08/23/16-03\",\"08/23/16-04\",\"08/23/16-05\",\"08/23/16-06\",\"08/23/16-07\",\"08/23/16-08\",\"08/23/16-17\",\"08/23/16-18\",\"08/23/16-19\",\"08/23/16-20\",\"08/23/16-21\",\"08/23/16-22\",\"08/23/16-23\",\"08/24/16-00\",\"08/24/16-01\",\"08/24/16-02\",\"08/24/16-03\",\"08/24/16-04\",\"08/24/16-05\",\"08/24/16-06\",\"08/24/16-07\",\"08/24/16-08\",\"08/24/16-09\",\"08/24/16-10\",\"08/24/16-11\",\"08/24/16-12\",\"08/24/16-13\",\"08/24/16-14\",\"08/24/16-15\",\"08/24/16-16\",\"08/24/16-17\",\"08/24/16-18\",\"08/24/16-19\",\"08/24/16-20\",\"08/24/16-21\",\"08/24/16-22\",\"08/24/16-23\",\"08/25/16-00\",\"08/25/16-01\",\"08/25/16-02\",\"08/25/16-03\",\"08/25/16-04\",\"08/25/16-05\",\"08/25/16-06\",\"08/25/16-07\",\"08/25/16-08\",\"08/25/16-09\",\"08/25/16-10\",\"08/25/16-11\",\"08/25/16-12\",\"08/25/16-13\",\"08/25/16-14\",\"08/25/16-15\",\"08/25/16-16\",\"08/25/16-17\",\"08/25/16-18\",\"08/25/16-19\",\"08/25/16-20\",\"08/25/16-21\",\"08/25/16-22\",\"08/25/16-23\",\"08/26/16-00\",\"08/26/16-01\",\"08/26/16-02\",\"08/26/16-03\",\"08/26/16-04\",\"08/26/16-05\",\"08/26/16-06\",\"08/26/16-07\",\"08/26/16-08\",\"08/26/16-09\",\"08/26/16-10\",\"08/26/16-11\",\"08/26/16-12\",\"08/26/16-13\",\"08/26/16-14\",\"08/26/16-15\",\"08/26/16-16\",\"08/26/16-17\",\"08/26/16-18\",\"08/26/16-19\",\"08/26/16-20\",\"08/26/16-21\",\"08/26/16-22\",\"08/26/16-23\",\"08/27/16-00\",\"08/27/16-01\",\"08/27/16-02\",\"08/27/16-03\",\"08/27/16-04\",\"08/27/16-05\",\"08/27/16-06\",\"08/27/16-07\",\"08/27/16-08\",\"08/27/16-09\",\"08/27/16-10\",\"08/27/16-11\",\"08/27/16-12\",\"08/27/16-13\",\"08/27/16-14\",\"08/27/16-15\",\"08/27/16-16\",\"08/27/16-17\",\"08/27/16-18\",\"08/27/16-19\",\"08/27/16-20\",\"08/27/16-21\",\"08/27/16-22\",\"08/27/16-23\",\"08/28/16-00\",\"08/28/16-01\",\"08/28/16-02\",\"08/28/16-03\",\"08/28/16-04\",\"08/28/16-05\",\"08/28/16-06\",\"08/28/16-07\",\"08/28/16-08\",\"08/28/16-09\",\"08/28/16-10\",\"08/28/16-11\",\"08/28/16-12\",\"08/28/16-13\",\"08/28/16-14\",\"08/28/16-15\",\"08/28/16-16\",\"08/28/16-17\",\"08/28/16-18\",\"08/28/16-19\",\"08/28/16-20\",\"08/28/16-21\",\"08/28/16-22\",\"08/28/16-23\",\"08/29/16-00\",\"08/29/16-01\",\"08/29/16-02\",\"08/29/16-03\",\"08/29/16-04\",\"08/29/16-05\",\"08/29/16-06\",\"08/29/16-07\",\"08/29/16-08\",\"08/29/16-09\",\"08/29/16-10\",\"08/29/16-11\",\"08/29/16-12\",\"08/29/16-13\",\"08/29/16-14\",\"08/29/16-15\",\"08/29/16-16\",\"08/29/16-17\",\"08/29/16-18\",\"08/29/16-19\",\"08/29/16-20\",\"08/29/16-21\",\"08/29/16-22\",\"08/29/16-23\",\"08/30/16-00\",\"08/30/16-01\",\"08/30/16-02\",\"08/30/16-03\",\"08/30/16-04\",\"08/30/16-05\",\"08/30/16-06\",\"08/30/16-07\",\"08/30/16-08\",\"08/30/16-09\",\"08/30/16-10\",\"08/30/16-11\",\"08/30/16-12\",\"08/30/16-13\",\"08/30/16-14\",\"08/30/16-15\",\"08/30/16-16\",\"08/30/16-17\",\"08/30/16-18\",\"08/30/16-19\",\"08/30/16-20\",\"08/30/16-21\",\"08/30/16-22\",\"08/30/16-23\",\"08/31/16-00\",\"08/31/16-01\",\"08/31/16-02\",\"08/31/16-03\",\"08/31/16-04\",\"08/31/16-05\",\"08/31/16-06\",\"08/31/16-07\",\"08/31/16-08\",\"08/31/16-09\",\"08/31/16-10\",\"08/31/16-11\",\"08/31/16-12\",\"08/31/16-13\",\"08/31/16-14\",\"08/31/16-15\",\"08/31/16-16\",\"08/31/16-17\",\"08/31/16-18\",\"08/31/16-19\",\"08/31/16-20\",\"08/31/16-21\",\"08/31/16-22\",\"08/31/16-23\",\"09/01/16-00\",\"09/01/16-01\",\"09/01/16-02\",\"09/01/16-03\",\"09/01/16-04\",\"09/01/16-05\",\"09/01/16-06\",\"09/01/16-07\",\"09/01/16-08\",\"09/01/16-09\",\"09/01/16-10\",\"09/01/16-11\",\"09/01/16-12\",\"09/01/16-13\",\"09/01/16-14\",\"09/01/16-15\",\"09/01/16-16\",\"09/01/16-17\",\"09/01/16-18\",\"09/01/16-19\",\"09/01/16-20\",\"09/01/16-21\",\"09/01/16-22\",\"09/01/16-23\",\"09/02/16-00\",\"09/02/16-01\",\"09/02/16-02\",\"09/02/16-03\",\"09/02/16-04\",\"09/02/16-05\",\"09/02/16-06\",\"09/02/16-07\",\"09/02/16-08\",\"09/02/16-09\",\"09/02/16-10\",\"09/02/16-11\",\"09/02/16-12\",\"09/02/16-13\",\"09/02/16-14\",\"09/02/16-15\",\"09/02/16-16\",\"09/02/16-17\",\"09/02/16-18\",\"09/02/16-19\",\"09/02/16-20\",\"09/02/16-21\",\"09/02/16-22\",\"09/02/16-23\",\"09/03/16-00\",\"09/03/16-01\",\"09/03/16-02\",\"09/03/16-03\",\"09/03/16-04\",\"09/03/16-05\",\"09/03/16-06\",\"09/03/16-07\",\"09/03/16-08\",\"09/03/16-09\",\"09/03/16-10\",\"09/03/16-11\",\"09/03/16-12\",\"09/03/16-13\",\"09/03/16-14\",\"09/03/16-15\",\"09/03/16-16\",\"09/03/16-17\",\"09/03/16-18\",\"09/03/16-19\",\"09/03/16-20\",\"09/03/16-21\",\"09/03/16-22\",\"09/03/16-23\",\"09/04/16-00\",\"09/04/16-01\",\"09/04/16-02\",\"09/04/16-03\",\"09/04/16-04\",\"09/04/16-05\",\"09/04/16-06\",\"09/04/16-07\",\"09/04/16-08\",\"09/04/16-09\",\"09/04/16-10\",\"09/04/16-11\",\"09/04/16-12\",\"09/04/16-13\",\"09/04/16-14\",\"09/04/16-15\",\"09/04/16-16\",\"09/04/16-17\",\"09/04/16-18\",\"09/04/16-19\",\"09/04/16-20\",\"09/04/16-21\",\"09/04/16-22\",\"09/04/16-23\",\"09/05/16-00\",\"09/05/16-01\",\"09/05/16-02\",\"09/05/16-03\",\"09/05/16-04\",\"09/05/16-05\",\"09/05/16-06\",\"09/05/16-07\",\"09/05/16-08\",\"09/05/16-09\",\"09/05/16-10\",\"09/05/16-11\",\"09/05/16-12\",\"09/05/16-13\",\"09/05/16-14\",\"09/05/16-15\",\"09/05/16-16\",\"09/05/16-17\",\"09/05/16-18\",\"09/05/16-19\",\"09/05/16-20\",\"09/05/16-21\",\"09/05/16-22\",\"09/05/16-23\",\"09/06/16-00\",\"09/06/16-01\",\"09/06/16-02\",\"09/06/16-03\",\"09/06/16-04\",\"09/06/16-05\",\"09/06/16-06\",\"09/06/16-07\",\"09/06/16-08\",\"09/06/16-09\",\"09/06/16-10\",\"09/06/16-11\",\"09/06/16-12\",\"09/06/16-13\",\"09/06/16-14\",\"09/06/16-15\",\"09/06/16-16\",\"09/06/16-17\",\"09/06/16-18\",\"09/06/16-19\",\"09/06/16-20\",\"09/06/16-21\",\"09/06/16-22\",\"09/06/16-23\",\"09/07/16-00\",\"09/07/16-01\",\"09/07/16-02\",\"09/07/16-03\",\"09/07/16-04\",\"09/07/16-05\",\"09/07/16-06\",\"09/07/16-07\",\"09/07/16-08\",\"09/07/16-09\",\"09/07/16-10\",\"09/07/16-11\",\"09/07/16-12\",\"09/07/16-13\",\"09/07/16-14\",\"09/07/16-15\",\"09/07/16-16\",\"09/07/16-17\",\"09/07/16-18\",\"09/07/16-19\",\"09/07/16-20\",\"09/07/16-21\",\"09/07/16-22\",\"09/07/16-23\",\"09/08/16-00\",\"09/08/16-01\",\"09/08/16-02\",\"09/08/16-03\",\"09/08/16-04\",\"09/08/16-05\",\"09/08/16-06\",\"09/08/16-07\",\"09/08/16-08\",\"09/08/16-09\",\"09/08/16-10\",\"09/08/16-11\",\"09/08/16-12\",\"09/08/16-13\",\"09/08/16-14\",\"09/08/16-15\",\"09/08/16-16\",\"09/08/16-17\",\"09/08/16-18\",\"09/08/16-19\",\"09/08/16-20\",\"09/08/16-21\",\"09/08/16-22\",\"09/08/16-23\",\"09/09/16-00\",\"09/09/16-01\",\"09/09/16-02\",\"09/09/16-03\",\"09/09/16-04\",\"09/09/16-05\",\"09/09/16-06\",\"09/09/16-07\",\"09/09/16-08\",\"09/09/16-09\",\"09/09/16-10\",\"09/09/16-11\",\"09/09/16-12\",\"09/09/16-13\",\"09/09/16-14\",\"09/09/16-15\",\"09/09/16-16\",\"09/09/16-17\",\"09/09/16-18\",\"09/09/16-19\",\"09/09/16-20\",\"09/09/16-21\",\"09/09/16-22\",\"09/09/16-23\",\"09/10/16-00\",\"09/10/16-01\",\"09/10/16-02\",\"09/10/16-03\",\"09/10/16-04\",\"09/10/16-05\",\"09/10/16-06\",\"09/10/16-07\",\"09/10/16-08\",\"09/10/16-09\",\"09/10/16-10\",\"09/10/16-11\",\"09/10/16-12\",\"09/10/16-13\",\"09/10/16-14\",\"09/10/16-15\",\"09/10/16-16\",\"09/10/16-17\",\"09/10/16-18\",\"09/10/16-19\",\"09/10/16-20\",\"09/10/16-21\",\"09/10/16-22\",\"09/10/16-23\",\"09/11/16-00\",\"09/11/16-01\",\"09/11/16-02\",\"09/11/16-03\",\"09/11/16-04\",\"09/11/16-05\",\"09/11/16-06\",\"09/11/16-07\",\"09/11/16-08\",\"09/11/16-09\",\"09/11/16-10\",\"09/11/16-11\",\"09/11/16-12\",\"09/11/16-13\",\"09/11/16-14\",\"09/11/16-15\",\"09/11/16-16\",\"09/11/16-17\",\"09/11/16-18\",\"09/11/16-19\",\"09/11/16-20\",\"09/11/16-21\",\"09/11/16-22\",\"09/11/16-23\",\"09/12/16-00\",\"09/12/16-01\",\"09/12/16-02\",\"09/12/16-03\",\"09/12/16-04\",\"09/12/16-05\",\"09/12/16-06\",\"09/12/16-07\",\"09/12/16-08\",\"09/12/16-09\",\"09/12/16-10\",\"09/12/16-11\",\"09/12/16-12\",\"09/12/16-13\",\"09/12/16-14\",\"09/12/16-15\",\"09/12/16-16\",\"09/12/16-17\",\"09/12/16-18\",\"09/12/16-19\",\"09/12/16-20\",\"09/12/16-21\",\"09/12/16-22\",\"09/12/16-23\",\"09/13/16-00\",\"09/13/16-01\",\"09/13/16-02\",\"09/13/16-03\",\"09/13/16-04\",\"09/13/16-05\",\"09/13/16-06\",\"09/13/16-07\",\"09/13/16-08\",\"09/13/16-09\",\"09/13/16-10\",\"09/13/16-11\",\"09/13/16-12\",\"09/13/16-13\",\"09/13/16-14\",\"09/13/16-15\",\"09/13/16-16\",\"09/13/16-17\",\"09/13/16-18\",\"09/13/16-19\",\"09/13/16-20\",\"09/13/16-21\",\"09/13/16-22\",\"09/13/16-23\",\"09/14/16-00\",\"09/14/16-01\",\"09/14/16-02\",\"09/14/16-03\",\"09/14/16-04\",\"09/14/16-05\",\"09/14/16-06\",\"09/14/16-07\",\"09/14/16-08\",\"09/14/16-09\",\"09/14/16-10\",\"09/14/16-11\",\"09/14/16-12\",\"09/14/16-13\",\"09/14/16-14\",\"09/14/16-15\",\"09/14/16-16\",\"09/14/16-17\",\"09/14/16-18\",\"09/14/16-19\",\"09/14/16-20\",\"09/14/16-21\",\"09/14/16-22\",\"09/14/16-23\",\"09/15/16-00\",\"09/15/16-01\",\"09/15/16-02\",\"09/15/16-03\",\"09/15/16-04\",\"09/15/16-05\",\"09/15/16-06\",\"09/15/16-07\",\"09/15/16-08\",\"09/15/16-09\",\"09/15/16-10\",\"09/15/16-11\",\"09/15/16-12\",\"09/15/16-13\",\"09/15/16-14\",\"09/15/16-15\",\"09/15/16-16\",\"09/15/16-17\",\"09/15/16-18\",\"09/15/16-19\",\"09/15/16-20\",\"09/15/16-21\",\"09/15/16-22\",\"09/15/16-23\",\"09/16/16-00\",\"09/16/16-01\",\"09/16/16-02\",\"09/16/16-03\",\"09/16/16-04\",\"09/16/16-05\",\"09/16/16-06\",\"09/16/16-07\",\"09/16/16-08\",\"09/16/16-09\",\"09/16/16-10\",\"09/16/16-11\",\"09/16/16-12\",\"09/16/16-13\",\"09/16/16-14\",\"09/16/16-15\",\"09/16/16-16\",\"09/16/16-17\",\"09/16/16-18\",\"09/16/16-19\",\"09/16/16-20\",\"09/16/16-21\",\"09/16/16-22\",\"09/16/16-23\",\"09/17/16-00\",\"09/17/16-01\",\"09/17/16-02\",\"09/17/16-03\",\"09/17/16-04\",\"09/17/16-05\",\"09/17/16-06\",\"09/17/16-07\",\"09/17/16-08\",\"09/17/16-09\",\"09/17/16-10\",\"09/17/16-11\",\"09/17/16-12\",\"09/17/16-13\",\"09/17/16-14\",\"09/17/16-15\",\"09/17/16-16\",\"09/17/16-17\",\"09/17/16-18\",\"09/17/16-19\",\"09/17/16-20\",\"09/17/16-21\",\"09/17/16-22\",\"09/17/16-23\",\"09/18/16-00\",\"09/18/16-01\",\"09/18/16-02\",\"09/18/16-03\",\"09/18/16-04\",\"09/18/16-05\",\"09/18/16-06\",\"09/18/16-07\",\"09/18/16-08\",\"09/18/16-09\",\"09/18/16-10\",\"09/18/16-11\",\"09/18/16-12\",\"09/18/16-13\",\"09/18/16-14\",\"09/18/16-15\",\"09/18/16-16\",\"09/18/16-17\",\"09/18/16-18\",\"09/18/16-19\",\"09/18/16-20\",\"09/18/16-21\",\"09/18/16-22\",\"09/18/16-23\",\"09/19/16-00\",\"09/19/16-01\",\"09/19/16-02\",\"09/19/16-03\",\"09/19/16-04\",\"09/19/16-05\",\"09/19/16-06\",\"09/19/16-07\",\"09/19/16-08\",\"09/19/16-09\",\"09/19/16-10\",\"09/19/16-11\",\"09/19/16-12\",\"09/19/16-13\",\"09/19/16-14\",\"09/19/16-15\",\"09/19/16-16\",\"09/19/16-17\",\"09/19/16-18\",\"09/19/16-19\",\"09/19/16-20\",\"09/19/16-21\",\"09/19/16-22\",\"09/19/16-23\",\"09/20/16-00\",\"09/20/16-01\",\"09/20/16-02\",\"09/20/16-03\",\"09/20/16-04\",\"09/20/16-05\",\"09/23/16-07\",\"09/23/16-07\",\"09/23/16-08\",\"09/23/16-09\",\"09/23/16-10\",\"09/23/16-11\",\"09/23/16-12\",\"09/23/16-13\",\"09/23/16-14\",\"09/23/16-15\",\"09/23/16-16\",\"09/23/16-17\",\"09/23/16-18\",\"09/23/16-19\",\"09/23/16-20\",\"09/23/16-21\",\"09/23/16-22\",\"09/23/16-23\",\"09/24/16-00\",\"09/24/16-01\",\"09/24/16-02\",\"09/24/16-03\",\"09/24/16-04\",\"09/24/16-05\",\"09/24/16-06\",\"09/24/16-07\",\"09/24/16-08\",\"09/24/16-09\",\"09/24/16-10\",\"09/24/16-11\",\"09/24/16-12\",\"09/24/16-13\",\"09/24/16-14\",\"09/24/16-15\",\"09/24/16-16\",\"09/24/16-17\",\"09/24/16-18\",\"09/24/16-19\",\"09/24/16-20\",\"09/24/16-21\",\"09/24/16-22\",\"09/24/16-23\",\"09/25/16-00\",\"09/25/16-01\",\"09/25/16-02\",\"09/25/16-03\",\"09/25/16-04\",\"09/25/16-05\",\"09/25/16-06\",\"09/25/16-07\",\"09/25/16-08\",\"09/25/16-09\",\"09/25/16-10\",\"09/25/16-11\",\"09/25/16-12\",\"09/25/16-13\",\"09/25/16-14\",\"09/25/16-15\",\"09/25/16-16\",\"09/25/16-17\",\"09/25/16-18\",\"09/25/16-19\",\"09/25/16-20\",\"09/25/16-21\",\"09/25/16-22\",\"09/25/16-23\",\"09/26/16-00\",\"09/26/16-01\",\"09/26/16-02\",\"09/26/16-03\",\"09/26/16-04\",\"09/26/16-05\",\"09/26/16-06\",\"09/26/16-07\",\"09/26/16-08\",\"09/26/16-09\",\"09/26/16-10\",\"09/26/16-11\",\"09/26/16-12\",\"09/26/16-13\",\"09/26/16-14\",\"09/26/16-15\",\"09/26/16-16\",\"09/26/16-17\",\"09/26/16-18\",\"09/26/16-19\",\"09/26/16-20\",\"09/26/16-21\",\"09/26/16-22\",\"09/26/16-23\",\"09/27/16-00\",\"09/27/16-01\",\"09/27/16-02\",\"09/27/16-03\",\"09/27/16-04\",\"09/27/16-05\",\"09/27/16-06\",\"09/27/16-07\",\"09/27/16-08\",\"09/27/16-09\",\"09/27/16-10\",\"09/27/16-11\",\"09/27/16-12\",\"09/27/16-13\",\"09/27/16-14\",\"09/27/16-15\",\"09/27/16-16\",\"09/27/16-17\",\"09/27/16-18\",\"09/27/16-19\",\"09/27/16-20\",\"09/27/16-21\",\"09/27/16-22\",\"09/27/16-23\",\"09/28/16-00\",\"09/28/16-01\",\"09/28/16-02\",\"09/28/16-03\",\"09/28/16-04\",\"09/28/16-05\",\"09/28/16-06\",\"09/28/16-07\"],\"Population\":[316,316,316,316,316,315,316,316,315,314,314,314,314,314,312,310,310,311,311,311,311,311,310,310,310,310,310,310,310,310,310,309,308,308,307,307,307,307,307,308,308,308,307,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,305,305,305,305,305,305,306,306,306,306,306,306,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,304,306,306,306,306,306,306,306,305,305,305,305,305,304,304,303,303,303,305,305,305,305,305,305,305,305,305,305,305,305,305,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,303,303,303,303,303,303,303,303,303,302,302,302,301,301,301,301,301,301,301,301,301,301,301,301,301,301,300,300,301,300,300,300,300,300,300,300,300,300,300,300,300,299,299,299,299,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,298,297,297,297,297,297,297,298,297,297,297,297,297,297,297,297,297,297,297,297,297,297,297,297,297,297,297,301,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,300,299,302,301,301,301,300,300,300,300,300,300,300,300,300,300,300,300,300,309,309,308,307,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,312,312,312,312,312,312,312,312,312,312,312,312,312,311,311,311,310,310,310,310,310,310,310,309,309,309,309,309,309,309,308,308,308,306,306,305,305,305,305,305,305,304,304,304,304,304,304,303,302,302,302,302,302,300,299,299,299,298,299,299,299,300,300,300,300,300,300,300,300,300,300,300,300,299,299,299,299,299,299,299,299,299,299,299,299,299,299,299,299,299,299,299,298,298,298,298,298,297,297,297,297,297,297,297,297,297,297,297,297,297,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,297,297,297,297,296,296,296,295,295,295,295,295,294,294,294,294,294,294,294,294,295,295,295,295,295,295,295,295,295,295,295,294,293,292,292,292,292,292,292,292,292,292,292,292,292,293,293,293,293,293,293,293,293,293,293,293,293,293,293,293,293,293,292,292,292,292,292,291,291,291,291,291,291,291,291,291,290,290,290,290,290,290,290,290,290,290,290,289,289,289,289,289,289,289,289,289,289,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,293,293,293,293,293,293,293,293,293,293,293,292,292,291,291,290,290,290,290,290,290,290,290,289,289,289,288,288,288,288,288,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,286,286,286,287,287,287,287,287,287,287,287,287,287,287,289,289,289,289,289,288,288,288,288,287,287,287,286,286,286,285,285,285,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,283,285,285,285,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,284,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,285,285,285,285,285,285,285,285,285,285,287,287,287,287,287,287,287,287,287,286,286,286,286,287,287,287,287,287,286,286,286,286,286,286,286,286,285,285,285,285,285,285,285,285,285,285,285,286,286,286,286,285,285,285,285,285,285,289,289,289,288,288,288,288,288,288,288,288,288,288,288,288,288,288,287,292,291,290,290,290,290,290,289,289,289,289,289,289,289,289,289,289,289,289,289,288,288,288,288,287,289,289,289,289,289,289,289,289,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,293,293,293,293,293,293,293,293,293,293,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,293,293,293,293,293,293,293,293,293,293,292,292,292,292,292,291,291,291,291,291,291,291,291,291,291,294,294,293,293,293,293,292,293,294,294,294,294,294,294,294,294,294,294,294,294,294,294,294,294,294,294,294,294,294,294,294,294,293,293,293,293,293,293,293,293,293,293,293,293,293,293,293,293,293,293,292,295,295,295,295,295,295,295,295,295,295,295,295,295,297,297,296,296,296,296,296,296,296,299,299,298,298,298,298,297,297,297,296,296,296,296,296,296,294,292,291,291,291,291,290,290,290,290,290,289,289,289,289,289,288,288,288,288,288,288,288,287,287,287,287,287,287,287,287,286,286,286,286,286,286,285,284,284,284,284,284,284,284,285,285,285,285,285,284,284,284,284,284,284,284,282,282,282,282,282,282,282,282,282,282,282,282,282,282,282,282,282,282,285,285,287,286,286,286,286,286,286,286,286,286,285,285,286,286,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,284,284,284,288,288,288,288,288,289,289,289,289,292,291,291,291,291,291,291,290,290,290,290,290,289,289,289,290,298,298,297,297,297,297,297,297,297,297,300,299,296,295,295,295,295,299,300,300,300,300,300,300,300,300,300,298,298,298,298,297,297,297,297,297,297,297,298,298,298,298,298,298,299,299,299,299,299,298,298,298,301,306,311,311,311,311,311,311,311,311,311,311,310,310,310,310,310,310,310,310,310,311,312,312,312,312,312,312,312,312,312,312,312,312,312,312,312,311,311,311,311,311,311,311,311,317,317,317,317,317,317,317,316,316,316,316,318,318,318,318,320,320,320,320,320,320,320,320,320,320,320,320,320,320,319,319,319,319,319,319,319,319,319,319,319,318,318,317,317,317,317,317,317,317,317,317,317,317,317,317,316,316,316,316,316,316,316,316,319,319,319,319,319,320,320,320,320,320,320,320,320,320,320,320,320,318,318,318,318,318,318,318,318,318,318,318,317,317,317,317,316,316,316,316,316,316,316,316,316,316,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,314,313,313,313,313,313,313,317,318,318,318,318,318,318,318,318,318,318,318,318,318,318,318,319,319,320,320,320,320,320,319,319,319,319,319,319,319,319,319,319,319,319,319,319,319,318,318,318,318,318,318,318,317,317,317,315,315,315,315,314,314,314,314,316,316,316,315,315,315,315,315,315,315,314,314,314,314,314,314,314,317,317,316,316,316,316,317,317,317,317,317,317,317,317,319,319,319,318,318,318,317,317,320,320,320,317,318,318,318,318,318,317,313,313,315,315,315,315,315,314,314,317,317,317,317,317,317,317,317,317,317,317,317,317,317,317,317,317,317,317,317,316,316,316,321,321,321,321,321,321,320,320,320,320,319,321,321,321,321,321,321,321,321,320,320,320,320,320,320,320,320,320,320,320,320,320,320,320,320,320,320,320,320,319,319,319,319,319,319,317,316,316,315,314,314,314,314,314,314,314,314,314,314,314,313,313,313,309,309,309,308,307,307,307,314,314,314,314,315,315,314,314,314,314,314,313,313,315,315,315,315,315,315,315,314,314,314,314,313,313,313,313,313,313,313,313,313,313,313,313,313,313,313,313,313,313,313,314,314,314,314,313,313,313,316,316,315,315,315,315,316,316,316,316,315,315,311,311,310,310,309,308,308,308,308,308,309,309,308,308,308,308,308,308,308,308,308,308,308,308,308,308,307,307,307,307,307,307,303,303,303,303,303,303,300,300,300,300,300,300,300,300,300,300,302,302,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,300,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,303,303,303,303,303,303,303,303,303,303,303,302,302,302,302,302,302,302,302,302,301,301,301,301,301,301,301,300,298,298,298,298,298,298,297,297,297,296,296,296,295,295,295,295,295,295,295,295,295,295,295,295,295,295,300,300,300,300,300,300,300,300,300,300,300,300,300,299,299,299,299,299,299,299,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,299,299,299,301,301,301,301,301,301,301,301,301,306,306,306,306,305,305,305,305,305,305,305,305,305,305,305,305,305,305,304,304,304,304,304,304,303,303,303,303,303,303,303,303,303,302,302,302,302,302,302,302,302,302,302,302,302,302,301,301,301,301,301,301,300,300,300,300,300,300,300,300,300,300,300,300,300,299,299,299,299,299,299,299,299,299,299,299,299,299,299,299,299,299,299,299,299,300,300,300,300,300,300,300,300,299,299,299,298,298,298,298,297,297,297,297,296,296,296,296,296,296,295,295,295,295,295,295,295,295,295,295,295,295,295,295,295,295,295,295,295,295,295,295,295,295,295,294,294,294,297,297,297,297,296,296,296,296,296,296,296,296,296,295,295,294,294,294,292,292,292,291,291,291,291,291,291,291,288,288,288,289,289,289,289,289,289,289,289,289,293,293,293,293,293,293,293,293,293,293,297,297,297,298,298,299,299,299,299,299,299,299,299,299,299,299,299,300,301,301,301,301,301,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,304,304,304,304,303,303,303,303,303,303,303,303,303,303,304,304,304,305,305,305,305,305,305,305,305,305,305,305,304,304,304,304,304,304,304,304,303,303,303,303,303,303,303,303,302,302,302,302,302,302,302,302,307,307,307,307,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,306,305,305,305,305,305,305,305,305,305,305,305,305,305,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,304,306,306,306,306,305,305,305,305,305,305,305,305,305,305,305,305,305,305,305,304,304,304,304,304,304,304,304,304,305,305,305,305,305,305,305,305,307,306,306,306,306,306,306,306,306,305,305,305,305,305,305,305,305,304,304,304,304,304,304,304,303,303,303,305,304,304,304,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,311,313,313,313,313,313,313,313,312,312,312,311,311,311,311,311,311,311,311,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,311,311,311,312,312,312,313,313,313,314,314,314,314,314,314,314,314,313,312,312,312,319,319,319,319,319,319,319,319,319,323,322,323,324,324,324,324,324,324,324,324,324,323,322,323,323,323,323,323,323,323,323,324,324,324,324,325,325,325,325,325,325,325,325,325,325,325,325,325,325,325,325,325,325,325,325,325,324,324,324,325,325,325,325,325,325,325,325,325,325,325,325,325,325,324,324,332,332,332,332,331,330,330,330,330,330,330,330,330,330,330,330,330,330,330,330,330,330,330,330,331,331,331,332,333,333,333,333,334,334,334,334,334,334,333,334,334,334,334,334,334,333,333,333,333,333,333,333,333,333,333,333,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,342,342,342,342,342,342,341,341,340,340,340,340,340,339,339,341,341,341,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,340,338,336,336,336,336,336,336,336,336,336,335,334,334,334,334,334,334,334,334,333,333,333,333,333,333,333,333,333,333,333,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,331,330,330,330,330,330,330,330,330,330,332,332,332,332,332,332,332,332,332,332,332,332,332,332,332,331,331,331,330,330,330,330,328,328,328,328,328,328,328,328,328,328,328,328,328,328,328,328,328,328,328,327,327,327,327,327,327,327,327,327,327,327,327,327,327,327,327,327,327,327,327,327,327,326,326,326,326,326,326,326,327,327,327,327,327,327,327,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,325,328,328,328,328,328,328,328,328,328,328,328,327,327,327,327,327,326,325,325,323,323,323,323,323,323,323,323,323,323,323,330,329,329,329,329,329,328,328,328,328,328,328,328,327,327,327,327,327,327,327,327,327,327,327,327,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,326,325,325,325,324,324,324,324,324,324,323,324,324,324,324,324,324,324,324,324,324,324,327,327,327,326,323,322,322,321,321,321,321,321,321,321,321,320,320,320,320,320,320,320,320,320,320,320,320,320,320,320,320,320,320,319,319,319,319,319,319,319,318,317,316,316,315,315,317,317,317,317,317,317,317,317,317,317,316,316,316,316,316,316,316,315,315,314,314,314,314,314,314,314,313,313,313,313,313,313,313,313,313,313,314,314,314,314,314,314,314,314,314,313,315,315,315,311,311,311,311,311,311,310,310,310,310,310,310,311,311,311,310,310,310,310,310,310,310,310,310,310,310,310,310,310,310,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,307,307,307,307,307,307,306,306,306,306,306,306,306,306,306,306,305,305,305,305,305,305,305,304,304,304,304,304,304,304,304,303,303,303,303,303,303,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,302,301,301,301,301,301,301,301,301,301,301,301,301,301,300,300,300,300,300,300,300,300,300,300,300,300,301,301,301,301,301,308,308,307,307,307,307,307,307,307,306,306,306,306,306,309,309,309,309,309,309,309,309,309,309,309,309,309,309,309,309,309,309,309,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,307,307,307,307,307,307,307,307,307,307,307,307,307,307,307,307,307,306,305,305,305,305,305,305,305,305,305,305,305,305,305,308,308,308,308,307,307,307,307,307,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,308,307,307,307,307,307,307,306,306,306,306,305,305,305,305,305,305,305,305,304,304,304,304,304,304,304,304,304,304,304,304,304,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,301,300,300,300,299,299,299,297,297,297,297,296,296,296,296,296,296,294,294,294,294,294,294,294,296,296,296,296,296,296,296,296,298,298,298,298,298,298,298,297,297,297,297,297,297,297,297,297,297,297,297,297,296,296,296,297,297,297,297,297,297,297,297,299,299,299,299,299,299,299,299,299,299,298,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,294,297,297,297,297,297,297,297,297,297,297,297,297,297,297,297,295,295,295,295,295,295,295,295,295,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,296,295,294,294,294,294,294,294,294,294,294,293,293,293,293,293,293,293,294,294,294,294,294,294,294,294,294,294,294,293,293,293,293,293,293,293,293,293,293,293,293,292,292,292,292,292,292,292,292,292,292,292,292,292,291,291,290,290,290,290,290,290,290,290,290,290,290,290,290,290,290,290,290,294,294,294,293,293,293,293,293,293,293,293,293,293,293,293,293,293,292,292,292,292,292,292,292,292,293,293,293,295,295,295,294,294,294,294,294,294,294,294,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,292,291,291,291,291,291,291,291,291,291,291,291,291,291,292,291,291,291,291,291,291,291,291,291,291,291,290,290,290,290,290,290,290,290,291,290,290,290,290,290,290,290,290,290,289,289,289,289,289,289,289,289,289,288,288,288,288,288,287,287,287,287,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,285,285,285,285,285,285,285,285,285,285,285,287,291,291,291,291,291,291,291,291,291,290,290,290,290,290,290,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,289,288,288,288,289,289,289,288,288,288,288,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,287,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,285,285,285,285,285,285,285,285,285,286,286,286,286,286,286,285,285,285,285,285,285,285,285,285,285,285,284,284,284,284,284,284,284,284,284,284,284,284,283,283,282,282,282,282,282,282,283,283,283,283,283,283,283,283,282,282,282,282,282,282,282,282,282,282,282,282,282,282,282,282,282,282,282,281,281,281,281,281,281,281,281,281,281,281,281,280,280,280,279,279,279,279,279,279,279,278,278,278,278,278,278,277,277,277,277,277,277,277,277,277,277,277,277,277,277,276,276,276,276,276,276,276,276,277,280,280,280,280,280,280,280,280,280,280,280,280,280,280,290,290,290,290,289,289,289,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,288,287,287,287,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,286,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,285,284,283,283,283,282,280,280,280,280,280,280,280,280,280,280,280,280,280,280,280,280,280,280,280,280,281,281,281,281,280,279,279,279,279,279,279,279,279,279,279,279,279,279,279,279,279,279,279,279,279,283,283,283,283,283,283,282],\"Pregnant Mothers\":[1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,0,0,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,2,2,2,2,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,3,3,3,3,3,3,3,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,2,2,2,2,2,2,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,2,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,2,3,3,3,3,3,3,3,3,3,3,3,2,2,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,3,3,3,3,2,2,3,3,2,3,4,4,4,4,4,4,4,4,4,4,4,4,5,4,3,3,3,3,3,3,3,3,3,3,2,2,2,2,2,2,2,1,0,0,0,0,0,0,0,1,1,1,1,1,1,2,2,2,2,2,2,2,1,1,1,2,3,5,4,4,4,4,4,4,4,4,3,1,0,0,0,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,0,0,0,2,2,3,3,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,2,2,3,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,2,2,2,2,2,2,2,2,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,2,1,2,1,1,2,2,2,2,1,2,2,2,2,2,2,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,0,0,0,0,0,0,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,2,2,2,2,2,2,1,1,1,1,2,2,2,3,3,3,3,1,1,1,1,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,1,1,1,1,1,1,1,2,2,2,2,2,2,3,3,3,3,3,3,3,3,3,3,3,2,2,2,2,2,2,2,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,2,2,1,1,2,2,2,2,2,2,2,2,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,5,5,5,4,4,3,3,3,3,3,3,3,3,3,3,4,4,3,2,2,2,2,2,1,1,1,1,1,2,2,2,3,3,3,3,3,3,3,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,1,1,1,2,2,2,3,3,3,3,4,4,4,4,4,4,4,4,4,4,4,4,5,5,4,4,4,3,3,3,3,3,4,4,4,4,4,4,4,4,4,4,4,4,5,4,4,4,4,4,4,4,5,5,4,4,4,3,3,3,3,3,3,3,3,3,3,3,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,2,2,2,3,4,4,4,4,4,4,4,4,4,4,4,5,5,5,5,5,5,5,5,5,4,4,4,3,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,3,3,3,3,3,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,2,2,2,2,2,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,2,2,1,1,1,1,1,2,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,0,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,3,3,3,2,2,2,2,2,2,2,2,3,3,3,4,4,4,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0]}},\"id\":\"09751f14-363e-4096-be27-e3bf1ce4fc78\",\"type\":\"ColumnDataSource\"},{\"attributes\":{\"days\":[1,8,15,22]},\"id\":\"759a8935-595e-482f-9b64-ed7ae793b1f3\",\"type\":\"DaysTicker\"},{\"attributes\":{\"below\":[{\"id\":\"d05c05d6-0807-4df8-aa9a-87b29190f0c0\",\"type\":\"DatetimeAxis\"}],\"left\":[{\"id\":\"b963823d-46bf-4c7b-a0d3-380e7c5566cf\",\"type\":\"LinearAxis\"}],\"plot_height\":150,\"plot_width\":1600,\"renderers\":[{\"id\":\"d05c05d6-0807-4df8-aa9a-87b29190f0c0\",\"type\":\"DatetimeAxis\"},{\"id\":\"36fcaefc-7e4c-47d4-bc8b-c7010f224007\",\"type\":\"Grid\"},{\"id\":\"b963823d-46bf-4c7b-a0d3-380e7c5566cf\",\"type\":\"LinearAxis\"},{\"id\":\"9f271225-28ff-4d64-8a82-2488ad65a90c\",\"type\":\"Grid\"},{\"id\":\"178d7500-8294-4489-970a-a5e47d438de0\",\"type\":\"GlyphRenderer\"}],\"sizing_mode\":\"scale_width\",\"title\":{\"id\":\"21872c55-2d33-40d2-ba04-ebf3db5a63e9\",\"type\":\"Title\"},\"tool_events\":{\"id\":\"6edb720f-299e-467d-a729-26251383602a\",\"type\":\"ToolEvents\"},\"toolbar\":{\"id\":\"786f34ed-2e4e-4811-83cd-395a04be5b23\",\"type\":\"Toolbar\"},\"x_range\":{\"id\":\"c9ab1709-3456-4d4a-afcf-e5b6953c7bee\",\"type\":\"Range1d\"},\"y_range\":{\"id\":\"3295f0c8-47e6-4945-912f-55a042a57270\",\"type\":\"Range1d\"}},\"id\":\"2ebbe383-aed7-471a-9394-cb067527920a\",\"subtype\":\"Figure\",\"type\":\"Plot\"},{\"attributes\":{\"data_source\":{\"id\":\"09751f14-363e-4096-be27-e3bf1ce4fc78\",\"type\":\"ColumnDataSource\"},\"glyph\":{\"id\":\"91379bec-9b6a-4676-aefb-25650069eb2d\",\"type\":\"Line\"},\"hover_glyph\":null,\"nonselection_glyph\":{\"id\":\"d3d666a4-9525-408f-ae1c-0d5d99a0a3cb\",\"type\":\"Line\"},\"selection_glyph\":null},\"id\":\"178d7500-8294-4489-970a-a5e47d438de0\",\"type\":\"GlyphRenderer\"},{\"attributes\":{\"max_interval\":500.0,\"num_minor_ticks\":0},\"id\":\"a1e78381-0e1a-474b-ad39-85b213ab9095\",\"type\":\"AdaptiveTicker\"},{\"attributes\":{\"plot\":{\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"}},\"id\":\"1cc2d776-7f8e-42b5-b316-4167f890ce28\",\"type\":\"ResetTool\"},{\"attributes\":{\"num_minor_ticks\":5},\"id\":\"a7f91300-a887-47cf-b18b-4be7c4c9bb33\",\"type\":\"DatetimeTicker\"},{\"attributes\":{\"plot\":null,\"text\":null},\"id\":\"eb3c4083-1eaf-4dc4-93d3-814e8b844c1b\",\"type\":\"Title\"},{\"attributes\":{\"days\":[1,15]},\"id\":\"8aea957f-368f-402f-a308-b0bf7d765c1e\",\"type\":\"DaysTicker\"},{\"attributes\":{\"plot\":{\"id\":\"2ebbe383-aed7-471a-9394-cb067527920a\",\"subtype\":\"Figure\",\"type\":\"Plot\"},\"ticker\":{\"id\":\"0ca5882b-d581-49f2-93f3-a07dfb3856d8\",\"type\":\"DatetimeTicker\"}},\"id\":\"36fcaefc-7e4c-47d4-bc8b-c7010f224007\",\"type\":\"Grid\"},{\"attributes\":{\"months\":[0,1,2,3,4,5,6,7,8,9,10,11]},\"id\":\"fe18b668-5507-48ed-8e58-b6976e7d7243\",\"type\":\"MonthsTicker\"},{\"attributes\":{\"plot\":{\"id\":\"cadfdbf4-663c-49e0-a0f5-064d9e09b9cd\",\"subtype\":\"Figure\",\"type\":\"Plot\"}},\"id\":\"b54047eb-194f-4e19-aef9-4a66ed72384f\",\"type\":\"PanTool\"},{\"attributes\":{},\"id\":\"8be3bc82-2e46-40aa-a62b-9524f689454e\",\"type\":\"DatetimeTickFormatter\"}],\"root_ids\":[\"751c511a-332d-4afb-8439-cad2e55a6a32\"]},\"title\":\"Bokeh Application\",\"version\":\"0.12.3\"}};\n",
" var render_items = [{\"docid\":\"99b5593e-368d-4de1-9ad5-3bf6e525c34d\",\"elementid\":\"3b840391-5260-4ada-9846-98fddc974d12\",\"modelid\":\"751c511a-332d-4afb-8439-cad2e55a6a32\"}];\n",
" \n",
" Bokeh.embed.embed_items(docs_json, render_items);\n",
" });\n",
" },\n",
" function(Bokeh) {\n",
" }\n",
" ];\n",
" \n",
" function run_inline_js() {\n",
" \n",
" if ((window.Bokeh !== undefined) || (force === \"1\")) {\n",
" for (var i = 0; i < inline_js.length; i++) {\n",
" inline_js[i](window.Bokeh);\n",
" }if (force === \"1\") {\n",
" display_loaded();\n",
" }} else if (Date.now() < window._bokeh_timeout) {\n",
" setTimeout(run_inline_js, 100);\n",
" } else if (!window._bokeh_failed_load) {\n",
" console.log(\"Bokeh: BokehJS failed to load within specified timeout.\");\n",
" window._bokeh_failed_load = true;\n",
" } else if (!force) {\n",
" var cell = $(\"#3b840391-5260-4ada-9846-98fddc974d12\").parents('.cell').data().cell;\n",
" cell.output_area.append_execute_result(NB_LOAD_WARNING)\n",
" }\n",
" \n",
" }\n",
" \n",
" if (window._bokeh_is_loading === 0) {\n",
" console.log(\"Bokeh: BokehJS loaded, going straight to plotting\");\n",
" run_inline_js();\n",
" } else {\n",
" load_libs(js_urls, function() {\n",
" console.log(\"Bokeh: BokehJS plotting callback run at\", now());\n",
" run_inline_js();\n",
" });\n",
" }\n",
" }(this));\n",
"</script>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"bokeh.io.show(layout)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
amkatrutsa/MIPT-Opt | Spring2021/intro_gd.ipynb | 1 | 62985 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {
"nbpresent": {
"id": "196b8a50-3d29-45c3-82b9-f4a09b49491d"
},
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Введение в численные методы оптимизации (Ю. Е. Нестеров Введение в выпуклую оптимизацию, гл. 1 $\\S$ 1.1)\n",
"\n",
" 1. Обзор материала весеннего семестра\n",
" 2. Постановка задачи\n",
" 3. Общая схема решения\n",
" 4. Сравнение методов оптимизации\n",
" 5. Методы одномерной минимизации\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpresent": {
"id": "2a573842-172b-4931-b0dd-9c9d3c47a450"
},
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Обзор материала весеннего семестра\n",
"\n",
"Также на [странице курса](https://github.com/amkatrutsa/MIPT-Opt/blob/master/Spring2021/README.md).\n",
"\n",
"1. Методы решения задач **безусловной** оптимизации\n",
" - Одномерная минимизация (**уже сегодня!**)\n",
" - Градиентный спуск и способы его ускорения\n",
" - Метод Ньютона\n",
" - Квазиньютоновские методы\n",
" - Метод сопряжённых градиентов \n",
" - Решение задачи наименьших квадратов\n",
"2. Методы решения задач **условной** оптимизации\n",
" - Методы проекции градиента и условного градиента\n",
" - Проксимальные методы\n",
" - Методы штрафных и барьерных функций\n",
" - Метод модифицированой функции Лагранжа"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Постановка задачи\n",
"\n",
"\\begin{equation}\n",
"\\begin{split}\n",
"& \\min_{x \\in S} f_0(x)\\\\\n",
"\\text{s.t. } & f_j(x) = 0, \\; j = 1,\\ldots,m\\\\\n",
"& g_k(x) \\leq 0, \\; k = 1,\\ldots,p\n",
"\\end{split}\n",
"\\end{equation}\n",
"где $S \\subseteq \\mathbb{R}^n$, $f_j: S \\rightarrow \\mathbb{R}, \\; j = 0,\\ldots,m$, $g_k: S \\rightarrow \\mathbb{R}, \\; k=1,\\ldots,p$\n",
"\n",
"Все функции как минимум непрерывны. \n",
"\n",
"Важный факт</span>: задачи **нелинейной** оптимизации \n",
"\n",
"в их самой общей форме являются **численно неразрешимыми**!"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Аналитические результаты\n",
"- Необходимое условие первого порядка: \n",
"\n",
"если $x^*$ точка локального минимума дифференцируемой функции $f(x)$, тогда \n",
"\n",
"$$\n",
"f'(x^*) = 0\n",
"$$\n",
"\n",
"- Необходимое условие второго порядка \n",
"\n",
"если $x^*$ точка локального минимума дважды дифференцируемой функции $f(x)$, тогда \n",
"\n",
"$$\n",
"f'(x^*) = 0 \\quad \\text{и} \\quad f''(x^*) \\succeq 0\n",
"$$\n",
"\n",
"- Достаточное условие: \n",
"\n",
"пусть $f(x)$ дважды дифференцируемая функция, и пусть точка $x^*$ удовлетворяет условиям\n",
"\n",
"$$\n",
"f'(x^*) = 0 \\quad f''(x^*) \\succ 0,\n",
"$$\n",
"\n",
"тогда $x^*$ является точкой строго локального минимума функции $f(x)$.\n",
"\n",
"**Замечание**: убедитесь, что Вы понимаете, как доказывать эти\n",
"\n",
"результаты!"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Особенности численного решения\n",
"\n",
"1. Точно решить задачу принципиально невозможно из-за погрешности машинной арифметики\n",
"2. Необходимо задать критерий обнаружения решения\n",
"3. Необходимо определить, какую информацию о задаче использовать"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Общая итеративная схема\n",
"\n",
"Дано: начальное приближение $x$, требуемая точность $\\varepsilon$.\n",
"\n",
"```python\n",
"def GeneralScheme(x, epsilon):\n",
" \n",
" while StopCriterion(x) > epsilon:\n",
" \n",
" OracleResponse = RequestOracle(x)\n",
" \n",
" UpdateInformation(I, x, OracleResponse)\n",
" \n",
" x = NextPoint(I, x)\n",
" \n",
" return x\n",
"```"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Вопросы\n",
"1. Какие критерии остановки могут быть?\n",
"2. Что такое оракул и зачем он нужен?\n",
"3. Что такое информационная модель?\n",
"4. Как вычисляется новая точка?"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"#### Критерии остановки\n",
"1. Сходимость по аргументу: \n",
"$$\n",
"\\| x_k - x^* \\|_2 < \\varepsilon\n",
"$$ \n",
"2. Сходимость по функции: \n",
"$$\n",
"\\| f_k - f^* \\|_2 < \\varepsilon\n",
"$$ \n",
"3. Выполнение необходимого условия \n",
"$$\n",
"\\| f'(x_k) \\|_2 < \\varepsilon\n",
"$$\n",
"\n",
"Но ведь $x^*$ неизвестна!\n",
"\n",
"Тогда\n",
"\n",
"\\begin{align*}\n",
"& \\|x_{k+1} - x_k \\| = \\|x_{k+1} - x_k + x^* - x^* \\| \\leq \\\\\n",
"& \\|x_{k+1} - x^* \\| + \\| x_k - x^* \\| \\leq 2\\varepsilon\n",
"\\end{align*}\n",
"\n",
"Аналогично для сходимости по функции, \n",
"\n",
"однако иногда можно оценить $f^*$! \n",
"\n",
"**Замечание**: лучше использовать относительные изменения \n",
"\n",
"этих величин! \n",
"\n",
"Например $\\dfrac{\\|x_{k+1} - x_k \\|_2}{\\| x_k \\|_2}$\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"#### Что такое оракул?\n",
"**Определение**: оракулом называют некоторое абстрактное \n",
"\n",
"устройство, которое отвечает на последовательные вопросы \n",
"\n",
"метода\n",
"\n",
"Аналогия из ООП: \n",
"\n",
"- оракул - это виртуальный метод базового класса\n",
"- каждая задача - производный класс\n",
"- оракул определяется для каждой задачи отдельно согласно общему определению в базовом классе\n",
"\n",
"**Концепция чёрного ящика**\n",
"1. Единственной информацией, получаемой в ходе работы итеративного метода, являются ответы оракула\n",
"2. Ответы оракула являются *локальными*"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"#### Информация о задаче\n",
"1. Каждый ответ оракула даёт **локальную** информацию о поведении функции в точке\n",
"2. Агрегируя все полученные ответы оракула, обновляем информацию о **глобальном** виде целевой функции:\n",
" - кривизна\n",
" - направление убывания\n",
" - etc"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"#### Вычисление следующей точки\n",
"\n",
"$$\n",
"x_{k+1} = x_{k} + \\alpha_k h_k\n",
"$$\n",
"\n",
"- **Линейный поиск**: фиксируется направление $h_k$ и производится поиск по этому направлению \"оптимального\" значения $\\alpha_k$\n",
"- **Метод доверительных областей**: фиксируется допустимый размер *области* по некоторой норме $\\| \\cdot \\| \\leq \\alpha$ и *модель* целевой функции, которая хорошо её аппроксимирует в выбранной области. \n",
" \n",
" Далее производится поиск направления $h_k$, минимизирующего модель целевой функции и не выводящего точку $x_k + h_k$ за пределы доверительной области"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"#### Вопросы\n",
"1. Как выбрать $\\alpha_k$?\n",
"2. Как выбрать $h_k$?\n",
"3. Как выбрать модель?\n",
"4. Как выбрать область?\n",
"5. Как выбрать размер области? \n",
"\n",
"<span style=\"color:red\">\n",
" В курсе рассматривается только линейный поиск!</span> \n",
" \n",
"Однако несколько раз копцепция метода доверительных областей \n",
"\n",
"будет использована."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Как сравнивать методы оптимизации?\n",
"Для заданного класса задач сравнивают следующие величины:\n",
"1. Сложность\n",
" - аналитическая: число обращений к оракулу для решения задачи с точностью $\\varepsilon$\n",
" - арифметическая: общее число всех вычислений, необходимых для решения задачи с точностью $\\varepsilon$\n",
"2. Скорость сходимости\n",
"3. Эксперименты"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Скорости сходимости \n",
"\n",
"_1._ Сублинейная\n",
"\n",
"$$\n",
"\\| x_{k+1} - x^* \\|_2 \\leq C k^{\\alpha},\n",
"$$\n",
"\n",
"где $\\alpha < 0$ и $ 0 < C < \\infty$\n",
"\n",
"_2._ Линейная (геометрическая прогрессия)\n",
"\n",
"$$\n",
"\\| x_{k+1} - x^* \\|_2 \\leq Cq^k, \n",
"$$\n",
"\n",
"где $q \\in (0, 1)$ и $ 0 < C < \\infty$\n",
"\n",
"_3._ Сверхлинейная \n",
"\n",
"$$\n",
"\\| x_{k+1} - x^* \\|_2 \\leq Cq^{k^p}, \n",
"$$\n",
"\n",
"где $q \\in (0, 1)$, $ 0 < C < \\infty$ и $p > 1$\n",
"\n",
"_4._ Квадратичная\n",
"\n",
"$$\n",
"\\| x_{k+1} - x^* \\|_2 \\leq C\\| x_k - x^* \\|^2_2, \\qquad \\text{или} \\qquad \\| x_{k+1} - x^* \\|_2 \\leq C q^{2^k}\n",
"$$\n",
"\n",
"где $q \\in (0, 1)$ и $ 0 < C < \\infty$"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import matplotlib.pyplot as plt\n",
"\n",
"USE_COLAB = False\n",
"if not USE_COLAB:\n",
" plt.rc(\"text\", usetex=True)\n",
"\n",
"import numpy as np\n",
"C = 10\n",
"alpha = -0.5\n",
"q = 0.9\n",
"num_iter = 50\n",
"sublinear = np.array([C * k**alpha for k in range(1, num_iter + 1)])\n",
"linear = np.array([C * q**k for k in range(1, num_iter + 1)])\n",
"superlinear = np.array([C * q**(k**2) for k in range(1, num_iter + 1)])\n",
"quadratic = np.array([C * q**(2**k) for k in range(1, num_iter + 1)])\n",
"plt.figure(figsize=(12,8))\n",
"plt.semilogy(np.arange(1, num_iter+1), sublinear, \n",
" label=r\"Sublinear, $\\alpha = -0.5$\", linewidth=5)\n",
"# plt.semilogy(np.arange(1, num_iter+1), superlinear, linewidth=5,\n",
"# label=r\"Superlinear, $q = 0.5, p=2$\")\n",
"plt.semilogy(np.arange(1, num_iter+1), linear, \n",
" label=r\"Linear, $q = 0.5$\", linewidth=5)\n",
"# plt.semilogy(np.arange(1, num_iter+1), quadratic, \n",
"# label=r\"Quadratic, $q = 0.5$\", linewidth=5)\n",
"plt.xlabel(\"Number of iterations, $k$\", fontsize=28)\n",
"plt.ylabel(\"Error rate upper bound\", fontsize=28)\n",
"plt.legend(loc=\"best\", fontsize=26)\n",
"plt.xticks(fontsize = 28)\n",
"_ = plt.yticks(fontsize = 28)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Значение теорем сходимости (Б.Т. Поляк Введение в оптимизацию, гл. 1, $\\S$ 6)\n",
"1. Что дают теоремы сходимости\n",
" - класс задач, для которых можно рассчитывать на применимость метода (важно не завышать условия!)\n",
" - выпуклость\n",
" - гладкость\n",
" - качественное поведение метода\n",
" - существенно ли начальное приближение\n",
" - по какому функционалу есть сходимость\n",
" - оценку скорости сходимости\n",
" - теоретическая оценка поведения метода без проведения экспериментов\n",
" - определение факторов, которые влияют на сходимость (обусловленность, размерность, etc)\n",
" - иногда заранее можно выбрать число итераций для достижения заданной точности \n",
"\n",
"2. Что **НЕ** дают теоремы сходимости\n",
" - сходимость метода **ничего не говорит** о целесообразности его применения\n",
" - оценки сходимости зависят от неизвестных констант - неконструктивный характер\n",
" - учёт ошибок округления и точности решения вспомогательных задач\n",
" \n",
"**Мораль**: нужно проявлять разумную осторожность \n",
"\n",
"и здравый смысл!"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Классификация задач\n",
"1. Безусловная оптимизация\n",
" - целевая функция липшицева\n",
" - градиент целевой функции липшицев\n",
"2. Условная оптимизация\n",
" - многогранник\n",
" - множество простой структуры\n",
" - общего вида"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Классификация методов\n",
"\n",
"### Какой размер истории нужно хранить для обновления?\n",
"\n",
"1. Одношаговые методы \n",
"\n",
"$$\n",
"x_{k+1} = \\Phi(x_k)\n",
"$$\n",
"\n",
"2. Многошаговые методы\n",
"\n",
"$$\n",
"x_{k+1} = \\Phi(x_k, x_{k-1}, ...)\n",
"$$\n",
"\n",
"### Какой порядок поизводных нужно вычислить?\n",
"1. Методы нулевого порядка: оракул возвращает только значение функции $f(x)$\n",
"\n",
"2. Методы первого порядка: оракул возвращает значение функции $f(x)$ и её градиент $f'(x)$\n",
"\n",
"3. Методы второго порядка: оракул возвращает значение функции $f(x)$, её градиент $f'(x)$ и гессиан $f''(x)$.\n",
"\n",
"**Q**: существуют ли методы более высокого порядка?\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"**А**: [Implementable tensor methods in unconstrained convex optimization](https://link.springer.com/content/pdf/10.1007/s10107-019-01449-1.pdf) by Y. Nesterov, 2019 "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Одномерная минимизация\n",
"**Определение**. Функция $f(x)$ называется унимодальной на $[a, b]$, если существует такая точка $x^* \\in [a, b]$, что \n",
"- $f(x_1) > f(x_2)$ для любых $a \\leq x_1 < x_2 < x^*$, \n",
"\n",
"и \n",
"- $f(x_1) < f(x_2)$ для любых $x^* < x_1 < x_2 \\leq b$.\n",
"\n",
"**Вопрос**: какая геометрия унимодальных функций?"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Метод дихотомии\n",
"\n",
"Идея из информатики первого семестра: \n",
"\n",
"делим отрезок $[a,b]$ на две равные части \n",
"\n",
"пока не найдём минимум унимодальной функции.\n",
"\n",
"- $N$ - число вычислений функции $f$\n",
"- $K = \\frac{N - 1}{2}$ - число итераций\n",
"\n",
"Тогда\n",
"\n",
"$$\n",
"|x_{K+1} - x^*| \\leq \\frac{b_{K+1} - a_{K+1}}{2} = \\left( \\frac{1}{2} \\right)^{\\frac{N-1}{2}} (b - a) \\approx 0.5^{K} (b - a) \n",
"$$"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"def binary_search(f, a, b, epsilon, callback=None):\n",
" c = (a + b) / 2.0\n",
" while abs(b - a) > epsilon:\n",
"# Check left subsegment\n",
" y = (a + c) / 2.0\n",
" if f(y) <= f(c):\n",
" b = c\n",
" c = y\n",
" else:\n",
"# Check right subsegment\n",
" z = (b + c) / 2.0\n",
" if f(c) <= f(z):\n",
" a = y\n",
" b = z\n",
" else:\n",
" a = c\n",
" c = z\n",
" if callback is not None:\n",
" callback(a, b)\n",
" return c"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"def my_callback(a, b, left_bound, right_bound, approximation):\n",
" left_bound.append(a)\n",
" right_bound.append(b)\n",
" approximation.append((a + b) / 2.0)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"import numpy as np\n",
"\n",
"left_boud_bs = []\n",
"right_bound_bs = []\n",
"approximation_bs = []\n",
"\n",
"callback_bs = lambda a, b: my_callback(a, b, \n",
" left_boud_bs, right_bound_bs, approximation_bs)\n",
"\n",
"# Target unimodal function on given segment\n",
"f = lambda x: (x - 2) * x * (x + 2)**2 # np.power(x+2, 2)\n",
"# f = lambda x: -np.sin(x)\n",
"x_true = -2\n",
"# x_true = np.pi / 2.0\n",
"a = -3\n",
"b = -1.5\n",
"epsilon = 1e-8\n",
"x_opt = binary_search(f, a, b, epsilon, callback_bs)\n",
"print(np.abs(x_opt - x_true))\n",
"plt.figure(figsize=(10,6))\n",
"plt.plot(np.linspace(a,b), f(np.linspace(a,b)))\n",
"plt.title(\"Objective function\", fontsize=28)\n",
"plt.xticks(fontsize = 28)\n",
"_ = plt.yticks(fontsize = 28)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Метод золотого сечения\n",
"Идея: \n",
"\n",
"делить отрезок $[a,b]$ не на две равные насти, \n",
"\n",
"а в пропорции \"золотого сечения\".\n",
"\n",
"Оценим скорость сходимости аналогично методу дихотомии:\n",
"\n",
"$$\n",
"|x_{K+1} - x^*| \\leq b_{K+1} - a_{K+1} = \\left( \\frac{1}{\\tau} \\right)^{N-1} (b - a) \\approx 0.618^K(b-a),\n",
"$$\n",
"где $\\tau = \\frac{\\sqrt{5} + 1}{2}$.\n",
"\n",
"- Константа геометрической прогрессии **больше**, чем у метода дихотомии\n",
"- Количество вызовов функции **меньше**, чем у метода дихотомии"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"def golden_search(f, a, b, tol=1e-5, callback=None):\n",
" tau = (np.sqrt(5) + 1) / 2.0\n",
" y = a + (b - a) / tau**2\n",
" z = a + (b - a) / tau\n",
" while b - a > tol:\n",
" if f(y) <= f(z):\n",
" b = z\n",
" z = y\n",
" y = a + (b - a) / tau**2\n",
" else:\n",
" a = y\n",
" y = z\n",
" z = a + (b - a) / tau\n",
" if callback is not None:\n",
" callback(a, b)\n",
" return (a + b) / 2.0"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"left_boud_gs = []\n",
"right_bound_gs = []\n",
"approximation_gs = []\n",
"\n",
"cb_gs = lambda a, b: my_callback(a, b, left_boud_gs, right_bound_gs, approximation_gs)\n",
"x_gs = golden_search(f, a, b, epsilon, cb_gs)\n",
"\n",
"print(f(x_opt))\n",
"print(f(x_gs))\n",
"print(np.abs(x_opt - x_true))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Сравнение методов одномерной минимизации"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"plt.figure(figsize=(10,6))\n",
"plt.semilogy(np.arange(1, len(approximation_bs) + 1), np.abs(x_true - np.array(approximation_bs, dtype=np.float64)), label=\"Binary search\")\n",
"plt.semilogy(np.arange(1, len(approximation_gs) + 1), np.abs(x_true - np.array(approximation_gs, dtype=np.float64)), label=\"Golden search\")\n",
"plt.xlabel(r\"Number of iterations, $k$\", fontsize=26)\n",
"plt.ylabel(\"Error rate upper bound\", fontsize=26)\n",
"plt.legend(loc=\"best\", fontsize=26)\n",
"plt.xticks(fontsize = 26)\n",
"_ = plt.yticks(fontsize = 26)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"%timeit binary_search(f, a, b, epsilon)\n",
"%timeit golden_search(f, a, b, epsilon)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Пример иного поведения методов\n",
"\n",
"$$\n",
"f(x) = \\sin(\\sin(\\sin(\\sqrt{x}))), \\; x \\in [2, 60]\n",
"$$"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"f = lambda x: np.sin(np.sin(np.sin(np.sqrt(x))))\n",
"x_true = (3 * np.pi / 2)**2\n",
"a = 2\n",
"b = 60\n",
"epsilon = 1e-8\n",
"plt.plot(np.linspace(a,b), f(np.linspace(a,b)))\n",
"plt.xticks(fontsize = 28)\n",
"_ = plt.yticks(fontsize = 28)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Сравнение скорости сходимости и времени работы методов"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Метод дихотомии"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"left_boud_bs = []\n",
"right_bound_bs = []\n",
"approximation_bs = []\n",
"\n",
"callback_bs = lambda a, b: my_callback(a, b, \n",
" left_boud_bs, right_bound_bs, approximation_bs)\n",
"\n",
"x_opt = binary_search(f, a, b, epsilon, callback_bs)\n",
"print(np.abs(x_opt - x_true))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Метод золотого сечения"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"left_boud_gs = []\n",
"right_bound_gs = []\n",
"approximation_gs = []\n",
"\n",
"cb_gs = lambda a, b: my_callback(a, b, left_boud_gs, right_bound_gs, approximation_gs)\n",
"x_gs = golden_search(f, a, b, epsilon, cb_gs)\n",
"\n",
"print(np.abs(x_opt - x_true))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Сходимость"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"plt.figure(figsize=(8,6))\n",
"plt.semilogy(np.abs(x_true - np.array(approximation_bs, dtype=np.float64)), label=\"Binary\")\n",
"plt.semilogy(np.abs(x_true - np.array(approximation_gs, dtype=np.float64)), label=\"Golden\")\n",
"plt.legend(fontsize=28)\n",
"plt.xticks(fontsize=28)\n",
"_ = plt.yticks(fontsize=28)\n",
"plt.xlabel(r\"Number of iterations, $k$\", fontsize=26)\n",
"plt.ylabel(\"Error rate upper bound\", fontsize=26)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Время работы"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"%timeit binary_search(f, a, b, epsilon)\n",
"%timeit golden_search(f, a, b, epsilon)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Резюме\n",
"1. Введение в численные методы оптимизации\n",
"2. Общая схема работы метода\n",
"3. Способы сравнения методов оптимизации\n",
"4. Зоопарк задач и методов\n",
"5. Одномерная минимизация"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Методы спуска. Градиентный спуск и его ускоренные модификации"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"## Что такое методы спуска?\n",
"\n",
"Последовательность $x_k$ генерируется по правилу\n",
"\n",
"$$\n",
"x_{k+1} = x_k + \\alpha_k h_k\n",
"$$\n",
"\n",
"так что\n",
"\n",
"$$\n",
"f(x_{k+1}) < f(x_k)\n",
"$$\n",
"\n",
"Направление $h_k$ называется *направлением убывания*.\n",
"\n",
"**Замечание**: существуют методы, которые не требуют монотонного убывания функции от итерации к итерации."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"```python\n",
"def DescentMethod(f, x0, epsilon, **kwargs):\n",
" \n",
" x = x0\n",
" \n",
" while StopCriterion(x, f, **kwargs) > epsilon:\n",
" \n",
" h = ComputeDescentDirection(x, f, **kwargs)\n",
" \n",
" alpha = SelectStepSize(x, h, f, **kwargs)\n",
" \n",
" x = x + alpha * h\n",
" \n",
" return x\n",
"\n",
"\n",
"```"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Способ 1: направление убывания\n",
"Рассмотрим линейную аппроксимацию дифференцируемой функции $f$ вдоль некоторого направления убывания $h, \\|h\\|_2 = 1$:\n",
"\n",
"$$\n",
"f(x + \\alpha h) = f(x) + \\alpha \\langle f'(x), h \\rangle + o(\\alpha)\n",
"$$\n",
"\n",
"Из условия убывания\n",
"\n",
"$$\n",
"f(x) + \\alpha \\langle f'(x), h \\rangle + o(\\alpha) < f(x)\n",
"$$\n",
"\n",
"и переходя к пределу при $\\alpha \\rightarrow 0$:\n",
"\n",
"$$\n",
"\\langle f'(x), h \\rangle \\leq 0\n",
"$$\n",
"\n",
"Также из неравенства Коши-Буняковского-Шварца\n",
"\n",
"$$\n",
"\\langle f'(x), h \\rangle \\geq -\\| f'(x) \\|_2 \\| h \\|_2 = -\\| f'(x) \\|_2\n",
"$$"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"Таким образом, направление антиградиента \n",
"\n",
"$$\n",
"h = -\\dfrac{f'(x)}{\\|f'(x)\\|_2}\n",
"$$\n",
"\n",
"даёт направление **наискорейшего локального** убывания функции$~f$.\n",
"\n",
"В итоге метод имеет вид\n",
"\n",
"$$\n",
"x_{k+1} = x_k - \\alpha f'(x_k)\n",
"$$"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Способ 2: схема Эйлера решения ОДУ\n",
"\n",
"Рассмотрим обыкновенное диференциальное уравнение вида:\n",
"\n",
"$$\n",
"\\frac{dx}{dt} = -f'(x(t))\n",
"$$\n",
"\n",
"и дискретизуем его на равномерной сетке с шагом $\\alpha$:\n",
"\n",
"$$\n",
"\\frac{x_{k+1} - x_k}{\\alpha} = -f'(x_k),\n",
"$$\n",
"\n",
"где $x_k \\equiv x(t_k)$ и $\\alpha = t_{k+1} - t_k$ - шаг сетки.\n",
"\n",
"Отсюда получаем выражение для $x_{k+1}$\n",
"\n",
"$$\n",
"x_{k+1} = x_k - \\alpha f'(x_k),\n",
"$$\n",
"\n",
"которое в точности совпадает с выражением для градиентного спуска.\n",
"\n",
"Такая схема называется явной или прямой схемой Эйлера.\n",
"\n",
"**Q:** какая схема называется неявной или обратной?"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Способ 3: минимизация квадратичной оценки сверху \n",
"#### (А. В. Гасников \"Метод универсального градиентного спуска\" https://arxiv.org/abs/1711.00394)\n",
"\n",
"Глобальная оценка сверху на функцию $f$ в точке $x_k$:\n",
"\n",
"$$\n",
"f(y) \\leq f(x_k) + \\langle f'(x_k), y - x_k \\rangle + \\frac{L}{2} \\|y - x_k \\|_2^2 = g(y), \n",
"$$\n",
"\n",
"где $\\lambda_{\\max}(f''(x)) \\leq L$ для всех допустимых $x$.\n",
"\n",
"Справа — квадратичная форма, точка минимума которой имеет аналитическое выражение:\n",
"\n",
"\\begin{align*}\n",
"& g'(y^*) = 0 \\\\\n",
"& f'(x_k) + L (y^* - x_k) = 0 \\\\\n",
"& y^* = x_k - \\frac{1}{L}f'(x_k) = x_{k+1}\n",
"\\end{align*}\n",
"\n",
"Этот способ позволяет оценить значение шага как $\\frac{1}{L}$. Однако часто константа $L$ неизвестна."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Итого: метод градиентного спуска — дёшево и сердито\n",
"\n",
"```python\n",
"def GradientDescentMethod(f, x0, epsilon, **kwargs):\n",
" \n",
" x = x0\n",
" \n",
" while StopCriterion(x, f, **kwargs) > epsilon:\n",
" \n",
" h = ComputeGradient(x, f, **kwargs)\n",
" \n",
" alpha = SelectStepSize(x, h, f, **kwargs)\n",
" \n",
" x = x - alpha * h\n",
" \n",
" return x\n",
"\n",
"```"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Как выбрать шаг $\\alpha_k$? (J. Nocedal, S. Wright Numerical Optimization, $\\S$ 3.1.)\n",
"\n",
"Список подходов:\n",
"- Постоянный шаг \n",
"\n",
"$$\n",
"\\alpha_k = \\overline{\\alpha}\n",
"$$\n",
"\n",
"- Априорно заданная последовательность, например\n",
"\n",
"$$\n",
"\\alpha_k = \\dfrac{\\overline{\\alpha}}{\\sqrt{k+1}}\n",
"$$\n",
"\n",
"- Наискорейший спуск\n",
"\n",
"$$\n",
"\\alpha_k = \\arg\\min_{\\alpha \\geq 0} f(x_k - \\alpha f'(x_k))\n",
"$$\n",
"\n",
"- Требование **достаточного** убывания, требование **существенного** убывания и условие кривизны: для некоторых $\\beta_1, \\beta_2$, таких что $0 < \\beta_1 < \\beta_2 < 1$ найти $x_{k+1}$ такую что\n",
"\n",
" - Достаточное убывание: $f(x_{k+1}) \\leq f(x_k) + \\beta_1 \\alpha_k \\langle f'(x_k), h_k \\rangle$ или\n",
" $ f(x_k) - f(x_{k+1}) \\geq \\beta_1 \\alpha_k \\langle f'(x_k), h_k \\rangle\n",
" $\n",
" - Существенное убывание: $f(x_{k+1}) \\geq f(x_k) + \\beta_2 \\alpha_k \\langle f'(x_k), h_k \\rangle$ или\n",
" $\n",
" f(x_k) - f(x_{k+1}) \\leq \\beta_2 \\alpha_k \\langle f'(x_k), h_k \\rangle\n",
" $\n",
" - Условие кривизны: $\\langle f'(x_{k+1}), h_k \\rangle \\geq \\beta_2 \\langle f'(x_k), h_k \\rangle$\n",
"\n",
"Обычно коэффициенты выбирают так: $\\beta_1 \\in (0, 0.3)$, а $\\beta_2 \\in (0.9, 1)$"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Анализ и мотивация подходов к выбору шага $\\alpha_k$\n",
"- Постоянный шаг: самое простое и неэффективное решение\n",
"- Априорно заданная последовательность: немногим лучше постоянного шага\n",
"- Наискорейший спуск: самое лучшее решение, но применимо только если вспомогательная задача решается аналитически или ооооооочень быстро. <br></br>\n",
"То есть почти всегда неприменимо :)\n",
"- Требование достаточного убывания, требование существенного убывания и условие кривизны:\n",
" - требование достаточного убывания гарантирует, что функция в точке $x_{k+1}$ не превосходит линейной аппроксимации с коэффициентом наклона $\\beta_1$\n",
" - требование существенного убывания гарантирует, что функция в точке $x_{k+1}$ убывает не меньше, чем линейная аппроксимация c коэффициентом наклона $\\beta_2$\n",
" - условие кривизны гарантирует, что угол наклона касательной в точке $x_{k+1}$ не меньше, чем угол наклона касательной в точке $x_k$, <br></br>\n",
"умноженный на $\\beta_2$ \n",
"\n",
"Требование существенного убывания и условие кривизны обеспечивают убывание функции по выбранному направлению $h_k$. Обычно выбирают одно из них."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"#### Альтернативные названия\n",
"- Требование достаточного убывания $\\equiv$ правило Армихо\n",
"- Требование достаточного убывания + условие кривизны $\\equiv$ правило Вольфа\n",
"- Требование достаточного убывания + требование существенного убывания $\\equiv$ правило Гольдштейна"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Зачем нужно условие существенного убывания?"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"%matplotlib notebook\n",
"import matplotlib.pyplot as plt\n",
"plt.rc(\"text\", usetex=True)\n",
"import ipywidgets as ipywidg\n",
"import numpy as np\n",
"import liboptpy.unconstr_solvers as methods\n",
"import liboptpy.step_size as ss\n",
"from tqdm import tqdm"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"f = lambda x: np.power(x, 2)\n",
"gradf = lambda x: 2 * x\n",
"\n",
"fig = plt.figure()\n",
"ax = fig.add_subplot(1, 1, 1)\n",
"\n",
"\n",
"\n",
"def update(x0, step):\n",
" gd = methods.fo.GradientDescent(f, gradf, ss.ConstantStepSize(step))\n",
" _ = gd.solve(np.array([x0]), max_iter=10)\n",
" x_hist = gd.get_convergence()\n",
" x = np.linspace(-5, 5)\n",
" ax.clear()\n",
" ax.plot(x, f(x), color=\"r\", label=\"$f(x) = x^2$\")\n",
" y_hist = np.array([f(x) for x in x_hist])\n",
" x_hist = np.array(x_hist)\n",
" plt.quiver(x_hist[:-1], y_hist[:-1], x_hist[1:]-x_hist[:-1], y_hist[1:]-y_hist[:-1], \n",
" scale_units='xy', angles='xy', scale=1, width=0.005, color=\"green\", label=\"Descent path\")\n",
" ax.legend()\n",
" fig.canvas.draw()\n",
"\n",
"step_slider = ipywidg.FloatSlider(value=0.8, min=0, max=1.2, step=0.1, description=\"Step\")\n",
"x0_slider = ipywidg.FloatSlider(value=1.5, min=-4, max=4, step=0.1, description=\"Initial point\")\n",
"_ = ipywidg.interact(update, x0=x0_slider, step=step_slider)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"def plot_alpha(f, grad, x, h, alphas, beta1, beta2):\n",
" df = np.zeros_like(alphas)\n",
" for i, alpha in enumerate(alphas):\n",
" df[i] = f(x + alpha * h)\n",
" upper_bound = f(x) + beta1 * alphas * grad(x) * h\n",
" lower_bound = f(x) + beta2 * alphas * grad(x) * h\n",
" plt.plot(alphas, df, label=r\"$f(x + \\alpha h)$\")\n",
" plt.plot(alphas, upper_bound, label=\"Upper bound\")\n",
" plt.plot(alphas, lower_bound, label=\"Lower bound\")\n",
" plt.xlabel(r\"$\\alpha$\", fontsize=18)\n",
" plt.legend(loc=\"best\", fontsize=18)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"f = lambda x: x**2\n",
"grad = lambda x: 2 * x\n",
"beta1 = 0.1\n",
"beta2 = 0.9\n",
"x0 = 0.5\n",
"plot_alpha(f, grad, x0, -grad(x0), np.linspace(1e-3, 1.01, 10), beta1, beta2)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## $f(x) = x\\log x$"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"x_range = np.linspace(1e-10, 4)\n",
"plt.plot(x_range, x_range * np.log(x_range))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"x0 = 1\n",
"f = lambda x: x * np.log(x)\n",
"grad = lambda x: np.log(x) + 1\n",
"beta1 = 0.3\n",
"beta2 = 0.7\n",
"plot_alpha(f, grad, x0, -grad(x0), np.linspace(1e-3, 0.9, 10), beta1, beta2)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Backtracking \n",
"\n",
"```python\n",
"def SelectStepSize(x, f, h, rho, alpha0, beta1, beta2):\n",
" \n",
" # 0 < rho < 1\n",
" \n",
" # alpha0 - initial guess of step size\n",
" \n",
" # beta1 and beta2 - constants from conditions\n",
" \n",
" alpha = alpha0\n",
" \n",
" # Check violating sufficient decrease and curvature conditions\n",
" \n",
" while (f(x - alpha * h) >= f(x) + beta1 * alpha grad_f(x_k).dot(h)) and \n",
" \n",
" (grad_f(x - alpha * h).dot(h) <= beta2 * grad_f(x_k).dot(h)):\n",
" \n",
" alpha *= rho\n",
" \n",
" return alpha\n",
"\n",
"```"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Теоремы сходимости (Б.Т. Поляк Введение в оптимизацию, гл. 1, $\\S$ 4; гл. 3, $\\S$ 1; Ю.Е. Нестеров Введение в выпуклую оптимизацию, $\\S$ 2.2)\n",
"От общего к частному:"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"**Теорема 1.** \n",
"Пусть \n",
"\n",
"- $f(x)$ дифференцируема на $\\mathbb{R}^n$, \n",
"- градиент $f(x)$ удовлетворяет условию Липшица с константой $L$\n",
"- $f(x)$ ограничена снизу\n",
"- $\\alpha = const$ и $0 < \\alpha < \\frac{2}{L}$\n",
"\n",
"Тогда для градиентного метода выполнено:\n",
"\n",
"$$\n",
"\\lim\\limits_{k \\to \\infty} f'(x_k) = 0,\n",
"$$\n",
"\n",
"а функция монотонно убывает $f(x_{k+1}) < f(x_k)$."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"**Теорема 2.** Пусть\n",
"- $f(x)$ дифференцируема на $\\mathbb{R}^n$\n",
"- $f(x)$ выпукла \n",
"- $f'(x)$ удовлетворяет условию Липшица с константой $L$\n",
"- $\\alpha = \\dfrac{1}{L}$\n",
"\n",
"Тогда \n",
"\n",
"$$\n",
"f(x_k) - f^* \\leq \\dfrac{2L \\| x_0 - x^*\\|^2_2}{k+4}\n",
"$$\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"**Теорема 3.**\n",
"Пусть \n",
"- $f(x)$ дважды дифференцируема и $\\mu\\mathbf{I} \\preceq f''(x) \\preceq L\\mathbf{I}$ для всех $x$\n",
"- $\\alpha = const$ и $0 < \\alpha < \\frac{2}{L}$\n",
"\n",
"Тогда \n",
"\n",
"$$\n",
"\\| x_k - x^*\\|_2 \\leq \\|x_0 - x^*\\|_2 q^k, \\qquad q = \\max(|1 - \\alpha l|, |1 - \\alpha L|) < 1\n",
"$$\n",
"\n",
"и минимальное $q^* = \\dfrac{L - \\mu}{L + \\mu}$ при $\\alpha^* = \\dfrac{2}{L + \\mu}$"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### От чего зависит $q^*$ и как это использовать?\n",
"Из Теоремы 3 имеем \n",
"\n",
"$$\n",
"q^* = \\dfrac{L - \\mu}{L + \\mu} = \\dfrac{L/\\mu - 1}{L/\\mu + 1} = \\dfrac{M - 1}{M + 1},\n",
"$$\n",
"\n",
"где $M$ - оценка числа обусловленности $f''(x)$.\n",
"\n",
"**Вопрос**: что такое число обусловленности матрицы?\n",
"\n",
"- При $M \\gg 1$, $q^* \\to 1 \\Rightarrow$ оооочень **медленная** сходимости градиентного метода. Например при $M = 100$: $q^* \\approx 0.98 $\n",
"- При $M \\simeq 1$, $q^* \\to 0 \\Rightarrow$ **ускорение** сходимости градиентного метода. Например при $M = 4$: $q^* = 0.6 $\n",
"\n",
"**Вопрос**: какая геометрия у этого требования?\n",
"\n",
"**Мораль**: необходимо сделать оценку $M$ как можно ближе к 1!\n",
"\n",
"О том, как это сделать, Вам будет предложено подумать в домашнем задании :)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Вычислительный аспект и эксперименты\n",
"1. Для каждого шага метода нужно хранить только текущую точку и вектор градиента: $O(n)$ памяти\n",
"2. Поиск $\\alpha_k$:\n",
"\n",
" - дан априори\n",
" - ищется из аналитического решения задачи наискорейшего спуска\n",
" - заканчивается за конечное число шагов\n",
"3. Для каждого шага метода нужно вычислять линейную комбинацию векторов: $O(n)$ вычислений + высокопроизводительные реализации"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Pеализация градиентного спуска"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"def GradientDescent(f, gradf, x0, epsilon, num_iter, line_search, \n",
" disp=False, callback=None, **kwargs):\n",
" x = x0.copy()\n",
" iteration = 0\n",
" opt_arg = {\"f\": f, \"grad_f\": gradf}\n",
" for key in kwargs:\n",
" opt_arg[key] = kwargs[key]\n",
" while True:\n",
" gradient = gradf(x)\n",
" alpha = line_search(x, -gradient, **opt_arg)\n",
" x = x - alpha * gradient\n",
" if callback is not None:\n",
" callback(x)\n",
" iteration += 1\n",
" if disp:\n",
" print(\"Current function val =\", f(x))\n",
" print(\"Current gradient norm = \", np.linalg.norm(gradf(x)))\n",
" if np.linalg.norm(gradf(x)) < epsilon:\n",
" break\n",
" if iteration >= num_iter:\n",
" break\n",
" res = {\"x\": x, \"num_iter\": iteration, \"tol\": np.linalg.norm(gradf(x))}\n",
" return res"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Выбор шага\n",
"\n",
"Реализации различных способов выбора шага приведены [тут](https://github.com/amkatrutsa/liboptpy/blob/master/step_size.py)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Зависимость от обусловленности матрицы $f''(x)$\n",
"Рассмотрим задачу \n",
"$$\n",
"\\min f(x),\n",
"$$ \n",
"где\n",
"$$ f(x) = x^{\\top}Ax, \\; A = \\begin{bmatrix} 1 & 0\\\\ 0 & \\gamma \\end{bmatrix} $$\n",
"\n",
"$$\n",
"f'(x) = 2Ax\n",
"$$"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"def my_f(x, A):\n",
" return 0.5 * x.dot(A.dot(x))\n",
"\n",
"def my_gradf(x, A):\n",
" return A.dot(x)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"plt.rc(\"text\", usetex=True)\n",
"\n",
"gammas = [0.1, 0.5, 1, 2, 3, 4, 5, 10, 20, 50, 100, 1000, 5000, 10000]\n",
"# gammas = [1]\n",
"num_iter_converg = []\n",
"for g in gammas:\n",
" A = np.array([[1, 0], \n",
" [0, g]], dtype=np.float64)\n",
" f = lambda x: my_f(x, A)\n",
" gradf = lambda x: my_gradf(x, A)\n",
"# x0 = np.random.rand(A.shape[0])\n",
"# x0 = np.sort(x0)\n",
"# x0 = x0[::-1]\n",
" x0 = np.array([g, 1], dtype=np.float64)\n",
"# print x0[1] / x0[0]\n",
" gd = methods.fo.GradientDescent(f, gradf, ss.ExactLineSearch4Quad(A))\n",
" x = gd.solve(x0, tol=1e-7, max_iter=100)\n",
" num_iter_converg.append(len(gd.get_convergence()))\n",
"\n",
"plt.figure(figsize=(8, 6))\n",
"plt.loglog(gammas, num_iter_converg)\n",
"plt.xticks(fontsize = 20)\n",
"plt.yticks(fontsize = 20)\n",
"plt.xlabel(r\"$\\gamma$\", fontsize=20)\n",
"plt.ylabel(r\"Number of iterations with $\\varepsilon = 10^{-7}$\", fontsize=20)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"- При неудачном начальном приближении сходимость для плохо обусловенной задачи очень медленная\n",
"- При случайном начальном приближении сходимость может быть гораздо быстрее теоретических оценок"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Эксперимент на многомерной задаче\n",
"Пусть $A \\in \\mathbb{R}^{m \\times n}$. Рассмотрим систему линейных неравенств: $Ax \\leq 1$ при условии $|x_i| \\leq 1$ для всех $i$.\n",
"\n",
"**Определение.** Аналитическим центром системы неравенств $Ax \\leq 1$ при условии $|x_i| \\leq 1$ является решение задачи\n",
"$$\n",
"f(x) = - \\sum_{i=1}^m \\log(1 - a_i^{\\top}x) - \\sum_{i = 1}^n \\log (1 - x^2_i) \\to \\min_x\n",
"$$\n",
"$$\n",
"f'(x) - ?\n",
"$$"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Точное решение с помощью CVXPy"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"import numpy as np\n",
"\n",
"n = 1000\n",
"m = 2000\n",
"A = np.random.rand(n, m)\n",
"\n",
"x = cvx.Variable(n)\n",
"\n",
"obj = cvx.Minimize(cvx.sum(-cvx.log(1 - A.T * x)) - \n",
" cvx.sum(cvx.log(1 - cvx.square(x))))\n",
"prob = cvx.Problem(obj)\n",
"prob.solve(solver=\"SCS\", verbose=True)\n",
"x = x.value\n",
"print(\"Optimal value =\", prob.value)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Решение с помощью градиентного спуска"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [],
"source": [
"import cvxpy as cvx\n",
"print(cvx.installed_solvers())\n",
"\n",
"# !pip install jax \n",
"# !pip install jaxlib\n",
"\n",
"import jax.numpy as jnp\n",
"import jax\n",
"\n",
"# from jax.config import config\n",
"# config.update(\"jax_enable_x64\", True)\n",
"\n",
"A = jnp.array(A)\n",
"print(A.dtype)\n",
"x0 = jnp.zeros(n)\n",
"f = lambda x: -jnp.sum(jnp.log(1 - A.T@x)) - jnp.sum(jnp.log(1 - x*x))\n",
"grad_f = lambda x: jnp.sum(A @ (jnp.diagflat(1 / (1 - A.T @ x))), \\\n",
" axis=1) + 2 * x / (1 - jnp.power(x, 2))\n",
"grad_f_jax = jax.grad(f)\n",
"print(jnp.linalg.norm(grad_f(x0) - grad_f_jax(x0)))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"Подробнее про jax, его возможности и особенности можно посмотреть например [тут](https://github.com/amkatrutsa/MIPT-Opt/blob/master/Fall2020/03-MatrixCalculus/jax_autodiff_tutorial.ipynb)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [],
"source": [
"gd = methods.fo.GradientDescent(f, grad_f_jax, ss.Backtracking(\"Armijo\", rho=0.5, beta=0.1, init_alpha=1.))\n",
"x = gd.solve(x0, tol=1e-5, max_iter=100, disp=True)\n",
"\n",
"x_conv = gd.get_convergence()\n",
"grad_conv = [jnp.linalg.norm(grad_f_jax(x)) for x in x_conv]\n",
"plt.figure(figsize=(8,6))\n",
"plt.semilogy(grad_conv, label=r\"$\\| f'(x_k) \\|_2$\")\n",
"plt.semilogy([np.linalg.norm(x - np.array(x_k)) for x_k in x_conv], label=r\"$\\|x_k - x^*\\|_2$\")\n",
"plt.semilogy([np.linalg.norm(prob.value - f(np.array(x_k))) for x_k in x_conv], label=r\"$\\|f(x_k) - f^*\\|_2$\")\n",
"plt.semilogy([np.linalg.norm(np.array(x_conv[i]) - np.array(x_conv[i+1])) for i in range(len(x_conv) - 1)], label=r\"$\\|x_k - x_{k+1}\\|_2$\")\n",
"plt.semilogy([np.linalg.norm(f(np.array(x_conv[i])) - f(np.array(x_conv[i+1]))) for i in range(len(x_conv) - 1)], label=r\"$\\|f(x_k) - f(x_{k+1})\\|_2$\")\n",
"plt.xlabel(r\"Number of iteration, $k$\", fontsize=20)\n",
"plt.ylabel(r\"Convergence rate\", fontsize=20)\n",
"plt.xticks(fontsize = 20)\n",
"plt.yticks(fontsize = 20)\n",
"plt.legend(loc=\"best\", fontsize=20)\n",
"plt.tight_layout()"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Pro & Contra\n",
"\n",
"Pro\n",
"- легко реализовать\n",
"- сходимость как минимум к стационарной точке\n",
"- параметры при выборе шага влияют на сходимость не столь сильно\n",
"- имеет многочисленные вариации\n",
"\n",
"Contra\n",
"- линейная сходимость для сильно выпуклых функций\n",
"- очень сильно зависит от числа обусловленности $f''(x)$, выбор начального приближения может помочь\n",
"- не является оптимальным для выпуклых функций с липшицевым градиентом и сильновыпуклых функций (см. [ускорение Нестерова](https://blogs.princeton.edu/imabandit/2013/04/01/acceleratedgradientdescent/))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Резюме\n",
"1. Методы спуска\n",
"2. Направление убывания\n",
"3. Метод градиентного спуска\n",
"4. Правила выбора шага\n",
"5. Теоремы сходимости\n",
"6. Эксперименты"
]
}
],
"metadata": {
"anaconda-cloud": {},
"celltoolbar": "Slideshow",
"kernelspec": {
"display_name": "Python 3 (cvxpy)",
"language": "python",
"name": "cvxpy"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.8"
},
"nbpresent": {
"slides": {
"b738dfa0-30f4-4350-8338-c31d236608ec": {
"id": "b738dfa0-30f4-4350-8338-c31d236608ec",
"prev": null,
"regions": {
"96278b08-d857-478b-803c-5921bd08bbcd": {
"attrs": {
"height": 0.8,
"width": 0.8,
"x": 0.1,
"y": 0.1
},
"content": {
"cell": "196b8a50-3d29-45c3-82b9-f4a09b49491d",
"part": "whole"
},
"id": "96278b08-d857-478b-803c-5921bd08bbcd"
},
"9b98a7cc-d9d4-4a02-ac7e-30168dcde7af": {
"attrs": {
"height": 0.4,
"width": 0.8,
"x": 0.1,
"y": 0.5
},
"content": {
"cell": "2a573842-172b-4931-b0dd-9c9d3c47a450",
"part": "whole"
},
"id": "9b98a7cc-d9d4-4a02-ac7e-30168dcde7af"
}
}
}
},
"themes": {}
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| mit |
LedaLima/incubator-spot | spot-oa/oa/proxy/ipynb_templates/Advanced_Mode_master.ipynb | 7 | 8193 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Apache Spot's Ipython Advanced Mode\n",
"## Proxy\n",
"\n",
"This guide provides examples about how to request data, show data with some cool libraries like pandas and more.\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Import Libraries**\n",
"\n",
"The next cell will import the necessary libraries to execute the functions. Do not remove"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import datetime\n",
"import pandas as pd\n",
"import numpy as np\n",
"import linecache, bisect\n",
"import os\n",
"\n",
"spath = os.getcwd()\n",
"path = spath.split(\"/\")\n",
"date = path[len(path)-1]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Request Data**\n",
"\n",
"In order to request data we are using Graphql (a query language for APIs, more info at: http://graphql.org/).\n",
"\n",
"We provide the function to make a data request, all you need is a query and variables\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def makeGraphqlRequest(query, variables):\n",
" return GraphQLClient.request(query, variables)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now that we have a function, we can run a query like this:\n",
"\n",
"*Note: There's no need to manually set the date for the query, by default the code will read the date from the current path"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"suspicious_query = \"\"\"query($date:SpotDateType) {\n",
" proxy {\n",
" suspicious(date:$date)\n",
" { clientIp\n",
" clientToServerBytes\n",
" datetime\n",
" duration\n",
" host\n",
" networkContext\n",
" referer\n",
" requestMethod\n",
" responseCode\n",
" responseCodeLabel\n",
" responseContentType\n",
" score\n",
" serverIp\n",
" serverToClientBytes\n",
" uri\n",
" uriPath\n",
" uriPort\n",
" uriQuery\n",
" uriRep\n",
" userAgent\n",
" username\n",
" webCategory \n",
" }\n",
" }\n",
" }\"\"\"\n",
"\n",
"##If you want to use a different date for your query, switch the \n",
"##commented/uncommented following lines\n",
"\n",
"variables={\n",
" 'date': datetime.datetime.strptime(date, '%Y%m%d').strftime('%Y-%m-%d')\n",
"# 'date': \"2016-10-08\"\n",
" }\n",
" \n",
"suspicious_request = makeGraphqlRequest(suspicious_query,variables)\n",
"\n",
"##The variable suspicious_request will contain the resulting data from the query.\n",
"results = suspicious_request['data']['proxy']['suspicious']\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##Pandas Dataframes\n",
"\n",
"The following cell loads the results into a pandas dataframe\n",
"\n",
"For more information on how to use pandas, you can learn more here: https://pandas.pydata.org/pandas-docs/stable/10min.html"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"df = pd.read_json(json.dumps(results))\n",
"##Printing only the selected column list from the dataframe\n",
"##Unless specified otherwise, \n",
"print df[['clientIp','uriQuery','datetime','clientToServerBytes','serverToClientBytes', 'host']]\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##Additional operations \n",
"\n",
"Additional operations can be performed on the dataframe like sorting the data, filtering it and grouping it\n",
"\n",
"**Filtering the data**"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"##Filter results where the destination port = 3389\n",
"##The resulting data will be stored in df2 \n",
"\n",
"df2 = df[df['clientIp'].isin(['10.173.202.136'])]\n",
"print df2[['clientIp','uriQuery','datetime','host']]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Ordering the data**"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"srtd = df.sort_values(by=\"host\")\n",
"print srtd[['host','clientIp','uriQuery','datetime']]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Grouping the data**"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"## This command will group the results by pairs of source-destination IP\n",
"## summarizing all other columns \n",
"grpd = df.groupby(['clientIp','host']).sum()\n",
"## This will print the resulting dataframe displaying the input and output bytes columnns\n",
"print grpd[[\"clientToServerBytes\",\"serverToClientBytes\"]]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Reset Scored Connections**\n",
"\n",
"Uncomment and execute the following cell to reset all scored connections for this day"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# reset_scores = \"\"\"mutation($date:SpotDateType!) {\n",
"# proxy{\n",
"# resetScoredConnections(date:$date){\n",
"# success\n",
"# }\n",
"# }\n",
"# }\"\"\"\n",
"\n",
"\n",
"# variables={\n",
"# 'date': datetime.datetime.strptime(date, '%Y%m%d').strftime('%Y-%m-%d')\n",
"# }\n",
" \n",
"# request = makeGraphqlRequest(reset_scores,variables)\n",
"\n",
"\n",
"# print request['data']['proxy']['resetScoredConnections']['success']"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##Sandbox\n",
"\n",
"At this point you can perform your own analysis using the previously provided functions as a guide.\n",
"\n",
"Happy threat hunting!"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"#Your code here"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.10"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| apache-2.0 |
debsankha/network_course_python | exercises/04-exercise-visualization.ipynb | 1 | 3137 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**3.Graph Layouts**"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"a) Which layouts do you think would fit best to which kind of graphs?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"b) Create a random graph containing about 50 nodes. Assign random values\n",
"∈ [0, 1] to the edges as ’radius’ attributes."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"c) Display the graph using the spring layout. Use the edge’s ‘radius’ at-\n",
"tributes as weights for the spring layout."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"d) Display the graph using the shell layout. Distribute the nodes across 5\n",
"different shells."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"e)** Try to display the graph in a 3-dimensional spring layout (hint: use mat-\n",
"plotlib’s mplot3d toolkit). Scale the color and width of the edges according\n",
"to their radius."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**E3.2 Graph Colorings**"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"a) Load the graph from the file `../data/visualization/huge_graph.xml`. How large is the\n",
"graph?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"b) Plot the graph using its ‘x’ and ‘y’ node attributes as coordinates and the\n",
"edge’s ‘radius’ attribute as edge-widhts. What kind of graph is this?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"c) Choose colors, linewidths, marker- and linestyles in a way that they sup-\n",
"port the information contained in the graph (very subjective :-))."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"d) What is the maximum degree of the nodes in the graph? Color the nodes\n",
"differently according to their degree. Scale the node sizes according to the\n",
"graph’s node attribute ‘conductivity’."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"e)* Color the thickest 15% of the edges differently than the rest to highlight\n",
"them."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"f)** Try to find the outermost cycle of the graph and color it differently."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.1"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| gpl-2.0 |
alexwhb/algorithm-practice | jupyter-notebooks/data structures/Binary Search Tree.ipynb | 1 | 6408 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Binary Search Trees (BST)\n",
"Binary Search trees are a data structure that has many advantages over arrays and linked lists. With a binary search tree you are able to both treverse the tree fast to find nodes, and you can insert and delete nodse much faster than in an array, because you don't have to traverse the whole array and move each element to the fill the blank space. They also can work as a sorting algorithem that is very effecent. O(nlog(n))\n",
"\n",
"BST are binary... meaning they have two children per node... a right and a left. The rule with a BST is that all children to the left of the node must equal to or smalller than the value stored in the parent node. All the values in the right node must be greater than the parent node. \n",
"\n",
"Now BST's are not ideal if they are very very unballanced, which can happen fairly easily, so there are lots of algorithems to not let the trees get too unblananced and force the hight to be more reasnible, which increases traversal effecency. \n",
"\n",
"there is a possiblity that a BST that is not ballenced with some algorithem, could potentally just turn into a linked list, where your lookup time will end up being linear time, which is not good in this case. \n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class Node(object):\n",
" def __init__(self, value=None):\n",
" self.value = value \n",
" self.lChild = None\n",
" self.rChild = None"
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"class Tree(object):\n",
" def __init__(self):\n",
" self.size = 0\n",
" self.root = None\n",
" \n",
" def insert(self, root, node):\n",
" if root is None:\n",
" root = Node()\n",
" else:\n",
" if root.value > node.value:\n",
" if root.lChild is None:\n",
" root.lChild = node\n",
" else:\n",
" self.insert(root.lChild, node)\n",
" else:\n",
" if root.rChild is None: \n",
" root.rChild = node\n",
" else:\n",
" self.insert(root.rChild, node)\n",
" \n",
" def in_order_print(self, root):\n",
" if root is None: \n",
" return\n",
" else:\n",
" self.in_order_print(root.lChild)\n",
" print(root.value)\n",
" self.in_order_print(root.rChild)\n",
" "
]
},
{
"cell_type": "code",
"execution_count": 35,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"3\n",
"12\n",
"33\n",
"50\n",
"65\n",
"88\n",
"93\n"
]
}
],
"source": [
"root = Node(50)\n",
"n2 = Node(30)\n",
"n3 = Node(70)\n",
"n4 = Node(65)\n",
"n5 = Node(55)\n",
"\n",
"tree = Tree()\n",
"\n",
"tree.insert(root, Node(93))\n",
"tree.insert(root, Node(33))\n",
"tree.insert(root, Node(88))\n",
"tree.insert(root, Node(65))\n",
"tree.insert(root, Node(3))\n",
"tree.insert(root, Node(12))\n",
"\n",
"# print(root.lChild.value)\n",
"tree.in_order_print(root)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"# The AVL method of bllencing BST's:\n",
"[Here](https://interactivepython.org/runestone/static/pythonds/Trees/AVLTreeImplementation.html) is the awesome resource I used to solidify my understanding of this info. [Here's a video on AVL trees](https://www.youtube.com/watch?v=rbg7Qf8GkQ4)\n",
"\n",
"Basicly the concept behind AVL trees is that you set a value for the hight of each node in the tree. If any side of the tree has a hight grater than the oppiste side by more than one we have to move nodes around in such a way that we satisife that condition. \n",
"\n",
"There are 4 types of cases where we need rotations: right right, right left, left left, left right. In each of these cases we do a diferent mode of rotation to keep the tree ballenced. \n",
"\n",
"There are two base cases to this, because this process is recursive: \n",
" * The recursive call has reached the root of the tree.\n",
" * The balance factor of the parent has been adjusted to zero. You should convince yourself that once a subtree has a balance factor of zero, then the balance of its ancestor nodes does not change.\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class Node(object):\n",
" def __init__(self, value, parrent):\n",
" self.value = value\n",
" self.parrent = parrent\n",
" self.rightChild = None\n",
" self.leftChile = None\n",
"\n",
"class AvlBst(object):\n",
" def __init__(self):\n",
" self.root = None\n",
" self.size = 0\n",
" \n",
" def add(self, node:Node):\n",
" if self.root is None:\n",
" self.root = node\n",
" else:\n",
" pass\n",
" \n",
" def find(self, value) -> Node:\n",
" pass\n",
" \n",
" def remove(self, node):\n",
" pass\n",
" \n",
" @property\n",
" def height(self) -> int:\n",
" pass\n",
" \n",
" @property\n",
" def ballance_factor(self) -> int:\n",
" pass"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.1"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| mit |
FranciscoBraga/AprendendoPython | conexão_com_banco_sqlite/Criando um Banco SqLite.ipynb | 1 | 6670 | {
"cells": [
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"ename": "SyntaxError",
"evalue": "invalid syntax (<ipython-input-9-a89637ef5f0d>, line 1)",
"output_type": "error",
"traceback": [
"\u001b[1;36m File \u001b[1;32m\"<ipython-input-9-a89637ef5f0d>\"\u001b[1;36m, line \u001b[1;32m1\u001b[0m\n\u001b[1;33m encoding: utf-8\u001b[0m\n\u001b[1;37m ^\u001b[0m\n\u001b[1;31mSyntaxError\u001b[0m\u001b[1;31m:\u001b[0m invalid syntax\n"
]
}
],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"#importando o módulo de acesso SQLite\n",
"import sqlite3"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"#cria uma conexão com o banco\n",
"#se o banco não exitir é criado\n",
"con = sqlite3.connect('escola.db')"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"#criando um curso para poder percorrer todos os registros de um banco de dados\n",
"cursor=con.cursor()"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"#cria uma instrução sql\n",
"sql_create = 'create table cursos'\\\n",
"'(id integer primary key,'\\\n",
"'titulo varchar(100),'\\\n",
"'categoria varchar(140))'"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<sqlite3.Cursor at 0x4116f80>"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"#executando a instrução sql no cursor\n",
"cursor.execute(sql_create)"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"#criando outra setença SQL para inserir registros \n",
"sql_insert ='insert into cursos values (?,?,?)'"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"#dados\n",
"recset=[(1000,'Ciencia de Dados','Data Science'),\n",
" (1001,'Big Data Fundamentos','Big Data'),\n",
" (1002,'Python Fundamentos','Analise de Dados')]"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"#inserindo os registros\n",
"for rec in recset:\n",
" cursor.execute(sql_insert ,rec)"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"#grava no banco\n",
"con.commit()"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"#selecionando registro\n",
"sql_select ='select * from cursos'"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<sqlite3.Cursor at 0x4116f80>"
]
},
"execution_count": 14,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"#selecionado todos os registros\n",
"cursor.execute(sql_select)"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"#recupera os dados\n",
"dados = cursor.fetchall()"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Curso: 1000, Titulo: Ciencia de Dados, Categoria: Data Science \n",
"\n",
"Curso: 1001, Titulo: Big Data Fundamentos, Categoria: Big Data \n",
"\n",
"Curso: 1002, Titulo: Python Fundamentos, Categoria: Analise de Dados \n",
"\n"
]
}
],
"source": [
"#mostrando os dados\n",
"for linha in dados:\n",
" print('Curso: %s, Titulo: %s, Categoria: %s \\n' %linha)"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Curso: 1000, Titulo: Ciencia de Dados, Categoria: Data Science \n",
"\n",
"Curso: 1001, Titulo: Big Data Fundamentos, Categoria: Big Data \n",
"\n",
"Curso: 1002, Titulo: Python Fundamentos, Categoria: Analise de Dados \n",
"\n",
"Curso: 1003, Titulo: Gestao de dados com MongoDB, Categoria: Big Data \n",
"\n",
"Curso: 1004, Titulo: R Fundamentos, Categoria: Analise de dados \n",
"\n",
"Curso: 1005, Titulo: Gestao de dados com MongoDB, Categoria: Big Data \n",
"\n",
"Curso: 1006, Titulo: R Fundamentos, Categoria: Analise de dados \n",
"\n"
]
}
],
"source": [
"#gravando registros no banco\n",
"recset=[(1005,'Gestao de dados com MongoDB', 'Big Data'),\n",
" (1006,'R Fundamentos','Analise de dados')]\n",
"\n",
"#inserindo um registro\n",
"for rec in recset:\n",
" cursor.execute(sql_insert, rec)\n",
"\n",
"#grava no banco\n",
"con.commit()\n",
"\n",
"#selecionando o dados\n",
"cursor.execute(sql_select)\n",
"\n",
"#recupera os dados\n",
"dados = cursor.fetchall()\n",
"\n",
"#mostranaod os dados\n",
"for linha in dados:\n",
"\n",
" print('Curso: %s, Titulo: %s, Categoria: %s \\n' %linha)"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"#fechando a conexao\n",
"con.close()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.13"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| apache-2.0 |
alfkjartan/nvgimu | notebooks/.ipynb_checkpoints/Get started-checkpoint.ipynb | 1 | 182290 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Getting started with the analysis of nvg data\n",
"This notebook assumes that data exists in a database in the hdf5 format. For instructions how to set up the database with data see [../readme.md].\n",
"\n",
"## Import modules"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"import nvg.ximu.ximudata as ximudata\n",
"%matplotlib notebook"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Load the database"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"reload(ximudata)\n",
"dbfilename = \"/home/kjartan/Dropbox/Public/nvg201209.hdf5\"\n",
"db = ximudata.NVGData(dbfilename);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Explore contents of the database file"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Subjects: [u'S10', u'S11', u'S12', u'S2', u'S3', u'S4', u'S5', u'S6', u'S7', u'S8', u'S9']\n",
"Trials: [u'B', u'D', u'M', u'N']\n",
"IMUs: [u'B', u'LA', u'LH', u'LT', u'N', u'RA', u'RH', u'RT']\n",
"Attributes of example trial [u'PNAtICLA', u'PNAtICRA', u'PNAtCycleEvents', u'cycleFrequency', u'verticalDisplacement']\n",
"Shape of example IMU data entry (87243, 10)\n"
]
}
],
"source": [
"dbfile = db.hdfFile;\n",
"print \"Subjects: \", dbfile.keys()\n",
"print \"Trials: \", dbfile['S5'].keys()\n",
"print \"IMUs: \", dbfile['S5/B'].keys()\n",
"print \"Attributes of example trial\", dbfile['S5/B'].attrs.keys()\n",
"print \"Shape of example IMU data entry\", dbfile['S5/B/N'].shape\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## The content of the raw IMU file\n",
"The columns of the IMU data contain: \n",
"0: Packet number, \n",
"1: Gyroscope X (deg/s),\n",
"2: Gyroscope Y (deg/s),\n",
"3: Gyroscope Z (deg/s),\n",
"4: Accelerometer X (g),\n",
"5: Accelerometer Y (g),\n",
"6: Accelerometer Z (g),\n",
"7: Magnetometer X (G),\n",
"8: Magnetometer Y (G),\n",
"9: Magnetometer Z (G)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Plot example data\n"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"application/javascript": [
"/* Put everything inside the global mpl namespace */\n",
"window.mpl = {};\n",
"\n",
"mpl.get_websocket_type = function() {\n",
" if (typeof(WebSocket) !== 'undefined') {\n",
" return WebSocket;\n",
" } else if (typeof(MozWebSocket) !== 'undefined') {\n",
" return MozWebSocket;\n",
" } else {\n",
" alert('Your browser does not have WebSocket support.' +\n",
" 'Please try Chrome, Safari or Firefox ≥ 6. ' +\n",
" 'Firefox 4 and 5 are also supported but you ' +\n",
" 'have to enable WebSockets in about:config.');\n",
" };\n",
"}\n",
"\n",
"mpl.figure = function(figure_id, websocket, ondownload, parent_element) {\n",
" this.id = figure_id;\n",
"\n",
" this.ws = websocket;\n",
"\n",
" this.supports_binary = (this.ws.binaryType != undefined);\n",
"\n",
" if (!this.supports_binary) {\n",
" var warnings = document.getElementById(\"mpl-warnings\");\n",
" if (warnings) {\n",
" warnings.style.display = 'block';\n",
" warnings.textContent = (\n",
" \"This browser does not support binary websocket messages. \" +\n",
" \"Performance may be slow.\");\n",
" }\n",
" }\n",
"\n",
" this.imageObj = new Image();\n",
"\n",
" this.context = undefined;\n",
" this.message = undefined;\n",
" this.canvas = undefined;\n",
" this.rubberband_canvas = undefined;\n",
" this.rubberband_context = undefined;\n",
" this.format_dropdown = undefined;\n",
"\n",
" this.image_mode = 'full';\n",
"\n",
" this.root = $('<div/>');\n",
" this._root_extra_style(this.root)\n",
" this.root.attr('style', 'display: inline-block');\n",
"\n",
" $(parent_element).append(this.root);\n",
"\n",
" this._init_header(this);\n",
" this._init_canvas(this);\n",
" this._init_toolbar(this);\n",
"\n",
" var fig = this;\n",
"\n",
" this.waiting = false;\n",
"\n",
" this.ws.onopen = function () {\n",
" fig.send_message(\"supports_binary\", {value: fig.supports_binary});\n",
" fig.send_message(\"send_image_mode\", {});\n",
" fig.send_message(\"refresh\", {});\n",
" }\n",
"\n",
" this.imageObj.onload = function() {\n",
" if (fig.image_mode == 'full') {\n",
" // Full images could contain transparency (where diff images\n",
" // almost always do), so we need to clear the canvas so that\n",
" // there is no ghosting.\n",
" fig.context.clearRect(0, 0, fig.canvas.width, fig.canvas.height);\n",
" }\n",
" fig.context.drawImage(fig.imageObj, 0, 0);\n",
" };\n",
"\n",
" this.imageObj.onunload = function() {\n",
" this.ws.close();\n",
" }\n",
"\n",
" this.ws.onmessage = this._make_on_message_function(this);\n",
"\n",
" this.ondownload = ondownload;\n",
"}\n",
"\n",
"mpl.figure.prototype._init_header = function() {\n",
" var titlebar = $(\n",
" '<div class=\"ui-dialog-titlebar ui-widget-header ui-corner-all ' +\n",
" 'ui-helper-clearfix\"/>');\n",
" var titletext = $(\n",
" '<div class=\"ui-dialog-title\" style=\"width: 100%; ' +\n",
" 'text-align: center; padding: 3px;\"/>');\n",
" titlebar.append(titletext)\n",
" this.root.append(titlebar);\n",
" this.header = titletext[0];\n",
"}\n",
"\n",
"\n",
"\n",
"mpl.figure.prototype._canvas_extra_style = function(canvas_div) {\n",
"\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype._root_extra_style = function(canvas_div) {\n",
"\n",
"}\n",
"\n",
"mpl.figure.prototype._init_canvas = function() {\n",
" var fig = this;\n",
"\n",
" var canvas_div = $('<div/>');\n",
"\n",
" canvas_div.attr('style', 'position: relative; clear: both; outline: 0');\n",
"\n",
" function canvas_keyboard_event(event) {\n",
" return fig.key_event(event, event['data']);\n",
" }\n",
"\n",
" canvas_div.keydown('key_press', canvas_keyboard_event);\n",
" canvas_div.keyup('key_release', canvas_keyboard_event);\n",
" this.canvas_div = canvas_div\n",
" this._canvas_extra_style(canvas_div)\n",
" this.root.append(canvas_div);\n",
"\n",
" var canvas = $('<canvas/>');\n",
" canvas.addClass('mpl-canvas');\n",
" canvas.attr('style', \"left: 0; top: 0; z-index: 0; outline: 0\")\n",
"\n",
" this.canvas = canvas[0];\n",
" this.context = canvas[0].getContext(\"2d\");\n",
"\n",
" var rubberband = $('<canvas/>');\n",
" rubberband.attr('style', \"position: absolute; left: 0; top: 0; z-index: 1;\")\n",
"\n",
" var pass_mouse_events = true;\n",
"\n",
" canvas_div.resizable({\n",
" start: function(event, ui) {\n",
" pass_mouse_events = false;\n",
" },\n",
" resize: function(event, ui) {\n",
" fig.request_resize(ui.size.width, ui.size.height);\n",
" },\n",
" stop: function(event, ui) {\n",
" pass_mouse_events = true;\n",
" fig.request_resize(ui.size.width, ui.size.height);\n",
" },\n",
" });\n",
"\n",
" function mouse_event_fn(event) {\n",
" if (pass_mouse_events)\n",
" return fig.mouse_event(event, event['data']);\n",
" }\n",
"\n",
" rubberband.mousedown('button_press', mouse_event_fn);\n",
" rubberband.mouseup('button_release', mouse_event_fn);\n",
" // Throttle sequential mouse events to 1 every 20ms.\n",
" rubberband.mousemove('motion_notify', mouse_event_fn);\n",
"\n",
" rubberband.mouseenter('figure_enter', mouse_event_fn);\n",
" rubberband.mouseleave('figure_leave', mouse_event_fn);\n",
"\n",
" canvas_div.on(\"wheel\", function (event) {\n",
" event = event.originalEvent;\n",
" event['data'] = 'scroll'\n",
" if (event.deltaY < 0) {\n",
" event.step = 1;\n",
" } else {\n",
" event.step = -1;\n",
" }\n",
" mouse_event_fn(event);\n",
" });\n",
"\n",
" canvas_div.append(canvas);\n",
" canvas_div.append(rubberband);\n",
"\n",
" this.rubberband = rubberband;\n",
" this.rubberband_canvas = rubberband[0];\n",
" this.rubberband_context = rubberband[0].getContext(\"2d\");\n",
" this.rubberband_context.strokeStyle = \"#000000\";\n",
"\n",
" this._resize_canvas = function(width, height) {\n",
" // Keep the size of the canvas, canvas container, and rubber band\n",
" // canvas in synch.\n",
" canvas_div.css('width', width)\n",
" canvas_div.css('height', height)\n",
"\n",
" canvas.attr('width', width);\n",
" canvas.attr('height', height);\n",
"\n",
" rubberband.attr('width', width);\n",
" rubberband.attr('height', height);\n",
" }\n",
"\n",
" // Set the figure to an initial 600x600px, this will subsequently be updated\n",
" // upon first draw.\n",
" this._resize_canvas(600, 600);\n",
"\n",
" // Disable right mouse context menu.\n",
" $(this.rubberband_canvas).bind(\"contextmenu\",function(e){\n",
" return false;\n",
" });\n",
"\n",
" function set_focus () {\n",
" canvas.focus();\n",
" canvas_div.focus();\n",
" }\n",
"\n",
" window.setTimeout(set_focus, 100);\n",
"}\n",
"\n",
"mpl.figure.prototype._init_toolbar = function() {\n",
" var fig = this;\n",
"\n",
" var nav_element = $('<div/>')\n",
" nav_element.attr('style', 'width: 100%');\n",
" this.root.append(nav_element);\n",
"\n",
" // Define a callback function for later on.\n",
" function toolbar_event(event) {\n",
" return fig.toolbar_button_onclick(event['data']);\n",
" }\n",
" function toolbar_mouse_event(event) {\n",
" return fig.toolbar_button_onmouseover(event['data']);\n",
" }\n",
"\n",
" for(var toolbar_ind in mpl.toolbar_items) {\n",
" var name = mpl.toolbar_items[toolbar_ind][0];\n",
" var tooltip = mpl.toolbar_items[toolbar_ind][1];\n",
" var image = mpl.toolbar_items[toolbar_ind][2];\n",
" var method_name = mpl.toolbar_items[toolbar_ind][3];\n",
"\n",
" if (!name) {\n",
" // put a spacer in here.\n",
" continue;\n",
" }\n",
" var button = $('<button/>');\n",
" button.addClass('ui-button ui-widget ui-state-default ui-corner-all ' +\n",
" 'ui-button-icon-only');\n",
" button.attr('role', 'button');\n",
" button.attr('aria-disabled', 'false');\n",
" button.click(method_name, toolbar_event);\n",
" button.mouseover(tooltip, toolbar_mouse_event);\n",
"\n",
" var icon_img = $('<span/>');\n",
" icon_img.addClass('ui-button-icon-primary ui-icon');\n",
" icon_img.addClass(image);\n",
" icon_img.addClass('ui-corner-all');\n",
"\n",
" var tooltip_span = $('<span/>');\n",
" tooltip_span.addClass('ui-button-text');\n",
" tooltip_span.html(tooltip);\n",
"\n",
" button.append(icon_img);\n",
" button.append(tooltip_span);\n",
"\n",
" nav_element.append(button);\n",
" }\n",
"\n",
" var fmt_picker_span = $('<span/>');\n",
"\n",
" var fmt_picker = $('<select/>');\n",
" fmt_picker.addClass('mpl-toolbar-option ui-widget ui-widget-content');\n",
" fmt_picker_span.append(fmt_picker);\n",
" nav_element.append(fmt_picker_span);\n",
" this.format_dropdown = fmt_picker[0];\n",
"\n",
" for (var ind in mpl.extensions) {\n",
" var fmt = mpl.extensions[ind];\n",
" var option = $(\n",
" '<option/>', {selected: fmt === mpl.default_extension}).html(fmt);\n",
" fmt_picker.append(option)\n",
" }\n",
"\n",
" // Add hover states to the ui-buttons\n",
" $( \".ui-button\" ).hover(\n",
" function() { $(this).addClass(\"ui-state-hover\");},\n",
" function() { $(this).removeClass(\"ui-state-hover\");}\n",
" );\n",
"\n",
" var status_bar = $('<span class=\"mpl-message\"/>');\n",
" nav_element.append(status_bar);\n",
" this.message = status_bar[0];\n",
"}\n",
"\n",
"mpl.figure.prototype.request_resize = function(x_pixels, y_pixels) {\n",
" // Request matplotlib to resize the figure. Matplotlib will then trigger a resize in the client,\n",
" // which will in turn request a refresh of the image.\n",
" this.send_message('resize', {'width': x_pixels, 'height': y_pixels});\n",
"}\n",
"\n",
"mpl.figure.prototype.send_message = function(type, properties) {\n",
" properties['type'] = type;\n",
" properties['figure_id'] = this.id;\n",
" this.ws.send(JSON.stringify(properties));\n",
"}\n",
"\n",
"mpl.figure.prototype.send_draw_message = function() {\n",
" if (!this.waiting) {\n",
" this.waiting = true;\n",
" this.ws.send(JSON.stringify({type: \"draw\", figure_id: this.id}));\n",
" }\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype.handle_save = function(fig, msg) {\n",
" var format_dropdown = fig.format_dropdown;\n",
" var format = format_dropdown.options[format_dropdown.selectedIndex].value;\n",
" fig.ondownload(fig, format);\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype.handle_resize = function(fig, msg) {\n",
" var size = msg['size'];\n",
" if (size[0] != fig.canvas.width || size[1] != fig.canvas.height) {\n",
" fig._resize_canvas(size[0], size[1]);\n",
" fig.send_message(\"refresh\", {});\n",
" };\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_rubberband = function(fig, msg) {\n",
" var x0 = msg['x0'];\n",
" var y0 = fig.canvas.height - msg['y0'];\n",
" var x1 = msg['x1'];\n",
" var y1 = fig.canvas.height - msg['y1'];\n",
" x0 = Math.floor(x0) + 0.5;\n",
" y0 = Math.floor(y0) + 0.5;\n",
" x1 = Math.floor(x1) + 0.5;\n",
" y1 = Math.floor(y1) + 0.5;\n",
" var min_x = Math.min(x0, x1);\n",
" var min_y = Math.min(y0, y1);\n",
" var width = Math.abs(x1 - x0);\n",
" var height = Math.abs(y1 - y0);\n",
"\n",
" fig.rubberband_context.clearRect(\n",
" 0, 0, fig.canvas.width, fig.canvas.height);\n",
"\n",
" fig.rubberband_context.strokeRect(min_x, min_y, width, height);\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_figure_label = function(fig, msg) {\n",
" // Updates the figure title.\n",
" fig.header.textContent = msg['label'];\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_cursor = function(fig, msg) {\n",
" var cursor = msg['cursor'];\n",
" switch(cursor)\n",
" {\n",
" case 0:\n",
" cursor = 'pointer';\n",
" break;\n",
" case 1:\n",
" cursor = 'default';\n",
" break;\n",
" case 2:\n",
" cursor = 'crosshair';\n",
" break;\n",
" case 3:\n",
" cursor = 'move';\n",
" break;\n",
" }\n",
" fig.rubberband_canvas.style.cursor = cursor;\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_message = function(fig, msg) {\n",
" fig.message.textContent = msg['message'];\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_draw = function(fig, msg) {\n",
" // Request the server to send over a new figure.\n",
" fig.send_draw_message();\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_image_mode = function(fig, msg) {\n",
" fig.image_mode = msg['mode'];\n",
"}\n",
"\n",
"mpl.figure.prototype.updated_canvas_event = function() {\n",
" // Called whenever the canvas gets updated.\n",
" this.send_message(\"ack\", {});\n",
"}\n",
"\n",
"// A function to construct a web socket function for onmessage handling.\n",
"// Called in the figure constructor.\n",
"mpl.figure.prototype._make_on_message_function = function(fig) {\n",
" return function socket_on_message(evt) {\n",
" if (evt.data instanceof Blob) {\n",
" /* FIXME: We get \"Resource interpreted as Image but\n",
" * transferred with MIME type text/plain:\" errors on\n",
" * Chrome. But how to set the MIME type? It doesn't seem\n",
" * to be part of the websocket stream */\n",
" evt.data.type = \"image/png\";\n",
"\n",
" /* Free the memory for the previous frames */\n",
" if (fig.imageObj.src) {\n",
" (window.URL || window.webkitURL).revokeObjectURL(\n",
" fig.imageObj.src);\n",
" }\n",
"\n",
" fig.imageObj.src = (window.URL || window.webkitURL).createObjectURL(\n",
" evt.data);\n",
" fig.updated_canvas_event();\n",
" fig.waiting = false;\n",
" return;\n",
" }\n",
" else if (typeof evt.data === 'string' && evt.data.slice(0, 21) == \"data:image/png;base64\") {\n",
" fig.imageObj.src = evt.data;\n",
" fig.updated_canvas_event();\n",
" fig.waiting = false;\n",
" return;\n",
" }\n",
"\n",
" var msg = JSON.parse(evt.data);\n",
" var msg_type = msg['type'];\n",
"\n",
" // Call the \"handle_{type}\" callback, which takes\n",
" // the figure and JSON message as its only arguments.\n",
" try {\n",
" var callback = fig[\"handle_\" + msg_type];\n",
" } catch (e) {\n",
" console.log(\"No handler for the '\" + msg_type + \"' message type: \", msg);\n",
" return;\n",
" }\n",
"\n",
" if (callback) {\n",
" try {\n",
" // console.log(\"Handling '\" + msg_type + \"' message: \", msg);\n",
" callback(fig, msg);\n",
" } catch (e) {\n",
" console.log(\"Exception inside the 'handler_\" + msg_type + \"' callback:\", e, e.stack, msg);\n",
" }\n",
" }\n",
" };\n",
"}\n",
"\n",
"// from http://stackoverflow.com/questions/1114465/getting-mouse-location-in-canvas\n",
"mpl.findpos = function(e) {\n",
" //this section is from http://www.quirksmode.org/js/events_properties.html\n",
" var targ;\n",
" if (!e)\n",
" e = window.event;\n",
" if (e.target)\n",
" targ = e.target;\n",
" else if (e.srcElement)\n",
" targ = e.srcElement;\n",
" if (targ.nodeType == 3) // defeat Safari bug\n",
" targ = targ.parentNode;\n",
"\n",
" // jQuery normalizes the pageX and pageY\n",
" // pageX,Y are the mouse positions relative to the document\n",
" // offset() returns the position of the element relative to the document\n",
" var x = e.pageX - $(targ).offset().left;\n",
" var y = e.pageY - $(targ).offset().top;\n",
"\n",
" return {\"x\": x, \"y\": y};\n",
"};\n",
"\n",
"/*\n",
" * return a copy of an object with only non-object keys\n",
" * we need this to avoid circular references\n",
" * http://stackoverflow.com/a/24161582/3208463\n",
" */\n",
"function simpleKeys (original) {\n",
" return Object.keys(original).reduce(function (obj, key) {\n",
" if (typeof original[key] !== 'object')\n",
" obj[key] = original[key]\n",
" return obj;\n",
" }, {});\n",
"}\n",
"\n",
"mpl.figure.prototype.mouse_event = function(event, name) {\n",
" var canvas_pos = mpl.findpos(event)\n",
"\n",
" if (name === 'button_press')\n",
" {\n",
" this.canvas.focus();\n",
" this.canvas_div.focus();\n",
" }\n",
"\n",
" var x = canvas_pos.x;\n",
" var y = canvas_pos.y;\n",
"\n",
" this.send_message(name, {x: x, y: y, button: event.button,\n",
" step: event.step,\n",
" guiEvent: simpleKeys(event)});\n",
"\n",
" /* This prevents the web browser from automatically changing to\n",
" * the text insertion cursor when the button is pressed. We want\n",
" * to control all of the cursor setting manually through the\n",
" * 'cursor' event from matplotlib */\n",
" event.preventDefault();\n",
" return false;\n",
"}\n",
"\n",
"mpl.figure.prototype._key_event_extra = function(event, name) {\n",
" // Handle any extra behaviour associated with a key event\n",
"}\n",
"\n",
"mpl.figure.prototype.key_event = function(event, name) {\n",
"\n",
" // Prevent repeat events\n",
" if (name == 'key_press')\n",
" {\n",
" if (event.which === this._key)\n",
" return;\n",
" else\n",
" this._key = event.which;\n",
" }\n",
" if (name == 'key_release')\n",
" this._key = null;\n",
"\n",
" var value = '';\n",
" if (event.ctrlKey && event.which != 17)\n",
" value += \"ctrl+\";\n",
" if (event.altKey && event.which != 18)\n",
" value += \"alt+\";\n",
" if (event.shiftKey && event.which != 16)\n",
" value += \"shift+\";\n",
"\n",
" value += 'k';\n",
" value += event.which.toString();\n",
"\n",
" this._key_event_extra(event, name);\n",
"\n",
" this.send_message(name, {key: value,\n",
" guiEvent: simpleKeys(event)});\n",
" return false;\n",
"}\n",
"\n",
"mpl.figure.prototype.toolbar_button_onclick = function(name) {\n",
" if (name == 'download') {\n",
" this.handle_save(this, null);\n",
" } else {\n",
" this.send_message(\"toolbar_button\", {name: name});\n",
" }\n",
"};\n",
"\n",
"mpl.figure.prototype.toolbar_button_onmouseover = function(tooltip) {\n",
" this.message.textContent = tooltip;\n",
"};\n",
"mpl.toolbar_items = [[\"Home\", \"Reset original view\", \"fa fa-home icon-home\", \"home\"], [\"Back\", \"Back to previous view\", \"fa fa-arrow-left icon-arrow-left\", \"back\"], [\"Forward\", \"Forward to next view\", \"fa fa-arrow-right icon-arrow-right\", \"forward\"], [\"\", \"\", \"\", \"\"], [\"Pan\", \"Pan axes with left mouse, zoom with right\", \"fa fa-arrows icon-move\", \"pan\"], [\"Zoom\", \"Zoom to rectangle\", \"fa fa-square-o icon-check-empty\", \"zoom\"], [\"\", \"\", \"\", \"\"], [\"Download\", \"Download plot\", \"fa fa-floppy-o icon-save\", \"download\"]];\n",
"\n",
"mpl.extensions = [\"eps\", \"jpeg\", \"pdf\", \"png\", \"ps\", \"raw\", \"svg\", \"tif\"];\n",
"\n",
"mpl.default_extension = \"png\";var comm_websocket_adapter = function(comm) {\n",
" // Create a \"websocket\"-like object which calls the given IPython comm\n",
" // object with the appropriate methods. Currently this is a non binary\n",
" // socket, so there is still some room for performance tuning.\n",
" var ws = {};\n",
"\n",
" ws.close = function() {\n",
" comm.close()\n",
" };\n",
" ws.send = function(m) {\n",
" //console.log('sending', m);\n",
" comm.send(m);\n",
" };\n",
" // Register the callback with on_msg.\n",
" comm.on_msg(function(msg) {\n",
" //console.log('receiving', msg['content']['data'], msg);\n",
" // Pass the mpl event to the overriden (by mpl) onmessage function.\n",
" ws.onmessage(msg['content']['data'])\n",
" });\n",
" return ws;\n",
"}\n",
"\n",
"mpl.mpl_figure_comm = function(comm, msg) {\n",
" // This is the function which gets called when the mpl process\n",
" // starts-up an IPython Comm through the \"matplotlib\" channel.\n",
"\n",
" var id = msg.content.data.id;\n",
" // Get hold of the div created by the display call when the Comm\n",
" // socket was opened in Python.\n",
" var element = $(\"#\" + id);\n",
" var ws_proxy = comm_websocket_adapter(comm)\n",
"\n",
" function ondownload(figure, format) {\n",
" window.open(figure.imageObj.src);\n",
" }\n",
"\n",
" var fig = new mpl.figure(id, ws_proxy,\n",
" ondownload,\n",
" element.get(0));\n",
"\n",
" // Call onopen now - mpl needs it, as it is assuming we've passed it a real\n",
" // web socket which is closed, not our websocket->open comm proxy.\n",
" ws_proxy.onopen();\n",
"\n",
" fig.parent_element = element.get(0);\n",
" fig.cell_info = mpl.find_output_cell(\"<div id='\" + id + \"'></div>\");\n",
" if (!fig.cell_info) {\n",
" console.error(\"Failed to find cell for figure\", id, fig);\n",
" return;\n",
" }\n",
"\n",
" var output_index = fig.cell_info[2]\n",
" var cell = fig.cell_info[0];\n",
"\n",
"};\n",
"\n",
"mpl.figure.prototype.handle_close = function(fig, msg) {\n",
" fig.root.unbind('remove')\n",
"\n",
" // Update the output cell to use the data from the current canvas.\n",
" fig.push_to_output();\n",
" var dataURL = fig.canvas.toDataURL();\n",
" // Re-enable the keyboard manager in IPython - without this line, in FF,\n",
" // the notebook keyboard shortcuts fail.\n",
" IPython.keyboard_manager.enable()\n",
" $(fig.parent_element).html('<img src=\"' + dataURL + '\">');\n",
" fig.close_ws(fig, msg);\n",
"}\n",
"\n",
"mpl.figure.prototype.close_ws = function(fig, msg){\n",
" fig.send_message('closing', msg);\n",
" // fig.ws.close()\n",
"}\n",
"\n",
"mpl.figure.prototype.push_to_output = function(remove_interactive) {\n",
" // Turn the data on the canvas into data in the output cell.\n",
" var dataURL = this.canvas.toDataURL();\n",
" this.cell_info[1]['text/html'] = '<img src=\"' + dataURL + '\">';\n",
"}\n",
"\n",
"mpl.figure.prototype.updated_canvas_event = function() {\n",
" // Tell IPython that the notebook contents must change.\n",
" IPython.notebook.set_dirty(true);\n",
" this.send_message(\"ack\", {});\n",
" var fig = this;\n",
" // Wait a second, then push the new image to the DOM so\n",
" // that it is saved nicely (might be nice to debounce this).\n",
" setTimeout(function () { fig.push_to_output() }, 1000);\n",
"}\n",
"\n",
"mpl.figure.prototype._init_toolbar = function() {\n",
" var fig = this;\n",
"\n",
" var nav_element = $('<div/>')\n",
" nav_element.attr('style', 'width: 100%');\n",
" this.root.append(nav_element);\n",
"\n",
" // Define a callback function for later on.\n",
" function toolbar_event(event) {\n",
" return fig.toolbar_button_onclick(event['data']);\n",
" }\n",
" function toolbar_mouse_event(event) {\n",
" return fig.toolbar_button_onmouseover(event['data']);\n",
" }\n",
"\n",
" for(var toolbar_ind in mpl.toolbar_items){\n",
" var name = mpl.toolbar_items[toolbar_ind][0];\n",
" var tooltip = mpl.toolbar_items[toolbar_ind][1];\n",
" var image = mpl.toolbar_items[toolbar_ind][2];\n",
" var method_name = mpl.toolbar_items[toolbar_ind][3];\n",
"\n",
" if (!name) { continue; };\n",
"\n",
" var button = $('<button class=\"btn btn-default\" href=\"#\" title=\"' + name + '\"><i class=\"fa ' + image + ' fa-lg\"></i></button>');\n",
" button.click(method_name, toolbar_event);\n",
" button.mouseover(tooltip, toolbar_mouse_event);\n",
" nav_element.append(button);\n",
" }\n",
"\n",
" // Add the status bar.\n",
" var status_bar = $('<span class=\"mpl-message\" style=\"text-align:right; float: right;\"/>');\n",
" nav_element.append(status_bar);\n",
" this.message = status_bar[0];\n",
"\n",
" // Add the close button to the window.\n",
" var buttongrp = $('<div class=\"btn-group inline pull-right\"></div>');\n",
" var button = $('<button class=\"btn btn-mini btn-primary\" href=\"#\" title=\"Stop Interaction\"><i class=\"fa fa-power-off icon-remove icon-large\"></i></button>');\n",
" button.click(function (evt) { fig.handle_close(fig, {}); } );\n",
" button.mouseover('Stop Interaction', toolbar_mouse_event);\n",
" buttongrp.append(button);\n",
" var titlebar = this.root.find($('.ui-dialog-titlebar'));\n",
" titlebar.prepend(buttongrp);\n",
"}\n",
"\n",
"mpl.figure.prototype._root_extra_style = function(el){\n",
" var fig = this\n",
" el.on(\"remove\", function(){\n",
"\tfig.close_ws(fig, {});\n",
" });\n",
"}\n",
"\n",
"mpl.figure.prototype._canvas_extra_style = function(el){\n",
" // this is important to make the div 'focusable\n",
" el.attr('tabindex', 0)\n",
" // reach out to IPython and tell the keyboard manager to turn it's self\n",
" // off when our div gets focus\n",
"\n",
" // location in version 3\n",
" if (IPython.notebook.keyboard_manager) {\n",
" IPython.notebook.keyboard_manager.register_events(el);\n",
" }\n",
" else {\n",
" // location in version 2\n",
" IPython.keyboard_manager.register_events(el);\n",
" }\n",
"\n",
"}\n",
"\n",
"mpl.figure.prototype._key_event_extra = function(event, name) {\n",
" var manager = IPython.notebook.keyboard_manager;\n",
" if (!manager)\n",
" manager = IPython.keyboard_manager;\n",
"\n",
" // Check for shift+enter\n",
" if (event.shiftKey && event.which == 13) {\n",
" this.canvas_div.blur();\n",
" event.shiftKey = false;\n",
" // Send a \"J\" for go to next cell\n",
" event.which = 74;\n",
" event.keyCode = 74;\n",
" manager.command_mode();\n",
" manager.handle_keydown(event);\n",
" }\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_save = function(fig, msg) {\n",
" fig.ondownload(fig, null);\n",
"}\n",
"\n",
"\n",
"mpl.find_output_cell = function(html_output) {\n",
" // Return the cell and output element which can be found *uniquely* in the notebook.\n",
" // Note - this is a bit hacky, but it is done because the \"notebook_saving.Notebook\"\n",
" // IPython event is triggered only after the cells have been serialised, which for\n",
" // our purposes (turning an active figure into a static one), is too late.\n",
" var cells = IPython.notebook.get_cells();\n",
" var ncells = cells.length;\n",
" for (var i=0; i<ncells; i++) {\n",
" var cell = cells[i];\n",
" if (cell.cell_type === 'code'){\n",
" for (var j=0; j<cell.output_area.outputs.length; j++) {\n",
" var data = cell.output_area.outputs[j];\n",
" if (data.data) {\n",
" // IPython >= 3 moved mimebundle to data attribute of output\n",
" data = data.data;\n",
" }\n",
" if (data['text/html'] == html_output) {\n",
" return [cell, data, j];\n",
" }\n",
" }\n",
" }\n",
" }\n",
"}\n",
"\n",
"// Register the function which deals with the matplotlib target/channel.\n",
"// The kernel may be null if the page has been refreshed.\n",
"if (IPython.notebook.kernel != null) {\n",
" IPython.notebook.kernel.comm_manager.register_target('matplotlib', mpl.mpl_figure_comm);\n",
"}\n"
],
"text/plain": [
"<IPython.core.display.Javascript object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"<img src=\"data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAABLAAAAMgCAYAAAAz4JsCAAAgAElEQVR4XuzdCZxNZQPH8d8sxm7s+y77kn3f17IURQuhJN5CUimpUJFEIpGtLKWNQhEia8iePbKv2Y3drO/nOefOzJ0xGIw7d+79n8+n9zX3nnOe5/k+z13O/z7nHB+0SEACEpCABCQgAQlIQAISkIAEJCABCUjAjQV83LhuqpoEJCABCUhAAhKQgAQkIAEJSEACEpCABFCApUEgAQlIQAISkIAEJCABCUhAAhKQgAQk4NYCCrDcuntUOQlIQAISkIAEJCABCUhAAhKQgAQkIAEFWBoDEpCABCQgAQlIQAISkIAEJCABCUhAAm4toADLrbtHlZOABCQgAQlIQAISkIAEJCABCUhAAhJQgKUxIAEJSEACEpCABCQgAQlIQAISkIAEJODWAgqw3Lp7VDkJSEACEpCABCQgAQlIQAISkIAEJCABBVgaAxKQgAQkIAEJSEACEpCABCQgAQlIQAJuLaAAy627R5WTgAQkIAEJSEACEpCABCQgAQlIQAISUIClMSABCUhAAhKQgAQkIAEJSEACEpCABCTg1gIKsNy6e1Q5CUhAAhKQgAQkIAEJSEACEpCABCQgAQVYGgMSkIAEJCABCUhAAhKQgAQkIAEJSEACbi2gAMutu0eVk4AEJCABCUhAAhKQgAQkIAEJSEACElCApTEgAQlIQAISkIAEJCABCUhAAhKQgAQk4NYCCrDcuntUOQlIQAISkIAEJCABCUhAAhKQgAQkIAEFWBoDEpCABCQgAQlIQAISkIAEJCABCUhAAm4toADLrbtHlZOABCQgAQlIQAISkIAEJCABCUhAAhJQgKUxIAEJSEACEpCABCQgAQlIQAISkIAEJODWAgqw3Lp7VDkJSEACEpCABCQgAQlIQAISkIAEJCABBVgaAxKQgAQkIAEJSEACEpCABCQgAQlIQAJuLaAAy627R5WTgAQkIAEJSEACEpCABCQgAQlIQAISUIClMSABCUhAAhKQgAQkIAEJSEACEpCABCTg1gIKsNy6e1Q5CUhAAhKQgAQkIAEJSEACEpCABCQgAQVYGgMSkIAEJCABCUhAAhKQgAQkIAEJSEACbi2gAMutu0eVk4AEJCABCUhAAhKQgAQkIAEJSEACElCApTEgAQlIQAISkIAEJCABCUhAAhKQgAQk4NYCCrDcuntUOQlIQAISkIAEJCABCUhAAhKQgAQkIAEFWBoDEpCABCQgAQlIQAISkIAEJCABCUhAAm4toADLrbtHlZOABCQgAQlIQAISkIAEJCABCUhAAhJQgKUxIAEJSEACEpCABCQgAQlIQAISkIAEJODWAgqw3Lp7VDkJSEACEpCABCQgAQlIQAISkIAEJCABBVgaAxKQgAQkIAEJSEACEpCABCQgAQlIQAJuLaAAy627R5WTgAQkIAEJSEACEpCABCQgAQlIQAISUIClMSABCUhAAhKQgAQkIAEJSEACEpCABCTg1gIKsNy6e1Q5CUhAAhKQgAQkIAEJSEACEpCABCQgAQVYGgMSkIAEJCABCUhAAhKQgAQkIAEJSEACbi2gAMutu0eVk4AEJCABCUhAAhKQgAQkIAEJSEACElCApTEgAQlIQAISkIAEJCABCUhAAhKQgAQk4NYCCrDcuntUOQlIQAISkIAEJCABCUhAAhKQgAQkIAEFWBoDEpCABCQgAQlIQAISkIAEJCABCUhAAm4toADLrbtHlZOABCQgAQlIQAISkIAEJCABCUhAAhJQgKUxIAEJSEACEpCABCQgAQlIQAISkIAEJODWAgqw3Lp7VDkJSEACEpCABCQgAQlIQAISkIAEJCABBVgaAxKQgAQkIAEJSEACEpCABCQgAQlIQAJuLaAAy627R5WTgAQkIAEJSEACEpCABCQgAQlIQAISUIClMSABCUhAAhKQgAQkIAEJSEACEpCABCTg1gIKsNy6e1Q5CUhAAhKQgAQkIAEJSEACEpCABCQgAQVYGgMSkIAEJCABCUhAAhKQgAQkIAEJSEACbi2gAMutu0eVk4AEJCABCUhAAhKQgAQkIAEJSEACElCApTEgAQlIQAISkIAEJCABCUhAAhKQgAQk4NYCCrDcuntUOQlIQAISkIAEJCABCUhAAhKQgAQkIAEFWBoDEpCABCQgAQlIQAISkIAEJCABCUhAAm4toADLrbtHlZOABCQgAQlIQAISkIAEJCABCUhAAhJQgKUxIAEJSEACEpCABCQgAQlIQAISkIAEJODWAgqw3Lp7VDkJSEACEpCABCQgAQlIQAISkIAEJCABBVgaAxKQgAQkIAEJSEACEpCABCQgAQlIQAJuLaAAy627R5WTgAQkIAEJSEACEpCABCQgAQlIQAISUIClMSABCUhAAhKQgAQkIAEJSEACEpCABCTg1gIKsNy6e1Q5CUhAAhKQgAQkIAEJSEACEpCABCQgAQVYGgMSkIAEJCABCUhAAhKQgAQkIAEJSEACbi2gAMutu0eVk4AEJCABCUhAAhKQgAQkIAEJSEACElCApTEgAQlIQAISkIAEJCABCUhAAhKQgAQk4NYCCrDcuntUOQlIQAISkIAEJCABCUhAAhKQgAQkIAEFWBoDEpCABCQgAQlIQAISkIAEJCABCUhAAm4toADLrbtHlZOABCQgAQlIQAISkIAEJCABCUhAAhJQgKUxIAEJSEACEpCABCQgAQlIQAISkIAEJODWAgqw3Lp7VDkJSEACEpCABCQgAQlIQAISkIAEJCABBVgaAxKQgAQkIAEJSEACEpCABCQgAQlIQAJuLaAAy627R5WTgAQkIAEJSEACEpCABCQgAQlIQAISUIClMSABCUhAAhKQgAQkIAEJSEACEpCABCTg1gIKsNy6e1Q5CUhAAhKQgAQkIAEJSEACEpCABCQgAQVYGgMSkIAEJCABCUhAAhKQgAQkIAEJSEACbi2gAMutu0eVk4AEJCABCUhAAhKQgAQkIAEJSEACElCApTEgAQlIQAISkIAEJCABCUhAAhKQgAQk4NYCCrDcunsSvHLVgIFAJSAM2A7UdJRSBhgFVADOAxOA92LVwPzdGUgHbAC6OfaR4BXVDiUgAQlIQAISkIAEJCABCUhAAhKQQKSAAizvGQsmvPoN6A7MAEIcYdU6IA2wG/gKeB8oAswDhgEjHUS9Hds+DOwF+gMdHOte8R5GtVQCEpCABCQgAQlIQAISkIAEJCABVwsowHK1eOKVtxxYA5ggKvbSERgC5ATCHU++DPQACjv+3gcMBz53/O0HHANeBaYlXrNUsgQkIAEJSEACEpCABCQgAQlIQAKeLqAAy9N72G5fSuAi8AlQFygE7AcGAz87gqnigJldFbmYGVt/AoGAr+O0QvOYCcEilwXAVuB172BUKyUgAQlIQAISkIAEJCABCUhAAhJIDAEFWImh7voycwGHgRNAM+Bv4FHge6CO47pWqYGnnapWzHF9qzyOAOsQYEKuXU7rmO0vAF1iNcmMKzOby4RmWiQgAQlIQAISkIAEJCABCUhAAq4QSOs4UyjCFYWpDNcKKMByrXdilWYuum4uzP4R0NepEvOBTUByRziVUDOwTGB2JLEaq3IlIAEJSEACEpCABCQgAQlIwGsFcgNHvbb1HtxwBVge3LmxmvYvMP0mAdZO4ONY18Dq6bho+62ugXUc6BXHNbBMYBZ0+PBh0qUz/9QiAc8U6Nu3Lx9++KFnNk6tkoBDQONcQ8EbBDTOvaGX1UaNc40BTxe4cOECefKYE4isy+CYM4W0eJiAAiwP69BbNMdclL2P4zpXW4AWjlMIawP/OE4NNHchHOS4cPtcxzWzIu9CaK5zZe5gaE5BNBd07wc8AxQFYt+F0AqwgoKCFGB5z/jyypa++uqrDB9u7m2gRQKeK6Bx7rl9q5ZFC2icazR4g4DGuTf0sne30QRYgYEmu1KA5akjQQGWp/Zs3O16E+jmeEGbGVkDgDmOVUsBY4AKJnwCvgA+iLUbs35XwJxXvN6xr+1xFKUAy7vGlde2Vl8EvbbrvarhGude1d1e21iNc6/teq9quMa5V3W3VzZWAZbnd7sCLM/v48RooQKsxFBXmS4XWLBgAU2aNHF5uSpQAq4U0Dh3pbbKSiwBjfPEkle5rhTQOHeltspKDAEFWImh7toyFWC51ttbSlOA5S09rXZKQAISkIAEJCABCUhAAhJwAwEFWG7QCfe5Cgqw7jOwl+5eAZaXdryaLQEJSEACEpCABCQgAQlIIDEEFGAlhrpry1SA5VpvbylNAZa39LTaKQEJSEACEpCABCQgAQlIwA0EFGC5QSfc5yoowLrPwF66ewVYXtrxarYEJCABCUhAAhKQgAQkIIHEEFCAlRjqri1TAZZrvb2lNAVY3tLTaqcEJCABCUhAAhKQgAQkIAE3EFCA5QadcJ+roADrPgN76e4VYHlpx6vZEpCABCQgAQlIQAISkIAEEkNAAVZiqLu2TAVYrvX2ltIUYHlLT6udEpCABCQgAQlIQAISkIAE3EBAAZYbdMJ9roICrPsM7KW7V4DlpR2vZktAAhKQgAQkIAEJSEACEkgMAQVYiaHu2jIVYLnW21tKU4DlLT2tdkpAAhKQgAQkIAEJSEACEnADAQVYbtAJ97kKCrDuM7CX7l4Blpd2vJotAQlIQAISkIAEJCABCUggMQQUYCWGumvLVIDlWm9vKU0Blrf0tNopAQlIQAISkIAEJCABCUjADQQUYLlBJ9znKijAus/AXrp7BVhe2vFqtgQkIAEJSEACEpCABCQggcQQUICVGOquLVMBlmu9vaU0BVje0tNqpwQkIAEJSEACEpCABCQgATcQUIDlBp1wn6ugAOs+A3vp7hVgeWnHq9kSkIAEJCABCUhAAhKQgAQSQ0ABVmKou7ZMBViu9faW0hRgeUtPq50SkIAEJCABCUhAAhKQgATcQEABlht0wn2uggKs+wzspbtXgOWlHe9Jzb52DfLnhwMHIEUKT2qZ2iIBCUhAAhKQgAQkIAHPE1CA5Xl9GrtFCrA8v4/jauFM4FGgIbDYsUIZYBRQATgPTADei7Wx+bszYAKqDUA3YHscBSjA8s5x5VGtPnwY8uaFI0cgVy6PapoaIwEJSEACEpCABCQgAY8TUIDlcV16Q4MUYHl+H8duYQegLdDI8Z8JsNIAu4GvgPeBIsA8YBgw0rGD3kB34GFgL9AfMPsy616JVYgCLO8bVx7X4sgAa9PuExTKm4q0ydN6XBvVIAlIQAISkIAEJCABCXiKgAIsT+nJm7dDAZbn97FzC3MDfwI1gUNOM7A6AkOAnEC4Y4OXgR5AYcff+4DhwOeOv/2AY8CrwDQFWN41kLyhtZEBFgN8qJq7KqufX+0NzVYbJSABCUhAAhKQgAQkkCQFFGAlyW67o0orwLojriS/8gLgR+BLR1AVeQqhCaaKO2ZXRTaymiPsCgR8HacVmsfWOCmY/W0FXleAleTHhhoQS8A5wMqYMiNn3jgjIwlIQAISkIAEJCABCUjATQUUYLlpxyRgtRRgJSCmm+/qJcd1r5o46mlmWkUGWBOB1MDTTm0o5ri+VR5HgGVmbJmQa5fTOt8DF4AuCrDcvPdVvTsWUIB1x2TaQAISkIAEJCABCUhAAokmoAAr0ehdVrACLJdRJ2pBBR2zqaoAh+MIsDQDK1G7R4W7o4BzgJUhRQbOvnnWHaupOklAAhKQgAQkIAEJSEACZmbFhQsEBpoTiDD/YyZaaPEwAQVYHtahN2mOucbVOMeLOLLPMwFBwA/AKmAokMPpGlg9HRdtv9U1sI4DvW52Daxu3boREBBgValJkybWf1okkFQEFGAllZ5SPSUgAQlIQAISkIAEvFVgwYIFmP/MEhwczOjRoxVgefBgUIDlwZ3r1LQUQMZYTT0CPAksBEIdpwaauxAOcly4fS7widNdCM11rsxdCJsB5oLu/YBngKK6C6F3DCJva6UCLG/rcbVXAhKQgAQkIAEJSCApC2gGVlLuvfjVXQFW/Jw8ca0woBGw2NG4UsAYoIJjZtYXwAexGj4A6AqkBdYD3RzXyYrtk87sIygoiHTpzD+1SCDpCTgHWOlTpOfcm+eSXiNUYwlIQAISkIAEJCABCXiJgAIsz+9oBVie38eJ0UIFWImhrjITVODIEchjbmEwwAcFWAlKq51JQAISkIAEJCABCUggwQUUYCU4qdvtUAGW23WJR1RIAZZHdKN3N0IBlnf3v1ovAQlIQAISkIAEJJC0BBRgJa3+upvaKsC6GzVtczsBBVi3E9Lzbi/gHGAFJg/kfJ/zbl9nVVACEpCABCQgAQlIQALeKqAAy/N7XgGW5/dxYrRQAVZiqKvMBBVQgJWgnNqZBCQgAQlIQAISkIAE7quAAqz7yusWO1eA5Rbd4HGVUIDlcV3qfQ1SgOV9fa4WS0ACEpCABCQgAQkkXQEFWEm37+JbcwVY8ZXSencioADrTrS0rlsKWHchrLkCOtVGpxC6ZRepUhKQgAQkIAEJSEACEogSUIDl+YNBAZbn93FitFABVmKoq8wEFbACrJc7QtmppEuejqA+QQm6f+1MAhKQgAQkIAEJSEACEkg4AQVYCWfprntSgOWuPZO066UAK2n3n2oPKMDSMJCABCQgAQlIQAISkEDSEVCAlXT66m5rqgDrbuW03a0EFGBpfCR5AesaWD2ehbJTdAphku9NNUACEpCABCQgAQlIwNMFFGB5eg+DAizP7+PEaKECrMRQV5kJKuAcYOkUwgSl1c4kIAEJSEACEpCABCSQ4AIKsBKc1O12qADL7brEIyqkAMsjutG7G2EFWN2fg3KTdQ0s7x4Kar0EJCABCUhAAhKQQBIQUICVBDrpHquoAOseAbV5nAIKsDQwkryAHWB14o3LkzieNSVTp11J8m1SAyQgAQlIQAISkIAEJOCpAgqwPLVno9ulAMvz+zgxWqgAKzHUVWaCCkQGWBGzJxGUHAKvRSTo/rUzCUhAAhKQgAQkIAEJSCDhBBRgJZylu+5JAZa79kzSrpcCrKTdf6o9YAVY3Z4n4pevuJAc0inA0riQgAQkIAEJSEACEpCA2woowHLbrkmwiinASjBK7chJQAGWhkOSF1CAleS7UA2QgAQkIAEJSEACEvAiAQVYnt/ZCrA8v48To4UKsBJDXWUmqIAdYHUm4pcvuRgAaa971ymE64+tJ3/6/GROlTlBXbUzCUhAAhKQgAQkIAEJ3A8BBVj3Q9W99qkAy736w1NqowDLU3rSi9tx9CjkfvEFIn6dyKUASONlAZbPez40LtSYBc8s8OJRoKZLQAISkIAEJCABCSQVAQVYSaWn7r6eCrDu3k5b3lxAAZZGR5IXUIDlQ/U81VnZaWWS70s1QAISkIAEJCABCUjA8wUUYHl+HyvA8vw+Ni0cDDQD8gGXgGXAG+Y61U7NLwOMAioA54EJwHuxeMzfnQETUG0AugHb4yBUgOUd48qjW2kHWF2I+HUCl5NB6mDvOoXQzMBSgOXRQ1yNk4AEJCABCUhAAh4loADLo7ozzsYowPL8PjYtHATMALYCqYAvgBJAOUfz0wC7ga+A94EiwDxgGDDSsU5voDvwMLAX6A90cKx7JRajAizvGFce3UrnAOtKMkilAMuj+1uNk4AEJCABCUhAAhJI2gIKsJJ2/8Wn9gqw4qPkees8CGwEMgJBQEdgCJATCHc092WgB1DY8fc+YDjwueNvP+AY8CowTQGW5w0Sb2+RdRH3F7sSMWc8CrC8fTSo/RKQgAQkIAEJSEAC7i6gAMvde+je66cA694Nk+IezOmD/wMKOipvgqnijtlVke2pBvwJBAK+jtMKzWNrnBpsru5sZnW9rgArKQ4D1flWAs4B1lV/SBnifacQ1shTgz87mbcBLRKQgAQkIAEJSEACEnBvAQVY7t0/CVE7BVgJoZi09tEQmAk8Bix0VH0ikBp42qkpxRzXt8rjCLAOOUKuXU7rfA9cALoowEpag0C1vb2AHWD9j4g541CAdXsvrSEBCUhAAhKQgAQkIIHEFFCAlZj6rilbAZZrnN2llObA145TBn9xqpRmYLlLD6kebiNgBVj/e5GIuWO55g8pvHAGli7i7jbDURWRgAQkIAEJSEACEriNgAIszx8iCrBc08ed4llMKDA1nuve6WrtHNevagMsirWxuRj7x7GugdXTcdH2W10D6zjQ62bXwOrWrRsBAQFWUU2aNLH+0yKBpCLgHGBd94Pkod53CqECrKQyWlVPCUhAAhKQgAQk4J0CCxYswPxnluDgYEaPHm3+aS6DY84U0uJhAgqwXNOhYYA5Be92S1bHqXy3W+9Onzd3DzR3F2wBrIxjY3MXQnNqoLkLobljoQmt5gKfON2F0FznyuynGWAu6N4PeAYoCuguhHfaI1rf7QWsuxB2fYmIuV+gAMvtu0sVlIAEJCABCUhAAhLwcgHNwPL8AaAAyzV9fBFIG4+izgEZ4rHena5i7iwYAlx3bGj63Uwnedgp0CoFjAEqOO5M+AXwQayCBgBdHW1ZD3RzXCcrdn3SmX0EBQWRLp35pxYJJD0B5wAr2A8CvHAGli7invTGrWosAQlIQAISkIAEvFVAAZbn97wCLNf08YuACYRut5g7A4693UpJ4HkFWEmgk1TFWwscOwa5XuhGxG9jUICl0SIBCUhAAhKQgAQkIAH3FlCA5d79kxC1U4CVEIraR2wBBVgaE0lewA6wuhPx22hCfCFZmPddA0szsJL8MFYDJCABCUhAAhKQgNcIKMDy/K5WgOX6PjbXlzoPnHJc76oPYC7ePgS45vrq3JcSFWDdF1bt1JUCx49Dzs52gBXqA/7hCrBc6a+yJCABCUhAAhKQgAQkcCcCCrDuRCtprqsAy/X9tg54HtgCfAo0cgRY5uLq5ppSnrAowPKEXvTyNlgB1vM9iJj3uQIsLx8Lar4EJCABCUhAAhKQgPsLKMBy/z661xoqwLpXwTvf/iyQGTAXVjd3JqwLXAI2AbnufHduuYUCLLfsFlXqTgT++w9ydLIDrDAf8NMMrDvh07oSkIAEJCABCUhAAhJwqYACLJdyJ0phCrBcz27uNJgRKAAsBvI7qhDfOxW6vsZ3XqICrDs30xZuJmAHWC8TMW+UAiw36xtVRwISkIAEJCABCUhAArEFFGB5/phQgOX6Pl4KLALyOoru4ph5tVYzsFzfGSpRAjcTOHECsj/bk4j5n1nTJX0jdA0sjRYJSEACEpCABCQgAQm4q4ACLHftmYSrlwKshLOM757KAGOA68CzwGGgI1DP8Xd89+PO62kGljv3juoWLwHnAMvaQAFWvNy0kgQkIAEJSEACEpCABBJDQAFWYqi7tkwFWK7zrgisd11xiVqSAqxE5VfhCSFgB1ivEDF/pL07BVgJwap9SEACEpCABCQgAQlI4L4IKMC6L6xutVMFWK7rDjPTKgyYCcwAzF0HPXVRgOWpPetF7VKA5UPNvDVZ8dwKL+p1NVUCEpCABCQgAQlIIKkKKMBKqj0X/3orwIq/VUKsWQV4HHgMSAXMBn4CljjCrYQowx32oQDLHXpBdbgnASvA6tiLiAUj7P0kkRlYL855kZxpc/JunXfvqf05XvehVNGaLHxBAdY9QWpjCUhAAhKQgAQkIAGXCCjAcglzohaiACvx+B90CrOyA786wqzfgeDEq1aClKwAK0EYtZPEFDh5ErJ1SHoBls979tt6RP97vOi8jw+/Vc5G0zX/JWY3eFTZ4zeM58ftP7Kog7mPhxYJSEACEkjqAttPbufjVR8zpeWUpN4Ut6j/W4ve4tVqr5IldRa3qI8qkfQEFGAlvT670xorwLpTsfuzfjHHrCwzM8vMyvrg/hTjsr0qwHIZtQq6XwJ2gPUqEQs+tYtIIjOwEjLA+itHOqoeC7pfxPdtv1P+nsKzs5+9qxAv6FoQQdeDyBsYeaPYhKtmmS/KsPXk1ruqV8LVwnv2dCXkCqmSmcnON182/7eZIpmKkDJZSpfAmPEVmCLwlmUtPbCU6nmqE+AXcFd1inC8V/n4JM5XvJCwEILDgkkdkPqu6u+qjfaf28/w1cMpkaUEL1Z68YZiL1y/QDLfZC4bGwnd7qAguHIFcuSI3rPpGz9fP3x9fONdnPlMmdduHg898FC8t4m94lebvuL5X573yPe+nvN68tnazxK1bdW/rM7gBoOpk7/OLfto28ltpAlIQ/70+e+6L503PHPlDBlTZiQh32vMePvsoc/oUaVHgtRRO/E+AQVYnt/nifPtxvNd76WFyYCQe9mBG2yrAMsNOkFVuDeBU6cg6zOvEfH7cHtHSTTAOhx0mGxpslkHYmERYfj7+mO+IE5vM53WJVrfHMnHh1VZ0jGtTRCjR9+bZUJu/eSMJ62Dr+8e/+6mu33hlxeYuGniXR1Q1JtSDxMgxDWDLSzcXMYQ6wDQhAQTN07k+fLPx/tgsPQXpTEHEJH7/vu/vymTrUy8tzdln7t6jlWHV9GsSLMY7b94/SImsDF9HXsx26RNntbqe3dehq4cyhuL3mDvy3sJuFyQ3LnvrbZmnG99cSulspaKsaNTl0+RdVhWLr51kbSD09Krai8+bPAh5uDeON2vZeHehTT+pvFtx+XdHMCFhcHUqfDcc1iv71EPj6J75e43bcqm45usgKxk1pKYg9Dsn2S3PFL4p7jj5g9eMZiimYvy+I+P80TJJ9hzdg8bj2+Ms53rj60nNDyUqrmr3nE5d7uBmdGx7dQ2fn3aTHSPXiLDfhNyXu57+Ybdm+dr56tNt1TL6NYNzGfCvSxVJ1a1woNHiz56w8G5CTbNcqtwMzwinF//Xs2j5WrEqxrly8OmTdEfXZ1md2LS35N4o/obDMn+DJQqBfEIOY3DgDoD6F+3/w3lVppQiZcqvmSFWznSRidlJsB0DmAj35PXvbCOijnNPY3sZeepnRwMOhhnOGYCROOSJzBPvNp7u5U++QRm/zudFTmeuGFsHn6NR+YAACAASURBVDp+lf/OXqRyyazWbupOrsvMJ2eSIWWGm+72u63fWf25aN8iK8BiQARnzkDGjNGbmLFuPoMLZCgQ/WB4OKHjxxLe+XkC/JPfrtoxnh+wdIAVuLct3faGsdylfBfGtRh3w/6GrRrGy1VetvrD9GVg8kDO9zl/w3r7zu2zPiOyps7KrtO7eDC7OVEk7sX0b/KBdt0ntJhA5/Kdb9uOoxeOMnLNSPaf38/kRyfHGXBH7vd271/OhZnP4u2ntlMyS8kEDdIiy3h38bvsObcH41srXy3m7J5Dy2Itb9terZB4AgqwEs/eVSUrwHKVdHQ5X92kyGvAAWA6sN/11UrQEhVgJSindpYYAu4aYF0Lvcb10OvWgU75ceXpVK5TjAPV2DOwzN/mgMUcBPSY18P64h752JBGQ2LSmm/f//wD/v5QtSqrcwRQPe0MIna1iLMLOv/SmeOXjjO37dx76iLzBTSuX3DNl/+X573MZw9/FhW+RLbv0luX2HturxUApRiYgvEtxtPhwQ5WPbr82oUJGycQ8m7IbUObYxePWdcMM4sJerINyUOIz2XL6eD5g+QfmZ9auevy/RPTePT7R7kacpVtL23jcvBl0gxOw6aumyibvewt2//2H29bBx1DVw21vmiH9QvjxKUT5Byek2wp8rCn527SpIhfcND1166M3zielsk+Z2bfbpiD0i4VutB7YW/+PPRnnKGBMetZpSeD6g/iYvBFsqcxZ61HLyZUqJCjwl1/+e81vxePl3jcuui/WcwB20PTHmL7S9sxbTcHNzEO4OLQ+n7b9zz909MxnnEOEU3f/LD9B/zC0rD+72uM6xp9wPT73t8JDcpO2ZwlyJndP6rfzM4Wtl9Iw4INMbPyjlw4YgUStSfXtso58foJsg2LGfjFDi73nt1L+hTpyZQqE/9d+o8tJ7bQuFDjOx7vZrZPx1kdWXFoxU0DLBNCZhmaheth1/m44cf0rtGbBXsWWAd8/6v4v1uW+ddfUK0aTNr4Nc/90oH2ZdoztdXUOLd5eNrDzN8z33puYL2Blk/VL+1A6dirx8icKrMddMcj3DDbRL4mYxfmbGkOdj9/+HO6zOlirXazU5yHrfqE5QeXM/KhEdaYMSFGvyX9rLA9cnxFllN4VGGeK/UiT5R5lNyBuewA8uc5kDMn1LFnouw4tYOSY0rGWWZkvdMGpOXCWxeiqm9e95dDLkdtl/F6ec4O3mD/hvHHH7B2Lbz11h2PAWenV6q8wqcP2bN7TRDS9ue2VnBgxuTNli9XzKHz4hZcfyuCAKfJeeHhcO0apEoFG45toOKEijxb9lkmtZxM3hw/ceiYmdwf3U+18tZieacVsHRplNOPP8LMmdDz1WAeLBsWNevMfN6kHJSSclmrML/DL1YdnZfINpnwwLwvRi7m8aiwyseHjwc3p++VOYT5Yb0XLmq/yPpMyvtpXg5fOBznDK8GUxuweP9iCmcszO4eu2/ubTomIoL/zexDsSyFeaR0AwpmKGivP3IkDBxopY/WcG7+P6g47obxF/hCay7k/sn6zJj1zyzaTG/D78/8zrw988iUMhNv1347RvnmM8v3fXsWW9Z9L3Oy4Gew5D32fPkuhQpFH1oN+XMIff7oE/W5261SN/pmaknOqo2oMbwkK3tFm0UWYJrTfuYzTNs6jZcrv8zIhx13Qnb0Ybrk6QjqE3NmtPG+WYBlnvu09HJ+Pt+fFYeXWD+YnHvzHKPWjIrRLrOe+aGrWfo3aD1hEOXrjMa3+0sUKRKdc07bMs36HmE+86t/Vd2q8tu13mZg/YGY64aePQvFi0dTzVq6n6plspA9YxpM+Pbesveinvyx9Y+0KdnGfm1GRLDz9M6o11zXPKMY2+nmAbxzZ5j3/ybfNLEe2tBlA+Wyl4vx3mVmIZrXhlnWHl1rPR8SHmJ9TpngPfZiQlWzXseyHa0gvsL4CtYq5n2/R+UetPiuxW1/hLj5YNUzrhBQgOUK5cQtQwGW6/1/AFoBmx2BVT7AHP2YnwbNJ655638EMNfCSqqLAqyk2nOqd5TA6dOQ4+lehCxyr4u4N53W1PpSHRlEmeBhfZf1UfV2PkgyXywHrRgUo1cr5azEumPreKz4Y8xoMyPmQWrr1vDTT/Ddd/D006zODdU7w6nep6yDWrNE/rL+ww/w1D/2R4j5QmxCGedfeq0nhgyBjRsJmjKeulPqWrM7FndYHOOUHHOAYg5UTHtMwJA6WWrrV28zy+jTvz5lxo4ZHOl1hFzpclm7jH2wPPup2Vaw1Kb4U/Sr049z107z9ZavrQDLBDZ189elxlc1+KDeBxwKOmTZmRBj2mPTovb3a+iT1Ok7jgLDynEm3P79wMzI6PHbK3z19wTr73YFezFtn33AefXtq5jQp9akWjECLBNAmPDhUvAly+Lzpp8TeQB4q5dWz3TLGdGrlrWKmWVhZmaZL83mYNYcwL/+++v47G9InoAyjLoUfYpI5Bgwv8abWQAnL5+M8cXahGRmRpYxa1CggeU/99+5N3z5Ns9HBj2mDiakeXDsg9ZBijkwXXN0jRUgmH4OCYGrVyGdeZd3LGZ7MwOjb82+1nVLzGlZxr9PjT58tPIja4aT+eJvgkKf8OQcOwb580PF8RX59vFvrQPanJ/k4vilYzGYzJgyY6Nt5qH0/LsOV0OvRD2/sv3f7Nzux7or0xn3z/vW4yn2t2LeO2+w49xGuv3WzXpsQbvfafxAo6hxM675OLrO6Xqr7ojhY9pmAo7KOarzx8EF9th4I4ym3RazeGJDfB1nYplA0wSucc2gmblzJo/9aIcIvVbB8AZD+KnQG7x+uBAPZi/Nl498aQVk5sCpxJgS1nomwArc3ptX/gvkasSFGHX6Zdcv+OxrTIkiKShUyG7KunVQuTIwwH5NmjD3yt6y/Be+jTHtX6XMuFLWTJnRzUbf8Br6tMmn9FrQy9pu9TPbqfZNSSsA+KjBR7Qq3or/TgWTJ18IwRcDSWbmiDste/fCA9/4QASkCIVrTs8HvxNMMj/7gdiv29gBlglizVh7feHrUXs3QasJDSOXFwsNZegTLxJyLTkfjz7J4GD7PeGBgFrkyuHLsoPLiBhgbpGTCp83rlA7b22WH1oetX1kmbt2wfQTA3l3iX2jCxNQLm96jpHf7mBmeEnSBMOh9LGGyK4WTHrjMTo+9RE+u3Zx6fpFK3AtlaUUby0OIV3dxtC4sRVMm5DHhH8j/hqBOXVuy4tb4jQwD4a+G4r/B9EzI00dTaie0j+l9T44csVE/EMDaV6wDdO3/0Tvda35+bEFPF62ISNH+FKi2R8MnbKdBUOfIeJKRpK/60Ohs1D2P/j2Z6jzLCybZF8P0fSBTzg031CaX+ZuZVafD2iV4l1q5KnBysMr4ev55Hh8GMdTLeKnqicYMSqUv8rlIuNVyHANHsnXiCG97a+m5r3OzFZ07tc5TyykWfGGUWWZzxcTbEfO8nq3HgysA3X3w2frM5P2z3VUHVuPE9fNb7fwdsXhfND0lajPpKKfF2X3GTu4svouNJSQjVsJL1cafMJI7pi9dPH9d0jbfxA+pu8dy+imo+la7Fk2pq9PpfA17Dy5k4YlUnCs6fNQcLEVAJkg6PjF45ZzimQpKdwDRnSfQ/PvmtvjKuMD1mzCyPJNQGreC83r3MzUNUvT3TAv+HEiSpn7McGWpy5Rumhqa7ZeypTQY153Ju8YHfV5bdb5/kRtnvxiORnehF3vnsB8pm84voHzb5633j9S/68JV3JEHwI4v1YivVd2WkmZrGXZsy+MsuGHGPNsKZZ078r0jmMxM4XN50iM1164H/iG0eRfWFTEz/rBx5zSaWZdmrDuheJ9ePzXulYb0l2sTNAnazmeBnJeiuDnn6GVOWoBWv/Ymp922m2NXMyMuqktp3KqcFeeLlOCus+nZlrySgye+gp9q5yg0LU2dG1eiQ9XDOb89XNR2/Wv058Bde1Oc36PNH/n2TqKg9O7x5ggaF4X5vU1e+lhWlWpwLIDK1h3ajn4hPLNTvtz2izms33WZ7XYkX4o5U79wOIpGzkaEf39YVij4fxzeicTN02w+sXMpDaBrwntJ/89medmP2ftZ8dLO6z34+wXoccaGN0qJ0OPl2H02fksGnslyZ5aHKPzPPQPBVge2rFOzVKA5fo+Nu+yqwHnmVjm3dL8lPGC+X4LmLnBlVxftQQrUQFWglFqR4klcPpkOJmz+UUXn8inEJpfC/OOyGvNnjEHdZHhReeLhRn38U6mbf2W9g+2tw4okoVCyM3OFosAH/ODtS/WrJvZtb8gV5ochKdMTWjmbAQQwvR+rWnz/gz+ygXjKkLtg7D1o15WoFTiJCzZU5Nsv6+IOlg2SJGnY5mg68Lla7TLNIpxfbuR7NIVRqyOPkBe23ktpbOVtg4Czl2+zBvTvub7M70J72d+0bZPb1jccTHVJlYjONy+n0WqYBjU4lMrPHtz0ZtxD4lTxSDLP9Zz5hfzM1fPkCegNIeDt8a5vjm4erjww6R/PzXBA6F8F9hkT8Qi02Xo98gwev4RfTBdIOWD7L9qfneIuWzsspFyOcpZD1aeUNkKB+90aenzFefyTqFa7mrWwdTN2vjsJrjuB9+VsUswv86bU1fMbJsFexdYAdbrRSYy9Onnmbp5qjXj549aETRYEfOjvvLR+qSvEMykFiusWSW5J/rQI/84Pm3/PKeunLLK/3PJVM6mhPOOS0N1iPgD/wKrOLqhLAvG1+ZCkA/pPrJnAgR+FGjNkvj37L9xNv31aq8zedEwzqWA8rzMuk/e4fRGH6qMzkKPtiN4IncTck0obo1JszTbBfszwPG8Gci/7xxj50CVLrB+HDR5Bmb8CHUPRhe1KxMUPQPZX4MTjjMA01yHlCFwKk3cvZHaPB8KFwOg7VaYVB4CQiHYDy6/fZn6U+qzsuNysr2dnDOpsYKRCl1gY054qcR7jNlun04186mZFM1U1DrQabAXvmwymnztXqLNu7MY81pjRnycksEBATy/MZQZJeCcY9KjT9lJ0NI+UDIzYvoXep5mvz9rlW8c/MOgw2a4kBx+Lg75MhZgX899XL8OKT7ygaX9KX32XbZs9rNeS2uHTODFuctpmPp73l0GJQfm5djlQzc0flWHTVSfao9X52XgH/DEdphVzPZYWBCGV4OA6w9S+MJm/s0IiwYFk/7af/x0ca0VsnSr3I3ly3ypt8yHN/6EIYvgm9LQ3txr2WmJYACHhw8g76vRD5ZN8xCbXpvHvn1Ahn0U+qyQFYK9vAaW5IedWSDU6e03cstfvoUWu+G1xjDcngBChvP1OJdmFd/Mvk47x8u9aHfwD4cdThOGTEDw1vz3GdtqKH7v+sXYf6u53VgTmoUdOwYQeB0rDDHjYcVX0KwdnHZczuv6dw8QsGtPjLDEjI0TObKSbfde2nZMS48Sz1Jt4GSyvQ4nTQhwAY62XU+27ytaf0cuJkya+eTPtJxuh5tmGfnQSIZ/15MwX9g95AqB76ey3p9ycIw+89dw9YNW9Flpr5vjsaH8V6Y35wZD03aQrXFLBnebRbEz0WW8Uw9e/+0c6c9f44EPc1DkDPz2rf18qydhexZ7zB9JhzU7yi/M/v/IZc14qOyUK5d7vx2/dnqHf2sWJ1fH7hT1+dxyuj4QnnsUvir/HkvbVufjAY0Y/yvkiZ7YZu3SuM7/GprshTJjyrDr4HmCU8YcpyNyLaZ718bkeOsB5kz6hxFV4dufIrjw2VDS9XwDnydbQvFZTGz4M4+VrsHKitlo/i80bQsfL4TyXe3Pv7DJBfA9YP8gsaBeFZosWcND7eBoOjiVCsoWqk6Whav4eqbdWrN9l3d+4YVJj1ivhT5/Yo3Z5rugcaUP+GLbdnbm/R7z3vHSOhha035faNABCp+B06ngo4azyfFOJ9I8locip3uTpsQKNvqNJSL3RAZO6cy7DextzFLoZdjndLrhr3X/pXGWEOY+XoLHnoKip+BMKpjSYSaVC9bk/Z+/ZdXynmywsxjr/WZPRjjgmKBlbF+s+KI1c8uEWKuaX+LBByH52z7kvAghfnD4UyjQ05cXWozk7T97kO4aBF6Dw0eegJI/guOjwtTxdErIcjXC+pw3gXiAbwD/nPnHmunrPIaLnYYrhfNzoNcBNmaHJ9rAv+MC8AkOtl8n5vvGe5DvFTgUCOmuQ/JQ+715UM3+9G34HrU/qsCKaxvIdhHyBcHa3ND4/EuM7dyW2RfX8deRv6wZuGZfaa9Dlm312Fd8K6Q+TYWjUPWI/V75dVl4rcwQvln5pvVZYNox36cBD4UvwlwTLv0IHzJu7U9I5nVczPEboS+dIcuwTMx+aQW18tWMczbpW8vhw8Xg1w/C7N9K7CWRvxM61UT/jCWgAMvzh4QCLNf38VnATGUIdyrafF0wV1cwH2XmPBIzh/zWV3l1fb3vpEQFWHeipXXdUuDYruPkLOZINBL5y8rZq2etU0PM9XNypMlhnbYXGWCZL2jTP3meJ4O+5Frv8zTunp6lU+CJ1jA95qV/LOcPF8Fbf9oHElaznH61juyIl5rCmN+wAqxsl6HA+ej1By2Cvmb7l0pw6Jsd1HoOQn3hqOMdyzcc6hyAxU5nL5myzOOj50KPpjcemJrn9p99lgIZJxMe69rCJU/Ati+gbFfYnAMa7oWNOeDsra/NHTWmzMHVqi+hWVt4fwl0fQTM6TL/pYED6WFsRbj8IdTvAEsKwkP/wrxpsOmBtPyY7yLzH4Av5kD9jlD4LBxOB8nD7C/R5uDitQbvELEkKxnKNaTbTnv2TA0T+GWzvmtzMdaZga+thB9KwZGbvMPnOQ/VD8PsYjFnszj31YTyWGHIirxQ8hSsdxzQmHXmTINe4RP5t31n6u+Dp7ZBl0cg6yX7YDpyP1bQEP69HaIku0rgVduppOOsDTMu/swDtZ6PfnmWPQ5H09oHHslD7GBz4QP28/nOQUCYbRoZnpqDETMr560Mrek6YAYf1IZ+9e31Nw7JQ7mrh3m3c0E+mGhSDBhbAZbns2eOmCX9mzBmLrTdBj797YOg2y0meHn8CZj/DVQ/As8/Al/+AtU7wSrHz0bflrL3aRYTzJh+NeHXf5/Yj42rFMDPRYPpMrsKj19cg28/CH8fxlSEV5vYB/y9V9mBTc4P0rN4xHnaPwbrHJMAInx88O0fwUOHGjHvq4VxVtnMbjSzZFK9E90n5l/rc0DNTjBgKVFBReNn7Bkw/Z78gvptWnH+nexUOAar88I7NfvTqNtkau9ySvSAeQ/A3gzw8sN2IBa5+IfCA+fs4O7Ip1DzOTiXEraPubVsUHL4pBq8vxSqdIY1E6FIdwjOV4yDl/9h+g/QemfMfbRpAzNKxnyP+aosdPo7er3f0pUia+ptVOoKGa/AmY/t55blg5nFIP012JAT9mWA11bF3PZ9M57MBIwB9ni8FnOyaYzKmEBryOxMtDwcne40ag+LHDPY4nofdN7Bd6Xg6W2wNSuUPgkB70CVo/YB+cERsCcD5HaMd+ftIsdfbF3Tp2+uxAqUHn3Kfu2scVzqKbIumd6AhVOh/E1uBGvGdJYrMPv7W/edCWYiQyvnNaeXgDY77EfMF9LpJeHJ7RDsC0V7QIivPUacF2M9fD70+st+1PTxgkJw4aOY6/3g2FfsmkWGzeZxs6/0V+22fzUb9qe3w1rnzw6zntl/k3VnmVIvIx03259LCwvBsOoQFKtcs36O1+zxfWnwjS5vNrRft2dSwuZsUN+e/GUtnR6xQ57IQMs8lvJtuOoYV4sKQKOOcGwY5LgUt/nnlaC74zcM854V+WNRZJ+aEHzD+OhtzftV3wawPmfM97cXWsAExyXbfikCXVpAqZOw6Gv7vfCjRfb4MW140HHWqfOPMOZHgI35MpLyylm++RmqHYku0wRuZhxfTG6/T9Y5CPVr12Hx8mWY16dp28P2xDPMayxZOPS1J9ZZ3xfM58479eHPvPD0Vvhmpt2XkW00fd98N6QOscM9854e4rg1Vbem0GWDXectWaH2c3B+CJR+EbJfgrnTICAcKr0Q/X5qPjdMX19IAdNmRL93J38Hgv1jvr+Y96YSS55g0t4fSdcnelzWYQnL6/0BdQbG6LjrQ1MTcPkyP331NQ/WLErZSZW5nBxrptqWbHA8Xczx7rzxB0vf59069ixOLe4loADLvfrjftRGAdb9UL31Ps23TPP7ZPQ5P2CuaGm+spvbXpnDnePmR0XXVy1eJZpDCHPxERNSbQDMeRrbY22pACtelFrJnQX2b9tHgdKOoxvrm5t9GoarlxUHVlF7Sg0WtFtIk2mNoop/rFhrfnx6Bn4R8HF1+1dLc/ARuQyoA1+Vsw98N4+1HzUH4C853nnMAZQJH2514Bb7YOOT+fCq48DF/JI93z4Lz1oW5495MODsZGYiZLsEW8ZC1+Ywbo79JfyTBTClLJxPYR8ElnrR/kXZHIiaA8YC56Dq0bjF/9fMDtbMl1vzhdPM0nr2bzC/BpuDghKn7Fk8JgDJdBVebwTDFsb8om32/HZ9GLTYLsMcjE03VyGMYxlRBV5ZE/MJcyC1Ip8dZjzQA+Z+Cw89A/tH2geB5ou4WSp3hrUT7dlDC76xD8wf2mPPADKhzafVoNZBOJgeFn5tbzOnMHxcA7qts8MIcxCw77OY5ZtZBOYAtkYnuOpvb2vaapYeD8OoeTHXN6HmjzPsx0yAYg5qDgTasyTMODLLK01g6oNw1hEkfF/Srl+NQzD8dziUDhY8APnPQ6N9kNXMMhkWXc7ZFFhhjrGIvZg+bbMd/O/ipXSzg/C4eythH92dEYqYn54cy47MUOK0/YcJgP6cdGN5Q6vbM4niCg5irx37oNbMmhm45OZtiDxI7tAS/s5uv65utphZb0vzQyt7cuJdL5eSwanU9mvOeTHjyBxsm5A5rmVTdih3kwDGef0r/pAq9O6qZ943blb+7fZowoFHbnF5pdttn9DPm5llnzjOHgvziX5dJnQ5d7u/gbXgnRUxtzZBswkhXL04B3DOZZsgZ6NTSOT8XJ8G8NEfd1dT8xr4rIr9A87NllGVocda+9nfHoCmjiAocv3uD8Pnsd6X49rXvvRQ8MbrrN+w6j+ZiDHjzgRJzkHw3bX0xq1mFbU/6yLHplnDfP6tzAuvrYYPa97cJVVfuPLhvdXkxxL2+5j5Yc15KdDT/ryNzzKpLPRpCCecPq/is93N1rFCO3Nqqxa3E1CA5XZdkuAVUoCV4KS33WEf4DXgS8CEWeYaWJ0A8zuX+b3oCcephNFHqrfdpctW6A2Y3+cfBvYC5hwKc9XkIkD0xUnscCsoKCiIdM4XSnFZNVWQBO5d4MjOQ+QuYV6ejuU+B1jmukLmwrx+fvDm7+/w8epB1pejgi2nsb/cM+C4hsXW0TChgj174zmnmQyxWzy/EDxkXqW3WJwDrXsXu7M9mBkd5lQdd1omloPOm9ypRqqLBCQgAQlIQALuJmBmKC4a0IGyr3xEGnLQuTOYa4NqSXwBBViJ3wf3uwYKsO63cNz7N6FPe8Cc+GHmF5jf3OO+XVDi1O9mpZrzPIYDnztWMKc+mqsjmCtbOM3FUIDlXt2m2tyNwNF/DpOruJkU6VhuEmCZuz/F8wZyN1Tj3DmoUgV277avc/vQQzBvHmR4pyTnk+2wTxOs+TE0epNlX0HtGy9pczdN0zYSkIAEJCABCUhAAvcgYC4pcJ30rBk9k2eW9SF8/F8xLjx/D7vWpvcgoADrHvCSyKYKsJJIR7lBNc2sKjOhuRrgfCKNuS2TuWxq9NWONQPLDbpLVbhXgfgEWFvWXKVe1SvsPZeJ9I67VpmLEptAy9zJ/XbL6C8O8saR/PyT6QvyvPaivXr+/Ph0PGBdTDXy9D5z/ZZdkbHx7Xaq5yUgAQlIQAISkIAEXCow68WxbGh9lEypMvJK1VdcWrYKixZQgOX5o0EBVuL0cQHgacAc4ppT8sxlcM29pmNdAjVxKneTUnMDZv5HcWCX0zrm8qHmPjNdnB7TKYRu1XWqTGyB4CsXSeafnAhfH/4umZnyuy/QqWk+alaoTcf2/YnIk4OdW7ZR2kyPciwR5o46/v6ERoRZ18P6oeCLtDtkzgSGpb2GUWvYKxAKrxRtw6gD9m2Nrv57BHJnJGDOHMKbNSPZ6TOEhQTjmy8/Edeu4pvGccs0dZEEJCABCUhAAhKQQJIWMJdmSF2tNh0/W5ak25GUK68AKyn3XvzqrgArfk4JuZa5B9MvwCrHbCZzBFsLMNfGapaQBSXwvjQDK4FBtbvEEQi/egXfVI57oidOFVSqBCQgAQlIQAISkIAHCkxu3phnfzUnqGhJDAEFWImh7toyFWC51tuUZm6wa+7jOhs457jbYErAXF8qh+urc0clxnUNLHPHxF5xXQOrW7duBJirUgNNmjSx/tMiAXcQqJnhazpmfosZVY/Sf1EKKpy8TvJw+24y/erCkdMNmLhtMb5E32FmQqlUnD74GOf9UzDk3MQYzTgb4M+n2RpQJMMC2m+xnzK3c654DEb/BgMKVea1w2t5rw6cOlmPB66c5wH28NDhi9ZdArVIQAISkIAEJCABCSR9gd7ZpzL0uLnUsRZXCSxYsADzn1mCg4MZPXq0+Weg4ywhV1VD5bhIQAGWi6CdijHXkXJcLQdzY+6MjuciwyzX1yj+JZrrXJlTHs1MMRNm9QOeAYrqLoTxR9Sa7idw+TKkjjUp69jfK8hZrnZ0ZWNdxH1s02/43zz7C8rJ7afIWiKz9e/Ub/tgbn9+beCtb6989upZSr+TidFzoaXTSbmT/dvwbOh0a1+N8/Xl94P3eP9p9+NWjSQgAQlIQAISkIBHCpyesZTMj9fxyLYlhUZpBlZS6KV7q6MCrHvzu5utdwCPAHsgKsAqBpgj1tJ3s0MXbzMA6AqYUx/XA92A7bHqoGtgubhTVFzCC9wuwIoq8fp1qMG2cwAAIABJREFUSJ486s8BSweQPkX6O7qAZ6lS8O7pl/mt7NsMGp+F3BGH4cwZ/stZnuw57LfpPL3g8KcJ307tUQISkIAEJCABCUjgzgXGpG3Bx3lqcmDHm3w98nnyV32IWpVb3/mOtEWCCSjASjBKt92RAizXd81rQDvgTUdo1Rz4GPgOGOX66tyXEhVg3RdW7dSVAsc2/0nOsubydI4l1gwsV9alytCnWXvF3C8BWu6EB/+qQ+Uz2dh06QFyB66kY5D7Xyz0ij+kCo2/2oc1oe+f8V//Ttbs3QiGLryTLe583cI9oMYh+PpBCHv/zrc3WzzX3J9Jc+4A7e6K0VYSkIAEJCCBOAXOpIRMV4VzK4EM6SM4Z86j0eIWAgqw3KIb7mslFGDdV944d+7rOPXO3F/VBD3mY2EsYE7Pu/U5R66v692WqADrbuW0ndsIHDm4ldz5y0TXJxEDLFOJGfNO0mZReUh3lJ6FRzGibXd8fOD1QjP5+GRHemf4kjl+j7L5v0wkv3qJ9q2g0V7o4Lgml9nHyjxQ43D8iDdlh3L/xW/djTxIeTbHufLgmvDWn7AxXRYq1HiKiHlx5/Qd6udi6uKjUfso3boEW2eYCas3Li2ZySxaxa9yjrXWU55zBTZx8Vhdnuu1hNYjh7ArpCx/ht7+2nzbs0DJU3EXV/tZWD455nO/FoFHLm6ACB9IdZqIfY1vWdf/UsObjeDUrLn8RjMuk5I0vhcg3I8IzEfG3S37yU8BDsR748qdYcTEalRndby3uZcVd2WComfuZQ+es+3vBaGxOTH/Dpc2bWD6dLjuB8nD7nBjN1l9UIEqvL1/jZvURtWIS2BGcWjtzvfJjlXp/ume570L9l2CXbl0fxg+n3fnJX5DO55hmrVhUHIIvH7n+7ibLQr0hP0jb73lX7mgavRHs7VyuoZdubBo3N0UeVfbtGcyX/PsXW173zdq3hx+/fW+F6MC4i+gACv+Vkl1TQVYidtzWQFzTazgxK1GgpeuACvBSbVDVwscDjrMl4/mZUDk5KZEDrAuXoT//Q/eHfkPhTMWxs/XzwqwypWDjRvNRSttoYAZ3/Le+HYMqGf/vebkJHpMysr+qxUJeicbuwZnJ3/YjclUM+Ywl+a81BQKn4W5hWHR1/Y++id7g/dCPiY1l2jHNC6Slu9oG9UlPkRQldXk5gjTeSJGVwVUG0Tw6rcZRXdeZhR5OMQh8oG/P9VDl7GKGtb6qaq9x9XV/YjA/ljy8Q0hU/h5TpOFUb5d6BE+nr0UpAW/spMSVt5fjyWspAbXSXHD8HihBXyZtTIRX66hA1P4mce4ZJ35DKQ4z+Lf0lO/vtmLD1spRWXWcpVUUfv5NEUHkl9LyUuMY49/Lh4Itb/BnyUDGTlHWTbyN+WpUvIV1mwfYT33WJpR/H6pA5cznIZzBaP2Fdmm8alb0uXyrBvqOsj3dd5J9g5cDySQ8/gRxlky2fvkJ37i1qcjRNbJecemT8wSWXbsQgOzLqPBydP8zOPWU49ke49fQ9qyr8qnFJg3hnB88COcEmxnByXJy0HLezLPWes/zG/Moyk10n3Lygv2WBiQsjsDrn5+Q/t+S1WJplfM/UtiLv7vQtjVrFQ+f5I1Me+LcMO6CfXAuoBiVAr+57a7O58c0sfjIPJlRvJIm59pON1+o/DJuoWIk3bw3ZMRhOFHai6TqdQo3th2FNMvtVnGMurGqEPrdMOZceHVm9ZrIG/ThAVUZh1vMIQh9GECnemSeiBczkaZFEvYfM3c5PjOl4+yNKfPqTm33bCKz5/87N+MxSEtaM831vpl2cTflLvttrFXOOObjkzhF6yHc/nsxz/Ch4LsYwl314Y7rkCsDU6lgixXbr+X9MUncn5n5zhXHJfuYdpfmce3yZvR+fLcW+7syaJP8cMue1ZtXEvpFlXY+mvMUK8ya1hLldtX8j6ssSwf1DkY945/phWPMdN6MsdrcPwTmFYa2m29fUWC02Ui4MIZNmaH0SUzsWfVWCoFLGFY0JiojXcly8UPqerTL8jxgXT73VqvMz9CCSXZTdd+pmI1DpdazTKnHyByFZrA0b0vMKgWvL3C3tRc09LP8fNy8WrPs3O1HYydIjNb0wWy+2Jdtjz8JWN+g0L+W9kbal8NpE2RZyi7Oy9vY1/HsrjPZkb6v8TvRa/w4Y5NBIRHV83U17xXjyvrz7Baoez+PgtzTlWhBXMoyF72UeiGdhQLWMM/wdHjYQ+F6JSlFwdONeeTunNps9Rc4QOmpG1Ax4t/ML6cD1022Q0JxQ9/wvBp8goRC+zPr7iWQfRhWOmcjI54mbAdTxAYfpVH+NX6LnCZNHzfbQVPjXaaqR6PvolcZQPluUQa6rA8aqs8j9fg8E8rrb+PkoN1/qVpGfo7uTnMEfLcdu8LaWh9J/AlnMXUJ5AgZtOSTJzmDJkJ9YGPI96iL4OtfeX03cex8OjPaucCnq01j8krHqbq8/BXXFlo/vyweTOkTYv1ZUyL2wgowHKbrrhvFdEr7r7RevWOFWB5dfd7RuNNgJV/eF7r9K+TqSDrZfebINm2LbRoAU8/faP5T3//zryD0xlcfQKNG0O2bLBgySUITmOt7BxshNauT7Llf9CgUG8WtxtGhGPST4S54h3w9dQIGlYK4rMpgXz0kf3Ynh4jKTTKTCTFOlhYtgzMDWAGfejDWLpSmH9pwGLrueW/XaJe0xSE4U/LlrBl1l72HvAnJGc+spb5ipL/5mNlWANrX31zTCL4+GmG0ZsvvoCnah+jaL2c+J08xnnSWyHT4cPw44/w2mtgvkPuP3DjR5lP5p1wKTtcs++ZkT49nDc/FwDbtkHJklh1mTXbh/4MoPys/jzaMno/dgBkDip8qcNS5ubqwo6jgeQc8gq532xHCq5yjZRUYD1TRl1k1Z6sdB1ZgkOHIG9e+PBD6NvXLi/SOvhKKIGpgvEnlBqsZD4PM5OWPMtkLhDIV19Bp07RfdmqFZQoAQMHxf1R/Wb9dQxZXIkDVZ4k/4GlcOKEtfGZGo8wu9NsihSBpZ9tYe/0DaylMttDirK6aR+qLfyEShUjKFoUvpnmw2+Fe9LsX/sgJuLSZUqn2cc2StOoEaxfj3VqhJ8fhIVBKi6Tg+PUf+EBjhyBefMgDRe5QirC8eMzetADO8QyhvVYbJVtwi8T5PzAU9ZzkX4pHuvOtXy/cOTTMHJxzHrO7MOEnWZpz1S2UYpNlI+GcfrXeQJJT1Ccz8V+8BKpGU8XXuX2F5PzKTuJzX8PpwxbOUrOqLqZfUYeUJZiK3tTlOLqVajku5of0tam0LWzEJyWJsxnCfUIJjk7dph+jGBs38PUapfXGhdm3Jkl3D8Zm8evZXCn3fzIkzGqPItHaZVsGoTYd5gwl9rLmRP277dXO3oUcuWy/12RdayjctT2GylHeTZZf18jOSm4znZKkJdDbH7oTWrOfzdq3WqsYjXVrb87MpkpPGuFxcbKBGVmeZpv+d7qO7vexdlhjeH9DV5gyhNzydXVXA0h5jJ6wCm2r77AmAXRB99/86A13jdTlqL8w+sM40W+oGu3ZJibRoXnyInPcXNzY/DJtpmIEw/GNEnWkJYhi3icGVHBrjlofYZvmEY7GvIHv9DCOsg2oUjW7/eQrW4xkmGfiruaqvxBA0qxjZbWzaDhWp4c/JjhuDVbtVXdUsxcuo3veZKJdOZvylqh/UheIZhkpOES1VjNTopb7Z/JY3Zdk12K6qcpUyCiY0c6MpXGLGAGrXmI+VFh/RSftnwa8boVgFcuuZC12xvFaKPpyw1U5PO+x+j2oaODgbosYSn1CGj9CE+H/sKUG7PwqLDl6zJQbktJSrGdGql+ZuUVu56xl9y94IjTy+EKKTlMHoqy2+pj+8cC6FclI++vMfcdil4iXwdDeR3/0iXIvfU3nnh1FcyaQqqs/5H/r3Is+ScnDxTzY45fI2qHrWUabWnHt9ZOFtGAhjs/p0nxg/yeojI9e/gzfVpajl3dR3BQIZKF2+83kT8sJCPYej3FtUQG7ea5RvxOhjaNrJmJcQX4jzLLCjUqPjmXDWnfI2Li2qhdWu/7A+wxbj7/TvQYyNujstGP9xmSdhADj7YhQ7qUDEn5POk/Gc//XrI/LH0DzvFhyEDejhhi/QARQjLCI3wZX2kCXdZ3sdbJwTHyV83BX2vCrHH1YMQ224A/yJ4tglMnwgg3M25zrSP8cGUm+z7Hc0y23kfjakerkruZub1IVN1nZOxCm7PjOHUKMqcLZlLj73hu2bNc2neSNAWzMpxe1g85v4z7j4zpw+HJJwkLjcDP327vLopQjF0Mpg99GGK3izDrM3D7yR08EFiCuclb0YpZVr9cITWnl24jc91SUXVYnRvaFerAvmVTeSLlGH68+hIXS1bhcuX6ZJ9kh0Zf84wVgPfjPZqteIvatcI50f8L0r/XC58U54i4lsFa7zjZqch6yrGJlhOaM/SFXdRO/isTrveOcwyYBxuwiMXY3yUi61+TP9mQug6XLvsQlDkv6U8f5Due4il+wIdwq301+JOh9I6efXzgAGTMyKUHy5Gu/V4ijldi4D/rokLNIt1h9yj3+054Uxgve0IBlud3uAIs1/Sx+boZn3e6uH8GcE0dE7IUBVgJqal9JYqACbDyjshrfYl11wDrTmHMd7JXX4VChWBoyckQGAjNmkFAgPXPCxegTLfBbMliJy/XpxYjYN8/4DT7bOhQeOMNMHduHJ/6FV5hJCM+jeAVO8uCs2e5GJGGnJmvkyX5RfZfz2ltHvkDpQmRTAg22P4ue8MPl2ammflB0+w/lWNC1NKlsGkTPPMMZM1qzzZLlszetkIFWL/B6aPsxAmW7shKvXrQsCEsWmSXY9o2ZAgMGoQVKBQv7qivjw+hy1fhX6sa25r3odRc+4u7OWioWdP+gdXUKSI4hJmzfGjV2g9CQ/EP8LF+3T+8+Sx5ymRgzBjo1s2mMiGWCRb8/e0yzMHHFkpTJmKLVefMmWH2bGhfw/yyXpChQ33o3RvCw8HXER527w6jIs+2jMR75BHGzclF1/AvOFPrUTItn4WV8jVpAt9/T8gfywhYvCAqoDNlm7CuXz/YsgX2mFuHXL1KjVQbyf5YDX76CQgJYf4fyejVC/5xdLUp1wRTJiA0IdXWrZAihW1n2vfHH1Ctmt0/pp3HjsFff8GlS9C94U62dh3ND1l7kKNuUasfzEw304fO4yBy7K5YAbVqmTuDjOU5JlFgYGcKvvM0R8lF4xQrWHvNzGbwYTm1/s/eeYDZVZRv/N1ANgVIQm8JHQSkKL0XASNdpImhCcIfSEBAVKpUaUJQJFQBpYNIB4kgXZqAICAdAiH0QBJa2JDs/3nvOSc5udzdvf2U+5vn2SebvXNmvvl9c+aeec83M1pfMzZF8+S61/LLad11pfsuelkvFw7DlW7f6jxtedv+028NC0kHXba6dt+9U0uv2E///PNY9R+6njb+6K+FKKgzF/2DLnlzE/1n8Nbq/Xaw3LKt9+daZMH+hfbeu8efteHeS2n3H04K7hWLTlM79c7DY/Tp3IvN6EdhXz7wwEB0/CKM5jFDt9t2WqC0aDi94/vD/fcv3JCPHna91jpzx+l2f7H3gdrwziP0xLgF9dJLQZ9pbw9EWAuKK64Y3COzB3q0TjvmM6164rY6bPk19J//narPTzpLs41/S/ee9R/NcupvtcHh6+rp/3Rq4kRpQx+OFYsYsKA6XOcURBpP/o/TcfruxSM029676Oqdb9KPr92ucD9E6b33pAUWCP735z9Le+zxzRv5oXuv1nobBWJlv37S5MnSx69P0PxL9NcUtU8vK/rF97RF6WG/WKAgxF48arKOOK6PFv/wsYJgOll99YqW1vL6n27VNhoyuFMLzD1F/36mXR3rbqw+/7qnEOU5QqOmT/h3nvUSXTvlpzMMCO/rqM6HtK7WvXDPwluAyxb8lXbX5Wrb9fvqvCKI+DjvlsHaZptARNm5/206/sWdfevrT38K7g/fA6MOH6unFtlWq+qpgo8++kjyOLvUYlM0lz7WEWfNr223lT74QFrkoG110OO76nrtqKHf79Sd/3ej9KMfTffF3xY5RGteNlyPj19SgwdLa6whdfburTZXKunFc+7WsiM2VdugN6RFH9C3nllDL7zQpgWXG6gDdK6mHvJLnXH781ppkV/p+Xl66ffXLKG9dGmBx+tafPpy4r9odx2vY3XnyBe01vEL6uOJq073xzNaSd8eO1o/GvK47tQP9JYW0QJ6X1vpVq2y7SL6983jtPs5a+qeEX/T5e0/0+SOXjpAo3Ru5wEeggp2u//7+8R9ba65guadql/r1zq9cO9M+XqqXj/gFA27eAs91blKsBT+MMnfLTvsoMK4dM9lr2njddvUtuQSOvts6cc/LpxrokV23UD9nwxDo8LB46yTv9ShR/bVQhqnL9VPn2guvfZaMPb13Xd3ff/9y3W7tigI6GvpUa2k/xbGi5tv6iy8aLhoniO00h3Bm5kX/tep5Y/cU5rvOe272Mk65xebqb1Pm666SgVB3z4eufgfdfKYXfRuxzyFe/KYY1QQjaZMkS6OReoUvjY7O/Xli2+q3/KLaw5N0iXXzaGddgpE/96aok80p07f+2X9+NhvFcYIv5xx8rWntgVCUuFlwzKduuKqmZeTf/X2h+ozeF5NGDNBgxYbpDuGXaktr/xJ/Ota+sc/VHiD1damM/QLnTznGbI+3GeWr1V467TJJnpxqS217Gt3yL6f5dlnNP8cX+i5q/+rF15t15HXr1Lwo+3xz2a97taB+qMu2Pxm3XHYPSoM8C6nrU2Db95I454+Rj9d9he68eqBhT4w5s02yW9ibrhBOuEE6dhjtfVWnbr1tjbp+us1cdPtCy+XPr/jfvXfYqOZxLr3NV+h791yi+RVetOHrKJop011l+7TRoXv472X/ZcueTEQ491sN9/PDA89JC39wi16dNoaWnu7BfTrfT7WicNeVPtG62hnXaPrtFNByJouFIbPPK+/Li25wnidcGwf7bvX59LYlzX/qhuoADEaBL8xmvGHpAkgYCXtgcbXj4DVeMauYe9YNY6BPUDSZZIsbC1eeMksOV76+OaY0/BaELAajpgKGk0gjwJWd8ws0jjK5uynTtUR/zxCL494WUt/b4dA+YgJWI7C8URi3nml8//wlbZb8x3Nt+bi04WXeB2vvBLkXWutIHrED6phkND0bH4WtWDl6C0LIJ4klJtuvDGIpHKkkZ9uO/v1U1uoHLhcP7TOPXcQOeR8ngd6Uui/R+JYvC6LA+/OuZyW04v62/WdhbxXXinde29gXzy5fLfrkXC7KJf9738Hk9ooRc/ZF/xmnH51wmya0Dmo8BB+1lkqCH6elF1/vQoP6NZGIoHHy0Iff3yGAFZQxDwb8I9VJishp/vsj5mTBTBHcF1wwUwHY34jn4vxpLAgPJSZLATaN8UraS1GWtC6665A6HNEoHnF5xh2iec4m28e/P3aa6Vf/zrwhydsFhTtn6hs5y9Ee/UPBJKf/Uya9FGH5hj3ot5ZY1st9NUY/fW6Tnn/J6NZZRWp//i39NZrXwcd8+yz1Xb0UfqrdtDeulj3PjmwIHTGbfcE12KhxSHb1fnOu5o0+hENeOo+vXHI2QXR5Rvzk48/VmFmvPrqJam5bVdcIQ3zMS2SzjwzmJiXtfrYMG6/XVpqqQBGmO65JxAASyXzHuBvWwURf0ccEeZyWb6Z407wDNtsomQFzJ9bNVp2Wc3d93ON/2p2LTPLa3qxY4kCG4tK7b079dK972iBVRcuCKC+DxxBZkHYQpqjDQvVtLUVoo3+oaHBH9wZw2Q/OkrNHGyaBXCL0d/5TmCmx4XpGyAfdpim3vkP9Xr2v/IBr7bDIoGxG80WW0iP3fGR9jtqHh11lNSvf5vkUNQrr9TibW/omMWu0HXfOkYbvPFn3Tv/LrrrgT7B2usLLtCrsyyjCw99SSNHBv3LKfLNX9qCiKn9LrhQH9+9TxC9ExPed965oBF36XdryEbs5dy21S8JnCy8u53x5PvfuqVF4UKyIuhBcLYg0m6m5EHJg8ybb0r77qtbf3m/Tn5448K1ttGCisdWC8grraRCFNtxxwX9+l8PTNWg2b/Wxj/oU+hSWz1/qm7TVnpVSxWWXb/wQsDd3WKp/92iabO2663+y2qxjRYrvOiwvuqIPyf74Q9/kA46KPi/XezPxjzyrp79YH6tslrXe/V5PNhorclqe+XlwMii5HvkgAOkJZaQLBh4PNlnnyCTmXoMj4T9wh+tTHjAsYOefroA2GLz0UcHoll0T0yvxsaOHq0Jq2+mQQOm6ajfzKItN5+mddabYfOHj7+heSe+WhjkbIe5RH3SX4Fxs933PW57rL3pJhUEyuhWe/55FV5mnHFGoJtGyVsk2VyPj/4O9BjnfmLOF10UfJdsv32g8zgV+uWECXr9wrs13wE7BEK11TGrXEsvHdxIdnz0xseRTZdLu+/exXjT1qaXtv2VvnVT8IImnnyfv3f9QxqwwiIatNIiM33me9Ac4mOhv+fMyH6Jp/++/1+9cN+K2mKLtgIP/8z2zivBxe7f4duvzmmd8s3d1veb0XSOLvU4s+ms9+mxNxfQ2j9dtnBP+TsxShb3Hxi4tRbafGWttGKnzrxyAa25RqdWuOpIndbvOJ16VlCuhyD7yd/JFlaj5LEo8o3bd/jhQb7VVpNuPCV8ixO+4XKUq6/1S5oFFwxLsErtG4+UWgIIWKl1Td0MQ8CqG8qyC3I8gGP347vkriXpJEmbll1KujMiYKXbP1hXBoFWE7AiJKMeH6URfx+hzmM7g1ACP2VvMiMkvwx0FWWZc04Voo+i5XYVXRzPbFXGs4BipanCAqOJbE+qgx/OHS3gSWRXySb5ofjYY4Ool2hCbOHNyxc9ifbPyy8HETXR5xtsEAg+eUyO6PKEwNFDTqXm7N2227Mtv/1edNHp2TxRseBn90fJwqkn8RZFPd81Z4sljUzFEWau2xNcizWNSK7PQqTF0EsvlfasZI/jSGCKKwPuiAU1uPLk/v3AA1Lno48Fk1WH4YTJQomFhbh/os8sWHgeHi2F7Kpmt9VCr8UCdwFHNxZMt7DjyWQFHcm27LZbsBTT0YVOJ+z/rg5b/X713yuIGosnR8w4ItL3ZankscCChcVU+8MTZAemmIcjRdOSLEhZvLMAc+GFQb8p956wTrTCCjNEdbfZWopfBjQ9OZzPyoMH2DD5v77fS+hjTTev2grdz6Lvk7JE76KKfI2/shf3a/Hi5DBcq4JDet5Hqlr7e7zOTrLSWggB7Tl5iNp77yDIeLrY28Nl1vMs4lrMr4ZhqeK7e4nQcyvIkQQBBKwkqDe3TgSs5vJ2bd611Au84+cF+bHaB7CG71Kbb1Sda0TAqjNQims+gbiA9eGss2veKZ8234gEapwydYqeeOcJrT0kFkqUgB0VVxmFa9Q6Y7TS4bUgPTwxe6LgyIXu5s2eyHqC6AiSKDnYwvuRFe/5Gokf/nueBayK/coFPRJwlICjYZLcR3i6gFXOZgk9tiibGTzhdmBM/H5PU0tsmyf4fmlQa3LkpCOdYhpSrUW2/PUWFy0yOtVLfGlFqGbnyEdH5pJakwACVv79joDVfB/7UHsfWhs/08Lb9h4iKTi6JPsJASv7Pmz5Frw96W0NOWtIYQ8snzY0b+eHLc8EAI0nYBHijjuCZW0kCGSFAAJWVjyFnWklEK2ItPCCgJVWL2FXFgggYGXBS7XZiIBVG79qrh4qFY6+ceC698BaLBSutpN0ZzUFpvAaBKwUOgWTKiPQ2dmpXsf2UeeJUxCwKkNHbghAoMUIeO+v889PaElZi7Gmufkm4K32vPk9CQIQqI4AAlZ13LJ0FQJWMt6yaPUTSd5W8G1JV4diVjLW1L9WBKz6M6XEBAi0bb+rOm+4EgErAfZUCQEIQAACEIAABCAAgUoIIGBVQiubeRGwsum3tFuNgJV2D2FfWQQQsMrCRCYIQAACEIAABCAAAQgkTgABK3EXNNwABKyGIy5UsI2kW8qoaitJt5WRL+1ZELDS7iHsK4tA2/bD1HnDVURglUWLTBCAAAQgAAEIQAACEEiOAAJWcuybVTMCVnNI++TBck4Y/FhSHla+I2A1p19RS4MJIGA1GDDFQwACEIAABCAAAQhAoE4EELDqBDLFxSBgNcc5X0t6uIyqfOjr7GXkS3sWBKy0ewj7yiKAgFUWJjJBAAIQgAAEIAABCEAgcQIIWIm7oOEGIGA1HHGhgmPLrMZC12/LzJvmbAhYafYOtpVNAAGrbFRkhAAEIAABCEAAAhCAQKIEELASxd+UyhGwmoK55SpBwGo5l+ezwQhY+fQrrYIABCAAAQhAAAIQyB8BBKz8+bS4RQhY+fdxEi1EwEqCOnXWnUAkYH2geTVf5wd1L58CIQABCEAAAhCAAAQgAIH6EEDAqg/HNJeCgJVm79THtt0k/Z+k5SRNk/SspKOL9uQaJGmUpC3DPLdLGiFpYsyEHSSdKGkRSWPCMm7swkQErPr4jlISJjBDwJpP83W+n7A1VA8BCEAAAhCAAAQgAAEIdEUAASv/fQMBK/8+3l/Sq6FgNTkUpixELSvpnbD5Fqx6S9pZkvvEtZI+l/TD8PM1Jd0naRdJt0raVtIVktaT9FQJhAhY+e9XLdFCC1inv3eVXnriMv3pK2vBJAhAAAIQgAAEIAABCEAgjQQQsNLolfrahIBVX55ZKe0TSXtKujkWUbWSpOfCBvj3p8PP3pZ0iaSBkraPNfAGSeMl7YOAlRW3Y2elBH7yt2G6+rmr1P/0Tn1uSZcEAQhAAAIQgAAEIAABCKSSAAJWKt1SV6MQsOqKs+zCzH31UCB6S9K/JXWWfXVtGR1N9aCkZcKlgNtIukZS/6JiHa3lZYO3hVFWjso6LZbniFDQWg0BqzaHcHV6CQyC3DYcAAAgAElEQVS7YZiuehYBK70ewjIIQAACEIAABCAAAQgEBBCw8t8TELCa7+MFJd0iaRVJjoSaMxSIvCwvWtJXjlWXStojFL5K+dFL/r5XVNAQSQ9IukzSseFnu0r6nSTbFU/vSTpU0lXhEkTnuSCWYb/wcwthxYklhOV4kDypJxAJWLP9rlOffZZ6czEQAhCAAAQgAAEIQAACLUsAASv/rkfAar6PHe1k7t6b6mNJc4UbqPcK96Aq1yJHTPXtJvMUSZ/GPl9K0j/C/a0cPRWl7iKwvGTQ+2N5nysisMr1DPlyQwABKzeupCEQgAAEIAABCEAAAjkngICVcweHQkr+W5muFr4r6VuOcIyZ5f2lXpK0QINM9Z5Wd0o6R9LJRXX4VME3JK0c2wPLv1u0WlRStAeWo6q8pDBKPe6BNXz4cLW3txfyDx06tPBDgkCWCCBgZclb2AoBCEAAAhCAAAQg0GoERo8eLf84dXR0aNSoUf7V8+v4fLvVsOS2vURgNd+1XprnaKj4gqQ5wmV68zfAnHXCkwOPl3R2F+X7ZEGfQjgsFDWvDu3bLszvfbPuDU8hdESWlzt6GeL6nELYAI9RZGoIIGClxhUYAgEIQAACEIAABCAAgW4JEIGV/w6CgNV8H3spnpf3HRCqwlaHHRnVR9JODTDnHkkbSPoiFnHnDeMdiXVqWN+g0Iatwj21LGiNKFKtvZzwpDAqa4ykIyXd1IW97IHVAEdSZPMJRALW7Gd06tP4gtzmm0KNEIAABCAAAQhAAAIQgEA3BBCw8t89ELCa7+OFwn2lVgz3wPIm7s9Jsng0rvnmNKRGBKyGYKXQZhNAwGo2ceqDAAQgAAEIQAACEIBAdQQQsKrjlqWrELCS8ZY3bF9Dkk8FHCvpcUnTkjGlIbUiYDUEK4U2mwACVrOJUx8EIAABCEAAAhCAAASqI4CAVR23LF2FgNVcb3lHc2+Ovpqkyc2tuqm1IWA1FTeVNYoAAlajyFIuBCAAAQhAAAIQgAAE6ksAAau+PNNYGgJW873iZYKL+5CE5lfdtBoRsJqGmooaSSASsOY4s1OTOMekkagpGwIQgAAEIAABCEAAAjURQMCqCV8mLkbAar6bTpD0laTfNr/qptWIgNU01FTUSAIIWI2kS9kQgAAEIAABCEAAAhCoHwEErPqxTGtJCFjN98yDktaU9L6kN4v2vvJpgXlICFh58CJtEAIWnQACEIAABCAAAQhAAALZIICAlQ0/1WIlAlYt9Kq79thuLju+uiJTdxUCVupcgkHVEIgErAEjOzVxYjUlcA0EIAABCEAAAhCAAAQg0AwCCFjNoJxsHQhYyfLPa+0IWHn1bIu1CwGrxRxOcyEAAQhAAAIQgAAEMksAASuzrivbcASsslHVLeMNks6TdFfdSkxfQQhY6fMJFlVBAAGrCmhcAgEIQAACEIAABCAAgQQIIGAlAL3JVSJgNRm4pHMkDZM0XtKFki6V9GHzzWhojQhYDcVL4c0igIDVLNLUAwEIQAACEIAABCAAgdoIIGDVxi8LVyNgJeOlfpJ2kbSvpO9IuimMyro/GXPqXisCVt2RUmASBCIBa+BZnZowIQkLqBMCEIAABCAAAQhAAAIQKIcAAlY5lLKdBwEref9ZwPqTpO9KekXSyPD/05I3rWoLELCqRseFaSJABFaavIEtEIAABCAAAQhAAAIQ6JoAAlb+ewcCVnI+nlPSHpL2kTRfuJTwdUk/l/SMpB8nZ1rNNSNg1YyQAtJAAAErDV7ABghAAAIQgAAEIAABCPRMAAGrZ0ZZz4GA1XwPrh8uHdxe0n8knS/pOklfhabMJWmspNmab1rdakTAqhtKCkqSAAJWkvSpGwIQgAAEIAABCEAAAuUTQMAqn1VWcyJgNd9zn0q6MhSunu6i+pMlHdl80+pWIwJW3VBSUJIE2AMrSfrUDQEIQAACEIAABCAAgfIJIGCVzyqrORGwmu+5OSRZxMpzQsDKs3dbqG0IWC3kbJoKAQhAAAIQgAAEIJBpAghYmXZfWcYjYJWFqSGZ1pPUK1byvyRNbUhNzS8UAav5zKmxAQQQsBoAlSIhAAEIQAACEIAABCDQAAIIWA2AmrIiEbCa55A9JW0rabuwyi8l9Ql/75S0q6Srm2dOQ2tCwGooXgpvFgEErGaRph4IQAACEIAABCAAAQjURgABqzZ+WbgaAat5XrpLkve2ujes8hNJ84S/byTpCEmbNtgcn3B4lqSTJP0mVtcgSaMkbSlpmqTbJY2QNDGWZwdJJ0paRNIYSUdLurELexGwGuxIim8OgUjAGvT7Tn3iO5YEAQhAAAIQgAAEIAABCKSSAAJWKt1SV6MQsOqKs9vC3pK0pKQpMQFrzvD3WSW9HopDjbLoW5LuCPffuqVIwLJg1VvSzpLcJ66V9LmkH4bGrCnpPkm7SLo1jCS7QpKXQT5VwmAErEZ5kXKbSgABq6m4qQwCEIAABCAAAQhAAAJVE0DAqhpdZi5EwGqeq7xxuzdwj9IKkp4L/2M/+PPZG2SO99p6OIwAO0TSgzEBK4qoWilmj3/3CYn+7G1Jl0gaKGn7mH03SBovaR8ErAZ5jWITJ4CAlbgLMAACEIAABCAAAQhAAAJlEUDAKgtTpjMhYDXPfeMkrRsuvyuudbFQYFqoQeZ4uZ8jsHYLlzDGBaxtJF0jqX9R3ZMledngbWGUlaOyTovl8ZJHC1qrIWA1yGsUmzgBBKzEXYABEIAABCAAAQhAAAIQKIsAAlZZmDKdCQGree67UtL7kg4tUeVISQtI+kkF5lwqaQ9J3gC+lB+95O97kr4j6abw3wklBCxvHv87SQsW1f1eaOtVkl4N81wQy7Nf+PkyCFgVeI2smSIQCVhz/qFTH3+cKdMxFgIQgAAEIAABCEAAAi1FAAEr/+5GwGqej1eU9Fh40qDFLEdkDZY0TNKPJXmfqWcrMMcRU327ye+9tnzS4ZOSjg1FLGf3JvLlRmA5wsr7Y3mfq4ojsIYPH6729vaCiUOHDi38kCCQJQIIWFnyFrZCAAIQgAAEIAABCLQagdGjR8s/Th0dHRo1ymeTFba/mdRqLFqhvQhYzfXyxpLOl7R0LHLK0U2OZrqnAaYsGm4O772qIl/7Zra45U3jLap5n6s3JK0c2wPLv1u08vXRHljemN1LCqPEHlgNcBhFposAAla6/IE1EIAABCAAAQhAAAIQ6IoAEVj57xsIWMn42ALWvJI+lPRKA02wf4uXBl4fRoKdGi5pdPU+WdCnEDoazNdcLekzSduFtjk6zJFbPoXQEVnbSrpM0vqcQthA71F04gQQsBJ3AQZAAAIQgAAEIAABCECgLAIIWGVhynQmBKxMu68q4x3p9VDsFEIXMkjSOZK2CiPDLGiNKAq79HLCk8KorDGSjowtSyw2xNFaEydOnKgBA/wrCQLZJBAJWHOd3anxjmMkQQACEIAABCAAAQhAAAKpJICAlUq31NUoBKy64qSwkAACFl0hFwQQsHLhRhoBAQhAAAIQgAAEINACBBCw8u9kBKz8+ziJFiJgJUGdOutOAAGr7kgpEAIQgAAEIAABCEAAAg0hgIDVEKypKhQBK1XuyI0xCFi5cWVrNwQBq7X9T+shAAEIQAACEIAABLJDAAErO76q1lIErGrJcV13BBCw6B+5IBAJWHP/sVMffZSLJtEICEAAAhCAAAQgAAEI5JIAAlYu3TpToxCw8u/jJFqIgJUEdeqsOwEErLojpUAIQAACEIAABCAAAQg0hAACVkOwpqpQBKxUuSM3xiBg5caVrd0QBKzW9j+thwAEIAABCEAAAhDIDgEErOz4qlpLEbCqJcd13RFAwKJ/5IIAAlYu3EgjIAABCEAAAhCAAARagAACVv6djICVfx8n0UIErCSoU2fdCUQC1jzndOrDD+tePAVCAAIQgAAEIAABCEAAAnUigIBVJ5ApLgYBK8XOybBpCFgZdh6mzyCAgEVvgAAEIAABCEAAAhCAQDYIIGBlw0+1WImAVQs9ru2KAAIWfSMXBBCwcuFGGgEBCEAAAhCAAAQg0AIEELDy72QErPz7OIkWImAlQZ06604AAavuSCkQAhCAAAQgAAEIQAACDSGAgNUQrKkqFAErVe7IjTEIWLlxZWs3JBKw5h3VqQ8+aG0WtB4CEIAABCAAAQhAAAJpJoCAlWbv1Mc2BKz6cKSUmQkgYNEjckEAASsXbqQREIAABCAAAQhAAAItQAABK/9ORsDKv4+TaCECVhLUqbPuBBCw6o6UAiEAAQhAAAIQgAAEINAQAghYDcGaqkIRsFLljtwYg4CVG1e2dkMQsFrb/7QeAhCAAAQgAAEIQCA7BBCwsuOrai1FwKqWHNd1RwABi/6RCwIIWLlwI42AAAQgAAEIQAACEGgBAghY+XcyAlb+fZxECxGwkqBOnXUngIBVd6QUCAEIQAACEIAABCAAgYYQQMBqCNZUFYqAlSp35MYYBKzcuLK1G4KA1dr+p/UQgAAEIAABCEAAAtkhgICVHV9VaykCVrXksnXdwpJOk/QDSe2S3pS0i6TnwmYMkjRK0paSpkm6XdIISRNjzdxB0omSFpE0RtLRkm7sAgMCVrb6B9Z2QeAvT/9Fe968p+Y7t1Pvvw8mCEAAAhCAAAQgAAEIQCCtBBCw0uqZ+tmFgFU/lmktaU5JT0n6q6STJU2QtGQoTn0UGm3BqreknSW5T1wr6XNJPww/X1PSfaHodaukbSVdIWm9sOzitiNgpbU3YFfFBNrapPnmEwJWxeS4AAIQgAAEIAABCEAAAs0jgIDVPNZJ1YSAlRT55tXrqKmhktboosooomqlWESWf386jLZ6W9IlkgZK2j5Wxg2Sxkvap0S5CFjN8y81NZgAAlaDAVM8BCAAAQhAAAIQgAAE6kAAAasOEFNeBAJWyh1UB/MeCZcMeunghpI+kHSlpN9K6pS0jaRrJPUvqmuyJC8bvC2MsnJUlpchRumIUNBaDQGrDl6iiNQSQMBKrWswDAIQgAAEIAABCEAAAtMJIGDlvzMgYGXXx5dK2iMUoUr50Uv+vifpFUmLS9pN0nWSvh2KUn+U9DtJu4b/LliE4j1Jh0q6StKrYZ4LYnn2Cz9fBgEru50Iy3smgIDVMyNyQAACEIAABCAAAQhAIGkCCFhJe6Dx9SNgNZ5xo2pwxFTfbgqfIulTSU9K6pC0dizv4eE+Vv5bdxFYXjLo/bG8h1bFEVjDhw9Xe7sDv6ShQ4cWfkgQyBoBBKyseQx7IQABCEAAAhCAAARahcDo0aPlH6eOjg6NGuWzyQrb30xqFQat1E4ErPx7+6Iw6mqdLgQs74H1hqSVY3tg+XeLVotKivbA8r5WXlIYJfbAyn/foYU+1YBN3OkHEIAABCAAAQhAAAIQSD0BIrBS76KaDUTAqhlh6gtYRdLDknaXdL2k5cKoqt9L8o+TTxb0KYTDwlMIr5b0maTtws99CuG94SmEjsjyKYSXSVqfUwhT738MrJHAQgtJW24pXWQpmAQBCEAAAhCAAAQgAAEIpJIAAlYq3VJXoxCw6ooztYVtKemUcC8s7211YbinVWTwIEnnSNoq3FPLgtaIorBLLyc8KYzKGiPpSEk3ddFiTiFMbVfAMAhAAAIQgAAEIAABCEAAAvkjgICVP58WtwgBK/8+TqKFCFhJUKdOCEAAAhCAAAQgAAEIQAACLUoAASv/jkfAyr+Pk2ghAlYS1KkTAhCAAAQgAAEIQAACEIBAixJAwMq/4xGw8u/jJFqIgJUEdeqEAAQgAAEIQAACEIAABCDQogQQsPLveASs/Ps4iRYiYCVBnTohAAEIQAACEIAABCAAAQi0KAEErPw7HgEr/z5OooUIWElQp04IQAACEIAABCAAAQhAAAItSgABK/+OR8DKv4+TaCECVhLUqRMCEIAABCAAAQhAAAIQgECLEkDAyr/jEbDy7+MkWoiAlQR16oQABCAAAQhAAAIQgAAEINCiBBCw8u94BKz8+ziJFiJgJUGdOiEAAQhAAAIQgAAEIAABCLQoAQSs/DseASv/Pk6ihQhYSVCnTghAAAIQgAAEIAABCEAAAi1KAAEr/45HwMq/j5NoIQJWEtSpEwIQgAAEIAABCEAAAhCAQIsSQMDKv+MRsPLv4yRaiICVBHXqhAAEIAABCEAAAhCAAAQg0KIEELDy73gErPz7OIkWImAlQZ06IQABCEAAAhCAAAQgAAEItCgBBKz8Ox4BK/8+TqKFCFhJUKdOCEAAAhCAAAQgAAEIQAACLUoAASv/jkfAyr+Pk2ghAlYS1KkTAhCAAAQgAAEIQAACEIBAixJAwMq/4xGw8u/jJFqIgJUEdeqEAAQgAAEIQAACEIAABCDQogQQsPLveASs/Ps4iRYiYCVBnTohAAEIQAACEIAABCAAAQi0KAEErPw7HgEr/z5OooUIWElQp04IQAACEIAABCAAAQhAAAItSgABK/+OR8DKv4+TaCECVhLUqRMCEIAABCAAAQhAAAIQgECLEkDAyr/jEbDy7+Nekk6UNEzSnJLekXSWpAtjTR8kaZSkLSVNk3S7pBGSJsby7BCWs4ikMZKOlnRjF/gQsPLfr2ghBCAAAQhAAAIQgAAEIACB1BBAwEqNKxpmCAJWw9CmpuADQ7FpY0n/k7SBpDslbSPp7tBKC1a9Je0syX3iWkmfS/ph+Pmaku6TtIukWyVtK+kKSetJeqpESxGwUuN+DGkkgdGjR2vo0KGNrIKyIZA4Afp54i7AgCYQoJ83ATJVJE6Afp64CzCgwQQQsBoMOAXFI2ClwAkNNuH3koZI2j5Wz78lXSfpd5IWlfSGpJUkPRfm8e9PS3K01duSLpE0sKiMGySNl7QPAlaDPUjxqSVw6KGHauTIkam1D8MgUA8C9PN6UKSMtBOgn6fdQ9hXDwL083pQpIw0E0DASrN36mMbAlZ9OKa5lOXDiKrdJD0j6XuheOVIrOfDSKxrJPUvasRkSV42eFsYZeWorNNieY4IBa3VELDS7H5sayQBHgQbSZey00KAfp4WT2BHIwnQzxtJl7LTQoB+nhZPYEejCCBgNYpsespFwEqPLyq15FJJe0jqDJf9FV/vJX8Wq/pJ+q2kg8L9rbzH1cGSzg8v2DWMxFqwqID3JB0q6SpJr4Z5Lojl2S/8fJmuBKyxY8dqwACvJiRBIJ8EjjzySJ188sn5bBytgkBIgH5OV2gFAvTzVvAybaSf0wfyTsAC1pAhXnxUWD00Ke/tbcX2IWBl1+uOmOrbjflTJH0qyULXCpJ2CpcK+vebw2gqb+TuvbC6isDyskPvj+V9riqJwFo4XHqYXbpYDgEIQAACEIAABCAAAQhAAAJZJDBY0rgsGo7N3RNAwMp/D/mvpIsl/SHW1DMlLRueOuh9rrwH1sqxPbD8u0Ur748V7YHlUCovKYxSd3tguV8tFApo+SdMCyEAAQhAAAIQgAAEIAABCEAgDQTmkPROuFIpDfZgQx0JIGDVEWZKixoladUwAustScuFJwleKenY0GafLOhTCIeFyxGvlvSZpO3Cz30K4b3hKYSOyPIphJdJWr+LUwhTigKzIAABCEAAAhCAAAQgAAEIQAACEMgiAQSsLHqtMpu91PBUST+UNCg8OfB6SUdK8jJDJ//9HElbhUq1Ba0RReuGvZzwpDAqa0x4/U2VmUJuCEAAAhCAAAQgAAEIQAACEIAABCBQOQEErMqZcQUEIAABCEAAAhCAAAQgAAEIQAACEIBAEwkgYDURNlVBAAIQgAAEIAABCEAAAhCAAAQgAAEIVE4AAatyZlm9YmdJw8PN2mcP97yaFmvMSpL+GO6XNUHSRZKOL2qs//8zSd7Q/cmwvOdTWEZWfYTdtROotZ97X7hjJH0R7gfXGe4Z5/3hopSWe6V2WpSQVQLd9XOfTus9Cr8jaUlJv5X0mxINZTzPqvdbx+5a+znjeev0lSy3tLt+voakoyWtLqmfpDclnSXpzzyfZ9nlLWl7rf2c8bwlu03pRiNgtU5n2EzSXJK8J9afigQsC1ovS7pE0gmSlpH0d0lnxE4v/GW4L9bmkl4LN4DfPczryX5aymgdj9LSUgRq7ef+gtxE0gZd4KWf0+/SQKC7ft5H0n6SnpZ0iqS7SwhYjOdp8CI29ESg1n7OeN4TYT5PA4Hu+rmfueeVdIekjyRtJOlmSbtJuiU0nvE8DV7Ehp4I1NrPGc97ItxCnyNgtZCzw6ZuKOmeIgFrD0mnSVpIUhSVdZCkAyUtHV73uqSR4Wbv/tMs4fGkh0ryiYZpKaP1PEqLSxGotp/39AVJP6e/pYlAqX4et8+nxz5YQsBiPE+TF7GlJwLV9nPG857I8nmaCPTUzyNbb5Tkw5QO4fk8Te7DljIJVNvPGc/LBNwK2RCwWsHLM7ex1MBhYWo5SX7TE6W1JT0kaaCkXpK8rNB/eyyWZ7SkZyUdFopbaSij9TxKi8sVsHrq55+FkYXuz44q9M/Dko4KHxZdT09lNOtewesQMIGeHgRLCVheAs54Tv/JEoFq+rnb5wkP43mWPN3atvbUz03H4/eLkn4t6fLw/4znrd1vstb6avo543nWvNxgexGwGgw4hcWXGji8pHA2SbvE7F1Wkve3GhIKWG+FItdLsTzXSJokad9wWWIaykghckxKgEA1/fwdSctL+lTSWEkLSvqdpLUked8rC1ppuVcSQEqVKSTQ04NgKQFrsCTG8xQ6E5O6JFBNP3dhjOd0qiwR6Kmf9w6XDfrf74crJhjPs+RhbC3nxVupfs54Tt+ZiQACVut1CCKwWs/nrdjiavq5I7CKU7ukiZK2DvcSIgKrFXtTetvc04SHCKz0+g7LyidQTT8vVTrjefnMydl8At31c2/g7qWDs0raJnyhZguJqG2+n6ixNgLV9HPG89qY5+5qBKzcubTHBpUaOLwZ++lFe2D9PNy0vbs9sN6VdLCkqyQlXYb3AvBeXCQImEC1/bwrAcsPjHfRz+lcKSNQ7cS+1B5YjOcpcy7mTCdQbT9nPKcTZYlAV/18kKTbw03cd5A0pahRjOdZ8jK2VtvPGc/pO9MJIGC1Tmfw3jwOy/TA4RMG55A0VVJHuHzQSwN9CqGPXLdo5S/LM2OnEHofiRGStpTkL0sfy76rpG+Fb4J8Olsaymgdj9LSUgRq7ec7hoccjJc0f7iEcD1JK0r6PDxtk35O30uaQHf9vFOSI02cx/sUei9Dny7rAzqiiQ/jedIepP5yCNTazxnPy6FMnqQJdNfP5wtfnnlLDz9z+7m9ODGeJ+1B6i+HQK39nPG8HMotkgcBq0UcHZ4SeKkkT26c7Hv/vrGkByStIOlcSauGS6bOk3RiEZ7jJP1fKH49IWl4uE9WlC0tZbSOV2lpMQGfElhLP/fx1N7zyvu5fRLeG8eEoi39nP6WFgI99fM3JC1SZOz9kr4X+xvjeVq8iR1dEai1nzOe07eyQKC7fr5ReBiB9+B0ip7hfbqsXyhHifE8C55ubRtr7eeM563df2ZqPQIWnQECEIAABCAAAQhAAAIQgAAEIAABCEAg1QQQsFLtHoyDAAQgAAEIQAACEIAABCAAAQhAAAIQQMCiD0AAAhCAAAQgAAEIQAACEIAABCAAAQikmgACVqrdg3EQgAAEIAABCEAAAhCAAAQgAAEIQAACCFj0AQhAAAIQgAAEIAABCEAAAhCAAAQgAIFUE0DASrV7MA4CEIAABCAAAQhAAAIQgAAEIAABCEAAAYs+AAEIQAACEIAABCAAAQhAAAIQgAAEIJBqAghYqXYPxkEAAhCAAAQgAAEIQAACEIAABCAAAQggYNEHIAABCEAAAhCAAAQgAAEIQAACEIAABFJNAAEr1e7BOAhAAAIQgAAEIAABCEAAAhCAAAQgAAEELPoABCAAAQhAAAIQgAAEIAABCEAAAhCAQKoJIGCl2j0YBwEIQAACEIAABCAAAQhAAAIQgAAEIICARR+AAAQgAAEIQAACEIAABCAAAQhAAAIQSDUBBKxUuwfjIAABCEAAAhCAAAQgAAEIQAACEIAABBCw6AMQgAAEIAABCEAAAhCAAAQgAAEIQAACqSaAgJVq92AcBCAAAQhAAAIQgAAEIAABCEAAAhCAAAIWfQACEIAABCAAAQhAAAIQgAAEIAABCEAg1QQQsFLtnlQZd6ykYyR9Icn9plPSrZKGpcpKjIEABCAAAQhAAAIQgAAEIAABCEAgdwQQsHLn0oY1yALWJpI2aFgNFAwBCEAAAhCAAAQgAAEIQAACEIAABEoQQMCiW5RLAAGrXFLkgwAEIAABCEAAAhCAAAQgAAEIQKCuBBCw6ooz14VZwDosXELoZYQPSzpK0phct5rGQQACEIAABCAAAQhAAAIQgAAEIJA4AQSsxF2QGQOWl/SppLGSFpT0O0lrSVopFLUy0xAMhQAEIAABCEAAAhCAAAQgAAEIQCBbBBCwsuWvNFnbLmmipK0l3V1kmPvVQqHglSabsQUCEIAABCAAAQhAAAIQgAAE8ktgDknvhIeO5beVLdoyBKwWdXwdmh0JWNtIuquovIUlvV2HOigCAhCAAAQgAAEIQAACEIAABCBQCYHBksZVcgF5s0EAASsbfkqDlTtKukfSeEnzh0sI15O0oqTPiwwc4OissWPHasAA/0qCQD4JHHnkkTr55JPz2ThaBYGQAP2crtAKBOjnreBl2kg/pw/kncCkSZM0ZMgQN3OgpEl5b28rtg8BqxW9Xl2bbw73vJpN0ieSHpB0jKTXSxRXELAmTpyIgFUda67KCIFDDz1UI0eOzIi1mAmB6gjQz6vjxlXZIkA/z5a/sLY6AvTz6rhxVXYIWMAaONDaFQJWdrxWmaUIWJXxInd5BBCwyuNErowT4EEw4w7E/LII0M/LwkSmjBOgn2fcgZhfFgH6eVmYyJRhAghYGXZemaYjYJUJimwVEUDAqggXmbNKYPTo0Ro6dGhWzbMQn3sAACAASURBVMduCJRFgH5eFiYyZZwA/TzjDsT8sgjQz8vCRKYME0DAyrDzyjQdAatMUGSriAACVkW4yAwBCEAAAhCAAAQgAAEIQAACtRBAwKqFXjauRcDKhp+yZiUCVtY8hr0QgAAEIAABCEAAAhCAAAQyTAABK8POK9N0BKwyQZGtIgIIWBXhIjMEIAABCEAAAhCAAAQgAAEI1EIAAasWetm4FgErG37KmpUIWFnzGPaWJjB5sjR2rLT00hCCAAQgAAEIQAACEIAABFJMAAErxc6pk2kIWHUCSTEzEUDAokPkg8AvfiGNHCl1duajPbQCAhCAAAQgAAEIQAACOSWAgJVTx8aahYCVfx8n0UIErCSoU2f9CQwbJl11FQJW/clSIgQgAAEIQAACEIAABOpKAAGrrjhTWRgCVirdknmjELAy70IaUCCAgEVHgAAEIAABCEAAAhCAQCYIIGBlwk01GYmAVRM+Lu6CAAIWXSMfBBCw8uFHWgEBCEAAAhCAAAQgkHsCCFi5d7EQsPLv4yRaiICVBHXqrD8BBKz6M6VECEAAAhCAAAQgAAEINIAAAlYDoKasSASslDkkJ+YgYOXEkS3djI4OqU+fAAGbuLd0V6DxEIAABCAAAQhAAALpJ4CAlX4f1WohAlatBFv3+hslbStpU0n3FGFAwGrdfpGflr/7rrTQQghY+fEoLYEABCAAAQhAAAIQyDEBBKwcOzdsGgJW/n3ciBbuLuknkjYLfxCwGkGZMpMlgICVLH9qhwAEIAABCEAAAhCAQAUEELAqgJXRrAhYGXVcgmYPlvSQpPUkvUUEVoKeoOrGEkDAaixfSocABCAAAQhAAAIQgEAdCSBg1RFmSotCwEqpY1Js1mhJ10m6WNI0BKwUewrTaiOAgFUbP66GAAQgAAEIQAACEIBAEwkgYDURdkJVIWAlBD6j1R4Q7ns1NLQfASujjsTsMgggYJUBiSwQgAAEIAABCEAAAhBIBwEErHT4oZFWIGA1km6+yl4iXDq4pqSxCFj5ci6tKUEAAYtuAQEIQAACEIAABCAAgcwQQMDKjKuqNhQBq2p0LXfhHpIukDRJUtRv5pY0UdK1kvaLESmcQjh8+HC1t7cX/jx06NDCDwkCmSGAgJUZV2EoBCAAAQhAAAIQgEBrEhg9erT849TR0aFRo0b514HhvLU1oeS41QhYOXZunZvWV9JcRWW+LWlnSXdJmlAsYE2cOFEDBljLIkEggwQQsDLoNEyGAAQgAAEIQAACEGhVAkRg5d/zCFj593EjWzhV0maS7imqpBCBhYDVSPSU3XACCFgNR0wFEIAABCAAAQhAAAIQqBcBBKx6kUxvOQhY6fVNli1DwMqy97A9IICARU+AAAQgAAEIQAACEIBAZgggYGXGVVUbioBVNTou7IYAAhbdI/sEELCy70NaAAEIQAACEIAABCDQMgQQsPLvagSs/Ps4iRYiYCVBnTrrSwABq748KQ0CEIAABCAAAQhAAAINJICA1UC4KSkaASsljsiZGQhYOXNoSzYHAasl3U6jIQABCEAAAhCAAASySQABK5t+q8RqBKxKaJG3XAIIWOWSIl96CSBgpdc3WAYBCEAAAhCAAAQgAIEiAghY+e8SCFj593ESLUTASoI6ddaXwDvvSAsvHJTZ2VnfsikNAhCAAAQgAAEIQAACEKgrAQSsuuJMZWEIWKl0S+aNQsDKvAtpgBCw6AQQgAAEIAABCEAAAhDIDAEErMy4qmpDEbCqRseF3RBAwKJ7ZJ8AAlb2fUgLIAABCEAAAhCAAARahgACVv5djYCVfx8n0UIErCSoU2d9CSBg1ZcnpUEAAhCAAAQgAAEIQKCBBBCwGgg3JUUjYKXEETkzAwErZw5tyeYgYLWk22k0BCAAAQhAAAIQgEA2CSBgZdNvlViNgFUJLfKWSwABq1xS5EsvAQSs9PoGyyAAAQhAAAIQgAAEIFBEAAEr/10CASv/Pk6ihQhYSVCnzvoSQMCqL09KgwAEIAABCEAAAhCAQAMJIGA1EG5KikbASokjMmDGbyTtLmkeSR2SnpR0uKRnStiOgJUBh2JiDwQQsOgiEIAABCAAAQhAAAIQyAwBBKzMuKpqQxGwqkbXchcuLekDSRMlzSrpIEm/krSgpM4iGghYLdc9ctjgmIB12dN/0e4rW78lQQACEIAABCAAAQhAAAJpJICAlUav1NcmBKz68myV0vpI2l/SmZLmkzQeAatVXN9C7YwJWANPGaCJh1u7JUEAAhCAAAQgAAEIQAACaSSAgJVGr9TXJgSs+vLMe2lbSLpS0kBJ0ySdJemXJRpNBFbee0IrtA8BqxW8TBshAAEIQAACEIAABHJCAAErJ47sphkIWPn3cSNaOEjSHpLelvQ3BKxGIKbMxAkgYCXuAgyAAAQgAAEIQAACEIBAuQQQsMolld18CFjZ9V3SlrvvfCJpfUnPFhlDBFbS3qH+2gkgYNXOkBIgAAEIQAACEIAABCDQJAIIWE0CnWA1CFgJws941d7I3ZsC7SbphlIC1vDhw9Xe3l74aOjQoYUfEgQyQyAmYM12wgB9fgx7YGXGdxgKAQhAAAIQgAAEINASBEaPHi3/OHV0dGjUqFH+1VveTGoJAC3WSASsFnN4Dc31qYPXhCcRzivpt5J2kLScpPdLCVgTJ07UgAEOxiJBIIMExo2TBg8uGN7riAGadjICVga9iMkQgAAEIAABCEAAAi1CgAis/DsaASv/Pq5XC2+VtJqk2UM1+9+STpD0VIkKWEJYL+qUkxwBBKzk2FMzBCAAAQhAAAIQgAAEKiSAgFUhsAxmR8DKoNMyYDICVgachIk9EEDAootAAAIQgAAEIAABCEAgMwQQsDLjqqoNRcCqGh0XdkMAAYvukX0CCFjZ9yEtgAAEIAABCEAAAhBoGQIIWPl3NQJW/n2cRAsRsJKgTp31JYCAVV+elAYBCEAAAhCAAAQgAIEGEkDAaiDclBSNgJUSR+TMDASsnDm0JZuDgNWSbqfREIAABCAAAQhAAALZJICAlU2/VWI1AlYltMhbLgEErHJJkS+9BBCw0usbLIMABCAAAQhAAAIQgEARAQSs/HcJBKz8+ziJFiJgJUGdOutLAAGrvjwpDQIQgAAEIAABCEAAAg0kgIDVQLgpKRoBKyWOyJkZCFg5c2hLNgcBqyXdTqMhAAEIQAACEIAABLJJAAErm36rxGoErEpokbdcAghY5ZIiX3oJIGCl1zdYBgEIQAACEIAABCAAgSICCFj57xIIWPn3cRItRMBKgjp11pcAAlZ9eVIaBCAAAQhAAAIQgAAEGkgAAauBcFNSNAJWShyRMzMQsHLm0JZsDgJWS7qdRkMAAhCAAAQgAAEIZJMAAlY2/VaJ1QhYldAib7kEELDKJUW+9BJAwEqvb7AMAhCAAAQgAAEIQAACRQQQsPLfJRCw8u/jJFqIgJUEdeqsLwEErPrypDQIQAACEIAABCAAAQg0kAACVgPhpqRoBKyUOCIDZpwiaUtJi0r6TNL9kn4l6e0StiNgZcChmNgDgZkErIGadvIEkEEAAhCAAAQgAAEIQAACKSWAgJVSx9TRLASsOsLMeVG/lXS9pGcl9Zd0nqTlJX0XASvnnm/V5r39tjRkSKH1vY5AwGrVbkC7IQABCEAAAhCAAASyQQABKxt+qsVKBKxa6LX2tStLekrSXJImFqEgAqu1+0Y+Wh8TsHbdup+uuOWLfLSLVkAAAhCAAAQgAAEIQCCHBBCwcujUoiYhYOXfx41qoZcP7idpiRIVIGA1ijrlNo9ATMAa37dNc385rXl1UxMEIAABCEAAAhCAAAQgUBEBBKyKcGUyMwJWJt2WuNGbSrpR0o8k3YWAlbg/MKARBGIC1sd92zQXAlYjKFMmBCAAAQhAAAIQgAAE6kIAAasuGFNdCAJWqt2TSuO2knS5pD0k3dKFhURgpdJ1GFURgZiA9Ulfac4vOyu6nMwQgAAEIAABCEAAAhCAQPMIIGA1j3VSNSFgJUU+m/UOk3SOpB0l3d1NEwoC1vDhw9Xe3l7INnTo0MIPCQKZIRATsCb0kQZNRsDKjO8wFAIQgAAEIAABCECgJQiMHj1a/nHq6OjQqFGj/OtASZNaAkCLNRIBq8UcXkNzR0g6QdLWkv7VQzlEYNUAmktTQgABKyWOwAwIQAACEIAABCAAAQj0TIAIrJ4ZZT0HAlbWPdg8+72D9RRJX4VVuu84JGXzEoIWAlbz/EJNjSIQE7Am9pEGEoHVKNKUCwEIQAACEIAABCAAgZoJIGDVjDD1BSBgpd5FmTQQASuTbsPomQjEBKxJ7dKAr1hCSA+BAAQgAAEIQAACEIBAWgkgYKXVM/WzCwGrfiwpaQYBBCx6Q/YJIGBl34e0AAIQgAAEIAABCECgZQggYOXf1QhY+fdxEi1EwEqCOnXWl8C4cdLgwYUyP22X5iACq758KQ0CEIAABCAAAQhAAAJ1JICAVUeYKS0KASuljsm4WQhYGXcg5kuKCVif9ZZm72AJIf0CAhCAAAQgAAEIQAACaSWAgJVWz9TPLgSs+rGkpBkEELDoDdknEBOwPu8tzYaAlX2f0gIIQAACEIAABCAAgdwSQMDKrWunNwwBK/8+TqKFCFhJUKfO+hJAwKovT0qDAAQgAAEIQAACEIBAAwkgYDUQbkqKRsBKiSPKMKNXGXmcxeuckl7rhIBVprPIlmICsU3cv5hV6j8l6dsqxawwDQIQgAAEIAABCEAAAgkTQMBK2AFNqB4BqwmQ61TF1DLLmSxptjLzNiobAlajyFJu8wjEBKwvZ5X6IWA1jz01QQACEIAABCAAAQhAoEICCFgVAstgdgSs7DjtC0mb92Cu/XmzpIEJNwsBK2EHUH0dCCBg1QEiRUAAAhCAAAQgAAEIQKA5BBCwmsM5yVoQsJKkX1nd/5K0bhmXPCBpgzLyNTILAlYj6VJ2cwjEBKzJs0h9v26hJYQvvyx961vS3/4m/ehHzeFNLRCAAAQgAAEIQCBtBDo7pU8/lQZ4ekNKOwEErLR7qHb7ELBqZ0gJ3ySAgEWvyD6BmID11SxSn1YSsOaaS/rkE2mDDaT778+eL7/+WurokPr3z57tWFwegQ8/lOaYQ+rbt7z85IIABCAAAQhUQ+Daa6Uf/1iykEVKPQEErNS7qGYDEbBqRkgBJQggYNEtsk8gJmB19JLap7bQg0tb+NWw/vrSAw7qzFjaZx/pT3/iYTNjbqvIXPfRn/xEuvLKii4jMwQgUAcC888v/fzn0pFH1qEwioBAygmcdJJ0zDE8U6TcTZF5CFgZcVQNZiJg1QAvwUsv6aJub+D+pqS/Snq9zvbtLGm4pJUlzS6pt6RpXdSBgFVn+BSXAIG0CljXXy+tvLLUp4/00EPSeutJiyzSPaCDD5Y231z6/velSZOkgT1sk5d1Act8/vtfHjYTuG2aVqX76GqrSf/+d3lVTpzYc78vr6Suc91zTxC1OOustZbU3OtXWEG67DJplVWaW29StX38sdS7dxDBl8f0/vvSbbdJe+9dunWOUD3rLOmww6RorK+Ug69bfXXp8ccrvZL8JnDJJdLii0sbb/xNHocfLq29trTtttlhNW2adN11QZRS3tKIEdKoUUGrbr01GCfHj5eWX16aZZa8tTYX7UHAyoUbu20EAlY2fXytpO0kPSNpjKRFJX3HQ6ukJSQtJ2kbSf+oY/M2kzSXJK/J+RMCVh3JUlQ6CcQErCm9pN5picAqnnDssIN06aXSn/8s+UFr0UWlTTaRDjlEWnFFaf/9pfPPDxh7X6uXXpoh7Hz0UbAEa3Zr0pI88XnuOWnTTWf4pJKQ+TFjpMUWa6w/L7pIWmqp0g/+Uc0rrSQ9+2ywjNAT1eLk5ZEW8caODXilKb3xhrTEEpKXLOy0Uzoscx/wBCUND+vjxkkWcS3KdjWBtl8tInm/ktlmk26+WfrhD0sLml98EfQD3xtR8n1gcSO+BHXKFGnffSX3v64EKt+bV1whDRtWX7+dfXYgRrgtjUi2+7jjpGOPrX/pH3wgHXpocB96nGp0mjAhuLe7Embcl3v1khZeWHrkEWnIkJ4tsvjpJased0olj5nLLCO1t3dd1r/+JT31lHTggT3X11MOC3B+EdHVWOs6zjknKKXU+P2f/wST8C+/rH4Jrvmuuab06KMzW+txd9llS4+7PbUric+fflpydI3HlGYm8xs0KFiqHyX3M38nR/3siCOkk0+e8bl9OXVq6fFn5Ehp+PDgxVYlyf3EZTqa7owzpI02Cl4MFCePD7vtJi25ZOnSfS+ts05Qlu+vyy+XvBXBlltWYk35ec3izTfLe9549VVpvvkq27/qppsC0cr2+1mqVLr4Ymmvvcq3mZxNI4CA1TTUiVWEgJUY+poqvkjSI36HEyvlp5LWkbSPJI+2P5G0ek21lL54Q0n3IGA1gCxFpotATMD6uk2adVoKlhCee27wkBpPftj1A1qlyRN3T9DXWkuad17Jy+5+9zvpwQdnLql4AhSJGV99Ja27bvAG3pPTaIPTt96aeVLoB/UTTwwe9BZaaEbZjvjw5PG++wKh5tvfDj6LNpDvSjhzefPME0wou0qOKHn+een006Vf/vKbuVyG7fFb8J4EOpfjtjYrOiWaeNvP0SS0Ut/WI//f/x6IhBY4jz5a+u1vS7O6/XbJIsVP/RVUZXIf8mS4O198/nkgxpqP+46TJ1qPPRZMmOIpYmj7775bsgDkSYgnqY5qiAtQFobcDywIWLTq10+aPFnabjvphhuCUh2xctppAQeLW54MlUqu91e/CoSgeu6/5nIt/uy5Z+l63UZPPKN2ud8fdFDX4oQ5W+h58slAFPPE8/jjpd/8JhCy/PsLLwRLZl5/PRB6uhNnbNWpp0ruM8V75sWFpGgCboHF9VhA8RgQ959ZVxrB5nI9+TZ7J0dG/PGP0ve+NzMvjzXur84bpXif89g1ePA3+5MnsXfcEUzOzdrL5v75zxkRfW6jRRCPNRYhXnxR8vLrUn2yuI+7LIs+juwoN626aiCGvfOOtOCCM1/117/OLHyvsUbQZgvQvpct6trvvnc8rtmvW28tWfT3Pd5V8mEeFrBdvlPk13h7IvHdfeHXvy63NY3J98QTgcC93HJBX+vqZUD0XdHT90DcSvvXDBdYIHhZ5Bc3fhFSbjRbJKJawPKP/eM+axHd33/x9ItfBN/5jtby97P7uP919Fxx//L994MfdM3T4/SOOwbjZ/TiJrL5L3+R9thD2nDD4Du5ODmfo7h9H5RKDz8cPA9EL42icuMHwfzsZ8G95zY7uU/6e9VC3c5e5NFN8jhvPr7W47O3CPA4Ypbe5sC+9tjtFw1up7/f7fvf/z7wyxZbBJydPMZ4jPSzk9t7zTXB/Rr/jt9ss+Be7y595zvBfViu3xvT0ym1BAEErPx3CwSsbPr4Y0nzFC3hcxyrZ3SOkvKutu9L6mGdUFWNR8CqChsXZY5A2gQsP1SWWm5QLVg/ePUkyvhh0csCPLn3pMkP0f7xRMXLHDxR8RvjuecO/rUQ5gdjP9BHKS4meImVHz4dpWLBLEqOWHFEjSdVfgj3w6bfPPvB1snXePLoyVY0kfYSGU8sS014LYb973/BRNOT8fiEOJq8eZnhM89IfgPv3+PJZTp5whZNrv2Q29VDtt/WOmotimTzg/oBB3yT7yuvBA/Wd97ZdTRNxMtt8yTcD+SO7ognT8bM5rvf7dn7jtawWOGoLicvffD+Nf/4x4wJvicAntR4UhD325xzBkKgH+5fey34xBMGT9os+sQnbRaY3K7o1Mo//CHgUbyMyWwtjjgCxkKPI80iMTKaRJqBxbtIrPU1550XiDIWS82kq+RJSvytvyeoFn484Yv6rkUs9223wZMys7Ao5T5jcdTJApSvsY133TVjYujJkft5lMzHbC1cRGKChTaLzW6P+5YZOMLB6ZZbAhHBy3+vvjrg6+QICvcbi2hRH3BdFpQdZWn/OAKiVHJ+1+dJ1wknBNEP5uD7yAKU22r/OXrCEZjug56Ex5OvsygTCVAWf3y/OnmfMUc1uX3RmOHJp1N0f1iI8pjp5H7raDULJPFTuxzR4Os88bT/HU3nKFG3y+KPxySPM6NHB20pNTG04O7JbHz/s67GRos3FobM31FBceEqanvU53xf2PfxfmdbPYm1GONxwmNAtETK94zHQEe92hb3MY+BHpecPCaYjcWhe++dca/FhZLPPpuxjDH6u+v3+Onxzsv84slRtv67+4mTx1C3yUvDLSw5IsVjw7vvznydfXHhhcE4Yv+7b2y1VfA3C8++pzz5933o8dGfe4LvyLLoxULkC9vs+8ECr5P7i5fNum770i8ynNwe921/f3gMdoq+IzzO2EYLwqVSNHabYankly8WXl2GRSQn9zXbbwHS/cdidXw88xgSRZCar/vomWfO6GNutzm4DaWSx1FHFDlZLLFAFrXJ/aZYPPI9aIHW7J1833gssBBtH0VCoD+zwO57oishxP3M45B9FKV4P/L4YKHI7XZfKE6OgCzuS85vsas4qtNCuP1bLCLHBUv/bnE/6gOuL4rAcp/xWBoX+S3K+fvA9/+NNwbRsE7x9no8tAAWT++9F9wfttF5d989eBnm5wXnd4rGNY9fFtyPOuqbUWu+1mKTIw/9LGNRMOobUVS6y4qP7f4+93jYU/KLjUg47ykvnzeNAAJW01AnVhECVmLoa6rY+1xtLyn8Bi2U5Zhfvy72ZjgWsPwEM2dNtZS+GAGrAVApMoUEYgLW1DZplqQjsLzPlZc61St5+UlcaOqp3O23Dx6Si5OXkHhy6IdCh9Q7eYLvh8FSy84sangSVCp5MuIH0eih35NHiyf+uycg0eSo+Fo/zPvB1BMyiw7RW/Uonz/39Z6YRQ/P0WeeeHsfJb+ZtrAWjwjx5DMeGRGfNPitvsvyg7EfkJdeOpisxUUlTy498fdEyzZF4k70sG5Bxg/pfvvtCY3fgJdK8XojAc5MPGkye0+uLLhYcIqWlHqibwHIPvE1Fgs8AYtPgtw+Cyr+1xNvv5G2yOYJcuTLYnsc9eFIOrP2BDqahDh6w5MHT+wtjkQ+tJjjN+Fuq6OsLD50leIClvPY/xbLPNn09fVOFrK8vLC7ZJ96WU60H439a6ElSqUmne4LnrRZcIgi0zyeWAAqXobpNnsZUTQ5tshm0cmpuOziSWN3NnjSa2bxqEdPOH3PeyJXnCJBuifGnjC6n0X2WiiwCOg2u29Um9znXI7HGSffX54Euz+7P1l4sa8igch5HDnmyA+LBV2Jez3ZU7wsy3sPORrJkXYWRLz0r1Syb3ytxUELxE4Whn1dPFm49OQ9ShbgPY57Ir/ffjP+brEjfm/6EwtObrsjtCx8OJqkp+RxwWNKPVIkEnpc7I6vOfQUhWL/enxxP4tSdL9bHPR9ZWHCdUVRRv6e8LhmccovSyxOWVhztFv0MsF9OT7mWhTz546siUcDOnJo6NBAVLTgZmHY43EUZRnZ5LHa4q37ocUSJ4s/FoH8/eGxzJ8V30NXXRWIm2bmlwvRS5HiMS0SXIr94+/K4kjSeB5Hz/lFTjxZEPJLGovnTtF46fvEApu/Sy2wRC+Ciuu0gOfv7XiKIrot8JixxWvfA77HipNFS4/v22wTtNf3jpP35YwEpuJr/CLCY6lfdhQvv7Nw6eccj7cWwopf0Hgs6G6pp1mbv18MFCf3nUhg7+re8LOJ702PQ8VLY8u5n/wdaIHZXP2d3J0/yymPPFUTQMCqGl1mLkTAyoyrZjLUTwD+1vFs0WKWN3HxQmy/rjtFkjdOcXiD962qd0LAqjdRyksngZiA5ViDXpUsMWhEi3qaIDSiznLLjKKZ4vk94Sn10FtumfXM58mFhZlSe/z4wdbCQrQZeLS0slT9fnj2ZNUTdS+3KhZAHIkTiQ/d2e9ImCiiyfks0HS3N45FOUcqeULb1VthR8sUL5lypIAFiyjCyYKT93CKJ7fJE4MoORLFEXVpSmnqS+YSHwu6ui8dgeeoqJ6SJ1uO3vEkPUqRSFjqWkcTuY9Gk7TuxAMLmNHmwz3ZUdwne8pf/Hk9hZN42eXY5aiRUsueym2DhSMLSLWmcsuxKFtOdIftKXdMqdX2Wq6PR6ZVUo6FCvd7R99G4pwFdQsiUdp110DUqjRZKPRytnjy+HfKKTOiLHsq08v6LEQUC4IWOH1ISDxZMLO4WnwwgMUcC0g97QVlsdmRWLUmR2FZqHMqFvEqLdt+8fdOcURfpeVUmr+rl2X+/iteYhkv26Jk8dLdSuuuZ/6knxnr2ZaMlYWAlTGHVWEuAlYV0FJyye6SvJ5gYUnjJPn1SLgxSEMtLFvAGj58uNrD5T5Dhw6Vf0gQyAyBmIBVsDmphxG/+fUeV5XskZIZyBk31Mtw4hEh1Tan1ISo0rIcqWBhg9R4At6DxpFmjbonHa3nCAQSBFqBQHGUWlbbXOoFQVbbgt21E0jqmbF2yzNZwujRo+Ufp46ODo0KXt54K51JmWwQRndLAAGLDlIuAe+S6+O8LGD9XZLPn57qccJT+6JCBshBzRMnakB8/4tyayIfBNJAoJkClvc98VvH4g15zSHNkVdp8FOSNng5mJcMkCAAAQhAAAIQgIAJeN87R4aSEiFABFYi2JtaKQJWU3HXVJn3s4qdt9tlWT7eI9yQoab6ii/25iw+AzsSq9x3/PvGkh5AwKorawpLA4FmClgWqRxp5c1KvQeFl6Z5KZr3gPESNxIEIAABCEAAAhCAQLoJ+JCRSk9STXeLMmcdAlbmXFaxwQhYFSNL7AKHQDqyqafkEwrDo1J6ytqwz4nAahhaCm4aAW/m6Q1Fo9SIcHBvyurTuLzPBgkCEIAABCAAAQhAIBsEvFm9D2/w/nfeB7D4kI5stCJ3ViJg5c6l32gQAlZ2fOwdXk8rw9yDyxS6yiiq6iwIWFWjrmtNuAAAIABJREFU48LUEGiGgMXywNS4G0MgAAEIQAACEIBAjwROPrnr0x17vJgMjSaAgNVowsmXj4CVvA/KteC+EntNlbrWe1IlvVs6Ala5XiVfMgS8CbOP2Pax2E4+wvqDD4Ile5GoVK6A5VPcfPKN38I5+ehvJy8HdJl+Mxcdue7T1HwEvY9bnjRJ8ilHJAhAAAIQgAAEIACBdBM48sjg+Y2UagIIWKl2T12MQ8CqC0YKKSKAgEWXSDeBciKfNtggOGksSnvsIT3xhPTaa9IJJwRHce+1V7rbiXUQgAAEIAABCEAAArUT8HYPfglJSjUBBKxUu6cuxiFg1QUjhSBg0QcyRaAcAatZDYpOsptrLunll6VFFw0iwxwlttxykkPV29ubZQ31QAACEIAABCAAAQjECTRiH1QIN4QAAlZDsKaqUASsVLkjN8YQgZUbV+a0IRaIzj5bOvhgaYstkmvkYotJb7zRc/0+0Wb//aWDDpJ695b++1/p66+l7bfv+VpyQAACEIAABCAAAQhUR+C006Rf/aq6a7mq6QQQsJqOvOkVImA1HXlLVIiA1RJuzlEjTzlF6tNHWmYZaemlpXvukQ44YOYGPvaYdMUV0tNPSw8+OOOz+Fu5Tz+VBoSHhTbjbd1//iNdc4209dbBPlylkiO7HPZ+4YXSvvvmyGk0BQIQgAAEIAABCDSQwOKLS6+/3sAKKLreBBCw6k00feUhYKXPJ3mwCAErD15s8TZM/scd6jt0y9JCVXds9t47OE652Rt9evP4Rx+VNttshnWXXCL99KfSv/4lrbuudPzx0p//LI0ZMyPPqadKP/tZsKcXCQIQgAAEIAABCEAgIOCXliuvDI0MEUDAypCzqjQVAatKcAlf1sfnpkmaErOjt6Rekr5K2DZXj4CVAidgQm0EJv9ztPpu+oPKBazaqq396o4O6fnnpW99S+rfv3R5Xn542WXB8kmfnug9we67T9p449L5v/3toMxa0g03SD/60cwleAnk3/5WS6nVX+ulm8cdJ/3lL9WXwZUQgAAE6k3A4/YXX9S7VMqDQP0IOFrde3bmOR1yiDRyZJ5bmNu2IWDl1rXTG4aAlU0f/1PS8ZJiR6RpA0nHSIqFXyTWOASsxNBTcb0IfHXf3eqzcex2asaSwHoZX205zz0nrbjiN68eOlQaPVpaddVgyaIFry+/lBZcUPrHP6Sf/ER66inpu98NNqD3EkvvGRFPb74ZbFAfJS9r9M9SS0nXXy+tsoq0xBJSv37B5O1//5MuuCDYqyyepk0LosjKPQHSfnM03MCBgZ2jRkm/+Y3kv7us3XeXrryyNLEXXgg20l9vPemhh2bOc9ZZkh9wnczE5W++ebXkZ77OvG2TRUNz8P5nf/pTEClnkfHttyXvi2b7SqVi1i7HS2THj5cGD5ZuvjlYImtB0T+77hqU4hM2v/pKWn754P+bbCL985/S978f+NnJfrKvq01exurlrE7uD7Y1SmuuKXmpbjwddljgP9sfT2+9JS2ySGVW7LyzdO21M67ZdFNp+HDJR6OfcYa0ZRhx6T7pN+7F4qr9+/e/z1znD38YCMVXXRX8fcqUYJ+6666Tdtrpm/a5Lf67748RI6TvfCdYAmx/RP1n4sTAR7vsEvjZffWRR6R11pH22SfYi8XXX3xx6faXsjOe05wnTZIOP1xadlnJ/3dyu+3bOeYI/u++5/7i9lj0NrsDD5QmTw4+97Ll+HJqR3PusENQTjydd570yitBf434+Z63gO0xxXXOPnvQ/zwp9n3v5drxFJ8wb7ttwKdU2mor6bbbgk8ef1xaYw1ptdWCCNOXXpqx5+B220k33hh87nzdJftn9dWDscLLzb1UPPJ3/Dr75qKLpA8/DPzjPuV09NHSSSdJXvLtMbJU8rjnMdX2+B7o6qCRqVOlyy8PXlCsvXZw//rlgJP7kvk7wtbjRXFyX73ppiBS1/U4+b5yn91xR+mvf51xRZS3ezJB369EbHPf8iluvn+j5Hvc7bdt5rfWWjM+s0322733SiutFNwPPuDE/dJj5IYbBnndb8aNk/r2DV7KuD2/+EVwv/z858FhKE4rrBD4xy9sovHQ/XvhhaV439lvP+n886UXXwzukXjysnwLG3vuKU2YEIwf557bPaniFzi+Vzyue8uCDz4IrnW/9fi60ELB/2+5JeDhvn/mmcHfzLr4xdTYscE96shvJ29j4Ihr31fvvz/DLo83vg8dpW3mTl4e5/vTbbQPvL+m73uPLT5t2f0gSi7PY6jHJUdzu/3u1/aN743i5Pzuax7b/LLM31sex8zePHy9v1ud3N/dp+3rePLYZ1/MN5904okBa/vS/dbfVVF7PZ55LP+//wv6STmp1L3va+2bJZcMuJMySQABK5Nuq8hoBKyKcKUm80eS/E31dcyiWSW9JykN64AQsFLTVTCkWgId99+r9o2+N+PyDAhYt7x0i9ZfZH3N2a+GY579YOrIJCc/qFu88DJE/1tJ8uTBD/me7Poh35MKT1rmnTd4UHaKxCiX7wdYPzxbCIoLXc7nEP533w0eKP1gaTHtBz8IJuF+EI8Ekcg+T/BtrwUxP6DHkyOu/OAc96eFNE98/O+QIZLFKU8sLGh4cuHJr21wsrDx5JPBBNA2ewIZCR3+vydSbq8/d3ssCPrvnmBss00gvlk4iYQaP/h7Qu6JmZd6+iHdv/dyQK0kixkWfSweeHmqJxWebEWf2RYLTVHyZNQnW8ZFvuK+a+6eiJhFJL44yi5aJuEJ/THHBJyjZAHPE3eLI26jJxtOFgE88bY46HZb6LJA44mfGToi0CKYDyzw9ZFI5Ym8JyEWEz1hc59wGU533BFECHqS4z4UCYWe+FiAtLjhaz0Ze/jhQATxxNRCgQUi225x1RNEt8HszcgTKrc3mpAWc/H/423z/12+RRffF+YaCQvRhN95/OPJlCeSbrPttwj5xBPBpM1c3Q99fTzZVz5h1H3B9lqQu/PO4Npyku+t994L2HqiGJ/4ux/ZN+7rZuh72j6xsOJ6ndzPnCxwmp+XIc82W881m5Hr3WCDYKLsSfKrr864zpNw3xO+B/13+90CVan07LOBbb6H5557Ro6IsyernrS6j7mP+B5xO4tZ2nb71te5je7jRxzxzRotfvhe9j1uIcjjVJTcP9y/LLTZ710lf26R1yKa710n9wGLWsOGzRhbonEgmpTbNrOy0GAx2rY4j/uGxx2PF25jJNbaXx43Lfg4+Vr/P57czj/8Qdpjj2C8jlKU1+OL2+lkYat4bI3yn3669Otff/P66C++B9xXfR/5nrJvPdH32GTu7v8e312vBZJ33gnsKRaeo/IsxLivue9HYlq8XZ9/Ln3ySSBUFSfXFZXrscr3XTkHmpi/+2VxJHC8fPdV961ikcjX2k+O3L3//qDvx5MFa9vs7zLbZ5HHL1/sV4/bFhTNxLaai8eJKNk/7nvuk07uFx6b/UKpq+TyXa6/S6Jk/5qLxxIn3xNOxfeex2Tv8+nv0J6S708LfX5x4nvQ35Olkscfj+3+vjrnnGBMufrqnkqf8blFsKhvenxxXf6eK9U3oqt8X3kst+Dt/h/va/aXxUt/53qc8z3vscTjnPvd3XcHLxCOPTYozd/xHhf9vVs8tpTfCnKmhAACVkoc0UAzELAaCLeBRX8oaYik8DVooSZ/q4yTFHsCbKAF3ReNgJUYeiquF4GOhx5Q+/rB292P+rVpni+8ajfdqe34Nh24xoE6e/OiqKVKzPbE16KCk6OP/DY2jclv0S2G+UHXE1U/PPth3m9q/UbZb21LJU80P/oouLZUchSIBYFyHmL9kOwogEh4iZcXRX/4b54UWUSJP/xHE3RHdDgSptZkYcuTTL/hjpIZuT1xYaPWeqLrPUm7665A5HNbIn/Uq3xHmnhSYeHM4lqtKT7p9WTd/oiEsUrKdoSL+5knhRZPLeRUm9xGT6486Xe/LUoOfnDgz1FHVVtB0XWeuFoILhYxfE84+sORRpUmt8HXR2JYpdd3ld/3jyfgnjjb7mIhxCKhBQOLJnERqqg8B+VEem+9TCuUE/WnKGo1EjK7G1siAyxsWESJxBlPri3eWexoRLK44jHIgkdXyRw9hrhPuw1RZIxFY4uLpSLOGmFrI8v0OGVR3NF3lSaLjrvtFkQcdSXKlSrTAqUFE483pPoT8H1oYbU4YtH/tzAYRRcX1+zPHd1mIZmUOwIIWLlz6TcahICVTR97CaFjvc+Pme/jxfz6eqMGN8lLFz3iW6R6UtJwv78tqhMBq8FOoPjGE+h4+CG1rxuc7PfebG1a4LN0CVhTp03VLL1mjuiwgLXD8jvo7B+crQXnCN/CVoiqc9IkfXHbjZpt2J5BlEGte19VWH/N2T358mSwqyU4NVcQK8B1OALKESeVJgs+FkP89rh4iUqlZZE/lwTcvRyQ6DkwqXICDjJxwFAGgmcrbxxXVE7AN5QjihyFQ8o3AfvaS/sdaVwqdSV85ZtKy7QOASv/rkbAyqaP15ZkEetuSV4w7oXa3qzHscTdxL3X3NhfShohyRu9vCbJsbde+O764zuOImDVjJoCkibQ8dgjal9rnYIZaROwPvj8A81/xvz69IhPNXv7jKU5FrCi1HlsZ1UI//L0X7TnzXuq06sI/aDvB34SBCBQNwKPvf2Y1hwc7jtVotQPP/9Q8/SfR716BffzpZcGKwFJlRHwqtsf/zg/ApZXCzog6nuxle2VEUlnbq8Ed6Clt0lqZrIwPGhQM2ukrqYRcGT0jjtqSlt7YTVwtFVa0+qnokQJIGAlir8plSNgNQVzQyrxmgqvkfEGL2MknVciEqreFb8uyUdynBMW7PCPdyQdKim+CzICVr3JU17TCXQ88bjaVw8mmWkTsJ5//0WtcP5yuuyHV2j9RdfVYoMWK9gZF7De+8V7mn/2ov1SyqB4zD3H6KQHTwoELO/f5H1ZSAUCn371qTrVqQF9PMSR0krAK4S8+jXat7knOx99+1ENGTBECw8I9xbr6YIKP7/3jXv14Rcfaqdv76SPv/xYc58+t948+E0tMrD0JvS+j6/b4TrttMKO02tqlSiiW1+6VS+Nf0mHrRNuMl0h63h2B2Dssu84dU5qjF9rMK2qS709mregy2pf8DkA3ovcWxTGA2R/+ctgv/urbxunH2/ZPF/ZBm9n1qwA2C0u31bX7HT59O+Pzzs+10NvPaShS5W5511Vvaa2i57/4Hl9e76el3B7DG2fpV2rLFhFNHJtJnZ7tffh91aI9bhnDj44WF3r7cnK2WGggc2i6B4IIGDlv4sgYOXfx/VqoWdsXsjg6K/4MVHe5dchGvGnTQSselGnnMQIfDVhvPrMGZyJkDYB65bHntG2d36nYNuaC6+pR3/2aOH3uIDl/5eKwvKWUd5nNTqwKA7YUfV7XXGUrnr75IKANXXFb2vMfTdrybmWrMgP0eFYnphUm/742B919L1Ha+LhE6stoqzrxkwYo0UHLqq2MpYcDh45WB1TO/TBL8NTo8qqQXJETb/e/aZHy30x5QsdfOfBunDr8DS+MsvJe7avp30tsyklEE7+erKmdU5T/979Z8Lw4JsParWFVivwjZJd6W1RokOqeuLm+2bVBVfVE/s+0VPWsj9/5r1ntMJ8KxSW+c5ywiwF230/RtGTrx74apf3le0Z+f2ROnS3b0tDD5H6TlDnmeP0WcdnmuOUOTTh1xM0sO/Asm1pRsY3J7ypIQOHyGKdD5GoZiJ73H3H6fj7vUtB6bGr0na0LXGPtMcm+urorwqT6zSkrvpxObb5kD6Ls56Mu49ctPVF+tkqM+/h88mXn0w/xOP+Mffr5fEva59V9ymn+Ibn8VZfPruh+KwAb0X3+ytelEYsp1dHvK5F5xyiWdpmKYzJnZ2dmto5Vf99etZuV2p/94Lv6pJtLtF3F/yunnznST341oM6eK2Du21T217r6849btPQDau7l+4bc59m6z2bVl949bLY2WcXr3+P9vrexoX8018WhdHS9t1cp89VuPcPWTs84baskmvPdN6/z9NzHzynUVuOKhw4+vHkDzVbe3/NfsrsOneLcwv9rPcsXe/jFT17zN1vbn30K58zlY509Blj9Nvn9tK6G3TowZ8+WNb3fGS5t/fzd0l0nkr8EaEeglg6COXTCgSsfPo13ioErGz62NPCB4qEJJ877PNow3Ob694wHwXjc4+XC5ctRhVcI2mSJO/BFSUErLrjp8BmE5g8cbz6DkqfgHXGw2fojXc+1bnPn1BAsvRcS+vq7a/WmY+cqaufm/nUny+O/GKmib3ze0sI7+kbTYL8t0jo2veAL3XR/IFAYAHrtUVm11J7fVZSCOvOH37Q84GBxSdiV+LDTS7bRPe8cU+XdX855UvtcdMeumaHa9SrLTix77aXb9PYiWO1/+r765Gxj2jtIdbbu09+8L79J7dri6V7Xr8SPaRXujzT160zZB39a6//Z+9MwK2a3jD+NmikQoMmSTRIppSQlCL9kXksZRZRJDJEqWQMUUIDIbMIaSCZMlQaJBQlUomiUXP3/7x773XPvufuM94z7HPO+z1PT3XO2mv4fWuvs9e7v7XWDCxaswhr/luDls+1jJlrpLaE+54iGsWUfcq6TiorSoYhruWEc/Ivk9Hh4A5YuhSo92IxjL9gPM5uFHnj5N5Te1v9eO1ta60opc13bs4XrI565ijM/XNufuQSxa5SA0tZEXH3tr4X95zoHDzgnMjOfZZ5SF80Rv80qdoE484Zh5cXvIz7290fzWVh05i+MuvqWWgxqoU1CXcLWEt6LMGBex/omUe+gDWVwc22UWCbcNEE1HqsFn7t+Wt+1GU8FeVEuXyp8iDDtf+ttYQnnt3A/eh5CJ8x3mM7du+wBMUf/v4BNfeq6SmcMfri2NHHYnTH0bjy3Sut+3HXPbsKVe3GD27EyfVORscGHUO223wR7T3GtrCOVcsX3gS/WJNXgfMuxsm1z8LUK962smabKHau37oeP675EYdXO7zQGOmuHPcapO8SIYCxv7Ku1cpXw5+9C27+T1/w3gknEvBQSe79bsbua466Bs+c8UwBluw7n3T9BCcecCKK31vcuj+iZWn4GJ8HO6nb+93wzLfPeOa3bec2bNm5BZXKBNbk8VA360DVAcXQaN9DMe74BZYIxb333Yf8MbJl6FtfA1cFxuuhpw5Fj2N64MEpz+P2ry8H+udZh+G5D1o09TP9j/+/tum11vjz2/rfwrZ79+48lBhYHB1WfoFR/Y63DkKN1cL9Hny5/Esr2vL0+qfnZ8v0Qw77GL3OtgWsPh/2wUNfPoRNvfPsgwL721OyE+uciMFtB1u/GcZ27NphiS8lizsnh0ZZWf7eNKjcAG3PW4Ih99TBEYcVvn7i4ok4/RW7nve0ugcDxn4O1J1u1ePT3z61Pu98WGecdvBpuOjQi6K+dyf9PAlnv3Y2tvYNDMRzVs1B02ebFtr+gPfZt6u+Bf+O5neblQh3bxpe5z70JN7dZo+jkYRs1m3pv0utfURpPFfjuOOACUcWw4/df0SjKg3z2x5KwOLBnDwfJtx5CVG6TsmKQEACVhHgZcilErAyxFFB1aSQdJgTEWW+4jnL8wF4r0koejtjjsDq3r07SvE1OHgqeHvrj0wEMoWAW8BaXa4Yqm1O7ybujOD4ac1PaPxU5HB+N+PgyQvfgM87qxjmXjsXfGtNYxouZ+DbVmMUsObuBxzVLSBwcdIXTeRHsaoLUbdaVSxdEOKkv6BOUOXhKuh/Yn9cdsRl1kP/8WPsZZF8i24mY8H9ZtaKWWg+qjm23LUFZUraR3uXva8sGOFA4a7c4HJYcN0CrNy40lqq1bBy4OHTnRcnFS+c9QIuPfxSS1jig2+oDfDdExY+7HLidH2z663s+N2A1gNw94l352dPnxVDMRQfUNza0+iDSz6w6vzF5V9YAhYjaSgOUHjr/WFvfHjph6jzeB2r/hTwuh3dDV0O5zaDsHzPujWp1iQ/f1OfxTcsxsg5IzF92XRQMKGxbCPs/fLPLzj4yYNRq0ItLL95edS3YDh/M//qQ6qDZTMq6qOlH6HGXjWsKCG2bfYV3+HoVmuBy9qg5zE9rQmZO3qKk/nuzbrjsVPto+M5eT90xKGWUMI86w+rjzW3rgEF2wdmPFCozozMq/iAHTlx23G34cGTH8RbP7yFfp/0w8Lu31sHPjLa0MvYrkoPVsLWu7ZaE7T2L7VHg30boGmNppaA5b5nKMy0qNkC/Vr3w4LVC3DVe1dh0Q3cerKg0TeMzqMwZPoD/+aEcPAXgy2xaHvf7Rgzdwy6TbRPyPy4y8doU9eezBq7YsIVeG7ecxhyyhDcMvWWAt+t6LUCNR+tmS9gHTj0QLSo1QIvn/tyfjrW0d1HKNgcMPQAS/jjfTJ75Ww0G9kMXQ/vavVfLtcjhzJ7lAa6tMNnA/pZE0jeC6e+dCrmr56PS5pcYnGh/XHzH5af6X8KovQb+zftuqOvw4jZI6zomR1378SuvJ3WhJtpO4/vbAnsFAq/uy6wLJl9+PH2j6Nni54FIkg335qXL3Kw/7JfnPnqmfm+ocA5qM0gK0qTY4bbZ39s+MPq68VubABUXmzV7dTaF6BW5QoYNXeUldbcO72P7Y2HT3m4AGdGf1KI4ZjQ8ZWOYKTNhjv4ns62C9+8EJ2adAopxJl0ph7m/8F7FLIvUBDgmNVyTEtLKGPfMteZ8cNEhwYLWGfVuhavdh0KjkVPzHwCY894BaXvt6MJKQYYo8DLsZVjS8v9W1qRKMbYZ0sPKo3ZV8+2+j/F1lkrZ1kCJPv+sA7DrDH0lHqnoMx99jhrWLsPErngjQvwxg9vWOMsJ/s0vsjgGRXXrnKmGv3tfRn/+w8oGwiYRM+ewBPjCwpYTMcoxfMefhLzygy1BKy//ip8eOz3fy5Ck2e8x3bWkyznrppr9ZFPfvsEz8973hqHG1U+BHWfOAAYPQOdTq+NQy5+EXd9fJd1L5QuWRrv/PSOJdi4BUUzbnC84fJ8c39yLOILEwqiHOvoL/dvBSMLrzzySuz/+P64sd6TuPvsC1GlfBXc9uFtePjLh/Hr5TtQ9/oeQDPuBBIwjn8U4zod1snK74j9jrB+T5ZvWI7jax+Pdy56xxJxeB+u2rjKytMIXIy+az224JlOJ+4YjMdv6GBFjR2878H5Bbn7JX+PNmwL9PUCFXL5nn2TS+o5jh5RvgPmbZ6Un9T8rvE3Z8m/Swr8Rpuyfr/pd0s4Zz68t7kvIMdW2rst/0LHdlUsoZbMxy0Yh2uaXmO17fHPRlnMVm5bjIP2OQgcG2gvnv2iJbIZY9nmO/MZf3fpN15H6znJ/l0yYzYjrFdsXGH1b748a3vPQyjz5mRsvb0YXjvvNVx46AX5+XNfwubNAYqvXP56GGdkTp+37pH4tiANxq3/x0BgypQp4B/a9u3bMdx+G8OHhNAdOob8ldRfBCRg+csf0daGN6PXJiwbAewVbSZxpPPaA2sVAMY6aw+sOIDqEv8S8JuA1e6Fdpj2K89uiM34MMaJPh9KOSE496R6mH92Mbx5/ps47w37TSMntn/1/gsVHggMKxSw5uwHNO1mv7nkUrsGwxqgV4te1hKVvq36WtdySdOr576K0+qfll8xPqSW/rsFtg77qsBnI04bYYkynBjVrVQXA9oMsIQVGifFnCh5GevGh3Nj05ZOQ7sXeWYF8NWVX1n5uY2RKpzsclJ29MijLTGMUSt84OYk64ojryhQr0aVG2F+t/koNSiwzIhiAevEtrB95zW6ECUH2T+ZrQ9obU1qaWYyx3TByyfM0jGmY4RIsxrNMPHniai3dz3rwZ5WsXRFrN/mvUyybd22+KgLz+oILA/lBLfN2DZg/YKXjJr6/LnpT0tcYgRT85HNsfDvwEGx5zQ6B92adsO6retwfuPz0eXtLnis/WP5kVkU/vj/MxuciRqP1sAb579h7Q9185Sb8dUfX+W3l5NuCoYU/7q8Y4tsFMwoSj0588lCbnRH5fy89mdLoKJ9dOlHOKnuSTjhuRMwY/mMAtcdWKEBlm4oLBYxESdz8/6cl5+ekTQUWyz7ugdQ53Og+lxLfGEkQfcPulsiEqPgGOnFtjzQ9gHcPu32/DzIZvyP4/MFjoXXL/QUjJ8/83l0PaIrXvruJbDvcOJ/7uvn5l/r9tedLe+0JlyMamE/uuitQATDjc1vtKJMGB1H0cgShQYUPFnUDYSTPk6CyXzgZwPx8z8/W/cuRVzah4s/xymvtMq/pHGVxtbk9rvVtmB0xRFXYMy8MYV8889t/2CfcnvnR4Dc3epuK38vm9ZlmiWu0h5q95AVrXDgE96RZEzD+67uUG7VGTAyua/tfVb0V+WHK1vi4dizxqLFaAaS29Z9188YXiIwyXZfb9X3oX1wWLXD8ttm7kMumeM49cjJj1iisJcZ4YvfldhWGdccf74lvFFQPOmFwA7pd7S8A49//bgVWUShiz665K1LsG3XNitbji9cJnrO6+fgnIbnWOMKRSj2dQqaRvChoMNI2ZIDA9EvRkQrtbUGtpcJjHu8H8zYxjJuPe5WKzr06dlPY8qiT7Fu6vXYMf0O7DHQXs7FJeTfrLB3dWj7+2eYtn/A/56Nd66hIMBoOXJnJGsou/XY2/HwVwUF5H6HvYh+Z3WyhMtDqhwC3ieNhjeyRHYa27b3g3tj3eAFuL5zLTxV1QhYu4F6U4FLT7WiXsfOH4vXF76OSrvqY91zzwNXBSKOTH2O2NrTFrBWHYkV/b9Bjf32sMRVCuUUjS4Zz8O3vY2n8faY3CPk99YXy1oBB3BBg21k/cHPH1j/ZkSh+a3gbwfbSIEj2Nh/KQTTKNJzaWen8Z2s/0/pPMUSyBkt9+ycwJJxjsFPf2sfJD6y7du4elroCNXvr/veEveDbUXPNag51I4SN3b5EZdbY8qM32fghkk8cylgzXYvqrQkAAAgAElEQVTehFklH7c+oPDN3yH2ca+8CxXmfMBngdFzxuD6D64LlaTQ5xRpB5802PIVRXPDaXrX6eBvQee3O2Ngm4G4e3rg5Q/efh7T36lj/dbRZl4101qq6fWbZwr89ppvrd8FjqPm/vCq5KgzRmHq0qlW36PxpQ9FXyPEu59Fygxdg609K+ORtkPR+wRXX+raBiVrLsDOEd/g9usOwP33lcDixUCDBnaJErCi7h5JSagIrKRg9VWmErB85Y6oK8PZCGcMgVdsQFNHRPJ+FRV11mET8mmQv4icqVLM4poNvvLgkK1TCBPDWLn4hIBfBCy+WT3lpVOs/SniMU4WGQESq1HA+rY6cPS19pUUgShiGeO+GNd/YEcf0Vb2WomGwxuiy2FdMGyWfc7Duxe9ay2h4ASw/GA7MoWRIIwEiMUoQnB5FzeU5cP2hY0vxGsLX4uYBZf9MMIg2BjtxYga91tqCgEUZdy2rOcyK3qFVmPPmli5qfDkhaIEI7yOG2NPvjghJKuh3wy1BI2i2pxr5uCeT+6xorSiNU6iuJdUKAHGKx9OqI7f/3hc+val1td8203Bx8uqlKtibUqeCGMkECeyfjJOrMzEKVS9fu+xCvs/Ud36elKnSegwjofzwhIND3riIKzaxHc70Vuf4/vgwRkPRn+BK2U09Y2Y8fIWQG17chnOSpconS/gREob6Xu3EBwpbTTfc8kVo8BMH47mmkSm4QT6mFHHWJFZFOfM8iuWEWosSmT5ZdY2w9Z97QhMv9ixmx7AV3s6IvHqJkC1EKfafns10HRk2GrfcvQ9GDLbXjovC0+AEXNTl0z1PSZGufGlTiRrd2A7HFDxACuCMhnmFi5D5r/oDKDBe8CwH4AbDslPVv/PO7H46fsKXMaTNfdKZjhBMiBkUZ4SsLLImSGaIgErM33MBd1cg9AHAOPj+Sqbm3ZwZE/WHliGFM8m45SWQzN3vO3ucfqh9sDKzH6lWrsIFBCwygPVNqUuJnz1ptW4/4v7UX/f+paoEryUKBWOooA1qwbQ3L27XSoKTlEZjG6KJ6ItRdWziuFyH55SJRMBERABERABEfApAS6Prfg7sD6wi4uisNLnKwlY6WOfqpIlYKWKdGLL4RoDHtXDeFZuWrMJANdsMCKq8M6piS07mtwkYEVDSWl8TWDLujUou7e9bG11kgQsLoXg/k9cpvXC/Bfw3uL3rPK4v0XwcqpUw6KANbMGcEyWClip5qnyREAEREAEREAEcoBA/zwtI0yjmyVgpRF+ioqWgJUi0Ekshgvg/XNmrd1QCVhJdLiyTgwBblrOzTv5N08sMvv8cP8KbsL691/LUKWavXcLBaznJt+PO6bdkV84l7VxDxseF99vej9rM1Cz2W60NeQmvtyHxI9GAeutRsB5F/qxdqqTCIiACIiACIiACPiPwHV1nsRTlxXcg8x/tczeGknAyl7fmpZJwMoOHzMKi7twclfFwjs9pr6NErBSz1wlxkAg3EagJpty24HNztZRFLD2uzV8Adx8t3HVxhj33Tjr1CDu1zR81nCcUf8M63Qi7if02Nf2iWuZYHX+BdaUAzaXzoTaqo4iIAIiIAIiIAIi4A8CwSdA+6NWuVELCVjZ72cJWJntY56nzl2UedwJfck9sHgiYLpNAla6PaDywxJIhoAl5CIgAiIgAiIgAiIgArlNgBH9v9/8e25DSGPrJWClEX6KipaAlSLQCSyGZyef7whXPDueZ7HXBHA4gF8SWE5RspKAVRR6ujbpBKIRsMpvAzbxaARnCeHqJfNRt5K9pJBLBfe6P/FHzDSq3MiK1pKJgAiIgAiIgAiIgAhkEIGhv+Djt+ugdasSMW8pkUGt9H1VJWD53kVFrqAErCIjTGkGXNB0BYBKAN4G8CyAT3iCvSNg/ZXS2oQuTAKWTxyhasRO4JUFr+DDpR/ign0vw6knnJgvYAWfQrg7bzc6j++MTds34c4T7kTJ4iUxes5oPP3t0/mFvnbea2hStQnWbllr7ZW1cdtGVC1f1Xqw2b5rO5jHkn+W4NAR9srfzXduxuRfJoNHOm/ctglVH6kCfNkLOO5RO8+nvgP2/hW4+MzYG6YrREAEREAEREAEREAEEkNgcxWg/N+BvPrn4a+/gCr2+T+yNBGQgJUm8CksVgJWCmEnoKjdzobtnQFMdeW3SgJWAugqCxFwEfjwi89x8gmtrE9iOYVw0s+TUG6PcjjxAFv8imTLlgFtJtRF68oXYcwl96OYMyr36AE8ybNFaV3aAQdOA3hUM62/hu5IXPW9CIiACIiACIiACCSFwPcXAKsPB9reBQzagg3/lEaFCsWwdStQWnuHJgV5tJlKwIqWVOam0ywos3x3ubNRe1MA8wA8A+BlAIsBHAFAEViZ5U/V1scEpn3+Odq2il3AiqVJ33wDtGgBjBkDXMHYSgZZPQWMGgXMmwfspmRtWR5QfBewu6T931IbgdO6A4e/GEtxSisCIiACIiACIiACIhAPgQmjgDOvsq58rk4eLr9qO9pf9TWu/18rdOwYT4a6JhkEJGAlg6q/8pSA5S9/RFubZs4eWBcA4BS3FICTAXwWbQZJTqclhEkGrOyTT2D6FzPQ5oSWVkGxRGDt3Mk9soASJSLX0URbRU4ZJgXFrBsaARVWAP13A/2LA7v2AD67C/jjWKDJOOCIF7wzWHUEUJ1aeIbZxOG2gCfLXAJ/HQJU/SFz66+ai4AIiEC2EPjgSeB/N2ZLa5LXjv55OOPljli1aRVmdJ2Fd94BLuBMTOYrAhKwfOWOpFRGAlZSsKYsU+6FxbiNawEcBOBDAKemrPTQBUnA8oETVIXQBGbPBo48Eti4EVi1CmjUqHDaz76YgVaOgPVqY+Ci753le0FJt2+3I6XKlLG/qFoVqF0b6NcP2GMPYN06YP164NxzgWnTgGbNgP33B37+GWjcOEFe+t8NQPPh9hLDEqxQSSCvuJ35WV0LClirmwBzrwBOvRkYNxHodBow5A/gllrxV2boL0BPDkEABuwA7uFZE1HYqC+Bq44LJFx8GlB/YvgLx70P/Hxa0ZZRThkCtL8ligoGJZl9DXA0tx5MsL3/FHA6D5T1qb3+evRP6d9dAuy1EqjL7RnD2JOLgBsb+LTBTrV+OAd4byTQZ9/k1fPl94C9lwAdboqvjG17AqU3xXdtIq7aUgkou65gTutrAxWXJyJ3/+exvRxQ6j+7nhx/tbzb/z7zaw3v3Qn0c6Ks3XXkC6ltFYByayPX/Pfjgf1nhE73RR/goMnAfvMLpnlkFdC7euT8k5nio/uBdncESlh7EDByFnB6N+DQ15JZsp33O88BZ3GhS5DlFQOK2c9/o2vn5UfLJ79CKiFeAhKw4iWXOddJwMocX0Wq6SkAugE4J1LCFHwvASsFkFVE/ARCRT716QO88QZQowZw150zcOr/WqJRd2DxvsCvV+Zhzz1tUWrDBvvvatXir0NCryzzL1Dra+CXDoWzbdcHaPlQYHI1/V7g03vsdHsvBXrWA/jweuWxQOmNwKzrgRMHFsxnxDyg5iyg49X256++DdSdBhwzzP6/e+Lm/jcnt7+dCDScACxtC7zxOnDUSODk253rnIgxU9rDq4HjHgGOfzhQ/rAfgBMGAw3fsYW3yUPt7yr+Btx8gP3vXSWBEjsD1zwzG7j26IJtePxXO5+mI0NPNMe/AJzTxds1b48F5ncByPr2feJz39NzgPMvAPZ1HRg7+VFg5o1A90b25//ta09Ulp0IHPBpYb4/ngU0eie+8qO9yi2KLG8BjP7Knph/+IAtMI5/McB+wcVAk1fsnB/4F9haCejUATh4sndpP50JVPoVeHo+cFdZYI+twHOfAJe39k4/aAvQt2zguzdfAc67ONqWFC2d2XOuOaMTegCzugHNAoc0hM3cREMGJ3pqAbDPz8BF5wDDFwJ/H+KkoPhRHFh+LFD7K2D2tcDR3CXAw9iPuh1lf/FXY6DqwsKJOOmlP65pBlRxTjZd/D+g/gfeeY6eAVx5fOA7t1/Np8yzxA6AfXZZa7sOnPTVmwI0eTVwLYW/Q8bb/3/0d6DX/qFRfXEb8P1FwJ9HFhZ/3nwZOO+SwLWMKm11H8BJ+pwrgbOcddfReHlzZaD8Gu+Uy1oBBwQFsIcSE4JzeOM14NBX7HvSPfa5D9+Y/Jj9wiDYpg0C2vYFvrwFOG5I4e/HfgT8epLdL2K1naWAktvtq2b0BmrOLNzGSHm+/C5wSdC6qLefB86+LHDli1OAI8cUFBiYZn7Xgv50ixP8XSi1GRj1NbCzNNDmnkB/cdeJ9xv7dp3Pw9f0n3rAZr45+ipSiwp+776PzDfhontZ10/6Ae3ujL6cT+8GDnkDGDPDFsL5gueYoUD73oE8TP/zEkC/vRp471mg2G7gktOBgycBFIhLbrH7s9sffJH0bz3gtsr2bwh/O7fvBfSqbZf1+R3ANJ4FFbSPphnn+AxxFQ83d2xjdftlmBGj+ZvEz9z3ukm7pB1Q76PQXPj7X+UHYC9u2euyV94BtlUEdpYB6nwaeDZgEva/xWfYbec2CnklCvYpjgPr6gCTnrDHhWMfs+/Bmw4AKv0WvY+YkkL04M3eAvTG/YC9/sReeTWxof8fseWr1GkhIAErLdhTWqgErJTizpnCJGDljKszs6HRLN0rs+88bFl7JCreDmxgdJV5yMu0JpfYZj+A/nOQPYlZfZj9sEjjg+FRowA+JHNiSttVCji1J9DiCfv/FDPu32j/+/gH7b24Pnce4E20gXnwXtMAGPYTsN88gG8t/6sMbKxpPxTyAfYF5wG33lTg0vY20z02AzvKsTJ2GY3eAi48L0A5HHc+xJfeYF/LCQzL4QPt48vsf3Nis7QdsORk4Mdz7YdgPkT/3Rio/q1d7g1GQHB8zM8pfj09F9iyN3B5K3sS8NT3rjoVA957BjjjWmBFMzuS7dxL7Af4e3cBh79gT8or/2S/Of+3LrDHf8CO8kCF5bY/jFgQ3L5DXwWOHgG8MC0QyRYsEJb/C7g1SD11i3YvTQJaDQTmXQYsa2PXu8fBBXvuiPnAdYcHPhv5jd1H2P6lJwce5D94whbY2Ja1B9uTCFrdj4GVTe3JB8XP2l8H7hH2KSN2su6MyGK7WJ8tLvGPvii7Fvj9BDvPnnWBvZcVrKfFJ8+eIFO4ihTlMvJr4OoWgTy+Zl92RE93zgsu8p6IvfsssO/PtohqfHPE8/abeVM2hZXvHRFt38VA+162sPfCVPuU0MWnAxtrAIe9aJfNyMI/WtiTQbINZeyzFDU+v8tO4Y7mYb/mpIwTvkVn2vfNXXsCfzcKCFTufE3dma7sP7aI9M2NwMEfAPsssVOyf5f9F3hxMrCkvR0JtrMscEtNgBw52VzRHKj4O7DqSPs+u7s08PhSYF1du36MiOSY4hapWE59RpbxPswDKi0DbqpbsNVDVtjlUMD66EH7u1NvAg4fG4jo4rXsI8c+Chw12p78m30Amf6is2xx/DWOGby/w5hXvxn1lT1hpxhWewZQ5Sfg44H2mPIhRX+PR2TD9YDpdtTr628CxXfYfl9bHyi+0+7Tm6vZE3LyI9Pe1YA9/wKMyGCqynuDfcWUZYRLjisjZ9qpKNbznjpxUKCBHGsrLwIGbwTu3At44UN7rOt4lV3up/2Acy6107Odm6oBNx1o///7C0NHtLz3NPDttcD+nwO/20voLdGfY+ghbwJf3mqP792OtAXtGX3sNJ3bA2sa2v+nyGHG876lgXdHA991ttv4U0eb2W5XlG6xXUCzp2yRmHw51lCk4e/UeRcBjd8M3ItnXA00HWWXacYmQ4X3ItkzCplCeoeegZcATMMxkp+z/nyRMGBXQR8b5sYXP55tv6iZPgD4pqddCn8z+zljYLAgbP7/+htAtfm2v7x+v1jHPpWBDTXscWHKY/Z4yvGRYx0FSyP4PfMtsMoRqzufChw0BaBoyrqWWWcLv7xn+Ps9x96byRpv+dtIMcvYjQfbIhp/J2lHPAc0ft2+d839x8/ZdvqPL7I4vvOlWAsKsL0CbWEf4/3IlxG8/2gcBzqdbv+b9/8x5gQapwLkYA6jYd33WgFUWFmQD+/BK50+xxdO65wXVIFWFPSXmy3bzPHEfMb8mw8DTnjAfbX9b6+XAxQnB2217zU+t3BspfGF0cSngE3V8eyzwNXOO7zCmeoTPxGQgOUnbySnLhKwksM123I9jO/WAfAJlrOmdgA+DtNICVjZ1gOyrD3RCFjgw7B7iVOcAlbDhkDFigCXLXbvDjzh6ELhkJ54IvDpp8D06UAbR39IqQu4r1b99+0Jyda9vR8kWSE+IPJBmZOacn/b4hcFjWALFrAO/AjoQpHEY1lmo/GBySg3TJ17ZfRNtwSs/YHHfwOOHWJHbLH+4ezk24BaX9miwJe9baHprvIAo854wpCXcTL63Gf2ZIiTU4pUfKvOZWDR9pMqC+3JFScKoezWKvZS0EdW21EOZ17pfRKlmUiauhuBwZ2vmZRxgr7gEuDfA4HTrgeajQCWnmQLZsHpJz0emLiFY3jVMUCtmQXbzkkVIzWi5cH8OSGjGHCbM8nictcR39klUxigCGYmwqY+920Cyqy3RYBya+zJh2nrlEeAb3rYURycsDF6z3zHyAj282MfB345BZg4wvYjr2dZjV8DFnSyS3G3peUD9gSNYqTbDprkHQEZfe+1hZ4NtQIiDSdhNWbb9xRF3xPuL8izVy170suoPUbwcHkQRQBaMHeKUBQxbmhoC0sPrgFKbrWXDj+2DFhfJ5aa2mlPuA/4qpctalNEmfqwLY5wksyj5SmccYJMu4GCy2Lg26vs8YJiDyPbFl5giz1uo6DBJTtGrKIIRzYUnoPt9orAiAXAzXWAFUcD1ecC4z4ANu1nRwJykuzmYfz/6njgp7OBdrfbkZUbagJ3VALcY85+cwORbqbcWPqzu6699wP2XB36fth3kV1n+poizQ/nA0sYWO+ytnfYE3KKzRxvDnvZzo8Rff8ECdTlVwOdO9g8KGBRKOELjKuPAcZ8ZkfsnnJbYZ6MxmU9kmHsD1srBkRwdxm87w/4pLDASzGR98Ea1zr/fX6xhXC3GB6qvl3aAgc6j6uhfEcWHD82V7HHc7JlhJh5UROc91mXAUeMtdlzj0kKZhSAmQfrxhcBHFsocH7hRBsH5xH8mxj8PYWyczoBE8bYdaIFn0acDB9RwKFwWOCedLYm2OUcrcdxg7/3HKsYrc02HvihLWC99RKw8EJb0DTczf3H6GWOC7z3T7nFFv35wivY2E8p/HpZ02ftF0fuezocBwrgFH+rfQfsLgG8M9Ye57m1wluMHM4DTultv5DgPWKsycvAuZ0ARlJOHWJt/9C6NVA8jmDIZLhJeYYnIAEr+3uIBKzs93EiWtiQsRcA5gKY5WwYLwErEWSVR9oJ7NoFrFwJXHYZULYs0KQJcNRRwAXdfikYteLx8MtlhNwDy21ffmnvh8U8Ihk3AD377ECqAQPs0whvugl4800gLw/480+gZEmgcmVg0CBg+XJYbwIzyviwziUGL3KbPid6p2vb8AIWI5kYxWXe5EfTYIoI6/f3nuhGcz3TmMiWcAKWV16VfwQuOL9gpFa0ZYZKV3q9/Q0ntQ3ftpeduSNrKBhak3zXTzmFCjIINoo/jKjgpCMaq/CHPSEze6mFu+bqZkDN2QX9SRGIb9S5hDRW45K08y+0l1Z9dnfhqxnFxrqV2uQtmJIbJylefYd9kSIFlzi5o3nC1TEeMS7WNkdKz0hKLvl1T+S9rnFHRXp9f9p1wGEv2VGVFJ8pgj36R2CSHKke8X5/Y307si1eAShSuYxq4QR7uxM5wfQUpxlJ99hvgXuCfH5tA4z1eISpusBe0mmiDJkHRZcONwKN3gaene1a8hmpQkHf31LdWoZUpPazLg0mAPMutyM+uXQ3HE8TLcS9BnmgR7CFizCLsXm+Tk5xjCJTsOgcb6U5tvF+LEp+FNt3lI0tD45DjOh8Zk68NU/edYzs5H6a7v5I5oyma/Au8FnfxJUdHPGbuJwL5sT7gxG8kx/H33/bz2CyzCAgASsz/FSUWkrAKgq93LyWi9EVgZWbvs+pVv/w5xI0fsbZmJzv6fp5b+JeFCgUqChiUfBi1FU5rqSDvbH8N98AZ53lnXtUEWRFqViir+WD4Gd3Ah/fZ+e855/2hrFek69goSbRdYmUHyf1fcsBw360I9D8YtwD7KKzizYBTlZbOvSwl4wkS5xIZL3ZF2MVJ91LCBNZl2Tk1c2JGuQeY34yLmHiHm+p7CMUGhjVx6g6Y4zg4N45XtFcyeR17sXAIW8BA4PeeMRbJiNkT+oLPB3hFFlGbs7r6h31xLJ5P/BFwaIzbNH37RfjrZGuy2UCfOHBvbZScX9f1QKo9U3yy+K9wWjbSU9YLxNlmUNAAlbm+CremkrAipdc7l4nASt3fZ9TLV/0169oOMLZMyRJAla8QPfZB/j338hXN28OzHS2UYmcOokpgk9GDFdUugUs1o3LtlYGbQKfRDxRZc3Ii4vPSv5De1SVCUrESA+KBYwI87sxcsIshYm2rpkkYNEPtGijy6JlUNR0PQ6y995KxQS3qHVNxvXWssjdBfd+SkY5sebJDdS5jPOvQ2O9UulFID0EvJasJ6Mm559vLSNtedCR+DzCOQLJKF55xk9AAlb87DLlSglYmeKp5NTzOQBd7UXgnut0eA76SUFFS8BKji+Uq88I/LLmNxw8PLCJaDIisOJtMvfH4n4MkaxrV2Ds2EipfPa9nyON0omKyzAuPjN3BYB0svfDEsJ0tj8RZee6gJUIhspDBEQAuLq5fSpyisTw//6zt5eQZQ4BCViZ46t4ayoBK15y2XEdFyw5x5F5NojHkjnHj+V/H7WA1b17d5QqZb+Rb9++vfVHJgKZQmDp2uWoNyywl5CfBCwyfOQR4NZbw9O8805701HunZUxJgHL21VcMnTJGSl7aM+Y/pKKitaYBVzTXOyLwpqbW3N/tl+D34kVJVNdKwIikHMEvPZcTCIELR9MItwEZj1lyhTwD2379u0YPnw4/8lThXhUtSzLCEjAyjKHpqA5UQtY69evR4UK3EhXJgKZR+CP9StQ+/HAhtd+E7AM0RIlgN28Kz2MG8xzo3mzZ9b11wM//ABMnQo42rL/HOPnpXLppHXwRPuUpxS9dU5nU1W2CIiACIiACHgS4IEp+80Hvr8o6YDeegs455ykF6MCEkxAEVgJBurD7CRg+dApPq0Sz89lf/kPQAcAXF7IzTZ2edSXqtV6CVg+9aSqFRWB9VvXo9KDlfLT+lXAoiD17rvAHXcAa9cC++4baJ55c1i+PHDXXQAjsowNGQL07g1wP61//okKSWoS1foKuOo4CTXBtL1OeUqNR1SKCIiACIiACOQcAUVfZabLJWBlpt9iqbUErFho5W7aOgB+dfbKclO4F8AACVi52zGyveV1+5yLZeXGW6c05fUPEebkEwg7dhSMtqpeHVi5MnzlGJnlOwGLVS6/GthcLWTlKcht3lx08AMGAPfcU/R8UpLDQZOBzh0k7KUEtgpJNYHx4xXpkGrmfijvhBOA0qWBjz7yQ21UBxEoSEACVmb2CAlYmem3WGotASsWWkobLQFFYEVLSul8TeCg2zpjSflxwNSHkTejt6/raipXuzbQqRPwwAORq+sWsCZNAjowtjKFxo1Rt2yJrkB3dFnlysCaNdFdFy7V++8Dp59e9HxSkkOVH4DujSVgpQS2Ckk1AU4UzVLnVJTNsjQ5TQXp8GUsXgxcdx0wbVr66xJLDbh0f5fX+oNYMnGlnT4daNMmtotPOcXeDiBZduSRwNy5yco9M/LVGJEZfgqupQSszPRbLLWWgBULLaWNloAErGhJKZ2vCeQLWP3zsnKyQwGnRg3g8MMBPpBTFKpSJTqXXHst8Mwz0aVlKj4I84HYbUcfDcyeHV0e7gluoh6s33sPOOOMwuXvvTfw77+FPz/tNGDixOjqm4hUjDJjtFm+FdsN5BVPRNbKo4gEDjsM+O670JnEcwIohdkDDwRmzixi5TLk8nPPBbjHDK0oAlalSsC6dYFGL1sGHBA4QNaTRqIFCBYSShS75hrg2WcD1ahbF/iVMe1RGJeGU+BhRC33M0y19e0b3yEg3D+5WjX7HmGka7DxcBHu3Ui/t2vnLWA98QTQo0foFv/2G1CzJrB8OdCqlf13JAv2RaT0ob5futS+V8NZ27YA6/jLL5HTvfkmwN+dWOzkk4EPPwxccfvt0b24cpfBCLi99gI++KBwyffeC/TrF7pGJuo7ljrHm/aSS4CXX4736tiuq1fPfg76+muJ3LGR809qCVj+8UWyaiIBK1lkcztfCVi57f+saX22C1hejuIkjBFc48YV/PaFF4AuXQKfBU9stm2zJ1pjxni7/88/gf32A/jG/eCDAU4yzz+/oIDVuDGwcKF9fZkywNatgbzMBJcTlbffBrp3B159NXJXY9qzz7bTcbKzYkXgmvnzbfEu2E48Efj0UyC4zdxH7L77IpeZiBRHHQXMmBHd8d08jfK22wLiY+vWwCef2G1jG6O1WEVJlvvwwwVzb9gQoB+NMBFN2dyP7ZZbQqdkP3njjWhystN88QWwYQPwv/9Ff00sKSkq9OoVXuwNJ8hceSUwenThEs3bfgpZjDgsqh1yiH1og5+sY0d7zz6KdBSwKWRwIs5IkngjsF5/HbjggsJjRbh2lyxpjzUNGhROZSIzKcJwnInWeN+xXZ9/DjRtGrhq/XqgIs/CcowMHn0UoJjy8ce2wHHQQYVLoYDgXuIciU+o8YljFr+LxugHRvYY40sN9kea15Jr3v9ep+Gavsy/6eNg+/tv+yARnvNDoYccgo3Xsky3iHLxxcArr9gp3dExfBHSrFkgB/YH9gu39ewJPP54/P2MUcoc33g4Sv36kfPp3x+YM8fu75s22YOHNswAACAASURBVL99HNeD7bnngLPOCi1gcby5/377KjfvYFHnm2+AY44pnH/w7547BccZ3gv0R3Af/OwzWxh0G9vNbQco7jACjUKw1/MCr6FISyGZ4hzvCfr4+++j6YWF0zz2GHDzzYU/Zx+iP0y/iEYIpz8GDwaqVrV9E2y8d5nvV19JwIrPW+m/SgJW+n2Q7BpIwEo24dzMXwJWbvo961qdqwLWO+/YD9RuoyDCCRqND9x8YHzpJeCqq+zPzGTipJMALodwGydeq1bZAhYna3zDSXv6aVv0MvbHH0At5+BHRmxdeKH90E/x4rzz7AkDRbSxYwG+neeE5IYb7AdjTtTN5NhdtpmA8e00J/S83kQG8AGWwhvFMrdxssGljfzO1Iffh4pGOPVUYPJk7+7PSYF5A89JK4WPSHbsscCXX9qp2DZO8MIZfUPRzUxwTfRPpCih4DwpCHLyTr9GYxTYjj++YEr6Y/XqwoITJ0kU0/76y14qw4k5hZw6dYCRI4Grr7bz4USfE363MQqD/o7GWKfjjgMYHRB80ib9TOGIfHbyCJIwRvE0uF8Yf5A1jZO3YGPZ9F24iZQ7coETUkbacRJmxNElS+x7jPUPFwERrv5sJ/s7+5IxMjfRMI0aAT/+aH/D6CD2HeODcPmybowgogBNhoze4CSQAiTvGxojar79tmAUIyMaOEnm0uZu3QKCDie5nBDT76wDI41YT+7fx0MmuD9SsB9M5Mn++wO//24LFcECFkVrjmOhjBPxRYsKixAUrIYNs/9wbONE3b20iwLIjTfavi9Xzp5Uz5plC3AcLzip59JoChVm+dXGjTYnGlmRD9NQ3OBkmRzZdvYLttUdneSu/913h4+GcgtY7dsDzonyVhvYLznWXnaZLXYHj9GmHHe/ZZQR/WIOBmEEDP9wjPBKz/GU9zcFbLdQceihtjhDYdkYx1fjV9aFXHnf88UBX3D8/LN9D/EPfzs4bpMx2ZBV8+YABRu38XP2L471jKCl8MPfGGNGwOLLmc6dvXsG+wX9yMgpjv28N4wQHryczIy3CxbYv2kU1jim0Vg+2XEc4X1hIpspgLHfuY33OvsrIwmDzfzecSxnOYxaoxjE/vP888BTTwWuoODCdAWidmH/7vIFktt4HX+PyNmYWyDlbzGFL/J2t5t8GFXH9vF3lN/Try1bBvLhPcA+7xZtvcrw8gDvP/Yv8qexnRSaeS97/XYygpxjBe/JJ5+068r2/8fjpjyMQqcRl91jBIVUvvSgURjksw4Z5foSSm+K/v9UApb/fVTUGkrAKipBXe9FQAKW+kVWEMhFAYtiCN+6coLGiQgnh3yY5IMkJ3Lcq4R/m4ddPjRTUHJPFNwPwmZCyId4TuI4iTVv9E0n4dIPMxnl3zQ+iHJZECcpnIzRmO+DD9oTMH7Ph1ROgvjQTgGLEzaTlptCc+LBclkehTDmzYkp62QmT0bo4MSZEyVTtqmbO4IglIBFoe211+wr2Jbrrwe4PJGTW04SBg60J+XMi5MzClp86ObDN40MjdBA8YhvtN0WLvKCvpowwZ78MKKDogcFH07o6ROTr1e0FEVBvh2nsb5mPzBOQCg4GTORXJywU6gzUQQUpNwCFidXNPaHyy8v2IZHHglEWTGiatAgO/qFbeMksUkTW7zgJJPtMcaJCSerl14a6APkyDfo7lM13f4y/w7mRjGREzYKBpxEcmJE33mZmbTRb/QfjWKKOyqQfZll8G+KRTRex4kQJ0TB5bNtQ4faadhPuPyHE1Q3a3dduKyHy1bDWXCkoknLtvGedS9zMm2iH3mfm2gNilHcRJuCDSenvJ8YFUeRgX/Yfk5UOTE0IlVwndheTlopVnCZLX1GIdMwIXuKXxQY+vTxbhF58cj64Oi9YI6MDOG9SLGD31HkpXAerg+wfhwPTNQmI08onAXnzXuxRYuC9TOCnWkL/+ZYQcGG4yT7PQUCcz+bdGRGzpzcc0LMe8ctLtAfFG/cdWd9yJv3BMU5t5lxxIse70kKwbznKUxS5DBt89rHJ9SYwrSMjCMvcuUYTPGJ47CJcKLgyv5FHzMf9jEuxeYYSJ+zD/F+DvYHhSOKdxRUvIz3Fvss+YdbvsV7h78lwYKPu52sV7BQxT5tRBCmDRZZKOqaiEWTF/OhkMU2By8r59jH8daIgTzNl2LfTz95R/aZNjNPviCiIMV7goI3eRmR083G1IOiGo1jkDETncb+x742b54ddUshk+MjjX2eywQp5hnzEv/4HevFlzHsR+bFjenf5loKjRzH3G1hO7z87e1le/wjZ/bv4ChZ/qawL5m+b8YD9iv+hlAkdEdR81mA/YXjJMVT9wsnPqtwX0/+xrMcjqfMn+Mbjb+JzJPGOrHdfFnE+9jr5UWo9uhz/xGQgOU/nyS6RhKwEk1U+ZGABCz1g6wgkIsClvvBlJNRPpzSOPHn21evyVCws92To2jSc+LCpQaMxuAyDe6N43UdJ8+cfAcvSaFQxLevFCYoYvFNvonIYD58k8roA6+lLHz450M6H345SaMQ4bW3CdvkjnDgUiFOBDiJ4oTFTMqMgEGRygg9rBdFDgo0fIhmOVwexOsZvcE6UGDjBMY9CTZcGYXDB/DgibV58A51s7FMTrJpnNgy8sUYy+OkzOxLxsgQ935gFGFMFJKJguED/0MPBfJgu/jQTyGKbdlzz8B3FCEokNEXnEBROOAEMdhGjbLfeNOvNE7s3AKW6Qd8Kx/sGwqYbkGA/MxbdOYVPEmnUBC8WTTFNkalBJsp1/iOfqEQSqZexnzZhxiZ6L6HuAyNkyxGI7BPcgIYzT3BPHgv0O/c+4iTMC/j5JfRNW7j5I+HOdDYN+lnsghevmT48L5j/SlgsW4UBm+6KdB3DEv6l5N+LzMCllkizPuBk076n98ZAYuRORTGvYyTRhP55P6eYxDHIkbrMeqD94wxihlsq2kL7y32RbcP+G9y5L1q9tFxCxT8nmNAqKg8LwHLuwUFP2WfoZgTLNiHu5Z9n5Pu4OhBXsP+TrGEk3W2173nkVefIhfWIThSiXlRqGO/ofBgxnh+HpwPxyaKyFzC5VUnd1v4coGCHfttPMYoRI419BHF3VDL0aPNm2M0RVr2KwpF7DvBUZOMHuK4yt8WfuclInFMIReviCJ3XZhmxAh7nPX6rTFpOQ5yeSHFPApTZszn+MryTdSl13jlLo9jAtvFqK5gEYljN+9VE/llIgJ5//E3wWuvS/YpvgByRxNz7DH3BaNr+TvrNhM1TRGcrJm3uz9F8hUjqyiQ8h4zL684/vBzCtUc3ylqGqMvKKRynIlmHOWYzL7LMZjilTtSmfxYfzP2Raqrvs8cAhKwMsdX8dZUAla85HRdOAISsNQ/soJArgtYnNyE26g6lJNjFbDc+TByKpSAlc5OxTe/nAQz4okRDpxssZ2cFPPNPIUzRjCFEhq86s48+BDufqseqY2MiDniCPsBnhbpIZ6RGKxz8H4mvI5/OFHgZvyMVjBLhbzqQAGKk5toNxpm3uRkIpMitct8z2VCJoouUvtMxIY5IMC99JLXUjDkpJSiAMUX/p9iSrDRjxQUKZ5QoDJLVt3pmCacgBWufZx08Xou+WF0XCSfmbw4qaZoSjGJ0RUUMLj0idFynHQx2oLiW7BQF23+5jqKFNwrLtx9x7TRCFimbLJmVJL5vxGwoq2bF09O9lkPLyGFnzOSLfj+Y4QhBQqKF1xWaZYsm3pQaGZUJAWHUKfKUdCmyEfRId4lndH2/2jTcaks28Wlmuzj7j23TB7heJk0nNy7l2YVxT/R1j1cOo5XjFgLFSEWaxn8/aI47rXHWKx5pSo9284xPpHL1xhhyTHD7KXl1RYjirrT8LeJv1M0E00dioNJF0noLCpH8+In3X21qO3Q9ckjIAEreWz9krMELL94IrvqIQEru/yZs63JdQGLofaxbAJuOgone5wQ8y2vWfoVbSfidVw24NeHU0az8I202bPHCFjRti9R6bi3F5f4uPf+iZQ3lxgyYormV76sG9+KU6jhErFw9TRLHc0+Z5zQM7LEmIkW8oqqcLOiiMHoHkYpMELBq0xOmrh0llEm8RqFIgpkFFMSaZx4ms23KaJS4IrGeJ0RbthmRmt5RckxL6YNjnBzl2EisAw7inWMlGIEGi0RAla4NjGyjZEske4Hr3a6OXiVYSKw/HzPRONvrzRcIs5ltGYpaja2MV426bqO9wr3owu11DZZ9eLLEQpW7ugxRj+ZZdORBKxk1Ss4XwlYqSKdueVIwMpc30VbcwlY0ZJSulgISMCKhZbS+paABKz4BKyiONTvApa7bYxK4jKd4I3Mi9L+ZF/LJWdc7sFle342ioQ8BfKKK6KrJUUILmHh3jnxGpebcM8fLpXNJGPbueTKnBDmXsoZrh0UCTlZZmRRJGMZFKmCN9g311Hc4/KxUAJIsgWsSPUP9z2jmShIc5mil2WzgEV/MVKO/mGEnwSsovSk7LuWYjvHRRr3djSCdDpbKgErnfQzo2wJWJnhp6LUUgJWUejp2lAEJGCpb2QFgVwXsLhEiUuXUmmZJGClkovKCk+AkQPcE4hLAXPNKC6ZvaeS1XYKHNzLjCemeRmjN7iEKNQ+QTyljafaZaJAwqWlXCIcbWRbsnyQzHy53JdLoYP3U0tmmcrb/wR4gAtFaz4LuA/iSGfNuQcWTxPMxLEkndxyqWwJWNnvbQlY2e/jdLRQAlY6qKvMhBM4+8XOeGfpOKB/Xs49LCVjH45oHCQBKxpKSiMCmUWAwgiXd2rSmVl+U21FgAS4TJundobbnD5VpCRgpYp05pYjAStzfRdtzSVgRUtK6WIhIAErFlpK61sCncd3xrgFErBS6SBuKn722ZroppK5yhKBZBP45x9g7Vp7w3SZCIiACMRLQAJWvORy5zoJWNnvawlY2e/jRLTwUgDXAuAh6LsBLADQF8CXITKXgJUI6soj7QRyXcA68khgzpzUukECVmp5qzQREAEREAERyBQCErAyxVPpq6cErPSxT1XJErBSRTqzy7kOwC+OYLUVwA0ABgJoCGClR9MkYGW2v1V7h4ARsIrdmweeIJZLxiWEErByyeNqqwiIgAiIgAj4m8DAgcCjj9p7tslEwIuABKzs7xcSsLLfx8lqIX86LgMwQQJWshAr33QTyHUB66ijgG+/Ta0XFIGVWt4qTQREQAREQAREQASyhYAErGzxZOh2SMDKfh8no4XHAPgcAA8bXyYBKxmIlacfCBgBq/iAPOza5Ycapa4OjMBq2tQ+7SeVJgErlbRVlgiIgAiIgAiIgAhkDwEJWNnjy1AtkYCV/T4O10IeiN0VQB4Ar77wCYCTgjKoDeAzAC8A6Bcicy0hzO1+lTWtNwJWiYF52Lkza5oVVUMoYB19NDBrVlTJE5ZIAlbCUCojERABERABERABEcgpAhKwst/dErCy38fhWlgOQJkwCXYA2Oj6/iAAUwG8BuCOMNdZAlb37t1RqlQpK1n79u2tPzIRyCQCRsAqOSgPO3g35JBRwOJmqTNnprbRErBSy1uliYAIiIAIiIAIiEAmE5gyZQr4h7Z9+3YMHz6c/6wIYEMmt0t19yYgAUs9I1oChwGYDGAYgMERLlIEVrRUlc7XBCRgpV7Amj4dOOkkII9xoTIREAEREAEREAEREAERiJKAIrCiBJXBySRgZbDzUlj14wC8B+BeAE9EUa4ErCggKYn/CRgBa4/78rB9u//rm8gaXnwxcO65wHnnJTLXyHlRuPrhB6Bx48hplUIEREAEREAEREAEREAEDAEJWNnfFyRgZb+PE9HCjwG0AvCfa68sxkcwEusBjwIkYCWCuvJIOwEjYJUanIdt29JeHVVABERABERABERABERABEQgBAEJWNnfNSRgZb+P09FCCVjpoK4yE06g0/hOeHnBy/i4VR7atEl49spQBERABERABERABERABEQgQQQkYCUIpI+zkYDlY+dkcNUkYGWw81T1AAEjYOX104ZM6hciIAIiIAIiIAIiIAIi4GcCErD87J3E1E0CVmI4KpeCBCRgqUdkBQEJWFnhRjVCBERABERABERABEQgBwhIwMp+J0vAyn4fp6OFErDSQV1lJpyABKyEI1WGIiACIiACIiACIiACIpAUAhKwkoLVV5lKwPKVO7KmMhKwssaVud0QCVi57X+1XgREQAREQAREQAREIHMISMDKHF/FW1MJWPGS03XhCEjAUv/ICgISsLLCjWqECIiACIiACIiACIhADhCQgJX9TpaAlf0+TkcLJWClg7rKTDgBCVgJR6oMRUAEREAEREAEREAERCApBCRgJQWrrzKVgOUrd2RNZSRgZY0rc7shErBy2/9qvQiIgAiIgAiIgAiIQOYQkICVOb6Kt6YSsOIlp+vCEZCApf6RFQQkYGWFG9UIERABERABERABERCBHCAgASv7nSwBK/t9nI4WSsBKB3WVmXACErASjlQZioAIiIAIiIAIiIAIiEBSCEjASgpWX2UqActX7siaykjAyhpX5nZDJGDltv/VehEQAREQAREQAREQgcwhIAErc3wVb00lYMVLTteFIyABS/0jKwhIwMoKN6oRIiACIiACIiACIiACOUBAAlb2O1kCVvb7OBEt7AhgIIDaTmZLAdwP4K0QmUvASgR15ZF2AhKw0u4CVUAEREAEREAEREAEREAEoiIgASsqTBmdSAJWRrsvZZWv7pS0yvn7BABTABwDYIFHLSRgpcw1KiiZBCRgJZOu8hYBERABERABERABERCBxBGQgJU4ln7NSQKWXz3j33qxzxwPYCqAzgDGS8Dyr7NUs6IRkIBVNH66WgREQAREQAREQAREQARSRUACVqpIp68cCVjpY59pJTOq6jcA5QDsAeBzAKcA2CYBK9NcqfpGS0ACVrSklE4EREAEREAEREAEREAE0ktAAlZ6+aeidAlYqaDs3zKeA9AVQB4Ar77wCYCTgqpfCsBpAOoDeMi5NriFWkLoX5+rZjEQkIAVAywlFQEREAEREAEREAEREIE0EpCAlUb4KSpaAlaKQPu0GEZTlQlTtx0ANob4fiKADwAM9/jeErC6d++OUqWodwHt27e3/shEIJMISMDKJG+priIgAiIgAiIgAiIgArlGYMqUKeAf2vbt2zF8uDU9rQhgQ66xyIX2SsDKBS8np43cA+snAD1CCVjr169HhQrUsmQikJkEJGBlpt9UaxEQAREQAREQAREQgdwjoAis7Pe5BKzs93EiWngpgK8BLAHAkKrLADwJ4AwAkyVgJQKx8vAjAQlYfvSK6iQCIiACIiACIiACIiAChQlIwMr+XiEBK/t9nIgW9gfQBUAVAFsBLAbwGIA3Q2SuPbASQV15pJ2ABKy0u0AVEAEREAEREAEREAEREIGoCEjAigpTRieSgJXR7vNt5SVg+dY1qlgsBCRgxUJLaUVABERABERABERABEQgfQQkYKWPfapKloCVKtK5VY4ErNzyd9a29vIJl+P5ec8jrx8P6pSJgAiIgAiIgAiIgAiIgAj4lYAELL96JnH1koCVOJbKKUBAApZ6Q1YQ+GfLP5izag7aHdguK9qjRoiACIiACIiACIiACIhAthKQgJWtng20SwJW9vs4HS2UgJUO6ipTBERABERABERABERABERABHKUgASs7He8BKzs93E6WigBKx3UVaYIiIAIiIAIiIAIiIAIiIAI5CgBCVjZ73gJWNnv43S0UAJWOqirTBEQAREQAREQAREQAREQARHIUQISsLLf8RKwst/H6WihBKx0UFeZIiACIiACIiACIiACIiACIpCjBCRgZb/jJWBlv4/T0UIJWOmgrjJFQAREQAREQAREQAREQAREIEcJSMDKfsdLwMp+H6ejhRKw0kFdZYqACIiACIiACIiACIiACIhAjhKQgJX9jpeAlf0+TkcLJWClg7rKFAEREAEREAEREAEREAEREIEcJSABK/sdLwEr+32cjhZKwEoHdZUpAiIgAiIgAiIgAiIgAiIgAjlKQAJW9jteAlb2+zgdLZSAlQ7qKlMEREAEREAEREAEREAEREAEcpSABKzsd7wErOz3caJb2BPAYwAGAbgnROYSsBJNXfmJgAiIgAiIgAiIgAiIgAiIgAiEJCABK/s7hwSs7PdxIlvYAMAHADYCeFcCViLRKq9MJDBlyhS0b98+E6uuOotA1ATUz6NGpYQZTED9PIOdp6pHTUD9PGpUSpihBCRgZajjYqi2BKwYYOV40uIAvgQwGMDNAD6XgJXjPULNR69evfDoo4+KhAhkNQH186x2rxrnEFA/V1fIBQLq57ng5dxuowSs7Pe/BKzs93GiWtgXACOwLgUwXQJWorAqn0wmoAfBTPae6h4tAfXzaEkpXSYTUD/PZO+p7tESUD+PlpTSZSoBCViZ6rno6y0BK3pW2ZjyOQBdAeQB8OoLnwA4CcARAN5x/l4XrYC1fPlyVKjA7bBkIpCdBO68804MHsygRJkIZC8B9fPs9a1aFiCgfq7ekAsE1M9zwcu53UYKWLVr1yaEigA25DaN7Gy9BKzs9Gu0rSoHoEyYxDsAbAHwLYB+jojF5JEisGoC+CPaSiidCIiACIiACIiACIiACIiACIiACCSIQC0AKxKUl7LxEQEJWD5yhk+rUgfAUgBrXVFaVLQpbvHzJh71Zr+q4Wz27tNmqVoiIAIiIAIiIAIiIAIiIAIiIAJZRmAvACudVUZZ1jQ1RwKW+kAkAuwj1YMSvQngGwAPAFgdKQN9LwIiIAIiIAIiIAIiIAIiIAIiIAIiIAJFISABqyj0cvfajwF8EeYUwtwlo5aLgAiIgAiIgAiIgAiIgAiIgAiIgAgknIAErIQjVYYiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAKJJCABK5E0lZcIiIAIiIAIiIAIiIAIiIAIiIAIiIAIiEDCCUjASjhS32Z4IYDuAA4HsCeAPQDsdtX2MABPAmgKYB2AkQDuDWoN/38VgArOyYTMb6EP8/CtE1SxpBMoaj/naZt3A/jPObQgD8B7ADqpnyfddyogegLh+jlPln0BwBEA6gG4L8Ryb43n0fNWyvQQKGo/13ieHr+p1NgIhOvnzQH0BdAMQFkAvwF4DMDzej6PDbJSp51AUfu5xvO0u9A/FZCA5R9fJLsmJwPYB0A5AKOCBCwKWosBjAEwAEB9AJMAPAJgqFOxWwHcAKADgCUAOJB0cdJysu+XPJLNUfn7m0BR+zn7dVsArUI0U/3c3/7PldqF6+elAXQDMA/A/QA+8hCwNJ7nSk/J7HYWtZ9rPM9s/+dK7cP1cz5zVwHwAYA1AFoDmADgUgDv6vk8V7pIVrSzqP1c43lWdIPENEICVmI4ZlIuJwLgJuzuCKyuAB4EUMMVldUDwI0ADnYatxTAowCGOf8v4RxP2gvAOAB+ySOTfKG6Jo9AvP080g+k+nnyfKacYyfg1c/duUwH8LmHgKXxPHbWuiJ9BOLt5xrP0+czlRw7gUj93OT4NoBlAG7W83nskHVF2gnE2881nqfddf6pgAQs//giVTXxGjgoTDVyoqtMPY51ThqsCKC4s6yQn33jqugUAAsA9HbELT/kkSqOKsffBOLp55ucyEL2Z0YV8s+XAO5yHhbZYr/cK/6mr9qlikCkB0EvAYtLwLlMXON5qrykcopKIJ5+zjI54dF4XlT6uj5VBCL1c9aD4/dPAPoAeNH5v8bzVHlI5SSCQDz9XON5IshnUR4SsLLImVE2xWvg4JLC8gAuduXR0NnfqrYjYP3uiFyLXGleBbABwDXOskQ/5BElBiXLcgLx9POVAA4BsBHAcgDVATwMoAUA7hFHQcsv90qWu0/Ni5JApAdBLwGrFgCN51ECVjJfEIinn7PiGs994T5VIkoCkfo5V05w2SD/PsVZMaHxPEq4SuYbAvH0c43nvnGfPyoiAcsffkhlLeKJTFEEVio9pLISQSCefs4IrGArBWA9gDOcvYQUgZUI7yiPRBGI9CCoCKxEkVY+6SQQTz/3qq/G83R6UWVHIhCun3MDdy4dLAmgo/NCjfkpojYSVX3vNwLx9HON537zYprrIwErzQ5IQ/FeAwc3Y38oaA+sns6m7eH2wFoF4CYALzsbuqczD+4FwL24ZCJAAvH281ACFh8YP1Q/V+fyGYF4J/Zee2BpPPeZc1WdfALx9nON5+pEmUQgVD+vBGCis4n7eQB2BDVK43kmeVl1jbefazxX38knIAErdzoDo6gYdsyBgycM7gVgF4DtzvJBLg3kKYQ8cp2iFX8sh7hOIeQ+EjyF8DQA/LG8B0BnAA2cN0E8nc0PeeSOR9VSLwJF7efnO4ccrAVQzVlC2BJAEwCbndM21c/V99JNIFw/zwPASBOm4T6FXziny+52TXw0nqfbgyo/GgJF7ecaz6OhrDTpJhCun1d1Xp4tdJ65+dwebBrP0+1BlR8NgaL2c43n0VDOkTQSsHLE0c4pgc8B4OSGRt/z320AfAbgUABPAWjqLJkaAWBgEJ7+AK51xK/ZALo7+2SZZH7JI3e8qpYGE+ApgUXp5zyemntecT+3f517425HtFU/V3/zC4FI/fxXAPsHVfZTACe5PtN47hdvqh6hCBS1n2s8V9/KBALh+nlr5zAC7sFJM8/wPF2WL5SNaTzPBE/ndh2L2s81nud2/ynQeglY6gwiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAK+JiABy9fuUeVEQAREQAREQAREQAREQAREQAREQAREQAQkYKkPiIAIiIAIiIAIiIAIiIAIiIAIiIAIiIAI+JqABCxfu0eVEwEREAEREAEREAEREAEREAEREAEREAERkIClPiACIiACIiACIiACIiACIiACIiACIiACIuBrAhKwfO0eVU4EREAERMDHBMypOge5TqrkKZj8/A+PkwDZlH7OH54mtQeA3U77+PcgAPd470snLAAAIABJREFUtPd5AG0B1I6DxWUAxgA4AMDvMVxfEcBNAHjyz7wYrouUlM8djwG4AEA1J/9zIl3kg+/D+cddvenOSWHuEx8TVX32Kx5Fzj4WjR0BoC+AZg7rfwD8BOBtAE86GZg+7JUf+2h1AH9FU5grTU+nr7GcaC1ebtH2b3Nfsj5s10YAKwB8BWAUgK+jrWhQujoAeOon6/FCnHkk8jIzviwB0BDALlfm9QD87KO6JrLdyksEREAERCBHCEjAyhFHq5kiIAIiIAIJJ8DJP8Whg4MErPMBlAZwCgBOzN32C4DKAPaKQcDi5JsC1v5xtMDUsW6MApaZmF/ltDGOoj0vIZvXANzsiAcUVcjE7xatgEXRgEahKNHGvlQCQKsoMqZo9ZkjzIwA8CeAWgBaAmjg9Cdmsy8AChtu47Ph+45fjo2irOAkFHQ+B9Alhmvj5RZt/+Y91AHAGQDYvvIOh84AjgMw2BH7YqiylbQUAAqFFIzWxnpxEtK7BfLrADzrKkMCVhKAK0sREAEREIHUEpCAlVreKk0EREAERCB7CIQSsCg2UcBgFNYVruZSPPgUwFgnSivaCKx0CFiM2FoKINECFifYjDKjEJMIo4CwPREZRcgjWgErmVWJRcBiNFA7R/TcGWOlTnD66fUAno7xWiaPRcAqqv9iEbBCicCMCGTU2LlOdFocTfbNJUbAmgKgMQBGh5r7QwKWb9ykioiACIiACMRLQAJWvOR0nQiIgAiIQK4TCCdg3QngKQBVAWx1QD0DoD6ATxwRJ9ECFqOshgFoDWATgFcA/ACAETjuCKwLAVwDoAmAss6yosddS6BM9BWXWpnnBP77cifNyc7ywiMBcKkhhS6KbMzDLIn06hsUNpi3yded534AHnKiZBidtsj5/zhXRma524kAbgTAejDPo0J0REbGMU9G2FRwlsJxqdjFTj1DLT/r7/iHy/WMsV33AdgCgJEtjFyaBaAHgPmudPQt07qXEDLijstDT3ei71jnRwGMDKo3RcOBjvC0t7PE7V0nWo3iFdvt9gnLCrVU8T0ABzoiRqz3KZfUdXKWD66L8WK2jZGC7udLLoGlkGu4st8NAXA8gI8AnO3cE25ujGC83/ExubA/k/etTt8w1UqEgMX7kMtrFzuMY2my1xJCs+T3LABPAOB9wvx7AfjA+Zv9dx8nQvNKV/RWqCWJ9D37AO9tRtaFMiMQMwKPvHo7S3aZXgJWLJ5VWhEQAREQAV8SkIDlS7eoUiIgAiIgAhlAIJyAxWVa3DvoagCvOksKVwG4xZngMwopkQIW82LUFyf+FM/+BnCtI+7UDBKw+P0GZ8LO6BwuSbvDEYW45IhRMf8DMN4RbSiG0MwyKeZLkYni2GYARzuCz3Cn7FCuO9yJdCG3Fo7IwTwpCnGfLYphrBsj17i0iyIKhTYKKjQjYC13xLmpAEoC4N9exv1+uKzrAedvcmC7KKaw3aHED68oMYorrNdvAB52OFNsopBFocwIPcF7OZHTbCf9AADLALR3+gGjfsiMRpGGggOFGopdXFZJIYjLUC8F0AjAS84eWGTC5zf6MNRSxbsB3AuAoimXuc4J2g8plI/KOMsNyZT7lMVq9PEkx5/kyHqyL1LYcu/PNNpZ3kiuFGSCuVFwpMg1DcBKABT0GBFGYYbLDc2+XIkQsNhGsmUEFpcWhhNhg3l4CU4Uc7mvG/vpI079zV5k9Df7CyPbuAfcUIfXRU7G4QSsjwG0iVLA4njwspOeQibvUwlYsfZmpRcBERABEfAdAQlYvnOJKiQCIiACIpAhBMIJWBQfuFSwiiOaUAygkMBII4pYiRawKJRxUkxhiEIIjb/xCxzxI9QeWEzDSCNGaVEcYLQILZY9sLgcsI/TLgo64YyiD0Uq9xLCG5yJPKNLuHeSsQ+dKDFuJM7IIyNgMXqJkSXhjPWgcNLR2c/JK22sAtYaR1QyEXVkRJGMkUIUZ2jBQgyFJIqDh7r2SWM6CoWM0GF/oGDCJX/8P8WN1SEaFssSQgpRjF5jnvQxRcIvALwBgOIReXoZo9Mo5pDbxDjvw1BLCI0wSOGOkYJui7SJO/soxVmyIVMKP7RECVjcA4t9mP5gv4nWQglY3P+LwvAMJyNGnTFSj5GFh7j4U6Rj/6e/6JNEClgUrCgyU8ikKCoBK1qvKp0IiIAIiIBvCUjA8q1rVDEREAEREAGfE4gkYHHPHUajcPNsigaMmGFUkZnIJzICi/mzPEbyuI1CGctzC1jcF4dCEvc64oTdLJWjMFPOuTicgMVrOClmJFENJwqKl0Vzap2XgMVN3blZePAm9YbvYQAWusQKLqeiGBPJGMXENnFpI5fbBW8WH6uARZGJyw7dxughlsFIKVqwEMN67nCWBbqv47K51wGwbd8DYHQer70kTKNiEbBMNoxWYtQZ+TJ6h8vWuD8SNzT3sskAGEXFaLVYIpHceUUSsNi3GM3mNi8Bi6Ivl90xmpHReaaPMaqM0Vi0RAlYFCFvc6KiKFRGa6EELEZzMYrMGO/1bU7EHZcPGjPCM08YZaRZIgUs+o/Ri6wL73+KujqFMFrPKp0IiIAIiIAvCUjA8qVbVCkREAEREIEMIBBJwOJvLJeMcS8qTsS5BxKXZnkJWBQ5uF/TXR7tpnDCDeC5FCiUcW8dTlCPCUrA5X7ci8sIWFwiRTGIS9UYdcL9q7jJMwUB7nFlIqNCCVhs00xH+GI7GFHC6B4KMoysinTaoZeAxUgrTvaD606BjO0ykVmGN/cR49LDSEYxj/suUcDhPlQUVrj8z2xMHquAxWsZpeM2RjQxooYbZtOChRjuq8TIF6/nLQp+3MOKG/vTBxTaKKKEsngELHdeXBpq9rfiaXxk6zYKk1z2xuimSBFu4dhHErBYj11BGQRzY/0mOHurkTFFJQoyFIQZGWYOR0iUgJXoJYReG8Z7HQQQPIYkWsCiMMY+yL5F30vAijRq6HsREAEREAFfE5CA5Wv3qHIiIAIiIAI+JhBJwGLVGdnBjae59ImRWBQtvASsFY64RREp2LjRNYUnRtGEslARWKYsIyzxZDpG4FAQ+8qVGZc7ct+pSAIWo7c4IWYkGYU5Y4zI4j4/8QhYjMDi0kdO3t0WKgKLy+wovMVijHTiUi2eqsjoIzLgZvbcJ4gRPu7oLG683T1omaNZ5hdrBBYZc78tbvbu9cxFAZD7EzH6hiIOuYayogpYzNcsZaNQxv2Z3MZ+yv3CuIz0u1jgBqWNJGC5Iw/NpcECFgUlLmmlb4xxvzOKpS8mWMBifSjccbldqE3xQ+EIFYEVr4DFfbEYjefe+41lc08tCnmx7IFlIugoXnGj+FOdJbrswxTFZSIgAiIgAiKQcQQkYGWcy1RhERABERABnxCIRsCi2PKgI06ZyB8vAYsTdk6eGa3DSboxRsVQrHksRHSWSUdhhkurKHIxQorG33guT+MyMiMscW+jt4P2yuIG2SyDUVBGwGK5FFW43MlsNM48KQRxw3WKP5xQ0ygA/OiUEY+AxeivJz1ENUarUXDhMkWzBxb3EYtHwGI9uaH6ekdQ5N5DFM2+dMSBd5y2sP2MUGMZ7n26KAYwCoiChfEPI7wo5jGSjZFetGAhhr6mcMZN2MMtTePJdYxiY3RZqD2wuLyPUXYUdiIZ/fenRyIuy+OhAtwY3n3CI5NStGJklNkHLVIZob7nxvLce+38oARe/d4kCebGAwQoXpnINqZj1BWjiMyphvwsERFYFHjYz7lfmDmwINq2J1rAYrnsX7yXb3JVgv2ebY1HwOI+fLy/uZyVS13NaaLRtlHpREAEREAERMA3BCRg+cYVqogIiIAIiECGEYhGwPJqktdEnpN1Ck+MXqG4wogQRjtxA3BuXn2U6+Q1rzyNiMTNoLkMkae0dXPECPcphFxKx2gjCi8UXfZ00pd1xDMj2vD5gHlQjGB+jBJi3TY613LJI+vG6CJOtFkGxbd4BCzuuzXXEdAYxWVOIeR+UIxEYXSZW6yIRsCi8MWlcIzuYnvZLk7cGclC4Yrl8TNzit/tzh5FFNMoNnE/rmABiz753YlcImdGnXFPKYpOoU4hpCjIKCzmRRGSEVeMpqOoyD3IKJrQKITQ/+RMQYx1ZsQel1FSbKJx8/rrHCGDSyiNL7z6w7sOz7ccEZPlN3fEO/qVItV/rgvZv3ha4s2uDdKD86VwxM3JzZ5poW5Xik/HOVE/FNEo3PH0xlgELPqdBwvQh+87oh2FQPYVLi2MZwkhI+/OdCrNfHjPMeqQ/YGbnBsR0rSLoqVbLPNqbzIELJbJfavYJ9lfTnM21adgGo+AxXqzfVziSyFYAlaG/dCouiIgAiIgAgECErDUG0RABERABEQgPgKhBCxGUgUvh3OXwIk8T1LjXkDujbIpnFAU4SbllZyJP5e6MT3Fk0jGCS5Pd+OeURRCuDyOy6IY+eUWlvg9RTKKKIyyokjAyB5u+O4WbRitRTGFghGXb5mJL6OwWA5Fj3+c0xUp7IyMUsCi8MX83MalU9wDjCIDI6U4cWfkmnuZohfvUEwYdcL8GJFGIYgbrTMq6D4AXJJpjMwZYXa00xZG43DD8GAWjEzitRR9uLyQvCg4MXKH+RpjJBF9yiVkxkx+FKso9FHsYvsoLnG5ojH6iELDyY6wyGWljAzj0j4aGVHMo/BF4ZF7Z4Va8sY8KABSnGEEG/sahUHue8Uygk/aY7speHLPpFCn8HHTeS49ZX7hjMIQT1lsCoDCKJenUnAK1e+ZVzA3Pp/yXuB1vBd4siaFUkYPMi2XxNFiicCi+EajiMP7gzwYgce6mpM7TbsocHGfOC4B9tqXzqTjfc7oJrco9Jzjl+AxgH2I7M2Jle76u0VZ9hf2C94LFAvJnZFhFPKiEbC8xhbmSdGTLMlUSwgjdGJ9LQIiIAIi4E8CErD86Zei1opLO/iAzZOE+JAbvN8EH2T5ppEPt3wbz4dVPvBwCUsoO885tYpvpbkpMd+S80FSJgIiIAIiIAIiYBP41hEKuFQv24yCGqPAKH5mu3GpHSO9GFVIkVcmAiIgAiIgAiLgAwISsHzghCRUgW9euayBbxC5X0SwgMWlBVySwretXBJCEYt7oPB0Gi/jyVA8gvxi5y0gQ/ApdvFN7Jwk1F9ZioAIiIAIiEAmEWD0FCPbGM3DDdK5XDCbjMtZuRSSUUXupYfZ1EZ3WxgpxSg7LtmUiYAIiIAIiIAI+ISABCyfOCJJ1eAylI+DBCwua6CAxYfQcBvKuqvEzUMZfs49GYxxj4u1AK5OUt2VrQiIgAiIgAhkCgEKVtxPiUu9uI8WlyzKREAEREAEREAEREAEEkhAAlYCYfowKy8Bi/s5nAGApxlxCSE34p3m7LFBQcrLGGXFjXC5H4kx7mFCQYv7hshEQAREQAREQAREQAREQAREQAREQAREIGkEJGAlDa0vMvYSsLjJLjc/5ZHlfZzNcnmUNk+S+l+IWvM0pIedY51NEi4/7OWcvuSLxqoSIiACIiACIiACIiACIiACIiACIiAC2UlAAlZ2+tW0ykvA4uarPZ3N3c0SB55S9EXQZ24ysUZgsV/xlCIe8S0TAREQAREQAREQAREQAREQAREQgVQQ4GnGPICDp87KsoyABKwsc2hQc7wErE4Anncir4yAxWPGPwNQAcAWDyTcA4vf8SRCY+H2wOIx4TyeWiYCIiACIiACIiACIiACIiACIiACqSRQCwBPz5VlGQEJWFnmUKc5xZ2N2ylgTXLEql0AtgMoC+BHAG8B4D5WewLgEkKKWWeFwMFTCKc7pxBOBMBTCF8AcEKIUwgpdq1fvnw5KlTgP2Ui4C8C/+34D23HtsVnl3+GPUrwkM6CVnlQRax5GBg4uise+XksZj4L3HYyMOHZ9fkJH/jiAdzf/36AxyI4VqpEKWzftR3r71iPivfz3IPIdsWRV2DMXGrEsK4zduEbF2LyL5Mx+szRuHICV/0Cv9/8OyqWsfPt8nYXTPhpQkxlRa4NMKnTJHQY1yGapL5OE4sPUtWQ2dfMxtHPFtw20Ph87qq5GPLVELy3iHuAA4tuWIQGwxqkqmpWOWc1PAvsjx1f6Vig3JqzamJFsxWoWaEmNmzbgI3bih5c27JOS3zxGwN/C9q629eh0gOVCn1+2/G34aEZD6WUhx8LK1+qPDZv35y0qnU+rDNe+o6HDEe2mVfPRPORzUMmvPboa/HM7Gfyv3/69KfR7X3uPuBte5fdG/9u+TdywTGmiDQW3Nj8Rjw580l7N1DXeG6KKVG8BHbt5iNU8mzFLStQcwjf/fnXWtdtjU9+5YHUmWumLxy///GY8fuMIjfknEbnYEj7IdinLA/+Bs5+7Wx8vJRnJ3nboJMGoe/HfT2/vO7o6zBi9gj80esP1HqU827b6u5dF/O6zct/pujbqi8GfTYIIzuOxAWNL8j/vHix4vj39n9xy5RbMGoODyAPYUH93PwGhXtmMWn47FT9kepWxjUq1MDKDQxwKZox7/NfPx98fnp/8fsFMnPXrVGVRli0ZhF25+220vC7mX/MxMkv8uD16OzBkx9Enw/7oEm1Jnj/kvdR5zGeZ2Xb0FOHoudkLlApur163qvocHDmP0cVnUR6ctiwYQNq167NwvnAvCE9tVCpySQgASuZdNOXd1cAz7nCJulnhlC2cSKt6gMYBoCRV5wxU5TifljrnCqPALA/gNNcTeCG7TxWmqP9MgB3AngnRBMtAWv9+vUSsNLXB1RyGALF7rWHPk7Y3/npHbSq0woTL5mIFqNaYOHfC1F2O/DfYKDPK1fioUWjsXAYcPOpwJQXA5HI/ab3w4A7BwCnBgr64+Y/wAe8g/c9GKaMWByR1y+Qv9f1a29baz0o84Hto6UfWVlv67sNpQeVjqWYsGlr7lUTKzZm/gurJT2WoN4T9RLGJVkZGZ9fPuFyPD+PwbG2Vd+zOlZtWpWsYkPm++5F76LjqwUFLOvID1c/T2al2Mf3fWjfQkX0Ob4PHpzhPkckmbXwb957FN8DO3bz7BX/2yFVDsEPf/+QX9Hnz3wel024LGTFOQE3k9NEto73WLjx+NbjbsXDXz5sH22Ton4e3L71t69HxQeie+mRSDa5lteWu7ag7H1lceR+R2Lun3MT0vzJnSbj+fnPo3Wd1hj/03hMXTI1ZL777bkf/tz0p+f3lx1xWYHfAHci9700sM1A3D39bozuOBozV8zEM98GRGL29e4Tu+Op2U+FbltQP+c1eXl5KD6A7769bc2ta1B9SHXM7zYfhzx1iJUoUc8K4e5Pfrdt5zaUua9MoYqVKFYC7138Hv73cqjte8O795Oun6D12Nb5iYZ1GIYbJt2QkD7B5zIKcrL0EKCAVbGiNZ5KwEqPC5JeqgSspCPOyQIkYOWk2zOn0ZHEpT23ARvvB2599Uo88tNoLBgO9D4FmPxSQGC6a9pdGNx3cP6E5+srv8YxtRisaNuBQw/Er+t+jQlKJAFrde/VqFq+alziWEwVyYLEiXybmkwc/935H35b/xsaDW+UzGKKlncaJ/ZFq7iuTieBTk06YdwCBnjbFknASlZdd92zCyUGlAiZfZfDu+CF+S+kVcD6qftPaDi8YbIQKF+HwIpeK1Dz0eREuh1Q6QDU37d+WAErnCNMBFZRnMVniNNfPh0Tf+Z76RAWNJ7vvHsnnpr1FHpM7hHyki+v+BLHjTkOC65bgCYjmljpauxVAys3Fj0C69VzX8VFb13kWTaFs8oPVw5ZrydOfSJsvcOxbFK1CRb8taAouENeu/ue3ShWTFPspMCNIlMJWFFAyvAkursy3IE+rb4ELJ86RtWyCUQSsCpsBdY/APR6/Uo89sNozH8KuL0d8ME4W8B6feHreOvHt/D6hNeBg+w3kQz7DzY+6K3YsAL/bv0X9fauB0aRXPP+NSHdwIfPhX8tRJmSZXDQkwcVSvfs6c/i6qZXR6y/3/3ctm5bTPuV6xhkJPDRpR+h3Yvt/AuD59AW7o7+ra9q5gsCI04bgesmXpdfl2ubXlsgWiRVlXzrgrdw7usMIo9g6ueRCGX897/d9BvqPB5YNpbIBpUuURrbdm1LZJYx5xUp2tDKMKiftzuwXX5Ed6gCv7j8C7R8riW+ueobHDPqGJQtWRZc8psIAYui3+K1i2Nuq58vcL+M9HM9s7VuErCy1bOBdknAyn4fp6OFErDSQV1lRk0gkoC193/APw8BPd64Ak8uHPN/9s4CSo6ia8Pvh364u7vbj2sCAYIH1xDcEix8uLtDCAQJIQR3d3cI7i6BENxdguQ/T/fWbm1v93T37EjP7L3n5LDMlNx6b3VN11v33tLL50uH9pA22X9oENoVdVnnhJ/wlzT57vfvgvCoize4WI+OfFSXvnJpuypv9H1DC523UGIzOyy+QxD22Osa0tA1riw63aJ69ctXG3cAFdb8/m3vz5XHo8LdW3OGQFUQGLzeYO12x25VadsaNQTKQWDE3iM059lzllO1InXWmWcd3fXeXRVpK66RTARWGb2fsNoJOuyhw7Ttotvq8lcvVzQ8uIwmm7qKEVj1Na8RWPXFvxa9G4FVC5S7Xh9GYHU9mzfUiNMIrKl/lb4+Tep7ww46//VhevEC6chVpTsScmqX+7KSpkdDgWrKlo3AyrOurMc/frzs+lbRECgiAhese4F2vzM5aXsRdTadmhuBeodqTjfRdPry1y+rBvKhKx2qE584sWrtk7T+pre4hNykFALlvhMaqpVBwAisyuBY5FaMwCqydRpXNyOwGtd2XULzNOJoup+lL86Qdr1hew15/RK9cIF0THfptpgUJcd0P0ZHdjuyLNzS9CirUatkCBgChkABEDh3nXPV765+BdDEVDAEDAFDoHYIGIFVO6zjejICq77416J3I7BqgXLX68MIrK5n84YacRpxNONP0qdnSjve2EfDXrtMzw2Wjl9FujUmzzYJULlmvRxJ06OcNq2OIWAIGAKGgCFgCBgChkB9EDACqz64u16NwKov/rXo3QisWqDc9fowAqvr2byhRpxGHM38ozRqgLTdTdvqslcv17MXSietJN0c3h7dTjrzopKmR0OBmlPZyf87uX7444ectRqr+LBew7TDrTs0ltKmrSFgCBgChoAhYAiUhcDvh/0eXMRjUj8EjMCqH/a16tkIrFoh3bX6MQKra9m74UbLjVSl8jjM9r004pz/aLsbttGVr16p4UPG6NQVpZuMwKqIrW/f6nb1vbOvRv00qiLtFbERn9jsykRlEW1jOhkChoAhYAgYAtVAoDOHmtXQpyu2aQRW81vdCKzmt3E9RmgEVj1Qtz4zI/DGV29o4fMXji2/59J76rGHhumFgb9ru2u31DWvX6Pnh42nE5f+QzfEXBDYmZeVrkhsXLXxVdpqka300IcPqcdlPTLbrBEKrjHnGsF14J//8rn+PLztOvWuaOdGsJfpaAgYAp1HYPbJZ9dHP3zU+YasBUOgCRDozDthEwy/EEMwAqsQZqiqEkZgVRXeLtu4EVhd1vSNM/CHP3xYf//7t5accUkNe2mYpphgCm264KaadPxJpXff1ehFFtR2V22m6964Tn/evZS2nvlZXR/hvBaYegG92e/NsgftiI05Jp9DH/7wYdnt1LviUd2O0jGPHtNBjYnHm1i/jP6l3ee3bHGLes3fK/iskYmdhaddWK9/9Xrr2Oadal69s+c7saYod5z/0X80RmPqbV7r3xAwBAyBRAQu6XWJtr91e0PIEGhqBD7p/4lmHjBz4hjf7Pum7v3gXu273L5NjUMjDM4IrEawUud0NAKrc/hZ7XgEjMCymdHYCLz9tv5cfBH1uWJj3fjmjfr7vuW05fRP6tpF2oZ1w2Y3aI251ggJrzLFERvv7vmu5h00b5mtZKs25xRz6vCVD9eOt+2YrUJKKdqDAPz4x4/1yu6vaLELFmtXg+vC55t6Pj028rHWz2/c/EZtOP+GGus/YwWflUvs+B0N32m4lh+6fK4xdZ+9ux756JFcdSg85QRT6t8x/wa5u3446Ae9+fWbWuHiFVrbSTp5rcQ4cytrFTqFwBLTL6GXvngpaOP/Zvg/vfj5i7HtTTTuRPr1r1871ZdVNgSyILD+vOvr9ndvz1K0pmUu3uDiiv2u1FRx66wkAg/2eTDVS3rfZffVWc+c1bRITjXBVPr292+D8X2636ea6cyZEsdqnlfFmQZGYBXHFtXSxAisaiHbtds1Aqtr27/xR//GG/p96SXU59Jeuvmtm/X3/cvr894basqd9tT7372vyf47mWaeNPkkLisABz9wsE558hTx4hNHchy04kHB9+XKZRtepj639NFn+32mCcedMNCbEDdkvkHzldts66a+22zddP2b12tU/1F655t3NP+587e2OfeUc2v3JXfX/vfvH3yGdxJeSr7kIXb6LtVX5z1/njZeYGPNMPEMuuyVy/TSbi9prinnyk2EXbHRFep9c+/c499h8R0EcXfi4yfqt8N+C+qDp8My6QV23OPGDci+rLLCLCvoqVFPZS1et3I3b3Gzfv/rd21909Z106FaHX934Hea8tQpY5t/f6/39c+YfwK7n9zjZG2/+PZaedjKeu+799qVP6b7MTrqkaOqpWLTtPtG3ze00Hkx8dlNM8LKDGTaiabVV79+VZnGKtjKXsvspXOePadDixBbPebsodnOmq2CvVlTtULgj8P+0H9PKJ2MnN/1ct8lkjy3azW+LP2QkH2vu/bSRS9dJDyw1r1qXb3y5SuxVY3AyoJobcoYgVUbnOvZixFY9US/efs2Aqt5bds1Rvbqq/ptxWXU+6J1ghPvvx5YQdp1V2mbbao2fkfmjP2fsYPNMeKfbPdetLeuePWKXP2XeqGadcCsmZOoQxgtNeNS7U7/Iaje26v9ht0npOafen691e+tkvoeeP+BOu2p04IycSTe+GOPrz//CXNJ4Z6/wDQLxLZXighz7Z7V8yz4cIPqAAAgAElEQVQ9/vHjmmbCaXT+eucHuc22unGrTHh+tM9HWuT8RXTFxldog/k26FCH/vst3U+D1hmU2N7m128ekH1Z5N7e96rnFT2zFO1UGXei/Poer2vBaRbUWMeGnnG7LbmbBr8wOLXtZk5U/8shv2jikyYuuVHB7k/t+JSWn2V5nfPMOdr7nr3blb96k6szz7FUsGMKbLXwVhr+yfCGzT+E/le/frX+PfLfYO6xxjz/2fO5oThs5cN0wuMn5K7nKswy6SyZ18KyO+lkxYNXPFjvfvduyctHOtlF2dX7L9dfhDuf+fSZ7dp4bPvHtPJsK6ceMMwz5Ty6uNfFAQlcKTlghQNaf1sq1Wa12llxlhUDEnyX23dp18Wqs6+qhz96uKxu15xrTd33wX1B3Q/2/kBznT1X7nb+PuJvjXPcOCXrQeZziITtnvj4iVx9FD30lPePPw7/Qz/9+ZMmO3ky/XrorwGBFfXeXnnWlQOv8ke2z+/VnQswK5wZASOwMkPVsAWNwGpY0xVacSOwCm0eUy4VgZde0i/dV1DvwT1153t36q8HV5R22knadtvUquUWcCTMsF7DtMOtOwTN+J5C2y22nS595dJczaedCGbxgBqy/hDt/H876+UvXtZt79wWeJSQ/+nC9S4MNu6++MnxH93+Ua0y2yol9T3swcN04hMnirFdsuElHTY66P/Pv/9ou1u209ANhmr8ccZPbC9pLLSx5117ik3uDJPM0Fr/2tev1ZY3bhn8/4f7fKg5Bs7Roe21515bd79/t0buO1KzTjZryb7xQjh77bNLjjcL3jRw/7b3a43L14htKyuROfrw0QHp9s638Xm5aPzL/b/UdKdPp9f2eC2wqdMP4nH1y1bXpz9/WnI81SKwTln9FB30wEFB3xCOX//2da55D5mI7re8fYse2e4Rdb+0e676FCYJ//jHx8+3pOeKk/pBzw0KyNhdbttFp6xxiqY6darWvhebbrHE03tfQTwVnadkKcUhgPDUG/njyNzjK0KFbRbZRle+dmUreZ00tzdZYBPd+NaNiSpD7kCUsLksR3i2CYWOytHdjtbRjx5dTpMd6rCGlOuJxLPJM3rS4yfp0IcOTdSHHI43vHlDRfSlEQioVS4pvYZTjsOBfZbbR8tdtJye+fSZ1v4f3+FxrTTrSqkEFs/Lr6N/1e537l7ykMYRnlkGeOJqJ5bEyrVx3jrnBd7JeXN4DVxroPa5Z58sqqSWYfwXv3Sxdrptp3ZlS4UupzXKhSL3j7g/eLbGjBnTejiRVs//3hHLperw20kSf2TqU6duDbfL0k8RCKxSHmRx6/xql67WgVRMez/IgoWVqSwCRmBVFs8itmYEVhGt0vg6GYHV+Dbs2iN4/nn9vEY3bXNeD93z/j0a/fBK0vbbS336VA0XPG44MeWUb6ITJwr6+e3Q3zThiRMGf3NCe8nLl+Tqv7MEFvm9fjz4x3Z9njn8TO265K4iQXtUCJMjXO7QlQ7VCT3SPSKOe/Q4HfnIkcFLNhIleNL09/svRWDFgXb9G9dr8xs2D77Cw2r2geFLuC+EXs545owBweVe0uPaGvz84MAzyyfI4splJbCcB9ayMy3bbkNIm30W6xOET6YJ2JG3ackLl2xX1Hn4sQGDQJj6tKmDHGaLTrdoK/7UZUxsKJMEQnHHJdryqcWN7YTVTtBhDx2mrRfZWle9dlXQFJ5e5A4rJYTlHfzgwUGRmza/SRtft3HacNt9j/7kKZvilCn0UJ+HtNplq8XWP37V43X4w4fHfvfPkf9o7GPHjv0uaV5+/vPnAcm721K7tdZzuNy59Z36+tevM22Uo+GLg9YepPOfP19vfP1GO322XHhLPffpc/rg+w8y4zPBOBPo979/z1y+0gXJGTbVhFMFhNHg9QZrtzt2ayWwkrxmCFGeZcAsiapwCcaIfUakEiVJDUBgjTPWOBrx/Yh2RfISWEmh4Myzg1c6ONWbhc7jSM6FpllIr/d9PSB3tr25/SEKBO+yMy+rO969Q1lCvvLYMyuBxVqy97J7a6WLV9KTo55s7cJ5Jz4+8vGAZCXBdZwXcVYi/OsDvtY0p02TaQhZCaz7et8X5LLMuja7zln/ooRTJsUkzTbZbO1IZ8Y/9MWh2vn2nbM2kVrOJ7AofPITJ+uQBw9prQexmOYxlTSf/c5H7D1Cc0wRHv7kJbAgD/ve1Td1LK7AcasepyMePiJz+SwFS4Uvx63zSw9ZuoOXKPkwSc9gUhwEjMAqji2qpYkRWNVCtmu3awRW17Z/44/+2Wf101qraetB3QNSafSjq0i9e4ckVpXkxz9+DFzTuaEPrwrynRCm516sd1x8R1388sUle4c4wqPJSRoBlPbSHpe3Km34tHnuOueq79LpL6bcUAi+5LVCOktgjTf2eNp+se114YsXpmLw1z9/adCzg7Tfffu1emDhMeYnnf/if19o+jOmF0n255lqnrShp37/6pevBt51EEvnrH2O9rp7r9Y6k40/mX78MyQLXfJcQvsWPr/91Zds4p7+5Olgrpwx/IzEPrE9Ced9EgZ8es7VMwgF5Xvm3OSnTK6Xd3tZi02/WDsCCyKm1zW95LzQoh1F59aDIx7U6pev3q6Y2wARCksiXEiyZWZaRrvfsbuufePaRN3x6Nj33vAmp3IJLObWJCdN0oql3xlkEgQXxBo57gj/2PDaDTvofuWrV8bmSkt7rvyGmNPLzbycuGzgrvfuivUS+u84/9Uff//RWs2FLxKacv6652uhaRfSb3/9pvOfOz/IKbf/8vvr9OGnC88jyGS8zfDS2ez6zfTAiAdKzsOfDv5Jk55c/sUTpRp3HlWlypDfjTFhnyVnWDLwktti4S2C/642x2pBqA7iyC3+dp6CkF8QoM999ly7LggB/Lj/x7lJCNcIBNaWC22pU586tV27eZOmJ234kwj6OJwWn37xwNs17nn78+8/A5yc5yhlILCYXzzTWTxm0hYp/0bcUgSW7y3HWrbnMnvqk58+0a637xp4rSLRsG+8aSFi/XWPcnEE1k5L7KShLw1tp+5X+3+laU+fNm0IwffVJLD2WXYf4SWalh8qSdHowQTjd+tVpsFlKET+yQteuKAdtqwNzrOXMQx8ZmC7lqLrEHpx8LDNTcmpE/AWXn3OcN3PS2DF2RgyiN+kOEGfTa/btKQ3ZgZo2hUpFa4ft87jWUs+LF84dMSLz6Q4CBiBVRxbVEsTI7CqhWzXbtcIrK5t/8Yf/fDh+mGDNbX1WSvrwQ8f1J8QWFtvLe0QhvbVUhyps/MSO3d4cYrq8eSOT2rFi1cMPibh6EyTJt+YQ5mf//xZi16waGwOHTYAh6zcdmKbdcyjfhwV9OtuGsxaj3KdJbDIpUJid5e7iNNVNrxJ8sUvX2iGM2ZoJbD8G5U+/9/ngZcZJAi5omacZMY8Q0kse/pTp+uA+w8IbjH0X9TJGfb2N28H9R7Y9oGADPrmgG8CDyknjgjh/yHD3M2Pa829VuAp6It7+R75w8hW7zIILMpCTrmwHbB6cdcXtcQMS7QjsCC/8EiBRPXbcH3Evdz79sNrhosO+IxQ2G0WbdsEXf3a1SUTv/sb5yQC6/ldntdSQ5ZqHfLSMy4d2OjWd24NxkZyebwXHZZx2PifJc29OJI3D4H17W/fBqGvzCVCebjZEK84SMPFBy+uPZbaQyevfnIrcYNOzvMSD4U9lt6jVU2eV8in53Z5Lhgr5MW4Y4/b+r3L1RI3+U5f4/SA/GKzRTsQs05u2eKWDgSe3wbhwrvesWvq/I/DOq5SKfwc3o7gxTtytslnC+ZRjzl6aPqJpw/CDn0hR99n//usUwQWuXwueP6CdnnM/HyEaYP39YyWzUpgcfMl3iw3vXVTh+6SvJSmnnBqQQq6ZzrtUCJtHD7xQwhgUl4qyNOTnzw5aA4PwX7L9Av+Pu3J03TgAwcGXq3YLSpuDic9j6w1eMNNN/F0QWJ/P5QWb2BHcFIfu3/+y+dBU3dsdYfWu3q91mav2eSadkRf0ridB9Y4x44T5J6M83qN1nW/K3FYc3EKByFxHr2unXXmWScgs51gW8i9tHxTabbzv8cb7/s/vg+eF1+czoRIszbhYexkrinmaufN6eZc3OGEq/Pszs9q6ZmWDv43L4HFQVe/u8J54+TnQ34OfnOROEKt1BqXBx9XtlRob9w6BYkMrrw3OAFLfltNioOAEVjFsUW1NDECq1rIdu12jcDq2vZv/NE/8YS+32RdbXXG8oGnyx+Pd5M23zzMg1VjcS+cWbwb2NhufePWQb6mB/qU9sRww1jqwqX0wucvdBgVIVTlkFCdgaczBNZYx4wVJB8nQbtrJ41ocAQWYRBznj2nfALL1cVTZ/L/xp8IlzNWiCFO2wnPdGFutAPZgwcDQg6qBc5dQN8f9H0QBueETYnLA/bal68F5CPC7YjDXh4W/L3A1AvorW/eivVq6DVfr6BMlOR5YdcXRL6VUrhlsY1fxt+0k8yccDcnUQLr2O7HBqGkTqhLmCEb2Nu2vE0bXNMxcT5lfPxOXf1U9V++f+DJBFmEh914x48Xm08sbl7MP2j+dvnCSpEOafMqbV64OcVmnpP7sccaux35gp0ZB3PkP/9pe00jT5BPOEb7YXOV5BVCONcKF68Q5PZisxW1FTnPIOvj5Patbtf6V69fcliEPU4xwRSZSKQsBBZeWnvcuUfrPMYDDWKDkMNoKLUjdnvf1LuV3EoKC04aBDrh3bTRtRu1K+KTJO4LNr08n+jkz1n+LkV4ppFL2J0bzpa9aNkOz34SgTXuWOMKQsQ90/4z4Q8kCx6QLxDNzmvTJ7CinirOC5A+fI/bu9+7W+tctU679SeKuY/DuvOsqzu2viPWLBC9eKsirIWsw35dFybH93hVuhxo3BQLIfnoyEe16qWrlpy30RDCLRbaIvAOdRdcxFX+9sBvNeUEU2rBcxcM1lpfPt73Y80y2SxBvjO8In2iypVbb971ghBaDiEQbBuXp8r3QkxbU6LfJz1j0TXex5MDIP8mVdcGNy/Pc068BzIHPY4kI9/fd79/10FVwushWJ2437Wz1zq7w8UX5G5k3UYg8sGRHIgOc9bFCU6YIC8c7cp3n717ayJ27DXrWfH5LUutU857mYbr8a7UKQC6QGUjsJrfyEZgNb+N6zFCI7Dqgbr1WTkEHn1U327ZS1udukwQUvbHE92lTTaRdml/S1DlOkxuCbf/4x47rl1omysNIcHGxQneR4RpIVnJp7icDu6luhbj8/vwX6YhkwasNSCzCpxgM2Y2/FkJrC9/+TLwRIHA4kbCAT0HBC+2nPKetPpJmfvuTEGnK94XeOc47BnPGI0JcoohhFcRWugEHWc+c2b9PPpnPb3T01pu6HLBV2zkHv3o0SCBuBP6YK7ctMVNQQjGzW/fHGyaINNISnvLlre02xzGvbg7Qsi1GVfm4AcO1ilPhv2678ldhGegnwR/jzv2CMJbnL6EKXKLnMtv4uqS74bk1f5pd7R/NlYQLPNNNV87sseFT8aFiMTpTnlIGrfh9Ams6SaaTl/++mUrnp0lsOLmCzmMHEnEJs73rHLlIUzIj+dCPuPaifPkOGKVIwKSY/mhy4ubxaKEGeNxoTmQW6P/Gd2uaeehRd0el/UINpR+HjOIBTalSBpJk7a24MHz1a9fBSG7Lj+Wrwxzm3kCKTrzgJmDrwivHtprqB768KFgrSSsCbKLcSQl4o9iBwaf/fyZZjqzvdeqn+uIUEXy4YGfH57bbbZurTeQgT8XELjwXkICWZezYOPmFW3QB5cwvP7V6+2eJ/7H5Rp0Y7h7m7t11tNn6Z7eoRdmEokGGRCXrN61g50JYXf18QDl+frqgK8CPP123c2PPBuP7fCYuHjAidM/bn7y2bSnTRvMoTPXPDNI/p70W7Xo+Yvqta9eazd+f36/3e/tYD4SQnvX1ncFN6duu+i22miBjYI2v/ntmwBDDiqSJEpgUf/yVy8PyBOIc4g6QnNZZ8mDCEFIaDkHCcwB2vefBUfo8B3C7wk6+kJoKmsuz/x5z52XaDdCQvlNgIRjvU8SCHsORXzJSmD5ecu4uXCtudYKwur959QR5659SHdH3pIn0uV+TCKwNl9oc133xnWt6qEbc4nf2/739u+gN9/hXcq8c7cl+89GnKdantx+kKZczoMk5ddz62Qi6N5zVo3fg1L92nfpCBiBlY5Ro5cwAqvRLVhM/Y3AKqZdTKusCDz0kL7ZdlPN1u/P4EVtzDNrSxtuKO2aHkaTtYu85eI2JdGktoRY4LWRRxyB5bx+XN16vJRBIrHp7L1I72ATUq688NkLOufZc4KbDUsJpAw31EEMEa5QD3F2ZROMx4C/cXD6cLsdecJWnSPZm6AUabfb7btpu8W3C0KNho8aHniwDF5/cIfhDnx6oCYab6Lg1sk4OfuZs1tv3sq6QYprZ8sbtgy8HEgkDPnkPNzwPHn202c7eG8ccN8BQc4nJ32X6qtz1z031Vxggm05/Xf5Xkiofdgqh8XWxfsGLxzfBn1u7qN9l9u3NRk+ZNCxqx6b2nc5BdxNZEmbJzbv3S7pJkg57JQk7kIIvr9q46u01SJbBWGDa1+5tvCq8UleN9Ytbtgi2GQ6zxM2hOvPt75mnmTmIAE53z+03UOtXToSIjpfySvn5zgizxUenu/t9V6rF0eWtcXlU7prm7ZQK3+8kFzcoJm2XiURapOMN0lASiCLTLuIXt0j9IbxQ3PxZnyz35taYvASQV6qqN7kJIMo8ZP2O32Yc8zl41c7vlXHfnf206ifRomwPwjReaecV2c9c1bJMRzx0BFBiBZeLL7EeTu673e8dccgNHWZi5bp0HYpgpGcRBdtcFHiAYCre/jKhwcEKzfSEvIVd6FHOfM/WsfPGedjzzrE/NxlyfBACRIG4j4pkfbG124ckPZOjul+TKA74nI4ubEd1e0oHfPoMa1EL2UmPWnSYK7EzVufZKOs8xTyxxINweMwAQIrKklerh9+/2HgIeyLf9FFXO6zrOuz83SlbYimaze9NsjByUUhF6wXHjIg0fmGtye/ndw27MLnOKxwXsSuf3KicdkH5LkTvoOsxwMrOi5HbvVfrr/O7HlmBwIrqotrE+KQgw7C4cnbRWJ+ftNZj1greK8Y/snwoDi3dUIME7KPRyprKnklOQRxt/ZmWaMIdYQ4zFK2Es+DtZEdASOwsmPVqCWNwGpUyxVbbyOwim0f0y4NgQce0Nc7bKFpdw7d4cc8u460/vrS7sm3sqU12dnv4zYe/unhjZvf2JoMPU9fJGjlhY+XsOMfOz7wbqjmJj2Pbl2hLHblenhe1te7ar1gs1/OCzHt4CXx1xF/VRU2btojN9aKs4a51qKChweebS4vSlyZnW7dKbiQIDrOda5cJ0gAHTf+Uhv2pAGTS2jD+TcMPfOOCV93SmHLLYGQL5Br0XJZ6ncWeG6Y45Y2NqR+6GA57R764KFBgvek2zPdeAj/YfPHBo5NJt4lkDXYtxQx4QisNFu5ixA+2PsDzXX2XKk2yDpW8ve4/HAHrXhQkEcsTuLWTZL3k5dtrGPHCqqQs4iNOOJv6N0muv89/QOiqZznMm08zNFNrtskNy5uXFz+8MPBP5QcO7nJeswZegGVIrAIvcNOSXPd//ylz1/S/134f+LCgVJkatr4074/5IFDglxbncXeH7ef0w1CFyLdfe9uxvP7W2XYKgH5Ebe24h0VXL7S4g0dhwfhgdh50+s3DYbLjcLDeoUh376gw6qzr6qHP3q43XygPnnf/BsoHdHj1rQk8iuuD38d9EMXCZ+8ZtNrSs6lUhe7fPTDR0G+RML8es7ds8PY3Ac+thw2EY7piCw3rss3ulxcFOC8Bv060bGSM3G+qecLCG0Xwpm0FoD9aWucpuUuWi7I99WZdR6PTca7/Cxt5FzafLbva4OAEVi1wbmevRiBVU/0m7dvI7Ca17ZdY2T33quvdu2t6Xb8JnyRfH49aZ11pD3aEirXGgjnteL3604d/RfSvHoRZsFL2JIzLtmah8O9POZty8rnR4DTbhKQ49HAppykxOROySuc0kNgkX+l6MKGj41fdPNA/pRPf/pUi0y3SIchcDmAy1VSzmZ2xjNmDLBNq4tXHrfc4a3mSy0ILDztBj03KFXHStgXDwQ2mngisfl78uMntdKwlQICiwTaaVIKDz+Zs7uIwHl2ET5121Zt+XDS+in1PeHd5IBi7UpKohzN3+MIC9rFG3GCcScQoYFTTThV0NV7376neQfNG4SOHd396ICcOenxk3ToQ4dWzS5gudmCm+m6zdrCrNJwyUJgEWJMeJ0/5/GsIZyX0K3obYcul1iSx5Fvc5eDr9oE1oH3H6jTnjqt09j7pAdE1DOfPBN4V0PsQXBz+QlrD7cLcsujjxmfk7g7bl12a/b3v3+vVS5ZpTXHXJz90IHDoQNWOECTjB8mKo+uMRDuUS9QVyZK4jvvL3R94uMnxC2d/I4Q4gcZmaQD5X45tC3k0LWbhcBKWz+T5q3rgzydS83YdvlGdGxuLMvPvHwQRkvIdOAFf9SY1qaTyDrCi7vN3i3x0aGeC5Ptfkn3wOO5MwRW2jNq39cPASOw6od9rXo2AqtWSHetfozA6lr2br7R3nSTvtlnF03jPLBe3EBac02pX/sbc2o58L539g2uIEd44SbHBiGDRz9ydJD7g9vFKiFsbLm5L2sOrUr0aW10LQQ49WeexRFVpZB455t3gpANCIu8AlELOeXyteStXwsCy5Et5W4S847JL3/zWzdr4+s21k8H/xS7uY62XQoPQnYITcYbj7FAdmBr6hA2tNeye3VG1dx183jvuXAtbrHbYuEtgr6YN9hmgWkWyN13lgroRwL1bRfbNkvxoIwbU5/F+ujSDS+NrVdqzkO8fPv7t0GSdEK3EW725Nki3xKETPQWQd/m7gKMat/Adu3r13YglDKD5BX0w/Dini+8Rv/858+AzHzj6zdyHyJAphKKVsp7kucAEizJuzLNiyo6j1cYukLgGZZnvSCnFPkU/fD6rATWQtMspNf7hjnZ8gphzeQPe2bnZ2KrujDP6FimP336INw2icAqRbrFrVmv7v5qsBaRhP3HP39sl5vRf67yYJoXCytffQSMwKo+xvXuwQiselugOfs3Aqs57dp1RnXddfp+71015R4/BmMe81IvqUcPaa/abrx8wH0PrGknmlZf7t+WVLrrGMZGagjUBwFu6Zt7yrnb5YWpjybV6RUvzNkHzp5rM1xKk3OfPTfIJUQi5npLHgIL8maykyfTPdvc0yEMqt7jqHf/hDri6UYC/UaUapLQkLWEu3WG+MhLYJFfasiLQzrVp7Mjfad5YO28xM4assGQqph++1u216WvXNphLISQ3vPBPa0XIfgkE55ceHRVUqo5Ryqpp7VVGgEjsJp/hhiB1fw2rscIjcCqB+rWZ+UQuP56fXJkf82y5achgfXKRlL37tLee1euj5wt7Xzbzhr60tCgFle7f/a/z3K2YMUNAUPAEOh6COQhsECn1zW9dOXGV1YtOXnXs0AxRlx0ciKNwALFIx8+Uj3n6hnkqOPGzgMfOLAiBNb+9+2vbRbZRkvMsESssfa9Z98gpx7e2dWQJAIrri+HE95yH/f/uKLqFH2OVHSwTdyYEVhNbNyWoRmB1fw2rscIjcCqB+rWZ+UQuPZajTruAM262aiQwHp1Y2nllaV9961cHzlb2v2O3YNQQWSmSWbSJ/t9krMFK24IGAKGQNdD4PZ3bg9yQXET2d7L1u8QoushX6wRH/bgYSKsMu4G1iJoCnmyw+I7BPnQCOGPJkKP6shYuAnziG5HFEH9Tumw3S3bBTcfZvFgy0tI51HMCKw8aBW3rBFYxbVNpTQzAqtSSFo7PgJGYNl8aGwErr5ao046WLNuEp7ujXl9U2mFFaT+/es2LnKWkHSUMI7pJppOX+z/Rd10sY4NAUPAEDAEDAFDoHIIcAPpxgtsHCRh72rS5+Y+uvzVyzMRWFe+eqV639xbc0w+h0bsM6KiUHGpChdb5M3PWFElrLFOI2AEVqchLHwDRmAV3kQNqaARWA1pNlO6FYErrtDI04/Q7Bt9FBJYb2wmLbus9L//1R0kTginnnBqfX3A13XXxRQwBAwBQ8AQMAQMAUOgMwhse/O2gsDL4oFFP7wH7bPsPjprrbM6063VbVIEjMBqUsN6wzICq/ltXI8RGoFVD9Stz8ohcNllGnnW0Zq914chgfXWFtJSS0n771+5PspsiRe32SabTR/tG5JrJnVE4JRTpJ12kqaeuo5KWNeGgCFgCBgChkDjIjBg+ADtd99+mQksbsmcZPxJNM5Y4zTuoE3zqiFgBFbVoC1Mw0ZgFcYUFVWEu5/7SVpM0sSSxpX0r9cDf/8h6W8OMtifS1pe0hsJWlCGnfuukqaTxK7+UEl3JpQ3Aqui5rTGao7AsGH66NwTNMf6H4QE1tGSunWTHnmk5qpEO9z8+s216uyrao+l96i7Ll1egf/8J/TKO/30Lg+FAWAIGAKGgCFgCJSDwJgxY4IcdeOPM740cKA011zSeuuV05TVMQRkBFbzTwIjsJrTxmtImlISgfQXJRBYPSQ9nHH4JP4h8+nakt6RtLmkyyQtK+nlmDaMwMoIrBUrKAJDh+rDwadoznXfayOwAiYLrtfEEGhBAAJr8cWll14qH5JrrgnbmH/+8tuwml0HgSFDpLXXlmaeueuM2UZqCBgCXQOByy+X+vQJx2rvW13D5lUYpRFYVQC1YE0agVUwg1RYnW6SHkogsFZv+S5Ll09LulnSKV7hxyW9KWk3I7CyQGhlGgqBIUP04UWna8513jUCq6EM10ll8bB79VVp74w3lUFgnXGGtN9+5XW8117SoEHScstJw4eX14bV6loIMOd23llafXWJvzfnPMnEEDAEDIEmQIA1zYkRWE1g0Bcw3O8AACAASURBVPoMwQis+uBey16NwKol2rXvqxSBxRVmhBaOlHRBi6dWkobPSLopQmA9KWk8SUsbgVV7w1qPVUbgggs04rKBmqvn2yGB9XgPaZpppKuvrnLH1nxdEZhjDumjj7Kf/PKyze2UT7IcliHuZX2ssaR//imjAavS5RBgzuy6q3ThheHQbZPX5aaADdgQaFoEjMBqWtPWcmBGYNUS7fr0ZQRWfXCvVa9JBNaqkp6SxI6JcMMrJR0iaXCCYny3u6T1W7yuyLF1qSQSBM1nBFatzGn91AyB887TB1edq7nXwMlQGvP9PtLYY4feNibNi8Ccc0offpidFHAv2yNHSv/3f9I33+TDxn9Zxxvr7LPz1bfSXQ8B5szuu0sXcO5kBFbXmwA2YkOgiRHwfxOPOko6mgSkJoZAPgSMwMqHVyOWNgKrEa2WXeckAivawpGS1pS0UkLTY0k6XFLvltxaD0j6S9KcklaMqRPkwOrXr5/GGw8nLalnz57BPxNDoCEQGDRIH1w/WHOv9nq4R7xqXundd7MTGw0xyCoqeffd0qOPSiefXMVOqtB0uQTWddeFoVx5vWH8l/WsZMS334Z9PfhgFQCwJjMjgO0OPFDiJspaCv3ONJP06adhr3nnXC11tb6aH4HTTpNmnVXagnPNTkrfvtI220grxr1WdrLtzlb/4w+pR4/wIpdxCV7oIsJ4b7lFOuus2gy4nN/E2mhmvRQcgXvvvVf8Q0aPHq1zzz2XPyeT9FPBVTf1ykDACKwyQGugKnkILNilPG8NL0i6Q9JRMXhYEvcGmiSmagwCAwfq/Zsv1jyrvhruEd0hIJtF/o0zjvTvv9Kzz0pLx0XRdnFU3Utoo22uufloxAgJjyo2ZUnyww/S3HNLkEkIidi33DK8jZBbCbNKOS/rd94Z3s7UaNhmxaRRytVjjp9wgnQ4Z0me2DxolBnTnHryHPCP38Ny5eefJcK3WU/xZH2B18uCyfvvS/PMI335pTTttOUpt9VW0sYbS5ttVl79etRaddWQtKvVOlPOb2I9cLE+C42AeWAV2jwVUc4IrIrAWLhG8JjiiAgC625Jk7SEC46WtLgk7P6aJN44uI2QxD54YQV0dYzwa00bhAxOJelQSZtIWkLS9zHljcAq3JQwhXIhMGCA3rvjMs27SnjJZjsCi1xFEFjIuutKd8DjmrRDoB6b+0qYAFLqgw9CQirOo4C8Q7vtJl12WdtNSfRLbjQ2J8Fk8W6qBAdyas02W7x25bysG4FVCUuX38bo0dL447fVr9XGjh6j8yU638ofldU0BMpDwJ+TSy4pPf98/nZef11aZJH6PFNp2rLWDxwYrvHzzSd9/bU09dTxtSaZRLrvPmn55ZPXew68OPgqsrz3njTvvBIeLDfeKD30kBFYRbaX6dYBASOwmn9SGIHVnDbeTtIwtlItw8PO/E3uK8ilUyVxB/ffLUncz5M0xIPifEm4H6zb8hmkFyTXTHhmSsJH80BJLTEMHUA0Aqs551XXGdUhh2jko7dq9p5vhZyE88DiBT16OlzLDWyjWKARCazevaUrSQfY4lEVR2BNOqmEt0BUqEfoSzBZIgQWhNM663Sss9JKHZO/Z5lLd90VEqd4PMQRGlnmCP2QOP6TT8JwtEoKG55NN63dhqcc3RddNMTwpJPy1/7xR2nyydvqZbEZJPf6pJCU9N130hRT5O+XGtUksLikgrBUsDExBLIiUA4J77d9003StttKv/2W75nKqp9f7uGHpdVWS16bOGzAE8w906+91vY8vP22NP/8YZ7DqTjHjcjii0uvvCIdeaR0zDHx2jXK7yIHOBzIsBa4dSHLOud+//htGTVKmpltRk7p7HzK2Z0Vb04EjMBqTrv6ozICq/ltXI8RGoFVD9Stz84hQMLQY48N2zjmGL351G1aaPkwlKGVwIrrIeuLXee0a6za7iV0iSWkF1+sj+5rrRWGa3BjWxbJ8uKchTDCk+DVMPQ0IBwgLyBLfGGzNtFEHbXKMpccgUXtzz8PN3/kxNpllyyjDMs4LyJO1gkRIecMSeQJg4wK3kZvvCHdcEPoedS/f+l+9tgjTDCeNhawIWH+7LNn17tUSRLgQ8Dcemt6e0kbya++kqabrrTueJj4YcOlxnniidJhh7XX54ADpFM5QypD0ggsvk8Lf03qlrrXXhvOpXrL999LU04pXX65BLHcCEL4MJ415MOrh/Acb7edtP32le+dkLfllosPjy61bnLgw/rvnpENNpBuv116661wrjFX8Xh97LH2OqetHeWO0A/BJaeV70lJm+Rt7N697XCAUEE8rpA335QWXDD8m/XQ/e10cThQH6IsKqwDrAcI6yOevOUK3mB4Rz3xRHoLs8wSehTH5RVD548/lijjC7aJ/hZktcnff4c5woYPD+dMXsnyOxxt0x3IsH5DuJl0eQSMwGr+KWAEVvPbuB4jNAKrHqhbn51DwH9x2morvfb7SC26OJd1ZiSw2MCwOf3sM2mGGTqnS6PX9rFkw89GptaCDpyKv/RStp6zvDhnIbBcb4SacnMlGzZyVvnCpiEurDDLJsEnsAhZcR5hWeo6HX79VZp44nDD1o1I8xahjWeeCTcerr3omA85JPRcSupvqaVCL8W479l4QbT98ktI7pEc+JxzpIUX7nySYDZheJQxLt9Lbo01Qs8J+nGSRGCxkQYPEqTPOGNY+qmnws0f42EzHp3LpXCPmy9smtk8O2FTzYbRkZ58jncdXgwQXcOGhRt+JInAeuedcIwIHn8IpGnWOYFXidv4MSdWWSXbMxPFc+WVO5IRfkuMg41/ml7nny+R0Jv2yL8DFvUQiAbICOyTJhBuEG9pY0trJ+l7bI8uECRRcfOC5xbioJQMHSodemiYyymLuLaZHxAESX27z6MeqHxOaDbr4AILhKUGDGgjwmnXkURxbWTVcdllpaefLl3aJ7Cwle9JSU1I8H32CZ9PnlP/eYO0WmihsP0oAUXuLj+skIsduOABYS2J80RyOPGs8zvBYcT002cZbZhMPmtYH2PgMOeee8K2o/aB8IdY9OX66+OJ7CxzG88r8kdCrpWTjD+6xkGIgU8pcWkdWKuTwjezIWulmgQBI7CaxJAlhmEEVvPbuB4jNAKrHqhbn+UjkEBM/KcldLCkBxanm2uvLU3GZScE7w6Tdtih48ti+drVryYvrL//Lk04YahDdBPF9z/9FL7s//e/YZmodxGb0d13bxvDX3+FHkDOA8l5Wzji76CDwg0CoVpRAVdejMnRQT8TTBDqxIkvnkHHHx9u/tGFzyFTnntO+vPP8P/5h84tt6MGzbNZceX9/vDm4WWYPpzkIbAgUSCYbrst3EBQl9xpbIQgbOIkaYMAZoQhPsAFsAmCnZwNovripUUuF6c/hAf5XKJC/2w+2ISAGTiVGvMXX4Tznn7ZaLCRcDpgd8gqxoxN8bZy3in04wisDTfs+Ky4E3X0xEOLNiAx+NzPQUUbeOhQDjs78T2J4sgq9xk6QVSxQbr44jZvPX8jBHZXXBE+B/w36unmb7DcXHLPSrK1wm8gG/wNF+NzHgx+XWfbOFuw6YVUZOMdZ880Hfje5bzhbzb5EBx5xNcL/XkGoze1MQYIzJ12Clvm/7Ep2Ec3qISgEoqK8Azh/edCv3gW3HqUR8eksugKubnvvqFObi1g/nIogYcQdvFt67fF2H07Rp/huHrUifPiSdLRhb6xvvkefegOGex+e1hXCHsDI7fe0KbTgWe6Vy+Jm7qS1hqeYf7x7LOGETbtJK5OHPHPHGC9cbamPoTkeWSrUOgpdumlydajH5559OBv9OY3Bu9IPIPISYVE9fPXQH6XmDvUpQ3s6hOhJGXn0g4nTz4pEdaNUJfx++sppLwjr487rv1lCtxQHF1PHVbOdtHRuu9d/i/qE6bohN8/7MoY+a30D0NWXz30No1b8/1+8HCLerjSL/OG30/w4TllTfWFkPg4z8eo/d1vBP/FXrTp5iJ4rrBC2Ko/p/h/5gy/BXhIR5/96HzyPeUc8R/9neMZYCx4O3Ng4frg94nfMze+tNsjmbeIy3GaPEPtm4IjYARWwQ1UAfWMwKoAiNZEBwSMwLJJ0TgIxL3ktWificAqNdIsJ5ZFRoqrs9k04aHhXgoHDZL69Qv/n/+6TYk70Y6+gLI53HPPtlH6hAKbQ07nEbcpIASPl/o47Ni48tLOd5x4cyMbG0/XJpsOXlYdQeM8EuI2WU4jvuN0GpIpTvyT8TwElmsLAmu//UJ9jziiYzih32fSfGHTlsULJFrf19eRRmnz1dXBSwu8s4wZTyqID59Eoh/IH8LAouJ0uflmaaONwm993f2LEvgO0ogE+s6DwuX/StKNOYGXh5uzrn36uP9+qSeX7nqyzDLtEysTRufw9vsgTCsaHoR3Hd4lELDkE8uDWxwuzFm84JIwK2W/uDpZyjvdKYu3CARmHvExYq5CPkU3xSSFZoMIaegEUgJCJTq3HWnoyhHa/fjjoe3oqzM33vnjYj7svbfEmuYk7jnBMw+vtCQCZ/DgtpAwvwxjnXPOcNz+Rp0x4EnJwUcWgbBhTkfJxYMPlvD2cUL+Jm5RxYYQIpAcjlyJjitprYF0gszFc5UQ8CheUX3j1lZu64MgKld8sgivSsYDyUq7eK6Sqyrpd5txkVdrk03C3y53ayd5qUgT4IRnjOfeibugg//n9y4pUbs/T9zfPP9RLyY3RyEL4+zs8HeXctCW+wwiC281l1vRkX/8fvAsRNf1OJwh4RyZ5H+PXpCgfv6/Ur8bpeyPHni+xa1X2Iq5h/A8MxaHSZL+cTpDTkHgoaMjIDnIwQsNwXsv7lZIDibwJMMLDE9OngvmUikBc4iwoifZL/e56kL1jMBqfmMbgdX8Nq7HCI3Aqgfq1md5CMSFBbW01EpgPbhyuIHKK5yEu9M8Xt54CTv66PDFGulMIu68umQtj46OQOCEFJKBDRgvnWzCfI8q561D2xARbDwIj4uKe0H2vUvYNFPW5cnYeuuQ6MFrCoH4Ii8TG0deXAmZgKCiDf7GIwOvJDYr0RNZbMVLK0L56ImqbxfGxYurC9OKw4mTXfrqbCjTGWfE55Hx+4zmIcpCILn6/kbE5Z/JanfKsZknjAYh9CVrgnfC7gg9KyWMw+nnCAGIDjaaiK87J/pRmzIPsD+bF0JD8erzPfv8vvFGgnz159uQISER5o+xlL7MBxfy5Moxj9wpvV8X3cmRQ4iRS9Kex255bJSnLM8IOZH69AnxZePK84uOznvlhx9Cb0c/pNVfl/jeJZ2HWHZhVE6PqMeYCwmjP9+jIQkPvGogiSGmyQuEZxLkC56tTiBqTj657f/dXOG/PMv0U45XFuSjC7kshSvkBrn0wA8SxPV/1VVt3rauvvMaYq2E0PVJEvLD0R/rHsS2S+zPfGauObKXuqw12A1PJg4JIDEcye8IMTyG8Bb0Ba+X6Gd870Kao2sFzxqeKfQXJY6jmESJjv33l1jTfIHgheitlBBCStgkRCAkBGsSnnHu1tdoP5TjtyiqV7QcaxBhuxyuQNT5oeasK3gBlxL/N4R8VP4hjasHOYvN4w5HSJAOieTnR7z77tCDiDHjZUVdnldfOCiKXgLhcgm6dwzI0Sih5trgcpIoYezsmrZmxRGxpTBiTjP/IZ75vacfSGuf3PbnFOHfHAD44vJagbfvOU0ZfhMuuii8MTFO+K0ARyfoT3/ufYB1kIT8hJ5CxPmHa5Wav9ZOXRAwAqsusNe0UyOwagp3l+nMCKwuY+oGHigvMmzOFlss0eOglcDazMt/kXfIbMw4iSSMCk8fPIwI80AIieO0u0hy5pkhyQI+JO8lfIdTSU458Zhi8wAJwMsfJ/6ML03iXpD9U3bqEzYEEQJpFSdsEpznFyfRbOaSxCewksqgEyEJfohgqXFkJT5KtQHhF0fw+XVcuJ/7LG1T4ddlTNiFTY7zbEuzTT2+d+Sk37fzzoEAgVSGfIlKnAdUnP7YCq8VH7s11wyvuM8qhLhkTWgO7s5rglN+8gvVI+9b3NjY6BO653uVsIGEoOT5xduKzSEbfyeQNRCAPBtsph0hgUcDzynPDe3hGZM0Px1JSZsQOX7ie19PNqX053tBpdnIrSeETjpiCxKOcDfmPgIhw4a4VP6crM8WXk6s34ToQeI5gXx1oY6+zniM4DmCJwcb4ziBRKA+64GPPWVZgyHz44R8S2y609bAaF0Iff8QBpuzVkAgEsbKd2mhU9gde7mw7zj8yP1U7iUFaXbP+j3zNsvvUtb2ksq5eYh3FwdTlRDIzJdfTm6JdwfeIXxhjvMuA1kT5w2VpldWAovnCyLKhf9nfX5c/2lefUntoR/vIDxTUcErMXpRRtp4Xeily29IeZ94dWtJWjv2fWERMAKrsKapmGJGYFUMSmvIQ8AILJsOxUeA0/NttimpZyuBtdbTHW/UYXMU90KVd+TRU+289StdHkzABr04rY27VSsrkeB0oy13Rbn7DO8HPJucOG+DpPHgDYa3VRYhV1Ha7WWcWkNQRMPesrRf7TJuTsR5IpXqO5qUvdp6ltu+SwTv1y9nI5LUP94QkGT+hoiwQcJ5qiGQCoSykEidTR6hMEUWCBPmGM8A3iaQJVEvBspAWOMJ5bxd2Cjj1eAIrSyhVtXAAbKFMGGILxeWBBGH95bv7cKaUirXUt4NOBv3qIdI0vggiCBzXChrXDnCAiEKowL5nBSCh5cWJDcEKYcA5QprC2uyy93kwq9LtYfHF4cIzAfmT178ytW1qPXcjZ+NjgOHBxDacReLxGHPuPGESyM8o3WdJ6H/OfOIZ5gLcCBu4ySPN3CWuUJ4KO8I/lqBJ9fOO7fVLtp7WZZxWZlWBIzAav7JYARW89u4HiM0AqseqFuf2RGAeOJE3eVvSqjZSmD1/SpMBopLPB5IeIewkXMJQ7P33LFk0V6UCDli04dehPXhvdFZcQlp/XZIoMsGuStJ2um6w8LNCcgF8ut0BSFXCYl/KyF4NuKB5SegzuuBlVcPP99O3rr1Ls/m8bTT4tcmwmuSbvbC2yPJw6jWY0rykHTJvH19OhN2mHVcSbmBstavdjkIV8IT8bbNI+RzItTNCKwQtWhoZh4si1K2HHKf9yBCSDsrzCO8L5M8rzvbftb6Ua/gor2XZR2HlQsQMAKr+SeCEVjNb+N6jNAIrHqgbn1mRyDDiemfk02s//YPXdbHHDWmY9tRj6LsvbcvWbQXJfIEcRqJXoRzuQTu5Y7P6uVHAOwJRdtxxzB/iEk+BPASIeS0loJ3CjdkNpPgGUEi8EoQ9fXEhZA3Di3wGmHtJ5zx+eerqxF5pSDKiix5PWn9sURDwIs8zmrqxi2g3HbX1QTv5Tjv7Lw4FJUIJadhNAdi3rFZ+bohYARW3aCvWcdGYNUM6i7VkRFYXcrcDTjYUgRWS46qP6aYRBPs83MwuFgCiy8yEGGp6BSNwCJxLAls0SvpRrTUQVmBTiFQ1Jf6Tg2qhpWzJGGuoToN2xXhxNwe1izChpu8fpVYt9MwaQQCK20M9r0hUG0E8ATkoKxoQvJ8DpCiieOLpqfpE4uAEVjNPzGMwGp+G9djhEZg1QN16zM7AnEbGE6juQ2LpMAbbqjvF5xDU24eXvleVQKL01s8BMifU28ZPjz0viKxPCRKVwphqzf2fv/k2XGJcoukV6PoQl4fciSZGAI+AiRNJ1SJW+1MDAFDwBAohQA3jlYqOb8hXVMEjMCqKdx16cwIrLrA3vSdGoHV9CZu8AHGEVjcfMZ12sgRR+jhecfTaiOOrD6BxXXaXOddBE8sHxf04er26DXeDW76hlCfpNpJCW0bYgCmpCFgCBgChoAh0MAI8P5T61D0BoarSKobgVUka1RHFyOwqoNrV2/VCKyuPgOKPv44AitCIN301k3a5LpN8hFY5IrJm7NoiilCD6wiEljkEkpJdF90UzekfjPPHObAMjEEDAFDwBAwBAyB2iNAOgV7/6k97hXo0QisCoBY8CaMwCq4gRpUPSOwGtRwXUbtDATWLW/foo2u3ag0gXXbbVKvXtKpp0pcLc2tPHPMUR6MRSSwapErpjy0rJYhYAgYAoaAIWAIGALVQcAIrOrgWoNWjcCqAch17sIIrDoboEm7NwKrSQ3bNMOKEjM33CCRH8WT2965Tb2u6VWawOLbffYJ82ZNMEFY+777wlxa22+fD656E1hXXCFtu22bzj//LE0ySb4xWGlDwBAwBAwBQ8AQMAQaHYHddgsvtDFpOASMwGo4k+VW2Ais3JBZhQwIGIGVASQrUkcEogTWP/9IY43VTqE73r1D61+9fjqBFTcMyChyJ5AwOKtUisB6990wjJHwvzwSxeSHH6TJJ8/TgpU1BAwBQ8AQMATaEFhoIemNN9IRmXRS6aef0stZCUOgVghwCysHeyYNh4ARWA1nstwKG4GVGzKrkAEBI7AygGRF6ohAlKz5998OV6vf9d5dWveqdQMlE28hTBvCIYeEua1OOaV9ycMOkyCI/AShlSKw3Niytnf11dL663f0tiIvF/m5TAwBQ8AQMAQMgXIQwIOF22ydrLKK9NhjHVt6/nlpqaXK6cHqZEFgxx3D24XzCF7pN96Yp0bzlc36HtV8I2/oERmB1dDmy6S8EViZYLJCOREwAisnYFa8xggMGCBx0xvy8MOx16rf8/49WvvKtYMiZRNY/rDw8hpnnPATXoree0+ad962EpV6UXIE1q+/ShNOmA4s5S+7TOrTp33ZBx6QVl89vb6VKB+B/v0l5qJJ5xBgnv/2W+fayFP7iCOk447LXmO++aRDDw1J8uhzlr0VK2kINBYC444r/fhj+9+hRRaRXnut4zj4/SNk68ILizXGXXetnE55141KIgG+eXNa3n23tPba0pZbStdcU0ltGqetSr2XNc6Im0JTI7CawowlB2EEVvPbuB4jNAKrHqhbnxVF4N7379VaV64VtFkRAouG3n5b+uWX8KT51VelxRZr07mzL0rPPCM98oh08MFhm9dfL226aTImfP/WW9JRR1UUt4ZuDOzIZ5YkhBPMPbe03HJhiZtvlt5/XzrggDCB/+mnS+uuK915ZzYYvvhCmn76bGWrUQoyZdppQ70bWaqdrw2PyRNOaP+s8qytumo6aoRQPf20NPHEYdnNNw+fTTaGPPP33JPehl/Cn6OECePF6W4yzddSfUovsYT00kv16bvRe51mGunrr4s3ij33lAYN6qiXO0RJI04++ECac07p008lbmBNkhlnlD77rLbjf/xxaeWVK9MnJHvSoRKHRRwaOZlpphCPSglrzUUXSbvskr3FJ56QVlopDO0kxLOWcskl+fOIVkO/zr6XVUMnazMVASOwUiFq+AJGYDW8CQs5ACOwCmkWUyoPAvd/cL/WvGLNoErFCCxfgRdeaB8yMfvs0oEHStttl81zKjqYFVaQhg9v+/Taa8PNcpKkbSrygBVX9sgjpWOP7Wwrta1/0EEdwz19DQi35DQa0oeNJC+3kFAzzBASHGusIc01lzTVVNn0pj5J/3v2zFa+0qXo/5VXpMUXr3TLtW3v77/bvBur0fNDD0mrrdbWMrixucuyscXrwn8OyKty1VXh3EHyPoeEO5PjbvRoaa21JLxc+AcZThgWt6B++GE1UKhMm5C7kLzNKISKs4ZUSzbeWLrppmq1Xn67hAQSGhiV33+X/vtfid865juXguCJGB2DTxLwu8UaO3SotNNO7Vv85JPSBFf5IwhrQp7RB+IIFHJK+p7S5fYBib3sssnrPeTSzju3tc7aAnnWGfnmm/C3xeGfZ72BZOd3DQLrjz9CO9ZK7r1XWnPN/GtjnH68E3G4x+FhOQnZ8ZCGoHXe87XCwPrpFAJGYHUKvoaobARWQ5ip4ZQ0AqvhTGYKRxF4cMSDWv3yMISuKgSWH1Lod37ppeWFGeEVxIuak27dJEgkf+PtvsNjpZonqv/7n3TMMW1eJ40yvchZttFG0jLLxGvsSEE2a2wu2Hh9+WXoRcWL7r77hvUcKbHhhtIttySPPi+JgRcPHnxOTjpJQufzz5e48jtN/FP9E08M60KI4FXmkx7jjRe+sOMxcNZZbeOKa7/Uppp5cMYZ8SGqabrm+b6c8Bg2i2was8ijj0o8T07oD9zwwIrL5+O3CUG46KJtn7A5g3hKs31cWG+wGLUQX65F5tqUU0rLLx96/uEJw4arqMLzwHPRjPLii9L//V8zjqz0mJynTrQUJCvkqi+QV5Ebf9vNaXJD4lEYRxxlfc7zkD/Dhkk77BBqyHM09dRh3847Fg9b1scsAjF9+OHSiBEdS/vPbRxpfeWVEuT28ceHbXCrMQRgnKAveqcJfbImrLdex/UGgmqzzZJboC7vE7xXVPuAIKpF2tqYNm73/SyzSCNHhr/HffuGv5PlyHPPWX62cnCrYx0jsOoIfo26NgKrRkB3sW6MwOpiBm/G4T784cNa7bLQ66IqBBYNx73IXn651Lt3fkghXXjR8mWyycJk8VHJ6/WRps0GG0i33dZWio0coUJJ/dx1l7TOOvGtojN5UxBur9p++47jiqvZGc8OXm7PO09yBNU884ShgVFx33/0kfTVV21EF4TBwIHS2GOHNdy4IbQggOLEfynOag889E49NWztqafCzYXboGRpY+GFpddfD+v7Gyr+9m/hJHSFvE2QZXx3xx1hHZL9R6VUeAkkLSFy2DqLfmnzLO575hLheHnbR2/mrHvWSm0Yb71V6tVLWnDBkJBkfjgp1S+b0q22aq8bxJfDhDYgwHxyjM/4Hs+JuLbjCKwFFgjbYc6eeWYYolhLIR8YnmZZ5MEHpR490ktCDpKfsBaC1yTeGXhQ+sJavO228Rrg8QY5iTjPndtvj39GKMPawPPQjIJ3kQur9scXczlKrMdpdE6zprFm+GvSk09KeBknPW+sURA1yN57h/m0Vlwxd2qMzgAAIABJREFU/P3zv4viT9/PPht6R/F8Q1x991247vl64D2GFw9z5M03wz7OPrutNedhxboePQBhHdh667aykM2U94W5wa3FhASnrWWO5EqbS4yBdvHyZY1E/EteSvVDXf653+rILc3tuk4jw9L0jLOJr6v/vQvVT2rThVXzvZ8HlM/5jS9H8GDrisR0OVgVpI4RWAUxRBXVMAKriuB24aaNwOrCxm+WoT/60aPqfmn3YDg1JbB42cVjg9NYt0HiBJiXUPKE+HLOORL5QyBJyKvFi5YvvHS7q8lffjkMyaBM2gtyXiMSPkeeICfuhY9wDE5Bo8LGJumFmBd4Xjbxavr885AwwCsqSVzYJBuocsflNjFgiF6QU+Dv5yShf9/LqhRGbGghgUolafc3bWxm2NSkCf3TZjApI5445DNjAxYnYET7eFzhtRVX38fO93RI8xz466/Qy4LkyyQ89iWtbtp40773yV7C55ZeOq1G2/dON4c98w7SCKIK4hSB7IP0I+yJ+YAHGwSrL3Fzjjwz3PoVt6mP0zDahtONDTPPAYQuG1BsHLU7zz/POWGtCCTnaadlx6ESJXme8dbIModdYmjXL7ec4ZHjh6FBXvz5pwTZxc1pYFlKwAjiwZdRo+LXnrh2WF+5VIOLPfxLFd55J8QbbPHO8cXdmrfkkuHaO3hw6LGYlOMIkhH7QZiSO4/NdVTIpQdpR9t5hfxYkNvOm6hSOYQgaSBrSgnPCSFmUU+l6FylDT5jPYJcQsjDh9dxnDC3XZuuLcgmyGbn1ehC7/geAojfCp477AABD+asCz6x5MhERzrRN88gdbGN09Pp9PHHoUcqObiY69gHkiq6ZlKe31t/jcCblbnsC2uMf+AT7S/tdyz6exuHXdTz05XBA3S22aT550/+vQRb9+7h6sXpRBnmPHgzB0jQj7BW8h6DJHkHu9+kqO60Q95AZxP/ew7GyIHmiMq4cbvfLuY/6Ric4BF+9NHx8yzt0ygBmVbevq87AkZg1d0EVVfACKyqQ9wlOzACq0uavbkG/fjIx7XKJWFej5oSWGxiIAQI8cLzA+8mXh55KSSJuC+Uw72fl7Y0Aotk7eTiyRqGkdWceC+wwdlnn7Ya/ollkheJ+zzqvYWX0xZbhGQBBBjeKO70OKoTHif07wTPKHIARYWNKB5FSRK30SJ8I7oZRa8stzE5W7hbp6KbcAgyNpy+pG1a2KjhjcYGCdLIERal2nAeJM7mzAFe5INJHROK5toqRWDhWYdHA/Zx7bhwH8ZAeCVJuglTzUJgQdKwmcorLvGzXw9cp5uufUvMRUiGqPi6QV4wjyAvCe9jk8fcoi3IITwefII2zW54CeQhkZIILL8f5t5113W0W3RccfPWL5MU5gYGhEAlXepQyvPBYQnxB+FXSljDfA9TR2CxjhF6Rb4hSBiefXJ9MZeYc1x6Mfnk0qyzdmwd4hGb+fL992EoWhbheYXg4LmCPB8yJKyFDm6eR23E5h0vLHRjA89G3ZG5cX2iD3Oxe/fwGYaUi4YX48kGhmlrzA03tL+gg7UNsh1SzD1L2BNPQfTGi4yQVKdzFkxcGXBJI4bdOpxlHrt2WTMgogjZ479J8u234ZynXNxzB6EUvdE3qS2nH3OM/v01AFszXyCxmHdxvwnRduMIrGh4PmOL3pAKueKIRtqEIPMPemjXv/3QP3igfBYCK6/+/tjwdMPjLQ5v/7Ok3xDeM0hfgOCtFnewkvQe4rcJCe0/73zHb6mfG435zprDM4FQBtu6ue/0JUQ+egAYtWcSWYsXLWujScMgYARWw5iqbEWNwCobuopVfCxjS39ICjNKF1+MwCq+jUzDFASe+PgJrTwsvH2opgQWHUIyuI0kIQAuNM1/uWNj59zak14G2Xxz2osHB+Et7gUvjSzJMjs4pcXrgOTzJC3nb07AEU693UYqjcDafff2yVXZpLvk84wLj42kcMO4l/Sk/tjgRUOE3DiTXvY5dffDfsjd407oS2HEho9Tekfs4EnGC7bDJ0nvpNvk8E4hmW6a3fzv8bjDRi7ZON/hsZekQ1YPLIcBHmZg6p9yOwKLE2s28z6ZGNUdUsklF04bVxzWSTaLtgWh42+QyRGFp0Bc0mn6YTxs9mmfjedEE4W2jCPBKB+nux+6kuVZyrLx5xmGoPVvLo1rG2+PuITLeC1APOKV4m5E9OszXogTNmtxUirPmm8LPCvYAEfF5eaK5vZyZIxrAyxYEyCz8Dp1z5BLCA6pHM0NxByHzCcMzEnSOOPG5m/YuYUUwgDxczhBcJBnzoXTOu887EHOJcaXtA4T7hv1TsMbxJHJ7pIA2oDcg6iLCiSH28w7D1byGJKfDfLDXRzhbMiGnecPW6M3hGr0WfD7iMt157yYeM5Jqh0nrE3uMgN/HvveTVmegbxlXF9ZiBrXtqvjbvyLq0v4IF4+aUSs/+xDjECoI1EPLDCMetsxh/xw7KgerDd4IbkDFMgTPwQRrzWeo6gQIkc4PCHJ3JKaJknrLr+/HCT54sqydr72WvhNVG9CLvE+Znzk8ULi8mfx28Rzk/RbHdev688l+XdleF5Ym5zXrL8G+O1Eb32OwybJa9MIrLSZVLjvjcAqnEkqrpARWBWHNHeD+BafmFILO+0nqcb32OYei6tgBFbZ0FnFoiDw1KintOLFYZhDzQks/wSTTRRhCNEXRjZZbLbc53EvgxBYnAj7krTJSgMeLyjIJCe8ULswAT5zhJq7QciVi+oVfXmN5vOIEljk4Ei6tSwPgYU+6IK3RDT/SNImaPzxw02sE7wz4q6Lj2LnCCyXCJjboNhgltp08R0vytx0GJWsmzTaIGk/nleEu/iCpxOn0u42paTT8+h88svRPiFq3LYWJ3wP0RZ3exbf+RsvkruT5D06HyErsQ8bySTBMyoaMpY03/znJ/oMxbUPaUVifjb/zpupVA6ULJuwtGcLcoKwHidZ7Z3ULps5vMkgvsk3RbgWm2DmAIQzpFzcHPM3hxAshFVy2yZkJcm3HfmZNj/jMEEnNuXR0DYIYbxefAIL7xMwwfuSz11d+o0+k3zm1hSfcIbIo2wW8dcy5vbBB4e1oknI0cWFPru8T5DEkJ5xc7mUPWmb9ZuDCggpvER5PrEZRLMftgfJR5glXq54ibhnJs4jFFtBIkB2YmvC2fBYITeaexbAFU9DX2gTbxl+a1yON+flCBntfoOoA5kFuRh9niA34nLsZbFB3jI8LxBDrK1ZhXmJBxyezRDCceHtWduiHM8ToaH8prhQdpeEnhBBvIshEKO/wRwm8V3a8+6eIw5R6MuF1uGNFjduF5YHWe0OrEqNhzWOeeILxCfewdE1wunCPCRcnOeLWwrjxCeB3dwGp+h4s6yd0YMVP2cgv5eQV9Gw7jideL5Kefq60MU4nYzAyvNUFKKsEViFMENVlTACq6rwZmqc3eUkGUp+LymjP3yG1qpbxAis6uJrrdcAgac/eVrLDw3zEtWcwPITBPt5VfyNLSechBIg3LTjb4AdPmw6fAImGMyYdE8eH188Tzi95ATf3bLH9+4WO1eWTSThNJxe+y+2/gshmytHrLjP2RwRJsJJLRsvP+QLXdlsJN1alkZg4fXAS70rRz9sKKIeKkmEAaE5eIA4wdPD5W4pNQcdgUW74OGPmc2h36Zrx+nGptMnZwhti0soH9c/mxpIy1Ibd7w2CD+MtomXmNPTnyM+NoTokQso6Upxwq0IjSIUKirYmzlEiCwSR2CBN/YH42gOFr899IdkipNofpnofM9DDvHsgCWbOuwSJ1k2YVnWq+hGLUudLGUgoPDk8DekzEn6c/aGXGXuQB5DiiAkwT799NADkQ1idNPt9x3FFPLReQRRzvXHuhD1JnEJ8n0CixxibKJZY6Jt40XpctPhpYX3iwvBgrx1id99z9U0nPwLFZijkLT+WuXXd3ZyekMOsaHn2SAXl29H9AFTHwu/LecVGh2jC5NCBwTcaJe1klBE5j//T/LsTTdtPzqXd5DfBPJHQVRBaGBPfz2KztsoUU2r7jNICOcFzOcQu6xL2NWv5zwW/bpp2Jf7vQtRznObLmPmcCjrhQNZdKNNLvGAdEQg1fiNARvWDLy98EzyBXKLdcpJ0ppE2gDmtjsQcDZzSeLJB+YLoY88H5CiWfI9RYnJUnbzCSwXrpeEj/+b7T/X0fFmWTuj66IjDWmLd6C435o4vRyxGP0u6o0XpxOe0aUOVLLMEytTUwSMwKop3HXpzAisusDerlPInp8yqJG1XIamql7ECKyqQ2wdVBuBZz99VsteFIak1JzA8gfHizqkRPTlMu7WwWqAwiaezSBkGPlzIGcgqzht9xOx8x1kF8SCn58JDxBCZKL686LIPzZHTtxY3UskL7+lkrjHvfj/8UdIsrDJQm828NG8SIyFl3eEPuNCqviOUCZCI524m7DScHa2ifNyIuwzmmzfb4/NqiOwHCHlez+k9Z32PSfn4BvXJp9DQmLLLbcMw0jyED5gCVnib3adPrTt8pvxmSMyfIKJsD5CotCBOebyNUFUYFMXWlUqRAa7MmfxjKFeZwgs9EwLRcuyCUuzCd9Xi8Aq1bfr04Xn8Zy6GwIhPLiZz5ekPDJxcwTvFsgU/7mnP+eZ4tp1N/f5G92ddw6fO/SKeoJgX/5Rnu/89dHZHiIFAizONlE8os8/pB0ka9K8d20yDrDiOfIJXfc9eacgopLI3uia5+vlbhYt9ewlzUufwGId5llEB0es+M8jf3NwwObcz8nnr7/R8s6erK2Q7tFcfH6uxSzzvpZlwIBw4lI36uXVh7kGye2veW5O8lvE54S3+uITPHhBsU7FCesY9nGhhC6/Fjna8GYllxdEpROeX3578oyxFJHp6+TKQZim3XLKvMUzCo/lShFY4My4wMPhSV5IPx9Wmu0cfqxr/LYj0XeE6HPi2szzO5imh31fdQSMwKo6xHXvwAisupugKRUwAqspzdq1BvX8Z89r6SHhrWZ1JbA4OXQb97hT8mqbxe/T5VOKy29C+AkhDhBGfsJdEizHhZvwQuzfkhh9WWZTwAaA0CXCFhD/OnSIHk654wSPEXKRJL10QobgyRAYN5LM3G+P3DG87DpPDz/fSyncSxFYjiBKqo9XDN5QabpVw+7YBBKSHCyEduKpUKkXdzZa5PBhQ0ebEJcudM5tjghRI0QKko+QVJfg3YVgQuyx4eB5iAuD8zEhhw2hZz6BVSr8sVw8oxvAuAT9WdquF4EV3UAz1/GuIYzPJ2/dGKLjhQzw88S5cjx/eP/4HpDUxWuEPvEOIozLeVz6G102pWxOOyvMOfp03qn+LXOu7ej8xjOQhPVJ896tR6xFcaHN9Ic3Dl5kWUMYo+Ok72hYaVYsXOLraGLwaP04kipqYx8DNy/S1iUIBg4xXPL7rHp3pXKEzW68cThiQuv47cwqzq7YL+ohDPmflNsvqf28BFZW7y7SC5CfqlIEVtQbkHeKVVdNJ4jj5j35w7iUg/cPlzvLL1epQ4msNrVyFUfACKyKQ1q4Bo3AKoZJcK/g3tinW9Q5VNI4nmpnS/ohh6rEAPSTtJikiSVx/OO5OQR/kxT+b8592cJJIlaq5e7wDj2NJYmYkG1awhjZNQ6QdGGCTkZg5TCWFS0mAi9+/qKWvDC8vayuBJYPjx/KlMW7oBLQ+psYkre6K7bdNeauDxK3c9sQp/n+7V+4+Lsbify2CP3gJZ6cOHEvmXzvNrjcEoa4W7Q4eebvuGTVlKNu9BY8v4+sBNbQoRLeII4EITEu3j9p0sgEVv/+Yb4cSAlOo/OE6KThwvcQWJBX/lzAzsxnPA3wFmHOcMpPSAxhWXmTotMPZCobQ2c7EmljlzjvsCx6J5VBd0cwQ8pwI1o5Ui8Cyz3PTmfwgpRi3rvb+PzxRNedUrYhBJCNorO1T8YTLkyIHN/5n9M+yaghjysltEmi8Qcf7Oh5GCWq3K2nSQSWu0EOzzFC8+LWrlJJ/ys1pqR2XKhUdB2O05PP4saZRG6VIr2qPa5mat+/gCVrXsW48fM7yHrj8rERakgOwjziP8+ENUZvxnRtMa9YFzg4yLKGohMh/KUIrLiwvuh8jJtz/nqRZ6yUpb1LL5U22yz8O+4dwgisvKgWrrwRWIUzScUVMgKr4pCW1SAZQ6dtSdROA79KerGlJe4E5yjy1BwtryFpSkkTttSNI7B6SHo4Y5tcLcaVIqtyKa6kVSTdI4kslA/EtGEEVkZgrVhxEXj5i5e1xOAlAgULQ2D5uTbqQWA593pCRyCBfMFLhjAUF47kvnPeNvy//+LrQgfjwjkIT2TDyUYWccm0OdknHDC66Y5OozQCC4KNl2DC6UqF5znd0Ru8XVLjtGlLbjJy6dCHL+CDDd0Nk3Ht4LngPMsq5f2Upq/7HtIKe1RzbpEji5xqbPKThHG7/Cx5chn57bFBIVcLbZXbRlbcHEECwVlueBIhZ1dcEeabis6brHrkLYfe5NsjXNMXPr/xxjYvEf87sPTD4krNUf/5iermQgyj9asxBxkPedXwIMXjBc8+f32K6lZqvkCscksbYWB+Im7/Gcqywc9rqzzls8x3PKWYq3HzlbUX+xDmG50X/H+t16U8Y2+UssxJvKVYM8pdb8mnSC5DPJUhYrKGuPsYkYD+mWfCT/KG5KVh7c9DN0Y/4T31/bH7t4G6titNmtJeXHh03Dz3P7M5n2btQn1vBFahzFEVZYzAqgqsuRslE+OOkl5vqcn1S253iGfWMEnL5G5VwlWA5DNxBNbqLd9lafYsSbNIaonjCao8J+k6SafFNGAEVhZUrUyhEXjli1e0+ODFAx2rTmBBCCUl+o2iRH4WyJFaSdFe3HgBTSOw0l56ITe4LZEwp6JJPTxxioZBJfRxoV61mL+ExOGxhLdRIwlzrRwPEDdHCRH0bybNM3Zy+ECQQKRUW9AXbxC88Byx6frMOz/cbWZJIYTVHks9209bV+upW6P1DZalcvllGQ9rDl7C7nbJcggsl3iffIOEt1dLCOmGZIseXLg5FXejJrpUes7RHnnuuDW0lERJxbzrRLVwtHYzIWAEViaYGrqQEVjFMB8JT/z7aLnX1l15hI0I2Uu4r7bkAEoRWF+0EFtkgCRTa6mEEwtKulbStgTxSFqthbzCEysu7NAIrGLMK9OiEwi89uVrWvSCRYMWqk5g4Y1UrudGJ8aYWpVNJu72RZJKEFicDIN5NLluEcZpBFblrICHXbl5iPJogQcE/ZTrSZGnr0qWxcsNb6G8aw/jXHvt8GbCcr2NeP54DmvxDKIv4aN4mkQvhci7MSXHH4nLIbII4epKgucq+ckgAEw6hwBzsnv3tlszy2nNPUM8v3hFlkNgsXaRHJ1cdOQerJa4PHnR9QIcOLwjd2DcOlRpAsu/9KHUWI3AqtZMqEm7RmDVBOa6dmIEVl3hb+38l5bcUi3XYrVTajxJZBueqAxVkwgsQgGf4v4NSYQbXinpEEnedVvteptA0gmS9m7JpUUOrX1biK84tYzAKsNYVqVYCLzx1Rta+PyFA6WqRmBxhTN5WdhEEcpDaFWRhPxDLqF4UfTipJarwjl9TpJKv/TWcuzkUyKvUt6NdS11tL66NgJcNECSf8JBG0Hmnz+8dWzffcOcQRBP5K8iZ9kA0nmaGAI1RmDOOcPbLiuR683lrcPDEE/DPALJj2dUtQmsUr/V5Mg85pj4EttvH4b6X311nlF1vqwRWJ3HsI4tGIFVR/Br1LURWDUCOqWbdyVtLimSiCKoxZEI3k/zlKFqEoEVbepISWtKSsr+SAgjO3l0/LDl71slnZKQyD0gsPr166fxWvLL9OzZU/wzMQQaBYG3vn5LC56H82EVCawoGJxuc/U6svjiHXPTVBI8crkQTuOLyzHlf9aIREojE1jcgsZmIpp/ppK2t7YMAUPAEDAEmgcBfvPKuQGV8EO8R+t18QC51shVuOyyxbKFEVjFskcGbe69917xDxk9erTOPfdc/pxMUgFzRWQYkBUpiYARWMWYIGdKYqe8botXlNOKmwjvaEmcvl8ZquYhsGCXVkzoA7eQoZIGet+fIWn+Fp2j1cwDqwxjWZViIfDON+9o/nOZ4jUksOiMxMCE5nCVPUnDqyVci84psC/kw+AmOCe8xLlk69XSoxrtNjKBVQ08rE1DwBAwBAwBQyCKAL/vhPXhaY3HtUmIgLvoxeHRiAd5XdiW5oHV/MY3AqsYNp5KElcy/dmSW+pTSTNL2lQS4XtLSvo2h6pjteS3gsC6W9IkLcTYaPw6SIso6bWWcEBuI8Q3Fy+sgK6OET5HBzywPpa0gKTbW0IPj4opbwRWDmNZ0WIi8N6372neQWGOk6qFEMYNncTi3ERWjvCSNfHEErcFpslHH0mE4/XtG974xvXwXMONOAKI/DSc0DaazDab9PHHFobXaHYzfQ0BQ8AQMAQMgXoj4EL5nR5GYNXbIrn6NwIrF1wNWdgIrOKYbTpJx0taR9I0kr6WdFcLsUSS9zyyXcvNhWNaKmFn/ib3FeTSqS0EGdf/kMSdu+qHeB2cL2lWz7sKl4yTJW0oafIWMu0GSYdKisvbZQRWHmtZ2UIi8P5372uec8LI3ZoSWD6BRD6L4cOz4+NesrIkk4bgwX0/Tlx9kqt+8032/otScvbZpZEjjcAqij1MD0PAEDAEDAFDoFEQ4BDRv6WYPFwtKVEaZQhdWU8jsJrf+kZgNb+N6zFCI7Dqgbr1WVEERnw/QnOdPVd9Cay8txM6Aov8VpvjMFlCPvlEmmmm+ALcRvTSS1KvXuGtXY0mRmA1msVMX0PAEDAEDAFDoBgIkJfLzxHKpRWHHVYM3UyLVASMwEqFqOELGIHV8CYs5ACMwCqkWUypPAh89MNHmmPgHPUlsCCksnhTuYH5bu4HHSSdirNlgpQisFwy+R12aEsqnwe8epcdOlR65BHp8svrrYn1bwgYAoaAIWAIGAKNhsBKK0lPPtmmtYURNowFjcBqGFOVragRWGVDV7GKn0maMUNr5J4irK8RxAisRrCS6VgSgZE/jNTsA2evH4G1+urS/feXT2Adcoh0MpG/CTJqlDQzqfZiZMcdpWHDpEYlsGxuGwKGgCFgCBgChoAhUC4CDzwgrbGGEVjl4lfHekZg1RH8GnVtBFaNgC7Rze+S+rYkVi+lzYCW60Drr3G6BkZgpWNkJQqOQF0JLDyneHFaYonyCaxDD5VOOikZZXJEzZrAiUNckdTdCKyCz1JTzxAwBAwBQ8AQMASqgoDvAW8eWFWBuBqNGoFVDVSL1aYRWPW3x0ctCdbTNOGGwvnTChXkeyOwCmIIU6N8BOpKYPlqp4UQcovgp59Kt97aPmn54YdLJ5yQDMCHH0rkioqT7baTLrvMCKzyp4/VNAQMAUPAEDAEDIFGRsAIrIa0nhFYDWm2XEobgZULLiucEQEjsDICZcWKi0DDEFgDB0qEA55+ensC68gjpeOOSwZ4xAhpjjDHVwd57TVp0UWNwCru9DTNDAFDwBAwBAwBQ6CaCBiBVU10q9a2EVhVg7YwDRuBVRhTNJUiRmA1lTm75mAahsAaNEjaZBPpmmukffdtM9auu0pDhsQbD3KLf2OPnWxcXtwshLBrTn4btSFgCBgChoAh0NURcAQWB3qvvNLV0WiY8RuB1TCmKltRI7DKhs4qlkDACCybHg2PwMc/fqzZzpotGMeYo8bUbzxJIYS33Sb98ou04YbSBBN01K9U6GGWXA7UX3ll6bHH6jd269kQMAQMAUPAEDAEDIF6IODeoyaaKHzfMmkIBIzAaggzdUpJI7A6BZ9VTkDACCybGg2PQOEJrDQSqhIEVsDe1ZG8a/hZZAMwBAwBQ8AQMAQMgYZE4IADwvQM9i7UUOYzAquhzFWWskZglQWbVUpBwAgsmyINj0DDE1i77y4NHhzaYf/9pbXWCsMGn3oqGynlCDAjsBp+LtsADAFDwBAwBAwBQyAnAlxmw6U2RmDlBK6+xY3Aqi/+tejdCKxaoNz1+jACq+vZvOlGXBgC6623QmwXXLA9xmnE0rHHSkcdFdZ57jlpqaUk91laXeoYgdV0c9oGZAgYAoaAIWAIGAIZETjmGOnoo43AyghXUYoZgVUUS1RPDyOwqodtOS2PJWlbSctImiTSQJ9yGqxTHSOw6gS8dVs5BApDYLkhrbeedOed4f+tuKL0xBOlB8tLFy9f5LBaaaWQkPrzzzAR6TIsMSlC+Y02km66Ka2kfW8IGAKGgCFgCBgChkBzITD//NI774RjGjpU2nHH5hpfk47GCKwmNaw3LCOwimXjCyRtJulBSb9GVNuhWKqW1MYIrAYylqkaj8CoH0dp1rNmDb6saxJ3p94PP0jffivNPbfUrZv0yCOlTXfKKdLBB2cLF4xrCQKLmwxdGKJNFEPAEDAEDAFDwBAwBLoKAvPOK733XjjaySeXvv++q4y8ocdpBFZDmy+T8kZgZYKpZoW+kbS8pJbVsmb9VrojI7Aqjai1V3MECkdgOQQgllZZRXr00dKY4G1F6CDeV+XIs89KCywgTRJ1Bi2nMatjCBgChoAhYAgYAoZAAyGw/PLS00+HCk8xhfTddw2kfNdV1Qis5re9EVjFsvFnknD5+LtYauXWxgis3JBZhaIhUGgCC7Cy5LEqGqimjyFgCBgChoAhYAgYAo2AwLBhbWGDU04ZesGbFB4BI7AKb6JOK2gEVqchrGgDR0r6WdKAirZa+8aMwKo95tZjhREwAqvCgFpzhoAhYAgYAoaAIWAINAoCQ4aEqRSc2MFhQ1jOCKyGMFOnlDQCq1PwVbzy4y0J3EdJwhvLl1Uq3lv1GjQCq3rYWss1QsAIrBoBbd0YAoaAIWAIGAKGgCFQNASuu07aYotQq4knln7Gx8Ck6AgYgVV0C3VePyOwOo9hJVtoufM+tsljKtlRldsyAqvKAFvz1Ufgk58+0SzacTQlAAAgAElEQVQDZgk6KkQSdzdkcmAFSo2pPgjWgyFgCBgChoAhYAgYAl0RAd6zxuKC+Bax966GmAVGYDWEmTqlpBFYnYLPKicgYASWTY2GR6DQBBa3C550UsNjbAMwBAwBQ8AQMAQMAUOgsAi4Q0MUNAKrsGbyFTMCqyHM1CkljcDqFHxW2QgsmwPNikBhCazRo6Vxxml/KtisRrBxGQKGgCFgCBgChoAhUC8EjMCqF/Jl92sEVtnQNUxFI7CKZap/4fdjVPpT0khJV0g6VdJfxVK7gzbmgVVwA5l66QgUlsBKV91KGAKGgCFgCBgChoAhYAh0FgEjsDqLYM3rG4FVc8hr3qERWDWHvGSH/SXtLulsSR9Jml3SXpKGtpBW/5N0maTDiqW2EVgFt4epVwYCRmCVAZpVMQQMAUPAEDAEDAFDoFkQMAKr4SxpBFbDmSy3wkZg5YasqhWeldRb0rteL/O2eF4tI2kpSddJmrOqWnS+cfPA6jyG1kKdEfj0p08184CZAy0KlcS9zrhY94aAIWAIGAKGgCFgCHQJBIzAajgzG4HVcCbLrbARWLkhq2qFHyVNJelvr5dxJX0rCVII+YXLXKuqRecbNwKr8xhaC3VGwAisOhvAujcEDAFDwBAwBAwBQ6CeCBiBVU/0y+rbCKyyYGuoSkZgFctceGDdKukET61DJG0saWlJuIM8I2mmYqndQRsjsApuIFMvHQEjsNIxshKGgCFgCBgChoAhYAg0LQI+gfXOO9K8BMaYFBkBI7CKbJ3K6GYEVmVwrFQrhAneJWm0pFGSZpE0nqR1JEFurSZpfknnVarDKrVjBFaVgLVma4eAEVi1w9p6MgQMAUPAEDAEDAFDoHAI7L23dM45oVqPPCItuqj0++/SjDMWTlVTKETACKzmnwlGYBXPxpNJWl8SK+Onku6QRGhhI4kRWI1kLdM1FgEjsGxiGAKGgCFgCBgChoAh0IUR+OknaTK2ZpLOOku6917p7belESO6MCjFHroRWMW2TyW0MwKrEihaG1EEjMCyOdHwCHz282ea6cwwWteSuDe8OW0AhoAhYAgYAoaAIWAI5EPgt9+kiSYK61xwgbQ7l8XzYjhG+vRTadpppXFJV2xSFASMwCqKJaqnhxFY1cO23JYXaAkVnFaSb58jczS4haR+khZrSfjOyvqvV5+//2hJFk8fYyQtL+mNhD7Ob7kdkXIIdVjNB0rqH1PHCKwcxrKixUTACKxi2sW0MgQMAUPAEDAEDAFDoCYI/PWXNB7ZXCQNGiTtuWf4NwQW+bF69JAeeKAmqlgn2RAwAisbTo1cygisYllvU0lXSXpT0oIt/11I0hOSVs2h6hqSppQ0oaSLJMURWD0kPZyjTb/oIpJelrSUpJeMwCoTRatWaASMwCq0eUw5Q8AQMAQMAUPAEDAEqosARNVYY3Xs47HHpFVWaSOzqquFtZ4DASOwcoDVoEWNwCqW4SCF8GoaJul7SVNI2kvSNJLyeGC5UXWT9FACgbV6y3flIHBBi3cXXltxYh5Y5aBqdQqFgBFYhTKHKWMIGAKGgCFgCBgChkDtEfBvIozrHZLLpDAIGIFVGFNUTREjsKoGbVkN/9RCWv0j6QdJk7fcQkimwJnLaLEUgfVFC7E1kqjuFk+tLF1M0pJcvq+kK4zAygKZlWlEBIzAakSrmc6GgCFgCBgChoAhYAhUEIHpppO++iq5wX//DcMJTQqBgBFYhTBDVZWwp62q8OZuHFJpDkm/S4K0WrnFE+tLSRBHeSWJwCIc8SlJEGWEG14p6RBJgzN0QPA33mAQaqONwMqAmBVpSAQ+//lzzXhmeE2yJXFvSBOa0oaAIWAIGAKGgCFgCHQOgXPOkfbeO7mNJ56QVlyxc31Y7YohYARWxaAsbENGYBXLNLdLGirpFkkXSppP0m8tuawgo/JKEoEVbQdCak1JK2Xo4HVJd0g6uERZCyHMAKQVKTYCRmAV2z6mnSFgCBgChoAhYAgYAlVHYOBAad99k7u5915pTbZRJkVAwAisIlihujoYgVVdfPO2Pr2ksVtC9AgfPEUSZNDhkj7I25ikPARWT0lpxwfdJXHVxtySPkojsPr166fxWm7u6Nmzp/hnYgg0CgJGYDWKpUxPQ8AQMAQMAUPAEDAEqoTAgAHSfvslN96vn7TuutLaa1dJAWs2DYF7771X/ENGjx6tc889lz8nk0R6HpMmQ8AIrCYzaMtwuC6DmwchsO5uCT8kXJCQv8UlYffXJP0ridsIr24JCwye9hJynaSJJK2bUs48sJpzXnWpUTkCa1ivYdp+8e271NhtsIaAIWAIGAKGgCFgCBgCks48U/rf/9KhuPhiqXdvaVy2YCb1QsA8sOqFfO36NQKrdliX6mnODGqQEyurbNdyk6G7FgM78ze5ryCXTm3JYfW3JJK4nydpiNf4+ZJmjRBV07WU3VjSXUZgZTWFlWtUBByB9ch2j6jb7OVE8DbqyE1vQ8AQMAQMAUPAEDAEDIEAgdNPlw44IBsYt94qbbBBtrJWqioIGIFVFVgL1agRWMUwB95RTnybQDo58onQwkYR88BqFEv9f3t3AmtZXd8B/Fsq0FJAgYEBlUHFBWytpC4VQcF12tiqiW0IaV1bqnVELalpxTowtcUAA9oorkSbNtbGmmi11kzaiqBia4qpVXDfStVhU3btlKX5M+faN89737vvvrv8zzmfm0x4zDv3f/7/z+83Z+77zlnMc6SAAEtzECBAgAABAgR6LvDmNyennz4eQrlf1ko3fB9vFFutQ0CAtQ68lrxVgFVHoW5p7in1tubspnJp3/JXOVOqLS8BVlsqZZ4jBXbeujNHXHBEnIGlSQgQIECAAAECPRXYtSvZd9/xFr91a7Jt23jb2momAgKsmbBWNagAq45y7J/kuUl+v7lfVXkC4buSXFPH9NY8CwHWmsm8oTaBQYB16QsuzROPemJt0zMfAgQIECBAgACBeQj81Jg/Mj/nOcn73z+PGdnHCAEBVvdbY8w/jd2HqGiFJyZ5SZJyAXW511R57MV3K5rfOFMRYI2jZJuqBQRYVZfH5AgQIECAAAEC8xEYN8DatCn5dpsumpkP3zz3IsCap/Zi9iXAWoz7anstAVC5W+CZSZ6a5JLV3lDZ9wVYlRXEdNYuMAiwLnvBZXnCUU9Y+wDeQYAAAQIECBAg0H6BcQOsstK7B8/Qav+y27gCAVYbq7a2OQuw1uY1660f01xGWJ70V0Krck+sHbPe6QzGF2DNANWQ8xUQYM3X294IECBAgAABAlUKCLCqLMuwSQmwWlOqiScqwJqYbqpvPC3Ji5NsTHJx8+s7U93DfAcTYM3X295mIHDNrdfk8AsOjzOwZoBrSAIECBAgQIBAWwTWEmC98pXJG97QlpV1bp4CrM6V9CcWJMCqo8blqYNXJvlwkjtGTGlrHVMdaxYCrLGYbFSzgACr5uqYGwECBAgQIEBgTgKf+1xy3HGjd/bMZyYf+tD/f99lhHMqzE/uRoC1MPq57ViANTfqFXf08XLF9ApblO89uY6pjjULAdZYTDaqWWAQYH3ihZ/IiZvKsxW8CBAgQIAAAQIEeimw9CysAw5IbrklefjDk6uuSu66K9lrLwFWBY0hwKqgCDOeggBrxsA9HV6A1dPCd2nZgwDrky/8ZE7YdEKXlmYtBAgQIECAAAECaxFYGmCdempy8cXJ3nvvHqH8d+n3nYG1FtmpbivAmipnlYMJsKosS+snJcBqfQktQIClBwgQIECAAAECBO4RWBpQbduWbF12dxcBVhWNIsCqogwznYQAa6a8vR1cgNXb0ndn4dfedm02bt8YZ2B1p6ZWQoAAAQIECBCYSGBpQPXBDybPetaewwiwJmKd9psEWNMWrW88AVZ9NenCjARYXahiz9cgwOp5A1g+AQIECBAgQGAgMAio7rxzz/tdLf/+zp3JxvJgea9FCAiwFqE+330KsObr3Ze9CbD6UukOr3MQYH3qRZ/K4498fIdXamkECBAgQIAAAQIrCjz60ckVVySj7m81CLjc/2qhjSTAWij/XHYuwJoLc+92IsDqXcm7t2ABVvdqakUECBAgQIAAgYkEHvGI5AtfGB1gvfSlycc/vvuphF4LExBgLYx+bjsWYM2Nulc7EmD1qtzdXOwgwLr8RZfn+COP7+YirYoAAQIECBAgQGB1ge3bk/e9L/nMZ1bf1hYLExBgLYx+bjsWYM2Nulc7EmD1qtzdXOx1t12Xw7YfFgFWN+trVQQIECBAgAABAt0SEGB1q57DViPA6n6NF7FCAdYi1O1zqgICrKlyGowAAQIECBAgQIDATAUEWDPlrWJwAVYVZejcJARYnStp/xY0CLA+/TufzuPu/7j+AVgxAQIECBAgQIAAgRYJCLBaVKwJpyrAmhDO21YUEGBpkNYLCLBaX0ILIECAAAECBAgQ6JGAAKv7xRZgdb/Gi1ihAGsR6vY5VYFBgPWBUz6QZx/z7KmObTACBAgQIECAAAECBKYrIMCarmeNowmwaqxK++ckwGp/DXu/gutvvz6Hnn9otp28LVtP2tp7DwAECBAgQIAAAQIEahYQYNVcnenMTYA1HUej7CkgwNIRrRcQYLW+hBZAgAABAgQIECDQIwEBVveLLcDqfo0XsUIB1iLU7XOqAoMA6+yTzs5ZJ5811bENRoAAAQIECBAgQIDAdAUEWNP1rHE0AVaNVWn/nARY7a9h71cgwOp9CwAgQIAAAQIECBBokYAAq0XFmnCqAqwJ4bxtRQEBlgZpvcAgwDrrpLNy9slnt349FkCAAAECBAgQIECgywICrC5Xd/faBFjdr/EiVijAWoS6fU5V4Ibbb8iG8zfkHb/2jpz2qNOmOrbBCBAgQIAAAQIECBCYroAAa7qeNY4mwKqxKu2fkwCr/TXs/QoGAdZVL70qxx56bO89ABAgQIAAAQIECBCoWUCAVXN1pjM3AdZ0HI2yp4AAS0e0XmAQYH1xyxdzzIZjWr8eCyBAgAABAgQIECDQZQEBVperu3ttAqxu1viUJFuSPDLJ/kn2TnLXkqWWr3+U5I6mB+5OcnySK1fguF+Sc5P8SpJ9knw7yalJvjDkPQKsbvZVr1YlwOpVuS2WAAECBAgQIECg5QICrJYXcIzpC7DGQGrhJk9LcnCS/ZJcPCLAekqSS8Zc20FJPpvk75Kck+TGJEcnuSnJ9QKsMRVt1ioBAVarymWyBAgQIECAAAECPRcQYHW/AQRY3a7xSUk+NiLAemrzvXEEXpdkc5LHjrNxEmdgjQlls3oFvv/D7+eQ8w6JSwjrrZGZESBAgAABAgQIEBgICLC63wsCrG7XeKUAa2cTbJVLAd/WnKk1SuPTzSWD5dLBMua1Sd7TnI219NLEwfsFWN3uq16sbhBgfWnLl/KwDQ/rxZotkgABAgQIECBAgEBbBQRYba3c+PMWYI1v1cYtRwVYT0pyeZI7k5TLDUsY9eokbx+xyK8meWCS5yZ5X5KfT/IPSd6U5Pwh7xFgtbFbzHkPAQGWhiBAgAABAgQIECDQHgEBVntqNelMBViTyrXjfaMCrOWz35rk6UlOHLGsK5Lsam70Ptjkj5M8a9nvDb53T4C1ZcuW7LNPOWkr2bx58z2/vAi0RWAQYH35ZV/OQw95aFumbZ4ECBAgQIAAAQIEeiOwY8eOlF/ltWvXrlx00UXly3snubk3CD1aqACr28VeS4BV0qUTRnC8sznr6vFLvr9qgHXTTTflwANLluVFoH0CAqz21cyMCRAgQIAAAQIE+ivgDKzu116A1c0a79Xc36oEWB9NckBzuWA5i+q4JKXun09S7l9Vnkb43iTlLKx74uohr19qLjl8XpL3Jzk2yUeSvLH5tfwtLiHsZl/1alUCrF6V22IJECBAgAABAgRaLiDAankBx5i+AGsMpBZu8vwk705ydzP3Uufydbn3VQmXzkty/yR3NDdnf0uScpbV4PXWJJuSPGPJ75WvX9/cC6vcAP4dI+5/Vd4iwGph05jyngI33H5DNpy/IS4h1BkECBAgQIAAAQIE6hcQYNVfo/XOUIC1XkHvHyYgwNIXrRcYBFhfedlX8pBDHtL69VgAAQIECBAgQIAAgS4LCLC6XN3daxNgdb/Gi1ihAGsR6vY5VYHrb78+h55/aARYU2U1GAECBAgQIECAAIGZCAiwZsJa1aACrKrK0ZnJCLA6U8r+LkSA1d/aWzkBAgQIECBAgED7BARY7avZWmcswFqrmO3HERBgjaNkm6oFBFhVl8fkCBAgQIAAAQIECOwhIMDqfkMIsLpf40WsUIC1CHX7nKrAIMD66ulfzYMPfvBUxzYYAQIECBAgQIAAAQLTFRBgTdezxtEEWDVWpf1zEmC1v4a9X8F1t12Xw7YfFgFW71sBAAECBAgQIECAQAsEBFgtKNI6pyjAWiegtw8VEGBpjNYLDAKsr53+tRx98NGtX48FECBAgAABAgQIEOiygACry9XdvTYBVvdrvIgVCrAWoW6fUxUQYE2V02AECBAgQIAAAQIEZiogwJopbxWDC7CqKEPnJiHA6lxJ+7cgAVb/am7FBAgQIECAAAEC7RUQYLW3duPOXIA1rpTt1iIgwFqLlm2rFBBgVVkWkyJAgAABAgQIECAwVECA1f3GEGB1v8aLWKEAaxHq9jlVgWtvuzYbt2+Me2BNldVgBAgQIECAAAECBGYiIMCaCWtVgwqwqipHZyYjwOpMKfu7kEGA9fWXfz0POuhB/YWwcgIECBAgQIAAAQItEBBgtaBI65yiAGudgN4+VECApTFaLyDAan0JLYAAAQIECBAgQKBHAgKs7hdbgNX9Gi9ihQKsRajb51QFBFhT5TQYAQIECBAgQIAAgZkKCLBmylvF4AKsKsrQuUkIsDpX0v4t6Jpbr8nhFxwelxD2r/ZWTIAAAQIECBAg0D4BAVb7arbWGQuw1ipm+3EEBFjjKNmmaoFBgPWNl38jDzzogVXP1eQIECBAgAABAgQI9F1AgNX9DhBgdb/Gi1ihAGsR6vY5VYGdt+7MERccEQHWVFkNRoAAAQIECBAgQGAmAgKsmbBWNagAq6pydGYyAqzOlLK/CxFg9bf2Vk6AAAECBAgQINA+AQFW+2q21hkLsNYqZvtxBARY4yjZpmoBAVbV5TE5AgQIECBAgAABAnsICLC63xACrO7XeBErFGAtQt0+pyowCLC++Ypv5gH3ecBUxzYYAQIECBAgQIAAAQLTFRBgTdezxtEEWDVWpf1zEmC1v4a9X8H3bvle7nvhfSPA6n0rACBAgAABAgQIEGiBgACrBUVa5xQFWOsE9PahAgIsjdF6gUGA9a1XfCtH3eeo1q/HAggQIECAAAECBAh0WUCA1eXq7l6bAKv7NV7ECgVYi1C3z6kK3PijG3PQuQflulddlw37bZjq2AYjQIAAAQIECBAgQGC6AgKs6XrWOJoAq8aqtH9OAqz219AKktz8PzfnwH1LO3sRIECAAAECBAgQIFCzgACr5upMZ24CrOk4GmVPAQGWjiBAgAABAgQIECBAgACBuQkIsOZGvbAdCbAWRt/pHQuwOl1eiyNAgAABAgQIECBAgEBdAgKsuuoxi9kIsGahakwBlh4gQIAAAQIECBAgQIAAgbkJCLDmRr2wHQmwFkbf6R0LsDpdXosjQIAAAQIECBAgQIBAXQICrLrqMYvZCLBmoWpMAZYeIECAAAECBAgQIECAAIG5CQiw5ka9sB0JsBZGP9Mdn5JkS5JHJtk/yd5J7lqyx/L1j5LckaT0wN1Jjk9y5YhZnZTkkiS3Nt8v7/lBkk0jthdgzbS8BidAgAABAgQIECBAgACBpQICrO73gwCrmzV+WpKDk+yX5OIRAdZTmlBqHIESYH0syb2asGu19wiwVhPy/U4I7NixI5s3b+7EWiyCwCgBfa43+iCgz/tQZWvU53qg6wICrK5XePfZN17dFRgET8POwHpqE0qNs/rBOPskuXOMNwiwxkCySfsFzjjjjFx44YXtX4gVEFhBQJ9rjz4I6PM+VNka9bke6LqAAKvrFRZgdb3CKwVYO5szs76d5G3NmVqjPAbj/HeSfZN8Psnrklw24g0CrK53lvXdI+CDoEbog4A+70OVrVGf64E+COjzPlS532sUYHW//s7A6naNRwVYT0pyeXM2Vbnc8D1JXp3k7SM4DkuysblH1s8meUmSP0vyy0n+c8h77gmwrr766hx4YPnSi0A3Bc4888ycc8453VycVRFoBPS5VuiDgD7vQ5WtUZ/rga4LlADryCOPLMu8d5Kbu77ePq5PgNXtqo8KsJavemuSpyc5cQ0c5Z5YJQT7kyHvuV+ScraWFwECBAgQIECAAAECBAgQmKfA/ZN8Z547tK/5CAiw5uO8qL2sJcAqd6I+YQ0T/Zck/5rkNUPeU/rqvkluWcN4NiVAgAABAgQIECBAgAABAusROCDJd8d8+Nh69uO9CxAQYC0AfQ673Ku5v1UJsD6apPwhLjdf35XkuOy+91m5j9VdScrTCN+bpJyFddGIuZWzs76SpNwv62eSvDjJ65vA67NzWI9dECBAgAABAgQIECBAgAABAj0WEGB1s/jPT/LuJalzqfPdScq9r8pNqc5LUk6rvKMJpd6S5J1LKN6aZFOSZzS/Vy4TPC3JwUl+2IRff5rk0m7yWRUBAgQIECBAgAABAgQIECBQk4AAq6ZqmAsBAgQIECBAgAABAgQIECBAgMBPCAiw+tMUpyTZkuSRSfZvLjEslxAOXr+Y5E1JHpXkxuaMrG3LeMr//25zFtcVzXhXVjhGf6pqpcsF1tvnZyV5bZLbm0tty5mLH07yW/pcs1UksFKfl8u8/6q5XPzoJH/eXCK+fPqO5xUV1FSGCqy3zx3PNVYbBFbq88c2D0t6TJLyFPByK483JPlLn8/bUFpzXCKw3j53PNdOPxYQYPWnGZ7WXAK4X5KLlwVYJdAq97h6V5JyaeBDm3tnbU/yFw3Rq5K8LMmvJvl6knIgeV6zbflhv5Yx+lNRKx0msN4+L31d7gv3xBG8+lzf1SCwUp/vm+QlSf6juVfhPw8JsBzPa6iiOawmsN4+dzxfTdj3axBYqc/LZ+5Dk/xjkuuTnJzk75M8N8mHfD6voXzmMKbAevvc8XxM6D5sJsDqQ5X3XOOwJxOWe2ad2zw5cHBW1suTnJ7kIc3bv5HkwiRvbv7/p5unO5yR5D1JahmjfxW14mECk/b5an9B6nP9VpPAak+avSTJJ4YEWI7nNVXRXFYTmLTPHc9Xk/X9mgRW6/PBXD+Q5FtJ/sDn85rKZy5jCkza547nYwL3YTMBVh+qvHqAVYKpY5uzqwZbH5/kk0nunaQ81bBcVlh+79+WDLejuaH7HzbhVg1j9K+iVjxugLVan9/anFlY+rmcVVh+XZ7kNc2HxbKf1caY158VVSdQBFb7IDgswCoP8nA81z9tEpikz8v6yg88judtqnS/57panxedcvz+UpI/SvLXzf87nve7b9q2+kn63PG8bVWe8XwFWDMGrnD4YQeOcknhzyU5dcl8j0lS7m91ZBNg/VcTcn15yTZ/m+TmJL/XXJZYwxgVkpvSAgQm6fPvJnl4kluSXJ3kiCTnJ3lcknKPuBJo1fJnZQGkdlmhwGofBIcFWOUJtI7nFRbTlEYKTNLnZTDHc03VJoHV+nzv5rLB8t+nJylXTDiet6nC5jrOP7wN63PHc72zh4AAq38NMewvyFrOKpnGPPpXUSseJjBJn5czsJa/9klyU5JfT1LuJTSNHp3GGKpOYJwPgs7A0iddEFjtB/tRl8o6nneh+v1Zw0p9Xm7gXi4dvFeSZzb/oFZknFHbn/7oykon6fNha/f5vCsdMcE6BFgToLX8LcMOHOVm7OctuwfWK5qbtq90D6zvJXllkr9pbui+yDHKvQDKvbi8CIz6wX6cPh/1A0/5wPhP+lxzVSYw6Q/2w+6B5XheWXFN58cCk/a547kmapPAqD6/T5KPNDdx/40k/7tsUY7nbaqyuU7a547neufHAgKs/jRDuTdPOS2zHDg+muSAJHcm2dVcPlguDSxPISyPXC+hVfnL8oIlTyEs95EoTyF8RpLyl+XWJL+d5GHNvwSVp7PVMEZ/KmqlwwTW2+e/meRjSW5IsrG5hPDEJI9IclvztE19rvcWLbBSn9+dpPzLZNmm3Kew3MuwPF22XG4y+MHH8XzRFbT/cQTW2+eO5+Mo22bRAiv1+WHNP56VW3qUz9zlc/vyl+P5oito/+MIrLfPHc/HUe7JNgKsnhS6eUrgu5OUH27Kq9S+fP2kJJcl+YUkb0nyqOaSqbcmed0ynrOTvLgJv/49yZbmPlmDzWoZoz9VtdLlAuUpgevp8/J46nLPq3I/tx80fzZe24S2+ly/1SKwWp9/M8mmZZO9NMmTl/ye43kt1TSPUQLr7XPHc73VBoGV+vzk5mEE5R6c5TX4DF+eLlv+QXnwcjxvQ6X7Pcf19rnjeb/7Z4/VC7A0AwECBAgQIECAAAECBAgQIECAQNUCAqyqy2NyBAgQIECAAAECBAgQIECAAAECAiw9QIAAAQIECBAgQIAAAQIECBAgULWAAKvq8pgcAQIECBAgQIAAAQIECBAgQICAAEsPECBAgAABAgQIECBAgAABAgQIVC0gwKq6PCZHgAABAgQIECBAgAABAgQIECAgwNIDBAgQIECAAAECBAgQIECAAAECVQsIsKouj8kRIECAAAECBAgQIECAAAECBAgIsPQAAQIECBAgQIAAAQIECBAgQIBA1QICrKrLY3IECBAgQIAAAQIECBAgQIAAAQICLD1AgAABAgQIECBAgAABAgQIECBQtYAAq+rymBwBAgQIECBAgAABAgQIECBAgIAASw8QIECAAAECBAgQIECAAAECBAhULSDAqro8JkeAAAECBAgQIECAAAECBAgQICDA0gMECBAgQETPZ0YAAATXSURBVIAAAQIECBAgQIAAAQJVCwiwqi6PyREgQIAAAQIECBAgQIAAAQIECAiw9AABAgQIECBAgAABAgQIECBAgEDVAgKsqstjcgQIECBAgAABAgQIECBAgAABAgIsPUCAAAECBAgQIECAAAECBAgQIFC1gACr6vKYHAECBAgQIECAAAECBAgQIECAgABLDxAgQIAAAQIECBAgQIAAAQIECFQtIMCqujwmR4AAAQIECBAgQIAAAQIECBAgIMDSAwQIECBAgAABAgQIECBAgAABAlULCLCqLo/JESBAgAABAgQIECBAgAABAgQICLD0AAECBAgQIECAAAECBAgQIECAQNUCAqyqy2NyBAgQIECAAAECBAgQIECAAAECAiw9QIAAAQIECBAgQIAAAQIECBAgULWAAKvq8pgcAQIECBAgQIAAAQIECBAgQICAAEsPECBAgAABAgQIECBAgAABAgQIVC0gwKq6PCZHgAABAgQIECBAgAABAgQIECAgwNIDBAgQIECAAAECBAgQIECAAAECVQsIsKouj8kRIECAAAECBAgQIECAAAECBAgIsPQAAQIECBAgQIAAAQIECBAgQIBA1QICrKrLY3IECBAgQIAAAQIECBAgQIAAAQICLD1AgAABAgQIECBAgAABAgQIECBQtYAAq+rymBwBAgQIECBAgAABAgQIECBAgIAASw8QIECAAAECBAgQIECAAAECBAhULSDAqro8JkeAAAECBAgQIECAAAECBAgQICDA0gMECBAgQIAAAQIECBAgQIAAAQJVCwiwqi6PyREgQIAAAQIECBAgQIAAAQIECAiw9AABAgQIECBAgAABAgQIECBAgEDVAgKsqstjcgQIECBAgAABAgQIECBAgAABAgIsPUCAAAECBAgQIECAAAECBAgQIFC1gACr6vKYHAECBAgQIECAAAECBAgQIECAgABLDxAgQIAAAQIECBAgQIAAAQIECFQtIMCqujwmR4AAAQIECBAgQIAAAQIECBAgIMDSAwQIECBAgAABAgQIECBAgAABAlULCLCqLo/JESBAgAABAgQIECBAgAABAgQICLD0AAECBAgQIECAAAECBAgQIECAQNUCAqyqy2NyBAgQIECAAAECBAgQIECAAAECAiw9QIAAAQIECBAgQIAAAQIECBAgULWAAKvq8pgcAQIECBAgQIAAAQIECBAgQICAAEsPECBAgAABAgQIECBAgAABAgQIVC0gwKq6PCZHgAABAgQIECBAgAABAgQIECAgwNIDBAgQIECAAAECBAgQIECAAAECVQsIsKouj8kRIECAAAECBAgQIECAAAECBAgIsPQAAQIECBAgQIAAAQIECBAgQIBA1QICrKrLY3IECBAgQIAAAQIECBAgQIAAAQICLD1AgAABAgQIECBAgAABAgQIECBQtYAAq+rymBwBAgQIECBAgAABAgQIECBAgIAASw8QIECAAAECBAgQIECAAAECBAhULSDAqro8JkeAAAECBAgQIECAAAECBAgQICDA0gMECBAgQIAAAQIECBAgQIAAAQJVCwiwqi6PyREgQIAAAQIECBAgQIAAAQIECAiw9AABAgQIECBAgAABAgQIECBAgEDVAgKsqstjcgQIECBAgAABAgQIECBAgAABAv8HhpT5oD15D1AAAAAASUVORK5CYII=\">"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
"<HDF5 dataset \"N\": shape (87250, 10), type \"<f8\">"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"db.plot_imu_data()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Implemented analysis methods "
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"['get_PN_at_sync', 'get_ROM_joint_angle', 'get_RoM_angle_to_vertical', 'get_angle_between_segments', 'get_angle_to_vertical', 'get_cycle_data', 'get_cycle_frequency', 'get_imu_data', 'get_minmax_angle_to_vertical', 'get_minmax_joint_angle', 'get_orientation', 'get_range_of_motion', 'get_trial_attribute', 'get_vertical_displacement']\n"
]
}
],
"source": [
"print [s for s in dir(db) if s.startswith(\"get\")]"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.12"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| gpl-3.0 |
egovernments/analytics | jupyter-notebooks/EDA/EDANotebook2.ipynb | 2 | 22400 | {
"cells": [
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"library(dplyr)\n",
"library(ggplot2)\n",
"library(plotly)\n",
"a = read.csv(\"/home/mansiarora/Documents/DataCor_egov/Data/ddive_rolled_seq.csv\")\n",
"str(a)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"a$Complaint.Date = as.Date(a$Complaint.Date, format = \"%Y-%m-%d\")\n",
"a$Month = format(a$Complaint.Date, format = \"%m\")\n",
"a$Year = format(a$Complaint.Date, \"%Y\")\n",
"a$Week = format(a$Complaint.Date, \"%W\")\n",
"a$Weekday = weekdays(a$Complaint.Date)\n",
"a$Week_Year = paste0(a$Week, \"_\", a$Year)\n",
"a$Month_Year = paste0(a$Month, \"_\", a$Year) "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Counts by complaint type\n",
"b = a %>% group_by(Complaint.Type) %>%\n",
" summarise(count = sum(complaint_count))\n",
"b = b[order(-b$count),] \n",
"b <- transform(b, Complaint.Type = reorder(Complaint.Type, -count))\n",
"ggplot(b[1:20,], aes(x=Complaint.Type, y=count)) + geom_bar(stat = \"identity\") + theme(axis.text.x=element_text(angle=90,hjust=1,vjust=0.5))\n",
"topcomplaints = unique(b$Complaint.Type)[1:10]\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Counts by Ward\n",
"c = a %>%\n",
" group_by(Ward) %>%\n",
" summarise(count = sum(complaint_count))\n",
"c = c[order(-c$count),] \n",
"c <- transform(c, Ward = reorder(Ward, -count))\n",
"ggplot(c[1:20,], aes(x=Ward, y=count)) + geom_bar(stat = \"identity\") + theme(axis.text.x=element_text(angle=90,hjust=1,vjust=0.5))\n",
"topwards = unique(c$Ward)[1:10]\n",
"topwards"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Counts by complaint type and ward\n",
"d = a %>%\n",
" group_by(Complaint.Type, Ward) %>%\n",
" summarise(count = sum(complaint_count))\n",
"d = d[order(-d$count),] \n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# top 5 complaints of each ward\n",
"e = data_frame(Complaint.Type = character(), Ward = character(), count = numeric())\n",
"for( i in 1:length(topwards)) {\n",
" x = d[d$Ward == topwards[i],]\n",
" others_sum=sum(x[11:nrow(x),]$count, na.rm = TRUE)\n",
" x = data.frame(x[1:5,])\n",
" #y = data.frame(Complaint.Type = \"Others\", Ward = topwards[i], count=others_sum)\n",
" #x = rbind(x, y)\n",
" e = rbind(e, x)\n",
"}\n",
"ggplot(e, aes(x=Ward, y=count, fill=Complaint.Type)) + geom_bar(stat = \"identity\", position = \"fill\")\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Counts by complaint date (month)\n",
"f = a %>%\n",
" group_by(Month) %>%\n",
" summarise(count = sum(complaint_count))\n",
"f = f[order(-f$count),] \n",
"ggplot(f, aes(x=Month, y=count)) + geom_bar(stat = \"identity\")\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"g = a %>%\n",
" group_by(Year) %>%\n",
" summarise(count = sum(complaint_count))\n",
"g = g[order(-g$count),] \n",
"ggplot(g, aes(x=Year, y=count)) + geom_bar(stat = \"identity\")\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"h = a %>%\n",
" group_by(Month, Year) %>%\n",
" summarise(count = sum(complaint_count))\n",
"h = h[order(-h$count),] \n",
"ggplot(h, aes(x=Month, y=count, fill=Year)) + geom_bar(stat = \"identity\", position = \"fill\")\n",
"ggplot(h, aes(x=Year, y=count, fill=Month)) + geom_bar(stat = \"identity\", position = \"fill\")\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Trend of top complaint types over time\n",
"i = a[a$Complaint.Type %in% topcomplaints,] %>%\n",
" group_by(Complaint.Type, Year) %>%\n",
" summarise(count = sum(complaint_count))\n",
"i = i[order(-i$count),] \n",
"ggplot(i, aes(x=Year, y=count, fill=Complaint.Type)) + geom_bar(stat = \"identity\", position = \"fill\")\n",
"\n",
"j = a[a$Complaint.Type %in% topcomplaints,] %>%\n",
" group_by(Complaint.Type, Month) %>%\n",
" summarise(count = sum(complaint_count))\n",
"j = j[order(-j$count),] \n",
"ggplot(j, aes(x=Month, y=count, fill=Complaint.Type)) + geom_bar(stat = \"identity\", position = \"fill\")\n",
"\n",
"k = a[a$Complaint.Type %in% topcomplaints,] %>%\n",
" group_by(Complaint.Type, Month_Year) %>%\n",
" summarise(count = sum(complaint_count))\n",
"k = k[order(-k$count),] \n",
"ggplot(k, aes(x=Month_Year, y=count, fill=Complaint.Type)) + geom_bar(stat = \"identity\", position = \"fill\") + theme(axis.text.x=element_text(angle=90,hjust=0.4,vjust=0.1))\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Trend of top wards over time\n",
"l = a[a$Ward %in% topwards,] %>%\n",
" group_by(Ward, Year) %>%\n",
" summarise(count = sum(complaint_count))\n",
"l = l[order(-l$count),] \n",
"l$Ward <- factor(l$Ward, topwards)\n",
"ggplot(l, aes(x=Year, y=count, fill=Ward)) + geom_bar(stat = \"identity\")\n",
"ggplot(l, aes(x=Year, y=count, fill=Ward)) + geom_bar(stat = \"identity\", position = \"fill\")\n",
"\n",
"m = a[a$Ward %in% topwards,] %>%\n",
" group_by(Ward, Month) %>%\n",
" summarise(count = sum(complaint_count))\n",
"m = m[order(-m$count),] \n",
"ggplot(m, aes(x=Month, y=count, fill=Ward)) + geom_bar(stat = \"identity\")\n",
"ggplot(m, aes(x=Month, y=count, fill=Ward)) + geom_bar(stat = \"identity\", position = \"fill\")\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"#install.packages(\"gridExtra\")\n",
"library(\"gridExtra\")\n",
"\n",
"# Density plot\n",
"C1 = a[a$Complaint.Type == topcomplaints[1],]\n",
"D1 = ggplot(C1, aes(x=complaint_count)) + geom_density()\n",
"\n",
"C2 = a[a$Complaint.Type == topcomplaints[2],]\n",
"D2 = ggplot(C2, aes(x=complaint_count)) + geom_density()\n",
"\n",
"C3 = a[a$Complaint.Type == topcomplaints[3],]\n",
"D3 = ggplot(C3, aes(x=complaint_count)) + geom_density()\n",
"\n",
"C4 = a[a$Complaint.Type == topcomplaints[4],]\n",
"D4 = ggplot(C4, aes(x=complaint_count)) + geom_density()\n",
"\n",
"C5 = a[a$Complaint.Type == topcomplaints[5],]\n",
"D5 = ggplot(C5, aes(x=complaint_count)) + geom_density()\n",
"\n",
"C6 = a[a$Complaint.Type == topcomplaints[6],]\n",
"D6 = ggplot(C6, aes(x=complaint_count)) + geom_density()\n",
"\n",
"grid.arrange(D1, D2, D3, D4, D5, D6, ncol=3, nrow =2)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Complaint Count by date\n",
"\n",
"C1a = C1 %>%\n",
" group_by(Complaint.Date) %>%\n",
" summarise(count = sum(complaint_count))\n",
"a = ggplot(C1a, aes(x=Complaint.Date,y=count)) + geom_bar(stat=\"identity\") + ggtitle(topcomplaints[1]) + theme(plot.title = element_text(size = 10))\n",
"\n",
"C2a = C2 %>%\n",
" group_by(Complaint.Date) %>%\n",
" summarise(count = sum(complaint_count))\n",
"b = ggplot(C2a, aes(x=Complaint.Date,y=count)) + geom_bar(stat=\"identity\") + ggtitle(topcomplaints[2]) + theme(plot.title = element_text(size = 10))\n",
"\n",
"\n",
"C3a = C3 %>%\n",
" group_by(Complaint.Date) %>%\n",
" summarise(count = sum(complaint_count))\n",
"c = ggplot(C3a, aes(x=Complaint.Date,y=count)) + geom_bar(stat=\"identity\") + ggtitle(topcomplaints[3]) + theme(plot.title = element_text(size = 10))\n",
"\n",
"\n",
"C4a = C4 %>%\n",
" group_by(Complaint.Date) %>%\n",
" summarise(count = sum(complaint_count))\n",
"d = ggplot(C4a, aes(x=Complaint.Date,y=count)) + geom_bar(stat=\"identity\") + ggtitle(topcomplaints[4]) + theme(plot.title = element_text(size = 10))\n",
"\n",
"\n",
"C5a = C5 %>%\n",
" group_by(Complaint.Date) %>%\n",
" summarise(count = sum(complaint_count))\n",
"e = ggplot(C5a, aes(x=Complaint.Date,y=count)) + geom_bar(stat=\"identity\") + ggtitle(topcomplaints[5]) + theme(plot.title = element_text(size = 10))\n",
"\n",
"\n",
"C6a = C6 %>%\n",
" group_by(Complaint.Date) %>%\n",
" summarise(count = sum(complaint_count))\n",
"f = ggplot(C6a, aes(x=Complaint.Date,y=count)) + geom_bar(stat=\"identity\") + ggtitle(topcomplaints[6]) + theme(plot.title = element_text(size = 8))\n",
"\n",
"grid.arrange(a, b, c, d, e, f, ncol=3, nrow =2)\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Complaint Count by Year\n",
"\n",
"C1b = C1 %>%\n",
" group_by(Year) %>%\n",
" summarise(count = sum(complaint_count))\n",
"a = ggplot(C1b, aes(x=Year,y=count)) + geom_bar(stat=\"identity\") + ggtitle(topcomplaints[1]) + theme(plot.title = element_text(size = 10))\n",
"\n",
"C2b = C2 %>%\n",
" group_by(Year) %>%\n",
" summarise(count = sum(complaint_count))\n",
"b = ggplot(C2b, aes(x=Year,y=count)) + geom_bar(stat=\"identity\") + ggtitle(topcomplaints[2]) + theme(plot.title = element_text(size = 10))\n",
"\n",
"C3b = C3 %>%\n",
" group_by(Year) %>%\n",
" summarise(count = sum(complaint_count))\n",
"c = ggplot(C3b, aes(x=Year,y=count))+ geom_bar(stat=\"identity\") + ggtitle(topcomplaints[3]) + theme(plot.title = element_text(size = 10))\n",
"\n",
"C4b = C4 %>%\n",
" group_by(Year) %>%\n",
" summarise(count = sum(complaint_count))\n",
"d = ggplot(C4b, aes(x=Year,y=count)) + geom_bar(stat=\"identity\") + ggtitle(topcomplaints[4]) + theme(plot.title = element_text(size = 10))\n",
"\n",
"C5b = C5 %>%\n",
" group_by(Year) %>%\n",
" summarise(count = sum(complaint_count))\n",
"e = ggplot(C5b, aes(x=Year,y=count)) + geom_bar(stat=\"identity\") + ggtitle(topcomplaints[5]) + theme(plot.title = element_text(size = 10))\n",
"\n",
"C6b = C6 %>%\n",
" group_by(Year) %>%\n",
" summarise(count = sum(complaint_count))\n",
"f = ggplot(C6b, aes(x=Year,y=count)) + geom_bar(stat=\"identity\") + ggtitle(topcomplaints[6]) + theme(plot.title = element_text(size = 10))\n",
"\n",
"grid.arrange(a, b, c, d, e, f, ncol=3, nrow =2)\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Complaint Count by Week\n",
"\n",
"C1c = C1 %>%\n",
" group_by(Week) %>%\n",
" summarise(count = sum(complaint_count))\n",
"a = ggplot(C1c, aes(x=Week,y=count)) + geom_line(group=1) + ggtitle(topcomplaints[1]) + theme(plot.title = element_text(size = 10))\n",
"\n",
"C2c = C2 %>%\n",
" group_by(Week) %>%\n",
" summarise(count = sum(complaint_count))\n",
"b = ggplot(C2c, aes(x=Week,y=count)) + geom_line(group=1) + ggtitle(topcomplaints[2]) + theme(plot.title = element_text(size = 10))\n",
"\n",
"C3c = C3 %>%\n",
" group_by(Week) %>%\n",
" summarise(count = sum(complaint_count))\n",
"c = ggplot(C3c, aes(x=Week,y=count))+ geom_line(group=1) + ggtitle(topcomplaints[3]) + theme(plot.title = element_text(size = 10))\n",
"\n",
"C4c = C4 %>%\n",
" group_by(Week) %>%\n",
" summarise(count = sum(complaint_count))\n",
"d = ggplot(C4c, aes(x=Week,y=count)) + geom_line(group=1) + ggtitle(topcomplaints[4]) + theme(plot.title = element_text(size = 10))\n",
"\n",
"C5c = C5 %>%\n",
" group_by(Week) %>%\n",
" summarise(count = sum(complaint_count))\n",
"e = ggplot(C5c, aes(x=Week,y=count)) + geom_line(group=1) + ggtitle(topcomplaints[5]) + theme(plot.title = element_text(size = 10))\n",
"\n",
"C6c = C6 %>%\n",
" group_by(Week) %>%\n",
" summarise(count = sum(complaint_count))\n",
"f = ggplot(C6c, aes(x=Week,y=count)) + geom_line(group=1) + ggtitle(topcomplaints[6]) + theme(plot.title = element_text(size = 10))\n",
"\n",
"grid.arrange(a, b, c, d, e, f, ncol=3, nrow =2)\n",
"\n",
"\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Complaint Count by Weekday\n",
"\n",
"C1d = C1 %>%\n",
" group_by(Weekday) %>%\n",
" summarise(count = sum(complaint_count))\n",
"days = c(\"Mon\", \"Tue\", \"Wed\", \"Thurs\", \"Fri\", \"Sat\", \"Sun\")\n",
"levels(C1d$Weekday) = days\n",
"a = ggplot(C1d, aes(x=Weekday,y=count)) + geom_line(group=1) + ggtitle(topcomplaints[1]) + theme(plot.title = element_text(size = 10))+ theme(axis.text.x=element_text(angle=90,hjust=1,vjust=0.5))\n",
"\n",
"C2d = C2 %>%\n",
" group_by(Weekday) %>%\n",
" summarise(count = sum(complaint_count))\n",
"days = c(\"Mon\", \"Tue\", \"Wed\", \"Thurs\", \"Fri\", \"Sat\", \"Sun\")\n",
"levels(C2d$Weekday) = days\n",
"b = ggplot(C2d, aes(x=Weekday,y=count)) + geom_line(group=1) + ggtitle(topcomplaints[2]) + theme(plot.title = element_text(size = 10))+ theme(axis.text.x=element_text(angle=90,hjust=1,vjust=0.5))\n",
"\n",
"C3d = C3 %>%\n",
" group_by(Weekday) %>%\n",
" summarise(count = sum(complaint_count))\n",
"days = c(\"Mon\", \"Tue\", \"Wed\", \"Thurs\", \"Fri\", \"Sat\", \"Sun\")\n",
"levels(C3d$Weekday) = days\n",
"c = ggplot(C3d, aes(x=Weekday,y=count))+ geom_line(group=1) + ggtitle(topcomplaints[3]) + theme(plot.title = element_text(size = 10))+ theme(axis.text.x=element_text(angle=90,hjust=1,vjust=0.5))\n",
"\n",
"C4d = C4 %>%\n",
" group_by(Weekday) %>%\n",
" summarise(count = sum(complaint_count))\n",
"days = c(\"Mon\", \"Tue\", \"Wed\", \"Thurs\", \"Fri\", \"Sat\", \"Sun\")\n",
"levels(C4d$Weekday) = days\n",
"d = ggplot(C4d, aes(x=Weekday,y=count)) + geom_line(group=1) + ggtitle(topcomplaints[4]) + theme(plot.title = element_text(size = 10))+ theme(axis.text.x=element_text(angle=90,hjust=1,vjust=0.5))\n",
"\n",
"C5d = C5 %>%\n",
" group_by(Weekday) %>%\n",
" summarise(count = sum(complaint_count))\n",
"days = c(\"Mon\", \"Tue\", \"Wed\", \"Thurs\", \"Fri\", \"Sat\", \"Sun\")\n",
"levels(C5d$Weekday) = days\n",
"e = ggplot(C5d, aes(x=Weekday,y=count)) + geom_line(group=1) + ggtitle(topcomplaints[5]) + theme(plot.title = element_text(size = 10))+ theme(axis.text.x=element_text(angle=90,hjust=1,vjust=0.5))\n",
"\n",
"C6d = C6 %>%\n",
" group_by(Weekday) %>%\n",
" summarise(count = sum(complaint_count))\n",
"days = c(\"Mon\", \"Tue\", \"Wed\", \"Thurs\", \"Fri\", \"Sat\", \"Sun\")\n",
"levels(C6d$Weekday) = days\n",
"f = ggplot(C6d, aes(x=Weekday,y=count)) + geom_line(group=1) + ggtitle(topcomplaints[6]) + theme(plot.title = element_text(size = 10))+ theme(axis.text.x=element_text(angle=90,hjust=1,vjust=0.5))\n",
"\n",
"grid.arrange(a, b, c, d, e, f, ncol=3, nrow =2)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"#Top wards of each complaint type\n",
"C1e = C1 %>%\n",
" group_by(Ward) %>%\n",
" summarise(count = sum(complaint_count))\n",
"C1e = C1e[order(-C1e$count),] \n",
"C1e <- transform(C1e, Ward = reorder(Ward, -count))\n",
"a = ggplot(C1e[1:10,], aes(x=Ward, y=count)) + geom_bar(stat = \"identity\") + theme(axis.text.x=element_text(angle=90,hjust=1,vjust=0.5)) + ggtitle(topcomplaints[1]) + theme(plot.title = element_text(size = 10))\n",
"topwards_C1 = C1e[1:10,]$Ward\n",
"\n",
"C2e = C2 %>%\n",
" group_by(Ward) %>%\n",
" summarise(count = sum(complaint_count))\n",
"C2e = C2e[order(-C2e$count),] \n",
"C2e <- transform(C2e, Ward = reorder(Ward, -count))\n",
"b = ggplot(C2e[1:10,], aes(x=Ward, y=count)) + geom_bar(stat = \"identity\") + theme(axis.text.x=element_text(angle=90,hjust=1,vjust=0.5)) + ggtitle(topcomplaints[2]) + theme(plot.title = element_text(size = 10))\n",
"topwards_C2 = C2e[1:10,]$Ward\n",
"\n",
"C3e = C3 %>%\n",
" group_by(Ward) %>%\n",
" summarise(count = sum(complaint_count))\n",
"C3e = C3e[order(-C3e$count),] \n",
"C3e <- transform(C3e, Ward = reorder(Ward, -count))\n",
"c = ggplot(C3e[1:10,], aes(x=Ward, y=count)) + geom_bar(stat = \"identity\") + theme(axis.text.x=element_text(angle=90,hjust=1,vjust=0.5)) + ggtitle(topcomplaints[3]) + theme(plot.title = element_text(size = 10))\n",
"topwards_C3 = C3e[1:10,]$Ward\n",
"\n",
"C4e = C4 %>%\n",
" group_by(Ward) %>%\n",
" summarise(count = sum(complaint_count))\n",
"C4e = C4e[order(-C4e$count),] \n",
"C4e <- transform(C4e, Ward = reorder(Ward, -count))\n",
"d = ggplot(C4e[1:10,], aes(x=Ward, y=count)) + geom_bar(stat = \"identity\") + theme(axis.text.x=element_text(angle=90,hjust=1,vjust=0.5)) + ggtitle(topcomplaints[4]) + theme(plot.title = element_text(size = 10))\n",
"topwards_C4 = C4e[1:10,]$Ward\n",
"\n",
"C5e = C5 %>%\n",
" group_by(Ward) %>%\n",
" summarise(count = sum(complaint_count))\n",
"C5e = C5e[order(-C5e$count),] \n",
"C5e <- transform(C5e, Ward = reorder(Ward, -count))\n",
"e = ggplot(C5e[1:10,], aes(x=Ward, y=count)) + geom_bar(stat = \"identity\") + theme(axis.text.x=element_text(angle=90,hjust=1,vjust=0.5)) + ggtitle(topcomplaints[5]) + theme(plot.title = element_text(size = 10))\n",
"topwards_C5 = C5e[1:10,]$Ward\n",
"\n",
"C6e = C6 %>%\n",
" group_by(Ward) %>%\n",
" summarise(count = sum(complaint_count))\n",
"C6e = C6e[order(-C6e$count),] \n",
"C6e <- transform(C6e, Ward = reorder(Ward, -count))\n",
"f = ggplot(C6e[1:10,], aes(x=Ward, y=count)) + geom_bar(stat = \"identity\") + theme(axis.text.x=element_text(angle=90,hjust=1,vjust=0.5)) + ggtitle(topcomplaints[6]) + theme(plot.title = element_text(size = 10))\n",
"topwards_C6 = C6e[1:10,]$Ward\n",
"\n",
"grid.arrange(a, b, c, d, e, f, ncol=3, nrow =2)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Trends of top wards over time for each complaint type\n",
"C1f = C1 %>%\n",
" group_by(Ward, Year) %>%\n",
" summarise(count = sum(complaint_count))\n",
"C1f = C1f[order(-C1f$count),] \n",
"C1f <- transform(C1f, Ward = reorder(Ward, -count))\n",
"a = ggplot(C1f[C1f$Ward %in% topwards_C1,], aes(x=Ward, y=count)) + geom_bar(aes(fill = Year), position = \"dodge\", stat=\"identity\") + theme(axis.text.x=element_text(angle=90,hjust=1,vjust=0.5)) \n",
"\n",
"C2f = C2 %>%\n",
" group_by(Ward, Year) %>%\n",
" summarise(count = sum(complaint_count))\n",
"C2f = C2f[order(-C2f$count),] \n",
"C2f <- transform(C2f, Ward = reorder(Ward, -count))\n",
"b = ggplot(C2f[C2f$Ward %in% topwards_C2,], aes(x=Ward, y=count)) + geom_bar(aes(fill = Year), position = \"dodge\", stat=\"identity\") + theme(axis.text.x=element_text(angle=90,hjust=1,vjust=0.5))\n",
"\n",
"C3f = C3 %>%\n",
" group_by(Ward, Year) %>%\n",
" summarise(count = sum(complaint_count))\n",
"C3f = C3f[order(-C3f$count),] \n",
"C3f <- transform(C3f, Ward = reorder(Ward, -count))\n",
"c = ggplot(C3f[C3f$Ward %in% topwards_C3,], aes(x=Ward, y=count)) + geom_bar(aes(fill = Year), position = \"dodge\", stat=\"identity\") + theme(axis.text.x=element_text(angle=90,hjust=1,vjust=0.5))\n",
"\n",
"C4f = C4 %>%\n",
" group_by(Ward, Year) %>%\n",
" summarise(count = sum(complaint_count))\n",
"C4f = C4f[order(-C4f$count),] \n",
"C4f <- transform(C4f, Ward = reorder(Ward, -count))\n",
"d = ggplot(C4f[C4f$Ward %in% topwards_C4,], aes(x=Ward, y=count)) + geom_bar(aes(fill = Year), position = \"dodge\", stat=\"identity\") + theme(axis.text.x=element_text(angle=90,hjust=1,vjust=0.5))\n",
"\n",
"C5f = C5 %>%\n",
" group_by(Ward, Year) %>%\n",
" summarise(count = sum(complaint_count))\n",
"C5f = C5f[order(-C5f$count),] \n",
"C5f <- transform(C5f, Ward = reorder(Ward, -count))\n",
"e = ggplot(C5f[C5f$Ward %in% topwards_C5,], aes(x=Ward, y=count)) + geom_bar(aes(fill = Year), position = \"dodge\", stat=\"identity\") + theme(axis.text.x=element_text(angle=90,hjust=1,vjust=0.5))\n",
"\n",
"C6f = C6 %>%\n",
" group_by(Ward, Year) %>%\n",
" summarise(count = sum(complaint_count))\n",
"C6f = C6f[order(-C6f$count),] \n",
"C6f <- transform(C6f, Ward = reorder(Ward, -count))\n",
"f = ggplot(C6f[C6f$Ward %in% topwards_C6,], aes(x=Ward, y=count)) + geom_bar(aes(fill = Year), position = \"dodge\", stat=\"identity\") + theme(axis.text.x=element_text(angle=90,hjust=1,vjust=0.5))\n",
"\n",
"grid.arrange(a, b, c, d, e, f, ncol=2, nrow =3)\n",
"\n"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "R",
"language": "R",
"name": "ir"
},
"language_info": {
"codemirror_mode": "r",
"file_extension": ".r",
"mimetype": "text/x-r-source",
"name": "R",
"pygments_lexer": "r",
"version": "3.3.1"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
| mit |
fionapigott/Data-Science-45min-Intros | count-min-101/CountMinSketch.ipynb | 14 | 14934 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Basic Idea of Count Min sketch"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We map the input value to _multiple_ points in a _relatively small_ output space. Therefore, the count associated with a given input will be applied to multiple counts in the output space. Even though collisions will occur, the _minimum_ count associated with a given input will have some desirable properties, including the ability to be used to estimate the largest N counts.\n",
"\n",
"<img src=\"files/count_min_2.png\">\n",
"\n",
"http://debasishg.blogspot.com/2014/01/count-min-sketch-data-structure-for.html\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Parameters of the sketch:\n",
"\n",
"* epsilon\n",
"* delta\n",
"\n",
"These parameters are inversely and exponentially (respectively) related to the sketch size parameters, d and w. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Implementation of the CM sketch"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import sys\n",
"import random\n",
"import numpy as np\n",
"import heapq\n",
"import json\n",
"import time\n",
"\n",
"BIG_PRIME = 9223372036854775783\n",
"\n",
"def random_parameter():\n",
" return random.randrange(0, BIG_PRIME - 1)\n",
"\n",
"\n",
"class Sketch:\n",
" def __init__(self, delta, epsilon, k):\n",
" \"\"\"\n",
" Setup a new count-min sketch with parameters delta, epsilon and k\n",
"\n",
" The parameters delta and epsilon control the accuracy of the\n",
" estimates of the sketch\n",
"\n",
" Cormode and Muthukrishnan prove that for an item i with count a_i, the\n",
" estimate from the sketch a_i_hat will satisfy the relation\n",
"\n",
" a_hat_i <= a_i + epsilon * ||a||_1\n",
"\n",
" with probability at least 1 - delta, where a is the the vector of all\n",
" all counts and ||x||_1 is the L1 norm of a vector x\n",
"\n",
" Parameters\n",
" ----------\n",
" delta : float\n",
" A value in the unit interval that sets the precision of the sketch\n",
" epsilon : float\n",
" A value in the unit interval that sets the precision of the sketch\n",
" k : int\n",
" A positive integer that sets the number of top items counted\n",
"\n",
" Examples\n",
" --------\n",
" >>> s = Sketch(10**-7, 0.005, 40)\n",
"\n",
" Raises\n",
" ------\n",
" ValueError\n",
" If delta or epsilon are not in the unit interval, or if k is\n",
" not a positive integer\n",
"\n",
" \"\"\"\n",
" if delta <= 0 or delta >= 1:\n",
" raise ValueError(\"delta must be between 0 and 1, exclusive\")\n",
" if epsilon <= 0 or epsilon >= 1:\n",
" raise ValueError(\"epsilon must be between 0 and 1, exclusive\")\n",
" if k < 1:\n",
" raise ValueError(\"k must be a positive integer\")\n",
"\n",
" self.w = int(np.ceil(np.exp(1) / epsilon))\n",
" self.d = int(np.ceil(np.log(1 / delta)))\n",
" self.k = k\n",
" self.hash_functions = [self.__generate_hash_function() for i in range(self.d)]\n",
" self.count = np.zeros((self.d, self.w), dtype='int32')\n",
" self.heap, self.top_k = [], {} # top_k => [estimate, key] pairs\n",
"\n",
" def update(self, key, increment):\n",
" \"\"\"\n",
" Updates the sketch for the item with name of key by the amount\n",
" specified in increment\n",
"\n",
" Parameters\n",
" ----------\n",
" key : string\n",
" The item to update the value of in the sketch\n",
" increment : integer\n",
" The amount to update the sketch by for the given key\n",
"\n",
" Examples\n",
" --------\n",
" >>> s = Sketch(10**-7, 0.005, 40)\n",
" >>> s.update('http://www.cnn.com/', 1)\n",
"\n",
" \"\"\"\n",
" for row, hash_function in enumerate(self.hash_functions):\n",
" column = hash_function(abs(hash(key)))\n",
" self.count[row, column] += increment\n",
"\n",
" self.update_heap(key)\n",
"\n",
" def update_heap(self, key):\n",
" \"\"\"\n",
" Updates the class's heap that keeps track of the top k items for a\n",
" given key\n",
"\n",
" For the given key, it checks whether the key is present in the heap,\n",
" updating accordingly if so, and adding it to the heap if it is\n",
" absent\n",
"\n",
" Parameters\n",
" ----------\n",
" key : string\n",
" The item to check against the heap\n",
"\n",
" \"\"\"\n",
" estimate = self.get(key)\n",
"\n",
" if not self.heap or estimate >= self.heap[0][0]:\n",
" if key in self.top_k:\n",
" old_pair = self.top_k.get(key)\n",
" old_pair[0] = estimate\n",
" heapq.heapify(self.heap)\n",
" else:\n",
" if len(self.top_k) < self.k:\n",
" heapq.heappush(self.heap, [estimate, key])\n",
" self.top_k[key] = [estimate, key]\n",
" else:\n",
" new_pair = [estimate, key]\n",
" old_pair = heapq.heappushpop(self.heap, new_pair)\n",
" if new_pair[1] != old_pair[1]:\n",
" del self.top_k[old_pair[1]]\n",
" self.top_k[key] = new_pair\n",
" self.top_k[key] = new_pair\n",
"\n",
" def get(self, key):\n",
" \"\"\"\n",
" Fetches the sketch estimate for the given key\n",
"\n",
" Parameters\n",
" ----------\n",
" key : string\n",
" The item to produce an estimate for\n",
"\n",
" Returns\n",
" -------\n",
" estimate : int\n",
" The best estimate of the count for the given key based on the\n",
" sketch\n",
"\n",
" Examples\n",
" --------\n",
" >>> s = Sketch(10**-7, 0.005, 40)\n",
" >>> s.update('http://www.cnn.com/', 1)\n",
" >>> s.get('http://www.cnn.com/')\n",
" 1\n",
"\n",
" \"\"\"\n",
" value = sys.maxint\n",
" for row, hash_function in enumerate(self.hash_functions):\n",
" column = hash_function(abs(hash(key)))\n",
" value = min(self.count[row, column], value)\n",
"\n",
" return value\n",
"\n",
" def __generate_hash_function(self):\n",
" \"\"\"\n",
" Returns a hash function from a family of pairwise-independent hash\n",
" functions\n",
"\n",
" \"\"\"\n",
" a, b = random_parameter(), random_parameter()\n",
" return lambda x: (a * x + b) % BIG_PRIME % self.w\n",
" "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# define a function to return a list of the exact top users, sorted by count\n",
"def exact_top_users(f, top_n = 10):\n",
" import operator\n",
" counts = {}\n",
" for user in f:\n",
" user = user.rstrip('\\n')\n",
" try:\n",
" if user not in counts:\n",
" counts[user] = 1\n",
" else:\n",
" counts[user] += 1\n",
" except ValueError:\n",
" pass\n",
" except KeyError:\n",
" pass\n",
" counter = 0\n",
" results = []\n",
" for user,count in reversed(sorted(counts.iteritems(), key=operator.itemgetter(1))):\n",
" if counter >= top_n:\n",
" break\n",
" results.append('{},{}'.format(user,str(count)))\n",
" counter += 1\n",
" return results\n",
"# note that the output format is '[user] [count]'"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"f = open('CM_small.txt')\n",
"results_exact = sorted(exact_top_users(f))\n",
"print(results_exact)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# define a function to return a list of the estimated top users, sorted by count\n",
"def CM_top_users(f, s, top_n = 10):\n",
" for user_name in f:\n",
" s.update(user_name.rstrip('\\n'),1)\n",
" \n",
" results = []\n",
" counter = 0\n",
" for value in reversed(sorted(s.top_k.values())):\n",
" if counter >= top_n:\n",
" break\n",
" results.append('{1},{0}'.format(str(value[0]),str(value[1])))\n",
" counter += 1\n",
" return results\n",
"# note that the output format is '[user] [count]'"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# instantiate a Sketch object\n",
"s = Sketch(10**-3, 0.1, 10)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"f = open('CM_small.txt')\n",
"results_CM = sorted(CM_top_users(f,s))\n",
"print(results_CM)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"for item in zip(results_exact,results_CM):\n",
" print(item)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Is it possible to make the sketch so coarse that its estimates are wrong even for this data set?\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"s = Sketch(0.9, 0.9, 10)\n",
"f = open('CM_small.txt')\n",
"results_coarse_CM = CM_top_users(f,s)\n",
"print(results_coarse_CM)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Yes! (if you try enough) Why? \n",
"\n",
"* The 'w' parameter goes like ceiling(exp(1)/epsilon), which is always >=~ 3.\n",
"* The 'd' parameter goes like ceiling(log(1/delta), which is always >= 1.\n",
"\n",
"So, you're dealing with a space with minimum size 3 x 1. With 10 records, it's possible that all 4 users map their counts to the point. So it's possible to see an estimate as high as 10, in this case."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Now for a larger data set."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"f = open('CM_large.txt')\n",
"%time results_exact = exact_top_users(f)\n",
"print(results_exact)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# this could take a few minutes\n",
"\n",
"f = open('CM_large.txt')\n",
"s = Sketch(10**-4, 0.001, 10)\n",
"%time results_CM = CM_top_users(f,s)\n",
"print(results_CM)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For this precision and dataset size, the CM algo takes _much_ longer than the exact solution. In fact, the crossover point at which the CM sketch can achieve reasonable accuracy in the same time as the exact solution is a very large number of entries. "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"for item in zip(results_exact,results_CM):\n",
" print(item)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# the CM sketch gets the top entry (an outlier) correct but doesn't do well estimating the order of the more degenerate counts\n",
"\n",
"# let's decrease the precision via both the epsilon and delta parameters, and see whether it still gets the \"heavy-hitter\" correct\n",
"f = open('CM_large.txt')\n",
"s = Sketch(10**-3, 0.01, 10)\n",
"%time results_CM = CM_top_users(f,s)\n",
"print(results_CM)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# nope...sketch is too coarse, too many collisions, and the prominence of user 'Euph0r1a__ 129' is obscured\n",
"for item in zip(results_exact,results_CM):\n",
" print(item)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The most common use of the CM sketch is analysis of streaming data. Why?\n",
"\n",
"* Becasue the data are arriving in real time, the hashing of the inputs is not a bottleneck as it is when the data are already collected.\n",
"* Similarly, the recalculation of the top-k list (implemented as a heap, in this case) is done on insert. No need to sort the entire list.\n",
"* The sketches are associative, meaning that the operation can be easily parallelized, and the results combined in the end.\n",
"\n",
"**Take away**: use the CM sketch to estimate of the top-k most frequent elements in a streaming environment. "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.8"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| unlicense |
tensorflow/docs-l10n | site/zh-cn/lattice/tutorials/shape_constraints_for_ethics.ipynb | 1 | 39559 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {
"id": "R2AxpObRncMd"
},
"source": [
"***Copyright 2020 The TensorFlow Authors.***"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"cellView": "form",
"id": "gQ5Kfh1YnkFS"
},
"outputs": [],
"source": [
"#@title Licensed under the Apache License, Version 2.0 (the \"License\");\n",
"# you may not use this file except in compliance with the License.\n",
"# You may obtain a copy of the License at\n",
"#\n",
"# https://www.apache.org/licenses/LICENSE-2.0\n",
"#\n",
"# Unless required by applicable law or agreed to in writing, software\n",
"# distributed under the License is distributed on an \"AS IS\" BASIS,\n",
"# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.\n",
"# See the License for the specific language governing permissions and\n",
"# limitations under the License."
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "uc0VwsT5nvQi"
},
"source": [
"# 使用 Tensorflow Lattice 实现道德形状约束"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "gqJQZdvfn32j"
},
"source": [
"<table class=\"tfo-notebook-buttons\" align=\"left\">\n",
" <td><a target=\"_blank\" href=\"https://tensorflow.google.cn/lattice/tutorials/shape_constraints_for_ethics\"><img src=\"https://tensorflow.google.cn/images/tf_logo_32px.png\">在 TensorFlow.org 上查看 </a></td>\n",
" <td><a target=\"_blank\" href=\"https://colab.research.google.com/github/tensorflow/docs-l10n/blob/master/site/zh-cn/lattice/tutorials/shape_constraints_for_ethics.ipynb\"><img src=\"https://tensorflow.google.cn/images/colab_logo_32px.png\">在 Google Colab 中运行 </a></td>\n",
" <td><a target=\"_blank\" href=\"https://github.com/tensorflow/docs-l10n/blob/master/site/zh-cn/lattice/tutorials/shape_constraints_for_ethics.ipynb\"><img src=\"https://tensorflow.google.cn/images/GitHub-Mark-32px.png\">在 GitHub 中查看源代码</a></td>\n",
" <td><a href=\"https://storage.googleapis.com/tensorflow_docs/docs-l10n/site/zh-cn/lattice/tutorials/shape_constraints_for_ethics.ipynb\"><img src=\"https://tensorflow.google.cn/images/download_logo_32px.png\"> 下载笔记本</a></td>\n",
"</table>"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "YFZbuZMAoBny"
},
"source": [
"## 概述\n",
"\n",
"本教程演示了如何使用 TensorFlow Lattice (TFL) 库训练对行为*负责*,并且不违反特定的*道德*或*公平*假设的模型。特别是,我们将侧重于使用单调性约束来避免对某些特性的*不公平惩罚*。本教程包括 Serena Wang 和 Maya Gupta 在 [AISTATS 2020](https://www.aistats.org/) 上发表的论文 [*Deontological Ethics By Monotonicity Shape Constraints*](https://arxiv.org/abs/2001.11990) 中的实验演示。\n",
"\n",
"我们将在公共数据集上使用 TFL Canned Estimator,但请注意,本教程中的所有内容也可以使用通过 TFL Keras 层构造的模型来完成。\n",
"\n",
"在继续之前,请确保您的运行时已安装所有必需的软件包(如下方代码单元中导入的软件包)。"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "o4L76T-NpgCS"
},
"source": [
"## 设置"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "6FvmHcqbpkL7"
},
"source": [
"安装 TF Lattice 软件包:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "f91yvUt_peYs"
},
"outputs": [],
"source": [
"#@test {\"skip\": true}\n",
"!pip install tensorflow-lattice seaborn"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "6TDoQsvSpmfx"
},
"source": [
"导入所需的软件包:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "KGt0pm0b1O5X"
},
"outputs": [],
"source": [
"import tensorflow as tf\n",
"\n",
"import logging\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"import os\n",
"import pandas as pd\n",
"import seaborn as sns\n",
"from sklearn.model_selection import train_test_split\n",
"import sys\n",
"import tensorflow_lattice as tfl\n",
"logging.disable(sys.maxsize)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "DFN6GOcBAqzv"
},
"source": [
"本教程中使用的默认值:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "9uqMM2joAnoW"
},
"outputs": [],
"source": [
"# List of learning rate hyperparameters to try.\n",
"# For a longer list of reasonable hyperparameters, try [0.001, 0.01, 0.1].\n",
"LEARNING_RATES = [0.01]\n",
"# Default number of training epochs and batch sizes.\n",
"NUM_EPOCHS = 1000\n",
"BATCH_SIZE = 1000\n",
"# Directory containing dataset files.\n",
"DATA_DIR = 'https://raw.githubusercontent.com/serenalwang/shape_constraints_for_ethics/master'"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "OZJQfJvY3ibC"
},
"source": [
"# 案例研究 1:法学院入学\n",
"\n",
"在本教程的第一部分中,我们将考虑一个使用法学院招生委员会 (LSAC) 的 Law School Admissions 数据集的案例研究。我们将训练分类器利用以下两个特征来预测学生是否会通过考试:学生的 LSAT 分数和本科生的 GPA。\n",
"\n",
"假设分类器的分数用于指导法学院的招生或奖学金评定。根据基于成绩的社会规范,我们预期具有更高 GPA 和更高 LSAT 分数的学生应当从分类器中获得更高的分数。但是,我们会观察到,模型很容易违反这些直观的规范,有时会惩罚 GPA 或 LSAT 分数较高的人员。\n",
"\n",
"为了解决这种*不公平的惩罚*问题,我们可以施加单调性约束,这样在其他条件相同的情况下,模型永远不会惩罚更高的 GPA 或更高的 LSAT 分数。在本教程中,我们将展示如何使用 TFL 施加这些单调性约束。"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "vJES8lYT1fHN"
},
"source": [
"## 加载法学院数据"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "Cl89ZOsQ14An"
},
"outputs": [],
"source": [
"# Load data file.\n",
"law_file_name = 'lsac.csv'\n",
"law_file_path = os.path.join(DATA_DIR, law_file_name)\n",
"raw_law_df = pd.read_csv(law_file_path, delimiter=',')"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "RCpTYCNjqOsC"
},
"source": [
"预处理数据集:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "jdY5rtLs4xQK"
},
"outputs": [],
"source": [
"# Define label column name.\n",
"LAW_LABEL = 'pass_bar'"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "1t1Hd8gu6Uat"
},
"outputs": [],
"source": [
"def preprocess_law_data(input_df):\n",
" # Drop rows with where the label or features of interest are missing.\n",
" output_df = input_df[~input_df[LAW_LABEL].isna() & ~input_df['ugpa'].isna() &\n",
" (input_df['ugpa'] > 0) & ~input_df['lsat'].isna()]\n",
" return output_df\n",
"\n",
"\n",
"law_df = preprocess_law_data(raw_law_df)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "YhvSKr9SCrHP"
},
"source": [
"### 将数据划分为训练/验证/测试集"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "gQKkIGD-CvGD"
},
"outputs": [],
"source": [
"def split_dataset(input_df, random_state=888):\n",
" \"\"\"Splits an input dataset into train, val, and test sets.\"\"\"\n",
" train_df, test_val_df = train_test_split(\n",
" input_df, test_size=0.3, random_state=random_state)\n",
" val_df, test_df = train_test_split(\n",
" test_val_df, test_size=0.66, random_state=random_state)\n",
" return train_df, val_df, test_df\n",
"\n",
"\n",
"law_train_df, law_val_df, law_test_df = split_dataset(law_df)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "zObwzY7f3aLy"
},
"source": [
"### 可视化数据分布\n",
"\n",
"首先,我们可视化数据的分布。我们将为所有通过考试的学生以及所有未通过考试的学生绘制 GPA 和 LSAT 分数。"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "dRAZB5cLORUG"
},
"outputs": [],
"source": [
"def plot_dataset_contour(input_df, title):\n",
" plt.rcParams['font.family'] = ['serif']\n",
" g = sns.jointplot(\n",
" x='ugpa',\n",
" y='lsat',\n",
" data=input_df,\n",
" kind='kde',\n",
" xlim=[1.4, 4],\n",
" ylim=[0, 50])\n",
" g.plot_joint(plt.scatter, c='b', s=10, linewidth=1, marker='+')\n",
" g.ax_joint.collections[0].set_alpha(0)\n",
" g.set_axis_labels('Undergraduate GPA', 'LSAT score', fontsize=14)\n",
" g.fig.suptitle(title, fontsize=14)\n",
" # Adust plot so that the title fits.\n",
" plt.subplots_adjust(top=0.9)\n",
" plt.show()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "feovlsWPQhVG"
},
"outputs": [],
"source": [
"law_df_pos = law_df[law_df[LAW_LABEL] == 1]\n",
"plot_dataset_contour(\n",
" law_df_pos, title='Distribution of students that passed the bar')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "ct-2tEedU0aO"
},
"outputs": [],
"source": [
"law_df_neg = law_df[law_df[LAW_LABEL] == 0]\n",
"plot_dataset_contour(\n",
" law_df_neg, title='Distribution of students that failed the bar')"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "6grrFEMPfPjk"
},
"source": [
"## 训练校准线性模型以预测考试的通过情况\n",
"\n",
"接下来,我们将通过 TFL 训练*校准线性模型*,以预测学生是否会通过考试。两个输入特征分别是 LSAT 分数和本科 GPA,而训练标签将是学生是否通过了考试。\n",
"\n",
"我们首先在没有任何约束的情况下训练校准线性模型。然后,我们在具有单调性约束的情况下训练校准线性模型,并观察模型输出和准确率的差异。"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "vrUZvP8V736o"
},
"source": [
"### 用于训练 TFL 校准线性 Estimator 的辅助函数\n",
"\n",
"下面这些函数将用于此法学院案例研究以及下面的信用违约案例研究。"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "ollW4xAZ72kz"
},
"outputs": [],
"source": [
"def train_tfl_estimator(train_df, monotonicity, learning_rate, num_epochs,\n",
" batch_size, get_input_fn,\n",
" get_feature_columns_and_configs):\n",
" \"\"\"Trains a TFL calibrated linear estimator.\n",
"\n",
" Args:\n",
" train_df: pandas dataframe containing training data.\n",
" monotonicity: if 0, then no monotonicity constraints. If 1, then all\n",
" features are constrained to be monotonically increasing.\n",
" learning_rate: learning rate of Adam optimizer for gradient descent.\n",
" num_epochs: number of training epochs.\n",
" batch_size: batch size for each epoch. None means the batch size is the full\n",
" dataset size.\n",
" get_input_fn: function that returns the input_fn for a TF estimator.\n",
" get_feature_columns_and_configs: function that returns TFL feature columns\n",
" and configs.\n",
"\n",
" Returns:\n",
" estimator: a trained TFL calibrated linear estimator.\n",
"\n",
" \"\"\"\n",
" feature_columns, feature_configs = get_feature_columns_and_configs(\n",
" monotonicity)\n",
"\n",
" model_config = tfl.configs.CalibratedLinearConfig(\n",
" feature_configs=feature_configs, use_bias=False)\n",
"\n",
" estimator = tfl.estimators.CannedClassifier(\n",
" feature_columns=feature_columns,\n",
" model_config=model_config,\n",
" feature_analysis_input_fn=get_input_fn(input_df=train_df, num_epochs=1),\n",
" optimizer=tf.keras.optimizers.Adam(learning_rate))\n",
"\n",
" estimator.train(\n",
" input_fn=get_input_fn(\n",
" input_df=train_df, num_epochs=num_epochs, batch_size=batch_size))\n",
" return estimator\n",
"\n",
"\n",
"def optimize_learning_rates(\n",
" train_df,\n",
" val_df,\n",
" test_df,\n",
" monotonicity,\n",
" learning_rates,\n",
" num_epochs,\n",
" batch_size,\n",
" get_input_fn,\n",
" get_feature_columns_and_configs,\n",
"):\n",
" \"\"\"Optimizes learning rates for TFL estimators.\n",
"\n",
" Args:\n",
" train_df: pandas dataframe containing training data.\n",
" val_df: pandas dataframe containing validation data.\n",
" test_df: pandas dataframe containing test data.\n",
" monotonicity: if 0, then no monotonicity constraints. If 1, then all\n",
" features are constrained to be monotonically increasing.\n",
" learning_rates: list of learning rates to try.\n",
" num_epochs: number of training epochs.\n",
" batch_size: batch size for each epoch. None means the batch size is the full\n",
" dataset size.\n",
" get_input_fn: function that returns the input_fn for a TF estimator.\n",
" get_feature_columns_and_configs: function that returns TFL feature columns\n",
" and configs.\n",
"\n",
" Returns:\n",
" A single TFL estimator that achieved the best validation accuracy.\n",
" \"\"\"\n",
" estimators = []\n",
" train_accuracies = []\n",
" val_accuracies = []\n",
" test_accuracies = []\n",
" for lr in learning_rates:\n",
" estimator = train_tfl_estimator(\n",
" train_df=train_df,\n",
" monotonicity=monotonicity,\n",
" learning_rate=lr,\n",
" num_epochs=num_epochs,\n",
" batch_size=batch_size,\n",
" get_input_fn=get_input_fn,\n",
" get_feature_columns_and_configs=get_feature_columns_and_configs)\n",
" estimators.append(estimator)\n",
" train_acc = estimator.evaluate(\n",
" input_fn=get_input_fn(train_df, num_epochs=1))['accuracy']\n",
" val_acc = estimator.evaluate(\n",
" input_fn=get_input_fn(val_df, num_epochs=1))['accuracy']\n",
" test_acc = estimator.evaluate(\n",
" input_fn=get_input_fn(test_df, num_epochs=1))['accuracy']\n",
" print('accuracies for learning rate %f: train: %f, val: %f, test: %f' %\n",
" (lr, train_acc, val_acc, test_acc))\n",
" train_accuracies.append(train_acc)\n",
" val_accuracies.append(val_acc)\n",
" test_accuracies.append(test_acc)\n",
" max_index = val_accuracies.index(max(val_accuracies))\n",
" return estimators[max_index]"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "jeEfKSA7_aOg"
},
"source": [
"### 用于配置法学院数据集特征的辅助函数\n",
"\n",
"下面这些辅助函数专用于法学院案例研究。"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "B6NU6EEKIYMJ"
},
"outputs": [],
"source": [
"def get_input_fn_law(input_df, num_epochs, batch_size=None):\n",
" \"\"\"Gets TF input_fn for law school models.\"\"\"\n",
" return tf.compat.v1.estimator.inputs.pandas_input_fn(\n",
" x=input_df[['ugpa', 'lsat']],\n",
" y=input_df['pass_bar'],\n",
" num_epochs=num_epochs,\n",
" batch_size=batch_size or len(input_df),\n",
" shuffle=False)\n",
"\n",
"\n",
"def get_feature_columns_and_configs_law(monotonicity):\n",
" \"\"\"Gets TFL feature configs for law school models.\"\"\"\n",
" feature_columns = [\n",
" tf.feature_column.numeric_column('ugpa'),\n",
" tf.feature_column.numeric_column('lsat'),\n",
" ]\n",
" feature_configs = [\n",
" tfl.configs.FeatureConfig(\n",
" name='ugpa',\n",
" lattice_size=2,\n",
" pwl_calibration_num_keypoints=20,\n",
" monotonicity=monotonicity,\n",
" pwl_calibration_always_monotonic=False),\n",
" tfl.configs.FeatureConfig(\n",
" name='lsat',\n",
" lattice_size=2,\n",
" pwl_calibration_num_keypoints=20,\n",
" monotonicity=monotonicity,\n",
" pwl_calibration_always_monotonic=False),\n",
" ]\n",
" return feature_columns, feature_configs"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "HSfAwgiO_6YA"
},
"source": [
"### 用于可视化训练的模型输出的辅助函数"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "HESNIC5H-1dz"
},
"outputs": [],
"source": [
"def get_predicted_probabilities(estimator, input_df, get_input_fn):\n",
" predictions = estimator.predict(\n",
" input_fn=get_input_fn(input_df=input_df, num_epochs=1))\n",
" return [prediction['probabilities'][1] for prediction in predictions]\n",
"\n",
"\n",
"def plot_model_contour(estimator, input_df, num_keypoints=20):\n",
" x = np.linspace(min(input_df['ugpa']), max(input_df['ugpa']), num_keypoints)\n",
" y = np.linspace(min(input_df['lsat']), max(input_df['lsat']), num_keypoints)\n",
"\n",
" x_grid, y_grid = np.meshgrid(x, y)\n",
"\n",
" positions = np.vstack([x_grid.ravel(), y_grid.ravel()])\n",
" plot_df = pd.DataFrame(positions.T, columns=['ugpa', 'lsat'])\n",
" plot_df[LAW_LABEL] = np.ones(len(plot_df))\n",
" predictions = get_predicted_probabilities(\n",
" estimator=estimator, input_df=plot_df, get_input_fn=get_input_fn_law)\n",
" grid_predictions = np.reshape(predictions, x_grid.shape)\n",
"\n",
" plt.rcParams['font.family'] = ['serif']\n",
" plt.contour(\n",
" x_grid,\n",
" y_grid,\n",
" grid_predictions,\n",
" colors=('k',),\n",
" levels=np.linspace(0, 1, 11))\n",
" plt.contourf(\n",
" x_grid,\n",
" y_grid,\n",
" grid_predictions,\n",
" cmap=plt.cm.bone,\n",
" levels=np.linspace(0, 1, 11)) # levels=np.linspace(0,1,8));\n",
" plt.xticks(fontsize=20)\n",
" plt.yticks(fontsize=20)\n",
"\n",
" cbar = plt.colorbar()\n",
" cbar.ax.set_ylabel('Model score', fontsize=20)\n",
" cbar.ax.tick_params(labelsize=20)\n",
"\n",
" plt.xlabel('Undergraduate GPA', fontsize=20)\n",
" plt.ylabel('LSAT score', fontsize=20)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "fAMSCaRHIn1w"
},
"source": [
"## 训练无约束(非单调)的校准线性模型"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "Iff8omH3Ij_x"
},
"outputs": [],
"source": [
"nomon_linear_estimator = optimize_learning_rates(\n",
" train_df=law_train_df,\n",
" val_df=law_val_df,\n",
" test_df=law_test_df,\n",
" monotonicity=0,\n",
" learning_rates=LEARNING_RATES,\n",
" batch_size=BATCH_SIZE,\n",
" num_epochs=NUM_EPOCHS,\n",
" get_input_fn=get_input_fn_law,\n",
" get_feature_columns_and_configs=get_feature_columns_and_configs_law)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "Gxfv8hXMh4_E"
},
"outputs": [],
"source": [
"plot_model_contour(nomon_linear_estimator, input_df=law_df)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "eKVkjHg_LaWb"
},
"source": [
"## 训练单调的校准线性模型"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "C_MUEvGNp6g2"
},
"outputs": [],
"source": [
"mon_linear_estimator = optimize_learning_rates(\n",
" train_df=law_train_df,\n",
" val_df=law_val_df,\n",
" test_df=law_test_df,\n",
" monotonicity=1,\n",
" learning_rates=LEARNING_RATES,\n",
" batch_size=BATCH_SIZE,\n",
" num_epochs=NUM_EPOCHS,\n",
" get_input_fn=get_input_fn_law,\n",
" get_feature_columns_and_configs=get_feature_columns_and_configs_law)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "ABdhYOUVCXzD"
},
"outputs": [],
"source": [
"plot_model_contour(mon_linear_estimator, input_df=law_df)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "fsI14lrFxRha"
},
"source": [
"## 训练其他无约束的模型\n",
"\n",
"我们演示了可以将 TFL 校准线性模型训练成在 LSAT 分数和 GPA 上均单调,而不会牺牲过多的准确率。\n",
"\n",
"但是,与其他类型的模型(如深度神经网络 (DNN) 或梯度提升树 (GBT))相比,校准线性模型表现如何?DNN 和 GBT 看起来会有公平合理的输出吗?为了解决这一问题,我们接下来将训练无约束的 DNN 和 GBT。实际上,我们将观察到 DNN 和 GBT 都很容易违反 LSAT 分数和本科生 GPA 中的单调性。"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "uo1ruWXcvUqb"
},
"source": [
"### 训练无约束的深度神经网络 (DNN) 模型\n",
"\n",
"之前已对此架构进行了优化,可以实现较高的验证准确率。"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "3pplraob0Od-"
},
"outputs": [],
"source": [
"feature_names = ['ugpa', 'lsat']\n",
"\n",
"dnn_estimator = tf.estimator.DNNClassifier(\n",
" feature_columns=[\n",
" tf.feature_column.numeric_column(feature) for feature in feature_names\n",
" ],\n",
" hidden_units=[100, 100],\n",
" optimizer=tf.keras.optimizers.Adam(learning_rate=0.008),\n",
" activation_fn=tf.nn.relu)\n",
"\n",
"dnn_estimator.train(\n",
" input_fn=get_input_fn_law(\n",
" law_train_df, batch_size=BATCH_SIZE, num_epochs=NUM_EPOCHS))\n",
"dnn_train_acc = dnn_estimator.evaluate(\n",
" input_fn=get_input_fn_law(law_train_df, num_epochs=1))['accuracy']\n",
"dnn_val_acc = dnn_estimator.evaluate(\n",
" input_fn=get_input_fn_law(law_val_df, num_epochs=1))['accuracy']\n",
"dnn_test_acc = dnn_estimator.evaluate(\n",
" input_fn=get_input_fn_law(law_test_df, num_epochs=1))['accuracy']\n",
"print('accuracies for DNN: train: %f, val: %f, test: %f' %\n",
" (dnn_train_acc, dnn_val_acc, dnn_test_acc))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "LwPQqLt-E7R4"
},
"outputs": [],
"source": [
"plot_model_contour(dnn_estimator, input_df=law_df)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "OOAKK0_3vWir"
},
"source": [
"### 训练无约束的梯度提升树 (GBT) 模型\n",
"\n",
"之前已对此树形结构进行了优化,可以实现较高的验证准确率。"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "mFaI9hB-rgoL"
},
"outputs": [],
"source": [
"tree_estimator = tf.estimator.BoostedTreesClassifier(\n",
" feature_columns=[\n",
" tf.feature_column.numeric_column(feature) for feature in feature_names\n",
" ],\n",
" n_batches_per_layer=2,\n",
" n_trees=20,\n",
" max_depth=4)\n",
"\n",
"tree_estimator.train(\n",
" input_fn=get_input_fn_law(\n",
" law_train_df, num_epochs=NUM_EPOCHS, batch_size=BATCH_SIZE))\n",
"tree_train_acc = tree_estimator.evaluate(\n",
" input_fn=get_input_fn_law(law_train_df, num_epochs=1))['accuracy']\n",
"tree_val_acc = tree_estimator.evaluate(\n",
" input_fn=get_input_fn_law(law_val_df, num_epochs=1))['accuracy']\n",
"tree_test_acc = tree_estimator.evaluate(\n",
" input_fn=get_input_fn_law(law_test_df, num_epochs=1))['accuracy']\n",
"print('accuracies for GBT: train: %f, val: %f, test: %f' %\n",
" (tree_train_acc, tree_val_acc, tree_test_acc))"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "AZFyfQT1E_nR"
},
"outputs": [],
"source": [
"plot_model_contour(tree_estimator, input_df=law_df)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "uX2qiMlrY8aO"
},
"source": [
"# 案例研究 2:信用违约\n",
"\n",
"我们将在本教程中考虑的第二个案例研究是预测个人的信用违约概率。我们将使用 UCI 存储库中的 Default of Credit Card Clients 数据集。这些数据收集自 30,000 名中国台湾信用卡用户,并包含一个二元标签,用于标识用户是否在时间窗口内拖欠了付款。特征包括婚姻状况、性别、教育程度以及在 2005 年 4-9 月的每个月中,用户拖欠现有账单的时间有多长。\n",
"\n",
"正如我们在第一个案例研究中所做的那样,我们再次阐明了使用单调性约束来避免*不公平的惩罚*:使用该模型来确定用户的信用评分时,在其他条件都相同的情况下,如果许多人因较早支付账单而受到惩罚,那么这对他们来说是不公平的。因此,我们应用了单调性约束,使模型不会惩罚提前付款。"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "tz5yduNuFinA"
},
"source": [
"## 加载信用违约数据"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "KuylMNBCILwy"
},
"outputs": [],
"source": [
"# Load data file.\n",
"credit_file_name = 'credit_default.csv'\n",
"credit_file_path = os.path.join(DATA_DIR, credit_file_name)\n",
"credit_df = pd.read_csv(credit_file_path, delimiter=',')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "Hv_GQcEHIf9v"
},
"outputs": [],
"source": [
"# Define label column name.\n",
"CREDIT_LABEL = 'default'"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "13oZWY0YIoy3"
},
"source": [
"### 将数据划分为训练/验证/测试集"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "dty5tXJqIscz"
},
"outputs": [],
"source": [
"credit_train_df, credit_val_df, credit_test_df = split_dataset(credit_df)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "_kAciWXHKGV7"
},
"source": [
"### 可视化数据分布\n",
"\n",
"首先,我们可视化数据的分布。我们将为婚姻状况和还款状况不同的人绘制观察到的违约率的平均值和标准误差。还款状态表示一个人已偿还贷款的月数(截至 2005 年 4 月)。"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "8CxacQxnkHWE"
},
"outputs": [],
"source": [
"def get_agg_data(df, x_col, y_col, bins=11):\n",
" xbins = pd.cut(df[x_col], bins=bins)\n",
" data = df[[x_col, y_col]].groupby(xbins).agg(['mean', 'sem'])\n",
" return data\n",
"\n",
"\n",
"def plot_2d_means_credit(input_df, x_col, y_col, x_label, y_label):\n",
" plt.rcParams['font.family'] = ['serif']\n",
" _, ax = plt.subplots(nrows=1, ncols=1)\n",
" plt.setp(ax.spines.values(), color='black', linewidth=1)\n",
" ax.tick_params(\n",
" direction='in', length=6, width=1, top=False, right=False, labelsize=18)\n",
" df_single = get_agg_data(input_df[input_df['MARRIAGE'] == 1], x_col, y_col)\n",
" df_married = get_agg_data(input_df[input_df['MARRIAGE'] == 2], x_col, y_col)\n",
" ax.errorbar(\n",
" df_single[(x_col, 'mean')],\n",
" df_single[(y_col, 'mean')],\n",
" xerr=df_single[(x_col, 'sem')],\n",
" yerr=df_single[(y_col, 'sem')],\n",
" color='orange',\n",
" marker='s',\n",
" capsize=3,\n",
" capthick=1,\n",
" label='Single',\n",
" markersize=10,\n",
" linestyle='')\n",
" ax.errorbar(\n",
" df_married[(x_col, 'mean')],\n",
" df_married[(y_col, 'mean')],\n",
" xerr=df_married[(x_col, 'sem')],\n",
" yerr=df_married[(y_col, 'sem')],\n",
" color='b',\n",
" marker='^',\n",
" capsize=3,\n",
" capthick=1,\n",
" label='Married',\n",
" markersize=10,\n",
" linestyle='')\n",
" leg = ax.legend(loc='upper left', fontsize=18, frameon=True, numpoints=1)\n",
" ax.set_xlabel(x_label, fontsize=18)\n",
" ax.set_ylabel(y_label, fontsize=18)\n",
" ax.set_ylim(0, 1.1)\n",
" ax.set_xlim(-2, 8.5)\n",
" ax.patch.set_facecolor('white')\n",
" leg.get_frame().set_edgecolor('black')\n",
" leg.get_frame().set_facecolor('white')\n",
" leg.get_frame().set_linewidth(1)\n",
" plt.show()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "VHXyYbyekKLT"
},
"outputs": [],
"source": [
"plot_2d_means_credit(credit_train_df, 'PAY_0', 'default',\n",
" 'Repayment Status (April)', 'Observed default rate')"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "4hnZBigB7kzY"
},
"source": [
"## 训练校准线性模型以预测信用违约率\n",
"\n",
"接下来,我们将通过 TFL 训练*校准线性模型*,以预测某人是否会拖欠贷款。两个输入特征将是该人的婚姻状况以及该人截至 4 月已偿还贷款的月数(还款状态)。训练标签将是该人是否拖欠过贷款。\n",
"\n",
"我们首先在没有任何约束的情况下训练校准线性模型。然后,我们在具有单调性约束的情况下训练校准线性模型,并观察模型输出和准确率的差异。"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "UEcHW1u3Jk_2"
},
"source": [
"### 用于配置信用违约数据集特征的辅助函数\n",
"\n",
"下面这些辅助函数专用于信用违约案例研究。"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "QBa-hczLi7DM"
},
"outputs": [],
"source": [
"def get_input_fn_credit(input_df, num_epochs, batch_size=None):\n",
" \"\"\"Gets TF input_fn for credit default models.\"\"\"\n",
" return tf.compat.v1.estimator.inputs.pandas_input_fn(\n",
" x=input_df[['MARRIAGE', 'PAY_0']],\n",
" y=input_df['default'],\n",
" num_epochs=num_epochs,\n",
" batch_size=batch_size or len(input_df),\n",
" shuffle=False)\n",
"\n",
"\n",
"def get_feature_columns_and_configs_credit(monotonicity):\n",
" \"\"\"Gets TFL feature configs for credit default models.\"\"\"\n",
" feature_columns = [\n",
" tf.feature_column.numeric_column('MARRIAGE'),\n",
" tf.feature_column.numeric_column('PAY_0'),\n",
" ]\n",
" feature_configs = [\n",
" tfl.configs.FeatureConfig(\n",
" name='MARRIAGE',\n",
" lattice_size=2,\n",
" pwl_calibration_num_keypoints=3,\n",
" monotonicity=monotonicity,\n",
" pwl_calibration_always_monotonic=False),\n",
" tfl.configs.FeatureConfig(\n",
" name='PAY_0',\n",
" lattice_size=2,\n",
" pwl_calibration_num_keypoints=10,\n",
" monotonicity=monotonicity,\n",
" pwl_calibration_always_monotonic=False),\n",
" ]\n",
" return feature_columns, feature_configs"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "iwxnlRrQPdTg"
},
"source": [
"### 用于可视化训练的模型输出的辅助函数"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "zVGxEfbhPZ5H"
},
"outputs": [],
"source": [
"def plot_predictions_credit(input_df,\n",
" estimator,\n",
" x_col,\n",
" x_label='Repayment Status (April)',\n",
" y_label='Predicted default probability'):\n",
" predictions = get_predicted_probabilities(\n",
" estimator=estimator, input_df=input_df, get_input_fn=get_input_fn_credit)\n",
" new_df = input_df.copy()\n",
" new_df.loc[:, 'predictions'] = predictions\n",
" plot_2d_means_credit(new_df, x_col, 'predictions', x_label, y_label)"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "UMIpywE1P07H"
},
"source": [
"## 训练无约束(非单调)的校准线性模型"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "FfXUKns5cPEw"
},
"outputs": [],
"source": [
"nomon_linear_estimator = optimize_learning_rates(\n",
" train_df=credit_train_df,\n",
" val_df=credit_val_df,\n",
" test_df=credit_test_df,\n",
" monotonicity=0,\n",
" learning_rates=LEARNING_RATES,\n",
" batch_size=BATCH_SIZE,\n",
" num_epochs=NUM_EPOCHS,\n",
" get_input_fn=get_input_fn_credit,\n",
" get_feature_columns_and_configs=get_feature_columns_and_configs_credit)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "5zQ_jm75kRX6"
},
"outputs": [],
"source": [
"plot_predictions_credit(credit_train_df, nomon_linear_estimator, 'PAY_0')"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "0aokp7qLQBIr"
},
"source": [
"## 训练单调的校准线性模型"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "wWCG7YrLUZDH"
},
"outputs": [],
"source": [
"mon_linear_estimator = optimize_learning_rates(\n",
" train_df=credit_train_df,\n",
" val_df=credit_val_df,\n",
" test_df=credit_test_df,\n",
" monotonicity=1,\n",
" learning_rates=LEARNING_RATES,\n",
" batch_size=BATCH_SIZE,\n",
" num_epochs=NUM_EPOCHS,\n",
" get_input_fn=get_input_fn_credit,\n",
" get_feature_columns_and_configs=get_feature_columns_and_configs_credit)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"id": "JCQ2eMdndFhR"
},
"outputs": [],
"source": [
"plot_predictions_credit(credit_train_df, mon_linear_estimator, 'PAY_0')"
]
}
],
"metadata": {
"colab": {
"collapsed_sections": [],
"name": "shape_constraints_for_ethics.ipynb",
"toc_visible": true
},
"kernelspec": {
"display_name": "Python 3",
"name": "python3"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| apache-2.0 |
sauloal/ipython | probes/probes_cfg_images.ipynb | 1 | 311910 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Parameters"
]
},
{
"cell_type": "code",
"execution_count": 391,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"CONFIG_LOCAL = False\n",
"#CONFIG_LOCAL = True"
]
},
{
"cell_type": "code",
"execution_count": 392,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"if CONFIG_LOCAL:\n",
" config = {\n",
" 'data_folder' : 'probes',\n",
" 'RUN' : 'run_BWA_JKL_23_JU_1_orig',\n",
" 'chromosome' : 'SL2.40ch12',\n",
" 'scaffold' : 'SL2.40sc05611',\n",
" 'out_folder' : 'reports',\n",
" 'out_extensions': ['eps', 'png']\n",
" }\n",
"\n",
" if True:\n",
" config['BAC' ] = 'JBPP0904'\n",
" config['BAC_coord_start'] = 967164\n",
" config['BAC_coord_end' ] = 970727\n",
" config['BAC_coord' ] = '%012d-%012d' % ( config['BAC_coord_start'], config['BAC_coord_end' ] )\n",
" config['RUN' ] = 'run_BWA_JKL_23_JU_1_orig_PROBES'"
]
},
{
"cell_type": "code",
"execution_count": 393,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"if CONFIG_LOCAL:\n",
" %run -i probes_cfg.ipynb"
]
},
{
"cell_type": "code",
"execution_count": 394,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h1>Singularity Report</h1>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"<h2>Run: run_BWA_JKL_23_JU_1_orig_PROBES</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"<h2>Chromosome: SL2.40ch12</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"<h2>Scaffold: SL2.40sc05611</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"<h3>BAC: JBPP0904</h3>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"<h3>BAC coord start: 967164</h3>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"<h3>BAC coord end: 970727</h3>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Config\n",
"\tBAC : JBPP0904\n",
"\tBAC_coord : 000000967164-000000970727\n",
"\tBAC_coord_end : 970727\n",
"\tBAC_coord_start: 967164\n",
"\tRUN : run_BWA_JKL_23_JU_1_orig_PROBES\n",
"\tchromosome : SL2.40ch12\n",
"\tdata_folder : probes\n",
"\tout_extensions : ['eps', 'png', 'pdf']\n",
"\tout_folder : reports\n",
"\tscaffold : SL2.40sc05611\n",
"Max Rows : 10000\n",
"Column Names\n",
"\tK-mer Coverage\n",
"\tSequencing Coverage\n",
"\tBLAST Coverage\n",
"\tNs\n",
"\tAGP Contig\n",
"\tAGP Gap\n",
"\tK-mer Coverage averaged: 500 bp\n",
"\tK-mer Coverage averaged: 5 Kbp\n",
"\tK-mer Coverage averaged: 1 Mbp\n"
]
}
],
"source": [
"if CONFIG_LOCAL:\n",
" %run -i probes_cfg_header.ipynb"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Imports"
]
},
{
"cell_type": "code",
"execution_count": 395,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Populating the interactive namespace from numpy and matplotlib\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"WARNING: pylab import has clobbered these variables: ['axes', 'f', 'axis']\n",
"`%matplotlib` prevents importing * from pylab and numpy\n"
]
}
],
"source": [
"import pandas as pd\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"from matplotlib import gridspec\n",
"import os\n",
"import operator\n",
"\n",
"#import pylab\n",
"#pylab.show()\n",
"\n",
"%pylab inline\n",
"\n",
"pd.set_option('display.notebook_repr_html', True)\n",
"#pd.set_option('display.max_columns', 20)\n",
"#pd.set_option('display.max_rows', 25)\n",
"\n",
"from IPython.display import HTML, display\n",
"def addHeader(level, text):\n",
" display( HTML('''<h%(level)d>%(text)s</h%(level)d>''' % {'level':level, 'text':text}) )"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Files"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Input Files"
]
},
{
"cell_type": "code",
"execution_count": 396,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h1>Files</h1>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"<h2>Input Files</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"KmerCoverageFile : True probes/run_BWA_JKL_23_JU_1_orig_PROBES/S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727.S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.sam.SL2.40sc05611.sam.cov.prop.cov.gz\n",
"SequencingCoverageFile: True probes/run_BWA_JKL_23_JU_1_orig_PROBES/S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727.S_lycopersicum_chromosomes.fa_S_lycopersicum_chromosomes.pos.SL2.40ch12.pos.cov.SL2.40sc05611.cov.gz\n",
"AgpContigFile : True probes/run_BWA_JKL_23_JU_1_orig_PROBES/S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727.S_lycopersicum_scaffolds_from_contigs.2.40.agp.SL2.40sc05611.agp.contig.agp.cov.gz\n",
"AgpGapFile : True probes/run_BWA_JKL_23_JU_1_orig_PROBES/S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727.S_lycopersicum_scaffolds_from_contigs.2.40.agp.SL2.40sc05611.agp.gap.agp.cov.gz\n",
"AgpOtherFile : True probes/run_BWA_JKL_23_JU_1_orig_PROBES/S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727.S_lycopersicum_scaffolds_from_contigs.2.40.agp.SL2.40sc05611.agp.other.agp.cov.gz\n",
"AgpUnknownFile : True probes/run_BWA_JKL_23_JU_1_orig_PROBES/S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727.S_lycopersicum_scaffolds_from_contigs.2.40.agp.SL2.40sc05611.agp.unknown.agp.cov.gz\n",
"NsFile : True probes/run_BWA_JKL_23_JU_1_orig_PROBES/S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727.S_lycopersicum_scaffolds.fa_NONE.tab.SL2.40ch12.tab.SL2.40sc05611.tab.cov.gz\n",
"BlastCoverageFile : True probes/run_BWA_JKL_23_JU_1_orig_PROBES/S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727_Product.fasta.blast.cov.gz\n",
"\n",
"all files present\n"
]
}
],
"source": [
"addHeader(1,'Files')\n",
"addHeader(2,'Input Files')\n",
"\"\"\"\n",
"S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.sam.SL2.40sc06147.sam.cov\n",
"S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.sam.SL2.40sc06147.sam.cov.prop.cov\n",
"S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.sam.SL2.40sc06147.sam.pos\n",
"\"\"\"\n",
" \n",
"KmerCoverageFile = \"%(data_folder)s/%(RUN)s/S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.%(chromosome)s.sam.%(scaffold)s.sam.cov.prop.cov.gz\" % config\n",
"SequencingCoverageFile = \"%(data_folder)s/mapping/out/S_lycopersicum_chromosomes.fa_S_lycopersicum_chromosomes.pos.%(chromosome)s.pos.cov.%(scaffold)s.cov.gz\" % config\n",
"AgpContigFile = \"%(data_folder)s/agp/S_lycopersicum_scaffolds_from_contigs.2.40.agp.%(scaffold)s.agp.contig.agp.cov.gz\" % config\n",
"AgpGapFile = \"%(data_folder)s/agp/S_lycopersicum_scaffolds_from_contigs.2.40.agp.%(scaffold)s.agp.gap.agp.cov.gz\" % config\n",
"AgpOtherFile = \"%(data_folder)s/agp/S_lycopersicum_scaffolds_from_contigs.2.40.agp.%(scaffold)s.agp.other.agp.cov.gz\" % config\n",
"AgpUnknownFile = \"%(data_folder)s/agp/S_lycopersicum_scaffolds_from_contigs.2.40.agp.%(scaffold)s.agp.unknown.agp.cov.gz\" % config\n",
"NsFile = \"%(data_folder)s/Ns/S_lycopersicum_scaffolds.fa_NONE.tab.%(chromosome)s.tab.%(scaffold)s.tab.cov.gz\" % config\n",
"infiles = [KmerCoverageFile, SequencingCoverageFile, \n",
" AgpContigFile, AgpGapFile, \n",
" AgpUnknownFile, AgpOtherFile, NsFile]\n",
"\n",
"if BAC_MODE:\n",
" \"\"\"\n",
"\n",
" S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727.S_lycopersicum_chromosomes.fa_S_lycopersicum_chromosomes.pos.SL2.40ch12.pos.cov.SL2.40sc05611.cov\n",
" S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727.S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.sam.SL2.40sc05611.sam.cov.prop.cov\n",
" S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727_Product.fasta.blast.cov\n",
" S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727.S_lycopersicum_scaffolds_from_contigs.2.40.agp.SL2.40sc05611.agp.contig.agp.cov\n",
" S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727.S_lycopersicum_scaffolds_from_contigs.2.40.agp.SL2.40sc05611.agp.gap.agp.cov\n",
" S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727.S_lycopersicum_scaffolds_from_contigs.2.40.agp.SL2.40sc05611.agp.other.agp.cov\n",
" S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727.S_lycopersicum_scaffolds_from_contigs.2.40.agp.SL2.40sc05611.agp.unknown.agp.cov\n",
" S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727.S_lycopersicum_scaffolds.fa_NONE.tab.SL2.40ch12.tab.SL2.40sc05611.tab.cov\n",
" \"\"\"\n",
" \n",
" config['in_base_name'] = \"%(data_folder)s/%(RUN)s/S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.%(chromosome)s.%(scaffold)s.%(BAC)s_primer.%(BAC_coord)s\" % config\n",
" KmerCoverageFile = \"%(in_base_name)s.S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.%(chromosome)s.sam.%(scaffold)s.sam.cov.prop.cov.gz\" % config\n",
" SequencingCoverageFile = \"%(in_base_name)s.S_lycopersicum_chromosomes.fa_S_lycopersicum_chromosomes.pos.%(chromosome)s.pos.cov.%(scaffold)s.cov.gz\" % config\n",
" BlastCoverageFile = \"%(in_base_name)s_Product.fasta.blast.cov.gz\" % config\n",
" AgpContigFile = \"%(in_base_name)s.S_lycopersicum_scaffolds_from_contigs.2.40.agp.%(scaffold)s.agp.contig.agp.cov.gz\" % config\n",
" AgpGapFile = \"%(in_base_name)s.S_lycopersicum_scaffolds_from_contigs.2.40.agp.%(scaffold)s.agp.gap.agp.cov.gz\" % config\n",
" AgpOtherFile = \"%(in_base_name)s.S_lycopersicum_scaffolds_from_contigs.2.40.agp.%(scaffold)s.agp.other.agp.cov.gz\" % config\n",
" AgpUnknownFile = \"%(in_base_name)s.S_lycopersicum_scaffolds_from_contigs.2.40.agp.%(scaffold)s.agp.unknown.agp.cov.gz\" % config\n",
" NsFile = \"%(in_base_name)s.S_lycopersicum_scaffolds.fa_NONE.tab.%(chromosome)s.tab.%(scaffold)s.tab.cov.gz\" % config\n",
" \n",
" infiles = [KmerCoverageFile , SequencingCoverageFile, \n",
" BlastCoverageFile, AgpContigFile, \n",
" AgpGapFile , AgpUnknownFile, \n",
" AgpOtherFile , NsFile]\n",
"\n",
"\n",
"print \"%-22s: %-5s %s\" % ( \"KmerCoverageFile\" , os.path.exists(KmerCoverageFile) , KmerCoverageFile )\n",
"print \"%-22s: %-5s %s\" % ( \"SequencingCoverageFile\", os.path.exists(SequencingCoverageFile), SequencingCoverageFile )\n",
"print \"%-22s: %-5s %s\" % ( \"AgpContigFile\" , os.path.exists(AgpContigFile) , AgpContigFile )\n",
"print \"%-22s: %-5s %s\" % ( \"AgpGapFile\" , os.path.exists(AgpGapFile) , AgpGapFile )\n",
"print \"%-22s: %-5s %s\" % ( \"AgpOtherFile\" , os.path.exists(AgpOtherFile) , AgpOtherFile )\n",
"print \"%-22s: %-5s %s\" % ( \"AgpUnknownFile\" , os.path.exists(AgpUnknownFile) , AgpUnknownFile )\n",
"print \"%-22s: %-5s %s\" % ( \"NsFile\" , os.path.exists(NsFile) , NsFile )\n",
"\n",
"\n",
"\n",
"if BAC_MODE:\n",
" print \"%-22s: %-5s %s\" % ( \"BlastCoverageFile\" , os.path.exists(BlastCoverageFile) , BlastCoverageFile )\n",
"\n",
"print\n",
"\n",
"\n",
"\n",
"if not all([os.path.exists(x) for x in infiles]):\n",
" print \"missing file\"\n",
"\n",
"else:\n",
" print \"all files present\"\n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Output Files"
]
},
{
"cell_type": "code",
"execution_count": 397,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h2>Output Files</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"BLAST Coverage Distribution :\n",
" - reports/eps/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.BLAST_Coverage_Distribution.eps\n",
" - reports/png/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.BLAST_Coverage_Distribution.png\n",
" - reports/pdf/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.BLAST_Coverage_Distribution.pdf\n",
"BLAST Coverage Stats :\n",
" - reports/eps/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.BLAST_Coverage_Stats.eps\n",
" - reports/png/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.BLAST_Coverage_Stats.png\n",
" - reports/pdf/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.BLAST_Coverage_Stats.pdf\n",
"Combined graph :\n",
" - reports/eps/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Combined_graph.eps\n",
" - reports/png/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Combined_graph.png\n",
" - reports/pdf/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Combined_graph.pdf\n",
"Gaps Distribution :\n",
" - reports/eps/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Gaps_Distribution.eps\n",
" - reports/png/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Gaps_Distribution.png\n",
" - reports/pdf/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Gaps_Distribution.pdf\n",
"K-mer Coverage Distribution :\n",
" - reports/eps/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.K-mer_Coverage_Distribution.eps\n",
" - reports/png/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.K-mer_Coverage_Distribution.png\n",
" - reports/pdf/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.K-mer_Coverage_Distribution.pdf\n",
"K-mer Coverage Stats :\n",
" - reports/eps/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.K-mer_Coverage_Stats.eps\n",
" - reports/png/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.K-mer_Coverage_Stats.png\n",
" - reports/pdf/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.K-mer_Coverage_Stats.pdf\n",
"Ns Distribution :\n",
" - reports/eps/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Ns_Distribution.eps\n",
" - reports/png/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Ns_Distribution.png\n",
" - reports/pdf/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Ns_Distribution.pdf\n",
"Sequencing Coverage Distribution:\n",
" - reports/eps/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Sequencing_Coverage_Distribution.eps\n",
" - reports/png/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Sequencing_Coverage_Distribution.png\n",
" - reports/pdf/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Sequencing_Coverage_Distribution.pdf\n",
"Sequencing Coverage Stats :\n",
" - reports/eps/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Sequencing_Coverage_Stats.eps\n",
" - reports/png/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Sequencing_Coverage_Stats.png\n",
" - reports/pdf/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Sequencing_Coverage_Stats.pdf\n",
"all_data :\n",
" - reports/eps/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.raw_data.csv\n",
" - reports/png/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.raw_data.csv\n",
" - reports/pdf/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.raw_data.csv\n",
"all_data_full :\n",
" - reports/eps/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.K-raw_data.full.csv\n",
" - reports/png/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.K-raw_data.full.csv\n",
" - reports/pdf/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.K-raw_data.full.csv\n"
]
}
],
"source": [
"addHeader(2,'Output Files')\n",
"\n",
"config['out_bn' ] = \"%(out_folder)s/%%s/%(RUN)s_%(chromosome)s_%(scaffold)s_prop\" % config\n",
"config['out_bn_img' ] = \"%(out_bn)s.%%s.%%s\" % config\n",
"\n",
"if BAC_MODE:\n",
" config['out_bn' ] = \"%(out_folder)s/%%s/%(RUN)s_%(chromosome)s_%(scaffold)s_%(BAC)s_%(BAC_coord)s\" % config\n",
" config['out_bn_img' ] = \"%(out_bn)s.%%s.%%s\" % config\n",
"\n",
" \n",
"output_files = {\n",
" 'all_data' : [ config['out_bn_img'] % (ext, 'raw_data' , 'csv' ) for ext in config['out_extensions'] ],\n",
" 'all_data_full' : [ config['out_bn_img'] % (ext, 'K-raw_data' , 'full.csv') for ext in config['out_extensions'] ],\n",
" 'K-mer Coverage Stats' : [ config['out_bn_img'] % (ext, 'K-mer_Coverage_Stats' , ext ) for ext in config['out_extensions'] ],\n",
" 'Sequencing Coverage Stats' : [ config['out_bn_img'] % (ext, 'Sequencing_Coverage_Stats' , ext ) for ext in config['out_extensions'] ],\n",
" 'K-mer Coverage Distribution' : [ config['out_bn_img'] % (ext, 'K-mer_Coverage_Distribution' , ext ) for ext in config['out_extensions'] ],\n",
" 'Sequencing Coverage Distribution': [ config['out_bn_img'] % (ext, 'Sequencing_Coverage_Distribution', ext ) for ext in config['out_extensions'] ],\n",
" 'Gaps Distribution' : [ config['out_bn_img'] % (ext, 'Gaps_Distribution' , ext ) for ext in config['out_extensions'] ],\n",
" 'Ns Distribution' : [ config['out_bn_img'] % (ext, 'Ns_Distribution' , ext ) for ext in config['out_extensions'] ],\n",
" 'Combined graph' : [ config['out_bn_img'] % (ext, 'Combined_graph' , ext ) for ext in config['out_extensions'] ]\n",
"}\n",
"\n",
"\n",
"if BAC_MODE:\n",
" output_files['BLAST Coverage Stats' ] = [ config['out_bn_img'] % (ext, 'BLAST_Coverage_Stats' , ext) for ext in config['out_extensions'] ]\n",
" output_files['BLAST Coverage Distribution'] = [ config['out_bn_img'] % (ext, 'BLAST_Coverage_Distribution', ext) for ext in config['out_extensions'] ]\n",
"\n",
" \n",
"for of in sorted(output_files.keys()):\n",
" print \"%-32s:\\n - %s\" % ( of, \"\\n - \".join( output_files[of] ) )"
]
},
{
"cell_type": "code",
"execution_count": 398,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"class size_controller(object):\n",
" def __init__(self, w, h):\n",
" self.w = w\n",
" self.h = h\n",
" \n",
" def __enter__(self):\n",
" self.o = rcParams['figure.figsize']\n",
" rcParams['figure.figsize'] = self.w, self.h\n",
" return None\n",
" \n",
" def __exit__(self, type, value, traceback):\n",
" rcParams['figure.figsize'] = self.o\n",
" \n",
"col_type_int = np.int64\n",
"col_type_flo = np.float64\n",
"col_type_str = np.object\n",
"col_type_bol = np.int8"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Read Files"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## K-mer Coverage File"
]
},
{
"cell_type": "code",
"execution_count": 399,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h1>Read Files</h1>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"<h2>K-mer Coverage File</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"addHeader(1,'Read Files')\n",
"addHeader(2,'K-mer Coverage File')\n",
"\n",
"col_info = [\n",
" [ \"Position\" , col_type_int ], \n",
" [ \"K-mer Coverage\" , col_type_flo ], \n",
" [ \"K-mer Coverage averaged: 500 bp\" , col_type_flo ], \n",
" [ \"K-mer Coverage averaged: 2.5 Kbp\" , col_type_flo ], \n",
" [ \"K-mer Coverage averaged: 5 Kbp\" , col_type_flo ], \n",
" [ \"K-mer Coverage averaged: 50 Kbp\" , col_type_flo ], \n",
" [ \"K-mer Coverage averaged: 1 Mbp\" , col_type_flo ], \n",
" [ \"K-mer Coverage averaged: 5 Kbp before\", col_type_flo ], \n",
" [ \"K-mer Coverage averaged: 5 Kbp after\" , col_type_flo ]\n",
"]\n",
"\n",
"col_names=[cf[0] for cf in col_info]\n",
"col_types=dict(zip([c[0] for c in col_info], [c[1] for c in col_info]))\n",
"\n",
"if PARSE_VERBOSE:\n",
" print \"\\n\".join( col_names )"
]
},
{
"cell_type": "code",
"execution_count": 400,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"probes/run_BWA_JKL_23_JU_1_orig_PROBES/S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727.S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.sam.SL2.40sc05611.sam.cov.prop.cov.gz\n",
"Loaded 3564 rows and 9 columns\n"
]
}
],
"source": [
"SKIP_ROWS = 1\n",
"\n",
"print KmerCoverageFile\n",
"\n",
"KmerData = pd.read_csv(KmerCoverageFile, header=None, names=col_names, dtype=col_types, nrows=NROWS, \\\n",
" skiprows=SKIP_ROWS, verbose=PARSE_VERBOSE, delimiter=\"\\t\", comment=\"#\", compression=\"gzip\")\n",
" \n",
"print \"Loaded %d rows and %d columns\" % ( KmerData.shape[0], KmerData.shape[1] )\n",
"\n",
"if PARSE_VERBOSE:\n",
" print KmerData.head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Sequencing Coverage File"
]
},
{
"cell_type": "code",
"execution_count": 401,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h2>Sequencing Coverage File</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"addHeader(2,'Sequencing Coverage File')\n",
"\n",
"col_info = [\n",
" [ \"Position\" , col_type_int ], \n",
" [ \"Sequencing Coverage\" , col_type_int ]\n",
"]\n",
"\n",
"col_names=[cf[0] for cf in col_info]\n",
"col_types=dict(zip([c[0] for c in col_info], [c[1] for c in col_info]))\n",
"\n",
"if PARSE_VERBOSE:\n",
" print col_names\n",
" col_types"
]
},
{
"cell_type": "code",
"execution_count": 402,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"probes/run_BWA_JKL_23_JU_1_orig_PROBES/S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727.S_lycopersicum_chromosomes.fa_S_lycopersicum_chromosomes.pos.SL2.40ch12.pos.cov.SL2.40sc05611.cov.gz\n",
"Loaded 3564 rows and 2 columns\n"
]
}
],
"source": [
"SKIP_ROWS = 0\n",
"\n",
"print SequencingCoverageFile\n",
"\n",
"SequencingCoverageData = pd.read_csv(SequencingCoverageFile, header=None, names=col_names, dtype=col_types, nrows=NROWS, \\\n",
" skiprows=SKIP_ROWS, verbose=PARSE_VERBOSE, delimiter=\"\\t\", comment=\"#\", compression=\"gzip\")\n",
"\n",
"print \"Loaded %d rows and %d columns\" % ( SequencingCoverageData.shape[0], SequencingCoverageData.shape[1] )\n",
"\n",
"if PARSE_VERBOSE:\n",
" print SequencingCoverageData.head()"
]
},
{
"cell_type": "code",
"execution_count": 403,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h2>BLAST</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"if BAC_MODE:\n",
" addHeader(2,'BLAST')\n",
"\n",
" col_info = [\n",
" [ \"Position\" , col_type_int ], \n",
" [ \"BLAST Coverage\" , col_type_flo ]\n",
" ]\n",
"\n",
" col_names=[cf[0] for cf in col_info]\n",
" col_types=dict(zip([c[0] for c in col_info], [c[1] for c in col_info]))\n",
"\n",
" if PARSE_VERBOSE:\n",
" print col_names\n",
" col_types"
]
},
{
"cell_type": "code",
"execution_count": 404,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"probes/run_BWA_JKL_23_JU_1_orig_PROBES/S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727_Product.fasta.blast.cov.gz\n",
"Loaded 3564 rows and 2 columns\n"
]
}
],
"source": [
"if BAC_MODE:\n",
" SKIP_ROWS = 0\n",
" \n",
" print BlastCoverageFile\n",
" \n",
" BlastCoverageData = pd.read_csv(BlastCoverageFile, header=None, names=col_names, dtype=col_types, nrows=NROWS, \\\n",
" skiprows=SKIP_ROWS, verbose=PARSE_VERBOSE, delimiter=\"\\t\", comment=\"#\", compression=\"gzip\")\n",
" \n",
" print \"Loaded %d rows and %d columns\" % ( BlastCoverageData.shape[0], BlastCoverageData.shape[1] )\n",
" \n",
" if PARSE_VERBOSE:\n",
" print BlastCoverageData.head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## AGP"
]
},
{
"cell_type": "code",
"execution_count": 405,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h2>AGP</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"addHeader(2,'AGP')\n",
"SKIP_ROWS = 0"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Contig"
]
},
{
"cell_type": "code",
"execution_count": 406,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h3>Contig</h3>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"addHeader(3,'Contig')\n",
"\n",
"col_info = [\n",
" [ \"Position\" , col_type_int ], \n",
" [ \"AGP Contig\" , col_type_bol ]\n",
"]\n",
"\n",
"col_names=[cf[0] for cf in col_info]\n",
"col_types=dict(zip([c[0] for c in col_info], [c[1] for c in col_info]))\n",
"\n",
"if PARSE_VERBOSE:\n",
" print col_names\n",
" col_types"
]
},
{
"cell_type": "code",
"execution_count": 407,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"probes/run_BWA_JKL_23_JU_1_orig_PROBES/S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727.S_lycopersicum_scaffolds_from_contigs.2.40.agp.SL2.40sc05611.agp.contig.agp.cov.gz\n",
"Loaded 3564 rows and 2 columns\n"
]
}
],
"source": [
"print AgpContigFile\n",
"\n",
"AgpContigData = pd.read_csv(AgpContigFile, header=None, names=col_names, dtype=col_types, nrows=NROWS, \\\n",
" skiprows=SKIP_ROWS, verbose=PARSE_VERBOSE, delimiter=\"\\t\", comment=\"#\", compression=\"gzip\")\n",
"\n",
"print \"Loaded %d rows and %d columns\" % ( AgpContigData.shape[0], AgpContigData.shape[1] )\n",
"\n",
"if PARSE_VERBOSE:\n",
" print AgpContigData.head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Gap"
]
},
{
"cell_type": "code",
"execution_count": 408,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h3>Gap</h3>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"addHeader(3,'Gap')\n",
"\n",
"col_info = [\n",
" [ \"Position\" , col_type_int ], \n",
" [ \"AGP Gap\" , col_type_bol ]\n",
"]\n",
"\n",
"col_names=[cf[0] for cf in col_info]\n",
"col_types=dict(zip([c[0] for c in col_info], [c[1] for c in col_info]))\n",
"\n",
"if PARSE_VERBOSE:\n",
" print col_names\n",
" col_types"
]
},
{
"cell_type": "code",
"execution_count": 409,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"probes/run_BWA_JKL_23_JU_1_orig_PROBES/S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727.S_lycopersicum_scaffolds_from_contigs.2.40.agp.SL2.40sc05611.agp.gap.agp.cov.gz\n",
"Loaded 3564 rows and 2 columns\n"
]
}
],
"source": [
"print AgpGapFile\n",
"\n",
"AgpGapData = pd.read_csv(AgpGapFile, header=None, names=col_names, dtype=col_types, nrows=NROWS, \\\n",
" skiprows=SKIP_ROWS, verbose=PARSE_VERBOSE, delimiter=\"\\t\", comment=\"#\", compression=\"gzip\")\n",
" \n",
"print \"Loaded %d rows and %d columns\" % ( AgpGapData.shape[0], AgpGapData.shape[1] )\n",
"\n",
"if PARSE_VERBOSE:\n",
" print AgpGapData.head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Unknown"
]
},
{
"cell_type": "code",
"execution_count": 410,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h3>Unknown</h3>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"addHeader(3,'Unknown')\n",
"\n",
"col_info = [\n",
" [ \"Position\" , col_type_int ], \n",
" [ \"AGP Unknown\" , col_type_bol ]\n",
"]\n",
"\n",
"col_names=[cf[0] for cf in col_info]\n",
"col_types=dict(zip([c[0] for c in col_info], [c[1] for c in col_info]))\n",
"\n",
"if PARSE_VERBOSE:\n",
" print col_names\n",
" col_types"
]
},
{
"cell_type": "code",
"execution_count": 411,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"probes/run_BWA_JKL_23_JU_1_orig_PROBES/S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727.S_lycopersicum_scaffolds_from_contigs.2.40.agp.SL2.40sc05611.agp.unknown.agp.cov.gz\n",
"Loaded 3564 rows and 2 columns\n"
]
}
],
"source": [
"print AgpUnknownFile\n",
"\n",
"AgpUnknownData = pd.read_csv(AgpUnknownFile, header=None, names=col_names, dtype=col_types, nrows=NROWS, \\\n",
" skiprows=SKIP_ROWS, verbose=PARSE_VERBOSE, delimiter=\"\\t\", comment=\"#\", compression=\"gzip\")\n",
" \n",
"print \"Loaded %d rows and %d columns\" % ( AgpUnknownData.shape[0], AgpUnknownData.shape[1] )\n",
"\n",
"if PARSE_VERBOSE:\n",
" print AgpUnknownData.head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Other"
]
},
{
"cell_type": "code",
"execution_count": 412,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h3>Other</h3>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"addHeader(3,'Other')\n",
"\n",
"col_info = [\n",
" [ \"Position\" , col_type_int ], \n",
" [ \"AGP Other\" , col_type_bol ]\n",
"]\n",
"\n",
"col_names=[cf[0] for cf in col_info]\n",
"col_types=dict(zip([c[0] for c in col_info], [c[1] for c in col_info]))\n",
"\n",
"if PARSE_VERBOSE:\n",
" print col_names\n",
" col_types"
]
},
{
"cell_type": "code",
"execution_count": 413,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"probes/run_BWA_JKL_23_JU_1_orig_PROBES/S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727.S_lycopersicum_scaffolds_from_contigs.2.40.agp.SL2.40sc05611.agp.other.agp.cov.gz\n",
"Loaded 3564 rows and 2 columns\n"
]
}
],
"source": [
"print AgpOtherFile\n",
"\n",
"AgpOtherData = pd.read_csv(AgpOtherFile, header=None, names=col_names, dtype=col_types, nrows=NROWS, \\\n",
" skiprows=SKIP_ROWS, verbose=PARSE_VERBOSE, delimiter=\"\\t\", comment=\"#\", compression=\"gzip\")\n",
"\n",
"print \"Loaded %d rows and %d columns\" % ( AgpOtherData.shape[0], AgpOtherData.shape[1] )\n",
"\n",
"if PARSE_VERBOSE:\n",
" print AgpOtherData.head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Ns"
]
},
{
"cell_type": "code",
"execution_count": 414,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h2>Ns</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"addHeader(2,'Ns')\n",
"\n",
"col_info = [\n",
" [ \"Position\" , col_type_int ], \n",
" [ \"Ns\" , col_type_bol ]\n",
"]\n",
"\n",
"col_names=[cf[0] for cf in col_info]\n",
"col_types=dict(zip([c[0] for c in col_info], [c[1] for c in col_info]))\n",
"\n",
"if PARSE_VERBOSE:\n",
" print col_names\n",
" col_types"
]
},
{
"cell_type": "code",
"execution_count": 415,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"probes/run_BWA_JKL_23_JU_1_orig_PROBES/S_lycopersicum_chromosomes.fa_S_lycopersicum_scaffolds.sam.SL2.40ch12.SL2.40sc05611.JBPP0904_primer.000000967164-000000970727.S_lycopersicum_scaffolds.fa_NONE.tab.SL2.40ch12.tab.SL2.40sc05611.tab.cov.gz\n",
"Loaded 3564 rows and 2 columns\n"
]
}
],
"source": [
"print NsFile\n",
"\n",
"NsData = pd.read_csv(NsFile, header=None, names=col_names, dtype=col_types, nrows=NROWS, \\\n",
" skiprows=SKIP_ROWS, verbose=PARSE_VERBOSE, delimiter=\"\\t\", comment=\"#\", compression=\"gzip\")\n",
" \n",
"print \"Loaded %d rows and %d columns\" % ( NsData.shape[0], NsData.shape[1] )\n",
"\n",
"if PARSE_VERBOSE:\n",
" print NsData.head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Merge"
]
},
{
"cell_type": "code",
"execution_count": 416,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h1>Merge</h1>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Saved 3564 rows and 16 columns\n"
]
}
],
"source": [
"addHeader(1,'Merge')\n",
"\n",
"Data = pd.DataFrame(KmerData, copy=True)\n",
"\n",
"Data.combine_first( KmerData )\n",
"Data[ \"AGP Contig\" ] = AgpContigData[ \"AGP Contig\" ]\n",
"Data[ \"AGP Gap\" ] = AgpGapData[ \"AGP Gap\" ]\n",
"Data[ \"AGP Unknown\" ] = AgpUnknownData[ \"AGP Unknown\" ]\n",
"Data[ \"AGP Other\" ] = AgpOtherData[ \"AGP Other\" ]\n",
"Data[ \"Ns\" ] = NsData[ \"Ns\" ]\n",
"Data[ \"Sequencing Coverage\" ] = SequencingCoverageData[ \"Sequencing Coverage\" ]\n",
"if BAC_MODE:\n",
" Data[ \"BLAST Coverage\" ] = BlastCoverageData[ \"BLAST Coverage\" ]\n",
"\n",
"print \"Saved %d rows and %d columns\" % ( Data.shape[0], Data.shape[1] )\n",
"\n",
"if PARSE_VERBOSE:\n",
" print Data.head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#Stats"
]
},
{
"cell_type": "code",
"execution_count": 417,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h1>Stats</h1>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"<h2>Describe</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
" Position K-mer Coverage K-mer Coverage averaged: 500 bp \\\n",
"count 3564.000000 3564.000000 3564.000000 \n",
"mean 1781.500000 0.987118 0.979846 \n",
"std 1028.982507 0.042654 0.023863 \n",
"min 0.000000 0.652174 0.868090 \n",
"25% 890.750000 1.000000 0.976048 \n",
"50% 1781.500000 1.000000 0.988024 \n",
"75% 2672.250000 1.000000 0.994012 \n",
"max 3563.000000 1.000000 0.998004 \n",
"\n",
" K-mer Coverage averaged: 2.5 Kbp K-mer Coverage averaged: 5 Kbp \\\n",
"count 3564.000000 3564.000000 \n",
"mean 0.972331 0.950346 \n",
"std 0.015624 0.020099 \n",
"min 0.921127 0.900498 \n",
"25% 0.960016 0.937013 \n",
"50% 0.977739 0.952210 \n",
"75% 0.987205 0.969478 \n",
"max 0.990404 0.976005 \n",
"\n",
" K-mer Coverage averaged: 50 Kbp K-mer Coverage averaged: 1 Mbp \\\n",
"count 3564.000000 3564.000000 \n",
"mean 0.644977 0.759933 \n",
"std 0.015788 0.000203 \n",
"min 0.622268 0.759625 \n",
"25% 0.629966 0.759754 \n",
"50% 0.645013 0.759918 \n",
"75% 0.659184 0.760043 \n",
"max 0.671427 0.760458 \n",
"\n",
" K-mer Coverage averaged: 5 Kbp before \\\n",
"count 3564.000000 \n",
"mean 0.862887 \n",
"std 0.052024 \n",
"min 0.796571 \n",
"25% 0.808638 \n",
"50% 0.883462 \n",
"75% 0.913017 \n",
"max 0.950810 \n",
"\n",
" K-mer Coverage averaged: 5 Kbp after AGP Contig AGP Gap AGP Unknown \\\n",
"count 3564.000000 3564 3564 3564 \n",
"mean 0.932908 1 0 0 \n",
"std 0.018178 0 0 0 \n",
"min 0.917816 1 0 0 \n",
"25% 0.921216 1 0 0 \n",
"50% 0.922416 1 0 0 \n",
"75% 0.948210 1 0 0 \n",
"max 0.976005 1 0 0 \n",
"\n",
" AGP Other Ns Sequencing Coverage BLAST Coverage \n",
"count 3564 3564 3564.000000 3564.000000 \n",
"mean 0 0 133.513187 1.024270 \n",
"std 0 0 39.100518 0.162556 \n",
"min 0 0 56.000000 -1.000000 \n",
"25% 0 0 102.000000 1.000000 \n",
"50% 0 0 132.000000 1.000000 \n",
"75% 0 0 159.000000 1.000000 \n",
"max 0 0 299.000000 2.000000 \n"
]
}
],
"source": [
"addHeader(1,'Stats')\n",
"addHeader(2,'Describe')\n",
"\n",
"print Data.describe()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Quantiles"
]
},
{
"cell_type": "code",
"execution_count": 418,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h2>Quantiles</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"0.010 0.782609\n",
"0.025 0.869565\n",
"0.050 0.913043\n",
"0.100 0.956522\n",
"0.200 1.000000\n",
"0.300 1.000000\n",
"0.400 1.000000\n",
"0.500 1.000000\n",
"0.600 1.000000\n",
"0.700 1.000000\n",
"0.800 1.000000\n",
"0.900 1.000000\n",
"0.950 1.000000\n",
"0.975 1.000000\n",
"0.990 1.000000\n",
"dtype: float64\n"
]
},
{
"data": {
"text/html": [
"<h2>Percentiles</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"count 3564\n",
"count == 1 3033\n",
"prop == 1 0.85101010101\n"
]
}
],
"source": [
"addHeader(2,'Quantiles')\n",
"\n",
"print Data['K-mer Coverage'].quantile([.01, .025, .05, .1, .2, .3, .4, .5, .6, .7, .8, .9, .95, .975, .99])\n",
"\n",
"addHeader(2,'Percentiles')\n",
"print \"count \", Data['K-mer Coverage'].count()\n",
"print \"count == 1\", Data['K-mer Coverage'][ Data['K-mer Coverage'] == 1].count()\n",
"print \"prop == 1\", Data['K-mer Coverage'][ Data['K-mer Coverage'] == 1].count() * 1.0 / Data['K-mer Coverage'].count()"
]
},
{
"cell_type": "code",
"execution_count": 419,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h2>Median</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Position 1781.500000\n",
"K-mer Coverage 1.000000\n",
"K-mer Coverage averaged: 500 bp 0.988024\n",
"K-mer Coverage averaged: 2.5 Kbp 0.977739\n",
"K-mer Coverage averaged: 5 Kbp 0.952210\n",
"K-mer Coverage averaged: 50 Kbp 0.645013\n",
"K-mer Coverage averaged: 1 Mbp 0.759918\n",
"K-mer Coverage averaged: 5 Kbp before 0.883462\n",
"K-mer Coverage averaged: 5 Kbp after 0.922416\n",
"AGP Contig 1.000000\n",
"AGP Gap 0.000000\n",
"AGP Unknown 0.000000\n",
"AGP Other 0.000000\n",
"Ns 0.000000\n",
"Sequencing Coverage 132.000000\n",
"BLAST Coverage 1.000000\n",
"dtype: float64\n"
]
}
],
"source": [
"addHeader(2,'Median')\n",
"\n",
"print Data.median()"
]
},
{
"cell_type": "code",
"execution_count": 420,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h2>MAD</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Position 891.000000\n",
"K-mer Coverage 0.021926\n",
"K-mer Coverage averaged: 500 bp 0.014734\n",
"K-mer Coverage averaged: 2.5 Kbp 0.013925\n",
"K-mer Coverage averaged: 5 Kbp 0.016092\n",
"K-mer Coverage averaged: 50 Kbp 0.013832\n",
"K-mer Coverage averaged: 1 Mbp 0.000161\n",
"K-mer Coverage averaged: 5 Kbp before 0.048236\n",
"K-mer Coverage averaged: 5 Kbp after 0.015645\n",
"AGP Contig 0.000000\n",
"AGP Gap 0.000000\n",
"AGP Unknown 0.000000\n",
"AGP Other 0.000000\n",
"Ns 0.000000\n",
"Sequencing Coverage 30.920078\n",
"BLAST Coverage 0.050039\n",
"dtype: float64\n"
]
}
],
"source": [
"addHeader(2,'MAD')\n",
"print Data.mad()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Plot"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## K-mer Coverage Stats"
]
},
{
"cell_type": "code",
"execution_count": 421,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h1>Plot</h1>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"<h2>K-mer Coverage Stats</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Saving Image: reports/eps/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.K-mer_Coverage_Stats.eps\n",
"Saving Image: reports/png/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.K-mer_Coverage_Stats.png\n",
"Saving Image: reports/pdf/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.K-mer_Coverage_Stats.pdf\n"
]
},
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAABFAAAAJpCAYAAACKIsZjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\n",
"AAALEgAACxIB0t1+/AAAIABJREFUeJzs3X+UbWlZH/jvk76AgMqPoJg0xh6VECTGVklDRqPXgUjH\n",
"HyExY1g4ukAz2DMGEyYmwdbJdDEus2QiiomOQcTcO4kRJ/6IxIgtGtsgYxQyNELoJnSkHbrBRGw6\n",
"BIOmG57545xLbXZf6tw6t27tt059PmvV6nrPj9vPfet799nnqf2+p7o7AAAAAHx0f2DpAgAAAABG\n",
"p4ECAAAAsIEGCgAAAMAGGigAAAAAG2igAAAAAGyggQIAAACwwcYGSlX9UFX9h6p68wGP+XtV9faq\n",
"elNVffbk9uur6vb1fS88qqIBAAAAjtOlXIHyD5Nc/9HurKovSfLp3f34JF+f5PvXt1+V5HvXz/2M\n",
"JM+uqidedsUAAAAAx2xjA6W7X5vkvQc85M8lOb9+7K8meWRVfVKS65Lc0d13dvd9SV6Z5JmXXzIA\n",
"AADA8TqKPVCuTvLOyfiu9W1/+KPcDgAAAHCinDmiP6e2fmJVH1ENAAAAAJesuy+5n3EUDZS7k3zy\n",
"ZPy4rK42edDs9k9e3/4Ahyl4V1VVmwemqmqvu/eWroNxyART8sCcTDAlD8zJBFPysHLYCzqOooHy\n",
"qiTPT/LKqnpqknu7+z9U1e8keXxVXZPkXUmeleTZR/D/g+Ed1ZVVVXXT5f4ZGnM75ZqlC2Ao1yxd\n",
"AMO5ZukCGMo1SxfAcK5ZugCGcs3SBZxEGxsoVfUjSb4wyWOq6p1Jbsrq6pJ098u6+2eq6kuq6o4k\n",
"v5vka9f33V9Vz09yc5Krkryiu2+7Qn8PGMpRNC1clQQAADCO6l52CxJvElfMA3MywVxVne3uW5au\n",
"gzHIA3MywZQ8MCcTTMnDymHfc2mgDMI8MCcTAAAAV85h33MdxccYczTOL10AMLaqOrt0DYxDHpiT\n",
"CabkgTmZYEoetnNUH2PM5Tu3dAHsq6p7kjxqgDqW/pjv93b3oxeuAQAAYHGW8MBFyOWKeQAAAHaV\n",
"JTwAAAAAR0wDZRDWoDEnE8zJBFPywJxMMCUPzMkEU/KwHXugAByDo9rPpuryVlRZkgUAANuxB8og\n",
"qmqvu/eWroMVuVwxD2Px8wAAgKNz2PNrDZRBmIex+HmsmIex+HkAAMDROez5tSU88FEM8BHCDGKU\n",
"j7VOhsilj7YeRFWd7e5blq6DccgEU/LAnEwwJQ/b0UCBj2Lp3/SPcFAb4M36KB61dB4SmQAAgCVZ\n",
"wjMI8zAWP48V87BiHvaZCwAAdsVhz219jDEAAADABhoo4zi/dAGMxWezMycTTMkDczLBlDwwJxNM\n",
"ycN2NFDGcW7pAgAAAICLswcKXIRcrpiHFfOwz1wAALAr7IECAAAAcMQ0UAZhDRpzMsGcTDAlD8zJ\n",
"BFPywJxMMCUP29FAAQAAANjAHiiDqKq97t5bug5W5HLFPKyYh33mAgCAXXHYc1sNlEGYh7H4eayY\n",
"h5WqWvZAORiZAABgF9hEFnaEdYlj6e5a+ivJFw1QA4NwjGBOJpiSB+Zkgil52M6ZpQuAUY1w1UHV\n",
"4u9X37t0AbCLjur4chTHCI0xADh5juJcwnnE4VnCMwjzwJxMjMPPYp+5GIe9swCAbTmPWLEHygll\n",
"HpiTiXH4WewzF+PwswAAtuU8YsUeKCfX+aULAMZmrSpwEMcIpuSBOZmAy6eBMo5zSxcAAAAAXJwl\n",
"PDAo/zbG4Wexz1yMw88CANiW84gVS3hgd7xo6QIAAABY0UAZhDWJXMQtSxfAWBwnxlFV91RVL/m1\n",
"rmPRGqrqnqV/FuxzjGBKHpiTCWbswbmFM0sXAAAn0KOWvuy1qs529y0L17DsOmAAYFvnli7gJLIH\n",
"yiB8DjeMy3Fqn7lYMQ8r5gEAOMkOey6jgTII8wDj8u9zn7lYMQ8r5gEAOMlsIgs7wjpV5mSCKXlg\n",
"TiaYkgfmZIIpediOBgqM67lLFwAAAMCKJTyDMA/MycQ4/Cz2mYsV87BiHgDgZLIH54o9UE4o88Cc\n",
"TIzDz2KfuVgxDyvmAQBOJq/hK/ZAObl8DjdwIGtVmZIH5mSCKXlgTibg8mmgjOPc0gUAAAAAF2cJ\n",
"DwzKv41x+FnsMxcr5mHFPADAyeQ1fOWw83DmShYDXJYXLV0A+6pq2W7zON67dAEAALAES3gGYU0i\n",
"F3HL0gWw0t01wtcgtTx66Z8HK143mJMJpuSBOZlgxh6cW9BAAQAAgNPl3NIFnET2QBmEz+EGNnG8\n",
"HIefxYp5AABOssOey2igDMI8AJs4TozDz2LFPAAAJ9lhz2Us4YFBWacKHMQxgjmZYEoemJMJpuRh\n",
"OxooMK7nLl0Aw7HZFwAALGTjEp6quj7JS5NcleQHu/vFs/sfleSHknxqkt9L8nXd/W/X992Z5H1J\n",
"Ppjkvu6+7iJ/vst/Yx54IJmAcfn3uWIeAOBksgfnypHugVJVVyV5W5KnJ7k7yeuTPLu7b5s85u8m\n",
"eV93f1tVPSHJ93X309f3vSPJ53b3PUdV8K4yD8zJBIzLv88V8wAAJ5PX8JWj3gPluiR3dPed3X1f\n",
"klcmeebsMU9M8otJ0t1vS3JNVX3CtKZLLeaUc2k+cCBrVcdSVX3av5b+GfCRHCOYkgfmZAIu35kN\n",
"91+d5J2T8V1JnjJ7zJuSfEWSX66q65J8SpLHJfntJJ3k56vqg0le1t0vP5Kqd9O5pQsA4NIt/Vub\n",
"qjrb3bcsXIMmCsAxOKrjbdXlvXQt/doHS9vUQLmUf6jfkeR7quqNSd6c5I1Z7XmSJJ/f3e9aX5Hy\n",
"mqq6vbtfO/8DqupckjvXw3uT3HrhpPBCp9TY+CSNs74q63Id0YvlFy09H8ZHM75w2yj1GMtDJpae\n",
"D2M/D2N52PHxZZ/PJfnF7q5B/j7Gjg9LjV+Q5Nrs9x8OZdMeKE9Nstfd16/HNyb5UM82kp095x1J\n",
"PrO73z+7/aYk7+/ul8xu79bJhCQf/gd+dj28KcmL1t/fcuEfPadX2exrGF67VswDwMnhmM2UPKwc\n",
"dh42NVDOZLWJ7NOSvCvJr+WBm8g+IskHuvu/VtXzknxedz+3qh6W5Kru/s9V9fAkP5fkRd39c5dT\n",
"8K6qWv5SbMZSVfd096OXroNxOF6OY4SfxQivGyPMA/tGyATjkAfmHLPHUVX3JHnU0nUM4L1Lv985\n",
"7L+LA5fwdPf9VfX8JDdn9THGr+ju26rqhvX9L0vyGUnO1WqpwVuS/OX10x+b5Cdrtc7uTJIfnjdP\n",
"gI80uwLlUVW1t/7eFSgAALAbHrV0M2uEJmudwL3UNu2Bku5+dZJXz2572eT7X0nyhIs87x1ZrS3i\n",
"0pxNcsvCNQBwQix90sN4ZIIpeQAO4hixnU0fY8zxuWnpAgAAgJ31os0PAQ5y4B4ox1KAtXhJzAMP\n",
"VFW/390PWboOxuE4MY4RfhajXHq79Dywb4RMMA55YE4mxjHC6+cIeRhkHo5uDxTgeM32QHmwPVCY\n",
"Ob90AQAAcFpZwgNwQnT3c5eugXFoqjInE0zJA3MywZQ8bEcDBQAAAGADDZRxuDQfONB6iRckkQce\n",
"SCaYkgfmZIIpediOBso4zi1dAAAAsLOeu3QBcNJpoAzCGjRgE8cJpuSBOZlgSh64iOcsXQDjcIzY\n",
"jgYKjOXarD6F5+x6fOH7axephqFMPpUJAAA4Zhoog7AGjbVbk9yy/srk+1sXqYbR3LR0Aeyrqj7t\n",
"X0neu/TPgX3OJZiSB+AgjhHbObN0AcBH+IV8ZGPzwhvmv53kquMvB7iY7q6la6iqHqEOAIDTwhUo\n",
"4zi7dAEM4VVJ/tP6K5PvX7VYRQCcCNazMyUPwEEcI7ZT3b1sAX6DlsQ8sLK+lO7senhTkhetv7/F\n",
"QQ7HCabkAYDDqKq97t5bug68hl8wwjwctgZXoMBYbCILwFasZ2dKHriIW5YugHE4RmzHHigwlluT\n",
"PHL9/Rdm/4XOJrIkyfmlCwAAgNPKFSgAJ0R3P3fpGhjKizY/hNPEUk+m5IE5mWBKHrajgQIAJ5B1\n",
"7AAAx0sDZRwuzQcOZK0qU/LAnEwwJQ/MyQRT8rAdDZRxnFu6AAAAYGc9d+kC4KTTQBmENWjAJo4T\n",
"TMkDczLBlDxwEc9ZugDG4RixneruZQsY4LOfYURV9YHufujSdTCOqtqz7wUAsA3vu8bhZ7Eywjwc\n",
"tgZXoAzCGjSSVQ6qaq+q9pJ8zIXv5YO1m5YugHFU1bmla2AsXiuYkgfgII4R29FAAYCTyaXYAADH\n",
"SANlHGeXLgAAOLmsZ2dKHoCDOEZsRwNlHC7NBwAArpQXLV0AnHQ2kR2EeWDOJrLMOU4wJQ/MVdVZ\n",
"v1HkAnlgTibGMcJr+Ah5GGQeDlXDmStZDHA4682czq6HH7PeTDZJbln6AMcQzi9dAAAAl6+qlr2S\n",
"YVXD0iWcOBooAMfgqF4kq+qyNg5dusvPkXIpNh9Bo50peWBOJhjQe5cu4LAs4RmEeWCuqn6ruz9p\n",
"6ToAAIDd4v3nymHnwSay43BpPqmqs1W1t16689gL3/ucdpIPL/GCJPLAA8kEU/LAnEzA5bOEZxzn\n",
"li6A5a0vrbwlSarqed29t2Q9AADsjOdmfZ4JbMcSHhjIbBPZm7K/x4FNZAEA2Jr3XbtlhE1ok5O/\n",
"v95h/11ooMCgquqO7v70pesAAODk874LHsgeKCeUNYkkD9gD5dPsgcKUHDBVVeeWroGxOEYwJQ/A\n",
"QRwjtmMPFBjIbA+Uv2oPFOAAz8lqPTsAAMdAA2UcZ2NTp1NvtgfKo9ZXoiT2QCEfbrABXJRjBFPy\n",
"ABzEMWI7GijjuCnJ3tJFAAAAR6eq7knyqKXrSIbYePS93f3ohWuArdlEdhDmgbmqen93f+zSdTCO\n",
"qjrrtwVc4HWDOccIpuRhHKMcr0fIxChzwRh5GMFhM+kKFBjIbAnPwy3hAQAAGINP4QE4ITTRmHnR\n",
"0gUwFscIpuSBOZlgSh62YwnPIMwDc5bwAACcfM7z95kLRnPYTLoCZRznly6A5VXV2araWy/defiF\n",
"731OO8mHl3hBEnnggWSCKXlgTiaYkoftaKCM49zSBQAAAAAXp4EyCGvQgE0cJ5iSB+Zkgil5YE4m\n",
"mJKH7WigAAAAAGyggTIIa9BYuzarjzE+ux5f+P7aRaphKI4TTFXVuaVrYCyOEUzJA3MywZQ8bEcD\n",
"BQBOpucsXQAAwGmy8WOMq+r6JC9NclWSH+zuF8/uf1SSH0ryqUl+L8nXdfe/vZTnrh/jo6ySVNVe\n",
"d+8tXQfLqqoP5uKNzQ9191XHXQ8wLq+fACeD4/U+c8FoDpvJAxsoVXVVkrcleXqSu5O8Psmzu/u2\n",
"yWP+bpL3dfe3VdUTknxfdz/9Up67TcG7yjyQaKAAl87rBsDJ4Hi9z1wwmsNmctMSnuuS3NHdd3b3\n",
"fUlemeSZs8c8MckvJkl3vy3JNVX1iZf4XOAjvSrJf1p/ZfL9qxariGFYqwocxDGCKXlgTiaYkoft\n",
"nNlw/9VJ3jkZ35XkKbPHvCnJVyT55aq6LsmnJHncJT4XAE6dqjp4/ewx/jl+EwgAcGk2NVAu5cTs\n",
"O5J8T1W9Mcmbk7wxyQcv8blJPvxJAneuh/cmufXC51Jf6Izt+ngyF0PUY7zMeO331l+PWP83WS2D\n",
"W7w+4+XzUVVnR6nHePtxd9co9VwwSj3Gfp7G8rBr4wu3jVKPsfEpH78gq084vTNb2LQHylOT7HX3\n",
"9evxjVntxfCAzWAnz3lHks9M8scv5bllHVwS88BKVX1vki9bDz8lyW+uv//p7n7+MlUBALAt5/n7\n",
"zAWjOWwmN+2B8oYkj6+qa6rqwUmeldleDFX1iPV9qarnJfml7n7/pTyXj3B+6QIYwtVJHrn+yuT7\n",
"qxeriGHMf6PI6SYPzMkEU/LAnEwwJQ/bOXAJT3ffX1XPT3JzVh9F/Iruvq2qbljf/7Ikn5HkXK3W\n",
"Yb8lyV8+6LlX7q9y4p1bugCGcHdWy9iS1RKeeye3AwAAsJADl/AcSwEu44IPq6r3J3n4Re763e7+\n",
"2OOuBwCAy+P9zj5zwWgOm8lNm8gCx+tcPsoeKItUAwAAQJLNe6BwTKxBY+3HsmqinFuPL3z/Y4tU\n",
"w1AcJ5iSB+Zkgil5YE4mmJKH7WigAAAAAGxgCc84zia5ZeEaWN61WWXhggvf3xv5OPUufH49JPLA\n",
"A8kEU/LAnEwwJQ/bcQXKOG5augCGcGtWjZJb1uML39+6SDUAAAAk0UABODGsVWVKHpiTCabkgTmZ\n",
"YEoetmMJDwxkfSndLUlSVd/S3XtL1gMAAMBKdfeyBfgs8CTmgZV1J/jsenhTkhetv7/FOkUAgJPH\n",
"ef4+c8FoDptJS3gAAAAANtBAGcf5pQsAxmatKlPywJxMMCUPzMkEU/KwHXugjOPc0gWwvNkeKDfa\n",
"AwUAAGAM9kCBgdgDBQBgt3i/s89cMBp7oAAAAAAcMQ2UQViDBmziOMGUPDAnE0zJw1iqqn3Vsksf\n",
"+AiOEduxBwoMxB4oAAC7Z4RlK1V1dukl4ZoonHT2QBlEVe15s4w9UAAAdov3O/vMBaOxB8rJddPS\n",
"BQAAAAAXp4ECcEJYq8qUPDAnE0zJA3MywZQ8bMceKDAQe6AAAACMyR4ogzAPJPZAAQDYNc7z95kL\n",
"RmMPFAAAAIAjpoEyjvNLFwCMzVpVpuSBOZlgSh6Ykwmm5GE79kAZx7mlC2B59kABAAAYkz1QYCD2\n",
"QAEA2C3e7+wzF4zGHigAAAAAR0wDZRDWoAGbOE4wJQ/MyQRT8sCcTDAlD9vRQAEAAADYQANlHGeX\n",
"LgAYm31wmJIH5mSCKXlgTiaYkoftaKCM46alC2AI12bVTDu7Hl/4/tpFqgEAACCJBgrAiWGtKlPy\n",
"wJxMMCUPzMkEU/KwnTNLFwB8hJfkIxubX7j+759O8tLjLwcAAIAkqe5etgCfBZ7EPPBAMgEAcPI5\n",
"p9tnLhjNYTNpCQ8AAADABhoo4zi/dAEM50NLF8BYrFVlSh6Ykwmm5IE5mWBKHrajgTKOc0sXwHCe\n",
"tnQBAAAArNgDBQAA4ArxfmefuWA09kABAAAAOGIaKIOwBo05mWBOJpiSB+Zkgil5YE4mmJKH7Wig\n",
"AAAAAGxgD5RBVNVed+8tXQcAAHB0vN/ZZy4YzWEzqYEyCPMAAAC7x3n+PnPBaGwiCzvCukTmZIIp\n",
"eWBOJpiSB+Zkgil52I4GCgAAAMAGlvAMwjwAAMDucZ6/z1wwGkt4AAAAAI6YBso4zi9dAGOxLpE5\n",
"mWBKHpiTCabkgTmZYEoetqOBMo5zSxcAAAAAXNzGPVCq6vokL01yVZIf7O4Xz+5/TJJ/nOSTkpxJ\n",
"8p3dfW59351J3pfkg0nu6+7rLvLnWwcHAADsJO939pkLRnPYTB7YQKmqq5K8LcnTk9yd5PVJnt3d\n",
"t00es5fkId1947qZ8rYkj+3u+6vqHUk+t7vvOaqCAQAATgrvd/aZC0Zz1JvIXpfkju6+s7vvS/LK\n",
"JM+cPebdST5+/f3HJ/md7r5/WtOlFnOaWYPGnEwwJxNMyQNzMsGUPDAnE0zJw3Y2NVCuTvLOyfiu\n",
"9W1TL0/ypKp6V5I3Jflrk/s6yc9X1Ruq6nmXWywAAADAEs5suP/gDVJWviXJrd19tqo+Lclrquqz\n",
"uvs/J/m87n53VX3C+vbbu/u18z+gqs4luXM9vHf9592yvu9skuz6OMnZJLeMUo/x8uPulgfjjxhf\n",
"uG2UeozlwXi88QWj1GMsD8YrjtfGxsOMX5Dk2uz3Hw5l0x4oT02y193Xr8c3JvlQTzaSraqfSfLt\n",
"3f269fgXkrywu98w+7NuSvL+7n7J7PZu6+DMAwAA7CDn+fvMBaM5bCY3LeF5Q5LHV9U1VfXgJM9K\n",
"8qrZY27PapPZVNVjkzwhyW9U1cOq6uPWtz88yRcnefOlFgan3fy3RyATTMkDczLBlDwwJxNMycN2\n",
"DlzC06tP0nl+kpuz+hjjV3T3bVV1w/r+lyX5O0n+YVW9KauGzN/q7nuq6lOT/ERVXfj//HB3/9wV\n",
"/LsAAAAAXBEHLuE5lgJcxpXEPAAAwC5ynr/PXDCao17CAwAAAHDqaaCM4/zSBTAW6xKZkwmm5IE5\n",
"mWBKHpiTCabkYTsaKOM4t3QBAAAAwMXZAwUAAOAK8X5nn7lgNPZAAQAAADhiGiiDsAaNOZlgTiaY\n",
"kgfmZIIpeWBOJpiSh+1ooAAAAABsYA+UQVTVXnfvLV0HAABwdLzf2WcuGM1hM6mBMgjzAAAAu8d5\n",
"/j5zwWhsIgs7wrpE5mSCKXlgTiaYkgfmZIIpediOBgoAAADABpbwDMI8AADA7nGev89cMBpLeAAA\n",
"AACOmAbKOM4vXQBjsS6ROZlgSh6Ykwmm5IE5mWBKHrajgTKOc0sXAAAAAFycPVAAAACuEO939pkL\n",
"RmMPFAAAAIAjpoEyCGvQmJMJ5mSCKXlgTiaYkgfmZIIpediOBgoAAADABvZAGURV7XX33tJ1AAAA\n",
"R8f7nX3mgtEcNpMaKIMwDwAAsHuc5+8zF4zGJrKwI6xLZE4mmJIH5mSCKXlgTiaYkoftaKAAAAAA\n",
"bGAJzyDMAwAA7B7n+fvMBaOxhAcAAADgiGmgjOP80gUwFusSmZMJpuSBOZlgSh6Ykwmm5GE7Gijj\n",
"OLd0AQAAAMDF2QMFAADgCvF+Z5+5YDT2QAEAAAA4Yhoog7AGjTmZYE4mmJIH5mSCKXlgTiaYkoft\n",
"aKAAAAAAbGAPlEFU1V537y1dBwAAcHS839lnLhjNYTOpgTII8wAAALvHef4+c8FobCILO8K6ROZk\n",
"gil5YE4mmJIH5mSCKXnYjgYKAAAAwAaW8AzCPAAAwO5xnr/PXDAaS3gAAAAAjpgGyjjOL10AY7Eu\n",
"kTmZYEoemJMJpuSBOZlgSh62o4EyjnNLFwAAAABcnD1QAAAArhDvd/aZC0ZjDxQAAACAI6aBMghr\n",
"0JiTCeZkgil5YE4mmJKHsVRV+6pO8t6lfxasOEZs58zSBQAAAOyqUZasWD4Dl88eKIOoqr3u3lu6\n",
"DgAAYPd43wUPdNh/FxoogzAPAADAleL9BjyQTWRhR1iXyJxMMCUPzMkEU/IAHMQxYjsbGyhVdX1V\n",
"3V5Vb6+qF17k/sdU1c9W1a1V9Zaqeu6lPhcAAADgJDhwCU9VXZXkbUmenuTuJK9P8uzuvm3ymL0k\n",
"D+nuG6vqMevHPzZJb3ru+vkuJYt5AAAArhx7LsIDHfUSnuuS3NHdd3b3fUlemeSZs8e8O8nHr7//\n",
"+CS/0933X+JzAQAAuMI0T+DybWqgXJ3knZPxXevbpl6e5ElV9a4kb0ry1w7xXPadX7oAxmJdInMy\n",
"wZQ8MCcTTMkDczLBlDxs58yG+y/lI3q+Jcmt3X22qj4tyWuq6rMOU0RVnUty53p47/rPu2V939kk\n",
"2fVxknMj1WNsbDzeOMm1VTVMPcbyYDzc+NokI9VjLA/GA40vGKUeY3lYaPyCrI6Pd2YLm/ZAeWqS\n",
"ve6+fj2+McmHuvvFk8f8TJJv7+7Xrce/kOSFWTVnDnzu+vZue38AAAAAx+iw/YhNS3jekOTxVXVN\n",
"VT04ybOSvGr2mNuz2ig2VfXYJE9I8huX+FwAAACA4R3YQOnVZrDPT3Jzkrcm+dHuvq2qbqiqG9YP\n",
"+ztJnlxVb0ry80n+Vnff89Gee6X+Iifd/FIqkAnmZIIpeWBOJpiSB+ZqtW0CJHGM2NamPVDS3a9O\n",
"8urZbS+bfP+eJF9+qc8FAADg0lXVpexNeSl/znMu5/m2XuC0O3APlGMpwB4oSZLyuewAAABwbA7b\n",
"j9BAGYR5AAAAgONz1JvIAguxLpE5mWBKHpiTCabkgTmZYEoetqOBAgAAALCBJTyDMA8AAABwfCzh\n",
"AQAAADhiGijjOL90AYzFukTmZIIpeWBOJpiSB+Zkgil52I4GyjjOLV0AAAAAcHH2QAEAAABOHXug\n",
"AAAAABwxDZRBWIPGnEwwJxNMyQNzMsGUPDAnE0zJw3Y0UAAAAAA2sAfKIKpqr7v3lq4DAAAAToPD\n",
"9iM0UAZhHgAAAOD42EQWdoR1iczJBFPywJxMMCUPzMkEU/KwHQ0UAAAAgA0s4RmEeQAAAIDjYwkP\n",
"AAAAwBHTQBnH+aULYCzWJTInE0zJA3MywZQ8MCcTTMnDdjRQxnFu6QIAAACAi7MHCgAAAHDq2AMF\n",
"AAAA4IhpoAzCGjTmZII5mWBKHpiTCabkgTmZYEoetqOBAgAAALCBPVAGUVV73b23dB0AAABwGhy2\n",
"H6GBMgjzAAAAAMfHJrKwI6xLZE4mmJIH5mSCKXlgTiaYkoftaKAAAAAAbGAJzyDMAwAAABwfS3gA\n",
"AAAAjpgGyjjOL10AY7EukTmZYEoemJMJpuSBOZlgSh62o4EyjnNLFwAAAABcnD1QAAAAgFPHHigA\n",
"AAAAR0wDZRDWoDEnE8zJBFPywJxMMCUPzMkEU/KwHQ0UAAAAgA3sgTKIqtrr7r2l6wAAAIDT4LD9\n",
"CA2UQZgHAAAAOD42kYUdYV0iczLBlDwwJxNMyQNzMsGUPGxHAwUAAABgA0t4BmEeAAB2Q1Ute4I9\n",
"EOe3wMgO+z78zJUsBgAAThtNA4DdZAnPOM4vXQBjsS6ROZlgSh6Ykwmm5IE5mWBKHrajgTKOc0sX\n",
"AAAAAFycPVAAAACAU8fHGAMAAAAcMQ2UQViDxpxMMCcTTMkDczLBlDwwJxNMycN2NjZQqur6qrq9\n",
"qt5eVS+8yP1/o6reuP56c1XdX1WPXN93Z1X9+vq+X7sSfwEAAACAK+3APVCq6qokb0vy9CR3J3l9\n",
"kmd3920f5fFfluQF3f309fgdST63u+854P9hD5QkVbXX3XtL1wEAAACnwVHvgXJdkju6+87uvi/J\n",
"K5M884DHf1WSH5nXdKnFnHI3LV0AAAAAcHGbGihXJ3nnZHzX+rYHqKqHJXlGkh+f3NxJfr6q3lBV\n",
"z7ucQuG0sS6ROZlgSh6Ykwmm5IE5mWBKHrZzZsP9h/mM4y9P8svdfe/kts/r7ndX1SckeU1V3d7d\n",
"r50/sarOJblzPbw3ya3dfcv6vrNJsuvjyVwMUY+xsfF44yTXVtUw9RjLg/Fw42uTjFSPsTwYDzS+\n",
"YJR6jOUNW/+EAAAgAElEQVRhofELsjo+3pktbNoD5alJ9rr7+vX4xiQf6u4XX+SxP5nkR7v7lR/l\n",
"z7opyfu7+yWz27vtgWIeAAAA4Bgd9n34piU8b0jy+Kq6pqoenORZSV51kf/pI5J8QZKfmtz2sKr6\n",
"uPX3D0/yxUnefKmFAQAAAIziwAZKd9+f5PlJbk7y1qyuMLmtqm6oqhsmD/3zSW7u7g9MbntsktdW\n",
"1a1JfjXJT3f3zx1t+Tvl/NIFMJb55XUgE0zJA3MywZQ8MCcTTMnDdjbtgZLufnWSV89ue9lsfD6z\n",
"BkB3vyOrtUVcmnNLFwAAAABc3IF7oBxLAfb+AAAAAI7ZUe+BAgAAAHDqaaAMwho05mSCOZlgSh6Y\n",
"kwmm5IE5mWBKHrajgQIAAACwgT1QBlFVe929t3QdAAAAcBocth+hgTII8wAAAADHxyaysCOsS2RO\n",
"JpiSB+Zkgil5YE4mmJKH7WigAAAAAGxgCc8gzAMAAAAcH0t4AAAAAI6YBso4zi9dAGOxLpE5mWBK\n",
"HpiTCabkgTmZYEoetqOBMo5zSxcAAAAAXJw9UAAAAIBTxx4oAAAAAEdMA2UQ1qAxJxPMyQRT8sCc\n",
"TDAlD8zJBFPysB0NFAAAAIAN7IEyiKra6+69pesAAACA0+Cw/QgNlEGYBwAAADg+NpGFHWFdInMy\n",
"wZQ8MCcTTMkDczLBlDxsRwMFAAAAYANLeAZhHgAAAOD4WMIDAAAAcMQ0UMZxfukCGIt1iczJBFPy\n",
"wJxMMCUPzMkEU/KwHQ2UcZxbugAAAADg4uyBAgAAAJw69kABAAAAOGIaKIOwBo05mWBOJpiSB+Zk\n",
"gil5YE4mmJKH7WigAAAAAGxgD5RBVNVed+8tXQcAAACcBoftR2igDMI8AAAAwPGxiSzsCOsSmZMJ\n",
"puSBOZlgSh6Ykwmm5GE7GigAAAAAG1jCMwjzAAAAAMfHEh4AAACAI6aBMo7zSxfAWKxLZE4mmJIH\n",
"5mSCKXlgTiaYkoftaKCM49zSBQAAAAAXZw8UAAAA4NSxBwoAAADAEdNAGYQ1aMzJBHMywZQ8MCcT\n",
"TMkDczLBlDxsRwMFAAAAYAN7oAyiqva6e2/pOgAAAOA0OGw/QgNlEOYBAAAAjo9NZGFHWJfInEww\n",
"JQ/MyQRT8sCcTDAlD9vRQAEAAADYwBKeQZgHAAAAOD6W8AAAAAAcMQ2UcZxfugDGYl0iczLBlDww\n",
"JxNMyQNzMsGUPGxnYwOlqq6vqtur6u1V9cKL3P83quqN6683V9X9VfXIS3kuH+Hc0gUAAAAAF3fg\n",
"HihVdVWStyV5epK7k7w+ybO7+7aP8vgvS/KC7n76pT7X3h8AAADAcTvqPVCuS3JHd9/Z3fcleWWS\n",
"Zx7w+K9K8iNbPhcAAABgSJsaKFcneedkfNf6tgeoqocleUaSHz/sc7EGjQeSCeZkgil5YE4mmJIH\n",
"5mSCKXnYzpkN9x/mM46/PMkvd/e9h31uVZ1Lcud6eG+SW7v7lvV9Z5Nk18eTuRiiHmNj4/HGSa6t\n",
"qmHqMZYH4+HG1yYZqR5jeTAeaHzBKPUYy8NC4xdkdXy8M1vYtAfKU5Psdff16/GNST7U3S++yGN/\n",
"MsmPdvcrD/PcsgdKkqSq9rp7b+k6AAAA4DQ4bD9iUwPlTFYbwT4tybuS/FouvhHsI5L8RpLHdfcH\n",
"DvlcDZSYBwAAADhOh30ffuAeKN19f5LnJ7k5yVuzusLktqq6oapumDz0zye5+ULz5KDnXvpfBU63\n",
"+eV1IBNMyQNzMsGUPDAnE0zJw3Y27YGS7n51klfPbnvZbHw+yflLeS4AAADASXPgEp5jKcDSlSTm\n",
"AQAAAI7TkS7hAQAAAEADZSQPWALF6WZdInMywZQ8MCcTTMkDczLBlDxsRwNlHOeWLgAAAAC4OHug\n",
"AAAAAKeOPVAAAAAAjpgGyiCsQWNOJpiTCabkgTmZYEoemJMJpuRhOxooAAAAABvYA2UQVbXX3XtL\n",
"1wEAAACnwWH7ERoogzAPAAAAcHxsIgs7wrpE5mSCKXlgTiaYkgfmZIIpediOBgoAAADABpbwDMI8\n",
"AAAAwPGxhAcAAADgiGmgjOP80gUwFusSmZMJpuSBOZlgSh6Ykwmm5GE7GijjOLd0AQAAAMDF2QMF\n",
"AAAAOHXsgQIAAABwxDRQBmENGnMywZxMMCUPzMkEU/LAnEwwJQ/b0UABAAAA2MAeKIOoqr3u3lu6\n",
"DgAAADgNDtuP0EAZhHkAAACA42MTWdgR1iUyJxNMyQNzMsGUPDAnE0zJw3Y0UAAAAAA2sIRnEOYB\n",
"AAAAjo8lPAAAAABHTANlHOeXLoCxWJfInEwwJQ/MyQRT8sCcTDAlD9s5s3QBfNi5pQsAAJZRVUey\n",
"prrq8lYDW04MAB+dPVAAAHaAcyoAOBx7oAAAnE4vWroAANhlGiiDsAaNOZlgTiaYkgcu4palC2Ac\n",
"jhHMyQRT8rAdDRQAAACADeyBMoiq2uvuvaXrAAAAgNPgsP0IDZRBmAcAAAA4PjaRhR1hXSJzMsGU\n",
"PDAnE0zJA3MywZQ8bEcDBQBgNzx36QIAYJdZwjMI8wAAXA7nEgBwOJbwAAAAABwxDZRxnF+6AMZi\n",
"XSJzMsGUPAAHcYxgTiaYkoftaKCM49zSBQAAAAAXZw8UAIAd4JwKAA7nsK+dZ65kMQAAu66q7kny\n",
"qKXrSFYngguX8N7ufvTCNQDAFWEJzyCsQWNOJpiTCabkYSiP6u5a+ivJFw1QwxCNJBwjeCCZYEoe\n",
"tqOBAgAAALCBPVAGUVV73b23dB0AwOE4l9lnLgA4SQ77uqWBMgjzAAAnk9fwfeYCgJPksK9blvDA\n",
"oKxLZE4mmJIH5mSCKXlgTiaYkoftbGygVNX1VXV7Vb29ql74UR5ztqreWFVvqapbJrffWVW/vr7v\n",
"146wbgAAAIBjc+ASnqq6Ksnbkjw9yd1JXp/k2d192+Qxj0zyuiTP6O67quox3f2e9X3vSPK53X3P\n",
"Af+PnbjUc4CPDUyS7MJcAsBJsivnMkfBXABwkhz2devMhvuvS3JHd9+5/sNfmeSZSW6bPOarkvx4\n",
"d9+VJBeaJ9OaLrWYk8zJAgAAAOyuTUt4rk7yzsn4rvVtU49P8uiq+sWqekNVfc3kvk7y8+vbn3f5\n",
"5e4ua9CYkwnmZIIpeWBOJpiSB+Zkgil52M6mK1AuZVnKg5J8TpKnJXlYkl+pqn/d3W9P8vnd/a6q\n",
"+oQkr6mq27v7tfM/oKrOJblzPbw3ya3dfcv6vrNJsuvjyVwMUY+xsfF44yTXVtUw9RjLg/Fw42uT\n",
"LFrPBYPMx2kfL54H47HGF4xSj7E8LDR+QVbHxzuzhU17oDw1yV53X78e35jkQ9394sljXpjkod29\n",
"tx7/YJKf7e4fm/1ZNyV5f3e/ZHZ7t+UvAMAJ5Vxmn7kA4CQ57OvWpiU8b0jy+Kq6pqoenORZSV41\n",
"e8xPJfn8qrqqqh6W5ClJ3lpVD6uqj1sX9fAkX5zkzZdaGAAAAMAoDmygdPf9SZ6f5OYkb03yo919\n",
"W1XdUFU3rB9ze5KfTfLrSX41ycu7+61JPinJa6vq1vXtP93dP3fl/ion2/xSKpAJ5mSCKXlgTiaY\n",
"kgfmZIIpedjOpj1Q0t2vTvLq2W0vm42/M8l3zm77jazWFgEAAACcaAfugXIsBVgrCwCcYFW17MnU\n",
"YJzXAXBSHLYfsfEKFAAADqZpsKKZBMAu27SJLMfEGjTmZII5mWBKHpiTCabkgTmZYEoetqOBAgAA\n",
"ALCBPVAAAC6Dc5l95gKAk+Swr1uuQAEAAADYQANlENagMScTzMkEU/LAnEwwJQ/MyQRT8rAdDRQA\n",
"AACADeyBAgBwGZzL7DMXAJwk9kABAAAAOGIaKIOwBo05mWBOJpiSB+Zkgil5YE4mmJKH7WigAAAA\n",
"AGxgDxQAgMvgXGafuQDgJLEHCgAAAMAR00AZhDVozMkEczLBlDwwJxNMyQNzMsGUPGxHAwUAAABg\n",
"A3ugAABcBucy+8wFACfJYV+3zlzJYgAAToOqWvY3UuN479IFAMCVYgnPIKxBY04mmJMJpuRhHN1d\n",
"I3wNUsujl/55sOIYwZxMMCUP29FAAQAAANjAHigAADvAORUAHM5hXztdgQIAAACwgQbKIKxBY04m\n",
"mJMJpuQBOIhjBHMywZQ8bEcDBQBgN5xfugAA2GX2QAEAAABOHXugAAAAABwxDZRBWIPGnEwwJxNM\n",
"ycNuqaoe4WvpeeDoOEYwJxNMycN2zixdAADAaXcUy5mr6mx333IE5QAAF2EPFAAAAODUsQcKAAAA\n",
"wBHTQBmENWjMyQRzMsGUPDAnE0zJA3MywZQ8bEcDBQAAAGADe6AAAAAAp449UAAAAACOmAbKIKxB\n",
"Y04mmJMJpuSBOZlgSh6Ykwmm5GE7GigAAAAAG9gDBQAAADh17IECAAAAcMQ0UAZhDRpzMsGcTDAl\n",
"D8zJBFPywJxMMCUP29FAAQAAANjAHigAAADAqWMPFAAAAIAjpoEyCGvQmJMJ5mSCKXlgTiaYkgfm\n",
"ZIIpediOBgoAAADABvZAAQAAAE4de6AAAAAAHDENlEFYg8acTDAnE0zJA3MywZQ8MCcTTMnDdjY2\n",
"UKrq+qq6vareXlUv/CiPOVtVb6yqt1TVLYd5Lh927dIFMByZYE4mmJIH5mSCKXlgTiaYkoctnDno\n",
"zqq6Ksn3Jnl6kruTvL6qXtXdt00e88gk35fkGd19V1U95lKfy0d45NIFMByZYE4mmJIH5mSCKXlg\n",
"TiaYkoctbLoC5bokd3T3nd19X5JXJnnm7DFfleTHu/uuJOnu9xziuQAAAADD29RAuTrJOyfju9a3\n",
"TT0+yaOr6her6g1V9TWHeC77rlm6AIZzzdIFMJxrli6AoVyzdAEM55qlC2Ao1yxdAMO5ZukCGMo1\n",
"SxdwEh24hCfJpXzG8YOSfE6SpyV5WJJfqap/fYnPTbL66KBLfewuq6rnLF0DY5EJ5mSCKXlgTiaY\n",
"kgfmZIIpeTi8TQ2Uu5N88mT8yVldSTL1ziTv6e4PJPlAVf2rJJ+1ftym5+Ywn7kMAAAAsIRNS3je\n",
"kOTxVXVNVT04ybOSvGr2mJ9K8vlVdVVVPSzJU5K89RKfCwAAADC8A69A6e77q+r5SW5OclWSV3T3\n",
"bVV1w/r+l3X37VX1s0l+PcmHkry8u9+aJBd77hX8uwAAAABcEdVt+xEAAACAg2xawgNwpKrKvkfA\n",
"R+UYwVytLV0Hy5MFjoocnW4Xfv5V9TGHfa4Gyo7zQsOoqurTquoxVfWYpWthWY5TzDLwoEWLYUjd\n",
"3VX1pPXeev/N0vWwnHUW/tg6D39w6Xo4OaavNW0ZxqlVVbU+jnxJkh+uqocc5vmbPoWHHbAOyH+b\n",
"5JOS/HZ3v3bpmjidJgesZyR5aZJ/l+Q9VfV/d/fNC5fHgta5+O+y+sS2B3f3y5euieM1OTY8s6re\n",
"neSfd/etS9fFsiavG09L8g+T/HKST6yqH+zuVy5cHsdodg7x3Ul+J8lbqur13f1DC5fHCbHO0Bcm\n",
"+dNJbk1yR3ffvnBZHKN1Bj4zyf+S5Ju7+/cP83xXoOy4yQvNDyV5RJJfqqqv9NteljBp5n1Nkq9K\n",
"8jeS/EKSb6yqP7locSxickL8p5KcS/KHssrDK5atjOO0zsDnJfmOJL+S5IlJvrqq/tKylbG0dTa+\n",
"IMmfTfKVSb4uyYuTfPP6/IZTYp2FJyd5QZI/n+TLszqHePK6AQ8HWmfoS5N8b5LfSvItSb6yqq5a\n",
"tjKOU1V9fFavJ5+Z1YfgpKouuS+igbLD1h8t/egkX5/kL2T12/43J3mty9Y4buurJh+S5JuSPC3J\n",
"m7r77Vl9UtdbkzxpyfpYxvpk5rokX53khd39HUk+J8mnV9XLlq2O47JeknFjkn/a3f8oyTckuSPJ\n",
"0w57aS0n32Rt+oU3Nf9rkm9M8q7u/r3ufk1WV6N87kIlckymv/Crqocm+XNJviBJuvveJL+U5L8m\n",
"uXaRAjkRJseUh2d15cmXZfW+6GOy+qTYD1bVxy1YIlfQdOlWVT2ou9+X5AeS/NMkX19Vf7S7P3Sp\n",
"FxhooOygydq+D3b3PUl+LclzknxXkr/Y3b9VVV9bVX9iyTo5HSYnwA9aXyL3jUnekeR8knT37yR5\n",
"f5LPWj/e1VE7bvIiduFn/TlJrk/yxKr6+O6+P8lfSvJHquoRC5XJFTb7bc/HJXlvkr9QVU9avzH6\n",
"wazeFH3GEvWxqAvZeGiSdPcXZ/VG+fzkMR9M8gR7KO22C7/wq6oHd/cHknxPkn+S5P+oqqu7+7eT\n",
"vCXJn6iqB8kCUxeOD+tf1nxRkj+Z5P6sXl9enOSZ3f2u9VUpT5Wf3bXOwDOTfH9V/XCSx2TViP8P\n",
"Sb6hqp54qRcYaKDskNlB4tqq+rb1XR+T1W93v6a776iqz0ryN7Na0gNXRFV9YlV9+rqr/2eTvLSq\n",
"/rckj8zqzfGjq+qXquorsvpNwM8nNvU6DSY/42uq6qHd/Q+yWof6+Umesr608lOzWs5jr64dc+GK\n",
"kvVvez6zqj43yW8m+dYkP5Pk+evL9D8lq8bKf1msWI5VVV1dVdeuXze+NMn5qvquqnrauolSVXV7\n",
"VX19kr+Y5J/12rKVc9Sq6hMuLO1dZ+EH1m96Hpfk7yf59ST/sqr+SpK/nOTHuvs+WWDqwvGhqv54\n",
"kr+e5N4kP53Ve6Mf6u53rpcQf3cS+dlRk31vvjXJXpKrk/ztrPbA+Ykkv5/VucfDL6WJVnKyOybN\n",
"ky9M8t8neUaSv9/df7+qfiSrNV73J/kTSfa6+6cuPGfBstlB6zdIL0jy+KyW6HxrkpdktYb93Vlt\n",
"AvirWR20PjbJ/9Ddb1pfVnffMlVzpVXVpyZ5dnd/e632Lvi+JK9P8uAkfyXJ52W1jOM310/5x939\n",
"k4sUyxVRVY9N8tysLpv99Kz25/rXWe158g1JPpDka7M6Vvy7JN/R3f/Sa9Xuq9VHST47q3z8QJIb\n",
"kvy9rM5Z/mCSW7v75VX1mqzy8oXd/e/XVyb814XK5gpYX7l6Y5JPzOoq6m/K6hd/fy6r14ub17d/\n",
"e5I/luTvdPerqurM+gpGSPLhLD0uq9eTH+jub6yqP5zV+6SnJbkqq2b9t3T3P/daszuq6g9094cm\n",
"4+cl+Y9ZXb34rUm+qrvfUVVnssrAme5+2yX92TKyW2q10do/yepE9AlJnpzk9d39nbXavPNRSX6r\n",
"u//NZKmPEHDkarWvxRcnuS7J67r7xVX1yKxOkD+7u79+/SL2PUl+t7ufu1y1XGnrtcUPSfKuJP8g\n",
"q4buj2e1nOsvJXlWVst4np7V1Sjf3d3/dP1cJzQ7oKo+McnHJ/m2rPY3+ZQk39/dv1JV/1NWV6L9\n",
"rST3JPmfkzw6ybd193+Ugd1WVZ+eVdPsp7LaHPQrk/xyd99YVR+b1dVpX53kG7r7fesmyoO6++xS\n",
"NXNlVNUnZ3Xl4e9ldS77R5K8r7u/cX3/DVm9Zjwzq3Par83qXPfru/u3FimaoVzs/U1V/c2sXnuu\n",
"7e7ba7UXykOzeh16X3e/3fui3VFVD0ryp7r7X1XVk5I8PKv3xV+Z1ZXwX7tuwH91kqcm+avTZssm\n",
"lvDsnquT/J/d/aok35/Vb2/+QlV9U3f/P939LzRPuJIm2fq1rC7HvzvJs6rqM9b7Grw8ybVV9dnd\n",
"/a6s3iw/tKr+0GJFc0Wtrzr4ke5+T5I/muRLk3xRrz5S/e7u/q6sPnnlK9ZNk3+U5Juq6gu8cd4N\n",
"66sLbs7qvONbkjw2q71NrkmS9TKuNyX59vWboJ/K6pLav15VD5GBnfeMJJ/R3f9fVo3Vf5nkOVX1\n",
"5O5+f3f/bFaZeUqSdPefSfJfquqPLFYxR66q/mCSNyb5saze5Lw0q98Yf3ZVnU2S7n5Zkvuy+kXM\n",
"O5P8cFZXMvoUFS64cEX+k2u15+OTu/vvZnUl0+vWe138bne/p7v/Ta8+0CCJ90W7oKqemNUSz8dX\n",
"1T9L8s+yurL5liSfkOTnkry/Vp/8981JXn2Y5kmigXKiXdjzZHbz7yX5H6vq8euTjtcl+fdJPq+q\n",
"vubCg6wZ5kpZv2idWX///2a1VvlfZPXRtJ+T1W+TPjbrfQ26+66sLqN790Ilc+V9bJKPq6qHd/ed\n",
"Sc4meVxVfdvkOHRvVvuepLu/P8krkvym49TOqCS/m+T3u/sdWf0m8A1JnrTeAyVZ7YP0n5MPHzv+\n",
"ryQv6dXm0+yg2v+EpfuSPChJuvvurDa9/64k315Vf2Z9hconJ3nPhed295esGy7siF5tKv8TWW0s\n",
"/5Kslvn970n+VZIvrapnV9VnZtWIv3f9nH+f1VK/u5epmlFU1cPWy7g+VFVfnuQfZ/WJO99cVS/N\n",
"asno307yxqr6Y/PnO984+arqk7JqkLwvqz7H52e13O8/rhuuz89qWehLsjq23Njd/+JS9j2Zsjnf\n",
"Cbd+s/qUrF5MXtfdP1mrj4P87qq6Mauf8dVZdeevXrBUdlhVXZ3VGvXf7u53d/f9F/Yz6e63VtVP\n",
"JPm6JK/OauO3F3b//+zdd7hkVZX+8e/bjSBpkJxUFHMAZAABdVBxAAEVwRFUgs4YGVGJww9JIqiM\n",
"BEUUlOAoKoIJVIKiOIQhCCqSUURxQEHCCJJTv78/1q7u0+W9Tbr3VnfV+3meeehbt6rdz9Tus/dZ\n",
"Z+21/JtedoHtRwY5/pgckpai2kv+DcD2Pe1M6g2qIqG/ajdGx1Np+3v0Pmv76EGMOSaWpGfZvt72\n",
"fZLuYVbg9AZJB1FPf/aTdB3VmvSA3mdtXzaQQceU6NXDkfQt4FbadaLVNLlT0vFUFsKpwLnAjrYv\n",
"SVba8OmrXXIaVQvpfKp99cepm51dqcDrVVS6/eW9GgdO7bSRpyoSuwvwUUm3ApsD77Z9nqTVqSOi\n",
"77N9WMt0egZwzeBGHJNkESqL8anAa6l95QpU167PtVMYu1P1GBe1fevjDZ5AAijztBY82RQ4GDgJ\n",
"+LCkw6nFZwbVmulB4L1Ui9iNU2wtJlo7W3g8cCNws6RbbO9h+6FOEOUSSV+i2pR+11UwNq3ihpik\n",
"hajjWQK+AtzZ6qDcA+Aq3PUyKqD2AuCd3XmRG6ShsbeqdeQLqMJtS1E3y7Tzxx8FDqJulN9t+1eZ\n",
"AyNjQWB1qrj9wsC0VpfgAQBXa9HPU8Ufr7L9i6wbw6el239Q0jG2f009PX4/dYNzItUxYx/gk9QT\n",
"5a/YvrrNhVwjAknzA5+iMpXuaS8vQRWJPa/tQV9A1Vo7zPb+7XMJxg4ZV7fZZwPvAz5g+zhVDdAt\n",
"gO0l/QpYnyoi281ofFzzIEVk5zHdjWV7cnsE8B6qIv2x1Pmun9n+sqQFqcVmbapo4+a2rxzIwGMo\n",
"SZpGpdlfavugdkO8D1WQ613tPTOfLElarD1ZzA3SkGtzY2MqfXZR6kbpU8ANVLDtaVR9nGWAlWyf\n",
"0z6XDc2QkXQCVe/kPirY+jD13d9LbXaXBP7Qnijn2jACev/OJT2HykJak7oW3EYd47qXesh3N5Vt\n",
"cH3mxnCS9Dkqrf5caj9xB1UP6a3AV4E3UsXnd6M6MT2UdSL6SdqC6uD1Sipg/yKqwPAZtk9oR8g/\n",
"3t5ze+bP8OisJ9Pa8a19gJcCVwLft/3rdlpjUyqItpurVugT/9/M/Jl39AVP1qE2oAtTNydfpDqe\n",
"bEulOX6MWogWpSL5J9u+agDDjiEnaW/gGtvfbnN0CeAY4Pe2d2nvyWZnhHQWs+nABtR1aQuqiNd1\n",
"1HVrufb2t+bGeTj1BU+PpNaiY6kMySWowMnSVObJRQMbaEypMTa7z6DSrJ9KZR9cSe1dlqKKTP9y\n",
"gMONKSDpUODd1LGLLamb3+WpYxc3Au8EfmH74oENMuZqkjajCtD/jOredAt1s/wRat+xJrCr7e8P\n",
"bJAx4frujZ8J3GX7ry0r6WDqgc1/2b68vX9Z2395svclCaDMg1QF944BtrV9haStgDfa3kbSulTw\n",
"ZEfbV7f359hOTChJ03t1SyS9g7pIvdqtknlLldyD6qhx7fh/Uwyr7k0SVdtiU2ohO6DVQlkaeMT2\n",
"/w10oDGh+moZ9AdRjgZWsb1O5/cJro6I7rrRfha1D50h6VlUSvXvgJNs/7bvfQmuDqG+68M3gGfZ\n",
"fqWk11PB91Ns/3dvH5vrRfT0XxckrUA1KVibyng8vN0jLUcF5G5tP+d6MkQ6e803U1lqt1H1k46l\n",
"9pz7APMDX7V9cef9CaCMkpbu+hPqwvCZ9tozqSJrlwBrAR+xfUbv6c7gRhvDSFWo653AQsBnbV8r\n",
"6YPUUbKtehtfSd9uvz9vcKONqSLpecDC7Qx777VuJsrrqFalDwCftH13//umfNAxodoc2IDaqNzT\n",
"eb17k/Qtqv3o89rPvSyEzIEh1lk3FgQOA25rTwm7QZTnUA+ArgcOsv23QY03Jlf333vf9eEkYBnb\n",
"r2w/5wFgjKmzv9iUOio8jbq2zKCaFiwPfN32hWN9bsoHHJNG0quoB7mbUoWE306dwjicqr32ceAL\n",
"tiesaHDaGM/l1HReup4qkrSjpKe1126kzopeAWzfgicprhUTrkXyTwWupdpO7iFpR+DbVFbUWZI2\n",
"lfQmYBVaMcAYbi3j6IfUU5/eazODJ+2p85lUm9pFqI3NTNnMzPtULSFPpOof3dNe661dj2hWa/Mt\n",
"gcvahodekD9zYHj1rRsPA7sD75T0jPa9947zXEcFUL6V4MlwkrRA9wkwgKtrX+/6sDlwg6Rr2s8J\n",
"nsSY2hx6PXXN+D51ROcw2zdRXVj+D/g3SYt176Oy1gylhYAPA+sA/9z+vAHV1W8RYKeJDJ5AMlDm\n",
"ep2F5h+Bp1OFtW4H9qWyTd5i+/b+z0AuEjHx2vGxPW1v0X5+I/Aa6pz6oZLeSRULfQ7wZVdb7UT7\n",
"h1h7avxd4PO2j+k9UaYuQb0njNNtP9IyURa3fdsc/sqYx0haHriQesLz6XYztBCVkXRTe4+A6X3H\n",
"e3JtGAFjrBtvoNaNPwPH9a4HyZodbpJWAf4D+BJwfn/mWV8myneBz9j+n8GNOOZ2kvai9h/Pp+bW\n",
"1oEodrMAACAASURBVK6C0/NR90zz2f7dIMcYU0NV8+RQ4Du2z5L0aaqY8E62fz/R/3tpYzyXa8GT\n",
"N1FRtDOoavUHUmeF9wd+LGmjbhAlG9KYaJ2NzdXACpLebvubtn8oycAbJb3M9lclfY1atB7sy56K\n",
"4bQ+MB34blvAPktF/K+XdK7tn7TgiVomSoInw2dZqnDfQ5KeTq1RBlaVdLjtY9q69HD3Q1mrhtsc\n",
"1o1T2rqxKXWTc1u7PiR4MqQkLQV8g1orNgFmSLqwG0TpZaLYftj2W9rnEmQNYGZnP/fNh4WoPcd0\n",
"qi7k9ZI2p64rX8g1ZTh1s9h686Hdc9wFfFzSQVTtvV0mI3gCOcIzV2und5amWm69mtqgLgxc0NIa\n",
"9wX+B3jewAYZQ09V1+B9kv7B9r3AkcAaktYHsH0KlSq5R/t5Ri/ttm2KsvkZYraPpo5wHUddo+4B\n",
"vkm1otxC0jLZBA83V92bo6nOSpdQ3Q8+AnwI+ISqa1yMkMewbpwK3Ekd50kwbfgtQO0RXkM9vN0K\n",
"WKdlJ7p3hIeqVzBT5kXAzCzWGW2urCXpVe3o8GeAlYGf2/69pFdTAfyrEjwZLn0lLZ4CsxUQnt5e\n",
"PwS4gDrC80nb503Wg9xkoMzdFqeO61xLBUvWBja3faukDYHLbe8IidLH5Gh1DY4HDu2cST8XWBF4\n",
"g6TFbX8XOJ06076A7dQ9GRG9ozm2P95SaZ9me7f2u98Cn4NsgodZ5+nx+W2fcp3to9qvz5F0An2Z\n",
"JzHcsm5EP9t/knSP7Tsk7UftabekMgfOpR4O3pm1IvpJWgY4XdLawAupIztnUdeTH1M1L06RtBJ1\n",
"ZGNn22fmvmj4tADaRsBmkm6iau9d1rKbacdBd5e0mO07JzMLPhkocylJz6CO6SwD3AW8Fti9RVj/\n",
"Cfg89bQPyA1KTLxW1+DHwAm2vy7pKZIWA26lzhleA+wi6UTgBOC0bIJHzoxe5N/2AVS7uJ6FgSXa\n",
"f2NI9dJo25/PB77W+52ktajuS3kSOCKybsR4WvBEriLT+1OB1X+WtBPwK0krtGMaETPZvgW4HPgt\n",
"8O9Ut8ftqM6PmwKvoIqH7gK81fapOT4+fNpe45VUhtEFVGvqbYB/6b2nc/34W/dzkzGeFJGdS6kK\n",
"M36DSnnsZaAsRNUP2AjYtR2diJgUkl5GpeFfRh3ROLD9ahXgP20f3zbGLwf+YvuyRPyHW7s5egpV\n",
"4+b37bW/K1otaTOqbdzetn8wiLHG5FJfwc/uv/02J9anMpB2bzUvcm0YAVk34tF0rx2Svk/VKnhP\n",
"y0qKmEmzuvgh6RPUPdEGts9sr20BvMr2zn2fyzVlyEh6NtWW+Hzbn1R1on0b1bjiw1MdiE8AZS4j\n",
"aUngXtv3SdqSirBuCSxGdTZZHrjW9kVj3bhETCRJrwA2A/6NerJ8ALUR/jZ1nOy8znszH4eYpBdR\n",
"c+Aq4NnAp23/sPN7UWvKDEkfB35l++TMi+EhaSHggc6GVlSnnbvHeO9WwE22z8kcGC1ZNwIevauS\n",
"pGWBK6ngSdaKGFNfEOVwYAvgRbb/JultwLuBNwH3Z+4Ml75g66rAbtQxrnfZvrLVTjoP+IDtS6Zy\n",
"bKmBMheRtDKwK7BAOyN6KrAq8ELbFwJ/7Lw3C01Mmkepa3C2pG8Cs0V7MxeHl6qzyreATwHfAzYH\n",
"Npf0U+DBVgfFqsKRv7W9T/tcrlNDoj3tOQY4VtKZrkLRn6DqWJzbeV/v2nFi72fIHBgFWTeiG2Rt\n",
"wfRxg6zUEZ7X2r4814no18kimaFZ3Zk+1G6a/yjpC9TN9Odt3zfY0cZEUquL1a4hqwDzA7+jSlu8\n",
"G9hB0rHAX4FFgXuneow5azhAatqf5weupzoZXEc9qXkHldq4c/9n2yYlC01MitQ1iD7PA75s+3jb\n",
"91NZKM+iMk4ekTS9nT39nKTVe+dQc50aHrbvAH4KfAB4ZXv5KNvn9r3P/T9nDoyGrBujrQVZjwM2\n",
"bHtaqCDr6mO93/btti/v/JzrxIjr3hfR6bTianE9f/t5e+rasiuwn+3v930u5mEtM21HSSurGqac\n",
"Th3dOp/Kfj61vfU7VHe3HWz/Zqq//2SgDFYv3X0T6piOgePb2a6zqdZc8wEbSXqu7d8NcrAx/Lrp\n",
"cr3NcFu87msXp25dg1/lnOlosP3fkq7vvHQ5FfFfuP33H2z/VdImc0rZjnlT7+kfVbhtG+Brkt5D\n",
"BVR671meOn5654CGGQOSdSNgZpHYXpD1fuC/qSDr9Y/hs5kPAcyx08qDkp5i+yHbH5b0edu/7X1m\n",
"oIOOCaHquLQo8DJgEWAlqjDwBZI+QB3h+Q9gP+AWqlHBFYMYazJQBqgFT9akiuJ8BbgB2FjSDsCF\n",
"tr9GBVY2TPAkJoukhTSrk8qMFshfpP08c1Fqf14K2N6tKORgRhxTqfNE+Q+dlxcAVgCmSVoPOKEt\n",
"fNO6n4nh0J7+vRb4OvBR6snPnsBrOteL/YHFBzjMmEJZN6KrHauACrIuSQVZXw/c2HnP8qoCwhFj\n",
"asGTcTut2H6od92hGmxkvzEkJD2V6uA2jdpnLAu8mMp2xvYXgUuBT9i+Gfg+dSR053bkZ0qDaAmg\n",
"TDFJz5G0taoYDsDzgZ/YPstVN+Ac4PXA0gC2b7T986SnxWR4rCm3nZvoE52ikCOl/ztuT4/vo7ps\n",
"bAYcDBxu+5aWpZB5MZz+ETjL9jm2d6Rq4hwDbOKqb7DbY3nSHPO+rBvRL0HWmAiqTit7AN9uD5H/\n",
"nap98TpJCwC4FZTtXUdyPRkaAu6haij9gbpe/AJ4iaQ12nt+CtwFYPtX1Dp0iKe4Aw8kgDKlJL2Y\n",
"ak28FLP+f3818LwWccX2yVRhrVW6n8058pgMTl2DGIdaHZN+ne99ceqmad/ek+UEeYfDON/lNVSB\n",
"8xUAbB9O1e3aUdU97o6pHWUMStaNGEeCrPG49e01FqUKg24u6SXtWnMMdaTjxYMYX0wuSc8CaA/m\n",
"7qEVhLV9A3AQlYmyn6TDgEOpzBPaey6zfesUDxlIAGXKSFoROBH4jO3DbP+6/ep/qXOim7TMlFWo\n",
"rJSbBjTUGBFJuY1+c0rLH8MlwDa2T8+T5eHTUqlfJ+kDkramMo6WAbaS9ApVUdA7qADa7fnuR0PW\n",
"jYAEWePJ62SUzJC0Sssy+COVuXQa1WllTaoOxkA6rcSU2FvS7yU9BXiESjIAwPZ1VEbbbcDTgHfb\n",
"/u7c8MBO2fNMDUnrAB+0vW27QZnR23BKei6wLrA1VXjrONvfG9xoY1S0lNvPAR8EtgDWoIoznUkV\n",
"CP0scECeGg0/ddrUAme2gm2fBE7vPlluR3jc/RkSPBk2kjag/v3vSFXB/1fq/PG7qUDKC6jgyQ8z\n",
"B0ZL1o3orQOSXkd1abuLOoJ+OHA28HPgIepm+NOurkwRwMxOK++iOo4+F/gycCFV8+TfgfuoNWdj\n",
"4LfAgbZ/1r//iOEg6QQqw+g+4HjqJMafqKDZPVSw/g+ei1qepwvP1PkHatOJq+2nOheCB6inuScA\n",
"C7sqmc8VEySG3syUW+AcSR+ibqI/aPtUSbvZ/utghxhTwY+xg0LbNM/cxOQaNVxagH9+4O3AO6mC\n",
"wZdS14kbJO1EZa8u337Ohnb0ZN0YcW0dGCvIug8VZH05s4Ks52dPGz2ahzqtxORS6/Bn+22SjgTe\n",
"T2W7zgBeQwVOlqYyTy6HuecakiM8U+c8YIm2+exNgF7xtTWBdVytue7o/X5umSQxHJJyG+N5vGn5\n",
"uTYNn861YVo7i3wVdUN0ELBVC5a8D3iTq1jwjeP8VTFEsm5EP0nTJS3IrCDrvcwKsl4G7ARsC2zW\n",
"y1DLnjZg3uu0EhOvs9/sFZ+er/15eyoDehXb77f9VtvrA6vavmhAwx1XAihToEXY7qEi82u2pzXY\n",
"fkDS6sDHgT/M6e+ImAipaxBjcToojKxuNqSqBtdRkhYC/gxsDuxk+3eqznEfYVYF/GQgjYisGwEJ\n",
"ssaEmKc6rcTEkvQ84H2SFu691hdEeS/wv5Ku7X6sfXaualKQAMok6X7RbSGBOt93ArCNpB9K+lz7\n",
"eW/bZ85tkyOGSyfl9nPAdcBXqRS5fajo/4eALwHH9lJuMydHSjoojKjOtWF7qh7Xp6iz6UcAe0n6\n",
"FnVG/aNZq0ZL1o1IkDWeLM2jnVZi4kh6IdVM5W8tqaB7r/xIJ4iyJXCZpFe1n2e0/85V15EUkZ0E\n",
"nYVmC2Al25/p+/1iwJuoqsK32b4450NjMmlWXYMvUDdFC1Ab4je3p0bTSF2DkTHW9UbSpsBmwMds\n",
"/7m9dhZVCPBtwP9lTgyn9uTvB1Qh8xWBdYCnADsAz6Sq3z9g+8qsVaMj60bAbHvaDaiAyfrUMYxd\n",
"gd2BtanijysD+9v+fuZCdEk6FngtVRfn+8Autq/u/H5pKpAi4DDbv8paMzwkLU8lEXzB9qdbsGQh\n",
"qu7nTe09AqZ3kg7+rmnB3CQBlEnSUlo/RlUfP7vz+rReNK3zWi4SMSk6G5+n2H5I0q7As4HVge3a\n",
"U6P3AbfYPrnz/rn2ohVPXud7TgeFEdY3Dza3vYOqleDzqRvlq4E9bd/Z/5kBDTmmQNaN6JcgazxZ\n",
"mgc7rcTEkPQyKjvtMiq79UDAwKrA4baPGeDwnpAc4ZkEqnagOwIr9oIn7UnOzFSkLjdTO8oYZkm5\n",
"jTlJWv7o6n6XnX/nNwNvlLSJq5j5ldRGZ2ngvZKmZUM7/LJuRL/Odf9pwEm2z6KOd36RCr5/Frjd\n",
"9q/adQPIXIhZOkcz3kY11FgLeCl187w18P+o+XSzO51WMoeGh+1fA0cDy1FdZ2+h1pAPAZ+QtM4A\n",
"h/eEpI3xBOhuLFuGyR2SjgAOkbS/7b1drYun235kwMONEdGXctura7ArlWa7l6Reyu3MugZZsIaf\n",
"0qZ25LVrw3pUq9GLgXOBXaguKksB1wKvAE4Glh0r8B/DKetGdPe0YwRZT7N9GnClpMuAFagg66Gd\n",
"j2Q+jDi19rQwq0ioq13t9i2gsortdTrvz3VkSPW+2/YwDuA620e1X5/TMpMeHv9vmDvlCM8E6Dyx\n",
"2ZBKa7wJOI3qbb4DcJXtAwY5xhg9SbmNrqTlR4+kjYHPAIdRLUePpmoaLEcd2/pb+++KwL8Db3Mr\n",
"+hbDLetGdK79/UHWLYD3Ud3arqWyT04GlrC926DGG3MXVaeVDYCvdteNblBFVZh8ddvPaz9Psz0j\n",
"+43h1P1eJS3oKibcK3fxX9Qe9FeDHOPjlSM8E6AtNOtTm9GzgU8A/wb8mqopsKak/QY4xBghSbmN\n",
"rqTlR/fYjqQVgQ8AbwB+A0yngmhvptKrX0PNi6Woa8VHEzwZflk3oqetFRsDR1G1KY6mMtR+CxwM\n",
"vJtqd/9eap/7QnXaksbo0pB1WoknTlVkHJh5TekF3O9rW5LXAV8B/p87RYPnFTnC8yS1CTId2ISK\n",
"zD8A3AB8xfa9kn4NfJoqmhQxKZJyG3OStPzR1XfE9HXAX4APAwtThdxWoY7rnAjcT3VcMfAc4E22\n",
"fzOIccfky7oRPX3XiW6Q9ZnMCrIuCBxCBVmnA+tRgbV/SZA1VJ1Wfkx1Wvm6Op1WgJva3Hqkc5zn\n",
"Le1z2W8MifZw7gHbj/QyiqhOO3d3v+M2F5YCtrd9zrwWPIEEUJ6Qvk3HDGCGpN9QhWOfAbzFVTtg\n",
"O+Ah29/sfS4XiZgs46Tcpq7BiGvzYg0q0r81lWWwDpUdN25afgyHTtrsmlSR4N1sXyHpNcDdLdB/\n",
"E/AL4LTOU8Njc40Yflk3IkHWmCDLAj8DHpL0dDqdViQdbvuYth7NVu8i90XDQdVA5RjgWEln2n6Q\n",
"OpFxOrWu9N7Xq4lyYu9nmPfmQY7wPEFtoVlV0rqSFqE6FqwMHGj7ekmrAbsDf+1+ZkDDjSGXlNsY\n",
"S9LyA0DSCtTNz2W2L2qZkxcD90s6A/ge8NkWWOltZnKjPOSybgTMSifqBFkXsv1HYBlakJWq7Tcz\n",
"yNpeOzbBk+jxEHZaicfO9h3AT6nstVe2l4+yfW7f+9z/87y450wGyuPQiZr10uGPp9LVVgNeRaU2\n",
"biHpA8CiVDr8j5J5EpMhKbcxlqTlR/8THdt/lvQFYB9Jx9u+QNK9VBemfwaub68l+2jIZd2IsXSC\n",
"rKeNE2RdCdixF2TtZGBHDG2nlXhsNKtA8AXANsDXJL2HCqj03rM8cK/tOwc0zAmVAMoTIGlRYDFg\n",
"s3axOISKzK9FBVWeTx3duS4b0pgMSbmNOUlafrQ5sC7wUip74GjgTuBLkt5n+0LgVmDmEdPe5wY0\n",
"5JhkWTeiJ0HWmEjtmtINolzS+52q08rrgK8OboQxmVytql8LfA74INWxa0/gYUlnUmvM/sAB1D5k\n",
"npcjPI+BmnaBeAPwI6reyRoAtnehbkR+Dyxv+xrb1/U+nw1pTLSk3MZ4kpYfbQ5sChxLHd/6CrCl\n",
"7WOpDc7xLbgy22eyVg23rBvR1QuySnpvu8ntrRVfkrROmy632v5mN3iS60T0aMg7rcTj8o/AWbbP\n",
"sb0jdVz8GGAT23dT9deuH+QAJ1ICKI9BZ9OxCrAlVXzxQmClFlDB9m5UL+sX9n92qscboyF1DaKn\n",
"F+Rtf06b2hHXsiS3BDak1qpHgFPbr78MHEQyUEdS1o2ABFnjiZO0kKTpUNeGtv1YpP08W6cVap+x\n",
"ve1TEjwZHt09Z8c1wAJtjcH24cD1VObzksAdUzvKyaVcCx9d22CsAFwHHGF7J0krAe8AlgDOt31S\n",
"5/2peRITbqynP5J2pp4kbtx5QrQUY6TcZk4Op3HS8u+iUia/QgVMemn5/8mstPytgXPyZHm4SFrR\n",
"9p8k7U0F9J8DvM1V3PxN1HXhsvberFVDLutGjKUFWT9Ppdk/m1oXNrR9c9vzvh+4wn0FIGO0qdNp\n",
"BTjT9oOSPgmc3p0r/WtLrifDpXMq43VUQ4K7gHOoBIOzgZ8DD1HXl0/bPn9gg50kyUAZh6qXNVAR\n",
"Vts3Umnv75f00pb2ehyVIr+epGU6788FIiZFUm6jX9Lyo0dVpG0PSc8C/kQFUA5owZO1qSNci/be\n",
"n+vCaMi6EV0tyHoX8DsqqH4QVePm5hZkfantI22fm6yB6PKIdVqJsbU1ZQMqW+06qr7Na6g96LOo\n",
"zktfovaZ54+TsTJPSwBlDJKWBX7a/oukaZKm2T4E2As4V9Jqtv9ERWE/b/uWAQ45RkBSbmM8ScuP\n",
"5m7qadCbgK8DZwHvkPQt6ujOLrbPG7aNTIwv60Z0JcgaT5Sk3rHPC4AlqU4rrwdu7LxneUmLDWJ8\n",
"MTUkTZe0IPB2qsj0vcClVP2Ty4CdgG2pRis/7GWrDNu1JGegxzY/cI/tv7Sfp7kqDC9u+1BJ9wEX\n",
"S1rL9qUDHGeMkL66Bs+mLlDdugZPIf+mR0L/E2Kng8JIk7QctU79uR3POAz4MVX1fnngGcBNti/P\n",
"HBgtWTeiTzfI+kXgJVSQdbv255lB1mG74YknxyPYaSVm6VwTprmKBF8F/CtVY28r2zdIeh9wi+2T\n",
"Jd04x79wHpdFs0PS01p62gxgkfaa2kVjJeAoSQfbPlLVtWLZQY43RkenrkEv5bbXVrKXcnu97SPb\n",
"e7PxGQG9tHzSpnakqYoG7wUsI+ko4GfUGeQXtiNadwBXdz+TOTAasm5ET4KsMUFmdloBzpH0Iaom\n",
"ygdtnyppN9t/HewQYyJ1946qZio7S/og8GdgZ2Bz27+TtCrwEeDDvfd3/ztscoSnkbQA8EtJOwG3\n",
"AUtLWrRNmOlUt4qf2P4JgO2DbZ+RhSYmW1Juo1/S8kdX9yyxpPnaUdI9ge8ABwI7UGeR91anNldP\n",
"5sBoyLoRPS3Iui9wuKSNqJb2vSDrHbavtn2G7ct7n8l8iHHqVoxUp5UonZon2wPrAp8Cvg0cAezV\n",
"OSb8UdtnjsK9cTJQGtsPSNoG+AG1qTgfeL6kh6jNx07AbS0d9u5hj6zFXCUptzGbpOWPtraZ2Qx4\n",
"cwv+72n7m5IuA1YGbqE2Ocu1P8foyboxovqeGM/XspD2BDaigqzHUUHWzSRd4L4afpkP0dPmUH+n\n",
"lfcCW0nqdVq5g+q0cvvgRhqTpc2BNagHdVsD5wHrUB13dgCeST3Ie8D2laMQPIG0Mf47bZL8iCqQ\n",
"dAy1CX0QuJ/ajG7idK6IKdCXcvsSKuX2g1Sb2jFTbrPxGX5Km9qRJ2kTKvX+rdTRrRWB7Wxf1H4v\n",
"qpPG5ZkDoyXrRvT+zfeCrEAvyPqHNidWBt4BbAas01svIvq1rIPPAjsCp1M1Ly4F3k11+nsBsK9b\n",
"sVDI9WSYdK4lr6OO6uwg6SnA86ls56upa8ud/Z8Z0JCnTI7w9LH9S2A96hjPxbZXsb0GsD6wfoIn\n",
"MRWSchtjSVp+tE3q2lQbyVWA6cAPge9KWgdmHte6fPy/JYZR1o2AmU+MN6Faiu5P1es7XdLLbV9p\n",
"+4dUAGVt25eNyhPjeOyUTisjq3t0q/N93gy8UdImth+yfSVwGbA08F5Vt9qRCqAlA2Ucktaioq3/\n",
"afug9to02zNGJboWU2eMlNuHJS1Bpdz+B5Vy+wZgMSoLKmn5I6gd3fkOdVzni9Q51OWp4zovAf5f\n",
"dzMzuJHGZGpPgJaiCgS/0/YfJf2KypTcyPZdAx1gTImsGzGWNi8+BpwCrEDd7F4MvA14q6vA+Gzv\n",
"z3oRMFvGwVNsPyRpV+qY8OpUluPvNHunld77M4eGROc7XQ94OXXtOJfquvQ+4OvAtVRm0snAErZ3\n",
"G9R4ByUZKOOwfTGwKbCvpGf2giftd7lIxITrpNweLel4YDHb3wS2AX5H1TJ4MXWULEaIpOUkrdBu\n",
"jHem6ho8m3q6uD913PBt3TTaGF62HwL+CtwArCHpFdTTwV0SPBktWTeiX9ujHgDcSAVP3tlucG4F\n",
"Dm2B+P73xwjrZR2068kqVNfRhahOK5sDO3n2Tit3wfB3WhlFbQ5sDBwF3EMdE96Fymg8mDq+9VGq\n",
"Fs6vgReqOtOOlBQZnAPbP2/1BtLPPCZVX8ptr67B6ZJ6dQ2ulHQKqWswcpQ2tSNprHTY7tM+6gHI\n",
"JVQw7XXAB2xfMGpptKMs60aMp2UPdIOsK1JB1qMSZI2xtOvJBlTApNdpZVeqZs5eku5rf57ZaSXX\n",
"k+HQl824InVE+A1UgdjpVAbSgsAhVAHq6VS5i88C/2L7ngEMe6ByhOdRJD0tpkJSbqMnafkBs609\n",
"r6CyB261fW7fexahNjLL2f5NrgujJevGaHsMQdYFqRuhVZkVZD01QdYYi6qJxg+oTisrUp1WnsIc\n",
"Oq1kDs37+vacr6MKjt8FLEx13nkN8ArgROA/gS8ApubJOR7R2qAJoETMJVLXICAdFGIWVSHQw6hN\n",
"y7HAVsB3xgvq5wZ59GTdGF0JssZE6MyjdFoZYZLWpDJMdrN9kaTXAPvYXr/tPQ+ljglf0d4/s7TF\n",
"KEoNlIi5ROoaBKSDQszsgLAEVbBtc+rs8eXAuXPatGZDO3qyboyutlZsBHyZykg8W9Jbe2tCu8m9\n",
"2/ado/qUOMbWq3kC6bQSIGkFKsPkshY8mUZlM94v6Qzge8BnbV/RmQMjGzyB1ECJmFKpaxCPpn3X\n",
"47WpfavtC9s8SJvaIdO7Fth+BPg/SRdRLSRfC7zF9s2S/hX4ZTKPRkfWjegnaToVNOkFWZcgQdZ4\n",
"HNr1o7/Tyi7AjpKWojqtvILqtLLsqN8wD5P+tcH2nyV9AdhH0vFt/biX2n/8M3B9d02JHOGJmFJJ\n",
"uY3HImn5o6XvDPLLqGDJ3pL2pSrdr2/7t5JWo+bE+/uvGzG8sm5ET//3Kml3YHEqyLq1q1NKgqzx\n",
"qFSdVj5DHRPdiSpC/WPqGrMn8Lf23xWBf6c6/Y1csdBh1FlT1gVeSnXTuQbYkuqy9D6PUUMLEoTt\n",
"yRGeiCmUlNt4LJKWP3rateHVVIvArSR9yPZ+1FPBfSV9lSrotoftc/MkaHRk3YjekYtekFXS/u1X\n",
"T6VaVm/bgierAbtR8yRipu6xHc3eaeU3zOq08mbgPKpw6ObUg5zPUp13EjwZEu06silVW+1p1N5i\n",
"S9vHUnVvjm/Bldk+k+DJLDnCEzFFknIbXUnLj55OKvU3qCd9/wu8StICtt/eAmiLA5+z/csET0ZH\n",
"1o3o6QRZ/wXYSNIttveT9EIqyPow1XFnZpA18yBg3E4rH6Y6rRxIHRfudVq5n1mdVp4DvCmB2eEi\n",
"aVEq22RD4NnAtsCp7ddfprovJUYwB/l/TsQkS12DGM94aflt03uvpKNIWv6oWBE4wvYP2nGM1YBP\n",
"t6/8kN6bEkAbDVk3oitB1ngyeuuFqtPKPlSnlStUnVbutn2vpJuAXwCn9bJNJB3r1D4ZKpJWtP0n\n",
"Sb+jOvz1gmQ3S3oTVe/kyPbe7DnHkSM8EZMkKbcxJ0nLH13dVOqO+4H3SHpe+97PA64DXilp296b\n",
"kkY73LJuxBzMDLICR1Kp9ptL2sX2+bZP7QZPcp2ILqXTysiTtDywh6RnAX8CXggcYPt6SWsDBwOL\n",
"9t6fa8j4koESMYmSchtjSVp+tGvD2sDzgfNsnyTp2cBnJO1Brc8rUhvcFQc41JhiWTdinCBIL8j6\n",
"bdvXAudJ6gVZb7H9tTE+EyOqfw45nVYC7gaeRx0N/yLwEuAdkrZrf97F9nlZUx5dAigRkyQpt9Ev\n",
"afkBsxVwOxg4CfiwpMOB04AZwH8BD1IdeFYDNpY0v+0HBzXmmBpZN6InQdZ4stoc6nZaORq4E/iS\n",
"pF6nlVup7m45IjqkJC0HTGtBtJ2pzks/BvYHlgeeAdxk+/KsKY9NAigRkyt1DWLcNrXMSstfvy8t\n",
"//2DG21Mhr458FyqVeBGwIuA7ahibvPZ/qykL1FHbNcGPgZsnuDJSMm6MeISZI0nqzOHDqLmy1eA\n",
"Q20f264dx0va2vYF3c8MZrQxWVQdl/YCllHV1fsZcDbwwnY8/A7g6u5nMg8eXQIoERMkKbcxJ0nL\n",
"H119wZN1qLPHHwaWBT5J3QBtC3y8nUs/DlgIWAd4s+2rBjLwmHRZN6InQdaYSEqnlZHUdx2ZpUAu\n",
"IAAAGt5JREFUz1Uwdk/qWnIgtb94DbCZpAts39L9fNaVxyb/cCImUFJuYyxJyx9tvQ2JpDWo4o/b\n",
"ugr1bQVcbft2ST8HrqSuGw8Ct0s6ODdFwy/rRiTIGhNJ6bQy0tp1ZDPgzZIWAPa0/U1JlwErA7cA\n",
"61IdIG+Zw18V40gXnogJ0kmX/Ar1xOjEVpjpNOCnVArlF6hN0WXASyTNP6DhxtRLB4URJuk5wLeB\n",
"42xf0V6+AFhN0nHUE8FDbF/dbpBI8GT4Zd0ImNVdqxNkXcz2NdTNztW2bwdmC7K21w5O8CS6lE4r\n",
"I61dRzah2lXvTwVhT5f0cttX2v4h8A5gbduX5YHdE5MASsSToKb9uZtyezZVmGlD4BW2Pwv8E7AB\n",
"dTH7GHBgbpCGU3dedKRN7QgZYw5cD5wD7Cjpae21G4G3AlcA29s+o30m3/8Qy7oRY0mQNSZIt9PK\n",
"14GzqE4r36Lm0MxOK4MbYkyW9r2uDXwAWAWYDvwQ+G7LbuvtMy8f3Cjnfco+PeKJGSfldmEqsv9F\n",
"ahO8LbArtfE9rv3u/cDJeWo0vHopsX1p+b9XVT9fH+il5R9MpeXfYfvAwY04JlpnDvwj8HTgUuB2\n",
"YF9gLaqQ8O39n4E8ERxmWTeip//fu6q9/bFUV7bVbN/RAiXPp26GL7J9Vq4TMRbN3mnlJVSnlQ8C\n",
"f2GcTiuZQ8NJ0lOApajuSu+0/UdJv6Ie5G1k+66BDnAIJAMl4glKym2MJ2n50ebAm6g5sB61kVkf\n",
"2JO6LvxY0pL9n8mGdrhl3YiuXpC1XSueDuwAfAs4WdKStmfYvsb2pxM8ifGoOq3sCxwuaSPgt8zq\n",
"tHKH7attn9HNOsgcGl62HwL+CtwArNHq7F1KZR8leDIBEkCJeBKSchs9ScuPnjYVlgbeBbyaahu4\n",
"MHBB+573Bf6HSrOOEZN1IyBB1nji+vYb89n+EzVvvkN1WtmB6rSyt6Rl+j+fOTTvG+uoeGdOiLrH\n",
"v4TKXjsR+I7tC8Y5Yh6PU47wRDwOSbmNsSQtP7okLQHcAXwKWIA6j7x1O8a1IXC57Zvae9MBYchl\n",
"3Yh+7btdCvgS8G6qI8angH+2faukp1I3wifYvnBwI425UeeI6GbAm6l1Zk/bf2jHd1amCoVuBqxj\n",
"+7IBDjcmQWcOvILqpnOr7XP73rMIVQNlOdu/yX5j4iSAEvE4pK5BzElLyz+G2dvUvtH2NpLWpYIn\n",
"O9q+ur1//jxZHi6SngHsCBwEvIcqEvsh2+dI+ifqxnkr25cMcJgxhbJuRL8EWePJUnVa2Z9aY46m\n",
"Ov1tZ/ui9nsBL3WreZI5NHzaca3DqFbVxwJbUZkmHus7zzyYODnCE/E4JOU2xpO0/GjmB15J1b75\n",
"CnAR8H5Jh1Gb3J0TPBktWTeiqwVZ9wSWAe6iMpF2b8GTfwI+Tz1RBhJEi7/XgiPptDKiJE1vQdj3\n",
"AZtTNW8uB86d0/Ui15KJkwyUiMcoKbfRlbT86Go3wPfavk/SllT2yZbAYsBzqDo419q+KHNgdGTd\n",
"iH4t2P4NqhvbtVQm0kLAbVTdrF1tnzK4Eca8QOm0MnL6M0gk7Q4sTu07t7b9O0n/Cvwyx7YmVwIo\n",
"EY9RUm6jK2n50SNpZaq+zQLAftQ82AM4pf+mOHNgtGTdiJ4EWWOitQDs0cBJwM3Ae4GjbF8w0IHF\n",
"hOqrs/cyan+5t6R9qe98fdu/lbQaFVB7f389lJhYOcIT8Rgk5Tb6JS1/dKlpf54fuJ7axF5HHeN6\n",
"BzUndu7/bObA6Mi6ET0tyLo/8HlJzwROpY73vdD2H23/zPY3EjyJru5a032t8990WhkRbc/5aiqT\n",
"cStJH7K9H3AusK+kr1L70T1sn5vvf3LNN+gBRMwjenUNTqEuUCtRdQ3eQqXcpq7BCOmk5b+LalO7\n",
"LtWW+ALbD7anAgtQbWpvH+/viXmWbM9oRfy2BAwcb/uTks6mOiDMB2wk6bm2fzfIwcbAZN0YUX1P\n",
"jLtB1o2pIOsxVJD1+dQ1ZKYETqKrzaG/67TS5sm9ko4inVaGWpsD61FH//4d+F/gVZIWsP32Nj8W\n",
"Bz5n+5cJnky+HOGJmIOk3MZYkpYfktaknvi9m8o8WgT4PXCk7UckPR1Y0fbPBzjMGICsGyFp2jhB\n",
"1p9IeiUVZN0eeAmwRoKsMR6l00oAkt4OPLs9qFkEWA34NPA924d03pc1ZQokAyViHN26BpL2o1Ju\n",
"V6VSbi8E/th5by5YI0Kzt6m9C3g91aa2m5a/FXATZE4Mi1b4cR0qOHYZ9eT4J7bPAs6S9GbqRvk7\n",
"wM22bwRuzLVhtGTdCIAWPFkTOJxZQdaNJb2ACrKeJ+m/qSBrgifxd1SF6RdjVqeVJUinlZEwztpw\n",
"P/AeSd+2fS1wnqTrgFdKusX218b4TEyS1ECJaFLXIB6jtKkdMZJeTKXOLsWsdfNq4HntaTK2TwYe\n",
"plpKzpRrw3DLuhE9kp4jaWtJq7aXZgZZbe8DnEMF3JcGsH2j7Z+nXkV0dW6eH7H9f9Qe453AoVTx\n",
"0Jsl/aukVXP9GF4tw2htSdtKWtn2SdQDus9IWkXS6sCKVAvjFQc62BGUAErELL2uKpsAR1GpkkvZ\n",
"/iS1+b2fTl2DAY4zBkDSkpIWtH0dtZHZA7gbOICaKxcB29k+JRvi4SFpReqozmdsH2b71+1X/wv8\n",
"N7BJu2lahbphumlAQ43ByLoRCbLGk9bbN7Trycsk7d9+9VRgG2BbV5va1YDdqOyUGEJtDmxKPaR7\n",
"EXCipO2A04CfAv8FfAH4MHAZ8JIWwI8pkhooER2paxBjUdrUjixJ6wAftL1tS6me0ftu2w3xusDW\n",
"1I3ycba/N7jRxiBk3RhtLcj6I+AA2yd2Xl+SqnOyIHAVdaNzIrCl7SsGMdaYe3WCJ68G/oUqNH24\n",
"7cMlfROYQQXgVgU+Zvv7qXcyPLp7x7a3OII6FvwiKjB/FvAz21+WtCAVqF0b+CKwue0rBzLwEZUa\n",
"KDHSUtcgxtK3kKWDwmj7B6oNLe1mWJ1N6wNUC8kTgIVt35Frw/DLuhF9ngH82vaJ3SCr7dslnUAF\n",
"Wbelgqx7JXgSY2n7jXRaGUF9e851gD9R2SXLAp+kCsZuC3xc0jTgOGAhah16s+2rBjLwEZYjPDGy\n",
"knIbc5C0/Og5D1hC0k4w8+a3lyq7JrCO7Yds39H7fa4NwyvrRoxhtiArzLohYlaQ9Y3Au2x/L0c8\n",
"Yw5WBI6w/QPgSOBzwOaSdrF9vu1Tu8GTXE+GQ29tkLQG9b0vZvsaqlvX1bZvB34OXAmcZ/vB9trB\n",
"CZ4MRgIoMZJS1yDmxLN3UPgKcAPVQWEH4EJXtfMtgQ2dDgpDS9J8tu8B9gHWlPQhANsPtAJuHwf+\n",
"MMgxxtTJuhHjSJA1HrdxAmm9TivPs3237fOogtSvlLRt702ZQ8OnZTZ+mzoK3MtSuwBYTdJxwJeB\n",
"Q2xf3bJQsP3gYEYbqYESIyl1DaJff1q+pHcA69n+QPt9Ly3/PbZv7nwuT4KGyFhnyiUtDrwK2Au4\n",
"hQqabATsbvvknEMfDVk3ol8Lsj4saWOq0OeFtg9vv1udSrXf0faZgxxnzH06NU/WpgKu59n+vaSd\n",
"qVpKe1CZrgcDFwN32D5wcCOOidS/d2xryrHAa4HV2pHgadTceBNwke2zsuecO6QGSoyq1DWImVpa\n",
"/peBbzJ7Wv67Jb3S9nntRvldVFr+zABK5sTw6GxotwBWsv0ZANt/BX4o6RxqI3Mb8DXbFycVf6Rk\n",
"3YjZgqy2H24vX0jtqfeStCGzB1nPTJA1+rW1ZlMqQHIS8GFJh1OdVmZQnVYeBN5L1cDYWNL8yToY\n",
"Hm0O/CPwdOBSYAdgX+BkSW9px3Suaf+XB3ZzkRzhiVGVlNsAkpYfs7TNzFpUN5VfdX8naZrtO21/\n",
"zfbp3eBJrg0jI+vGiOsGWXvzACrIavuHwIbAt4DTgW16GWqDGm/MXbrHdlrW2keoQNvZwPLU/HmF\n",
"7c8C/wRsQBUS/RhwYIInw6NdR95EHRNfj3qAtz6wJ1Xv5MeqTl6zfSZrytwhAZQYOalrEH1m66DQ\n",
"uSm+nXqafA1V/Xx/0kFhqEl6GrAj1XL27PbadKi6OP3vz2ZmdGTdCEiQNZ647lxoxwEf4O87rfyC\n",
"6rTyHuAR4KnM6rSSNrVDosXRlgbeBbwa+BmwMHBBC5LtC/wP8LyBDTLmKEd4YiQk5TbmIGn5I6pv\n",
"Qzutfb9HAIdI2t/23m1OTHfrrhGjI+tG9BsvyGr7kfGCrFM9xpg79eaCZnVa2db2FZK2onVakTRb\n",
"pxXgdkkHJ/Nk6CwO3A5cSwVL1gY2t31rW1cut70jjF2XLQYvRWRj6I1X16Dz+8WYVdfgtjw1Gi2S\n",
"FgbOAo7vzQ1JC7Qny5sDS9o+ZpBjjMnRuTZsSD3lu4k6f74SdRb5KtsHDHKMMRhZNwLGDLLOULWr\n",
"PgT4ie292/sSZI1HpSpW/xPg8M5+45nAqdTDmrWAj9g+ozffBjfamAySnkEFYQ+iGhO8FfiQ7XMk\n",
"/RNVSHYr25cMcJjxKBJAiZHQUm4/Bny699Sovf53C1Q2waND6aAw8iStD3wB+ADVQvBw6uZoNWB3\n",
"4FLb+w5uhDEoWTciQdZ4MvqvC0qnlZHXgmjfoLos9TJQFqKC8RsBu9o+ZXAjjMciAZQYei3l9gvA\n",
"S2y/rL2Wp0Ujaqx0SKVN7chpm9bpwKeA71PHtY6kzprfIGlBYHXgvjwJGj1ZN6InQdZ4ojoBuG6n\n",
"ldupm+a1gF6nldk+AwmeDJtWEPZe2/dJ2pLKPtkSWAx4DlVE+FrbF2UOzP0SQImhk5TbGE/S8kfb\n",
"WN+lpPcCr6eKCW9p+3pJ2wEP2f5m73P5/odb1o3olyBrTARVp5UDgDOAVwAHAj+iCtO/DtioP4gS\n",
"w0XSysCuwALAflQQbQ/gFNsX9r03e855QLrwxFDqpNzu1W6Qrgd2Bp4jaa/2nmyCR0ybF+mgMMLa\n",
"HFhV0rqSFgEuA1amWkReL6n3VPmv3c8MaLgxhbJuhBqozlu2HwJ+Q9Us+DyVMXBDC7K+2fb5ti/p\n",
"fSaip02ldFoZQd3riKT5qbXkaOA6KovtHVTr4p37P+tm6kYbT0QCKDF02iZ4feAw4GzgE8C/Ab+m\n",
"Um/XlLTfAIcYA6K0qR1JfdkFGwBnAh8ELqDaVB8CbCHpDOCLwEdt/yg3RaMj60b0JMgaE6S/08re\n",
"zN5pZXHbO9q+MGvN0OllO28CHEXVvVnK9iepoMn9VDe3jSQ9d4DjjCcoR3hiqCTlNrqSlh8w29Gt\n",
"RanaNn+2fb6kQ6gjW2sBf6MK+T1k+7pkH42OrBvRPabXgqzHAz+m6py8CngjddRvGWBRKpjy/Rzv\n",
"i7EonVZGnqQ1gROpjOf1gUWA3wNH2n5E0tOph3k/H+Aw4wlKACXmealrEOPp3Ding8II6gugvYE6\n",
"c2zgRM/qtnQQtcFZxfafup/N9WF4Zd2IrgRZYyIpnVZGTvvO1wEut32ZpHcA69n+QPv9m6lg2nts\n",
"39z5XK4j86Ac4YmhkJTbGEvS8kdb7wiWpFWoaveHAxcCK7WACrZ3A/4LeGH/Z6d6vDG1sm5Er1ZB\n",
"J8j6IypzYA0A27sAJ1NPjpe3fY3t63qfz3yILklLSlqwzZFDqQDK3VQR2WOBi4DtbJ/SrZMR8zZJ\n",
"L6YCZksx6976auB5LesZ2ycDDwOrdD+bo+LzpmSgxDwrKbcxJ0nLjzYHVqAKtx1heydJK1EF3JYA\n",
"zrd9Uuf9uTYMuawbMZYWZN2NylBcs718Vi9LoGWinGb7zAENMeZySqeVkSRpRSrweoDtEzuvLwls\n",
"DywIXEUF6E+kshuvGMRYY+IkgBLzrKTcRr+k5YekhWzf2/faLlTLyJfbvqJteN4LLAZ8yvYtAxhq\n",
"DEDWjehKkDWeqL4jovNT2QWrARsDmwHHANsCN9vecmADjUklaR3gg7a3VTUlmNEJ0j8XWBfYmioc\n",
"e5zt7w1utDFRcoQn5jlJuY05SVr+6JK0LPDT9l8kTVMVDz4E2As4V9JqrdbJscDnEzwZDVk3okfS\n",
"Qr0/u1oV3wh8FHi/pJfa/iNwHHAPsJ6kZTrvzzyInnRaCYB/oDIWZ7a57xzNegC4hMpsfJft7+Xo\n",
"1nBIBkrMs5JyGz1Jyw+Y2fngy7Y3aD/PZ/thSYvb/quk7al6OGvZvnSgg42ByLox2lpw9SSqnexf\n",
"WgYKrg5tO1OtZl9j+9J2PZm/G0iL6FI6rYw8SQsDZwHH2/5Me20B2w9I2hxY0vYxgxxjTLxkoMQ8\n",
"pz1VfjrwC+B22ydQxSFvB17dLljY3sX2mYn0jo6Wlr8YsJntbYAzqHlyCrAd8GFgm17wZHAjjYkk\n",
"6WntjzOoDWwvqPZwS8c/QdIGto+knjQvO6ChxoBk3YhmfuAe239pP/fa2y9u+1Dq+nBxy1S7IcGT\n",
"6JL0HElbS1q1vfR84Ce2z7K9D3AO9bBmaQDbN9r+ebIOhlN7SHMPsA/VlOBDAC14sjrwceAPgxxj\n",
"TI4EUGKekJTbGEvS8kPSAsAvJe1EtYhcWtKibU5MBz5LbXB/AmD7YNtnZDM7/LJuRE+CrPFkKZ1W\n",
"gtmO52D74fbHC4ETgG0k/VDS59rPeycgP5xyhCfmekm5jUeTtPzRJmld4AdURsFzqWM6DwF/oo5s\n",
"3QYIuDub2NGQdSN6WpD1KuDzwBHAlcDqtu9qQdbvAOfZPrjvczniGUA6rUTpPLDbAlipd2Sn8/vF\n",
"qGLktwG32b64FzzJtWS4zDfoAUQ8BmOl3PbqGhwq6T4q5TZ1DUaMZnVQ+AXVQeEESRdQHRReLekp\n",
"tk9qmSjZEA8p2xdIej21wV2SKt63LvBg+/NywCa2fzO4UcYUy7oRwMx0+m2oIOuiwPnA8yX1gqw7\n",
"Abe1I6Azg6xZK6LjGcCvbZ+oTqcV27dLOoFab7al1pu9EjwZTi14shZV8+bT3d+pCtbfCXyt81qC\n",
"J0MqAZSYa0l6mu07GD/l9ihJB9s+shVxSsrtCFCnTa3tGcCNkj4K7C/pWFeb2uOoNrXrSTrPrdNK\n",
"FrHhZfuXktYDzgYutv0+mPn0ebl2XCOGXNaNGEuCrPEkzdZppXt8mFmdVk4AFrZ9R26ch1M7Crgj\n",
"VRj47PbadNuPtP3obPL9D6/UQIm5UuoaxFiUNrUxB7avBjYFPiVpt/baA8ANMPvZ5Rg+WTdiTmz/\n",
"EliPmhsX217F9hpU95T1EzyJOTgPWKJdW3o3xvO3360JrGP7oRa8Tc2TIdELlLU/T2vf7xHA/ZL2\n",
"h5kBtemDHGdMvdRAiblW6hpEP6VNbTwGktYGzgReDNw41pOhGE5ZN+LRtBT804H/tH1Qe63XjSfH\n",
"PGM2nX3GxsA2wIW2D2+/W50qRL1jaqwNn07Nkw2BdYCbqFp7KwE7AFfZPmCQY4zByBGemGsl5TZ6\n",
"kpYfj4erbeSK7TxyjJCsG/FoWmHHTYEzJZ1IJ8ia4EnA7PXSPHunlfmAvdoN9R+AjYDd3TqtZP4M\n",
"lxY8WZ8KxH8A+Da1hhxCBel3l7Sf7X0HOMwYgGSgxFxP0ouougZ72j66vZa6BiNC6aAQT0DnyVHm\n",
"wQjKuhGPRtJiCbJGv87akU4rI0zVpGA68Cng+1StmyOBN9u+QdKCwOrAfbYvGdxIYxASQIl5QlJu\n",
"R1vS8iPi8cq6EXOSIGuMp107PgZ8ulcstL0+rf9IaIInw2Os71LSe4HXU52YtrR9vaTtgIdsf7P3\n",
"uXz/oyUBlJhnpK7BaJO0BrPS8o8hafkR8SiybkTE49E6rXwBeIntl7XXptt+ZLAji8nWCaquCiwM\n",
"XA68BPgisL/t70laDTge2MX2jwY43BigBFBinpKU29GWtPyIeLyybkTEeLpZB50MtVdSdS5+Ynvv\n",
"9r4EUYZUN4NE0gZUgOTHwGrAq4A3Ulkoy1BZzwfa/n4yT0ZXAigxT0nKbSQtPyIej6wbETGedFqJ\n",
"zhxYlCoM/Gfb50s6hKp3sxbwN+D51NGd63J0a7RNG/QAIh6PTlX0XLBGlO2LgU2BfSU9s3smOfMi\n",
"Ivpl3YiI8fR1Wjkb+ATwb8Cvqbpra0rab4BDjEmips2BN1DHxHcE1gCwvQtwMvB7YHnb19i+rvf5\n",
"rCmjKxkoETFPSlp+REREPFHptBIAklYBdqMyj9ZsL59l+5T2+0OA02yfOaAhxlwmAZSImCclLT8i\n",
"IiIej3RaiZ4WQFsBuA44wvZOklYC3gEsAZxv+6TO+zMHAsgRnoiYRyUtPyIiIh6vXqcVSetKWgS4\n",
"DFiZKg56feu0sjvw1+5nBjTcmECSFur92fYM2zcCHwXeL+mlrSHBccA9wHqSlum8P3MggGSgRERE\n",
"RETEEEunlZC0LHASsLntv7QMFFoTgp2BvYHX2L5U0jOA+bs1TyJ65hv0ACIiIiIiIiZb67SyGLBZ\n",
"p9PKL6hOK8czRqeVGBrzA/fY/kv7eZrthyUtbvtQSfcBF0tay/alAxxnzOUSQImIiIiIiKHTrXnS\n",
"Oq3sARg4kapxsYukGVSnlVVsX9P9fLJP5n2Snmb7DmAGsEh7TS14shJwlKSDbR8paWFg2UGON+Z+\n",
"OcITERERERFDK51WRpOkBYCrgM8DRwBXAqvbvkvSdOA7wHm2D+77XI5uxbgSQImIiIiIiKGTTish\n",
"aV3gB8DhwHOBw4CHgD9R9W5uAwTcne8+HosEUCIiIiIiYihIWsj2vX2v7QLsD7zc9hWSVgTeS9VD\n",
"+ZTtWwYw1JgiktYAfgQsCRwDrAs8CNwPLAdsYvs3gxthzEsSQImIiIiIiHleOq3EeCS9CDgb2NP2\n",
"0e21BYDlWvviiMckRWQjIiIiImIYpNNKjMn21ZI2BU5vhWUPsv2ApBsgx7fisUsAJSIiIiIi5lnp\n",
"tBKPhe2LWxDlTEknAjfantF+l+BJPCY5whMREREREfOkdFqJx0vSYrbvHPQ4Yt6UAEpERERERMyz\n",
"0mklHo9e8CxBtHgicoQnIiIiIiLmWbYvkPR6ZnVauZ90Wolx9IImCZ7EE5EMlIiIiIiImOel00pE\n",
"TLZkoERERERExDwvnVYiYrIlAyUiIiIiIoaGpLWBM4EX0+m0EhHxZCWAEhERERERQyWdViJiMkwb\n",
"9AAiIiIiIiIm2N+gju0MeiARMTySgRIRERERERER8SiSgRIRERERERER8SgSQImIiIiIiIiIeBQJ\n",
"oEREREREREREPIoEUCIiIuL/t2MHAgAAAACC/K1HWKAwAgBgCBQAAACAEbhjKkbh+W3VAAAAAElF\n",
"TkSuQmCC\n"
],
"text/plain": [
"<matplotlib.figure.Figure at 0x7f85575a8650>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"addHeader(1,'Plot')\n",
"addHeader(2,'K-mer Coverage Stats')\n",
"\n",
"with size_controller(FULL_FIG_W, FULL_FIG_H):\n",
" bqc = Data.boxplot(column=[\"K-mer Coverage\", \n",
" \"K-mer Coverage averaged: 500 bp\",\n",
" \"K-mer Coverage averaged: 2.5 Kbp\",\n",
" \"K-mer Coverage averaged: 5 Kbp\",\n",
" \"K-mer Coverage averaged: 50 Kbp\",\n",
" \"K-mer Coverage averaged: 1 Mbp\",\n",
" \"K-mer Coverage averaged: 5 Kbp before\",\n",
" \"K-mer Coverage averaged: 5 Kbp after\"], return_type='dict', rot=45)\n",
" \n",
" plt.setp(bqc['boxes' ], color='black')\n",
" plt.setp(bqc['medians' ], color='black')\n",
" plt.setp(bqc['whiskers'], color='black')\n",
" plt.setp(bqc['fliers' ], color='black')\n",
" \n",
" for of in output_files['K-mer Coverage Stats']:\n",
" print \"Saving Image:\", of\n",
" savefig(of)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Sequencing Coverage Stats"
]
},
{
"cell_type": "code",
"execution_count": 422,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h2>Sequencing Coverage Stats</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Saving Image: reports/eps/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Sequencing_Coverage_Stats.eps\n",
"Saving Image: reports/png/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Sequencing_Coverage_Stats.png\n",
"Saving Image: reports/pdf/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Sequencing_Coverage_Stats.pdf\n"
]
},
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAABEgAAAHfCAYAAABDIO2KAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\n",
"AAALEgAACxIB0t1+/AAAIABJREFUeJzt3XuwrWddH/DvFw4XIdWQwSaA2DACtbFgUIkXqhx0ytTa\n",
"Al4Gb+3Eyzh2dFRs7Rh0rEltx9vo2Io6Y6ue1Ao1amHwCsHheCkVR8zhkoCAw+kYhSBKLGithDz9\n",
"Y7+72Tmcs07YZ+/97ne9n8/MnrzPu9611m/trJm1znc/z+/pGCMAAAAAa/aguQsAAAAAmJuABAAA\n",
"AFg9AQkAAACwegISAAAAYPUEJAAAAMDqCUgAAACA1dsYkLR9eNvXtj3T9o623z2dv6LtrW3f2vaV\n",
"bS/fc58Xtn1b27e0ffZhvwAAAACAS9UxxuYL2keMMf6q7Ykkv53kW5I8J8l7xhjf1/ZbkzxqjHFD\n",
"22uSvDjJ05M8Lsmrkjx5jHHvob4KAAAAgEtw0SU2Y4y/mg4fmuTBSd6bnYDk5un8zUmeNx0/N8lL\n",
"xhgfGGOcTfL2JNcdZMEAAAAAB+2iAUnbB7U9k+SuJK8eY9ye5Moxxl3TJXcluXI6fmySO/fc/c7s\n",
"zCQBAAAAOLZOXOyCaXnMtW0/Kskr2j7rnNtH203rdD7ktotcDwAAAHAoxhg93/mLBiR7HuAv2v5y\n",
"kk9Oclfbq8YY72r7mCTvni774ySP33O3j5nOPeCCAAA2aXt6jHFy7joAgOXZNGHjYrvYPHp3h5q2\n",
"H5HkHya5LcnLk1w/XXZ9kpdNxy9P8iVtH9r2CUmelOR3L618AGDt2p5se2PbG5M8c/e47cmZSwMA\n",
"tsTGXWzaPiU7TVgfNP389Bjj+9tekeSWJB+b5GyS548x7p7u821JvirJPUm+aYzxivM87jCDBADY\n",
"j7ZvH2M8ce46AIDl2ZRHXHSb38MgIAEA9qvtmTHGtXPXAQAsz6Y84qK72AAAHDNn5i4AANg+D7hJ\n",
"KwDAXKZeIyen4fVtz07Hp8cYp2coCQDYMpbYAACL0vb9Y4zL5q4DAFgeS2wAgG1yz9wFAADbR0AC\n",
"ABx7bV/U9uy0tOajdo/bvmju2gCA7WCJDQCwKG3/fIxxxdx1AADLY4kNALBNHjp3AQDA9hGQAABL\n",
"c8fcBQAA28c2vwDAsXfONr9Pb3vjdGybXwDgQOhBAgAsStszY4xr564DAFgePUgAAAAANrDEBgA4\n",
"9s5ZYvOJltgAAAfNEhsAYFHavnmM8ffmrgMAWB5LbACAbfJxcxcAAGwfAQkAsDQfnLsAAGD7CEgA\n",
"gGOv7Uvb3t327iQP3z1u+9K5awMAtoMeJADAorT9P2OMj5i7DgBgefQgAQC2ycPmLgAA2D4CEgBg\n",
"aY5++isAsPVOzF0AAMDFtH1BkudNwwe1PT0dv2yM8UPzVAUAbBMBCQCwBE9McvWe8dV7zgMAXDJN\n",
"WgGARWn7wTHGg+euAwBYHk1aAYBt4o8sAMCBE5AAAEvzgbkLAAC2j4AEADj22r607d1t707y0N3j\n",
"ti+duzYAYDvoQQIALErb948xLpu7DgBgefQgAQC2yUPmLgAA2D4CEgBgaf733AUAANtHQAIALI3l\n",
"NQDAgTsxdwEAABfT9gVJnjcNH9729HT8sjHGD81TFQCwTTRpBQAWxfcIAGC/NGkFABat7R+2vbft\n",
"vdP43unnD+euDQDYDmaQAACL0vbeMYY/8gAAHzYzSACAbeKPLADAgROQAABL88G5CwAAto+ABAA4\n",
"9tq+qO3ZtmeTPHj3uO2L5q4NANgOepAAAIvS9p4xxom56wAAlkcPEgBgm/gjCwBw4AQkAMCxd84S\n",
"mwdZYgMAHDRLbACARWn752OMK+auAwBYHktsAIBt8oi5CwAAto+ABABYmvfNXQAAsH10gAcAjr22\n",
"L0jyvGn46Lanp+OXjTF+aJ6qAIBtogcJALAobf96jPHwuesAAJZHDxIAAACADQQkAMCxd842vw+z\n",
"zS8AcNAssQEAFsU2vwDAflliAwBsE99fAIAD5wsGALA075y7AABg+9jmFwA49tqeTHJyGn582xun\n",
"49NjjNMzlAQAbBk9SACARWl7Zoxx7dx1AADLsymPMIMEADj2zplB8olmkAAAB80MEgBgUdq+f4xx\n",
"2dx1AADLYxcbAAAAgA0EJADAsdf2RW3Ptj2b5JG7x21fNHdtAMB2sMQGAFiUtmfHGFfPXQcAsDyW\n",
"2AAAAABsICABAJbmj+YuAADYPgISAGBpPmHuAgCA7SMgAQCW5vK5CwAAts+JuQsAALiYtieTnLxv\n",
"2Bun49NjjNMzlAQAbBm72AAAx17bNyS5Zho+OMkHp+M7xhhPnacqAGBpNuURAhIAYFHa3jvGsEwY\n",
"APiw2eYXAAAAYAMBCQCwNHfPXQAAsH00aQUAjr1zmrQ+SpNWAOCg6UECACxK2zNjjGvnrgMAWJ5N\n",
"eYQZJADAsXfODJJPNIMEADhoZpAAAIvS9tQY4yvmrgMAWB672AAAAABsICABAJbmzNwFAADbxxIb\n",
"AAAAYBUssQEAAADYQEACACzKtKMNAMCBEpAAAAAAq6cHCQAAALAKepAAAAAAbCAgAQAWRQ8SAOAw\n",
"CEgAAACA1dODBAAAAFiFffcgafv4tq9ue3vbN7X9xun8jW3vbHvb9PO5e+7zwrZva/uWts8+2JcC\n",
"AAAAcPA2ziBpe1WSq8YYZ9peluR1SZ6X5PlJ3jfG+MFzrr8myYuTPD3J45K8KsmTxxj3nnOdGSQA\n",
"wL60PTnGOD13HQDA8ux7BskY411jjDPT8fuTvDk7wUeSnO8Bn5vkJWOMD4wxziZ5e5Lr9ls4AAAA\n",
"wFF4wE1a216d5GlJfmc69Q1tX9/2J9pePp17bJI799ztztwXqAAAXDKzRwCAw/CAApJpec3PJ/mm\n",
"aSbJjyV5QpJrk7wzyQ9suPvRd4EFAAAA+DCcuNgFbR+S5BeS/NcxxsuSZIzx7j23/+ckvzgN/zjJ\n",
"4/fc/WOmc+d73FNJzk7Du5Oc2f2LUNuT0/MYGxsbGxsbG99vvHvuuNRjbGxsbGxsfKzHL8jO5I6z\n",
"uYiLNWltkpuT/NkY45v3nH/MGOOd0/E3J3n6GOPLel+T1utyX5PWJ45znqSatAIA+9Rq0goA7M+m\n",
"POJiM0iekeSfJXlD29umc9+W5EvbXptkJHlHkq9NkjHGHW1vSXJHknuSfN254QgAwKUQjgAAh2Hj\n",
"DJJDe1IzSAAAAIAjtimPeMC72AAAHAe7a4sBAA6SgAQAAABYPUtsAAAAgFWwxAYAAABgAwEJALAo\n",
"epAAAIdBQAIAAACsnh4kAAAAwCroQQIAAACwgYAEAFgUPUgAgMMgIAEAAABWTw8SAAAAYBX0IAEA\n",
"AADYQEACACyKHiQAwGEQkAAAAACrpwcJAAAAsAp6kAAAAABsICABABZFDxIA4DAISAAAAIDV04ME\n",
"AAAAWAU9SAAAAAA2EJAAAIuiBwkAcBgEJAAAAMDq6UECAAAArIIeJAAAAAAbCEgAgEXRgwQAOAwC\n",
"EgAAAGD19CABAAAAVkEPEgAAAIANBCQAwKLoQQIAHAYBCQAAALB6epAAAAAAq6AHCQAAAMAGAhIA\n",
"YFH0IAEADoOABAAAAFg9PUgAAACAVdCDBAAAAGADAQkAsCh6kAAAh0FAAgAAAKyeHiQAAADAKuhB\n",
"AgAAALCBgAQAWBQ9SACAwyAgAQAAAFZPDxIAAABgFfQgAQAAANhAQAIALIoeJADAYRCQAAAAAKun\n",
"BwkAAACwCnqQAAAAAGwgIAEAFkUPEgDgMAhIAAAAgNXTgwQAAABYBT1IAAAAADYQkAAAi6IHCQBw\n",
"GAQkAAAAwOrpQQIAAACsgh4kAAAAABucmLsAAOB4aXv000u3jJmyALA8AhIA4H6O+z/uLdUFAA6D\n",
"JTYAAADA6glIAAAAgNUTkAAAAACrJyABAAAAVk9AAgAszU1zFwAAbJ+OcfQ7+ek+DwAAABy1TXmE\n",
"GSQAwKK0PTl3DQDA9hGQAAAAAKtniQ0AAACwCpbYAAAAAGwgIAEAFqXtqblrAAC2jyU2AMCi+B4B\n",
"AOyXJTYAAAAAGwhIAAAAgNUTkAAAAACrJyABAAAAVk9AAgAszU1zFwAAbB+72AAAAACrYBcbAGBr\n",
"tD05dw0AwPYRkAAAAACrZ4kNAAAAsAqW2AAAAABsICABABal7am5awAAts/GgKTt49u+uu3tbd/U\n",
"9hun81e0vbXtW9u+su3le+7zwrZva/uWts8+7BcAAKzO9XMXAABsn409SNpeleSqMcaZtpcleV2S\n",
"5yX5yiTvGWN8X9tvTfKoMcYNba9J8uIkT0/yuCSvSvLkMca95zyuHiQAwL74HgEA7Ne+e5CMMd41\n",
"xjgzHb8/yZuzE3w8J8nN02U3Zyc0SZLnJnnJGOMDY4yzSd6e5LpLfgUAAAAAh+gB9yBpe3WSpyV5\n",
"bZIrxxh3TTfdleTK6fixSe7cc7c7sxOoAAAAABxbJx7IRdPyml9I8k1jjPe1981GGWOMtpv2Cj7v\n",
"bVODtbPT8O4kZ8YYp6fbTk6PbWxsbGxsbGx8v/Gu41KPsbGxsbGx8bEevyDJtbkvf7igjT1Ipgd7\n",
"SJJfSvKrY4wfms69JcnJMca72j4myavHGB/f9oapkO+Zrvu1JN85xnjtOY85hrXDAMA+tL1xjHHj\n",
"3HUAAMuzKY+42C42TfITSe7YDUcmL899HeSvT/KyPee/pO1D2z4hyZOS/O6lFA8AsJdwBAA4DBfb\n",
"xeYfJPnNJG9I/v9SmRdmJ/S4JcnHZmeayvPHGHdP9/m2JF+V5J7sLMl5xXke1wwSAGBf2p7cnTYL\n",
"APDh2JRHXHSJzWEQkAAA+yUgAQD2S0ACAAAArN6+e5AAAAAArIGABABYlLan5q4BANg+ltgAAIvi\n",
"ewQAsF+W2AAAAABsICABAAAAVk9AAgAAAKyegAQAAABYPQEJALA0N81dAACwfexiAwAAAKyCXWwA\n",
"gK3R9uTcNQAA20dAAgAAAKyeJTYAAADAKlhiAwAAALCBgAQAWJS2p+auAQDYPpbYAACL4nsEALBf\n",
"ltgAAAAAbCAgAQAAAFZPQAIAAACsnoAEAAAAWD0BCQCwNDfNXQAAsH3sYgMAAACsgl1sAICt0fbk\n",
"3DUAANtHQAIAAACsniU2AAAAwCpYYgMAAACwgYAEAFiUtqfmrgEA2D6W2AAAi+J7BACwX5bYAAAA\n",
"AGwgIAEAAABWT0ACAAAArJ6ABAAAAFg9AQkAsDQ3zV0AALB97GIDAAAArIJdbACArdH25Nw1AADb\n",
"R0ACAAAArJ4lNgAAAMAqWGIDAAAAsIGABABYlLan5q4BANg+ltgAAIviewQAsF+W2AAAAABsICAB\n",
"AAAAVk9AAgAAAKyegAQAAABYPQEJALA0N81dAACwfexiAwAAAKyCXWwAgK3R9uTcNQAA20dAAgAA\n",
"AKyeJTYAAADAKlhiAwAAALCBgAQAWJS2p+auAQDYPpbYAACL4nsEALBfltgAAAAAbCAgAQAAAFZP\n",
"QAIAAACsnoAEAAAAWD0BCQCwNDfNXQAAsH3sYgMAAACsgl1sAICt0fbk3DUAANtHQAIAAACsniU2\n",
"AAAAwCpYYgMAAACwgYAEAFiUtqfmrgEA2D6W2AAAi+J7BACwX5bYAAAAAGwgIAEAAABWT0ACAAAA\n",
"rJ6ABAAAAFi9E3MXAABr0/bPkzxq7jqWrO3Rd5nfDu8dY1wxdxEAcBwJSADg6D3KLizMQbAEABdm\n",
"iQ0AsChtT85dAwCwfQQkAAAAwOp1jKOfadl2mFoMwFr5HGQu3nsArN2mz0IzSAAAAIDVE5AAAIui\n",
"BwkAcBgEJAAAAMDq6UECAEfM5yBz8d4DYO30IAEAAADYQEACACyKHiQAwGEQkAAAAACrd9GApO1P\n",
"tr2r7Rv3nLux7Z1tb5t+PnfPbS9s+7a2b2n77MMqHABYpzHG6blrAAC2zwOZQfJTSf7ROedGkh8c\n",
"Yzxt+vnVJGl7TZIvTnLNdJ8fbWuWCgAAAHCsXTS8GGP8VpL3nuem83V9fW6Sl4wxPjDGOJvk7Umu\n",
"u6QKAQD20IMEADgMlzK74xvavr7tT7S9fDr32CR37rnmziSPu4TnAAAAADh0J/Z5vx9L8m+n4+9K\n",
"8gNJvvoC147znWx7KsnZaXh3kjO7a4p3/zJkbGxsbGy8jeNdx6Ue43WNdx2XeoyNjY2NjQ95/IIk\n",
"1+a+/OGCOsZ584v7X9ReneQXxxhP2XRb2xumQr5nuu3XknznGOO159xnjDHOt0QHALaez0Hm4r0H\n",
"wNpt+izc1xKbto/ZM/z8JLs73Lw8yZe0fWjbJyR5UpLf3c9zAACcz7kzIQAADsJFl9i0fUmSZyZ5\n",
"dNs/SvKdSU62vTbJSPKOJF+bJGOMO9rekuSOJPck+brxQKaoAAAAAMzoAS2xOfAnNb0TgBXzOchc\n",
"vPcAWLsDX2IDAAAAsE0EJADAouhBAgAcBgEJAAAAsHp6kADAEfM5yFy89wBYOz1IAAAAADYQkAAA\n",
"i6IHCQBwGAQkAAAAwOrpQQIAR8znIHPx3gNg7fQgAQAAANhAQAIALIoeJADAYRCQAAAAAKunBwkA\n",
"HDGfg8zFew+AtdODBAAAAGADAQkAsCh6kAAAh0FAAgAAAKyeHiQAcMR8DjIX7z0A1k4PEgAAAIAN\n",
"BCQAwKLoQQIAHAYBCQAAALB6epAAwBHzOchcvPcAWDs9SAAAAAA2EJAAAIuiBwkAcBgEJAAAAMDq\n",
"6UECAEfM5yBz8d4DYO30IAEAAADYQEACACyKHiQAwGEQkAAAAACrd2LuAgBgjdoefROwLdJqowEA\n",
"HCwBCQDMQKNM5iCYA4ALs8QGAFgUPUgAgMMgIAEAAABWr2Mc/UzLTfsOA8C28znIXLz3AFi7TZ+F\n",
"ZpAAAAAAqycgAQAWRQ8SAOAwCEgAAACA1dODBACOmM9B5uK9B8Da6UECAAAAsIGABABYFD1IAIDD\n",
"ICABAAAAVk8PEgA4Yj4HmYv3HgBrpwcJAAAAwAYCEgBgUfQgAQAOg4AEAAAAWD09SADgiPkcZC7e\n",
"ewCsnR4kAAAAABsISACARdGDBAA4DAISAAAAYPX0IAGAI+ZzkLl47wGwdnqQAAAAAGwgIAEAFkUP\n",
"EgDgMAhIAAAAgNXTgwQAjpjPQebivQfA2ulBAgAAALCBgAQAWBQ9SACAwyAgAQAAAFZPDxIAOGI+\n",
"B5mL9x4Aa6cHCQAAAMAGAhIAYFH0IAEADoOABAAAAFg9PUgA4Ij5HGQu3nsArJ0eJAAAAAAbCEgA\n",
"gEXRgwQAOAwCEgAAAGD19CABgCPmc5C5eO8BsHZ6kAAAAABsICABABZFDxIA4DAISAAAAIDV04ME\n",
"AI6Yz0Hm4r0HwNrpQQIAAACwgYAEAFgUPUgAgMMgIAEAAABWTw8SADhiPgeZi/ceAGunBwkAAADA\n",
"BgISAGBR9CABAA6DgAQAAABYPT1IAOCI+RxkLt57AKydHiQAAAAAGwhIAIBF0YMEADgMAhIAAABg\n",
"9fQgAYAj5nOQuXjvAbB2l9SDpO1Ptr2r7Rv3nLui7a1t39r2lW0v33PbC9u+re1b2j77YF4CAAAA\n",
"wOG56AyStp+Z5P1J/ssY4ynTue9L8p4xxve1/dYkjxpj3ND2miQvTvL0JI9L8qokTx5j3HvOY/rr\n",
"BQCr1fbop2/CjveOMa6YuwgAmMumPOLExe48xvittlefc/o5SZ45Hd+c5HSSG5I8N8lLxhgfSHK2\n",
"7duTXJfkd/ZVOQBsIX8kuDT+0AIAHIb9Nmm9coxx13R8V5Irp+PHJrlzz3V3ZmcmCQAAAMCxdcm7\n",
"2IydNTqbpgqbRgwAAAAcaxddYnMBd7W9aozxrraPSfLu6fwfJ3n8nus+Zjr3IdqeSnJ2Gt6d5MwY\n",
"4/R028kkMTY2NjY2NjY+d7zruNRjbGxsbGxsfKzHL0hybe7LHy7oAW3z250eJL847t+k9c/GGN/b\n",
"9oYkl4/7N2m9Lvc1aX3iOOdJau0wALBPvkcAAPu16XvERWeQtH1JdhqyPrrtHyX5N0m+J8ktbb86\n",
"OynM85NkjHFH21uS3JHkniRfd244AgBwiW6auwAAYPs8oBkkB/6k/vIDAAAAHLFNecQlN2kFADhK\n",
"u2uLAQAOkoAEAAAAWD1LbAAAAIBVsMQGAAAAYAMBCQCwKG1PzV0DALB9LLEBABbF9wgAYL8ssQEA\n",
"AADYQEACAAAArJ6ABAAAAFg9AQkAAACwegISAGBpbpq7AABg+9jFBgAAAFgFu9gAAFuj7cm5awAA\n",
"to+ABAAAAFg9S2wAAACAVbDEBgAAAGADAQkAsChtT81dAwCwfSyxAQAWxfcIAGC/LLEBAAAA2EBA\n",
"AgAAAKyegAQAAABYPQEJAAAAsHoCEgBgaW6auwAAYPvYxQYAAABYBbvYAABbo+3JuWsAALaPgAQA\n",
"AABYPUtsAAAAgFWwxAYAAABgAwEJALAobU/NXQMAsH0ssQEAFsX3CABgvyyxAQAAANhAQAIAAACs\n",
"noAEAAAAWD0BCQAAALB6AhIAYGlumrsAAGD72MUGAAAAWAW72AAAW6PtyblrAAC2j4AEAAAAWD1L\n",
"bAAAAIBVsMQGAAAAYAMBCQCwKG1PzV0DALB9LLEBABbF9wgAYL8ssQEAAADYQEACAAAArJ6ABAAA\n",
"AFg9AQkAAACwegISAGBpbpq7AABg+9jFBgAAAFgFu9gAAFuj7cm5awAAto+ABAAAAFg9S2wAAACA\n",
"VbDEBgAAAGADAQkAsChtT81dAwCwfSyxAQAWxfcIAGC/LLEBAAAA2EBAAgAAAKyegAQAAABYPQEJ\n",
"AAAAsHoCEgBgaW6auwAAYPvYxQYAAABYBbvYAABbo+3JuWsAALaPgAQAAABYPUtsAAAAgFWwxAYA\n",
"AABgAwEJALAobU/NXQMAsH0ssQEAFsX3CABgvyyxAQAAANhAQAIAAACsnoAEAAAAWD0BCQAAALB6\n",
"AhIAYGlumrsAAGD72MUGAAAAWAW72AAAW6PtyblrAAC2j4AEAAAAWL0TcxcAABwvbY9+/e2HqT3e\n",
"K3UtJQaA5RGQAAD34x/3AMAaWWIDACyKHiQAwGEQkAAAAACrZ5tfAAAAYBVs8wsAAACwgYAEAFgU\n",
"PUgAgMNwSQFJ27Nt39D2tra/O527ou2tbd/a9pVtLz+YUgEAkiTXzl0AALB9LnUGyUhycozxtDHG\n",
"ddO5G5LcOsZ4cpJfn8YAAAfFH18AgAN3EEtszm1u8pwkN0/HNyd53gE8BwAAAMChOYgZJK9q+3tt\n",
"v2Y6d+UY467p+K4kV17icwAA7HX13AUAANvnxCXe/xljjHe2/egkt7Z9y94bxxij7Xn3Eb7QeQCA\n",
"i2l7/dw1AADb5ZICkjHGO6f//mnblya5Lsldba8aY7yr7WOSvPs89zvvnsMAAAAAc9j3Epu2j2j7\n",
"t6bjRyZ5dpI3Jnl5kt2/6lyf5GWXWiQAAADAYeoY+1vp0vYJSV46DU8k+Zkxxne3vSLJLUk+NsnZ\n",
"JM8fY9x9ALUCAAAAHIp9ByQAAAAA2+IgtvkFAI6htt/e9k1tX9/2trbXzV3ThbT95bYfeUCP9eS2\n",
"v9L2rW1f1/Zn2/7tg3hsAGB7mUECAFuo7acn+YEkzxxjfGBaAvuw3Qbr26rtw5O8Ick3jzF+eTr3\n",
"zCTvGWPcfgjPd2KMcc9BPy4AcPTMIAGA7XRVdkKBDyTJGOPPd8ORtp/c9nTb32v7a22v2nP+9W3P\n",
"tP3+tm+czn9F2x/efeC2vzSFDmn77LavmWZq3DI1bk/bs21vnM6/oe3fnc5f1vanpnOvb/v5e66/\n",
"ou3Vbd/c9sen2S+vmEKPtH36dL/b9tZ3ji9L8prdcGR67b8xxri97cP3PPfvtz05Pe7/bHvNntd3\n",
"uu0ntX1k259s+9rp+ufs+X28vO2vJ7l1uu5Ve17rc/Y81ne0fUvb32r74rb/ajr/cW1/dfp/8Ju7\n",
"vx8AYD4CEgDYTq9M8vi2f9D2R9p+VpK0fUiSH07yhWOMT0nyU0n+/XSfn0ry9WOMa5OM6ed8RpLR\n",
"9tFJvj3J54wxPjnJ65L8yz3X/Ol0/seSfMt0/juSvHeM8dQxxicmefWe63c9McmLxhh/P8ndSb5w\n",
"T31fM8Z4WpJ7LlDfJ0x1nM/XJ/ngGOOpSb40yc1tH5bkZ5M8f/r9PCbJVWOM359e26+PMT41yWcn\n",
"+f62j5ge62nZ+R0+K8lfJ/n86bV+dnZm7qTt05N8QZKnJvncJJ+yp+YfT/IN0/+Df53kRy9QMwBw\n",
"RE7MXQAAcPDGGH/Z9pOTfGaSZyX52bY3ZCc8+IQkr2qbJA9O8idtPyrJR40xfnt6iJ/Ozj/qL6RJ\n",
"Pi3JNUleMz3WQ5O8Zs81/3367+9nJyhIks9J8sV76jzfTnfvGGO8YTp+XZKrp/ouG2O8djr/4iT/\n",
"ZENt5/OMJP9xet4/aPu/kjwpO7vvvTLJjdkJSn5uuv7ZSf5p291w52HZ2aVvJLl1T+0PSvLdbT8z\n",
"yb1JHtv2yun5XjbG+Jskf9P2F5NkmmXzGUl+bvq9JTu/OwBgRgISANhSY4x7k/xGkt+YlqNcn53A\n",
"4fYxxmfsvbbt5efcfW/IcE/uP+v04XuObx1jfNkFSvi/038/mPt/57hQgHHu/Xbv+xHnueZCj3F7\n",
"kmdueOwPud8Y40/a/lnbp2QnIPnaPTd/wRjjbfd7gPZTk/zlnlNfnuTRST5pjPHBtu/Izu9onPN8\n",
"u8cPys4smqdtqBMAOGKW2ADAFpp2cnnSnlNPS3I2yR8k+ei2nzZd95C210yzIe5u+4zp+i/fc9+z\n",
"Sa7tjscnuS47//j/nSTPaPtx02M98pznPJ9bs7PUZbfOc4OZ8xpj/EWS9/W+nXi+5AKXvjjJZ7T9\n",
"x3ue47PafkKS39p9XW2fnJ3ZIH8wXfazSb41yUeOMd40nXtFkm/c8zi7gca5IctHJnn3FI48K8nf\n",
"yc7v539kZwbKw9peluTzptfyviTvaPtF0+O27VMfyO8BADg8AhIA2E6XJTnV9va2r0/y8UlunJq2\n",
"flGS7217JsltST59us9XJvmRtrftfaBp2c07ktyR5D9k6vExxnhPkq9I8pLpOV6T5HzNRvf2M/l3\n",
"SR7V9o3380JZAAABBklEQVTT85+8wPXnG391kv801feIJH/xIXcc46+zs/TmG7qzze/tSf5Fkndn\n",
"p8/Hg9q+Icl/S3L9bhPbJD+fnaU/t+x5uO9K8pCp8eqbktx0nteTJD+T5FOmx/3nSd481fJ7SV6e\n",
"nV11fiXJG/fU/OVJvnr6HbwpyXMCAMzKNr8AwIdo+3eS/NIY4ylz17Kr7SPHGH85Hd+Q5MoxxjfP\n",
"XNZGuzVPzV1/IztNZs/MXRcA8KH0IAEAzqe58C42c/m8ti/MzveXs9mZvXLc/fi0hfDDk5wSjgDA\n",
"8WUGCQAAALB6epAAAAAAqycgAQAAAFZPQAIAAACsnoAEAAAAWD0BCQAAALB6/w+s2ZHAlOFxtAAA\n",
"AABJRU5ErkJggg==\n"
],
"text/plain": [
"<matplotlib.figure.Figure at 0x7f8557ce3f10>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"addHeader(2,'Sequencing Coverage Stats')\n",
"\n",
"with size_controller(FULL_FIG_W, FULL_FIG_H):\n",
" bqc = Data.boxplot(column=['Sequencing Coverage'], return_type='dict')\n",
" \n",
" plt.setp(bqc['boxes' ], color='black')\n",
" plt.setp(bqc['medians' ], color='black')\n",
" plt.setp(bqc['whiskers'], color='black')\n",
" plt.setp(bqc['fliers' ], color='black')\n",
" \n",
" for of in output_files['Sequencing Coverage Stats']:\n",
" print \"Saving Image:\", of\n",
" savefig(of)"
]
},
{
"cell_type": "code",
"execution_count": 423,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h2>BLAST Coverage Stats</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Saving Image: reports/eps/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.BLAST_Coverage_Stats.eps\n",
"Saving Image: reports/png/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.BLAST_Coverage_Stats.png\n",
"Saving Image: reports/pdf/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.BLAST_Coverage_Stats.pdf\n"
]
},
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAABE0AAAHfCAYAAAClCSbOAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\n",
"AAALEgAACxIB0t1+/AAAHS9JREFUeJzt3XGsbWlZHvDncQakopZY7CAwOqaACmIZ245TrOVUKx1p\n",
"O1RjFWoC1yZKTI1iNaG1tJxpk9r+YWoJETFR5phWQW0yGQSDo+UqqTotDgOIMwqp0wyoYyIORagR\n",
"8OsfZ185HtY9c/fe99x19zq/XzLJfvdee6/3kJB8ee633q9jjAAAAADw533K3A0AAAAAXI2EJgAA\n",
"AAAThCYAAAAAE4QmAAAAABOEJgAAAAAThCYAAAAAE7YKTdpe3/Ytbd/d9tfbfsdFrntl2/e0fUfb\n",
"G7e5JwAAAMCVcO2W3/9oku8aY9zb9tOT/Frbu8YY9124oO3zkjxljPHUtl+W5NVJbt7yvgAAAACn\n",
"aqudJmOM3xtj3Lt6/UdJ7kvyxGOX3ZrkYHXN3Uke1/a6be4LAAAAcNou20yTtjckuTHJ3cc+elKS\n",
"B4/U70vy5Mt1XwAAAIDTsO3jOUmS1aM5P53kO1c7Tj7pkmP1mPiNT3oPAAAA4LSNMY7nFkkuQ2jS\n",
"9lFJ/luS/zLGuGPikvcnuf5I/eTVe5fcJADASdoO6wgAYBMnbeLY9vScJvmRJL8xxviBi1x2Z5IX\n",
"ra6/OcnDY4yHtrkvAAAAwGnrGJs/FdP2byX5pSTvzCceufneJJ+bJGOM16yue1WSW5J8OMk3jzHu\n",
"mfgt/0IEAGzEOgIA2NRJ64itQpPLyWIHANiUdQQAsKmT1hGX7fQcAIAZ3TZ3AwDA8ghNAIAlOD93\n",
"AwDA8ghNAAAAACaYaQIAAACcWWaaAAAAAKxJaAIA7Ly2e3P3AAAsj9AEAFiCc3M3AAAsj5kmAMDO\n",
"s44AADZlpgkAAADAmoQmAAAAABOEJgAAAAAThCYAAAAAE4QmAMAS3DZ3AwDA8ghNAIAlOD93AwDA\n",
"8ghNAAAAACZ0jDF3D0lOPhcZAAAA4DSclEfYaQIAAAAwQWgCAOy8tntz9wAALI/QBABYgnNzNwAA\n",
"LI+ZJgDAzrOOAAA2ZaYJAAAAwJqEJgAAAAAThCYAAAAAE4QmAAAAABOEJgDAEtw2dwMAwPIITQCA\n",
"JTg/dwMAwPIITQAAAAAmdIwxdw9JTj4XGQAAAOA0nJRH2GkCAAAAMEFoAgDsvLZ7c/cAACyP0AQA\n",
"WIJzczcAACyPmSYAwM6zjgAANmWmCQAAAMCahCYAAAAAE4QmAAAAABOEJgAAAAAThCYAwBLcNncD\n",
"AMDyCE0AgCU4P3cDAMDyCE0AAAAAJnSMMXcPSU4+FxkAAADgNJyUR9hpAgAAADBBaAIA7Ly2e3P3\n",
"AAAsj9AEAFiCc3M3AAAsj5kmAMDOs44AADZlpgkAAADAmoQmAAAAABOEJgAAAAAThCYAAAAAE4Qm\n",
"AMAS3DZ3AwDA8ghNAIAlOD93AwDA8ghNAAAAACZ0jDF3D0lOPhcZAAAA4DSclEfYaQIAAAAwQWgC\n",
"AOy8tntz9wAALI/QBABYgnNzNwAALI+ZJgDAzrOOAAA2ZaYJAAAAwJqEJgAAAAAThCYAAAAAE4Qm\n",
"AAAAABOEJgDAEtw2dwMAwPIITQCAJTg/dwMAwPIITQAAAAAmdIwxdw9JTj4XGQAAAOA0nJRH2GkC\n",
"AAAAMEFoAgDsvLZ7c/cAACzP1qFJ2x9t+1Dbd13k8722H2z79tV/L9/2ngAAx5ybuwEAYHm2nmnS\n",
"9iuS/FGSHxtjPHPi870k/3yMcesj/I6ZJgDARqwjAIBNnepMkzHGW5P84SP1sO19AAAAAK6kKzHT\n",
"ZCR5dtt3tH1T26dfgXsCAAAAbOXaK3CPe5JcP8b4SNuvSXJHkqdNXdj29iQPrMqHk9w7xji/+mwv\n",
"SdRqtVqtVquP1xdcLf2o1Wq1Wq2+quuXJnlWPpE/XNTWM01WN7whyRvGxEyTiWt/O8lfG2N84Nj7\n",
"Y3gWGQDYgHUEALCpk9YRp/54Ttvr2nb1+qYcBjUfeISvAQCs47a5GwAAlmfrx3Pa/kSS5yR5fNsH\n",
"k7wiyaOSZIzxmiRfn+Tb2n4syUeSvGDbewIAHHN+7gYAgOW5LI/nXA621QIAm2q7d+E5ZQCAdZyU\n",
"RwhNAAAAgDNr1pkmAAAAALtIaAIA7LwLRwkCAFxOQhMAYAnOzd0AALA8ZpoAADvPOgIA2JSZJgAA\n",
"AABrEpoAAAAATBCaAAAAAEwQmgAAAABMEJoAAEtw29wNAADLIzQBAJbg/NwNAADLIzQBAAAAmNAx\n",
"xtw9JDn5XGQAAACA03BSHmGnCQAAAMAEoQkAsPPa7s3dAwCwPEITAGAJzs3dAACwPGaaAAA7zzoC\n",
"ANiUmSYAAAAAaxKaAAAAAEwQmgAAAABMEJoAAAAATBCaAABLcNvcDQAAyyM0AQCW4PzcDQAAyyM0\n",
"AQAAAJjQMcbcPSQ5+VxkAAAAgNNwUh5hpwkAAADABKEJALDz2u7N3QMAsDxCEwBgCc7N3QAAsDxm\n",
"mgAAO886AgDYlJkmAAAAAGsSmgAAAABMEJoAAAAATBCaAAAAAEwQmgAAS3Db3A0AAMsjNAEAluD8\n",
"3A0AAMsjNAEAAACY0DHG3D0kOflcZAAAAIDTcFIeYacJAAAAwAShCQCw89ruzd0DALA8QhMAYAnO\n",
"zd0AALA8ZpoAADvPOgIA2JSZJgAAAABrEpoAAAAATBCaAAAAAEwQmgAAAABMEJoAAEtw29wNAADL\n",
"IzQBAJbg/NwNAADLIzQBAAAAmNAxxtw9JDn5XGQAAACA03BSHmGnCQAAAMAEoQkAsPPa7s3dAwCw\n",
"PEITAGAJzs3dAACwPGaaAAA7zzoCANiUmSYAAAAAaxKaAAAAAEwQmgAAAABMEJoAAAAATBCaAABL\n",
"cNvcDQAAyyM0AQCW4PzcDQAAyyM0AQAAAJjQMcbcPSQ5+VxkAAAAgNNwUh5hpwkAAADABKEJALDz\n",
"2u7N3QMAsDxCEwBgCc7N3QAAsDxmmgAAO886AgDY1KnONGn7o20favuuE655Zdv3tH1H2xu3vScA\n",
"AADAabscj+e8NsktF/uw7fOSPGWM8dQk35rk1ZfhngAAAACnauvQZIzx1iR/eMIltyY5WF17d5LH\n",
"tb1u2/sCAAAAnKYrMQj2SUkePFK/L8mTr8B9AQAAADZ27RW6z/GBKpPTZ9venuSBVflwknvHGOdX\n",
"n+0liVqtVqvVS6yTvCVspe3VMd1+B10Yfne1/P9BrVar1epTrl+a5Fn5RP5wUZfl9Jy2NyR5wxjj\n",
"mROf/VCS82OM163q+5M8Z4zx0LHrxjD1HgDYgHUEALCpk9YRV+LxnDuTvGjVyM1JHj4emAAAAABc\n",
"bbZ+PKftTyR5TpLHt30wySuSPCpJxhivGWO8qe3z2r43yYeTfPO29wQAAAA4bZfl8ZzLwbZaAGBT\n",
"1hEAwKbmfjwHAAAAYOcITQCAJTiYuwEAYHk8ngMAAACcWR7PAQAAAFiT0AQA2Hlt9+buAQBYHqEJ\n",
"AAAAwAQzTQAAAIAzy0wTAGDR2u7P3QMAsDx2mgAAO886AgDYlJ0mAAAAAGsSmgAAAABMEJoAAAAA\n",
"TBCaAAAAAEwQmgAAS3AwdwMAwPI4PQcAAAA4s5yeAwAAALAmoQkAsPPa7s3dAwCwPEITAAAAgAlm\n",
"mgAAAABnlpkmAMCitd2fuwcAYHnsNAEAdp51BACwKTtNAAAAANYkNAEAAACYIDQBAAAAmCA0AQAA\n",
"AJggNAEAluBg7gYAgOVxeg4AAABwZjk9BwAAAGBNQhMAYOe13Zu7BwBgeYQmAAAAABPMNAEAAADO\n",
"LDNNAIBFa7s/dw8AwPLYaQIA7DzrCABgU3aaAAAAAKxJaAIAAAAwQWgCAAAAMEFoAgAAADBBaAIA\n",
"LMHB3A0AAMvj9BwAAADgzHJ6DgAAAMCahCYAwM5ruzd3DwDA8ghNAAAAACaYaQIAAACcWWaaAACL\n",
"1nZ/7h4AgOWx0wQA2HnWEQDApuw0AQAAAFiT0AQAAABggtAEAAAAYILQBAAAAGCC0AQAWIKDuRsA\n",
"AJbH6TkAAADAmeX0HAAAAIA1CU0AgJ3Xdm/uHgCA5RGaAAAAAEww0wQAAAA4s8w0AQAWre3+3D0A\n",
"AMtjpwkAsPOsIwCATdlpAgAAALAmoQkAAADABKEJAAAAwAShCQAAAMAEoQkAsAQHczcAACyP03MA\n",
"AACAM8vpOQAAAABrEpoAADuv7d7cPQAAy7N1aNL2lrb3t31P25dNfL7X9oNt37767+Xb3hMAAADg\n",
"tF27zZfbXpPkVUn+bpL3J/lfbe8cY9x37NJfHGPcus29AAAuZoxxfu4eAIDl2XanyU1J3jvGeGCM\n",
"8dEkr0vy/InrDHgFAE5N2/25ewAAlmfb0ORJSR48Ur9v9d5RI8mz276j7ZvaPn3LewIAHPeKuRsA\n",
"AJZnq8dzchiIPJJ7klw/xvhI269JckeSp215XwAAAIBTtW1o8v4k1x+pr8/hbpM/M8b40JHXP9v2\n",
"B9t+1hjjA8d/rO3tSR5YlQ8nuffCM8oXpuKr1Wq1Wq1WH68vuFr6UavVarVafVXXL03yrHwif7io\n",
"jnEpm0Uu8uX22iS/meSrkvxOkv+Z5IXjyCDYttcl+f0xxmh7U5KfHGPcMPFbY4xh9gkAsDbrCABg\n",
"UyetI7baaTLG+Fjbb0/y5iTXJPmRMcZ9bV+y+vw1Sb4+ybe1/ViSjyR5wTb3BAAAALgSttppcjn5\n",
"FyIAYFNtbx9jnJu7DwBg95yURwhNAAAAgDPrpDxi2yOHAQAAABZJaAIA7LwLU/EBAC4noQkAAADA\n",
"BDNNAAAAgDPLTBMAYNHa7s/dAwCwPHaaAAA7zzoCANiUnSYAAAAAaxKaAAAAAEwQmgAAAABMEJoA\n",
"AAAATBCaAABLcDB3AwDA8jg9BwAAADiznJ4DAAAAsCahCQCw89ruzd0DALA8QhMAAACACWaaAAAA\n",
"AGeWmSYAwKK13Z+7BwBgeew0AQB2nnUEALApO00AAAAA1iQ0AQAAAJggNAEAAACYIDQBAAAAmCA0\n",
"AQCW4GDuBgCA5XF6DgAAAHBmOT0HAAAAYE1CEwBg57Xdm7sHAGB5hCYAAAAAE8w0AQAAAM4sM00A\n",
"gEVruz93DwDA8thpAgDsPOsIAGBTdpoAAAAArEloAgAAADBBaAIAAAAwQWgCAAAAMEFoAgAswcHc\n",
"DQAAy+P0HAAAAODMcnoOAAAAwJqEJgDAzmu7N3cPAMDyCE0AAAAAJphpAgAAAJxZZpoAAIvWdn/u\n",
"HgCA5bHTBADYedYRAMCm7DQBAAAAWJPQBAAAAGCC0AQAAABggtAEAAAAYILQBABYgoO5GwAAlsfp\n",
"OQAAAMCZ5fQcAAAAgDUJTQCAndd2b+4eAIDlEZoAAAAATDDTBAAAADizzDQBABat7f7cPQAAy2On\n",
"CQCw86wjAIBN2WkCAAAAsCahCQAAAMAEoQkAAADABKEJAAAAwAShCQCwBAdzNwAALI/TcwAAAIAz\n",
"y+k5AAAAAGsSmgAAO6/t3tw9AADLIzQBAAAAmGCmCQAAAHBmmWkCACxa2/25ewAAlmfr0KTtLW3v\n",
"b/ueti+7yDWvXH3+jrY3bntPAIBjXjF3AwDA8mwVmrS9JsmrktyS5OlJXtj2i45d87wkTxljPDXJ\n",
"tyZ59Tb3BAAAALgStt1pclOS944xHhhjfDTJ65I8/9g1tyY5SJIxxt1JHtf2ui3vCwAAAHCqtg1N\n",
"npTkwSP1+1bvPdI1T97yvgAAAACn6totv3+pR+8cn0I7+b22tyd5YFU+nOTeMcb51Wd7SaJWq9Vq\n",
"tVp9vL7gaulHrVar1Wr1VV2/NMmz8on84aK2OnK47c1J9scYt6zqf5nkT8cY//HINT+U5PwY43Wr\n",
"+v4kzxljPHTst8Zw5DAAsIG2t48xzs3dBwCwe07KI7Z9POdtSZ7a9oa2j07yjUnuPHbNnUletGrk\n",
"5iQPHw9MAAC2ITABAE7DVo/njDE+1vbbk7w5yTVJfmSMcV/bl6w+f80Y401tn9f2vUk+nOSbt+4a\n",
"AAAA4JRt9XjO5eTxHABgU233LjynDACwjtN8PAcAAABgkew0AQAAAM4sO00AgEVruz93DwDA8thp\n",
"AgDsPOsIAGBTdpoAAAAArEloAgAAADBBaAIAAAAwQWgCAAAAMEFoAgAswcHcDQAAy+P0HAAAAODM\n",
"cnoOAAAAwJqEJgDAzmu7N3cPAMDyCE0AAAAAJphpAgAAAJxZZpoAAIvWdn/uHgCA5bHTBADYedYR\n",
"AMCm7DQBAAAAWJPQBAAAAGCC0AQAAABggtAEAAAAYILQBABYgoO5GwAAlsfpOQAAAMCZ5fQcAAAA\n",
"gDUJTQCAndd2b+4eAIDlEZoAAAAATDDTBAAAADizzDQBABat7f7cPQAAy2OnCQCw86wjAIBN2WkC\n",
"AAAAsCahCQAAAMAEoQkAAADABKEJAAAAwAShCQCwBAdzNwAALI/TcwAAAIAzy+k5AAAAAGsSmgAA\n",
"O6/t3tw9AADLIzQBAAAAmGCmCQAAAHBmmWkCACxa2/25ewAAlsdOEwBg51lHAACbstMEAAAAYE1C\n",
"EwAAAIAJQhMAAACACUITAAAAgAlCEwBgCQ7mbgAAWB6n5wAAAABnltNzAAAAANYkNAEAdl7bvbl7\n",
"AACWR2gCAAAAMMFMEwAAAODMMtMEAFi0tvtz9wAALI+dJgDAzrOOAAA2ZacJAAAAwJqEJgAAAAAT\n",
"hCYAAAAAE4QmAAAAABOEJgDAEhzM3QAAsDxOzwEAAADOLKfnAAAAAKxJaAIA7Ly2e3P3AAAsj9AE\n",
"AAAAYIKZJgAAAMCZZaYJALBobffn7gEAWB47TQCAnWcdAQBsyk4TAAAAgDVdu+kX235Wktcn+bwk\n",
"DyT5hjHGwxPXPZDk/yb5eJKPjjFu2vSeAAAAAFfKNjtN/kWSu8YYT0vyC6t6ykiyN8a4UWACAAAA\n",
"7IptQpNbkxysXh8k+UcnXOsZYwAAAGCnbBOaXDfGeGj1+qEk113kupHk59u+re23bHE/AICLOXjk\n",
"SwAA1nPiTJO2dyV5wsRH/+poMcYYbS92DM+XjzF+t+1nJ7mr7f1jjLde5H6353A+SpI8nOTeMcb5\n",
"1Wd7q3up1Wq1Wq1WH6/PXWX9qNVqtVqtvnrrlyZ5Vj6RP1zUxkcOt70/h7NKfq/t5yR5yxjjCx/h\n",
"O69I8kdjjO+f+GwMRwUCAAAAV9BJecQ2j+fcmeTFq9cvTnLHxI0/re1nrF4/Nslzk7xri3sCAHyS\n",
"C/+CBABwOW0TmvyHJF/d9reSfOWqTtsntn3j6ponJHlr23uT3J3kZ8YYP7dNwwAAAABXwsaP51xu\n",
"Hs8BAAAArrTTejwHAOCq0HZ/7h4AgOWx0wQA2HnWEQDApuw0AQAAAFiT0AQAAABggtAEAAAAYILQ\n",
"BAAAAGCC0AQAWIKDuRsAAJbH6TkAAADAmeX0HAAAAIA1CU0AgJ3Xdm/uHgCA5RGaAAAAAEww0wQA\n",
"AAA4s8w0AQAWre3+3D0AAMtjpwkAsPOsIwCATdlpAgAAALAmoQkAAADABKEJAAAAwAShCQAAAMAE\n",
"oQkAsAQHczcAACyP03MAAACAM8vpOQAAAABrEpoAADuv7d7cPQAAyyM0AQAAAJhgpgkAAABwZplp\n",
"AgAsWtv9uXsAAJbHThMAYOdZRwAAm7LTBAAAAGBNQhMAAACACUITAAAAgAlCEwAAAIAJQhMAYAkO\n",
"5m4AAFgep+cAAAAAZ5bTcwAAAADWJDQBAHZe2725ewAAlkdoAgAAADDBTBMAAADgzDLTBABYtLb7\n",
"c/cAACyPnSYAwM6zjgAANmWnCQAAAMCahCYAAAAAE4QmAAAAABOEJgAAAAAThCYAwBIczN0AALA8\n",
"Ts8BAAAAziyn5wAAAACsSWgCAOy8tntz9wAALI/QBAAAAGCCmSYAAADAmWWmCQCwaG335+4BAFge\n",
"O00AgJ1nHQEAbMpOEwAAAIA1CU0AAAAAJghNAAAAACYITQAAAAAmCE0AgCU4mLsBAGB5nJ4DAAAA\n",
"nFlOzwEAAABYk9AEANh5bffm7gEAWB6hCQAAAMAEM00AAACAM8tMEwBg0druz90DALA8dpoAADvP\n",
"OgIA2JSdJgAAAABrEpoAAAAATBCaAAAAAEwQmgAAAABM2Dg0afuP27677cfbfukJ193S9v6272n7\n",
"sk3vBwBwgjfP3QAAsDzb7DR5V5KvTfJLF7ug7TVJXpXkliRPT/LCtl+0xT0BAKb86twNAADLc+2m\n",
"Xxxj3J8k7Ymn+92U5L1jjAdW174uyfOT3LfpfQEAAACuhNOeafKkJA8eqd+3eg8A4HK6Ye4GAIDl\n",
"OXGnSdu7kjxh4qPvHWO84RJ+f6zTTNu1rgcAuKDti+fuAQBYlhNDkzHGV2/5++9Pcv2R+voc7jaZ\n",
"uteJz/kAAAAAXEmX6/GciwUeb0vy1LY3tH10km9McudluicAAADAqdnmyOGvbftgkpuTvLHtz67e\n",
"f2LbNybJGONjSb49h8cA/kaS148xDIEFAAAArnodwxgRAAAAgONO+/QcAGAB2n687dvb3tv219r+\n",
"zdX7N7R91wnfu6Ptrxx77wvanl/93m+0fU3b567qt7f9UNv7V69vn/jNp7V9U9vfWvXy+rZ/+bL/\n",
"0QDAmXfiIFgAgJWPjDFuTJK2z03yfUn2TvpC28cl+eIkH2z7+WOM31599Mok33/hJL62XzzG+PUk\n",
"P7eq35Lku8cY90z85mOS/EyS7xpjvHH13nOSfHaS39/6r/zk+127etwYADiD7DQBANb1F5N84BKu\n",
"+7okb0jyU0lecOT9J+TwhL0kySowOe5iQ+b/SZJfvhCYrL7/i2OMd7d9TNvXtn1n23va7iVJ219p\n",
"+/Q/++HDXS5f2vaxbX+07d2r629dfX6u7Z1tfyHJXavrfn61q+WdF65bXfuvV7ti3tr2x9t+9+r9\n",
"v9L2Z9u+re0vtf2CS/jfCwC4ythpAgBcir/Q9u1JHpPkc5J85SV85wVJ/k0Od4DckcPdKUnyn5L8\n",
"97a/nMPdJa8dY3zw2HcvNnTtGUl+7SKf/bMkHx9jfMkqpPi5tk9L8vok35Bkv+3nJHnCGOOetv8+\n",
"yS+MMf7palfM3W1/fvVbNyZ55hjj4bbXJPnaMcaH2j4+ya8kubPt38hhMPQlSR6d5J4cnhyYJD+c\n",
"5CVjjPe2/bIkP5jkqx7pfzAA4OoiNAEALsX/O/J4zs1JfiyHj95MantdkqeMMX51Vf9J22eMMd49\n",
"xri97ZuT3JLk+Ule0vavjjH+5BJ7udgulC/P4aM/GWP8Ztv/k+SpSX4yh+HMfg7Dk59aXf/cJP+w\n",
"7fes6k9N8rk5DGzuGmM8vHr/U5J8X9uvSPKnSZ64+vu+PMkdq77/pO2Fx40em+TZSX6q/bNWH32J\n",
"fxsAcBURmgAAaxlj/Grbx692XVzMNyT5rLYX5ph8RpIXJnn56jd+N8lrk7x2NUj2GUnefgm3f3eS\n",
"55zw+ScFKmOM32n7B22fuerrJUc+/roxxnv+3A8c7gz58JG3vinJ45N86Rjj46u/6TE5DFeO3u/C\n",
"609J8ocXQiYAYHeZaQIArKXtFya5JskfnHDZC5P8vTHG548xPj/JX89qrknbW9o+avX6CUn+Uo7M\n",
"OHkEP57k2W2fd6Sfv932GUnemsOAI6vHcj43yW+uLnt9kpcl+cwjM1TenOQ7jvzOhZDjePDymUl+\n",
"fxWY/J0kn5fDwOR/5HCnyqe2/fQkfz9JxhgfSvLbbb9+9btt+yWX+PcBAFcRO00AgEtxYaZJchgq\n",
"vGiMMVaPn3xB2wePXPufk1w/xrj7whtjjAfaPtz2piRfneQH2v7x6uPvGWNc0sk3Y4w/bvsPVt//\n",
"gSQfTfKOJN+Zw7khr277ziQfS/LiMcZHV1/96VVf//bIz/271e+8M4f/kPS/k9yaw0Dk6EyV/5rk\n",
"Davr3pbkvlUvb2t7Z5J3JnkoybuSXJjN8k2rXl6e5FFJfmJ1HQCwQzrGxeasAQBwkraPHWN8uO2n\n",
"JfnFJN8yxrh37r4AgMvDThMAgM398Oo448ckuV1gAgDLYqcJAAAAwASDYAEAAAAmCE0AAAAAJghN\n",
"AAAAACYITQAAAAAmCE0AAAAAJvx/uF6S+3lo04MAAAAASUVORK5CYII=\n"
],
"text/plain": [
"<matplotlib.figure.Figure at 0x7f85749f3690>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"if BAC_MODE:\n",
" addHeader(2,'BLAST Coverage Stats')\n",
" \n",
" with size_controller(FULL_FIG_W, FULL_FIG_H):\n",
" bqc = Data.boxplot(column=['BLAST Coverage'], return_type='dict')\n",
" plt.setp(bqc['boxes' ], color='black')\n",
" plt.setp(bqc['medians' ], color='black')\n",
" plt.setp(bqc['whiskers'], color='black')\n",
" plt.setp(bqc['fliers' ], color='black')\n",
"\n",
" for of in output_files['BLAST Coverage Stats']:\n",
" print \"Saving Image:\", of\n",
" savefig(of)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## K-mer Coverage Distribution"
]
},
{
"cell_type": "code",
"execution_count": 424,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h2>K-mer Coverage Distribution</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Number of rows: 3564\n",
"Saving Image: reports/eps/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.K-mer_Coverage_Distribution.eps\n",
"Saving Image: reports/png/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.K-mer_Coverage_Distribution.png\n",
"Saving Image: reports/pdf/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.K-mer_Coverage_Distribution.pdf\n"
]
},
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAABFQAAAHfCAYAAAB+sozsAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\n",
"AAALEgAACxIB0t1+/AAAIABJREFUeJzt3X+MZed93/fPV6KJlX80C8EBl6KIkkCl2CxcUElBF7HT\n",
"UIYlyEYgyShgyYBdoVUNA0psywFSUQZSDWwszQS1kwKF/U/kmFYTpkSCFag0kkUrEmAjMAUXpC2L\n",
"ZiUCJGC6XqpN5CSqTWAVPf1j78hfPVnu7tHOmXt25vUCBrrnzL0zz5x541L88j53aowRAAAAAK7f\n",
"K/a9AAAAAICbjYEKAAAAwEIGKgAAAAALGagAAAAALGSgAgAAALCQgQoAAADAQtc1UKmqV1bVk1X1\n",
"kd3xq6vq8ar6XFV9vKrOtvu+v6o+X1XPVNWb11o4AAAAwL5c7ytUfjLJ00nG7viBJI+PMV6f5BO7\n",
"41TVPUnekeSeJG9J8otV5VUwAAAAwIlyzWFHVb02yfcn+QdJanf6rUke3t1+OMnbd7ffluSRMcal\n",
"McbzSZ5Nct9RLhgAAABg367n1SN/L8nfSvKVdu62McaLu9svJrltd/s1SV5o93shyR03ukgAAACA\n",
"Lbnlap+sqr+W5AtjjCer6v4r3WeMMapqXOlzh3e5wte92v0BAAAAVjHGqGvf69quOlBJ8peTvLWq\n",
"vj/JmST/SVV9KMmLVXVujHGxqm5P8oXd/f8wyZ3t8a/dnfuPHNUPwMlQVQdjjIN9r4Nt0AMzTdDp\n",
"gZkm6PTATBN0R/kCj6tu+Rlj/PQY484xxt1J3pnkX44xfiTJY0netbvbu5J8eHf7sSTvrKpbq+ru\n",
"JK9L8umjWiwn2l37XgCbcte+F8Dm3LXvBbApd+17AWzOXfteAJty174XwObcte8FcDJd6xUqs8NJ\n",
"zkNJHq2qdyd5PskPJskY4+mqejSX/yLQl5O8Z4xhew8AAABwotQ+5h1VNWz5oauq+8cYn9r3OtgG\n",
"PTDTBJ0emGmCTg/MNEF3lPMIAxUAAADgVDjKecT1/NlkWN3L/RUpTic9MNMEnR6YaYJOD8w0wVoM\n",
"VAAAAAAWsuUHAAAAOBVs+QEAAADYIwMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAAAAAW8h4qAAAA\n",
"wKngPVQAAAAA9shAhU2wr5FOD8w0QacHZpqg0wMzTbAWAxUAAACAhbyHCgAAAHAqeA8VAAAAgD0y\n",
"UGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCHvoQIAAACcCt5DBQAAAGCPDFTYBPsa6fTATBN0\n",
"emCmCTo9MNMEazFQAQAAAFjIe6gAAAAAp4L3UAEAAADYIwMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoM\n",
"VAAAAAAW8h4qAAAAwKngPVQAAAAA9shAhU2wr5FOD8w0QacHZpqg0wMzTbAWAxUAAACAhbyHCgAA\n",
"AHAqeA8VAAAAgD0yUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCHvoQIAAACcCt5DBQAAAGCP\n",
"DFTYBPsa6fTATBN0emCmCTo9MNMEazFQAQAAAFjIe6gAAAAAp4L3UAEAAADYIwMVNsG+Rjo9MNME\n",
"nR6YaYJOD8w0wVoMVAAAAAAW8h4qAAAAwKngPVQAAAAA9shAhU2wr5FOD8w0QacHZpqg0wMzTbCW\n",
"W/b1javqzn1971Pu/x5j/Id9LwIAAABuZnt7D5VXvepV/9+xf+NT7k//9E+/McmfH2P8632vBY5D\n",
"VR3/Exxf5b2yOE083+yP5xpOE881++X55mQ4yvdQ2dsrVN73vvd9076+92l1/vz5ly5durTvZcCx\n",
"Ojg42PcSTiXXndNI98fPNec00v1+uO5cyd4GKuzN/1tlsAqsz39FA46D5xrgWp577rncfffd+14G\n",
"J5CByim0xenqSX+SOzg42OR136qj6sE136+jvP4n/TniqJyW55ot9nAarvtWHRwcbLKJk27Lzzcn\n",
"uYetXnM4ra76V36q6kxVPVFVT1XV01X1c7vzB1X1QlU9ufv4vvaY91fV56vqmap689o/ACfDSf2H\n",
"Hl8fPTDTBJ0emGmCTg/MNMFarvoKlTHGS1X1xjHGn1TVLUl+s6q+O8lI8gtjjF/o96+qe5K8I8k9\n",
"Se5I8utV9foxxldWWj8AAADAsbvqK1SSZIzxJ7ubtyZ5ZZIv7o6v9EYcb0vyyBjj0hjj+STPJrnv\n",
"CNbJCffcc8/tewlsiB6YaYJOD8w0QacHZppgLdccqFTVK6rqqSQvJvnkGOOzu0/9eFX9TlV9sKrO\n",
"7s69JskL7eEv5PIrVQAAAABOjGu+Ke1uu869VfXnkvxaVd2f5JeS/MzuLj+b5OeTvPvlvsSVTl64\n",
"cCFnz16ew5w5cybnzp376t62wwmi46M9PrSV9dxs6/PzuV6O/f62fnx4bivrcez4OI4Pz21lPafl\n",
"+PDcVtbTj09yD4e2sp6b5fjw3FFd/92/E2eM8SnHN8Xxe5Pcm+T5HLEaY1z/nav+dpI/HWP8z+3c\n",
"XUk+Msb4jqp6IEnGGA/tPvexJB8YYzwxfZ3hHaqP3/nz51+6dOnSGdf++G35nfBPMtd9f1z7/XDd\n",
"98e13w/XfX9c+/1w3ffn4OAgY4za9zq4cVU1jup3ea2/8vOth9t5qupVSd6U5MmqOtfu9gNJPrO7\n",
"/ViSd1bVrVV1d5LXJfn0USyUk22e+nK66YGZJuj0wEwTdHpgpgnWcq0tP7cnebiqXpHLw5cPjTE+\n",
"UVW/WlX35vJ2nueS/FiSjDGerqpHkzyd5MtJ3jOWvAQGAAAA4CZwrT+b/Jkkf/EK5//bqzzmwSQP\n",
"3vjSOE36/kbQAzNN0OmBmSbo9MBME6zlmn/lBwAAAICvZaDCJtjXSKcHZpqg0wMzTdDpgZkmWIuB\n",
"CgAAAMBCBipsgn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxkoMIm2NdIpwdmmqDTAzNN0OmBmSZY\n",
"i4EKAAAAwEIGKmyCfY10emCmCTo9MNMEnR6YaYK1GKgAAAAALGSgwibY10inB2aaoNMDM03Q6YGZ\n",
"JliLgQoAAADAQgYqbIJ9jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDCJtjXSKcHZpqg0wMzTdDp\n",
"gZkmWIuBCgAAAMBCBipsgn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxkoMIm2NdIpwdmmqDTAzNN\n",
"0OmBmSZYi4EKAAAAwEIGKmyCfY10emCmCTo9MNMEnR6YaYK1GKgAAAAALGSgwibY10inB2aaoNMD\n",
"M03Q6YGZJliLgQoAAADAQgYqbIJ9jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDCJtjXSKcHZpqg\n",
"0wMzTdDpgZkmWIuBCgAAAMBCBipsgn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxkoMIm2NdIpwdm\n",
"mqDTAzNN0OmBmSZYi4EKAAAAwEIGKmyCfY10emCmCTo9MNMEnR6YaYK1GKgAAAAALGSgwibY10in\n",
"B2aaoNMDM03Q6YGZJliLgQoAAADAQgYqbIJ9jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDCJtjX\n",
"SKcHZpqg0wMzTdDpgZkmWIuBCgAAAMBCBipsgn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxkoMIm\n",
"2NdIpwdmmqDTAzNN0OmBmSZYi4EKAAAAwEIGKmyCfY10emCmCTo9MNMEnR6YaYK1GKgAAAAALGSg\n",
"wibY10inB2aaoNMDM03Q6YGZJliLgQoAAADAQlcdqFTVmap6oqqeqqqnq+rndudfXVWPV9Xnqurj\n",
"VXW2Peb9VfX5qnqmqt689g/AyWBfI50emGmCTg/MNEGnB2aaYC1XHaiMMV5K8sYxxr1J/oskb6yq\n",
"707yQJLHxxivT/KJ3XGq6p4k70hyT5K3JPnFqvIqGAAAAOBEueawY4zxJ7ubtyZ5ZZIvJnlrkod3\n",
"5x9O8vbd7bcleWSMcWmM8XySZ5Pcd5QL5mSyr5FOD8w0QacHZpqg0wMzTbCWaw5UquoVVfVUkheT\n",
"fHKM8dkkt40xXtzd5cUkt+1uvybJC+3hLyS54wjXCwAAALB3t1zrDmOMryS5t6r+XJJfq6o3Tp8f\n",
"VTWu9iWudPLChQs5e/byW6+cOXMm586d++retsMJouOjPT60lfXcbOvz87lejv3+tn58eG4r63Hs\n",
"+DiOD89tZT2n5fjw3FbW049Pcg+HtrKem+X48NxRXf+quj9JxhifcnxTHL83yb1Jns8RqzHG9d+5\n",
"6m8n+dMk/0OS+8cYF6vq9lx+5cq3VdUDSTLGeGh3/48l+cAY44np64yDg4Mj+hG4XufPn3/p0qVL\n",
"Z1z743dwcBDX/fi57vvj2u+H674/rv1+uO7749rvh+u+PwcHBxlj1L7XwY2rqnFUv8tr/ZWfbz38\n",
"Cz5V9aokb0ryZJLHkrxrd7d3Jfnw7vZjSd5ZVbdW1d1JXpfk00exUE62eerL6aYHZpqg0wMzTdDp\n",
"gZkmWMu1tvzcnuTh3V/qeUWSD40xPlFVTyZ5tKrencsvm/nBJBljPF1VjyZ5OsmXk7xnLHkJDAAA\n",
"AMBN4KoDlTHGZ5L8xSuc/zdJvvdlHvNgkgePZHWcGn1/I+iBmSbo9MBME3R6YKYJ1nLNv/IDAAAA\n",
"wNcyUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQA\n",
"AAAAFjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoM\n",
"VAAAAAAWMlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTB\n",
"WgxUAAAAABYyUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/M\n",
"NMFaDFQAAAAAFjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJO\n",
"D8w0wVoMVAAAAAAWMlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphp\n",
"gk4PzDTBWgxUAAAAABYyUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0e\n",
"mGmCTg/MNMFaDFQAAAAAFjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNME\n",
"nR6YaYJOD8w0wVoMVAAAAAAWMlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w\n",
"0wSdHphpgk4PzDTBWgxUAAAAABYyUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6\n",
"PTDTBJ0emGmCTg/MNMFaDFQAAAAAFjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+\n",
"Rjo9MNMEnR6YaYJOD8w0wVoMVAAAAAAWMlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGChaw5U\n",
"qurOqvpkVX22qn6vqn5id/6gql6oqid3H9/XHvP+qvp8VT1TVW9e8wfgZLCvkU4PzDRBpwdmmqDT\n",
"AzNNsJZbruM+l5L81Bjjqar65iT/Z1U9nmQk+YUxxi/0O1fVPUnekeSeJHck+fWqev0Y4ytHvHYA\n",
"AACAvbjmK1TGGBfHGE/tbn8pye/n8qAkSeoKD3lbkkfGGJfGGM8neTbJfUezXE4q+xrp9MBME3R6\n",
"YKYJOj0w0wRrWfQeKlV1V5I3JPmt3akfr6rfqaoPVtXZ3bnXJHmhPeyF/NkABgAAAOCmdz1bfpIk\n",
"u+0+/zTJT44xvlRVv5TkZ3af/tkkP5/k3S/z8DGfuHDhQs6evTyDOXPmTM6dO/fVvW2HE0THR3t8\n",
"aCvrudnW5+dzvRz7/W39+PDcVtbj2PFxHB+e28p6Tsvx4bmtrKcfn+QeDm1lPTfL8eG5o7r+VXV/\n",
"kowxPuX4pjh+b5J7kzyfI1ZjjGvfqeobkvzzJB8dY/z9K3z+riQfGWN8R1U9kCRjjId2n/tYkg+M\n",
"MZ5o9x8HBwdHsX4WOH/+/EuXLl0649ofv4ODg7jux8913x/Xfj9c9/1x7ffDdd8f134/XPf9OTg4\n",
"yBij9r0OblxVjaP6XV7PX/mpJB9M8nQfplTV7e1uP5DkM7vbjyV5Z1XdWlV3J3ldkk8fxWI5ueap\n",
"L6ebHphpgk4PzDRBpwdmmmAt17Pl57uS/HCS362qJ3fnfjrJD1XVvbm8nee5JD+WJGOMp6vq0SRP\n",
"J/lykveM63kZDAAAAMBN4poDlTHGb+bKr2T56FUe82CSB29gXZwyfX8j6IGZJuj0wEwTdHpgpgnW\n",
"suiv/AAAAABgoMJG2NdIpwdmmqDTAzNN0OmBmSZYi4EKAAAAwEIGKmyCfY10emCmCTo9MNMEnR6Y\n",
"aYK1GKgAAAAALGSgwibY10inB2aaoNMDM03Q6YGZJliLgQoAAADAQgYqbIJ9jXR6YKYJOj0w0wSd\n",
"HphpgrUYqAAAAAAsZKDCJtjXSKcHZpqg0wMzTdDpgZkmWIuBCgAAAMBCBipsgn2NdHpgpgk6PTDT\n",
"BJ0emGmCtRioAAAAACxkoMIm2NdIpwdmmqDTAzNN0OmBmSZYi4EKAAAAwEIGKmyCfY10emCmCTo9\n",
"MNMEnR6YaYK1GKgAAAAALGSgwibY10inB2aaoNMDM03Q6YGZJliLgQoAAADAQgYqbIJ9jXR6YKYJ\n",
"Oj0w0wSdHphpgrUYqAAAAAAsZKDCJtjXSKcHZpqg0wMzTdDpgZkmWIuBCgAAAMBCBipsgn2NdHpg\n",
"pgk6PTDTBJ0emGmCtRioAAAAACxkoMIm2NdIpwdmmqDTAzNN0OmBmSZYi4EKAAAAwEIGKmyCfY10\n",
"emCmCTo9MNMEnR6YaYK1GKgAAAAALGSgwibY10inB2aaoNMDM03Q6YGZJliLgQoAAADAQgYqbIJ9\n",
"jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDCJtjXSKcHZpqg0wMzTdDpgZkmWIuBCgAAAMBCBips\n",
"gn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxkoMIm2NdIpwdmmqDTAzNN0OmBmSZYi4EKAAAAwEIG\n",
"KmyCfY10emCmCTo9MNMEnR6YaYK1GKgAAAAALGSgwibY10inB2aaoNMDM03Q6YGZJliLgQoAAADA\n",
"QgYqbIJ9jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDCJtjXSKcHZpqg0wMzTdDpgZkmWMs1BypV\n",
"dWdVfbKqPltVv1dVP7E7/+qqeryqPldVH6+qs+0x76+qz1fVM1X15jV/AAAAAIDjdj2vULmU5KfG\n",
"GP95kv8qyV+vqm9P8kCSx8cYr0/yid1xquqeJO9Ick+StyT5xaryShiuyr5GOj0w0wSdHphpgk4P\n",
"zDTBWq456BhjXBxjPLW7/aUkv5/kjiRvTfLw7m4PJ3n77vbbkjwyxrg0xng+ybNJ7jvidQMAAADs\n",
"zaJXjlTVXUnekOSJJLeNMV7cferFJLftbr8myQvtYS/k8gAGXpZ9jXR6YKYJOj0w0wSdHphpgrVc\n",
"90Clqr45yT9L8pNjjH/fPzfGGEnGVR5+tc8BAAAA3FRuuZ47VdU35PIw5UNjjA/vTr9YVefGGBer\n",
"6vYkX9id/8Mkd7aHv3Z37mtcuHAhZ89efh/bM2fO5Ny5c1/d23Y4QXR8tMeHtrKem219fj7Xy7Hf\n",
"39aPD89tZT2OHR/H8eG5razntBwfntvKevrxSe7h0FbWc7McH547qutfVfcnyRjjU45viuP3Jrk3\n",
"yfM5YnX5xSVXuUNV5fJ7pPzrMcZPtfN/d3fu71TVA0nOjjEe2L0p7T/O5fdNuSPJryf5z0b7RlU1\n",
"Dg4Ojvpn4RrOnz//0qVLl8649sfv4OAgrvvxc933x7XfD9d9f1z7/XDd98e13w/XfX8ODg4yxqh9\n",
"r4MbV1XjqH6X17Pl57uS/HCSN1bVk7uPtyR5KMmbqupzSb5nd5wxxtNJHk3ydJKPJnnPuNbUhlNv\n",
"nvpyuumBmSbo9MBME3R6YKYJ1nLNLT9jjN/Myw9evvdlHvNgkgdvYF0AAAAAm7Xor/zAWvr+RtAD\n",
"M03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxUAAAAABYyUGET7Guk\n",
"0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQAAAAAFjJQYRPs\n",
"a6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAAAAAWMlBh\n",
"E+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxUAAAAABYy\n",
"UGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQAAAAA\n",
"FjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAA\n",
"AAAWMlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxU\n",
"AAAAABYyUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFa\n",
"DFQAAAAAFjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0\n",
"wVoMVAAAAAAWMlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4P\n",
"zDTBWgxUAAAAABYyUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmC\n",
"Tg/MNMFaDFQAAAAAFjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6Y\n",
"aYJOD8w0wVquOVCpql+uqher6jPt3EFVvVBVT+4+vq997v1V9fmqeqaq3rzWwgEAAAD25XpeofIP\n",
"k7xlOjeS/MIY4w27j48mSVXdk+QdSe7ZPeYXq8qrYLgm+xrp9MBME3R6YKYJOj0w0wRrueawY4zx\n",
"G0m+eIVP1RXOvS3JI2OMS2OM55M8m+S+G1ohAAAAwMbcyKtHfryqfqeqPlhVZ3fnXpPkhXafF5Lc\n",
"cQPfg1PCvkY6PTDTBJ0emGmCTg/MNMFabvk6H/dLSX5md/tnk/x8kne/zH3HlU5euHAhZ89ensOc\n",
"OXMm586d++pLsQ6Dd3y0x4e2sp5+fPHixU2tZ43jQ1tZz5aPT0MPJ/340Fa/3kk9Pjy3lfXcLH05\n",
"vrmPD21lPafl+PDcVtZzWo4PbWU9N8vxxYsXj+TrHaqq+5NkjPEpxzfF8XuT3Jvk+RyxGmNc+05V\n",
"dyX5yBjjO672uap6IEnGGA/tPvexJB8YYzwxPWYcHBzc4NJZ6vz58y9dunTpjGt//A4ODuK6Hz/X\n",
"fX9c+/1w3ffHtd8P131/XPv9cN335+DgIGOM2vc6uHFVNY7qd/l1bfmpqtvb4Q8kOfwLQI8leWdV\n",
"3VpVdyd5XZJP39gSAQAAALblev5s8iNJ/lWSv1BVf1BV/32Sv1NVv1tVv5Pkryb5qSQZYzyd5NEk\n",
"Tyf5aJL3jOt5CQyn3vwyOk43PTDTBJ0emGmCTg/MNMFarvkeKmOMH7rC6V++yv0fTPLgjSwKAAAA\n",
"YMtu5K/8wJHpb3AGemCmCTo9MNMEnR6YaYK1GKgAAAAALGSgwibY10inB2aaoNMDM03Q6YGZJliL\n",
"gQoAAADAQgYqbIJ9jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDCJtjXSKcHZpqg0wMzTdDpgZkm\n",
"WIuBCgAAAMBCBipsgn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxkoMIm2NdIpwdmmqDTAzNN0OmB\n",
"mSZYi4EKAAAAwEIGKmyCfY10emCmCTo9MNMEnR6YaYK1GKgAAAAALGSgwibY10inB2aaoNMDM03Q\n",
"6YGZJliLgQoAAADAQgYqbIJ9jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDCJtjXSKcHZpqg0wMz\n",
"TdDpgZkmWIuBCgAAAMBCBipsgn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxkoMIm2NdIpwdmmqDT\n",
"AzNN0OmBmSZYi4EKAAAAwEIGKmyCfY10emCmCTo9MNMEnR6YaYK1GKgAAAAALGSgwibY10inB2aa\n",
"oNMDM03Q6YGZJliLgQoAAADAQgYqbIJ9jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDCJtjXSKcH\n",
"Zpqg0wMzTdDpgZkmWIuBCgAAAMBCBipsgn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxkoMIm2NdI\n",
"pwdmmqDTAzNN0OmBmSZYi4EKAAAAwEIGKmyCfY10emCmCTo9MNMEnR6YaYK1GKgAAAAALGSgwibY\n",
"10inB2aaoNMDM03Q6YGZJliLgQoAAADAQgYqbIJ9jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDC\n",
"JtjXSKcHZpqg0wMzTdDpgZkmWIuBCgAAAMBCBipsgn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxk\n",
"oMIm2NdIpwdmmqDTAzNN0OmBmSZYyzUHKlX1y1X1YlV9pp17dVU9XlWfq6qPV9XZ9rn3V9Xnq+qZ\n",
"qnrzWgsHAAAA2JfreYXKP0zyluncA0keH2O8PskndsepqnuSvCPJPbvH/GJVeRUM12RfI50emGmC\n",
"Tg/MNEGnB2aaYC3XHHaMMX4jyRen029N8vDu9sNJ3r67/bYkj4wxLo0xnk/ybJL7jmapAAAAANvw\n",
"9b565LYxxou72y8muW13+zVJXmj3eyHJHV/n9+AUsa+RTg/MNEGnB2aaoNMDM02wlltu9AuMMUZV\n",
"javd5UrfsIo3AAAPaElEQVQnL1y4kLNnL7/1ypkzZ3Lu3LmvvhTrMHjHR3t8aCvr6ccXL17c1HrW\n",
"OD60lfVs+fg09HDSjw9t9eud1OPDc1tZz83Sl+Ob+/jQVtZzWo4Pz21lPafl+NBW1nOzHF+8ePFI\n",
"vt6hqro/ScYYn3J8Uxy/N8m9SZ7PEasxxrXvVHVXko+MMb5jd/xMkvvHGBer6vYknxxjfFtVPbBb\n",
"+EO7+30syQfGGE9MX28cHBwc5c/BdTh//vxLly5dOuPaH7+Dg4O47sfPdd8f134/XPf9ce33w3Xf\n",
"H9d+P1z3/Tk4OMgYo/a9Dm5cVY2j+l1+vVt+Hkvyrt3tdyX5cDv/zqq6taruTvK6JJ++sSUCAAAA\n",
"bMv1/NnkR5L8qyR/oar+oKr+uyQPJXlTVX0uyffsjjPGeDrJo0meTvLRJO8Z1/MSGE69+WV0nG56\n",
"YKYJOj0w0wSdHphpgrVc8z1Uxhg/9DKf+t6Xuf+DSR68kUUBAAAAbNnXu+UHjlR/gzPQAzNN0OmB\n",
"mSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAAAAAWMlBhE+xrpNMDM03Q\n",
"6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxUAAAAABYyUGET7Guk0wMz\n",
"TdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQAAAAAFjJQYRPsa6TT\n",
"AzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAAAAAWMlBhE+xr\n",
"pNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxUAAAAABYyUGET\n",
"7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQAAAAAFjJQ\n",
"YRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAAAAAW\n",
"MlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxUAAAA\n",
"ABYyUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQA\n",
"AAAAFjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoM\n",
"VAAAAAAWMlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTB\n",
"WgxUAAAAABYyUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/M\n",
"NMFabrmRB1fV80n+XZL/kOTSGOO+qnp1kv89yX+a5PkkPzjG+OMbXCcAAADAZtzoK1RGkvvHGG8Y\n",
"Y9y3O/dAksfHGK9P8ondMVyVfY10emCmCTo9MNMEnR6YaYK1HMWWn5qO35rk4d3th5O8/Qi+BwAA\n",
"AMBmHMUrVH69qn67qn50d+62McaLu9svJrntBr8Hp4B9jXR6YKYJOj0w0wSdHphpgrXc0HuoJPmu\n",
"McYfVdWfT/J4VT3TPznGGFU1rvTACxcu5OzZs0mSM2fO5Ny5c199KdZh8I6P9vjQVtbTjy9evLip\n",
"9axxfGgr69ny8Wno4aQfH9rq1zupx4fntrKem6Uvxzf38aGtrOe0HB+e28p6Tsvxoa2s52Y5vnjx\n",
"4pF8vUNVdX+SjDE+5fimOH5vkntz+T1ej1SNMY7mC1V9IMmXkvxoLr+vysWquj3JJ8cY3zbddxwc\n",
"HBzJ9+X6nT9//qVLly6dce2P38HBQVz34+e6749rvx+u+/649vvhuu+Pa78frvv+HBwcZIxR+14H\n",
"N66qxlH9Lr/uLT9V9Y1V9S2729+U5M1JPpPksSTv2t3tXUk+fKOLBAAAANiSG3kPlduS/EZVPZXk\n",
"iST/fIzx8SQPJXlTVX0uyffsjuGq5pfRcbrpgZkm6PTATBN0emCmCdbydb+HyhjjuVzehzSf/zdJ\n",
"vvdGFgUAAACwZUfxZ5PhhvU3OAM9MNMEnR6YaYJOD8w0wVoMVAAAAAAWMlBhE+xrpNMDM03Q6YGZ\n",
"Juj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxUAAAAABYyUGET7Guk0wMzTdDp\n",
"gZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQAAAAAFjJQYRPsa6TTAzNN\n",
"0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAAAAAWMlBhE+xrpNMD\n",
"M03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxUAAAAABYyUGET7Guk\n",
"0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQAAAAAFjJQYRPs\n",
"a6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAAAAAWMlBh\n",
"E+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxUAAAAABYy\n",
"UGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQAAAAA\n",
"FjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAA\n",
"AAAWMlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxU\n",
"AAAAABYyUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFa\n",
"DFQAAAAAFjJQYRPsa6TTAzNN0OmBmSbo9MBME6xllYFKVb2lqp6pqs9X1fvW+B6cLBcvXtz3EtgQ\n",
"PTDTBJ0emGmCTg/MNMFajnygUlWvTPK/JnlLknuS/FBVfftRfx9OlpdeemnfS2BD9MBME3R6YKYJ\n",
"Oj0w0wRrWeMVKvcleXaM8fwY41KSf5LkbSt8HwAAAIC9uGWFr3lHkj9oxy8k+c75Tr/yK7/yb1f4\n",
"3lzFl7/85W/Z9xpezh//8R/vewlsiB6YaYJOD8w0QacHZppgLTXGONovWPXfJHnLGONHd8c/nOQ7\n",
"xxg/3u5ztN8UAAAA4DqMMeoovs4ar1D5wyR3tuM7c/lVKl91VIsHAAAA2Ic13kPlt5O8rqruqqpb\n",
"k7wjyWMrfB8AAACAvTjyV6iMMb5cVX8jya8leWWSD44xfv+ovw8AAADAvhz5e6gAAAAAnHRrbPm5\n",
"qqp6S1U9U1Wfr6r3Hff3Zz+q6vmq+t2qerKqPr079+qqeryqPldVH6+qs+3+79818kxVvXl/K+co\n",
"VNUvV9WLVfWZdm7x77+q/lJVfWb3uf/luH8Ojs7LNHFQVS/snieerKrva5/TxAlWVXdW1Ser6rNV\n",
"9XtV9RO7854nTqmrNOF54hSqqjNV9URVPVVVT1fVz+3Oe444pa7ShOeIU6yqXrn7vX9kd7z+c8QY\n",
"49g+cnkL0LNJ7kryDUmeSvLtx7kGH/v5SPJckldP5/5ukv9xd/t9SR7a3b5n18Y37Fp5Nskr9v0z\n",
"+Lih3/9fSfKGJJ/5On//h6+m+3SS+3a3/0Uu/0Wxvf98Po6siQ8k+ZtXuK8mTvhHknNJ7t3d/uYk\n",
"/1eSb/c8cXo/rtKE54lT+pHkG3f/e0uS30ry3Z4jTvfHyzThOeIUfyT5m0n+UZLHdserP0cc9ytU\n",
"7kvy7Bjj+THGpST/JMnbjnkN7M/8153emuTh3e2Hk7x9d/ttSR4ZY1waYzyfy4HfdywrZBVjjN9I\n",
"8sXp9JLf/3dW1e1JvmWM8end/X61PYabzMs0kfzHzxOJJk68McbFMcZTu9tfSvL7Se6I54lT6ypN\n",
"JJ4nTqUxxp/sbt6ay/+R9ovxHHGqvUwTieeIU6mqXpvk+5P8g/xZA6s/Rxz3QOWOJH/Qjl/In/3D\n",
"kZNtJPn1qvrtqvrR3bnbxhgv7m6/mOS23e3X5Gv/1LZOTqalv//5/B9GFyfRj1fV71TVB9vLMjVx\n",
"ilTVXbn86qUn4nmCfE0Tv7U75XniFKqqV1TVU7n8XPDJMcZn4zniVHuZJhLPEafV30vyt5J8pZ1b\n",
"/TniuAcq3gH39PquMcYbknxfkr9eVX+lf3Jcfk3V1frQzgl2Hb9/TodfSnJ3knuT/FGSn9/vcjhu\n",
"VfXNSf5Zkp8cY/z7/jnPE6fTrol/mstNfCmeJ06tMcZXxhj3Jnltkv+6qt44fd5zxClzhSbuj+eI\n",
"U6mq/lqSL4wxnsyVX6G02nPEcQ9U/jDJne34znztBIgTaozxR7v//X+SXMjlLTwvVtW5JNm9vOoL\n",
"u7vPnbx2d46TZcnv/4Xd+ddO53VxgowxvjB2cvnlmodb/TRxClTVN+TyMOVDY4wP7057njjFWhP/\n",
"22ETnicYY/zbJP9Hkr8UzxHka5r4Lz1HnFp/Oclbq+q5JI8k+Z6q+lCO4TniuAcqv53kdVV1V1Xd\n",
"muQdSR475jVwzKrqG6vqW3a3vynJm5N8Jpd/9+/a3e1dSQ7/D/RjSd5ZVbdW1d1JXpfLbw7EybLo\n",
"9z/GuJjk31XVd1ZVJfmR9hhOgN0/6A79QC4/TySaOPF2v78PJnl6jPH326c8T5xSL9eE54nTqaq+\n",
"9XDrRlW9KsmbkjwZzxGn1ss1cfgvzzueI06JMcZPjzHuHGPcneSdSf7lGONHcgzPEbes8PO8rDHG\n",
"l6vqbyT5tVx+46APjjF+/zjXwF7cluTC5SZzS5J/NMb4eFX9dpJHq+rdSZ5P8oNJMsZ4uqoeTfJ0\n",
"ki8nec9uysxNqqoeSfJXk3xrVf1Bkv8pyUNZ/vt/T5JfSfKqJP9ijPGx4/w5ODpXaOIDSe6vqntz\n",
"+eWYzyX5sUQTp8R3JfnhJL9bVU/uzr0/nidOsys18dNJfsjzxKl0e5KHq+oVufwfhD80xvjErg3P\n",
"EafTyzXxq54jyJ9t7Vn9/0eUf08FAAAAWOa4t/wAAAAA3PQMVAAAAAAWMlABAAAAWMhABQAAAGAh\n",
"AxUAAACAhQxUAAAAABYyUAEAAABY6P8HvvQvYScmiioAAAAASUVORK5CYII=\n"
],
"text/plain": [
"<matplotlib.figure.Figure at 0x7f85748f9d50>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"addHeader(2,'K-mer Coverage Distribution')\n",
"\n",
"with size_controller(FULL_FIG_W, FULL_FIG_H):\n",
" hf = Data[ Data[\"K-mer Coverage\"] > 0 ]['Position']\n",
" \n",
" print \"Number of rows:\", hf.size\n",
"\n",
" if hf.size > 0:\n",
" hs = hf.hist(color=HISTOGRAM_COLOR)\n",
"\n",
" for of in output_files['K-mer Coverage Distribution']:\n",
" print \"Saving Image:\", of\n",
" savefig(of)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Sequencing Coverage Distribution"
]
},
{
"cell_type": "code",
"execution_count": 425,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h2>Sequencing Coverage Distribution</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Number of rows: 3564\n",
"Saving Image: reports/eps/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Sequencing_Coverage_Distribution.eps\n",
"Saving Image: reports/png/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Sequencing_Coverage_Distribution.png\n",
"Saving Image: reports/pdf/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Sequencing_Coverage_Distribution.pdf\n"
]
},
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAABFQAAAHfCAYAAAB+sozsAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\n",
"AAALEgAACxIB0t1+/AAAIABJREFUeJzt3X+MZed93/fPV6KJlX80C8EBl6KIkkCl2CxcUElBF7HT\n",
"UIYlyEYgyShgyYBdoVUNA0psywFSUQZSDWwszQS1kwKF/U/kmFYTpkSCFag0kkUrEmAjMAUXpC2L\n",
"ZiUCJGC6XqpN5CSqTWAVPf1j78hfPVnu7tHOmXt25vUCBrrnzL0zz5x541L88j53aowRAAAAAK7f\n",
"K/a9AAAAAICbjYEKAAAAwEIGKgAAAAALGagAAAAALGSgAgAAALCQgQoAAADAQtc1UKmqV1bVk1X1\n",
"kd3xq6vq8ar6XFV9vKrOtvu+v6o+X1XPVNWb11o4AAAAwL5c7ytUfjLJ00nG7viBJI+PMV6f5BO7\n",
"41TVPUnekeSeJG9J8otV5VUwAAAAwIlyzWFHVb02yfcn+QdJanf6rUke3t1+OMnbd7ffluSRMcal\n",
"McbzSZ5Nct9RLhgAAABg367n1SN/L8nfSvKVdu62McaLu9svJrltd/s1SV5o93shyR03ukgAAACA\n",
"Lbnlap+sqr+W5AtjjCer6v4r3WeMMapqXOlzh3e5wte92v0BAAAAVjHGqGvf69quOlBJ8peTvLWq\n",
"vj/JmST/SVV9KMmLVXVujHGxqm5P8oXd/f8wyZ3t8a/dnfuPHNUPwMlQVQdjjIN9r4Nt0AMzTdDp\n",
"gZkm6PTATBN0R/kCj6tu+Rlj/PQY484xxt1J3pnkX44xfiTJY0netbvbu5J8eHf7sSTvrKpbq+ru\n",
"JK9L8umjWiwn2l37XgCbcte+F8Dm3LXvBbApd+17AWzOXfteAJty174XwObcte8FcDJd6xUqs8NJ\n",
"zkNJHq2qdyd5PskPJskY4+mqejSX/yLQl5O8Z4xhew8AAABwotQ+5h1VNWz5oauq+8cYn9r3OtgG\n",
"PTDTBJ0emGmCTg/MNEF3lPMIAxUAAADgVDjKecT1/NlkWN3L/RUpTic9MNMEnR6YaYJOD8w0wVoM\n",
"VAAAAAAWsuUHAAAAOBVs+QEAAADYIwMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAAAAAW8h4qAAAA\n",
"wKngPVQAAAAA9shAhU2wr5FOD8w0QacHZpqg0wMzTbAWAxUAAACAhbyHCgAAAHAqeA8VAAAAgD0y\n",
"UGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCHvoQIAAACcCt5DBQAAAGCPDFTYBPsa6fTATBN0\n",
"emCmCTo9MNMEazFQAQAAAFjIe6gAAAAAp4L3UAEAAADYIwMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoM\n",
"VAAAAAAW8h4qAAAAwKngPVQAAAAA9shAhU2wr5FOD8w0QacHZpqg0wMzTbAWAxUAAACAhbyHCgAA\n",
"AHAqeA8VAAAAgD0yUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCHvoQIAAACcCt5DBQAAAGCP\n",
"DFTYBPsa6fTATBN0emCmCTo9MNMEazFQAQAAAFjIe6gAAAAAp4L3UAEAAADYIwMVNsG+Rjo9MNME\n",
"nR6YaYJOD8w0wVoMVAAAAAAW8h4qAAAAwKngPVQAAAAA9shAhU2wr5FOD8w0QacHZpqg0wMzTbCW\n",
"W/b1javqzn1971Pu/x5j/Id9LwIAAABuZnt7D5VXvepV/9+xf+NT7k//9E+/McmfH2P8632vBY5D\n",
"VR3/Exxf5b2yOE083+yP5xpOE881++X55mQ4yvdQ2dsrVN73vvd9076+92l1/vz5ly5durTvZcCx\n",
"Ojg42PcSTiXXndNI98fPNec00v1+uO5cyd4GKuzN/1tlsAqsz39FA46D5xrgWp577rncfffd+14G\n",
"J5CByim0xenqSX+SOzg42OR136qj6sE136+jvP4n/TniqJyW55ot9nAarvtWHRwcbLKJk27Lzzcn\n",
"uYetXnM4ra76V36q6kxVPVFVT1XV01X1c7vzB1X1QlU9ufv4vvaY91fV56vqmap689o/ACfDSf2H\n",
"Hl8fPTDTBJ0emGmCTg/MNMFarvoKlTHGS1X1xjHGn1TVLUl+s6q+O8lI8gtjjF/o96+qe5K8I8k9\n",
"Se5I8utV9foxxldWWj8AAADAsbvqK1SSZIzxJ7ubtyZ5ZZIv7o6v9EYcb0vyyBjj0hjj+STPJrnv\n",
"CNbJCffcc8/tewlsiB6YaYJOD8w0QacHZppgLdccqFTVK6rqqSQvJvnkGOOzu0/9eFX9TlV9sKrO\n",
"7s69JskL7eEv5PIrVQAAAABOjGu+Ke1uu869VfXnkvxaVd2f5JeS/MzuLj+b5OeTvPvlvsSVTl64\n",
"cCFnz16ew5w5cybnzp376t62wwmi46M9PrSV9dxs6/PzuV6O/f62fnx4bivrcez4OI4Pz21lPafl\n",
"+PDcVtbTj09yD4e2sp6b5fjw3FFd/92/E2eM8SnHN8Xxe5Pcm+T5HLEaY1z/nav+dpI/HWP8z+3c\n",
"XUk+Msb4jqp6IEnGGA/tPvexJB8YYzwxfZ3hHaqP3/nz51+6dOnSGdf++G35nfBPMtd9f1z7/XDd\n",
"98e13w/XfX9c+/1w3ffn4OAgY4za9zq4cVU1jup3ea2/8vOth9t5qupVSd6U5MmqOtfu9gNJPrO7\n",
"/ViSd1bVrVV1d5LXJfn0USyUk22e+nK66YGZJuj0wEwTdHpgpgnWcq0tP7cnebiqXpHLw5cPjTE+\n",
"UVW/WlX35vJ2nueS/FiSjDGerqpHkzyd5MtJ3jOWvAQGAAAA4CZwrT+b/Jkkf/EK5//bqzzmwSQP\n",
"3vjSOE36/kbQAzNN0OmBmSbo9MBME6zlmn/lBwAAAICvZaDCJtjXSKcHZpqg0wMzTdDpgZkmWIuB\n",
"CgAAAMBCBipsgn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxkoMIm2NdIpwdmmqDTAzNN0OmBmSZY\n",
"i4EKAAAAwEIGKmyCfY10emCmCTo9MNMEnR6YaYK1GKgAAAAALGSgwibY10inB2aaoNMDM03Q6YGZ\n",
"JliLgQoAAADAQgYqbIJ9jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDCJtjXSKcHZpqg0wMzTdDp\n",
"gZkmWIuBCgAAAMBCBipsgn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxkoMIm2NdIpwdmmqDTAzNN\n",
"0OmBmSZYi4EKAAAAwEIGKmyCfY10emCmCTo9MNMEnR6YaYK1GKgAAAAALGSgwibY10inB2aaoNMD\n",
"M03Q6YGZJliLgQoAAADAQgYqbIJ9jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDCJtjXSKcHZpqg\n",
"0wMzTdDpgZkmWIuBCgAAAMBCBipsgn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxkoMIm2NdIpwdm\n",
"mqDTAzNN0OmBmSZYi4EKAAAAwEIGKmyCfY10emCmCTo9MNMEnR6YaYK1GKgAAAAALGSgwibY10in\n",
"B2aaoNMDM03Q6YGZJliLgQoAAADAQgYqbIJ9jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDCJtjX\n",
"SKcHZpqg0wMzTdDpgZkmWIuBCgAAAMBCBipsgn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxkoMIm\n",
"2NdIpwdmmqDTAzNN0OmBmSZYi4EKAAAAwEIGKmyCfY10emCmCTo9MNMEnR6YaYK1GKgAAAAALGSg\n",
"wibY10inB2aaoNMDM03Q6YGZJliLgQoAAADAQlcdqFTVmap6oqqeqqqnq+rndudfXVWPV9Xnqurj\n",
"VXW2Peb9VfX5qnqmqt689g/AyWBfI50emGmCTg/MNEGnB2aaYC1XHaiMMV5K8sYxxr1J/oskb6yq\n",
"707yQJLHxxivT/KJ3XGq6p4k70hyT5K3JPnFqvIqGAAAAOBEueawY4zxJ7ubtyZ5ZZIvJnlrkod3\n",
"5x9O8vbd7bcleWSMcWmM8XySZ5Pcd5QL5mSyr5FOD8w0QacHZpqg0wMzTbCWaw5UquoVVfVUkheT\n",
"fHKM8dkkt40xXtzd5cUkt+1uvybJC+3hLyS54wjXCwAAALB3t1zrDmOMryS5t6r+XJJfq6o3Tp8f\n",
"VTWu9iWudPLChQs5e/byW6+cOXMm586d++retsMJouOjPT60lfXcbOvz87lejv3+tn58eG4r63Hs\n",
"+DiOD89tZT2n5fjw3FbW049Pcg+HtrKem+X48NxRXf+quj9JxhifcnxTHL83yb1Jns8RqzHG9d+5\n",
"6m8n+dMk/0OS+8cYF6vq9lx+5cq3VdUDSTLGeGh3/48l+cAY44np64yDg4Mj+hG4XufPn3/p0qVL\n",
"Z1z743dwcBDX/fi57vvj2u+H674/rv1+uO7749rvh+u+PwcHBxlj1L7XwY2rqnFUv8tr/ZWfbz38\n",
"Cz5V9aokb0ryZJLHkrxrd7d3Jfnw7vZjSd5ZVbdW1d1JXpfk00exUE62eerL6aYHZpqg0wMzTdDp\n",
"gZkmWMu1tvzcnuTh3V/qeUWSD40xPlFVTyZ5tKrencsvm/nBJBljPF1VjyZ5OsmXk7xnLHkJDAAA\n",
"AMBN4KoDlTHGZ5L8xSuc/zdJvvdlHvNgkgePZHWcGn1/I+iBmSbo9MBME3R6YKYJ1nLNv/IDAAAA\n",
"wNcyUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQA\n",
"AAAAFjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoM\n",
"VAAAAAAWMlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTB\n",
"WgxUAAAAABYyUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/M\n",
"NMFaDFQAAAAAFjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJO\n",
"D8w0wVoMVAAAAAAWMlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphp\n",
"gk4PzDTBWgxUAAAAABYyUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0e\n",
"mGmCTg/MNMFaDFQAAAAAFjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNME\n",
"nR6YaYJOD8w0wVoMVAAAAAAWMlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w\n",
"0wSdHphpgk4PzDTBWgxUAAAAABYyUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6\n",
"PTDTBJ0emGmCTg/MNMFaDFQAAAAAFjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+\n",
"Rjo9MNMEnR6YaYJOD8w0wVoMVAAAAAAWMlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGChaw5U\n",
"qurOqvpkVX22qn6vqn5id/6gql6oqid3H9/XHvP+qvp8VT1TVW9e8wfgZLCvkU4PzDRBpwdmmqDT\n",
"AzNNsJZbruM+l5L81Bjjqar65iT/Z1U9nmQk+YUxxi/0O1fVPUnekeSeJHck+fWqev0Y4ytHvHYA\n",
"AACAvbjmK1TGGBfHGE/tbn8pye/n8qAkSeoKD3lbkkfGGJfGGM8neTbJfUezXE4q+xrp9MBME3R6\n",
"YKYJOj0w0wRrWfQeKlV1V5I3JPmt3akfr6rfqaoPVtXZ3bnXJHmhPeyF/NkABgAAAOCmdz1bfpIk\n",
"u+0+/zTJT44xvlRVv5TkZ3af/tkkP5/k3S/z8DGfuHDhQs6evTyDOXPmTM6dO/fVvW2HE0THR3t8\n",
"aCvrudnW5+dzvRz7/W39+PDcVtbj2PFxHB+e28p6Tsvx4bmtrKcfn+QeDm1lPTfL8eG5o7r+VXV/\n",
"kowxPuX4pjh+b5J7kzyfI1ZjjGvfqeobkvzzJB8dY/z9K3z+riQfGWN8R1U9kCRjjId2n/tYkg+M\n",
"MZ5o9x8HBwdHsX4WOH/+/EuXLl0649ofv4ODg7jux8913x/Xfj9c9/1x7ffDdd8f134/XPf9OTg4\n",
"yBij9r0OblxVjaP6XV7PX/mpJB9M8nQfplTV7e1uP5DkM7vbjyV5Z1XdWlV3J3ldkk8fxWI5ueap\n",
"L6ebHphpgk4PzDRBpwdmmmAt17Pl57uS/HCS362qJ3fnfjrJD1XVvbm8nee5JD+WJGOMp6vq0SRP\n",
"J/lykveM63kZDAAAAMBN4poDlTHGb+bKr2T56FUe82CSB29gXZwyfX8j6IGZJuj0wEwTdHpgpgnW\n",
"suiv/AAAAABgoMJG2NdIpwdmmqDTAzNN0OmBmSZYi4EKAAAAwEIGKmyCfY10emCmCTo9MNMEnR6Y\n",
"aYK1GKgAAAAALGSgwibY10inB2aaoNMDM03Q6YGZJliLgQoAAADAQgYqbIJ9jXR6YKYJOj0w0wSd\n",
"HphpgrUYqAAAAAAsZKDCJtjXSKcHZpqg0wMzTdDpgZkmWIuBCgAAAMBCBipsgn2NdHpgpgk6PTDT\n",
"BJ0emGmCtRioAAAAACxkoMIm2NdIpwdmmqDTAzNN0OmBmSZYi4EKAAAAwEIGKmyCfY10emCmCTo9\n",
"MNMEnR6YaYK1GKgAAAAALGSgwibY10inB2aaoNMDM03Q6YGZJliLgQoAAADAQgYqbIJ9jXR6YKYJ\n",
"Oj0w0wSdHphpgrUYqAAAAAAsZKDCJtjXSKcHZpqg0wMzTdDpgZkmWIuBCgAAAMBCBipsgn2NdHpg\n",
"pgk6PTDTBJ0emGmCtRioAAAAACxkoMIm2NdIpwdmmqDTAzNN0OmBmSZYi4EKAAAAwEIGKmyCfY10\n",
"emCmCTo9MNMEnR6YaYK1GKgAAAAALGSgwibY10inB2aaoNMDM03Q6YGZJliLgQoAAADAQgYqbIJ9\n",
"jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDCJtjXSKcHZpqg0wMzTdDpgZkmWIuBCgAAAMBCBips\n",
"gn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxkoMIm2NdIpwdmmqDTAzNN0OmBmSZYi4EKAAAAwEIG\n",
"KmyCfY10emCmCTo9MNMEnR6YaYK1GKgAAAAALGSgwibY10inB2aaoNMDM03Q6YGZJliLgQoAAADA\n",
"QgYqbIJ9jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDCJtjXSKcHZpqg0wMzTdDpgZkmWMs1BypV\n",
"dWdVfbKqPltVv1dVP7E7/+qqeryqPldVH6+qs+0x76+qz1fVM1X15jV/AAAAAIDjdj2vULmU5KfG\n",
"GP95kv8qyV+vqm9P8kCSx8cYr0/yid1xquqeJO9Ick+StyT5xaryShiuyr5GOj0w0wSdHphpgk4P\n",
"zDTBWq456BhjXBxjPLW7/aUkv5/kjiRvTfLw7m4PJ3n77vbbkjwyxrg0xng+ybNJ7jvidQMAAADs\n",
"zaJXjlTVXUnekOSJJLeNMV7cferFJLftbr8myQvtYS/k8gAGXpZ9jXR6YKYJOj0w0wSdHphpgrVc\n",
"90Clqr45yT9L8pNjjH/fPzfGGEnGVR5+tc8BAAAA3FRuuZ47VdU35PIw5UNjjA/vTr9YVefGGBer\n",
"6vYkX9id/8Mkd7aHv3Z37mtcuHAhZ89efh/bM2fO5Ny5c1/d23Y4QXR8tMeHtrKem219fj7Xy7Hf\n",
"39aPD89tZT2OHR/H8eG5razntBwfntvKevrxSe7h0FbWc7McH547qutfVfcnyRjjU45viuP3Jrk3\n",
"yfM5YnX5xSVXuUNV5fJ7pPzrMcZPtfN/d3fu71TVA0nOjjEe2L0p7T/O5fdNuSPJryf5z0b7RlU1\n",
"Dg4Ojvpn4RrOnz//0qVLl8649sfv4OAgrvvxc933x7XfD9d9f1z7/XDd98e13w/XfX8ODg4yxqh9\n",
"r4MbV1XjqH6X17Pl57uS/HCSN1bVk7uPtyR5KMmbqupzSb5nd5wxxtNJHk3ydJKPJnnPuNbUhlNv\n",
"nvpyuumBmSbo9MBME3R6YKYJ1nLNLT9jjN/Myw9evvdlHvNgkgdvYF0AAAAAm7Xor/zAWvr+RtAD\n",
"M03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxUAAAAABYyUGET7Guk\n",
"0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQAAAAAFjJQYRPs\n",
"a6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAAAAAWMlBh\n",
"E+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxUAAAAABYy\n",
"UGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQAAAAA\n",
"FjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAA\n",
"AAAWMlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxU\n",
"AAAAABYyUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFa\n",
"DFQAAAAAFjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0\n",
"wVoMVAAAAAAWMlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4P\n",
"zDTBWgxUAAAAABYyUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmC\n",
"Tg/MNMFaDFQAAAAAFjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6Y\n",
"aYJOD8w0wVquOVCpql+uqher6jPt3EFVvVBVT+4+vq997v1V9fmqeqaq3rzWwgEAAAD25XpeofIP\n",
"k7xlOjeS/MIY4w27j48mSVXdk+QdSe7ZPeYXq8qrYLgm+xrp9MBME3R6YKYJOj0w0wRrueawY4zx\n",
"G0m+eIVP1RXOvS3JI2OMS2OM55M8m+S+G1ohAAAAwMbcyKtHfryqfqeqPlhVZ3fnXpPkhXafF5Lc\n",
"cQPfg1PCvkY6PTDTBJ0emGmCTg/MNMFabvk6H/dLSX5md/tnk/x8kne/zH3HlU5euHAhZ89ensOc\n",
"OXMm586d++pLsQ6Dd3y0x4e2sp5+fPHixU2tZ43jQ1tZz5aPT0MPJ/340Fa/3kk9Pjy3lfXcLH05\n",
"vrmPD21lPafl+PDcVtZzWo4PbWU9N8vxxYsXj+TrHaqq+5NkjPEpxzfF8XuT3Jvk+RyxGmNc+05V\n",
"dyX5yBjjO672uap6IEnGGA/tPvexJB8YYzwxPWYcHBzc4NJZ6vz58y9dunTpjGt//A4ODuK6Hz/X\n",
"fX9c+/1w3ffHtd8P131/XPv9cN335+DgIGOM2vc6uHFVNY7qd/l1bfmpqtvb4Q8kOfwLQI8leWdV\n",
"3VpVdyd5XZJP39gSAQAAALblev5s8iNJ/lWSv1BVf1BV/32Sv1NVv1tVv5Pkryb5qSQZYzyd5NEk\n",
"Tyf5aJL3jOt5CQyn3vwyOk43PTDTBJ0emGmCTg/MNMFarvkeKmOMH7rC6V++yv0fTPLgjSwKAAAA\n",
"YMtu5K/8wJHpb3AGemCmCTo9MNMEnR6YaYK1GKgAAAAALGSgwibY10inB2aaoNMDM03Q6YGZJliL\n",
"gQoAAADAQgYqbIJ9jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDCJtjXSKcHZpqg0wMzTdDpgZkm\n",
"WIuBCgAAAMBCBipsgn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxkoMIm2NdIpwdmmqDTAzNN0OmB\n",
"mSZYi4EKAAAAwEIGKmyCfY10emCmCTo9MNMEnR6YaYK1GKgAAAAALGSgwibY10inB2aaoNMDM03Q\n",
"6YGZJliLgQoAAADAQgYqbIJ9jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDCJtjXSKcHZpqg0wMz\n",
"TdDpgZkmWIuBCgAAAMBCBipsgn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxkoMIm2NdIpwdmmqDT\n",
"AzNN0OmBmSZYi4EKAAAAwEIGKmyCfY10emCmCTo9MNMEnR6YaYK1GKgAAAAALGSgwibY10inB2aa\n",
"oNMDM03Q6YGZJliLgQoAAADAQgYqbIJ9jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDCJtjXSKcH\n",
"Zpqg0wMzTdDpgZkmWIuBCgAAAMBCBipsgn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxkoMIm2NdI\n",
"pwdmmqDTAzNN0OmBmSZYi4EKAAAAwEIGKmyCfY10emCmCTo9MNMEnR6YaYK1GKgAAAAALGSgwibY\n",
"10inB2aaoNMDM03Q6YGZJliLgQoAAADAQgYqbIJ9jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDC\n",
"JtjXSKcHZpqg0wMzTdDpgZkmWIuBCgAAAMBCBipsgn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxk\n",
"oMIm2NdIpwdmmqDTAzNN0OmBmSZYyzUHKlX1y1X1YlV9pp17dVU9XlWfq6qPV9XZ9rn3V9Xnq+qZ\n",
"qnrzWgsHAAAA2JfreYXKP0zyluncA0keH2O8PskndsepqnuSvCPJPbvH/GJVeRUM12RfI50emGmC\n",
"Tg/MNEGnB2aaYC3XHHaMMX4jyRen029N8vDu9sNJ3r67/bYkj4wxLo0xnk/ybJL7jmapAAAAANvw\n",
"9b565LYxxou72y8muW13+zVJXmj3eyHJHV/n9+AUsa+RTg/MNEGnB2aaoNMDM02wlltu9AuMMUZV\n",
"javd5UrfsIo3AAAPaElEQVQnL1y4kLNnL7/1ypkzZ3Lu3LmvvhTrMHjHR3t8aCvr6ccXL17c1HrW\n",
"OD60lfVs+fg09HDSjw9t9eud1OPDc1tZz83Sl+Ob+/jQVtZzWo4Pz21lPafl+NBW1nOzHF+8ePFI\n",
"vt6hqro/ScYYn3J8Uxy/N8m9SZ7PEasxxrXvVHVXko+MMb5jd/xMkvvHGBer6vYknxxjfFtVPbBb\n",
"+EO7+30syQfGGE9MX28cHBwc5c/BdTh//vxLly5dOuPaH7+Dg4O47sfPdd8f134/XPf9ce33w3Xf\n",
"H9d+P1z3/Tk4OMgYo/a9Dm5cVY2j+l1+vVt+Hkvyrt3tdyX5cDv/zqq6taruTvK6JJ++sSUCAAAA\n",
"bMv1/NnkR5L8qyR/oar+oKr+uyQPJXlTVX0uyffsjjPGeDrJo0meTvLRJO8Z1/MSGE69+WV0nG56\n",
"YKYJOj0w0wSdHphpgrVc8z1Uxhg/9DKf+t6Xuf+DSR68kUUBAAAAbNnXu+UHjlR/gzPQAzNN0OmB\n",
"mSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAAAAAWMlBhE+xrpNMDM03Q\n",
"6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxUAAAAABYyUGET7Guk0wMz\n",
"TdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQAAAAAFjJQYRPsa6TT\n",
"AzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAAAAAWMlBhE+xr\n",
"pNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxUAAAAABYyUGET\n",
"7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQAAAAAFjJQ\n",
"YRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAAAAAW\n",
"MlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxUAAAA\n",
"ABYyUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQA\n",
"AAAAFjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoM\n",
"VAAAAAAWMlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTB\n",
"WgxUAAAAABYyUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/M\n",
"NMFabrmRB1fV80n+XZL/kOTSGOO+qnp1kv89yX+a5PkkPzjG+OMbXCcAAADAZtzoK1RGkvvHGG8Y\n",
"Y9y3O/dAksfHGK9P8ondMVyVfY10emCmCTo9MNMEnR6YaYK1HMWWn5qO35rk4d3th5O8/Qi+BwAA\n",
"AMBmHMUrVH69qn67qn50d+62McaLu9svJrntBr8Hp4B9jXR6YKYJOj0w0wSdHphpgrXc0HuoJPmu\n",
"McYfVdWfT/J4VT3TPznGGFU1rvTACxcu5OzZs0mSM2fO5Ny5c199KdZh8I6P9vjQVtbTjy9evLip\n",
"9axxfGgr69ny8Wno4aQfH9rq1zupx4fntrKem6Uvxzf38aGtrOe0HB+e28p6Tsvxoa2s52Y5vnjx\n",
"4pF8vUNVdX+SjDE+5fimOH5vkntz+T1ej1SNMY7mC1V9IMmXkvxoLr+vysWquj3JJ8cY3zbddxwc\n",
"HBzJ9+X6nT9//qVLly6dce2P38HBQVz34+e6749rvx+u+/649vvhuu+Pa78frvv+HBwcZIxR+14H\n",
"N66qxlH9Lr/uLT9V9Y1V9S2729+U5M1JPpPksSTv2t3tXUk+fKOLBAAAANiSG3kPlduS/EZVPZXk\n",
"iST/fIzx8SQPJXlTVX0uyffsjuGq5pfRcbrpgZkm6PTATBN0emCmCdbydb+HyhjjuVzehzSf/zdJ\n",
"vvdGFgUAAACwZUfxZ5PhhvU3OAM9MNMEnR6YaYJOD8w0wVoMVAAAAAAWMlBhE+xrpNMDM03Q6YGZ\n",
"Juj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxUAAAAABYyUGET7Guk0wMzTdDp\n",
"gZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQAAAAAFjJQYRPsa6TTAzNN\n",
"0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAAAAAWMlBhE+xrpNMD\n",
"M03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxUAAAAABYyUGET7Guk\n",
"0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQAAAAAFjJQYRPs\n",
"a6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAAAAAWMlBh\n",
"E+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxUAAAAABYy\n",
"UGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQAAAAA\n",
"FjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAA\n",
"AAAWMlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxU\n",
"AAAAABYyUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFa\n",
"DFQAAAAAFjJQYRPsa6TTAzNN0OmBmSbo9MBME6xllYFKVb2lqp6pqs9X1fvW+B6cLBcvXtz3EtgQ\n",
"PTDTBJ0emGmCTg/MNMFajnygUlWvTPK/JnlLknuS/FBVfftRfx9OlpdeemnfS2BD9MBME3R6YKYJ\n",
"Oj0w0wRrWeMVKvcleXaM8fwY41KSf5LkbSt8HwAAAIC9uGWFr3lHkj9oxy8k+c75Tr/yK7/yb1f4\n",
"3lzFl7/85W/Z9xpezh//8R/vewlsiB6YaYJOD8w0QacHZppgLTXGONovWPXfJHnLGONHd8c/nOQ7\n",
"xxg/3u5ztN8UAAAA4DqMMeoovs4ar1D5wyR3tuM7c/lVKl91VIsHAAAA2Ic13kPlt5O8rqruqqpb\n",
"k7wjyWMrfB8AAACAvTjyV6iMMb5cVX8jya8leWWSD44xfv+ovw8AAADAvhz5e6gAAAAAnHRrbPm5\n",
"qqp6S1U9U1Wfr6r3Hff3Zz+q6vmq+t2qerKqPr079+qqeryqPldVH6+qs+3+79818kxVvXl/K+co\n",
"VNUvV9WLVfWZdm7x77+q/lJVfWb3uf/luH8Ojs7LNHFQVS/snieerKrva5/TxAlWVXdW1Ser6rNV\n",
"9XtV9RO7854nTqmrNOF54hSqqjNV9URVPVVVT1fVz+3Oe444pa7ShOeIU6yqXrn7vX9kd7z+c8QY\n",
"49g+cnkL0LNJ7kryDUmeSvLtx7kGH/v5SPJckldP5/5ukv9xd/t9SR7a3b5n18Y37Fp5Nskr9v0z\n",
"+Lih3/9fSfKGJJ/5On//h6+m+3SS+3a3/0Uu/0Wxvf98Po6siQ8k+ZtXuK8mTvhHknNJ7t3d/uYk\n",
"/1eSb/c8cXo/rtKE54lT+pHkG3f/e0uS30ry3Z4jTvfHyzThOeIUfyT5m0n+UZLHdserP0cc9ytU\n",
"7kvy7Bjj+THGpST/JMnbjnkN7M/8153emuTh3e2Hk7x9d/ttSR4ZY1waYzyfy4HfdywrZBVjjN9I\n",
"8sXp9JLf/3dW1e1JvmWM8end/X61PYabzMs0kfzHzxOJJk68McbFMcZTu9tfSvL7Se6I54lT6ypN\n",
"JJ4nTqUxxp/sbt6ay/+R9ovxHHGqvUwTieeIU6mqXpvk+5P8g/xZA6s/Rxz3QOWOJH/Qjl/In/3D\n",
"kZNtJPn1qvrtqvrR3bnbxhgv7m6/mOS23e3X5Gv/1LZOTqalv//5/B9GFyfRj1fV71TVB9vLMjVx\n",
"ilTVXbn86qUn4nmCfE0Tv7U75XniFKqqV1TVU7n8XPDJMcZn4zniVHuZJhLPEafV30vyt5J8pZ1b\n",
"/TniuAcq3gH39PquMcYbknxfkr9eVX+lf3Jcfk3V1frQzgl2Hb9/TodfSnJ3knuT/FGSn9/vcjhu\n",
"VfXNSf5Zkp8cY/z7/jnPE6fTrol/mstNfCmeJ06tMcZXxhj3Jnltkv+6qt44fd5zxClzhSbuj+eI\n",
"U6mq/lqSL4wxnsyVX6G02nPEcQ9U/jDJne34znztBIgTaozxR7v//X+SXMjlLTwvVtW5JNm9vOoL\n",
"u7vPnbx2d46TZcnv/4Xd+ddO53VxgowxvjB2cvnlmodb/TRxClTVN+TyMOVDY4wP7057njjFWhP/\n",
"22ETnicYY/zbJP9Hkr8UzxHka5r4Lz1HnFp/Oclbq+q5JI8k+Z6q+lCO4TniuAcqv53kdVV1V1Xd\n",
"muQdSR475jVwzKrqG6vqW3a3vynJm5N8Jpd/9+/a3e1dSQ7/D/RjSd5ZVbdW1d1JXpfLbw7EybLo\n",
"9z/GuJjk31XVd1ZVJfmR9hhOgN0/6A79QC4/TySaOPF2v78PJnl6jPH326c8T5xSL9eE54nTqaq+\n",
"9XDrRlW9KsmbkjwZzxGn1ss1cfgvzzueI06JMcZPjzHuHGPcneSdSf7lGONHcgzPEbes8PO8rDHG\n",
"l6vqbyT5tVx+46APjjF+/zjXwF7cluTC5SZzS5J/NMb4eFX9dpJHq+rdSZ5P8oNJMsZ4uqoeTfJ0\n",
"ki8nec9uysxNqqoeSfJXk3xrVf1Bkv8pyUNZ/vt/T5JfSfKqJP9ijPGx4/w5ODpXaOIDSe6vqntz\n",
"+eWYzyX5sUQTp8R3JfnhJL9bVU/uzr0/nidOsys18dNJfsjzxKl0e5KHq+oVufwfhD80xvjErg3P\n",
"EafTyzXxq54jyJ9t7Vn9/0eUf08FAAAAWOa4t/wAAAAA3PQMVAAAAAAWMlABAAAAWMhABQAAAGAh\n",
"AxUAAACAhQxUAAAAABYyUAEAAABY6P8HvvQvYScmiioAAAAASUVORK5CYII=\n"
],
"text/plain": [
"<matplotlib.figure.Figure at 0x7f8557ddcd50>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"addHeader(2,'Sequencing Coverage Distribution')\n",
"\n",
"with size_controller(FULL_FIG_W, FULL_FIG_H):\n",
" hf = Data[ Data[\"Sequencing Coverage\"] > 0 ]['Position']\n",
" \n",
" print \"Number of rows:\", hf.size\n",
"\n",
" if hf.size > 0:\n",
" hs = hf.hist(color=HISTOGRAM_COLOR)\n",
"\n",
" for of in output_files['Sequencing Coverage Distribution']:\n",
" print \"Saving Image:\", of\n",
" savefig(of)"
]
},
{
"cell_type": "code",
"execution_count": 426,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h2>BLAST Coverage Distribution</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Number of rows: 3560\n",
"Saving Image: reports/eps/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.BLAST_Coverage_Distribution.eps\n",
"Saving Image: reports/png/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.BLAST_Coverage_Distribution.png\n",
"Saving Image: reports/pdf/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.BLAST_Coverage_Distribution.pdf\n"
]
},
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAABFQAAAHfCAYAAAB+sozsAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\n",
"AAALEgAACxIB0t1+/AAAIABJREFUeJzt3X+MZed93/fPV6KJlX80C8EBl6KIkkCl2CxcUElBF7HT\n",
"UIYlyEYgyShgyYBdoVUNA0psywFSUQZSDWwsrQS1kwKF/U/kmFYTpkSCFag0kkUrEmAjMAUXpE2L\n",
"ZiUCJGC6XqpN5CSqTWAVPf1j78hfPVnu7tHOmXt25vUCBrrPmXtnzpx541L88j53aowRAAAAAK7f\n",
"K/Z9AgAAAAA3GwMVAAAAgIUMVAAAAAAWMlABAAAAWMhABQAAAGAhAxUAAACAha5roFJVr6yqJ6rq\n",
"o7v1q6vqsar6XFV9oqrOtvu+v6o+X1XPVNWb1zpxAAAAgH253leo/GSSp5OM3fqBJI+NMV6f5JO7\n",
"darqniTvSHJPkrck+cWq8ioYAAAA4ES55rCjql6b5PuT/IMktTv81iQP7W4/lOTtu9tvS/LwGOPS\n",
"GOP5JM8mue8oTxgAAABg367n1SN/L8nfSvKVduy2McaLu9svJrltd/s1SV5o93shyR03epIAAAAA\n",
"W3LL1T5ZVX8tyRfGGE9U1f1Xus8YY1TVuNLnDu9yha97tfsDAAAArGKMUde+17VddaCS5C8neWtV\n",
"fX+SM0n+k6r6cJIXq+rcGONiVd2e5Au7+/9hkjvb41+7O/YfOaofgJOhqg7GGAf7Pg+2QQ/MNEGn\n",
"B2aaoNMDM03QHeULPK665WeM8dNjjDvHGHcneWeSfznG+JEkjyZ51+5u70rykd3tR5O8s6puraq7\n",
"k7wuyWeO6mQ50e7a9wmwKXft+wTYnLv2fQJsyl37PgE25659nwCbcte+T4DNuWvfJ8DJdK1XqMwO\n",
"JzkfTPJIVb07yfNJfjBJxhhPV9UjufwXgb6c5D1jDNt7AAAAgBOl9jHvqKphyw9dVd0/xvj0vs+D\n",
"bdADM03Q6YGZJuj0wEwTdEc5jzBQAQAAAE6Fo5xHXM+fTYbVvdxfkeJ00gMzTdDpgZkm6PTATBOs\n",
"xUAFAAAAYCFbfgAAAIBTwZYfAAAAgD0yUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCHvoQIA\n",
"AACcCt5DBQAAAGCPDFTYBPsa6fTATBN0emCmCTo9MNMEazFQAQAAAFjIe6gAAAAAp4L3UAEAAADY\n",
"IwMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAAAAAW8h4qAAAAwKngPVQAAAAA9shAhU2wr5FOD8w0\n",
"QacHZpqg0wMzTbAWAxUAAACAhbyHCgAAAHAqeA8VAAAAgD0yUGET7Guk0wMzTdDpgZkm6PTATBOs\n",
"xUAFAAAAYCHvoQIAAACcCt5DBQAAAGCPDFTYBPsa6fTATBN0emCmCTo9MNMEazFQAQAAAFjIe6gA\n",
"AAAAp4L3UAEAAADYIwMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAAAAAW8h4qAAAAwKngPVQAAAAA\n",
"9shAhU2wr5FOD8w0QacHZpqg0wMzTbAWAxUAAACAhbyHCgAAAHAqeA8VAAAAgD0yUGET7Guk0wMz\n",
"TdDpgZkm6PTATBOsxUAFAAAAYCHvoQIAAACcCt5DBQAAAGCPDFTYBPsa6fTATBN0emCmCTo9MNME\n",
"a7llX9+4qu7c1/c+5f7vMcZ/2PdJAAAAwM1sb++h8qpXver/O/ZvfMr96Z/+6Tcm+fNjjH+973OB\n",
"41BVx/8Ex1d5ryxOE883++O5BoAljvI9VPb2CpX3ve9937Sv731anT9//qVLly7t+zTgWB0cHOz7\n",
"FE4l153TSPfHzzUHYJ/2NlBhb/7fKv8hB1if/2IPHAfPNZw2XpW1XFXdP8b49L7Pg5PHQOUU2uJ/\n",
"zXnuuedy99137/s0VnNwcLDJ675VR9WDa75fR3n9T/pzxFE5Lc81W+zhNFz3rTo4ONhkEyfdlp9v\n",
"TnIPW73mcFpd9a/8VNWZqnq8qp6sqqer6ud2xw+q6oWqemL38X3tMe+vqs9X1TNV9ea1fwBOhpP6\n",
"Dz2+Pnpgpgk6PTDTBJ0emHl1Cmu56itUxhgvVdUbxxh/UlW3JPnNqvruJCPJL4wxfqHfv6ruSfKO\n",
"JPckuSPJr1fV68cYX1np/AEAAE4N29z2x3YrZtfc8jPG+JPdzVuTvDLJF3frK8X0tiQPjzEuJXm+\n",
"qp5Ncl+S3zqCc+UEO8kvzWQ5PTDTBJ0emGmC7qT3YNvPckfRhOvOlVx1y0+SVNUrqurJJC8m+dQY\n",
"47O7T/14Vf1OVX2oqs7ujr0myQvt4S/k8itVAAAAAE6M63mFyleS3FtVfy7Jr1XV/Ul+KcnP7O7y\n",
"s0l+Psm7X+5LXOnghQsXcvbs5TnMmTNncu7cua9ODZ977rkksT7i9aGtnM/Ndn5+PtfL2u9v6+vD\n",
"Y1s5H2vr41gfHtvK+ZyW9eGxrZxPX5/kHg5t5XxulvXhsaO6/rt/J/7qe7NYb3793iT3Jnk+R6zG\n",
"GNd/56q/neRPxxj/czt2V5KPjjG+o6oeSJIxxgd3n/t4kg+MMR6fvs7wkqnjd/78+ZcuXbp0xrU/\n",
"flt+J/yTzHXfH9d+P1z3/XHt98N13x/Xfj9c9/05ODjwHionRFWNo/pdXuuv/Hzr4XaeqnpVkjcl\n",
"eaKqzrW7/UCSp3a3H03yzqq6taruTvK6JJ85ihPlZJunvpxuemCmCTo9MNMEnR6YaYK1XGvLz+1J\n",
"HqqqV+Ty8OXDY4xPVtWvVtW9ubyd57kkP5YkY4ynq+qRJE8n+XKS94wlL4EBAAAAuAlc688mP5Xk\n",
"L17h+H97lcc8mOTBGz81TpO+vxH0wEwTdHpgpgk6PTDTBGu55l/5AQAAAOBrGaiwCfY10umBmSbo\n",
"9MBME3R6YKYJ1mKgAgAAALCQgQqbYF8jnR6YaYJOD8w0QacHZppgLQYqAAAAAAsZqLAJ9jXS6YGZ\n",
"Juj0wEwTdHpgpgnWYqACAAAAsJCBCptgXyOdHphpgk4PzDRBpwdmmmAtBioAAAAACxmosAn2NdLp\n",
"gZkm6PTATBN0emCmCdZioAIAAACwkIEKm2BfI50emGmCTg/MNEGnB2aaYC0GKgAAAAALGaiwCfY1\n",
"0umBmSbo9MBME3R6YKYJ1mKgAgAAALCQgQqbYF8jnR6YaYJOD8w0QacHZppgLQYqAAAAAAsZqLAJ\n",
"9jXS6YGZJuj0wEwTdHpgpgnWYqACAAAAsJCBCptgXyOdHphpgk4PzDRBpwdmmmAtBioAAAAACxmo\n",
"sAn2NdLpgZkm6PTATBN0emCmCdZioAIAAACwkIEKm2BfI50emGmCTg/MNEGnB2aaYC0GKgAAAAAL\n",
"GaiwCfY10umBmSbo9MBME3R6YKYJ1mKgAgAAALCQgQqbYF8jnR6YaYJOD8w0QacHZppgLQYqAAAA\n",
"AAsZqLAJ9jXS6YGZJuj0wEwTdHpgpgnWYqACAAAAsJCBCptgXyOdHphpgk4PzDRBpwdmmmAtBioA\n",
"AAAACxmosAn2NdLpgZkm6PTATBN0emCmCdZioAIAAACwkIEKm2BfI50emGmCTg/MNEGnB2aaYC0G\n",
"KgAAAAALGaiwCfY10umBmSbo9MBME3R6YKYJ1mKgAgAAALCQgQqbYF8jnR6YaYJOD8w0QacHZppg\n",
"LQYqAAAAAAsZqLAJ9jXS6YGZJuj0wEwTdHpgpgnWYqACAAAAsJCBCptgXyOdHphpgk4PzDRBpwdm\n",
"mmAtBioAAAAACxmosAn2NdLpgZkm6PTATBN0emCmCdZioAIAAACw0FUHKlV1pqoer6onq+rpqvq5\n",
"3fFXV9VjVfW5qvpEVZ1tj3l/VX2+qp6pqjev/QNwMtjXSKcHZpqg0wMzTdDpgZkmWMtVBypjjJeS\n",
"vHGMcW+S/yLJG6vqu5M8kOSxMcbrk3xyt05V3ZPkHUnuSfKWJL9YVV4FAwAAAJwo1xx2jDH+ZHfz\n",
"1iSvTPLFJG9N8tDu+ENJ3r67/bYkD48xLo0xnk/ybJL7jvKEOZnsa6TTAzNN0OmBmSbo9MBME6zl\n",
"mgOVqnpFVT2Z5MUknxpjfDbJbWOMF3d3eTHJbbvbr0nyQnv4C0nuOMLzBQAAANi7W651hzHGV5Lc\n",
"W1V/LsmvVdUbp8+PqhpX+xJXOnjhwoWcPXv5rVfOnDmTc+fOfXVv2+EE0fpo14e2cj432/n5+Vwv\n",
"a7+/ra8Pj23lfKytj2N9eGwr53Na1ofHtnI+fX2Sezi0lfO5WdaHx47q+lfV/Ukyxvi09U2xfm+S\n",
"e5M8nyNWY4zrv3PV307yp0n+hyT3jzEuVtXtufzKlW+rqgeSZIzxwd39P57kA2OMx6evMw4ODo7o\n",
"R+B6nT9//qVLly6dce2P38HBQVz34+e6749rvx+u+/649vvhuu+Pa78frvv+HBwcZIxR+z4PblxV\n",
"jaP6XV7rr/x86+Ff8KmqVyV5U5Inkjya5F27u70ryUd2tx9N8s6qurWq7k7yuiSfOYoT5WSbp76c\n",
"bnpgpgk6PTDTBJ0emGmCtVxry8/tSR7a/aWeVyT58Bjjk1X1RJJHqurdufyymR9MkjHG01X1SJKn\n",
"k3w5yXvGkpfAAAAAANwErjpQGWM8leQvXuH4v0nyvS/zmAeTPHgkZ8ep0fc3gh6YaYJOD8w0QacH\n",
"ZppgLdf8Kz8AAAAAfC0DFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQAAAAAFjJQYRPsa6TTAzNN0OmB\n",
"mSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAAAAAWMlBhE+xrpNMDM03Q\n",
"6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxUAAAAABYyUGET7Guk0wMz\n",
"TdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQAAAAAFjJQYRPsa6TT\n",
"AzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAAAAAWMlBhE+xr\n",
"pNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxUAAAAABYyUGET\n",
"7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQAAAAAFjJQ\n",
"YRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoMVAAAAAAW\n",
"MlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTBWgxUAAAA\n",
"ABYyUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQA\n",
"AAAAFjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoM\n",
"VAAAAAAWMlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTB\n",
"WgxUAAAAABa65kClqu6sqk9V1Wer6veq6id2xw+q6oWqemL38X3tMe+vqs9X1TNV9eY1fwBOBvsa\n",
"6fTATBN0emCmCTo9MNMEa7nlOu5zKclPjTGerKpvTvJ/VtVjSUaSXxhj/EK/c1Xdk+QdSe5JckeS\n",
"X6+q148xvnLE5w4AAACwF9d8hcoY4+IY48nd7S8l+f1cHpQkSV3hIW9L8vAY49IY4/kkzya572hO\n",
"l5PKvkY6PTDTBJ0emGmCTg/MNMFaFr2HSlXdleQNSX5rd+jHq+p3qupDVXV2d+w1SV5oD3shfzaA\n",
"AQAAALjpXc+WnyTJbrvPP03yk2OML1XVLyX5md2nfzbJzyd598s8fMwHLly4kLNnL89gzpw5k3Pn\n",
"zn11b9vhBNH6aNeHtnI+N9v5+flcL2u/v62vD49t5XysrY9jfXhsK+dzWtaHx7ZyPn19kns4tJXz\n",
"uVnWh8eO6vpX1f1JMsb4tPVNsX5vknuTPJ8jVmOMa9+p6huS/PMkHxtj/P0rfP6uJB8dY3xHVT2Q\n",
"JGOMD+4+9/EkHxhjPN7uPw4ODo7i/Fng/PnzL126dOmMa3/8Dg4O4rofP9d9f1z7/XDd98e13w/X\n",
"fX9c+/1w3ffn4OAgY4za93lw46pqHNXv8nr+yk8l+VCSp/swpapub3f7gSRP7W4/muSdVXVrVd2d\n",
"5HVJPnMUJ8vJNU99Od30wEwTdHpgpgk6PTDTBGu5ni0/35Xkh5P8blU9sTv200l+qKruzeXtPM8l\n",
"+bEkGWM8XVWPJHk6yZeTvGdcz8tgAAAAAG4S1xyojDF+M1d+JcvHrvKYB5M8eAPnxSnT9zeCHphp\n",
"gk4PzDRBpwdmmmAti/7KDwAAAAAGKmyEfY10emCmCTo9MNMEnR6YaYK1GKgAAAAALGSgwibY10in\n",
"B2aaoNMDM03Q6YGZJliLgQoAAADAQgYqbIJ9jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDCJtjX\n",
"SKcHZpqg0wMzTdDpgZkmWIuBCgAAAMBCBipsgn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxkoMIm\n",
"2NdIpwdmmqDTAzNN0OmBmSZYi4EKAAAAwEIGKmyCfY10emCmCTo9MNMEnR6YaYK1GKgAAAAALGSg\n",
"wibY10inB2aaoNMDM03Q6YGZJliLgQoAAADAQgYqbIJ9jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAs\n",
"ZKDCJtjXSKcHZpqg0wMzTdDpgZkmWIuBCgAAAMBCBipsgn2NdHpgpgk6PTDTBJ0emGmCtRioAAAA\n",
"ACxkoMIm2NdIpwdmmqDTAzNN0OmBmSZYi4EKAAAAwEIGKmyCfY10emCmCTo9MNMEnR6YaYK1GKgA\n",
"AAAALGSgwibY10inB2aaoNMDM03Q6YGZJliLgQoAAADAQgYqbIJ9jXR6YKYJOj0w0wSdHphpgrUY\n",
"qAAAAAAsZKDCJtjXSKcHZpqg0wMzTdDpgZkmWIuBCgAAAMBCBipsgn2NdHpgpgk6PTDTBJ0emGmC\n",
"tRioAAAAACxkoMIm2NdIpwdmmqDTAzNN0OmBmSZYi4EKAAAAwEIGKmyCfY10emCmCTo9MNMEnR6Y\n",
"aYK1GKgAAAAALGSgwibY10inB2aaoNMDM03Q6YGZJliLgQoAAADAQgYqbIJ9jXR6YKYJOj0w0wSd\n",
"HphpgrUYqAAAAAAsZKDCJtjXSKcHZpqg0wMzTdDpgZkmWIuBCgAAAMBCBipsgn2NdHpgpgk6PTDT\n",
"BJ0emGmCtVxzoFJVd1bVp6rqs1X1e1X1E7vjr66qx6rqc1X1iao62x7z/qr6fFU9U1VvXvMHAAAA\n",
"ADhu1/MKlUtJfmqM8Z8n+a+S/PWq+vYkDyR5bIzx+iSf3K1TVfckeUeSe5K8JckvVpVXwnBV9jXS\n",
"6YGZJuj0wEwTdHpgpgnWcs1Bxxjj4hjjyd3tLyX5/SR3JHlrkod2d3soydt3t9+W5OExxqUxxvNJ\n",
"nk1y3xGfNwAAAMDeLHrlSFXdleQNSR5PctsY48Xdp15Mctvu9muSvNAe9kIuD2DgZdnXSKcHZpqg\n",
"0wMzTdDpgZkmWMt1D1Sq6puT/LMkPznG+Pf9c2OMkWRc5eFX+xwAAADATeWW67lTVX1DLg9TPjzG\n",
"+Mju8ItVdW6McbGqbk/yhd3xP0xyZ3v4a3fHvsaFCxdy9uzl97E9c+ZMzp0799W9bYcTROujXR/a\n",
"yvncbOfn53O9rP3+tr4+PLaV87G2Po714bGtnM9pWR8e28r59PVJ7uHQVs7nZlkfHjuq619V9yfJ\n",
"GOPT1jfF+r1J7k3yfI5YXX5xyVXuUFW5/B4p/3qM8VPt+N/dHfs7VfVAkrNjjAd2b0r7j3P5fVPu\n",
"SPLrSf6z0b5RVY2Dg4Oj/lm4hvPnz7906dKlM6798Ts4OIjrfvxc9/1x7ffDdd8f134/XPf9ce33\n",
"w3Xfn4ODg4wxat/nwY2rqnFUv8vr2fLzXUl+OMkbq+qJ3cdbknwwyZuq6nNJvme3zhjj6SSPJHk6\n",
"yceSvGdca2rDqTdPfTnd9MBME3R6YKYJOj0w0wRrueaWnzHGb+blBy/f+zKPeTDJgzdwXgAAAACb\n",
"teiv/MBa+v5G0AMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/MNMFaDFQA\n",
"AAAAFjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJOD8w0wVoM\n",
"VAAAAAAWMlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphpgk4PzDTB\n",
"WgxUAAAAABYyUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0emGmCTg/M\n",
"NMFaDFQAAAAAFjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNMEnR6YaYJO\n",
"D8w0wVoMVAAAAAAWMlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w0wSdHphp\n",
"gk4PzDTBWgxUAAAAABYyUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6PTDTBJ0e\n",
"mGmCTg/MNMFaDFQAAAAAFjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+Rjo9MNME\n",
"nR6YaYJOD8w0wVoMVAAAAAAWMlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2wb5GOj0w\n",
"0wSdHphpgk4PzDTBWgxUAAAAABYyUGET7Guk0wMzTdDpgZkm6PTATBOsxUAFAAAAYCEDFTbBvkY6\n",
"PTDTBJ0emGmCTg/MNMFaDFQAAAAAFjJQYRPsa6TTAzNN0OmBmSbo9MBME6zFQAUAAABgIQMVNsG+\n",
"Rjo9MNMEnR6YaYJOD8w0wVoMVAAAAAAWMlBhE+xrpNMDM03Q6YGZJuj0wEwTrMVABQAAAGAhAxU2\n",
"wb5GOj0w0wSdHphpgk4PzDTBWq45UKmqX66qF6vqqXbsoKpeqKondh/f1z73/qr6fFU9U1VvXuvE\n",
"AQAAAPblel6h8g+TvGU6NpL8whjjDbuPjyVJVd2T5B1J7tk95heryqtguCb7Gun0wEwTdHpgpgk6\n",
"PTDTBGu55rBjjPEbSb54hU/VFY69LcnDY4xLY4znkzyb5L4bOkMAAACAjbmRV4/8eFX9TlV9qKrO\n",
"7o69JskL7T4vJLnjBr4Hp4R9jXR6YKYJOj0w0wSdHphpgrXc8nU+7peS/Mzu9s8m+fkk736Z+44r\n",
"Hbxw4ULOnr08hzlz5kzOnTv31ZdiHQZvfbTrQ1s5n76+ePHips5njfWhrZzPltenoYeTvj601a93\n",
"UteHx7ZyPjdLX9Y39/rQVs7ntKwPj23lfE7L+tBWzudmWV+8ePFIvt6hqro/ScYYn7a+KdbvTXJv\n",
"kudzxGqMce07Vd2V5KNjjO+42ueq6oEkGWN8cPe5jyf5wBjj8ekx4+Dg4AZPnaXOnz//0qVLl864\n",
"9sfv4OAgrvvxc933x7XfD9d9f1z7/XDd98e13w/XfX8ODg4yxqh9nwc3rqrGUf0uv64tP1V1e1v+\n",
"QJLDvwD0aJJ3VtWtVXV3ktcl+cyNnSIAAADAtlzPn01+OMm/SvIXquoPquq/T/J3qup3q+p3kvzV\n",
"JD+VJGOMp5M8kuTpJB9L8p5xPS+B4dSbX0bH6aYHZpqg0wMzTdDpgZkmWMs130NljPFDVzj8y1e5\n",
"/4NJHryRkwIAAADYshv5Kz9wZPobnIEemGmCTg/MNEGnB2aaYC0GKgAAAAALGaiwCfY10umBmSbo\n",
"9MBME3R6YKYJ1mKgAgAAALCQgQqbYF8jnR6YaYJOD8w0QacHZppgLQYqAAAAAAsZqLAJ9jXS6YGZ\n",
"Juj0wEwTdHpgpgnWYqACAAAAsJCBCptgXyOdHphpgk4PzDRBpwdmmmAtBioAAAAACxmosAn2NdLp\n",
"gZkm6PTATBN0emCmCdZioAIAAACwkIEKm2BfI50emGmCTg/MNEGnB2aaYC0GKgAAAAALGaiwCfY1\n",
"0umBmSbo9MBME3R6YKYJ1mKgAgAAALCQgQqbYF8jnR6YaYJOD8w0QacHZppgLQYqAAAAAAsZqLAJ\n",
"9jXS6YGZJuj0wEwTdHpgpgnWYqACAAAAsJCBCptgXyOdHphpgk4PzDRBpwdmmmAtBioAAAAACxmo\n",
"sAn2NdLpgZkm6PTATBN0emCmCdZioAIAAACwkIEKm2BfI50emGmCTg/MNEGnB2aaYC0GKgAAAAAL\n",
"GaiwCfY10umBmSbo9MBME3R6YKYJ1mKgAgAAALCQgQqbYF8jnR6YaYJOD8w0QacHZppgLQYqAAAA\n",
"AAsZqLAJ9jXS6YGZJuj0wEwTdHpgpgnWYqACAAAAsJCBCptgXyOdHphpgk4PzDRBpwdmmmAtBioA\n",
"AAAACxmosAn2NdLpgZkm6PTATBN0emCmCdZioAIAAACwkIEKm2BfI50emGmCTg/MNEGnB2aaYC0G\n",
"KgAAAAALGaiwCfY10umBmSbo9MBME3R6YKYJ1mKgAgAAALCQgQqbYF8jnR6YaYJOD8w0QacHZppg\n",
"LQYqAAAAAAsZqLAJ9jXS6YGZJuj0wEwTdHpgpgnWYqACAAAAsJCBCptgXyOdHphpgk4PzDRBpwdm\n",
"mmAtBioAAAAACxmosAn2NdLpgZkm6PTATBN0emCmCdZyzYFKVf1yVb1YVU+1Y6+uqseq6nNV9Ymq\n",
"Ots+9/6q+nxVPVNVb17rxAEAAAD25XpeofIPk7xlOvZAksfGGK9P8sndOlV1T5J3JLln95hfrCqv\n",
"guGa7Guk0wMzTdDpgZkm6PTATBOs5ZrDjjHGbyT54nT4rUke2t1+KMnbd7ffluThMcalMcbzSZ5N\n",
"ct/RnCoAAADANny9rx65bYzx4u72i0lu291+TZIX2v1eSHLH1/k9OEXsa6TTAzNN0OmBmSbo9MBM\n",
"E6zllhvjmN8fAAAPcklEQVT9AmOMUVXjane50sELFy7k7NnLb71y5syZnDt37qsvxToM3vpo14e2\n",
"cj59ffHixU2dzxrrQ1s5ny2vT0MPJ319aKtf76SuD49t5Xxulr6sb+71oa2cz2lZHx7byvmclvWh\n",
"rZzPzbK+ePHikXy9Q1V1f5KMMT5tfVOs35vk3iTP54jVGOPad6q6K8lHxxjfsVs/k+T+McbFqro9\n",
"yafGGN9WVQ/sTvyDu/t9PMkHxhiPT19vHBwcHOXPwXU4f/78S5cuXTrj2h+/g4ODuO7Hz3XfH9d+\n",
"P1z3/XHt98N13x/Xfj9c9/05ODjIGKP2fR7cuKoaR/W7/Hq3/Dya5F272+9K8pF2/J1VdWtV3Z3k\n",
"dUk+c2OnCAAAALAt1/Nnkx9O8q+S/IWq+oOq+u+SfDDJm6rqc0m+Z7fOGOPpJI8keTrJx5K8Z1zP\n",
"S2A49eaX0XG66YGZJuj0wEwTdHpgpgnWcs33UBlj/NDLfOp7X+b+DyZ58EZOCgAAAGDLvt4tP3Ck\n",
"+hucgR6YaYJOD8w0QacHZppgLQYqAAAAAAsZqLAJ9jXS6YGZJuj0wEwTdHpgpgnWYqACAAAAsJCB\n",
"CptgXyOdHphpgk4PzDRBpwdmmmAtBioAAAAACxmosAn2NdLpgZkm6PTATBN0emCmCdZioAIAAACw\n",
"kIEKm2BfI50emGmCTg/MNEGnB2aaYC0GKgAAAAALGaiwCfY10umBmSbo9MBME3R6YKYJ1mKgAgAA\n",
"ALCQgQqbYF8jnR6YaYJOD8w0QacHZppgLQYqAAAAAAsZqLAJ9jXS6YGZJuj0wEwTdHpgpgnWYqAC\n",
"AAAAsJCBCptgXyOdHphpgk4PzDRBpwdmmmAtBioAAAAACxmosAn2NdLpgZkm6PTATBN0emCmCdZi\n",
"oAIAAACwkIEKm2BfI50emGmCTg/MNEGnB2aaYC0GKgAAAAALGaiwCfY10umBmSbo9MBME3R6YKYJ\n",
"1mKgAgAAALCQgQqbYF8jnR6YaYJOD8w0QacHZppgLQYqAAAAAAsZqLAJ9jXS6YGZJuj0wEwTdHpg\n",
"pgnWYqACAAAAsJCBCptgXyOdHphpgk4PzDRBpwdmmmAtBioAAAAACxmosAn2NdLpgZkm6PTATBN0\n",
"emCmCdZioAIAAACwkIEKm2BfI50emGmCTg/MNEGnB2aaYC0GKgAAAAALGaiwCfY10umBmSbo9MBM\n",
"E3R6YKYJ1mKgAgAAALCQgQqbYF8jnR6YaYJOD8w0QacHZppgLQYqAAAAAAsZqLAJ9jXS6YGZJuj0\n",
"wEwTdHpgpgnWYqACAAAAsJCBCptgXyOdHphpgk4PzDRBpwdmmmAtBioAAAAACxmosAn2NdLpgZkm\n",
"6PTATBN0emCmCdZioAIAAACwkIEKm2BfI50emGmCTg/MNEGnB2aaYC0GKgAAAAALGaiwCfY10umB\n",
"mSbo9MBME3R6YKYJ1nLLjTy4qp5P8u+S/Ickl8YY91XVq5P870n+0yTPJ/nBMcYf3+B5AgAAAGzG\n",
"jb5CZSS5f4zxhjHGfbtjDyR5bIzx+iSf3K3hquxrpNMDM03Q6YGZJuj0wEwTrOUotvzUtH5rkod2\n",
"tx9K8vYj+B4AAAAAm3EUr1D59ar67ar60d2x28YYL+5uv5jkthv8HpwC9jXS6YGZJuj0wEwTdHpg\n",
"pgnWckPvoZLku8YYf1RVfz7JY1X1TP/kGGNU1bjSAy9cuJCzZ88mSc6cOZNz58599aVYh8FbH+36\n",
"0FbOp68vXry4qfNZY31oK+ez5fVp6OGkrw9t9eud1PXhsa2cz83Sl/XNvT60lfM5LevDY1s5n9Oy\n",
"PrSV87lZ1hcvXjySr3eoqu5PkjHGp61vivV7k9yby+/xeqRqjHE0X6jqA0m+lORHc/l9VS5W1e1J\n",
"PjXG+LbpvuPg4OBIvi/X7/z58y9dunTpjGt//A4ODuK6Hz/XfX9c+/1w3ffHtd8P131/XPv9cN33\n",
"5+DgIGOM2vd5cOOqahzV7/Lr3vJTVd9YVd+yu/1NSd6c5KkkjyZ51+5u70rykRs9SQAAAIAtuZH3\n",
"ULktyW9U1ZNJHk/yz8cYn0jywSRvqqrPJfme3Rquan4ZHaebHphpgk4PzDRBpwdmmmAtX/d7qIwx\n",
"nsvlfUjz8X+T5Htv5KQAAAAAtuwo/mwy3LD+BmegB2aaoNMDM03Q6YGZJliLgQoAAADAQgYqbIJ9\n",
"jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDCJtjXSKcHZpqg0wMzTdDpgZkmWIuBCgAAAMBCBips\n",
"gn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxkoMIm2NdIpwdmmqDTAzNN0OmBmSZYi4EKAAAAwEIG\n",
"KmyCfY10emCmCTo9MNMEnR6YaYK1GKgAAAAALGSgwibY10inB2aaoNMDM03Q6YGZJliLgQoAAADA\n",
"QgYqbIJ9jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDCJtjXSKcHZpqg0wMzTdDpgZkmWIuBCgAA\n",
"AMBCBipsgn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxkoMIm2NdIpwdmmqDTAzNN0OmBmSZYi4EK\n",
"AAAAwEIGKmyCfY10emCmCTo9MNMEnR6YaYK1GKgAAAAALGSgwibY10inB2aaoNMDM03Q6YGZJliL\n",
"gQoAAADAQgYqbIJ9jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDCJtjXSKcHZpqg0wMzTdDpgZkm\n",
"WIuBCgAAAMBCBipsgn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxkoMIm2NdIpwdmmqDTAzNN0OmB\n",
"mSZYi4EKAAAAwEIGKmyCfY10emCmCTo9MNMEnR6YaYK1GKgAAAAALGSgwibY10inB2aaoNMDM03Q\n",
"6YGZJliLgQoAAADAQgYqbIJ9jXR6YKYJOj0w0wSdHphpgrUYqAAAAAAsZKDCJtjXSKcHZpqg0wMz\n",
"TdDpgZkmWIuBCgAAAMBCBipsgn2NdHpgpgk6PTDTBJ0emGmCtRioAAAAACxkoMIm2NdIpwdmmqDT\n",
"AzNN0OmBmSZYi4EKAAAAwEIGKmyCfY10emCmCTo9MNMEnR6YaYK1rDJQqaq3VNUzVfX5qnrfGt+D\n",
"k+XixYv7PgU2RA/MNEGnB2aaoNMDM02wliMfqFTVK5P8r0nekuSeJD9UVd9+1N+Hk+Wll17a9ymw\n",
"IXpgpgk6PTDTBJ0emGmCtazxCpX7kjw7xnh+jHEpyT9J8rYVvg8AAADAXtyywte8I8kftPULSb5z\n",
"vtOv/Mqv/NsVvjdX8eUvf/lb9n0OL+eP//iP930KbIgemGmCTg/MNEGnB2aaYC01xjjaL1j13yR5\n",
"yxjjR3frH07ynWOMH2/3OdpvCgAAAHAdxhh1FF9njVeo/GGSO9v6zlx+lcpXHdXJAwAAAOzDGu+h\n",
"8ttJXldVd1XVrUnekeTRFb4PAAAAwF4c+StUxhhfrqq/keTXkrwyyYfGGL9/1N8HAAAAYF+O/D1U\n",
"AAAAAE66Nbb8XFVVvaWqnqmqz1fV+477+7MfVfV8Vf1uVT1RVZ/ZHXt1VT1WVZ+rqk9U1dl2//fv\n",
"Gnmmqt68vzPnKFTVL1fVi1X1VDu2+PdfVX+pqp7afe5/Oe6fg6PzMk0cVNULu+eJJ6rq+9rnNHGC\n",
"VdWdVfWpqvpsVf1eVf3E7rjniVPqKk14njiFqupMVT1eVU9W1dNV9XO7454jTqmrNOE54hSrqlfu\n",
"fu8f3a3Xf44YYxzbRy5vAXo2yV1JviHJk0m+/TjPwcd+PpI8l+TV07G/m+R/3N1+X5IP7m7fs2vj\n",
"G3atPJvkFfv+GXzc0O//ryR5Q5Knvs7f/+Gr6T6T5L7d7X+Ry39RbO8/n48ja+IDSf7mFe6riRP+\n",
"keRcknt3t785yf+V5Ns9T5zej6s04XnilH4k+cbd/96S5LeSfLfniNP98TJNeI44xR9J/maSf5Tk\n",
"0d169eeI436Fyn1Jnh1jPD/GuJTknyR52zGfA/sz/3WntyZ5aHf7oSRv391+W5KHxxiXxhjP53Lg\n",
"9x3LGbKKMcZvJPnidHjJ7/87q+r2JN8yxvjM7n6/2h7DTeZlmkj+4+eJRBMn3hjj4hjjyd3tLyX5\n",
"/SR3xPPEqXWVJhLPE6fSGONPdjdvzeX/SPvFeI441V6micRzxKlUVa9N8v1J/kH+rIHVnyOOe6By\n",
"R5I/aOsX8mf/cORkG0l+vap+u6p+dHfstjHGi7vbLya5bXf7NfnaP7Wtk5Np6e9/Pv6H0cVJ9ONV\n",
"9TtV9aH2skxNnCJVdVcuv3rp8XieIF/TxG/tDnmeOIWq6hVV9WQuPxd8aozx2XiOONVeponEc8Rp\n",
"9feS/K0kX2nHVn+OOO6BinfAPb2+a4zxhiTfl+SvV9Vf6Z8cl19TdbU+tHOCXcfvn9Phl5LcneTe\n",
"JH+U5Of3ezoct6r65iT/LMlPjjH+ff+c54nTadfEP83lJr4UzxOn1hjjK2OMe5O8Nsl/XVVvnD7v\n",
"OeKUuUIT98dzxKlUVX8tyRfGGE/kyq9QWu054rgHKn+Y5M62vjNfOwHihBpj/NHuf/+fJBdyeQvP\n",
"i1V1Lkl2L6/6wu7ucyev3R3jZFny+39hd/y103FdnCBjjC+MnVx+uebhVj9NnAJV9Q25PEz58Bjj\n",
"I7vDnidOsdbE/3bYhOcJxhj/Nsn/keQvxXME+Zom/kvPEafWX07y1qp6LsnDSb6nqj6cY3iOOO6B\n",
"ym8neV1V3VVVtyZ5R5JHj/kcOGZV9Y1V9S2729+U5M1Jnsrl3/27dnd7V5LD/wP9aJJ3VtWtVXV3\n",
"ktfl8psDcbIs+v2PMS4m+XdV9Z1VVUl+pD2GE2D3D7pDP5DLzxOJJk683e/vQ0meHmP8/fYpzxOn\n",
"1Ms14XnidKqqbz3culFVr0rypiRPxHPEqfVyTRz+y/OO54hTYozx02OMO8cYdyd5Z5J/Ocb4kRzD\n",
"c8QtK/w8L2uM8eWq+htJfi2X3zjoQ2OM3z/Oc2Avbkty4XKTuSXJPxpjfKKqfjvJI1X17iTPJ/nB\n",
"JBljPF1VjyR5OsmXk7xnN2XmJlVVDyf5q0m+tar+IMn/lOSDWf77f0+SX0nyqiT/Yozx8eP8OTg6\n",
"V2jiA0nur6p7c/nlmM8l+bFEE6fEdyX54SS/W1VP7I69P54nTrMrNfHTSX7I88SpdHuSh6rqFbn8\n",
"H4Q/PMb45K4NzxGn08s18aueI8ifbe1Z/f9HlH9PBQAAAFjmuLf8AAAAANz0DFQAAAAAFjJQAQAA\n",
"AFjIQAUAAABgIQMVAAAAgIUMVAAAAAAWMlABAAAAWOj/B43INz4mxF3OAAAAAElFTkSuQmCC\n"
],
"text/plain": [
"<matplotlib.figure.Figure at 0x7f8575387950>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"if BAC_MODE:\n",
" addHeader(2,'BLAST Coverage Distribution')\n",
" \n",
" with size_controller(FULL_FIG_W, FULL_FIG_H):\n",
" hf = Data[ Data[\"BLAST Coverage\"] > 0 ]['Position']\n",
" \n",
" print \"Number of rows:\", hf.size\n",
"\n",
" if hf.size > 0:\n",
" hs = hf.hist(color=HISTOGRAM_COLOR)\n",
" \n",
" for of in output_files['BLAST Coverage Distribution']:\n",
" print \"Saving Image:\", of\n",
" savefig(of)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Gaps Distribution"
]
},
{
"cell_type": "code",
"execution_count": 427,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h2>Gaps Distribution</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Number of rows: 0\n"
]
}
],
"source": [
"addHeader(2,'Gaps Distribution')\n",
"\n",
"with size_controller(FULL_FIG_W, FULL_FIG_H):\n",
" hf = Data[ Data[\"AGP Gap\"] > 0 ]['Position']\n",
" \n",
" print \"Number of rows:\", hf.size\n",
"\n",
" if hf.size > 0:\n",
" hs = hf.hist(color=HISTOGRAM_COLOR)\n",
" \n",
" for of in output_files['Gaps Distribution']:\n",
" print \"Saving Image:\", of\n",
" savefig(of)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Ns Distribution"
]
},
{
"cell_type": "code",
"execution_count": 428,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h2>Ns Distribution</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Number of rows: 0\n"
]
}
],
"source": [
"addHeader(2,'Ns Distribution')\n",
"\n",
"with size_controller(FULL_FIG_W, FULL_FIG_H):\n",
" hf = Data[ Data[\"Ns\"] > 0 ]['Position']\n",
" \n",
" print \"Number of rows:\", hf.size\n",
"\n",
" if hf.size > 0:\n",
" hs = hf.hist(color=HISTOGRAM_COLOR)\n",
" \n",
" for of in output_files['Ns Distribution']:\n",
" print \"Saving Image:\", of\n",
" savefig(of)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## CSV Output"
]
},
{
"cell_type": "code",
"execution_count": 429,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<h2>CSV Output</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Original Size 3564 rows and 16 columns\n",
"no need to sample\n",
"Saving data to : reports/eps/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.raw_data.csv\n",
"Saving data to : reports/png/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.raw_data.csv\n",
"Saving data to : reports/pdf/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.raw_data.csv\n"
]
}
],
"source": [
"addHeader(2,'CSV Output')\n",
"\n",
"SAMPLE_EVERY = 1\n",
"\n",
"while ( Data.shape[0] / SAMPLE_EVERY ) > MAX_ROWS:\n",
" SAMPLE_EVERY += 1\n",
" \n",
"print \"Original Size %d rows and %d columns\" % ( Data.shape[0], Data.shape[1] )\n",
"\n",
"if SAMPLE_EVERY != 1:\n",
" print \"SAMPLING EVERY %d ROWS\" % SAMPLE_EVERY\n",
" \n",
" for of in output_files['all_data_full']:\n",
" print \"Saving full data to: \", of\n",
" Data.to_csv(of, sep='\\t', index=False)\n",
" \n",
" DataSampled = Data[::SAMPLE_EVERY]\n",
"\n",
" print \"New Size %d rows and %d columns\" % ( DataSampled.shape[0], DataSampled.shape[1] )\n",
" \n",
" if PARSE_VERBOSE:\n",
" print DataSampled.head()\n",
"\n",
"else:\n",
" print \"no need to sample\"\n",
" DataSampled = Data\n",
"\n",
"\n",
"for of in output_files['all_data']:\n",
" print \"Saving data to :\", of\n",
" DataSampled.to_csv(of, sep='\\t', index=False)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Combined Graph"
]
},
{
"cell_type": "code",
"execution_count": 436,
"metadata": {
"collapsed": false,
"scrolled": false
},
"outputs": [
{
"data": {
"text/html": [
"<h2>Combined Graph</h2>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"i 3 y 9 col 3 num cols 9 col name Ns\n",
"i 4 y 10 col 4 num cols 9 col name AGP Contig\n",
"i 5 y 11 col 5 num cols 9 col name AGP Gap\n",
"i 6 y 12 col 8 num cols 9 col name K-mer Coverage averaged: 500 bp\n",
"i 7 y 13 col 10 num cols 9 col name K-mer Coverage averaged: 5 Kbp\n",
"i 8 y 14 col 12 num cols 9 col name K-mer Coverage averaged: 1 Mbp\n",
"For axis 0 col name K-mer Coverage\n",
"K-mer Coverage 0.0 1.0 1.0 0.2\n",
"For axis 1 col name Sequencing Coverage\n",
"Sequencing Coverage 0.0 300.0 300.0 60.0\n",
"For axis 2 col name BLAST Coverage\n",
"BLAST Coverage 0.0 2.0 2.0 0.4\n",
"For axis 3 col name Ns\n",
"For axis 4 col name AGP Contig\n",
"For axis 5 col name AGP Gap\n",
"For axis 6 col name K-mer Coverage averaged: 500 bp\n",
"K-mer Coverage averaged: 500 bp 0.0 1.0 1.0 1.0\n",
"For axis 7 col name K-mer Coverage averaged: 5 Kbp\n",
"K-mer Coverage averaged: 5 Kbp 0.0 1.0 1.0 1.0\n",
"For axis 8 col name K-mer Coverage averaged: 1 Mbp\n",
"K-mer Coverage averaged: 1 Mbp 0.0 0.8 0.8 0.8\n",
"Saving Image: reports/eps/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Combined_graph.eps\n",
"Saving Image: reports/png/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Combined_graph.png\n",
"Saving Image: reports/pdf/run_BWA_JKL_23_JU_1_orig_PROBES_SL2.40ch12_SL2.40sc05611_JBPP0904_000000967164-000000970727.Combined_graph.pdf\n"
]
},
{
"data": {
"image/png": [
"iVBORw0KGgoAAAANSUhEUgAAAn8AAAR+CAYAAAChwlNkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\n",
"AAALEgAACxIB0t1+/AAAIABJREFUeJzs3XmcLFV5//HP987dgcsOl31RFFCEsLkhO4SgKDERcUFR\n",
"EwRJ3I0aCZcmJm4RNYYfRqOixA03NK6IioqIyCKisqhwZYcryHo37p3n98epZmrqds9095yeXub7\n",
"fr36Nd3VVdWnn6mufvrUU6cUEZiZmZnZzDCr1w0wMzMzs+nj5M/MzMxsBnHyZ2ZmZjaDOPkzMzMz\n",
"m0Gc/JmZmZnNIE7+zMzMzGYQJ39m9hhJZ0gaLW5LStNnSfrf0nM/lbR+L9uai6S9JX1S0h8krZB0\n",
"v6RrJX1A0u69bp+ZWW6ze90AM+tbASnxAz4FvLiYfjlwVEQ83KuG5SLpNODM0qQA5gJPKm4Ab5ju\n",
"dpmZdZN7/sysKUkCPgm8pJh0BXBkRDzUu1a1RtLcInFt9vyJjCV+K4HXAVsA84GnAO8Blne5mVMm\n",
"aUGv22Bmg8XJn5k1MwJ8AjiheHwVcEREPDjZgqXDwzdLOkjSVZJWSrpa0uGSNpD0EUn3Sbpb0rmS\n",
"FlXWsbGk90m6oVj2QUkXS3peZb4TS6/3aknvl3QHsALYtkn7RoB/K016W0R8OCLujYhHI+LXEfF2\n",
"4PTSMrMlvaF4L48UbfqNpJqkhcU8cyTdU7Tluspr7lpq56dK058m6atFHB6VdEdxGHqHyvIXl5Z/\n",
"kqQLJT0CfKt4/lRJP5J0Z9G2FZKuk/Tu6iH6Iv4fk/TnIq6fl/TU0vp/WJl/N0nnSbpd0uriPX5R\n",
"0h6NtwAz62sR4ZtvvvlGRACcAYwWt3tL968CNm5jPfXlHiL1nq0tTXsEuKy4X57+idLyWwC/L82z\n",
"tjLvm0vznliavqyyzPZN2rdfaZkHgdmTvJ8RUpI1Wll//fEVwMJi3veX5tmrtI4zS9MPLKYdB6xp\n",
"8j7/BDyhtPzFTd7nD4rnvzNBvL5fWo+A7zV4L7eVpv2gNP8Bxf+w0bqXAwf0erv1zTff2ru558/M\n",
"mtm4+LsMODwi/tzBOtYDPgBsCHyxmLYA2A14GvA4oF47+KLScmcCO5OSjL8BFgLbAT8unn+npMVN\n",
"Xu94YH3g8UXbG9mpdP8PEbFmkvdxPHBUcf+qot1bAd8tpu1NOmwMqbcUUpJVr5OEsff3h4j4cdFb\n",
"eA7pCMyVpJjMBw4DVgObAO9r0p6lpJrEhcDJxbQPAHsBm5LqFrcjJYQAh0jas7h/ePEaADcBuwPb\n",
"FPcb+VjRrqXAPsX9fUixnQ+c3WQ5M+tTTv7MbDKbA6/vcNnVwJmRTg4pH0q8ICIuj4ilwLXFtLmS\n",
"tizuH1P8HQG+QjqEextwYH1e4KAGr/fpiDg/IlZExM0RsaLDdlc9u3T/XyNiaUTcA7y1NP1ogIj4\n",
"DfCLYtoLASTtR0oYAc4t/j6TsQR7H+B6YBXwA9L7AziiSXv+MSKui4hVEXFjMe1PpJ7b35JqGG9j\n",
"LGEFeELx97DStP+MiBsi4i7Gn/hC0e5dgCcWD3ckJb6rir+bF9P3KP3fzGwAOPkzs2Z+Cjxa3D9N\n",
"0r/Un5C0Y6k+rGGdWOGeiFhV3F9Zmv7H0v1HS/fnFX+3KE2LJrdNGrze1ZO9qUK5l+txkuZMMn89\n",
"0QngltL0WxrMA2O9f9tKehZjPYBrGUv+yu+xvu7qbV6DEzqCyvuUtDPwE+BYYDFp3x6V5err2axJ\n",
"+29lXa20sdn/wsz6lJM/M2vme6TDnfVDojVJb6vMU00CqpodTp3sMOvdxd+HgXkRMdLgdk6D5Vrt\n",
"6bsKuLO4vz5wSqOZihNDyu0RUD4RY/vS/XtK9z9PSnZFOlP6uGL6hRFxR2WdAB9r8h5HGvVelhLq\n",
"uueSDsECnAdsEhEjpEPBVeVD4eUTYrZrMG/5PX1vgjZe12BZM+tTTv7MrKmI+CopeVlbTPp3SW8q\n",
"DnvOqiQAh2Z86W8Uf9cHPi5p2+JM2p0knSTpV1NZeUSMAqeVJr1b0j9I2rQYImYPSe8B/rV4/pul\n",
"ed9R9HxuCby7NP2xeSLiAdLhaoBXkuoDYaxHEOBSoF5H+XJJL5K0vqT1ijNv3yfpgy2+pXLv6Qpg\n",
"laSnAy9rMO/3S/f/QdLjJW0FLKnOGBG/A+qHlQ+X9DpJG0maL2lPSadL+nyLbTSzPuHkz8wmFBFf\n",
"JA33Uk8A3yfptS0urjZeqjzv6cDNxf0TSIcnVwF/AD7C2ADMHYuITwI1Uo/lfOA/Sb1iK4FrgLcw\n",
"1pv2BeDbxf19SIeN72Sspu7KYvmyeqJXH0z/T8DXSq+/HDiVdNbsXOAzpDOPHwJ+BrwJGDf8TaFR\n",
"TL/D2GH1k0hn4f4UuK/B+74IuKh4+ARScnc76QSbx2Yr3T+JsV7MDxTrXE469HwG6x4aNrM+13by\n",
"J+lASV+XdFtR5/PyFpbZoxh/anmx3L9MtoyZ9URU/qYHEZ9nbEiVAD4g6WQmVj0U3HDdjaYXJ1Ps\n",
"C7yXdCLESlJSdAMpSTq+hfVOKiJqwFNJVzC5idRr9gDwa+BDpDNd6z2FzyUlZFeThqtZSTq54kzS\n",
"0C0rKuv+AekM2XocPlM9q7iI6wHAl4G7SD1495BOGHk3adiYSd9nRPyhaN/VxXu4iXQo+7NNlvkb\n",
"4H+A+0kJ5/mkJK/u3tK6f0xKeD9NqgtcXTx/DSnh/edqe8ysvymivf2lpL8inaV2NWlncEpEfHqC\n",
"+ReRflleTNpJ7ka6YsAZEXFWZ802M7NOSdobWBYRtxaPNybtl59bzHJyRHy0V+0zs+5qO/kbt7D0\n",
"EHDqJMnfKcC7gC3rRcqS3kFKGhuOvm9mZt0j6T+AN5J6OR8BtiQNqwPprOHDWhj70MwG1HTU/D0d\n",
"+Enl7LQLga2rly8yM7NpcTHwI9Ih3M1JZ1VfBrwBJ35mQ2/25LNM2WLGjyUFY0McLGb8eF9mZtZl\n",
"EfENxs6oNrMZZjqSv7aOK0vq/Di0mZmZ2QwTEe2MrDAtyd9dpB6+si1Lz60j0vALU/FM4FwiPgOA\n",
"9DHSNTB/1+Z6ng58iYiPFes5lXTZqcum2L5ObQw8iYjDi/bsSxp64fuNZt4GTr49DYuRyyzg2UTs\n",
"89gU6VJSjVCuy2j1wtOBrxKRYiW9nzR472+gK3GcyIbAXkQcUrRlT9K1Uy+aaKFBMc2x7FfPBo4i\n",
"4l4kkU6eu6B47nDgH4kYu4KHtD/prN9xn/M2Y7kzEES8vFjnC0hjGP6YiJOKaS8hndH900nWdTRw\n",
"DBF3F8vtShrW5sIW29Kp8Z+NiUg/Bi5n7LrRE+rCdvkU4EYi3la05x+A59C7745pUYrj04DvEpEG\n",
"GZfOJF3q8HVEfKeY9iXS2ea3TbLaA4CPEfGFcVOlDUiXjJxqD/aGwJ7UxymV/gL4MJPvc58M/JGI\n",
"N5XadAHpyOadzRaawNOAbxHxnwCbS7csg+tIwz5VHQK8g4hL0su232k2HTV/PwOeJWleadoRwO0R\n",
"0c1DvuXEdoQ0REUnRprc74XRShtmM0HP6o5Nkuspv376wqobYWz8t0EVrBvXx7aXHfPHcSJrG7Rl\n",
"aHrDd5zeWPar+rh+UNnWWHdbbDQP0HYsq/uO+ue2vJ+cQ2vbWrDu/nU6ttHqZ2Mibe3zd8y/XVZj\n",
"NB0dLT2341gcR1l321Lxt242rX13VGNZXj7Hdtfos9HKeqvvsd6mqXwfPtaObRtfbrEuGB/LtnUy\n",
"zt96kvaStFex/A7F4+2K598lqZwxf5Y0IOi5kp4k6fmki6F3c5iXRhteJ8lfow9wp0lkDtWd34Q7\n",
"623Sr6rcqrGdxXAkf+UP0ri4dimOzbT1Px400xzLflXer1S/wIKxxLCu4U6+zViOsu423umXXvXz\n",
"MrfF5aaq3eSv5f1SF7bLtTSO91ArxXEt47fj2aTkr7q9tRKTZslfru2uul21ut7qZwqm9kNoXMy2\n",
"Tlf/abauRj8S29JJz99+pOtiXkUa/b5W3K8fql1MaaT4iHiQ1NO3NXAFqTv1P6LeHdw9nWxkjXTy\n",
"y7hb2ur5WzQ24n9OjX71D/pOrVHP32NfHF2KYzNt/Y8HzTTHsl+Vk6fqF02jnXrDz1ibsWyU6DVK\n",
"CDvp8Ziunr/qe5jILNrYL3Vhu6zGqNcdB9OiFMdmPZ/Vnr+pJH/92PM3wuTXLW9pfRuOXVWnkSn3\n",
"/LXdFR0RFzNB0hgRr2gw7dfAQe2+1hRUAzOb1PvYrurOcS4D1PO3f3cOsdV7JlaQLnqvidowIKr/\n",
"53E7pS7FsZmh7vmb5lj2q/L+qVHPX3WnXu0JBNqOZaNDvNVp7fQkzK3cH+ievy5sl9XEoNffHdNi\n",
"//GHfSfraW41QW+W/OXaN3a6z61+fmBqSf64mD0txXL9JvM2i0nLhvnavjl6/vrt19so4/9nE/5C\n",
"OSldWiq3iQ5ZDapGPxYe+z93KY7NVP/HwxJjYNpj2a/Kn6FqUtBop95wv9NmLJv1/HXypVf9Yp/O\n",
"nr/Jv7NSTXJb+/wubJf99t0xLUpxbPaDujqt1V6yZslfjph2us9t1BM9lSNh4z77r03D4DVb1/TX\n",
"/A2IXB+8cmE29L5uox96hcoxGZZfs9X6nF7uqKsn1QxV8mfAuj1/zZ6jyTydaLZP7OTwbTVBna79\n",
"UKMTzhrph0SrUU9rr9s0narvv/4/6bTGtFnyl0P6Xh3brjr9EQRtlhs0aEe1R32i3usp1fwN6xlI\n",
"a4G/RTqseLw16w403Yp++/U2CsxD+mbxeBHpQvANfRR27MIv2mHs+VsLHIlUH8JmMXBl/ckuxXEi\n",
"I8A3SafvL2LwT6h5TA9i2Y9GgLOQVpB28NUfHicA3yxNa/hl1GYsVwNblfYdGxXTti9N2xi4t4V1\n",
"LSjaWP+MTOd+YA7wZuB9SDsC55IuT7caOB14ZzFPW4lBF7bLtcBTSrHdjBlwQYNSHNcCB5Te/5ak\n",
"Xr6/K4YZAtiECb6/SiZK/nJ9H89h/D63lR7JZmfmd7q/Hpdv/Dc8/tUTf65eh/QK4A+dvNiwJn/X\n",
"kHZkdTfR2k6tqlndQi99j/G/Dh6a5tefqFh9UP2G8TU/S4FlvWkKkMaX6uX/2LrrEtK4o3Xlkw2u\n",
"B3apzJ/jsOoDpPE4y0d77id90dWnLSWdYTiZ3wPblB5P5xGI35HGV4M0lp5I+/q5wO7AVsAvgBum\n",
"qT3N3ML4sU+X0tl30KC6kfHvdynwIGl7q/s9rY0P26iHDfL+6Ojke3UN6+ZQU+n5G/c+Z03c2fQL\n",
"UizXB/bq5MWGNflbQ54v734b6gXSTrwlrvlr2SgTbC896Klq+X88aNzrB6SeqkcmeK66j2mYXHUQ\n",
"y0bJRycJycOM/xKfrpo/SJ+NcgIrUsyCNPrESjrY93dpu+zlD8ieqNT8NXr/ncSkWX1bzh8dnexz\n",
"G/VITmXc23Hr+3u4g3V/CNatIsVyOaXRVdoxrDV/uTQaq2loDsF1qPxBHKozUc36QLOhXvpJo3FU\n",
"p2s/UK17rtdpjZKSP++Phk/1e7iu150P4+saOzjRaML1tZZvtDP80ThO/ibWbzV/bfko7NiF1ZYH\n",
"oe31h29adCmOM5JjOalGw5k0rfmbjgY10Gi/OF37gUaDzNdfe0Gn7fB2mUcXv3O63fPXiUZD10Dn\n",
"bRq3bX86xXKyfKOd4Y/GcfI3sV7u5PpVuWdiWM72NesXjXbm/dbz1+hMzulS3SfXxxlNJ8N5/zyM\n",
"Gg2mDNNbbtBI7tE3xr1Ptfb+Whv+qAEnfxNrNC7RwBz27WLNX7nnb+i5Ti0fx3JSjQ7jNPzR2cNY\n",
"9nIsymbJH0wh+fN2mUeX4tgs+eu3nr+pnhA67n2eAPcweb7hnr8uqQZ2oA77dkm5568fzn42GyaN\n",
"dub99iOrl0dEqr2O5Zo/9/wNp36t+et0kPRmqp/9VuoHA/f8dUUA2yKdgnQKaRiBgUl2ulh/cWwR\n",
"j7+l+bUHh4brgfJxLCfV6DBOwx9ZPa75K39J7c/09vxtVOx/jmR8zd+ena7U22UeXYpjs56/p9Hb\n",
"759uHPZdXM83Lkjbcyv5Rkc5Sb/9ouw3d5MG/D22eLwC+FPvmtMXbiONs1Ufa+vWHrbFbNgEIKQR\n",
"IuqHfPrtiEP1S28/4JfT9Nr3k4blqO+TR0iHGtcjDSTcyWD+1t+aJX8Hkr6jeyV3z9+9pKFbjiWt\n",
"aC2tvb+OXtPJ38RWAJf1uhGd6lL9xe+L24zheqB8HMuW1Mf7qid/DU+s6mEsGx2anq4fgWuBnzd5\n",
"7qZOV+rtMo8uxbF6qL9uDb1N9huVhU0l+VtFKd/469aX6+iHoQ/7mpn1l+o1xfut52+sx0MaYfxJ\n",
"F2a5Nbu821TG1MuhWqIxUKNfOPkbYq5jycNxzMexbEn1y67fav7WMvbd0eui+yy8XebRxZq/Rid8\n",
"TOVqGjmknr80uDNkPpLaRizd82dmNgTKwylB/51VX651GqjeDhtIza5i0euev7p6HtWrz2lHP76c\n",
"/A0x17Hk4Tjm41i2pKVrivd4nL96j8dQ9Px5u8yjizV/zZK/Xo+7Wy7RyPpZaCOW7vkzMxsC1ctZ\n",
"9VvPH4wlqHMZguTP+lqzs31n0R+fi3rbej3odFuc/A0x17Hk4Tjm41i2pJr8Nez564NY7ghsxxCM\n",
"9dkHsRwKXaz5W4C0wWNTUq9zPxz27VrPXxux9FAvZmZDoKXkr8dWA58hJX6retwWG27LgS2AzwLH\n",
"FNP6pZetfDJKr9q0upOFnPwNMdex5OE45uNYtqRa89ewtqnHsfx2D187O2+XeXQpjo8APwSeVJrW\n",
"T6UQXUn+2ojlH4CD212/D/uamfWX6tAW/fRFZ9YL1YGe+7Hnb4T+aFNLnPwNMdex5OE45uNYtqRR\n",
"z986XyqOZT6OZR5djGN1QOV+Sf6gSyd8dHubdPJnZtZfGtX8relRW8z6QaPr6PZDb3i552+gyuic\n",
"/A0x17Hk4Tjm41i2pJr8Nez5cyzzcSzz6GIcq2P99UvPX7mXvlc1fx1x8mdm1l+Cdb/oej2YrVkv\n",
"9XPy55o/6y+uY8nDcczHsWxJtedvFg2SP8cyH8cyj2ms+euXK8t0refPNX9mZjNLS5d3M5tBypcU\n",
"hP7t+RsYHSV/kl4j6WZJKyRdIemASeY/WtJlkh6UtEzSBZJ26azJ1irXseThOObjWLakUc1fP13b\n",
"d+g4lnl0OY7lH0X92PPXq2v7dqTt5E/SC4EPAu8E9gIuBb4tabsm8z8euAC4uJj/cGA+8K3Ommxm\n",
"NvRGKvfd82czXflSau75m6JOev7eCHwyIj4eETdExGuBO4FTmsy/V/E6b4+ImyLiGuA9wOMkbdJR\n",
"q60lrmPJw3HMx7FsSaOeP9f8dZFjmUeX49ivPX/1pG94a/4kzQX2Bi6sPHUh8Iwmi/0UeBj4e0kj\n",
"ShdnPhG4PCLua6+5ZmYzgnv+zMZzz19G7fb8bUZ6g3dXpt8DLG60QETcCRxNOky8ErifdI2+YxrN\n",
"b/m4jiUPxzEfx7IlLfX8OZb5OJZ5TEMc6z1//TSsSr1Nc8k4JFO3Y9n1Eakl7Uyq+fsk8FlgEXAm\n",
"cL6kQyNinX/gM+HYbVKSyCJYuT/cVQ9EvSvUj/3Yj/14GB9vDhv9dbFvlnTw/8GGzyl6/vqhfX7s\n",
"xz16PHo4HPh96e5IiVb0un0XwEbXwJ5L4CvA7C/DxvfCjt1+fYCLYMfbYaMFsJAOqEHu1XzmdNj3\n",
"EeD4iPhyafrZwO4RcUiDZd4DHB4R+5SmbQPcChwQEZdW5o+AWtvvxNbx0dJGaJ1zHPNxLFvydOAC\n",
"Is4phra4CvhadSbHMh/HMo8ux/EvgROI+D3Ss4E3AT/u0mu16pnAuUR8BukM4C+Aq3OsuI1Ybit4\n",
"VUSonfW3ddg3IlYDVwJHVp46gnTWbyNi3XqV+mOPM2hmNl65sN37SLMkfS6kTYGD6Z/Dvk9Hegmw\n",
"G/3Tpkm11fMHIOk44DzgNaSE72TgFcCTIuJWSe8C9ouIw4v5DwB+BJwBfB7YAPh3YFdgt4hYUVm/\n",
"e/7MbCZ7GvBdIj6AtAC4BPi/HrfJrNeOIOUbuwBLgF8Bf+hpi9Jh2K2L+wJuBJZNcxs66vlru+Yv\n",
"Is5XyrxPA7YCrgWOjohbi1kWAzuX5r+kGBvwbcA/AcuBnwFHVRM/MzNjLWNnNXa9LttsQNR7xOeQ\n",
"EqxeJ36QDssu7XEbOtLRIYWIOCcidoqI+RGxX0RcUnruFRGxc2X+L0XEvhGxQURsGRHHRsT1U228\n",
"TaxcHGqdcxzzcSxbMsr4MwgbDvPiWObjWObR5TjWz4LvlzH+uqrb26TrSczM+ssoY0O9zIgvOrMW\n",
"1Hv+3BuegZO/Ieaz1/JwHPNxLFtSPuFjLk2SP8cyH8cyjy7HsdzzN/SDnnd7m3TyZ2bWX8o1f3OY\n",
"AV90Zi2oX0ptoK6k0a+c/A0x17Hk4Tjm41i2pFzz1/QQl2OZj2OZxzTU/M2lfy7t1lWu+TMzm1nK\n",
"NX/u+TMbMxf3/GXR9jh/3eZx/sxshtsV+DMRpyDtCZwNXNTjNpn12sGkH0LfAA4HLu9pa/pH96/w\n",
"YWZmXbeWscO9M+IQl1kLrgHW4M9EFk7+hpjrWPJwHPNxLFsyytihraZDvTiW+TiWeXQ5jvVa2KZj\n",
"Xw4T1/yZmc0s1Zo/93KYjf0och1sBq75MzPrL9sD84l4MdIhpOuYXtzbJpn13ELg6cBPgN1Ih4HN\n",
"NX9mZkOhPNSLe/7Mkvrnwj1/GTj5G2KuY8nDcczHsWxJueZvBNf8dZ1jmUeX47iWlLPMiCt8uObP\n",
"zGxmcc2f2brqP4pmRPLXba75MzPrL5sDOxFxNNL/AI/HNX9mAM8DLgM2BG7scVv6hWv+zMyGwChj\n",
"++Zd6fIF3s0GzDzc8zdlTv6GmOtY8nAc83EsW1I+4WMNcF+jmRzLfBzLPKYhjqOkcf7665BlF7jm\n",
"z8xsZqme8LG2h20x6zfz8GdiylzzZ2bWX9YH9ifiQKRLSeOarehxm8z6wbOBO4B7gVt63JZ+4Zo/\n",
"M7Mh4J4/s8aCGXJ5t25z8jfEXMeSh+OYj2PZkrWMJX+zaPJF51jm41jmMQ1xnDHJn2v+zMxmlvpg\n",
"tuCeP7Oy+hiY/kxMkWv+zMz6yyzgOaT94BnA13raGrP+8VfF3yuAZb1sSB9xzZ+Z2RAYJQ3v8jrg\n",
"Tz1ui1k/uQdYDjzY64YMOid/Q8x1LHk4jvk4li27BPgx8NNmMziW+TiWeUxDHK8EfgSs6vLr9Jxr\n",
"/szMzMwsG9f8mZmZmQ0m1/yZmZmZ2cQ6Sv4kvUbSzZJWSLpC0gEtLPN6SddLWinpDknv6uS1rXWu\n",
"Y8nDcczHsczHsczHsczDccyn27GcPfks40l6IfBB4BRSUfKpwLcl7R4RtzZZ5izSZVneDFwLbAhs\n",
"1WmjzczMzKwzbdf8Sfo58MuIeHVp2o3AlyLinxvM/0RSwrdHRNzQwvpd82dmZmY2ue7X/EmaC+wN\n",
"XFh56kLgGU0Wex5wE3C0pJuKw8XnStq8ndc2MzMzs6lrt+ZvM9Llhu6uTL8HWNxkmZ2BHYDjgJcB\n",
"JwC7Av8nqa1M1drj+os8HMd8HMt8HMt8HMs8HMd8+q7mrwOzgHnACRHxewBJJwA3APsCv6gu8Ew4\n",
"dhu4H2ARrNwf7joJlsJYQPzYj6fr8eWwuJ/aM8iPLy9+JPZLe/zYjynpl/YM6mN/vqdve70Idrwd\n",
"NloAC+lAWzV/xWHfR4DjI+LLpelnA7tHxCENlqkBb4+IuaVpAlZX11M855o/MzMzs8l1v+YvIlaT\n",
"Lq9yZOWpI4BLmyx2CTBb0s6laTuTDh//sZ3XNzMzM7Op6WScv7OAEyW9StJukj5E6ur9CICkd0m6\n",
"qDT/RcBVwCck7SXpL4BPAJdFxBVTbL9NoHpIwzrjOObjWObjWObjWObhOObT7Vi2XfMXEedL2hQ4\n",
"jTRW37XA0aUx/haTevbq84ek5wD/SbpQ+QrS2cFvnGLbzczMzKxNvravmZmZ2WDytX3NzMzMbGJO\n",
"/oaY6y/ycBzzcSzzcSzzcSzzcBzz6XYsnfyZmZmZzSCu+TMzMzMbTK75MzMzM7OJOfkbYq6/yMNx\n",
"zMexzMexzMexzMNxzMc1f2ZmZmaWjWv+zMzMzAaTa/7MzMzMbGJO/oaY6y/ycBzzcSzzcSzzcSzz\n",
"cBzzcc2fmZmZmWXjmj8zMzOzweSaPzMzMzObmJO/Ieb6izwcx3wcy3wcy3wcyzwcx3xc82dmZmZm\n",
"2bjmz8zMzGwwuebPzMzMzCbm5G+Iuf4iD8cxH8cyH8cyH8cyD8cxH9f8mZmZmVk2rvkzMzMzG0yu\n",
"+TMzMzOziTn5G2Kuv8jDcczHsczHsczHsczDcczHNX9mZmZmlo1r/szMzMwGk2v+zMzMzGxiTv6G\n",
"mOsv8nAc83Es83Es83Es83Ac83HNn5mZmZll45o/MzMzs8E0fTV/kl4j6WZJKyRdIemAFpfbRdJD\n",
"kh7q5HXNzMzMbGraTv4kvRD4IPBOYC/gUuDbkrabZLm5wOeBHwH91d04pFx/kYfjmI9jmY9jmY9j\n",
"mYfjmE8/1vy9EfhkRHw8Im6IiNcCdwKnTLLce4BfAl8E2uqeNDMzM7M82qr5K3rvHgGOj4gvl6b/\n",
"F/DkiDi4yXLPBj5A6ik8DvhwRGzQZF7X/JmZmZlNrqOav9ltvshmwAhwd2X6PcDiRgtI2hr4KHBs\n",
"RCyX3OlnZmZm1ivtJn+dOA84JyJ+0eoCz4Rjt4H7ARbByv3hrpNgKYwdB/fjyR+Xawb6oT2D+vhy\n",
"WPw/cFm/tGeQH/8dPM2fZ3++++1xfVq/tGdQH/vzPT2fb4CLYMfbYaMFsJAO5Drsezawe0Qc0mCZ\n",
"UWBteRKp1nAtcEpE/E9lfh/2zeSjsGN9o7HOOY75OJb5OJb5OJZ5OI75tBHLjg77tj3On6TLgGsi\n",
"4tWlaTcCX4yIdzSYf/fKpGOBdwD7AXdExP2V+Z38mZmZmU1uWmr+AM4CzpN0OWmYl5NJ9X4fAZD0\n",
"LmC/iDgcICJ+W15Y0v7AaHW6mZmZmXVf20O9RMT5wOuB04CrgWcAR0fErcUsi4GdJ1tNu69r7SvX\n",
"B1jnHMdHKIxHAAAgAElEQVR8HMt8HMt8HMs8HMd8uh3Ljk74iIhzgHOaPPeKSZY9Fzi3k9c1MzMz\n",
"s6nxtX3NzMzMBtP0XdvXzMzMzAaTk78h5vqLPBzHfBzLfBzLfBzLPBzHfLodSyd/ZmZmZjOIa/7M\n",
"zMzMBpNr/szMzMxsYk7+hpjrL/JwHPNxLPNxLPNxLPNwHPNxzZ+ZmZmZZeOaPzMzM7PB5Jo/MzMz\n",
"M5uYk78h5vqLPBzHfBzLfBzLfBzLPBzHfFzzZ2ZmZmbZuObPzMzMbDC55s/MzMzMJubkb4i5/iIP\n",
"xzEfxzIfxzIfxzIPxzEf1/yZmZmZWTau+TMzMzMbTK75MzMzM7OJOfkbYq6/yMNxzMexzMexzMex\n",
"zMNxzMc1f2ZmZmaWjWv+zMzMzAaTa/7MzMzMbGJO/oaY6y/ycBzzcSzzcSzzcSzzcBzzcc2fmZmZ\n",
"mWXjmj8zMzOzweSaPzMzMzObmJO/Ieb6izwcx3wcy3wcy3wcyzwcx3z6tuZP0msk3SxphaQrJB0w\n",
"wbwHS/qapDskPSLpGkmv6PS1zczMzKwzHdX8SXohcB5wCnAJcCrwCmD3iLi1wfxvBxYA3wbuBI4C\n",
"Pgy8LCI+V5nXNX9mZmZmk+uo5q/T5O/nwC8j4tWlaTcCX4qIf25xHV8ARiLibyvTnfyZmZmZTW56\n",
"TviQNBfYG7iw8tSFwDPaWNWGwH3tvr61zvUXeTiO+TiW+TiW+TiWeTiO+XQ7lrM7WGYzYAS4uzL9\n",
"HmBxKyuQ9BzgUNpLFs3MzMxsijpJ/qZE0jOBzwD/GBFXNJrnmXDsNnA/wCJYuT/cdRIshbFs2I8n\n",
"f3wSLO2n9gzy47p+ac+gPq5P65f2DPJjf779uN8e16f1S3sG+fFEn2+Ai2DH22GjBbCQDrRd81cc\n",
"9n0EOD4ivlyafjbphI9DJlj2AOCbwL9ExH82mcc1f2ZmZmaTm56av4hYDVwJHFl56gjg0mbLSToQ\n",
"+BawpFniZ3lVe62sM45jPo5lPo5lPo5lHo5jPt2OZaeHfc8CzpN0OSnhO5lU7/cRAEnvAvaLiMOL\n",
"xweTevz+C/icpHpt4NqIWNZ5883MzMysHR1f21fSKcA/AVsB1wJviIhLiuc+CRwUETuXHr8MqHZL\n",
"Lq3PU1qvD/uamZmZTW76xvnrJid/ZmZmZi2Znpo/Gxyuv8jDcczHsczHsczHsczDccyn27F08mdm\n",
"ZmY2g/iwr5mZmdlg8mFfMzMzM5uYk78h5vqLPBzHfBzLfBzLfBzLPBzHfFzzZ2ZmZmbZuObPzMzM\n",
"bDC55s/MzMzMJubkb4i5/iIPxzEfxzIfxzIfxzIPxzEf1/yZmZmZWTau+TMzMzMbTK75MzMzM7OJ\n",
"OfkbYq6/yMNxzMexzMexzMexzMNxzMc1f2ZmZmaWjWv+zMzMzAaTa/7MzMzMbGJO/oaY6y/ycBzz\n",
"cSzzcSzzcSzzcBzzcc2fmZmZmWXjmj8zMzOzweSaPzMzMzObmJO/Ieb6izwcx3wcy3wcy3wcyzwc\n",
"x3xc82dmZmZm2bjmz8zMzGwwuebPzMzMzCbm5G+Iuf4iD8cxH8cyH8cyH8cyD8cxH9f8mZmZmVk2\n",
"rvkzMzMzG0zTV/Mn6TWSbpa0QtIVkg6YZP49JP1I0nJJt0n6l05e18zMzMympu3kT9ILgQ8C7wT2\n",
"Ai4Fvi1puybzLwK+B9wJ7Au8DniLpDd22mhrjesv8nAc83Es83Es83Es83Ac8+nHmr83Ap+MiI9H\n",
"xA0R8VpSYndKk/lfAswHXh4Rv42ILwPvKdZjXXQ5LO51G4aB45iPY5mPY5mPY5mH45hPt2PZVvIn\n",
"aS6wN3Bh5akLgWc0WezpwE8iYlVl/q0l7dDO61t7HkxJt02R45iPY5mPY5mPY5mH45hPt2PZbs/f\n",
"ZsAIcHdl+j00z1IXN5j/7tJz1iW3w0a9bsMwcBzzcSzzcSzzcSzzcBzz6XYsZ3dz5YVOTifeMXcj\n",
"ZqLbYXscyylzHPNxLPNxLPNxLPNwHPNpI5bLO1l/W0O9FId9HwGOL2r36tPPBnaPiEMaLPMpYNOI\n",
"eE5p2n7Az4GdIuKPlfn7a+wZMzMzsz7W7lAvbfX8RcRqSVcCRwJfLj11BPDFJov9DHiPpHmlur8j\n",
"gNuriV/xGm29ATMzMzNrXSdn+54FnCjpVZJ2k/QhUu3eRwAkvUvSRaX5P0vqljxX0pMkPR94a7Ee\n",
"MzMzM5tGbdf8RcT5kjYFTgO2Aq4Fjo6IW4tZFgM7l+Z/UNIRwNnAFcB9wH9ExAem2ngzMzMza0/f\n",
"Xd7NzMzMzLqno8u7mZmZmdlgcvJnZmZmNoM4+TMzMzObQZz8mZmZmc0gTv7MzMzMZhAnf2ZmZmYz\n",
"iJM/MzMzsxnEyZ+ZmZnZDOLkz8zMzGwGcfJnZmZmNoM4+TMzMzObQZz8mZmZmc0gTv7MzMzMZhAn\n",
"f2ZmZmYziJM/swEh6SmSzpd0k6RVku6VdF0x7dhet6/fSDpD0mhxO6gP2rOxpNMk/VzS/ZJWSrpZ\n",
"0lclHdfr9pnZzDG71w0ws8lJOgD4AWOf2QA2AjYGngg8AFzQm9b1rShulP72hKR9ga8BWxWT6u3Z\n",
"HtgBOBg4f/pbZmYzkXv+zAbD20iJ31rgecB6pMRvX+AM4A89a1mfiohaRIwUtx/3qh2StgC+yVji\n",
"91XgycBcYBvgFcB1vWld6yTNleTvDLMh4A+y2WDYpfj7EPC9iFgZEQ9GxFURcWZEvLs8s6T5xSHG\n",
"ayUtl/SIpMslvaK6Ykm7S/qepBWS7pT075L+vnTIdElp3qXFtJsr62g2fVtJ5xSHN1dL+rOkb0l6\n",
"VmW+8iHa50o6W9Ldkh6Q9F1Jj6/ML0mvknRJMc+qog2fabLOg0rT69N+KOloSb8o3vvvJb2lQXyO\n",
"lnRNcZj2ekknSDq3jUPKbwI2L+5fFRF/ExHXRcTaiLgrIj4FVOPxLElfl7RM0qOS7pL0OUl7lOb5\n",
"QKkNT60s//Ni+kOS1iumbSzpfZJuKN7Lg5IulvS8yrInltb7aknvl3QHsALYTtJekr5SxOvBUvu+\n",
"LGmfBvF7uaQbi9e8WtJRxevWX2P70rwtb7dmNgUR4ZtvvvX5DfgeMFrcbgHOAV4G7Nhg3oXAZaX5\n",
"1xa3+uMPl+ZdDCyrzDsK3Faadnpp/puLaTdVXnOd6aTD0csqbaivfw1wXGneM0qvd1+lLaOknrFZ\n",
"xbwCvtjk/a1tsM61wIGl6fXl7m8Qm1HgJaV5Dy7a2iw+49bd5H/3m9LyL2rhf/3SSpvK91cABxXz\n",
"7VGa/sHS8o8rTf9EMW0L4PdN/hejwJtLy59Yml79/20PHN9gPfV1PQzsWlrXCZXYrgVWA3eVHm/f\n",
"7nbrm2++Te3mnj+zwfBBxurEtgVeDZwL3CTpp5L2LM37WmD/4v6pwCLSl3+9puxUSX9R3H8DsGlx\n",
"/6vAZsDeND8qoDamf6hY9/3AIcACUkJ4fbH+/5LUqO74fmBP0iHR+uHQJ5be0wuAvynu3wYcCawP\n",
"PJ6U8LXa5kXAv5MOn/9DafoJpfv/xlgsTgc2BF4MbD3Just2Kt3/7UQzFr10Hy7W+yhwbNHOk4tZ\n",
"5gH/DRAR1wJXFtOPKx2SfVHxN4BPFPfPBHYmJVN/Q0q0tgPqh8PfKWlxgyatR0r26vFdVrzmX5Ji\n",
"MJ8Uk1OL+ReStk2K9vx7aV2vLOZ9O2l7rGpnuzWzqeh19umbb761diP1Qn2f1HMyWrndAqxXzPfT\n",
"Bs9Xb28t5v05Y70sTy691pmlecs9f0tp3PM3bjop0VvTQjueWsx/Rmnaa0rrfV9p+nHFtP8tTTth\n",
"gniV19mo5+8OQMW09UrTf1uaVu95Wlaft3jukkbrbtKO5aV595xk3iNL83618txVpf/VzsW0U0rz\n",
"H1ZMq/c03lBa9vYW/hcvLOY9sTTtIw3auAh4DymRXd5gPd8s5tu1NO2qyjpuKb2Xes9fy9utb775\n",
"NrWbe/7MBkREXBwRh5Hqx54DfITUOwSpN/Bpxf1yr0o0uW1SPL9pad7bSvdvb7N51R68TRjfezhZ\n",
"O8puKN1fXro/v/i7ZWmdE/akTeIPEVHvTW30Ohsz1rN3e2legFvbeJ2bSvd3n2TezUv3b6k8V35c\n",
"/x9/FlhZ3H9x0QO8W/H4Ew3mh/b+F1c3mHY+8BZScjeP8WdVQ0r8IfUiN3svjbavTttoZm1y8mc2\n",
"ACRtUL8fEQ9ExLci4jWkQ7919S/Gu+uzAtvG2Bmv5dtbi3mWlZbfrnR/2yZNWVX8rSdI9UOVW1bm\n",
"u4/UqwNwY5M2jETEtxu8xqOl+42GaLmr/tJMnkxN5LHXqSR2dfXaQ4CtJJUP8W7XYP5mvlG6/6ZG\n",
"M0gaKe7eXZq8Q2W27Uv374G0LTA2xM/zSb12kHpdP1Wav77eh4F5Tf4X5zRo2opKOzcm9U5C+j88\n",
"KSJGSIfpq/5Uuv/Y9lTEsdH21c52a2ZT4OTPbDB8TdJ5kp4taTNJcyQ9GaifaRqM1cfVkw0Bn5D0\n",
"+GL+bSW9pDhDtp5Y/LA0b03SJkVd1d81acfS4u9iSfsVdV01YKQ8U0SsIB2iBniCpPdI2lxpuJBd\n",
"Jb1R0vdZVyvj8X29dP/fJB0qaaGkHSWd3uE6110oYjnpBARIPXJvlrSBpOOBZ7SxqrMYS4T2lvRF\n",
"SbsV/5PFkk4kHfIE+Bnw5+L+X0k6RtL6kv4e2KuYfkNElHsT6z185dq770bEXaV56tvE+sDHi21h\n",
"jqSdJJ0k6Vctvpc1jMVzLfCQ0lA272ww7w2M9SbvLelFxY+YN5HqOava2W7NbCp6fdzZN998m/wG\n",
"/ISJa6G+Upp3AXD5BPOW66w2Z+zMy/KtXCNWrvl7WWW+h0k9aCuLxzeX5t2VlPQ0a0f5zOAzStMP\n",
"bDL9ZaXp5zdbbwvrrE/7QSXG9enl93BQ8f4mis+zWvj/7U+qMWwWi/tK876Y5vWSy6nUGJKSpaWV\n",
"+f66Ms8WpLEgm24TpXlPbBTz0vMXNlj+htL9H5bmfWmDeVeTevnq2+J27W63vvnm29RuE/b8STpV\n",
"aXyrB4rbpZKOrsxzhqTbizGZfihp98rz8yR9WGm8qoclfU1So199Ztbcv5DOnv0FKYlYDTxCqsl6\n",
"O/DC+oyRet0OBE4DrinmW0768v8K6azLO4t5l5FOJLmIdIjvLuBdwGNj+1WcB7yDlGysKF7/8GJ9\n",
"42q/IuJ6Um/VOcVrryKdyfsb4H8YO4OV0nLVXrqG0yPiOODvST1mDxTxuA34fAvrbDatPr38Hn5E\n",
"GlT72qL9N5AS4KtK89/bZF3l9l5OGtj5dOAK4MFifUtJV/54dWnez5L+J98gJc+Pkv4vXwD2j8qA\n",
"1RERjB3+D9Kh/K9X5rmHNCD4e0lnW68kjRl5A/AZ0hm95RiU/1a9tGjLfaT/53mMbX/V+P0vaRDr\n",
"3xfv95fAMYwvN7ivmLfl7dbMpqZ+plvjJ6Xnkj6wvyMdIj4R+Cdgv4i4RtJbSV8ELwduJO3YDgCe\n",
"GBEPF+s4B3guaYd5H+kQyEbAPhExipn1neJQZP1w4hkRcWYPm9MzxVA0h5J6CdcU044i1dnNJZ0I\n",
"0k7934xS1AjuDlxaJKnVbeuyiGjnELqZZTDhtX0j4uuVSadJOgXYv6gReT3wroj4KqSR3EmFyC8G\n",
"PippQ9KvtRMj4vvFPCcAfyT1FlyY882YmWU2H/gOsEbS3cAGpKFOIPXIndKrhg2IbUglC6sl3UM6\n",
"g3q94rmHSGP7mdk0a/mED0kjRaHzfNLAoDuRzvB7LIGLiJXFc/VfcvsAcyrz3EYqTPevPbP+Ndmh\n",
"v5liJems2ZtJRyzmkX68nkc6AvKNCZa1VNv3BVKpwqakE4N+Rxqoes+IuKKHbTObsSbs+QNQupbk\n",
"z0g7vRWkgVZvkFRP3u6uLHIPY6PfLyYVEldrYu5m3aEhzKxPRLre7KcmnXHIFYd6fV3ZDhU1pS+a\n",
"dEYzm1aTJn+k4uCnkIYReAHweUmHTLJMx70FkmZ6T4OZmZlZyyKilUtNPmbS5C8iHmVshPqrJe1H\n",
"GkuqXgC+JeOvDLAlY4Ow3gWMSNq00vu3mLFrSjZ6zbbehDUm6eKIOLjX7Rh0jmM+3Y6lavop8GAs\n",
"ib/q1mv0C2+X+TiWeTiO+bQTy046zToZ5HkEmBURN5OSu/po70iaTzrb99Ji0pWkoujyPNuSxv+q\n",
"z2Pds7TXDRgSS3vdgCGytMvrF7BINb1SNe3a5dfqtaW9bsAQWdrrBgyJpb1uwBBZ2s2VT9jzJ+nd\n",
"pLGmbiOd5fZi0qCnRxWzfBD4Z0nXk4p4TyOdwfVZSJcekvRx4L3FmV71oV6uIY0rZmaW0yrSVSxe\n",
"QboEW623zTEz6z+THfbdEvhf0mHaB0hJ21ER8T2AiHivpAXA2aRT+C8DjoyIR0rreD1ptPovkEZw\n",
"vwh4aX3MJ+uqX/a6AUPCccyn27FcRfqhOoc0QPAw83aZj2OZh+OYT1djOeEgz70gKVzzZ2btUk0j\n",
"pJEJZpN+cH45lsR7etsqM7Pu6iRvauVsXzOzQTCfdNUNSLXJ/hFpZtZAJyd82ICQdHCv2zAMHMd8\n",
"uhzLhaR92oLi71Anf94u83Es83Ac8+l2LN3zZ2YDTTVdDBxGSv6Wk+r+FpDq/szMrMI9f0MsIi7u\n",
"dRuGgeOYT+5YqqY5pP3YCcD2pB+0N5EOAS/I+Vr9xttlPo5lHo5jPt2OpZM/Mxtk65Pq+14JbE4a\n",
"V/QG0vBUQ538mZl1ysnfEHP9RR6OYz5diOVCUvI3m3Syx8PAKHAHsEXm1+or3i7zcSzzcBzz6XYs\n",
"nfyZ2SDbi5QAzgFOLk1/BNioJy0yM+tzTv6GmOsv8nAc8+lCLE8mHd6dS+r9qw9cuooh3795u8zH\n",
"sczDcczHNX9mZs1tSNqP1ZO/0WL6o/hsXzOzhpz8DTHXX+ThOObThVjOJo3ndxfjB3Zew5Anf94u\n",
"83Es83Ac83HNn5lZc7OAZcCvSInfmmL60Cd/Zmad8rV9zWxgqaYrgJ8Dq4FDgeuA60k9gkcAz4gl\n",
"sbZ3LTQz665O8ib3/JnZQFJN9SFelpFq/WYDDxZPR3Gb15vWmZn1Lyd/Q8z1F3k4jvlkjuVcoN6r\n",
"N0qq+VtVelyfZyh5u8zHsczDcczHNX9mZo0tZCzJG2V8zV+QLvH2AdV0ag/aZmbWt5z8DTGPuZSH\n",
"45hP5ljOZ3zyN4uxnkBIh4GfCByX8TX7hrfLfBzLPBzHfDzOn5lZY/NYt+evnPyNkPZx3s+ZmZV4\n",
"pzjEXH+Rh+OYT+ZYlvdfjZK/R4H1GBv7b6h4u8zHsczDcczHNX9mZo3NYuxybvXDvmtKz3+FlPyZ\n",
"mVnJ7F43wLrH9Rd5OI75dCGW9V69AFYwdhi47mrgzsyv2Re8XebjWObhOObjmj8zs8bKPX8A5zeY\n",
"51GG9LCvmVmnnPwNMddf5OE45tOFmr9WLlE0lMmft8t8HMs8HMd8XPNnZtZcK4ndUCZ/ZmadcvI3\n",
"xFx/kYfjmE/mWIrJe/6qNYBDw9tlPo5lHo5jPq75MzObGvf8mZmVOPkbYq6/yMNxzKeL4/xN+LIZ\n",
"X7NveLvMx7HMw3HMxzV/ZmaNzegTPszMOjVh8ifp7ZJ+IekBSfdI+rqkJ00w/39LGpX0psr0eZI+\n",
"LGmZpIclfU3SNrnehDXm+os8HMd8ehDLYEiTP2+X+TiWeTiO+fS65u8g4L+ApwOHkkbPv0jSxtUZ\n",
"Jf0tsB9wB+v+Gv8g8HzgeOBZwCLgG5Lc82hmnWpl/9FKz6CZ2Ywy4c4zIo6KiE9FxG8j4tfACcDm\n",
"wDPK80nagZTgvYg0qGr5uQ2BVwJvjojvR8TVxXqeAhye7Z3YOlx/kYfjmE+PYjmUPzK9XebjWObh\n",
"OObTbzV/i4pl/lyfIGk28DngXyPihgbL7APMAS6sT4iI24DrqCSRZmZtaKXmb2gP+5qZdard5O9D\n",
"pGtl/qw0rQbcExH/3WSZxcDaiLi3Mv1uYMs2X9/a4PqLPBzHfLowzt+M5e0yH8cyD8cxn27Hcnar\n",
"M0o6i9RTd0BERDHtYODlwF7V2afSKEnnAkuLh/cDv6wHot4V6sd+7Md+zA1syEPsyL7F/uIKdgR4\n",
"7PGv2ZJgLYVet9eP/diP/XiqjwsHQ7G/64AiJq+HlvQB4DjgkIi4sTR9CXA640fRHyke3xER20s6\n",
"FLgI2DxKvX+SfgOcHxG1ymtFRMzoX/S5SDr4sS9J65jjmE/OWKqm/YH3A9+fYLbHAWtjSZyY4zX7\n",
"ibfLfBzLPBzHfNqJZSd506SHfSV9CHghcGg58Sv8P2APYM/ithfpbN+zgMOKea4knQRyZGmd2wK7\n",
"Ape201gzszaNwsw+PGxmVjXhYV9JZwMvBY4FHpC0uHjqoYh4JCKWAcsqyzwK3BURvwOIiAckfRx4\n",
"r6R7gPtIyeE1pB5B6xL/AsvDccwncyxbHeR5KHm7zMexzMNxzKfbsZys5u8U0s61eljlDODMNl7n\n",
"9aQxAr8ALCAlfS+NVo45m5k11uoJa0M51IuZWacmG+dvVkSMFH/Lt6aJX0TsFBFnVaatjojXRsRm\n",
"EbFeRDwvIm7P9SassUpxqHXIcczHsczHsczHsczDccyn27H0L2IzG1Qe58/MrANO/oaY6y/ycBzz\n",
"cSzzcSzzcSzzcBzz6XYsnfyZ2aBqpUcv8H7OzGwc7xSHmOsv8nAc88kcyxm9//J2mY9jmYfjmI9r\n",
"/szMOueaPzOzCid/Q8z1F3k4jvn0aJy/oUz+vF3m41jm4Tjm45o/M7OpGcrkz8ysU07+hpjrL/Jw\n",
"HPPJHMtWkrrRyWcZTN4u83Es83Ac83HNn5lZYzP6sK+ZWafUb1dYkxQR4Z21mTWkml4AnFo8DOBH\n",
"E8y+LbBhLIkXdL1hZmY90Ene5J4/Mxs0WwBzmfza5HX+MWlmVuLkb4i5/iIPxzGfTLG8HVgPmNfC\n",
"vKMMafLn7TIfxzIPxzEf1/yZ9THVNEc1bdjrdswURawXAwtJPX8jvW2RmdngcfI3xDzmUh4RcbFq\n",
"erlqatSD9Dbg69PdpkGVYZv8OvAiYCkp8ZvTwjJD2fPnz3c+jmUejmM+3Y5lqzUzZjNWkfS9CrgC\n",
"+E3l6cfhz1HXqaaLgeeRkr1ZwGpS3Be0snj3WmZmNnjc8zfEXH+Rydk8m5Rk/GuTOfw5atEUtslZ\n",
"wDbA/aQEMIrbo5MsN7SXd/PnOx/HMg/HMR/X/Jn12l4cBGwAbFX0QJWtZUiTiz4zAryJVO8nUlJ3\n",
"MXDJJMuN4p5ZM7NxnPwNMddfZPJMHiElEOsDI6rpyFL9n5O/Nkxhm5wH7EM60UOkpG4Z8MAkyz0I\n",
"bK2aNujwdfuWP9/5OJZ5OI75+Nq+Zr23IXAtaWy5BcA7Sb1OkJKQWappn940bfgVifZsYFExaQ7w\n",
"cIuLryD1Eu7QhaaZmQ0kJ39DzPUXmVzLbqQk4uek8eXmA3NU0w6kEw/mAu9XTW/pXSMHQ4fbZP0y\n",
"bp8GPk9KBB9qY/mHgZ1U06aqaVfV1MoZwn3Pn+98HEvI0TvuOObjmj+zHlJN+zCXHUgnFtxESvZG\n",
"SEngE4HdScnffOA5vWrnkKtew3cO7SV/axgbkudzwMvyNc1s8KmmLYFv9LodNn2c/A0x119ksQNP\n",
"JICVxeOvAteQatBGSIeBFwCbAjf3pIUDpMNtcjbjk7/LgD+3sfxCUr3mBqRD+Bt10Ia+4893Po4l\n",
"BwLzVdM/TGUljmM+rvkz661NSScW3FmadiPps/NWUgJ4JylBGZ321s0M1bN1f9fm8vNIPbMXkcZp\n",
"3C1Ho8yGyHakH0jH9rohNj2c/A0x119MjWraBngp1zW8huwcUuI3m3RY8ZvAXsUyQ0s1XaSafqKa\n",
"Xt7R8m1sk6qpPrTOh5l6Yj2bdObvfcBTmlytZaD4853PTI5lUQP7dFL5yuyp1MTO5Djm5po/s97Z\n",
"DFhANBxI+GekHqV6r9SfSIeGPzuMw4qUbEI6jPpK1dQoKc7pUNIX0i6MP+zbrqsZuzLLfaT/2e5T\n",
"a5rZ0NiT1Bs+h/R5u6C3zbHp4ORviLn+Ysq2BzZgd37a4LkVpORvPVIPIKQewIXAk6anedNLNW1M\n",
"eq/zi9t27a6jzW1yS1J8qzV/7boVuKq4v5J0eOuZU1hfX/DnO5/piqVqumCqdXVdMB+4F7ieNJzS\n",
"5p2uyNtkPq75M+udbUgnFqxs8NwjFIdJgCuLaQ+QkpVdpqV10+9ZpN6Bu0kJ1Hpdfr3U85p3P7UK\n",
"+AMpSTebblsAL1BN+/e6ISUjpB9Xj5A+F3NU00m9bZJ126Q7VUkHSvq6pNskjUrja30kLZL0/yTd\n",
"Kmm5pOslvb4yzzxJH5a0TNLDkr4mDXdtVD9w/cWUzQUe5Ap2bPDcSlLi90XSr2aA20i/ok+YltZN\n",
"o+JQ9mmk9/xj0mHuRRMu1Gg97W2TG5GSzdw/Uh9lCM749ec7n2mM5WzSfuXAaXq9VtSvlX0taTSD\n",
"9elwOCRvk/n0Q83fesCvgNcxNlp+2QeBvwReCuwK/BvwbkkvrczzfOB4Uu/BIuAbktzzaP1sHs1P\n",
"NKgnf+VewbuBLwCbF4dIh8lXSL1w9c//WtpI/lTTKarp4jYvhLeIlGjOZvLLuLVjFWnIl7appheq\n",
"pp+ppi+opmNU079lbJcNvxHSD49Het2QknryB2n8zMtJl7F0XewQmzT5iohvR8RpEfFlGn8R7gd8\n",
"OiJ+FBG3RMR5pHG49geQtCHwSuDNEfH9iLia1DPyFODwXG/E1uX6iymbD6xhX5Y2eG6UlOhVPxOr\n",
"SL/sP5z7hAjV9HzVtCDnOttQP/z6peLxKC0OmaKatgNeAsxlyWOHyOvP7a+aDmmwzAGkw+crSV9O\n",
"Oc/OXUUHvZaFvyPVRD0ReDFwcKY2tc2f73ymI5aq6fGkfcMcUkdKvygnf5Bql9cDdmp3Rd4m8xmE\n",
"mr9vA8+VtC2ApGcAewHfKZ7fh7RxXVhfICJuA64DnpHh9c26ZQGph6uZRrWAkHqqnkjxAyijNwB/\n",
"mx41DNoAACAASURBVHmdrVpASsDqZz6vAbZqcdmnkU7eWMC6h1tPB2oNlnkn6YtyBWn/kXMMxeXA\n",
"nqqpk96/8gko2zJ2so/ZZLYnlYjcBIRqep5q+uR0N6K4LGVZ9YSq20k/fJ/cYF4bEjmSv7cCvwVu\n",
"kbSadMH7f4qIbxXPLwbWRsS9leXuJn0hWJe4/mLKFgBrmtT8TWQE2Jg0hELu9jw+8zpbJcYnOveR\n",
"rpjRig1In/d5fIkjKs/V6/qq6ldOeRi4gzSwdi53kJLJts5qVE2zSAnpnaQvx43p4Ulz/nznM02x\n",
"XEDa7oL0eXoD0/x5Ln7wfLoyzmX187ca+CXph+Z57SSA3ibz6Yeav8n8B/BU4Bhgb9IG/X5Jf5lh\n",
"3Wa9tIh0iLATq4HjVNPzczRENR1J+vI4UjWdnmOd7TaB1NtXt5zUw9+KDUi1RMtYf52evyCdXVg9\n",
"rDtCqrlcA/yQsZNqcllFKmxvxzmkL8p7SPFYiEdMsNaVfzyVB4kfRzXtq5p+1KU2HEr64TJXNV1c\n",
"vM7JjP9sQ+rQWUja57Taw28DZJ0Nrx2S1iOdCPLXEfHNYvKvJe0FvBn4LnAXMCJp00rv32JSMXej\n",
"9Z4Lj9VZ3Q/8sn78u54N+/HkjyPi4n5qzyA95gwuB/bgVywjXd4tqfcC1usAGz++hH3ZENiaX3Oy\n",
"pPsytGcX4M/cyGIe5TDgzGmLh4AlAHyx9H7vBEb1HH2MG7k4bozPNF3+OezFvjwKrGUOCyUdzBn8\n",
"DjiXG9kCMYddeDJwben1Avhsi/Hu5PEaYIM24v9k4Cn8jo14gD+zL58H5nAjx2lTHR33piMd/nz7\n",
"8QSP53A9GxKsZTeeDKzHjaynOTqU09gdeAHXsoLgUZ7CfNW0J2ewcc72cCnPYjM25Ql8B5jHjWxM\n",
"sJoncitQ/bzM53cs5Hc8lSVc1tL6i2l9Eu+BfjzR57twMLR9VOoximh97FRJDwGnRsSni8frk87C\n",
"e24p+UPSfwOPi4jDlU74uAc4MSI+Vzy/LfBH4KiI+F7lNSIiBv7SSzbYVNMewP8CX6OzerPdgScA\n",
"t8SSeO4U2zIH+Bzpl/gTgC/FknjbVNbZ5uuPAL8Avl6aPJt0lv8q4KexJN46wfKfIrV9E9JwEueR\n",
"hro4nlRD9xApmf0zqUfkSuAnwP/lfi8lxwN3xZI4uJWZVdOPST2Rm5K2i7pjgJfFkvhNwwXNCqrp\n",
"eOBVpDri64EjST3HF5JOnJxHqnEdJZVDfD2WxDsyt+FrwE6knvtNSDW8q4BbSId6yzYk9RS+JZbE\n",
"hVjf6iRvamWcv/Uk7aXUmzcL2KF4vF1EPAx8nzS0y0GSdpJ0Iuls3q8CRMQDwMeB90o6TNJfkHb+\n",
"15AutD70VNPGqmnLqVwzsaPXdf3FVGxO6nUe7aDmD9JnZT6whWp6wRTbchDpahr3k744pnuYiIWs\n",
"e2LD2mLaXNLAtRN5HCmxW8ON/BXwDtIXywbFOpaTvvjOIpWRbM66h6Fyq9fvtTP/LNKP1rKHab32\n",
"MSt/vvOZpliWz6qdTzqi8DPSYOZzSTWkm5B+YMwhHXJtm2qaU/2uUU1vVE0vIQ1cL9LnbTVjn+H7\n",
"GqzqAVK5RcvfW94m8+l2LFupV9mPdGmkq0gbbK24Xz9D7yXAz0m/hn8D/BNwWkScXVrH60nJ4BeA\n",
"S0gXWD8m2ul2HFCq6QhS79EFwId63Bxr3UZMLQEZIfWOzQemmvytZGxnfR3tJS05HNPgNetF67OY\n",
"4IxX1TSX9CV2J/AAYiEpka2f6DFC6unYm5RErV+8XreTv0tor55zhPRer6xMX0v7tYM2M5U/J1uT\n",
"PkMrSWeNrwWuIO0vbiF9Njqtc/0g8OnKtONI39X1IZvqwzZ9u2hXs6FngjaSPxsck9b8FceamyaJ\n",
"EbGMNPbVROtYDby2uA2VYgyzsyc4tLcFxSVzgCdPW8PwmEtTtDH1YV4aj/M3mUcYuw7uLZ02QjXt\n",
"C7yXlPytKtp0sGo6GTgklsQLO113G06icaI0SkoAHzfBstuRDi0F8Ft24UbgWNJJYrNJ72cx6fDS\n",
"3cV8uzDxEDs5PER7CWb9C7M6vM9aetTz5893Pt2OZTHo+3qM9fwtIu0f7iX9EApS50m5fODZqumI\n",
"VksTSp5A6fKFRS9gfTiX+0nbcf3SjGuKdjQ7mjBK2ve0ZJi2ySJuXwL+LpbEssnmz63bsfSZalO3\n",
"DbBJg7MVy9YnfYDmqKbcw39YZkVv1Uvo/ExfgN8DnyXVuE3lc7YtKbmoDzEySkoojwe2zT2QdBPz\n",
"aHw5tLmk9zauDarp+NIVTrZnfBzXkL5o5pMOK42QeiM2IL23VaSziDu6Akcb1tJCj4ZqOlI1PYOx\n",
"w8TV+s9RpvlHnQ2kC0hHAEaLWz3xW0P6cdToEO+GdNbLX7/6UN3bGPsMzy+eq39frS0eTzTo9JRO\n",
"DB1ExbWXP0c603nrHjenK5z85TGb5heKf5T0Ab+RlAS+c7oa5fqLju3J2IkIdFjzB+l/v5qp9QzN\n",
"IiUp9QTqT4x9KSyE9kfh78BcSoO0l6wgfYnMVk2blqafCvyjatqetPN89LFnUizXK24XAt8CvkmK\n",
"0R3FOtdnrGeiW1YBGxbXLJ7I6cB7SO+z0Rfxanr05eDPdz7TEMs5jPXejxaP65+Lb5LKEMoepbga\n",
"iGraUDVd3MZrPVwsd1TRKbE/6fO0CWP7ovoh6JXAj2Cdy7bWrQV2bvWFh2ibPIF0BGIOPSrr6Iea\n",
"P5vYAtIHqVnyN4/UY3NNcX/z4uxJ6zOqScXOch7p//pQhtWuAvaYwmXZRopb/cvhHlLCMZu0Y+r0\n",
"MmUtKeIRpEOyVX9irFfgmNL0ecBhpBO7NmXdQ7iXkX4MLScVvf+ZVKO0tFjf+lAMPdE9q0jxe3aj\n",
"J0s9+fWe1vVJ77fqAaa/BtMGSDFI8mzSj7ZbGev5vq2YZZR1S0N+T/rMrSEN5zFPNf11C6/1ZlKy\n",
"Nh84jXRG/v3ApcW0X5Fq9peWFquexFT2MPkHqx8Es0mJ8nx6VNbRbU7+pq5+JmSznop5/H/23jtc\n",
"sqrK+/+s27f79u1M7qYJLUpQRJCgZBpEFJQxDpjj6yiDYxqdGWNTo77ovP5Q39HR8TWBY8aECiio\n",
"GAgiCIiSQyOxaYFuoHP33b8/1j59zq1buXbdqlv1/TxPPVXn1Am7Vp2zz9prr+A3dzbNNJdJKmvX\n",
"T/4Xk8TH8KCc2fj/thpo1ecv4954vMUt7p9FmN4XlwM+hZTVCP2PNtrWCJlyWc0Hbxqey7M4Ojby\n",
"YJBTKE77uizvwZ3bK7EK/22dSnJbZDqe4HYcVrLTgd/GBLhzYntGqGz93EwTPlEp0f2djg7L8in4\n",
"cyKz/D2GX1O13EpWA7/ElY9P44rjP9dyL7KSHY/7084ln+Z9Mt7/rAfOBv6MGyOubLDtK2jCCt9H\n",
"1+QocCmurP9brMs8qcjnr/eZiT9Ejqnyfab8gd98K1B0YK/yNPIpkntxy1S7bMGj27dvcf/M8lZk\n",
"M3nUXqetTodXOH9GVvJtCy674vrsu1Gq10CuxF34fTIZDFNZcVtC7h81Gre7lMpy2BS3E6Ias/AB\n",
"0p241W8F3r/Uuy/G4r7F63C/ShvG4IQz8WfRdDwDx9+Al+B+w5sq7dcAa+m8C0ZNrGTPsJJNZl7T\n",
"/YB9cZmNUbkm+ZRHyl/7ZCVwquU6m8l4J/FAFUuBlWx3K9lTUjWsj/wvJou7cGXqiRQtXa37/GUM\n",
"03q6l2ouAhfH72Z02I1gEdWV4CH8tz0EbG8lW2IleyfRDxB/CM2kWJe3fVmmJIvgLedBfIA2iv+G\n",
"YapbaTbTpWlf3d/p6LAsZ+L9/u/i+yZ8MNEI9+HPi5vxZ81pVUpGLo7nyVIn3RJfWf3pdpS/eY3W\n",
"9+2QHP8Oj3xuqhZ3GxyIK3vT8GnyOXQh3Y18/noUK9kucbSV3VzVHsBFyx/UUP7w2qGfT9ZI0Syb\n",
"8f/yibTeWVbiHqpbz+pR7R5dST4t1HDh9RZYQnXl7zrcf+9xXFF6N/AKxit/a+l8zr5W+RmVfRln\n",
"4j5Xd+O/8eYq24Esf6I+s2itShD4QGQYtxjOwlMivb/CgO8YfBAyAw+iAlccH8L7kFbvwex5dXad\n",
"jBZJiUEumcUxSwL/wUk6fZbj9e547gep7tM/ZRm4EO4UWMmGgO/hvhj7k4fuV2IO4xWJQHVLwTa0\n",
"3klMoI/8LyaLYfx/3IXiw749nz+ofX3Uo9YA7R7cN6jVYJKaxHQtJ+GlqCqxFrcuzMentefH1wZc\n",
"AZxJeafZvixTkqW5KGcE98u6roFjbKRD8q+H7u90dFiWO+PXSStswq/RP+NBIRuAY/GZpvsL221L\n",
"nnqp+Ly5CziY9gazM+PrBbi/cVUSyvEL+LT16XhfPAt/Pk4G84DbyRXmLXRB+ev0/S3lrw5xGvaz\n",
"wMlhWXg8rt4Bvxh2wR962eisEtsx3rdjGK/v+LXCOQ4G3hO/G7KS7YVf/M8Ly8Jkl/Ka8sRR8S9x\n",
"RfsteNmwt4Zl4Y46u07HO88daSMxcwXGaN3KbtQeEIzROZ+cT+LX+W11tttI/uCZjqdrGYmvSmWj\n",
"eoUxPE3NImA4LAtZhPHuNG4pWQfMtJJZWNb/FYtES+xC65kDNuH3USALQPNrcz7jlb89cAv1MOMt\n",
"9Q8wPq1MK3wfHwTWK+OYkl3xVExLgNfjMtjNSjYtLAudTgD/HMYr64E+tO5r2rc+O+E3WjHX0Xa4\n",
"Jec5+KjucarLcjYTR30jZWb75+P52jbiF9rn8Bv2I9HK2BID7BP0L+SJkT+Mjxif3MB+WTm2aRQV\n",
"9vb91AKtD7QasRhWqy7TLk+kMX+29fh1bnj5uZ8A5wFfj59zesvnbzN+bXwL+HpM9bMfsDeNK61Z\n",
"FP/HG/WLSsUA39/J6bAsF+JBX61wF34fFTE8grjIQfj1XJ4vcE18teN68RiuRNY9Rgo5xqpZ2SzM\n",
"e/F7NEuntku7x2+A8tx+m+mC8iefv+5j+MWwa2HdE/AbYhG5paPaQ3qU8crfVfiDsmjC3p28kPfD\n",
"uLI5HTfXdzSPW59yEnmE1t64AlNTiYpTnNuT+5fUynjfLO1Y/urttwI4IXWljzg4Mepb/cCV20vx\n",
"tm7BrQzr8U6zl61hWX3iaXhn/zT8v59Bc5Hea4CleG5DMcWwkh3KSMtuGfWO/SVyA0GrlFu6tuCz\n",
"T9k55uP9XbVawD9o49wZG5i8qc+n4333SlzJHQF+iw/oX2UlW2Ql27eD5x/G8yJmZBG/fYWUv/oM\n",
"x1cxT9tTGO/XVMuna5TxJvc1uOK4I4CVbCYeVm74w/Jx/CbLIoxaHnEMsE/QKD5t+wD+IG8kWuvD\n",
"+H+SRfzm/1n7fmqB1n3+6jlZ3xWPfVqLx6/GyTRXl3g5ufJXnd7z+TP8epmFP1Azp/lmpsk24LKa\n",
"1HQQA3x/JyMGMZzFe+veZ+X7NXo/743fnynSRmVkAVYZr8Cv2TsTnqOcLTTgXpLompyPDx6ze/Ma\n",
"/Letw8tavhX4XBuJ86sSr4cxxivrtYI0O4by/HWfLB1E0fJ3LD4qyeqablX+rGSft5J9Mn7+IpVT\n",
"ZWzCpwLAp9amk/t2rYrHzPIH9p2vQSeJnfIQHoX6G9zqOo3CtKuV7N1WsnLH5YB3OneRPqy/HeVv\n",
"iNrWs8xS2YnckTPw67wRAt7WqVQHcx15UMoQLsN5uDLXzMN6ZTzGpE77iiRkOfSOqrWRlezNVrLz\n",
"4+f9gF83GP06jYnpvtplM+MVsXtorw55I2xi8vL9HYbLa4TclQR8MD8Lz3U4k9YT59ci8/suTnFv\n",
"oUuJ3DuJlL/6ZA/tZ1nJToyfp+M3nJH7BmWyfCqQZQPfC79Yy4M2NpJfuJk/SOYs/1c8GOQR/OHb\n",
"8uhmQH2CsoSmmcL0fXzUWPS5ez7ut1nkITyqdSXlSYbT+Py1eq/VUxq3kA8UUrIWl1kzFrD612pv\n",
"+fyNkd9nj+APt4VULuNWixvxgcbhVrLnJm1hDQb0/k7NAmCYP7Jnne32wXNZvgIfsM/EB4v1yNwn\n",
"UrKJ8YO96XQ+sGojnu/vXVay51TbKNE1OR9PU7MYvzczxfn3eOWfHXBlrBNl1+YxcfYi0IVpX/n8\n",
"dZ8h8hxLr4zrZuFm6cwqU5z2LU59XQMVp7nGgOdbyY7C/cyyXGFFp+ALyS0TogFieaMdmOiYHICT\n",
"Cn5xM/Co6v2sZFkgzyLa88upRTs+f4dR39fmPrxiQErWMXHQUo8LqVwCrZfJfBUfxh8mi2gtLcdq\n",
"XJGYlNKNIhkLgCGm1X2474YrXG/BB5jT8TQkVSnUxf5egnYW2QTsXQgwypJId5KNuGX7peTPweTE\n",
"Mmp74n1PJV/t9figdKthxEq22Er20Zh3t12WMLGv3gg8rWD8SYKV7IREbW4JKX/1Mbxjnw6siSb/\n",
"rFZiJr+iZccKn6fjFoVKLAY+Sj7SuCK+MjbhD+CWnWwH0CfoDLxjKp9imYlbY7PSSCO4zD8LfDGu\n",
"W0g15S+Nz99eVrJWFIM9Ge9yUIm1pL+Xs8SyzbCSehGBveXzB36PnY23ewfc77OVYJ/VuMVwUbqm\n",
"1WYA7++2qVAlYm9giP3rBtYtIvfFPgrvQ15SberXSnYo8G38vmw1x181NuP91cetZNvhOf46rfyt\n",
"xl06hqkx/ZvgmnwHrtRtwGVd3q+tIZ+aXRTTon0az7yRojrWE5jYh63Dlf9StsJKNhKNB+0ECn2A\n",
"6mVh5fPXAwzjisKV+IP48+RRjHfjuZWKlr+i8lce7FFkNO6TWaNuZ6LfRidzuPUVcQQ1CziEicpf\n",
"Vh9zl9hZD+HT9sUorvmkdcouMoaPVF/VzE4xGGgET/Baj9TRitPo7Ujd1DyGW3QW0Fwt4iJ/ohCF\n",
"KXqLaOU/t2z1O2nMvWYGcANuHR7Bc+xlfqKVWIoraKkVP8gTP4/gbi2n0vlneZYuZojOzkbNJS8Z\n",
"OQyU52bNKgZtwJNOfwOX82zSDLzmMjEtz+P4/1xU9F+Ou2cd28pJotI4nc77alZFSZ6rYCW7hDzl\n",
"g+F/0mz84shyKf0qvu8DTLOSnYDLNLtIRqmsUGzGH65DcZtqEZJtKX9mtnSArAMfxJW8jUwcuWUP\n",
"9nfgitQwPsKD/B6YSbUb8SqWtGmxypS/bZvcbzd81Hl1ne2M9H5Fw3RC+Wtflp1iPZ5iIuBKXCtk\n",
"fcSkMGD3d8vEvhz8HhyOA8AfAP+B3/ePc3N1y5+V7DC8v/4LPlOzHbkF6gAr2b/E9WeEZSF7Jiym\n",
"eZ/ZRtmEPzvmkSti1WaYUrGFXEGuGtHfzjUZ/5e9cbk9QrnvtRPw3KFPwH3qZ5NX6mnEB7MeBzNR\n",
"kc6qKD0c2zkbn/6fS4N5B+N09peA08KycAP5lHbVQXun7++BtPzFZK4ftJLVchidjt/kWV3GdXHd\n",
"vbiPVZHMp+sV+Agh+0OrWf6y3GJZGpJqHURfZhbvEHvh1tMsUXOR3+AjyCxCLFPQZ+K+fy+ls6Ow\n",
"1eSKaV2y6xOfZmnk4dFOQEk1XklnHKp7lU34/Tqd1hPybqAP84H1ATPwe31b/P99G24tOhlX4n5H\n",
"bcv5k+MxstRA8+L2K+PnHfF+fP/CPgfSfmWNamzG+7BsRmM2na+fnSl806iXzql1jsR/SyOzGJnv\n",
"XyaHaXjKtHaZx0T/6Y3Ad4A50cBzBP7f3kbjeXiPwX/bTnE5s3Ae0W6DW2UglT98avB51PalmoWn\n",
"/cgyjWfaf6UH+FrcGfbJuIk4xJJRI1W2z445HPerdjMFcj+1phkwq8A8PFJ6HhP9JAMefDOKJ9fO\n",
"5D2C3wPvwP+LyukY2rdUPQb8gjpVRqxke1nJXoj7r5yAX5+NPjwavpetZMfEkoK12JM0I+nx9KbV\n",
"D/zhmQ3GWi3FleX7mxQG7P5ul3l4P7AZd7+Yi1/fM4B17F3TzzNz69mMDyRvw+s+Z5H2M8j7n8zS\n",
"mE0Pd+J6WBWPu10898005hrSDltwGUynxoxhK9dk9J87Engh/pxtJGhsfWzLWlwGD1Ej1ZKV7MgG\n",
"E+HPprIRIKti9H58enkd/myfX/gNtXwOd8WfS9nAMqtAVbXNmSytZLtH386kDKrydzIu/IrBFAUn\n",
"3t/H7TI/nmp+UA/iI8mZwB/xm/Jsqlt7DL+BpuOBCNWUvx3x0ZCoz2y8I7iOiSWOwG/eTfh/swH/\n",
"LzNLzxw6n8dpRQPbfBh3Av4Qfu3sRmP5wapGE0crohWXgY8Bn4wdllXZfrjaMfuYdn/zZtyS3LUI\n",
"PlGRNbg157fkrjvr8QfyKP4gtxr/W5ancwved1yPD/LHyJ8Ny4G5MePADPz+nY0/G1KzgVwBuym2\n",
"J2UewUpks1BZBZyUvBEPfjwM/58eaGCfDeTGlWHch3vnGgrefwCNROtmwZyVWBvbNhe/pjYAO0b/\n",
"vdfi8QDVWEw+4wdZlHlj/c05eJ31pAxa556xFL9gPlzl+ywpZ3G0A9UT7maJhA3vFEbwKYY5VB5F\n",
"3EPuQ1GeULJIVm2gJQYlD1hUVjLl7y9U73Bn4HVwH8Nl/+e43wi1lL80uem24H6htaY0NpNPKc3A\n",
"O6tGffmqHfdjuFN0RuYnNAe3RpanbfgV8KZ43majfevTW3n+imQR040o6bVoqBJCCgbl/k7AKHAt\n",
"7q7zMK6o/Qp/IG8GtnAr83GrTjUqDfy3xa2ImWXw5fGVPT/OwxWzTjAN91u8rkPHr3bOa6lhzWzx\n",
"msxmwUZovM9ZH9txO3kA30Iq+wmCP8O3b+C4tZS/7L98Ja70b8CnbUvkVVaqsQN+TWRK+7MpKz5Q\n",
"TkGWQ3RgFmbglD8r2Yvxqb/pVJ+vL2Zkz6wgULtMT6YkPop3NvOoPk38VzwNwHXUVv7WACOyJNTl\n",
"Rfh/Vs8X5XbcmroeH5nfjXcW0/Cpk05TKzoQ/Nq6mTyVwQjV63UWqeXz9xQ8yjlTSPYjdxafhQ+E\n",
"iszAOyYDzm/g3P3CGvxauKjN42xB9bh7hhjhO49cqbgYT6m1luKAyRgB9ijb97g4hTuC9x3lbIzH\n",
"Xkk+BbgKv68uwqcwOxUxfzZp6483wjRccd7GSrZbigNayU7FB+SZRbHR3zSGy+Cm+P4Q8EsmJu/P\n",
"KBpxKrVjsZXsHPw5Uk3524AHeMyK7c3S0WwXl6fXqPoyN26f9dMnUlD+rGSfqJEKLHsWJGXglD9c\n",
"U78X+Bkws9xMHC0zLyVX/raQy+m75KVmytlc2O4n+M1fz3chM1lXU1oujO8t1QwdIJ+gJ9BYGbLl\n",
"eAd9D57yIbMQFiO0J5LOT20MOLrSFzH/2D64VXIm+Ui40eNOuJdjDqzMr+mjsQD83+PX6h14Z1ge\n",
"oDCMOyXXr9PbCr3r85eKLUxSoMwA3d/tsJjK1qSsfNgqAJ7EjXgqlyIvwe+duVSeVr0EuAyPxh/D\n",
"76f7aa4s4lTiu3j/tJYqpdVauCZfifdBmRtWO0F3a4Fty/3jrGQvIWbWsJK9sIqC9hy8cssQ1afQ\n",
"N+L/cVZ27m7cGjgvrsuCT8YR/f+3wZXKbMCR+f1nCukzKQv+KMjS8GCTJ5GQQVT+FuA35gpc+M8o\n",
"+/55wGvITbgX4Ioi1M4D91u8WgC49W8l9cPvN+IXS7Vpys3xtWOd4ww62+Cj7HqsxkeK9zH+v/w1\n",
"7qvZaVYAh1jJplnJdgIfbERn57fgHcgmfICRdSS3NHjsStMHS/GR6lzgUOAAvJNZQO43VKx5PEI+\n",
"Gq01KBHVkeWvtxihuiUnCxQAVwKXlH2fWXiKQWJFNuA+YJvw9EDTcEWz0Xt2qpH1metJF9W+DT7Y\n",
"vAv3sW810h78eToCvM1KtjOAlWwb4O24AjUbz+tYqQTja6idlxf8GpiF9+MX4VbdlXj/GuK+lQw1\n",
"z4/n34i7/pxMHj2+2Ep2bFzelD0XyjBcBzilRtuaZhCVvxnk06xr8dxeAETB/xv+Z2YX92oa8wNa\n",
"SYz2aoKHcB+UWkrlGB6d3DQD5BO0HY0n5v0TE0d2d1FrxJnOT20Fbu5/LT6KBvev+yQeCZwl/r4e\n",
"9625nsYUsGrTvjPwgcUwrpDMIU+cmhWDL/rvPA/vILNRaWfy/PU3k6b8DdD93Q4jVL+Ov0GmqP2J\n",
"UeBpZd9nVrxtqR91v57xDv39TDE5/jhauCZX4P3NZbSvNAdcOZsHfDOuO5dcic8C+95nJSu3XP4N\n",
"7/vK07gVyVLsXENu2FlHnt5ta/RvGQfg/XDWTz8n7rM5nvOs2OYXA/+d7VSQ5QbcQnhIDNJ7X4VK\n",
"NU0zUMqfleypeAqLTPl7FI/QuiQuH8/4h2SneQT3QanFCuDN8vurjJXsPXhOrXZGjJPFcvzaehO5\n",
"0vUyfLSY+bxk1931NO7MXU35G8EHF9/AByevjOt+j1ssfgXsVqgROhu3gBSr1IjmyKwDojeopfxt\n",
"Lnx6BJ8WvMJKdomV7Ao8N9sIrhQ2kkdvjMHIy1pV+WuGaJXbFbiq7RblXIXPeMyKFZKyXIgj5Ol3\n",
"ZlMoqxangRfh/e/fahw7U/6KxppM+cvSCFVS/opR38O4QWkY9z2dE/d5PJ5/cYVp6bXA5Xje1+Nw\n",
"t7Sn1mhnQ/RkB99mvbxaPJHx01mb8HxqM6Jy9QzcH/BGemcE90dc62+2OsSg+AQdjN9cjUz7tnqG\n",
"5QmPNoYre5lzcDbFuiOtDziqKX9/V/h8P+7Q/jj5g2w13nllUxUz8XvC4vbpGQyfv1pBPckYkPu7\n",
"KWK91Q/Hz08H/pFG0qAcyG34/7Y9/hCeTx4okt0X9cgq+QwCr4++bONo8pp8IvlMQypuwF21RvCU\n",
"blkJ1d/hs3zT4jmLaV8OxP/7y/EZkWpk2T+KQZzZVPMQHtH70gr7zY7bBbxvPQp/ri/HB+bnxO1G\n",
"4+tZ4LK0ks3Ap8Wz6eW34Apt237FdZU/MzvazM4zs3vMbMzMXlv4btjMPm5m15nZ42Z2n5l93cx2\n",
"LTvGiJn9p5mtjNv9yGyC2bXIL9v4TbXYjCtSxVFcZnF5Cn4R3IebdX/SoTa0wgbcN0JM5GZ8JQZg\n",
"ggAAIABJREFUyiV9WpLOMYPcSjAD7xC2xS19rUQdDwHHVBgxDpN3Erfh11C5VaoYLJL5vGQJbUXz\n",
"dMTyF5WaQaq40iqvAE6OydIPobq/XiWuwO+TYXwm4S94OqRbmFhjthIjeK66Tufc6zYBHzD+S6sH\n",
"sJI9A1fG1pM+Hc5GvG89He/bpuH92nz8+f8n/HmfsXfc7tY6x11P5QwIs8jz9pbHEEA+eAi4X+kC\n",
"8n4+s0pvh/fVq4GnxPt9Np4EOit3t4U8sXfblUEasfzNxoX1dtxKEMq+ezrwkfj+AtyMe6HZOOvd\n",
"p/D57JfhWu884CdmVu38nUy4O5PcSrRdbMuC2LastMsYjaXYmCw204Ly148+QTFAYoeCojNC7dFa\n",
"+6T1U/sd/pDZglsZpuODnXvwTrAVP7s9cDkcWLZ+Jnknsxm4kol1grMEtuAK6Dq8X2i1ykVt+t/n\n",
"b4xOVEaB/8Ir0WylH+/vdrCSvQBPU7QFr/W9M3kQVW38urwdvz/m4PfOTbil/BYaK82YVfroVHqX\n",
"XmE+rqgcVv5FE9fkJ3B94RE6oyyvwZWmUVypy+r/3obP7A0VniGLcaNPI/9bpSjuNXgfej+VjRAz\n",
"8Gtwe+BUKv/m3+DR4w/j8v0Mv+cTeCaLzKXJcEXzb1RPadMwdZW/EMIFIYQPhBC+V97gEMLqEMIJ\n",
"IYTvhhBuDSH8AXgz7ry+D4CZzQfeALw7hPCLEMI1wKtxP4rj2/0BTTILD8rIbuR7yHPxHUvtnHvd\n",
"pJovwSDyJtwqm0Vs7Udn6md2ivvxzmgz7vg7jF+Tl9P6Q+NOfHBQPurcwvhgpdupHJSU9QO74j5/\n",
"svy1zjrcfyg1I7SY8mmAeAXex1+IPyifh/fvzSTu3oQbAO5q4fwPx/d+t/yNEhPFW8n2r7dxOVHp\n",
"GsX7m07N2NyAt/EWvG9dhfe1WVqeGcCB0cXsRbSXmP0KfHYuGyyUk802zo6fK/nvL8f75k1kz4Vp\n",
"zMCrPWXBHT+Ov2kdCYLKOuHzlykpWTTMQfiP3ZrzLoRwD659V0tqmCx5pZXsiVayXeMFdzrjO+Yb\n",
"8ASRl5GX+upFWlL++sEnyEr2RStZsb7xYvzCz7K1Z+H2naMzfmrb4NUBUihZV+MKYLmfqlFfoQzk\n",
"PjeLcKt45/xd+9/n7zHc4pSaaZQpf/1wfydmDbmlbwTv079GIzMD46/LS2kt9dPD9O4zJCXr8H5r\n",
"FXCWlext2RcNXpNZGcW5dG7gvg5XtrLp+jXkvnVZG96Bz0jOp/FsEZV4AK+28jhlFrkYVTwf/50b\n",
"Y5sW1jjWarKg04O3+kRmlr8s6tdIEFiUVPkzsxnA/wecF0LIQqYXAltCCOXTqCtwR8ZKJHn4xOL1\n",
"ZwPfwufI51BZw3+U6hp5LxDItf+BIYazPw2vf5yxM+NL9WQ1N6caQ+RpCVKwBR8xlp+jnhUikE+B\n",
"bEseddbINJeYyGqq92vt0IgiP+iMkSttjVz7qbkXv6c7YfntJX4GfB/vK2bilrNmmIP/N9/G/So7\n",
"wT24Bbia+8ow7n+3CDdUXVplu2Z4FJhXlpljH1xGm3GZzcUH6tW4C88ZnCXn38L4jCCr8Snqtl3j\n",
"kil/ZjYM/A/+MHt9Wwf7Fnub2Rnx9Y6iH4GZLW1ieRtuZTG3sD1wJjCL67h2nN/RVSzharbFBf1n\n",
"rmLJhO+7vXwD84lKazO/P/vchvy6vXwwt7Ijv+HgrelI/sKe3MwmYImVbHduYgeuLYykOiH/H3Fo\n",
"B44/DMzhz9ye6HhzgG3L5GdczW4197+J+ZzPQbE9M7ianbieW8nKWaWW5484tOv3UyeXr2Y7bmFR\n",
"5k+U5H4YsqV4X72pz+7v1MujXM+c+H9MB7Y0/P9l69r7/x/lNnbgpkL0arevx84s70pWh/wWduTG\n",
"3KDSyPOas3l23H9Dh9u7usb3twP38Hv25kaGyQZW7Z0vcDOz+FIhy8KlnMitzMIH05u5it9yFXfX\n",
"Od5s4OfcwnbczAyuKswkXMWfuQbjZnazISuZ2VfN7Ku0gIXQ+GDSzB4DTg8hnFO2fhhPqrgvsDSE\n",
"8GDhu+NwzXWHovXPzP4CfCeEUCo7VuAMrgXOCMvCj1r4TfmxvKzLO/HpkoAreN+ssvmJuON9O+Vl\n",
"OsWBwB/CsvDhZnYys6VTeWrISvZG4L3AD4FDwrJwjJXsInyENYanR5mNV+joTIAC+A2ZfrryMDzn\n",
"5NdJY7ncFQ+6emZYFjZF5eMaXHa1WIoXJr8Gv087G+XeGVn2GicDR4dlIYk/UyxX9Svg0rAsnLZ1\n",
"/RS/v1NjJfs+Hqh3Lx5YeBuNpixKd11O1ZmIVtgZz5f317AsPBsauyZjvt3/pv062u2wO64P/Am/\n",
"VlLlGnw28KawLNwAYCX7HB60cUWTxxniVl7FnjxM5T75RcBpYVm4DFxvCiFYcydoEzObjptvnwoc\n",
"W1T8IleT59PL9tkFN4deVuWwM/HAkdbb5WHSh+MJEq/BzaTX1tjlAnpT8YMW80f1wYPhePy3H4HX\n",
"YX46PqX2AG6uH8Wnwzrb2XZGWbkc90FJ1fa78dF0lg5kiMamCbNo3/lMRpBH/yt+4NflJ61kZzez\n",
"k5XMrGS/sZJ9Ny5fYCX7Ij5dlFVd2Uof3N/JiFNti8jdFX5LM7kq012Xg6L4gU8/zqDgo9/gNTmX\n",
"7stpA244yNJupWJrhR8r2SfwdEO1qoZUY4w9t+YQrMRMfDazZeomVzSz2biFAvyBsruZHYCPsO7D\n",
"y1QdjI92zcyyKbhVIYT1IYTVZvYl4D/M7EHcKfYsPKdZteoWgfp1cevxXDxZ4rV4JM0RTF0/pqxo\n",
"+MBgJTsXH539GU9lEvA6tX+Lr6wKyxiKTM3wqRi/x5oZ2A3j92S3O+R+4X5gL5q/Z+fhSvhotNxu\n",
"gyuSI/FYvZJ4vhd5KnmeNDF5XE7zsy6z6X5E9HrcP7MTyt/seP9mJTtbNSpltaKrfdeW318jD4hD\n",
"cCfaP+LaZil+LuEP47/DR1xX48pg9ioWIX4HHg3zbTzP2aPAyaH6nPOVtP+HLMKDSpbH5R+T+TFN\n",
"PbIcRU3RaM4lK9nuVrI9mj1+p7CSDeGBQgvwmzSLcHoTfl0E8ofhVXRaqS/6ZPQ2AU9YCrli3Mg+\n",
"O+Dy7nxZsqkjy3bI+rVm79kT8Wt6GJ8+yqx9I7hz/bj+utH7e0DIShm21hcMxnXZCdYC+1vJlgDY\n",
"0+yNsWxbLWbT/eCljfjg6kjSK38fAr6MR/4O0+o1eQ1XU8iSUsYFwEiFxP4N00iev0tCCEPxNa3w\n",
"+Q0hhLsqrM9e5xSOsTGE8LYQwvYhhNkhhBeEEO6tcdrNtF8mZxHjw7fbtSR2k0zZyaazkxGP93ng\n",
"CymP2yZPwBWR6Xgal6wKxpPIR/bT8VFRpbx1g8wT4nszlr/t8A55UsqSDQC7EQcsTZaqPJ1c0TsF\n",
"V/yMvOZoT5bj7BFeg/sAi8llBd53nG0lM/blbcC/19lnJt1X/tbjluIdSGtRz0rA7UVeuq415W8L\n",
"66luNXwI15Nazv3Zq53JFsrSJVjJ/j6m/miUefSuD1+zFH3+zo+lcerSoP/F+bisemlK6VV4my7B\n",
"FbwhxmdrB+90aoXMp2Pq+KmtJvf5yyPYahNwhSPLvdVZpo4s2+FGfPp2Gl7JoFFGcCXvDvJ0GL/A\n",
"/6OHkc9fLfajnet3MK7LTrAJH6g/AuzJPmxiYqWhcqbTfeVvDFfKppG23xsjz8OXHbu1HIL1r8kx\n",
"2hiw96ry9zAw30q2yEo220o2CrwbnwqpipVs1Eo2N05hzmHq+viVswk4yEqW1SH+aIqDRmV6JL5m\n",
"W8k6VVO5WUbxKKzl+H/4Nfx3X0p+I/2CzuWImqpswpOqQ3MBH6N4RyV/qTRcgz8QK5Xcq0icvjE8\n",
"48Am3Mo9Df9/ziUvISUqI5/I7nE1np9uAd6XjNaZjkztZ9cqWSBVSl/nLXjfm1XzODvx8YvMAZrK\n",
"AFKkV5W/zGL3DeD95Fm46/kSfAbPNfg1PJq4X5S/2/GHyTn4A2VOI3P9tXyCrGSvxP0SRuOxt6H9\n",
"qfZUzGZi5vfv46kbJp+p4w+0nDx7/OtovHb3Utzi1Nk0LzCVZNku36S5qkFPxR9Em+JrDp7epYh8\n",
"/ipgJZuD94vNlHEbz+Bcl51gI55m6t3cvFWp+9caLkq9YPnLSJ2aZxN+H9+AD9pap/41OQ14qpWs\n",
"2STbQO8qf+Btm4dH6WbTki+3kp1RaeOYC+vJuP/STFyR6ZdpX/AHyS74w3pWXG6H0/Eo2lFc1vfR\n",
"pRq50bp7bEGh3YGJEbzJSv71MauBBbHTfTGNKR474dfTZnpjNN4vbMIzDUyLFvt6PIu8v1qJB9UV\n",
"LbFjVLBsWcmmW8mObMfxeyoTfSp/gsu7mnO86CxZKbVFhK2K1IvwZ/c4rGRz8RynvaJ7/JK0M0ij\n",
"5KlsOq1/XIFf9y9rZede+QMqkc2bj+IRxWvx0d3RVbZfiI+W5+APvdl0MvHv5HMT/vtvwW+27Wpv\n",
"Xt0nKHaYmX/RLbiP0p9or75hO/wdnmokq+H7RHppCnLq+AONxdeh+L3TiEJwJXkqkc4zdWSZghvw\n",
"fuiYBrZ9Mbnz9hh+XxYZo6y/jvf3McAn8SCTQeRNeF/4s7aOMljXZWoewq/dEfbhUXyQMopbAykb\n",
"mJyBz8r1SnDOPaQd9N6K96f160nXo/41uRwfYLaUpaGXlb9p+ANpCL+5b8CteY9X2X6PuH32ILsc\n",
"Vxj7hT+T+yfMxae3W+V1+AXzKzxVynW46b5da2KrbI//pi9byb6K/+flycJFYzyM1+idkBS4Cjfh\n",
"8lauxPRswXP+1az1aiV7OX7vraxzrEpuGR/GFcxdW2zjVOc1uOyUo7J7rMeVkFHySloj+EwVwK+t\n",
"ZFmRh2FcUexXS/VDuJ/fZBkvHgcWt7Jjryt/Ab9Y7sWFmqVBIAaBFNkNjzi6EPcNu2vSWjo5rMdl\n",
"MT2+ZlvJ9q21QyWfICvZe/AO8+ayr9bgU4bdGJHNi+3ZBk8o3iv+IM7U8gfajI+qswjpRvgeHlnd\n",
"eaaWLFMwRv1krPvgg59f19jmMWCRlSwL6MHm23PxB+0KXOHva7I+30pWnEpfjT8b2mPwrsvUXA+M\n",
"cAMzcEU8AE+3ki3Gr+13W8n2x2ebRugvl6zO0Ng1uYYWB+69rPytw+e0sxHxo/hFsyUmkbzISlZM\n",
"B5NVNliNRx/1G1lU5jzgp7hyfEgLx3kufgOW+zmM4Tfka9toY9PEDv043PJ4Pm6R7CeL7WSzGf+P\n",
"DU8EKrpLZgmpxd/w/q1WJ565vZy+dc0itsfvm4XAP7fVyknCSravlezgFvZbgvf5o3gS3a/Hr6bh\n",
"rgui+/yMddyG1+z9Ef6semf8bg/gs7gV/Drkn5mSlnz1m64aMYn8KL4Xc7n9Ar+gdsCVhHOtZNcC\n",
"++Md7AOT2sLJ53f4KPdR3KdgfyuZhWWVK6WU+/wVSkb9nsoXzCbgZCvZp8KyMFnBH/vgkdzZCH6o\n",
"Stu6x9TyB3oUt54O0YuJzaeWLFNQ0/JnJdsVd3uoNeWbMZM8iTe8nOW4wng73if2LFFpG8MrQ20H\n",
"HFv2vQHzwrJQbbpsD/z3b4/7Bu8cfZe3AVa13cDBuy47wUMcNM4KuwV4Jt4n/RmPaN8Tf6b3SyaO\n",
"ztH4Nfm3Vg7fy5a/SjyGdwLLyKNqDsV9XrbHi9v3M3fiNxL4VM9SPDiiUd6ATxlXu/F2wDvYyRwU\n",
"jOD/ZXYBK1dXezyE/4cDVQu6h9lCFYfsqLx8H4/0bWTAM43xzukLcOXvr7T4AJhE/gf4NN5Pz6zw\n",
"/SnkA37A85AWfMUW4QP8I3BL5xCwMy4P+fv1JlnfPoIPUAz3TW1/ml4UaWTgOIGppvytxi1/++AX\n",
"02zyslSPM1gX1T34b36hley3sT7vwVayX1vJPgAVff6OoHZQx2q8g21Z+bOSzbeSXWolO77BXbKo\n",
"4/vicqOVKSaPqeUPtJbJV+AbZ2rJMgWbqX7PvQzvu2bSmPJ3HhDifX4uV3Mq/kDdAsxLXfqxEaxk\n",
"F8U+p16w2M54WqEhKj93FjPxmn0t8MH4OctDehpuOZwGvJRUFqTBuy47w3g5rsWv7zVxeTr+3JK/\n",
"XyN0+JqcasofuPVvBh4g8ACuPMwAftvNRnWJgFsN5uPm9GfiD5ITixtZyV4ZnW3X4/4W1biAQl1l\n",
"K9k2VrIfxIopjbINbpF9V4PbjzDemjEd5Ztrh3V4ctGv19tQTAprqB7t+yJ8ynIONDTFsx4P7DgC\n",
"2IU5HIT3gVmJrf/TbmNbYBY+IN+9znYzcAtlAIYrKItDTLT6ryH3l9yWPIp0Gi6zUyrsI3qHC4Ef\n",
"4u5K4IOgfp+dmzL0pnWgNlfjuf7W4j6Ai/C0IINo+t+Id4Kj+HRKlupmDMb5/P0TnjdsR2pnwQ9x\n",
"3+y6eD6wBM/N9JoG2zQL75Dr5iGMHFq2/DN6zVdt6vkD9e7IeurJsl1W464q44hWuj1x5/iF5NaR\n",
"WqzDlaQjgG3Zm+n4DMgQPuh7WqI218VK9m/AM/DZh23xsoI3Rd+9U3GF9MKwLKyJ64bwvmQ63l89\n",
"hfGBeZWi0/cCRmJi4EPx3z+HXOGbS6oEvYN3XXaG8XLczPggpovJZ3hEPTp8TU5Fy9862BpODp5H\n",
"axAVP/AbaS7eae6CK25zgSErWdHnaxr+oFlEfd+gQO4v9jzcqtiMfEfwqagZ9aoOxNH/CxmvkD5I\n",
"rwV8CNE6j+P3UDlL8AHs4zRXtvAxPK3Vo3hqmE24sp/5ViXFSjZiJft4ha+eiSut2+D9yz/E9Qfg\n",
"ddjfB/xrXLd93OZJ5NkbtloKYz8xgldDKSqAs/C+6D/xPv/i+H4Rnv5rFp6gXkwNpPj1EFNR+XsE\n",
"T3UiXJEbxk3pu+Ad8c24H+TZBZ+/zM9mmPpVT7JpmecC++L5m5rJI/Qp8uosLy1+YSXbz0pWzGWW\n",
"Oazf1MTxJx/5A6Vj8GS5AbdelQ+Enk1riW7/it83v+SqcesvJsEgOCp7bym0dxFwRIUSdfPx6d4Z\n",
"jLfa7YIPQOfjA8B98KCWzbiSm5USfKeV7BVxn1OBl8RjFPMVZgPbPfG+bT2ej/J+3M1nXIBIWwze\n",
"ddkZJMd0dFiWU3HaFwYrsKMW6/AR9Vr8gTAb9yH6C3ACz+IEK9kDeAdtNOYfkyXW3hb3J1pFWZ6y\n",
"+CD4LPDOsCyUK5OZT86deIddZDf8QTgNz0X3XqbuNShEI4wRLeHE6Xgr2afwacxWLCG3xlc5K0hz\n",
"L70Qd/G4Fs+zuh1ufdvXSnYNbsV7GO9vMkUus/RPw11L/ooramvIrX2PANfE15PwoL1/tJLtArwA\n",
"DwR4Au7H95nYlvnx3HPxweQ68hrfm+mlEpBCTDGmouVP5GzGFa0NeGe6P94hrgHu5SiW4klhN+Ed\n",
"cCP/t+Gd/2LyNAo7WsmeUdjmCbh/0biyMlayWfE8P4377Vl27P3i9y8D/gXv1LtVT7hx5A+UjsGU\n",
"5Wb8Ws84GFeibmjrqONlOYa7e7QbALEJ96ubF5dfht+zn8UT9v4Y72c2Ad/F/a6/hQ/6tseVxU2x\n",
"Pc/Glck5jM/FtzFuPxefHdiGrELE+NmC+fggsvMVIQbzukyP5JgO+fyJGmRWusfxDnY+uU/fcny0\n",
"fAI+ih+hsf/7LuBkvOpGwB9c2wJnFbbZDbdkHB6rrWQ8D1fmVuMj9PJ6o/vG/d5KrowOqr+mGBy2\n",
"4Pdncflm0tZTzoK12q3PfTx+j2bK6sFxeTZulZsT123E7/EVuLL3GN5PLMYVtYV4n3Mwbr0rDvIe\n",
"wPuZLGnzLXGfG4H5VrKvWMkuiftfgfcTD7f5u4QQBaT8TX2+hUf8Tcc740yZWsVt7IRbF/5KHhVY\n",
"jxtxZ+r5+MPpUXyKpzj1uwP+kDkd+DfYWqngXeRTT6uZ6NO0I7kVclv8YdX7TsDyY0nHYMpyM648\n",
"ZcENc3CFpz0mynILBeXPSnaclezwRg8XB3IH4/1IFqQyPy5PB/6AK2GvYOIU8ybc6vdUfObhJtx6\n",
"+Ag+OC0GdW0ErsIHqhfjg1Pw6N9hPBJ4FO9zNgPfptO1pwfzukyP5JgO+fyJOmRJTr85Yf0qLiLP\n",
"H/YIjTuY34lP7d6Jd9znAs+zku0UloUV+Ih8GO/cj7eSvR2P8puHj+jBO+2t15eV7P24M/jN+PTv\n",
"/zTYFiGmOmPklr9FuJLWCX+1MeBpVrIr8X7hI/FcRzW4/2txhWsFMCdmDDDgclwZewj3Jz6OiVbL\n",
"acAxuB/gvbjCeDTef/yaylxUYd0weULnNeSzD0KIhEj562fG+wzcQOM+Rg/h1QQyP5tNeFDJQvzB\n",
"MAOP3FuHK3J/jz8cRsk76i3kyaIPxX1//ohbINPk5pos5MeSjsGU5VbLH57+JE2/O1GWW4AP4/fu\n",
"DbgiFqxkcysEZo0j5tJ7DT44m4Vb/DJL/YOFTVfgieLLFbIH8Hq9I+QD0nNovlrPDFwxfoDmSle2\n",
"x2Bel+mRHNPRYVlK+RPVKHew3gwcjnf8T8dH+n/C/Xa2wa1+F5BHYo/hKWMOxtM4BNySCPLzE4OF\n",
"4dOpv8STIc+pvXnLBNxF46W41Ww0vm9rJfsx8JywLFQLnFiAK3o34gO6w4C9qZwhoNIg8lbcVziQ\n",
"39+tlGk8D1ced0HPJyE6hnz++pm0PgOrcYdv8Gi/RbiCl6WYWBlfWWm2zeQJWg/HLYVTs2yb/FjS\n",
"MZiyXIJXy4E8L177TJTlL4Dv4IrcTDx9SojnHsaj9icoc9Ev8MxCu+7Arfz7kpfmqsdGXHlsN9o4\n",
"Cxa7Ffham8dqnMG8LtMjOaZDtX1Fj3AdsJ2V7Hm45SLz7csija8t234TbhHcBrdAKCeXGFTuBWZa\n",
"yRbh06IP1tm+Xc7Dp5ln4QFbL8CVv2/g08LlnEJecQTcWjgXt1g2U2rxevIpXyFEDyOzej+T1mcg\n",
"C+B4f/x8ZVy/konBJpAXZX8QtyKsqrDN1EB+LOkYTFlejgdJfAIfBP0yyVGry/JR3Oo+E/ed2xFX\n",
"5jbgkbTlDOMDuDsK636PV9JohjvJXTumFoN5XaZHckyH8vyJHmIGnuZler0NyWsEr8KTPnc2SasQ\n",
"vUuWKuVJTJ5l7H586nQIV/zuwYM45gBYyU60kr0rbpvl8ivW/b4NH8AJIfoQKX/9THqfgZ/hubgu\n",
"b3D76bgSOLWnfOXHko7BlGXALXBpk5rXluUleGDGMD7VfHlsQxaQ9SHgpVayo3CFMEutMpgM5nWZ\n",
"HskxHVPB58/MFpnZ2Wb2oJmtM7O/mNnRZducYWb3mtlaM/uVmVWafhC9zUo8ees9DW7/IJ5gWohB\n",
"5yo8GKKVCNh2GCZ377kW2DOmdRnGfQIPwoO2vstUH6QJIRqmbeXPzBYAl+Kd2kl4jdm3UnBqNrN/\n",
"xas/vBU4JH53kZl1KuWBgF7wv/gZuaVh6tJ9OfYPgyvLTeRWuDQ0JsurgZ/HzytxBfRM8qjco3Af\n",
"wcF2yxjc6zItkmM6pkCev38B7g0hvK6wLosExcwMeAdwZgjhB3Hda3EF8BXAFxK0QQghep3M2jaZ\n",
"bGR8abUH8Tx+s/CB2W7ANZPcJiFEl0kx7ftC4Eoz+7aZrTCza8zs9ML3TwB2Ih99EkJYD/wGz/8m\n",
"OoX8L9IgOaZjsGU5RPt58HJal+Uc3H1jFI8Ibjaqt/8Y7OsyHZJjOqaAz98ewD/i0WEnAJ8GPlZQ\n",
"ABfG9xVl+z1Y+E4IIfqdIbofZJfl3bwWn4LOgrKEEANEimnfIeDKEML74/J1ZrYncDrw2Tr7Vu50\n",
"vsQLmRvzwo2wnsU8sHX+O9OGtVx/+WCW91R7pvJyRq+0Z6ouZ+t6pT2TuzzELczl0US/v5X7+wbW\n",
"M4SxDwBruI2dWTWw/4eWdX/37nKt+xvgDpbwGAsYbs2VxEJob9BnZsuBn4cQ/qGw7tXA50IIc8xs\n",
"D9wqeEgI4erCNj8FHgwhvL7seIEzKLXVKCGE6D1eDTwG/LDbDYkcCTwROLvbDRFCtMwunMEbQwjW\n",
"zE4ppiAuhTiOzNkLto4E7sTzS52QfWlmM/GO57IE5xfVKLdaidaQHNMx2LIcIuUUa/uyvBQv+SYG\n",
"+7pMh+SYjg7LMsW07yeBy8zsfXhR8acD/wS8FyCEEMzsU8D7zOwmPOv8B/ARsDoeIcSgcAF5/dxe\n",
"IOApaIQQA0bb074AZnYS8L+BvfE0L58JIXymbJtlwJtxh+MrgNNDCDdUOJamfYUQQggh6tPStG8K\n",
"yx8hhPOB8+tsUwIpdUIIIYQQ3aTbaQdEJ5H/RRokx3RIlumQLNMhWaZBckxHh2Up5U8IIYQQYoBI\n",
"4vOXEvn8CSGEEEI0RNdSvQghhBBCiCmClL9+Rv4XaZAc0yFZpkOyTIdkmQbJMR3y+RNCCCGEEKmQ\n",
"z58QQgghxNREPn9CCCGEEKI2Uv76GflfpEFyTIdkmQ7JMh2SZRokx3TI508IIYQQQqRCPn9CCCGE\n",
"EFMT+fwJIYQQQojaSPnrZ+R/kQbJMR2SZToky3RIlmmQHNMhnz8hhBBCCJEK+fwJIYQQQkxN5PMn\n",
"hBBCCCFqI+Wvn5H/RRokx3RIlumQLNMhWaZBckyHfP6EEEIIIUQq5PMnhBBCCDE1kc+fEEIIIYSo\n",
"jZS/fkb+F2mQHNMhWaZDskyHZJkGyTEd8vkTQgghhBCpkM+fEEIIIcTURD5/QgghhBCiNlL++hn5\n",
"X6RBckyHZJkOyTIdkmUaJMd0yOdPCCGEEEKkQj5/QgghhBBTE/n8CSGEEEKI2kyq8mdm/2hmd5rZ\n",
"OjO7ysyOnMzzDxzyv0iD5JgOyTIdkmU6JMs0SI7p6BefPzM7FfgU8BHgAOAy4AIz23Wy2jBw3MvC\n",
"bjehL5Ac0yFZpkOyTIdkmQbJMR0dluVkWv7eBXwlhPClEMLNIYS3AfcDp01iGwaLDczsdhP6Askx\n",
"HZJlOiTLdEiWaZAc09FhWU6K8mdmM4ADgZ+XffVz4PDJaMNA8hgLut2EvkByTIdkmQ4KYvv4AAAg\n",
"AElEQVTJMh2SZRokx3R0WJbDnTx4ge2BacCKsvUPQkXT5i4db9Eg8Ci7Ilm2j+SYDskyHZJlOiTL\n",
"NEiO6WhclqOtHH5SUr2Y2c7APcDRIYTfFdZ/CHhFCGGfwrreyj0jhBBCCNHDNJvqZbIsf38DtgA7\n",
"la3fCff720qzP0AIIYQQQjTOpPj8hRA2AlcDJ5R99Ww86lcIIYQQQkwCk2X5AzgL+JqZXYkrfG/B\n",
"/f0+P4ltEEIIIYQYaCZN+QshfMfMtgM+ACwCrgdOCiHcPVltEEIIIYQYdHqutq8QQgghhOgcqu0r\n",
"hBBCCDFASPkTQgghhBggpPwJIYQQQgwQUv6EEEIIIQYIKX9CCCGEEAOElD8hhBBCiAFCyp8QQggh\n",
"xAAh5U8IIYQQYoCQ8ieEEEIIMUBI+RNCCCGEGCCk/AkhhBBCDBBS/oQQQgghBggpf0IIIYQQA4SU\n",
"PyEEZnaGmY2VvTaa2T1mdq6ZHVS2/dLCdr9q8BwnlB3/2zW2PcrMfmpmd5vZBjNbaWbXm9n/mNnR\n",
"Ndpc7XVMA+3b08w+Y2Y3mtnjZvaYmd1kZl8ws2c28huFEGIqMNztBgghepIATAN2Bl4MnGRmB4UQ\n",
"bqyybSO8umz5ZDObG0J4rLjSzE4Fvll2/G2B7YB9gRuA38T1xXNbjTbVbKOZvR74HDCjbPs9gb2A\n",
"HYAX1TqGEEJMFWT5E0KUc0YIYRqucP0srpsJvLLVA5rZLOCFZatnAi+tsPkH4/tq4ChgFNgROBz4\n",
"D+B+gBBCKYQwLXsBZxeO8fridyGE39Ro23HAF3HFLwAfBnYFRoC9gfcBDzfze7tBlLEQQtRFyp8Q\n",
"oiIhhNXAeYVV27ZxuBcBs+Pnr5Bb1sqtgeDWNnAl77IQwsYQwkMhhCtCCP8WQvhKlXNYlfX1OLOw\n",
"76dDCMtCCPeFEDaHEG4LIXwM+IdxJzJ7nZldGqeGN5jZbWb2STPbrrDNNXHK+REzm1FYv8DM1sfv\n",
"fl1Y/2Qz+5qZ3Run3B80s++a2X5l5/5qYTr7yDgtvxr4c/z+VDO7KE6Zr43tu8PMPmdmO5Yda7qZ\n",
"fdzMHjCzNWZ2QZz+zo5/Z9n2u8Tj3Bnb+IiZnW9mR7UoeyFEF5DyJ4QoxwDMbD5wclwXgGvaOGam\n",
"5AXgU8CVcfkYM1tctu1f4/s+wI1RqTrVzBa2cf6KRGXokELb/k+l7UIIWwr7/DfwZeAwYBbuPrMH\n",
"8HbgKjPbKW765fg+DzipcLgXk1sZvxSPeSRwNW5dXYhPuW8HvAT4ffy+Ej+Ix5tTWHcs8Cx8yn4k\n",
"tm8J8Gbg12Y2vbDt54D34JbVmcAJQNGHc+t0uZntjV8DbwZ2i22cBzwX+JWZnVKljUKIHkPKnxCi\n",
"nGVmNgY8gj/YAb5FVFSaJSpDx8fFW0MI1wPfy75m4nTyWYXPe+FK1TeBe6OVafdW2lGFJYXPj4YQ\n",
"7q+1sZkdAbwpLi4HDsCVtMwauTvw7/Hz14GN+G98ReEw2efHgO/Gz/8PV76WAwfFzwcBK+Pnz1Zp\n",
"0mrgUHxqPFMwvw48E/dTnIErk1+N3+2dbWdmewFviOsfxpXZ7YHLqpzr0/G3rsIVzNF4vJvwZ8ln\n",
"yhRLIUSPIuVPCFGJ8mCKY8gtZM3ycvK+5ntl7wCvGnfiED4HnAL8HhgrfGW4Mvp9M2t1irddnlf4\n",
"/OkQwvUhhFXAuwrrTwIIITwM/Cjbz8zmROvl0rjuOyGEdWa2J65EgSujfwQ2xPcd4vr9yqdsIx8I\n",
"IVwZp8ZviuseAN4GXAusA1YAryvss1d8P66w7px4nEdwH8dxmNkouQK/ALgEWA/cgltowRXHAyu0\n",
"UQjRY0j5E0KUkwV8jJJbqXYG/qfF4xX9+m4ws31x/7874rqnmtn+xR1CCOeGEA4DFuFTn18nV0YP\n",
"AJ7YYlvKWV74PM/MFtXZfofC52x6OvOPfLTCNtnU70zc7/FUvN/dOuWLT7kWCVVe21XYbtxUfJyq\n",
"/x1uTd0Fn5otV+RH4/v2lX4LcDcT2Zbxz4tqbWzHL1QIMUlI+RNCVCRak74FPBRX7WFm29fapxwz\n",
"ezLw9MKqrwHXA3/C/eQyXlXYZ16hDStDCD8IIbwa+EW2CbBNM+2oRgjhQXL/Q8P93yZgZtPixxWF\n",
"1bsXvl+A+78BPFjY5ufAvfHYL48vgBtDCL+vcMyLyqKUi69KaXbWlS0fS658Xgwsior8Oyrsu7Lw\n",
"eZfC510rbPswkPk93lKjjRdU2FcI0WNI+RNClJMFfIyY2cvJLU6bgccrbL+dmT3HzJ5beD0nKkzF\n",
"Kd1KlqKMok/cH8zsv8zsODPbxsxmmNlhQGYd3IxPN6bi/eTTy28zs2VmtihGwu5pZu/DffIAflrY\n",
"721m9tSo+H2isH7rNiGEQJ6C5tnAM+LnrxS2uY389xxvZm+PEcEzzWx/M/uQmX2rwd+yqfB5A7A2\n",
"Wlr/qcK2vyx8frWZHWhm2wL/u3zDEMI6cuV7rxghvEP8b/Yxs3eZ2S/K9xNC9CghBL300mvAX8AZ\n",
"uAJU6/X/CtsvbWD7Bfi06hhuNdq7wnl/V9j++Lju7jrHPavKb/hqYZvXNPn734grS9XO+f3Ctp+v\n",
"sd0dwI5lx35i2TYbgB3KtjkaWFvjuL+s8jt3KzvOAtySWL7/zYXPHyps/8UK295b+Hx7Ydt9gL/V\n",
"+u3dvo710kuvxl5NW/7M7L1m9gczWx3zUJ0XR5b19tvPzH4d807dY2YfrLePEGLSCIX37DWG+7H9\n",
"AfhnPMVHre3LX/vhKUECcFUI4eYK5z2ncJws6vd04L/xgIUVuDXrUeAK4LTYlnq/oSlCCF8Cngb8\n",
"F64orcWtnDfhCtLHCtu+BXg9cDkesbsRuB1PYXNw8Knk4rFvZ3xFkvNDCCvLtvkNHt17Dq78bsSn\n",
"268D/i/jgzCq/s7gwScn4kr1GlyRW1Zof/k+b8HT2zwYf/OFjE+8nU35Ezyg5AA8PcztuBK7CvhL\n",
"lNFbytsjhOhNLITm+kkzuxBPu/AHfNr43/EUAU8JHilWaZ95+LTGJXH7J+PTHmeEEM6qtI8QQojO\n",
"Ymb7AGMhhFvi8iieaidT9D8WQpgQ/SuEmNo0rfxNOIDZbDzX1AtCCD+tss1peBb9nUIIG+K69wOn\n",
"hRB2qbSPEEKIzmJmb8Uti4/jVrydgCxX343AEdGaKIToI1IEfMyLx6lo9YscBvw2U/wiPwd2Tpyw\n",
"VQghRONcjddvfhxPObMBTx+zDHiGFD8h+pPhBMf4NN5ZXF5jm4WMzyMFeXqDhcBdCdohhBCiCUII\n",
"l+M+gkKIAaIt5c/MzgIOB44MteePG55bNrP25qGFEEIIIQaIEEJTVY9aVv7M7JN4CaZjQwjL62z+\n",
"AG7hK7JT4btxNPsjRGXM7JIQwtJut2OqIzmmQ7JMh2SZDskyDYMkRzMOx2MZtscj9IeAxXhaqxE8\n",
"H+k6vLrPuXhpyFl4uqRFwDeA5wCvDWFi3tJmZNmK0awlnz8z+zRepui4LEqsDpcDR5nZSGHds4F7\n",
"Qwia8u0cy7vdgD5hebcb0Ecs73YD+ojl3W5AH7G82w3oE5Z3uwGTSKY/VTNWGS2knSqwvI1969JK\n",
"nr/P4kXCXwmsNrOF8TW7sM2ZZnZxYbdv4Dmkvmpm+5rZi4F/xVMKCCGEEEL0A7WUwey95ZykqWjF\n",
"8ncaMAcv9XNf4VVMvLqQQt3OEMKjuKVvZ+Aq4D+BT4QQPtlas0WDXNvtBvQJkmM6JMt0SJbpkCzT\n",
"IDk2RlFBrKaHdVSWbef5S42ZBfn8CSGEEKJXMeNI4KPADng2k8znbwyYgfv+rQFGcZ+/58fPD+Np\n",
"lb4JnAC8IQRuaq8tzetNKfL8CSGEEEIMEtbAe29Z1wpI+etjzGxpt9vQD0iO6ZAs0yFZpkOyTIPk\n",
"2BANWeg6LUspf0IIIYQQ7VG08lmFdcX1lfaZVKT89TEhhEu63YZ+QHJMh2SZDskyHZJlGiRHoDHL\n",
"XlHpq6iHdVqWUv6EEEIIITpLuU9g+edJRcpfHyP/izRIjumQLNMhWaZDskzDgMmxnSTPdad75fMn\n",
"hBBCCDE1qGfNK34vnz+RHvlfpEFyTIdkmQ7JMh2SZRoGXI5Ga9O4FfeRz58QQgghxNSmp/L/Sfnr\n",
"YwbM/6JjSI7pkCzTIVmmQ7JMw4DJcQhX4srTulQK7Gga+fwJIYQQQkw9Kln4eqJ8rZS/PmbA/S+S\n",
"ITmmQ7JMh2SZDskyDZJjOuTzJ4QQQggxNagV+FHpu67oYVL++pgB87/oGJJjOiTLdEiW6ZAs0zDg\n",
"cqyl8JV/rzx/QgghhBBTjHqBHc2un1Sk/PUx8r9Ig+SYDskyHZJlOiTLNAy4HMujfZvZZ+IX8vkT\n",
"QgghhOgL5PMnOsuA+18kQ3JMh2SZDskyHZJlGiTHdMjnTwghhBCi92g1j58qfIjOMeD+F8mQHNMh\n",
"WaZDskyHZJmGAZNjpj81GtjRVOUP+fwJIYQQQvQ2SQI9Jgspf32M/C/SIDmmQ7JMh2SZDskyDZIj\n",
"kCjJs3z+hBBCCCF6m65b85pByl8fM2D+Fx1DckyHZJkOyTIdkmUaBkyOzfr81Vs/Dvn8CSGEEEJM\n",
"DRpR+rpuJZTy18fI/yINkmM6JMt0SJbpkCzTIDk2RNHvL1BFWZTPnxBCCCFEf9KVWr9NK39mdrSZ\n",
"nWdm95jZmJm9tsH93mFmN5nZejO7z8zObL65ohkGzP+iY0iO6ZAs0yFZpkOyTMOAy7FRJc5oYNq3\n",
"07IcbmGf2cCfgLOBc2jgR5jZWcDzgHcD1wPzgUUtnFsIIYQQottUC/joT5+/EMIFIYQPhBC+B4zV\n",
"297M9gbeCvxdCOHHIYTlIYTrQggXttBe0QTyv0iD5JgOyTIdkmU6JMs0DLgcG1XoGrIQ9oPP3wuA\n",
"O4CTzOwOM7vTzL5qZjtMwrmFEEIIIbpBuUJYSfGbGj5/LbAHsDtwCvAa4NXAPsCPzawrP3pQGHD/\n",
"i2RIjumQLNMhWaZDskzDAMqxnrWvmrI3JX3+mmUIGAFeHUK4DcDMXg3cDBwM/KF8BzP7KrA8Lq4C\n",
"rs0EkZlCtaxlLWtZy1rWspa7tGzwwwUwOgrPwblgFgzNgOes9+Ufz4PhWXBi/P7CURgbhpMe9+Xz\n",
"5sMPDoKvXNXM+SNLgSW0iIXQut+hmT0GnB5COKfGNiXgvSGEGYV1BmwEXhbcd7C4fQghyCKYADNb\n",
"ml00onUkx3RIlumQLNMhWaZhkORoxonAe3AF7BZgGrAYmFnY7AE8wPW7wItxQ9gGIAA/AJ4FvDME\n",
"rpp4/MZl2YreNBnTvr8Dhs1sj8K6PXBB3TUJ5xdCCCGE6AXKp32nhs+fmc02swPM7IC4/+5xedf4\n",
"/ZlmdnFhl4uBPwJfjts9HfgycEUIYYK2K9IxKCOwTiM5pkOyTIdkmQ7JMg2SY0uKXMV9Oi3LVix/\n",
"h+DK3B9x82Ypfi7F7xfilj0Ags8rPx94EPgNcCHwVzwKWAghhBBiqlPNh65SHsApmefvkhDCUHxN\n",
"K3x+Q/z+9SGEPcr2eSCEcEoIYV4IYacQwqtDCCtT/QhRmTLnUNEikmM6JMt0SJbpkCzTMGByrJXk\n",
"2aqsb5hOy1K1fYUQQgghJoeeqPQh5a+Pkf9FGiTHdEiW6ZAs0yFZpkFynEAjSZ4r6mG96PMnhBBC\n",
"CDHoNBO1a2XvXUXKXx8zYP4XHUNyTIdkmQ7JMh2SZRoGTI7VlLlqPn/NHbzDspyMCh9CCCGEEP1E\n",
"ptz9FrgXOCgu34RnNJkH7Fpl365H+0r562Pkf5EGyTEdkmU6JMt0SJZpGFA53h7fM4Xuivh+H7BL\n",
"qweVz58QQgghxNSj0tRv+bqu6GFS/vqYAfO/6BiSYzoky3RIlumQLNMgOVakJd8/5fkTQgghhOgt\n",
"Gkni3HXfvmpI+etjBtT/IjmSYzoky3RIlumQLNMwgHJsN21LVeVQPn9CCCGEEP2JfP5EWuR/kQbJ\n",
"MR2SZToky3RIlmkYQDl2bFpXPn9CCCGEEL1F+ZRvM4pg130Bpfz1MQPof9ERJMd0SJbpkCzTIVmm\n",
"YcDk2NEybfL5E0IIIYSY2vRETd8MKX99zAD6X3QEyTEdkmU6JMt0SJZpGHA5tqrcVdxPPn9CCCGE\n",
"EL1H1333WkXKXx8zYP4XHUNyTIdkmQ7JMh2SZRoGTI4d1Z/k8yeEEEII0Xv0lB9fM0j562MG3P8i\n",
"GZJjOiTLdEiW6ZAs0zDgcmx1Clg+f0IIIYQQA0RXrIdS/vqYAfO/6BiSYzoky3RIlumQLNMwgHJs\n",
"xNpnVT7XPrB8/oQQQggheopyRa5Rxa4n/ASl/PUxA+5/kQzJMR2SZToky3RIlmkYQDm2q8hVtRzK\n",
"508IIYQQovdpRRnsih4m5a+PGUD/i44gOaZDskyHZJkOyTINAyjHUOVzJZpSDOXzJ4QQQgjRW0xp\n",
"/WlKN17UZgD9LzqC5JgOyTIdkmU6JMs0SI7p6EmfPzM72szOM7N7zGzMzF5bZ/ulZvYjM7vPzNaY\n",
"2XVm9vrWmiyEEEII0VNUmtZtNhXMpNGq5W828Cfg7cA66v/Aw4DrgJcA+wKfA75gZi9v8fyiAQbQ\n",
"/6IjSI7pkCzTIVmmQ7JMg+Q4gZYVu07LcriVnUIIFwAXAJjZVxvY/syyVZ83s2NxZfCbrbRBCCGE\n",
"EKKLtFrSret00+dvPvBwF8/f98j/Ig2SYzoky3RIlumQLNMwYHJsRH9qWTnstCxbsvy1i5k9HzgO\n",
"OLwb5xdCCCGEaJPitG4ril7XLIeTrvyZ2RHA14F/CiFcVWWbrwLL4+Iq4Nps/jvThrVcfzmEcEkv\n",
"tWcqL2f0Snum6nK2rlfaM5WXdX9rudeWs3W90p7O/94fbgMPLoF/WO7LF8yCuwvL5y2A6bPgxCid\n",
"C0chjMGJa3z5Rwvg10+Hs35Zfvxa93dkKbCEFrEQ2lM8zewx4PQQwjkNbHsk8FPggyGE/1tlmxBC\n",
"6Inad0IIIYQQ5ZhxKvC/gEvjqsOB3YBvFTY7Htg+rjsFmA5sAdYAPwaOAT4aAhe315bm9aZJ8/kz\n",
"s6OB84Fl1RQ/kZZyq5VoDckxHZJlOiTLdEiWaRhwObaa6qXywTosy5amfc1sNrBnXBwCdjezA4CH\n",
"Qgh3m9mZwCEhhOPj9ktxi99ngG+a2cK475YQwsp2foAQQgghxCQzpWcoW7X8HQL8Mb5mAqX4uRS/\n",
"XwjsUdj+tXG79wD3A/fF1+9bPL9ogKIfhmgdyTEdkmU6JMt0SJZpkBxrYoX3UGH9ODoty1bz/F1C\n",
"DcUxhPD6Csuq6CGEEEKIQaKehXBKVfgQU4AB979IhuSYDskyHZJlOiTLNAy4HOv59zXl/9dpWUr5\n",
"E0IIIYRojmb1p57yEZTy18fI/yINkmM6JMt0SJbpkCzTIDmmo9OylPInhBBCCNEerVr2uqKHSfnr\n",
"Ywbc/yIZkmM6JMt0SJbpkCzTIDmmQz5/QgghhBC9RU/58DWLlL8+Rv4XaZAc0yFZpkOyTIdkmQbJ\n",
"MR3y+RNCCCGE6G1aKeXWcvm3dpHy18fI/yINkmM6JMt0SJbpkCzTIDm2RMXpY/n8CSGEEEL0HnXL\n",
"tJXRM36CUv76GPlfpEFyTIdkmQ7JMh2SZRoGTI4d1Z/k8yeEEEII0XuUW/J6xrJXj+FuN6ASZryx\n",
"223oDz6+N/zrzd1uxdRHckyHZJkOyTIdkmUaBkqOhyQ4hgHPNmPniV81LMuWgkZ6UvkDTul2A/qD\n",
"vbYB9u92K6Y+kmM6JMt0SJbpkCzTMHByvLvN/e8F9o2vMhqW5WgrJ+5V5e/ybjegP3hRtxvQJ0iO\n",
"6ZAs0yFZpkOyTMNAy7GaBc6qvAPcFl8VaFiWuwBHNbpxhnz+hBBCCCEGCCl/fc0XlnS7Bf2B5JgO\n",
"yTIdkmU6JMs0DLQcEwd7dFaWUv6EEEIIIQYIC6Fr1UUqYmYBQqnb7RBCCCGEaJAjgN2AbxbWPQvY\n",
"CfgG8DI8zmIMeBT4SaLz7gL2xhBCU5ZHWf6EEEIIIQYIKX99zUD7XyREckyHZJkOyTIdkmUaJMd0\n",
"yOdPCCGEEKKX6S0fujrI508IIYQQoj3k8yeEEEIIIXoTKX99jfwv0iA5pkOyTIdkmQ7JMg2SYzrk\n",
"8yeEEEIIMZUpTst23d9OPn9CCCGEEO1Rz+fv5cA03OdvNfDTROedPJ8/M/tHM7vTzNaZ2VVmdmSd\n",
"7U8ysyvM7FEzW2lmPzSzPVs5txBCCCFEj1HPktZTlramlT8zOxX4FPAR4ADgMuACM9u1yvZPAn4I\n",
"XBK3Px6YCZzfWpNF48j/Ig2SYzoky3RIlumQLNMgOdagydq/vefz9y7gKyGEL4UQbg4hvA24Hzit\n",
"yvYHxPO8N4RwRwjhOuDjwBPNbNuWWi2EEEII0TtUU+7K1zepBHaGppQ/M5sBHAj8vOyrnwOHV9nt\n",
"UuBx4E1mNs3M5gKvA64MITzcXHNFc/zD8m63oD+QHNMhWaZDskyHZJkGyTEdnZVls5a/7XGHxRVl\n",
"6x8EFlbaIYRwP3ASPk28HlgF7Auc3OS5hRBCCCFEmwx3+gRmtgfu8/cVPOJlHvDvwHfM7LhQMdz4\n",
"iBfC4lX+ed56eMYDuRaczYNruf5y0WegF9ozVZevXAhfvKJ32jOVl//XobqfUy3r/k63nK3rlfZM\n",
"1eVBv78vHIW/LsmXz5sPM0bhueTfE+C5q+ofr9b9DXDxErh3AYzOogWaSvUSp33XAC8LIXyvsP6z\n",
"wFNCCMdW2OfjwPEhhIMK6xYDdwNHhhAuK9teqV6S8YUl+UUjWkdyTIdkmQ7JMh2SZRoGWo5HUDnV\n",
"y0Lg6+SpXgI+A1on1UvDsux8qpcQwkbgauCEsq+ejUf9VsLwvDZFsmUlme4oA3sTJkZyTIdkmQ7J\n",
"Mh2SZRoGWo7NpHJpYNvOyrIV5ess4HVm9kYze7KZfRrXbD8PYGZnmtnFhe3PAw40sw+a2Z5mdiA+\n",
"BfxXXJEUQgghhBgUmrLSdYKmlb8QwneAdwAfAK7Bo3xPCiHcHTdZCOxR2P53wKnAC4A/AhfggR/P\n",
"DSGsa6v1og5F/wDROpJjOiTLdEiW6ZAs0zDQcmxEoWtC6eusLFsK+AghfA74XJXvXl9h3bnAua2c\n",
"SwghhBCij+h6tQ/V9hVCCCGEaI8jgN3xrCYZ5QEfw3jMwyOkq3I2ebV9/3/27jxOsqq+///7zQwz\n",
"wwAj47Aq4ICKCCj8RlFUREEwbkETE0GEiF83UL6uMZqIbCKiqLjEQDQybBKXr1EjioAL4JIIOBhR\n",
"EQ0wsjMsDjMwCzDz+f1xbtGn79yq7uo+3dVd9Xo+HvfRVafOvXXup6urPn3u594CAABAR1Nrdi1D\n",
"8tfXBrr+oiDiWA6xLIdYlkMsyyCONeM4sWNiY0nyBwAAMD5TdpavCTV/AAAA40PNHwAAwIDLZ9d6\n",
"fm2/HMlfX6P+ogziWA6xLIdYlkMsyyCOozDKJJCaPwAAgOloSs34tVDzBwAAMD5NNX8HSHqcpPMl\n",
"HSZphtKh4PtEzR8AAAAmC8lfX6P+ogziWA6xLIdYlkMsyxjoOBY+jErNHwAAwFQ2JWv72qHmDwAA\n",
"YHyo+QMAAMDURPLX1wa6/qIg4lgOsSyHWJZDLMsgjh10eViYmj8AAAAUQs0fAADA+IxU8/c6pQk3\n",
"av4AAAD6wNSaSRsByV9fo/6iDOJYDrEsh1iWQyzLGOg4Fr7UCzV/AAAAKISaPwAAgPGh5g8AAABT\n",
"85s/SP762kDXXxREHMshluUQy3KIZRnEcRRGmQxS8wcAAIBCqPkDAAAYn3Y1f4+XdJ6Gav4k6R5J\n",
"FxV6Xmr+AAAApqgpU/9H8tfXqL8ogziWQyzLIZblEMsyiGM51PwBAABMdVNmZm8kY0r+bL/N9k22\n",
"V9u+2va+o1zvybZX2l45ludFt96ytNcj6A/EsRxiWQ6xLIdYlkEcy5nYWHad/Nk+RNKnJZ0saS9J\n",
"P5d0ke0dRlhvlqSvSLpc0+w78AAAAPrFWGb+3iNpcUR8KSKuj4h3SLpD0tEjrPcxSb+S9HVNo6nR\n",
"6Y36izKIYznEshxiWQ6xLGOg41h4UmsK1fxVs3eLJF1Se+gSSc/tsN7LJb1c0v8ViR8AAOgv0yq3\n",
"mdll/y0lzZB0V619maRtm1aw/ThJX5D0qohYZU+r+Exz1F+UQRzLIZblEMtyiGUZxLGDLpOfiY1l\n",
"t8nfWJwn6YyIuGr0qzzvVdLjl6fb89ZIz7pzKBCtqVDuc5/73Oc+97nP/aly//ubSDcvHLr/n4+R\n",
"Zs2RXpLu6uI5UsTQ/bE+nyT9YKF02xbSJnM1Bl19w0d12PdBSYdGxDey9s9L2i0i9m9YZ72kdXmT\n",
"0uHmdZKOjoh/q/XnGz6K+cLCoRcNxo44lkMsyyGW5RDLMgY6js+TtFDSl7O2/Bs+DlfKfUKj+oaP\n",
"UcdyTN/w0dXMX0Q8ZPuXkl4s6RvZQwcpncjRZI/a/VdJ+qCkvSXd3s3zAwAAYHzGctj3U5LOs32l\n",
"0mVejlKq9ztTkmx/VNLeEXGgJEXE7/KVbT9L0vp6OybCwP4HVhhxLIdYlkMsyyGWZRDHciY2ll0n\n",
"fxHxNdsLJB0raTtJ10p6WUTcUnXZVtLOI22m2+cFAACY5ro6PDtRxvQNHxFxRkTsFBFzImLviPhp\n",
"9tgbIqJt8hcRZ0fEvLE8L7qVF4di7IhjOcSyHGJZDrEsgzg2GGOyN7Gx5Lt9AQAABkhXZ/tOBs72\n",
"BQAA00y7s323l3Suhs72laS7NeLZvqM2prN9mfkDAAAYICR/fY36izKIYznEshxiWQ6xLIM4lkPN\n",
"HwAAAAqh5g8AAGB8qPkDAADA1ETy19eovyiDOJZDLMshluUQyzKIYznU/AEAAKAQav4AAADGh5o/\n",
"AAAAPGpKfKdvC8lfX6P+ogziWA6xLIdYlkMsyyCO5VDzBwAAMN20q6vreb0dNX8AAADjM1LN3xFK\n",
"E24haZmk7xd6Xmr+AAAAppB6UjYlav9I/voa9RdlEMdyiGU5xLIcYlnGwMexYE+KBZ0AACAASURB\n",
"VGJHzR8AAMB0M7Xq6jLU/AEAAIzP8yTtJOn8rG1/STtKOkdDNX+SdJeo+QMAAMBkIfnrawNff1EI\n",
"cSyHWJZDLMshlmUQx3Ko+QMAAEAh1PwBAACMTzc1f3dKurjQ81LzBwAAgM5I/voa9RdlEMdyiGU5\n",
"xLIcYlkGcSyHmj8AAAAUQs0fAADA+FDzBwAAgKlpTMmf7bfZvsn2attX2953hP5Ps3257VW2b7X9\n",
"obENF92h/qIM4lgOsSyHWJZDLMsgjuVMsZo/24dI+rSkkyXtJennki6yvUOb/vMkXSrpDknPlPRO\n",
"Se+z/Z6xDhqjdeW2vR5BfyCO5RDLcohlOcSyDOJYzsTGciwzf++RtDgivhQR10fEO5QSu6Pb9H+d\n",
"pDmSXh8Rv4uIb0j6WLUdTKgVc3o9gv5AHMshluUQy3KIZRnEsYGzn87uj2BiY9lV8md7lqRFki6p\n",
"PXSJpOe2We05kn4SEWtr/R9n+wndPD+6ddsWvR5BfyCO5RDLcohlOcSyDOJYzsTGcmaX/beUNEPS\n",
"XbX2ZZLaTVFuK+nmWttd2WN/alhn6y7HhUa3bi9iWQBxLIdYlkMsyyGWZQx0HOdXP/P93yJry2f8\n",
"5mnEOI06lo8Z3fCG6+pSL7YfJ+lWSftFxE+z9uMkHRYRuzasc7GkWyLiTVnbjpKWSnpORPyi1n9q\n",
"XXsGAABgCuv2Ui/dzvzdI2mdpG1q7dso1f01uVMbzgpukz02TLc7AAAAgNHrquYvIh6S9EtJL649\n",
"dJDSWb9N/kvS823PrvW/LSKaDvkCAABggozlbN9PSTrS9httP9X2Z5Rm9s6UJNsftf2DrP8FklZJ\n",
"Otv27rb/WtL7q+0AAABgEnV72FcR8TXbCyQdK2k7SddKellE3FJ12VbSzln/FbYPkvR5SVdLuk/S\n",
"JyLi9PEOHgAAAN2Zct/tCwAAgInDd/sCAAAMEJI/AACAAULyBwAAMEBI/gAAAAYIyR8AAMAAIfkD\n",
"AAAYICR/AAAAA4TkDwAAYICQ/AEAAAwQkj8AAIABQvIHAAAwQEj+AAAABgjJHwAAwAAh+QMwsGyf\n",
"YHt9tayzvUft8Ttbj/dqjABQGskfACSWdGKtLWo/AWDaI/kDgCGvsr1ndt89GwkATBCSPwBI1ql5\n",
"9m8Y22+2fbXt+2yvtX2b7Uts/93kDBMAxofkDwCSL1c/D7a9qKmD7b+V9K+SFkl6jKSZkraVdKCk\n",
"V0zGIAFgvEj+ACC5StKF1e2T2vTZr/q5UtJTJM2RtFDS30r6/kQODgBKmdnrAQDAFBGSjleawXup\n",
"7b0b+txY/dxM0ockLZH0O0mXRsSKSRklAIwTM38AUImIayR9W6n27yRteJbvv0j6uqT1ko6QdLqk\n",
"iyXdZfv9kzhUABgzkj8AGO54paTvLyRtmT8QEWsj4hBJ8yU9T9IbJP1C0mxJp9h+3CSPFQC6RvIH\n",
"AJmI+LWkb1Z3Z+SP2X617WMkbS/p15K+Uf1sefykDBIAxoGaPwDY0PGS/kobXufvqWp/MsgdGp4I\n",
"AsCUxMwfgEHW+A0eEfFbpdq+qD32A0kXSPqj0hm/j0i6XdK/S3pBRKyd6AEDwHg5gm8tAgAAGBTM\n",
"/AEAAAwQkj8AAIABQvIHAAAwQKbc2b62KUIEAAAYpYioX5mgoymX/End7wSa2f5VROzV63FMd8Sx\n",
"HGJZDrEsh1iWQRzL6SaWY5k047Bvf/tVrwfQJ4hjOcSyHGJZDrEsgziWM6GxJPnrb0t7PYA+sbTX\n",
"A+gjS3s9gD6ytNcD6CNLez2APrG01wPoI0sncuMkf/1tea8H0CeIYznEshxiWQ6xLIM4ljOhsST5\n",
"629MwZdBHMshluUQy3KIZRnEsZwJjeWU+4YP28EJHwAAACMbS97EzB8AAMAAIfnrY7Zf2Osx9APi\n",
"WA6xLIdYlkMsyyCO5Ux0LEn+AAAABgg1fwAAANMUNX8AAADoiOSvj1F/UQZxLIdYlkMsyyGWZRDH\n",
"cqj5AwAAQDHU/AEAAExT1PwBAACgI5K/Pkb9RRnEsRxiWQ6xLIdYlkEcy6HmDwAAAMVQ8wcAADBN\n",
"UfMHAACAjkj++hj1F2UQx3KIZTnEshxiWQZxLIeaPwAAABRDzR8AAMA0Rc0fAAAAOiL562PUX5RB\n",
"HMshluUQy3KIZRnEsRxq/gAAAFAMNX8AAADTFDV/AAAA6Ijkr49Rf1EGcSyHWJZDLMshlmUQx3Ko\n",
"+QMAAEAx1PwBAABMU9T8AQAAoCOSvz5G/UUZxLEcYlkOsSyHWJZBHMuh5g8AAADFUPMHAAAwTVHz\n",
"BwAAgI5I/voY9RdlEMdyiGU5xLIcYlkGcSyHmj+Mx169HkCfII7lEMtyiGU5xLIM4ljOhMaS5K+/\n",
"bdHrAfQJ4lgOsSyHWJZDLMsgjuVMaCxJ/vrbwl4PoE8s7PUA+sjCXg+gjyzs9QD6yMJeD6BPLOz1\n",
"APrIwoncOMlff2MKvgziWA6xLIdYlkMsyyCO5UxoLKfkpV56PQYAAIDpottLvUy55A8AAAATh8O+\n",
"AAAAA4TkDwAAYICQ/AEAAAwQkj8AAIABQvIHAAAwQEj+AAAABgjJHwAAwAAh+QMAABggJH8AAAAD\n",
"hOQPAABggJD8AQAADBCSPwAAgAFC8gcAADBASP4AAAAGCMkfAADAACH5AwAAGCAkfwAAAAOE5A/A\n",
"pLL9c9vrs2XXDn3n2D7K9g9sL7P9UPXz17bPtH1Qrf/6hmW17d/aPtH2Jl2Mc5HtxbZvqLax3Pa1\n",
"tk+3vdt4YjDK53+C7RNsH2/7BQ2PX9bax4keC4D+MrPXAwAwOGw/UdI+teYjJH2woe9Okr4jKU+0\n",
"QtICSVtK2kPSCyQ9tc3TRfVzVtXnQ5L+wva+EfHICOM8VtJJtW3NkrR7tUjSuztto4CdJB2XPf/l\n",
"tccjWwBg1Jj5AzCZDm9oO6zeYHu2pO9pKPH7b0n7S9pU0lxJe0p6v6Q/tnmeiIgZSv/gPkfSvVX7\n",
"syS9ttMAbR+pocRvjaR3Stpa0hxJT5f0MUmrOm1jArjeEBH7R8SMiOCfeABdIfkDMJleV/1cLekr\n",
"1e0n2N6v1u8Nkp5S3b5D0kERcXlErImItRFxbUScFhEHd3qySK6UdEHWvHe7/rZnSPpI1vSBiPhc\n",
"RNwbEQ9HxG8i4h81NCMn2zNtv9v2EtsP2l6THWaeW9t+61D0j22/zPZV1SHl/7X9vqzf2ZJ+lK16\n",
"fLbu8VWfxsO+tnexfbHtVbbvsH2K7TfX1wcwuPiPEcCksL2PpCdVdy+SdI6kQ6v7h0u6Iuv+l9nt\n",
"f46IB8f59DNG2W+RpO2q2w9I+pemThGxTno0WfxPSS9pPVT9bB1mfrnt/SKiPlP4/ykd0pbSrN7O\n",
"kj5m+/aI+LKaD+VG7We9Xba3Ujo8vE3VNFvSByTd3tQfwGBi5g/AZMkP+f4/ST+UtLy6/ze2Z2WP\n",
"75Tdvq51w/a7Gk7oeHm7J7S9ke1na/ih3l90GGP+vDeMVBuolLy2Er8lkp6olDxeXLUtUjpsXDdP\n",
"0imS5ks6Jms/QpIi4g1Kh7lbTqgO8c6IiLwWse5dGkr8LpS0laRnavTJL4ABQPIHYMLZ3ljSIdXd\n",
"NZIurBKr1uzXFho+25eLNrdb95tmslwdDn1E0n8pJVmSdJWGDjeXkCeeH46IpRGxTKkeseVlDevd\n",
"Kem4iFihNAPasmN2e4M6v1F4UfUzJB0bEfdFxBJJXxrDtgD0KZI/AJPhJUpn6UpphuwJtveQ9Ous\n",
"Tz4zeGN2+9FLwUTEZyJiIw0lTJ0SpFZiuEZp9vAjkvZvHbJtI3/eJ1ZJaydbZc91c9Z+c0Of3A0R\n",
"0Upa80PCc0Z4vpFs2WYMt4xzuwD6CMkfgMmQJ3bPlXStUuJ3Wtb+UtutGboLs/a3264nRSPNikV2\n",
"mHRuROweER9qqL2rW6J0gokkbSbp6KZOVa2fJN2VjecJWZd8Bm9ZwyYezgfabh9GGGuTu7Pb22e3\n",
"dxjDtgD0KZI/ABPK9jwNP6Qbar5G3SwNHRpeLOkP1e3tJX3X9t62N7a9QOnSK8VFxHpJx2ZNp9o+\n",
"xvYC27NsP832xyR9uHr8u1nfD9peaHsbSadm7XmfbtyT3d6tVhPZzg+rn5Z0gu35thdJetMYxwCg\n",
"D5H8AZhof6Ohw5lfzWbkZlTX4ntx1vdwSYqItUr1dK0EcH+lEzXWKs1u1c+urRtLvZyq514s6cRq\n",
"23MkfbZ6zjWS/kfS+/L9UTpzWZKeoXTY+I5sfL+s1h+tfNz/q6EE8DWS1lQnuNQvi5Ov82mlekJJ\n",
"+mul6xteLSk/1M3ZvsCAI/kDMNFa1/YLSec2PP5DSbdVjz/H9kJJiogblM6Wfbekn0q6T+kEjhVK\n",
"h4y/KOlgDZ1Z2zLub72IiBMlPVuptvBGpesS3i/pN5I+Uz13a6bwYEnvlXSNpAeVksTfKV0oer+I\n",
"WN0wvsanzR+rEuBDlBLIBxv2a4NLv0TEPZJeKOnSasx3SvqopM9l690rAAPN7ctNAADTje0DJF1d\n",
"nUks209Wmp3cWdJ6SXtExO97OEQAPcZFngGgv3xc0iLbrZM/8jOSP0HiB4DkDwD6y9eU6gB3Uvou\n",
"5GVKh46/EBHf7uXAAEwNHPYFAAAYIFNu5s822SgAAMAoRURXVziYcsmfJJ1wwgkn9noM/eCTn/zk\n",
"Ue9973vP7PU4pjviWA6xLIdYlkMsyyCO5XQRy+1POOGEN3a7fS710se22GKLO0fuhZEQx3KIZTnE\n",
"shxiWQZxLGeiY0ny18c233zz5b0eQz8gjuUQy3KIZTnEsgziWM5Ex5Lkr4/Nnj17Ta/H0A+IYznE\n",
"shxiWQ6xLIM4ljPRsST562OPf/zjmYIvgDiWQyzLIZblEMsyiGM5Ex3LKXepF9vBCR8AAAAj2v6E\n",
"E054Y7dn+zLzBwAAMEBI/vrY1VdfvbDXY+gHxLEcYlkOsSyHWJZBHMuZ6FiS/AEAAAwQav4AAACm\n",
"J2r+AAAA0BnJXx+j/qIM4lgOsSyHWJZDLMsgjuVQ8wcAAIBiqPkDAACYnqj5AwAAQGckf32M+osy\n",
"iGM5xLIcYlkOsSyDOJZDzR8AAACKoeYPAABgeqLmDwAAAJ2R/PUx6i/KII7lEMtyiGU5xLIM4lgO\n",
"NX8AAAAohpo/AACA6YmaPwAAAHRG8tfHqL8ogziWQyzLIZblEMsyiGM51PwBAACgGGr+AAAApidq\n",
"/gAAANAZyV8fo/6iDOJYDrEsh1iWQyzLII7lUPMHAACAYqj5AwAAmJ6o+QMAAEBnJH99jPqLMohj\n",
"OcSyHGJZDrEsgziWQ80fAAAAiqHmDwAAYHqi5g8AAACdkfz1MeovyiCO5RDLcohlOcSyDOJYDjV/\n",
"GLPbbrtt216PoR8Qx3KIZTnEshxiWQZxLGeiY0ny18fWrl07p9dj6AfEsRxiWQ6xLIdYlkEcy5no\n",
"WJL89bGVK1du0esx9APiWA6xLIdYlkMsyyCO5Ux0LEn++tjy5cuZgi+AOJZDLMshluUQyzKIYzkT\n",
"HcspeamXXo8BAABguuj2Ui9TLvkDAADAxOGwLwAAwAAh+QMAABggJH8AAAADhOQPAABggJD8AQAA\n",
"DBCSPwAAgAFC8gcAADBASP4AAAAGCMkfAADAACH5AwAAGCAkfwAAAAOE5A8AAGCAkPwBAAAMEJI/\n",
"AACAAULyBwAAMEBI/gAAAAYIyR8AAMAAIfkDMGXZ/rnt9dmya4e+c2wfZfsHtpfZfqj6+WvbZ9o+\n",
"qNZ/fcOy2vZvbZ9oe5Muxvl02/9q+/e2H7C9yvZN1VjeY3ur8cQBAEpyRPR6DACwAdtPlPTHWvNH\n",
"I+KDDX13kvQdSbtlza03N1c/r4+Ip2brrG/om/e/UtK+EfHICOP8gKSPZOs1beu1EfHVTtsBgMnC\n",
"zB+AqerwhrbD6g22Z0v6noYSv/+WtL+kTSXNlbSnpPdrw0SyJSJihqSZkp4j6d6q/VmSXttpgLZf\n",
"L+kUpSTvIUn/KGlHSbMkbSfplZIuqB4DgCmB5A/AVPW66udqSV+pbj/B9n61fm+Q9JTq9h2SDoqI\n",
"yyNiTUSsjYhrI+K0iDi405NFcqVSstayd7v+tmcoJX4t/xQRH4uI2yJiXUQsi4jvRMThEfHNbL1D\n",
"bF9q+5bq8PBa2zfaPsP21rXnWFodjr7J9j62f1qtc7vtU23P7LRPANCE5A/AlGN7H0lPqu5eJOmc\n",
"7OH6jOBfZrf/OSIeHOfTzxhlv0VKs3uS9KCkz45yvf0lvUjS4yTNVppxXCjprZIut71xwzpbSfqh\n",
"0szkbEnbSvoHSV8a5XMCwKNI/gBMRXmC9/+UEp/l1f2/sT0re3yn7PZ1rRu239VwQsfL2z2h7Y1s\n",
"P1vDD/X+osMY8+e9Ia8NtL289rxXZX2/LOnZSgndLKVE7uzqsadIelnDc82VdJak+dW6y6r2I2w/\n",
"vcMYAWADJH8AppRq5uuQ6u4aSRdWidV3qrYtNHy2LxdtbrfuN53h5urkj0ck/ZdSgiVJV2nocPNI\n",
"Rnqu/Padkt4h6VdKh7TvknRk9vguDdt/SNL7ImJFRFwt6d+yxw4c5RgBQBLJH4Cp5yWSFlS3lyjV\n",
"+e0h6ddZn3xm8Mbs9qOXgomIz0TERho6ZGy110rW1ijNHn5E0v4Rsa7DOvnz7pzX30XEfEk711ew\n",
"/RhJP1WqZ9xe6RBzPVFsusTMvRGxJrt/S3Z7Qb0zAHRC8gdgqskTu+dKulYp8Tsta3+p7dYM3YVZ\n",
"+9ttz6ltr1PSJ1Vn+1bL3IjYPSI+FBGrRlhvidIJJpK0uVLN3kjPu7/S4V5J+oGk7aozjd81wnMt\n",
"qF13cMfs9j0jrAsAw5D8AZgybM/T8EO6UVtaZmno0PBiSX+obm8v6bu297a9se0FkoadQVtKRKyX\n",
"dGzW9HHbx9jesqpJfHLDavk1A9dKWmV7d0n/d4SnmyXpVNvzbO8t6U2tYUi6dGx7AGBQkfwBmEr+\n",
"RlJr5u6r2YzcjGqG7MVZ38MlKSLWSnq5hhLA/ZVO1Fgr6W6lw8hSc72fNPLMYFsRsVjSidW2N1E6\n",
"43eZ0uHjixtW+Wk1JlVjXqE0sznS1fYfUKoLXK60b63Zw/Mi4jdjHT+AwUTyB2AqaV3bLySd2/D4\n",
"DyXdVj3+HNsLJSkiblC69Mq7lRKs+5Rm2VYoHTL+oqSDtWFC1u4kkFGLiBOVzsA9R6kOcLVS4nmr\n",
"pEskfUDSq6u+yyW9tBrjg9W+HC/p1Gw8Te6R9EJJV2joJJGPS3rjeMYOYDDx9W4AMEXZXqpU37c0\n",
"IjY4gQQAxoKZPwCY+sZ8aBoA6kj+AGDqajrZBQDGhcO+AAAAA2TKfSm4bbJRAACAUYqIrkpDplzy\n",
"J3W/E2hm+7KIeGGvxzHdEcdyiGU5xLIcYlkGcSynm1iOZdKMmr/+trTXA+gTS3s9gD6ytNcD6CNL\n",
"ez2APrK01wPoE0t7PYA+snQiN07yBwAAMEBI/vrbr3o9gD5BHMshluUQy3KIZRnEsZwJjeWUO9vX\n",
"dlDzBwAAMLKx5E3M/AEAAAwQkr8+ZvuFvR5DPyCO5RDLcohlOcSyDOJYzkTHkuQPAABggFDzBwAA\n",
"ME1R8wcAAICOSP76GPUXZRDHcohlOcSyHGJZBnEsh5o/AAAAFEPNHwAAwDRFzR8AAAA6IvnrY9Rf\n",
"lEEcyyGW5RDLcohlGcSxHGr+AAAAUAw1fwAAANMUNX8AAADoiOSvj1F/UQZxLIdYlkMsyyGWZRDH\n",
"cqj5AwAAQDHU/AEAAExT1PwBAACgI5K/Pkb9RRnEsRxiWQ6xLIdYlkEcy6HmDwAAAMVQ8wcAADBN\n",
"UfMHAACAjkj++hj1F2UQx3KIZTnEshxiWQZxLIeaPwAAABRDzR8AAMA0Rc0fAAAAOiL562PUX5RB\n",
"HMshluUQy3KIZRnEsRxq/gAAAFAMNX8AAADTFDV/AAAA6Ijkr49Rf1EGcSyHWJZDLMshlmUQx3Ko\n",
"+cN47NXrAfQJ4lgOsSyHWJZDLMsgjuVMaCxJ/vrbFr0eQJ8gjuUQy3KIZTnEsgziWM6ExpLkr78t\n",
"7PUA+sTCXg+gjyzs9QD6yMJeD6CPLOz1APrEwl4PoI8snMiNk/z1N6bgyyCO5RDLcohlOcSyDOJY\n",
"zoTGckpe6qXXYwAAAJguur3Uy5RL/gAAADBxOOwLAAAwQEj+AAAABgjJHwAAwAAh+QMAABggJH8A\n",
"AAADhOQPAABggJD8AQAADBCSPwAAgAFC8gcAADBASP4AAAAGCMkfAADAACH5AwAAGCAkfwAAAAOE\n",
"5A8AAGCAkPwBAAAMEJI/AACAAULyBwAAMEBI/gAAAAYIyR/6gu0TbK+vluOz9o1sn5899jPbm/Vy\n",
"rKXYXmR7se0bbK+2vdz2tbZPt71br8eHwZb9zd00jm0szLbTtLy1YZ0jbV9p+0HbK2xfZvvlbbb/\n",
"CtuXV/0etP0L268f5diOzMYxqnWAqWJmrwcATICQUuIn6RxJh1XtV0p6SUQ80KuBlWL7WEknZU0h\n",
"aZak3atFkt492eMCGsQEbmdYm+1TJH2g9th+kvaz/daI+GLW962Szqj13VvSYtu7RMQHuxhXqX0E\n",
"JgUzf+hLti1psaTXVU1XS3pxRKzs3ahGx/asKnFt9/iRGkr81kh6p6StJc2R9HRJH5O0aoKHOW62\n",
"N+n1GKYr23N6PYZJFpL2j4gZteULrQ6299RQ4vcbSTtJ2lPSHVXb6ba3rvpuI+lTVfvtSn83O0n6\n",
"bdX2fttPG+XYPNadAnqF5A/9aIaksyQdUd1fIumgiFgx0or5oSrbL7C9xPYa29fYPtD25rbPtH2f\n",
"7btsn217Xm0b822fZvv6at3WoadX1vrlh43eavuTtm+XtFrS9m3GN0PSR7KmD0TE5yLi3oh4OCJ+\n",
"ExH/KOm4bJ2Ztt9d7cuD1Zh+a/tE23OrPhvbXlaN5brac+6ajfOcrH0f29+s4vCw7durw9BPqK1/\n",
"Wbb+7rYvsf2gpO9Vj7+9OvR2RzW21bavs31q/RB9Ff8v2v5zFdev2H52tv0f1/o/1fZ5tm+z/VC1\n",
"j18f7Qe77TOquN1d7ePK6tDgUVmfPbPnP6O2/tHZY0dm7YfZvsL2/bbX2v6D7ZPrCXG+X7b/yvav\n",
"bD8k6f2jHV+2rV1sX2x7VRXrU2y/2Q3lElX/l1T976tit9T2Z20vqPWbVb3e76peX9+1/aQOMR3r\n",
"4eCRkqy/y26fGhE3R8RvNDS7N1fSa6rbr5HUivW/RMRvI+JmpX+cpPTZ2M2h3I1tf9j2rdVr+Ke2\n",
"nzVs8Cl+rfeWfao+q6q/m1NtcyQOkyciWFim/SLpBEnrq+Xe7PYSSfO72E5rvZVKs2frsrYHJf13\n",
"dTtvPytbf2tJ/5v1WVfr+/dZ3yOz9rtr6+zYZnx7Z+uskDRzhP2ZoZRkra9tv3X/aklzq76fzPrs\n",
"lW3jpKx9v6rtNZIeabOf90jaJVv/sjb7+aPq8e93iNcPs+1Y0qUN+3Jr1vajrP++1e+wadurJO07\n",
"itfD6tq6+diOy/r9Mtu/mVn7FVX7/VmcP9fh93GlpDkNr8d7a/E+rsvxbaU0A5Y/7/pa7PL+720Y\n",
"Y2udGyRtlfU9u6HvbVnbjW3+xm4cRfwXZv2XSXpY0nJJP5D08lrfK7Ix7Jm1/3W2jbOrtnOztldm\n",
"fRdl7ZePMLYjs763anhc10t6QNLuWf+lWfuDDb+vc3r9PsoyOAszf+hH86ufd0s6MCL+PIZtbCrp\n",
"dEmPkfT1qm0TSU+VtI+kJyq9iUvSa7P1TpK0s9Kb+quVZht2UPpgkqSTbW/b5vkOlbSZpCdVY2+y\n",
"U3b7hoh4ZIT9OFTSS6rbS6pxbyfp4qptkdJhYynNlkopyWrVSUpD+3dDRFxRzRaeoTQ78kulmMyR\n",
"9CJJD0l6rKTT2oxnqVJN4lxJrdmp0yXtJWmBUt3iDkoJoSTt73Q4T5IOrJ5Dkm6UtJukx1e3m3yx\n",
"GtdSSc+obj9DKbZzJH2+zXq5/yNpF0nzJM2uxnlr9dg7s36t2C2Q9GJJsr2DUgIqSV+PiFW295H0\n",
"9qptsdLvYlNJ/1C1PVPS0Q3jmC/p/Kr/fKVa1m7G9y5J21S3L1RKBp+p9M/BMNW4P1rdvUgpAdtE\n",
"Q6+JnSQdW/XdVUMzbndLepakLTX0em+n2xq5UIrtRkr7eoCk79h+W9Znm+z2/W1ub91F3626GN9M\n",
"pfeF+UrJvZRe4yc19J2r9HqZL+nZSkmtJB1h++ldPCcwdr3OPllYSiwaPvOXLyd1uZ3Wemskza7a\n",
"jlLDf+eSfqah//a3qdpuazOOfDmk6ntk1nbmKMf3mmyda0bR/4Ksfz7D8fSs/SdZ+y+qtj9V9/OZ\n",
"xn+q2g4axT6uyrZ5Wda+T8MYnyHpP5Rqrx5u2NbfVv1Ozdreka1/YNbemk188ijGuL71e+sQv0Oq\n",
"8d+n4bM0rd/7VlW/LZRm4dZLOq9qe1/W77lV20dGMaaLGl6P9ymbERzD+PIZ66dn65+c9W/NJr55\n",
"FGO8rup7dNb2iWy7O2ftI87wdYj/lpL+Sen1OlcpIftotu0VkmZVfa/P9nFhm9fH96q2i7O2F2Z9\n",
"n5S1/26EsR2Z9f1w1r6JpLWt8WXtSzX03pLP7ua/g/dM5PskC0trYeYP/ehnSkmEJB1r+0OtB9x8\n",
"6YgfN2xjWUSsrW6vydr/lN1+OLs9u/q5ddYWbZbHNjzfNSPtVCWf5Xqi7Y1H6N+avQhJN2ftNzf0\n",
"kYZmsLa3/XwNzfasUzq8Jw3fx9a268vsev1a1T5sP23vLOknkl4laVulmZ36rFBrO1u2Gf8t2tBo\n",
"xtjud9Ea26GS/l3pbNEtsu1sMLaIWC7pW1XbwdW+t2J3fUT8vGFc3Yzp+ojIX4ddjU/lY9caY17/\n",
"d2t2+7aG7XYtIu6JiFMi4tcRsSoi7o5U0/rHqsumkvaobt+ZrbpFdjuvyW3Nst3VRd/ReDSmEbFa\n",
"KRmXpE0b/kbvrf0u89/BAgGTgOQP/ehSpcOdrUOiJ9r+QK1P/cOsrt3h8/PGDgAAIABJREFU1JEO\n",
"s7Y+VB5Qmjmsn504IyLOaFhv9QjbbVmiobMXN1PzIcLWiSH5eCwpPxFjx+x2/iH3FaVk10pnSrcK\n",
"5C+JiNtr25SkL7bZxxnVh+AwWULdcrDSIVhJOk/SYyNihtKh4Lr8UHh+QswODX3zfbq0wxiva1i3\n",
"5dDs9jGSNqnG1i5RX1z93EzphIw9a+3S8Ngd3mZMz27YdtPro5vxdRO7fIwfbDPG1mHTfLv5thpP\n",
"WOqW7XYneTj72fr7vSpr2z3rm99u9bmyzeNNfUfj0b+tqiyilcStjIiHa30X1P4xyv8W7+niOYEx\n",
"I/lDX4qIbyolL+uqplNsvzcilkbERrUPsgMKPvWF1c/NJH3J9vZOZ9LuZPsttn89no1HxHpV9VaV\n",
"U20fY3tBddbl02x/TNKHq8e/m/X9YDXzuY3SIVTV+0TE/UqHYKVUT7ZddfusrP/PJbXqKF9v+7W2\n",
"N7O9qdOZt6fZ/vQodyn/YFwtaa3t52j4mZstP8xuH2P7Sba3k3R8vWNE/FHSH6q7B9p+p+0tbM+p\n",
"zs49zvZXuhjbSkkzbL9Bqa6uyaVKszhWOlQppX8Wzs36XJjdPtn2c23Ptv3Y6uzaC2y/TqPTzfha\n",
"sbOkE5zOSF8k6U0NfS/W0D85f2/7L2zPtT3P6Qz4M22/v3r8smy9I2w/0/Z8DT8jfZguz/Y9xfZn\n",
"qu3Osb2V7VOVDs9K6XX4m+r2uRpKBD9g+wlOZ3W3/kF6UNLXqttf09DlkN5mew/bC1WdRa30vvHo\n",
"me2j8Cbbe9t+jNLfVuvM3R809J2l9Hc7z/beGvodhNJrCJh4vT7uzMJSYtHwmr/8rMVDNbyO7B0j\n",
"bKfV76as7cg2274sa9+xatta6WzIdrVS69ps9++63N/jtWGNV758quq3kVJy167fVUozRvm2D6j1\n",
"WabaWcUamlltt92zmuLUsB9P1NAZuflyvRpiI+mShr55nWV+dvB+bbY9rD6wQ4wPa1jnQaVDfMN+\n",
"79k6J9X6f7thu5/vMKb6/rYdazfjUzrse/sIsftQtu33NfTNl/zvYHHD48uy2zfVxj3qWkClGeB2\n",
"Y3hE0mG1/u1qKtdJenOt71s69D15FGM7Mlvn1obtrJS0W9Z/adW+QunEknr/s3v1/skyeMukzfzZ\n",
"3s/2f1bXQeLrcFBa1H6mOxFf0dCbdChd6HWDa6A1bCtq9zfYdlN7RCxTOovy45J+r3QIdaVSMvNl\n",
"DT9U1267I4qIE5XOFDxHqQ5wtdIHym8kfUbpTFdFmik8WOnSHdcoJQdrJP1OKVHZL2qHZyPiR0of\n",
"VK04fDlqZxVXcd1X0jeUaq0eVvrAv0pp5uOTo9nPiLihGt811T7cqDRTc0GbdV4t6d+ULvexQmkG\n",
"5y3Z4/dm275C6WSSc5Vm5B6qHv8fSZ/V0Oxco4i4QOlbUm6qxnaV0pnTN7TbH6VEKC8nOKthu2+X\n",
"dLiky6v9eKga34+Ukq7v11cZ7/gi4h5JL1SaWVqt9Dv7qIbOTJWGx+40SS9TOtv3HqXf7x1K9bTH\n",
"afis2FuUft93KyXbl0p6QTaGpvGP9jW/WNKnlV4frXHcqTQ7/fwqBkMbTd/K8QalSxitUvrbu1zS\n",
"X0b27R5V3y9I+kulM5Nbl3a6StIbIiKfXW8nf10fp3Tixu1Kf18/l/SiiPhdw3qt38UVSr+Lu5Te\n",
"L944iucEinBE1587Y3si+6WSnqf0R3yupKMj4tzOawHAkOpQ5d0RcUt1f75SgnBw1eWoyL71AUNs\n",
"HyDp6qgudm77yUrJXevM3D0i4vc9HGJfs71Uqb5vaUTs3OPhYMBN2hXFI+IipTca2T57sp4XQF85\n",
"TNJ7bN+vNIu5jYauVfcTNcy04VEfl7TIduskjfxM8E+Q+E0avg4OPcfXyQCYTi5TOpS7m1Ly8oCk\n",
"6yR9VdLn64enMczXlBKPnZQukbJM6SLdX4iIb/dyYAOi09UFgEk1aYd9hz2pvVLS2znsCwAAMLmm\n",
"3Myfbf4rAgAAGKWI6KqcYMolf5L0y8MPP0vp63FGOstytLdb1ildHuAhDZ392bde9a1vHfmtV73q\n",
"7F6PY7ojjuX0YSzrb7jW8AsQb1Qt9fb6T2f9Z0raOFta2xj2PIdceOH+X33FK+rfTtM0npHGXR/H\n",
"jDbjbsnfN+9X+jaL1lnL01Ifvi5LqL9O6+0btL3q298+4luvfOV52vD11XpdjbSt/P7GSt9QM7f6\n",
"ubGGXpud1m16bYeGXxC8qX+rz/qsr5W+vWm2pP9VOov8Dxq66Hoo5Sp3SLpp0XnnFcspbF8WES8c\n",
"Zd+un3dKJn9q/sohdOmxc+Ys7/UY+gFxLKcPY9npH9MJtenMmU9RqnfEOPXh67KEri9F9djZs/+s\n",
"kb8FaTraWOlbaw6Q9HINT0BnKCWHq5ccccQvlC7s/d+LzjtvxTifc+k41+9o0pI/25sqfdm6lAL3\n",
"BNt7KX3PIcneRGj7zUjoCnEsh1iWQyzLIZZl9G8cH1a6nmanb6WZL2kXSXtL2mzJEUe0kuDW95W3\n",
"jjyGhl+ofLXSNSYfrJ5njaQ/bbfpplsvOeKIjRedd1796wGLmMyZv72VLmIqpZ0/sVrOVvoaKRS2\n",
"07x5d47cCyMhjuUQy3KIZTnEsowBj+OfNfS1l1b6Gr/8MHJeTtFa8hKPTav7MyTt8fKddnqSpMuX\n",
"HHHEdUqzgGurbSl7DtXaRq0nZ/t2Yjt+efjhJ/Z6HAAAAD20idLh5s3VPFkXkjZ9xvnnv6AvTvgA\n",
"AAAYcKsl/XGEPttr6OsUR23SvtsXk+8//vjHhb0eQz8gjuUQy3KIZTnEsgziWM5Ex5LkDwAAYIBQ\n",
"8wcAADA9bf+M889/Y7c1f8z8AQAADBCSvz5G/UUZxLEcYlkOsSyHWJZBHMuh5g8AAADFUPMHAAAw\n",
"PVHzBwAAgM5I/voY9RdlEMdyiGU5xLIcYlkGcSyHmj8AAAAUQ80fAADA9ETNHwAAADoj+etj1F+U\n",
"QRzLIZblEMtyiGUZxLEcav4AAABQDDV/AAAA0xM1fwAAAOiM5K+PUX9RBnEsh1iWQyzLIZZlEMdy\n",
"qPkDAABAMdT8AQAATE/U/AEAAKAzkr8+Rv1FGcSxHGJZDrEsh1iWQRzLoeYPAAAAxVDzBwAAMD1R\n",
"8wcAAIDOSP76GPUXZRDHcohlOcSyHGJZBnEsh5o/AAAAFEPNHwAAwPREzR8AAAA6m9Tkz/bbbN9k\n",
"e7Xtq23vO5nPP2iovyiDOJZDLMshluUQyzKIYzl9U/Nn+xBJn5Z0sqS9JP1c0kW2d5isMQya395z\n",
"z7a9HkM/II7lEMtyiGU5xLIM4ljORMdyMmf+3iNpcUR8KSKuj4h3SLpD0tGTOIaB8sDDD8/p9Rj6\n",
"AXEsh1iWQyzLIZZlEMdyJjqWk5L82Z4laZGkS2oPXSLpuZMxhkF096pVW/R6DP2AOJZDLMshluUQ\n",
"yzKIYzkTHcuZE7nxzJaSZki6q9a+TFLT1CYvoALuXLXq8SKW40YcyyGW5RDLcohlGcSxnC5iudlY\n",
"tj8pl3qx/ThJt0raLyJ+mrUfJ+mwiNg1a5ta154BAACYwrq91MtkzfzdI2mdpG1q7dso1f09qtsd\n",
"AAAAwOhNSs1fRDwk6ZeSXlx76CCls34BAAAwCSZr5k+SPiXpPNtXKiV8RynV+505iWMAAAAYaJOW\n",
"/EXE12wvkHSspO0kXSvpZRFxy2SNAQAAYNBNue/2BQAAwMThu30BAAAGCMkfAADAACH5AwAAGCAk\n",
"fwAAAAOE5A8AAGCAkPwBAAAMEJI/AACAAULyBwAAMEBI/gAAAAYIyR8AAMAAIfkDAAAYICR/AAAA\n",
"A4TkDwAAYICQ/KFv2T7B9vpqOT5r38j2+dljP7O9WS/HWortRbYX277B9mrby21fa/t027v1enwY\n",
"bNnf3E3j2MbCbDtNy1tHsY2u3htsv7CpPzBdzez1AIBJElJ6c5d0jqTDqvYrJb0kIh7o1cBKsX2s\n",
"pJOyppA0S9Lu1SJJ757scQENYgK30+22R3xvsD2e7QNTDjN/GBhO7+CLJb2uarpa0osjYmXvRjU6\n",
"tmdVH07tHj9SQ4nfGknvlLS1pDmSni7pY5JWTfAwx832Jr0ew3Rle06vxzDJQtL+ETGjtnyh2w1N\n",
"5/cGYCxI/jAoZkg6S9IR1f0lkg6KiBUjrZgfqrL9AttLbK+xfY3tA21vbvtM2/fZvsv22bbn1bYx\n",
"3/Zptq+v1l1h+zLbr6z1OzI/fGX7k7Zvl7Ra0vZtxjdD0keypg9ExOci4t6IeDgifhMR/yjpuGyd\n",
"mbbfXe3Lg9WYfmv7RNtzqz4b215WjeW62nPumo3znKx9H9vfrOLwsO3bq8PQT6itf1m2/u62L7H9\n",
"oKTvVY+/3fbltu+oxrba9nW2T60foq/i/0Xbf67i+hXbz862/+Na/6faPs/2bbYfqvbx67af1vwK\n",
"2CDeZ1Rxu7vax5W2f2H7qKzPntnzn1Fb/+jssSOz9sNsX2H7fttrbf/B9sn1hDjfL9t/ZftXth+S\n",
"9P7Rji/b1i62L7a9qor1Kbbf7DaHOG2/pOp/XxW7pbY/a3tBrd+s6vV+V/X6+q7tJ3WI6VgPB3vk\n",
"LiPq9r3Btt/lVFrReh94aa1D/vp+iu2LbD9g+17b/2p78wLjBsYuIlhY+nKRdIKk9dVyb3Z7iaT5\n",
"XWyntd5KpdmzdVnbg5L+u7qdt5+Vrb+1pP/N+qyr9f37rO+RWfvdtXV2bDO+vbN1VkiaOcL+zFBK\n",
"stbXtt+6f7WkuVXfT2Z99sq2cVLWvl/V9hpJj7TZz3sk7ZKtf1mb/fxR9fj3O8Trh9l2LOnShn25\n",
"NWv7UdZ/3+p32LTtVZL2HcXrYXVt3Xxsx2X9fpnt38ys/Yqq/f4szp/r8Pu4UtKchtfjvbV4H9fl\n",
"+LaSdEftedfXYpf3f2/DGFvr3CBpq6zv2Q19b8vabmzzN3bjKOK/MOu/TNLDkpZL+oGkl0/Ee4Ok\n",
"F2Z9WvHJ4/qwpAPbvL6XNfT/kST3+j2SZXAXZv4wKOZXP+9WepP+8xi2samk0yU9RtLXq7ZNJD1V\n",
"0j6SniipVTv42my9kyTtrPTm/2pJcyXtoJQESNLJtrdt83yHStpM0pOqsTfZKbt9Q0Q8MsJ+HCrp\n",
"JdXtJdW4t5N0cdW2SOmwsZRmRKSUZLVqoaSh/bshIq6oZgvPUDqa8EulmMyR9CJJD0l6rKTT2oxn\n",
"qVJN4lxJrdmp0yXtJWmBUt3iDkoJoSTtb3vP6vaB1XNI0o2SdpP0+Op2ky9W41oq6RnV7WcoxXaO\n",
"pM+3WS/3fyTtImmepNnVOG+tHntn1q8VuwWSXixJtndQSkAl6esRscr2PpLeXrUtVvpdbCrpH6q2\n",
"Z0o6umEc8yWdX/Wfr1Sv1s343iVpm+r2hUrJ4DOV/jkYphr3R6u7FyklYJto6DWxk6Rjq767Svq7\n",
"qv1uSc+StKWGXu/tjKVWb4HSa26epAMkfcf227rcTrfvDfMlvbR6zvdXbTOUSiua/EQptk+VdH3V\n",
"9kJJr+hynEA5vc4+WVgmatHw/+7z5aQut9Nab42k2VXbUVn7OVnfn2nov/xtqrbb2owjXw6p+h6Z\n",
"tZ05yvG9JlvnmlH0vyDr/8qs/elZ+0+y9l9UbX+q7uczjf9UtR00in1clW3zsqx9n4YxPkPSf0i6\n",
"XWlWpb6tv636nZq1vSNb/8CsvTWb+ORRjHF96/fWIX6HVOO/T8Nnc1q/962qflsozcKtl3Re1fa+\n",
"rN9zq7aPjGJMFzW8Hu9TNiM4hvHlM9ZPz9Y/Oevfmk188yjGeF3V9+is7RPZdnfO2kec4esQ/y0l\n",
"/ZPS63WuUmL10WzbK1T9nZZ6b9Dwmb/zao/dnMVxfu31vU7SE7O+b8q289mJfg9kYWm3MPOHQfEz\n",
"pSRCko61/aHWA26+dMSPG7axLCLWVrfXZO1/ym4/nN2eXf3cOmuLNstjG57vmpF2qpLPcj3R9sYj\n",
"9N8qG8vNWfvNDX2koRms7W0/X0OzPeuUDu9Jw/exte36Mrtev1a1D9tP2zsrzZa8StK2SjM79Vmh\n",
"1na2bDP+W7Sh0Yyx3e+iNbZDJf27pP2UkrvWdjYYW0Qsl/Stqu3gat9bsbs+In7eMK5uxnR9ROSv\n",
"w67Gp/Kxa40xr/+7Nbt9W8N2uxYR90TEKRHx64hYFRF3R6pp/WPVZVNJe3SxybbvDW3cXLuf79eW\n",
"2lC72C6odwQmC8kfBsWlSoc7W4dET7T9gVqf+odZXbvDqSMdZr2r+vmA0oxE/ezEGRFxRsN6q0fY\n",
"bssSpdotKR0ibjpE2DoxJB+PJeUnYuyY3V6W3f6KUrJrpbMhX1O1XxIRt9e2KUlfbLOPMyJig33K\n",
"EuqWg5UOwUrSeZIeGxEzlA4F1+WHwvMTYnZo6Jvv06Udxnhdw7oth2a3j5G0STW2don64urnZkqH\n",
"CPestUvDY3d4mzE9u2HbTa+PbsbXTezyMX6wzRhbh5Dz7ebbajxhqVu2253k4ezn+i42OZr3htyj\n",
"fzPVWPL9uqdTfw3/G2vqC0wKkj8MjIj4plLysq5qOsX2eyNiaURsVPsgO6DgU19Y/dxM0pdsb+90\n",
"Ju1Ott9i+9fj2XhErFdVb1U51fYxthdUZ10+zfbHJH24evy7Wd8PVjOf2ygdQlW9T0Tcr3QIVkr1\n",
"ZNtVt8/K+v9cUqtW6vW2X+t0cdxNnc68Pc32p0e5S/ns6WpJa20/R0N1ZLkfZrePsf0k29tJ2uBC\n",
"vBHxR0l/qO4eaPudtrewPac6O/c421/pYmwrJc2w/QaluromlyrN9ljpUKWUkoxzsz4XZrdPtv1c\n",
"27NtP7Y6u/YC26/T6HQzvlbsLOkEpzPSFykdmqy7WEPJ0d/b/gvbc23PczoD/kzbrfq3y7L1jrD9\n",
"TNvzNfyM9GG6PNv3FNufqbY7x/ZWtk9VqouV0uvwN6PYzqPavTe06f5Xtg+qzth9n1KNqZRKLur1\n",
"glb6e1xgexelk2ZaLu1mjEBRvT7uzMIyUYuG1/XkZy0equF1ZO8YYTutfjdlbUe22fZlWfuOVdvW\n",
"SmdDtquVWtdmu3/X5f4erw1rvPLlU1W/jZSSu3b9rlKaMcq3fUCtzzLVzirW0OxJu+2e1RSnhv14\n",
"oobOyM2X65tiI+mShr55nWV+dvB+bbY9rD6wQ4wPa1jnQQ3VfT36e8/WOanW/9sN2/18hzHV97ft\n",
"WLsZn9IhyttHiN2Hsm2/r6FvvuR/B4sbHl+W3b6pNu5R1wIqzQC3G8Mjkg4r/d6g5rN98+UhSS9q\n",
"8z7Q1P+HI42RhWUil0mb+bO9n+3/tH1r9R/e6yfruTGwovYz3Yn4ioaSrJB0uhuugdawrajd32Db\n",
"Te0RsUzpLMqPS/q90iHUlUrJzJc1/FBdu+2OKCJOlPRspbM+b1SaNbtfaRbkM0pnuirSTOHBSrMQ\n",
"1yglB2sk/U4pUdkvaodnI+JHSmfItuLw5aidVVzFdV9J35B0p9KH6DKlZPJUpcvGjLifEXFDNb5r\n",
"qn24UelQ9gVt1nm1pH9TutzHCklfk/SW7PF7s21foXQyyblKM3IPVY//j6TPamh2rlFEXKD0LSk3\n",
"VWO7SunM6Rva7Y9SIpSXE5zVsN23Szpc0uXVfjxUje9HSknX9+urjHd8EXGPUlJzadX3TqUTJz6X\n",
"bTKP3WmSXqZ0tu89Sr/fO5Rq5o7T0NnGUor/J5UOAa+qnuMF2Riaxj/a1/xiSZ9Wen20xnGn0uz0\n",
"86sYjKTb94a8/xc0FOO1Sq+dV0ZEPgudP8/zlf7ZekBpVvKLkl7Z0BeYNI7o+jNmbE+ULoL5PKU/\n",
"2HMlHR0R53ZeCwA6qw5V3h0Rt1T35yslCAdXXY6KMXzrwyCwfYCkq6O6oLHtJysld60zc/eIiN/3\n",
"cIjTku3LlGaZI1LNJTClTNp3+0bERUpvKrJ99mQ9L4C+d5ik99i+X2kWcxsNXavuJ2qYacOjPi5p\n",
"ke3WSRr5meCfIPEbtxLfQAIUN2nJHwBMkMuUDuXuppS8PCDpOklflfT5+uFpDPM1pQRlJ6VLpCxT\n",
"ukj3FyLi270c2DQ35vINYDJM2mHfYU9qr5T0dg77AgAATK4pN/Nnm/+UAAAARikiuioxmHLJn9T9\n",
"TqCZ7V9FRLvrj2GUbP9KEXsr/b3MUDpM1lpU+xkauuREftmTiB4eAvLQeFv7kC8b1e7P1NA1QDfS\n",
"0Lqtfd8oW5riIA3f16F4bb75+Vq58g21bebb2ahhyZ+7Xezz/htXy2yli0XPztryfdg4W+q/23zs\n",
"Uvv9zp9fbdZvio9rj9djOTxuG64n7bLLIv3hD0uyx0ZzNnp9HK39af3uW2PppL7t5vG1X28ko3n/\n",
"7/YzovW32WzXXXfV738/Un1j6b/f/Pe7TsMv05SfHb4+e/7677j+2PpsO+uqtta2H6qWNUpnYK9R\n",
"Olv5YW14iahHsmVdrT2yba8fdnuLLT6n5cvfXhtr08+mC+q3+9myvtbeeu78vTYfaz7GeozqS2t7\n",
"eZ/62NY1tEV1o/h7ezef32OZNJuSyR+K+VVTY5UIzFL6YNxE6cNxVrW0PvxnaOhDcWbWNjNrz9+8\n",
"NtKGH2JNH47SyB8WTR+MeVLSblutP9j1VfvG1T5tUi1zs33Ok4I8IdpI9ed/9at3kHRlbYxNl6uI\n",
"DvvT+lqC1hhbb1oPK70ht97AmpOm4W3t+uS/g3x/Ns5u59to9yZcf5NV7X5TktHUf8PHDzhgc6Xv\n",
"ju20zdE+R/12Hps8Ea9/sKl2v/6BUI9x/Q1/vZrHvb62Tqfx5tttiv3I295uu/lK37tcf801vQbb\n",
"fTi0njv/YBvPB9lI645l22Mdz+jXW7BgI0n/OcbnKaHdPz3Shv9ANN2XNnwPzv+Ba70nzFaq7Wyd\n",
"FDWztk6+RLZ+/vdVf0/So/df8IK5kv6h4XE1tLVL4MfSr9M/Vp221+mzqN39DdbJGjq9b9QTy059\n",
"QgcfvK2lH2vos6KVxOfvaw8r1Th3bdKSP9ubKn2xupReTE+wvZeke1uXaHi0byrarichrWWWNkxE\n",
"Zmvov/xWn3yd/I+p9UfQlETUf6n1GQlp+Adou//w8/v1P9Q8kWmNsz7j0DSu+gtvRpvHh9qOOWYn\n",
"p+uE5X/8rWRHGv7B1/SzKRloetEqa2v3H3apD4V2H075m1L9v7U80XpE6Vpw92r4f7frNfyPa+g5\n",
"NtpoPw3/1oJuNL2BNP0+6olnS7tELFf/XdUTmnxWYbwf7uMze7aUrmWH8dpmm3uVzm7GeD3+8ct7\n",
"PIL8H5Ppa/bsGZKu6PUweqhTEip1TurzNmuzzWYpTeDUc5b8M3+mhr5hpiuTOfO3t1IiIqUPnxOr\n",
"5Wylr4zKtb5aqj79PdIsRSsBaPfffX2buXb/qdfbRztD0Wn9VlLSmoLv9J9Au/HlbxRNCUJo/foZ\n",
"Si+ePKFrJUG9SwCmm3nz1oxj7abXRP67G+339/aH8cUSOWJZDrEsgziOdCRk9DbZ5H6li/SPZN3I\n",
"XTY0mdf5u0yj/y7h703gUAbHnnsuVZrlwng861l39noIfYNYlkMsyyGWZRDHciY4lj251EsntkPp\n",
"a6oAAADQ3vay39jtibKT9t2+AAAA6D2Sv372hS8s7PUQ+gJxLIdYlkMsyyGWZRDHciY4liR/AAAA\n",
"A4SaPwAAgOmJmj8AAAB0RvLXz6i/KIM4lkMsyyGW5RDLMohjOdT8AQAAoBRq/gAAAKYnav4AAADQ\n",
"GclfP6P+ogziWA6xLIdYlkMsyyCO5VDzBwAAgFKo+QMAAJieqPkDAABAZyR//Yz6izKIYznEshxi\n",
"WQ6xLIM4lkPNHwAAAEqh5g8AAGB6ouYPAAAAnZH89TPqL8ogjuUQy3KIZTnEsgziWA41fwAAACiF\n",
"mj8AAIDpiZo/AAAAdEby18+ovyiDOJZDLMshluUQyzKIYznU/AEAAKAUav4AAACmJ2r+AAAA0BnJ\n",
"Xz+j/qIM4lgOsSyHWJZDLMsgjuVQ8wcAAIBSqPkDAACYnqj5AwAAQGeTmvzZfpvtm2yvtn217X0n\n",
"8/kHDvUXZRDHcohlOcSyHGJZBnEsp19q/mwfIunTkk6WtJekn0u6yPYOkzWGgXPlldv2egh9gTiW\n",
"QyzLIZblEMsyiGM5ExzLyZz5e4+kxRHxpYi4PiLeIekOSUdP4hgGy4oVc3o9hL5AHMshluUQy3KI\n",
"ZRnEsZwJjuWkJH+2Z0laJOmS2kOXSHruZIxhIN122xa9HkJfII7lEMtyiGU5xLIM4ljOBMdy5kRu\n",
"PLOlpBmS7qq1L5PUNLW544SPaBDcdtsOIpbjRxzLIZblEMtyiGUZxLGc0cfyMWPZ/KRc6sX24yTd\n",
"Kmm/iPhp1n6cpMMiYtesbWpdewYAAGAK6/ZSL5M183ePpHWStqm1b6NU9/eobncAAAAAozcpNX8R\n",
"8ZCkX0p6ce2hg5TO+gUAAMAkmKyZP0n6lKTzbF+plPAdpVTvd+YkjgEAAGCgTVryFxFfs71A0rGS\n",
"tpN0raSXRcQtkzUGAACAQTflvtsXAAAAE4fv9gUAABggJH8AAAADhOQPAABggJD8AQAADBCSPwAA\n",
"gAFC8gcAADBASP4AAAAGCMkfAADAACH5AwAAGCAkfwAAAAOE5A8AAGCAkPwBAAAMEJI/AACAAULy\n",
"h75j+wTb66vl+Kx9I9vnZ4/9zPZmvRxrKbYX2V5s+wbbq20vt32t7dNt79br8WGwZX9zN41zOx+y\n",
"fWn1+m5t8+tdrJ+/N6y3/bmGPv9c65O/h5ydte84nn0BemlmrwcATLCQUuIn6RxJh1XtV0p6SUQ8\n",
"0KuBlWL7WEknZU0haZak3atFkt492eMCGsQ413+vpHkFt3mE7fdHxCpJsr2ppCNGsf3x7gfQU8z8\n",
"oe/ZtqTFkl5XNV0t6cURsbJ3oxod27OqxLXd40dqKPFbI+mdkraWNEfS0yV9TNKqCR7muNnepNdj\n",
"mK5sz+n1GCbRYklvlnRUoe3N09A/hFJ6j9i80LaBKYvkD/1uhqRMaa0IAAAWz0lEQVSzNPTf/BJJ\n",
"B0XEipFWzA9V2X6B7SW219i+xvaBtje3fabt+2zfVR0Smlfbxnz7/2/v3KPsKqo0/vsIkvAYNIIm\n",
"kIDhIQsfKAM6EoyICMjgWj6XgIwj4BtxgW9FJQQGAQWB4DAyOhKEERFlfAwKJIoIAipBxgdCnAEC\n",
"JEASQF5JSCDZ80fVtatPzu3u2306t9P9/dY6q8+ts6vurq/r9q2u2lWlMyQtyHkfl3StpDdX7I4s\n",
"3u+Dkr4i6X5gJTC1jX/jgC8WSZ+NiK9GxMMR8XRE/CkijgdmFnk2lvSxXJfl2afbJJ0kabNs8yxJ\n",
"S7Mvt1fec9fCz28V6XtJ+kHW4WlJ9+dp6BdU8l9b5H+JpLmSlgM/zc+PkfRLSQ9k31ZKul3S6dUp\n",
"+qz/NyT9Net6qaRXFeX/omL/IkkXS1osaXWu4/ck7VbfAtbR+2tZt2W5jk9I+o2kDxU2Ly/e/2uV\n",
"/EcXz44s0g+XdJ2kxyStkvQXSadUO8RlvSS9VdL/SFoNfGag/hVl7SLpakkrstanSnq/aqY6s/1B\n",
"2f6RrN1CSedK2qpit0lu70ty+/qJpJ370LSj6eCI+FhEfBP4y0Ds++Ge/LPUp3W/cAD5J0n6ttIU\n",
"9BOSvitpcuuhpGlF/eZIOiq35VWS7pB0RAN1MGZwRIQvX6PqAmYBa/P1cHH/O2BiB+W08j1BGj1b\n",
"U6QtB36d78v0C4r8zwf+r7BZU7H9ZGF7ZJG+rJJn+zb+vbLI8ziwcT/1GUfqZK2tlN96PR/YLNt+\n",
"pbDZvSjj5CJ9n5x2CPBMm3o+BOxS5L+2TT2vyc+v6kOvnxflCJhXU5dFRdo1hf2M/DusK3sFMGMA\n",
"7WFlJW/p28zC7paifhsX6dfl9McKnb/ax+/jt8CEmvb4cEXvmR369zzggcr7rq1oV9p/osbHVp47\n",
"gecVthfW2C4u0u5q8xm7qz/9K/n2LfJeNsi/DbNIo+VrSZ+lV+X7lcAJbbQo69fSq9T5z8Cm2XZa\n",
"kb60xnYtcFS3/176GpuXR/7MaGdi/rkM2D8i/jqIMjYHzgaeDbSCyzcFXgTsBewEtGIH31nkOxnY\n",
"kfQH/+3AZsB2pE4AwCnlSEHl/Q4DtgB2zr7XsUNxf2dEPNNPPQ4DDsr3v8t+bwNcndP2IE0bQxot\n",
"hdTJKqfFWvW7MyKuy6OFXyPNItxC0mQC8HpgNfBc4Iw2/iwkxSRuRs+Iy9nA7sBWpLjF7UgdQoDX\n",
"SXp5vt8/vwfAXcCLgSn5vo5vZL8WAnvm+z1J2k4AzmuTr+Q9wC6kqcLx2c9F+dlxhV1Lu62AAwEk\n",
"bUfqgAJ8LyJWSNoLOCanzSH9LjYHPp3TXgEcXePHROA/s/1EUixrJ/59FJiU768gdQZfQfrnoBfZ\n",
"79PyyytJHZpN6WkTOwBfyLa7Au/O6cuAfwC2pqe9t6Nb8XPLgMvz/dH0aP1fpM5afywEtie10Rty\n",
"2q7A+2pstyZpsyU94ScAp0ly7L1Z/3S79+nLV9MXvf+7L6+TOyynle8pYHxO+1CR/q3C9gZ6/rOf\n",
"lNMWt/GjvA7NtkcWaecP0L9Dijy3DsD+ksL+zUX6y4r064v03+S0e/LrcqTxczntgAHUcUVR5rVF\n",
"+l41Pu5J+vK9H3i6pqx3ZLvTi7Rji/z7F+mt0cQXDsDHta3fWx/6HZr9f4R1R3DWkEfAgOeQRo/W\n",
"AhfntE8VdnvntC8OwKcra9rjIxQjgoPwrxyxflmR/5TCvjWa+P4B+Hh7tj26SDuzKHfHIr2jEb4+\n",
"fhf7FmUOduTvw6QO+VrSSP7yrMkMen/O2438vb5Nu/txTptWpF1f8eNXxe9gj+H4O+jLV1+XR/7M\n",
"aOcGUicC4AuSTmg9qMTk1MaJZZZGxKp8/1SRfk9x/3RxPz7/fH6RFm2u59a83639VSpTjnLtJOlZ\n",
"/dg/r/Dl3iL93hob6BnBmirpNfSM9qwhfQlC7zq2yq5e46vxazm9Vz0l7QhcD7wFmEwaTayOCrXK\n",
"2bqN//exLgPxsd3vouXbYcB3gH1InbtWOev4FhGPAj/MaW/KdW9ptyAibqzxqxOfFkRE2Q478o/m\n",
"tWv5WMb/LSruF9eUOyKIiF8Bt5G02RT4c07rNyvttduKdbm38rplrzb2xgwr7vyZ0c480nRna0r0\n",
"JEmfrdhUv8yqtJtO7W+adUn++SRp5HBczfW1mnwr+ym3xe9IsVuQpojrpghbC0NKfwSUCzG2L+7L\n",
"6a5LSZ1dkaaqDsnpcyPi/kqZAN9oU8dxEbFOnYoOdYs3kaZgAS4GnhsR40hTwVXKqfByQcx2NbZl\n",
"neb14ePtNXlbHFbcf4QU1zWO9h31OfnnFqQFGS+vpENv7d7VxqdX1ZRd1z468a8T7UofP9/Gx9YU\n",
"clluWVbtgqURxPnFfd3nsY6+PkMP1di/oPK6P3tjhhV3/syoJyJ+QOq8rMlJp0r6REQsjIiNKl9k\n",
"+zX41lfkn1sA35Q0VWkl7Q6SPiDpD0MpPCLWkuOtMqdL+oikrfKqy90kfQn4l/z8J4Xt5/PI5yTS\n",
"FCpVm4h4jDQFCymebJt8f0FhfyPQiqM8QtI7JW0haXOllbdnSDpngFUqR09XAqskTacnjqzk58X9\n",
"RyTtLGkb4MSqYUT8Lz2rQ/eXdJyk50iakFfnzpR0aQe+PQGMk3QUKa6ujnmk0R0Bn8tpzwAXFTZX\n",
"FPenSNpb0nhJz82ray+RVMaHNeVfSzsBs5RWpO9Bfaza1fT8k/NJSW+QtJmkLZVWwJ8v6TP5+bVF\n",
"vn+W9ApJE+m9Ir0Xna72zb5uTYq/bTE+t/mtBxk/dxHwA1Jbv6gf25ITJU2RNIXe7W5eje3eSqu6\n",
"t5B0ODA9py8BhvR3wJhB0e15Z1++mr7oHddTxuscRu84smP7Kadld3eRdmSbsq8t0rfPac8nrYZs\n",
"Fyu1pk257+6wvieyboxXeZ2V7TYide7a2d1MXqlYlL1fxWYplVXF9Iystiv3gjqdauqxEz0rcstr\n",
"QZ02wNwa2zLOslwdvE+bsnvFB/ah8eE1eZaTpvN6/d6LPCdX7H9UU+55ffhUrW9bXzvxjzTte38/\n",
"2p1QlP2pGtvyKj8Hc2qeLy3u76743VEsIGmRRV++vLaDvw0f7sNuIDF/i2re/zZyPCa9Y/7q4n/X\n",
"AEeu77+PvnxFDDLmT9KHlfY+WylpvqQZ/dgfLOnXSntxLZP0Q0kvHMx7GzMAovIzvYi4lJ5OVgBn\n",
"q2YPtJqyovJ6nbLr0iNiKWkV5ZeBO0hTqE+QOjPfpvdUXbty+yUiTiJtU/EtUhzgStJ2In8CZpNW\n",
"uhJppPBNpK07biV1Dp4ibU9xMmnrlpWVsq8hfeG2dPh2VFYVZ11nkFZOPkjqYC8ldSZPJ20b0289\n",
"I+LO7N+tuQ53kaayL2mT5+3AfwCPkra6uQz4QPH84aLs60iLSS4ijcitzs9/D5xLz+hcLRFxCemU\n",
"lLuzbzeTVk7f2a4+pI5QGU5wQU25xwDvAn6Z67E6+3cNqdN1VTXLUP2LiIdICybmZdsHSSt6y6PO\n",
"Su3OAA4mrfZ9iPT7fYAUTzuTntXGkPT/CmkKeEV+j9cWPtT530mbbxcb2VfYRt17DdauTH8LqW0+\n",
"Svpcfw/YLyrxmJmrSR3024FVpJHooyLiwn78MGZYUERn3zWSDiXF4xxNWrF0DHAU8OKIWCdgOG/w\n",
"+WfgLODrpN3TvwTsFBHuABpjBkWeqlzW+ruTpxjnkDqQAB+KiK93y7+RjKT9gPmRNzvP/4xfSc/K\n",
"3JdGxB1ddHGDR9I0ehZlXRgR7+meN8b0ZjAjfx8H5kTENyNiQUQcS/ovsDbYnBRzshFwfETcFRG/\n",
"J3f+JLVdXWeMMf1wOHCP0gkfi0ijja2O3/XUjLSZv/Fl4FGlkziWkEajdySNaJ3pjp8xo5uOOn+S\n",
"NiFtBDu38mgusHebbDeQVju+X9I4SX9Hmnr7bUQ80pm7xhjzN64lTZeuJm1R8yRpD7uPkfZg6281\n",
"9ljmMtL0+rNIW8MsJY38vS0iqqvhzdDoOJTDmOGmo2lfSduSglz3iWIvJEkzgcMjYtc2+fYm7Xs1\n",
"kdThvBX4x4hod3KBMcYYY4wZBob9WJm8cesPSbE4l5COtzkZuEzSflHpfUryf0nGGGOMMQMkItSJ\n",
"faedv4fIx1dV0ifRs9lslQ8C90VEay8oJL2LtKJtOmmfsF7MmsUbKknVDmF/lRyJHcj17tPs2Xzq\n",
"uOPanqvaNGX9OmqEbeyb0KsJP5g9m08edxxnDqHsTv0YjQTAuefyiWOP7bX6tyt+bGDU+lzTLofS\n",
"zoaqSyv/QH0Y7PsNy2epzWe8STbEdtcxA/jO6VSHMaFbHeecw6c/+lG+PADTmDWLazotv6POX0Ss\n",
"lnQL6bDyy4tHB9Bz4H0VkVaPlbRet4s5PL4Tv0w9L3wh04DPd9uPDZ2so9tkA+y8M9MAx5Q1QG6X\n",
"fW5RYwaGtWwGf+c0xy67MA04oT87Utxuxwxm2vcs4GJJvyWN2n2IdA7n+QCSTgNeGRH7Z/sfA5/I\n",
"Z6peStrq5VTS5qO3tHmPXw7CL1PhyScR1nLIWMfmsJbNYS2bw1o2g3Vsjg60nAq8utPyO+78RcRl\n",
"krYiHSu1DfBH4OBij7/JpC0DWva/ynsDfhb4NGnjz5uAg6obyppmGT+eus1GTYdYx+awls1hLZvD\n",
"WjaDdWyO4dZyUAs+Ih1GX3sAdkQcVZP2feD7g3kvM3imTOHBbvswGrCOzWEtm8NaNoe1bAbr2BzD\n",
"rWXHJ3wMN5Ji1ixO6rYfxhhjjDEjnKmzZvHeTlf7DupsX2OMMcYYs2Hizt8oZv58pnXbh9GAdWwO\n",
"a9kc1rI5rGUzWMfmGG4t3fkzxhhjjBlDOObPGGOMMWbDxDF/xhhjjDGmb9z5G8U4/qIZrGNzWMvm\n",
"sJbNYS2bwTo2h2P+jDHGGGNMYzjmzxhjjDFmw8Qxf8YYY4wxpm/c+RvFOP6iGaxjc1jL5rCWzWEt\n",
"m8E6Nodj/owxxhhjTGM45s8YY4wxZsPEMX/GGGOMMaZv3PkbxTj+ohmsY3NYy+awls1hLZvBOjaH\n",
"Y/6MMcYYY0xjOObPGGOMMWbDxDF/xhhjjDGmb9z5G8U4/qIZrGNzWMvmsJbNYS2bwTo2h2P+jDHG\n",
"GGNMYzjmzxhjjDFmw8Qxf8YYY4wxpm/c+RvFOP6iGaxjc1jL5rCWzWEtm8E6Nodj/owxxhhjTGM4\n",
"5s8YY4wxZsPEMX/GGGOMMaZv3PkbxTj+ohmsY3NYy+awls1hLZvBOjaHY/6MMcYYY0xjOObPGGOM\n",
"MWbDxDF/xhhjjDGmbwbV+ZP0YUl3S1opab6kGf3Y7ybpl5JWSFok6YTBuWs6wfEXzWAdm8NaNoe1\n",
"bA5r2QzWsTlGXMyfpEOBc4BTgN2BG4ErJW3Xxn5LYB7wAPAK4DjgU5I+PlinzcBYvJjJ3fZhNGAd\n",
"m8NaNoe1bA5r2QzWsTmGW8vBjPx9HJgTEd+MiAURcSypY3d0G/t/AiYAR0TEnyPicuBLuRwzjKxa\n",
"xYRu+zAasI7NYS2bw1o2h7VsBuvYHMOtZUedP0mbAHsAcyuP5gJ7t8k2Hbg+IlZV7LeV9IJO3t8Y\n",
"Y4wxxgyNjTu03xoYByyppC+FtkOUk4F7K2lLimf31OSZ2qFfpoaVK9kWazlkrGNzWMvmsJbNYS2b\n",
"wTo2RwdaDmqEsKOtXiRtCywC9omIXxXpM4HDI2LXmjxXA/dFxPuKtO2BhcD0iPhNxX5k7T1jjDHG\n",
"GDOC6XSrl05H/h4C1gCTKumTSHF/dTzIuqOCk4pnvei0AsYYY4wxZuB0FPMXEauBW4ADK48OIK36\n",
"reMm4DWSxlfsF0dE3ZSvMcYYY4wZJgaz2vcs4EhJ75X0IkmzSSN75wNIOk3Szwr7S4AVwIWSXiLp\n",
"bcBncjnGGGOMMWY90um0LxFxmaStgC8A2wB/BA6OiPuyyWRgx8L+cUkHAOcB84FHgDMj4uyhOm+M\n",
"McYYYzpjxJ3ta4wxxhhjho8Rc7Zvp0fGjTUkzZK0tnLdX2OzOB+j9wtJL648Hy/pq5KWSXpS0o8k\n",
"TVm/NVn/SNpH0o/z0YJrJR1RYzNk7SRNlHSxpEfzdZGkZw93/dYn/Wkp6cKadnpjxWbMaynpeEk3\n",
"S3pM0tKs6Utq7Nwu+2EgWrpdDgxJx0j6fdbyMUk3Sjq4YuM2OQD607LbbXJEdP7U4ZFxY5g7SNPq\n",
"rWu31gNJnyGdmvIR4JWkvRfnSdqiyH8O8DbgMOA1wJbAFZJGRDsYRjYH/kA6WnAl0Gu4u0HtLiG1\n",
"3zcAB5E2RL94GOrTTfrUMr+eR+92enDFxlrCa4F/JW2Cvx/wDPAzSRNbBm6XA6ZfLXG7HCj3AZ8G\n",
"/h7YE7gG+KGkl4PbZIf0qSXdbpMR0fUL+A3w75W0vwCndtu3kXIBs4A/tnkm0lY7xxdpE4DHgQ/k\n",
"188GVgHvLGymkrbuObDb9VuPOj4BvLtp7YAXAWtJe1e2bF6d03bpdr3Xh5Y57ULgv/vIYy3rddmc\n",
"1Gl5Y37tdtmQlm6XQ9bzYeD9bpPNaZnvu9omuz7io8EdGTdW2TEPt98l6TuSdsjpO5D2TvybhhHx\n",
"FHAdPRruCTyrYrMIuJ2xrfNQtZuek6YDT0bETUXZNwLLC5uxQAAzJC2RtEDS1yU9r3huLevZkjQT\n",
"89f82u1y8FS1BLfLjpE0TtJhpA7edbhNDpoaLaHLbbLj1b7DwGCOjBuL/Bo4gjT1O4m02vrGHNvS\n",
"0qlOw23z/WRgTUQ8XLFZwrqbdo8lhqrd5MJmWfkwIkLSWGvHVwGXA3eTvixOAa6RtGekfUKtZT2z\n",
"gVtJ+6KC2+VQqGoJbpcDRtJuJO3Gk0I7DomIBZJaHTy3yQHSTsv8uKttciR0/swAiIiripd/knQT\n",
"qdEcQZo2b5t1WB0b3fSnnU+jqRAR3y1e3ibpFtL53W8EftBH1jGrpaSzSCMnMyLP2/SD22Ub2mnp\n",
"dtkRdwAvI007vgO4VNLr+snjNllPrZYRMb/bbbLr074M7si4MU9ErABuA3amR6c6DVtH6D0IjFPa\n",
"o7FkMjXH7I0hWnUfjHZVm3LIHkkCns8Y1jciHiCdB75zTrKWBZLOBg4F9ouIhcUjt8sO6UPLdXC7\n",
"bE9EPB0Rd0XErRHxOdKs0zEM7XtmzOkIfWpZZ7te22TXO38xuCPjxjySJpCCPR+IiLtJv+gDK89n\n",
"0KPhLcDTFZupwK6MbZ2b0u4mYAtJZZzFdFLw+ZjVN8ewTKHni8NaZpROR2p1Vv5Seex22QH9aFln\n",
"73Y5cMYBGzX4PTNWdYSsZd2D9d4mu736JY/MH0Ja1fJeUodmNmkF0Xbd9m2kXMCZwD6k2IBXAVcA\n",
"j7Y0Ii0pfxR4K/BS4FLSfxGbF2X8G2n5+etJy89/AfyOvNn3aL3yB2H3fC0HTsj3jWoH/JS0Dcpe\n",
"+QP4R+BH3a7/+tIyPzsz138asG/+43SvtVxHx/OAx4DX0Xurh1Int8sGtHS77EjL00mduWmkrcRO\n",
"I83MHeA22ZyWI6FNdl2gogJHk/7bfQq4mRSz0XW/RsoFfAdYTOokLwK+B+xasTkRuJ8UWPoL4MWV\n",
"55sA55Km2pcDPwKmdLtu60G7fUlL39fmD1/r/oImtQOeQ9pf6bF8XQRs2e36ry8tSSvZriIFJK8C\n",
"Fub0qk5jXssa/VrXzIqd2+UQtXS77EjLOVmfp7Jec8kdP7fJ5rQcCW3Sx7sZY4wxxowhuh7zZ4wx\n",
"xhhj1h/u/BljjDHGjCHc+TPGGGOMGUO482eMMcYYM4Zw588YY4wxZgzhzp8xxhhjzBjCnT9jjDHG\n",
"mDGEO3/GGGOMMWOI/wf3gnYrw4JUVgAAAABJRU5ErkJggg==\n"
],
"text/plain": [
"<matplotlib.figure.Figure at 0x7f855513e050>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"addHeader(2,'Combined Graph')\n",
"\n",
"num_cols = sum([1 if x is not None else 0 for x in cols_to_plot])\n",
"#print \"num_cols:\", num_cols, \" :: \", \", \".join(sorted(list(set([x[0] if x is not None else None for x in cols_to_plot])-set([None]))))\n",
"#print \"\\n\".join( [ str( (x, y[0]) ) if y is not None else str( (x, \"None\") ) for x,y in enumerate(cols_to_plot) ] )\n",
"\n",
"with size_controller(CHROM_FIG_W, CHROM_FIG_H):\n",
" if True:\n",
" #fig, axes = plt.subplots(nrows=len(cols_to_plot)+2, ncols=1)\n",
" f = plt.figure()\n",
" \n",
" plt.subplots_adjust(wspace=0.5, hspace=0.5)\n",
"\n",
" num_extra_rows = 3\n",
" num_row_span = 3\n",
" \n",
" num_cols_e = num_cols + (num_extra_rows*num_row_span)\n",
" axes = []\n",
"\n",
" axes.append( [ plt.subplot2grid((num_cols_e,1), (0 , 0), rowspan=num_row_span) ] + cols_to_plot[0] )\n",
" axes.append( [ plt.subplot2grid((num_cols_e,1), (num_row_span, 0), rowspan=num_row_span) ] + cols_to_plot[1] )\n",
" \n",
" #print \"num_extra_rows\", num_extra_rows\n",
" #print \"num_row_span \", num_row_span\n",
" #print \"num_cols_e \", num_cols_e\n",
" \n",
" if BAC_MODE:\n",
" axes.append( [ plt.subplot2grid((num_cols_e,1), (num_row_span*2, 0), rowspan=num_row_span) ] + cols_to_plot[2] )\n",
" else:\n",
" axes.append( None )\n",
" \n",
" col_num = 3\n",
" plot_num = 0\n",
" for i in xrange( col_num, len(cols_to_plot) ):\n",
" y = (num_extra_rows*num_row_span)+plot_num\n",
" \n",
" try:\n",
" cold = cols_to_plot[col_num]\n",
" except:\n",
" continue\n",
" \n",
" while ( cold is None ) and ( col_num < len(cols_to_plot)-1 ):\n",
" col_num += 1\n",
" #print \" cn\", col_num,\"l\",len(cols_to_plot)\n",
" cold = cols_to_plot[col_num]\n",
" \n",
" if cold is not None:\n",
" #print 'i', i, 'y', y, 'col', col_num, 'num cols', num_cols, 'col name', cold[0]\n",
" axes.append( [ plt.subplot2grid((num_cols_e,1), (y, 0) ) ] + cold )\n",
" col_num += 1\n",
" plot_num += 1\n",
"\n",
" #print \"num_cols\", num_cols\n",
" #print \"axes\" , len(axes)\n",
"\n",
" axis_j = 0\n",
" for axis_i, axis_data in enumerate(axes):\n",
" if axis_data is None:\n",
" #print \" skip\"\n",
" continue\n",
" \n",
" axis, col_to_plot, col_ylim, col_yticks, col_color = axis_data\n",
" \n",
" #print \"For axis\", axis_i, \"col name\", col_to_plot\n",
" if axis is None:\n",
" #print \" skip\"\n",
" continue\n",
" \n",
" p = DataSampled[col_to_plot].plot(ax=axis, kind='area', fontsize=14, stacked=False, color=col_color)\n",
" \n",
" axis.set_title(col_to_plot, fontdict={'fontsize': 16, 'fontweight': 'bold'})\n",
" \n",
" if col_ylim is not None:\n",
" col_ylim_min, col_ylim_max = col_ylim\n",
" \n",
" if col_ylim_min is not None:\n",
" axis.set_ylim( bottom = col_ylim_min )\n",
" \n",
" if col_ylim_max is not None:\n",
" axis.set_ylim( top = col_ylim_max )\n",
" \n",
" \n",
" if col_yticks is not None:\n",
" if col_yticks == 0:\n",
" axis.set_yticks([])\n",
" \n",
" else:\n",
" ylim_min, ylim_max = axis.get_ylim()\n",
" ylim_diff = ylim_max - ylim_min\n",
" ylim_step = ylim_diff / (col_yticks*1.0)\n",
" #print col_to_plot, ylim_min, ylim_max, ylim_diff, ylim_step\n",
" axis.set_yticks(np.arange(ylim_min,ylim_max+ylim_step,ylim_step))\n",
" \n",
" plt.tight_layout()\n",
" curr_fig = plt.gcf()\n",
" #curr_fig.set_size_inches(CHROM_FIG_W/5.0, CHROM_FIG_H/5.0)\n",
" for of in output_files['Combined graph']:\n",
" print \"Saving Image:\", of\n",
" curr_fig.savefig(of, dpi=300)\n",
" #curr_fig.set_size_inches(CHROM_FIG_W, CHROM_FIG_H)"
]
},
{
"cell_type": "code",
"execution_count": 431,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Saulo Aflitos Last updated: 30/06/2015 \n",
"\n",
"CPython 2.7.9\n",
"IPython 3.0.0\n",
"\n",
"numpy 1.9.2\n",
"scipy 0.15.1\n",
"matplotlib 1.4.3\n",
"pandas 0.16.0\n",
"IPython 3.0.0\n",
"\n",
"compiler : GCC 4.4.7 20120313 (Red Hat 4.4.7-1)\n",
"system : Linux\n",
"release : 3.13.0-46-generic\n",
"machine : x86_64\n",
"processor : x86_64\n",
"CPU cores : 80\n",
"interpreter: 64bit\n",
"host name : assembly\n",
"Git hash : 5f46e34ab0d66890231b7cebb0d492969ea23a90\n"
]
},
{
"data": {
"text/html": [
"<script>\n",
"\n",
"scroll_show=true; \n",
"function scroll_toggle() {\n",
" if (scroll_show){\n",
" $('.output_scroll').css('overflow', 'visible');\n",
" $('.output_scroll').css('height' , 'auto' );\n",
"\n",
" var classes_to_hide = ['div.input', 'div.output_stderr', 'div.output_prompt', 'div.input_prompt', 'div.prompt', 'div.out_prompt_overlay.prompt'];\n",
"\n",
" for ( var c in classes_to_hide ) {\n",
" $(classes_to_hide[c]).hide();\n",
" $(classes_to_hide[c]).css('visibility', 'hidden');\n",
" }\n",
" } else {\n",
" $('.output_scroll').css('overflow', 'scroll');\n",
" $('.output_scroll').css('height' , '2.4em' );\n",
"\n",
" var classes_to_hide = ['div.input', 'div.output_stderr', 'div.output_prompt', 'div.input_prompt', 'div.prompt', 'div.out_prompt_overlay.prompt'];\n",
"\n",
" for ( var c in classes_to_hide ) {\n",
" $(classes_to_hide[c]).show();\n",
" $(classes_to_hide[c]).css('visibility', 'visible');\n",
" }\n",
" }\n",
" scroll_show = !scroll_show;\n",
"} \n",
"$( document ).ready(scroll_toggle);\n",
"</script>\n",
"<form action=\"javascript:scroll_toggle()\"><input type=\"submit\" value=\"Click here to toggle on/off the raw code.\"></form>"
],
"text/plain": [
"<IPython.core.display.HTML object>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"if CONFIG_LOCAL:\n",
" %run -i probes_cfg_footer.ipynb"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.9"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| mit |
Jackie789/JupyterNotebooks | CorrectingForAssumptions.ipynb | 1 | 87042 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Engineering Existing Data to Follow Multivariate Linear Regression Assumptions\n",
"\n",
"Jackie Zuker\n",
"\n",
"### Assumptions: \n",
"1. **Linear relationship** - Features should have a linear relationship with the outcome\n",
"2. **Multivariate normality** - The error from the model should be normally distributed\n",
"3. **Homoscedasticity** - The distribution of error should be consistent for all predicted values\n",
"4. **Low multicollinearity** - correlations between features should be low or non-existent"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The model in use has problems with heterscedasticity and multivariate non-normality. "
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"import math\n",
"import warnings\n",
"\n",
"from IPython.display import display\n",
"from matplotlib import pyplot as plt\n",
"import numpy as np\n",
"import pandas as pd\n",
"import seaborn as sns\n",
"from sklearn import linear_model\n",
"#import statsmodels.formula.api as smf\n",
"#import statsmodels as smf\n",
"\n",
"# Display preferences.\n",
"%matplotlib inline\n",
"pd.options.display.float_format = '{:.3f}'.format\n",
"\n",
"# Suppress annoying harmless error.\n",
"warnings.filterwarnings(\n",
" action=\"ignore\",\n",
" module=\"scipy\",\n",
" message=\"^internal gelsd\"\n",
")"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>TV</th>\n",
" <th>Radio</th>\n",
" <th>Newspaper</th>\n",
" <th>Sales</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>230.100</td>\n",
" <td>37.800</td>\n",
" <td>69.200</td>\n",
" <td>22.100</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>44.500</td>\n",
" <td>39.300</td>\n",
" <td>45.100</td>\n",
" <td>10.400</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>17.200</td>\n",
" <td>45.900</td>\n",
" <td>69.300</td>\n",
" <td>9.300</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>151.500</td>\n",
" <td>41.300</td>\n",
" <td>58.500</td>\n",
" <td>18.500</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>180.800</td>\n",
" <td>10.800</td>\n",
" <td>58.400</td>\n",
" <td>12.900</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" TV Radio Newspaper Sales\n",
"1 230.100 37.800 69.200 22.100\n",
"2 44.500 39.300 45.100 10.400\n",
"3 17.200 45.900 69.300 9.300\n",
"4 151.500 41.300 58.500 18.500\n",
"5 180.800 10.800 58.400 12.900"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n",
"Coefficients: \n",
" [[ 0.04576465 0.18853002 -0.00103749]]\n",
"\n",
"Intercept: \n",
" [ 2.93888937]\n",
"\n",
"R-squared:\n",
"0.897210638179\n"
]
}
],
"source": [
"# Acquire, load, and preview the data.\n",
"data = pd.read_csv(\n",
" 'http://www-bcf.usc.edu/~gareth/ISL/Advertising.csv',\n",
" index_col=0\n",
")\n",
"display(data.head())\n",
"\n",
"# Instantiate and fit our model.\n",
"regr = linear_model.LinearRegression()\n",
"Y = data['Sales'].values.reshape(-1, 1)\n",
"X = data[['TV','Radio','Newspaper']]\n",
"regr.fit(X, Y)\n",
"\n",
"# Inspect the results.\n",
"print('\\nCoefficients: \\n', regr.coef_)\n",
"print('\\nIntercept: \\n', regr.intercept_)\n",
"print('\\nR-squared:')\n",
"print(regr.score(X, Y))"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX0AAAETCAYAAADah9Z7AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XlcVOX+B/DPAUKTRUPbzDQtEb3mEqQggkoCiuCSWyJk\nP03KNEMTcUEwF9wtw6tm3np5VfSmmUteV9RAUPI1bSBKhrmQCLixqgzM8/vDnJsBwwgcBng+7788\nZzjP833OjJ955pwzZxQhhAAREUnBzNQFEBFRzWHoExFJhKFPRCQRhj4RkUQY+kREEmHoExFJhKFf\nB7Vr1w5+fn4YNGgQBg8eDG9vbwwdOhRJSUmVbnP27NlISEgotT4pKQkeHh6Vbjc9PR1du3at9PbV\nISwsDMnJyY+8XUhICH799ddyH9+5cyfeeeedqpRWJQcOHEBgYGCZj40dOxY3b958pPa2b9+OLVu2\nAACioqIwb968Ktf4V+W9xv7KUL9/rS85ORlz5syp1vpkwdCvozZu3Ijdu3dj165dOHjwIHx8fLBg\nwYJKt7dw4UL06NGjGiusPRISEvCoX0f573//CxsbG9jb26tUlbri4+MfeRuNRoO7d++qUM19VX2N\n/bW+jh07ori4GMeOHauu8qRhYeoCqOqKi4uRkZGBxo0b69etXbsWhw4dgk6nw3PPPYeIiAg8/fTT\nOHToENauXQtFUWBubo7p06fj1VdfRWBgIEaPHo1+/fohOjoaGzduhLW19UOhFxUVhVu3biE8PLzU\n8k8//YRly5ahqKgI2dnZ6NGjByIjIw3WfezYMXzyySfQ6XRo1KgRPvroIzg4OODIkSNYvXo1SkpK\nYG1tjZkzZ6JTp04G+w8MDESXLl3www8/ICMjA46OjliyZAlWrVqFrKwsTJs2DUuXLkVmZmaZ4/+7\nqKgorFq1CgCQnZ2N0NBQ3Lp1CwDQq1cvBAcHP/T3Bw4cwPLly7F+/Xq0adMG27dvx9atW6HT6dCk\nSRPMmTMHWq0W77zzDr777jsAwLhx49C0aVMsXboURUVFcHNzw+HDh5GdnY2FCxfi9u3bKCkpQWBg\nIIYNGwYAWLVqFfbu3YsmTZqgVatWZe7XmTNnAgDGjBmD9evXIz8/H/PmzcPt27ehKArGjh2LwYMH\nP7TN4cOHcfToUcTHx6Nhw4YAgAsXLiAwMBDZ2dlo1qwZVq5ciaeeegqZmZmYN28eMjIyoNVqMWDA\nALz77rul6ggMDETjxo1x4cIFjBo1CocOHdK/xnbu3In169ejYcOGcHZ2xr///W+kpKSU2+/PP//8\nUH2jR4/GyJEjMXfuXPTp08fg64z+RlCdY29vL3x9fYWfn59wdXUVHh4eYv78+eL69etCCCG++eYb\nERwcLLRarRBCiG3btom3335bCCHEa6+9Jn788UchhBBxcXEiKipKCCFEQECA2L9/v0hJSREuLi4i\nKytLCCHEnDlzRJ8+fYQQQnz66afio48+0tfx1+UpU6aIU6dOCSGEyM/PF927dxdJSUniypUrokuX\nLqXGkJ2dLRwdHUVKSooQQoiDBw+KcePGid9++0306NFDXL58WQghREJCgnB1dRV5eXkG+w8ICBCT\nJ08WJSUlIi8vT/Ts2VOcPHlSCCFEnz59xC+//GJw/H+VmpqqH7MQQqxevVrMmTNHCCFEQUGBCA4O\nFrm5ueLrr78WQUFBYs+ePWLAgAHi6tWrQgghEhMThb+/vygsLNT3079/fyGEEB4eHiI1NVXcuXNH\n9OnTR7i7uwshhDh+/Lh4++23hVarFT4+PiI5OVkIIURubq7o37+/+PHHH8Xhw4eFj4+PyMvLE1qt\nVgQFBYmAgIBS9Qtx/zVy48YNodVqxWuvvSYOHjwohBDi2rVrws3NTfzwww+ltgkNDRUbNmzQ71sP\nDw9x48YNIYQQEyZMEKtXrxZCCBEYGChiYmKEEELcvXtXBAYGin379pVqLyAgQMycOfOh5f3794vz\n588LFxcXkZGRIYQQIioqStjb21fY71/re8DZ2Vn/WiHjcKZfR23cuBF2dnZISUnB+PHj0bVrVzRt\n2hTA/Rl0UlIShg4dCgDQ6XS4c+cOAGDAgAGYNGkSevXqBVdXV4wfP/6hdk+ePAlXV1c8+eSTAICR\nI0fixIkTFdazePFixMbGYt26dbhw4QLu3r2LwsJCNGnSpMy//+GHH9C2bVu0b98eAODl5QUvLy9s\n2bIFzs7OeP755wEALi4usLOzM+qYfJ8+fWBmZgZra2u0atUKOTk5pf6movED92eaLVu21C+7ubkh\nKCgIGRkZ6NGjBz788EPY2NgAuH/OIy4uDrNmzcKzzz4LADh+/DguXbqEN954Q99GTk4Obt++DU9P\nT8TGxsLe3h7du3dHamoqzp8/j5iYGHh5eeHixYu4fPkyZs2apd/27t27SElJQVpaGjw9PWFtbQ0A\nGDp0KDZt2mRwn1y8eBH37t2Dl5cXAODpp5+Gl5cX4uLiKjzX4urqCjs7OwCAg4MDbt68icLCQpw+\nfRo5OTn6T0KFhYU4d+4cfHx8SrXh5ORUat2JEyfg6uqKZ555BgAQEBCAqKgog/2W5/nnn8fvv/+u\nf71QxRj6dVyHDh0wc+ZMhIWFoXPnzmjRogV0Oh3efvtt+Pv7AwCKior0AThlyhQMGzYMJ06c0H/E\n3rlzp749RVEeOv5tbm5e7mNarVb/79GjR8PBwQFubm7o378/fv75Z4PH0c3NzaEoin5ZCIHU1NQy\ntxFCoLi42GD/APSHJcqq9YHyxm9m9r/TW2ZmZigpKdEvd+rUCTExMTh58iROnTqF4cOH45///CcA\nwMbGBitWrEBwcDB69+6t3/+DBg1CSEgIgPtvullZWWjcuDE8PT3xySefICsrC66urmjatClOnDiB\n2NhYBAcHIzs7G7a2tti9e7e+/+vXr8PGxgbLli0r97kpj06nK3d/VsTC4n/x8GB/6nQ6CCGwbds2\nPP744wCAmzdvokGDBmW20ahRo1LrzM3NDY6jrH7LU1JSYtR+oP/hidx6wNfXF126dNEfQ+/Zsyd2\n7NiB/Px8APePA0+fPh3FxcXw8PBAYWEhRo0ahYiICKSlpT0UAD169EB8fDyuXbsGAPjmm2/0jz3x\nxBM4c+YMhBAoLCzUfwLIyclBcnIypk2bBi8vL2RmZuLy5ctlBs4DnTt3RlpaGs6fPw8AiImJQUhI\nCJydnREfH48rV64AuP/JIyMjA507dy63/4qYm5ujuLjYqPEDwAsvvID09HT98vLly7FmzRr07dsX\ns2fPxksvvYSLFy/q/9bFxQWBgYEIDQ2FTqeDq6sr9u3bh6ysLADA1q1bMWbMGABA165dcfnyZRw/\nfhw9evSAq6srNm7ciBdeeAF2dnZo3bo1GjRooA/9jIwM+Pr6Ijk5GW5ubjhw4AByc3Oh0+keemMo\nb8ytW7fGY489hkOHDgEAMjMzcfDgwTJPqD7YxhBra2t06dIFX375JQAgNzcXo0aNQkxMjMHt/qpn\nz544efIkMjMzAdy/KscYf69PCIE//vgDrVu3Nrpv4ky/3pgzZw4GDhyIuLg4DB8+HJmZmRgxYgQU\nRcGzzz6LxYsXw8LCArNmzcK0adNgYWEBRVEQGRkJS0tLfTvt2rVDSEgIxowZAysrK3Tq1En/2IP2\nvby88PTTT6Nr164QQqBx48YICgrCkCFD0KRJEzzxxBN45ZVXcOnSpXI/djdr1gzLly9HaGio/oTt\nxx9/jJdeegkRERGYNGkSSkpK0LBhQ6xbtw42Njbl9l+Rvn37YsqUKViwYEGF4wcAe3t7NGjQAGlp\naXjxxRcxZswYzJgxA76+vrC0tES7du3g6+uLb7/9Vr/Nu+++i6NHj2LDhg0ICgrC+PHjMXbsWCiK\nAmtra6xevRqKokBRFPTq1QtJSUmws7ODo6MjcnJy9IdfLC0tsWbNGixcuBAbNmxAcXExPvjgAzg6\nOgIAUlNTMXToUNja2sLBwUF/cvnvPD094e/vjzVr1mDNmjVYsGABoqKiUFJSgokTJ8LZ2bnUNu7u\n7pg/f36F+3P58uWYP38+/Pz8UFRUBF9fXwwcOLDC7R5o3bo1Zs6ciXHjxsHS0hLt27fXf2ow5K/1\nvfPOO0hKSkLLli3RvHlzo/smQBHG/K8hkszevXuh0Wgwd+5cU5dS71y5cgW7d+/Ge++9BzMzMxw6\ndAiff/650TP+B2bMmIF+/fqhd+/e6hRaT3GmT1QGPz8/xMTEIDU1Fe3atTN1OfXKM888g6ysLPj5\n+cHc3Bw2NjYVXt77d0lJSVAUhYFfCZzpExFJhCdyiYgkwtAnIpJIrT6mr9FoTF0CEVGd9OCKr7+r\n1aEPlF+4qWg0mlpXU1XUt/EA9W9MHE/tVhvHY2jCzMM7REQSYegTEUmEoU9EJBGGPhGRRBj6REQS\nYegTEUmEoU9EJBGGPhGRRBj6REQSqfXfyCUi8vuw/F8JU9PeFYNM0q+aONMnIpIIQ5+ISCI8vENE\nRqu2wyzR6RX/DalC1dD/7LPPcPToUWi1WowaNQrdunXDjBkzoCgK2rZti4iICJiZ8cMGEVFNUS1x\nExMT8eOPP2Lr1q3YtGkTrl27hkWLFiE4OBjR0dEQQiAmJkat7omIqAyq/UbuihUroCgKzp8/j/z8\nfEyfPh3vvfceYmNjoSgKjhw5gvj4eERERJTbBn9Ehah2mSvZYZm5/i1MXUKl1fiPqNy6dQtXr17F\nunXrkJ6ejgkTJkAIAUVRAABWVlbIy8ursJ3a+OMEta2mqqhv4wHq35hq1XgkC31j9nuten7+ZGjC\nrFroN2nSBG3atIGlpSXatGmDBg0a4Nq1a/rHCwoKYGtrq1b3RERUBtWO6Ts6OiIuLg5CCGRmZuLO\nnTtwcXFBYmIiACA2NhZOTk5qdU9ERGVQbabfp08fnD59GsOGDYMQAuHh4WjRogXmzJmDlStXok2b\nNvD29lareyIiKoOql2xOnz691LrNmzer2SURERnAi+SJiCTC0CcikghDn4hIIgx9IiKJMPSJiCTC\n0CcikghDn4hIIgx9IiKJMPSJiCTC0CcikghDn4hIIgx9IiKJMPSJiCTC0CcikghDn4hIIgx9IiKJ\nMPSJiCTC0CcikghDn4hIIgx9IiKJMPSJiCTC0CcikghDn4hIIgx9IiKJMPSJiCRioWbjQ4YMgbW1\nNQCgRYsWGDlyJBYuXAhzc3P07NkTkyZNUrN7IiL6G9VC/969exBCYNOmTfp1gwYNQlRUFJ5//nkE\nBQUhJSUFHTp0UKsEIiL6G9UO75w7dw537tzB2LFj8eabb+L06dMoKipCy5YtoSgKevbsiYSEBLW6\nJyKiMqg202/YsCHGjRuH4cOH4+LFixg/fjxsbW31j1tZWeHKlSsVtqPRaNQqsdJqY01VUd/GA9S/\nMdW38dQVxu73uvT8qBb6rVu3RqtWraAoClq3bg0bGxvcvn1b/3hBQcFDbwLlcXR0VKvEStFoNLWu\npqqob+MB6t+YatV4otNNXUGNMma/16rn50+G3oRUO7yzY8cOLF68GACQmZmJO3fuoFGjRrh8+TKE\nEDhx4gScnJzU6p6IiMqg2kx/2LBhmDlzJkaNGgVFURAZGQkzMzNMmzYNJSUl6NmzJzp37qxW90RE\nVAbVQt/S0hIrVqwotf6rr75Sq0siIqoAv5xFRCQRhj4RkUQY+kREEmHoExFJhKFPRCQRhj4RkUQY\n+kREEmHoExFJhKFPRCQRhj4RkUQY+kREEmHoExFJhKFPRCQRhj4RkUQY+kREEmHoExFJhKFPRCQR\nhj4RkUQY+kREEmHoExFJhKFPRCQRhj4RkUQY+kREEmHoExFJhKFPRCQRhj4RkURUDf0bN26gV69e\nSEtLw6VLlzBq1Cj4+/sjIiICOp1Oza6JiKgMqoW+VqtFeHg4GjZsCABYtGgRgoODER0dDSEEYmJi\n1OqaiIjKYaFWw0uWLMEbb7yB9evXAwDOnDmDbt26AQDc3d0RHx8PT0/PCtvRaDRqlVhptbGmqqhv\n4wHq35jq23jqCmP3e116flQJ/Z07d8LOzg5ubm760BdCQFEUAICVlRXy8vKMasvR0VGNEitNo9HU\nupqqor6NB6h/Y6pV44lON3UFNcqY/V6rnp8/GXoTUiX0v/76ayiKgpMnT+Ls2bMIDQ3FzZs39Y8X\nFBTA1tZWja6JiMgAVUJ/y5Yt+n8HBgZi7ty5WLZsGRITE9G9e3fExsbC2dlZja6JiMiAGrtkMzQ0\nFFFRURg5ciS0Wi28vb1rqmsiIvqTaidyH9i0aZP+35s3b1a7OyIiMoBfziIikghDn4hIIgx9IiKJ\nMPSJiCTC0CcikghDn4hIIgx9IiKJGBX658+fL7Xup59+qvZiiIhIXQa/nKXRaKDT6RAWFoaFCxdC\nCAEAKC4uxty5c3Hw4MEaKZKIiKqHwdBPSEjA999/j6ysLKxatep/G1lYYOTIkaoXR0RE1ctg6L//\n/vsAgF27dmHw4ME1UhAREanHqHvvvPrqq1iyZAlycnL0h3iA+7+GRUREdYdRoR8cHAwnJyc4OTnp\nfwiFiIjqHqNCv7i4GKGhoWrXQkREKjPqkk1HR0ccPXoURUVFatdDREQqMmqmf+DAgVL3wlcUBWfP\nnlWlKCIiUodRoX/ixAm16yAiohpgVOivXr26zPWTJk2q1mKIiEhdj3zvHa1Wi6NHj+LGjRtq1ENE\nRCoyaqb/9xn9xIkTMXbsWFUKIiIi9VTqLpsFBQW4evVqdddCREQqM2qm7+Hhof9SlhACubm5GDdu\nnKqFERFR9TMq9Ddt2qT/t6IosLW1hbW1tWpFERGROowK/ebNm2Pr1q04deoUiouL4ezsjICAAJiZ\n8TdYiIjqEqNCf+nSpbh06RKGDh0KIQR27tyJK1euYPbs2WrXR0RE1cio0I+Pj8euXbv0M/vevXvD\nz8/P4DYlJSUICwvD77//DkVR8NFHH6FBgwaYMWMGFEVB27ZtERERwU8LREQ1yKjQLykpQXFxMSwt\nLfXL5ubmBrc5duwYAGDbtm1ITEzExx9/DCEEgoOD0b17d4SHhyMmJgaenp5VHAIRERnLqND38/PD\nm2++iQEDBgAA9u3bB19fX4Pb9O3bF7179wYAXL16Fba2tkhISEC3bt0AAO7u7oiPj2foExHVoApD\nPycnByNGjED79u1x6tQpJCYm4s033zTql7QsLCwQGhqKw4cP49NPP0V8fLz+0k8rKyvk5eVV2IZG\nozFiGDWrNtZUFfVtPED9G1N9G09dYex+r0vPj8HQT0lJQVBQECIjI9GrVy/06tULK1euxIoVK+Dg\n4AAHB4cKO1iyZAmmTZuGESNG4N69e/r1BQUFsLW1rXB7R0dHI4ZRczQaTa2rqSrq23iA+jemWjWe\n6HRTV1CjjNnvter5+ZOhNyGDZ1GXLFmCFStWwN3dXb9u6tSpiIyMxOLFiw12umvXLnz22WcAgMcf\nfxyKoqBjx45ITEwEAMTGxsLJycnoQRARUdUZDP3c3Fx079691Ho3NzfcunXLYMNeXl5ISUnB6NGj\nMW7cOMyaNQvh4eGIiorCyJEjodVq4e3tXbXqiYjokRg8vFNcXAydTlfqskqdTgetVmuw4UaNGmHV\nqlWl1v/9x1iIiKjmGJzpv/rqq2XeS3/NmjXo2LGjakUREZE6DM70p06diqCgIOzduxcvv/wyhBBI\nSUmBnZ0d1q5dW1M1EhFRNTEY+tbW1tiyZQtOnTqFs2fPwszMDKNHj+YJWCKiOqrC6/QVRYGLiwtc\nXFxqoh4iIlIRb3xDRCQRhj4RkUQY+kREEmHoExFJhKFPRCQRhj4RkUQY+kREEmHoExFJhKFPRCQR\nhj4RkUQY+kREEjHqh9GJqPbw+3C3qUugOowzfSIiiTD0iYgkwsM7RETlMPpQWnR6tfe9d8Wgam8T\n4EyfiEgqDH0iIokw9ImIJMLQJyKSCEOfiEgiDH0iIomocsmmVqvFrFmz8Mcff6CoqAgTJkzASy+9\nhBkzZkBRFLRt2xYREREwM+N7DhFRTVIl9Pfs2YMmTZpg2bJluH37NgYPHgwHBwcEBweje/fuCA8P\nR0xMDDw9PdXonoiIyqHKVLtfv3744IMPAABCCJibm+PMmTPo1q0bAMDd3R0JCQlqdE1ERAaoMtO3\nsrICAOTn52Py5MkIDg7GkiVLoCiK/vG8vDyj2tJoNGqUWCW1saaqqG/jAerfmOrbeKhiaj3nqt2G\nISMjAxMnToS/vz/8/PywbNky/WMFBQWwtbU1qh1HR0e1SqwUjUZT62qqivo2HqD+janUeFT4yj/V\nPlV5DRt6w1Dl8M7169cxduxYhISEYNiwYQCADh06IDExEQAQGxsLJycnNbomIiIDVJnpr1u3Drm5\nuVizZg3WrFkDAJg9ezYWLFiAlStXok2bNvD29laja6IaU6P3tefsnqqJKqEfFhaGsLCwUus3b96s\nRndERGQkXihPRCQRhj4RkUQY+kREEmHoExFJhKFPRCQRhj4RkUQY+kREEmHoExFJhKFPRCQRhj4R\nkUQY+kREEmHoExFJhKFPRCQRhj4RkUQY+kREEmHoExFJhKFPRCQRhj4RkUQY+kREEmHoExFJhKFP\nRCQRhj4RkUQY+kREEmHoExFJhKFPRCQRhj4RkURUDf2ff/4ZgYGBAIBLly5h1KhR8Pf3R0REBHQ6\nnZpdExFRGVQL/c8//xxhYWG4d+8eAGDRokUIDg5GdHQ0hBCIiYlRq2siIiqHhVoNt2zZElFRUZg+\nfToA4MyZM+jWrRsAwN3dHfHx8fD09KywHY1Go1aJlVYba6qK+jYeoH6OieSi1mtYtdD39vZGenq6\nflkIAUVRAABWVlbIy8szqh1HR0dV6qssjUZT62qqivo2HqAGxxSdXvHfEFVSVV7Dht4wauxErpnZ\n/7oqKCiAra1tTXVNRER/qrHQ79ChAxITEwEAsbGxcHJyqqmuiYjoTzUW+qGhoYiKisLIkSOh1Wrh\n7e1dU10TEdGfVDumDwAtWrTAV199BQBo3bo1Nm/erGZ3RERUAX45i4hIIgx9IiKJMPSJiCTC0Cci\nkoiqJ3KJ1Ob34e6yH+AXp4jKxJk+EZFEGPpERBJh6BMRSYShT0QkEYY+EZFEGPpERBJh6BMRSYSh\nT0QkEYY+EZFEGPpERBJh6BMRSYShT0QkEYY+EZFEeJdNqhbl3u2SiGoVzvSJiCTC0CcikghDn4hI\nIgx9IiKJMPSJiCRSr6/eUe2Kkgp+f3XvikHq9EtEVEU1Gvo6nQ5z585FamoqLC0tsWDBArRq1aom\nSyAiklqNHt45cuQIioqK8J///AcffvghFi9eXJPdExFJr0ZDX6PRwM3NDQDQpUsXJCcn12T3RETS\nq9HDO/n5+bC2ttYvm5ubo7i4GBYW5Zeh0Wgq3d9c/xaV3rYqqlKzKVRHvaba10T1lVo5UqOhb21t\njYKCAv2yTqczGPiOjo41URYRkTRq9PDOK6+8gtjYWADATz/9BHt7+5rsnohIeooQQtRUZw+u3vn1\n118hhEBkZCRefPHFmuqeiEh6NRr6RERkWvxGLhGRRBj6REQSYegTEUmkXt97Rw15eXmYMmUKCgsL\nYWlpiWXLluHJJ580dVmVVlJSgkWLFiE5ORlFRUV4//330adPH1OXVWVpaWkYMWIEEhIS0KBBA1OX\nUyV5eXkICQlBfn4+tFotZsyYga5du5q6rEdW327DotVqMWvWLPzxxx8oKirChAkT8Nprr5m6rApx\npv+Idu7cCXt7e0RHR8PHxwf/+te/TF1SlezevRvFxcXYtm0b1q5di0uXLpm6pCrLz8/HkiVLYGlp\naepSqsWXX34JZ2dnbN68GYsWLcK8efNMXVKl1LfbsOzZswdNmjRBdHQ0NmzYgPnz55u6JKNwpv+I\n7O3tceHCBQD3w8XQl8vqghMnTqBt27YICgqCEAJz5swxdUlV8mAMU6dOxXvvvWfqcqrFW2+9pX8D\nKykpqbOfXOrbbVj69esHb29vAPdfd+bm5iauyDh1O7FUtn37dmzcuPGhdeHh4YiPj4ePjw9ycnKw\nZcsWE1X36MoazxNPPIEGDRrgs88+w+nTpzFz5sw6M6ayxtO8eXP4+PjAwcHBRFVVTVljioyMRKdO\nnZCdnY2QkBDMmjXLRNVVTWVuw1KbWVlZAbg/rsmTJyM4ONjEFRlJ0COZOHGi2Lp1qxBCiLNnzwpf\nX18TV1Q1wcHB4sCBA/rlHj16mLCaquvbt68ICAgQAQEBomPHjsLf39/UJVWLc+fOCR8fH3H8+HFT\nl1JpkZGRYt++ffplNzc3E1ZTPa5evSqGDBkitm/fbupSjFY332JNyNbWFjY2NgCApk2bPnQvobrI\n0dER3333Hby9vXHu3Dk8++yzpi6pSg4fPqz/t4eHB7744gsTVlM9fvvtN3zwwQf45JNP6uwnGOD+\nbViOHTsGHx+fenEbluvXr2Ps2LEIDw+Hi4uLqcsxGr+R+4gyMzMRFhaGwsJCFBcXY/LkyXB1dTV1\nWZVWVFSEiIgIpKWlQQiBuXPn4h//+Iepy6oWHh4e2L9/f509Bv7AhAkTkJqaiueeew7A/RsXrl27\n1sRVPbr6dhuWBQsWYP/+/WjTpo1+3eeff46GDRuasKqKMfSJiCTCSzaJiCTC0CcikghDn4hIIgx9\nIiKJMPSJiCTC0CcppKeno2PHjhg0aBAGDRoEPz8/eHh44NNPP33ktmbPno2kpKRS62fMmIGdO3dW\nqj4PDw+kp6dXaluiR8EvZ5E0nnrqKezevVu/nJmZCW9vbwwYMOCRrhdfuHChGuUR1QjO9Ela2dnZ\nEELAysoK69evx5AhQzBw4EAsXboUQgjk5+cjKCgIr7/+Ol5//XXExMQAAAIDA5GYmAghBBYtWgRv\nb28EBgbi8uXLAO5/qvDw8ND3ExUVhaioKADA5s2bMXz4cPj6+sLPzw9paWk1P3CSGmf6JI2srCwM\nGjQI9+7dw61bt/Dyyy9j9erV+PXXX5GcnIwdO3ZAURSEhIRgz5490Ol0eO6557B+/XqkpaVhx44d\nD90v/eBaTtdSAAACKElEQVTBg0hJScG3336LvLw8DBw40GD/+fn5OHLkCDZt2oSGDRti1apViI6O\nrvN3NqW6haFP0nhweEen02Hx4sVITU2Fs7MzVq5ciV9++QWvv/46AODu3bto3rw5hg4dipUrVyIz\nMxO9e/fGxIkTH2rv+++/h5eXFx577DHY2dnB3d3dYP/W1tZYsWIF9u3bh4sXLyIuLg7t27dXbbxE\nZWHok3TMzMwwffp0DB48GF988QVKSkowZswY/N///R8AIDc3F+bm5rCyssL+/fsRFxeHY8eO4Ysv\nvsD+/fv17SiKAp1Op19+cItgRVHw17ubPLh9cEZGBgIDAxEQEAB3d3c0a9YMZ8+eraFRE93HY/ok\nJQsLC0yfPh3r1q1Dhw4dsHv3bhQUFKC4uBgTJ07EwYMHsXnzZkRFRaF///6IiIjAzZs3kZeXp2/D\nxcUFBw4cQFFREXJychAXFwfg/p1Yc3JycPPmTRQVFenXJyUloVWrVnjrrbfQuXNnxMbGoqSkxCTj\nJ3lxpk/Scnd3R5cuXXD69Gl4eXlhxIgRKCkpgZubG4YMGYKCggJMnToVfn5+sLCwwKRJk2Bra6vf\nvm/fvkhKSoKvry+aNWumvwLIxsYG48aNw7Bhw/DMM8/g5ZdfBgC4urpi69at8PHxgaWlJTp16oTz\n58+bZOwkL95lk4hIIjy8Q0QkEYY+EZFEGPpERBJh6BMRSYShT0QkEYY+EZFEGPpERBL5f5Br1CCJ\nxDMgAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x110137588>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX0AAAETCAYAAADah9Z7AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztnXl4E1X3x79Zmja0QAuFUjYRka1QwCKbFKHslUJRQGUR\nra++KrIKKFBEWRRZfBVEVF71RX4o7oAKL/hSka1lqSJtQVSQtXvp3jRpkvv7oyYm6cxkJs3anM/z\n+EgnM3PP3Llz7rnnnnuujDHGQBAEQfgFck8LQBAEQbgPUvoEQRB+BCl9giAIP4KUPkEQhB9BSp8g\nCMKPIKVPEAThR5DSt0OXLl2QkJCACRMmIDExEaNHj8YDDzyAjIwMh++5bNkynDhxos7xjIwMxMXF\nOXzfGzduoE+fPg5fL4aTJ08iOjraXB8TJkzA/fffj5SUlHrfe9y4cTh58iTy8vLw0EMPCZ57/fp1\nzJ49W3IZ77//Pl544QXz33l5eXjqqadgG7nMV5ebN2/GypUr7Zbz1ltv4X//+59k+TzBypUrsXnz\nZoevT0pKwq1btwAATzzxBP744w/eczMyMjBnzhwAwLlz5/Diiy86XK63kJycjMzMTADA9u3bsXv3\nbg9LJIzS0wL4Atu3b0ezZs3Mf7///vtYvXo1Pv30U4fut2bNGmeJ5hHat2+PPXv2mP/+9ddf8fDD\nD+PQoUNW9eQoERER2LVrl+A52dnZ+PPPP+tdVnJyMubMmQOZTFbve1ly8uRJdOrUyan39FaOHz9u\n/ve2bdsEz+3Zsyc2bdoEAPjjjz+Ql5fnUtncwYkTJ/Dggw8CAKZPn45JkybhnnvuQYsWLTwsGTek\n9CWi1+uRk5ODpk2bmo9t3boVBw8ehNFoRJs2bbBixQpERETg4MGD2Lp1K2QyGRQKBRYvXoy7774b\nM2bMwLRp0zBmzBh8/PHH2L59O0JCQtC5c2fzPTdv3ozi4mKzJWT599mzZ7F+/XrodDoUFBRg0KBB\neOWVV3hlfv3111FRUWG+15EjR7B582Z88sknWLVqFX766ScEBASgbdu2ePXVVxEcHCypTrp27Yqg\noCDcvHkTO3fuxNmzZ5Gfn48uXbpgw4YNvPXzxx9/YOnSpdBoNOjYsSOqqqoA1FrZCQkJ+Pnnn6HX\n67F+/XocPnwYCoUCffr0wYoVK5CcnIy8vDw8/vjjeP/99/HTTz9hw4YN0Gg0kMlkmD17NoYNG4aa\nmhqsXr0aJ06cQPPmzdG8eXM0btwYAHD27FkUFRWhZ8+ekp7XRHl5OdasWYPffvsNNTU1GDhwIBYv\nXoxPP/0UmZmZWLduHRQKBe69915s2LABp0+fhsFgQPfu3ZGcnIyQkBDExcUhOjoaFy9exIIFC9Ch\nQwesXLkSJSUlkMlkSEpKQmJiIiorK7FkyRJcvXoVcrkcUVFRWLlyJeRyOb744gt8+OGHkMvlCAsL\nw2uvvYbIyEikpKRg69atqKmpQVBQEJ5//nn06dMHFRUVWLZsGX799Ve0bNkSCoUCMTExAIAffvgB\n7777LnQ6HW7duoXExETMmzePt/xly5YBAGbOnIn33nsP06ZNw5tvvomePXtyynXt2jWsWrUK27Zt\nw6ZNm1BeXo4lS5ZAoVCgWbNmWLBgAQBg7969OHDgALZs2WJV53FxcRgxYgTOnDmD8vJyPPbYY5g6\ndSpOnjyJNWvWoFGjRqiqqsIXX3yBY8eOcT7/pUuXsGzZMuh0OjDGMGnSJEybNg0A/7c8Y8YM9O7d\nGz/99BNycnIQExOD1157DW+++Sby8/OxcOFCrFu3Dr169cLYsWOxbds2LF261KF25XIYIUjnzp3Z\nuHHjWEJCArvnnntYXFwcW7VqFSssLGSMMfb111+zefPmsZqaGsYYY7t27WL/+Mc/GGOMDR8+nP38\n88+MMcaOHj3KNm/ezBhjbPr06Wz//v3s/PnzbODAgSw/P58xxtjy5cvZsGHDGGOMbdq0ib388stm\nOSz/nj9/PktLS2OMMVZRUcH69+/PMjIy2PXr11nv3r3rPMO1a9dY//79mVarZYwxNnfuXPbZZ5+x\n06dPszFjxjCj0cgYY2zdunUsPT1dsD7S0tLYfffdZ3XswIEDbNCgQayqqopt2rSJjR492lwfQvUz\nYcIE9tlnnzHGGDtz5gzr0qULS0tLs3qO7du3s2nTpjGNRsMMBgObO3cu+/rrr63kKCkpYaNGjWLX\nr19njDGWm5vLhgwZwm7evMn+85//sEceeYRptVpWWVnJJk6cyJ5//nnGGGNr165lmzZt4nzO69ev\ns65du7Lx48db/Tdo0CDze3jhhRfYRx99xBhjTK/Xs4ULF7L33nuPMfb3O2aMsc2bN7O1a9ea63nj\nxo1sxYoVjDHGhg0bxt566y3GGGM1NTVs+PDh7MCBA+bniI2NZT/99BP7+uuvWVJSkrmsZcuWsStX\nrrALFy6w/v37s+zsbMYYYx9++CFbvnw5+/PPP9m4cePYrVu3GGOM/fbbb+yee+5hlZWVbM2aNWzx\n4sXMaDSyoqIiNmTIELZp0yZmNBrZ9OnT2Z9//mkuv1u3bqyoqIi3fMZqv5GioiLz85w7d45XLsv3\n9uWXX7Inn3ySMcbY+fPn2T333GNuJ1OnTmVHjhyp816GDRvGli9fzoxGI8vJyWH9+/dnv/76K0tL\nS2Ndu3ZlN27cYIwxwedfsmQJe/fddxljjOXn57N58+Yxg8Eg2FanT5/O5syZwwwGAysvL2eDBw9m\nqampVs9s4rfffmNDhw7lbFfeAFn6IjC5d86fP48nnngCffr0QfPmzQHUWkYZGRl44IEHAABGoxEa\njQYAcN999+HZZ5/Fvffei3vuuQdPPPGE1X1TU1OthoEPPvggjh07ZleetWvX4siRI3jnnXdw+fJl\nVFdXo6qqCqGhoZznt2vXDl27dkVKSgoGDhyI1NRUrFmzBgaDAQqFApMnT8bgwYMxevRoREdH2y3/\n2rVrmDBhAoDakU+rVq3w9ttvQ61WAwB69+4NpVIpWD/FxcW4ePEiEhMTAQAxMTG4884765R14sQJ\nTJgwAUFBQQCAN954A0Ct+8TE2bNnUVBQgFmzZpmPyWQyXLx4EampqRg3bhxUKhVUKhUSEhJw8eJF\nAMDly5cRHx/P+5xBQUFWbizg7xEXABw+fBgZGRn44osvAADV1dWc9zl8+DDKy8vN8zg1NTXm9gMA\nffv2BQBcuXIFWq0Wo0aNAlDr5ho1ahSOHj2KiRMn4l//+hdmzJiBQYMGYebMmbjtttvw4YcfYvDg\nwYiMjAQAPProowCAnTt3Ij8/3/y3qU6uXbuG1NRULF26FDKZDM2aNcPIkSPNv7/zzjs4fPgwvv32\nW1y6dAmMMWg0GsTExHCWz0dqaiqnXJbvzZJu3bqhbdu2OHz4MG6//Xbk5+dj8ODBnOdOnToVMpkM\nrVq1QmxsLI4fP46oqChERkaiTZs2AGpdTnzPP3LkSDz//PM4d+4cBg4ciOTkZMjlcsFvGQCGDRsG\nuVyOkJAQ3HbbbSgtLeWUr3379sjOzoZWq0VgYCBvHXkKUvoS6N69O5YsWYLk5GT06tULbdu2hdFo\nxD/+8Q9MnToVAKDT6cyNYf78+Zg0aRKOHTuGr776Cu+99x6++uor8/1kMpnVBKJCoeD9raamxvzv\nadOmoWvXroiNjcXYsWPxyy+/1JmItGXy5MnYvXs3ioqKMHLkSLMLZ8+ePfjpp5+QlpaGefPm4ZFH\nHrH6ULiw9enb0qhRI/O/+erH5EO3lNvUUVhie6ywsBBGo9HqmMFgwB133IHPP//cfCwvLw/NmjWr\nM+9iW8e295KC0WjEm2++iTvuuAMAUFZWxjk3YDQasXTpUtx7770AgMrKSmi1WvPvpvrikoUxBr1e\nj3bt2uH777/HyZMnkZaWhsceewzJyclQKBRWZVZXV+PmzZswGo0YOHCguZMEgJycHLRs2dJ8XxOm\nOqmqqsLEiRMxYsQI9O3bFw888AD+97//gTHGW/6YMWM464ZPLiGmTZuGL7/8Eh06dMCUKVN451ks\n24TRaIRcLreqR9Nxvufv2rUrDhw4gBMnTiA1NRVbtmzBrl27BL9lAGbDA6j7fVpiMBggk8mcPk/k\nLCh6RyLjxo1D7969zT70wYMH44svvkBFRQUA4M0338TixYuh1+sRFxeHqqoqPPzww1ixYgUuXboE\nvV5vvtegQYNw/Phx5ObmAgC+/vpr829hYWHIysoCYwxVVVXmEUBpaSkyMzOxcOFCjBo1Cnl5ebh2\n7Zpd5TVy5EhkZWXhs88+w5QpUwDUWuGPPvoo+vTpg9mzZyMxMRG//vqr8ypLoH5CQ0MRFRVlVtRZ\nWVn47bff6lw/cOBAfPvtt9DpdDAajXjppZfw3XffQaFQmDvC3r174+rVqzh9+jQA4MKFCxg9ejTy\n8/MRGxuL3bt3Q6vVQqvVYt++feZ733777bh+/Xq9nu0///kPGGPQ6XR4+umn8X//938AapWe6V0P\nHjwYO3fuND/D8uXL8frrr9e53+23346AgAAcPHgQQG3HdeDAAQwaNAgff/wxlixZgsGDB2PRokUY\nPHgwfv/9d/Tv3x+pqanIz88HAOzatQvr16/HgAEDcPz4cVy6dAkA8OOPP2L8+PHQarWIjY3FF198\nAaPRiNLSUhw6dAgAcPXqVVRUVGDevHmIi4vDqVOnzDLzlW/7rCb45LLE9rrRo0fjwoULOHjwoNna\n5sIUHZOdnY3jx49jyJAhdc4Rev7nnnsO+/btw3333YcVK1YgJCQEOTk5vG3VHrbPcf36dbRt2xYq\nlcrutZ6ALH0HWL58OcaPH4+jR49i8uTJyMvLM1smkZGRWLt2LZRKJZYuXYqFCxdCqVRCJpPhlVde\nsWoIXbp0waJFizBz5kwEBwdbuVZM9x81ahQiIiLQp08fMMbQtGlTPPnkk5g4cSJCQ0MRFhaGu+66\nC1evXkW7du14ZVapVIiPj8eJEyfM5QwZMgRHjhzBuHHj0KhRIzRt2hSrVq0CUBtW2qNHDzz88MP1\nqiu++gFqJ5iXLFmCXbt2oX379ujYsWOd6x966CHcvHkT999/Pxhj6NevH2bMmIHKykooFApMmjQJ\nn3/+OTZt2oR169ZBq9WCMYZ169ahTZs2eOihh3Dt2jWMGzcOoaGhVi6J0aNHY82aNeYQQqksW7YM\na9asQUJCAmpqajBo0CD84x//AFDrCnjttddQU1ODZ555Bq+99homTpwIg8GAbt26WYWNmggICMDb\nb7+N1atXY/PmzTAYDJg1axYGDBiA6OhonDp1CvHx8VCr1WjdujUeeeQRNG3aFIsWLTKX26JFC7zy\nyiuIiIjAypUrsWDBAjDGoFQqsXXrVjRq1AizZ8/GihUrMHbsWDRr1swcQNClSxcMHToUY8eORZMm\nTdC+fXt06tQJV69eRWJiImf5QK1BMXXqVLz99tvmZzG1bVu5rly5Yj6nT58+eOONNzBr1ixs2bIF\nKpUKo0ePRmFhoWAU2I0bN3D//fejuroaycnJ6NixIwoKCqzOufPOO3mf/5lnnsGyZcvw6aefQqFQ\nYMSIEejXrx/uvvtu3rYqxIgRIzB//nysXr0agwcPxtGjR3lHQN6AjNnzCxBEAyYpKQnz5s0TNZdB\nuJaqqipMnz4dK1asQK9evTjPiYuLM0cHeSMGgwETJ07EBx98gPDwcE+Lwwm5dwi/ZuXKldiyZYvd\nORHCtRw9ehRDhw5F//79eRW+L7Bjxw7MnDnTaxU+QJY+QRCEX0GWPkEQhB9BSp8gCMKP8PronfT0\ndE+LQBAE4ZOY0mtY4vVKH+AW3BOkp6d7jSzeCNWPMFQ//FDdCONI/fAZzOTeIQiC8CNI6RMEQfgR\npPQJgiD8CFL6BEEQfgQpfYIgCD+ClL4F1To9cgorUa3T2z+5AZRLEIT/4RMhm67GYDDig2+ykJaZ\ng4ISDVqEqjGgRySSEqKgULiuX/RUuQRB+C+k9AF88E0W9h69bP47v1hj/vuJRNdl8/NUuQRB+C9+\nb05W6/RIy8zh/C0tM8dlLhdPlUsQhH/j90q/uEyLghIN52+FJRoUl2k5f/PVcgmC8G/8XumHNQlE\ni1A152/hoWqENXHNxsaeKpcgCP/G75V+kEqJAT0iOX8b0CMSQSrXTHt4qlyCIOriTxF0pFkAzIzv\nhsxLhbiSWwajEZDLgQ6tmmBmfDeH7let06O4TIuwJoGCyjspIQpArQ+/sESDcIvoHYIgpCP22zPh\njxF0pPQBbN93AZezy8x/G43A5ewybN93QVIUjdQGpFDI8URiT8yI7yapoRIEYY2jytsfI+gaZlcm\nAWdG0ZgaUH6xBoz93YA++CZL8LoglRKR4cGk8AnCQRz59vw1gs7vlX59o2hMvsDSCq3DDcif/IkE\n4WwcVd7eHEHnSp3g96alKYomv7juyxeKorEdTjZrHISismrOc00NKDJcyXmP1IxsFJRUo0VoEAb2\nbN2g/YkE4WzEKG/bbw9w/Nu3ROocgj343FS92rB639uE3yt9UxSNpV/PhFAUja0vkE/hA/wN6N97\nM/HtsT/NfxeUVGPv0cswMoZ/ToyW8hgE4bc4qrwd/faB+k0AC3UUfHMMeZ1D0O9uwduKxu+VPiA9\nikZoOMkFVwOq1ulx6PQ1zvMPnb6Gmfd1Jx8/QYigPsrb0Qg6RyaA7XUUQnrl4k0NqnV6p+gE0iqQ\nHkUjNJwEgGZNAlFSrhVsQLlFVdBoDZzXa7QG5BZVoUNkE7uyO3t4SRC+iKPK25EIOntzCDPiu3He\nw15HIaRXSisNvG4qqbhVS9TU1GDp0qW4efMmdDodnn76aQwfPtydIghSG0Vjv0qEhpMtw9R4fd69\nqKrW22lA9nx0wr8bDEa8tzsDaZk5uFWmRcuwhh9fTPg3QgaOFOXNdR+x3z4gbPTlF2vwzpfnMHtK\nb6vvUExHIaRXmgYrnLZK361Kf+/evQgNDcX69etRUlKCxMREr1L6YrE3nGwaEoimIcIvqFXzYKgD\nldBo687OqwOVaNU8mPdag8GIBW/8aLW2wB/iiwn/RIr/XEh5O2shlpByBoBDZ64jWB1g9R2Km2wO\n5tUrXdqonTaSd6tJOGbMGMydOxcAwBiDQqFwZ/FOJSkhCuNjO6JlmBpyWa2FPz62o+jVtEEqJYbf\n3Y7zt+F3txN8we/tzrBS+JakZmTjSk6pV4Z/Umgq4Qh8Mfjv7c5wyn3sraOxRSiFignbUFGxubb4\n9Mqou5pKklEIGWPMebFAIqmoqMDTTz+NKVOmICEhQfDc9PR0h8rQ6Y2o0BgRopZDpXRd31afcgxG\nhoM/leLXG1UoqzKiSSM5urZthFF3NYVCLuMtb/M3uSjXGAXv3TRYga5t1IL3ctZz2MP8nDc1KK00\nSJaN8F90eiO2fJeH0sq6818yADF3BmNsTKjddiR0n9BgBZ65L0JSuzcYGb45WYyzf1Zx/i4DMDuh\nFULUcvN3dehsGU7+VlHn3P6dQzC2b2gdeZ3xPcbExNQ55vaZv5ycHMyaNQtTp061q/BNcAnOhytz\naaSnp0uSRQz97pY2GZtTWImK6my79y2tNODkbxWIiGgp6O5xZn3x1c+23RlWjV2sbA0NV7SfhgJf\n3eQUVqKsiru9MwBnfq9E61YRdtuR0H3KqgzocEd3RIbzu1S5iO6lxzOvHUJBSd1w7fDQIPxRFIQz\nF/LM31W/qFYY17IFTmXl1plstvetOdJ2+Axmt7p3CgsLkZSUhEWLFmHSpEkuKcNZQzh3Yi8Ng6Vb\nRGiYyIW91cDv7c5wSn1V6/S4Va6vU5a/LnUnnIOY9i6mHbkilXmQSomBPVtz/ta4kQr7Tlyx+q6+\nPfYn5DIZtiyOwzsvjMCWxXF4IrGn2wMv3FraO++8g7KyMrz99tuYMWMGZsyYgepq/kVNUmloCqZS\no8O/PvkJz6xLwT/X/g+z1qVgx74L6BfVSvQ98os1+PHnGyitsF5SbjAYsfXLX/DftCuc14mtL4PB\niG27MzBrXQo2fZOLWetSsG13BgyGWveTNy91J7yfIJUSfbtFCJ4jph25KpU5lw8+flAHVGhqOM83\n6SdP5tpya6nJyclITk522f0dXY7tbZhcLt+fumoVy2+ywscNvh3jYzuaY5JDGwdCo9Xzxv2/9dkv\neAu/4LZWjbFoRgwimgVjx74L2HfiCq8MBcUaXLxajC63hQk2Tnuxx85Y6k74J6bv4PT5XMHzxLSj\nap0eYwd1gN5gxJkLeU5LZc4VKlpcpsX+1Cuc53uDHvJ+DSiB+ioYb1noZKtIbTmVlYsti+OsGtqO\nfRcErwGAq7nleHb9YbQIU6OiSid4rkwOLH/3hKCPX+wiFUdXSxL+jb3vwESIOoC3HXHNWfXtFoGE\n2I4ID3VeGKRlqGhYE3i1odOgvjhHFYw3baQgJsWDZVxvZLgSBoMRRsagDlTwWvuWFPDEF1ti/Cs4\nyGS5V2hqkJQQZbXoTOzIylWbxXhLJ004HympTsqrdLwpCrhGovtOXIHyLwvdFXi7odPgvhRHFIw3\nbaRgL8UDUNda+OCbLKvEba4g5cx1HE6/DiOrtWJ6dgrHzPhuoiwaZ28W402dNOEaxHwHJopKqzld\nJo6mS+BDipHhzbviNTilL1XBOLth1Bd7q/0Aa2tBavK3+mD8a0VHQYkGKWeuIzUjGwFK7gV2IeoA\nBEhYLSkFb+qkGxqeGD1ZRn6ZyhTzHZjgc5k4a47PESNDSA95eoTa4JS+CbEKxtsmf4WGhupAJUb2\na29lLUixiLjuF6JWoqi0GuGhavTp0hIHT16F2OV6Gq2B1510ObsMH3yT5VQlXK3TI7eoEqkZ3PHW\nnuikGwqeGD1ZlplfrMGuYynmMoW+A1v6dov4S4nC6t07K4hAyMiwZ1xa6iFvGaH6/dfhjdEltkPD\n5k2DEN2pBZ5M7IFGapXVuVIsIltG9mtfJ+rgQNpVpzwD4DwlbPWxFGt4U9F5Q2SEr+KJ0ZO9Mrm+\ng8aNVKjQ1Fj9feZCHvanXqmjRJ3hWxcaSX9/6hpSM7JRWFotSoF7ywi1wX8d9oZS7pp0kTKkk+Ki\nEpI/flAHDL+7PYrLNTidlYeffyvgXAloHXUQxLnC0BH4Mg5KRWwUh6c6aU8P1+uLFBens55VbJlc\n34FJht0//mEVdsylROvrWxcaSdeGSet5y3bked2B77VQkUgZSrly0qU+Qzo+F5Xthyckf20ZYegf\n1VpUBziwZ2tRClYsh85cR6BKgcR7OzmkKKTMWXDNI7gSbxmucyFFOYtxcbYMkzvtWat1ely8Wsw7\nOrUcsfGlQQ5rApy5kMd5vaUSrW8QgdSRNJ8C9yY3coNV+lKGUs6OLnFUDnsIKRkx8ouZ57DsQAqK\nNQgKVIAxoFpnPxSUj/+mXeEcfotBypyFK+YRhPCW4boljnREYlycznhWW9nk8r9Dg23LbBocgG1/\n7RfB9RxC7aKguK4SdTSIQMrcAsCvwL3Jjdwg49scTcdgLweOu+Tgw15eIWfIb+oAtyyOw7tLRuCj\nl8Zgx8tj8N6SEdj+4igM79sOLUKDIJcBMpEJMo1GOJzXx9m5hpyFt6b8kJJ7ypTTCYBgigIATnlW\nW9m4FL6pzJ0HLvI+R7VOD22NHuFNgzivl8mB3T/+YU4FUl+4Ui2oA7mj1vgUuKvSQDhCg7T0vWUo\n5Uw5XOkTFLOTkOnf8x6+yzw8T37nhEPlSfETO8vScjbe0sYsEdtGuEYD/aJaYdzg2zkzQOYXaxx6\nVsv3apKBC5PFb9r9beroLpiz8TDnud+fuorUv9yYfO3daIRTF2BxeQL4VsALKXBvid1vkErfW4ZS\nzpTDFUrGUZ90kEqJLreFoWWYY1FDUv3EXB9LeZWOM1xUar06OjHpDW3MVnaxbYTLVfPtsT8xPrYj\ntiyOqzNpqq0xIDxUzbmSm+tZudpVjzvC+dsKAx6JC0fCyP4IUimRU1gpMHlqgEar+evfwiMMZ0+Q\nWhpCjihwV7qRpdAglb63LIN2phyuUDL18dPaW09QrdVDJuCzleIndpalZUl9J2E92cb4ZJ86uovd\nNiJmNBAZHmzOnmr2v/P48rieleu9ppy5zpsmJDxUjbbhKocWZgnhyhFXfRS4sxYpOkqDVPqA9wyl\nkhKioDcYkZaZg+IyLVqEOSaHs5WMM9xFtnXcpJECQ+66DdNGd0FpZU2dkDpLeU3XSSm/vpaWJc6Y\nmPRUGxOSXaiNABAdNWNbhoFjxV7H1k3qPKtwtBV/x6FS/p0AUKpLjw93jLg8rcAdwbeklYA3DKVM\nFtmZC3koLteiWZMg9O0W4XBInzOVTH3dRaUVWlzJKcOUEZ3NdXzl0nkM7F+rMBupVXgysSeUCjmn\nvI76iU3U5/06a37EE22sWqdHqoDsm58bav63qc77RbWCkTHMWpdiN2rG3mjAkgpNDWoMRqu2LNSu\ntDo9hvdth4xLhXXaw9mzP1udy7Uwq0Kj53TpKOQA15ytNyQ380YafI14sie2tZaKyqrrNcHkTCXj\nqLtIp9Nj0eajuJJbBqOxdhKuQ6smWD87Ftk2e3kKyWuvfG2NgTdzoiWOvF9nz4+4q40ZDEa88+U5\n3iyphSUalFbW2HWF8aXZMClJIZ+6bXm2dWXvvT71QDQA2G2/Ulx6XAqfaxTiCnxxYV6DDNn0BlwZ\n0ueM0EyhELKed4TzXrdo81Fczi4zW4pGY218/KLNRyXJK1R+eZUOczb+UGcXLjFYbi3Jhyu2znMH\nH3yThUNnrvP+bim7qc4B4agZGf7e7WnsoA6StuTkqisxoYlS2q/lubahky1Cg6AO5L6HaRTiKix3\njDPtaie1rXoK3+iafBBvDOmzhWshFiBDSvp1ZFwqrDOxWVqhxZXcMs57XcktQ2V1I4fLLyzRIFCl\ntNoBTIqf3d7ErK1F5oycLM608OzdT4zLhUt2wcVtDHj5yQFIy8ytk7+mX1Qru+m6+TYvcdVch631\nr63R84Z2uvob88aFeWIhpe8ivCGkzx6WH9HWL88hxcKK5GrEV3LKeBfUGI1AXom00Ytl+blFlVj5\n7zROn+0KGiQkAAAgAElEQVSJczcxsn97tGrObx3yfYRGxiCXyep0BjPjuwEQp5gsFXKAwnnpCADx\nUUT2VibH9W3HKbu9dpiWmcuZv8ZyS06+iV++zUuc4Ya0t3bDlKLBE9+YN+XRcQTvlczH8ZawUbFk\nXirkPG7ZiDtENuGdBJTLgYhQx54pSKVEYIAShaXcid4KS7WYveGwefGOrUIU+ggPnb5u1ZHYdmZC\niolLIYeoA3A5u4z3flIRazEKKe8WoUF4+oFozk5HqB327RbBm7/GtCXnyP63YfaGHzjP4du8pD5I\nCaX11DfmC6N4Icin70K4lm+Pj+3oFbvnWCKmEQNA05BAdGjVhPO89hGNERzkeEMX40fmSylgLxMi\nF6Z5FSH/MldKA0uFz3U/KVTr9Lx7A6RmZFvdT8hXPrBn6zryW85t8LXDhNiOgu89t6gSAEOLUO50\nB3zWdKVGh3998hOesfB3b/3yF9zIL7dbR1LSSACe+cZ8dU7IhPd2Rw0AbwgbFYMUV9T62bG10Ts5\nZeadtACgrEKLb08Xo3dvo0NuDimx2WmZOZgyorN5v15HFvPYs8ik7kjmiIVX21lxj24KSupa0TPj\nuyHzUuHfkVMyoH2rxmZXFVDXUg632IuBK0UxX70FqpRY+e80FJZW87ZZW2vaVPb3p65aLcIy7Uu7\n78QVztGaaees0gqtZLeJJ74xXxvF2+Ld0jUQvH0Bh5RGrFIp8eZzw/DWZz/jwMlr5uO3ynW4Va7D\ngjd+xOvz7nV4HUKlpkYwQgWoVSJzNx7GrfK/N6/o2z0C+45f4Xg2Oap1df1R9iwyqTuShYao0MjO\nSEenNyKnsNKsmBRyGeQyWHWeJuRy1Lnf9n0XrEYaRgZcySnHos1HzXVu6y4qKKnGoTPXcSIjB8Ni\n2iIhtqP5N6H3bpkr3vR/daACWp2Bd/5DzL4Hlu6rpIQoq52zmv94GEVlPC4+O52qu78xb1n86Qje\nq4kItyKlEVfr9Pj5twLO+1zOLsN7uzPw9AO9JMugUMjx1APROHepkDcW3YRJOZiUSIfW3G6nVuEh\nuMLhkrFnkUkdPZg6PC7/s8kC/vGnPJRVZZvnBorLqzkVPlA7b1JVrUfTkNqOSWjkYarzxxKieM/R\naPWc1raUvEaNG6mwbvYAtGreiNOdJGVkdPxcNrQ1Bqud2vgUPuB9bhNfGcVz4RtSErw4K3RQSiO2\nZwUfOnMNj8R3Q7DN1o5iCFIpMdCBJfjXeEJJqzQ1iB/UAafP56KwpBrhoUEY2LO1XYssSKVE324R\nnGkk+OCbhOWarLXXmbQMs1Zy9uo8LTMHYwd1EDU6sZXTOgzSgDkbuSduC0s0CAxQcLYLqSOjotJq\nfH9S/Nac3uo28fZRPBc0keujuGpxiJiFM2FNAtGsMffkHgBodUa8tzvTYRlMk3N8E4hc8IWSFhRr\najeAMSUME7sJAGDlCpFCWmYOSiu0yCmsRHGpBgclKDcTtkrOXp3XTrbLHN57wPTeWzVv5NAkpdR9\nDwBut5aJZk0CBSdmxSzCI7hxexdlNBrx0ksv4eLFi1CpVFi9ejVuu+02d4vh83hycUiQSon+PVoJ\nWsGZlwqtYrgd3SM4t6gSL29LRWGpVvAavlDSoECF1fqDAgn1FB6qdih9dH6xBnM2/oBbZVpeuYRQ\nByoxbXQXq2P26rxFmBqtmjeq994Djk5SOjIy4qNlmBqvz7vXPFHPNVnsjVtU+goyxvgycbiGgwcP\nIiUlBWvXrsXZs2fx7rvvYuvWrbznp6en4+39RW6UkB+tTodAlXSXhbNhrNb/aeQwleRyGZo3CZJi\n0DomA4BbpdUwCJhrzZsGQS6XoaKqBtoaA4xGBrlchsAABUIaBfDkXLTGYGQo4onft0SpkEFvqCuL\n7C9ZbRFbT+VVNXbztruC5k2DoJBbC8cAFJdVcz6nOlCJxo0CwABUVNWgWqvnfG5LuOqA63oZgKBA\nJe87M12j1emtrHe5DFAFKCCTAVqdQdCy53wWBvPiOpOMfO/DdE1DxRHd88zY5oiJialz3O2Wfnp6\nOmJjYwEAvXv3RmamfTeAVqeze467cLksFg2dTysajYxT4Zt+q9ZqIZe7UOszQKMzwihgL8hkgL6m\nBhqdETr93+cZjQwarR4GgwHqQBGWGau9F19RMhkQoJBBrZJDozOixsDA/rpGKZehhkNBmuQQU08q\nBWBQyqzua+pIXGUumepOzyFacGDd5wxQyKBSMHPbVCkARZAcVVqjoKJVygFdjXV71mit3xdQ+6wG\ngwE6HffNuK4BajviwL/0cIBCjnKNUbDOLJ+lpLy6zjPWRmJx79VcrdNDpWDc34yIb8oXcJbucbvS\nr6ioQEhIiPlvhUIBvV4PpZJflP9bOc4dotklPT2ds+d0BlKGrdU6PWatS+F0O7QMU2PL4jiXTnpt\n251h14WQMLgjZsR345UztHGQaDn5yhvYIxKzJvcyR7gAdbfos1dPQN2Mj1yuKNtj1To9Cks0+Obo\nZZy5kIfCEg3CmgSJGpXYI2FwR7uuJy4ZLdtQfnFtCmU+c79Dq8bYOHcIVBb1L9Su+N6XlGv43mP8\noA7o1LwasYNiEKRS1jmPMUCnZ4jt3Rop6dzhvDIA6+cOMyeZs60PX3cFOaJ70tPTOY+7XemHhISg\nsrLS/LfRaBRU+P6CFB+9JxeH2AvNswwHrG/OfBN8ieHSsnJw6WaJ1YdsG03BV08xXVtix74LdfaJ\nBWpTENgqCdv7BqmUaNuyMZ5+oJdZATcKUmLBGz/Wa8en4Tw5dGzhihqxbUNCcwlXcsuxfd8Fq7bl\nSHoBKdcIhQWfPfuzuTPla1/n/iiQtG2jLydFcyVu17Z33XUXfvjhB8THx+Ps2bPo3Lmzu0XwOhxJ\n4OTsxSFiJ1rtheYtf3wAOkTWxsw7K+mc1MRwliQlRMHIWJ0cPAfTrsLS82PaJ9YSsUrCUgHXZ8en\nlmG1+eYdsUKlxskDtakeLNuWI+9LyjViwoKF2ldRaTWGxrSzev8mbI0dX0+K5krc/tQjR47E8ePH\n8dBDD4ExhldeecXdIngdjlhYzlocInUILPSRhwYr0Kr53+mVXTEi4UsMd+yXm5gyorOVqweorSe5\nTFZn8o/H1c+JFCXBPSoB52InW+ozSpMaJw/UTfXgyPty9Bq+EZ69TuTJxB4IUQfYNXZ8PSmaK3H7\nU8vlcqxcudLdxXo19bGI67s4ROoQWOgj79JG7dIRidCHfKtMi7kbD+OeXq3r5HXhS2omFilKgqsz\nzi2q4s1UCdRG6twTbX/BmCW2IzNH8g9xpXpw5H3Zu0ZKuK69TiRYrRJl7PhCanNP4Z9dnZfhKR+9\no0Ngvo+8V5u6sfTu2uIRqA1jte2whJKaicURJWHZGbdq3og33r9Zk0C8uWBonREKH0IjM6muJdtU\nD4Bj74vvGtMCQqkTqWI6HnvGjq8nRXMl/vvkXoYnEjg5OgTm+8j5ogUA5yxXF5uJ07LDqu0oguql\n+OurJITkHtyrjWiFDwiPzLjaUN9uETh9Ppfz+W1TPdjKLPV92V7j6ESqswwFX06K5kpI6XsJnkjg\nVN8hsCfyjpg+2GO/3MStMu5VupYdVpBKiYE9W/N2FJaZIy2jd5ytJJISopCXl48/CwwoLNGg+V8p\nj21X3gohZmTG1YaUCrnPjCItqW/78uWkaK6EasDLcKci9cUhsOlDnjKiM+Zu5E7Fa9th/R3Bc808\noaoOVGL43e0wfUxXlFXWWCmEmfd1d7qSUCjkGNs3FF2798R7uzORcamQdy9iPsSOzGzbkC+NIl2B\nLyZFcyVUE36Orw6Bm4YE4p5e3Ba8bYelUMjxz4nRmHlfd+QWVQFgVvvt2mYDlaokpExUfnzgoqSQ\nU0scHZn54iiScB2k9D2Ms1IjO3ovXx4CS+2wglRK8xoCZyA13FWnN9bL5VHfkRmNIgmAlL7HcOYS\ncWfcyxeHwGI6LGd2qrZInais0Bjt7kkbGKAUlNUbRmZi69SXZPUnqBY8hDOXiPv7cnOuDsvVeVcc\nmagMUctF7UkrJKsnR2ZS69SXZPUn/PvpPYQ9hSFlYwhn3ssXELt5hqkjzC/WgLG/O8IPvslyStli\nJiptUSnlGNAjkvMajVaPgpJq0bKaNj0B4LbNRBytUzEb8zgbV7z/hgJZ+h7AmZEN3hQl4UqkZiF1\nZt4VrrL7dotwaKJSyp60QrLyyZQQ2xHhoXVXRtcXX8pl40uyegL/fXIP4szIBn+JkpDiwnKkIxTy\n/XKVve/EFXRs3YSz3oUmKm1dHvb2pOXrtPlkstz4fOroLnXCUR3Fl4wLX5LVE/jvk3sQZ0Y2+EOU\nhFTLTUpHaG8EIVR2eZUO8YM6mPPpS5moNM1DVOv0kjttexk1TR3i96euolpncIo/25eMC1+S1RP4\nvkbwUZwZ2eANURKuRKrlFqRSol9UqzqpkgGgX1Qrqw7C3gjCXqrfxHs74bGEKIcnKh3ptMVm1DS5\njJwxse9LxoUvyeoJ/PvpPYgzIxt8OdZeDGItN9tds+whZgQhpmyu6CEpoYJSO21HMmpaPpOjbcOX\njAtfktXdNBzN4KM4Mz7em2Pt6xMvbc9yC1DIrbI5hoeqUVHFvZ/oqaxczLyvO4JUSpEjiGBJVqOQ\nu4gPqZ222MRz/M/U8I0LX5LV3VAtEC7FWfHSQpabrYuGazs9E5aKT+wIQorVKOQuuqud8DOK6bRN\nnacpUZtpP1wxOMufbSunNy+A8mZDyFNQbRAuxVkLx/gsN6nbBFoqPrG+X7FWoz13UY/IMNFy2sLX\neW56biiKy7VWG7QHqpR1dgqzfSZnQAugfBNS+oTLKK3Q4tgvNzl/c9S/bGu5Sd0m0FbxSbHi7VmN\n9txFFZqmouW0xV7nablBe9PgAOw8cNHl/mx/Xwnuq5DSJ5yOyQI8/ku2qJz39UHIRaMOVCJErURR\naTWv4nPXzl7hoWqEqB2zfsWGrFp2Sq72Z9MCKN+F3grhdGwtQC6c6V/mc9EM6hmJxxKiUFWtFzU5\n6sqdvQb0iIRKyT25bA9HFxu50p9NC6B8F3K8EU5FrI/dmf7lpIQojI/tiJZhashQuxuWOlCJlPTr\nWPDGj/j22GUE1NPHLDbnj6UsclntloTjYztabRIuNVeOaQTBhacWG3mjTIQ4qCsmnIo9H3uzJoEY\n3KuNU/3Lli6arV+ec3iTEi6clVnSYDBi/5kSvL0/RfKkpzcuNvJGmQhx0JshnIqQX7t50yC8uWCo\npI3ApZJ5qZDzuKN+ZkcnK7k2CT/5W4Xk+5jwxsVG3igTYR9S+oRTEbIA74luLUnhS43/draf2VmT\nlc64jzcuNvJGmQj70BsinE59LUBH4r8NBiN2//gHZDKAsbq/B6qUaBocIOk5nNWJOLMz8sbFRt4o\nE8EPvSnC6dTXAnTEpfLBN1nYd+IK7z01Wj12Hrgo2q9frdNDW2NAeKiac4WvlMlKyvpIeBOCX2J2\ndrbgxa1bt5ZUWHl5ORYtWoSKigrU1NTghRdeQJ8+fSTdw5vw5uXn3oAjFqAjrhCxEUNiXCm2o4wg\nlYLzPCmTlUIur77dIqjtEG5FsLVNnz4dMpkMjGO8LJPJcOjQIUmFffjhhxgwYAAeffRRXL58Gc89\n9xy+/vpraRJ7AbT83HU44goRuypXjCvFdpRhSk+sDlTUyU0vhaSEKOTl5ePPAgPyizWQywGjETh9\nPhdKhZzaDuE2ZIxLo7uIsrIyqFQqBAUF4ffff8fy5cuxa9cuwWvS09PdJJ149p8psYrEMNG/cwjG\n9g31gEQNB53eiC3f5aG0su72gaHBCjxzXwRUSrnoa8RcL+U+TRrJ0a1tI4y6qykUcpngc1RojAhR\ny63K+/ZUMc78UVnnfGo7hCuIiYmpc0zUuPLy5cv4+OOPUVVVBcYYjEYjbty4gZ07d/Je8/nnn2P7\n9u1Wx1555RVER0ejoKAAixYtwtKlSx0W3BOkp6cjqmcvvL0/hfP3PwsMiOrZy2+H6+np6U55V5k5\nGZyukCF33YaB/bl98nzXiL0eqN1gvKxK2KVZVmXEyd8qEBHRknN+QGgUeOpMOq4VGTnv6+1tx9Wu\nTGe1nYaKI/XDZzCLenvz58/H8OHDkZ6ejokTJ+LIkSO48847Ba+ZPHkyJk+eXOf4xYsXsWDBAixe\nvBj9+vUTU7xXQcvPXY8j0T+W1xQUaxAUqAAgg1anFx09JGVzkrTMHEwZ0blOigehSegOoUafazvk\nymx4iGphRqMRc+bMgV6vR/fu3fHQQw/hoYceklzYH3/8gblz5+KNN95A165dJV/vDVAkhutxJPqH\n6xoAkqxTKZuT5BdrMHfjYdwqrzYrwgdH3InvT13lPD8tMwddhjX1ubZDmTQbHqK6arVaDZ1Ohw4d\nOiArKwsqlQpaLXf2RCE2btwInU6HNWvWYMaMGXj66acl38PTmBQDF7T83LnURv8ES94o3nSNI9cn\nJURheF87u538RVFZNRj7WxE+v+W4eeLXlsISDbQ18Km2Yy+SSkr+IMJ7ENXKxo8fj6eeegobNmzA\ngw8+iKNHjyIiIkJyYVu3bpV8jTdCy88bLgqFHE89EI1zlwoFd+DiIruw7uS+ieZNgxCiliMp1nfa\nDrkyGyai3tj06dORmJiIkJAQ7NixAxkZGRg8eLCrZfNaaPl5wyZIpcRAB/agNXLP0QIAoju1gErJ\nfKrtkCuzYSKqtb311lt1jl28eBHPPvus0wXyJWj5ecPFZHkfP5eNotJqUdeYYu9tUQcq8WRiD1w4\nn2E+5gtthzJpNkwkT7/X1NQgJSUFRUVFrpCHILwCk0X+5oKhaCbSou3Qqgnn8ZH92qORWuVM8dyG\nvf0BCN9DVFdta9HPmjULSUlJLhGIcC2UOkIaTUNq8/9zWbvqQKVVSOjM+G7Yvu+CT/jrxSK0IX1+\nsYbakQ/i0NuqrKy0m5eH8C68Ld7alzofvon7aaO7oLSyxuoZfMVfb0LsezC5owwGI7btzvCadkRI\nR1SLjIuLg0xWu+ScMYaysjKy9H0Mb4m39rbORwxCk69cbhtHE825s6Nw9D14SzsiHEdU69qxY4f5\n3zKZDE2aNEFISIjLhCKci7M2A3EGvqw0XDH56qlOkO896A1GJN7bibPz8aZ2RDiO4BvavXu34MWJ\niYlOFYZwDd4Sb+1qpeFLLiMTnugEhd7Df9OuYH/qFc7Ox1vaEVE/BN/QyZMnAQDXrl3D1atXce+9\n90KhUODYsWPo1KkTKX0fwVvirV2lNHzRZQR4znIWeg+mkFOuzsdb2hFRPwRb1KuvvgoAmDFjBvbu\n3YtmzZoBAEpLSzFr1izXS0c4BaF46xB1AAJcqBgtrW9XKQ1fdRl5ynKWmljO1PlQ3H7DQNTXnp+f\nj9DQv3N9q9VqFBQUuEwowvkkJUShY+u6ceSXs8vwwTdZTi/PFOUxa10K/rn2f5i1LgU79l1Av6hW\nnOdLURrVOj1yCitRrdP7dH4Yk/LlwpWWs1D+KFtMnY8Jitv3fUR9ZUOHDsVjjz2GUaNGwWg04r//\n/S/Gjh3ratkIJ1JjMKJCU8P5mytcCXzW97jBt2N8bEeHYtm53Dg97gjntVi93c/sScvZNhW1jGc1\nsW3n40tpJAhuRL2tJUuW4MCBAzh16hRkMhmSkpIwfPhwV8tGOBF3uhKErO9TWbnYsjjOIaXB1ZGk\nnLkOdaCCM7ulL/iZPZW8z1Z57/7xD86N5fk6H19II0FwI/jWsrKyEBUVhdOnT6NZs2YYM2aM+bfT\np0/j7rvvdrmAhHNw5yScuA4mWJLSEN78nHvbQl/wM3vacjYp7ycTe0KpkDeo1cQEN4Kta9euXVi1\nahU2bdpU5zeZTIaPPvrIZYIRzsWdrgRXdDBCHYlWp8fwvu2QcanQZxWWpy1nT3c+hPsQfKurVq0C\nYL04CwAqKipocZYP4i5Xgis6GHsdyVMPRAOQtlMWURdPdz6E6xH1dn/44QecOXMGzzzzDCZNmoRb\nt25hzpw5mDZtmqvlI5yIO5NnObuDEduRkMIiCGFE59Nft24d9u3bh+joaLz44ouYMWMGKX0fxR3J\ns1zhLmjoO5b54opiwvcQ3bLuuOMOvP766xg/fjyCg4NRU8Md/kf4Du5Y1ORMd0FD9Tv76opiwjcR\n1aLCw8OxatUqZGZmIjY2FmvXrkXr1q1dLRvhQnx5UZMjG557M6bON79YY7XRuisWzRGEKKW/ceNG\n9OzZEzt27ECjRo3Qrl07bNy40dWyES5ETFgl4Xp8ufMlfBNRSj8kJARyuRxffvklNBoNgoODKXrH\nx/FUCgDCGup8CXcjSulv2LABR44cwcGDB2EwGPDll19i7dq1rpaNcCFC+Vd8YVFTQ4E6X8LdiFL6\nx44dw/r16xEYGIiQkBB8+OGHOHLkiKtlI1wMJc/yPNT5Eu5GVIuSy2v7BtOWiTqdznyM8F3cGQ1D\n4Yj8NPRQVMK7EPX1jRkzBvPmzUNpaSn+85//YM+ePRg3bpzDhV66dAlTpkzBiRMnEBhIw1dP48pV\nmBSOaJ+GGopKeCd2W9bly5cxYcIEdOvWDa1bt0Zubi4effRRnDlzxqECKyoq8Nprr0GlqruhNNHw\n8NUNTjwBpUAg3IGgqbV582Y88MADGDNmDORyORYuXIhmzZrh5ZdfRnZ2tuTCGGNYvnw5FixYALWa\ne/KKaDhQOCJBeB8yxhjj+3H48OH45JNPkJ+fj02bNqGmpgaFhYVYvHgxYmNjBW/8+eefY/v27VbH\nWrdujfj4eCQmJiIuLg779++3695JT0+X8DiEN3GrXI9N3+Ry/iYDMDuhFZo1JstWCJ3eiAqNESFq\nOVRKae6w+lxLNAxiYmLqHBNU+uPHj8fevXsBAAMGDEBiYiIWLVoEhULhkAAjR45Eq1a12+WdPXsW\n0dHR2Llzp+A16enpnIJ7Am+SxRuxrZ9qnR6z1qVwZsZsGabGlsVxfuW7ltJ+6jMX4ovzKPRtCeNI\n/fBdI/jFWUbohIWF4YUXXpBUqC3ff/+9+d9xcXH44IMP6nU/wruhjbQdpz5zITSPQggh2O2bQjQB\nICgoyOXCEA0PWgsgnfrMhdA8CmEPQVPr999/N++Fm5eXZ/43YwwymQyHDh1yuOCUlBSHryV8BwpH\nlE599jN2517IhG8i+PYPHDjgLjmIBg6FI4qnPttNunMvZMI3EfwK27Rp4y45CIL4i/rMhdA8CmEP\nagEE4YXUJzUDpXUghCClTxBeSH3mQmgehRCCWgJBeDH1mQuheRSCC+9cqUEQBEG4BFL6BEEQfgQp\nfYIgCD+ClD5BEIQfQUqfIAjCjyClTxAE4UeQ0icIgvAjSOkTBEH4EaT0iQZJtU6PnMJKSiVMEDbQ\ncj2iQeGLu0YRhDshpU80KGjXKIIQhkwfosFAu0YRhH1I6RMNBjG7RhGEv0NKn2gwmHaN4oJ2jSKI\nWkjpEw0G065RXNCuUQRRC30FRIOCdo0iCGFI6RMNCto1iiCEoa+BaJDQrlEEwQ359AmCIPwIUvoE\nQRB+BCl9giAIP8KtTk+DwYBXX30VmZmZ0Ol0mD17NoYNG+ZOEQiCIPwatyr9PXv2QK/XY9euXcjL\ny8P+/fvdWTxBEITf41alf+zYMdx555148sknwRjD8uXL3Vk8QRCE3yNjjDFX3Pjzzz/H9u3brY6F\nhYWhbdu2eOWVV3D69Gm8+eab2Llzp+B90tPTXSEeQRBEgycmJqbOMZdZ+pMnT8bkyZOtjs2fPx9D\nhw6FTCZDv379cOXKFVH34hLcE6Snp3uNLN4I1Y8wVD/8UN0I40j98BnMbo3eiYmJwY8//ggA+PXX\nXxEZyZ0nhSAIgnANblX6U6ZMAWMMU6ZMwfLly/Hyyy+7s3iCIAi/x60TuSqVCq+++qo7iyQIgiAs\noMVZBEEQfgQpfYIgCD+ClD5BEIQfQUqfIAjCjyClTxAE4UeQ0icIgvAjSOkTBEH4EaT0CYIg/AhS\n+gRBEH4EKX2CIAg/gpQ+QRCEH0FKnyAIwo8gpU8QBOFHkNInCILwI0jpEwRB+BGk9AmCIPwIUvoE\nQRB+BCl9giAIP4KUPkEQhB9BSp8gCMKPIKVPEAThR5DSJwiC8CNI6RMEQfgRpPQJgiD8CFL6BEEQ\nfgQpfYIgCD9C6c7CysvLMX/+fFRVVUGlUmH9+vVo0aKFO0UgCILwa9xq6X/11Vfo3LkzPv74Y8TH\nx+P99993Z/EEQRB+j1uVfufOnVFZWQkAqKiogFLp1oEGQRCE3yNjjDFX3Pjzzz/H9u3brY69+OKL\nWLp0KVQqFUpLS7Fz50506NBB8D7p6emuEI8gCKLBExMTU/cgcyOzZs1in3zyCWOMsQsXLrBx48bZ\nvebMmTOuFks03iSLN0L1IwzVDz9UN8I4Uj9817jVvdOkSRM0btwYANC8eXOzq4cgCIJwD251qs+d\nOxfJycn4+OOPodfrsWrVKncWTxAE4fe4VelHRERg27Zt7iySIAiCsIAWZxEEQfgRpPQJgiD8CFL6\nBEEQfgQpfYIgCD+ClD5BEIQfQUqfcCnVOj1yCitRrdN7WhSCIODmkE3CfzAYjPjgmyykZeagoESD\nFqFqDOgRiaSEKCgUZGsQhKcgpU+4hA++ycLeo5fNf+cXa8x/P5HY01NiEYTfQyYX4XSqdXqkZeZw\n/paWmUOuHoLwIKT0CadTXKZFQYmG87fCEg2Ky7RuloggCBOk9AmnE9YkEC1C1Zy/hYeqEdYk0M0S\nEQRhgpQ+4XSCVEoM6BHJ+duAHpEIUtFUEkF4Cvr6CJeQlBAFoNaHX1iiQbhF9A5BEJ6DlD7hEhQK\nOZ5I7IkZ8d1QXKZFWJNAsvAJwgugr5BwKUEqJSLDqZkRhLdAPn2CIAg/gpQ+QRCEH0FKnyAIwo8g\npU8QBOFHyBhjzNNCCJGenu5pEQiCIHySmJiYOse8XukTBEEQzoPcOwRBEH4EKX2CIAg/gpQ+QRCE\nH/i4CPEAAAazSURBVEFKnyAIwo8gpU8QBOFHkNInCILwIygTlkgmTpyIkJAQAEDbtm3x6quvelgi\n7+CXX37Bhg0bsGPHDly9ehUvvPACZDIZ7rzzTqxYsQJyuf/aFZZ1c/78efzzn/9Ehw4dAAAPP/ww\n4uPjPSugh6ipqcHSpUtx8+ZN6HQ6PP300+jUqRO1nb/gqp/IyEintR9S+iLQarVgjGHHjh2eFsWr\n2LZtG/bu3Qu1unaXrFdffRXz5s1D//798eKLL+LQoUMYOXKkh6X0DLZ1k5WVhcceewxJSUkelszz\n7N27F6GhoVi/fj1KSkqQmJiIrl27Utv5C676mTVrltPaj392pRL59ddfodFokJSUhEceeQRnz571\ntEheQfv27bF582bz31lZWejXrx8AYMiQIThx4oSnRPM4tnWTmZmJw4cPY9q0aVi6dCkqKio8KJ1n\nGTNmDObOnQsAYIxBoVBQ27GAq36c2X5I6YsgKCgIjz/+ON5//328/PLLWLhwIfR6vafF8jijR4+G\nUvn3YJExBplMBgAIDg5GeXm5p0TzOLZ1Ex0djcWLF2Pnzp1o164dtmzZ4kHpPEtwcDBCQkJQUVGB\nOXPmYN68edR2LOCqH2e2H1L6Irj99tsxfvx4yGQy3H777QgNDUVBQYGnxfI6LH2wlZWVaNKkiQel\n8S5GjhyJHj16mP99/vx5D0vkWXJycvDII49gwoQJSEhIoLZjg239OLP9kNIXwRdffIG1a9cCAPLy\n8lBRUYEWLVp4WCrvo3v37jh58iQA4MiRI+jbt6+HJfIeHn/8cZw7dw4AkJqaiqgo/90ruLCwEElJ\nSVi0aBEmTZoEgNqOJVz148z2QwnXRKDT6bBkyRJkZ2dDJpNh4cKFuOuuuzwtlldw48YNLFiwAJ99\n9hn+/PNPLF++HDU1NejYsSNWr14NhULhaRE9hmXdZGVlYdWqVQgICEB4eDhWrVpljgbzN1avXo39\n+/ejY8eO5mPLli3D6tWrqe2Au37mzZuH9evXO6X9kNInCILwI8i9QxAE4UeQ0icIgvAjSOkTBEH4\nEaT0CYIg/AhS+gRBEH4EKX2iwXPjxg306NEDEyZMQGJiIu677z489thjyM3Ndeh+X331FV544QUA\nwBNPPIG8vDzeczdt2oQzZ85Iun+XLl0ckosgxEBKn/ALWrZsiT179mD37t347rvv0KNHD6xatare\n9922bRsiIiJ4fz99+jQMBkO9yyEIZ0FZNgm/pG/fvkhJSUFcXByio6Nx4cIFfPzxxzh69Ci2b98O\no9GIqKgorFixAoGBgdi9eze2bt2KkJAQtGnTBo0aNQIAxMXF4aOPPkKLFi3w8ssvIz09HQEBAXjm\nmWeg0+mQmZmJ5ORkvPXWWwgKCsJLL72EkpISBAUFYfny5ejevTtu3LiBRYsWoaqqCr169fJwzRAN\nHbL0Cb+jpqYG+/fvN6+qHjJkCA4cOIBbt27hs88+w65du7Bnzx40b94c77//PvLy8rBhwwbs3LkT\nn376KSorK+vcc8eOHaiqqsL+/fvx4YcfYsuWLYiPj0ePHj2wevVqdOnSBc8//zwWLVqEr7/+GqtW\nrcL8+fMBAKtWrcL999+PPXv20EpvwuWQpU/4Bfn5+ZgwYQKA2rQa0dHReO6553D8+HGzdX3y5Elc\nvXoVU6ZMAVDbOXTv3h0///wz+vTpg/DwcABAQkIC0tLSrO5/+vRpTJkyBXK5HC1atMB3331n9Xtl\nZSUyMzOxZMkS87GqqioUFxfj1KlT2LhxIwBg/PjxSE5Odk0lEARI6RN+gsmnz0VgYCAAwGAwYOzY\nsWalW1lZCYPBgNTUVBiNRvP5limT+Y5dvXoVkZGR5r+NRiNUKpWVDLm5uQgNDQVQm5YaAGQymTnF\nMEG4AnLvEMRf9O/fH99//z2KiorAGMNLL72E7du3IyYmBr/88gvy8vJgNBqxb9++Otfefffd2L9/\nPxhjKCoqwvTp06HT6aBQKGAwGNC4cWN06NDBrPSPHz+OadOmAQAGDRqEvXv3AgAOHjwInU7nvocm\n/A6y9AniL7p27Ypnn30WM2fOhNFoRLdu3fDkk08iMDAQycnJePTRR6FWq9GpU6c6106dOhWrV6/G\n+PHjAQDLly9HSEgIYmNjsWLFCrz22mtYv349XnrpJfz73/9GQEAA/vWvf0Emk+HFF1/EokWLsGvX\nLvTs2RPBwcHufnTCj6AsmwRBEH4EuXcIgiD8CFL6BEEQfgQpfYIgCD+ClD5BEIQfQUqfIAjCjyCl\nTxAE4UeQ0icIgvAj/h+Tlf0p2ZFX7gAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1106ddda0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Extract predicted values.\n",
"predicted = regr.predict(X).ravel()\n",
"actual = data['Sales']\n",
"\n",
"# Calculate the error, also called the residual.\n",
"residual = actual - predicted\n",
"\n",
"sns.set_style(\"whitegrid\")\n",
"\n",
"# This looks a bit concerning.\n",
"plt.hist(residual)\n",
"plt.title('Residual counts (skewed to the right)')\n",
"plt.xlabel('Residual')\n",
"plt.ylabel('Count')\n",
"plt.show()\n",
"\n",
"plt.scatter(predicted, residual)\n",
"plt.xlabel('Predicted')\n",
"plt.ylabel('Residual')\n",
"plt.axhline(y=0)\n",
"plt.title('Residual vs. Predicted( Heteroscedasticity present)')\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"As shown above, the error from the model is not normally distributed. The error is skewed to the right, similar to the raw data itself. \n",
"\n",
"Additionally, the distribution of error terms is not consistent, it is heteroscadastic. \n",
"\n",
"### Inspect the Data and Transform\n",
"\n",
"The data is skewed to the right. The data is transformed by taking its square root to see if we can obtain a more normal distribution. "
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAW8AAAD3CAYAAADSftWOAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAADTBJREFUeJzt3X9IXfUfx/HX0VVbVy4SFQRrpZsxbETsivbP7J/sjsC2\nYGQ6HOT+iDHYLs2lM6cbSia2oqSoRn/ppEZF2R/9UVJcyHH/OLDF7voBMQS3Ea0Y6SX0muf7x7ev\n3/2we+/0Hu993z0ff/nznvfHo897ONzjcTzP8wQAMKUo1wMAAG4e8QYAg4g3ABhEvAHAIOINAAat\nWomNuK67EpsBgIITCoUW/fiKxDvVAIXAdd2CXt/1WG9hY735I9WBL6dNAMAg4g0ABhFvADCIeAOA\nQcQbAAwi3gBgEPEGAIOINwAYRLwBwKAVu8ISNtQf+DyzLxyZzOp2vzi2LauPBxQ6jrwBwCDiDQAG\nEW8AMIh4A4BBxBsADCLeAGAQ8QYAg4g3ABhEvAHAIOINAAYRbwAwiHgDgEHEGwAMIt4AYBDxBgCD\niDcAGES8AcAg4g0ABhFvADCIeAOAQcQbAAwi3gBgEPEGAIOINwAYRLwBwCDiDQAGEW8AMCijeP/+\n++96/PHH9csvv2hiYkKNjY1qampSd3e35ufn/Z4RAHCdtPFOJpPq6urS6tWrJUl9fX2KRCIaGRmR\n53kaGxvzfUgAwLXSxru/v1/PPfec7r33XklSPB5XdXW1JKm2tlbj4+P+TggAuMGqVJ/89NNPdddd\nd2nLli16//33JUme58lxHElSIBDQ1NRURhtyXXeZo+a3Ql+f3/L955fv82Ub681/KeP9ySefyHEc\nnTp1Sj/88IPa2tr0xx9/LHw+kUgoGAxmtKFQKLS8SfOY67qFs76RyZxsNp9/fgW1fzPAevNHqieV\nlPE+ceLEwtvNzc06cuSIBgYGFIvFVFNTo2g0qsceeyx7kwIAMnLTLxVsa2vT4OCgGhoalEwmFQ6H\n/ZgLAJBCyiPvqw0NDS28PTw87MswAIDMcJEOABhEvAHAIOINAAYRbwAwiHgDgEHEGwAMIt4AYBDx\nBgCDiDcAGES8AcAg4g0ABhFvADCIeAOAQcQbAAwi3gBgEPEGAIOINwAYlPGddAA/1R/4PGfb/uLY\ntpxtG1gqjrwBwCDiDQAGEW8AMIh4A4BBxBsADCLeAGAQ8QYAg4g3ABhEvAHAIOINAAYRbwAwiHgD\ngEHEGwAMIt4AYBDxBgCDiDcAGES8AcAg4g0ABqW9Ddrff/+tzs5OnT9/Xo7j6OjRo7rjjjvU3t4u\nx3FUUVGh7u5uFRXxPAAAKyVtvL/55htJ0ocffqhYLKY33nhDnucpEomopqZGXV1dGhsbU11dne/D\nAgD+K+3h8hNPPKGenh5J0sWLFxUMBhWPx1VdXS1Jqq2t1fj4uL9TAgCukdHd41etWqW2tjZ99dVX\neuutt/Tdd9/JcRxJUiAQ0NTUVNrHcF13eZPmuUJfXyHLZN/davuX9ea/jOItSf39/WptbdWzzz6r\nmZmZhY8nEgkFg8G03x8KhZY2oQGu6xbO+kYmcz3Biku37wpq/2aA9eaPVE8qaU+bfPbZZ3rvvfck\nSWvWrJHjONq0aZNisZgkKRqNqqqqKkujAgAykfbI+8knn9ShQ4e0c+dOzc3NqaOjQ+vXr9fhw4f1\n+uuvq7y8XOFweCVmBQD8I22877zzTr355ps3fHx4eNiXgYCVVn/g8/Rf5MPppC+Obcv6Y+LWwYuz\nAcAg4g0ABhFvADCIeAOAQcQbAAwi3gBgEPEGAIOINwAYRLwBwCDiDQAGEW8AMIh4A4BBxBsADCLe\nAGAQ8QYAg4g3ABhEvAHAIOINAAYRbwAwiHgDgEHEGwAMIt4AYBDxBgCDiDcAGES8AcAg4g0ABhFv\nADCIeAOAQcQbAAwi3gBg0KpcDwDcquoPfJ6zbX9xbFvOto3s4MgbAAwi3gBgEPEGAIOINwAYRLwB\nwKCUrzZJJpPq6OjQhQsXNDs7qz179mjDhg1qb2+X4ziqqKhQd3e3iop4DgCAlZQy3qOjoyotLdXA\nwICuXLmi7du3a+PGjYpEIqqpqVFXV5fGxsZUV1e3UvMCAJTmtMnWrVu1f/9+SZLneSouLlY8Hld1\ndbUkqba2VuPj4/5PCQC4Rsoj70AgIEmanp7Wvn37FIlE1N/fL8dxFj4/NTWV0YZc113mqPktm+s7\nMjKZtccCFpPu97XQ/16vZ3G9aa+wvHTpkvbu3aumpibV19drYGBg4XOJRELBYDCjDYVCoaVPmedc\n183u+og3fJbq9zXrv895Lp/Xm+pJJeVpk8uXL6ulpUUHDx7Ujh07JEmVlZWKxWKSpGg0qqqqqiyO\nCgDIRMp4v/vuu/rzzz/1zjvvqLm5Wc3NzYpEIhocHFRDQ4OSyaTC4fBKzQoA+EfK0yadnZ3q7Oy8\n4ePDw8O+DQQASI8XaAOAQcQbAAwi3gBgEPEGAIOINwAYRLwBwCDiDQAGEW8AMIi7xwO3oLR3rvfp\n/+tw1/rs4cgbAAwi3gBgEPEGAIOINwAYRLwBwCDiDQAGEW8AMIh4A4BBxBsADCLeAGAQ8QYAg4g3\nABhEvAHAIOINAAYRbwAwiHgDgEHEGwAMIt4AYBDxBgCDiDcAGES8AcAg7h4PYMWkvWu9TwrxrvUc\neQOAQcQbAAwi3gBgEPEGAIOINwAYlFG8z5w5o+bmZknSxMSEGhsb1dTUpO7ubs3Pz/s6IADgRmnj\nffz4cXV2dmpmZkaS1NfXp0gkopGREXmep7GxMd+HBABcK228161bp8HBwYX34/G4qqurJUm1tbUa\nHx/3bzoAwKLSXqQTDoc1OTm58L7neXIcR5IUCAQ0NTWV0YZc113iiDYU+voAy9L9fVr8+73pKyyL\niv5/sJ5IJBQMBjP6vlAodLObMsN13eyub2Qy/dcAyFiqv8+s//1mUaonlZt+tUllZaVisZgkKRqN\nqqqqaumTAQCW5Kbj3dbWpsHBQTU0NCiZTCocDvsxFwAghYxOm6xdu1YnT56UJJWVlWl4eNjXofLF\nTf0THU51AFhBXKQDAAYRbwAwiHgDgEHEGwAMIt4AYBDxBgCDiDcAGES8AcAg7h4PoOClveDOx4vs\n/LpzPUfeAGAQ8QYAg4g3ABhEvAHAIOINAAYRbwAwiHgDgEHEGwAMIt4AYBDxBgCDiDcAGES8AcAg\n4g0ABhFvADCIeAOAQcQbAAwi3gBgEPEGAIOINwAYRLwBwCDiDQAGmbh7fNo7PwPALYYjbwAwiHgD\ngEHEGwAMIt4AYBDxBgCDlvRqk/n5eR05ckQ//fSTbr/9dvX29uqBBx7I9mwAgH+xpCPvr7/+WrOz\ns/roo4904MABvfrqq9meCwCQwpLi7bqutmzZIkl69NFHdfbs2awOBQBIbUmnTaanp1VSUrLwfnFx\nsebm5rRq1b8/nOu6S9mUJOlI09olfy8A5NJy2pfKkuJdUlKiRCKx8P78/HzKcIdCoaVsBgDwL5Z0\n2mTz5s2KRqOSpNOnT+uhhx7K6lAAgNQcz/O8m/2m/73a5Oeff5bneXrllVe0fv16P+YDACxiSfEG\nAOQWF+kAgEHEGwAMIt4AYJCJmzHks2eeeWbhNe9r165VX19fjifyx5kzZ/Taa69paGhIExMTam9v\nl+M4qqioUHd3t4qKCus44Or1njt3Ti+88IIefPBBSVJjY6Oeeuqp3A6YJclkUh0dHbpw4YJmZ2e1\nZ88ebdiwoWD372Lrve+++0zuX+K9DDMzM/I8T0NDQ7kexVfHjx/X6Oio1qxZI0nq6+tTJBJRTU2N\nurq6NDY2prq6uhxPmT3Xrzcej+v5559XS0tLjifLvtHRUZWWlmpgYEBXrlzR9u3btXHjxoLdv4ut\nd+/evSb3b2E8nebIjz/+qL/++kstLS3atWuXTp8+neuRfLFu3ToNDg4uvB+Px1VdXS1Jqq2t1fj4\neK5G88X16z179qy+/fZb7dy5Ux0dHZqens7hdNm1detW7d+/X5LkeZ6Ki4sLev8utl6r+5d4L8Pq\n1au1e/duffDBBzp69KhaW1s1NzeX67GyLhwOX3MFred5chxHkhQIBDQ1NZWr0Xxx/XofeeQRvfTS\nSzpx4oTuv/9+vf322zmcLrsCgYBKSko0PT2tffv2KRKJFPT+XWy9Vvcv8V6GsrIyPf3003IcR2Vl\nZSotLdVvv/2W67F8d/X5z0QioWAwmMNp/FdXV6dNmzYtvH3u3LkcT5Rdly5d0q5du7Rt2zbV19cX\n/P69fr1W9y/xXoaPP/544d/h/vrrr5qentY999yT46n8V1lZqVgsJkmKRqOqqqrK8UT+2r17t77/\n/ntJ0qlTp/Twww/neKLsuXz5slpaWnTw4EHt2LFDUmHv38XWa3X/coXlMszOzurQoUO6ePGiHMdR\na2urNm/enOuxfDE5OakXX3xRJ0+e1Pnz53X48GElk0mVl5ert7dXxcXFuR4xq65ebzweV09Pj267\n7Tbdfffd6unpuea/alrW29urL7/8UuXl5Qsfe/nll9Xb21uQ+3ex9UYiEQ0MDJjbv8QbAAzitAkA\nGES8AcAg4g0ABhFvADCIeAOAQcQbAAwi3gBg0H8AeJyninXLCLoAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x10c4b6668>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.hist(actual)\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"sqrt_actual = np.sqrt(actual)"
]
},
{
"cell_type": "code",
"execution_count": 33,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAW8AAAD3CAYAAADSftWOAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAEDlJREFUeJzt3X9MVfUfx/HXAUYqeHNu+Zfh0GzlXGUwrE3hj1Tc1EhF\nEdy1jWa/p5QY4lBwmsqctWK1tLXVQJYMneUfrRm6saSY3U0q/LWoLNKZWky4Ej/kfP+o7y0Q78XL\nvffcDz4ff+E93nve+3Dvk+PxHq5l27YtAIBRYpweAABw+4g3ABiIeAOAgYg3ABiIeAOAgeIisROP\nxxOJ3QDAiJOSkjLo7RGJt78BIsnj8UTFHANF61wSswUrWmeL1rkkZrvVfm+F0yYAYCDiDQAGIt4A\nYCDiDQAGIt4AYCDiDQAGGtJbBRcvXqzExERJ0sSJE5WTk6PXX39dsbGxmjVrll5++eWwDgkA6C9g\nvLu6umTbtiorK323ZWVlqaKiQvfee6+effZZnTp1StOmTQvroACAfwU8bXLmzBl1dnYqPz9fq1at\n0okTJ9Td3a2kpCRZlqVZs2apoaEhErMCAP5hBfowhrNnz6qpqUnLli3Tzz//rNWrV8vlcungwYOS\npNraWv3666965ZVXbvkYXB6PaFZW3erMfvMmOrJfmCXoy+OTk5M1adIkWZal5ORkjR07Vm1tbb7t\nXq9XLpcr6AEiKVovv43WuaQ7ZDaH4u3U5dYj/vsZBkZeHl9bW6udO3dKki5duqTOzk6NGTNGv/zy\ni2zb1pdffqnU1NTQTQsACCjgkXd2draKi4uVm5sry7K0fft2xcTEqLCwUDdu3NCsWbP08MMPR2JW\nAMA/AsY7Pj5eu3fvvun2mpqasAwEAAiMi3QAwEDEGwAMRLwBwEDEGwAMRLwBwEDEGwAMRLwBwEDE\nGwAMRLwBwEDEGwAMRLwBwEDEGwAMRLwBwEDEGwAMRLwBwEDEGwAMRLwBwEDEGwAMRLwBwEDEGwAM\nRLwBwEDEGwAMRLwBwEDEGwAMRLwBwEDEGwAMRLwBwEDEGwAMRLwBwEDEGwAMRLwBwEDEGwAMRLwB\nwEBDivfVq1eVkZGhlpYWnT9/Xrm5ucrLy1Npaan6+vrCPSMAYICA8e7p6dHmzZs1atQoSdKOHTtU\nUFCg6upq2baturq6sA8JAOgvYLzLy8u1YsUKTZgwQZLU3NystLQ0SVJ6eroaGhrCOyEA4CZx/jYe\nPHhQ48eP1+zZs7V3715Jkm3bsixLkpSQkKD29vYh7cjj8Qxz1NCIljkGita5JGYLF6dmj+Y1Y7ah\n8xvvAwcOyLIsffXVVzp9+rSKior0xx9/+LZ7vV65XK4h7SglJWV4k4aAx+OJijkGita5pDtkturW\n4T9GEJxY1zvi+xkGTs3m7weG33jv27fP97Xb7VZZWZl27dqlxsZGzZw5U/X19XrsscdCNykAYEhu\n+62CRUVFqqioUE5Ojnp6epSZmRmOuQAAfvg98v6vyspK39dVVVVhGQYAMDRcpAMABiLeAGAg4g0A\nBiLeAGAg4g0ABiLeAGAg4g0ABiLeAGCgIV+kAyC0Fq37xJkdV7fq8O4sZ/aNkOHIGwAMRLwBwEDE\nGwAMRLwBwEDEGwAMRLwBwEDEGwAMRLwBwEDEGwAMRLwBwEDEGwAMRLwBwEDEGwAMRLwBwEDEGwAM\nRLwBwEDEGwAMRLwBwEDEGwAMRLwBwEDEGwAMRLwBwEDEGwAMFOf0AIAkLVr3SXB3rG4N7SCAITjy\nBgADBTzyvnHjhkpKSvTTTz/Jsixt2bJFd911lzZs2CDLsjR16lSVlpYqJoafAwAQKQHjfezYMUnS\nxx9/rMbGRr355puybVsFBQWaOXOmNm/erLq6Os2dOzfswwIA/hbwcHnOnDnaunWrJOnChQtyuVxq\nbm5WWlqaJCk9PV0NDQ3hnRIA0M+Q/sMyLi5ORUVFOnLkiN5++20dP35clmVJkhISEtTe3h7wMTwe\nz/AmDZFomWOgaJ1Liu7ZEJxo/Z5G61xS9M025HeblJeXq7CwUMuXL1dXV5fvdq/XK5fLFfD+KSkp\nwU0YQh6PJyrmGCha55IiOBvvGomoaHy+8ToYfL+3EvC0yaFDh7Rnzx5J0ujRo2VZlqZPn67GxkZJ\nUn19vVJTU0M0KgBgKAIeec+bN0/FxcVauXKlent7tXHjRk2ZMkWbNm3SG2+8ocmTJyszMzMSswIA\n/hEw3mPGjNFbb7110+1VVVVhGQgAEBhvzgYAAxFvADAQ8QYAAxFvADAQ8QYAAxFvADAQ8QYAAxFv\nADAQ8QYAAxFvADAQ8QYAA/EBxMAdKOgPfB6mw7uzHNnvSMSRNwAYiHgDgIGINwAYiHgDgIGINwAY\niHgDgIGINwAYiHgDgIGINwAYiHgDgIGINwAYiHgDgIGINwAYiHgDgIGINwAYiHgDgIH4MAYAERPw\nQyCqW8Oy35H4IRAceQOAgYg3ABiIeAOAgYg3ABjI739Y9vT0aOPGjfrtt9/U3d2tF154Qffdd582\nbNggy7I0depUlZaWKiaGnwEAEEl+4/3pp59q3Lhx2rVrl9ra2vTUU0/pgQceUEFBgWbOnKnNmzer\nrq5Oc+fOjdS8AAAFOG0yf/58rV27VpJk27ZiY2PV3NystLQ0SVJ6eroaGhrCPyUAoB+/R94JCQmS\npI6ODq1Zs0YFBQUqLy+XZVm+7e3t7UPakcfjGeaooREtcwwUrXNJ0T0bMBSheA5H2+sg4EU6Fy9e\n1EsvvaS8vDwtWrRIu3bt8m3zer1yuVxD2lFKSkrwU4aIx+OJijkGita5pAjOFqaLMwBp+P1x6jXq\n7weG39MmV65cUX5+vtavX6/s7GxJ0rRp09TY2ChJqq+vV2pqaghHBQAMhd94v/fee7p27Zreffdd\nud1uud1uFRQUqKKiQjk5Oerp6VFmZmakZgUA/MPvaZOSkhKVlJTcdHtVVVXYBgIABMYbtAHAQMQb\nAAxEvAHAQMQbAAxEvAHAQMQbAAxEvAHAQMQbAAxEvAHAQMQbAAxEvAHAQMQbAAxEvAHAQMQbAAxE\nvAHAQMQbAAxEvAHAQMQbAAxEvAHAQMQbAAxEvAHAQMQbAAxEvAHAQMQbAAwU5/QAABBui9Z9MvwH\nqW4N6m6Hd2cNf9+D4MgbAAxEvAHAQMQbAAzEOW/0M+i5wSDP9QEIH468AcBAxBsADES8AcBAxBsA\nDES8AcBAQ4p3U1OT3G63JOn8+fPKzc1VXl6eSktL1dfXF9YBAQA3Cxjv999/XyUlJerq6pIk7dix\nQwUFBaqurpZt26qrqwv7kACA/gK+zzspKUkVFRV67bXXJEnNzc1KS0uTJKWnp+v48eOaO3duwB15\nPJ5hjhoa0TLHQNE6F4DhCddrO2C8MzMz1dr670Uatm3LsixJUkJCgtrb24e0o5SUlCBHDB2PxxMV\ncwwUVXNxQQ4QUsN5bfsL/23/h2VMzL938Xq9crlcwU0FAAjabcd72rRpamxslCTV19crNTU15EMB\nAPy77XgXFRWpoqJCOTk56unpUWZmZjjmAgD4MaRfTDVx4kTV1NRIkpKTk1VVVRXWoQAA/nGRDgAY\niHgDgIGINwAYiHgDgIGINwAYiHgDgIGINwAYiA8gjkKDfggwAPwHR94AYCDiDQAGIt4AYCDiDQAG\nIt4AYCDiDQAGIt4AYCDiDQAGIt4AYCDiDQAGIt4AYCDiDQAGIt4AYCDiDQAGIt4AYCDiDQAGIt4A\nYCDiDQAGIt4AYCDiDQAGIt4AYCDiDQAGIt4AYCDiDQAGinN6gKFYtO6T0D1YdWvoHiuUonUuAFEp\nqHj39fWprKxMZ8+eVXx8vLZt26ZJkyaFejYAwC0Eddrkiy++UHd3t/bv369169Zp586doZ4LAOBH\nUPH2eDyaPXu2JOmRRx7R999/H9KhAAD+BXXapKOjQ4mJib4/x8bGqre3V3Fxt344j8cTzK4kSWV5\nE4O+LwA4aTjt8yeoeCcmJsrr9fr+3NfX5zfcKSkpwewGAHALQZ02efTRR1VfXy9JOnnypO6///6Q\nDgUA8M+ybdu+3Tv9/90m586dk23b2r59u6ZMmRKO+QAAgwgq3gAAZ3GFJQAYiHgDgIGINwAYaMTG\nu6mpSW63+6bbP/zwQy1YsEBut1tut1s//vhjxGbq6enR+vXrlZeXp+zsbNXV1fXbfvToUS1dulQ5\nOTmqqamJ2FxDmc2pdbtx44aKi4u1YsUK5ebm6ty5c/22O7lmgWZz8rkmSVevXlVGRoZaWlr63e7k\nmgWazek1W7x4sW/fxcXF/bbV1NRoyZIlWr58uY4dOxbRuQZlj0B79+61Fy5caC9btuymbevWrbO/\n++47B6ay7draWnvbtm22bdv2n3/+aWdkZPi2dXd323PmzLHb2trsrq4ue8mSJfbly5ejYjbbdm7d\njhw5Ym/YsMG2bdv++uuv7eeff963zek18zebbTv7XOvu7rZffPFFe968efYPP/zQ73Yn18zfbLbt\n7Jr99ddfdlZW1qDbfv/9d3vhwoV2V1eXfe3aNd/XThqRR95JSUmqqKgYdFtzc7P27t2r3Nxc7dmz\nJ6JzzZ8/X2vXrpUk2bat2NhY37aWlhYlJSXp7rvvVnx8vFJSUnTixImomE1ybt3mzJmjrVu3SpIu\nXLggl8vl2+b0mvmbTXL2uVZeXq4VK1ZowoQJ/W53es38zSY5u2ZnzpxRZ2en8vPztWrVKp08edK3\n7dtvv9WMGTMUHx+vsWPHKikpSWfOnInofAONyHhnZmbe8orPBQsWqKysTB999JE8Hk9E//mTkJCg\nxMREdXR0aM2aNSooKPBt6+jo0NixY/v93Y6OjqiYTXJ23eLi4lRUVKStW7dq0aJFvtudXjN/s0nO\nrdnBgwc1fvx43+8f+i+n18zfbJKzz7NRo0bpmWee0QcffKAtW7aosLBQvb29kpxft8GMyHjfim3b\nevrppzV+/HjFx8crIyNDp06diugMFy9e1KpVq5SVldXvxT7wVw54vd5+TxYnZ4uGdSsvL9fnn3+u\nTZs26fr165KiY81uNZuTa3bgwAE1NDTI7Xbr9OnTKioq0uXLlyU5v2b+ZnP6eZacnKwnn3xSlmUp\nOTlZ48aNi5p1G8wdFe+Ojg4tXLhQXq9Xtm2rsbFR06dPj9j+r1y5ovz8fK1fv17Z2dn9tk2ZMkXn\nz59XW1uburu79c0332jGjBlRMZuT63bo0CHfP59Hjx4ty7IUE/P309bpNfM3m5Nrtm/fPlVVVamy\nslIPPvigysvLdc8990hyfs38zeb067O2ttb3660vXbqkjo4O32wPPfSQPB6Purq61N7erpaWFsd/\nLciIvcKytbVVr776qmpqanT48GFdv35dOTk5OnTokCorKxUfH6/HH39ca9asidhM27Zt02effabJ\nkyf7blu2bJk6OzuVk5Ojo0eP6p133pFt21q6dKlWrlwZNbM5tW7Xr19XcXGxrly5ot7eXq1evVqd\nnZ2+76eTaxZoNiefa//ndrtVVlamU6dORcWaBZrNyTXr7u5WcXGxLly4IMuyVFhYqKamJiUlJemJ\nJ55QTU2N9u/fL9u29dxzzykzMzNisw1mxMYbAEayO+q0CQCMFMQbAAxEvAHAQMQbAAxEvAHAQMQb\nAAxEvAHAQP8DyqAo+vq1gW0AAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1107607f0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.hist(sqrt_actual)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"That's a little better. Has this helped the multivariate normality? Yes. "
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX0AAAETCAYAAADah9Z7AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAFytJREFUeJzt3XuUZGV57/HvMM1ARhptFn0QEjwcjXmiHhUcFFyojIAi\nUUTB3ESijCwPiC6QEO4IIgl4ASF6DIZxMsaAGhDwEkZGHWdE5OIMoBDJAxpZMQuVjmeQ0dHoOH3+\n2Lulpuiuqp7pXd3l+/2s1WtV7dv7dF1+teutvd89b3x8HElSGbab7QIkSf1j6EtSQQx9SSqIoS9J\nBTH0Jakghr4kFWRotguQ2kXEOHAv8GtgHFgIPAqckJlrt3KbS4FPZuaX2qbvC1ybmXtt5Xb3Au7N\nzJ22Zv2ZEBFXAldk5rrZqkGDw9DXXPXSzPyviTsRcSrwQeCFW7OxzDxupgqbg14GfGS2i9BgMPQ1\n50XEEPAU4P+1TDsbOIqqi/JB4K2Z+VBEHAmcA2ym+qbwV5n51YhYDXwoM6+NiBOAdwA/Ae5p2eb5\nwK6Z+bb2+xGxP/BeYAdgd+CLmfnmLnW/CriwrvFnwPGZ+c2IeA1wHjCf6hvMKZl5R5f2VwO3AgfU\nj8XNwBuBdwN7AFdFxF8AvzvZ/9/bI60S2KevueorEfHNiHgIuL+edixAHW7PBl6QmXsDNwJL62Xe\nR/UBsC9wLrC4daMRsTdwPvCSzHw+8Mse6zkJeGdm7gc8E3h1RCyaauGI2A34J+BNmfmcuq6LI+IP\ngSuAo+rp7wQ+ExE791DD0+r/59nAQcCBmXk28BBwdGbeTpf/XzL0NVe9NDOfC7ySqk//65n5cD3v\nVcD+wNqIuBt4OxD1vE8C19d9+CNUe+etDgZWZuYP6/t/32M9bwSeFBFnAR+ua+rUj38AVV//3QCZ\neV1mHkYV1l/OzH+vp68CHgam/ABp8bnM3JyZG4DvALtMsky3/1+FM/Q1p2XmXVRdMUvrH02h6hZ5\nT2buXe/p70sVstR7vgcAa4E3AbdGROvrfByY13J/U4d5C1pu3wz8EfBvwAXAf7Yt225TvT0AImJe\nRDyHyd9z2wHbd2kf4OcdagV6+v9VOF8MmvMy8xNU/dmX1ZNuAo5r6RK5APh4RAxFxIPAEzLzCuCt\nwDOoAnXCF4GXR8Tv1fff1DJvDFhUB/QTgJcDRMQI1QfL6Zl5HVW/+e9TffhM5XbgGRHxrPr+EVTd\nPavq9p9ab/sgYM96+Unb78EmYPse/38VztDXoHgbcFhEHErVf/954LaI+FfgOVR955uAk4GrI+JO\n4BpgSWb+98RGMvMe4DTgyxGxFtixpY2rqIL3AarfCW6t11kPXATcWa9zJnALVfBPKjN/BBwNfKzu\ngjoF+LPM/DZVGF8XEfcCFwOHZ+ZPpmq/BzcAn6LqOur4/0vzHFpZksrhnr4kFcTQl6SCGPqSVBBD\nX5IKMqeHYRgb29D1V+aRkYWsX7+xH+VstUGoEQajzkGoEaxzJg1CjTC36hwdHZ7yHJKB39MfGup0\nqPTcMAg1wmDUOQg1gnXOpEGoEQanzoEPfUlS7wx9SSqIoS9JBTH0Jakghr4kFcTQl6SCNHacfkTM\nB66kurjFOHA88AtgeX3/XuDEzNzcVA2SpC01uad/OEBmHkB1zc6/Bi4FzsnMF1NdAOKIBtuXJLVp\nLPQz8wbgLfXd/wk8QnVJuDX1tBXAIU21L0l6vMbH04+IjwGvBV4HLM/MPerpB1Fd4OENU627adOv\nxwflLLfSHf6Xn5mVdj93iV8WpUlMOQxD42PvZOYbI+J0qsvB/U7LrGGqvf8p9TKOxejoMGNjG7ap\nxqYNQo0wOHW2mqv1DspjOQh1DkKNMLfqHB0dnnJeY907EXFMRJxZ390IbAbWRsTietphVBebliT1\nSZN7+tcB/xARX6W6MPPJwH3AlRGxoL59bYPtS5LaNBb6mfkz4E8mmXVgU21Kkjrz5CxJKoihL0kF\nmdNXzpLmsiUXr5qVdpedcdCstKvfDu7pS1JBDH1JKoihL0kFMfQlqSCGviQVxNCXpIJ4yKaknnmY\n6uBzT1+SCmLoS1JBDH1JKoihL0kFMfQlqSAevaOBNltHk0iDyj19SSqIoS9JBTH0Jakghr4kFcTQ\nl6SCGPqSVBBDX5IKYuhLUkEMfUkqiKEvSQUx9CWpII2MvRMR2wPLgL2AHYALge8DnwceqBf7u8z8\nVBPtS5Im19SAa28AfpyZx0TELsDdwAXApZl5SUNtSpK6aCr0rwGurW/PAzYBi4CIiCOo9vZPzswN\nnTYyMrKQoaH5XRsbHR3etmr7YBBqhMGps2Qz/RwNwnM+CDXCYNTZSOhn5k8BImKYKvzPoermWZqZ\n6yLibOA84NRO21m/fmPXtkZHhxkb6/jZMesGoUYYnDpLN5PP0aA854NQ41x6LDt9+DT2Q25E7Al8\nBfh4Zl4NXJ+Z6+rZ1wP7NNW2JGlyjYR+ROwGrAROz8xl9eSbIuIF9e2DgXWTrixJakxTffpnASPA\nuRFxbj3tFOADEfEr4IfAWxpqW5I0hab69E8CTppk1gFNtCdJ6o0nZ0lSQQx9SSqIoS9JBTH0Jakg\nhr4kFcTQl6SCGPqSVBBDX5IKYuhLUkEMfUkqiKEvSQUx9CWpIIa+JBXE0Jekghj6klSQpi6iIqkh\nSy5eNdslaIC5py9JBTH0Jakghr4kFcTQl6SCGPqSVBBDX5IKYuhLUkEMfUkqiKEvSQUx9CWpII0M\nwxAR2wPLgL2AHYALgW8Dy4Fx4F7gxMzc3ET7kqTJNbWn/wbgx5n5YuAVwIeAS4Fz6mnzgCMaaluS\nNIWmQv8a4Nz69jxgE7AIWFNPWwEc0lDbkqQpNNK9k5k/BYiIYeBa4Bzg/Zk5Xi+yAXhit+2MjCxk\naGh+1/ZGR4e3vtg+GYQaYXDqVFkG5XU5CHU2NrRyROwJXA98ODOvjoj3tsweBh7pto316zd2bWd0\ndJixsQ1bXWc/DEKNMDh1qjyD8LqcS++fTh8+jXTvRMRuwErg9MxcVk++KyIW17cPA25uom1J0tSa\n2tM/CxgBzo2Iib79k4C/jYgFwH1U3T6SpD5qqk//JKqQb3dgE+1JknrjyVmSVBBDX5IK4oXRf4t4\nwWxJ3binL0kFMfQlqSCGviQVxNCXpIIY+pJUEENfkgpi6EtSQQx9SSqIoS9JBekp9CPiWZNM23/m\ny5EkNanjMAwRcQAwH1gaEW+muvThxHpXAH/QbHmSpJnUbeydl1ENh7w7cEHL9E3AR5oqSpLUjI6h\nn5nnA0TEMZn58b5UJElqTK+jbH41It4H7MJjXTxk5pJGqpIkNaLX0P9nqmva3gyMN1eOJKlJvYb+\n9pl5aqOVSJIa1+tx+l+LiMPri5pLkgZUr3v6rwPeBhARE9PGM3N+E0VJkprRU+hn5h5NFyJJal5P\noR8R75xsemZeMNl0SZpJs3X952VnHDQr7Tap1z79eS1/C4BXA7s1VZQkqRm9du+8q/V+RLwbWNlI\nRZKkxmztKJs7AU+ZyUIkSc3rtU//ezx2UtZ2wJOA9zVVlCSpGb0esrm45fY48EhmPtptpYjYD3hP\nZi6OiH2AzwMP1LP/LjM/NZ1iJUnbptfQ/w/geODgep1VEfGhzNw81QoRcRpwDPCzetIi4NLMvGQb\n6pUkbYNeQ/+9wNOBZVRH8BwLPBU4ucM63wWOBCZG51wEREQcQbW3f3JmbujU6MjIQoaGup//NTo6\n3HWZ2TYINUra0nTft4PwPu819F8O7DOxZx8R/wLc02mFzPx0ROzVMukOYGlmrouIs4HzgI7j+axf\nv7FrYaOjw4yNdfzsmHWDUKOkx5vO+3Yuvc87ffj0evTOEFt+QAwBv55mHddn5rqJ28A+01xfkrSN\neg39q4DVEfH2iHg7sAq4eppt3RQRL6hvHwys67SwJGnmde3eiYgR4ErgLuCg+u+yrbiS1gnAByPi\nV8APgbdMc31J0jbqdmH0fYAbgWMzcwWwIiL+Brg4Ir6Zmd/qtH5mPgjsX9++EzhgRqqWJG2Vbt07\n7wf+PDO/MDEhM88ClgCXNlmYJGnmdQv9kcxc3T4xM28Cdm2kIklSY7qF/vYR8bhl6mleRUuSBky3\n0F9DdTx9u3OAtTNfjiSpSd2O3jkTuDEijga+QXU27vOAh6nG1JckDZCOoZ+ZGyLiJcBLqU6m2gz8\n38y8uR/FSZJmVtfj9DNznOpkrNm5XpkkacZs7UVUJEkDqNcB1zQNs3URZ0nqxj19SSqIoS9JBTH0\nJakghr4kFcTQl6SCGPqSVBBDX5IKYuhLUkEMfUkqiKEvSQUx9CWpIIa+JBXE0Jekghj6klQQQ1+S\nCmLoS1JBDH1JKkijV86KiP2A92Tm4oj4fWA5MA7cC5yYmZubbF+StKXG9vQj4jRgKbBjPelS4JzM\nfDEwDziiqbYlSZNrsnvnu8CRLfcXAWvq2yuAQxpsW5I0ica6dzLz0xGxV8ukeZk5Xt/eADyx2zZG\nRhYyNDS/a1ujo8NbVaMkdTLdbBmELGq0T79Na//9MPBItxXWr9/YdaOjo8OMjW3YhrIkaXLTyZa5\nlEWdPnz6efTOXRGxuL59GHBzH9uWJNHfPf2/BK6MiAXAfcC1fWxbkkTDoZ+ZDwL717fvBw5ssj1J\nUmeenCVJBTH0Jakg/ezT77slF6+a7RIkaU5xT1+SCmLoS1JBDH1JKoihL0kFMfQlqSCGviQVxNCX\npIIY+pJUEENfkgpi6EtSQQx9SSqIoS9JBfmtHnBNkrbFbA7auOyMgxrZrnv6klQQQ1+SCmLoS1JB\nDH1JKoihL0kFMfQlqSCGviQVxNCXpIIY+pJUEENfkgpi6EtSQfo+9k5E3Ak8Wt/9XmYe2+8aJKlU\nfQ39iNgRmJeZi/vZriSp0u89/ecCCyNiZd32WZl521QLj4wsZGhofteNjo4Oz1yFkjQHNJVr/Q79\njcD7gaXA04EVERGZuWmyhdev39h1g6Ojw4yNbZjRIiVptm1LrnX6wOh36N8PfCczx4H7I+LHwO7A\n9/tchyQVqd9H7ywBLgGIiD2AnYEf9LkGSSpWv/f0Pwosj4ivAePAkqm6diRJM6+voZ+ZvwRe3882\nJUmP8eQsSSqIoS9JBTH0Jakghr4kFcTQl6SCGPqSVBBDX5IKYuhLUkEMfUkqiKEvSQUx9CWpIIa+\nJBXE0Jekghj6klQQQ1+SCmLoS1JBDH1JKoihL0kFMfQlqSCGviQVxNCXpIIY+pJUEENfkgpi6EtS\nQQx9SSqIoS9JBRnqZ2MRsR3wYeC5wH8Dx2Xmd/pZgySVrN97+q8BdszMFwJnAJf0uX1JKlq/Q/9F\nwBcAMvM2YN8+ty9JRetr9w6wM/CTlvu/joihzNw02cKjo8Pzetno6OjwpNM/d8kR0y5Qkn6b9XtP\n/1GgNaG3myrwJUkzr9+hfwvwRwARsT9wT5/bl6Si9bt753rgZRHxdWAecGyf25ekos0bHx+f7Rok\nSX3iyVmSVBBDX5IKYuhLUkH6/UPuVomIJwL/RHWc/wLglMy8tT4C6HJgE7AyM9/Vtt6uwNXA7wAP\nAcdm5saGa30t8MeZ+fr6/uqW2X8ILM/MM1qW3wW4H7i3nnR9Zl7eZI1T1Pla4P3A9+tFzsvMNS3L\nz4XH8mDgQuBXwMPAX7TWEBHzgP8EHqgn3ZqZZzZZ4xR1zrnXZd3uGcAr6rtPAp6cmU9uW+YzwK5U\nj/HPM/Owputq18vzGBHnAa+keoxPzsw7+lzjpJnUtszlVCekbqgnHZGZP2GWDUToA6cAX87MyyIi\ngE8AzwOuAI4C/h34l4jYJzPvalnvncDVmbm8fsH/H+ADTRVZP8mHAndPTMvMxfW8pwL/TBVarZ4H\nfCIz395UXe0mqxNYBJyWmZ+eYrVZfyypxm16SWb+KCIuAo4D/rZl/tOAOzPz8Kbq6rHOOfW6nJCZ\nFwMX13V/HjhtksWeDjwrM2fzCI+Oz2NEPA84ENgP2BP4NPD8/pUHTJ1JrRYBh2bmf/W5to4GpXvn\nA8BH6ttDwC8iYmdgh8z8bv0CvQk4pG293wz7AKyYZP5M+zpwwhTzLgNOz8yftk1fBCyKiDURcU1E\n7N5ohZXJ6lwELImImyPikoho3yGYC4/l4sz8UX17CPhF2/xFwO9GxFci4sb6zdi0Leqco6/LLUTE\nkcD6zFzZNn03qm8An4uIr0XEq/pZV4tuz+OLqL5BjWfmfwBDETHa5xofl0mtM+vBJZ8O/H1E3BIR\nS/pc35Tm3J5+RLwZeEfb5GMz8xsR8WSqr1QnU32terRlmQ3AU9vWax32YQPwxIZr/FRELJ5k+ecA\nO2fmlyfZ3L8B6zLzSxFxNPBB4HWzUOcXgRuA71HtqR4PfKhl/qw/lpn5g3qdI4GXAue2rfcD4KLM\nvCYiXkT1WpmRPcBp1Dlrr8tWnd5HwJnAn0+y2gKqQRAvB3YBbomIOzLz4Zmur0udJ9L5edwZ+HHL\n/YnHcKyPNU6WSa2eQPVevhSYD3wlItZm5reaqHE65lzoZ+ZHgY+2T4+IZwOfBE7NzDX1HlXrkA7D\nwCNtq00M+/DzKebPaI0dvAG4cop5q4CJ/tzrgQu2obQtTLPOZZn5CPymX/eotvlz4rGMiHdQfSi+\nIjPb9/TXUvXxkplfi4g9ImLeTHRVTKPO9qFG+va6bNXhffRM4JEphjT/IXBFPTTKwxFxFxBUv580\nYrI6I2IhnZ/HXh7jRmus69wik9pmbwQun/itJiJWUQ0pP+uhPxDdO/UL9Rrg9Zm5AiAzHwV+GRFP\nq3/4ORS4uW3V3wz7ABw2yfx+OZjHvs63W8pjAXswsK4vFbWoH79vRcTvdahj1h/LiDgbeDFwyBT9\npOdR73FFxHOB7/e7b3oAXpeHUHUpTTXvGoCI2An438B9faqrVbfn8Rbg0IjYLiKeQjWGV1/7zSfL\npDZ/QPVNaX5EbE/VJXVnP2ucykCEPnARsCNweUSsrvdEoeqCuAq4A7grM2+PiF0i4rp6/oXAn0XE\nLcAL2bK7op+enJm/+TraVuMZwAn1UT7HAyf1u7j6DXUccF1ErAEWAlfOpcey7m8+D9gDWFG/Dk6o\n562MiAVUP1IeWP8PlwJv6meNLeby6zKofmB+bELEeyPiBXV43R8RtwErgbNm6UfISZ/HljrXUX1Q\n3kr1I+6Js1DjpJkUEadExKsz8z7g48BtwBrgHzPzX2ehzsdxGAZJKsig7OlLkmaAoS9JBTH0Jakg\nhr4kFcTQl6SCzLmTs6QmRMReVAPbfbuetB3VmZ0fy8zzprmtpVQnMa1tm74cWJ2Zy7eivgephpl4\ncLrrStNh6KskD2Xm3hN3ImIP4IGI+GR9XHVPMvO4RqqT+sDQV8l2p7pW84Z6tMs/oRon5SbgdKrT\n+z8BTAw//K7M/Gx9It35VCfdXAK8imqI5PnA6vpbxerM3AsgIs4HyMzzI+JtwDFUY7NsBv50Oh84\n0rYy9FWSPSLibqozKXcFvgG8lmq4gUVUg3qNU51JeTRViD+Yma+MiGcAS4DPtmzvKGAf4FlUo1N2\nHFelHi/qNVTdOD+PiAuAtwJ9G1Zb8odclWSie+eZVMG+gGrAu0OoxmZfRzU+yr5UQf514DURcQPV\n2CnvbtveYuC6zPxVZo4BN3ZqvB6X5/VUQzBcBBwO7DQz/5rUG0NfxcnMzcBfAbsBp1Lt0V+WmXvX\nHwr7AX+dmQ9QXe3sKqqB3u6oB1GbMM6W76FNLdNbl9seICL2pBov5klUg54tb1tOapyhryLVwwef\nCpxFtXd/TETsVF885gbgdXX/+7sy8xqqbpj/wZZj338J+OOI2CEiRnjsUoSPACMRMRoRO7RMfz7w\nncz8AHA71Qib8xv9R6U2hr6KlZlfoBoF8UCq0Rpvp7pW8d3Ax4B/BCIi7gG+Cpw/cc2Bev3PAKvr\ndT5LfThofR3U91H9ZvAlqtE2oRq5cruI+Hbd7oPA/2ryf5TaOcqmJBXEPX1JKoihL0kFMfQlqSCG\nviQVxNCXpIIY+pJUEENfkgry/wFg4x8q1ojgSQAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x10c4ba470>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Extract predicted values.\n",
"predicted = regr.predict(X).ravel()\n",
"actual = data['Sales']\n",
"\n",
"# Calculate the error, also called the residual.\n",
"corr_residual = sqrt_actual - predicted\n",
"\n",
"plt.hist(corr_residual)\n",
"plt.title('Residual counts')\n",
"plt.xlabel('Residual')\n",
"plt.ylabel('Count')\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Transforming the data into the sqrt of the data lessened the skewness to the right, and allowed the error from the model to be more normally-distributed. Let's see if our transformation helped the problem with heteroscedasticity. \n",
"\n",
"### Homoscedasticity"
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYsAAAETCAYAAADH1SqlAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xlc1HX+wPHXMDgMgtxoWJqZ5QHinUdqm2apeZCKeWeU\ntm5aluJPy7SStFJrNy1b01q3rVS2UkstXW/yHrWE0g5vRQHlHIYZmJnfH8jkwDAznDPA+/l49Ij5\nXvOej194z/dzKsxmsxkhhBDCDg9XByCEEML9SbIQQgjhkCQLIYQQDkmyEEII4ZAkCyGEEA5JshBC\nCOGQJAvhFlq2bMngwYMZOnQoUVFRPPLIIwwfPpyTJ0+W+5ovv/wy+/fvL7H95MmT9OnTp9zXvXTp\nEh06dCj3+c44dOgQkZGRlvIYOnQow4YNY+fOnRW+9qBBgzh06BDXrl1j1KhRdo+9ePEi06ZNK/N7\nrF69mtmzZ5c3ROGGPF0dgBBF1qxZQ1BQkOX16tWriYuLY926deW63htvvFFZoblE06ZN2bhxo+X1\nqVOnGD16NDt27LAqp/Jq1KgRa9eutXvMlStXOHv2bIXfS9R8kiyEWyooKCA5ORl/f3/LthUrVrBt\n2zZMJhO333478+fPp1GjRmzbto0VK1agUChQKpXMmjWLLl26MH78eMaOHUv//v35/PPPWbNmDb6+\nvtx7772Way5btoz09HTmzZtX4vWJEydYvHgxBoOB1NRUevTowcKFC0uN+Z133iEnJ8dyrb1797Js\n2TK++OILFixYwLFjx6hXrx533HEHixYtwsfHp0xl0qpVK9RqNZcvX+azzz7jxIkTpKSk0LJlS5Ys\nWVJq+fz++++89NJL6HQ6mjdvTm5uLlD4hDR48GCOHz9OQUEBixcvZvfu3SiVSjp06MD8+fOZO3cu\n165d46mnnmL16tUcO3aMJUuWoNPpUCgUTJs2jQcffJD8/Hzi4uLYv38/wcHBBAcH06BBgzJ9PuHe\nJFkIt/HEE0+gUCi4ceMGXl5ePPjggyxatAiADRs28OuvvxIfH4+npyfr1q1j7ty5fPTRR7z99tss\nWbKE9u3bk5CQwKFDh+jSpYvlur/88gvLly9n48aNhIaGWv6YO/Lvf/+b5557jq5du6LVaunbty+J\niYkEBATYPD46Opro6Ghmz56NSqXiq6++YuTIkZw4cYLDhw+zZcsWFAoFixcv5vTp03Ts2LFM5bNt\n2zY8PDxo0aIFu3fv5vLly3z77bd4enraLZ+ZM2cyduxYoqOj0Wg0jB07tsS1P//8c5KSkti4cSMq\nlYoXX3yRLVu2EBcXx4IFC1i9ejWZmZnMmTOH1atXc8cdd3Dt2jVGjhxJy5Yt2b59O+fOnWPz5s0U\nFBQwbtw4SRa1jCQL4TaKqqF+/vlnJk2aRIcOHQgODgZg165dnDx5kuHDhwNgMpnQ6XQAPProo0yd\nOpUHHniA+++/n0mTJlld98CBA9x///2EhoYC8Pjjj5OQkOAwnjfffJO9e/fy4YcfcubMGfLy8sjN\nzS01WTRp0oRWrVqxc+dOunfvzoEDB3jjjTcwGo0olUqio6Pp2bMnjzzyCJGRkQ7f/8KFCwwdOhQo\nfNK67bbb+OCDD/D29gagffv2eHp62i2f9PR0Tp8+TVRUFACdOnXinnvuKfFe+/fvZ+jQoajVagD+\n/ve/A4VtJ0VOnDhBamoqzz77rGWbQqHg9OnTHDhwgEGDBqFSqVCpVAwePJjTp087/Iyi5pBkIdxO\nmzZtmDNnDnPnzqVdu3bccccdmEwmnn76acaMGQOAwWAgMzMTgBdeeIERI0aQkJDAV199xcqVK/nq\nq68s11MoFNw6BZpSqSx1X35+vuXnsWPH0qpVK3r16sWAAQP48ccfcTSVWnR0NBs2bOD69ev069fP\nUtW0ceNGjh07xsGDB5k+fToTJkxg4sSJdq9VvM2iuPr161t+Lq18FAoFgFXcRQnmVsW3paWlYTKZ\nrLYZjUbuvvtu4uPjLduuXbtGUFBQiXalW8tY1A7SG0q4pUGDBtG+fXtLG0HPnj3573//S05ODgD/\n+Mc/mDVrFgUFBfTp04fc3FxGjx7N/Pnz+eOPPygoKLBcq0ePHvzwww9cvXoVgK+//tqyLzAwkKSk\nJMxmM7m5uZYnjszMTBITE5k5cyYPP/ww165d48KFCyX+gBbXr18/kpKSWL9+PSNHjgQKv/VPnDiR\nDh06MG3aNKKiojh16lTlFZad8gkICCA8PNzyBz4pKYlff/21xPndu3fn22+/xWAwYDKZePXVV9m8\neTNKpdKSQNu3b8/58+c5cuQIUFi998gjj5CSkkKvXr3YsGEDer0evV7Pli1bKvXzCdeTJwvhtl55\n5RWGDBnCvn37iI6OttSRKxQKwsLCePPNN/H09OSll15i5syZeHp6olAoWLhwISqVynKdli1bEhsb\nyxNPPIGPj49VFVDR9R9++GEaNWpEhw4dMJvN+Pv7M3nyZB577DECAgIIDAykY8eOnD9/niZNmpQa\ns0qlYuDAgezfv9/yPr1792bv3r0MGjSI+vXr4+/vz4IFC4DC7r0RERGMHj26QmVVWvlAYcP7nDlz\nWLt2LU2bNqV58+Ylzh81ahSXL19m2LBhmM1m7rvvPsaPH49Wq0WpVDJixAji4+N57733ePvtt9Hr\n9ZjNZt5++21uv/12Ro0axYULFxg0aBABAQHceeedFfo8wv0oZIpyIYQQjkg1lBBCCIckWQghhHBI\nkoUQQgiHJFkIIYRwqNb2htJoNK4OQQghapxOnTrZ3F5rkwWU/qGrm0ajcZtY3JGUj31SPqWTsrGv\nrOVj70u2VEMJIYRwSJKFEEIIhyRZCCGEcEiShRBCCIckWQghhHBIkoUQQgiH3CJZmEwm5s2bx+OP\nP8748eM5f/681f7169czbNgwRo4cya5du1wUpRBC1F1uMevstm3b2LlzJ2+++SYnTpzgn//8JytW\nrAAgNTWVmJgYvvzyS/R6PWPGjOHLL7+0moLaFo1Gwwdbr1dH+A7pDQa8HMRbl0n52CflUzopG/vK\nWj5/GxDs3oPyNBoNvXr1AgoXWElMTLTs++mnn+jQoYNlucamTZty6tQpp5al1BsMVRZzWblTLO5I\nysc+KZ/SSdnYV1nl4xbJIicnB19fX8trpVJJQUEBnp6e5OTkWC387uPjY1kNzJH/vD6o0mMtDxll\nap+Uj31SPqWTsrGv1o3g9vX1RavVWl6bTCbLmsDF92m1WqvkIYQQouq5RbLo2LEje/fuBeDEiRPc\ne++9ln2RkZFoNBr0ej3Z2dn88ccfVvuFEEJUPbeohurXrx8//PADo0aNwmw2s3DhQj755BOaNm1K\n3759GT9+PGPGjMFsNvPCCy/g5eXl6pCFEKJOcYtk4eHhweuvv2617e6777b8PHLkSEaOHFndYQkh\nhLjJLaqhhBBCuDdJFkIIIRySZCGEEMIhSRbF5BkKSE7TkmcocHUoQgjhNtyigdsdGI0mPv4miYOJ\nyaRm6AgN8KZbRBgxg8NRKiWnCiHqNkkWN338TRKb9p2xvE5J11leT4pq66qwhBDCLchXZgqrng4m\nJtvcdzAxWaqkhBB1niQLID1LT2qGzua+lHQdH375E0ajqZqjEkII9yHJAgj08yI0wLvU/TuOXuTj\nb5JK3S+N4kKI2k7aLAC1ypNuEWFWbRbFHUxMZvzA1qhVfxZZUaP4gcRk0tJ1hAR6010axYUQtZD8\nRbspZnA4fTo3KXV/WoaO9Cy91bZVmxLZtO8Mqek6zEDqzUbxVZsSbV9ECCFqKEkWNymVHkwZHklo\ngNrm/pAAbwL9/pzAMM9QwI4jF20eu+PIRamSEkLUKpIsbqFWedK9bWOb+7pFhFlVQV29rkWnt50Q\ndPoCrl7X2twnhBA1kbRZFBMzOBwobKNIy9ARcsvgPGsKB1dytF8IIWoOSRbFKJUeTIpqy/iBrUnP\n0hPo52X1RFEksIH9NTUc7RdCiJpEqqFKoVZ5EhbiYzNRAOTm2W+TcLRfCCFqEkkW5RTo50XDQNtj\nMxoGWjeGCyFETefyaqjs7GxiY2PJyckhPz+f2bNn06FDB6tj4uLiOHbsGD4+PgB88MEHNGjQwBXh\nWtgbm1G8MdyWPEOB3WouIYRwJy7/K/XJJ5/QrVs3Jk6cyJkzZ5gxYwZff/211TFJSUmsWrWKoKAg\nF0Vpm/ON4X+S2W2FEDWRwmw2m10ZQFZWFiqVCrVazW+//cYrr7zC2rVrLftNJhM9e/akY8eOpKWl\nMWLECEaMGOHwuhqNpirDtmIoMJGjM+Hr7YHK0/4f/K1HMzj0a06J7V3v9aVvez+nryOEEFWhU6dO\nNrdX65NFfHw8a9assdq2cOFCIiMjSU1NJTY2lpdeeslqf25uLuPGjePJJ5/EaDQyYcIEIiIiaNWq\nlcP3K+1DVzeNRkOnTp3IMxTwwdadNo/56XweZ1IKSMvMq3NPG0XlI2yT8imdlI19ZS0fe1+yqzVZ\nREdHEx0dXWL76dOnefHFF5k1axb33Xef1T5vb28mTJiAt3dhY3K3bt04deqUU8nC3dib3VanL7AM\n8pO1NIQQ7sblX1t///13nn/+eZYuXcoDDzxQYv+5c+cYPXo0RqOR/Px8jh07Rnh46W0C7szR7LbF\nyVoaQgh34fIG7qVLl2IwGHjjjTcA8PX1ZcWKFXzyySc0bdqUvn37MnToUEaOHEm9evUYOnQo99xz\nj4ujLh9nZre9VdHkhWEhLv9nEkLUcS7/K7RixQqb25988knLz08//TRPP/10dYVUpWz1oMrONaDT\nG0scW3zyQiGEcBWXJ4u6xtZ0Ip9u+cXm00bn1o1uTkio4Lbg+jIeQwjhMvLXxwWKD8gr/rQR7K/G\np76KXZqLbNl/DgBvLyV9uzTl6SERlh5SMrBPCFFd5C9MNbI3IO/Wp40Ne363JIkiOr2RbxPO4qFQ\nEDM4nI+/SWL/T5dJy9QT4u9Fj8jb60xXWyFE9ZNkUY0+/ibJqrqpeBdZtcqTQD848su1Uq9x4OQV\n8vIL2HbwgmVbWqaeTfvOUGAyMWVYu6r7AEKIOku+hlaTPEMBBxOTbe67tYtsepaetHTbYzEAUjPy\n2HH4gs193x84J11thRBVQpJFNbE3IO/W9b0D/bwIKWU2WwB/H0+MJtv7jCa4cDW7wrEKIURxkiyq\nib0Bebd2kVWrPOkeEVbqdVo2C7b7PplaffmDFEKIUkiyqCZFA/JsKT6leczgcAb1vAtvrz+3eXsp\nGdTzLqYOt98mcW+TQPIMBZxLzuJccqZUSwkhKoU0cFcjZ6c0Vyo9eOaxSJ54tE2JcRZGo4kGPiqy\ntYYS17891IfPvvuF3ccuWQb5eXt50rdLE6sut0IIUVaSLKqRs+t7F1GrPGkW5m+17eNvkmwmCoDL\nqVoup2qttun0BZYutzIpoRCivOSrpgs4Wt+7NPZ6VDkikxIKISpCnixqEHs9qhxJzdBx9XouXvWU\n1Fd7kp6dh0wjIoRwlvyVqEGKelSl2BmHURq1Ssnrqw6WSDa2phERQoji5K9DDWKvR5UjOr3R5lNJ\n0TQiKzecJDlNK1VVQgib5Mmihineo8pLpbQ5vXkRtUqJQoHdYwC+O3COrQfO1bklXYUQzpFkUcMU\n71Hl51OPz78/bdUdt3PrRjzc7U6UHgoAnlu62+F1TebC/8uSrkIIWyRZ1FCFPaoK//nsdcfNMxSU\nq51j34lLhDcPIrx5CP6+sgCTEHWdy5OF2Wymd+/eNGvWDID27dszY8YMq2OWL1/O7t278fT05KWX\nXiIyMtIFkbq3W5NH8e1lWcq1SHq2gUVrjgLQrLEfS6f1QiW9poSos1z+23/hwgXCw8P58MMPbe5P\nSkri8OHDxMfHk5yczLRp0/jyyy+rOcqaraidI+HHy9zIKvvcUeeuZPH8u3t494UHpJutEHWUy1sw\nk5KSuHbtGuPHj2fSpEmcOWP9DVij0dCzZ08UCgWNGzfGaDRy48YNF0VbMxW1c7w340GC/dTlusal\nlBymvLWDjzacxFjatLdCiFqrWr8mxsfHs2bNGqtt8+bNY/LkyQwYMICjR48SGxtr9eSQk5NDQECA\n5bWPjw/Z2dkEBQU5fD+NRlN5wVeQu8TS4jZPrmeV79y0jDw27TvDtWspDOgc4PiEMnCX8nFXUj6l\nk7Kxr7LKp1qTRXR0NNHR0VbbdDodSqUSgM6dO5OSkoLZbEahKOzJ4+vri1b753xHWq2WBg0aOPV+\nnTp1qqTIK0aj0bhNLO3b/7m0a3kG9wGcTTXSomUEuXkFlbL+tzuVjzuS8imdlI19ZS0fe4nF5dVQ\ny5cvtzxtnDp1irCwMEuiAOjYsSMJCQmYTCauXLmCyWRy6qlC2FZUJfXKU93KfY2UdB3PLd3FM2/+\nj7+9vZN3vziGVmd7ckMhRO3g8tbKyZMnExsby549e1AqlSxatAiAt99+m/79+xMZGUnnzp15/PHH\nMZlMzJs3z8UR1w63BdenYWD5pg4BLA3lqek6dh69yIGTV+h3350ymE+IWsrlycLf35+VK1eW2D5r\n1izLz9OmTWPatGnVGVatZ69L7cAezejbpSnr/3eaQ0nXnLqeTm9k074zaHX5/HV4pPSaEqKWkd/o\nOszeYkxKpQdznrjP0r6RlqEj0E/N9cw8u9fccfQix39NoVtEGJOj2spThhC1hCSLOszRYky37r96\nXYsh38SiNYdJy7CfMG5k6dmy/xw//Z7G0ud6Ud9bVdUfRQhRxSRZiFJHfwMYjSY+3fILBxOTSc3Q\n4VVP6fR1L6Xk8MTr23i4q7RlCFHTSbIQdn38TZJVu0aewf7stcXlGaQtQ4jaQH5zRakqsoxrcTuO\nXuTH31OJbBHK5KgIfKRqSogaRZKFKFVFlnG1JS0jT7rZClFDyW+qKFWgnxchAd6Vft2ibrYff5NU\n6dcWQlQNSRaiVGqVJ23vDqmy63934Cy7jl7g5wtaMnPKPhuuEKL6SLIQdk2OisDby7keUH06N2HN\nvIfp07kJoQGOZ7c1FJh554vjrE9IZ9z875i6eAcGWQNcCLckyULY5eOtot99dzp1bOIfadT3rscL\nozvywf/1pU/nJmV6r/NXc5i4YJtMgS6EG5JkIRyKGRzOkF7NaRjojcLOcWkZOtJvzhmlVnny3Mj2\n9C1jwsjOzee5d3ZJwhDCzUiyEA4VjeR+f1Yf3pv5IKGBthu9QwK8CfTzsjrvr8MjCfEv24JLF67m\nsHLDyQrFLISoXJIshNPUKk+ahfnRPSLM5v5uEWElBt2pVZ70iGxc5vc6mJhMZo6e5DSt5f950p4h\nhMvIOAtRZvYmICzteJPZzOYfzmI2O/ceN7L0PL90F9ez9Hh4gMkEoQFqurdtLOMzhHABSRaizBxN\nQGjr+Gcei2RMv5bELt/H5VRtqcfe6vrN9g/TzeaL1JvLugJMimpbsQ8hhCgT+Xomyq1wAkIfp+d7\nauDrxYezH+Lf8x7mtqD65X7fg4nJUiUlRDWTZCGqXaC/Nx/O7svAHs0I9its/Pa42c1KVc/xLXlr\nryshRPVweTXUypUr2bdvHwBZWVmkpaXxww8/WB0zZcoU0tPTqVevHl5eXqxatcoVoYpKpFR6MGV4\nO54cHM6+/Rru69yeT75JYsfRiw7PDfZXE+jnRZ6hwKlqMCFExbn8N2zy5MlMnjwZgGeeeYbY2NgS\nx5w/f57NmzejUNjr5S9qIrXKk6AGnniplJz8I82pcyLuDrFaYyO02Ap/QojK5za/Wdu2bcPPz4+e\nPXtabU9LSyMrK4u//vWvjB49ml27drkoQlGV0rP0pKQ7N8NtPaWCTfvOkJKuw2yGlHSdTEwoRBVT\nmM3OdmasuPj4eNasWWO1beHChURGRjJ8+HDeeecd7rzTemqJ5ORktm7dyoQJE8jMzGT06NF88cUX\nBAcH230vjUZT6fGLqmMoMLHkqys4027dwNuDbF3JEd7+9T0Y80AogQ2UqDzd5nuQEDVKp06dbG6v\n1mqo6OhooqOjS2z//fff8fPzK5EoAEJCQhg1ahSenp4EBwfTunVrzp496zBZQOkfurppNBq3icUd\naTQaOnTogHJjChTYzxYBvvXIyMm3uS8z18SKrdcIDVBbFlmqDet/y/1TOikb+8paPva+ZLvF16/9\n+/fTu3fvUvc9//zzAGi1Wn777TeaN29eneGJapCepXeqO6w+3/GcUakZeew4epEnXt/G0v8c5cyl\ndOlqK0QFubyBG+Ds2bPcf//9Vtvefvtt+vfvzwMPPEBCQgIjR47Ew8ODF198kaCgIBdFKqpKoJ8X\noQHeDtstdHrn1wDPMxjZffwyu49fxtvLk75dmvD0kAhpBBeiHOwmiytXrtg9uXHjss/5Y8v8+fNL\nbJs1a5bl55dffrlS3ke4L7XKk24RYZYR2pVNpy/g24SzeCgUMvpbiHKwmyzGjRuHQqHAVhu4QqFg\nx44dVRaYqHuK5pb64acrXM/Mc+ochQICfVXcyDY4dfz2w+cZ8WAL8vJNMj5DiDKw+5uyc+fO6opD\nCMucUyMfupfnlu7ihhOjtEMDvOncuhFb9p9z6j10eiNPLdxOfoGZYD81XSNuY3JUW6maEsIBp75W\nnTlzhs8//5zc3FzMZjMmk4lLly7x2WefVXV8og7y9/WiZ7vbnaqSKhqM56n0YPMPZ3BmzaT8gsIn\n5etZeWzZf45T527wzvQHJGEIYYdTvx0vvPACfn5+/PLLL7Ru3Zrr169zzz33VHVsog67dXU+D0Xh\n9OTNG/tZXjcM9GZIr+aWUdvjB7YmyM/2okyOnLmSJYstCeGAU08WJpOJ5557joKCAtq0acOoUaMY\nNWpUVccm6rDSpkEvbT6o9Cw9aZnOjQC35X+Hz9OxVSit7gzG39fL8QlC1DFOJQtvb28MBgPNmjUj\nKSmJzp07o9fLrJ+i6hVOg+5Z6usizna9LY2hwEzcx0fw8IBmt/mxeFovVNL4LYSFU9VQQ4YM4a9/\n/St/+ctf+M9//sPTTz9No0aNqjo2IZxW1PW2okymwmqp2GX7KiEqIWoPp746jRs3jqioKHx9ffn0\n0085efJkiQn/hHA1W8u9+nrX48yVrDJf69zVLDJz9HiplDINuhA4mSyWL19eYtvp06eZOnVqpQck\nBFCutSpstXMYjSaeXLCtTCO/ofAJY+l/NFxMySItUy/rf4s6r8xflfLz89m3bx/t2rWrinhEHWc0\nmvj4m6QKrVVxa7tGcpqWPEPZEkWR47+lWn4uWv/bZDbzzGOR5bqeEDWZU8mi+BPEs88+S0xMTJUE\nJOq2j79JshpfUbRWBVCuaToq2vBd3P8OX+CJR9tIlZSoc8r1PK3Vah3OGyVEWeUZCjiYmGxz38HE\n5HLNHFtZDd9F8gxGlq8/gVZnuPnUIrPZirrBqa9Hffr0sSxpajabycrKkicLUenSs/SkZth+AkjL\n0JGepbfZbdYRWw3fai9PLlzNLlece45f5tDPV9HrjYQEetNdlnQVdYBTv3mffvqp5WeFQoGfnx++\nvr5VFpSom+xVGYUEeBPoV77BcrYavtMydEx5q/xzn+XdbDBPvVlNJm0Zorazmyw2bNhg9+SoqKhK\nDUbUbfamKe8WEVbhdoJbG75DArxpGFh5bRk7jlyUtgxRq9m9sw8dOgTAhQsXOH/+PA888ABKpZKE\nhARatGghyUJUOltVRkW9oSpTZa+fodMXcOFqFg3qe8mYDFEr2b2jFy1aBMD48ePZtGmTZYW6zMxM\nnn322aqPTtQ5pc0JVRWKEtD2w+fLPA7DlpdW/IDeYKJhYNm7+wrh7py6k1NSUggICLC89vb2JjU1\n1c4Z9m3fvp0ZM2ZYXp84cYLo6GhGjRplcwDgjRs3iImJYcyYMUyfPh2drnKqDoT7Kqwy8qnSb+hF\ns9X61lfZ3B/UQMXKOX3p07mJZbZbe/SGwvnRi7r7rtxwknPJWZxLzpReU6LGc+o38S9/+QtPPvkk\nDz/8MCaTie+++44BAwaU6w3j4uJISEigdevWlm3z589n2bJlNGnShMmTJ/Pzzz/Tpk0by/4PPviA\nQYMGMWzYMFauXMm6deuYOHFiud5fiFulZ+lJK6UHVkaOAVDwwuiOlhHlX+/+ja0Hzjt17S37z1kW\nZZI1wEVN59RdO2fOHMaMGcOZM2c4f/48MTExTJ8+vVxv2LFjR1599VXL65ycHAwGA02bNkWhUNCz\nZ0/2799vdY5Go6FXr14A9O7du8R+IcqrqAeWLbf2wCp60nnmsUj6dm5S5vcpWgP842+SKhSvEK5i\n98kiKSmJ8PBwjhw5QlBQEP3797fsO3LkCF26dCn13Pj4eNasWWO1beHChQwcONDScA6FyeLWbrg+\nPj5cvHjR6rycnBwaNGhg2Z+d7Vz/eI1G49Rx1cGdYnFHriyfu0KVpKTb3p508scS27s2N3HkZw+y\ncp1Ylq+YXUfP4qvI5PaQeviona9ik/undFI29lVW+di9W9euXcuCBQt47733SuxTKBT8+9//LvXc\n6OhooqOjHQbg6+uLVqu1vNZqtfj5+dk8Rq1W29xfmk6dOjl1XFXTaDRuE4s7cnX5tG//53xUxXtg\nlVZllJh8slw9qbJ1Zj7fex0PD2jaqAEzx3WiUZD9thlXl487k7Kxr6zlYy+x2E0WCxYsAKwH5UHJ\np4GK8PX1pV69ely4cIEmTZqQkJBQYi6qjh07smfPHoYNG8bevXvl5hCVqjw9sG7t4puaocNsLtt7\nmkxwLjmbqYt3S+8pUSM4dWfu2rWLxYsXo9VqGTBgAH379uWzzz6rtCBee+01Zs6cyYgRI2jTpg3t\n2rUjIyPDkjSmTJnC5s2bGTVqFMePH2fcuHGV9t5CFClLD6yiBPP+rD68N+MvhAaoy/2+Rb2npD1D\nuDOn17N4++232bJlC5GRkcybN4/x48czduzYcr1p165d6dq1q+V1+/btWb9+vdUxAQEBlm60ISEh\nrF69ulzvJURVUqs8aRbmT/e2jSs8wO9gYjLjB7aWAX3CLTn9zHv33Xeze/du+vTpg4+PD/n5+VUZ\nlxA1SsxbdwnmAAAcbUlEQVTgcAb2aIZHBWqRUtJ1XL2uldlshVty6itMSEgICxYsIDExkcWLF/Pm\nm2/SuHHjqo5NiBpDqfRgyvDCBcGKxlaUx2urDnI9M89q0Sch3IFTyWLp0qX873//44knnqB+/fo0\nadJEllQVwobJUW3xVHqw7dA58gxl71qblpEH/NmOkZKuo9e9ZWw9F6IKOPXQ7Ovri4eHB19++SU6\nnQ4fHx+ZolwIG4oavtfMe4QmDSv+O3IwMZklX11lyls7yM7Jq4QIhSgfp5LFkiVL2Lt3L9u2bcNo\nNPLll1/y5ptvVnVsQtRY9b1VLJv5IAN7NCPYX40Cyt2eYQYupeQw7tXvWR5/AqOx7E8sQlSUU7dv\nQkICixcvxsvLC19fXz755BP27t1b1bEJUaMVtWN8OLsv/5zzEP27NbN5nLNJxGSG7w+eZ9z8rWTn\n6CsvUCGc4NRt6nHzbi5aWtVgMFi2CSHsKxq/MTmqLUN6NbfMYNsw0Ju/dLwdv/r1ynS9HF0BY+d/\nx4ovf5SnDFFtnGrg7t+/P9OnTyczM5N//etfbNy4kUGDBlV1bELUKrZGiqdn6dl97HKZr2WmsNfV\n8V9TeGpwBK2aBeHvW75lZ4VwhsNkcebMGYYOHUrr1q1p3LgxV69eZeLEiRw9erQ64hOi1rl1eddA\nPwgN9Ca1nMu7JqflEvfJYQDuCmvAkud6o5JBfaIK2K1LWrZsGcOHD6d///54eHgwc+ZMgoKCeO21\n17hy5Up1xShEraVWedI9IqxSrnU2OZvYZfsq5VpCFGf3K8iGDRv4/vvvSUlJ4b333mPVqlWkpaXx\nj3/8w7K+hBCiYmIGh2Mym9lx5CI6feHIbbXKgw4tG3Lg5NUyXevMlSzSM3UE+tteo0OI8rKbLHx8\nfGjYsCENGzbkp59+IioqilWrVqFUKqsrPiFqPaXSg2cei+SJR9tw9boWUHBbcH0A/vb2zjJXUa34\n6iQvPXlfFUQq6jK71VC39ngKDAxk9uzZkiiEqCJFkxI2C/NDrfIsdxXVbxdvyNxSotLZTRZFXWUB\n1OryT8EshCifmMHhdL7Hp0wD+m5k6UnPsh6HkWcokAkKRYXYrYb67bff6Nu3LwDXrl2z/Gw2m1Eo\nFOzYsaPqIxSiDlMqPRjUJZCGoaFOT1AY7K+2rB1uNP65CmBKuo4AXxVdw29jyvB2stCSKBO7yeL7\n77+vrjiEEHYUTVDozMp8kS1CLWtifPxNktU6Gxk5Br4/dIGEH6/w0ZyHaCBjM4ST7CaL22+/vbri\nEELYceuAvgtXs5n53t5SE8aEga2Bwqqng4nJNo/R5hWOAn+05108PSRCnjKEQ3KHCFGDqFWeNKiv\nsvtkoc83kWco4PT5dFLs9KQyA98mnJXlXIVTXDLUc/v27Xz33XcsXboUgAMHDvD3v/8dT09PgoOD\neeutt/D2/rOfuNlspnfv3jRr1gwoXIZ1xowZrghdCJcL9PMiNEBNakbJKctD/L3YsOd3jv5yjdQM\n57rcbj98nrGPtKS+t6qyQxW1SLUni7i4OBISEmjdurVl26uvvspnn31GSEgIS5cuJT4+ngkTJlj2\nX7hwgfDwcD788MPqDlcIt6NWeZa65refj1eZV+rT6Y2s3JDIX4dHWo3zkLXAxa0UZrO9B9rKt2XL\nFoKCgli3bh3vvvsuACkpKTRs2BCAt956i2bNmvH4449bnfPRRx/h6+uLWq1mzpw5NG/e3O77aDSa\nqvsQQriY0WRm27FMTl/Wkak14u+jpEWYmt+u6MjMLftMtEoP8FBAvrHwdT0lRDarz8AugSg9FPZP\nFrVKp06dbG6vsq8O8fHxrFmzxmrbwoULGThwIIcOHbLaXpQotm3bxqFDh5g+fbrV/tDQUCZPnsyA\nAQM4evQosbGxfPnllw5jKO1DVzeNRuM2sbgjKR/7Siuf+7oUNmLfOoPtM2/+r1zvYTSB8ZbX+UbQ\n/JFLus6Td6Y/4LYN4HLv2FfW8rH3JbvKkkV0dDTR0dFOH/+vf/2L7777jlWrVuHlZd2dLyIiwjJy\nvHPnzqSkpFjGeghRl5WYwTbA22ajtoeicPGksjpzJYu3/3OU0Q+35LZgH6maqsPc4l9+xYoVJCUl\n8a9//cvmSPHly5cTEBDApEmTOHXqFGFhYZIohChGrfKkW0SYzbaM/t2bEfVAC77c+SvfH7pQpuvu\n/ymZ/T8l41XPg35d75SutnWUy5NFWloa77//Pm3atGHSpEkADBgwgDFjxhATE8OHH37I5MmTiY2N\nZc+ePSiVShYtWuTiqIVwTzGDwwE4mJhMWoaOkABvukWEETM43LLMq5fKk4QfL3Mjq2xLs+rzTXyb\ncJaCAiPDHryXQD8vedKoQ6q9gbu6uFNdpjvF4o6kfOwrT/nc2pZh6w96Zo6e55fu5npWye63zmoY\naJ2IXEHuHfvK02ZR2vHyLClELVS07ndp3/z9fb24v13jCr1HSrqOTfvOsGz9CZmgsA6QZ0gh6qii\nKqsDJ6/YHODnrB1HL/Lj76m0axHK5KgIGdxXS8mThRB1VNF8Ux/8X1/6dm5SoWulZeSx4+hFJi7Y\nzkcbTmI0ln2sh3BvkiyEEJz8I61SrqPTF7Bp3xmZb6oWkmQhRB2XnqV3eh4pZ+07cYlfL6RLW0Yt\nIm0WQtRxhRMT2h7M1zDQm0V/60nydS1NG/ry6qqDnLmS5fCa6dkGZvxjL95eSvp2aSpjM2oB+dcT\noo4rGsxnS7eIMBoG1afdPaF4e9cjR5dfpmvr9Ea+TTjL0s81nEvOlCeNGkyeLIQQdgfzFalIddW+\nE1fYd+KKPGnUYJIshBBWK/GVNpjPXnWVs4qeNDwUCiZFta1o2KIaSWoXQljYG8xnr7qqrA4mJkuV\nVA0jyUII4bSYweEM6dWchoHeVGQqz9QMHellnJtKuJZUQwkhnHZrddXV67m8vvogqeWollKrlAT6\neTk+ULgNebIQQpSZWuVJszA/updSLeVocT2zGfQGI8lpWjJz9CSnaaVays3Jk4UQotxs9aKKuDuE\nnUcv2j0vz2Dkqbht6PNNeHiAyQShAWoiW4TyxMDW5OWbZAp0NyP/EkKIcrPViwog8Y80h72m9PmF\n80eZbk4jlXpzfqkdNxNNaIA33du6dgp08Sf5FxBCVNitvagqq9dUakbhFOirNiVWQoSioiRZCCEq\nXVGvqdCAksskl9X2w+fJzJGeU67mkmSxfft2ZsyYYfX6oYceYvz48YwfP57Dhw9bHX/jxg1iYmIY\nM2YM06dPR6er3EnPhBCV69bpz5fNfJCQCiQNvcFETNw2PvjvCS6lZEtDuItUe5tFXFwcCQkJtG7d\n2rItMTGR2NhYHnnkEZvnfPDBBwwaNIhhw4axcuVK1q1bx8SJE6spYiFEeRX1murRtjGb9p0p93UM\n+Sa2HjjP1gPnCQ30pnuxqUhE1av2Nbi3bNlCUFAQ69at49133wXg6aefxsPDg5ycHCIjI5k5cyae\nnn/msccee4yVK1cSGhrKqVOneOedd1i5cqXd99FoNFX6OYQQzjOazGw7lsnpyzoytUZUngrMmKnI\nQ0LnFvXp0doPX28PVJ5So15ZSluDu8qeLOLj41mzZo3VtoULFzJw4EAOHTpktf3+++/noYce4o47\n7mD+/PmsXbuWcePGWfbn5OTQoEEDAHx8fMjOznYqBndZyF0WlbdPyse+2lI+93WBPEOBVa+p9Cw9\nXvU8WLPlF/b/dJk8g/Mr7B39PZejv+cSGqCme9vG0mvKhrLeO/a+ZFdZsoiOjiY6OtqpY4cPH46f\nnx8Affv25fvvv7fa7+vri1arRa1Wo9VqLccKIWqWwl5Tf/7ZKfr5hdEdmRwVwYdf/cSeY5cpS3VH\nakYem/adwWQ288xjkZUcsSji8jRsNpsZMmQIV69eBeDAgQOEh1vXRXbs2JE9e/YAsHfv3lrxLUsI\nYc3HW8WMsZ0Z0KNZuc7fceSCNH5XIZcnC4VCQVxcHFOnTmXcuHHodDpGjhxJRkYGU6dOBWDKlCls\n3ryZUaNGcfz4casqKiFE7TI5qi2Det6Ft5eyTOfp9EYuXM2WqUOqSLU3cFcXd6rndadY3JGUj311\ntXzyDAVcvZ5L/I7T7D1+xalzgvy8SM/WE9jAi/DmwQzvcw+3h/rW2WlDytNmUe0N3EIIURFF3W5f\nHN2JAF81B05eITUjz+45N25Oe34jS29Znc+rnoIekbfz18faUt9bVR2h10qSLIQQbq34/FNf7/6N\nrQfOO32+Pt/MLs0lDpy8Qvt7GzFlWFuC/L2rMOLaSZKFEKJGKOpJ9cxjkdTzVHIwMZnUdB2Bfl6W\nJwp78gwmDiYmczAxmeaN/Vg8rReqOlo9VR4ub+AWQoiyKHrSeH9WH6YNvo33ZjxIsF/ZphM5cyWL\nGcv2VVGEtZMkCyFEjaRWeRLUwBN/Xy+6RtxW5vPPXcnil3Np0nPKSfIMJoSo8SZHteXUuRucuZJV\npvNmLfuBID8vurRuRNRfWhAS4F1ne045IqUihKjxlEoP3pn+AP/8+id2ai6hNxidPvdGlp7vD13g\n+0MXZOoQOyRZCCFqBaXSg7+NaE/MkAiuXtei0+fzzb6z7Dvh3BgN+HPqEIBJUW2rKtQaSVKnEKJW\nKRyf4U/rZiHMGt+Fh7rcUeZrHExMlraMYiRZCCFqtanRHWjeuGyTj6am60h3ojtuXSLJQghRqxW1\nZwzs0Yxgf+e62Ab6eRHo50WeoUDmmrpJ2iyEELWeUunBlOHteHJwOGkZOhatOcyFqzmlHt+5VUPe\njz/BT7+nkZ6tJzTAm86tGzG4V/M622Oq7n1iIUSdpVZ5ckfDBrz34oNMf3c355JLLqTWwEfF/45c\nxHTLFKsp6Tq27D/Hlv3naBjoTbeby7rWpR5TdeeTCiHETUqlB39/4S8M7NGMID8vFECwv5pmYQ3I\n1hqsEkVxKek6Nu07w8ffJFVbvO5AniyEEHXSrVVT6Vl66qs9eeHve5w+/2BiMiMfupfcvAIC/bxq\nfdVU7f50QgjhQNEEhclpWtLSdU6fl5Ku4/mlu7mRnUdoQO2vmqqdn0oIIcoo0M+LkMCyTV1+PSsP\ns7luVE25JFls376dGTNmWF6PHz/e8t/999/PkiVLrI7PyMiga9eulmPWrFlT3SELIWo5tcqT7hFh\nFbpGbR7MV+3VUHFxcSQkJNC6dWvLtk8//RSAixcv8vzzzzNlyhSrc37++WcGDRrEK6+8Uq2xCiHq\nlpjB4ZjMZnYcuYhOX/hHX1VPQViwLzp9AWkZOgIalL5+RlpG4WC+sJDaV8Nf7Z+oY8eOPPTQQ6xb\nt67EvjfeeIPY2Fh8fHysticmJpKUlMS4ceMICgpi7ty5NGzYsLpCFkLUEUqlB888FskTj7bh6nUt\noOC24PqoVZ7kGQosDeEv/n0PKTbaN0ICvAn086r+wKtBlSWL+Pj4EtVFCxcuZODAgRw6dKjE8adO\nnUKr1dK9e/cS+5o3b05ERAQ9evRg06ZNxMXF8d577zmMQaPRlP8DVDJ3isUdSfnYJ+VTuqoum+s2\n5iG8K1RJSrrt7Uknf7TaZigwkaMz4evtgcqz+mv+K6t8qixZREdHEx0d7fTxmzZtKvX4bt264e1d\n2PDUr18/pxIFQKdOnZx+/6qk0WjcJhZ3JOVjn5RP6VxVNu3bm/j4myQOJiaTlqEjxEZvKKPxz2NS\nM3Qu6TFV1vKxl1jcpmLt4MGDTJo0yea+uXPn8vDDDzNw4EAOHDhAeHh4NUcnhBB/KlradfzA1qRn\n6W2Os/j4myTLdOfwZ48pqJnTn7tN19nU1FQCAwMtrzMyMpg6dSoAM2bM4IsvvmD8+PGsXbuWl19+\n2VVhCiGEReEYDZ8SiSLPUMDBxGSb5xxMTCYzR1/jJih0yZNF165d6dq1q9W2ffusF08PCAhg+fLl\nADRp0sTSY0oIIdxdepae1AzbA/xS0nVMW7KLjGw9Qf5q2t0TyuSoCHy8VdUcZdm4zZOFEELUFoF+\nXoQGlD7ALz1bjxm4npnHzqMXmfj6Nj7acBKj0VR9QZaRJAshhKhkapUn3cowwC/PYHT7EeCSLIQQ\nogrEDA5nSK/mNAz0xkMBQQ0cVzO58whwt+kNJYQQtUnxHlNnkzNZ9K8jds9Jy9Bx9XouXvWUbjeT\nrftEIoQQtVDRrLb11Y7/3HqplLy++iBpLhqXYY/rIxBCiDrA39eLu8Ia2D1GpzeSmq5zy5lsJVkI\nIUQ1WfJcb5o39kNRbHuIvxfeXrafPIraMfIMBS4dmyHVUEIIUU1UKk/+MeNBMnP0nEvOIizYB6PJ\njD6/gOeW7rZ5TlqGjuXxJ0j8/bpLF1qSZCGEENXM39eLdveEWl7nGQoIDfC2OZOth0LBnmOXLa9d\nNW2IVEMJIYSL2RuXUWAy29xe3d1sJVkIIYQbKD4uo2GgN16q0v9EFy20VF2kGkoIIdxA8XEZ+nwj\n05bsKvX4QD91tS60JE8WQgjhRopmsr0tuD4NA0ufX6pr+G02Z7utqh5T8mQhhBBuqKgd49Y1MYo0\nb+zH5Fsat0tbaKnd7bbbO8pDkoUQQripmMGFC70dTEwmNV1HoJ8X3SLCmBzV1qrbbGkLLV2715f7\nulROLJIshBDCTTmzIp+9hZZOX9aRZyiolDmmpM1CCCHcXGkr8oH9hZYytcZK6zFVrU8W2dnZxMbG\nkpOTQ35+PrNnz6ZDhw6cOHGCN954A6VSSc+ePS3LqRa5ceMGM2fOJC8vj4YNG7Jo0SK8vUtv+BFC\niLqiaKElWwP6/H2UldZjqlqfLD755BO6devGf/7zHxYtWsTrr78OwPz581m6dClffPEFP/74Iz//\n/LPVeR988AGDBg3i888/p02bNqxbt646wxZCCLdlb0Bfy9u9K22a82pNFhMnTmTUqFEAGI1GvLy8\nyMnJwWAw0LRpUxQKBT179mT//v1W52k0Gnr16gVA7969S+wXQoi6zNaAviG9mvNwR/9Ke48qq4aK\nj49nzZo1VtsWLlxIZGQkqampxMbG8tJLL5GTk4Ovr6/lGB8fHy5evGh1Xk5ODg0aNLDsz87OdioG\njUZTwU9RedwpFnck5WOflE/ppGwKdWwCEWGB5Oj88fX2QOVpABSVVj5Vliyio6OJjo4usf306dO8\n+OKLzJo1i/vuu4+cnBy0Wq1lv1arxc/Pz+ocX19ftFotarXa5v7SdOrUqWIfopJoNBq3icUdSfnY\nJ+VTOikb+8paPvYSS7VWQ/3+++88//zzLF26lAceeAAoTAT16tXjwoULmM1mEhIS6Ny5s9V5HTt2\nZM+ePQDs3btXbg4hhKhm1Zosli5disFg4I033mD8+PFMmTIFgNdee42ZM2cyYsQI2rRpQ7t27cjI\nyLD0ipoyZQqbN29m1KhRHD9+nHHjxlVn2EIIUedVa9fZFStW2Nzevn171q9fb7UtICCA5cuXAxAS\nEsLq1aurPD4hhBC2yaA8IYQQDinMZnPlzTTlRqSHhBBClF1pbcK1NlkIIYSoPFINJYQQwiFJFkII\nIRySZCGEEMIhSRZCCCEckmQhhBDCIUkWQgghHJJlVavYY489ZplV94477mDRokUujsj1fvzxR5Ys\nWcKnn37K+fPnmT17NgqFgnvuuYf58+fj4VG3v8PcWj4///wzzzzzDM2aNQNg9OjRDBw40LUBukh+\nfj4vvfQSly9fxmAwMGXKFFq0aCH3z022yicsLKzS7h9JFlVIr9djNpv59NNPXR2K2/joo4/YtGmT\nZaXDRYsWMX36dLp27cq8efPYsWMH/fr1c3GUrlO8fJKSknjyySeJiYlxcWSut2nTJgICAli8eDEZ\nGRlERUXRqlUruX9uslU+zz77bKXdP3UzBVeTU6dOodPpiImJYcKECZw4ccLVIblc06ZNWbZsmeV1\nUlIS9913HyALW0HJ8klMTGT37t2MHTvWsv5LXdW/f3+ef/55AMxmM0qlUu6fW9gqn8q8fyRZVCG1\nWs1TTz3F6tWrLTPrFhQUuDosl3rkkUfw9PzzgdZsNqNQKICyLWxVWxUvn8jISGbNmsVnn31GkyZN\neP/9910YnWv5+Pjg6+tLTk4Ozz33HNOnT5f75xa2yqcy7x9JFlXorrvuYsiQISgUCu666y4CAgJI\nTU11dVhu5db65bIsbFVX9OvXj4iICMvPxdenr2uSk5OZMGECQ4cOZfDgwXL/FFO8fCrz/pFkUYX+\n+9//8uabbwJw7do1cnJyCA0NdXFU7qVNmzYcOnQIKFzYqvjCV3XdU089xU8//QTAgQMHCA8Pd3FE\nrpOWlkZMTAyxsbGMGDECkPvnVrbKpzLvH5lIsAoZDAbmzJnDlStXUCgUzJw5k44dO7o6LJe7dOkS\nL774IuvXr+fs2bO88sor5Ofn07x5c+Li4lAqla4O0aVuLZ+kpCQWLFhAvXr1CAkJYcGCBVZr1tcl\ncXFxbN26lebNm1u2vfzyy8TFxcn9g+3ymT59OosXL66U+0eShRBCCIekGkoIIYRDkiyEEEI4JMlC\nCCGEQ5IshBBCOCTJQgghhEOSLISw4dKlS0RERDB06FCioqJ49NFHefLJJ7l69Wq5rvfVV18xe/Zs\nACZNmsS1a9dKPfa9997j6NGjZbp+y5YtyxWXEM6SZCFEKRo2bMjGjRvZsGEDmzdvJiIiggULFlT4\nuh999BGNGjUqdf+RI0cwGo0Vfh8hKpPMOiuEkzp37szOnTvp06cPkZGR/PLLL3z++efs27ePNWvW\nYDKZCA8PZ/78+Xh5ebFhwwZWrFiBr68vt99+O/Xr1wegT58+/Pvf/yY0NJTXXnsNjUZDvXr1+Nvf\n/obBYCAxMZG5c+eyfPly1Go1r776KhkZGajVal555RXatGnDpUuXiI2NJTc3l3bt2rm4ZERdIE8W\nQjghPz+frVu3Wkbg9+7dm++//54bN26wfv161q5dy8aNGwkODmb16tVcu3aNJUuW8Nlnn7Fu3Tq0\nWm2Ja3766afk5uaydetWPvnkE95//30GDhxIREQEcXFxtGzZkv/7v/8jNjaWr7/+mgULFvDCCy8A\nsGDBAoYNG8bGjRtlVgBRLeTJQohSpKSkMHToUKBw6pbIyEhmzJjBDz/8YPk2f+jQIc6fP8/IkSOB\nwqTSpk0bjh8/TocOHQgJCQFg8ODBHDx40Or6R44cYeTIkXh4eBAaGsrmzZut9mu1WhITE5kzZ45l\nW25uLunp6Rw+fJilS5cCMGTIEObOnVs1hSDETZIshChFUZuFLV5eXgAYjUYGDBhg+WOt1WoxGo0c\nOHAAk8lkOf7WacdL23b+/HnCwsIsr00mEyqVyiqGq1evEhAQABRO7w6gUCgs03QLUVWkGkqICuja\ntSvbt2/n+vXrmM1mXn31VdasWUOnTp348ccfuXbtGiaTiS1btpQ4t0uXLmzduhWz2cz169cZN24c\nBoMBpVKJ0WikQYMGNGvWzJIsfvjhB8aOHQtAjx492LRpEwDbtm3DYDBU34cWdZI8WQhRAa1atWLq\n1Kk88cQTmEwmWrduzeTJk/Hy8mLu3LlMnDgRb29vWrRoUeLcMWPGEBcXx5AhQwB45ZVX8PX1pVev\nXsyfP5+33nqLxYsX8+qrr7Jq1Srq1avHu+++i0KhYN68ecTGxrJ27Vratm2Lj49PdX90UcfIrLNC\nCCEckmooIYQQDkmyEEII4ZAkCyGEEA5JshBCCOGQJAshhBAOSbIQQgjhkCQLIYQQDv0/i173zUE9\nYJEAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1106eac50>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.scatter(predicted, corr_residual)\n",
"plt.xlabel('Predicted')\n",
"plt.ylabel('Residual')\n",
"plt.axhline(y=0)\n",
"plt.title('Residual vs. Predicted')\n",
"plt.show()\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"There was a big improvement here as well. Success!"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| gpl-3.0 |
pycroscopy/pycroscopy | jupyter_notebooks/image_registration.ipynb | 1 | 25183 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {
"hideCode": false,
"hideOutput": true,
"hidePrompt": false
},
"source": [
"<font size = \"5\"> **[Image Registration](image_registration.ipynb)** </font>\n",
"\n",
"<hr style=\"height:1px;border-top:4px solid #FF8200\" />\n",
"\n",
"by \n",
" \n",
"Gerd Duscher and Matthew. F. Chisholm\n",
"\n",
"Materials Science & Engineering<br>\n",
"Joint Institute of Advanced Materials<br>\n",
"The University of Tennessee, Knoxville\n",
"\n",
"\n",
"# Registration of a Stack of Images \n",
"\n",
"We us this notebook **only** for a stack of images."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"## Prerequesites\n",
"\n",
"### Install pycroscopy \n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"scrolled": true
},
"outputs": [],
"source": [
"import sys\n",
"from pkg_resources import get_distribution, DistributionNotFound\n",
"\n",
"def test_package(package_name):\n",
" \"\"\"Test if package exists and returns version or -1\"\"\"\n",
" try:\n",
" version = (get_distribution(package_name).version)\n",
" except (DistributionNotFound, ImportError) as err:\n",
" version = '-1'\n",
" return version\n",
"\n",
"# Colab setup ------------------\n",
"if 'google.colab' in sys.modules:\n",
" !pip install git+https://github.com/pycroscopy/pyTEMlib/ -q\n",
"\n",
"# pyTEMlib setup ------------------\n",
"else:\n",
" if test_package('sidpy') < '0.0.4':\n",
" print('installing sidpy')\n",
" !{sys.executable} -m pip install --upgrade sidpy -q \n",
" if test_package('pyNSID') < '0.0.2':\n",
" print('installing pyNSID')\n",
" !{sys.executable} -m pip install --upgrade pyNSID -q \n",
" if test_package('pycroscopy') < '0':\n",
" print('installing pyTEMlib')\n",
" !{sys.executable} -m pip install --upgrade pyTEMlib -q\n",
"# ------------------------------\n",
"print('done')"
]
},
{
"cell_type": "markdown",
"metadata": {
"hideCode": false,
"hidePrompt": false
},
"source": [
"### Import the usual libraries\n",
"\n",
"You can load that library with the code cell above:"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"hideCode": false,
"hidePrompt": false,
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Populating the interactive namespace from numpy and matplotlib\n",
"The autoreload extension is already loaded. To reload it, use:\n",
" %reload_ext autoreload\n"
]
}
],
"source": [
"# import matplotlib and numpy\n",
"# use \"inline\" instead of \"notebook\" for non-interactive\n",
"# use widget for jupyterlab needs ipympl to be installed\n",
"import sys\n",
"if 'google.colab' in sys.modules:\n",
" %pylab --no-import-all notebook\n",
"else: \n",
" %pylab --no-import-all widget\n",
"\n",
"from sidpy.io.interface_utils import open_file_dialog\n",
"\n",
"from SciFiReaders import DM3Reader\n",
"import SciFiReaders\n",
"\n",
"%load_ext autoreload\n",
"%autoreload 2\n",
"\n",
"sys.path.insert(0, '../')\n",
"import pycroscopy as px\n",
"\n",
"__notebook__ = 'Image_Registration'\n",
"__notebook_version__ = '2021_10_04'"
]
},
{
"cell_type": "markdown",
"metadata": {
"hideCode": false,
"hidePrompt": false
},
"source": [
"## Load an image stack :\n",
"\n",
"Please, load an image stack. <br>\n",
"\n",
"A stack of images is used to reduce noise, but for an added image the images have to be aligned to compensate for drift and other microscope instabilities.\n",
"\n",
"You select here (with the ``open_file_dialog`` parameter), whether an **open file dialog** apears in the code cell below the next one or whether you want to get a list of files (Nion has a weird way of dealing with file names)."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "3db76f26919446f5ba497a06f440c888",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"FileChooser(path='.', filename='', title='HTML(value='', layout=Layout(display='none'))', show_hidden='False',…"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"if 'google.colab' in sys.modules:\n",
" from google.colab import drive\n",
" drive.mount(\"/content/drive\")\n",
" drive_directory = 'drive/MyDrive/'\n",
"else:\n",
" drive_directory = '.'\n",
"\n",
"file_widget = open_file_dialog(drive_directory)\n",
"file_widget"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Plot Image Stack\n",
"Either we load the selected file in hte widget above above or a file dialog window appears.\n",
"\n",
"This is the point the notebook can be repeated with a new file. Either select a file above again (without running the code cell above) or open a file dialog here\n",
"\n",
"Note that the **open file dialog** might not apear in the foreground!"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"sidpy.Dataset of type IMAGE_STACK with:\n",
" dask.array<array, shape=(512, 512, 20), dtype=float32, chunksize=(512, 512, 20), chunktype=numpy.ndarray>\n",
" data contains: intensity (counts)\n",
" and Dimensions: \n",
"x: distance (counts) of size (512,)\n",
"y: distance (counts) of size (512,)\n",
"z: distance (counts) of size (20,)\n"
]
},
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "9eec2a83025248ecba978ddadbd9afb6",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"Canvas(toolbar=Toolbar(toolitems=[('Home', 'Reset original view', 'home', 'home'), ('Back', 'Back to previous …"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "0718fe47a1334c62a3eaccd1a7f9c029",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"HBox(children=(Play(value=0, description='Press play', interval=500, max=20), IntSlider(value=0, continuous_up…"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"try: \n",
" main_dataset.h5_dataset.file.close()\n",
"except:\n",
" pass\n",
"dm3_reader = DM3Reader(file_widget.selected)\n",
"main_dataset = dm3_reader.read()\n",
"\n",
"if main_dataset.data_type.name != 'IMAGE_STACK':\n",
" print(f\"Please load an image stack for this notebook, this is an {main_dataset.data_type}\")\n",
"print(main_dataset) \n",
"main_dataset.dim_0.dimension_type = 'spatial'\n",
"main_dataset.dim_1.dimension_type = 'spatial'\n",
"main_dataset.z.dimension_type = 'temporal'\n",
"main_dataset.plot() # note this needs a view reference for interaction"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {},
"outputs": [],
"source": [
"main_dataset._axes\n",
"frame_dim = []\n",
"spatial_dim = []\n",
"for i, axis in main_dataset._axes.items():\n",
" if axis.dimension_type.name == 'SPATIAL':\n",
" spatial_dim.append(i)\n",
" else:\n",
" frame_dim.append(i)\n",
" \n",
"if len(spatial_dim) != 2:\n",
" print('need two spatial dimensions')\n",
"if len(frame_dim) != 1:\n",
" print('need one frame dimensions')\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Complete Registration \n",
"\n",
"Takes a while, depending on your computer between 1 and 10 minutes."
]
},
{
"cell_type": "code",
"execution_count": 53,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Rigid_Registration\n",
"Stack contains 20 images, each with 512 pixels in x-direction and 512 pixels in y-direction\n"
]
},
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "a93afdca35b046f2b999ddcac4329783",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
" 0%| | 0/20 [00:00<?, ?it/s]"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Non-Rigid_Registration\n"
]
},
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "e7538be9e7db43ef87ba108502734ab6",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
" 0%| | 0/20 [00:00<?, ?it/s]"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
":-)\n",
"You have successfully completed Diffeomorphic Demons Registration\n"
]
},
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "15e613a3040f4d358b25b5d2c642bc7b",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"Canvas(toolbar=Toolbar(toolitems=[('Home', 'Reset original view', 'home', 'home'), ('Back', 'Back to previous …"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "76a5ba9fcf3141e7830c48138d30f831",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"HBox(children=(Play(value=0, description='Press play', interval=500, max=20), IntSlider(value=0, continuous_up…"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"<table>\n",
" <tr>\n",
" <td>\n",
" <table>\n",
" <thead>\n",
" <tr>\n",
" <td> </td>\n",
" <th> Array </th>\n",
" <th> Chunk </th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" \n",
" <tr>\n",
" <th> Bytes </th>\n",
" <td> 34.01 MiB </td>\n",
" <td> 34.01 MiB </td>\n",
" </tr>\n",
" \n",
" <tr>\n",
" <th> Shape </th>\n",
" <td> (20, 453, 492) </td>\n",
" <td> (20, 453, 492) </td>\n",
" </tr>\n",
" <tr>\n",
" <th> Count </th>\n",
" <td> 1 Tasks </td>\n",
" <td> 1 Chunks </td>\n",
" </tr>\n",
" <tr>\n",
" <th> Type </th>\n",
" <td> float64 </td>\n",
" <td> numpy.ndarray </td>\n",
" </tr>\n",
" </tbody>\n",
" </table>\n",
" </td>\n",
" <td>\n",
" <svg width=\"199\" height=\"180\" style=\"stroke:rgb(0,0,0);stroke-width:1\" >\n",
"\n",
" <!-- Horizontal lines -->\n",
" <line x1=\"10\" y1=\"0\" x2=\"29\" y2=\"19\" style=\"stroke-width:2\" />\n",
" <line x1=\"10\" y1=\"110\" x2=\"29\" y2=\"130\" style=\"stroke-width:2\" />\n",
"\n",
" <!-- Vertical lines -->\n",
" <line x1=\"10\" y1=\"0\" x2=\"10\" y2=\"110\" style=\"stroke-width:2\" />\n",
" <line x1=\"29\" y1=\"19\" x2=\"29\" y2=\"130\" style=\"stroke-width:2\" />\n",
"\n",
" <!-- Colored Rectangle -->\n",
" <polygon points=\"10.0,0.0 29.548557181801698,19.548557181801698 29.548557181801698,130.0363620598505 10.0,110.48780487804878\" style=\"fill:#ECB172A0;stroke-width:0\"/>\n",
"\n",
" <!-- Horizontal lines -->\n",
" <line x1=\"10\" y1=\"0\" x2=\"130\" y2=\"0\" style=\"stroke-width:2\" />\n",
" <line x1=\"29\" y1=\"19\" x2=\"149\" y2=\"19\" style=\"stroke-width:2\" />\n",
"\n",
" <!-- Vertical lines -->\n",
" <line x1=\"10\" y1=\"0\" x2=\"29\" y2=\"19\" style=\"stroke-width:2\" />\n",
" <line x1=\"130\" y1=\"0\" x2=\"149\" y2=\"19\" style=\"stroke-width:2\" />\n",
"\n",
" <!-- Colored Rectangle -->\n",
" <polygon points=\"10.0,0.0 130.0,0.0 149.5485571818017,19.548557181801698 29.548557181801698,19.548557181801698\" style=\"fill:#ECB172A0;stroke-width:0\"/>\n",
"\n",
" <!-- Horizontal lines -->\n",
" <line x1=\"29\" y1=\"19\" x2=\"149\" y2=\"19\" style=\"stroke-width:2\" />\n",
" <line x1=\"29\" y1=\"130\" x2=\"149\" y2=\"130\" style=\"stroke-width:2\" />\n",
"\n",
" <!-- Vertical lines -->\n",
" <line x1=\"29\" y1=\"19\" x2=\"29\" y2=\"130\" style=\"stroke-width:2\" />\n",
" <line x1=\"149\" y1=\"19\" x2=\"149\" y2=\"130\" style=\"stroke-width:2\" />\n",
"\n",
" <!-- Colored Rectangle -->\n",
" <polygon points=\"29.548557181801698,19.548557181801698 149.5485571818017,19.548557181801698 149.5485571818017,130.0363620598505 29.548557181801698,130.0363620598505\" style=\"fill:#ECB172A0;stroke-width:0\"/>\n",
"\n",
" <!-- Text -->\n",
" <text x=\"89.548557\" y=\"150.036362\" font-size=\"1.0rem\" font-weight=\"100\" text-anchor=\"middle\" >492</text>\n",
" <text x=\"169.548557\" y=\"74.792460\" font-size=\"1.0rem\" font-weight=\"100\" text-anchor=\"middle\" transform=\"rotate(-90,169.548557,74.792460)\">453</text>\n",
" <text x=\"9.774279\" y=\"140.262083\" font-size=\"1.0rem\" font-weight=\"100\" text-anchor=\"middle\" transform=\"rotate(45,9.774279,140.262083)\">20</text>\n",
"</svg>\n",
" </td>\n",
" </tr>\n",
"</table>"
],
"text/plain": [
"sidpy.Dataset of type IMAGE_STACK with:\n",
" dask.array<array, shape=(20, 453, 492), dtype=float64, chunksize=(20, 453, 492), chunktype=numpy.ndarray>\n",
" data contains: intensity (counts)\n",
" and Dimensions: \n",
"z: distance (counts) of size (20,)\n",
"x: distance (counts) of size (453,)\n",
"y: distance (counts) of size (492,)\n",
" with metadata: ['analysis', 'input_crop', 'input_shape']"
]
},
"execution_count": 53,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"## Do all of registration\n",
"notebook_tags ={'notebook': __notebook__, 'notebook_version': __notebook_version__}\n",
"\n",
"non_rigid_registered, rigid_registered_dataset = px.image.complete_registration(main_dataset)\n",
" \n",
"non_rigid_registered.plot()\n",
"non_rigid_registered"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Check Drift"
]
},
{
"cell_type": "code",
"execution_count": 54,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "22c9608a9f884158955866d43235ebc3",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"Canvas(toolbar=Toolbar(toolitems=[('Home', 'Reset original view', 'home', 'home'), ('Back', 'Back to previous …"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"scale_x = (rigid_registered_dataset.x[1]-rigid_registered_dataset.x[0])*1.\n",
"drift = rigid_registered_dataset.metadata['drift']\n",
"x = np.linspace(0,drift.shape[0]-1,drift.shape[0])\n",
"\n",
"polynom_degree = 2 # 1 is linear fit, 2 is parabolic fit, ...\n",
"line_fit_x = np.polyfit(x, drift[:,0], polynom_degree)\n",
"poly_x = np.poly1d(line_fit_x)\n",
"line_fit_y = np.polyfit(x, drift[:,1], polynom_degree)\n",
"poly_y = np.poly1d(line_fit_y)\n",
"\n",
"\n",
"plt.figure()\n",
"# plot drift and fit of drift\n",
"plt.axhline(color = 'gray')\n",
"plt.plot(x, drift[:,0], label = 'drift x')\n",
"plt.plot(x, drift[:,1], label = 'drift y')\n",
"plt.plot(x, poly_x(x), label = 'fit_drift_x')\n",
"plt.plot(x, poly_y(x), label = 'fit_drift_y')\n",
"plt.legend();\n",
"\n",
"# set second axis in pico meter\n",
"ax_pixels = plt.gca()\n",
"ax_pixels.step(1, 1)\n",
"ax_pm = ax_pixels.twinx()\n",
"x_1, x_2 = ax_pixels.get_ylim()\n",
"ax_pm.set_ylim(x_1*scale_x, x_2*scale_x)\n",
"\n",
"# add labels\n",
"ax_pixels.set_ylabel('drift [pixels]')\n",
"ax_pm.set_ylabel('drift [nm]')\n",
"ax_pixels.set_xlabel('image number');\n",
"plt.tight_layout()\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Appendix"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Demon Registration\n",
"\n",
"Here we use the **Diffeomorphic Demon Non-Rigid Registration** as provided by **simpleITK**. \n",
"\n",
"Please Cite: \n",
"* [simpleITK](http://www.simpleitk.org/SimpleITK/project/parti.html)\n",
" \n",
" and\n",
" \n",
"* [T. Vercauteren, X. Pennec, A. Perchant and N. Ayache *Diffeomorphic Demons Using ITK\\'s Finite Difference Solver Hierarchy* The Insight Journal, 2007](http://hdl.handle.net/1926/510)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This Non-Rigid Registration consists of the following steps:\n",
"\n",
"- determine ``reference`` image\n",
" - For this we use the average of the rigid registered stack\n",
" - this averaged stack is then smeared with a Gaussian of sigma 2 pixel to reduce noise\n",
" - under the assumption that high frequency scan distortions cancel out over several images, we, therefore, obtained the center of mass of the atoms. \n",
"\n",
"- perform the ``demon registration`` filter to determine a distortion matrix\n",
" - each single image of a stack is first smeared with a Gaussian of sigma of 2pixels\n",
" - then the deformation matrix is determined for these images\n",
" - the deformation matrix is a matrix where each pixel has a vector ( x, and y value) for the relative shift of this pixel.\n",
" \n",
"- This deformation matrix is used to ``transform`` the image\n",
"\t- The transformation is performed on the original image.\n",
"\t- Important, here, is to set the interpolator method, (the image needs to be interpolated because the new pixels are not on an integer grid.)\n",
" \n",
" \n",
"Let's see what the different interpolators do.\n",
"\n",
"|Method\t| RMS contrast |\tStandard |\tMean |\n",
"|-------|:--------------|:-------------|:-------|\n",
"|original |0.1965806\t|0.07764114\t|0.3949583\n",
"|Linear\t |0.20159315\t|0.079470366\t|0.39421165\n",
"|BSpline\t|0.20162606\t|0.0794831 \t|0.39421043\n",
"|Gaussian\t|0.14310582\t|0.056414302 \t|0.39421389\n",
"|Hamming\t|0.20163293\t|0.07948672 \t|0.39421496\n",
"\n",
"The Gaussian interpolator is the only one seems to smear the signal.\n",
"\n",
"We will use the ``Bspline`` method a fast and simple method that does not introduce spurious features and does not smear the signal.\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Full Code of Demon registration "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"import simpleITK as sitk\n",
"\n",
"def DemonReg(cube, verbose = False):\n",
" \"\"\"\n",
" Diffeomorphic Demon Non-Rigid Registration \n",
" Usage:\n",
" \n",
" DemReg = DemonReg(cube, verbose = False)\n",
"\n",
" Input:\n",
" cube: stack of image after rigid registration and cropping\n",
" Output:\n",
" DemReg: stack of images with non-rigid registration\n",
"\n",
" Dempends on:\n",
" simpleITK and numpy\n",
" \n",
" Please Cite: http://www.simpleitk.org/SimpleITK/project/parti.html\n",
" and T. Vercauteren, X. Pennec, A. Perchant and N. Ayache\n",
" Diffeomorphic Demons Using ITK\\'s Finite Difference Solver Hierarchy\n",
" The Insight Journal, http://hdl.handle.net/1926/510 2007\n",
" \"\"\"\n",
" \n",
" DemReg = np.zeros_like(cube)\n",
" nimages = cube.shape[0]\n",
" print(nimages)\n",
" # create fixed image by summing over rigid registration\n",
"\n",
" fixed_np = np.average(current_dataset, axis=0)\n",
"\n",
" fixed = sitk.GetImageFromArray(fixed_np)\n",
" fixed = sitk.DiscreteGaussian(fixed, 2.0)\n",
"\n",
" #demons = sitk.SymmetricForcesDemonsRegistrationFilter()\n",
" demons = sitk.DiffeomorphicDemonsRegistrationFilter()\n",
"\n",
" demons.SetNumberOfIterations(200)\n",
" demons.SetStandardDeviations(1.0)\n",
"\n",
" resampler = sitk.ResampleImageFilter()\n",
" resampler.SetReferenceImage(fixed);\n",
" resampler.SetInterpolator(sitk.sitkBspline)\n",
" resampler.SetDefaultPixelValue(0)\n",
"\n",
" done = 0\n",
" \n",
" for i in range(nimages):\n",
" if done < int((i+1)/nimages*50):\n",
" done = int((i+1)/nimages*50)\n",
" sys.stdout.write('\\r')\n",
" # progress output :\n",
" sys.stdout.write(\"[%-50s] %d%%\" % ('*'*done, 2*done))\n",
" sys.stdout.flush()\n",
" \n",
" moving = sitk.GetImageFromArray(cube[i])\n",
" movingf = sitk.DiscreteGaussian(moving, 2.0)\n",
" displacementField = demons.Execute(fixed,movingf)\n",
" outTx = sitk.DisplacementFieldTransform( displacementField )\n",
" resampler.SetTransform(outTx)\n",
" out = resampler.Execute(moving)\n",
" DemReg[i,:,:] = sitk.GetArrayFromImage(out)\n",
" #print('image ', i)\n",
" \n",
" \n",
" print(':-)')\n",
" print('You have succesfully completed Diffeomorphic Demons Registration')\n",
" \n",
" return DemReg\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"hide_code_all_hidden": false,
"kernelspec": {
"display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.9.7"
},
"toc": {
"base_numbering": "2",
"nav_menu": {},
"number_sections": true,
"sideBar": true,
"skip_h1_title": false,
"title_cell": "Table of Contents",
"title_sidebar": "Contents",
"toc_cell": false,
"toc_position": {
"height": "calc(100% - 180px)",
"left": "10px",
"top": "150px",
"width": "174px"
},
"toc_section_display": true,
"toc_window_display": true
},
"varInspector": {
"cols": {
"lenName": 16,
"lenType": 16,
"lenVar": 40
},
"kernels_config": {
"python": {
"delete_cmd_postfix": "",
"delete_cmd_prefix": "del ",
"library": "var_list.py",
"varRefreshCmd": "print(var_dic_list())"
},
"r": {
"delete_cmd_postfix": ") ",
"delete_cmd_prefix": "rm(",
"library": "var_list.r",
"varRefreshCmd": "cat(var_dic_list()) "
}
},
"types_to_exclude": [
"module",
"function",
"builtin_function_or_method",
"instance",
"_Feature"
],
"window_display": false
}
},
"nbformat": 4,
"nbformat_minor": 4
}
| mit |
surchs/Logbooks | cluster_pheno_demo_10_24_14.ipynb | 1 | 3639519 | null | gpl-3.0 |
ORNL-CEES/Cap | python/example/EffectsOfInhomogeneitiesOnEIS.ipynb | 3 | 2923 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Studying the effect of pore size distribution on impedance spectroscopy"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false,
"scrolled": false
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"from pycap import PropertyTree, EnergyStorageDevice, Experiment\n",
"from pycap import NyquistPlot\n",
"from helpers import RefreshDisplay, PrintColumns\n",
"\n",
"# build the energy storage device\n",
"ptree = PropertyTree()\n",
"ptree.parse_info('super_capacitor.info')\n",
"device = EnergyStorageDevice(ptree)\n",
"\n",
"# set up the experiment\n",
"ptree = PropertyTree()\n",
"ptree.parse_info('impedance_spectroscopy.info')\n",
"eis = Experiment(ptree)\n",
"\n",
"# attach observers\n",
"observers = [\n",
" NyquistPlot(),\n",
" RefreshDisplay(),\n",
" PrintColumns(),\n",
"]\n",
"for o in observers:\n",
" eis.attach(o)\n",
"\n",
"# run the experiment\n",
"%time eis.run(device)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"# Save the impedance spectrum data into a file\n",
"from pickle import dump, load\n",
"with open('homogeneous_electrolyte_conductivity_5.5e3.dat', 'wb') as fout:\n",
" dump(eis._data, fout)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from pycap import plot_nyquist\n",
"from matplotlib import pyplot\n",
"fig = pyplot.figure(figsize=(14, 14))\n",
"\n",
"plot_nyquist(load(open('inhomogeneous.dat', 'rb')), figure=fig, ls='b:')\n",
"plot_nyquist(load(open('inhomogeneous_electrolyte_conductivity.dat', 'rb')), figure=fig, ls='g--') # 1e3 to 1e4\n",
"plot_nyquist(load(open('homogeneous_electrolyte_conductivity_1e3.dat', 'rb')), figure=fig, ls='k:') # 1e3\n",
"plot_nyquist(load(open('homogeneous_electrolyte_conductivity_1e4.dat', 'rb')), figure=fig, ls='k--') # 1e4\n",
"plot_nyquist(load(open('homogeneous_electrolyte_conductivity_5.5e3.dat', 'rb')), figure=fig, ls='k-.') # 5.5e3\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.1+"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| bsd-3-clause |
gfabieno/SeisCL | docs/notebooks/Accuracy/AnalyticalSolutions.ipynb | 1 | 614 | {
"cells": [
{
"cell_type": "markdown",
"id": "royal-facility",
"metadata": {},
"source": [
"# Analytical Solutions\n",
"\n",
"Under Development ..."
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.3"
}
},
"nbformat": 4,
"nbformat_minor": 5
}
| gpl-3.0 |
dirmeier/dataframe | examples/demo.ipynb | 1 | 4121 | {
"cells": [
{
"cell_type": "code",
"source": [
"from sklearn import datasets\n",
"import re\n",
"from dataframe import Callable\n",
"import numpy"
],
"outputs": [],
"execution_count": 1,
"metadata": {
"collapsed": false,
"outputHidden": false,
"inputHidden": false
}
},
{
"cell_type": "code",
"source": [
"class Mean(Callable):\n",
" def __call__(self, *args):\n",
" vals = args[0].values\n",
" return numpy.mean(vals)"
],
"outputs": [],
"execution_count": 3,
"metadata": {
"collapsed": false,
"outputHidden": false,
"inputHidden": false
}
},
{
"cell_type": "code",
"source": [
"iris_data = datasets.load_iris()\n",
"features = [re.sub(\"\\s|cm|\\(|\\)\", \"\", x) for x in iris_data.feature_names]\n",
"data = {features[i]: iris_data.data[:,i] for i in range(len(iris_data.data[1,:]))}\n",
"data[\"target\"] = iris_data.target"
],
"outputs": [],
"execution_count": 4,
"metadata": {
"collapsed": false,
"outputHidden": false,
"inputHidden": false
}
},
{
"cell_type": "code",
"source": [
"from dataframe import DataFrame\n",
"from dataframe import group, aggregate, subset\n",
"frame = DataFrame(**data)\n",
"frame"
],
"outputs": [
{
"output_type": "execute_result",
"execution_count": 5,
"data": {
"text/plain": [
"\n",
"A dataframe\n",
"\n",
"petallength petalwidth sepallength sepalwidth target\n",
"------------- ------------ ------------- ------------ --------\n",
"1.4 0.2 5.1 3.5 0\n",
"1.4 0.2 4.9 3.0 0\n",
"1.3 0.2 4.7 3.2 0\n",
". . . . .\n",
". . . . .\n",
". . . . .\n",
"5.2 2.0 6.5 3.0 2\n",
"5.4 2.3 6.2 3.4 2\n",
"5.1 1.8 5.9 3.0 2"
]
},
"metadata": {}
}
],
"execution_count": 5,
"metadata": {
"collapsed": false,
"outputHidden": false,
"inputHidden": false
}
},
{
"cell_type": "code",
"source": [
"frame >> group(\"target\") >> aggregate(Mean, \"m\", \"sepalwidth\")"
],
"outputs": [
{
"output_type": "execute_result",
"execution_count": 6,
"data": {
"text/plain": [
"\n",
"A dataframe\n",
"\n",
" m target\n",
"----- --------\n",
"3.418 0\n",
"2.77 1\n",
"2.974 2"
]
},
"metadata": {}
}
],
"execution_count": 6,
"metadata": {
"collapsed": false,
"outputHidden": false,
"inputHidden": false
}
}
],
"metadata": {
"kernelspec": {
"name": "python3",
"language": "python",
"display_name": "Python 3"
},
"kernel_info": {
"name": "python3"
},
"language_info": {
"version": "3.5.2",
"mimetype": "text/x-python",
"nbconvert_exporter": "python",
"file_extension": ".py",
"pygments_lexer": "ipython3",
"codemirror_mode": {
"version": 3,
"name": "ipython"
},
"name": "python"
}
},
"nbformat": 4,
"nbformat_minor": 4
} | gpl-3.0 |
ImAlexisSaez/deep-learning-specialization-coursera | course_1/week_3/assignment_1/planar_data_classification_with_one_hidden_layer_v1.ipynb | 1 | 557787 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Planar data classification with one hidden layer\n",
"\n",
"Welcome to your week 3 programming assignment. It's time to build your first neural network, which will have a hidden layer. You will see a big difference between this model and the one you implemented using logistic regression. \n",
"\n",
"**You will learn how to:**\n",
"- Implement a 2-class classification neural network with a single hidden layer\n",
"- Use units with a non-linear activation function, such as tanh \n",
"- Compute the cross entropy loss \n",
"- Implement forward and backward propagation\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 1 - Packages ##\n",
"\n",
"Let's first import all the packages that you will need during this assignment.\n",
"- [numpy](www.numpy.org) is the fundamental package for scientific computing with Python.\n",
"- [sklearn](http://scikit-learn.org/stable/) provides simple and efficient tools for data mining and data analysis. \n",
"- [matplotlib](http://matplotlib.org) is a library for plotting graphs in Python.\n",
"- testCases provides some test examples to assess the correctness of your functions\n",
"- planar_utils provide various useful functions used in this assignment"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Package imports\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"from testCases import *\n",
"import sklearn\n",
"import sklearn.datasets\n",
"import sklearn.linear_model\n",
"from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets\n",
"\n",
"%matplotlib inline\n",
"\n",
"np.random.seed(1) # set a seed so that the results are consistent"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 2 - Dataset ##\n",
"\n",
"First, let's get the dataset you will work on. The following code will load a \"flower\" 2-class dataset into variables `X` and `Y`."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"X, Y = load_planar_dataset()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Visualize the dataset using matplotlib. The data looks like a \"flower\" with some red (label y=0) and some blue (y=1) points. Your goal is to build a model to fit this data. "
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXYAAAD8CAYAAABjAo9vAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXd4VGX2xz/33inpPUAghBB67713pKlYUNfe/enau6u4\nNuxtxd214dpAKYqgIEWq9NBCT2jphfQymXLv+/tjIDBkJgSYFML9PI/PLre899zMzLnvPe853yMJ\nIdDR0dHRaTjIdW2Ajo6Ojo530R27jo6OTgNDd+w6Ojo6DQzdsevo6Og0MHTHrqOjo9PA0B27jo6O\nTgNDd+w6Ojo6DQzdsevo6Og0MHTHrqOjo9PAMNTFRSMiIkRsbGxdXFpHR0fnkiU+Pv6EECLyXMfV\niWOPjY1l27ZtdXFpHR0dnUsWSZKOV+c4PRSjo6Oj08DQHbuOjo5OA0N37Do6OjoNDN2x6+jo6DQw\ndMeuo3OZIDQNe3EZQtPq2hSdGqZOsmJ0dHRqDyEEe977id0zZmMvLsMY4Evnp6fR9ZkbkSSprs3T\nqQG8NmOXJEmRJGmHJEmLvTWmjo7OxbPrtW/Z+fI32PKLEQ4VW0EJu1/7nu0vzqpr03RqCG+GYh4B\n9ntxPB0dnYtEtdpIeOcnHGXlLtsdZeXs/XBepe06DQOvOHZJkqKBicAX3hhPR0fHO5Sm5HjcJyky\nJcnZtWiNTm3hrRj7h8DTQKCXxtNpgBw/kscfv+4jM72YVu0iGD+lI+GR/nVtVoPGt3EowqG63afZ\nHPg2Dq1li3Rqg4uesUuSNAnIFkLEn+O4eyVJ2iZJ0racHM+zCJ2aoyQlm7/u/4C5cTexsNd9JM5a\nWmsZElv+OsZrzy5lw9pjHD50gpVLDvH8w79y/EherVz/csUY6EeLqUOQFNefumRQaHHVYMyh+lys\nIeKNUMwgYIokSceAOcBISZK+O/sgIcRnQojeQojekZHn1LDR8TLFxzJZ2P0eEr9aQsmxLPJ2JLHp\n4X+x/u53PZ5TmppDyu+byUs4clHXdthVvpq5CZtNRWgCANWhUW5x8PV/Nl/U2A0dzaFybME61t46\ng40PfkjO1gNoqsrut2YzJ/p6vvGfwO9DHyV70z6PY1jzixFCuGwTmiC0W1xNm69TR0hnf+AXNZgk\nDQeeFEJMquq43r17C10ErHZZd/tbHP5+BUJ1naErviamxP+XkPYxFds0u4N1d77N8fnrkM1GhN1B\nULvmjPltBn5NwiqOE0Kw78P5JLw9B0tOAUGtm9F7xj20uHqwyzUSD2Tz7j//pNxir2SXLEv8Z/YN\nmM165u3ZqFYbS0c/Rd7OJByl5SBLKD4mAuOaUnwkHbXMWnGs4mdm/PJ3CO0aR8GeY5gjgglq1ZSS\n5CwWtL8dtdxWaXxzeBA3Zi/QUx4vISRJihdC9D7Xcfqv6TIh9Y+tlZw6AAIyVm53cezbX/6a4wvW\no5bbKhxCfsJRVkx+gSlb/11x3NYn/8PB/y7CcdLBFB1KZc0tbzD4iyeJu2FkxXEGgwJenEBcLhz8\nbDG5OxJPO3BNoJZZKdhztNKxapmV1Te9TnlOAbJBQbM7COkYS6fHr0M2G906dmteMXOaXoe9sJTw\n3m3p98GDRPRqW9O3pVMLeLXyVAix+lyzdZ26wejv43a7ZFAwBp1ewBRCcOCTX1AtVpfjhEOlYP9x\nCvYdA5yv9wf+/WuFUwdwGIykhTVj3ttLSU8tqNjeIi4Ms4/7OYQQguf//isnsksu9NYaLImz/nCZ\nlZ+L0uNZqGVW7EVlqBYbeTuTiH/uczRr5TclAISgPCsftdxG9vo9LOr3fxybv8ZL1uvUJbqkwGVC\nu/sno/iZK+/QNGKuHHj6n3YH9hL3uc2y0UBp2gkA8vccRTYbK/blNmrGhrHXk9hlAPubdeClx35j\n5stLObEjCQnBQ88Mw+xjqPTaLwTknijjoxmrL/4mGxhCdZ/NUv3zNaz5xYT1aO3yWXlEE6y+8XWs\neUUXdV2dukd37JcJnR65hqjh3TD4+yAZFAx+ZhRfM8N/mo7pjBm7YjISENPI7RhquY3QLs4FN5+I\nkIrXe7vRxN7eI9AMRlSjEU0xYLdrbNuWwZfTPuTHmBsIys7gzU+mgFQ5JCM0QWZaERlphTVw55cu\ncTePRvE1XdwgqkDxN6PZPMzaz0I4VA7NWnpx19Spc3THfpkgGw2MXvQG45a/Q89X7qDPew9wffJs\nmk/oV+nY3m/fV2l2r/iZaXXzaPyahJH0/QoW9fu/CmeR0zQWqOywNYOB5KatsaTnsnzS86h5Bcge\nFurUUgvb3ltQKXvjcqbD/11JUOtmGM4Ioxn8fWh540h8o8IwBvrCORY+haaRuWKHu4/HI7nxhy7U\nZJ16gr54ehkhSRKN+nekUf+OVR7X8rphIEH8s59TfCQDU0gAHR+9hm4v/I1tz31OwltzXI63G81o\nsuJ2LIfJOePU7CrH//cHoeEhnMgurXSckGROfPkL+1uG0PHvV1/gHTYsjP6+TNo0kyPfr+Do3DUY\nA/1od89Emo7tjdA0NvzfRyR9/QfC7nB7vmw2Ihncfy4eUWR8m4RRfCyTwNgmXrgLnbrAq+mO1UVP\nd6zfWAtKyNuRiDk8iJBOsZRnF5CyeBMF+4+z/18/V8quKQyNZNeAsWiGs+K4mkZUciLtdm8EoMXU\nIYQ8fRefvrMWu/30GLLDTkzibmITE/BtEsYN6XNr/B4bAosHPkTOJg/yTLJEy2kjSFu2DVvu+cXM\nZZMRSZEIiG3C8Nn/IKxrKy9Yq+MN9HRHnfOmNCOXlVe9SO7WgyBLSIqCKTQAe2EpkiKjltvBTaVq\nUH4OIblZFDZuhsrJ0ICmYXDYaZG4GwDF10xE3/Y093PQfddaDjRpR1lgMObyMmISd9M41VkEZcnK\nQwih51ZXA2Ogn8d9Bj8fhsx6msX9HyTPk2OXJLdpqKdCbIX7k1ky/HGuPfydXqF6iaHH2HUAsGTn\n83OH251OHUATCLsDa3YBmtXuTLvzID8gAV22r2Z4Bz8iInwx2sppnHaEXmsW4WMpBUlCMRtpddMo\nlox4HP+kJHqt/40hS36g76pfaJJ65NTjgICYxrpTrybt7ptcSSqgAk3j+M/r6frc30B2f0yXZ28k\nesoAkD3/vVWbncPfLveGuTq1iO7YdQDY895c7EVlF3y+ZHcQ/MdyHrs2hrffGsVgJRt/Rzmy0UBk\nv/ZM3PAvMtfsQvWUU30SW1EZO1/9FtVauaDGXmKh+GgGajUzPBo6La4ejMHPfX2Co8xK4b7jxF47\nlLgbRyCbTr+cS0aFbi/eTM9/3k7OX3tB8xyOVcus5LspiNKp3+ihGB0AUhZtuOgx8nYm8ee1LzP4\ny6eYsuXf2ApLQJIq0imTf15fqfDpbGz5xex+czaZa3Yxbvk7SJKEo9zGpgc/4sjsP5EUGUmW6fLs\njXR99vLuACRJEo2HdSX1t02Vsl4MAb4Etm6GJEkM+/Z5Oj48leRf/kIxG4m9fjiZa3Yxu8k12PKL\nq7yG4msirLseY7/U0B27DgDG4POQz5VPxmbdTPTUMitbHvuUltcNwxQc4LIvrHsrFD8zjmJLlcOr\nFis5m/eTvWEvjQd1Zu2tM0hdvMmlLH73G9+j+Jro/Oi11be7AdL12ZvI+HOHa4WqJKH4moi9dmjF\npsg+7Yns0x5wSkbsfv179xITZyNJNBrQiRVTXiBteTyyQaHlDSPo89a9mMOCvH07Ol5CD8XoANDx\nwatQfDwUw5wxK5ZNRgJjm3DF6vcxBPi6PdxWUIIlK7/S9qZje+MfHYlsPPd8QrXayVqfQElqNim/\nbqikdeIoLWf3a99d9o2ZGw/sxJCvnsYcHoQhwBfF10Rol5ZMXPcRBt/KlcbxL37Frle/rZ5TlyU6\nPTKVpaOeJOW3zWhWO47Scg5/s5zFA/6uh8TqMfqMXQeAuJtGkb5yO0fmrHLRFokc3JlGfdtz9Kc1\nIAQtpw2n2ws3O7vde2jgIDThNmNDVhQmrvuIjQ9+xPGf1yNUDdlocCtQpZiN2IstLOr1AJrNfZ62\nragMR2l5ldkhlwMtrx9Oi6lDKDyQjMHfh8CWUW6PKzyYwt735la7WOnUZ+AoK3fJntHsDsoycjn+\n83ripo3wxi3oeBndsesAIMkyQ2Y9Q6fHryPtj23IJgOx1w3FPyoCgL7vPuByvDk0kLAerTmx5YDL\n7E82GWg+ZQBGD7N5c1gQw2e/iGZ3oNkdHF+wjg0PfOiUpT0DIQT7/rWgyrCNMcDXpSrzUkIIgfVE\nIarNQcrijdjyimk8tCuNBna6oHUD2aAQ2rlllcckL/yrmjN1GRA0GtiJ9JXb3T5YHSUWstYn6I69\nnqI79ssYIQRZa3eTl3CUwJZNaDauD2Fd4gjrUr0GDCPnTmfJiMcpy8yryKwIbt+cQZ89cc5zZaMB\n2Wgg7m+jydq4j6RZSysWRoUQtLl9HIe+WuLxfIOfmc5PTUPykMpXnzk6dw1bHptJWU4BhQFhlIaE\n4VtWQsQbP9B4QEdGL34dxVQN0S4v49+iEZaMfISqIlRB5updHo+VzUb8o/WGOfUVvfL0MsWaX8zS\nUU9QlJSOcKjIRgVTcABXrPnA46u8O4Smkbl2N8WH0wnpFEtkvw4XNOMsPppBxp87MAb503xiP7a/\nNIu9789zf7Ak0fXZG+n56h2XnGNP+2MrK6+ZTrlNsGvAWMoCgwGQhMBos9Jr+5/0f3IqXZ+7yevX\nLjyUwsLu97oNfQW1aYY5PIiczQeqpZ2v+Jm5NvFb/KLCvW6njmeqW3nqjZ6nPpIkbZEkaZckSXsl\nSfrnxY6pU/NsuP8DCvYdx1FiQS23YS+2UJaey8qrXzqvcSRZJmp4d9reNYFG/TtecPphYMso2t41\ngZbXDcPg50N4z7buF2cVmVa3jKHX63chyTKaqpK1YS8Zq3fiOEcqZX0g/oUvUcusHOo2gNKgUDSD\n8aQqpolyX392dRnEgc8W1ci1g9s2p9OT1zkF3k5+ToqviZBOLZi0aSYnth5069RlsxHZZMAY5Ffx\n38h5L+tOvR7jjVCMFRgphCiRJMkIrJckaYkQYpMXxtapARwWK8kL/6oUOxWaRlFSGoWJqQS3ia4j\n65zEXjOE+Oe/QC23uSzSGnxMdHveOZvNXLubVde97JQ6kJyLtgNmPkzrW8bWldnnpPBQKqqscKJJ\nDEI5S6BLlikLCKHQcZ7CXedBr1fuJHp8Pw598Ru2ghJipw4h9rphTkfv4aGsmIyMmPcyjlILitlI\n1MgeKOaLlBPWqVEu2rELZyznVPsb48n/dO3VekxVRUKyQcGWV3XRSm2gmE1M2vgJG+57n9Q/toKA\n0K5xDPz0UYLbNseSlcfyic9VWnTdcP+HBLePqcjZrm/4N4vAciTb435JaIQO6V6jNjQe2InGAztV\n2h41ojsZK3dUSiGVzUaiRnZHPvtBpFNv8criqSRJChAPtAZmCiH01vP1GFNoIH5R4ZQcz6q0T6ga\noV3rR/d6v6hwRv/6OqrVhlA1l/L5xG+Wuc3wUMtt7H1/LsNnv1ibpp4Ta7mdDWuOcnjMJIpXb8Vo\ns2LzdZOmKcuMmH5D7RsIDPzPYyzq9yBqWTmOMiuyyYhsVBg++x+6U7/E8IpjF0KoQHdJkkKAnyVJ\n6iyE2HPmMZIk3QvcCxATE+NmFJ3aQpIk+n/yMKuuf8Vl9m7w86Hna3e6LWypS9y99hcfznC7CIgQ\nFB3OqAWrqk9BXhkvP7WEshIbVqsDKbYDQoCkqi7hGAWNKVM7Et6ubsJggS2juDbxG5L+t4zsjXsJ\nahNN23smEtDcfUctnfqLV9MdhRAFkiStAsYDe87a9xnwGTizYrx5XZ3zp/nE/oxd8ibbX5pFwd5j\nBLRoTLcXbqbF1YMBZ9bM8Z/XYy8sJWpUj3qnyd1oQEcSZy1122TCp1FIHVjkme++3EZhvgXtZEqo\nONmURHLYCcjLpSwgGB9LKT18irnqjtvq0lRMwQF0fHgqHR+eWqd26FwcF+3YJUmKBOwnnbovMAZ4\n66It06lxmgztyoTVH1TanrJ4I6umvYokS2gOFUmRiZk8kKHfPVdvXsmbTx6AcLivSM2NP1RvNN2F\nEOzYnFLh1M9EEoKWB3cQluN8wzCH1632SllmHtv/8SXHf16PJMu0vGEEPV+5Q9divwTxRhJwFLBK\nkqTdwFZguRBisRfG1akDrPnFrJr2KqrFiqO0vEKLPWXxRg598Xtdm1dBydFMDP6etWrKsytr1dQV\n7pz6KYR0+ifo1yyiNsxxi62whEW97yfpm+XY8kuw5hZx6PPfWNTvQRzuQl469ZqLduxCiN1CiB5C\niK5CiM5CiFe8YZhO3XB8/lokN40XHKXl7J/5Sx1Y5B5zeJBHrRrAo0BZbSNJEp17RLnNJBSSREiu\ncwHb4OdTI0VJ1eXg579hzS9x+ZtqNgeWjFyOzvmzzuzSuTAurbI9nRrHWlCK5qE5sq2gchPquiIw\ntgmhXeMqdRCSTQZiJg/A6GE2XxfcfHdf/PxNGI1OWyUJFE2l/cFt+PibUXxMdHnmhjrTXbHmF5P0\nv2Vu02AdpeWkLdOrxC81dK0YHReiRnZ3drY/q3hJMihEX9G3jqxyz8h5L7NkxONYsvMRqkCSILhD\nDAOroVVTm+TmlBAe4U9qcgEGo0xMbCi33NuXoOKB2PJLiOjdtpJ2fU1TlpFL0jfLSF26lewNezyK\ng0kGRa8wvQTRHbuOCxE929JsXB/S/tha0bxBMigYg/zo9sLf6tg6V/yjI7nm4P/IWL2LkiMntWou\nQtagJkjYkc7HM1ZjszlDHJomSE0uYOPao/ztrj51YlPq0i2suvZlNIfqURL5FLLRQNt7JtaSZTre\nQhcB06mEpqoc+PevHPh0IfYiC83G96b7S7cSENO4rk275Hj2wYVkpBVV2m4wynzwxTUEBdeu7LCj\n3MacxtdgL65Gf1sJhsx6mta3jqt5w3SqRXVFwPQZu04lZEWh40NX0/Ghq+valEsSe3EZW576L4nf\nrSBj1DS3GixGo8LxI3l06dG0Vm1LW7K52mJpio+ZRoO61LBFOjWB7th1GiSaqpKxYjslydmEdW9V\na9oxQgh+H/kEycmFlAeEI6kOhKGytrqmilqfrQMkvPtTldlEZyIpsvvqXp16j+7Ydc6b/D1HObHt\nIH7NIoga2aPeFC2douhwOktHPo6toARN1ZAkibAerRn7+5seOzt5i72/bGFpaGfKG/siCeGsMtW0\nk12JnEgShEX4EdMytEZtOZvynAJOxB+q9vEGfx9COujyH5ciumPXqTaq1cbKqdPJXLMLSZKQZBlj\nsB/jV7xLcNvmdW0e4Jwxr5jyAqVpJyq6OgGc2HqQzY/OZPAXT9bYtTVN8N85hyjzCXBx5GgaqCoK\nAqO/DwFBZp54aWStL/KWpGRj8DFhP8eCqSTLyD5GBn/x5CXXyETHie7YdapN/Atfkblqp8vrub3E\nwvIJz3FN4rf1IhulYO8xSpOzK5x6cXA4Rzr0pCg0kg0pNkoX7mXM5I7IboqwLpZD+7IpVyVXpw4g\nyxjLy+huTWfUGw/QrlPjGrn+uQiMa+oxC0bxMxF3w0jydh4mpFMsnZ+4rt7pA+lUH92x61SbQ58v\nrhxzFQJLdgEnth4ksm/da6CXnyh05uEDRSER7Bg4DqEYQJJQjSbmzIrnyIEsHnhmpNevnZ9b5ry2\nGw0b1Whm8n1jaNGlidevW11MQX6EdW9Fzqb9LtudVa830u2Fm+vIMh1vo79n6VQLIQT2knK3+1Sr\njbxdh2vZIveE92iNZrUDkNSxt3Ph8ow3CQ2JTRtSOLrtiNevHds6zKMuTGSgUqGcWVdseuQT8nZX\nvu+YqwfT9fn6VaOgc3Hojl2nWkiSRGjnlm73CbvKlif+TcGB5Fq2qjKm4AC6PHMDBn8fisMiPRwl\n8csM7/cVjWoWTOfuUZhMrovJRpPC7c+O9vr1zgdLdj6JX/5eUXR2Jjmb99WLMJqO99Adu0616ffh\n/6H4uO916SixsO2Zz2rZIvd0f+lWBv77UcCzs0pNrxndmwefGsroie3w8XVGOZs1D+aR54bTsWtU\njVyvuuTtPIzsoU9p8eEMj/pAOpcmeoxdp9pEjehBq5tHe5TvTV+xvZYtco8kSbS6eQzBS3+goMR9\nzrav3XLB4wshSPrfMna/+QOWjDxCu7Sk1+t30WRYN4xGhWm39WLabb3QNFEni6Tu8I0K85i/bvAz\nV6xL6DQM9Bm7znlRZdu5+uHDKrjyxu4gKotbyZpKjy6ewjTnZvtLs9j00McUHUrFXlxG9oa9LJvw\nHGl/bHW9Tj1x6gBhXeIIjIuqpIap+Jpp/8AUPRTTwNAdu855odnsHvcFtqzbcMPZDB3XnhZN/JDV\nk2EGIZBVO9FFWUx898Ja0Fnzi9n73lwcZa4LyarFyqZHZ16syTXK6MVvENSmGYYAH4xBfig+JqLH\n96Hna3fWtWk6XsYbrfGaA98AjQEBfCaE+Ohix9Wpn0SN6M6JLQcqx2RliXb3T64bozxgMMhM//Qa\n1i9KYM3Pu6C8nP59mzHywb9h8Lmwht252xORzUa3pfbFiWk4ym0YPKxD1DUBzRtx9d5ZnNhygNLU\nHMK6tyaoVe1q1ejUDt6IsTuAJ4QQ2yVJCgTiJUlaLoTY54WxXcjJKiEzvYjGUYE0aqL3YawLOjx4\nJftn/uJsunFKGVSR8WsSRpvb658KoKLIDLuqG8Ou6uaV8Xwigj3GqmWzAcVUt8tW5TkFlGXmEdSq\nKQa/ylo0kiQR2a8Dkf061IF1OrXFRX8LhRAZQMbJ/18sSdJ+oBngNcduLbfz6bvr2LsrE4NRxuHQ\naNepEQ89PQxf38oCSzo1h2/jMCZtmsnmhz8hfUU8kiwTNbongXFRrLvtLSL7d6DtXRMabAPk0K5x\n+EdHUpiY6iJZoPgYaXXLmDorwbcVlrDmlhmkL49HMRnRVJUuT99A9xdv0ePnlyFe1WOXJCkWWAt0\nFkIUnbXvXuBegJiYmF7Hjx+v9rj/eX892zYmY7efnikZjDLde0fz92eGecFynQtBCEH6inhWXv0S\n4mTTBsXPjMHXzKSNnxDUulldm1gjnBYZK0WoGgJBRJ/2jP3tDbez5Nrg9+GPkbNpv8saiMHfh14z\n7tbll0+iaYKCvDLMPkb8AzyHy6zldnJzyggJ88XPv36F1Wpdj12SpABgPvDo2U4dQAjxGfAZOBtt\nVHdcS5mNrRuP47C7Zjc47Bo7t6VSUmwlIPDC4qWnsNtVFv6UwJpliZSX22nboRHTbu9FTGztqu9d\naghNY83f3nApelHLrKjlNv66732uWPleHVrnXewlFg5+/htH565Gtdgw+PsiNEFQ66Z0euJ6YiYN\nqDPbCg+mcGLrwUoL247Scna89DUdHryqQc/aHQ6NHVtSSDp4gohIfwYMbUlAkKtP2LbxON9+tpXS\nUhtCE7Tv0ph7HxlEcMhptU9N1fjp2x2s/P0gsiLhcGj0HxzLbQ/0R5Jg8fw9rF6WiM3qoFO3KK67\npQeNo4Jq+3arhVccuyRJRpxO/XshxAJvjHmKokIriiJXcuzgXBwrKii/KMcuhOCD1/7k0P4c7Cfb\nl+3ZmUHis0t5+Z0JNG0eXOX5drvKhtVH2Lj2KAaDwtDRrenRN5rSYit+AeZKVYgNidz4RDSrG71u\nTZC1LqHeLiQKIchcvZPCg6kEt4umybBuVYZQ7MVl/NLjXkqOZ8FZvUEtWfnk7pzB5C2fEtwmuqZN\nd0tRUhqyyeC2GbWtoITNj86k/0cP1YFlNU9JkZVXnllCQb4Fa7kDo1FmztfxTJzaiYnXdMZsNnBg\nTxb//eCvivaEAPt2Z/LG88uY8cmUirTUn+fsYsXvB7DbTn/Gm/86jsOhUZBv4fChExU+YtumFPbs\nzODVDyYR2bh2+9VWB29kxUjAl8B+IcT7F2+SK+ERfh7To4UGEY38L2r8I4m5JB047dRPYbM6WDB7\nJw88MYRNa4+x7s8kNA0GDW/JoOFxGIwKJcXlTH/id/JOlFVohOzb7czzlk/mCw8d1Yob7+yN0djw\nHLzQNLfdgU4fUPttF8+FJSuPJSOfoDQlB6FqSIqMf3QE4/98H78mYW7P2fXWD5QccX6upQHBJLfp\nSlFoJGZLCTFJCYSdyGTbM58xasErtXkrFQS3j6kyDfXQF7/R/v7JhHRoUYtW1Q6f/2sDWRnFFf+2\nn5wALvwpgd9/2cPwsW1ZsyzJxamDs9FJQV4Ze3dl0KVHUxwOjd9+3ovqcP3O2m0qWzccRzHILj5C\naAJruYNF8xK488G6e1vzhDdm7IOAW4AESZJ2ntz2vBDCfXnieWIwKky+rgsLf9qNzXr6D2syK0y4\nuiMm88XdQtKBHFQ3wk1CwIG9Wbw9fQVHEk9UXPto0gmWLT7AsDGtWPD9LiwW17Q/VRUn/9d5/Mol\nh9i+OYXbHuhHh85N8PE1kpNVzC8/7mbfrkz8AkyMmdSeoaNa16uCluoQ0bsdkrsmGyczLwy+Fxci\nqwnW3DyDoqQ0xBnrNUVJ6ay9+Q3Gr3jX7TmHPnd+lYtCwtk5cDyarIAsYwkIoig0krh98RiWx9eK\n/e4IatWUJsO6OQuk3DxLNYdK8q8bLknHnptTys5tqciyRI8+0YSE+VXsy8ooYufWVI/n2m2C5YsP\netzvcGikpRTQpUdT9u5Kr+TUz+RM33MKTRPs251ZzTupXbyRFbOeGq45nDi1Ez6+Bhb+mEBxkTP0\nMvnaLoydfPEysUHBPhg8hHpKS2wc2JPlss1mVUk9XsAPX8ZXe0Kan2fhozdWYzDIjL+yEyt+P4C1\n3I6mQV5uGd9/sZWk/Tnc/fDAi76f2kQ2KAz95llWTXsFzeZAOFQUHxOKj4lBnz2ONb+YxK//IG9n\nEqGdW9LmjvH4RFQd2qpJyk8UkrU+wcWpAwiHStZfe7Bk5+PbqPK6iuOkqmVil/5oZ7W50wxGjnTs\nTYtt2TVneDUYMXc6P0ZPw15YWQNHkmXkS1AyYOFPu1k0d4/zpVCC77/YxrTbejJmkvN3v2jenosa\n32CUaXKjtyOPAAAgAElEQVQyRr5upWd10lOTNXcoioyqaihK/ar1vCS0YiRJYvSE9oy6oh2qQ0Mx\nyF5bDOrZvzn/++9mt/u0Kj7Q840yCOF8TfxtwR40IVxmVjaryqb1x5h4TSeimtWd47sQmk/sz5Xx\n/2XfJz9TlJhKowGdaH//ZKy5RcyNvQm13IZmd6D4mtj1+neM//M9Inq2rRNbbYWlyAalQtb3TGSj\ngq2gxK1jD2jRmPyDKRSHRLgdVxIaAdeO9bq954PR35du/7iZ7S/OQjureEqSJFpcM7SOLDtNUYGF\n1cuTyEgtJLZ1OINHtPKYnXJoXzaL5+9xyYQD+GHWNhbN30O5xY6mVZ6MVRdJAj9/E116Ogu0cnMu\nTBQuN6eUR+6Yx+MvjiSujfvvR11wSTj2U0iShMHLsWqz2cCTL43i/df+RFMFAoHNqnrU1b5YPI0r\nAfsTsohqFozV6mD54v2s//MIQsDAYS2JbhHCgtm7SE8pJCDQzLjJ7ZlwdaeKWH5dEtyuOQP+9XDF\nvx0WK/Pa3Iqj5LTQlmqxoVpsrJ72Ktcc+qZOsjQCWjRGNhuhtLKuvGw0Ehjnvgqz52t3smraK0hC\nQ0iVv3+SItP53vFet/d86fDgVRxfsI78hKM4SixIioxsMtLjn7cRGFt3DT4ADh/K4e2XVqCqArtd\nZevGZH6evYt/vDme6JiQSsevXHKwUlwcnJOtwvwLF3A7RWTjAJ59dWzFTLtdx0YcP5qP6ji/h4Xd\nrmK3q7wzfQUfzbr2okPD3qJ+WFHHtG4fycezrmXPrgzKSm0sW7Sfo0l5tWqDLEv4+hlx2FVef+4P\n0lMLKxZrFs5NQFW1ill+UWE5C+cmkJVZwl0P1b+Fm82PzHRx6mdSfCSdoqS0OskgkQ0Kfd97gI0P\nfuSSoqn4menz7n0ewxUtrh5Mp0emsm9tMjmNYxBnrSsERATSunPdl+YbfExMWPMhKYs3krxoA6bg\nANrcPq7OW9wJIfj0nXWUl59ej7LbVOw2lRcfXcx9jw2i/xBXrf/iYqvb9QJvoCgS9zw8iPDI04kX\nY6d0ZPXyJCxn/M4k2a2GnFs0TbB9S0ql+6gr6n66V08wGBW6945m4LA4WsSF1+hCprvJqgB69Ilm\n64ZkMtOLXFbgVYdW6Utus6psXHOE/LyyGrPzQjkye6XnnQIyVu30vL+GaXPbOEb8NJ2I3u0whQQQ\n0bsdI36aTts7rvB4jiRJ9H33AR7/6jZCA42cUg0wmw34+hl59PkR9WbhWzYotLhqMEO+fJp+7/9f\njTv1osJysjKK0VTPHjAjtYjiosqpmOB0iF98vIFD+13XKLr3jsZkrv7budmn+seGhvvRpoOrumdY\nuB8vvXUFHbs0QZKczr/PgBa079y4ysSvU1htDv73ny3cd+Mc3nt1JcnH8qttT03Q4Gfs2ZnFZGcW\n06RpEBGNqpdvOm5KBzasOeJ2JfxcmMwK/YfEsmH1UVRVqxSLN5kVYuPCOXYkF9UhMBhlEPDws8Pw\n8TUSvzkZa3n1mh4YjArHD+cRekamQF0jhKikfHg21hOFtWSNe5pP6EfzCf3O6xwhBDa/QO57fjRF\nhRbSkgsJi/Cj7+DYy1LWIj+vjE/fWUfSwRwkyfnw69Q9iolXd6Jtx0YuoTZV1apMr7DbNRbP28Pj\nL57uQzt0VCuWLdpPfm4ZjnOERwICzdx6X18cdo1N64+xZ0d6Rcjz1KxbUSQURSYkzJcnp492Gwps\n2jyYZ14Zg6aJinvKTC/in0/9js2muk2wOIXQoKzUubaxOz6dfbsyeXL6SDp0iaKowMKeXRkYDApd\nejatle9Lg3XsFoudT95aw8F92RgMzqyXzj2i+L8nhpwzDtY0OpiHnx3O5x/9hcVi9+jgzT4GBo+M\nY++uTIoKyolrE861N/egZetwpt3Wi13xaaxbeZhD+7LQNIhpGcot9/ahTftGHEk8wYG9WQQEmOk9\nIKaidNk/wIQkVW9xVtMEwaG+Hvfn55Wxb3cmZh8DXXo0xVwL8T9Jkgjv1ZbcbYfc7pd9jATUcbz3\nfDl+JI+PZqympNiKLEtomuDGO3oxbEybujatTtBUjVeeWkJe7plvi4Jd29LYuzODLj2b8vAzwyrW\nf5rFhGA2G6qcsGSkuT7sfXyNvPzuBBbNS2Dz+uNICEpL7ZXGMJkUxkxqT7/BsQAMGhGH3a6iqRpF\nheWUWxz4+BlJOZpPcKgPcW0izrm+c+bbV5OmQcz45Eo+mrGKo4m51U6acDg03pq+gkHDW7F53VEU\ng/NvoamCex4ZSN9BsdUb6ALxqlZMdendu7fYtm1bjV7jozdWs3t7msvT3mhU6De4Bfc8MqhaY2ia\nID2lgNXLElmzIqnCwRsMMmYfA/98bwKRjc8tdqWpGpomqrXwe/jQCd58cdk53xYkWaJJVCAzPqnc\nJEEIwbzvdvDHrwdQFAlOPij+/swwuvSoHAvOTCti3g872b87Ez9/I6MntGPMxPYXvDCb9dcelo5+\n0m32iTkiiOuTf6wXFan5e49xbN4ahKbR4qrBhPeo7KjLLXYeu3tBxWzsFCazwuP/GEmHLpfWQ6o6\nFBZY2LE1FaEJuvVqRliEaxHgrm1pfPD6nx6dnNls4OZ7+zB0VOuKbQk70vnw9VVuZ9+SBD37Nefh\nZ4dXaVfq8XzeemkFNpsDIZy/z649m/F/Tw7BYKjZqPKDt/5EiYdwkiRLiPNItjCZFN7415QLqlit\nrlZMg3TsxUXlPHrXfLevTkajzPtfXoMiy/j5G5EkCZtNJflIHj6+BprFhLh9oifsSGfpr/sozLfQ\nuVsU467sWGMhkIU/7mbRvD1UfDaScxX/RFYpikFGCEFIqC9PvTza7ZcjflMy//1gPdazHg4ms8J7\nn00lKPi0UFVmWhHTn/wNa7mj4odqNMlEx4QQHhlAoyaBjJ7QzmWhqTrkbD3AutveovBAMsgSstGA\nf3Qkoxe+SkjH2PMaqyaI/8dX7P1gLppdRWgCxcdI61vHMmDmIy6f/+rf9/Pt51txiMrfic7do3jq\n5bptUu1tVi45yOyv4pGdEUKEJph8XReuvL5rxTHzvt/BorlV55DHtY1g+tuu6xYpx/J45ZmllSYt\nJpPCCzPGEdsq/Jz2qarGnp0ZFBWU06ptxDklP7zFvTfMdvvGYTTKgFQpLbMqFIPMpKmdmHpT9/O2\no9ZFwOoTBXmWivDL2aiq4JE75iEhER7pR7fezVi74jCyJKGqKn7+Zm66qzd9B7Vw+YF36dHU7Wy3\nJrhyWlf6D23J9s0pCCHo2bc5TZoFkZNVzLGTMfVW7Ty/Uv7x6/5KTh2cs/bN648xZuLpwq75P+x0\nceoAdpvG0aS8isygJQv3ce+jgxg4tPor/pF92jN13ywcFiu5O5IwBvoS2rllvRCjytm8n70fzkO1\nnJ6Fq2VWDn+7nJgpA4ke37di+5aPF+EwN3EbI87JKqkNc2uN1OQC5syKr+SkFs/fQ/tOjWnXqTGA\ni3CWJ2zWyk6weWwYb828ks8/ci6WShIEh/px+wP9quXUwVkQ1K1X7auGdu4WxfYtKZXeUjQhMJmU\n83Ls6kntmZqkQTr2Rk0CPOaLn94uyM4sqVRybLNZ+PTddcz/fqfHGXFt0DgqkCuu6uiyLbJxYLVC\nP4WF7hcv7TaVogLXffsTMs8ZNxSa4PMP/6JHn+jzXvgx+JppPLDTeZ1T0yR+vdSlA1JhaCSpLTtg\n9/El77MN3D24G/4BZk5sO4hyMAmlYziq0TV0JAmNlq2r54wuFdYsT3QbKrHZVFYuOVTh2IeNbs33\nX2z1+L0xGCT6DnIvXxAW4c8zr46htMSG3eYgONS3Xjzsz8X1t/VkX0ImNqujohLVbDYwZlI7evaL\n4fXn/6h2DrzZx0DHrjUbwmuQ6Y5mHyPjp3Q4r3Sps8nOLObtl1dQF6Gqi6VT1ybO2PpZ+PgYaNux\nkcu26upNa5pgy1/V19Cvz9hLLBVNMlLiOrJrwFhymsVSEBHFLjWU5/6+iIK8Mk7EHyL8RBpGWzlo\nrjMySdOYfF2XujC/xiguLHc/IRLO8OYpTGYDN9zey20aoGKQCQnzY/SEquU+/ANMhIT5XRJOHZyL\nqK9/NJlhY9rQpGkgbTs24r7HBnHtzT1o1TaC1z6YiMlscLkfk0nGZFJcFmMNBpnwCH9694+pUXsb\n5IwdYOpN3fHzN7F4/l5KS6yYzAZsVke1V7WFgMJ8C4cPnqB1+wvvaF8XTJzamY1rj2Ips5+OmxsV\noqKD6dTNteH06Intmfvt9mqldhYV1OzrY23R4uohJC/cQJlNcLRDTzTl9M9AlWSKi8qZ//1OxsZF\nYpBleq77jUNdB5DbpDkCCf/iAnoWHiE65o46vIvzo7TERsKONEqLbaQl57NnVyY+vs6F8sEj4pAV\nma69mrF9S6rbzJNuvV0LysZf2ZHmsaHM/2En6SmFSBIEBvkweGQrRk9oV+8aVHiD8Eh/brvffZps\n0+YhvDVzCr//so89O9MJCvZh3OQOxLYKY/73O9m+JRVFkRkwrCVTb+zm9Qr6s2mQi6dnIoTA4XA2\n5fji4w2UW6qXIw7g62fkrocG0GdgC5KP5fPnkoPk55bRqXtThoxqVa/zl7Myivjpmx3s2ZGO0aQw\nZFRrrprWBbPPWSJWqsZ/PviLHVtSEFBJvvhM3v73lR4bCxw7nMvaFUmUltjo0Tea3v1javzLe6Fo\nDpWlo54gIc3Ggfa9Kwl7gfNNZub/ruWnmBuwZOWDEGiSjJAlzD5G+n/yMG1uq389Xt3x16rDfP3v\nzW4/X7PZQLfezXjwqaHY7SrTn/iNrIziivUpg0EmONSX1z+eXK+/75cLl3VWjDscDo3H7ppHUaH7\nlCV3GI0KMz6ZzP7dmc7MCIczbdFkVvAPMPPP9yZUayHpUiA1uYCDe7PYsTmZhJ2VpUhbt4/gxTfd\nV2cuXrCHhXN2Y3doCE1g9jHQpGkQL8wYVyu58xeCarPzy6sL+X1XMQ65so0BgWZmfns9BQeSWT7p\necqzC5AUGc1qp+Oj19Dr9bsuiTBCRlohLz32m1vdlVOYzArPvz6Olq3DsVjsLJ63hw1rjqCpgr6D\nWnDl9V0rdSS6XFFVDZvVgY+vsU4+f92xu2HR/ATmfbezWhoUBqNMr37Nue3+/jxy57xKMx1FkRgw\nLI57LjGp3XOhaYK532znj0X7UTWBLEn0GdiC+x8b5DavPSerhOce+tVtVkCPvtEuhSrnZYeqYiso\nwRQcUGOSs6UlNrefrcEgM3xcG265x5kdI4TgxLaDWHOLiOjTDp/wS0eBc/asbSxbdKBKUTtZlph6\nUzcmX9uw1gy8ic2mMvurbaz/8zCqqhEU7MO023sx4DwyxbxBraY7SpL0FTAJyBZCdPbGmDWBj9mI\n0Si7tL7yREioL02aBfPJ22tw9yRQVUH8xuQG59hlWWLa7b245uYezn6yAaYqQyrbN6fg6Um5Y0sq\nM99dx9+fGYamCYoKLJh9jVW+0gshSHh7DrvfnI1abkM2Gej06LV0f+kWZHdNPS4C/wATdzzQn1n/\n3oSmaqiqQJHAZJBp37kxmiaQZQlJkojsc/Ha/3VBQZ7lnEqlikHG5zIPs5SWWNm09hj5eWXEtY2g\ne69mLhOST99Zy55dGRWTgPw8C199shGjSanxhdALwVvvyV8DnwDfeGm8GqFT9yj4pnqvTyeyS/lt\n/p5z6lQ0VAwGmZAq5ApOIYSockF69/Y0Fs/fw/LfDlBabEMIQZceTbn77wPdvt7vev17Et6cXaE3\no1nt7H3vJxxl5fR95/4Lvh9PDBoRR5haypcv/0ZOWBQqgjKL4D9vriK2fWOeeXXsJd23tnP3pmzd\neLzK7kAI6DPw0uuu5C0O7s3inX+urHi4m0wKkY0DeGHGePwDTGSmF7k49VPYbCpzv9leLx27V9Id\nhRBrgdrVub0AmkYHM3Boy2rHfaty6ooi0XtA/ftAa5vufaKRqlA2tNtUFvywk4I8C3a7isOhsXt7\nOjNeXEZhgYWtG46za1sadruKarOT8PacSiJijjIr+z/5hYKDyV63X3OobL3tdXJDGoMsg6yAJOGQ\nFI4czGHWzI2Ulrhp2O0lhBBkb9rHsflrKT6a4fXx+w2JrXIdSJYl7nyof7Ue4g0Ru13l7ZdXYLep\nFfnpNptKemohc752tjtMPV6AwUM4MSuzfhap1c+VrRrkjgf7075LY5b/dpCSIiv5eaXVCs2cicms\nEBBo5rpbe9SQlZcOTZoGMW5yB35bsMfjzP3s1mKqqpGRWshjdy3AWDEbFlwxtiVlZn9MbrTcNaud\nhd3uofHgLgz/8UWvxbkzV+8k0z/CreqahsTGtUfZujGZq6Z1ZdI13o0ylhzP4o+xT1OWkYskS2g2\nB82nDGTYt88hG73z0zSZFF79YBIzXviD1OTTQluyDEHBvjw/YxyNm5y76K2hsmzRfrcV6kLAhjVH\nuOuhAYRH+ju7nrnhTHmO+kStOXZJku4F7gWIiam7ma4kSQwcFsfAYXEApKcW8tEbq8nLLUWRZewO\n5+uWuw9blqFrr2i69Ihi8IhWl31c8hTX3dIDh0N1u0hXtbMXqJbTf+efFyYi9x9PYMEJOm9ZhdHu\nmsGk2RxkrUtgxaQXmLTxE6/Ybs0rRlMUj7KyQjjfOhb+tJtmzYPp0be5V64rhGDZFc9SfDgdcUaL\nt5RFG9nxz2/o9dqdXrkOODN8XvtoMgk70lmzLAmLxUbfQS0YOCyu3nT8qSt2bEnxuO+UD4htFUaj\nJoGkJRe4fL9NZoUJV3f0dHqdUmufqhDiM+AzcGbF1NZ1z0XT6GDenDmF9NRCLGV2wsL9ePqBXyod\nJ8kSvfo356Gnh9WBlfWfabf2JDe7lF3b03DYVZSTzjI4xIcT2dXvJ6kpBgpDI9ndfxQ91i9BPuvJ\noNkd5CUcIS/hCGFd4i7a7sgBHQnN+he0rlqQyWZVWbxgr9cce+72REpTsl2cOoBqsbJ/5i9edezg\nnNB07dmMrj1rX2elvmC3q2SlFxEQaCbkpICfUkXGVXCIczYuSRJPTh/FxzNWk3IsH8Ug47CrjBzf\nlnGTO9SK7efL5f24PokkSTRrfrrv4nW39GDe9zudub/Cmfro42Ng2m296tDK+o2syDz0zDCOJJ5g\nz84MfHwN9B3YgiNJufz7vXXn17REVigOiWT9FTfR4uAuYg7vcZlQywaFosQ0AmIbYwy4uLL0gOaN\naDmgLcnHDpLeoq3bYqVT5Od6r1uVJSMXyUOWj72wFCHEJZEnXx8pyCtj+5ZUtJOyw5GNA1jx2wHm\nfrcTEKgOjbi2Efzfk0PpN7gFiQdy3Oq8nDkbDwn15aW3ryAro4iCPAvRLULwD6i/uf3eSnecDQwH\nIiRJSgWmCyG+9MbYdcG4KR2JbRXOskUHyMstpVO3KMZMat9gipFqkrg2ES7d2nv29eOG23vx0zc7\nAIGqCnx8DJSW2KpOw5MkNIOR4+26IWsazY/uq9hlLypj1bUvO/8hS7ScNoKh/3v2gvPdS45m0OpA\nCsG5WRxt142yoLBK/QslWaJVW+91oQ/v2QbN5tSrF0BxSDjFIRGYyi3EhUq6U79AVvx+kDmz4p3N\naoA5s+Lp1rspu7enu0wuEg/k8NaLy5n+7hUsX3yQ7MziimQJWZaIbhHCmEmVZ+ONo4I8Vl/XJy6r\nAqXaJiOtkEXz9nD4YA7hkQFMnNrJRaslO7OY5GP5hEf4E9sqrEH/mO12lfSUQvwDnBoi/3hkMRZL\n5UYc7jDYyhm0dE5V3dWI7N+RSRv+dd52CSH42jCmYjFAAPHDJlMaEIw4Q0PGbDbw0jtXEB0T4mGk\n82f9Pe+S+OMadnYZQlFoBEgSkhCYA3x4/s0raB4b6rVrXQ6kJhfw8pO/V5bFkHBbamH2MfDEiyOJ\niQtj2aL9bFx7FFmWGDKyFaMmtK+Xaa565WkdczQplxn/WIbdplbMTE1mhetv7cnwsW3493vr2B2f\njsEoo6mCyCYBPDl9VL3qX1qTpKcWMmdWPAln9Kf0hKRpDF09H8VmRbN51vppc/cEBn/2xHnb8kPk\n1Vhziyr+7TAYSerUh+zoOIRiIK5tBH+7u88Fz9iTvl3Orle/pTQ1h6A2zej56p3ETBmIpqr866HZ\n7ExzoMmuTiQ0zJf3v7im3jTJvhT4/OO/WP/nkWofbzYb+NvdvS+pFofVdewNUra3PvDNZ1uwljtc\nnJbNqvLj19uZPSuehO3p2O0qljI7VquD9JRCPnx9VR1aXLs0jQ7m8RdHMmvBzdz99wEEBXuOV/oE\nmLn+wCx6vFq1mmLil0tYf8+7WLLPr0N8x0emovidvr7BYafDnk1MOrKOL+f/jZfevuKCnfrut+ew\n4b73KUpKQy23kZ9wlNU3vcbh71cgKwr7CgyVnDo4e/YmHci5oGtejmzfksKG1UfP7yQJl7W1hoTu\n2GsAVdU4mnjC7T67XWX1H4mVRJk0TZCWXEB6SqHb805hszrYviWFzeuPUeShocalxpBRrfn46+vo\n2rMpBqPrV9JkVhg/pQMBTcMJan2OjA4hSJy1lJ873XlexT5dn7uJltcPRzEbMQb5Y/D3Iahtc8Yt\nfRPlAvu+ApSmnyD++S9cmnqAs1vTlif/g9A0rOWewlESJSXVF6y7nHHYVT778C+Pb34Gg1ypP4Fi\nkGkSFUirdt5bN6lP6FkxNYAkSc4Gt6r7L5qqui+Ists1MtMLPfZx3BWfxsx31las6zkcGldN69og\nxJskSeLBp4by2Ud/sSs+DYNBQVU1Ro5vy5ST/TZjJg3A4O+Do7SKB5omsOWXsOXJ/zBq/j+rdW1Z\nURjy1dP0fOUO8nYm4ds0nPAebS56zWPllS9WNPQ4G3thKZasfFq2ieDIocqTANWh0tqLi7UNmcQD\nOVXKWgSH+jD52s7M/34XVqsDTT0pa/HwwAa7rqU79hpAliWax4Zy/PD5qyykJhfQs1/lAq6CfAuf\nvLWm0kx/0dw9tGwdTufutdOPtSbx8TXy8LPDKSospyCvjMgmgS6CYbLRwMSNn/Brn/sRbnpqnkJo\nGqm/bz7v6/tHR+If7Z2mKsVH0inY6zk0oGkaxiA//nZnb96avtwlY8NkNjDqirYENdAsrKyMIhbM\n3sW+XZn4+RsZNaE9o69oe0EqoHByIuXBP0sSvPzuBIKCfRk2ug35eRZ8/YwNshHImeiOvYYYNb4t\nsz7d5HYmYTDIHnVoMtOK3W7fsPqI2zZ9VquDpb/up3P3pmzfksLvC/aSl1tG63aRXDmtyyUZQwwK\n9vFYqh3WuSU35//Krz3voygpHeFwnx9/oamPmt3B4e9WcGjWEoSq0ermMbS5YzwGn3M7gqy/9rD/\nk18ozysipF1zZJMR1UOoJWZSf4z+vrRu78vzr49j/vc7OZp0gqAQXyZe3YlBIy6++Ko+kpVRxPTH\nf6fc6kBogqLCcuZ+u53E/dk8+NTQCxqztYdwiiRLdOkeRVCw8wEpKzLhkf4XbPulhO7Ya4gBQ1sy\ne1Y8ljLXH7bZbCC2dTiH9mVVcvpGk0J0C/eOuCDfgt2NzAE4pVkXz9/Dwp92V8z88nLL2Lktlede\nG9vgmi4bfMxcufNzkr5ZzsYHPkCcFdqSjAqx1zidxIltB0n83x84ii3EXDWI5pMHeJT/1VSVZROf\nI2fjvopwT/6uwyT97w8mrP0QxeS+eEm12fl9+KOc2HSgYlvGqh3g4eEtGRUGfflUxb9btg7nyemj\nqv8HuMSwltspyC8nNMyXBbN3VTj1U9isKju3ppJ6PJ/oFuef4mkwKtz36CA+fXcd6hkKjSazgVvv\n6+vNW7lk0B17DWEyG3jmlTG8+8rKk5oTzhZ9w8a0Zvi4Nrz85O+VqjEVRWbIqFZux2vXsRGrlyVW\n6kepGGTatI/klx93u+TvCk1gLXfw3RdbefHN8V6/v7pGMRlpd/cEfBuHsPqG1xCqimZzYAjwxSci\nmD7v3MeOl78m4d2f0MrtaJrG0QXriOjRmnHL33HrpFMWbyJn036XGL6jzErB3mMcnbOK1reOrXSO\n0DR+7nQHxYfPWqw96dQlg4w4w8ErPib6ffwQ5uAAL/0l6i8Oh8YPX25l7crDyLKEEAJNFS5O/RQC\nwf49WRfk2AF69G3Oqx9OYuWSg2RnltC2YyOGjW5NQGD9rQ6tSXTHXoO0bB3Ox7OuZX9CJqUlNtp2\nbFSRp/7o8yP47KO/sJTaEUIQGu7HA08MITDIfQiie59oIhsHkJlWVBHGkSTnG0DrdpFsXHvUbb/S\nwwdzGnR5eszkgUzdN4tDXy2hNCWbJsO60fL64ZQczyLhnR+x2VQOd+xDZkxrNMVAQHE+ytu/Mu4f\n11Qa6/iCdTjcKEs6Sss5MudPt45915uzKzv1M5AMCoqPGbXchjk8iJ6v3kG7uyde3E3XEiVFVjat\nP0ZBXhmt20fStUfT84qDf/vZFjasPlJlH91TyLJ80XHvJk2D+NtdfS5qjIaC7thrGEWR3S5sduoW\nxQdfXENmehGKItOoSUCVzldRZP4xYxzzvt/JhtVHcThUuvRoyrTbelGQV+Y2/g7O19SG6tRPEdCi\nMT3/ebvLtmPz16LaVXb3G0NxaATaySrSkqAwftxSTOtDJyrlppccy/J4DYOf+5nf/o8WVGmbMcCP\nGzLmopZZMQT4XjKfxf6ETD54bRVCCGw2FbOPgUZNAnnhjbH4+p3bAZeV2vhr1RG3LRPdIYSgVz/v\nCKzp6I69TpFliabR1dcV9/Uzccs9fSt6cZ4ispE/ZrOBcotrmMZgkBk4rOqejA67ysZ1R1m38jC+\nvkbGTelAx65RVZ5zKSDsKkVBYRSHhFc49VOoksz873fw9D/HuGwvPHDc43jNJvR3u91WVLVyZctp\nw5EVBTnw0qkotttVPp6xGusZmUfWcgcZqYXM/XYHt97X75xjnMgpRTHI1XbsN9zeS5fB9iK6Y28A\nyMZP5hEAACAASURBVIrMoy+M4O3pK9A0gc3qwGw2ENkkkBvv8KxIabOpPP/3heRknXZOO7elMWBY\nS+5/bHBtmF5jxFw5kNI58bgVWpckjp2Viio0jfIc98VhktGAT2Qwfy49xOL5eygssBDVLJjrbulB\nWNc4Tmw96PY8Y5AfPV+pulq2PrJvd6bbbC6HQ2PDmqPVcuzhEf6oHjKWzsZoUujS49JP161P6I69\ngRDXJoIPv7yGbRuTyc8tI7Z1OJ26RVWpNTL3m+0uTv0UG9ccZdQV7WjT/tw53Qk70vnj1/0U5lvo\n1D2K8VM6VGhd1yXhPdoQO7AdSdnuQ1TBZ7WCk2QZn0YhlGcXVDpWNiisO2xn7cb4illsyrF8Pnlr\nDdfffT3KnrdQLa7VpebwIK49+j2mgLr/W5wvNqvDQ3tyqhUvB2ej8P5DW7Jp3bEqz5EkZ2y80WXc\nxakm0CUFGhA+vkYGj2zF5Ou60KVH03MKSK3787DHfYvnJZzzegt/2s3Hb64mYUc6ycfyWb74AM8/\nvIicrNO5+DlZJWzblMyRxBMe1wHAGWMtt9jRPFTlXgjX/fd+fAJ9OFvaz2RWmDTV2ebOXmph86Mz\n+S54snPGftbfTDYZCOrTkdUb0lxCE+B841myJY+RC14hpJOzGbTia6b9g1cyLfVHrzl1IQSJB7L5\na9URjh3O9cqYVdG+c2O3+uRI0LFrk2qPc/v9/Rg4rCVGo4KPrwGj0blAajYrKAYZH18DwaG+PPys\n3rzG2+gz9suYquKfJedo4FxYYGHR3ASX3HqHQ0Mts/PjNzu4/7HB/PeD9ezYkupUsNQE4ZH+PPnS\nqEpFIpvXH2PO1/EU5FswKDJDRrfmhtt7XbRsqtGo8MLbE3jvlT8pKbYiyxJ2u8rYSR0YOLylsz3d\nuGfIjT+Eaj1Zb3DyGSAZDSAEQW2bE/3ULRi+3+925lmQV0b40O5cnfAVQtOQ5OrNlQ7uzSIjrYgu\nPaIIjwwg5VgeG9YeI+VoPoFBZvoNjqVLz6Zs35zC1//ehKXMjqzISBLExIbyxEujaqx6MjDIhynX\n/T97Zx0exfm14Xtm1iKEuEAgQUKCO0GKW3GqtP3q7vKjSl0odVfq7rTFpThFgzsEkpAQd9mszcz3\nx0Jg2d0kkI1A974urovszM68k+yeeee85zxPF+b9saeqJFeUBPQ6DVffVKOwYBUarcTN9wzg6pt6\nU1RQSXCoLzq9hr07s8hIKyYs0p8efaLRaLzzS0/jEdleQRAuBt4FJOBzVVVfqW7//4Js7/nAs9MX\nOOWaT3Ll9T2ZcKl78+YNq1P4+pONTgu2AAaDhlET4lky74BDMDy5WPzSuxOrqkO2bjzGJ2+vc6jp\n1+okunSP4sEnhzsdu6LcwpK5+9i0Lg2NVmTo6DhGjI3jeHoJC+bsJT21kFaxwUy4tDMxbYMBkG02\n1n6/gR37CvCNCKJ9tB8hx45QmZ7LoS8XIRvNlDcLJC8qFqtOhyJKWHUGmpUW0Co7BatGR9LgidhU\n109Avr5aDBqV0CA9Nq2B5kE+jBwf7zJvfCylkJkzljj83nz9tPanldMmyScbbMrLnIXANBqRnomt\nuPccOzVry86k4yz6ey/FhZUkdIlgwqVdCIu48OvvmzINpscuCIIEHAJGAxnAFuBqVVX3uXuPN7A3\nDVKPFvLc9AVOC2UGHw0ffHslWq37GXPShmN89t6/LgO7r58WRQGTCyMNvV7DU6+MpXUbe9B97J6/\nyT5e6rSfVicx892JDm41lUYLTz+0gKJCY5XRsE4vERHVjKxjxfb6flEERUGjEbn/yRG0kMv4+dp3\n2BZvX/BTJA2SzYrObKLXvwvRmio5mtCTjLad7abWLgg9nkKlfwDGgGDU6mbkqlrlvKTXaxg9MZ4r\nrutVtVlRVG6f9qPbDuKzQaMR+fC7K72VJP8xGlKPvR+QrKrqUVVVLcDPwBQPHNdLPRPbNpjHXhhN\nULAPgmCPSW3jQpj1wZRqgzpA155RrnVwtCKDhrV1GdQBBFTWzviaP7vczNLxj5OT4boSRRIgPdVx\nIXPF4kMUF1VWBXWwt6OnpxbZGz1PBl1RxKbA7FeWs3DsY2yP64MiaarKHmWNFpPBl+SOvSkJCiOj\nbScUjYaqX8IZ//JbtsGqM6CvKEOyWRFtVlxe/Gk16mazjSVzD5CXU1712rqVRzwS1MGug2I8IVdh\nKSln73tz2PTgh6Qv3FTtWoaX/waeyLG3BNJP+zkDqLkeykuToGPXSN758nIqyi1otCJ6fe0+EnqD\nljvu689Hb61DlVVkBPR6ifCoZlx2bU92bcskJ8tZ0MxitFC+YiWWSiPF+9LQjmmDxeC8yGg1mmnu\n7ziWpI3HXFdYqLisajSaZLJDWrrcqEoSeS1iUcGpzt0JQcBi8CXm8E6C87JIa9+FwohaNNMIsGvr\ncUaOjwcgPeXsDECqw+CjITDIh+PLklg2YUaVGNq+9+bg0yKESw98fV5W5HjxDA22aiEIwu2CICQJ\ngpCUl+d1hmlq+PnrXAZ1VVEo3pdK2dFMh9eNWQUcueYJBqz+m5i9SbRK20/8llXcfVksPj5arr7J\nefFTUmxEpCejqzRWvdYqebd9Bnw6ioKPsQx5wzaHl318zm6xUEVAsbqX91UEkdyWbZyMq10iiuRE\nt6N5YS4BxQWuZ+xnvkUA6TTjkIQuEbUadxXuuok1Ilfd0BvVZmPZxBlOCpeVmQUsG/eEy/daSso5\n9PkCdrz0PceXJaEqnqtC8tJ08MSM/Thw+vQl+sRrDqiqOhuYDfYcuwfO66WeSV+wkXW3vI611Ihs\ntSFqNcRcOpg+M29h4wMfYMwqRLLJtC48NRNdfeXzTMv4hZ79WnHPo0P45ZttZGWU4OenI3zbdlod\n2OVwjuij+zH7+HM8Nh5RkVEFCb+yIrpsXkFJt3EO+44Y14Hkg3lOQmgAKMqpVMyJn/3Li4kszeGQ\nq7z4yaApnMXc5sRbwo8fJS2uK2oN8yJFgV59o6t+7pXYCl8/LcaKM25kp+XmT3+zoCqIGg2n+7X4\n+Gm5/YFB9OrXiuTvlqK6qWzKXb/HqUonZ91ulk54AhQVm9GMxs9A8/hWjFv5Flr/s9d+r8wtwpxf\nQrN2LZD0F7a++fmGJwL7FiBOEIQ22AP6VcA1Hjiul3qkYPthSo9kEjm0Gz5hzop6hTuPsHLaC8jG\nU1UZimwh5cflpM9dj63SDC5qzmWjifwtBwnv34kefaLp0cce2MxFZfwc9SXKGTXlAtB+7xZiDu2k\nIiAInakS34pSNH4GAjvFOuzbO7EV/QfHsmF1CjabgigKCIJAgi2PA2ZfZFFC0WgRbVYkRWZMSytq\nSQTtD2wlOb6XfXFUEE8F9VqWJgIIskxkhr3u389spMORXRyK73VKqVAQqgK0oCpo9Fquu62vg1mG\nIAjM+mAyM59YQm52edXbWolGivPKKA8MBVXFYCyn9eHdhJXkEPLuk+zYm4/BoGX42Dj6DYqt6k8o\nO1qN/Z9qFy/TnpAyUKw2/pnyNLayUyJntvJKivaksHXG5/R/775a/R5M+SXsfv0XDs6ej7XMiKTX\nIWoker54I53vdxZW89I41Dmwq6pqEwThXmAJ9nLHL1VV3VvnkXmpF0qTjzN/wL2YC05VokQM6crF\ny9900Cnf/fovTt2UJ3GlgFiFIKCYXVTDBDUjLLEjuf/udfn4r7VaCCzIqTqGZNDR9uoRZxxa4OZ7\nBjBqQgI7kzLQaCT6DmxNc1+JZdNeZNeBEowBQfiWFtG9SwijZ89AscmEPvIpzeat5FBcT8oCQ6vO\n4ZbTUyCCgEYjEBrqRyI+mHVtiBjUheEX92X1jG84qA2juHkogiLjX1GKf/sWtB/dg2ETOhHZIsDp\n0IFBvrz+ySVUlJspKzERFtmMyow8/u59B7byShSL/WlE42eg0wOX0vumRC5xM8zWUway4/lvXW4T\nNBIav1NKoVkrd6DKzrN7xWwl+dultQrsFSfGac4vqXp6kSvNyEDS459hCAuk3dUXrq78+YRHGpRU\nVV0ILPTEsbzUH6qi8HevO5wCc86a3ay47DlG/fVi1WvF+9JqlUd2PodKaGJHl9uGfPsE8wfci6XM\niOzGt1TQSAR1a8uwH550mx5oHRtE61jHp4zxC15mcGo2ZcnHCegQjX9rez5bsdrIzSnncFwPe1Cv\nTT79jH0EUeTZ96bg63sFAJU5hfzR4QbkMiPtOdW9q/E1MOW3OwloV7PuiZ+/Hj9/u2Kkf0wEl+z+\ngj1v/krm0q0YIoLo/MCltJo4oNpjhPSIIyA+mtKDGU7bOt13iUMaxlrNzfhMs213JM343D4hcPGx\nUExW1t74GmF9E2o2HfdS73g7T89DFFnGeDwfXXM/dGdh2HBs3ga3s+30eRtQTuTRAYJ7tKNw1xG3\nZsyCJCL56JDNNlSrzT7L9tEx4MP73drI+cdEcPnRH0j7fTU5G/aR+++eqhuILiSA3i/dTKvxifi2\nODcT52axkTSLPdXyrqoqXzz4E+uUGAgUag7qrnLdADYbh/bm0uNEvvzQF4tcLsrKViv73ptD/3fv\nPeux+0aF0O+Nu876fZO3fsqyCU+Qs8YuASFIAgl3TaHvG3c67Bc5uGvV08CZRA7tXqtzpc/b4Pbz\nAKBabSwa/j8uT/mB7BU7SP52KbLZQttpw2k99aJztiv0cvZ4A3sTx+6j+SfGrEKiL+6HLqQZ25/6\nCmt5Jaqi0GJkL+LvmIQhrDmhfePd2r4BFG5Pdn8iVaUytwi/lnbhr66PTCPl11UOOfaTCJJI9PhE\nEt+9lz1v/krehn00axtFl+lXEuZmtn4SjUFHu2tH0+5au2SuzWhCNlnQBTXzqFZ5ZaWVpx+cT162\nWrtcuqK4DfyKxUZF2aknjKLdR13Ocit0vqw9WEHaN1vp0SeaDp3C611/XetrYPzKt7GUVmDKLcY3\nOszljdUQFkjXx65izxu/VjlECZKIxldPvzdrd0Op7rN1EmupkX8mPUnuuj1V5zm+eAuBb/xKcPd2\nlB3NJGJQFxLumoxPRPBZXKmXs8EjkgJni7fz1DVlKVkc/GwBZUeziBzSDUtxOTtf/sGe61ZVRJ3G\n9axLFND46tH4Ghj+27NEDu7m8viZK7azZNTDrk8uClxfsdChuiF79U5W/d9MKjNPCU9pfPXogpox\nceMHVTeBpoaiqMy4fy5ZGc4drU6c+PxHNJcwp2ZSHBTuVCkjyjIzXxtDi472FMuu135mx/PfIlee\nuulltOnI0U69QZJQENDrNXTuEcU9/xsEqlorM+yGIO3vf9nzxq9UZhUQMbgb3Z/8v1qnTjbe/z4H\nPp3nthIHQNRrQVXdfk5RVESDDo1Bx4T17xOY0PpcL+U/SYNJCpwL3sDuTPqCjaya9gKKze7dKfnq\nXc6Wa0LjZ+DyI9/jE+7aO/LHiMsw5zlL08ZcNoQRvz3r9LqqqhTtSSHtr3VUZhUSltiRNlcOQ+PT\nNL0ky8vMzHx8CZnHXXe0no4g2BUx73tsKG0i9XwZfxvbBo1HljSnZvmyTIvsFF7696kqn1RTfgm/\nx12HtcQueVzp24wtw6c4NTppUIjbvZGI1MPogvxpOaYP3Wf8H0Fdqjc/aapYSsqZP+A+ytNzq10j\nObOu3vWOAhGDuzJ+1dseHuWFTUNKCnipI7LZwur/exmb0Vw10zmXoA6gygrJ3y51u/2SvV/g3/Y0\nhyQBosf1Y9hPT7ncXxAEgru2pefT1zPwoweJu2Fskw3qO7Zk8MBNv9cqqIPKhMu68NZnl9K5exQ5\nq3fhbyyjy6Z/EFXltDp3yGnZln17TzXVGUKbM37NOwT3aIeo15IX086lhowNkYyW7UFVsRSWkfLz\nSv7qfiv/TH262sXMpoquuT9TdszmotnTiR6fiHBGzlzUazGEBdZugVpVyf13D7K55oXbspQsUues\nJW/Tfq9cQi3x5tgbEUWWSftjLXve+g1bhWe+6LLJQmlyptvtPqGBXJH8PcacIsqPZhLYKeasFmCb\nKmWlJj58Y02V0bdbVBWNJHD/jOF073Oqr+7w14tRbTLp7buiCOKp4CRKyMDHb67lva+vqJKYDe7a\nlinbZlOZU8jffx7g6GLX2vZOcgUqpM9dzx8drmPkny8Q2q/jeeODCiDptLS9egRtrx7B8WVJbHrw\nQ0oPZiDqNLS7bjSxVwxlxSXPVOXXq0Wg2puAYrWx+rpZpM9dj6jToCoKfi3DGLPk1aqqJy+u8Qb2\nBsRWaUZVFLR+PqiKwopLniFr5Y7afQlqicbfQHj/6hcwAXwjgvCNcJ2uOR/ZvC7NZRnemYRF+PPy\ne5PQGRxVERWrjIpAUXhLl4utsqxy5GAe8Z0dA4pPRDB9hsWxYmWakxGHKNsIy0xxOY7K7CIWDHmQ\ngHYtGfnXCzTvcP4ZObcc3YdL936FzWRB0mkQRBFVVWkzbTgpv6ys9nMtiCJRw3tVpbdcse3Zr0mf\ntwHZZKlarC5NPs6y8U8wdfcX59UNsaHxBvZ6xlxYyurrX+H4ok1Vgce3VRhd/neFx4O6IInomvvT\nZpqzjvn5jKqq5G3aT+mhDJrHtyK0X4LTl7q83FyjcXL3Pi156MnhLgNCu/8bSc6m/biRXEcQ7Iuy\nrmgXH0q33i3ZtfWUy5Io29CZjESnHHB/XVaZkoPpLBr2P65M+6mq1PR84/SFYUEQGPTZdNpcOYzD\n3yxBMVsI7BTL3rd+P7F+ZEXjq0fyNTDwkwerPe6Bj/52WKAGe6qxPC2Hwh3JhPSMq5fruRA4Pz9J\n5wk2k4W/ut+G8Xi+w+vG9Dw2/++jWs0wXSEadMTfPoFWEwew47lvyNu4H0SB6PGJ9jryJpoDPxdM\nBSUsGf0opYczsD+7qwR0iGbs0tcwhDSv2q9jl0gW6Pe61JERRejZtxX3PT7U7Syv7TUjOfDJPAIL\ncigOjnCatasqtHfjASsIAnc/PJgNa1JYufgQpkorhtXriNi3E82ZAmdnoqrYKkykz99IzCXnt4H4\nSQRBoOWYPrQcc2qNr8Ot4zk4ewGlhzMIH9iZuBvHVpsCVBUFa6nR5TZBI2HMKiSkp8eHfsHgDez1\nSMovK52CehXVBHVDWHM0zXypSM91Ki0TJJG2Vw2n35t3IUoSLUf1RrZYEUTxgmwAWXPtLIr3pjo0\nBBXvSWXNdbMYs/CUUVdcxzDax4dyaH+eg7SvJAnceFd/LhrRrtpHd8VqozK7kPjibJIGjkPWaO3B\nXVURRIFLruparUa9KAoMGtaWQcPaAlC0pwvLJs6gIj2vxg5e2WyhPDW7xt/F+Yx/6wh6v3RzrfcX\nRJGADtGUHnLuqpVNFkJ6tj+r81fmFGIuLLMLllWT/rlQ8FbFeBhTQQnFB44hmy1kLt9W/c4uAo3G\nz8Cgzx5mctInRA3rgWTQoQnwRdRpiBrZk8sOfcvgLx91aBaRdNoLMqib8kvIWrXDqctTsdrIWrkD\nU8Gp6hdBEPjfUyOYOq0boeF+NAvQM2h4W177eCpDRrWv0dj7yPf/YC4oxVBagt502kxREFBV+PPn\nXQ4m3TUR1KUNV6T8yLjVbxM+qItLvfiTiDotQd3autymyDLG7EJstWz7v5Do9+ZdSGc8fUq+etpf\nNxrfqBC377OZLChWG5aScspSs5g/6D5+iZ7GX91v44fAyex5+7f6Hnqj452xnwU563az/+O5mHKL\naDGyF4Iokr/1EAHtW9LmquFse/orji/ZUpUrDe3Todrj+UQGYy2twGY026s1/AxET0ik1cT+CKLI\n2CWvUZ6WQ0V6Ls3jW9lLyf5DmAtLEbWSS1ExUSNhLixzSMdotBITL+vCxMvce7W6I33eBmwVJgrD\nozH7+DulYixmmfl/7OWmu/vX+piCIBB5UVcmrH2Xwl1H2DnrR1J/X+OgiinqNDRrE0nUCOe8wr73\n5rD1qS+RzRYEUSTuxrH0e/ueJtPsVN+0mtCfEb8/y5bHZlOy/xj6kAA6P3Q5XR6+0uX++UkHWX/3\nOxRsO2yXPjipuHkask1my/RPKN6XRsnBdGSThTZXDiPhzsnnJF3cVPE2KNWSna/8yK6XfrDL1Z5W\n44xq/3IqNtleFXBac4Zk0CGb3dioARO3fIRcbuLIj8tRFYW204YTNbKXd7X/BIrVxk/hl2I50Qh0\nOrpAP67OmeORBcfS5OPM6XIzqsXG0fgeHOvQ3eXTVGSLAF79qG6uj8eXJbHhnveoSMumOCicgoGD\nkNq0okvvaEaPj6+S+d3+/DfOyo2iQOspgxj5x/N1GsOFSMnhDOb2uuOcihEkHz3+MRFM2vxRkw/u\ntW1Q8s7Ya0HF8Tx2vvCdsz7IiXh9sqlIVRzz4Sc1UCzFZU459d6zbiWst90yrbYiTP81RK2G3rNu\nZfPDnzg0bEm+enrPus1jVSRbn/zCLmQG6M2ViLINReOchw0MrPuidMvRfbjs4Dcs/n0X637bi8Uq\nw5Eijh4pYt5vu+nRN5pp1/dkx4vfOb9ZUTn2978kf7+M9PkbyV1nb/CJGtGTXi/dTPO4aOf3/EfY\n/drPtVapPBO50kx5WjYHP1tAl4cu9/DIGgdvYK8FGQs323UuzgFraQX/VzSXfe//Rd76vQR1a0O3\nx6++IJqCGoKEOydjCAtk+7NfU56ajX9sJD2fv5HYy4Z47ByZy7ae5o6UwpFOzhMi0Walk+oZz1Jj\nhYU/ftvr5N+qqrB9cwb7tmfSza85fmXO0g8oKmtvfM0uWnaC1N9Xc3zJFiYnffKflczN27AP1YXx\nS22RKy2k/LLSG9j/SwiSeM7pEd/oMHQBfvR48v88PKoLn/27s/lnwUFKSirp9uxDXDquQ5WGuSeR\nfPRQbHc00lotdNv0D3v6jkA98TdXRZGYQ7tQjxth1tV1Pt++XdlIkogV13X3ZqvCkU696bZpuesD\nnGlUooK13MT2579h6Hcz6jy+85Fm7VrYJaDrwIVUJlynqhhBEK4QBGGvIAiKIAg15n3OV1pN7H9O\nswGNr56ez91QDyO68Jn76y7eemkFSRuPcXh/HnN/282M++ZRXOR5jZX428YjnWaUHViQw8Alv9A5\naRUJO9YxYOlvxCTv9ljlkSSJ1RXJAFAcElnDHmegKGSt2H7OYzrf6frINCTfcw/MGj8D8bdP9OCI\nGpe6ljvuAS4F1nhgLE0Wn/Ag+r1zD5KPHkE67Vd24ttpN53QE9a/I6Jei8bPgLa5H71m3kLcDWMb\nZ9DnMUWFRub+tgeL+dSM1mqRKSs18edPOzx+vs6PXoVpYH/29xvGgR4DKQ6OQFAVgvMyCcs6htZq\nRvLVE3fzuJoPVpvz9YhCqaFoQa+TnES2akIX1KwuwzqvibioK/3fvw+Nv8+pm/QJ8xdDeCCRI3sS\nflEX+r5+Bz2euQ7JR2f//Qr2oB49rh9tpg1r1GvwJHVKxaiquh8476s4FJuMbLJUuyKecPtEIgZ1\n4dDnCzDlFhM+sDPGrALyNu4nIC6aTvdNJbBTLObicsz5Jfi1Dv9PNELUB7u3ZSJKApxR5SjLKkkb\n0rnp7uot484Gm03hrZfXkBwYh9XPfiPJb9WeyPRDtN+1GRQFjb8PoX3iib91vEfOqddruPOhi/j4\nzbVYLM7pGK1WYuTkznSf+BC7XvmJyuxCAjvHULg92a0LkuSrp9N97txR/xt0uGkcba8eSf6WA4ha\njX3CpdcS1LWtU4xqM204R39eiVxppvWUQYQP7OwyjpkLS7GWVeLXKszBarCp85/OsVvLK9l4//sc\n/WkFqk1G42dA1GrQhzYn4Y6JdLxnqkPlRVDnWBLfvqfaY+oD/dEHehdG60J1qQpJ8uwkYsncfezf\nk+Pwmk0QyW6TQP/+0QRZyomZehEtx/WrlYNQbemV2IpZH0zmz592sn5NCqIooMgKWq2GNu1DmDKt\nOzqdRIfTnhI2PvABh79YhM3oWNInajW0uXwo8bdNcHjdWl5J8rdLyVy+Db/oMBLunERgxxiPXUNT\nRGPQuTWaOZ3AjjH0ev5Gt9uNWQWsuW4WOev2nNBg8qX/+/d7dNG+Pqmxjl0QhH8AVwm/J1VV/fvE\nPquAh1VVdVucLgjC7cDtAK1bt+6dlla3hQ5PsGDIA+RvOeiyAUby1RM5pBujF8w6759I6ouSg+kY\nswoI6trGoVGorlSUm3ng5j+cqkY0WpHRExO46obeHjmPqqrcPu0nl7NmVJWh/aO4+YnRHjlXdVRW\nWtm64RilJSbaJ4QRlxDm8jOnqir7P/yLPW/+himvGL+WobSaNID42ybSPN5RHbIyp5C5fe/CUlSO\nrcKEoJEQtRoGffY/2l0zyunYiiyTuWwrFel5hPSKI7R39c11Fwon49/pv29FlpkTfwPlx3Id+1J8\n9IxZ9AqRQ07dOGSLFcVqQ+tXc/17yeEMrKVGgrrEOjiVnQ0eq2NXVdX5U3AOqKo6G5gN9gYlTxyz\nLuQnHbQ/2roI6mA3ushZu5vcf/cQcVHXBh5d08aYmc/yqU9TtDfN3pxlttLh9okkvnXXWT2u5mSV\nsm7FEUpLzHTt2YKe/aKRJBE/fz033pXINx9vQpYVZFlFb9AQFu7PlCtrno3VluPpJdUqQmat2QlP\njCbtaCF5OeW0bN2cqJaeu4GdxMdHy0Uj2tW4nyAIdLr3EjrdW3PKZcujs6nMLqoKTKpNRrbJ/Hv7\nW7SePMgh7VhyOIPFI6ZjLTWiyAqgEtYvgdHzX0bjazjn62rKlKVms+mBD8hYtBlBFGg1sT+J79yL\nX3QYxxdvoTKv2MkJSq40s/35bxi3/E0qc4tYf+fbZCzYhKqqBHZszYCPHyJiYGenc5UczmDFZc9R\ndjTT/tQnQN837yL+Fs+k9lzxn03FFGxPrkmbCZvRTOby7d7AfhqqqrJ03OMU70tDlZUqWdVDny/A\nv1UYXaa7bvc+k7X/HObrTzejyAqKAhvWpBDZIoAnXx6D3qDlouHtaB8fxtrlRygtrqRLzxb0hNXl\nkAAAIABJREFUTmyFphohrrOlvNSMCG6KDsGw/yDPPbyAjLRiRFQUBOI7R3D/40PRG5r2+knanLUu\nLepEjUTmP1uJmWpXklRVlX8mzsCYWeDQIZ23cT+bH/mUgR8+0GBjbijMhaXM63c3lsIyVEVBBY79\nvZ7c9fu49MDXlBw45nbCV7L/GIrVxoKB9znM6It2p7B0zKNM3PQhQZ1jq/aXzRYWDXmQytxiUNWq\nz9qmBz7Av3U4LUfXTzFhXcsdLxEEIQMYACwQBGGJZ4ZV//jHRiBK1V++pNeiC/RroBGdHxRsO0zZ\n0Syn8k/ZaGbPG7/W6hh//LCDzz/YiM2qVJVkm002MtNLmPfH3qr9IlsEcMV1PbnlvoEkXhTr0aAO\n0LpNkFuRTdFqJb1tR1IP5WO1KpitKlarwv4dmXzz6SaPjqOhUU/TlS/YfhhjVoGzporJQvLXiy9I\nK7qDn87HVmFCPa0fQJUVLKVGkr9dSkBctNtUSUBcS9Lnb3Q9ozdZ2Dnze4fXjs3dgNVocv79Gs3s\nnPmDh67ImToFdlVV/1RVNVpVVb2qqhGqqjbZ2r68TftZPOYRfgydyp9db6EyuxBtoF/1HaUCF5xp\nhTtUReHg5wv5q/ut/BpzFetufZ3ytByn/SqO5TqWfJ6GKb9mr9Hliw8y97fdLrdZrTLrVri2mKsP\nDAYNoeH+zlo+qkqHQ1sp8Qt28jKVEdi4KgWL2XV1SlOh1eQBLv9OitVGi1G9qn42F5QiuFkUlk3W\n2hlTn2dkrd7hZOABIBtNZK/eRfT4RHRB/k6/P8lXT49nrqdwRzK2Mud+ClVRKNh6yOG1sqOZyJWu\npQ7KjmbV4Sqq54JOxdhMFo4v3kzuhn3sf//PKi0Jc2EZa298FY2fD/qgZtiMZlSbbJeHlUR7maKq\nctGXj+IbGdzIV9EwrLv5dVJ/X1NVcZH8zVLS5qxj8tZPaNbmlPl1ULe2bkvumtWinf3376pvopHr\n0BZ+tuzYepySEpOT4JeoyGg7xCIoMrgIeqosYzRa0emb7ten3+t3kr1yJ5bSCmSjGUESEXVa+n9w\nH7qAU0+hob07uE07NO/Y2qEqrDK3iMNfLKJoTwrBPdsTd9PFHl00byj8Y6MQJNHpqVPQauxP8hqJ\n8WveYeWVz1O44wiCJCEZtCS+ey8tRvai4lguGj+DS8ExB6N47PLNGh8d1jNvBIJAcLc2Hr+2kzTd\nT2Ydyd2wl2UTnkCVVbsjvNOsDGzllSgWK4bwIAbNno6uuS+5G/ah9fch5tLBGELPvw/tuVC8P42U\n31Y7zGJOPppuf/Zrhnz7RNXrAe1a0PLivhxfssVhJiL56unzym3VnkdVVYwV1TsK9enf+hyv4uzZ\nvC7NpeOSImkwRrVGzXLd5SrZrAQ0b9qLir4tQrl0/1cc/HwhWcu34dcqnI53TyG4u+MirT7YLoW7\n7905DmWUko+e/u+cKu3N33qIxSOmo1htyCYLqXPWsvOl75mw7j2CutRfgKoPOt07lSPfL3MQlgP7\n+kPCHZMASJ+/kaI9qSdMtFUkg47ABPtnM/aKoWye/rHTcSVfPd0evcrhtZYX98UnMhibKdvBNEfy\n0dHjmfrrSj9/Ku7PAlulmaXjHsdSXIG1zFitg41isWEuLKX0cDrhAzrT5X9XEH/7xPM+qKuqyqEv\nFvJrzFV8JY3i15irOPTFQhRFoTK3CGvFqaCVtWK769+RonB86Vanl4f99BTxt09E8rV34vq1Dmfw\nV48RM2WQ2/EossL2LRkI1aS+dDqJqVd5ruqlJqxunjwApAA/YlL3IZ5hbSfabHQuPIpwrr6GDYiu\nuT9dp1/JmIWvMOjT/zkF9ZP0eulmEt+/j4D4VmgDfIkY3JWxS16lxSh7Wamqqqy++iWsZcaqp17F\nbMVaamT+oPswF9XegKQpENSlDYM+m27vEA/wtf9r5sPQH2YQ0L4lmcu3kfTop8hGM7ZyE7LRTGVW\nIYtHPYK1zIjW34dxK9/CLyYCjb8P2gBfNP4+JL5zD1HDe1KaksWOF79j0cjpLB4+nXbXjabFyF6I\nOg2iTot/myhG/vE8Yf0S6u0aLxg9dsUmc3xpEpVZBZiLytj61Jeo1XxxzyRqZC8uXvY6ssVK0e4U\ntM18GsU5XlVV8jbuoyIjn5BecQS0a+GwPT/pIDtnfk/e5oPoQ5rR4Zbx9kaqM9rP97z5K9uf/cZh\nFibqtXaNeJMFVGg1IZFBn00nfcEmNtzzLrZy5xlqs3YtuPywCwlZ7PW+ssmCxtdQba2/zaYw68kl\npCQXIMvuP28vvTORVrFBbrd7mvdfXU3ShmMut3Xv05JuSavYvK+YlDadsBh8MFSU0+bANloUZeIT\nHsTFK950SFNdqJQdzeTPrre6zEsDhPZLYNLGD6s9hrWiEmtJBYaIII82etUFm9FE9ppdCKJIxJBu\nVQYmS8Y+alf8PAONn4HEt++mw632RjBVVSnceQRbeSUhvTugygorp71A5tIkhzSPaNDh3zqccSvf\nsjdAhgScc2/Mf0qPvXhfKotHPmzPlcsKNosVzmbRRxAwhAZw+OvFbHrQ/gFVbDL+MRGM+OP5qkew\n+qY8LYclYx7BmFWIIAooFhvRExIZ+sOTSDotaX//y+qrX0Q22WeRlVkFbH7oI/a8/gtTts+ucliS\nzRZ2vPCdU4eiYrY65FPT529k0YjpjFv9NhvufsdpPJKvnoS7JrsdryhJiLVozPj+8y0kH3Tj/QqI\nksDd0wc3aFAH+w3HLSoM//Vpgp77hj1v/YbNqpAa353D3QawX6vDv7SQoitf57bNb17wDWyKTa72\nGgt3HSV7zU4OfDyPtL/WgaLScmwf+r15F4aIINbf9Q5pc9YCoPX3oc9rt9PhJs/o7tQFja+B6Iv7\nOb3uzn/WVmGiPD2v6mdBEAjpccp7deWVz5O1fJtT7l4xWag4lsuhLxbS46nrPDT66jnvUzGqorDk\n4sepzC3GWma0B7OzXMnX+OoJS+zIhnvfw1pqxFpqRDaaKTmQzsKhDzaI36Sqqiwd/wRlR7KwlVfa\nx2CykLFwM9uf/RpFlll/+1tVQf10jJkF/HvHW1U/l6fl1KpMTbHaKDuaRdGOIwz/7Vk0vno0fgYE\nrYTGz0DUiJ50uv/SOl2XxWxj1ZJDbrf36hfNF79eQ9+BDd/q3rFLBDqd8+xRp5Po2CUCSael54s3\nIUgi+3oPJaNtZ2w6PQgC5c1D2BDZlaT5nhclqwuVRgu52WXYqmm8OlsC4qLRBbsXGBO1GlZc9hyp\nf6yxTx6sNtLnb+SP+Bv4IWgyKT+tqJpUmAtKWX/7Wxz50Y0kcSOjyLJbAxeNv49bE21zYSnH5m1w\nW1ggmywc/WmFx8ZZE+f9jD13/V6sJeU1OsE7IAoIooAgigiiSJeHryR9wSanxRRUFbnSQtqctbS7\nZqRnB34GhTuSqTiW41BbC/ZutwMfzaX9DWPti8BuSJ+/EdliRdJpMYQ2dzKAdodqkynak0LHe6Zy\nZfovpM1Zi7mwjMhh3Qnre+45wIxjxeRll5GdWVrtnyaiRbMa+wnqi8Ej27Ngzl6sVrlqjKIooDdo\nGDLa/gVWrDLlGl8KI1qiSI5fF0XSMHfBEfpOcvYrbWjMJitffbSJpA1piJKIIMDkK7ox/pJOdX6i\nEASBId8+zuKR052cwMD+GVVl2XVppIv9VVlh/V1v1/t36lzY9uQXrssQBQHfqGBaTXQtQFeZU4R0\nogvbHZ5y/KoN531gN+WXuPSndIUgiVWfM9WmIOgkgnu2p9sT1zAnwfUKtc1oojzF9aNZ1T4nyior\nMvIo2nWU40uTEDQScTeMpcv0K2rVlm3MKnQr02otM7Lv/T+r/dCoqopitSHptOiDA4gen0jGwk3V\nvgfsH7ZmJ0q09EH2nH1dKC8189bMFaQdLcRmrbl0sVe/hl/HOImfv47n3hjP959tYefWDAC69W7J\ntbf2rTL00Bh0WDq0Q1BUcPHnySpwnXduaD58fS37dmVhtSpw4vf+1y87MfhoGDkuvs7HjxrWg96z\nbmPrU1/AaSksyaBDF+RPZVbhWR3PVlaJKb/Eo0UKqqKQNmcth75YiGyx0e6akbS7dlStdVlsJgv7\nP/zbtcWeACPnzyR7zS7MBaWED+iEX3RY1Wb/2EiHxq8zEX10dLil4dJP531gD0vsaDeMdoHG34Aq\nq4g6DbLJYn9MOm36qFisFO48wsHZ8wnu0Z7ytFynmb/G14ClrILFox/BWlpBzCWDSbhrUpW1Xc66\n3Syb9CSqomArd+ww2zXrR47NXc/EDR/UaNIQ0ivOvWejAIc+W+A0mz+doE4xDkJEg796lOVTniZv\n8wFErWS/fptsd28/eVhRRBfkT4sxnmtr/uC11aQkF6BUs0h6OsGhjdfZa8ovwU+EB2YMcykGdZKe\nt49j198pLo/RLKDxyx7zcsrYtyvbHtRPw2KW+euXXR4J7ADdHr0KrZ+Bbc98Zf/OKSqxlw/BJzKY\nfe/NcZuGcIkgUJGe67HArqoqq656kYxFm6vqy/M27efAp/MZv+adqoXR6jDlFrl8wgC7u9LCgfdX\nXaNisdL+5nEMeP8+BFFE46On8/Qr2PvGb05rW4JOQ1jfBOJPlFI2BOd9YPeNCiH+9olOcqaSr54x\nC19BH9yM0iOZ5Py7l33v/IFicbwJyEYzhz5fyEVfPsLxpUkO6ZiTQvz7P/ir6vWi3SkcnD2fyVs/\nQdRpWDZhhr2k0gWyyULJwXSO/f1vjXKfvpHBxN14McnfLXWREqLaDkDJoGPAGZoeugA/xq18i+J9\nqZQcPk7zDtFkLt/G1hlf2BdmrTKBnVoz4vfnPValUJBXQfLB/FoHdVEEH99zU7mrCwU7kll746uU\nHLBXxAR1acPgrx9zW489+Oah/LE6m5Iyq8PToU4vMXZKxwYZc3VkZ5ah0YouBc1Ki03YbAoajWfS\nXR3vmUr8HZMwZhWgD26G1s+HstRs9n/4N1D7wC6IAv4erCjKXrXDIaiD/btdsi+NI98urZU7kiE8\nCNVNZLdVmJwako58s5Tgrm1IuNNeYNDz2RvQBfixa9aPWIrKEPVagnu0p9vjVxM9PrFBq4HO+8AO\nkPjOPQR2imHPG79iyismpHcHes+8hfD+nVBVlfK0HDLmb3AK6ieRzVZCe3VgwIcPsP7Ot6vSF4Io\nIJutDmWTssmCMauAPW/+RmBCqxoXKW3llWQs3ETsZUMoT89FtdrwbxPlcmY44MP7adY2ir1v/Yap\noBRDaHNM+cWoLqo3BK2ELtCfiMHd6Pns9QR3bevy/IGdYgnsFGv/f8cYOtw6geK9qeiD/GnWtoXL\n95wtqqqyY0sG837fg62WnaOiKNC1Zwv8/Bs2sBsz81k09CGHm3HB9mQWDH6Ayw99W1VZdDqiJDLj\n1Qm8/vw/lJeaEUQBq1Vm0LC2jJnY+IE9PLKZ27RXswC9x4L6SUSNhH+r8FPniI1k2M9PsebaWfYS\n2DMnJmcgaCTibr7Yo74FqXPWYnNxXpvRxJEfl9cqsGsMOhLumsyBj+c6XMPJJqUzJ1c2o4k9b/1e\nFdgFQaDL/66g80OXI5ssSAZdo1VMXRCBXRAEEu6YVNU1djob7nmXI98tc9n+C/ba7rbThmEzmkh6\ndLZD8Hf3aKmYraT+toqEu6bU+PgpaCRUReHPrrdQdiQTRAFDaHMGf/UoUcMdF90EUaTrI9Po+sg0\nAHbO/IHtz33t8rgB7Vpy6b6vqj23KzQGnce1tn/4PIk1/yRjroV+iiiBVqshPMKf2x4Y6NFx1Ib9\nH89DPvMGr6ooZisHP19A9ydcm45HtgzgjU8vIflgHqXFJtrEhRIc4tsAI66ZiKhmdOgUzsF9OQ4B\nXqeXmHRFwyiTtp40kKtz/yB79S6OLdjA4S8WIWokVFVFlRV7/llVQRRIuHMSfV+9w6PnF7Uau1Wl\ni3mWqKt9mOsz6zZM+SWk/LgCQSuBohLSpwP5Ww+5fGo25xc7vSYIQqMbY18Qgd0dBdsPk/yti9TG\nCSQfPb5RwXR68HJSflmFrdLsNsfm9F69joiLuiBqJLdPAgCiViJtzjqHGWLFsVz+mfwUk7d+Um0T\nVPSERHbO+sFp/JJB12T8GTMzSli17LCTKYY7Lr+2J+07hNGhU3ijzGbyN+9zuaAsmyzkb3Fflgn2\nL2xcQni1+zQW9z0+lM/fW8+OpAw0GhFVgfGXdGLMxPrrbjwTSa+j5Zg+tBzThz4v30rehn2Iei3h\nAzqDqmLKK0YfEnDOJhPV0fbqERycPd/pu6LxM9S6Zl6x2lh97cukz9uAqNeiKgo+kUF0e/xqVl7x\ngsv3hNahcqw+uaADe9pf/7qs+wZ7Dr7nczcQf/tEdAF+FO1Ncdl56e69HW4bT2ifeCIGdyV7zS6n\nrjzRoEOAE9Upm52OIZut7H37dwZ+/JDb84T0aE/bq0aQ8svKqieOqpvRA5fVaqz1za5tx6utBjid\nNu1DmHBJl3oekXuOL0sie41rZUlRryXwNB3t8w0fHy33PTaU8lIzpSUmQsP9GlWkTOvnUyVJcBLf\nFqH1dr6wvgl0vGsy+z+eay9CUFQ0/j5EjehJ7JVDa3WM7c9/ay8bPq2IofxYLpsf+oio4T3IWrnd\nSR+p98u3evxaPMEFHdhFSUQQBVQX6cfAjjF0fXiaw8/uFNsESQRRRLXa0Pj7ENY3vmqFe+TfL7L7\n1Z858Ok8bGWVhPbpQFhiR/xahdN66iC2PfWly1Zs1SZTuPNojdcw6LPpRI9P5OCn8+xVOZcNqboZ\nNQU0Gqla/RewpwQMBi13Pzy4gUbljDEznxWXPOO2/FPUaki4o+Y8bFPHP0CPf0DjpgEai76v30ns\nFcM48sM/yGYLbS4fStTIXrV+Mjzw0V/O31VFxZhVyEVfPUpwz/Yc/GQe1lIjof0S6PfGnU3WQrBO\ngV0QhNeBSYAFOALcpKqqc9KpkYi9fAi7Xv0Z+YzcmOSrJ+6mix1eazNtOEmPf2ZfgDltQVTy1TP0\nhycp2HYYa0k50eP702JUryoLOEmnpcfT19HjadetwkHd2iL56p0eEQWN5FaUyWE/QSD20sHEXtp4\nQbE6+vRvxc9fOetqaHUSXXpEERTiS2zbYPoPjm1U16HD3y5FcfNkcdLL8vS6ZC/nJ2H9Es5JXEtV\nVSwlrqvbBFHAXFBK7xdvpveLN9d1iA1CXZfLlwFdVFXtBhwCnqhh/wYlsFMsXR6+wq5CeCIQa/x9\nCO3dgQ63OjbiaP19GL/2XYK6tkEy6ND4GfCJDGb4r88SM2UQvZ6/kcR37qXlmD5n5evZ/voxdn33\nM2YNkk5L54eaRjqlLgQG+zJqfAeHy9NqJWLbBnP3w0O44Y5Eho6Oa3QruYpjuShu+gQCO8cQMahu\nKSJrRSVFe1IwF5bW6TheGgdBEAjs5FrWQrHYmuzM3B11mrGrqrr0tB83ApfXbTiep9fzN9Fq4gCS\nv16CtbySmEsuotXEAS4bhgITWjN1x2eUp+ciV5oJaN/yrIK4K/RBzRi/5h1WX/sypYcyQBDwiQhi\n8FePNop6pKfZsSWD5YsOOfR1qapK/yFtXOqwNBYRg7pw5Pt/nNZRRJ2WqGE9zvm4qqKwdcbn7Hv/\nL0SNhGyx0nrKQC764pFaOdc3FHk5ZSxbcJCM1CJi2oUwanw8IWFNI53XVOj35l0sv+QZh3SM5Kun\n3TUj63V9oD7wmGyvIAjzgF9UVf2+pn3rQ7b3fKDieB6K1a4aeSEoAqqqyvTb/qQgv8Jpm8FHwwff\nXonWwz6l54pstjCn081UZOSeMjwQBHTN/Zi6+3P8Wp5bGmbxE9+xeF02pQHBaM0mWh3ZQ6ucVKLH\n9mHkny968ArOnQN7c3jrhRXYbDKyrKLRiEgakcdfHE3buPMrYNU3mf9sZctjn1G8JwV9iN2EpPP/\nLm8yUsMek+0VBOEfINLFpidVVf37xD5PYm87c+vOKgjC7cDtAK1bN5xLTlPiXINHU6WsxERJibtK\nIoHjx4qJbRfSoGNyh6TXMWnTh2ye/jGpv61Gscm0GNWLxHfuOee/y6F92fyyx4YSHAGCgKzVcaRz\nXyoCghCWJFFxPK/R/+aqqvLp2+scegxsNgWbTeGzd9cz6wP3ssz/RVqM6s2Urb1r3rGJU2NgV1V1\nVHXbBUG4EZgIjFSrmf6rqjobmA32GfvZDdNLU0Rv0Lit+1dkBV+/hpcLqA5DaHOGfPM4Q7553CPH\n++mLJGfFR42WrNYdaJedTNnRrEYP7DmZZZSXue7jyM0po7jQSGBw02i08uI56pRAFgThYuBRYLKq\nqq6XlL1csOgNWrr2bIF0huyuIApERQcQHulew/tCIC3VdQGYqMgU+wQSUAtz7/pGqO4brlJjqaqX\n85O6VsV8ADQDlgmCsEMQhE88MCYv5xG33DeAiBbNMBg0aLQiBh8NgUE+3PdY7ZpCzmcMPm4qfQSB\nlv3i8I1q/DRUeGQzt8bb/gF6jqUUUVlZvbSzl/OPulbFuLYT8fKfoVmAgZnvTmL/7myOHysmLMKf\nbr1bOs3iGxpFUUlPLUJRVGLaBNWLmcfwsR1YMm+/o5yCqqLXiVz29X0eP9+5IAgC7TqEkZ/rvMBd\nXFjJe7NWoaoqV17fizGTGl/QzItnuKA7T700DKIo0Ll7FJ27Nw1j5/27s/nozbVYTPYFQ61O4o6H\nLqJrT8+oWZ5k6lXdSE8tYv/ubBDsGlQ6vYbHXhiNrhbmKg3F7u2ZbrdZTtyUfvoqiciWAXTr1fjp\nIy91x2PljmfDf7Xc0Uv9U5BXwRP3znVSmtTpJV58eyKRLQI8fs701CKOHM4nMNCHLj1beFwmt67c\nesWPLrXazyQiyp/XPr6kAUbk5Vypbblj0/oEevFSR1YsOYTsQhNetin8s/Cgx89ntcrs2p7Jgjl7\n+eaTTfz0VRIlxbUTk2soErpE2B8naiA3u7z+B+OlQfCmYrxcEBQVGvnzp538u/IoNhfGJLKskpVR\n4tFzKorKG88v5+ih/KqUxsrFh9myPo2Z705CoxFRFLXKP7WxuOqm3hx+LBeL2UY17opn5QfvpWnj\nDexezntKS0w889ACysvNbm35tFqRdvGe7bLctyuLlOSCqqAOIMsK5WVmnvnfAkqKTCBAi+gAbr5n\nQKN1eUa3DuSFtyYw97fdJG04hqnStSGK6C19vGDwpmK8nPcsmbsfo9Hi3mtVAI1WYsTFnjF1Psne\nHVmYTc5BUrapFOYbkWUF2aaQnlrMK08vIy+nzKPnPxsiogK47f5BPDhjuNva9nYdvPICFwrewO7l\nrLCYbaxdfoSvPtrIgjl7KG0C+eSdW4+79fwUBGgXF8pTs8YSGORZUS5ff12tF0ptVpnFc/d79Pzn\nQkKXCGLaBDsFd41W5Po7ExtnUF48jjcV46XWFBYYeeGRhRiNVswmG1qdxN+/7mb60yOI7xzRaONq\n5sZYQpIEJl7elUuv7l4v5x04tC1//+rakelMZFkl5XBBvYzjbBAEgcdfGsPPX21l/aqjWCwybeJC\nuO62vrSODWrs4XnxEN7A7qXWfPPJJkqKTVWGFScbcz54bQ3vfnlZvTQB1YbEi2I5sCfHyUhDlESG\njqq/HrqQMD9uuqs/X328EUGwL6aeTAc5jUUUaBHdvN7Gcjb4+Gi56e7+3HhXot1f2ptbv+DwBnYv\ntcJmU9i17bhLFyKLxcbR5ALaxze84FV5qZnfv9/uclw33JlY75rjg4a3pWuvFmzdeAzridnvG8+v\nwHRGm75GKzJ2ctPq7BQE4Uz/Fy8XCN7A7sUJi0UGVXU0Q1ZVt+VwAoLLEsOGYMWSQ5hcLGDq9BK2\nWjTleIKA5gaGjz3lsPPYC6P48LU1lJWaARVBFBg6qn2TU7v0cuHiDexeqsjJKuOrjzZycF8OqNAu\nPpSb7u5Py1aBaLQS7eJCST6Y5/Q+VVUbrZRv/+5sR62WE1jMMvt35zgE3IaibVwob8y+hH9XHeW7\nTzcDsGpZMisWH2LI6Diuu63vBWG04qXp4q2K8QJARbmFFx5dxIE92SiyiqKoHD6Qx4uPLaa4yF75\ncsNdiRh8NEgnKkEEwT4zvv7OxEazwQsJ9XMpPStJQqNav5lMNr6bvRmTyYap0obZZMNqVVi7PJl/\nVx5ttHF5+W/gDexeAFi7PBmLxeaYblHtZXorFtlb8VvHBvHye5MZcXEH2rQPod+gWGbMHMugYW0b\nZ9DAqAnxaLXOH2NJEhk2pvHER7duPObShMRibhpljzarzMa1KXz54Qbm/LiDvByvnMCFhDcV4wWA\n5IN5WMzOKQ2rVSH5wKn0S0iYH9fe2rchh1Ytse1CuO7Wvnz32Ra7VPCJ6pTb7h9IRJTnBb9qS1mJ\nGaubdYeyUlMDj8aRinILLz62iMICI2aTDUkjsuivfdz6wEAiIptRmG+kVWwQYRH+jTpOL+eON7B7\nASCyRQAajei0CCqKApEtGy9A1oYho+Poe1Es+3dlI4oCHbtFotc37kc7rmMYGklEPuP3KYgCCY1Y\n8w8w5yf7DP3k31q2KcjAR2+sRasVEQQBq0XG10/HmIkJjJ6Y0Oh6N17Ojrpa470oCMKuE+5JSwVB\n8KzgtZcGY/jYDi7NMTRakVETEhphRGeHj4+WXomt6NE3utGDOtjb89vFh6I9fe1BAL1e4pKruqMo\nKru3Z/Ld7M38/t12MtM9K1BWHRtWp7iuYlLBalGwmGVU1T6z//vX3Tz14PxGf8rwcnbUSY9dEIQA\nVVVLT/z/fqCTqqp31vQ+rx5702Tvziw+fnNtlXa3KIrc8eAgevSNbuSRucdaXom5qAzfqBBETeMs\n4LrDapWZ99tuVi49jNlkI6FzBNNu7EVEVABvvbic5IP5mE02RElAkkSuuLYHYyd3qvdx3Xn1z2dl\nh6fRiIwaH8/VN9coA+6lnqmtHrvHjDYEQXgCaK2q6l017esN7E0XRVZIOVKIqqrEtguwy1kaAAAS\ny0lEQVRpcqYRJ7GWV7L+zrdJ/WMNgiQi6bT0eulmOt49pbGHViPLFx3k56+3Oq1paHUSs96fRFhE\n/ZqAf/j6Gjb/m3ZW79EbNHzw7ZWNVv3kxU6DGW0IgjBTEIR04P+AZ6rZ73ZBEJIEQUjKy3OuhfbS\nuKiqypp/kplx/zzefGE5f/60k/TUokYfU96m/WQs2oQp3zFVseKy50j9Yw2K2YpsNGMpLmfLo5+S\n/N3SRhpt7Vm19LDLhWpVUdn877F6P39cx7PvEDabbHz69rp6GI2X+qDGZKQgCP8AkS42Pamq6t+q\nqj4JPHlixn4v8Kyr46iqOhuYDfYZ+7kP2YunUWSFl59cyuHTql/27Mji0P5cHn1+FHEJ4Q0+puJ9\nqSydMANzQSmCKCKbLXR+6HJ6z7yF0kMZ5KzbjWJ2TCfIRjPbnvma9teNafDxng3ulCgVRcFmq/9u\nWa1WQqsTsVrOrlt4Z9Jx8nPLCQ33Vss0dWoM7KqqjqrlsX4AFuImsHtpunz89jqHoH4Si1nm+8+2\n0D4hjH9XHsVqkYnvHM41N/chOqb+lAAVq41FI6ZjyitxsPXZ/96fBHaMQRvgi6iVkF0oBlccy623\ncXmKxItimP/HHqxnBHiNVqJHn/pfz+jULQpU152vggiqm3iv0YpkZpR4A/t5QF2rYuJO+3EKcKBu\nw/HS0BTmV5C0wf3jf+qRQlYtPUyl0YrNprB3ZzYvPr6YnKz6M43IWLQZudLi5NVmM5rY9epPBLRv\nieJmZuvbIqTexuUpxkzqSFCIr0PFjN6gof9FscS0Da7380dENWPIqHYO1UOSJODnr+ONTy7Bx1fr\n8n2yTfEG9fOEutaFvSIIQjygAGlAjRUxXpoWqUcK0WhELLL7FMCZqQOLWWb+77u55b6BHhuHzSqz\nfnUK61cfxZSZj61NV0qaBWMx+BJQmEvM4V34lZdgyi4kqHMsIT3ak590EMVySgBM42eg+5P/57Ex\n1Re+fjpeeHsiq5YcYvP6Y/j4aBg+tgN9BrRusDFcd3s/OnQKZ+m8A5SXmenaM4oJl3YhKMSX8Eh/\n0o6esb4iQEy74CYjPeyleuoU2FVVvcxTA/HSODQPMpz1exRF5cDeHI+NwWaVefmppaSnFp1aVIxJ\n4KSmrMnHj/yo1vRct4ioXrEAjJo3k9XXzCR71Q5EvRbVJtP10WnE3zHJY+OqT3x8tIyb2plxUzs3\nyvkFQaD/4Db0H9zG4fXtm9PJznR+GhOAyVd0baDReakrjd/J4aVRaRsXSlCw71mnVgKDfWu1X1mp\nibwc+4JbQHPXN5ENa1LJSC12rBQ5Xf1QFFFEkSPdE7n6pYkA6IOaMWbRK1TmFFKZU0RA+5ZofM/+\nJuXFkdX/JLv0cQXYtjmdbr1aNvCIvJwL3sD+H0cQBB55biSvPfsPJUWVWKyy28Wzk+j0EuOmVt9I\nY7PKfPXRRjatS0WjlbBaZXontubW+wY46rwD61cfxWx2HUxOpyQ4grB+jl2wPhHB+ETUf166IbCU\nlJP8zVLyNu+neUJrOtw8Dt8WDSuH7EoCGezLHe62eWl6eAO7F8IimvHax1M5cjCft2euoLzM4nZf\njVZk3NROVFZYefKBeZQWm2gXH8ql1/Rw8Mz8/vMtbPo3DatVqar+2LY5na8+ErjjoYucjlkbtBdw\nc0zpkUzmD7gH2WjGZjQjGnTsfvVnRi+cReTgbk77FxdVkp9bTniEPwGBtTPpLi8zs3LJIfbvyiYk\n3J/RE+JpFRtESbEJg0GDwUdL4uBYDu/Pc7rR6g0a+g6I8ci1eql/vIHdC2CfubdPCEOrdR88I6L8\neeqVcSyYs4dvPtlU9eXfsSWDvTuzmTFzDG3ah2A2WVl3ojzydKwWmS3rj3HtbWYHUakhI9tzcE9u\ntbN2jUZk4NDGkweub9bd+gbmwjI4YfGnmCwowKqrXmJa+s8Iov3mZzHbmP3uenZsSa96Euo7MIZb\n7h3g9m+nqiqb1qXy2XvrkW1Klc/p+lVH0ersTlOqCt16t+T6O/rRolVzjqefSo3p9RLt48Po1tub\nhjlfaJr94l4ajeq+vJde0wNFUVm+8KBDEFZVe8D56Uu7TERpiQnRjUOQpBEpKnQsQO/dvzVde0ZV\nO66o6ACuurFXbS/jvMJaUUnuv3uqgrrDtjIjhTuPVP385Ycb2ZGUgdWq2EtQrQpJG47x/WdbqvYp\nyKtg2fwDLJ2/n7ycMn78MolP3/4Xm1WpqiBVFBWbzX4Mq1XBZlPYufU4b76wgidmjuGqG3vTPj6M\nDp3Cuf6ORKY/M8Jren0e4Z2xe3Fg0uVd2bQuFVPlqcAtCBAdE0i/QbFs3XgMSSM5NdcAVbZ5zYPc\nL6wqskLoGc5Goij8f3t3Hh1VfQVw/HvfmyWBQBKyYAiJCWFHRAoq1ogCLiAKKrUVq5XqqVq6iOJW\ncau2dpGKp9TW0kU8ra31HJe6oBb3agUREHoApajIYkhCWLMw669/vICEmSFBkpnJy/38BXnDvN/8\nwtz5zW+5l+lXjuaD97fGzTro9VrMvHEsmd1cWjM0TkA/QDiwZ7+hPsCydz+L2X4aCkZ4541PuPTK\nUSxe9BHP/H21s43FwD8WLscY4hb7PlQkHKVm214+3VDHhEmDmDBp0NG8KpVCOmJXLRT0zuLuuedy\nwol98fltuvfwcc6UIdzx84lYlnOIJW5pIMCf4Rxs8flsJk4dgs/fcmrA57cZd85A/BkeAoEw0cgX\nAcrrs51gFJekRSrejuLt0Y1eJ1TEvWZ7PeSNdM4B7tzRlDApm4kaFj2zlmceX0UoFCEUjBAKRQiH\nDZFI2zN4mKhJagph1THc+25RX1pRcTbXzxkX99qgYb3x+uwWI3pwRtWnn/lFcLrgkhFYtlOZJxKO\nYtnCWZMHU1Key/VXPcWunY1YljBidF+uvaGS7JxMSo7NZePHdS0PnAr07tMjpfVLk6HyDzeyaOws\nIoEQ0WAIsS0sv5fTFt5yIB1xfkH3hEE6HI7y7BOriR5Z+pcYliUHKifV1TZQXbWH3kU9Xd//btNu\naXuPhKbt7dw+3VDHL+9aTDgcJRox2LZFef88Zt85PmYrYzgcpaHeWSxdvWIrD/3yrZjplm7dfTz4\n52nsrGvk3ltfIhSMENgXxu/34PFazPnZORSX5CTzJaZEw5Za1s5/mu3vfUjPQSUM++GF5Awta/GY\nxxcu59UXP4qbHfJoiUB+YRb3zjuPhx/4N2tWbcPjtQiHIgwfWcy1sytd/c2pM0h6PvYjoYE9/UWj\nhuVLNvHmYqfI9ZjTyqgcV4HP72Hp2xtZ+LslBIMRolFDfkF3brh9PEWtHDe/ZeYzcU81Apx+dn+u\nnHkK+5pCLHl7I1s27qS4NIcxY8vJzIyfu6Qr2bmjkZefW8e6/1YTaApRV9tAsI37yvcveh5unl0E\nyvvn8f2bT+cfjy5nxdLNLdZRvF6bE08t5ZpZlQmfQ3U8DezqSzPG8PADb7Ny2ZYDpxB9fptjinoy\n/apRzLv39RZBRQSyevp5YMFF+PwejDEs+fdGXn52HfV7AwwbUcSUi4dzw9VPJZqeJyPTy+//fkky\nXl6ns+3zPfz4pkUEAxHn246Az2u3KbB7vBYFhVlYtrB1U/y5cxEnq6PHY5OTm0ltTQMmzoeA12sx\n/9GL3buI3QkkrdCGcp//ratl5XtbWhwtDwYibKvaw19+vywmoDjbHSMsa84S+dc/LOORh5bw6YY6\naqvreevVDdw+6zn8GYm/xh+8kKpa+tuf3j+QXRMAA8FghAQ7Sh3N17JzMrnhjnExRbUPZgxEI87v\nsGZbfdygDmDZFnt2B77kq1DJpIFdxVi+dDPBYOxhoWAgQk11/KmUwL4wNVV7qa3ey5uLN7TY5x6N\nGJqawuTlJV6AO26k1kFPZM2qqkMzGAPOTqKEpQubH79rRyNz73mNgt7OqP1oCNArv205glRqaWBX\nMWxbEo4GMzI8ca9lZHjoU5LN2tXb4h5kMVHDzh2NlFXE5nXJyPTwjW+58/BRe0gUkG3L4uLLT2Dg\n0EJ8fjtuv0cihurP9/LRmmqiR7Dt8VA+v4fJFw077MlklT40sKsYY04rw+OJfQP7/R7Omjw4JmeL\niBCORHnysZW888anCfejZ2R6uXvuuXznB1+luDSHvILunHH2AH7y4PkcU9yzI16KK5x06rHYdvy3\n6oRzBzPnvnP41YKLONx6WbC5DJ6IM++enZvZppTNIpDVw8+0S0dwvqbt7TTaZe+SiMwG5gIFxpjt\n7fGcKnVKy3sxceoQXnp2HaGgk0fEn+Fh8LDenH/xcCoGFfDIb5ewZ9c+IpEoxhjCIUN1Vb0zR5tg\n2uCMs/ojIlROqKByQvwDOSrW9BmjWb+2ht279hHYF8brtRBLmHnTaXi9NuvX1jD3nlfj9vuhjHE+\noH/9yNd4753P+OOv/5MwR4/HY3H/7y4gN78bctgJfZVujjqwi0gJcDbQ8eXVVdJM++ZIRo0p5Z03\nnGReo8aUMmxEEZYlDB/Zh18tuJCqrbu58/oXCIW+iCj7g4uIE8xDwQg+v4fy/nlMnnZcil5N55bV\n089986fw/rubWL+2ml753akcX0Fur25EI1Hm/+LNhDnU42locLJ3DuuXRUVjFevohWlOMobIgd/d\n17/1FXrpwaROqT1G7POAm4F/tsNzqTRSVpFHWUX8GqIiQl1tY3OGwdgdF8bAJTNG0VAfZNDQQgYO\nLdRR31Hwem1OGVvOKWNbVjz65H91cRe6D6e4JIdoOMKiyuvovbmGbNvHjsI+7M4tJNAjm4rxxzH5\nshPpNyC5ueBV+zmqwC4iU4GtxphV+qbtevzNe9bj8Xgsxk8cqMG8g4XD0cP2sddnEQp+8cHr89lM\n//YoNj//Lvu278KEI/jDTRRt/piizR+DCKWF9fQbMCkZzVcdpNXALiKvAMfEuTQHuA1nGqZVInI1\ncDVAaWnyivaqjtN/UD4+nycmb4zHY3FyZZkG9SToNzA/4YnS/oPyOX5UMYuf/5D6+iDFJdlcMmMU\nw0f24YMXXiPcsC/2HxnDjpUbOrjVqqO1GtiNMWfG+7mIDAfKgf2j9b7AChE5yRizLc7zLAAWgHPy\n9GgardKDZVtcd9sZ3H/3K0SjhmAggj/DQ6+8blx6VauH41Q78PlsrrjmZBY+vOTAQrftsfB6La74\n7hhKy3KZ+vXYCkw9+hXh6ZZBuL4p5lrPAVpQo7Nrt5QCIrIRGN2WXTGaUsBdGhuCLH17Izu2N1Le\nP48Ro4sTbs9THePj9dt56dm11FTtZcCQQiZOGUJ+YVbCx4ebAjxx7HQCdXs4eDuN3c3PWc/9lKJx\nI5PRbHWEkp4rRgO7Up3Lrg838dq0u6j/rBrLtsESTp43kwEzJqa6aSqBtgb2dsvBaYwpa6/nUkp1\nvJzBpVy05hF2r99MaG8TucPLsX2aSdMNNLmyUl1c9sCSVDdBtTOdCFVKKZfRwK6UUi6jgV0ppVxG\nA7tSSrmMBnallHKZlNQ8FZFa4LMOevp8QFMHt077qXXaR63TPmpde/bRscaYgtYelJLA3pFE5P22\nbODv6rSfWqd91Drto9aloo90KkYppVxGA7tSSrmMGwP7glQ3oJPQfmqd9lHrtI9al/Q+ct0cu1JK\ndXVuHLErpVSX5urALiKzRcSIiBZvPISI3C8iH4rIahF5WkRyUt2mdCEiE0XkIxHZICK3pro96UhE\nSkTkdRFZKyJrROS6VLcpXYmILSIrReT5ZN3TtYFdREpwyvZtSnVb0tRi4DhjzPHAeuBHKW5PWhAR\nG3gImAQMBaaLyNDUtiothYHZxpihwBjge9pPCV0HrEvmDV0b2IF5wM2ALiLEYYz5lzFmf7HSJTil\nDRWcBGwwxnxijAkCjwNTU9ymtGOMqTLGrGj+816cwKU19Q4hIn2BycAfk3lfVwZ2EZkKbDXGrEp1\nWzqJK4EXU92INFEMbD7o71vQgHVYIlIGjASWprYlaelBnAFmNJk37bSFNkTkFeCYOJfmALfhTMN0\naYfrI2PMP5sfMwfna/VjyWybcgcRyQKeBGYZY/akuj3pRETOA2qMMctF5Ixk3rvTBnZjzJnxfi4i\nw4FyYJWIgDPFsEJETjLGbEtiE1MuUR/tJyIzgPOACUb3ve63FTi4pFDf5p+pQ4iIFyeoP2aMeSrV\n7UlDpwJTRORcIAPoKSJ/NcZc1tE3dv0+9iMpst2ViMhE4AHgdGNMbarbky5ExIOzmDwBJ6AvAy41\nxqxJacPSjDijpkeBHcaYWaluT7prHrHfaIw5Lxn3c+Ucu2qT3wA9gMUi8oGIPJzqBqWD5gXl7wMv\n4ywIPqFBPa5TgcuB8c3/fz5oHpmqNOD6EbtSSnU1OmJXSimX0cCulFIuo4FdKaVcRgO7Ukq5jAZ2\npZRyGQ3sSinlMhrYlVLKZTSwK6WUy/wfuoiIWc8YlM0AAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x20f62675390>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Visualize the data:\n",
"plt.scatter(X[0, :], X[1, :], c=Y, s=40, cmap=plt.cm.Spectral);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"You have:\n",
" - a numpy-array (matrix) X that contains your features (x1, x2)\n",
" - a numpy-array (vector) Y that contains your labels (red:0, blue:1).\n",
"\n",
"Lets first get a better sense of what our data is like. \n",
"\n",
"**Exercise**: How many training examples do you have? In addition, what is the `shape` of the variables `X` and `Y`? \n",
"\n",
"**Hint**: How do you get the shape of a numpy array? [(help)](https://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.shape.html)"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"The shape of X is: (2, 400)\n",
"The shape of Y is: (1, 400)\n",
"I have m = 400 training examples!\n"
]
}
],
"source": [
"### START CODE HERE ### (≈ 3 lines of code)\n",
"shape_X = X.shape\n",
"shape_Y = Y.shape\n",
"m = Y.flatten().shape # training set size\n",
"### END CODE HERE ###\n",
"\n",
"print ('The shape of X is: ' + str(shape_X))\n",
"print ('The shape of Y is: ' + str(shape_Y))\n",
"print ('I have m = %d training examples!' % (m))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Expected Output**:\n",
" \n",
"<table style=\"width:20%\">\n",
" \n",
" <tr>\n",
" <td>**shape of X**</td>\n",
" <td> (2, 400) </td> \n",
" </tr>\n",
" \n",
" <tr>\n",
" <td>**shape of Y**</td>\n",
" <td>(1, 400) </td> \n",
" </tr>\n",
" \n",
" <tr>\n",
" <td>**m**</td>\n",
" <td> 400 </td> \n",
" </tr>\n",
" \n",
"</table>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 3 - Simple Logistic Regression\n",
"\n",
"Before building a full neural network, lets first see how logistic regression performs on this problem. You can use sklearn's built-in functions to do that. Run the code below to train a logistic regression classifier on the dataset."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"c:\\anaconda3\\envs\\tensorflow\\lib\\site-packages\\sklearn\\utils\\validation.py:547: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().\n",
" y = column_or_1d(y, warn=True)\n"
]
}
],
"source": [
"# Train the logistic regression classifier\n",
"clf = sklearn.linear_model.LogisticRegressionCV();\n",
"clf.fit(X.T, Y.T);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"You can now plot the decision boundary of these models. Run the code below."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"scrolled": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Accuracy of logistic regression: 47 % (percentage of correctly labelled datapoints)\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYQAAAEWCAYAAABmE+CbAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvXmUHPl92Pf5VlXf19z3AAMMzgUW2Jt7kMtdLineFCVb\nMinqYBKZsezEcaQX2WIcx1ZeHEXJYyTF9osYS886HIl6EkUuD/FYkrs89r4A7AKLczD3ffXdXccv\nf1RPY3q6ezAAZqZngPq8N29mqqp/9avqqt/39/ueopTCw8PDw8NDa3QHPDw8PDx2Bp5A8PDw8PAA\nPIHg4eHh4VHCEwgeHh4eHoAnEDw8PDw8SngCwcPDw8MD8ASCxy5FRD4jIt+5yc++LSJPbHKXdjwi\n8nci8iuN7ofHzkW8OASPrUZErgK/qpR6pgHn/k/AmFLqX95iOwPAEJApbZoD/h+l1O/cSrseHjsJ\no9Ed8PDYZTQppSwReQB4TkReU0p9dzNPICKGUsrazDY9PDaCpzLyaCgi8g9F5JKILIjI0yLSs2rf\nT4nIeRFZFpH/ICLPicivlvZ9VkR+XPpbROT/EpEZEUmKyBkROS4inwM+A/ymiKRF5Gul46+KyPtL\nf+si8nkRuSwiKRF5TUT6r9dvpdSrwNvAPav62yMifyMisyIyJCL/dNW+kIj8iYgsisg5EflNERlb\ntf+qiPxzETkNZETEuE57D4nIq6XrnRaRL5S2B0Xkz0VkXkSWROQVEeks7Xt21f3TRORfishw6b79\nqYgkSvsGRESJyK+IyIiIzInI/3jDX67HrsMTCB4NQ0TeB/xvwM8D3cAw8JelfW3AXwO/BbQC54FH\n6zT1U8DjwCEgUWpvXin1ReA/A7+rlIoqpT5e47O/Dnwa+AgQB/5LILuBvj8MHAculf7XgK8Bp4Be\n4Cngn4nIB0sf+Z+BAWA/8AHgF2s0+2ngo0AT4Fynvd8Hfl8pFQcGgb8qbf+V0j3ox71v/wjI1TjX\nZ0s/T5b6FAX+3Zpj3g0cLp37X4nI0fXuicfuxxMIHo3kM8AfK6VeV0oVcAf/R0r6+o8AbyulvlxS\nn/wBMFWnHROIAUdw7WLnlFKTG+zDrwL/Uil1XrmcUkrNr3P8nIjkgBeA/wB8pbT9QaBdKfXbSqmi\nUuoK8P8Cnyrt/3ng3yqlFpVSY6XrWcsfKKVGlVK5DbRnAgdEpE0plVZKvbhqeytwQCllK6VeU0ol\na5zrM8AXlFJXlFJp3Hv/KRFZrUb+N0qpnFLqFK5gOrnOffG4DfAEgkcj6cFdFQBQGpjmcWfEPcDo\nqn0KGFvbQGnf93Fnt/8emBGRL4pIfIN96Acu30Cf23Bn078BPAH4Stv3Aj0lNc2SiCwBnwc6S/sr\nrmfN37W2Xa+9/wp3RfROSS30sdL2PwO+DfyliEyIyO+KiI9qKu596W9jVftQKYCzpev2uI3xBIJH\nI5nAHfgAEJEI7ux2HJgE+lbtk9X/r0Up9QdKqfuBu3AHyv9hZdd1+jCKq3LZMKWZ9xeAPPCPV7Uz\npJRqWvUTU0p9pLS/4npwBVFV02v6Vbc9pdRFpdSngQ7gfwf+WkQiSilTKfVvlFJ34arYPgb8co1z\nVdx7YA9gAdM3cCs8bjM8geCxXfhKBs+VHwP4C+C/EJF7RCQA/FvgJaXUVeAbwN0i8snSsf8E6KrV\nsIg8KCLvKs2EM7gDtVPaPY2rI6/HfwT+FxE5WDJOnxCR1g1e0+/gGqyDwMtAqmQYDpWM1cdF5MHS\nsX8F/JaINItIL/DfXKftddsTkV8UkXallAMslT7jiMiTInK3iOhAEleF5NRo/y+A/15E9olIFPfe\nf8nzbrqz8QSCx3bxTVzj5srPvy7FJfxPwN/gzqAHKenIlVJzwM8Bv4urRroLeBUo1Gg7jqtfX8RV\nfcwD/0dp3x8Bd5XULl+p8dkv4A7W38EdQP8ICG3wmr5ROuc/VErZuLPxe3DjFeZwhU2idOxv46q8\nhoBncA3mta4FcFch12nvQ8DbIpLGNTB/qmR76Cq1nQTOAc/hqpHW8sel7T8stZ8H/tsNXrfHbYoX\nmOaxKyh58YwBn1FK/aDR/blVROTXcAfx9za6Lx4eK3grBI8di4h8UESaSuqkzwMCvHidj+1IRKRb\nRB4r+f8fxjVK/22j++XhsRovUtljJ/MI8P8BfuAs8MmSWmQ34gf+ENiHq/P/S1y3VQ+PHYOnMvLw\n8PDwADyVkYeHh4dHiV2lMmoy/KrLF250Nzw8PDx2Fefzy3NKqfbrHberBEKXL8wfH3h3o7vh4eHh\nsat47K1vDF//KE9l5OHh4eFRwhMIHh4eHh6AJxA8PDw8PEp4AsHDw8PDA/AEgoeHh4dHCU8geHh4\neHgAnkDw8PDw8CjhCQQPDw8PD8ATCB4eHh4eJTyB4OHh4eEBeALBw8PDw6OEJxA8PDw8PABPIHh4\neHh4lPAEgoeHh4cH4AkEDw8PD48SnkDw8PDw8AB2WYEcDw+PraFYcFhatLBtiEQ1YnEdEWl0tzy2\nGU8geHjc4aSWLSbHTZQq/Z+0WZy36B8IoGmeULiTaLjKSER0EXlDRL7e6L54eNxpOI5iauKaMABQ\nDhTyiuVFq3Ed82gIDRcIwH8HnGt0Jzw87kTyOafmdqUglay9z+P2paEqIxHpAz4K/K/ArzeyLx67\nh7zm53TTIYbDPYTtAncvnWdPbqrR3dqVaJqg6uzzTAh3Ho22Ifwe8JtArN4BIvI54HMAnb7QNnXL\n40bIZmxmpkwKeYWuQ0ubQXOrsSVGybzm56/7P0heC2BrOgvAVLCNBxbOcHL5wqafb7djWQrLUvj9\nUtMeEAgKmgb2msWACDS1NHp48NhuGvaNi8jHgBml1Gsi8kS945RSXwS+CHAk1FRvMuPRIPI5h7Hh\nYlkHbdswN2NhW4r2Ln/FscWiw/KChWmWPFkSetUg5diKbMYBgXBEq9r/VvxgWRisYGkGr7TczdHk\nFfzqztR7ZzM2c9MmhYLC5xNa2g3SSYd0ykbEVQG1tBu0tlULalVDM6QU+PzV2z1ubxo5BXgM+ISI\nfAQIAnER+XOl1C82sE8eN8jcTKVBEtzBZHHBprVDlQf0TNpmfOSa4EinbBbmLfbuC6Dp7jGppMXk\nmFlWVSgFPf1+orFrg/9IpLtCGKygK4e5QDM9+dnNv8gdTjZjVwjlQkExOWaW969sX5i1QClME2xL\nEYlpGEb9Vdz8jEU4qggEhFBY89xQ7wAaZlRWSv2WUqpPKTUAfAr4vicMdh+FQp1Fm4BpuvuUUkyO\nFSs9WRSYRcXCvDujt0x3EFMKHMf9sRGGp4Tiqkl/xMpRJYGAouZjLNRRVx9+OzM7XS2Ua6EUzM/a\nJJdsMmmH2SmLmcn6n02nHGYmTUavFhm6WMBeq1fyuO3wlIQet0QgIFhmjRFFga80+ywWFE4dtUQq\nadPW4SOVtFd/lOGDJxg9cBxH03lZWTy4cIZjyUucWD7PWLgLS9Y8uiKcaTqCEo13LZzZxCvc+RTy\nNycGlQJrgxo201RcvVRg/6Ggt1K4jdkJbqcopZ5VSn2s0f3wuHFa231V3igikGjWy6ogWecp00r7\nbFuVZ6ojB+5m5ODd2D4/StcpGgFeaDnJD5e7URcneHj6dUQ5VSsFSzM4kzhEca2wuM0xfLc2QG90\nfLcsyKa9VcLtzI4QCB67l1BYo3ePH7/fHVU0zfUy6ujylY/x+7Xy/tWseLIkl62y6kgBoweP4xi+\nimMdw8fVw/eSStqET50jZqZrj2S2w3TxzvJGa203qm/FDciIjaibVkin7esf5LFrubOmUh5bQiSq\ns++gjlKqrjqhZ4+f0aHCNfdGBfGETrHgsDB3bZBxdB1L99VsoxgKA2BailguSdIXrVp+KE0jeXWJ\nfJ8QDN0Z851Ek4HjKOZmLNdjSKCl1SAUFqYnTEzzuk1sGNtSFPIOgeCdcW/vNDyB4LFp1BMGjuOQ\nzThE4xqIYOhCsehQKDjklyqnp5pt4y/kKIYiVe2Ek0vuHwqOjL3F1NEu7FUCQbNM2ieuYhSLLMzp\n9PTfOX6TzS0+mpoNbBt0/dp3oWkWbKKpPZV0SKcKBIJC394Auu7ZE24nPDHvsaWkUxYXzxWYnjBZ\nWnBYmreZm7FILjnkc9UDlQCDb7+CtsbaqVkWg2dfLR/Ump3n2Ms/IJhJIo6DZln0DF/g8KkXADfm\n4U5DRDAMqRDM69lvojENo/ZibF2UgnxOMTVevIleeuxkvBWCx5ZRLDqMj9y4vqJz4iq6bTF+4j5S\nRpRwaon9Z1+jaWEaBHw+YWHOpMUc513f+zKObqDZNquTMPh8sq4K606hudWoiElYTSbt0N5lMDNZ\n7WokAj4fFNcZ8zNpB8dRXkbU2whPIHhsGUsLNx813DY9RvszY7S0GxRyDpm0G70cT+g0teiMDLkj\nlQC6XX2eTNph+EqBPQNu4JtSilTSZnnRxnEgntBoajaQ23wwi8V1JqktEFTJjpPPKZJL1+w4mu4K\nkoXZ9b8/pUpRzp6e4bbBEwgeW0axeGu6a6Xc6NqBAwF6/ddGHXMD6iCl3PiHmWmTrh4/0xMmyWX7\nWjRv3iGVtOkfCNzWqwgRIRzR3HQgawgEBF3X6O7109rukMs6aJobfT4/a13X9GD43OjyVNJxPcaa\nDSIxL6J5N+PJdo8tIxze+OOlV2ejAErBa8uVro4+v4ZvA773K5/N522Wl+yqSOl8XpFJ3f62ho4u\nXzneYwUR6OypdA2OxXVmp02KBTZkhxaBmSmLbMZdwU2MFZmZ2kSXJo9txxMIHltGotnAqLMGFXFj\nFkRc42ZLWw1f+hK1/OR7+v3lz6+HUjB2tbYiXDlujqXbnUBQY2AwQHOLTjAkJJp1BgYDhMKVUnh+\nxsTcoJ1Y08A0qRKyy4v2HWnQv13wVEYeW4auC3sHg8zNmKRLqSkiUY2Obh+m6eYyCgQEf0CjWHSY\nm6lt3IzGq5cPgaDG4OEgqaSNZbr2gVopHJRyM7DW7eM6yd12CpalyOdsTFORzypEc2MPQjewAvP5\nNTq613fDXV7auHDUNHDqmBiyGQe/35tr7kY8geCxqSjlqmGWlyzXaNmk09nto6uncjDSdQgGr/3v\n92u0thvMz1rlWacI7qy2ThCUpgmJJvcRjsV1RoYKOKWMFiLuj6Ooq/4QgURTHV3VDkApxdy0ycK8\nTTrWxPjAEQrhKM0z4/SMXqSzxaa1/Sb8Ruud7waOrZcDSQQvNmEX4wkEj01lrfE2m3FILdv09Puv\na2xsbfcRiemkliwUEE8YG4429gc09h0MklyyKBYUwZCGbStma6w6Vujp9+PbwTPZ1LLN4oLNbNce\nzt33OI6mgaax1NrJ+P67eOBHXyPRpG45l9EKsbjO8uKtq9Ai0Z17Tz3WxxMIHptGIe9UCANwZ+uZ\ntOvBEo5cfzYeDGoEu24uwljXhebWazPmXM5BsKpmviLQ3ecjEtVYXrJYWrBKrqg6zS1GOSlfo1mY\nt7ARzt/zKM4qY4xj+CiIMDJ4jL7kW+VV0q3S3uEjm3awLFWxSmvvNJibsWpmrAVXfaRKv/v2BLy4\nhF2MJxA8No1M2qlpAHaFgr0hgbCZhEIa4ahGdlW/RNyykdGYzvSkSXKV99H8rEVy2Wbv/p0xqDk2\nZKMJVI2CQEo3mOvai5Z+e9POpxvCwIEA6aRNLufg9wvxJgPTVKg6lejiCY1Es1uFLRgSz+V0l+MJ\nBI9Nw82hU+0V1Ei9cm+/n6UFi+VFu6SG0mludQe5ZA1XVLPoGqg3a9Z9s2T0ELMH9pAsGKg6g6xh\nFjddPaNprhCIN63eBn6/VBVDEoHmNl9dG4/H7sMTCB6bRjSuMz1l1rROxhONedREXDXSalUSQC5r\nu2HONcp/ZlIOiSYaxpn4QV5qPQkolKNwRHNLyGmVifxOpC5uy0pGROgbCDA+WqCQU1Ay2Hd2e8Lg\ndsMTCB6bhq4LfXv8jI9UOrN39/kxfEI+d63oezyhN9SgaxhS361GGleIc9EX46XWE9fqRq/cIqXQ\nLBNRCkfTOTB3kbussW3rl2EIewYCmEWF4ygCQS8i+XbEEwgem0o4onPgSJBc1tXbh8IamiZMTxZd\ntc0qfX1Ht5uyuTH91OoWhinWqxO9DVyM7nVXBGsQ26Lv8tvEl+aJLc3RHiwifduX3ju5bDE7bWGZ\nCk1zcx25hXk8oXA74QkEj03HzZ9zzRCay9oVwgBc1czMpEk0pruz9W1mvSphjRQIjmioGuXOBAjk\nc7RNjwJgxLbv1c2kbabGzfI9cxxYmLNwHEXHTXqEeexMPAWgx5az1hW1jDQudcRK4FotGhm9vC8z\nhqFq3BMRWkvCwE0kt30eW6uDBVdQCpYWbBynccLTY/PxBILHllNXq9DAsUREaGrRq/omAi2tjYte\n7iwsMJAeQ1NOOb+0Zlvse+d1QoUsugG9e7Y+oM5xFNmMzeRYgVy2fm4i2/IEwu2EpzLy2HLiCYOl\nhdqrhGi0cYNve6cPx3ZXMCseR82tBk0tjXstTscPMRTtw0FBSXV0OD3EI9plnP0B/IGt9fVXSjE/\nZ7FQY1WwFhEaou7z2Do8geCx5QRDbjbThTlr1TAHXb2+hqpnRISuXj/tXQrLVPh80tAo5ZQR5uXV\nHkZuL7kQ28fx6GVaistb34dle0PCAHAz1O6AAD6PzcMTCB7bQluHj3hCd91ONSEWb4wxuRa6Lg1N\nyGZbitkZk7MtAzg1RmJHNIYivdsiEGZnzA0JA8PnCgSP2wvvG/XYNvwBjZbAzjdbKaXIZR2yGQfd\nEOIJfcsEhnIUV0Zsppr7WU6017GrqPXdojYJs+hgbbC+jZtRdmcIdI/NwxMIHg3FcRSpZZtsxsHn\nFxLNxoaqoW0VSinGhovlOAoRmJ026d/rryoosxkMOS0898QT7rk1rWbeIk0pBjOjm37utSzeQA3s\n8BbcC4/G4wkEj4Zh24rhKwUss5RdU1z/9r69/m1PhLfC0qJVFgYARcNPsrmDVKrAvaEU2ibOim2E\nZ/e/F9u3xpdfKcRxEFEIwkPzZ2gy05t23npstAa2pkFbhzd03I5436pHw5ifNTFNdU1NUvpzctxk\n/8HGpEZYnfBuZPAYQ0fuRUp5n8+qIp+YfI6EtTmD82SoHVXHKBtJLXI4fZXD9iQxK7sp57se4bBW\nt8Z0MCTYtntMS7vhVUS7TfEEgkfDSCWdmjpz2yp5/fgbpzpabO1i6PC9KN1AlRYrWeXjq51P8Evj\nX68RS3zjOKLVbkeEYD7L/flL2yoUTbP2CiEW1+np9yKS7wQ8Me/RMOp5LCp1Y/rszcTN7Q+j++9C\n6WvUViLkAmEuWy2bcq7u3CyqRt4i3TI5bo9uqzDIltKL1KKj25s33il4AsGjYSRqRAqvsDhvrxsh\nu1UkmnTCUY1cLFE3xPqKv3NTzuVTNu+deRndsdBK6SoMx6S3MMvB/PimnGOjrK0NsYJobhlUjzsD\nT/R7NIzmFoPlRbtuMrnkkkUovL2qChGht99Pwk6TU/GaQkFMG27Q5u04yq3IVq4XrdPa7uNAZpT2\n0UUuxPZS0ALszU7Ql5vaFJWUh8eN4gkEj4YhIhgGFAu191t2Y/LkiAgnMpeZivdU73McevPTENl4\ne0opxq4WyOev1SpeWrDJpB0GBgMkrDQPLm5eKcybIZ7Qa68SFEQamF7EY3vxVEYeDWW9ZJmNrMY1\nkJukNT2L2Nf06mJbNC9McdC/dENt5bJOhTCAUrlOU5Gu49Wz3YTCGonmVSq8lapoPb6GRnF7bC8N\nWyGISD/wp0Anrq/JF5VSv9+o/ng0hkhEJ5+tbUCOJRo3MxXgZ2ae443QIBfi+8BR7Ju7xP3m0A0H\nzuVzTk39vHLcWhGxeONn4CJCZ7efRJNb1U7T3Pvv83lzxjuJRqqMLOA3lFKvi0gMeE1EvquUOtvA\nPtVk3p/gjaajLASaaC0sct/iOZrNZKO7dVvQ1GKwtGCxaiKOCISjWkPTYwPoODyQu8gDuYvXNt7E\nG+Pza2ilssirEWFb/fmVo0gu2ySXbTQdmpqNKnVQMKQRDHlC4E6lYQJBKTUJTJb+TonIOaAX2FEC\nYTLYxje734stGko0lnwxrkb6+NjED+gsLDS6e7sewxD2DgaZmzbdYjkCjg2ZtMPVdAGf3zXy+ndB\nDqR6RKMaogE1BMJ2rYKUUowOF8jnrqmuMqkiza0G7Z2+bemDx85nRxiVRWQAuBd4qca+zwGfA+j0\nhba1XwA/absPS7t2m5RoWKLxfNu9/Mz492663ZQR5kziELOBFlqKS5xYOk/CymxGl3cdPp/Q3een\nWHS4eqlQHrAUbjnL0asF9h8K7spkavmcQyppEY5oZNIOTmkl5A9AT19g2/Tz6aRTIQzAtWMszFs0\nNetbXnBnO3AQJkIdFDQ/XflZIna+Yv/lSB9vNN9FVg/RmZ/loYUzNJup8v6iGLzScpxL0b0AHEiP\n8ODCGXRlczm6l0vRfvyOydHkFXrzM9t6bdtFwwWCiESBvwH+mVKqSg+jlPoi8EWAI6GmbVUiKGDe\n31Rz32zg5oOTFnxxvtL7fmzRcDSd6WArF2IDfHziWTrWWXWYYnA+NsBUsI2EmeJo8go+ZaEpB1+t\nsou7jKWF2nn4Hcf1hd8J3i6Oo8ik3al+OKKtO6BPTRRYXqw2GotAKKTjD2yfgEul6pQxVTAxVmTP\nvsCuFLgrLPgTfL37veXJmy06e9NjPD73GkGnyKnEIV5tubu8/2qkl/FwFz879l2azBQOwld738ei\nL15OMHg2PshYqIOgU2Qu0Iyl+UAphiO9nFx6hwca7Bm2FTRUIIiID1cY/Gel1Jcb2ZdaCOBzTEy9\n2hc+4GwwT3ANnm+7F1Mzyj7uK6uOH7Xfz09N/YRTicNMh9pIFFPcs/QObcUl5n1xvtr7FJZmoERD\nHJvXm48hKEDRl53myZmXCDnFm+5Xo6mXelkB1g4o1ZhJ24yPFssxAkq5XjiJpurXKJuxysIg2dTG\n1UMnycaaiC4vsPfCKVheINGsb0kG1VoY67zp+Zzr7bQTjNs3gwKe7nmSguaviBsZivYzFOmlOzfD\nZLirMqZENCzgtea7eGrmJYbDPSz6ExWR446mk/RFSQH2ipZABEsM3mw6ytHk5apVyG6nkV5GAvwR\ncE4p9YVG9eN6HF++yOmmw9ceCMBwLI4vnb/pNqeC7TUDnub8zXyp/8M4JXvFnL+JoUgf3bkZxsOd\nlH0BoTyLUaXhaTTczZ/v/QT3LJ7jSHoIn2PxfOs9DEX7ARjIjPHo3JuEnDpO/zuASEwjXWsmq1y3\nyEZi24rxkaJb5njV9ukJk1BYqzIOL8y5K7bFtm7OPPQUjq6BaORDERY6ejn5wrdpSi5sm0BINNUv\nYwqwvGjtaIFgis6FldVxMcXR1JXyYPxG05EqYQC4/4teLQxKKNGYCra5bTQfLb9Lq3FEr/lZDYeJ\nUAcH0yObcHU7h0auEB4Dfgk4IyJvlrZ9Xin1zQb2qYoHFt8mqwe5FBtAVza26BxKXeXepXduuk1D\nWdh1Ql3t1Q+gaDgC45Fuysn56yGCg8brLcd4s/loaWXjcx9o4Eq0n+lgK/9g5O/QG+2+U4dYXGdh\nzsIsXtN1i0C8SSefc5gYKWLZilBYo73Dt62G5nSytkpOKbfsZGt7ZV8sy10dXDz+EM7q6bmm4Wga\nl44/xL5z39qy/q4lENRoatFZnN99qsWcFuDLfR8gr/uxNB+6Y3O6+QhPTr+IT1mcSRy67rtRj7iZ\nwUGYDzTXP67Gu2eJzqy/mf2Moa/1FtjFNNLL6Mew8yP0NRRPzL3KwwunSfkixMwMwVtUyxxbvsSp\nNauOjQz416V0jCM6BdEqPuOITl4PMhzpZX9mDHDdaTN6iLbiIkG7yHiok2VflJbiMt352W3/cjRN\n2LsvwOKCRWrZRjQ3vUUuazM5dk2flE46ZNIFBgYD2+a2udZltHJftYANhXXyeZtsrLYNKp1oIV5D\n1bSVtHf4aq4SRNykftvNxWg/r7ScIG1EiFoZHpo/zYEahYBeaTlO1giWJze2pmOj852ud+N3TIra\nzXlJGY7FvUtnXQ/CegfVee+UaJxNDDIdaucT49+/bYRCw43Ku4WgUyRY2Bz9/H2Lb5P0RRmK9KEr\n232gt8GgZ4rBgj9Bd26Wb3Y/zpI/jigHW3QMZaFEw0HQUCSKKT4+8QP8anuzjmq60Nruo7Xdfckz\naZulGoZZ5cDslEnvnsC29CsS1Zidrt4uApFY9Wqvtc3H4oKNbpnVBXAAv1UksM2utKIJvXv8jI+4\nz/HKHCQW14nGtrcvF6N7+GH7g2Ujb8oX5XudjzCRbOfdc2+weoi+GuktC4MKRCjWsO9tCKV4fPYV\n+nKut1DCTLHkT1Qds957aWs+FvwJLsQGOJq6cnP92GHsfl+zXYiO4qmZF/nUyDf4wPTzNBdvLBVC\nmRuss+tTFk1mku91PsxCIIGlGZi6H0fTKWp+TM2HrRmYpQf95Za7b65fm8jMVH0hvOLtsx34AxrN\na7KzikA0rhOqEchl+IQ9A376h86irbGWG47FvcmbVzneCpGozuChIB1dPto6DPbsC9Dd5992D6OX\nW05UuHMDIMK5+AG+0/VYxYxd3wIPuubicoX+/z2zr2E4VrkYkmzwnJZm8FrzXfyg/UGGwr04O1/p\nsS7eCmGLSBlhRCmidq7uMVE7RzSX42B6hNd8sUoV0kZZbxajHDd/MSDKwe+YdOXmeLb9XdUzrjVt\nOJrOxdgA755/48b7tInUS3wH7qU7jkKrV1hhk2nv8hOJ2SSXbBzlJoSLROtXdgtHdB6Xy/wkGeNq\n0140pXBEOLZ8kRPLF7alz7XQDaGpZWte/alAK8+33sN8oBmfYzKQGefk8vkKf38FpI1w7QZEGA91\nMB1soys/B8DR5GVebz52/fejli6sBrpj89hc5XPdk5/lZ8e+y5tNh1n0J+jIz6Mph3OJA9WCa805\nM0aYC/H9XIrupa2wyE9PfB9BMe9vwhKd9sLirlEpeQJhk5n3J3im8xFSRhSAmJXmA9Mv0FJcrvuZ\nY8uXuBC/5N8jAAAgAElEQVTbR9oIuw9frUG+9LBrykFDoRDuXzhNzgjzTnw/phis+L/oyuFI8jIZ\nI8JwxM3YuSc7yXtmX8MSveSqen2cevpTYCLYQc4I0pGfJ76FAXWGAVZjauXUJBzRN1Tv2RSDZzse\n5Gq4Fw2FoSzuXTjLXakhfNushtsuZgItPN3zZNkDrqDpnI/v50J8H/vTo7xv5iW0ki9PxMqR8dUW\nCpboTAQ7ygLh5NJ5ZgKtjIW70FDus17j/ejNTfOhqR+R0UOcjR9gItROXvOjcA35tui0FJd4aOEM\n3aW2V9NsJnly9pXy/w6Cqfl4J77f3VDrfVhtp9N0ZoKt/EX/h12PMt2PKBAUT868xEB24gbuZmPw\nBMImUhSDr63xh17yxXm650k+M/z1ugOBX1n87Nh3uBAb4EJ0L7PB1goXOE3ZdObm+MDU84xHurBF\noz87Sdh2p8+Pzr/Jki/KlUg/jgj7MuO0lgTQytC/0pqD4HOs6lnPGiEkymEgU12kJWlE+FrPExT0\nACi3DOSh1BDvmXutYrFc0Hy83HI3l6N7ADiQGuHBxTM3HL/R0mYwM1X7voXC2ratDlZjmYrlRYtC\nQREKC4kmA21NgNoznQ8zFurC0dy5oYXBq60n6Cws0FWY3/Y+bwY2wnCkl9lAMwkzzWB6tOKZ/nHb\nvdUV4ERQCFcjvbwT28ddJV37Qwunea7jwZq2AUM5BFe5R+soPjT9Exb8CWYDzVjovNh2TzmdjKZs\ndOXw6NwbGMohYWV4ZOHULV+vhuLhhVOcjw2UhVwFtSZuIqR90fLfK3yv8xF+bvRbWzp52gw8gbCJ\nXIn2Y6/x7kEEWzRebz5KZ36ervwcurIZivSR04N05ufoLMzjUzbHkpc5lrzMaKiLH7ffT8oIl2f7\nD8+fRsfhQB2/5yYzzX1L56q2rx0uNVxj2vc6H7n2QjkWjujojoWtGRiOScAxeWS++qX6TtdjZIxw\nxYt/MTZAV36OQ+lhwBU6X+l9iqQRxSlHfe7nfGwAvzJpLSzxyPypDSUIbGoxMIuKxYVKna5uQHfv\n9ufgyeccRq+66TWUgnQKFuYs9g4GMQz3bqe1IGOhzvK1r2CJxpvNR/jQ1E+2vd+3SkHz8ZXe95Mx\nQpiaD8Mxean1BJ8c/x4JMw2UovrrrCptzeDtxIGyQDiUHsbUdH7c9kCNzyj2p6u9jVqKy+WVdl9+\nmlOJwyz4E7QXFjixfIGYld28Cy5hioGG4oasGDXugSPCO7F9PLT41qb1bSvwBMImktVDWFJ9Sy0x\nOJ04jB534xjcOZNyhQdCyMrzxMxL9Jfyo/Tnpvj0yDcwRUcvqYg2k4HsBJ8cf4YziYOkjCi9uWkO\npIYZjXSz6IvTXlxkMD2KscawljQiLPliVbNAq/SyrwiEkXA3GSNcMSAqTcdSGpb4yOohxsJdfGz8\nB/QUqpfuqxEROrr9tHY4JJcdbEvhDwjRmN6Q1cHkeLHCBdUSnbzuZ3baLAuoibQfsZ1qlw3RyqrE\n3cYrzXeTNCLl79TSfFhK5wft7+KTE25OL0PZFNcZUuw1q4FjySu0FpN8q/Oxcru6svmpqZ9c17U7\nYaZ5fO61W7mkDRGxc/gdk1zVitop2YQ2FszniE7WCG5BDzcXTyBsIu2FeQxlYUn1zNVVHZQenjVL\nzawR4ls9j3N86QKPLJwub9/K/EStxWWemH21Ytux5OV1P2NpRl37g7nKF3w+0FSyaayhHHDnisTv\ndz7ML458fUP91XWN5pbGRyuvlPt0RLhy1wNM7D0MAppt8+jSKY4kr2CPzaOOVvdVHJvu3O5MinY5\ntqdqxYNozAZbKIqBX1kcSV7hdNOR2pG9jsVgjVl/V36OXx5+mrlAMwBthcVNnwDdCgI8PvvqmhW1\njU9ZvHfmZb7b9Zir3l19zTVUSYZj0p+d2t7O3wSe2+km0pebprWwhO6s0nnX0TOu/d8RnbcTB1ne\nwTPIpmKyatUAoDsW+1PXVFlxM7Mhw2nGCO+gV//6rP7aVoSBYxg4uoHlD/B8231cjfSimRZ7Lp2u\ndDd1HHTL4p5biHDfakzRKYrOlUgfb8UPMLcqsaOs4+K8clseWjhDwkxd8/Yp/RbHJm5lOVnn2jUU\nHYUFOgoLO0oYrDCQneAT499nf3qU9vw8x5cv8nOj32JfdoK/N/qdkruq+17ojuXaNFaNAYZj0VJc\nZl8Nm9xOw1shbCICfGzyOU4nDnEhNoCpGeQ1P06t2XIdRsNdJJKXWPDFmQq1E7Zy9GendoTbmlby\nlvhu52M4JSFmOCZRK1fhRrkvM8YLrSexRK82Mq6hntJnzt/EfKCJuJmmKz+3I7y7NU0IRzVSWSkL\ng9VYmsFrLce433+FvRdOE8qkGD1wnKI/RPPcJIeuvkm0Z+d5GE0HWvhh+4Ms+uPubFcppLSe7c9O\n8v7pFziYusrbiYPYq1YJohy6crNl4a+j+LnRb3Mp2s/52AAFPUDEyjGYGWUwPYKhGv8M3yztxUXe\nP/Ni1fZWc5nPjHydd2L7mQs00VZY5HBqiMlQB2fjg1hicCA9zJHUlR0p7NbiCYRNxlA29y2d476l\ncxTF4E8GfnrDn5WSe+L3Ot7FUKQPcAdh3bH5xMT3K3y5G8We7BR/f/TbnI0PkjbC9OemOJAeqVg5\nGMrmZ8af4dn2h5gMtVcvqQGUoquG+sQSjW91vYfpYBsrPlJxM8PHJ35wyylDNoPuXj+ZCa2uJMsY\nETq6fYyPFOkcH6JzfAhwL79vrx/q5LBqFEkjwtd7nnBTO68ggsLNBjoa7uad2D4eWHybiVAHy/4Y\ntmjojoNfmTwx+3JFezoOh9PDHC7Zk24n1nrsrRB0ityzXLn62Z8ZK6eI2U14AmEL8SuLo8krvJ04\nWDuuoErX6qbWvRrpKwfh2LhL+W93vZt/MPp3O2KmnLDS13Xri1lZPj75LJboTPlb+Wbv4yhKHlhK\nEbCLfGjqx1Wfe7X5OFPBtoogpAV/gqd7nuDvjT1zQyslpRSWqdB02bRCNIYhHOxXvFDLgKoUbfkF\nIlGd/gE/czMWxaIiEBDaOnw7sjTlW4mDVcbe1Viawbn4IHelrvCz499lPNTJvL+JmJVhb2ZiR6xc\nt5qcHuDHJXWgQtibmeDdc6/ddqmvwRMIW05bcamUJbU6TL8CpWjPz/PyqiIe147VyBhhkr5o2cVv\nt2Aom77CDL909WnOxgdZ9MXpz01xMD1Scwl9Pr6vOiJVhEV/E1/reYJPTPyAZV+MjBGkrbBUd9WQ\nSlpMT5hlj6BIVKOr178pgkEXeHjhNM+33Xvtu1Ku51h3bhoHIRTW6R/YWauBWqytAVALZyXaHddO\n1perkdRpF6OAiVAHF6J7UaJxIDVMf24K4ZoLdcoIo0qCczjSw2ywhU8Pf+O2E4ieQNhi1quAtpbJ\nUMc6ybTUujO5nU7IKXJ/jTiJtdRLC464KYq/1P9hskYIrZSU7+TSOR5YfLti5ZTPOUyOmRWZDNJp\nh4nRIv0Dm5MM72jqClo2x/Od91MMuhG3SjRebzrGeKiLj079cFfojDvyc4yFOus+d5pjczB1dXs7\ntc38qO0+3ontdwWjCFcifQymR3hi9hVGwt3k9GBZGID7PRc1H0PRvrpxQbuVnbeGvc1oKS6zNzuB\n4VzHmCg19Oyr8DkWzeukv7hd2Jsdd3Mw1cDSDJK+CJZmUNT92JrOqaYjPNd2P0/3PMm3Ox9jLNTJ\nwlyNUpzKLcM5O13Etm99oFZK4VyexPIHKr472/AxEergm92PV3jpbMb5Uss2Y8MFxoYLpJZt1A0m\nN6zFseQl1/5Tqy2laCkucTx56ZbPs1OZDLRyLn7AjURe+Q41g4vRvcwEWljyx7FqTMRMzceiL77d\n3d1yvBXCNvDU9IucjQ9yNj5IQQ+Q0wOVy/R1EtTpjo2geGr6xR1hP9hqHp4/xXC4x41rqGl3qZzD\n2JrB+fh+d7tSDEd68LXk6Bq5RP/ls/jMyux4C3M2S4s2e/cFbqnAjllUzDV1udkx144XmsZ4qJOv\n9j7F47Ov3HJVLaUUk2NmRTW5bKZINKXT03eT6Z9LhO0CPzv6Hb7a+xQF3V+28YDi7qULPLxweles\ndG6WV+pk9FWicTXcQ2dhAUPZmGueO59j0mzefhM0TyBsAxqK48lL5ZnW+egAL7aexNR87qsmXAta\nW0E5JIopDqWHOZy6SmSdrKm3ExE7z6dGvslf7P0YFrXLF1ax8rKWAt6KwQijg8eZ6j/AA889jX9N\nylTHhqkJkz37bkF9JGDUKwJd6oslBj9qf4B9mbFbcrl0ax5XFrZRyq3ilss5NdNv3wjNVopfHv4q\nQ5FehiM9hKwCR1JXdoRX21az5I/XT7chOnuyk4StPCmfVo5KFuUQsIvsS+/8uIIbxRMIDeBw+iqH\n0lfJ6wEM2+Qv936MrB6seDAN5fC+2ZdvyAZxuxB2Cnxy/Bm+3fVucnoQUG5lLPFh6RvLX6R0nWIw\nzCtPfJLBs6/SOXa5YoWVyzoopW66DoDPJ7QtTq4bsLXCnL/5lhLaZTO1ayErBdm0fcsCAdxJy2Bm\njMFd6CpZC4XrnVbQ/LQXFjGUxdn4IKeaDlPQAnTlZ3l4/jRxM0POCNVs40DJ8eGnx5/h+bZ7GYr0\no4CB7DiPzb1x2xmUwRMIDUOAUClb6UcnnuWbPe91K6cphSMaj8y9eUcKgxVai8t8euQbLPliOKLR\nUlzmcqSf5zoewhKtpCJyoFaMwwoimMEQF048TCaaYPCd1yt2Xzjrug1GYxrdff4byo0kIoQDcOLF\n73L64fdjGX7QqgdmheC/wQyva9F0KWtyHBEW23qwfT6a56fQ9N1XI3mrSeshvtn9OClfFFEOjmh0\n5WeZDraXvcJGwt1Mhjp419ybzAWaKwLuUIqmYpKO4iLgOkQ8NfMS8FIDrmZ78QTCDqDFTPKZ4a8x\nHWyjqBl05eZuqHTloi/Oa813MRdopslMcd/i2bIwSRlhJoPtBJ0ivdkp9F2kDxaoUFscyIySmEhz\nOnGItBGhubDEhfi+apfeNTiGj7HBu9hz+S18ZrWbajrlcOVinv0HA2g1BvV65HIOcWuOR7/9JUYO\n3M3woZMovTKSN2plNpTVtarPjirZqoVYXGd2yiSVaOXUIx8o258cTeeB+TM0p87fcPu3KwrK5WFX\n2+nGQ11rshC7gXdzgRbuW3yb15uPISgchJbiEh+Z/NG2930n4AmEHYJAuSDIjTDrb+bp3veVE28t\n+2KMhzr5wNRPGA13cS5+AFFuYT9d2Xx84ge03MQAtVNoLyyWZmsuHcUFftJ2f6lQev3VguY4ZONN\nJOZrJ5ezLRi9WmTPvsCG1UiaJtgoNKUYuHgapWmMHLgbzbHRNCHoFPjw5I9uyBmgkHeYmiiSz7mC\nOxbX6ezx0b0nwI+PfADLX5kx84224/QU53ZtjYXNZiLYXiUM6qFEYzrYynvHXuVY8hLz/ibCdp6m\nXWo7+fxH/3H9nW99Y0NteAJhl/NC28nKQLaSMfP7nQ9ji1ZaCruzVlMZfKv7PXx65Bu3jcfSkdRV\nBtOjjIa7eK35OAv+ODXVSLpGT6xIZp1xM59TDF8u0N3nJxC8/oDS1KwzN3PNxXXf+TfpHXqHQncH\nfa0OnYX5G7rPlqUYvlKosBekkjbFooNxbA8Y1e6Plmici++na9YTCDk9UKrHvH5lszLKKQ/+Acek\nJz+7xT28MR498xu8PjfEr/+fXdt2Tk8g7HJmA601t6+u2lZGhLQeYt7fRFtxqeozec3P6cQhRiI9\nhK08J5bP74qoVJ+y2Z8ZZ39mnKFwD9/rfLQiiE9zbLryc/RFClzUXS+jehQKipGhAgODAXz+9YVC\nc6tR9gBaGYOiUuBocAajcOMid3ykUNN4XCwoiqYOtdR9olHUbs319HbhdOKwW4+kzuAvULFyMJTD\nvRsIltws7vmwqwYO/+4/54l/sQGvwX+RA7ZPGIAnEHY9Rq1ymOugRGPBn6gSCHnNz1/3f5C85sfW\nDOYDMBlq56H509ydvLjZ3d4y9mUneP/08/yw/QFMzYeDsCc7WU7C1tHpY2pifSOv48DivEVH9/oD\nrYjQ0++nWHDI5x18Po1gSG7KcymXdcpqorUooGVpGmdPtYAyHJPBTHWdgd3ESo3u+UATCTNFf3bq\npmIfxsLVVercEyhCdo7+7DSXo3tQIoStHO+Ze432wuKtXwDwpT/8BU49vcFAxI0IgwbhCYRdTm/O\nfchr1lyoE/BWK8LyrcTBsjBYwdIMXmo9wZHUEEXN4HJ0D0XNR1926obVIdvJQHaCvcNPkzbC+Evl\nQFdINBsUizYLc+u7DObqDM618Ac0/AGNfM5hacFGN9hQRTelFNmMg2Uqstl1li0KYj6LR+be5IW2\ne3BK9iLDMWnPL7CvRuGZ3YJZqkO+6I/hoKHjELQL/PT49244eVzEyjLnb6565gXFRyd+SKuZ5PHZ\n17A0Hb9jrvv8PnrmNwA2NpMHePqGurpj8QTCLueepXNcifZX6U3Fsesa1lQNITEc7q5OKgdoyuHt\n+CCvthwH3GCdU01H2JsZ56mZnRs9LVC3xm57Z4BwxGZ8pFhTRQMQCAqO46qDbAtCYa1uttKKSGJK\nmSww6R8I1P1MKmUxMbIxd1S/XwgGNY6lLtNZmOdcfD8Fzc++zBj7MuO7MpLYQRAUL7ccZ96fKM/s\nHXQs0Xmu/UE+MnVjnj4nli4wHuqqKGOrKZuO/DytZpJ7PmzxEe2fbqyxHTyL30o8gbDLaSsuM5AZ\nZ2TVgK47FjEr4xa5X5OHxVB2zTztETvHXI0VhSMar7Ucq1w5iMFwpIerkd5dUQWqFpGozoEjQUaG\nChTylQOqiJsd9fL5PAp3oaVEiEc1uvt8VSqh5LJdEUmslKsGGR8tsv9gtddScslicnzjsQluHQWX\ntuIS75l7fZ2jdzbz/gQ/bH+AmUArmnLc+7tGzaNEYzzchV1aMVyPL/3hLwBw6ukmIkt5WmYyZXNL\nLhzglUOHeeneo5t9KbclnkC4DXj/9Auci+/nbHwQR3QGU8OcXL7Audh+Xm6921Ux4BrRjiQv1wx4\nqzW7cv3os24U9RoszceF6MCuFQjguo3u2RdgZsokueQO6IGA0NHtY3LcxFIaV+66n4m9h3B0g0hy\nkYcnX+WAr1LvvDhfI5keYFtuDeZA8JpAcGx1XWGwWn509fqua9zebkzRuRzdw1SwjYSZ4khqqBxk\nuR4ZPchXe95XzlPliF47qR6ALvyrD//XqI0EC65S12SagmTiAXxFG0cXbN/uzRDcCDyBcBugoTiW\nvMyx5OWK7SeSF+jPTXExugdHNPZnxupGP/fkZ8s66pXoztbiEieWzvNc+4M1PyO7UFWxFk0Tunr8\ndHaX6v+KUMg72Jbi3L3vYb5rT7lUZibRwrPRJ2kdf6Yi2Mwy6xuD1453qeT6kcWaBm2dPkRcO4Rh\n7CylXE7z8+W+D5DXA1iaD92xeKP5Lj4x/v2anmur+Xf3f4r4fK4yxXIN9aUCsgHfxoRBLTTBDHpD\n283g3bXbnGYzyUOLb23o2LtSlzmYvsqCP0HQLpCwMtho/LC9+ljDMTmcGqrZjo3wYusJ3okNYms6\nbYUF3jfzEk07uLjParWOUlAIhpjv3oOjV74itui82XSEJ0teS46jsOuN8cq1Rcz7m0gaEdqKi5jX\nyZAZT2g0t+zc1/KVlrvJ6qGyzt/WDGwUf3HgI0zuW9/Lpn0sueF8+/Pd0VvsqcfNsHOfPI+G4FM2\nnatWEToOH5h+nm93vRtw8yxpSnEgNcKe7GTNNr7W8wTTwfby7G820Mpf9X+YTw9/jdh1PEcs0ZgJ\ntOJTFm2FxYYYrQNBoRCJ1U1tvRBIlP917FUZo9dgB/x8pe8DLPgTpVWXzp7YMHvnflRXVdLW0diY\ngkf++AQAT/7Nu2vu77u4gF5VT0LwFWw028HR6w/5haBBMGOiXWdh6eiC5fdUPY3AEwge16UvN81n\nhr/GUKTPdTvNTdNaRz2w6ItVCAPATUut4Cdt9/Oh6Z/UPc/lSB/PdTwESqFECNpFPjz1I1q2uTCQ\niLAvkeONGnmNRDm0512BaZmKpcX69oAL972bOX9ThW/8aNMeAofuouv825XtarD/oB/9FlVETkmE\nrvU8WjetwWr+Zv3drodafRXZeqSbgsQX8m6W2VWfWX3FjkCypdpm5bE9eALBY0MEnSJHU1eue9yV\nSH/tHSJMBWvonkos+WI82/GuiiC7tBh8rfsJPjP8NOfj+3m9+Rg5PUjCTPHI/JtVK5SpQCunmo6Q\n8kXozU5zcvk84ZsshN4atDiYusql2F7slZTbSqErm5NL58llbUav1ndbtQ2D2dbeqkApSzMY33eU\n44vnWV6yQUG8SaOlzVc3bsFBsEXHUBaCa5yN/sFnsUz47a85mEEDo2DROpUhkHOjYQshg/nu6KbP\ntFNNARLzuYpZvgLyYR9qndUBgGNoTA0kaJ7OEMyaKBFsQ/AVHRxNEKXIJAIkW2qno/bYejyB4LGp\nxKxM3X1+pzrT6ArnYvux18ZNiDsQ/rjtPi7HBsrCYskf57udj/LBqR+XU2tcjO7hh+0PuuUORVj0\nxbkQH+Dvj36nqrjQki/G2/EDpIwwfblpDqeuktWDnIvvJ2OE6M9OMZge5fH514nbWc4kDlHQ/cTM\nNPdPvQmzi4xPu55FluFjvrOfoj+II4Lt89E6PUYom6o7Y04bIZ67+4MkCssYmsKvbD528gr9wcXK\ntAaOQ+dIkkD+mpHC0sGwgS+4nk7dgGVoGJbrnrkiUgI5i66ry4wPNl13oL4Rkq0hglmLQO7aysg2\nNOZ7Nqbzt/w6s/2VgZGa5WCYNpZfX1fl5LH1rCsQRCQOtCulLq/ZfkIpdfpWTy4iHwJ+H1dT+x+V\nUr9zq216NJYD6RGe63iorLoooxT3LdbPG5M1gjUD6RRwKTZQFTRnaQYvt9xN3/g0NsKP2+6vWF04\nmk5BwWvNd/H43Gvl7cPhbp7pfLScHXY83MXrTUcpan4cEZSmMxTq5c34YT428gz6xRGs+w+jWRZp\nPcxzvY/Sobo4PPE88519nL3/CZQIapV6aeTQSTTLxJfPUQxXDpQKQNOZDbcxG24rb39z9AjLrSGS\nqwKiuq8u4ytW3knDpsquYlhVdxsBRCmiywVSmznjFmFmTxx/3sKft7B8GvlwjXKnN4BjaBQNTxDs\nBOoKBBH5eeD3gBkR8QGfVUq9Utr9n4D7buXEIqID/x74ADAGvCIiTyulzt5Kux6NRUPx4Ynn+Lue\n91YIhcH0CIfTtb2SAPZmJ7ga6cXSKiuiOaJVj4AlFo0Yl8/nyEQS2HtruC+Kzlj4WnIwB+HZjocq\nBIelGeVVxQq24WOZGM+rfYyevAvLV1lqc6Z3H4mFaS7e/UjZJXUtjuGjaPjAtpCSoGF1hbY1A6im\nIDGfI5MIYPt09IJVJQyg9q2oNxRrCnwFd3XRNj7BsZdfRbctzt9zkvHB/bc0iBeDBkXPtfO2Y71v\n9PPA/UqpSRF5CPgzEfktpdTfUv8ZvBEeAi4ppa4AiMhfAj8NeAJhl9OXn+GzQ19mKNJLQfOzJzdF\n4joup/vSY7wZPcRSIIFtuELBcEyOLl/mfHw/Rb1aFx5KLWNZILmCKzhqYOSvzbiXfTF38F9LjYHR\nMQwmeg9g1xjwHcPHyIETOOsV0ym1qSnounqeqb0HcYzrl/8MpU3SzTr+/K1XQnOAYlDnoe8+w5E3\nTpW3910ZYqa3h2/9wqduSSh43H6sJxB0pdQkgFLqZRF5Evi6iPRzfYeCjdALrM7KNQa8a+1BIvI5\n4HMAnT7P2LRb8CmbQ+mRqu22rUguWRTyDj6/Riyh4/drJBeKHHvn75jsO8BM3z50y6R/5Dz3x+aI\n2HlebTleMbPXLIt977wBgL+Yp2lukqW27oqKZZpl0nXlHJ//+V8DEXTTpufK0nXdHleQdfJk5yKx\nDQ6mis6JIZKtnaSbaqcqrzyp+6sYugFjcI2UIwpwNMDJceSNU1UzuI7xCQbfepvLdx8vbwtks9z9\nwkvsuXQJ0+/n3H33cunE3Z7QuINYTyCkRGRwxX5QWik8AXwFOLYdnSud94vAFwGOhJp2f2jsHUyx\n4DA8VFhVj8BhbsYiFBZyOYWmoHf4PL3D10pCLhZ1TvjOoyubMwMnSWZ0osU0A2+8RMvsRPm4u17/\nIW8/8ATJlg7EcVCisffCaTqGryAlN1bbp2MG3Nl3xRC34iq0auDTLJP+S29z+e6qOcq1AXiDA6Vu\nW/QOneP8iYdBX1/Nko25cQi236Do1/CvVRutHfyVKv04oF0rkFoIGcz1RLnvuWfrnuvoq6+XBYKv\nUOBjf/LnhDIZdMc1UD/0/R/QNjXFix/8qQ1dZ3x+gQNn3qJlZoZsLMb5e04y3729+fw9bo31ns5f\nAzQRuWtFr6+USpUMwZ/ahHOPA6t9FPtK2zx2IY6jmBovkk65g0koLHT3+TFWGQsnx4s1i9PksgpH\npGbWzis08Xsf/ey1DUrx7m+8TMtM5aPiM4vc88J3yIWiFIMhIslFDNtiqbWlwuA72xujcySJbjlu\nYTUFkeQclj+CrRuAoDShY+wKS21RDp36Me/c+17XcKzrdVOKr/Rt7WDtL+SIJBfx59K0tXcz17uP\ntRpXcWwcw2CuO1rhZTM1kKB9LEUo67qSKqBr7DLpRAuFYIRAIUfnyEVap0Z4/sOfwDYCmH6ddHMQ\nM+C+2ppTew4luIWDVhg88xbBXK4sDNx7ajH41lnOPPIwmXh1yvQVjKLJe//2K/QOj5TbVsC+c+/w\nyvue4MI9J+t+1mNnUVcgKKVOAYjIWyLyZ8DvAsHS7weAP7vFc78CHBSRfbiC4FPAL9ximx4NQCnF\nlQv5ihQO2YziyojFn/6jf4Lj86GbJr/we/933dQFUsehPxeNrDlQOPvg/9/eewfJdd33np9zQ8fp\n6Thr7nsAACAASURBVMkBwACDnIhEkCDBBEZRFKlgBcuyJVmynmXv7qt9rvWWd/1c+8du7T8uu97b\nffW85ed95V2vJduyqECJosRMUQRJEIFEjoMweTC5u6fTDWf/uD2NaXT3YICZ6R4A51PFIub27dun\nb3ef7zm/uJtV586j2XbR+cFUgmAqgQRsw+DA008VPO6YOv1r6vClbQzLJRM0kFodO999j9beIVzd\nRAqbjx97iOFly7j3nXdpu3ya/rVbZxeD3Nhm3BQcXeCKBOd2bCNZE2HrRx/SeeYThpevIRMMEYpP\nMNnYwMV7tjDZWFMcHqppDK+M5q+HEEh9nH0//4WX0JU7dmr3LgbWlF6Jn9q9m42fHC06LoHz27bl\n/26/0o1R4n66uk7j4NCsgvDga2/Q3t1TIHMCMGybB15/k6vLlzHRXD4HRbF0mEuYwAPAXwLvAxHg\n+8DD831hKaUthPi3wKt4Yad/L6U8eYOnKSqAdCWuZ4HIR8VMt/8DimrKd546zWOnXimyU7sph13v\nvc/hJ7wVdtkaD3gZsC6gz3jcNgxOPFBcWG+stZV3P/s8D772Ov5kCi33nOmVqatp9K5ZzbGH9jLW\n1lr8YkKQDZpkZ7ikjjyxz4sCkjK/o2i71MdEwzqcNv/N29GFQAo4f+82zrONfT/9OYZt47Pi1Jy/\nNkEnr4Y48sQDN75+7vHe9et48Y//kJXnLmBaFr1rVxNraCj7tHhjPV1bt7D2pBerMX2PYtEoZ3bv\nyp+XqKvD0QT6dTsKISXJmvI5Bppt03n2bMHndv3zn/v+v/CjP/o3tPT109bdQ7KmhotbN5MOh0s+\nR1E95iIIFpACgng7hEtSyhsXKZ8DUspXgFcW4lqKWyOdcjmyoQPrRIrBjg7C8Tirz59FuC7pUIhz\nO7Yx1trKkLUCy+8veY2O810ljwtgxcWLHH5iH65h0Ne5iuUXL5XcJbiaxkh7G02Dg7iajpCSw/se\nZaCzs+S1e9avo2fdWsKxOJHxcTrPnsXMZLm8eRM969bemiNUiHzzoPrBBP60H8fHja9VZucwnSwG\n0NrbmxeuadKBEEMrNtDcO0GiLkyqZm7x/JlQiPM7t9/4/eTY//xzXNq8ie0ffIiZzXJux3bO79he\n4IA/s2snG44eA/ea8LtCkKitZWQWP4Bu2+VLWJMzTTkOL/zDPxJIpTEtC1vX2fnefq5sWE84kWC8\nqYnT991Lom6OLSgVi8ZcBOEg8BJwP9AE/K0Q4ktSyq8s6sgUt0y59n/CcVh3/ATrTpxCCsFoawsb\nzh6n/lIXmpS09PZ5CU2588OJBDv3f4BtGAjgo6ee4PyO4oloKlranCCB5IxV4PuffpbPfO+fqIl5\npaOnX8fK7QSOPfwQoViMQDLFZGMDjnmDME0hmIrWMhWtZbBz1Q3uytyJDk8RmcjMSQiE63q1l0qE\np/pTU4BnKkmHggST1zq4jTUv48T9T3r9fadcAsk4Wb+OYyaxfT4mmhoXNLqnf81q+tesLvt4vKGe\nt3/r8zz8yq8wMxk0KRlub+Pdz70w6zgsv5+p2lpqJ8qXvjYch3A8kRdEI2dbXHvqNAJo6e1j/fET\nvPbVrzCyrP3W3qBiQRByFnUHEELcJ6U8dN2xb0gp5+tDuGk2Bevk368rXYXxTmbaXDPn9n+lkJKn\nf/gjWnr7MO1rTsqbmXJsw+CVr3+N8ZaWguNmOs3X/tPfwHXXk8Avvv67jM74kQvXpfP0GTYcPUbt\n+ARTkQgn99zHlY0bqh7eKFxJ/WCCmlj2hvdlOqwzHbTY9ZsPOb99b6EouC7R0csce9Qzea05eYoH\nX3sd07JxheD9Z38H21e449Jsm84zh+m4dMbruNa5ioNPPUF8FpPQgiMlkYlJLJ85Z5NO25VunvzR\nT9Btu/TuD+ZU9nq0pZmXv/XNmxmtYo78+i+fPyylvO9G591wh3C9GOSOVVwM7kT2/v12/sTywv6O\n/mxxt8udp08XiAHcfHah5jisP3qcj54pdNRagQBvfukLPPGTn6HNiFI5vO/RAjEAkJrGpa1buLR1\ny02/h8VEOC7tlyYw7Ou7U19HbgE13hImXh/gno8O0tbbxVhbByPtq66JmoCJ5tXoloNj6lzcspma\niQm2HTjIZH1zyb7WrmEwsmw1Ky96K+cVly6z4r/+Pxzd+wBHH3m4MoIpBPH6m/suDq5aySvf/D22\nHDhI59lzBcLgTo/5BgtPgPrhETTbLpv93drdw+bDRwgkU3SvX8e5nduxfdUtF36noXLPF5Cdz9kE\nv+JV9ChXT76AG5QaXgjqRkbY99LPqR0bLxvJM1c0KfGnS1cP7Vu7lu/96Z/QfuUKRjZL/+rVNzb5\nLCEi42n0OYmBS//qeqyA9946LnThGD7GWldcV/JbAyS1Y2nGW8MgBMcefohT999H3dVxglNGyQQ5\nbUao1vTVdnxwgM6z5ziy71F61q2r+k6qFBNNTbz//HMcfPpJ9rzxFqvPeH6owZUdDHZ0sO3AAUyr\nOIppJlLTCkKEZ7Ll4CF2/mY/hu1VfG0cGmLDsWO8/M2vK1FYQJQgzJGFqie/WAjXZd2xE2z/4AP8\n6QyxuiiHH9/Hvp//Al86vSC1RizTpHvD+lkGIco6gZcCumVhZrKkw6GiSTWUyM5q1pBAOmhwdVW0\n4LnJmhC+VLRkMx2BwJ8s7Jdg+3yMLG9hedcE4rqidJpt0X7lXNFrC6BubJxHX/4lp+/dycf7Hpvb\nG64Clt/P/uefY/9nPu0dEALhujRcvcqKi5fyiXS6W/jebV3n0pZNJQXBzGTYlRODaQzbJhSLs+7Y\ncc7ct3uR39Xdw10rCIG3vwjA//DXt38mpXBdnvveP9E0OJT/kTUMj/DMD3+Eq+s3LQaSXCOU3I5C\nwxODkbY2utevW8CRVwbdstj76ut0nj2HBLKBAB8+8xQ9M8TNSwgrXapC4vUBGG8rDr88vXs3j/7s\nlZITmQRss4TMCMHVFV6CnJASzXXRXJfm/su09JcvAGhaFlsPHeHM7ntJzRIKuiSY2ZJU0/j1Fz5H\nw9AQLb19pINBVp6/QMeFLlxDR3Ncri5fzkdPPVXyUk0DAyXrRpm2zcrzXUoQFpA7RhCmzTV/Yt0z\nN3v8Xy/+mCpF5+mzBWIA18wNWomGv7LEeTMfS4eC/Ozbv0/t2Dgbjh7DzGa5vGkjlzduKLulX8o8\n+vIrLL94CT13L4ypKR57+RVe/Z3fzke1xOoD+JNWUeMXgMmmIJONpetojbS3IYQkOjrIeGNbQWkK\nSfnuX1bAoHddPaFEFt2yefD1X9HWc+WG4u3oOs39A7Pv1JYoY62tjLV6eSGXt2wmPBmjbmSEeH3d\nrLkUmUCwpLnTBW+3N0fCsZgX+TZLkt3dzm0lCH11zbObbqpkrqkGZiZD4+AQ6XCINSdP3dQuwDEM\njj74AJuPfIyZzWLaNtOu4MubNnLoycdJh8Okw2GudqxYhNFXjmAiwfKLl/KhjtNots09Bz7ind/6\nPADpGh+TjUGioymkEAhX4hiCqx212P7yP5O1J0/hS6dZe+Ighx//PHJGToIAgkmbbKiMjVsTJGv9\ngJ+3v/g5Nh0+wrYPD2BaVtnPU0hJOlQsTv5kknAsTrwuihW4PVpQTocM34ix1haSNTVEJiYKcjkc\nw+D0vbtKPieQmMKXSYOE6NgYD7z+BsGkF4adrKnhzS/9FhMtKnv6em4rQbibaBgcYtd7+6m/Okwy\nUkPW5yccjzPZ2ECiNsLGo8dxdQ3hurhCmzWE1DZ0DNvJ/3uspZkTex/g7O5drDlxiub+fiYbGzi/\nY/sdlz0ajsdxdR2uFwSgdny84FisKUSiPoAvZXtNW/z6DR24a06ewrRtLq7ejETmnMkeAqgdTRGr\nDyL12a9j+0xO7H2AE3sfYNWZM+z+9W+omYxd129YkA4Fubp8+bXXcBz2vfQyHV1d+cilszu3c/Cp\nJ5ek8/mWEII3vvIlnn7xx4TicaQQaK7LoSf2MbxiecGpgakk+372c5r7+gsi3mBGfk08zmf/4R+Z\nqo3gS2cY6ljB4X2PEmucQzXaOxwlCEuQ5r4+nvnBi/nwvXAikZ/wa8fGriWP5Xxs5dLGJZAMhTh9\n/32sP34cgAtbt3L6vntBCCy/n7O7d3F2d+lV1p3AZENDQRG3aRxNMLSiePfj6hrpmrlFrdSNjNDc\n51VcnWxs9Wp9XI8A03LI3qDK6UyubNrElU2bWHXmLA/96jVsw+TyxnsZXtaJq+u0dseYaA6RCZk8\n8dOfsaLrovd9yK2eN318lKmaCKce3EPt2BjBqSRjLc1lM81vBxJ1UX76nW9RPzyMP5VmpL2tOLpI\nSp7+4YvUDQ+jzxJQN32vIpNeguSKC120dffws29/k6lodLHewm2BEoQlyH1v/7ogXwBm+ARKnK8B\njhBFpREcXeeXX/8aU3V1nCxRE+huwPL7OXn//Ww5dCgf9jjd+/jEA3vmde3t73+Yt20Hk3GSkbri\nTmiOi3OL7SGvbNpIz7q1LLs4juZq+YWAP2XT2h3DMgVN/UNFO0NNSu59bz+79r+P5jg4hoFAcuzB\nBzn+0IO3NJYlgRBFSZEzqb86TO34xKxikL/UjH9rgG5b3HPgIAc+9fS8h3k7owRhCdIwdPWmn+OY\nJr9+7lmWXb5MOBbnyvr1dO1QzU2QktP33s9kfQubjxwkMjnBYEcHRx57ZE7269loGLqaF+iV548z\n3rSsIKlKODb1w/30r47gGLdm1/dlJEJqJQMGTMvl2N5PseetnxSLwoywzumqsNsOfMREcxM9t2Gk\n2FwIJRIlE/7mgu5Kmvv7b3ziHY4ShCVIOhyiJha/qecIKelfs5qejRsWaVS3H3rWobXH631g+xo4\n/sCzxOsDTDQX5yHcChNNjUTGx9GA6Pgwmz7+Dee3PYhjmEghaBroZs3pg1zZtIyxtlsTBCNbvmub\nQJANhIjVNxMdH77usWJMy2LrwUN3rCCMtrbmI8luFleIWSOd7haUICxBjj/4APe99U6R2WgamftP\nw/MfuIbBwScfv60ygytBS18cw8qtlHNmhMh4mkzQIBWZvz392N4HaRgaYaJ5OUhJ88AVHnrtB2QC\nIQwri+HY2LpOYh47Edt3g1aaUpL1z721bGBGgb07jXRNmDO7drDhk6OYdqEwyOv/r2kFzYBcXS9Z\nav1uQwlCNciVgLANo+Qkfm7HdvzJFNsOfATkSgwjsQ0TzXXp3rCe8YZ6Oi5dIVkT5tR9u4uiLe52\njKyDkXVK2Nehdjy9IIJgGxEOPf55hCsRSC5tvpe1xw+wvPt87nGDrq2byQZvvRd4OmRg+3TMTPF7\nAbBNk2BiosCHVG7v4whB75o1tzyW24FDTzzOWGsrWw4eIhzzIpLSoRBdWzcz0dTk1Ytqa+O+t99h\nzanTXr+HSA0fPvN0PkdiGjOdJjiVJFEX9SLV7gJuWO10KRFpXy93//7/We1hzIvW7h4e+tVrhGNe\nlqqradiGQc+GdRx57NGCsE/NtgnHE6TCYYR0iYxPMBWtJTOPCeZuwZe2ae2eRCsRgpX16wysnl8x\nQTNp0d4dK5p8hePwwJs/QnNtTu/exdGHH5p3Mp/muNQPThGOZ73XyB13BcTrAsQa/Sy/dBlfOo3m\nOtz/1jtFdYO8JK4wP//WN/PJXGY6zcaPP6Gj6xLJSA2ndt97Vy0sNNvGsCyygUCBCVG3LB761Wus\nOnceV9OQQnDksUc4Wybn4XZgwaqdKhaO2rExnnrxxwWmIM1xMByHNSdPs+zyFX76nW/nw+lcwyio\nPFmy+9cdQjCRoPPMOQwrS9/q1fN+r1m/jsz3B7uGK2AqMv9iaI1DU/kWljORQvD2F77M1ZULl/Tk\n6hqjyyOMOS6RsRThhIWrCeL1AZIRHwhR4BcwMxY7978PUmI4Dlmfj7M7tnNqz31kQp4Y+NJpPvv/\n/iOBqSkMx8EFlndd5KOnnuTCjm0Frx8dGWXD0WMEkkl6167xMtbvgBWz1DRqx8fRXJeR9vb8LmDv\nq6+z8tx5dMfJ+yR2v/MuyUgkf5/rr14lMjHJWEtz2cY+ZibDynPn8afTDKxaOWuE1FJBCUIF2Xzo\nSFmnl+66+NIZVp86zfm7rCl5x7nzPPbyK4BEc1y2f3CAri2b+fDZZ+bUpKZ2LEVkPIOQklTYZKI5\nhGPqjLWFaRxIIKS3qnYFOKZGvH7+mbxmxik9NiFov3SZZKSGYMLC1b3Xywbn/1OTukasOUzsBlpz\nas99nN21g9rxCVLhcMnyDpsPHc6LAXj+KM222fPW21zasilvyuw8dZqHf/UamuOgSUnHhS42Hz7C\nr7721bJlqm8HmvoHePLHP82ZYz0hf/dzLzC8rN0r4X3d79S0bbZ9eIDBjhU888MfUzcyjBQamuvQ\nvW49773wXMFOsKW3l6df/DFIb9EnNY3LGzd4Rf+WcOTf7VeY5jYmOjpWlCswE9OyaOm7u0LfjGyW\nR3/xCoZtY9jepGPYNmtOn2HZ5SuzP1lK2i5NUDecwrBddEcSjmVpvzyJcFyStX4GO6PE6/wkwybj\nLSEGOuuKm9nfAoLyn2Mq0kTjQJzQlEXNZIq2KxOEJ0qXDV8sHNNkvKW5bK2fjgsXi8p5gDcx1g+P\nADnTyauvY9h2/ntrWhZ1wyOsPXH7tj83slme+dcXCSaT+LJZfNks/kyGJ37yEtGR0ZKF9ABC8QQP\n/eo1GoaGMC0bXzaLYTusvHCBLR9daxsjXJcnfvISZtbCtCx018WwbVadO8/Kc+cr9TZvCSUIi4mU\nNPf2seO9/Ww+dJixlibsWbbatqEz2Xhnhb4ZmSxrj5/gngMfeVm91wli+5VupCj+GhqWxZpcY/iS\nSMnyC+P4sm5RjL5wJTW5CdjyG4y31TDcUUuiPojUFmZ1lvVpxU1fpMTIpLB8wWtZy0JDIGgcTCDc\npeOvK1UPCbz8hUzQ20E19w+UjOs3bZvVp88s6vgWk5XnL5TuDSIlbd09JQXBFYLhZe10XOgqiE4C\nrxT3po8/yf/d3N+P5hQ7r0zLYv2x4/N/A4vI7bvnW8IIx6FuZJRdv3mPtp5eDMvC1TSElF7rRYqV\n2GvJqHNh27biC96mNAwO8ewPfohwXTTHxtUNBld28PZvfX6Ojtbyk3ftSBLdKd3QRpMQSNncXCbH\nTSAlepl6IaaVJRUoXpUbloUvZZEJL41mLqfuv4+Wvr4C57MrBBONjcTr6wGvvlK5pkozy2AI16X9\n8hWCU1MML1tGbIkvanzptNe/4jp0x8GfTnHoiX3seeOtvK/PFQLbNDnxwP10XOgqeU3Tutb3QsxW\nNmOJB/EoQVhgOk+f4cHX3kBzPBPI9IQ1vaqY7jVgaxoIgWbbSCGYbG7ivec+fVPlfJc0UvLET17C\nl8nkD+muRduVbtYdO573kwysWlXyR2KbJl33bC57+ZrJ8n2PJWDdKH5/HvhTNppd7FBGShyjdC6I\nFAJfJrVkBKF/dSdHH9rLzv0feIsV1yXWUM9bX/xC/pyRtjYygQDGddVXLdPkXO7zi4xP8Ow//wAz\nm0VIiXBdrmzcwHvPP7dkbeWDK1eWHJttmvSv7mSyoYFYfR0NOdNZ1u/nNy98htH2duJ1ddSNjRU8\nzxWC3jWr838PL2sveX3LNOnaunVh38wCowRhAWkYHOLhV35V0jY7jcBbJbjAT7/zbdKhIJrr3laF\nx8KTk9z/5tssv3wFx9A5v20bRx96kNDUFOlQiGwgQN3IaMl2m6Zts/7Yibwg2D6Tdz/7PPt+9jLg\nrTalptG1dQsDq1aVfH0j6xRVsryehXAcl0O7rtPZtQc0hGOh2RbuTGFwXfzpJOnA0qrDf/KBPZzb\nuSNfRn2iqanwBCF488tf5FM/+KHnfM11Ojt97y76chPg4z99ieDUVIFvbM2p07iaxvvTXdOWGBPN\nTVzatJHOs+fyK3vLNLi6fBmDK1bwxf/77wklEvnP2JdO89jLr/CjP/o3vP/cszzzry+iOQ6662Ib\nBrZp8vEjD9Nx/gKdp09TMxlnuK2N1r5ekN7OwzZNBlZ1cHnzxuq98TmgBGGeGJksq8+coXZsjOa+\n/rmnzgvB8ouXuLx5I8suXUYKQf/qzooIQ/3VYZZfuoRtmlzeuCGf+6DZNvd8+BGbP/4EI5slVhfl\n0JNPMLC6M/9cXzrNC//f972Y95wDeMvhI2w5dBjHMLzEufXrODlLF6vrHbK969byoz/6Q1adPYuZ\nzdK3ZnXZEL1APENLX6LstSUw3B7GMRdvh1DODyGBTDjIynMn6V13T94sYWSzrDnxEVsPTPLa136b\neEP9oo3tZrH8fgZXrSz7+ERzEz/8b/+I9ivd+FMphjpWkIxEAKiZmKR2fKIoUEIAa0+c5MqmjfSt\n7iQyMYmQLrH6+vzKORhPUD88TCIarYqJ6f3nnqVv7RrWHz2G5rp03bOVi1s2s6LrIr5MuuA9aXiR\nQqtPn+Hczh289Ae/z+bDHxMdHWNoxTKuLl/O8//4fQKpVP79u3jZzxe3biEdCtHfuYqhjhVLdtc0\njRKEeRAZG+cz3/9ndNvGtCxcZrN6FyKFoOHqVe5/+x3c3ASjuZJ3X/hMQWvHBUVK9rzxFuuPn8iv\nxHe/8673muvX8dSLP6Gtpyf/Y6gfHeOZH/6Ijx95iOMP7QVg3bHjGJZV+IPJTXxabrXVcf4CUkqy\nfl+BbRXAMgwu3FO8bU6HQzdM/BGOS0tfougez5yOJusDpKKL2yBGK+McFkAyHGayKcieN37ERGML\n/au3EK9r4szufQBsf/8I+18o3SpyqSI1jf7VnUXH9Zy5sxQasOvd33D/m28Rjnvl2zOBAGfu3UnT\nwCAdXRe9RkRSMtLexptf/mJld8lCcGXjBq5cV/urZnISzS5e1JmWRSTXP2MqGuXQk497l3FdvvJ/\n/RcCqVRRBVXNcVh+8RIv/jffXfJCMI2KMpoHD//yVXypVH7S07g+Dcqj1DEhJWtPnMSwbXxZC1/W\nwrBtHnv5FQJTi1Nvpq27h3W515wOhTNsm0d/8QotPb209PUVTPTT5ZZ37v+AYNxblTcNDBY0Oy+F\n4TisutDF/uc+jWWaWIbh2fVNk+Flyzi/Y/stjb92NFXyuABcDfpWR5lsXfwGP9mAgSzx+3YFpMM+\njj38EFOREEMr1xOva0LqOo7pwzF99HfeQ93QePGTK4GU+FIWdVeniI4kZy2cNxcmGxtwZslFaMiV\nozZsG9O2qUkk2P3ue6w6f8H7/uXMLi19/Tzx45fmNZaFomHoalEUEXjf3dG24v7rbd096LZddiHo\nT6cJJcrvaJcaShBuEd2yvPCy647P5uiU5CIWDJ2LmzaVjThYde7cDV9fcxw6zl9g/dFjREdH5zTm\nNadOYVy3YgeQQmP9seNl7fISWHb5MuCZEGYLnZ3G1TQS0Sgv/vEfcviJfRzd+yBvffHzvP7VL99U\nXRhfyqK5J8aK82PUjqXL3l9X13BmaXW5kNg+nWTEhztjMBJwdUGizlvluqaPica2ooxe1zAIJWb3\nfywKUtIwOEVrd4zasTTRkRTtl+aZHyEEv3n+uZILHhdvF1xU2oPi34gA2np6MNIZForo6CjLLl0m\nMDU15+c09/ax6uy5kjvQZDhUso+1mc3Oek0hJdb1jXyWMMpkdItIIbxtYIlJfWY7y+lH818yKXGF\nRjbgLykIwnWpmZhg48efkAqF6F27Jp8RWjs6xgNvvEnble7cqljzIkRgblmQZQTIsCxWnz5TVqCk\nEPlyGud2bGfrwUNIxyl4j0U/Ik2QiNYidZ2zu3aWH9MsBKayNPfG85nGZV8Lr1RFJRltryEbSBMZ\nTyNcSSriY6IplE96u7xhE5rr4pQYVqm8i8XGn7QJxzJoMz5iIaFhaIpUxId7i8l6/WtWc+SRh9i5\n/wP03PfHhVxYsSy9PS5De3cPPRvmV5rbl0rx5I9/SuPQVVxdQ7Mdzu3czsEnn7ih2WbdiZP5zOWZ\nuJpGJhTid/7T3yCF4OKWTRzZ9xiW38/QiuVl/YauEPStroxfcKFQgnCLuIbBwMqVtF+5UmBmsTWN\nVE0N4fi1KPjrzTCa6+LLZHB1Pd+8JP+4lGw64iW5uLqOq+v86mtfJRMM8pnv/RNmJpPfleium9/e\nrjp3noFVK7lYwj4/zcWtW+g8e77Iri+knHWr6Op6PqwuHQ7zy9/9GntffY3mgUGkEEgpC65hGwaH\nHt8373o3DYNTBRMYlN+BpRegNMRcaO3uYef+94mOjjHe3MQnjzzM8PJlReed33EPK7qKTUMSSTpU\n+RVjOJ4pGx8fTFhMRW990jrx0F4mm5vZ/sGHhOIJhpe3c2XDeva++ga6W7wjLYflm3/59kd+8Uua\nBga930Xup7X+2HHGm5u5sH32HB/NcUp3JHRdGgcG8p3Y1h87QXP/IC///tfJhEJ8/MhD7Nj/AUbO\ndDRtDbi6rJ33lmikVTmUIMyD/c89y3Pf/2f86RSa4zlpJxsbePV3fhsjm+W+t96h82yx+cdwHAKp\nFF1bN7P++MnCJJlcQTIAckXHnvjJT7m4ZXO+x3IpTMti4ydHubRlM6F4nGwgULQyGVy5kq6tW1h3\n4qRXXyXXrLyck1YCjmHw1pe/WFCme6K5iV9+/XcRuRotkYkJduz/gJbePpKRCMf3PpAPS7wVNMel\nZjyFYc3NtCKBzBz7IM+H5V0Xefyln+d9KIEr3bT09fPGl7/I0MqOgnOtgI+R1hoaRlJMy5iXfKgR\na1xcp3cpSqfwAYKS/pCbpWf9usLGO1Ky9sQpWnv7buhzAi8H4GpHcY/rm8GXTrPsSneRD8C0bLYc\nOnxDQbi8eROrzhUvmICCtpy661I7Pk5bdw+Dq1Zy8oE9DC9fxoZPjhGcmmKstYULW7Yw2bJwBQ4r\nhRKEeZCK1PCT736H5RcvEZmYYLy5mcGVHdSOjfGZ73nRR3oJM4xtGAy3t9E4OIQrRMGHUFS/pMdc\nKQAAG9lJREFUH6+GSktv36z5DQDBxBS//Td/i56LAupZu4b9n/n0tWbkQnDgU09zfsc2ll+8THR0\nlJXnzpfs33y1rZXjD+2lv3NV2SJm0zuAeH09773wmVnHNld0y8nVIio7hRXgCkhGfFgV8B/sefPt\ngslN4JUtuP+td3j5W98oOj/eFMYOmNSOptBtl1TYJNYYXNSQ2HJMRX3UTKaLdwkSUouRLCcEb37p\nt9j4yVE2fvwJteMTgLdbnjkEKQSupvHOFz43754DZjZbNurJNwf/RN/qTnrXrGblhS40x8lXFyhV\nf0y4LvXDw/mQ3asrVnB1xfwEbSmgBGGeSE2jd93agmN7X329wLQzE8+pbNC3ZjU73v/whpM8AEIQ\na6j3Vltlzrd1nVA8XiBAK7ou8tjPXuatL3+x4Nyx1lbGWlupHR1jVYliW5Zpcn7njqL3VQnqrybR\n5iAGEsgEDRJ1AaZqF393IByHyMREycfqRkbKPi9V4yNVgd3LjcgGTWINQWrHCiO1RpZHkPrihERK\nXefM7ns5s/te/MkkGz85SnNfP+NNTQwvX0b98AjZgJ/LmzYtSIb+VCRC1u8v2pG4Qsxpx7r80mVW\ndHXlgz+Qkr5VK2nr6y/aNbi65uVV3GEoQVhghOvS2tdfckKTQM/aNRx68nFqJidxDR3mIAiWz8ex\nvXtZc+pMgZ1z2sFqmSauJvBlCq9lOA7tV7oJxeP5ZKKZxBob6F6/jo7zF/K7BFvXSYXDXNq86Wbe\n9oIRnLLmJAbxOj/jbTWVGBJIyWM/f7nsw+nQ7VFuZLI5xFTUT2DKQgrm5Uy+WTKhEMdyuSzTLHi+\njRC8/+lP8fhLP8+X67Z1Hcvv4+jDe2d9qpnJsO+lnxW13mzv6cUxDNwZHekcTSMdDpfMzbjdUYKw\nwEghcIUoaSrK+v28k6sV42payQSYaTuz7rrYuo7UNN797POka8K88vWv8cAbb9HW3YOj60w0NTLR\n1OTtNvZ/gD9THH7q6jrBxFRJQQB47/nn2PDJMTZ+8gmGZXF54wZOPPhA1fozu6J0LPS0+LkCbFNj\norlyk/Dq02dYfulKSaGyDJ3jD+6p2Fjmi+3TSSxinadq07d2Db/4xu+y5dARIuPjDK7s4My9u/KN\ngcqxoutiyegvzXXp2rCeSCxGW3cP5OoWffjsp+bdCW8pUhVBEEL8FfBZIAt0Ad+WUpbej99u5DIg\nV509V+DcsnWdrhkRQMnaWnrWr6PjQld+iyvJReg88Th1o6Mka2roumcLqRpvJRxrbOT1r36l5Mu2\n9fRQOz5e5FDTXJfJhvKlAaSmcfbenZy999ZCQxeaeF2A6FiqILpI4pWbzoRMMiEz3yWsUqw9cbKk\no1EClzZvvuWwWsXiMNHczPvPPXtTz9Fct2xJbFc3eP2rX8kHf9yJQjBNtXYIrwN/LqW0hRB/Cfw5\n8D9VaSwLzofPPEXt2DjR6aqIUjLa1sqRxx4pOO+9559jx3vvs/GTo5jZLMPLl3Hg6SdvqdXe8Qf2\nsPrUGUQ2m9/aWqbJiT33Y/urb8OeK44hENeFr9uGxtCq6II0trkVyjkqLZ/PE/mbFCdfOs09Hx6g\n88w5HMPg7K4dnN21s7oTjSsJJbJoriQdMrHv4F1EKfo6O0uWxHZMk+6NnmnrThaCaaoiCFLK12b8\n+SHw5WqMY7GwAgF+8c3fo7l/gNqxMcabm0v2CHZ1nY/3PcrH+x6d92sma2t5+fe/wY7977PsyhVS\noRAnHtjD5U1Lu7riTHTLoeFqssg0ozteNzS7SnPUhW330NrbV7RLkJpWMgdhNvRslodfeYvxphV0\nbd1La99Fdr77Hi29fbz7+c8u5LDnjC9l09IT84oO5pQ4XhdgoiV029TgmS/pmjCHH3+M3b/+DZrj\neKXMTZPLG9czeF1I8Z3MUvAh/AHwg3IPCiG+C3wXwF97G8X1CsHw8mU3PWHMh0RdlP3PP1ex11to\nQvHSZQCE9B6LNZbu8rXYXNm4gZXnL9Bx/gKa6+TCIwVvf+FzN71q7Dg/wOUN9+bLY8fqm4isWMM9\nH71FdHSUycbGRXgHsyAlLb0x9OsK9kUm0qTDJuklECFVKc7svpfBlStZc+oUumXTvWH9bVGhdCFZ\nNEEQQrwBFFeDgr+QUr6UO+cv8PIJv1/uOlLKvwP+DiDSvn5ptxtSzI/pFM+lhhD85rPP0zgwSHt3\nN5lAgCsbN5AN3FyCmZF1kCJUYPpyDZN4XRNjrctpGhisuCD4U3ZJ27kmoWYifVcJAnhJl0f2PVbt\nYVSNRRMEKeXTsz0uhPgW8ALwlJRLvK+coiKkIj7qRpJFoiAFJJfAxDTa3sZoe6k1ztwIJEuXcXAN\nk7GmZUxFKhRGO4PZWjpqVajBp6guVfGSCCE+DfwZ8Dkp5eLUelbcdtg+ncnGIK6YWR0WYo1B7AoX\nr1sMXE2UjPsXjoMmHa+1Y4XJBE2vGt11SEC3HWpHkyUbxivuTKrlQ/jPgB94XXj2uQ+llH9cpbEo\nlhCxphCpiI9QzPMnJGsrU5ZiJkbGITKewsw4ZEIm8foArjH/tVOyxkdDmQq5J/Zsq4qtWgq8TGWn\neEy+rIs5nKJ2NMVgZ91dF3l0N1KtKKP51bhV3NFYfoPJ5uqsVfxTFi29sXzJbX/aJjKeZmB1dP41\niDTB1ZW1NPfGvK5ruTl4ZGUdqUh1TGKaI0t2gBMz/q+50NQfZ7CzrqJjU1SeOz+wVqGYK1LSOJhA\nm9F/QZNey8y64YWxbGYDBgOdUeJRP+mQyXhTkHSoOlnhUL4/9EwE4Es7ZftpKO4clkLYqUJRdXTb\npXYkWbLktsCrsbQQGBmHtiuTuSqanqO5bizNQGcUZ9osVUHTkdQEybBJMGHdcHWoOxLHuHtCMO9G\nlCAo7nr0bK7ktlu+yqo7h5X0XGgcTKDNeB1NgnQk7ZcmPdONgKmIj7HWcMUys0fba2jpjeNL2wXd\n6a7HVVpwx6NMRoq7nrqRJJpbvmucKyBevwBNbaT04v6vO+zZ6T2REBJCsSytPbGKmWik7pUGGeiM\nlk0DkbnzFHc2aoegqCpG1iE6ksSfsvNhp5kK29TLldyW4K3Ya/0LIwizMPP1NcDMOPjSDtkKtQYF\nsP0GE81B6oZTBeIogYnm6mSJKyqLEgRF1TAyDu1XJhCuNyGalos/aTHaXkOytnKNyV1doJcIuwTo\n76xbuBwIIUhGfITi2Rt3gxNgZisrCADxhiBCQnTkWiOdWGOQeIMShLsBJQiKqlE3PJUXg2k0CQ1D\nUxUtcW0ZGka2sLe0C6RqzAVPiBtrC2NmHYxsrhdGzmZf9E4lZKuRjCcEsaYQscYguu3i6BoskP9E\nsfRRgqCoGoES9nQA4UpvMqpA7+FAIltyHAIYbQsv+Ou5usZAZxR/ysbMOliGRvNAoqBtqAtkAjpW\noIo/TyGq0vtZUV2Ul0ixuLiSyGiK9osTtF+aIDKWyjtLnTLZvwIq1tqxZiJd0IxnGql5mbqLghBk\nQiaJugCZGh8Dq6Ika0xcrnWGC6QdGvvjiBJJYwrFYqEEQbF4SElrT4y6kSS+rIMv41A3nKQlF0Ez\n2RAsCmV0BUxF/HNKmFoIZivgNlvht4XE8elMNoVAXDMfTZf8buqLV2QMCgUok5FiEQkkbXxpu2AF\nrkmv5LI/aZOs9WFYQaKjKRACISWpGh9ji2CqKcdUrQ9/yireJchc4bcKUTuWQlw3hunENd1yKmu+\nkZJA0iYUywAwFfVXPPJLUR2UICgWDX/KKprkwFv9+lMWmbBJrClEvCGIkXVwDG1BisjdDFNRPzWT\nmbxwSbyCb6Nt4YrtUsCLKCoZ+irAsCrjT5mmYWiK8GQm/9mFYxkStX5sv46QkAqb1fVvKBYN9akq\nFg3H0JCCIlGQotB/IDVRvQlGCIZW1hJMZAnFsziGRiIaqHi57UzQxJcuFgVNglXBKqO+lE14MlOw\nYxISIpOZvH+jbtj7DGMNgZypS0Uh3SkoQVAsGlMRH/VXkwUZt16yl6honsENEYJUxE8qUr0xxRoC\n3kQ8o6yFKyBR58ewHOp74/gyNq6uMdkQIFEfWJSJOJjIlt7VURgaKyTUjqXRHclYW+Ub+ygWByUI\nikVD6hpDK2tp6ouj25731jE0hpdHKmqOKUcoFmPTx59Qf3WYkfY2zu7aSTpcOf/FTBxTZ7AzSt3V\nKQJJG1cXxOoDZIIGbd2x/Ipds13qh5PojmSyObTg47iZz8Vrs5lhojGIq0JU7wiUICgWFdvQiEf9\n+DI22YBJvM4PFa6JI1wX3Xawfdcco/VDV/n0P/8LuuOiOw5t3T1sPvwxv/jG7xFvqK/o+KaxfToj\nK2oLjjXnejPMRJOeEzrWGFxwYZ2KmNQN39xzGoamisatuD1RgqBYNEKxDE39CSCXW5CwiEykGeyM\nViTPQLNt7nv7HdYfP4nmOMTr6vjwU08xuGoVe197HTN7rYaR4ThojsOet97mzS9/cdHHNlfMEn4F\nAATolrvgvo6b/VwEEExYmGlbOZrvAFQegmJR8KUsmvoTBbZnTXoRM/WDCVq6J1lxfozWy5MEprKL\nMoZHfvFL1h8/iWHbaFISHR/nqR/9lIbBQZoGh4oduEDble5FGcutYvv10hVIZfnEvvkgNYEsc9ly\nWRmeKCzOZ6ioLEoQFItCw0CidFkKIBy3CCZtdEcSSNs098YJ5mLeF4pAYoqOC10Ytl1wXHMcth44\niKuV/urb5tKKt59sDCJLJO8lon6vF/JCIwSx+hIJg4BlipKiIMXN+R4USxe1x1MsPFLOWvahVGhl\nw9UkfQtQ0C4wlaVuOIUvbXFo3+dwdRPLHyCQjLPm1GGaB7upGxuna8tm1pw6jeE4+efahsG5Hdvn\n9foLTSZkMrw8QsPQFIblInO9GSYWwaE8zWSTV9m0dsyreCqFYKI5iG3qtPSWyJyWXolwxe2PEgTF\nwiMEUhM3VYdHt12EpGg1fDMEYxmaBhK5iBxBuiaafyxVE+X0vY8hP36XieYoB598gsjkJM39A7ia\nhua69Heu4ugjD936ABaJdI2P/hofuNOlURd5NS4Ek80hJpuCaI7E1QUIQfvFiSIxl0AmaFQ8oVCx\nOChBUCwKsfoAtaOpOdskpSZmFQMzY1MznsawXNJhk0Q0UGgykZL6q8mSheqmcQ2DS5t307e2Adtn\n8trv/DZ1IyNExseZaGyqWnTRnNEK328okcAxDDLBRepVIARuroey5riYWaf4FMBX4rji9kQJgmJR\nmGzy6umHJzOl6/3PwBUQr/NTM+ElZqVqTCz/ta9mMJ6lqT+e7/cbSFpExq+LVpJg2DeuTpqsqSVe\nX5f/e6KpiYmmplt7k1WipaeXR175JcHEFALJ8LJlvPvZ50nVzDNBTEp8aRvdlkWrfjnLrmS2xxS3\nF0oQFIuDEIy11zDRHGL5hfGyLSolkKzxERlPe0+TEB3xMnTHW7wkscbBRFGBPGyX2tEUE7lzEOBq\nAv0GZir7Nk+gCk/GePrFH2NaVv5YS28fz/7Lv/LT73w7b04y0zb1V5P40zaOLphsDDIV9Zc1N/mS\nFi1918ptCyAdMNAdFykEiboAqbBZ1G50WswVdwbK8KdYVFxDwzHKryD7VkcJJbJo0pvoBdcyYP1J\nr4lMKV+EJiE0M9RRCGINAWbbI7iwqM7YSrD+6FE0t/BdalISiido6esDPPNa25VJAkkLzZWYlkvD\n0BSR0VxbTCnxJy1CsQxG1iEymvSyoR157XOQXgMjX9bFn3GovzqFK8Dy67g58XWFV+gu1qjaa94p\nqB2CYtGJNQQ9+/6MY54zUsefdTwVuG7OFxJqYhkmmspPNteHjsYag4TiWXyZ4mQuCcTq/UurhtIt\nUDs+ge4U2+wlEI55EUDR4WTevDaNJqFuNEWy1k9LbwzDcvNPLGfSu/75oSmLgVVRNCkxLJes36h4\nEUDF4qJ2CIpFJ1EfYCrqR+KZGFy8fsHD0+UOyll5pMQxdawSyVmu8CZ4M217/YmlBCGwfXpp85QG\nVgX7GywWQx0dWEbxOk6TLiNtbQD4y2Q3CwktPZOYWTe/E7jZCcCftskGTZK5ctiKOwu1Q1AsPjl/\nwmRTEF/GwTa1vNM4XabxihRerwKA4eURWnpi+Th8LVeTv2FwKu9bcDUYXlFLMuIjmDNBFV4Q0uHb\nXxC67tnCPR8dREsk0HOmI8sw6Fm3Lh8lZfm0sg5205JFYnEzLmHH0PClbIKJLFITTNX6VO/lOwgl\nCIqK4Zg6KUPDsFw0x8XVNaSuMdoWpmlgKn+eFF6i07RYOKbOwOq6fASMowtau2MFq1vNhdbuGP2d\ntaRDpmc/n9HwZrwlVLE+zYuJ7fPx8jd/j+3vf8iq8xewTYMzu3ZydtfO/DnxugD+ZKJo9T+fWCCJ\nJ7qheIZwzCuRLYHoSJLRtjDJaGAeV1csFZQgKCpGaDJNw1ASIb1VajJsMtpWQ+14GolnvnABJJ6t\nfzoiRkoCU56DNB0yqR1NllzlSqBxcIqhVVGCCYtQPIOraySi/juq8FomFOLg009y8OknC47rtktT\nXxxf2kaIa20obiQE05upcudJwNEgHg0QHU/nd18i92Dj4BSpGh/yDhDcu50751eiWNL4kxaNM0w8\nAMEpi7Yrkxi2m1/NTv+/qT9O77p6zIxDa0/sWsN7CZaplXWC+jJOruGNj1TEt3hvaKkhJS3dnn9g\n5r0p654hV4EWzx+jlzlx+rDuQt1YuvRJwvssb3eHvUIJgqJC1I6WbiJvWm7pyd2VmGmb1t44ulP4\nRDPr5ie063Hv0iJrvrSNUeZeXn+vZv4t8EKDdau0z2FOd3PuFUoUSxy1x1NUhHKT1WyYWefazmAG\n0+ahEn7juzYmXrdlydlb4PlQXHHtnonrHjdzYlDqfs6VVM1dtBu7g1GCoKgI6ZBRdoK5fm0qyWUs\nDydLzkoCSAd1LJ+Wn+QkXknoeP3d6dzMBvSSvZBdARNNQUaW1ZAJlI4GEjP+mw4NLrcDmyYfQixg\nZNnSaImqmD9VNRkJIf4U+GugWUo5Us2xKBaXWGOQcCxb1ER+sjGImXUIxb2s4+lJTQA+W5YUEVdA\nss4rxaBbDoblYvn0u7ripmPqJKJ+wpOZa6G4eB3QEnUBoqMp/JkbF6ETgGXqxOr9NMxSLNDRBZNN\nIZIR31193+80qiYIQogO4FPA0mpRpVgUvNDRKHUjKQJTFo4hiDUE847IWNqmdiRJKGEVbFtnJjEL\nPDHIBgyman3566o4eI+x1jCZoEFkLI3mSpIRH7HGILotiYynS+4gSiGkRGpZmga7GW9chtRz91eI\nfBjv6LLIHZHXoSikmjuE/wj8GfBSFcegqCCOqTPaXroipxUwymbOSpEzOWkayYiP5AI00rkjEYKp\naICp63ICaiaKHfpQ2iwk8ZIFn/rxj4mOjDAVbWRgxVpiDS3YPj+psJ+hlU1kgyoe5U6kKp+qEOLz\nQJ+U8qi4wQ9bCPFd4LsA/trmCoxOUS1sUytru441hsiUyWpWzI6b6zVR0sfANRGWeH0pXD1DZHwc\nXUpqJ0aonbhmze1d3UnPxi9VYNSKarBogiCEeANoK/HQXwD/Hs9cdEOklH8H/B1ApH29CnC7g0nU\nB6iZzBRMXBKvXEJGrUhvmWTER/3VqaLjUsBYS4jIZBbddkmHDCabQtQPDyHL9JwOpFKLPVxFFVm0\nX5mU8ulSx4UQ24DVwPTuYAVwRAixR0o5uFjjUSx9LL/ByLIIjQOJfLip5dMZXhFRJqJ54Boao+01\nNA4kCo6PtYU9E1N9YajuWEtzyXBfW9fpXrduUceqqC4VX3ZJKY8DLdN/CyEuA/epKCMFQCrio7fG\ny1B2NYHjUw7jhSBZ6ycVNgklvMY6qRqzbG0nxzQ58NQTPPjGW2i2jQbYhkGypoYzu3dVcNSKSqP2\n4YqlhxB3VO2hpYLUtXwF2RvRtX0bk81NbDp0hFBiit51azi3fTu2XyWg3clU/Vcnpeys9hgUCkUx\nI+3tvPfZ56s9DEUFURklCoVCoQCUICgUCoUihxIEhUKhUABKEBQKhUKRQwmCQqFQKAAlCAqFQqHI\noQRBoVAoFIASBIVCoVDkUIKgUCgUCkAJgkKhUChyKEFQKBQKBaAEQaFQKBQ5lCAoFAqFAlCCoFAo\nFIocShAUCoVCAShBUCgUCkUOJQgKhUKhAEDIEs20lypCiGHgSrXHUYYm4G7vC63ugYe6D+oewNK6\nB6uklM03Oum2EoSljBDikJTyvmqPo5qoe+Ch7oO6B3B73gNlMlIoFAoFoARBoVAoFDmUICwcf1ft\nASwB1D3wUPdB3QO4De+B8iEoFAqFAlA7BIVCoVDkUIKgUCgUCkAJwqIghPhTIYQUQjRVeyyVRgjx\nV0KIM0KIY0KInwgh6qo9pkohhPi0EOKsEOKCEOJ/rvZ4Ko0QokMI8bYQ4pQQ4qQQ4t9Ve0zVQgih\nCyE+FkK8XO2x3AxKEBYYIUQH8Cmgu9pjqRKvA/dIKbcD54A/r/J4KoIQQgf+BngO2AJ8TQixpbqj\nqjg28KdSyi3Ag8B/dxfeg2n+HXC62oO4WZQgLDz/Efgz4K701kspX5NS2rk/PwRWVHM8FWQPcEFK\neVFKmQX+Bfh8lcdUUaSUA1LKI7l/x/EmxOXVHVXlEUKsAJ4H/mu1x3KzKEFYQIQQnwf6pJRHqz2W\nJcIfAL+s9iAqxHKgZ8bfvdyFk+E0QohOYBdwoLojqQr/B96i0K32QG4Wo9oDuN0QQrwBtJV46C+A\nf49nLrqjme0eSClfyp3zF3gmhO9XcmyK6iOEqAF+BPyJlDJW7fFUEiHEC8BVKeVhIcTj1R7PzaIE\n4SaRUj5d6rgQYhuwGjgqhADPVHJECLFHSjlYwSEuOuXuwTRCiG8BLwBPybsn0aUP6Jjx94rcsbsK\nIYSJJwbfl1L+uNrjqQIPA58TQnwGCAC1QojvSSm/XuVxzQmVmLZICCEuA/dJKZdKtcOKIIT4NPAf\ngH1SyuFqj6dSCCEMPCf6U3hCcBD4XSnlyaoOrIIIbyX0D8CYlPJPqj2eapPbIfyPUsoXqj2WuaJ8\nCIqF5j8DEeB1IcQnQoi/rfaAKkHOkf5vgVfxnKn/ejeJQY6HgW8AT+Y++09yK2XFbYLaISgUCoUC\nUDsEhUKhUORQgqBQKBQKQAmCQqFQKHIoQVAoFAoFoARBoVAoFDmUICgUC4QQ4ldCiInbrcKlQjGN\nEgSFYuH4K7w4fIXitkQJgkJxkwgh7s/1ewgIIcK52v/3SCnfBOLVHp9CcauoWkYKxU0ipTwohPgZ\n8L8DQeB7UsoTVR6WQjFvlCAoFLfG/4ZXrygN/PdVHotCsSAok5FCcWs0AjV4dZsCVR6LQrEgKEFQ\nKG6N/wL8L3j9Hv6yymNRKBYEZTJSKG4SIcQ3AUtK+U+5XsrvCyGeBP5XYBNQI4ToBb4jpXy1mmNV\nKG4GVe1UoVAoFIAyGSkUCoUihxIEhUKhUABKEBQKhUKRQwmCQqFQKAAlCAqFQqHIoQRBoVAoFIAS\nBIVCoVDk+P8B2BAvSDnlqLAAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x20f65682ef0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Plot the decision boundary for logistic regression\n",
"plot_decision_boundary(lambda x: clf.predict(x), X, Y)\n",
"plt.title(\"Logistic Regression\")\n",
"\n",
"# Print accuracy\n",
"LR_predictions = clf.predict(X.T)\n",
"print ('Accuracy of logistic regression: %d ' % float((np.dot(Y,LR_predictions) + np.dot(1-Y,1-LR_predictions))/float(Y.size)*100) +\n",
" '% ' + \"(percentage of correctly labelled datapoints)\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Expected Output**:\n",
"\n",
"<table style=\"width:20%\">\n",
" <tr>\n",
" <td>**Accuracy**</td>\n",
" <td> 47% </td> \n",
" </tr>\n",
" \n",
"</table>\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Interpretation**: The dataset is not linearly separable, so logistic regression doesn't perform well. Hopefully a neural network will do better. Let's try this now! "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 4 - Neural Network model\n",
"\n",
"Logistic regression did not work well on the \"flower dataset\". You are going to train a Neural Network with a single hidden layer.\n",
"\n",
"**Here is our model**:\n",
"<img src=\"images/classification_kiank.png\" style=\"width:600px;height:300px;\">\n",
"\n",
"**Mathematically**:\n",
"\n",
"For one example $x^{(i)}$:\n",
"$$z^{[1] (i)} = W^{[1]} x^{(i)} + b^{[1] (i)}\\tag{1}$$ \n",
"$$a^{[1] (i)} = \\tanh(z^{[1] (i)})\\tag{2}$$\n",
"$$z^{[2] (i)} = W^{[2]} a^{[1] (i)} + b^{[2] (i)}\\tag{3}$$\n",
"$$\\hat{y}^{(i)} = a^{[2] (i)} = \\sigma(z^{ [2] (i)})\\tag{4}$$\n",
"$$y^{(i)}_{prediction} = \\begin{cases} 1 & \\mbox{if } a^{[2](i)} > 0.5 \\\\ 0 & \\mbox{otherwise } \\end{cases}\\tag{5}$$\n",
"\n",
"Given the predictions on all the examples, you can also compute the cost $J$ as follows: \n",
"$$J = - \\frac{1}{m} \\sum\\limits_{i = 0}^{m} \\large\\left(\\small y^{(i)}\\log\\left(a^{[2] (i)}\\right) + (1-y^{(i)})\\log\\left(1- a^{[2] (i)}\\right) \\large \\right) \\small \\tag{6}$$\n",
"\n",
"**Reminder**: The general methodology to build a Neural Network is to:\n",
" 1. Define the neural network structure ( # of input units, # of hidden units, etc). \n",
" 2. Initialize the model's parameters\n",
" 3. Loop:\n",
" - Implement forward propagation\n",
" - Compute loss\n",
" - Implement backward propagation to get the gradients\n",
" - Update parameters (gradient descent)\n",
"\n",
"You often build helper functions to compute steps 1-3 and then merge them into one function we call `nn_model()`. Once you've built `nn_model()` and learnt the right parameters, you can make predictions on new data."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 4.1 - Defining the neural network structure ####\n",
"\n",
"**Exercise**: Define three variables:\n",
" - n_x: the size of the input layer\n",
" - n_h: the size of the hidden layer (set this to 4) \n",
" - n_y: the size of the output layer\n",
"\n",
"**Hint**: Use shapes of X and Y to find n_x and n_y. Also, hard code the hidden layer size to be 4."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# GRADED FUNCTION: layer_sizes\n",
"\n",
"def layer_sizes(X, Y):\n",
" \"\"\"\n",
" Arguments:\n",
" X -- input dataset of shape (input size, number of examples)\n",
" Y -- labels of shape (output size, number of examples)\n",
" \n",
" Returns:\n",
" n_x -- the size of the input layer\n",
" n_h -- the size of the hidden layer\n",
" n_y -- the size of the output layer\n",
" \"\"\"\n",
" ### START CODE HERE ### (≈ 3 lines of code)\n",
" n_x = X.shape[0] # size of input layer\n",
" n_h = 4\n",
" n_y = Y.shape[0] # size of output layer\n",
" ### END CODE HERE ###\n",
" return (n_x, n_h, n_y)"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"The size of the input layer is: n_x = 5\n",
"The size of the hidden layer is: n_h = 4\n",
"The size of the output layer is: n_y = 2\n"
]
}
],
"source": [
"X_assess, Y_assess = layer_sizes_test_case()\n",
"(n_x, n_h, n_y) = layer_sizes(X_assess, Y_assess)\n",
"print(\"The size of the input layer is: n_x = \" + str(n_x))\n",
"print(\"The size of the hidden layer is: n_h = \" + str(n_h))\n",
"print(\"The size of the output layer is: n_y = \" + str(n_y))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Expected Output** (these are not the sizes you will use for your network, they are just used to assess the function you've just coded).\n",
"\n",
"<table style=\"width:20%\">\n",
" <tr>\n",
" <td>**n_x**</td>\n",
" <td> 5 </td> \n",
" </tr>\n",
" \n",
" <tr>\n",
" <td>**n_h**</td>\n",
" <td> 4 </td> \n",
" </tr>\n",
" \n",
" <tr>\n",
" <td>**n_y**</td>\n",
" <td> 2 </td> \n",
" </tr>\n",
" \n",
"</table>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 4.2 - Initialize the model's parameters ####\n",
"\n",
"**Exercise**: Implement the function `initialize_parameters()`.\n",
"\n",
"**Instructions**:\n",
"- Make sure your parameters' sizes are right. Refer to the neural network figure above if needed.\n",
"- You will initialize the weights matrices with random values. \n",
" - Use: `np.random.randn(a,b) * 0.01` to randomly initialize a matrix of shape (a,b).\n",
"- You will initialize the bias vectors as zeros. \n",
" - Use: `np.zeros((a,b))` to initialize a matrix of shape (a,b) with zeros."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# GRADED FUNCTION: initialize_parameters\n",
"\n",
"def initialize_parameters(n_x, n_h, n_y):\n",
" \"\"\"\n",
" Argument:\n",
" n_x -- size of the input layer\n",
" n_h -- size of the hidden layer\n",
" n_y -- size of the output layer\n",
" \n",
" Returns:\n",
" params -- python dictionary containing your parameters:\n",
" W1 -- weight matrix of shape (n_h, n_x)\n",
" b1 -- bias vector of shape (n_h, 1)\n",
" W2 -- weight matrix of shape (n_y, n_h)\n",
" b2 -- bias vector of shape (n_y, 1)\n",
" \"\"\"\n",
" \n",
" np.random.seed(2) # we set up a seed so that your output matches ours although the initialization is random.\n",
" \n",
" ### START CODE HERE ### (≈ 4 lines of code)\n",
" W1 = np.random.randn(n_h, n_x) * 0.01\n",
" b1 = np.zeros((n_h, 1))\n",
" W2 = np.random.randn(n_y, n_h) * 0.01\n",
" b2 = np.zeros((n_y, 1))\n",
" ### END CODE HERE ###\n",
" \n",
" assert (W1.shape == (n_h, n_x))\n",
" assert (b1.shape == (n_h, 1))\n",
" assert (W2.shape == (n_y, n_h))\n",
" assert (b2.shape == (n_y, 1))\n",
" \n",
" parameters = {\"W1\": W1,\n",
" \"b1\": b1,\n",
" \"W2\": W2,\n",
" \"b2\": b2}\n",
" \n",
" return parameters"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"W1 = [[-0.00416758 -0.00056267]\n",
" [-0.02136196 0.01640271]\n",
" [-0.01793436 -0.00841747]\n",
" [ 0.00502881 -0.01245288]]\n",
"b1 = [[ 0.]\n",
" [ 0.]\n",
" [ 0.]\n",
" [ 0.]]\n",
"W2 = [[-0.01057952 -0.00909008 0.00551454 0.02292208]]\n",
"b2 = [[ 0.]]\n"
]
}
],
"source": [
"n_x, n_h, n_y = initialize_parameters_test_case()\n",
"\n",
"parameters = initialize_parameters(n_x, n_h, n_y)\n",
"print(\"W1 = \" + str(parameters[\"W1\"]))\n",
"print(\"b1 = \" + str(parameters[\"b1\"]))\n",
"print(\"W2 = \" + str(parameters[\"W2\"]))\n",
"print(\"b2 = \" + str(parameters[\"b2\"]))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Expected Output**:\n",
"\n",
"<table style=\"width:90%\">\n",
" <tr>\n",
" <td>**W1**</td>\n",
" <td> [[-0.00416758 -0.00056267]\n",
" [-0.02136196 0.01640271]\n",
" [-0.01793436 -0.00841747]\n",
" [ 0.00502881 -0.01245288]] </td> \n",
" </tr>\n",
" \n",
" <tr>\n",
" <td>**b1**</td>\n",
" <td> [[ 0.]\n",
" [ 0.]\n",
" [ 0.]\n",
" [ 0.]] </td> \n",
" </tr>\n",
" \n",
" <tr>\n",
" <td>**W2**</td>\n",
" <td> [[-0.01057952 -0.00909008 0.00551454 0.02292208]]</td> \n",
" </tr>\n",
" \n",
"\n",
" <tr>\n",
" <td>**b2**</td>\n",
" <td> [[ 0.]] </td> \n",
" </tr>\n",
" \n",
"</table>\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 4.3 - The Loop ####\n",
"\n",
"**Question**: Implement `forward_propagation()`.\n",
"\n",
"**Instructions**:\n",
"- Look above at the mathematical representation of your classifier.\n",
"- You can use the function `sigmoid()`. It is built-in (imported) in the notebook.\n",
"- You can use the function `np.tanh()`. It is part of the numpy library.\n",
"- The steps you have to implement are:\n",
" 1. Retrieve each parameter from the dictionary \"parameters\" (which is the output of `initialize_parameters()`) by using `parameters[\"..\"]`.\n",
" 2. Implement Forward Propagation. Compute $Z^{[1]}, A^{[1]}, Z^{[2]}$ and $A^{[2]}$ (the vector of all your predictions on all the examples in the training set).\n",
"- Values needed in the backpropagation are stored in \"`cache`\". The `cache` will be given as an input to the backpropagation function."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# GRADED FUNCTION: forward_propagation\n",
"\n",
"def forward_propagation(X, parameters):\n",
" \"\"\"\n",
" Argument:\n",
" X -- input data of size (n_x, m)\n",
" parameters -- python dictionary containing your parameters (output of initialization function)\n",
" \n",
" Returns:\n",
" A2 -- The sigmoid output of the second activation\n",
" cache -- a dictionary containing \"Z1\", \"A1\", \"Z2\" and \"A2\"\n",
" \"\"\"\n",
" # Retrieve each parameter from the dictionary \"parameters\"\n",
" ### START CODE HERE ### (≈ 4 lines of code)\n",
" W1 = parameters[\"W1\"]\n",
" b1 = parameters[\"b1\"]\n",
" W2 = parameters[\"W2\"]\n",
" b2 = parameters[\"b2\"]\n",
" ### END CODE HERE ###\n",
" \n",
" # Implement Forward Propagation to calculate A2 (probabilities)\n",
" ### START CODE HERE ### (≈ 4 lines of code)\n",
" Z1 = np.dot(W1, X) + b1\n",
" A1 = np.tanh(Z1)\n",
" Z2 = np.dot(W2, A1) + b2\n",
" A2 = sigmoid(Z2)\n",
" ### END CODE HERE ###\n",
" \n",
" assert(A2.shape == (1, X.shape[1]))\n",
" \n",
" cache = {\"Z1\": Z1,\n",
" \"A1\": A1,\n",
" \"Z2\": Z2,\n",
" \"A2\": A2}\n",
" \n",
" return A2, cache"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"-0.000499755777742 -0.000496963353232 0.000438187450959 0.500109546852\n"
]
}
],
"source": [
"X_assess, parameters = forward_propagation_test_case()\n",
"\n",
"A2, cache = forward_propagation(X_assess, parameters)\n",
"\n",
"# Note: we use the mean here just to make sure that your output matches ours. \n",
"print(np.mean(cache['Z1']) ,np.mean(cache['A1']),np.mean(cache['Z2']),np.mean(cache['A2']))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Expected Output**:\n",
"<table style=\"width:55%\">\n",
" <tr>\n",
" <td> -0.000499755777742 -0.000496963353232 0.000438187450959 0.500109546852 </td> \n",
" </tr>\n",
"</table>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now that you have computed $A^{[2]}$ (in the Python variable \"`A2`\"), which contains $a^{[2](i)}$ for every example, you can compute the cost function as follows:\n",
"\n",
"$$J = - \\frac{1}{m} \\sum\\limits_{i = 0}^{m} \\large{(} \\small y^{(i)}\\log\\left(a^{[2] (i)}\\right) + (1-y^{(i)})\\log\\left(1- a^{[2] (i)}\\right) \\large{)} \\small\\tag{13}$$\n",
"\n",
"**Exercise**: Implement `compute_cost()` to compute the value of the cost $J$.\n",
"\n",
"**Instructions**:\n",
"- There are many ways to implement the cross-entropy loss. To help you, we give you how we would have implemented\n",
"$- \\sum\\limits_{i=0}^{m} y^{(i)}\\log(a^{[2](i)})$:\n",
"```python\n",
"logprobs = np.multiply(np.log(A2),Y)\n",
"cost = - np.sum(logprobs) # no need to use a for loop!\n",
"```\n",
"\n",
"(you can use either `np.multiply()` and then `np.sum()` or directly `np.dot()`).\n"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# GRADED FUNCTION: compute_cost\n",
"\n",
"def compute_cost(A2, Y, parameters):\n",
" \"\"\"\n",
" Computes the cross-entropy cost given in equation (13)\n",
" \n",
" Arguments:\n",
" A2 -- The sigmoid output of the second activation, of shape (1, number of examples)\n",
" Y -- \"true\" labels vector of shape (1, number of examples)\n",
" parameters -- python dictionary containing your parameters W1, b1, W2 and b2\n",
" \n",
" Returns:\n",
" cost -- cross-entropy cost given equation (13)\n",
" \"\"\"\n",
" \n",
" m = Y.shape[1] # number of example\n",
" \n",
" # Retrieve W1 and W2 from parameters\n",
" ### START CODE HERE ### (≈ 2 lines of code)\n",
" W1 = parameters[\"W1\"]\n",
" W2 = parameters[\"W2\"]\n",
" ### END CODE HERE ###\n",
" \n",
" # Compute the cross-entropy cost\n",
" ### START CODE HERE ### (≈ 2 lines of code)\n",
" logprobs = np.multiply(Y, np.log(A2)) + np.multiply(np.log(1 - A2), 1 - Y)\n",
" cost = - 1 / m * np.sum(logprobs)\n",
" ### END CODE HERE ###\n",
" \n",
" cost = np.squeeze(cost) # makes sure cost is the dimension we expect. \n",
" # E.g., turns [[17]] into 17 \n",
" assert(isinstance(cost, float))\n",
" \n",
" return cost"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"cost = 0.692919893776\n"
]
}
],
"source": [
"A2, Y_assess, parameters = compute_cost_test_case()\n",
"\n",
"print(\"cost = \" + str(compute_cost(A2, Y_assess, parameters)))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Expected Output**:\n",
"<table style=\"width:20%\">\n",
" <tr>\n",
" <td>**cost**</td>\n",
" <td> 0.692919893776 </td> \n",
" </tr>\n",
" \n",
"</table>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Using the cache computed during forward propagation, you can now implement backward propagation.\n",
"\n",
"**Question**: Implement the function `backward_propagation()`.\n",
"\n",
"**Instructions**:\n",
"Backpropagation is usually the hardest (most mathematical) part in deep learning. To help you, here again is the slide from the lecture on backpropagation. You'll want to use the six equations on the right of this slide, since you are building a vectorized implementation. \n",
"\n",
"<img src=\"images/grad_summary.png\" style=\"width:600px;height:300px;\">\n",
"\n",
"<!--\n",
"$\\frac{\\partial \\mathcal{J} }{ \\partial z_{2}^{(i)} } = \\frac{1}{m} (a^{[2](i)} - y^{(i)})$\n",
"\n",
"$\\frac{\\partial \\mathcal{J} }{ \\partial W_2 } = \\frac{\\partial \\mathcal{J} }{ \\partial z_{2}^{(i)} } a^{[1] (i) T} $\n",
"\n",
"$\\frac{\\partial \\mathcal{J} }{ \\partial b_2 } = \\sum_i{\\frac{\\partial \\mathcal{J} }{ \\partial z_{2}^{(i)}}}$\n",
"\n",
"$\\frac{\\partial \\mathcal{J} }{ \\partial z_{1}^{(i)} } = W_2^T \\frac{\\partial \\mathcal{J} }{ \\partial z_{2}^{(i)} } * ( 1 - a^{[1] (i) 2}) $\n",
"\n",
"$\\frac{\\partial \\mathcal{J} }{ \\partial W_1 } = \\frac{\\partial \\mathcal{J} }{ \\partial z_{1}^{(i)} } X^T $\n",
"\n",
"$\\frac{\\partial \\mathcal{J} _i }{ \\partial b_1 } = \\sum_i{\\frac{\\partial \\mathcal{J} }{ \\partial z_{1}^{(i)}}}$\n",
"\n",
"- Note that $*$ denotes elementwise multiplication.\n",
"- The notation you will use is common in deep learning coding:\n",
" - dW1 = $\\frac{\\partial \\mathcal{J} }{ \\partial W_1 }$\n",
" - db1 = $\\frac{\\partial \\mathcal{J} }{ \\partial b_1 }$\n",
" - dW2 = $\\frac{\\partial \\mathcal{J} }{ \\partial W_2 }$\n",
" - db2 = $\\frac{\\partial \\mathcal{J} }{ \\partial b_2 }$\n",
" \n",
"!-->\n",
"\n",
"- Tips:\n",
" - To compute dZ1 you'll need to compute $g^{[1]'}(Z^{[1]})$. Since $g^{[1]}(.)$ is the tanh activation function, if $a = g^{[1]}(z)$ then $g^{[1]'}(z) = 1-a^2$. So you can compute \n",
" $g^{[1]'}(Z^{[1]})$ using `(1 - np.power(A1, 2))`."
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# GRADED FUNCTION: backward_propagation\n",
"\n",
"def backward_propagation(parameters, cache, X, Y):\n",
" \"\"\"\n",
" Implement the backward propagation using the instructions above.\n",
" \n",
" Arguments:\n",
" parameters -- python dictionary containing our parameters \n",
" cache -- a dictionary containing \"Z1\", \"A1\", \"Z2\" and \"A2\".\n",
" X -- input data of shape (2, number of examples)\n",
" Y -- \"true\" labels vector of shape (1, number of examples)\n",
" \n",
" Returns:\n",
" grads -- python dictionary containing your gradients with respect to different parameters\n",
" \"\"\"\n",
" m = X.shape[1]\n",
" \n",
" # First, retrieve W1 and W2 from the dictionary \"parameters\".\n",
" ### START CODE HERE ### (≈ 2 lines of code)\n",
" W1 = parameters[\"W1\"]\n",
" W2 = parameters[\"W2\"]\n",
" ### END CODE HERE ###\n",
" \n",
" # Retrieve also A1 and A2 from dictionary \"cache\".\n",
" ### START CODE HERE ### (≈ 2 lines of code)\n",
" A1 = cache[\"A1\"]\n",
" A2 = cache[\"A2\"]\n",
" ### END CODE HERE ###\n",
" \n",
" # Backward propagation: calculate dW1, db1, dW2, db2. \n",
" ### START CODE HERE ### (≈ 6 lines of code, corresponding to 6 equations on slide above)\n",
" dZ2 = A2 - Y\n",
" dW2 = 1 / m * np.dot(dZ2, A1.T)\n",
" db2 = 1 / m * np.sum(dZ2, axis=1, keepdims=True)\n",
" dZ1 = np.dot(W2.T, dZ2) * (1 - np.power(A1, 2))\n",
" dW1 = 1 / m * np.dot(dZ1, X.T)\n",
" db1 = 1 / m * np.sum(dZ1, axis=1, keepdims=True)\n",
" ### END CODE HERE ###\n",
" \n",
" grads = {\"dW1\": dW1,\n",
" \"db1\": db1,\n",
" \"dW2\": dW2,\n",
" \"db2\": db2}\n",
" \n",
" return grads"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"dW1 = [[ 0.01018708 -0.00708701]\n",
" [ 0.00873447 -0.0060768 ]\n",
" [-0.00530847 0.00369379]\n",
" [-0.02206365 0.01535126]]\n",
"db1 = [[-0.00069728]\n",
" [-0.00060606]\n",
" [ 0.000364 ]\n",
" [ 0.00151207]]\n",
"dW2 = [[ 0.00363613 0.03153604 0.01162914 -0.01318316]]\n",
"db2 = [[ 0.06589489]]\n"
]
}
],
"source": [
"parameters, cache, X_assess, Y_assess = backward_propagation_test_case()\n",
"\n",
"grads = backward_propagation(parameters, cache, X_assess, Y_assess)\n",
"print (\"dW1 = \"+ str(grads[\"dW1\"]))\n",
"print (\"db1 = \"+ str(grads[\"db1\"]))\n",
"print (\"dW2 = \"+ str(grads[\"dW2\"]))\n",
"print (\"db2 = \"+ str(grads[\"db2\"]))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Expected output**:\n",
"\n",
"\n",
"\n",
"<table style=\"width:80%\">\n",
" <tr>\n",
" <td>**dW1**</td>\n",
" <td> [[ 0.01018708 -0.00708701]\n",
" [ 0.00873447 -0.0060768 ]\n",
" [-0.00530847 0.00369379]\n",
" [-0.02206365 0.01535126]] </td> \n",
" </tr>\n",
" \n",
" <tr>\n",
" <td>**db1**</td>\n",
" <td> [[-0.00069728]\n",
" [-0.00060606]\n",
" [ 0.000364 ]\n",
" [ 0.00151207]] </td> \n",
" </tr>\n",
" \n",
" <tr>\n",
" <td>**dW2**</td>\n",
" <td> [[ 0.00363613 0.03153604 0.01162914 -0.01318316]] </td> \n",
" </tr>\n",
" \n",
"\n",
" <tr>\n",
" <td>**db2**</td>\n",
" <td> [[ 0.06589489]] </td> \n",
" </tr>\n",
" \n",
"</table> "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Question**: Implement the update rule. Use gradient descent. You have to use (dW1, db1, dW2, db2) in order to update (W1, b1, W2, b2).\n",
"\n",
"**General gradient descent rule**: $ \\theta = \\theta - \\alpha \\frac{\\partial J }{ \\partial \\theta }$ where $\\alpha$ is the learning rate and $\\theta$ represents a parameter.\n",
"\n",
"**Illustration**: The gradient descent algorithm with a good learning rate (converging) and a bad learning rate (diverging). Images courtesy of Adam Harley.\n",
"\n",
"<img src=\"images/sgd.gif\" style=\"width:400;height:400;\"> <img src=\"images/sgd_bad.gif\" style=\"width:400;height:400;\">\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# GRADED FUNCTION: update_parameters\n",
"\n",
"def update_parameters(parameters, grads, learning_rate = 1.2):\n",
" \"\"\"\n",
" Updates parameters using the gradient descent update rule given above\n",
" \n",
" Arguments:\n",
" parameters -- python dictionary containing your parameters \n",
" grads -- python dictionary containing your gradients \n",
" \n",
" Returns:\n",
" parameters -- python dictionary containing your updated parameters \n",
" \"\"\"\n",
" # Retrieve each parameter from the dictionary \"parameters\"\n",
" ### START CODE HERE ### (≈ 4 lines of code)\n",
" W1 = parameters[\"W1\"]\n",
" b1 = parameters[\"b1\"]\n",
" W2 = parameters[\"W2\"]\n",
" b2 = parameters[\"b2\"]\n",
" ### END CODE HERE ###\n",
" \n",
" # Retrieve each gradient from the dictionary \"grads\"\n",
" ### START CODE HERE ### (≈ 4 lines of code)\n",
" dW1 = grads[\"dW1\"]\n",
" db1 = grads[\"db1\"]\n",
" dW2 = grads[\"dW2\"]\n",
" db2 = grads[\"db2\"]\n",
" ## END CODE HERE ###\n",
" \n",
" # Update rule for each parameter\n",
" ### START CODE HERE ### (≈ 4 lines of code)\n",
" W1 = W1 - learning_rate * dW1\n",
" b1 = b1 - learning_rate * db1\n",
" W2 = W2 - learning_rate * dW2\n",
" b2 = b2 - learning_rate * db2\n",
" ### END CODE HERE ###\n",
" \n",
" parameters = {\"W1\": W1,\n",
" \"b1\": b1,\n",
" \"W2\": W2,\n",
" \"b2\": b2}\n",
" \n",
" return parameters"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"W1 = [[-0.00643025 0.01936718]\n",
" [-0.02410458 0.03978052]\n",
" [-0.01653973 -0.02096177]\n",
" [ 0.01046864 -0.05990141]]\n",
"b1 = [[ -1.02420756e-06]\n",
" [ 1.27373948e-05]\n",
" [ 8.32996807e-07]\n",
" [ -3.20136836e-06]]\n",
"W2 = [[-0.01041081 -0.04463285 0.01758031 0.04747113]]\n",
"b2 = [[ 0.00010457]]\n"
]
}
],
"source": [
"parameters, grads = update_parameters_test_case()\n",
"parameters = update_parameters(parameters, grads)\n",
"\n",
"print(\"W1 = \" + str(parameters[\"W1\"]))\n",
"print(\"b1 = \" + str(parameters[\"b1\"]))\n",
"print(\"W2 = \" + str(parameters[\"W2\"]))\n",
"print(\"b2 = \" + str(parameters[\"b2\"]))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Expected Output**:\n",
"\n",
"\n",
"<table style=\"width:80%\">\n",
" <tr>\n",
" <td>**W1**</td>\n",
" <td> [[-0.00643025 0.01936718]\n",
" [-0.02410458 0.03978052]\n",
" [-0.01653973 -0.02096177]\n",
" [ 0.01046864 -0.05990141]]</td> \n",
" </tr>\n",
" \n",
" <tr>\n",
" <td>**b1**</td>\n",
" <td> [[ -1.02420756e-06]\n",
" [ 1.27373948e-05]\n",
" [ 8.32996807e-07]\n",
" [ -3.20136836e-06]]</td> \n",
" </tr>\n",
" \n",
" <tr>\n",
" <td>**W2**</td>\n",
" <td> [[-0.01041081 -0.04463285 0.01758031 0.04747113]] </td> \n",
" </tr>\n",
" \n",
"\n",
" <tr>\n",
" <td>**b2**</td>\n",
" <td> [[ 0.00010457]] </td> \n",
" </tr>\n",
" \n",
"</table> "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 4.4 - Integrate parts 4.1, 4.2 and 4.3 in nn_model() ####\n",
"\n",
"**Question**: Build your neural network model in `nn_model()`.\n",
"\n",
"**Instructions**: The neural network model has to use the previous functions in the right order."
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# GRADED FUNCTION: nn_model\n",
"\n",
"def nn_model(X, Y, n_h, num_iterations = 10000, print_cost=False):\n",
" \"\"\"\n",
" Arguments:\n",
" X -- dataset of shape (2, number of examples)\n",
" Y -- labels of shape (1, number of examples)\n",
" n_h -- size of the hidden layer\n",
" num_iterations -- Number of iterations in gradient descent loop\n",
" print_cost -- if True, print the cost every 1000 iterations\n",
" \n",
" Returns:\n",
" parameters -- parameters learnt by the model. They can then be used to predict.\n",
" \"\"\"\n",
" \n",
" np.random.seed(3)\n",
" n_x = layer_sizes(X, Y)[0]\n",
" n_y = layer_sizes(X, Y)[2]\n",
" \n",
" # Initialize parameters, then retrieve W1, b1, W2, b2. Inputs: \"n_x, n_h, n_y\". Outputs = \"W1, b1, W2, b2, parameters\".\n",
" ### START CODE HERE ### (≈ 5 lines of code)\n",
" parameters = initialize_parameters(n_x, n_h, n_y)\n",
" W1 = parameters[\"W1\"]\n",
" b1 = parameters[\"b1\"]\n",
" W2 = parameters[\"W2\"]\n",
" b2 = parameters[\"b2\"]\n",
" ### END CODE HERE ###\n",
" \n",
" # Loop (gradient descent)\n",
"\n",
" for i in range(0, num_iterations):\n",
" \n",
" ### START CODE HERE ### (≈ 4 lines of code)\n",
" # Forward propagation. Inputs: \"X, parameters\". Outputs: \"A2, cache\".\n",
" A2, cache = forward_propagation(X, parameters)\n",
" \n",
" # Cost function. Inputs: \"A2, Y, parameters\". Outputs: \"cost\".\n",
" cost = compute_cost(A2, Y, parameters)\n",
" \n",
" # Backpropagation. Inputs: \"parameters, cache, X, Y\". Outputs: \"grads\".\n",
" grads = backward_propagation(parameters, cache, X, Y)\n",
" \n",
" # Gradient descent parameter update. Inputs: \"parameters, grads\". Outputs: \"parameters\".\n",
" parameters = update_parameters(parameters, grads)\n",
" \n",
" ### END CODE HERE ###\n",
" \n",
" # Print the cost every 1000 iterations\n",
" if print_cost and i % 1000 == 0:\n",
" print (\"Cost after iteration %i: %f\" %(i, cost))\n",
"\n",
" return parameters"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"c:\\anaconda3\\envs\\tensorflow\\lib\\site-packages\\ipykernel_launcher.py:26: RuntimeWarning: divide by zero encountered in log\n",
"C:\\Users\\cucoa\\OneDrive\\Documentos\\git\\deep-learning-specialization-coursera\\course_1\\week_3\\assignment_1\\planar_utils.py:34: RuntimeWarning: overflow encountered in exp\n",
" s = 1/(1+np.exp(-x))\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"W1 = [[-4.18494482 5.33220319]\n",
" [-7.52989354 1.24306197]\n",
" [-4.19295428 5.32631786]\n",
" [ 7.52983748 -1.24309404]]\n",
"b1 = [[ 2.32926815]\n",
" [ 3.7945905 ]\n",
" [ 2.33002544]\n",
" [-3.79468791]]\n",
"W2 = [[-6033.83672179 -6008.12981272 -6033.10095329 6008.06636901]]\n",
"b2 = [[-52.66607704]]\n"
]
}
],
"source": [
"X_assess, Y_assess = nn_model_test_case()\n",
"\n",
"parameters = nn_model(X_assess, Y_assess, 4, num_iterations=10000, print_cost=False)\n",
"print(\"W1 = \" + str(parameters[\"W1\"]))\n",
"print(\"b1 = \" + str(parameters[\"b1\"]))\n",
"print(\"W2 = \" + str(parameters[\"W2\"]))\n",
"print(\"b2 = \" + str(parameters[\"b2\"]))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Expected Output**:\n",
"\n",
"<table style=\"width:90%\">\n",
" <tr>\n",
" <td>**W1**</td>\n",
" <td> [[-4.18494056 5.33220609]\n",
" [-7.52989382 1.24306181]\n",
" [-4.1929459 5.32632331]\n",
" [ 7.52983719 -1.24309422]]</td> \n",
" </tr>\n",
" \n",
" <tr>\n",
" <td>**b1**</td>\n",
" <td> [[ 2.32926819]\n",
" [ 3.79458998]\n",
" [ 2.33002577]\n",
" [-3.79468846]]</td> \n",
" </tr>\n",
" \n",
" <tr>\n",
" <td>**W2**</td>\n",
" <td> [[-6033.83672146 -6008.12980822 -6033.10095287 6008.06637269]] </td> \n",
" </tr>\n",
" \n",
"\n",
" <tr>\n",
" <td>**b2**</td>\n",
" <td> [[-52.66607724]] </td> \n",
" </tr>\n",
" \n",
"</table> "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 4.5 Predictions\n",
"\n",
"**Question**: Use your model to predict by building predict().\n",
"Use forward propagation to predict results.\n",
"\n",
"**Reminder**: predictions = $y_{prediction} = \\mathbb 1 \\text{{activation > 0.5}} = \\begin{cases}\n",
" 1 & \\text{if}\\ activation > 0.5 \\\\\n",
" 0 & \\text{otherwise}\n",
" \\end{cases}$ \n",
" \n",
"As an example, if you would like to set the entries of a matrix X to 0 and 1 based on a threshold you would do: ```X_new = (X > threshold)```"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# GRADED FUNCTION: predict\n",
"\n",
"def predict(parameters, X):\n",
" \"\"\"\n",
" Using the learned parameters, predicts a class for each example in X\n",
" \n",
" Arguments:\n",
" parameters -- python dictionary containing your parameters \n",
" X -- input data of size (n_x, m)\n",
" \n",
" Returns\n",
" predictions -- vector of predictions of our model (red: 0 / blue: 1)\n",
" \"\"\"\n",
" \n",
" # Computes probabilities using forward propagation, and classifies to 0/1 using 0.5 as the threshold.\n",
" ### START CODE HERE ### (≈ 2 lines of code)\n",
" A2, cache = forward_propagation(X, parameters)\n",
" predictions = (A2 > 0.5)\n",
" ### END CODE HERE ###\n",
" \n",
" return predictions"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"predictions mean = 0.666666666667\n"
]
}
],
"source": [
"parameters, X_assess = predict_test_case()\n",
"\n",
"predictions = predict(parameters, X_assess)\n",
"print(\"predictions mean = \" + str(np.mean(predictions)))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Expected Output**: \n",
"\n",
"\n",
"<table style=\"width:40%\">\n",
" <tr>\n",
" <td>**predictions mean**</td>\n",
" <td> 0.666666666667 </td> \n",
" </tr>\n",
" \n",
"</table>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"It is time to run the model and see how it performs on a planar dataset. Run the following code to test your model with a single hidden layer of $n_h$ hidden units."
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"scrolled": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Cost after iteration 0: 0.693048\n",
"Cost after iteration 1000: 0.288083\n",
"Cost after iteration 2000: 0.254385\n",
"Cost after iteration 3000: 0.233864\n",
"Cost after iteration 4000: 0.226792\n",
"Cost after iteration 5000: 0.222644\n",
"Cost after iteration 6000: 0.219731\n",
"Cost after iteration 7000: 0.217504\n",
"Cost after iteration 8000: 0.219504\n",
"Cost after iteration 9000: 0.218571\n"
]
},
{
"data": {
"text/plain": [
"<matplotlib.text.Text at 0x20f65704b70>"
]
},
"execution_count": 23,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYQAAAEWCAYAAABmE+CbAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvXeUJNlZ4Pv7IiIjfWWWr+pqb2ZG40ca+VlpxEiA1MIv\nTgdhxCJBs1ixmIa3y4MVy9vHLotfCdADIVgJEIJBBoTeamSQN+M0RjM9bct1ufQuzN0/IjIrbZnu\nqsqq6vid06ezMsy9ERlxv/vZK0opAgICAgICtH53ICAgICBgdxAIhICAgIAAIBAIAQEBAQE+gUAI\nCAgICAACgRAQEBAQ4BMIhICAgIAAIBAIexIR+bCI/MAG9iuIyPGd6FO/EJELIvLqHWrr5SLyjH9f\nv3ULzvdnIvKf19je8/cTkR8UkU+tcexDIvLvrrePXc77qyLy7q0+71YiIl8Vkfv73Y+9SCAQtgl/\noCqLSF5EMiLyaRH5URG57nuulHqtUurPN7BfQin13PW2107TtRVEZEVEPigih7a6nV3IrwG/79/X\nv9/uxrbr99vvKKVuU0o9tB3nFpFXiohaS5DvZQKBsL18k1IqCRwBfhP4BeBP+9ulLeOblFIJYBKY\nB36vz/3ZFCJiXMNhR4Cv7mB7AeyeeyciIeB3gM/1uy/bRSAQdgClVFYp9SDw3cAPiMjtACISFpHf\nEpFLIjIvIv9TRKL140TkW0TkYRHJicg5EflG//uGOUBETorIx0UkKyKLIvLepuOViJz0P6dE5F0i\nsiAiF0XkV+raSt384PdlRUTOi8hrN3htFeBvgVub2l2rrRaTg4gc9ftpNF3br4vIv/ra1UdEZKRp\n/zf651wSkV9u7ouIvEhEPuNrZLMi8vsiYrbdjx8XkWeAZ0TkD0Tkv7Wd40ER+Zn26xSRc8Bx4B99\nzSgsIgf8/ZdF5FkR+ZGm/X9VRP5WRN4tIjngB3vcwkFfw8qLyOdE5ERbf+u/37DfVk5EPg+caD6J\niLxGRJ7yn4PfB6Rt+5tE5En/9/1nETnS1s6PimcOy/j3peX4XojI34jInN/uJ0TkNv/7F/rPtN60\n77eLyCP+Z01EftF/rpdE5K9FZMjfVn8mflhELgH/u0u7IyLyAb+/yyLyyaZnrGFG9LcX/H9F/7xH\n/W2vF+/9qmvwd65zuW8FPgI8tZF7sxcJBMIOopT6PHAF+Df+V78J3ATcDZwEpoD/CN7gBrwL+A9A\nGngFcKHLaX8d7yEdBA7Se6b+e0AKb1B7JfD9wA81bX8x8DQwAvxX4E83MiiISAxP0H12E22txxv8\n/ccAE/g5v61bgT8C3ggcAIbxrrmOA/yMfw0vBR4AzrSd+1vxrvVW4M+B720aSEaAVwN/1d4hpdQJ\n4BK+ZqSUqgLvwfs9DwD/FvgNEfm6psO+BU9YpoG/7HGt3wP833i/37PA23rs9wdABU8je5P/j6Z+\n/x3wK/61nwNe3rT9W4CzwLcDo8Angf/Vdv7XAy8E7gS+C/iGHv1o58PAKbzf6sv416mU+gKwBHx9\n075vxHumAX4C77d4Jd79W/GvsZlXAs/r0Ze34t37UWDcv76OOjxKqbT/eyXwZvefBKZF5B7gncBb\n8J6jtwMPiki420X6AvRNeGbD/YtSKvi3Df/wBu9Xd/n+s8Av483gisCJpm0vBc77n98O/HaPcz8E\n/Dv/87uAdwAHu+yn8ASNDtSAW5u2vQV4yP/8g8CzTdti/rETa1xbAcgAFjAD3OFvW6+tXwXe3bTt\nqN+W0XRtv9K0/QzwT/7n/wi8p2lb3G+r4z77238aeH/b/fi6tn2eBF7jf/73wIc28psCh/AEULJp\n+38B/qzpOj+xzjPyZ8CfNP39OuCpHr+fBdzStO03gE/5n78f+GzTNsEbLOvPyIeBH27argEl4EhT\nO/c1bf9r4Bd79Lnl92vblvbPlfL//gXgL/3PQ36bk033/YGmYyf9azSanonja9y7XwP+ATi5kXcP\nb9JyARj1//4j4Nfb9nkaeGWP9v4B+O6m3+0/r/Xb7tV/gYaw80wBy3gzmxjwJV9lzQD/5H8P3oBz\nbgPn+3m8AeDz4kVXvKnLPiNACLjY9N1Fvy915uoflFIl/2NijXa/VSmVBiJ4A+nHRWRig22tx1zT\n51JTPw4Al5v6WcSbhQIgIjf5ZoQ530zzG35/mrnc9vefA9/nf/4+4C822McDwLJSKt/0Xft1trfV\njV7X2swo3kDZfL7m+9t+X1TbvkeA32l6zpbxnpmuv/8a/WhBRHQR+U3f7JNjVYOt3/N3A98kInE8\nreOTSqnZpj69v6lPT+IJ2PGmJta6f/8vnkb1ERF5TkR+cY1+3gP8PvBtSqmFpvbfWm/f78MhvHvZ\nfvw34Qn+97Zv228EAmEHEZEX4r2EnwIWgTJwm/LU2rRSKqU81Ra8l+FEj1M1UErNKaV+RCl1AG8m\n/od1u3MTi3izryNN3x0Gpq/vikAp5Sil/g7vZb5vA20V8QRhnYlNNDeL99ICDXPVcNP2P8Kz755S\nSg3gmRHazV7tZoV3A98iInfhmSc2Gj00AwyJSLLpu/Z7ulWlhBcAm6Zr99uq035fpG3fy8Bbmp6z\ntFIqqpT69HX26w14ZrFX45kIj9a7AKCUmgY+g2eqeiOtwvYy8Nq2PkX8Y+r0vH9KqbxS6q1KqePA\nNwM/KyIPtO8nImN4v+mPK6W+0tb+29rajyml2k1p4Jke7/UnGnN42sZPi8g/9Lwze5RAIOwAIjIg\nIq/Hszm/Wyn1mFLKBf4Y+G3/oUVEpkSkbi/9U+CHROQB3wE3JSK3dDn3d4pI3Y6+gvcSuc37KKUc\nPDPA20Qk6dtDfxZvMLzeaxPfRj0IPLmBth4GXiEih0UkBfzSJpr7W+D1InKfeM7iX6P1GU4COaDg\n36sfW++ESqkrwBfwBqv3KaXKG+mIUuoy8Gngv4hIxHdI/jBbcE+7tOXg+Qh+VURivi+lOQ/lg8Bt\nvtPWAH6SVkH7P4FfanL4pkTkO7ega0mgiqelxfA0snbehafF3uFfQ3Of3uY/H4jIqP8cbQjfIXzS\nF35ZvAmJ27aPgffMvFsp9ddtp/hj4EdF5MX+MxwXkdNtAr7O/8Wqr+9u4EH/+M34xfYEgUDYXv5R\nRPJ4s5FfBv47rQ/RL+CpvZ/1Ve6PAjdDwwH9Q8Bv4z3wH6d11l3nhcDnRKSA96D+lOoeu/4TeLPz\n5/A0lL/Cc6pdz7UV8AbgtwE/oJSqh2T2bEsp9S/Ae4FHgS8BH9hog/75f9w/3yyeALzStMvP4c1a\n83gv7EZV/D/HG7A2ai6q8714s+IZ4P3Af1JKfXST59go/x7PjDOHZ8P+/+oblFKLwHfiBSks4Tl5\n/7Vp+/uB/wd4j/+cPQ5sKIpsHd6FZ7qaBp6gNbCgzvvxzUNNpkjwHLwP4pl88v6xL95E26fw3pcC\nnhbyh0qpj7XtcxAvgOOnmyKNCiJyWCn1ReBH8ExJK3jv4Q92a8jXRubq//A0+6JSankT/d0TiO8k\nCQi4YRGRV+DN7I+o4IXYcsQL2X3LNgrLgC0i0BACbmjESzb6Kbxon0AYbDEi8h14ZsyOXIKA3ceu\nyAAMCOgHIvI84IvAI+xDe3C/EZGH8PI93uj7zAJ2OYHJKCAgICAACExGAQEBAQE+e8pklDZMNRGK\nrb9jQEBAQECDpyvZRaXU6Hr77SmBMBGK8c6T9/W7GwEBAQF7ipc//sGL6+8VmIwCAgICAnwCgRAQ\nEBAQAAQCISAgICDAJxAIAQEBAQFAIBACAgICAnwCgRAQEBAQAAQCISAgICDAZ0/lIQQEBAQEbJyz\np/0lxR//4Ib2DwRCQEBAwD6jIQg2yZ4SCNPpUe5+rc3DH95T3Q4ICAjYEa5VENTZcz6E12k/ed0X\nHRAQELDf2Ipxcc9OtesX/xsf/MM+9yQgICCgf2zlBHnPCoQ6gWAICAi4EXnpO+/kVe/b2mKfe85k\n1Iuzp8/w0nfe2e9uBAQEBGw7Z0+f2XJhAPtAQ2jmVe+7D07fF2gLAQEB+5Lt9p/uK4FQJzAjBQQE\n7CciH/t2fva3Jra9nX0pEOoEgiEgYGPUqi6ZFRvHgXhCIzmgIyL97lYA/jj2WzvT1r4WCHXOnj7D\nXd+c4bvf8lf97kpAwK4jn7WZnbZQyv8757CyZHPoaBhNC4RCv+hHeH3fncoioovIV0TkA9vZziMP\npjl7+gwve+yt29lMQMCewnUVczOrwgBAuVCtKLIrdv86dgPzssfe2rdcq74LBOCngCd3qrH7f7Ec\nJLYFBPhUym7X75WCfK77toDt4+zpM9z/i+W+td9Xk5GIHAROA28DfnYn2w78C3uXimbyaPomLsYO\nEHOq3JF5msPluX53a0+iaYLqsS1wIewcu2WS2m8fwv8Afh5I9tpBRN4MvBkgPDC65R0IBMP1Uyo6\nXJ2zqFYUug5DIwaDw8a2OCUrmsnfHvoGKloYR9NZBuYiI9y7/Bh3Zb+25e3tdWxbYdsK05Su/oBw\nRNA0cNqUARFID/V7eLgx2C3CAPooEETk9cBVpdSXROT+Xvsppd4BvAMgOXmq12Tmugkcz9dGpexy\n5WKtYYN2HFi8auPYitEJs2XfWs0lu2xjWX4kS0rvGKRcR1EquiAQi2sd2x8fONUQBnVszeALQ3fw\nvNxzmOrGtHuXig6L8xbVqiIUEoZGDQo5l0LeQcQzAQ2NGgyPdApq1cUypBSEzM7vA7aO3SQI6vRz\nCvBy4JtF5HVABBgQkXcrpb6vXx165ME0j5w+E2gLm2DxaqtDErzBZGXZYXhMNQb0YsFh+tKq4Cjk\nHZaXbI4cC6Pp3j75nM3sFathqlAKDhwySSRXB/9L8ckWYVBHVy6L4UEOVBa2/iJ3OaWi0yKUq1XF\n7BWrsb3+/fKCDUphWeDYinhSwzB6a3FLV21iCUU4LERjWhCGukXsRkFQp28CQSn1S8AvAfgaws/1\nUxg0E5iRNk612kNpE7AsbzBRSjF7pdYayaLAqimWl2xGxkLYljeIKbU6gLkiXJwTTkXB9J/UuF1m\nQakOA3dNC3ElOsZkZYEbbdhamO8Uyt1QCpYWnMbfpaKLrtPz2ELepZD31IdQSDhywkTXd0Mcyt7k\nZY+9ta8O440QGAnXIBAM6xMOC7bVZURREPJnn7Wqwu1hlsjnHEbGQuRzTvOhXDx1J5dP3o6r6Xxe\n2bxw+TFuyz3LndmnuRKbwJa2R1eEx9K3oETjxcuPbeEV7n6qlWuzpCoF9gYtbJaluPBsleM3RQJN\n4Ro4e/oM7HJhALsj7BSl1ENKqdf3ux+9OHv6DO99+xv63Y1dyfBoqCMaRQRSg3rDFCRrPGWav81x\nVGOmeunkHVw6dQdOyETpOjUjzGeG7uIT2UnUMzO8ZP7LiHI7pra2ZvBY6iZq7cJin2OErm+A3uj4\nbttQKgShqJvh7Okzu9pE1M6uEAh7gXpi292vvTGdlr2IxjSmDpuYpjeqaJoXZTQ2EWrsY5paY3sz\n9UiWXNZmecm7rwq4fOp2XCPUsq9rhLhw8z3kcw6xR54kaRW6j2SOy3wtunUXuAcYHjU6b8UmZMRG\nzE11CgVn/Z0CgN3tK+jFjTWV2gJep/0knA7MSM3EEzrHTukopXqaEw4cNrl8vroa3qhgIKVTq7os\nL64OMq6uY+uhrueoRWMAWLYiWc6RCyU61A+laeQuZKgcFCLRG2O+k0obuK5i8artRQwJDA0bRGPC\n/IyFZa17ig3j2IpqxSUcuTHu7bWwFwVBnUAgXCOBf6GTXsLAdV1KRZfEgAYiGLpQq7lUqy6VTOv0\nVHMczGqZWjTecZ5YLuN9UHDLlceZe94ETpNA0GyL0ZkLGLUay4s6Bw7dOHGTg0Mh0oMGjgO6vvpb\naJoNPVPPNk8+51LIVwlHhINHwuh64E+os5cFQZ1AzF8ngX9hbQp5m2eerDI/Y5FZdsksOSxetcll\nXCrlzoFKgBNf/QJam7dTs21OPPHFxk7DpSVu+/zHiBRziOui2TYHLn6Nmx/5DODlPNxoiAiGIS2C\neS3/TSKpYXRXxtZEKaiUFXPTtWvo5f6jn7WHtppAQ9gC6vkLH3J/l4c/HNzSOrWay/Slzdsrxmcu\noDs203c+n7yRIJbPcPyJL5FengfxQiCXFy2GrGle/P//Ha5uoDkOzUUYQiFZ04R1ozA4bLTkJDRT\nLLiMThhcne30i4lAKAS1Ncb8YsHFddUNXRF1r0QPbZRg9NpCAv9CK5nla3fAj8xfYfSjVxgaNaiW\nXYoFL3t5IKWTHtK5dN4bqQTQnc52igWXi89VOXzUS3xTSpHPOWRXHFwXBlIa6UED2eeDWXJAZ5bu\nAkH5fpxKWZHLrPpxNN0TJMsLa/9+SvlZzjegnWEv5BRcC4FA2AYC/4JHrXZ9tmulvOzaoyfDTJmr\no461AXOQUl7+w9V5i4kDJvMzFrmss5rNW3HJ5xwOHQ3vay1CRIjFNa8cSBvhsKDrGpNTJsOjLuWS\ni6Z52edLC/a6rgcj5GWX53OuFzE2aBBP7v+M5v2mFTRzA8r2neNG9y/EYht/vPTOahSAn7yWbQ11\nDJkaoQ3E3tePrVQcshmnI1O6UlEU8/vf1zA2EWrke9QRgfEDraHByQGdhXmLWpUN+aFF4OqcTano\naXAzV2pcndvCkKZdxl7LKbgWAg1hm7mR/QupQYOVJbtrNqwIjaJr8YRGNKZ5YZPdkp67fHfgkMml\n89WWUhfdUAquXOhuCFeuV2MpMdBDGu0TwhGNoyfCrCzZlMteyOjQsIEZbpUSS1ctrA36iTUNL5y1\nTchmVxwGh11Mc//MNfe7EGjmxhqh+siN6F/QdeHIiQiLVy0KfmmKeEJjbDKEZXm1jMJhwQxr1Gou\ni1e7Oze7DdjhiMaJmyPkcw625fkHupVwUMqrwNqzj2sUd9st2LaiUnawLEWlpBDNyz2IbkIDC5ka\nY5Nrh+FmMxtPOtM0cHu4GErF/SMQbiRhAIFA2HH2u39BKc8Mk814s/2BtM74ZIiJA62Dka5DJLL6\nt2lqDI8aLC2sagkiMDikE+mRBKVpQirtPcLJAZ1L56u4fkWLugbiKnqaP0Qgld692oFSisV5i+Ul\nh0IyzfTRW6jGEgxenebA5WcYH3IYHr2GuNFe7W1i3141kETYF7kJN5ogqBMIhD6xXwVDu/O2VHTJ\nZx0OHDLXdTYOj4aIJ3XyGRsFDKSMDWcbm2GNY6ci5DI2taoiEtVwHMVCF62jzoFDJqFdPJPNZx1W\nlh0WJg7z5PNfgatpoGlkhseZPn4r937yH0ml1XXXMqqTHNDJrlx/aYp4Yvfe0/WIfOzb+dnfmuh3\nN/pGIBD6zNl95F+oVtwWYQDebL1Y8CJYYvH1Z+ORiEZk4toyjHVdGBxenTGXyy6C3THzFYHJgyHi\nCY1sxiazbPuhqDqDQ0ajKF+/WV6ycRCevvtluMbq8+EaIaoiXDpxGwdzjze0pOtldCxEqeBi26pF\nSxsdN1i8anetWAue+Uj5/x88HN6zeQlnT5+B3+p3L/rL3h+F9gH7xb9QLLg9ncLFgrMhgbCVRKMa\nsYRGqalfIt6ykYmkzvysRa4p+mhpwSaXdThyfHcMaq4DpUQK1WVBIKUbLE4cQSt8dcva0w3h6Mkw\nhZxDueximsJA2sCyFKrHSnQDKY3UoLcKWyQqezLk9EY1D3UjEAi7iL1uRvJq6HRG/fTTrjx1yCSz\nbJNdcXwzlM7gsDfI5bqEolo1z0G9VbPua6WoR1k4eZhc1UD1GGQNq7bl5hlN84TAQLr5OzBN6VgM\nSQQGR0I9fTy7nUAQdBIIhF3IXhUMiQGd+Tmrq3dyINWfR03EMyM1m5IAyiXHS3PusvxnMe+SStM3\nHhs4xeeG7wIUylW4ooHr0pxMoNkWd+af2RFNRkQ4eDTM9OUq1bIC32E/PhkIg/1GIBB2MXvNv6Dr\nwsHDJtOXWoPZJw+aGCGhUl5d9H0gpffVoWsY0jusRrauOuhmWQkl+dzwnavrRtdvkVJotoUohavp\nnFx8hlvtKzvWL8MQDh8NY9UUrqsIR/ZmRnIgCNZmb4w0NzB7zb8Qi+ucvCVCueTZ7aMxDU0T5mdr\nntmmyV4/NumVbO5PP7WeCW21XutE7wDPJI54GkEb4tgcPPdVBjJLJDOLjEZqyMGdK++dy9oszNvY\nlkLTvFpH3sI8e0Mo3OjRQxslEAh7hL1kRvLq56w6Qsslp0UYgGeauTprkUjq3mx9h1kru7mfAsEV\nDdVluTMBwpUyI/OXATCSO/fqFgsOc9NW4565Liwv2riuYuwaI8J2irtfa3uTqhs8emijBAJhj7GX\nBEOd9lDUBuINNv1w4DaXzminn9nLx4pX+GrqFHb7utAiDPvCwCskt3MRW83JgnWUgsyyw8jY7i1/\nHZiHNs/e9AgFcPb0GV76zjv73Y0N0dOq0L+JOCJCekjv6JsIDA33L3t5vLrM0cIVNOU26ktrjs2x\np75MtFpCN2Dq8PYn1LmuolR0mL1SpVzqXQDQsfv4I/bgvW9/QyAMrpFAQ9jDvOp998Hp+3a9tjCQ\nMsgsd9cSEon+Db6j4yFcx9Ng6hFHg8MG6aH+vRaPDtzE+cRBXBT4pqObC+d5qXYO93gYM7y9sf5K\nKZYWbZa7aAXtiNAXc99anD19Bh7sdy/2LoFA2AfsdjNSJKoxNGKwvGg3DXMwMRXqq3lGRJiYMhmd\nUNiWIhSSvmYp540Yn2+OMPJ6ydeSx7g9cY6hWnb7+5B1NiQMAIZGds8CQ4FGsDUEAmEfsZsFw8hY\niIGU7oWdakJyoD/O5G7ouvS1IJtjKxauWjwxdBS3y0jsisb5+NSOCISFq9aGhIER8gRCvwmih7aW\n/v+iAVvO2dNn+Nh3fIrPvOnRfnelBTOsMRTe/W4rpRTlkkup6KIbwkBK3zaBoVzFc5cc5gYPkU2N\n9vCrrLPowxZh1VzsDa5v41WU7Z8QDaKHtodAIOxT9op/wXUV+axDqegSMoXUoLGh1dC2C6UUVy7W\nGnkUIrAwb3HoiEk0tvX+jvPuEB+//36vbU3rWrdIU4oTxctb3nY7K5tYAzu2DfdiowTmoe0jEAj7\nnN1sRnIcxcXnqtiWX11TvPj2g0fMHS+EVyezYjeEAUDNMMkNjpHPV7knmkfbwlmxg/DQ8VfihNpi\n+ZVCXBcRhSC8aOkx0lZhy9rtxUbXwNY0GBnb+aGjoRUEbBuBQLhB2I2CYWnBwrLUqpnE/zg7bXH8\nVH9KIzQXvLt04jbO33IP4td9fkLV+ObZj5Oyt2Zwno2Oono4ZeP5FW4uXOBmZ5akXdqS9tYjFtN6\nrjEdiQqO4+0zNGrs+IpogVawMwQC4Qbj7Okz3PXNGb77LX/V766Qz7ldbeaO7Uf9mP0zHa0MT3D+\n5ntQuoHylZWSCvEP4/fzxukPdMkl3jyuaN3PI0KkUuIFlWd3VChaVncNITmgc+BQfzKSA0Gws+x+\nD1/AlvPIg+ld8aL1ilhUanP27K3Eq+0Pl4/fitLbzFYilMMxztlDW9LWZHkB1aVukW5b3O5c3lFh\nUPLLi3RjbHLn541nT5/ZFc/ojUYgEG5g+v3SpbpkCtdZWXLWzJDdLlJpnVhCo5xM9Uyxfs4c35K2\nQsrhlVc/j+7aaMobjA3XYqq6wKnK9Ja0sVHa14aoI5q3DOpOEgiC/hGYjAL65l8YHDLIrjg9i8nl\nMjbR2M6aKkSEqUMmKadAWQ10FQpiObBJn7frKm9FtsZ60TrDoyFOFi8zenmFryWPUNXCHCnNcLA8\ntyUmqb1GIAj6TyAQAhrstGAQEQwDatXu222nP3VyRIQ7i+eYGzjQuc11marMQ3zj51NKceVClUpl\nda3izLJDseBy9ESYlF3ghStbtxTmtTCQ0rtrCQri21xe5KXvvNMLkw7oO4HJKKCDs6fP8N63v2FH\n2nLXGPP7uRrX0fIsw4UFxFm1q4tjM7g8xykzs6lzlUtuizAAf7lOS1HoEdWz00RjGqnBJhNefVW0\nA6FtzeI+e/pMIAx2EX3TEETkEPAuYBwv1uQdSqnf6Vd/Alp55ME0j5w+s+3aQjyuUyl1dyAnU/1L\nfhLg265+nK9ET/C1gWPgKo4tPssLrPObTpyrlN2u9nnlemtFJAf6d511RITxSZNU2lvVTtO8+x8K\nbY9QDsxDu5N+moxs4K1KqS+LSBL4koj8i1LqiT72qSuhik1qqUyoalOLGOSGo1jhG8Patt1mpPSQ\nQWbZpmkijgjEElpfy2MD6LjcW36Ge8vPrH55DT97yNTQ/GWRmxFhR+P5lavIZR1yWQdNh/Sg0WEO\nikQ1ItHt61MgCHY3fRvVlFKzwKz/OS8iTwJTwK4SCOGSxdjlHOKtLU6oViOWrzF/eIBaNLTu8fuF\n7RIMhiEcORFhcd6iWPDKULsOFAsuFwpVQqbn5DX3QA2kXiQSGqIBXQTCTmlBSikuX6xSKa+aror5\nGoPDBqPjO/McB8Jg97MrprkichS4B/hcl21vBt4MEB4Y3dF+AQzOF9GaZqqCtwb70HyJuaOpaz6v\nbjkklyuEKza1sE5+KIpt9t90sB7bIRhCIWHyoEmt5nLh2WpjwFJ4y1levlDl+E2RPbN+bzOVsks+\nZxOLaxQLLq6vCZlhOHAwvGNVVgs5t0UYgOfHWF6ySQ/q27rgzo4JAqWIlCw0R1GNhXCM1muK5aoM\nLJUxbJdK1CAzGsNu0vTFcUkvlonnvCiHYjJMZjSK0oR4rkYsV0VpQj4doRrfn5PBvgsEEUkA7wN+\nWimVa9+ulHoH8A6A5OSpnTUiKIVZ7Z6sY1auPXEqVLWZuJhDXG/13HDZJpGtrqt1iKuIZypEyjaW\nqVNIh3E1z/vXqwTCdnH29Bk+5P4uD3946x6hzHL3Ovyu68XCb3e0y0ZwXUWx4E31Y3FtzQF9bqZK\ndqXTaSwC0aiOGd653yyf77GMqYKZKzUOHwtvucDdyeihUNVm/FIOUV79E1FQSoRYnkzg6hrJpTLp\nxVJjchcrWERLWWaPpLHDOijFxKUcRtVpRNokshUixRquoWFWbDS/tEq0UCM3FCU7GtuRa9tJ+ioQ\nRCSEJwwTdnpPAAAgAElEQVT+Uin1d/3sS1f8gVa6hMK41zGzG5wvNYQBNGkdc0UWDiYZWCoT9gf9\n3HAUK2JgVGwmL2URt7G4F6mlcuOc5bjB0mQS19g508rrtJ+E01unLfQqvawAexcs1VgsOExfrjV+\nN6W8KJxua0KXinZDGOTSI1y46S5KyTSJ7DJHvvYIZJdJDerbUkG1G8Yab3ql7EU7baVz++zpM96b\nvRMoxfjFHFrTOwX+oP/MCtWITqTitGwTABdSSyWWDiSJFGqEqq37aAoMywXbbQiS+ruaWi5TSEdw\ntsnp3i/6GWUkwJ8CTyql/nu/+rEeucEIA8vlFrORK97310qkbHVNPDKrDgeeyzT8FWbVIV6oUY4a\nRP1InGYh0ky0aDP17Aq54QiFVASlC4PzRWL5GgClpMnKWHxbBMZWmZHiSY1Ct5ms8sIi+4njKKYv\n1VCq1dc9P2MRjWkdzuHlRU+zXBmZ5LEXPYCrayAalWic5bEp7vrMP5POLe+YQEiley9jCpBdsbdE\nIGyXeUhcRTxbaUyUiulIwyQ0sFTuEAbgD97QIQyat4f99yq9WO6yx6oAaEfh+RdLqfC1XdAupZ9v\n2cuBNwJfJyIP+/9e18f+dCU7EqU4EMYVcDVQAsVUmNxw9JrP6a5h3qkLA1h9GGNtwqDrcf6/1FKF\nA89lOHBuhXiuhqa8mU48V2PiYnZbF1q53lIYyQGdkCktycEiMJDWqZRdLjxb4dmny0xfrlKr7mz8\nfiHX3XSolLfsZDu27fXvmdtfhGsYXg0IAE3DNQyevf1FPct2bAfhiEZ6aHuFz3YJA812OfBchsGr\nJRK5GqmlMgfOrRDN14gULZLL5XXfjV44ptYwDffar9sbI8o3G+/AwkU7ST+jjD7F2r/V7kCE5ckE\nmbEYRs3FNjVvtncd5NOdWkfzWsNdu7GRrjb9r1w6VGTddonla5QGvFlNqGKj2y61iIGrC5GiRchy\nqIUNqlGjZy2f9bjWFds0TThyLMzKsk0+6yCaV96iXHKYvbJqTyrkXIqFKkdPhHcsbLM9ZLR1W+eg\nEI3pVCoOpWS66zGF1BADXUxN28noWKirliDiFfW7Vq5VEMSyFdKLZQzLxQ5pZEailFKdmndqsYRu\nu43nuf7ejE7ncTVBu8a5gSuQHY511QDq9HoDBEiuVIiULeYOp3pXatxj9N2pvFdwdY3aFsVnZ0ei\nGJZDLF9DiXRVd7cDURCqOWi2y9jlHKGaA+L5SFxNEFbtIZapM384hbpGX8m1rtim6cLwaIjhUc+5\nXiw4ZLo4ZpULC3MWU4d3RmWPJzQW5ju/F4F4snPmPTwSYmXZQbetzgVwANOuEd7hUFrRhKnDJtOX\nPDNifUW45IBOIrn5vlyPRhDLVhieW43gC1kuI7NF8iWLlYlEy2Qknq/1NPnoa6W6r4EClibiVPxo\nIcvUMGtuxz5rPf0aEKo6JLIVCoPXbjHYTQQCoR+IsHQgScZyCNUc0vNFwrXNT3PWe2A79hdvoB+Z\nya+qyP50sV0ohWoO6YWi93JeB9frX7g6V+u5rR7tsxOYYY3BIZ2Vphm2CCQGdKJdJgpGSDh81OTQ\n+Se4dPw2XGM1esxwbe7JPbVTXW8hntA5cVOEfM7BcRTxhL7pRLStiB4aXGjVkMGfdWdrGE6ehalk\nQygoTWCL61pZptaijSxPJFryjTbamqZoBIGUkmHKidA1a9a7gUAgbBO65dmVnVBvu60T0nFCOqUB\nm9BS5wuyEdYSCs3bFF5kVCVqMDJrd3XANVP3O6xMbL5P3bhWwdCr8B14ssx1FdoOqeujEybxpEMu\n4+AqryBcPNF7ZbdYXOcVco5/zSW5kD6CphSuCLdln+HO7Nd2pM/d0A0hPXRtr/560UPhkkV6vohZ\ndVCaF/qZG26N90cpdLu7MBcgUrQIl22qMU+I5lNhUht4P9o393wvBJbHWyc61ViIuaMpBpYqhGo2\n1YiBEkhmqmu2qwDDVoRyNeK5GrWIwdyRAcDTHkQpapFrN7/uNIFA2GJCFZuRmbwXrgbYIY3FqeSa\npS7yg1ESuSpYbiPWuf3xUc3/+xszw1EMR5HIVFrsoEqgkI5gWA7Rgmd7LydCLI/He56/G9LLYaYU\n4ZKN7nj+h80k1G3Wv2AYYPdnrZyuxOL6htZ7tsTgobEXciE2hYbCUDb3LD/BrfnzhNQuuqANshHz\nkFm2GLuUW41UcSGRs0jkshSTJksHfFOQCI6hYfQSCgoiJashEHLDUcIVm0jRamzv9n5UYgZXDw5g\nWA6JTNVPUvNW5asHaFhhncxorHHuZqyw4fWxcVKF5kIi681Kepmtmj+bFZsD51YQxGtbQCEsTSYo\nJ/uz6txmCATCFiKOYvxSazx0qOYyfjHH9MnBnsljShdmj6aJZyrEc1XCldaoFQVUogYLU0miJQtx\nFeWE2QghXRmPY9QcYrmql5CTNLEi/k/bbN/w/+6mgrcLCYV3nnaMmsPYpRy663pHKEUxFWZ5PN4y\nC9Icl9RCiXjOM/kUB0wyozGUrm3KvzA0YnB1rvsAGo1pO6YdNGNbiuyKTbWqiMaEVNpAa/O1fHT8\nJVyJTuBqOi5gY/DF4TsZry4zUV3a8T5fDw1hoBSxfA2zYmObOsWBcMszPThX7Kl5xvI1qplVW3tm\nJMpwl/3Bm9A4zYEbIiwcHCBUtTErNuIqBq+WWsw7SvPeAzTBDhtkxrdgaBNhZSxGIlvt3k86hYTg\naQyeGPB3QjEyk2f2WHrXVyMIBMIWEstXEaU6Zg2iFAOLJWrRENWYgRIhlq+h2y7VqBfRozShMBSl\nMBQlUqgxNF/EsFx/th9mZcwbcOsRQu3Ypk5upEvmZLuqKsLSRIKRmXzjhfKHdlzxTEWueE70lbHO\nov+j03mMRsSHJ1Ti2SrVaIhiPSbbTxQyak1Zn5kqiWwVVxNqEYPMWGxDZqT0kIFVU6wstwpJ3YDJ\nqZ0vH1Apu1y+4JXXUAoKeVhetDlyIoJheHeloEW4Eh3H1Vpffls0Hh68hW+c+9cd7/e10KwViOMy\ncTGL4WuxrkB6ocTckVRjkFsrdFPDM7/UBUIxHUFcxdDVUtdjSgOdkxErbDQ07UrcJLlcxqw41KIG\nuaHImubZa0VzFUq65yL0oqsmoSCeqZDt8k7tJgKBsIUYttv1wREFAysVyFRWR98mtdc2PJWyGvde\ngkrCZCZhIv7DuNX2x3LSZO5IiuRKBcNyqMRCFAfCRIs1QjWXWkSnlAx3aDRGzcGodb70mvJC8OoC\nIVqwMCynJclFwxtADUehFy2i57PMHU5Si5lrCgYRYWzSZHjMJZd1cWyFGRYSSb0v2sHsdK0lBNUW\nnYpusjBvNQTUTMFEHLczy0c08sb1Oel3gm7mofRCCaPmNi5JU6AcxfBMgXm/ppfqUsCvmfaM/8KQ\nl4U/eiW36usSYWEquW5ot23q1x3wsBEcQ/NCW7to1JsRFALofVrwaTMEAmELqUaNng+J5mmRgB/u\n17TNsBXjl/PkBiNkxldnENtZn8iKGCxPtr5QBXPt0LmePgVaX3azancXjG3/j8wUmDm5umD9Wv4F\nXdcYHOp/tnJ9uU9XhOduvZeZIzeDgOY4vCzzCLfknsO5soR6XmdfxXWYLF/d6W5vmJc99lbu/8Xu\nGbvxfK1TvgHhio04CqULhVSEgZVK1xmyCxS7aLfVWIgrp4YwKw6wCx2wIiy3adQKL7l0cTLO2HTB\n263pkG6mJFdohLjuZvZXIY4+U4mFqIUN3KanoZedsf1vAZKZCkate0bsbsAy9a5CyhXPR1DHDume\nZrMOhq06Mj1f9b77dm2Z5OZxqi4MXMPA1Q1sM8ynR57PhfgUmmVz+NlH0ZqLM7kuum1zd6Y/4abr\ncfb0GV718yVwXGK5KsmVMqGNFnCsBzmMxbBDWmsABJ4wsE2d3FCPci8i1KKGV9hxNwkDn3LSZP5I\nilLSpBrxrmP2WJpKMszM0ZRnYvX3dcUXGE2X4QrUwnpXn9xuI9AQthIRrh4eILlc9hxRSqHZm0s6\nixZr5M0ooapNuGTjGNruiW0WYXEyweh0k/9BvEiqfFNtp1LSJH1VEGcD197juv7TA2/GrNi86UsP\nMlFZ3BUp7ZomxBIa+ZI0hEEztmbwpaHbeIH5HEe+9ijRYp7LJ2+nZkYZXJzlpgsPkziwuyKMzp4+\ng1m2mDyfIdRU2bcezVaOmyxOJSgMhElmKh3Z9ZWYsTpJEGHmeJp4tko8W0VzXBxDo5QKU0yG93Q2\nby1isDiV7PjejhjMnBwkkalgVhyqEZ1iKkykZDei/4pJk0I6sjve4XUIBMIWozQhNxIjNxJDHMXB\nZ5Y3dbwrwvBMvlGUrn7OucMpr0xvn6kkTGaPpUlkKhiWSyUe6og2UZowdyTF8FyBSI86TF7kVJfr\ncRVjV3KEy95xf3/wAWxT50ee+lsibu8ktZ1icsqkOKP1jNstGnHGJkNMX6oxPn2e8enzgDcWHDxi\nAv3/DeucPX0Go+Z4kXFdksRQ3gQlkamQHY0RKVmEag6iPH+Bq3m+r9YDhWI6QjF97cUfdy3tEXs+\nrq6RG24N6CgN6D0DQHYzgUDYRpQuFNJhkpnOsLVeuQDieqF9LTMxRzE2nWPmWHpXzDJsUyezTrSE\nY+pcPZxCXEWoVGPiyqqt1bPBwsLBgY7j0oslwmW75fpDVYd33PwdvOtnnuCLb35kw/1USmFbCk2X\nLVuIxjCEU4cUn1EOtfbXRylGKsvEEzqHjposXrWp1RThsDAyFtrWpSk3Q7NJLrlSWdMxqikvQqww\nGGXuaIpIycKsONghzTOB7ILncbvRbJehpsrBXk5PYt+VvoZAIGw7VsRASbXjpesmIKoRg/RCqets\nTbdcrwjYLo9jbkdpQi0R5srJEIlMhVDVoRwPeWWDuwwmiWxnZqgAZs3ljb97O/Ovexn/4V/+kqIR\nYaSa6ak15HM28zNWIyIontCYmDK3RDDoAi9ZfpRPj9yDra3mewiKyfI8LkI0pnPo6O76rbr5ZkLV\nzqz1dhrbRajETSq7O3Jy8yhFpGQTz1YAz/ldiftmWqUa4bb1+xAtWExUskwfT+9pM1g3AoGwzVSj\nG7/FkfLaL+daUT67HdfQuudJtNFrtrqaBZrhPUdeCwIh2+GuzJPcu/LVlvtWKbvMXrFa/NWFgsvM\n5RqHjm6NGv+8/HNopTKfHn8BtYh3XUo0vpy+jenoBKfnPsGqe7W/rBU9VI2GiJR6P3cuUOiSE7Cf\nGJwrkMjWGsEdsVyN0oDJ0mSCaMFCd9yW+yN4iZexQm1PmoXWIhAI24wVNijHTaLF2po1UdabZ7ia\nYO0x7eBaKCVCxHPdq1tqCqSeFKfA0XS+OHQ7RT1Czhwg7NS4Lfcs2uXLXRfZKRVdFuZrDI2ErltT\nUErhnpvFPtSq6ThGiBltjA9NvoKXLD3CSC1zXe00t1fIuWQznm8llTZIDPSuo1Tn7Okz0EMYAOT9\nBaCa82IabQJWWNs3lTy7YZZqJLOtz5uGJxTyg7bnM+mSW6EpT7uCQCAEbJLFqQSJlYpXKMtx0dui\nb9aqLVQPX1s8kLwh7LWZ0ThR34eyEb+LBjyVOtmo3HoxfoDQUJmJS89y6NwThKzW6njLiw6ZFYcj\nx8KY11F+2qopFtMTiOt2+ok1jenoOP8w9QCvWPgCpwqXrrkd8ITB7BWrZTW5UrFGIq9z4GD32ft7\n3/4GHnmw+1oMzbiGxuzRFBNNS1DWZWluMOz5ivbxc5de6L1SWjRfpRY1u+YWucKa9cn2KvvvinYj\nslqWArwU9sEFb13lbjMz8GdnpkZxIEwxFd6WtPzdiBPSmDk+yNRzKz3vTTvNNm6FUIvEuXziduYO\nneTejz+I2VYy1XVgbsbi8LHrmN0JGL0Wgfb7YovBJ0fv5VjxCoa69lLd3prHrQvbKOWt4lYuux3l\nt8+ePgMPbvz8dtjgyqlBYvka0UINR9copCO7Iqptuwl1ybyvoymhnAjhGBrS5EPwKgdrlBL7z5QW\nCIQ+UExHKKbCaI7C1WDqXKZTaxBYmkxS24QPYr/ghjTmjqQYnc43yiS7mreQj75Bs7zSdWqRGF+4\n/1s58cQXGb9yruX+lksuSql1TS69CIWEkZXZDfl1Fs3B6ypoVyp2XwtZKSgVnIZAuK6EPr9O1r6x\niStFqOqguV72sxJIZCoMLFfQHUUlaviJdDqG0z03pDjgRVHNHUkxeNWLMhKgFDdZnojvO4cyBAKh\nf4jg+sXQrh4eYOxyDs1RKBFEKVbGYjekMKhjRQxmjqe92kl+2eJYrupVyGxbxKTnaymCFYnytTtf\nQjGR4sRTX27Z/LUnvKiSRFJj8qC5qdpIIkIsDHd+9l949CWvxjZM0DpNUArBdNfQJDaApks94AVX\nhJWRAzihEINLc2i6s2szu/uFbjmMXc5jWE7D3FOJGEQqq+HM0aJF5GKWldE4ZtXuSLizTM3LnMYz\nqy0dSLK3atReGzfuiLOLsMIG0ycGCZe90r7VqIHaxLrNoarNwGKZcMXGMnWyI9HGw6zXHCJlG0eX\n1VC6vYJIy8IqpVQE2zRIrnjr8NbCup8RvvZpXCPElRO3cvjc44SszjDVQt7luWcqHD8VRusyqPei\nXHYZsBd52T+/l0sn7+DiTXeh9FUziyiXhF1k0Mpt+JyNPrvKXzpASA7oLMxZ5FPDPPLS16DE66Or\n6WSH98mMfqtQirHL+VVTUF0AtEXwCYDrRa5lh6OklsqN72umztVDnTkyNwKBQNgtiHRdtGM9zIrN\n+MVsY9ZsWC6RksXCVIJI0SKZ8e3n4lWSnD88sKedYbWowVJ0tYRALWIwNF9sCIWe9mDXpTSQJrXU\nvbicY8PlCzUOHwtv2IykaYKDQlOKo888itI0Lp28A8110DQh4lZ57ewnN1V2o1pxmZupUSl7F5Qc\n0Bk/EGLycJhP3fIabLM1AziRtSkNWNf07OxHwkVrTb9AMwKEyzbLk2nygxHMqoOjazeE76QXe3dk\nCAAgPV9sUXcFT0UemSl6tZSaKo0pvNnT9IndkfG8FRTTEUoDYSKFGunFMiG/OGD71dmhEI/f+3xe\n8pF/Ru9h96+UFRfPVZk8aBKOrK8ppAd1Fq/aDfv+sacfZur8U1Qnxzg47DJeXdqUMLBtxcXnqi3+\ngnzOoVZzMW47DEbnQCXKs40HAsHLKB6dKXTdtlbgBoDSNaqx/Zd5vFmCO7DHCfeoSKm5qmvGr2a7\nLUXMWo7xVzmbPJ9h7HKOSLH/tYM2gtKE8kCY2eNpFqYSHZVWXbxKtM/edRvV2Nox9dWq4tL5KlZt\n/aigwWGDRFL3TDua9y8hVe6OXGVik8IAYPpStavzuFZVlCydaqhz0Bc61xm4URlYLiNu94KKTdXn\nV78TOmoQ3egEAmGPs9k1E4R6Qk0rmuMyeT7DwHIZs+oQLVqMXsmTWO6d1LQbKSfDLB5IYuvilSIW\nr/bMgl+p8suvfMW6+cOuCytL61clFREOHDI5eiLMxIEQh46EOXoi3Fg5bVP9LrkNM1E7Vd3g44du\n6RzR8OLh93xkkFKEixbJ5TLRQq2jJPpGiRStrgOaAhzNy7iul6e2DI2FqRszim8tgruxxylHDeIF\nq+saC70S3rppCMnlCprTqlVoCgYXShTTETRXEctV0RxFJR7ySnLsUrNTOWkynRhEt11cTVoc9Odu\nv4348gp3f/Zza87gyz0G526YYQ0zrFEpu2SWHXSDDa3oppSiVHSxLUWp1HsdDN11yYyOYIViLWsJ\nu+L5UPZCnf1eiKsYv5T1nkn/gXUMjfkjKRxjc/NVx9BQPZbxnD88gB0JsawUmqtwNdm1z28/CQTC\nHic3HCVe6AxrXGs46/YaRAs9SmuIkFwpk1r0ozCUp5qXEiZLBxK796US6ZnM9+gr7mP+6GEeeN/f\nY1idwhQgHBFc10sIc2yIxrSe1UpbMom9phEsDh0N9zwmn7eZubR+OKoCcoODrIyNAl7toUTGi6Uv\nJc29W3HU1wLSCyUvX6DJ1yWWy9BsgYVNRvrkhqNESlZL1JnCqydmR3xzmwjuFlW+3Y8EAmGPY0VD\nlBKmN6D739UXrTFqbsdgpwRKyU4TQ8/ZlVKkFsotqrgovMJehRrlLufaC8wfPsx7fuIM3/C/3svw\n/FX0poWSrVCIeALOPV3xbM/Ki9AaSGhMHgx1RCHlsk5LJrHyEtCZvlzj+KnOqKVcxmZ2emO5CUqE\nj3zXd6z2LWLsyFrC20WoYjM0V/R8X35uRbelOaNFC1y1qeSvaizE8nicoavFxoyoGu2+sE1AdwKB\nsA9YnEqQyHi1kkQpCgNh8kNREisV0oulxoxJCeTT4a5209xQ99mVY2jojtuxeLqmIJ6t7lmBAOAa\nBv/8vd/NC//3Q5x8/Kvots3y2Ciffc0DvOIfP0RMOZy/9QXMHLkJVzeI51Z4yewXORlaaTnPypLd\n1ezt2N4azOHI6qDmOmpNYeDdc8NPUHT51OteSyW5uwY0cRXxXBWzbGObGoVUBHcD5h3ddpm4lFt1\n/K5jlZP1d+mgmI5QHAgTqjm4em8tMaA7gUDYD4hQGIx2VKXMD0epJELEcl7yVinZXRgAVOMhVsY8\nG3X9TbTC3vqxw3PFHbiI/uAaBp/7+lfzudc8gLguStdJLywSKZd56p77WJo43Fgqs5ga4qHEqxie\n/mhLspltdR+26tpFM/nc2mtml6NRHr3vZTi6zuWTJ6jGdlcUjGa7TFzMotsumvK00dRSmbnDKazI\n2sNJYqUCbVFAvSKCqlFj0wETq52UdfsS0J3gru1zrLBBdnRjP3NhMEoxFSFUtXF1zVuMx1UMU6J9\nruYKvZdJVIr0fJGkn0VcDessHUi0ZB3vOkQaWcaa61ALR1iaPIyrt/bZEZ2H07fwqoXPA15GsdNr\njFeeL2LJTJMz4ozUVrCsbM8uKODCLTfz9D13b8UVbQupxVLLYjGa8oTeyGyB2WNrV1c1q/aGwxo7\nluYM2BF28Rsa0A+UJo2yFwBowsJUgtErecDzHyjxVpUqx7snQ41fzBKurPojwlWHA+ezTJ9Ir6/C\nu4pwxUaJUIvofXGYroyOUkyme5a2Xg6nGn+6TmNhrQ6csMnfH3wNy2YKUS6u6BxOXuRY9lO4bXkO\nXiikwSP3vWzrL2gLiec716rwQpkdNMfFXaPkSjVieKGh65Ua0WXPrQy4XwjyEALWpRI3mT45yMp4\nnMxojLkjKZYnu0cYGRW7RRjAqllgaB3TUyxX5dCzy4xdyTN+KcvUuUzXnIntRmkaX37FS3G1zkFJ\nAefHJnnpO+/EthSZld7+gK89/z4WzTS2ZmDpJo6mc274OI/f9iKcpppJCqiFTf7mx95MLXqdi9Eo\ndc1x/Bs6/RoCer1WC+kISqRlv/ZjXIHcUA/NM2DbCTSEgA3h+jXy1yNe6J7dXK8b0wuj6jA8W/Bn\nj94wIbbL+KUcV06kSWSrpBbL6I7CMjVWxuJU2urRh0tecpNhuVTiIXJD0Q05O7sxf+QQo5cyxIqW\nl4Ls98rLbo3yXb97jNec/zIhq7u9yDEMFoanOoSKpmDm2PMoJ0OcfOxxRCmevf1WvvqiFzZ8FR0o\n1dDMEEGzvIKF4pd2tiIGRtVmeK7YuMfVqMHSZGLLZ9r5dJjUUrmjOmglFlq3IKNraMwdTTE4XyRS\nslAiOIYQqnn5IqIUxVSY3ND+XaFttxMIhIAtxVpjAF4r/juRqXRULfXqMikG54skcqt5EmbNZXQ6\nz8LBJJW4JxRi2UpLaWyz6pDIVpk9muowUxlVh+RKBcN2KMdCFNMRdNv14vttl0rcpJg0WTiUYmCp\nTGqpjCiFHdKphR0OPfM0L/zYxwlZFrYRYmn8EDUzgiuCEwoxPH+FaCnfc8as2YqlkRMsft1RatEI\nrq6j2+C2v42uJxDDlVWhY+tgtMkg29Aw/HUjGma6ss3EBc9Mt5nKuevhxfrbhMurmpFjaF5Oygaw\nTb0jv0CzXQzLwTb1NU1OAdvPmgJBRAaAUaXUubbv71RKPXq9jYvINwK/g2ep/ROl1G9e7zkD+ksp\nFYYupiEFZId7z/zaFzJv4NIiDOpoyktqmouboBRD86WOIn+aoxhYKrfE7UcLNUam8w3BESlapJbK\nGLbjB8XrJFdKDIZ0lsdN7n3oIS7c/EIUgu44hCswMpMnXCqxOH6QJ15wv2cGaTIBXbrpLjTbIlQp\nU4u1DpQKz05rWt6ncM3TqJKZCtnhKLmR1aiiyQtZQm25JIbTGZlj2J33ri5ME9kq+a2ccYtw9fAA\nZsXGrNjYIY1K7PrKqruGRu0aNbmAraWnQBCR7wL+B3BVRELADyqlvuBv/jPg+dfTsIjowB8ArwGu\nAF8QkQeVUk9cz3kD+owI84eSjF/Ot3xdTJoUU71zFsoJk1i+c+BfK149Uqzyb//w7RQTAzz1/Ffh\nGq1ObgGiBYtG1oBSTWYpD015M1SvOp2/m24Qsmzu/NRXuHzyHpxQq2lqcfII84uzPHPHS3uaeVwj\nRM0IgWMjIihN90w/9YGzbQDVlBe+WV8uVa/aHcKgcT828F39nPUyJSPTM9z2+S+iOzZP330X0yeO\nX9cgXosY1ILQzn3HWr/oWeAFSqlZEXkR8Bci8ktKqfezsaVu1+NFwLNKqecAROQ9wLcAgUDY41Tj\nJpdvGiKa92sfJcx1bdmlpMnwrIO4eIMnnoMxnwqTzNW6VvSM51aIFwqEanZj0Zh2IuUCMAj46+d2\nqwzaZWB0dYPM2EEcvfMVcY0Ql07eibvWYjr+OTUFExeeZu7IqQ6B1Y1owaIwqGNW1s5X2AguUIvo\nvOhfPsotX3mk8f3B585zdeoA//SG79mbZS+2iYd+c3t8F5++479ty3k3w8s3uN9aAkFXSs0CKKU+\nLyKvAj4gIofYfAJhN6aAy01/XwFe3L6TiLwZeDNAeGB0C5oN2AmUJpRSnU7oULXK8a8+QWpxieJA\nkqlvaLUAACAASURBVPPPu4VSKsVNX3mY53/iUyxOHuPqwWNots3o7HN88vRrcEJR0outJiHNsTn+\n1FcAMGsV0ouzZEYmW1Ys02yLm574IsmzXkSUm1Pk/hjY4Firub13LMeTGxxMFeMz58kNj1NID6/d\nngEH7ykRvrOCk3HJv2Nj/USpzr4oRcyp8P0P/TVXnil1HDI+PcPP/+XvkR5cHQJsW7G8YFHIu4gG\ng0M6qUHjmted3mt8+oP97kH/WUsg5EXkRN1/4GsK9wN/D9y2E53z230H8A6A5OSpPV/4/UPu727L\neR/+8O5X32tVl4vnqzSPs/d+4lNEY+JVF1UwdfFppi4+3dj+o3/9J4xOmHx14CRfHryVsh4hVspx\n/PEvMLQw09jv1i9/gq/eez+5oTEv41g0jnztUcYvPse/ectMY1D7u6lXs2gOttj8G2GaTQOfZlsc\nfvZxnrnjJZ0XUh+ANzhQ6o7N1PknefrOl0AXjaOxX9Xmu/7oH4m4nl/hb6a+nuVw22JG7YO/H2Yq\nroPSjca1TFQWeGD+sxSWqj3bW1myGgLBcRQXz1WwmwLBrs7ZVMqKiamNVVOtVhxyGYdKRREKCakh\ng2iP4n4Bu5O1RpEfAzQRubVu11dK5X1H8PdsQdvTwKGmvw/63/VkKrPAb3zwD7eg6f7x8D4N7HJd\nxdx0jULei3aJxoTJgyZGk7NwdrpGt0l3udRbzhcLLmPA7blnuT33LAqYvVIjn209UciqcfdnPkI5\nmqAWiRLPrWA4NqYpLTPcr5/7Vz5w4H5KRhQUuKIxcfUCC6kJHCMECEoTJi4/y6niJUJfrvH4va/y\nHMe63n02XqfLYB2ulInnVkjkV8gNjTJ76FSn/8BxEA0emP9sQxgAfNv0R/nIxMu5HJsEwHBtRq6c\nJzc4QjUSJ1wtM37pGSamn6N6xymupiYZsArcnn22UVqjuMYUSjWtJJRdsTsyrpXyCvcNj7qEzDWi\nx1zFlUtVym2N5bIOoxMGg0PBam57hZ6jk1LqEQAReVxE/gL4r0DE//9e4C+us+0vAKdE5BieIPge\n4A3Xec6APqCU4v+09+YxkmT3nd/nxZl3Zt1VXX13z3A4nBkOryFnSIgUSVBHU6JMybteemXrAAhj\ndqEVloZMjeAFbBgLC5K9/mO9WBE2AQNLW1wvJZESRYmkOLIO3qQ45Mxwru7po6rrrrzPOJ7/iMys\nysrIOrMys6reB2h0d17xMjLifd/7nbdeqXVMKJWy5NYrda69wUbXNXxf9mwAsxs7m80IYHzCoFTw\nQvOvotUS0WrQRlEImDnXORklvCr/+N6XWLEnqBhRpmsbxJ0KqzddXtenqVsRpkprXBmrEzlnwtoa\nG6+/yOL1R3YXg9YBW0iJpws8rURmTMcw4KEffoMLr/6IlflrNKIxYsUcEdNnIi24WruP7XcmuRn4\n/Ozy3wYf1/zuxYLL0g+djsfGxnWmKq9C5dWuIWUmDHLZcNNXZmzLvFYp++H5bIJgxb/LJmHlvtMl\nBs1TwOqSSzSqEYmqzOOTwH6Wq+8Efhf4OpAEPsP+fRQ9kVK6Qoh/DvwlQdjpp6WULxz1cxVHR/oS\n3wdNZ1/242LeC63nIyVsrLlMzx6ugYsQMD7ZfYlGohrnzlssLzXweuS6xZMak1NmaD8CAczWN6Bl\nTdEEM7Mm03IzeD4tAJ17XpK/fOv78Sz74M5XIZACXn3ro7z61kd575/8KZfXXiFWKXHl1S0Hr27A\ntQcje57n1rPJlEH0QZ1SwcP3IZEMmvP0wrY1UmmNQr6zVIZhBC1AW1iWIDSPXHaL8nZ8X+5ZsO/e\n7QZXHrCpVSWVkodhClIZ41Cd5RTHy34EwQGqQJRgh/C6lHLvhrP7QEr558Cf9+OzFIejVvXJbrg4\njiQaE7hOUJFTEvR0T2V0ojGdaExD75FYViz2nhDKRR9mQdME8YRGuRR+6QgBkYigVpPt2kBTMwbx\nRPjKMpHSuZaM4DqSRkNSzHv4viSZ1pt9jg8+2Wx/z99NPM4L6Qe3BrcbPXYOrWQxgJmFha7na5EY\nKxeucX88ycX6ChcrS2j7iNcwDEFmfP+mx7nzNsm0y8aai/QhPaaT2eEszowHO4mduwTTEkSiu5Sr\n2EelDCnhzs06ng/SD07V2opLMqXheWDZgrEJA2sXs5RiMOznqvoO8HngHcAk8O+FEL8opfzPj3Vk\nir4jpSSXdSnkPAQCKwKF3JapoLojGMV1YXPdQ4hgwp+eNciE2INNs/eEsd2HOnvO4s7rNdwd5X9a\nO4HJaRPH8fHcYJLYqwWlEALTEpgWPYXjMHw383AgBvsQAuH7ICUyJB/BrpaBIDKuFosSrWyd4M2p\nczz/jvcjRZD38Kp/hcl6lg/cfBZT+Fi26Gt0TyJpkEj2vt0tW2P+otXh52ntxHYbh6YFv7/TowQ4\nBIKw3Vndut6KhUAwK2XIZz0uXLaJxpQoDJP9nP1fl1L+KymlI6VcklJ+BPjCcQ9M0V+klCzcabDW\njBypVn3y2R524673Nu3Byy61WvcKfyLErNNiamZLQAxTcPWBCHPnTCJRgW4Eu4K5eYuJZolu0wxa\nVe4lBseBIwyenXoH3xt/ZE8xkICnC0opnwd++A2Eu8N25ftEymvt/z7/zidwzOA7+kLw4tvei28Y\nQWQQ4Gomq+YY3/YvcvtmnVderHHvdo16H/IR9ks8oXPtwQiXr9tcfTDCxSs2xi5iD4Eoz5wzj5zO\nICWs3A+vg6UYHHsKgpTyuyGPHdWhrBgwhbxHpbI/AeiFlJDf7Dba64bG/IXuncPkdGBu2o4QgtSY\nwaWrEa6/IcqlaxGS6cOZePpJQxj8v+c/xCvJK7uLQVMds1MxFq6PM7t4l9mFm0ysLnTaTgTkpq6g\nN4vf3Xr4jTz/xDtwDYPs5Gxo1VDfMFk5f639/0pZcvtmg7WVBvIYK5huRwiBZWkHsu/HEzqXrtok\n09qRhKFel/hhiYNNKmWPxbt17r5eZ3PdwfdOfBT6yHE6YyAVbeo1n/sLDRr1/tw8vZrBJFIGDz6s\nUyn5+H7g1B3GKv+wPJ9+gLIR3VsM8Ll/ZQyn2bT9wms38QyLzZnzne8VGiBJbdbIzsRBCH747qd4\n8R1vJ7OaJVo2QvsCaCEneHPdo1jwmJqxSCS1oYtnGHZE49x5G8+TrC45gR9KQiyuEY0JNtfDo8K2\ns1tqx+a6w/rqVqvSWtUnl/W4fNVG26VoouJgKEE4JbT8AxtrLr4XOAOnZgyWFp3Q2P/DIAQkU71t\n9UII4snRDS/0fYnvBX6NnZPq7fg8vtb7dpBALWqweindMWtVEjGsajq0mY5AYFc6HSauZbE+P838\nzRxiR1E6zXWYu/NK6PGdRpB/MTauM3XIqK1BoOtB/slsc+YWQiClpF6T7YCCMGEQgp47Rc+THWLQ\n+oygH4XL+KTKc+gXyoNzCpBScudWjdUlF88NbpZGXbJ418HvSzxYMwooqpFInbxLxvclSwsNXnup\nxq1Xa9x8pUaxsGX6eubG09ydmO35fknQB2D1cqZrCfvjt70No1HrzHze9j7XDDlfQrB6PomvCXwB\nSB/Nc5m6f5vp+6/3HoeE7KbXs4fzKCHEllNcCMH8RZuLV2ymZkxm543mTidwSgsB0ZjGzFz4xF6r\n+qE7BylpJ0Iq+oPaIZwCinmPeq3Hk4eYO3QdLl+P0KgH23Lfl6RS+kjY+g/D0kKDcmnLf+K5sLTg\n8PDHfH55/jcBKIxFsCtOV+MXgPxktGfp7vW5WYSQpDeWyU7MdoRVSXp3/3IiBgvXx4iVGuiOy7u+\n8hfM3ruzZ9VIIaBa9Unu1Yp0BIlEtXZeSDoDTsOnXpdYltg1l0LXRc/L+CC+DqfhgwgCFxThKEE4\noXiepF7z0XVBPncwm5AQQWTQ5mYQl759K55MaUzPWhiGwDB0YvGTN/Fsx3Vkhxi08CT8n9++Av9Z\n8P9awiI/ESW9UUUKgfAlniFYvZDCtXvfJtdeeBGrVuPa89/he+/7SOD8ba2MgWjFpRHrYeLRBJWU\nDdg8+9Gf56HvfZ9Hv/ktTMfpKQySQLC7vqcrcR2JaYme+SKjhmlpu2ZAt7AjAsMQOI3OH1EIyEyE\nX5+uI/G8YPfQqEuWl7ZMp4YB8xctlT0dghKEEaVW9VlfdYJJ3wxi8j1HYtkCwxTks95Wc/c97v/t\nTeCFCG6w8SmDzIRBIedSrUpsW5AeO33Zo44jO75/Cw1IZbMdjxUmY5TGIlhVN2jaYut7hp9efeFF\nTNfl1pU3IpHtdpsQ/CypjSqFsShyj0natUyef/KdPP/kO7n00ku87f/7WxL5QsdP6wuBpdMRqy+l\n5P69RofpJDOuMz1rnsjdXBhCCM5fsli80+j4PadmDWI7othcNzgf1UpvU5Lrwp1bDQwTfC84n1Oz\nJvYuu5SzghKEEaRa8bh3u9GexFxX0jJgNLatktqT3C5mIU2D8SmDfLOeTTqjMzYRZKnqOoxNmM1u\nAacTyxahTkxPE6ycP9/1uK9rXb2ae5FZX2dqMai4mp+YCWp97ESA6Xg0dqlyupM7Dz3EnYce4tJL\nL/PUX3wZ1zC5/Ya3snbuMr6u89DFMg9+/Rucq2+weKdOeUcdodymh2HCxKRFo+7juhI70jvT/CRg\nWRqXr9tBaKoniUS0ruiiINemTr22PztpK0GyXPKp3qpz+Zq9axG/s4AShBFkddk5Ur5AGwGXrtlY\nlsbEGY3E0HXBD971Lh7+7ncxncCR3Op9/Pw7nzjSZz/29W8imj9UtFKkkux2Omuej3fI9pB3HnoD\n965f49ytLJqvBW0xgZfuxnnp/AeZqG3y4K2/IhJShWh9xWNjtdpRVWN8ymBy6uReB0IIIpHeolav\nyUOHV/s+bKy7zJ4b3QiuQaAEYQTZ7wpnO5oWVPYslzxcJ/AFnKXmJmE8c+PpoAR1xSE/Ns0bv/8d\nkvkcyxcu8P2feA/ldGrvD9mF8ZXVdpjexVd/RHbyXEdLTeG5jK3d5/6VJJ4R7lzeC6suEVLrMB21\n/r0RGeO5Jz/EE1/741CrYWtR0fp7c83FtrVdQ4dPMq4bbh7cL7WqilhSgjCC6IY4cGihlJBI6qTS\n6ieFQAz0hsfMvQK66+Na4/zonT9FcSxCbirWl9aRuckJktksGpDOrvHQP/wtrz76LjzDRArB5NJd\nrv74O9x56Bybs4cTBKPRO2BAIGhEYhTGpkhn13q+roWUkN1wT60gRCLakXbWqrieEoSRZHxSZ23Z\n3ffFLURQeO4kZQYfF8/ceLr97+nFIobTTP5qnstktkY9alBN2kc+1g+ffBfjK+vkpuZBSqaW7vDU\nlz9LPRLDcBoYnour65SOsBPZqxc1UtKw998LOPBHnU4MU5Ae08lt7iPqTtDhe+tVav2soc7AEJAy\nyJgVGqGTeGbMwPOCLX7w+uDx1qI2qIEvKJckhhnUtd8ZbXHW2C4EEKysjYbXZUrRJKSytb4Igmsk\n+e77PoLwJQLJ6298K9d+9C3m777afN7g5pveSCN6+ObttZiBa+mY9e7vAuCaJtFSDk8ItFZ28C6f\nl0ie7lXw9GzQA2Nz3cF1gntGNwSptIYd0dp+iNUVl2I+KKdhmoKZue7eGZ4n8dygHag4I4stJQgD\nplL2WF50tsoFi62SEFMzJoYRZHhOTpmMTxi4rsQwgkgZpxFcnHozNHRyeohfZER46kef4H2frHY9\nrvmyaxXYfq4PRdHMikNmvYpAgBYkTkngtUffxcTqIprv8uO3vYXn3v3U0Q4kBCsXU4wtl4kXg2qg\nranJF1DMRPnjj/8q86/fxqrV0HyPd3ztr9sO9O3oBh1lHjxPktt0KRX9U7OwEEKQzhikM7tPbXPz\nFjNzEhnSCCpoB+tQKnrB/QlMThuMTZxch/x+UYIwQBp1n4U7jU5TULO0dCHnUSl5XLkeaYfTaZrA\nsrYuVH2XRiUnHdcJOm/5viSe0EM7ne3kmRtPQ4gYADRsHRmiCL6AcvLokSQTK+UgwmiHL0IKwbO/\n8EusXpw68jFa+LrGxnySTc8nuVklXnLwNUFxLEIlaYEQ3Hvgevv1Zt3h8b//OkiJ4Xk0LIvZRFDz\np5Vn4nmS2zdr7VInVKFcbDA9Z5AZ65z46jWffNbFdYMdxknNWN+JEFBvSKSURKNaexewfD8QA9lU\neUnQ0McwtxzytZqP05DYEdHT9+B5klLBw/MksYROJDL6uzMlCANkc2N3v4DnQT7vnrmm5MWCy9JC\ns09ws+1mKq036+x3Tzwd5iEpSW1WSWbrCCmpxk1yUzE8U2dzNs7EUgnR3Cz4AjxTozh2OAfvdsy6\nF+6YFoK5129TSSaIlhx8PTheI3r0W03qGoWpOIU9tObFJ97Oy295M6lsjmo8Ti0eaz/3r7/47wDY\nXN+qe9X+/GbPi1R6yx+Vz7ms3N8Kgy4VPbKbLhcu2yfaZ1Wt+CzerdPaSAKcu2ARiWqh/bqlDCqu\nxuJaO9ehFdGUSOrMne+8Vitlj4W7jfaCT6wGzvzZ+dFOGBx9yTpF7BUjLSXUKqfX6ReG70mWFpyO\nVoxSNvs3lLvDAHeKwezrOTJrVQzXR/ck8UKDudt5hOdTSdksX05TzNhU4ibZ6RhLlzNI/eiXfe/q\nOlBNTjKxVCRWdkjkq8zeyRHP9So2dTx4pkl2eqpDDCA4f5/9g49RLoWXoxZshT37vmRlyekSjXpN\nks/1aGZ9AvC9IIHN84KWnn7zz+LdBvX6LhnOjmR5sUGtKpEyeE9QYM9jc33rfLSyx7eXhZEyaE07\n6sX41A7hGJEy6ExWLnrohoYdEdSqveOkhQgya08TvheYglxXEosHxc22r5DKZT80dlxKyOe8dmvM\nnU5jpGT+tSy6J7ti9IUvSeRqFCdiOLZBdjbR9+/VsDTsut+5S5ASo17FsaJbWcsiyCGYWC5RSdnI\nEVhVP/eFDFOzF5m/fafrOSm3aiXVqn6oG0ZKKOZ9xsaPfajHQrHo9ZTzatnrmcsQiWqhE7qUQXb4\nRDPpr9qjEZWUkM+OdtivEoRjQEpJreazsepSKbcujr1D4YSA9Njp+UlqVZ97t+vt1b8QQcOU+Ytb\nfXp3mx4FIULQJLVe6RKDFpqESNWleORv0AMp0Xss9EynQTUS63rccBysqkM9PhqZsC++4+1MLy52\nOZ8te6vyqBC990Hbq31LKamUghIZ0Zi2a+XSUcD3CA02kDIw207NGqwudZp3NS0ISy0Vw9t87tbp\nbecxRpnTM/uMCIWcy8qSg79Vfqgn21citi2YnbdOTXE5KSWL9+od/RikhErZJ5fd8pPEEuHJRCKm\n859+6hd6fn4i39i1IqizV/z+EbCrLprb7VBGSjwj3P8jhcCqV0dGEO5fucxzTz3J43//DXxNQ/g+\nCcPj/MWtcNxIVKBr4O4QPyEgMx5MHY2Gz73X63g+7es9kdKYm7dG1lYei4cLlhBBO1DLFliWR71p\n4tU0mDtvEo3pWJboqCfWYntjqGiPgAghglpio4wShD5Sq/osLTp7v5Dg4rhy3UZvhpSepMJjTsNn\nddmhXPKbuxqdickgd0I3gvLLjbrECzEzSwmFrNcWBE0TnLtgcf9eo/28axi89uCbWLp0KfT4RsND\n26PzTz8cx73QdnQ623pCQ3gOmuvgbxcG38euVahFjlYqo9+88M4neOXxNzOxvEItHiM3OQlsOZ6D\nKqM2927XOxY4Y+M6ieYEuHi3gbvjdy7mfYRoMDd/9FyP48COBJFSrTwE2GrSE40JXn+13vGdfB+W\nFh2uPhA4hbcXnmw1+ZmcNigWPAp5F9eRRKJau+Jqe3ecCI47yihBOCK+JynkPRoNn0r5YH0JyiWf\nZFqnXAreF0/oAxGGWi3wa2iaIJnW27sS35dsrDnksx6+D6ZFs4/v1kXseZI7t+rt3spBOQSP7IbX\naiNMIqkz1qNOPXRvnBJJnasPRvjMhacwGw0Wr14hOx2eZBEp1pleLO362WtzcbxjbCDTyw8ggXo8\nysVXXmDh+iNBW03AaDS4+vy3edO38nz5n/wjiuOjU1/WsW2WL13seOyZG0+3RcGOaFx7Q4RK2cfz\nJNGYjmkG37/R8Lt6FLQo5HySKY94QgtybmTQ1rW1a3CdoJ+HuUdznONi9pxJIqGTywamofSYTiqt\nUyr6eCFrDekHjagy4wZXrttkN10a9cBEFolp3N12TzTfAQQ7At0I7u1obDT7YW9HCcIRaNR97r5e\nb0cbHJRaNVhpt5eb0mFu3iR5TPWIpJSsLgcTfmvVsrbiMHfeJJHUWbhbp7qtlHKjHqwAJ6Z0JqcD\nU0c+6/Zsyymbjwcx3BJNp2uX0Gvb/K8+8s/2HL/wfKYXS12r8+2nPj8WoZo+vt0BNJPeQhBAJR4n\nPxnlia9+jtzENPevPEwxM8lLb3svAI99/fv8/Yc/cKzj6wct382//uK/C3plJ7p/M7lHwMzaSoPV\n5a26XJoemJpqVT/YXRLcN5FosBMZ5C5ZiGAxtHPF7jgy9HtJGQggBI19ppt9raWU3Hy5tkMMtiiX\nPK4+GBl5IWihBOEILC82el4I+6Hd6Wzb/LK06BCN68fiS6iU/bYYwJaILS04nL8oeoa8bqx5ZMYk\nhimoVsMjKLYjZbD7OXexaQpqOZW1wL6a2eY47+U0DiO1EZ6EJgBPg6VLabxdupv1i0bEQAoQO86D\nL6AWt/jhu5/i4suvsHLxAYqZSaSu4zVDd+5ffoTMSpbczBB2CVJi1VxixQZSE5RT9p61krYLw04s\nW6Bp9LwHGnXYfnF7LmysbgvPbP5dq0oW79a5eOV4hXw/1KrhX6bVU3wnW0Ej4Xhe0JDHPCGpRUoQ\nDonvS6rVw4UMCAHJtEYhF77EKhY8xsZ3/2mkH7SGdF1JNK7tq9tTIR8ee46gvXXuRbnkkR4ziNga\nZbG3KABYpuDaAxEKBQ/X8YnFdWLxYNu8XyGwqg7p9Sp2zUX0iCqCIJt3EGIAQcG5StIiVmy0ezBL\nwNcFpUxgN/dNi9zELHJHv0vfMIiVfHIzAxnqFlIyvlwmXqi3hSy1UWVzJk45s/dEHCYMQgjm5k0W\n7u7Pb7Yb1UrQ8lLvQ44IQL3u4zpBY6D9Lq4qFY9SIfye1A1IJrvFcw9XFtAZkTXqKEEYEnovO7QM\nnLbZTRfDEMQTWjsjtFH3WVlyOhK2WjvRfWVB9pjEpQ/FHjdCi9YY0uPGnhnXrXG1bMY7xW2/YhAp\nN5haKLYzjSH4CmEmo4Y9WGfdxlyCRqRGMltD+JJq0iI3GWsnvd1+8CE038cLGZYUg58h7IpLvFBv\nCxgEO5zxlTLVpIW/z4n4mRtP8+wv/h3f+LUfAhBPGkxM+2ys7lhZ96gjtRuVsk8ydbRz47mShbud\nmcTpsf21FC1keyyYAMMQvPpSrbmYC+qO6bogGtu95HYsfrI61SlBOCSaJojFtdBsWsPcas8XhgQ8\nvzPsdDvZDQ8hggQZIeDC5SAa6c6teteKpPX+YsEjltB2LeqVyugUQ9Ly90IIiDerZBqG4OIVm+X7\nQcZmr9dPzXQ35zmIeQhgfLncMYFB77yFWh9KQ+yHmbv3ePzvv056Y5Ps1CQ/eM+7WZs/1/W6V9/8\nCOdvZrsel0hqscGHnsaL9S4TV4toyaGc3n9E0E9+7j1w4z3t3cLklIVte2ysOcGONaqRSOkdJS/2\nQz/M7EuLW9dl69j5rIdtCzJ7lITZbazbPzOf86hVfS5dtTEMwcSUwcZa9yIpEoW586MRZrxflCAc\ngbl5izuv1/E9ie8HNnLLEly8bOP5ktWlBqViWAZMEK2TSutbfoSdL9lWymHxXoNUaveVSJAtGdQA\nch2JpouulUksrpHK6BRy+xcFIeD8Jaujbo0d0bh0NYJsfojTkKyvuVQrPoYpmJg0OiKTIs9+lH/5\n+7P7OyBB28lEtorh7C/NXwL1ffZBPgrzN2/xvs//KUYzJjFy5y7Ti/f56i99lJWLFzpe60Qs1mcS\njK9XacmYBHxNozAxeFt5T2ObAHnIiXi7GSmZ0jsycKWUFHJez6zdrmEIiMePtsvzPBm6QJMSspve\nnoKQTO9zwSSDMjSVsk88oTMxZRKNaeSyHp4bFLxLZ3TsyGiHmIahBOEIGKbg6gM25ZJPoyGJRIIt\nZKMhuXurvmuJimhUo9rDgbUT15H7cua6bhDx0NpFxJMac+esdvVUIQSz5ywyYz7lkke97gemopDP\ntSMwOW0Ri2s9i5i1dgCWLTgXshJ6/Gdcflb7Dfj9fX1NAHTHa9Yi6u0v2I4voJK0cAbgP3jir55t\niwEE07zhurzja3/Nn/3KL3e9vjgZx42YpDaq6K5PNW5SmIgea0hsL8ppi0S+1r1LkFA9YrJcL//C\n+UsW2U2X3KaLE57g22b+onXkngP+LmXNd3uuRTyhEU9qlIv7CJwA6nVJvFkVJfCPnTwB2IkShCMi\nhOhYDQOs3G/s6mwSGsQSOhtr+y8QZlka1couqxfRbaYqF33uLzQ4f6nTHBCJBjWFGnWfUqHepQdB\nJqrZ9b0OwkHNQy3GVito+xADCdSjBqVMhHLq+HcHwvNI5nKhz2XW13u+r5qwqA5g97IXjahJYTxK\narMzUmt9Ponsk417p39BCMH4hMn4hInrSvKbLtWqj2UHC6d6TaLrnbkwR8EwRWioMxAaNruTcskP\nnMrbhhKLC6oV2XXfCUFHafrTghKEPiOlbGcohpFIakzNmjiN/TcE13QYnzJ6RgkJrVneecdzrVIR\njiPbyUTbsezA1ru93K8QwY2VOmRG5WGFoEW07OxLDIoZ+1iK1oUfUPITf/pnPZ+uxbprF40i+akY\n5bRNpOwgBQdyJu+Xnf6FFoYhmJjuNNkk+5y43doB37/XnUm889g78TzZzpbfvkKqlCWa1n2ftgI+\nThtKEAaIpsF8s1aM2EfoZsvJdu68hWlqXLxqs7otysiOCOyIRiKhs7bawA/ZlgsRmJLCBAFgfBUO\n0wAAGmlJREFUbt4kFxXksh7SD+rQTEyZh6p1f1QxgMAEFHabtaKLfAGuqZGbGtwkfOXHLzH/+p1Q\noXIMnR+964mBjeWouJZO6RjrPLXYLX/hOEkkdS5dtcluuDQaQSbx2ISx5w6kXPJ6RkYlUhquQ/u+\nSyQ1Zs6Nbq2mozAUQRBC/B7wc0ADuAn8qpQyfD9+wmhlQBbz3o7HOzN0TVMjkdS3OjO1XwjTswaN\netA6M50xMJqTuW1rXLgcHg1SLuvkG90+CSnB3mVrK4RgbMI8UnvAfghBi2ImQnqz2hFdJAnKTddj\nJvWY2e4SNiiuPf8CptMdNiaB19/4Rl5+y+MDG8tJYxjCYEc0ZucPZqbbbXGmCcGFy1Y7iOI0CkGL\nYe0QvgL8tpTSFUL8LvDbwH83pLH0nZk5k0bd72iIE4lqTM50Trpz8ybra0Etdd8PimtNz5mHarU3\nMWVQzHsdvgshgpK92jHFQX/2Dz7Gc1/I9PUzPUMgZOdCzTU0Vi6l+9LY5jDIHhOAY1ncfORNBxYn\nq1bjkW9+i8svvYJnGLz8ljfz8lseRw4zg8mXxEoNNF9Si5l7ZjAflJ3+hVEjHtdBdot+K+8g+Pfp\nFYIWQxEEKeWXt/33m8AvDWMcx4WuCy5dtalVA1GwI1po2rvQBFMzFlN9yFo1TY1L12w2Vl3KZQ/D\nEIxPGsfSjKMdPfSF/n6u7niMr1a6TDO6F3RDc4cUxPHao48ws7DYtUuQmhaag7AbeqPBu//8a2Qn\nz3PzTU8ys3iLx//m75heWORvPvJz/Rz2vrGqLtP3CkEXuFZeSyZCbjrW151YL//CKGCYgqlpg7VV\nt8P/kEwFRenOCqPgQ/g14LO9nhRCfBz4OMCMGR3UmI6MEIJoTCc6QH+jZWnHngjTT/PQTmI9mo8I\nGTxXmBjO73/nDQ9y8dXXuPDqa2i+h6/rgODZX/j5A6/qL7y6xO0H39ouj10YmyR5/iqPfPtrpDc2\nyE9MHMM32AUpmV4ooO+ISEjmatTiJrVjiJAaln9hL8YmTWIJnXwuEIWWGJyFnUGLYxMEIcRXgbBs\npN+RUn6++ZrfAVzgM70+R0r5KeBTAA9FM4crHqQ4MscpBG221dwfKYTgb3/uBhNLy8zdvUs9EuHO\nGx6kETlYgpnR8JAi1mH68g2TYmaSzZl5JpeWBy4IdtVFhBjQNQmJXO1YBKHFKAqDHdmqZHoWOTZB\nkFJ+cLfnhRC/AnwY+ICU+82bVQyDgYgBQRhkZr3SJQpSQGUEYvk35mbZmNt/xvVOIpXweia+YbI5\neY5yckBhtNsIE4MW2oD6wY+6f+EsMawoo58Gfgt4r5SyMowxKPZmUELQwrV08hNR0hvVdkatFFCY\niOIOuHjdceBrAl/XuuszeR6a9Fi+eDH8jcdIPWpCWP1/QHc9UhsVSplI3/MVdjLK/oWzxLB8CP8W\nsIGvNO1z35RS/jdDGotiB4MWgu0UJmNUkxaxQuBPqKQGU5ZiO0bdI5mtYtY96jGT4lgE3zj6hFhJ\nWIz3yEZ8/olHBxpK20IKgkzlkNIOVsPHXKuS2qiyfDnT98ijMEbRjHSWGFaU0fVhHFexN8MUgxaO\nbZCfGs5axS47TC8U2iW37ZpLMltj6Ur66DWINMHqxRRTC4Wg61pzDl6/mKGaHI5JTPNkaAc4se1v\nzYfJ+0WWL/c3xHg3lDAMh1GIMlKMAKMgBENHSiaWSx0mHU0G5UgyaxU2ziWPfIhGxGDpcprURhWz\n4VONGdRiw2un1as/9HYEYNW8rW7xA0T5FwbL2QmwVYTy5KcfU2IA6K7P2Eo5tOS2IKix1A+Muse5\nW3mSuTqxssPYepX5W1l0x+useT4gpCaoxM0wN0IX+j4qhh4HP/m596hrdECoHcIZ5pkbT8Pnhj2K\n4aM3miW3/V1adB6xNHOLieUS2rbjaBKkJ5l7PR+YbgSUkxabM/GBZWZvzCWYXihi1dyO7nQ78Ycc\njq/MSMePEoQziFptdZJZr3RM0jvxBRTH+tDURsog7n/Hw4Gdvnl8CbFCA7PhsXwpPRATjdSD0iBG\n3WXu9XzoeZDN140CShiODyUIZ4hRFAKj4ZFer2BX3XbYaX3ANvVeJbclBCv2lN0fQdiF7cfXALPu\nYdU8GgNqDQrg2ga5qSiZtWqHLVkCuanRqxKg/Av9ZzQkX3HsjKQY1D3mbueIFxqYjk+07DB9r0Cs\nUB/oOPxdiv/dv5xhcy7Rn5W6EFSS1v6SsQWYIdVrj5vieJT8ZBQf2n/yE1GK46MnCKD8C/1G7RBO\nOaN8s2TWygh/x+pYwvhKeaAlrh1Dw2j4HePwgWrC7HtC3OZsHLPhYbQm+6bNvuubSmgMIxlPCAqT\nMQoTUXTXx9M16JP/5DhRZqT+oAThlPLkpx8Lsj9HmEiIPR1A+DKYjAbQezhSaoSOQwAbs/G+H8/X\nNZYup7GrLmbDwzE0ppZKHW1DfaAe0XEiQ7w9hRhK7+ejooThaCiT0SnkmRtPj44Y+JLkRpW5Wznm\nXs+R3Ky2Qyu9Htm/Ao69VEKLRK7WVUoCQGpBpu6xIAT1mEkpE6GesFi6lKaSCEI/W53hIjWPiftF\nREjSmGJvnrnxNJFnPzrsYZw41A7hFDFy5iEpmblXwKq57Uk3s1YhWmqweiFFfjzalQjmC6gk7X0l\nTPWD3Qq47Vb4rZ94lk5+Mka0nG/XcKJZ8lvziqxd6HPz4TPCv/z9WbjxtNotHAAlCKeAkROCJpGK\n2yEGEPgI7KqLXXGppCwMJyhmhxAIKakmLDaPwVTTi3LKwq463bsE2Sz8NiBSm1sF/VpoMqiQqjve\nYM03UhKpuG3nfjltDzzyq58oM9L+UYJwwhlVMQCwq07XJAdBwxu76lCPmxQmYxTHoxgND8/Q+lJE\n7iCU0zaJfL0tXJKg4NvGbHxguxQIIopCQ18FGM5g/CktxlfKxPP19m8XL9QppWxcW0dIqMbN4fo3\nDokShr05eb+qAhhtIWjhGRpS0CUKUnT6D6QmhjfBCMHKxRTRUoNYsYFnaJTSkYGX265HTaxatyho\nEpwBVBltYVVd4vl6x45JSEjm623/RmatWZZ8PEJ+sr9tNgeBEobeKKfyCeMk1R4qh4SOBslegkrK\nHsqYQhGCatJm41yS3HR8KL0XCuMRfE105Cj4AooZG8PxmLmd58LLG8y/liWxzTHfb6KlRviujmCy\naIXIahJSmzXGV8rHMo5BcFLuo0GidggniJNWe0jqGisXU0wuFtHdwHvrGRpr88mBmmN6ESsUeOgf\nfsDY6hrrc7O8/JbHqcUH57/YjmfqLF9Ok1ktE6m4+LqgMBahHjWYvVtor9g112dsrYLuSfJT/W/Y\nfZDfJWizWSc3EcU/gSGqoHYLOxEnqXvlQ9GM/PT1EQmnHCAneSWjuT7xXA2r7tKImBQzNgy4Jo7w\nfXTXw7W2HKNjK6v89P/zh+iej+55uLqOZxh88Zf/S4rjYwMd325MLRSIlrpLa/gCFh4Y77uw6g2X\n+Vvh9YzCkEAlYbJ+/nREQp1WYXj381/8npTy7Xu9Tu0QRpjIsx8NQudOKLFCncn7JaCZW1BySOZq\nLF9ODyTPQHNd3v7sX/PAj15A8zyKmQzf/NAHWL50iSe//BXMxtZEa3gemufxxNee5a9+aXTi180Q\nvwIAAnTH77t566C/iwCiJQez5p5IR/NOzvqO4eT/gqeUZ248Db8/7FEcHqvqMHm/1FWWQjg+Y8sl\ndE9i1T0cUyc/FaUW73/HsPd88UtcuHkLw3UBSGezfOBzf8KXPvaPmVxe6XbgArN37vZ9HEfBtXUM\n1w8tbdErse8oSE0gNRA9+iyHZpYT+B5OgyC0OKvCoJzKI8YzN54+0SaiFuNLpZ6TR7zoEK246J4k\nUnOZWigS7XNBu0ipzIXXbrbFoIXmebzpW9/B18IvfdccrXj7/EQUueNE+gJKaTvohdxvhKAwFu3q\nfeADjilCC/NJcTDfw0niNNyLB+H0SPoJ56kffYL3fbI67GH0Byl3LfsQFlo5vlphsQ8F7SLlBpm1\nKlbN4bvv/Xl83cSxI0QqRa6++D2mlu+S2cxy8+E3cvXFH2N4WxVFXcPglTc/dqTj95t6zGRtPsl4\ns5ubbPZmyB2DQ7lFfjKobJraDK5HKQS5qSiuqTO9UOx+gwxKhJ9WztJuQQnCCPDMjafhtIgBgBBI\nTRyoDo/u+ghJ12r4IEQLdSaXWqUwBLVEuv1cNZHmx2/9CeQ//A25qTTfef9Pksznmbq/hK9paL7P\n/cuXeO49Tx1+AMdELWFxP2GB3yqNesyrcSHIT8XIT0bRPBmUBxeCuVu5LjGXQD1qDDyhcBicBWFQ\ngjBETvN2tDAWIbVR3bdNUmpiVzEw6y6JbA3D8anFTUrpSKfJRErGViuhhepa+IbB6298G4vXxnEt\nky//F/+IzPo6yWyW3MTkSEUXhaJ1ft9YqYRnGNSjx9SrQAh8Izim5vmh/RkEYA2hb8MwOc3CoARh\nSJxmMYDA7KC7flACgd59emErASuRq6P5kmrCxLG3Ls1oscHk/WK732+k4pDM7ohWkmC4e1cnrSRS\nFMcy7f/nJifJTU4e7ksOiel7C7znz79EtFRGIFk7d46/+bkbVBOJo32wlFg1F92VXat+ucuuZLfn\nTjOnsWObEoQBc9qFoI0QbM4lyE3FmH8t27tPL1BJWCSzteBtEtLrUMrYZKeDJLGdFVE1Cbg+qY0q\nueZrEOBrAn0PM5V7QhOoWsTzBT74n/4I03Haj00vLPJTf/gf+ZNf/9W2OcmsuYytVrBrLp4uyE9E\nKaftnuYmq+IwvbhVblsAtYiB7vlIIShlIlTjZle70ZaYn1V+8nPvgRvvOTW7BSUIA+LMCMEOfEPD\nMwSaGz5RL15JM38731U7J5GrU0nY+Ea4L0KTECs1tgmCoDAeIb3e20zlw7E6YwfBA889h+Z37oQ0\nKYkVS0wvLrJ6/jxm3WX2Tr69o9J8yfhKGc31KU7GQErsqovu+jQiBtFinbG1wIe1fbLf3jjIXC1T\niZs4th50exMCpKQaNylMjGZ7zUFyWsxIShCOmVMVPXRICuPRwL6/7bHAGaljN7xgFtox5wsJiUKd\n3GTvyWZn6GhhIkqs2MCqdydzSaAwZo9WDaVDkMrm0L1um70E4oUgAii9VmmLQQtNQmajSiVlM71Q\nwHD89ht7mfR2vj9Wdli6lEaTEsPxadjGUOo+jTInXRhOf2jAEHnmxtNnXgwASmMRymkbSWBi8An6\nBa+1yh30svJIiWfqOLbe9RJfBBO8WXODFauUIASupYebpzRwBtjf4LhYuXABx+hex2nSZ302yGq3\ne2Q3CwnT9/KYDR9NBpP8QScAu+bSiJpUmuWwFeE8c+Npnvz0aIUw7we1QzgGzqp5qCdNf0J+MopV\n93BNre00rvVovCJF0KsAYG0+yfS9QjsOX2vW5B9fLrdNTb4Ga+dTVJIW0VIjtOFNLX7yBeHmIw/z\nyLe/g1YqoTdNR45hcO/69XaUlGNpPR3spiO7xOIgLmHP0LCqLtFSA6kJyinrRPZeHgQn0b+gitv1\nGSUGe9A0N/i6aEcIxfI1Jpe2yihLESQ6bc7Gt5yg2yJgPF0wc7fQZYICuH85xdhalUjF6Wh4k52O\nURo7HbZuu1Lhsa9/k0uvvoZrGrz0lsd5+S2PI5smtGizhlQ/t/8S8HSoJizihaBEdjPdg43ZOJV0\npI9HO50MUxj2W9xOCUKfUEKwN7F8jfGVCkIGq9RK3GRjNsHMQgGz5qERmJMA1i6ktlb0UhIpO2i+\npBYzSW1USGXr4UlSEZ2VS2miJYdYsY6va5TS9qmqs9ML3fWZXCxi1ZrO4OatvdcOoDUD9HqdBDwN\nipkI6Wyta/flC1i4PoYccBXbk8owhEFVOx0QSgj2h11xmNhm4gGIlh1m7+QxXL+9mm39PXm/yML1\nMcy6x8y9wlbDewmOqfV0glp1r9nwxqKa7H/BvJFFSqbvBv6B7eemp3uGZgVaggld7/HC1sO6D5nN\nWviLRPBbnnSH/aB45sbT/PX/HOXrj/4vwx5KF0rSD0nk2Y8qMTgAqY3wJvKm44dmFwtfYtZcZu4V\n0D2J5hP8kWA2/J4TnX9Ki6zthVVzMZyQqqh0i8L2qqUCdi07IUL+7HkAxZ6875PVkZw/1A7hEJz0\n0tTDoNdktRtmw9vaGWxje5TqztXwWY2J110ZHr5LsAOQbPW2FjueN5shqDvLW/cqdx1GNXGGdmN9\nZNTCVJUgHICT3rBmmNRiRjDBhzznQ5eDWMggnj5s9SmAalTH8CTmtqqqpbRNcexsOjcbET20F7Iv\nIDcZxbV0UhtV7Fp4PaIWLSf8zjyGnbReB7B+bjRaop5kRkUYhioIQohPEKy1p6SU68Mcy16oXcHR\nKExEiRcaaP5W2KMvgnr/ZsMjVmwAnatYy5Wh1ghfQCUTlGLQHQ/D8XEs/UxU3OyFZ+qU0jbxfH0r\nFJegA1opEyG9UcWu712ETgCOqVMYsxnfpVigpwvykzEqSetMn/d+M2z/wtAEQQhxAfgQMFotqnYw\nina+k4hn6ixdSZNZrxIpO3iGoDAebTsiCzWX1HqFWMnp2C3sNA/5AhoRg3LKan+uioMP2JyJU48a\nJDdraL6kkrQoTETRXUkyWwvdQYQhpERqDSaX75KdOIfUm+dXiPbOYONc8lTkdYwi7/tkFW48PZTd\nwjB3CP8G+C3g80McQ0+UEPQfz9TZmAuvyOlEjJ6Zs1IEJiepaVSSFpU+NNI5lQhBOR2hvCMnIJHr\nduhDuI9AEiQLfuCP/oj0+jrl9ARL569RGJ/GtWyqcZuVi5M0osrafNwMw4w0lF9VCPERYFFK+ZzY\n48YWQnwc+DjAjDkYh6ESg+HgmlpPR2ZhIka9R1azYnf8Zq+JUB8DWyIsCfpS+HqdZDaLLiWp3Dqp\n3JY1d+HKZe694RcHMGpFi0EKw7EJghDiq0CYB/Z3gGcIzEV7IqX8FPApCBLT+jbAEJQQDJfSWIRE\nvt4xcUmCcgl1tSI9NJWkxdhquetxKWBzOkYy30B3fWoxg/xkjLG1lXbW804iVVWba1gMwr9wbHeZ\nlPKDYY8LIR4FrgCt3cF54PtCiCeklMvHNZ7dUNFDo4FjG6yfSzKxVGqHmzqWztr5pDIRHQHf0NiY\nSzCxVOp4fHM2HpiYdpT02JyeCg33dXWdu9evH+tYFbtz3P6FoZeuEELcBt6+nyijfpeuePxnXH5W\n+42+fZ6iT0iJWffwNYFnKYdxvxCeT6wUNNapJsytbnMhXPvhj3jXV7+G5rpogGsYVBIJ/uy//qc4\ntspIHhX2KwyqdMUeKPPQCCPEmag9NGikrrUryO7FzcceJT81yUPf/T6xUpmF61d55bHHcG2VgDZK\n9Nu/MPQdwkHoxw5BCYFCoTiN7OZf2O8O4UxllCgxUCgUp5V+1Ec6E/tyJQQKheKscBQz0qkWhM/+\nwcd47guZYQ9DoVAoBs5hhOFUCkI7eugLwx6JQqFQDJdnbjwNz39xX689dYKgzEMKhUJxOE6NICgh\nUCgUiqNxKqKMlBgoFArF0TnROwQlBAqFQtE/TqQgKCFQKBSK/nOiTEaJy1ElBgqFQnFMnChBeDkX\n3lxFoVAoFEfnRAmCQqFQKI4PJQgKhUKhAJQgKBQKhaKJEgSFQqFQAEoQFAqFQtFECYJCoVAogBPW\nMU0IsQbcGfY4ejAJ7NkX+pSjzkGAOg/qHMBonYNLUsqpvV50ogRhlBFCfHc/LepOM+ocBKjzoM4B\nnMxzoExGCoVCoQCUICgUCoWiiRKE/vGpYQ9gBFDnIECdB3UO4ASeA+VDUCgUCgWgdggKhUKhaKIE\nQaFQKBSAEoRjQQjxCSGEFEJMDnssg0YI8XtCiJeEED8UQvyxECIz7DENCiHETwshXhZCvCaE+OSw\nxzNohBAXhBDPCiFeFEK8IIT4F8Me07AQQuhCiH8QQvzZsMdyEJQg9BkhxAXgQ8DdYY9lSHwFeERK\n+RjwCvDbQx7PQBBC6MD/DvwM8DDwT4QQDw93VAPHBT4hpXwYeBfwz87gOWjxL4AfD3sQB0UJQv/5\nN8BvAWfSWy+l/LKU0m3+95vA+WGOZ4A8AbwmpbwlpWwAfwh8ZMhjGihSyiUp5feb/y4STIjzwx3V\n4BFCnAduAP/HsMdyUJQg9BEhxEeARSnlc8Mey4jwa8CXhj2IATEP3Nv2/wXO4GTYQghxGXgL8K3h\njmQo/G8Ei0J/2AM5KMawB3DSEEJ8FZgNeep3gGcIzEWnmt3OgZTy883X/A6BCeEzgxybYvgIIRLA\n54DflFIWhj2eQSKE+DCwKqX8nhDifcMez0FRgnBApJQfDHtcCPEocAV4TggBgank+0KIJ6SUywMc\n4rHT6xy0EEL8CvBh4APy7CS6LAIXtv3/fPOxM4UQwiQQg89IKf9o2OMZAu8Gfl4I8bNABEgJIf6D\nlPKfDnlc+0Ilph0TQojbwNullKNS7XAgCCF+GvhfgfdKKdeGPZ5BIYQwCJzoHyAQgu8AH5NSvjDU\ngQ0QEayE/i9gU0r5m8Mez7Bp7hD+Wynlh4c9lv2ifAiKfvNvgSTwFSHED4QQ/37YAxoETUf6Pwf+\nksCZ+h/Pkhg0eTfwy8D7m7/9D5orZcUJQe0QFAqFQgGoHYJCoVAomihBUCgUCgWgBEGhUCgUTZQg\nKBQKhQJQgqBQKBSKJkoQFIo+IYT4CyFE7qRVuFQoWihBUCj6x+8RxOErFCcSJQgKxQERQryj2e8h\nIoSIN2v/PyKl/CugOOzxKRSHRdUyUigOiJTyO0KILwD/ExAF/oOU8vkhD0uhODJKEBSKw/E/EtQr\nqgG/MeSxKBR9QZmMFIrDMQEkCOo2RYY8FoWiLyhBUCgOxx8A/z1Bv4ffHfJYFIq+oExGCsUBEUL8\nV4Ajpfy/m72Uvy6EeD/wPwAPAQkhxALw61LKvxzmWBWKg6CqnSoUCoUCUCYjhUKhUDRRgqBQKBQK\nQAmCQqFQKJooQVAoFAoFoARBoVAoFE2UICgUCoUCUIKgUCgUiib/P6Sg9jy2lE3+AAAAAElFTkSu\nQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x20f6569dda0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Build a model with a n_h-dimensional hidden layer\n",
"parameters = nn_model(X, Y, n_h = 4, num_iterations = 10000, print_cost=True)\n",
"\n",
"# Plot the decision boundary\n",
"plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)\n",
"plt.title(\"Decision Boundary for hidden layer size \" + str(4))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Expected Output**:\n",
"\n",
"<table style=\"width:40%\">\n",
" <tr>\n",
" <td>**Cost after iteration 9000**</td>\n",
" <td> 0.218607 </td> \n",
" </tr>\n",
" \n",
"</table>\n"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Accuracy: 90%\n"
]
}
],
"source": [
"# Print accuracy\n",
"predictions = predict(parameters, X)\n",
"print ('Accuracy: %d' % float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100) + '%')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Expected Output**: \n",
"\n",
"<table style=\"width:15%\">\n",
" <tr>\n",
" <td>**Accuracy**</td>\n",
" <td> 90% </td> \n",
" </tr>\n",
"</table>"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Accuracy is really high compared to Logistic Regression. The model has learnt the leaf patterns of the flower! Neural networks are able to learn even highly non-linear decision boundaries, unlike logistic regression. \n",
"\n",
"Now, let's try out several hidden layer sizes."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 4.6 - Tuning hidden layer size (optional/ungraded exercise) ###\n",
"\n",
"Run the following code. It may take 1-2 minutes. You will observe different behaviors of the model for various hidden layer sizes."
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"scrolled": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Accuracy for 1 hidden units: 67.5 %\n",
"Accuracy for 2 hidden units: 67.25 %\n",
"Accuracy for 3 hidden units: 90.75 %\n",
"Accuracy for 4 hidden units: 90.5 %\n",
"Accuracy for 5 hidden units: 91.25 %\n",
"Accuracy for 20 hidden units: 90.0 %\n",
"Accuracy for 50 hidden units: 90.75 %\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA7IAAAWhCAYAAACoEqz7AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XmQ5Old3/n387vyqjzqvvrununRjDSakUb3wYzkBUkD\nBoQPIIDFiwHHRBg2EOuAcQS2w2Zj/1DYQHg3jHbNYgOxFiAWRiB5DQIdowPr1mg0o5np6a6u+67K\nO/N3PPvHLysrqyqzuqq7qvKXVd9XxITUlVmZT1Zl/T75XN9Haa0RQgghhBBCCCF6hdHtBgghhBBC\nCCGEEIchHVkhhBBCCCGEED1FOrJCCCGEEEIIIXqKdGSFEEIIIYQQQvQU6cgKIYQQQgghhOgp0pEV\nQgghhBBCCNFTpCMrzhyl1PNKqcc73Pa4Umpmn+/9XaXUvzm2xvUQpVRCKfVxpdSmUuqPDvF9F5RS\nRaWUeZztE0II0Tskm4+GZLM4S6QjK04VpdQtpdTf2fW1n1ZKPbv1b631Q1rrT5944/axu4094u8B\no8Cg1vrvH/SbtNa3tdZ9Wmv/qBqilHKUUn/c+P3rTh+GhBBCnDzJ5hMVpWx+q1LqL5VSa0qpZaXU\nHymlxo/q8YWQjqwQAhU67PXgIvCS1to7jjbdhWeBnwAWut0QIYQQ4l6dgmzuBz4CXCJsVwH4v7vZ\nIHG6SEdWnDmtI8ONJTi/q5RaV0p9B3jTrvs+qpT6mlKqoJT6KBDfdfv3K6W+oZTaUEp9QSn18K7n\n+WWl1LcaS3w+qpTa8f0HbO8/Ukq90GjDq0qpn2+57dtKqR9o+betlFpRSj3a+PdbG+3aUEp9s3Wm\nUin1aaXUryulPg+UgSttnvs1jfttNJZ9/d3G1/8V8GvAP2wsRfqZNt/7ZqXUV5RSeaXUolLq3za+\nfqkxa2oppd7W+P6t/6pKqVuN+xlKqV9RSt1QSq0qpf5QKTXQ7mekta5rrX9Da/0scGSjyUIIIU6G\nZHPzvqcpmz+ptf4jrXVea10G/j3wjsP+rIXoRDqy4qz7F8DVxn/fB/yPWzcopRzgT4HfAwaAPwJ+\npOX2R4HfAX4eGAR+G3hGKRVrefx/ALwPuAw8DPz0XbRxCfh+IAP8I+DfKaXe0LjtPxPOQm75ADCv\ntf66UmoS+Avg3zTa/8vAx5RSwy33/0ng54A0MNX6pEopG/g48N+AEeCfAn+glLqutf4XwP8KfLSx\nFOk/tmn3bwK/qbXOEP58/3D3HbTWX2x8fx/hyO3fAv9P4+Z/CvwQ8D3ABLAO/O/7/qSEEEKcBpLN\npzOb3w08f8D7CnFH0pEVp9GfNkYpN5RSG8D/sc99/wHw61rrNa31NPBbLbe9FbCB39Bau1rrPwa+\n3HL7zwG/rbX+W621r7X+T0Ct8X1bfktrPae1XiMMnkcO+2K01n+htb6hQ58hDK93NW7+feADSqlM\n498/SRjuEIboJ7TWn9BaB1rrvwS+QhioW35Xa/281trTWru7nvqtQB/wvzVmPP8a+HPgxw7YdBe4\nppQa0loXtdZfusP9f4tw2dE/b/z7nwD/XGs9o7WuAf8S+HtKKeuAzy+EECI6JJtDZzKbG7Pivwb8\nLwdspxB3JB1ZcRr9kNY6t/Uf8NQ+950Aplv+PbXrtlmtte5w+0XgQ7uC+Xzj+7a07tcsE4bPoSil\n3q+U+pIKiyVsEIbdEIDWeg74PPAjSqkc8H7gD1ra9/d3te+dQGuhhdbXvtsEMK21Dlq+NgVMHrDp\nPwPcD7yolPqyUur793mNPw88Dvx4y/NdBP7flra/QLhsePSAzy+EECI6JJu323emslkpdQ34JPCL\nWuvPHbCdQtyRzGyIs26eMOC2lrpc2HXbpFJKtQTmBeBG4/9PE44Y//pxNa6xFOpjwE8Bf6a1dpVS\nfwqolrv9J+AfE/49f1FrPdvSvt/TWv/sPk+h97ltDjivlDJaAuwC8NJB2q61fhn4MRUWqvgg8MdK\nqcHd91NKvQv418A7tdb5lpumgf9Ja/35gzyfEEKIU0OyubOeymal1EXgr4B/rbX+vTvdX4jDkBlZ\ncdb9IfCrSql+pdQ5wr0fW74IeMAvNAo1fBB4c8vt/yfwT5RSb1GhlFLqSaVU+i7bopRS8db/AAeI\nAcuAp5R6P/C9u77vT4E3AL9IuC9ny+8DP6CU+j6llNl4zMcbr/Mg/pZwpPqfNV7/48APAP/lgC/m\nJ5RSw42g3Wh8Odh1n/OEv4Of0lrvDuH/APx6IwRRSg0rpX5wn+eLqe2CHU7j9apO9xdCCBFZks2d\n9Uw2q3A/8F8D/15r/R8O9OqEOATpyIqz7l8RLsm5Sbi/pTlaqLWuE45W/jSwBvxD4E9abv8K8LOE\nVfjWgVe4u4IRW94OVNr89wuEgbIO/DjwTOs3aa0rhCPDl3e1bxr4QeBpwrCdJtybcqC/+8br/wHC\nJVErhPuZfkpr/eIBX8/7gOeVUkXC4hI/2mhrq/cSLkf6Y7VdHXFrBP43G6/1vymlCsCXgLfs83zf\nJfx5TQL/X+P/XzxgW4UQQkSHZHMHPZbN/5iw6vK/bHmc4gHbKcQdqZ1bDIQQvUgp9WvA/Vrrn7jj\nnYUQQghx7CSbhTheskdWiB6nwvPbfoawKqIQQgghukyyWYjjJ0uLhehhSqmfJVyW9Emt9We73R4h\nhBDirJNsFuJkyNJiIYQQQgghhBA9RWZkhRBCCCGEEEL0FOnICiGEEEIIIYToKT1V7ClnOXrMTna7\nGUIIIU6J71Y3V7TWw91uRy+TbBZCCHGUDprNPdWRHbOT/M61d3a7GUIIIU6Jd3z7L6a63YZeJ9ks\nhBDiKB00m2VpsRBCCCGEEEKIniIdWSGEEEIIIYQQPUU6skIIIYQQQggheop0ZIUQQgghhBBC9BTp\nyAohhBBCCCGE6CnSkRVCCCGEEEII0VOkIyuEEEIIIYQQouuefvKpA9+3p86RFUIIIYQQQghxujzy\nfo8PGL9wqO+RjqwQQgghhBBCiK44zCxsK1laLIQQQgghhBDixN1tJxZkRlYIIYQQQgghxAm6m6XE\nu0lHVgghxJnTDNBv/0W3myKEEEKcKfcyC9tKOrJCCCHOlKMKUCGEEEIczlFmsHRkhRBCnAlHsYxJ\nCCGEEHfnqAeSpSMrhBDi1JNZWCGEEKI7jiuDpWqxEEKIU006sUIIIUR3HGcGy4ysEEKIU0k6sEII\nIUT3HHcOS0dWCCHEqSOdWCGEEKI7TiqDpSMrhBDi1Pjob/8433wm1+1mCCGEEGfSSQ4kS0dWCCHE\nqfD0k0/BM91uhRBCCHE2nfRqKOnICiGE6Glv+52HeeJj7+x2M4QQQogzqVuroaQjK4QQomc9/eRT\n8LFut0IIIYQ4m7q5Gko6skIIIXrO25/7EI//SqXbzRBCCCHOrG4XVpSOrBBCiJ7y9JNPgXRihRBC\niK6I/80H+aUPj3W7GdKRFUL0LrcesLHu4bqQShmksyaGobrdLHFMohKcQgghOpNsPt2efvIp+HC3\nWxHqekdWKWUCXwFmtdbf3+32CCF6Q7nkMzNVR+vw38W8z+qKx8UrMUxTAvO0iVJwngWSzUKIu1Eq\n+sze3pnNa6seFy/HMCSbe1oUj7czut0A4BeBF7rdCCFE79BaMz+zHZTh18BzNWsrbvcaJo5Ft/fg\nnFGSzUKIQ+mUzW5ds7bqda9h4p49/eRTkevEQpc7skqpc8CTwP/VzXYIIXqLW9f4/t6vaw2FfHDy\nDRLH4uknn5JObBdINgsh7ka9pgn03q9rDYXNNqEtekKUc7jbS4t/A/hnQLrL7RBC9BC1z14bIwrr\nTMQ9i3JwngGSzUKIQzMMoE1HFkBJNvecXqhL0bWOrFLq+4ElrfVXlVKP73O/nwN+DmDUTpxQ64TY\nyVUWc4lhDB0wUVnGRGb9usm2FU5MUavuTEylINtvdqlV4ihEcQ/OWSLZLHpJXVnMJUawtM+4ZHPX\n2Y6B4yhqtb3Z3D/Q7bkzcRi9Upeim++qdwB/Vyn1ASAOZJRSv6+1/onWO2mtPwJ8BOCBRK7DOI84\nrbTWVKsaQ4ETUyh18oUCXkmd5zMjb0bpMCAV8H0LzzJRXT7xtohtk+cdpm7W8Fu23fRlDHL9Epa9\nqpuHqosmyWZxRzrQVGvdzeaX+i7y2eHHMHQAKAwC3rfwLGPVlRNvi9g2ccHh9qu1Hdt/0hmDTE4G\nmXtFL62I6tonPq31rwK/CtAY9f3l3UEpzrZiwQ+LBgBosGzFuQsOTuzk1qdsWik+PfJmfGPnn8p/\nHX8XP3nrGWwtxQuOkudpgkBj23f+YFQq+Ts6sRDunUUTjjaIniGzsNEh2SzupLDpsTAXFtXTXcrm\nDTvNZ4cfwzcsWndefmLs3fzk1J9ha9mPeZQOk83lor+zhoUC15Wxrl7QC0uJd5OpCxFJ9VrA3PTO\nynduXXP7Vo2r98c7Xkhr1YBaNcB2DOKJex8lfil9Cd3uMTTcSk1wX/H2PT3+WVQp+6yteLiuJpky\nGBi0QcHcdJ1qJZz1NkwYn3RI9bUfwQ18zdL83kGEWlWT3/TJyqxsz5BZWCF6R70WMD/r7snm6Vs1\nruyTzdVqQL0aYMcM4vF7z+bvpi8RtNt0qeB2cpyrpZl7evyzqFzyWV9tyeYhGzTMzWxns2nC2D7Z\n7PuapYVd2ayhWmlkc06yOap6ZSnxbpF4R2mtPw18usvNEBGyse7tCMotQQDlUrDnIhoEmtnbdSrl\nIJyN0+Fyp/OX9p4p6vua5QWX/KaP1pDqMxgdt7GdvaFYNxyCNsW9A6VwDfueXuNZtLnhsTi3/SGo\nVvXZ3PCxTKjXt+/nezB7u86lqzGcmIEONBqaB6pXKgFKsec9ojXSke0RvbR06aySbBa7bazdezbH\n4opzF++QzbRks703g2uGg27TkdVINt+NzXWPxfmd2Zzf8DEMcFtOtPO2svlaDMdpk83lztlckI5s\nZPVyHss7SkSSt8+KXc/bm6Kryy6VchBePJsXYs3inMvEead5P601M7dq1Gq6eaEtFQOmXq1x+b74\nnmC9WJ7jxcxlPLU3GM+VFw79us4yrTVL8+6egAt8qHc4Smd12cXzoVwMR4MTSYOxSZt9B/MVLMzV\nqdc08YRiYNDGsmWtcZT0cmgKcZa5HbJZE3ZEd1tZ2pvN1apmcd5l4tzObJ6+WaO2tT0EKBUCpso1\nrtwXx9iVzZfKs7ycvoi3q9OqUUxWFu/25Z1JOtAsLezNZt+n4zF3a8surhsOXgAkUwZjEzaG0bFo\nMQALs3XqdU0iqegfkGzutl5cSrybFMMWkdTXZ7TvrOiwM7Pb5rrfdpS4kPfRLTdUygG1ut7bmQog\nv7E3oScri5wrL2IFjSFJrUFrfGXyyfF3MRcfPszLOtPqdb1vwLVTyAfNTiyEv7/br9aIxVXHUv7l\nYsDmuk+lHLC+6vPqy1WqVdkvFQVyLqwQva0vfQTZrNtnc93Ve3pBQQCbm3uz+Xx5gYnKUptsNvjk\n+Lslmw/hbrI5vxk0O7EQdminbobZ3Ol0vFIxYHMjzOa1lTCba5LNXfP0k0/1fCcWpCMrIiqdMRuV\nELe/tnW0itNmCXC7A7i3tIZovbYzKANlMHXttXzxPR/kmYd/mC8OvJ5aywivAr538fM8sfTfSbkl\nQIcNUYoNJ8snx9/NqiNFag7CNNX+Q7VttLt7EEAxHzSWpjXOpttnUFdrmL5ZJ9jvTSKOnXRgheh9\n6YyJ47TP5nZLgNsNMIc37PxnbXc2Gwa37nsdX3zPj/Dx1/0wXxp4mLraXkQYnh4QZnNyVzavN7J5\nzcne9es8S+4mm9sJAigWtrPZOEA235Zs7orTlMfSkRWRpAzFhcsxhkYsYnFFImkwPukwMtZ+70tf\nX/u3cjyumns3INw32+q5t7yXqfsfoZrKUI2n+Hb2Pv5k7L2sbQbNJcwKGK8uUzXje0709pXB13Kv\nuYdXenZYliKR2vt7UipclrR7lL/TwepaQ70eYNuK3ICJZd65SHEQhPtzRXecptAU4iwzDMWFK7uy\n+VznbE51yuZdxRgdRzUv5Br41lv+B27f93qqqTSVeIrnsvfzJ+PvZWPDb2azgWa0ukKtQzZ/I/fA\nvb/gM8CyVdvZdKUg0SGb2w1Q6CAs/GU7imy/iXmA03aCINw7K07G25/70KnLY9kjKyLLMBQDQ3ZY\nOe8OhkdtyqUaQRBeYBsDs4xOOjvu58QUlq1w65p8bpDNgRECa/vPIDBMSnaS5/UEoy/dZHjUon/Q\npmClMLSPz84rs1YG607maF7wGTBxzmHudn1HsaaBYYvBIYvNdY/1NZ8g0JgmuPX2j6EMcByDWzeq\neG77+7RTzAf0DxzN6xAHc9oCUwhxuGweGbOplPdm89jEzmyOxRWW1cjm/mHy/UN7srlop/i2Hmfk\npSmGxyz6B8JsNjtk85otM7IHNXHOYbZxcsBWNg8OWwwMWWyse2ys+QS+xrT2z2bbUdx8pbrnaLz9\nFPJSoPEkPP3kU/ArlW4348jJO0ecCrZjcPm+OJvrHpVKQCxmkOu3moUEdKCZn6tT2Ayao76F3DDt\nNvv4ls1G/wgjszdZXvRIpkyyRoFA7R1eVEFAfGmZUtHvWI5ebDNNxfnLMdx6OOPtxIxmga3cgE22\n32Lq1Rr12t59zFssU1Gr+YfqxAKYlhSVOCmPvN/jA8YvdLsZQogusx2Dy9fibGx4VLeyecDCalyP\ng0CzMFunkG/N5qG2FYl9y2YzN8zw3BTLC9vZ7LfJZoKA+NKSZPMBmVa4Cq5eD/A9TSxmNAts9Q/Y\n5A6SzZaiWtl7vvtBnlscr9M8qCwdWXFqmKZqO0KstebWq1Xqta0vhP8TqxQxdECw6/6G55IoFxrf\nGy5JHYkbvCZ/gxczV/CMln06gc/5l55jtrx9VIy4M9sxsJ29Xy8Vg7DwRJugVAoyWZOhUZtbN6qH\nfs7+AfkwcxJOc2AKIQ7PtBSD7bI50Ey1zeYSJgHerllWw3OJl4vhXXVYoHE4Vuf+wk1eTl/azmat\nMQOfcy99m9nK9lEx4s4cx4C7zObhUZubrxw+m3MD0hU5Lm9/7kM8fgpnYVvJu0ecevOz9e2gbDGw\nNIvpuvimtWP0V2nN6MyN5r91o6f79tWvE6sUeS53Hc+JkV5f5tq3v0yylEcD62seo+NtEkAcWLUS\nNH/euw0OWwwOhx+GOt2nHaUgkzMo5H1Wlz3iiZ0zAuJovO13HuaJj72z280QQvSITtk8uDgTZrNh\nbmez1mE2z77avN9WDrxz5WvEywWe77+OZztk1pa49vyXSZQLaMKzb0fGJJvvRaXsHyibg7vJ5k2P\n1SUt2XzETutS4t2kIyt6nu8HFDZ9qtWAWNwgkzEplzTrax6+H7QNSgBDa97whU9y4x2Ps+L0o7Um\nUS7ymq99FqfxTUpBX6YxKqw1l259h/Tyt9o+nluXynv3ynbCY3XaBWa55DfD0okpqpX2P+9sziDZ\nZwKalUUP14XN9Z3HBKyvely8IjPoR+XpJ5+Cj3W7FUKIKGlmcyUgnjBJZwxKpYCNNf8O2Rzwxi98\nglfe3pLNpQKv+drnsBsbNFuzWemAyzefJ/vlb7Z9vLpk8z2zHQOl2h9zWCn7wHY216r7Z7NGs9op\nm9ca2Swz6PfkLK2Mko6s6Gnrqy5LC60bMgKW5r1msYI76Vdlfnj2U1QMh9X1gPJsofl9W0GZTBlo\nrZmbqVPMtx9u3Kq8K+5NOmOyON9+82ulrKk1BiuGR22mp+p7qhonUwZjkzG01tx8uYbb5qEaxw2y\ntOBy7mLsGF7F2SGzsEKIdtZWXJYXt7N5cyNgcZ6DZzNb2Rxjdc2nPLczm9MZk0Sykc3TdYoFyebj\nlMmYLHXI5nJJU6uF+5+HR21mbu/N5lTfdja/+lIVr80+Wq1B+7C84DJ5QbL5bpylDuwW6ciKnlUs\n+Ls6sdsOEpQAI6PhKGIiqHMuC1UnxuaGhw4gnTUbx8IoCnmfUoegBDBNpOreETAMRa7fZH11bzl+\nrcPfeSxukEyZjI3bLC24YfgBfWmD8UYlzEo5wPP3fxO0HuYuDk9mYYUQ7RTy/o5ObKuDZvNwM5tr\nnMtBNdbIZh12YpvZvOlT2udabpqQy0k23yvDDI/U2Vhrn82lgk8sZpDqMxkdt1luyeZ02mRsMvx9\nlkvBHZcf7/f7FJ2dxU4sSEdW9LCVxUOWrd0lnlAsLbpkMiaZrIkyFPGEQTyxdy9NftPrGMBOTGFa\nisU5l9yASTIlRYXuhW23X8KkVHi+8JZsv0UmZ+K6GtNUzerHQPOcwf0YMkh/185qYAoh7uzesxmW\nF13SGZNMzkSpO2Rzh37PVjYvzDeyOSnZfC9su3HWb7tsbjkBItdvkd0nm++UzoZskT2Us1DQaT/S\nkRU9y3UPt+9l6zprmuB5NPZYaiqlgI11jwuXYzsuxju+l85XVreuqdfCthQL/o7CBxBWTS7mw+fQ\nGtJZg1zO2tEpE9vSGZPlDh+E0pmdH0SUUjjO9s8xCDQbax75zc6FKbZk++VDzWFJB1YIcSd3nc0W\neC5UKwAB5VLA5obP+UtOx2zeJ5p3ZnPeZ2jE2nGygdaaQt5ncz0cOM3kTLKNjrPYK501WVny2nZE\n75jNvmZj/WDZLFWMD+6sFHTaj8xJiJ7lxA4eNkrBpasxrtwXx9+1MkZrqFXDQOsk22+2O3K2+f2t\n/3912dsxI7g45zI/W6dcCqiUA5YXPKan6uiDrrE6YyxbMTZpN2ZgG/8pGJuwwxHhDoJAM/VqjZUl\nr2OxiS2GCUNbVRZ9TbHgUyr68jvZh3RihRAHcehsvhbj8n3xPeePah1Wsu+0/xUgm7MOnM0rSx5+\ny5aThVmXhVm3mc1L8y4zks0d2bbB6ESbbJ60sY4om00zrIIM4DeyuVySbG5HMjkkwx6iZw2P2o3Q\n2fl1ZYQHc3uubgbc2KSDEzPIb3ptl8ZoDYV8QCbb/rmSKYNsv8nmur/je9pRKtyjmc6Y1GpBOAK5\nK1CrlYBSMaAvLbOC7WSyFqk+k1Ix/Hmn+swdy5N201oze7vWHH2/k2QqXEq+ueGxOOdufxBScO5C\njERSxvi2nPVlS0KIwxketZm9vTebDSM8793ztrN5/JyD4xhsbnTO5mLe3zPjtyXVtyubVefj2bay\nuS9tUqsGFPJ7s7ki2byvbM6iL21SKvigDpDNgWZmqnbgytHJvnBGfHPdY3F+O5uVgsmLMRIJyWYp\nsriTdGRFz0qmTCYvOCwvuNTqGsOAbM5sFomo1zU6gFhcNZcK7XfBNffJLaUUo+MO/QNhyBkmlIs+\n+c32ibm1/7JUaF+ufqs4goRlZ6apyGQPdomam6lTLh0sKJWC/gGTei1gcc5tVjHeMjNV4+r1OIYs\n/ZZlS0KIQ0v1hdm8tOBSr2lMM1y2e9fZvE8MbGVzbiCg3MjmUsGn0OGEga1sLnbK5iA86k2yuTPT\nVGQOWEBrdqZOpXyYbLaoVQMW59tk8y3JZimyuJd0ZEVPS/WZpK61D5xYm+VNyZSBoWD3ImKlDrYv\nw4kZzbNHYzGDQr7WtihRIqlYXnRZW2lfuRHAlEO/j0S9HuxbURq2ilGEoTg8apFMmSwt7J0xgHBC\noFQMOs4AnAUyCyuEuBepPpPLh8jmVMoIr9G7vq5UOAt4J7GYQayRzY5jUCzszWbDCIs8Li/UWWtT\nGX/r+fbrVIuDq9fCwYX97MjmMYtE0tg3m8vFoHl+8FkjS4nbk46sOFOUUpy7FGNmqtZcfqQ1jIzb\nxOOHW7ISTxgMj1ksL3jN5S+GAecuxshvBqyvdu7EhuF8Oi/GQRAm0EmNmtaqet+zCS0LJi44+J5G\nodCEe286HgGgw32zZ5XMwgohTpoyFOcvNrK5cfnVGkbHbWKHzOZE0mB41GJ50Wt2js2tbN7wWW9z\nhEyrg3Sce1E3srndcvEtlg0T5xx8f2c2794r3coPzl42y1Li/Z3Ov1Yh9hGPG1y9P06lEqADSCQM\njLscge0fsMlkLSrlAMMIA1QpxdxM+xFFCDuxE+cdbOd07PXwXM3mhketFlCrbleJTCQNxibs5gz2\ncXEc1fFnbRhw/nIMrWFuro4fNHJVQyZrdOwAJ1On43dzGPG/+SC/9OGxbjdDCHFGxRMGV6/HqZQD\ntA4z5G47Xf2DNplcI5vNMOeVUsxO75/NkxecfQsX9ZJ9s3nSxjnmzyC202aKvcEw4fylGDqAuel6\nc2B562QHZbTZ66whdcaON5SlxHcmHVnRM3QQlm/f3PDDpcCNc0TvplS+UurIzpQzTbVnP43f6RxT\nBZevxU5NJ7ZS9sMKzAFs9g8z/bqHqCb66F+e4/yr36F+s8qV+493T0ssbhBPKKoVvfMDioKLVxxs\nW/HqS1W8xijv1l3ymwFOTFGvbX+fUtA/aJ2a389BPf3kU/DhbrdCCNGLgkY2548qm4+os3KobAau\n3BfDsk/Htb9c8pvFMDcHRhrZnGJgeZZzr36H+qu1Y8/meMIgFldUq3pnh1bBxSuxPdm8pdAhmweG\nrFMzyHAQspT4YKQjK3qC1prpqTrVStC8sC1WXYoFn8kLse42ro1EyqDYptiEaXJqLsRaa+ZmXHQA\ni5OX+e7r30FghjX5S5l+Fi7cx5s++wz5TY9c//Feas5diLEw74ZHKOlwD9Zoo1J1pezjt1lGrHU4\nmzswZJHf9DGUIttvkuo7OyO+MgsrhLgXWodVaVsHEherLqViwMR5p7uNayORNCi12bdpWaenboXW\nmvnGqrCFc1d56eG3EZgmKEUpk2tmcyHvH/sy6nMXYyzOuRQKjWyOK8YmwkrV5ZLfdouP1uERTgOD\njWw2FLkB88gGOKLukfd7fMD4hW43o2dIR1b0hHIpoFoNdsy4aR0W5alWAuIRK8k+PGJTLtZ2XKSV\ngtHxvQe7e54mCDS2re5qBLtbXFfje5pAKV5+3VsJrO3LiTZNPOVw69rrGJv/6rG3xTAVE+cctA4/\nTLWOMgd+5206vh8e9XPQ6siniczCCiHuVZjBek82Fwt+NLN5zKbyaptsnmifzTrQWL2WzXWN70Og\nDF5+3VvnNibkAAAgAElEQVR2ZbOFi2LqymsZXfr6sbfFNBUT5ztk8z51oAIfMjnrwNWRTwuZhT28\ns/UOET2rXPLbng2ndXhb1MLSiRlcuhpjdcWjUg4aM3/2jvNJPS8cNa2UwxdmmDA+4ZDqkbL/RiPY\nK6kM2tj789eGyfroOWIbxx+WW5RS7P68EU8abfdEKQV9mWi9b06KhKUQ4iiUS+2PsYHwzNaoZXMs\nZnDxaoy11mwetnecT7o7m00zPIu+V1brbGVgOZ1te7s2TdZGzxEvfOsE27Q3mxOJztl8Fk8NkFy+\nO9KRFT3BsgyU2huYyojuciDbMRib6Ly0amaqFlb1a/A9mJ2uc/FK7NBVGrvBshVOTGG5dYIOo9VO\nvUq6yx1z01TNCpat+22cmDq11Sk7kaAUQhwl01Lti+ap/c9/7SZnn2zWWjNzq0attv2CPA9mb9e5\ndDV27MULj4LtGDiOwqrX2g4yA8TcKn3p7r4W01IMjVisLO3M5lhMkc6enY6sLCW+NxG9zAixUzpr\nsrzo7vm6ojdH7qrVoFlBsJXWsL7m7dsBjpKJ8w7+zQq5tUU2BsbQ5vbvwvRdHiu/hIrA4eX9gzbx\nhMnGmofva/oyJpmseaYOVpdOrBDiqGWzFqtLe89LUbCn0FIvqFU19XrnbB4d751s9m6Vyawvs9k/\n0j6bI7BcemDIJp402FjzCXxNOmOSPkPZLLl876QjK3qCZSnOXXSYm2mUadfhaN7keacnL3ie2/ns\nU7dNiEaJq0y+1v8gL6cvoVFMZG9y/ze+wIuPvotC/xAqCMA0eHTjRa5VZ7vd3KZE0iCR7I0PIUfp\no7/943zzmVy3myGEOIUsu5HN03UCzXY2X+jNbHb3yeZ2HdwocZXFV/sf5OX0RWhk8/WvPcsLb3w3\nxewgSofZ/MaN73ClNt/t5jYlk+aRnSLRS6QTezSkIyt6RjJlcvX+OLWqbi4NjcKI4t2Ix9vvDQFI\nJKP7mjTw5xOPs+r04xth8NwYvc5c3ziPfeYZaok+avEEmeI616+a0IMfZE6Tp598Cp7pdiuEEKdZ\nMmVy9fopyeZE53PJkxHP5mcmnmDdyeAb4Uf7G2P3M983xmOf+TiVVB/1WIJMYY3r1yzJ5i6SpcRH\nSzqyoqcopYgn2l+AtdbUqppAaxJxIxJLWjuxbEUy1f4YgE4hGgVziRHWnGyzEwth4Yhaoo/V0fMM\nL9wmUS5gGFAqqp5c9n0ayEivEOIkHSSbtdbEE0akO7m2bZBIGJTLvZXNM4kxNpx0sxMLYYXiaqqP\n1dFJhhZnSJYKKAPKJaMnl32fBpLNR086suJUqFYDZqdq+EG4Nwdg/JwT6Yu157ZPxY01n6ERHcmw\nX471E6i9BSJ826aQG2J44TYQjg7rCKW+72s21z1qVU0sHhZ5imqRsHshI71CiCipVgJmb/dYNvvt\ns2t91WdwOJrZvBLrx1d7f6a+aVPMDjK0OAM0jqKLTjTje5rNjZZs7rcwzej9fO+VZPPxkY6s6HlB\noJm+VSPww39vXaPnputcvhbDdqJZZdDt0JENdHiGWhQrPqbdEmYQhIertzA8l3i5sP0FDamIHF5e\nrwdMvVpDB2GAqzysrnhcvBLDieh7427ISK8QIkqa2dyY3NyRzffFsO1oXn871akIgvA/MxrRtkPa\nK2FpH3fXQLPpe8Qrxea/tYZkKho/93otYOrmzmxeW/G4INksDuH0vFPEmVUqBtsJ2UJr2Fz3T75B\nB+TE2o86GkZ4pmwUXSrNYWkvLBqxRQcYgc/I7E0gLJ8/MhadGc/FeZfA3x6F1o2BgsW5vVWwe5UE\npRAiaooFv100o4H8Ru9ls2mG+RxFl0ozWIG/M5uDAMP3GZ6bAhrZPB6dGc922ez7sDQv2SwOLoJz\nPkIcju/rjktlOi0RioLhUZuZqfqOtisFQyNWJJcuAZgE/NDsp/jrkbewHB8AYKC2ydtufQEjozEM\nk2zOitQ5uOU2+5AByqUAraO5TOyg4n/zQX7pw2PdboYQQuzh+7QdZEaD50U7m2dv91Y2WzrgB2f/\nir8efSsrsX4ABusbvO3mF1AZjWmYZPotYhE5B1drTbnUPptLHb7eS2Qp8cmRjqzoeclk+wuzUpDq\ni+jUJmGlx8kLDsuLLvWaxrIUg8MW2f5o/1lmvBI/NPfX1AwbgFjggg1E8OzbWrVzICpFZD+UHMTT\nTz4FH+52K4QQor1OS1ijns2pvkY2L7jU641sHrHI5qKdzVmvxA/PfmpnNjtELpvD4l/7Z3Mvk1nY\nkxXtv0ohDsCJGWRyJvkNvzmCqlRYRr8vHY3Rx05SfWakA303H4MXMld4OX0RUwe8Jn+Da8XbRCl3\n6rWAaiVgdcXFrbe/j1KQyfbOz72VjPQKIXpBLGaQyZrkN3dns0Gqrwey+VrvZISnDF5IX+GVRjY/\nuPkKV0vT0czmZRe3w+rhXs5mkE5sN0hHVpwKo+M2qT6TjTUPHUA6Z5DLRXcZUC8KUPz5xOOsxPrx\nGiX+l2MDzCRGeWL5y11uHQS+Zna6TqUc3LEqYyyuGBmzT6ZhR0hCUgjRS0YnGtm87qE1pLOSzUct\nQPHxiSdYdXLN43eWY/3MFkb5npWvdLl14fav2dt1qpUDZvNo72UzSD53i3RkxamgVHhmqZxbenxu\nJ8dZieWanVgAz7C40XeBRzZepN8t7PPdx29h3j1QJ1YpmLzgYESk4MVBvO13HuaJj72z280QQohD\nUUqRzpqke3iWLepupSYb57u3ZrPNy+mLvH7zRXJucZ/vPn6Lc+6BOrFKwbmLvZXNIB3Ybov22g4h\nRCR4nmYqNopntB8pnU+MnHCLdgoCTTHvH/h8vFKhd4pJPP3kU9KJFUIIscd+2azQzMcjkM2FA2az\ngmIPZTNIJzYKZEZWCNGR52nmZ8LlurWggMr66N1nyGpN3K91qYUhz+tcuXq3sMR/dCtmbnn7cx/i\n8V+pdLsZQgghIsbzNPPTdSqVgBpFVGZvNisg4Ve708AGr37wbKZxNF6vkE5sNEhHVoiI0lpTr4UJ\n4MRUV/YUzd6uUa4pfMthZPoGU/e9fudpClpjEHChPHfibWu1uuQd+L5KQTLiBbaefvIpkE6sEEJE\nTjObFThOd7J5ZqpGuW4QWA6jt19h+upr92SzGficLy+ceNtaLS8d7kzYTpWuo0Q6sNEiHVkhIqhS\nDpibroXn8AGmpZg87xBPnNxFvlRTfOP621icvAJKEauUufjSN5m+9lB4KryhiPt13rfwLJbu3nIg\nrTWF/MGGcZWCdNYkHqFzbneTkBRCiGiqlH3mputdzeZCTfGN17yDpYnLoCBWKTWy+bVgKDAUCb/G\n+xaexaS72XzQpcJKQSZnRuoM+nYkn6NHOrLi1PN9zfKCSz7vg4a+tMnIuI1lRbOggO9rZqZqBC3X\nf8/VTN+qcfX++IkVQvj05NtY6htHm+FloppKM3X/63nk858gljCZHLcYqG9Eorz/fkuXxs/ZbK77\nKAXZfiuyRzJJQAohzpI92ZwxGRmLcDZ7mumpOrpdNl+PYxgnlc3vYLlvtLmUuJrKMHX/wzz67CeI\npSwmxkwG6puRyOb9jE/abG5EP5u3SEZHk3Rkxammteb2zRr1umZr3U0h71Op+Fy+dnLBcxiFzb2F\nETzLpp5IslasM5Q9/jYUzQTz6QkCY+cS3MAwmLn6Wt41/QUG69Eoka+UItlnUC7uHflN9RlkshaZ\nbLQvdRKQQoizpJnNte2wK2z6VMoBV67FUBHM5vymD+2yOdnI5szxt6FgJVlMjxIYOzMtMExmrj7E\nu2a/FK1sThmUS3uzuS9tkMlZZHLRzmaAj/72j/PNZ3LdboboIPrvICHuQbkU4Lp6T/j4XtihzUbw\nItpauEijePm1b2Lh4v2oIOArhsHr8i/zlrVvHetoa9FKYmofn117SQ2DcjpD/0C0fm5j4za3bmzP\nYisVrn4eHY9GoHcS/5sP8ksfHut2M4QQ4kSVio1s3sX3NYWCH8nBR8/bPkImUIpXXvsWFi5cQwUB\nXzUMHt58iTetP3es2VywUpg6YM9mGsOg0pclF7FsHp2wmdqdzSaMjDvdbdgBPf3kU/BMt1sh9hOt\nd7wQR6xW1bTbvqk11KrRLPOeSBooA3QAt64/zPyF+8LlvY0+5XOZa8S9Ko/kXzq2NuTcAr7aWxBJ\nBT7ng3XMCC390lqzueE3xyoMA9JZg5HRaJ9H9/STT8GHu90KIYQ4ebVa0D6bg0Y2n8DKo8NKpkzW\n13x0ADevP8r8+Ws7svmb2ftIeBVeV3jl2NrQX893zma9hhmhzNNas7m+M5szOYPhkWhn8xZZKdUb\nor0gXYh75MQUqsO7PIrLiiGs2pdIGKBg+spDaGvnrGJg2nw19yD6wDXtDy8e1Hkw/wpW0FINWAdY\n2ufR/IvH9rx3Y2nBZW3Fa34oCgLIbwTUatE8Yif+Nx+UgBRCnGmOY/RkNsfjYTbPXnkN2tq1vNe0\n+XLuoWPN5kRQ44HCjR3ZrHSArX0eyX/32J73bizOu6yv7szmzfWAWj2a2bxFMrq3yIysONVSfQaW\npXDbXDhXlz1sW5Htj9afgVKKcxcc1tZ9Aqv90ljPctjMB+Syx3eMzNtWv0HWLfDN3APUDIfx6hJv\nXf0Waa98bM95WIHfGPHd9evVGlaWXc5fjHWnYR3ILKwQQoR7JE1T4QV7s3llycOyVeS2/iilOHfR\nYW0jIDDbt821Y+QLmmzm+Drj71j5Otl6kedy91MzHCYqS7x17Zv0+dE5ss33NfmN9tm8uuRyLmLZ\nvEUyuvdE6yohxBFTSnHhcoyZqRq16t7AXJx3SWfNyI0AK0MxOGhhaJ9Atfsz1SwEGXKUjq8NwEP5\nGzyUv3Fsz3GvXC88y2/3HmhgRxGRbpO9sEIIsU0pxcXLMaanam2v1YvzLulM9LLZMBRDAyZKB+g2\nS3xBs+inyHJ8nUoFvC7/Mq/Lv3xsz3GvPFejVPsTBaKUza1kFrY3SUdWnHp3KuVfKQek+o5vZvNe\npGtFNhN7q+WpQOMor8133J3AD0MnipUi92Pbqm0nFiAej8ZrkRFeIYTYy7L3uUZrqFYCkqloZnNf\nvUQhvrdMsWRzyLZVx2PxYolovRbpwPY26ciKM6HeYU+G1nTcpxMFb9x8gU87b9q5jCkISJbynEtU\nuNdt7pVywMJcPRwhVZBOm4xO2JEqGLEfw1D0D1rhPpyWX7FSMDjc3YrFUrJfCCE601q33fYT3hbO\n2kbVGza+w+eGH9uTzaniBhPJGveazeWyz+KsS70edmT7MiZj43ZPFEkCMExFbsBkY82PXDa3kk5s\n75OOrDj1gqB95eItiUR0e7LXSreZtQd5OXcF1ahfb7l13nP7szj32O56PWD6Vm07ZDQUCj7e7YAL\nl+P32PKTMzRiYVqwtuLh++FM7MiYTbyLv1cp2S+EEPsLgvZLT7fEIzZz1+p6aYo5Z4gb2UvNbLbd\nGk9Mf+7es7kWMHOrvn0Mn4Zi3mfW1Zy/HM29pe0Mj9pYlmJttTWbnbBgVpfJQPPpIR1ZceopRce9\nGqYZ7VFfBTy+8XXeUPgu08YgcbfCpWAZ8wgCfmPXLCbQWM6lqVUDYhEIm4NQSjEwaDMwGI1RXhnh\nFUKIOzOMfbLZin42v2f9q7wx/wIzxiAJt8zFYOVIsnn3CiMIf0aVSkC9FuDEeiibh2wGhqKRzVtk\noPl06VpHVil1HvjPwCjhLrePaK1/s1vtEaeXUopsv7mnuq1SMDDUG2M5Gb/MQ36jWvAR7ZXpdDyN\nUuC6mljvTMpGgnRgxWkg2SxOilKKTNYkv9lm+WmPZHPWL5M9wWyu1zVO70zKRo7k9OnTzSuFB3xI\na/01pVQa+KpS6i+11t/pYpvEKTU8auN7UCz4zRHgbL9J/2BvhOVxSCQNKuWg7civE4vuSHgUSTiK\nU0SyWZyYkXEbP9CUCsGObM4NnOVsVlQq7ClkqDXEIlLEsNfIyQGnV9euFFrreWC+8f8LSqkXgEmg\np8IyQDGbGKVgpxiurjFcX+92k0QbhqGYOO/guRrXDXAcA/MO1YxPu9yAxfqah/a3v6YU9KVNHCc6\nS5c8N1zqbDmKWMSWVEkHVpw2pymbZxKjFO0UI9VVhuob3W6SaMMwFJPnY41s1jiOOvPZ3D9gs7Hm\nE+yapU5nTGw7OhkY5WxuJScHnG6RGPJSSl0CHgX+trstOZySmeDPJt9D1YwRoFDAWHWZ980/i8k+\n1YVE11i2wrLDcv7VasDmeliEIJ0x6Usbkd6Tc9QsS3HxSoyVRZdSMcAwINdvMTAcicsCWmsW513y\nG9uz6LG44tzFWNerKj/yfo8PGL/Q1TYIcdx6NZuLZoI/m3wvNdNpZvN4ZYnvW3gWs9N5XaKrwmwO\nr+vVSpjNQRBW6z1z2WwrLl6NsbzgUi41snnAisxWKK01i3Mu+c3tbI4nDCYvOF3P5t1ksPn06/pf\nhVKqD/gY8D9rrfNtbv854OcARu3ECbduf389+haKVhLdcn7LfHyYb+Qe4I0bPTV4feZsrLksLWwX\nVCjmfRJJg3MXnTMVmI5jMHE+mhtuNtY88hvh3qmt31O1olmYrTN5oXttlmAUZ0EvZ/OnRt9GyUrs\nyOa5xAjfyl3n0Y0Xu9gycSfray7LLdlcOMPZ3M2c28/6mtfc17z1e6pUwqP8JiPyeUKWEp8dXe3I\nKqVswqD8A631n7S7j9b6I8BHAB5I5CIzlFozbBbiQzuCEsA3LF7MXDnSjqwGFuND3ExOYGmf+4q3\nybmFI3v8s8b39Y5OLDQqApYDCnmfTLbr4zvHSgeaSiXcG2uYUK9pbFuRSEZr1Ht91/lzW4rFgMDX\nJ36eXiRmYbVGBaANwrVmbVg1n+xqGafq4cYsNgcTuPE272mtSa9V6dusobSmlI2RH0igGwVLTDcg\nWahh+JpKn009bnV8TnG69HI2Vw2HpfhA22x+IXPlSDuyGliID3ErNYkdeNxXnCLrFo/s8c8a39M7\nOrGwnc3FQkA6Y3avcSdAB5pyOVzNZxhhYacoZvPGapts1lAqBASBxjiiold3qytLiQ+QzXbNI7Na\nwal61GMW+X2zuULfZh2lNcVsjMKObPZJ5usYQSObE9GqCn3Sulm1WAH/EXhBa/1vu9WOuxXQ+Q/V\nV0e3V0ADnxl+jBt9F/GUiULzzdwDvH3l6zxYePVQj+UqE1MHGGd8aVW5FIS189sUUihsnu6ObLnk\nMzNVZ3eFSFS41PjCpVhzeVe3BX6H96mGtVWXoRHnxNoShVnYRLFO/0IJywvQCoq5GOsjqR2h6VQ9\nRqc2UTp8i9v1OolinaXzGWrJlrDTmuHpAvGKi9H4MWdWKyQKdRYuZUkU6gzNhx/IlYbMWoVy2mF1\nvE86s6dcr2ezrwyUhnYRHaij6whp4G+G38zNvnPNbP5G7gHeufI1HijcPNRjSTaHyqXtgk+ttrL5\nNHdkS0Wf2du9kc1+0P59qjVsrLoMDJ9cNu/WjaxOFGoMLJYxG9lcyMXZGEnuzOaKy+jt/I5sTnbI\n5pHpPLGK18zm7GqFZLHOwsUsyUKdwfkiNB4ns1ahlImxNpY6s9nczU/s7wB+EnhOKfWNxtee1lp/\noottOrBEUCdbL7DuZHe8eYzA50px+sieZy4+EnZijfBXpVH4yuALQ2/gcmmWRFA7wGMM87nhx9i0\n+zC05v7CTR7ZeIE1J0fSrzJcW9unW376GPuMM3R7JPGgfE+zse5RLgXYjqJ/wLrjua++r5meqrft\nwKPBrWvmZupciMiB66m+8FiGdlaXfZIpn2Tq+D/YRKET61RchmYLzWBTGtLrNRKFOuujKSp9DihF\n/2KpeR8Ig05pGFgoMX9l+/B3p+oRL7u0vmMMDXbdJ5GvM7RQ3Pk4GpKFOuWMGz6XOM16OptTfpW0\nV2LDyez4epjNt4/seWYSo2En1gg/hGrAV/Ds0Bu5VJolHtTv+BiziRE+N/RG8nYfhg64XrjJ6zde\nZM3JkfIqDNXXz1Q27zcHsF9uR4nvadbXPCrlRjYPWncshOR7mpmpve+X1myen61z/lJ0srnQIZuX\nl3wSqYBE8mR/YW9/7kM8/iuVE31OgFjZZWiuuCObM+tVkoUa66N9VPpsUIqBDtncv1hi4fJ2Nscq\nHrGytzeba36zE7s7m1P5GuW0Q/WMZnM3qxY/S9sx097xnqW/5ZmJJwiUgW9YWIFLwq/y2PrzR/Yc\nN/rO47UZRVYETCfHuK84xct9l/hm7jo10+FceYHH1r5Nnx/+Qd9MTvKXY29vLrPyFbyQucILmas4\ngUugFGmvzJNznyHln/xFoBuSKSMc9d31daUgOxD9EV/P1dy6USUIGkFXgvyGz+QFh1Rf5/YXNrzm\ni67FEtx48DFWxy6gdMDo9CtcfvHrVCoevqcjUTVyaNSiWPAJOtRNW1/zjrUjG4UO7JaBxXI4y9RC\nAbanGZotUk1ZGJ4mVmv/4cKu++GbpTHolszX2158DQ2pQo120yKGhtRmTTqyp9zpyOYv8fGJJwhQ\nzWxOelXeuH50W35u9F3AU3s/QhkEzCRHuVqc5rvpS3wre5266XCuPM+b1p5v5uyN1CSfGm3NZoPv\nZK7yncy17Wx2Szw5/xlSfvXI2h1lqVT7zo9SkO2P/kop19VM3UU2b254zf9fiyd55cHHWBs7jwoC\nxm6/zOXvfp1y2cf3dSSKKQ2PWJT2y+ZVj0TyhFdMdaETC2FHtHM2F6ikLCxP43TIZqd28GxOFmpt\nVxNudWalIysObai+wY/d/gu+m77Mpp1mrLbC1eJtLH10FYtNHRC+a3e+tZUGQwf894HX8e3s/c0Z\n25fSl7iVmuR75z9H0U7x6ZG3oHf/WTSCs26Gb/p1O8Mfnftefmj2U2S8UnN506bVx9f7X8NSfJBc\nPc+j6y+ciuOFlAor387cqoWvtHFRGBy2SCaj35FdWXbxd10TtYaF2TpX7o933EtTroTvS9+0+Oq7\nv596LNEc5p67dJ1C/zBv+Pwn2u5L7QbbNhidsJmfcdve7nttv3wkTrQTqzV2zcf0A+pxi8Dc+WHO\nqvs4Va9jz8IAEqXwh9HpPnrXDalC+5UcGgiMNmv7hOghw7X1MJv7LpO3U4xVV7hSmj7SbDZ0gELv\nzVfA0JovDbye72SvtWTzZaZSk3zv/LPk7T4+M/LmO2ezk+WPG9mc9srNbN6w+/h67jUsxwfpr2/y\n6PoLp+J4IWU0snkqvD5t5fPgiHXiM3x3Y3WpQzbPuVy5r/M+10ojm72tbHbi29l8+QEKuSEe/eJ/\njcxl2XYMRsdt5mc7ZHOnbUHH4FizuiWba3ELvTubaz5Ozd83m5N3ymZDba/q1Jpkodb2vgHgt5uB\nEdKRvVeJoM4jm989tse/v3iLFzJX9uy7DZRiLj7MC9lrO5Y2a2VQMxw+PvkeQHGgNfNKUTNjfPTC\nB7ACl0c3XuRCeY5nJt+Lp0y0Mli300wnx/nehWc5X1k84ld58hIJg2vX45RKYeGgZMrcsf8k8DXV\naoBpRe98tFKh/cie74eztbbTodCAbQABS5OX8Wxnx1otbVoUM/2UhkcwrT0FSrsm1WeilLsnwMPz\nbo/+9/K233mYJz72ziN/3E5M12dkuoDl+milUFqzOZggP5Rs3ie9dufZmP3+ygMFhf5481pgugGG\n3+7jdyhe8faMMG89TjEbjaVtQtxJwq/xyObxVSi+XrjFy+lLeLuyWaOYjo/wYptsrhoxPj7xRDgL\ne8Bsrppx/suFJ7EDl0c3XuBceYFnJt+Dj4k2wmy+nZzgfQufY7KydNQv88QlkgZXr8cpl8LCQcmU\niWX1RjYXix2y2dP4HlgdavLYjc8ei+eu4ln2jmwOTItCbpDy0DCWFZ1CYqn0yWbzbse9lDjM5jyW\nu11TZWMoSWFwu0J7ev3Oz3+nbM73x7ef0wswOuw/VkCiQzZrBaVsfO8NZ4R0ZCNuuLbOG9a/w9f6\nH0IRbpjQKFJehe9mLrcPw60KAYfReBzPdPh6/4N8t+8SrmqpUqoMPGXw7PBj/Ojtv+jtdWcNylD0\npffOwK6vuCwvec3VlU5Mce5CdAotGKYCr/3Fbr89vpmsydqKRyE7SNAhUY3zw6hqdCpim6ZiaMRi\nZWm7kqVS4Tl7uSNeavb0k0+FdVrvVdCownCAD6rDMwXsemNEt/ECs6sVPMvA0GFAWfXOs7H72XqH\nlNMxNoa3O8Za7T9za7k7S9ltPY7SMDxboJSJsTGS3DNzLMRZMlpb5fUbL/KN3AMAGI1sTngVXspc\n6ZjN+rAFpxqP45oOX+t/iBfTl8Mlzbuy+XNDb+RHpz95Ly8pMowO2by64rIa5Ww2FH6HKbP99v9m\nchbrqz6FXOdsNi8MQTU6HVnTVAyOWKzuymbbUce+DPyulxIfIptHZgrY9UYWNl5fbqWMbymMIMxK\nu3Zv2VzKxNgcaj26TN11Ng/N5ClnY6wPJ/fMHJ920pHtAW/YeIH7ilNMJ8cxtY8VeHxm5M0Exl3+\n+lrW47fjGRZ5J932PgUriassHL29rjNAUTdsnMBtLn3KWynydh/99c2e2t9T2PRYWgxf29bFuVbV\nzNyucelqNEa8+gfMPccHQTiSvd/e1ljcIJM1SBY3MDx3T2AaCoZU6TiafE8GhmziCYP1VQ/fD0d7\nc/3WkR2/c1SzsE7FZXChhF3zwxHSTIz10VSzZP5uVt3f7sS2MDQMLZSay4GVDpcVHTaaFODaBqsT\nfTu+HlgG9ZiJU9353IGiWVFx9+NsbW5QjX2ysYrH/OXsgT4QCHFaPbb+PNcLN7mdHMcOfJT2+dzI\nmwiMu9yicpBstttnc97uw1Mmlt6eFdzK5liwve9u00pR6MFszm96rLTJ5tnpGhevRCeblxf3ZnMy\nZey7tzUeN0hnDVLFTQzPI7B2frYzFAwRvWweHLJJ7M7mAetYi2bezVLiWNllYLElm7Nhxf+O2Vzz\nsDZQX14AACAASURBVDpl8/zRZHPdNlgb35nNvm1Qd8w9y5UPks2mhtRGI5svna1slo5sj0h7ZR7M\n3wDgq/0PhrOld2trOPMu3uiGDppBqYGv5R7km/0P4GNga49H155nNjnGXGIEUwf4yuRqcYrvWf5K\n5I8W8H3dcc9Hraqp1wKcCCxlyvZb1KqazQ1/x8j0+Lk7b/Qfm3SwS7eZ0o8SBEFzCZOhfVJ+hcmI\nLhtPpsxjKex0VLOwVt1n9HZ+R+XC1GYNu+azeDHT9m/N8NsfAwXbncZWHU4U6UgDtUT768TKRJrR\nqc1wGVPjgWsJi1iHpUutz2sAluuTKEkFYyHSXpmHGtn85f6HcI17ONPxHrLZ1AFmSzZ/pf8hvpW7\nTtDI5jeufZvbqQnm48PNbL5WuMW7V77aG9ncoVZCtaKp1wMcp/vZnBuwqNU0+ZZsjsUV45N3vk6O\nTzrYpVtM6YcJtNGcwjW0T9orMV5dPu7m35Xjyubd7nbA2aqFS4Rbs7lvo4ZV81m6mG37Paav2xY8\nhKPL5nqnbJ5sZLOmOYNcS9jEK27HzwpbDMLPIvGSe6YKP0lHtgel3RK29nDV3QWmEbiYGlzD6hiY\nTuDiN6oxbzEDjwcKN5uh9/XcA3yj/zXNYhY1TP526BGU1gSGyda48Kt9F8i6Rd6w8cJdtfekbK7v\nHUltValEoyOrlGJ0wmFwONwrZNmK+B2O3mn93qE+zQfn/4rPDr+JhfgQCrhQmuPdy189FUvGD+Ko\n99ek1yp7ws0AYlWPsZsbLF3M7lmKW49ZbYOpXShqBbW4he36aBSWFxYH2e/3pRXkBxJtb/Mck9lr\n/SSKdSw3oJawqMctBueLpHZVTWzXHqXBrnrSkRWiRdorYwVu80iewzKC8Egsj87ZHAvq+Mps5i6E\n2fya/I3m3+lX+x/kW7kHdmTzF4ce3ZPNN9IX6XcLvP4Y63wchY21/Sv71SrR6MgqpRhrZHOtGmDb\n6o7H4rV+73BfwAfnP8Vnh9/EYnwQheZSaY53LX/lzGRzO/cy4Jxpk82KsBbE2M11li60yea41bYT\n2zGbExZ23UdrsBqFru6YzYOHy+ah2SLJYvuKxjtemw4rIVf77nDHU0Q6sj3ocmmGLw49gqvN/Tde\nAOhwTf1WiX8z8Bis5/k7C8/y+eHHuJ0cDysntoSmGXi8c/krrMQGeD577f9n772CJDnvBL/fl7a8\nad89M909Dm4czMCRIAEsQZBLLHdXS665Cz0oQheSjg96uDdRcQ+Ki1AoQvsgKaSQ7kJxodPdxfFW\nt467SweSAAEQfgAMZgYDjO2Z9q66y5vM/D49VLWprqx2Y9AmfxEMoquysrJ6qvOX/y//Bk1JpNAZ\nLo7z7Fx9rKACzqcebpIpjfdZ2yHV1QwuJY/v+EC2WFy/o2W17EFq5/zJGKYgZm5vJTTlFPj9idfw\n0ACFvsNX5O8m96JVf7vOhQKwapLOiQKzh5rnWqIJMr1ROhrt+9vcnF2mlLQppOopdGbFJZEpY1U8\nNE8ipEJpAk0qhALH0sn0RXFC63xfhaAcb27etNATxS676K5ENGp02zWXsBpButQ1ch2hfbUCHBDg\nx9HCKO92nsFVcstuNqRLZ3WRl6bf4c3uJxj1cbMhXb42+yFToS4uJ46hKQ8pdA4Xx3h6/lOgnk68\nOohdfrs2br6QPL7jA9nSBm6uVCRx/5trXwqmKTC36ea0k+cPJn6Nh4ZA7fi75feSu7Hg3K6OVQBW\nVdI5WWD2YLOb1RbdXEzYFBtutiou8Yabhaw3Vmxys62T6Y3i2Ftzc6Yvij3i1n2/ys1+gbW55GZD\nI5fe+27eOVflAZvGVB5/MP4rft3zDPN2Col/B0ShJF+ZPUdY1ricOIqrGRzL3+Kh/A0MJfn21Ft4\nCMZDPZzrPMmCmSTuFngyc5Hh0gTHi6M8vvgZOTNGzC0R9lZGdnhCr9/R3SS17dbz3kfMDRpGtO/z\nunvRuXvjKHY6odf+iH/2532b2taoeiTnSthlF9cU5DoiVBqDzf1YTsv1eU4A4ZKD8GRLE4ZiKoRj\n68QXKhiOpGbrxLJV3+CxHF25y+OEDOYH4q0bre66sQ2koTFxJEUkXyO6WCFUatSksSJMRV2g4aLT\nSNfysMsO2Y4wuVVNpQIC9humcpfdnLGT67r5q7PnsKXD5cRRPE3neH6Eh3I30ZH87tRbeGiMhbs5\n13GKRStBwinwZOYCQ6VJjhbHOLtwiawZJ+4UCcsVN7tCx9tCQ6k7SoW+T2zo5j0Y6+0nN/vRbsHZ\nrLok58pYFRfX0Mh1hqlE27u5FjKxK+0XmsMFZ3kheDVLbk5kKmiuxLE1Ytmav5tXBYq1e+jm8SMp\nIoUascUK9jpujhRqdTdXPeySw2JnmHzX3nXzzo8u9ihTdifnUw+RN6MMlKc5s/jFlhovpJwCfzT+\nSyqaxVi4l9/0PNW0AmtIl8cXLnEyfwOAo8Ux3/3oKAYr0wyO+9dG2tKhu9o6O1ZXHhGvQtHYxB+H\nkgzsgrEA6Q6D7IJ/+3whIJ7Y+TNmN2Iy1MWF5AOUjDCDxQlO5K5hS//ao73ED1/5Afz55rY1qy59\nN7P1WhjAdCE0Xu/knE/VGzitlVE+HSK+WAXpv9yhqDeK8Pt21cIm8+Hmi8nVwawSsNgdwdvMCv/d\naPAgBFLXCJXdpiYWS/52Ta0+JmCV0DUFqfkyniEoJUIk50pEc/Xh7fXOjJG2jTUCAnYSU6Euzicf\nJG9GOVCa4kz2CpEtuDnt5Pne+KtUNIvRcB9v9DzZ4uazmYucaLj5WHHUdz86kqHyNEPruLmnmml5\n3FQutlelbPinLq5G7BI3pzoNsovt3ezX4Xi3MRHq5kLyOGU9xFBpghPZa01NNfcT7Ro6mRWXvpFV\nbnYkobG6m3Npm8WeVjfnOkPEcu3djMA3kIW6m+cONNysFIIi0TVuXuiJII1NpI/fDTdrAqkL7DZu\ndkwNw8fN6bky0tAoxS2Sc+VlNxcSNrk94OYgkP0SuBY9VA88Rb2gf8FMcCV+mO+P/pyYt7U0ipCs\ncaw4ijYjebfzUfJGFFvWeGzhM05nr9yjT1A/iTwz90lLAK1JF4FACoESGpr00JXHs/Pn191fRbP4\nLHGE6VAXqVqOk7lrxN3Suq+RCDyhY6jttUBfix3SODBoMTFaa1rhFQJiCX1XDGRfj8/iR3in6zFc\noYMQzFkpLieO8P2xX+zpYHarXQ5TM8VlUS6x9N9LAWZrt0GdyaFkfe6cK1u+j56h4W2yy/JCX4xi\n0iaSr6EElBL2+mlI9wC/ml9BvXui1AWmz9dFAB3TJZLzFXRvRabxhQqhksPU0P7qpBiw+7gaG+SN\n7ieXz5ELZoIribqbt9rhNyRrHC/eXnZzwYgQklUez3zGydzVe/QJGm6eP8+b3Wc3dLOhPJ7ZwM1l\nzeJy4ijToU7StRwnvgQ3h0Ia/QfNejPGNW6O7wE3X0gc4/3OMytuttN1N4/+Yl8FsxulEqen27s5\nvlhFU5Dpa3Xz1FCCnts5dJ/56a6hITfjZlFPNy4kbSK5GkqDYiKEa9/fRZREptIUqMKKm5UmWp5b\ner5jqkhqroy2ys2JhXrWVbuGlLuFIJC9z0gEb3U/0SQYqenUlOBc+gTPz324rf0eKY5zpDiORNy3\nmopjxVHMaZcPOk6RN6Kka1meylwg4pX5NPkgGStJb2WeU9kr6wboBT3MXx58GUcz8DSDsXAfnyWP\n8XsTv6G3Ot+yvUTwXsdpPksewxMaUbfMV+Y+4nBp4o4/Uyyuc/zhEPmcR7FQD0jiSZ1IVEPswD/0\nWlWyuODiOBCLacSTum/re0fUm32s/t55mkGZEBcSxzm7+Nn9POz7QksAqxShooNdcfEMjWLcRvkI\nLFRqf/GlKYjlqiz0tM5qc22d6eEk/TcXEVLV58BSX7Wd74ttSRS1sEkt/OWl/GleazAO1O/WaqJt\nl0YNEGsCeU2BWfUIlRwq0b1dqxOwe/EQvNXV6uaqgo/Sj/C1uY+2td+jxTGOFsfuq5sfKNzCkg4f\ndpwkb0TpqGV5KvMpIa/KheQDLFhJeitznMpeWTdAzxsR/urgyzhCX+Pm133vBnsNN19ednOJ5+Y+\nYqg0ecefKZE0iCd08tmGm8UucnNcI55o52aD9zrPNDXW9DSDEmEuJY/x2OLn9/OwvxQU8C+e/yfY\n/+U8UVOjlLB97xK2K9+Bumei2SoL3dEWrzu2wdRwkv6RbKub+7fgZiG+fDe7bVLOG4vMW3WzVXWx\nyy7VyM4vMWhHEMjeZ/JG1Ld+RQmNsYh//Z6C5flwG/253e/GAEOlSV9JfX3u3Kb38V7naaq6tdz0\nQmo6Ep3f9DzJn4z+rGX733Y9zpX48PIFR8GM8qveZ3l6/jxSaCTcIoPFiW03MBJCkEgaJHZQ8wg/\nCnmv6e5xMe+RmXcZOmy3zFidt5IgZcvAM08zuBUd2HOB7NogVkhFz+1svSlTo1FCaqbE9GCipSHS\nRt8aBeiuxPUZOu41akyXalhcSyefDuFauyv1rRyzsKrl1tVdpch2RrDLOd9aIfCXqFBgVTwq0bt9\npAEBd4ecGUP5XNAqoe9KNw+XJhj2Wdzdipvf7TxDRTOXG1ctufmN7rN8f+wXLdu/2fUE1+JDy0FZ\nwYzxau9Xlt2cdAocKk3emZtTBonUtl5+3yjkPCbG1rh5zmXoiN0SzM5aKUQbN49ED+z5QNYROv/n\nI39K93h+2c3pmRLTQ4nWTKSNui4Buidx9VbfeqZed/NCBbvs4lg6hd3o5riFWfNzM2Q7w9jl/Nbd\nHASyAVvBljXa3OtAVx4/HniRrBmjq7rIE5mLjEV6OZ96GEczCHsVnpn/hOMF/5qa3crtyMByELua\nrBmnqplNaa81YfBFfLhp9RLqJ/23ux5f/jkkq/zR2KsbpkDtVpRSTI43p0ArBU5NsZBx6exuPinl\nJ0vIPv/0q9VNvHY77Ro6xTNlrKrXNEtOKUX3RJ6JI+mmbcsxi2h+/Tb369WrSl0j1xmBzu18gp1B\nPh0ilq1Co95mafV6oSdCNWqS6Y3QOVVqWw/s10nRNXd3+l/A3qbuZv/vqCYlfzvwIjkzRnd1YXkm\n6/nkg7iaQcSr8Ozcx217UexWRsP9vt2XM1YSR+iYaqVutaqZXIsP42nN50ZP6M1u9qp8b+wXWy6j\n2i2s6+Z5HzdPFZF9PmdSpYi4W0tn3208+69P84f/1+MkMuUWN3dNFJg83LxiUY6aRArOum5216lX\nlbpGbpc3PcqnQ8QWq+CtdXOUatQi0xOhc7rVzUtfx5bHNfB2uZuDQPY+E5I1DpanGAv3IVed8DXp\nkTeiZK16G/DbeojRcC8aLIuhZET4dc+zfJQ+wfMzH9Dnk3a7GzGlS033SzlU6Ko5jaJkhNFQvk1z\nVqeHVDSbn/U9xx/7rBrvBapV1dKpUQqNcjSOKlWbYijPVaipBSKFLIVEGrSVk5buufe0lvp+sl5D\np1i26ltXojsS3fGaAtOFviiRQg18WttL6vPfdntzhI1QusbkcJL4YoVw3sEzBPmO8PKqbTEVRniK\n9Gy56dJfAmiiqbGGol67U9rjIwACdjcRr0p/eYaJcE+Lm3NmjEWtnqJzSw9xO9xX91BjQbVoRPhl\n71c4V8vy/OyHviUxuxFDuTi03qkRKLQ1AirqYTQkHmsW+dbc5a7oNj/v+yrfG//lXT/enUC10no7\nTGoa5Ugcys1udl2FmMwQPp6nGE81u1l6nNojbvZjaTbsQG7B181GzUN3Jd6qwDTTGyVcXPR3s4DF\nznDdP3sYqWtMHE4SX6gQLvi4OR1G81S9HnbV6xTU7/rL5i7HUghK8d3t5iCQ/RL4nZn3eLX3K0yF\nuhozWjU0JXFWB3ONmW8tAZsQLFpJ/mHgBV6ZeH1PBLOP5K7yUfpE011WTXoMlSYwVPNvIOaWNjcG\nRwgyVoqaMPZkswRtTYrNxOBxrp94EgCl6dysTPI70+9hKRfHUQgBp977JZ8+8xLlaAKhFEpoHL32\nMQdN/66Yu4X/+C//Med/fPdyzaSuMXk4RcdUYXn8DIBrCLJdEYpJe51X7x1U485yrs2d5UJnvU44\nOV9GdyU122CxJ4Kna3RN5rEq9b/dashgfiC25y8wAnY/L828wy/6vsq03YmuJJ7QEErh6quCOaGh\nUHhr05CFYMFO8fcDL/Ddidd8a0h3G49kr/FJ+uEWNx8ujrWMh4m7xbbZZk0IwZzd0XJHd68gtOZx\nQONDD3DjkbPQaLJ1szzB78y8h6k8nNqKmy888xLlSHzZzcevnmPAmv3yPsg9ZDMNGP2yiKWpMznc\ncHN5n7u5K0Kuy//5fGcYaTS7eaG33p24c6KAVW24OWxsrUZ4hxIEsl8CtnT4vcnfkDciFPUwcafI\nvx/+7pb24WoG73ee5vcnXrtHR3n/eHTxC+atNLeiA2hKooRGRy3L87MftGxrKI9HFy7zSfrhloHv\nfighNi563IVYtoZpCWpVRaa7n2snn0IaKxdbo+F+ft37DN+eegvTFCgFdrXMk7/5O4rxFDUrRDw7\nTzoi4dDuXY374Ss/gB9vvF0haZOcb64rUYBr6r5pwq6lMzOYrF+R7PKT/L2kmAotD4JfzdRwCs2r\nX+hKn1rigICdiC0dvjvx+rKbY26J/zD0SuuG65wTXKHzfscpfm/yN/fuQO8Tjy1eJmOnuB3pX3Zz\nZ3WRr/nU2ZrK48zi53yaemhzbt6Dc9kBLEtgmoJaTTHfc4DrJ55sdnNkgNd6nubl6bcxrbqbQ5US\nZ1//McV4CteyiS3O0xFTcHD3utmPZ//1aV78y+eaHmvnZsfSfcfauLbOzFDg5nURor2bD9fdrKCl\nYeVuJQhkv0Tibom4W0Ii0JVXH8ezBTLWDu9GtEk0FN+ceYesEWXeTpFwinTVFttu//jiZ0S8Mh+n\nH6Gs27jCaD2hKYUpnT09VubAoMXozSq3j59qEiXUm3KMhfso6TYRqiRSOrlFD6Ugml8kSv1X1tm9\nO1cwl1Z0NVcSKjkoIFyoES45KE2QS4UopEPL34tcR5hw0cGquMsNJZQQzB2IrfMuBKK8A4IANmC3\nsuRmD4GmFHIrpwEhmLd2eDeiTaKjeHn6bbJmjHkrSdIp0rmOm88uXCLqlvkk/fC6braksyczpaDe\nkOrAoMXoiL+bPU3nVmSAsmYRNmrEk/VOzCiI5Rcb+4COXermJUq6zVSoG4lgNNLLZ+lj/O//syCW\nLlNIrbg53xEmXHCwqg03a3U3zw7E13+DwM3bZq+5OQhkdwAaipPZq1xIPtDcxGgpP6XNH2xsVSMj\nBUyEepiz08TdAkPFyZbUn51O0i2SdIsbbieAh/M3eTh/E4B30yc5n36k5ff0tdmNRxmVNZtb0QEE\nisHiBGFZ29axfxlYlsaRB0K8F/MPxjQkZT1ExKvS229iGIKFjIv0wA4Jevst7NDuO6EtBbHxuRKp\n+XrDkKUuffVvgCI9W8KqeivzXjXB9GACu+Quj98pxa09X+saEBCwfXQUj2SvcSl5bEtujq/ymALG\nwz3MW2kSToHB0vY76n9ZJJ0CSaew4XYCeCR/g0fyNwB4p+MMn6YebPk9fd0n22otZd3mVqTu5qHi\nBKHd5Ga77uZ3Y/5t2nUkFd0mLGv0DZiYpmBh3kVKCIUFPX0Wtr373LzEudQjfJx+BIHEFQZKCAxP\ngadIzzTc3Jj3qjTB9FCCUMnFCtwcsA2CQHaH8GTmIjejB8iaqwYTCwFKgmykUKySgSFdzmYuAvX2\n5X8/8AIZK4lEQ0diSYc/GP/Vnu3au5qnFy4S8aqc6zhBTbOIuiW+NvshQ+WpdV/3RWyIN7ufRDQC\nftX1BF+f/ZAHCrfux2HfFYQQHKzO8Lkda+n8rICkk1/erqvHpKtn97ZYX11XY5ccUvM+LegbaAqi\nuSrZrvBK6rAQVKMm1eju/R0EBATcX57OfMpIdICcGW91s2r06F7r5oVLQH1G6N8NvMiiFcdbcrNX\n4w/Hf7Vnu/au5pnMecJumY87TlDTTGINNw9u4ObP44d5q+uJuptVfazPCzPvc6y4eyY2CCE4UJ3l\nihVtncqgIOEUl7fb7W5ezXi4p1FXrUOj8dfa2aXRbJVsZ7ObK1GTSuDmgG0QBLI7BA1F0Yi2rvAK\njXqLtsbjSmEol+dmP1qeEXcufYJ5K7W8YizRcYXOaz1P74ka2o0QwOncVU7nrm76NQU9zJvdZ5tO\ntgC/6T7LQHlmV11kPLZ4meuxQRzNWBamIV2emv8UQ+2uu/LtWNscIrZYaTsrbRlRn11aXmdUTkB7\nhCeJ5mvojqQaNuoXGUE6V8A+Q0NRaOdm1exmU7n1QK0xW/2DjpNkrOTy5IElN7/e89SeqKHdCAE8\nmrvCo7nNd9/NGVHe6nq8xc2v9TzFwO1ZIt7uGUnz+MJn3IwebHHz0/Pnd13G3Gb5LHEUV2zgXAFW\nNXDzdgnc3EwQyO4g2l6Xr/6CCoFUguHS+PJDV33mqiqhMR3q2rNde++UG7FD+I2HlkLnbw98gz8c\n/yXRbQrT8xTlkkTTIBzREPf4BBN3S3x/7OecSz/CRLiXqFvm0cXLDDUupnY7fh0ONW8TrULU7p+P\n9mVhVlz6budAqeWa4ppdb4AVpHwF7DvafeXXuNlTYjmIBbgaH2qZq6qExkS4Z8927b1TbsQO+TaC\nkkLnbxpujmxz9vmym3UIh++9mxNuseHmE0yEe4i6JR5bvMxgaf070ruZqmZtHFSp9ee9BrTHqrj0\nrnVzyGD6UGLfTgYIAtkdxOHiGDdih5AbrGbpSnI1OshsqIOCEaW2TofAvdq1907xhIb0O9kKQcGI\n8JP+r/P9sV8gqA96d4VBxCtvGDwtzDvMTrvL53FNg4ND9j2vRY27JV6Y/ZBiWXHFPsjFziFGQv2c\nKNxYt3HWTma9Fv2lhEW42H4w+lLXw5odrPiuRUhFNFshVHJxTY18OtTcuVkpuifyiFWzYIWqr6DH\nM+VdP1A+IGCrDBfHuRk92JoiugZDSa7FDjFjd1EwIjhivUus/XnRuRGe0OrXLWsRgrwR4ad9X+d7\n468CW3NzZs5hbqbuZgXoGhwctu95LWrcLfH8zPsUK4IroYNc6BhmJDTAicJ1OmvZe/re95tHf9fl\nf8weoWO6tL6bbR0nFIQfaxFSEV2sECq7OKZGwcfNXeN5NLlyUS9UPbiNL5TJd+5PNwffpB3EV+Y+\nYSbUSVkP4QgDgaqvTK45qXtC492ux5CNuWTLtTqrt1OSzurCnu7aeycMFSc4lz6B53dhIgQ5M86k\n3c3HHQ8zEe5BKEXYq/LCzPscqMz47rNcksxOuyi10gtEShi7VeXIA6F7uvqrlGJiwuONky9RSHTU\nOyVKydXkYb4699FyY6zdwKO/6/Id7b9dd5tiwiaeqWBVvRZhKurz0WYPxPd1uo0fmifpu7mI7ioa\nRQvEFyrMHEosD1TXXYnutE6E1BTEstUgkA3Yd3x17iNm7A6qur2umx2h807n4xu6uacyjxlkSvky\nXJzg49TDbdyssWglmAh18VH6BJPhboSCiFfmhZn3Gaj4z10tlTzmZprd7EoYG7k/bh6b8Hjz1MsU\n46llN19JHua52XM8VBi5Z+99P1leeE4q4gtVzJq/mythg7mDG3Qk3odorqT/5iKat+LmxBo3G45E\nd1tT0uturu3bQDa4t7+DCMsqf3L7p7ww8z5nFy5yNnMRfW3qkZJIoeNp+srqcOP/tca2RmPszIsz\n793Pw99VdDg5TmWv1C80fBBK8nrPk4yHexq/b4OCGeVn/V8ja/h3CV7MuE2D0JfwZD3IvZcU8pJr\n8aGVIBZA0/A0g992PU5t3TsDO4cfvvKDDYNYAIRgajhJOWrW56E1/icF5NI200NJ3xl0+53UdBGj\nEcRC/Z6QpqBrPI/vl3ctwbpAwD4k4lX5s1VufiJzqdXNsj5ndSM3h2SNF2ffv5+Hv6vorC1yIntt\nXTe/1v00E8tu1smbMX7a/3Xyhv+F/OK819bNlfI9dnNOci05vBLEwoqbu5/A2aiedBfQlD2lCSYP\nJylHfNzcEWJmKLnnxr/cDdLTRXSv1c2dE5t08z5md1zd7iN0FEeKY9Do3h/xKvy263FEYxh5xC1R\nMsK4Yk13NyEIOVWOF0ZIOkWOFm4HtbEb8HTmAo4w+Cx5rCVlzNN0SiKEWiMZTwje7zhFzoqRsVLY\nXpVHFy5zKncVz/M/2SgJE2M1Ekmdjq76GJy7TW7RZeaR4ZaZdfVj1vn3Q9/lwfxNzmYu3rPvhZSK\n+VmHxQUPJSES1ejpN7GsjaXlNyh9Q4Rg9lACq+wQzdVHMxQTFrVw0PnQF6WI5Wq+sajmKXRH4lk6\nnqnjmnrLiroU9eH1AQH7ER3Z5OawV+GdrseW3Rx1SxTbuDnsVDhWuEXSKXKscDu4G7sBz2bO42gG\nnyeO+Lq5LOyWx6UQvNtxmqyVIGMlCTfcfDJ3FU+2d/P4aN3NnV0m+j1wc3bRZebUYV83u0Ln3w39\nPg/mb/Bk5tI9+15IqZibccgubt3NG+FbAiQEs4Nr3WxTCwchhy9KEc37u1l3FborG17W8EwNUZOB\nm1cRfKt2OA/lb3KscJs5O43t1TClw48GX/HdNu4WeSZz4T4f4e7myYWL3IoeoKyHlptyGNJlsDjO\naKSfta04lNC5GVuplSobYd7tPMOl5DEGoqOkLl4mVGqdt+e5sDDvkc96DB8Loet3X5i6U2tNYwMQ\ngppucSlxjIlwD99r1P7ebSZGa5SKcnnxsFiQ3LpR5fCx0LrB+w9f+QH85fbftxY2g+B1E5jV9o1l\nBDQ1cZo7EKP3Vg6xpqFELh2+D0caELDzeSR/g+OFW8zbaWyviq4kf3Ho277bJpxC4OYt8lTmArej\nA5Q1G7nWzdGBFjdLoXMzdmjZzSUjzDsNN/eFb9Px2WXsUuuces+FhYxHPucxfPTeuNnYwM2fddmL\nGAAAIABJREFUJY4zFermPxv/5T1x8/jtGuVSq5uPHAttO3hfr4fFEoGbN4e1WTcLwexAnN7bzW6u\nhg3yHaH7c7A7kCCQ3QUYyqOvMrf8c1dtgRm7o2lF0pAOp7Obb3EfUMeWDt8b+wWfph5gJHqQkFfl\n1OIVumoL3IoebH2Bki0dFZWmk7MSFHoeQrzwAKfffZVkxr+O1vPqKcid3Xf35J5IGRy4fYX5vkO+\nK78AUtPJmTHGwn0c2mCO31apVmVTELuEkpDNuHT6zMjbTC1swN1DKIUS+I4tUoKmVGzHNhg/liaS\nr6G7kmrIoBoxgprjgIBVmGvc3FHLMWelUNpqN7ucym5+NFxAnZCs8b3Rn/Np6iFuRQcIuRVOZ6+Q\nrmW35OaslSDf9zCi50HOvPNzEgtzPq+tB7TZBZeOrrvr5mTK4MCtL8j0HGjrZk/T67W/4R4OlP2v\nHbZLtSKbgtgllITFha1fiwTevvsI2d7NUqMpFdsJrXFz2KAa3t9uDhLVdyHfnPot6VoWQ7qYXg1d\nepxavMrh4tiXfWi7kpCs8VTmIn8y+jN+f+I1DpfGibsljhVuYciVVB+hGqmWbU4YUtPxDJMrZ5/D\nDPlvoxQUi3e/JicW1zhYm2Hw6qdonluPmH1whc68nbrr71+rKN/6SaWg7FODtOla2IDtoeqpwquv\nXmohw7cbqKJeu9TyuCYoJm1ynWGq+3xOXUDAZvjW1FuknByGdLAabj69+DmHV43LC9g8YVnj6cyn\ndTdPvs5waYKkW+RwcbTJzdom3Xz17HNY67m5cA/cnNA4VJ7m0LWLiHXc7KExb919N1er0vfXotTW\n64MDb98FZKubqyHD//oJyHW0ZkE1uTkSuDm4I7sLiXoVvj/2C+atFCU9RHd1gbDc3ly1gPY8P/sB\nXdUFLiaP42gGQ8UJFs0Ek+HudU8cRTvO69/4Rxy8cpHBq5+2nJ9M8+6fdIQQuI5i+OoFBm5fZeT4\nGaaGjiP15j9xQ3rEndbU5zvFtNuMeRJgr7lw2ExKUsDm0B0P3VU4tl5PP1KK5FyZRKZc30DAYmeY\nfEcYhGC+P0bXRB7RWHeQoj6mKLdPux0GBNxNol6ZPx77+So3ZwjL2pd9WHuOF2fe51Iiw6XkMRzN\nYLg4zryVYjrcve7r8qEkr33jH3HwygUGr15odbN1bwICx1UcvnKegVtXGHnwUaYOHUWtcbOOJO60\npj7fKZal+fYKEoItjQUMvL01NnazaLg5BJpgri9G12Sh2c227hvIBjQTBLK7FAG7dj7obkEAJ3PX\nOJm7tvzYlN3JPwy8gLteF2AhcHSLW8dP4ek6Rz7/uOlpw4TrV8pID6yQoLffJBS6s86F1YqkWqnb\nyqpWOHr5Q2YPDCOFVh9mS73bo6kchosTd/RefoRCGqGwoFJWTdLUBKQ66qlLgQjvHsJTdE3kCZWc\nRhENZDvrwktkymhL/wYKUnNllCYopMOU4xaTh1PEFivorqQcsyjFNzHAPiAgYFMEbr73aChO5a5y\nKreSsj0Z6uIn/c/japtx82mk0Dh85XzT04ax4ma74Wb7jt2sqFXrJ2S7WubopQ+YHRjCXe1mKbG8\nGoOlu+9mOySwQ4JKRTUtNgsBqfTGIUCQSrw1hCfpHi9gl1fcvNgVQVNqjZsVqbkSUhcUUyHKCZvJ\nkBG4eRsEgWwAClg04wgUSacQTNhYh77qPC9PvcXbXY+xaCbqD7ZLZzJMxo88wuGr59FUPb3HtiEz\nu5JaVCkpbl2vcWjYIhLdvjAdR9UHvTdOkrrn8dhbP+GLR58jl+4GAf3lWV6YfR+dezNu4OCgzfSk\nwy27l2uPnKUUSxJ1y8iFi/yb5/0blAVsj87JehCrLc02AJJzZRCsiLKBpiA5X6HQaNTkWjqLPdH7\ne8ABAQFbpu7mBBqSRODmdemvzPHNqd/ydtdjZM3GnNJ13Dx27CTD1z5FUwqhgW0L5le5uVxSjFyv\nMXjYIhy5e242PJfH3/wJnz/2VfKpupsHKjO8MPM+um9a050hhODgkM3MpMPNUB/XHz5LOZYg6pZg\n4SLHC7fbvjZYfN46XZMF7JJTr9ts/HOmZkvruLlMMVUv7QncvD2CQHafM2V38su+r1DVLAAibpmX\np39LZy0LQFmz+DxxhHkrRXd1gYfyN7Cl82Ue8pfOofI0fzr6MzwEr/U8zUj0AJ7QfaUpNEHfg0nC\n1RJCg5tX/VPAx27VOPrg9jsm2qHW9KFIMc/jb/+URI9NZ7eJuXbu4TZRSuHUFLoumjoearrAO36I\ni33P4TVWxQtWjF/3PUNsobwcSAXcGZoniRSdlsYQGu3HzfkNUQ8ICNi5TIa6+GXvs9Q0ExBE3RLf\nmvotaScHQFm3uRw/QsZK0l3N8FD+5r5382B5isHRn+Ih+HXvM9yKHMATmn9AqwkGHkxg1yogFCPX\n/FPAR0fuzM2hkPBxc44nfvtTkr0hOrqMe+5mXRc4xwf5rO+rq9wc543uJ3GFwcP5Gy37CoLYraO5\nknDRaVlwCtx8bwmaPe1jyprFTwaep2hEcDUDVzPImTH+buBFXKGzYMb50eArnEuf4Hp8iA86TvKj\nwVfIGcGKEdRn/r408y5/PPoz0o3Afy0CRVzUsEMa5VL7E5ZScPtmFbXNwdemKUgk9RZfaxp0pcRd\nE2Vu0eXaFxVGrle5fqXC2K1q0/zc9ztOL4ty+Rga6a3BUO+7g1V2/euR16Fm31l6XEBAwP2jpNv8\npP/rlIwIrmbiagZZM8aPD7yIh0bGTPCjQ9/ho/QjXI8P8WHHKX506DvkjaDWHepu/ub0O/zx2M9I\nNQL/lm2UJKY52CGNSqn9CVUpGB25AzdbGvFEOzdz19ycXXS59vmKm8dvV5Gr3dzZ6mZXM3i/41SL\nToIgdntYpa272QncfMcEgew+5lp8CLl27UgIXKEzEj3Am91nqWnG8snP0wyqmslvux77Eo5255J0\ni3x99kN02TzM3JAujy1cWk7l3WhFt1ZVTI7VcJ3tCbN3wKS718C0BLoOiZTO0NH1Z7huhVLJY3Lc\nQXp1uS91YJ4YXVnJXrTivq/VPIVoM5Q+YPNYZZfu8bzvcwqohHXkmn9uKWAhSFcKCNg1XI0Nt4yS\nQWg4wuBWdIA31rjZ1QwqusXbnY9+CUe7c0k6Bb4++2FTh2Oou/mJzCW0RtShbeDmakUxOe5s2819\nB0y6ltxsQDKl39WZtaWix9S4g5Sr3FyQTIytuHk53XoNVd3CFfVg6oev/CAIYreJVXbonlzPzUbg\n5ntEkFq8jynq4ZYVOgBP6FyLHmIq1NqdVwmN0XDfpt9j6bS/12t7+qrzfGfyDd7tfJR5K0nEq/D4\nwiUeyt9c3iYa1ZpqZfzI5yTFQoXBw/aWOgpCvRYm3WmS7rw3A8inJ3xSrxSUSxKnJjEtjWI45Dvc\nW2piZah3wLZJzxRb6myg/ncmNcF8fxzTkSRnS5iOh2PpLHZH6i36AwICdgVFY303z4Q6Qazxg9AY\njfRv+j32i5v7K3N8e/JN3u06w4KZJOKVeXzhEg/mR5a3ica05cY87chnPYp5b9tu7ug06biPblYK\nSkWJ6ygMUxBziyxayZbtLOlgKC8IYO+QjukN3DwQw6x5JGfLmI5Hza67uRYO3HynBIHsPqa/Mst5\n9aCPEAXj4V6UkiC2l/ZQ0m3e6nqCW9EDKGCoOMFzc+eIepU7P/AdykBllj8af7Xt80ITHDpscfvG\n+uMYpKyLafBI62zPL4t8zqPWZsKTEKD9by/ww9dOEs7X6JrIN53QpYBsZyjovncXsCpu2+cmhxN4\nlo5n6VSirRcsAQEBu4OB8gwXksd93TwW6UO1ibha7uL6UNRDDTcPIICh4jjPzZ0j4u3dEX4HKjN8\nb6y9mzVNMDhscfvmJtw86TB42L7bh7ht8lmPWpvDFgJctx7IPpW5wK97nmnq6mxIl8czn/HfB0Hs\nHWNV2qeITw4n8Ewdz9SpRK37eFT7gyC1eB9zqDTVVntKaKRrOf/bh0KQNWNt9+sh+JsDLzESPYAU\nGkpo3IoO8DcHXsLb51+5cFjn2EP2Utf9tpTLats1OfeC+dn2TURqQud/+NkDAJTjFvP9MVyjnrTl\n6YLF7kh9juk+Q3MlZsWFu5hSLXX/L44S4JlBrU1AwF5gsDTZ1s2eppOsFXzdrIRYt4eFh8bfHHiJ\nW9EBlNCQQmMkeqDh5v290BiO6Bx9cBNuLskd5ea5ddwsJVh2/d/1cHGcr8++T9QpglKEvArGSyY/\neu4b9+tQdwz6PXGz/9+P0gI332uCO7L7GA1FR3WR+VCHz3OSiFdhwecumiE95q0kSafgu99b0QEq\nuo1atZqshEZVt7gZPcCx4ujd+xC7EF3XGD5aH1VTLPg3gNppNy+dWrs7APDZE4/j2iurjKWETSlh\nr1xo7bQPc48RnqR7okCo5KAa6WoLPZG70rU51xEiNVtqueOdTwd3vAMC9goailQtx4KdannOkB4R\nr0JWtGZdGNIlYyVJuEXf/d6MHqCqWy1urug2t6IDHCmO370PsQsxDI2hhptL67hZ7KBz7Xp1ux1d\nOtqqkp7jhVGOF0bxEPzz7/w3MCH2fm75KjRP0jVeIFRuuBnI9ESXx9/cCdmOMKm5Vjfn0uHAzfeY\nIJDd5zy1cIFXe7/akm5yZuFzXM1gMtyD1JpXk5QQbYNYqM+9c3xSkh1hsGgloAh5I8K7HWcYi/Rh\nSoeT2auczl5Zbr6w1zEtjYNDNtMTVRYXmoUpBI0OxNs/+bmOYn62HijrBnR0mcQTm1sVVEqRz3os\nLriAIJnSsUOCsk9nR9c0+eTrz/nvaJ+evLsnCtiNFvxLI3LSMyVc687TivLpELoriS9UQNT3X0za\nLHYH3UoDAvYST2Uu8KveZ1vc/OjiZSqazXS4C7nGs1Jo67vZSuCI1ss+R+iNuejj5Iwo73WeYSzc\niyUdTmavcCp7dd+42bI0Dg3ZTE1Uyfq5OXVnd9echptL23RzLuuSXfBYcrNlCyrl1n8bTYOuHv/6\ny3/+yj+9k4+wa+kaz2OX3CY3d0wXcU2davTOalXzHQ03L1aW662LSZts1/7LRrvfBIHsPmewNMUL\nM+/xbuejFIwItqzx6MJlzmS/oKiHuZQ8hmTlJKtLj67qwvKcWT/StRym8nDW1PeY0iVdy1LWbf7y\n4MtUNROERk23+LDjJAt2khdn3r9nn3Un0t1nUXNqlIty+eQXCmv09K+cVGs1SakgERrE4vqGnQ5d\nVzFyvYLXKNlwHJgcq1HtNujqXv9kLT3FzWsV3OVSTEW5JLFDoqVRlWsYfPA7L6A2ysXaR+iuJFTy\nmSOnIDFfufP6GCFY7ImS7YpgOF49hbtNunFAQMDuZbg0wfMz7/Nu5xmKDTc/tvAZp7NXKBgRPkse\nbQpkNenRW51fnjPrR7qWxZQujt7sAVN5pGs5inqIvzr4MjXNQC27+RQLZoIX5j68Z591J9LTZ+HU\navWxeQ03hyMaPX2tbtYabt6o+7HrKG75uLnWbdC5gZs9TzGySTcLAT19Zsti+H/8l/+Y8z9uvcu/\nH9AdD7vsthS3aQoSmTKzdxjIIgSLvQ03u4Gb7ydBIBvA0eIYR4tjeGhoqwbyxLwy3x1/jTd6zjJv\npRAoDhdH+drsuXX3N1SaIOxV8IS2LFqhJCFZZbg4wUfph+vt3lcFup5mcD06yFnjInG3dK8+6o5D\n0wSHhmyqVUmtorBs0dQRcXbaYWG+YS4B0xMOBwYtorH2K7gLcw7emqwopSAz65LuMNoGwkopblxd\nkexqqlXFwL94gnP/aoaOmRmK8Tjnv/oVbj9wfMufeS9hVlxSsyWsiotr6RQTFgr/bC3dvTvzAgGU\nJnDs4PQdELCXOVYc5VhxtMXNcbfEdyde543us2SsJEIpjhVv89zsR+vub7g4wXudVVxNX04v1pRH\n2KswVJrgg46TOEJvSj12NYNr8WGeXLi4p5s1rkXTBIeGbaoVSa3q4+apGguZxjldAJMOBwctItH2\nbs7MOy1+VQrmG25uFwhLKblxtYps4+buXoNCTlKtSExT0NnTepf3h6/8AH68qY++J7AqLsnVbo63\nb9BlOP5p5NtB6QJHD9x8Pwl+2wHLLM07XU13bYHvjb2KK3Q0JTeVXqSh+MOxX/F216PcjB4CYLg4\nxlfmP0ZHMhXq8h0toCmPBSu5rwLZJWxbw15zni0VPRbmXZSCSijCXP8gSmiUZ0Y5FXGaal9WUyxK\n3zECQkC1KolE/EU7PdEq2WUUvPrXig//7E+28Kn2NlbZpfd2FqHq1zFG2cUu+3cVVkAlGIETEBCw\nDfzc3FPN8P2xX2zJzTqSPxz/JW93PsZI9CBQd/NX5z5GQzEV6m4pJQLQlUfGShIt759Adgk7pGGv\nKaEsFjwWMt4qNw+hhKAyc5uTYbetm9eru61WFeGI/+umJhzfIBYABZ6r1u2kvN9G61hlh97buc27\n+U7vxgZ8qQSBbMCmMNTW7iaFZZVvzLwHvNfyXLqWYzLc07TqC/X6nrjj36RiP5JdrIty8uBRrp55\ntp46JODmw49Tmb7A0+Urvq9rN65VSjCM9ndjc9n2/8YSqET3SB2mUiQyZWKLVYRUlOIW2a4I0tha\nGlBqtnVunN9vV9Fo+tAZ1MoEBATcXbbq5ohX5aWZd32fS9eyTIc6W9zsCa1tA6n9yJKbJwaPc+3U\n08tLCDcffpzq1Kc8Wbnq+7p2bSPqbm73nCKfW/+OYbssq9Brf8Q/+/O+dV+7o1CKxHyZWHbJzTbZ\n7nDbbv3tSM+UNu9mLXDzbidI4A6475zKXkVXzSdmTXr0VDPr1vfsN5SEqh3m6plnkbqBMgyUbiB1\ngwt9p8iYidbXKEWtTYdh3ag3svDD89adBY8SghsnHtnOx9hxdI/nSc6VMR2J4Snii1X6bmURW2zF\nb68zN24t+Y5w0II/ICBgR3Mqe8XXzX2VuXWbSO03lFJUQhGunXq67mZ9xc3n+0+zaMZ9X1Nr02HY\nMOsNIP3wvI0bCyeSrVHwD1/5we4KYoHusTzJ+RU3xxYr9I1ktzwmZ71562vJdYTxtriIHbCzCP71\nAu47SbfAdyZ/Q6qWq6dEKY/DxTG+Pfnmpl5f1EN8kHqEX/Y8w+X4Yd8OyXuBREpnvv+Qb4Qphcb1\n2GDL405NIdss3mrrdBHW9fZ3chXw5u99h1K8Vc67DbPiEio6Tau1gnqTpmiuuqV9eW3ubq9FifYz\n5gICAgJ2Cmknz+9OvkGylq+7WXocKY7y8tRvN/X6oh6uu7m77mZ3r7o5aTDfP9jGzYLrjbTt1dRq\nCtXGzetNKDCM9QcADBw0McyVDUKv/dGuTCW2Ki6hUrObNRpuzm/VzZsLbepuDsKg3U6QWhzwpdBf\nmeNPR39KVTPRlYfR7gy/hkm7k7878CIKDYTgemyQ9zpO82ejPyUka/f4qO8v0ZiGLTXWv1fajGgX\njbLSW6uohzmfepCpUBdJp8CZxc/pqi3S1W0wMQ/GSlvEehD7nW9z6+GHtvkpdhbtVmo1BXbJobCF\neXLZzjAdU83pxe0aPZXid9itOCAgIOA+MFCZ5U9Hf0Jti26eCHXz9wPPr7g5Psj76VP82dhPsaVz\nj4/6/hKLa1hSW55F2ozAzwLrqJmlxv+FhpunQ10knTyPLn5OZy1LR7fB/Izb1JkYoO+gQXzV3dgf\nvvID+PMtf5wdwfpudim2jk1uS7YzTMf05txcjgVu3u0EgWzAl8pWBKeAn/V/DbV6lVcIqrrN691P\n8u3pza0aA3hoTIc6ESh6K/M7ckaeEILT5jSf+RhQU5IjxbGWx01TYNmCaqX58wgBqbROzojylwdf\nxhU6UtOZs9OMRA8wPpimErM4cvESZ95+h0ihyGJXJx++8DzTg4fu2We837RL75UCHGtrdw+KyRCa\nq0jNl5bXGmq2sSLkxj/bQk8kSCsOCAjYNQi24ea+51rcXDFCvNF1lm/OvLPpfblCY9ruQkPubDdb\nU3wuYG2BiaYkh/3cbGlYlqBa9Xdz1ozxVwe+iavpSLHk5oN8a+otDnROoeuQmfVwXYUdEnT3mk0d\nknfjXdjVuIa2POZoNVKA2ybtuh3FpI3mNbu5ausr5UANN2d6o3hmcEd2txMEsgG7hpwRpab5rJ4J\nwWikf9P7uR3p55c9zyy/VleSb029RV9l7i4d6d0jJis8O/cJ73Q9ikKghEBTkjOLX9BZW2zatlaT\nVCuKrm6T6ckaUq7MlovFdVIdBr/qOIXTmBEIoISGKzQ6p4qMHzW5cfIEN06euN8f875RiRh4hoZw\nZMvqbHELd2OXyHeGlwehS11DaQKj5hHO10DU78QGQWxAQMBeZsGM42g+nV+FYCQ6sOn9jEQG+HXv\nMyx1NtTx+PbkW/RW5+/ewd4lEl6Zp+c/5b3O0yghUNTd/OjCZTrW9PpYcnNnj8nMZK0+Hm/JzQmd\nZNrg1Y7Tvm5+o/ss/+j2P5BKm6TSrb/jXdfQqQ2VqImnawi5xs0CCsktulmIFTc7EmkEbt7LBIFs\nwK7B8RnZs4Rar4hkFUU9zKu9X8FdtS8H+En/1/nPR36MpVwUMGN3cDsygKFcjhVurzsSyBE6WTNO\n2Kvckzl7J/LXOVSe4kbsEBLBcHG8SZRKKSbHHQq5elcIJcG0oLfPREkIRTRsuy7H8XBvS0dKAN2T\naJ5CbrLu845QCrvsEsnXU8GLCZta+D6dioRgejBJ52SeUMkFAa6pMdcf337DByGahOhaOvmgC2JA\nQMA+wTeIbeDnGz/yRoRf9T67xs1m3c23foypPBQwbXdyO9KPuQPcfCp3lcHSJDdiB1EIDhfHSDv5\n5eeVUkyOORTyzW7ua7g5HNGwGm6e8JnkAFA0wlQ1y7d06q6nEi+5OVcFISgmbWqh++nmBF0Thfqo\nHAGOqTE/EN/yRIHV+/SswM17nSCQDdg1pGt5BAq19l6aUiRqef8XreFqfLD19dQXR0eiBzleGOE3\n3We5Hhtans93Ln2C52c/4HjhdsvrPk08wAedpxBIJDoD5Rlemn4bS22+a95mSLhFHl383Pe5hXmX\nQq4+DmBpldepwdS4Q2+/SbkoqZYlsbiOLWtU8F/dVOsV8ayHlISLDlITVCMmCIFVcYlkq1gVF6XV\nhViKWxiOpGs8h1VdqbuKLVbIdYTJdt+f8T6eqTEzmETz6vN2ty3JgICAgAC6qot+WaGgFOna5iYR\nXIkN05onAwrBregBjhZu81r3U9yMHWpy84sz73HUJ5X3k+SDnOs4iVAKKTQOlKf4xvS7d93NSbfA\nY23cnJl3KeTbuHnApFSUVCqSWEzHkjWqus8sWAWGzzFvKpXYz81lh0iuilXxmt1c8+iayLe4OdsZ\nJtd1v9ysMz0UuDlga6wbyAohEkC3Uur6msdPK6U+vdM3F0J8G/hfAR34v5VS/9Od7jNg76IjeTzz\nGec6TjS18RMoXpxpnVfrR0Wz8XxWPSUaVd1kPNzL9djg8qqwbNT8/Kb7SQZLk011QyORAT7oPNW0\ngjwe7uFXvc/wu1Nv+b6/I3SuxIcZiR4g7FU4kb1GbzWDh+BG7BAjkfrjD+dv0FnLNr3WlTAW6aNm\nhOgrT2PkC6BgMbPSBKIQT1GKpzBqVRzLZlII0nMThNwqTDp87ZFL/J37DGLVBYOkfleyezSHQOGY\nAscyMB2FY+sUk3bbzn7x+RLp2fLyzwpwbB2rulI5JIBQySExr2NWvZZWGEJBIlOmmLRxt1ineicE\n3QoDdiuBmwN2EjqSMwuX+ST98IqblUKgeGGTbq7qFtLPzUJQ0SxGI33cjB1scfPrPU9zaGSqKUC9\nET3AuY6TTW4eC/fxWs/TfKtNLw1H6HwRP8yt6ACRhpt7qhk8NK7HDnErMkDYq/BI/gYda9zseIKx\nWB+ObtNfnkbP1UcVLc6vcnMiTSmWRK9VcS2bSSXonB3HkjXA4aHo53zc/yjuqrvbmnRJOzn+of95\nhFL0lGaJ/dcP8rNfxohnyhSSNqqNxxJzJVJz7d285OCN3JycL1NM2E13Nu81gZsDtkLbQFYI8SfA\n/wLMCCFM4L9QSn3QePr/AR6/kzcWQujA/wF8ExgDPhBC/Fgp9dmd7Ddgb3N28RIJt8D7Haeo6DYd\ntSzPzX1ET21hU68/VJ7iUvIYrmhOhRIoDpSm+TT1IK5o/bPQlGQs3Nu08ns+9VCTKAGkpjMe7qOs\n2YRlc8t4R+j89YGXyJux+uuU5Gb0EE/PfcKV+DAZK4mnmyAlnyeO8LXZczxYGKFWlVxdjPDeEy8j\nNR1EvVb2wK0vOPbZBygJnqZz8alvkO3oqdfraM0iiGYznH73F7h/fYUDJ5JMDj2AJiWeriM0HbMm\nsagX1dbv1zogBFJAcq7M1FAS124WmV2qkZ4tN4sPsBpCbP79+T++mnChRr4jSPsJCFiPwM0BO5Gn\nFi6QdPJ82HGKim7RWV3kubmP6F7Ty6Edh0pTfJ44giNa05QPlqc5l36kKchbQijFeLiXw6Xx5cfO\npx72dfNopJ+KT5quIwz+6uBLFIwormYglORG9BDPzn3M5cQRFsxEk5uXMrRqVckX2SgfPP4yUtOW\n3Xzw5mWOfn6u7mbd4MJT3yCX7kIJrcXNsew8p995lci5S/SejDI59ABCSqSmoYRg3krVRw4oxWS4\nB/4TxEV1xc3DyZYFYLtYIzV3F91cdCjcx0A2IGArrHdH9ofAE0qpSSHEU8C/FUL8d0qpv2bj+cyb\n4SngmlLqBoAQ4kfAHwCBLAPW5YHCLR4o3NrWawfKMwyUZ5gI9y6LzpAOx/K36XByiOUcoDVfcSEQ\nKGo1iZRg24Ki7p+iqyGp6FZLIPt5/Ag5M4a3JNhGM4e3ux6ri0tvSFrT8NB4s+sJhvO3uX2zzAcv\nfhfHCjXdiR4ffIDk7BRd06PcePgJFjt7ULr/n3Qx2cE7L/8pZ975BQ9cfJ/DX5ynGE8VnDeYAAAg\nAElEQVRx++gJMn2HVva7ptZYU/U6n86pAtNDzf3vU6vuxDb9qnwf3fiksdk654CAfU7g5oAdhwAe\nKozwUGFkW68/WJ6irzzHZLhrOWA1pMMD+RFSTh5NqXoTKB9PLLlZSbDWcbNAUtVbA9lLiaPkjeiy\nm5caLb3V9bivm9/oOstQboyRm2U+/J3fx7HspuMaG36I5NwUnTPjXH/kLNmO7rZuLiQ7eedbf8qZ\nt3/G8YvvM3TlPKVYktFjJ5nvPbgyN6+NmzsmC8yscXN6xr9ueLsnB/8xQwEBO4P1AlldKTUJoJR6\nXwjxIvD3QohDbGWwZXsOAKOrfh4Dnr4L+w0IaIsAvjX1W67HBrkSH0JTkofyNxku1ldzHyiMcC0+\nhLsmxUkhkJduMVKqpxYrBTFjgvzgMdCaVyqVVCScYst734wdXAli1+xbGT7NMqTkppumGA/hmnaL\nyKRhMj78IF3To0wNHmsryvoHFyAEF55+iWdf/QtMp0oqM83Fp15cf9o6jVEMZRekahqGpzvrr+K2\nflD/i5AlVs9a7b85wpOvvU40lyfb0cG7L79Epq93K+8WELBXCdwcsOcQwLen3uRabJCrDTc/nLvB\nUGkCqLv5RuxQS8aUAryLtxipuMsNleLmBMVDR1cGtC69hyeJ+7h5ZItuVlJx002RS4TxDNPXzRPD\nD9I5M87UoaMbulkJwafPfJOv/OIvsGpVrMwMFzr7VoLYdi8FQmW3xa2a61dtvM5+NnBzeZWbB27c\n5OxrrxPNF1js6uTdb77EQm/PFt4tIODust5fSV4IcXTph4Y4X6C+Mnvf5nMIIf4rIcSHQogPF73W\nrm0BAVulUnSJXL7Cqd++ylMXXmMwN7Z80u+vzHEiexVduujSw5AOunQ5+dHreEWHpUVhgKEr5zFc\nFyFX6kE11+HYhffxaq3NGWyvSstE8yX8HhcCt1TD1XTaXZ9Kw8A1zLpMN4OA2YHh5R91dwuNL9Z4\nrhIx/Y+q3Wek9VMo6jW6c/2x5cYORz+9wDf/v78kPTePVavRNTXF7/2//46+ke3dhQ8I2GMEbg7Y\nk1SKLtHP6m5++uJrDObHl7UzUJ7h4dx1dOmiNdxsNNzsluu1qKrRp2j4yicYrgNLblYKzXU4euE9\nPGft5NeGm7eCEHilmm/wu4SnGziGhVwviF2FEoLZ/qHln3V383N811KJ3mU3N2pWH/j4E176T39F\nej6DVavRPTHJd//Nv6X39uja3QUE3DfWC2T/KaAJIR5ZekAplQe+DfyTu/De48ChVT8fbDzWhFLq\nXymlziqlzqZ0nxmiAQE+KKVQPifthYzD2K0ahZykXJbMz7rculHF81a2fSbzKd8f+zlPZT7lK3Of\n8L3Lf0N6qrUrYqhS4uzrf8vAyBdEcgukZ8Y49f6v6B+7RqkgW7Y/mb2GodZIVEnsWhnNWxNQKoXu\n1OhzMiRz/vNtNdehe+wmnz7zTf5/9t4zSI7zTNB8vjRV1VVdpr138AAJRxB0Iil6TxnKjIYys7Mz\nO7Oj2dmIu/2zobjYXxcXuxcb93v34lajkcZIougkURp6EvQGNPBAN4BGe99dXb7SfPcj21WX6W6g\nG+hu5BNBQajKyvwyUZVPvp953+UOxNhCYOoLRz7PgJUv9pymAMny/F7nqVo/C5Ixzm2LlIjZAHkm\n8lcsk9Zzn4OQ2IpT5Fzi1HXt2xYhFfLObX/ba2/kre0BuOv3fyjaRsU0aT3XyY4vviQ8tv5qDrq4\nrCKum102LEXdPDbj5pjj5rERk+4LGewZNwvgjvEv+FbfK9w64+anTr9AxXDeVxNfKuG4+dI5/LFJ\nKkf62ffRazT0Xyji5k40O9fBYtbNiwNKaaNlM9Sak4SjowVHMhXToLb/Il/e/tAKrswiN3efnQ/E\niyCZmclUwM2z7y/ctqibz36OFBJbEXNuTvn1PDcffuOtgm6++3cvFW3jQjeHxl03u6w+RbuKpJRf\nAgghTgghfgH834Bv5s+bgV9c4bE/AbYLITpwJPk94Okr3KfLdU42YzM0YJBKOrLyeAQVVRqhiDP9\nd3TIzOmUlBJMQzI1YVJVMz+qGTHiRKLnAIhlisvEl06y/cTHOa8JJW+2MQBN6REOTZzg08q9KNIC\nIfBZGe679AZf0sKlbXtRbKfdimVx6LPXqKxVmZ602PnFu5w5eDe2IkBRUUwDfyzKZHUD0xU1+TIt\nMlVIsSWh8WEATE2lvr+LswdvxpOViEXPFs7aIAXDozJRX563L1tT6d8aoXoghjfl1MlLhDx0nPqU\n8HiSWKQKxbapGBukergPKeDDh+9CMxQUyybj1/OTVKTTBUeJBVCWTBY8r8joGA//8tcoljV3/S7u\n2sH7jz6y5LRpF5eNhutml41IQTdXa4TDKraE0ZEibp40qayed3OFEaMi6pTbm86YRftwfekkO44v\nypisgKLmO6ElNcxNkyc5WnHjnJvLrDT3db/B50o7PVtvRJkJKlXL5ObPX6OqVmN6MsP2Y+9zbt9X\nctwcmJ5ivLaJeKRq2W4WSEITs27WqOvr5Nz+m5Zws8ZEfSBvX7Nurlrk5i3HPyYUTRMLV6PY1oyb\ne5FC8MGjd6NnRVE3+5JJ1AKd3gIoS+RP1waoGBnloV/+GsW259x8YfcuPnjkIdfNLqvGcuY83Ar8\nN+B9IAj8E/CVKz2wlNIUQvwH4GWcFP8/lVKevNL9uly/WJbk0sVMTidmNisZHjQYHzWoqdcRIn92\njZQQj1k5gexCfH6x4pVn5cHCGf4ORM+yO3aBYV81XitLbWYcoYFv4iSNr58jWlXn9PbGhmlp9aAo\nCm1bvPiH+wm9+1sGmrcjg34qpkc423gj8XBlYSEIAbY9tzYWnFHQVMjLxRu2UzESYbyuls79+8j4\n/WhZi7pLQ9T2DxOcHAPF5sKeGxlrrCPt14pKx9ZVRtoiOa+ly2/maz/9B5ounXUSdACGrnHy8GEM\nnw+jcB4OZzvPCkd2pOS+517Am8rN0Nh+tpPBtnYu3rB7RbsTtk1LZydbT5wiPDFBPBLh+G23MtzS\nvLJ2ubisPa6bXTYERd08YDA+YlBTV8rNNpXVhfdbVrayMi0CCJQX/szBqTPsnr7AiK8Kn5WhJjOB\n0OHWieM0vX5m3s3xYVpbPAhF8PO//htuOvIuez98mZHmrUzU1uJNTJMOVBMrFMTCjJstp8d7gZuT\nQQ8XbthJxego4/V1jpvLymbcPEht/zChyTEsBS7ecCNjDbVkSrjZKuDmjP8wX/vZP9DUvdDNOsdv\nvQXT68UsUMZ2lqy3xJuFkJL7nnsebzqd4+aOM2cZbG+je/euFe1OWBYtnV1sO3GS0OQksUiE47ff\nykiz6+brneUEsgaQAspwen0vSinz52ZcBlLKPwDF5wu6uADZrMXokEk6ZePxCmrqPfh8+TKanjIp\n9s00TZiasIouEdG04r2Duq4QrlCJThb/PMzHjE1tHhSl+P68tkFrcjDntUilTigiSacHUMsE3tp5\naaiqoL7RQz0GN3KGt/03c7z6FieNf7FeTdt2ZKlqWAIMr0as0kcy6GGk9fbc88tk2HLyFFXDw0zU\n1nLitrsxfCWizSVIBoP8/s9+yIF336PhUg9pfxknbrmFi3uWFpetqkQjEcJTUznyk8BETXX+aOzY\nOL5kMi+xhW4Y7PziyxUFso0Xu/nqi79Dzzrr/QQQnpyirrePdx99mEsrFK+LyxrjutnlmpLNWIwO\nz7jZJ6it8+At4OboUm4u4dZSS0x1j0IoojI9tQw3K9Dc6i3pZp+dzXNzRaVOeMbNWpnAU+vlJ4//\neO79Dx9+0Pk/tqR6KE5gKpLTgZyHbTv/qQq2gKxXY7rKR6rcw2ghN584RdXIjJtvvwdjpQHlAhLh\nEL//kePm+p5e0n4/x2+7ZVlBpa1pxEIhgtPTeW4er8tPxFgxMoo3lS7o5h1fHltRINt0/gJ3//b3\n6IYzzVsAockp6nv7eOfxR+nZuWPZ+3LZfCwnkP0EeBE4DFQD/0MI8S0p5XfWtGUuLkAqadFzcT6R\niGlKLp3P0NCsEwrnfn2zGVlSZqmkje4BY1FeEiGgoqr0T6G2XqfMrzA5bpLNyrylK8GQQrhCwx9Q\nEJc5ZUZRBH5/4ZFcy5RMTFl82HY7Q/4WpFqippuUSEVBzGRsVCWIjIml5Qe+gelpHv/5P6Fls+im\niaGdZf97H/CHHz5NrKLiss4DIB4J8+4Tj13WZ1/93nf4xv/6ezTDRDBTyF3XefNb38zbVrGsomV7\n1MXrjkvgj8W49/kX0QpMa9ZMk9tefZ1Lu3a606Fc1hOum12uGcmERW/3AjfHJd3xDA0tOqHQIjen\nl+FmHYxFy1GFgIrK0m6ua9Dx+xUmJ9bezQceNXlM+Q8573mTSXZ88SWWUkEiXJWXKTmHRW52aria\nTjKlRW0rn4ry+C/+CdUw5t38/oe89MPvE4+EC+19WcQqIrzz5OOX9dlXvvddvv7TnzlJLlng5qe+\nnretWsrNZum1vwsJRKe558Xf5blZMOPml1+lZ8d2183XMcsJZP9CSvnpzP8fBL4uhPjhGrbJxWWO\ngd7C2TCH+g2CITVHTL4yBRG1ivb8AjS3eejvMTCycm4qU3Wthj9Quti3EIJQWJsLno2sTTzmHKg8\npKLra3cTNbI2R+M1nLjpLiwtP7FDDjN1cMWiflBFQmQ0mVcL9pbX3sCbSs1NM9JNE9WyuO2V13j1\nT67N83AyFOKXf/e3bDl5iurBIcYb6rmwZzeWnj/1e7K2BrtAUG9oGuf3LH80dsuJUyUzOnrTae7+\n7e858rUnXGG6rBdcN7tcMwb6iri5zyC4O9fN3jKBiJa8xc672Zh3c03dMt0c0QhF8t0cDKloq+Tm\nhaOws5RPRbn9j2/QdeNt2AXK8ORQws3hsSQjrbluvvW11/Gk03luvvXV13n9O09d8flcDolImF/9\n3Y+dGVxDw4w1NnBx966Cbh6vq3VmjS3C0DQurMDNW0+cQNjFH+p86TR3vvRH3n38UdfN1ylLBrIL\nRLnwtStNJuHisiRSSopVh5ESjKzE452/cQXDKmMjBmaRe16gXMHjUWnfqpDNSCxL4vMpBZM/LIXu\nUaioWtn6nMvBRvC+Zydnbj649E3athHYSCmclW2L8KTz0/k3XeyeE+UsipTU9/QuWfd1LbE1ja79\n++jav6/kdlJROPLkY9z33IsIKVEtC0PXmaqu5tyB/cs+ni+ZRCuRvVkAzRcu0tLVRe/27YQmJmjt\n7ALg0vbtxCovf/TaxeVycN3scq2QUlJswstskibdM++OcFhjYtQs6vPyoILHq9K+TSGTkdjrzM2F\nglikZOuxLs4duGt5bpYWIJBqftu8qfwL09h9qaCbG7u7V9Dy1cfSdToP7Kdzie2kqnLkice494Xf\nImwb1bYxdJ2J2ho699247OP5EinUEoGsAFo7u2i6cJH+rVsIjU/Q2tmJFIKeHTuIVUSKftZlc7C8\nAlcuLsvAMiXJpI0iwB9QMAzJ2IhJMmmhaYLKai1vOvAVscgdiiJo2+JjeDA71yMLjmNUFeoaPTN/\nF3h967/nLitUftP8EDE9uLQopSRbpqJlY2iGH7tAJOvJpPJesxWlYCZCW1FQDQsUxZmSvI4ZbG/n\n+X/3b9l6/CT+eJzB9jZ6t20t2BtcfB9t7Dh2fG4NTiF0w2Db8ZMEJ6c4+O77c73E+9/7gM/vvIPu\nXTupGh4mWR5kvL7O7R12cXFZF5imJJWwUdQZN2cloyNOBmFNE1TV6ARDpUc+rwRFddw8NJAlsaD8\njVBm3Nww72bfOnNzoSBWWDYNF6eYqmlbxigsZMo0PJlpVDNQMG+kJ5MEqnJesxVlLtPvQixVRTWc\nabv2OnfzwJYOXvjLP2friZP44kkGO1rp27pCN3e0se3kyaXdfOIkFSOj7P/gwzk3H3jvA47efRe9\nO7ZRNTRMPBRioq7WdfMmww1kXS6b2VpwQggmxw1Gh825+8NsR+Lsn5YpGewzGBk0UFRBMKRSWa2h\nluhxFULgKxOkU/m3fkWh4HReTRc0tXqRUhKP2WQzNrpHEAyqiBJJHtYbEni+6cElg9jZOq7DbWGy\nfp0tJ4douNDNwJY9zlSnGRTTJDzeS255SDh/w262Hz+ZE8xOVtZy4tb7aLwYRQBZr8pYYzAvHf96\nIhkMcvyO2y778/1bOhirr6d6YAC9xMisls1y8N33c9fr2DaH3jrCTe+8h6WqCCmJRSK8+t1vkw74\nL7tNLi4uLpfDQjdPjBmMjSxw88z/LHTzQF8WdaY0TSisUlmllRwNne0MzqQLuFl1RkUXo+mC5rZc\nN3s8CuVBZV26ueAoLICUNHRH0czSM5YkIIVguDVE1q+z7Xg/dZd6GWjflefm0EQfi918cfcuOk6d\nzpkpNFFdz8nD99J4YWrOzaNNQSx9/bo5EQpx7I7bl96wCH1btzBRW0Pl0HBJN+uZDPs/+DDPzYff\neJOb3z4y5+bpigpe/e63yPhdN28W1nd3jsu6ZDpqcv5cmnOn0nSdTTM8mGV02KkBN5uQT8rC62Es\ny5kSPDlu0nMhg22XrmvT3OYpWJO1uc1TMnGDEE6wXFXjJIVaj6IsxftV+5nyhJbs7U2W6wxuiZD1\nO2IcbG2l/ewXtJ07hpbNgLTxpuJsO/Y+o801ebs4+tWvMlFbg6HrGLpGIhDk+O0PYek+FAlCgidt\nUdcTpbp/kJbOLnzxwjXjNjRC8Np3v8Un99/LcGMDdoHrbug6yfLygut1BE5yC082i24YhMfHuPt3\nv78KDXdxcXFxmJ6ad/P5GTePjSxys13AzXLezRNjJpcuZpDLcXOBJ8iWttIl1Ba6ORhefx3MBx41\niwexQMVwAs2w87Lx5lDIzW2ttJ/+jNbO46hG1nFzMs72L99jpCU/6+8n993DVHX1vJvLg5y49QEs\n3Zvj5vpL01T3DzhuLlLPdSMjFYVXvvddPr3vnpJuTvvLEIszfZHv5sjYGHe99Me1b7jLVcMdkXVZ\nEfGYxVC/MSdC23LK2qwUKcEwJLFpi3Ck+NdQVRW27fQRi1okErZTRL1KK5lCfyNjCpX3qw5wOryt\n9Ia2RSLkZaw5lPNy5egoihC0dR0nNDFMz479pP3ljDW2MdTSnn88r4c//OBpagYGiIyNkyivRTU1\nlAXPMALwpLPs/fA9qkb6UU2TlN/P8VsPc+7gAWxtc9xGbFV11v4c2E/jhYvc88JvETg95pau07t1\nC1PV1cDZvM8u/jaqtqS2fwBvMun2/Lq4uKw5sWmLoYF5N1tX4uas4+ZQCTdrmsK2XT6moxbJhI3X\nK4hUbmw3lwpghS2pGIpTPp0tGcQK2yIW9jLelOvmihHHze2dxwhPDNOzfR9pfzkjTe0MN7fm7cfw\nennpR9+npn+AyHgpN2fY98F7VI4OzLv5tls4d2D/pnLzuYMHOHfwAE3nL3DPi78DJIppYekaPdu3\nMVVVCXO5lOfJd7NN/aUe9HT6isoMuqwfNse33OWqMTZiFBxpvRykhGTcJrzEWvz5rISrc9z1Skrx\n8nzzA0zr5SVFKZGMN4ZIhPPryR088i6KbTPS0MaZg3c5GX2FIOUPUn9pmsH2CKZ30RC3EIw2NTHa\n1ETFUJzQVKbAUQWW7p2btuNPJjn85tvs/fgT/vD9p0lcQTmA9cjAlg6e++t/R/uZM3jSGQY62hhr\naKA8GuXA++/DMqp1SiHQDINCVzN/Y0nFyCgImKypcdfwuLi4rIhVd3PCXtK5QgjCEW1Jh28ESgWx\nimnT0B1FNUuPxEoko00hkqF8N9905B0U22a4sZ2zB+6cCzJT/iANl6YZbA/nL98RgtHmJkabm6gc\njBOMFrZJnpvfeIsbPvqEf/3Bn5IIby4392/dwrN/9Zd0nDmLns0w0NHOWEMDoYkJ9n/wkTPtYAmk\nItANY3mB7JybBZMFatm7XHvcQNZlWRiGJD5tkc2skilnWMuyNRuNjyv3lgxiZ6/8SHOIdHnh6VvB\nqSkk0LX31tzeWEVBSIiMJvJGcReS8evY0UxOr+/cvifHcv6uAGWJJN/46c/4ww/+lMna2qL73Yik\nA37OHLop57V4JMLRu+/m0NtH5l5TLAuEyMswmfH5SISKX+tZavoHuOeF36JnnXIWWa+Xt775NcYa\nGlbhLFxcXDYzhmETn7ZX1c1CkJN1eDPj1Ib9jyW3qRhJlAxiZ6/8UEuIbKCwm8ujUSSCrr235bvZ\nloRHk4w3BYu2IePXCUwXcrMgODma84oCBBIJvvG/fsZLP/w+UzXVpU5vw5EuD3D65lw3T1dW8vmd\nd3DwnffmxmUV28kUvdjNaX+AZHn5ksep7etzathmnURTWZ+XN7/xdcYb6lfpTFxWAzeQdVmSyQmD\n0SGnt2+1enzBkWW4Yv0mKbia/OTxH9N8bgJ1iXVJA+0hTF9+zbZZpisqCE5NY+r5MhWAr0Ca/4Uk\ngx7CYyqaYc0JUzFNKkYHCE5PFNynapo88Q//yEBHO0e/ehdTNflrcTcTZ26+ib5tW+fK7wy1NHHf\ncy/iSafRTRNLEdiqynuPPbxk760nnebBZ36Dnp3PyKgbBg/+6jf85m/+CsOb37Pv4uLiAswlWVwL\nSk0r3iyUGoVdSFncWGIkFgY7wpje4tcsFqnAH0tgqfnbCMCXLJ6VFyAR9BAeV8Cw591smVSO9FEe\nmyq4T9U0efJnP6e/o53P7rl7ZmnM5uXULYfp2bGd1s4uJ9FWcxP3P/sCnkwGzTSxFAVbUXjv0aXd\n7E0meeCZ53KyJeuGwUO/foZn/uavMT2l14K7XD02/53KZdlk0hZTkyaWJQiUK4RCKqYpGR0yryiA\nbWjW8XoFg/3GXK+xqkJDs6dgdsPrjTmZlriv2sB4Q6BkEAvw2Vfv5Ksv/B5ZZGdWgRp2OQjBUFuI\n0HiKQMwZIdx2+hhtXceLfwQQUtJ44SJ1vX289KPvE62qKrr9ZiAeCXPq8KG5v7/4F/+G7V8ep+FS\nD9MVEc7edIDpysol99N++iwU6LwQUtJ29hxd+/auZrNdXFw2IJm0xdSEiWULyssVgmHVKaEzfGVu\nbmzxoHtgqJCbN/lsqeUGscDSbm4sLxnEAnz21bu483d/QBYJoJYsc6cIBtvChMdT+GfcvP30F7R2\nnSzZbCElTRcuUt/bx+//7AfL8tJGJh6JcOrwzXN/f+Ev/g07vjxOfU8v05UVnLnpALGKpeu+d5w5\niyjw4xK2pO1cJ+dvvGE1m+1yBbiBrAu2LentTpNeUGY0FrUYGTSIVKoF657NoqpOUolCCAH+coVg\nSEUIQftWFcOwkbYzbalU1uHNRCplE500kTYEwyqBcgUhRJ5I42Evwcl0ztQhJ4U/jDWWkwouPTo3\n2N7OO08+Rm1vH5M1TcgFvb+2gOmqsiX3IVWFaG2AaG0AAM1so+XiKYRpluyVVgBMk/3vvc+Rrz25\n5HE2E4bXy6lbbubULTcvvfECfMlkbrmAGVTTpCyRXK3mubi4bECKuXl40CBSqZUMYpdyc6B8pvTN\nrJuzNlJeH26edW/1wCDbTpxANUy6d+2kf0tHwZG6eMhLcKqAmxUYawiSCi49Ote/pYP3Hn+E6v4B\notUN2Jfp5qnaAFMzbtaNdpovnlm2m/e9/yHvPvHYksfZTBg+HydvPczJWw+v6HO+RAK1gJsVy8Ln\nunld4QayLowMGTminMW2YXrKWpwEbo6aOo2KKo3u8xmMrMyRqqJATb1OOKLmSFHXr68R2PFRg/HR\n+V7zWMyicYvg//rm/5a3bbTajzdl4knP3DyFM4I63BZeurd2AXo2y9ZTn3Jxl814XevMflSiVWUk\nQiufDtOzcwcvVVay7/0PaD3XiSKLjfeCIiXVg0MrPsb1ynBLM6au5xV7tzSNoZbma9QqFxeX9UBp\nNxeeUiwEVNfqVFSqdF8o7Obaep3QYjdfB7OjFnYe7/3gQ/Z98BGKZaFIZ5Stb0sHR772RF4wG62Z\ncXMm181DbWHsFbjZk8mw9cRHXNx9MxN1LXNunqoqK5ggaiku7drJdGUle9//gNbOriXdXDMwuOJj\nXK8Mt7RgfvpZnpttVWHYdfO6wg1kr3OklE6wWgTTdO7pi3t+hYDyoCPC1g4vE6MG01F7bt3rZi6R\ns1xMQ+YEseDU8Ou+pNF0sdvp/V2AVJzi6Z60iSdtYeoK6YC+oix59Zcu8ZU/voxmmuz88kO6bjAZ\na2hF2DaK7UNIZ4R3pUzVVHPk60+iGAYPPPs8tf39KFbh5BfxTZYlcS0ZbmlmuLmJut4+9JneX0N3\ngtjRpsZr3DoXF5drhZSS6GW4GaA8pCAUx83jowaxBW6urNp4ddVXg4VBrD8WY9/7H6ItGLLWDYPm\nCxdpuNTDYHtbzmelIhhuC+FNmegZC9OjkPavzM2NF7u5/eVXHTcf+4CuG0zG61sR0ka1fQhbIi/j\n32WytoYj3/gaimHw4DPPUTM4iGJZeW6WwHTFJkgvfZUYbGtltKGBmoGBHDcPtLcz5iZ7Wle4gazL\nkmtsKqpUJsetue2EgMoaDY/X6YlUVUFNvYca97edQyJhFSprhm4YtJ7rzAtkARCCbJlOtqz0Wthi\n7H//QzTTxFYUjt79OBlfAKk6CbVCE2m8KZPh1tBlp5C3dZ1XvvddgpNT3PbKq9T29ec8DJiaxpd3\n3H5Z+74uEYI3nvoG246fYPvxE05Wy3030rX3xhX/G5XF4xx6821au85jKwqd+/byxZ13YOmX911y\ncXG5xlyGm6tqNDyeeTfX1nuovc7dvHgZT+PF7oJrVTXDoOVcV14gC4AQZPw6Gf9luvm9D2YSDql8\ndvcTZLz+VXfzy0//CcGJSW5/+RVqBgZz3GxpGsdvv/Wy9n1dIgSvfecpth87wbYTJ5BC0Llvr7M2\ndoX/Rv5YjJvfeIvm8xecmrj79/HFnXdsmjq/1xr3Km4ypJSYhkTVBIoikNKZVqDCW5wAACAASURB\nVDQ7OppO20yOmxhZSaBcIVKh4fMJ0unCxtR0qKnzEArbxKadm2IwpOL1bf5pSFeKUuRmZwtBdo0y\n3pVPRQEYbWgn6y2bEyXMFk838abMy5bxLLGKCK9/+ykOv/4m206cREhJxufj4/vvZbi1pfCHpKS+\np5eOU6cBuHDDHmeKziZfj7UUUlXpPLCfzgP7l/2Z8Pg4HSdP40skUWwLxbZp7TqPZsxn17zhk0+p\n7+nlpR8+TWhyCtWymKquQirub9fF5WqzpJtTM242ZtxcqeH1CTJF3Kx7Crg5rOL1ur/vWYoldDJ1\nvWAgK4XA9K5Nx195dMbNTe1kPb6CbvakzcvuxJ4lVlnBa9/5Fre8/iZbT5xE4JSC++iB+xhpLjIl\nVkoaLvXQcfo0Uijzbr7OkarKuYP7OXdw+W6OjI3Rceo03kQS1bYRtk1rZxfa7Dpm0+TGjz+hrq+P\nP37/TwlNTKDYtpNR+jp/Frpc3EB2EzE5YTC2IIuh7oHsTP1sj1cQCqmMj82/n07ZTE6YNDR56LuU\nLbjPxhYn4PL6FDd4XSGBoEJG8+DJ5l5bW1U5v3f1M96VxePomczMFKJqbK2wED2ZKw9kwTmPjx56\ngE/uuwc9myVTVlbyRvyVP/wrW06fQcwULN9y6jTnDuzjk/vvu+K2XE/s+OxzDr91BGVBgo/Zgf+F\nV18AVcPDfOt//n/4UinnIU3XOfLkYwy1FRhxcHFxWRMmxw3GRha4WYdZLXi8gmBIYWLMynHz1IRJ\nfQk3NzW7bi5FqazEfVu3FFwWY6sq529YfTf7YzE0I4sEopHa4m5OW1ccyALYmsaHDz/Ix/ffuyw3\n3/X7l2g/2znv5pOnOHPTAY7ee88Vt+V6Ytenn3HoyDvLcnPNwCDf+h//L95UGoTA9Oi8/eQTxQcC\nXIri3v02CbFpi9EhE9t2pgpLOR/EAmQzkrHF6zUlWCbEYxZbdnjxB8Tcva4sINiyw0tZmVvn9XL4\nyeM/5v948m9546lvkPV4Zv7TMVWVT+65e01qrd77/Ivo2SwCKItHUczCdelMfXX/TW1NI+v1UTGc\noPncBC3nJqgajKGY9tw2DRcusvXkKRTbWVcrAM2y2Pn5l0RGR4vu2yUXXyLB4TffRjNNFJi7lkDR\nJB+BWAzNNNENg7JkkvueewF/LHZ1Guzicp0zHTUZHV7k5gWxaTYjGR+18txsmpCIW3Rsy3Wzf8bN\nXtfNRVmqtI7p8cy4Wc9x88f330u0evVLx9337AtoWWe2jD8+hVIgGy6AucrJMGfdXLnAzZWDcRRr\n3s3NnefpOH02z827j35OeHx8VduzmSmLxTn09pEVujmOPuvmRJL7n32esnj86jR4E+GOyG4SxkeM\ny64nl4jZ1DUotLT7VrdR1ykLJTrc2sKv//bf09h9CdU0GWxvc3pHV5nyqSgVo2NzPVN1fRfp3nUT\ntrRBzLxq23iNDCn/0jXUVoSU1PdMo2WsueMHolkC0SzxkIep2gAH332v4EcV26als4uyeIIdXxyj\nvrcXRUp6tm3l6D13kw4EVretG5ymi93O1OBidTUKsFiiii3ZduwEx77irmV2cVlrFif8WwnxmE1t\nvevm5fKr//k0X/52eQmNhtpa+fXf/g2N3d2oprVmbg5NTBCemJhzY33feS7tPIAt1flRUtvGm02T\nXgs3X5pGy867uTyaoTyaIRb2EK0JcOC94m5u6jxPIDrN9i9n3QyXdmzj6FfvJuP3r25bNzjNFy5c\nsZuFbbP1xElO3OauZV4JbiC7STDMy6+Krrgdu6vC7T/dx73P3pn3uqXr9G7ftqbH9qTT2AvWPupm\nloPv/oEzB+8kHq4CJOHxYbYd/5Bo1WOMNjet2rF9CSNHlDB/gy6fzlKWMCiLJ4v2Su778GMny+KC\n0gEdp89Q39PLC3/5526yogXYinJZWacXoloW/rg7IuvicjUwjct3s+q6edn85PEfw29X9hnHzdvX\npkEzeNKZXDcbWQ6890fOHLyTRKgSkETGhth24kOm6p5krKFh1Y5dljDQjMJuDkaz+BMGvhJuPvj+\nB3lu3nLytOPmv/hzN1nRAqxV+LFqloU/5o7IrhT3W7hJ8JUpJOP20hsuQgioqHK/BlfKTx7/MTyb\n+5pi2U4ZHU1getf2Gk8VmA4ViEc59M5LmJqOkBLVMjE1jcrR0VUNZD0ZC1HkWU3gjAD2btvD7i8+\nKriNVmCalWrbeNNpOs6cdTL4ugDO2i7FLv5gvHAtjg0gBGLRcJCh6wy6a2RdXK4KvjKFZMJ181qy\n1FTixcy7WcH0rm1vwURtTd49uDw2xc1Hfp/jZkPTqBgZXdVAVl/KzZakb+sedh7/pOA2xdzsS6Zo\nP3uOCzfsWbW2bnT6tm1FvPJa0feX6+ahtta1auKmxV0ju0moqdWXTHgmBHg8zp+K4vwZqVQJhd1u\n38vl9p/uy5eolIRHkzR1TVLTP01Dd5T67qmcNaOrja1pfPjg/ZiaxuxRZm+RmmmgWo6QbEUQi6xu\nLTnDo5YcJVQkDLZtw1yULVdSuqatbhhUDQ6tTiM3CYbXy9tfewJT0zA0zbmGgKUomJrKaEM9Q40N\n9Ha08+ZT3+Di7l0YC0a0TU0jWllBzxrPEHBxcXGoqVuGmxXweHPdXFGpEgy5bi6F782nVhbESklk\nJEFT1yTV/TEauqeo647mrBldbWxN46MH7lvSzVKsvptNXUGWeMpXJAx0bMdcVL9WzrSnGLphUDU0\nvEqt3BxkfT6OPPFYYTerKqMNDQw11NO7pYM3vv0U3Tt3YOjzHVWmpjFVXUXvtq3X7Bw2Km533ybB\nV6bQusXL2LBBOmWj6QKvV5BI2NgWlPkVaut1vD6FTNrGNCVen4Kmuem+L5dCo7AA/liW0EQKZfZO\nhpONsHogxkhreM3ac/GGPUxXVrL706OUR6epGh5GseanFVmKIB0IMLjKPX6pch1LVRCmXXCKkgRi\nkSCfffVuDr7zLuCsv5mORAhOTxdNfGFoGtGqylVt62agb9tWfv3jv6al6zxq1sD06ii2ZLSxkelF\n16tv6xa2njzFjs+/RDNNLuzZzZmbDuSUfnBxcVk7fGUKrR1exkYcN+u6wOMVJOI2tp3r5nTaxnLd\nvCx+8viP4b+v7DOB6SzByfSMmx05e9Mm1f1xRlpDq9/IGc7vvZFoVRW7j35GoKCbFVLBcoZWOWNt\nMuihYkRB2MXdPF0Z4vO77+LAu+8DC9wcjaIUWe9p6DrRylVez7sJ6N2xnWdm3KwYBqbHg2LbjDQ1\nEVt0vQba2xw3f/ElimVxYc8ezh7c75bHuwzcQHYT4fMpNLd5l9zO61NYeiuXYtxx/D9xz39OFX0/\nNDEjygUIwJcyUUwbW1ubG5WeNkEG6Nr7FdJ+HUmaO155merBIRCCwfY23nvk4dW/UQrBcFuYyqE4\nZQknU/JCaUoB8Qofp+sOce7APsLjE6QCATTT5Gt//w8Fd2kDtqa6U5eKYPh8XLhxGWUihOD8jTc4\nRdxdXFyuCb6y5bnZ55bRWRYrnUo8S3C2g3kBjpuNNXezpJzOGTcLUtz+8svOqKYQ9Hd08MEjD61+\nHVEhGGoLUTUYx5d0OowXuzkW8XHqlsOcPXjAcXN5AD2T5cl/+EXBXdo460Ev7tm9um3dJGR9vmX5\nVioKXXtvdJdOrQJuIOvisgJ+8viPoUQQCxSdpiRn3lsLWfriWWr6Ywg5W1zdwlYEr373T5DCRgqx\npokZLF1htCWEYlhUD8bxpUxnWo2mMF5fjulRZ7bTmaivm/vc2f372HHsOLrhBMCzzxhjDfW899gj\nZH1utk4XFxcXl8sPYGdRrMILRiVOLoe1mGBcFs9SvcDNetpCKgovf+97wNVws8pIa9hx88CMm8WM\nmxvKsQq4OVUOXXtvYOuJU3luHm1s5P3HHsbwusMhLusDN5Bdx5imZGLMIB6zURXw+RWklHi9CqGI\nhqq6U4+uJsuVaCrgQZtK503lkULMBXSripRUD8RzepqdJEs24dEk403B1T9mEewZaQrLRrHB0kTJ\nXuZP77uHwY52tn95DNU06d65k0s7t2OWkqSUVI6MUJZIMlZf55YBWAV8iSQHj7xDa9d5LFXl3P69\nnLj1FjcrpYtLAXLcrDojrlJKfD6VYFh13bwGXGkQC84yGG0qk+9mRax6DVdnx5KqRW5WAGnbREaT\njDdeZTe3hVEsG7EMN3/0wP30d3Sw7dgJVMvi4u6d9GzftrSbh0coS7puXi188QQ3vfMOLV3nsTSN\nc/v3OW52lwfN4T6lrFMsS3LpfBrTAiQYQDrtrFcQwmZsxKS1w4vXnYq05qxUoNHqMvyxDIotUeR8\nUqOJ+sDqTx0CvCmjYCZbgaB8OnVVA9lZpKpgLec+KwT9Wzro39KxrP2WxeI8+MyzlEejSCFQLItT\nhw/x+V13rsm1vR7Qslke//k/UpZIoNrOmMTejz6hZmCQ17/zrWvcOheX9YVlzrh5Zmm/AaRTjpun\nhc3oiEFbhxeP13XzarCS2rBLMV3tJxDLIha5eby+fG3cnCjh5mjqqgays9iqAst0c9+2rfQtM/mQ\nPxbjwV//hsB0DCkEqmVx/NZb+PLOO66swdcxWibLkz//Bd5kEnXme7T3w4+pHhzijW998xq3bv3g\nBrLrlKkJ06mrXGAmjJTOf4P9Wdq3ulMvl4uUkkTMJjZtoagQrtCWXJN0Ob3AtqYwuCVC+WSasoSB\nqSvEKsvI+tbm5+aPZpw07gVE7Emn0bIGpmdz1GK994UXCY+PoyxIW7/76OeM19XRs3NH3vaeVIo9\nn3xKa9d5MmVlnLr5pjWvG7geEbZNbf8AwrYZaWrMGWntOHUabzo9F8SCU3ahvrePipERJmtrnRel\npHpwkNDkFJM11fOvF8GbTLL15CkC0zFGmpvo2bbVTTLlsuGZnHVzAaQEaTlubtviunm5SCmJx2zi\n0xbqjJu9PuWyasOWwtIUBjoiBCfT+JKOm6cryzDWyM2B6eJu9qaSqIaxaeqk3/vci4QmJnPcfMMn\nnzJRV0tvgSz53lSKGz7+hObzF0iXlXH65kMFt9vsCMty3CwlI81NOSOtW0+cRE9n5oJYcNzccKmH\nyNgYU9XVzotSUjMwSHBqionaGqZqakoe05dIsuXkKQKxGMMtzfRu27qhk0y5gew6JRG3kYWXc8yR\nSUssS7rTmJaBlJL+nizJxPx1jU5a1NRrVFTmi6RkACsl5VNpyqMZhIR4yEuswgcLUtjbqsJ0tZ/p\n6tU+k3w0q7AokZLIaD/VgzDU2oI/lkUzbLJelXRA33AjmIHoNBWjozmiBKcUwJ6jn+UFsnomw5M/\n+wW+ZBJt5smzamiIk4cPX1e9xLV9fdz73IsoCwLVI08+Tv/WLc77/QNz66AWIoWgctgJZD3pNA/+\n6jeEJyac9WRSMtzcxBtPfaPg9OPqgUEe+tUzCCnRTJPtx46zLxLhj9//HqbHs2bn6uKy1ix0SDHS\nKYltSxRlY91jrwVSSvouZUmlbOTMLWpq0uK9hx68nJ3NuRkJibCXWGSRmzWFaI2f6Cq1vxRqCTdX\njPRTPaQx3NSEPz7jZp9K2r/x3BycnCKyqIMZHDfvPvpZXoDqSad58mc/x5tMzbm5emiI47feyvE7\nbrtq7b7W1PX0cu8Lv0UscPPbX3+SgY525/3+fvQCVR1m3TxVXY0nleLhXz1DcHJqzs1DLc28+c2v\nF3RzTX8/D/76WYS00UyL7ceOE62s4F+f/t6G7VTZuCH4JkfXl3cj21i3u2tHPGaTTOY+gEgJo0Mm\nlpl7811qFLa6P0bFSBJv2sKTsYiMJanrmWbJp5s1IhXQwS4wRCAlrV3HMTUPTecnqRqMExlNUNMf\no747iiiS+GK94smksYv0GnpT+Qm4dn7+Jb7UvCgBdMPkxo8+Lrj9ZkTPZHjgmefwpdN4stm5/+55\n8XeUxeIARCsrMQuMlEogHnbKRd32ymtUjI6iGwYew0AzTer6+jjw3vv5B5WSu3/3EvrMduA80IQm\nJrjhk0/X7FxdXK4Gblmc1SU2bZFKzgex4Kj0ltffRM9klr8jKalZ4GZvxiIymqSu99q5OV3Czc3n\nT2AsdnPfjJsLTEdez3jSK3Pzrs8+x1vAzfs+/BA9nV6zdq4n9HSa+599Hu9iNz//Ir5EAoCpqqqC\nbgaIzbj5jpdfITw2nuPm+t5e9n7wUf6HpOTu38662bn2umEQGR9n96dH1+ZErwJuILtOqajSluyU\n8/sVFHc0dlnEolaOKGcRwulhh2UUV5eSyoEY/riRm7xBgidjzpWeudokwj5sRSAWCtM0aD5/Eqkq\naBkPWtZCkc7aHEWCN20QGUtek/ZeLlNVVUiRf8syVZVLBaYLN168OBdILcRW1eummHvruc7Cb0jJ\nllOnAejadyO2quasYrAUQTIYZLilGWHbtJ7rzJl6DMz05p7I23V5dJqyGRHnbG9Zc8d0cdmoVFYv\nw80BxR2NXSaxqFUwzrQVhfqe3uXtZMbNZYXcnDbxXSM3xyM+pEJuMGsatHQex/LoeFMampHv5vAG\nc/NkbeGprKaqcmlH/pKfpgvdc4HUQmxVpWp4ZNXbtx5pP3uu4OtCSjpOnwGgc/9eZ03zAixFIR4O\nMdrUiGKaNHddKOjmnV8ey9t3aHISbzq/Y0EzLbZuYDe7gew6QEpJMmExPmrMrI2V+MoU6pt0FDV/\nlomigKZDfbM7RS+btZmcMIlOOtetGKWm/wvFGYX93/97fcljRYYTlE9nC46CKxK8yWsjS9W0kaqK\nnP2iSBvdNKgavshr3/4m3rSVfwGEQnByY41KSlXlg4cfxNQ07JlzNTWNdMDPqcOH8rZPBkNz2y1E\nSEkqcH1kU/RkMjnTlmZRLQvPjNDSgQAv/+l3maypwVIULEVhsK2Nl//0uyAEwraddV4FUAt1FCii\n6AiIpbhrZF02DkXd3KijKPluFgpouqChyXXz8t1cPOA39eWtfqscTlAeMwq6WUgnIeK1QDVtbFWb\n/6LYNh4jS8VoD68/9U08Rdwc2mButlWVDx96IM/NqfJyTh86mLd9IhQsWOpIWDapQGCNW7s+8KQz\nKAUW26uWhSfljEqnyst55U++y2R19ZybB9rbePl7jpuVUm62CrlZRRT5Kdob2M3uGtlrzOK1m0LA\n8JBBXb1GMKyxbadKNiMRCpiGJJOW6B5BoFxBbLB1FKvN2IjBxNj8j3V40KCxxUN5MP8HGa5QmS7Q\n85v1e/iv31lGQidbEiqQtn/ubQGWem36haoG4059vNnRSqGQ9ZXx7uPfBpzAu9C9q1AQst65tGsn\n0xUV7D76GYHpGP1b2uncv69gTbvThw7Sdu4cyoLztIUgFokwuUQyhM3CYFtrwfVWpq4z0DGfKXqi\nro7f/fmPZqaIqTnJwWxNY7y+jurBoZzvvy0E/Qv2MUsyFGK6spLI6GhOT6mpaZzbv3c1TsvFZc1Z\nvHZTCBgZMqit1wmGVbaFXTcXo5Cbm1o8BAq4ueYX9zHx1Jt5s2dsRWGopWXJYwlbUl7CzVKwJrXb\nl0OemxWFTJmfd5/4NoqVQSALu7lAzoL1zsU9u4lWVrLrs88ITMfp39JB5/69Bd186uZDtHSdz3Gz\npQiiVVVEq6uuZrOvGQPtbc7SnEUdzY6b2+f+Pt5Qz2//7Z8VdLPp8TBZW0Pl8Eiem/u2bMk7ZjwS\nJhYOOwkzF7xuzJT12ai4gew1IhG3iE5aZDI22aycizRmA63hQZORIZPKao3qWueL6/GA//rorFqS\nVNJmYszMC0wHerNs2+nLm3Jd5lepqtEYH3VunEJAWvfw2te/tax6XJq5dKn0RPjqFwgXtsSbMvMk\nLhD4YwYZf5ryqWlikeqcnl9hWUTGB4DSo9Drkcm6Wt5/7JEltxtvqOe9Rx7i9ldfA+nU1Z2sqebN\nb349L7ir6+nl0FtHqBgbIxks54s7bufiDXvW6hSuGlM1NVzYs5uO02fmEjoZus5gWyvDLc1z2ymm\nSdu5TiKjY0SrKrm0c0dO4of3H3mIR//5lyimhWZZGJqG6dH59L6vFjzuW19/kkf++ZdopoFi20gE\nQ60tnD14YG1P2MXlCnBGYG2mJi0yGQsjs/A958/hQYORIYOqGo2qGtfNi0klrYJu7u/Nsm2XL2cE\n9ieP/xjehb23Jdn3wYdIRUEKgRSC17/z1LKynKvGMtwcWl9uDsSyGN4kgWiSeLhykZvNGTc3XNX2\nrgYT9XW8/9ijS2431tjABw89wK2vvQE4bp6orXHcvIj6Sz0ceusIkfFxEsEgX9x5B927d6162682\nk3W1XNy1g/aznTlu7u9oZ7SpcW47xTRpO9tJZGyMaHUV3Tt35CRxeu+Rh3nkX36FYs272fB4OHrP\n3QWP+9Y3nuSRf/kVqmmh2BYSwWB7G+cObNxAVshrtAj+cthVFpE/3XbntW7GFTM6lGVyovC6kMUI\nAQ1NHoLhjTvsvxYMD2SZmsyflqEoUNeoEwoX7qMxDcnfb78P0+PcMApldSuEsCUt5yYK9vpKYKQ5\nSLr8GkwnsyWtRdplCRjqCPG1n/6cY7c/jKVq2JqOamTxZFLo2ZHrIkOgYllExsbI+HwkZhIkLKS2\nt48Hn3k2Z0TA1FQ+ueernLspf1rUhkNKWrrOs+3YCRTb4sINe+jetXMu3b4vkeDxX/wz3lQK3TAw\ndB3D4+GlHz5NMhSa240vkWD7l8eoGBtntKGerr03YviKlxhRLIvm8xfwx+OMNjQw3rA+O03e/m+P\nH5VS3nyt27GR2SxuHhnKMrUSNzd7CIZcNy9kaCBLtICbhTLzLDNzvRbnoyiLx2m41IPh8azMzZZN\nS+dkUTcPNwfJXAM3l3pmsBQYagvytb//R8fNioqt66iGgSedQDPHOXH7LVe9zVcbxTSJjI+T8ZWR\nCIfy3q/r6eWB3zy3yM0aH99/L50beARxDilp7exi2/ETCFty/kbHzbMd7WXxOI/94p/xptNzbs56\nvfzhh0+TDM7XIPbFE+w4dozw2DijjQ2c33tjwZHwWRTTpPnCRfzxOCONjUzU1635qV4Oy3WzOyJ7\nlclmbSbGixShK4CUMDFubPpAVkrJxJjJ5LiJbYOvTKG2XsdXVnhKULHnDClLvAn8l2/87YrbJmyJ\nP5Yh61HwZO0cMUkgVaZdmyAWQBHYikCxZV67TN2ZhnLy8EEOvfkCk3UtpP3l+ONTlE+N8tq3r4+C\n2raqMlFX/EZ905F38qa1aabFra+/yUB7O/HKirVu4toiBL3btxWt0Xf49Tcpi8fmatXphoFqmtz2\nymu88e2n5rZLBwIcv+P2gvtQDIOmi920dHWBEFzYs4eh1hZ6dlx/NXtdNibZjM3kit1sbvpAVkrJ\n+KjJ1MQCNzfoRWuwl+oEkFJyx/H/xD3/OX8NaKq8nAsrnAXjuDmLoSvoRr6bkwHtmgSxAFIRyJl1\nPQXd7PVw+tB+Dr39PJM1M26OTVE+PXb9uFnTSrr50NtHCrjZcdNAe1vBjukNhRD07Nhe1JO3vvY6\n/nh8rqzRrJtvefV13nrqG3PbpcsDHCvh5uaL3bR0dmErChdu2MPwJnOzG8heJWZHvmcz5K6EAmu2\nNwS2LYnHLLIZia5DMKSiFFlHOjJoEJ2a7wlPJW16LmYIBBXSSRuhCCIV6kw2Z0EwpDI9VbjnPFBe\n+MFiqbI6hdCylpMOX0qEzI+RUwGN0eb8nsSrhbDsvCAWHHHOToc+e+gmotXV7PnkU6oHnREyS1V5\n/J9+OTedJ32dJFgoRGRsvODrQkoe/tWvefbf/9WGq+u3Elq7zucUXAenFl3TxW7mFu4XQc9kuP3l\nV2k7ey4n6UT7mXN07tvLJ/ffu1bNdnFZFa7MzRtnRttCbFsSn7bIZiW6LgiGFZQiGRGHB4yc/BKp\npE3PBcfNqaSNssjNobBaOBOxhP/nqb/ivxYIYi8HLWNRf2nezTOHmCNVrjHWdO3crFg2YlEQC7lu\nPn34EFM11ez59Cg1g+cpiyccN//jvzBeV8ub3/w6Gf/1kZiwEKXc/NC//Jrn//ovN7Wbm89fyKvN\nq0hJy4WLy3Pzv75C+7nOud4lCXScOcPZA/s5eu89a9jyq4sbyK4x6ZTN8GCWdEoiBPjKVv6j85c7\ngjGyNuNjJqmEjaYLqmo0/IFr0xucStqMDhukUzaqJqisVolUaHNJLrJZR3YLk7INDZhU16hU1eb2\nkFqmzAliZ5ES4tOzDxeSsRGTVMqmqcWLP6AQCucmcBICaus11EV1/i4ngJ2lrieaEygKwAbiYQ+T\ndYHS6ZCvBiVuZHLBW0NtrdiqwoO/fhYQTNY2kygP449Huef5F/nXHzy99m1dp8TDYbwj+Sn/BU59\nvLrePoZbmqnv6aG+p5d0IMDFXTvnHjDKYnF2fv4FVcMjjNXXcfbgAdLlG6djQBb7Di3jAeG+Z1+g\nZmAgT7a6YbDjy2N07tvLVE31ajTTxWVVyXfzyvcRmHFzNmszMWqSTNroHkFV9bV188hQlkxaomqC\nqmqV8EI3Z5xO4lw3Q02tSmVNrptNUxZMkrjQzdaMm9MpSWOLB39AIRhSiU3nuvmdRx4mW2IpwkpZ\n7GZw3ByLeJiqK7/mAU6pLo6F99zB9jZsReH+3zwHCCbqWkgGQo6bX/gtLz/9vTVv63olHg5RUSCY\nFUBZMknNwACjjY00XLpEXW8fqUCA7t27yJQ5P2Z/LMbOz76gcnSUsfp6zh7cv6E67fOHKGZeX8Z3\n+/7fPOckaFzw4xWAYpjs+vxLOvftZbpqcyTWcgPZNcTI2vR0Z+bql0oJqeQSPbiLUsyqKlTV6GSz\nNpfOZ+YSnGWzklQyS12jTjhydf8Z02mb3u7MnKRMQzI6ZGKZzCWmGurLUiCzOGOjFrrXzFnDms06\nDxJLrUuSEhIxm0zGxutVnHOvUIlPWwjF6Qn2eHMDyysJYsums6hm/q1EzY+niQAAIABJREFUAfwJ\ng8lrHcTiTF9K+3V8ydzSA7bITz6155OjGJqHz+96HFPzzK3J0YwM4bHx6yZb4GK+uPMO7n3+xbxg\nDACh4I/FeOCZZ6ntH0AzDCxN46a3jnDs9ltJBwIcfv1NVMtCtW0aurvZc/QzXvrh0xtGEr1b2mk/\n15Vz/pai0Ltta8mHwfD4ONVDQ3k17GYRtk3ThQtuIOuy7sgWdPMKdiBAVaCqWiebsbl0Yd7NRlaS\nSmSpb9QJXW03p/LdPDJkYlnMJaYa7C/s5tERC91r5UyVzmbtZbvZmX1l4/E6pQPDFSrxmEXbf/wK\n/6VvG7GK1VuiURZNo1qF3RyIm0zVX/tROqkqpMs0fIsSPtkC4ovcfMPHn2BqHj6/+wksTcPSPKhG\nFs3IEJyYJLbRl7dcJp/f9RXueeF3Bd0sFQV/LM5Dv3qG6sGhOTcfeusIx+64jXRZGYffeBPVsmfc\nfIk9nx7l9z/6wYa5nv0d7bQsGpW1FIVL27eVdHNkdJTK4ZGibkZKmi90c2qDPKMshRvIriGTE+ac\nKJdDoFyhqkZjYszEMCT+gEJllY6mCwb6jMVZupHSKQcQCqtXNd3/+IhRsId2YszJsoyEVKq4+cZH\ncwNZ3SOWlVwDAOHI2ut1ShyU+VXK/Pk931cSwM4SiBafAlWsFte1YLyhnLqeKOqCzMpZn0a0OndK\nkj8ep2vfbWS9ZXMjyZauY6kq5ZMm0XUabyiWjZ62sHQF07P6oxx927bSeeMN7Dh+Iv/ByLIITMeo\n7etHn1mrM7tm56Z33kMK4Uxtm9lelRIlm+Wu3/+Rl/7sB6ve1tWm7fQZWrsuIOR8GQhbESRCQT56\n8IGSny2fijoZv4uUcbIVBdPj1tN0WX9Mjq/MzeVBhYpqjckZNwfKFSqqdDRNMNBb3M3Bq+zmsSJu\nHh8zqajSkBLSpdw8YuQEsh5dWZmb004gK4TAH1D5P7/7d5AAVjluKI8WL7ez/AavPeON5dRdmka1\n5r8gmTKNaFXu8L8/nuDc/jvIenwL3OzBUlVCEwaxyqva7GWjmDZ6Zu3c3Lt9O+f37GbbyVMF3Rya\nmKRmYHDOyXNuPvJuvpttGyWb5c6X/sAff/j9VW/ratNx8hRNF7tz3GwpColwiI8fuK/kZ4NT0blk\njoWQisBYUJVgo+MGsmtIJl3ihrpo5FUIqKjUSCVtNE0QDKuUB9W5VPWpROEkFNIGw5B4PFdPluli\n5yWcHuDFU3sXYxq5n9c0kTcVqRS6Xnz/Bx41eUz5j0vvpAiKaaNnLQxdQbXy17fATIIn//r56Vi6\nwsCWCL6EgWbYZH0qWZ+W12PX19FOtLI5fzq0oqDa1350OQ8piYwmCU6m534vmTKN0aYgcpVr9n7y\nwH3U9/URiE6jzTyVGrpG14030nL+/FwQuxABBYuRC6BqeBhh2yVlcq3xpNPc+ceX0RYPzwiFdx9/\nlHSg9NqsyZrqnDqAixHApR07VqGlLi6rSyk3Lx6BFAIilRrpBW4OBlXEjJuTycJutm1nam4pX602\nmXSxERinLaqyhJsXrfnVdEF50BlZXZ6b5+93q9GZvJBcNxdujARSgfXzgG7pKgNbl+fmyZrGAm5W\nUZaff+zqISWRkSShqfRcQqu1cvPHDz5AbX8/genYAjfrnNu/l9aurrxkUFDazTWDQ0uuL73WeJNJ\n7nj5lTw3CyF454nHllw3PVFbg2IX/+IICT073WRPLsvA6xMkE4Xfi1Q4yYpsGzweQaRKY6Avi5TO\nbywatdA0k7YtXlRVoGoiTzKzqOryfpCWKbGlJJ2SRCdNhIBQRKM8uLIC7h6PyAtGAcciwkma4fEI\npz5uAQplIq5v0lE15kof6B6BYeRnV9I1QZm/8I3yisQpJVWDCQKxTM4xZ04pj6R//cgSACGWzJx8\n5qaDNHYnCq7dWT992PMEohmCk2mUBZmovUmT6sH4qifYsnSdl370A3Yf/Yz2M2cxPF7O3HSAi7t3\n8cg///Ky9lkxMrpmae096TQdp89QFo8z0tzMQHvbisXcfP4CdoHPCNum/fRZRpuaEJaFalqY3vzv\nVjIUonvXTtrPnpt7mJj9HpmayjtPPr5kMOzici3w+UTRqcThiJN7wbbB4xVUVGoM9C5w85TFuMek\ntcNxs6aKokmflgocZzFNiZSSVNJmesq6bDfrHgWzRM3z2TW8xgrc3NCkMzIM0UnHzcXcrusCX5ng\n9p/u495nV7EUk5RUDcYJxLLLcnNqA7r59M03UX9pJXPbry3lU2mCU2knmdWsm1MmVUPxVU+wZXp0\nXvqzH7Ln06O0nf3/2bvT4Miu80zQ73eX3DfsQO0LtbC40yQlklooUaREUbbU8tLTCu8dIU+zZ9wd\nlsNtUzHd0RM9PzqsaPeP7oiRY8LRM2N7JNm0LMqyNlqUbVmiFpIqksW1WGSxFiyFLfflLmd+3ASQ\nibyZSACZuJnA+0SUqEokEgcJVL75nXvOd16FFQ7jpdtvw5vvfAc++qd/vqPHHLl2DSuTkz0d55pQ\nuYyTL72MSLGEhaNHMHv82I6yWYkGYFMh67o48fKrWJqZ8bLZcXxXPRXTabz1trfh2GvnfbLZwN9/\n/GfX9xHvByxk+2hkzER2xWladiTiLSGemglhasbrmCgieON8pel+a1dal65ZmJwOYWzCxGy90G18\nrERSg6YB5bILu6YQjgpCoeYwqtVczF6u+S4pKhZqSKZ0zBzpfgng2ISBcql1LOGI4M3z1S331ExM\ntQaNiGByOoSJKbX+93LJwewVC7blLa2IxTTMHA61BHsvgjO9WEYsX+1qybACoLdf2DSwarEYSvEq\noiWn6YVVASglB28JaGqtiG2gAYgWLYjj9nzm1wqH8dw9d7e0sX/t5pswOr/ge1W2HVekb1djx2dn\n8cAX/xLiujBsG7b5DJamJvHtX/qFrs9eXOP7W6wUNMfB3d/4Fk6dexGaUsinU3jqwQcwd/xY012/\n/9CHsTIxjuufeRahag0rY2O4cMP1uHDDGS4rpoE1MmYgu9qazYmkjqlDIUwd2sjmC69tymbl7YNd\ny+bRCQNzVyyfbNYhmtd8ybZ2ls2ptI7pw93/OxqfNHD54s6zedwvmzXB1EwIk9Mb2VwqOpi7YnkF\nOOrZfCSEz37sXwOPdT3crmSulRDL17aRzcOnGo+jEq8h4pPNxVT780CD4pvNCogVLIijoLq8uNIt\nKxzG2Xvvwdl772m6/bWbbkTm2uK2s9nV+vNbMnHlCh740mMQpaDbNuyfmFicmcYTv/jz3jacLnVa\nNi+Og3u+/g2cevFliFLIp9P4wYcfwPyxo013/d7DD+GGH/0Y73z2pzBqFlbHx/D6DWfwxpkzsEMD\nNtmzSyxk+8g0BcdOhrEwZ6FUdKFpQHpEX2+IBHihYNvK/+qlAvJZB5PT3tE1tQkDS9fs9TCKJzSM\nT5m4+HrV+/z6Eo9EUsfMERMiAuUqr0Nhm3/nSgH5nIORstv2zNbNYnEdh46GsDBrwbK8Rk2JlIZ8\n1l1/zI3vz2tY5Z0/J5iYDrU9f27t+VgTjek4eZ0Gx/YOU/e78vzow4/0JDiTPi/M7QfpLaMJWmJ1\nFafOvYhQpYrL153C3LGtZ/4WD6cxfTEL3XEhrtfZ2DE1rwPzgNEc/ysLCoDmKjh79I7lwg1ncPT8\n6zj05pvQbadp30278ZUTCaz0o8mRUnj/X38VoVpt/SbTsjA+N493/PQsXrrjZ7p+qCunTkJ8Ngo6\nhoHMotfIaW1pU3plFR987Mv421/5FFYnJjaGo2l48a478eJdd+7imyLaW2ZIw7GTYczPWvUjZIDM\nqI7xiU3ZbCnf1Udebrrr2ewVtpuz2WjJ5mRKx/RhL5tdV7V09t/8NXJZB5kxt2NmNorFvexfmLNh\nWwqieZPdW2VzNCaYmAoh3GU2x+I6Tr5tI5vf++Lv+p4N2wvJ1eHL5uTKCk6dewlmrYbLp09h7tjR\nrrJ56qLX60KUl822qWN1cvBWtWgdlnZ72bw3E/3nb74JRy5cwMzFS9Atr+HlVtlcSiaRHevDpmOl\n8P6vfBWmZa3fZFoWJq7O4m1nn8Mrt9/W9UNdPnUK73KfaLndNQyMz81jbH4e+no2r+D+v/wrfO1X\nf7mpYafSNLzw7nfhhXe/axff1HAI/l/8PheOaDh6ovOMWsd/8g0vfmMT5vqRM7rudem9ermGarX+\nolL/TyHvYGVJMDpuolBwt2xqoRRQLDhdF7KAVyzHE9r6VoPZK5b/HQWYORLa8VEEIgKjzeRRL/fg\naG53SekKUE6EYEWC/adz4qWXce/XvwlxXWiui7c/9zyunjiO737i5zoGpmt4+2mjBcvbbxTSUU6Y\nA7lfpBI3Ec/WWv59uJrAMfZu76nSNHz3n30c47OzmH7zLbztuecRLRZh2vb60lwFACJwNA3K0PGd\nT36iL89penkZ4UrrG0bDtnHd8+e2VchWo1H84MEHcPe3nvCuwrouXF3HhTPX4/S5F1v25+iOgxt/\n+GN872Mf3fX3QRS0cMQrZjvq8E94/Ug2keZsNrxsvvJWazbncw4iUcHImIlC3sFWsaMUUCo4XRey\nAJBMGUgk9Y1svtwhm4+GEPNpltiNtWx+9OFHgD4VsVAK0uH9S+PyYle8lUVWONhsPvXCOdz9rScg\nrgtxXbz97HO4fPoU/uFnH+6YCc56Ntdg1lxYYd3b7zuA2VyOm4jnfLJZ1+Bs0SOll5Sm4cl/9gkv\nmy++hbc/9zwixZJ/NusalG7gyT5lc2ZxEaFqreX2tWzeTiFbicfw1AP3491P/J23fLuezedvPIPr\nXjjnm803/Pgn+P5DH9719zGMWMgGSCmF1WUbqyv+U7Ii3n6dNdkVG/Oz1vor9/ysf0Ap5e01HR03\nYdVUS0dFv6+zdrXTdRWsmoJhypZ7b0Vk/fXAbTNDJ8CWX3+7elXAiquQXiwhnqu23W8DeC+Eti5w\nDQ2FTBiFTO/OwtsJo1rDvV//ZlOTA9OycOjNizh6/jwuvW2LTfwiKCdD6NNbj55ZHY8hmrcgroIG\n7+egBFieDuaMwMWZGSzOzODFu+7AiZdfwbFXXkM1GsGrt94CV9cwdekyKrEYLl13Gk6fOgIqSNsN\nzarL/XiNLtx4A+aPHcXxl1+F7ti4fPo0zFoVJ195FZsvFWlKIb20vJNhEw2Vxmz2++cm4q2uWrO6\nbGFhzt7I5qvts3ll2cHImAnLUltOMosA2i6z2emQzWqXjYR63dBpjTgK6SUvm7di6QLX1JDPRFqO\nnNtrZrWKu7/1RFM2a5aFI69fwJHXL+Dydac7P4AIysnwcGRzoTWbl6bje5/NIlg8dAiLhw7hxTvv\nwMmXX8GxV19DJRbDK7feAiWCqcveGbOXrju97e032xlHO92c+7rZ6zffhLnjx3HilVegOS4uXXca\nkVIJJ196BYbtk80+5+0eFCxkAzR7xUKhTadeESAa07zjbODtpZmfre/D6eLioVuf6o1EBaJhy8BM\nJDUsLlhYXrQ3lkGldUzPmOvdGTtJpnWUiq5v6/92zZl2omfBqRSmLmZh1pz1ZUuditm5k2m4xmDs\nvpm+dAmuz/5L07Jw6sWXty5kh4Rj6rh6KoPUchnhkgU7pCM3Gg38arir67hwwxlcuOFM0+39ah7R\nKDc6gko8DiObbfpdtQwDr910444eUwG4cvokciMjUJqGcKnk243Y0TQsHpre2cCJhsjsZattp971\nbB6rZ3PVxcKc3XU2q3o2R6Pa1tkszdm8tnQ5mdYxfcjsqhFUMq2jXOptNt/z/Gf6tpQYSmH6rSyM\nLrN59lSm5/0Sdmrm4ltts/nESy9vXcgOCSekY/ZUBsnlMiIlC9agZLNh4PUbb8DrN97QdPvKVP+z\neXVsDNVopGlpMeCdfvDazTvLZghw+fQpZEdHARFEikXfLs2OpuHaoZmdfY19gIVsQGpV17eIXWsS\nMTJmeEVoPahyq921v1+TSHpFVzSmIRLRUCm3BploXjgcOhpCoeBgebE5jPNZB5oGTM1s3WwildKR\nXbZRqaj1ryMCTEwbXXdV7qTXnRAjRaupiAU2TkTaPFrb1AamiAXgG5SAN3ZnGw0FhoFraFidHLz9\nu4ERwZOf+Dl8+Atfgua60BwHrq5j/shhvHrLzdt6qFg+j/v++nGMLFyD0jTYpoF/+uhDuHLqJF67\n+SZc9/wL6000XHh7Z1/gXlja56oV17eI9XpBeNkcbdiGk121t5XN8YZsDocF1YbMXLP2En/4WAj5\n3EY2q51kc1pHdsVu+joiwOS0sX61dzv6upQYXjM/o8tstkL6wBSxQPtsdoGBeg/RCw6zuZkInvzE\nx/HgF/+iKZvnjh3F+Ztv2tZDxbM53PfXX0FmaQlKNNimie89/BCunjyB8zee8fZfN2azaeDFO7vf\nVrTfsJANSLnstpwlC2wE1eaZUtVpM03D43hLkbDeUEpEcOR4CMuLNrKrDqAUEikNsbh3Rm0spkE0\nwYXX/A9Sz644mJxSW16VFU1w9GQY+ayDfM7bw5sZNba177adXjV0ahSq2G27ILpA03KZxUOJ3n7x\nXdBsG9MX34JZa92LYZsmzu/wqhwNj5WpSfzlv/otHHvttfrxO4dx7dCh7S3pUgoPfuFLSK5moSkF\nOA5My8J9f/04vvrrv4IffeiDyI9kcOYnTyNUqWL+yGE8/YH3o5hO9+8bIxoAlXKbJnP1PafR6OZs\n7vBgm7JZ35TNR0+EsXTNRi67kc3xuA5Nl/oVW8HslQ7ZPK22vCqraYJjJ8LI5RwUct4e3szIzrK5\nX0uJG20nm5dmBqeQ0i2rbTY79TPJaX9bnp7CX/6rT+PYq68hWixi/ugRLM7MbDubP/yFLyGey3nZ\njHo2f/krePw3fw0/fOBDyI2M4szTT8Os1jB/9Ah+ct/7UUr19tijYcJCNiBGhw3xps8kayKlY2XZ\nf5b48PEQinkHtZpCLKYhPdJ8FVTTBOOTZlO35M3anYOn4O1x7WbSU0SQyhhIZXrza9XP5UuOqUMJ\nWgJTCVBOmBDlzfbmRyJwzMGZSb3/sS9j8sqV9ZnpteE7uoaXb7u15XgU2p/skNmytHk7Jq5cRaxQ\nrAflBnEdvOPZs/jx/R/AS3f8zLaaRxHtB4YpvpPMEO8kgs0SKd3bS+uTzUeOh1DYIpsnpkzfI+nW\ntNvjqpRXREsX8SSaIJ0xkN5hNvf8bNgObENrm82lhAltELNZKXzoL/8K41dnfbJZx0s/czsWjh4J\nanS0h+xQCBc2LW3ejqlLlxEul1qyWXNdvP2nZ/HMfe/Hi3fdgRfvumO3Q903WMgGJBbXoOsCe9OV\nVhEgM9L6Y4lENSTTOvJZp2l50MiYgXhcR3yHXYEbH79UbJ1aNnTvCu9e6/fypVIyhJEFgXJUU/Ao\nTbA0k9xR45x+G52fx8SVq00b/QXe/ogX3nUXzr7n3uAGR0MlViz6NqDQXYV4NhfAiIgGQyyuQdcA\ne1McCoC0TzZHYxoSKb1pq5AIMDpuIBbXd9yxf/3x22Wz6fW/6Ld+rIjqpJQKY+RayTeblwc0m8fm\n5jE2N9/UTVbgFbHP3f0uPL/pbHKidmKFAvx2hOuuiwSz2VcgmwtE5A9F5GUReU5EviwimSDGESQR\nwbETofo+WC/4DMObwTVDrT8WEcH0IROHj4WQzuhIj+g4eiLUcSZ3OyamzZbVDyLA5Ex3DSV6JfLk\nJ/dk+ZLSBHPH06hFdKxtC65FdMwdTw9kUALAyLVF3yUquusiuZoNYEQ0rBZnpqH5HGBpGQZmTxwP\nYEQ0CJjN9Ww+GUY40pDNprdFx++KrIhg5vDmbA53XAG1HRNT/tk8tQfZvBdZvJnSBHPHNmezMdDZ\nPLqwAL+N0rrjIJllNlP3rh065J/NJrO5naCuyH4bwB8opWwR+c8A/gDAvwtoLIExQxqOn4rAthRc\npWCa0jGYRATxhI54oveXSCMRDcdPh7G0YKNSdmGGBGMTxq5nk7fj0YcfAT63Z18Omqu8ZhEAqlET\nubEo3D08n3S78hn//Ym2oWO14SBsoq0UUymcv+lGnD53DqblNY1wdB3lRLyl4yMdKMxmeNl84vSA\nZHNUw/FT3l7aStlFKOxlc3SH5792Yy+XEvtpzOZKzER+LAp3gJo6bZYbGfGdZLYNA6tj4wGMiIZV\nIZPGhRvO4ORLL61ns63rKCUSuHDm+oBHN5gCKWSVUt9q+OtTAH4hiHEMCsMUdDx5fY+EwxoOHd26\nC2KvRZ78JH7nc3t7rEcsV8XYbME7bBpAqOogkavi6snMwBazC4cPI59JI720DL1+OK8C4Go6zt+0\nva54vpTC6RfO4cYf/QThchlzx47i2fe+B/mRwb4oY1Zt6LZCNTJYHSwH3Q8fuB/XDs3g+meehVmt\n4c13vA0v3nUn7FB/zsClwcdsbjYw2RzZu2ze66XEm8WyFYzNFVuyefbE4Gbz/NEjKKZSSK6srGez\nC29y8PWbejAxqBSue/4F3PCjnyBcqWD2+DE8+973oNBmcntQMJt35gcffgALhw/hnc/+FGathjff\n8Xacu+vOvp1PP+wGYY/sbwL4YtCDoGDs9VVYAIBSGJ0vNrX31xSgHIX0Yhkr04PTCbGJCL71P/0S\n7v7mt3Dk/AWIUliamsL3H3oQlXhs1w9/6z9+D0devwTLjCNaKOH4K6/i0Btv4qu/8asoDmBHPM12\nMXkpB7PmrDdnyY5FkRvf/XNxIIjgwo037KoxBe1rzOYDJoilxE2Uwuh8qSWbxVZILZWxOjW42fyN\nf/FLuPsb38KRC2942Tw9je8/9CCq0eiuH/62v/9HHH7jEqxQAtFiGSdefgWHL7yBx3/z11BKJnvw\nDfSWbrmYvJyD0ZDNq2NR5JnN3RHB6zfdiNd5CkVX+lbIisgTAPwus31WKfWV+n0+C8AG8GcdHufT\nAD4NAFPm7l8QaHAEFZpGzYX4HGckAKLFGlYwoGEJoBqN4ruf+Dg0x4G4bs9m6CLFMsrxI3jxzrcB\nSkFpGg698TJOvPwMbvjhj/GjB+7vydfppcnLeYSqjne9pP7jTC+VYYUNlJN7v7KAaBgwm2mzWx+y\n8VHtt4MeBsyaA/HZayoAYoXa4BayAKqxGL77yU/0PJuj+SJKyWN48Y63A1BwNQ1HLryI46/8FGd+\n/BP85IMf6MnX6aWJKzmYm7I5s1SGFTFQSTCbqbf6VsgqpT7U6eMi8usAPgbgfqXaHyeulPpjAH8M\nAO+MZrZx7DgNqqBnfV1d2i4Wc3dwQHwQXF33DiXskfErBVSiCaDhQPerJ96B1Ooipi5f6dnX6RW9\n5sCs2i0/R00BqZUyC1miNpjN1CjoPG7kdmjm5AzosuLNep7NV0uoRONN2Xzl5PVIrSxi6tLlnn2d\nXjFqzkYR20BTQGq5wkKWei6orsUfAfB7AH5OKVUKYgwUjEEITdfQUIkaLccEugLkRg/elQWj5kBz\ntaagBADXMHH55PXIjQzePhzNVW23rmltzkQmos6YzQfLIORxI8fUUYu0y+ZIIGMKklFzIKpTNo8E\nNLL2NMdtm82603qMFNFuBbVH9r8BCAP4dr0T4FNKqf85oLHQHgiioVMni4eSmLych1m11/dw5Eaj\nKB3AK3niKigNEJ+Msc0Qzr3rrr0f1BaskI71H1wDF0ApwYYIRDvEbD4ABmUpsZ9rh5OYvOwtTW3M\n5nIyHPTQ9pzmdMjmUBjn7rpz7we1hVrY2BzLALzJiBKvxlIfBNW1+Logvi4FI5CGTltwDQ1zJ9Iw\nqg4M20Utog90e/9+ssI6lE9RKI6DQjqCxZmZYAbWiSZYnoxidK6Etb6iCt7/yR/AmXuiXmA273+D\ndhV2My+bMzCqNgxbHehsrkX8J2zFsZHPRLE8PRXIuDrSBMuTMYzNews6GkefHzl4kxHUf4PQtZj2\nqS9+/lM4+/hgH91ih3XY4b07K3cgiWBpOo7xhuOIFAArYmL2xOCegae5AASQekoKvDPppy7l4eiC\nciKEQiYC1WHfFRHRQTHoRWwjO2zAPuh1Tz2bG48KdAVwIiHMnpgIenRtaa6CEqx3n17L5slLebi6\noJQIochsph5hIUt98ejDjwCPBz2K4Raq2AhVbNimjkrM8D1wvVfKqTDmwjoSKxUYloty3Bz4oEkt\nlZuOaQC8Tf9m1UEIQLhkI7lSxuzJkYH+PoiI+m2YitiBphRCFQehqg3L1FHtczaXUmFYjdmcMFFM\nD3Y2p5crvtm8dsqAl80VzJ3MDPT3QcOBhSz1FMOyB1yFycs5hMv2+k2OqWHuWLqvB8JbYQMr04m+\nPX6v6Y5/U6e1WNQAiKWQXCojN8Hz64jo4GEm947UsznUkM22qWGe2dxE6yKbTctFYrnMs2Vp1w7m\nxgPqCwZmb6SXygiXbWgK63+Mmoux2ULQQxso3v6hzgRAcrXS/8EQEQ2QWx+ymck9ll4sIbQpm82a\ni7E5ZnMjq4vtWgIgtcJspt3jFVnaNYZlbyVWW5flCIBo0ap3GO7TUhylEC7bCJcsuLqGUio00E02\nVibjmLyUa9rX6/fMtLtyS0S0HzGT+yORrfpnc8ECXAX0OZsjJQuOoaGYDEENcDYvT8YxeZnZTHuD\nhSztCgOzh5RCqGJ7Z6R2uE/bQ9p2+bUnruQRKVoQBSgBRhaKWDiaQjU2mMfZVGMm5o+nkb5WQqhk\nQWcmEtEBx0zug3ohKR2yubW3cO++9sTlPCKl5myeP5pCLTqg2Rw3MX8s7V3BZjZTn7GQpR0Z5HPo\nhpFRczD5Vg6663phheZyVQGohfW+zcLGc1VEitZGl8H6fyeu5HH5VAaRsg1RCpWYOVAzwbWIgWtH\nUzArNmbezPrexx2c4RIR9Q2L2N4zqg6mLuWgOR2yOaL3baVUYrWCSGlTNisvm6+czCBatoFBzOao\nl82hso3pi8xm6h8WsrRtDMseUwqTl3IwbLclINfa7UMESzP9a/Yj33wiAAAgAElEQVSQWG1dMgV4\nzS2Onl8BpD4eBSxPxVHMDNZZrVZYh2o4imeNAlBIHfQzHIhoP2Mm94lSmLqUgx5gNsdzNd9s1uyN\nbF67FDyI2VwL675LixWAfJrZTLvHQpa6xquw/RGqOi1BucYyBPmRCIrpSF+7Iraztselcc3U6HwR\n1ag5WOfvimB5Ko7RuSIE9TcZAFwdyLErIhHtUyxi+8fb6tMumzXkR8IoZiKB9JIQbFydXTM6X0Q1\nZsIODVA2a4Llab9sFnYspp5gIUtdGfqwrO9xAYBqtL/nvm2X5ijfDTYCwDZ15Mf6/2JfyIS90O5i\nL4soIJGtYHUy3vdxbUcxE4EV1pFarkC3HJQTIRRGgnmTQUTUb0Ofy8DAZ7PyCWcBYIe0PcnmYiq0\nrWyOZyvITgxeNtshHcmVMnTLZTZTT7GQpY7u/pOb8YHH3hP0MHYlXLIwcSUPUV4SKAiuHU6iGh+M\nRgnViOHbJcIVoJQM7ckYiqkwYvlaU7OntfVAm5frCtC5IVWAalETi4cH4+dKRNQP+6KABRApWhi/\nkofUA1BJPZsHpMFgNWqsv29otJfZXMhEEC1YTc2e1mzOZgDQ3D0Z1rZVY+bA/Fxpf2EhS209+vAj\nwGNBj2J3NMfF5KXcptlM71DzK9eNDMSMoNIFKxNRjCyUN5beCGCH9L3b71J/A7F+/I6hoRoxfJs0\nuAKUEnsT4kREtGG/FLGa7WLisk82X8rh8nUjA9G4SOmabzZbIR3F9B5m85HmbK5EdMxczLWOV4Ay\ns5kOGBay5Gu/hGUsV+v4scJI8I0RjJqD1HJ1fXmxAlCOG1g6lOrfmbF+RFpmTXNjUaSWyut7ZV0B\nKnETlQG5mk1EdFDsl1wGgHi+2uFjNRQGoGmRUXWQbslmE4uHkv07M9aPXzaPRpFabs7mcjyESoxv\n6+lg4W88NdlPQQl4S2D9lt+IAnRnANbgtOlYHC3aCJftwAvG7HgMlZiJRLYKcRWKqZA34ztA+5iI\niPazL37+Uzj7eCboYfSU5rTPZs0ZgK0rbToWR4sWwhU78GWy2YkYKnETidUKRHnbg8oJk9lMBw4L\nWVq334pYAKjEDP9jWcSbWQ1au47FooDESjnwQhZo3tsijgvDcmGbGgOTiKjPHn34EeDxoEfRe5WY\niZSUfbO5MgB7KUMV2zs7dtPtooDkSiXwQhZgNhMBLGQJw13Aao6L5HIF0UINrqEhNxpBJb6xR6QW\nMVBOhBAtbJzFtrYEpxYJ/tdfOnQs1gdhVnqNUhidKyKRq3pDFWBlPIbCaDTokRER7Uv7JZsdQ0N+\nUzZXowYqcRORotWczYkQatHgs1lz22ezNgiruda4CmNzRcTza9ns9dwojDCb6WAI/tWCAjXsQTnz\nRhaa43pBWHUQLllYnYghv1ZgiWDxUAKxfA2J1QoAoJCOoJQajOWxtWjwHYu7MTpfRDxXbTpXduRa\nCa6hoZTioeZERL0y7EuJvWxeheao9WyOlCysTDRMftYbDMZzNcSzFQCCQiY8MLk3CKcJdGN0vohY\nvjGbFUYWSnAMHeUBGidRv7CQPaDuef4zuO/3y0EPY1cSK5WNIrZOU0DmWgmFdARKrxeqIiilwgNZ\ncClNsDwVx+h8salpgx3SB6LZBQCIqxDPVlvOsdMUkFoqD+TzSkQ0jPbDUuLkcmWjiK3T6pOfxUxk\no4mhCIrpMIrpwcsQpWtYmYxhZKHUlM172rF4C+IqJOoTzI00BaSXSixk6UBgIXsAPfrwI8CQF7EA\nEGtYLtxIiSBUDb4ZQ7eKmQissIFkvTAvJ0wU05G97VjcQafGG4Y9QEusUA/21QpiuRqULshnImyA\nQURDYZhXSDWKtslmiCA0AI2SulUYiaIWWctmhXIyhEIqvLcdizvQHHftuPcWujWA2bxSQSxfz+aR\nCI8Kop5gIXuARJ78JH7nc9NBD6NnbENDCI5PMwYFRx+MoOlWLWpgKZoIehi+HEO8onpTQavg7XMa\nGK7C1MUszJqz/iYqXLKQH4lgdSIGs+bAFYET0oMdJxFRg/2WzY6hQVVbsxlKwTGCPx92O2pRE0vR\nwSy8HUODEgHU4Gfz9MUsjE3ZnBuNIjse9bJZEzgms5m2b4B+06mfHn34EeBzQY+it/KjUUSLVtOy\nGgVv6Y8d5q92z4hgZSKG0fnieggpeN0lVydigQ6tUTxfaypiAW+JVXK5sn58EBTg6oLCSAT5TATu\nkL2pIqL9ZT9mc240ikjJJ5vDOmxOJPaOCFYmBz+bE7lqUxELrC1/LiO5WmnK5vxIBIWRCFyd2Uzd\n4bv9fW7Ym0Z0Uo2ZWJmMY2ShuN5d0ArruHYkFfTQ9p1iJgLH1JBeLMOwHFQjBrITMViNEwZKQVxA\naQhkKW+75Wxel8mND4ijkF4sI7VUxrXDSVS4vImI9ti+zua4ub6/tDGbF5jNPVfMROAYGtJLZRiW\ni2rUwOp4DHa4YcJgQLMZaD6dQRyFzGIZ6aUyrh1JNnW5JmqHhew+th+aRmylMBJBMR2GWbXh6hpn\ne/uoEg+1DZb4agUj10rQHAVXE2THIl7n6D0MTUfX2u4XarT2cVHAxNU8Ll03OjB7noho/zsY2RxF\nMR1hNu+BSiLUdkI2sVJGZrHckM1R5Ecje5rNtrGDbL5SwKXrRpjNtCVeu9+n9kvTiG4oTVCLmkMZ\nlOmlJRy+8Aai+ULQQ9mxWLaC0fkidEd559+63qxqcrmyp+MojPh3vuwYgwqIlKy+jIeIaDNm83BI\nL9azuTC82RxfrWBkobQpm0tIruxxNrc5gaFziaoQKTObaWu8IrvPHKSQHGZmtYoPPvZljM/Nw9E1\n6LaD1288g6cefGDoOuxmFsu+R/Okl8p7OvNrhXS4ALbzlkkUkFitoBJnZ2Mi6p/91tBpvwpVKvjg\nY1/G2PwCXF2DZjs4f9ON+OED9w9dRqSXOmTzyB5mc1jv6opsI3Hr2RxjNlNnLGT3kQNXxCqvnXsi\nW4UAKKTDe/rivCWlYNZqsE0TSmte/HDv17+Bidk56I4Dw/ZuO3XuJayOj+Pln7k9gMHunN7mCB7N\nVRDlNZ7YC5qrvFVIfkcywT9EBUC0YCGeraI4IOf2EtH+sh8bOnWkFJL1bAaGLJu/9g2Mz85Bd12g\nns2nXziH5ckJvHbrLQEMdueMNkfwdDpSrx80R63vld6sYzbnLcRztYE8Z5gGBwvZfeDAFbAA4LqY\nvphDqKHFf+ZaCbFCDfNHU4EH5tHXzuOuJ76DWLEIV9Pwyq234On3vxdK12HUajhy/oIXlA1M28b1\nTz87dIWsFdIRrjottzu67FkRCwCuJlAiENWalo5Wb/rktoamBiC1XGEhS0Q9d+Dy2XUx82YOZq05\nm6OFGhYGIJuPvfIq7vrOk4gUS3B1DS/fdhuefd97oDQNZrWKw2++6ZvNZ37y9NAVslZIR6jmk82G\ntqc/B1eXtoWsrXlXiTXVLpvLLGSpI+6RHXIHLiQBQClMXWouYgHvhTBUthEp2RBXIZarIrlchlmx\n93R4k5cu431f/RoS+Tw014Vh23j7T8/iXU98BwBgWHbbEAlVq3s51J5YnYzB3fTtuOLdvqdvWkSw\nOhrxHcvSoSRmT4345SgAQHcG6/B4IhpukSc/efDyWSlMvdVcxAJeNofLNsLlYLN5+uJbeO/Xvo54\nvgDddWFaNq5/5lnc+Z0nAQBmrdZ28jVUre3hSHtjpU02r0xE93YgIsiORn3Hsnw4idmT6bbZrDGb\naQu8IjukDlxANoiUbITKPoetw9vzGM1XMX4l712Zq69bKcdDWDyc2JPC6pbv/wCG3RzQpm3j9Avn\n8PR970MlFkUpEUcym2u6jyuCKydP9H18vVaJh3DtSAqZhSLMmgPb1LE6EUU5ufezqPmxKKCJtzfI\nUbBNDSsTMa+jo1JwDYFmtx4eX44P5oH3RDR8DtxS4rpI0UKo0j6bY7kqJi7nm1bNlBIhLB0KLpsN\n28bbnnsBz7zvvSglEqhEY0jk8033cUVw5dTJvo+v1yqJEK4dSSKzUGrI5hjKyb0/1iY3FoXanM2T\nce8kBKWgdAGc1myuxJjN1BkL2SFz60M2Pqr9dtDDCFSkUGvbNEABiOdq3v7MhhujxRoS2Wrb7nm9\nlFxZ9b3d1TVEC0VYY2F8/yMfxv2PfRma40BTCrauww6ZePZ97+n7+PqhEjcxd3IAzkQUQX406h39\no1TzmyMRrEzEMD5b9P4K7/fF1QTZ8cE5PJ6IhtdBnmSOFq2ODX3iuRp0t7lYiRVqqOzRPsh22axE\nECmVUMhk8P2HHsQH/uor0Buy2QqH8NP33NP38fVDJR7C3MkBOI91q2wej2JsvuT9FYALr+v16gSz\nmTpjITtEDnJANnL19lEpANBYxNZpCkis9qmQVareMKgCUcCFd96CUMVBdmIGoUoJx84/j/H5yxBX\noZhKAgDmjh/DV3/tl3Hm6WeQWlrG/JEjeOX221CJ80W7ZzbN8OuWg9GFjaBcezu1MhEdyuMhiGhw\nsCuxNynYibitC0i1euf4vhSy9WxOZCuAAi6881YYlkJ2fBrhShHHXnseYwtXAAClRAIAMHviBL72\nq7+M659+GqnlFcwfO4qXb7sV1RizuWd8snnkWtn7EDYaQC1PxeCYzGbqjIXskGARu6GYCiO9VIZs\nykSF9h3wvDv0p1Pf6HwR8Wx1vc398vQpb2wiqMSTeDE9imOvnsXKVAqOubFMJjc25h23Q3siXT8U\nfv3Q9fp/RxbLXqOnQemoSURD5aAuJd6smA4jtbz9bPZr0NcLo3NFxHMb2bx46HRTNp9Lj+H4y8/i\n2pExuMbG2+Hs+Bie+vCDfRkTtcpcKzWtoltvErZQQjEVZjZTRyxkBxwL2FZOSMfSTAJjs/WDyuvd\n7tb++HEFfZnxNap2UxELAAJpGohrmHjz+tvx1tvHev71qXvtlr2Jq2BYLq/KEtG2MaM32CEdS9Nx\njM0VvcK1y2wupHqfzWbFbipiAf9sfuOGO3CR2RyoSMk/mzVXQbddXpWljljIDjAGZHulVBjlRAjh\nkoV4rop4rrWj4NoMsCtALWwg3+2yYlchnqsiWqzB0XUURsKwwv7/VKJFq7uH1HUYlgtLZ6PwoLi6\nrJ8L2EjQebk6EdFm9zz/Gdz3++WghzFwSukIysmwl83ZKuL5LbI5YqAwsoNsNnTkMxHYYf8iJ1Ky\nfI97aXlIXYNpM5uD5GoagNZjggRbL1cnYiE7gNjQqTtKE1QSIWSuldrepxrSkJ2Me11pu1ieIq7C\n9MUsjJoDTQEK3v6apZkESj6zxm6X4SdKwTUOVlCOzs3jZ/7+HzA2N49yIoGz97wbb17/zsDGkxuN\nYnSu0DRDrwCUY2bXP0ciokcffgRgEdvWejYvFNvepxLWkZ2IobKdbH4zC8NqyObVChZnEij7ZbPW\n/uzSpsdVgHPAXv/HZudw+9//I8bm51FKJnD23ntw8R1vD2w8udEIRueLTdnswmsiqQ7Yz4a2j4Xs\ngOFV2O0Tn+ZOa/KjEZQTXsc+o+pgdL6ASMmGEqCQDmN1Mg7VMOOXWKmsF7FAfUmUAsbmiiglQsCm\n2cFSIoTRLcLSFa+FvHOACtmR+QV85M+/AMO2IQDC1Sru+cY3ESmW8PIdt/t+jm450B0FK6Q3/Uy2\nYtQcpJbKCJdtWGENubEYahED4irvx1J/rGIqBLMaQWql4p0VqLyrAUuHErv+fonoYGBGd09U+2wu\njEa8Y9EAmFUbI3NFRMr1bM6EsTrRnM3JlfJ6EQs0Z/PlZKilGC4lQxidb19IA/VsjpsHapJ5dG4e\nH/7/vtiUzfd+7esIl0p49bZbfT+nN9msIzsWheWXzekwzKqD1GpDNkcNLM4wm2lrLGQHxN1/cjM+\n8NhwHr0StFrMhJmt+gbmWhGr2S5mLmbXi15RQCJbhVlzsHAsvX7/eL55T80GhVDVRi3afKaZ0gUL\nR1KYuJRrCljvMzyVuHngXpBv+94/Qa8H5RrTsnHbP/0TXrntFih9YzmY5rgYv5JHuGyvz6CvTMRQ\nGN360PZYrorxq95eaQFg1hxEC1nYpgaz5h2kXomZWJqJwzF1rE7GkRuLwqw4cEyN+2KJqCvM6O2r\nRU2Ylv9xeaV6NuuWi+mLueZsXq3CqLm4djS1fv9YruabzQKFUMVBLdr8dlbpGhaOds7mctzE0qHk\nrr7HYXP7P/zjehG7xrRt3P4P38Nrt9wMpW0U9ZrjYuJyHqFKQzZPxlAY6SKbs1WMz27O5lr7bJ6q\nZ3OV2Uzbc3CmoQbYow8/woDchexYFEqaL4q6APKZEFzDezFMrlSATbPDmgLCZRtmdWPjpKu1+Seh\n0HYmshozUcx4S5sa7yEAlACLM4kDtzxmbG7e98VFXBexQvMs+fgV7yq5pgDN9X4uI9dKiBQ27a1S\nCuKo9e7TI/OFpiJ27b+aAsyau95gJFKyMH0xt/55rq6hGjcZlETUFWb0zmTHYi2LlVwAuUx4PROT\nK+WWI/M05b1uG9WNfZOqXR8D1X4fZTVmel1v4Z/NSzPJbV1h3A9G5xd8JxZ0x0Gk2LxNa+KyN8Hc\nlM0LJUSKHbJZKYzOFZqK2LX/bpnNBrOZto9XZAPEZhG9YYd0zB1PY2ShiHDZhqsLciNR5Ec3GkiE\nqrb/lVYBzKqz3swpPxJBuGy17KN0DA1WhxfXcMn2X0IlArPmoBY9WIVsIZ1GrNi6rEsUUI1uzObq\nloNwubVjoaaA1HLZW3qmFNJLZaSWKxBXwdEF+UwYiVX/q/BA65sWzXURy9d89zkTEbXDpcQ7Z4d1\nzJ9IIzNfRLhiw9U15EYjyDc0dzKrju+kpxLvKt5aM6d8JoJQubXHgW1qbRs+AUCk3C6bUc/mg/U2\nuJhOIVr2f99ZjW78XHTLQajS+tx52VxBJV7P5sUyUitliAs4hqCQCiPeZoUc4J/N0YKFcjK0m2+L\nDrCD9S94gLBZRG9ZEaNpifBmtbCBSNFqLWYVYDWEYDlhIp+JILlaWb/N1QULR1MdG1LYpoZQ1Wl9\n8VbqQO2NXXP23rvxgS9/BYa9cbXbMgycv/lG2KGN5dmao7zn1eccQd32lh+lF8tILZfXf3aGo5BZ\nqrTcvxNxAcNyd/CdENFBxKXEvVGLGFg43j6brbAOt2i1FLOi0DR5XEqGECqHkVyt1u/graC6diSF\nTrylrH7ZjAOZzT+99x7c95WvtmTzq7fe3HSWrm6rts2y9HqWZq6VkFypbGSzrZBe3kk2t3YsJuoW\nC9k9xquwwciP1Jv8NCwvdgWoRo3mo3VEsDoVR340gnDZhqNrqMaM9SJWXAWtflWwsbDNjUW9c0ob\nu+4JUI2aB/IMtKsnT+D7H3kQd37nuwhVq1AiePWWm/H0B97fdD8rpPsWsQrecrHEchmppXLrmxx0\ndbLCxuMJUOswa09EtObRhx8BHgt6FAdDfiSK5GoVyt2UzTGz+UqrCFanEsiPRredzZFSazZX4iYc\n8+AVsldOn8JTD9yPO777DzBrNbgieOW2W/DM+9/XdD8rrPuGrALg6kBiuYzkcqUn2dzueEOibvC3\nZw/xKmxwXEPD7PEURueLLV2L/TimjlJDASqut+8jnqtBwXvxXZ6MoVRvelCLeg2dxuaL600rynET\nSzMHq5FEozfOXI83rn8nwuUyrHAYru5TSGqClckYRhZK67O6ayEYrjgIVUttlyh1yxVv+Xkl3nAl\n2HahuQq2qXV19AMR7X+caN57jqlh7niquWvxrrM5jlJ9+XI1ZmJpJoHRxmxOhLB0wBowNnr9phvx\n+o03dMxm1Smbyw5Cld5ksxXSUYltlCLMZtouFrJ7hPtsgmeHOy8/7mTsah7RgrXepAAKGJ8vIWu7\nyE54gVtOhXE5GYJuu3A1OXANnnyJoBqLdbxLYSQKO2QgtVyGWbGhOxsz89Jhatc2BLqjgPoKqM2R\np+p/CukwVidigEi9Q3IBkbLlfVwTLE0nuD+H6IDjRHNwrHDn5cedjF/NI9KSzUWsOg5y4142l1Jh\nlJjNzbrOZh2ppQrMah+yORPZyGbbxfjVTdk8k1g/eYKoHRayfcYCdo8p5TUoUN6y4cYZvWi+hvRS\nGbrtohI1kJ2IddUdT7NdxAqtDYkEQHqpgvxIdOMcOpEDuZR4R5RCqOpAs13UogYWjqYwdTELo2y3\n3hXNYegKsHQoCaPmYGyu6BuUrgBzJzNNP+O1Lozr4eoojF/NY+54GlaEL4dEBxFzeg90m80xA9nx\n7rJZt1xECj77awFkFisojETh6szmbduczcdSmH5zFYbTupfVL5sXDydhVreXzZOXcwhVnOZsvsJs\npq3xt6OPGI57K1S2MXE5B01tvLReO5RAJRFCYqXctEQmnq8hVqxh9kSmJTA1x4Vmu7BNHdAEuu22\nvFg3ihVqKGQibT5KfnTLweSlHAzLhRKBphSyHc6NVQLYujfLa4UNrEzGUI2ZSC2X2/5cFg8lYFgO\nzKqDSsyAbivfLoxS75B80M4TJDro2NBpb4TKFiYv5yGud4lOQbC4ls3LZYxca8jmXA2xgoXZE+ku\nstmniVODaL6GIrN5W/yyeXUsirbvgASw6tlcCxtYnYyhFjWRXmyfzdcOJ5uy2bBdmD7NMkV5Rycu\nH+Bl4LQ1FrJ9wH02e09chalLOWju2noX778TV/K4ejKNkWvlpo7FAgAukF4sbRQwrsLYXAHxfG19\nL8jqeAyFkUjnvSDb6WxAALwro2vnya01e0otl1FIhxGqtB6V5AqwOhGDQFCOm+tXwDXH/8lXAoxf\nLawvNev08xOwozHRQcOGTntjI5vrNyjvf7xszjQVscBaNntHrq3tY5V6Nsc2Z3Om83Fq3GG5fZM+\n2Zxe8rLZ9DnG0NGkTTb7Z6oS731Z19lcY0dj6oyFbI9xn00wooUa2rXYS65UfDvjegdybyxjHZ0v\nIpavQRpeXDOLJTimhkK7c0vFO7KHumfUHN/jEDTlnSlYiZuI1DtAK9n42Njcxrm0K5MxFEai3pEM\nPoWvKPifTehzmytAJcafIdFBwdVSeyeWr7Wd7E2ulH3b3AqAcMla//voXAFRn2y2QxoKqTASuTbZ\nHOf+yu0wqg6Mdtlcc1CJmesdoFX956a5qimbl6fiKGYiXjZXy7vP5jizmTpjIdsjkSc/id/53HTQ\nwziwtHpjgZbb4Z1T1m7Wz6633xdXIZ6rtrzoasqbjZw9kYZuuYgWN8JV1a8Sct/N9nhnx8L/fDpX\nYfZYCqGKvd5dOrNpxh4ARhZKqIUNlBIhJFarMCwH2tqvQP1YWr+f+dqXXfvYWlOJ/AiXnxHtd1xK\nvPc0x/V9rRe18cfPejY7CvF6Edv0uMo7Y3zuRBqG7TRNSivxJjsP4vE6u6G5btts1hyFuRMphMs2\nwmUbrqDlajrgXRCwQjpKyTAS2dqustnVBAVmM22BhWwPPPrwI8Dngh7FwdbYvr2RK0A5GYKmFGL5\nWtOLritAdszbl9luiSoA6LYLiODa0RTMio1YvgpAUEyFm8+5o65457m2pqUr3qH3EEEtaqIWNRHP\n+h+uLgqYfisHCFAzNWRHIwhXHLi6wArpSC+V214FkPrXcnUNpYSJ3Hhso1kXEe1LXEocjErM9C2O\nVD2bddubIN6czbm1bHbb96hYy+aFY2mEKjaia9mcDnfVLIqa1cKGb242ZnM1ZqIaM5FY7SKbQxpy\noxGEKg5cQ4Nlaltnswa4mpfN2fHYRrMuojZYyO7CFz//KZx9PBP0MAje0TrFVLjpqqorXnfEStx7\n4QU29r8qEaxOROEYGsIlC9WwDqUJsKmgVah3WKyzIgay7KC3O5pgaSrmdTRUG4WlY2gtV0alw9bV\ntT02oZoLY7WKK6dHoDSvjX9mqf3yfgUgPxJpe04hEe0vXEocHCtioJQMNU0kr23nqMRMVKMmxmYL\niBU2snllwus2HC5ZqEZ0KJGW7UEKqOe6pxYxUGM2744mWJ6Ke2fubpHNnXqDrGdz1YVhV3H59IjX\nnMtyvEK2DRdALhNBltlM2xDov3oR+Qy8a5kTSqnFIMeyXY8+/AjweNCjoEbL03FU4iYS2SrgKhTT\nYRTTYUAEqn5cy7LjemehuS4mLxegOaX1YwDyqRCS2WrT4d9K85YPU2+V0hHYYQPJZe/IhXLcRCET\naTrfL1qoeV2J/Zalbfr/Ur/iXkyH4RoaVsaiyCyVm/ZUrVECLiUm6mCYs7nRrQ/Z+Kj220EP48Dz\nzgOtIbFaBaBQTDVn8+LhJGQtmx0Xk1fWshkApH02jzObe62YicAKG0iurGVzqJ7NzccldZ3NrkKs\nUEMpFYZj6siNRZFqk83QwKXEtG2BFbIichTAgwDeCmoMO8GZ3QEm4h18nmrfyVDpGmxN4cj5LLS1\nw73rM73JbBVL03EkslUYlotq1EB2LMblw31Sixhtj7yJFGsYv5JvWm7WmJktbfrd+jKzuvx4DK7u\nIrVcgeZq3uHs8JY1L08nuK+ZqI1hzebNmNUDZDvZfLExm73/SWarWJ6KI5GrQl/L5i7PmqXtq0UN\nLEXbZHOhhvGr/tnsu/dVNZ8KkB2PwW6XzTPMZtq+IK/I/hGA3wPwlQDHsC0Mxv3B64irfM8sC1Ud\nLBxLBzIu2pBZaG0isbbNym+/lBKgFvECULNt3P3Nb+Pky6/A0XVorovn3nUnXnj3u5uu+BKRr6HL\n5s2Y1cMpWrAgrn82GzUH88zmwPk1eFrLZhetHYmVbGzP0mwb93zjWzjxyqvr2Xz27nfh3F13MZtp\nxwIpZEXk4wCuKKXOigzHSV8Mxv1Db9PhWNB8VY+CY1rtz46zQhpMy23ab1UL6+tH6Nz5ne/ixCuv\nQncc6I73ODf96McopVJ4/aYb+z52omE1jNnciEuJh1u7s0cFWL9yR8HqdK6rHdJgbM7miLFeyL7r\nie/g+KuvNWXzzU/9EMVUGm/ccH3fx077U98KWRF5AoDfeSy0o84AACAASURBVDSfBfAovKVL3TzO\npwF8GgCmzGjPxtctFrD7TyXaocNxgufODQLL1BGutgamqwnmj6eRWiojkasBAArpsNfhUgSa4+C6\nF87BsO2mzzMtGzc99SMWsnTg7Zds3oxZPfyqbc7z5nmig8M2dYR8illXE8wdSyO9XEY85zXuKmTC\nyI162axbFk6dexGG0/y5pmXj5qd+yEKWdqxvhaxS6kN+t4vITQBOAlib8T0C4BkRuUspNefzOH8M\n4I8B4J3RzJ5OyTEY9ycnpCOfCSO52tzh2ArrXot5CtzqRAwTm/bIrh2XpHQN2cm4b2dDo1aDuP6z\n+pFSqV/DJRoa+yGbN2NW7w92SEchHUYiW9204sZgNg+I1YlYyx5ZV4DV8SiUoWF1Mu57IoBZq7V9\nzEix2I+h0gGx50uLlVLPA5hc+7uIvAngjkHqjMhQ3P9WJ+OoxkJIrlYgrkIx6XXmwxAup9uPKokQ\nFmcSGLlWgmG5cHXB6lh0y46GtUgElXgM8Xyh6XYF4NqhmT6OmGi4DUM2+2Fe7y8rU97pA8mVKkQp\nFFMhFNLM5kFRToawNJNApjGbx6Pe+6cOKrEYapEwjGLzhLILYOHI4T6OmPY7HrrVgPtrDhARlJMh\nlDnLO7DKqTDKqbDXVbrbNzEi+OH9H8T7/uZvodt2/Rw8gWMYePq+9/V1vES0d1jA7lMiKCfDKCfb\ndzimYK13oN5BNr/3b7+xvvVnLZufed97+zha2u8CL2SVUieCHgPAUCQaWNucib/09rfh27/087jp\nBz9EamUVizPTOHvPu5EbG+vTAIn2n0HJZj/Ma6IBsM1sfuud78AT8Thu+sFTSK5mce3QDJ67593I\njY72aYB0EAReyAbt7j+5GR947D1BD4OIemjhyBH83S8eCXoYRNRDkSc/id/5nF+fKiIaBvNHj2D+\n6C8EPQzaRw50Ifvow48AjwU9CiIiIurk0YcfAT4X9CiIiGiQHNhClkuTiIiIBht7VxARUTsHrpBl\nAUtERDT4mNdERNSJFvQA9hJDkYiIaPAxr4mIaCsH4oosGzoRERENBxaxRETUjX1fyLKhExER0eBj\nAUtERNuxbwvZe57/DO77/XLQwyAiIqItsIglIqLt2peF7KMPPwKwiCUiIhp4LGKJiGgn9lUhy8PS\niYiIhgMLWCIi2o19U8jysHQiIqLhwCKWiIh2a+gLWe6FJSIiGh4sYomIqBeGupDlXlgiIqLh8MXP\nfwpnH88EPQwiItonhraQ5YwuERHRcHj04UeAx4MeBRER7SdDV8iyoRMREdHw4MQzERH1w1AVslcy\nEyxiiYiIhgAnnomIqJ+GqpAlIiKiwceTBIiIqN+0oAdARERE+weXEhMR0V7gFVkiIiLaNS4lJiKi\nvcRCloiIiHaFS4mJiGivcWkxERER7diVzETQQyAiogOIhSwRERERERENFRayRERERERENFRYyBIR\nEREREdFQYSFLREREREREQ4WFLBEREREREQ0VUUoFPYauicg1ABeDHscujANYDHoQQ4rP3c7weds5\nPnc7N0zP3XGlFNvu7gKz+UDjc7czfN52js/dzg3Tc9dVNg9VITvsROQnSqk7gh7HMOJztzN83naO\nz93O8bmjYcLf153jc7czfN52js/dzu3H545Li4mIiIiIiGiosJAlIiIiIiKiocJCdm/9cdADGGJ8\n7naGz9vO8bnbOT53NEz4+7pzfO52hs/bzvG527l999xxjywRERERERENFV6RJSIiIiIioqHCQjYA\nIvIZEVEiMh70WIaFiPyhiLwsIs+JyJdFJBP0mAadiHxERF4RkfMi8vtBj2dYiMhREXlSRF4UkXMi\n8m+CHtMwERFdRJ4Vkb8JeixE28Fs3j5m8/Yxm3eG2bw7+zWbWcjuMRE5CuBBAG8FPZYh820ANyql\nbgbwKoA/CHg8A01EdAD/HcBDAM4A+BcicibYUQ0NG8BnlFJnALwbwL/mc7ct/wbAS0EPgmg7mM07\nxmzeBmbzrjCbd2dfZjML2b33RwB+DwA3J2+DUupbSim7/tenABwJcjxD4C4A55VSF5RSNQBfAPDx\ngMc0FJRSs0qpZ+r/Pw/vhf9wsKMaDiJyBMDDAP6voMdCtE3M5h1gNm8bs3mHmM07t5+zmYXsHhKR\njwO4opQ6G/RYhtxvAvh60IMYcIcBXGr4+2XwBX/bROQEgNsA/DDYkQyN/wqvGHCDHghRt5jNPcNs\n3hqzuQeYzdu2b7PZCHoA+42IPAFg2udDnwXwKLylS+Sj03OnlPpK/T6fhbe85M/2cmx08IhIAsBj\nAP6tUioX9HgGnYh8DMCCUuppEbkv6PEQNWI27xyzmQYJs3l79ns2s5DtMaXUh/xuF5GbAJwEcFZE\nAG/5zTMicpdSam4Phziw2j13a0Tk1wF8DMD9iudGbeUKgKMNfz9Sv426ICImvKD8M6XUXwU9niFx\nL4CfE5GPAogASInInyqlfjngcRExm3eB2dxTzOZdYDbvyL7OZp4jGxAReRPAHUqpxaDHMgxE5CMA\n/guA9yulrgU9nkEnIga8xhv3wwvJHwP4lFLqXKADGwLivZv9vwEsK6X+bdDjGUb1Wd/fVUp9LOix\nEG0Hs3l7mM3bw2zeOWbz7u3HbOYeWRoW/w1AEsC3ReSnIvJ/Bj2gQVZvvvG/APgmvIYIX2JQdu1e\nAL8C4IP137Wf1mcyiYioGbN5G5jNu8Jspha8IktERERERERDhVdkiYiIiIiIaKiwkCUiIiIiIqKh\nwkKWiIiIiIiIhgoLWSIiIiIiIhoqLGSJiIiIiIhoqLCQJdqHROQbIrIqIn8T9FiIiIiI2UzUayxk\nifanP4R33hoRERENBmYzUQ+xkCUaYiJyp4g8JyIREYmLyDkRuVEp9XcA8kGPj4iI6KBhNhPtDSPo\nARDRzimlfiwijwP4TwCiAP5UKfVCwMMiIiI6sJjNRHuDhSzR8PvfAfwYQAXAbwc8FiIiImI2E/Ud\nlxYTDb8xAAkASQCRgMdCREREzGaivmMhSzT8Pg/gfwPwZwD+c8BjISIiImYzUd9xaTHREBORXwVg\nKaX+XER0AN8XkQ8C+I8A3gkgISKXAfxLpdQ3gxwrERHRQcBsJtobopQKegxEREREREREXePSYiIi\nIiIiIhoqLGSJiIiIiIhoqLCQJSIiIiIioqHCQpaIiIiIiIiGCgtZIiIiIiIiGiosZImIiIiIiGio\nsJAlIiIiIiKiocJCloiIiIiIiIYKC1kiIiIiIiIaKixkiYiIiIiIaKiwkCUiIiIiIqKhwkKWiIiI\niIiIhgoLWSIiIiIiIhoqLGSJiIiIiIhoqLCQpQNHRM6JyH1tPnafiFzu8Ln/Q0T+U98GN0REJCoi\nXxWRrIj8xTY+75iIFERE7+f4iIhoeDCbe4PZTAcJC1naV0TkTRH50Kbbfl1Evrf2d6XUDUqp7+75\n4DrYPMYh8QsApgCMKaV+sdtPUkq9pZRKKKWcXg1ERM6IyE9EZKX+5wkROdOrxyciop1jNu+pgcnm\nRiLy70VEbf49INoNFrJEBPFs9/XgOIBXlVJ2P8a0TVcB/HMA4/U/jwP4QqAjIiIi2oV9kM0AABE5\nDeAXAcwGPRbaX1jI0oHTODNcX4LzP+pX8V4EcOem+94mIs+ISF5EvgggsunjHxORn4rIqoh8X0Ru\n3vR1fldEnqsv8fmiiDR9fpfj/Q0Reak+hgsi8lsNH3tBRH624e+miCyKyG31v7+7Pq5VETnbuGxL\nRL4rIv+HiPwTgBKAUz5f+/r6/Vbry75+rn77fwTw7wH88/pSpH/p87l31a+S5kRkXkT+S/32E/VZ\nWUNE7q5//tqfioi8Wb+fJiK/LyKvi8iSiHxJREb9niOl1KpS6vX6TLIAcABct93nmoiIgsFsXr/v\nvsnmBv8dwL8DUOvy6SXqCgtZOuj+A4DT9T8fBvBrax8QkRCAvwbw/wIYBfAXAH6+4eO3AfgTAL8F\nYAzA5wE8LiLhhsf/JQAfAXASwM0Afn0HY1wA8DEAKQC/AeCPROT2+sf+HwC/3HDfjwKYVUo9KyKH\nAXwNwH+qj/93ATwmIhMN9/8VAJ8GkARwsfGLiogJ4KsAvgVgEsD/CuDPROQdSqn/APz/7L17cGTZ\nedj3O/fefncDjTdmMJjXvkhJ3F0+RGmXK3tZkmztwpYVyo5jlmSn5FhyIQmd0iouGq5KOZWyI1VR\nKotOucwkZsWyoxRdWklmWWRiy1rJFrmURJm7XJHUkrM7M8BgBm+g0e/7OvnjNp59uwHMoNG3u79f\nFWp3+nn6dX/3O+f7vsM/Aj7XSEX65yHj/mXgl7XWQwTv778+fgOt9euN+2eBEeAPgP+ncfV/D/wY\n8GeBy8A2gQxbopTaAWrAP2mMTxAEQeg9xM194mal1F8B6lrrL7S6jSA8LBLICv3IbzZmKXcagc0/\nbXPb/xL4h1rrLa31EvDpQ9d9PxAD/rHW2tFa/xrwR4eu/2ngM1rrP9Bae1rrfwHUG/fb49Na6/ta\n6y0C8Tx71hejtf6txmqj1lr/HoG8fqBx9b8CXlZKDTX+/ZMEcodAol/QWn9Ba+1rrf898FUCoe7x\nf2mtv6G1drXWzrGn/n4gC/y81trWWv8O8G+Bv3bKoTvA40qpca11SWv9lRNu/2mgCPz9xr//NvD3\ntdb3tNZ14B8Af1kpZbV6AK11HhgG/jvga6ccpyAIgtB5xM0BA+NmpVSOILD+O6ccmyCcCQlkhX7k\nx7TW+b0/YL7NbS8DS4f+fffYdctaa93i+mvAK8fEPNu43x4rh/6/QiCfM6GUekkp9RWl1FbjOV4m\nqANFa30f+BLw40qpPPAS8H8fGt9fOTa+F4BLhx7+8Gs/zmVgSWvtH7rsLjBzyqH/TeBJ4E+VUn+k\nlPoLbV7jzwAvAh8/9HzXgN84NPZvEaQMT7V7Uq11GfhnwK8opSZPOVZBEAShs4ibD8Y3KG7+B8C/\n1FrfOeXYBOFMtFzZEIQB4QGB4L7R+PfVY9fNKKXUIWFeBd5p/P8SwYzxP+zU4BqpUK8Cfx34N1pr\nRyn1mwR1oHv8C+C/Ifg9v661Xj40vn+ptf5bbZ5Ct7nuPjCrlDIOCewq8O3TjF1r/R3gr6mgUcXH\ngF9TSo0dv51S6geA/wV4QWu9e+iqJeCntNZfOs3zHcMA0gRiX3uI+wuCIAjdQ9zcml5y8w8CV5RS\ne5MWE8C/Vkr9gtb6F04zXkFoh6zICoPOvwb+nlJqRCl1haD2Y4/XARf4RKNRw8eADx+6/v8A/rZS\n6vtUQEYpNddIpXkYlFIqefgPiAMJYB1wlVIvAX/u2P1+E/gAQerOrxy6/F8Bf1Ep9eeVUmbjMV9s\nvM7T8AcEM9V/t/H6XwT+IqfsBqyU+gml1ERDtDuNi/1jt5kl+Az+utb6uIT/GfAPlVLXGredUEr9\npRbP9cMqaP5hNlK5fomgbudbpxmrIAiCECnEza3pGTcTBLLfQ5C6/SxBEP4znNDvQhBOiwSywqDz\nPxOk5NwmqG/Zq2FBa20TzFb+18AWwfYuv37o+q8Cfwv43wiCpls8XMOIPZ4HqiF/nyAQyjbwcYKt\nZfbRWlcJZoZvHBvfEvCXgAUC2S4B/yOn/N03Xv9fJEiJ2iCoZ/rrWus/PeXr+RHgG0qpEkFzif+q\nMdbD/CBBOtKvqYPuiHsz8L/ceK3/TilVBL4CfF+L58oTNKIoEMzKPwb8iNa6dsqxCoIgCNFB3NyC\nXnKz1npTa72y90eQgryttS6dcqyC0BZ1tMRAEIReRCn1PwFPaq1/4sQbC4IgCILQccTNgtBZpEZW\nEHocFezf9jcJuiIKgiAIgtBlxM2C0HkktVgQehil1N8iSEv6otb6P3Z7PIIgCIIw6IibBeFikNRi\nQRAEQRAEQRAEoaeQFVlBEARBEARBEAShp5BAVhAEQRAEQRAEQegpeqrZU96K6+lYutvDEARBEPqE\nt2uFDa31RLfH0cuImwVBEITz5LRu7qlAdjqW5rOPv9DtYQiCIAh9wkf+5LfudnsMvY64WRAEQThP\nTutmSS0WBEEQBEEQBEEQegoJZAVBEARBEARBEISeQgJZQRAEQRAEQRAEoaeQQFYQBEEQBEEQBEHo\nKSSQFQRBEARBEARBEHoKCWQFQRAEQRAEQRCEnkICWUEQBEEQBEEQBKGnkEBWEARBEARBEARB6Ckk\nkBUEQRAEQRAEQRB6CglkBUEQBEEQBEEQhK6TfO1jp76t1cFxCIIgCIIgCIIgCMKJLMzNw6dOf3sJ\nZAVBEARBEARBEISu8Pxbr/DiJ6tnvp8EsoIgCIIgCIIgCMKFszA3Dw8RxEKP1cgu5yeCFysIgiAI\nQiRYzk90ewiCIAhCj/H8W688clzXU4HsHhLMCoIgCEJ0EC8LgiAIp2Vhbv6hUomP07OpxXvS/Ee/\n9U+7PBJBEARBEMTLgiAIQjuSr32Mn/3U9Lk9Xk+uyB5GZoEFQRAEIToszM3z3Gef7vYwBEEQhAix\nMDd/rkEs9EEgC8EbIwGtIAiCIESDj776gnhZEARBADq38NizqcVhSFqTIAiCIESHhbl5fvfnU3z5\nfb/Y7aEIgiAIF0ynJzT7YkX2ODILLAiCIAjR4MVPVsXLgiAIA8ZFHPf7MpAFSTcWBEEQhCixMDfP\n82+90u1hCIIgCB0k+drHLiwG69tAdg8JZgVBEAQhGsjqrCAIQv/SiYZO7ej7QBZkdVYQBEEQosTC\n3DzJ1z7W7WEIgiAI58DnPvPxrsRaAxHI7iHBrCAIgiBEg5/91LR4WRAEocdZmJvnzc/nu/LcfdW1\n+DRIZ2NB6B9qVZ/tTRfH0aQzBiOjFqaluj0sQRDOwMLcPM/86A5/9Wd+tdtDEQThHKhVfbY2XVxH\nk8ka5EctTFPc3G9EYSKy6yuySilTKfU1pdS/vcjnlaYTgtDb7BZcFm/X2S14VCs+Wxsut9+p4bq6\n20MTegApOWnPRbv5zc/n5fMQhD5gdydwc7Hh5s11lzu3xM39RlSO110PZIG/A3yrG08sTScEoTfR\nWrP6wEHrw5eB58LWutO9gQmRp1t1PD1IV9wsEwyC0Lu0crPrwtaGuLlfiNIxuquBrFLqCjAH/J/d\nHIc0nRCE3sKxNdoPv65UbHGFMPB0s46nl4iCmxfm5nn2JbdbTy8IwkNg1zWt1l3Fzb1PFCcau10j\n+4+BvwvkujyOoFX03LzUzgpCD2C0qbUxun1UEyJH1MTbA0TCzS8bn4A56WkhCL2CYSpaRbKmebFj\nEc6PZ19yg+NxBOnaiqxS6i8Aa1rrPz7hdj+tlPqqUuqrTqXQ8XEtzM3zuc98vOPPI/QWJTPFt3I3\neTt3nZoR7/ZwBh7LUqRSzYcvpWB0TCJZIeDZl1wJYs9IFN28MDfPc599uqPPIfQmJTPFNxturhux\nbg9n4InFFMlU80SzUjA6Lp9PL7IwNx/ZIBZAad2d4mul1P8K/CTgAklgCPh1rfVPtLpP7tIT+oN/\n45cvaIQyCxwFPE9TKfsYBqQzBkpdfNe7rw89yR+OPY1CAxqN4gdXv8KNyvKFj0U4wHU1i7frOPbB\nMWxk1GRiOtaV74kQLU4bwP7eL8z9sdb6Qx0eTs8QdTeLl6NBFNz8Rv4pvjryPQ03g0bxw6tf5lrl\nwYWPRTjAdTWL79ZwDpXEjo6bjE+Km3uJbq/CntbNXVu60Fr/PeDvASilXgR+rp0ou4Fs1dNddrYc\n1lZcVCNTRSm4cjVBKn1xiQRb8WH+cOx9eMbRnJj/MPX9/OTdz5PwpXnBeaG1xq5rPF+TTBoYRnvh\nFbaD1v6HKZV8xnXwXREGE1mBfTSi7mbZqqf7bG85rK+4oEDRcPO1BMmQLJlOsRHP88cj34N3rJbk\nt6ee5yfEzeeK1pp6XeOf0s07Wy7usfL2UtFnbELc3Cv0kkej0LU48vTSB9ov1Go+aysuWoPvg/bB\n9+De3Tq+H55FoLWmXPLY2nAo7nqclG3g+xrPa3+b72Su4quQFFY0dzIzp39Bwj7FXY8779S49XaV\n+0s2dt3Htn3u3Kpz9906y3dtbr1do7DTutGL52o2112Of8Suo9nZlgYxg8jzb70ix+oBQbbq6R61\nqs96w83aD/zsebB0t44+hZtL5+Xm3DXcFm5eTF86/QsS9gl1c93n9q06i6d0s+tqtjaa3ezYuu39\nhOjQa8fWSBSTaa1/F/jdLg+jLbI6e7HsbjcfCCFYma2UfbK5oyuknqdZulPHbnSzVQaYpuLajQRW\n7OgUoOtoHizbVMpBB71EUjE9EyeZbJaiZ5gt+hYofJkHOjPbGw7rawefbXHXo1zyUEawdQ6wf93q\nfYdEwiCZMnCcIK3bshRKKapVP1ipP/bhaA3los/o2IW9JCECLMzNwyer3R5G3xF1N4uXL56dFm5G\nQ7mFmxdv13GcAzdbpuLqKd18aSZOIszNLfyrIXTyWWjP5obDZpibVTBRAUfdnEwaJJIHbo7Fgve8\nVvGDZfoWbh4ZvZCXIzwEvRbA7iG/9jMiTScuhr0DZxMa/JCZ2vVVJ2j73ujurv2GFO/bR++uNYt3\n6vuiBKjXNEu366Gbdd8sLWGF7PPio7gidThnwvc16yGrqL5/EMQeRmvYXHe4c6vG7e/UuP2dOrdv\n1alVfUxTtWzxjwpW7t/9do37Szb1mrT871eiuBWAcPHId+Di8Fu4WUNottT6qrM/wQyBmx1HsxLm\n5tvNbl68XQ9dnb1ZvoelmwfjY4ibz4jv6yNB7MHl4ediWsPGusPtw27+To1azcdsszymgaU7DTff\ns6nXxc1RoZePoRLIPgQfffWFnv7Qe4HskEmrSdV0prmHe7Hghc4SV0r+kXSnStkPDVi1ht2QtJep\n+iZPFm9j+W5wo8afBn599s9xKzN76tc06DhOy9CzJaWiT72u9996xw5W3mPxYFY/jErJp1zycRzd\nSJWqUym1mhkRehHpRiwcRyY1LobckBle56hbuzls1rFc8o+kGJdLPm5IwKo1oSmpl2rrPF5cbLjZ\nP+LmX7vyI7wrpT+nxrF1sIp6Bkq7frB40HCzbQcLAvG4wmzj5kq54eaCx51bdSplcXM36QeXRiK1\nuFdZmJvntR//fV7/qa93eyh9RzZnkEoZVCv+foCqFIxOWE3pSCehOThGO7Y+IlXXivHOez/I2pWb\nYBhcq97n+Y2vkfFqwXMCL2z8Z54o3uV3Jr+PYiwDykArkxomvzf5YbL3K0zXNx/5Nfc7Vpv95VrR\nKn24uOtz5Xqc5bv2foDcruxqadHm8aeSLQUr9A69Ll2hs0i6cWfJDhkktw1qx9w8NmFhWc3H19Me\n8h0nxM3f9SHWZm6AYXC9sszzm2+QPuTmP7PxVZ4q3eE/TH4fJSt94GbD5LXJ7yd7/zUm61uP9oIH\nANM6RzcXfWavx7l3195vxtjWzXdtnngq2XZveKEz9ItLZUX2EZHV2c6glOLKtTjTMzGyOYOhYZMr\n1+KMT4TvQ5YdCt9pO5U+2mHvcFdFDbzx3J9n5eoTeLE4nmlxO3OFVy//MGtb/n7aiwJyboVKQ5SH\ncZXJGyPvebQXOyCYliKba57NVwpyw8aRy5UKNk8PrZPW4Do+hgr2qzOM9qIM7hR0ORZ6F1lxE86C\nfFc6g1KK2WNunr0eZ6yVm3Phbj6+ZU8yefD/GvjaR15iZfaxfTe/m53l1y79EOubQQMiCNyccStU\nzWSImw3eyIubT4NlKTI5I9zNQ2d1s0YpRSqlQoPd5jvBjjSBulCe++zTfXV8lBXZc2Jhbp7f/fkU\nX37fL3Z7KH2DUoqhYYuh4ZO/phNTMarlIDVJ+8HB1jBgeuaoXA0T4nFF3dYURqeoZofR5oFotTKo\nGzG+ac1y+Z1bjX1J45StFIb28DgmZaXYtbLn8noHgemZGKv3g0YSEJx7TE7FGB6xKBW9Rtv+YGa+\nXm/RZsuARMLg9q0a/hlKbMoln9Hx83gVwkXy3Gef5qOvvtDtYQg9iKzOdoazuHlyOka14uN5B82e\nDAXTl4+52YBYXGHbmu2xS9TSOfShgkutDGwzzjetGS698y6j4xbjkzHKZgpD+zQlqCpD3HwGLs3E\nWVl2KBUPuXk6xnA+cPP2pht8hhrsNm6OxRV3zujmSkkaNF4UC3Pz8Gq3R3G+SCB7jrz4ySrMzYs0\nu4BlKW48nqBY9KhXfeIJg9ywub8a63uae4t1qpVDNTlDI+iQ/dB8K0ZxeAy9dIvtLY/skE9e7YZv\nw+N7pB88oLDjMpyXn9NJGIbi0pU4k57G9zRWTO3PymdzJpmswe1b9SAFPASlgomISsU7kygBYmdM\nSRe6Tz9KV7h4Fubm+YL/ad74ohyjL5o9N5dauNnzNMt361Srh3pZDOXxjZBOxVaM0vAY+t67bG24\nZHMmI0YLN3seqfv32d1xGRI3n4hhKC7PxvFauTlj8O6tetPe7XsoBYm4olw6u5vPWi4mnJ3n33ol\niFH6EEkt7gALc/MkX/tYt4cxcCgjmCWemI4zPGIdBLG+5vat2pEgFiBdKmCEFIYYrkOmuAM0mkAV\nXOLa5f3b3woaS+zh+5iuy+y332L1vkOtKh34TotpKmLxo6llEDR3CmvGFdwHRsctrt5IUNo9+3ud\nH5OTmV5B0oiF8+Zl4xPyneoSRis3ew03V4+5ubyLSfMxPszNCd/hmZ0/bXaz5zJ76xus3Hekc/0Z\naOXmYtFrubevaQVunr2RoFI6+3s9Mipu7iQLc/N9G8SCrMh2jJ/91LSszkaE+0s2bkgJRn79AYlq\nGT+Tw1eNlGHfx/Q8ppbfbbr9B3a+Sapc4GvD78WOJxnZeMD1t98gWauggZ0tl+mZeGdfTJ9Tr/mE\n7HYEQH7UZHwySEc7se7mEIYRNCjZXHdw6ppkymB03CKekHm8qPG5z3ycNz+f7/YwhD5GmjRGh+Ul\nO3TrtZHV+8RrFbx0Fn3EzS4Ty7ebbv+h7W+QLhV41K/GZQAAIABJREFUY/g9gZvX73Pj7TdINNy8\nveUyfVnc/Ci0dfPIgZtDdmBqiWFAbthkY83BsRtunrCIx8XN58UgTN5JINthFubmeeZHd/irP/Or\n3R5K3+I4PlsbLnbdJ5kygnrLXY+dbQ/f0y33pFXA+7/8Re4//xFuZ66ggfzmCk+9+TqW6wS3URzU\nAWnN+NJtPvTGrdDHa7WSKJyeeEKhDEKFWS75jE0EjSQSyaCjdRjjkxbpjIHnaVaWHTwPdncO7U1Y\n99jd9bh6PXGk+ZfQXRbm5uHz3R6FMAh89NUXYO4FmWjuMI7ts7W552aT/IhJcddjZ8vD99u5WfPB\nL3+Rpec+wt3MDBoY2XjAk19/HasR+Ta5efFdPrT1ndDH88TNj0wiYUBzJTLAkb1/kye62cR1fVbu\nO/geFLYPHnPPzdduJEgkxc2PwiAEsHtIIHsBvPn5PG/K6uy5o7VmY9Vha/PgQFgpe2xteKfrlgeM\nxB2+e/X1YEV1x2O9sUm7JhBlftQklTbQOti/9Hh68h5KQSYnB95HJZszMZQTqst6TVOralJpxcR0\njKXb9abPODdkMDYRQ2vNO2/XWp4oaR/WVhyu3kic+2sQzoaswgrdQpo0dgatNesrDttbh93ssrXh\nntrN+bjDd61+OVhR3fbYeGDvFwIpBSOjJsmUgfY1i3fq1Krt3BzeOVk4PdkhE3PFCXVqraqpVYOF\nhImpGEt3mt08lDcDN/uad74dBLFh7Ll59rq4+WEZpCAWJJC9UKSD4vmyu+MdCWIPc9rU0/GpIB1G\nASN5k2wmQbHgoXUQVO3NChYLXltRxuJKmj2dA4ahGBqx2N5ozjfTOpioSKWDPYZnrsZZvW/jOMFn\nMDxiMtn4PCtl/8QUJ6lp7j6yCit0G2nSeP4UdtwjQexhTuvmicnApwoYHTHJZRIUd5vdvLvrUa+1\nd/PQsASyj4phKIbyJtsh51xaQ7nkkUwZpNIGl2fjrD04cHN+1GSi4eZy2T/xO9BqRVdoTz83dGqH\nnHl3gQWR5rmwGRLsnIV4ApYXbXJDJiNjVtDkIGYwOt68sron0DBicUAHG3uPjJrkhsymRgnC6YnH\nwvefU4ojm6ZnsiY3n0zh+xqlOPKet2pKcRhDzm26xqDNGAvRZ2Funl/6uRVqH/31bg+l59lab7Hc\ndkriCbi3aDM0bDIyamE0GhCFurlwgpuBe3dtRsYssrnmJkbC6YnFDJRqfr+DvWUP3tdsziSbC3ez\n39jCpx2muPnMLMzNwwAGsSCBbNeQ1dlH56x1L6YJqGAPO8cBuw6g2dpwKRY8rj2W2O+meJzDAdRx\nbJsg6rI1K1WfasVn6tJBYwmtNdubLoXtQAC5YYOx8VjbxxxkckMmaytOy+uOc/gzc13N1rpDsei1\nbEyxh3RKvHgkgBWijDRpPB/O2i+ilZs31112Cx7Xbj6kmxuPA5pa1d7fF36PZjebjI1b4uYW5IZN\n1ldbuDlk1TvUzW0WBfYYkR0GTk3ytY8Fx60BRor6uszC3DzPvvRoK4uDylmaASgF124muHYj0dTB\nWGtwHM1uofUscn7EouVE7qGDstZB8wLn0F5ry0s2G2sutq1xHM32psfd23X0Wdr7DRCmpZi5Gscw\nOPI3czWOZbU+wfA8zd13amxvebjhrj30HMF2ARB89jvbLrs77qlWcoWz8/xbr0gQK/QMC3PzfO4z\nH+/2MHqWszTRUwZceyzJ1VZutjXF3XZuNlu7+dhjBW7QjX9rlhePu9ll8XYdfZa2+AOE1cLNV67F\nj6zIHsdzNXf23HzC6a5lHQSyjuOLm9uwMDc/8EEsyIpsJHjZ+ATMyersWZmcjjWkc/RyKwaxmKJa\n1SiCg+/0TIxY3GC34AZFN8fus1fjkR8J/0mk0gbjkxYba41mFYR31oUgaK5VfWIxk1rVp1I6WhOy\nL+eid9B1UThCJmvy+HuS+7UyqZSBajEjD0G60tKd+omS3H/8TJD+vbnhsLnWuJMC7jtcno2TleYg\n58YgpzwJvYs0aXx4WjX8icXAiqn9fhNWTHFpJkYspijseK3dXPQZbtEPLp0xGZuw2Fx39wNa/wQ3\nZ2MmtaqmUm52s+1oSkU/NPtHaLj5qSTVRo+JVLp9urbvBc24wrZZavX4Sik21x0214+6eeZqnExW\nPhdpkHgUOYuOELK/3dlIpgyu3kiwseZQq/qYpmJkzCLfSBn13KAWw7QOajTarejFYu2ndUfHYwzn\nLSoVH8MI6mYPt47fQ3NQ41EqhafRBI2LfIaGT/daBxGlFOnM6aR1b9Fu2fCj+XGDGd9a1WdzzT34\nfBr/vb9k8/hTSUkve0Qk5UnoB6QM6Oyk0sfcbDXcPNLezSFxLHBQ69qKsYkYwyMW1T03F7wgMD6G\nJsj4gWDiOtTNPlTLngSybVDGWdxcx66f3s35MYtq1WdzvdnNy4s2j78n2TLNfBCQBonNSCAbMWR/\nu7ORTBlcuRbept0MCVpTaQPTVLjH0nqVouVq7PHH3BOcZSl2d5plaJmKZErxYNlmN0Sme88Xiw/u\nwfg8qdf8kzsQKxpNJ2DqUoxkymBtxQ6v1VHBBISslj8c+wHsp7o9EkE4P6RJ49k4q5vTGQPDaF5N\nDTrSn3wstg652bQUuyFNoCxLkUjCg3t2y1IipYKVYuHRqdX8lrs97NPwsqFg6nKcZNJg9X5rN5dL\ng7laLhPDrZEztYgi+9t1BqUUV6/HWV60sW2932BieiZOPHG2kvFE0uDSlTgry4397TTEE4qZ2Tg7\n2x7FNjW3KPp2ux7H8UEHJwMX0SHStnXbvQkTiaCux/U0jq3xPbBtv2X6GZx+iwjhKAtz8xLACn2L\nrM52DqUUszcSLC/aOIfcfOlKnHj8bG5OJg2mZ2Ks3g+aJeg9N1+Ns7Plta25VQqG+tXNdiC9i3Kz\nU9eh6eJ7JJKKK1cTOK6PU9d4nsax22/PM4i9RcSr7enPX2ufIPvbdYZY3OD648n9YCaRePiDem7I\nJJtLUq9pDJN94e5stphRJGhmcHk20TbNuZeo1322N13qNT8IFBsBohVTXL4SP1Pjj4chkVBt3+sr\n1xM4tube3YMJB4BMtsW4NFKHc0akkZMwSEgZUGeIxw1uNNys/SD4fFg3Dw1b5IbMJjdvb53g5qt9\n5Oaaz/ZW99wcT6qWQWwsBleuJXBsv9nNOSN8clpDesDcLG49GQlkewDZ3y7A9zQb6w7Fgt9Y0TQZ\nHbceul7irLO8rVAqSCU+jN9q1lDB1ZsJYrH+aBheKnrcXwpODNanr7L4xPuwk2mGN1a4/u038O4U\nuflksm1Hw0clnjBIZ42mplpKBd0wTRPuLNabVmDLJZ902qBaPbifUjAxZfXNiUynee6zTwflEIIw\nYEgZ0AGep9lcd4IsJKV6083AtccSWFYfuvnSNRYf/x7sZJr8xgOuv/0G3p1Sx92cSBikM0ZTUy1l\nwNWbgZtv37Wb3Vz0SaYNapWjbp6cHhw3S0On0yOBbI8w6Pvbaa25e7uOYx9spr214VIpe8xeT0Ru\nk/NM1gytwYlZqm8OxFprVhq1LEs33svt934A34oBsDZzg83pWb73P36e3UK943u2zlyJs7HusLMd\n7B+bzhhMTsewLEWl7BF27qI1GGawdUBx1wtqsfLWmbZ1GmQW5ubh1W6PQhC6y6CnG2utWTziZt1w\ns8/s9Xgk3RxW9hOLq44GdReJ1jooedKw+Nh3c+epZ/fdvDpzk43pq3z49/4NxYK93xyzU1yejbO5\n5rCzc8jNlwI3l0vhKd5ag3XIzYaCoRGLxBnLv3oVaeh0NiSQ7TEGVZqloo/j6COzelpDraqpVvxT\nd9C7KManYpRLHr7PkRnF6ZnYEbFrrbHrGt/XJJJGT3Xjc5yg3tQzTO4cCmIBMAw8LO488QyXl77S\n8bEoQzExFWdiqvk63aZMR+tg+4aofX+ijKQ6CUIzg9oMqrjrHZlghj03B034UuloHVsnJi0qYW6+\n3EdubqQRe6Z5JIgFDtz8+NNcuv+HHR+LYSgmpuNMhPQpalcL6w+gm8WtD4cEsj3KoEmzVvFC923d\nE2bUDnaxmOLG40l2toOZ6XhCMTJqHWko5dg+9xqNLfb2pp2ajp2qQ2MU2BN7LZ0NN5JhsDM2RWqr\nu59NKm2EDk8pGBqO1vcmykjXREFozyBONB9O/zyMJphoTqUvfEht2euRUdh2qVR8EnFFfsw6ks5s\n2z7Ld20c55CbL8V6pkHjnpurmSFUCzcXxqdI73TXf2lxMwDPvuTysvGJbg+jZ+mNX6UQyiBJMxY3\nUKq5nb4yiGy9qWkpxiZijE00X6e1ZuluozsjB3Hg6gOHRNLoeBOG88CyFMmUQd2u4Rvh403Xyq2b\nKl0QhqGYnomxsuwczMAbkEoZ5AZIlo+CdE0UhNMzSBPNVlyFNuaJ8jY21p6bQ67TWnPvThDEBv8O\nLl+975BI9IibY4pkUlGvV9Et3JyqlUl3282mYupy0F368Op4OmMMzBY7sgr76ET/FymcyCD8EHLD\nJmGlNoYRdLjrNWo1jes0T0VqDdubbhdG9HBcno2TUzbjq0sY3tFxm57L91f/NBI1UkPDFtcfTzA6\nbjI8YnL5Spwr16JXvxU1PveZjw/E8UUQzpuFufmB+O0M561QN5sGZHvRzVUf1wt3885WL7k5QZY6\no2vLqDA3196OhP+G8xbXHztw88xsnJmrg+HmQTg+XASyItsn9PvqrGkqrt5IcP9esIqpgWRScelK\nvKdqV/bw3NZ7n7putPdJqxlxvjT+fm5nZtEKpkaXuPHGV8HXbFy6htI+Fj7Pbb7BbH2t28PdJx43\nmJiKd3sYPYM0nBCER2cQ3Dx7I8GDY26+fKU3gxHXbd1TIepurhoJvjT+fu5krqCB6dElHvv6H6L8\nD7ExfXXfzR/Z/BpX6uvdHu4+8cRguVk6Ep8vEsj2GQtz83zB/zRvfLH/PtpEMthjbk8mvdz9N5UK\nrw0BSGej+7p8FL8584MUYxl8FaT+PBi7ytZHxvnw7/wG+uuv48STJGslnngyAX3SBXKQkFliQTh/\n+jndOHnIzYqgrKZXSaWNpu1g9khnovu69txciqX33Xx/fJat58f48H/4DTzTwo0nSNZKPP5UAnpw\nAaAfkAni86f/oh0hKBqf698Z4FYBrO/rYL8yH9JZI9Kt9E1Lkc4oyqXmaNa1uzCgU7KUnqZipfZF\nCYBh4MQSbFy6xtTyu1iug2FApeRLDWoPIQGsIHSWfl+dbevmko8mqH+MspstS5HJtnBzhDOL76Yv\nU7WSx9xsNtx8lcn7d4i5NoYR7KE+KDWoUUEaOnUOCWT7mH6X5mEqZY/lxYMIUGuYvGSRH4m1uVd3\ncVoErIUdj8lLOpJpWdvxIVzVXPfkx2KUcwepMhqC/KyI4Ng+25sutZommVSMjFnE4r1Xv9UJnn/r\nFV78ZLXbwxCEgaGfM6eOUy553F866uapS9Huzm+3cPPOtsfEVDTdvBMfwlHNwalnHXVz1LAbbq73\nsZtlkriz9Ne3RQil339Evq+5t2jj++z/aQ1rD1zq9RY5QhGgVb2NhpapTd0mbxexQvZBMl2bdGnn\n4AINmUw0Di+1ms/td+psb3lUKz7bWx6336lTq0b0Tb5AFubmJYgVhC7wsvGJvnez52mWl5rdvPrA\nwY6ym0MaMQJon9BtAKNA3tklpr2my03XIVM8cLPWdH0ngT1qVZ8779TZOeTmO+/Uqdci+iafkec+\n+3Tf/8ajQDS+zULH6ecOiqWiF7r4pzUUtqObC5RMhv/8TDPoxhxFrlYekHJrGIeF6fuYjsPE/bso\nFbTPvzQTw4hI+tjaA6fp5EP7sPYgwjncHSb52sf69nggCL3Ewtw8z3326W4PoyOUis2BFQRu3i2E\nXxcFWm2xY1nB1m1R5Gr5PkmvjjrkZuX7WI7N+Mrivpsvz0anQebqA7vJzb4fTHT0Ogtz83z01Re6\nPYyBIKI/SaFT9OPJq/bDu/9CdFc2ASamY03bFigFk1OxSKYuARhofmz5t7lRuoehPZT2uVa9z19a\n/PdMTSgmpmLcfDJJbjg6aWPVSviXoFrV6FZfnD5mYW6en/3UdLeHIQhCg4+++kLfujm0/S/Bam1U\nmZgKd3Pg7Gi62UTzXyz/NjfKywdurizzo0v/nskJg4npwM3ZXDRqY7XW1Krh34FWzu4Fnn/rlb78\nLUeZ6JxtChdGv9XOttrUWyki3dAgmTK4eiPBxppDreYTiynGJ2NkstEdM0DKt/mhta+gGzvrKAiO\nJOPRqkfWOmj+1WqbI2UQ2ZOSTiByFYRoszA3z+/+fIovv+8Xuz2Uc6FVCmvU3ZxKH3VzPG4wNmFF\n381enR9efX1/7iDKbi6XWq/IRzUj7SQW5uZBSnUuHAlkB5h+2Q4gFjMYHbfY2nD3AxZlBDWa6YjU\nabYimTK4ci3R7WGcGltZfG3ku7iVvYqhfd67+w7vK3wbs9W0+wWjtaZa8alWfbYb34fQIFZBfiTa\nJyXnhQSwgtA7vPjJKvSLm+MhblaQzZmk0uLm86RuxPjP+ffybvYqpvZ47+47fE/hO9FzcyVo7uS3\nGJZSkB/tPTeLZ7uHBLIDTr+szgYrmQaFbQ9fw9CwSSZrDNSKW6fxMPiNKz/ErpXFNwLRfHX0e7if\nmuTllf/U5dEFzbOW7tRxHH1iQ45M1mB8Mlqz1OfNc599Wmp0BKFH6ZfV2fHJGOmMwe6OuLlTuMrg\nN2Z+iKKVOeTm9/EgOcGPrH6py6NruPl2w80nxNXZnMH4RO+4WQLY7hPtKTHhwuiHhhOptMn0TJzL\nV+Jkc6aI8py5nb1CyUrvixLAMywepCZZj490cWQBK8s2dv3kIFYpmLocnYYXnUAaTQhC7/PiJ6t9\ncaKczoibO8m7mauUrdQRN7uGxXJ6ms1497feebBsY9snB7FKwdSlOKpH3NwPv81+QAJZYZ9+bTgh\nPBpaa+o1nyVzDNdoninVwFpy9OIHdgjf15RLp28QUdqNbsfMR+Fzn/m4/IYFoc9YmJsn+drHuj0M\nIWJoranVfJascDcDrCW67GZPUzmtm1XrTtdRQho6RQtJLRaa6Jd0Y+HRcWyfe4s2jq3xKGDkXXzr\n6GHD0JqsW+nSCANa7fvXin5sVrwwNw+f7/YoBEHoBD/7qem+qZ0VHh3b9lm+a+M4Gt8ooPIu2jzq\nZoUm02U322dxs6Zl7WxUkIZO0UNWZIWWyIxTdwlWGT3KJQ+/C0d3rTX37toUSVLK5pm49w7qWN6u\n0j5x7TBbWbnw8R1mffVs+85FZUP486Cf94gWBOEoC3PzfO4zH+/2MAaaw27W3XLzHZuiSlLKDDOx\n9A7GsdlZpX0Sns2V6uqFj+8wG33iZtl7PbrIiqzQln5and0LBnuhNrJc9Lh/zwaC1F1FsJH5Rbb/\n33Vi/NEHfoCdsalAklpz5Z0/Ye3KY9RTGVCKMXuHH1p9HaOLnRG11pSKp0tdUgpGxiziiWjK8ix8\n7jMf583Pd7/+SRCEi+XNz+d5s49WZ3vJzaWGmw+PdOZqnHTm4ty848T4ow/9GQqjUxjaR/k+V269\nxeqVx7FTaVCKcXs7Em4+bcmPUjA6bhGPR8/NC3Pz8Kluj0JohQSywqlYmJvnC/6neeOLvfeVcR3N\ng2WbSjk4oKZSiumZeGSDGdfVLC/ZR9JfNbC8aPPYk0lM62Jk/zuzL7CTGkebJntVK0uPP83TX/l3\n5HWF2VmLtFe/kLE8CrPX4+wWPBQwlLciv+3DaZA0YkEQen2i2XE0K4fdnDaYnolFMpiB4FzifsPN\nh8PDe3dtHnsqiWlelJv/DIXUaMPNQQC99PjTPPPl/5e8UWP2ikVK3PzIJF/7WJDSL0Sa3otKhK7x\nsvEJmOstaWqtuXu7fqSGslrVLN6uc/OJJMYFiecsFAvNzQ5qqQzV7BDZapnLubOl6jwMu1aGzfQY\n2jg6y+ybBvce+26eWPxPpL1otMhXSpEbMijuNs/85oZN0hnzQmfLO4mkNgmCcJxenGjWvmbx3Rqu\ne3BZteKz+G6dm08mI7k6u1twmy6rprLUsrnAzdnOu7kQy7KdHgl38+PfzeP3vkQqQm7O5ozQjKmh\niLtZVmF7h9456gmRoZf2tysXfTyvObXG92G34JEfjd5PwPMO2tT7hsE3P/Bn2ZqaQfk+b5kGN8vL\nvLj2Bx3d6LxiJjG0T1NIrQzq6Sz5kWi9b5OX4lQrNVwP0KAMsCzF5HQ0hP6oSAArCEI7em2iuVTy\n8UKyTn0/mMwdjphj4KibPcPkmx/6s2xPXEb5Hm+ZFo+VF3lx7Y86ms5bNlOYPeTmqUtxqtUaXg+5\nWXzbW0TrGy/0DC9+stoTHRRtO3xfUa2Drn9RJJM12dpw0Rreee+H2JycCboRNiYu303PkM1/F9+3\n842OjWHULuCr5jQfw/e46a5GaiXb9zXrqw6eF9QSo4LZ3qlLsZ7fr/D5t14JfmuCIAinoFfSjW3b\n70k3b296aA23vvt72Zy4DKYV/AHvpGcZGi7yocK3OjaGMXsHL9TNLje91UitZO+52T/k5uG8yeR0\nNN0sAWxvEq2EdKHniPr+domkIuSYDwTNBaJIMqXIDpmg4P61J9HHtrvxTYuvDz/Z0U7Gce3ywe1v\nYPkHqVSG9oj7Dk8Xv92x530YVu47FAvBycXe3+6Ot1931asszM1LECsIwkMR9ZPyZNJo4+ZoyjmV\nNsjkDFCwcvXx/QB2D9+0eGP4PR11c8J3eHb7W01uTvgOT+9+p2PP+zCsLDsUd4+6ubDtUa1Ez81R\n/70IrZEVWeGRifL+dumMQTyusOu6ae/QrQ0Pw3QYG49WiotSikszMTJDFtoMrx/xzRg7u5rRfOeE\n//6dPyVvF/l6/ikqZpLZygPev/OtSDV48jxNqSHKw2gNm+vuhXZ5Pi+kwYQgCOdBlFdn99xcrx/r\nnERw7DYNGImgmy9fiVMo0lSjuodnxdjd9cnnO+eeD+18k1GnwNeH30PNjDNbWeH9O98i5dsde86z\n4rmaUrG1m6NSGyvd/3sfCWSFc2Nhbp5f+rkVah/99W4PZR+lFFevJ7i3WKdaaZ4l3VxzyY9YF9Zt\n8LQopRgeUhi+h2+G/Ey1ZpUco5Q7Oo4blWVuVJY7+hyPguvqIGcpZALcOctG7BFBGkwIgnDeLMzN\n89qP/z6v/9TXuz2UfZRSzF5PcO9unVq1+Vi9vuYyFFE354fA0D6+CgnGtGZN58hT6eg4bpaXuVkW\nNz8K0v2/P5BAVjhXorg6a5gKz2194KxVfDK5aMwOHidfL7CVHmu6XGlNmvPpkKi1xrE1hqGwYtE6\naTiJWJvxRq2VfzskrUkQhE7y0VdfgLkXIuVm01ShzRj3qFX9yGbVDNV22UmPNF2utCalzmdltKfd\nHFehQSxAKtVdN4tv+4veOdMTeoqFuXk+95mPd3sYQEMGLWI+rYlU46LjfO/ONzC8Yy3/fZ9cYYPL\n6dojP36p6PHO2zXuvFPn3e/UWDy2VVHUMQzF+ITVVO+sDBifiP483cLcvEhVEIQLI2pudtu4OWqr\nsYf53kK4m4e315jOPPokc2k3xM1tJuSjhmEoxiab3WwYMNZFN4tv+w8JZIWO8ebn85E4aOw1GWhF\nMhVdWV6vPuDZzT/B8FxMx8ZwXXK7m/y5lS8Re8RN4+s1n/tLNp538B5VKz737tbR7d6wiDE6HuPS\nlTiJpMK0IJszuHYzQTwR3cPbsy+5kfhtCIIweETFzb7f3s2JZHTdfLOyzDOb3zzi5qHdTX549ctt\nM4VOQ63mc/9euJt7ibHxGNMzsX0354a652aZNO5fujYtopSaBX4FmCJIQPjftda/3K3xCJ2j2w0n\nlApW6MJa/VtWdDsk7vG9xbd5uvwuq2aepF1lgiIq8ehj3t5yQ08ibFtTr+lIB/jHyQ2Z5IaimYJ2\nHJGpEGXEzYNDt91sGIGfwzwUi6nIu/nDxW/xTPkWq+Zww80l1DkE3zubLdxc19RqPslkdCdpjzM0\nbDE03N3sKHFuf9PNX4MLvKK1/i7g+4H/Vin1XV0cj9BhFubmefYl9+QbnjNKKUZGQ9JPFYxNRj/9\nFIKW+1eddSZV6dzk3qrhglL0VApTryAzwkKPIG4eMLp1XArcbIa7uQdKQ2DPzRtMqvK5udlu5+Ye\nKv2JAuLc/qdrRwqt9QPgQeP/i0qpbwEzwDe7NSah87xsfALmLn4GeHzSQmvNzpYXXKBgbNxiON8b\nsuwEmYxBteyHtsfvpRnfqPP8W6/IfrBCzyBuHky6tTo7PhXDb+wvCgdB7PDIYLu5Vmnh5i43SuoV\nJIAdHCJxpFBKXQfeD/xBd0dydpSvSe/WsRwfO2lRzcZoml4Umrjo7QCUUkxOxxmf1HiuxrIUyhjs\nz2l4xGJ708U9tEiuFAyPmJHqkFir+dSrPlZMkc4YkU83O8zC3DxIECv0KH3j5pRFNSNuPg3dcPPU\npTgTU+LmPfKjFjtbzW7Oj5pYVnTemz03x+KKVDoabn72JTdYMBEGhq4HskqpLPAq8D9orXdDrv9p\n4KcBEkMTFzy69lh1j+nFAsrXKA1agRs3Wbk6jI5wt72o0I3tAAxDYcSDz6Zc8tjedPF9yA4Z5Ecs\njAESqGkqrj2WZGvDobTrY5gwMmYxNByNWlOtNctLNpVSo7hZgWUF+wJHKdAOQzZZF3qdXnZzrO4y\ndXcXpQ/c7MRNVq8NowfoGP+wdNvNpaLHzlbg5tyQwfCgunndoVQM3Dw6ZpGLipv9hpvL0XKzrMIO\nJqqb3UmVUjHg3wL/n9b6l066fe7SE/qDfyM6PSem7+wQr3kc/tn6CoojSXYmM10bVy/yuz+f4svv\n+8ULe76NNYetjYOGCkpBPKG4eiMxUMKMMpvrDpvrzU0v0mmD2RuJ7gzqFIhMe4vf+4W5P9Zaf6jb\n44gSve7mS7d3iNWb3bw7kqQgbj4TF7k6C7A/hLAIAAAgAElEQVS+6rC9KW6OMptrDpsbIW7OGMxe\nv3g3P/fZp4PJF6GvOK2bu9m1WAH/HPjWaUQZNQzPbwpiAQwNmd36+QayWpMu2qR362hDUconqadj\n5/f4EeDFT1Zhbv5CZoBdVx8JYiGoPbHrmmLB6/vaHM/TlIsevg42WndsTSymyA6ZkTpR2Nn2Qjs3\nVio+nqcjt8fghQSwWmPZPr6l8M3wWqlExWF4vULc9nBiJoWJNLVM8/FC+Zr8eoXMbh00VHJxdibS\n+FbwuLGaS7ZQx/B8Krk41WxcUjMHgJ53s+sTs8PdnN21zzeQHQA3X+TqrOvoI0EsHHLzrtf3PS08\nT1MqemitMQ2FbWticUU21yNuLvv4nsa4QDcvzM0HeSPd5pRuzq9XiNkeTtxkZzxNPczNnt9wsw00\n3DyZ3n/cWM0lu1PH8H0qucTAlzR286jwEeAngbeUUm80LlvQWn+hi2OKHlozca9IsuJg6GAvhHTR\nZnc0RWEifabHsRwf32z9I4sCC3PzHV+drVb80Jb/WkOx2N+B7G7B5cG95s3alQHGisPVG9HZf7Vd\ntsjGqs3U5Wisyl7UCmxmp8boWgW0RgGVTIzNy7kjqZKJssPkvV2Mxltnei7xe7tsXM5SzR16v7Rm\narFArO7t3zZbqJOsONy/kSdbqDOyVkZpUATHnHrKYm12aKCFOSCIm0+D1kwu7ZKoukfcXBhLsTsu\nbn4YKhUvOOCEuLlU7O9AdnfH5cFyiJsVGIbD1ZsJ4o+4d/x50dbN6w6T0/GOjyFKtbDZ7Soj69UD\nN2fjbF7KHnFzsmwzca944Oaqy+S9XdZnctSyh94vrZla3CVmh7j5Zp7sTo2RtcoRN9fSMdav5AbW\nzd3sWvz70DRp2jP4poGdtIjX3Kb0pfLQ+Z1gp8rOfhALwRumNAxtVSnlE3ixk2sm0rt1RlfLQS0v\nUE3H2B1LEbM9PNOI3GxOp1dnTbPJk/tEqZFCOxzbZ3PDpVoOGi2MjlukM+2/C66rm4JYXxmAxvA1\nHnD/ns31x5KdG/gZyObM/U6Wxyns+GRzHplc92qGLrIbcbJsM7pa3j8OAKRLDslbW+yMpymNBJ/Z\n6GrpyG0gWIkaWascCWQTFZdYzTuy/5oCTNcnsxsEsYcfx9CQqLqkizaVczy+CdGj591sGdhxk3hI\nanFp+BzdXLL3g1g4cHN+s0o5n8SzTg460oUao6uVoJYXqGZiFEZTxAfWzSosjgXAilgGTits22dr\n3aVaabh5wiKdPsHNjm4KYvfdrDWeBw/u2Vy7GRE3D7V2886WRybrkcl2zs1RKt9JlmxG1ipH3Vy0\nSZaPunlkpRzq5tHVMvcPBbLJihNMMB+63b6bC/Wm5zJ0cJ9BdnP/Tm9dABuXs0zfPdrsyUmYFM4y\nG3sCqaLd9OXfI1l2KA8bDG1WGdquoXxNPWWxPZXBSQQfbWa7xthq+YjQU2WHVNlBNy7UClau53Hj\n0WgksMfC3Dy/9HMr1D766+f6uKm0gWmA6x+9XCnI98BqrG373H2nju/v/VtTKdtMXY61nbHe3Tlo\ngVjJDPH2M89TGJ1EoRlbuceTX/8y1Ou4jc6R3WZ8Mkap6OGFbD2sNWxvu10LZC+6G/HIarMEFWD6\nQZCaLdQwPI3VYv9fy/GDN61xUpwu1kMjFUMHx5yws0lDB5NigypLoXfYmMk1udlOmOyOpc7tOdIt\n3KxpuHkoztBGlaGdPTfH2J5K77s5t1UNVlYO3TdVckiVDtzsK1gdIDenMwbKAMLcPNoDbq773H23\n2c3TMzGGhluPv3DIzeXsMG8/8zy7oxMorRlbWeKpN1+HWh3P1ZhRcfOuhxcSy2oNO9tuxwLZKAWx\ncLKbM4U6lutjeqd0867d2s2lNm4e4EA2GnkKPYobN7n32Aibl7LsTKRZv5Jj5Zy7IvqmCl89VMF1\noytlhjermJ5uzMy4TN8pkC7UGVovNwWxjbuiCL78hgbDD5pjJEt1lHdgkHjVYXJxlyvf2WL6ToFk\nyT6313VafvZT0+d+4FJKMXs9QSymgpRaIziGTF2K9cQebRtr7r4o99Aa1lectik/tVpwnWPF+c8/\n8DKF0UkwDLRhsjl9hTc+8lInh31mLEsxfTnWckHCD58Q7ijPv/XK+YtUa5Ilm0yhhmU3v6hYzSVm\n+yF3DDCAeN0n5uqWy2j+4WOS1mSK4bLUgBczmk4k966Tjq9CL+DGTZYfG2Fr+sDN592x2DeNlpk9\nvqEYe1BieOuwmx2m7wZuHl4vNwWx0Oxmc9/NdoibC1z5zhZTdwoky/3lZiumGim1DTdfjpHogb3N\nN9acUDevPTjJzcGdnFicr73wMrujE6Aabp6a5Wsf+ZGW37VuYFmKqcuta8E74ebnPvv0xQexh9xs\nhrg5XnOJOe3dnKh7WF4bN5vqIOuiUXPfys2upVq62R9gN0d/iivqGKqjsyCl4QS57Roq5CiW2amR\nLh9NbVYAGsYflA7+fQJ795m8F9ynlE9QGooztVTcz8M3PZeJ5SKb0xkqwxef3rIwN88zP7rDX/2Z\nXz2Xx4snDG48kaBe0/i+JpkyjjRTcBxNteJhmtHbu7RaDreE7wcpSrF4+FjjjctXr9zEN8zgLKGB\nNkzqyTSlS5exrO3zH/RDEqRLh9cN5YYv9sSmE6uwVt1jarGAofX+LGt5OMHWVGZfbrnt2omP0+7b\n6SvYHU3uP57p+ii/9WlRyyD3nFMzBaGTaENR7uD3tTScILvT7GatFJntKulKiJv9h3VzEU3g5kou\nzuThWjvPJX6vyMalLNUurMict5sTCYObbd3sU634kXTz/nY0x/B9cF2ItYj9gtpXn5XZJwI3q0Nu\nNk3qqSyV6WlMq9CBUT8cmayJUk5TrxGlOPct/LrR0ClWd5laDLbw2nNzKZ9ge/KQm7ce3c2F0YMs\nEcvxg+drQbboiJtDkEA24rgJi62pDKOr5f1fhEahFU1B7B4Pc1g/fJ9MoR6a0rxXa1cZSnSlbufN\nz+d58xzrc5RSJFNHX4fWmvVVh52toOmEIoj3Zq9HpwmSaSncFimk7boFDuVNNtddKrk8vtVsVK0U\n1uURqEYnkDWMYOZ39f6BMJWCRFJdWOOPM80Ca43p+OjTNG7Rmsl7u5jHZmszhTpuzED5OvhMQjqw\nnmoojf/ujqaOpFRqQ7V8PK3AODaevcdRGqaWitQyMTanM6eqzxeEfsVJtnFz5fzdrAiavoSlNBsa\nRtcqLOe601n8oty8tuIEtZmNq8wIutlrkULaTgfDeZOtDZdybhjfavaaVhCfGYFqdALZVm5OJtW5\nBbLnuq3OGd08ca/Y5MLsTh3XMjD23Rz+Oz9xKI3/7o6mKI4eLAz5j+Dm6cVdqpkYW9PZIKtqgJBA\ntgco55NUcnGSFRdtBK25xx80pwyfFk17oRoaVKuDsaeDE+xDAZPyfCzHx42bQeqW1iSqLpbjYydM\nnOT5fs32AotONJwobLtsbzZWPBsTcb4P9xZtbjyeiMTs7+i4xcry0ZlQpYLmSO22pInHDUbHLXKF\nTQzXaQpmDQOm9G6nhv3QDOctkimDwraL60B2yCA3ZHb8szhrGlOqZDP6oITRaKpWS8fYuJxtKc2Y\n7QWro8cuNzTk14+u/PqcvQ5EAXbMaOpu7psGtZRFstLcqG4vA+P44xw+ZiTLDtN3d1l+LB+pRjSC\ncNEcd7Ph+oytdMnNrr9fD7x/e8/H7BM372y5wQQz7J/Buz4sL9pcj4ibx8YtVu6HuHnIbDvJHE8Y\njI6Z5AqbrLVw84QfUTcnG252ITdkkh06n1Xy81yFTRVtxlZKRxqebrZzc721m0fOy83xEDdbBvWk\nRaL6cG5OlYPyhUFzswSyPYI2Daq5oLPZ8EYlNNX4tBz/8p9pHOpQnZzWjK6Ug30oG/vZlIYTJKou\nsUP1BPWUxdqVITjnHP6FuXm+4H+aN754Pl9j19WsPgjpLAQ4tsauaxLJ7h8choYtHFuzue7ubyOU\nzhpMz5y8f+HEVIwPVO5x13uW2qH0YtP3GLULTNU2Oj38hyKRMC6kpT88XFv/WM1lfLl4ZKUkWXaY\nulvgwY1wqSif0MYNEP7bPKswNbTc03Ljco6pxV0s5+B3WsnFg/qcE8ajAMP3B7q5hCDsccTN682N\nX878eDykmw11EMSGuLmYT5IqO0d+87VUY9uODrj5PINZ19WsrYS72bY1tq1JJLrv5tywiW0H+9Tv\nuTmTNZhuU0+6x8R0nA9Wl1j0nqF+xM0u4/UdJutbnR7+Q5FIGkxeOj83n/duALGay/j9o25OneRm\nrTvu5lorN8/kmFwsBE2gGpSHEmR266dzs+eTKjn7x6RBQALZHsSJm8HKbOsa87b4BAXmx1Maj9zG\nVChfH/nxB7V2qf0ffn6tQma3HtymMQWZ26kDR39ciapLfqPCznluRN/gZeMTMHc+M8A7W+Gi3KNW\n9SPTcGJsIsbImIVdDzoMW7HTS3woDX/5wW/zlbFnuJOZwdSaJ4q3+fDWn/TunhvnxMM2kwirY1dA\nzPaZubXNyvXhplRcO2miQ2wZdiKrVbA1x57c4rYH+uik1OH76cZ9WnVp9S2DBzeGidcaqzNJCzdu\n4q+UyBbqR373YeNRPqGNqQRhkHHiFr7ioYNZzclu9kyFEermgzr4kbVyk5uHGrX2hx83WXUY3qye\nbU/6U3Keq7Pbm6dwcwTSi5VSjE/GGB2zsG2NFVNn2gFgOKX5Kw9+m9fHnuFu5jKm9nmyeIfv3Xpr\nINzciT4UQ1vVlm6+/M42q9fC3GwRFsmem5uNxrl0CJ5l8OBGft/N9aSF1+haninUTwyYlQ6yvS5u\nT4XuI4FsD1LJxRlZM1B+c+rDcfYWfWj811cHKY/59QrZwsEsz94PTivYuJTFsj1GNqr7IiyOJCmM\nN358WpPbqYW2HT+OoYPank4EsnsszM3z2o//Pq//1Ncf+jGqlfYzA7Wax3CEfjKG0VxHdFoyXo0f\nXPuDcx5R7/Kos8CxFnWsiiAdf/x+idVrw8euVGxezjK+fNBUrd35bzUbp5wP6mlMxyO7XSNe9zBc\nH8Pz0IYRdEjd2+pjMt1+2w6lsFMx7EM+3ZnIkKi5xOoHQWrYLLAm6JCeu7WFbxgURxKU8gcn0oIw\niFRycUbWFapNB/E9Qt2cibExnSW/0drNm5eyxOoe+c1jbh47cHN2p356N+/UOhLI7nEeAW212t7N\n9ZpHlE5nDfNR3Fzlh9a+cs4jijad3JPdssPPkxVguZqxByXWrja7eeNSlvH7p3RzLrHfWM60PXI7\ntWAvWM/HcAM3W42yvHo6cLN3RjdvT6aDLsn2UTc3BdZAomwzs13FNwx2R5PB2PrYzdH55QunRylW\nrg8zslIiXQo6uoZ9RTWwMZPFNxWZgo3ha8pDcarZoCHE9nSW7ekssZrL8EaFeN3DiZsUxlPYqSDt\noTSSxHQ1nqmOph/p8BPclkNu04ntvPjoqy/A3AsPLcxEQlEpt74+CjU4wvkTNgucqDjk1yvEqy6u\nBaWRNOXhBL4VPh9aS8eI19zQlRhFkJVgeH5TTU41G+fBjTyZnRqW62PHTfKbzTPIe7fdw4uZFDow\nMaRNxcq1YRKVYKUmUQlWQg7PKO+dgCcrex0UPUbWKsTqHtvT2XMfkyD0DEbw+xldLZNq52YF65ez\naEOR3bVRvqY8lKCajZ3KzbUsFEeTmK6PZxpH3Kz8s7r5EV/zKXmUdON4XFFt5+aBWK/sT866Cpuo\nOOTXKsRrLq6lKI2kTnCzFbg55LrAYy7K89HH3ZwL3JzdqWG6Pk7cZLilmw/ShL242ZFFG20arFw/\nnZtT+/0vPEZXy8RqHjvTnVtI6jYSyHaJVNFmeLOC6frUkzF2JtK4idN3evMsg40rQ0HzhopzpB0/\nBLO725MZqrlglqiebp0v7ySt4LHCUAovLG3VULgxI3QPrePpFxqoZi4uX/9hV2fzYxbbW+HpksF2\nL73/c3k3c4U38++haia4Ulnhg9vfJOMNUhLKAa3SiPf2T97TWtyFkfUKI+sVKtkYm5dzTftRFkeS\n5HZq6FYpgW2mdN14c1Ca3zz6mWxOZ1qK+txRCsNvBN+HLt4bvhMPfveHjzeGDsoKPNOgNJJkdLVM\numSjCVapticvcPyC8AikinWGN6qYnk891XBzu9WTY3gxk/UT3Lw1laG25+Y2bjzZzc3j0ga4lkHM\nPerm/Q6nxy47fBLeaR52dXZ0zAq6FYfQD27WwDuZWb6ef4qamWC28oAPbH+TjHfy9i69zFlLeRKV\n427WJ7t5NEWuUG/tZlrr2T0WlCpg6LibL7VuGnXuqKDsoK2bbf/IdYaGoZ0anqWoDCcZWS2RLjsH\nbp7KXNz4O4T6/9l77yDJ7vvA7/N7oXOePJtmI0AkkogECTCLAgmFO+pI6WifJZ/vqCNOJ9uqctUZ\nrrtzlctXkk6us1QWbckqlixKdwqmLJFikBggiCBBEoSIRIDA7mLD7OTQufvln/94PT3d0697ZnZn\ndie8T9XW7r5Or193v8/7/X7fMKhJ814jPXFW3vfzv3mrd+OGSRWb5BcbbbmtxczPnchtazDbSXuW\nynJwNIXycGLXC7HEahYjG8IiJbRNqUhf2lIRzAXkCHaiWi6Z1SaxpuPPPA/FN62oqLgeiitxdKVv\n2MR2hdlsuMxctXA7nCkE5AsqIzep2NBu8f3cHbyYfwuO4h9XIT2insXHpv+axAEXZid/8juf4MXP\n5/rePnqlRLzZp1cv/oVf0MWlanuMTFeIbAgzlvh57XOn+r/mRjTLJV6zkELQSEdu+iBwdLpCvN7b\nv9cT/nuJmv2Pj1RFV5sACTi6wuypvVlJ8elfe/x5KeX9t3o/9jMHxc3plSa55QA3T+W2NZjtJNqw\n/YgFy8HR/FXV3XZzvGb1pCwEudlTBPNTuYHtOrSWm6NNByuiUtkhN//tr8b59t3/25bfU6PuMjNt\n4W1085DGyNjNG4zvBs/l7+Kl3G0dbnaJuTYfm/4Kcc+8xXu388Se+ii/8hvj237c2OUSMWOAm9MR\nlo+ke25TbZfRqxV02+t1c1T1iz5tkVvu5qtl4o3enHFP+APvyCA3K6LdVQHWrk2UvkWvbjVbdfP+\nnsbaj0h/BqlzhlYAeH414pWAH+FWMBM6C1PZze+4gxipCAvHM2SXm+iWixXTKA/HcVWFVCtHwIpr\n1LLRnrCNTjTTZeJKuV0aXTf9E8XSkTRGqnfwKDw/r2FtxQchKI7EqeV7k+effPyJbQkznlA5c3sc\nw/CoV/0TQiqt7pkiTxtpNlxWVxwcW5JMqeQLGmpAcQlT0Xkh/xZcZf0nL4WCJXRezJ7j4dXrzy3e\nLzhC5dfe+fPE/i+brN6glosGTq5E+4gS/MqEibqN4ng9AnN1hcUTGcYvl1Edr32xiBAsT24v5NaJ\nqFT7FIO4GfRr8YEQuJqCNINzghXomfkW+K1BDlslxZB9hie7BrGwwc2T1+/m+Zvs5uYGN5stN3sd\nbjbjGvVN3KybDuNXyn64Mr6bEzWLpaMZjGTv4FF4kqHZanvFRwpBcTTRzu3v5L3/ugnbCDdOJFXO\n3h7HaLrUa/5q8152c6PhUmy5OZVWyRW0wPZ4pqLzYu52XGXdRVKoWAq8nDvLg6uv3Mzd3nWefPwJ\n+I3ubcKTJCsm0YaNE1GpZa/TzTUrMIXH1VUWprLBbp7YX25WvH5uBkcT6GaffHhAer1u1hyPWN0O\nvNbeL4QD2ZuMZnt9S3rHmsGV+YQrUV0PR1N2vEz+jWLFdZaO9QqtMrz14hH5pXp7EAv+sRASCgt1\nZpN6z0zR0FyNeM1aT3SXkvxCA81yUTyJFVWpZ2NtQW9XmACxmEJsjwpyjXLRYWFuvWedaTiUiw4n\nTsd6KiWuammE5/XUiPcUldn42E3a41vH//TYv2DicpnCgt8ew8OvZrh4LNPTokZuUtlB4q84BM3E\neqrC7MkcyapFpGnj6OrA/J29SiMTIWIG5fxKSsNxPz+2v097tx3CSooh+wvd7hO6ih9mH3jbQXfz\nYqM9iIUON8/XmD2d77n/0GyVeN3ucnNhvu4Xvmm7uXvw/OTjT/DWnyrxs7/4n7a0T7G4Six+favj\nN4tS0WZxzulyc2nVYep0rGeieVnPIjwXlO735CoqM/Ex4GAMZPutwiqu1z3AxA/fDXKzp4A6oO6X\n72aJF/D16HFzpOXmfRZWW09H0c1Gj5slgtJwglijsj03e/4ElbGPy1vsr0/wAOCq/csSeAImLxY5\n9voKE5dKxGomhfkaRy+sMnGpxLHzq6SXGzd1f28GsYYTeEw02+uZfVJcz5912/BDVYBM0SRdtigs\nNjl6oYhudl98PPn4E8Se+ujO7vwtwvMki/PdjdelBMeF4nJvSGhtpoonAn7u0iPtDKiisc+JPfVR\nnnz8CbIrzbYowf++KBKGZ2uwIb2ikY4MrFCIEDgDwuRRBPVslOJ4iupQfN8NYgFquRh2RPVnrWm1\nBRGwMp7CjussHUkFHqN2COPG7YofkhwSsldxNaWvm2WHm8cvlYjVLApzHW6+sEp65eC5Odou6NaN\nZns9URuK4/nRKoFuNkiXTQqLDY5eKKJtCH988fO56259ttfw3ez0uNl1YTWgjVBtuoIXdCkuPdL2\nwXDzk48/0TeUOLPcRLV73Tw0F+Dm1GA3S+HXbulLp5sL8X03iAW/AKsT5OYJ383Lk9t0s+C6Uxr3\nCvvvU9znSFWhno60v4Tt7fhyWCuiEjFdRq/V/L5Rkvaf/HKTo+dXiVcOTt6EGxBuA4AAb8NqrOLK\nvieyjbPGI9eqPff5ld8YPxDCtMzeo2DrEYpD48zL7hA4x5HIpQqZ1SWE230BoXoe95Re39V9vRU8\n/Jl7uuSZqPZOfoA/MaJtKFhWHE3hKSLwe+YJKI7E99zqy04jFb8y+up4ino6QjUfY24q187tM1JR\nlscTdB65NVG6avex87cpN7WoTEjIdvFUhUaqj5utdTdHTZfRa9VuN3uQX2py5Pwq8Zp1S/Z/N+h3\noS+FPznViep623BzJfB+Tz7+BH/yO5+4rn3dK5hmb1EhW4+yOjTOgtdd1M+2JWK5TKq8Euzm8hu7\nvLe7y5/8zic2vd5KVq3AgYjqeKgbCpYVx5J4SvCAzC9wmtiTuZ47iVQEcyfW3VxpuXktbaeZjrIy\nFuxmL8jNmkIzIE1gPxGGFt8CVsZTQJ1k1WznkQgpey601076G7eprmR4rsaSKjBuYjXg3aJSiHUV\nvwL/pFTPRHsGDO3iEZsUKRO0VnQD8iVgZ5u13wpUdf0QSODybW9l+szdrfBhhfN2mQ/Pf5O4a+LY\nEiHgzuee4rX73k1xeAIhPRTP5S2vfZfx1MotfS87zZOPPwGf694mB8htY5VDqQpmT+XILdVJVP0Q\ndtkqclQeTuzrXJJtIfzZ67X+eBtp5OJ4ukp2uek3bo+38vAUhcJCrd1+pJGKsDqePPAXGCH7n5WJ\nFIX5Gsmqte5mT/ZcaAt6w/QEoLmS4Zlq3xzS/UalECO3FODmgL6U9qAolQ4E+EV3XIkMmMR+8fM5\nXryBVj23mo1uvnTb25k+cyeK5yEVhfN2icfmvkncs9puvvt7X+fV+95NaWjdzXe8+h1G06u39L3c\nCE8+/gR8fvP7yf7rGD3elqrC3Mk8uaV6O71MCr9gU3k4cSCuh7eEMtjN9XwcV/fbBa25uTScQCp0\ntQZrpCOsju1/N4cD2VuBIliZTLHqJlE8D08RHDtf3N5TSMgtNZg/AD/cWi6GZnmkS0Z7kNpM6hTH\nAvpetQo7baz63DckbJPXvpHedrcSPaIQjQmMpmR54gTTp+/CUzVoXUssKzm+OvZOfmr2KfSIQErQ\nHYt7vvs1rEgUR48Sa1TJ5xQ4IAOzQU3Vq7loT5G1tYqFblCuq6awOpFmdWKXdvaAYCQjgRcPa+1H\ngH0vyZDDg1QEK5NpVl3pDzwEHL1Q2tZzKBKySw2M5M0t8LQbVPMxNNslVTK73Lwa1CdTERRHEl3n\n2UFu3qz1636dbI5EFCJRgWlIlianuHb6DqSq4bbdnOfrYw/zE3NPE4m23GxbvPU7AW7eh8Xxthvx\nVs33TpZIwIxpgWk5rq5cd+G1w4SRigROuh9EN4cD2VuIVAVua/rOUwRqv2pkfdCsAVnv+wkhKI0l\nqQzH0SwXV1MHtgOo5eM4HbNNG8NPoBVGoYiBFRnX2K/CPHI8yrUrJtOn78DTNhYsUlmMDlFX4yRp\nkh/SKK74eTsRyyRimSgKFIb39ymgqKeZiY/zhTseIf6JeY43HTwhqOWilIYT7RX9Wj5GrOl0hf25\nqsLSdVYJD9kCB0SSIYePTjdLxS+Ish36FY7adwhBcSxFeTixNTcX4rgRlcxyEy0gNBQ60g+2mJ7x\n5ONP8CXvt3jhy/vHVUePR7l21WT69J09bvaEynxshIYaJYFJvqBSXHV73Dy0D93cOYjVTYdY3QYP\n4nWLmNHh5pH1EOBqPka0YXe1e3M1ZduV/kO2wQFz8/77pRxEhKA8FPdnpTo2rw1r+33luoqneNKv\nxmY42LqyaVn9vYinKljxre1z52xTarVBYbHZ1RsLYGkLJ0LNdElU/Xzjf/vBX+Rr/zG1rd52txJN\nE0ydjvFsMrgUvIKHqUZIuk2GRzX0CKwuu7iuJJFQGB7TiUT213dkDQl8a/jtvJw7BxLyS36hFQGo\nUpIuGuiW688+gl9m/0gazXSIGg6upmAkeitih4SEhLQRgnIhTna5Gbp5i25upiI019y80qCw1Ovm\nrQxSdNMhXrVACH4q/S9xHlf3zWSzpvtu/nait+0QgMDDVCIkXJPhMR09IlhdWXfzyJiOvs/c3B7E\nSklhoU6ybHalxnW6WbPc9V7sQrB8NINuOkQMB1dTMRJa6OaQLRMOZPcI1UKMVNlAt7yuwggSvxz5\nxpwcT+DPahFQvlxAbrnJwokMdvTgfwrtnTUAACAASURBVMS1QgJXU8gt+bPAdlRlZSyJHR+co5Re\nbpBbabZPttmVJj/5zy2q+yzceKoxyyt6Em9D+X4hJVnLL6ohhCCX18nl93/eFsD/8p5/xshMNbCA\nE/jhfbG6jWa5OB0XlU5UwzkEv4mQkJCdoTIUJ1kxr8/Njsf4lV43z5/I7vtKoVuhNpTA0xQ/j97x\nsKIqq+NJ7NhgD2WWG2Q73bzcoDSS4MnHn+Cpn3mGZ//p/uh7frw5x2uRBJ7o/qxV6ZG1a0DLzQWd\nXGF/unljKHG8ZrcLoQWhSIgHuNmOaofiejVk5wm/NXsFIfwCCBs3b/h7LWR2+UgKs1VMIrvU8Mvh\nt+6jSJBSMjRXY34qt/v7vgdoZmI0M8Gzn0Folktupdl1shWtvONmSt9X4cZvK/2IC+njmET9purS\nQ5Mejy59H3XTLOH9xds+7PAR5ZcZvlbpK8o2wu+P5oRtX64LtZUbp9kuRkKnkYluORwwJOTAIETX\nILa9ecPfa1VBlyfT7f6XuQFuXpja/zm0W6GRjdHIbt3NuumQDXLzYoNGUud9n3sEHn9kX7j53tJr\nvJk6hqXouIqGkB5qy83KAXBzUD5sqmRs6mYp/L7ioZuvD9V2SRUNNMfDSOiBhVEPE+FAdg8hRW+V\nYuie7RWAIiVWx8xVsmoFSjZiuAjX23dhTDeDtWq0GxHA+JUK81NZnIh6XcWgbMujXvdQFUEyraDs\n8gkm7pl8bPqveSVzhmuJcdJOg7vLbzBq7t+Kh0F0SnNLR1SCs8/Cs/YK0YbN6HQFpN+jLVG1yK40\nmZvKhueTkEPHVt0sPInVsdKa6OPmqOEgPBlODAUQH+DmiQ1u/ttfjW8rFciyPBo30c0J1+Bj01/h\nh9mzXIuPkXbq3FN6gxFre8U99xo32sJQyLCv+PUSrduMXqsgpP+bSFQtMqt+lMdhdXM4kN1D1DJR\nUgNCMtaQQpAqGcQatj/bO7BIVCjK7SAAxZOMTleYPZUDIfi3H/xFFE/yb77xe6gMrvqxtGBTXGt6\nLvznO3oiQjyxuyftmGdxX/GHnL72Gq+kTvO3I28jKSzurl7geHN+V197t3n4M/f4s/Ad1DNR4jW7\n77fbA8x4GKoUhOJ4pFebxBo2TkSlWohjxTqOk5QMz9a6zkOKBByP7EqTUlDF0pCQA0w9E/XDJTe7\no6DbzZu0iQsJoE9uZJCbP/jf11De/0n+zTf+74HRR1JKlhZsSqtu+8l8N0eJJ3b34j/uWdy3+gqn\n6q/ySvoMT428nSQWb62e52hzYVdfe6dZi4gaRD0TJV7fzM16uBobgOJ4ZFabRFturhTi2D1urva4\nWbM9MqsG5VZKw2EjvMrbQ5RGkkQNB930T7Zrs5I9JwRPdoXerDU77ryfBIyEFtinLcTvn5VdbvSd\n+VUdj1jVIr/cRLNdEPC7Zz/Oh2af4XT9WuBz1mtuuzIwANL/HK5dsThzewyxi8ULpJRcnvZ45v7H\nMOIpPE2jCMwlRrm39Br3ll7btdfeTYJ6woL/+RkJjVjD6fl9yNbtqxNh1cONqLbLxKUSwvNXWqXh\nkqhYLB9Jtxuqr/Vf3ogi/dnfcCAbctgojiaIGA66tZmb2Zqbk3q4GtuHrbg5XrPaYdsI+J2zP8t/\n9z/ksT75fwY/Z92j1KoMDLTdPHPV5PRtu+/mS9MezzzwYcxYssPNY9xffIW3lV/ftdfeSba6CtvI\nRDDKA9ycibA6Hrp5I6rtMvFmCSE73FxtublVPE2zPJSAhStFQrJiHtqB7OFch96jSFUwfyLLwvEM\nxbEkK+PJnjnGNSl25Y903OYJ8BS/fPlKeCHfFyeiUhxJ9J/DFTC0UEe3XBQJiufPBv/NxLv4dx/4\npN/nTNFxO07V5WKHKDfQqO9uq6Rq2eXS8CmMuC/KNVxV5/n8nTSVm9ePTkqJt81WUht58vEnBotT\nCBaPZajmou2iKx7+9391NM7KkXR4oRhAfr7uf5db/xf4/x6aq7Z7yw06bhsb1IeEHAakqjA/lWXx\n2A26WYCjh24ehBNRKQ1v4ua5Orrltd2sepLf/PVV/t0Hg91cKjqBbpYSmo3ddXOl5HJp5Ex7ELuG\nq2o8V7gLQ7l5RZ6u183bCiVec3M2yM0JViZDNwdRmPejoLrcLKEw2+nm/o8/zMc0XJHdawiBFdex\nWhV3PU2hMFdD8SQCMKMaEdPpma0UgKMKKsN+j9VmMmwtshm1QhzF9citGL15TJL2Md+4PbdY59O3\n/WMito0iJW8pX+Ch1ZeQfUaxngczVy1SaZXhMW1XWt5Uyi7Ldx3r6VkH4AmFz079NCfqMzy6/DwJ\n19zx1wdwXcnCrE216oKEaEwwPhkhtsW2DQCxpz7Kr/zG+NbuLATF8RTVQrzdH7aRiuCGIUvBSEmi\nT8iX8PyVWCei4moKdlT1c+w77uMJqOaiN2tvQ0L2FkJgJvR2ISdPVRiaryE63Ww5PT1nBWBrCtWh\nGLauYoRu3pTqkO/m7Gqvm5Eg6OPm+TqfPvdzqK5E9xzuWHNzn7Gq5/kRU6m0ysiYtistbypll+Wp\nY12D2PbrC5U/mPoHnKxf45Glvyfu7S03X3curBAUJ1JUh+KtFkr+Srurh24OREri9d4VbGhN1Dge\nrq7i6ip2RCVihm7uJBzI7nGaqQgzZ/JotoenCoSEIxeDCwXYUZVqPrinaEgw1aEEyZpfCl5phRtJ\nAbVMhFTVYmNKrADirZAZT6h4Al7JneON9BRj+XlGX3mJVKm3yJKUUK241OsuJ8/E0LSdvZARCkSM\nhm9mZYOchK/9K8kjrETz/NzVL+1KxcRrV0wMQ7abBZqG5Oplk5NnYuj65u/3ycefgN/Y/uuu5XmG\nDCbSSlkIQuBXXF1j6UiasasVVGf9B9BIRajlt159NCTkINNMR7iW6nCzJ5l8sxR4Xyd087apDCdI\n1Gw0u9vN9UyEZNVio8IEEG+uDwYcRePllptHc3OMvvIyqXJ/NzfqLlO74GZFgYjRHOjmS8kjrETy\nfHz6yzvuZikl1y633NzCNCTTLTdrfdx8owWdoOXmofB7vxkRw+l7m8DvVLLG0pE041crfohxa/Gk\nkY5Qyx1eN4cD2f2AEF2J8UZCJ1q3u+LCPQGV8GJ+20jFD+dOlg0SVQtXU6jmYzi6Srpi9d6f3rwo\nKRRMLcbV/HGuvesod33/KQoLM8Gv50FxxWFkbGfDiXJ5jaOXf8TS5Em8jbLs2E9DjXI1McFUY3ZH\nX99oepgdg9j2a3pQWrUZGesf2rwTwgzZArJ/9VVPEXgdFQ9dXWX2VI5Yw0F1PMyYdij6XoaEbItO\nN6t+gbmNuYGhm68PqQjmp7IkSwaJ2rqbXU0huQ03G1qMq4UTXHvkGHc/9w3yi8Hu8zworToMj+6s\nm7N5jaOXXmN5/PgAN6s0tBjTiXFONOZ29PUNQ2KavSd9KaG42nstspWCTiE7zyA3d1YjdiMqM6dz\nxBo2qiMx49qhL5wV5sjuQ5Ym/R6yfj6swBN+MQojdfPyIA8SUhHU8nEWj2dZmUxjxXU8TaGSj+F1\nmNHbbKJWKHiqxhtvfxd6NvizkBKazZ3PyUmmVI5R5OxLz6I6NrjBq2+OUClFMjv++rYl+xbINo3g\nGeZN82BDrhvF8YgYTlfRJiumBubRSKA8HHChLQRGUqeejYaD2JCQLbB8JI2R6HCzAsXRpB9OHLJt\npCKoFbrd7Ooq1dwNuDk9wM27kC+bTCkckyuceeW7KAPc7KJQ0nfDzV5gJLuUYJnd7/fJx58IB7G7\nzJqbRZebtb5uLo30c3PEd/MhH8RCuCK7L5GqwuKxDKrjoTie34/rECd67xalkQRmXCddbKK4kkY6\nQrTpDCwtD9CMJPj6oz/L2NULnH35uygbEnQikZ3/rKSUNBqSidJFRmcvc/XMXUyfuasnZ1aTLnmr\nvOOvH42JntVY8FPBNrY3CGqnE3IdSEnEdFFtDyvm588gJYX5OqmK2Z7hrWajFMeSIARLR9J+f1j8\n26TwIzyqYchwSMgN46kKi8czqK3K36Gbd4fSaAIzoZEpGghX0shEiDY2d3MjmuQb7/lZxq6e58zL\n30XZUNciGt2dz6rRkEyWzjM28yZXztzNtdN39rhZxaOwG26OKoGFroSAWMvNoZN3mC43a7i6AlIy\nNFcjWbWQApBQzcUojSZ8N0+mGb3W6+bDHDK8VcKB7D7G1RRcLVxU3zWEoJmOtNuSAOiGQ6xRbhWc\n6PMwwFNUFo6dRiA599J3NtxDcv61Jp4Hui4Ym9RJpm5sVs00JLbj20r1XE5ceJmF42cwFAUU/7kV\nzyXhNDnW2Pm+spGoQjKlUK95yFaEsavp6NIhm18/zfRrpxOyPRTHY3S6gm657QFrPRvFUwTJiuk3\nS29dvKTKJo6uUB1KYCZ0Zs7kSVQsVNfDiOuYCS0sPhMSsoO4uuJfvIbsDkLQTEdpptcL3OhJ381B\n4ZnthwGuojJ//AzC8zj7yve6bndlt5vHJ3USN+hmoylx1tzsupw4/zILx85gKmo7Z1bxXFJOg6O7\n0PM9GlNIJBUa9W43R6RDLq+FTt5hFMdjbLqC1nKz0ppMlggSVavLzemSgasrVAtxzKTOzOk8yaqJ\n4kqMhI4ZD928FcKBbAh4kljT8cvWhxe1A7FjGgsnsuQW60RbuVB9G3+rGrPHz3Hm1edQHBc9IlAV\nKBfXV2htW3LtisXkMZ105vp/jo7jV3Fcc7jiedz7zS9y/s4HWZk4jiLgZG2ad668sCuFngAmj0ZY\nXnJ4LXGCC2+5H0ePoEmXaul1/uXTj/H+J41ded3DyPBsdb1yYevjTJZMRECejSIhu2pQHfJ7zHmq\nEhZtCgnZD3iSWNNGChFe1G6CHdNYOJ4lt7QFNysas1O3cea17yNcj0hEIBRJZYObp69YHDmuk0rv\nnJtVz+Xeb36RC3c9yMr4MRQBp2pXeefKCwNXk2+EyWMRVpYcXk2d5OJt9+LoEaIJlc+l4n6Mcfi9\n2jFGZqroG9ycKpmB30dFQma12S5W6WlKWBTuOggHsoeceM1ieLba+p9AAktH0+0WA5rlkl5tEjFc\nrJhGZSh26EuoWzGNxeNZkJLcYoN0yfBn2QLu66kKf/ypT/GFn3yWZz/1Mpcv9hapAJidtjl1Tt1S\ndd8gYvHe8KGIaXDXD/6O4RmNwvDO5Wh5rsQwPFRNEI2urzoIRVA9NcX50XfgKP6pxUble8N387VP\nrsLw4WzWvdMojkes2VuqX4G+fYwVd3cmL0JCQnaHeLXlZgGbujmuUSmEbrbiW3ezq6r85yeeQAjJ\n//jF3+PyxeDWNzNXbU6fU/tW992MeICbo2aTu/7+aUbGNPJDO+dm15WYhoemCSIdblYUQfnUKS6M\nPth2s2FA1mwigWro5h1BcTyiRh8393tM6OYbJox9OcSotsvwTBXFo/VHonqS0emKP0vZdJi4VCJd\nMokZDumSweSlEvqAUuGHCiEojSWZOZPHjGmBJyopBHYswmNfey9/eNv7Bz7d1Utm3160m6FpgvyQ\n1jWxKoS/PZffufmqlWWbC68bzFy1uHLR5PJFA8de3+fv5+9qi3INf9bR6D/KCtkWsXpv64nNMGPh\nnGVIyH5BtV2GZ6socoObr1UQniTStLvdXDSYvFRGN0M3A11utmJqsJsV381WLMYfnX3PwKe7ITfr\ngnxB7XWzLsjmdtDNSzYXW26+vOZmp8PNhWA3Z0M37xihm28N4UD2EJOsBM9ACgmJqkVhoYbSMZsp\nAOFBfrF+0/ZxP+CpCqvjSeSGekdr1aTXDNZIJQee4xxbMn3ZwjSur3LiyJjOxNEI8YRCNCooDGuc\nOB1FUXcmbKhec1lecJDSb1UgpZ+bOzO9/j2q6cnAxwpPIrxQljdKrG4zNF8PXGGQQCPlV0yVHds8\ngV/sKSQkZF+QLJvBxfM8SFRNhubrAW6W5BcaN3M39zyeqrAyntrUzc3kYDfbtuTaZQvTvD43Dwe5\n+dTOublWdVleDHDz1XU3F6PBFZEVTw7MKw7ZGrGaNdDN9dDNu0Y4FXCIUdz+J7BkxSRi9JaJF0Cs\nsfVZ37X2H509Kg8idkxjfipLdqlBtOng6iql4XhXS6T548cxo1Giptk3F6bZ8LjypsmxqQjxxPbD\nxNIZlXRm58PLpJTMzwaHRZuGxLI8Hvxpj+rVOLGAFXtPFYHl5UO2R27Rv4DdiARcFVbHU6iOR3al\niW46WDGN8lAcJxqe6kNC9guKK/s6IlG20M1gN0cb9jZe4xC5+USW3HKDSNPB0VXKG9w8e3IKKxIh\nYll9j3uj4XHlosmxqWhPJf7NEELsqpsXBrjZtjz+3T/8JcYvlYgGfG9cVfhVdENuiPxio7+bNUFx\nPEXF8ciuNNBNt+XmRNjabgcIr24OMc1kxA/53IAvRCewwfhW0SyX4dkakdagxoqpLE+mD3TPKzuq\nsXy0fx84qSj81c//l/zk7/8BEat/mwApYWHWZurM3jlWlZKL0+caSQj4P97xMywrE0RHbUanK10n\ndE9AcSQRFpTYASJWcA9CgNmpHFJT8DSF5SPpm7hXISEhO4mR0skUg90ca9p93byVM6zv5mp7otqK\naSxPpg62m2MaS1ty82fR7cFuXpyzOHF67xTLKxcdnD5rC1o6wm8+/DEASqNJRq71urkUunlH0Ae6\nOdvh5p3vFXzYOdhTcSEDMRP95zGEADsi+obbDMqTFZ5k/ErZb/qML9eI4TJ+pXzow0vruRx/+ktP\nUE+n8QbIwzTldefk7AYry/0/b1PRKA4P+/9O6Cwey2DGNDwBVkRlZSJF/bD1QpPSb9VUs9orHzuB\n06fdlqcIZNiKKyTkQGAk+hcAEnKwm7WAVbf2Y9tudjvc7IRuBmr5PH/6S5+ikUoOdLNh7C03r670\n/7zrTUlpeAgAI6mzeDSDGVPbbl6eDN28U/RrhempAqkd3EmivUC4InuYEQIzphILCCH2hMDVVITV\nO4CRCmi2i90nST1etfycyM6XwpdoompSz3acONeEcIhmBD1N469+4Z/wtm8+w20vvBQ8s77HxiRu\nn8p6EnjhkXfh6usXXmZCZ34qe5P2bO/R3UdOIKSkUohTHo7f8Pe8PBSnsFDvmVUvD8UO1W8oJORA\nIwRWVA0MBfVUgacqCAJuU/yVoX7hiomq2dfN8apFI7vel/UwtmVxdZ0v/MJ/xb1/9wxnX3o50M2K\n4ocK7xVcp7+bn3/Po3ja+nWamdSZT+Zu0p7tPVTb77+u2R1uHopT3oGqzaXhfm4O2+nsNuFA9pBT\nGk0GhoKWRuIort9ftifuX/phtP3QbDcw91ZI0Gx/Bkw3HArzdaKGgxRQy0YpjSYPTR6lGY/z3Q/9\nGM1Uiru+8z30jtggISCXV29IlpbpsThv02x4KKqgMKSSK2hbek4pJStLNpWyCwgyWZV4XKFe6529\nNONxXn3gvuvez4PIyLXOPnL+DyGz2sSOqjQy0YGP3Yx6LoaQktxSE0VKpIById7uQxcSEnIwKI4F\nu7k4kkCzPaLNZk9InZBgD8i502xvgJv9gXGk5ebImptzUYojSTgsbk4kePaxD9FMJrjjuee73Oxo\nGqO5G1uNNU2PpZabVVWQ346bPcnKsk2l5ILw3RyLCxr13n0yEgneePvbbmhfDxojMxV0a4ObV5pY\nUY1mOjLwsZtRz0YRniS3vOZmQbkQoxr2bN91woHsIWctFDS/2EA3HVxNoTQcp5GNoTgemVUDKddn\ncD3hh6gMyqexYhpS0CNMKfzbVNtl/GoZ4bVmgyWkyiaa7bF07HDlD7z8jodIliucevU1PE1FdVwu\n33aO2m8/xMd/6U+QUmI0JbWqg6IKMhkVPTJ4uda2/IJRXmvc6XmSpQUHy5KMTQw+WTuO5M3zBrI9\nZpWsLDnoEVCSGk7D9U/SgKtpPPuhDx66WftBqLZLxAzoIychXTRueCALUMvHqeViKJ7EU0R4/ENC\nDiBmwg8FzS/V0U0XR1coDydoZKIojke6aCC9bjc3b9DNmuUydqXcHjwLCalSy80DckwPIi++650k\nqzVOvvYj3A43/6fHPsQXxW/zgy+pGE2PWtVFVQXprLZpH3jL8rga4GbbloyOD3azbXtcOm92dMpZ\nd7Mb1xBGt5u//diHQjd0oFnu+gRzB76bmzc8kEUIaoU4tXzo5ptNOJAN6RsK6mkK81NZ8ot1YnUb\nqQh/5XSTMAwjqWNHVHTLbQvRE+BEVJpJndxioz2IXUOREGvYaJZ7oItObEQqCs9++Mf5wbsfJV0q\nUs3mMFJJ+DK88JFP8a9+9zepVlxfXgJWFh3Gj+hksv1/uqvLTluU7deRUC66DI9IVC345Op5Hm++\nYQa2lGt4Gs8//G6G5+YZmZ2jms/x0jseYunokRt49/ufWN3yJ4EsF0dTqGX6y3An83EQAm+HWjeE\nhITsTfqFgrbdvFAn1vDdXM3F/PSFAawNdLUNbrYjKkZSJ7/Q6BnkKtJv+6VaLu4hc/O3PvIYz7/n\nUdKlEtVcDiPpt0r5iPxXPCq/xOnLP2q7efkG3FxadRkakah9zumet3EQu07D03juPe9lbGaW4bk5\nKvk8Lz/8EEtHJq/3rR8IYjWL/NLW3Kz2SZ26LkI333TCgWzIQJyIuv2ZWCFYOJElu9zwe9VKP+yi\nPORXxwtasfIf18rvOUSyXMNIJjCS3RMERy5dZqWhoEuXaqbAwtFTSCEozV3h/lSlbw+6ZjN4wCQE\nmJZHok/hgblrdt++6LrjkCmW+NbjH976mzrgROs2I9eq7QtC3fbIrfRWGgXwgGbqBmd8Q0JCQlo4\nEXX7EUxCMH88S3al4feqFVDPRP0cwQFulkKg24drILuGkUy2B7BrHL34JscuXERKqGYLLBw5BUJQ\nnrvMfekqSp8wbKPR382WKYkngh83Oz3YzelymWd+InTzGrG6xcjMFt0soBG6eV8TDmRDdgWpCEqj\nSUqjvc2erZhGtOH0lsyW/sxwiM/JV19Dt22unLmbK+feiqf4R2zuxDlqxTd5f+WFwMcJRUBATUvP\nA13vU1nPk9Sq/VcMPSGoZQ5GaJnwJLnFOqmKiZD+KsXqaHLbF2n5pd6+cf2aoXuqoBIWfQgJCbnF\nSHUTNzd7B7NCytDNHZz64avots3lc2/l6pm7/V68EmZPnKOxeoH3VF8KfmBQgjJrbu63GisD61O0\nbxeCeuZgtFsTriS/VCdZNhG03DyWxNW3993LBfR07edmVxVUC2Ee635mj9VGDTkMVPMxULrbB2wl\n9/aw4SmCZjzFldve6lceVBRQFDxN583CaRajhZ7HSCmxjGDpafogWTKwCaEnBG/e+ZbreRt7CykZ\nvVohVTZRPP+6Il6zmbhSRmwz9HdQ37iNVPMx/2InJCQkZI9SKcSQCj1ubqYi2x5MHGSkotBIprl6\n9m7fzWLdzeeHz7Ic6Q0Hl1JiW8HPp0dA6+Nm1x2caukJwaW33H49b2NvISVj02WSZRNFdrj5chmx\nzdDf0M2Hi/DTC7npuLrK/IkMRkLzV6sUQTUfY2lya7OKuulQmKkydqlEdrGO4uxg7uEe4s0772Rp\n8kRgSJGrKFxK9Oan2pbsG4I0CFWFZrw391m2/nz9Yz+DmbjxEvW3mojhEDG7K3GvtZ9Ilc1tPZfd\nZ3V7I1IQijIkJGTP4+oq88ezGHHfzW7LzcuTqS09vtPNmaX6ztYF2ENcvKvl5oDbHEXjcrLXzZYp\n+/b+HTSLvDZO3siam7/68X+EFd//0T7RpoNuuoFuTlaCw4L74Wxx0kUKkKGb9z1haHHILcGOaiwe\n336v0VjVZHSmBvgnuajpkikazJ7KHbgZ4/njxxiaKyLoFaAUCqrsnXXslzcLtAtJrOoZni/cxUJ0\niLRT477iq3z6/T/D1Kuv8a6v/A1aq92AxM+N+uo/+ijzJ47v1Nu6pegBfRnBL2gSMXp7Jg+iPJJg\nuCMPB/xjFvQJNG60ImJISEjITcCOaSye2L6b4xWTkdluN2dXDWZP53G1gzVYmJ06QX6+hJDBg9Ov\nnXuA+7/7w65tiiqCMn4AfyIZYCWS5fv5O1mKDpFxatxb/CFHm4v83Yd+nHd89es9bv6bj3+MxePH\ndu6N3UL6raL6bt76CitAaSTB8Gzo5sNCOJAN2T9IychsraeZOxKG5mrbGhgrrkesZoOAZjKC3ItV\n5oTgtfvv5uiFYs8JWAr4/AOP8ueR9/Lvv/jp9nZNE8TiCs0NRSWEgMKQxkoky18c+QCuUJFCoa4n\n+EJilETZ4PIdb8FMxHnrt75DqlxmeWKcFx55J6WRkZvwZm8O/ULXPQHWgN7IQTRTEVYmUuQXG6iO\n54eCJzUSVbs1lQxIWJ5I4R2wC7mQkJCQNlIy3MfNhbkqS8e24WbHI163kXvdzQ/c09fNjUyUJx9/\ngqd+5hme/ad+vqyuC6IxgdGUG5+K/JDGciTHXx75AI5QoMPNKxMpGpkozWSSe579DqlyhaXJCV58\n5J2Uhodv0hveffrlYHticG/kIJrpCCvjSfJLzcFunkyH0VIHgHAgG7Jv0Cw3uJk7EG1sfTUtWTIo\nLNTXH9w6od1wH7FdwNMUliZTDM/VurYXRxPtQdmTjz/B//pXv43R9DCakmxOxfMklikRwi/vnyuo\npLMqXyncjSPUrlglRUJhsUEjE2Vuaoq5qamb+RZvKmZc81tDmW47r2Jtdrue236P10Ym6veGXYvn\nFoKi6xGr24BfrCIMXQoJCTnI6EZwtWMBxOo35ualI2mMPVhV1tMUlidTDG1w8+pYsu3m933uEb74\n2PN8588VjKYkV9AoLvs93dfcnC+opDMqXyrc03Lz+pFUJOQX6jTSEWZPnWT21Mmb+h5vJmZcw2m5\nee0IrLm5lr0ON2djNLKxXjfv9QWMkG0TDmRD9g8Dcj+3ejrSLJfCQn095KT19/BslZkz+Vb1QUm8\nZpGoWniKoJ6NYcX7/1QUxyNq6fSCDgAAIABJREFUODia4s8c7nAT7GYmykxSJ16zQUqaqUjXCp/i\nODxdG2Fyerr9llQFJo9qCEUhGlPQWr1jF2NDgQk3wpMorsTr02N2R5GSRNUiWTaRAurZGM2UfnOa\nhwvBwvEMhYU6yaoFEoyExup46sZmZjv23VMVf3AbEhIScsi5UTePzFS5dibvTwi23BGvtdyci2HF\n+rtZdTwiu+jmRiaKMcDNqm3zW382xsTMTHubosLkMR0hRICbe/dPvZVuzsVoJm+um/MLdZIVvyrW\nmptvaDJ4o5uvY1AcsrcJB7Ih+wanT3iJBKwthp4kWi1XAm+rWtSyUUauVYk1bBTpP3eqbFIaTlDd\n2D5FSnKLDTIlA9maXnUiKgvHMjseSuqpCvU+J+C7vvs9RmZnu4o8uS7MTDsUhlWaDQ9FgXRWJeEY\nGGpwqXnZp/fdZiiOR6pk4KmCeiaKVATxmi/DiOkiFUEtE6GWj6MbDsMzVTRXti9w4nWbeibK6sTW\nCorcKFJVWJlMs9IxUxsSEhIScn3YfQaTEjBjW3NzsjzAzTWLeibK6HSVaLPbzcWRBLVCr5vzi3XS\nJX9Attbab/Emu/nuZ7/L8Nx8t5sdmLlqUxhWadRdVFWQzmokXANL7V15Xmvfdj10urmWjYGAeNUi\nWfHd7Cm+s6v5GBHDYWSmirrBzbVslOL4zXGzt+bmidDNIVtn4EBWCJEBRqSUFzdsv0dK2adR1tYR\nQjwG/CagAr8npfzVG33OkAOMEKyOJSgsNLpCT4AtV1UUA0r6Ck8Sr9ntQSy00ikk5Jcb1LPRLgkm\nKxbpkoGQ68+rmy4jM1UW+hTLUFyPzEqTeM32e4sW4jTTEYQrSZeaxKv+9mohhpHskJqUZFZLaBY4\nkRi2DqOz0yiey7kXX0ZzXCRQHJmkns4hPBdH1bik6QzPXSFdLbK86LB6m4JEIjrmyT3A0QQTl0rg\nSTzVw47qqK6fN1rNx/r2WM3PVUmX13sKFBYauJpAdWT7+AHklpukiyaq47VTVNrHREKyYlItxLC3\nmad6Q4SSDNmnhG4O2VMIwepogsJir5tXtjhBKbxBbvYnmtcGsbDu5sJSg0Y22hVRk6yYpEpmy83+\ntojpMjxb7VtLQ3E8MqstN2uCSn7NzR7pouGvAqsK1UIcI6mvP3CDmx1dMjI7jZCSsy+/gub2cbOq\nMTx3lUzNd/Odn2jwzN+ne9xsa4LJiyVA4ikdbo613NynyGWgm1WB6na7WV9ukC4aaK3uDxvdnCqb\nVPPxvgsJu0Lo5pBt0PeqUQjxceB/BxaFEDrwC1LK51o3/z5w7428sBBCBX4b+DHgGvCcEOLzUspX\nb+R5Qw42tXwcJ6KRW6qj2h5mQqc0kthy/9lmKkJm1Qic+W2mImSXextpgy/lWMPuChlNF5uBTbcj\nhoPqeD2VGoXrMXGpjOJ47fzMyGyVSiFGqmygWZ7fKxZI1ExWR5JUhxMU5he4/6lvc/7uhwHwFAfF\n88gv1bjthWfQbRtbj/DCuz6MEU/iahqdOrpy7q3oZpO3fvuvec8X/pwrZ+9i+sw9SCHwFAWhqOi2\nRCD9fBIHoqYNQhBrOKRLBgvHsz3h1bGqRbps9YSOqY7s2aZIEK1BbCASYnX75g5kQ0L2IaGbQ/Yi\ntYI/2MktNVBtDyOhU96Om9OR9sRwz20pnfxiHzcL3x2dbs6sGoFujjUdFMfrWZVVXI+JyyUUR/pu\ntiDSrFLOx0iXDTTb9WOCpUOiZrE6mqA6lGB4bo63P/0dLtzV6WaXwmKNsy99i4jlu/kHj3wEM5bo\ndfNtb0M3GrztW18h8T9/hZNn7+bq2Xtaz+W7ObLmZgC5wc1Fg4UT2Z7w6ljVDHazex1uBuINi2p0\n/7f4CTmYDIqxeBK4T0r5NuC/Bj4rhPiHrdt2YrrkQeCClPJNKaUF/DHw0zvwvCEHHCOpMz+VY+Zs\ngeUj6S2LEvxZzHomiifW+7B5AiqFOE5ExVNE31RcKWBkZobJS5fRTAvN6l/EIqiBd7pooLhe149O\nkZBdMdBNpz2I9Z9AobBUJ1Jv8qE//jPevOMBPE3H0/RW43WN4sgkxdGjCODCHQ/QSGZw9YifAytE\n1x87Guf77/sHLE6cYOr8K7zrr/+Y+5/+PPmlWYTskFvn4/B/6IqEwnx3QQuA3HIj+L33OyZ9j5Z/\no3edoc0hIYeM0M0hexIjGWm7eWWbbjbjGo10pMfN5aE4rr65m0evXfPdbPV3swSUgJVf382yx825\nVQPdcvxBLLTdWFisE6s3+OCffo4373hwg5t1VkePUB4+ggDO3/UQzUS6v5tjCZ77wEdZGj/G1PmX\neeQr/5n7n/48ueX5bjd3vD5s4ualHXQz/qA6JGSvMmj5Q5VSzgFIKb8nhHgf8FdCiGMMLLuzZY4A\n0x3/vwY8tAPPGxLSHyFYHU9Sz0RJVtaKDUWx4n6oUD0XIxWQqyOQfPiP/oCo0QQJmm1z8Y77mT35\nFqTaLWvNsXEivSf+eN0OnFEWUiLV3p+i6jhM/egi9UweT+m9IPA0nbnj5xibucTSkame/dj4vgF+\ndO+7yX3t/yVqNknUq1Tzo1sK44mYLsKTXXm0ijt4FrcHKQe+Vmc/tzMvvsS9f/cMUcOgkUrxnQ99\nkJnTp7bzaiEhB5XQzSEHDyFYmUhRzzokKqZfST4babu5lvOd3bNiKyUf+ezvE7EskBLNtrlw14PM\nnbit1822jaP3ujlWs7bt5hOvXaCWKSADiid6ms7csTOMzl5mafLEltz82n3vIffVPyNimS03j2zN\nzYbb41YlYOV1IIPcLKCxVjVaSs6++BL3fvNbRAyDRjrFsz/2Y8yePrjVlEP2PoMGslUhxOm1HBwp\n5ZwQ4r3AXwB33oydAxBCfBL4JMCYHu/qmRkSshmxpz7a9X8pJeXPX2Xx06/hrpqkPzDJ2CfvQh9b\nD5t54WsKz3xOQVFbM5UC7vne10hVKl3PdeLCyywdOYmjR/E0DTwPxXO58+Vn+Of/+m5it3Xn4nz5\nd1XeeE7408fdewWe7F6RBRCChzMzlN3BzcDNaBwvQLb9WJ44wZHLPwJAt0ycyBaq+AXsdiMdIVM0\ne4U5QIobm5KvzbovHc20KxPe9e3vcO8z32rfL1Wt8oHP/X88/ZM/wZW33Lb5voaEHGz2nJujmYPT\nazrkFiElUz96nTuee56o0eTaqVO8/PBDgD+QteI6peHEeiSQAIngnme/SrLW3cN26o2XWJ44scHN\nHrf/4JssT36QaiHf9dKupiBxAwZ/rapSG3wmFd/NxUFuFgIzGkcGTEL3Y3niBJNX3gB8N7v6FtoO\nBai2mY6glW7MzSDRo/DT/63LkXMLAMz/h5dY+JuX2/dIVar82Of+nBOfeZTcTxzffF9vArf/+p/y\nwpfDFKWDwLu2eL9Bn/anAEUIccdaboyUstoqAvFzN7qDwAxwrOP/R1vbupBS/i7wuwC3x3M7Mdsc\ncsCRUuI4/vnaeN+fd922vGizuuy0qwiufOYNSv/PG0ydibXL4N8OnFAizMTH0KVDfmmWhasG3obX\niVgmDz71F8yeOEdx5AixRpUjl14jXStR+vgsuUL3z+vOaIE3J9+Ho6xvF9Ij3qhiRJPd4TueR8Ro\nMPqDHyErLsLb+OqgODbj0+d58Z0/vq3j43bMDh+9+AoX73pw4EBY8VzO1K7yL770J13bLaHyhyd+\nClvpKM8vJYrnguf5oVYtNMvk3A+/y7U7305DjyOkxFVUzlYu8+jy86gXZOvhkjdeM3r2QQDv/+Jf\ncfbNrwe/J0dSKbs4jkciqZJIKoiwYMSWeduHt97r8aCRvNU7sH32nJvTE2dvuZu/5P3Wrd6FG+ag\nX4B3ulnb0E5mad6iuOq23XzH3/+Au1/6ASdPx1A77ttUoszER9fdvBTkZoMHnvpLZqfOURyeJN6o\ncvTSa6RqJT71pc+Sy3cf5/noEF+cfO8GN7skG1Ua0WSXy/A8YvUaw6+/gVd2AwtI+m6+wAvvemwb\nR0fgdnj46MUf8uad9w90s+o5nK1e6XGzKTT+cOqncIQW4GbpD+5b6JbB2R9+j+k776WpxxASXEXh\nXPkSj6z8PeovSgz8z27h1V43A0z/s28Se0twDq3jSKotNydTKvHE7rr5hbAZy6FDyAFVXAGEEK8A\nnwV+HYi1/r5fSvnwDb2wEBrwBvABfEk+B3xCSvnDfo+5PZ6TnznzyI28bMgBx2h6zF6zsC3/e62o\nkM2rDA3pIODi6wYbv/JCQH5IZWQsePazWnGZn7EIGEsGoigwfiRCOtM7E3s+dZxnhu9DIvCEYNgq\n8Z7L3+QFc5QLdz7ohzIJQaxR44EXv85tEw5XL5nMJ8d46cEPAAJPVVFch+zqIo6qUi2M9c6y9mkt\no7gO93/zCyQqZYTwj8/CQw/xw/y5nhApxXUQimDMWOGx+WfQZe9gxxQa3x56O1eSR1Clyx2VCxx5\n/SUuahNUMwUU1yG3vECmvIIiJKdvj7EaL9BUooyaq8Q8q+v5XEdy4fVgWQKcuyPWI8FGw+XaFb8n\nrJR+GlI8rnD0RCQczIZsyrte+eLzUsr7b/V+bJfQzSH7iWbDY26m2825vEphWAcJF98IdnNhWGN4\nVA94RqiUHeZnbeQ23DxxNEIq3evm11NTfGv47YDAEwoj5irvvvxNfmCPc/GOB9pujjeqPPDiNzg3\n4XDlTZP59DgvP/B+EAJPabl5ZQFbj1ALCg8e4OYHnv5L4rWq72YN5h96mB/mzgbeVyiCcWOZH59/\nBl32rgybQuNbw/dyJTGJJl3uKp9n/PWXuahPUsvkUV2H3PI86fIKigKnb4uxEh/CUCKMmStEPbvr\n+RxbcvGN/m6+7c7egWyj3nIz64vBiaTCkeOhm0M2Z6tu3srUxUPArwHfBtLAH7H1Fd++SCkdIcQv\nAX+NX+L/M4NEGRKyGY4jmb5sdg04PReKyy7lVZfRCZ1Wu9cupIRGvb8J4wml5zGDEAKSqeDiCGdr\nVzlVu0YxkiHqWaSdBujwgHGFya++STkzhGZbDHsVjhzxT/bHpqKkVpbJPf055iemUDNxtHqNV07e\nh6tFgkOFhADHho7ZXE8RVIYSnEo3MHWVaEwhnVE5U3qJ+yuvcUUMMW8n0Gp1cmYZbSLPiKiRt6t9\n32tUOrxv+TlYfq69zRnSqF2cZnhhup2xJwSMjGuoimDELPZ9vm1EYQH+LPHstNV1ISM9/6KpVHTI\nF4IvgPrhupJS0aFScnFsiaYLhkd00tmb2HogJGRrhG4O2Rc4jmT6itl1nvZcWF12KRVdRseuz82J\nhArS7nv7Rga5+bbaZc7Urna7OQL3Ny9x5GtvUk4X0C2LEVlh4qjv5uMno6RXlsg//TnmJ0+ipmNo\n9XrLzfoANzvQERnlKYLYQwonf2BgRjvcXHyB+8uvclUUmLcT6LU6OauMOr41N79/6Xtd25xhjfqF\nq7gLV7vcPDrmu3nUXO37fIPSfINou1l2bvM/z3LJ7VkV3wzXlZRWHT/yas3No3rggkHI4WIr3yQb\naAJx/FnfS1Judf5rMFLKLwFf2onnCjm4NBsui3M2piXRNBgdD55RrZScvgNOz4PiSv/b9YACEGto\nmmBoRGNlqf/jYT1c6sjxCMqACrwqHsNWqWtbKq1yLqVg22VURaBq63mriiIYGtEZGoFT4hpfGXqU\nuclhfwW136ym9EBRka08IjOhUR5OYCZ0fu2/+OWuXHPbllRW6sSNGrfHBPmChp5RwJnr/2YHoGmC\nqdMxiis29aqHpgvyQxrJ1ObCEUIQjQlMo/dAx+O9IUmmIQNXyqWEStHd1kC2XHKYn+m+KLJMydyM\nheNq2x4Uh4TsMqGbQ24pjbrL0rzvZl0XjI7rgef5ctHpW4bMc6FUHOTm/i7VdEFhWOtKFwpCCP++\nm60EBrk5k9VIZ+Smbj7ZcvP85NAW3Kz4bhYCM65RGklg1XTe8wl44cvrkWG27VFZqRE3qr6bh3bA\nzWdiFJdt6jWvffwSyS24WRFEogLLDHBzovf6yTBk4Gey5ubtDGTLRX/lvRPLlMxds3DHNXKhmw81\nW6mp/Ry+LB8AHgX+sRDiz3Z1r0JCWtSqDlcvWf5J0QPbgpmrFsWV3jBX2wo+ca5hGpKgukZCQH54\n8El1aETn6Ak/XDgSWX/cGoVhlROnopw8GyUau75S9UIIIhGlKx9oDcvymF6Q/EXmncxFh/0CEn1F\nKX2RKgoCgQJEm05X24EnH38CANPwuHzBYHXFpVH3KK64XLpoYjRv7HpY0wQjYxGmzsQ4eiK6pUHs\nGkdPRHpmfxUVJo8HhH4Pik7aRuSSZXkszAbP7EsJS/MO3lZjy0NCbg6hm0NuGbWKw/TldTdbpuTa\nFYvSaoCb7cFuNpoD3Dw02M3DozpHjkdIZVT0ADcPjWi+m89EiUZ3x81XF+Avsu9kPjq0PTfLlptb\n7fo+ovxy+66+m02KHW6+fMHENHbAzePrbt7KIHaNYyciPVFTqgZHjvW6WTCghPp23Gx6LMz1d/Pi\nQujmw85WpkT+Gynl91v/ngN+WgjxT3Zxn0JC2mxcIVtjcd4mV1C7ZlfjSYVyyR0ozKPHo8zN2DQb\nHrRaso1N6MTjmwvOLyLkn8VdV7ZDnpJJBUXdvXwP0/T4jnWM1x96x2BJQis2SyI2mEKRkF1q0Eyt\nC+fJx5/gU7/9H3tWNKUHC3MWJ07FdvBdbB1NUzh9W4x6zcUyJZGoIJlSA2fSo1GBqoCz4T0IAdlt\nzPhWNvneSAnXrlgcm4qGuT0he4XQzSG3jLk+bl6Ys8nmN7g5oQw8xwoBR45HmV9zM36tg7EJndgW\n3JxMqe3JUteVNGq+35MpZWB01I1iGh7fdk9w/qEHt+jm3jGcIiG33GS+5eYnH3+Cf//FT7MwZ/e4\n2fP843v85BY6DewCmq5wZqtujgkUBdxAN2998FweEGkH/vXKtas2x8KaGIeWTa/0OkTZue2zu7M7\nISHrSCkZVN3esiTR6PqJK51WWYk4gaEvAOmMiqYrHJuK4jgS15VEIuK6Tn6qKm5KboYtVL6ReStX\nj9y2aU854bpI4YFU/My2DUTM3pnyajPwrhhNiZTylolBCEEqrfmZf5vcb/J4lGuXTeRasScBiZRC\nNrf1z8f7/9l78yDZrvrO83vO3XJfal9eLW/RkwRIAhkDwgJJYAJE2W5bNs207bYxMbajn3sYR9sx\nQz/P/DExMx2ObuzocUxMN55uYv6YdowXAQZjN5jNCC0YJHggCdDy3qtX+5b7ctdz5o+bmZXLvblU\nZVZmVZ1PhAJerqcy897P/Z3zO78fa2PKCnrZrb4YjUsolxhyWffHGYtLPc1qCwT9QLhZMCw4997S\nUcWyXLdWicYkHOzZtUJPDRD3fqXOzczhUI7j5hOoaWARCV+OvwXr863FmJqpuplw4tmXVjEaJwWu\nr1zDr3/ijz1fqxroD4te3Dy/oGF9tdHN4QhFrIfvh7XvPggA0EsM+ZyDaKzRzfGEhGBIuPmsI+pU\nC/qGaTAUCwyUApGYBNPg2N02YegcVALGxmUkx+Wu5dTpcc0TrYS6xRcOdk2k06yhmIGqEkzP1rWD\nkUlL+f9Ro0xV/PnC4zAkrauZ3kJcQ6iwC9kMN7TYqaLqRQATDbfZigLJMFpfkhLsaOOQwDFhpntr\nrn7CBIMUl68GkM85sG2OUFhCINjbRVAkKiGT6rwqm8s6KJcZsunDx+YyDhJjEmJxGeUyg6IQhCOi\n/Y9AIBgNWt3MsLttHbp5QkZyrHs3d4I2V9mlBEuXNOzvmsg0u1kjmGpyM0bczSVJw19ceByG5FNs\nsQrnAHHdHM5vgzoxOB5xlVYuoNnNpixDNVtXvblEsa2NQ+YOxs3MaLs5RHHpagCFnAPb4QiFJM/9\ntO2IxKSOmXY1N1cKSdW7OTkmIRKXoQs3n1lEICs4Epxz2BaHJBNQSmo94Kpsb1oNVQgdG9jbsbG3\na4MSN3CYnFYgtynkAAChMEGp2HoGkyRAUVtPiJJEMDWrYXKGQy9zGAaDqpKB9y7rNwwEf7Xw/o5B\nLAfAJIrt5ThsVcLFlzex+OoNrN79lobed9S2EUutA1hqeP4rD9yPe1/4LmT7cLU2NT2PHz74brdX\nAQFUx8Tj29/EeFMRjFGCSqSnVOJmgiGKSFRCId9emIyjIYgF3N94+sBBpvr7J4BEgYWLGlSP36hA\nIBAMCs44bNt1MyHA3o51eG6Cj5u3bext26BSnZvbBJOEEIRCBKVS68lSluHpdUkimJ7VMFXvZo14\nFvEbZRwQ/NWF93cMYpvdHHtxHQuvfh93rj7Q4uZoZhPAcsPzX73vPtx94wZk+/C7O5i+gB/9xLvd\n/GRCoDkmHt9+CmNmtr9/ZB+RjunmUJgiHKEoFljHFOPmgJdzIHXg1K5NCXEvaxYvap7Xj4LTifgm\nBT2T3rfw2o903HrNwGs/0rFxx6g1Mq/+B7SW0ndvdPd55LIOVm/qYE77lM75RRVKU0E6QoDFi949\nXw8f4waviaRbke80iZID+MrU21GSgh1ne3NJDZuXErBVd5p38+IyLtz8Ia7eeBbBQtaVZHoPb/jO\nV7F1ab7lJb73rp/CxsVl2JIEU1VRiMTw4lsfg6VosCQFFlVQlEP4/NyjyOTd8vfHLTYxihBCMHtB\nwdyCikiUehajIARQZJ/fNQ5/+5y53RU210zvBwoEAkGf4ZzjYN/Caz8+dPPmulnLNOnoZrhpnLmM\ng9XX9Y7bLeaXVMhNbqaVCbx2NLg5dPrc/OWph1CWAp3dPBZocvNFLLz+Eu76/nMIFHOgjo1oag9v\n+PZXsHXxQstLvPDIu7C5vAxbrrg5msDLb30UlqzCklRYVEFBDuHzs2ffzXMLKuYutHez3IWbWdXN\n68LNZwmxIivoiWzGXVWtP2EU8kc7eTqO+3rJcf/S6ZRSXLoaRLnkoFhg0DSCSOx0ya8XylTF1yd/\nEnfCc20rH4JzZMcDyExHGu6avb0KEIKZjZugzMHq1QdQDsdw+5634GCqNZBlkoSv/8I/QSSTQfwg\nBVOJI1BqmuEiBDYjeMmewsTWnepNiCcpJqZUSAMsdHWSuHt/JESi7j6b9VXDzYCr/NYTY5K7ypFr\nPzNcxTR4rd+dQCAQDJJcxsFBs5tzR3dzLmO3bWtCKcXlq0GUSg5KBQYt4J4/z66bNXx16m1YD810\ndHNmIojsVLjhrrlbtwBCMLv+OiTm4PbVB1COxHDr3geRmppteSkmy/jaEz+PaDqNWCoNq+Lmhncm\nBBaneNmaxPjWWvWms+nmmIRITEK55GB91Wxwc7LiZuQO09bboetu1sKoby8TdIcIZAU9kerQS7UX\nOHcL6HRDMHT2N+3n5RA+feF90Kl/OjGHWzFhZzEGI9y6Kv3A089CYgwbS1fx+hvfBia7h3hBmcD0\nWg47S3GYgdbDvpBIoJBIILldAC157JklBKZyWMWYcyCTYsimdSwsq2fuuwmGKpWT8wwO4wiFKVSV\nwrI4DnZbi2b5wcHRTa8Bxtwq2ARu9e1BVtoUCARnj4MOvVR7oRc3h0ISQmfs/N9MTg7j0xfeB4P6\npxN3dPOzz0FiDOvL9+DmG36ill5sKxOYvpPD9lIcloeb88kk8skkxrYKIPBxc11v23o3Ly6rCJyx\n7yYYkhrcHA5TKCqFZTLs79rdxLGukbs8VoSbRx8RyAq6Qi8z5LM2TK+qg0ekWuhB4PKtsfthyBrA\n/UQJAARbyzFYAe+Z8lChAEYIbt37E7Ug1n0aAeFAYreE3cWY7xj0sIpI1gBt/poJQfxgp3VMHLhz\n28TCknrmKvdS2lr9UlEIZuYUtzl75WviPosestJdQbFC3qmlOlV7781fUBGOnq3PUyAQ9J+qmz0r\nAh8R4eZGnht/ALqk+U5JVt28uRyH7RGMAkCw5uYHG/bI1ty8V8LeQjs3KwjnvN2c8HHz6m0Ti2dw\notnTzSrF9Jzi9oPv4GZFIV1lSuVzNrbWrYa5i7kFtdbqSTAaiEBW0JH9XQupPs72Vum11+dZ55X4\nMqQ2+5I4ATYvJeEo/lvbU1NTSO4dgHlULSbwbsFTTzmiwAzIUHW7JkxqW5hev4lwwaegBAfWbpvQ\nKtUnz1pA20wsISMclVAsuAUkgkGK9TsmLJPXWgwQAsxe6NzXzrY5NtfMw71rlds31kxcuhoQqU8C\ngcCXapHFgbg5IdwMAG9+3MZ/eG0BtE2WNifAxuUkmOzv5vTkJGLpHLiHEwgAVW/v5lJURTQlQTWc\nBjfPrL2OYCnvMzDgzq3z4+Z4Qkakzs2BIMX6qgnb5uCs0c2dsC2OrXWrYW85AGzcMXH5asBNZRaM\nBOJMJQDgFooo5h2kUzYcB4hEKZLjCmybHyuIJQRYWFYhKwQ7mxaKBdcGWoBgZl4VF+pwe8YBwPxr\nKcBDlrzy3958tG0QCwDPP/ouvO8vnvRNm7HbiBaAmxq1EEMkqyOcM8EJcN+3nsX8rR93/DsMg2N9\n1cTCRQ3BLprYn2YkiSAWPzx9Ll/SkM+75f8VlSCWkLv6beez/k3y8jkHyTFxihYIzjOccxTyDjIp\nGw4DIpGKmy1+rCC2WjRRklvdPDuvigt11LmZpEA9pFpz84Vo2yAWAL7z6CN47199xjc12VY6BJmE\nYGcxjkhGRzjv7hG9/7mnMbf6ase/o+rmxYsaAufNzZc1FHIOyqXe3JzL+k8s5HMOEsLNI4P4JgRw\nHI7br+uw61qWGbqD1L7bH9NPlIS46ZOWxT0DJ0KAWPxwb+uFJc2thMjddinnAc45igWGTMoGY0A0\nThFPyKCU4M2P2/gg/VjtsflEAPGDckPqEAfgSAT781EYIf/CG1X25+bwpQ9/CBde2UBufL4hvZgR\nIDsR6jxoSlBIBlFIBgEAL+IBTK/fhGxZHXd7cg4c7Fq4sNS+cuVZg1BXnrF4b89jjHseX5yjY0Vv\ngUBwtnFsjts3m9xcdt0WVv2dAAAgAElEQVQcT7Z3s6IQmG3cHE9KCATPt5sLeYZs2nVzLCEhHpdA\nKnsgq0EsUHFzytvNexeiMIOd3bx3YR5f/qe/iPnXNpEbnwOTmt0c7DxoSlAYC6IwVufmjVuQbLs7\nN+9ZmF88X26m1A1eY4nenuc4bdzcoaK34GQRgawAO1tmgyircO5WQqxt3KuDEGBiSkFyXMLabRN6\nubGSqywDM/MqQuHG2b/ztlF+d9tq6DuqlxnyGQef/J3fBaeNn01uPAjVcBAsmLXP3NRk7C5EwaXu\nZ1Gn19bwhu8+h9tX34ztxatglMKRKNLTYZSjnVNqmtlZXMBn/tuP4t7nn8fd370BpUNAaxjiJN8t\noYgE4lFAjRCIfTgCwTlnu42b/bI5CAEmpxUkxiSs3TKg640X5LICzMwJN3u5OZdx8Mlr/32rmyeC\nUA0bwaJ16OaAjN0LPbr5zhre+PxzuHnPg9hZuKvm5tRMGHqkdzdvLy3hM7/5UdzznYqbOwS0hi7c\n3C2RqIT0QWvGg3Dz6CEC2XMO5xz5rP/mD8dxD1yv01807jYyX1hSkUnblaCXIJGUEEuc3TL83WKZ\nrEGUQGVywJax8OpruHP31cYnEHflVTYdKIYDW6GeVQzbsfjKq3jz089CsSwsvv4SyuEY0pNzkByG\nQMlCOaqC9SDeKuVoBC88+gi+++534R1f/BIuv/wjUMfxlKYmioR0TTBIEY1JyOcOfyfVTIajpoDx\nygud9+NPIDjNcM7bts+pudlDztFKi7oLyxoyaRv5qpvHJMTiws2m4eNmS8KF129i7a4rjU8gBPsX\nYsdy89KPfowHnnkWim1j8fWXoIdjSE/MQnIYgkULeuRobi5Fo3jhsUfx3UfejXf+3Rdx8Uc/AnWY\nt5sD5/t774VAkCISk1BodnNCghYQbh4lRCAr6MjktIy9ncb9AlOzCpTKfk1CCZLjStt+sOeRUtH7\nIkSxLFy4eas1kK1gq1KtiXqvvOlb34ZiWbAlGc+/62dgqZrbpR5AOGdC1R1sXYy3b+beBk4pnn38\nA3j+sUfxk1/+KpZ+/AoU53BloLpSL+iemXkF0biEbMYGQBBPSAhHehelaTBsbZi1thmRKMXMnNjr\nJhCcVbzcPD2n1CqyUkowNq5gTLi5gXZunr91qzWQrXAcN9/3rX+EYtuwZQUvvGsFltLkZsPB1vLx\n3Pz0yuP49nsexdv//itYePW1FjePT4rfQbcQQjA7r6AYk5DN2iAgiB3RzYbBsF3v5ljFzeckjX/Q\niED2jOE4HKbBa+XFHYfDcdx/E0JQLDhI7duwLLc35viEjGCIoFzyTjlRVSA5riAak1HIu2nGkagk\nijR1gSQRz7Rsh1KUQ13sVT0CwWIBALA7fxGOLNdECbhDkS0HgZIF3aPPXS+YgQCeXnkc2YlxvPHb\nz0PTdaQnJvCT//cDkP/gac/nuKv/DrIZV67xpFRbOTjPEEIQiUqI9NBup1R0kEk7sC0GgIBz3tL3\nsZBnWL2pY/mKBr3sVm0UffAEguHQ4mabgzEOuc7NB/s27KqbJ9u7WdOIcPMRkeSTd3OgWAQA7Fy4\nBEfycLPpQCvZMMLHCzbNYBBP/ewK3vTct1w3GwZSk5N42396APK//qbnczjnyGUdN6sOws1VCCGI\nxCREYt27uVhwkE07sO02bs4xrOoGli+rrpu527teuPloiED2jMA5x/6ujfSBXUs3ovQw/YhSIByl\nyGcP97JmTQf5rIP5BRVrq6bn685XivbIChFV2npk7Nkn8Ppdn4VW1hvSfDileO3+N/X9/aKpNLRS\nGRxAMZZs7FVXh2I40MN9eENC8OI73o4X3/H22k2ff5oDH7wf/+Zv/0PDQzl3qybWz4SXSwz5nIO5\nLtrUCA7Z27GQPqjfV+u/78mygNd/bNT+zTkwM6cgJlprCAQnAucc+zsW0inH182RGEUu0+TmnIP5\nBQVrtz02yQKYW3QnI4WbeyccoVDCEsx84z5jTilef1P/3Rw7OIBW1sEBFKJj/m42nWMHsgBcNz/0\nDrz40DtqN/3NUxz44H2ebl67baJcOnRzqcRQyDPMddGmRnBIazusNm42eaub55WGisuC7jjbdbjP\nEdmMXbu4Zcw9KKpZJdX/Xy/KKowB2ayDK/cEEE9SSBJAJSCepLhyjwZVFT+Ro3B95Rp+/0/m8aUP\nfwilSASWosBUVZiqgqdWHkc+mezvG3KO93zms7XqhZFsCtSrSggAS+v/iVKyGSbXclj8cQqLP07h\n39/3K/izf/vPavfns05LOhfn7sxk/Wwl57y2j0TQimWypiC2M4wd/sc5sL1pwTTaNEUUCAR9I5O2\naxe3fm7Opj3c7AC5LBNuHgD/08/+Dp584p+hFA7DVKtuVvGNn11BIdFj6flOcI73PvnZWk2JSO6g\njZv7X0RIshxMNbj5V2H+1RO1+7MZpyGIdcfsOlsvH94u3Nwe02Q9t8NqcfOGBdMUbu4VEfqfEdL7\nR+8nVyoySBLBzJwGzPV3XOeN+pL9AJCemsJf/YvfwsT2NiTbwd7sTENLnH4RS6URyeZqM1NTm7dx\n694HYVKplsJEHAchvQA92P8geno1C9k6LDARKNnIfRL49/f9Cn7jR3+N1P6+79MLORuGTpFN29Ar\nVRVDIYrpOQWqJi7W6vHb29ULnLsTX5PTYrZdIBg0XpVPu0W4ub889Kn78diTDwMAUtPT+Mtrv42J\nrW1IzuDcnDg4QLBYrLl5ev0mbt/9ZrBmN5fzMAL9d/PMag6SXe9mC5/6HxWU7/sVfPSHn23r5nzO\nRrnsurla8TgUrrhZTKQ0UCr0x825jIOJKfHZ9oL4tM4IzjF6Tg7g3H3uuL5yrSWIrUEI9mdnsbNw\nYSCiBADJtsHr9ldIjo0Hv/E3mNi+A+I4oLaN6fWbeODZL2L2zlpf3ztYsBpECbh7fgjcgPa/LP8M\nDrSY7/NTBw52tqxaEAu4qU13bhnH+l2fRSit7O06Jo535w6BQNBnHPs4bhZbLvrF9ZVrtSC2BiHY\nnxuwmy0bvG7rjOzY+ImnvoDxnfWam2fWXsMDz34R0+sbfX3vUN4EZd5uDpZs/JeLP4tcJOr7/NS+\ng90tq6FtT6nIcOemIfqcN0El9MnN4nPtFRHCnBGCYdq2VL8fhADjE6KS3VGpn+FtRjYdaGUbjkyh\nh+QjVyPshszkBBwqQcFhylJAL+FN3/l6w+NsWUYslcLW8lLf3lsxHRCfcy8BQDjH7av34b7veBea\n8IMxIJexRTXsOsJR6lWjpCdIpSiMQCAYPKEwRSF/NDePTYhLtH7QPMlcdbMtUxgDdnNqarIhkAWA\nQLmI+7791YbbLFlGLJXGzuJC395bthiIz0+v6uZby/fhDalnenpdxoBc1hF7s+uIRCQQWMLNQ0D8\nCs8Ik1MKSgUDrI0vKXX7iOllXusNOzEp91SRTXDI9ZVrwJMed3CO8a0CQvnDAlqORLGzFIOjDOaz\n5pTiqZ/5IB777OdAGIPEGDhaJwg5IchMTvb1vU1NAifwDWYpB3YvLMN54RlI7X6gTXAOGIaYnayH\nUoILSyrWV00wjlpEW71OCkcoQNyK2YmkjHzWbti3Q4hbHfEoLQQEAkHvTE4rKBU7uFkCAhpBuc7N\nk1OyuKg9Ji1ZUs1uJhU3Lw7QzZKEb648jkc+9zdt3QxCkJkc7+t7W2pnN28tXsLd33vuCG4Weznr\noRLB/KKKjTsmOEeDc4HKJDQhoBRIJGVkM3ZDL2NC3EmvUFi4uVdEIHtGUDWK5csaDvZt6CUGRSXQ\nAgSFPINjA6EIxcSkDEWlsG0O2+ZQVSLKfR+Bd/7g9/Dox8u+90cyupvSUycPYjNMbuSxvZwY2Lg2\nL13EX3/0I7jrxvcRyeYwf+sWFMOo7R9wJIrs2Bh2Lsz39X31sAJblaAYjmdmDQNQSETw1MrjePuX\nvwrFcCv1zcwwHGzBd/8YIW5TckEjwZCEK/cEUCq6BWIkCjAOaAHakooYCKoIRdxWPZxxxBKirYJA\ncJJ4u5mikHPgOO7k0/iUAkUhsC0O2xFu7gdeW31a3MwBwhgmNwrYXu5zkac61q9cxud+49dx5fs/\nQCSbxfzNW1BMs+ZmW5KQmZjA3lx/N0KXIwpsRXKzpjzuZwTIJ6N4+oMfwE9+5atQDDfAn55hSLVz\nMxVu9iIUlnDl7gBKJea21pIIGAcCAdrSz10LKIhEJGQyNjiDcPMxIKepCtk9wQT/1BXvNE6B4CTw\n3Qdbx+ytDFSjdRMiI8DmpcTAZn4DRQvx/RJki8EIyjCCHG956h+w8PpNMEpx8w334PlHHoGt9b/I\nD3EYEnslRDNukFo9FXMAnAKbFyt/N+cIFEuwNBWaruMX/vQ/Q/bZsCnJwKW7AuKCTjBQfurFLzzP\nOX/rsMdxmhFuFowK7SaaZ29moJqtvuEEWL+cBJMHE5wFiibi+2XIFoMelGEGGR78xj/gws1brpvf\neC+ef+TdsNX+u5k6DIndEiJZLzcTbFxKuH93nZsDpTJ+/j99ytfNsgxcFG4WDJhu3SxWZAWCLugm\ngK1CmP/kkN9+leMSyuoY3y7WZpqlvIlgAXj2A4/jGwNot9MMlyjSMxFkpsJI7hQRyRkAB4yAjNRM\n+DB4JwR6xG1iW1IUfO/hd+LNTz8Lmdnu0m2FSJRgalYTojxhOOdiRlggEJxKrq9cA9pkSxGfhRsO\ngDKOQeg5nNExtnPo5nDeRKgIPP34CuwBtNtphkkUqdkI0lNhJHfr3Bx03VwL3uvcXIwr+P4734H7\nn/0WZMduKMoQiVJMz6rCzSeMcLM/IpAdYSyTYW/HRrHggFJADbg/4oBGkRhz04QFg6WXALZKMaoi\nltYbUosBgFECexDfGecNQSxQmXXlHIm9EvYu+FcM7vtQKEFqNoLUTLgykPYn3pfe/jZsLS/h0osv\nQ3Ic/HT6hwiFadsTNuccxQKDY3MEQ1S06OkDpsmws2mhVGQgBIjFJUzOKJAkIU6BoBnTZNjbsVAq\nsEY3BypuVsQ56STptN2nSimqIurlZonCHsR3xnlDEAtU3Mw4EntF7J+km6Xe3PyDh96BjYsXcfml\nl0EdB+/L/BDBkHDzSWMaDDtbjW6emlFAhZtriEB2RLFtjts3DbBKZgdjgF1wz4algoN02sHCkoZg\nSJwoBsGbH7fxQfqxIz03Nx5EuGACFgPllRQeAhzMRQdSHTFQND2LORAQhHNl7OHkZHn45t3/nanp\naaSmpwEA38JP4+t/GMQz9/2R52NNg+HObQOcHe7ficYkzMwrYrbyiDgOx2rduYZztyKloTMsXtLE\n5yoQ1GFbHKuvHxZvanFzysHCsoag2EN4InRaha0nNx50Cz3ZjW7en4sMxM3BvL+bI7ky9kfdzTPT\nSM0cuvmBn8vgw7/9Z56PNQyGtVtGQxHCaFzCzJxw81FxbI7VWx5uNhgWLwo3VxGB7IiSPnA3gPvB\nGbC9YeLiXYGTG9QphzGObNpGPscgSUBiTEY40prac5RV2Hq4RLG1nEAoZyBQtGArFIVEAI46mDSi\nUM50U6Y8TmpquQxV12EGTs/v5NGPl4GVa/g3X/i/Wu7bWDPh2I235XMOQmGKeLL1dGaZDHu7NkoF\nB1QiSI5JSIzJ504AjsNRLDgAB8IRqaHwRDbdeq6pVozWyxzBEKncxlHIM5gmQ0CjCEXaz86bBkMm\nZcM0OUIRikRCFrPIglNP6sBqW4GYM2Bnw8TyldNzzh023bq5nsDXnsC/+sRMb+8jUWxdTCCcM6BV\n3ZwMDKxuRShv+LpZKxWhGAYsTRvIew+CG59L4IaHmznn2LhjtvQnz2cdhMMUsUQXbh6XkEgKN9e7\nOePnZp3D0DkCwYqbGUehUHFzgHbMajMqbrYsjnCYIn7K3SwC2RGlXGK+FeOqmBaHY/OWamiCVjjj\nuHPLgGnw2udaLJgYm5AxMeX2Ke02PYkwjthB2S2ewDlKMQ2ZiSC4dDgDzylBMRFAMTH4ixmJeYsS\nnGNsdx35cYKdhQWEswZk04EZkFGKaeAjvsfl+sq1htVZ02CwzNaDgnMgk7JbAlnbdlcaq3J1HI69\nHRuGwTEz1/+iGqNKPmdja93CYQNaC1OzChKVz8vQue+5xjQYgiHqrkLd0uE47oU6oYCiECxe1DzT\nj4sFp9aGAABKRYb0gY3lSwFxvhKcavRS5wKZhsHBHH6qLw5PCtaFm5u5vnIN+ETr7YRxxPZL7j5Q\nAMWohqyHmwuJAAon4GbK4Ovm8Z01ZKYU7M3PI5w1oJgOjKCMUvR0uBlALaA1TQ7b8nZzOuW0BLK2\n1Zhx6Dgce9s2TINjevb8uDmXtbG9YdVV4LIwPacgnujgZuIGo4EghWVx3Lmpw2GHblZVgsVlzfP8\nU8g72Fyrc3OBIX3gYOmyt8tPAyL3ZURRte5+UER8g12RyzkNogTck2xq34ZtcVxfudZVEAvOMXUn\ni9hBGbLNIDsckYyOmdWcf636AVOKaqgZoR7OsPD6D2BoIcy9nkFyt4hYxsDYThFzNzOg9uj3gXv0\n4+WaNLln8z0Xr/pa6QO7ZeWEcyCXcTylexaxbY6tdcvta1dJx+Yc2N2yYJruh6MFiG+2WXWP09am\nCdtCbXaYM/fiZW/HankO5xxbG2bLsWbbwMF+6+MFgtNEV24m8D1XCRrJZ9u42W49T/tmTHGOqdUM\nYikdss0h2xzRobtZ9XXzhddfgqmFMF9xczRjYGy7iNlbp8PNwOF3wRl8f+9enVHSB1bLx8I5kE07\nnt/5WcS2ObY36txc8fPOpgWr6uagj5s5oFXcvL1hwrab3Gxw7O16u3nb080cqVPsZhEGjShj43LH\nrQyRCBWV47qkkHc8XWYoKv7zPT/d3Ytwjsm1HDTdaThwKAdkyzlssn7CFGMqHImgtvTIGGBbuPTy\nC9DDYQSLFJLDQCqmccdrI7FXHMp4j8L1lWv4X574HXj93KsFEJrxy2og5Pw0cy/kvNsncO5eQAJA\nPCmDNpmAEDfADQQJOOcoFTw+r7rXqMcyuee1GzhQyJ2Pz11wdkl24+aocHO35H3cTIh7Dq9yfeVa\n+yD2Tg6awTzdHCwM5yK9GNM83Xz5pW+jGI8hlHfb49S7WTFtxPdLQxnvUbi+cg3/6xPXenJzqeTt\nAUIAQz8fjsi3c3PlvkRCblmsIsQNcANBCsY4SsXWz6u6l7YZ0+Sek/7ue57ez10EsiMA57ySYmBi\nb8eEaTKoGsWFJRWK2nR2IIcXmecpPdILzjnKJYa9HRP7u4crTF60S5kwgt2lGI1vFhAs2Z4Tj5QD\natn2uGfwKIYDQiTURyMyY5CtAr7yxM9DNllrehOhiGT1Ex7pMSEEf/tLv9TwpxDiptEkx1t3Sfit\nnHAOyMr5uMhstxDBKkaTJILFSxpCEff3U734WFiqFJPocYK83QU8HXy3CYGgb9S7eX/HXSnRAhTz\niyqU5nNIxc0B4eaKm52u3Cz7uJkDkCrni051KyY28giU/d2slYcTyKqmAwLa6GbHgeSU8dWf/ydQ\nfNwczXRXvGpU4JTivz7xi5BChx4mxHVwYszDzT7dGzhH63F1RuHMf0tPNZNMkgmWLmoIhevcnHDd\n3PkNWm+i1N/nzZPZpwmxR3bIMMaxdsuAYfJaakBq38HYhIxEUsLFKxqY46YQ25a7wVtRSSUd8Hwc\n8F5wzrGzaSGXPZzNTe3bDXv/6kmMychlGmd+OQBbUbCzsNDx/QjjCOdN32wxRgB7QMWcOjG+XXB7\n11Z/D5TCUjW88O73QzWMw62RTcjWcALv47C9tIS//O3fxJXvv4hHXv5HhCIU0agE4hE8JT2+cxAg\nEKS1tJx6OHfFQgjOzLEVjlLs7bTeTggQiR4eJ6pKfeVIKEEoTD1nfiOx1t+8rBAEAgTlcuOvjhD3\nOxEITgNeezcP9m3XzWMSLt7l7ebAOa9WzDnH9qaFfJOb6/f+1ZMYkxs8XkWiwP/2oX/ZscoucThC\nBWs03bxVcFvv1LtZC+CFd78fgbJ/sCpbpy/Nc/PiMv78n/8GrvzgB3jk5W+7bo5Jni4dm5CRzzV+\n54QAwaB3y56z6OZIVML+rt3yu3fdfPh7VTWKhWVvN1NKEAzRhsyFKlGPlXBFcWMH3cvNHosBp4Xz\nfcYdEpxzZDM2Vm/quPmqDl3nLZXJUvs2br1mYGfTApXcH6yqUUTjEgLB9hXJzgPlEmuRX3Xvn+Ox\nxyIQoPjG4x+ApSgwVRWWoqAYi+JLH/4QeBdTUVKbPSscAIib4nvSEMah6k6LxAmAUNGCYpmIH2y1\n7NMhjo3E3tqJjbOfFGMx3Hj4nfiT3/pdxOKyZxALoLZyIiukIkA3HX9+sfV7ymVt3HxFx6s/1PHa\nj3Qc7Fmee3tOG6pKMTYht6xixxJSQ+sux+Y42LewsWbgYM9q2ac0PadAkg735BPiSnFy2rsYy9yC\nBlUlIJXFiOp7xhJiSVYwunDuVs9dvanj5iu6Z7GV1L6NW68a2NnydvN5p1RkDUEscLj3z3E83Byk\nmJpVQEjlXEHdybC//PWPdNUqprObCYrRk68MTBwGxWhN7yQAggXXzbHULpoLOVDHRmJv/YRG2V+K\n8RhuPPxT+JPf+l384S9/zPc61cvN4SjFnIebs5kz6maNIjkmtbg5nmw8jzg2x8Gev5tn5iturrwO\noYCiEkz6FEqbW9CgNLk5npQ8U8BPC6c3BD/FbG9YLbNRXlTz3IMh79YiZxHOea3yWrtg3WsGt0qx\n0Fglrz4tafXuq5jc3IKlqjiYme66p5ott79A2bkQa6iMeFLwNsPn4DiYnsK7//oLeOlt74WpBcEr\nf28kl0K5Q3uD00Bz9cRmwhEJl+6icGz3pO1Xxa9adAFwrysO9mxwzjExdfpTBCemFIQjEnIZGxxu\n2nB9EGuaDKs3D3vzFvMMqX0bi5e02sq1qlJcuhpAPufANNz0Sr+VcMC9EF2+okEvc9g2RyBAoPik\nkwkEo8LWhoVCt27OVNzsscp4Fqm6uVMl5uYgtgapuDnusSqblBGLSyiXGL7yP38Az/34StdudpT2\n55XthRj4MKqxthk/JxwHM9N41+f/Di++/X2wVA2cUAAc0ewBih6f0Wnkuk8bPaBLN+cc7GyeXTdP\nzqiIxJi/mw2G1Vutbl66pNVWrmtuzjqV9jsSIjH/xS5FIbh4RYNeZrBtdyLptKdzn42j5RRhGMxz\nE7Yfbvny1tYiZw3GOHa3rVoqqKIQTM8pvr3kfA+7umqRD33qfjz25MMNdzuKgu2lxZ7GRm2GSEaH\npVAoFmt4bw6gEFVhhrxnvwYOIeAELU3XOQBHpmCyjO889i781N99HtmxaRjBCILFLBSziGce/wBq\n+TqnnOsr1/C37E/wvb9rPU4IIZDbfD37u1bLhRfnwMGeg3DUQTB4+gP+YIgiGPIW/+5WYwXJamXj\nnU0LixcPVzIoJb4X7abprsIU8k7lcRKiTVIWCEYZQ2eexcv84NytjH7WA9kWN6sE07P+bm5Xrbnd\n5DSlBP/7h/874JX2r1GPZDOE27k5psIKDuf74QT+bpYkOIqCFx75KTz0xc8hOzblurmQgWyV8fQH\n33+m3Ax4TzZ3cvNeGzdHog4CZ9zNO35u3rIa0o0pJb4xgmky5DMOCoWKm5MSojEJwdDp/+yqnO0z\n8IjAOa/NOpU99pl1wrMC6IjAGPfdt2DbHLmMDb3MoKjupn/FZ/Z0e8NqqCxsWW6DbS1AYOjue8QT\nEiamFVBKEEvIyDbvfwRqTaWvr1wDnjz+36eWbUzfyYJw163N314+oSI9HTn+Gx0R4rAWUQLuWKVK\nCsrqvfcgOzGBu7/3PcysriGaTsORZbzn05+FHgrhSx/+JRQSiZMd+AD4IP0YsOK/OuuHV2/aKuu3\nTVy5J3CmU/m99r4C1arPvO3fbtscG3eMpj03bhG2Qt7B3MLJp/QJBN1S72a/SqrtaG7vNUp0cnM2\nbcPQO7t5a91EsXBYAd4yXTcHAgS6p5ul1toEQMXN3u/RqZiTF2rZwvSdnK+bcwkNmelwz6/bL6jD\nfd0sO+5ob73xDchMTuLq925gdvUOIpkMHFnGTz/5WZTDYXzpwx9CMR472YEPiHaTzX5Ybdrkra2a\nuHL3+XRzqdiFmy2OjTU/NzPMXTj9K9pVRCA7YIoFB9ubh/s2lV5/OwSIxNyTv64z7O1Y0MsMskww\nPil7pumcBIW8g90tC5bFQSiQHJMwMaXUDixdZ1i7ZTSIPrXvIJ6kmJ5VGw5A2+ae7XE4R+0g5BzI\npB3oOsfiRQ3BkLv3L7XfWLDoPZ/5EH7tmd5WXH3hHFNrObdYQwU3+QfIJzSkZ4YXwNYgBH7VnOqb\nqmcmJ7B++TIuv/gymKxia/EuFONJRLIpPPKZv8EXPvIrZ2L2F3CF+ce/vw39sU939XhVay1+UIVx\nVxqhEEUu56CYZ5AVNxWumtpj6AwH+zZM3U25HZuUPYtJjSqEeFc37vRz4Jxj/bYBw2h9MudAIc9Q\nLjGxKisYSZrdrPboZkKAaNXN5YqbddfNE5OKZ7GVk6DVzTImpuRDN5cZ1m63ujmRpJhqcrNl8YYg\ntgrnqBVzq7rZMDgWljWEQhKS4zLSB41unltQPSuaHyWIBWOY9nVzAOmZ4QWwVXib6u2s7r701CQ2\nLl3E5ZdehqNU3BxLIpJJ4ZG//jz+9td+5SSGeyL0Otmsqe5kiReMuZOtgSBFvhs3BynGJ2TPYlKj\nSjs3twtiOedYW3UL1bXe56Zs62V2Zvb0i0B2gJgGw8adxubDpuH/+Orvsvp4Qtzy2+MTCgyd4c5N\no3af6bjNlG2LY2ziZNNaSyUHm2uHfxdnQPrAAWPA9Kx7NbC9YXrOVmfTDFrARnLscMyWyX0P2Hrc\nwJbVDsCJKQWxhIRinoFQ4P/4xd/E//NMsF9/JkJZA9Sj6RYBEM6bSM/07a2ODKcEpbCCYMFqqNzG\nCJBPNq6G3fPCd1aa0oMAACAASURBVGGpQbzwrhUwSQKTZOzPLIEyG8mdA6RnJk528APkX31iBmiz\nP6eeyWkFa7e9ewATAtgWw+otq6F6afrAQTwpQZbdNKcqhuEgn3OweFE7NZIIR2hLDzlC3KqH7WRp\n6Bxmm9VszoFS0RGBrGDkMPRWNxvt3FyJkurdLMsEYxMK9DLDnVuNbt7aMGHbMpLjJ+zmopeb3T2F\nUzOum7d83JypuDlR72aLde3mconBqEzmTU4riCckFAuum6NRCZLceC45UgBbIZI1QDz+BgIgVDCQ\nxmgEsuWI6+b6v9x1c2PLv3uffwGmFsJ3H/4gGJXAZBn7M4ugjoPE7gEyU+MnO/gBc33lGr7+h0E8\nc98ftX3cxLSC9VVvN1PiTrTsbBmwzFY3S5I7QVPFMBzks6fPzYV8q5s7FWYydN4206zq5tPyOXTi\nbPwVI0rqoLW0djsiUYrlyxqSYxLCUYrJaRkXL2uQZNJmH58N7tXheIAceJQM5xzIph0wh8Nx3FYE\nfqQPGnOlVY10/zkRd59x7bkqxb/7tY/h3/7qx2AE+xfEAkA4Z3S7VWeoHMxGYAUkMAIw6oqyHFGR\nG2v8PFRdxyv3vwO2rIBJ7hwWk2XYsopQfnRz5GTTQShrQCtZna+omri+cq3jBVMoLGFswkcMHDAt\n3hDEVsmmnYYgtvYUDmyue8t31EjvWy2iBABVA6Zm2l+E2zZvu2pbnYgTCEaNdM9ullrcvHxFgyT5\nu9ltrXGybt7f83ZzJuWAMbfwmtcqTZUWN6v06G7WKJLjMhJJua9BLACE2rTCGyUOZiMwm9xciqot\ngayq63jlgYdgKwqYXHWzAltREc6N7t6y47j50Y+XO/4OwhEJyXFvN3PuLhbVB7FVsmmnIYitf87W\nKXHzwb6FYsHDzYEu3Gx14eZhFEAbEGJFdoC0mxFpnuWstqfIpGyYJkcwTBFLyLVKbnrZO9DgHLBs\nDlU9uR+l7yoMcS9u5Q4Xr83tcSTJ3YCeTXeuFgmOWmrIcWXohWLYUAwHjkQ9V2MrQ0ApPKTiTh5w\niWJ7OQFFtyFbDJYmefbNu331LpSis605o5RCGkVXco7xrQJCebOWPm0rFLuLcTgdqkg30656IuBW\n9i0VWUO7DULcfndFj7T3TlgmB2fct6rvKGBbHHs+fewmp5WOogsEO1zkEiDq0WdWIBg27TIJWtxM\ngVic1twcqrqZHm6j8YJz14cnWRHUMvwnJG2bdzymm9vjyHKPbu6iMvlRva3oNhTTgS1TUI82PpUh\noDxCbmY9uLmQ8OiiQCnoiLp5YrOAYKHezRJ2FmNgR3Bzu61Ak1MKykUGw2h08/ik7F8huw2myTvu\nLx02lsU9F4wIAaam1Y6Vwzu5mZwxN4tAdoBUGxV7/aDGp2Rk0w4cmyMQpIjGKDbXDmd2S0WG9IGN\n5UsByAqBrFLYPv3S5C5mVjh3Z2IZ5ygXDysnxxMSEmNyTwe1phHYXpvwuVtgIpthUDX/NOpQuPVE\nNzWjQFEJ0gcOHMdt16GXm2baCKAFCN7xCw5WpH/Z9Xi7gTCOyfUctLLdUKCBw7uAoh4avUPHCsiw\nAv73v/rA/bjwehactJ7A+AjmZkTTOkJ5090HVflOFJNhfCOP3aV4z6/XqXri4rKGXNZNDaaUIDEm\nIRSWKgUXel9Z0XWOYGgwsjRNhmzKhmW56UfRuOS5/6wdxYLjub+acyCfYwhH3Itf5nC371zTOUKW\nCZJjEtKp1osJSoH5RfVMzfoKzg7BEIVe9nHzpFtIsOrmiI+bly4HIMsEikI8e5cD3a161Lu5VHSQ\nzzCAHNHNAQrbYxUHcIPUYp5BUQHLZ1HK181Kxc3M282EAFqQtE1VPGoA27Obh1SluB2d3Pzjt7wF\nF27mau3x6vG6bdhEUzqChWY3O5jYLGB3sffiVO22AhFKsHCx4uasA0k6dLObTdS7mw2dIxAcnJsz\nKRu25fbGjcaO6GYPXDc7CIWl9m5W/CegKAUuLHUOhk8To3fEnyESYzIyKRtO3W+ymt8+PqFgvLK3\nlXOOW68aDT84zgHHdluDzMyrmJiUW/b0VFdxCXU3b1uWe3AGgo09pPQyw8aa6Rl87u3YKOQZLiyp\nXQvTXb0yWsaiagR3bpm18XtRXe1pvZ1gbFzBWN2eIkNn2NmyUC6x2gzSf/zIv8Anpf5XQk3sFqGV\n7YbiEX5wALRdA9cRxdY0FOIawjmzsunLhRGgEBu96rLRjN7yfRAAAd0GdRjYEfv2+q3OkkoJ++Yy\n9skxGXrZ7Hnmlw5owrNYcBrOBYW8g9SBjaWLWk9yIh0+vrVVo1ZlnVBgekZp6M8MuHuYtCBF+sCG\nYwOBoFtRPBzx72MnEAyb5LiMbLrVzfGEhPFJBeOTh26++Yre4ma76uY5FeOTSsO+1NprJSUQ4l54\n2m3dbMC2Wse4t2OjWGCYXzy+mzWNYK3qZp/nEuI+v/V2dy9wfS0OQ2fY2TRRLvPafvppn3THNz9u\nu0V+jkiyVzefiqTjRuyAhmJURajQ6uZi/BS5uWyBOAz8GG5+4Ocy+PBv/1nD7ZQSJJJumno9yXEJ\n2xveE1LtoAOauC/kG/eoF/JOre9rL8Fsp8N97baBcqnOzbNKS+HXqRkFwSBF6sAGY0AgcHbdLALZ\nASLLBEuXA9jfsVAsOKCSu4KRGGv82B3bXfnwolCZmQlHJEzPKdjbtmqFGuJJCckxCTdf0eHUTUwF\ngtSdcaEEjPGWCoX1VIs0lEsMoXB3V96BIMXCsobdbROGziHJBJEIQSbt/SaaRsA4RygsYXxChtJF\n+hHgzi4vXtTAOcdffPKXcePzya6edxQiWaMrUQIACKCPQPrSxOYWrn7vBjRdx+rdV3HrnrvBpfbf\n4cFMFLKVg2IcXsGZARmZqeEXx2jGq5gHUJmJZxw4RqDYbnW2mUiMIl6qzG5WB9ABRcFA0v0559ha\nN1surC2TI3Vge16I+hGJSABvvYImxL3Art/nzh1ge9OCotKG4k2EEMTiw6ueLhAcBVkmWLqkYX/X\nbutm2+YNwW49xbx7RyQqYXpWwd5Oo5sTHm4OhijmFytudjq7uVRk0MvdZ3a4blaxu23V3ByOUGTT\nHn8EcavCMsYRjkoYm/BvwdOMFqBYvBSo7QH2uzA+9vYfzhHu1c3D6ulex+TGJu66cQOqYWL17qu4\nfffVjm7en4ti+k4Oilnn5qCMzGRo0MPtGdKmLgvhR1kjPeTG5xK40WWhxmjMzZjKZXpws4qBVC7m\n3C3y5uXm9IFdmxzrhkhUwg683VwqOg3Zjtxx21eqKm3IiCDEDVybJ5/PImf/LxwyikIw26FfE6H+\nx1/9LE48ISMQJMhnGSgFonEZW2sG7MYq99DLDKl996K2kHc6HtvVYLbbQBZwhbx06TBXZmPNp7Ic\nBSZn2jRP70BtNvfzR3p613j1e/OCEaAQ1zz3uZwk937neTz4jW+C2jYogNnVVVz93g188b/5p22F\nySWK7aU4VN2GYjJYqgRzBFOxAKAUURHN6C3z645Me94j60c3ve0IIZieVTE2zlAsOsimnYa9tIeP\nc/9XkoELy9pAZj3dFMTW26spR70EslQimF9UsXHncJ8TgFq6sNd7pA4szIdGb4VAIOgVRaUd3Uzb\nHMMNbk5W3FzZlhCLy+5Ka5ObyyVWu6jNd7H33nVzb5W/gyEJS5cOHbBxx3uPDyXA1KzSk/eb8TvH\nPfSp+/HYkw8f+XUb3qPNZ1SfXsyI23pn2G5+wz9+G2/+5jOQKm6eu72Kqze+jy99+EPgbZYC3VoX\ndW7WJJiB0XRzOaoikmkthmnLFKxPKavdTDYTQjAzp2JsgqFUdJBJOZ6FGasDVWSCC0uD6Z/qdU0A\nVNycdXoKZCWJYG5BxeZak5vHpZaCbNX3SO3bmFs4O71he2E0j5JzAmMcB3uWO1vqcQAQAiTGDk/K\nB3uWW6UY7m97b8dufRIOKwhPTCmw7c7F5KqtBAC3AIxhMCgK6W3Wqs2bHLVw4yCKOdVDbYbkTtFN\n54H/nhsOwFApHFVCMREYejEJrVzGg//wFOS6pQLFsjG2u4flH72CW2+8t/0LEAIzqMDsb5HnvpOd\nCCJUMEEdBlqZ5eXErQTZz5633fa2U1SKhEoRT8goFRmKeXclJ55w29SUywyS5E7yDCp1p9oGxIuj\npEuFIxIu3x1AseCAM/ffpsWQ8Snu0q6AnUBwVmCMY3/Xcld6unDz/q6F1H73bh6fVODY3he+De9D\nDyt/19yskq6KKtW/51HuOyrXV64BTx7vNajNMNaFmwHXzbYqoZAIDD1TKlAs4cGnnobU4GYL49s7\nWHzlVazec3f7Fzglbs5MhNw9sg4H5QADgAG4GehusllVKdQ6Nxfy7l7aeEICCIFeYpDkwbqZtnVz\n7+8ZiVbcXJnwCkekyv5bHzdbo9t5YtCIQHaIbNwxPYtBVY+zaExCspLqZOjMDWIrj+1cQNB9RChE\nveq5tLxfJEqxvWEil3VqVRuDIYr5he42hccSMoqF1n2EnHsXkGhH4GtPuJv/BwnnmFnNQrZYTZDt\nPqPdxRi4PBpV3qbW18EkCc05b4plYemVLgLZUwKTKTYvJRDO6AiUbdgKRT4ZgKMM5nvoNt2YEIJw\nRGrJMogOaFz1qCqFopKWFhruhXXvp/NqoRlJIghGKSglINS/4mGvx7JAcBpZXzU9i0HV3Bw/TEOu\nZkB17eZamrEEQtq3ASJw3by1YSLf7OZKinInYgk3/bLFzUDfezz3ZfK5RzfvLMWPvCez30yvrcGR\npIZAFjh0c8dA9pTAZIrNi0mEszoCZQuWIqEwQDd3O9ns52alQ9/VfqCobuG35orohAAJnxZC7ai5\nWSYIhtq7mRAcK7PitCMC2SGh68y7ojEBonGKiUmlYS9pLttD3zsCxCqltQNBinCEoljwlrIkE8wv\nqMhmHOQqpcyrjyuXGLa3LMx1SL8CXNk2vw8hwMy80tNs1PWVa8Anun74kQkWTEg2a5jlrQb89bdx\nAKYmjUwQCwCWqnpOpTNCYAbalEY8hXBKUBgLonCC79mpVc+wmV9UsXbL3VtX3RcUi0sdm6Q3Y+gM\n63cMONXixdwtGhFPyhibkBsuzgFAktBQ8EUgOIvoZeYbxB7XzdXXANzCaKEIRcnHzbLsphdmUk6t\nzUi9m3e2LMzOd3ZzNCYhl3XcYJYBIO7xPjvfXSDcDf3MngrlTUhOl24OSCMTxALt3WycNTdLVTef\n3PJxN6uzw4IQd6tOdd97zc0JqedWN4bOsL56uH+ec2B6TkE8ISM5Lrf0wabULWB3Xjm/f/mQMXTm\n2foCHOCMdF0QCTicJea8IkCFYLxur9zcgopcxkEm7f74o3GKUNgtCa5WSndvrHmvphZybiP1TsIj\nxJVuuXSY1hGLS13/HYNOI25GMRzfvTcMAIW754YTgoO5yEkOrS2KruOuGz+AYrUWAmCShFceuH8I\nozp79FIM6qRRVYpLVwMoFRlsmyMYoj2lGgLubO/aqgGnkgFZPRR2tixoAYqJKQWaRpE6sODYQChC\nMT6pdOwRLRCcdow2fWGB47lZUUltrxwhh5PI2YqbYxU3k3o33zE83ZzPOpiZ69wPs/o+pSJDsVBx\nc0LqurBTJ/rtbsV0fAv9Nbt5fzba1/c+Dmq5jCvff9HXza/eL9zcD7pdnR0GqtYnN982WorM7Wxa\nCAQoJqZkaAGC1L4N5rhunjjnbhaB7JBQfCqakkqv1GaiMRnpg9bceEKAxUsaSkUHlukeONGoK8LD\nx3i3FamH+TUY554TjD5jJwiFpZ5SHE46gK1iqxI4aS0kwSvFnEAILIWiGNdGZ8aXc7z/z/8Sib39\nlpQrR6J4/t3vwv7c7LBGdyYZ1dXZagrVUamtzjTBOZBJ25gJqojGJURPICVLIBglFJV4TjJXW8w1\nE43LnvvWCAGWLmko1rs5JjUEnoR4txWpx2lT1ZgzwKMteAt+KZfHoZ8Fneqx2rk54a5qjqSb/7+/\nQPwg5enmbz/6bqRmpoc1ujPJ9ZVr+NovfhPPfvT7wx5KA/1ws19Bx0zaxvSsKjoFNCE+iSERDFKo\nCoHhsdfNK+AMBGlLSgEhwOSMjECAIhA43gk9FKaV5tKNKCoZSM+t4/aWOy6lqIrEHgVp2ofDJIr0\ndLjvBQv6weTmFmKpNKS6fg0EgEMpfvD2t+FHb31weIM7w4zy6uxR8Wv5AQCOTyswgeA8EAxRd6+b\nl5s9WlkEg7RW6bvezVMzMrQAhXZcN4fcLTvNqCrpqW90P+lHQSc/ShEVSYmC2I1udmSK9FRoJN08\nvb6BaCbb6maJ4sY7H8IrD75leIM7wzz25MPAysNnys2Oz6ISgFoGlaCRoQSyhJB/B+BnAZgAXgfw\nG5zzzDDGMiwIIVhY1rC9adYCSC1AMDOv+qYITE4riMUlFCr966Jxqee0BT8mZ9xG6vUXuIQAM3NK\n36u8DWsVtgFCsL0Ux9h2AaGCmwpUiihIz/S/6l6/iKXTnrdLjCGWyZ7waM4f11eu4et/GMQz9/3R\nsIdybIIh/6IRkR738wjODsLNh27eqXNzIOi2+fB184yKWIIhn3NAqFujopcU5HZMzShYvdnq5um5\nk9+v/s4f/B4e/Xh5sG9CCbaX40g2uTk1ym5OpTxT1ySHIZY5V4fPUDhLk82hkH9/90hsRDIQRoxh\nfSp/D+BNnPP7AbwC4F8PaRxDRZIJ5hc1XL03gLvuDWD5cqDjyqoWcPeqjU8qfQtiAXff3cUrAYyN\nSwiGKOIJCUuXtb5WQnvnD35vNILYCqpuQ3I4bJmgGFORngr3rT/pIEhPTMCrfqMly9ifHXCVZwEA\n4NGPl0fqN3xUZJlgbEJuuC6spk72WphCcKYQboZ7fNS7eelSoOPKanVv+fiE0rcgFnD33S1fCSBZ\ndXNSwnKf3dwN11euDT6IrVDv5kJMRXo6DDbKbp6c8AyyLUXGwbRw80lxJtysECTHW92sBYSb/RjK\niizn/Et1/3wOwC8NYxyjAqHEt0faSSIrBJMzg2mofH3lGnBCEuyGSLqM5G4JtBIXyjkToYKFreX4\n0Buq+5GamcbBzAwmNrdqPWQZIbBVBa+/6Y3Hfn3CGO577lu49/nvQjEM7M/O4B/f+57R3tvDOQIl\nC5LNYQTlE/vurq9cwx///jb0xz59Iu83CCamFARDFJmUDcdxi8DFE3LfKpkKTh/CzY2MipsVhWBq\nQG7uxIm0w6sjkiojuefh5ovxgbV3OS77s7NIT05ibGenwc2WouL1N77h2K9PGMP9zzyHe174LhTT\nxP7cLP7xvY8hNX063KwHZTgn6GbgdK/OTk4rCIVdNzPmrsTGE/LAeuCedggfREfsXgZAyOcB/Dnn\n/P/t9Nh7ggn+qSv9Ly4gGBwjOUPGORZeTYM27ajnAIpxzW3qPaJIloW3fOObuPLiS5AcBxuXlvHt\n9zyGYix27Nd++xf/HvGDPJisIp7aRSSXhqUo+Jtf+1Xkxsf6MPr+IpsOpu/kQGu17t3vL3XCe5xP\nszAFwE+9+IXnOedvHfY4Rg3hZsGJ+5txLLyaqgWxVTiAQkJz04tHFNm08JZvPIUrL70M6jhYv3QJ\n337voyhFj19Z+aH/+kXEUiU4soL4wQ4i+QwsRcHnP/LPkU8m+zD6/uK6OeteY1W+y0JcO/H6I6d9\nsvm8062bBxbIEkK+DMBrGu8POOd/XXnMHwB4K4AnuM9ACCG/BeC3AGBaCf7Ep+9+z0DGK+gvf/7J\nX8aNzyWGPQxPZMPB7GoG1KPgjaVQbF4ePTEMmlC2gNnbWXBKwSgF4cD4zhrueeEp3HzjvXjmgx8Y\n9hBbmL2ZcVs11N3GCJCaiaAY1050LA/8XAYf/u0/O9H3FPSH8xbICjcLumEYk9CKbmPmTla4uY5I\nOo/ptRw4OXTzxPYq7v7uN/Ha/ffhufe/b9hDbIRzzN3MQLZYi5sPZiMoxU7WzYCYbD6tdOvmgaUW\nc85/ut39hJCPAPgZAO/1E2Xldf4UwJ8C7qxvP8coGAzXV64Bnxv2KPxhMvHtITvKe2QHBucY3y7D\nVrXabCkHcDB9AbsLlzG+szvc8Xkgmw5ky2lJ+6MciGT0Ew9kb3wugRsj2qpHIKhHuFnQjmFmUTky\n9XWz3ae+t6cKzpHc1WErjW7en1nE2PwljG9vD3d8HiimA8lmnm6OpvWhBLJnId1Y4M9QzgyEkA8A\n+B8A/BznvDSMMQj6z/WVa6OZStwEkyhKYQWs6UzLCJAdDw5nUENENitt5ptSfpisYHPpqlvIYsQg\njMNv81pzyvhJclqOAYHAC+Hm882wz11Mpij7uDl3Dt2smA7aunlqajgDawNh8HUzGaKbgeH/vgWD\nYVhTXP8ngCiAvyeEfI8Q8h+HNA5BH3jz4/apO0EczEVRDivgxJUko0B6KgQ9MpyCGsOEeFRCruJI\nEl58x9tOcDTdYWkSuMdeG0aAYnT43+FpOx4EggrCzeeQwNeeGJlz1v5sFHqDmwnSU2Ho4eGf10+c\nNnGfI0l48W2jtyPCDEjgHpEsI0AxNvzvUEw2nz2GVbX4yjDeV9B/TusJgVOC/QsxUIeB2gy2IgHn\ntFqrpUpglIA2NeImjoPMRBSZidFbkQUh2J8JY2qj4P4TrvM5gHwiMMyR1RDpTILThnDz+eP6yjXg\nE8MexSFcIti7EAO1GajD3Er057Raq6VJ4JQALW62kZqOIzc+PqSRtYEQHMyEMbnZ5GYCFEbEzYD7\nu//aL34Tz370+8MeiuCYDCWQFZx+TmsA2wyTKJh0Dvfe1EMI9uejmFrLAXD3sjACWGEVO4vxIQ/O\nH1V3wAlqFS4JAMKBudsZMEpQjqjIjQWH3n/w+so1/C37E3zv78TpViAQjAajXJARcNOMh33uHjqE\nYH8uisn1Rjeb4QB2Fo/fqWBQaLrd6mYGzN0aLTc/9uTDwMrDYrL5lCOurAQ9cdI95c4tnCNYsKAa\nNmxFQimqujOzA8IIKdi4nEQkq7t930IKyhFlpGfCYxm9pU0DBUBtd21WTukIZ3VsXUoOfbLig/Rj\nwIpYnRUIBMNn1AsyjjR1brYqbh5kNpceVrB5KYlwVofknA43RzLGqXEz4B4PX//DIJ6574+GPRTB\nERCBrKBrRi0F6axCHIaZOznIpgPC3ZSc5C7B9lLcTbMaEEymyI2HBvb6/aY5FbrlfgDEAWIHZWSm\nwiczqA6IdCaBQDAszkom1bAgDsPMas6tmN/kZmeAbnYUitzEKXJzh6JOVTdHD8rIjoibH/14GRCd\nB04lw58KEYw8YnP8yZLYK0M2HdBKYV7K3aBtfKsw7KGNFEZQblcLA4D7+YUz+kkMp2see/JhcTwJ\nBIITRZxzjk9ir9TiZsnhGN8Wbq7HCHReIyMAIllj8IPpkesr1xD42hPDHoagB0QgK/DloU/dL+Q3\nBML51rQcAkAr24MtX885QjkDY1sFxHeLkE1ncO/VB1LTYXByWNjR75OR2EmNqDeur1zD/8/enUe5\ndtV3ov/+ztEsVUk13qo7+F4bY8DgCTBwbdNth3TgWgTS0N10vDI1GehVr9v0sv2ySGV1uvM66UVe\nG5Kw0r1iXj930klIm+Q64AackMHOwxgIngcMeLrzrVu3BpXm4Zyz3x9HUkmlo7qqKklHR/p+1rrg\n0rhLUp2vfnvvs/dNz9/tdjOIaMgxx7sjmi63fGkWAKF8H7P5Yh76gGfz+lwUVifZfIlZVW656945\n/s14CKcWU4uj919rnwR/3O2WjBhLIZItu7PXmqWw79QGAiW7t1kBGF8vYmX/GAoDsJ2Nk0rIh/OX\nJzC2VkAoX4G/PKAV6zY4nYmIeoVfxrtDLIVwtgxR/c9mqWazvzGb1wq4eGBsYLcLLFezeXytgGCu\nAn/Fe9kM2H8/n71nCcXbHnS7KbQNjshSk8Xkgl3EUl8FigYOvrKOqaWsfe7NlusVqlNpe7SoRCxV\nrBexwOa0qenzWWiGiViqiNh6ceBGaY2AjvW5GFb2j7W9jeWBoxxHZ4mom1jEdkegUMGBV9Yxdb59\nNhcjvc1mv1M2n8tCq2xms14ZvGxem4th9UD7bDb1wV2wqoajs4OPI7IEoGEUlvpPKcyeTkPfMhJb\nn5ZT3RR+dT7WsyZEM+WW6cwAAEvh4KuppvDemAoP3MITlaAOS2udRqwApCcGZ++67XB0loj2il+6\nu0gpzJ7JuJvN6dZTjQB7pPbga5vZPLEMpKbCyAxYNpeDOiwB9C2/gwKQmQi60qbdWEwu4LoPpfCx\nT3zB7abQFh4Yq6Be4yisuwJF5/NrBEDFr2F1Loazb5jo6YrFqk3HaG1vVq3hX3y1gEDR6FlbdqW6\n356FzS8ZFoBKQEdmcrCC/VK42AQR7dT1xwwWsV0WLBiO04kFQCWgYXXezmbT38tsdg5np2xOrBbg\nH8BsXh2SbH72oQT/xgYQR2RH2Cj9QYppIZyrAAAKUT/UAOxdViMW7FRy6HU1/Rry8d73WmYTIQQL\n2aae33ZnA4kCohsllDtYmbCfirEAzl+RQCxVhK9ioRD1Iz8e7On+u71y171zHJ0loo54OcubszkA\nNUDTTbc7J9bw68iP9z6bMxMhBIo7yOZ0CakBy+bCWDWb14vwGXY258aDPd1/t5dqf2/M58EwWJ92\n6osH7rsDzz6UcLsZfRNOlzB9PmsXiwCggNX5WF9CqBOlsPOfoSWwD/Z9kB8LIJgPbi6H31BYi1Nq\nurDoRSeMgD4we8Z2A6czEdF2vFzERtIle1u5hrxZmY+hMDDZ7HesGi1B374/5McCCOWDiHaYzY55\nPQCMgI7UvuHJZsD+2/ua9Tk88zBLKTfx1R8xi8kF4CG3W9E/mmHZCxYpNAXS1PksShE/TN8AjMxq\ngpV9UUyfz9nThWAHZTnsQ64Po7EAABGsz8WQmQwjmK/A0jWUQjoOvJZquanqY4iTPZ3pWY7OElED\nLxewAKBXK5JSEgAAIABJREFUTEw5ZPP0+SzORvywBiCblSZY3RfF1FJzNpfCPuTG+7RisAjW5mJI\n17LZp6Ec1LG/TTb3rV0EALhduxNIcnTWTSxkR4TXQ2+3oun2G25H0iVkJsN9bI2zQNHA1IV8vafV\nXgXRj4sHYkCb82N6xQjoTefirs9GMbGcq/fyKgFy8WDbUWTqHU5nIiJgOPI8kilve112ABbpCxQq\nmFzeks1RPy7uH4RsjmBiOd+Uzdl4EOWwv6/tItticgGPfPQxfOvjz7ndlJHDb6ND7vpjht1jNKJE\ntZ9+48p+rVu1WbE4lK8gnDNc38M1OxFCMepHNF2CWAr5sQCD0mWczkQ0mm56/m57dfMhoFmqbTZr\ng5LNDisWh3IVhPKG63u4ZifCKEYD1SnHCoVYEGV2MLvqtuO3AMlb2NncZ/zUD7Fh6LXdq0LUj/hK\nazGrBCgMwGbigaLzqoiasvePc7uQBeye4I3qkv562UQwX7G3uxmgBbNGDaczEY2WxeQCMCRFLGDn\n7/hqoU02u99Z2m7F4lo2u13IAtVsnrGz2cdsHhicPdVfLGSH0CgVsHrFROJiHqHqeZ3pyZC9QFJ1\n2k8l5EM2EUQsVWqZglMZgJX97DY5L1m83YqJ/SamwszZDIKFCpQINKWQToSQmo30fYoVbeLoLNFw\n8+oe763ZHLbP36zmRTlkrwER3WjO5kwiiErQ/ePZdvmrWW2v6jsxrWo2G5vZPBFCaobZ7LZFrm3R\nF+4fLahrQo98xN62Y0RohoX51zfsKUoAYJiYXMrBXzKbVq5dn40iHwvWz5fNjQdRigzGR78U8sGp\niO3nisWdmFrKIlioVBfmsNs7liqiEtSRS7h/LtMo4+gs0XBaTC4Ax91uxc7pFdMhm7PwlcP1EUQA\nWNsXRX4siEgtmwdo/YXtVizu2yKMHZg6n0Uwb0ADNrN5vYhKsI+LRVJbHJ3tPc4/GBKLyYWRKmIB\nYHytAKkFZZWm7IO4ZjZ0mYqgFPVjbT6GtfkYSlH/4PRUaoKV+TFY0rBZeG1VxAEJIbEUItly0z52\ngP1aj68V3WkUtVhMLuDo/de63Qwi2qObnr/b0zOrxteKm0VslZ0XBciWbC42ZnNkcLJZaYKV+Zhz\nNg/IysBiWojkKi1f5GuvNQ2OxeQCHrjvDrebMZQGo+uLds3LYbdXoXzrARwAIIC/ZKIU8UY/TWEs\ngHOXJxDbKEEzLRSjAfscoQEJdM1SUACcWqObAzTHCoBmWhhfKSCSKUNpgsxEENlEaGBey17jYhNE\n3jYM58IG8xXHvIAIAl7K5vEgzod8iFazuRALoDhAHeHbZbM2aNlsWIivFhDOlKF0QSYxWtkMcCu9\nXmEh61GjNo3YSSWgI1A0Ww/iCoOxP+wOmA2LNgwaUxdYugbNaA5GBaAQcX9RjhqxFOZObECvWPUO\njonlPIIFA2tzsfr5vaWwb+jDczG5gEc/Hcbj13zG7aYQUQeGaUViw68hUHLKZgXD761sNgY5m30a\nLE2gmc3TpWpb+A0KMRXmT2xAN6zqVHM7mwNFE+v7oggWKrA0QTk0/NkMcLpxt7GQ9aDF5AJwr9ut\ncF9mMoxIpty06qEFe+pP435rtEciWJuLYvpsxt62CHZQWpoMVMBHU0XohtU0Sq8pIJIuI5JZsy+o\ndl/nxgNIT0ZgBIf3c3LrpwoAe3+JBt4wjMI2Sk9FEM5tNGez2Oedmv7hPeb2nQjW5mKYPteazakB\nyubYhn2619ap5tGNUn3tkprceADpqchIfIfjYlDdwULWQ0Z5GrGTcsiHlf1jmFzK1s/HKUb9WJmP\nud20oVOIBbB0OI7x1QL8ZRPFiB+ZyVDTlxKxFHTDgqlrUHr/e1VDtcWothBs2X5JAbGNMqLpMtbm\nosjFh3uxqsXkAj57zxKKtz3odlOIaIthzPVy2IeV+RimLuTq61gUon6sMpu7rjAWwIVqNvsqtWwO\nN81Kq2ezT4PSXMjmfIfZjM1sXp2LIj/k2QxwdLYbWMh6gFeX3++HwlgAZ2MT0A0LliZQ3D+tZyoh\nH1YPjLVeoRTiK4WmxSWy8SDW90X7Ok3I8OtQaHNu1ha1AJ1cyiEfC7pSePfTXffOcXSWaIA8cN8d\nePahhNvN6JnCeBBnxgLM5j4oh3xY6TCbM4mgvavDgGfz1FIOhbGgK4W3GxaTC3jko4/hWx9/zu2m\neA6PLANuMbnAIvZSRGD6de8FpVKYO3kKVz73PCaWl91uza7FUkWMrxWgKdT/xTZKSFzM97Ud2Tbb\nAF0qBkOFSvcbM6AWkwtDOQJE5CWLyYWhLmLrPJzN8ydOVrP5otut2bXYems2j6VKiK/0dxp7ZmJ3\n2RzMj042A/ZijcznneOI7IDih3m4hbNZvP9PH0A4m6v2QCosXXYIj/zTD8PSvXVuSHy16Lg1z9h6\nsa+bsht+re0Kju2IAsZWCygM0EqU/cBzc4j6b5gWdBpWkUwG7//TBxDK5+3zTpXCuSOH8eiHfxzK\na9lcLWIbaQoYXy9iYzrcv2z27S6bx9cKA7VKdL9wdHZnPNZNNvweuO8OFrEdEkshsZzDgZfXcODl\nNSQu5Jr3qHOZZpoYX11DoND6xeWWrz6MsdQGApUK/JUKfIaBuVOn8dbvfNeFlu5Nu2X+7S8BfWyH\npdrmXbtmCIBgwcDY+ujth8vRWaL+WUwujEwRK+aWbF62z5UdFJph2NlcbD3uv/crX0NsI41AeTOb\n50+cxNVPPOVCS/dGN5xf836/F5ql2lax22Zz3kBsBLMZ4OjsTnBEdoAsJheAh9xuhUeYFva/noJu\nbG66PpYqIpyv4PyRuOs9eFc9/Qze8fffgCgFzbJw+so34JvHPgAj4Ie/VMK+02egqeZDuM8wcNVz\nz+H5m97jUqt3pxz0IVQ0Wi43/P1dWMLSBJYm0M3WaDT8GqAUfA2flxoN9uhxZjLcl3YOmsXkAr5m\nfQ7PPMw4IOq2UdsqT0wL+19LQTcbsnm9iFCugqUByOY3P/kUbvjGN+vZfPKNV+LxY++H6fcjUChg\n5tz5lmz2Gwbe9OyzePHdN7rU6t0ph3QEi2bL5YZf6+v7YOkCJQJseV0VgIpfoFlo+rzUaADGU0Vk\nRzSbAW6l1wmOyA4AjozskKrtSaZalnP3lU2EsxVohoWx1QISyzmEs+WWA2gvHXj1Nbzzkb9HoFyG\nv1KBbpo4+MqruPnhv7TbabUfNdaN1tAZdOv7IrBks2dVwd5qYX1ftL8NEcH6jN2WRpYAq/MxLB1p\nf07aII0WuOF27U4eg4i6bDG5MFJFbD2bzdZs9pdNhHK1bM4jsZxDqM/ZfOjlV/D2v/9GUzZf9sqr\nOPqXX7fbuc2MLt1o7awddOuzUcdsXnMhm1Mz4ZZsVgKs7h/D0pF4+5HZEc9mwN5Kj/ncHrvgXXT9\nMQO3a3e63QzPCWcr8FUsx5kqooBwtozpcxkAdoBa60WUQz5cODQO9GGE8Jpv/wP8W0LPZ5o49Mqr\nCBQKKIXDSE9OYGJltek2pqbh5FVv7Hn7uq0c9mPpcByJFXuD80pAx8Z0GCUXNmTPJUJQmiC+UoDP\nsFAO6kjNROy2KAXDr8Ffaf6yomCvfk3cCoCoG4Z9ReJ2wtky9G2yOZIpY+bsZjaP1bL5svG+jBA6\nZrNh4MgPX8Z3SiUUoxFk4+OIr6033cbUNJy46qqet6/bShE/LhyOI34xj0DJ3WzOToRh6VpTNq/P\nRlAO29ls+TRoRms252PBvrd1UHErPWcckXXJYnKBRewuhfKVbT+4kXSpvkIfYP9/oGhgLNWfcy0i\n2Yzj5ZamIZS3z5F67PZjKAcCMKqLR1T8fhRiMTxzy019aWO3VUI+XDw4jrNXTmD5snFXgrImPx7E\n+SsSOH3VJC4cjm+2RQSp6QgUNnuoLQCmz76cNrH3l2h3RmZFYgehXPtsVgCibbK5X+dBbpfNwUIB\nEMFjyWMoB/xN2ZwfG8NzNx/tSxu7rRzy4eKhwczmcngzm9dnwg7ZrNmLUlHdXffOMZ+34Ihsn/ED\nuHemT2ChtRemdgB0WmBIU0B0o9Sb8yCVQixVRGyjBFHA9689Cn/FQmZiBv5yCYdeeR77T/4QSgTZ\nRBwAsDa3D3/xix/Hlc89j/h6CssH9uO1q98C0+9eyAw7X9nE1IUcgM11JwTAxmQIlo99eltxdJZo\nZ0Y9302f1jabBc6ziDUFxNKl3pwHWcvmVAkC4PvXHYVuCjKJafjLRVz28vOYP/UyLE1Dbszeh3Vl\nfh5/8Qs/jzc+9zzG19dx4dBBvP6WNzObe8hXcs7mFLO5rcXkAq77UAof+8QX3G6K61jI9gmX3e+e\nbDxk74PWEIqN54C0naDUo6lL02czCOcq9V7m7MQ8RKnqHnoBvPrWG5GPjmPlQLxpa51iNIoXjnpr\nYScvi1/MQ6zmc7cEQGKliOxE/7Yi8Bpu1UO0vVEvYGty8SDiqzvPZtWLY69SmDmbsUeJq41ITx5o\nyuZX3vYuFKIxLB2eadpapxiLem7RRS9LXMxBLLRk88RKAbmJELO5jWcfSuBZ5jML2X5YTC4ALGK7\nxvJpWD40jpmzGXshgOrK7rV/jvcRIJvo/rkWgaLRVMSi1oaGA6/l8+PMlW/F6TdOdf35qXOhgtHm\n3C0FX8WCEfDWHoH9xNFZImcsYjeZfh0XD45j+txgZHOog2w+9cZrcfoqZrObgttks25YMP3M5u2M\nej5zzL6HuCds75Qifpy5cgJLh+PIjTsv1KNgn2dhCVCIBpCNdxaWmmlhfCWPuRMpzJxJI5irtL1t\nMN/+uqa2aAJfxXsrEndFH1el3I7ZZoqSADB19vh2gsczIhvz3Vkx2pDNbRbRa8zmfCyA3Hjn2Ryv\nZvP0mfS2+RvMGx3tY85sdl+7bAYAS2eZ0qlRPR5xRLZHuCdsH4igEvIh6LCHaU0ppCM1F0M5tPlR\n10wLSsRxj1PNtDD/+gY004KmAAV7y4D12Yg9/XSL7Q7ATU1Vnd92WMyfOIF3/e0jiK+uoRQO44V3\n34gXb3yna9OENqbCmD6XaeqhtwTIjwWgGJYdG/XeXyLm+yXUsrm0TTaHfVjfF0Wlls1KQbPUJbI5\nBc1U9iJRMBHOVbC2L4pcItRye8unQWmAtN9Rp/q8o5fN+197HTf+3aOIr62hGAnj+Xe/Cy+98x3u\nZfN0GNPnss7Z3Me96IfBKOYzC9kuG9UeEVep9tOWshOhehEbKFQwfT4LX9k+GaMQ9WN1PtbU4xdb\nL9aLWKA6JUoBE8t55OKhloNqPhbApCZQDpt519QOyKO0aMHsmTP4kQe/DF91q4NQoYDrHnsc/lIZ\nz7z35tY7KIVA0YRuWCiFfTt6rQJFA4mLeQSKBip+e3uBYtQPvWK/z7VpSYWxANZnI5i4mK9/Zgqx\nANbmYt34lUfOYnIBj3z0MXzr48+53RSivmC+75Bqn4uZiVC9iA3mK5g6n4WveszOR/1Y25LNY2vF\nehELbGbz5IUc8uPB1mweC2DigkBh+2zOjQdHatRv36nTuO1LD9WzOZwv4IZvfBP+csV5ZWalECga\n0E2FUmiH2VyoIHGxgECpms0zYRQjTtkcxPqMhYmVPAD7fc2PBbDKbN61UcpnFrJdwoBzTzHqh7+6\nKuFWheoeZHrFxL5T6c0eP2XvRzt7Ko2lI/F6T2QkW27qFawTQaBotC5drwkuXDaOmdNp+Az7jrV2\n1B4mFw9ibbbPG5C77PrHHq8HZY3fMHD1E0/iuaPvhuXbPPToFROzp9P1LzGigPRECKmZyPY9xEph\nbL2IieVq+AHQTQOBsxlYsrnFg+HXsXIghkrQh+xEGNl4CL6KBcsnI/UFphduO34LkLxlpHp/aTQx\n43euFA04ZrMCUIzZ0459Zfv435LNp9NYOrK5jVH7bAb8JWNzK5faw9Sy+YydzY1tqD1MNhHE+ohl\n8w3f+KZjNr/tH76LF97zrqYFKZ2yeWMybG+Jc6lsXi1uFqaoZvOZLdkc0HFx/xiMoI7sZBjZhJ3N\npk84S6oLRiWfWcju0dH7r7U/LOSa9FQY0XQZWsOKtBbs6Sqqeu7j2Hqx5XwZAeAvmwiUzPqoralr\nABzOl1Gqel2rStCHYtSP2Ea5ZdU9S2DvUTpi02Piq6ttrwvncsjF4/WfZ85m4C9b9mtXfY/G1oso\nh3zIN5w7JaYF3VQwfBogwPS5LCKZcsuXJE3ZgVu73F82se9kGmevnLB77TWBEeTiEd00itOZaDSw\ngN29jakwIg7ZnJoO10dQnbJZA+AvmfAXjfqorenTgJJTNrc/j7IS8qEU8cOXLjddXsvmjelLdJYO\nofG1NcfLRSmE8nnkq9sQAcDMmdZsHl8roBzSURhrn80zZzMIZyuO2dzYGeEvmZg7tYEzb5iwvyMx\nm3ti2POZXR57sJhcYBE7AEy/jvNH7EWfDJ+gFNSxuj+G9HSkfht/2XSeXiR2j3BNZjIMa8sNFYBK\nQN/2ABsotnt8gb88egtJpKbarwJZiG72gOtlE/5S62unKfsLDgBAKUyez+LQK+uYfz2FQy+vYWIp\ni3C2tYit2dqhIFCIZMptbk3dwi/9NEz4ed4b069jySGbMw3Z7GuTzUpgjwRWpSdCztkc1Lddcb59\nNsM+zWjEbExNOl6uRFCMNL8vTt+bNAWM17LZas3myfM5hHKtRawTASCWQiTLbO6HYT2ecUR2F4b1\nw+BlZkDH6v6xttcXw76WpfgBAApNC0EVo36sz1TPoxQBlEIloOPiofFtn78S1BFwKMhq9x81z7z3\nZsw+8OdNU5gqPh9evPGdTdOKNas6dOowZUwz7QsnLuQQTZeaRlnHNnYWfGIBujF6X1rcMOy9vzT8\nrj9m4HbtTrebMRSMS2RzKexDKN+azaKAcrBxb9cAUtMRJFYasjmoY/ngpbPZqSATBRj+0RvLeea9\nt+BH/+x4czb7fXj+3Tc2TSvuJJsnl1uzOZZ2Ps2rHVHM5n4axnwevb/iPeBy+96VS9gLNTUeky2x\nF/vZ2pubnQzjzBsnsXxwDOePJLB0eaK+qqFeMREoGvYeeQ3SU2GoLUfv2uOP0iJPNRcPHMDffvQn\nsDY9DSWCQiSCp997M57dsphEJag7LsWhqv8bX84hliq1fsnZYXuU2F+YqH8Wkwu4/lj7VUuJBtFi\ncoFFbB9lJ5yzOT8WgLklmzNTYZy5siGbjyTq+VrLZmzJ5o022ZwbsQUYay4cOohH/umHsT41BQWg\nEI3gqfe+F88ffU/T7exOBOdsVkohcSGHaJts3smmPsxmdwxTPosakH2kOvHmcELdf6U7U3lZwHqf\nXjGRuJhHOFeBEkF6IojM5CUWLajSTAvTZzP23nTVyzYmQ9hoWCgimK9gcikHf9mEEiCTCCI1Gx25\nc3B2KpwuYfp8tt6rWzsibf3vrVSby7eyBCiHfbhwaLz+XvhLBjRToRzycXn/Phjk3t+bX/jqk0qp\nd7rdDi9zM5u7haOw7mnKZk2QToSQmQx1nM0zZzIIFIx6ZmxMhZCeacjmXAWTFxqzOYTU7OidH7tT\nkY0ippZyPc3mUtiP5UNj9VF2f9lkNvfZoOZzp9nMbpBLYAE7PEz/9lOctjN9NoNQQxELAPE1e6ue\n9Xn7MUsRP85fkdjcZJwh2ZHCeBBLAR1j60UE8xX4KlZ9qki7V1ABqPg1+CpW/TZOK2Namt0jn5mw\nOyz0ionZMxn7vOhqcLbbI5i6Z5S2AiDvYc67ay/ZPHMmg2DBaMqBxGoRuqmwXt2+pRRlNu9GPh5C\nJejbeTYHNPgbzj9un82ReoeFvUJyBr7KZja32yOYusvr041Hb15Fh64/ZjDcPEgshXCmhEi6BM1s\nOO9CKcTWCzjwyjoO/WAV+05uIFCodPSYesVsGomtPxfsczX1ypbFnEQYlJ1QCuFsGdFUEUoTrM3H\noHRxPCipLf+tBFg5MIa1+SiUOAelqQHnL59AZqq6arRSmD2dgb9k2qsnWvaehBPLeQTznX0WaPdu\nO34Lj6k0UI7efy0/k33SmM2yNZvXtmZzZ1Me9YpZH4ltei4AY6mSvV9p0xXM5o44ZbO2s2xendsm\nm3Xg3BUTyEyF60XrvtNpezS2IZsnL+Q6/p5Ge+fVYyFHZB149c0cdaFcGTNnMk0budZ69OKrBYyv\nFurnc4QKBvadSmPpcLy+vH+Nr2zCV7FQDuqwfBo0s/2G6oC95112YvQWdNoLX8nEvlMb0JSqJ2Fu\nPNiyKmWNEvucHd1QKIV0bMxEUAn6MHEx77i3oBJgdS6GUL4CsRSKER/EUvBVnBf9GFsvtO4RTD2x\nmFzAo58O4/FrPuN2U2iELSYXgONut2I0hLJlzJzdks1zUeTiIcRXChhf25rNG1g6EkcluH0268Yl\nsjlXRpYjejviL9nfjaQxm+PBlvOMa5QA5YAO3VQohX1ITYdhBH2YuJBru+/vylwM4VwZYgGFqA+6\nqaA3zK6q37S6e8FqmNncL14cnWUh24AFrHdJ9TwZTaGpi3DyQg7lkK+piK3fRwHxlTxWqqseimlh\n5qw9Tam2+XcmEcT6dGT7cz7YwbszSmH2TBr6lg6CaLqEbDyIYNFseq/sHlxBbiwAgaAQ89e/4Gxd\ndKvRzLmsfZtLNEcA6IZ31goYBrd+qgAkFzwVljQ8mPX9o1VztSWbl3IohXxNRWyNnc0FrBywpxuL\naWH2TMZezKl6gmYmEcLG9PanhPCovkNK2d+jtmbzRgnZRBCBUptsHrezOR8L1Lcp3Lo3cON9Zs/u\nJJu5orEbFpML+Jr1OTzz8OCXiYPfwj646fm77S9W5FmRrPP0E1FALFV0vg5AsLg5LXjqfBbBvGFP\nn6kehGOpEioBHempEOKrxdYDrwD5WGCvzR8pvrIJ3WjtfdWUvedfNh5EbKNkX1j90uIzFRIXCxAA\n8RUgPRnGxkwEuXgQgaLh+EWo0/4FS4B8jD2+blhMLuCz9yyheNuDbjeFRgAL2P4Lt9m/uzba5rTM\nrQB20Vo1fT6LQKE5m8dSRVSCOjYmQ4ivtWazEqAwxmzeCX9p+2zOxYOI1rIZ9lvRnM15pKfC2JiO\nIDce2FE2O9W9tZ0fyB23a3cCycEfnR35c2QXkwssYofAdiNz7diLElR7D02FSK7S8gdR2/x7YyaK\nTCKIWqeygn2QXZmLjuQS/nvRrqfWvs5eoOP85QmszcWwui9av48GOwA1BYyvFRDZKKEU1FEO+epT\nkmvn6LSbBlW7TY0lgOnTOP3MRXfdO8cCg3qOnzF3aNtksxLnPGjOZgvhdtm8VsTGbBTZeKAlm1fn\nY7B0ZvNOyDZTz0QprNWzOYrVuSgEDtm8WkA4XUIp5GvKZgvbZ/PW/gxm8+BYTC7g6P3Xut2MtkZ2\nRDb0yEdw171zbjeDuqQYdR5RUwLkx4MAgNhG855nSlCfmqQp1Xb6cG3z7/W5GNJTYYSzlfpILIvY\nnasEdXtZfbP5G4wlQG7c7n01AjqMgN5+NF3ZvfRKAEsTpKbD8FUsWLoGUxdMrOTbzisTAIYuMP0a\n8rEAMhMhKH7hcd1icgHXfSiFj33iC243hYbI0fuvxW3Hvb01kJcVYgEkLuZbLrdHTIPQlD11tW02\nW9tks2VPO12bH8PGtMls3qNyqLavu1M229+j6tm83j6bZ841ZPNMBL6yCcunwdQEEw6fhfp90ZDN\nYwFkEmFuwTMgbjt+C5C8ZSBHZ0fuL722SiGL2OFiBHSkJ8OwZPMQXNtUvRT2YX1fFJmJUP36il/D\nynwMmqUQSZegoBx7b+0NwzeLZNOvIzsRQjYRYlDulghW5mMt71UloLdug9Ow4ETTQ2CzB9hnKiRW\ni0jNRLAxE0E+Htz25ChLgGwihKUjCaSnIyxiB8izDyU4ckZds5hcYBHrMiOgN2VvbcS0ls1r+6LI\nJJqz+eL+GHSzms3VgmgrBaAY3Zx2ymzuAhGs7nfI5qDeOjLaaTavFJCajWJjOlIfVGjHEiAzUc3m\nqQiUziJ20CwmF3DT83e73Ywmro7IisjdAO4FMKOUWun183GVwuG2MRNBIeZHLFWCKIXceNAeqa0u\nt5+ajSI1E4Eo+/ybmTMZSO1IrFA/N7N2DocFQFV7FKm7irEAzl2eQGyjBF/FQiHmR34s0LQ1QjRV\nrJ97c0lKIZIpI5cIwdI1rO2LYvJCrj5trWGxTCgRZCY4XWmQeXHlxGHS72zuNq57MVhSs1EUYgFE\nN6rZHA+iGGnI5n1RpGY3s3n2TAZoyOZMPIixrdms2zNxqLsKsQDOX55ANGXvxVuMtmZzbL2AxMoO\nszkehOW7dDZzKvHgG7TFGl0rZEXkEIAfA3Cq18/FHv7RUQ77sbbdUu3VPctmz2Razt2JbZSwMh9D\nJFuGr2yhFPHZo7zs3e0JM2Bvo+Mkki5hcsvy/Y3vltMy/XrDVOVcIgRfJY/YehGWHoTPtN/3YtSP\n9Vme1+wVXlo5cVj0M5t7YTG5ALCIHTiliH/7Lc7q2ZyGtmWh2rEt2VyM+JBhNveMEdCxMRt1vC6y\nUcTEcn5n2dyw8nAuEYK/nEMsVYLJbPa0QVms0c1vB78N4JcBfLlXT8BzY8hJKFeB05wYUfYedqv7\nx/rfKGoSX3HYkgGbU9OcVqgshe3Dma9Uxm1f+jJmz56DpWvQDBOvvfVqfOv9/6SpV5m8wSsrJw6R\nnmdzL3DdC+8LZ8vO01UVECwymwdBYhfZXKx2YPhLJdz24Jcxc/48TF2DzzDx8jVvw3f+yfuYzR51\n171zro/OutL1ISIfBnBWKfVsr56D58ZQO5rV/tyO7VZYpP7xGWbb60rhzZUQAfu8mmLEXy9kj379\nr7HvzFn4DAOBUhk+08Tl33sJb3niyV43m3poMbmA648Zl74h7Vo/srkXuO7FcGi3+4Bgc9FFctd2\n+7qWwnprNkcDKNey+S+/jplz5+AzDARLZeimiTe88CLe9PQzvW429dhicgGhRz7iynP3bERWRP4G\ngFN+VDh0AAAgAElEQVSy/CqARdhTlzp5nF8C8EsAsM9/6fMhOI2YLqUY9Tue22FxT9iBUQ74ECq2\nFi2WLlg+NIbYRgmxDXt/wmwiiGw8CIhAMwwc/uHL0M3mQthvGHjLk0/jpRvf2Zf2U29wdHbv3Mrm\nXrj+mGF/JmgotNt9oLY4FLmvEtQRLLZ2NJu6YPnQOGKpEmLpEhQE2UQQubi9wJOvXMFlr7zqmM1X\nP/EUfvD2G/rSfuodt0Zne1bIKqV+1OlyEbkGwOUAnhV7KsFBAE+JyLuUUksOj/N5AJ8HgDeHE227\n5Li4A3XK9GlYnw7bixXUFo+ojuoVYtucw0N9k5qNYPZ0umkKkyXA+kwE0DRkJ8KtKxwD8BmGvZqi\ng0Cp5Hg5ec9icgGPfPQxfOvjz7ndFM/pdzb3Cjuth4/p17ExFUZ8dUs2R/1ti1zqr/WZqH0e89Zs\nnq1m82QY2UmHbK5U2j4ms3m49Huxxr5PLVZKPa+UmlVKHVFKHQFwBsDbnYKyU4vJBRaxtCOZqQgu\nXDaObDyI3FgAK/vHcPHgGM/TGBCliB/Lh8ZRDPtgaYJyUMfK/hhyl1jRsBwMIjc+3nK5JYLzhw/3\nqrnkgtuO38Jipot6kc29wvd9eKWnN7M5O17N5gPM5kFRilazOWRncymoY2X/GPLx7bO5GAkjH2td\nQMoSwbkjzOZh1K/jtKeXgmSY0V5ccoVjclUp4seFw/Gd3UkEj3/gx/C+P38QumlCUwqmrsPw+fDk\nre/tTUPJVYvJBTz66TAev+YzbjeFeowLOo0GZvNgK0X8uHBkd9n8I8e/VM9mQ9dh+v146h9xPZth\n1Y/RWVFtpuENojeHE+r+K+0PPItYImpnfHUVVz/xJOKra1g+cADff8cNKMRibjeLemw3YXnzC199\nUinFk6f3oDGbe4WZT+R98RU7m8fX1nDh4AF8/+1vR9FhpJaGz0636uk0mz1XyM598gtuN4OIiAZU\nr8KS2utlIfvAfXfg2YcSPXlsIiLqr047nDvNZk/tPHw2MeN2E4iIaIDdde8cR++GxGJygUUsEdEQ\nWUwudDWjPVXIEhERdcLNfe1ob7r9RYeIiAZLt47xLGSJiGgocXTWe/h+ERGNhm50WrKQJSKiobaY\nXMAD993hdjNoG0fvv5ZFLBHRCFpMLuDo/dfu6r4sZImIaOg9+1CChdKAWkwu4Lbj3IKDiGhU7XZv\neE/vI0tERLQT/djXjjrHzgUiIqpZTC7gug+lgJu/2tHtWcgSEdHIWUwu4GvW54AX3G7JaGIBS0RE\nTnayWj0LWSIiGkm3a3cC+Cu3mzFSrj9mVF93IiKivWEhS0RERD3HUVgiIuomFrJERETUM0fvv5aL\nORERUdexkCUiIqKeWEwuAMfdbgUREQ0jbr9DREREXcepxERE1EsckSUiIqKuCT3yEdx175zbzSAi\noiHHQpaIiIi6YjG5ANzrdiuIiGgUsJAlIiKiPeGCTkRE1G88R5aIiIh27WxihkUsERH1HQtZIiIi\nIiIi8hQWskREREREROQpLGSJiIiIiIjIU1jIEhERERERkaewkCUiIiIiIiJPYSFLREREREREnsJC\nloiIiIiIiDyFhSwRERERERF5CgtZIiIiIiIi8hRRSrndho6JyEUAJ91uxx5MA1hxuxEexddud/i6\n7R5fu93z0mt3WCk143YjvIzZPNL42u0OX7fd42u3e1567TrKZk8Vsl4nIk8opd7pdju8iK/d7vB1\n2z2+drvH1468hJ/X3eNrtzt83XaPr93uDeNrx6nFRERERERE5CksZImIiIiIiMhTWMj21+fdboCH\n8bXbHb5uu8fXbvf42pGX8PO6e3ztdoev2+7xtdu9oXvteI4sEREREREReQpHZImIiIiIiMhTWMi6\nQETuFhElItNut8UrROS/iMj3ReQ5EfkLEUm43aZBJyIfEJEfiMgrIvIpt9vjFSJySEQeEZHviciL\nIvJJt9vkJSKii8jTIvIVt9tCtBPM5p1jNu8cs3l3mM17M6zZzEK2z0TkEIAfA3DK7bZ4zF8DeJtS\n6loAPwTwKy63Z6CJiA7gvwI4BuBqAD8pIle72yrPMADcrZS6GsB7APwffO125JMAXnK7EUQ7wWze\nNWbzDjCb94TZvDdDmc0sZPvvtwH8MgCenLwDSqmvK6WM6o/fBnDQzfZ4wLsAvKKUek0pVQbwvwB8\n2OU2eYJS6rxS6qnqf2dgH/gPuNsqbxCRgwCSAP67220h2iFm8y4wm3eM2bxLzObdG+ZsZiHbRyLy\nYQBnlVLPut0Wj/s4gIfdbsSAOwDgdMPPZ8AD/o6JyBEANwD4jrst8YzfgV0MWG43hKhTzOauYTZf\nGrO5C5jNOza02exzuwHDRkT+BsCcw1W/CmAR9tQlcrDda6eU+nL1Nr8Ke3rJn/SzbTR6RCQG4DiA\nf6eUSrvdnkEnIh8EsKyUelJEbnW7PUSNmM27x2ymQcJs3plhz2YWsl2mlPpRp8tF5BoAlwN4VkQA\ne/rNUyLyLqXUUh+bOLDavXY1IvJzAD4I4H2K+0ZdylkAhxp+Pli9jDogIn7YQfknSqkH3W6PR9wM\n4EMicjuAEIBxEfljpdRPudwuImbzHjCbu4rZvAfM5l0Z6mzmPrIuEZETAN6plFpxuy1eICIfAPBZ\nAP9YKXXR7fYMOhHxwV54432wQ/K7AO5QSr3oasM8QOxvs38IYE0p9e/cbo8XVXt971FKfdDtthDt\nBLN5Z5jNO8Ns3j1m894NYzbzHFnyit8DMAbgr0XkGRH5fbcbNMiqi2/8GwB/BXtBhC8yKDt2M4Cf\nBvAj1c/aM9WeTCIiasZs3gFm854wm6kFR2SJiIiIiIjIUzgiS0RERERERJ7CQpaIiIiIiIg8hYUs\nEREREREReQoLWSIiIiIiIvIUFrJERERERETkKSxkiYaQiPyliKRE5Ctut4WIiIiYzUTdxkKWaDj9\nF9j7rREREdFgYDYTdRELWSIPE5EbReQ5EQmJSFREXhSRtyml/hZAxu32ERERjRpmM1F/+NxuABHt\nnlLquyLyEIDfABAG8MdKqRdcbhYREdHIYjYT9QcLWSLv+78AfBdAEcCdLreFiIiImM1EPcepxUTe\nNwUgBmAMQMjlthARERGzmajnWMgSed99AP49gD8B8Fsut4WIiIiYzUQ9x6nFRB4mIj8DoKKU+oKI\n6AAeF5EfAfDrAN4MICYiZwD8vFLqr9xsKxER0ShgNhP1hyil3G4DERERERERUcc4tZiIiIiIiIg8\nhYUsEREREREReQoLWSIiIiIiIvIUFrJERERERETkKSxkiYiIiIiIyFNYyBIREREREZGnsJAlIiIi\nIiIiT2EhS0RERERERJ7CQpaIiIiIiIg8hYUsEREREREReQoLWSIiIiIiIvIUFrJERERERETkKSxk\niYiIiIiIyFNYyBIREREREZGnsJClkSMiL4rIrW2uu1VEzmxz3z8Qkd/oWeM8RETCIvK/RWRDRP5s\nB/e7TESyIqL3sn1ERDS4mMXdwSymUcZCloaKiJwQkR/dctnPichjtZ+VUm9VSj3a98ZtY2sbPeKf\nAdgHYEop9c87vZNS6pRSKqaUMrvVEBE5IiKqGsq1f/++W49PRESdYxb31SBl8XtE5K9FZE1ELorI\nn4nIfMP1IiK/JSKr1X+/JSLSreen0cNClohq4bLT48FhAD9UShm9aNMuJarBHFNK/Se3G0NERNSp\nIcjiCQCfB3AEdrsyAP5Hw/W/BOAnAFwH4FoAPw7gE/1tIg0TFrI0chp7iqtTcv5ARNZF5HsAbtxy\n2xtE5CkRyYjIAwBCW67/oIg8IyIpEXlcRK7d8jz3iMhz1Sk/D4hI0/07bO+/EpGXqm14TUQ+0XDd\nCyLy4w0/+0VkRURuqP78nmq7UiLybOM0LhF5VER+U0S+CSAP4AqH535L9Xap6jSwD1Uv/3UAvwbg\nY9XRz593uO+7ROQJEUmLyAUR+Wz18troqU9Ejm4ZRS2KyInq7TQR+ZSIvFrtuf2iiEzu9PUjIqLB\nwyyu33Zoslgp9bBS6s+UUmmlVB7A7wG4ueEmPwvgM0qpM0qpswDuBfBzHb0BRA5YyNKo+w8A3lD9\n937YB1kAgIgEAHwJwB8BmATwZwA+2nD9DQDuh92bOAXgPgAPiUiw4fH/BYAPALgcdu/jz+2ijcsA\nPghgHMC/AvDbIvL26nX/E8BPNdz2dgDnlVJPi8gBAF8F8BvV9t8D4LiIzDTc/qdh95COATjZ+KQi\n4gfwvwF8HcAsgH8L4E9E5E1Kqf8A4D8DeKA6+vn/OrT7dwH8rlJqHPbr+8WtN1BKfas2ggq7J/c7\nAP60evW/hd1z+48B7AewDuC/bvtKASdF5IyI/A8Rmb7EbYmIaDAwi4cri2v+EYAXG35+K4BnG35+\ntnoZ0a6wkKVh9KVqr2VKRFIA/ts2t/0XAH5TKbWmlDoN4HMN170HgB/A7yilKkqpPwfw3YbrfwnA\nfUqp7yilTKXUHwIoVe9X8zml1Dml1BrsILp+p7+MUuqrSqlXle3vYYfZe6tX/zGA20VkvPrzT8MO\ne8AO1a8ppb6mlLKUUn8N4AnYAVvzB0qpF5VShlKqsuWp3wMgBuDTSqmyUurvAHwFwE922PQKgCtF\nZFoplVVKffsSt/8c7GlIv1r9+V8D+NVqz20JwH8E8M9ExOdw3xXYPfiHAbwD9peBP+mwnURE1H3M\nYtsoZXFddVT81wD8nw0XxwBsNPycBhAT4XmytDssZGkY/YRSKlH7B2Bhm9vuB3C64eeTW647q5RS\nba4/DODuLUF9qHq/mqWG/87DPojviIgcE5Fvi714Qgp2+E0DgFLqHIBvAvioiCQAHMNmAXcYwD/f\n0r5bAMw3PHzj777VfgCnlVJWw2UnARzosOk/D+AqAN8Xke+KyAe3+R0/AeBWAHc0PN9hAH/R0PaX\nAJiwF7VoUg3nJ6pfAi4A+DcAfkxExjpsKxERdRezeLN9I5HFDY9zJYCHAXxSKfWNhquysEe0a+IA\nslveW6KObdubQjQCzsMOvNrUl8u2XHdARKThIHsZgFer/30adg/yb/aqcdWpUccB/AyALyulKiLy\nJQCNvZd/COAXYP89f6t63kmtfX+klPrFbZ5iu/A4B+CQiGgNgXYZgB920nal1MsAflLshSs+AuDP\nRWRq6+1E5L0A/hOAW5RS6YarTgP4uFLqm50839anr/4/O+uIiAYfs7g9T2WxiBwG8DcA/pNS6o+2\nXP0i7IWe/qH683VonnpMtCP8kkej7osAfkVEJkTkIOxzQWq+BcAAcGd14YaPAHhXw/X/D4B/LSLv\nFltURJJ7GAUUEQk1/gMQABAEcBGAISLHAPzYlvt9CcDbAXwS9nk6NX8M4MdF5P0iolcf89bq79mJ\n78Duuf7l6u9/K+wVBv9Xh7/MT4nITDV4U9WLrS23OQT7PfgZpdTWUP59AL9ZDUWIyIyIfLjNc71b\nRN5UXZRiCvbUqEeVUhtOtyciooHCLG7PS1l8AMDfAfg9pdTvO9zkfwK4S0QOVG97N4A/6OT3IHLC\nQpZG3a/DnqLzOuzzXeq9h0qpMuzey58DsAbgYwAebLj+CQC/CHtVvnUAr2Bvq+/dBKDg8O9O2AGz\nDuAOAA813kkpVYDdU3z5lvadBvBhAIuww/c07HNVOvq7r/7+Pw57itQK7PObfkYp9f0Of58PAHhR\nRLKwF5v4l9W2Nnof7OlJfy6bqyXWemd/t/q7fl1EMgC+DeDdbZ7rCgB/Cfu8nhdgnx/V6flDRETk\nLmZxGx7L4l+Ancf/seFxsg3X3wf7HOXnq/++Ur2MaFeE09KJvE9Efg3AVUqpn7rkjYmIiKjrmMVE\n/cVzZIk8Tuz93H4e9iqJRERE1GfMYqL+49RiIg8TkV+EPU3pYaXU/+d2e4iIiEYNs5jIHZxaTERE\nRERERJ7CEVkiIiIiIiLyFBayRERERERE5CmeWuwp4QuoOX/E7WYQEdGQ+EFxY0UpNeN2O7zMH4mr\nUHy2/vOB1EUXW0OD4Gyi+U+Kn4nu096UwOkL/r48F98/6rdOs9lTheycP4L7r7zF7WYQEdGQuPmF\nr550uw1eF4rP4h0/+7tNl332niUUb3uwzT1o5Ey/ye0WDJ2bnrkbt35q63awvfGfv/rf+vI8RDWd\nZjOnFhMREVFX3XXvHBaTC243g2hoPX7NZ/ryPCxiaZCxkCUiIqKeYDFLRES9wkKWiIiIemYxuYCb\nnr/b7WYQEdGQYSFLREREPXXrpwocnSXymEc/HXa7CUTbYiFLREREfcFilsg7+nUeLtFusZAlIiKi\nvuFUYyIi6gYWskRERNRXnGpMtHe9XFH4ug+levbYRN3CQpaIiIhcwdFZosH0sU98we0mEF0SC1ki\nIiJyDUdniYhoN1jIEhERketYzBINBq5WTG7aSRb4etgOIiIioo4tJhfw6KfDXC2VyEX8+yM37KYz\nkyOyRERENDA41ZiIaLTs9pjPQpaIiIgGDotZokv77D1LbjeBaNeO3n/tno71LGSJiIhoIC0mF3D0\n/mvdbgbRyOjllj5EjRaTC7jt+C17egxPFbJnEzO4/pjhdjOIiIioT247fgtHZ4mIhsT1x4yuHdM9\nVcgCwO3anQw0IiKiEcPsJ2pVvO3Brj0WpylTry0mF3C7dmfXHs9zhWzNYnKBo7NEREQjhFONiXqn\nm0UxUaO9ngvbjmcLWYCjs0REtHvMD2/iVGMiIu/oxrmw7Xi6kK1hDy0REe0ECyHvW0wu4Kbn73a7\nGURDgdOKqdt6NQrbyNfTR++j247fAiRv4WprRETUFgvY4XLrpwpAcoHZT7RHnFZM3bSYXACO9/55\nhmJEttFicoFfVIiIqEk3V0mkwcP3lohoMPTzeDx0hWwNQ42IiIDur5JIg4mnGdGo2uu0YE4rpm4I\nPfKRvtdfQzO12EntxeSUIyKi0cMOzdHD04xoFL35//4isIfOOk4rpr1aTC4A9/b/eYd2RLYRe2mJ\niEYLi9jRxvefiKj3bnr+blePt0M9ItuIvbREwyeXMbG6YsCoKESiGqZmfPAHRqJ/jtpgAUM1i8kF\nPPLRx/Ctjz/ndlOIeuqZh31Acnf3/Zr1OTzT5XIgmzGxxmweeovJBeBTBVfb4PqnSkR0EXlaRL7S\nj+fjYlBEwyG1VsHZ02UU8hYqFYWNlIkTr5ZQKVtuN41cwmN79/Q7m3uFe84Sbe+Zh7tbxK6vVnDO\nKZsrzOZh4fYobCPXC1kAnwTwUr+fdFDeACLaOWUpXLxgQKnmyy0LWL1ouNMocg07KHvClWzuFX4+\niFpd96FUVx/PshQuLjObh9licsHe9mxAuFrIishB2JMh/rsbz88vP0TeVK4oqDbX5XPs9R0Vg9Qr\nPEzczuZeWUwu4Ppj/DJNVPOxT3yhq49XKbdLZmaz17mxInEn3B6R/R0AvwzA1U83F4Mi8hZdF7Sr\nZH1+6W9jyBWD1is8ZAYim3vhdu3OgfwyRrRX3R5d3Q3dx2weRovJBdx175zbzXDkWiErIh8EsKyU\nevISt/slEXlCRJ6o5Dd61h6eR0PbWQkk8MTEW/FU4i3Y8EXdbs7I8/kE0ZgG2ZKLIsDk9MisYTeS\nBrVXeFgMWjb3Cjuwh8PFwAS+O/FWPJ14M9LM5h155KOPdf0xfT5BJOqczVPMZk8a9Lx181N1M4AP\nicjtAEIAxkXkj5VSP9V4I6XU5wF8HgDG5t/Yfs5ClywmF/Dop8N4/JrP9PqpqAOVsoVc1oJoQGxM\nt0fi+uxbk9fhe/ErYYgGDQpPTVyNm1aextWZ1/reFto0d8CP0yfKKBU3DwtTMz7ExnQXW0W95NY+\ndSNmILO5F7ibwe6VyxbyLmfzN6duwPfHr7CzWSk8OfFW3LLyFN6ceb3vbRkEP3tVEXft4Pa9Ws17\nvpbNpYZsnvUhGmM2e8kD992BZx9KuN2MS3JtRFYp9StKqYNKqSMA/iWAv9salG659VOFge+BGAUr\nyxW8/koJy0sVXDhXwas/KCKXNfvahuXgpF3Eaj5ANFiiw9R8eHz67cjrob62ZdgppZDLmshsmDCM\nS38vXlk2UC413y61ZsA0PfmdmrbBUdj+GeRs7hV+tnbm4oUKTriczUuhabuIrWWzZmfzY9PvQEEL\n9rUtg6J424Md33Yn05B3lc1bzpVNrTKbvWQxueCJIhYYoX1kd2MxuYDP3rO0o4MDdUchb2FtpXXl\nu7OnyrjyzSFoWmvvr2UpZNImigULgYBgPOHbtpe4XLagFBAICGTrPJiqV2OHYEhrL6LAwsnIfryF\no7I7opRCas3A2ooB0wSCIcHsXAAiwJmTJVi191vZo6tTM37HxzEqChvrZsvnwzTtYrbd/ch7OApL\n/cA9ZzuTz5lYX3XI5tNlXPmmbbJ5w0SxaCEQFIzHL53NUIB/u2yOHoIhrWMxmrJwKjqPN2VO7Oj3\nGjVbF3lSSmF9zcB6NZtDIcHMfAAC4PTJEqCqp74qYHrWh8lp54ytbbfjlM0b60bb+9FgCD3ykYE9\nF7adgShklVKPAnjU5WY4uuveOSC5wKlHfbaRag1KAIAAuayFsfHm4tIwFE6+VoRpAErZ52OsXDRw\n+PIgAsHmsCuXLJw9Xa6vrqfrwPzBACJRh4JVKdiH79Ywlbbr5lI7K8tG05egYkHh9IkSROzl+Rut\nXjQQjmoIhzWUigpKAaGw/cWmWLQggpbPiFL2yohTM/35fah3vDKtaZgNcjb3AqcaX1raoUgB7ITM\nZy3EtmZzpZrNFqAsO5tXlw1cdkUQgUAH2XwogEjEqTO5Tf5KLbdpJ1YuVLC+tvneFgoKp193zuaV\nZQPhiI5QWFAs2hVuPZsL7bM5l7MwOd2f34d2zqudxm6vWuwZi8kFhB75iNvNGB3b5JByCKmLSxUY\nlc2Dp1KAZQJL5yot9z11ooRyyS6MlAIMAzhzsoxKpfVxr8yegq5aF+60RMOB/IWd/U4jzrKUY0++\nUq1BWbt8ddnAqz8s4tSJEk6fLNWnsPn84tzRUXXilSJefqmAU68Vkc/1d8ob7Z2XpjXR8OFU4/as\nbbO59bLlpQoMwy5ia7cxTeDC1my2FE697pDNJ8owHLL5jdmT8DlkswkN+wvM5u1sXeTJMlVTEVuz\nbTZftKeUn2nI5nzOhP8S2fx6LZtfL6GQZzYPggfuu8PTxzwWsjtw171znn6zvWQsrresegcAUEDU\nYeQ0m3E+IBbyFqyG5M1lLThkH0xNw/pG69F3upzC29e/B90yoVmmncbVlP3iZcfw3PgbO/6dRl2l\nopwGtreVz1n2KHu1N9807enlPp8gEHR+sHzOQqmkYFnVXuUTZaQ3uHekF3BvbxoU3HPW2XibbFYK\niMRav1K2y+Z8zmrqlM5mLcci2dI0rDlk80xpHdelvg/dMrZks4UHLkvihfErO/+lRszW6fOVinL+\nvrWNXNaCadqFbi2bz5wsw+ezT9dyks9aKNeyOW/h1OtlZNIsZt00DJ3GAzG12GtqX7Q4/ah3IlEN\nsXEd2fRmL6EIMDvvs/cp22qbg3DjVUZFNfUWloMhfP+6m7E+ewAQYLa4hlsv/gMSlUz9Nm9PvYQr\ns6fwlflbkfFHABFY4oMF4LtT12KiksGhwtKeft9R4Ntmf7m2BI73yWyYOHg4iPOnyygUrG17gAHg\n/JkKIlHdbgMNnOuPGbhdu9PtZhA1uV27E0gy6xtFY87ZvG/e73jeq9M0UyeGoZqO9aVgGD+4/mas\nz+wHBNhXXMWtF/8B8Uq2fpt3rr+IN2ZO4Cv7b0XWV81m3Q8LwHemrsNEJY0DheU9/sbDxemzfKkZ\nTjuRSVs4eCSIc6fLKHaQzeeq51Y7fq+jnhmmU3c4IrsHHDnoHRHB/AE/Dh4OYGJKx9SMD0feEERi\nwnmhgHibXuJoTIM0LD4Rjmx+5BUET998DGuz+6E0DUo0XAhN4sH59+HMBXuVvlqPsUAh7wsBWxaX\nMDQfnktc1YXfePjpuiA+0fo+iQATU82XiwA+HxyLWHvKmWWvgKh19iUJsBeBosGzmFxgEUsDjVm/\nqV02xyecx0Xaza6KjWlNCzmFw5vZaong6Vtux9rMZjYvhaaq2WwhnzMbRnMFBb1NNsdHL5u/Zn1u\nx/fRdXEcaW+bzW3Wa7KnjSuYhuq4AwMAUuvM5n4ahlHYRixk94hT4XpHRBCJ6pidC2B61t+yaFOj\n6Vk/gkGBiH2gFc1e8XDuQKB+G6UUTEshGLJvtz4zj3IwDGgNU5VFgykafhA7grOnyjh/tgKlFIp6\nEFqbo3JOC3ftdx52s3N+TEz56t85/AHBgUMBzM4FcNnlQcQndERjGnx+gdEm20QDgiENJ18tIZ91\nmCfeRiHf+W2p947efy2PneQZnGq8aSfZPLvPj0BQIFpzNu/b35zNlqXs2wmwNnsAlUAQ0BoeVzQY\nouPl6GGcOVnGhXN2Nhf0IDSn84UA5HRmc6NHP93+9di334+JSb05my9rzuZILZsrzo8hGhAICk6+\nVkI+13ne5pnNfTOMmcupxV2ymFzA16zP4ZmH+ZK6QdMFl10RRCFvoVRUCAQEkdhmj69hKJx6vYhK\nBfVRvkJsHEprDWDL50c+FodSQDZtIp/QMaGloZxmNJsmYqdPY3W1wi1fOiAimNnnx/SsD1BoGi0P\nhTXMBv147WV79Wnn+9s999l0m1Wtt9HuvB3qv8XkAnDc7VYQ7QynGu+cpgsON2ZzUBCJbsnm14qo\nGKhncyk2BktrXQujMZvTGybGEzqmtBSUwzY8YhqInTqFtfUKt3ypevyaz7S9TkQwMxfA9D7VPpt/\nWITZ5pRWESAS0ZDZ2Hk2B5nNPTeMBWwNR2S76HbtzqH+sAy6Wi/xxJQP0TG9HpSmofD6y0VUymia\nqhpLrzku4a8ZFYxvrABAvZj1KRNHV56BzzLq82XENOCvlHDo1RewetFAnivwdUxEmoKyJps2YQcJ\nc4MAACAASURBVLV5Gf0Bwb55e0pbLrezpLSnSLGTyW0chaVhwM/wzjRlc0xvKmJff7m5gxkAohvr\n0NE6SqcZFYylVgFsZrNfmXj36rN2NteezzTgL5dw8NWXsLJsjNRsnHaDKZ+9p7N1PNplcyZttl2x\nOlDN5gOXBZDfRTYnmM09NezHK356eoCLQQ2Ws6dLjkvIj68uI5ZeRzY+CVOr/ilYJvzlEmbOnqjf\nrtbZe3XmNYQyG3gqehVKoQgml8/i4GvfQ6BcggKwsWY67ndHnSuXVdve3PG4tnke1jZZufXcHN1n\n9xSfP1NGxVAIBjVMz/qbzpem3uMoLA0T5vzenT3lnM3xlSVEMinkxidhVkdmxTQRKBUxc/5E/Xa1\nbH5b+hWE0yk8HbsKpWAYUxfO4OBrL8FfqWbzuoFwJNDyPKOkeNuDe7p/ueS84wMAjDVm8zbaZfO5\n02UYtWze5286X5p2b9gL2BoWsj20mFxgyPVBIW9i9aKBSsVCKKQjMakjs2FiI2U6hmSNALj+O1/H\n+rvfiR+MHYGpBNPnT+GK7z0JvTosKAKMJ+w/E8tUCC+dwzWpM46PZ263wR51JBTS2q9UnLYwNaMg\nIghHNOTanB+7b96PcFRDuWTh3OkKTMO+b03esHD6RAkHDwcQcdjKibrrpufvxq2fKrjdDKKeYM63\n15LNUzoyqc6y+YZv/xXW3nMjfhg7AtMCps+fxBUvPQmtekcRYDzekM3nzuKa9GnHxzPN0crmz96z\nhLvunav/3I3PZyisA2I6ZnM2s5nNoYjWdu2KjrL59RIOHQkgzEGBXRu1XQBYyPYYe217Ryn1/7P3\nZjGyJeed3z/irLlvtS937W6yyVazqYVUNymhKXkkdRdG9lAaD0DYMDCGNHAZIAxRMIh6sccPxhjg\nCBi9GBrbhGcMC5AhasZ8kDQDDVsSaJEcDalutjhNsrd7q27tVbkvZ43wQ2Rm5XJO1nIrK09Wxg+4\nffvWllGZeeJ3vogvvg/7T5y+idCxfVQrF0/xzcQ5Plp8Cy8X30Kj7mN32xEWbWfWzC2oME0Kxjge\nt5u1B0EIkErLifdpSaQoVBWBxSRcl6PZYEgkFcwvamg27KHd22xeQSanitfrfTd0d5dz4PjAxd2H\n8jUbJ1sbm4AMYiW3HFkjox/OOfZ2HNRrAW4OWagcJJvg+Ojpm3jl9E3Uaz72dtpupuL75xdVGG03\nP/rAhuuEuJmKysmzhPW5P8Infu8LAIB/8I9+/1p+ZjJFoSgIrF/h2BytJhMFwBY1PA5wc65wcTcf\nHbi4+2C2XrPrYlZ2YXuRs+4NsbWxid/57YOnTu+QnFEuen1B7GUhBJhfOCsCkUgqeOYjJup1H5yJ\nf6uaiGgrZS9clAQwY6J8veTpIIQgnVFRPBm2JW83UU8kFRgmxZ37Bo4OXFgtBkURZ2A752CbDXbu\nvZIdsigheXrMNz7ftyMgkdx2ZCGoM0qnXl8Q28cFpl1CRCeCDsmUgocfMdst8dpubvcdrZQ8eO4I\nN5t0JheZryuA7UAIQSYb4maObiBrmBTr9w0c7zuwLA5FAfJzKrJ54eawTKpebEu6+SrMYhALyED2\nRvmtrywBMg3p2iiePkVxpXYbgEfvW0imFMwtaFA1AqqQbrpSL416eGNvVRMrkh++ayObFwUtevvj\nSS6HrpPAHnSif11/JcU7943An8HZ+Qv/sgH7eNja2AS+MulRSCSTQaYai0D2ynTc/F7bzYsaVJW0\ne51ezs2aLs52fvhe28156eanQdMu5uZYjOLOAzPwZ3DOz13LUKWbL8WsBrAdZCA7AbY2NvGJXy1f\n+4rZrMEuee5F0wkoFd/nuuhWx62UfTTqPu49Y0JRgifQUROr64i/fZ/j5MiDZXGsrJ0VlmCM4+TQ\nRaUizpckUwrmlzQ5WYeQSis4OhhOPbpI+rbjMBwfuGg22MgzWABQmJu9Vfpx8ge/94Vb1WRdIrkq\ns55qHNaiJYyOm32fwwtw8/1nTNAruNmxO+PhODn0YFscyz295ZnPcXLU4+a0OLYi3RxMKqPg+DDE\nzamLubnRCC8a1SE/L918UWY9iAVk+52J8dbXs/IN+JRcpuospcCd+waW13R4AYvFvi/Sh8PI5lVc\nZCG30xLAcVj73xw7j2yUS6KtDGOi/93j9y0wWRwqEKoQrN8zuqu/hIiV4PV7RuhCAyBaOTx+30a9\ndn4Qq2roVlm0WgwnRy6KJy5cZ3baNFwnWxubMoiVSHqY5XZ8scQV3LyqB56/vE431yp+d44PdHPZ\nx+MPbOnmEJS2m9VBN983QhcaAMBzz9x8XhCraUAmK918Hi+95s3s/DLIbC4XRghZDOrqzC9paH0w\nXL7fjBFoOkG9KlKOYnGKxWWxytps+IGpMZwDrQYDCsGPZZoUiysajvbd7tf3/t0HAewWh64DrZZo\nAj/4dT4TUr1IyfpZxIxR3H/W6J5L1nQyMiXM8zgef2CdG8B26PQyPNx3UCn53dfn5MjD4rImX5cL\nIkUqkYxmFlONFxY1PG7aQ0FLLE6gakTUtui4eUW4uVEPLgQlzl9y5MLcHBM/43DfFd8+ws2EAJbF\noeniTKcd0O7N9zhqVb8bTEn6MWMUD8bp5vbO7sGeg2q57WbSdvOKJl8XSO8OIt8REWHWU5GugmFQ\n3Hto4PRENDxXVSA/pyGRFBMhbxuqd5LVNBJ6PkM3Ri/rZrIqUmkFtsVAKUGl7KEUdE6XA6oufla9\n6gcKlTMR5GZy5/+eswoh5NzXBBCv85PHdmCl4+CfC+QLKpoNvy+IFT8LONx3kUwp8gztCGatvL9E\n8jTMWjBrmMLNxV43z2tIJEa7OQhCLu/mctFDuTTsZs7b9wCcCzcHBFeci53AjEwwCeUybt55ZAdm\nwQX/XCCXV9FqsrMgFgC4WN843Gu7ecTu723m5a++iM997bOTHkbkkFFThJBVDy+PplMsrQQ3Og9a\nJTRjFJpGhtroEIpuVb1RUEq6/c2yeRXl4nCgqhsEug7sPLLRagYvQ15EzpKLYVs8tC3SIJpOsLSi\nQTcoSqdOaJGQel2uyIchV4Mlkssza9lX+iXdHItTaCqBM9gdgADZC2TI9Lo5V1BRKQ+72TBEAPbk\nsTPSzYYhT91dB1aLh3Z7GETXCRbbbi6GuZkAjbofWPTrtrO1sQl8bdKjiCbyao0gWxubePmrL056\nGLcSQsQZj3iSdvvF6jrB+l0Dmna5y0HXKdbu6t2znCBAIkmxdtdA6dRHqxleTZEQ3MpAiXPRT67V\n9Lur7uPGdfnIM1KxOMWzz5u494yBbE5Bs9EeX9jePOm2EZb0IM/kSCRPj7yGgiFEnLWMd87Xthd7\nO2cyL4NuhLv59Ngb7eZb2nd2Em72XD5SpvFEj5vzatvNLHR8s+jlV97+kpwzzuH23UnfEj73tc8C\nG5+dmdXbm0RVReDKfA7Gn67Uezyh4P6zFL4vgtNOykvQanAHwwSW10YXLpommg0fxRMPts26xTo6\nNw8ra3o31XtcmCYJf64NgtU7OloNht0dUV6ac6B4IloEBMLPzulIBFKkEsn1MWupxhdFVUXget1u\npgTdYkTVshfqCzNGsLyqz4SbV9d1xBPj9ZwRI6E98AyTYHVdR7PBsNfnZg+xePDz3+khPCtsbWwC\nX25NehiRRwayEWdrYxN//k9i+Kuf+KeTHsrE8TyOo30X9ZooCpFOizY2V5UOVci1pCQQQqAOXEmh\nK54EWLtr3pry/pWyh8M9F4wDe/c+iu1nXoCrm0iVT/DwB38Nvn2KB8+N9/fVdIp0RkG10r94QBVg\n/b4BQoC9J87QWdhWiyGZot0+hJ1d3aXVq7+nbhvyTI5EMh5uU6qx53IcHUyLm8O/fu3u7VlgrpQ8\nHO4LNz+5/zyePPMCXM1AqnyMZ37w1+CPi2N3s65TpNIKagO1QhQFWL9nAGFubvJANy/PkJvl4vHF\nkanFU8CrX27N/JuaMVH5rjMhciZ2Pbc/tG8sTeYyhPU71XVya4JYzsXCAufAhx/5JN7/2E/BjifB\nVBWVuSW8+ZlfQT2VRXVE64TrYnFFw/yS2n5+gUxOwf2Hoi9w2FkozsWfew8NzC+qmF/S8OA5cybP\n3wSxtbEpg1iJZMxMu9sD3VzxsRNRNydD3GyY5NYESZzxbi/2D57/KXz4/E/CjiXabl7G33zmNTSS\nGdQql2z4ewWWVjXML6rQ2m7O5hTce6bt5gYLTBfuvG3uDrg5NQNu3trYnPo54aa5/e+KW8Qs787W\nq35gk3XX5Wg2WOTSTebmNTTqDJ7LuyuKhKCvGTsggsFmQ/Q9jcXpVAW5brt1gaeoePLw42ADS9+M\nKnj07Cew/vibYx8LIQS5vIZcXrvk94nzVHlZ3KPLK29/Ca/KdCaJ5MaY5t3ZWtWHP7hWyAEnqm5e\nEG72vX43L90iNzuuqADhqRp2HzwPpgS5+UWsbf/V2MdCCEGuoCFXCHDzqKe0XXRrlgpvyQD2ashA\ndsp49cstYAbP19hWcCNtzsTnoiZLRSW499BArSqKPuk6QTqr9snQthh2Htl9fe8K8yoK85cLxiZF\nZ/XajidBgl4cSlHLFhA/mexrE48Hi5AQIH0LC249DfJMjkQyOabx7KzVCnEzBxybI5G8+TGNQlUJ\n7j/T7+ZMVu1rt2ZZDE8G3bygojA3RW7mQCueAmEMGFQwpahl55AoTtbNsRFuvo3FMMOQi8dPx+ws\nddwyZi39QDcpSMC7lVCxoxZFKBWCXFrRkZ/T+oLYTu9T3wcYE384B06PPTQb40/3uQ4UlSCRpDCs\nJhgNeA04R6pVPatCOSEIJVhZ17sr74D4O5VWkExF871z08jKiBJJNJi269AwaWDVeNruCBBFBt2s\nDLr5UYCbjzw0m9PhZlUliCcoTKsORgOCVc6QblVCA8mbgoa4OZ1RkEjOhpu3NjZlEPuUzMY75RYz\nbdK7Kqm0gqBYSW0HU9NGqyVSlgbhHCgXp0OWDlFRWI8jrbtY2nkf1HP7Pq8wH6+03gnsGXjTJJIK\nHj5nYmFJw9yCijv3DSyv6ZEY26SRIpVIosU0LVSnQ9ysqES0uZsyWk0GFnC0l3OgMk1uvhNHRnOx\nsPsBqNdfp0JhDK9YEXTzonDz0urtd7P5xuen5hqPOrOzd3+LmebzNReFUoK79w0c7Lto1kUEmExR\nLK5M54THR/jQ96NXIKOXmhrHGwufxqE5BwBIz5/i2e9+E6rrYPf+R8GogoTTwM+Xvoclpzjh0Z6h\nqATZvJzyOkiJSiTRZhpSjalCcOeBgcM9F81G281pisXl6XQzY+LoZpCFo+7mqprAGwufxpFZAACk\n50/wzHe/Cc11sHf3I2CUIunU8fPF72HBKU94tGfMmpu3NjaBr0x6FLeH2XnnzAC3vRiUplOs3zW6\nlRCnUZIdzDgN3JEFgFQ6uqvYPij+9eovoqWY4O1c73KqgDc/8xo+/Wd/iAfvfBeMKlC5j5XnTGCK\nCmTMEjKIlUimg2kIZnWdYv3e7XBzbISbkxF2s0eEmy3F6HHzHN76zGv42T/7Qzz8wV+fufkjJnBL\nKjRPE3/we1/AW1/PTnoYt47oXpWSKzELrXoIIYGi9DyOctFD6dSD44SYKCIoCkEyHSySsHYxUeBx\nYgUu0bqiBABQCl9RcLx6HwQipRgEU3PWd5aYppRFiUQi2NrYxB/83hcmPYxzuS1uTqSC3Ww1o7sj\n+yixCo+qw26mCo6X73XdTAi6O+eSm2NrY1MGsWNC7sjeUmYh3biXasXDwe7ZGc3jQyA/p2JuIbpV\nBq2QY4m1KsMi46A0eiumVS0BP+BAFFM1tOKp7r8JABqhVXmrxXB67MK2OQyDoDCvwYzNzjreS695\neJ1+cdLDkEgkV+Str2fx1hTszg4S5OaoV+e3Q9xcrfhYXOGR3HGuqUl4ZLiwE1M1WPH+0tFRGv6Q\nmxc0mObtcrNcPB4vt+vdIhlia2MTL3/1xUkPY6z4PsfBrmj+3funeOLBakV35ZGFnLfpjD+KzNkl\nKAG9FhTXRapy2vexqBT6aDZ8bH9oo15jcB2Oeo1h+0N7ZnaMtzY2ZRArkdwSpumm2POC3Xx67MGy\noutmP6jaE9rjj+iwC3YJakDxDcXzkKz016qYdCeBDoFu/sBGa0qqQ5+HzIC6GaLxbpaMlc997bO3\n+mKq14InPc7FanBUCSt9r2kksApkFFhtHSHrVKGws+eVMB+G1cDc4TYIBSgFVu/okdlRPjpwhxYG\nOAeO9t3gb7glSIlKJLeTrY1NmG98ftLDOJdGTRwzGYRzoFqeQjfrBDSiZ0vXWwdIu3VQdnY/RJkP\ns1VH4eQJaNvNa3ej4+bD/dvrZunem0OmFs8Qt7oYVEiZwajubALA/JKG1gd2X2EJQoDFFS2SqUuA\neJr/7t4b+A+5j+Pd1D1wEDysb+OTR2/DW1ZBqWiHFBVRAoBtBb8JbJuD82imiT0tUqISye3mt76y\nBEQ81Zh3/zNdLCxq2G4GuHk5uunQBMCv7n4D3819HO+m7gIgeKb+GC8d/S3cpei5mXMOxw5+c1gh\nzp4GZEGnm0cGsjPGq19uRV5+lyWRVAA+vIJHCJDKBDQDjwiGQXHvoYHTdgq0rlPk59TIn93UuI+X\ni9/Hy8Xvn31QAZCN1nTCfI5aTRS3CFrQoMp0V9cMQgawEslssbWxid/57QNYn/ujSQ9liGRSwRFC\n3JyOli96MUyKuw+N7vEkXafIz6uRP7upcw8vF9/Cy8W3zj4YVTdXw92sRPe2bSRbG5vA1yc9itkj\nWu9uyY0RZfldFlUlWFhScXTgdSdFQoBMTkE8Hu0ZUdMpllb0SQ/jwjQUE98qvITHiRVQzvFs7RE+\nXXwbGo9GmhhjHPWaj1aDoVL2Q3fkCQFyt6xvnQxiJZLZJKq7s6pGML+k4jjAzWHpu1FBnzo3x9pu\nXgblHM/VPsSnim9DG9W0/ga5lJsL0+Vm6d7JMl3vFsm1ElX5XYVsXkM8qaBa9sE5Ryod/Z3NacMl\nCv7V2t9Bs6eH7DvphzgyC/h7u38WdBTqZsfnMDz+UKSDnVeQI5NTUJi/HdOflKhEIgGi2XM2l9eQ\nSCioVqSbx4VLVPzR2t9Bq6eH7Dvphzg28vhP974xcTc7jijixNj5x70yOQX5uelxs/Tv5JGziWRq\netSdh65TzC1omF/UpSjHwPvJO7Bpfw9ZRhWU9DQOzLkJjkywv+vC984PYgkB8nPRPYd8GaREJRJJ\nL1H0uW5IN4+TH6fuwhnoIetTFadGFkdGYYIjE+w/ceD75wexhACFKXGz+cbnpX8jgpxRJABEjzp5\nUUqC4JyjUfexiww8OlzsgoOgqE+2uAFjHK3mxfsi1KvRSLe6KrIisUQiCUP6fDbouHmPZAPdDBAU\n9cyNj6sX3+ewWhcv3hTWhSJKbG1sioxGSSSQgaykD3mDLOnFthje/5GF3R0H5LAI6g0X7qDgyLi1\nCYzuDMeOaHO/a+aVt78kr0+JRHIh5Fxxe7Habt7bcUAPT0G94ToVRLr52pHXVPSQgawkkK2NTbz0\nWjQK+MwqvsdRKXuolD343s2Xo+ecY+exjUoih9P8Mgr7O6JHXU9PAsp9xL0WVluHNz6+Xo4PL/de\nTaanb+rb2tgUVcclEonkgkxLz9lpwut1sz85N5cTeZzkl1HY2w50c9JtYNk6vvHx9XJpN6eiWaBT\nbvJEl+k5US25cV6nXwQ2ELniEVfFdRnARSXFqJ/BqJQ8HPY0BT+Ei6UVDekbLKN/6pr49md/Ga14\nEoRzcEqx8uE7qGXnUSksgAC409jDzx9/d6LFJDjnaDYutupLCDC/pELTpieQlfKUSCRPQ9QLO7qO\nmL+nwc3lkoujfa/bu/4QLpZWNaQzN+fmE8/Et3/uV2DFEl03r77/H1EtLKCSXwAFcK+xi5+LgJsv\neuSHEGBhSYWqRev1f+k1T9wLSyKLDGQl57K1sYk/Zr+LN/9kOt8ujs2wu+PAdcTKqaoSrKxHt+iE\n6zAc7rtDhREO9lzEE8qNTfTfuPvzaJoZcHr2PO3d+yg+/td/jpW3DnDnngEakW73Yf3oAODeMwbq\n7Z51ybQCXY/m6x6EDGIlEsl1EbWqxrbFsPekx80awcpadN3sOAxH++1WQj2+Odhtu1kdv5s5gH93\n91U0jTTQ4+bdB8/jJ/79N7BsHWH9bvTdTAhw9+GZm1NpBVrE3Cz9Ox1E610jiSyv0y9O5UXNGMf2\nhzYcm4NzMaG6LsfOI3si6boXoVb1+xTEAVSzczhYe4BtL30jYyhrKdTMdF8QCwBM1bD78Hlk0iRC\noiRIZxQMLuR3+hUaBkVhXkN+TpuaIFamMUkkknEQlVRjxji2Hw242Wm7eQLpuhehVunvf9rr5h33\nZtxc0tJoGMm+IBYAmKLiyYPnkU3TSLk5lVYwuC0c5OYoBbEvf/VF6d8pYjq32CQTo3NxR2lVdxT1\nmg8WMKdzDlQrfiQbb/eu9nqqhrde/iU0UqIq8I8Jwd86Rby2/5djbXRuUx0kpI+NZ5jI3GCK80VY\nWNJgtXzYtvg3IYBhEiwsBlVyjC4yjUkikYybKKQa16t+4E4d5yJgzOaj5Rigf2fRVXW89fIvoZnK\ngHDgx5Rg0T7BawffhDpONys6aJCbCYFnmkhnonXGdGFZg231u9mMUcxH1M1bG5vA1yY9CslliM4S\niGSqmJbVKi+kr6jYmY1mNb1k6mx38d0XPoVaOgemamCqBl9RcaAX8O3si2MdQ8EpgwecVaLMw3Pe\nHiiNzjkW3+fY3XHgOOg+b5msgrsPTFAlOuM8j62NTRnESiSSG2OSHvc8Pt1ufvFnUW+72deEm/eN\neXwn+8JYxzBnl8DI8K274nv4iLcHEjE37233uLm9E3vnvhGpe4gO03JfK+lHBrKSKzMN6Y+xGBlK\nOe3CRTGCqGGYFNm8SMc5XH0AKP0r01xR8E7mAdgY069U7uMzJ38DlZ2tBCjMQ8K38EL1vbE97lXY\nf+Kg2WTd9DQAqJR91KakV6xMY5JIJJNia2MTr7z9pRt/XDNGERCPAUB7Lo+em80YRSanAITgaOUu\noPTvfnJFwQ/SD8GC0sCuCY37eDnQzS18vPr+2B73KuztDLiZA5WSH7k+7tNwLysJJ3q5G5KpY2tj\nE2/82jfxrX/4/UkPZQgzRhGLU7Tak2kvpaIPEGBhSZ/M4EawsKQjmWZD52A6cKrgtMoxnxvfquZH\nax8i51TxduZZNNUY7jT28LHq+9B5dNoyeV67YvHAa8s5UDxxxfmcCCPTmCQSyaR59cutG081jsUp\nzBiFFeTmUx8EwHwE3by4rCOZYQiLwrmiolhhmMuNzz0fq32AvFPB37bdfLexh+ej5mY3uGIx50Dx\n1EMyIm6WAez0IwNZybXwua99Ftj4bOTOzhJCsHZHx5NtG83G8CppuegjP8dvpNrgZYnHKRTmw1cC\nLlPOcUzSmEd9rGNYtE+xeHQ61sd4GpjPu20QBvGj4/QhXnn7S7InrEQiiRQ3WdWYEIL1Ozp2Htto\nNYcn8FLRRy6ibk7EKSj3wUiwm09ICnNojnUMS/YpliLsZn+Em70IFNp8+asvivtWydQjA1nJtRLF\nYlCEErhu+MRptVhkm3DnW0UcJxeGPk44RxrWtTwGYxxWi4FSAsOMfh+/XjSdhLkS8WQ0T05sbWwC\nMoiVSCQR5CYdfp6bbYtBTUbVzSWcJOaHPk44R+q63OxzWNZ0ulkf4eZEYrJulplQt4to3ulJpp4o\npWtwzuG5YZ9D5Bpw9/Lpyt+CDmwtEt9D7mQfS8mQX+oSlEsu3vuhhd1tB9sf2vjwPRuOHc1CG0EQ\nQrCwrA2dg6YKUJiPVlVE843PR+q6kEgkkjBuYq7inIdmznCOSO7GdvhUOcjNPgrHu1hMPv0Z0HLR\nxXs/GnCzM0VupgQLS8NuVibo5lfe/pJ08C1EBrKSsRGVA/S9RYCCMM3oXgar1jE+c/QfoLo2qOeC\n+D7mTvfwy6ffemrJW62z5u6M9fTxe+xEstBGGJmsirW7OhJJCsMgyBUU3H9oQovQAsXWxqZoeSGR\nSCRTwrgLQXW8E4YRYTevW0d45ei7UD2n6+b5kyf4pdJ3ntrNraaPo4NhNz+ZNjfnht1876E5kc2D\nrY1NeZznljKx1GJCyDqAfwlgESL74J9zzv/ZpMYjGR9bG5v4Y/a7ePNPJvN2I0Ts0LGARVJNj06w\nE8bHmo/xke1tVJQETM9GnLiA8fQ/t3TqBd5E+L5INY7Fo5nSFUQ8oSCeiN54zTc+LwNYyVQh3Szp\nZZyFoCgVf1jARqM+BW7+ePMRPvr4cb+br6E+Vek0uMeu53LYFocZi/5z02HSbpb1KG4/k1zu8gB8\niXP+MQA/C+C/JYR8bILjkYyR1+kXJ7Y7SwhBYU4dSnEhBJFtyj2IAo68XxeivCb8kPY9BIAfrer4\nU4nchZVMKdLNkiHG4W9CCPLSzUOEupkAfgQKJU0Lchd2NphYIMs53+ecf6/9/zUA7wBYndR4JDfD\n1sYmXv7qizf+uLmCivlFtdv2TVWBxRUt8u1ZxkkiSQN77HIOxGLRTemKOlFJqZdIroJ0sySMcaQa\n5+dUzC2ooD1uXlrRItOeZRIkUuFuNuPSzRdBOnh2iETVYkLIPQCfBPCdyY7k8igeQ6JsQXN82DEV\njYwJTqcn7WMSTKJVDyEEuYKGbF4FuChEMOtkcirKJR+uw7tpTIQAhXkVSkSKbHAu+sRaLQZVI0il\nFdCIvnYvvebhdfrFSQ9DIrk2ptrNLkOiIt183Vx3qrHYldWQK0g3d8jmVFSKPlx3wM0LKhQlGs8P\n5xzNOoNlMWgaQTIibpYB7Owx8UCWEJKEKIT933HOqwGf/00AvwkARnq41Pkk0VseFrcrAADKgXjN\nQebUwv69DJgqV83OY2tjE3/+T2L4q5/4pzf2mIQQgIhJuFrxUTr1wHwgmaYozGmRCeBuIRrcpgAA\nIABJREFUAkoJ7j4wUC56qNcYFAXI5lUkItLugDGO7Q9tOA4Hb/efPz5wcee+Ad2I1vUl5Sm5bUy3\nm10sblcBLtLO4jUH6aKFg3sZMCVac8e0ct09Z3vdXCl5KJd8MAakUhT5eS0yAdxN0HVzyUO9yqCo\nEXOzz7H9qMfNBKAHLu48MKDrk7u+pIdnk4nO6IQQDUKU/zfn/I+CvoZz/s855z/NOf9pLZ652QGe\nQ2G/BspFEAuIvxWPIXMy3kbYt4lXv9yayORzuO/icM+FbXG4Lkep6OPRBzZYyNmU2wqlYjX8zn0D\nq3eMyIgSAE6PXTi2ECUAcCbO7u49cSY7sB5ees2bfnmeV9ZbMnNMtZs5x9xeXbi5/SHKAdVlyBzL\n83LXyThSjQ/3XBwdeMLNjnDz4/dtMDZbcxRV2m5+ED03nwy6mQs370/Izbe2tZ1084WYZNViAuD/\nAPAO5/x3JjWOq0I9Bs0dLrVHIFZ/S9dY44UwjmTZQqJqgxOCWs5EM6Uj8BDFlLK1sYnf+e0DWJ8L\nvGe6VlyXoVoeqArIRRGFctlDvjAdRSauiuMw1Ks+GOMgRDSk1zSCTE6NVN++apkFzuG2xeF7fOK7\n55MQJ/EZdMuHr1J4RvCNTazmIHfUgOoyeBpFeS6GZsYc+jrqMeQP6ojXRZESK67hdCkBXxc/12w4\nSJUsUJ+jkdLRyMrUzFlg2t2seByKF+Lmuo0SEtf2WIRxJEsWEjUbjBLUs7fPzedxnanGjsNQrfS7\nmXPA88QubW5W3Mw5CNpu1gky2Yi5uRJcVdlqcfg+v9Hd862NTeArN/ZwoVCfQbN8+BqFpwe7OV61\nkT1uXsjNhYM6Yh03J9pu1tpurrfdzISb61kTmGE3TzK1+DMA/ksAbxNC3mx/bItz/scTHNOF4QSi\nMUEQ1/mG4hyL2xVott/d+dWtOsymgeJS8sI/hjAO3fLgKwSeMfGM8kB+6ytLYyvz34vV4iBkeKGL\nc6BZZ8gXxvrwE6VUdHG0P9yBnhCgeOJh/Z4BMzKFnsJXIvf3HKyu6yId7YZ5+asvinPeN0zmuIl0\nsSXuyDngGgqO1tJ9xxhiNQdze7XuXKG5DIWDBggHGtkeYXKOpccVqC5D5xk0my6WH1ew+zCHdLGF\n9GmrZ87xkKzYOLibmWlhzgjT7WYKhL1D+XXOF5xj8XEFmnPmZqNVh9E0ULqMm30O3fbgK+GLU9PA\ndaQaWy3Wnd964RxoNhhyt9nNJy6ODkPcfBw1N4dzuOdgeW38bo5MazvOkTlp9bnZMVUcr6X6jjHE\nqzYK+/UhNwPoD2aD3NxwsfSogr2HOaRPxWP1ublq4+DO7Lp5YhEN5/ybCPdN5OEKhRVXYTa9vl+C\nEaCWuYYmn23iNacviAVEmlSiYqOaj52t/HAOwhG4Y5IstpA7bqITvXkaRaUQg+Yw+CpFI62DR+jc\nUGena1wBraqS0BBpGvrKAoBlMZwcumi1GFSVYG5eQyoz+ibIdVlfEMsB2GYchHMYdguci7TdB88O\nrxBOgnRWCe2n16wz1Kvs3N/5utna2BQJlzdMvGqfyasrMB9r75VQzZuozMXBCZA/bPTNFYCYL7In\nzb5A1my4UHpECYjJmDCORMlC5rQFMjDnaI6PRNXuD4glt45pdzNTKGxThdEKcPM1vncTVacviAXE\ndZKs2Khd0M2pYgvZHje7GkV1Lg7NFjs7jVS03HweWxubeOPXvolv/cPvX+n7R+06To2bWwzHRy6s\nFoOmEhQWzu+O4DisL4jlAOxYApT50G0LnAP7uw7uPxONuTedUVAuBru5XmOo19hYO0JEZRcW6Jy/\n73ez0fKw9m6/m3NHwW7OHbf6AtlY3YXiDbuZMo5E2UKmGOBm20ei5qBxjbHHNBHNrbkp4WQlhaXt\nikhjar+xrISGaiF2bY8Ra7hDb/4ORtOFr1LkjhpIVGwQDrg6RXEpCTsuUnAyxw1kTi1xUbRnHc1h\nmNsXK0Ec4gI7XE/DiUcrbee6i0l0MGMEmkrgOP1PLCFALh/9S8K2GLY/sLsScXyO/V0HnqsiNxf+\nGlbLZ81hq9k5vPOTPwc7lgAHQbJaxMe++xcgrTo8l0PVJn/TUJjTUKv6cAOO3XAOVMrejQWyk26q\nnj1qDs0DnVcoVbQQr1igDKFzheK1z9q0V8njVTswUqFc7Mxygj5Zdj4XrzsykJVEnpOVFBa3K1D8\nMze3Ehpq+et775oNJ9zNLU+4+bCBZNUWGRS6guJS4szNRw1kiv1u1h2Gub06gLabDxs4vJuBY0bf\nSx2epitBLE6hqgRugJuzueg/B1aLYfvDMzfbPsf+EwfekopcfoSbS2duruTm8c5P/hwcMy7cXDnF\nx7/7F4DVgOfxSKQYz81rqFd9uAGtczkHKiVvLIHspLKhRhEUoA66WWHDPu0g4ocBNwd8LeUiHuAY\nXmWkHIjV7ZkNZKdnqS+CMJVi734WR6tpFBcTOLiXwfFa+lrPx3hKyO4hEY8/t1tDomyDcvHm1h2G\nhZ0q0ict5PdrZ0Fs/7d2/1CIi2Bpu4pksQXFOZtQzbqD5Q/KuPPDU6y+V0KibF3b73VRxtGTkxDS\nTtMhIES8XIoCrKzrkauGG8TJkRuYFn1y7IGPKIhhW+Jzjm7irZd/Ca1kBkxRwRUFtUwBf/OZ1+AT\nEpnjXVQhWFzWQsdzUzUQxt1UnfiihVf6tAWj6Q79YnrLhRpw5q8DBaD6gMLDt9GYQs7mJc4Rr7uB\nX8sBeJoCEvBwHIA/RbtDktnF1yj2HrTdvCTcfHLNbvZVGprZ4ytEuLl9Uyrc7GNhp4rUaQv5vdpZ\nENtDoJsfVYSb3TM3x2oOlj8o4c4PT7EyITefx1W8HehmFVi9M+VuPvTARwjLdsSEaxsxfP/lX4KV\nSJ+5OTuHv/nMa+CIlpsXRrh5HGxtbN54EEt8hmTbzXpr2M1G0xWLxCF03ExHuNlXab+bG06om12N\nBga5s+7m6C9xRR1CYCc02BjPbmYjayJdsvrevCKDgSB93IBhs2EZtlMJgYvnhxEA+aMm+FETVlJD\nLWNgfu8sn1/1GPKHDRDOUc9d347zRbnu3VlVI7j7wITncjAmCir0numwWgzNhih7n0opoBEq/d9q\nBQc1nAOux6GHpGAZJkGtChysPwQjA5MepfBVDfXVNSjqyXUP+crEEwoIGb45IATIZMe7G3sTu7B6\ny8XijmgTQrg4e28lNByvprpyS5XOv0kd9e5kBCjPnV2zisdARtxUparBj8cJRCEbiWQaGLOb61kT\nqSA3U4LsUQO6E+zm3PHl3Az0u7meMbpVmQFAa7sZQOSyJa6Saqy13ey6HHyEm1UVkeld2sEa4WbP\nA7SQt6JhUNTBsH/nmeFz3JTC03Q0VlehKKfXPOKrM9rN1xtaTKKwYpCbWwkNJ2N0s+qeZZAEkara\ngR/nBGgmZ3M3FpCBbOTxdAXHqynM7dVBwEV1XZWC+gyGzQMvkqtO652VYLPhQm8OpzSLs3YtUSFt\nAkuD4zg7K1Joz34Xzjn2d13Uq+L8B6HA0b6LtXsGYhEptKBpBH7IKqA6IuDOZFWcHHmw4ilwdfjS\n54TCXE4DjegEsoQQrKzr2N0W+cWdDJx4ko41rXhrYxO4QhBLGIdme2D0AoVbOMf8bg20596HcMCs\nuyJdyefghEB1/Ctd050jO6WFeN/iE6NkRDEcgLD+OYT3/M/8bk3MSSvJyBaNk0huAk9XcLKSQmF/\n2M26c31uJj1/mw0XRoibc8dNkVoYlW27NldNNdYC3Lz3xEGjxrpuJvtupIogaTqB3wp2szJCB5mc\ngtNj4WamBLmZCDc3oxPIUkqwsqZjd6ffzYkkRTJ9Pa/HH/zeF/DW17PX8rMu6+aFJ8NujtVdZI+a\nUHwGTggU9+ncXFxM9C0+MeXqbl7YrbbdnJrqonFXQd6JTAFWUseTZ3PQLR+ciCpl+cPGlQPWoBz7\nXigPz+enPgdhHLwnYFIdH6rrw9UVUR6cc8RrDlSXwTEUWAntWuU6zmJQpyceapWzFC7eXiDb3bbx\n8DlzIlVyB5mb17C74/SthBIiiiON2jlWNYKFZRVHpUMcrj+Er/YvD1MKLLmlcQ37yiSSCh48Z6JW\n8eF5DImkglicjuW1eJqV30TZEjsjnaJquoKjtVS3ZP4gmu2DBvQtpgBSJbuveCfD5c+BEIgz84MZ\nFFyhaCa0ofP3rH0uNijdkXcev11YYulxFbvP5GQ7HslM00rpeJLMQbc8cEqgt1zkD5tjdXNYMgX1\neXfnqMNNu3kUT1sI6vTYQ716Fln0uvlBRNxcmNewF+DmTG70zrGmUSwsqjgoHuJo9T7YgJsJJVjy\niuMa9pVJpBQ8eNZEterDv2Y3b21sAl+/hkECSJYs5I7O3OzqCo5HuFm3fJCAY1oUEBmSuA43K0MZ\nFEyhaCU0mHW372deys3bFTx5mJupCsYykJ0WCIETEy9XvO6EBpoX5TxhhsEo6d68EiZ2lIymC04I\nCOdoJTQYlg/qs3alRnHm7uBO+tqrL153urHrcpweDZe/BwDfE2lDsfjkV7oSKQWLKxqOD1ywttcz\nOQULS+en0OXyGn7aPsCO00CDpsCo+H1U5mGldYR5J3qBLCCqWeYK452uniaIFTew7aIPnaJqti9K\n5t/PgquXe++Tgb+BM2HygM8FwQFYieBU4NPlJOZ36zBablfu1XwMqZIFJUDgZOD/SfuGeFaLS0gk\nXQiBExNzb7xqhxaAuihXdrNCukEsYRzzT2owWsLNlHM0ExoMywNlHISJgNfVFRzeyfQtTI+Tq+7O\nug7D6XGwmz1PFEA0Y5N3czKlYHFZw/HhFdw8p+FnnD08cZto0mSfm9eaByg4lXEO/cqoGkH+Gt18\n3WnERtM9K8jUKapm+1h6XMHegxGLsb3R6sCHe/8G+t18kSuJA2glg98TJ8tJcV/d8vrcnB6oVjw4\nns7/E8YRrztopmfHzTKQnUIcUw2sKnpROABPp9ACzvB08FQKxWdDOzaVuVh3BTd32DhLc2pPEPF2\nA+fuxc4A1faRPW5eqrfeRbnO3dnyaUAJvh4sKxqBLCDShNMZBb4vdlIvc04oZgC/dvgNvJl9Hu8l\n16FwhuerH+CFyo/HOOLoch3iHDwrB4hrQPE5Vt8v4fBeBu5AKq5rKGCUDO3KBslQnE81QBkDx1n1\nQsrPvr73+zjEolM1pEorVyiO7qShOD5Uj4mxKBSEc9FofeDcX9BZP2VEASqJZBZxTBWMhFcPPw9R\nbI1Cc0e4WaNQvGE3lwtnbs4fiEWqkW7moqVW9qSJ0mLiagO+IpddhC6dBgexHaISyAJAJqcinVXg\newBVLufmuA78+sG/w/eyz+OD5B0o3MfHqu/jhcq7YxxxdBjHWdhUQABIICr5r75bxMG97FAqrmMq\n7bPKF3NzI22IdGMINwPnuFkhqOaDa80IN2egOj4UT2ROcIWCMI5U2Tp3biG8fdZ2hpCB7BTSSmjw\ndAXqQA+7QTp5+H059e2LrrgYR7pkiR2Y9nnLzgXHCXCymoTqMmSPm1BdBqYQlAsx1HPtG2POkQwo\nEx40ZVOInnulMfau3trYxO/89gGsz/3RlX+GZY2eIWwrWpMDIQQBR10vhMFcfLr4fXy6eLU0r9vC\nueLsKYs/isGerB0IhNAKe3Uc3B8460MITlZTWNipin/y0Su6VkLr7oASn7X7WHpQXAbqMzBKoXoM\nii8yIypzsdDUqQ6+rsDXz76mPBeH5vgwG6IFDw15y3OI3afMSROcEtSyZt8il0Qyi7SSOjyt7eYR\nXxfq5oyB4nzbzeUQN68koTo+csctKF7bzXMxUbsCADhHojactRXoZg4kqvaNB7LA5VKNLXu0my2L\nIXNdA7sGCCFQr1hjzGAuXi5+Hy/PkJuvFMBe1M1e+Hl1yoG5/RoO7g27+XjAzaEQ4ebODmjXzbYn\nFpw8H1xRoAy4mZ2TpeXpylkvagDl+babm/1uHgqs0e/matZE9Za7WQay0wghOLiTRva4hUTN7u7o\nBK0UHd5JgylUpDwxjmZK76ZBVQtxVAtxKK6PVNGCYXlwDQXVdjN3JwZxcQZNGB0TR4jf+soS8BTp\nxmaMoNkI/3yUqiNKno7zxBmr2cgdNqB6HAxAI6OjnovBDenn2Eq20/ZCUn90xwf12JC87LiG3Wdy\niFcdKD6Dq1IUDhuB4mz2pCJxhZ4tKl0nlOB4LQ3V9pA/aMBoeUMryqzzO9ntQhc+R7rYgmZ7osVJ\nG+KLQz3yHK1kZiAEB3fTyB43kag54txqwJdxChyuCzeLHvADbp6Lozon3JwuWtAtD46hoNZ1s4Zm\nxgx0M7msmyfo8YumGpsmQWuEm5UZbj0y7Vw2iI1VbeSO2m5uL/7Usia8EW7W7RFutnwQnw0dfRty\ns0ZROAhwMxcLWN1/jtPN68LNhYMG9Au6OVNsQXd8UW25zW1zswxkJwHnSJYsZIoWqM/gGiqKi/Gu\nxC70IxSK0lICpaUENMvD0uOKKBPe/jwjIte+V4xh+JqC8qgV2aCVHErgGgp02+/7cND5PY6bbdtx\n1d3ZXF5D6dQPLKYxjpLyNw0H8HbmOXw/8xwcRcdy6xg/e/oWcm510kO7MS4iTbPhYG633t1RUQCk\nKg5SFQeOqeBoLT0UkNazMaTKNkhYSuCIrVY2ID4CtItGdf7FcbyauvYz5qPQLV8E5gMf5wBsU4Fp\n9VdrpFykLub266jlTRT2GzAskQ5ox1ScLCf7dn4lkkgy4GbHUFG6kpuTKC2JwoyLjyvdQi3dXdUe\nN1fmR7t55G5pgJs5JXB1Ct3pT6cIcjMD0EhPvqXWeanGuYKGcjHczeOsYH8TMBC8nXkOb2eeg6No\nWG4dtd1cm/TQxsplg1iz7ojWU+1/KxxIlW2kyjYcU8XRegpswJO1nIlkZYSbRzDkZj7s5qPV9I0G\nhIblQQ9xs2MqMILcXHOQO6ijljMxt1+Hbon7dium4nQleW7mVtQho5o0R43U8rP8p/6rfzbpYTw1\nmeMm0sXW0BmXw7sZOCGrSueh2R4yJy3olgdPU1CZi8GOj6d/Xge95WJxuzokaU4JCOOgXPxevkpx\ncC8zNMH0jd/ykD1uno1/PhZaqKZD5wxB53xfEJfdnbVthv0dB3ZPKhMhwPyCitzceJ/PcfPNwifx\no/QDeLT9HuMMGvfx93f+FCmvOdnB3QAXlebSB2UYjh/4OQ7Aiqs4ujOcyEZ8hvknNZjtldLe73FM\nZTh9aQTEZ+IcLCGwEtqNr5wubFcQaw6fS2MUcDUFhh38/DAAGKiwyAH4CsFuRCsp/sX/svFdzvlP\nT3oc08xtcXP2qDF0RpwR4OBuJjQb4zw020PmuAnd9m/MzUbTxcLOmZsZ2tWM20UZu27WKA7ujnaz\nbrXHb3nwdAWVubiodjyCwfN9F2VUqrFtMezu2HCds48RAswvqcjlp9vNfzn3U3g3da/fzczDf77z\np0j64+1lPgmuehZ2+f0S9JDzn8LNGo7upIc+R3yGhZ3qUJDHIRZaD+9ePDGd+qx99IagldBu3GmL\njyswWwFuJiIdeXBzqft5INjNatvNEUw9vqibp3uLaQohjA8FsYB4c2VOmjheG74IL4JrqH2pAzeB\nE9Owfz+LVLEF3fZhx1TUcqZIZa45UB0PrqGK3dgRF8ngqrXqe9Cf1HC6lBDpUwPQdsCgW173wqzk\nY4Fn9LY2NvGJXy3jH/yj37/Q72QYFPeeMeH7HI2aWAFOJJV2v9noUav6KJ648DwgkaAozKvQ9OEb\nhxbV8cP0Q/i0Z+WNUHgA3sx+FD938r2bG/QN05Em9RmSJQuxhgtPo6jmg1OFtZAgFhDvT7PlBaYJ\nc4XieD2Nhe0qdNvrtsLglOBk5XLXJlfoRKsOjjoT5Gn0LHVpAIp2tmPvzwJAZ7CSomS6IGy40Blw\n5uaTp3HzFb/3qtjxIDfHwBSCeNWG6vpwTFWkRI5y88BitdryoD+p4nQ5GXgtU59hfqcG3fa6BSmr\n+djIXedeRqUaGybFg2dj/W5OKVDVKXBzkqIwr7V74/bTVAz8OHV/yM0+VfBW9iP4zOmbNzjq8fLS\nax5ep18c+jj1GFIlC2bThasrqOXNoeKIAKCNKGIk3OyGuvnoTgaL2xVott91M6MEp8uXK0LKJuzm\nUUcBXE0Rv1/A50Ld7HPE6g5aqel1swxkb5iwSp+dXH3wnl5wbcEorg/VZXB15dwD4jeNpyuB1YhF\nUZqLXRjZo8ZQjyzKgdxRU0wYA6Kd26t3z+51Lur0qTijp/gctqGiVjC76RJvfT2Lty55dlZRCNIR\nTyU+PXFxeuR1060qZR+1mo97D80hYRaVFIjvizKKPXBCcWQUbmrIN043iPUYVj4sdzMFeEuk25ys\npNAaSHtnynAl4V44xOTPAt4enBIc3k3DbHrt7AKKZlKP5E7kKOoZQ6QvDTwNnBCU5+OINSqhwW5g\nYY0ZrKQomS5U1w9sudE5czbSzSOygiZFqJuzFz+/lztqDs0BXTcHLFDP7dZgWEFudqH4gG2qqOXN\nc1MZR6UaT4Wbj12cHve4ueSjVvVx/6E5tCh+StMgnRLHPTCi4Micu6khj52wXVjFZVh+dOZmo+Uh\nUbVxvJqClRxwMyWB7eE6cIhF0yDTcEpwcDcz9W5uZPTAM7+cEpTnY4g1wttz3lY3R3s2uIX4IYEo\nh0gNWHu3BMo4/HaV4HjT7aYxUMZRz+goLiZEz5VbwmC6RweFcTEp9fS4ox6D2XSHvp5CnNEjEBNh\numzh4E4KTvxsIrzOVj2ThjHeF8R2P+4DxWMXiyv9Amhul8BWh98zhDFkb+EZ2UFpZk6afYVXCMQE\nXjio40myP62mkTGQLlqh52k4JfACdr27tNOBz0u/izKNjIF4zRHXWufmHcDJSgqeoeJwPY2l7Wpg\nxUQguPCcY073ORzJ7cZTaeBuR6d20vq7JZC2m0tzMSTrbreHOmUctYyB0mL8VrlZt4Lb3igeE71o\ney5p6rGhYxVAx83emZtLFg7ups89d7y1sYk/Zr+LN/9kum5Tmc/7gtizjwPFExcLy0FuHp4bCWPI\nRrR37GV4+asvip32EELdvF/H7jMDbk7rohZFyM/ilMDTbreb61kT8ZojNnN63Hy8enU3B+1+TxO3\nZ8adEjglqGcNsIArUXUZFMbb6bUchaMmzLroBdf5eLLiYP3dEpKl23NuwgtJDeIQK3C9UMZDMyv6\nJkIA87v1wK/b2tjES6+N7ksXdRybD2WEteIpHKw9wI65gN6yBq7LwUsN5A93xcpvD4QzvFT+4U0M\n+UYw3/h84MpvZ5FjEML40GpkeS4OX6VD77POYlNxMRHJ8yTXCiE4XkvheC2NSsFEeT6O3Ye57g2A\nE9dwtJYSZ+/a39J5fjyN9q2IMwK4ugJrzOcCJZKngSsUjUy4m2mPm+cOmzAb/W5OVey2m62bHvrY\nCF14J6Lyci+03UcziIu6eZDX6RfH0lt0nNgBbm4m2m42FvqeI9dhIKUacsd7oANuptzHS+UfjX/A\nY2RrY3NkEAtA7CAGfJwyPpTBWF5IwFdJqJtPl5Iz4eaj9TSO11J9bu6cu3fiGo4H3Mwwws2GAis+\n3YHsdI9+SiktJMAoRbrUAmHizUU9BiUgpWnwkuysVuWOmpPP1b8mKoUYCgeNoQIbtaw5NCl5GhWF\nb0akfnZQfC76awakfL1OvwhsTO/urKqS7oovB/CjT7yCo7UHIIwBBPgRd/Gre99AymvC94RYn//e\nX+K9Fz6Fw/WH4ITCbNbwsXe+jUJ++ld9gfYu7FeCP8cUAgSsXRAML5aAEuzdzyBdskRrDMbBKYFt\nKqgV4lcuyDZ1nLN6bSV1HNzLiNY7jg8rpqGWN8Eo6bYGA4B62hBn5G77DYZk6ikuJsAoQapsdd2s\neGz43GzA9565uQFfpUNHFqaRSiGG/GGAm3MBbtYVcEIQWFp4AMVjgS1PwjivqnGUUDX0ufmHL30G\nx6v3QRhvu9nG3917AymvCc8TT+PHvvsXePeFT+No7YFwc6OGF975FnKF6c2WuugCBKMUwHBdCoLh\n9jCcEuzdzyJdtJCoirZVjBA4poJqIX7lgmxTByGwEnpoQdTWoJvjGmr5GDgRxWYTNVExrZ4xUJmb\nfjfLqsWTpP3cEw6s/7h46dLgjqFg//7FK6FGmdRpC9nTVvc5qWcM0XYg4AKLV20U9ut91ZKDnjsO\nYOe5/LkVXy/alD1qPHlso9lg2Ft7Bu/+xKfBejqwE86Qdyr49Sf/FoxxvPdDqytXRggYVaD6HnJ5\nZSjVadr4g9/7At76urgOCON9Z9g6JCo28gf1vhuyUVUOJbODrFr89NxWN1PGsfZu6dJutg0FB7fB\nzZwjVbSQPW12t3dqWQPlhRA3V6xur83z3Lz9XP7S5xOnJZjdeWSj2WTYW38W773wqSE3z9klfH73\nz0a7uaBgYWn63BwWwIa6uWwNLZZwAK2EhuN16eZZRlYtngbaFzSHOAeqXGCXsRdlyg9o91IrxFDL\nm1A8sYM6Kvhspg14moJ0sQXF9UVD64Gv6ZQVv0jbkos2ZY8ay2s69p842Lv/0T5RAqKIU1lLoabG\nkfKamF9UcXwozu1QzkF9D4oC5Ke4pRAH8D+9+huI/e8Ocr5oe6O1eyc2UjqKS4nuin8jrUOzTKTK\nFni7BYVrKDhZuVzFQolEMgO03cworuRmNaSo49RByOXcnDHh6QrSRWukmz2VXKnIzrTUuVhZF27e\nvf98oJuLehZ1JYYkWphbUHFydDvc3A1iOYfZ9GDWHRDOYDY8UXGYtN28mARv1z5pZAzotodU2QZr\nu9kxRH9TieQiyEA2ChCC0nwc+YNG36HlXnUGyaA3xZH6DMmyBaPpwTUU1LImfH3KiqsQcuHGzE7s\nrN1QvGJhbr8hfgTOnrfj89oRcQ6jKSrkAcA//txv4E/+i+/g2//1dOzOKgrB2l2fPMeQAAAgAElE\nQVQDSkjRDAIOj4j3SK6gQTcoTk88+C5HPElRmNMi21boPLZe/28wv1vDwpNqt0Jf728SrzlQPXbW\nH44QlBcTqBZi0G0PvkqnvsCBRCIZM4SgPBdD7rD5dG4uWTBabTfnzq/aGzku5WYNJ6vCSfFyC3MH\nokd5r5uP1s53s9n0EG+7uZEx+nrvRj3V+EJupgrgi4BVNyiKJx58jyORosjPaZFtKxREX0EnzkU/\n9XahQKDnGuEdN1dxeOfMzaXFJCqFOHTbg6dSeNLNkksg3y0RoZE1kS5a0By/rzACgO7h7M6/OUSx\nhXK7N5vi+lh+VDlrLdJwkSpZOLxzfmXA20AzY+JQU5A5bkJ1GWxTQXkhDl8f/fbOHTWQLNvdyTZR\ntfH5//UllKdsd/ZhYwdvagn4tP/31ZjfV5E4kVSQSE7ZDdQAnT508ardLbYSBIWouKlZXt+5GaZS\nWOr0pWtJJJLJUM/FkCpa0FzW5+ZONePOv4EzN5ekmwEAzWwMh7p6aTfnDxuiPkGPm2tZE+XFRPdr\npmF39kFjB99XPwI20FpHZw4y7lnBq2RKQTI1nW7e2tgEvnb273hVVLsPdTMH9JYH1fb6AlbpZslV\nkYFshOgNYnvpLfrEAfgKwfF6urvqmz0OL1++/yA39nFHATuu4aiz+3YBNMtDsmz3TbaEA6mSjUbK\nmApJdnix/CO8n7yDuhqDRzVQ5oOC4xeOvn3ps11RpvfsTaJqh4qyCxHVRt2Lt02U9KBZHtLFFlSX\noZXQUM+ZkeuVKZHcBL1BbIfBBefOcZajtXR38Sx7FNb2q3Fr6lucx2XdrFseEpUgN1uoZ3R4Zv8C\nQJR3Z18q/xAfJtbRUGPwqNrj5u9MvZtfeftLePXLw90zLuJmTsQ15U1/rdKJIN3cjwxkI0RYs2cy\n8P+dPrMdYo3g1iKaw0Kr9s46sXpw02gCYGmnisO7GTimemlJcs5htTgadR+KQpBKK2NP39W5h197\n8m/xXvIOnsQWkfKaeL76PtJeY6yPe1ME9aG70Ik1LkrLSy5PrOZgbq/WLdqiW6L/4979LFhISw6J\n5LbCKUACjr0Oudnnfb6Nh7nZ9i9VtXeWiNXC3bz8uIqDu5mh6rQX6Tk75OaMMvb0XYO5+PUn/6bH\nzQ18rPo+Ul5zrI87brY2NoGAIPaiEC6KlUouT6xqY66n2KlueUiVLezfm103y0A2QtSzBlIl6/yd\nJogqv/GmC+pxkBGVp/mUl9UeF5wScIIhYXZWzBd2qnjyjNjN/sev/gYo4/jvv/kvYDA3/GdyjoNd\nF7WqD85FvZDjQxcr6/rY04ZU7uO5ygfI7D7Gm3M/gX+98CpMuHix9i4+Uvtwald/B9OWOtSzZmhv\nWECk47eSOrxpOyd+A6iOj8xJE0ZLnBWuFGKwkj0pXZyjMFDhmXKA+xyZkyZKS7IIh2S2qGVEobhz\nd5oApIpNxOsuqM9HtqKRbg6GUxJY7bjr5idV7D4UbjabHgjjsOIqXlfCW+pxzrH/xEW91u/m1XUd\niRtyc3p3G2/NvYB/tfg5mNzBS9V38Wz90VS5uXO0ZxT1rBm6uQIINzdT+vSdE78Bum5uevA1ispc\nrL/FDucoDFR4phwgHkfmtCU6fcwgsxm+R5TyfBythAZGxO5s7xmcPrhovq45TDRj58NfxwG0ktqF\nqvbOIs3U6JwWwjjiFRtr75Ww8KSKuf0avvrg86j/z78Z+j2NGusGsYC4h+Ec2HvigAXstF8njHG8\nv8Pxpx99HTsrz6IVS6IUy+GbhU/i/yt8cqyPPQ5e/uqLI/vQWQkN9bQeeH1wANW8KSsSB6A6PpY/\nLCNRdaC5DGbLw/yTGhJl6+xrXCZ6Hg5AAMTq4Qs5EsltpTwfh3UBNxMOpMo2NDfczZ0b+atU7Z0F\nGmk9uGdPG+pzxKvCzfO7Nczt17D2XgnJktghDPJGvca6QSxw825+dwf4N8+/jp3VZ9EykyjF8vjL\nuZ/Et/KfGOtjXydbG5vnBrGAuO9spEa7+XRZunkQ1e5xs9d2886Amx1/hJudGxxttJCBbJQgBCdr\naezfz+JkJYnD9ZTou9UDQzuFqff8SPtvjna7ACLSNuRkEY6vUZwuJ8NTVAmQP2qA+qJIB2XiOf+/\nvlrB//gLvwEfFCUtBYuerZZVKl7gAjwB0KwPN/y+TiplD4+WnoWnGeDK2Uqnr2h4J/0QRe2cKpHX\niOdxOA7DVXtUb21sDqUSD0EIiisplOZiYBDXBSPiz8lKEpWQPoezTv7gLCWpAwWQO2x0d48YJeGr\n6Yp8TiUzCCU4viY3u6aC06XZ3Dm5CL4mnp+Rbj5sQPE5KONdN+eOmtAtD2Ac/8N/8pv9bi4HuxkA\nmo0xu7nk4dHKc3BVHZz2u/kHmWdR1m7uPu2qbh61qDwEIThdDXbzsXRzKIX989086ijCLB8hlKnF\nEcTTlW5K5OGdNAoHDWi2DxDRJDrWdIfO6xAArkpQXkjA05W+8v+SYJppA0WfIX/YHL5x5/1FtjoQ\nDuQO6vjnz/x9AIDq+7jX3MWrR/8+4KsFjAG7Oy7MmIfFZR1m7PonnHqVoXR3GUwdft0ZofjD9V/B\nvF3ELxx+BxmvHvATnh7P5dh74sBqiTenogBLq/qFKyWHFY8YRW0ujnpOpDIB4vqQ585CaLe0CCwo\nx8VOrKcronpkTBPtE3q+hhGglo/d1GglksjR6+aj9TTyh8LN/Bw3OxpFZT4OV1eGzndKhmlmTBQ9\nhtxJazidmwebtuNm3RaB6f/54O+hmdTxxbd+P3xhjgG72y5iMQ8LKzpMcwxurjGUHiyDh7j5/1l/\nDfN2Eb94+O2x1bXwXI7dHRu2JZ7Mi7r5Kk7uUJuLo5EzYUo3nw/nMKxwNyseg68p8FUKx1RhtLwh\nN1fzs1vVUr6rIo4T07B/P4vt5/LYfi6P4lIysBACB+AaKpppQwaxl6CeNWHFVbD2rMDRvmHPmoG2\nJAAMm4ldWg4wquDD5Dr+xb3/DN/56V9GcWEl9LGsFsf2IxuuE1A15ClRVAKzURdmHho0AScUx0Ye\n/+/qL8Ij13/Zc86x89hGq8m6aVueB+xuO3Ds83/frY3NKwuTKxTNtIFm2pCiHIFueaGfI0BfAbmT\n1SQcUwEjgE9J95popGV7BIkEENV4O27eabs5aBtRuFlBM23IIPYS1PMxOOYl3Wz5XTeTds/S/+3h\nr+M7P/MrKM0vhz5Wq8Wx86EN173+NGOqEMQatQu52R/DLTnn4r7DavFhN4+4F3kaJ3dg0s0XwmiN\ndnPvbuvxamrYzTlTHFeYUeQ7a1qgBCAETKVoJvXu5N6BE6BakLsll4YQHK2ncbKSQi1joFIwsX8/\ni+pcLPSmZNChHAQ+VXGcXMAPfuYXcLj2IPThOANKp+GT1lXJ5RWsP/qPoCw8TYoTCo8qeJRYvfbH\nt1ocrjP8hHEOlIvhv6/5xucvl7YkuTKckKF0yA6+QvpuNJhCcXAvi4N7GZysJrH7MCd6OMqUMImk\nnx43d2pc9CLdfEUIweGdXjfHhJsLF3dzJ9X7OLmAv/3UL+Jo5V7owzEGlE+vvwZALq9g/f9n7z2D\nJLmuA93vpivv2vd0j5/BABjMwHsSIAh6yC2l1YqkKHG1slyFXoSkH1wo1kS89/hWu5Ji5aXVSk/7\ntDJcGYoGIEUDCgQN3MCDwAzG90z77vIu3X0/sqq6qququ9rMYLo7vwjEoMtkZrn88tx77jnnVnez\nJTQuRLoPhK+XcsnFtnt3s+/kq8+qbm5aT+9qHdy8w9O1/UB2CzI/GqUYDyCFJ0lbE8yPRqmGt3+D\n9SuCEJRjBoujUbKDXmq2qyqkB8O4YsmZzf/fDUfVOH38brThWNfzSqWy+aO+obDKeKDA0ef/GaNS\ngi7StIVKQdv89Vm23SXfCzA7BLjgjfj+8m+MbPqx+HiFI0J5E81c+h5YAe973akwXGYw3HE7VkCj\nEjF2bFl/H5+1sLArtszNCvO7Ypgh383rosXN4cbSh8xAu5tXw1E1XrvjQbTBq+vmcERlXM9z44kn\n0Svlrm52hEL+Srm5C8sHn30nX3k6udkMqh3rT0ggPdT5O+G7eQk/z2UroggWR6MsDkdQXOn9AHbw\naMyVotAXwgxpXkskV1KKBQgWTCJ5c8WS+aYW4Ik7f4jk3CQ3Pv8kmtM66hkMbf5nJaUkl3Hoty9z\n71f+N1N7DnP6prtwtdYLKFU6DFQXN33/wWDnKF8ICEdbT7Sf+eOP8vLnk5t+DDsOKQkVLVTLpRrS\nsIIawpUMXsoTKFuN9lKViM7cWMzLPhiPMTyRa6l8WIwHKCb8zvQ+PhtF+m6+KuT7PTdHM0tuDhVM\nwqu4WSD46r0/zMD0RW488U3UZjeLK+fmfNZhwL5E/1c+w+S+I5y58Y42Nyu4DF4JN4eU7m6OeG4O\nfuPDfgC7mXR1c45A2W64uRwxmB+L1twcZ/hirqWdZjERoOQv51kVP5DdyigC1y/hf0UxQzoLTaPp\n1ZBGuGiBK7sKU+Ctnc0Mj3Hq5vu48YVvLt0nvFHQk697a08UBYZGdBKpjf0UK2UXx13a/8jEaS7v\nv4FSNI5UvW2rrk2fmWWsPLuhfXVCNxTiCZVc1mtx4Cgq1VCEsFMmkVwqKPHoI5+Ez2/67nccqukw\ncjGL4i7196hEdBxVEChbXoGU2u3BokVyrkRmKIIV1Lh0MEWoaKI6kkpIx/Yb0/v4bC6+m6841bDe\nkoVWDWmEiia43bv31G9fHBrjzZvv5egLT7XcV60sc/OoTiK5MTeXS61uHr1wisv7rqcciTc6DKiu\nzUA1w2hlbkP76oRhKMTiaqM1oKPW3VwhkVQ8J//Gpu92x6KZDsPL3FyO6LiKIFC2W9wcKpok5ste\nIbigxqVDTW4O643Ccj4r4weyPii2S6hoNSov+ovyu2MbKlP7EiTmSwSLFqrTPaB1UZgd28f1r34H\nxbIJhRVs26WQXyqw4LowPWkhpSTZt/70M9crat0YeFWk5NZvPc6F625mdvcBNBWuy5/n1swbV6wB\n+/AunUBI8ELiRs4eOIYCSEVhJn+OL991lz8zsYkMTuZR7dbvXrBgday0rUiIZqreOhoARVBepY+y\nj4/P24/v5t7x3Jz03FwwUVcIaKWiMje2n/L3nidUKROOKFiWS7GwzM2XLZCSRGoDbnbb3Xxb3c3j\nB9BVyXX5c9yaefOKuXlkTCcQFryQPMq5/cdQkEhF8IW+iLdY1nfzpjFwud3NoRXcHMtUyNaX9vhu\nXhd+ILvDiWQq9M20lnyfH41Sjns/JqNsk5gvoZsOZkAlOxDe8ZUXbUNlYZfXlzW6WCY1X0Z0maF1\nFYW/+sVf5L/+uzky9/4dF85UO25zZsoLdAPB9Y3ABcNKW588zbE59OYJ7s28TGoDQfJyLMulXHLR\nNEEorCBqEhRCMLP3Os4PHMdVNOqXBK8nD5GcLXnFgnw2jGK7GFWnXYp0X8OtrLOnr4+Pz9tDNF0m\nNVvy/qhFQvNjMcpRL9XQKFsk5su+m5todnNsoUxyoYToEtBKReHvPvnzuJrCf/i73+PC2c5unp60\nCYVVjMD6BhFCndxsWxx643nuz7y84WysZizTpVzu7ObpvUe4MHCsxc2RbBVXEUuDnD4bQrUcdHNt\nbm5e5uOzPvzhvR2MZjr0zRQb5err/w1MFVBsl2DRYvhillDRQrdcwgWLkQtZAqXNr+y3VSn0hZg4\nnPJGyzvc7yoCR1P45d8Y4S+PPLTitibOm7jrPKmpqmBwWGsZWBUCjIDYcGpUHSklM1Mm596qMj1p\ncemiydlTlZb2Oi8mb8BWWvdXH3Xs2pHeZ02Ec5WuVmzKWmq5reIXm/Hx2TJopkNqtrTkZbfm5st5\nFMclWDAZvphrc7NR9t1cJ98fYuJwH+VwZzc7qtIosPPXhx9YsZDjxXNV5Dr9paqCgaF2NwcCglhi\nc1JHG24+3eTmt6ot7XVeTN3Y2c1p382bRThX7dgesxsSb0mQz8bwA9kdTLcfndd/rUqqFuTWz7/1\nUvap2SvTtHvLIgTp4QiuIhoyrPe8WxyJNtJ28onEirJ0HLhwpkqp2L1M/0qk+nV27wsQT6hEogpD\nozp79gdQNmmtViHnkln01tlI1/uv3o+uLvmy1rkpt5D+yONmEMpXSc2VO8/+CyjGDWRTbQ+XWgEa\nfzbcx2fLEMl2d3MobzYGoNvcPFO6mod57SME6ZEIsqObl1qW5JMrFx90HDh/pkq5tD439w3o7N5n\nEKu5eXhUZ/cmujmfc9rdbEkuXzQbjymEOztA1Hru+myMcK5Kcr67mwuJQFulbVcRXasS+/TOzs5D\n2eGIFUbhwjkT3ex80jYqPZ7MpUSrpVlYhrqt12HYhsrU/gTxhQrBsoWlK+T6w5ihpZ/Y7PgYpWiE\ncKHYdS2MaUouXTAZ220Qia19tDYUVgiFN7/KXX3EtxOWJTFNSSAgyEVDBEt22+tzNKWlF5rP+kjO\nebM0y5F4rT7SwxGyg2Fi6QpGxcYMauT7Qjh+iX4fny3DSoN+kWwVzXI73mdUeuxRLiW66XjnjR3g\n5sn9CeILZQJlG9uoubkpDXt6z27K4RChUudABMCsSibOm4ztMYhE1+NmlVB484v3eG7uPBNvmRKz\n6vKfPvyLDF/IErTavx+2rnTtYerTOyu6WVdJD0XIDoSILVYwqjbVkE4+FfTb52wCfiC7gylHDRIL\nlbbbBXglwuleLGG1AgFGxWbwkpcGBeCqCnNj0W3dT8/RVdIjK4yuCcEXPvETPPI//xfRfL57IQoJ\nM9MWB9YRyF4p0os2TrfxCwG/d++PsDA6glGxGb6QhabZAlfA4lB4W18sXS30LhewAFN7E6AqOCr+\nmicfny1MOWYQT6/dzb2cYY2yzeDlZW4ej7UEdtsNz83R7g8Qgi/860/wyP/8/4isMNAsJcxOW+w/\ndA25ecHu1poWU9f57ft/1HvcUIThi1lvBpbaMhQB6eGI7+ZNoNvgEsDUvjgoAkdV/VohVwB/KGAH\nY4Y6rx0B77xmBpSu9680Kyscl+GLOTTbbazx0WzX61/pdP+x7wSq4TCf/bmfZnFoEFvtLkPLlOte\nk3MlyCx0/7wrmsHi0CAAZlBjel+CUlTH0hTKYZ3Z3fFG8bAdg5Rez+FMpaXx+Uax9M7fGVcV0KGh\nuo+Pz9ajGuoeVHoZTt3drK8wKyscl+GJbLubL+YQzrXjm7eDSiTMP/zcz5Ae6F/RzWb12nJzerG7\nXxyhkBkcAMAMaUzv9dxsawqVupujO6xP6RVys613DqccTXi9nHyuGNt3CM6nJ6ohjWC5QyqoInBV\nBUF74CkVUG2Hbl+fcN7sXDxAQiRvUkjW1lFKieJIpBDIHXQRLhWFL33sI9zw/Alu/dZ3OlaUVRQa\nFQc3tK/atje6LadLqpsEnn3PQ41+eABWQGN+PL6h/W1lGn3kmi4MSzGDhdHohke+M4NhBibzLSlM\nroD0oD/j7eOzbRCCSkglVG6/0HY0r0hR5yr53syQ1blUAZG82blQnJSE81WKy92siB21JESqKl/6\n8Y9xw/PPc8u3v9vRzaq6eW7ejO24XQYgJPDMex9GNgVRVnCHu7lac7Nc6vFajAda1kuvl/Rg2CuU\nuszNmYHwhrbrszp+ILvDSQ9HGOmQCpoejqBaLsF6A+dmJCumIamO7FqoQrW9wDhQtOifLqDV/i5H\ndBZGo7g7pE+eo+u8du892IbBbd98Cr1p7YoaVEjFN/Y+lEsuM1Mm1YpEKJBMqQwO6YgeLkpcVzIz\naVLIu0gJ8YRKOKy09L+tU4zFOHv06IaOdbsxeKm9j1w4b1IJN10orpNyzGB+V4zUbBHNcnE0hcxA\naMPb9fHxubbIDEcJXFhKBYWlZRq66RColNvcLCSYK7RwU213VTcHiyb9U0XUWvZUqebmndLD1jZ0\nXr3vXhxd55anvo1uL7lZCOjr39hlc6nkMDtpUa1KFAWSfSoDQ3pPQa3reLUq8nkXam4OhZWW/rd1\nCokE52+8YUPHuq2QkqHLOe/6tOnmSK5KNaxTTGwsa6wcDzAPpOZKaJaLrXtuLiV8N19p/EB2h2PV\nUkETcyUCFQfbUMj0h6lGdITjEk+XEU0X5V5l1ABOlxRH8GZ5pWivhCcFVEM6WtVh6FKuRcKhgsXg\nRJ6ZfYnNf5HXMG/editGpcJNzz4PeAW4Xrn5Vl584J18+vE/REpJIe+SzzooKiRTGsHQyhcU1arL\nxPlqY1JcupBZdLAt2LV75TSiatXh/OnWok7ZjIOqgaKCiYrmOLjCW+/x7Q99wJ8JlN7AjRTebIhm\ndegjJyGW2XggC14wW47tsHQwH58dhhn0UkET856bLUMhOxCmGtapOi6xdAXhLHNzYjU360hR7uzm\nsI5erdW2WObmoUt5ZvbuLDd/747bMSpVbnzuec9xUvK9O27nX+ZeBrwZ1ULOJZ9bg5srLpfOmw03\nuy6kFxxsG0bH1udmTfcyuEzRwc07nWY3my6q5XZ0czRT2XAgC14wu+OWUV0D+IGsT9dUUKkqTO1L\nkpgvES6YuIpCPhVYSg3uQjWkUQ3pBMpWQ4iu8G6vhDVSM8U2kQrAqNroVRsrsIO+lkLwyv338drd\ndxEuFClHwji6VxDr1z748/z8H/425bKLrA245jIOg8Maqf7uRbMW5+22zG4poZB3sC2JpncOPB3H\nbRNlnQoaJx56gFCxyNCly2T7+3jj9tvI9fev/TVvIyLZCsnZEmotDa8Q17v2ePXbD/n4+KyFbqmg\nrqowtX/tbq6ENaohjUBTppVbG2CuhjT6ptvdrOAVb9SqDnbg2ilydMURgpfeeT+v3Ht3i5tf4h0I\n1/XcXHIbrs1lHAZHNFJ93d280MXN+azD4LBE07q42e7u5rLUeO7hB4nkCwxdvky2v5837riNXF/f\nul72diGSqZCaKzVS5PNxw3fzNmUHRQw+68HVFNIjUdJreZIQzO6OEU1XiGargNdDq5AKghDoZvuM\nVf15muVi7cABLVfTKCRbR7x3v3WarKmiuS6Lg2NM7TmEVBRGLp/lHnumq/Sqlc4FtYQA03TRuozY\nX57oLEoA3baJpzM89/BDPb6iax/heutk1rs+O5Q36ZsuNi4IhSuJZTq/h/Uerz4+Pj6bwfrdHF+z\nm6UQaPYOC2RrdHLz3pOnPDdLl8Whcab2HAIhGLl0hrudWbQuTjFXcLNldg9kV3NzLJvjhXc90OMr\nuvbZqJvDuWqj13J9e/FMteNjXQEl381bGj+Q9bkyCEGhL0ShL9R2VyWst4wIN5AScweKshv7Tp5C\ntyxO3XQX03sO42reSG96cBfZ/BQfWvxu5xYMXc79rgtGoHPqk+tKysXuo5KuEGT7Umt9Cdckiu3S\nP10gVPB675kBlYXRKNYa208k59v7xnW8CAQcVSHf4bfg4+Pjc1VZxc1Gpd3NipSYOylTahX2vXkS\n3bI4efweZsYPNty8OLiLXG6SD6Sf7jJY33l7rgu60flO15GUSyu7Obed3DxVIFSsuTlYc/Mav3uJ\nNbjZ1hTyKd/NW5mdsXrf55qikAx61RCbbutl7e1OwzIMCrEk03uva4gSwNV0puOjTAUH254jpaRa\n7Sw9XafriK+7QlckLxBTObcdCkdIyfDFHKGChaCe0u4wcjGHYq+tNdRKfeOWU0gGdlT1Tx8fn61H\nPtXZzYVEAFfzLxfrmAGDfCzJzPihNjdPJnYxExxoe47rSswubjaMld3cbXDaC8Q0zl9/ZM2v4ZpD\nSkYuZgkVm9xccRi5kGv0PO6Vtbk56Lt5i+MPsflcdVxNYWpfguRciVDRwlUEuVTQS2/qgUDJIjlb\nQrMcqmGdzGAY29h+AfBbNx8jWOx8QrYVjYvhUXZV5lpuN83uI7crrQJRVdB0gW21Psprmi54/GMf\nwQps/ZzvQNluK8Yk8AYAopkKuTWUyjcNleAKPRvrSIF/Eejj43PNs1E3B4sWiTnPzZWam53t6Obj\nxzGqKrJDhGkrGhOhYUYq8y23W2at/HSnzoSyeyClap6f7WWqabj54x/FNrZ+amywZLcVY6q7OZKp\nku/vfdbUMlQC1dV7xHpu9oPYrY4fyPq8LTi6ysKu2JqfF0mX6Z8pNU52at4knDeZ3J/A3mapT/Oj\no1w6kOnYk9cVgoDbvm5GU0XXiLU+4jsVHODp/ptZNJKEnTK3Lb7OJ34nwe//1zEe+sfPo9g2Cksz\nsY/9+EfJDA9t4it7++jWAF2RoK+xOXpmKMzQRGv1bUnnFKaiX2XYx8dnC7BeN0cXy/TNLrk5kjeJ\nbFM3z42PMTmbQ0gXSWugrkoHw20f4FS1FdxcK8A4GRzk6f6bSRsJwnaZO9KvcbhwkX/6gR/igc9/\nEc22G7Gwo6o89hMfIzvQPvu7FdGszXRzhMFLPbhZQCnqu3mrs73OLj7bGynpawpiYWmAc2CywPT+\nZM+b0kyHUN70TmQx45pNaT59/Ajjp9Pt64kF/MNdD3LrV95suVnVBJGo11euOf4VAvoHdaYD/Tw+\n+iC24v30c0qMJ0bu4e//JEzhQIgvfezHOPrs88QX08yO7eL1u+6gFN8+DdS79T+uV9VeC9Wwzux4\nnNRcEb3q4GgKxbhBPF0vKiGRCObGYzumB6OPj88ORMqWIBaW3Nw/VWBm3xrcXHUIF0zkte7mm48w\n1sHNlqpx9M+Pwr842XK7pgnCEYVi0W0JaIWA/gGNqeAAXxp9YMnNRoxvjdzJ3w49TCEV4ssf/TFu\nevY5Yuk0M+PjfO+uOyjF1j7gcK3SrT6KK8Bco5srEZ258TjJ2SK66WDrCqWo0VTwSSKFYG7Md/N2\nwA9kfbYMWtXuXNwIb51jr8TnSyQWyo0huuRcicXhyKb0+NxspKowuzvO4KU8jZVLEuZHozi6yqOP\nfJJPP/YHjX6zlZJDKKzgSigXXa/9HTA4qBGNqXyj71hDlHUUCcn5MoVUkDW9bscAACAASURBVMXh\nYZ76/keu/gu9SljB9tZQEnBVQXEdjcurEZ3pSOtFWnYgTKBkQz043ul9dn18fLY1RpclFgIIVHp3\nc2K+RHyh3Oj9eS272VUV5sbjDF7OQ7Obd8X4D//DgGY351wqZYdwREFKKJea3DykEYmpfLXveJub\nTamRnCtTSAZZHBnmmz/wfVf9dV4tzKCGGdIwmgqBem5WKK6jN2slordNbmQHwgTKvpu3G34g67OF\n2PhJR6/aJBbKS6OotX/7ZopUogaOpoDrrZeM5E1cRVBIBilH9a4nPb1qEyjb2JpCJdL9ceulGta5\ndDhFsGSB9P5uLk7wH9/zb/jEH/0+liUb/WaFgF27dTRdwTAESu3xi4HOI+NCSlRH4lyN9SKuJJbx\n2j/IWiGRQjJ41aQyOx4jsVAmmqkgJJSjOumhyOYVfBCCaqR7L0EfHx+f7YS7CadOvWITb3KzaHJz\nOWrgagqi5uZwzc35VJDKCqmhesUmULlybq5EdCYOpQiWu7j54Z/iE3/0B1h2k5uVzm5OG4lOu0CR\nEsWRV2ctpyuJpStEc2+Dm4VgdjxOYr7ktYaSUI4ZpAfDm+dmxXfzdsQPZH22DHZARQraGrZLvEbv\nvRDOmW3PrxPKmxSSAUYuZtGrTkOowZJFPhUkMxRZtmPJwGSBUKG2VlWAqwhm9iQ2v/iUEFQinYV9\n/DtPU7YVVHdp5FtKuHzRIhZXEEKgKJBIacSsAhW18+ims05ZaBWbeLqCVCDbF0KqCpFMmWjWRLPc\nWopYgOxgiEDJon+qgOIuDUvoVa+wyNxY7OoIUxFkB8NkB3sv7OTj4+Pj0xk7oHV1c7lHN0dy1a5u\nDhdMCvEAwxey6Garm3N9ofZzuZQMXM432riAN7M3sye++W5Wurv5lm99h7KzzM1uzc0JBYFAUWtu\ntossqO3bqWcMrQe9YhNLV5CKINsX7OzmeIDMQIhgseZm2ermYNFmfvzqpDBLRZAZirRfa/n4rMCK\nZxghRBwYlFKeWXb7cSnlKxvduRDiA8BvAyrwP6SU/3mlx49l5vj0Y39A8Bsf7nkfv/wbIxs7SJ9r\nByGYH40yOFnw/qReuQ8WRqM9bmSl2r1eoNscxIKXehtPV8ingi3rdaKZCqGC2TK7K1zJ4OU8U13W\n66qW01oRsi9IIRlEcSSJ+RKhgoVUBbm+EMW40QjshOMwdHkaxVaphiK4qsvwxBlUx+Xg699DdRwc\nVWV2134Kca+nnK1qSFWjf/oiQ1MXyWaq5PabnknF0roQF3BUwfhbi96+pI1taICKZSjkBsJd15YO\nTGQJF5fSymLpKlIB4bbOn8cyFe9CxZVtPb8U6VW7NCo2ZsgfLfXxWY1rzc0+OxwhWBiNMtDBzYuj\nmxMERfLVliAWPHckFr1lMU5TZfhYukKoaLU8VtguA5N5prus19VMh8RciVCp1c2qI4nX3Oyqgvwy\nNyuOw+ClaRRHoxoK46oOIxfPokiXA2+8saKbB6cvMDB1kWza4Yj2It+57l2d3Xxq0fOptLEMDYGK\nFVDJ9oe69j8fnMgSanFzBVfQEqjWb49ku7s5VDQ9N6+xz7qPz9Wi6zdTCPGjwH8DZoUQOvAJKeVz\ntbv/HLhtIzsWQqjA7wPvBS4BzwkhPi+l/N5qz6089A897+fT6z7C1bn3z473/NiH/v4dV/BIdg7l\neIApQyW+UEY3HcoRnXxfqOf2JqVYgPhipePIbzmqk5xrb6QNnpQDJZtSYimQjWWqHZtua6aDajlt\nRSoU22X0XBbFlQhAdSSp2RJ62SaaN71eaYoCNgxM5jDKIdIjUUbPX+DYd07w1s33IxEYpoliWxiV\nIMee/iqaY1MNhDjxwPdh64bX105KT7RSMjt+gJOOzU3PPsE9X/8npsYPcOGG26kGQgjXQWg6mi2X\n5CZVjKoE4aCbDqFilrnxWNuoczhbJVzssG55WRBbf1/qr7sTQnrvrx/I+viszLXsZp+dS6nm5sRC\nGW0dbi7GA8TSnd1cihr0zRRWcLNFqWkdZbSLm/Wqg2q5OHrrMamWy8j5Dm6u2ERzrW4OTObQKyEy\nw1F2nTvP0adf5PTx+5Ci2c0Bbnr2a2i2TSUY5oUHvg9b0zu6WXEsjj39dVInL3Jd6ducv/42zEAI\n4boITWtzc6DZzQWT2fF4W7psJFMh1MHNy4PY+vuykpuR3vvrB7I+1yorfTMfBW6XUk4JIe4C/kII\n8e+klJ9lMxYrwl3AaSnlWQAhxN8APwhsGVl+96d6H/j+NBseJN8wt3zQ5kPKL73dh7FhrKDGwtj6\nRnmtoEauL0R8sdwQphSQHgrj6CquqnRtoQIue0+eQjdNpvbsRq+aQOc0pU4yji+WEcuEoUiI5UwU\nx0GqTdsSCvHFMpUwPPjZz/Pse34EV136ubqaTiHRx9zYfnZdfIu3jt2NGQh5soWlFN3av66q8cq9\n7+Pgq0+z+/xJRi+dxVU1Xr3r3WQGRltTepv+X9ReS990kcmDrYFsYqHc+bV3vHXlk0bHXqtSoto2\njuYXZfDxacJ3s881iRXUmN8kN0sAAYvDEVxNwenmZiFAuux98ySaZTG1Zw+6uZKb2+UcS5fbgjlF\nQizb2c2JhTJmQPLg577AMw+3uzmf7Gd+dB+jE6d569g9mEZwBTfrvHz/Bzj8yncZu3CK0YkzuKrK\nK3e/l+zAsozCTm6eKTJ1oHWWOb6JbkbQMtsNgJRolo2t+272eftZKZBVpZRTAFLKZ4UQDwFfFELs\nZrX8zN4YAyaa/r4E3L0J2/Xpwktf0vg0f/B2HwZAz+nhVyI1PDsYphg3CBe89TOlmNFYN5NPBhpF\ngOp48pT8wJ//KUJKhOOgOQ7nj9zMxKFjLRID0KsVbL19FDpQtttSd8ATa4soa6iOzb43z1BI9HV8\nHa6mM7P7ILsuvsXC8PiSKDtRk83Zo3cxOHOJYLmI6tgUEv09iUizXIQrW4suyBVGcTtRH4lefjNe\nY/dSvdeqlNzyzW9x9PkTqI6DZeiceOCdnLrt1rXszcdnu+K72Wdbkh0MU4obhGpuLsYMnJqbC6kg\n0Wy13c3S4Qf+3z9F4CJcF812OHv9rVw6eBS5zM1GFzcHS1bnjgjSXcHNp8klOvdwdTWdmfEDjE6c\nZnF4rCc3n77pbgZmLhGolFAdp6v3l6ObTptbxWa7Obrk5tuefIobT7yA4jhYhsFz73qA07fcvJa9\n+Szjt351+opsdy3Zq9ci9/f4uJUC2bwQ4mB9DU5t9PddwD8CRzd4fD0jhPhZ4GcBhvXQ1dqtzxWm\n1x/YZqeGSylJL9ikFxxcVzKyX3DzgyrxvtpJXIcTw3v4i5l7EEIipSCiVjnyz18lUK22bGv36deZ\nG91HJRzF1XSEYyOk5IYTT5IZepjFkeGWx1uGSqDcqYWQBFe2yU4KwcPp57lsdy9OoTgOpUgMqfRY\nwELA3Ohedp/1JleMSgnbWL20fUDYfEH+HoorG7P6xXgAfaHc/no6SVFKkF7vtuZ7vMbugtnd8UaQ\nfMfXv8GNL7zYeJxhWtzztScQEk7e7gezPjuea87Ngfjg1dqtzzZFuC43PH+CG068iFGtMrVnNyfe\n9SD5Pm9dqRXQWBiJ0D9dbKTmuqrgjm88TsBsdfPe06+xMLqXSiiCq+kojg1ScuPz/8ziyPtID7V+\nXy1DJVixaF8lCrhuu5sVhYfTJ5iwu1dMVh2bUiSOFL32KZXMj+xh7LzXG96olinr3bffeFaHiLUY\nD5BYrGyOm/fEoebmu7/6NY689EqTm03u+8rXEMBbqwSzj7u/s+pr2SgvfWlrpj9XHnu7j2Brs9Kn\n/guAIoS4sb42RkqZrxWB+LFN2PdlYHfT3+O121qQUv534L8DXB9KbsZos882R0pJpeKNSAaCAtF0\n4p6ZsshlHOrZRZNnJNPnbPYdCqDXRmpVJvlx8Y/MBfrQXIfQwjxTGRN32X40x+aOJ7/A3K69ZPpH\nCJQLjF48TdAs89Nf/QzJvtaf16Ie57Pj723pFae4DrFCmnw4gdskS+E6RPIZIvNF4lkL1bZwlklN\nsS1GL5zipfs+sJY3p+XPfade5s1b78dVu69NVV2b63JneeXLXrBcn9V3UPjLvY9QVkONCwsA3axi\nq6oXXNfe+1Ahy5FXn2bq+K3MhwdQpFcx8db097g18ybiVP3wJKe+V2k7BgHc+8QT/OT0dzseo1l1\nyaRtnh++jsn9+zh/5DpcbWtKzcdnFa45N8dGD/tu9gHg5h/I8K9+7q863ielpFKWCAUCgVY3T102\nyWeX3Lz39Bn2nz3DvkNBdH3pcbZQmQuk0F2bwMIC09kObrYt7njy88zu2ke2b7jFzT/zlb8mmWp1\nw4KR5B/HHsZucrDq2sTyi+QiqVY3Ow7R7ALhxRKJbA7FsTu6eeTiW7x4/wd7f+Pq6dQ19p56mVM3\n39eW8dWM6tocz57mFx5/ueV2Wyj81Z7vo6wGV3VzuJDl8GtPM3X8NhZCfSi1o7ht8XVuzp5ccrMr\nOfVGZzff/7Wv8a8vf7vjMdbd/LgN0ahCLK4iNqudjo8PKwSyUsqXAYQQrwkh/gL4L0Cw9u8dwF9s\ncN/PAYeFEPvxJPljwEc3uE2fHU6x4DB5yUS6tXO3gFhMYWBYR1FESxBbx3UhPW8zNLokI026jFbm\nAcgvE0wzinQZvnyO4cvnmm4ETW8/UfdZOd4//S2eHLyTshpECthXmuTeyad5JZfizeP342gaUigk\nF2e4482niI+q5HMOx5/9Oi/d+36kEEghQAj6pyc4c8NtmMFw51FWaLtdAIMzF8HbBOMLF4jPx3h2\n8GZcUZ/V9d441bGRisKB4iXuWWgVJYCKy8cuPMbLySOciu1Fcx1uzbxB8vw5zpkJ8vE+9GqZeHqe\ngFlBUeCuqW9Q1MNU1QBJM4e67BKkqUtBG97AsWy5+AEo5B0mJ0ykhIMLb3DojTd4z9e/zJ79gUaP\nvvXQaV+9ct+rv9LzY9/1qc7rmXx8OuG7+eryW786zW0D+zd1m9859pubur1rii6zS4W8w9RlE9el\nrhjicYWBIR0hREsQW8d1Ib1gMTTS7GZnyc3LI9gmFNdl5NJZRi6dbdwmFFqC4jr9Zob3Tn+bbw7e\nQUUNIoF9xcvcM/UsL+X7OXX8XhzVc3NqYZo7Tn7Lc3PW4eZnv85L97yvxc0DUxc5feOdWIEOPVi7\nuVnA4GzNzcDeuXMkFmI8N3Bsyc21GVXFsUFROFiY4K7F9vormnT52IUv8lLyet6K7UV3LW5Nv0Hs\n/HnO20kKsRR6pUw8M0fArKIocPfUExS17m52VnJzl88hn3OYumQ2XnIh57C4YL+tbvbZfgjZYeF7\nywOEiAC/DtwOxIC/BH5dym5f3TXsXIgP4VVfVIE/k1L+3ys9/vpQUv7ZIb/6r09nLEty7q1KmwzB\nk8TQiMbcjO2JdBnBkGDvgWDH7TqO5MzJztvthKbBgeuCXU+0EiirAXTXQZdeefxyyWFq0iKrRdFt\nk4GQzdCoF3xLKcllHdJZydzAOGoiiGm6vLr/Tm+0tst+FLOKWxsplsJLVb5/9gUOTr6JWZUYAUE4\n4vWZdRAsyAiXzQiiWKHfyqKOJklRJuRWO26/G64jOX+2im3JFmePjOnEEyvPknabka1z3Y2t76uU\nktNvVto+UyFgYEijb2BtVZAt02Vh3qaQc3AcUFXoG9BI9WtbTpy3fNBe/UE1tkMRuPXy5K8/ckJK\necfbfRxr5Vpy820jCfmtn7h3zfvZqqmAPmvDMl3Ona52dfPgiMZ8FzeHwgp79nfpfW5Lzpzq3c26\nLth/ONCDm2106UVupaLD9JRNVot4bg7bDI0sc3NOMts/jpYIUa26vHbgTlxV7dnNhia5a/IF9k+e\nwjSXu1lhnjCTlTBKsULKyaGPJElSIuSavb3w+vvlSC50cPPouEEsvvLypNXcfORo69I/6UpOn+zi\n5mGNvv51uHnOppBvcvOgRqpv67nZpzfuf+2xntzci0UsoAyE8EZ9z22GKAGklI8Dj2/Gtny2L/mc\nzcyUhWN7J6+BIY1kX/tJMJexu86cSgnpxfYR3zpGoPs6FlUVDI3qzE5ZqwozGBLsGjdWPLEKIOy0\nBoehsMqBQyquayGEQIilEWghBImkRiIJw0qaL4y+m4waaUkPakNKXF33RomBSkQnPRzhb468l08/\n9haRpra71YoniGqlzFBwgf5BnWBQATez8ovtgqIK9h0MkE3bFAsumi5I9WkEgquvFRJCEAoLyqX2\nNzoSVdre12ql8wciJeSyzpoC2YU5i/nZ1uDPcWB+1rvAGhjaWq2B1hIkXCtF4D7zx71P/L38+c79\nIHcQ14ybS1nhB6U7kFzWZna6yc3DGslU+3ky2yETqo6UkE2v5ObuLlU1wdCIxuy0vaqbQ2GF0XW4\nORzp0c1qhs+N3kZODffuZgGVsM7kcISfOnkGYiqRpod6bjapVkoMBxX6B2seXaeb1Q26ORgSVMod\n3Bxrf35lBTfns86aAtmubp6xkS70D24tN/tsLr2Y5zngc8CdwADwR0KIH5ZS/ssremQ+PkA2YzN9\n2Wr87TgwM2VjWZLB4dZ1Kba9Qg4wYFYl4YgXJDVLTwjo61/5p5BMaYTCCtm0jVmVlEru0r4EjOzS\niURUVG1jI4Pd0m0qZZeLuQDPHX0nBS22chXERuEGr3iDwKvKaJRtbEPl0Uc+yacf8wKXcsll4vzS\nSLlpSor5KuN7DcKRHgtIdXkdqX6dVP/anzu+N8D5MxWspsFmI+ANECynaflPx2PolXow3wkpYWHe\nJtmnovXYE9FnfXRbW9fxsZu0z14rI16D+G72edvIpC1mJpfOmY4DM5M2tiUZGOrg5hWoViShsBck\nLXdzajU39+mEwirZTM3NxaWxHCFgeFQnEr2ybr6QC/DcTQ9Q1KJrc7OsubnS7p5yyWHivNnkZodC\n3mF8n0E4/Pa4efe+djcHurlZ2Rw3V8qruHnOc7Oq+m7eqfQSyP4bKeXztf+fAn5QCPHxK3hMPj4N\nZqasjrcvzjsMDLWuk4hEVW/kt8uchBCwa7fB7LTdWI+jG4KRXXpPI5KBgNJYq+MVrfB2FAy1zxRu\nJuWyy1PqEc7ffXzlkV7wFhUJEMvqFSoSEgslSgkvRasezM5Om22ykRJmpyz2HVq/LDeCoggOHA5R\nrbiYVYkeEN4McQeMgEDTBZbZ+iKEgGRf78efy64yoi9h4rzJ3gMbW9vj47OJ+G72eduYneocXCzM\nOfQPtru5U32KOkLA2B6D2SmbfG6Zm1fIlqoTCLa6uVx2EXgziFfUzSWHbxo3cuHumzbo5nLLADN4\n1z5d3Xzw2nCzERBdr50CAYGmCSyrk5t7z95Yzc2y5uaNrrv12bqs+m1qEmXzbRstJuGzQ5BSIl1v\ndG6tQqk/txtmVRIINstSIRjsnJYqBMST3qjd6JjByKhsdLxZj+i8FNgrL5OKYvD48J3MD4yt2u9V\nODaOCoojOvaC183Wag2PPvJJfvK/dC46Uq3Kt72gQiCoEOi8bLmBEILxPQYXz1eX1uJISCTVVdf8\nNNPLGivLlGQzNsmURj7nkMt472e8ti9/nY7P1cR3s89G2LCbVzhnWrV1nnWiMYVAsHNaqhCQSNXc\nPG4w4npuVtX1nU+FEBuaseyVsmLw2MidLKzBzaoDssPMoV71BgUefeSTAPzzfw5xUvm/Om6r23Ka\nq0mvbh7bazBxropbP2TpfdbRDqnI3ejFzWZVks86xJNeccxs2ql9rzSisSs70eDz9uMvavHZFKSU\nlEsuxbyDUATxpIpZlcxOWViWbMhqcFirrTNZ/cSy2mOWi04IwfjeAJlFi4V5B9dZ8ksoojA0srSO\nQiiiU6x3TZHVIvzt7g/giJVHemUtxzkzGCW5MIFuR7HUZT2XpSRYzuFlIC5RDoUIldur5jqGwbno\nOKp0GSvPoG3O0rsrghFQOHhdkFLRxbYlobCCYawtzSgW18issIYaPKEWcg7loqSQX3psqeiSzzok\nUhrlkoOuK8QS6rovxHx8fHw2i7qbC3kHpcnNM1MWds3NyT6VgaHe3bwaSgc3795Xc/Oc401O1h4S\njigMDm8tN6e1KH+/+/2rurlu58xglNTcBVQngb28nY50CZTzNLv5XZ8q82PBAIFKe6FFJ2BwNjKG\nJl3GSjNt1YWvJQIBhYNHgpQKLrYjCYcV9DW6OZ5QV1xDDbV1tzkv9bpYcJvcbBKNKcQTGuWy7+bt\nih/I+qwLx5Fe2qcuUDWYvmw1UoKAtjUNUkJm0SGz6M1ihSMKw6P6ikWWAGIJhXy2/USt651b3CiK\noG/AoG/Aq3JXrUoMQ6y6n2sNB4V/GH9fD0EsOJrC9N4kjq6QXBTse+MEZ266Z6mPqut6/Wqzk8CB\nlud/747bOf7dp9Htpc9revdBTh2/F7VpwfEHpp9iV2VuM1/ipiKEIBJd/+VPKKyQSK0uTBAtQSzU\nAty8S7Fg1rojOMzNWOzeH+iaEu3j4+NzJVju5qlLVss5a2HO9gon1P6WEtILDumF3t0shCAaVyjk\nOrjZAK3DetRmN5vmUmrqWgcd325sofLZ8feu6mYXcDWVqX0JXE2hb16w/3snOHPTXbhaLXCvuTma\nm6bNzbffxrFnnkNrcvPUnsO8dezumpslAs/N9XZE1yJCCCKxjbhZ7cnNUnqDysvdnM+5FPKtbt6z\nP9DTcjKfrYH/SfqsCSkls9MmZ05WuHShytm3Klw8V20JYnuhVHS5cLaKs0oRiJFdOqFwqyw0DXZ3\nKcffjG4oRGPqlgtiXQSPjT6Aqegrj/ZKSXoozOSBFI7uvcbJfXsZnTjDsWe/TmJ+mkCpwMD0RY5/\n+8tcvK69F+Jr99zF6eM3YasqpmGQj6c4dfxeXFXDUvXGf18afSezGZibMSkWHFZr27UVGR412LM/\nQKpf6VivQwivfcNK1Tfr/7ouTF1aW2sEHx8fn/UipWRmqtXNE+fMtoE378Hdt1Mqulw4V8VxVj7H\nj47pBEPtbt6zb3U3G3U3b7Egtu5mqwc3Z4bCTB5I4tYKBF7av4/RidPc9Nw3SCxMEygXGZy+yO3f\n/CKP/s71bZt49d57OH3T0Yabc4k+Tra42cBUDb408gBzabnt3by75mbRxc2a1j0NebmbJ303byv8\nGVmfNZFZtBspmPWTQ6d1L70gpVeVeKUWKYqisGd/ENt0KZVcjIAgGLrWE4/WT06L8NWhe5gP9q9Y\nvh8kC8MRCn2tKcT73ziJVBSS81MMxJJcPHyc+dG95JID5BOD7dsSgmff8zAvveN+opksuEGiOZvl\ne5aO5CQjDM2fY3HeG7mPxATDo4GODea3KsGQQjAUIJFyuXS+iuPWJi+k1/ZJKAKR7W3QxjIlliW3\n1fvj4+NzbZJetBuzVvXzU7m8vrRT6dbcvEKLFEVR2Hugyc1BQTC4fd2c1SJ8dfg+FgKp1d08EqGQ\nanXzwdffQCoKqblJirEkFw8fY250L6V4kid+8Rvw7h9u3ZSi8Mz73sOLD7yDaCaLcIJE8u1udl3J\nSYYZnL/QcHO05uZOWWtblVBIIRQKkEi6XLqwVBNDShgc1gBBPuf27Gbblh0zB3y2Hn4g67Mm0gtr\nm3ldCSl7L1ygGQrxLTZ6u1bSeozPjr8XS/FOyp2QgCsE0/uS2MH2n+9Nzz6H6jicP3yci4ePNVKY\nzHCUwct5ZsfjVCPtFydmMMjiSJDUTBFor0YphWhb21PMS87mK4zt1onGt9epJBBQOHBdkHLZxXW8\n1GNVFdi2ZG66cyXtTvSqSdv21t0KIBJTfcH6+Pisic12s+m7ucGikeAfxx7GElrXILbh5v1J7EC7\nD48+/zyq43DuyC1MHDzacHMxmuQr4XfwKz84w29+brjteXU3900VEF3d3Or0Ql5SyFcY26MTjW0z\nNwdrbi65uO4yN8/07uZe8d187bO9vuE+VwQpJcWCSy7jtJVS3whC0FJ1eKfzdP/NmIreNfiRgBQw\ntT+BY3T+6QbKZVyhMHFoKYito0hIzpeYiSS6HkM5qhPNVBDLP2Yh6Jub7PicyxMWI2NeUYbtVB2w\nU/VLTROM7TGYnFhKTXK7THrUWwOtRiZtM9vcZmrKYnhUJ5HyT88+Pj7daXaz7bv5ivHdvl7dnMQx\nOs9KB8oVHEVtCWLr2IrGd/7jDNzWHsjWKcUMIrkqylrcfNFidJxtV1VfCNHW5365myWNCfI2jFpr\noNXILFrMTtcGDwSem3fpJJK+m68l/E/DZ1VmJi1yue79WXuiqbhEHUXBv1ivcd+rv8Iffvgyitv9\nYsRV4PLBVMfy/XVmx3bRPzmD7NJPbXkLnuVUwjrliEGoaKJI7yNTbZvdZ14jWC52fd70ZYu5GYuh\nEZ14Ynt/ppGoyqHrvRFh8C74Ll+0qJS9tCahgCLo2CR+OZbpMtuhX+DMlEU4qvppyT4+Ph2RUrYV\nWVwzHbwMnpvj/sV6g4vR0fYAsglHgclV3Dy3a5TU7ELX+9NGfMVjqER0KhGdYNGquVmi2g573nqF\nQKXU9XlTlyxmtR3k5iPBRkp9ICi4fMGkUl1qNdWrm03TZXa6qYdt7d+ZSYtIRN1Wadtbne39rfbp\nGdeVZNM26UUb6XqVCweGdBwHcj2uCeyEELDvYABNE8zOWOSyDkhv+0Ojul8GnVrvuE+V2aWKjoFs\nfbR3bjy+oigBTjz0IB/4X3+D6PKBWV1GixsIwfxYlFDBIpKrIgXc/uSTjEycW/V1OLYX0Gpa+2jp\ndmP5iPDufQblkkul7KLpgmhM7ak5ez7ndK27Usg5pPr9U7SPz07GdSXZRZt0uubmqMLAoI5ts6Eg\nVgjYdyiApra6ORL1WtX5bl7q6zp2Oo1it4/kN9y8e3U3P//Qg7z/r/931/tTZm7lgxGCubEYoYJJ\nJGfiKnDnE//EyOULq76OHeVmZZmb9wfW5+YVrnvzeYdUn+/mawX/MZiI7QAAIABJREFUk/DBtiTn\nTldaUiRzWZdctkoiqXb9Mauql6JRLnV+gBDQN6A1qgaP7DIY2bXZR39tI6Ukk7bJLjq40kvx6RvQ\nUFXBfa/+Cu/61FIP11xfkNRsqWXkVwKWrjA3HscOrC6gzMAAj/3kx9j/+nnyqV24TetaXQGZwfDq\nBy0E5ZhBOeaNWj737nfw/r+ZxKh6Pe1W7JonYX7OZs82l+Vy6oHtWi8SuqU+eQVbtl/1SR8fn96x\nLMn55W7OuOQyVeJJZUNu7h/UGlWDd6ybF20ytQJZsbhK/4DW6IFbD2LBc3NybmNuTg8N8fjHP8pd\nz7zImd2t6cWqa3NH+jX+vfs1PqT8UveNCEE5FqAc8ypDP/fwO3n/Z6bRe3Tzwpy97QPZ5WzIzeu4\nz+fq4weyPkxPmV3X+eVzDkK0/3A9Eeok+1SmLpkU8q3V4gJBGB3ze3Ut7+GXXrAp5B3+9N/+Em5T\nEAtQSAbRTJdYpoIUAiEl5YjOwq5Y11ThNqTkyAsvceSll7m0/wYuHzyKZQSxNMHiaIxquHsVym6k\nh4f4u1/4OQ689hrHn36GcKG4ojAt0z/L90o0prIwZ3f8fUU30HvPx8dn6zMz2d3NhZzb1c0DQzqJ\nlMrkhEmx4Lu5E5OXTIpN1y0NN//i/4Grtp5786kgquUQy1SX3Bw1mB+NermqvSAl1594kbHXXkKW\nqlw4dBzLCBI3c7xz4UVGK/O89CUNHun9NSyODPO3v/CzHHz1NY49/Szh4ipu3sR11NudaFxlcb7d\nzQDR2M7+7Vxr+IHsDkdKSTHfffGr63avNB+rFfcZHTco5F1yWRuBIJFSCUeUbVVcYD1Uq25bDz8p\noehq7HvzJGdvOtr6BCHIDEfIDYTQTAdHV3G0tZ0wD7z+Pa575RU0x2Fg5hJzYwewdQPdEiQWylgB\nFUdfe4BkGzqnbruVU7fewtFnnuX4d59Bt6yO0gyF/JN8rwSCCql+jfTCkjCXZzKsBSkljg0I/OqK\nPj5bmHohp26s6OZacZ9du2tuztgI4bk5EvUHyKoVtyWIhSU37z15inM33tD6BCHIDEfJDYTRTAdb\nVxv9YXvl0CuvcujV10BCYm4GY3cFWzPI61FeSN1I0swRdcqrb2gZtmFw8vbbOHnbrRz77tMce+Y5\ntC5uDvpu7plgUCHZpzbaTUKTm9dRpbvuZiFA9d28qfiBrM+qjIzpTF+2GtKUEnbtNhoXykIIYnGV\nWNwXZDOVUueLEN2yGLk40R7I1nBVBXOdwrnx+RPolo2lG7z4jg/iaEbjaidQthm5kOPyweTKzdxX\nQghev+duvnfnHdz87e9y43PPoztO8930D/mnlbUwOKwTi6vksl51xHhCW9cFR7nkMnmpil0rgBwM\nCnbtMdB1/+LFx2c7MjKmMX3Z9mZma7eN7TYaF8q+mztTXsHNwxMT7YFsjQ25+cQL6LaNpQd46f4P\n4Gh6w8PTgQE+N/ZuPnLxcX7rV6f55d8YWfsOhODV++7ltbvv4panvsUNJ15suNkFjKjBwKAfQK2F\noRGDWMIlv2E3O0xOmNi1AsjBkGDX7oBfzHGT8K84txmW6VKpSHRdEAwpmFUXx5EEggpCQC7jsDhv\nY9uSYFhhcFgnElO6zsoGQ4J4QiMaUykVvceEI0pPi+V3OpouOlaFdFSVYmLlCoXrJVCpADAzdgAp\nlJaAVQCK6xIqWI31r+tFqiovvfN+sv39HH/6GYLFInO7Rvnpd05w/vnOJ3rXlaQXbHIZT67xlEqq\nT/O/S3gj5cFQb5+JlJJ81iGTdrAt7zcpEW3tNyoVyYUzVfYdClCqpRdGon61RR+ftwPTdKlWJLoh\nCAbb3ZytudmxJaG6m6NK11lZz81en1DfzWtD00XHtGxbVSnGr6ybp3cfRCqtbpaKQpUAl0LDXLfB\n/UhV5cUHHyDbP8CxZ54lWCoxOzbGiw++g8zAAJ9+7A/antPiZgGJpOdm4X+XCIUUQmtwcy7rkF10\nsO26m2kMLteplCUXzlbYd9B382bgB7LbhOZS/M0naCm9UvpSQjgiKBVl475SweViscrYHoNysX0t\njlBgbI/3A1YU4a/ZWyMPn/5Vfr/vdwkXCihNxnQVhbeOH9v0/fVNzxAqFJFAORpr61UHgATNWrkF\nT88IwbmjN3Du6NLo9ZO2C++T/J9f+ePW3UrJhbNVzOrS+zA/Y1PMO+zeF9jxaehrYWbS6lBJvPPa\nJ8eBs6eqTQMqFgNDGn0Da18r7ePjs3aklI1aCd3cHIoIyk1uLhZcSqUq43sMSiWzrfWd4rt5Q0Si\nCspQCHum0uJmqSicPnbTpu9vYGqKQMlLGy5F4i1FGOu4CPJ6hMpD/wBNhabWhRCcPXaUs8eWsr5U\n20W1XB595JMtwayU3oCn2VTbYm7GplBw2L3Xd/NaWEs7LMdud/PgsEaq33fzWvED2W1CesFu/ICW\n/4jqAWqx0KG1i4Rs2ubQ9UGvum6tgl8iqZLq1/yT2Dp59JFPwq9ViX7kX/Guz32exPwCUhGYwSBP\nPfIhSrHY5u5QSh767OdQax92fHGe6d0Wjt5+UqyGNv9nr5kOg5fz6KbXTuZ3b/gIC6NR/tMTfwJA\nZtFpCWLrlEuScsltVBS0ba95rT8y2Rmz6q65HdbyysjzszbhqEpwhxd78fG5GizWigit5OZSJze7\nkEk7HD5Sc3PGa4+TSKkk+3w3b4Rf+75/Syyd4cHPfYHE4iISqIZCPPX9H6IcjW7uzqTkXU1uTqRn\nmdl9sG2gWQBD1cXN3TegVW0GJwtotR7ytq7yn979M3zlt+N859hvkl60W4LYOuWi7+a1UK24a26H\ntdzNczOemwPrqI+xk/ED2W1C84L0tVIuS4QQpPp0Un3+aNBGeHTZSGohmeCLP/lxwrkcqu2QT21g\nfeoKJBcWGqlLAINTFzh//S1UlCiyVoFRcWyiuTSXDiU3d+euZORCFsWRCDwh66bLyIUcv3vDR/j3\nw49z7k9muj49n3UoFhxyGQe7VgxB170iYn5xilZKXdZ2rQUpIZexCY5sLL3cx8dndTbi5krZRSiC\nVL/uz9RsAsFvfLix/jSfSvLFT3ycSC6HcgXdnJqdw6iajb8HJy9w/sgtVBUFqSy5OZ6eZaCyuKnH\nIFzJyMVcw80AuukwciHHR360wMLDP8vH//C3uz6/kO/gZkMwOua7eTnd1l2vhbqbB4d9N68F/5u4\nTXDd9ZdV1w1/hG0zWB7ENlOKx8n3pa6IKIG2oX5Futz21GPsOv8mRqVEoFRg9+lXuem5rzF27vym\n7jpcMBGubKmSWA9oDdPl/7n0AeYifV2fn0k7LM47jUIIUoJpSibOV71RYJ8GmipWbhbYI8tTFX18\nfK4MG3KzP/u1aTz6yCc7FlEqXmE3i2XLPlTX4fZvfpHR86cabt5z6hWOPfu1xlrnzSKcX9nNwxey\nLIa7D2ynFzq4ueq52fHd3IKq+W5+u/BnZLcJkahKLrv2tY9CwMCg/zXYCB0DWCkJlG0CZRtHUyjF\njN57wa6DzMAAZiCAbi1VFdAtk8OvP8fh159r3GZrGpF8flP3rVkuYgWnCQlnj9zMLU8/sabzfH10\n0l/PuUQkqqAI2MgqZyG81lk+Pj5XnkhUJb9ON/f7bt4wn/njj/Ly55uCtSY325pC+Qq7eXFoCNvQ\n29x83WvPcN1rzzRuE2Lze7Cr9spuRsL5Izdz7Nkn1+zmbNamz88SaBCJKi3Vw9eDEBD13bxm/BnZ\nbcLAsI6qdh9UFAI0DeJJ78fm9bLyWuvU10D4rI37Xv2VrkHs0ESOoYkcybkSfdMFxk6n0av2lTsY\nIfjnH/p+LEPH0jSWLb1YOjQB8yPrKO2/AtWQhlzBggJY2DWOo67te1afmfVZQiiC3fvay/YL4RVn\nS/Wr9A2oDA5rHDgcYHBYazknCOH1mAyF/VO/j8/VYHBYW93NuiCe8N282Tz6yCdbg1hXMtzk5v7p\nAmNn0mhX2M3H/uZ+ljUR6Mhmp+uawZXdrACz43vW5ebNDrq3Oooi2NOrm68LMDDU7uZ4QiXkp2yv\nGX+4b5ug64L9h7yiEOWSi2EIAkGFfM7BtiXRmFdOXdUEw6MS16UmVz91aT08+sgn4VOdm5fHFisE\nyjZKvYm29CoDDl7OM3kgdcWOaX7XLv7u53+WfW+cJJzPc/D11wkVi6i11DZb05gdG2NhdPMDWTOo\nYVSWXnMzroB8MsLXf+TD3Pm1J0gtLGAaBgMPD1H48qWu68eEAmE/4GojEFTYfziAWfWqnKoauI63\nRGB5642+AYVwVCWXsZGuNxMbCiv+797H5yqh68rqbu7XUFXBsOu7eTPotswnni5jLHezIxmcLDC1\nf5NrRzShfupbHDwcJJfzWqZlMw5OU+wshNc6abMD2Uq45uay3XHWyhWQS0V54of/BXd+7QmSi4uY\nhsHhD+5j4vOnurtZ4A+GdmAtbu4fVGqZlL6bN4ofyG4jVE3QP9ia6pFItX/EiiL+f/beLMq167zz\n++99RhzMQI237nwpUhJFirIlWaSoFtmeRJYtO7S75ZZ7dbfdsZWUEz1ITsIuJ2sl8UovZzXth6yk\nV9sPfOqoo3RTjmnJ7UFu2hoouS1RnGVSInmnmqswAwdn2jsPB0BhOECh6haAg8L+rUWRqgHYVQWc\n3/n2/gZQcQ06Ee3NIvoRK1o9AR0BIDkMsu3BVUezy24U60jtmzCN8yimZbx5/wfw3hf+FpffeAOM\nSnjz/vfh9Q9/6PSfmBDsXEggkTORPDBB+GGpCAfAKUElpaM0dxF//M//mb+dSwi0Wg2/KP0BZDc4\n7U6WCWIJcSIRBCEEmt4mvAEZXrpORWMngWCCCDePj0G9Kvq5WbY9SI4HTxmBbzjHG7FLeCF9L2qy\njjmrgA/vvQjp5nZjXCJBMi0hM+e/HvTnngCeOqXnHsLN1ZSOcvYSnv0vf6XlZr1axS/QtyB7wW5W\nVIK4cHMgx3LzMebHC/ojAtkpgHMudmlCwPrq2ukJ5pSJ5Uyk92otSet1F+qOi5cf/Ci+8/cfGf0C\nKEFpzkApG0HiwEQ8XwflgBlVkF8wwOS2u7PGa9kyDHzrp34SD/7ZX0CRObjFWp9OZSRk55WeXUzB\naPFcDkIAKonfu0BwFMLN4WJQEAvgzgoYT0g8V8fX5z8Ij/q329uRefzJ+UfxSfqfcM3K93z9URvl\nx6bNzcl9E7GC7+ZaVEFhwQCTet1cj0bx7Z/8cXzkq38JlTAwh7c+3XSzeN2PF+Hm/ohANsTU6ww7\nmzbqJm+0Pfc/rmn+7p1ofz4eeppFHEE1qULeN3t2fj2ZwlVG8DfjvCOIbUI5kNqrYfdi8vSfsx+k\nIc05Y6gvf/t992L70kVceuNNSJ6HX9j4z0fOUPM8jnLJg+dyRAwq0nFOgbrJsLVh+7N+iZ/Svbyi\nipmBAkEAdZNhZyvAzXrDzWJG81g5MoBtUElqSB50upkD8BQ6mtNYxpDeq7WC2CYukfCf0/dhdftr\np/+c/SAExXkDxfnh3PzW/fdh6/IlXH7jByDMwy8O6+aiB88Tbj4tTJNh+7YN2/Hn+Bqxhptl8Xtt\nIgLZkOLYDDffsVqtuP225/5/25aHStnDykUV0ZhI7xgl66trwLPH+55SOoJI2YFquX4NDgFACPZX\n4iNp8R8p2307ExrlOoAxBrInoBaP4/sf/FEAwKv4MADgX37lXwd+bd1kuHXdAuetLChEDIrzF1UQ\ncXp7IlzXH6fAmm3/OVCrMty8buHKXZq4EREI2rBt/73R180l4eZx8cBjLh6nnx3668uZCIyKDcXy\nOty8dy4+kvUZZbsxfqfrGkoI9pTezfFhA/JxUUsk8PqHfDe/hg/39TLgz1G9fSPAzZdU4ZAT4jq+\nm9tH8tQq/j3Q5WvCzU1EIBtS8gfuwHlSnAPbmw6uvkvseA2L53Hk9h2USwyUAumMjERKCvz93ZFQ\nKMHOpQT0qgPNdODJEqoJFVwazS69UbZAmuboQjOr0KtV1KPRkTz3qFhfXeuRJuccG7fsw4AL/vvA\nrDHk88GjAKw6w86WA7Pm/81TaQlzC8rMBb2OzVAuMQB+cxm1bWe9mHcDm3q4LodZY63OqZ7HUSq4\nsC0OPUIRT0oDU7/NmofcvgvH4TCiFJmsIk54BVNPfv9oN+9sOrgi3Dw0nttwc7nh5qyMRDLYzU1O\n4mhOCbYvJQ/drEioxkfpZhtBcSwASPU6XJdP1cna+uoa/up3Inj+vt/t+DjnHJu3rEA3F/Iu0ple\nN9frDLvtbs403Dxj7xnfzX4tcrebC33c7Di9bi4WXDhDurlW9ZA/aHPznDJVr8NuRCAbUur1o4s5\nXJeDeX5nNMFgGOO48bYF1+GtC8POlgPTZFg6d1hsP8wOL/UY0jvVxm6rX2uSX4zBUzprTeoxFfXY\n6Av5CUfwSS/nmNu6idIcxZ6iI5avQ7E9WBEZlZTeWbcaQpo3Ks2A1rZ54BB2zoFS3usJZJtZDU25\nMgbkcx5sh2PlgjbaxYeIQs7B7rbrl4dxYH/XRWZexlyj+Uyzw2IPzRELUcC2GG40MkQ4B0jRw/6u\ng0tX9cDgtFhwsbPptB7XqnsoFTxcuqb3jCcQCKYJawg3O85h92HBYJjHcf1tC57b5uZNB3WTYXG5\n15+DHN3j5piK3GK0p0fD2NzceL4eOMfSxtuwHYaansCryXeh9NF3IbFTC72bH3nSBLo2mm2LI6gv\nVNPN3YGs3ZVxyBiQP/Dg2MC5C7PT/Cifc7DX5ebsvNxqDGdbvG9dt9OoW7Yshptvt52EFzzs7zXc\nHBCcFvMudrZ63Xz5WrDLp4HwvltmHD1y9AuKwB9RIjiaYsHtCGKBxkW24MGx/avp+ura0WlKnGPx\negHRkg3K/SDSqDhYulEAYZOZq1ZLaH6P924Yw/m3X0Ndj2P5nQKSORNG1UFqv4Zzbxcg2cEdCcPG\n+uraiXbf8wduxw4x4P/Nq2XW+pufdRyH+0Fs22BhzoHcngur7v8OdIP0zXjXGnX425sOmIfW+4cz\nwHWB3R2n53s459jddnqCY88DDvZ6v14gmCa0YdxMgBlL+jgxhYLbEcQC/nWmmPdaN+tNBjqacyy9\n0+Xmso3l60VgQm6uJjRQL+Caxzycf+f7OEjM499f+AReTdyFG69R383vFCA54XfznWStBWUccg5U\nyr1/87OKYzM/iO1y88GeC7vR+DLSz80crTr87Q0/S423PYbrAHsz5GYRBoWUdFYe2IafECCeGJw+\nIDikVmHBp04EuPC/Pj7cRZn5olQc3pEpRABQj/tpRBOgFlfhqBStSKMRZdz90vMozGcRLXG/uUXj\nikhAIHl+E4pp4n/5L34DUsAOIyFAIt179NEvq4EQ/3R3FqiUg2+IOEcrnSmZknuyOlpzDXUKxvw0\npiCqAY/v2Lxv6mWtMhsbCIKzSzorD9xAJgR+Wqxw81D0czMhfk8EAHjw6fsHOpowjuW3C5DdIDez\nibn5rk/XMG/mDt3MGOC5eM/3voGYxvCN5R+DS2VwKjXWSyC5DKnd6XDz+uoaHnrl81A1Eph90NfN\nZrAHCEEriDvrVMrBP2ePm7t+fYT4DZ+0hpvrZvC9TKXU62bb4n0bd1er0/t7F4FsCGCN2s1b1y1s\n3bZhmgyKQnHhinY4dLpxdSbk8CZz8dyAAVUzAOd+99rNWza2N2yYtf67mIoafFNhSwqefHa4VJaF\n2yWoNgsqdwHlgFJ3Az4zejTTheQRcEr9FwcHJHBUExE893OfhBSQjgtCEC3Vx7/YO4EQ/OE/+mXY\nqtrapWw2lEgHzGTU9eC/Oef9Xw+zCKUEl67qSKYlSJI/vzc7J2OlkeI1sGQp4HODxgOIMgjBNNHt\n5rrJoKoUFy/3d3M0RrGwLNzc6eb+N8n9rsUc/rVofXUNjz7z8MDnm79dguL0d7NqTcbN7i3gwMiC\ngLQupBJjWHLzyFyMoqwE9K4gBLHy9Lj5kSdN/NbP/AbOXdDQvAUBDt2cCnCz1qerN+eAqgk3Nzd2\nqERw6ZqOZKrhZoUgO3/o5kEEeVuSSN9U5aBDgmlB3FZMGM/rrd0sFT3EExTpOQUXrxzW8nkuh2Uz\nKAqBMooxLlME5xwbN23Uqqzj99ZeX9BOKi2jkPM6dn4ZITCjUeyeXzny+YjHoNfcQFH6jwU42mQK\nojLblcY4gcbqKIVLKX7wwIOIlcsgjb6J3cjOZHap74Tc0iL+w3/967j0xpv4TPmrKG7IfVv8p7My\nCgWv43SwuZupqr3vH844nEbzjbOS6RCLS9jb7k0ZamZ0NJFl4teKn+t9DEIIYnHas4NMCJBM9r7m\nZZnAiFJUK71fH9SQSyAII57HceMtC67b5eak37gs2M105mvAOee4fcMPXjvcvCAjOxfg5oyMYt7r\nOZWNJYHf/sXfOPL56FBunsCtLueIfY2g2j56h1J4RMb1930Qyze+1fdb5WYb7Cnit//Bf4Pffvb/\nGmo0XmZORqnQ+TcnBIjGaeC9LWO81Rjr7LiZYm+n9+OEAPFkl5tXggNXSgmisWDXJlIBblYIIgZF\nrRrk5ukNB6d35VMMZxy5AxeFvNdTG9KkXGKolC0YUYqVi377ckkmMGTRPQIAqhWGWo311NUc7LlI\npuSeonVV83+PW7dt1KkCwhjy83P4q5//5FAjcSSvfyoqh98NsZYYfwMhwjiUgHpPAkCvOjATDJmd\nTeQWzoO3HYdR10F69yaAo4P4sOFoGn54/33473AfgP6jepTGyUn7vMdkWsL8Yu/NVG7fwcHeYYfA\nZErCwvL0d1BUFIL5JbmjoQQh/o1E+664YzPkDlzUTQZNp8hk5Y7uiYvnVFjv+Df1zS6cmkYwtxAc\nmC6fV7F5y7+ZJcR/b2bm5A5BCwRhgzGO/L6LQmGAm4sMlZIFI0axckG4uZtKmXUEsUDDzbsNN3ed\n/GgaxbkLaqvWDwB2lpfx73/uZ4dyMw3KOGo+L3w3V+PjbyBEGMfeptPbyIRQbEQWITMX83u3sTd3\nHrwtf9R38y0A58e74FPgf/rkbwR2Ne5GVSkuXmlzMwVSKQlzXW7m3L9XPthzWyeJybSEhaUz4GaV\nYn5Rxt7O4X0HIUB2Xu6Y12vbDLl9v6eFplNk5uSOjfilcypuXu9slqbp/d187ryKjVt+dknTzdl5\nuWNje9oQgewE2LjVeZLYD96Y55g/cJEJ2Mk8i3guh+dxKCoZeKGqlLzgOjwCVKsekqnel/b/9qn/\nFuAciVwOrqKglkgMvS73iBPw7YsJ8AnsFPIBT8kowcHiIj7+h38MR42gksyAcA5OKTK7GyhmhxuM\nHnbWV9fwe7+5jfqjX+r5nB6huHRVB+e87+upVHSxv9vZ5r5Q8NPUF89NfwfFdEZBLCahXPJ3wOOJ\nzhb/9XpnB8m66XcxvNCWPinLBFfu0lCrMtg2h6aRgcPuJYngwmUNjs3guhyqRv20JoEgpDSzfLqD\nsOCv9Ws7CzkX6RnJMvCnJAzp5j79KGpVD4lkr5tjcQnX7tFh2xz/6if/KWrx4ee6HuXmrYvJiXTe\n4oSAcx5YfiEz13fTq3+L+gciqCTSLTdnt28hvxAb+3pPi6CuxkEM5eaCh4MuNxfzHgiAhYCO1tNG\nOqsgGpf89wyAeNf4nbrZObO6bnooFT1cvKxBbzRilJUuN+sEkcgAN8sEF69osG0Gz+XQNDqwHGga\nEIHsmKmbrCcNYBCcA8WCd+YDWc/j2Lptt1IeCAEWlhUkUzKY58ugPaWEDtg86k49+eLvfxovPdsY\nPk4IStnssdYmWy4SuTpcmfQ0k+AAiikN7iRSl5prII0RPO0fA8Akv272+cd/Go9+6f9DLZaEoxnQ\naiUwmeJ7H/soqOuCydN/GfjcU0sD5Tnoxqv9JLYFBwp5D7GEi2hs+n8/ikqRmQu+4dvdcgI7SO5s\n2bh8TW99jBCCaExCd1UX534zqGLBRa3KQAhBMiUhnZWhqBTK9N9vCGaAusl7Uu4G0eyse9YD2R43\nU2BxSUGin5v7xJUEvW5u57d+5ug04m4Uy0U8V4crEchegJszOrwJlfyAABQcPZ07OIfOLL+u9J3r\nePQP/wjVNjd7CsXe+el3c7+Zs90MdPN+r5s598foxRIujOj0/n6aqAPcvLNl97qZ+R+/dPX4bqaE\nIJmWkM40TnXPiJun/1UwBXDGYVkcVOrfrW3g94e0wSrnHI7DIUkk8LTFtvx0RavOICsEmayMiBEs\nlc1bNmo11tGGfGfTwcGeg2YpZyxOsXROhSQTJFO9Na+AL8to7PCisL66Bjx78p9Rr9iY3yiDNDZW\n2zqlgxGgOGegnI2c/AnuEMp4TxAL+GttNnnaunwJf/hr/xxXX3sdV19/HUa1DEYIHvrTPwenFH/2\nS/8A+YWF8S58RKyvruH9nyzgU5/5wtDf4w5o979x08Fd7z7b3cH7NWKx6nzgbjngpz3dvm53jUzg\nONhzUa0wXLisTn0KmODsctbdLEsk8LSl3c2KQpCekxGJBLu5eUrdemzPH8e1v+vAcQCQNjdLBMm0\njGIh+FTWiAbfsJ9klEu3m9v/eow23JyZoJs9Dh50HEsI7JR/4rx55TL+8Nd+FVdeex3XXut0M5Mo\n/uyX/iEK8/PjXfgpMuzpbD/cAWnjt284eNe7z3Z38H4dievmEG62GG7f6HXz/q7v5vOXzo6bRSA7\nYkoFf/gw4EvvuAPSm638AaBa8bC37cCyOCTJrzlLZ+WJvBgLeRd7bfOo4gkJi+eU1g1/rerh9g37\nUGYmR6VkIxo7rPlt4jh+TU13RyLOgfZ+RJUyw63rFi5d06DpFAtLMna33WajXhAAK5dUUEruaMZZ\nC8Ywv1FuNFLyaQaz1YSKg3PDpz+NCkbI4aK6P9d2A2PGY6ikkogXS7B1A7eu3otKMoN4YR8f/fKf\n48u/8stD1SNNAy89m8JLx5CnHultftCEw0/vjxgUhZyLatkx6pNRAAAgAElEQVTflElnpdamTK3q\nYX/Xn/2m6RRzC/03bMIIlYLHEB/1cuCcBwSxzc/5gYFZYzCi0/O7EMwOxYKL3TY3D8ryCaK9oUq1\n4mF324HddPO8jHRmQm7OOR11d/GkhMXl/m6umxzlko1o/LDmt4lts8AAn3P4QSwAcKBSYrhlW7h0\n1U95bNb+tf/45xtubuehVz7vBzvHJcDN1F8KKkkNueXJp+ZySvo2oMp7h0dhtXgctUQCsVIJViSK\n21ffi0rCd/PDX/kzfPmfTr+b108YzOo6HdjxulZj0CPdbpZbJTEtN9sMmkYxt6AcdhufAihFq268\n++ODri2cc9y6YcENGA3Lub95bZoMxhTdpwxCBLIjpG4ybG92Dh92B3SBJ80rMfwXGyF+K/LMnAyz\nxrBx81A+ngfs77rwPAQ2rxkl1bLnpyO2/VzN+rtzF1Rwznt+7tb3VvzC9fbOwq6DVtH5Udg2R91k\niBgSUhkF8YSMWqOhjBGl+JFVD4/TUwhiAUQLVt/Tzkg1JMOjKUEloSFasjqkzghQyugdX3r3Sy+j\nbiTw4kc/AY9SgEoop+ewfeluzG3uYn9lccyLHy3NzYyjBDq/qODG28FdIinxU+uuv9XWTMH0X+9G\njECWCErFQ9PUqgy3rttYuagiGpsOSUSjFOVSQEfitDRQlnWTwx3UBK0hTBHICsKGaTLsdDnKG+Bm\nSg/9xLnvalX1b5prVa/XzTsumIe+DVdGRaXsYXe7Mx2zXPR3qZZXGm7e6OPmcm8/Ds/lw7vZ4rDq\nHHqEIJ1VkEjKfqkB9a8x3Sdn66trwEmCWADxQr2/myvh6MbPKcHV6k28Hb0Ar61zMSNAseuk+O4X\nX4IZTeHFh34arOnm1By2L74Lme195Jan91S2ybCpxu3MLym42cfNhACew3F9ow6vMaa36eZojECS\nKUqFwx3amusfhJy/pE6FkzjnMGIUlT5uHoRpMnj9p1H6G821sxPITs/WxBSSzwXU3g0gnpBw9W4d\ncwsy0hkJy+dVXLqqgVKC/d1e+XAO5A9cMDbe/KZ+dQuVsgfP42Ae4Nj911TIdb7DNI0M/3sinY8t\nyQTxhIRYXML/+LO/gcfpZ4f9MY4kWrb77qgOarI0bvKLUZhRBYz4DZ4YAcppHZVUZyAruS7evP8j\n8GSldfzAqQRPkqFXQ3op4BxazUH8wIRRsoATvNbXV9fwwGP971KbJwh9nh62xQI7mNYqvCOIbf+e\n7Y1w3Ewdxd62HTiY3YiSIzfImBeYONeCUPR0DxcIwkD+4JhuTna5eaXdzcE+zO1PwM17wfcJ5aLv\nZs8bnK7Z7WZVo8dys93WQV+SCeJJ383tQaz+3BN3nDEVGeDmMJ1efmzvuzhvbkNiHhTPBmTfzdVk\n54QDyfPw5v0PgrW7WZLgyTIilUmsfAhO4OZHnjSP9bePRCjmF/q72ayzwyC2jWqFdwSx7d+zdXtK\n3LzjoBrg5miMYv6IDTLmBfYYa0HI2XKzOJEdIYNq77p3OSn1O/ftbNlwLI5IlEKPHHYHtKz+6RWu\ny6H2GSo+CoJSCQEAxN/BlZX+6a4AwLquOlTyhzwHNt3phvcO037gMfd0AljOodccKJYHTvz5dH2W\ngFo0PA0+OCXYP5+A5DJIjgdHlcCl3sD0rfe+B7Y+1/sAhICyEF7UGMfirRLUugvC/c2DDCXYvpSE\nqx5vJ/Fx+llgtf/pbDrrn+zXKocdS/2GY8G12Efhuv4ojzDX1jo2Qz6ozpwAqYxy5Np1Y/BNbves\nWoEgLBzXzdGYhJ1NG47ddPNhV1B7gJs9l4OO0c2Dfi7P82tmB71nuwNvSfIzwnIBm9c9BLi5m/XV\nNeCpIx4n8LEP3cwIafV/CFgCqrHwuFnhHj6x/U1UJR1X/uf78Wvf/JG+bq4bmd4HIBTS8Uu3Rw5h\nHAvtbqZAmhDsDOnm46Qap+cabq6xVuMjQoDFZeXYG1LAdLjZtllwDxjiz10+qi44EjnCzY1446wg\nAtkREo3RwFb+hABLKwoKOQ+u44sxEqHYun2YnmRZ/giMS9c0qCqFplHU3OArWvdctiA446jVGJjn\n/7tc8luYx5MS5uaVY7Xfjhi0la7UjeMwFAsMqkpgW8HvpFhAymV2XoGqUeT2HbguYBgElTLrqA9o\npg+3y/JUamHhB62LN0qQHa8jZalZe9uNrYfvrePJFJ7c/0birffdi4tv5jrmyTZhIbyoJ3Im1Lrb\nSpkmHOAex9xGGdtXUid6zPXVNTz3C9/At3715Y6PE0KwckFFreq/NygFkml/nlu5yNB3V2YAVp0j\nYozm92qaDPl9F67LEY1RpDLyscfb9K0LbmRXxOISrDqD53Foeu/4HEkiyC7IPeMRAEBRgJWLWqhv\nFgSzSzRGUTf7uPmcgkLed7MRpVB1Eujmy9c0KCqFqvWv45OGcDNjfmfRbjcnUhKy80dvKLUTMXrL\nBJo/l2MzFCsMitrZe6KdoJvbuQUFmkZxcODAc30HV0per5tjtGP+ZTsdkwOOyfHdHL4b9C//6yf8\nn7/P0n5w/324+IM8OOn9glC6+aDLzQwg4JjbrGD7cnKox+jn4m4IIVi5qKJaYaiUO91cLHpAn/vM\nQdiWnwI/Csyan6J/R27uM9mk6WYjSmFb/qhKXe8dnyPJ/Q+HFPXsuTl8d+NniGRaRj7XOVidEP/0\nJ5GUW/PUOOd46816zwuOMb8O9tx5FXMLMm5dtzu+hhAgnZHAOVDI+QXtkYiEWKJzhlR7DU/3cxRy\nHmpVhktXtaEbU8zNy6iWe0WmKH6X10E7QZSiZ+h1k3hC6jjBcRzeSK/wQCiQTMnIzvu/swefvh+P\nPvPwUOsdhvROFYrtDUzHaMIxuNA+rDBFQTEb9euL2n5SRoBKShvwnZMhVuys+wX8GxfV9kBdBjYg\naB/Eo888DKw+3LMj3Gph37XR4teo28fe+T1uY7dhKRbcjvq+uunPs7x0TR9qU6sJlfpnThAA139Y\nh20f1sjNLcg9Y8CycwoiEYp8zoXnchgGRTwpQQvhzaRA0CSVkVHIu/BcdLg5MycjkfL/ARpufqO/\nm5cbbu5obNj2WP6oEBeO7fd1iMU73VyteNi8Fezm3IHv5otXhndzdkFBpWJ1jOzw0wiHcLPUv6Y3\nnpQQT7a5eYFhb9tFteK7OZWWkZ0Lvp2808kB6e1junmorxwPrY32I35+pigopSOIFa0eN5e7SoTC\nQF83111Qj4EFnDoH0c/F3RBCEItLPRstmayMzTC5Oe83d+128+Vr+lCbWk2oNLhvzPW3LDhtbp5f\nlHvGgGXnlVYjLM/jiBgUiTPqZhHIjhBJIrh8TUNu30Wl7EGS/OYQ3el2nhvcNRQAahX/ExFDwspF\ntbMzYlaGEaN4uxEEcw4UqAdlzx94LEkEnsd7JNsO534DpVqVDd2cRtUoLl3VsL/rwqx5kBWCSFRC\noU+aRzRGwRhHNCYhlZaHfkMrCsG5872DrtZX14BnhnqIoTEG1dx0QwBz0qnFnOPCD3+Id7/wItR6\nHTfuuQd/9yMPwFUHDwbLL0QhuQyRqgNOCAjnMGMqCvPGmBY+PEHNPFqfO4XHH3ZHOBqTWrubwHCN\nTzQdHYPNTwvOeE+jNc4B1wNy+w4WloYfDBeN0cA4lhCgWvVapzbN59rfdaHptOc6YUSlqWieIRA0\nkSSCy1d15A4O3ZzJyoh1udl1eGDXUMB/jwD+63/loordLQe2fThRIBLtcnPeg6IQXLqigTbc3N4k\nqgcOWNbx3Ky13OzArPmjdfyO68HlEU03x+ISkunhT44UheLchcHXmlPJluJ8YK+KbggB6tEJD8fk\nHBff/AHe/b0Xodg2rt9zD974wANw1cH3DLnFGCSPQ29zcy2uojg3uRFC/elfXnaC5KUTdzWOxU/m\nZkU9fTczxrG73etmzwNyBw7mF4d/XcbiEnbQ21CUEH/zq9vNezu+m7s9HLQxfxYRgeyIkSS/acqg\nximE9DaSaX1/W9BnRCkWzykoFVxQSmDEJGxv2h2i5cxvhnSw59/UVsoDWpe1fU/dHF6WgH+T3i6y\njZtW4M9Aqb/7fRr5+Cdu1X8EpM8s1ibtn+IEKGQj8JTJXhw+8LWv4z0vvAilMQMhtX+Aa6+9hi//\nk38MTxkgzGY9reNBsf162kn/LP2oJFQk8vWOnV8OwFGkgSnUx2HYHeHsvIJURoZZ81DMe6hWWCu1\njTcW1twd1SMEKxdHc8Jt2Tz4PoH7XUexNPxjUUpw/pLW8d7lHMjOSzjYC26UkT9wZ0KMgrOPJA/h\nZtr/5liWAtxcPHTz1u3+bp5fUlEuDedmq348N2saxcqFw+vP7Rv93ZzOyiN5P59WyQ8Z0BUdCHDz\nnAFPmWzjwg8+99e4+6WXu9z8Or78T34ZTB5wy00J9s4nINkeFCfcbq4mNMSD3KxKJ86UGnZjuZtA\nNzd93FjYONzcr5SON9w8f4yhEL6bVdy+aXdMMmkP2rufI3/gzuyGsghkJ4jncexsOX3rTZtpyE12\ntx0U84c7q/mD4O9rdilcWOp/0tv9PEqjg1m9zlpD0iMGHT6FdsDXnUYW7p206u+HbHvIblWgmY3d\nPPQ/6TMNGa4mo5rUJl4fG6lUcO93XoDU1l9d9jxESyVcfe11/OCB9x/5GJ4SXkk2Kc0ZMKoOZNsD\n5X6aFScE++dOf0bgMKN6JIkgFpcRi8uw6gzVCoMkAbGEBEL8G05JIiM5iT1cA/rueB8ndalJxKC4\ndo/u1/IzIBKlsOoMuf3gExxvQMdTgeCs4HkcO5tO32CzmToM+OnHO5sOSsXh3FwqMswv+V2/jzpB\nItQ//QTa3KwSRCLDu3nQl42iQuY0gtiTuLmS1OBM2M1GuYx7vvci5HY3uy5ixSKufv/v8MP73nfk\nY3iqBO+YzQzHTTEbQaTiQHZO183Dbix3M9DNAOoWgzxiN1Op/6bXcXrQNIkYEu5qupn7rq6brG/K\n8aBu5GcdEchOCM45bl23YAXs4jTlks7KSDYGrps11hHEHo3/IEaMAjuDv5JS/+tu37AOG8A0gtsL\nl7Wh6u5SKQnVcvD6jDsYQH1aO7s9MI7FG0VIbSNEBv1q91figd0GJ8H85hY8SeoIZAFAcVycf/ud\noQLZaYBTgq3LSUQqDjTTgatIqCbUkf4dhk1x0nTa06EzMoaZbIpCoekEdbPz1dq96TUsjHFUK8xP\n/Y9KoJRA04M7HhICRM9Qp0OBIAjOOW69M9jNmTm5VTNqmqwjiD2K5mNEY1Lg6J52KAUiUYJb163D\nhlIEUBtuHmbzKpmWUa0EpzBH7sDN3ZzaKSzjWLpRBJ1CNy/c3gCTJHQP8VQcBytvvT1UIDsNcIli\n60oSkYoNzXRP3c0nTTUGgt08jnmpqtrfzZk+9eODaLqZMw6j4WZ9gJvPUhfi4xKOd/8MUje5n4oQ\n0DUxkfJPSeYXldaua6U8fJtx/zH8F7WmUSTTUt+dVz1CcPGqhnyjsUSznoczP1Vi2HmYRuzweVr/\nUGDlonpkq/B+jCyIBWBUbFDWOQczqLyDA7AicmhECQB1I4KObh4NGCGoxU7/tHKiEAIzrqKwEEUl\nrY/l77C+ujbS196dsnJRg6YTEOLf6DZFedxRN2bNw1tv1LG9YWNny8HbP6jjYM8BpQTzS3LHNYMQ\n/8T3JMGyQDBNmDUGO2AOOiFAMiXh2j065hba3Fw6XhDb3JzWdIpE6gg3X9GQP3BbpzJNN1sWx/bm\ncG6Oxg6fp8fNp3Qke5rXS6Ns++U+bR/r5+a6ETY3G4HHZYwQ1OLxCaxohBACM66NzM1HzX8PIysX\nAtw8f/zSulr10M3bm21ulgjmF3vdLMsEqczsunl2f/IJY9ss8OrMOcA80tN0YZBwKPUfhjP/Ra3r\npNXdFwAWlhTEYhIKBX9ydCIlI2L4M2qbz1MsBNfRNE9rjmrVTQjB4rKKVMafxUmpn9Zx3LbjwGgD\n2Cay7fWti2Vo/GkIwKTRpLKeFKNcxge+9k0ojtuTbsUkCW984IFJLe3Msb66hvd/soBPfeYLk15K\nB7JMcPmaDqvO4LoceqR3NM5RcOY3getuZHOw58KIUqQz/sgNf4wAEIufbIyAQDBtOAFBLNBwM0OA\nm/s/Fm3c27OmmyMU6bbTmcVlBbG4hGLBBTiC3dwnE6tS9k9rjtooJoRg6ZyKdIahVmWgkn96cxrv\n5VG4unvMTjudbqY4WA6Rm0slPPD1b0JxnGA3P3D/pJY2tRw1/z1syMqdu5kxvwlcsJslpLMKNF24\nuR0RyE4ITaPBYy8IAudbJZJS4FByQoArd2kwTQ7HZtAjtKe2lRCCaFwamBY4aEf5OK3NNa3/LLmj\nGOcpmK3L4NSff9YOJ379B6cErkJhxtTRFBKdBM7x0//u/0WsWOyQpN9kQcHzn/hpFObnJrW6M8lL\nz6bw0h2kOY0STac4aduKWp+5l83uqhFDEt2IBTNJvzq6/m6WkT/oDTZbbq5xOI4/tzLIzUFjRdoZ\n6GYM38E9KOXypDzwmOsHGSPA1mRw0tu13nezAU4BV5FgxpTQuJkwhk984YuIlss9brZVFc8/9tMo\nZbOTWt7Uc9JGUJPijtxcZYGp9Jz7o/cihirc3IUIZCeEHqHQI71D2ZvDnrtRNYr5JRl7252pFksr\nCmSFIq4AfadtD0EsJqEU0HRK03pPh0fBuFM561EFriK1GgkBfsMCV5FQykZCI8h2lm7egl6tgnbd\n2TBK8foHfxQ33n3PhFZ29hmmGdQ0wVj/ujPGZrdphECgRwg0ncCq8x43N+fLtqPpFPMLMvZ2G25u\nZFotn2+4OXln64nGpcCGkJpOjsyUGgWjdrUZa3Nz42OM+B1xS1k9lG5evnETWt0MdPNrH/4gbt5z\n94RWdnY4aSOoaWOQf4dp3jqLTCSQJYT8KwA/C8AG8BaAX+GcFyaxlkly/pKK/R0HxYK/mxuNUSws\nKX0Dx3RGQTwuo1rxAHJ66UEAML+ooFb14PnZx61amqWV0c5km1gtIiHYvphEar+GaMkC4LeUL8yF\nM4gF0LPb20RiDPFCcezrmUXupAlFmDCi/TNCEgmxvzmrCDf7p6QXLmvY23FQanfz8gA3zymIJ0fr\nZjZmN3fz4NP3+8HEqCEE25cSSO2bLTdXEhqKc0Z43VwqgQQEIBJjiBVLE1jR2eWsOLgf0agE8OAZ\nss0Gc4JOJnXH8hcA/gXn3CWE/O8A/gWA/2FCa5kYlBIsLKtYWB7+e2SFBJ7Y3imyQnDlLh3FggvT\n5NA0gmRKhqyMRhxjk2I/OIdRthCp2CAcsHS/fX+YGkd0s7+0BBKQZ+YoMnYunD+156GeB8lx4Gha\naG8cJslZOJ2VJIKFJRm724flCoT4XUxjifC+BwQjR7gZvpsXl1UshsDNSpub6003p+WhpgmcFuur\na8AzY3oyzhEtdbq5mtTAQ1wDuL+8HLjJ7CgKdoWbT51pSzU+Dv58axl7O21upv70j1hcuDmIiQSy\nnPM/b/u/3wbwi5NYh6ATKhGkswrSI36esUqxD8kDE4kDs5VWrNccLN0oYvtyEo4WzhOp4lwWG1cv\n49zb16G4fhqbRynqhoG33/ueO358yXHw4b98Dldfex2Ec9TicXz7p34Cm1cu3/FjjwrCOIyyDcll\nqBuyP+N3TIKfdpmmMgoiht9oxnOBeEJCNH6M2dGCM4dwcziRJIJMVpnIc487ayq5byKR63Xz1uUU\nXC2cJ1L5hXlsXr6E5es3Dt0sSTBjUbxzCiU/kuPgx776l7jy+t+BcI5qIo5v/9RPYuvypTt+7FFB\nPA6jYkFy+UjcfJZTjdNZBZGohFLehccabo4JN/eD8ON08hnFAgj5YwBf5Jz/26O+9t2RFH/6rgme\n4gnuiIde+TweedKc9DJAGMf5H+RaomzCAdTiKvZXwtsmnzCG93z3Bdzz4kuQXBc37r4bLz/0EViR\nyB0/9sPP/gkUm8BVdSQPdpDZ24Ary/jTX/4l5BYXT2H1p4tSd7F4swTCOQj3m4HUDQV75+Nj360+\nizKdFT766le+yzn/4KTXETaEm2ebSZT9DHJzNaHi4FyI3ex5DTe/DMnzcP0e3822rt/xY/+9P/oy\nJFeCq+hIHWwjvbcJT5bxJ//408gvzJ/C6k8X1XSxeKsEtLs5qmBvZTRuFv49mwzr5pEFsoSQrwJY\nCvjUb3HO/6jxNb8F4IMAnuB9FkII+XUAvw4Ai0rkR790z98fyXoFoyVMczlly8Xy9WKPLAHAUSg2\nr436TDp8xA9KmNuqASBgkgTquYgXD3Dft/8Ct+66hq/93M9OeomdcI6VtwqQ3c7uu4wA+QUDlfSd\nB/bH5a9+J4Ln7/vdsT+v4M6YtUBWuFlwFJPytVJ3sXSzBBpQbzqrbk7uFZDZqQOEgFEJkucint/H\n+/7mq7jx7rvxjZ95fNJL7GSAm3OLUVRTdx7YB/En7P/Ai/8xnNl0gpMxrJtH9lfnnP/EoM8TQv4Z\ngJ8B8OP9RNl4nD8A8AeAv+t7mmsUjB79uSfwuaeC7pkmhyfTwHoWDr9r8czBOVL7Nph8mLrGZAXl\n5By2Lt6NZG5/gosLRrE9UK93hAzlQKxoTSSQfeRJEzjjjSgE049ws6Afk+5d4Sk0cN6QP2JuNt2c\nPHA73OzJCkrpeexcvAvJg9wEFxeMYg1wc8EaWSA7bTNnBafHRCqHCSGfAPDfA/gk57w2iTUIRs/6\n6lroglgA4BJFJaGBdUWznADFufEHQJNGsT0ETSNksozti3dh79wxOp6EgQnfUq+vrkF/7onJLkIg\nOAHCzbPL+uraZBswAmASRS2uCjc3UCwPPCAVl8kyti68C3srIXVzn+xhMgY5hyn7TzAeJtUC6/8E\nEAfwF4SQFwkh/2ZC6xCMAP25J0J/McktRVFO+cEsB+DKFPvLMVjGZBpqTBLezzoNXv2xD49pJcPj\nqBJYQBdLRoBq8qSjyE+Pzz21FPr3gEAQgHDzjPHg0/eH6lp1sBxDJdnl5pU47MjsuXkwHK99+EOT\nXkQPjiYFB98EqIzJzeura3jgMXcszyWYPJPqWnzXJJ5XMHrWV9eApya9iiEgBIXFGAoLURDGwSmZ\n2Xb2rkr9dGuHdYS0hHnYO5dFJZWc2Nr6Qgj2lmNYulXu+dS4ZDkM66treP8nC/jUZ74w6aUIBEci\n3DxbhGGCQA+EIL8UQ35RuNnRJDCJgnbVmxLPw86FeVQTiQmtbACEYH85hoXbnW7mBKgmxudmkWo8\nO4ihRIJTYX11LVS7ukNDiD87dkZFCcAPClfiYJS0dsEZAaoJHXvnM5NeXV+iFX9oOGn7Bxw4/8M8\nzv8gh7mNMmTbm+AKfV56NjWd7w2BQHAmeeiVz4f/miTc7Lv5fK+bK0kd+yvhdXOkYoOTTjcTBpx/\ny3dzdqMMaUxuDv3rXHDHiBZfgjtGXChOH8I4osU6NNOFo0moJHUweXT7To4uY+OuNIyyDeoyWGOe\nyXoSYkWrJymaAr7tPX++rF6xsXU17TcRmTDN94nYIRYIBJNifXUNCMEYvGll3G62dRm3O9yswI6E\n+9Y9VrR6pkJQAGAAwBEt24hUbGxeS4/0d9dkXTRhPNOE+90gCDUigB0N1GX+eCCPgXJ/BzZ5UMf2\nxQQcfXRvWU5JKOpLh4UcMTqMwO+UmNivIr8cnvmD66trYlSAQCAYK2GcIDBtSC7D0vUCqMc73Xwp\nAUcTbm5Cjujp1HRzcq+G/HJsLGsSG8lnl8kfUwimjrA1hzhrpPZqkFzW2tGk3N8Fzm5VJruwkGEa\nypE9EAmAaNkex3KOxeP0s+I9JBAIxkJYJwhMG6ndKiSXCzcfQX1INxuV8btZNII6e4hAVnAswtCi\n/6xjlO2elFkCQLU8kID5bKcFYRzxnImFm0VkN8tQTWdkz3Ua5BejrdohoP/UHTq6X9kdI0b1CASC\nUSI2zE4Po+IEu7nugbDRjZYhXrebwx2I5ZaGc7PkTWZWnthIPluI3DbBUIg3/eihLkO0bA1OmR1R\nzSrxOJZvFCA5/kkwhx9Q5xajIxtgfqe4qoTNaynECnXoFQd6yOXej889tQSIGh6BQHCKCGefHtRl\niJYsYICbRxWSEc8vNWpmaU2Nm6823Fy1oZuTb7oYhKidPRuIE1nBkQghjh696mDlrTxSuzUQ3itF\nDsCMKv4oghEQL5itIBY4rGHJ7FSh1F0k92pI7VZDd0rLJIpS1kB+Kdr3a7yAebNhZGo7fwsEglAh\nriOnh161fTfvDXBzTAFG5eZ8vaPUqOXm3SrkMLtZpijNGcgv9q+BDYObRarx9CNOZAV9ETIcE5xj\nbqPc0+WPw5+9BgCuQnEwwqYIRtnuef7mIpZvFFv2jufrqCY15Bajoepo7KgSPAmQuzZ+OYBSJpy7\n1v1YX13D7/3mNuqPfmnSSxEIBFOEaOh0yjCO+Y3KEW6WcLA0ATcz4FyXmytJDfkRruUkOJoEjwJy\nV4kPB1AMiZvFzNnpRpzICnrQn3tCBLFjRDPdnrobwN95dRUJu+cT2LqSGmmbek8KfmwCvwNhcxYc\n5UC0aEELWxovIdg7nwAjjQ7/8P9tRWSU05FJruxEfO6pJfEeFAgEQyMaOp0+frlKbxRJADiKhN0L\nCWxdSY7UzewYbo4VrdCdzIIQ7Le5maPhZkNGJRMuNwvnTifiRFbQwfrqGvDUpFdx+kiOB6PRvbYW\nV+Ep0oRX1E1whY2nUFhRZeTPXs7o0GtOx85vv5ofwgGjZMEyRr+u42BHFGzclUa0aEFyGeqGgnpU\nCdXJ8XFZX13D+z9ZwKc+84VJL0UgEISQL/7+p/HSs6lJL+PEhNnNvgMJgmzoKXQsDixndGjm8G6O\nlmzYkXC52TIUbFxLI1pquDmqoG6E082ibnb6EIGsAMD0y3AQsbyJ9G6t9f9TezXkFwxUQnJSZ0Vk\n8ABZMgJUxjQ7rh5VUcxGkDwwwQkB4RyMElDGg2fChQEwBkkAACAASURBVFBAgL97XQ7ZLu+d8tKz\nKbwk5CoQCLpYX10Dnp30Kk5OLGcivRdiNxtyYNDICFBJjcfNZux4bubhVDOYPD1uFjNnpwsRyAqm\nXoaDkGwP6d1aT41JereGelSFq4Zg95cQHCxHMbfhz6JrhrS1mIpaXB3bMkpzBippHarpgkkUjkJw\n/q1Cz9dxgqkazn5WEHIVCATA2UiBlG0P6b1gN5uxkJzMEoLcUhTZzS43x1WYsQm5WaZwZYKVfm5O\nCDefFuJ0djoQNbIzzCx0STUqdnAeDkcrnWnS6FUHc5sVgKBVK2tFZByci4395JNJFPWYCjsig8sS\n9pdjfm1L2z/FbAS2LvbAJoXosigQzC5nxdlG2Q7O9kGY3Gwju9XlZkP2Gy9Oys26DCZLOAhwcyEb\ngSPcfKqclffbWUa84meQBx5z/S5tM0CzGULPx8e+kj706Vis1V0YJRu1CZ98mgkNG1HFv7HgQD2q\nhOMUe8YRXRYFgtniLJf/dDCqgazHpU/HYs10YZRt1CZ88llLaKgbSmuz3owp4TjFPoOIXhXhRpzI\nzhjrq2szE8QCfgpQUM0IJxhr2m4//I7Fveb2OxDWJ7CiXphEUUnpqKQ0UI/BKFmQ7XAOOJ81xOms\nQHD2WV9dO3NBbC2mBNdzEow1bbcfWp+Oxc3O/WGAyYdullzh5lHy0rMpcTobUsSJ7Izw4NP349Fn\nHp70Mk4dpe4ivVuFZrrglKCU1lHKRlppP64qoTAXQWrfbKUx8UZ6bPhPFkNzbgzqMizeKnVIshZT\nJ5L+LOhEnM4KBGeXab15brpZN12wIDdrcquJUbubC3NGiNwc3LE4TFCXYfFmCbLT5ua4OpH051lA\n9KoIHyKQnQHWV9eAZya9itNHsj0s3SyCsEbI53EkD0zIDkNu+XAoeDlrwIxpMMoWCIBqXIWrheOl\nb0VkcNKnY/GYuiIOw9xmBYrldYTWRsWGnaujnJ2OToRnnfXVNTz3C9/At3715UkvRSAQ3CHTGsAC\nfiOnpRvFVmmP1HSzy5BbOnRzac5ALa4iWrYbTZQ0uFo4gtgwdCwehrnNMhS7y81lG5ZeD92c1rOE\naAQVHkRq8RnmoVc+P9UyPIpEzjwMYhtQDkRLFqjLOr7W1SSU5gwU54zQBLEAAEKwtxJvNWvg8P9d\ni4+3Y/EgiMegm07P+TDlQLwQjvRngc+jzzx8pt/zAsFZ54HH3Kl/Dycap6zdbo4Vg9wsozhnoDRn\nhCaIBTDQzWFIfQYA6jHophvo5oRw88iZ9vfpWSFEd/SC02R9dQ140pz0MkaKVu+9gAMACKBYHix5\nOvZpLEPB7bvSiJZtUI+jbiiwI+F5axLuSzywnImFK+1Kcjykd2qIVG1wSlBJaijMGQCdrRSr9dU1\n/NXvRPD8fb876aUIBIIhOSs3xmofN3NCoNhT5Oaogo270jCabo4qoerYTxifHjfbHtK7VUSqDjgl\nKKd0FOciU5/+LFKNJ890XE0EQ3PWT2HbsbXg1B9wwFWn66XNGw2VStlIqIJYAGASgRdw48EBmCE5\nNQb83enl60UYFRuU++ls8Xwd8xtlSC5DtGjBKFmhE/yoeORJc2auBQLBNPPg0/efqfeqo0l93MxD\nVP86HKzdzSEKYgHAk2lfN9dCcmoM+HW8yzeKMCpOy82JnOm72fHdHClPt5vP0vt32gjXu1JwR8zC\nKWw7pUwE0ZLVMYuOEcCMijb0pwohOFiOYeFWqZUuxogf4BbmjEmvrkW0UAdhvCedTa86WPlhvnVj\nRQDUDT+dzTKUCax0vIgdY4EgvJzFHhalbKRnTixrdCMOCrwEJ6SvmymKIXJzrJ+bKw5Wqnnwxutk\n2t0s6mYng7iinAG++PufnsndIFeTsHshAbux+8sIUElq2D8Xn/TSzhyWoWDzagqljI5aTEFh3sDm\nlRRY200JdRm0qgPJmUz7f810e2b+Ab4cCfyLHW38t15zsXCrhPjB7Gz8zOI1QiAIM2f1Pelosu9m\ntc3NKQ37bU0YBaeDZSjYutLt5mSHm6VJu7k+wM082M2x3HS6eX11DV/8/U9PehkzhTiRnXLWV9eA\nZye9isnRvIgfbulNd71FmPEUCYWFaO8nOEdmu4pYyfLnAnL/VHz/XHystamOJoNVnUBhdtMUaGq/\nhmpKA5NmY09PnM4KBJPnrAaw7ViGgq2rws3jwFX7uzm7VYVRtlqThCbiZlUCgzPUyVnTzem9GqpJ\nDXwK3fzSsym8JE5nx8b0vUIEAHwRzoIMh4aQqROl5Di48tr3cf/z38bK2+8cCn/KSByYrRRvyvyU\noUjVQWa3OtZ1VNJ6qzFVO0e9KrSaM6olhZb11TU89MrnJ70MgWDmmDlvT6mbr772Ou771rdx7p3r\n0+vmfRNG2QLtcnN6b7xuLqf14IZUR3zftLt55t7rE0KcyE4h4s0x/cTzeTz2f/87yI4LyXHgKQpK\nmTT+9B99Cq4aniYNwxDP13tOQSkHokULucXo2G5iPImA43i7c4QDyT0TZlSduc7GjzxpAmLXWCAY\nCw8+fT8efebhSS9DcASJgxwe+8L/A8k9dHMhm8Wf/9I/hKtOV91mohDs5ljBQn5hfG5mEu3bXbkf\nfsaUie0pd/P66hp+7ze3UX/0S5NeyplFBLJThAhgO6EuQ3qnimjFBgDUoipyS9GO2pBJopom0nv7\nMGNRlDKZjs997Mv/EVrNbAVd1HGQ3D/A/c9/Gy888vfGv9g7gPbpNEg4+s/tGdE6+j1V3xEFABTb\nQzJnhqo5xjgR6cYCwWg5iw2dBkFdhsxOFUbTzTEVucXwuFkzTaT29lGLxVDOpDs+97EvfwWq2enm\n9N4e3vc3f4MXPzZdGxED3TxGCOOt1OZuBrrZ8pDImShNuZs/99SS2DQeISKQnQJEANsLcT2ce7vY\nEbwYFRvadRcb11KTTWXiHA98/Zu492+/AyZJoIzhYHEBzz3x87AiEaj1OjI7Oz0nh7Ln4errr09d\nIGtFFOg1p0dGjiqNdSeVUX9MkOyyjo9zoNEQjEOzWO/wePg71LMayDYRHRcFgtPloVc+72c+zBDU\n9bDydrGjS61RtqHWXWxenbybP/DXX8e9330BniyBegz7S4t47omfh63r0Go1pPcPAt187dXXpy6Q\nrUdk6LXemb62Jo3178AkAkYJqNcZyXIAli4BfICbi9bUB7JNhGNHQzi2xwR9EUFsAJxj+Xqx5wSO\nwJ8lapRtyJaH9E4Vc7dLrdbv4+Ly372B937nu5A9D6ptQ3ZdzG1t42N//JUjv3fcO6WnQX7RAKeH\nm63NLpW5pYDmE6OEEOQWDDDSuRZOgIPlGPYuJAd88xT+4keAqL0XCE6H9dW1mQtiwTiW3yn2jFoh\n8DvnRio2ZMtFett3c7RQB8bo5quvfx/v+d73IHkeVMt38/zmFh7+8p+MbQ3jJL8QBSfhcHN+MQrW\n9qJoujm3HMP++f5unsZ7okEIx54+4kQ2pIgXen+Msg3JDU4jJdz/fHar0pqrFqk6iOdMbF9KgUuj\n34W892+/A8V1Oz4mMYalW7ehV2uoRw3kFheQ3dru2ElyJQlv3fueka/vtHE0GZtXUkgcmNDqLmxN\nRikTgauNf5avmdCwK1MkD0zItgdLl1Gci8DV5MZaJSiW1/HaYQSoxrWxrzXMrK+u4a9+J4Ln7/vd\nSS9FIJgq9Oee8FMJZ5Bo2Qb1Bri5ZMOo2B1uTuTq2L6cBB9D9s57//Y7UJxeN5+7cROqacIyDBTm\nskjv7Aa4+b0jX99p4+gytq6kEM9N3s21hAZPpkjum5AdD1ZERjFrtNbiqBSKzXrdnJiuniHDIk5n\nTw9xIhsyHnrl8yKIPQLNdPu+cDkBIhUblB/WXVAOyA5DPD+e3XHNrPtrAek452OUQrX8z3199XHY\nkQhsRQEH4CgKitkMXn7wwbGs8bTxFAn5pRi2L6eQW45NRJRNLEPB7oUENq+lcbASbwWxAFDM6AAO\nd6gZAFemKM5Fxr/QkPPIk6a4FgkEx2B9dW1mg1gAUM3+I1Y4/PKfXjd7iE3YzZwQqJZfz/u1n3kc\ndkSH0+bmwtwcXv3Ij41ljaeNq4bMzRcbbj4X71hLMes7uMfN2bORVhyEmDl7OogT2RCxvroGzFoq\n0glwFQqG3l0Y3vifoH1dyv3d4lHUWhDGkdivIdYYQfPKhx6B5BGYsSQk18HKO9/H5TdehCdJKKdS\nAIByJo3/8F/9Gi69+QPEikUcLC5i88plcCr2lkaFUneR3a52vj4IUJnSWXXjQpzOCgSDmeVT2HZc\nRervZhKcJko5EC3ZKI8gYCGMI7lfQ7RkARx49UOPgoDCjPpuPv/267j8xktwVBWVZAIAUMpm8cxn\nfh2X3nwT0WIJB8tL2LhyeepGCE0TaoCbScvNZ/v3LmbO3jkikA0BQoLHo5rUkNo3wdvqcJp+HHTJ\nY6NIXeIcC7dKUOtuq829ZaRb6/AUFbev3gtLj2D7YqYjUPUUBW9PYbrStJLar/XcSFEOpA5MlDOR\nqW7xP2rEqB6BIJj11TXgqUmvIhxUkxpSB33cPKDWkY0iWOEcCzeLUC2v5WYzlulw861r98LSIti8\nttARqLqqgrfed+/pr0kQSGqv182EA6mciXI2MhObCCLV+OSIY4gJM+upSCeBSRTbFxNwNKmjkQFp\n+6fne4g/lPu00Uy3I4htrqPjuWUZ2xffhdvvetepP79geNR6b/fGJt2djgXBrK+uQX/uiUkvQyAI\nBSL1vhMmN9yshsDNNbcjiG2uo3O9CrYu343bV6+e+vMLhkfp52buNwmbFYRfT4Y4kZ0QX/z9T+Ol\nZ1OTXsbU0mxiQF2G1F4VsaLd8zUtfxGgktJQiw/XNEByPCT3TUSqDjyJoJSN+N8bsCuo1t2hGt5y\nSiA5DGzWUlg5h16rwdY0MHmylxtXkSB3NeFq4oVkvuE0IGbiCWYdEcD2x9FlbF313ZzerSJaCnZz\nM924nNJhxk7gZpmglImglghu1KfV3aE63nJKILsMzoy5mTAGzTTD4WZVgmwGu3nW7pmEX4+PCGQn\nwPrqGvDspFdxNmAyhRYwJ62JacjILcfgKY2mApxDsT1/5qjS2/SAuswf7dPovCi7QHarAsWKoDjf\nW8PjKpKf13DUpiH3a3tniauvvoYPPffXkG0bIARv3n8fvvPox8GlyTSbKMwZWLhd6tihZ806HJFW\nfGzWV9fw/k8W8KnPfGHSSxEIxoYIYoeDyRSqOcDNMQX5xejQbpYcD8vvHI7da7pZtr3A3heuQsEp\nQIZxszy5BkiT4NrLr+CDf/01yLYDEII3Hrgf333k4xPr0VGci0C9Xe5xczmlz6ybRarx8IhAdowI\nAY6IAde5SkpvSTFSaYzlacytczQJeyvxDmkmcmbP+ADK/Y+XMnpPUyAzpoBRCsJYR01Qdwv5Smq2\nGgqde/sdPPjnX+04Ab375VdAOcPf/ORP9H4D54hUHEgegxWR4WjDX5r0io30bg2K7bU6EFeTmn9a\nDsDWZYAQWFEF+8sxZHZrkFwG3khpKwRsUAiGQzSqEMwKIovqJPQ/Eq0k29zcGpk3yM31ntnxlAPJ\nAxPldKSnKVAtriK9Szpm2ga5uZzSz3xDoXbO//AtfOSr/6nDzfe8+DLAge/8+KO939Dm5npE7pgC\ncBQdblYoilnfzZrpgpNDN9ejKg6WY0gLN3ewvrqG3/vNbdQf/dKklxJqRCA7Bh54zMXj9LOTXsaZ\nxYypkHP1wE6J9UbKkmx5mNvo3PFT6x4Wb5aweTXVShvWq05wXEwIVMuDZdCej29fSmD+dhlqYz5p\nuzQ5/N3GUma2xru8//lv9aTxyq6Lu155Dd/9+Mfhqsrhxy0PSzeL/k1M4+9Ti/tiG9jkgXOkdqpI\nFKzW71xxGTI7VWS2q/5JOfdTx/ZW4rAMBWZCw0ZcBWEAp5iJJhLjoLlJJwJawVlEZFGdDDOmQcnX\ne5zKAdSjvgMUy8XcZq+bF26VsHWlzc21/m5WbBd2ROn5+PbFJOY3+ru5MGegnDn9+tww8/5vBrv5\nnpdexgsf/1hHmrFiuVi8WWpt/gNDuplxpHeriLe72elyM/yxR7vn47AjCmoJv/xLuLkTkWp8NLNz\nRDQh1lfXRBA7YkqZCJhMWtm9HH6mb37RaKWlxPP13q54ACSPQWurzXAVGryHzHnfOkpPkeAEzGYj\n8K/F1YQ+cxflWLEU+HFOAM1sGzHFOeY3SqAeB2X+DjvlgFG2ES1aHd8r2R60mgPqMoBzLN4sdQSx\nTSj3L2zNx5M8joXbJRCv8QohxN+Bn7G/yThYX13DA48F1zoJBNPG+uqayKS6A0rZCDyp1825pWir\nS3ysj5tlh7WyaoATulmV4Kq9n2u5OanNnAeipWA3A4dzdgH4br5d9t3Mu9zcVfcsB7g5fpSbme/m\nxVttgbJwc1/Edag/4kR2RDz49P149JmHJ72MmYDJFFtXUojn6ohUbHgyRSkbgWW0nfq5Xt8M5Pau\neKVsBJGq0yFWBsCKyHDV/nU0ihX8+JwQyI4Hb8bqY/eXlnD+rbd6T8kpRS0Wbf1/2WGQHRYovHih\njmpKB2Ec8xtlaDWnNYvQjMgDuxD30BBwNTVbu++T4HH6WWBVnM4Kphtx43jnHLq50aBJoShlutwc\ncP0H/E1PyT0UcSkT8TOmetysBNbUNlGs/o8vOwz2jDX6yy0t4tw713t+J54soR49TOWVbQ+SG+zm\nWL6OalID8RpuNn03gwOmoUC1TuDmZHDTLsEhYqZ7MLP1Dh4T66trIogdM0yiKM4b2L6Swt6FRIco\nAf/iygJt5gepTeyIgoPlmL+LTHzZ1aMK9lbiA5/fjsiBu8WE88DT2rPOix/7KDyl83fiKDK+9/BH\nO5o9NWuigmg26chsV/zdXu7v4hIORGqdI4+OgjROZgXjY311DQ8+ff+klyEQHAtxCnu6MJmiuBD1\n3Xy+1831aLCbKfe92sQyFBwsReHRNjfHFOytxAY+f383A07Aae1Z54WPPQxX7nKzLOOFjz3c0eyJ\ndBcUt9H0dna7As08dDPlgFF1juVmcIB6szNi50555ElTXJ+6ECeyp4g4hQ0v1ZSORL4OuKx1kW12\nrO3ezW3WasgOA5PIYft3zqHWPb8hkS6Dte3kljIRREsWwA6v/c3Hn7X28QCQX5jHn376l/AjX/sG\nslvbqMVjePnBj+DGu+/p+DpHlcAoAe0KMjn88QDZjTKiZbvHp6T5NUOuhxOg3nUDJRg9jz7zMLD6\nsDidFUwF4gZx/FSSOuIBbi6n9J6U4VpSRy2h9XGzC8njPW4uZiMwShbAO93sN3maPTfnlhYbbv46\nsts7qMVjeOmjD+Hm3Z1z7h1NAidN0x7C4Qee2Y0yjFNwM4SbT4RoBHUI4QNORMLGuyMp/vRd4QwU\nhQDDD/EYErk6jLINTglKaR21RPB82G4kx8PCzSJk57ADYjWu4OBcvPX9iuUivVuDVnPAJIpSRvcH\nvYt6j4FoVQcLt0v+ziwOtUm6/rubYWXJCFCLqThonqpzDr3mgHoclqGIGbJjJIwB7Udf/cp3Oecf\nnPQ6ppkwu3lYhMMnB/UY4gcmjIoNRinKGb3v7Pb/n707D3Lsvu5D/z33XuxA79tMz8ZltDmk5FiW\nRYqOSNsliWwtLsqJYpXsOPKzlOoktEvUc9HtSvL8XqySK5Rsq2KVqZfw2Y4lh4qp2LQoyVuGTkmk\ntZqrSHEZzj4903tjB+695/1xgW6gG+hpdAO4F+jvp6rJaaynsf1w7vn9zm8rs+xg8twazJqxOTMQ\nxnJNQ6JQoTI25zk2tyKaLWH8QrqzY3Mq7H2PAurG5kI8VHdAgpoL4rjaDrsdm5nI7tOtz9yL2+/L\nX/uCFAzVzrgt7k029eoKwlvW2iiAfCKEhaMD7YzwQDLLDhJrRcTTJYSKzjXXPCiAYtT0ulHWfIRt\nfX4cU7Aymdj4UmRVujAaldeBAFgbabxHMHVG0AZdJrL7F8SxebeYwAbEHsfmQ6dXECptH5tzyRAW\nj3Bs3q+9jM2FqInINcZm2xKsTmyOzRsdkis5iahXTV9rsEcwbRe0cbUddjs2c2rxPszNzAJMYgPF\ntF3E0iWIKvLJ8GaDJlUMLuYxsJyHqNcBcXkysbE9z463WXIaNowQALFsGVbJ2bERFDUmjotEugTD\ndlGMh7A+GkM8U2o4UG49EuwagqXDKURyZYxcyW5bk6MA7JBg/sRQ3fSzyfNpmFv2CR5YzqMYs3b1\nWqD941Y9FATcFq+7zLKLWKbx2Dy0kNvYWaCVsdkqObBKjcfmeIZj8141GpsT6d2PzcuHU4hkyxi5\n2nhsLocMzJ8Y3JzarYqJ897uBXVj81IexVhoY6smau4gTzVmIrsH0VN3e3s7UaDE1woYnc9u/D60\nkMPaaAzrY3EMX80iuVrc+FANlV2MX0zj6tbGUKqI5G1YZW8drB0xt23CvlUsU0L6gO0Tu1/hfBmT\n573pxKKASh6FeAhOk6PxKl7DLstxUYiFkB6JwgmZGJnPNGwsoQKsjMUrWzsoCjELogrDadIheaXA\nRLbL5mZm8cb3ruIDH/2C36HQAcMqbHclVgsYuVI/Nq+OxZEejWHkShaJte1j85VjA/V7w+5hbI5m\ny8gwkW3JnsbmRAiW7aIQDyE9HIMTMjB6ufnYvDoeqxy48MZmQ7EtiQW8+0+u5JnI7tJB3XOWiWyL\n5mZmgfv9joK2MmwXo/Pbj/4NLnkfwrVJbJUoMLiYx9VjoY3bmDy3Bqu82UEvnwhj8XBixzUfbotT\noQ48VYxfzMCoaVQo6m14nxmMwM3XdyRWAI5lwAmbcNVAIRne1brWscvZjeds8BqXNdwGIy513FOP\nDOGpAzjwkj9Yhe0+w3YbzpoZWsyhELOQXCtu30e2MjYvHPXGZrPsYvL8GszasTkZxuKhncdm5djc\nmuresY3G5qEoIoXtY7NtGXBCJlzLQD4RhmNd+zEfu7S7sVnAsXkv5g7YmMqV1LsUPXU3j+IGWCxT\nani6KLxuwo3OAxAqORu/j13KIFRy6zb/jmVLSK0UsDwRb9jCXyvNCmj3QkWnYbt9Q4FIwcbqWAyu\nYGObBcfwpoynVgpIrhYxfmEdo5ezgCoyQ9GGWzdIpTmFNPjZyhUgO8Dn0E/c8oQ6bW5mlkmsD+Lp\n5mNzcr0IbfT5ja1jcxrW1rE5U0JqtYiV8VjzsZmzbFoSLjoNE0dDgXDBxtro1rFZYNWMzRMX1jFS\nmRXXrrE5N8D9ZfdibmYWtz5zr99hdAUT2V2Ym5nlVOKA2+kYoDbpTKgASlFv2pE4LqL5cuNpp6tF\nZEdiWBnzBkyF9wHrCrBwJHUgW/h3Uno0jgs3DmNxOomF6dTGF5fqYGcoEE8XkVrOewNdIuztK4jN\n56XRl6Oq6nOIyuXLEROZwWjH/y66Niaz1Al8XQWTGrJ1dxfvdAClyv7rhuMiUrCbLgnJjMaxunVs\nNoCrRwagJiuy7bQ+FsfF6th8OAVDddvYnFgvIrWUh2N4U463jc073P7WsbkUMZFhIrtnB2XPWU4t\n3sFBeAH0i3wyjOGaNThVWjmip4ZgYDlfPy1GgNVKR7ytU5tqSeUIZXosjsxwDNFcGais2Wy1wyJ5\niaNrGjDs+qpsdd9dAFDTQCERRnKl0PA2RIHhhTy0cgxhZTwOQ+HtLSioWyu97boAypagFLOQT0a8\naiy3YQgMNoOiduEY7r98MoThq9tPVwGylSQltVLYNjZXu9WKq02nD1c73K6PxZEejiKaszf3DOfY\n3LJSxPQOLmzZ190VIFsZm91djM1DC7mNMll1bHYqBxVGrmaB7ROyvOtic2zOJSO73h6RdtbvU41Z\nSmqCA2BvcSwDKxPxjSN+1SOA6eEoSjELa2MxrEzEYVsGXAEKUQsL0ylECjZSy3kYjgs7tP3toKif\nOqymIJ8KI58Mc6DcKxEsTCfhGqg7WluMhZAZqq+M6sZ/ttwEqutnvJ/hhRwyQxFkhqLIp3Y+glt9\nXSxOD3iDMwfKQJqbmcUtD97sdxjUoziGB4MTMrEyvn1sXh+JoRy1sDoex8p4zdgcqx+bxdWGPRG8\nLXY2P+vVNJBPhb2mfRyb90YEC9OpbWNzIR7aOMi8obpd0tabgJdYbB2bs0OVvYF3KBq4AqRHYlic\nHkCOY3Nb9fN46mtFVkTuhdc6aVxVF/2MpYqDX+/KDMdQSIQRT5cgriKXCqMcrbzERZAZjiEz7HUX\njmVKGL+Y3rju0AKQTUVglosbm3+74h195D5m7VeKhXDhhmEk0iWYlW6HxZi1OXDVbpe0y9uMr5eQ\nGY5CDW8wHr+Y3qi0V29D4VVttybMFEx3PHwbMHNbXx9NDqIgjs27dcuDN3uvGwqMzEgMhWQY8XWv\nsdO2sXkkhkyl839svdhgbA7DtEt1Y7NjGlgb424B7VaMd2BsTpeQGYpCTQOLh5MYu5RpPjZvTZip\nbfp1PPUtkRWRowDeAeCcXzHUuvWZe3E794TteXbYxProzoObOIqxi+ltXRQT6SIWDicRKTgIlRwU\nYhayQ1F2PuwQNY2mCWVytbh9KnjN+Y3a9Nc2qSgkQijG8oinSyhFUwC87XdyyTDWxuJc19xj5mZm\n8dgnY3j8pk/5HUrfC9rY3Iq5mVngYb+joEbssIn1axwUFsfFWINtWxLpEhYOe1XaUMlBIW4hO8ix\nuVN2HpsLLY3N0M3lWYC3DKwUzSGWKaMYHYDA5NjcZf02nvpZkf1tAL8K4M99jAFAZfBjEntgxLKl\nzd27a4gCsWwZK1NJX+KiTVsHSmDzKWu0Xqq6lx0ARHI5vOtPvojE+rp3PVXMHz2CU3f/NFyTewr2\nqtvvyx/IPfJ8EJixebdYhe0PsUy54emiQCxXxspkossR0VaDS4WWxmYINvaBjWazeOeffBGJtFdx\nF1VcPn4Mp376vVCOzV3VT+OpL4c+ROR9AC6qqA1aBwAAIABJREFU6lN+3H8Vt3w4wJqs09ip6RN1\nj+k0fyJyqVBdW3+30jSkOlXtbV/5GlIrKwiVywiVy7BsG1PnL+CmJ77Z6bCpCw7StgLdFpSxuRVz\nM7NMYvvEjvVV5eAcBI22zqvKJRuMzYMRlCPe2Hzbo19DarV+bD509hx+6Fvf7nTY1EQ/5EAdq8iK\nyN8AaLRnza8DmIM3dWk3t/MRAB8BgMlQ+9ZD9MOTR3tTPTq4VbXDMfmvGLUQzW3fDsmxDCwdSiKX\ntZFYLwDw1tRUn1OzXMbhM2dhuvWDrWXbOPn003jqtlu78wdQR/XT0eRuC/rYvFtcDtR/8hybA68Y\ntRDL29tOt0MGlqZTyGXKSKwVvLXPNWNzqFjE1LlzMLfsU2vZNl771NN49pa3diV+2q7Xpxp3LJFV\n1Z9qdLqI3ATgOgBPibd4/AiA74nIW1R1vsHtfA7A5wDgdbGhfR+SYwJLrmlgeTKBkSvZjQpsdSuA\nQpw7UgXBykQcU2fXvPU1qExbEmB5MgEYXnfKfGr7ZveG2/xosWk7nQuYfDE3M4tPf3wehTu+5Hco\nPSOoY3MruByoP7lWk7F5MOI1HCLfrU4mEDm7Bmk0Nos0H5ud5uOvaW9PjKm7evngcNc/GVT1GQAT\n1d9F5AyAN3e6M+Kb7rRxl3FPJ++Cekh2KIpiPFTpoqheA4JY46PB1H3lqIXLJwYxuJhHpGCjXGni\nVYzv/ByVIxGsjY5ieGGhrprrGILzJ2/obNDki4/dP9WzA3CQ+DU2t4oHo/vb9rE5ghKT2MAoRS3M\nV8bmcGVsXhuLXfP7UzEex/rwMIaXlupOdwwD506e7GTI1IJe3HP2QHw6cOCjRnbTRZH8Y0csLE2n\nWr7eN+56J975J1+E4TqwbAflkIVSJIrv/fiPdyBKCorq53yvDcK0OxzHDw6OzcFWjlhY3NPY/C68\n46EvwnBcWI6DsmWhGIvhydve1oEoaa/mZmZx6v1fxxMfftrvUHZFtIcW0L8uNqQP3rj7pg4PPfBB\nPPXIUAcjIqIgimazOPnUMxhcXsbC4cN45YfeADuyfboT9adWktm3Pfvod1X1zR0Mp++1Oja3ikks\nUX+IZTI4+fQzGFhewdXpaZz+odfDDnNsDio/Dwzvdmzu24rs3Mws8IjfURCRHwqJBJ65lc0jDipW\nZ/sDGzoR9Zd8Momnb73F7zBol3phqnHf7TzMLXWIiAjwxoPoqbv9DoP2YG5mlkksEZHP5mZmccuD\nN/sdRlN9lcgygSUiolofu3+KY0MPiZ66m88XEVGA3PHwbYH9XO6LqcVBfXCJiCgYON04+OZmZoH7\n/Y6CiIgaCeKesz1dkb3lwZuZxBIR0a7Nzczi1mfu9TsMqvHQAx/kWE5E1ANuvy8fqM/rnk1k52Zm\nccfDneuSSERE/SloA/FBNjczy90FiIh6TFDG0J5LZFmFJSKiduBY4p9bn7mXjz8RUQ8LQiOonkpk\nLw6NswpLRETUw9iRmIioP/jdCKqnElkiIiLqXazCEhH1H78+25nIEhERUUexoRMRUX/zY6oxE1ki\nIiLqGDZ0IiI6GLo91ZiJLBEREbXd3Mwsq7BERAdQtz77mcgSERFRWzGBJSI62OZmZhE9dXdH78Pq\n6K0TERHRgcEEloiIqj52/xQwM4tPPPrZjtw+K7JERES0b0xiiYiokU41gmIiS0RERHsWH1QmsURE\ntKNONIJiIktERER79pJM+B0CERH1iHYms0xkiYiIiIiIqCvaNdWYiSwRERERERF1TTumGjORJSIi\nIiIioq7bTzLLRJaIiIiIiIh8MTczizfdabd8PSayRERERERE5Ju7jHtars4ykSUiIiIiIiLftZLM\nMpElIiIiIiKinsJEloiIiIiIiHoKE1kiIiIiIiLqKaKqfsewayKyAOCs33HswxiARb+D6FF87PaG\nj9ve8bHbu1567I6r6rjfQfQyjs0HGh+7veHjtnd87Paulx67XY3NPZXI9joR+Y6qvtnvOHoRH7u9\n4eO2d3zs9o6PHfUSvl73jo/d3vBx2zs+dnvXj48dpxYTERERERFRT2EiS0RERERERD2FiWx3fc7v\nAHoYH7u94eO2d3zs9o6PHfUSvl73jo/d3vBx2zs+dnvXd48d18gSERERERFRT2FFloiIiIiIiHoK\nE1kfiMi9IqIiMuZ3LL1CRP6TiLwgIk+LyP8UkSG/Ywo6EXmXiPxARF4Wkfv8jqdXiMhRETklIt8X\nkedE5Jf9jqmXiIgpIv8gIl/2OxaiVnBsbh3H5tZxbN4bjs37069jMxPZLhORowDeAeCc37H0mL8G\n8I9U9WYALwL4NZ/jCTQRMQH8HoA7AbwBwM+KyBv8japn2ADuVdU3AHgrgH/Nx64lvwzgeb+DIGoF\nx+Y949jcAo7N+8KxeX/6cmxmItt9vw3gVwFwcXILVPWvVNWu/Pr3AI74GU8PeAuAl1X1tKqWAPx3\nAO/zOaaeoKqXVfV7lX+n4X3wT/sbVW8QkSMAZgD8F79jIWoRx+Y94NjcMo7Ne8Sxee/6eWxmIttF\nIvI+ABdV9Sm/Y+lxHwbwVb+DCLhpAOdrfr8AfuC3TEROAPhhAN/0N5Ke8TvwkgHX70CIdotjc9tw\nbL42js1twLG5ZX07Nlt+B9BvRORvAEw1OOvXAczBm7pEDez02Knqn1cu8+vwppd8vpux0cEjIkkA\nDwP4FVVd9zueoBORdwO4qqrfFZHb/Y6HqBbH5r3j2ExBwrG5Nf0+NjORbTNV/alGp4vITQCuA/CU\niADe9JvvichbVHW+iyEGVrPHrkpEfgHAuwH8pHLfqGu5COBoze9HKqfRLohICN5A+XlV/ZLf8fSI\ntwF4r4jcBSAKYEBE/lhVP+RzXEQcm/eBY3NbcWzeB47Ne9LXYzP3kfWJiJwB8GZVXfQ7ll4gIu8C\n8GkAb1fVBb/jCToRseA13vhJeIPktwF8UFWf8zWwHiDet9k/BLCsqr/idzy9qHLU9+Oq+m6/YyFq\nBcfm1nBsbg3H5r3j2Lx//Tg2c40s9Yr/DCAF4K9F5EkR+X2/AwqySvONfwPgL+E1RPgiB8pdexuA\nnwPwE5XX2pOVI5lERFSPY3MLODbvC8dm2oYVWSIiIiIiIuoprMgSERERERFRT2EiS0RERERERD2F\niSwRERERERH1FCayRERERERE1FOYyBIREREREVFPYSJL1IdE5GsisioiX/Y7FiIiIuLYTNRuTGSJ\n+tN/grffGhEREQUDx2aiNmIiS9TDRORHReRpEYmKSEJEnhORf6Sqfwsg7Xd8REREBw3HZqLusPwO\ngIj2TlW/LSKPAPiPAGIA/lhVn/U5LCIiogOLYzNRdzCRJep9/zeAbwMoALjH51iIiIiIYzNRx3Fq\nMVHvGwWQBJACEPU5FiIiIuLYTNRxTGSJet8DAP4dgM8D+C2fYyEiIiKOzUQdx6nFRD1MRH4eQFlV\nvyAiJoDHReQnAPwGgNcBSIrIBQC/qKp/6WesREREBwHHZqLuEFX1OwYiIiIiIiKiXePUYiIiIiIi\nIuopTGSJiIiIiIiopzCRJSIiIiIiop7CRJaIiIiIiIh6ChNZIiIiIiIi6ilMZImIiIiIiKinMJEl\nIiIiIiKinsJEloiIiIiIiHoKE1kiIiIiIiLqKUxkiYiIiIiIqKcwkSUiIiIiIqKewkSWiIiIiIiI\negoTWSIiIiIiIuopTGSJiIiIiIiopzCRpb4nIs+JyO1NzrtdRC7scN0/EJH/2LHgeoiIxETkL0Rk\nTUT+RwvXOyYiGRExOxkfERERER0cTGSpp4nIGRH5qS2n/YKIfL36u6r+kKo+1vXgdrA1xh7xMwAm\nAYyq6j/d7ZVU9ZyqJlXVaVcgInJCRLSSIFd//l3N+SIivyUiS5Wf3xIRadf9ExEREZG/LL8DIKLu\nqyR1oqpuC1c7DuBFVbU7FNZeDDWJ5yMAfhrAGwEogL8G8CqA3+9ibERERETUIazIUt+rrdpWpsf+\ngYisiMj3Afzolsv+sIh8T0TSIvIQgOiW898tIk+KyKqIPC4iN2+5n4+LyNOV6bcPiUjd9XcZ778U\nkecrMZwWkY/WnPesiLyn5veQiCyKyA9Xfn9rJa5VEXmqdkq1iDwmIr8pIt8AkANwfYP7fn3lcquV\nKdnvrZz+GwD+PYAPVKqfv9jgum8Rke+IyLqIXBGRT1dOr1ZPLRG5ZUsVtSAiZyqXM0TkPhF5pVJF\n/aKIjLT6+FX8CwCfUtULqnoRwP0AfmGPt0VEREREAcNElg6a/wDghsrPO+ElPAAAEQkD+DMA/w3A\nCID/AeD9Nef/MIAHAXwUwCiABwA8IiKRmtv/ZwDeBeA6ADdjb8nTVQDvBjAA4F8C+G0R+ceV8/4I\nwIdqLnsXgMuq+g8iMg3gUQD/sRL/xwE8LCLjNZf/OXjVyhSAs7V3KiIhAH8B4K8ATAD4twA+LyKv\nVdX/AOATAB6qTBP+rw3i/l0Av6uqA/Ae3y9uvYCqPlG5fhLAMIBvAviTytn/Fl4V9e0ADgNYAfB7\nOz5SwFkRuSAi/5+IjNWc/kMAnqr5/anKaURERETUB5jIUj/4s0oFcVVEVgF8dofL/jMAv6mqy6p6\nHsBnas57K4AQgN9R1bKq/imAb9ec/xEAD6jqN1XVUdU/BFCsXK/qM6p6SVWX4SWFb2r1j1HVR1X1\nFfX8HbzE8scrZ/8xgLtEZKDy+8/BS7wBL8H9iqp+RVVdVf1rAN+Bl+xW/YGqPqeqtqqWt9z1WwEk\nAXxSVUuq+r8AfBnAz+4y9DKAG0VkTFUzqvr317j8ZwCkAfx65fd/BeDXK1XUIoD/C8DPiEijJRCL\n8KrpxwH8CLzE/PM15ycBrNX8vg4gyXWyRERERP2BiSz1g59W1aHqD4DZHS57GMD5mt/Pbjnvoqpq\nk/OPA7h3S9J8tHK9qvmaf+fgJVQtEZE7ReTvRWS5ch93ARgDAFW9BOAbAN4vIkMA7sRmAnccwD/d\nEt9tAA7V3Hzt377VYQDnt6ybPQtgepeh/yKA1wB4QUS+LSLv3uFv/CiA2wF8sOb+jgP4nzWxPw/A\ngddgqk4lUf5OJSG/AuDfAHiHiKQqF8nAq2hXDQLIbHluiYiIiKhHsdkTHTSX4SWfz1V+P7blvGkR\nkZqE5xiAVyr/Pg+vmvubnQquMk35YQA/D+DPVbUsIn8GoLaS+IcA/g94798nKmtAq/H9N1X9pR3u\nYqdE7hKAoyJi1CSXxwC8uJvYVfUlAD8rIgaAuwH8qYiMbr2ciPw4gP8HwG2qul5z1nkAH1bVb+zm\n/rbefeX/1YNzz8Fr9PStyu9vxOZzTkREREQ9jhVZOmi+CODXRGRYRI7AW5dZ9QQAG8A9lSZKdwN4\nS835/y+AfyUiPyaehIjM1FQBWyUiEq39ARAGEAGwAMAWkTsBvGPL9f4MwD8G8Mvw1sxW/TGA94jI\nO0XErNzm7ZW/cze+Ca+K/KuVv/92AO8B8N93+cd8SETGK0nwauVkd8tljsJ7Dn5eVbcmyL8P4DdF\n5HjlsuMi8r4m9/VjIvLaSoOoUXjTlB9T1ep04j8C8DERma6sHb4XwB/s5u8gIiIiouBjIksHzW/A\nmy77Kry1p9X1pVDVErxK4i8AWAbwAQBfqjn/OwB+CcB/hteI6GXsrxPurQDyDX7ugZfsrQD4IIBH\naq+kqnl4VdvrtsR3HsD7AMzBS4TPA/g/scv3eeXvfw+86cqL8NYa/7yqvrDLv+ddAJ4TkQy8xk//\nvBJrrZ+EN1X4T2s6F1crpb9b+Vv/SkTSAP4ewI81ua/rAXwN3hrbZ+GtVa5dy/sAvDXKz1R+vlw5\njYiIiIj6gHDJGFHvEZF/D+A1qvqha16YiIiIiKjPcI0sUY+p7K36i/A6FhMRERERHTicWkzUQ0Tk\nl+BNGf6qqv5vv+MhIiIiIvIDpxYTERERERFRT2FFloiIiIiIiHoKE1kiIiIiIiLqKT3V7CkUH9To\n4ETdaUcny3B/sNrkGtRvLg6Nd/T2p1cXOnr7fuv049dJ/f7ckD9+UFhbVNXefWMQEREdUD21RjZ1\n6KT+yL/43YbnfeLRz3Y5GvLL3MxsR273ILyGbn3mXtx+39atXYPvK+5n8ORXe+q4G/WItz376HdV\n9c1+x0FERESt6ZupxXMzs3jogQ/6HQZ1QScSzoOQxALA4zd9yu8Q9oRJLBERERHV6ptEFgCeemSo\nY9U6CpY3vrd908k//fH5tt0WtV87n2siIiIi6g99lchWMZntfx/46BfadluFO77UttvqBb1WfW7n\nc01ERERE/aEvE1nAS2ajp+72OwzqoE88+tl9V+t6LakjIiIiIqI+TmQB4GP3T7E62+c+8NEv4LFP\nxvZ03YOcxPbKdOqvuJ/xOwQiIiIiCqC+TmSrmMz2t8dv+lTLldmDnMQCvTOdmk2eiIiIiKiRA5HI\nApxq3O8+8NEv7Do5PehJbK849f6v+x0CEREREQXUgUlkAU41PgiulaQyid0U9ETxiQ8/7XcIRERE\nRBRQByqRrWIy298+8ehntyWsjU476IKcKAY9ySYiIiIifx3YBWhzM7N47JMxPH7Tp/wOhTqEiWvv\nCnKSTf1h44Dms4/6GwgRERHtyYGsyFbdfl+e1Vk60HqlezFRO/Fzn4iIqPcd6ES2il9q6KAKYvdi\nVtKpU+ZmZvl5T0RE1CeYyFbMzczi1mfu9TsMIiLqACawRERE/YWJbA1ONaaD6CvuZ/wOYcNjn4z5\nHQL1meipu/m5TkRE1IeYyDbA6iwdJE9+NTg939h8jdppbmYWH7t/yu8wiIiIqAOYyDbB6iwRUW96\n6IEP8vObiIiozzGRvQZ+GaKD4I3vXfU7BDZ5oraYm5nFU48M+R0GERERdRgT2V3gVGPqdx/46Bf8\nDoFoX9iRmIiI6GBhIrtLnGpM1Dls8kT7wc9mIiKig4eJbIv4hYn61an3f923+2aTJ9oLVmGJiIgO\nLiaye8CpxtSPnvjw077cL6uxtBdMYImIiA42JrJ7xKnGRO3Baiy1ip+9RERExER2n/iFivpJt7sX\nf/rj8129P+ptnEpMREREVUxk22BuZha3PHiz32EQ7Vu3uxcX7vhSV++PetOb7rSZwBIREVEdy+8A\n+sUdD98GzNzGvTCJukRVsbZqY3nRgWMrojED41MhRKM8PtdPmMASERFRI75/4xMRU0T+QUS+7Hcs\n7cAvXUS78xX3M/u6/tKCjauXbZRLCtcFclkX504XUSy4bYqQ/HTLgzfz85SIiIia8j2RBfDLAJ73\nO4h2mpuZxZvutP0Og2hPurUNz5Nf3fuEENdVLC/aUK0/XdVLcKm3zc3MerNciIiIiJrwNZEVkSMA\nZgD8Fz/j6IS7jHtYTaCe1I1tePbb5KlcVkAan1fIsyLby/i5SURERLvhd0X2dwD8KoC+/ebJL2VE\n2+23yZNlCaCNzwuFm2S4FGjsSExERESt8C2RFZF3A7iqqt+9xuU+IiLfEZHvlHNrXYquvTjVuLcp\ngHPxQzg1/hb83dibMR8Z9Tukjtvv+tVOM01BatCEbMlZRYDRcfaw6zVMYImIiKhVfn7jexuA94rI\nXQCiAAZE5I9V9UO1F1LVzwH4HACkDp1sUoMJvruMe4AZsKtxi/I5F5m0DcMQDAyaCIW7e+xFAfzt\nxFtxNnEYthEC1MXLqeN44+oLePPKc12NpZue/KrlTfrvgHa9ByYPWSgWXBQL3seCCDA2YSGeMNty\n+9R5tzx4M9fCEhER0Z74VpFV1V9T1SOqegLAPwfwv7Ymsf2Ie87ujqpi/mIJ588UsbzoYPGqjVdf\nLmJttbuV7UvRic0kFgDEgG1YeHLo9Uhb8a7G0k9UFa6r0JpuTY6jWFuxsbJko1i89mqD+Ys2SsXN\n61cbPdnlnj3edaCwoRMRERHth99rZA+kOx6+jVPpriGXdbG+5tR1pVUFrlwqw3EaJyq2rVi6WsaF\ns0UsXCl5DYGaUFXkcw5yWQeu2/xyZxKHYcv2Cp9AcT5+aPd/UA967JOxtt/mb37593B1voSXni/g\npecLePWlIjJp73l45QcFXLlcxsKVMs6+UsSVy6W6RLdWueQik3a2dS12FVhZLrc9bmofbqtDRERE\n7RCIRFZVH1PVd/sdR7fxy1xz6bXtSQoAQIBsxtl2cqnk4tWXC1hatJHNuFhedPDqy4WGHWwLeRev\nvFjA+bMlXDxXwss/KGB9rXGlN+TakAZdhQQKy+3vdc+5X/2ttt/mlctlrC5vPrflsuLS+RIunC1B\nFXU/aysOchkXrqvIpB2k1x24lYMYxaJuWx8LAFCgkPcu0ywJJv+wCktERETtEohE9iBjI6gmmjSe\nFQDS4MyF+TJcB/UVXBeYv1Squ5zrKs6fKcKxvfNdt3K5i2WUStuT3tdkzsBokBC5MDBeWGrpT+o1\n+9nntZG/fOdjWF/dfoCimrhupQosLdp4+QcFXL5QwuWLmwcdwmFpfKADXgL78gt5vPj9Ak6/2Pwg\nBXXPrc/cywN3RERE1FZMZAOAe85uNzC0vSMt4CU3ieT2l20223hNZbGgdVOHs5nGl8tH4riUi26r\nvQ6VM7ht8bswXRuWW64rGT589F14YuSNzXaBoS0e/+izTQ9QNJPPuXUHHFS9gw5iALGY0fA1ks8p\nnErRvlxWXL5QxsoSpxv7ZW5mFrffl/c7DCIiIuozTGQDhMnspnjcxPCIl8zW/hw+GoZhbs9ejGYJ\nUuV6VY6jdZW8XCKF77z9PfjWT96Nv3nTe/Anx2ZwZcv2Oq9Ln8HPnX0EUacEQAEROKYFxzDx/cEb\n8WriyP7/4ID69Mfn23I7j30yhlCo+d6vzTQ7mLG+6mD6WBipgcYHPLa6Om+jXO7b7aoDKXrqbn6m\nERERUccwkQ0YTjXeND4VxokbIhibDGFiKoQbXhNFMtV4a5XBYWt7QiOoJDqbZ8QTmy95VwRPvu1O\nZFLDcE0LjmkhHUriL6bejlcuCdZX7Y11lgUzgrwZAaT+LWMbFp4ZPNmePziACnd8qS238/hNn4Jh\nCEbGtj9PIsDYZP3pIkBoh+nDrqsoFl3k803WUjewssT3VbfMzcziY/dP+R0GERER9TEmsgHEqcab\nwhEDI6MWhkYsmFbz0tvYuIVE0ptqahheIhSNCiYPhTYuo66imFdEogIRYHnyCBzT8q5Qw4Xg9Mh1\nmL9UrjQhUpQk1HCtLAAUJdTwdPKcev/XN/49Om5hfMqCFfKeg1jcwLHrIhgdC+G6kxGMTVgYGDJg\nmEC51PjxFgEiUQPnXi2hXGp4kYaq+81SZ/Gzi4iIiLqhvd1cqK3mZmbxiUc/63cYPUEMwfSxCEpF\nF8WiIhQWRKObCWqp6ODcqyU4LrzprQKUYnGosf1YjloWCrEkVL01mtmMixFZbdi92HBsDL16GleW\nSpiYCtVVf8nzxIef3vi3iGB4JIThke3JfyhkYHhE8MqLBbhNZgFLpcq+vof9hCNRPjedxASWiIiI\nuokV2YDjl8PWhCMGUgNmXRJbLrk480rJawBUzUUVSC0vNOw9ZJbLGFq+4l1MgUzagQnF2xe+BdO1\nUc2yDLuMSC6D6Vdf8LaKadJwqtd1Yj/ZZtLrzacKR2OCw0fDmJoOIZ9rrbpqGMDwKCvnncLPKSIi\nIuo2VmR7QPVLIquzral2K75wrtQwOUqtLWN48RJWxw/DNry3guHYiObSGLt8duNyZmVZ7vXZi4i8\n+DX8Q+QGFKIJjFy9gKkLr8B0HCi8fU8TycZreHvZ4zd9CthjotLqa9a2tWkiG08YTddI1xKp384n\nFBJYYeDc6QJsGwiHBeNToV3dFu0seupuroUlIiIiXzCR7SGcatzY+pqNpQUbtq2IRAyMjJpYW3OQ\nWb92hfSm755C4S034/nU9SjagokLp3H05Wc31sOKAIND3tvEthV6aRknM4sNb0t323WImorGmk8S\nWV9zMDahEBEkUibSa07Dy00fCyMaM5DLOrh8oYxyWVGu2X2nVFJcOl/C4aNhJrP7MDczC9zvdxRE\nRER0UDGR7TFMZjepKs6fKdZNM83nXFzM7X6K7+CAgdesvYib1170rnuuCFe95sSqwNThEMIRA46j\nOPuKV9FrRAQYGOLbqdZeXqfxhIFwBCgVt5/nON4+wMmUifEJC5m0A93yVI9OmEgkTbiOt39ss2ML\nqsDClTIT2T146IEP4qlHhvwOg4iIiA44fvPuQZxq7FlesFteK1nLMIGxic11k7G4gRteG0U+50LV\n+92obFC7tmJ7a2wbEAESSQPJFJec75eIIDVgYWlh+xEDdYFC3ktkQ2EDJ26IYPGqjXzWgWkJRsdC\nSA16iWk2626bYrxVs67I1NzczCzwiN9REBEREbHZU0876A1WVlf2vi+oCOA6wMsvFHD+TBGlols5\nXRBPeFW9ahILALms2zQpsiwgk3bx8gsFXL1c2libu5Wq9uz041YPmuznIEs4LNv3BIZXJQ+FpeZy\nBg4fCeOG18Zw4oboRhILeI91k6dhgxViF+PdmpuZPfCfN0RERBQsTGR73EH+ctlsi5ZmojFBImnA\nCtVX6nJZF2dPF2HbzTOfcLh50lNdf+m6wOqKg4vn6jc3tW3FxfNFvPj9Al78fgHnXt1MnPvRpz8+\nv6/rJwfMrVv7AgCMytY7OynkXZw9XcDlC2U02C2pztgEJ6TsxkH+jCEiIqLgYiLbB+ZmZvHQAx/0\nO4yuS7SwvtE0gSPHIxibCMFpUMhV9aYPNzM0YjWsEja6nXzORbHgVn731vHWNp7K51ycfbUIx+nN\n6uy1FO740r6ubxiCY9dHEI1tPuDRmODYdZG6KvlW5ZKLc68WUchf+3ENhQUDgxZUFZm0g8sXS5i/\nVEIh378HGFr1pjttJrFEREQUWExk+8RTjwwduC+d45PWxtY4tVIpwciYCdP09g9NDZo4fkMEpiko\nldyGCakqdkxiwhED08fCsCxvWrIIGlYrTF5kAAAgAElEQVQNAQAClIpeMpXLuiiXtydW6gLrq3uf\nGu2H/VZaWxEOGzh+fRQ3vs77OX59FOFI848rb6/g4o5rYmslkwZUFZculHDpfAnrqw7WVhyce7WI\npYXytW+gz83NzOIu4x6/wyAiIiJqinPr+sxB6mocChm47sYoVlds5HMurBAwPBpCpJLwjE9uv044\nbDRMdkR23voFABJJE9e/Jgq7rBBDsLJkY3nJ3j6FVYFwRKCqSK9v76wLeIlzsdh/Fdl2v/ZM89pl\ncK/qXdr1VHPDAIZHLeSyLrKZ+rXPqsDSgo3BIetArqF90502E1giIiLqCazI9qGD1JjFtASj4yEc\nOR7B1OHIRhLbTDRmIBrb3kxIBBgcvvZxHRFBKGzAsgTDIxa2znStJsShkODsK0WsrzZudbybxDlo\nrjVl+NT7v96lSOoV8i7sa0zTrlbPY3EDx66LIBQ2mh5kgADZTJMW1X2MVVgiIiLqJb31TZpaclCS\n2VYdORbBwJC5kczGEwaOXx+BZbVWgbNC3rrNWNx7G3l7yZo4cjyMxYUySiVtOtXVNIGBwf7aw/SJ\nDz8N1/Wq0Ol1p2trgG0b2OmZS6YMnHx9DCdu9NbdLi/aSK87EGkenxygT0auhSUiIqJexKnFfa4f\n95ytbm+zU+OfnRimYOpwGFOHvWmpspsuTk1Eol6Fr7qtTvW20mtO0yQ2mTQweTi85/iD5vgLP8A7\n/vJRvFRWOC6gpglLvb9/8nAIg0Od/ZiJxRtPFweAeEJw+EgYa6s2rlwqb1wuve4gHGn++CdbaCTW\ny5jAEhERUa9iIntA9MPa2VLRxfzFEvKVrrTxhIGp6TBC+1jLuJ8kdk+3I8DUdBhmi9XfoPjEo5+t\nS35e/+3v4pYn/jcKJeDV1/0ILl73OrimiWg2g5PPfBO4dBHxuIFQuHMlTssSDI9aWFmyNxJVEa9i\nPn0sAlXUJbGAtxa2VFSkBg2vo7R4VV0FcORY/xxkaOaWB2/GHQ/f5ncYRERERHt2gCbQUS9XX1xH\nce7V4kYSC3gdgc+dLmxUQ4OkdupyrWhUejaJrap2LzZsG7d++3E4BRcv3fRWL4m1QoAYKCQH8NyP\n3oHVoXGsr3V+ven4ZAiHj4QRTxiIRAWj4xZOXO9t15PPN+9U7TrA9a+JYupwCFPTYdz42ijiif6u\nxs7NzDKJJSIiop7HiuwBMzczize+dxUf+OgX/A6lJevrTsOutI4LZNIuUgPBSj5Gx0PIZVwUSwp1\nvTWXhgCHjoTrLuc6inTagesA8aRxzWZVQVC440v4BLwK+ZlcCbYVwvzRG6Bm/ceJa5o4e/JmXHf6\nsa7ElRwwkWzwOhDZ3lh64zzDq+gODB6Mj8JePphFREREVOtgfHujOk89MoSnemyqcbnoNlwHqa63\nhygQrETWMATHro8gl3VRyLsIhQXJlFk3ZTWXdXDhXMn7RQFcAQaHTEwcCrVtynMnmZaXIRZjCRiu\nC2frUyCCXGoQyZS/HzOxuAFDgK11YRFgaBedqvsBE1giIiLqN8Ev/1DH9NKX20jMaDg9VAyv4VIQ\niQgSSROj4yEMDFp1Sayq4uL5EtT1knFV72dt1UE2s8sNUX1mmoLUoIloPgM1GjwHrovh7DKiMX+T\nchHBkeMRGKb3ehHDS2KHRy0kksE6ANIJvfQ+JyIiItqtYGYA1DVzM7OInrrb7zCuKZUyYW1p6iQC\nhMOCeKL3Xsb5nNtwvqsqsLZidz+gFimANSuJyLERDCcVR155DoZdrruMqS7eVng+ENXlaMzAja+J\n4vCRMCYPhXDdySjGJ0N+h9VRtzx4M5NYIiIi6lsHY14d7ehj908BAZ9qLIbg+HURLFwte3uAwtuH\ndWyiN6bhbrVTf6oA9q6qsxwexF9N3oqMFYcAsCYLeP23H0O4kMf5kzehHI5gOLOEf5J+GqPldb/D\n3SCGHKxtdR72OwoiIiKizmEiSxuCvkWPaW3u/9rrYnEDbrN9ZgeCW2Eui4lHDt+BohFGda63HUvi\n6Vvegbf+zZ/iyJkXAFSm7p6MAvvYGolad+sz9+L2+/J+h0FERETUccH9xky+6JWpxo0Uiy4Wr5Zx\ndb6EfM4J5LY8VYYhSKUav/2y6eCukT2TOAIXBrYuWFYxcHX6+rrT8tnOb7tDm+ZmZpnEEhER0YHB\niixt0wtTjbdaWS5jYd7emJa7uuxgYNDE5OHgTj3O5xonrJmMC9fVuuZQQZEzo3AaNHZyLQvFaHzj\ndxHAMIMTfzbjYPFqGaWiIhwWjE2G+qbRU/TU3d57loiIiOgAYUWWmuqVRjG2rXVJLOCtM11fc5om\ni0HQaF9cAIAGd53sZGERhm4P3CyXMbh8ZeN3ESCRDMbHSybt4OK5Egp5hesChYLi4rkSMunerxjP\nzcwyiSUiIqIDKRjfNCmw5mZmcesz9/odxo6yaQdoUPxTBdJrwU1WEk0aD4UjAjNA1cxak8UlHMov\nwHI3Oyubjo1EehljixchBmBZwJETkcBUwhfmy9sODKgCV+fLja/QA6Kn7u6ZA01EREREncCpxXRN\nt9+XD/RU453yJQnwoZrxSQu5jAPX3azAigFMHQ77G9gOBMA757+O5wduwPMD10MheE36DN6w+iLK\nR8MwDEE0JoFJYgGgVGpc3i6XFKoaqFh3Y25mFrjf7yiIiIiI/MVElnYtqF2NEykTuLS9uiYCDAwG\n9yUeChm47sYoVlds5HMuwhHB8IiFUDjA2TcAE4rXr5/G69dfgVndDFeAcMDWnNplxdqq7WXfDXJZ\n00JvJrFERERExESWWjM3M4vHPhnD4zd9yu9QNpim4NCREC5fqE9mR8ctRGMBTwotweh4yO8wdm01\nlMTfjf8orkTHAADHcpfw9oXvIOYUfY7M49he8prLushmmq+PFgFGx3rn448JLBEREVG9YH/Lp0C6\n/b584L5YpwYs3PCaKCYPhTAxFcJ1N0Z6KkHsBUUjhD+b/inMR8egYkDFwLn4Ifz54Z9oVPDsumLB\nxemXCli8au+YxALeQY6hkd5IZIP2XiMiIiIKAiaytGdB+4JtWoLBYS9BCfr03F70UvI4HDHrFh6r\nmMhZMVyMTfoYmefyxVLdeuNmRIDUoBn4acUPPfDBwL3HiIiIiIKC3/ZpX3qhqzHtj+Mo1lZszLtJ\n2Mb2KqYLwVoo5UNkNTE4imJh93XhbDq42zIB3vvqqUeG/A6DiIiIKLB6Y24dBVrQuxrT3uVyDi6c\nLQEKWOYCjNHr4Vr1U7YFipHSqk8RegqF1hLToBZjWYElIiIi2h1WZKltWJ1tr1LRxdJCGUuLZZSK\n3a8gqiounC9jcXQal6dvwMDKAkLlEuBu7s1rug5GSmuYKix2Pb5aC1da2xM2ORCsDssAk1giIiKi\nVrAiS20V1OqsqqKQVwCKaMwI/PrIpYUylhbsjfWeS1dtjE1YGBnrXgOreSeJb/zEe+GYFgCBGoLx\nC6ehhonlQ0dhiuJk+gzesvwM/Hw0N5/b5mqf7qnpECwrOM8/E1giIiKi1jGRpY4I0p6z+ZyLi+eL\n0GpRU4DDR8JIBGzf0yqvEmvXNS1SBRav2kgOmAh3oZGVAjh14u0ohaN1zZ0Wpq/D6/7h63jzi9/A\n0RORjsexGyICMbD5/NYwDOC6k1FkMw4E3p7DpskkloiIiKjXMZGljgnCnrOuo7hwtgh3S5Jz8VwJ\n15+MwgoFJ6mpSq87dUmsK4KlyaPIJwdQNtJ4PRZgdHjDm5XwIPKhWF0SCwCuFcKlE6/DG89d6uj9\nt2poyMTqSv3jJgIMDZuwLMHgULA+6pjAEhEREe1PsL7dUd/xe6pxOu00TfnW1myMdnGq7q7V5Nal\nSBTfu20G5XAEjmnhnDp41snjfRf/FlG31LEQbDEhTfax0UgIqcFgVbNHJywUCi7yOd2YRpxMGRib\nCN7zyySWiIiIaP/Y7Im6wq8v767TeF9RVcC1O1vV3KtUytxIxl686a0oxOJwQmHAMGCbIaxaSXx9\n+I0djWG0uAJpcAjAdGy8oXguUGuM7bLi3KslFPLqTTFWIDlg4NCRMMQITpxvutNmEktERETUJkxk\nqWvmZmZxy4M3d/U+YwmjaSMi21Fok6qjn8IRA2MTFiDA4tQxwNhS/TQMvDJwHE4HE3ETijuufhOW\na8NQr0ux5ZYxXF7HG9KnO3a/e3HpQhGlokJ1c51sZt3F+pqz8xW7aG5mFncZ9/gdBhEREVHf4NRi\n6qo7Hr4NmLmta1ONo1EDqQFz27pTAFhfdQEt49CRcFdiacXIWAiJAbP5hqdiYCEtmBruXAwncpfw\nM+e/hhcGbkDWiuJobh7XZy7ARPe3AmrGLjfuWKwKrCzZvq+NveXBm73XPBERERG1FSuy5ItuTrGc\nmg4hnmicEKbXHZTLwUnMakXCBizXbnieqItlJDsew6CdxY8tP42fuPotnMycC1QSCwCu27wq7fpc\nkJ2bmWUSS0RERNQhTGTJN92aaiwiKBabJzzFQvCmF1dNZBeaLPIFhiXXlvuwy4r1NRuZtAPdITEM\nolBYYDT5FEsO+PPxdsuDN3MtLBEREVGHMZElX93x8G0d/9KvqnAaFzah6iVDQfXW9WdhbCktGraN\nifkzmEjtv+S4eLWM0y8VMH+pjMsXSnjlxQIK+WBVXXciIpiaDtfNwBYBLMubnt1trMISERERdQcT\nWQqETiazqo2LmlWRSHDfBuPFFbxj/uuI59MQ14Xh2Dh6+WW8M/0dmOb+EvBc1sHyor3RJMl1AccB\nLpwtBrIJVjPJlIkTN0QwNGIikfQaZZ24MQrL6u4BClZhiYiIiLrHt04oInIUwB8BmASgAD6nqr/r\nVzzkv7mZWXzF/Qye/Gp7X5YigGmhYVU2EgluNbbqeOEKPnTpKyiLBVMdmFCgDcXG1eXtDbAAwFUg\nn3MRTwRrr9idhCMGJg/507SLCSwRERFR9/lZirIB3KuqbwDwVgD/WkTe4GM8FAB3Gfe0PTEQEYxP\nhLY1ABYBxqe6P/10LwRAWG0viW2TZo2SBF51lq6NSSwRERGRP3xLZFX1sqp+r/LvNIDnAUz7FQ8F\nS7sThMFhC4eOhBEOC0SASFQwfSyMRLJ3qo7tlho0G+7uowrE48Gdbh0EczOzTGKJiIiIfBSIfWRF\n5ASAHwbwTX8jaV2oaCO1XECo5KAQDyE9HIVrMQloh3ZPNU4NmEgNHNzEdauBQRNrKw4KeXdjirEI\nMHHIgrHP9bft4rqK9JqDfM5FKCwYHLa6vvZ1KyawRERERP7zPZEVkSSAhwH8iqquNzj/IwA+AgCR\ngfEuR7ezaLaE8QtpiFamfhZspFYKuHzdIJwQE6Z2uMu4B5gBPvHoZ9t6u6qKpQUbays2XBdIJE2M\nT1oIhQ/OQQgRwdETYWTWXaTXHZiWV7mORoPxGDi24uzpImxboeol2cuLNo6eiCAa636Mtz5zL26/\nL9/1+yUiIiKi7Xz9xioiIXhJ7OdV9UuNLqOqn1PVN6vqm0Pxwe4GuBNVjF7OwqgksQBgKGC4iqGF\n9uzvSZvaXQW7dL6E5UUbtu2tB02vOzh7ugjH7p1uve0gIkgNmjh8NIzJQ+HAJLEAsLhQRrmsG9Vi\nVe+5unyx1PVY5mZmeyuJVYXhuDu3664wbBeGzUXRRERE1Fv87FosAP4rgOdV9dN+xbFXhqMwne1f\n/gRALFtu8325GFjMI5EuQQVID0WRHomi4QLHPjY3M9uWymyp6CKbcbd9x3ddYHXFxuh4bzSA2qt8\nzsX6qg3HVRgClMuKcNjA8KiFcIC2IkqvN94nt1RUlMsuQqHOxxo9dTc+dv9Ux+9nt6ySg3DBhmMa\nKMathp8ByZU8hhbyMFyFGoLVkSjSo7Ftl7VKDsYupREueo9zOWRi8XAS5agFqCKxXkJq2budXCqM\n9dEYXDM4rw8iIiI62PycWvw2AD8H4BkRebJy2pyqfsXHmHZNjeZJpLvDea0SVzF1Zg1m2d0onw8t\n5hDNl7FwZGDXt2OWHUTyNlzTQKHJF+BeUK3M7iehLRYVItuLVVrZdqafLVwpY3lx+z5EuayDtVUn\nUA2wvGNdjSuKly+UcPREpHKZzpibmQXu79jNt0YVI/NZJNaLG1NAHMPAlWMpOOHNj/HEagHDV3Mw\nqmueXcXQUh4wBOmRWN3tTZ5dg+noxoySUMnB1Ll1XLhhCMMLOSTWihu3k1ouIJ4u4fKJIWhA1k8T\nERHRweZbIquqX8fmrNyeo4YglwghlinXzc92BVgfjrbtfuLrRZi2W3cfhgLRbBmhgu1VT+BVbQ1H\nYYeM+iRVvanOqZWC97sIXFGsD8cRLtmwLQOZoSiccDCSl93aT3U2FJKmMy57YV9ZAMhmHCzMl1Es\nKkwTGBmzMDxq7ZjYlYpuXRLriiAzOApxXSTXlwEF5i+Vcf1Jo6MJ4m4NDZtYWrAbPleFvGJ91cHg\ncPs/wh564IN46pGhtt/ufiTWikisVxLLjSTVxfTpNWRTYaxMJaAAhhc2k9gqQ4HBpTzSw5uzOGKZ\nEgxX6z6ABd7a8dRKAcm1IqTmdgwAsF0k1wr1CTERERGRT3xv9tTLlg4lMXEhjXDBhorAUEV2MIJM\nGxPZaK687YtpVbhgwwkZGL2UQSxXhsJLsJcmE8gPRLwqzuUMkuulzS+s6n15HV7MoVrvGlguYOFI\nEoVkZPudqMJw1asyByC5qbXX6mw0ZiASFRTy9Q+sGMDQSPDfEvmcg4vnShsJnuMAi1e9plVjE82n\nRa+vbU7VXRqfxvM/8k+g4j2vVqmIm771t0ilV2DbQCgAs6tHRi1k0s625wnwqufra+1PZOdmZoFH\n2nqT+1c5GLX1c6D6bkykS4ilvfd4s3eo4dRfOb5en6huXE6BcN6GCradXz2AxkSWiIiIgiD439oD\nTE0DV44Pwio6sGwHpYjV9q13ymETrmB7MisCxzIwcX4d4YKz+SXWUYxdziCTK8MqO4hl7W1fbrdW\nYQTAxIUM1odt5AbCKEW9qceJ1YJX4XEUagDrIzGsNVhr57e9VGePHI/gyqUS0mkXUCAcEUwdDvdE\n1+LFq9urlKpeR9+RMQtGk6ntpaI3bboQjeO5H70DrrX59ndMC0/e+k7c+tdfhBGQh0AMwcRUCOfO\nlBrOMG7ny9DPLXXMsoPEWhGW7aIQDyGXCtf9cdFcGabT5GgWvPevgZ2ntzhWzUwNVcQz5YaXVwB2\nyIBkm59HREREFARMZNvAjpiwI52ZmpsdimJwqb5bqgJwDWDkchqWs/0LrCiQWi16/97l/QiAgZUC\nUisFlCMm0sNRjFzJ1qy1AwYqcayNxff893RKq3vOmqbg8NEIXFcBRd2+qaqKbMZFLuPAtASDQxas\nUHCS92Kx+Tpe21aEw41jjcYNpNddzB+90avE1hKBioHMsWMwzSvtDHdfojEDpuFVnWuJoG3VWD+T\n2OoWXlAvGU2sFTGwbGL+2CBQOSCRrLyXd7LTq9MVYGVi8z1rlndeB55aa3x/KkAhHsLGXkhERERE\nPuLh9YBzLANXjg2gHDLgivdlshg1IY42TGKBzSprq181q5WdUNHBcE0SW2UoMLCc39WWHn64y7in\n5aTEMKQ+iXUV588Ucel8CSvLDpYWbJx+qYBspnEHXT9EdugsbFnNn/XBQS/xK0ViUHP7gRcVA7Hx\nxP4DbCMRwfTxCAzDm/pdmQmNgSETydT+P77ancQatov4ehHRbPna7xNVjF3KeNt2Va+vQKjgYOxy\nBpNn1zBxbh1mydlzMwEXwOJ0CrmBzWUDO80a0crsj633V/1Lxi5ncOTlFYTz7e3MTkRERNQqVmR7\nQCkWwqXrh2DaLlQEsUwJI1eye/5yq9g5yTXQ/Du4uN6PVvMgVUTyNqySg3LUQilqQRwXybUiQiUH\nxaiF3EBkxy7P7bafRlBXr5SQz23+8dXH4dKFEm58bTQQTZBGJyzkz5TqniMRYHi0+bRiADAtwaEj\nISwuXsKVYzfCseoXwooBTJcWOhX2nsViBm54bRSZtAPXAeIJY9/bBHWiCjuwmPNmTwgACFwDuHJ0\nAHak8cdsuOhAGrzRDADx9Oa6dleu/Z5txg4byCfDdaepIcgORDabR9XcT6N1s6jc98Z5jmLy/Dou\n3DAM5XY8RERE5BN+C+kVInBCJlzLgGW7Tb9w7tZer+6aAq28agzHxdSZNUycX8fIlSwmz65h8swq\npl9Z9TolrxYxciWLw6dXYdjd3dZmL4lKqehidblxnK4TnK154nET08fCG1OITRMYHbcwNnHt41ID\ngxbeMriI4fwKTGezg7HllnFj5hyGy+mOxb0fhiEYGLQwNLL/vW47kcRGs2UMLuW96qoLGK7CtBWH\nzq7BLG3f7gjwqp/N3oi1SWs12XQrF69pXLwjBZBLNWjgBmB5MoHsQAQqXgLrGoKViTjc3W6to16T\nKSIiIiK/sCLbg4qxEFTye05mvenJFiIFu2FHZIXXZMoqO9sqNivj8Y31cSPzWa+qVHPdSMGbgls9\nzVBAbBfDV7NYOpzaW8B71GpX45XlxglHVbHgIp4IxjZFiaSJ606aUNWWq8QhC/jpq3+HFwauw4up\nE7DUwevXXsEN2fMdijYYOrkWNrmy/f0oAOACh0+v4crxAZRi9RXwctiEYxmQsnvNaqsKkBmMVm5U\nkVgv4f9n786DJE/v+s6/n9+R91l319HnzGik0WhmNELoQkiyQEbDYQO2WWMMxjY2E6xj17AR9uyG\nN8IbQdgOcCx4jQnHBmvA2BgbbBASlmQhDiEJgaTROYdmpq86us6svPN3Pc/+8avKqqzMrK6qruqu\nrv6+IkbdnZX3UcrP7/s836/SpnubuzOxim8W7VjUR4Z0ULcUG+dyVCYy2LvGdlmR6Qby7m3TXw1W\nJu6ErLSJA/kpWKkghBBCiAeLBNn7UCcTL+FNDAmi27YrN4qt6s+W2mjcfThb88lX2iQ6EYa4PK+3\nvpSuzeSwIkNppUXCjwgdi83xDO381jJFY3qWP24btmc30whYP/IjvjMHXWrse/sfGfA6p6Miu9tR\nlzrbaB6rvcpjtVeP+R6dPk9+R8gHrX9w+Asagx1qtG3ddmn83pms27b3qo8tNli8XOoNfEqxOptn\n8kYtDqQmbjw2bH+7l3G6e10rE4Z0I+5MboUaO4oDpRNo7EjTyiVolFPo2yz9NbZFuOvYTG00jR3G\nWwNQ8TaCgZcDcpsdSqstUNDMJ9mYyt7VLQRCCCGEeLBJkL2XTFxROXRFQymW5wrkK21yVR97q3K6\n9xq0pVi6WMDYVjxn0kAn6xIm4m+uzWKSZjHZ3dOabIf4SZtGKdVtCLN8sXg8D/VYruXoDhJmM1mL\nVnN4WHXOyOiR+ACHwrrnr8rJO2oVNldpU1ppdSueXtqmNpqhk3UHflZb+QTJ9vADS3aosSKD3tOM\nK0g6zD9UJt0IsCON79pMztf6qrtGqd69rkrtHFQ6TkpRmcpRHUszcbOO60Xxnnl2fr/orb+7292P\nDWRrHk4QsXxh6/eFMThbP9+u9gohhBBCHCcJsveCMfEe0koHZeLOxBuTGdpD9rMNZCnqoxnqoxkc\nP2LqWrVbFTLE4XhtJk+UiF/iZmnIEkPiqkx9JM2hdkcq1V2evPsr6u7ljdu0gkbxEI/thDz3zLM8\n8d2b/LW/9x8G/rxUdthYC9EDsux2p9z7WYTFn448zgvFhwiVzYhf5VvWPs9UZ+1e37UTcdQQm6l5\nlJdbPQ0EUu2I1Hyd0LFYvlAgcnvfC41iilzV68503qt7wGqQPaF0dSbP2GIDRVyh1bZidbZwV6ud\nmbqP60fd52D7lg1xqE+1e7t4KyDZDhm/WaM6lmZssYG9tS8+cixWZ/IEKfm/GyGEEEIcH2VO6SiV\nQfLnHjZP//DP3eu7ccfKtxrkqv0dQ1fmCngZd/gF92EHEflKh2QrJEzY1EZTBEO6pR4X1wuZul4D\nY7AM3fFA2ra6X2IB/KTDyvn9v4inmn7PMubqaHrf8L3dLdkONX7K6VaZD2pYdTYIDLcWfVqNrfuv\n4i/pUzMuheL9/UX8f0y8jWvZGSJr53E4OuR75z9OOajdw3t2vO50L+y5VyskhsxaNYCfsrl1sdT/\nQ20YXaqTrQd9B3c6GYeV84dY3bD1/jZK4afsu17RnLxeJdXu3zOuLQhcm6Q3eByVBlD07bHVlmLh\nofKpXHr8h//8mc8bY95yr++HEEIIIQ7n/v5mfh9SkekLsRB/8SuutVk5f7QgG7k2mxN3dwZokHRY\nuFwiV+3gehF+yqFRjEftpFoBjq8JkjZe2tn3i3iyGTA+X+8+J26g4/FCxtAop/vObwcRkzdqcVje\nKkG38gnWz+UO/IV/2FJj11XMXUhijKHd0hgD6Yy171ibe8UYw+ZGyMZ6RBQZ0mmL8SmXVKp/CXTT\nTnEtO0tk9Qb+SFk8X3qU965+7m7d7RO1X4i1/YjieptUKyB0LWqjaTrZ/uW5zpAQC1tLar0IO4j6\nqrJYivXpPGqhTrq5M2c1ci3WDtvoTKkjH9Q6DkOrxwb8pN3X5G3boNFd8eieeE998xSszBBCCCHE\n2SBB9i6zo+Ffkl0/Qum4wUzoWGApMIZEJ8IJoiNVHk+adixqo5m+0zvZBBwwV5dWWwODfWm1TaOU\n6gunYwsNnO1Or1uXy9R8HK+KrQ1+wqY6nrntUsb9lhorpU5Nh+Jh1pYDKhtRNzi0mpobVz0uXk72\njaipqCwqimBPkDXKYiN5PPug76XbNXRy/Ihz16pxp1/igyXJdj0eQ7On8q/tuHvvfoZ2DFeKtdkC\nrheS6ESErnXbAzmnUaOUItlu9H0uta2ojmfINgIY0uBqEGXoWaUhhBBCCHGnJMjeZZEzuGHQ9r7W\n2W9sdE+rlVOkmwGuH3XP5KVtVmcKmCHXcz9K+IOXKVrGYGnTM9vSDjUJL+z7Am0Bya0qkRNoMs0q\nK7M5Orn9K0Bf+p0SXzpgV+PTJIdJOVEAACAASURBVIpMT4jdZjSsr4acm+2tNDavrhPN9r9nlNGM\ndzb6Tr+fHGQpcXGt1Q2x2ywD5ZVWXCXcFTRrIynKq+2hIU1bKm5gtI8g6Zz40v6T1MonSDWTZGte\n9zSj4r26kWuzdKEQHxjY+/4bcn1GEQd6IYQQQohjIt8s7jJjKaqj6b5ZjQB2oHsazBQ3OkBv46RU\nO2LulQq1kRSbu2a63s8C1xq4584ohd6zpFfp4ZUytefPscUm8w8nDvQcHXbm7L0W+AaldpZxGqA2\nMkG1PE4m6jCmlnFN/Jz6vkbVPSbnX2Vl5jLa2VqyagxWFPHE5kv35kHcobf/0pt472++60DnTbX6\nD35AvOTVCXTPSof6SDyaau/y2e2DTevT+TPxuduXiufM1kdSJFsh2o67Jm/vcQ2TDsvnC93RQYp4\nj7y2IHTjpcfbv9/0VoiVICuEEEKI4yTfLO6B2mgabVsUNtrdZkWJdsjeGs+wuZQA+UqH0LVplPdp\niHSf2BzPML5Q72t+VR3pX1YcuhbatrAOsEzR0mbgyJP9HHTm7L3muKobYrVSfPWtf4HN0UmMZWHp\niG8ow3ctfpJRv4qO4qfxdV/6LKlWk4XLryd0EhQqq7z+5c9RnGzf2wdzBM898yz85sHPHzkWzoD3\njIKein98ouLWxSLZqke25sXvITvu0t0op/r3xp5h+1WW/bTL4uUSuUoH14/wMm68R16p7mgwtjqW\n18v9n2UhhBBCiDshQfZeUIpGOdUNoUob5l4+3PJOy0Bho30mgmwnFzdqKq+0sEON3qpa10cGPDal\nWD+XY3x+pxK0e8blXkfpkno/hFnHUeTyNo16xOKF17E5OoV24o9zZNlExvCxyXfyAzc/QjIZPwcK\nw8VvfJmL3/hy/G8F5VEHuHdNhQ7rHV/5Sd7zj4YE763qqrZUdw7ytupomrHF/oMl7ayLtgcsE1aK\nZim1f+dsQeTaVAc0mdseDSaEEEIIcVIkyJ4CRg2vGO3ndg1p7ietQpJWIbmzVnaf6k0n67J0qURu\ns4PjR6QbQV+QNcTV26OO+7jdzNnTYGrGZXUZPnfhkW6I7VKKlpOm5uYoBg0mz7ncWgx6nl7bUYyM\n3T+/Ap575lnYHWKNIVPzyTQ8lIZkO+ge3PBSDqsz+W6gbecTbI5nKK224pFKJg6x64ftJiyEEEII\nIU6F++db7FmmFBsTGcYWGz3Li3fH1EFBzcvsvHx2EFFYb5Nsb8+RTePfpmvvqXTA5YdhYmfcUKrh\nMTHfiC/O1l5GYHmusP+VbI0EyW3GDW0apSSt/M6e2tPeCMqyFJPnEiRSFs0h59lub1QoOSSSFpX1\nkDA0ZHMWxbKDvXdZ7SnV19DJGCav10h4IZbpr8on2yGTN2osXSp2X8/6SJpGKYUTRES21Ve1FUII\nIYQQ9w/5JndKtAtJwkTvy6HY+XK+Hc66f7cUlfE4yDl+xPTVKvlNj6QXkan7TF6vkmr4d+ne31ud\nXJLFyyXqhQSdlE11JMnCw2Wi/UYVGcPYYoPRpQbpVkC6FTC61GBssdE3CPMgXXHvpUfq17B12Hd6\nKvIoBvWdf6ctzs0mmLuYZGTMvS9C7Nt/6U0Dn/9szeuGWOg/0BN3r45IdHqbiBlLESQdCbFCCCGE\nEPc5+TZ3irj+4KXFatd/BohsxdLFImEyDmqllWbPaBFFvId29FazL5SdVWHCpjKdZ/liiepEbvC+\nx10SnZB0w+/ZM2kZSNd9ks3+AwDPPfMsqU9+73Hf7WPxxto3GPcquDqI94nqEFcHfNvypw885/M0\neu6ZZ4d2Jc7U/L6u33sZJbNL70Sq6TNxo8r0qxVGlho4Q8ZkCSGEEELcC/fh2tOzS9sK+zb7XhVx\nN97dho0WsSN96K69D4p0M+ibgQnx8zs532BlTtHJ9s5i/Yc/MwW3WWpsjKFR1zTqEbYNxZJDMnWy\nx4sco/nuxd/nZnqK5dQYmajNQ40bJHVword7UvZt6LRF22rfJl8Q74P1Uw9Oh+HjlN3sMLLc7B4s\ncKoe2bofH0Dbb6WDEEIIIcRdIkH2FKmVUwPnyw5SWGuRaQRY2rDf2ffOYRWxyLYwW01/duvOoF1o\nMP9wGbVVpbW0oZN1CRP20K7Gxhjmr/u02xqzVQjc3IiYOOdSKp/sR00BM40loqUNvjj7NJ+ZewLX\nhDxWe4WnNl/A3vddcnr0NXQaolFKka0NXzqvgWYx+UCNyjmoRDuktNIk2QmJHIvqaJpmMbmzP90Y\nyiutnt9DCkAbimstaZAlhBBCiFNBguwpUhtNY0c6bj6kQG2Fob79fwaydb9nf+De6pRWxI2LJMgO\n1CokKK8Ma5EUP5e5SofyWqun61a9nGJzItvdt7k70NZrEe2W7lnNbQysLAUUCjbWCe5JjSLDSzcV\nn/mWDxI6LlgWES5fLL2ezUSB96989sRu+7gcZi+yl3GpjqQobnQGNkKrTGZoyOicPm4nZPJ6tbun\nxAo0I7ea2KGmNhaPy3ECjRqwJUERr/4QQgghhDgNZI/saaIUlckc8w+VWT5fZPFiAWOpnlra9o6/\nQVVbQ1yB1SoeUbMxlbsLd/r+pG2LldkCw3dQGkqrLSwdP9fb/+UrHVLNACvUpJoB/+T9f697iVo1\nGrwlWUG9HmFOcL9ytRJyY+5RItsGa+djrW2Hq9lZbqYn7kpN1hhDp6NpNSO0PtgtPvfMs0dqqFWd\nyLI6nSNS8YEbrSCyFMtzBRrl9IE7YD9IRpfqfcHfAoprbdh6vbSthi7ZDqVJlhBCCCFOCanInkLG\ntvC3mhUtXShSXmmSagUYS9HMJcjVvW61dpsCAkexNpMncixZUnkAXtZlfTrH6FKj/8CAGbz/Uhko\nLzdwAo1RCmUMP/fYDzLxdzXf+v2/PPB2jIZbCwHrKyGT0y7Z3PG/Ns2GpnZpHGP3f6S1svjo1LtJ\nRx2+/dafMO5Xjv32AXxPM3/DJwwMSsUHVibPuRRLw3/N3GlH6HYhyXw+QbIdVwq9tCMBdhhtSHh6\naEh1Qk2YsNG2RSvrkm4GPZ8LreJVI0IIIYQQp4EcXj/lwqTN6lyBm68bZf7hETYnMgObFBnATzn4\naVdC7CG08glauQR6K3htV/aqo4Mreoq4u7RlwNYGy0CyE1L9V5rffs8PcmvuytDKZxAYFm74eN7x\nd9J1XUWmXkHpAZ1llSKybBpult+dfg+BOv7jV8YYbl7zCHyDMaB1HOCXFwM6nf7H+46v/OTxjTVS\nCi/j4mVcCbH7SHjDlwUrINpVbV2fztPOuhgF2oo/E5XxDO18Yuh1CCGEEELcTVKRvc8Y26JeTJKr\nej3VEqOgurXHTRyCUqzP5Km3Q1KtAG0pWoUERimK6/1NhwZ1yu2OPTIWLz75TkI3wdzVFwYuMzYG\nKushU9PHGwhKow5zV19g6cIjGGv4gQytFK/lZnld/dqx3n67pYkG5HNjYHOj9/EetKGTOF7GUgMb\nnAFEjsLs2k9vLMXabAEr1NiRJnBt2W8vhBBCiFNFKrL3ocpklupommhr/6yXtFmZKxCk5LjEUflp\nh9pomkY5hbYtjKVYn8p2K7Xb1Vpzu+/yyuLlN34z/OjTQ2fD+P7x71ZNpSxmsm2e/PRHyVbX4wQ5\nIElHyqZtH38TpCgaPgonDHfux7FVYcVwxpBsBuQ2OyRbQfd9ECRsQtfqWzFggI3J7MCr0o5FkHQk\nxAohhBDi1JHkcz9SitpYpttlVJyMVjGFn3bJVj0sbWjnXNI1j3zV339+KfD7q4+Te/c0T3zmYyR8\nb+dnCtJpC2MMxhgs63iOJRlj2NyIKERrfNMffoi1iRm+/pb3oB2353y20Uy1V4/lNndLZ6yBFWil\nIJe3DzQbVhyOijTZuo8daLy0QyfrYmnD5I0ajr+zxDxI2iyfL2IsxcpsgcmbNexwp3xeG0nTzifv\nxUMQQgghhDgyCbJC7CNM2FTHdw4YBAmHbCNAbe2PHWQ75DYLZb7+9Lt58jMf3/mZgmYjZGNtZ7/i\n6LjN6LiLuoP9nXvH/oyuLFCorFErj6Od+GPu6JDp9jKT3vqRb2cYx1GURx0q6yHGgJ9M0cqXyAcN\nfvav/Sj/QkLssXI7IZM3aihjUCZeKRAkbULXxvWingMtrhdRWmlSmcoRJWwWL5dIdELsyOClHLR0\nIhZCCCHEfUiCrMDxIzJ1H0M8X1WaRQ0XuRaLl0rkKx0ydQ/XH94FFmWxOTZNZXSMdKvJuOvRbmm8\nTu/Z1lfj6tnYxNH3ze6thirgTZ/9OIsXHmHl4kMkE4pHa6/xaP3qvtXkOzE+6ZLKWHxq7Gnmzz2E\nm1B0tMXIrTZrM07PHkxxZ8YW61ja7NqfDW4nItGJ+sfrGMjVfCpT22dW+GkXIYQQQoj7mQTZB1xh\nrUVxvR1XdYDSWovKRCaewwmkGj6l1RZuoAkSFpvjGTrZB7tzqXYsquMZquMZMjWP8koLOxwcaLWl\n+PAP/xCRYzG2uMgz//4/DrzO9dWITDYikz3aQYRBS3sto5m7/iLfFLxKYZ8ROIfVaWtaTY3jQK5g\nY+0KqK/Nvp7FkStoy8bb2jebagWM3GqyPi1zjY+DHUQ4Aw6gWDB8VvAJzjAWQgghhLgXZE3ZA8z1\nQorrbaytmakWcfWmvNLCDiLSNY/xhTpJL8LShmQnYny+Tqrh3+u7fmq0CkkWrpRoFBIDQ0TkWER2\nHDmK6xvDgwawcMNH66MFDstSTM24PdNnlBUH3HzxeCrsxhgWbnrcuOqxuhxwayng1Zc6dNo7+y2/\nUnyE0OoNzZaBbN2TMHUcjCG36Q2tqhvVH2YN0M5KBVYIIYQQZ4sE2QdYpuYPHMWhDGTqPuXVVt8+\n0O2gK3ZRis2JLJGt0FsJY7vL8fq5XHe26ebY2L5XozW89nKHem3ALNgDKBQdLj6UZHTMoVS2mZ5N\nMHshcUd7b3erbUY0ajt7cY2O7/PCTQ9jDO/4yk9STw6puhpQRwzpYke26lHYaA+u/iuol5Joa+d9\nqBVEtqIypCuxEEIIIcT9SpYWi4EyNQ8nGDAYFHD9AwYtY0i14qZGnfTZHuGhHYvFyyVymx1SrZAg\nYdMopwgTO9XQ9alJNkdHKK1vDK2oRREszfvoaZfiEZYDJxIWY5PHf3zKaMPKrWDgz6IQfuatf5X/\n/R+1Gc84pBtB3+MLXQtjy3GzO7W9gmIvA/hJm83xLNWxDLmqh+tF+CmbZiGFsc/uZ08IIYQQDyYJ\nsg+wViFBcb2/m6wCkp0IrcAeVkQzBvap9KWaPuMLDXYWOipWp3N0cmd3f62xLeqjGeqjQ86gFB/5\nob/Bt//H/8TY8vLw5aEG1lbCIwXZk7KxFqIHH9fAd1yUiX9YmciSalVhqxGRIV7uuj4l+2OPgxMO\neRGA5bkCWAqDoj6Svov3SgghhBDi7pMSyQMsSDr77tkMEtbAnxsFyXY44CcxK9KMz8ddVS3N1n+G\n8YU61j5fxB8EYcLlI3/zB1m8eIHAHb5vMQziObOnxWZleBU+dBwq4+Px3xM2i5eK1MopOimbRjHJ\nrYtFvAdsj6aKDNnNDoW1FslWcGz7g/3k4P3OkWOd6RUPQgghhBB7nZ6Sj7gn2jmXzJCloNq2UAwI\nnioOq8NkasObQWVr3k61yBhcL8JYqmcJ7pmnFJ/4/u/l0gsv8vb//jGcqD8k2jZ3vLfVGEMUgmWB\ndYSlpdtBWik1NFQb4NN/8dsx1s4xsci12XyA92Qmtma80p3x2sZLO6zMFfZdxXAQlYksEzdrPcuL\ntYKNicwdX7cQQgghxP1EguwDbnMiS3rAUtCNqSyOH5Fqh3178pQBb585lJY2Q5tIWVsNfzLVDiPL\nrThAG0OQtFmdyT8wM2yNZfHaY2/AAO/46Mdxwp0Kt0rbjJbuLJQ06hHLiz7bGTmXt5madg8UaINA\nszTv025tvVZZi3TWolHrP3hRHRlh/uGH7ui+ninGMLZQ777PIX7fJ9sh+Urnjpf8ehmXlblCPBLL\njwhdm83x9AM/EksIIYQQDx4Jsg+47aWg+Y0OqXZAkLCpjaQJUg4qbchXPJwg6oZZraA2kkY7w1el\nd7IuZo2+MGtUPAbE7YSM3mr2BOREJ2LiZo2lS6UHqrJ09bE3YEcRT/3xp0i32nipFF9859t5+akn\n+emP/Bu0NlQrIfWaxrKgNOKQy+8f9jttzeJNv2c1a6MesTBvmLuQ3Pey7VbIjau9TZ1azfi2m/kc\niY6HGwSEto22bf74Oz945Md+ZmiDE2oiW2GHBnvA8nnLQK7qHcveVS/jsnyheMfXI4QQQghxP5Mg\nK4YuBTWW4tbFIvlKm0zdR1sW9XKKdm7//Y5+yqGVT5Cp+z0BuJVL4KccRpeafSFXAU6gSXgRfurB\nelu+8qbHeeXxN2JFETpeUwzA//GBH+Pv/MLP43umG0pbTZ/yqMP45PDXYGMt7NuSaQy0m5rA17iJ\nwQchwkD3hdhtnuXwlbe+FW1bTCwsUh0Z4ZU3vZFO9sFdQowx5NfblHY1TGtn3f5BrkIIIYQQ4tg9\nWIlBHJqxFLXRDLXRzKEut34uRysfkKt2wECjlKSdS4BS2GE0uGOvUg9uMyil0E7vx/Hiiy/RiBwc\nE3Jr7gqLFx7BWBZTN1/hXeENks7gxOR5gxszKQVBYHCHrEJduDl8b7MbhhQ2K/zZX3gf33jyiYM9\nplPODiKUifeDH2UVQLbqUdozDifTGHwgQAON4v7VcCGEEEIIcXASZMXJUIp2PkE735+a2tkEyQF7\nbzHmgavG7mfu1ddwg4CvPv0eNiZn0E5chX0tV2Kzc5m/vPwHDOorbVnbu517aQ3J5OBqrI4Mnfbw\nUqJWio3JyaM9kFPG8SPGFurdecjatlg7lzt0Z+VBM10HxWEDBEmbejl1tDsshBBCCCH6yPgdcdc1\nSkkix0Lv+tZ/kL23D5p2JkO1NNoTYgG047CZLjOfmeq7jNYGrzM4kLoJsJ3BlUe9z3JYA/jJBNde\n98ih7v+pZAyTN2okvHjft2Xi2awT8zXsYPiIoUHs6OBriFv5xAO191sIIYQQ4qRJ+Uvcdca24r23\nG514762tqI2k4qXHB5CpdiittrEjjZ90qExlz2Ql9+UnnyBTDzCqP9yHtstCaoLzraWe04PAwOCC\nbM++WQNEysI2Ot6f7CjchCLwey9ogMi2+NAP/xDRPnNv7xepVoCldX/l1EBu06M6fvAl9F7KJtUK\nBy+T333VigemG7cQQgghxN1y9r79i/uCti2q45lDBQeA/GqT8nqnGx6SnZCpa1WWLhQI9hkJdD/a\nHB/j6qOPYGmNoTcIaQXZqN13GcdRQ5sNJbaaPL2WneEzo0/RdDK4OuCJzRd5+2++nt/+Sc23/cZ/\nwYoibK3RShG6Lr/zt/4mreLZ6JJrB3rg82MBziErspsTWSavV8HsLCk29C4vjsdZqbgiK4QQQggh\njo0EWXH/MKYnxMJO8XFsscHSlfKBryfZDsnU4+ZGzWLy1FZ0bzx6idlXNlDaoPbU/n7jbe/jTR99\nuec021bkizb1atRTgVUKRscdbqYn+f2JtxFZ8eP17QR/OvYmPv6P01RnMvz2j/4Ir3v+eQrrG6zM\nzvKNN72RIHV29nYOm3+sFYeexeqnHG5dKFJca5HsRAQJi1Y+Ge+djeKmZZFjsTqTx1iyrFgIIYQQ\n4jidzm/vQgzgeuHA0xXgBgfvdlxebpKret0RQLnNDtXRNLWxw1WH7wZjKW6dLzK+UO/OJzWWYnUm\nj3YsnnvmWX76w7+AjgybmyHtpsZNQK5g0ajF57dsmJhyyWRtPjryeDfEbrMMFDbaVMfSNIsFvvCt\n777rj/NuCZP2wNFQoWvRPELVNEg5rM0Wek5rlJI4vgZ19I7IQgghhBBifxJkxX1j0F7Rw0q0Q3JV\nr6fbrDJxB9pWIUmYsFGRprgez841lqJeStIopQYHEmNItQKS7ZDIicOQsY+3YVWQcli8XIq77Jq4\nA+7u+/JP3/Mj/Mgv/xs6zV37YBWcm3HIZB3i0bTx+Wtubujt2JEhGtIM6jipSFNca5OteaCgUUhS\nG8vctarl+rkcXrpDftNDaUOzkKQ2koLjun2lCJOyJ1YIIYQQ4iRJkBX3jTBhoS2w9xRfDdA64OiU\ndGOnEtv3s6ZPw0lx7loVO9TdsFteaZFsh6xP53svoA2TN2skOiHKxE19yistbp0vEBz3UmWlCJKD\nr/PJT/0JjVbcuKnLwNJ8SCodAgrbVpRGHMp+laX0xMDrj+yjBblU3aNQ6aAtRXUkTZSwya+3ydW8\nbmffds5lYyJDuhFQXmmh2NlLWqh0SLUCli8U7071Uika5TSNcvrkb0sIIYQQQpyIfb9tK6UKwLgx\n5tU9p7/JGPPlO71xpdRfBH4OsIH/1xjzz+70OsUZphSrs3kmb9TjfxKHWG0rNqaHVxp3M/sEJaMU\n2WqnJ8RCvPQ2U/ep+hFhYqfSVqi0SXR25uEqA8YYxhfqLF4uDQxlbidkZLlJsh2iLUWjlGRzPIMT\naMorTVLNAG0p6uUUtdF09zrcTofpawsYUnjpLOAz89oL2FHExZdextYaP5Fk8cLrqJXHUMYQuAlQ\nFqPL88xefYHWTZ/2dBVSY7Cruq0BjeH8SxuAQZmIyLZA2QSuTXU8PXj/qDFMXauS8HaaJGUaQbfh\n0e5Hn24ETDfjxkh769WWgYQXkWyFh57lKoQQQgghHkxDg6xS6q8C/zewopRygR8xxvzZ1o//HfDm\nO7lhpZQN/Gvg24B54M+UUr9jjPn6nVyvONu8TIKFKyVylQ6uH9HJuDRLqQMvS20V4mY8g6qyrVyC\nkeVmT4jtUpBshz1BNlv1+86rADvUOIHuOS+A7UdM3aii9Nb5tCFf6eB6EemmjzIGlIUVGcorDRKd\ngLXZIhe//gIPfeUVXn3jW9HKItWOsEJNOzvLU3/8uzhRSCub5wvf8p1Eto2xnXiNsVJgDLWRCa4+\n+hSPfOnTPPHZP2Fj/DWuPfo0jUIZJ/DwUxkcvesRKGer6m2wo5DEfJ31czlahWTP48ltdkh40cDx\nM3tPU/HVDR1Vo0zcgVqCrLhTf/DP0nz68Z898PnfeYL3RQghhBAnZ7+K7HPA08aYJaXUW4FfVUr9\nY2PMf2X499HDeCvwijHmNQCl1K8D3wNIkBX7ilyb6kT2SJcNEzaViSzllWbP6WvncmjHInCtvhEq\n26zQ49HPfw3XD7g1N0uiY4N18OBV2Oh0Q2z3Og2kmwFWpDH2ruBr2eRqPl6lyts+9gn+9P3fj7Z3\nPq7acelkctw6/whzV7/ON974zYSOC9ZWvXO7Grzrz5effCftbIErL36B0dXfBeAL7/oOgtT+Ta4s\nEy+ZbuUTPVXm/EbnQCH2dqcDGGurMdIujueTbjVp5vNoR3ZBHKd/+VO3jnS5znt/65jvyfH79Ifv\n9T0QQgghxN2w37dD2xizBGCM+ZxS6r3A7yql5hg6qfJQZoCbu/49D3zzMVyvEPtqlFO0ci6Zho+x\nLFo5t9ugqVFKUah0eiq2BlA64rt++d+jMFhhXIW8efkxrj36VG/IMoZUu0Xo9I8CSnjh4OBn9oTY\nLVYUcv7FmzQL5bhau4d2HFanLzB39etsjp/bCbHDKMX8lceYmn+VbKMKQCtX2v8yW+xQd/cBH9l2\nlXjvyYDeNWtVRRHv+vB/5+JLL6GMwVgWX3v6Kb7w3vfcwY3fXZ/8vk8d+jKf+dE73q1xYB0Je0II\nIYS4z+0XZOtKqSvb+2O3KrPvAf4b8NjduHMASqkfA34MIFkYv1s3K84oKwx5+g//mIe//BWcIGBj\nYoLPfvv7WZs+B0CUsFmZLTC21OjOAg0SFu/87/8VN+wd/zN77QXWp2apl8bQlo0VRVhG84bP/wHV\n8fexMjvbc34/aZNsDw6zaN0XRI1lka1VcHxv6N5eN/CoF0cO3NHZKFifnO0G2VSrTiORvM2l4orp\n3hBbL6cY2Wrc1HvmAYHVGJTRaGX1zMM1xM/L2ky+e5l3feT3uPTiS91zKa154599nshx+Wu1Lx3o\ncd5rn5GgKIQQQghxovYLsj8OWEqpN2zvWzXG1LcaNP3AMdz2AjC369+zW6f1MMb8W+DfAuTPPXwc\nlWBxBuy3NDKqBzT+ZBnlKnLvmsJK2rx57BKffvxnWbjp0azr7pia0ZUVvvPX/gMXryRJJHfCoAFq\nTg7HhJjNJktNn72Tai2tefLTH2VzdIrayDjJTovxxes4OuRHPvlblEZ6P141J8t/nvsA4a7lyLYO\nGd1cZq0wgd4VZFUUUlxf5v2Vr7NQ90l2WrQz+Z6wa4UB566+yPNv/8CBu/0qY7CineZMl176Il97\ny3t7li3v5eiQN228yI9/42s9p2sUvznzbWwke6u6mWaVVjoX36etgF1aW+Khr3+O9See5HphDhSk\nQ4+3r3+RK8357oYCow0vv9Dpv9/AU5/9LLxhcKfhdktTWQ8JQ0M2Z1EacbCP2IVZCCGEEEKcfkO/\nvRpjvgSglPqqUupXgX8BpLb+fAvwq3d4238GPKyUukQcYH8A+Ot3eJ3ihH1E//yBz/v8753cvsZh\nSyOrmyHLiwGwM1M1nVFsTiWwHdUTYrcZAxtrIVMzO515FVAMGwA09rkfCiiv36K8vitYW5BI9oeo\nQtjkuxc+yafG38xKchTXhDxafZU3r36Jr349x4uPv51mvoQyhsmFq7z5+p+Tm7YpFm2e+NOP8/zb\nvp0gkQbi5baTN1/lxTe/m8gd3FE4voN77odSTNy6HudLA3ONJSZWPsunxt6C5yR3LqvioG4peGP1\nZd5S6Q2x8cM0fP/Cx3g1O8eLhcs4OuTpytewl1aZryVp5MokW3WyjWrc3MqGN699lnDjzwmVQ0p7\nfdVcvfdowZ6HZIzpzsTdVq2ELC8F3YfcaWs2KxEXrySPHGaNMURRfNzAukvzbYUQQgghxMEdJGl8\nM/DPgU8DeeDXOIZGj8aYXbnj3wAAIABJREFUUCn1E8BHicfv/JIxpv/b8gPiie/ePND5fviRzj1t\nuPL8KR497Pua5cWgL6i2W4YbVz3GJpztRr59PG94gspkrYGXGcZ1FenM4KW+436Fv7zwid6GUg48\nPlJj8vO/S6NjYRMxUrYZPRc/15PTLvmmz8Tnf5tKYQxVyrIWZXjh4lMD99YCoBR2u0WUSsPWPlOj\nYH2mwMMzmsBLkEgqkikLWgs8dGOBTmix4KfRzYCS1SI5miOLj91Xi951M8BDzZs81NzZ7q7LDvVq\ni9RaE6N3svS52QRKKVwT4Zpo4PVZQx7OMFoblm/1vubGQBQaKushYxOH64LcbmvWVnzazZ0rLJZt\nJqbcvgAthBBCCCHunYOkkgBoA2niiuxVY8w+dZODM8Z8BPjIcVzXUfzBPxu8THGYw4x0OLQD7qnr\nX3R59m2sBaythN2tl6VRm4nJ/ipkbTMaGjiNgc2N4T9PpobvMbUsxfRcgsWb/m0Dbb5gM3nu9qFn\n70+TSYu5C9t7VXvDl1KKbM4mm7PJOSH/beabaKvE8BALYAxRKo1WCpSik3FYn86hHZt/+n0/wU9/\n+Be6Z201I9ZWQjxPk0i0GJtwyeYcjvpusyzF+UtJmnVNsxnhOIpiycFxbx8ElVLk8haNev+vmHzR\n6ntevY7pzhPezRho1KJDBdnlJZ/Njf6AXa3Ep02eG1D5FkIIIYQQ94Qyt/lmrpT6EvDbwP8FjAG/\nCPjGmL9y8nev16Ppkvmlh951t29W3EMbawGry2Hf6YWSxbmZ3iZFw4LIbvlCHJJ2v+2VRbxHNrF/\nw6QwNNSrEb6nadQjoigOTI4L07MuqbR9YlW7RiPilXaRLz3+LXTSuf07FBuDUfQ0VdIKKhMZGuWd\ngzc//eFfoNmIWLjRG9CVgum5BLn8Icujx8QYw/x1n1ZzJ8xmshaz5xOoPct8fU9z7VVv4AGGTNZi\n7uLtG1lBvMf25rXB17Pt8iNJXPdgTbXE/eOdX/3w540xb7nX90MIIYQQh3OQiuzfNsb8+dbfl4Dv\nUUr90AneJyG61lb6QyxAbVMzec707F/M5W2qleFVV2XB1IzLxlrE5kZIFEE6YzFxzr1tiAVwHEV5\nNP7ITBhDEMTVQPcAl70TjUbEJ0pvYfmxy3EVdr+wrONBtYre+2SZeI7t7iD73DPP8nd/7l8O3DO8\nshTcsyCrlGLuYpIwNPieJpGwhlZzE0mLRFLhdcye66D7Wh1EvRbettp+4zWfSw8lsaSJlBBCCCHE\nPXfbb3q7Quzu0+600ZN4QBhjCHyDbSts53ABwBizb7gIfEMytXOdmaxFNjd4WapSUC7bWJbF2IR1\n6L2T/denSCROPtDUnAy/c+mdNPPl23YmVlFIkFA4PvGu8z2coP+gQMeHQTE8CMzAxkp3k+MoHOf2\nYXr2fJL56x6+b7p7oEfHnUMF8YM8zCgybFZCSiMOmxsh1c24+l8s2ZRHnL5qsRBCCCGEODmnt3OP\nuK8YY2jUNLVahG1BsezgeRGrt8J4/6KBbC6ufiqlcA4Qam8XovYGY6Xivaz1WsTaSkDg7wSUQtFm\nbPLOwuvdtpIo899m349B7Zu0DAajFJXpAqOL10h6GbxMrvdMWpNubQK9s5jb2SzZRn9fZi+X42vF\nS9hGc7E5T1r7x/GQToTjKi5cSeJ5hig0pNLWobsVF4oOlfXh1XyIA3KzHtGoazrtneXpaysh9XpE\noWDTbhncBJTKzolX6oUQQgghHmQSZMWR+L7G6xjchCKZVMxf92m3dr7cb1erdmvUNY26h1Jx+Dg3\nkxja3XdbacQeuO81mRochpVSFIoOhaJDFMXVYNc9fDX4XguUw+/MvG//EGsM2lKErsPyhQLatiiv\nOVz5wud48al3x3NpLQsVRVg6ItNYBh7uuYovv/2becsf/CHurmrtzUcf5+pDT6AAheFPxp7ifSuf\n5XKzb8zzqaGUIpU6+mucTFmMTjisr9xmibFSPSEW4oDbaRm89s5lK+sRsxcSZLL3Znm2EEIIIcRZ\nJyUDcSjGGBZv+lx7xePWgs+N1zyuvtLpCbG3v454WfDN6x5hsP+FJs8lyBd736bJlOL8AZr42LaK\nq3P3WYgNlcV/nfkLROo2+2ExrJ3LsXSpiLbj52jp/HlGb93kzZ/6MJMLV8lVVpm8+Q2e+qMPce31\nj/Rdw8tPPsGX3vF2/ESC0HGojEzw6sNPoS2HyHIILZfIcvj9ibcxvwqLN302NwLC8Fgal58qo2Mu\nlx5OMj7lYA84xKdUPFppWM/2veF2aSHgds30hBBCCCHE0UhFVhzKxlpIox4vwdz+jh4cddWpgc3K\n7Wd9Ts8m0dNx4x/HtQ60LPl+tZoo87HJd9Bws/tWYgFWZvK0C72B/tEvPo+xLDL1TVyvTevcBVqF\nMqszl/GThf7rUoqvffNb+fpbnibVbpNqQH7T6xsPZLTh1cQ5plZeo16D5aWQZArOzST3HV10v3Fd\ni5FRi3zBYeGGh++Z7sswec5FG6hV91+CvC0KDWEQr1oQQgghhBDHS4KsOJTNjdt3dz2o7crsQViW\nIpU+28s0V5IjfGj6vQSW0xcktxlA24rFyyX0gEZIj37xeZwo4pXHvonFC4+gna2PuA0jy020bdHO\n989DNbZNO5cj1WwOvX9G9QZWrwPXXvWYmHIoj95f+49vx3UVF6+k8H2NjuJVAEoposiweis48Gfg\noA2gvI6mXouX0OeLNsnk2Tk4IIQQQghxEiTIitsyxlDdjKhWQsLB03CORClIZaRate2zo28ivE2I\njWwVLyUe0s3X9QMiy2bxwut2QuwWy0BxrTUwyG5r5RPkNjuovUFNKUZX5gdeZuVWSBQZRsbcnnFI\nZ8HesUy2HY8GWrzpE4bxk7TdKXlvuE0N2ce91/pqwPrqzgGijbWQ0XGH0fGzdXBACCGEEOI4SZAV\n+zLGsHDDp9U8+B7YvaytLKD37C20HSiW5C0I8UzXuZc3sPTgJ9kAoa1YvFKGfcLi4sULTF67ybA0\n7Nxmb6uXdmgUk+SqXjfM2lHIla9+joTXGXq59dWIjbWIsQmHkbGzHcBSaYtLDye7qwkcF24txEvu\n4xm+cUftc3O338fte7onxEIciNdXQ/JF+0DzjYUQQgghHkSSIgQQ7+dbXfWpVzVGx0spJ6ZcjOGO\nQqxScPFKEsdVbKyFVCsR2hhyeZuxibNXwTuK5555FoDQUSQGLLU2gLEUq3OFfUMswJ+/59088yu/\nhhVF6L0di4zhQm2JeUaGX4FSVKZyNIsp0g0PlOJtH/swE/M3bvs4jIlH0SQSFrnC2V4GrpQikdx5\nLabnEvhePJbHcRXpjHWgGbz12uD9tsZAoxYxMiZBVgghhBBiEAmyAt/TXH3VixPTlk7bcOOqT75o\nDQ2xbkKRSivq1cFVPqVgYmpnnubouPvALZfU2rC+GlCtxIEll7cZn3RxXNUNsNuqo2lGbzWxdlfn\nAC9lszpbQDu3DzXNYpHf/ts/wsNffIlm8Rza2Xq+jcExEW/d+Ap/whtvez1+2sFPx78ePv0d38YH\nfv0/kW40UcYMXfq8dTOsrwVnPsgOkkhaJA65t3VY1o1Pl4M8QgghhBDDyOF+wa1FvyfE7tao6YFf\ntpWCkVGH6dkkpRG77zzZvMXlh1OURh6s4LrXwg2fynpEFMVLq2vViMXFDv/k2/5O33lbxRSV8Qza\nUmgFWkGtnGL5QvFAIRZAac3bPvY/eOJP/4g3fPGPyVQ3sAOfidYq37Xw+4z7FX76w79wqMdQL5f4\nzb/3d/n9v/w9bIyPD3urdB3nPuqzLlfo/+xsyxfk17MQQgghxDBSkX3AGWNot4ZHE2NAWfQHXRV3\nV4V41muhqKnXQhSQLzmkztBIlqPqtPXA+bo1z+Xy117g5aee6LtMYyRNo5zCDjXatjCHXHr9ui8+\nz+xrV3HCEMfzCJMpjFKsJct8YvLtfODWpxgJaod+LMayWHjoCgsPXeHS177Om//oU2Tr9YE1w2xW\nXvuDSiQsxicdVpd70//4rpUMh2GMwevEI4MSSXWg5c1CCCGEEPcjCbLitmbnEiwu+N1mTZYFM3MJ\nbHvnS3I6Y5HODO+G+yDyOoOXXLtBwPjS0sAgC4BSRO7RluY+8vyXccIQP5niy297/87SYqBmHD40\n815+8PqHjnTd264+9gauPvYGHvrSl3nrJz6Ju1WCjSxF6CYYHb+jq3/glEddcnmbRj1+v+QKNq57\n+ADaqIcszQfdz6njwOyFszXnVwghhBBimwTZM8QYQ6dt6HQ0rqvIZBWdtiEK46BpO/Foj431EB3F\nFZvJcy6FokVtyD7XTNYik7O58kgKrxOXFrdnaor9uYmtFrZ7KrKh47A5uk/DpTu5zSAA4NbsFcze\n10gpImVzIzPNv/ypW/zDn5m6o9t65Yk30SiVePyzf0q2Xmfp/Hm+8ra38uuFAh/RP8/zv9f76yWK\nDKvLAfVq3N23UIwbfu0+IPKgchMW5dGDBU5jDBvrIZvrIVG0s892b1fwMITrVz0uXk7SqO/s0ZZg\nK4QQQoizQILsGaF1PCan3dr5NmtM/CV3e85lIgm7J6j4nmH+us/MhQStlk8Y9F6n48D0XFzRUypu\n7CQO7n2//iQ/98wr5Cub2FspwwDasnjl8ds3XDqsqevXSdfrWw2iMpi9XYsBjaJlp47tNm9dOM+t\nC+fjfxhDwotItEM+mPqf4RnV3Y9rjOHqKx2iXStoNzciWg3NxYeScmDkEPaOw9qvo7jRcPUVr3tA\nZX01pDRiMzElqyeEEEIIcX+TIHtGbKyFA/djGrPzRXfQGFBjoLIWcvnhFM2mplYJMUCxaJMryNvj\nqJ575ln4LUj+T0/zjt/7GDNXr6KAjfFxPv0dH8DLZI719pTWvPtDH8beerHL67dYuvBIz9LibVOd\ntWO9bYBEO2R8oYYVGVBgUGxMZnnugz/OR8y/4hO/YnpC7DbfNzQbmlzexhiD7xmMkar/MJ22Pto4\nrF2hd3MjIl/QpDNSmRVCCCHE/UuSyhmxPd7lKDzPoJQil7PJ5R68sSnHbfdYHS+T4ZPf95ewwhBL\na8LEyVTCSmtrOMFOUhy9NU+2VqFZGEE78cfcCgNGVuYZ6VSO9baVNkzerGHp7bQU/8/YUoNoGb53\n+u/zHf6vUKA68PL1WkStGtKo6e4qAsuCc7MJsvJ+7NFpD94CcBjGQK0ayp52IYQQQtzXJMieEea2\nQ1GGSyal8nUc9s6F3U07DnceQYaLbLtnjanC8OSnP8rixUe5NXcZS2umr7/M9PwrNGdcjrMenKn7\nA9e3KsDRML5QJ7STQy9f24x6/m0MRFG8hPbSw6kjNT46q9yE6m4VuBPyjAohhBDifidB9ozIF2w2\nN6Lbn3EPpWB04sGe9Xoc+kKsMWTqPslWQORaNIqpA8+CPYrayAitfI58ZbM7HNrWEXOvfY251762\nc0YFYXiHKWgPK9Sofa5SGbj6+icpf+pjhwpQBqhthoyOy/tzWyZrYdkKrQ/4Gg5oNqZUPCJLCCGE\nEOJ+Jt9mzoixcZdmQxMGZmC1Rqm4mpMvWGxuRERRXImdOOeSTsteuaMaVIVV2jB1vYrjR1gGtILi\nWpuVuQJe5oRCmVJ88nv/Eh/4j/+JTKcdvweGZJ1MxrrjjsW7eRkXoxgaZhWwMTlN6Dg4YXjwMGsg\nDI43dN/vlFKcv5Rg8aZPp9373DgOjIw5KKVQVtyhuFmPuLUYd3HbXrZdHnXkMy+EEEKI+54E2TPC\ndhQXryRp1CJaLU0ioUilLWrViCg0ZPM2haKNZSnGJu71vT0bhi0lzm+0uyEW6P45tthg4UppZ17K\nMauOjvJf/v6P8b/9519EhxGbGyHBrlW/SsUzSo97/IqfdmjnEqQbfvex7qYV1MsZfu9v/HWe/sM/\nYmxhkU4mw63zczz2ja8RDtn3qRRkZI9sH9e1uHA5FVfWDSjLYIzCtulrkFUoOWSyNvVahDGGXN4m\nkZQQK4QQQoj7nwTZM8SyFIWSQ6G0c1omK0HguL3jKz/Je/5Re+jPczVvYKCzIo0TaMLECbwmxlBY\nbzOzscmvP/kD5MMmb1v9ImM3r1OrRiilKI3EBzP228t7VGvTObI1n9JKEzsy3aqrBrQdL602dpr/\n8Ve+r3sZ1/O4/MILuEN2DydTilxeQtcwjrP9LO9/YMRxFeVR+VUvhBBCiLNFviWecsYYwtCgI1li\neRo898yz+4ZYALNPxdWcUJed4lqL4nqblk6CUtTdHJ+cejutuVkuXklx4XKSYsnhnV/9qZO5A0rR\nLCZZeKjM+lQWL2kTuBb1kRRLl4oYu/+BB8kkf/A9303gOvgJt5vHbAfGpxzmLsp82bvJGIPX0fj+\nSbYlE0IIIYQ4HnKY/hRrNiKWFwPCMN73atvxtsdk0mJ03JHRJHdR6pPfe+B9pfVikvJqq6cqa4Aw\nYRO5J/CaaU1xvdNXlwsthz8rv5HZ9nL3tNuF8DumFM1SimYpdaCzL16+xG88++PMvvYaltb8Pz+x\nzPM/9cK+lwl8TbUSEYSGbNYiX7BRlgTeO9FsRCzN++itvdVuQjEzl5BlyEIIIYQ4tSTInlKep1m4\n4fc0boq2mhK3W/HPJqdditJ99MQ998yz8DMHP3+jnCLVCkg3g+5p2lKszuRP4N5BtuYP/VnFyXX/\nfhJLio9DmExw7fWPAvDBT74BnnkvP/3hXxh43mYj6vlc1KsRG2sh5y8nsYaEWWMMWm/Pp5XAu1fg\n9/+u8T3DzWselx9JSVVcCCGEEKeSpKBTqrIe7jsr0hhYvRVQKNryRfOAgsCwuhzQrEdYFhTLDqPj\nztDn73ZVWKXjZjt9y2aVYm22gNsJSbZDIseinXNPrMlTuuEP3SXpttsEgeb//Es/cSK3fVKee+bZ\nvjBrjGFpvjdwGQO+b6isDx7T02rGXXsD38TNrvI2U9Mu1oClzmdZp62pboZgIF+0SWes7vt+sxIN\n/F0TaWg1NNl8vIogCDSV9RDfM6TSFqURZ9c+3X71WsT6aryiJJOxGJtwpcIrhBBCiGMjQfaU8r3b\n74nVOq7SOvIq3lYUGa6/2ulWtbWGjbUQr6OZOZ/sO/9+VVg7iBhdapBqhQD4KYe1cznCZO+y4SDl\nEKTuwoszLCAbw/TKq/zik99JohNSWGvh+hov7VAbTZ9M06lj9Nwzz/IR/fM8/3vxc+h7hkHjU42B\nWjXqC7K+p5m/vhN8jYFGPWLhhmHuUv9rflatrQRsrO0cGKtuRhRKNlPTCWCfEUdmZ+Zwp625cc3D\nbG2fbTU1lY2QC5eTJBL94bSyFrC6snOb9Zqm2fDi80uYFUIIIcQxkG8Up1RcMbn9+Wx5BQ+kWgnR\ne3rYGAPNhsb3dn7w3DPP7r8E1ximrlVJteJ5qApIdEKmrldR0b1pktMoJkFHfadbUcjEKy/RzhSZ\nul4lW/dJ+BG5aodzVzdxvfAe3NvD+aD1D7qvh1IMnY07aMXwxoBVDcZAu937mp9lvq97QixsBf/N\niPbW2KNMzkIN+T2SzsQ/uLXod0Ps9nXoKF4VspfWhtXV/udea1hbPf3vOSGEEELcHyQGnVLlUQdr\nn1dHKSiWpcnNQbVbeuDySaWg04m/od9uD6mKNDOvVHrGy0AcZpUx++5VPUmdrIuXssHorYShUWHA\n67/whyydP0++EqIM3cqtQmFpQ2m5eU/u71E898yzfOuvPYmb6H+/KwWlkf7K97BVDUrFy8wfBM36\n4MBuDDRqcajMF2xcV/UcOFMqXoKcSFpobfA6g5+vZqP/+odWeIk/h0IIIYQQx0GC7CkQhoaVJZ+r\n3+hw46pHox7hOIoLl5Pkiza2DdauVaBKQaFkMzHVvyfwQaK1obIecP01j5vXPOq1CDNkY3EiOawR\nELgJ60CNkCZv1PpC7DbLgOP3V0XvhnQzwA22xv4oBSoOq4sXzvOpD34H9qC7pRSZ5r0J3kf13t98\nF7/+Q38L2wHL2nqoKg5ihVL/Mul0Rg0csWoMD8zy1v1WdWzvkbUsxYVLSUbHHRJJRSqtmJx2mZp2\nu9cx7HoGHWyzHTW0cu66cuBNCCGEEMdDdlfeY2FouPbKzt5NfMPCDZ9UWjE65nJuxkWpeC+b0YYg\nNDi2euCa1exlTNxV1euYbqW13fIplm0mzyX6zl8acalsRD3LIwFWJyb4d9/3N257e1akSXjR0KZK\nWoGfvgcfJ2Mo32pujfrZunfKQjsWi5feQHGjAmZwaHP9zl27m8elPlLm//tf/lf+8W/8a6LQkM5Y\nQ0NpecRlcyPq2Ve7XWkcFKii0OD5Gte1zkzgyhVsVgYs/90+GLbNshWj4+7AhllKKfIFe+tAUe91\nFMv973nbVuTyNo16//lHx+X/coQQQghxPB6MssQpoyPDrUWfl19o8+pLu0LsLp22YXHe5/prHnrr\nm7iyFImE9cCHWIg7onqe6dv7V61E+H7/8kXXVcxdTPZUZq8//BAf///bu/MY2e7rPvDf87v31r71\n3v1ev52yaFukaEeWLYqZULKgiGzHmkgD2xESx5ARK9MzowSi4ZFbGAxmMDAcmHECI2OMPBMiAWwn\nSkIbokNJ3kInUijJjmVutkSK21v69b7UvtzlN3/c6qW6qvpVd1fVrar+foAH6dVy6/equ4r33HN+\n5/zE/9BRN2Hlti+X1AA8Q6GUbA6ge008wHRal2uGyw60EkwvvwHlNO5NVI6NsbWb/Vhi12ml8Es/\n9b/gI7/7g8dmVk1LcOVGGMmUglL+3yenzf1M4/7xtMb6ag1vvFbB8k2/MuLOzYPP3TAzTalfDAPk\nUBZ7es5saNJUKXu4c7OKN17z/+1HS4Bn5ixEoqo+wsg/RjyhMNkmMJ29aPnzfQX7z5mZszj7moiI\niLqGl8f7bD+TeCQIa/1Yf5/f9qaDyenzUUZcrXpwHY1wRME4JmAvFrym7OqectFr2Uk1GlW4dl8E\n//uHfhaeUnCtzt9Tx1LQAn+vaQsrV1M9G69zHK38QLrVK3tKsD0zjfk3n4FnWNiavQTxPGilMHvr\nu1i9MtHv5XbVB55+BFh4pO3MWQAIhRQuXDq+Q/HutoPdbT97uPeZLBY8rC7X7vncYZBMm4glDBTz\nLjSAeMJoGJtTKrm48/ZBd2fH1igVq7h4ObQfeCpDcPlaGNWKh1pNIxyWYy8iKCWYmw9hxtVwXQ3T\nEo4JIyIioq5iINtn5bKHSlW33UN21N5okVEPZB1b486tKmpVf96n1n4Z4vikCbumoZTAPFTu2Xbk\nkNT36LXw0GMOHlefPvHawiUb6a0yvEOB7N4raAA7U1F4ZoCZphbdfDX8QBYi+M8f/Vv48L/7D7jy\nnW/BCUcQKeZRTsSxMxNHuFRCNRYLYtVd02rm7EnsbLWeo5rPecjt2khlhv+zZxiCVKb1h2ZjxW7Z\n3Xl9xca1dzT+XocjCuHIkcd6Gvm8i91tB5WK3t+3PDVjweA2CCIiIuoRBrJ94Loa5ZIHZQDVitdx\nELvncCJDaw3X9Uv1VMAdi11Xo1b1YJoCq0UGtFzysLVho1rxYFqCsQmzXm7YvO7l29X9zqh7J9Vb\nG07D6JBwRHBhPgQrpJDOmC0DEFUveTyqk2ZOrcSyFUyuFgHdGC96AFxTsDMdRzkVXNZOebplllgA\nmPVy6K25Wfz7//FTuPzaa3jgm38Kw3WQ2drCX/vPX8UP/pev4Y8//rexdvlSfxfeZUdnzp6Ee0zZ\n+Mqyg0TSHOlgrNKmI3GtpqG1PjaTWil7uH2z2jD9ScOfVVsuebh6I8xMLBEREfUEA9ke2960sbnu\n+FlGtC4BPY4IkK43ZcntOlhftffnoabH/M7F/T5R1FrvB5l72dNIVOHi5dB+OXAh7+Lu7UPlio7G\nyh0b2xEbl69FGoLwWs1rOd7jcKkn4O8bvv12DdfeEUYorDA3H8Lqst95V8PPOs1fDjW8H6fNwgIA\nXA+TK8WmUTsaQCVhYWM+dbrjdpGnpG3Js2MeBPROyILSGvFcDuV4Gje/590opjJIZHfwQ//pq3j2\np38K+rh5T0PgcfVpYAEnzs7G4gqFNmNqRIBi0UMkqrC1YaNU8GCYwPikvwcUAHJZB5vrDmxbI2QJ\nJmcO7hsGhoGW+/Tv9eugtV9F0WKEMaD9EUfFgodEcnjeCyIiIhoeDGR7qFR0sbnuNARkxyVj90bs\naO2PBBUBojGFsQkTxYKL1buNJYDZHT8jOXuhv02GCjlvP1N60DHYw8qdGuavhKG1xtrdWstyzWoF\n2NqwMTVzsGbXxX5AfC9OPbsdixtIpgwkEhFUKh5EBOFI4z6802Zh9yR3Wnf1FQDhktPyvr4TQT4T\nQXK3Uu9c7PMEyE5GGx564+VXUEhN4uUf/hA8QwGiUIkmsD1zEVPL61i/NNvnxffGSUuNp2YsFPLV\nlveJ+Bnbm28cNGWzbeDu7RpCYYFpAqXiwRtfq/lN2uYuWkilB//rVWuNWFwhn2sM5EX8WdbHXSQr\nl9rvUwf877BqhYEsERER9cbgn2kNsb0GMp1KpY36SbULx/aD2EjUD862NpyW+9hyuy6mZ3RfSx+3\ntpr31AFAqejBcfw7nGNGqmZ3XUzNHPw9HJYTVVs79sGjRQmiseYT5bMGsQAQLdbaj9sJuKz7sN3p\nGAQaid16MCaCnckoSkdKnrUIXn/gh+Ed3mCsFDwohCrHRCRB0hqxfA3hsgPHUiimw34Qfg97P/9O\nAtpQWGH2ooXV5eYxNVr7wVirjGWtqlFrFf9qYG3FHopAdnXZbpmNTmXUPUfl3Ou7TRRghQbnc0JE\nRESjZfDPtIbYcXvvDmcgRfxsbCSqcPvtKmxbIxJRiCfUfkbEbjFSZo/jaoT6GMi6xyQjvb0OpTgm\n+3x0X6sSTM+aWF9pDtZbPTcSbR/InCWAFc8PmqyK/w802oy10UAgo3baEsHOTAK7U3Eo14NrqpYd\nlL/74APwVKblIZTXZ4YCAAAgAElEQVQ7eGXF4nqYvZmDabtQ2s8yZzbLWLucQi3S2VdXp9nZVNpA\nueQht+tffNp7+y7Mh7C50Rzg3ovn+p//4zpvB61a9ZpmwwL+vz0Wb72X/bBoTB37eTUUmI0lIiKi\nnmEg20OJlPLL71qcKF68EkJ2x4VT04glFJQBrB0qHS4WPJSKVVy+HkYkohCJtt7HJwJYbbr0HuY6\nGoWCC9fRKBU9lIr+sRJJA9NzVsM4jnuJJxSyO80pKlFAueyisK5hWoBda/38RIv9g5kxC6Gwws6W\nA8f2yx1zWReu0xjwJ1NG27EfZwliDdvF7M0slKuhDjWVbrev2bYGL0DRSuCq9oHD2997P65+ewOe\n0fyx9wYw4EpvlfeDWAD+/2qNibt5rFwf6/g4nTSCEhHMXgghM+6hmHehlCCZ9sfUZHedlnu476VW\n9VpWC3RDIe9ia9OBW/+sTEyZLRuuHeforNg9WgOlgodkyv+ucB2NaFzBshqPr5Rg5oLV8L21JxoT\nzF0MBd6QjoiIiEYXA9keSmdMZHdc1A7NjBUBpmZMxOMG4nH/JFdrjddfrbQsHd5cszF/JYzJaQvF\nQrXhMSL+iBrH0djdsVGr+iec6YzZkAnKZR2sLrcuB87nXFQqHq7d13l30YkpC4Wc21BuKeJnYNbu\nHp9VNS1gqs0ooVjMQOzQif/4pMb2po181oNSQHrcQGas+Vf2fU896M8UPYOxtSIMR+8Hrce9Exq4\ndyecAaSVwvZ0EumtEuTQv9ATIDseOeaZwYjnag37fveYtgfD9uBanf8MOm0EFYkoRCKNxx2bNFEs\ntN7zfZyTXBw6iZ1NGxvrB5+z7K6LfN7F1RvhpmDznutrUzohCnjztQo87+BCUmbc3/pw+HsinTER\niShkdx24DhBLKCSSCkYH5d9EREREZ8FAtoeUEly+FkYu66KQc6EMwdi40ZSlcRy0bZpSKft3hCMK\nl6+FsbFmo1L2x9lMTJmwLMFbb1T3n18seNjZdHDlRgSmKXAc3TaIPXh9jULe67jTqmUJrt6IYHvL\nRqnowbIEobC0nceZGTOgoRGN+Q2aOs3SGIZgaibUsJ/2qKWFReDpjg53rFjB7ryjtADlRMClxVrj\nnX/xIu7/1rdg1Wzcvu8GXnz/w6jEj58Jm52MQnmev5+2HsTkMxHkx6PHPi8Ius0PRI65715OM3M2\nFjMwc8HC+spBx/B7PieuTpwh7YTn6YYgdv921x9XdZLGb/GEghLgaG2FCFDIuXCObCHY3Xb3P8OH\nhSMK07MDVGpPRERE5wID2R5TSpAZM1tmEvdp3TbQNA+VsIYj/rFyygHEn5m6smw3BMFa+4Hx5rqN\n2QshFHLHdF3ae47nl0ECnZdBmpY0nLzeuVlt+W9QCognja7vlXv45Sfw6GfLZz+Q1jBtr21mCodu\n3guetmfi8MxgM04Pf/n3cfXVV2HZfrTxjpdexqXX38AXf/ZnYIePmWu7t592MgbT8eCYBvQAlhUD\nQCEdRnqr3JCV1QBqYeNM7/9pZs6mMyZSaQO1mkZ2x8HutgscSmgKAK/eaTyeUJi92JvArlbTbTt8\nl4sna9gl4l9ou3Or5jdQq3+nTExb2Fht3fhqd9sZqtFCRERENLoYyAbIsf1RHeVy+xmWE1N+Ga7W\nGndv11AsHOy5LeTan7gW8m79efdehyi/c6vW/p64StmDFRIkkp1nT9t1TdbofhXu0sIi0IUg1qo4\nmFrO+02d9PFzfvOpEJyIiVIyBNcK9kQ+ns3i2re/A/NQbbfheQhVKrjvpZfx7R96zz2PoQ0Fe8DL\nP3MTUURKNsLlempQ/G7RmxeSZz72aWbOigjCYf8CzviERqnkwlCCWMJ/H23bb+7UywZPpiEdXfTq\nVCiscO2+MOyahqf9DuKVcvtg2fNOvleYiIiIqBcYyAZEa41bb1dh11qfGCoFTM6Y+9mPcslrCGLv\nRdX3sSWSChtrxz/WMASxmODmm1XUatqfYasApWxcuRbuqEQyM2ag0KIDqqrPwu2GrmVhAYirMXMr\nB+XpjkqKd2fi0AMS+E2srsEzDBydCWM5DmZv3e4okB0KIli/lEKo4iBcceCYBsoJq2VH5tM6Takx\n4AeNR8frhPowasa0BLG4QqnoNe2XH588+de542jkcy48TyOeMOrzmFs/dq/ZGhEREdEgGIwz83Oo\nXPK7gbaSGTNw3/0RjI0fNEUq5DufSSviN2YBACvkdzRtd+6fSClcuR7G1objN6WqJ3m154/ZWWkx\nW7OVWNzYfx1R/h/DAOavdN5E6jhLC4tdC2IBIJavQnRzEHv0LdYAynFrYIJYACglE5AWmzVdpZAf\n67yb71AQQS1qIT8WRTkZ6moQu6cbM4f7aW4+hFhc7X/WlAKm50zEEycLMgt5F2++VsHGqo3NNQe3\n3qxi9W4NIsDMBavhrRYBQmFBZpzXPomIiGgw8KwkILat285ZdV00BX/HlSuaJuDubfPUfhZ2bOLg\nRzsxZSGeNJDbdQANJNPG/izWvdfJZVsHyuWSB8/VbUuHD5uYspAeM1EuelAG6ifbZws8Is99DJ95\ncvZMx2jFcDxImx+AB/iXeDTghAxszSW6/vqnldrawiPPfhmm4zSVQntK4dUfeCiopQ21vWD2NNnZ\nfjMMwfyVMBxHw3U0QiGBnHDMjef52xoOf+a1BnK7LpIpA6m0iXBEIbvjwLGBeFKdqFEbERERUa8x\nkA1IJKpaj70QIBpvPllMpQ1sbTR3KxUFXLnh73GzbY1IRLWcsxqJKET60FnUNP35m92wtLAIPNmV\nQzWpRi1oKTcFs1r8Zk5aCRxLoRYxe5IFPA3xPPzNf/vvESkWGwJYDaCUSOBrC48hP5YJankj4bSl\nxkEwTTn1iJ9S0WvZ30xrf5xPPGEgHGY3YiIiIhpcgdRLisiviMh3ROQlEfldETl3Z9/hsEI8qZpi\nJMMUpDPN1xeskMLsRb/cT6mDksL5yyGYpkI05mdRWgWxnUimjJadjiJR6Sgb2229LvesxkxUoya8\nQ/80T4BaxEQxHUYpFUYt2t39mGc19/ZNmHat6UPrKYU3vv97sXrlciDrGjXDVmrcdeznREREREMg\nqIzsHwL4Ra21IyL/BMAvAvhfA1pLYC7Mh7Cz5WB3x4X2NBIpA5NTVtvyvVTaRCJp+GM2BIjF1IlL\nCtuZnLFQKnl+yXN9jIhSwFyPxoi007cgot5IKLldRiJbA+CPe8mPRQYqeD0sUiq1LIc2PA/xfLH/\nCxphw1RqfBqxuGq5lUAESGXY0ImIiIgGXyAZWa31H2it6zM18A0A80GsI2gigvFJC9ffEcGNd0Yx\nMxeCcY9SQaUE8aThdxjt4n41wxBcvRHG3MUQxicNzFywcP17IqfO8J5GXzNhWiO9WUZmqwKr5gLQ\nsCOm32Z5QK3PX2zZ5Mm2LCxfv9q114kUS0hvbUHce88gHnWjmp1VSjA371d47F23EfG3MMQTg9PY\njIiIiKidQdgj+0kAXwh6EeQH1smU0fcRG71q6HScsfUiErtVqHpWKlTzMHUnh7XLKb+keAAVMhm8\n/sC7cOMv/wqW7XeTdkwTubEx3Hzn95z5+Falgv/u957F3K3b8JSCpxT+9Ec/gDff9f1nPnavGLaH\neLYCw/FQiVsoJ7rf2XiY9s2eRDJlIvoOA7mcC8/VSCQPmsARERERDTrRnc50OemBRf4IQKvo5HNa\n6y/WH/M5AO8B8DHdZiEi8nMAfg4AZqzoX/udd36wJ+ulYASR8RJXY/717f0gds/eqJ2NS6m+r6lj\nWuPKq6/hnX/xAqyajbe+7368+tC74VpnD74f/Z3fQy2UQi0Sw/jGXUwvvwVPCf7oJz6O9fnBK5oI\nF21M38kBAJT29zjbYQNrl9PQPcisv/vHd/GTn/rtrh+XgvX+V579c631iAxfJiIiOj96Fsje84VF\nfgbApwD8qNa61Mlz7o9m9FP3PdLTdVF/fOHzn8CLzwTT48usOph7O9sUyAKAbSncvTFis1g7kFnb\nxdhGFVoJtDKgHBuRUgE/8NVnsXLtCp772H8f9BIbaY3513dguI0/RE+A3cko8hOxnr30KGZnzzMG\nskRERMMpkNJiEfkIgF8A8Dc6DWJpdCwtLALPBPf6rtW6dFrDz+idO1ojtevAMw++DjzTQiWexPL1\n70VqdzXAxbVmVV2I13wlQmkgkav1NJAd9UZQRERERMMgqD2y/wJAGMAfir+f7Rta638Y0FqoTwal\ncY5WgvxYBMmdSkNWVguwO9m7AGhQWVUXGtI0fckzTKxfvI5ievBmiepj9sEed183jereWSIiIqJh\nEFTX4vu01pe01g/V/zCIHXGDEsTu2Z2KYXcyBtcQaADViIH1Sym/c/E5c9x+UuW5eOW9P9TH1XTG\nCSm4pmoaeeoByGfCfVvHoP1eExEREZ0X5++snfpqYE/0RZCfiCI/EQ16JYFzQgackOGX6x6+w3Nx\n99oMKol4UEtrTwSbcwnM3so1BrPiN+zqp6WFRTaCIiIiIuozzlqgnhnYIJaabFxMwjUVPAE85TdN\nyo/HsDOdDnppbSWyVWgAcviPBubf2MXl72xh5u0sQhXn+IN0yYvPZPj7TkRERNRHDGSpJ3hSfzbK\n8ZBeL2L6ZhZjqwWYNbenr+eEDCzfyGBjPoWtmQRWrmWwPZvo+kzWbornqk1fYIeD2kjFwczb2Z6/\nd4fx956IiIioP1haTF3FE/mzM2suZt/OQjwNBSBSdpDIVrF+KYVqrIdlsyKo9Lkst9cEQHqjiK2L\n/ZsNzFJjIiIiot5jRpa64qHHHAaxXZLZKEHVg1jAD8aUBiZWC0Eua+CUE6GmZk9HCYBowe7Hchqw\n1JiIiIiotxjI0pktLSzicfXpoJcxMiJFu2kUDgCYNQ/K9Xr2usrxkFkrYu7NHczczCKar/Xstbph\neya+v68XQNugVt0r2u0hBrNEREREvcFAlk7tfU89yBP1LjKrLjLrRYhuE3kJ4PVoz6pyPMy9tYvU\nTgWhmodI2cHk3TxSm6WevF43eKbC8nV/L28+Nbgl0UsLi4g897Ggl0FEREQ0UrhHlk5laWEReDro\nVYyOWK6KiZUCRPvlsHvdePd44pfS4piZr2eR3KlAebrhNZUG0ltl1CIm4vkaxNMopkL+OgalCZQS\nFNNhVCMmErndlg9xzODX+pknZ4GFRfzSs78e9FKIiIiIRgIzsnQiD7/8BLOwXSaexsRKAUofBK97\nwawn/p9a1MTWbO/muUaLtdYluBqYWs4jnq0inq9h8m4BU8t5oF3WOCBOSMExpam82AOQG6BZwfzs\nEBEREXUHA1nq2NLCIh79bDnoZYycUNlBq02xAsAOKaxczWDtchra6N3H1TFVyz2me42m9pantL+H\nN1LsfwOlY4lg41IKniF+8A//TzkZQiETCXp1DVhqTERERHR2DGSpI8OeSQpVHGTWi8isFf3AcYDo\nYz6FrmnACRs9X0N+PAp9JJg+rnlSrDB4jaDssIk7N8awNZfAzkwcq1fT2LyYHJwy6EM+8+Ts0H+m\niIiIiILEPbJ0rFE42U5vlJDaLkPqkVlyt4LceBTZqViwC6urRUx4SiBH9qh6AuTH+pNNrMYsbM/E\nMb5eAqABDTiWgml7++/bHg3A69Fe3TNTglIqHPQqOrbEfbNEREREp8KMLLU1CkGsWXWR2i7vl8fu\nlcqmtsuwqgOSmRXB1kwcGvUgsf4nn4mgEu9fN95iJoLb7xjD6uU07l7PYPVqpmXJsxagkB6eYHHQ\nLS0s4uGXnwh6GURERERDhYEsNRmlhk6xQq0powgAooFoYTD2ecZyVUzdLewH2hDADhvYnYr1vyxW\nBHbEhGsZ0EqwPp+CpwSeAlzlZ4m3Z+Jwwizm6KZHP1semc8cERERUT8wkKUGo9bQSQua9n4ed3u/\ntepYrDRg1VwkspVA1wb4Jce37xvDxoUktuYSuHPfGIoD1jxplDCYJSIiIuoMA1kCMPxZWPF0y5Ew\npWSo7XOOu69f/I7FzRG10kAsNyANlZSgkvDnx0ZKNpLbZYRL9sCN4BkVLDUmIiIiujfWB5IfwA5p\nFjZcsjG+WoBV86AFKKbC2JmJQ9ebEbmW4TcxWis2PG97Jg7X6n034HvRCm0DQj1ADZWMmovZW1ko\n128EBfGbVK1dSgEDtM5R8ehnywAbQRERERG1xYzsORZ57mNDnYW1qg6mb+cQqnn7TZziuSom7+Yb\nHlfMRLB8YwzbM3Fsz8SxfGNwymNrEROeIU2jbjwBCn3qWNyJyZUCDEdDaf9LQ2l/pFF6azgvgAwL\nzpwlIiIiao2B7Dm1tLCIzzw5G/QyziS1VWlq5KQ0ECnaMGy34XbPVChmIihmIvDMAfq1l3pDJcNv\nqOTJwdidch87Fh9HuR7CZaepgbHSQCJbDWRN96Rbl5oPI86cJSIiImrG0uJz5guf/wRefCYT9DK6\nwqo1B1cAAAHMmjcQpcOdsCMm7tw35gfgrkYlZg7W2uulxE1p4/07B4dVcTC+WkS44gACFJMhbM/E\noY0BunhxSpw5S0RERHRg+M/uqGNLC4sjE8QCQDVitQyjRPvja4aK+A2ViunwYAWx8LPZdshoWf5c\nTA7OPFnleJi9lUO44l/gkHrDrJnbeVhVB6mtMpI7ZSjHC3qpp8ZGUEREREQ+BrLnxCiWJuYmItCq\ncX+pJ0AhHR6s8uERsDmX8OfJ1lPgngCOZSA7GQ12YYckdiuA1g1ZegV/L+/s21lkNkrIrJUw//oO\n5t7cQSxXHcryY86cJSIiImJp8cgb5RNe1zKwciWF8fUSwiUbnqGQGwsjPz44wdWosCMmlm9kEM/V\nYNZc1KKmP77o0Oggq+rAqrpwLAO1iNFyrFAvhSoOVJu4dO/2vRWFah4mVgoIlSPYnYn3ZX3dxlJj\nIiIiOs8YyI6wUQ5i9zhhE+uXUkEv41zQhmrdSdnTmL6TR7hs+8Gr1rDDBtYupfq6N7UWNREt2m2D\n2aOUBlK7FeQnonCHNIO/tLCIP/nlKJ5/4J8GvRQiIiKivmIgO4LOQwA7CiLFEu57+RWkdnawfvEC\n3vre++Fag9Gp+CQymyWEy/UAsl6qa1VcjK8VsXUh2bd1FDIRpDfL+72pOqEBhEo2yqnB2et7Upw5\nS0REROfRcKYhqK3zGMSK60Hc4WrgM766hr/9//5LvPv55/GOl1/Be//4OXz0X/4rhEuloJd2Yols\ntSkLqgDEc7W+7kH1RCC6OYg9LqgVDYytl4bu96eV8/jZJyIiovOLGdkRcR5PYs2ai4mVAsJlBwBQ\njZjYupCAExqMrr/JnV1MrqyglEhg7dJ8w57RR770ZYRqtf2/W7YN5bp46GvP45sf/lAQyz018Y4J\nVk+SHj0jdUzQvHdPqyDXcDykN8tDu1f2sKWFRTz38a/h6598KeilEBEREfUUA9kRcB6DWKPqYu7t\n3YYMXLjiYPZmFss3xqBVfxsNNdAa7//SV3D11dfgiQACVGIx/P5P/QRKqRTC5TJS2ztNTzM8D1de\n++7QBbLluIVYwW4IEjWAWsQE+vhz8JTAsRQsuzG7qgFUoiY8BcSKzbOHFYB4vjoSgSwAfODpR4CF\nR1hqTERERCONpcVDbGlh8VwGseJpzN3cbSojlfp9sXwV4ZKNyTs5zL69i/RGCaqPpaPvePElXHn1\nNZiOg5BtI1Szkcjm8OgXfw8A4Kn2HzvXGIxs8knsTMfhGY2jebQSbM32OTAUwdZswn/9+k0e/AB3\ney6B7WP36wZ44aNHzuN3AxEREZ0fDGSH1Hk+SY3lqhCvdeghGojma5i+nUOsYCNccZHaLmPurV0o\npz/B7P1/8QIsx2m4TWmNsfUNRPMF2OEw1ucv+tnaQxzTxHff/UBf1thNbsjA3esZ7E5GUUxayE5E\nsXw9AzvS/4KPatzCytU0CukwKlET+fEIVq5l4IQMeIZCNWriaAGyJ0AhM7zNno6ztLCI9z31YNDL\nICIiIuo6BrJD5qHHnHMdxAJAqOq2/cXVAKIFv4PuXpioNKAcjdR2uS/rM20HGkA1EoNrHARzWgSm\nYwMAvrrwOArpNGohC7ZpwjFNrM3P45Uffm9f1thtnqGQn4hh82IKuckYvADH2ThhE9tzCaxdSWN3\nOg7XOlhLPu0HrLr+xwNQCxvIjvDs4Q88/ci5/84gIiKi0cM9skOEJ6M+O2zAQ/NVGA0A4mdlj1Lw\nA9zd6e6vR7kextaKiOVrEA288CMfhtIKnmlCQzB99y18z0tfRy0SQT6TAQCUkwn87j/4JOZu3kIi\nm8XW7Ay2Z2a6vzjaFy7ZmFgrNu7lFaAatfq6lzcoSxzRQ0RERCOEgewQeOgxB4+rTwe9jIFRTIWR\n2ShBu3o/KNnvStti/MoetxdZQq0xczMHq+buv64biuFwEfPGhatwTAt3r082dC6GCFauXun+mqil\n9Ga5eUyQBpK7FWSnYsE2COuTpYVFfMn7NbzwZX71ExER0XDj2cyAYxa2mVaClStpTKwVESna+7cf\nF4Z4AuTGI11fS6Rkw7TdpqZTDa9tmNicu4L1i2Ndf33qnFVz2t5nON7AjG3qtcfVp4EFMDtLRERE\nQ417ZAfU+556kEHsMdyQgfVLKdx65ziKqVDLx+zvgxRgdzKGSqL1446yqg6mb+dw6dUtXHx9B8mt\nMtBmRqlVddHUPajVWpQfLJ03Zs3G2No6IsVi0EtBLdzc6GlPT7L1A47fL0RERDTMmJEdQEsLi8DT\nQa9iSIggXG6eDbqnmLCwPZeENvxHiKcRLtvwlPhzTo90DjZrLmZvZve7IivHQ2azBMt2sT2baDq+\nHTL8B94rmNU4Nxm/Pe/6xjfx7ue/AU8pGK6LO9ev4as/9jhcy+r+i2kN8bRfHiytfxuykzFEStmG\nPdR+pj56LsqKW9kLZpmdJSIiomFz/tIQA+zhl59gluQU9DExSDEd2Q9i47sVzH93G1PLeczczuHi\nG7uwqo3lpsntctNoH6WBRLbacnxPJW7BsYyGOHYvE7zHEyA7cb6Cpavf/g4efP4b/izdWg2G6+Li\nm2/h4a/8QcvHi+shsVNBerOESLHWNgPeSny3gvnXd3Dpuzu49N1tpDdLEMdFLFdFNF+FeP6xalET\n65dSqEb8n5djKuxMxZCdHN2OxZ3i9w4RERENG2ZkB8TSwiLw2f6Mhxk1xVQY5ma56aqMB6CS8LN/\noYqD8bWi3+ynHiOJ52H6Vg7L943tZ/HaZXc9EVg1F9WjJagiWLuSwsRyHtGS/9zDDai0AFuzCZTa\nlD+Pqnd980+bZumarosrr30X36hWYYcP5raGyg5mbmcB7Tfr0gLUIibWLqWO7SYsrsbESgGxQm3/\nPRcPSG2VkdosQ6v6z0IDmxeTKCdCqMYsrF7NdP8fPAKWFhbx3Me/hq9/8qWgl0JERER0T8zIDgBm\nQ84mPxaFEzL2OwXvzQfdupDYD1ATO5WmsTwCQHka4dJBwGWHjZZVwqI1HKv1x8UzVMts694t1Vhz\nCfOoixZLLW/XIghVqodu0JhazkN52J/9q7R/4SG5W2l4XKhsI5arwqy6gNaYvZltCGL3KO1/sRke\n9o87uZxvmVGnRpw5S0RERMOCGdkA8YSxO7QhWL2aRjxbQbRowzEVCmMR2OGDX2/D9VrvoxVAeQcB\nTm4iuj8Pdo8nQDluwbXa73E17XbHFxiOd+xzR9HqpUu4+uqrUEdKhB3LQil5sNfYrLlQbnOAuVfO\nnR+PQjkeZm7nYNZc/4KA1rBDRlO36HuJ5WsojHW/c/Uo4sxZIiIiGnTMyAaEQWx3aSUojEWxMZ/C\nzmyiIYgFgFIyBK9F1CMaqEYPmg/ZYRPr8ynUQmq/43ExHcbmheSxr1+JWa37PdWDrvPmhb/+MJyQ\nBa+eifb3pJr45oc+CK0Of+3cOxSdWC3Aqrp+ptXTfsa2/veOaezvlaXOLC0s4qHH2o8sIiIiIgoS\nM7J99vDLT+BR7oXtu2IyjOROZT8g2tu/mp2Iwjuy77Uat7Byfczvgis4KAvWGtGCDcP1UI2aDcFy\nfiLqN4Ty9H5o5omf4dXG+btelB8bw+/9/Z/GA9/4JqbvLKOQTuGVH/lhrF2ab3icE1JwTQU5ktHW\nAAzbxczbWYQrzfuW9xpFd5yRlYP90tQ5zpwlIiKiQSX6BN1Bg3Z/NKOfuu+RoJdxaszCBszTSGQr\niOVr8AxBPhNFNd5ZcGNWXcze3G3oaFyNGvWGRH6gatgu0ptlRIs2XFOQG4+ilAq3PygBAKyKg9lb\nOX+EzqGvo8NNs1oFrJ0EsnsXLPKZCHZn4v5xXY1YoQbleqjELNgRXs/rxKgGs+9/5dk/11q/J+h1\nEBER0ckwkO2DyHMfw2eenA16GQR/zIvh1hs3ddqASWtceHMHpq2bsobViIE1dsE9M/E0YrkqEtkq\nQmXnnnseNIByzESo6sJw/e+woz9NDcAOKWzPJPYbboXKNmZu5w5mJAlQSoaxNRc/dw25TuNL3q/h\nhS+PVuDPQJaIiGg4jdYZyQBaWlgEngx6FeeHVXUQz1YhGiimQqjt7X/1NCZWC4jna/UsnWBnOoZi\n5t7Nf0zbg3EkiAX8wClccWFVHGb1TsGwXSR2qzAcD5W4hWLaL/9uFcTuxZ0Kfsm2pwTbc0lE81WM\nbZSa9svuXWRYv5w+6CitNabv+B2SDz8wlq+inLCYPe8AS42JiIhoUPDsu0e+8PlP4MVnmKnrp+RW\nGZnN0n55amK3gmI6jO3ZBCZWC/vdiP3Zohrja0W4pkIlcWjGq+eXnZq2h1rERCVmQnRzEHtYpGQz\nkD2hSLGGqTv5/Z9HPFdFasuAYwpC1RbZVQEK6XB9f7KFQjoMbSjE87WWTZ+0+POFx9aLkPpztPhj\nlI7a65DMQLZz7GpMREREQePZdw8sLSwCzwS9ivPFsF1kNhszc6KBeLaKYiKE+JGROoAfwKS3yvuB\nrFlzMXMz66K2aSkAAAzmSURBVDds0n4wVAubWL+UrAdBza+rAbjnsJnTmWiNybuFhp+V0oBVc1GN\nhqHFaXivNQDHUv6II904t9drMb8X8H9WY+slCOqBct6+55roZBjMEhERUZB4Bt5lbOgUjGixdaAi\nGvvlxK2Y9kGd6eTdPAzXH+8iQH3Mi4PUdgWbc4nWx1CCcjLU6h5qw6q6LUfhKA2Eyw62Z+Nwlfgl\nxAI4psC0PcSKNqIlG+OrBUzdyQNaozAWaRqrtHdkhYPMrhz6c5Q/YonzZU9jaWGR33lEREQUCGZk\nu4Qnc8E6Lp/mGnIwr+XIcyox/yOgXA+hqtsU6OyVnS7fN4ZNrTGxWtzP1nqGYGM+dbAHkzqij3m7\ntBIU0xEUU2FYNRfK1Zi+nWvK3kZKNjLrRdghA4V0GIls1b9zf/ZR+47Gh38NtPgzgIspXow4C2Zn\niYiIqN8YyHYBg9jglZMhYK3YdLsWoJQOw7UUxtYPSo81AK2A7GTs0A3tju7fUUpHUEqFEao40CKw\nwwY73Z6CEzJazo71BCjsNd8SgR02kdiptDyGaCC1U90PinenovAMA64hEE9jcrUItMj6An6AW7MU\nyskQKnELlZjFn2MXMJglIiKifmIgewYMYAeHZyhsziUwuVJouH1nKgY7bMIOm3BNA+mtMgzH3W8Y\nFM9WIZ5GORlCLWw0ZWW9etOgfSIHnZDpdESwPp/C7K2s33ypHm8WU+EWmdH2wShwsG85s1HG3etj\ncC0FeBoazRc19ngC5MciKIxHz/bvoCZLC4t494/v4ic/9dtBL4WIiIhGXKBzZEXkCfjDaaa01pv3\nevwgzZFlEDuYlOshWvAbO5XjIT+waSG+W8H4WnE/ENIClGMWImUHov19sp742cPVy2logxm7rtMa\n0aLtj9+JWXBCRsN946tFJHJVQLcvE97jCbA7FUO+HpyGyjamb+chnm7YG+sJ4FoKK1czLAnvsWHJ\nznKOLBER0XAKLCMrIpcAfBjAraDWcBoMYAebZ6h7Nu5RrofxtWJTh+NoycbmhQQMV8Os+VnbcoJl\npz0jgnKi9d7U5HYZ8Vy1qXvx/lOPHko3dpV2LIHhriNatFFITcAOxyFao5QMIZ+JMojtg73vymEJ\naImIiGi4BFla/M8A/AKALwa4ho499JiDx9Wng14GdUHkmA7H0YKN7blEn1dER6V2qk3zYff6dWm0\nnjNbqnePjmezePw3/w3MWg2m48A1TeTGxvCVv/OTcMJs6tRv3DtLREREvRDI+B0R+SiAZa31i0G8\n/kktLSwyiD0njuuoS/2j2jRqAoD8WBieHAS1ngC58eh+afIjz34FkVIJIduG0hqWbSO9tYWH/uvz\n/Vk8NWElCxEREXVbzzKyIvJHAGZb3PU5AEvwy4o7Oc7PAfg5AJix+t+chSdgo6ddOasWoJgOt7yP\n+qscMxEr2E2ZVyeksDuTQCkVQSxXBerNuOyI/1Vm1mqYvnsX6sjef9N1cf2vvo3/9sFH+7J+asZS\nYyIiIuqmngWyWusPtbpdRB4AcA3Ai+LvPZwH8C0Rea/WerXFcX4DwG8AfrOnXq33KAawo0srwcbF\nJKaW8w2358aj7Eg8IHan44iUshBPQ6GefRVga9Yv+65FTdSiLb6+jv2GCK6xHR1gqTERERF1Q99L\ni7XWL2utp7XWV7XWVwHcAfCDrYLYoDCIHX2VRAh37hvD9kwcO9Nx3L2WQXYqFvSyqM4JGVi5lkF+\nPIJK1EQhE8bK1QyqseMvNDjhEDZnZ+EdadDlGAbeuv/+Xi6ZToDfsURERHRWgeyRHVQPPebwBOsc\n0YZCMRNBYSwC9/DoFxoIrqWwOx3H2pU0tmcTcMKd/Yy+tvAR1CIR2JYFDcC2LBQyGbzw19/f2wXT\niSwtLOILn/9E0MsgIiKiIRXoHNmT6uUcWQawRKPDsG1cffU1JHaz2J6Zxp0b16EVr9sNqiBLjTlH\nloiIaDgFOX5nILzvqQfxgad7ExwTUTBcy8Ib7/r+oJdBHeK+WSIiIjqpc52iWFpYZBBLRDQAlhYW\nEXnuY0Evg4iIiIbEuQxkH375CZYSExENmM88OcvvZiIiIurIuQtklxYW8ehny0Evg4iI2mAwS0RE\nRPdyrgJZnhwREQ0HlhoTERHRcc5FsycGsEREw+czT84CbARFRERELYx8RpZBLBHRcOP3OBERER01\nsoEsGzoREY2OpYVFPPzyE0Evg4iIiAbESAaybOhERDR6Hv1smRcoiYiICMCIBbKR5z7GkxwiohHH\nRlBEREQkWuug19Cx+6MZ/dR9j7S8jwEsnRftGt/wM0Dn0VkbQb3/lWf/XGv9ni4th4iIiPpk6DOy\nzMLSefFLz/76sSftv/Tsr+NXf361jysiCh6//4mIiM6noc7I8gSGzoPTZJz42aDz5ld/fhWVD/zO\niZ/HjCwREdFwGsqM7Bc+/wmeqNO5cNqySc7dpPPmM0/O8r8LRERE58jQBbJLC4t48ZlM0Msg6rmz\nBqMMZuk8YjBLRER0PgxVILucmQp6CUR90a0g9LmPf60rxyEaJpw5S0RENPqGKpAlGnXPffxrXc2k\nfv2TL7EBFJ1LnDlLREQ02hjIEg2IP/nlKL7+yZe6ftzTNMAhGhUMZomIiEYTA1miAfDuH9/F8w/8\n054dn/tl6TxjqTEREdHoYSBLNAB+8lO/HfQSiEYaS42JiIhGCwNZooD1K1vKrCwRS42JiIhGBQNZ\nogD1O7j8k1+O9vX1iAbR0sIi3vfUg0Evg4iIiM6AgSxRQILIkPZyHy7RMPnA048wO0tERDTEGMgS\nBSDIMt8veb8W2GsTEREREXUDA1miPgu6vPeFL5uBvj4RERER0VkxkCXqs0Eo7/3Vn18NeglERERE\nRKcmWuug19AxEdkAcDPodZzBJIDNoBcxpPjenQ7ft9Pje3d6w/TeXdFaTwW9CCIiIjqZoQpkh52I\n/Det9XuCXscw4nt3OnzfTo/v3enxvSMiIqJeY2kxERERERERDRUGskRERERERDRUGMj2128EvYAh\nxvfudPi+nR7fu9Pje0dEREQ9xT2yRERERERENFSYkSUiIiIiIqKhwkA2ACLyhIhoEZkMei3DQkR+\nRUS+IyIvicjvikgm6DUNOhH5iIi8KiKvi8hng17PsBCRSyLynIj8lYj8pYj8o6DXNExExBCRvxCR\n/xj0WoiIiGh0MZDtMxG5BODDAG4FvZYh84cA3qW1fhDAawB+MeD1DDQRMQD83wAeA/B9AP6OiHxf\nsKsaGg6AJ7TW3wfgRwD8T3zvTuQfAfh20IsgIiKi0cZAtv/+GYBfAMDNySegtf4DrbVT/+s3AMwH\nuZ4h8F4Ar2ut39Ra1wD8WwAfDXhNQ0FrvaK1/lb9/+fhB2UXg13VcBCReQALAP6/oNdCREREo42B\nbB+JyEcBLGutXwx6LUPukwC+HPQiBtxFALcP/f0OGIydmIhcBfADAL4Z7EqGxj+Hf6HOC3ohRERE\nNNrMoBcwakTkjwDMtrjrcwCW4JcVUwvHvXda6y/WH/M5+KWfv9XPtdH5IyIJAE8D+Mda61zQ6xl0\nIvJjANa11n8uIo8GvR4iIiIabQxku0xr/aFWt4vIAwCuAXhRRAC/NPZbIvJerfVqH5c4sNq9d3tE\n5GcA/BiAH9WcG3UvywAuHfr7fP026oCIWPCD2N/SWv9O0OsZEu8H8OMi8jiACICUiPym1vrvBrwu\nIiIiGkGcIxsQEXkbwHu01ptBr2UYiMhHAPwqgL+htd4Iej2DTkRM+E2xfhR+APtnAD6htf7LQBc2\nBMS/0vSvAWxrrf9x0OsZRvWM7M9rrX8s6LUQERHRaOIeWRoW/wJAEsAfisgLIvL/BL2gQVZvjPU/\nA/h9+M2K/h2D2I69H8DfA/DB+u/aC/UsIxERERENCGZkiYiIiIiIaKgwI0tERERERERDhYEsERER\nERERDRUGskRERERERDRUGMgSERERERHRUGEgS0REREREREOFgSzRCBKRr4jIroj8x6DXQkRERETU\nbQxkiUbTr8CfhUpERERENHIYyBINMRH5IRF5SUQiIhIXkb8UkXdprf8YQD7o9RERERER9YIZ9AKI\n6PS01n8mIs8A+L8ARAH8ptb6lYCXRURERETUUwxkiYbf/wngzwBUAHw64LUQEREREfUcS4uJht8E\ngASAJIBIwGshIiIiIuo5BrJEw+/zAP43AL8F4J8EvBYiIiIiop5jaTHREBORnwZga61/W0QMAM+L\nyAcB/B8A7geQEJE7AH5Wa/37Qa6ViIiIiKhbRGsd9BqIiIiIiIiIOsbSYiIiIiIiIhoqDGSJiIiI\niIhoqDCQJSIiIiIioqHCQJaIiIiIiIiGCgNZIiIiIiIiGioMZImIiIiIiGioMJAlIiIiIiKiocJA\nloiIiIiIiIbK/w9DyeUVvISwbwAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x20f666e20f0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# This may take about 2 minutes to run\n",
"\n",
"plt.figure(figsize=(16, 32))\n",
"hidden_layer_sizes = [1, 2, 3, 4, 5, 20, 50]\n",
"for i, n_h in enumerate(hidden_layer_sizes):\n",
" plt.subplot(5, 2, i+1)\n",
" plt.title('Hidden Layer of size %d' % n_h)\n",
" parameters = nn_model(X, Y, n_h, num_iterations = 5000)\n",
" plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)\n",
" predictions = predict(parameters, X)\n",
" accuracy = float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100)\n",
" print (\"Accuracy for {} hidden units: {} %\".format(n_h, accuracy))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Interpretation**:\n",
"- The larger models (with more hidden units) are able to fit the training set better, until eventually the largest models overfit the data. \n",
"- The best hidden layer size seems to be around n_h = 5. Indeed, a value around here seems to fits the data well without also incurring noticable overfitting.\n",
"- You will also learn later about regularization, which lets you use very large models (such as n_h = 50) without much overfitting. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Optional questions**:\n",
"\n",
"**Note**: Remember to submit the assignment but clicking the blue \"Submit Assignment\" button at the upper-right. \n",
"\n",
"Some optional/ungraded questions that you can explore if you wish: \n",
"- What happens when you change the tanh activation for a sigmoid activation or a ReLU activation?\n",
"- Play with the learning_rate. What happens?\n",
"- What if we change the dataset? (See part 5 below!)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<font color='blue'>\n",
"**You've learnt to:**\n",
"- Build a complete neural network with a hidden layer\n",
"- Make a good use of a non-linear unit\n",
"- Implemented forward propagation and backpropagation, and trained a neural network\n",
"- See the impact of varying the hidden layer size, including overfitting."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Nice work! "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 5) Performance on other datasets"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"If you want, you can rerun the whole notebook (minus the dataset part) for each of the following datasets."
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"scrolled": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAAD8CAYAAAB+UHOxAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXd4VGXah+9zzvT0QhqBhBZK6NJBihSliIK6dt3PgmUt\na9u1rK4odtG1u+jqWlZQEVQUpUuRGnqHkB5CSO9TTvn+GIiEmUkCpEHOfV16wZzyPmcS3ve8T/k9\ngqZp6Ojo6Oi0PsTmNkBHR0dHp3nQFwAdHR2dVoq+AOjo6Oi0UvQFQEdHR6eVoi8AOjo6Oq0UfQHQ\n0dHRaaXoC4COjo5OK0VfAHR0dHRaKfoCoKOjo9NKMTS3AbURHh6uxcfHN7cZOjo6OucNW7duzdc0\nrU19zm3RC0B8fDxJSUnNbYaOjo7OeYMgCOn1PVd3Aeno6Oi0UvQFQEdHR6eVoi8AOjo6Oq0UfQHQ\n0dHRaaXoC4COjo5OK6VFZwHp6Oi4qapysXbFEfbuzCE0zMYllyXQLj6kuc3SOc/RFwAdnRZOcVEV\nzz66mIpyB06HgijCulVHuPnOQYwc17m5zdM5j9FdQM1IYUElBXkV6G05dWrjm8+3UVpchdOhAKCq\n4HQofD5nM5UVzma2Tud8Rt8BNAOZaUV8+OY6co+WgiAQEmrlzgeGk9AjorlN02mBbN2YiaJ4viRI\nksDenTkMHBbXDFbpXAjoO4AmprzUwQtPLiErvRiXS8XlVDh+rJzXZ67g+LGy5jZPpxGpKHeSk12C\n06k0tyk6OoC+A2hy1q5IRpZVj89lWWHpov3cdOegZrBKpzGxV7n4z3sb2LYpE0lyv3NNmZ7I5df0\nQhCEOq+/aEg7Nq5J9dgFKIpGYp/oRrFZp3Wg7wCamIy0Ilxe3gAVRSM9tagZLNJpbN57bQ3bN2Ui\nu1QcdhmHXWbRd3tZ9tOBel1/7a39CQy2YjJLAIgimMwSt941CJufqTFN17nA0XcATUxsfAjGDRke\ni4AoCbSLC24mqy5sVFWjIK8cs8VIYJClScfOyy1j/+5cXK6auz6nQ+bHb3czfkq3OncBQcFWXnp3\nKutWHmHPDj0NVKfhaJAFQBCET4ApwHFN03p6OT4a+AFIPfHRAk3TnmuIsc83Ro7txKJvd3ssAAaD\nyKVTuzeTVRcu2zZl8t8PN1FV6URVNDp2CePuhy8mrI1fk4x/7GgZBqOIy+W56ysvc6DIKgajVOd9\nrFYj4yd3Y/zkbo1hpk4rpaFcQP8FLqvjnLWapvU98V+rnPwBAgItPDFrAjHtgjCaJEwmibA2fjzy\n9FgiowOb27wLisMHjvPB7LWUFLlTKGVZJflgPrOe+NVrHKYxiIoJQHZ5H8s/wIxk0L2wOs1Hg+wA\nNE1bIwhCfEPcqzUQ1zGUl96ZSkFeBYqi0ibSv17BQJ0z44dvdntk3KiqRmWFkx1bshgwtH2j29Am\nMoDuvSLZv/tYDTeQySwx9ZpeuFwqSxftZ83yZBRFZeDwOKZM74l/gLnRbdPRacoYwDBBEHYB2cCj\nmqbtbcKxWyRN5YZobHZuzebnBXspyCunU0I4U//Um9j2zR/POJpZ4vVzp0MmJ8v7scbgvr+N5ON3\na2YBXX5VT8ZOTODFp5aSnvpHYsCyRQfYvC6dWf+aogd4dRqdploAtgHtNU0rFwRhEvA90MXbiYIg\nzABmALRv3/hvaDrnxpIf9zH/fzuqq1QL8ivZviWLvz83ns5d69WVrtGIjg2kIK/C43OT2UBU26Zz\nt5ktRv7y6Egqyp2UldoJDffDZJLYtjmTzPTiGvEgWVYpLbGzaskhJk/3CKfp6DQoTeKA1DStVNO0\n8hN/XgwYBUEI93HuHE3TBmiaNqBNm+adQHRqp6rKxfwv/5j8ATRVw+lQ+GLOlma0zM0V1/SuTp08\niSAKWKxG+g2MbXJ7/PxNRMUEYjK5bdq1NRuHXfY4z+VU2LYps6nN02mFNMkCIAhClHDCyS0IwqAT\n4xY0xdg6jUfKoXyfQcz0lIImC7T6IqFHBHc+MIyAQDNmiwGjUaRD5zD+8dJl9cq8aWz8/M2IkvfY\nj5+/HgPQaXwaKg10LjAaCBcEIQv4J2AE0DTtQ+Bq4B5BEGSgCrhO0xXQznssVgOa6v3HKEkiotj8\nge1Bw+MZMKQ9ucfKsFiNhITamtukakZc0pEli/ajKjUD1WazgUsmJjSTVTqtiYbKArq+juPvAu82\nxFg6LYcOncOx+pmwn+bGMBhEBg6LaxELAIAoiUS3DWpuMzyIbhvEDbcN4Kv/JCEI7gwlQRQYPaEz\nfS5q29zm6bQC9EpgnbNGFAUeemoMLz+9DEVRcTpkzGYDoW38uHnGwHO6d1mpnb07czAYJHr2jcZi\nNTaQ1S2LSy5LoN+gWLZuzESWFfpeFNukAWqd1o3Qkj0xAwYM0JKSkprbDJ06cNhdbNmQQWF+JXEd\nQunVLxpROvvw0uLv97LgfzuRDAIgoKoqdz00ggFDzs+sMEVR2b45i707jxIQZOXiSzrSJjKguc3S\nuUARBGGrpmkD6nWuvgDotCT27z7GG7NW1sgsAjCZJF5+74rzrnbCXuXihSeXkJtThsMuIxncsZHb\n7xvK0JEdmts8nQuQM1kA9Dp0nRbF0p8OeEz+4PaPr115pBksOjd+/HY3OVkl1emeiuzuAfGfdzdQ\nUe5oZut0Wjv6AqDToigurPT6uSyrFBV4P9aSWbcqxUMJFNzxkx1J2U1qS2pyAauWHGLXtmxUpXlT\ndHVaBnoQWKdFkdg3hoy0Ig8BNYvFQI/eUc1k1dmj+KqF0DRkLwqhjYHD7mL2cytJPeIuvRFFEavV\nwOOzJhAVowecWzP6DkCnRTFhclcsFiOnauMZDCIh4TYuGtyu+Qw7S/oPjvVa7KWqGr36N02q59xP\nt5JyOB+nQ8HpULBXuSguquKNWStpyTFAncZHXwB0WhSBwVZmzp7EoBHxWCwG/PxMjJ7Qmadfntgi\nqnfPlOk39MU/wIzxFNtNZonJV/UkNKzxi9JUVfPqhtI0KC6sIkPvQteq0V1AOi2O8Ah/7n3k4uY2\no0EICbXx0ttTWbb4ALu2ZhMYbGH85G707BvTJOOriurT1SSKAuVlvgPRDruL3TtyUGSVxN7R+Afq\n8hQXGvoCoKPTyPgHmpl2XR+mXdenycc2GCWi2gaSk1XqcUx2KcR3CvV63bZNmXzwxlpEUQQ0FFnl\nqhv7MvHKxEa2WKcp0V1AOjoXODffOahagfQkJrPExCt7eBWdK8ir4IPZa6vjBfYqGZdLZcHcnRzY\nm9tUZus0AfoCoKNzgZPYJ5rHnh1HQo8IrDYj0bGB3HrXYKbf0Nfr+WtXHkH1IvLndCgsXbS/sc3V\naUJ0F5BOiyUro5jVSw9TXFRFr/4xDBkRj8ms/8qeDQk9InjqxUvrdW5RQaVPKe/zsRZDxzf6vyad\nFsma5cl8Pmcziqyiqho7t2bz0/w9PPPqRL1fbiPTvVckG9akejSrMRhFEvtEN5NVOo2B7gLSaXGU\nlzn4fM5mXE6l2hXhsMsU5FWwcN7OZrbuwmfAkPaEhtlqNPsRBLBYjEyY0q0ZLdNpaPQdgE6LY9e2\nbK+9BGRZZePaNG6+c1Ct1+/ffYzvv97F0awSoqIDuPK6Pvqb6xlgMEo8/cpE5n+5nY1rU1EUjT4X\nteXaW/sTGGxtbvN0GhB9AdBpcWi1yNT46kB2ks2/p/HR2+urBeVKi+3868VV/PnuIQwf07Ehzbyg\n8fM3cevdg7n17sHNbYpOI9IgLiBBED4RBOG4IAh7fBwXBEF4WxCEZEEQdgmC0L8hxtW5MOnSo43X\nIKQkCQwcFufzOlXV+GLOFg81UadD4X//2YKiC6Dp6NSgoWIA/wUuq+X4RKDLif9mAB800Lg6Fxg/\nLdjDU/cvqqEFBO689cBgK9Nv8F1MVZBXgd3u8npMllVyc8oa0lQdnfOehuoJvEYQhPhaTrkC+PxE\nI/iNgiAEC4IQrWlaTkOMr3NhkLQhgx++3oXTWfMNXpIEpl3bmzGXJWC1mXxeb7UaURXvLiJVUbHZ\nzs+2kqqqsWV9OquWHMLhUBg8PI7RE7pcsG0ydZqOpooBtAUyT/l71onP9AVAp5pF83d7bQZjNElE\nxATWOvmDW3IhoXsEB/bm1ihkEkWBuE5hBIc2nPiaw+5i3aoUtm3KxD/AzJjLEuiWGNlg9z+Jpmn8\n+811bN+chcPhTsvMSivit6WH+efrk7Dqi4DOOdDi0kAFQZghCEKSIAhJeXl5zW2OThNSmO+7GUxh\nXkW97nHXQ8MJj/DDYjVgMIhYrAZCw2wNKi5XUe7k6Yd+Zt5/t7JnRw4b16Ux+7kVjZKieuRgPts2\nZ1ZP/gBOp0J+XgUrfznY4OPptC6aageQDZwq5h574jMPNE2bA8wBd0/gxjdNp6UQ1zGU3duPenwu\nSSLt4kPqdY/gUBuvvHcFe3bmuNNAYwLp3S/mnJrUn87ihXsoyK/4o2mN5g40//zdXkaM6USbSP8G\nG2t7UpbXXZHLqbBxbRqTp/dssLGamuQDeWxYk4qqaQwaFke3npEIpwd/dBqVploAfgTuEwRhHjAY\nKNH9/zqnM+36Phzcm1sjBmAwiETFBNKtZ/3dK6Ik0rt/W3o3UsOVDWvSPDqWnWTHlizGN2CxlNEo\nIUqC19iG8TzsjwBut9YXczazduURXE4FDfh9VQr9BsZy10MjvNaA6DQODZUGOhfYAHQVBCFLEITb\nBUG4WxCEu0+cshhIAZKBj4B7G2JcnQuLTgnhPPz0JcS0C0IUBQwGkcEj4nj8+fEt6s3Q5wQlgNDA\nk9fgEXFIXnYvZrPE6Eu7NOhYTcXBfcdZtzIFp0NB0wDNXem9fUsWO5Kymtu8VkVDZQFdX8dxDfhL\nQ4ylc2HTvVcUL70zFadDxmAQG9R1UxtOp8LOpCwqyp0k9IggJjbI57nDx3Tk5+/24jq90YoG/QfF\nNqhd0W2DuPK63nw/b1e1LpLZYqBbYiTDR5+fhW3rf0vB4ZQ9PnfYZdauOEL/Qedf68/zFb0SWKdF\n0pSqn4cPHGf2c+7+uKqqoWnQf3A77v7rcK8L0MQrerB1YwbHj5XjsMvVu5WrbuxLaLhfg9s3ZXpP\n+g2MZcNvqTicMv0HtTuv/eWyrIKP6J6v7mU6jYO+AOigqlqr9bs6HTKzn1tJVWXNArLtmzNZ9vMB\nLp3aw+Mai9XIs69NYvP6dHZsycY/wMSo8V2I6+i9u1ZD0LZdMFff3K/R7t+UDBoWR9KGDA+1UbPZ\nwJCRHZrJqtaJvgC0YnYmZTP30yRyskux2oyMndiVadf3wWBocdnBjcbOrdm4PZQ1cToUlv180OsC\nAG7BtGGjOjJs1PnphmlOel/Ulm6JkRzYm1u9CJjMEu07hjB4RHzzGtfK0BeAVsqubdm8++rq6oyb\nqkoXSxbt5/ixMv7y2Mhmtq7pKC9z+KweLsoqZM+/5pP44FXnjbvF6VRwORVsfsYWa7MoCvz1ydFs\nWpfO2pXJqKrGsNEdGTayQ6t6+WgJ6AtAK+Xrz7Z5SC64nArbt2SRl1tGm8iAZrKsaUnoEeHdHa2q\nBOXnsP3pBchllfR9+pamNu2MqCh38OkHm9i+KRNNg9BwG7fcNajRUmHPFVESGTqqA0NH6S6f5kRf\nblspRzNLvH4uSQLpKUVNbE3z0bZdMP0GxtZsmq6qSKpCx/3bkCvs7H71a2S7s/mMrANN03jpH8vY\nvikTWVZRFJW83HLeeXk1h/Yfb27zdFow+gLQSvHVVlHTICSsdTX9uOfhEUyaEI+lqhyD00FYbib9\n1/6MX/mJRVIQqMjIRdM0jq3dxe7Xvib586W4yqua1M60IwW899oannpwEf9+cx1Z6e6F+sCeXI4f\nK/OQ0HY6FRbO1Tuo6fhGdwG1Ui6d2p0fvtlVQ2ZAEAVCwmx07BLejJY1PaIkMunq3pTe/xyqw1NO\nWnXJGAJsLB71Vwq3J6M4XEgWExsfeIcJv7xMxNDERrdxx5Ys3nt9jbtyVnPv4JI2ZvDQU2PIyij2\n2esgM6317OZ0zhx9B9BKmXRlD4aN6ojBKGK1GTGbDUS3DeSxf45tscHDxsQc7E/ctBFIlpqKo5LF\nRNy0Eex7cz75SYeQK+xosoJcXoWrtJJlU55CdXkWNTUkqqLyn3c3/FE5izt11+lQ+M+7Gwlr4+cz\neBoe0XC6RBcqGWlFLP5+Lyt+OUhpcdPu6pobfQfQShElkf+7dwjTrutNekoRwaFW2ncIaZWT/0mG\nf/QIcnkVR5dvQzIbURwuosf2Y/hHj/BN3PWoXuIAmqJwdMU2Yi+rvU/xuXDsaFkNNdBTKSmuon2H\nUCxWIw67zKkZrSazxNRrejWaXec7qqrx8Tvr2fJ7OoqqIYkCcz/dyu33DWVoK6lH0BeAVk5wqK1B\ndfLPZ4x+Vsb9+ALl6bmUHs4isEss/nFuETq5wu79Ig1cpd5lrBvMLpNUo79BjeFVDYvFwJMvXMpb\nL60iL7ccSRRRVY2rbuxD/8G6rIIvNqxOJWl9RnU23Eln6H/e3UC3npEUF1bx04I9HMsqJa5TKFOm\n9ySmnW+JkPMRfQHQafFomsbKXw+xeOE+SourCDO46Hr0APERFno8MJ3IEQ37lusfF1k98Z8k8uJe\n5Czf5nGu4nQReXHjvWW7KqrI+3op1spyXJKFU3tlCgLEdwolINBCQKCFF9+eytGsEiornLSLD8Hc\nhHIa5yPLfznofWelaXz7xXa2rE//I+aSVcKW9ek8+sxYujZC45/mQo8B6LR45n6ylXn/3Ur+8XKc\nToWcSpE1/glsX32YJZf9nX3vLGx0Gwa9fjcGfyuC+Mc/GYOfhR73T8MWHVave1QdLyJl3krSf/gd\nucpR5/muskoWDbyXpCc/puuaXzG4nIiyO0htthjwDzRz10MjalwTExtE565t9Mm/HlRVeE/tlWWV\nzevSvMZcPnl/YxNa2PjovyWthJTD+Xzz+XZSk/PxDzBz6eXdGTe5W4vXACotrmLlrwdxnaa/rxoM\nJPcYSMjqH0n6+xw63TQOc0jjFa+F9u7E5ZvfZ+esLzi2ZjfWyBB6PnINHa4dU6/rd8z6kl0v/g/R\nKLlf3TWN0V8/U2vsYP97P1CedgzF7sQPB0OWfcvxth2oCgll2H2TGXvTYH2iPwf6Doolb9EBj/RZ\ng1HC17+K/NxySkvsBAZZGt/AJkD/7WkFHDmUx8tPL6tO+bRXyXz75XYy04u4/b5hPq/b/Hs6C+bu\nIC+3nLA2fky7rjdDRzat9k1qciEGo+SxAABUBIagAaLRQM6KbcRfPapRbQnu1p5RXz51xtdl/bqZ\n3a/MRbE7UU4JJay6eiZXH/kCa6R3EbmUuStQTgk8GxSZmIzDkCUSlZGA2Tz8jG3R+YNJV/Tg91Up\nVJQ5q9NoTWaJDp3CSEnO93qNBhiNF47j5MJ5Eh2fzPvvNo+2gk6HwobVqeQfL/d6zaolh/jo7d/J\nySpFdqnkHi3jk/c2snTR/qYwuZqAILPPAKikyO43NQFE0x/N0VVZYc8b3/Jtxxv5KvxKVkx/huL9\n6U1jsBf2vjnfaxBZU1WOfLXC53WnPlMNVJWMhesoz8htKBNbJYHBVp5/cwqXTEwgrI0fMe2CuObm\n/jw2cxyhYZ6y3qIo0KVbG6w2k5e7nZ/oC0ArIOWw97cZySBy5JDnMUVR+faL7V4XjQVf7WxSzfYO\nncMICrZwenaqqMhEp7mbomuKSsy4/tXHVt8wi23PfEp52jEchWVk/LCeRYP/0iyLgOqSKTmY6fWY\nYndSlVPo89out03EYPNesV20L40fB9yNPa+4QexsSooKK0k7UoDD7ll0Vx+OHS3l1x/2sXTRfgry\nKs7JluAQKzfdMZA3PprOS+9MZcKUbhiNEvf9fRQ2PxMms1sixGwxEBhk4c4HfO+Yz0caxAUkCMJl\nwFuABHysadrLpx0fDfwApJ74aIGmac81xNg6dWOzmSgt8Z7G6E0SojC/wuckr6Fx/Fj5WafDyS6F\nlUsOs2b5YRRZY8jF8Uy4vJvPtypBEHjkmbG88swyKsuduCrsaEBQ/jE6pexCspoZ+eWTGGxun2zR\nnlQyf96EcmqQVdOQK+1se/oTLpk/86zsPhtKjxxl8ci/Ys/3Pkkb/K0eGUyqolCelosp0EbXOyaR\nvnAtuWt3e1YoqxpyuZ39731Pv2f/3EhPUJO0IwWkJhcQEmqjZ7+YM1buLC918P7sNRzadxzJIKGq\nKhOv7MG06/rUu/7k68+3seynA2iqhiDAN59v56ob+zDxyoatxm4fH8IbH09n45pUjh0to318CAOH\ntW/SRkVNwTk/jSAIEvAeMB7IArYIgvCjpmn7Tjt1raZpU851PJ0z55KJCSxesNdD/dNkNtDdS7N1\nm58ZxYdEsiyr+Aec3RZYVVRefXY5qckF1buLRfP3sH51KjNnT8Ji9e7yiIoJZPa/p7F/Ty4FuaUY\nk1NQthXgd+m1dPm/iTVSNnPX7vYxuMax1bvOyu6zZcW0Z6jKLQQvLizRbCSgUwyxkwdXf3bkq+Vs\n+ut7KFVOVFkhYlgiIz9/nN/veJ3sJUke91DsTrKXbm30BcDpkHnzhVUkH8wDDURJwGQy8Pis8bRt\nF1zv+7wxayVpKYUoslod0/nl+/0EBloYN7lbndfv3ZnDip8P4jrt93jBVztJ7BNN+w4N25DHajUy\n5tKEBr1nS6MhXECDgGRN01I0TXMC84ArGuC+Og3E5Vf3ome/GIwmCbPZgMVqJCDQzGPPjvPa8tDP\n30Sv/p5veJIk0i0xksBg32JxLpfCxrWpLJy3k41rU2v0zd25NZu0I4U1XEsul0JhQQVrlifX+gyi\nJJLYJ5qRE7oy9N6JjPj4UXo+di0I1JBiMIcFIvp4MzUFN50sQsnBTMpSjnqd/AESbpvI5DX/QpTc\nLobsZUn8PuMNHPmlyBV2VIeL3LW7+fWSRwgf1A3R5OVdTRCwtT0z3aYjh/J54/mVPHT7d7z0j6Xs\n3ZlT5zXffrmdw/uP43QoOJ0K9iqZ0lI7r89c4TM+czqZaUVkphehnC5Y55BZ9N2eet1j1ZJDXvP2\nXS6FNSuO1OseOjVpiP1MW+BUJ2cWMNjLecMEQdgFZAOPapq2twHG1qkHBoPIg0+MJjuzmCMH8wkM\nttCzb+1b+DsfGMbrM1eQlVGMKApoKkS1DeSehy/2eU1ebhnPP/4rjioZu13GYjHw1SdJPP3yZbSJ\nDGD7liyPNoDgji1s2ZDBhMu7+7y3q6KK0sPZWCNDMIUEsPH+t0n53woEUUAwSPR+6iZ6Pfon2k0Z\ngkfAAJBsZno8MK2Ob8pNWWoOuev2oKkqWYs3kbV4E4IoEn/1SAa8MgNLeN3uL2dxOaJBwpsjTTQZ\n6D/rNowBf1Rg75j5OUplzdoATVaoPFZIYOdYBEkCan53ktVE4oPT6/VMALu3H+Xtl39z7wQ1KCyo\nJOVwPjffMZCR47v4vG7N8mTPLCwNKsudpBzKp3O3NnWOffxYGZIkgpdvpKSofvo7FeXe8/Y1zd0P\nQefMaSqH1jagvaZp5YIgTAK+B7z+xgmCMAOYAdC+ffsmMq910LZdcL237H7+Zv752iRSkwvIyS4h\nKiaQDp3DavXVvj97HaUlDrQTb4V2u4zDqfDB7HU88+pErDYjogiqF+FKq827+0fTNHbO+oJdr8xD\nNEioThljgA1XWWWNFMmdMz/DYDHR4/5pjP/pRZZNeRJN09BkFdBof8Uwut1b+8ZUU1V+v3M2KXNX\nIkgicqW9RvPyI18uJ2fVdqbt+aQ65uCLkN4d0bw9KOAX2wZTsD+aqqIpKqLRQMmhLK/nqk4ZZ0kF\nI794grW3vowgiWgaaC6Z/rNuq3cVtKZpfPbhJq+B/a8+2cqw0R0xGCWv19m9LNrgVo8tL6vfxNu2\nXbBHvv1J6itYd9HgdiQfyPNwZZotBvoN1CUvzoaGWACygVO//dgTn1WjaVrpKX9eLAjC+4IghGua\n5pGComnaHGAOwIABA+q3v9RpNDp0DqND57orXYsLK8lILaye/E+iqRrpqYUUF1UxYkwnli8+iHra\nxCiKAiPHdvJ634P/XsTuV75GqXRUvzsqXkTZ5EoHO57/nO73XUnkiF5clzOfrJ834igsI/LiXgR3\nj6vzGQ58uIjUr3/zen9wu5rseSWkzFtFwm0Ta72XwWrmohfuYOsTHyGf8mYvWc0MfP1uNvzlLZI/\nW4JidxHUrT2WNkE48j2b9KgOF6XJ2fS470raXjqAo0u3ojhdxIzrjyWsfoH4kkOZ7H77eyJ/3o4p\nNJJj7TqjGP+I42hAZnqx15+zIAjEdQglPcUzW8nlUujYpX5V0FFtA+maGMHBPbk1dhMms8T0G/rU\n6x4Xj+3E0p8OUJBfgXziHkaTRHTbQF3z6CxpiBjAFqCLIAgdBEEwAdcBP556giAIUcKJV0dBEAad\nGLegAcbWaSE4HIrPqmJRFHDYZWLjgn1WrnpLRwXY+eL/3G/i9cBZXFF9rsFqJv7qUXSdMaVekz+c\nyNevYyy5ws7R5Vvrdb8e909j1Ff/IHxgVywRwUSP68+ly15j71vfkfzfJShVTtA0SvanU5p81Kvr\nCuDAnEXkrNqO0c9K3LQRdLx2TL0n/7Tv1vBDv7tInrOI8KPpdNi/jUErF2Ku+iN9UlVVnzswgBtv\nH1CdDnkSs9nAuElda40Hnc4Dfx/F4BHxGI0SRpOEf4CZG24bwLBR9SsuNFuMPPv6JCZemUhElD9R\nMYFceW0vnnzxUr2X8FlyzjsATdNkQRDuA5bgTgP9RNO0vYIg3H3i+IfA1cA9giDIQBVwnaZp+tv9\nBUSbSH+sVqOHiwHAajPRJtKflMP5Xt0Aqqqxaslhrr31Io9jlUfr/55g9LfW6ZqpDUdhWZ3nCEYD\nfu0i6n3P9lOH0X7qH7nj+VsPUbDloMcuQ6ulp4Bmd7Hr1XlEj+lX73EB5CoHa//v1RopsQZFRlJk\nOu3ZzL6BYxAEaBMZQFRMoM/7dE2M5PHnJzD/y+2kHSkgKNjKpGmJXOxj1+YLs8XInQ8O55a7B1NZ\n4SQoyOLN7qTSAAAgAElEQVQ1CaE2bH4mrr6xL1ff2PeMrtPxToPEADRNWwwsPu2zD0/587vAuw0x\nlk7LRBQF/nzvED6YvbY6yIgAJpPEn+8ZjCgKlBbbfe4SqqpcaJrmEWMIiI+iLKXuTBXJZqbn3671\nuF6utHPo019Jn78aY4CNhDsn027KUK+xjIjhiWT9vAlqeTcRDRIJd0zyebz4QAb73/2e0sNZRAzv\nSbe7L8caEVJ9vGDbYTSfSjO+KU89dsbXHFu9E8HL9y0A4bmZmM0GDCaRvzzmO7B/kk4J4fz9ufFn\nbIM3zGaDrmHUQtB/CjoNRv9B7Xj8+Qksmr+b7Ixi2rYP5vKre9EpwZ2q2KFzWI200FNpFxfsdVLu\n99z/8fuM2TUyZASTAVOQH67SSiSzEdWl0OP+afT+23U1rnWVV7Fo8L2Up+dWX5+zagedbhrHsA8e\n8hjrolm3cWzVDg/ZBkESMfhZ0GSF4f95jKAusV6fIWPRen67bhaqS0aTFXLX7mbfv75jyoZ3Cerq\n9lH7tWuDKIles4Nqo82guvPkNU3DWVSGZDVjsJprXcgAZFkBNGY9voQbb7uIEWM7n6FVOuc7+gKg\n06B0Sgjnr096V8gMDrUxalxn1q48UsNVZDJJXP9/A7zf74axyBVVbH3yP8iVDjRVJf7qkQz74CGU\nKgeVOQXY2oZTmZVPRVYe/u3/KArb/85CylOP1XC3yBV2kr9YRte7Liesb80JL7R3JyatfYukv8/h\n+Pq9GANtdLltIiGJ8UhmEzHjL8Lo793nrbpk1t76Sg13i2J3ojhc/H73G0xa9SaA+x6BNndD+VMm\naMliQlNVVKenK0g0G+n9xA1exz1J5uJNbLzvbSqPumMpMeMuwuBv9dqsRgMKI2JRFA1FUcCh8Nmc\nzQSH2ejZN6bWcXQuLPQFQKdJuenOQUTFBPLLD/soL3XQLj6EP93Sn25eKpJP0vXOKXS5bSJVxwox\nBftj9HNPwkZ/K6nf/EbSEx8jCAKqSya0byfGfPtP/Nq24chpaponUR0uMhdt8FgAAML6dubSJa+e\n8XPlbT7gPe1T0zi+bg+Kw4lkNiFKEpetnM3yKU9ReTQfwSChOlwkPnQ1osnA7lfmoTic1emn5rBA\nxi16odZAdu663ay6ZmaNxSdr8Sav5wpmIy4kDvesKUPtdCj88M1ufQFoZegLgE6TIooCEy7vXmvR\nl9frJAm/tjULjtIXriPp73NqpFnmbznIL6Mf5qqDnyEaffx6i4LvY2eJIAo1agZqHqRGhk9Ql1im\nH/gvhTuScRSUEta/C+ZQdxC2w7VjSPt2NYrTReykIUQO7VHn2Nv++d+a2ke+zJBEzAN7sT64Ow7R\nM+vn2NFSL1fpXMjoC4BOg6FpGpt/T2fxwr0UF1XRpXsE067rfUZ6MWfCjuc+rzH5g1sZtOp4ETmr\ndpBw20S2/H2OR4WtaJCIu6ruwOeZED6wm7vZy+mIAlGj+yKdJu0sCAJh/TxrIYO7tafv0zef0djF\ne1LrPgn3d2MLsiHYrOCluKuxfk46LRd9AdBpMOZ/uYNlP+3HccK/n7Q+nV1bs3nyhQnEd6pfwZAv\nNE0j/bs17P/gR5xFZbSfOoyyVO/ZQZqiUpqcTcKdk0mbv4b8rYeQy6sQJBHRZKTPUzf6DOSeLaJB\nYtRX/2DF9GfQZAXVKSPZzBhsZoZ/6Blwbkj84iKx53kWkZ2OYJSISYwlqMSK83g56imCfyazxJXX\n9fZ6XVFhJYsX7mX3tqP4B5qZMKU7A4e1r7eCp07LRWjJ6fgDBgzQkpI8VRB1Wh6lxVU8fOcCr527\nuiZG8OQLl57T/dff8yZHvlxenaEjWoygaDWE4E5i8LcwYfHLRI7ohaooZC3eRMaP6zEG2Oh8ywSv\nvv+GoiztGAfn/ETp4Wwihvagy20TMTeyCF3Gj+v57fpZdbqBJKuZK3bMQQsP46O3fufAnlxEUcDm\nZ+LmGQMZMNQzzlCQV8EzD/9EVZVcLeRmNhsYOa4zN905sFGeR+fcEARhq6Zp3rMqTkPfAeg0CIcO\n5CEZvLduTD6Qd073Lt6XRvLny2pMcKrdhWCQwCDCKcVlotFAYKe2OArL+GnY/VRkHCdsQAL9/nmL\nV5dLffFWo3ASV3kVKV+toGD7YYK6tqPXo3+q9un7ojwjl8xFGxAkifZTh2KLqZ+qZ9XxItK/W4ur\nvIqY8RcR1rcz7acOI2HGZPa/tcDndaLFyPA5D1fvfB57dhwV5Q7sVTIhYTaf9RnffLGNinJnjYxS\nh0Pmt2WHuXRqN9pENl4fZp3GR18AdM6Y3JxS9u48hsVqoN/AWKw2EzabEV9R0HNtopH1y2Y0xXNh\n0WQFc3gQokHCWVyOpmq0vWwg4QMSWH3DC9WyDpWLCshZvpXxi18maqR3N4cv8rcdYtOD73F8w14k\ns5GO149l0Oy7MQW53+rLUo7y09D7kSvtyBV2JJuZ7c9+xmUrZhN+kXct+R3Pf8Gul77iZD/LzQ+/\nz0Uv3UHig1fVakvqN6tY++dXQRTQXArbZ35G+yuGMeqLJ+l+z1QOzfnZ6y5AMEhckzoXW2RIjc/9\n/M34+XvvOAbuXd2mtWleywkEAfbsyGHMpfoCcD6jLwA69eakouS6VSkIuDN6Pn1/I395bCS9+sVg\nNErYq2q6ZEQRBgw7N1VXyWpG8CEZYAkLZNreT6g6VuiWVxYE5kZe5aUjmION97/NlTs/rve4xQcy\n+GXUQ9VuJ6XKyZEvl5OfdJArtv0bQRRZ+3+vYi8oqdb9Pylat2zSE0SO6o052J8ut00kYog7myd3\n3W52nWgQfypbn/wP0aP7EtrHu7xCVW6hW9bh1OtcMpk/biD5s6V0+b/LCEyIpXh3ao10VNFsJG76\nxR6Tf32Y++lWn7VkAue+sOs0P7qCkk692bAmlfW/peJynmgMYpdxOhTee20NVRUuHvrHJZgtNScF\nVYPN69LPyQ0UN/1ir1WtktVMwp2TEUQRW0w4xgAb+UkHfaZ4Fu9LR/ah9Algzy9h4wPvMC/6aua1\n/RMrr3rWY6JWnS7KUnLIXpqEs6ScvI37vTZ9secVkz5/DYc++YVfxz3K9pmfAbD/gx/dInCnoThc\nHPz4Z5+2pX6z2uvncoWdfe99D8DYhc9hiw3HEGB1VwP7WQjt3ZFh7z/o8761sWVDhs9jiqLRb2DD\nBtJ1mh59CdepN0sXHfDakQkNNv2extiJXYmI8iczrbjGMYdd5oM31vL6v6edVeaILSqUIe89wMb7\n3kZT3NWyBn8L4QO60f2+K3GWlJPz205Eg4Q5NBBN9S60IBgkRIOXVE3AVVbJjwPvoSqnoLoatyrH\nuxCdXGEnP+kQ4QO7Uqesj6qhVDrY/eo8Ot4wFkdBqXeJBlX1KgddbV9pJYq37x5wlbiVPQPio7j6\nyJfkLN9GWdoxQnt3pM2QHmedrXO6tPepXHZFd2x+Z9caVKfloC8AOvWmwkfzD5dLoaLcSWmJnZws\n78VEpSV2jh0tJbrt2TWTT/i/iUSP6UfK/5bjKC6n7YQBxIztz8GPfmbzQ+9Xt0xUZQWjvxW5vKae\nj2gyEH/VSJ8LwKFPfsGeV+xViuF0DDYztpgwLGFBBHZuS/G+9Dqv0WSVjIXraH/5UI6v2+1Rv2Dw\ns9Bu8hCf18eM68+ul7/y0CkSjYYaaqOiJNH2Us/snLLUHA5+9DPlqTlEXtybzrdM8ClrcZJe/WLY\nkZTlsV4ZTRJTrq5fIxqdlo3uAtKpNz37xSBJnm+TJrOBbomRtYqPCdSpTVYnAfFR9HnqJga9djdt\nxw8gb/MBtjzyAYrdiau00v2WXOnAfrwY0WTE4G9FMEgY/K0EdW3HkHcf8HnvrMWbPArGfD6LJNLh\nmlEADP/4UQx+FndGUi1oaGiaRuc/X4o1OqxGj1/JYsK/QxTxJ+7pjfBB3Yge2x/J9kfQVjQaMAX7\nu3sj10LmTxtY2Ot29s7+ltSvfyPp73NY0O1WKrJrd8vdcPsAbP4mjEb3NCGcUHe96Y6BWK2++wfo\nnD/oOwCdenP51T3ZuDYNe5Wzuq2j0STRKSGcLt3bIAgCkTEBZGd4ujJs/mai29aeGnmm7Ht7AbIX\nfzqAKsuEJMbR4bpLCO3biZix/RFE3+87lja1V8GKJgOS2YRkNTHuh1nV/XwjhvTgiu1z2DP7W/K3\nHkKTZYr3p6Oe5q4RDRJxV47A6Gfl8s3vs+ulr0j9ehWCKNLp5vH0+tt1SGbfLhVBELhk/rMcnLOI\nAx8swlVeRfvLh9L7iRuwRYX6vE5xOFl904s1Fje5wo5id7Lpr+8xeu7TFO9NQ7KaCOwSW8NdFBEV\nwMvvTGX54oPs332MsDb+jJ/SrVrdVef8Ry8E0zkj8nLLWTh3J7u2ZWM2Gxg1oQuTruxR3U82NbmA\nl59eiuxSkWUVySBikEQe+scYuveKalBbfh7xAMfX7/V5XLKYuHLXxwR2blvnvXLX7+WXMQ+h+ZCr\ntkSGMOabZ4gYlogo+X7bd1VU8fOw+ylLyXG7awQBg9VM9/unMeClO+p+qDPAUVTGvre+I+27tRj8\nLHS763I63TK+hn3Zy5JYdc1Mr6qggkHE4G9DUxQ0RcWvXQSXfPtPQnp2aFA7dZoWvRBMp9FoE+nP\njL8O93m8Q+cwXnpnKit+OUhqciGxccGMn9y1UQqGoi/pR/7WQ6gOl9fjoslA4a4UylJzqMjMI6x/\nF59VwJHDEomdNITMH373etwWFUrUxXXXEBj9rEzZ9D6pc1eStmAtpmA/ut4xmahRf/S9Lc/IdQu+\n2V3EThp0VgVqjqIyfug3g6rcourn37g3jcyfNjBm/rPVb/Le6idOoskqruLy6r+XHsxk8aiH+FP6\n3DrjAzoXBg2yAxAE4TLgLdwtIT/WNO3l044LJ45PAiqBP2uatq2u++o7gObH6VTYtDaNpI0Z+PkZ\nGTW+C10TfUs3NyVVx4tY2OM2HIXeA8+SxYQx0OYOuGoaaBrhg7szftELXltHVh0v4tv4GzxSPw02\nC4PevJeud04+Z5v3v/8DWx79EE3V0BQF0WykwzWjGfHJYwiC4E4t3XQAY6CNNoO6+XRbbZ/5Gbte\nmYtqr7n4GfwsXLr0VSKGJgLujmhzI6/yCB77wuBnYfCb95Jwx7k/q07zcCY7gHMOAguCIAHvAROB\nHsD1giCcrmE7Eehy4r8ZwAfnOq5O4+Owu5j52GK+mLOJHVuy+H11Kq8/t4Lv/re9uU0DwBoRwuWb\n3yO4Z7znQVFAcTixHy9GLq9CrrAjVzrI27CPzY9+6Hn+iftd/NnjHqqeikvGVVpBycHMc7K3NDmb\nLY99iGJ3ojpdaIqKUukgbf5q0r5dza5X5zEv+hpW/ek5llz6N76Ju56C7YcBqDyaT96m/dWLXdp3\nazwmf3BP+Fm/bK7+u8FmYdiHDyHZ/iimkywmn4V1coWd0uTsc3pOnfOHhnABDQKSNU1LARAEYR5w\nBbDvlHOuAD4/0Qh+oyAIwYIgRGuaVnezV51mY8miA+TmlOFynvCLa+7GIb/8sJ/hYzrV2kj8dIoP\npJP2zWoki4m2EwcR2qtjg9gY0DGGK3d+TNLjH7H/nYWIZmP1BOtNmUKxO0n+bAlD333A69u1OSzQ\nndFzSixAc8lseezfbH36U8L6dGLsD8/X6PNbfZ6qVlcknwwSn8qR/y1HlT1jDHKFnc2PfICzqMzd\nRezEDkQuq+KXsY8QMTSRY6t2VD9blz9fViMb6FREgwGDX83dTacbxxHSswP73llIWWoO0aP7Urjr\nCBkLf/doYmPwt+oxgFZEQywAbYFTX42ygMH1OKctoC8ALZj1v6X8MfmfgqpqbNucyaQrE+u8h72g\nhF/HPUbRziPVn239xyd0umkcI/7zWINICguCwMBXZtDnyRso2pvOoTk/kfy/5eDD/604XKgu2WvW\nzd7Z33it1AVQ7U7ytx1ixRVPM2XDuzWOpXy9is1/fQ9nSQWaqhE7aRAjPn60hiicq6zSZ5C5Mjvf\n6+dyWRVHl21Fk5XqhSH5i6VEje6Lwc/itX9xh2s9W3KG9unEiI8frf570Z5Usn7ZXLPXsiRiDLAR\nd7XvdFSdC4sWVwcgCMIMQRCSBEFIyss7NxVJnXPEx9xc3ylb0zR+Gf1wjckf3CJuKXNXkjpvFUdX\nbmfRkHv5wn8y8zvfxMGPf+Zs41KmIH8ihyVScjjL5+QP7o5cp0/+mqZhzyumLO1Y7c/kUijcnULx\ngT9kErKXbGHd7a9RlVtUvfvIWryJJeP/VuNZYicNweDvGXuodTxFRTtt16BUOshdvZOYCQPdb/uC\n4E5TtZgYNPseAuLrzrYK6dmB8T+9iH+HKASDhCCJtBnSgykb3sFg0St8WwsNsQPIBtqd8vfYE5+d\n6TkAaJo2B5gD7iBwA9inc5YMH92RhXN3oiieP4aLBtct8Ja3aT+lh7O8HlMdLnbM+oLytNxq4bay\nlBw2//V9ylJyGPDi2adMBveII3/zAZ8ZMJbIYAp3HqkWXstYtJ6N971N1fFid38BAd/tHXFLShz/\nfQ+mQBu2mHC2Pf2pRxGZ6pQpOZTJ8Q37iBzm3ilFj+mLX3wUJXvSzvrZqu8vKwyf8xClh7PJ+mUz\nRj8L8X8aXa/J/yTHN+6jIjvfXZQmCBRsPUTOqh10ufXcejfonD80xAKwBegiCEIH3JP6dcANp53z\nI3DfifjAYKBE9/+3fDp3bYPiRQ9GQ8OvHjowJQcza51Iy5KPejR0kSvt7PvXd/R67FrMIWeXOpr4\n16tJ/nwpePe2kLtuDz8Nv59x3z+PaDS4m6nUswoYQC6tZNOD77HxvrcJ7de5xm7gVDRVZcO9/6L0\ncDaS2Uinm8djP1Z0No/kgcFmwRTsT8SQHtVKo2fCsTW72DXrf2hOGeUU+YsN975FxNAeBCW0q+Vq\nnQuFc3YBaZomA/cBS4D9wDeapu0VBOFuQRDuPnHaYiAFSAY+Au4913F1Gp/liw96ncAlUWT96pQ6\nrw9KiPWZbYKA125e4JYwLtiefCameox7eg/eGpwQaPv9rjfdDdW9Tf6SWKuvS660ozhc5G85iOLw\nHjNQqpwU7UpBqXLgLC7nwL8XucXg6osgYAj0DCYDJNw5qdaCtLrY/+5CZC+9A1RZ5tAnv571fXXO\nLxqkEEzTtMW4J/lTP/vwlD9rwF8aYiydpuP4sTKvnzudis9jp9JmSA8CE2Ip2p3isZAYA6woTtlr\nKqPmkrFGnH2D8sLdKQg+OlydSlVOAc5TCqFORTQaGPDKDMyh/mx78j9UZheA4FlYpSkqotGEIIo1\nC9IEwUP8SKuH0FzNCzTksiqvh0r2+ZZqrg9Vx4u9ijNpLgV7bqHP6xwOmS2/p5OdUUx0uyAGD4/D\nbNF1gc5XWlwQWKd+bFqXxmP3fM+fp3/Jg7fNZ/nPB846eOqLTgnhiF7E3ywWAx06160HIwgCly17\njRAvTU5Up0LsxEFIpwUcBVHEPz6K4MT4s7bbYLPUWgF7Ek1V8Y+L8HpMAI58vpT079Yx+J37ubHs\nJ6w+mqposkLbCQMw+FsxBtiQLCYks+9J0eeuyONEwedCdnRlnXWUteLtuwd3GmjbCd57/ebmlPHI\njAV8Pmczi7/fx5cfbeHhGQs5ln0GuxqdFoW+AJyHrF2RzMfvrOd4ThmaqlFcWMXXn29jwVc7GnSc\niVcmYjytKEoUBax+JgYO92wg7g1TaIDXFEfF7iRz0UZC+nZCspkx+FswBFjxi4tk3E8vIggCitNF\n1i+bSPl6FZU+tPm9EdS1Hba2tS9QgiTSZmgi/Z79MwYvOfWKw0nB1kNkfL+ONTe+yIa73ySou/dn\nNlhNJNwxieuPL2DSmn8x/eBntBnq3S8vWoz4x0W6nznA6l4MfKTCnl6QVsO+KmetzW3qoutdl2MO\nDaihYiqajfi3jyDuqou9XvPhG2spL3XgsLt3Mg67TEWZg/deX3PWdug0L7oW0HmGqmp88/l2nI6a\nEc6TBVqTpvdsMKneyOgAnpg1gc//vYm0I4UIAvTq35Y/3zMYk6l+/uei3ak+8+o1WaE8NYfJa9+i\ncFcK/u0jiBrVB0EUyV23m+VT/+EuVNI0FKdM4oNXcdFLd9RZOyAIApd8N5PFox5Cdbr+yJU/kd1j\n8LdiCrQx8rO/498+kgGvzCDpiY8RRAGlyuku1jplNyVX2En5aoW7uEsU4ZTiKUESMYcFETtpMKIk\nVWcW9Xz4GvI3H/CUYFA1Eu6YREifTriKK/CLi6B4fwZ73/iW0sPuxDjRbMRoszD0wwdZddVMr88o\nmiSOr9tNzLiLav0ufGEO9ufypA/Z/ux/SV+wFkGS6HTTOPo+fbPX+ElJcRUZaUUeXiNNg5ysUgrz\nKwgN9zsrW3SaD30BOM8oL7VTWel9QjUYRHKySujYpeHkejt0DuOfr03C6ZARRaFa9bO+iEZDrY0A\n5AoH9rySGqmHztIKlk1+Atdp/u/dr31NytyVdL//Srr/5UoMVt8NzUN6duBP6XNJ/eY3So9kE9y1\nPYpLpjz1GCGJ8cRNH4FkNiFXOZAsphMLj0DJ4WxKvWT1aIpaI15wMnUyYmgPRn7xhEdAtt3kIfR8\n7Fp2vzwXwSihOmR3dTKw47kv0DSNdlOG0PPha0i4bSJdb5+EpmmUHMhAdckEJ8a7K5Ul0WtNg2gy\n1nAlOQpLOb5hH8YAGxHD/1AszV6aRNKTH1OyLx1rdCi9H7+ehDsmIwgCtqhQhn/4MMM/fNjn91j9\nM3EoiD4WXkF0x4V0zj/0BeA8w2IzIfhIT5FdKkHBjaPieLYNwIN7xGEOC/QtRqbh4d5J/26t93aE\nmkZF5nG2//MzUr/+jcm/v11rto/R30rCbRO9HnMUl7N95ufsfeNb9xu/qkE9AscnMfhZmLbvU2yR\nvrX4+z1zC93uvpzDn/7K9mfdPYFP7TiW/t1ashZvwj8ukkuXvoZfbBuCT3MztZs8hMyfNnj0HRZE\nkYjhPQHY8fwX7HrpK0STAVVWECWJ/i/eji06lDU3v1xdZ1GeeozND39AeVouF71we72fFSA8wg//\nADOFBZ6y0labiYiohld71Wl89BjAeYbJJDFkZLyHb16SBDomhBPWpmVtwwVBYPS8p32qWmqqSpuB\nXWt8drKi1hdKlYOSgxmkzT8737OztIIfL7qbPa997Z6QT06uqua1wbs3VJeMs7DuTChrRAgVmXke\n1bwnUaqclB7OZsWVT1d/Vp55nINzfuLwp7/Sb+atWNsEI51QLxVNBiSbmVFfPolkMpK+cB27X51X\n3RVNqXTgKqtk0/3vsOra56sn/5PIFXb2vjkfh4/sJ18IgsBt9w3FZJaqQxaCACazxG33DkE8g8VT\np+Wg7wCaAEVR2ZmUTU52KVExAfQZEIvBcPZr780zBlFcVMWBPbkYJBFV1YiODeS+v41sQKsbjogh\nPbjkh+dZOe2ZGhOhZDUTM74/wT3ia5zfZkh3JIupVgljudxO+oI1dLph7Bnbc+CDH6nKKfCdKSQK\nCJKE5qNOAdxa+t4E32qco2lUZudTmZ1fuy6/olJ8IIOSg5mkzF3B7lfmgSQiCAKaojJw9t1oikru\nml0EdIqh64wpBHSIBmDXq/N8f08+xhTNRop2HqnRo6A+9OoXwz9euoyfF+whK72YmPbBTJmeSHyn\nsDO6j07LQV8AGpnC/ApmPbGEinIHTqeCySRh8zPxj5cuO+u3dbPZwKPPjCUnu4TsjBLaRPoT19G3\nK6Il0H7yEC5b8TqbH/mAwu3JGAP96HbP5fR95haPc6NG9SGkd0cKtyf73gkIAsYg9/enndD6r63l\n46mkfbem1h0GqoamyV5z+cHtfgnuGY9fbBuftzi2eidrb3+NqqMFbheTKNS6uxCNBjIXb2LP7G9R\nTmtws+XRf3PFjjn0uG+ax3VVR72LyNWGYndgDju79pxxHUO599GW+aKhc+boC0Aj8+Gb6ygqqEQ9\n8Y/fXiXjdCi89/oannnFu3+6vkS3DSK6bVBDmOkT2aXw/de7WLXkMJWVTmxWI6oGQcEWLp3anVHj\nu9R7+x91cW+mbq67FcTJ+oHtz37GwX//hKvM0+9ssJqJu3IEq659jozvf0dVFCIv7sXQdx8kpI4a\nAoOtHnESrfp/NW0zSljCgxjz9TM+Ly0+kMGyyU+4G9HUE9XhImfFNq9v86qskPzfX7noBU99pDZD\nE6nIXl1v1xWA6lJYMe0ZJq35F7Zo/e29NaPHABqR0hI7Rw7mV0/+J1FVjfSUQooLPSe2lsY7r6zm\n1x/3U17mQFU0ysudVFY4ycku5atPkvjkvQ2NMq7BZmHgq3dxU8kiev3tWiSr2a1aaZCQrCa6/eUK\nNj7wLukL17klJVSN3DW7+XnY/ZRn5NZ67+gxZ+b6OJ3Lkz6sdsGAW/K6eH96dV7+nte/8XiLB/fi\nYQiwekhMGPws9Hhgms+qZM0lY88r8Xqs3zM315oN5RVVozw9lzU3v+S+v6ah1qNwTufCQ98BNCL2\nKpe7ktaLK1mSROxVZygN0IgUFlSSkVJISJiN9h1CEASBzLQi9u065rUnALhTAzeuSePyq3sRGd14\nWSADXp5B51svJeN7d7/e9tNGkL/lIAc++LFmcFXTUOxO9v7rOwa/4VtuKmJoIoJR8qnNXxsGm4WS\n/Rn4RYfhLClnza2vkL1kizvdFejz1I0UbDvs1eevuRQ63zme2ElD2PrER5QczMQaGUKvx6+n291T\n2f3yXAq2H/aom3BX53rv8BfcI56Jq95gxfR/UplVf/l0TVbIXbebj19azsZtuciySnznMG6+cxCd\nEhoujbih0DSNNcuT+eX7fZSVOuiUEM5VN/Zt8a7Plo6+ADQi4RH+WKxGj6ItAKNRIiLKvxmsqomi\nqHzy3kY2rU3FYJRQFY3wSD8efWYsRw7n1yn+L4pwcG9uoy4AAMHd42qkSO57ewFyuadOjuqSyV27\nuydvx9kAACAASURBVNZ7RQxPRDRIKGexAKguGVuUWxJi+RVPk7dxP6rTVa0DtHPWl4T07IAgiR6L\ngMFmIbhHHO0mDabdpNN7JkHXuy9n/3vfUyUXVy9OksVEYKcY2l8x3KdN4QO60v+5P/P7Pf9C87Lz\n8IWswrY1ybjM7lhK6uECXn56Kf98bRKx7c9ei6kx+PLjJNYsP1z9b2nntmz27znGE7MmNGjdS2tD\ndwE1IqIocMuMQR5VsyazxC13DUKsryZMI/Ljt7vZvC4Nl0ulqtKFwyGTk1XKazNXEBhkqdO/L4gC\nNv+GbSCiqWqdukb+HaK8atkgCAR08K2Jr2kae9/8Dk0+c5eHIIkEJbQjuEc8xfvTyU86WF3cdRK5\nwk5Zag6iFy0gwSjR6cZxPu9vDglg6rZ/0/XOyVgiQ7DFhpP48DVMWvtW9Q7DF+EDu/n8WZ0q91DD\nVoORClPNTCaXU+GHr3fVOlZTU1RYyeqlh2q+SJ1oTzrv063NZ9gFQPPPQBc4A4fF8diz40jsE01I\nmI0evaN45OmxDB4R39ymAbDspwMeVZyqqlFwvIKgYItHvcHpCIJA7/5tG8SWY6t38kO/GfzXOIEv\nA6ew8cF3vUoWA3S5ZYJXUTXJaiLx4Wt8jpHy1Qp2vzzXpxS1N0SzEYO/lcCEWMYtmgVA6eFsRIP3\nSdmeV8Lob56pqTEkCChVDtJ/+L3WsawRIQx990Guz5nPtRlfc9Gs2zD61x20DkmMJ3p0X49FUbKa\n3TGU0/WOTEaSew320CHSNDhy6MwzixqTw/vzkHykTbc0W883dBdQE5DQI4K/zfT95tdQOBwy639L\nYde2bAKDrFxyWUKtPlJN06go954OKUoCpcV2/v7ceJ5//NdqAbDTueJPveqtC1QbxzfsZenkJ6q1\n+eUKOwc/+pmiPalMXDHb43xrZCjjFr3AqmtmnpjMBTRFYfBb99XaIGXnC/9DrvRdX3AqotHA2EUv\nIJdW4NcugvBB3ap1iIK6tvO5iPjFhqM55Zo5RJqG6pTZcPe/iBrZ54w6d9WXSxbMZNvTn7ozp8qr\nCOndgcFv3Ev0mH5Ej+nHjuc+p/RwNkHd22OYOp4NG4rAy881NKz2+oYzRXYpbNucRU52CVExgVw0\nuN0ZSYr4+Zvw5Ys0W/Up7FzQv70LhPIyBzMfW0xJkR2HQ0YQBdb/lsKfbu3P+MndvF4jCAJRbQO9\nyvnKLpX2HUIJa+NHVNsA0o9472TlTRrg/9u7z8CoqrSB4/9z77QUSCghJCGhV+m9SZUizYptbeta\nV3FfV3fVRddVd9Vde0FXLGvvDSxIU6nSQQRCJ5QAIZXUqfe8HyZEwswkk0ySScj5fSGZuXPvyTBz\nz73nPOd5qmPjA2/6llW0O8lcm0rWxt20HNDF5zUJY/pyxbHPOLF6Ox6Hk/gRPTFFVlxzt7gKcfOG\ny03Sef39ri+I6ZpMq+E9yFi5rVwdAFOkjb4PXUvqnK/8Fpox3B72vreYfg9cE3Q7gqVbLQz6zy0M\n+s8tSCnLJc1LHN+fxPH9y353ONx8se5zn31YrCamXnxOjbUpM6OQf93/PSXFLux2NzabiQ/e3MAD\nj08mLj64ObBuPeOxWHTsJeWH28wWnTETO9dYWxsjNQR0lvjq463kZBXjcHiv6KQhcTo9fPzWJvLz\n/BcVAbjy+gG+cxQWncEjUsoWqkVF+Q8z1HWNyCBKQwYje9OewM9t3B3wOc2k03pUb5ImDKz05A9U\nqc5AREJzb6EXjwdnfpHPvMT4Lx4h5YLh3iGiKBvmmCj6PXo9nX9/Po5s/2kipNvD3rcWeheHASUZ\nOeSlHsSZXxR0u4JRWcZUq9XEvY+cR2zzCGwRJiIizZgtOhde3ot+g2uuHOR/n1lBXp4de+mdht3u\n5mSenVeeXhH0PnRd456HxhMVbcEWYcJs0bFYdbr2aMVFV4QW0tvYhXQHIIRoDnwMtAPSgMuklD6X\nikKINKAAb5VWt5TSf0xbDSnMd5CXW0xcfHSjqVa0dmUabj8Tm5ou2LIxnVHjO/l9Xd9BbfjjPefy\n0dubOJ6eT2SUhQlTu3LB5b3Lthk/pSv7dmWVdS6n73v46A410v6I1s1xnfQ9CWq6Xmlu/1Oyt+xl\n/T3/JWPVNsxREXS5cQp9/3EdptPGxQf88wYWT5vtkyPHH0d2AcuueZyDX67AcLqxxcUy8N830enq\nCQCYm0Qy9qO/4zxZiCM7n8g2cWXJ6ZKnDyV3R5rfKmDF6Vls+sdbpH2yjIJ96WXrzZr17sDYTx8i\npnOboP7eULXr2IJnX7+E/buzKClx0bFLyxrr0MGbQjptf45PYj9pSA4eyCEvt4TYZsElL2zboTnP\n/+9SftmQzsncEjp0aUn7TmoRW6hCHQK6D1gqpXxCCHFf6e/3Bth2rJSyVmdsHHYXr734M5vXHcZk\n0jE8BhOnd+OS3/VrvMmqKlkg6nZ5iIuP5t5HJhDbLMLv+zRgSDIjx3Vg+dJ9SEMiNIE0JGMndaZJ\n0youQvJjx9Zj7Dh3MscTTxBz4ijJ+7Zjsxd7a+JG2Uia5L9C1enydqTx3bl/KltJ63C42PHCF2Su\nTWXyD0+XXREnjO3H2I8fZOklD1W6DsBwudj/0Q9lOXVKjmWz+tZnvbnzrxxXtp0lJhpLTPnhjB53\nXsyO57/A5acDMBwufn38A5//m9yt+/lm6B3M3P+ez/5qyvZfjrFwfiq5OcWc0yeBSTO606lb4JQW\nobCXuNE14W8ZDJomcNhdQPDZa81mnYHDUmqsfUroHcAFwJjSn98GfiJwB1DrXn56Jdu3HMXtMnC7\nvF/aRd/sxBZhZvqlvcLVrDoxZGQ7fvh+N54z7gIMQ9J3gP8onaULdvPpO5uQSDylC4Fu/8somjUv\nPwlYXOSi6znxtGrdhMyMQn5efgCXy8OKpfv4ceEeLpjZi+kzq/f+Lpy/g8/e3+IN8WvSjKLIpmS0\n7cyg9YtpEaUx4bsn0AKEMZ5u0z/e9okY8tidZG3YReaaHbQa9tu4dsL4/kGVjETik1DNU+xg099e\nL9cBlD3ncLL/ox858PGPmCKttJkyhAMf/+i/Ew7QMbsKitn77mK/eX9C9c0X25j38daycMqjh0+y\nbPFeHn56Sq2kc46L966DcfhZB2OLMBMXr1JIh1uoHUC8lPJY6c/HgfgA20lgiRDCA7wqpZwb4nF9\nZGcWsX3LMVyu8l9Yp8PDd19uZ+rFPc/qu4ALL+/NlvVHOJlXgtPhQWgCs0lj5jX9aOqnRsCmtYf5\n6K0N5WKr9+3K4vHZi3hizgVl79XyxXt457X16LoASdlYrpf3tfM/+5WENjFVvjorKnTw6Xtbyq00\nlrqOB528q6/ilqemVzqWfcqJVdv85sMxXG4y16SW6wA0swnNbCpfxL0KCg9mYHg8CE0ja91O0hdv\nRLea2ffBEgr2Hi27C9EjrN6Vcmd2NgGSzIF3jiBr/a5qtasiBfl2vvpwK67T7nrcbgOPx8nHb29i\n1r2ja/yYmia49tYhvPrsynKfM4tV57pbh5zV38eGotIOQAixBPAXszb79F+klFIIEWjAYaSUMl0I\n0QpYLITYKaX0m8xdCHEzcDNASkrwJ5TMjEJMZq3cB/wUh92Nw+GusVKJ9VF0Eyv/en4aq37azy8b\n0olpFsHYSV0CjpN++dEvPiuUDUNyMreEnduO06N3AofScnn3tfW4nB4qOlU6HR6++XxblTuAndsy\n0HUNF+XbIYE9BwvKTv5SStxuA5NJC9gh2Fo1o+RYjs/jmtWM7Yxi7ppJp8PlY9n/0Y8+C7mCYWnu\nvXL9cebDpC9cj7vE6Y1SPPNuocSB0DU0m6Us+6hmNqFZTN67FT8dltA1n6IwNWHH1uPoJoHrjD9X\nSti6Kb3Gj3fKwKEpxD4ygfmf/Er64TySkmOZMbNXrQ07KVVTaQcgpQwYwC6EyBBCJEgpjwkhEoAT\nAfaRXvrvCSHEl8BgwG8HUHp3MBdg4MCBQac4jE9sgjvAmK4twoy1mhWtGhKrzcy4yV0ZN7lrpdtm\nnfCfeMyQkoxjBfToncAPC3b5nVj2pzrhoGaLHjDThG7SkFKy6OtU5n+6jaJCJ9FNLMy4rDcTpnb1\n6Qh63T2T1bc955NNU2gabS/0TaMw5IU7yN2RxsmdhzFcbjSThsfhRgiB0DUik1qimXTy9x8tN1dg\nirTS888z2fPm96R/v77SNQXSkLQe0wf7iTyc+cWkTB9Gp+sn8u2wO/2+VrdZ6Pz7SX72FBrve+3/\n3TYFGGKTUlKQ78BqM4X0/enUNY4/P+g7ZKaEX6hnxfnAdcATpf/OO3MDIUQUoEkpC0p/ngg8EuJx\nfTRrHkmfQW34ZUN6uSEFi9XEjJm91O3mGVonNmX/nmyfx4UQJLbxppjOzSnxyWTql4AO1YjI6N6r\ntd/1PSaTxtBz2zHv4618++X2sjuVgnwHn767CYfd5TOn0+F355G9ZS+pc+aVReJoFhMTvnnMb3io\npWkU09e+zIlV28jevJeolFYkTxmC82QRhtNFREILHFknWXrR38nevBfNYsJjd9Lp95Ppfd+VzB90\nW3ALyoSgeZ+ODHz8pnIPn//TMyy54IHf7loE2OJiGf/Vo0RUUGayunr2ScDwM+xkMmkMH93O5/FN\n6w7z3tz1nCwNIe4zMIkbbh9GdJPQJ/2V+kNUlnOlwhcL0QL4BEgBDuINA80RQiQCr0sppwghOgBf\nlr7EBHwgpfxXMPsfOHCg3LBhQ9DtcTo9vPPqWtYsP4CmaQgB0y7pybRLewY9ltxY/Lr5KC888VO5\nYSBd10hs05RHn5uGEILF3+7kk3c2+U1mdzqLVeeBxydXKzPjti1Hef7xn5AGuFwebDYTzVpEcu8j\nE7j3j/N8Qk8BbDYTL717md80FcVHs8hYuQ1LbDQJY/tWmkMnGPl70yk+mk3sOW2xtfB2jp93vZb8\nPZUPnegRVqaufJ4W/XwXLEkpyd+TTl5qGk06JHqTyNXi5/SXDem89J9lSClxuQxsNhMt4qJ44InJ\n5cI/d27L4OlHl5b/bJg0EpN++2wo9ZcQYmOwofYhdQC1raodwCn2EhcF+Q6aNY+o0pLzxubn5Qf4\n4I0N2EtcGIbknL4J3HznCKJLQztLSlz8bdZ8TuaW4PF4Pye6LjCZNDweA49HktyuGdfcPJgu3VtV\nux0n80pY/dN+crKL6dK9Ff0GJ3PiWAEP//U7vymzrTYTjz47rUoZSKWUpH26jNSXvsSRW0jy9GH0\nvOtSbHHVy3q5/q+vsuOFL8oVefen590zGfTkrdU6Rm3IzSlm9U/7yc0poWsP73t9ZnnSf/1tIbt3\n+I7mWm0m/vzAOLr1DBTrodQHjb4DUIJnGJLc7GIiIs1+FwGdzCvh03c3s+HnQwAMHJbCZdf0o0mM\nDcOQ6LWU0bSo0MGdv/+sLJz3dCazxktvzyQiMvhFS6tve5Z97y0pmyPQrGassdHM2DyXyNZVv3Ox\nZ+bxVd+bsGeeDFjwHeA656Kgwljrg4XzU/ns/c0B7/jMFo0rrh/IeVMqn2NSwqcqHcDZPzOqVEjT\nRIW1iWNiI7hx1nBunDXc5zldr72hgKhoK/0GJbN5/eFyncCpxUBVOfnnpR5k7zuLyhVaMRwu7Dn5\nbH3sfYa+MKvK7bPFxXLhltfYMPt19ryxwG9cv7VlTFAnfyklWet2krl+F5EJzUmeNhTdWrMptiuz\n8OsdfPBmxamVdV0jrlX4a1goNUd1AEq9deOsYcx50kXqtgxMJg232+Cc3q35/R/LF1NJ/fU48z7e\nytEjJ0loE8MFl/WiR+/fSjamL9rgk44AvBW6Dn65slodAHg7gZFz76Fgz1FO/LyjXEipKdJGn/uv\nqnQf7mI7i6beT/aG3RgeA82so1vMTF7yFM37dKxWu6rKMCSfvbelwm2EJoiMstCrX4Lf56WU7Npx\ngqwThSS3bVZrlbpysoo4kVFIfEITnwWLStWpDkCpt2wRZu7++3gyMwrIOFZAfEJTnwySa1em8fqL\nq8uGLU7m2dm/O4sb7hjGsFHtAW8BeU3XMfysZjCdmSe/GsZ/9QjLrn6MY0s3o1lMGC4PPe66hB7/\nd0mlr904+02y1u4sWydg2MFNCYum3s/lhz7ym4m0phUVOgKW/QTvurWUdrHMuneM3yJGOVlFPPHg\nYk7mliDxdgbtO7bgzw+Ow1ZDa28cdhevPLOSbZuPYjLruF0e+g5K5ub/G1Ej6cgbK5UNVKn34uKb\n0LNvos/J3/AYvDt3nc+YtdPp4f3X15cVOm970Uik9J1L0COsdLlpaoXHNtyeSquTWWKimfD1Y8w8\n8D5Tlj3HlRmfM+DRG4KKltnz5oKyk//pXAXFZKzaVunra0JEhLnC0p8DhqbwyDPTAqZvfv7xn8jM\nKMRud+Owu3E6POzbk8W7c9fVWBtff+lntm0+Wla5zuUy2LLhCO+8urbGjtEYqQ5AabAyTxT5DRMF\n7+rkExnexW62uFhGvHY3us1SVqrRFG0jbmh3etx5sd/XH1mwls+7X8/b1km813Qaa+96GY/Df/Gc\nUyLim9O8T8egKnid4iryn6pbCIEz1/9ivZpmMusMHOp/FbcQcPFVgVMuHz+az9HDJ33Wi7hdhjdD\nbTXqLp+psMDBprWHfdK8uJwe1iw/4FMnQAmeGgJSGqyICFPAhWoewyAi8rfhh45XnUfrUX3Y/+FS\nHLmFJJ43gISxff1epR9dspEfLn24LGW0u8jOrrlfk783nQlfB7WEJWhxg7qRuTbV53HD6SZuaPca\nPVZFbrlrJBnHF3Bo/2/Z3IWA3904iKTkwKGyBfl2b7lGP0NIhvQWngk1FDsvt8Q7B+QnIkzTNAry\n7TU21NTYqA5AaTAK8u0sX7qPI2m5pLRrxrnjO9Gxc0v27Mws1xFomqBDpxbEnJEEL6pNHL3+ckWl\nx9lw32s+9QI8JU6O/bCZvNSDNZqrZ/Czf+T78+7xRiiVDjWZIm10u/0CIlo1q+TVNcds1nn0mWkc\nSstlzfIDNI21MWp8p0rrA7Rp2yxgupCYWFuN1BeIaxUVsKMXAmLVZHC1qQ5AaRAO7s/h8QcW4XEb\nOJ0e1v98iHmf/srt95zLi/9eXm4oSEpZ7fTUALnb0/w+Lkwa2Zv3VqkD2LH1GN/PTyU3q5huPeM5\n/8IeNG/5W9htq6E9mLL8OTY/9BaZa3cS0boZvf5yBR2vDq2GtNPpIW1vNharTtsOzXG5DL79Yhs/\nLdqD0+GhZ78EZl7dzycNdEq7ZqS0C77jiYgwM+3ic8ql7ABvVbmrbhhYI6uGrTYzE6Z1Y/E3O32y\nik69+By/K8KV4KiFYEqDcN8d8zh2xLd2cUysjeJiJy5n+avQJk2tPPfmpT6rXIPxccoVFB/J9Hnc\nFB3BhG8eo/Wo3n5e5WvBvB188cGWcicts0XnwX9Pom370KpZ5eUUs2zJXjKOFtCxa0uGj+lQlu12\n+ZK9vP/6eoQQGFISFW2hSVMrR4/kl0X7CE0QEWHin89Nr3AdSDCklKz8YR9ff7aN3JxiEpJimHlN\nP3r1Swxpv6czDMnXn21jwVfejsYWYWLapT05/4IeKjXFGdRKYOWsknWikPvumF9hqOKZzBaNW/98\nbsDJzYrsePFLNtz/Wrmi7kLTiGobz6V73gkqNLOo0MGfbvjcb5tNJo0n5syodkGUXdszePrRHzA8\nBi6XgcWqY7WZeOg/55OTVcxTjyytNH8TeEt6jp7QietvHVqtdoSDYUjsJS5sEWaV4DGAqnQAKgpI\nqfcMQ1YUpeiXy2nwytMr2LblaJWP1/2OC+l601R0mwVzTBSmKBtNu7Rh8tKngo7LP1XrwB+32+DV\nZ1dVuV3gfS/mPLUch91dFhXjdHgoLHDy5pw1PkMxFe7LI9m+5VjlG9YjWumCNHXyrxlqDkCp9+Li\no2kSYyM707dovNmiB7wzcLsMXnh8Gc++cTFR0cEv+BJCMOTZ2+nzt9+RvWkPtvhmNO/TsUpDDWaL\n7nf18SkH9mZTmO8oS7wXrIP7c/wmyJOGZNf2DOKqWNqxSVPfVNlK46HuABoYp9NDdmaR38pnZysh\nBDf/aQRWqwmtNP+QrgusNhNX3zQIizXwJKBEsm7VwWod1xYXS9KkQbTo26nK48yBah2UtUtKHJVk\nEvXHMAwCNUVKaN+xedBXx1ariUkz6i7UVKl/1B1AA+HxGHz67maWLvDWixUIJkzryiVX9fW7PP9s\n061nPI8+N5WF81M5fDCPtu2bMXF6d1q1bkLb9s351/3f+ywUAnC7PBQWOPzssXaZzTp3/HUUTz/y\ng9/nPYbkhcd/4v5/TqxSDHvbDi3QAgxDtevUghmX9WbT2iPloqI0XRAdbcVud6FpAmlIDANGT+jE\n4BE1X35SaTjUJHAD8d7r61m2eI9PGNx5U7tx+bX9w9iy+uHNOT+zYuk+n3hxq83E3Q+Oo+s5weew\nz8wo4IM3NrJ1czqaEAwYmsJVNwygaWzwK3xPWfXjPl57YbXfGvAms8bYSV24+sZBVdrnxjWH+O+z\nK3G7DAxDYjJpmMwasx+bREr75uzbncnb/13L4bQ8hBD0GZDE9X8cgs1mYsuGdBx2Nz16t6alyux5\nVlJRQGcZe4mLO6771O9Yt8WqM+edy7A0gprHFcnMKOTBu77BXuIqO9maLTodu7TkvkcnBD2Ek3/S\nzv13zKOoyFU2hq/rgtjmkTzx0owqvc9FhQ5efGIZu1JPYHj8f880XTB4eFtGT+hULoNpZQ6n5bLo\nm50cP5pPxy4tmTitW7n1BeBdhatrQhVFamTqrB6AEGIm8A+gOzBYSun3bC2EmAw8D+h4S0U+Ecpx\nG5vsrCJ0XfjJZekdH8/NKalSdayzUVx8NA8/PYVP39vC9i1HsVhNjJnYmWmXVK0c6NIFu3DY3eUm\ncD0eSWGBgzUr0xg1vlPQ+5rz5HLvKuUAJ3/wRuKsWZHGpnWHGXd+V668fkBQ+05u14w/3DEs4PPb\nfznG4m93UpDvoM+AJMaf36VKE+FK3SsscLBi6V4O7MshKTmG0RM6E9us6nedVRHqZeM24GLg1UAb\nCCF0YA4wATgCrBdCzJdS7gjx2I1Gs+aReAIstzcMSWwzFckBEJ/QlDv+MiqkfezYetzvXILD7mbn\nrxlBdwDZmUXs3pEZME3CmZwODz98t4tR4ztWmHsnGF98+EvZginwRg4tXbCLR5+ZWq1hLKX2HT18\nkkfv+x63y4PT6cFs1vjui+385eHz6NQ1rtaOG9LsoZQyVUq5q5LNBgN7pZT7pZRO4CPgglCO29hE\nRlkYNrq9T95zi0Vn1PiOWG0qEVZxkZNvPv+Vf9zzHU88uIj1qw9WmsbZn5ZxUX6jbEwmjeZxweec\nyckuwmSu2tfL7THYtOZwlV5zpuzMIr77ovxaAJfTQ8FJO199vDWkfSu1Z+4LqyguduIsHeZ1uQzs\ndjevPLWiWp/jYNVF+EgScPqn+kjpY0oVXHvLEIaMbIfZrBMRYcZs1hg+pgNX/aFqE4hno6JCBw/e\n9Q1fffwrB/Zmk/prBq+9sJo3Xvq5yvuaMK2b39wymiYYfV7noPYhpcTp8OAMkKo6EIE3RUMotm5K\nR/j5Vns8kvWrD4W0b6V2FBY4OHQg129Z0YJ8h98UKDWl0iEgIcQSoLWfp2ZLKefVdIOEEDcDNwOk\npFR9Gf/ZymzWufHO4Vx5wwCyM4toERdNVHTd1o2tr76fn0pebkm5dMEOu5u1K9KYMLVblcoTdujc\nkt/dOIj3X1+PZtJAek/ot/55ZMCCKKfLOFbA048sJS+3xJuq8oxvtcWq07t/Els3ppdd7Z2i6RoD\nhiYH3VZ/dJMWcM5Dr0ZeJKX2SVnBSnfhXftRWyrtAKSUoaUlhHTg9E91m9LHAh1vLjAXvFFAIR77\nrBMVbT0rJ/MK8u0s/W4X27Yco1mLSCZM7UaXHq0q3P7IwTyat4xk3aqDfnPFu90Gi7/ZycVX9fGJ\nkKnImImdGXJuO1J/PY6uaXTvFR9U9I9hSP7998XkZBX5Dfts2tTKJVf3Y/jo9jw2exFHD5/E4XAj\nhDdiafKM7iQkxQTdTn/6D0rmnVd9K3GZzTojx3YIad9K7WjS1EbrpKYcOZjn85wtwkxiiHNCFamL\n2MH1QGchRHu8J/4rgMqrZSuNRnZmEQ/d/S32Em+pPwRs2XCES3/Xl0kzepTb1vAYvPvaepYv3YvZ\nrON2B14ZaxiSn1ccYM2KA/QdlMwtd40IOnVwRISZ/oOrdjW+a3sGRQUOvyd/AJfboH2nFlisJh54\nYjIb1xxiw+qDRERZGDW+E526BT/Z53S42bH1OG63Qfde8WUXBdFNrVx3y2DefnUdhsfA45FYbSbi\nE5ow7ZKeVfp7lLpz46zhZenO3W4DTReYTBo3/2l4reY9CmkdgBDiIuBFIA7IA7ZIKScJIRLxhntO\nKd1uCvAc3jDQN6WUQZVVUusAGodXnl7BulVp+LvT7T8kmSt/P6Asb/28T7byzefbyk1ynuoAKvoo\nmy06547ryHW3DqnJppez6sf9vPPqWuz2wGP/8QlN+PfLF4SUwnjL+iO8/PQK73yBlHg8ksuu6cfE\n6b+ldTh+NJ+VP+wj/6SdXv0S6Tc4uVqpsZW6k51ZxOJvd3JgbzZJyTFMnN6d1olNq7wftRBMaVBu\nueLDgCdNISAi0sK/np9GsxaR/PHqTygu8q3NK4R3mOPMcfXTmS06r7x/ea0VEEk/nMdDd39XYdpq\ni1Xn0WenVeuLDZCTVcS9t8/zyfhpser85aHzKhw2UxoHlQ5aaVAqymUkpXdC99svt2MY0u/JH7wp\nH2Zc1oshI9sGvtKVkpIAr68JScmx9OjdGnMF4Z9CiJAKpa9Yus/vwjKn08PC+b61hRWlIqoDUGpV\nUaGTvNySCmOZh57brsIIFY/HYPsvx9B1jRYBJnM9bsmIMR24/rahAUMprTYT0U1qdwJ91r2jtrQp\nSAAAEDZJREFUGX9+14DzElaricQ21Z/ozcku9r+4THrXHihKVTTuBDJKrcnJKmLu86vZnXoCIbyr\nmX//x6Gc08c3382lV/dl+9ZjZJ0oCrjiuWmMd7Xzpdf05X8vr/GpP9t/SHJZpM+4yV34ceFun8R5\nF11Z+5lTzWadK28YyIBhKTz50BLcbm/CNk0TmMwaf5g1LKQ2dDsnnp+XH8BxxpCZyazRw89729AU\n5jv48K0NrFt1EMMjOadPAr+7cSDxCdUbMlMqpuYAlBrndnm459avOJlbUi47p8Wq88Djk/3G5btc\nHpYv2cN7r23wzehp1bnlrpEMKC3vuOrHfXzyzmby8+2YTBrjJndh5jX9y4Z+DEPy7RfbWPDVDoqL\nnMTERnDxVX0YPSG4hVzVYRiSBfN2sGh+KoUFDpJSYpk4vRt7UjM5uN+b22XyBT1IrkLBdX9cLg+z\n7/ya7MyisjsBoQkiI8089uKMWs8dU5tcLg9/mzWf7MxiPJ7Sv610DujxF6cT2zz4ldiNmZoEVsJq\n7co03nzpZ5+JXSFgwLAUZv11dMDX/rIhnTlPLUcIgZQSw2MwcXp3Zl7Tr1zkjJQSh92Nw+5i9U8H\nOHL4JG07NGfk2A5ERlnKtvG4jVrPhlmQb+epR5ZycH8O8rQbGItF509/G0PPvjVXHB28K0c/eWcT\na1em4fFIevdP5Irrf4uUaqh+XnaA/72yxvfuxqQxaUZ3LlNpz4NSZ9lAFcWf9MMn/Ub1SAmHD+RW\n+No+A5N48a1L2brpqDdvfZ8EmrfwvfITQnD8aD5PPLgYt9vA5fSwblUaX330Cw/+ezIJSTEIUfup\nkI+n5/PQPd9hL/HN1ep0evjwfxv51/M12wFEN7Fyw+3DuOH2wNlAG6Kd2zN8Tv7gXdCX+uvxMLTo\n7KcmgZUa16p1NFab/2uLYMIfrTYzg4a3ZeS4jn5P/uC9up/z5ApKil1lYZdOh4fiIievPle9guvV\n8ebLa/ye/E85ciivVpN5nU1axEX5T6AnqNJKbiV4qgNQatyg4W0xW3SfmrgWq860S2tmNWrGsQLy\ncot9Hj91l1GQb6+R41TE6fSwJ/VEhdtERlpCWvTVUBiG5JeN6bz93zV8/PYmjhzyTWtQmZHjOvpd\n9Wqx6Kp2cS1RQ0BKjbNaTcx+bBIv/WcZmccL0XSBrmtce8tgunSvmYVKHo8R+MQqvNkvw81k1hh/\nfpda2XdBvh0pf4uOCie3y8NTjyxl/55sHHY3miZY8u1OLrqqD1MuPCfo/TRvEcmse0cz58kVZdcO\nbo/B5df2r7HPjVKe6gCUWpHYJobHXphBxrECHHYXSSmx6DUYgpmQFIPNZvI7ZhzXKrpOomEsFp3O\n3Vuxe0eG3zQUfQcmceEVfWr0mEcO5jL3+dWkl15ht05qyk13DqddxxY1epyq+GnRHvbtzioLuzUM\nidPp4Yv3f2Hg0JQqTU737p/ES+/MJPXX47hdBt16xpdN6is1Tw0BKbUqPqEJKe2b1+jJH7z5+W/6\n0wgsVr1s2EDXBVariRtnDa/RY1XkhtuHEhll8Q554a3xq5sEf5g1jFn3jqnR/Dv5J+388/6FHNyf\ng7s0adiRg3k8/sAicnN8h8PqyrLFe31SUwAYsno1CMxmb8rs/kOS1cm/lqk7AKXB6tUvkYefmsr3\n83eQfiiPdp1aMGl69zoNh2yd2JT/vHwhPy3ew56dmSQkNmHc+V1rpQ3LFu/xuwrY7TZY+t0uLr26\nX40fMxhuj//Fe9IwcLurn/ZCqX2qA1AatMTkmLCHQ0Y3tdZJquUDe7P9JppzuwwO7M2u9eMHMnRk\nO77+bBuuM3IcmUw6fQe2CVOrlGCoISBFaSDapMT6DZPUTRptUmqvaEhlJk7vRvOWkeVqVlutJoaN\nal+lamxK3VN3AIrSQIyZ1IXv56f6VD/TdY3zpnYNU6u8qRoeeWYqyxbvYd3qQ0REmBk7qTP9h4RW\n3lKpfSoVhNIgORxuVv6wj/WrDxIRaWHspM706pd41sfc79l5gleeXklBvh2BIDLKzC13jaR7L39l\nu5XGSOUCUs5qJSUuHv7Ld2RnFpVFn1itJs4d35Frbh4c5tbVPiklx9LzkVKS2CbmrO/0lKqps4Iw\nQoiZQojtQghDCBHwgEKINCHEr0KILUIIdUZXQrLo61SyMorKhR46HG6WL9nLkYMV5xo6GwghSGwT\nQ1JyrDr5KyEJdRJ4G3AxsDyIbcdKKfsG2zMpSiBrlqf5RJyANxxx87ojYWiRojRMIU0CSylTAXUV\notQpTff/eRNC1HrBF0U5m9RVFJAElgghPMCrUsq5dXTcBk1KydqVaSz6eieFBQ569Utg6sU9G31m\nxHPHdeTz97f4FIDXhGDgsJQwtSp4xUVOMjMKadEyiuimtVuiUlEqUmkHIIRYAvgLMZgtpZwX5HFG\nSinThRCtgMVCiJ1SSr/DRkKIm4GbAVJS6v+XuTa9+9p6Vizdh9PhzXeTdaKQn5en8fDTU4mLjw5z\n68Jn/JSubPj5EIfScnHY3QjhTR8w47LexCfU36IoHo/Be6X/p7pJw+P2MGBoCn+4YxgWq4rIVupe\njUQBCSF+Au6RUlY6wSuE+AdQKKV8qrJtG3MUUMaxAmb/6WuflZ+aBsNGdeDm/xsRppbVDx6PwZb1\nR9i07jARkRbOHdex3i86+vDNDfzw/e5ydy5mi86AIcncdve5Qe8nM6OABV/tYO+uTFq1bsr5F/ag\nY5eWtdFkpQGqVxXBhBBRgCalLCj9eSLwSG0ft6HbsfUY/qZWDAN+2Zhe9w2qZ3RdY8DQlLI6wfWd\n0+nhh4W7fYatXE4PG9ccoiDfTpOmlad2TtuXzWOzF+F2efB4JIcO5PLLxiNcf9tQRozpUFvNV85S\nIXUAQoiLgBeBOOBbIcQWKeUkIUQi8LqUcgoQD3xZOlFsAj6QUn4fYrvPelabCS3A5LrVWrtlDpWa\nV1jg8M6E+WEy6eRkFQfVAbz137XlUmBL6a2E9s6r6xg8oi2GIVn5wz7WrkzDajMxZoJ3Ra4K1FD8\nCTUK6EvgSz+PHwWmlP68H6jZpOiNQL9Bbfjfy2t8HjdbdEZP7ByGFimhaNrU6rfaFXizebZsVfmc\njtPp4eC+HL/PCWDX9gw+eGMDmScKy9ZI7Np+gsHD23LjnXWXIltpOFTMXD0VEWnh9ntGYbHoWCw6\nQnjvCjp2acmUi4KvsqTUDyazzuQLe2A54+7NYtUZOa4DUdGV573XBD5lNk+RUrJ5/RFOZBSWXyBn\nd7N2VRr792SF0nzlLKVCD+qxvoPa8PRrF7N2ZRpFhU669mhFt57x6na+gbrgst4AfP/VDozS4Isx\nEztz+XUDgnq9yazTq18iv246imGUH0+yRpjZveOE33TRLqeHTWsP06GzmihWylMdQD3XNMbGhKnd\nwt0MpQZomuCiK/ow/ZKenMyz0yTGVi6FcjCuv20oj/x1AcVFThx2N2aLjq4J7rx3NO+/sd7va4QQ\nNVqZTDl7qA5AUeqYyazTIq56i/mat4jkP69cyLpVaezfk02r+GhGju1IdFMro87rxJFDeT7lGXWT\nxuAR7Wqg5crZRnUAitLAWCw6I8d2ZOTYjuUeP3d8J9avPsjeXVnlFshNu6QnickxYWqtUp+pDkBR\nzhImk8Y9D53Hti1H2bjmMFabiRFjOtT7BXJK+KgOQFHOIpom6N0/id79k8LdFKUBUDNDiqIojZTq\nABRFURop1QEoiqI0UqoDUBRFaaRUB6AoitJIqQ5AURSlkVIdgKIoSiOlOgBFUZRGSnUAiqIojZTq\nABRFURqpkDoAIcSTQoidQoitQogvhRCxAbabLITYJYTYK4S4L5RjKoqiKDUj1DuAxUBPKWVvYDdw\n/5kbCCF0YA5wPtADuFII0SPE4yqKoighCqkDkFIuklKeqlC9BmjjZ7PBwF4p5X4ppRP4CLgglOMq\niqIooavJOYAbgAV+Hk8CDp/2+5HSxxRFUZQwqjQdtBBiCdDaz1OzpZTzSreZDbiB90NtkBDiZuBm\ngJSUlFB3pyiKogRQaQcgpTyvoueFENcD04DxUkrpZ5N0IPm039uUPhboeHOBuQADBw70tz9FURSl\nBoRUEEYIMRn4KzBaSlkcYLP1QGchRHu8J/4rgKtCOa6ihIvT6WHjmkOcOFZAYnIM/Qa1wWSuWmF3\nRakvQq0I9hJgBRYLIQDWSClvFUIkAq9LKadIKd1CiDuAhYAOvCml3B7icRWlzmUcK+Cf93+P0+7G\nbndjizAREWnhwScmV7vIu6KEk/A/alM/DBw4UG7YsCHczVAUAP7+5285dCCH078ymibo3C2Ovz02\nKXwNU5TTCCE2SikHBrOtWgmsKEHIzizi6JGTnHm9ZBiSfbuzKMx3hKdhihIC1QEoShAcdjeaJvw+\nJzSBw+H2+5yi1GeqA1CUILRObII5wGRvkyZWmreMrOMWKUroVAegKEHQdI1rbxmMxXpaJyDAYtG5\n/rahlAZBKEqDEmoUkKI0GkNGtqNZi0i+/vRXjqXn06ZtLDNm9qJD55bhbpqiVIvqABSlCrp0b8Xd\nfx8f7mYoSo1QQ0CKoiiNlOoAFEVRGinVASiKojRSqgNQFEVppFQHoCiK0kipDkBRFKWRqtfJ4IQQ\nmcDBcLfDj5ZAVrgbEWaN/T1o7H8/qPcA6ud70FZKGRfMhvW6A6ivhBAbgs22d7Zq7O9BY//7Qb0H\n0PDfAzUEpCiK0kipDkBRFKWRUh1A9cwNdwPqgcb+HjT2vx/UewAN/D1QcwCKoiiNlLoDUBRFaaRU\nB1BNQognhRA7hRBbhRBfCiFiw92muiSEmCmE2C6EMIQQDTYKojqEEJOFELuEEHuFEPeFuz11TQjx\nphDihBBiW7jbEg5CiGQhxI9CiB2l34E/hbtN1aU6gOpbDPSUUvYGdgP3h7k9dW0bcDGwPNwNqUtC\nCB2YA5wP9ACuFEL0CG+r6txbwORwNyKM3MDdUsoewFDg9ob6GVAdQDVJKRdJKU8Vgl0DtAlne+qa\nlDJVSrkr3O0Ig8HAXinlfimlE/gIuCDMbapTUsrlQE642xEuUspjUspNpT8XAKlAUnhbVT2qA6gZ\nNwALwt0IpU4kAYdP+/0IDfTLr4ROCNEO6AesDW9LqkdVBKuAEGIJ0NrPU7OllPNKt5mN95bw/bps\nW10I5u9XlMZKCBENfA78n5QyP9ztqQ7VAVRASnleRc8LIa4HpgHj5VkYT1vZ399IpQPJp/3epvQx\npRERQpjxnvzfl1J+Ee72VJcaAqomIcRk4K/ADCllcbjbo9SZ9UBnIUR7IYQFuAKYH+Y2KXVICCGA\nN4BUKeUz4W5PKFQHUH0vAU2AxUKILUKI/4a7QXVJCHGREOIIMAz4VgixMNxtqgulE/93AAvxTv59\nIqXcHt5W1S0hxIfAz0BXIcQRIcQfwt2mOjYCuAYYV/rd3yKEmBLuRlWHWgmsKIrSSKk7AEVRlEZK\ndQCKoiiNlOoAFEVRGinVASiKojRSqgNQFEVppFQHoCiK0kipDkBRFKWRUh2AoihKI/X/4ZB+p5aK\nKJAAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x20f65cd9b38>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Datasets\n",
"noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure = load_extra_datasets()\n",
"\n",
"datasets = {\"noisy_circles\": noisy_circles,\n",
" \"noisy_moons\": noisy_moons,\n",
" \"blobs\": blobs,\n",
" \"gaussian_quantiles\": gaussian_quantiles}\n",
"\n",
"### START CODE HERE ### (choose your dataset)\n",
"dataset = \"gaussian_quantiles\"\n",
"### END CODE HERE ###\n",
"\n",
"X, Y = datasets[dataset]\n",
"X, Y = X.T, Y.reshape(1, Y.shape[0])\n",
"\n",
"# make blobs binary\n",
"if dataset == \"blobs\":\n",
" Y = Y%2\n",
"\n",
"# Visualize the data\n",
"plt.scatter(X[0, :], X[1, :], c=Y, s=40, cmap=plt.cm.Spectral);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Congrats on finishing this Programming Assignment!\n",
"\n",
"Reference:\n",
"- http://scs.ryerson.ca/~aharley/neural-networks/\n",
"- http://cs231n.github.io/neural-networks-case-study/"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"coursera": {
"course_slug": "neural-networks-deep-learning",
"graded_item_id": "wRuwL",
"launcher_item_id": "NI888"
},
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.4"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
dtamayo/rebound | ipython_examples/HyperbolicOrbits.ipynb | 2 | 68225 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Loading Hyperbolic Orbits into REBOUND\n",
"\n",
"Imagine we have a table of orbital elements for comets (kindly provided by Toni Engelhardt)."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"from io import StringIO\n",
"import numpy as np\n",
"import rebound\n",
"epoch_of_elements = 53371.0 # [MJD, days]\n",
"c = StringIO(u\"\"\"\n",
"# id e q[AU] i[deg] Omega[deg] argperi[deg] t_peri[MJD, days] epoch_of_observation[MJD, days]\n",
"168026 12.181214 15.346358 136.782470 37.581438 268.412314 54776.806093 55516.41727\n",
"21170 2.662235 2.013923 140.646538 23.029490 46.292039 54336.126288 53673.44043 \n",
"189298 15.503013 11.550314 20.042232 203.240743 150.855761 55761.641176 55718.447145 \n",
"72278 34.638392 24.742323 157.984412 126.431540 178.612758 54382.158401 54347.240445\n",
"109766 8.832472 9.900228 144.857801 243.102255 271.345342 55627.501618 54748.37722\n",
"\"\"\")\n",
"comets = np.loadtxt(c) # load the table into a numpy array"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We want to add these comits to a REBOUND simulation(s). The first thing to do is set the units, which have to be consistent throughout. Here we have a table in AU and days, so we'll use the gaussian gravitational constant (AU, days, solar masses). "
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"sim = rebound.Simulation()\n",
"k = 0.01720209895 # Gaussian constant\n",
"sim.G = k**2"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We also set the simulation time to the epoch at which the elements are valid:"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"sim.t = epoch_of_elements"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We then add the giant planets in our Solar System to the simulation. You could for example query JPL HORIZONS for the states of the planets at each comet's corresponding epoch of observation (see [Horizons.ipynb](Horizons.ipynb)). Here we set up toy masses and orbits for Jupiter & Saturn:"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"sim.add(m=1.) # Sun\n",
"sim.add(m=1.e-3, a=5.) # Jupiter\n",
"sim.add(m=3.e-4, a=10.) # Saturn"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"Let's write a function that takes a comet from the table and adds it to our simulation:"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"def addOrbit(sim, comet_elem):\n",
" tracklet_id, e, q, inc, Omega, argperi, t_peri, epoch_of_observation = comet_elem\n",
" sim.add(primary=sim.particles[0], \n",
" a = q/(1.-e),\n",
" e = e,\n",
" inc = inc*np.pi/180., # have to convert to radians\n",
" Omega = Omega*np.pi/180.,\n",
" omega = argperi*np.pi/180.,\n",
" T = t_peri # time of pericenter passage\n",
" )"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"By default, REBOUND adds and outputs particles in Jacobi orbital elements. Typically orbital elements for comets are heliocentric. Mixing the two will give you relative errors in elements, positions etc. of order the mass ratio of Jupiter to the Sun ($\\sim 0.001$) which is why we pass the additional `primary=sim.particles[0]` argument to the `add()` function. If this level of accuracy doesn't matters to you, you can ignore the `primary` argument.\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can now set up the first comet and quickly plot to see what the system looks like:"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAU0AAAFCCAYAAAB1po8RAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XlwXNWdL/DvUbdaLaul1r7vliyveLdsDFiGYGPMQFYq\nA2QjE4ZJwstMXjKEMATXo8IkpDI1ZKYmkwqQhCUBQjwODhibJcLGE8sLXvAia98X093aet/O+8OS\nIoxs60rd9/by/VSpqnVb0vldkL86595zzxFSShAR0cwkaF0AEVE0YWgSESnA0CQiUoChSUSkAEOT\niEgBhiYRkQJ6rQuYCyEE50sRUVhIKcV0x6O+pyml1Pzj0Ucf1bwGnhPPSe0Pl8uFs2fPoqWlBT6f\nLybOaeLjSqK6p0lE2ujt7YXFYkFhYSFycnK0LkdVDE0imjG/34/m5mZ0dHRg8+bNMBqNWpekOoZm\nCNTV1WldQsjxnKKDmudkt9vR3t6O9PR0bN26FQkJ4bm6F+n/n8TVxu+RTAgho7l+omgQDAYxMDAA\ni8WCsrIymM1mrUsKOyEE5GVuBLGnSUSX5fF48N577yEzMxNLly5FYmKi1iVpjj1NIpqWzWZDd3c3\nsrKyUFxcrHU5qmJPk4hmLBAIoLu7Gw6HA9XV1Zg3b57WJUWUqJ+nSUShY7VasX//fgghsGjRIgbm\nNDg8JyIAwMDAAPr6+pCZmYny8nKty9HUlYbnDE2iOOfz+dDe3g4pJSoqKmAwGLQuSXO8pklE0+ru\n7obVakVeXh7y8/MhxLQ5QVPwmiZRHAoGg+jq6kJjYyOKi4tRUFDAwJwhDs+J4ozL5UJ7ezuMRiPK\nysqg0+m0LinicHhORAAu3uwZHBxEcXExsrKytC4nKjE0ieKA3+/H6dOnYbFYcN1118XlQhuhwuE5\nUYwbGxtDR0cHMjIyUFhYGLaFNmIJh+dEcUhKib6+PlitVpSXlyMtLU3rkmICQ5MoBnk8HtTX16Ok\npASLFi3iQhshxOE5UYyZWGgjLS0NFRUVWpcTlTg8J4oDE3MvudBGeLGnSRQDLBYLWltbkZeXh9LS\nUt7smSP2NIli2ODgIFpbW1FQUBD3C22ogT1Noijl8/nQ0dGBQCCAiooKJCUlaV1SzGBPkyjGWCwW\n9PX1ITs7m8+Nq4wXPoiiiJQSXV1dOHjwIMrKylBYWMjAVBmH50RRwuPxoK2tDYmJiSgvL4dez4Fi\nuHB4ThTlJuZeFhQUIDc3V+ty4pqmoSmEKAbwLIA8AEEAv5RS/kwIkQHgJQBlADoA3CmlHNGsUCKN\nBAIBHDt2DD6fD6tWrUJycrLWJcU9TYfnQoh8APlSyhNCCBOAYwDuAPAVAFYp5RNCiAcBZEgpvzfN\n93N4TjHL6XSira0NSUlJqKio4HBcRVGzR5AQYheA/xz/2CSlHBwP1nop5cJpvp6hSTFpcHAQAwMD\nKC0tRUZGhtblxJ2oCE0hRDmAegBLAXRLKTOmvGeTUmZO8z0MTYopbrcbJ0+ehNls5txLDUX8jaDx\nofkrAL4lpbQLIS5NQiYjxbzR0VG0trbCYDCgpqaGU4kilOahKYTQ42JgPiel/OP44UEhRN6U4fmF\ny33/jh07Jl/X1dWhrq4ujNUShd7UdS+rqqqQmpqqdUlxp76+HvX19TP6Ws2H50KIZwFYpJTfnnLs\nxwBsUsof80YQxTK73Y7u7m7OvYwwEXtNUwixEcB+AB/g4hBcAvg+gMMAXgZQAqATF6ccDU/z/QxN\nilpDQ0P4y1/+goULF6KyslLrcmiKiA3NuWJoUjQKBoPo7u7G2NgYKisrue5lBGJoEkUIl8uFtrY2\nzJs3D6WlpdxzPEJF/N1zonjQ3t6OxsZGrFu3jnuORzH2NInCLBAIoLOzE06nEyUlJTCbzVqXRFfB\n4TmRRhwOB9ra2pCeno6ioiJuQxElODwn0sCZM2fg8/lQXl6O9PR0rcuhEOGfPaIQ8/l8aG5uhtVq\nxYIFCxiYMYbDc6IQGh0dRUdHB7ehiHIcnhOFWTAYRE9PD4aHh1FRUcFHIWMYQ5NojrxeL44ePQop\nJdatW4fExEStS6Iw4vCcaA6Gh4fR2dmJ3NxcFBQUaF0OhQiH50QhJqWcHI5XVVUhJSVF65JIJbx7\nTqSQw+HAO++8A4/Hg8WLFzMw4wyH50QKTOwKOW/ePFRXV2tdDoUJh+dEczR1ZaLq6mquTBTH2NMk\nuorh4WF0d3fDZDJxZaI4caWeJq9pEl2B1WrF4cOHkZqaioqKCgYmsadJNJ1gMIiuri44HA5UVlYi\nOTlZ65JIRVzliEiBiYWCU1JSUFpaypWJ4hBvBBHNUGdnJ86cOYPa2louFEzTYk+TCBeH4xMLBRcX\nF3Oh4DjH4TnRFUwMx00mE0pKSjgcJw7PiS6npaUFdrsdpaWlyMzM1LocigL8k0pxKRgMor29HV1d\nXZg/fz4Dk2aMw3OKOxyO09VweE407sMPP0RfXx+Ki4t5d5xmhaFJcSEYDOL48eMYGxvD+vXrYTQa\ntS6JohSH5xTz3G43WltbkZycjNLSUuj17CvQlXF4TnHLarWip6eHw3EKGYYmxSS/348PPvgABoMB\nCxYs4LPjFDIMTYo5Ho8Hzc3NcLvdWLZsGYfjFFK8pkkxZWhoCF1dXSgsLEROTo7W5VCU4jVNinnB\nYBC9vb0YGRnhyuoUVgxNinperxcHDhxAVlYWli1bxoWCKaw4PKeoNjo6io6ODmRlZaGoqEjrcihG\ncHhOMUdKif7+flgsFlRWVsJkMmldEsUJ9jQp6rjdbpw+fRppaWmoqKhAYmKi1iVRjGFPk2KGw+FA\nY2MjdDodqqurIcS0v9dEYcPQpKhx4cIF9Pf3o6qqiiurk2Y4PKeIFwgE0NnZCY/Hg8rKSiQlJWld\nEsU47ntOUcvtdmPPnj3w+/2oqalhYJLm2NOkiDXxdE9ubi4KCgq0LofiCG8EUVSRUqKnp4dP91BE\nYk+TIorT6URzczNSUlJQUVHBp3tIE7ymSVFhbGwM77//PnQ6HaqqqhiYFJE072kKIZ4GcBuAQSnl\nNePHMgC8BKAMQAeAO6WUI9N8L3uaMWJwcBCDg4MoLy9HWlqa1uVQnIv0nuavAGy95Nj3ALwlpawB\n8A6Ah1SvilQRDAbR1tYGm82GhQsXMjAp4mkemlLK9wAMXXL4DgC/GX/9GwCfVLUoUoXD4cDevXsh\nhEBNTQ0MBoPWJRFdVaTePc+VUg4CgJRyQAiRq3VBFFrDw8Po7OzEokWLUF5eHrZ2pJTwer0AAL1e\nP/nYJfc6p9mK1NC81GUvXO7YsWPydV1dHerq6lQoh2ZLSom+vj7YbDZUVVUhJSVlTj/P5/PB5XJh\neHgYAwMDMJvN8Hq9aGpqQn5+PhITEzE8PIyEhARkZWXB6/Wip6cHVVVV0Ov1sFqtyM/Pn7wsYDQa\nYTab+Ux7nKmvr0d9ff2MvlbzG0EAIIQoA7B7yo2gcwDqpJSDQoh8AH+WUi6a5vt4IyiKuN1udHZ2\nQgiBysrKWe3dMzIyAqfTCbvdjra2NrjdblRUVCApKQlerxeFhYVISkpCQkICDAYDdDrdtAHo9/vh\n9/sxNjYG4OKjmh9++CHcbjeSk5ORmJgIr9eLiooKzJs3jz3TOHOlG0GREprluBiay8Y//zEAm5Ty\nx0KIBwFkSCm/N833MTSjhMvlwsGDB5GXl4elS5cq6slduHABLpcLVqsVra2tqKysREFBAUwmE0wm\nU8gDLRAIwG63w2KxICEhAW63GyMjI6iqqkJ6ejo3aosDER2aQojfAqgDkAVgEMCjAHYB+D2AEgCd\nuDjlaHia72VoRgGbzYbu7m6UlJQgMzNzRt/j8Xjw4Ycfor+/H01NTVizZg3y8vI0GTr7/X5cuHAB\nwWAQdrsdXq8XRUVFyMzM5DA+RkV0aM4FQzOySSnR29uL4eFhzJ8/f0Z7jzscDrS3t+PQoUPYsGED\nCgsLkZ6eHjHhFAgE0N/fD6/XCykljEYjsrKyYDQatS6NQoihSapzu904fvw4srOzUVFRcdUhrcVi\nwZEjR5CamoqioiLk5+fPKGS15Ha70d7ejmAwiLy8PA7dYwhDk1TldDrR1NQEAFi+fPkVe4ljY2Po\n7OyE1WpFSkoKVq5cGXWPT/p8vskVmQoKClBQUMAbR1GOoUmqsVqt6OnpQWlpKTIyMi77dYFAAOfP\nn8f+/fuxZcsWlJaWRn0vze12w2azwev1Ij09Henp6VqXRLPE0KSwm7qc29WuX7a3t6OnpwdpaWkh\nmasZaVwuFxobG5GZmYmioqKo/2MQjxiaFFZ+vx/79+9HRkYGrrnmmssOr/1+PxobG3Ho0CFs3749\nphcWllJiZGQEIyMjmDdvHnJycrQuiRRgaFLYuFwutLS0wGQyoays7LLX8np6etDS0oKMjAwsWbIk\nbnpfHo8H58+fR15eHnJycnitM0owNCksJm5+XO36ZW9vL9566y2sXbsWixcvVrHCyCClhM1mg8vl\nQkZGRsxdjohFDE0KqWAwiPb2djidTsyfP/+y21EEg0GcOnUKQ0NDWLNmDVJTU1WuNLLYbDb09/dj\n/vz5nNcZ4RiaFDKBQADnzp3D4OAgNm3adNlhdiAQwIEDB9DT04M777yTy76N83g8sFgsSE1N5dqh\nEYyhSSHhdrvR2tqK1NRUlJSUXHb+pc/nw7Fjx6DX66Ny3mW4+f1+NDU1IS8vD1lZWVqXQ9OI9JXb\nKQqMjIxM3tAoLS29bGD6/X4899xz8Pv9WL16NQNzGnq9HgsWLIDf78fo6KjW5ZBC7GnSVZ0+fRoe\njwc1NTUwmUyX/Tq/349Dhw4hKSkJa9euVbHC6DTxHLtOp4vp6VfRiD1NmpWJGz5jY2NXDUyfz4fd\nu3fDaDRizZo1KlYZvXQ6HXJzcxEMBuFwOLQuh2aIoUnT8vl8aGpqgpQStbW1VwxMADh58iT8fj9W\nrlwZMSsSRQODwYC8vDzY7XbY7Xaty6EZYGjSxzgcDjQ2NsJsNqOysvKqE7Kbm5sxOjqKT33qU7yG\nOQt6vR5msxn9/f3w+/1al0NXwdCkj+jt7cWf//xnlJSUzOg6W0tLC15//XWsX78+bp7yCQej0YiS\nkhIMDw8jGAxqXQ5dAUOTJvX29sJms+G6666b0Qo9brcb58+fx6c//enLTnCnmTMajUhMTER/f7/W\npdAVsGtACAQC6OjogN/vx6JFi2bUYwwGg9i/fz/Ky8tRUlKiQpXxIS0tDU6nEy6XK+IXYY5X7GnG\nObvdjsbGxsm5gzMdYp86dQqtra1YtOhjm4TSHAghkJOTA4fDweubEYqhGcfsdjsOHDiA5ORklJWV\nzfiut9PpRGdnJ+6++26u2hMGer0eRqMRAwMDWpdC0+DwPE5NrLC+ceNGxc9Av/HGG6ipqeGz02Fk\nMpng8Xjgdru5uEeEYWjGmak7RNbU1Cj+B9nV1YWBgQHcfvvtYapw7lwuFxwOB7xeL+x2OwwGA8bG\nxmAymSClhF6vR0pKCnQ6HdLS0iK2t2w2mzE2NgaDwRCxNcYjhmYc8Xq9OHXqFNLS0rBw4ULFU4SC\nwSDOnDmDT37ykxE1vcjv92NoaAi9vb0IBoOw2WwoKiqCTqeDwWDAvHnzkJiYiKSkJPj9fng8Hjid\nTthsNuh0Ouj1ephMJmRlZUXUzRe9Xj+5Fmd2drbW5dC4yPnNp7Dyer1obGyElBLV1dWzemqnoaEB\nAFBYWBjq8mbF5XLh7Nmz8Pl8EEKgoKAAWVlZM17kt6SkBIFAAG63G1arFX19fXC73SgoKEBaWlpE\n/GEwm80YHR1FIBDggwMRQvvfCgo7u92OtrY25OfnIzc3d1Y/IxAI4MyZM7jppptCXJ1ydrsdra2t\nsNlsKCgoQFlZ2ax7iDqdDikpKZNB63A4cOHCBYyMjCA5ORl5eXmaPhaq0+lgNBrhdru54nuE4CpH\nMW7ihk95eTnMZvOsf05rayu6urqwefPmEFanjN/vR2dnJ86dO4clS5agqKgobIsbu91uWCwWeDwe\n5ObmarrqvJQSfX19yMvLi4jebzzgIsRx6sSJE3A6nVi5cuWcrtUFg0H8+te/xvbt25GXlxfCCmfO\narWiubkZgUAAa9asQVJSkirtjo6OYnR0FEIIFBYWatbrdDqdSEhI4J10lXBpuDgTDAbR1tYGIQRW\nrVo155sb7e3t8Pl8mgVmX18fjhw5gry8PGzcuFG1wAQuPqGTn58Pg8GAjo4O+Hw+1dqeymg0wuv1\ngp0E7bGvH2N8Ph9aWlqQnJyMa665JiQ9o+7ubnziE58IQXXKdXR04OTJk9i8ebNm80L1ej1ycnJg\nMBgwODiI7Oxs1Xt8CQkJCAaDcDqdvLapMfY0Y8jEI5EZGRkoLy8PSWBaLBZ0dnairKwsBBUq09LS\nglOnTmHr1q0RMZHebDbDbDZjaGgIbrdb9fa5KEpkYGjGCJvNhr1796KwsBD5+fkh+7lnz55FUlKS\n6jcgGhsb0dzcjC1btkTUdbzU1FSYTCaMjIyoPlQ3GAyQUnLpOI0xNGPA4OAgenp6cPPNN4d8d0O7\n3Y66urqQ/syr6e7uRk9PDzZs2BBRgTkhNTUVycnJsNlsql9jFELA6XSq2iZ9FEMzikkp0dnZCavV\nioULF4Z8CDs0NISRkZFZz+2cDbvdjubmZixYsGBGa3pqJS0tDUajEVarVdV2uX+89hiaUcrr9eL0\n6dPw+XyoqakJyz+m999/Hy6XS9Xnnk+cOIHk5GSUlpaq1uZspaamIiEhQdVN0RITE5GQkMC76Bpi\naEYhj8eDY8eOwev1Yv78+WF7vE4Ioepk9ubmZgwPD6O2tla1NuciISEBKSkpcLvdql5nFELA6/Wq\n1h59FEMzytjtdpw/fx5VVVVYvXp12CZbB4NBDA4OhvSm0pX4/X50dHRg5cqVUbWiz8RNMjV7mwkJ\nCQgEAqq1Rx8VPb+dBJvNhtbWVpSXlyMnJyesbTU3N6Orq0u1VX+6u7vh8/lQVFSkSnuhlJqaCp/P\np9pK61wqTluc3B4lTp06NbmHjxpBFgwGsXr16rC3M9HW4cOHVb9LHyoJCQlISkqCz+dTZWrW+CN+\nkFJyj3kN8M9VhJNSor29HQ6HAwsXLlSt5zexJqUaBgYGkJWVpdljmqGQlJSk6oR3KSX3ENIIQzOC\n+f1+NDU1IRgMora2VtUnQk6cOKFae83NzcjIyFClrXDR6/WTvU01GAwG9jI1wtCMUB6PB42NjUhJ\nScH8+fNVv4blcrmQmZkZ9nb8fj96e3uxePHisLcVbjqdTrUbNAxM7TA0I5DNZsO+ffuQn5+P4uJi\n1dt3u92qrSFps9kibpuJ2dLr9aoOmbVacSneMTQjjM1mQ3d3N9atW6fZvjBWq1W1nm1zc3PMbOOg\n0+mg0+lUmbOZkJDABYk1wv/qEaS/vx8WiwULFizQtOc1MDCA4eFhVdry+XyYP3++Km2pQQiBYDAY\n9j86QggO0TUS0T1NIcQtQohGIUSTEOJBresJl2AwiNbWVgwPD6t6h/xyUlNTsXTpUlXaslgsMbU+\n5MQOkmrgo5TaiNjQFEIkAPhPAFsBLAHwt0KIhdpWFXqBQAANDQ24cOECampqkJiYqHVJ8Hq9qi0M\nMTIyosqd87GxMaxduxZ2uz1sbQQCAbz22mt4/PHH8ac//SmsN4Um2nrsscfC3hZ9VCQPz9cBaJZS\ndgKAEOJFAHcAaNS0qhDyeDxoaWlBUVERiouLI+YpD4/Ho0po+nw+pKenq/KH4vXXX8fRo0fx+uuv\n48477wz5zw8EAti6dSsaGhrgcDiQkpKC2tpa7N27N+TXbNVsiz7uqv9KhRAPCCG0mERXBKB7yuc9\n48digsPhwPnz55GTk4PS0tKICUwAWLZs2eQe5+EUCATQ19cX1ja+9rWvIS0tDV/4whcAAPfccw/S\n0tJw3333hbSdPXv2oKGhAXa7HVJK2O12NDQ0YM+ePSFtR+226ONm0tPMA3BECPE+gGcA7I2kLSB3\n7Ngx+bquri4qHsXr7u6G1WpFeXl5RK4ZaTAYVLkzq9frQ75o8qW+//3vo6GhAS0tLZOPOZaXl+Oh\nhx4KaTvHjx//2KIdDocDJ06cwG233Ra1bcWL+vp61NfXz+yLJ55hvdIHAIGL1xZfBNAC4HEA82fy\nvbP9ALAewBtTPv8egAcv+RoZbQYHB+Ubb7whrVar1qVcVnd3t3ziiSfC3o7b7Zb/9m//FvZ2du7c\nKfV6vTSZTFKv18udO3eGvI3du3dLk8kkAUx+mEwmuXv37qhuK16NZ8u02TSjMeH4DxkY//ADyADw\nihDiiZlF86wcAVAlhCgTQhgAfB7Aq2FsL6yklOju7obFYsHmzZtVedpmtgYHBzE6Ohr2dnQ6HZKT\nk8M+r/GVV15BamoqfvjDH8JkMuEPf/hDyNvYtm0bamtrJ7fnMJlMqK2txbZt28LWlk6ngxAirG3R\nxwl5lZG2EOJbAL4IwALgKQC7pJS+8bvbzVLKsE2yE0LcAuBJXLz2+rSU8keXvC+vVn8kCAaDaG9v\nRyAQCOuiwaFy+vRpWK1WbNq0KextvfTSS7jtttvCOu3ogw8+QEFBAbKzs2GxWDAwMBCWKVWBQAD/\n9E//hKamJnzzm9/Etm3bwvb/OhAIYOnSpbjppptwyy23hLWteDS+ktS0E2FncuEqE8Cn5fhd7AlS\nyqAQIqwXUKSUbwCoCWcb4eZyudDQ0ICysjJUVlZGxYRknU6n2uR2u92OwcFBVFZWhq2NZcuWTb7O\nzs4O25NWOp0OS5cuxZYtW8J+bTEhIQFZWVl4/PHHI2J743hy1eG5lPLRSwNzynvnQl9S7HC73Whu\nbkZOTg4qKiqiIjCBv97ZV0NNTY0qlwLU0t7erspkfYfDAZ1Ox8DUQCTP04xqY2NjaGtrQ3Fxcdjv\nEIdaVVUVzp1T5++h0WjEwMCAKm2Fm9PphMPhwPr168PeVktLC5KSksLeDn1c5EwOjCE2mw1tbW2o\nrKyMusAELt7EsNvtqiw8UVVVhba2NlU3JguXpqYmZGZmqvIYbH9/f9SvQRqtGJohdu7cORw7dgwL\nFixQZWm1cNDr9WhtbcXg4GDY20pPT0dubi76+/vD3la47d27V7XV7oeGhrBu3TpV2qKPYmiGiJQS\nnZ2dCAaD2Lhxo+aLbszVmjVrwvqc9lQmkwmnTp1Spa1w8Xq9sFgsuPXWW1Vp7/Tp01G5CV0sYGiG\nQCAQmHziZNGiRapuSxEuZWVlsFqtqrR1/fXXo7OzEy6XS5X2wuHw4cMwGo2qBdn777/P9TQ1wtCc\nI6fTicbGRiQlJWmyLUW4GI1GvP/++6q0lZKSgqKiIjQ2RudaLFJKvPrqq7j55ptVac/tdsPn8/GR\nSY3Exr9wjbhcLuzfvx8GgwGlpaVRM6VoJgoLCzE0NKTamo3Lly/Hu+++G5VbOOzfvx9paWm49tpr\nVWmvsbERZWVlk08fkboYmrM0NjaGpqYmrF27FtXV1VqXE3J5eXkoLi6GxWJRpb3S0lIsXLgQb7/9\ntirthYrX68Xbb7+N1atXqzZcfv755/n0j4YYmrNgtVqjekrRTGVnZ6t6g2b16tUYGBiIqjvpzz//\nPJKSknDLLbeo1qbT6cRdd92lWnv0UQxNhc6dO4fe3l7U1NRE7ZSimVL7rvbE2qJvvvmmqrs6ztbx\n48fR3NyMe++9V7VLM2NjY2hpacGGDRtUaY8+jqE5Q1JKdHR0oL+/HwsWLIiL60kbN26EwWCA0+lU\nrc3NmzfDaDRi165dqrU5GzabDbt378bGjRtRUFCgWrvPPvsscnJy4uL3L1IxNGdgYkqR3+9HXV1d\n3PzC6vV6lJSU4PTp06q1KYTArbfeCo/HE7HXN91uN55++mlkZGSofge7ubkZW7ZsUbVN+iiG5lX4\nfD40NTXBYDDE1JSimZo3bx727dunapsmkwmbN29GZ2cnDh06pGrbVxMIBPDkk09Cr9fjG9/4hqpt\nDw8Po6mpCZ/73OdUbZc+Kr4SQKHh4WHU19cjIyMDZWVlMTWlaKbq6uqQmZmJoaEhVdstLCzEzTff\njCNHjuDw4cOqtn05Xq8Xjz/+OMxmM/7hH/5B9T+gv/jFL7BgwYKYeHgimjE0L2NsbAzt7e2orq5G\nfn6+1uVoRq/XY+nSpTh+/LjqbZeUlODuu+/GgQMH8Pbbb2t6c+jChQt47LHHUFZWhnvvvVf1SzTB\nYBCHDx/GjTfeqGq79HEMzWlMrFJUVVWF8vJyrcvRXFVVFV588UV4vV7V287MzMQ3v/lNtLS04MUX\nXwz77pXTqa+vx5NPPolVq1bhnnvuUW1P+KmOHj2KjIwM/M3f/I3qbdNHXXW7i0gWju0u+vv7YbFY\nUFVVFfWLboTSzp07UVpaijVr1mjSfjAYxIEDB3DkyBGsWrUK119/fdj3S7fZbHjqqacgpcSNN96I\ntWvXhrW9K7nnnnvwuc99DnfccYdmNcSTuW53EReklDh16hRsNtvkVBv6q2uvvRY7d+7E8uXLwx5W\n00lISMCmTZuwfPlyvPDCC2hpaUFNTQ2uu+66kD8dMzg4iAMHDqChoQHXXXcdbr75Zk2vI545cwYX\nLlzATTfdpFkN9FfsaeKvG5/5/X5UVFQwMC/j0UcfxerVq3H77bdrXQpOnz6N48ePo6urCxs2bEB1\ndTVKSkpm/fP8fj/Onj2Lv/zlL+jo6MA111yDTZs2obCwMIRVz853v/td3HDDDRyaq+hKPc24D02/\n34+WlhYYjca4vUM+U93d3di1axfuu+++iNlqoaWlBefOncPZs2dhMBhQXV0Ns9mMxYsXIyMj47J3\nuN1uNzo7O9HT04Oenh6cPXsWJSUlyMnJwe233x4xl2ZeffVV/OpXv8LLL7+sSQ8/XjE0L2N0dBQd\nHR3Izs6OiB5FNPjTn/4Eo9GIT3ziE1qX8hFSSpw9exYWiwUnTpxAIBCA3W6HEAI5OTkYGhqC2WyG\n0+nE6OgokpKS4Ha7sWTJEmRkZGDVqlXIycnR+jQ+IhAI4Mtf/jI2btyI+++/X+ty4gqvaU7D4XDg\n0KFDqK4BvJVUAAAODElEQVSuZmAqsH79evzzP/8zli9fHlEhI4TAkiVLAGByv3afz4eBgQFIKWGz\n2SZ3bkxLS0N6enrEL+L72muvITc3F3//93+vdSk0Rdz0NAOBAPbs2YPjx4+juroaCxYswPz582E2\nm8NcZew5ePAgOjo6cNddd/FyRph0dnbiq1/9Kn75y1+ioqJC63LiTtz3NAOBALZu3YqGhgY4HA4k\nJydj3bp1eOutt7QuLSpt2LABjY2NePfdd1FXV6d1OTFHSon//u//xsaNGxmYESguJrfv2bMHDQ0N\nsNvtkFLC6XTi6NGj2LNnj9alRaWEhARs2LABL7/8suqPV8aDvXv3Ynh4GI888ojWpdA04iI0jx49\n+rGdFR0OB06cOKFRRdFv8eLF+NKXvoSdO3dGxdqX0eL8+fP44Q9/iG9/+9sRf801XsV8aI6MjGDX\nrl0fmwCdkpKCFStWaFRVbFi3bh30ej2efvpprUuJCS6XC//+7/+O+++/Pya3UIkVMR2avb292LRp\nE6699lps2rQJJpMJQgiYTCbU1tZi27ZtWpcY1YQQ2L59O7q6unDy5Emty4lqwWAQjz32GKqrq7mV\nRYSL2f7/gQMHcMstt+CRRx7Bgw8+iGAwiD179uDEiRNYsWIFtm3bxs2pQiA7Oxv/+I//iGeffRZp\naWm8cTFLv/jFL3D8+HHs3LmTMxIiXExOOTpw4ADuvvtu3HffffiXf/kXDSqLP6dPn8ZPfvIT/OhH\nP1J1+4dYsGfPHrzyyiv46U9/ivT0dK3LIcTZE0G///3v8Z3vfAe/+c1vOB1GZQ0NDXjvvffwla98\nBZmZmVqXExWee+45/O53v8NTTz3FhywiyJVCM2auaQaDQTzxxBN4+OGH8dprrzEwNVBbW4tNmzbh\niSeeQFdXl9blRLz33nsPe/bswYMPPsjAjCIx0dOceEZ34omfuax2Q3P33HPPobu7G3/3d3+H3Nxc\nrcuJSM888wzeeecdPPbYY7wOHIFiuqfp8Xjwta99DSMjI/jggw8YmBHgC1/4Am699VY888wznAt7\nCSkl/ud//gc7d+7EAw88wMCMQlF/9/wzn/kM8vPz8corr3AdzAiyYsUKjIyM4Oc//zm+8Y1v4Jpr\nrtG6JM15vV787Gc/Q1dXF379618jOztb65JoFqI+NFetWoUdO3bE3da60WDTpk2oqanBCy+8gPb2\ndmzfvj1un3IZGhrCI488AovFgmeeeYY7SkaxmLimSZHN4XDgBz/4weQyZ/E2rea9997DM888gy1b\ntuCzn/1s3P7hiCZxNeWIIlMgEMCBAwdw8OBB3HDDDbj++uu1LinsPB4PnnvuOfz2t7/Fv/7rv6K2\ntlbrkmiGGJoUMTo7O/GDH/wAN9xwAz7zmc/EbK/zzTffxK5duzB//nx85StfQUZGhtYlkQIMTYoo\nPp8P7777Lg4ePIjS0lLcfffdMXMTz2q14oUXXsC+fftw3333RcQmdKQcQ5MiUkdHB37+858jPT0d\nW7duxcqVK6P2uWun04mf/OQnOH/+PG677TZ8+tOfhtFo1LosmiWGJkW01tZW7Ny5E2fOnMEDDzyA\nFStWRM1iKhaLBW+++SbefvttFBYW4vOf/zwWL16sdVk0RwxNinjBYBCHDh3CiRMnYLPZkJ2djbvu\numtyM7RI09XVhX379mHnzp1Yt24d7r//fuTn52tdFoVIRIamEOKzAHYAWARgrZTy/SnvPQTgXgB+\nAN+SUu67zM9gaMagpqYmPPvsswgEAqipqUFZWRk2btyo+XXP0dFRHD58GE899RSSk5Oxfft2bN68\nGVlZWZrWRaEXqaFZAyAI4BcAvjMRmkKIRQB+C2AtgGIAbwGoni4dGZqxzeVy4dixY3jqqaeQl5eH\nJUuWoKCgAKtXr1ZlFSUpJfr6+nDy5Ek8//zzSE5OxsqVK1FdXY0bbrgBycnJYa+BtBGRoTlZgBB/\nBvB/p4Tm9wBIKeWPxz/fA2CHlLJhmu9laMaJkZERnDlzBi+99BL8fj+Ki4uRnp4+GaL5+flITEyc\nUxvDw8Po6OjAwMAATp06hf/93/9FeXk5li1bhtTUVGzbtg2pqakhOiOKZNEWmv8B4C9Syt+Of/4U\ngNellDun+V6GZhwKBALo7e1FfX09+vr6Jj8fGhrC+vXrkZGRgcHBQdTU1CAjIwN2ux1CCGRkZMDl\ncqG1tRX5+fmw2+1oaGhASkoKRkdH0d/fD7PZjOuvvx5lZWVIS0vDihUrovaOPs2eZvueCyHeBJA3\n9RAACeBhKeXuULSxY8eOydd1dXVcRzMO6HQ6lJaW4otf/OLkMbfbjfb2dkgpMTQ0hP7+foyOjmJ0\ndBStra0IBAIoKSmBz+dDa2srzGYzzGYzVq9ejcWLF6OiogJms5kBGafq6+tRX18/o6+NxJ7mpcPz\nNwA8yuE5EaklGtbTnFrcqwA+L4QwCCEqAFQBOKxNWUREH6VZaAohPimE6AawHsCfxm/4QEp5FsDL\nAM4CeB3A19mdJKJIofnwfC44PCeicIiG4TkRUVRgaBIRKcDQJCJSgKFJRKQAQ5OISAGGJhGRAgxN\nIiIFGJpERAowNImIFGBoEhEpwNAkIlKAoUlEpABDk4hIAYYmEZECDE0iIgUYmkRECjA0iYgUYGgS\nESnA0CQiUoChSUSkAEOTiEgBhiYRkQIMTSIiBRiaREQKMDSJiBRgaBIRKcDQJCJSgKFJRKQAQ5OI\nSAGGJhGRAgxNIiIFGJpERAowNImIFGBoEhEpwNAkIlKAoUlEpABDk4hIAYYmEZECDE0iIgUYmkRE\nCjA0iYgUYGgSESnA0CQiUkCz0BRCPCGEOCeEOCGE+IMQIm3Kew8JIZrH39+iVY1ERJfSsqe5D8AS\nKeUKAM0AHgIAIcRiAHcCWARgG4D/EkIIzaokIppCs9CUUr4lpQyOf3oIQPH469sBvCil9EspO3Ax\nUNdpUCIR0cdEyjXNewG8Pv66CED3lPd6x48REWlOH84fLoR4E0De1EMAJICHpZS7x7/mYQA+KeXv\nwlkLEVEohDU0pZQ3X+l9IcSXAdwK4MYph3sBlEz5vHj82LR27Ngx+bqurg51dXXKCyWiuFZfX4/6\n+voZfa2QUoa3mss1LMQtAH4K4AYppXXK8cUAXgBQi4vD8jcBVMtpChVCTHeYiGhOhBCQUk57Azqs\nPc2r+A8ABgBvjt8cPySl/LqU8qwQ4mUAZwH4AHydyUhEkUKznmYosKdJROFwpZ5mpNw9JyKKCgxN\nIiIFGJpERAowNImIFGBoEhEpwNAkIlKAoUlEpABDk4hIAYYmEZECDE0iIgUYmkRECjA0iYgUYGgS\nESnA0CQiUoChSUSkAEOTiEgBhiYRkQIMTSIiBRiaREQKMDSJiBRgaBIRKcDQJCJSgKFJRKQAQ5OI\nSAGGJhGRAgxNIiIFGJohUF9fr3UJIcdzig48J/UxNEMg0v8nzwbPKTrwnNTH0CQiUoChSUSkgJBS\nal3DrAkhord4IopoUkox3fGoDk0iIrVxeE5EpABDk4hIAYbmHAghnhBCnBNCnBBC/EEIkTblvYeE\nEM3j72/Rss6ZEkJ8VghxWggREEKsuuS9qDufCUKIW4QQjUKIJiHEg1rXMxtCiKeFEINCiFNTjmUI\nIfYJIc4LIfYKIcxa1qiUEKJYCPGOEOKMEOIDIcT/GT8e0efF0JybfQCWSClXAGgG8BAACCEWA7gT\nwCIA2wD8lxBi2ovKEeYDAJ8C8O7Ug0KIRYjO84EQIgHAfwLYCmAJgL8VQizUtqpZ+RUunsNU3wPw\nlpSyBsA7GP/9iyJ+AN+WUi4BsAHAN8b/30T0eTE050BK+ZaUMjj+6SEAxeOvbwfwopTSL6XswMVA\nXadBiYpIKc9LKZsBXBqIdyAKz2fcOgDNUspOKaUPwIu4eD5RRUr5HoChSw7fAeA3469/A+CTqhY1\nR1LKASnlifHXdgDncPHfUESfF0MzdO4F8Pr46yIA3VPe6x0/Fq2i+Xwurb0H0VP71eRKKQeBiwEE\nIFfjemZNCFEOYAUudj7yIvm89FoXEOmEEG8CyJt6CIAE8LCUcvf41zwMwCel/J0GJSoyk/OhqBWV\n8weFECYArwD4lpTSPs3864g6L4bmVUgpb77S+0KILwO4FcCNUw73AiiZ8nnx+DHNXe18LiNiz2cG\negGUTvk8mmq/mkEhRJ6UclAIkQ/ggtYFKSWE0ONiYD4npfzj+OGIPi8Oz+dACHELgO8CuF1K6Zny\n1qsAPi+EMAghKgBUATisRY1zMPW6ZjSfzxEAVUKIMiGEAcDncfF8opHAx/+/fHn89ZcA/PHSb4gC\nzwA4K6V8csqxiD4vPhE0B0KIZgAGANbxQ4eklF8ff+8hAF8F4MPFYcc+baqcOSHEJwH8B4BsAMMA\nTkgpt42/F3XnM2H8j9uTuNhJeFpK+SONS1JMCPFbAHUAsgAMAngUwC4Av8fFUUAngDullMNa1aiU\nEGIjgP24OGtDjn98Hxf/IL+MCD0vhiYRkQIcnhMRKcDQJCJSgKFJRKQAQ5OISAGGJhGRAgxNIiIF\nGJpERAowNImIFGBoUkwTQqwRQpwcfwQ0ZXyR5cVa10XRi08EUcwTQvw/AMnjH91Syh9rXBJFMYYm\nxTwhRCIuLtzhAnCt5C89zQGH5xQPsgGYAKQCMGpcC0U59jQp5gkh/gjgdwAqABRKKR/QuCSKYlyE\nmGKaEOILALxSyhfHN1k7KISok1LWa1waRSn2NImIFOA1TSIiBRiaREQKMDSJiBRgaBIRKcDQJCJS\ngKFJRKQAQ5OISAGGJhGRAv8fIZ3Pkw1x1G4AAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1053af490>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"addOrbit(sim, comets[0])\n",
"%matplotlib inline\n",
"fig = rebound.OrbitPlot(sim, trails=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now we just integrate until whatever final time we’re interested in. Here it's the epoch at which we observe the comet, which is the last column in our table:"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAU0AAAFCCAYAAAB1po8RAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl81NW9//HXSYYsJEDIQhL2JSwCKiCCLaKxIBChRcGl\nautGobeiUotaFG9BbUsRr8rVKxd64boUEREU8crmEgGFgALRIEHWhASyEkK2yWzn90dCfgECZCDJ\n+c7k83w88jCZzEzeDpN3zvku56u01gghhKifANMBhBDCl0hpCiGEF6Q0hRDCC1KaQgjhBSlNIYTw\ngpSmEEJ4wWY6wOVQSsnxUkKIRqG1VnXd7vMjTa11k3/MmjXLyM/1pUxWy2PFTBfLU1BQQGpqKllZ\nWXg8HktksuLr1BgfF+LzpSmEv9Fak5mZyebNm+natSsdOnRAqToHPcIAn56eC+FvHA4Hhw8fJiAg\ngLFjx9KiRQvTkcRZpDQvQWJioukI57BaJqvlAetlOjvPyZMnycjIIC4ujtjYWEtksgKrZVIXm79b\nmVJK+3J+IQA8Hg+7du2ivLycQYMGERYWZjpSs6eUQp9nR5CUphAG2e12Dh06REBAAN27dycoKMh0\nJMGFS1Om50IYUlhYSFZWFh06dCA6Otp0HFFPUppCNDGn08nu3btp2bIlvXr1IjQ01HQk4QUpTSGa\nUHl5OQcPHgSgT58+BAYGGk4kvCWlKUQTycvL4/jx43Tq1InIyEjTccQlkh1BQjSyyspKMjIycLvd\ndO/eneDgYNORxEVcaEeQnBEkRCMqLS1ly5Yt2O12+vTpI4XpB2SkKUQjycnJITc3l65du9KmTRvT\ncYQX5DhNIZqQ0+nkyJEjeDweunXrJsde+iCZngvRRIqKili7dm3N4URSmP5HRppCNACtNcePH6eg\noIC4uDjatWtnOpK4DDI9F6IROZ1ODh8+DEC3bt1kZSI/IKdRCtFIjh49WnPsZVxcnKx72QzINk0h\nLoHWmuzsbDIzM+nSpQvx8fFSmM2ETM+F8JLD4eDQoUPYbDa6du2KzSYTNn8j03MhLpHb7Wbt2rXs\n2rWLgQMHMnjwYHJzc40uFCzMktIU4jzcbjejR48mJSWFsrIyQkNDSUhIYNOmTXKwejMm2zSFOI+1\na9eSkpJCaWkpWuuaFYo2b95sOpowSEpTiPPYtWsXZWVlZ9xWXl7O7t27DSUSVmC8NJVSi5VSuUqp\n72vdNksplaWU2ln9McZkRtH8VFZWsnTp0nOugR0WFsaAAQMMpRJWYLw0gf8FRtdx+8ta60HVH+ua\nOpRovg4ePMjw4cPp1KkTP//5zwkPD0cpRXh4OEOHDiUpKcl0RGGQ8R1BWustSqkudXxLDnoTTW7l\nypVMnTqVZ599lqlTp+LxeFi7di27d+9mwIABJCUlyWrrzZwljtOsLs01Wuurqr+eBdwPnAK+BaZr\nrYvreJwcpykaRHFxMb/97W/Zu3cvy5YtY/DgwaYjCYN88TjNN4DntdZaKfVX4GVgUl13nD17ds3n\niYmJlruwvLC+Q4cOcccdd1BcXMz27dvlUhTNUHJyMsnJyfW6ryVHml58T0aa4rKsWrWKxx57jGee\neYY//OEPciqkAHxjpKmotQ1TKRWntc6p/nICkGYklfBbJSUlPPvss6xbt46PPvpIpuOi3oyXplLq\nXSARiFJKZQKzgJuUUgMAD3AE+L2xgMLvHD58mJ///Of06NGDlJQUIiIiTEcSPsQS0/NLJdNz4a2P\nP/6YRx99lEceeYTp06cTEGCFo+6E1fjC9FyIRuVwOHj22Wf55JNPWLlypUzHxSWTP7PC73377bf0\n7duXI0eO8PXXX0thissipSn82rp167jzzjsZMmQI7733Hm3btjUdSfg4mZ4Lv+R0OvnrX//KihUr\nWLZsGUOHDjUdSfgJKU3hd1JTU3nqqacIDw9n8+bNREVFmY4k/IhMz4VfSU5OJjExkYSEBFasWCGF\nKRqcjDSFX3C73bz00ku8/fbbrF69mhtuuMF0JOGnpDSFzysoKGDKlCm4XC6++OILuXaPaFQyPRc+\n7YMPPqBv374MGjSIVatWSWGKRidnBAmfpLVmwYIFvPbaa/z+97/nj3/8o+lIwo/IGUHCrxQXF/PY\nY4+Rm5vLxo0b6dixo+lIohmR6bnwKatXr2bkyJF07NiRNWvWSGGKJielKXyC1pqlS5cyadIk7rnn\nHv72t7/RokUL07FEMyTTc2F5FRUVzJgxgx9++IFt27aRkJBgOpJoxmSkKSzt0KFDjBs3Dq01n3zy\niRSmME5KU1jWggULGDJkCA8++CDz58+nZcuWpiMJIdNzYT0ul4s5c+awbt06lixZwq9+9SvTkYSo\nIaUpLCUnJ4epU6fSunVr/u///k8uRSEsR6bnwjLefPNNxo0bx0033cTixYulMIUlyUhTGKe1ZtGi\nRbzwwgu8+OKL3HPPPaYjCXFeUprCqJKSEp544gkKCgrYsWMH8fHxpiMJcUEyPRfGpKenM378eOLj\n43nvvfekMIVPkJGmMGL+/PnMmTOHhQsXMn78eNNxhKg3KU3RpBwOB3//+9/ZsmULS5cuZcSIEaYj\nCeEVKU3RZI4fP860adOIiYnhww8/pFWrVqYjCeE12aYpmsRbb73FxIkTufnmm3n99delMIXPkpGm\naFRaa5YsWcILL7zAvHnzuOOOO0xHEuKyGC9NpdRiYByQq7W+qvq2tsByoAtwBLhTa11sLKS4JKWl\npcycOZPc3FxSUlLkUhTCL1hhev6/wOizbpsBfKa17g18ATzd5KnEZTl48CB33XUXUVFRvP3221KY\nwm8YL02t9Rag6KybxwNvVX/+FnBrk4YSl2XRokXcdNNNTJ48mb/85S8EBQWZjiREgzE+PT+Pdlrr\nXACtdY5Sqp3pQOLi3G438+fPZ/369SxcuJCkpCTTkYRocFYtzbPJJSctrqioiCeffBKbzcby5cub\nfLENt9uNy+UiICAArTUejwen00lAQACBgYE196usrCQ0NBSoueIgADabjYAA4xMv4QOsWpq5SqlY\nrXWuUioOyDvfHWfPnl3zeWJiIomJiY2fTpzh008/Zf78+YwdO5ZHHnmkUcvH7XbjdDopKSkhJCQE\nt9uNx+PB5XLh8XgICwtDKVVTnqcpVXU11tq3n36c1rrmeZRSuN1ugoKCCAwMrHmu048X/ik5OZnk\n5OR63dcS1z1XSnUF1mitr6z+ei5wQms9Vyn1Z6Ct1npGHY+T654b9tFHH/H4448ze/Zs7r///gZ/\n/tMF6XQ6a0rMZrPhdrtp2bJlzQixoYpaa43L5ar52uPx1BRqSEiIlGgzYenrniul3gUSgSilVCYw\nC/gHsEIp9RCQAdxpLqGoi8PhYN68eezcuZMvv/ySrl27Nsjzut1uioqKsNlsZ0yvw8LCCA0NPWOq\n3RiUUnVe5dLj8aC1RmuN0+nE7XZjs9mw2WxSoM2MJUaal0pGmmbk5eXx1FNPER0dzXPPPUdYWNhl\nPZ/b7cZut2O323E6nbhcLqKiomqmyFZUu0ShqmxPj0Kh6v9p7dq17Nq1i4EDB5KUlGTZ/xdxrguN\nNKU0hVfWrFnDk08+yVNPPcUDDzxwWdNiu93OiRMnKCkpITY2lpCQEIKDg31y5OZ2u9Fao5TC4/GQ\nlJRESkoKZWVlhIWFMXToUNavXy/F6SOkNMVl01qzcuVKFi1axN13382DDz54Sc/jcDiw2+2Ul5cT\nGBhIaGgoLVu29Ks91x9//DH33nsvpaWlNbeFh4ezbNkyxo0bZzCZqC9Lb9MU1udwOJg7dy579+5l\nyZIldOzY0evncLlclJaWcuzYMSIjI4mMjPTbg95TU1MpKys747aysjK+++47KU0/4D9/3kWj+PHH\nH5k8eTJ2u53Fixd7XZh2u52ioiJycnIA6NWrF3FxcX5bmAADBw48ZzuvzWbj/fff5z//8z/P2Dsv\nfI+UpjivXbt2ceutt9K7d2/++te/1hwUXh8ej4eioiL27t2L2+0mPj6eiIgIbDb/n9wkJSUxdOhQ\nwsPDUUoRHh7ODTfcwH/8x3+wb98+7rrrLj777DNk05Jvkm2a4hynt1+++eab/Pu//ztDhw716vGl\npaWcPHmSkJCQZlOUZzu993z37t0MGDDgjL3n27dv57XXXqO0tJQpU6bI6aYWJDuCRL05HA5efPFF\n9u/fz5w5c2jfvn29H1tZWUl6ejrR0dFER0cTHBzciEl9m8fj4ZVXXmHjxo2MGDGCP/zhD4SHh5uO\nJapdqDRlei5qpKenM2bMGBwOBwsXLqx3YWqtOXHiBLm5uXTu3JkOHTpIYV5EQEAA06dP5/3338fl\ncnH33Xfz6aef4vF4TEcTFyEjTQHA999/z8yZM+nZsycvvfRSvQ8BKi4u5tSpUwQHBxMZGdksp+IN\nYffu3fzxj3+kX79+zJ07V0adhsn0XJyX1pqPP/6YJUuW8Mwzz3i1/bKoqIgjR47QpUsXIiMjGzFl\n81BSUsLChQvZunUrs2fP5sorrzQdqdmS0hR1qqio4LXXXmPPnj38/e9/p0OHDvV6nMvlIi8vD4/H\nQ1xcnIwuG9jmzZuZO3cugwcPZubMmXWeCy8al5SmOEdhYSHjx4+nW7duLFy4kJYtW9brcUVFReTm\n5hITE0NkZKRPnvLoC44fP86kSZO44ooreP755y/7/H7hHdkRJM6Qnp7Oww8/zH333cebb75Z78Is\nKSnh+PHjREVFERUVJYXZiOLj41m9ejVxcXH827/9G9nZ2aYjiWoy0mxmNmzYwIIFC5g+fTrXX399\nvR9XWFjIqVOnaN++vewZb0Jaa1atWsWSJUu47777uOuuu0xHahbk3HOBw+HgmWeeIScnh1deeaXe\n6196PB72799PaGgonTp1ku2XTUwpxcSJEwF44403iI+P54YbbjCcqnmT34BmoKSkhL/85S+kpqay\ncuVK2rZtW6/Haa3Jzs7G4XCQkJAgy5oZNHHiRPr378+MGTMoLy9nzJgxpiM1W7JN089lZGTw6KOP\n0qdPHzZu3FjvwvR4PGRnZxMQEED//v2lMC2gd+/evPrqqyxevJiFCxeajtNsyTZNP7Z161Zefvll\npkyZws0331zvx7lcLjIzMwkJCSE+Pl52+FhMRkYG9913H7///e+55557TMfxS7JNs5nRWvP000+z\nbds2/vu//5s+ffp49dgDBw7gcDjo1q2bFKYFdenSheXLl/PYY48RGRkpU/UmJtNzP1NZWcncuXMp\nLCzkn//8p1eFCXDs2DFatmzJlVdeKYVpYXFxccybN49Fixbx1VdfmY7TrMj03I/k5+fzwgsv0Llz\nZx577DGvF/rNzc2loqKCzp07+9XlJ/zZ/v37mTRpEn/+858ZO3as6Th+Qw5ubwa2bt3K448/zg03\n3MD06dO9LsyDBw+SlZVFx44dpTB9SM+ePZk5cyaLFy/m2LFjpuM0C/Lb4QfWr1/Pgw8+yKRJk7j9\n9tu9nlaXlpZit9vp06ePHIfpg0aPHs19993Hs88+e861iUTDk9L0YW63m8WLF7Nq1SrWr1/PTTfd\n5PVzOJ1OsrKy6NKli5zf7MNuvfVWrr76ambMmIHD4TAdx6/JNk0fVVZWxrx583C73Tz11FO0atXK\n6+dwuVwcOnSIyMhIoqOjGyGlaEpOp5PbbruNpKQkpk6dajqOT5Ntmn5m586d3HvvvbRv357Zs2df\nUmFC1U6EkpISKUw/0aJFC958802++uor0tLSTMfxW1KaPiY1NZW5c+fys5/9jClTplzymTolJSUo\npRgwYEADJxQmRUdH8/jjjzNnzhxKSkpMx/FLMj33EVpr1q5dywcffMD06dPp16/fJT+Xy+Vi//79\ndOrUSS6r4KdeeeUVfvjhB/7nf/5Hjoa4BD47PVdKHVFKpSqldimltpvOY4rL5WLhwoWsX7+eOXPm\nXFZhAuzbt4+IiAgpTD82ZcoUCgsL2bRpk+kofsfSpQl4gESt9UCt9RDTYUwoKSlh3LhxpKenM2fO\nHGJjYy/r+QoLC8nPz6ddu3YNlFBYUVhYGH/7299YtGgRpaWlpuP4FauXpsL6GRtNdnY2zzzzDL/6\n1a946aWX6r3C+vm43W5ycnIYPHiwrFrUDPTv35+hQ4eyZMkS01H8itULSQPrlVI7lFKTTYdpSrt3\n72bWrFlMnDiRhx9+uEEOOs/NzaVVq1YyLW9GJk2axMaNG/n4449NR/EbVj/9Y5jW+rhSKgbYqJTa\nq7XeYjpUY/J4PLzzzjt8/fXXPPnkk/Tu3btBnre4uJjjx49z9dVXN8jzWY3D4SAzM5PKykpSUlKI\niori8OHDpzfoU1RURPv27Tl69Cg9e/aktLSU6OhoYmNjCQwM5Morr6R169Z+t9MkPDyc2267jU8+\n+YRx48b53f+fCZYuTa318er/5iulPgSGAGeU5uzZs2s+T0xMJDExsQkTNiyXy8Ubb7zBihUrWLFi\nBXFxcQ323IcOHSI8PNyvTpMsKipi27ZtZGZmUlJSQnl5OYMHDyYiIoIePXrQr18/WrVqRcuWLQkI\nCCAgIIDy8nIA8vLycDgcFBQUkJmZyaFDhzhw4ADDhg2rWeWpvgs2W90DDzzA7t272bx5MzfeeKPp\nOJaUnJxMcnJyve5r2UOOlFItgQCtdalSKgzYADyntd5Q6z5+c8hRaWkpr776KsHBwTz66KOEhIQ0\n6HMfOXKEvn37+vxI4+TJkxw4cIANGzYQGBhIQkIC8fHxDBw4kNDQ0Mt67qKiIvLz89m0aRNaa4KC\ngujduzfXXnutz28DTk1N5dVXX2XRokVyHfV68MnrniulugEfUrVd0wYs1Vr/46z7+EVpHjt2jHnz\n5nHttdfy61//usGL7aeffvL5UyWzs7PZs2cPX3zxBQMGDGDAgAEkJCQ02sjZ5XKxc+dOsrKyyMnJ\noXPnzowcObJB/5g1tT/96U/Ex8fz5JNPmo5ieT5ZmvXhD6X50Ucf8fbbb/PYY481yqaF/Px8cnNz\n6devn08uKnx6Cv7ll18ycuRIrrvuOlq3bt2kGbKzs0lLSyMjI4PY2FhuueUWnxytbdmyhXnz5rFi\nxQqvlw5sbqQ0Lerzzz/n7bff5q677uKWW25plJ+xZcsWOnbsWO9L9lqFx+Nh27ZtrFq1iptvvpnr\nr7/e+CpMeXl5bN++ncLCQrp3787111/vc3+IZs2axXXXXUdSUpLpKJYmpWkxbrebd999lz179vCn\nP/2p0Q40Ly0t5fDhw/Tv39+nfrlzcnL4r//6LxISEhg9enSD7hBrCPv37+ebb74hNjaWa665hpiY\nGNOR6i0tLY1XXnmFRYsW+fx22sYkpWkhpaWlLFiwAK01jzzyyGUfsH4hhw4dIiws7LLPImoqHo+H\n1atXs3//fq655hpuuukmy+64crvdfP755+zfv59bb72VDh06mI5UL1prpk2bxvDhw7njjjtMx7Es\nnz333N/k5eXxq1/9iqCgIKZPn96ohWm32zl16hRRUVGN9jMaksPhYM2aNaSlpXHXXXcxYsQIyxYm\nQGBgIKNGjWLixImsXr2azz77DF/4A66UYvDgwXz00Uemo/gs674r/cz+/fuZM2cO06ZNY9q0aY0+\nNdqzZw9aa584LtNut/Piiy9y7NgxnnrqKbp06WI6Ur3FxcVx9913U1ZWxvr163E6naYjXdQ999xD\nYGAgGRkZpqP4JCnNJrB161Zef/11HnroIcaPH9/oP09rTUBAAD179mz0n3W58vPzWbBgAf3792fy\n5MkEBwebjuS1tm3bkpSUxLFjx/jiiy9wu92mI12QzWZj5MiRbNiw4eJ3FueQ0mxEHo+HhQsX8uGH\nH/LUU09x5ZVXNsnPLS4uJigoyPLnmFdUVPDOO+8QFhbG+PHjfWJUfD5BQUHcf//9KKV45513LF+c\no0aNIjk5GbvdbjqKz5HSbCROp5NXX32VTz/9lJkzZzbpjoKCggLLH8hut9v5xz/+QY8ePZg8ebJP\n7d0/n8DAQH7xi1/Qtm1bUlJS8Hg8piOdV1xcHHa7nXfffdd0FJ8jpdkITp06xUsvvUSbNm344IMP\naNOmTZP9bLvdzr59+yy9A8jtdrN69Wrat2/PuHHj/KIwT7PZbNxyyy2kp6fz5Zdfmo5zQQ888ACF\nhYWmY/gcKc0GlpWVxd///neuuuoqHnrooSY/c6S4uJjo6GhLT3WXLVvGTz/9xEMPPeSXxwq2aNGC\niRMnUlJSwoEDB0zHOa/hw4ezc+dOueSvl6Q0G9Dq1auZMWMGEydOZOzYsUZGUCUlJZbe+3zw4EEy\nMzOZNGmST56KWF9t2rRh0KBBfPLJJ5SVlZmOU6eIiAi6devG7t27TUfxKVKaDSQ5OZkNGzbwu9/9\njmuvvdZIBq01J0+etOySZg6HgwULFnDjjTfSvn1703EaXefOnRkxYgSbN2+27PbNK664QrZreklK\n8zJ5PB7ef/99Nm/ezPPPP290Pc8TJ04QEBBg2cN21q1bx8CBAxk2bJjpKE2mb9++ZGZmkp6ebjpK\nnQYPHszRo0d94sB8q5DSvAzl5eUsWLCA3NxcnnjiCeM7XzIyMnC5XEYznE9GRgaff/4548aNMx2l\nSQUGBnL77bezd+9eS17grE+fPkRGRnLs2DHTUXyGlOYlOnHiBHfffTcej4eHH374shfAbQhBQUH0\n6tXLdIw6ffbZZ0yYMKFJjySwisjISJRSfPfdd6ajnEMpRf/+/UlLSzMdxWdIaV6CzMxMXnnlFaZM\nmcLUqVMtsQfY4/FQWlpqyQPad+3axZ49e5rVtPxsSUlJnDhxglOnTpmOco7+/fvLziAvSGl6KTU1\nlQULFnDnnXcyduxYyywqUVZWRmhoqCUPNdq1axcTJ060ZLamcvrf5ttvvzUd5RwdOnRg3bp1pmP4\nDGv8xvsAj8fDu+++y8qVK3n44Yeb7JTI+jpy5Igl99Du3buX77//niFDhpiOYtxNN91EaWmp5U5d\n7N27Nx07duTkyZOmo/gEKc16cLvdLF26lJUrVzJt2jQ6depkOtI5XC4XERERpmOc46effuIXv/iF\nXx+TWV/h4eFUVFRYbiqslKJbt24cOXLEdBSfIKV5EXa7nX/+859UVlby7rvvGt9DfiFWO9+8vLyc\nL7/8kuuuu850FMsYPny45UaagJSmF6Q0L+DEiRPMnz+fdu3a8dBDD1n2+EetNRUVFZbYg1/b4cOH\n6dixY6NdzsMXxcXFkZ6eTm5urukoZ2jbti1btmwxHcMnSGmex/bt23nyySf5+c9/zoQJEyyzw6cu\nFRUV2Gw2y+1o2bhxI1dccYXpGJYSEBDAgAEDKCkpMR3lDHFxceTn55uO4ROs2wQGpaWlsWrVKm67\n7TaGDx9uOs5F5ebmkpOTYzrGGbTW5OTkSGnWIS4uznLbNa+44gpLHDrnC6w1NDFMa82mTZvYsmUL\njz76qM9cLCskJITevXubjnGGw4cPY7PZ6Natm+kolhMbG4vL5cLj8VhmBtO6dWsqKyux2+2EhISY\njmNp1vgXswCXy8WqVavYuXMnU6dO9ZnCBKisrLTc9tYff/yR8PBwv1ors6GEhobSunVrS80OlFJE\nR0fLFL0epDSpKp3p06eTlpbGww8/bMlDdy7E4XBYrjQrKioYOnSo6RiWZbPZKCgoMB3jDIWFhaSk\npJiOYXnNvjSLi4tZuHAhw4YNY+bMmZYrn/rIy8szHeEc27dvl5VzLqBHjx6WOxmhf//+lj6kziqa\ndWkeO3aMBQsWMGjQIO644w7L7X2ur5KSEstsGzstLCzMcmdNWYnT6bTccnFRUVGyins9WLollFJj\ngFepKvfFWuu5DfXcmzZtYtOmTdx6663079+/oZ7WiOjoaMLCwkzHqOFwOMjPzycyMtJ0FMuKj4+3\n3AyhZcuWVFRUmI5hedYantSilAoAXgdGA/2Au5VSfRriubdt28aCBQu47bbbfL4woeo0TyuNNE8f\naG+lQ1hKSkq49tprLbOmpc1ms+T1g6xW5FZknd+0cw0B9mutM7TWTuA9YPzlPKHH42Ht2rXs2LGD\nN954g379+jVIUNOsdOgKwMmTJy13rvmnn37Kt99+y6effmo6CgDBwcGW2+FYWFjIoUOHTMewvIv+\npimlHlVKmbjoTAfgaK2vs6pvuyROp5Ply5eTk5PD7373O8teR+dSHDhwwFI7Xex2u2V2ckyePJnW\nrVvz29/+FoDf/OY3tG7dmilTphjNZbPZsNvtuN1uozlqS0hIkJMR6qE+2zRjgR1KqZ3AEmC9ttBv\n6OzZs2s+T0xMrPMaPXl5efzjH/9g2LBh3HnnnZaaNjaEdu3aWWqkGRYWZpltrM888wwpKSkcOHAA\np9OJzWaja9euPP3006ajWe7SJFrrZntcbXJyMsnJyfW670VLU2v9rFLq34FRwIPA60qp96naMXPw\ncoJeRDbQudbXHatvO0Pt0qxLfn4+S5cupW/fvkyYMMEv3xTh4eGWGmkWFRVRWFhoOgZQtXrPc889\nx5133kl4eDh2u53nnnvO+JlKHo+HqKgoS/0Bb86lefaA67nnnjvvfes1PKkeWeZUf7iAtsAHSqkX\nLyfoRewAEpRSXZRSQcCvgY+9eYIjR47w9ttvM2LECH73u9/57RsiICDAUqXZuXNnS6249MEHH9Cq\nVSv+9re/ER4ezsqVK01Hwul0Wu5iZllZWWRlZZmOYXkXHWkqpaYB9wEFwP8AT2qtndV7t/cDTzVG\nMK21Wyn1CLCB/3/I0d76Pj41NZWNGzcyceJE46OKxuZ2uy011QsMDOT777/n+eefZ9CgQSQlJRkd\nUc2YMYP58+cTHR3NPffcY4nTF10ul+W2HwYEBNC6dWvTMSyvPts0I4EJWuuM2jdqrT1KqUa9HqvW\neh3g9UoU7777Lps2beKFF14gJiamEZJZS2ZmJgkJCbRq1cp0FNxuN7feeiubNm1i3bp1hIWFMXTo\nUNavX2+sOGsfZB8dHW2JxZoLCgosdxplSEgInTt3vvgdm7mLTs+11rPOLsxa36v3yK8puN1u1qxZ\nQ0VFRbPQudRpAAAWK0lEQVQpTKha1ssqh/isXbuWlJQUnE4nWmtKS0tJSUlh7dq1pqNZTseOHU1H\nOENZWZllduBZmXV2uV4mu93O8uXLsdvt3Hfffc2mMKHqeudWOf1t165dlJWVnXFbWVmZ5daPNC03\nN9dS230BSktLpTTrwS9K8+jRoyxevJjo6Ghuv/12y4y6mkpwcLBlSnPgwIHn/OKFhYUxYMAAQ4ms\nyYrXqN+6datckbIefL40c3NzmT9/PjExMYwaNcpv95BfSGVlpWWuOZOUlMTQoUNr1tIMDw9n6NCh\nJCUlmY5mGW63m8rKStq3b286yhni4uK46qqrTMewPEsv2FEfK1asYMqUKfTq1ct0FGOCgoIss3hs\nYGAg69evZ+3atezcudMSe8+tprCwkLKyMkvNiOx2O3a7XRZZqQefL80JEyZY7i92U7PaRbECAwMZ\nN24co0aNIiAgQArzLKdOnbLc5oqCggJiYmIsdWaZVfn8K9TcCxOqthlWVFRY6gB3qDq/ujluLrmY\nXbt2WW6x63379lkuk1X5fGmKqpFdixYtLLcWolKKyspK0zEspbS0lA4dOljuGlQHDhyQP3D1JKXp\nJ/Ly8jh69OjF79iElFIEBgZaaiUf03bv3k1QUJDlpsFOp5NRo0aZjuETrPUvJy5Znz59LDc9h6op\nuow2q7jdbjweDz179jQd5RwZGRl+f7pxQ5HS9BOxsbGUlJSYjnGO0zuBrLK+pkl79+4lMDCQNm3a\nmI5yhrKyMoqLi4mLizMdxSdIafqJNm3aUFxcbMnRZlBQEHa73XQMozweDydPnqRHjx6mo5xj06ZN\nOJ1Oy20ysCp5lfxEcHAwdrudEydOmI5yDpvNhsfjadbbNvfs2YPNZrPkaK64uJjrr7/edAyfIaXp\nR5RSlluj8bTQ0FDKy8tNxzDC6XRy4sQJS44yoWrP+bBhw0zH8BlSmn5k4MCBlt3pcnrbplXOkW9K\nO3bsICYmxpKLyJSXl5OdnW3ZQrciKU0/Eh0dTWFhoWWnwWFhYZSXl1tqweTGVlRUhNPppHv37qaj\n1Gnr1q20b9/eUqd0Wp2Uph8JCgqidevWltyuCVUrg5/eKWTFHVYNraKigi1btnDVVVcREhJiOk6d\nvvnmG1mt3UtSmn5Ga01KSorpGOfVsmVLoOr8a3/m8Xg4dOgQPXr0sOzlol0uFwUFBdx7772mo/gU\nKU0/c8UVVxAYGGjpkVxoaChaa7/evrlr1y6Kioosdx2g2tLT02nXrp0lLv/hS6Q0/Uzbtm1p1aqV\n5a4/U1tgYCCtW7emqKjIL4/fzMjIICAggEGDBln6fO4dO3YwePBg0zF8jpSmH+rQoQPZ2edcIt5S\nAgICaNu2LZWVlX5VnMePHyc1NZU+ffrUbIqwIrvdzvvvv0+/fv1MR/E5Upp+KD4+ntTUVMuXUVBQ\nECEhIZw4cQKn02k6zmVLT08nKyuLUaNGWe76P2fbvXs3N9xwg+Uu7uYLpDT9UEhICG3atCEzM9N0\nlIsKDg6mXbt2FBUVWfLc+frQWpOZmUlhYSG9evWy7J7y2r766itGjx5tOoZPktL0U8OGDbP8FP00\nm81GREQEDoeDU6dO+dTiHm63m507d5KRkcGQIUMstxhHXbKzsykoKJDrAV0in7/chahbTEwMWmsK\nCgp8Yu9oUFAQbdu2JTc3l8rKSiIjIy1/mYzCwkLS09Pp1KkT7du3x2bzjV+nJUuW0K9fP5/JazUy\n0vRj3bt354cffjAdo94CAgKIj48nPDycrKwsy07XXS4XBw8e5OjRo3To0IHOnTv7TAGVlJRw+PBh\nEhMTTUfxWVKafiwuLo7U1FSfu5Z1aGgocXFxuN1usrKyLHUZj4KCAtLS0sjPz6dfv3507drVdCSv\nfP7554wYMcLncluJJUtTKTVLKZWllNpZ/THGdCZfFBISwtixY9m/f7/pKF4LDg4mIiKC8PBwSkpK\nOHbsmNHyLCoqIi0tjbS0NBISErjuuut87nztsrIy2QHUAKw8p3hZa/2y6RC+rlu3bmzcuJHi4mKf\n2ElxtoiIiJpts8XFxRQWFtK6dWtatWrV6AeOOxwOioqKyMnJoaSkhP79+9O3b1+fXaz3X//6F717\n9/aJbdxWZuXStO6pFD7EZrPRs2dPfvjhB59daFYpVbNj6+TJk1RUVFBYWFiz8yg4OLjBdhq53W7y\n8vKoqKigoKCA4OBgevToQVhYmKXP7rmY0tJSvv76a5544gnTUXyelUtzqlLqt8C3wHStdbHpQL6q\nS5cufPTRR/To0YP4+HjTcS6ZUqpm8QuHw0FpaSlFRUWcOHGC2NhYKisradu2LTabjRYtWly0SD0e\nD3a7neLiYgICAjhy5Ajh4eFA1emo11xzjeX34NfXJ598wrhx4+QwowagTC3soJTaCMTWvgnQwExg\nG1CgtdZKqb8C8VrrSXU8h7bywhRWcvjwYQ4fPsxNN93k0yOmurjdbiorKykoKCAkJIS8vDxatGiB\n1hq3211znntUVBSFhYWEhIRQXl6O0+kkMjKS0tLSmjNj2rRp4zN7wuvr+PHjvPzyy8yaNavmj4K4\nMKUUWus6f1GMvTu01jfX867/BNac75uzZ8+u+TwxMVEOpTiPbt26kZGRQUZGht/tOQ0MDKRly5Z0\n7twZgHbt2gFVl5lwOp0opQgLCyM0NJRWrVoRFBREYGAgNpvN7/6A1GXhwoWMHj1aCvMCkpOTSU5O\nrtd9jY00L0QpFae1zqn+/HHgWq31PXXcT0aaXjh58iSbNm1i5MiRll5MQjScHTt28Nprr7Fw4ULL\nnw9vJRcaaVp1N+CLSqnvlVK7gRuBx00H8gcRERG4XC4+++wz01FEEygrK+PDDz9k1qxZUpgNyJIj\nzfqSkab3Kisr+eyzz7jmmmsseTlZ0XDeeecdQkJCuOOOO0xH8Tm+ONIUjSQ4OJhrr72Wb7/91q9X\nTm/u1q9fT2pqKr/85S9NR/E7UprNULt27ejQoQNbtmwxHUU0glOnTrFmzRpGjhzpE8vU+RopzWaq\nX79+7N69m3379pmOIhqQ1pp33nmHMWPGMGaMnH3cGKQ0m6mgoCAmTZrE3r17fW5BD3F+GzZswOVy\nkZSUZDqK35LSbMbatGnDwIED+frrr2X7ph/48ssvWbZsGffff7/fnMlkRVKazVyXLl2IiYlhxYoV\nPrViujhTXl4eGzdu5MEHHyQiIsJ0HL8mpSkYMGAAWmu+++4701HEJSgrK2PRokX88pe/5MYbbzQd\nx+9JaQqCgoK48847yc/PJz093XQc4QW73c4bb7zBVVddxc9+9jPTcZoFKU0BVBXnjTfeSHp6OgcO\nHDAdR9SD2+3m9ddf59ixY3I8ZhOS0hQ1wsLCGD58OEuXLuXIkSOm44gL0FqzbNkyWrVqxdy5c5vF\nwiNWIadRinPk5eWxefNmhg4dWrNkmrAOj8fDihUrKCgoYPLkyQQFBZmO5HcudBqllKaoU2FhIcnJ\nyVKcFuPxeJgzZw4lJSXMnj1bzvhpJHLuufBaVFQUiYmJLF++nJ07d5qOI6i6dPDSpUsJCwvjz3/+\nsxSmITLSFBd0+PBhduzYUXNRMWGG3W7nrbfeIjg4mN/85jd+t7q81chIU1yybt26ccstt3Dw4EF2\n7NiB/JFqegUFBUybNo1WrVpx3333SWEaJiNNUS8Oh4N169Zx7NgxHnroIdn50ESOHDnCv/71L7p0\n6cK9997rs5cP9jWyI0g0CIfDweeff47dbicxMbHmypCicWzbto3169dz11130adPH9NxmhUpTdGg\nDh06xPbt2xk8eDAJCQmm4/idyspK5s2bR2lpKdOnTycmJsZ0pGZHSlM0uJMnT7J06VIiIyOZMGEC\nwcHBpiP5hczMTJYvX050dDQTJkygTZs2piM1S1KaolGUl5ezY8cOcnJyGDZsmBzPeRmcTicbNmxg\n165djB8/niuvvNJ0pGZNSlM0qmPHjvH111/TunVrhg0bJtfX9lJWVhYLFy7E4XDwzDPPyOjSAqQ0\nRaNzOBwsW7aMsrIyRo4cSc+ePeV86IuoqKhgw4YN/Pjjj4wZM4arr75a9o5bhJSmaDL5+fls3boV\nrTXXXXcdsbGxpiNZjtvt5tNPP2Xjxo2MGDGCUaNGyXXJLUZKUzQprTUHDhxg+fLlJCQkMHr0aDk8\niarXJS0tjc8//5ygoCAGDx7MkCFDTMcSdZDSFEaUlZWRnp7O3r17iY+P55prrmmWl2LQWpOcnMw3\n33xD27ZtGTVqFD169JDNFxYmpSmMcjqd7Nmzh40bNxIVFUVSUhJxcXF+XxpOp5PU1FS++eYbysvL\nGTBgAKNHj/b7/29/IKUpLKGsrIwff/yRgwcPYrPZ6Nu3L927d/e71XpOnDjB8uXLycvLo0ePHlx/\n/fV06dJFytKHSGkKS9Fak52dzdatW0lJSWHs2LH07NmT9u3b++ze44qKCtLT09m9ezf5+flER0dz\n44030qNHD9PRxCWwZGkqpW4HZgNXANdqrXfW+t7TwEOAC5imtd5wnueQ0vRxxcXFHD58mAMHDlBW\nVkZISAiDBg2ie/fulr92d1lZGfv37yctLY21a9cyduxYBg4cSM+ePWUlIh9n1dLsDXiAhcATp0tT\nKXUF8C5wLdAR+AzoWVc7Smn6l6KiItauXYvWmrKyMjp27EhcXBzt2rWjQ4cOxqe3LpeL7Oxstm3b\nRlZWFi6Xi+7du9OrVy86duxIVFSU0Xyi4ViyNGsCKPUlML1Wac4AtNZ6bvXXa4HZWuuUOh4rpemn\nKioqOHr0KDt37uTHH3+kU6dOxMbGEhsbS0hICJ07dyYiIqLRitTlclFYWMjx48f5+uuvCQsLIzc3\nl5iYGMLCwujUqRNDhgyREaWfulBpWvFfvAOwtdbX2dW3iWYkNDSUXr160atXLwBKS0vJyckhNzeX\nNWvW0KpVK2w2GxEREbRs2ZLi4mKuvvpqQkNDadmyJQEBAQQHBxMaGkpAQAABAQForfF4PLhcLpxO\nJ6WlpRQWFhIUFERJSQklJSX88MMPuFwuAgICiIiIIDo6GpvNxg033EDHjh1lHVHRuKWplNoI1D4l\nRAEamKm1XtOYP1v4l/DwcBISEkhISGDYsGFA1RJqJ0+e5Pjx46Snp1NUVER2djYVFRXs27cPrTUx\nMTG43W48Hg+7du2ib9++hIeHY7PZqKysJD8/n8GDBxMeHk5UVBTDhw8nJiaGzp07yyhS1KlR3xVa\n65sv4WHZQKdaX3esvq1Os2fPrvk8MTGRxMTES/iRwhcFBwfXTNkHDBhgOo7wYcnJySQnJ9frvlbZ\npvmE1vq76q/7AkuBoVRNyzciO4KEEE3IkhdWU0rdqpQ6ClwHfFK9wwet9Y/A+8CPwKfAw9KMQgir\nMD7SvBwy0hRCNAZLjjSFEMIXSWkKIYQXpDSFEMILUppCCOEFKU0hhPCClKYQQnhBSlMIIbwgpSmE\nEF6Q0hRCCC9IaQohhBekNIUQwgtSmkII4QUpTSGE8IKUphBCeEFKUwghvCClKYQQXpDSFEIIL0hp\nCiGEF6Q0hRDCC1KaQgjhBSlNIYTwgpSmEEJ4QUpTCCG8IKUphBBekNIUQggvSGkKIYQXpDSFEMIL\nUppCCOEFY6WplLpdKZWmlHIrpQbVur2LUqpcKbWz+uMNUxmFEOJsNoM/+wfgNmBhHd87oLUeVMft\nQghhlLHS1FrvA1BKqTq+XddtQghhnFW3aXZVSn2nlPpSKXW96TBCCHFao440lVIbgdjaNwEamKm1\nXnOehx0DOmuti6q3dX6klOqrtS6t686zZ8+u+TwxMZHExMSGiC6EaEaSk5NJTk6u132V1rpx01ws\ngFJfAtO11ju9/b5SSpvOL4TwP0optNZ1bia0yvS8JpxSKlopFVD9eXcgAThkKpgQQtRm8pCjW5VS\nR4HrgE+UUmurv3UD8L1SaifwPvB7rfVJUzmFEKI249PzyyHTcyFEY/CF6bkQQvgEKU0hhPCClKYQ\nQnhBSlMIIbwgpSmEEF6Q0hRCCC9IaQohhBekNIUQwgtSmkII4QUpTSGE8IKUphBCeEFKUwghvCCl\nKYQQXpDSFEIIL0hpCiGEF6Q0hRDCC1KaQgjhBSlNIYTwgpSmEEJ4QUpTCCG8IKUphBBekNK8BMnJ\nyaYjnMNqmayWB6yXyWp5QDLVh5TmJbDaPyJYL5PV8oD1MlktD0im+pDSFEIIL0hpCiGEF5TW2nSG\nS6aU8t3wQghL01qrum736dIUQoimJtNzIYTwgpSmEEJ4QUrTC0qp25VSaUopt1JqUK3buyilypVS\nO6s/3jCZp/p7Tyul9iul9iqlRjVFnjryzVJKZdV6XcYYyjFGKZWulPpJKfVnExnOppQ6opRKVUrt\nUkptN5RhsVIqVyn1fa3b2iqlNiil9iml1iul2hjOY4n3UG1Smt75AbgN+KqO7x3QWg+q/njYZB6l\n1BXAncAVQBLwhlKqzo3aTeDlWq/Luqb+4UqpAOB1YDTQD7hbKdWnqXPUwQMkaq0Haq2HGMrwv1S9\nLrXNAD7TWvcGvgCeNpwHDL+Hzial6QWt9T6t9X6grgJq8lK6QJ7xwHtaa5fW+giwHzD1i2mqrE8b\nAuzXWmdorZ3Ae1S9PqYpDP/+aa23AEVn3TweeKv687eAWw3nAfPvoTNIaTacrkqp75RSXyqlrjec\npQNwtNbX2dW3mTBVKbVbKfU/TTnVq+Xs1yILc69FbRpYr5TaoZSabDpMLe201rkAWuscoJ3hPGD+\nPXQGm+kAVqOU2gjE1r6Jqjf4TK31mvM87BjQWWtdVL1t8SOlVF+tdamhPE3mQvmAN4DntdZaKfVX\n4GVgUtOntKRhWuvjSqkYYKNSam/1SMtqTB+TaLn3kJTmWbTWN1/CY5xUTyu01juVUgeBXsBOE3mo\nGll2qvV1x+rbGpwX+f4JmCj5bKBzra8b7bXwhtb6ePV/85VSH1K1GcEKpZmrlIrVWucqpeKAPJNh\ntNb5tb409R46g0zPL13NdhalVHT1DgeUUt2BBOCQqTzAx8CvlVJBSqlu1XmafA9t9S/daROAtKbO\nAOwAEqqPcAgCfk3V62OMUqqlUiq8+vMwYBRmXhuoet+c/d55oPrz+4HVJvNY5D10Jq21fNTzg6qN\n4keBCuA4sLb69tP/mDuBb4FbTOap/t7TwAFgLzDK0Ov1NvA9sBv4CIg1lGMMsI+qHWIzLPA+6lb9\nmuyi6ggII5mAd6natFQJZAIPAm2Bz6pfrw1AhOE8lngP1f6Q0yiFEMILMj0XQggvSGkKIYQXpDSF\nEMILUppCCOEFKU0hhPCClKYQQnhBSlMIIbwgpSmEEF6Q0hR+TSk1uHqx3yClVFj1os19TecSvkvO\nCBJ+Tyn1PBBa/XFUaz3XcCThw6Q0hd9TSrWgauGOCuDnWt704jLI9Fw0B9FAONAKCDGcRfg4GWkK\nv6eUWg0so2p1ofZa60cNRxI+TBYhFn5NKfVbwKG1fq96zdOvlVKJWutkw9GEj5KRphBCeEG2aQoh\nhBekNIUQwgtSmkII4QUpTSGE8IKUphBCeEFKUwghvCClKYQQXpDSFEIIL/w/sYlalxXOMt8AAAAA\nSUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x107b76f90>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"tfinal = comets[0][-1]\n",
"sim.integrate(tfinal)\n",
"fig = rebound.OrbitPlot(sim, trails=True)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"REBOUND automatically find out if you want to integrate forward or backward in time."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For fun, let's add all the coments to a simulation:"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAU0AAAFCCAYAAAB1po8RAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XlwXFeZN/7v0Wa11Nr3XZYsWYvlXXZwcBDBiTEJGDKE\nJAwTYCCZFMP8mGIIBF5qSAHzDlAMTOadClsKQoaEACY4iRPHWRzHZLESW4s3SZa19KJWd0ut3td7\n+57fH7Y0lrV1t7r73m49nypVSa2+957W8vS55znnOYxzDkIIIaFJkbsBhBCSSChoEkJIGChoEkJI\nGChoEkJIGChoEkJIGChoEkJIGNLkbsBqMMZovhQhJCY452yxxxO+p8k5j+nHd77znZhfQ+6PtfAa\nE+l1er1eDA8PK/41Tk1N4Uc/+hEEQUi63+VyEj5oEpJs/H4//H6/3M1Y0c9//nOUlJQgLS2hb1jD\nRkGTEIUJBAIQBEHuZizL7/fD4XDglltukbspcUdBcwVdXV1yNyHm1sJrBBLndaanp6O4uDiiY+P1\nGnt6erBp0yZUVVXF5XrXk/N3yVa6f1cyxhhP5PYTshiLxYJAIICKigq5m7Iozjl+8pOf4ODBg9iw\nYYPczYkJxhh4siaCCEk2kiQhNTVV7mYs6fjx4+jp6UFjY6PcTZEFBU1CFEYURaSkKPdfc2RkBHff\nfTcYW7QjlvSU+5shZI2anJyE2+2WuxmLstlsuHz58ppMAM1aW3MFCEkAxcXFyM/Pl7sZi3rzzTex\nc+dOZGZmyt0U2VBPkxCFUeqYZiAQwA9/+EPs3LlT7qbIioImIQoTDAYVOabZ29uLD33oQ2hoaJC7\nKbJS3m+GkDUuGAwqcpXNa6+9ho997GNyN0N2FDQJUZjJyUm5m7CARqPBzMwMtm7dKndTZEdBkxAF\n4ZxDpVIhPT1d7qbM893vfhfl5eWKHDaIN/oJEKIgwWAQubm5cjdjHpfLhWAwiHvvvVfupigCBU1C\nFESJmfMTJ06gs7MTpaWlcjdFEShoEqIgSlsNJEkSjh07hv3798vdFMVQzm+HEAK/36+osnCHDh3C\nuXPn1uw688VQ0CREQZRWgHhgYABf+9rX1uw688UoImgyxlIYYz2Mseeufl3AGHuZMTbEGDvGGMuT\nu42ExENGRgZKSkrkbgaAK1OfhoeHceutt8rdFEVRRNAE8BUAF6/5+iEAr3LONwI4DuCbsrSKkDhT\nUiLo+eefx759+5CRkSF3UxRF9qDJGKsG8BEAj13z8EEAv736+W8BfDze7SJEDqIoKiJoer1e/OAH\nP8DevXvlboriyB40AfwUwIMAri3BXsY5NwEA59wIgOY6kDVBkiRFZM9PnDiBu+66ixJAi5B1gStj\n7DYAJs55H2Osa5mnLrmnxcMPPzz3eVdXV8LsA0PIYiYmJlBRUYHCwkLZ2sA5x+HDh3H//ffH/FpO\npxNqtVr2RNOJEydw4sSJkJ4r6x5BjLH/C+AzAEQAKgA5AP4CYCeALs65iTFWDuB1znnrIsfTHkEk\nqYyNjaG4uBg5OTmytaGnpwePPPIIHn/88ZgFM1EUMTU1BQAoLS1VxJDEtRS7RxDn/Fuc81rOeQOA\nuwEc55z/HYDnAXzu6tM+C+BZmZpISFwpIRH07W9/G7W1tTELmBaLBYODg1CpVCgvL5f99YZLefWn\nrvgBgD8yxv4egAbAp2RuDyFxIUmSrGXhLBYLgsEg/uVf/iXq5w4Gg7BarXC5XKipqUFeXmLOJFRM\n0OScvwHgjaufzwDYJ2+LCIk/uQsQP/fcc9i3b1/Ut9vw+XwYGBhAWVkZamtrFZHsilTitpyQJGQ0\nGmW7XfX5fPjzn/+MO+64I2rnlCQJU1NTMJlMaGxsRGVlZUIHTEBBPU1C1jpRFJGVlSVbJvk3v/kN\ndDpd1KYZiaIIg8EAh8OBlpYWRVajj0RyvApCkoAkSbLuQnn69Gn88Ic/jMq5zGYznE4nioqKUFNT\nI/uUomiioEmIQgSDQdluzYeHh6HT6bBv3+pSCZIkwWKxwGq1orKyUtapU7GS2IMLhCQROacbPf74\n47jzzjtXdQvtcrlw7tw5AEBTU1NSBkyAepqEKIbP54MoinG/rtVqxaOPPore3t6IjpckCXa7HQ6H\nA9XV1SgqKopyC5WFgiYhCuHxeOD1euN+3eeeew6f//znUV9fH/axoiji8uXLSElJQUNDQ9Ike5aT\n/K+QkAQhxy6UkiThySefjCgBZLFY4HK5UFZWhoKCghi0TploTJMQhZAjEXT06FGoVKqw9jOXJAlG\noxE6nQ6lpaVrKmACFDQJUQw5EkHf+c530NzcHPKUILvdjpGREaSlpWHz5s1QqVQxbqHyUNAkRCHi\nXYBYq9VCEIR55RWXwjmHzWbD1NQUCgoKUFxcnPAreyJFY5qEKITBYMC6devidr0nnngCd955J7Kz\ns5d9niAIGBwcREFBAerr69dEsmc5a/vVE6Ig+fn5yMrKisu1rFYrnnrqKbz00kvLPs/hcMBqtaK8\nvFwxG77JjYImIQqRkpISt+z5I488AlEUUVtbu+j3JUmCXq+HzWbDxo0b49oDVjoKmoQoRLyy55xz\nnDhxAj/72c8W/b7NZoPD4UBWVhYqKyvX/O349dbmSC4hChSv7Pm7774Lt9uND37wg/Me55zDarVC\no9EgNzcXxcXFFDAXQT8RQhRAEATY7fa4VAP6z//8T3zxi1+cl/32er3Q6XTIzc1Fe3s7BctlUE+T\nEAWIV8V2rVaLP//5z7jtttvmHnM6nZicnERWVhbKy8spYK6AfjqEKADnHMXFxTG/zu9+9zvcf//9\nqK6uhiRJuHz5MlJTU1FdXU3JnhBR0CREAeIxnikIAh577DE899xz8Hg8sFgsyMnJQUlJCfUuw0C3\n54QogCiKMb89//Wvf42GhgaUl5fj4sWLKCwsREVFBQXMMFHQJEQBBEGIeRLou9/9LpqamiCKIjZv\n3rziSiCyOHqLIUQBbDYb/H5/1M8bDAZx9OhRPPvss/B4PPj617+O8vLyqF9nLWGcc7nbEDHGGE/k\n9hMyy2QyISUlJapLFYPBIG655RZ0d3fD4/EgIyMDe/fuxbFjx2TbViNRMMbAOV+060+354QoQCxW\nAz377LNzARMAAoEAuru7cfTo0aheZ62hoEmIAkQzaHLOMTExgddff33B9hlutxt9fX1Ruc5aRUGT\nEAWI1pSjQCAAo9EISZLwwQ9+cEGyJzs7O6wq7WQhCpqEKMDk5CSCweCqzuF0OtHf349169ahpqYG\nBw8exI4dO5CVlQXGGNRqNXbv3o0DBw5EqdVrEyWCCAnD7N9btKcHnTt3Dhs2bIho+whRFDE1NYVg\nMIiioqJ55+jv78eFCxcwOjqKrVu34sCBA5QECsFyiSCackRIGILBIDjnUa97mZ6eHtE5fT4ftFot\n0tLSUF9fP2+CvMfjwdjYGO666y4KlFFEQZOQMPj9/qivoOGchz2myTmHXq9HMBhEVVXVohPVLRYL\nOjs7KWBGGY1pEhIGURSjfms+W+Eo1POKogij0Qiv14uKiopFA6YkSZiZmaEtKmKAepqEhMHpdCIz\nMzOq5xQEAT6fL6TnzszMwGAwoLq6GuXl5UsGWoPBgOzsbGRkZESzqQTU0yQkLH6/P+rjmYIgrLiE\nMhgMYnp6Gk6nEzU1NcjPz1+2ZzowMBC3TdrWGuppEhIiURQBIOrViFJSUpZdD+73+zEwMICSkhLU\n1NSseH2n04nKykpUVlZGtZ3kCgqahITI4/HA6XRG/bzLVW23WCxwuVxYv3498vLyQjqf2WxGaWlp\nNJtIrkG354SEKBAIQK1WR/28wWBwQUZeFEVotVoYDAZUVVWFHDA9Hg9sNhuKioqi3k5yBfU0CQmR\nz+eLSc3L63uaFosFTqcTeXl5qKmpCeuaY2NjkCQpLvsNrVX0kyUkRGazOSZB02Qywel0QpIkWCwW\nmEwmFBYWoqCgIKzrSZIEURTR0dER9TaS/0U9TUJCxDmPye15fn4+AGBwcBDFxcVoaWmJqKdotVqR\nlZUV9SlRZD7qaRISounp6ahPNwIAh8MBq9WKwsJClJaWRnxrrdfrKQEUBxQ0CQnB7AqbnJycqJ0z\nGAxiaGgIU1NTc5PVI2Wz2aDVakNOGJHI0e05ISHwer3IycmJ2rpzt9uNmZkZFBQUICUlJaLqRtey\nWq3YtWtXVNpGlkc9TUJCYLPZ4Ha7V30ezjnMZvPc+GVpaSksFsuqEkyCIMBut6O4uHjV7SMro54m\nISGIxtxHj8cDi8WC9PR0dHR0zK0L55yvqhKRwWBAYWEhVTOKE+ppEhICn8+3qsy5y+XCyMgI0tPT\nUV5ePhcwJUlCXl5exLf9nHOcPXs2qmOtZHnU0yQkBMPDw6ipqQn7OFEUodfrkZaWhubmZqxbt27e\n91e7oZrVasXGjRtRUFAQ8TlIeChoEhICxhiqqqrCOsbv98NkMkEQBNTU1CwaHBdbQhmOqakplJWV\nRXw8CZ+sQZMxVg3gCQBlACQAv+Kc/xdjrADAHwDUARgH8CnOuV22hpI1z2q1LlrsdykTExNwuVyo\nrq5e9jhBEBDpPlcOhwN+v5+mGcWZ3GOaIoCvcs7bAbwPwD8yxloAPATgVc75RgDHAXxTxjaSNU4Q\nBGg0mpBugYPB4Lze5UqB1uVywWq1RtSuoaEhMMZisrSTLE3WoMk5N3LO+65+7gIwAKAawEEAv736\ntN8C+Lg8LSTkSi+zurp6xdtol8uFvr4+pKWloa6uLqQiwJmZmRHVvRRFEenp6WhtbQ37WLI6ihnT\nZIzVA9gK4BSAMs65CbgSWBljtDaMyGZqagqCICz5/dnVQh6PB01NTcjNzQ353JEmgqanp5Gfnx/1\nTd7IyhTxE2eMqQEcAvAVzrmLMXb9IA9tbk5ko9frlwyEgiBgZGQEaWlpWL9+fdgBMJJEkCRJmJyc\nxMaNG8M6jkSH7EGTMZaGKwHzfzjnz1592MQYK+Ocmxhj5QDMSx3/8MMPz33e1dWFrq6uGLaWrEWB\nQAAVFRULHp+ZmYHT6URZWVnEU36CwWDYRUAmJydhNpuxbdu2iK5JFjpx4gROnDgR0nNZpJm7aGGM\nPQFgmnP+1Wse+yGAGc75Dxlj3wBQwDl/aJFjudztJ8nvP/7jP9DS0oLbbrsNwJWe3vT0NCYmJtDS\n0rKqdeNnz55FaWlpWMU6Ll26hJKSEpqbGUOMMXDOF82wyT3l6EYAfwvgHGOsF1duw78F4IcA/sgY\n+3sAGgCfkq+VZK1zu91oaGgAcCXZMzU1BbVajS1btqy6Qnp6enpYQdfr9cLn883V4CTxJ2vQ5Jy/\nBWCpQaB98WwLIUvxer0oKiqCw+HAxMQECgsLUVJSEpVzZ2RkhLU3+eTkJEpKSmiakYzknqdJiKK5\n3W6MjY1hZmYGDocDjY2NUV2BI4piyIkgQRDQ29uLwsLCqF2fhE/2RBAhSqbRaFBRUQGVSoXKysqo\nb1gmSVLIGXeLxYLt27cvWL9O4ot6moQsYWJiAmfPnkVmZibq6uqiHjCDwSC8Xm9I5+WcY2pqiraz\nUADqaRJyHVEUMT09DUmSYLfbY1Z2LRAIwOFwhPRcq9WK9PT0sNa/k9igniYh13C73ejv70daWhqq\nq6vBOceGDRtidr1Qy8319vbSLpMKQUGTEGBuz3GLxYLm5mYUFxeDMYbh4eGYLVUMdTzT6/WiuLgY\ntbW1MWkHCQ/dnpM1TxRFjI6OAgAaGhrmBUm73Y6mpqaYXTeUoGk2m1e1tS+JLgqaZE1zOp2wWq0o\nLi5Gfn7+vMAkSRI8Hk/YxYdDFcq6c0EQYLVa0d7eHpM2kPDRWxdZkzjnmJ6extDQEIqKilBYWLig\nJ2c2m2Gz2WI2L9JiscDpdC77nEuXLsHv94e9Pp3EDvU0yZrj8/kwNTWF9PR0bNu2bclbZK1WG9G+\nQKHKzMxctqfJOYckSWhra4tZG0j4qKdJ1hSv14uxsTEwxlBeXr7smKLBYIjpRHLG2LLrzu12OzIy\nMminSYWhoEnWBEmSoNfrMTU1hfXr16O6unrZ5weDQfzxj39EX18fjhw5gmAwGPU2rVSAeDYBRJSF\nbs9J0hNFESaTCS6XC42NjSuODwaDQezfvx8nT56EKIro7e3F7t27cezYsVVtt7vYdZY638zMDAYH\nB2OWuSeRo54mSWpWqxXj4+PIzs7Gxo0bQ0qoHD16FN3d3XM7RbpcLnR3d+Po0aNRbZvT6VxyGpHD\n4cC2bduompECUdAkSYlzDpvNhqmpKRQVFSE/Pz/kANTb2wu32z3vMbfbjb6+vqi20WazLRo0RVGE\nzWZbtFo8kR/dnpOkM7tvT25u7oLJ6qHYtm0bsrOz4XK55h7Lzs7G1q1bo9ZGzjlKSkoWraU5NTWF\ngoIC2jRNoainSZKKz+eD0WhEdnY2ysvLIwo8Bw4cwM6dO6FSqcAYg1qtxu7du3HgwIGotXOp1UCS\nJOG9995DUVFR1K5FooveykjSmJiYgNPpRG1tbUh7ji8lNTUVhw4dwqFDhzA1NYWtW7fiwIEDUU8C\nLRbQbTYb6uvroVaro3YtEl0UNEnCm93oTBCEVQfMWaIo4uabb45Z9nqpzLnZbKbCHApHt+ckofl8\nPpw7dw4AohYwgSsbqMVyYrvVaoXVap33mNvthiiKyMvLi9l1yepR0CQJy+VywWQyoaqqKiZVgGJZ\n8DcjI2PBuGV/fz+ys7NpmpHC0e05STicc2g0Gni9XjQ0NMSkR2i1WmOejLm2qHAgEABjLGYVlUj0\nUNAkCUUURUxNTSEjIwPV1dUxm5YzmzWPlWAwOC/YT01Nobq6OqztfIk86PacJAyPx4P+/n6sW7cO\nlZWVMQuYoigCQEznSV475Wg2kUXrzBMD9TRJQrDb7bDZbGhubl6y6k8wGITNZoPf78fMzAzWrVsH\nk8mEwsJCWCwWFBQUwOfzQa1WIyUlBZmZmcjKyoJKpYJKpZobE3W5XOCcx/T1OJ3OuYTP6Ojogp4n\nUS4KmkTRJEnC2NgYAoEANmzYsGDteCAQwMTEBDwez1xgzM7ORlFREbKzs1FZWTkvGEmSBEEQEAwG\n4Xa7547PyclBMBhEZWUlAoFAzAoPz7Lb7XO1Om02G00zSiAUNIliCYIAs9mM7Oxs1NXVzbtddjqd\nGBwcnOsdNjQ0YOPGjSHdUs+OG+bm5gLAXKB0OByYnp7G6Ogo1Gp1TMcYCwoKoFKp4HA4kJWVRbfm\nCYSCJlEkt9uNixcvoqmpCfn5+XOP22w2jIyMwOv1oq6uDmVlZVEJbBkZGSguLkZxcTF8Ph8CgQAm\nJyeRmpqKioqKqK4Gmq3InpaWBpPJhLKysqidm8QeBU2iODabDQ6HA62trXMZbJ/PB51Oh5GREWzb\ntg0lJSUx3Z1xdqL89PQ09Ho9cnJyonbLPpsEstlsMBqNaGxsjMp5SXxQ9pwohiRJGB0dhcFgQGVl\n5VzAtFgseOeddxAIBLBv3z6UlZXFNGBOTU0hMzMT6enpqKioQFlZGQKBALRaLQRBWPX5RVGc62UW\nFxfT1rwJhnqaRBFmxy+zsrJQW1uLtLQ0SJIEnU6Hc+fOYe/evXFZXji7jPHa5FFmZibKy8thsVgw\nNTWF3NzcVc3hdDqdMJvNUKlU2LRpUzSaTeKIgiaRndfrxYULF7B+/fq5VTiSJOH06dMQBAG33HJL\n3KbjeDwe+Hy+Rb9XVFQEl8sFp9MJSZLmEknhSk1NBWOMamYqlE6nW/b7dF9AZGW322E2m9Ha2jov\nYL7xxhtQqVTYvXt3XOcv+v3+Zccu1Wo1CgsLYbfb4fF4IrqGIAgwmUyUMVcgvV6PJ598ctnnUNAk\nsuCcQ6fTQavVorKycq44hiiKOH36NAoKCtDW1hb3nlggEFhxH6HZFUnT09MRBU6j0YjU1NRlt+8l\n8ffuu+/i1Vdfxd/93d8t+zwKmiTuRFGE0WhEeno6Wltb5wWpkZERuN1udHR0RHWaT6hsNltIU5hS\nU1NRWVkJh8MRduCcmZnBli1bIm0iibJgMIjDhw/jT3/6E+64444Vi6ZQ0CRxFQgEcPbsWaSkpKCs\nrGxeT3JkZASXL1/G3r17ZQmYAJCenr7kMs3rpaWlIT8/H16vN+Ss+myQvXbuKZGP0+nEM888g5SU\nFHz/+98PaZyagiaJG7fbjcnJSWzYsAFlZWXz6kZaLBaMjY3hpptukjU5MtsDDtXs1CSn0xnS88fG\nxpCSkhLzte1kZWazGQ8++CByc3Px0Y9+NOSxc0rdkbgwm82YmJhAa2vrvDqSwJXbo8uXL6OysjLk\nXl4szCaBwl1hlJubC5vNBqfTuWz73W43tFotGhsbY1rgmKxseHgYR48exX333YcdO3aEdSwFTRJT\nkiTBYrFAEAS0tbUt+m5+6dIlzMzMYNeuXVG9rtPphMPhmCvQAVxJ4mRlZSE7O3tBIsbr9UKSpIiu\np1ar57arWKqnbDabsWPHDtjtdtmGH9Y6zjmeeOIJDA0N4Z/+6Z8i2luegiaJmWAwiKGhIWRnZ6Om\npmbRlS8+nw96vR579uyJyjYPNpsNOp0OVqsV69atg1qtniv/JkkSOOeYmZmBwWBARkYGCgoKUFRU\nhLS0NLjd7ojnXqalpSE1NRVer3fR3mYgEIDdbsfGjRvhdrtX+zJJBARBwHPPPQeHw4Evf/nLEQVM\ngIImiRG/3w+z2YzS0lIUFxcv+TytVov09PRVr/bxeDy4ePEiHA4HqqursWPHjhVvgZ1OJ6xWK4aH\nh1FcXAxBEFY1JzQ7OxsOh2PR3qbBYEBxcTE45zShXQYGgwGPPPIIdu3ahQceeCCscevrUSKIRJ3T\n6cS5c+eQn5+/bMAUBAH9/f3Yvn37qq6n1+vx1ltvQaVSYe/evWhubg5pzDAnJwe1tbWor6+H1+vF\n0NDQqv6ZGGNIT09fkEkXRRFnzpyZmxTvcrkivgYJn1arxeOPP47m5mZ84hOfWNXvGKCeJokyu90O\nu92OlpaWFddnm81mVFVVRXxLDFwZDx0bG8P27dtRUlIS0TlUKhVqa2uh1+ths9mQk5MTcY8zMzMT\nNpsN69atmxuOmJ6exrZt25CVlQW73U5JoDh65plncPHiRXzyk59ES0tLVM5JPU0SFZxzjI+PL6hQ\ntJyenp5V7fg4PDyMsbEx7NmzJ+KAOWt2nLG0tBRms3lun6BwpaSkQKVSzR0vSRLMZvPc+BljbFVv\nEiQ0kiThyJEjeOGFF3DnnXdGLWAC1NMkUTAbGMLZIdLtdiMtLS3iWpJmsxmDg4O48cYbozJNSRRF\nVFdXzwU0i8UScc3O1NRUCIKAjIwMzMzMzCWigCtDErR8MrasViueeuoppKam4r/+67+i3rOnniZZ\nldlxScYYKioqQk5yzK6/jiQpIkkSenp60NraGrXCwGazGYFAAMCVeZez2fRIpKengzGGYDCId955\nZ97qH0EQVj2mRpZmNpvxrW99C1arFffdd19MhkKop0ki5vP5YDabUVNTs2zCZzEGgwH19fURXXdg\nYADp6enYsGFDRMcvJi0tbd62E3l5ebBarcjOzg67t8kYQ0pKCqxWK+rr6+f9bPx+PwXNGDl79iye\nfvppfPrTn8bevXtjdh3qaZKIWK1WDA4Ozu2rEy63242CgoKwj5MkCcPDw2htbQ372OXOqdPp5gWz\ntLQ0qFSqJWtrriQ1NRUGg2Fux0ngf8d9aWJ7dHHO8eyzz+JrX/saPve5z8U0YALU0yQRmF0y2NTU\nhKysrLCPDwQCMJlMESWB9Hr9XIWhaHG5XKirq1vQA8zKygp5Tfli5+Scz7s1F0URDQ0NtL1FFImi\niKeeegpjY2P49a9/jerq6phfU9G/PcbYhxljg4yxS4yxb8jdnrWOc47Lly9jenp6Xg3McPl8PlRU\nVEQUPPR6fVQDJnBlHGyxKkUpKSlIS0ubW4IZjp6engUT9mk8M7rsdjvuuusuTExM4Otf/3pcAiag\n4KDJGEsB8N8A9gNoB3APYyx68wZIWCRJgtFohEqlQn19/apWtUxOTkY8wdtisUS05a3T6URnZ+ei\n12WMzbuNnhUMBvHyyy/j+9//Po4cORJy8HS5XFCpVOjt7cX3vve9uWMpaEaPRqPBd7/7XRw4cADf\n+MY34jojQcm357sADHPONQDAGHsawEEAg7K2ag0KBAIYGBhAZWUliouLV71GXK1WR5wEcrlcEY2h\nvvjiizh9+jRefPFFfOpTn5p73G63Y2pqasHUp2AwiP3796O7uxtutxvZ2dnYvXs3jh07tuKYpF6v\nx0MPPYTe3t55xz755JNR2aN9rXvyySfx7LPP4qtf/SpuuOGGuF9/xZ4mY+yfGGPhj9ivXhWAa3c4\n0l99jMSRz+eD0WhERUUFSkpKolJUAwAuXLgQ9jHBYBB5eXkLSsst57777kNubu7cFgaf+cxnkJub\ni/vvvx/AlYTUxo0bFxx39OhRdHd3z41NulwudHd34+jRo8tez+Px4NVXX0Vvb++CYw8fPhxxFSVy\nZXjo0KFDeO211/DlL39ZloAJhNbTLAPwHmOsB8CvARzjCqqg+vDDD8993tXVha6uLtnakmwsFgsM\nBgMaGhqiOt+tsLAwoi1wZ8vMheNb3/oWuru7cfnyZQiCgLS0NNTX1+Ob3/wm3G43xsbG8L73vW/B\ncbO9xGu53W709fXh9ttvX/J6586dg0ajWfTY8+fP44477gir/eQKq9WK73znO8jPz8dPf/rTqG/n\nfOLECZw4cSK0J3POV/wAwHBlbPFpAJcB/F8AjaEcG+kHgBsAvHTN1w8B+MZ1z+EkNmw2Gx8bG+N2\nuz3q59ZoNPzXv/512McFg0H+yCOPcFEUwzrumWee4WlpaVytVvO0tDT+zDPPcM451+l03GQyLXrM\n888/z9VqNQcw96FWq/nzzz+/5HXcbjc/fvw4P3z48KLH/uIXv+A+ny+sthPOjUYj/8d//Ef+xS9+\nkfv9/rhc82psWTQ2hZQIunoS49UPEUABgEOMsR+FFpoj8h6ADYyxOsZYBoC7ATwXw+sRXHkTHR0d\nxfT09LwPJyp8AAAgAElEQVRlhdEkCAJqa2vDPi4lJQUFBQWw2WxhHXfo0CHk5OTg3/7t36BWq/Hn\nP/8ZJpNpbqnkYg4cODC3fTBjDGq1Grt378aBAweWvM7k5CTa2tpw++23Y9euXXMrg2aPfd/73keJ\noDC9/PLLeOihh7B//3788pe/VMaY8FLRlP9vb+4rAM4AOAbgTgDpVx9PATCy0vGr+QDwYQBDAIYB\nPLTI92PxJrNmBYNBbjQa+fj4OBcEIWbX0Wg0/Lnnnovo2GeeeYafO3curGPOnj3Lp6amOOecT01N\n8Z6eHn7p0iVus9mWPU4URf4P//AP/N577+XPP//8sj1cj8fD+/v7eTAY5JxzPjExwe+44w7+ve99\njz///PPc6/XywcHBsNq91r3wwgv8hhtu4C+99FLcr41lepqhjGkWAriDX81iXxNsJcbY0oM7UcA5\nfwnAwlF6EnWBQACXLl1CSUkJamtro5bwWczsEsVIlJeXY2JiAps2bQr5mI6OjrnPCwoKMDY2hvz8\n/BXHxURRRE1NDT7/+c+vODd0aGgI5eXlc3NP7XY7tmzZgm9/+9sAriSIFNFLSgA+nw8///nPMTAw\ngEOHDq24pW68rRg0OeffWeZ7A9FtDpHD7AqdgoKCiOZAhkutVmPdunUIBAJhB5Lm5mY8//zzER07\nO9e0pKQkpFJyf/3rX6FSqVYMmG63GwaDYV4gP3/+/Lxk1/T0dNjDCmuR3W7HF77wBTDG8Jvf/Cai\nhGGsKXZyO4kPu92O4eFh5Ofnx+0dPTU1FZIkYWxsLOxji4qKkJeXh97e3rCPvXTpEux2O+rq6lZ8\nriRJ6O/vR3t7+4rPNRqN2Llz57wJ/36/f976+IyMDJSXl4fd5rVkZGQEX/7yl7Fv3z78/ve/V2TA\nBChormlutxsWi0WWrXNbW1vh8XgiOnb79u04f/58WKuKdDodVCoVmpqaQhp6OHnyJERRxM0337zs\n89xuNzwez4IJ9/39/fPehARBiGid/lpx+PBhHDx4EPfeey8eeOABRe+jREFzjdLr9TAajaiuro6o\n2tBqZWVl4ezZsxEdW1dXh/Lycrz22muzCcFl6fV6mEwmVFdXh5S9npqaQnd3Nz70oQ+t+Pzx8fF5\nY5mz11OpVGhra5t7LBAIUOZ8EZxzPP7443jiiSfws5/9DLfccovcTVoRBc01hnOO6elp+P1+VFVV\nyZacaGxsRFZWVtiT1WfdfPPNsNlsOHny5JLP4Zzj4sWLEEUR27ZtC6kkm8/nw5NPPomamhrs3Llz\n2efOzMxgZGRkQbWm7u5u5OTkzOstzVZyJ//L4/HgwIEDOH78OH75y1/GvKRbtFDQXEOCwSCGh4cR\nCASwfv36sJYjRltqairUanVE45rAlc3Qbr/9dly6dAl//etfF3xfFEXo9XqkpaWhuro6pIDpdDrx\n2GOPQaVS4a677lrx+WazGe9///vn9TI55zh//vy8VUOBQABer1fRt5zxNjk5ifvvvx/r16/Hf//3\nf0dUT0AuFDTXiGAwCJPJhPT09AW3k3Lp7OxEX19fxJuYFRUV4eDBgxgeHsZf/vKXuYLBs28OszU/\nQwlWly9fxmOPPQa1Wo0vfOELKwZZm80GSZIWbLcxOjoKURTR1NQ095jH45nbSoMAv//973HXXXfh\ntttuw6OPPppwG83RW98a4PF4oNVqUVZWFvValKtRXFyM0tJSjI+PR7x1RWlpKe6++268+OKL+O1v\nf4vW1ta5LXlDKTBitVrx0ksvQavVYuvWrbjllltWfEOZrfS+2Kqmp59+Gjt27FgQqJU211Auf/rT\nn/DTn/4U999/P+655x65mxMRCppJzufzwWQyIT8/X5aEz0o2btyI1157bVUVzbOysvDJT34Sp0+f\nxsmTJxEIBNDe3o4NGzYsOgwxMzODwcFBDA8Pw2w2o7y8HJ/73OdCnqOq1WphMpnmTZoHgMHBQQSD\nQezbt2/e436/P+J91JOF1+vFgw8+CL1ejz/+8Y8RlwZUAhZK9lGpGGM8kdsfC8FgEEePHkVvby8a\nGhqwY8cO1NbWKna6iyRJePnll1FYWIhdu3ZFfB6v14uLFy+iqqoKXq8X58+fh9FohMvlQmpqKhhj\nkCQJoiiCc47c3FzU1dWhs7MzrB0tJUnChQsXUF9fP2+aFuccP/7xj1FZWYm//du/nXeMVqtFXl5e\n1CvzJIqZmRncf//9mJiYwMsvvxz36W2RYIyBc77obQr1NJPI9YVzVSoVOjs78dprr8ndtCWlpKSg\ntbUVJ06cQHt7e0Ql6CwWC4aHh9HR0TF3/Pr16wFcSQhZLBa43W4wxpCbm4uCgoKIe7VmsxnZ2dkL\n/vFffPFFCIKAu+++e8ExgUBgzfY033rrLfzrv/4rbrvtNnzlK19Jik3l5M8GkKi5vnCux+PBmTNn\nViycK7e6ujrU1dXhL3/5S0jzLq+l1WphtVrR1ta2aMCd3Zq3oaEB69evR1FRUcQBUxRFmEymBeOT\nJpMJPT09+PCHP7wgKEiSBI1GsybnaL7wwgu455578NnPfhZf/epXkyJgAhQ0k8rp06cXrJKZLZyr\ndHv27EFubi7efvvtkJ4vSRImJydhs9lQWVkZlwxsb28vGGPzeo3BYBD/8z//g8rKSmzfvn3BMYIg\noLi4OGkCRihEUcSPf/xj/Pu//zuef/553HvvvXI3Karo9jxJWCwWnDt3DhkZGfOmt2RnZ2Pr1q0y\ntiw0GRkZ6OzsxAsvvIC6urpldxaUJAmjo6NwuVzo6OiIS0Dy+XxIS0tbsDXGr371K6hUKnzuc59b\n9Di/36/IBFysOJ1OfOQjH4EkSTh8+HBIhVESDfU0k8DMzAx+8pOfoKOjA+9///uhVqtDLpyrJBUV\nFdi3bx/+8Ic/LLlSSBAE9PT0IDMzE5s3b45bD2526+Bre5mHDx+Gy+XC3XffvWQ7IqnGlEiCwSCO\nHDmC733ve3jsscdw2223YceOHTh27FhSBkyAsucJr6enB0888QT279+PD3/4w5AkCUePHkVfXx+2\nbt2KAwcOJNyt4cjICF566SV8/OMfnzd+6HQ6odfrkZeXF9f5pg6HA1qtFu3t7XPzPk+ePIlXX30V\n991336Lb/86amJhAVlZWUvY2r088AkBLSwvOnj2b8KuflsueU9BMYENDQ3j00Uexe/dufPrTn5a7\nOVHV09OD8+fPo7OzE62trbDZbDAYDMjLy4vrRHHOOY4ePYqdO3eitLQUkiThpZdewptvvokHH3xw\nxWA4ODiImpqaqG5MpxRHjhzBPffcM28cXa1W4/e///2ym88lAppylIQOHTqEd955B1/60pcW3YI2\n0W3fvh0pKSl455135qoGbd26Ne41Fqenp1FTU4PS0lIEAgH88pe/hNfrxTe+8Y2Q5l3q9Xo0NDTE\noaXxd+bMmYh27Ex0FDQT0PHjx/Hmm2/is5/9bFIGzFlbt26FKIo4cuQIduzYEfZ0pNUSRREGgwHN\nzc3QarV47LHH0NHRgY985CMh9RwFQUBNTU1SjmkKgoCKigpkZmbC6/XOPZ4oicfVoNvzBCKKIn7x\ni1/AbrfjgQceCGslS6IJBoMYGhqCSqVCWVkZjh49CqvVio6ODnR2dsal4IhWq4XP50N3dzc0Gg26\nurpw4403hrx/ktPpxMzMTEiV4hOJ2WyGwWBAaWkp7r333rkxzezsbOzevRvHjh1LuHH069GYZhIQ\nBAG/+93vMDQ0hIceegj5+flyNylmfD4fDAYDBEFAU1PTXICcmJjAM888g+LiYrS2tmLLli0x2wDO\nYDDgiSeegN1ux86dO3HTTTeFnQ2enp6e65ElC4vFgosXL6KxsRGVlZVzy3YTOfG4GAqaCc5iseBX\nv/oVKisrcc899yT16hKv14vh4WHk5OTMLYW8Fuccp0+fxvnz5+H1etHZ2bnkaqBIjI+P4+zZs3jp\npZfQ1NSEj370oxFXYEqmzLkkSRgfH0cgEEB9fb2stVjjgYJmArPZbPj5z3+OjIwM/PM//7Mi6mDG\nitPpRF9fHzZt2rRioOGco6enByaTCadPn8amTZuQm5uLjo4OlJSUhPxzCgQCOH/+PGZmZvDee+8h\nIyMDWVlZ2Lx5M/bs2bOqnuypU6fQ1taWcPUiryeKIi5evAin04kbbrghKXqSK6GgmaDOnz+Pw4cP\n4wMf+EDCbAUQKZ1Oh5mZGTQ2NoadIfd6vRgcHMTly5dhMBggiiIyMjJQU1MDt9uNuro6WCwWFBQU\nwGq1QhRFuFwumEwmcM7BOceOHTuQn5+Pbdu24eLFi2hoaFhVpp5zjjNnzmDLli0JfWfgcrmg1WpR\nUFCA8vLymA2HKA0FzQQ0Pj6Oxx57DDfccENST9+YXRLJOUdlZWVUbrN9Ph+Gh4fBGMPg4CBKSkqg\n1WpRWloKl8uF4uJiZGZmory8HGVlZfNuNXt6epCSkrLqDHAgEMD4+Diam5tX+3JkMz09jVOnTmHP\nnj1JnXRcDAXNBPPKK6+gp6cHd955Z9LO8QOuBBaDwQCn04mWlhbZe2Q+nw8XLlxAW1sbVCrVqs7l\ncDhgs9kWre6udJxzGI3GufYn48T8lSwXNJN3gCxBnTp1Cq+//joOHjyY9AHz0qVLCAQC2LRpk+wB\nE7gyxaimpmbVARNI3GrtoijirbfewvT0NJqamtZkwFwJTW5XiGAwiEOHDsFqtYa82iRReTwe9PT0\noKWlRTG7EM7MzEAUxagVmXA6nQmXNfd6vRgfH0d1dTVqa2uTOum4GvRTUQBRFPHss89iaGgIn/nM\nZ5I6YBqNRgwNDWHz5s2KCZiiKOLkyZOorKyMWqLDYDAkVNJEr9fjzJkzKC8vR319PQXMZdCYpswc\nDgcOHTqEgoICfPSjH0346jDLGRsbgyAIKC8vV9Q0HJ1OB5/PN2/b3dWQJAlDQ0NoaWlJiMBpNBph\nNBpRU1ODoqIiuZujCFSwQ6FcLheeeuopMMZw8ODBpH13n13D7XA40NLSoqixPo/Hg5mZGbS3t0ft\nnH6/HxkZGYoPmLNzVHNzc7Fp06akfsOOJvopyWR0dBSvvPIKduzYgZ07dyr+HyxSgiBgdHQUgiCg\no6NDcW8MGo0GVVVVUQ0YiZAE8vl8GBkZQWpqKhobG5P27y8WKGjKYHJyEocOHcKOHTvQ2dkpd3Ni\nxu/348yZM6ivr49r0eBQjY6OwmAwoLW1Narn9fl8il5maDAYYLFYUFVVtebmX0YDBc04O3PmDPr6\n+nDXXXclXfWba01PT2N8fBxtbW2KLC4iCMLcssBo0+v1i66bVwKj0YiBgQFs37494bL7SkFBM44u\nXryIl19+GZ/61KeSOmBqNBr4fD40NDQoMmACVwJbUVFRTOYhpqamKm5+YyAQgFarBQDcdNNNipgX\nm6goaMaBJEl4/fXXMT09jS996UtJO6VIkiRMTEzA4XCgsbERWVlZcjdpURaLBS6XK6rJn1mCIECl\nUinq9tzn8+Hdd99FUVER2traaPxylZQ1Kp+EJEnCyZMn0d/fj9tvvz1pA6YgCBgfH4fFYkFbW5ti\nA6YkSXjvvfdQUFAQk6SU3+9XVMC02Wy4fPky2tvb520MRyJH8zRjyOfz4ZVXXkFmZia6urqS9pYo\nEAigv78fJSUlqKurU/Q/psFggNfrRWNjY0zOPz09DVEUUV5eHpPzh4pzjpGREYyPj2PPnj2KfRNT\nKpqnKQOfz4cjR47A5/PhtttuU9xUm2hxOBy4ePEimpubFZ+J9fl8mJqaQltbW8yuYbPZZE+wiKII\nrVYLxhj27t2r+OlPiYaCZgyYzWa89dZbaGpqwubNmxXd81qNiYkJ2Gw2bNy4UfZAEYoLFy6gpqYm\npj3+6elpWVfVuFwuvPPOO2htbUVVVVXS/u3JKTm7PzKy2Ww4cuQISkpKYrqHjdy0Wi0cDgfq6uoS\nImBOTk7CZrPFdL27JEnIy8uTbcaA1WrF+Pg42tvbUV1dnbR/e3KjnmYUDQ8PY2BgALfeeiuqq6vl\nbk5MiKKIiYkJzMzMoKOjIyGW3omiCLPZjD179sR0mESu5ZOcc/T394Mxhubm5qiUtiNLo55mlOh0\nOhw/fhybN29O2oApCAIGBgbg8/mwdevWhAiYwJXfTVFRUcyDic/ni/v4oSiKGB0dRUpKCjZu3EgB\nMw4S469e4fr7+2EymXDPPfcoqnpPNHm9XvT09KC5uTlqNSfjYWJiAmazOS7LVeO9fHJqagparRZV\nVVVoaGig2/E4oZ7mKnDOce7cOfT09ODGG29M2oBpMpkwODiI9vb2hAqYkiRBr9ejuro6LrMXxsfH\nEa8pcBaLBWNjYygrK1tTG54pAc3TjJAoijh9+jQAYPv27cjIyJClHbE2NjaGQCCAsrIyxS6JXIpe\nr4cgCHFbB37u3Dls3Lgxpn8Ls7fjkiStif3H5UJ7BEWZKIp4++23YTKZ0NnZmZQBMxgMQqPRwOl0\noq6uLuECpsfjgcViQU1NTVyuFwgEkJGREdO/hUAggIsXL2JmZgbNzc0UMGVCY5phcjqdOHv2LEpL\nS7F3796kvC0KBAJzRTc2bdqUcBPzOed48803sXnz5rglq3w+X0yTMBaLBUajEeXl5SgtLY3ZdcjK\nZPtvYIz9iDE2wBjrY4z9mTGWe833vskYG776/VvlauP1vF4v/vrXvyIjIyNhtjIIl9/vR29vL1Qq\nlSKLBofCbDajpKQkrksZY5kEMhqN6O7uRnV1NQVMBZBtTJMxtg/Acc65xBj7AQDOOf8mY6wNwJMA\nOgFUA3gVQNNig5fxHNM0mUwYHR1FfX09Kioq4nLNeLNarRgcHERra2vC3Y7P8vv9GBwcjPu2Ghcu\nXEB5eXlUVwMJggC9Xg9RFFFXV5eUw0BKpcgxTc75q5xz6eqXp3AlQALAxwA8zTkXOefjAIYB7JKh\niXOsVitOnTqFqqqqpA2YGo0Gk5OTaG9vT9iACVzJYJeVlcV9vqTL5YpqT9Pr9eKNN96AIAjYsGED\nBUwFUcqY5t8D+P3Vz6sAvHPN9yauPiYLnU4Hk8mEm2++GTk5OXI1I2YkScL4+DgEQUB9fX1CV8PR\narUYGxvD/v3743pdURSRl5cXtcLDVqsVExMT2LJlS0JN8VorYho0GWOvACi79iEAHMD/4Zw/f/U5\n/weAwDn//SKnkJXBYEB/fz+6urqgVqvlbk7UBQIB6HQ6uN1utLW1JcwKn8WIogir1Yobb7wx7mPN\n0dpIjXOOCxcuwGazYfv27Qn9BpbMYvpfwjm/ZbnvM8Y+B+AjAG6+5uEJANfOE6m++tiiHn744bnP\nu7q60NXVFX5DryNJEkZHRxEIBHDrrbcm5a2Rz+fD0NAQsrOz0dHRkfBJrdmlknLcDXi93lXfmguC\nAI1Gg3Xr1mHXrl1J+TenZCdOnMCJEydCeq6ciaAPA/gPADdxzi3XPD6bCNqNK7flryCOiSBJknD5\n8mWYTCa8733vS+je11Lcbjd6e3vR1tam+BqYoTCbzZicnJQt26/T6aBWqyOu9jQ9PY2zZ8+ivb0d\nZWVlKx9AYk6RiSAA/w+AGsArjLEextijAMA5vwjgjwAuAngRwJfilSIPBAK4fPky1q1bhxtvvDEp\nA+bk5CQGBgawZcuWpAiYkiTh7NmzKC4ulm161OjoaMQ9dZPJBKPRiNbWVgqYCYKWUV4liiIGBgaQ\nmpqK1tbWhL9dvR7nHMPDwwCAysrKpBmj1el0CAaDqK+vl+X6kiRhaGgo7Hm7giCgp6cHBQUFqK+v\np9txhaHtLlbgcrkwOTmJqqqqpOh9XW92+1ZJktDQ0JA0/6ButxtWqzWm21esJJIaml6vF+Pj48jK\nysKGDRsScgHBWrbmg6bP58Pw8DAqKyuTMmB6PB5MTEwgGAxi48aNSdODliQJp0+fxqZNm2QdRgl3\nJdDo6CicTidqa2sTouI9WWhNB02bzTa3x00yTu/weDy4cOECKisrUVUl21TXmJicnERmZqas+/EA\noQfN2T3hjUYj2traEnoBwVq3Zu8LXC4XNBoNSkpKkjJgWq1W9PT0zG2wlUx8Ph+mp6exbds2uZsC\nnU63Yk93dsfOYDCI3bt3U8BMcGuypzkzMwO/34/29vakzJDP9qCTdYK0RqNBRUWF7GOznHOkpKQs\n+zN2OBw4d+4cSktLZUtWkehKvoixAqvVCovFgoaGBqSmpsrdnJjIyspCTk5OUr6+wcFBTE9PY+PG\njXI3BYFAAHl5eYtuCSxJ0txqqy1btiTNbAWyhoKmJEmwWq1ISUlBY2NjUmcs5e6BxUogEIDX68Xm\nzZvlbgqApcczBUHA4OAg7HY7brjhhqS8m1nL1sRvczZgCoKAsrKypMkgrzVarRbl5eWK2YvJ6/Uu\nKDxss9kwMTGBkpISbNq0if7WklDydreuEkURTqcTKpWKNqBKYEajEYFAIK6FhVditVrn3ZpPTk7i\nrbfeQk1NDf2tJbGkDpqSJMFutyM1NTUpEyJrhSiKePfddxV3lzA1NYX09PS5zc5cLhf27dunmJ4w\niY2kDZqCIMDr9SI3N5cG4ROcTqfD9u3bZZ+Tea3ZoR4AeO211wAAGzZsiHvxYxJ/SRk0JUmC1+tF\nenr6oplNkjjsdjvcbjcqKyvlbso8Xq8XPp8Po6Oj2LlzJxoaGhTVCyaxk3RBMxgMQhRFqNXqpM0i\nrxWBQAD9/f2ora1V1GyHYDCI7u5uGI1GNDU1KaoHTGIv6bLnkiQhPT2d3vWTgFarRVZWlqLGCL1e\nLzQaDbKysuK+eRtRBuW8fUcJBczk4HK54PF4FLFUcpZOp8OpU6dQWloalWrtJDElXU+TJD5JkqDR\naFBbW6uIVU2SJEGv18PlcmHbtm1Qq9WoqKiI2kZqJLEkXU+TJL6+vj4EAgFFFLZwOp148803AQAt\nLS3Iz8+Hz+ejgLmGUU+TKIrH44EkSbIWFp41u5VuTU0Namtr5x4Pt4YmSS4UNIlicM6h0Wiwfv16\nWRcjBINBnD17FhkZGWhsbFywVHJ2/i9Zm+j2nCiGXq9HWlqarFN4/H4/Ll++DMYYmpqaFgRMAJiY\nmKD5v2sY9TSJIni9Xrz33ns4cOCAbG3QaDSYmZlBTU0NiouLF31OMBgEALo9X8Oop0kUQavV4v3v\nf/+iPbtY45xDr9fDYDCgrq5uyYAJXOmJlpaWKmqyPYkv6mkS2U1NTYFzjpKSkrhf2+FwYHx8HLm5\nudi1a9eKU5wWKwdH1hZ6uySycrlcGBwcRH19fdwXJdhsNgwMDEClUqG+vj6kOaGUOSfU0ySyGh8f\nR0FBQVwDkSRJGBkZgSiK6OjoCCtTb7VaaevdNY56mkQ2MzMzSElJQXt7e9yu6ff7ceHCBUxNTaG5\nuTmsgClJEkwmE/U01zjqaRJZiKIInU6HpqamuN2WG41GTE9Po7y8HB0dHWEf7/P5UF9fT0mgNY5+\n+0QWp06dQmZmZlwmsXPOodPp0N/fj7q6uogTTj6fj5JAhHqaJP5sNhuysrLQ2NgY82s5nU5MTk4i\nPT0d+/btW1UBEEoCEYB6miTOgsEgtFotmpubY761rc1mw9tvv43MzEysX79+1RWTqBwcAainSeJs\nZGQE+fn5Md23SRRFGAwGuN1u7N27NypDAJIkYXh4GPX19atvIElo1NMkcWO1WjE4OBjT/X78fj/e\nffddWCyWsLPjK5031LmcJLlRT5PEhSRJmJiYwAc+8IGY3ZZbLBZMTk6iqakp6quLfD4f7WpKAFDQ\nJHEyMTEBtVqNvLy8qJ9bkiRcunQJBoMBN9xwQ0wy8pQEIrPo9pzEnNlshkajQXV1ddTP7fV6MTw8\nDJVKFbXxy6WuQ9ONCEBBk8SYJEnQ6XSoqamJ+m252WzG8ePHUVRUhLq6upjVuJwdWqCeJgHo9pzE\nmNFoRH5+Purq6qJ2ztmNzjweD2666Sbk5ORE7dyL8fv9yMrKoiQQAUA9TRJDbrcbU1NT8/bXWS2v\n14vXXnsNgiCgubk55gETAAKBAEpLS2N+HZIYKGiSmOCc4+TJkygsLIzabbPFYsHIyAg6OjrQ2NgY\ntzXgNJ5JrkW35yQmTCYT6uvrUVNTs+pzBYNB9PT0zFVEivfYos/nW7aaO1lbKGiSqPP5fDCZTGht\nbV31uTweDzQaDQoLC1FXVxfzpZeLsVqtMcn8k8REQZNEFeccFy5cQE1NDTIyMlZ1rrGxMeh0OnR0\ndMhW+Nfj8cDpdMoSrIky0ZgmiaqJiQnYbLZVJU6CwSDGx8fh9XqxZcsWWSulC4JA683JPBQ0SdQE\nAgFYLBbceOONEZ/DarXizTffRFpaGlpaWmKygigcVEOTXI+CJokajUaDsrKyiBM1ZrMZExMTaGxs\nRHV1tSIqpNPySXI9GqghUXHp0iVYLBZs2LAh7GMFQcDp06dRWFiIpqYmrFu3LgYtjAzV0CTXk/+t\nnCQ8QRBgt9vR0tIS9n4/LpcLw8PDyM/PV1zA9Hg8mJiYiNnyTJKYqKdJVk2r1aKqqirshM2FCxcQ\nCATQ2NiI3NzcGLUucqIooqGhQe5mEIWhniZZFbPZDJ/Ph4qKipCPEQQBo6Oj8Pv9aG5uVmTABK6M\nZ2ZnZ8vdDKIwsgdNxti/MMYkxljhNY99kzE2zBgbYIzdKmf7yNJEUcTbb7+NysrKkG/LJycn0dfX\nh6ysLGzbtk3RQYmSQGQxst6eM8aqAdwCQHPNY60APgWgFUA1gFcZY02ccy5PK8lSdDodduzYEdJt\nOeccJpMJer0eNTU1KC8vj0MLV8fr9YbVgyZrg9w9zZ8CePC6xw4CeJpzLnLOxwEMA9gV74aR5dnt\ndrjdblRVVa34XJfLhd7eXng8HmzdujUhAqbH48H09DQlgcgCsgVNxtjHAOg45+eu+1YVAN01X09c\nfYwoRCAQQF9fH+rq6lacS+lwOHD58mVkZmaioaEhYYJQIBBAfn6+3M0gChTT23PG2CsAyq59CAAH\n8ETZR+8AAAj8SURBVG0A38KVW/NVefjhh+c+7+rqQldX12pPSVag0WigVquXrWUpSRIGBwcBABs2\nbEi4TckEQaDKRmvIiRMncOLEiZCey+QYKmSMbQLwKgAPrgTSalzpUe4C8PcAwDn/wdXnvgTgO5zz\n7kXOQ0OdceZwOKDRaNDW1rZkJXO/34+xsTHYbDbs2LEjYXqX19JqtcjLy5N9GSeRB2MMnPNFs5uy\nJII45+cBzA1sMcbGAGznnFsZY88BeJIx9hNcuS3fAOBdOdpJ5pMkCRqNBrW1tUsGTJ1OB6vVioqK\nCrS0tMS5hdHj8/kSYuyVxJ9SJrdzXOlxgnN+kTH2RwAXAQgAvkTdSWU4c+YM0tPTF+19zW4+NjY2\nJmspt2jw+/1wuVyrLm1HkpMigibnvOG6r/8dwL/L1ByyCJfLhbS0tEULC9tsNuj1euTk5ODGG29M\n+A3I3G43JEmSuxlEoeSeckQSwOxteX19/YK14RaLBefOnYNarUZdXV3CB0zgyuulSu1kKYroaRJl\nGxkZgUqlmnfLHQgEMDY2BgDo7OxMqpUzXq9XsUs7ifyop0mW5Xa7MTg4OG9ljMfjwblz5+B2u9HU\n1JRUAROg5ZNkedTTJEvinEOj0WDPnj1z1cu1Wi0cDgcaGxuTcvK3KIoQBIGSQGRJ1NMkSzIajcjI\nyEBRURFEUcTw8DBGRkbQ1NSUlAETuLLdxszMTNh1QcnaQUGTLGpmZgbnz59HbW0tLBYLLl26hOzs\nbHR1dSmqUHC0McaohiZZFgVNsgDnHAaDAY2NjbBarTh9+jTKysrCKgGXqHw+H7KysuRuBlEwGtMk\nC5jNZgSDQQSDQbhcLtx8880JuRQyEj6fj9ack2VRT5PM4/F4MDIygsnJSQBIqMpEqxUMBiEIQlIP\nP5DVo54mmSNJEl544QWoVCp0dXUlXGWi1QgGg/jDH/6AkydP4vbbb8eBAweSYqI+iT5ZqhxFC1U5\nip5AIIA33ngD09PT+Ju/+Zs1NeUmGAxi//79OHXqFDweD7Kzs7F7924cO3aMAucatVyVI7o9J5ie\nnsaFCxeQlpaGT3ziE2sqYALA0aNH0d3dDbfbDc45XC4Xuru7cfToUbmbRhSIguYaJkkSRkZGcObM\nGdhsNjQ3N6/JlTC9vb1wu93zHnO73ejr65OpRUTJKGiuUW63G8PDw0hNTcWWLVuQkpKyZjcR27Zt\n24JpRtnZ2di6datMLSJKRkFzDbJYLHj99ddRUFCAqqoqmEwmdHZ2rrjfT7I6cOAAmpqakJqaCsYY\n1Go1du/ejQMHDsjdNKJAlAhaQwRBgMFggNfrRU1NDbKzs+cqGFVWVsrdPFn95Cc/wYsvvoiuri5s\n3bqVsudrHCWCViHUzZaUzuPx4OTJk/B6vWhubkZ2djY0Gg1GR0cxNDQkd/PiYrnfpd1uxwMPPIBv\nf/vbuP322xM2YCbL3+tK5HydFDRXkAx/hGazGaOjo9i2bRtaWlqQkpICURRhs9nQ2dmJN954Q+4m\nxsVyv8uBgYFFq9InmmT4ew2FnK+TJrcnMVEU0dfXh0AggB07dsxb6aLT6VBUVJS01YrC4fP5oNPp\n0NTUJHdTSAKgoJmknE4ndDodysvLUVlZOS/JMzk5CYfDgY6ODhlbqBxnz55FdXX1mpufSiKT8Ikg\nudtACElOSyWCEjpoEkJIvFEiiBBCwkBBkxBCwkBBcxmMsX9hjEmMscJrHvsmY2yYMTbAGLtVzvat\nFmPsR1dfRx9j7M+MsdxrvpdMr/PDjLFBxtglxtg35G5PtDDGqhljxxljFxhj5xhj/9/VxwsYYy8z\nxoYYY8cYY3lyt3W1GGMpjLEexthzV7+W7TVS0FwCY6wawC0ANNc81grgUwBaARwA8ChL7P0fXgbQ\nzjnfCmAYwDcBgDHWhiR5nYyxFAD/DWA/gHYA9zDGWuRtVdSIAL7KOW8H8D4A/3j1tT0E4FXO+UYA\nx3H195rgvgLg4jVfy/YaKWgu7acAHrzusYMAnuaci5zzcVwJNLvi3bBo4Zy/yjmXrn55CkD11c8/\nhuR5nbsADHPONZxzAcDTuPJ7THiccyPnvO/q5y4AA7jyOzwI4LdXn/ZbAB+Xp4XRcbUD8/+3d/+u\nVWRhGMe/z+KGFbWTjfg7YmmhsFhoE6xEIaUKIoqlKPbRykpLsV1tLBSxSQI2gtgIouAPFP0DVDDW\ngrgij8UZYQgxcIzrZCbPp7r33Lnwvkx47px7z5wcAP5tDXfWY0JzHpImgDe2X8x5aQPwpvX8XTM2\nBCeBO83jIfU5t5e39LeXH5K0FdhJ+fAbtT0LJViBv7ur7Jf4fgHTXurTWY/LdnG7pLvAaHuIclLO\nA5OUqXnvLdDnOdszzTHngC+2b3RQYiySpNXAbeCs7Y/zrF/u7bpCSQeBWdvPJI0vcOhv63HZhqbt\neUNR0g5gK/C8+R5vI/BE0m7KFdfm1uEbm7El60d9fifpBGXqs681/A7Y1Hq+5PtcQO/OWQ1JKyiB\ned32VDM8K2nU9qykdcCH7ipctL3AhKQDwEpgjaTrwPuuesz0fA7bL22vs73N9hhlOrfL9gdgGjgs\naUTSGLAdeNRlvYshaT9l2jNh+3PrpWngyED6fAxsl7RF0ghwhNLfUFwDXtm+3BqbBk40j48DU3Pf\n1Be2J21vtr2Ncu7u2T4GzNBRj8v2SrOCKVNabL+SdIvyK94X4FTPN/S8AowAd5sfxx/aPjWkPm1/\nlXSaslLgD+Cq7dcdl/VLSNoLHAVeSHpK+VudBC4BtySdpKz+ONRdlf+bi3TUY26jjIiokOl5RESF\nhGZERIWEZkREhYRmRESFhGZERIWEZkREhYRmRESFhGZERIWEZgyapH8kPW9uCV0l6WWzX2jET8kd\nQTF4ki5QNntYSdny71LHJUWPJTRj8CT9Sdm44xOwp6/30cfSkOl5LAdrgdXAGuCvjmuJnsuVZgye\npCngBjAGrLd9puOSoseyNVwMmqRjwH+2bzb/ZO2BpHHb9zsuLXoqV5oRERXynWZERIWEZkREhYRm\nRESFhGZERIWEZkREhYRmRESFhGZERIWEZkREhW/IjtgecSmH+AAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x10904d090>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sim = rebound.Simulation()\n",
"sim.G = k**2\n",
"sim.t = epoch_of_elements \n",
"sim.add(m=1.) # Sun\n",
"sim.add(m=1.e-3, a=5.) # Jupiter\n",
"sim.add(m=3.e-4, a=10.) # Saturn\n",
"for comet in comets:\n",
" addOrbit(sim, comet)\n",
"fig = rebound.OrbitPlot(sim, trails=True)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.10"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| gpl-3.0 |
wathen/PhD | MHD/FEniCS/ShiftCurlCurl/CppGradient/Efficient/.ipynb_checkpoints/Untitled4-checkpoint.ipynb | 1 | 10513 | {
"metadata": {
"name": ""
},
"nbformat": 3,
"nbformat_minor": 0,
"worksheets": [
{
"cells": [
{
"cell_type": "code",
"collapsed": false,
"input": [
"from dolfin import *\n",
"import numpy\n",
"nn = 1\n",
"mesh = UnitCubeMesh(int(nn),int(nn),int(nn))\n",
"order = 1\n",
"parameters['reorder_dofs_serial'] = False\n",
"Magnetic = FunctionSpace(mesh, \"N1curl\", order)\n",
"Lagrange = FunctionSpace(mesh, \"CG\", order)\n",
"print Magnetic.dim()\n",
"def boundary(x, on_boundary):\n",
" return on_boundary"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stderr",
"text": [
"DEBUG:UFL:No integrals left after transformation, returning empty form.\n"
]
},
{
"output_type": "stream",
"stream": "stderr",
"text": [
"DEBUG:FFC:Reusing form from cache.\n"
]
},
{
"output_type": "stream",
"stream": "stderr",
"text": [
"DEBUG:UFL:No integrals left after transformation, returning empty form.\n"
]
},
{
"output_type": "stream",
"stream": "stderr",
"text": [
"DEBUG:FFC:Reusing form from cache.\n"
]
},
{
"output_type": "stream",
"stream": "stdout",
"text": [
"19\n"
]
}
],
"prompt_number": 11
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"B = BoundaryMesh(Magnetic.mesh(),\"exterior\",False)\n",
"numpy.sort(B.entity_map(1).array().astype(\"float_\",\"C\"))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 6,
"text": [
"array([ 2., 4., 5., 7., 11., 12., 13., 15.])"
]
}
],
"prompt_number": 6
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"E = EdgeFunctionBool(mesh)\n",
"print E.array()\n",
"VertexBoundary = numpy.zeros(mesh.num_edges())\n",
"VertexBoundary[E.array()] = 1\n",
"print VertexBoundary"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"[False False False False False False False False True True True True\n",
" False False False False]\n",
"[ 0. 0. 0. 0. 0. 0. 0. 0. 1. 1. 1. 1. 0. 0. 0. 0.]\n"
]
}
],
"prompt_number": 13
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"B = BoundaryMesh(Magnetic.mesh(),\"exterior\",False)\n",
"print numpy.sort(B.entity_map(0).array().astype(\"float_\",\"C\"))\n",
"bb = numpy.sort(B.entity_map(0).array().astype(\"float_\",\"C\"))\n",
"print numpy.sort(B.entity_map(1).array().astype(\"float_\",\"C\"))"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"[ 0. 1. 2. 3. 4. 5. 9. 10. 14. 15. 19. 20. 21. 22. 23.\n",
" 24.]\n",
"[ 2. 4. 7. 11. 13. 15. 20. 27. 33. 40. 45. 46. 49. 52. 53.\n",
" 55.]\n"
]
}
],
"prompt_number": 14
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"B = BoundaryMesh(Magnetic.mesh(),\"exterior\")\n",
"B.entity_map(0).array()"
],
"language": "python",
"metadata": {},
"outputs": [
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 16,
"text": [
"array([ 0, 1, 5, 2, 3, 4, 9, 10, 14, 15, 19, 20, 21, 22, 23, 24], dtype=uint64)"
]
}
],
"prompt_number": 16
},
{
"cell_type": "code",
"collapsed": false,
"input": [],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"vert 0\n",
"\n",
"edge 1\n",
"\n",
"edge 2\n",
"\n",
"edge 4\n",
"\n",
"vert 1\n",
"\n",
"edge 0\n",
"\n",
"edge 2\n",
"\n",
"edge 6\n",
"\n",
"edge 7\n",
"\n",
"vert 2\n",
"\n",
"edge 5\n",
"\n",
"edge 7\n",
"\n",
"edge 10\n",
"\n",
"edge 11\n",
"\n",
"vert 3\n",
"\n",
"edge 9\n",
"\n",
"edge 11\n",
"\n",
"edge 14\n",
"\n",
"edge 15\n",
"\n",
"vert 4\n",
"\n",
"edge 13\n",
"\n",
"edge 15\n",
"\n",
"vert 5\n",
"\n",
"edge 3\n",
"\n",
"edge 4\n",
"\n",
"edge 18\n",
"\n",
"edge 20\n",
"\n",
"vert 9\n",
"\n",
"edge 13\n",
"\n",
"edge 14\n",
"\n",
"edge 16\n",
"\n",
"edge 27\n",
"\n",
"vert 10\n",
"\n",
"edge 19\n",
"\n",
"edge 20\n",
"\n",
"edge 31\n",
"\n",
"edge 33\n",
"\n",
"vert 14\n",
"\n",
"edge 27\n",
"\n",
"edge 28\n",
"\n",
"edge 29\n",
"\n",
"edge 40\n",
"\n",
"vert 15\n",
"\n",
"edge 32\n",
"\n",
"edge 33\n",
"\n",
"edge 44\n",
"\n",
"edge 46\n",
"\n",
"vert 19\n",
"\n",
"edge 40\n",
"\n",
"edge 41\n",
"\n",
"edge 42\n",
"\n",
"edge 53\n",
"\n",
"vert 20\n",
"\n",
"edge 45\n",
"\n",
"edge 46\n",
"\n",
"vert 21\n",
"\n",
"edge 43\n",
"\n",
"edge 44\n",
"\n",
"edge 45\n",
"\n",
"edge 49\n",
"\n",
"vert 22\n",
"\n",
"edge 47\n",
"\n",
"edge 48\n",
"\n",
"edge 49\n",
"\n",
"edge 52\n",
"\n",
"vert 23\n",
"\n",
"edge 50\n",
"\n",
"edge 51\n",
"\n",
"edge 52\n",
"\n",
"edge 55\n",
"\n",
"vert 24\n",
"\n",
"edge 53\n",
"\n",
"edge 54\n",
"\n",
"edge 55\n"
]
},
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 13,
"text": [
"array([ 4., 7., 11., 15., 15., 20., 27., 33., 40., 46., 53.,\n",
" 46., 49., 52., 55., 55.])"
]
}
],
"prompt_number": 13
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"b = SparsityPatternBuilder()"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 33
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"B = EdgeFunctionBool(mesh)"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 2
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"B = BoundaryMesh(mesh,\"exterior\")"
],
"language": "python",
"metadata": {},
"outputs": [],
"prompt_number": 12
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"bb = B.entity_map(2).array()\n",
"print bb"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"[ 0 3 4 6 7 9 10 12 13 15 16 17]\n"
]
}
],
"prompt_number": 15
},
{
"cell_type": "code",
"collapsed": false,
"input": [
"k = 0\n",
"VertexBoundary = numpy.zeros(3*bb.size)\n",
"for face in faces(mesh):\n",
" if face.index() == bb[k]:\n",
" k = k+1\n",
" print \"\\nface\", face.index()\n",
" for edge in edges(face):\n",
" print \" edge\", edge.index()\n",
" VertexBoundary[kk] = edge.index()\n",
" kk = kk+1\n",
"VertexBoundary"
],
"language": "python",
"metadata": {},
"outputs": [
{
"output_type": "stream",
"stream": "stdout",
"text": [
"\n",
"face 0\n",
" edge 1\n",
" edge 2\n",
" edge 0\n",
"\n",
"face 3\n",
" edge 4\n",
" edge 5\n",
" edge 2\n",
"\n",
"face 4\n",
" edge 1\n",
" edge 7\n",
" edge 6\n",
"\n",
"face 6\n",
" edge 5\n",
" edge 8\n",
" edge 7\n",
"\n",
"face 7\n",
" edge 9\n",
" edge 10\n",
" edge 6\n",
"\n",
"face 9\n",
" edge 8\n",
" edge 11\n",
" edge 10\n",
"\n",
"face 10\n",
" edge 12\n",
" edge 13\n",
" edge 0\n",
"\n",
"face 12\n",
" edge 4\n",
" edge 14\n",
" edge 13\n",
"\n",
"face 13\n",
" edge 9\n",
" edge 16\n",
" edge 15\n",
"\n",
"face 15\n",
" edge 11\n",
" edge 17\n",
" edge 16\n",
"\n",
"face 16\n",
" edge 12\n",
" edge 18\n",
" edge 15\n",
"\n",
"face 17\n",
" edge 14\n",
" edge 17\n",
" edge 18\n"
]
},
{
"metadata": {},
"output_type": "pyout",
"prompt_number": 24,
"text": [
"array([ 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])"
]
}
],
"prompt_number": 24
}
],
"metadata": {}
}
]
} | mit |
getsmarter/bda | module_4/M4_NB3_NetworkClustering.ipynb | 1 | 24094 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<div align=\"right\">Python 3.6 Jupyter Notebook</div>\n",
"\n",
"# Finding connected components using clustering\n",
"\n",
"<br><div class=\"alert alert-warning\">\n",
"<b>Note that this notebook contains advanced exercises applicable only to students who wish to deepen their understanding and qualify for bonus marks on the course.</b> You will be able to achieve 100% for this notebook by only completing Exercise 1. Optional, additional exercises can be completed to qualify for bonus marks.\n",
"</div>\n",
"\n",
"\n",
"### Your completion of the notebook exercises will be graded based on your ability to do the following:\n",
"\n",
"> **Understand**: Do your pseudo-code and comments show evidence that you recall and understand technical concepts?\n",
"\n",
"> **Apply**: Are you able to execute code (using the supplied examples) that performs the required functionality on supplied or generated data sets? \n",
"\n",
"> **Analyze**: Are you able to pick the relevant method or library to resolve specific stated questions?\n",
"\n",
"> **Evaluate**: Are you able to interpret the results and justify your interpretation based on the observed data?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Notebook objectives\n",
"By the end of this notebook, you will be expected to:\n",
"> \n",
" - Find connected components in networks (using the techniques of hierarchical clustering, modularity maximization, and spectral graph partitioning); and\n",
" - Interpret clustering results.\n",
" \n",
"#### List of exercises\n",
"> - **Exercise 1**: Understanding hierarchical clustering.\n",
"- **Exercise 2 [Advanced]**: Interpreting the results of hierarchical clustering.\n",
"- **Exercise 3 [Advanced]**: Summarizing clustering results based on modularity maximization and spectral graph partitioning."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Notebook introduction"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Community detection is an important task in social network analysis. The idea behind it is to identify groups of people that share a common interest, based on the assumption that these people tend to link to each other more than to the rest of the network. Specifically, real-world networks exhibit clustering behavior that can be observed in the graph representation of these networks by the formation of clusters or partitions. These groups of nodes on a graph (clusters) correspond to communities that share common properties, or have a common role in the system under study.\n",
"\n",
"Intuitively, it is expected that such clusters are associated with a high concentration of nodes. In the following examples, you will explore the identification of these clusters using the following approaches, as discussed in the video content:\n",
"\n",
"- Hierarchical clustering (using a distance matrix)\n",
"- The Louvain Algorithm (using modularity maximization)\n",
"- Spectral graph partitioning"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Import required modules"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"import networkx as nx\n",
"import pandas as pd\n",
"import numpy as np\n",
"\n",
"%matplotlib inline\n",
"import matplotlib.pylab as plt\n",
"from networkx.drawing.nx_agraph import graphviz_layout\n",
"\n",
"from collections import defaultdict, Counter\n",
"import operator\n",
"\n",
"## For hierarchical clustering.\n",
"from scipy.cluster import hierarchy\n",
"from scipy.spatial import distance\n",
"\n",
"## For spectral graph partitioning.\n",
"from sklearn.cluster import spectral_clustering as spc\n",
"\n",
"## For Community Detection (Louvain Method).\n",
"import community\n",
"\n",
"\n",
"import sys\n",
"sys.path.append('..')\n",
"from utils import draw_partitioned_graph\n",
"from utils import fancy_dendrogram\n",
"\n",
"plt.rcParams['figure.figsize'] = (15, 9)\n",
"plt.rcParams['axes.titlesize'] = 'large'"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 1. Data preparation"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"You are going to read the graph from an adjacency list saved in earlier exercises."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"call_adjmatrix = pd.read_csv('./call.adjmatrix', index_col=0)\n",
"call_graph = nx.from_numpy_matrix(call_adjmatrix.as_matrix())"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# Display call graph object.\n",
"plt.figure(figsize=(10,10))\n",
"plt.axis('off')\n",
"\n",
"pos = graphviz_layout(call_graph, prog='dot')\n",
"nx.draw_networkx(call_graph, pos=pos, node_color='#11DD11', with_labels=False)\n",
"_ = plt.axis('off')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 2. Hierarchical clustering"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This notebook makes use of a hierarchical clustering algorithm, as implemented in [Scipy](http://docs.scipy.org/doc/scipy/reference/). The following example uses the average distance measure. Since the graph is weighted, you can also use the single linkage inter-cluster distance measure (see exercises)."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"def create_hc(G, linkage='average'):\n",
" \"\"\"\n",
" Creates hierarchical cluster of graph G from distance matrix\n",
" \"\"\" \n",
" \n",
" path_length=nx.all_pairs_shortest_path_length(G)\n",
" distances=np.zeros((G.order(),G.order())) \n",
" \n",
" for u,p in dict(path_length).items():\n",
" for v,d in p.items():\n",
" distances[list(G.nodes)[u]][list(G.nodes)[v]] = d\n",
" distances[list(G.nodes)[v]][list(G.nodes)[u]] = d\n",
" if u==v: \n",
" distances[list(G.nodes)[u]][list(G.nodes)[u]]=0\n",
" # Create hierarchical cluster (HC).\n",
" Y=distance.squareform(distances)\n",
" if linkage == 'max':\n",
" # Creates HC using farthest point linkage.\n",
" Z=hierarchy.complete(Y) \n",
" if linkage == 'single':\n",
" # Creates HC using closest point linkage.\n",
" Z=hierarchy.single(Y) \n",
" if linkage == 'average':\n",
" # Creates HC using average point linkage.\n",
" Z=hierarchy.average(Y)\n",
" \n",
" return Z\n",
"\n",
"def get_cluster_membership(Z, maxclust):\n",
" '''\n",
" Assigns cluster membership by specifying cluster size.\n",
" '''\n",
" hc_out=list(hierarchy.fcluster(Z,maxclust, criterion='maxclust'))\n",
" \n",
" # Map cluster values to a dictionary variable.\n",
" cluster_membership = {}\n",
" i = 0\n",
" for i in range(len(hc_out)):\n",
" cluster_membership[i]=hc_out[i]\n",
" \n",
" return cluster_membership"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Below is a demonstration of hierarchical clustering when applied to the call graph."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# Perform hierarchical clustering using 'average' linkage. \n",
"Z = create_hc(call_graph, linkage='average') "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The dendrogram corresponding to the partitioned graph is obtained as follows:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"hierarchy.dendrogram(Z)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"You will notice that the full dendrogram is unwieldy, and difficult to use or read. Fortunately, the `dendrogram` method has a feature that allows one to only show the `lastp` merged clusters, where $p$ is the desired number of last `p` merged clusters."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"plt.title('Hierarchical Clustering Dendrogram (pruned)')\n",
"plt.xlabel('sample index (or leaf size)')\n",
"plt.ylabel('distance')\n",
"hierarchy.dendrogram(\n",
" Z,\n",
" truncate_mode='lastp', # show only the last p merged clusters\n",
" p=10, # show only the last p merged clusters\n",
" show_leaf_counts=True, # numbers in brackets are counts for each leaf\n",
" leaf_rotation=90,\n",
" leaf_font_size=12)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This dendrogram can help explain what happens as a result of the agglomerative method of hierarchical clustering. Starting at the bottom-most level, each node is assigned its own cluster. The closest pair of nodes (according to a distance function) are then merged into a new cluster. The distance matrix is recomputed, treating the merged cluster as an individual node. This process is repeated until the entire network has been merged into a single, large cluster, which the top level in the dendrogram above represents. You can now understand why this method is agglomerative.\n",
"\n",
"The linkage function is used to determine the distance between a cluster and a node, or between two clusters, using the following possibilities:\n",
"\n",
"- **Single:** Merge two clusters with the smallest minimum pairwise distance.\n",
"- **Average:** Merge two clusters with the smallest average pairwise distance.\n",
"- **Maximum or complete:** Merge the two clusters with the smallest maximum pairwise distance."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now, you can finally retrieve the clusters, based on the analysis of the dendrogram. In this post-processing, there are different ways of determining $k$, the number of clusters to partition the data into. Scipy's hierarchical flat clustering function - \"``hierarchy.fcluster()``\" - is used to assign cluster membership by specifying a distance threshold, or the number of clusters required. In the function definition (above), you have been provided with a utility function, \"``get_cluster_membership()``\", which does the latter.\n",
"\n",
"Selecting the number of clusters $k$ is, in general, an ill-posed problem. Different interpretations are possible, depending on the nature of the problem, the scale of the distribution of points in a data set, and the required clustering resolution. In agglomerative clustering, as used in the example above, you can get zero error for the objective function by considering each data point as its own cluster. Hence, the selection of $k$ invariably involves a trade-off maximum compression of the data (using a single cluster), and maximum accuracy by assigning each data point to its own cluster. The selection of an optimal $k$ can be done using automated techniques or manually."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Here, identification of an appropriate cluster is ideally done manually as this has the advantages of gaining some insights into your data as well as providing an opportunity to [perform sanity checks](https://joernhees.de/blog/2015/08/26/scipy-hierarchical-clustering-and-dendrogram-tutorial). To select the cluster size, look for a large shift in the distance metric. In our example with dendrograms plots shown above, say a case has been made for an ideal cutoff of 3.5. The number of clusters is then simply the number of intersections of a horizontal line (with height of 3.5) with the vertical lines of the dendrogram. Therefore, 3 clusters would be obtained in this case as shown below."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"fancy_dendrogram( Z, truncate_mode='lastp', p=12, leaf_rotation=90.,\n",
" leaf_font_size=12.0,\n",
" show_contracted=False,\n",
" annotate_above=10,\n",
" max_d=3.5)\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"opt_clust = 3\n",
"opt_clust"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"You can now assign the data to these \"``opt_clust``\" clusters."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"cluster_assignments = get_cluster_membership(Z, maxclust=opt_clust)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The partitioned graph, corresponding to the dendrogram above, can now be visualized."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"clust = list(set(cluster_assignments.values()))\n",
"clust"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"cluster_centers = sorted(set(cluster_assignments.values()))\n",
"freq = [list(cluster_assignments.values()).count(x) for x in cluster_centers]"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# Creata a DataFrame object containing list of cluster centers and number of objects in each cluster\n",
"df = pd.DataFrame({'cluster_centres':cluster_centers, 'number_of_objects':freq})\n",
"df.head(10)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"<div class=\"alert alert-info\">\n",
"<b>Exercise 1 Start.</b>\n",
"</div>\n",
"\n",
"### Instructions\n",
"\n",
"> 1. How many clusters are obtained after the final step of a generic agglomerative clustering algorithm (before post-processing)?\n",
">> **Note:** Post-processing involves determining the optimal clusters for the problem at hand.\n",
"> 2. Based on your answer above, would you consider agglomerative clustering a top-down approach, or a bottom-up approach?\n",
"> 3. Which of the three linkage functions (i.e. single, average, or maximum or complete) do you think is likely to be most sensitive to outliers? \n",
">>**Hint**: Look at this [single-link and complete-link clustering](http://nlp.stanford.edu/IR-book/html/htmledition/single-link-and-complete-link-clustering-1.html) resource."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Your markdown answer here.\n",
"\n",
"1. \n",
"2. \n",
"3. \n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"\n",
"<div class=\"alert alert-info\">\n",
"<b>Exercise 1 End.</b>\n",
"</div>\n",
"\n",
"> **Exercise complete**:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"<div class=\"alert alert-info\">\n",
"<b>Exercise 2 [Advanced] Start.</b>\n",
"</div>\n",
"\n",
"### Instructions\n",
"\n",
"> In this exercise, you will investigate the structural properties of the clusters generated from above.\n",
"\n",
"> 1. Assign the values from your \"cluster_assignments\" to a Pandas DataFrame named \"df1\", with the column name \"cluster_label\".\n",
">> **Hint**: The variable \"``cluster_assignments``\" is of type ``dict``. You will need to get the values component of this dict, **not** the keys.\n",
"> 2. Add a field called \"participantID\" to \"df1\", and assign to this the index values from the previously-loaded \"``call_adjmatrix``\" DataFrame.\n",
"> 3. Load the DataFrame containing the centrality measures that you saved in Notebook 1 of this module, into \"df2\".\n",
"> 4. Perform an inner join by merging \"df1\" and \"df2\" on the field \"participantID\". Assign the result of this join to variable \"df3\".\n",
"> 5. Perform a groupby on \"df3\" (using \"cluster_label\" field), and then evaluate the mean of the four centrality measures (using the \"`agg()`\" method). Assign the aggregation result to \"df4\".\n",
"> 6. Review \"df4\", and plot its barplot. \n",
"> 7. Merge clusters which share the same mean values for a centrality measure into a single cluster. Assign the smallest value of the labels in the set to the merged cluster.\n",
">> **Note**:<br>\n",
"Combine clusters such that, given a cluster with centrality measures $[x1, x2, x3, x4]$, and another cluster with centrality measures $[z1, z2, z3, z4]$, the following holds true:<br>\n",
"$x1 = z1$ <br> $x2 = z2$ <br> $x3 = z3$ <br> $x4 = z4$<br>\n",
"> 8. Print the size of each cluster, in descending order, after performing the cluster merging in the preceding step."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# Your code here.\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"\n",
"<div class=\"alert alert-info\">\n",
"<b>Exercise 2 [Advanced] End.</b>\n",
"</div>\n",
"\n",
"> **Exercise complete**: \n",
"> This is a good time to \"Save and Checkpoint\"."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 3. Community detection\n",
"Community detection is an important component in the analysis of large and complex networks. Identifying these subgraph structures helps in understanding organizational and functional characteristics of the underlying physical networks. In this section, you will study a few approaches that are widely used in community detection using graph representations."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 3.1 The Louvain modularity-maximization approach"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The Louvain method is one of the most widely-used methods for detecting communities in large networks. It was developed by a team of researchers at the Université catholique de Louvain. The method can unveil hierarchies of communities, and allows you to zoom within communities in order to discover sub-communities, sub-sub-communities, and so forth. The modularity QQ quantifies how good a \"community\" or partition is, and is defined as follows:\n",
"\n",
"$$Q_c =\\frac{1}{2m}\\sum _{(ij)} \\left [ A_{ij}-\\frac{k_ik_j}{2m} \\right] \\delta(c_i, c_j)$$\n",
"\n",
"The higher the $Q_c$ of a community is, the better the partition is.\n",
"\n",
"The Louvain method is a greedy optimization method that attempts to optimize the \"modularity\" of a partition of the network via two steps:\n",
"\n",
"1. Locally optimize the modularity to identify \"small\" communities.\n",
"2. Aggregate nodes belonging to the same community, and create a new network with aggregated nodes as individual nodes.\n",
"\n",
"Steps 1 and 2 are then repeated until a maximum of modularity produces a hierarchy of communities."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 3.2 Spectral graph partitioning"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Spectral graph partitioning and clustering is based on the spectrum — the eigenvalues and associated eigenvectors — of the Laplacian matrix that corresponds to a given graph. The approach is mathematically complex, but involves performing a $k$-means clustering, on a spectral projection of the graph, with $k$=2 (using an adjacency matrix as the affinity). A schematic illustration of the process is depicted in the figure below.\n",
"\n",
"**Optional**: You can read more about [spectral graph processing](https://devblogs.nvidia.com/parallelforall/fast-spectral-graph-partitioning-gpus/)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now, apply spectral graph partitioning to your call graph, and visualize the resulting community structure. You can read more about [Scikit-Learn](http://scikit-learn.org/stable/index.html), and the [Spectral Clustering](http://scikit-learn.org/stable/modules/generated/sklearn.cluster.SpectralClustering.html) function utilized in this section. Spectral graph partitioning needs input in the form of the number of clusters sought (default setting is 8). There are various approaches one can take to optimize the final number of clusters, depending on problem domain knowledge. Below you will use a value of $k=9$."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# Create the spectral partition using the spectral clustering function from Scikit-Learn.\n",
"spectral_partition = spc(call_adjmatrix.as_matrix(), 9, assign_labels='discretize')"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"pos = graphviz_layout(call_graph, prog='dot')\n",
"nx.draw_networkx_nodes(call_graph, pos, cmap=plt.cm.RdYlBu, node_color=spectral_partition)\n",
"nx.draw_networkx_edges(call_graph, pos, alpha=0.5)\n",
"plt.axis('off')\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"print(spectral_partition)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"<div class=\"alert alert-info\">\n",
"<b>Exercise 3 [Advanced] Start.</b>\n",
"</div>\n",
"\n",
"### Instructions\n",
"Compute the size of each the clusters obtained using the spectral graph partitioning method.\n",
" "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# Your code here."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<br>\n",
"\n",
"<div class=\"alert alert-info\">\n",
"<b>Exercise 3 [Advanced] End.</b>\n",
"</div>\n",
"\n",
"> **Exercise complete**: \n",
"> This is a good time to \"Save and Checkpoint\"."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## 4. Submit your notebook\n",
"\n",
"Please make sure that you:\n",
"- Perform a final \"Save and Checkpoint\";\n",
"- Download a copy of the notebook in \".ipynb\" format to your local machine using \"File\", \"Download as\", and \"IPython Notebook (.ipynb)\"; and\n",
"- Submit a copy of this file to the Online Campus."
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.6"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
mjbommar/cscs-530-w2016 | samples/cscs530-w2015-midterm-sample1.ipynb | 1 | 19277 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Midterm \n",
"\n",
"### Goal\n",
"\n",
"I will explore whether a network-theory driven approach shown to improve the efficiency of an agricultural extension program is sensitive to the models and parameters originally used.\n",
"\n",
"### Justification\n",
"\n",
"Social networks have been shown to be important vehicles for the transmission of new agricultural methods or 'technologies' (Bandiera and Rasul 2006, Conley and Udry 2010). These types of dynamics and time-varying agent behavior are best captured with through network modeling.\n",
"\n",
"My project is based off a recent paper which used network modeling in conjunction with a large-scale field experiment (Beaman et al 2014). I wish to test the robustness of the findings of their model and so will employ a similar network modeling method.\n",
"\n",
"### Background on base paper\n",
"\n",
"Beaman and co-authors aimed to improve the rollout of an agricultural extension program using predictions from network theory to optimally select 'seed farmers'. 'Seed farmers' are the select farmers in a village that the agricultural extension program trains. Because it is costly to train farmers in this way, it is most efficient to pick seed farmers such that their adoption of the agricultural technology will lead to the greatest spread of the technology throughout the village. \n",
"\n",
"Beaman and coauthors first elicit the social networks of various rural villages. Then under the condition that the extension program only trains two farmers in each village, they take every possible combination of two nodes in a village network and simulate an information diffusion process for 4 periods. They take a measure of information diffusion at the end of each simulation and the pair of nodes which gives the greatest diffusion is their optimal seeding pair. \n",
"\n",
"Their findings are then used in a field experiment where a random half of total villages are seeded according to their simulated optimal seeds while the other half is seeded according to the extension program's default procedure, usually based off of a field officer's own knowledge of the village and its influential farmers. They find evidence that network-theory informed seeding leads to increased technological adoption over baseline seeding procedures. \n",
"\n",
"### My extensions and measures of interest\n",
"\n",
"I wish to recreate and expand upon their simulations in the following ways:\n",
"- I will compare optimal seeds found with their method against optimal seeds found with an extended process of information diffusion. The extended process will include the possibility that households can reject a new technology even after being exposed to it by multiple connections. The original process assumes that a household will automatically adopt a technology after the number of connections who have adopted the technology passes a certain threshold\n",
"- I will also sweep across the number of periods simulated and the alpha which the adoption threshold is normally distributed around to see if this produces alternate optimal seeds.\n",
"\n",
"### Outline\n",
"\n",
"The original paper looks at rural village in Malawi. I do not have access to their network data but I have a dataset of social graphs from 74 villages in South India. Though there may be differences in network structure between villages in these two locations, I will assume they are reasonably comparable.\n",
"\n",
"First, I will recreate results from Beaman et al by selecting all combinations of node pairs in a subset of 25 villages. For each pair, I will run them through a information diffusion simulation for {3,4,5,6} steps. I will also sweep through values {1,2,3} for a alpha parameter. Each household has an adoption threshold, T, which determines whether they adopt the new technology or not. If X number of connections have adopted the technology and X=>T, then the household will adopt the new technology in the next period. Each household independently drawns a threshold from a normal distribution N(alpha, 0.5) bounded positive, so sweeping through alpha parameters will push up and down the distribution of household thresholds T. \n",
"\n",
"To mitigate stochasticity, I will repeat 2000 times, and take an average measure of information diffusion (given by percent of households adopted at last step). The pair of nodes which give the greatest information difussion are my theory-driven seed farmers equivalent to those found in Beaman et al. I will examine whether the determination of these optimal seed farmers depends on the number of steps run and the alpha parameter used. Then, I will run the same simulations except using the extended information diffusion process described above. I want to see whether seed farmers selected through this method are different than those selected by Beaman's process. For the midterm, I will concentrate on coding the re-creation of method from Beaman et al.\n",
"\n",
"\n",
"### I. Space\n",
"I will model space with an undirected social network. Each node represents a rural household and each edge represents a social connection. \n",
"\n",
"### II. Actors\n",
"Each node in my network is a household. They are modeled simply and have only a few properties:\n",
"- id: household id\n",
"- adopted: whether they have adopted the new technology or not\n",
"- threshold: the threshold above which they will adopt the new technology in the next period. This threshold will be drawn from a normal distribution with mean alpha and standard deviation 0.5 which is bounded to be positive.\n",
"\n",
"In each step, each unadopted household will count the number of connections who have adopted the new technology. If this count exceeds a household's adoption threshold, it will also adopt the technology in the next period.\n",
"\n",
"### III. Model Wrapper\n",
"I will wrap my model in a function which loops through each village, and in each village, loops through every possible pair of nodes. Then, I will sweep through my parameters, number of steps and alpha. I will repeat this under the alternate information diffusion process. I will also determine and collect optimal seeds here.\n",
"\n",
"### IV. Initial Conditions\n",
"Each model will start with a list of adopted households. In the first step, only seed households will be in this list which will be read in through the wrapper.\n",
"\n",
"### V. Model Parameters\n",
"My model will have the following parameters:\n",
"- network: adjacency matrix that is read in from wrapper\n",
"- alpha: parameter determining distribution of adoption threshold\n",
"- HH_adopted: list of adopted households, in first step these are seed households given by wrapper\n",
"- HH_not_adopted: list of all not adopted households\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": false
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
":0: FutureWarning: IPython widgets are experimental and may change in the future.\n"
]
}
],
"source": [
"#Imports\n",
"\n",
"%matplotlib inline\n",
"\n",
"# Standard imports\n",
"import copy\n",
"import itertools\n",
"\n",
"# Scientific computing imports\n",
"import numpy\n",
"import matplotlib.pyplot as plt\n",
"import networkx\n",
"import pandas\n",
"import seaborn; seaborn.set()\n",
"import scipy.stats as stats\n",
"\n",
"\n",
"# Import widget methods\n",
"from IPython.html.widgets import *"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Household class\n",
"Below is a rough draft of the household class. It only has one component:\n",
"\n",
"- constructor: class constructor, which \"initializes\" or \"creates\" the household when we call Household(). This is in the __init__ method."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class Household(object):\n",
" \"\"\"\n",
" Household class, which encapsulates the entire behavior of a household.\n",
" \"\"\"\n",
" \n",
" def __init__(self, model, household_id, adopted=False, threshold=1):\n",
" \"\"\"\n",
" Constructor for HH class. By default,\n",
" * not adopted\n",
" * threshold = 1\n",
" \n",
" Must \"link\" the Household to their \"parent\" Model object.\n",
" \"\"\"\n",
" # Set model link and ID\n",
" self.model = model\n",
" self.household_id = household_id\n",
" \n",
" # Set HH parameters.\n",
" self.adopted = adopted\n",
" self.threshold = threshold\n",
"\n",
" def __repr__(self):\n",
" '''\n",
" Return string representation.\n",
" '''\n",
" skip_none = True\n",
" repr_string = type(self).__name__ + \" [\"\n",
" except_list = \"model\"\n",
"\n",
" elements = [e for e in dir(self) if str(e) not in except_list]\n",
" for e in elements:\n",
" # Make sure we only display \"public\" fields; skip anything private (_*), that is a method/function, or that is a module.\n",
" if not e.startswith(\"_\") and eval('type(self.{0}).__name__'.format(e)) not in ['DataFrame', 'function', 'method', 'builtin_function_or_method', 'module', 'instancemethod']:\n",
" value = eval(\"self.\" + e)\n",
" if value != None and skip_none == True:\n",
" repr_string += \"{0}={1}, \".format(e, value)\n",
"\n",
" # Clean up trailing space and comma.\n",
" return repr_string.strip(\" \").strip(\",\") + \"]\""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Model class\n",
"\n",
"Below, we will define our model class. This can be broken up as follows:\n",
"- constructor: class constructor, which \"initializes\" or \"creates\" the model when we call Model(). This is in the __init__ method.\n",
"- setup_network: sets up graph\n",
"- setup_households: sets up households\n",
"- get_neighborhood: defines a function to get a list of connected nodes\n",
"- step_adopt_decision: method to step through household decision\n",
"- step: main step method"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class Model(object):\n",
" \"\"\"\n",
" Model class, which encapsulates the entire behavior of a single \"run\" in network model.\n",
" \"\"\"\n",
" \n",
" def __init__(self, network, alpha, HH_adopted, HH_not_adopted):\n",
" \"\"\"\n",
" Class constructor.\n",
" \"\"\"\n",
" # Set our model parameters\n",
" self.network = network\n",
" self.alpha = alpha\n",
" self.HH_adopted = HH_adopted\n",
" self.HH_not_adopted = HH_not_adopted\n",
" \n",
" # Set our state variables\n",
" self.t = 0\n",
" self.households = []\n",
" \n",
" # Setup our history variables.\n",
" self.history_adopted = []\n",
" self.history_not_adopted = []\n",
" self.percent_adopted = 0\n",
" \n",
" # Call our setup methods\n",
" self.setup_network()\n",
" self.setup_household()\n",
" \n",
" def setup_network(self):\n",
" \"\"\"\n",
" Method to setup network.\n",
" \"\"\"\n",
" ## need to flesh this out. will network be an input given from wrapper? \n",
" ## what do I need to do to set up network?\n",
" g = network\n",
" \n",
" def setup_households(self):\n",
" \"\"\"\n",
" Method to setup households.\n",
" \"\"\"\n",
" num_households = nx.nodes(g)\n",
" # Create all households.\n",
" for i in xrange(self.num_households):\n",
" self.households.append(Household(model=self,\n",
" household_id=i,\n",
" adopted=False,\n",
" threshold=stats.truncnorm.rvs((0 - alpha) / 0.5, (alpha) / 0.5, loc=alpha, scale=0.5,size=1) \n",
"\n",
" \n",
" \n",
" \n",
" def get_neighborhood(self, x):\n",
" \"\"\"\n",
" Get a list of connected nodes.\n",
" \"\"\"\n",
" neighbors = []\n",
" for i in g.neighbors(x):\n",
" neighbors.append(i)\n",
" return neighbors\n",
" \n",
" def step_adopt_decision(self):\n",
" \n",
" \"\"\"\n",
" Model a household evaluating their connections and making an adopt/not adopt decision\n",
" \"\"\"\n",
" will_adopt = []\n",
" for i in HH_not_adopted:\n",
" adopt_count = 0\n",
" for j in get_neighborhood(i):\n",
" if j.adopted:\n",
" adopt_count+=1\n",
" if adopt_count >= i.threshold:\n",
" will_adopt.append(i) \n",
" \n",
" \n",
" \n",
" def step(self):\n",
" \"\"\"\n",
" Model step function.\n",
" \"\"\"\n",
" \n",
" # Adoption decision\n",
" self.step_adopt_decision()\n",
" \n",
" # Increment steps and track history.\n",
" self.t += 1\n",
" self.HH_adopted.append(will_adopt)\n",
" self.HH_not_adopted.remove(will_adopt)\n",
" self.history_adopted.append(self.HH_adopted)\n",
" self.history_not_adopted.append(self.HH_not_adopted)\n",
" self.percent_adopted = len(HH_adopted)/len(households)\n",
"\n",
"\n",
" def __repr__(self):\n",
" '''\n",
" Return string representation.\n",
" '''\n",
" skip_none = True\n",
" repr_string = type(self).__name__ + \" [\"\n",
"\n",
" elements = dir(self)\n",
" for e in elements:\n",
" # Make sure we only display \"public\" fields; skip anything private (_*), that is a method/function, or that is a module.\n",
" e_type = eval('type(self.{0}).__name__'.format(e))\n",
" if not e.startswith(\"_\") and e_type not in ['DataFrame', 'function', 'method', 'builtin_function_or_method', 'module', 'instancemethod']:\n",
" value = eval(\"self.\" + e)\n",
" if value != None and skip_none == True:\n",
" if e_type in ['list', 'set', 'tuple']:\n",
" repr_string += \"\\n\\n\\t{0}={1},\\n\\n\".format(e, value)\n",
" elif e_type in ['ndarray']:\n",
" repr_string += \"\\n\\n\\t{0}=\\t\\n{1},\\n\\n\".format(e, value)\n",
" else:\n",
" repr_string += \"{0}={1}, \".format(e, value)\n",
"\n",
" # Clean up trailing space and comma.\n",
" return repr_string.strip(\" \").strip(\",\") + \"]\""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Wrapper with parameter sweep\n",
"\n",
"Below is the code which wrappers around the model. It does the following:\n",
"- Loops through all villages we wish to examine\n",
" - Pulls network data from a csv and puts in the appropriate format\n",
"- Loops through all possible pairs of nodes within each village\n",
"- Sweeps through alpha and number of steps parameters\n",
"- Runs 2000 samples"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"\n",
"## cycle through villages:\n",
"## (need to create village list where each item points to a different csv file)\n",
"num_samples = 2000\n",
"\n",
"for fn in village_list:\n",
" village = np.genfromtxt(fn, delimiter=\",\")\n",
" network = from_numpy_matrix(village)\n",
" for HH_adopted in itertools.combinations(nx.nodes(network),2):\n",
" HH_not_adopted = [node for node in nx.nodes(network) if node not in HH_adopted]\n",
" for alpha in [1,2,3]:\n",
" for num_steps in [3,4,5,6]:\n",
" for n in xrange(num_samples):\n",
" m = Model(network, alpha, HH_adopted, HH_not_adopted)\n",
" for t in xrange(num_steps):\n",
" m.step() \n",
"## I need to collect adoption rate at each final step and average over all samples\n",
"## I am not sure where to fit this in\n",
"\n",
"\n",
"## I also need to write a function which determines optimal seed pairing\n",
"\n",
"#######\n",
"#######"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Results\n",
"I hope to present charts which list optimal seed pairings at each parameter level and information diffusion process. This means optimal pairing will be given for alpha = {1,2,3} for each of num_steps = {3,4,5,6} and this will be done for both the original information diffusion process and the extended process.\n",
"\n",
"## Hypothetical results\n",
"\n",
"I expect that the optimal seeding is dependent upon the alpha parameter though I suspect it may not be as dependent upon the number of steps parameter.\n",
"\n",
"I am more interested in whether optimal seeds given by the extended information diffusion process are different than those given by the original process. I am actually not sure but I suspect that they will be different. If so, they could provide improved predictions to test in the field which hopefully may lead to even more efficient seed farmer targeting."
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.11"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
| bsd-2-clause |
ppyht2/tf-exercise | 012. Unsupervised MNIST/Unsupervised MNIST.ipynb | 1 | 59721 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"# Unsupervised Learning on the MNIST dataset "
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": true,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"import tensorflow as tf \n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"import os\n",
"from tensorflow.examples.tutorials.mnist import input_data\n",
"% matplotlib inline"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"# 1. Loading the data set "
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Extracting MNIST_data/train-images-idx3-ubyte.gz\n",
"Extracting MNIST_data/train-labels-idx1-ubyte.gz\n",
"Extracting MNIST_data/t10k-images-idx3-ubyte.gz\n",
"Extracting MNIST_data/t10k-labels-idx1-ubyte.gz\n"
]
}
],
"source": [
"mnist = input_data.read_data_sets(\"MNIST_data\", one_hot=True)"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"### 1.1 Plot a few examples"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeMAAAMzCAYAAACV1no+AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XmcFNW5//HvM8MAAoKAiMgiKItr1LjvGjTiEreYRJMb\nETGYqIlGk2hiboxJrjGbue7KFYPmejX+1AhR4kbcF1xRWWRxQUEEwQVEtpk5vz+mqerToWd6ppdT\nXfN5v168fE6fmq7HeabmTNXpOmXOOQEAgHBqQicAAEB7x2AMAEBgDMYAAATGYAwAQGAMxgAABMZg\nDABAYAzGAAAExmCcw8ycma0ys/8qcPtLM9s7M+tQ7vzQOtQzfdpQ07Fm9lnm64aWOz+0DsdoE2PR\nD5+ZOUnDnHPzN9J3qqRbJH3HOXdT1uuDJb0tqc45V1+hVFGAjdUz89rnkjb88N/hnDsjq3+wqGdi\n5dbUzIZL+oOk/STVSnpB0g+cc3Oa+zokA8dok9T8VVFuZtZT0s8kzQydC0piF34pp8ZmkiZLGiNp\npaRfSJokabuQSaFo7eoY5TJ14X4r6SpJy0InAiDmnHveOTfBOfeRc269pD9LGmFmvUPnBhSKwbgA\nZraXpD0k3RA6F5TME2b2gZndk7nkhfQ4SNIHzrnloRNBUdrVMcpg3AIzq5V0naRznHONofNBSRws\nabCaLmO+L+m+NH0QpD0zswGSrpV0fuhcUJR2d4wyGLfsLEmvOeeeC50ISsM594Rzbp1z7hNJ50oa\nImn7wGmhSGbWR9JDkq5zzt0eOh+0XXs8RlP9l0aJjJR0sJkdlWn3krSbme3qnDsnYF4oHSfJQieB\ntst8wPIhSZOdcwXdIoOqkvpjlMG4ZadJ6pzVvkfSXZImBMkGRTGzHSXVSXpd0iaSfiNpkaTZIfNC\n25lZd0kPSnraOXdR6HxQnPZ6jHKZugXOuU+ccx9s+CdpnaQVzrlPQ+eGNukr6W+SVkh6S03zUsdk\nPoWL6nSCpD0ljcks7rHh36DQiaFN2uUxyqIfOcxsjaS1kq5yzv1nAdtfoqYPi3SS1NU511DmFNEK\n1DN92lDTMWq63amzpB2cc2+VOUW0AsdoEwZjAAAC4zI1AACBFTUYm9koM5tjZvPNjA9OpAA1TRfq\nmT7UNJ3afJk6sxjGXEmHS1qopsXZT3HOzSpdeqgkapou1DN9qGl6FXNr016S5m/4MISZ3SHpOEl5\nfyg6WifXWV2L2CWKtUartM6tzXe/XqtqSj3DK2U9JWqaBByj6dJCPSPFDMb9Jb2X1V4oae/mvqCz\numpvG1nELlGsaW5qc92tqin1DK+U9ZSoaRJwjKZLC/WMlH3RDzMbJ2mcJHVWl3LvDmVGPdOHmqYL\n9axOxXyAa5GkgVntAZnXPM658c65PZxze9SpUxG7QwW0WFPqWVU4RtOHYzSlihmMX5A0zMyGmFlH\nSSer6QHfqF7UNF2oZ/pQ05Rq82Vq51y9mZ2jpjVhayXd7JybWbLMUHHUNF2oZ/pQ0/Qqas7YOTdF\n0pQS5YIEoKbpQj3Th5qmEytwAQAQGIMxAACBMRgDABAYgzEAAIExGAMAEBiDMQAAgTEYAwAQGIMx\nAACBMRgDABBY2Z/aBLTVR6fv67Wf+fU1ebets9ooXu8avL6/r+oVxYM6fOT17Z61jn72e+S+z4i7\nz/L6hv1gWt5c0Da1I4Z67dk/6pl32wN3mhPFt279hNeXW/98Ftav9tpfeuiHUTzsL+u8Pnvm1YLe\nE+XVof9WXnv94C2i+JOhm3h9y3d1Udxl8Aqvb8vuK6P4ge0m5d3fY2vqvPYZj4+J4u1//JbX17Dc\n/93SWpwZAwAQGIMxAACBMRgDABBYu50zrtl00yiu39Wfq6p58pWi33/9Ybt77Ydv+Z8o/tY7h3l9\nH+9f3FxDWvUf7c/JNKox77brXf7tjuu6LO/XZW+Z/R6573PdURO9vj/+/VtRXPvoy3nfH82rHTok\nio+/9xmv7+/dFxT0Huudf07R3M9JtgEd/DnGN466Lor/eYg/X33JNadG8ZZX+nmi9Wp79/LaKw8a\nFsULj/APxK0Gx8fv9dv9n9fXp6Y+ijev9euZrUbmtRvlsuL8Dum83mvPPeLGKH7ooK5e3x/P/o8o\n7vjgi828a74cAQBAUAzGAAAE1m4vU7/xu+2j+H9H3eD1/WqbLxb9/m+f5N8mk31ZZFTvGV7f7fI/\nro8mMxf1818YuvHtKuHQTT7z2hecszaKBzxa6WzS461vxzUe0/09r6+wi83lcWSXj7321V9ZGDeu\nrHAyKVHzhe2iuNt1H3p9k4Zcl7v5xt9DHb32c2vj9uOre3t9P330a61N8d9suuVKr33Vzn+L4s1q\nPvf6lo6Lb5Ub8GDr98WZMQAAgTEYAwAQGIMxAACBtZs543d+7S+tOP3YK6J4/vra3M2L9rsv/a3l\njdCsPpM6+y8cnH/bqz+Ob404u+ccr+/R1d2ieMtaf1m87TsW9vfoKW8e5bXt+R4FfR2at81Vb8SN\nM8Ll0ZIp298dxcdqz4CZVI9l4/zfuQO/Fd+qePuQh72+19fFtyh96+XTvb4OT8THWrfF/icJuk+e\nHsWNa9Z4fcP1fCszbtlv9YUorunSxevrv2txwylnxgAABMZgDABAYKm+TF3bvXsUn3HCQ15fF8v+\niHxhT3lpSfZH93fv9FROb/7VYVC8Rw4eHMVTu+3o9bk18W1I1iHnR75DPEWx/MD+XlfvJxdFceMS\n/1aM/mtYhakUsp908+VZJ3p9fx1xWxS/Vd/N6zv9nu9G8VZP+Zcuu7y3KordSzO9vvovxSvjDbps\nrtc3fuBjBeW84Ff+5detf/FsQV/XHnxwb3zL6Mt7Xpt3u1rzzwN/vuD4KB7w1Zm5m+cV8va3xs/9\nW5uKfbIXZ8YAAATGYAwAQGAtDsZmdrOZLTWzGVmv9TKzh81sXua/+Z8CjsShpulCPdOHmrY/hcwZ\nT5R0jaRbs167SNJU59zlZnZRpn1h6dMrzucHjoji83rmX7Pwz4u/nPPKJ23a36oh8Rz1oA6JniOe\nqCqoae06/+kta1x8+4M/5y/NuXh4FA89/7m879mhv7/0qPssnl/s9U9/DrFxXfzEltzbJhJmoqqg\nni3peLj/lKZvj/phFHd5fZHXt+2i/DV2eXukDv96KYofe92/Ralx4L8KyFIaPMm/Pa65/RVhoqqw\npuOGx5+VaWzmO7PHf53ltfvdVvg8cVq1eGbsnHtCUu4z/o6TdEsmvkXS8ULVoKbpQj3Th5q2P239\nNHVf59ziTPyBpL75NjSzcZLGSVJndcm3GcIrqKbUs2pwjKYPx2iKFX1rk3POmVne6xHOufGSxktS\nd+tVpis6G/fuEYV9Pu2Z+dt47WEq78PiL332K157uF7Ks2UYzdW0kvXs8vdpXnu3kedF8ewTrvH6\nttklvoxZs+mmXl/9rvHjnr5yo3+L2+eNneKvM/9GiZmfxbc6vXqdfztL73viJ281rvSf7JI0ST5G\nm9PxgReiuL6Z7VrDdo9ve7vpSzcX/HU3fRr/jsi9XSqEpByja4/0L/Xv2vnGvNtu/1i8xNqwW1/3\n+hoSfgxVQls/Tb3EzPpJUua/S0uXEgKhpulCPdOHmqZYWwfjyZJGZ+LRkiaVJh0ERE3ThXqmDzVN\nsUJubbpd0rOSRpjZQjMbK+lySYeb2TxJh2XaqBLUNF2oZ/pQ0/anxTlj59wpebpGljiXkvvqAYU9\ntWPzf3VqeaMC1G9S2IUGW1FXkv21VbXWdPsrlkTx7KP9+d3bh98RxXteea7X98YR1xf0/jU5f5s2\nbjYvblz2mNe386h4/mvbsfO8vtxl8sqtWusZwvv/Gf/cHNR5ndfX3NKKN10bf85jC5V/KdRqqWnH\nFeu99jYdsn/2/ds7Zx9yUxR/4/5RXt+i/9kpijf7a/tcXpQVuAAACIzBGACAwFL91Kadu7xX0Ha5\nKz01J/uB0rmXIz84al3u5hvV/7HE3D1SVerfeieKP2n0L4HtWBNfLiv0snQxXj8ovuT2hYt/4PUN\nvrh9XmZLiuxj9M0Jw7y+mXvGtzPVyHK/MoouW7az19PvjjeiuDTPeEsHe3q6197/HxdE8UVf+ofX\nN7b7wij+f9s+6L/R5VntnJnwOz7rE8XX/uJrXl+Pf7wWxZWeHio1zowBAAiMwRgAgMAYjAEACCzV\nc8b3Lt0tik/Z9IG820353RVee8yZJ0TxjOf9pTJdv/jpPcP/uNbr+8Ve9+Xdx3oXzzR1Wbw673Yo\nzBn3jvPas0++NlAm0gP/8Qev/d2LDwiUSfuUPUcsSXPHx09rm3XQeK/Pv30p51a2rN6JL+zn9Q1f\n/mJRObYXw86Ol7C947Ajvb4/HRw/ae0XX7/T6/t6t/yLiWX3nXzFdV7frgPPieIBN/pLbCZ9mdpc\nnBkDABAYgzEAAIGl+jL1x5cNjuI//H4Hr+/HvWdFcbcafwWu/zd0StwY6nV5t0M0Hlr4LUpXfxw/\nLUbPvZZ/QxRk2wv8h8uP3e/QKJ4w6NG8X7eswZ8iOHVevNBRw2+38PrqHomfprVsnP/Upu+ff3cU\nf2vTxV7f/Cv2ieKh5/t5ovTePXdXrz3r0Cvb9D6vrI3PTUZc6/+ccDNi62UfP5I0+JE4vu2/d/H6\nbjww/kW78Hj/5rHnRl4Vxb1r/FsaX/7h1VG896pzvL4+11fXLYacGQMAEBiDMQAAgTEYAwAQWKrn\njDs+8EIUP/bpPl7fhK/Hc4xjR/pzjBf2np33PWst6+8X19xzXnw1Vvi2aL0Fl20XxTOvetjrm752\nYBRfd/lXvb6eE+N5pRrlXz518/H+/NP1q+P3Oe6yP3l9T530xyg+ZeoPvb5O978gFO/N2+LbFmcf\ncrXXV+iR9m69Py980ffjWnV6hTqVU8Pyj7z2JvfGT9gbdq+/7TcP/X4Uj7nBf4Rz9m1PY86Z4vU9\n8GD8M5K9lG5ScWYMAEBgDMYAAASW6svU2ezZV7320Kyrjk/U9fD6Ht/9tCj+YN9uXt/ne8ZPBjl8\n2Bte35VbPZ13/zc+cHgUbytudym1zv+IL3P9ZLm/Olfdgg+juOei0tzukP0A9N1Hft/rm3N4vOrT\nooP9Q2yb+0uy+3ahuacvzc56alZzT1/KlX1petyYc72+Tv/i0nQS1T76chRfNvEbXt/J51wTxTt3\n9qeZ7nurZ3kTKzHOjAEACIzBGACAwBiMAQAIrN3MGTfHrV/nv5C1XOWWzUzv/uvOnf0XsuaM365f\n43UN/8vHUewv9oa2cPv6y+nNGxf/KG/xr45e32bPvF/WXLZ4uM5/If54gC4//jav6+YbvhTF1XC7\nRUhzLo+Pr9kHXeP1Ffr0pVyHPRDfvjScOeKqs+mB/tOdGrMWKn19zcDczasKZ8YAAATGYAwAQGBc\npm6lDlv2jeK79xqf0xtfHr1x2YFeT8PMOeVMq91ZcHTOA+W/HF/GnHqg33fVy8dHcTnq0OO2nLmM\n38fhMV2Xe11X7LFlFHfjMrVnzTF7ee07vnJNni3b7saRE6P4vhf9pz01uvznJm+fFD/Rq35B/pXa\nUDzr4A9Law6PV9J6epcbvb7sCYnxc/f3+rbSLFUTzowBAAisxcHYzAaa2aNmNsvMZprZuZnXe5nZ\nw2Y2L/Pf6rrDup1qVKOoZ7pwjKYLx2j7VMiZcb2kC5xzO0jaR9LZZraDpIskTXXODZM0NdNGdaCe\n6cIxmj7Us51pcc7YObdY0uJMvNLMZkvqL+k4SYdkNrtF0mOSLixLlgny4ahtonh4Xce8202Z5D8l\napCeKVtOrVGjGjnnXpaqu56Df+4va7nk1HiZw5Gb+NuOfOj/ovjqj/1lFW+7+ogo3vKh/LdAvf2t\n/l579YD6KH78qCu8vjqLl1Bd71R2aTlGb77W/z4O6NCp5Ps4eJN4OdtDN/Hn+pu7JeqETieXPJd8\n0nKMtkb2Z3Fm/WqQ1zf36BuyWrlLn8a2/FP+38fVoFVzxmY2WNJukqZJ6pv5JSBJH0jqm+fLkFDU\nM32oabpQz/aj4MHYzLpJulvSec65Fdl9zjknaaPnAGY2zsxeNLMX12ttUcmidKhn+lDTdKGe7UtB\ntzaZWZ2afihuc87dk3l5iZn1c84tNrN+kpZu7Gudc+MljZek7tarAhftymt9t/yXSZY0xJdKt7nF\nv/2hPnfjgNJYzwOnnB/Fb3zl2rzbnd3Tv7Xp7F/E7ZpfFL6Sk8+/nLrexWusFf4exanWmi741b5R\nPLjDy15f48bHmn/Tmqc2Nfd1P3z/gCj+55wdvL6hc18p6D1LpVrq+emUoV675pbNC/q6Vf38Go35\nzpQonrzZP3O2zv8794R5x8T7fmp6QftOqkI+TW2SJkia7ZzLntSZLGl0Jh4taVLp00OpuaZfcNQz\nRThG04VjtH0q5Mx4f0nflvS6mW340+Nnki6XdKeZjZW0QNLXy5MiSqmhaWVs6pkuHKMpwjHaPhXy\naeqnlP86wcjSpoNy66AOcs5RzxThGE0XjtH2ieUwW8m+vDxv388WHRXFLJlXWSP+Z1UU79zjDK/v\n9YNuqnQ6kdtX+rdEbfb0u1GcpM8RBJM15uTOERc+3174XP+jq+Pbzm5YdIjXt/zKwVE89J5pBe67\nfftSv7le+9Ir/lbQ1+XO12fXvrmq/275jv7XfWeTPFtWH5bDBAAgMAZjAAAC4zJ1K1230/+1vBEq\nzr00M4q3Hbep13fQCT+I4hsv/W+vb/uOpf97dFnWLW7XXf5Vr6/nomdzN2/XesyPL0/+ZYX/cPjR\n3Re06T1/+H78xLQXrtvN6+szLZ5mapjlX2LtoiVt2l97dsere3rtnx/2YhTXWW2b3vOVdf6F6jHj\nz43iAb/NXcnwrTbtI4k4MwYAIDAGYwAAAmMwBgAgMOaMW+kLHRuyWv6cyPlbPhzFPzrke15f7WP+\nUn8on8aVK732ZrfG87QXTz3B61t+aPyEmKVfXuf1zR55Y0H72/6RM/32z+NVCnu+xxxxczb7a/z9\neeosf2nF5uaMd3xsXBT3eqiz19f7nhlx30r/+98glNKw017y2l+89LwovuPUP3t9O3aMh5upq/0l\nZM98fHQUj7hutdc34KVkPPGu3DgzBgAgMAZjAAACs6YncVVGd+vl9rbqXs1t4c/2i+LpZ1/t9W33\naLzy0/Az/dsmGletUhJMc1O1wn2U/zEorZCGela7UtZToqZJwDGaLoXWkzNjAAACYzAGACAwBmMA\nAALj1qZWGnBZ/DH7Yy7b3esbqleiuNDnzQAAwJkxAACBMRgDABAYgzEAAIExGAMAEBiDMQAAgTEY\nAwAQWEWXwzSzDyUtkLS5pGUV23F+SclDqlwuWzvn+pTijRJYTyk5uVRdPaWopquUjO+hlJx6SlVY\nU47RZiWqnhUdjKOdmr3onNuj4jtOaB5SsnJprSTlnpRckpJHWyQpd3IpjSTlnpRckpLHBlymBgAg\nMAZjAAACCzUYjw+031xJyUNKVi6tlaTck5JLUvJoiyTlTi6lkaTck5JLUvKQFGjOGAAAxLhMDQBA\nYBUdjM1slJnNMbP5ZnZRhfd9s5ktNbMZWa/1MrOHzWxe5r89K5DHQDN71MxmmdlMMzs3VC6lEKqm\nSalnZr+pqSnHKPUs4b4TUc/MfhNf04oNxmZWK+laSUdK2kHSKWa2Q6X2L2mipFE5r10kaapzbpik\nqZl2udVLusA5t4OkfSSdnfk+hMilKIFrOlHJqKeUkppyjEaoZ2lMVDLqKVVDTZ1zFfknaV9JD2a1\nfyrpp5Xaf2afgyXNyGrPkdQvE/eTNKeS+WT2O0nS4UnIpdpqmsR6VnNNQ9czqTWlnumqZ1JrWsnL\n1P0lvZfVXph5LaS+zrnFmfgDSX0ruXMzGyxpN0nTQufSRkmrafDvYZXXNGn1lDhGi0E9NyKpNeUD\nXBmu6U+jin203My6Sbpb0nnOuRUhc0mjEN9DalpeHKPpwjHqq+RgvEjSwKz2gMxrIS0xs36SlPnv\n0krs1Mzq1PQDcZtz7p6QuRQpaTUN9j1MSU2TVk+JY7QY1DNL0mtaycH4BUnDzGyImXWUdLKkyRXc\n/8ZMljQ6E49W0zxCWZmZSZogabZz7oqQuZRA0moa5HuYopomrZ4Sx2gxqGdGVdS0wpPmR0maK+lN\nSRdXeN+3S1osab2a5k7GSuqtpk/QzZP0iKReFcjjADVdCnlN0vTMv6NC5FLNNU1KPdNWU45R6pm2\nelZLTVmBCwCAwPgAFwAAgTEYAwAQGIMxAACBMRgDABAYgzEAAIExGAMAEBiDMQAAgTEYAwAQGIMx\nAACBMRgDABAYgzEAAIExGAMAEBiDMQAAgTEYAwAQGIMxAACBMRgDABAYgzEAAIExGAMAEBiDMQAA\ngTEYAwAQGIMxAACBMRgDABAYgzEAAIExGAMAEBiDMQAAgTEYAwAQGIMxAACBMRgDABAYgzEAAIEx\nGAMAEBiDMQAAgTEYAwAQGIMxAACBMRgDABAYgzEAAIExGAMAEBiDMQAAgTEYAwAQGIMxAACBMRgD\nABAYgzEAAIExGOcwM2dmq8zsvwrcfqyZfZb5uqHlzg+tQz3Tpw01vTSzvTOzDuXOD63DMdqEwXjj\ndnHOXSxJZjbczCaZ2Ydm9pGZPWhmIzZs6Jyb4JzrFi5VFCCqpySZ2Xgzm2NmjWZ2WvaG1LNqeDXd\nwMxOzfySPmPDa865SyTtWNHs0FrZv3MPzAy22f+cmX1VSu8xymDcss0kTZY0QlJfSc9LmhQ0IxTr\nVUlnSXo5dCIoHTPrKelnkmaGzgVt55x70jnXbcM/ScdI+kzSA4FTKysG4xY4557P/CX2kXNuvaQ/\nSxphZr1D54a2cc5d65ybKmlN6FxQUr+VdJWkZaETQUmNlnSXc25V6ETKicG49Q6S9IFzbnnoRAA0\nMbO9JO0h6YbQuaB0zKyrpJMk3RI6l3JjMG4FMxsg6VpJ54fOBUATM6uVdJ2kc5xzjaHzQUmdqKYr\nHY+HTqTcGIwLZGZ9JD0k6Trn3O2h8wEQOUvSa86550IngpIbLelW55wLnUi58TH/AmQ+GPKQpMnO\nuYI+fg+gYkZKOtjMjsq0e0nazcx2dc6dEzAvFMHMBko6RNKZgVOpCAbjFphZd0kPSnraOXdR6HxQ\nPDPrqKarQiapzsw6S1rHJc6qdZqkzlnteyTdJWlCkGxQKt+W9Ixz7s3QiVQCl6lbdoKkPSWNybnv\nbVDoxNBmD0laLWk/SeMz8UFBM0KbOec+cc59sOGfpHWSVjjnPg2dG4pyqtrBB7c2YDD+d2slvWRm\nv5Yk59wtzjlzznXNvvfNOfeuJJnZGDP7JPN1nFklj1dPSXLOHZKpafa/xyTqWSX+rabZMvW9aUPb\nzC5R073layWlfu6xCm20ns657Zxz/3Z1I63HqLWDeXEAABKNM2MAAAIrajA2s1GZNX7nmxkfbkoB\napou1DN9qGk6tfkydeZG+7mSDpe0UNILkk5xzs0qXXqoJGqaLtQzfahpehVza9NekuY7596SJDO7\nQ9JxkvL+UHS0Tq6zuhaxSxRrjVZpnVtrebpbVVPqGV4p6ylR0yTgGE2XFuoZKWYw7i/pvaz2Qkl7\n525kZuMkjZOkzuqivW1kEbtEsaa5qc11t1hT6pksxdZToqZJwzGaLi3UM1L2D3A558Y75/Zwzu1R\np07l3h3KjHqmDzVNF+pZnYoZjBdJGpjVHpB5DdWLmqYL9UwfappSxQzGL0gaZmZDMssLnixpcmnS\nQiDUNF2oZ/pQ05Rq85yxc67ezM5R07rNtZJuds7NLFlmqDhqmi7UM32oaXoV9aAI59wUSVNKlAsS\ngJqmC/VMH2qaTqzABQBAYAzGAAAExmAMAEBgDMYAAATGYAwAQGAMxgAABFbUrU2Js9fOXvPdozaN\n4sbtP8v7ZT0nd/HaPeatihvPv16a3JB48/+6m9e+df8JUfzLMWO9vprHX6lITgDaB86MAQAIjMEY\nAIDAqu4ytXXyn0Iyd/yOUfzwIVd5fYM6bJL3fWoUP16y8QDn9b1bvzqKr152iNc35cE9o3jolW96\nfQ1LlubdH5Kpw9bxmvtvfOkmr69RjVG8ya8We31rDy5vXqi8Pac3RPGUGw7w+vrc8Gyl00E7w5kx\nAACBMRgDABAYgzEAAIFV3Zzx27eO8NrP73d1FO/58HleX5/H6wp6z1XHrvDahw+eE8V/2HKa1/eH\n0XF75in1Xt9Jd58bxdv+6LmC9o2w5n9nQOgUEEju5082rf0oio/73uNe3/MPDI3i+nfeLW9iaJc4\nMwYAIDAGYwAAAqu6y9SzDpjotff47Y+jePg1z7TpPXve4rfndO4cxccO/5bX1+fG96P4L4Me8/pe\nOzm+tWrUzt/w+roc/V4Uu3r/8jaA1llxyj5R3P32tk0JNe6+nde+sPctebaUhn83vpdtyEVcpt5g\n7ZF7eu2Hb7oh77Y7Tzgnijeb699O2uN/mdbjzBgAgMAYjAEACIzBGACAwKpuzjhX3+fi25JcM9u1\nRuOaNXHjtTe8viX7xvHQ8Wd6fXOPjudLpu50l9c34oqzonjYD/zbpRBO912Xh04BBajZyZ/fvfG3\n/x3F/7HV+V5fvz8V9tmR7a6aVXxi8GQvIZvr9bHXRPHihtVe36XnjIri6Tf7T9/zWE67mV/6fR+L\nlyde36+711f72br4Lef6nwFoXLky/5uWEWfGAAAExmAMAEBgVXeZetc/n+O1By6YF8UNuRuX2fBx\nL3jtEVfHl6LnnXi91/ePY+PLamc/+AOvr9P9/vugcv60w51RXGe1Xt/6rEtgs58b4vVtow/Kmhd8\nb1zQ1Wt/oWN8++Hpp0/x+h68fqsobvz8c69v1Vf3juI/9bsuZy9x/e9Y2dPrGTphSRRX+vdMknV5\n3n9y3c5Pjo3i1w+ckPfr+tb6q59dN/DRuHHJo8qnJuf8sbnL4n85b3AUD+64zOtb0Rj//ExftbXX\n9+JZu0WxPftq3vcvNc6MAQAIrMXB2MxuNrOlZjYj67VeZvawmc3L/Ldnc++BZKGm6UI904eatj+F\nnBlPlDTMyjlHAAAgAElEQVQq57WLJE11zg2TNDXTRvWYKGqaJhNFPdNmoqhpu9LinLFz7gkzG5zz\n8nGSDsnEt0h6TNKFJcwrr63+6N+2kKT5m+E/fCmKh24yzuube+SNUbz7r17y+mbcX968ciWtppXU\nYcu+XruzrY/i9c7/23TyqvjEY/iNi72+JC1omtZ61m4/LIpfP/zanN54zm+HTou8ngdrB0Zx7pOZ\nOpwZz/3mfkYg2y//drLX3nresy3mW0rVUtOG5R957aE/7xHFbz2y3u+r82tRbmN6vJO3r0bxZwmO\n6+rPJ4/qvlcUdyx5Vvm1dc64r3Nuw2+nDyT1bW5jVAVqmi7UM32oaYoV/QEu55xTM7dem9k4M3vR\nzF5cr7XF7g4V0FxNqWf14RhNH47R9GnrrU1LzKyfc26xmfWTtDTfhs658ZLGS1J361WqRbISKftp\nTH2eqvM7j4zDy7f0b2U6RruXM61CFVTTaq/noq9v67V3aeY61IzVA6K4/q13ypRR2VT/MXrdqijs\nVtM572a/mv8Vr9115VtRXNunj9f32E735n2fzxrjlfeG3POp15f/BpqKSvwx2jD/7Sg+87zzvL4P\nd80/3Fxyyu1RfEK3vD+qZfHrD7/otbvMiy9bV3I6qq1nxpMljc7EoyVNKk06CIiapgv1TB9qmmKF\n3Np0u6RnJY0ws4VmNlbS5ZION7N5kg7LtFElqGm6UM/0oabtTyGfpj4lT9fIEueCCqGm6UI904ea\ntj9VtxxmpdV06eK13Y7b5tlS+nj7blG82Tz/qSRz18dPCRle509U1vbdIoobllR2vgRIig79t/La\nJ275ct5tG1w8i/v5vf6HirsqnjP+fK/BBe//gvcPjeLG6TzRqVib3Pu81x6Uf7pef/llvCTlrX33\n9Ppm/zprucqcpzYN3SZelnbKds3sIEf2bW0vf22Y19fw1lu5m1cEy2ECABAYgzEAAIFxmXojPvta\n/GSX3X4y3ev781YTo7gm55pJY3NPum5mLZeB/4gfZv3e0f6tGA0fftjMe6K1Dvj2Sy1vlPG/M+OV\neLbR9Ga2RCnM/b7/9JyxPabk2VLa55V4haw+N/irY2VP+4y4ZIYKNe9nO0RxnQr/OUFp5U7VDR+X\nf+rusBnx787mnuCUe/tS9qXpxrffbW2KZcGZMQAAgTEYAwAQGIMxAACBtds547VHxx+fv/7aK72+\n4XX5b6nI/mz999/fz+s5pMfsKP5q148LzuXGAfGcV8N0f97jG299OYqXXTbE6+v0T39ZTWxc9u1p\nQ7u87/dl/T2a+xSfrs/6t7WhvDp9Yi1vlPHIrrdE8YQZO3p9R3aLn+y2fUdqmCZLz/J/547u8Yes\nlv+5nJs+3SaKp9xwgNfXp8JP4SoEZ8YAAATGYAwAQGDt5jJ1TdeuXjv70nTuQ6/nro+f3nLUIz/w\n+gZNiv9+6fwPf4WZBf32jeJLT9vG65t+ztV5c9vp6W9H8V92n+j13TA4ay348f7X7TklfirK8DO5\nZJ3Pp1/5QhR/b7PHvb7sSYHZ6/zHzfV79KONbofyGHTTHK9962mbR/Gp3f0HwPeo2SSKz++Vu2IS\nl6aTIPsWM0nSZt3zbuvei6eP3Hr/WUnv/mSPKP7mN/7l9fWoiS9N/3ixfwl7/jcHRXGfucm7LJ2L\nM2MAAAJjMAYAIDAGYwAAAms3c8Zzf7Oz1x5e92QU//GjEV7fE8fGy+INf/vFgvdRvzh+gojrsE3e\n7f6+qpfXHvS116P4Eu3u9a3/cjxf8lm/Oq/PXzgTxVrS0M1rN854I1Am7VPDsuVe+45jD47iS87v\n7fUNHbY4in85ZJLXt3/nws4xtrnrTK+9/Yx3orheaIvseeJdH/jA67t0i39Gce7Slfu8GH9u5rNV\nnb2+GQfHn++pyTl/zH6X+57zl7wcNndaYUknBGfGAAAExmAMAEBgqb5MvfTs+KPuL570R6/v7lX9\noviJ4/wVfOrffqdN+3vzD/GtTc+d/Iec3vjSy4WPfd3rGa78tyXVPRRfJu/ZpqxQqDEPnuG1h+v5\nPFuiEhrmvhnFw7/7Zt7tzjn7HK/9ysXX5d326o/jJ0ONuHiW11e/cmXu5mitrNuXsi9LS/4Kd+tz\nHnD3/B63NfOm+VfJy36fy798h9f36598K4q3+v0zSjrOjAEACIzBGACAwBiMAQAILNVzxpseG9/+\n0K3GX/Jy6ifx7Uv1b73Tpvdffsa+Xvuxb8TzxNnL9Un+7Uzb/8xfvq+hTXtHoTqcvqSg7Tp+VNvy\nRkic2rWu5Y0yrnjyiCgevpLPBJSaffZ5FI//dLDXN67HO1H85Vknen2/3faeKN6tU/7FZ/d8+RSv\n/cmM+Ja3YRP843xQ/aIoroZb1TgzBgAgMAZjAAACS/Vl6j8P/1sU1+T8rz5z525RvJUK/9h74wG7\nRvH3Lvi719evNn5azPR1/oWRG846KYrrlr1U8P7QetbJn5IY3D1e2Sl3BR+k29KGVV57+yvinwWm\nh0qvflH89KX7T/Kn8e4aNCqKnflf9/jvt4vi3Tr5t5xtN+WsKB7+Hf820Oy1DKu9nvxmAgAgsBYH\nYzMbaGaPmtksM5tpZudmXu9lZg+b2bzMf1mTogo0qlHUM104RtOFY7R9KuTMuF7SBc65HSTtI+ls\nM9tB0kWSpjrnhkmammmjOlDPdOEYTR/q2c60OGfsnFssaXEmXmlmsyX1l3ScpEMym90i6TFJF5Yl\nyzb60/vxbQy3DH7E6/tsu3UFvcfKk/fx2uf96vYo/mrXj72+Me8eEsXv/sp/ElSnR/IveVlJNaqR\nc+5lqfrqWaiGvXbw2v8zaHwU579ponpV8zFabisb/duespfYTKq0HKMNs+Z67Y5ZU8Fnz/P7jujy\naRSvcf7nbbrN8Z9Wl1atmjM2s8GSdpM0TVLfzC8BSfpAUt+SZoayo57pQ03ThXq2HwUPxmbWTdLd\nks5zzq3I7nPOOUkbvfPezMaZ2Ytm9uJ6rS0qWZQO9Uwfapou1LN9KejWJjOrU9MPxW3OuQ1LpSwx\ns37OucVm1k/S0o19rXNuvKTxktTdehW+VE4JPPvasLiRc5n6/H0fjuK/nnaU1/fZwPhz90+M85++\n1KMmfvrS0IfGeX3bnx+vrNXp42Rclt6Yaq1nuW26IHQGbdfuamrxMfr5qPxPW5rw0X55+5Ks3dUz\ny64P+0/hGv7H5D9xqRQK+TS1SZogabZz7oqsrsmSRmfi0ZImlT49lJpr+mOaeqYIx2i6cIy2T4Wc\nGe8v6duSXjez6ZnXfibpckl3mtlYSQskfT3P1yNBGppujaee6cIxmiIco+1TIZ+mfkqS5ekeWdp0\nUG4d1EHO5a5/E6GeVYhjNF04RtunVC+Huf2fPoziy/bb2ev7+eYzovi7/3VN3vd4dm1Xrz06a554\nuwtmen0Nq/yl91Bdev/Ps6FTQIE69N8qimft9795t7vrgf299hBR4ySoNf8mwx++f2AUDx/TPpcL\nZjlMAAACYzAGACCwVF+mbpj/dhQ/f9xQr2/7y/eI4vq1/rdh0+nx7Uv97/vA6xs+L34geRpXc2pv\n9vrDuVG8ZSue3oXk+rRxdRQPmcTUUVK8/5P4NrMDOvvTBZPzTpG3H5wZAwAQGIMxAACBMRgDABBY\nqueMs9W/867XHnLyu3m29DWUIxmUVc2Tr3jtY/vvmXdb5omr0+c7xbc23buqm9d35fe/E8Udn0vu\nsrTtzfqsu0Q7mz/0PPf+4CjeUrMrlFGycGYMAEBgDMYAAATWbi5TA0iPjg/El5+vH+bftthRXJpO\norqsu8zWuHqvr9f1XdXecWYMAEBgDMYAAATGYAwAQGDMGQMAym6r38e3EZ50hP8o5i7zlkWxP5vc\nfnBmDABAYAzGAAAExmVqAEBF1Yx8z2u310vT2TgzBgAgMAZjAAACYzAGACAwc85VbmdmH0paIGlz\nScta2LwSkpKHVLlctnbO9SnFGyWwnlJycqm6ekpRTVcpGd9DKTn1lKqwphyjzUpUPSs6GEc7NXvR\nObdHxXec0DykZOXSWknKPSm5JCWPtkhS7uRSGknKPSm5JCWPDbhMDQBAYAzGAAAEFmowHh9ov7mS\nkoeUrFxaK0m5JyWXpOTRFknKnVxKI0m5JyWXpOQhKdCcMQAAiHGZGgCAwCo6GJvZKDObY2bzzeyi\nCu/7ZjNbamYzsl7rZWYPm9m8zH97ViCPgWb2qJnNMrOZZnZuqFxKIVRNk1LPzH5TU1OOUepZwn0n\nop6Z/Sa+phUbjM2sVtK1ko6UtIOkU8xsh0rtX9JESaNyXrtI0lTn3DBJUzPtcquXdIFzbgdJ+0g6\nO/N9CJFLUQLXdKKSUU8pJTXlGI1Qz9KYqGTUU6qGmjrnKvJP0r6SHsxq/1TSTyu1/8w+B0uakdWe\nI6lfJu4naU4l88nsd5Kkw5OQS7XVNIn1rOaahq5nUmtKPdNVz6TWtJKXqftLyn5Ux8LMayH1dc4t\nzsQfSOpbyZ2b2WBJu0maFjqXNkpaTYN/D6u8pkmrp8QxWgzquRFJrSkf4MpwTX8aVeyj5WbWTdLd\nks5zzq0ImUsahfgeUtPy4hhNF45RXyUH40WSBma1B2ReC2mJmfWTpMx/l1Zip2ZWp6YfiNucc/eE\nzKVISatpsO9hSmqatHpKHKPFoJ5Zkl7TSg7GL0gaZmZDzKyjpJMlTa7g/jdmsqTRmXi0muYRysrM\nTNIESbOdc1eEzKUEklbTIN/DFNU0afWUOEaLQT0zqqKmFZ40P0rSXElvSrq4wvu+XdJiSevVNHcy\nVlJvNX2Cbp6kRyT1qkAeB6jpUshrkqZn/h0VIpdqrmlS6pm2mnKMUs+01bNaasoKXAAABMYHuAAA\nCIzBGACAwBiMAQAIjMEYAIDAGIwBAAiMwRgAgMAYjAEACIzBGACAwBiMAQAIjMEYAIDAGIwBAAiM\nwRgAgMAYjAEACIzBGACAwBiMAQAIjMEYAIDAGIwBAAiMwRgAgMAYjAEACIzBGACAwBiMAQAIjMEY\nAIDAGIwBAAiMwRgAgMAYjAEACIzBGACAwBiMAQAIjMEYAIDAGIwBAAiMwRgAgMAYjAEACIzBGACA\nwBiMAQAIjMEYAIDAGIwBAAiMwRgAgMAYjAEACIzBGACAwBiMAQAIjMEYAIDAGIwBAAiMwTiHmTkz\nW2Vm/1Xg9mPN7LPM1w0td35oHeqZPtQ0XdpQz8My9Ww0s8PKnV+lMBhv3C7OuYs3NMxsvJnNyRT/\ntOwNnXMTnHPdKp4hWiOqp5ltbmZPm9lyM/vEzJ41s/03bEg9q0Z2TQ/M/HLO/ufM7KsSNa0Sub9z\nv2RmL5vZCjN7y8zGbehzzj2Sqee7QTItEwbjwrwq6SxJL4dOBEX7TNLpkvpI6inpd5L+YWYdgmaF\nNnPOPemc67bhn6Rj1FTnBwKnhjYwszpJf5d0o6Qekr4h6Qoz2yVoYmXGL6ACOOeulSQzWxM6FxTH\nObdG0hxJMrMaSQ1qGpR7SVoaMDWUzmhJdznnVoVOBG3SS1J3SX91zjlJL5jZbEk7qOnEKJU4M0a7\nZGavSVojabKkm5xzDMQpYGZdJZ0k6ZbQuaBtnHNLJN0uaYyZ1ZrZvpK2lvRU2MzKizNjtEvOuS+Y\nWWdJJ0jqGDoflMyJkpZJejx0IijK7ZJuknRlpv0959x7AfMpO86M0W4559Y4526XdFHa56PakdGS\nbs1c3kQVMrPtJN0h6VQ1/aG8o6SfmNnRQRMrMwZjQKqTtE3oJFAcMxso6RBJtwZOBcXZSdJc59yD\nzrlG59wcSfdLOjJwXmXFYFwAM+uYuaRpkurMrHPmwz+oMma2j5kdkKnpJmZ2oaS+kqaFzg1F+7ak\nZ5xzb4ZOBEV5RdKwzO1NZmbbqukT8q8FzqusGFAK85Ck1ZL2kzQ+Ex8UNCO0VSdJ10paLmmRpKMk\nHe2cez9oViiFU8UHt6pe5o+p0yVdJWmFmub/71bTHHJqMRj/u7WSXjKzX294wTl3iHPOcv49Jklm\nNsbMPsl8XWOYlNEMr57Oucedc7s45zZ1zvVyzh3snHtiw8bUsyr82zEqSc657ZxzE3I3pqaJt7Hf\nuXc653bKHKcDnHMXOucaJcnMRmbq2VdNtyamgvE5BwAAwirqzNjMRmWWiZxvZheVKimEQ03ThXqm\nDzVNpzafGZtZraS5kg6XtFDSC5JOcc7NKl16qCRqmi7UM32oaXoVs+jHXpLmO+fekiQzu0PScZLy\n/lB0tE6us7oWsUsUa41WaZ1ba3m6W1VT6hleKespUdMk4BhNlxbqGSlmMO4vKXtFlIWS9m7uCzqr\nq/a2kUXsEsWa5qY2192qmlLP8EpZT4maJgHHaLq0UM9I2ZfDzDz6apwkdVaXcu8OZUY904eapgv1\nrE7FfIBrkaSBWe0Bmdc8zrnxzrk9nHN71KlTEbtDBbRYU+pZVThG04djNKWKGYxfUNMqKUPMrKOk\nk9X0BBxUL2qaLtQzfahpSrX5MrVzrt7MzpH0oKRaSTc752aWLDNUHDVNF+qZPtQ0vYqaM3bOTZE0\npUS5IAGoabpQz/ShpunEcpgAAATGYAwAQGAMxgAABMZgDABAYAzGAAAExmAMAEBgZV8OEyiHml13\n8NrXTBofxYM75F8CsNb8vz8vXLJrFN81czevb8tJHaO42/+b1qY8AYSx6qR4ye57/3yF13fQDT+O\n4oGXPet/YRufZFgszowBAAiMwRgAgMC4TL0R2ZdAB41/2+ub8cddorjbnc9VLCf4Gjap89pXfnho\nFG9Su97r+80WL8UN15i3z9tO0vpDGqJ49u/9/X/n9+dG8RY3+V/n1q9rJnMAldD1rnhq6Xid7/U9\n/ec/RvHXnzjb66t58pXyJpYHZ8YAAATGYAwAQGAMxgAABMac8UYs+mX80fZ/DvA/9v6Fbw6O4u6T\nO3t9jWvWlDUvxOzZV732nD2y+jr4P9bH7vTtKH7/kM28vhW7rI3in+7zT69vx04Lo3ivTv7tDi/8\n/Noo3nnzc7y+gb9+prnUAVRY9vyxJJ145ilRvGyfTby+rZ6sSEr/hjNjAAACYzAGACAwLlNvxOnD\n4kvTDTm3wly4/UNRPHHvY72+msfDfCQePldf77enz4riLaf7226ZFd+tLby+SUP2jOKet33q9d2y\n9b+i+Csn+pelX/1tfFjl5gKgeTWbbuq3u8Yr6uUeTw3LlrdpH4s/7h7F6/s3NrNl5XBmDABAYAzG\nAAAExmAMAEBgzBm34PV1/tKKv7j/a1G83fx3vT5mB9Ol/u0FUfzc0/v6nVlzxif08JfDnDHghPg9\n3vF/RgD8uw4DB0TxHvf5SxBf2ie+12hh/Wde34FT42VpB91d6/V1feKNuLFFb6/vkX2uj+Jj/viT\n1idcBpwZAwAQGIMxAACBcZm6Bf9atb3XrlsZ//1Sv+j9SqeDClp00X5RPOeb13h9tRb/HIy+7Xte\n3+B3ch5WnkL1I3f32lNuvSGKO8i/XPhcvMiZzpt1stf33W2fiOKxPT7w+rJvK3yzfrXX963Xx7Qu\n4VaqudO/rLnZremvaSVlX5aWpN3+EU8JXdpnZt6ve7+hk9d+cuSVUTzgiG5e348/2C2Kn126udc3\nY11c360mzvD6GhQGZ8YAAATGYAwAQGAtDsZmdrOZLTWzGVmv9TKzh81sXua/PcubJkqJmqYL9Uwf\natr+FDJnPFHSNZJuzXrtIklTnXOXm9lFmfaFpU8vjBvvPCqKZ4zz5wqv7puKG5gmqp3VNJ/aHUdE\n8fqrPvf6nh7xpyhuVEevb88XvxHFgy95vkzZFWyiKlzPlQP870fuPHG2fbKm+Z7b7Y682zW4vF3a\ntoP/ZJ3m3qcUbthma689+dbeebYsm4lK8TE65/I+Xvv+Le6L4qmr/Z+ln//nd6K4532zvD4NiBe0\nnf0D/4lsbx87Pm5s6S9VvN1N8ec8tl6RjM8DtHhm7Jx7QtJHOS8fJ+mWTHyLpONLnBfKiJqmC/VM\nH2ra/rR1zrivc25xJv5AUt8S5YNwqGm6UM/0oaYpVvStTc45Z2Z5LzCZ2ThJ4ySps7rk2yxR1m6e\n/8PtnRen/26w5mpajfXMtvr4vbz2b66IL2Xt28mv+1pnUfy1+Ud5fVuO+TCKGxpD3QxRmHIco71u\ne8Fr7979nHh/+a9Y/5tuo+LbmRbP9y9durr41qYRw/zbCOfM7R/F3bdc6fX1676i8ASy/GrIvVF8\nYrfZXt9kHdCm9yyXajxG1x4dPwXtXwf+2euburpHFP/u1G97fd2ffi6Kc4+0mrr45+A3h97t9b22\nbk0U/8fV53t9g6+JV81rZnakotp6ZrzEzPpJUua/S/Nt6Jwb75zbwzm3R5065dsM4RVUU+pZNThG\n04djNMXaOhhPljQ6E4+WNKk06SAgapou1DN9qGmKFXJr0+2SnpU0wswWmtlYSZdLOtzM5kk6LNNG\nlaCm6UI904eatj8tToA6507J0zWyxLkkRs1ay9tXuzZvV9VIfU1r/EnLd34VzxPPGnOt19fYzIzR\nF+4+L4qHnftc3u1CC1FPV+/f4tf36mfa9kb/HYfD9Fb+/eW0h2tRwdsWasxP4ycAPfK937fxXUoj\njcfokt3ronhQB3/pynPePjyK6xZ86PU1donnvedduovXd8tX4+O5s/k/k9/7SXz89rvT//lMyjxx\nNlbgAgAgMAZjAAACS/99Om1Qsz7/ZepBN82J4mTf0NJ+ZV+WlqQZY7JXUctf21yXH3l7FP9+xje9\nvt7/k4xVe1A6Aw9f0PJGaLPBkz+J4qXfWeX1TR72QBTfMdVf5fOGBQdH8fydrvf6DplxYhR3+aH/\nyfFuM5M7tbQxnBkDABAYgzEAAIExGAMAEBhzxpK0185e87Sj/5V300+/NCyKu925vGwpoe2OOXKa\n167Jmif+3fLtvb6nlm8bxV/d8mWv77Tu8RKMjT/ynxJ0w/snRXGn+/2lIVGdlqzcNHQKqdY4PX7i\n0vE/usDr2//C+Jj9Q84Tlk7eKV6m9KDXT/D6uh63OIob1qxRNePMGACAwBiMAQAIjMvUkvT8617z\n6SPjS5erp73q9X20ffz3i7+GDJLijeO38tpHDhgTxbWvzvP6Gj+PL0Xfs/WeXt/ce9+L4t9s8ZLX\nd8O5WasE3d/mVJEgn34Sr/R0zKune32ba26l00m1ulWNXvvoHq/m2dI3css5Xvu52p55tqw+nBkD\nABAYgzEAAIExGAMAEBhzxhtRvyieRzxhztcCZoK2qH9vode2rHZj7sbZX7fgPa/9j3v2i+LffNef\nMx606UdRvLSDfxjlPtEIyVTbdwuv/dyXro7iQ6adWel0Uu+zr+0dxdf/4Uqv76OGeL5+x2vO8vqu\nP+O6KL6kzyyvb9Twb8WNV2aWIs1gODMGACAwBmMAAALjMnUrHXHs81E8+9KAiSCovwx6LIqP7XOU\n11e/+IMKZ4O2+GzfwV67d80mYRJJqbVH+7cKnvnru6P4w4auXt9Pfz0uigdMfMbrm/bN+FbTgzq/\nWcoUE4UzYwAAAmMwBgAgMAZjAAACY864Besbar324T1mRPG8ASO9vvqFiyqSEypj9aD1efumru4U\nxW7N2kqkgxJbvn3+X38Ns3mCU1t02GZwFI+4dLrXd1y3+NbBw/7zfK+v18Rn4/fYeqDXd3jXu6J4\nYb1/TNasip/U1ND6dBOFM2MAAAJjMAYAIDAuU7fkyj5e89AbV0Txj87Y2usb9EsuU1ezhkO/6LX/\ndli88k+N/OmKqxYeFn/dx4uF6rN6hD+9UJ91obPvi9V+0TOMd0+Kn5h2/1b3en3b3HVeFA/7y7PK\nZ9ZP+3ntXTvFU0Lb3P0Dr2/Y3GltyjOJODMGACAwBmMAAAJrcTA2s4Fm9qiZzTKzmWZ2bub1Xmb2\nsJnNy/w3PU95TrFGNYp6pgvHaLpwjLZPhcwZ10u6wDn3spltKuklM3tY0mmSpjrnLjeziyRdJOnC\n8qUaRqf7X/Daj67pHsUHHfWK1/fOLyuRUUm023rmqt1xRBRv+qt3vb7dOsZ/q76w1nl96y7uG8Wm\n4HPG7foYbY0O/baM4qmH+k8OempNjyjeZNLzCqwq69l/1IIoPnH+4V7f8Avi35f+0SStOGWfKP77\nEVfm9MZzxls8Z0XnmFQtnhk75xY7517OxCslzZbUX9Jxkm7JbHaLpOPLlSRKp0Y1op7pwjGaLhyj\n7VOrPk1tZoMl7SZpmqS+zrkNpwQfSOqb52vGSRonSZ3VZWObIBDqmT7UNF2oZ/tR8GBsZt0k3S3p\nPOfcCrP4coFzzplZ7pWHDX3jJY2XpO7Wa6PbVJNznviPKJ52uH85ZfROY6O4ccYbFcupLZJSz89P\n2Ntrd1jdGMWdlnzepvf8eKfuXnvZF/On+ZfjbojifTv5t7PMXh+v9nP6BH/FoIFP+0+WSYKk1DTJ\nXK/4UvSgDv5AdcQz8bE9RK9WLKd8qqGeVtfRa+/b++0ofuFj/9bPj0/ePYo/2tl/nxe/eUUU98h5\netaQyfETnYbf7k8bpklBn6Y2szo1/VDc5py7J/PyEjPrl+nvJ2lpeVJEqVHP9KGm6UI9259CPk1t\nkiZImu2cuyKra7Kk0Zl4tKRJpU8PpeaaPjpBPVOEYzRdOEbbp0IuU+8v6duSXjezDSt//0zS5ZLu\nNLOxkhZI+np5UkQpNTStMkQ904VjNEU4RtunFgdj59xTkvJ9nnxkntdTq9+D8bds1Uh/OuaNH3aL\n4uFjlUgd1EHOucTUs25lvdeeMCGehx/QwZ87qsn6MWz8t5sjClOT86Oc/T7PrvWXvDz/snOieOBN\nyZsj3oBjtHDvnNg7dAotStox2qwaP80utfESo/cN/6e/7e+ae6P4WB/yj+94PcPPeiluNKZ3mVJW\n4AIAIDAGYwAAAuOpTa206d+ei+Ivf/HHXt/Pj/17FN+1y6FeX+Ors8ubWJWqe+Qlr/29E8+M4kU/\n95h5jEsAACAASURBVC9F77xFvNLVLYMfadP+zlq0v9d+4v7donjwpE+8vt7T8z9ZBtWpoVP+6Y2u\nT3atYCbp4Nb6T766fmq86taPv/am1/fQ53VR/N/v+atzrbs0Xhlt+OMv5uwk1XfbRTgzBgAgMAZj\nAAACYzAGACAw5oyLMPSvH3vtB/ffMYpX/X6N17fJERVJqeq5l2ZG8VYn+H3Ls+JjtLvaZrXXGqT4\nlqXG3E2ROgcd/loUf9zo/yxs8eLKSqeTOsPOjT9Tc8S5uzaz5fteqzan3R5xZgwAQGAMxgAABMZl\n6iLkPpnp0wPieBPvoiqAEDoM8Z8cdF7fO6L4imX7+hs//3olUgI2ijNjAAACYzAGACAwBmMAAAJj\nzhhAar15Wn+vvV1dpyj+20z/9riheqUiOQEbw5kxAACBMRgDABAYl6kBtEuu0UKnAEQ4MwYAIDAG\nYwAAAmMwBgAgMHPOVW5nZh9KWiBpc0nLKrbj/JKSh1S5XLZ2zvUpxRslsJ5ScnKpunpKUU1XKRnf\nQyk59ZSqsKYco81KVD0rOhhHOzV70Tm3R8V3nNA8pGTl0lpJyj0puSQlj7ZIUu7kUhpJyj0puSQl\njw24TA0AQGAMxgAABBZqMB4faL+5kpKHlKxcWitJuScll6Tk0RZJyp1cSiNJuScll6TkISnQnDEA\nAIhxmRoAgMAYjAEACKyig7GZjTKzOWY238wuqvC+bzazpWY2I+u1Xmb2sJnNy/y3ZwXyGGhmj5rZ\nLDObaWbnhsqlFELVNCn1zOw3NTXlGKWeJdx3IuqZ2W/ia1qxwdjMaiVdK+lISTtIOsXMdqjU/iVN\nlDQq57WLJE11zg2TNDXTLrd6SRc453aQtI+kszPfhxC5FCVwTScqGfWUUlJTjtEI9SyNiUpGPaVq\nqKlzriL/JO0r6cGs9k8l/bRS+8/sc7CkGVntOZL6ZeJ+kuZUMp/MfidJOjwJuVRbTZNYz2quaeh6\nJrWm1DNd9UxqTSt5mbq/pPey2gszr4XU1zm3OBN/IKlvJXduZoMl7SZpWuhc2ihpNQ3+Pazymiat\nnhLHaDGo50YktaZ8gCvDNf1pVLH7vMysm6S7JZ3nnFsRMpc0CvE9pKblxTGaLhyjvkoOxoskDcxq\nD8i8FtISM+snSZn/Lq3ETs2sTk0/ELc55+4JmUuRklbTYN/DlNQ0afWUOEaLQT2zJL2mlRyMX5A0\nzMyGmFlHSSdLmlzB/W/MZEmjM/FoNc0jlJWZmaQJkmY7564ImUsJJK2mQb6HKapp0uopcYwWg3pm\nVEVNKzxpfpSkuZLelHRxhfd9u6TFktarae5krKTeavoE3TxJj0jqVYE8DlDTpZDXJE3P/DsqRC7V\nXNOk1DNtNeUYpZ5pq2e11JTlMAEACIwPcAEAEBiDMQAAgTEYAwAQGIMxAACBMRgDABAYgzEAAIEx\nGAMAEBiDMQAAgTEYAwAQGIMxAACBMRgDABAYgzEAAIExGAMAEBiDMQAAgTEYAwAQGIMxAACBMRgD\nABAYgzEAAIExGAMAEBiDMQAAgTEYAwAQGIMxAACBMRgDABAYgzEAAIExGAMAEBiDMQAAgTEYAwAQ\nGIMxAACBMRgDABAYgzEAAIExGAMAEBiDMQAAgTEYAwAQGIMxAACBMRgDABAYgzEAAIExGAMAEBiD\nMQAAgTEYAwAQGIMxAACBMRjnMDNnZqvM7L8K3P7SzPbOzDqUOz+0ThvqOdbMPst83dBy54fW4xhN\nF47RJuacC51DopiZkzTMOTc/57XPJW34Zt3hnDsjq3+wpLcl1Tnn6iuXLVqSW08z21zSJEnbSaqV\nNFvSj5xzTzf3dUiOPMforpImSNpeTTUd65ybntU/WByjiZSnnuMlHSxpmKTTnXMTC/m6asaZceF2\ncc51y/w7o+XNkVCfSTpdUh9JPSX9TtI/OGOqXmbWUU1/YP2vmmp6i6RJmddRnV6VdJakl0MnUikM\nxmhXnHNrnHNznHONkkxSg5p+gfcKmxmKcIikDpL+2zm31jl3lZpq+6WgWaHNnHPXOuemSloTOpdK\nYTAu3BNm9oGZ3ZO55IUqZmavqelAnyzpJufc0sApoe12lPSa8+fcXsu8DlQFBuPCHCxpsJrmGd+X\ndB+XNaubc+4LkrpL+qakpwKng+J0k/RpzmufSto0QC5AmzCgFMA590QmXGdm50paoaYPirweLisU\nyzm3RtLtZjbbzKY7514NnRPa5DM1/WGVrbuklQFyAdqEM+O2cWqak0I61EnaJnQSaLOZkr5gZtnH\n5BcyrwNVgcG4BWa2o5ntama1ZtZN0p8kLVLT7ROoMma2j5kdYGYdzWwTM7tQUl9J00LnhjZ7TE0f\nxPuBmXUys3Myr/8rXEooRub47Kymk546M+tsZqker1L9P1cifSX9TU2Xpt9S09zxMc659SGTQpt1\nknStpOVq+qPqKElHO+feD5oV2sw5t07S8ZJOlfSJmm5dOz7zOqrTQ5JWS9pP0vhMfFDQjMqMRT9y\nmNkaSWslXeWc+88Ctr9E0vlq+iXf1TnXUOYU0QptqOcYSX+W1FnSDs65t8qcIlqJYzRdOEabMBgD\nABAYl6kBAAisqMHYzEaZ2Rwzm29mF5UqKYRDTdOFeqYPNU2nNl+mNrNaSXMlHS5poaQXJJ3inJtV\nuvRQSdQ0Xahn+lDT9Cpm0Y+9JM3fMHluZndIOk5S3h+KjtbJdVbXInaJYq3RKq1za/PdI92qmlLP\n8EpZT4maJgHHaLq0UM9IMYNxf0nvZbUXStq7uS/orK7a20YWsUsUa5qb2lx3q2pKPcMrZT0lapoE\nHKPp0kI9I2VfDtPMxkkaJ0md1aXcu0OZUc/0oabpQj2rUzEf4FokaWBWe0DmNY9zbrxzbg/n3B51\n6lTE7lABLdaUelYVjtH04RhNqWIG4xckDTOzIZmHeJ+spsfRoXpR03ShnulDTVOqzZepnXP1mTVg\nH5RUK+lm5xwLs1cxapou1DN9qGl6FTVn7JybImlKiXJBAlDTdKGe6UNN04kVuAAACIzBGACAwBiM\nAQAIjMEYAIDAGIwBAAiMwRgAgMDKvhwmAITy4PvT2/R1py44yGsv2XdFKdJBG9TuOCKK53ynp9fX\nZ/iyKO5x1PyK5VQOnBkDABAYgzEAAIGl+jL1796eFsW7dvIXTB9y33eiuPfz/reh903PljcxtEnN\nrjtE8ZzzOxf8dQP6fhzFR281w+u78ZUDo7jffR29vk3//nIUu/XrCt4fKuvzE/wnCD557Y1Fv+et\nWz/hv/B+HB549pleV5e/TxNKJ/uytCTtd/urUfz33q/n/brb3+jvte884eAobpg9r0TZlQ9nxgAA\nBMZgDABAYAzGAAAElqo54/f+cz+vvWPHl6J4vWvw+uYefUPcd5Tft/aS+ij+4kM/8PrqltRFcdf3\nzevb4ppnWpkxctV07RrFb07Y1ut7cN/ronhAh028vkY1tml/5498I36Pkf577LH1uVG81R+obZLM\n//M+UfzmN25oZsvSy52TPlDxHDLzx8XLvX2puXnibN/adLHX/lvH6hreODMGACAwBmMAAAKrrvP4\nFmz+er3XXtawOu6r3SR380id1eZtzx2V/zaJtW69117y4/o8W0ovrBkYxZfeforXN/DBVVFsz76q\n9uydC3aJ4tcPvDKnt5Py+ahhbRTPq+/m9W1WsyaKR9T5tW7O/2/vzsOjKtI1gL9fSEgAQQlgCFsC\nJEGiI4s4AzKiXmAQhgs6oyJuOKKgogJ6VXDGBUcZR1FmVBwuigL34jLXDVxGVNQBkVVFZJFNdgib\nyL5kqftHmnNOtZ5Op7c6ffr9PY8PVamTPp/5OFS6qqvqaOPIhr4p9oKXLyV6aDqU7d3s6aqCtwwG\n4hPfXT5Bq6fKU8h3xkRERIaxMyYiIjKMnTEREZFhvpozrvX2Iq2+fby9vWHDEFOFnRZfo9Wbnrrf\nKs8oesf1+zIlQ6u3SM9wuRJocYp9usjvb3pGa9v6B3tuu8ec27W2gmu/dn1NP8ofZ5+yc0FnfW79\n3+1escpdHrpNa6u7xZ6vr/nBYq0tvXkzqzz0k0+0tt61D0YeLMWVc544FltcVkfwqU0/2R7TwTl/\n3Wtk+7jFRP7Gd8ZERESGsTMmIiIyzFfD1MFufdDeQemNR57Q2nIcS53SPtR3fFFTN1vl7j1u0dpK\nBtrLZK5uu0Rrm76qk2ss2fWOWOW57V7T2mo4NvIa+Av9NT/vbe80lPkvffjVjyqO2D+n7Kt2a23F\nD9lD+AXPh3+ylsqypyuypDTEleQlLe9ZFdfXb/3azVq9YOQCq7xufLF+cYhhaqJY4DtjIiIiw9gZ\nExERGVZlZywiL4rILhFZ7vhatoh8JCJrA3/WD/Ua5C3Mqb8wn/7DnKaecOaMpwB4FsA0x9dGAZit\nlHpMREYF6vfGPrzonDbNnldc+YD+9zanlj33m95nj9ZW8Zy9PWWtGfpyqZYz7PKixs31tpJlrrFI\npr2VY/+Cq/TGMvvUKNmvL7XJLInLPPEUJEFOy3/cr9ULRixwuRKocWYbq7ypXwOtbeltzwRfbkmD\nPWE/8PveWlvhQyussse35JuCJMhnVXLm19PqoZYTOQUvQ5q3wJ7vdc4DA/pyqYK33P8+NZmj9C8M\nCCuUWJoCH+Q0kVaV6p8HkRPu2xN7UZXvjJVScwD8EPTl/gCmBspTAVwS47gojphTf2E+/Yc5TT2R\nfpo6Ryl18vDIEgA5bheKyBAAQwAgC7UjvB0lQFg5ZT6TBp9R/+Ez6mNRL21SSikRUSHaJwGYBAD1\nJNv1OpOm/+Ilrf7JyiLXa9/ddbZV/vGZFlpbnTd2un6fOm6fKlS+YnV1Q0yoUDn1Sj7XTjlHq799\noX3SS/DJTKGGmMfs7miVD97dRG886D7tkEy8/Iw6h42n5UW2y9aGx9tq9VDDz7XfWhjWazpPYqqK\nPkx+IOzvi0YyPKOJ1v8TfVe+olVLXK70pkg/Tb1TRHIBIPDnrtiFRIYwp/7CfPoPc+pjkXbGMwEM\nCpQHAZgR4lpKDsypvzCf/sOc+lg4S5teATAfQBsR2SoigwE8BqCniKwF0CNQpyTBnPoL8+k/zGnq\nqXLOWCk10KWpe4xjiathr9+o1Vde+6xVbpmepbUNPnUz3DjbJj7cSmv7YIk9n1y2aUtEcSaCH3K6\nuuckrV6BEMdyhbDkB3vef90V+odd2uwvtMpq0zb9fo5tO01LpnyuG99ZqztPPKqO84cNtcrhzgPH\ni7aUCu7z1dWRTDmNtQzRn+XSMGe9G8x3PzUvGXAHLiIiIsPYGRMRERnm61ObnBot1cc6dl511Co7\nT3ACgPnH7WGSxzb10doea/mmVb75tO+1tqeH2dcWTdCaPD1snYxmH9WHlC+qdSii13mnzUyrXNEm\naBGUY9elkdvP15pW/ck+oavmrORaQpFozuVLkQ5L/+SEpRDLl2Ih0jgpMuvH2dMXpepLra0ixOLE\np/edYZUbVOMkNy/iO2MiIiLD2BkTEREZxs6YiIjIsJSZM677qj7H1KfpPVY5a48+n5y90p5/VIu/\n1dpuvH6kVX7hofFa28qr7eVSZx++XWtrMYZzxrE0/hr9GJ1bb7H/Kl961lKtbWzj6Je+jG8yV6sv\nn2ifKDT6miFam8zT75/q5k6IbJtL5zxx8OlL8eCc2waYw3hKy9KXk2a2POhyZWgvvdrLKjfHF1HF\nZBrfGRMRERnGzpiIiMiwlBmmDpb7pPuQRqgNX+pPsT8+f2VffVevb7pMtcrv3/C41jbomzutcq23\nF4UZJblaoJ+oVOgYxVwedGk/nOv6Mkf7/9IqN7xrg9Y2rdU7VjlT9N19zq5pl8dN15fBDB9qnx6T\nisue9OFeINIh30QMTTtFOpye6Dj9QLVtrdW/6jzFUUvN94ip+X9NRETkIeyMiYiIDGNnTEREZFjK\nzhnHwukv6dtoootdbJaut2XevsOuvB3HoKhaas2w5+8PB50Oe+6D9jz/X66ZprX1rr3PKrfN0OeT\nD91+wCpnz4pFlMllezeJ6Pt6NWkf40hCi3Ru23liFADUhtlTo/wgzfG+MNJTm5Id3xkTEREZxs6Y\niIjIMA5TR6HOV/quWv+5up9Vdp4GBACX5NpDYDPRIL6BUUy0GGMvf/vrmmu0tt7jnnH9vvfavWSV\n/9D0cq2tbNv2GEXnXV4+8WjdePt0oEjjrP0Wh6WjtfV+ve48mSl4WNrZtvC4PiXU9LMjMY/NFL4z\nJiIiMoydMRERkWHsjImIiAzjnHEUynaUaHV1v700Y/PLR7W2nnW+s8r//M+RWlvWO9we0+vSj4W/\nvuK70jpWWZWVxSMcz3HOxVZn+0vtZCbEflvJ4OVLkc4TO5czcSlT9FrU31f1RT/jYIV+2lPGD/ac\ncXlUEZnHd8ZERESGsTMmIiIyjMPUMeQ8VP7GNVdrbR8Wv2mV1W279W98B5Qgu249T6sPGva+VX5x\nch+tLfcpe2nT3jP1XYFCuWvlFVY5e+ea6oaYlJrMcQzjDwj/+7p2XmmVd0Z47+Ch6Jb3rLLK0/LC\nP4npuk3drPKGx9tqbVzO5A1bTujLQstX+uf54jtjIiIiw6rsjEWkuYh8KiIrRWSFiAwPfD1bRD4S\nkbWBP+vHP1yKVgUqwHz6C59Rf+EzmprCeWdcBuAupVQxgM4AholIMYBRAGYrpQoBzA7UKTkwn/7C\nZ9R/mM8UU+WcsVJqB4AdgfJBEVkFoCmA/gAuDFw2FcBnAO6NS5Q+c2v+Z1r9JeQl7N5pSINS6ivA\nv/mUjJpaffWz7azymr76Npbzjtnb6x3K1xdHbH7Anl9eNjR4+0v3U2ZqvXBateKNlheeUeec6nX3\ndNPapuXNcf0+rS1op1DnHG7I76vGUqpQr7+zi33alsnlS6nwjKaJvlQw3FObMiTZFzC5q9acsYjk\nA+gAYCGAnMA/AgBQAiAnppFR3DGf/sOc+gvzmTrC7oxF5BQAbwAYoZQ64GxTSikAP7srgogMEZEl\nIrKkFMejCpZih/n0H+bUX5jP1BLW0iYRyUDlX4rpSqmTa3R2ikiuUmqHiOQC2PVz36uUmgRgEgDU\nk+y4HhN9+Pf6EocDefZwR7Op32lt5Xt/iPp+kpmp1Tf+saNVfjjvZa3tuCq1yqM/0U/yKUJid+BK\nlnxGatvITlr9u75/t8oVQdfe8j/2DlB12+u7As2+9AXH9+lD306Xre+l1U+Zv9EqJ2pQzUs5DV4W\nhAnuw9ShhBrejpRzaNo5LO01XspnPFQo0ethntrUOONHra1GsZ3PZF/mFM6nqQXAZACrlFJPOZpm\nAhgUKA8CMCP24VGsqcpfpplPH+Ez6i98RlNTOO+MuwK4FsC3InLykxL3AXgMwD9FZDCATQCucPl+\n8pDyyvdqzKe/8Bn1ET6jqSmcT1N/DkBcmrvHNhyKt3SkQynFfPoIn1F/4TOamny1Hea+NvpH4r8a\nZs8VTrihjdb28eXn2JXd4c8frx9eZJVP7bhHa/u2/bNWuVTps4WP7P6lVS66hac0xZrqYi9fmnzL\n30NcqVt2k71kqeInM8ru88TLT9gTW4f76B+SqTh4MOz7+1Hw1pGtu9nz8pGemhQp56lQAFAwMvYn\nQ1Hi9KilP1t3/66hVW7u9zljIiIiii92xkRERIb5api62dgvtPrng+2DqG+vv1Zru/1jvR6+D11b\nDlXYw5Ud3xmhtRXdyqHpeErfe8gq15XSoNYMROKtQ6db5UdX9tbamt9knzFUcXBvRK+fKpxDw62h\nDxvHYtg61FB0ATgs7UVb383Xv3BneN/XdvZQrd76syOxCcgD+M6YiIjIMHbGREREhrEzJiIiMkwq\ntzhNjHqSrX4lZpbJbX7wPK3+2h/sjW3aZkQ2pzjzsH6c6AuX/9YqV3yzKqLXjLeFajYOqB/c1jBW\ni8l8hlJ/XrZWn5o/y/Xath8PdW07Y6y9XWL56nXRBxYHscwn4N2cppJUeEZTSbj55DtjIiIiw9gZ\nExERGearpU2htBijL3u6e0znONzFm0PTqWZfV31HtX441/XaQnzl2ubfY8yJyGv4zpiIiMgwdsZE\nRESGsTMmIiIyjJ0xERGRYeyMiYiIDGNnTEREZBg7YyIiIsPYGRMRERnGzpiIiMgwdsZERESGJfTU\nJhHZDWATgIYA9iTsxu68EgeQuFjylFKNYvFCHswn4J1Yki6fgJXTw/DGzxDwTj6BJMwpn9GQPJXP\nhHbG1k1FliilOiX8xh6NA/BWLNXlpdi9EotX4oiEl2JnLLHhpdi9EotX4jiJw9RERESGsTMmIiIy\nzFRnPMnQfYN5JQ7AW7FUl5di90osXokjEl6KnbHEhpdi90osXokDgKE5YyIiIrJxmJqIiMiwhHbG\nInKxiKwWkXUiMirB935RRHaJyHLH17JF5CMRWRv4s34C4mguIp+KyEoRWSEiw03FEgumcuqVfAbu\n65uc8hllPmN4b0/kM3Bfz+c0YZ2xiNQAMAFAbwDFAAaKSHGi7g9gCoCLg742CsBspVQhgNmBeryV\nAbhLKVUMoDOAYYGfg4lYomI4p1PgjXwCPskpn1EL8xkbU+CNfALJkFOlVEL+A9AFwCxHfTSA0Ym6\nf+Ce+QCWO+qrAeQGyrkAVicynsB9ZwDo6YVYki2nXsxnMufUdD69mlPm01/59GpOEzlM3RTAFkd9\na+BrJuUopXYEyiUAchJ5cxHJB9ABwELTsUTIazk1/jNM8px6LZ8An9FoMJ8/w6s55Qe4AlTlr0YJ\n+2i5iJwC4A0AI5RSB0zG4kcmfobMaXzxGfUXPqO6RHbG2wA0d9SbBb5m0k4RyQWAwJ+7EnFTEclA\n5V+I6UqpN03GEiWv5dTYz9AnOfVaPgE+o9FgPh28ntNEdsaLARSKSEsRqQngSgAzE3j/nzMTwKBA\neRAq5xHiSkQEwGQAq5RST5mMJQa8llMjP0Mf5dRr+QT4jEaD+QxIipwmeNK8D4A1ANYD+GOC7/0K\ngB0ASlE5dzIYQANUfoJuLYCPAWQnII5fo3IoZBmApYH/+piIJZlz6pV8+i2nfEaZT7/lM1lyyh24\niIiIDOMHuIiIiAxjZ0xERGQYO2MiIiLD2BkTEREZxs6YiIjIMHbGREREhrEzJiIiMoydMRERkWHs\njImIiAxjZ0xERGQYO2MiIiLD2BkTEREZxs6YiIjIMHbGREREhrEzJiIiMoydMRERkWHsjImIiAxj\nZ0xERGQYO2MiIiLD2BkTEREZxs6YiIjIMHbGREREhrEzJiIiMoydMRERkWHsjImIiAxjZ0xERGQY\nO2MiIiLD2BkTEREZxs6YiIjIMHbGREREhrEzJiIiMoydMRERkWHsjImIiAxjZ0xERGQYO2MiIiLD\n2BkTEREZxs6YiIjIMHbGREREhrEzJiIiMoydMRERkWHsjImIiAxjZxxERJSIHBaRR8O8fkzgeiUi\n6fGOj6qH+fSfCHI6WEQOBb6vIN7xUfXwGa0kSinTMXiKiCgAhUqpdUFfOwLg5A/rVaXUjY72fAAb\nAGQopcoSFy1Vhfn0H5ec1gAwBsANAOoCWAfgIqXUj6G+j8wLlRcRuQ7AVAA3KaVecHw9Hz57Rn3z\nW0UCtOND7CvMp7+MAXAegC4ANgM4E8AxoxFRVESkPoD7AKwwHUsisDMmoqQW+Ed7BCp/wdoU+PJy\ngyFRbPwFwNMArjAdSCJwzjh8c0SkRETeDAyRUHJjPv3jFwDKAFwWyOkaERlmOiiKnIj8EkAnABNN\nx5Io7IzDcwGAfABnANgO4F0/fXAgBTGf/tIMwKkAigC0BHAZgIdEpKfRqCgigfn/5wDcppSqMB1P\norAzDoNSao5S6kTgwyDDUfnAtzUcFkWI+fSdo4E/H1ZKHVVKLQPwKoA+BmOiyN0KYJlSaoHpQBKJ\n7wYiowCI6SAoZpjP5LYs8KdzaQiXiSSv7gAuEJGTv0xlA+ggIu2VUrcZjCuu2BlXQUTOBJAB4FsA\ntQA8AmAbgFUm46LIMJ/+o5RaLyJzAfxRRO4A0ArAlQAGmo2MInQ9gCxH/U0ArwOYbCSaBOEwddVy\nALwG4ACA71E519hXKVVqMiiKGPPpTwMB5AHYC+A9APcrpWabDYkioZT6USlVcvI/ACcAHFBK7Tcd\nWzxx048gInIMwHEATyul7g/j+gcB3AkgE0AdpVR5nEOkamA+/SeCnP4BwHhUvtsqVkp9H+cQqRr4\njFZiZ0xERGQYh6mJiIgMi6ozFpGLRWS1iKwTkVGxCorMYU79hfn0H+bUnyIepg4szF4DoCeArQAW\nAxiolFoZu/AokZhTf2E+/Yc59a9oljb9EsC6kx+GEJFXAfQH4PqXoqZkqizUieKWFK1jOIwT6rjb\nmtpq5ZT5NC+W+QSYUy/gM+ovVeTTEk1n3BTAFkd9K4BfBV8kIkMADAGALNTGr6R7FLekaC0Mvdqj\nypwyn94SbT4B5tRr+Iz6SxX5tMT9A1xKqUlKqU5KqU4ZyIz37SjOmE//YU79hflMTtF0xtsANHfU\nmwW+RsmLOfUX5tN/mFOfiqYzXgygUERaikhNVG4/NzM2YZEhzKm/MJ/+w5z6VMRzxkqpMhG5DcAs\nADUAvKiUWhGzyCjhmFN/YT79hzn1r6gOilBKvQ/g/RjFQh7AnPpLKubzyKX255nmTvhvra31azdb\n5YKRyXlCXyrmNBVwBy4iIiLD2BkTEREZxvOMiSipOYelgZ8OTRMlA74zJiIiMoydMRERkWHsjImI\niAzjnHEUNjzWRavPuPJJq1yUkaW1/WbVJVY5vcfm+AZGlEK2d6tyD35LkzmRnVJHFG98Z0xERGQY\nO2MiIiLDOExdhbSzz9DqjSfZe7K/33yC1nZc2T/OfRVHtbZLcr+xyu+ifixDJEo568Z3tsrrB0x0\nve66Td20eu23FsYtJr+Sc87U6je88q5VvrTOD1pb9+WXWeVavTbENzCf4TtjIiIiw9gZExER3aKF\nhAAAEYdJREFUGcbOmIiIyDDOGQPYf3VnrZ41qMQqv952stZ2apq9ZOnhPWdrbe8+Z89PHW2kL7e4\nZeB7UcdJlKqCt7wMNU/stLPLgXiEk1LWDDpFq/evs8cqVwRd+9FZ/7TKfS8YorWl/fvrmMeW3rSJ\nVS75bZ7rdQ0nzY/5vWON74yJiIgMY2dMRERkWMoMU5f2OEerl9x83Cov6vw3rS1TMqzy/ON1tLZB\nH9pDL2fctUJra3jYHgo5fJk+rPbUgp5WuQhLwg2b4sy5bKO8dk3X64401tv2DzwU3uuLvuPTod32\n36e2o9fr12bYf+9OFDbR2tLmxn6Iz+ucQ9PVOYnp/GFDrXJtcClTtP7W+38i+r5RL07T6k9d2Nsq\nl23ZGtFrOoelAeDEtBpW+Ysznnb9vjPaD9Prdy6zyhXHjkUUS6zxnTEREZFh7IyJiIgMY2dMRERk\nmK/njGvknG6V88eu1No+ajrPKu8qL9PaOn5hzwu3HntCaytatsgqB3+s36nO6/pcVdHrVYZLUXDO\nLwZveai6trfKG/SpI7zX1d7SNC9dnxdOc/yuWhEy2+7Sgn7fdb7OA+eeq7Vlpx+2yiOy39Xa+jXV\nr00F4Z7GxC0vvalblv5v55NZ7p/JCFfw8qVQ88ROa/r/Q6sXH7zNKre61xvLnvjOmIiIyDB2xkRE\nRIb5epi6okWOVX6u6Qda28ayI1a538R7tLaWf/nCfo04xUbVt/3u86zygGs/0dqG1R9vlf8xpoPW\n1qeuvSymbc3g3z+jHzqL1MOnL3ZtazfvBq2eh2/jHY7ndO28suqLAMxbUKzVC7AgHuGQj9Qr3ms6\nhJ/gO2MiIiLDquyMReRFEdklIssdX8sWkY9EZG3gTx7Qm0SYU39hPv2HOU094bwzngLg4qCvjQIw\nWylVCGB2oE7JYwqYUz+ZAubTb6aAOU0pVc4ZK6XmiEh+0Jf7A7gwUJ4K4DMA98YwrpioUbLPKn9w\ntLbWdrjC/qUy7/92aG3l8Q3LuGTJqerSTqvPvuMJq3xqWvBcr72V5N0N9LnGCo/OxtxXom+Z2jhz\nv1VuffePWpu++E6XLPmsrml5c8K6rmCk/+aIvZTTMeMGafXeDzwb1vdlSA2tvnu83d1k940+LuCn\nSwfDjaVfC2vAAYtaFWltZd9vjDquSET6r1SOUupkD1YCICfUxZQUmFN/YT79hzn1sajfMiilFADl\n1i4iQ0RkiYgsKcVxt8vIQ0LllPlMPnxG/YfPqP9EurRpp4jkKqV2iEgugF1uFyqlJgGYBAD1JNv1\nH4R4cJ4M8qcVl2htSzq9bJU3vLVca/vgvy6wyjVnpcwJS2Hl1GQ+07Sy+++RwUNSpWFGuei4vuPT\nDS8Pc7lSV/DfW7R6+CfS6AvnlqOuo6a/ZgSS4hl1Wje+c9BXlrpem6InM5l5RoNeIdzd6IKfu4oY\n/M2qu0WfsPnS8btGh0z3uIJjGdXwG6t8ceF5WlvNJBumngng5ETCIAAzYhMOGcSc+gvz6T/MqY+F\ns7TpFQDzAbQRka0iMhjAYwB6ishaAD0CdUoSzKm/MJ/+w5ymnnA+TT3Qpal7jGOhBGFO/YX59B/m\nNPX4ejtMp8ZX6XNwAz74jVV+pdUsrW3wC/Zc1W++1rclPP3P9pIatTj1tihMJJn/jVa/8fvfWeXX\nCt4Nvtzyk7mqMOe4xl70O62evym801xCLTui8K0fMDHsa+NxMlPO/Hqubc4tN/24lCpZZP5L30L2\nf/fa870dmnwe0Wvub5mh1RtF9CrR8+YCTCIiohTCzpiIiMiwlBmmrjh8WKsfuTTLKrd56iatbXX3\n563ywnNe1trwtl0smnGL1tTyTXvvroyPv4w0VHJx6KGmVnnQI720tqn5s4Ivr7b6rxzU6j/c1MYq\nl69YHfXrk3lHLrV3PdveTV/KNisvxDC5YzewXiPbxzyuVHBarWNWOT2vudZWtinqpXwRO/2KzVpd\nhT9bElN8Z0xERGQYO2MiIiLD2BkTEREZljJzxsHK9+y1yoXX7dXa+hfbS/zqPb9Ha3u42TtWecMl\nk7S2sb+25xgnf3yR1tbmH/bOdeVrv48gYqrx6VdWuWTsuVpbxxuut8pLO0+L6PUn532k1ds9aC9r\ny7siopekKuhbYLpvf9n6tZu1egEiW17U8p5VVnlumKdCUWy83/YNq/zp7FO0tls+uc79G51T+0HL\nFkfWj+xZdzr+11ytXhPbon7NSPCdMRERkWHsjImIiAxL2WHqUMpXrrHK+7rqbSPaXm+V117fUGv7\n8MonrPLdA/QD7qf1tpflTHz8Uq0t+6XwdnoiW+Z7+k48zd6zy/3Oulpr2/igvcPO0vNeDPseX503\n2Sqf+dxtWlvRrYvCfh2KXqS7XgXvqjWNQ9PVp68AC3limlOo09O61zqita35rft6IufrlKpy1+tC\nvbcMeZKbBP0PGsJ3xkRERIaxMyYiIjKMnTEREZFhnDOupvJVa61yq3vXam23vjLEKu99tFRrm9f+\nVat83SPPam0dG9xulZuM+yImcaayiuXfafUWl9vlsx+5Q2t7+5onrXJBRqbWlplmzzMN/rU+1zgX\nWaDEcW5jCYR/ahPniKNXd7N+LtmXx+1yh0z3E9EiPT0t1OvE4jWCX6fdo19rbWu+b22Vy9esj+h+\nkeA7YyIiIsPYGRMRERnGYeoYqlhqL2dq8Ht9GLPNX4dZ5dWXTdDanrjZXkLzzGs9tbayLVtjGaLn\n1WhkH+393QOttLbC26M/UD7/T/oysts+sacIXnjp71pbs/RaVrlv3W+0tmljR1jllvdxaVqkmsxx\njB8OcL/OuXMWAOx8y/3acHf1qo7rNnVz1A7E5DWTRea/9GWED1xt70y3cbg+/vvt+ZORbP7aWH9+\nz77W3t0v/34OUxMREaUMdsZERESGsTMmIiIyjHPGcVJx7JhWb/u3HVZ5Xt8Mra1nraNW+W85p+kv\nlGJzxhuHFlrlD/o9obVdtfS/rHKDyZHN06Y3baLV6/95g1Vukp4ZfLmlbU3999ayOsrlSqoObYnS\nBPfrfrJEabtdDD7Raf0A960VI7Xh8bZWuTai/+xCMpP59ucnClbo2412HXBH8OU/62ALvT52wHTX\nazPEXlo1/POBWtvCHk9b5VPTaoZ176qU1TXzbPOdMRERkWHsjImIiAzz9TB1jXr2EIpq1Uxrcy5D\nSoSDZ+dY5fOz9B1tagh/JzrpxRuescp56fqw0++Gf2KV572Xr7WVley0yjvvOE9rS+ux1yrf1eZj\nre2yU0oiivOs9hut8nH3y6gaejVpr9WdJy6F2kkrHsPS5w8bqtXD3fEr1ZQf0Jd5NXg+vOmjBkH1\nSfe3+tnrghXhS63+8OL/sMpPNvk8rNcI9vqhxlq9cOpBq5zIAWv2AkRERIZV2RmLSHMR+VREVorI\nChEZHvh6toh8JCJrA3/Wj3+4FK0KVID59Bc+o/7CZzQ1hfPOuAzAXUqpYgCdAQwTkWIAowDMVkoV\nApgdqFNyYD79hc+o/zCfKabKOWOl1A4AOwLlgyKyCkBTAP0BXBi4bCqAzwDcG5coI7TzyjOt8sH/\nOKy1tbwyvvdW57XT6n968iWrXBE0EzH9QEOrXGPnj1qbPrscvTSkQSn1FeDNfJ7jWF0UfD7LXQ2W\nW+Ue85drbUcq7G/smqXPK0V60ovTwuP6crSjD+Ra5TRENu8cK8n8jIbiXE503T16WzxOY3LOWZtc\nvuT1Z9RL0sR+ttNCvLfMkBpa3XmKk3PpVOCFjKjWbUUkH0AHAAsB5AT+EQCAEgA5Lt9GHsV8+g9z\n6i/MZ+oIuzMWkVMAvAFghFJK+widUkrB5YNnIjJERJaIyJJSfu7UM5hP/2FO/YX5TC1hLW0SkQxU\n/qWYrpR6M/DlnSKSq5TaISK5AHb93PcqpSYBmAQA9SQ7oVubZP1o3+6+jm9rbfc9erVVbj1OP4y+\nfN++sF4/eDenkr55VvnxeyZpbd2yTri+zrjnr7DKuVu+COve0fByPs94zT7d6vPLxmltDWvYpyh1\n+MlmO6VWKdSQVHXMP26/zqOt9GU3afg6+HKjvJzTSDmXEwWf0tQLdj70U5p0wcuenKcv7ezi3dOX\n/JjPeHjvu7Os8hO57v92Bv8b4Jy66l9nj9b2eEd7SV0DfcYrrsL5NLUAmAxglVLqKUfTTACDAuVB\nAGbEPjyKNVX5yzTz6SN8Rv2Fz2hqCuedcVcA1wL4VkROHg56H4DHAPxTRAYD2ATgCpfvJw8pRznA\nfPoNn1Ef4TOamsL5NPXnAMSluXtsw6F4S0c6lFLMp4/wGfUXPqOpydfbYZ42d6NVXn5U3w5z5fX2\nETGfXakvW/n0YLFV7nfqV66vX1dKtXpBhvupP875x2ETb9Xamk20T0GJfhFOciu4c4FV7pmvb0n4\n5a+mhPUaoeaHgr2w396Gr3VNfQrulg8HWeUiLArr3pR4BSMXuLb1Gtk+6CvenSem6ms+3dGFXWQu\njljgdphERESGsTMmIiIyzNfD1GU77J2RFvUv0NraDr3AKr818Cmt7cFGSx01999X0pCl1f+y1x7e\nfvMf+phJ44/tU4WarNU/gp/qQ9NumozT/3p26jrcKrfs+73W1qfRt1b5g91naW3Llra0ymkN9XWX\nRXdssiuN9dOeilZwaJrIy+os22aVR24/X2sb32RuWK/hnKoCgNP/bU9XlUcRW3XxnTEREZFh7IyJ\niIgMY2dMRERkmK/njJ3KNm7W6i1H2/U7R3eJ+f0aYb5WT+Tcg1/IF99o9SaOqfbjT+jXvtO8g1Uu\n27JVayvETrjR8rL3h+qGSEQGlW3bbpXnT9U/84HR7nPGf97d0Sq/P/HXWlujNfODL08IvjMmIiIy\njJ0xERGRYSkzTE3+Fjw0TUSp5fRn9SWj/Z49N6zvC55SNIXvjImIiAxjZ0xERGQYO2MiIiLD2BkT\nEREZxs6YiIjIMHbGREREhrEzJiIiMoydMRERkWHsjImIiAxjZ0xERGSYKKUSdzOR3QA2AWgIYE/C\nbuzOK3EAiYslTynVKBYv5MF8At6JJenyCVg5PQxv/AwB7+QTSMKc8hkNyVP5TGhnbN1UZIlSqlPC\nb+zROABvxVJdXordK7F4JY5IeCl2xhIbXordK7F4JY6TOExNRERkGDtjIiIiw0x1xpMM3TeYV+IA\nvBVLdXkpdq/E4pU4IuGl2BlLbHgpdq/E4pU4ABiaMyYiIiIbh6mJiIgMS2hnLCIXi8hqEVknIqMS\nfO8XRWSXiCx3fC1bRD4SkbWBP+snII7mIvKpiKwUkRUiMtxULLFgKqdeyWfgvr7JKZ9R5jOG9/ZE\nPgP39XxOE9YZi0gNABMA9AZQDGCgiBQn6v4ApgC4OOhrowDMVkoVApgdqMdbGYC7lFLFADoDGBb4\nOZiIJSqGczoF3sgn4JOc8hm1MJ+xMQXeyCeQDDlVSiXkPwBdAMxy1EcDGJ2o+wfumQ9guaO+GkBu\noJwLYHUi4wncdwaAnl6IJdly6sV8JnNOTefTqzllPv2VT6/mNJHD1E0BbHHUtwa+ZlKOUmpHoFwC\nICeRNxeRfAAdACw0HUuEvJZT4z/DJM+p1/IJ8BmNBvP5M7yaU36AK0BV/mqUsI+Wi8gpAN4AMEIp\ndcBkLH5k4mfInMYXn1F/4TOqS2RnvA1Ac0e9WeBrJu0UkVwACPy5KxE3FZEMVP6FmK6UetNkLFHy\nWk6N/Qx9klOv5RPgMxoN5tPB6zlNZGe8GEChiLQUkZoArgQwM4H3/zkzAQwKlAehch4hrkREAEwG\nsEop9ZTJWGLAazk18jP0UU69lk+Az2g0mM+ApMhpgifN+wBYA2A9gD8m+N6vANgBoBSVcyeDATRA\n5Sfo1gL4GEB2AuL4NSqHQpYBWBr4r4+JWJI5p17Jp99yymeU+fRbPpMlp9yBi4iIyDB+gIuIiMgw\ndsZERESGsTMmIiIyjJ0xERGRYeyMiYiIDGNnTEREZBg7YyIiIsPYGRMRERn2/15Eq87eY5CpAAAA\nAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f82b81db4a8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"def show_examples(size, width):\n",
" # Calc the depth needed\n",
" depth = int(size/width)\n",
" # Load the images and labels\n",
" images, labels = mnist.test.next_batch(depth*width)\n",
" # Config Subplot\n",
" f, axarr = plt.subplots(depth, width)\n",
" for d in range(depth):\n",
" for i in range(width):\n",
" axarr[d,i].imshow(images[d * width + i].reshape(28,28))\n",
" # Fine the index where value is 1\n",
" axarr[d,i].set_title(np.where(labels[d*width+i]==1)[0])\n",
" axarr[d,i].set_axis_off\n",
" f.set_size_inches(width*2, depth*3)\n",
" return\n",
"show_examples(20,4)"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"### 1.2 Prep for test set embeddings"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"LOG_DIR = 'tmp/tb/1'"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"# 2. Modelling "
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": true,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"n_features = 28*28\n",
"# Four Layer the autoencoder\n",
"#dimensions = [512, 256, 128, 64, 2]\n",
"dimensions = [512, 256, 128, 64]\n",
"learning_rate = 1e-4"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"### 2.1 Define the graph"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"tf.reset_default_graph()\n",
"\n",
"\n",
"##\n",
"x = tf.placeholder(tf.float32, [None, n_features], name='input')\n",
"\n",
"current_input = x\n",
"n_input = n_features\n",
"\n",
"ws = [] # list of all the weights \n",
"\n",
"# Building the Encoder\n",
"for layer_i, n_output in enumerate(dimensions):\n",
" #print('Creating weights with {} by {}' .format(n_input, n_output))\n",
" layer_name = 'encode_layer' + str(layer_i)\n",
" with tf.name_scope(layer_name):\n",
" w = tf.Variable(tf.truncated_normal([n_input, n_output], stddev=0.1), tf.float32, name='w')\n",
" h = tf.nn.relu(tf.matmul(current_input, w))\n",
" # Tensorboard Recording\n",
" tf.summary.histogram('weights', w)\n",
" tf.summary.histogram('activation', h)\n",
" ws.append(w)\n",
" current_input = h\n",
" n_input = n_output\n",
" \n",
" \n",
"\n",
"z = tf.identity(current_input, 'inner')\n",
"## Test \n",
"#embedding = tf.Variable(mnist.test.images, name = 'test_embedding')\n",
"\n",
"\n",
"## Building the Decoder \n",
"wd = ws[::-1] # Reverse the weights \n",
"dimensions_d = dimensions[::-1][1:] + [n_features]\n",
"\n",
"for layer_i, n_output in enumerate(dimensions_d):\n",
" layer_name = 'decode_layer' + str(layer_i)\n",
" with tf.name_scope(layer_name):\n",
" w = tf.transpose(wd[layer_i], name='w')\n",
" h = tf.nn.relu(tf.matmul(current_input, w))\n",
" # TB summary\n",
" tf.summary.histogram('weights', w)\n",
" tf.summary.histogram('activation', h)\n",
" current_input = h\n",
" n_input = n_output\n",
" \n",
" \n",
"y = current_input\n",
"y = tf.identity(y, 'output')\n",
"\n",
"\n",
"## Measure output performance and optimiser\n",
"with tf.name_scope('Cost'):\n",
" cost = tf.reduce_mean(tf.squared_difference(x, y), 1)\n",
" cost = tf.reduce_mean(cost)\n",
" tf.summary.scalar('Cost', cost)\n",
" \n",
"with tf.name_scope('Training'):\n",
" optimizer = tf.train.AdamOptimizer(learning_rate).minimize(cost)"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"### 2.2 Training"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true,
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Epoch: 0 Cost: 0.18830522894859314\n",
"Epoch: 1 Cost: 0.0434880293905735\n",
"Epoch: 2 Cost: 0.02912084572017193\n",
"Epoch: 3 Cost: 0.02431577816605568\n",
"Epoch: 4 Cost: 0.020580973476171494\n",
"Epoch: 5 Cost: 0.01844988390803337\n"
]
}
],
"source": [
"batch_size = 128\n",
"n_epoch = 5\n",
"epoch_cycle = 500\n",
"n_iter = n_epoch * epoch_cycle\n",
"\n",
"sess = tf.InteractiveSession()\n",
"tf.global_variables_initializer().run()\n",
"\n",
"\n",
"#tf.summary.image('input_images', mnist.train.images, 10)\n",
"# Image must be a 4d tensor? what? \n",
"#saver = tf.train.Saver([z])\n",
"merged_summary = tf.summary.merge_all()\n",
"writer = tf.summary.FileWriter(LOG_DIR)\n",
"writer.add_graph(sess.graph)\n",
"\n",
"for it in range(n_iter+1):\n",
" batch_x,_ = mnist.test.next_batch(batch_size)\n",
" optimizer.run(feed_dict={x:batch_x})\n",
" \n",
" if it % epoch_cycle == 0:\n",
" epoch_value = int(it/epoch_cycle)\n",
" cost_value = cost.eval(feed_dict={x:batch_x})\n",
" print('Epoch: {} Cost: {}' .format(epoch_value, cost_value))\n",
" \n",
" # Record variables and write to disk\n",
" if it % 10 ==0:\n",
" s = sess.run(merged_summary, feed_dict={x:batch_x})\n",
" writer.add_summary(s, it)"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"# 3. Reporting"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"### 3.1 Cost of test set"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Cost of test set: 0.018090857192873955\n",
"Test to Train ratio: 0.9805404543876648\n"
]
}
],
"source": [
"test_x = mnist.test.images\n",
"test_cost = cost.eval(feed_dict={x:test_x})\n",
"print('Cost of test set: {}'.format(test_cost))\n",
"print('Test to Train ratio: {}'.format(test_cost/cost_value))"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"### 3.2 Visual Inspection"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"test_out = y.eval(feed_dict={x:test_x})"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.image.AxesImage at 0x7f82aa708cf8>"
]
},
"execution_count": 17,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXQAAAC7CAYAAAB1qmWGAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAFQdJREFUeJzt3XmQleWVBvDn9AKN7M0O3WwKKHEBacCIJhiIUUcHmaTc\nZqaIZUKYjI5WnKpQTCVqYlJq4lIZt6AyYI0jY0ZUoiaKyCBGaWyQrdltISzN1iCr9HbP/NGXqZZz\nGm73Xfp+L8+viuru0+fe773Ny+mP+26iqiAioujLae0GEBFRarCgExEFggWdiCgQLOhERIFgQSci\nCgQLOhFRIFjQiYgCwYJORBSIpAq6iFwjIhtFZIuITE9Vo4haG/s2RZG0dKWoiOQC2ATg2wB2APgE\nwK2qui51zSPKPPZtiqq8JB47BsAWVa0AABGZC2ASgCY7fRtpqwVon8QliZp2AsdQo9WSgqdi36as\nkmjfTqag9wOwvdHXOwCMPd0DCtAeY2VCEpckalqpLkzVU7FvU1ZJtG8nU9ATIiJTAUwFgAKck+7L\nEWUM+zZlm2QGRXcCKG70dVE89hWqOlNVS1S1JB9tk7gcUcawb1MkJVPQPwEwREQGiUgbALcAmJ+a\nZhG1KvZtiqQWv+WiqnUicieAdwDkApilquUpaxlRK2HfpqhK6j10VX0bwNspagtR1mDfpijiSlEi\nokCwoBMRBYIFnYgoECzoRESBYEEnIgoECzoRUSBY0ImIAsGCTkQUCBZ0IqJAsKATEQWCBZ2IKBAs\n6EREgWBBJyIKBAs6EVEg0n4EHaVebo8eJrb+wYFurrSrT/h5z3vG5uat3+rm1n9xKOHnJUpG7cRR\nbnzfSHtKVEGVurm51TZeuGyvm6tt25hYbO2G0zUxa/AOnYgoECzoRESBYEEnIgoECzoRUSCSGhQV\nka0AjgCoB1CnqiWpaBQ1qL/qUjfe/oHtJrbh3KeTvl7OBPv7/cpVN7u5nX450MTk41VJtyFbsG+n\nTm73biZWN6TIzd12/TkmVtO3xs2dONz2t2k9F7m5K0/0N7EHP7rezR0wT0ysTcdL3Nxs6/OpmOVy\nlaruT8HzEGUb9m2KFL7lQkQUiGQLugJ4V0SWi8jUVDSIKEuwb1PkJPuWyxWqulNEegJYICIbVPWD\nxgnxfwxTAaAA9v0xoizFvk2Rk9QduqrujH/cC+A1AGOcnJmqWqKqJfmwK7uIshH7NkVRi+/QRaQ9\ngBxVPRL//GoAv0hZy0KQk+uG84r7mljFlGITe/8Hj7iPL8zNXPFYfMnLbnzX3GoTm/D6v7q5Q+5e\nmtI2pRv79pnVj/dnYB0aZPvmweE2r+3gw+7j646fMLFbL1zu5u6p7mRio5xl+wDQJWeLiX126TI3\nd+6Jr5vYsOdq3dy6K0eaWM6ST93cTEjmLZdeAF4TkZPP81+q+ueUtIqodbFvUyS1uKCragUAf3Im\nUYSxb1NUcdoiEVEgWNCJiALB/dBTJG+AHdTceKe/vLn8tt8l9Jw5aOfGH9x/sYltPtrTzR3Swe75\nPKP7yoSufzp98+zg1+wbnnVzH3rquyZWv+mzpNtAmXHgdjtI+MUwP3f0lXbf8BjsUvpNVXZPfwDI\n6xgzsf/50zj/YvZpMajwAjf1vm++YWI/7vaRm/veQPviNkzr6uYOe/64ifk7smcG79CJiALBgk5E\nFAgWdCKiQLCgExEFggWdiCgQnOXSTHl9ervxIfMqTWxe73lJXau8ps6Nl35/hInpp+Vu7hddupvY\n5Tf/i5u79OdPNqN11ti2/vLoo/9uZy60+05Sl6I0OHrTZW688B/sgSpDCo4l/Lz9Cr4wsYPt/c3M\nquba2WJF7+1yc+u7dTQxqbN9DQAeaHODiW0Z6S/9v2WA3WpgZ+8ubu7aaf71Wgvv0ImIAsGCTkQU\nCBZ0IqJAsKATEQVCVDO3ULWTFOpYmZCx6yXLW/K89MGn3NxYGhb8XrN+shvPm/jXlF8LAIqWdjCx\nZ4sXp+Va1/cblfLnLNWFOKwHnAXh6Ze1fbuJPflrv2UH1ns/UOHmts+rMbFjdf6+48ed+Oq1A02s\nQ4XfrqI/2TO569dtcnObQ8fZ17v5dn9OyMPf+IOJvTB0UMLXymnf3o3HjiU+kHyqRPs279CJiALB\ngk5EFAgWdCKiQLCgExEF4owFXURmicheEVnbKFYoIgtEZHP8o79ZMFEWY9+m0CSy9H82gCcBvNgo\nNh3AQlV9SESmx7/+aeqblxmxb9qTuwHglft/Y3ObOHQihsSXAH9t7l0m1neJszz+dX9pcrpseOxC\nE4s9viijbciw2Qi8bx++ZbQbP1pk7+Umd/FnuZyTU21iv6+40s099hd7cMU59TavV9mX7uNjm/w2\nJEv+Yg91yfmev9VBv7yDJnbZKv+wmuUH+5tY7Xi7DUimnPEOXVU/AHDglPAkAHPin88BcGOK20WU\nduzbFJqWvofeS1VP/hraDaBXitpD1NrYtymykh4U1YaVSU2uqhGRqSJSJiJltbD/dSPKVuzbFDUt\nLeh7RKQPAMQ/2pOI41R1pqqWqGpJPuzBwkRZhn2bIqul+6HPBzAFwEPxj/ZI7SxVdYddzj/rZ4+7\nud7J9s0xfvUtbnzIz1abWOy4PT0807qU7jSx1472dHMnd2iyzkVdZPv2se+ONbGqi/zV4rH+dlBy\nxRE7wAcA5VX2DIDjS+zgJwB0qbCD+20O21HRnMWfuo9P10YkeYMH2tgx/2fzi8GXNuOZW28A1JPI\ntMWXAXwMYJiI7BCRO9DQ2b8tIpsBTIx/TRQp7NsUmjPeoavqrU18Kwt3IiJKHPs2hYYrRYmIAsGC\nTkQUCBZ0IqJAtHSWS9ar+qGdzQIAb//8tybWOcffrL85vOX83mwWIDtmtHjqttnT3d+susTNndxh\nQbqbQ81UdZE9NKLvqF1u7qhu9pCUd/96vpv7ZUUnEytaVevmttt11MRkp50R5ewGkFYnBnUzMRlq\n2woA15fbpf/HY36NKD040MSOfWNf8xqXQrxDJyIKBAs6EVEgWNCJiALBgk5EFIggBkXz+tilyVN/\n4q/Ybs4A6KNVdn/wV5/6lps79L/XmVh9lg5+UrRVX+vvcZ578SET27HPP5/j3E777fNu6OzmDnzX\nbjyWu2iFm5v4qQDpEbvSP9tg3yV2G48R/T53c9vm2AHfE+qXyg177WacxeCgKBERJYkFnYgoECzo\nRESBYEEnIgpEEIOi6x/ua2Kvd3qriWz7O6yy3j+w9vXH7ABo99kfu7mZXvmWDhWP2NW1bw54sons\nxO8FymvqWtgi8hy4IN+N9+/qrHDs4E8CeH+tXRU65I/+IL58tKoZrWtducvs5AQAOD7JDpZuqvL3\ndB/VeZuJPV8+zs2NbWvfjNalH+/QiYgCwYJORBQIFnQiokCwoBMRBSKRM0VnicheEVnbKHa/iOwU\nkZXxP9elt5lEqce+TaFJZJbLbABPAnjxlPjjqmo3F28FFw6wez7HmrEIefr2G9x41yZmtERdzojh\nbnzd39sZLc35OZZW+7Mv7p/2IxPLR1nCz5tGs5HlfdvT47odbrz+KvvvYPvjl7m5A96187JylpW7\nudqMtrW2L6/29++vL7QzrXq0P+bmfv6lnf1SU1Xg5vZanV0/nTPeoavqBwAOZKAtRBnFvk2hSeY9\n9DtFZHX8v63+DkBE0cS+TZHU0oL+DIBzAYwAUAng0aYSRWSqiJSJSFkt7K5tRFmGfZsiq0UFXVX3\nqGq9qsYAPAdgzGlyZ6pqiaqW5MNuYUmUTdi3KcpatPRfRPqoamX8y8kA1p4uP91ePc8u829qKK9e\n7SDGxhf9w3G7I0KDojn2gGAAOHSb3Tv7pV81Nd7XLuHLeT/H2+dPc3PPe3dpws/b2rKtb3vyJtoD\nngGg18f2MOetC8XNLdhnt7vQusxt0ZDbybYVAOQc2wfrdu9xc2NXjDCx7RP9e9TRQz8zsTY5/oYd\nSysHmFj+Yf/fV+f/zK4accaCLiIvAxgPoLuI7ABwH4DxIjICDQPgWwHYaQxEWY59m0JzxoKuqrc6\n4RfS0BaijGLfptBwpSgRUSBY0ImIAsGCTkQUiCAOuGiO0aW3m1jR77NrpPpM8gYUm9jGO4vc3PLb\nfudEk59i5/0cz7snOrNZomz0Sn92RsUxOxOj7UF/louWZW7yTt7A/jZYXePmHrrczjCpKxjk5u7/\nmxMmdnG/z93cjnl2nUDpLnstAKhdb2fgFC3y25tteIdORBQIFnQiokCwoBMRBYIFnYgoEGfdoGj1\n1o6t3YSEbf+3y9341X+3zMTm9Z6XljZMWHOzGx8www4y+UN1lIwtT9j9zDsf3ezmllXYQb7OdoV/\nWuV26WxiNcXdTKzycn+bibr2dkuJwVduc3OHFhw1sXa5tW7u1iO2DXVrbFsBoP+C4yaW8+FKNzfb\n8A6diCgQLOhERIFgQSciCgQLOhFRIFjQiYgCEcQslxx4y5v931WTxtsZIkumfN3N7faHVSYWO25H\nwJsiJRe68SODO5jY0J/YE9ff6f+0+/ha9eaTJP+7edi8H5vYkLtK3VzOaMkMbzuFH2yxfQUADl3x\nNRPb+qDft2WUzdXl/vN6h6dUf+dSN3XvpfkmVtPVHjdT38E/TGPauEUmdm3HNW7uO0fta5i90c4K\nAoDYKjujpXiRPwUoKjNaPLxDJyIKBAs6EVEgWNCJiAJxxoIuIsUiskhE1olIuYjcHY8XisgCEdkc\n/9g1/c0lSh32bQqNqHN6+1cSRPoA6KOqK0SkI4DlAG4E8H0AB1T1IRGZDqCrqv70dM/VSQp1rExI\nTcsbeXPnchOLwQ7ENNeM3WNNbF+NHdAEgJja341PFL/l5nbMaZPQ9XOa+H3bnNdWWm0Hqe795T+5\nuYX/Ea194U9VqgtxWA/4G4A7otC3Nz09xsQuuGCHm9vdWQr/yQ5/z++8ZXYLjHb7/FpwvLf9kcrY\nL9zcu87/XxO7o5Nt79Y6f3LB5lq7RP/Xn13n5m6v6GFiXVfZAVwA6PHs2dG3z3iHrqqVqroi/vkR\nAOsB9AMwCcCceNocNPxDIIoM9m0KTbPeQxeRgQBGAigF0EtVK+Pf2g2gV0pbRpRB7NsUgoQLuoh0\nAPAqgHtU9XDj72nD+zbu/9dEZKqIlIlIWS3sDn1ErY19m0KRUEEXkXw0dPiXVPXkPq174u9Bnnwv\ncq/3WFWdqaolqlqSn4KzLIlSiX2bQpLILBcB8AKA9ar6WKNvzQcwJf75FABvpL55ROnDvk2hSWSW\nyxUAlgBYA/z/9IoZaHiv8RUA/QFsA3CTqh443XOlaybAw5/b5ekXtEnPFPtUzDxJ9lrlNXbZ9Pfm\n3e3mDn2kwsTq97g3nJHXglkuWd+3PUf/PNiNX97Tnni/+mA/N3dblZ2J2a/wkJubn2M3ephWvNjN\nrVE7yyTXecdq8eFh7uPf2mC3y+j1pv+/n66Lt5pYXeVuNzfqEu3bZ9zLRVU/BNzNUgAgMz2YKA3Y\ntyk0XClKRBQIFnQiokCwoBMRBSKI/dBnjLZLg3c839PNfX/U8yaW6FL8dHrvS7sU+9db/CXPXX5Y\nY2Lnbrf7ZgPctzzqcjt1MrEO19iBbgD44ysXmdiFfSqdTD9+vM7/d9CpzQkTq3e2ugCAdw7YNqzY\nU2RiRzf62+Oc/5TdJqBu23Y3199R/ezGO3QiokCwoBMRBYIFnYgoECzoRESBYEEnIgrEGZf+p1Im\nl0c3xTvtfOvf2hPBAaBmoB3dT4UeC+1S5u5LdplY3efb0nL9UDV36X8qZUPfxhg7w2TLbe3d1DYH\n7L1cj3H+jJiDx9uZ2NHd/kEvfRfZ5y3YX2tiee/bQ2moaSk74IKIiKKBBZ2IKBAs6EREgWBBJyIK\nRBBL/5tDl5eb2IAsGJ/hMmZK2rI1JnT+zr5u6rFL7D7psqy7m1u064iJxVYva2bjKBN4h05EFAgW\ndCKiQLCgExEFIpFDootFZJGIrBORchG5Ox6/X0R2isjK+B9/r1eiLMW+TaFJZFC0DsC9qrpCRDoC\nWC4iC+Lfe1xVf5u+5hGlFfs2BSWRQ6IrAVTGPz8iIusB+EeJE0XI2dC363baLSUAoG0TcU8sVY2h\ntGvWe+giMhDASACl8dCdIrJaRGaJiH8ECVEEsG9TCBIu6CLSAcCrAO5R1cMAngFwLoARaLjLebSJ\nx00VkTIRKatFdQqaTJRa7NsUioQKuojko6HDv6Sq8wBAVfeoar2qxgA8B2CM91hVnamqJapakg+7\nyyBRa2LfppAkMstFALwAYL2qPtYo3qdR2mQAa1PfPKL0Yd+m0CQyy2UcgH8EsEZEVsZjMwDcKiIj\nACiArQB+lJYWEqUP+zYFJZFZLh8C8DZWfzv1zSHKHPZtCg1XihIRBYIFnYgoECzoRESBYEEnIgoE\nCzoRUSBY0ImIAsGCTkQUCBZ0IqJAsKATEQVCVDVzFxPZB2Bb/MvuAPZn7OKZw9fVegaoao/WuHCj\nvh2Fn1NLhfraovC6EurbGS3oX7mwSJmqlrTKxdOIr+vsFvLPKdTXFtLr4lsuRESBYEEnIgpEaxb0\nma147XTi6zq7hfxzCvW1BfO6Wu09dCIiSi2+5UJEFIiMF3QRuUZENorIFhGZnunrp1L8RPi9IrK2\nUaxQRBaIyOb4x8idGC8ixSKySETWiUi5iNwdj0f+taVTKH2b/Tp6r+2kjBZ0EckF8BSAawEMR8NR\nX8Mz2YYUmw3gmlNi0wEsVNUhABbGv46aOgD3qupwAJcB+Of431MIry0tAuvbs8F+HUmZvkMfA2CL\nqlaoag2AuQAmZbgNKaOqHwA4cEp4EoA58c/nALgxo41KAVWtVNUV8c+PAFgPoB8CeG1pFEzfZr+O\n3ms7KdMFvR+A7Y2+3hGPhaSXqlbGP98NoFdrNiZZIjIQwEgApQjstaVY6H07qL/7UPs1B0XTSBum\nEEV2GpGIdADwKoB7VPVw4+9F/bVRy0X97z7kfp3pgr4TQHGjr4visZDsEZE+ABD/uLeV29MiIpKP\nhk7/kqrOi4eDeG1pEnrfDuLvPvR+nemC/gmAISIySETaALgFwPwMtyHd5gOYEv98CoA3WrEtLSIi\nAuAFAOtV9bFG34r8a0uj0Pt25P/uz4Z+nfGFRSJyHYAnAOQCmKWqv8poA1JIRF4GMB4Nu7XtAXAf\ngNcBvAKgPxp237tJVU8dYMpqInIFgCUA1gCIxcMz0PB+Y6RfWzqF0rfZr6P32k7iSlEiokBwUJSI\nKBAs6EREgWBBJyIKBAs6EVEgWNCJiALBgk5EFAgWdCKiQLCgExEF4v8AJ2R4mt+8ujwAAAAASUVO\nRK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f82aad782b0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"index = 60\n",
"plt.subplot(1,2,1)\n",
"plt.imshow(test_x[index].reshape(28,28))\n",
"plt.subplot(1,2,2)\n",
"plt.imshow(test_out[index].reshape(28,28))\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 3.3 64D Compress output for tensorboard"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false
},
"outputs": [],
"source": [
"compressed = z.eval(feed_dict={x:mnist.test.images})\n",
" \n",
"metadata = 'compressed_metadata.tsv'\n",
"test_labels = mnist.test.labels\n",
"\n",
"with open(metadata, 'w') as metadata_file:\n",
" for i, v in enumerate(test_labels):\n",
" c = np.where(v==1)\n",
" metadata_file.write('{}\\n'.format(int(c[0])))\n",
" \n",
"\n",
"np.save('compressed_output', compressed)"
]
},
{
"cell_type": "markdown",
"metadata": {
"deletable": true,
"editable": true
},
"source": [
"#### 3.4 2D Compressed Visualisation"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": false,
"deletable": true,
"editable": true
},
"outputs": [],
"source": [
"sample = 1024\n",
"compressed = z.eval(feed_dict={x:mnist.test.images})\n",
"labels = mnist.test.labels\n",
"metadata = np.empty(len(labels))\n",
"for i, v in enumerate(labels):\n",
" metadata[i] = np.where(v==1)[0]\n",
"\n",
" \n",
"for i in range(10):\n",
" index = np.where(metadata==i)\n",
" plt.scatter(compressed[index,0], compressed[index,1], label=str(i))\n",
" \n",
"plt.legend() \n",
"fig = plt.gcf()\n",
"fig.set_size_inches(18.5, 10.5)\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true,
"deletable": true,
"editable": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.2"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| gpl-3.0 |
OceanPARCELS/parcels | parcels/examples/tutorial_sampling.ipynb | 1 | 252044 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Field sampling tutorial"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The particle trajectories allow us to study fields like temperature, plastic concentration or chlorophyll from a Lagrangian perspective. \n",
"\n",
"In this tutorial we will go through how particles can sample `Fields`, using temperature as an example. Along the way we will get to know the parcels class `Variable` (see [here](https://oceanparcels.org/gh-pages/html/#parcels.particle.Variable) for the documentation) and some of its methods. This tutorial covers several applications of a sampling setup:\n",
"* [**Basic along trajectory sampling**](#Basic-sampling)\n",
"* [**Sampling initial conditions**](#Sampling-initial-values)\n",
"* [**Sampling initial and along-trajectory values with repeated release**](#Sampling-with-repeatdt)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Basic sampling\n",
"We import the `Variable` class as well as the standard modules needed to set up a simulation."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"# Modules needed for the Parcels simulation\n",
"from parcels import Variable, FieldSet, ParticleSet, JITParticle, AdvectionRK4\n",
"import numpy as np\n",
"from datetime import timedelta as delta\n",
"\n",
"# To open and look at the temperature data\n",
"import xarray as xr \n",
"import matplotlib as mpl\n",
"import matplotlib.pyplot as plt"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Suppose we want to study the environmental temperature for plankton drifting around a peninsula. We have a dataset with surface ocean velocities and the corresponding sea surface temperature stored in netcdf files in the folder `\"Peninsula_data\"`. Besides the velocity fields, we load the temperature field using `extra_fields={'T': 'T'}`. The particles are released on the left hand side of the domain."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYsAAAD8CAYAAACGsIhGAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAAAfO0lEQVR4nO3df5BV5Z3n8fcH/En7W9TBbkBnQ7lj3I0/KKLr7pSRmCDbFdwtextqE8msU0xEqpKdsBMcquiFXXbNLkmmrE5r2OiKjlHAxEixGKU0rMmUUdH4i8aOHQ3Q0CshJkK6/THY3/3jPg23L7f73gvd93YfP6+qU/fc73mec58TIl+e5znnOYoIzMzMhjKu1g0wM7PRz8nCzMxKcrIwM7OSnCzMzKwkJwszMyvJycLMzEpysjAzqyJJkyX9VNJ2SdskfTXFz5K0WdIb6fPMQerPktQhqVPSkqq1289ZmJlVj6RJwKSIeFHSqcALwA3Al4F3IuL2lATOjIhvFNQdD/wKuA7oAp4H5kVE+0i32z0LM7MqiojuiHgx7R8AtgP1wBxgTSq2hlwCKTQD6IyINyPiQ+ChVG/EHVeNHxkJ0vgYp+Nr3QwmcGqtmwDAhONGR96vG/9RrZvAySd8WOsmAHDCye/XugkAjK/rq3UTAOg79aya/fYvX/7tvog451jO8dlrp8Q775T3Z/rLl3+7DcgvvDoiVheWk3QBcBnwLHBeRHRDLqFIOrfIqeuBXXnfu4BPl9WoYzRmk8U4Hc/JJ0yudTO4bNxnat0EAKafcXKtmwDA5WcfqHUT+NT5u0oXqoKp/6yj1k0AoO6qP9a6CQD0/vmNNfvt0869c8exnuOdd97n/24u7xpOO/fO9yNi+lBlJJ0C/BD4WkTsl1TOqYsVqspcwuj456iZ2ceIpOPJJYoHIuJHKfx2ms/on9fYW6RqF5D/r+QGYM9ItrWfk4WZWRUp14W4G9geEd/OO7QBmJ/25wOPFqn+PDBN0oWSTgDmpnojzsnCzKy6rga+BFwr6aW0zQZuB66T9Aa5u51uB5B0vqRNABFxEFgEPE5uYnxdRGyrRqPH7JyFmdlYFBE/p/jcA8DMIuX3ALPzvm8CNo1M6wbnnoWZmZXkZGFmZiU5WZiZWUlOFmZmVpKThZmZleRkYWZmJTlZmJlZSU4WZmZWkpOFmZmVlJlk0dTcSHvHFvb3dtDesYWm5sZaN8nMLDMysdxHU3MjrW0rqaubAMCUqfW0tq0EYP3ajbVsmplZJmSiZ7F8xeJDiaJfXd0Elq9YXKMWmZllSyaSRcPkSRXFzcysMplIFl27uiuKm5lZZTKRLFqWraKnp3dArKenl5Zlq2rUIjOzbMlEsli/diOLFi5l547d9PX1sXPHbhYtXOrJbTOzYZKJu6EglzCcHMzMRkYmehZmZjayMtOzMDMbKyTdAzQCeyPikhRbC1yUipwB/CEiLi1S9zfAAeAj4GBETK9Ck50szMxq4F6gFbivPxARzf37kr4FvDtE/c9ExL4Ra10RThZmZlUWEU9LuqDYMUkC/h1wbVUbVYLnLMzMRpd/BbwdEW8McjyAJyS9IGlBtRrlnoWZWRnGHXiHCU8/VG7xiZK25n1fHRGry6w7D3hwiONXR8QeSecCmyW9HhFPl9uwo+VkYWY2/PYdzcSzpOOAfwtcMViZiNiTPvdKegSYAYx4svAwlJnZ6PFZ4PWI6Cp2UFKdpFP794HPAa9Vo2FOFmZmVSbpQeAZ4CJJXZJuTofmUjAEJel8SZvS1/OAn0t6GXgO+D8R8ZNqtNnDUGZmVRYR8waJf7lIbA8wO+2/CXxqRBs3CPcszMysJCcLMzMrycnCzMxKcrIwM7OSMpMsmpobae/Ywv7eDto7ttDU3FjrJpmZZUbZyULSeEm/lLQxfT9L0mZJb6TPM/PK3iapU1KHpM/nxa+Q9Go6dkdaAwVJJ0pam+LPDrZmymCamhtpbVvJlKn1jBs3jilT62ltW+mEYWY2TCrpWXwV2J73fQnwZERMA55M35F0Mbl7hT8JzALaJI1Pde4EFgDT0jYrxW8Gfh8RnwC+A3yzkotYvmIxdXUTBsTq6iawfMXiSk5jZmaDKCtZSGoA/jXw/bzwHGBN2l8D3JAXfygiPoiIt4BOYIakScBpEfFMRAS5pXlvKHKuh4GZ/b2OcjRMnlRR3MzMKlNuz+LvgL8B+vJi50VEN0D6PDfF64FdeeW6Uqw+7RfGB9SJiIPk1nE/u7ARkhZI2ippa8RHh0+0q7tooweLm5lZZUomC0n9b3N6ocxzFusRxBDxoeoMDESsjojpETH98MgWtCxbRU9P74CyPT29tCxbVWaTzcxsKOX0LK4GvpBe5fcQcK2kvwfeTkNLpM+9qXwXMDmvfgOwJ8UbisQH1EmrLp4OvFPuRaxfu5FFC5eyc8du+vr62LljN4sWLmX92o3lnsLMzIZQMllExG0R0RARF5CbuH4qIr4IbADmp2LzgUfT/gZgbrrD6UJyE9nPpaGqA5KuTPMRNxXU6T/Xjek3juhZDGX92o1cfNE1nDbhIi6+6BonCjOzYXQsCwneDqxLqyXuBJoAImKbpHVAO3AQuDUOTzDcQu7dsycDj6UN4G7gfkmd5HoUc4+hXWZmNswqShYRsQXYkvZ/B8wcpNxKYGWR+FbgkiLx90nJxszMRp/MPMFtZmYjx8nCzMxKcrIwM7OSnCzMzKwkJwszMyvJycLMrMok3SNpr6TX8mL/WdJuSS+lbfYgdWelFb07JS2pVpudLMzMqu9eDq+6ne87EXFp2jYVHkwreH8XuB64GJiXVvoecU4WZmZVFhFPU8GSRnlmAJ0R8WZEfEhuCaY5w9q4QRzLE9xmZh8bH/WMo+eZU8os/fuJkrbmBVZHxOoyKi6SdBOwFfh6RPy+4HixVb0/XWajjol7FmZmw29f/wrZaSsnUdwJ/BPgUqAb+FaRMmWt0D0SnCzMzEaBiHg7Ij6KiD7gf5Ebcio02KreIy4zyaKpuZH2ji3s7+2gvWOL379tZmNK/ysfkn8DvFak2PPANEkXSjqB3KKrG6rRvkzMWTQ1N9LatvLQe7inTK2ntS23jqGXKjez0UbSg8A1wERJXUALcI2kS8kNK/0G+KtU9nzg+xExOyIOSloEPA6MB+6JiG3VaHMmksXyFYsPJYp+dXUTWL5isZOFmY06ETGvSPjuQcruAWbnfd8EHHFb7UjLxDBUw+RJFcXNzKwymUgWXbu6K4qbmVllMpEsWpatoqend0Csp6eXlmWratQiM7NsyUSyWL92I4sWLmXnjt309fWxc8duFi1c6vkKM7NhkokJbsglDCcHM7ORkYmehZmZjSwnCzMzK8nJwszMSnKyMDOzkpwszMysJCcLMzMrycnCzMxKcrIwM7OSnCzMzKwkJwszMyvJycLMzEpysjAzs5KcLMzMrKTMJIum5kbaO7awv7eD9o4tNDU31rpJZmZFSbpH0l5Jr+XF/qek1yW9IukRSWcMUvc3kl6V9JKkrdVqcyaSRVNzI61tK5kytZ5x48YxZWo9rW0rnTDMbLS6F5hVENsMXBIR/xz4FXDbEPU/ExGXRsT0EWrfETKRLJavWExd3YQBsbq6CSxfsbhGLTIzG1xEPA28UxB7IiIOpq+/ABqq3rAhZOLlRw2TJ1UUNzOr1IfvncSOVy8qs/SuiQVDRKsjYnUFP/cfgLWDHAvgCUkBfK/C8x61kj0LSSdJek7Sy5K2SVqe4mdJ2izpjfR5Zl6d2yR1SuqQ9Pm8+BVprK1T0h2SlOInSlqb4s9KuqCSi+ja1V1R3MxshO2LiOl5W9l/oUtaChwEHhikyNURcTlwPXCrpD8fhvaWVM4w1AfAtRHxKeBSYJakK4ElwJMRMQ14Mn1H0sXAXOCT5Mbk2iSNT+e6E1gATEtb/5jdzcDvI+ITwHeAb1ZyES3LVtHT0zsg1tPTS8uyVZWcxsyspiTNBxqBfx8RUaxMROxJn3uBR4AZ1WhbyWQROX9MX49PWwBzgDUpvga4Ie3PAR6KiA8i4i2gE5ghaRJwWkQ8k/5HuK+gTv+5HgZm9vc6yrF+7UYWLVzKzh276evrY+eO3SxauNTv5DazMUPSLOAbwBcioneQMnWSTu3fBz4HvFas7HAra84i9QxeAD4BfDcinpV0XkR0A0REt6RzU/F6cpMz/bpS7B/TfmG8v86udK6Dkt4Fzgb2FbRjAbmeCSpo+vq1G50czGxMkPQgcA0wUVIX0ELu7qcTgc3p38q/iIivSDof+H5EzAbOAx5Jx48DfhARP6lGm8tKFhHxEXBpuu/3EUmXDFG8WI8ghogPVaewHauB1QDjx51UtItmZjbaRcS8IuG7Bym7B5id9t8EPjWCTRtURbfORsQfgC3k5hreTkNLpM+9qVgXMDmvWgOwJ8UbisQH1JF0HHA6BbeVmZlZ7ZRzN9Q5/U8SSjoZ+CzwOrABmJ+KzQceTfsbgLnpDqcLyU1kP5eGrA5IujLNR9xUUKf/XDcCTw02uWNmZtVXzjDUJGBNmrcYB6yLiI2SngHWSboZ2Ak0AUTENknrgHZyt3/dmoaxAG4h9+TiycBjaYNc9+t+SZ3kehRzh+PizMxseJRMFhHxCnBZkfjvgJmD1FkJrCwS3wocMd8REe+Tko2ZmY0+mVjuw8zMRpaThZmZleRkYWZmJTlZmJlZSZlYddbMzI4k6awyivWlZ+iG5GRhZpZde9I21Fp744EppU7kZGFmll3bI+KIRx/ySfplOSfynIWZWXZdNUxlspMsmpobae/Ywv7eDto7tvj922Zm8J8kfX2oAumh6JIyMQzV1NxIa9vKQ+/hnjK1nta23APkXrbczD7GvkTupXUDSPpL4JyI+O/lnigTPYvlKxYfShT96uomsHzF4hq1yMxsVHhvkBcp3Q98sZITZSJZNEyeVFHczOxj4r3+V0nki4gPyC30WrZMJIuuXd0Vxc3MPia+BTwqaWp+ML3ZtK+SE2UiWbQsW0VPz8CeVk9PLy3LVtWoRWZmtRcR64HvAi9I2ijpv0r6b8A/ABX9BZmJZLF+7UYWLVzKzh276evrY+eO3SxauNST22Y2Kkm6R9JeSa/lxc6StFnSG+nzzEHqzpLUIalT0pJSvxURa4ALgXXA8cD7wLyIeKCSNmfibijIJQwnBzMbI+4FWoH78mJLgCcj4vaUBJYA38ivlF5C913gOnKvo35e0oaIaB/qxyLiQMFvVSwTPQszs7EkIp4m91bQfHOANWl/DXBDkaozgM6IeDMiPgQeSvWKknRV/2uxj5WThZnZ8JsoaWvetqCMOudFRDdA+jy3SJl6YFfe964UO4Kk/wKcA3yvsqYXl5lhKDOzkfTehyfw8p7J5RbfFxHTR6AZxRYEjEHK/gPw58CvhuOHnSzMzEaHtyVNioju9GzE3iJluoD8jNVAblXZI0TET4CfDFfjPAxlZjY6bADmp/35wKNFyjwPTJN0oaQTgLmp3ohzsjAzqzJJDwLPABdJ6pJ0M3A7cJ2kN8jd7XR7Knu+pE0AEXEQWAQ8DmwH1kXEtiF+58Uy2lKyDHgYysys6iJi3iCHZhYpuweYnfd9E7CpzJ/6M0mvDHFcwOnlnMjJwswsu/5pGWU+KudEThZmZhkVETuG61yeszAzs5KcLMzMMkrSsI0eOVmYmWXXc8N1IicLM7PsKvbE91HJzAR3U3Mjy1cspmHyJLp2ddOybJVXoTWzj7tzJP31YAcj4tvlnigTyaKpuZHWtpWH3sM9ZWo9rW0rAZwwzOzjbDxwCsPQw8hEsli+YvGhRNGvrm4Cy1csdrIws4+z7ohYMRwnysScRcPkI95HPmTczOxjYtjmLDKRLLp2dVcUNzP7mDhi+ZCjlYlk0bJsFT09vQNiPT29tCyr6H3kZmaZEhGFb+M7aplIFuvXbmTRwqXs3LGbvr4+du7YzaKFSz1fYWY2TDIxwQ25hOHkYGY2Mkr2LCRNlvRTSdslbZP01RQ/S9JmSW+kzzPz6twmqVNSh6TP58WvkPRqOnaHJKX4iZLWpvizki4YgWs1M7OjVM4w1EHg6xHxZ8CVwK2SLgaWAE9GxDTgyfSddGwu8ElgFtAmaXw6153AAmBa2mal+M3A7yPiE8B3gG8Ow7WZmdkwKZksIqI7Il5M+wfIvZ2pHpgDrEnF1gA3pP05wEMR8UFEvAV0AjPSO2VPi4hnIiKA+wrq9J/rYWBmf6/DzMxqr6IJ7jQ8dBnwLHBeRHRDLqEA56Zi9cCuvGpdKVaf9gvjA+qk1wa+C5xd5PcXSNoqaWtEWe/rMDOzYVB2spB0CvBD4GsRsX+ookViMUR8qDoDAxGrI2J6REw/PLJlZjZ2SLpI0kt5235JXysoc42kd/PKLKtRcw8p624oSceTSxQPRMSPUvhtSZMiojsNMe1N8S5gcl71BmBPijcUiefX6Urrr58ODNv9wWZmo0VEdACXAqT53N3AI0WK/iwiGqvYtCGVczeUgLuB7QUrFG4A5qf9+cCjefG56Q6nC8lNZD+XhqoOSLoynfOmgjr957oReCrNa5iZZdlM4NfD+frTkVJOz+Jq4EvAq5JeSrG/BW4H1km6GdgJNAFExDZJ64B2cndS3RqHJxhuAe4FTgYeSxvkktH9kjrJ9SjmHttlmZnV1ERJW/O+r46I1UXKzQUeHOQcV0l6mdwIzOKI2DbcjaxEyWQRET9n8MWoiq47EhErgZVF4luBS4rE3yclGzOz0ajno/G8+LtTyy2+LyKmD1VA0gnAF4Dbihx+EZgaEX+UNBv4MblRmprJxHIfZmZj0PXAixHxduGBiNgfEX9M+5uA4yVNrHYD8zlZmJnVxjwGGYKS9Cd5K1zMIPd39e+q2LYjZGZtKDOzsULSBOA64K/yYl8BiIi7yN3oc4ukg8B7wNxa3/TjZGFmVmUR0UvBg8cpSfTvtwKt1W7XUDIzDNXU3Eh7xxb293bQ3rGFpuZRc3uymdmYl4meRVNzI61tKw+9h3vK1Hpa23I3Y3nZcjOzY5eJnsXyFYsPJYp+dXUTWL5icY1aZGaWLZlIFg2TJ1UUNzOzymQiWXTt6q4obmZmlclEsmhZtoqent4BsZ6eXlqWrapRi8zMsiUTyWL92o0sWriUnTt209fXx84du1m0cKknt83Mhkkm7oaCXMJwcjAzGxmZ6FmYmdnIcrIwM7OSnCzMzKwkJwszMyvJycLMzEpysjAzs5KcLMzMrCQnCzMzK8nJwszMSnKyMDOzkpwszMyqTNJvJL0q6SVJW4scl6Q7JHVKekXS5bVoZ77MrA1lZjbGfCYi9g1y7HpgWto+DdyZPmvGPQszs9FnDnBf5PwCOENSTd/mlplk0dTcSHvHFvb3dtDesYWm5sZaN8nMPr4mStqaty0oOB7AE5JeKHIMoB7Ylfe9K8VqJhPDUE3NjbS2rTz0Hu4pU+tpbVsJ4GXLzWxY9B7sY+sf3iu3+L6ImD7E8asjYo+kc4HNkl6PiKfzjqtInSj3x0dCJnoWy1csPpQo+tXVTWD5isU1apGZ2eAiYk/63As8AswoKNIFTM773gDsqU7ristEsmiYXHwob7C4mVmtSKqTdGr/PvA54LWCYhuAm9JdUVcC70ZEd5WbOkAmhqG6dnUzZeqRw3ldu2r6v62ZWTHnAY9IgtzfwT+IiJ9I+gpARNwFbAJmA51AL/AXNWrrIZlIFi3LVg2YswDo6emlZdmqGrbKzOxIEfEm8Kki8bvy9gO4tZrtKiUTw1Dr125k0cKl7Nyxm76+Pnbu2M2ihUs9uW1mNkwy0bOAXMJwcjAzGxmZ6FmYmdnIcrIwM7OSnCzMzKykkslC0j2S9kp6LS92lqTNkt5In2fmHbstrZTYIenzefEr0iqLnWk1RaX4iZLWpvizki4Y5ms0M7NjVE7P4l5gVkFsCfBkREwDnkzfkXQxMBf4ZKrTJml8qnMnsIDDKyn2n/Nm4PcR8QngO8A3j/ZizMxsZJRMFmm9kncKwnOANWl/DXBDXvyhiPggIt4i90DJjLRa4mkR8Uy6f/i+gjr953oYmNnf6zAzs9HhaOcszut/9Dx9npvig62UWJ/2C+MD6kTEQeBd4OxiPyppQf8qjhEfHWXTzcysUsM9wT3YSolDraBY9uqKEbE6IqZHxPTDo1tmZjbSjjZZvN3/Io70uTfFB1spsSvtF8YH1JF0HHA6Rw57mZlZDR1tstgAzE/784FH8+Jz0x1OF5KbyH4uDVUdkHRlmo+4qaBO/7luBJ5K8xpmZjZKlFzuQ9KDwDXk3vzUBbQAtwPrJN0M7ASaACJim6R1QDtwELg1Dk8u3ELuzqqTgcfSBnA3cL+kTnI9irnDcmVmZjZsSiaLiJg3yKGZg5RfCawsEt8KXFIk/j4p2ZiZ2ejkJ7jNzKwkJwszMyspM8miqbmR9o4t7O/toL1jC03NjbVukplZZmTifRZNzY0D3pQ3ZWo9rW25aRO/48LM7NhlomexfMXiAa9UBairm8DyFYtr1CIzs+IkTZb0U0nbJW2T9NUiZa6R9K6kl9K2rBZtzZeJnkXD5EkVxc3Maugg8PWIeFHSqcALkjZHRHtBuZ9FxKgZT89Ez6JrV3dFcTOzWomI7oh4Me0fALZzeK28USsTyaJl2Sp6enoHxHp6emlZtqpGLTIzKy29v+cy4Nkih6+S9LKkxyR9srotO1ImhqH6J7GXr1hMw+RJdO3qpmXZKk9um9mw6eUAL/b9tNziEyVtzfu+OiJW5xeQdArwQ+BrEbG/oP6LwNSI+KOk2cCPyS2fVDOZSBaQSxhODmY2SuyLiOmDHZR0PLlE8UBE/KjweH7yiIhNktokTYyIfSPT3NIyMQxlZjZWpMVU7wa2R8S3BynzJ3mvnp5B7u/q31WvlUfKTM/CzGyMuBr4EvCqpJdS7G+BKQARcRe5FbhvkXQQeA+YW+vVuJ0szMyqKCJ+TvGXvuWXaQVaq9Oi8ngYyszMSnKyMDOzkpwszMysJCcLMzMrycnCzMxKcrIwM7OSnCzMzKwkJwszMyvJycLMzEpysjAzs5Iykyyamhtp79jC/t4O2ju20NQ8al4wZWY25mVibaim5kZa21Yeeg/3lKn1tLatBPCy5WZmwyATPYvlKxYfShT96uomsHzF4hq1yMwsWzKRLBomT6oobmZmlclEsuja1V1R3MzMKpOJZNGybBU9Pb0DYj09vbQsW1WjFpmZZUsmksX6tRtZtHApO3fspq+vj507drNo4VJPbpuZDZNM3A0FuYTh5GBmNjIy0bMwM7OR5WRhZlZlkmZJ6pDUKWlJkeOSdEc6/oqky2vRznxOFmZmVSRpPPBd4HrgYmCepIsLil0PTEvbAuDOqjayCCcLM7PqmgF0RsSbEfEh8BAwp6DMHOC+yPkFcIakmj44NmYnuPvig309H3TuqHU7fkbncJ1qIrDvqNvx3nA14xgVf7TlmK6tYq9V7ZeGvq4nqtaOkTACf2Y1/cfx1GM9QV988HjPB50Tyyx+kqSted9XR8TqtF8P7Mo71gV8uqB+sTL1DPZfWBWM2WQREefUug3DSdLWiJhe63aMhKxeW1avC7J9bUcrImYN06lU7PRHUaaqPAxlZlZdXcDkvO8NwJ6jKFNVThZmZtX1PDBN0oWSTgDmAhsKymwAbkp3RV0JvBsRNV2/aMwOQ2XQ6tJFxqysXltWrwuyfW01FREHJS0CHgfGA/dExDZJX0nH7wI2AbOBTqAX+ItatbefImo6DGZmZmOAh6HMzKwkJwszMyvJyWIYSZos6aeStkvaJumrKX6WpM2S3kifZ+bVuS090t8h6fN58SskvZqO3SFJKX6ipLUp/qykC6p4feMl/VLSxoxd1xmSHpb0evqzuypD1/Yf0/8XX5P0oKSTsnJtVmUR4W2YNmAScHnaPxX4FbnH+f8HsCTFlwDfTPsXAy8DJwIXAr8GxqdjzwFXkbvf+jHg+hRfCNyV9ucCa6t4fX8N/ADYmL5n5brWAH+Z9k8AzsjCtZF7iOst4OT0fR3w5Sxcm7fqbzVvQJY34FHgOqADmJRik4COtH8bcFte+cfTf5CTgNfz4vOA7+WXSfvHkXvKVlW4lgbgSeDavGSRhes6Lf2FqoJ4Fq6t/yngs9LvbgQ+l4Vr81b9zcNQIyR1xy8DngXOi3SPdPo8NxUb7JH++rRfGB9QJyIOAu8CZ4/IRQz0d8DfAH15sSxc158CvwX+dxpi+76kOjJwbRGxG1gF7CS3TMS7EfEEGbg2qz4nixEg6RTgh8DXImL/UEWLxGKI+FB1RoykRmBvRLxQbpUisVF3XclxwOXAnRFxGdBDbmhmMGPm2tJcxBxyQ0rnA3WSvjhUlSKxUXltVn1OFsNM0vHkEsUDEfGjFH67f8XI9Lk3xQd7pL8r7RfGB9SRdBxwOvDO8F/JAFcDX5D0G3IrZF4r6e8Z+9fV/7tdEfFs+v4wueSRhWv7LPBWRPw2Iv4R+BHwL8jGtVmVOVkMo3SHyN3A9oj4dt6hDcD8tD+f3FxGf3xuuqPkQnJr1z+XhgYOSLoynfOmgjr957oReCoiRvRfchFxW0Q0RMQF5CYxn4qIL47160rX9v+AXZIuSqGZQDsZuDZyw09XSpqQ2jQT2E42rs2qrdaTJlnagH9Jrgv+CvBS2maTG8N9EngjfZ6VV2cpubtOOkh3mKT4dHKLbf8aaOXw0/YnAevJLQPwHPCnVb7Gazg8wZ2J6wIuBbamP7cfA2dm6NqWA6+ndt1P7k6nTFybt+puXu7DzMxK8jCUmZmV5GRhZmYlOVmYmVlJThZmZlaSk4WZmZXkZGFmZiU5WZiZWUn/HxBwloDiCsncAAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 432x288 with 2 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Velocity and temperature fields\n",
"fieldset = FieldSet.from_parcels(\"Peninsula_data/peninsula\", extra_fields={'T': 'T'}, allow_time_extrapolation=True)\n",
"\n",
"# Particle locations and initial time\n",
"npart = 10 # number of particles to be released\n",
"lon = 3e3 * np.ones(npart)\n",
"lat = np.linspace(3e3 , 45e3, npart, dtype=np.float32)\n",
"time = np.arange(0, npart) * delta(hours=2).total_seconds() # release each particle two hours later\n",
"\n",
"# Plot temperature field and initial particle locations\n",
"T_data = xr.open_dataset(\"Peninsula_data/peninsulaT.nc\")\n",
"plt.figure()\n",
"ax = plt.axes()\n",
"T_contour = ax.contourf(T_data.x.values, T_data.y.values, T_data.T.values[0,0], cmap=plt.cm.inferno)\n",
"ax.scatter(lon, lat, c='w')\n",
"plt.colorbar(T_contour, label='T [$^{\\circ} C$]')\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To sample the temperature field, we need to create a new class of particles where temperature is a `Variable`. As an argument for the `Variable` class, we need to provide the initial values for the particles. The easiest option is to access `fieldset.T`, but this option has some drawbacks."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"WARNING: Particle initialisation from field can be very slow as it is computed in scipy mode.\n"
]
}
],
"source": [
"class SampleParticle(JITParticle): # Define a new particle class\n",
" temperature = Variable('temperature', initial=fieldset.T) # Variable 'temperature' initialised by sampling the temperature\n",
"\n",
"pset = ParticleSet(fieldset=fieldset, pclass=SampleParticle, lon=lon, lat=lat, time=time)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Using `fieldset.T` leads to the `WARNING` displayed above because `Variable` accesses the fieldset in the slower SciPy mode. Another problem can occur when using the repeatdt argument instead of time:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"<a id='repeatdt_error'></a>"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"tags": [
"raises-exception"
]
},
"outputs": [
{
"ename": "RuntimeError",
"evalue": "Cannot initialise a Variable with a Field if no time provided. Add a \"time=\" to ParticleSet construction",
"output_type": "error",
"traceback": [
"\u001b[1;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[1;31mRuntimeError\u001b[0m Traceback (most recent call last)",
"\u001b[1;32m<ipython-input-4-43d86eef917d>\u001b[0m in \u001b[0;36m<module>\u001b[1;34m()\u001b[0m\n\u001b[0;32m 1\u001b[0m \u001b[0mrepeatdt\u001b[0m \u001b[1;33m=\u001b[0m \u001b[0mdelta\u001b[0m\u001b[1;33m(\u001b[0m\u001b[0mhours\u001b[0m\u001b[1;33m=\u001b[0m\u001b[1;36m3\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0;32m 2\u001b[0m \u001b[1;33m\u001b[0m\u001b[0m\n\u001b[1;32m----> 3\u001b[1;33m \u001b[0mpset\u001b[0m \u001b[1;33m=\u001b[0m \u001b[0mParticleSet\u001b[0m\u001b[1;33m(\u001b[0m\u001b[0mfieldset\u001b[0m\u001b[1;33m=\u001b[0m\u001b[0mfieldset\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0mpclass\u001b[0m\u001b[1;33m=\u001b[0m\u001b[0mSampleParticle\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0mlon\u001b[0m\u001b[1;33m=\u001b[0m\u001b[0mlon\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0mlat\u001b[0m\u001b[1;33m=\u001b[0m\u001b[0mlat\u001b[0m\u001b[1;33m,\u001b[0m \u001b[0mrepeatdt\u001b[0m\u001b[1;33m=\u001b[0m\u001b[0mrepeatdt\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0m",
"\u001b[1;32mc:\\users\\gebruiker\\documents\\github\\parcels\\parcels\\particleset.py\u001b[0m in \u001b[0;36m__init__\u001b[1;34m(self, fieldset, pclass, lon, lat, depth, time, repeatdt, lonlatdepth_dtype, pid_orig, **kwargs)\u001b[0m\n\u001b[0;32m 284\u001b[0m \u001b[1;32mfor\u001b[0m \u001b[0mi\u001b[0m \u001b[1;32min\u001b[0m \u001b[0mrange\u001b[0m\u001b[1;33m(\u001b[0m\u001b[0mself\u001b[0m\u001b[1;33m.\u001b[0m\u001b[0msize\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m:\u001b[0m\u001b[1;33m\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[0;32m 285\u001b[0m \u001b[1;32mif\u001b[0m \u001b[1;33m(\u001b[0m\u001b[0mtime\u001b[0m\u001b[1;33m[\u001b[0m\u001b[0mi\u001b[0m\u001b[1;33m]\u001b[0m \u001b[1;32mis\u001b[0m \u001b[1;32mNone\u001b[0m\u001b[1;33m)\u001b[0m \u001b[1;32mor\u001b[0m \u001b[1;33m(\u001b[0m\u001b[0mnp\u001b[0m\u001b[1;33m.\u001b[0m\u001b[0misnan\u001b[0m\u001b[1;33m(\u001b[0m\u001b[0mtime\u001b[0m\u001b[1;33m[\u001b[0m\u001b[0mi\u001b[0m\u001b[1;33m]\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m:\u001b[0m\u001b[1;33m\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n\u001b[1;32m--> 286\u001b[1;33m raise RuntimeError('Cannot initialise a Variable with a Field if no time provided. '\n\u001b[0m\u001b[0;32m 287\u001b[0m 'Add a \"time=\" to ParticleSet construction')\n\u001b[0;32m 288\u001b[0m \u001b[0mv\u001b[0m\u001b[1;33m.\u001b[0m\u001b[0minitial\u001b[0m\u001b[1;33m.\u001b[0m\u001b[0mfieldset\u001b[0m\u001b[1;33m.\u001b[0m\u001b[0mcomputeTimeChunk\u001b[0m\u001b[1;33m(\u001b[0m\u001b[0mtime\u001b[0m\u001b[1;33m[\u001b[0m\u001b[0mi\u001b[0m\u001b[1;33m]\u001b[0m\u001b[1;33m,\u001b[0m \u001b[1;36m0\u001b[0m\u001b[1;33m)\u001b[0m\u001b[1;33m\u001b[0m\u001b[1;33m\u001b[0m\u001b[0m\n",
"\u001b[1;31mRuntimeError\u001b[0m: Cannot initialise a Variable with a Field if no time provided. Add a \"time=\" to ParticleSet construction"
]
}
],
"source": [
"repeatdt = delta(hours=3)\n",
"\n",
"pset = ParticleSet(fieldset=fieldset, pclass=SampleParticle, lon=lon, lat=lat, repeatdt=repeatdt)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Since the initial time is not defined, the `Variable` class does not know at what time to access the temperature field."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The solution to this initialisation problem is to leave the initial value zero and sample the initial condition in JIT mode with the sampling Kernel:"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [],
"source": [
"class SampleParticleInitZero(JITParticle): # Define a new particle class\n",
" temperature = Variable('temperature', initial=0) # Variable 'temperature' initially zero\n",
"\n",
"pset = ParticleSet(fieldset=fieldset, pclass=SampleParticleInitZero, lon=lon, lat=lat, time=time)\n",
"\n",
"def SampleT(particle, fieldset, time):\n",
" particle.temperature = fieldset.T[time, particle.depth, particle.lat, particle.lon]\n",
"sample_kernel = pset.Kernel(SampleT) # Casting the SampleT function to a kernel."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"To sample the initial values we can execute the Sample kernel over the entire particleset with dt = 0 so that time does not increase"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"INFO: Compiled SampleParticleInitZeroSampleT ==> C:\\Users\\GEBRUI~1\\AppData\\Local\\Temp\\parcels-tmp\\95267e2b33bce749036c721bfb587691_0.dll\n",
"WARNING: dt or runtime are zero, or endtime is equal to Particle.time. The kernels will be executed once, without incrementing time\n",
"INFO: Compiled SampleParticleInitZeroAdvectionRK4SampleT ==> C:\\Users\\GEBRUI~1\\AppData\\Local\\Temp\\parcels-tmp\\7e5de9a8e76698139bc7c407a0d61d6f_0.dll\n"
]
}
],
"source": [
"pset.execute(sample_kernel, dt=0) # by only executing the sample kernel we record the initial temperature of the particles\n",
"\n",
"output_file = pset.ParticleFile(name=\"InitZero.nc\", outputdt=delta(hours=1))\n",
"pset.execute(AdvectionRK4 + sample_kernel, runtime=delta(hours=30), dt=delta(minutes=5),\n",
" output_file=output_file)\n",
"output_file.export() # export the trajectory data to a netcdf file\n",
"output_file.close()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The particle dataset now contains the particle trajectories and the corresponding environmental temperature"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZkAAAEKCAYAAADAVygjAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAADa90lEQVR4nOydd1hURxeH39lGk46gItjF3nvvvRt7iRpLYkzUGFuM0Zhoihpji93Yu8Ya7L13xa4ICCIgTTpsme+PRXQDKvmCirrv8+wjzp65d+6F3d+dOWfOEVJKzJgxY8aMmdeB4m0PwIwZM2bMvL+YRcaMGTNmzLw2zCJjxowZM2ZeG2aRMWPGjBkzrw2zyJgxY8aMmdeGWWTMmDFjxsxrwywyZsyYMfMOIITwEEIcEkLcFEJcF0IMTW13EkLsE0LcTf3X8QX9mwkhbgsh7gkhxryxcZv3yZgxY8ZM9kcIkRvILaW8KISwBS4A7YA+QKSU8udU8XCUUo7+R18lcAdoDAQB54BuUsobr3vc5pmMGTNmzLwDSCkfSSkvpv4cC9wE3IG2wPJUs+UYheefVAHuSSnvSylTgHWp/V47qjdxkuyEi4uLzJ8//9sehhkzZt4BLly4EC6lzPlfjtG0WRkZER6XyfP5XQeSnmtaKKVc+E87IUR+oDxwBnCTUj4CoxAJIVwzOLQ7EPjc/4OAqpka1H/kgxOZ/Pnzc/78+bc9DDNmzLwDCCEC/usxIsLjOHP+h0zZqkTPJCllpVeMKQewGRgmpYwRQmTm0BkZvRFfyQcnMmbMPPVDZvLDacbMf0IiMRj0WXIsIYQao8CsllJuSW0OFULkTp3F5AbCMugaBHg89/+8QHCWDOoVmH0yZrIt/v7+3LhxA4PB8EIbvV7PsmXLaFa/Ec3qN2L58uXo9Rl/oP39/WnXsjUWGg221jb06/0xUVFRr2v4ZswYkRKDITlTr5chjE9FS4CbUsrfnntrO/Bx6s8fA9sy6H4OKCKEKCCE0ABdU/u9dswiY+aNodfr2bdvH8uWLePmzZsvtPPz86NaxSqUL1WWRjXqkT9vPvbt25fOTkpJ148688vX4ynsq6Owr46fv/qW7p278s+oydjYWGpXq4Hd1SBWlmzHvCLNCN1/lmYNGqWzNWMmK5FIDFKXqdcrqAn0AhoIIS6nvloAPwONhRB3MUaP/QwghMgjhPgbQEqpA4YAezAGDGyQUl5/PVdsinm5zMx/5ubNm5w+fZo8efLQqFEjlEplOpsHDx7QqF5DdE+ScVE68lVCAM1btWDF6pUm9nq9nqYNGlMq0ZVuebqgQHA74SGdO3zExauXKVCgQJrtiRMnOH34GJPyNEetMB6jgq0n4/d74+3tTdmyZUlJSSElJYVVq1aRT1rR2bUEADZK+DRXeYY/OMThw4epX7/+a75LZj5cJPLVAvLqo0h5nIx9KwANM7APBlo89/+/gb//80D+JWaRMZMhUkquXLlCXFwclSpVwtLSMp2NXq+nT68+7Ny+k3yWnkQbnqCwVXDg8AETMQDo2aUHBWNdqW1XHgCtVXXW7N3DvHnzGDJkCElJSURERLBr1y5SohJo4FYmrW8xm7yUTcxHh3btKVy0CLGxscTGxuLr60tFlVuawABoFCpKq11p2bKlyflVKPjYvaxJmxCCYpZO3Lx50ywyZl4jWSMy7ypmkfkASUlJQaVSoVBkvFp669Yt2rZqR1RYFJYqS2J1McxfNJ8uXbqY2C1evJjjfx+jl2031Ao1ABdiLtGtUzeOnz5OWFgYISEh3Lhxg/MXzjM6T5+0vmqFipqaMowdMZrRo0eTkJCQ9l5JG890Y3JT2XPZ9wrJ2hRsbW2xtbUlV65chD+ISWcbJZPo2rUrDRo0QKPRoNFoOHLkCFe37DHZQCCl5GZiBCNLlsz8zTNj5t8iJdJgFhkzHwBHjx5l6OfD8LlxFStLawYMGMDPv/6ERqNJs9Hr9TRt1BSPmMLU1DRBCEG4DGNgv4GULl2aYsWKERYWRlBQEL/98hvllWXTBAagnFUZ5l1ciFqtNjm3pdCg/IcL0EKosbS0pHf/Pjg7O+Ps7ExKSgrfjhpLkiEFS4VxXFJKbhiCmTF7Jn379k3rHxkZSeH8BbkcG0g5W2PgzOXYQO7pItkzbx4ODg5ptq1bt6bk9p2sCb1GS+fCpBj0rAu/iVsBT+rUqZNl99iMmQwxz2TMvMtcvnyZX36ays3rNylfsTyjx46kWLFiJjbXrl2jVYvWlDDUoG2OT0mUcWxZupPHjx+zcvUKwPhlvmXLFrQxerwsSqX1dVG5kj+lKDWq1SA+MR6dzviB0QgN5ZxKm5xHgQKN2oKBAwdRsmRJcuXKhZubGz06d+dWoh/FrQumnetCym36fzaQn37+yXSsl32Y/5c3DaxKYqXQcDrpLgpXa7p162Zi5+TkxLZdO+jeqQubY68hAYNGwfa/d5oIDECOHDk4dvokI4cOZ6D336hVarp27cIv06eZQ5nNvGYMSH3i2x7EW+ODy11WqVIl+a5sxoyMjGTdunUEBwdTq1YtmjRpkm6J6/Dhw7Ru2ZY8+pLY4kqMCCFEeYvDRw9SoUKFNLs+vfpwcctdvNQV09q0MgXv+GVUrlaJ0NBQAgMDSU5OJo/ag2b27U3OczvpGiEuAXTu1pm8efPi7u7Orp27OLnxBE2sG6Z9Ud9P8uOKzTV8A3xNvryPHz9OmxatKa7Jj5O05b54hHDRcPz0iXSCYDAYWLFiBUvmLSQ+Lp52nTsybPgw7OzsMrxPer2eCxcuIISgQoUKGQYemDHz/yCEuPCqzZGvonz53PLIkb6vNgTs7X/6z+fLbphF5i0gpeTcuXOEh4dTtWpVnJ2d09mcOXOGJo2bYYMbJFmSYhlGibJF2btvt4kTvkzJcnDPDTdVwbS2IO0NZP7HtG3fGn9/fwICArh60YfKmia4qjxMzrM3bjWexfNQsmRJPD09sbOzY8oPU2iXowdWCuu08R7S7eL7WRPo3bt3Wt+YmBhqV69NwqN4PPR5iVHGck/ry7ad26hbt266a3r48CFLFi/hgV8AterVpmvXrhkGFJgxk13IGpHJJY8c6v1qQ8Decep7JzLm5bIs5smTJ0RFReHh4ZHhE7W/vz9NmzQnNCQcC5U1sYnhfDv+W775ZmyajZSSrp2745xcFkdVPlCD1Bm4dek448aNo27duvj7+3P//n2u3bhKA6sBJudwUxXk6N3j/P67L56enuTLl4/8BfPxOOChicgkGxLRq5M5dOgQLi4uae2J8YksnruEorIUGmGJv+IOOQu5pHP829nZcfbiWTZs2MDRQ0fxyOdBv0/6kTdv3gzvjbu7O99N+O7/uq9mzLyzSAkfsOPfPJPJJFJKkpOTsbCwyHANPzY2lk/69Wf7ju2oVBqsra2YM2cWnTt3NjlG6VJlCfMzYKvIjxACnSGRKMUl1m9cTcWKFQkICODkyZOMGfktxZTtTM4Vo3/I/eSjGNACYGlpiTZFR1VNZ6wVz5aSnujDeOhwhsDgB2nLa/fu3aNS+coU1Jcjr6owCTKWW+IM7Xq2Ys4fs9Nd686dO1n4xyLiYuNo37kdAwYMwMrK6l/fNzNm3mWyZCZTzk0eOdDl1YaAvcvs924mY97xDy9NW2IwGJg06QccHR2xsclBgQIF2bJlSzq7bt26s8f7GDbKYlhRlJRYR/r168/JkycB0Gq17N27F3+/gDSBAVAprLDQutO6VVtcXV2pXLkyQ4cOJSUlfYoJiaRAgfycPXuWsLAwEhISGD58OP6qM2il0T5FJvJAfZ5hI4aZ+G8KFy7MkeOHcammYb92DbdynOCLbz5j5uzf051HCEHr1q3Z4b2dQ8cP8uWXX5oFxoyZ/xMhDQhdUqZe7yMf9HLZmjVrGDt2LA8ePCBXrlxMmDCBQYMGmcwexo8fz6yZf6BNsUGjtOfRwwR69eqNnZ0djRo1AiAwMJADBw5io/DCWBsI1Moc6LSOtG7VBitrS4KDg5FSohY2CBvTmZBSWOLq6sboMV+TL18+PD096dSxC1EP7+OkKgSAQeqJUd/ju69GUrly5bS+U36aTER4BOvXr8fOwomYpEgG9B3AiBFfpbvesmXLsvfgniy/j2bMmHkZ5uWytz2GN8rT5bLNmzfTu/fHJCbqASVgwNpaya+//sLgwYMBSE5OxsnJGb3WAYV4psc6fRz2jgqKFy9GYGAggYGBSIMKJ2vTcN4UfQxSFcpHnTrg6elJrly5+Gr4CJxFJSyUxuUtKSVPxDVGf/c5I0eOTOt79epVGtRrhMZgh0ixIkEZQs3a1flr2+Z0e1AAHj9+TEBAAIUKFcLRMcPqq2bMmPmXZMVyWYWyzvKod8tXGwK27ivfu+WyD3YmM27cOBIT9Yg08VCSkKBnxIiv2bNnD8HBwTx48ICEhASsNC4mfRUKC6KiwhBCULNmTXLmzMkfc+ehNySjVFg8Z5jAx316MXv2M5+HpaUlXwwZiqUuLwppgV4Tgat7Dj799FOTc5QpU4YHQf5s2bKFR48eUatWLapVq/bCPR05c+YkZ87/VFvJjBkzrwMJZFGq/3eRD1Zk/P0DMM5gnkdBUlI8vr6+5M2bl1KlSrFmzVoMUotCPJs9SJlMvXr12L//WWZgR0cnpk2dgU7rhFJhgV7GoLJKZNSoUSZn6NOnDyVLlmTunHmEhITQslVf+vXrh42NTboxWltb07Nnz6y8bDNmzLxxJOIDXi77YEWmUKGC3Lx5H9NbYCBXrlz4+PikzRhKlizJxIk/oE22QiHU6A2JqC2S+OGHSSbHGz/+W4oWLcLUX6cTGhZKwwYNmfj9BDw8TPelAFSuXJllyyunazdjxsz7iDTPZD5Efv75Z7p27Upiog7jjEaPlZWSyZMnmyxJjRgxAkdHR378cQohIY8oV64M06dPpXr16ibHE0LQtWtXunbt+mYvxIwZM9kbKRG6lxcke5/5YEOYW7duzdq1aylaND9KZTL58uVmwYL59OvXz8ROCMEnn3yCn58viYkJnD17mtq1a7+lUZv5r0gpuXz5Mrt27SIkJOSV9mFhYZw8eZKwsIwq2poxkwlk6kwmM6/3kA9WZADatGnDrVs30Wq1+PndN/s/shFPxeDkyZMkJ7/4KTAlJYXx34wjd043bKysadO8Jbdu3crQNiwsjJqVq9CqXiMmDfwSr4KFGPnViAwrY2q1WgZ98glF8hfgs46djf/2H5CWHPSfBAYG8tXQodSuXIleXbpw7ty5/+/CzbyXCIM+U6/3kQ9aZMy8eXx9fblw4QIpKSkvtLl58yYlihajRb0m9G7TBfdcedi8eXOGth9374n3onUMc6jJtPztsL3ymDo1ahEcHJzetlsP3EOSmFeoMd/lrsr8os3YvnwNK1euTGf746RJXNm1l3Vl6jG3UCXWlanHxZ27+XHSpHS2vr6+VClXjshdO+ktJbmvXqFlw4Zs3/5GSqibyfZ82DOZD3afjJk3S1BQEJ3af8Ttm7fJobEmUSYze96cdD4snU5HoXwFqGkoSHXbYgghCEgKY3HEAU5fOIuXl1ea7b1796hctgLT87dDo3jmXlwRdgb7WsVp37EDSUlJJCUl8fjxY36d/BMrS7XB4jnbM9FBrEy4T+dePVAoFAghUCgUzP5tBnOLVSO/tW2arV9CDMPunWfRsmXY2NhgY2ODtbU1kydOJNfNG3xa8Fk10LORkfwU+pg7/v4vLA5nJvuTFftkKpa0lSfWZ+4QVqUPv/R8QoilQCsgTEpZKrVtPfD0g+EAREspy2XQ1x+IBfSA7k3tx/lgHf9msoa1a9cy+fvJBAQGUKZkaX78ZXK6UsZSSlo1bYlLqA1funRHKRQEJ4cxuP+neHl5Ub58eaSUREVFsWnTJlQJkhquxdP657N0paJFAZo3bY6LqwtRUVFpr0KWLiYCA+Bl4crirdvZtMV09mOr1KARpmHrDmorHj9+zKxZszAYDBgMBqSUGPR6cltYm9jmtrAmKjaWjh07mrRbK5WsrVbFpK2yoyPRt+7w6NEj3N3d/91NNfN+ISVC9+KZ+79kGTAHWPHs8DItMZoQYjrw5CX960spw7NqMJnB/IhlJh1SSs6cOcMPP/zAzJkzX+ggX7hgIcMGDcXrcWF62XbD4Z497Vu35/DhwyZ2J06c4FFgMHVyVEApjH9yeSxcKa8pRoumzfH09MTCwgJnZ2cGDRqERUr6P0tnlS1JCQm4uLhQuXJlunTpwoABAwjVx6H7xzKDb0ok3Xv35Pbt2wQEBBAaGkpkZCQOOZ3xiTN14B968oBPh3xOYmIiycnJaLVadDoddapV50D4QxPbA+EPqVq+ApcvX+bEiRPs27ePrVu34pE3Lw8TTYtSxeh0pOj12NvbZ+qem3nPyaLlMinlUSAyo/eEMSy2M7A2awf/3zDPZD5ApJQvzBwgpaTvx/3Y+ddO3GV+dKoUxn8znrUb1tKy5bPUGAaDgQnjJ9DYoiFuGlcAilkVxSAN9O7em4pVK/LgwQMCAgKIiIjAXeOa7pzOKgeEFDRo0IBcuXKRO3duVCoVY0aMIl6fhI3SWGvGICU++iCmzpxOjx49TI4RHBDIogun6eJUDlulJSeifTmT+IBL3+/A09PTxHbe4kX07tqd5g4FyKvOwbmkMPxVySwZOybdffjl9xm0aNyEMF0ypW0c8ImP5q+IILxX76Ns2bImtpGRkUwdPYqiOWxxtbQgUa/n1/t+fNShAzly5Mjkb8XM+4tEvCQJbxZSGwiVUt594UBgrxBCAguklAvfxKDMIvOBIKVkzpy5/DLlF4JDgylepDi//vaLiXAAbN++nb3b9tLCohPq1CwHBfGie5furF63mqCgIO7fv8/NmzcJjwjHLZerSX9Pi7zsDznI3bt38fT0pEqVKjg5OTFj2m/E6uKxVT3LbHDH8IBR345m2LBhJsd44OfP3CUrqWNRHCulhnPJvjgUdKNTp07prmvd5o2MHjGSccuXkZicRM0q1dk390A6gQFo2bIlR0+fZN7sOdz0D6BZgzYMGDgwXWVOgKpVq3Li7Blm/DqVjVevUqpqdU6M/DpdWWswZnHw9/Wl44wZ5LO3JzAmhoYNGzJr/vwX/j7MfED8u7QyLkKI553GC/+FGHTj5bOYmlLKYCGEK7BPCHErdWb0WjE7/t8DwsPD2bRpE3FxcTRr1oxSpUqls/n1l6lMn/w7JQy1cFC4EKp7wA1xnE3bNtKoUaPUMG4/BvQbiO6ygmJWpsk+t0atIVJvXMrVaDTkz5+fgPsBdHPshJPaKc3uXqIvDz1COH/F9B5P/G4Ci2YuoLqmDDmU1lzT3iPOUcu5S+extbU1sZVSsn37dhbPW0h8bBztunR8ZT0bKSUGg+Gtll6Ojo7m5s2beHh4vLBwm5l3iyxx/Be3lqf+LJopW4vqV155PiFEfmDnU8d/apsKeAhUlFIGveo8QoiJQJyUclqmBvYfMIvMO86uXbvo2rkbzkoPFHo1EQTQr39ffvt9etrylE6nw9XFjYq65tgpnwlCoPY29y0u4eBsh7+/P3q9HiUqqtjUorhVGZPz7E7awrDvvqRr1664u7ujUCiY8uMU5k+bRwNNXZxUTgSnPGJ/8iGWrl5KmzZtTPpLKdm2bRvzZv1BVFQUrdq24sthQzOcRZgxk13IKpE5vbRwpmw1NXz+X5FpBoyVUqave2583wZQSCljU3/eB0ySUu7O5GX835iXy7Ip4eHhfDVsBJu3bEZKSZs2bfl95m/kypUrzSY+Pp5uXXtQXN8Ie9wA8JQVWL5kJfkKeGJra8udO3fw8fEhNiYWO1snk3M4K/NwJfYIDZvUp2vXrhQpUoTHjx8zddI0ChuKoVZoAAjRPiRREc+XX36JhcWzLNNjx41FqVQybeo0YqJiyO2Wi99//z2dwIAxc0K7du1o167da7hbZsxkY6QEnTZLDiWEWAvUw7isFgRMkFIuAbryj6UyIUQeYLGUsgXgBvyV+uCpAta8CYF5ejIzb5grV66wdu069Ho9nTp9RJUqpuGver2e2rXq8uQBFJTNEUJwbPs1qp+uya07N7CwsODJkycsXrwYa+mAvdItra9aWOCSXIQRw7/GgB6NRkOhQoVQqpTE6CNNZjIR+mAqV6rM+vXr09qklNy7fY8NazeQV1EAnSqFIF0Am7ZsNBEYMArH6LGjGTl6JElJSVhZWb0woMCMmQ8WKSGLHP9Sym4vaO+TQVsw0CL15/tA2X/avAnMIpOFSCm5ceMG8fHxlC9fPsPiYpMnT+HnKb9gYcgFEhbMW8Snnw3k16m/pNl4e3sT8SiGvNRHKIxf2rlEeXxD9lK2bFmioqLScmnZCVf4h6tCKIwRWwsXL8DT0xOlUsnUX6cx7YffKKGrhb0yJ6G6AG6Ls2yZvMm0rxDMXzSfTz//lL1792JnZ0enTp1wdnZ+4XUrFAqsra1f+L4ZMx8672vKmMxgFpl/wctCf+/cuUObNu14+DAYlVKNEAb+XLaUtm3bptn4+voyZfJP5BTVUKmM4bl6mZ+5c+fhlssVnU7HvXv3OHDgACLBFqExPZe1dCMhIYrWrVtTtGhRPDw86N9vADGGcOwUxsJqOplChMaXWaOWU6DAsx3oX48cgY2NNT9P+YXgkIcU9yrB2mmradiwYYbXU65cOcqVK/dfbpcZM2YAY1qZNxLCnC0xi8wr0Ov1/PjjZGbOnEl0dBRlypRl9uxZJpmY9Xo9Deo3JCZShYWiMEIKtPo4unfvycWL53F0dOT+/fvMnTsXjXRBlbr/A0ApNKh1Lnz99dcAuLq64uTkRLgiPJ2oSatYfvppisleEY1Gw8e9+pBTFEDo1ESq/OnUuSNNmjQxuQ4hBIM/H8zgzwe/rltlxoyZjJB80CLzQe/4P3XqFA0bNsTV1Y2aNWuyf//+dDZDhw5j2tQZJMRaYKHy4Ma1IJo1a86lS5fSbP7++29iYxOxULqkiYJamQOptaF06TK4ublRvXp1Vq1ahVabPqOwQikYMmQI0dHRhIaG4uPjQ25PJ0K5hFYmoZPJhBquoLbVp0tp0rFjR27fvcUXk/rw8dg27Du0m0VLFpp9I2bMZBtSZzKZeb2HfLAhzEeOHKFFixYkJup5VrRMxapVK2nfvj1g3PeQO3ce0Dsjnst5pdPH4JrLhjx5cuPv78/jx49RK+2wtzSNhU/UhuGe35rBgz+lUKFC2Nra0rx5S5ypiIXSDgCtIZ5weQ6fa1coWLBgWt/Hjx/zxZChbN26BYOUtGrZmtlzZprzYJkx8wbJihDmSkXU8szvLpmyVbUK+c/ny2689uUyYfx2Pg88lFK2EkI4AeuB/IA/0FlKGZVqOxb4BGOW0C+llHtS2ytiTAxnBfwNDJVSSiGEBcZEcRWBCKCLlNI/M+P6+uuvSUzUI8RT57yCxEQd/fp9wp49e3jw4AF37twhOVmLpdp0g59CWBAW9piSJUtQvnx57O3tmfn7LAxSh0IYb6mUEpVFEt9++yO9evVK67t48UL69x+IbWpEWKwuhBm/zzARGICcOXOybv2atFon5pmJGTPvMO/pLCUzvAmfzFDgJmCX+v8xwAEp5c9CiDGp/x8thCiBMda7JJAH2C+EKCql1APzgIHAaYwi0wzwxihIUVLKwkKIrsAvQBcygY/PNdJfvpLoaGMm4Hz58uHl5YW/fwBS6k1mMggtbdu2YePGDWlNyckpLFu6EoPWHgVKhDqWgoXz0rlzZ5MzdO/enSZNmrBjxw70ej2tWrUy2fvyT8zikvUkJSVx//59cufOjaOj4yvtU1JSMBgMWFpavtLWjJl0mH0yrw8hRF6gJbD4uea2wPLUn5cD7Z5rXyelTJZS+gH3gCpCiNyAnZTylDQ+1q/4R5+nx9oENBSZ/FY2frH/8xcvsbe35/Hjx1y4cIFdu3YxePBgVJo4DIYUpDSg08ehVCfx7bfjTHr+/vsMlvy5gCo1CuJVxpnxE0dy/PixdHtLAFxcXOjbty/9+/d/qcCYyRwHDhygS/uPaFynHtOmTiM2NvaFtr9Nm467ay5a1K5PPve89Ov1MUlJSRnahoaG0qldO+xtbbG3taNxnbrcvn37hceWUnLkyBGWLFnCuXPnMqy4aeZD5MP2ybxux//vwChMv83dpJSPAFL/fZph0R0IfM4uKLXNPfXnf7ab9JFS6jDWUUi3oUMIMVAIcV4Icf7x48cAjBv3DdbWSqQ0Dk1KA9bWCr7++muT2cOMGb8xZuzX2Dro0BqCKVOuIHv37kmXiVcIwUcffcSBg/s5e/Y0I0aMMO8d+T9JTExk+rTp1KhYlQa16rJy5UoML/gA/jZtOj07dMHqbDClApRsnraQmlWqERcXl852w4YNzJr8Mz951mZugYYsKtqcu/uOM2zIF+ls9Xo9jevWxeLyLbZWaIh3lSaUCI6ifq3aPHmSvlxHREQEVcuXZ2Cnj9j102Q+atqU5g0bkpCQ8MLrjIqK4siRI9y9+6KkuWbeCyRgkJl7vYe8tuUyIcTT6m0XhBD1MtMlgzb5kvaX9TFtMGYxXQhGxz9A//79iY6O5ocffkSn06FQCIYNG8o333xj0lepVDJu3DjGjRv3z8Oa+Zf4+vpy8OBBHBwcaNWqVYYJL7VaLQ3r1CfJP5JqFoVJMej4fuhYjh48wqI/F5vYRkdHM3HCBCblbYGLxphSv4KtJ3PCjjFt6lS6de9OQkJC2uv7b76lt3Nx3C2NCTlzqDR86laWAStXUrp8OaytrVEqlSgUCq5du0ZyWASflqie9tDROXcBrifGMnv2bL744gtsbW3Tql4OHTyYIrFPGFO+DEIIdAYDY27d5fsJE/hl6lSTcUsp+fH7iUyfNo2iTnYEPImjTLnyrNvy10s3vZp5V5Gg073tQbw1XqdPpibQRgjRArAE7IQQq4BQIURuKeWj1KWwp1WkggCP5/rnBYJT2/Nm0P58n6DULKT2vKCgzz8RQjBy5EiGDRtGWFgYLi4uGS5tmfnvSCkZ9fUoFs5fgJdNAeJkIoMHfcau3X+nS6nz119/EekXwmCnpihSv9yL23jww/r1FC9dArVazePHjwkLC8PHxwdXhU2awIDx91rF0oNff/yJ7ydNMjm2pUKFe3HTCEAHtSVCp2fIkCHpxt3M1SOdT8xLY83E775j/PjxCCGwtbXFzs6OkOBgDtetlWavUij4zNOdAYsW0aJVK/LkyUOePHmwsbFh48aNrPpjNnvqeuFmpUFrMDDlph+f9OrJ1r+9040jNDSUmb9N5+Thg+TOm5fBw0aY7NMyk815OpP5QHltIiOlHAuMBUidyXwtpewphJgKfAz8nPrvttQu24E1QojfMDr+iwBnpZR6IUSsEKIacAboDcx+rs/HwCngI+Cg/JcL4Wq12hwW/H+SnJzMwoUL2bh6AxaWlvQd2JeuXbumq2nv7e3N6iUrGezcBevUjag34+/TvnU7jpw4SmBgIAEBAfj7+7Nx3XpKKPKkCQyAhUJNAaUrI0aMAIxC4uLiQo4cOYjRJqTbtBqhjadi5UoMHvoF1tbWWFlZYW1tzZTvJ3H61kM+srRLs70VF46DkxPXz51BCIFer8dgMHDmzBm+HfIleilRPnfsCwnR9O7Th1KlSvHkyROePHlCZGQka1evwlJpet02ShUxsbHUq1cvrc3Ozg6NQc+kUnlwszImIFUrFIzyykX1fYd5+PChyd/jo0ePqFaxPA1dYIi7Bb4hwXRt25Ipv83i4z59/s/fnJk3jnw//S2Z4W3s+P8Z2CCE+AR4AHQCkFJeF0JsAG4AOuDz1MgygM94FsLsnfoCWAKsFELcwziD6fqmLuJDR6fT0aRBEx7dCKaEohhaqWP04NEc2n+IRUsXpdklJSUx67eZVFIVTxMYgOI2BdkTdJwiRYqktQkhsM1hi6MyvaswXq1lzpw5dO7cGScnJ5RKJVJKypYohXfUDZo5lkAhBI+Sn7A//h7bZuyievXqJseYPmsmtavXQIekYg43/BOfsC7qNr/9MYf8+fOb2BYqVIjFf8zjRz8feucqgIVCweawB0RZWzB37tx0S32P/P3ZHPyI7h7PJt3rHj6iRYsWfD5sGMHBwWmvDSuWkTtVYJ5ipVKi0uvw9PQkX758FCpUiEKFCnH75nUaOxv4qUpOAOq6Q2VXK3qMGE637t3RaEyPYyY78v76WzLDGxEZKeVh4HDqzxFAhgmzpJSTgckZtJ8H0lXiklImkSpSZrIGg8HAnNlzmPnbLB5HPKZWjZr8PO1nypQxrS+zY8cOAm74096qDQphFIWChvz8uXolSdokHj9+zO3btwkICECNilbO6ctc2FjmoO+gATRv3pz8+fOTN29eQkNDKVOiNLcTgvCyzotBSk7F3iLRQs/AgQNNko4KIdjuvYv2rdpwOGgHDhobghOj+HXatHQCA1C8eHFOnTvLzz9OZsnJU+QrWoA1YzbToEGDdLZCCHbu3cPE8d8xdvVqUrRa2rZty9Gff8rQlzRz/nwa1qnDjcQkSlhYcCExibt6A8fmz083U1ZKyfa9f1HO6dky36XIOBSW1oz+6nP8/Py4f/8+mzZtIiUmiq+bmlb5LO1sia1acPv2bUqXNi0uZyYb8oEvl32wO/4/VOLj41GpVC/0P40cMZJ1izdQTlTFVmmPf8o9borLnDl/hiJFihASEsL169eZNHES+BionKOiSf+dkd74GwIoVaoUXl5eeHl5ERYWhvfqHfR2aIUydb9RcHIY6+L2EBz6KN2X9r59++jb82NEioFkvZZc7rnZ8NemDEsfg9Hnc+3aNSIjI6lUqRI2NjYZ2r1uIiIiWPbnn9y9eZOylSrRs2fPdFU/wbgEVr1SBWrkUNLIxYb78Sks8otg9qLF6fZVNa1Xm/bCj46F7NPaEnUGym0O4PodX3Lnzv3ar+tDJkt2/BdQyDMTMjfjVPVNNu/4N/NucuXKFQb1/5SLly+iEIK2bdoxb+EfODk9qy8THR3NvHnzaWPVFSuFMfy6uGUZEhMSqF+nPknaJCIjn8VVlLYume48eis9axevpUOHDmltOp0O/3t+/Hl2O14iHwmKZHwS77Bk+dIMZwWNGzcmIDgQHx8fLC0t8fLyeummVCFEtniid3Z2ZkRqotOXkTt3bs5dvsqcWTNZd/gweUp6snPRcCpXrpzOdsiIUQzr14tKrlbks9WQrDcw6WIktWvVMgvMO4KUIHUf1sP885hF5j0gLi6OW7dukStXrgxry4eEhFC/TgMKaMvR0qo/OrRc3n2epo2acfLMCe7evcvVq1fZs2cPGoNFmsA8JY/aA7+4O3Tp0ZlSpUpRqlQpHBwcqFe7HoHJQXhY5EVKyc3EW8SrE2jZsqVJf5VKxQ7vnXh7e7N7lzdOLs6s6LMhXSqd51Eqle91qYGcOXPy/Q8/vtKudevW3B09jibff08+ByuCniRQpWpVVq5e9wZGaSZLkKTf9/0BYRaZd5xff5nKpEk/kENtT1zyE+rWrcPaDWuws3sWQbVo0WJySk/yq40zDw1KSipqsufqcmxsbNBqjaVhlUolQipIMSSjUTxbTovQP6ZFy+YsWLDA5NwbNm/g4x4fo0xQojNosXd2YO+2vRkuxSkUClq2bJlOgMy8mq++HsmAQZ9y/fp1cuXKlS5Iwcw7gFlkzGQ3pJQcO3aMc+fOkS9fPlq3bp3uy3vLli388sM0yhhaY6W1Qy90XDt2mt49+zDpx4lcvXqVq1evsmblWly1ReC5ZWEhBE4qN8o28qJr166UKVOGYsWKMaDfAE7sOERFZU1sFDl4kHKfm/IKf4yekW6MTZs2JSgkiMuXL2NhYUGpUqXMudZeE7a2tlSrVu1tD8PM/8uHu1pmdvxnR5KSkmjetCVXLl3DSu+KXh2H0krHsRNHTJaYalarQ8wlS1xVhdLadDKF44nLMWCM/tZoNOTMmRMRbkUVi+Zpdgap55BhLcdOHTHxZ6SkpDDq69EsWbKY5JRkihQsyu9zZtC4ceM3cOVmzGQvssLxX9FTIU+PzpzjXzPk5Y5/IcRS4Gk2lVKpbROBAcDjVLNvpJR/Z9C3GTATY22TxVLKn//Ndfy/fNBFy94GQUFBfPbpYIoULkatmnXYunVrOptffvmVGxf8ya9rQi4q4K6tgzIqF21bt2fBggUMGTKEunXrcu7cWSwVdiZ9VUKDlcaG6dOnc+3aNeLi4rh+/ToGx0Ru6s6QYIghWv+Yi+ynVu1a6RzmGo2G32fNIDommqjoKK7fvmYWGDNm/iuGTL5ezTKMWej/yQwpZbnUV0YCowTmAs2BEkC31Mz3rx2zyGQh8fHxeHt7c+DAgTQ/x/M8evSICuUrsmHFPhKCnblzIZaPe33C1F+f5baKi4tj0YIlOOq8EOLZr8dZ4cX1G9f59NNPWbFiBTqdjsJFChEu75ucI8bwGCsbC7744gtKliyJWq3G3t6eM+dOU7FtUc4odnArxzF6f9mFzVs3vvBalErlWwsFNmPmvUKC1Cky9XrloaQ8SiZTZ/2DKsA9KeV9KWUKsA5jFvvXjtknk0WsX7+eTz7pj4U6B1IaEEo927dvo2bNmmk206ZOx5Boh73SmD/LQumAhcGBcd+OZ9/+fdy5c4eAgAAUqChiYbr3VCBQq9WcOHmaihUrIoTgwYMHVCxfGb+kMzjo85IgnxCi9mH2zJkmmxYB8ubNy8o1K1//jTBjxsw/EGDItK/SRQjx/Hr+wtQEv69iiBCiN8YCkSOeFoJ8joyy3FfN7KD+C+aZzCvQarVMmDAB15yuWFlZ06xZc27evGli4+vrS7++n6DWe6LQ5kWp80QX70Tz5i25fv063t7e/P7776xYsQq13jTLrlphjdQp8ff3p2bNmvz444+0bd+GKMUdk3okkXpfShQvQaVKldKc656enly+epE2/esiiwbj1cSJHd7bTCpxmjFjJhsgReZeEC6lrPTcKzMCMw8oBJQDHgHTM7DJVMb618EHPZPx9/dn2rRpnDt3jlKlSjFy5Mh0u8p79/6YHTt2o0u2RAhnDh04S/Vq1bl+4zru7u5IKZk79w8U0g6V8tn+Eo3Knuj4R5Qq9WxGolFbYquIw+q5kjcGqUdjqeDAgQN4eBiTUMfGxlK7Zl2CAg6jSnQGywSSNRHsWHUo3TW4u7vz+8z0kV8fElJKQkND0Wg0JptLMyIsLIzZM2dx8shR8np6MGT4sAw3QT4lNjaWtWvXcvPadUqXK0uXLl3My4hm/h0SZOZnMv/+8FKGPv1ZCLEI2JmB2Yuy3L92PtjosmvXrlGjRg2Sk/VotQaUSoGFhYI9e/akLXE9ePAAL69ioHcx8Y/oZTSe+VyxsrLE19eXhIQErNR5sNHkMTlXoj6A9h81ZeDAgRQrVoybN2/SskUb7AylsFDaY5A64rhHxRpF2bPXNMW7Tqdjx44dnD59hgIF8tOtWzfs7e0xY8q5c+fo/3Ff/P390UsDNatVZ8nK5RluSg0ODqZqhUqUVtpTxdqVoOQ4tkbdY/6fS/joo4/S2fv5+VG3Rg0KKy0prrbGJyWehwoDx86cJk+ePOnswZhZYdmSJTyJjKRZmzZ06NABleqDfpZ7p8mS6LK8SnlySI5XGwKWY2NeeT4hRH5g53PRZbmfFoIUQgwHqkopu/6jjwq4gzFv5EPgHNBdSnn9X17Ov+aDFZlGjRpx8OBxhHjmu5BSi7t7Tj755BP8/f25ePEiN67fRaNyMzmG3pCASpNAw4YNKFy4MCkpKfy5dBVWolCaGBmkjkR5Fx+fKxQq9CzEeMWKFQwbOhyDXpCsTaRhg4asXrPSLCDP4e3tzYxfpxMc9JBadWsz5ttvMtyAGBISQkmv4nS1K0tV+wLopJ5dUde5aRPHtds305UcGDpkCIF/HeKT3M+qmt6MC+f3qKsEBD9EqVSa2Ldt3oJctwPo7V44rW1h4G30Vcuxan36HfdLFi9m7Fdf0Sm3G45KJbuionErUYIdu/ek85E9RUpJTEwMNjY2ZjHKhmSJyLir5InB6XPYZYTVt9GvCmFeC9QDXIBQYELq/8thXP7yBwal1uvKgzFUuUVq3xYYqxUrgaWpCYlfOx+syFhbW5OUpDDZPCilRMp4wOgod3Nz4/LlK6gVeUw3GSri6D+gB7NmzQSMmYvbtW3P0SMn0SfbABKhiWHQoP5MnWZaFRGMfp579+7h7OyMq6truvc/ZObPm8/EMd/SxKosrhoHriUFcFEXwLlL58mXL5+J7ZQfJ3Ngzhr65nzmv5RS8m3ATso3rImjoyOxsbHExsYSExPDzctXmZi/FkVsTP1iPa5swWClwcLCApVKhVKpRKlUEhQYyO5qzbFWPvvyj0hJosulQ4wZNw4XFxdcXFzImTMnFhYWtGjShNUVypLfxrhsqjMY6O9zg2FTp9GzZ89017p582a+GfEVD0NCsLCw4LPPPmPij5PNYpONyDKR+TRzD5FW30WaE2S+L9jZ2ZGUFINR1J8isbCwJDo6CktLY+2TVi1bcfjwSfRaa0CJ3hCPhSaFYcOGpvVSKBT8tXULmzdvZs2atVhZWtHvk74v3F+iVqspXrz467u4bEZERAQjvxrJ5s2bMBgMtG/Xnmm/T08nsMnJyYwb8w2DHBqT28LoW8ln6YohUtKza3eq1KhGYGBg2ivsUQhd3Uw/j0II3BQ27N27F2dn57TKlba2ttjY2PA4JcFEZJIMOlKEpEeXLqjVavR6PTqdDq1Wy7rVa0gx6E1EJsVgQOoNTJw4Md11lrSzTRMYMFbHbOvixMypv2JnZ0ehQoUoWLAgVlZWHDx4kCGf9OW3cu5Ur1yWoIQUxqxextjkZKbO+P2F9zIxMRG1Wm0WoncI+Zp9MtmdD/Yv9YsvvmDKlJ9JTDRWVZRSYmmp4JNP+qUJDMDGTRsZPvwrli9fTkpKMuXKVWD+/D/SJXdUKpV07tw5Xar2Dx2dTke9WnWxCVXziUNHBHBmz1VqV6+Fz81rKJXGyLqbN29y6NAhRIohTWCeUsY6H3PP7uTClUt4eHiQN29eGjVqREREBJdPXKWxLJ4209Qa9ATIGE6fPp2uBs66desYN3goXjbOOGus0Rr0rAi9RtPGjVm0aBH/RGh1LD95ni89iiGEwCAly0Pu03/AAH6fM5uIiAjCw8MJDw/n8OHDrJ01K90xnqRo8bl3m7Ztn21JyJMnDzIpkZFFc1LD1biZ1sPGghnl8tB40SIm/jg5XXDBmTNn+OrzTzl/xQeNWkWP7t2Y9vtscuTI3Fq/mbfJvwphfu/4YJfL9HpjEazVq9dgZWVFUlIiLVu2ZNWqVSYi8xSDwYBer3/h2vqHhk6nY9GiRaxYYtwY2qVHFz4f8nm61P07duxgWJ8h9MrR2mTJcenjLYicakJDQ0lKSkprVytUTC7QG0vFszQcZ2Pu8LCIngNHD5kcIzExkYplypM7Rkl928IkG7TsiL1J4Rrl2LTtr3RjllIyacJEpk+bRgF7F4LjoilboTwb/tqSYVRaREQEjevWIyksnOJWdvjER+Ocz4M9hw6aJCB9ej8KeXrypaszTXMZfXhhScl8fOUac5cvx83NDV9fX+7fv4+vry/bN65nXc1CFLU3zXhdccdlajVtTo0aNShbtixlypQhISGB6hXLM6m8Le0K2hGZpGfixWiS85djm/fezPy6zPyfZMVyWYU8anm8v2OmbG1+ePzeLZd9sCLzlJCQEG7fvk2hQoUyjEgykzEd23Xk0uFLlFGUQimUXDfcIGcxVw4fP4wQgrt373LhwgXmzZuH/mocTR1rmfQ/FH2Ghy5RtG3XluLFi1OiRAmKFy/OwH4DCDp2g/b21bBUaHiUHMnS6AMsW7+KZs3SZ9OIjIxk8qQf2LZlK5aWFnzcvx/Dhg9/6cNAVFQUV69eJU+ePCblnzPCYDBw4MABbt++TcmSJalXr94Lk4BevHiRts2b46pS4qRWc+5xON98+y2jxo5NZ9ulXVuKB1yhb5FnQSX3YxNpffAWDjldefjwYVq7rY0VvQpa833VZ8uLKXpJxb+COHz6PF5eXibH9vPzY9ovUzh/+gSe+Qsy9Osx1Kplev/NZI4sEZncann8E+dXGwI2k0PNIvOu8y4kyHybpKSksG3bNu7fv0+FChVo2LBhuiit8+fP07x+M7rl6IJKGFdcDdLA2icbyFkwJw8ePCA2NhYw1pJxVTkx0M10GXF93G6+nfU93bt3N2mPi4vjk4/78re3N/YWOUiSWib/PIVBnw56jVeddWi1Wvbv309MTAz16tXDzc0tQ7tLly7RuG4dvi7qQsPcDtyJSeSHm2EM+HoMI0aNIjIyEh8fH65cucLc335lTGFoXcB09tR6VyBuVRrStWtXKleuTMGCBbl37x61q1WmVzEFTfKpuB6u45fzKcycv9S8lPt/kDUio5FH+7hkytb250dmkXnXMYvMiwkICKBOzTooEzTYah14rHyER+G8HDi8P23t//Hjx4wbN46z687QIEc9k/5nYs/hbxtA+w7tqVixIhUrVqRw4cKUL10Ot2h7qluXQwjBmfir+FuHcPPurQyXJgHCw8MJCwujUKFCLywV/a5z7tw5Jn4zhrPnzpM3T26GjR5L7969082UJoz/lqDti/mlyrMlvXitgVJr76EVKpKTkwFwcnLCzlpDj/yJjK72LGT29MNkBh4R+AY+SvfAEBkZydatW4mPj6d58+YULlwYM8/IEpHJpZFHP85cFKntrw/NIvOu8yGLzKNHj9BqtXh4eGS45NO4fmOizydS2qIiYPRhnEjZj2cVd3LlduP06dP4+voCkFudi64upk/GB5MO8/H4PgwfPtykPSQkhGFDhvLX9q0gJa1btub3OTPNy5OZJCQkhPKlS/JJQTVdC9kSmqjjh8uxFKrdjPlL/uTatWucO3eOs2fPsnntCvZ3caKo8/P7vyQF5j9mxfotNGnSJG0p0dvbm55dO1G/sBp7jZ7tN3QM/nIY3/8w5W1darYjq0TmSK+MZ7T/xG5akFlk3nU+RJG5f/8+Pbr0xOeaD0qFkjx58rB89TKqVKmSZhMXF4ezkwtdbPuhem6DaqQunF1PNpIztwvVq1enWrVqlC9fnh5de1BWX5qSlsZs4b7J9zmmO8Ed3zvkzJkzw3E8/VszFzb799y9e5fvxoxi/4ED2NvZ0m/gZ4waMyZdKHOtyuX40iOI5oWeBWBEJOrxmv+IFD1YWVlRqVIlKlasyJ+L57Oth5JqnsZjPI43UGuRgVVbdpt9OKlkhciUz6WRR3rmypSt/fTA905kPtgQ5g8FrVZLvdr1cYzypJG6FwIFDx/eo0mjpmz+axM3b97k1KlTnDhxAp1Wyz/z6AkEzs5OPHz40EQcDh45SJeOXTgfdBGlQomdox271u56ocCAWVz+C0WKFGHt5vQRc//k869GM3HEp5RwUZPPXkVsioGRR5P4qEMH2n7UhVOnTnHq1Clmz55NxTxQzfPZUmROGwUDKuhYt3qFWWSyEinA8OHmIjaLzDtMZGQk34wdx6aNm1EoFHTt1oUfJ/9gEl7r7e2NTFBSSF0urS2vugjBCfdp1KgRYNy3UaNGDdRCw+3HPpS0LA8YZx63DVfp2r1rOoEoWbIkPjd98PX1RafT4eXlZRaRbEDXrl154H+fOj9Nwd3egofRSbRs2ZIFS5djbW2d5vxfvXo1K38anK6/RinR6dLXQjLz3/iQN2Oal8veUbRaLWVLlychUEFuQ0kkEKzwwaWwJafOnuDatWucOnWKFStWEHolloqWjUz630m+SN66dixctCDNR3P37l3q1KyLrdYem2R7Ii1Csc9jx9ETR3BwcHgr12nm/yMuLo67d++SJ0+eDCPcoqOjKejpzoG+Ckq4GbNexCVLai6WzPpzE02aNHnTQ86WZMlymaulPNQlc/5Hxzm+5uUyM6+f5ORkpk6dxp9LlpGSkkLHjzowYeJ3ODo+29C1fft2oh/FU0w2RSiMT0mFZS3O3diAra1tWmVOZ2dnEg3J6KUepTB+mUgpeWLxiPH9vsTT0zPtmEWKFOGe3102bNiQFsLcunVrcwqTd5AcOXJQvnz5F77v4ODA7HkLaDx4IJ1Lg71Gx4YbKhq3/shcbvs1YJ7JfEBkh5mMMRGnTBdO+pRmTVtw8cTN1BLMKp4o7mHnLrhy9RIJCQmcO3eOn376iYATcRTUmNZCuas9Sb6qdgwZMoTq1avj4eFBu9btuXjUh/z6MihQEqS4iW1+DWcvnEGj0WQ4hveZuLg44uLicHNz++CX+Pz8/Fi7di3xcbG0bNWa6tWrf/D35HmyYiZTztVSHvzI89WGgPO8u+/dTObD9Ua9BfR6PRMnfo+TowsqlYpSJcty4MABE5tz585x+sQZ3A01sFHmxFrhSC5ZidCAaPLly4ezszPNmjXjyJEjxBCS/hzWcQwbNowuXbrg6emJEIJNf21k+MQhRHve51Gua3T7sj3HTh59LwRGSsn169fx8fHBYDC81DYmJoaeXbqSK6crxQsVwatAIfbs2fPSPocPH6ZxnbrkdXWlYa3a6X5f7zoFChTgm2++YfKUn6hRo4ZZYF4HqQkyM/N6HzHPZLIQX19fzp07R548eahVq1a6mcqXXwxl1bKNWBuKoBY2JOhDiVfc5dDhA+TLl49Lly4xb948Tnhfx0NVzaRvmPYGFnmfMGBgfypXrkzx4sWpVKEyOZ7kI48ogQQeyqtoXR5z1/f2eyEgr+LixYt0+6gzMZHRKBBY2tmwav1aqlevnqF9y8ZN0F8PoK9raWyUai7GPGJW6CUOnThO6dKl09nv2bOHnp0682nuQpS1c8YnJpL5j+6xdO0aWrZsmeE5EhMTWbduHWdPniRfwYL07dfvhbv+zWR/smQmk9NK7u+QP1O2ORfeeu9mMmaRyQIMBgP9PxnAuvXrsdI4oJdJuLo5c/DggbQNhzExMeRyy01ORXWUimdhozEp/sQr/ElKSkhrs1I6UMyilck5QhTn+fr7AXz11VdpbX5+fgzoN4ijx48A0LBBIxYtWfBOb3JMTk7mwIEDJCYm0qBBAxM/1PPExcVR0DM/nWxKU9WuAAAXYx+w8skF7vr5miS8TElJ4fz587Rq3JSlXi1QK56Vd1gfeoOwojn5csRwVCpVWhp9tVrNgN4f011lTx3n3Gn2JyNDWSNjuXQjfUHByMhI6lSrhlNiAjVzWHMvRcvhiCj+3rfvpSWezWRfskpk9rUt+GpDwHXJjfdOZMwe3VeQnJzMzz//zJIlS0lJSeGjjzry/fff4+z8LOHd4sWL2bx5O1aiKAqdEiElIUFhtGvXgR9++J5r165x/PhxdFpQWpmmSLFQOqJVBjN5+g+UL1+e0qVLU6VyNcJCruMivBAoiNL7k2gZSu/evU36FihQgP2H9qZlMX5RipZ3hRMnTtCudVtcVHZYCDV9Y4OZNmM6AwcNTGe7adMm8qudqGb/7MNb0S4fJ2PvU7NmTaytrYmIiCAiIoK4uDgAClg5mAgMQAELezYfPsKeg/vTnUMBVK1hOmOp4piTUSfO0LhxYzw8PHB3dydv3ry4u7uzad06immTmViyaNqy067gED7t25cL165leM06nQ5vb28CAgKoVKkSVatWNS9ZvW+Y68l8uMTGxrJixQrOnz9PqVKl6Nu3b7qU761bteHkqXPoki0AwdIla/D23s21az5YWVmh0+mYMWMmpDigUBm/wIQQaMjJhQsXaNGiBQC5cuXCIFPQGZJQKZ6JQbKMolHjhiYzlCNHD9G7Vx9OndqGEIKiRYvy14oDuLhknGTvXRcXMC4ztW3Zmo421SlhY3SSPrZ6wpgRo8jjngeDwcCtW7fSXpcvX6amZf50x8mlsiM4JpyCBQtSsmRJnJ2dcXZ2Rq1W88OEiTzRJWOveib0FxPD6Na7JwM/+xStVptWsEyr1TKg98fcjXtCKbtnfxP34mOwt7LmyZMn3Lhxg5CQkDRfkLVSyYqqFUxEolluNyYfOcmJEyeoVq2aSYnngIAAmtSri70uEa8cGqY/jqNEhUps2bHzvc3X9iEiEUj54bq/P1iRCQwMpHLlKsTFJZCQkISVlQWTJ0/m5MmTFCtWDDA64U+eOoU+xRFFapiw1Kt5GBRKrVq1SEpK4t69e6Sk6LC3LPqPMwgsLCz588/FNG3aFCcnJ0aNGsOi+cuw1hVCrchBvC6UJGUg479bbdLTw8ODQ4cPEBUVhU6ne+ku+uzOvXv3mPLDFM6cPI1nfk9Gjh1FgwYN0tnt3r2bXGqnNIEByKmxp4KmAG1bt8GAcVk3V65ceHl50aRJE07uO4zWoE+bneikAR99KMuWr0zbaPo8j0NC+XHlOno4FcNZY82R6AecT4ng0k9TyJUrfdqPcRMnMv27iUzIX4r81rY8SIxjWtAtJk2ZzJfDhhnPqdMREhLCw4cP6d6xAwl6vckxtAYDSSlaatWqhbW1NaVLl6Zs2bKULVuWlUsW0cZO8kWxfGm2n573YdrUXxn37fj/74abyZZk1UxGCLEUaAWESSlLpbZNBVoDKYAv0FdKGZ1BX38gFtADuje1LPfB+mQ6derM1q07MRieXz7RUbJkEYYMGYKvry/79u3j2tW7qJSmtSB0+hhsbCV169bFy8uLq1d9OH7kIhYib9pTbIruCXY5k3nwwD+tzWAwMGPGDKZPm0F4xGMqVqjE9N+mUqNGjTd1+W+UO3fuUL1yNcqoilJY7UmYNoLjKZeYOW8W3bt35+bNm5w+fZpTp07h7e2NfbSSQe6my1OHoq4QU8KSn379CS8vr7RNoVJKOrZtz52Tl2hkXQSFEBxMuEeuMoXx3r83wyUnKSULFy5kwaw5REZG0qBxI76b9D358+fPcPxSSmZMm8bPU35Cr9WiUKkYMWoko8eOzfD4v/7yCztmz2RWSS80qUEf8/wCuGLnRL/PPuPy5ctcuXKFK1euEB0djUYh8GlfAUvls6fcC+FxfBuQxPV799MdPzw8nHlz53LqyAHyeORj8NDhVKhQIbO/DjP/B1nhkynrbC13t/znQ2jG5Fl55aXnE0LUAeKAFc+JTBPgoJRSJ4T4BUBKOTqDvv5AJSll+L+/iv+fD1ZkcuTIQUKCRIhnH3Dj/pV4ANRqNa6uroSFRqBSmEYHKdXxTPx+DCNGjACMRbAqV65KxONYdEkWKFR69CKabdu20rBhwzd3cdmMHl26E7rPn1q2FdPagpJDWBv1NypLFTExMQA4OjpSrlw5Th8/yei8nXBQGcsK6Ax65kTuYs7KhRlGc+l0OpYsWcLqP1dg0Bvo+nEPBg4cmOWRdTqdjoiICJycnF5aDE2r1dL9o484ceQI1V2cuBufgD6HLXsOHTIJxpBScvnyZepUr8aV1mVQKZ4J1vWoBDofvkXNBo2oXbs2derUoXLlykRHR1O9UgVqOupplkfN3Sc65t+K548ly+jYsWOWXq+ZZ2SVyHi38Hq1IeC+6vIrzyeEyA/sfCoy/3ivPfCRlLJHBu/5YxaZ189TkXF0dOLJk+R0IqNUJnPnzp20nfBFi3gR/DAKpA0gMMh4rGx03Lt3z8RHEh8fz6pVqzh44BD5C+Rn0KCBFCyYuYiSd42zZ88ybvQ4zl84j3sed0Z9M4pevXqZPN0nJCRQyLMgHTQNyak29XP9+nAx7bt0oEmTJlSrVo2iRY2O8l9++plpU36lmpUXlqi4oPOjXK1KbNq65YUbV7Mjly9f5vz58+TLl48GDRqY+GGep3qFcnRUxdC5gPHvSErJ1xcC8bPLRZJWx/Xrxgg2CwsLcuV0poFDEr/WeFaX5GxIAp+eTcQv6NELz2Hmv5EVIlPG2Ub+3bR4pmw91l4IAJ4XgYVSyoX/GFN+XiwyO4D1UspVGbznB0QBEljwz+O+Ll6bT0YIYQkcBSxSz7NJSjlBCOEErAfyA/5AZyllVGqfscAnGNcMv5RS7kltrwgsA6yAv4GhUkophLAAVgAVgQigi5TSPzPj+/jj3ixYsJjkZIkQAiklGg20bduRAgUKpNkdPXaE3r0+5viJY4CgWPFiLF++LJ0T3sbGhkGDBjFo0LtRwfH/5eLFizRu0JjKqkp8ZNWR8McRjB4ymrCQMGrWrsmBAwfYv38/p06dAq0kwjnaRGQS9IkoNErmz5+Pra2tybFHjx1DnXp1Wb50GQnxCUzv9BVt2rR5pwQGoFy5cpQrV+6VdvP/XE7TBvU5GZ1MMSsFR6K0JNg6cujQYRwcHIiIiOD48eMcO3aM5Qv+oGsl08JXVXJZQ3IkN2/epFQp0++ba9eu8fu0X7h1/SolSpdj+MgxFC+euS86M1nMv4suC/9/RU0IMQ7QAatfYFJTShkshHAF9gkhbkkpj/4/5/pX43pdMxlhfKy1kVLGCSHUwHFgKNABiJRS/iyEGAM4SilHCyFKAGuBKkAeYD9QVEqpF0KcTe17GqPIzJJSegshBgNlpJSfCiG6Au2llF1eNq6nM5n4+HiaNWvGpUuXEUIJGChYsACHDh1KF2EGxn0uWq3WJHT5Q6Rdq3Y8Of6EstZl0toidZGsDV+HTuoQQlCuXDkaNmyIRqNh6ezFfJSjCc5qB5IMyXjHH6Ni6+osXb70LV5F9iEyMpKVK1cScN+XytWq07FjxwyX+xrUqMrHOR7SssAzYU7QGSi2/C5KKxsaNmxIkyZNaNKkCSEhIbRv1YzPy6mpllvFiYc65l/VsWvvAZMaQmZeTZbMZJxs5M7GJTNlm2/Duf9ruUwI8THwKdBQSpnwor7P2U8E4qSU0zI1sP/Aa5vJSKN6xaX+V536kkBboF5q+3LgMDA6tX2dlDIZ8BNC3AOqpK4j2kkpTwEIIVYA7QDv1D4TU4+1CZgjhBAyE8ppY2PD0aNHOXfuHD4+PhQtWpRatWq9cI/C8+nz30fi4+P59ptvWbliFSkpybRs2ZKpv0018SVER0dz6tQpmqpNM/Q6qZywVFvyy4xf6Ny5s8ksz9nJmUkTJ2GjsuJJUiwd2rdn7vy5b+y6sjtOTk4MHTr0lXYDvxzOD8M/o5KbFW7WKnQGyZSL0ZQtW4YylaqyZ88etm3bZjxmDgum1rOmcwlrAGp5WpDbJp5xI4ez78iJ13o9ZjJGyte3T0YI0Qzjd2jdFwmMEMIGUEgpY1N/bgJMem2Deo7XGsIsjFOEC0BhYK6U8owQwk1K+QhASvkodeoG4I5xpvKUoNQ2berP/2x/2icw9Vg6IcQTwBnTNU2EEAOBgYBJ1mEhBFWqVPngn+6klLRo2pJHVx9TW9kctYWam97XqH68OqvXrebo0aPs3r2b06dPozAoCLMLw+m5JbA4fRwooU+fPlhbW5sc+6sRX/HZ4M/w8/PDzc3tg58J/r906dKFW9d9qDVjBiXdbPGLSqR4qdLs/Gs7zs7OSCm5d+8ee/bs4csvv6Cdl+l97lDMiuFzz2AwGEyWH6Ojo5n6y0/8vW0TNjY29PxkMAMHDnznliizNTLr8pIJIdZifEh3EUIEAROAsRjdEvtSH5JPp67u5AEWSylbAG7AX6nvq4A1UsrdWTKoV/BaRUZKqQfKCSEcMF5gOkfVc2T0W5AvaX9Zn3+OYyGwEIzLZS8b8/tKeHg4KpUqw7owZ86c4ebVmzRTd0aRGghRzqIa+yK2UrduXQAqVqzImDFjcHFxYdK3k8iRnAN3jTsx+hiOphxjwMAB6QTmKVZWVpQoUeK1XduHgBCCiT9M5othX3H58mXc3d3T9nM9fb9IkSIUKVKEHyaMwz9aR1HnZ5Fw/tF6VNJArly5aNq0Kc2aNaNWrVq0bdGY0jbB/F5XEpMEP00fxYUzJ1n054q3cZnvJRL+sVXiPxxLym4ZNC95gW0w0CL15/tA2SwZxL/kjWzGlFJGCyEOA82AUCFE7tRZTG4gLNUsCPB4rlteIDi1PW8G7c/3CRJCqAB7IPK1Xcg7yOXLl+nb+xNu376FxEDNGrVYtvLPtGUwrVbLli1bcDC4pAnMU/KqCuBVvTDrNqzF1fWZ09nd3Z1Rw0eyK+xvLCwsGPz5YCb9+EZm3h88zs7OrwyLH/TZ54zcMI/lzZU4WCqISNQz6mgyrdp1QG1hye7du1m1yhh8VKeQmkU9LdOWiWsWkBSfsYlR34ynSJEi6Y6dkJCAUqk0ZyT4lxhe43JZdue1zYmFEDlTZzAIIayARsAtYDvwcarZx8C21J+3A12FEBZCiAJAEeBs6tJarBCiWmowQe9/9Hl6rI8wbkj6IGcqGREeHk6Deg0Rdx1ppOlDI00fHp2No3aNOixYsICOHTvi4uLC1KlTCU4M5J+3LkYTQZt2rU0EBqBTp07cD/QjNDyU8Khwpvw85Z0obBYUFMTSpUtZv359Wj6zV5GYmMjp06e5c+fOax5d1jF+wvd41etA6aVR1FmfSNml0ZRv1pU169azatUqQkNDOXv2LFUrlKZTaaWJH9JGI6iZT8GuXbtMjnnr1i2aNqiJs5M9jva2dOnQitDQ0Dd9ae8mMnNp/t/X/GavM7qsDEbHvhKjmG2QUk4SQjgDGwBP4AHQSUoZmdpnHNAPYxjeMCmld2p7JZ6FMHsDX6SGMFsCK4HyGGcwXVOnhS8kOxQtyyoCAgLYsmULer2etm3bpnvy/O233/hj4jJKUdek/UDcauJkFB4eHjRt2pSmTZvyw8Qf0T9QUEpVCZVQcTflOn6am9y+d/uFmZDfJX6ePIWfpkyhkkNe4qWOu/HhbNr6F/Xr139hnz+XLuXr4cPJZWVDeEICRYp5sf6vLbi7u7+wT3bi8ePH+Pn5UahQoQx9Yd+NH0fUkVlMa2G6V6zEtDj8IiVeXl40bdqUGjVqMPzLTxlVP44BNQXJOpiyR8H+IE8uXr31XvtvsiK6rJSDrdxS58VVSp/Ha8ex9y4L8we7GfNdZ+GChXw1fAQuigIgBeHSj2/Hj2PM2NHodDrOnz/P0C+HEX9VRWGN6R/4Vd1hen7dnu+//z7tKTYyMpIvBn/B5i2b0Rv01KlVlz8WzMXLK3M7ld8kiYmJTPxuAiuWLScxKYnmzZrx87RfyZcvX4b2Z86coW3jZvyUrx7OGqPf6GpsKL+HXSDwUTBWVlbp+pw8eZL2zVswrVB5CtrYoZMGVjz05ZqDJWcuXXzh2FJSUtixYwe+vr6UKVOGJk2aZNsv4YCAACqVK8nCNgaaF1Oh1cNvx/WsuePEwM+HsW/fPo4cOUJSUhKtygj++uyZj0dKSfXfrJgydyNNmjyLNtTr9Xh7e3P0yCFc3XLTq1evd7qeTlaJzObamUv/U2znUbPIvOu8KyLz5MkTHj9+jKenZ7p9E0FBQXgVKU4pWmGtsAcg2RDPJf0WatSuxvnz59NStjir81DTov2z/GlSzwk2sueQN5Uqpf9b1uv1GAyGl6ZPedu0bNKM8Mv3aWNXGmuFhiMxd7jAI3xu3TAJbIiJiSEwMJBvRo3B9nIgnXOZ7lUY43uAPJVKUbBgQZRKJSqVKu3f/X97UydJ0MW9UJq9Xkq6+hzD++hhypZN70N9+PAh9WvVwlGbQgkrC87FxpMjjzt7Dx/OtiHwhw8f5tNPehH3JIrEFD3ly5Xjz9Ub8PAwukeTkpLo0a0T1ZTeDG9k6rzuv9JAgnt7vvvuO0qWLElKSgptWjQiPPAq7Sok4RduwY6Lko1bdlCvXr23cHX/nawSmU21Kr7aECi+68h7JzLZfyH9AyMpKYlBAz9j48YNaFRWCIWBKT9P5rPPPkuz2bp1Ky7KfFhL+7Q2C4UNzroCXLp4ia5du9KoUSOqV69Oo/qNuf7oGB6GEujR4a+4QuXqlTMUGAClUvlWUpQYDAbu3LmDlZXVC2ckkJqy5fRZJudthyo1UKGdc3kehcTQonlzHBwdefDgAYGBgWlCqxYKPnYvl+5Yaim4dOkS169fR6/Xo9fr0el06PV6FCkpdCls2kcpBNY6A5UqVaJw4cIULlyYQoUKpf37+6+/0FCjZEhq1JeUku9u3+O7ceP4ffbsrLlRWUy9evW4ee8B9+/fx9ramty5c5u8b2lpSeu2HVk/8wjDGyWntesNkv03DTw8uZGNGzfi6upKXnd3HPS3OPW9Mq0w3+7Levp93JV7fsHZdkb3upFSoNd/uGl/zCLzhpFSEh4ejrW1NTY2Nune/3TQYHZvOUZB0QKVwYJEXRRjRn5LcnIyCoWCo0ePsmfPHqyS3IyR8c+hUqkZOmwoEyZMSGs7eeYEEyd8z1+b/kJjoWHAJ30YNWrk677Mf8XBgwfp16sviXHxJOu0FCvmxZqN60xyv+n1eq5fv87MmTPxVDmmCcxTSli4sfnyZYqU8KJIkSI0aNAADw8PPDw8CAoK4o8pU2liKIyFwvgnH5wUg582Bn+/wAwzPPz6yy8cmL3ApCpmSFICIfpkPv/8cwIDA7l37x6HDh0iPt6YVFUpBD80rJ1mL4SgX948DFy79oUio9Pp2LVrV9qG4LZt277xyC0hBIUKFXrh+126dOGXyRP4alMoQ+oaSNRKJu/RUKJsZY4uWcnhw4c5dOgQ3ts38N0gJcrnEn42LatEvTqBq1evZirVzvvK69yMmd0xL5e9QQ4fPsyA/oMIDAoEKWnVqhWLlyxKW+J5WqK5oGiBSjz7oonS+ROUcgYDOvLnz0+FChXYtcObcsp2WCmMyzDJMp5rYgenz518p/akPHjwgLIly/BRjpoUs/bEgOR4rA8+Fg+Zu3AeZ86c4eTJk5w+fZrY2FgAHNTWTC/cFcVzUVErIs7Q+ItujB33TbpzGAwGenfrwYl9B6ltnYdEqeNgzAN+nj6NAQMHZDiuJ0+eUL1iJfIlG2hs78rj5ERWhwcydOwYRjwn0lJKQkNDuXHjBs2aNOFkg1pYPTcTfJCQQIcTZ6laqzZ169albt26VKtWDWtrayIjI2lUpxaK6Aiq2au5Eq8nRKo5dOJktiuhHRoayoRvx7B921Y0GhXdevRh/ITvTfZGNW1YgwHlLtG+iqnvpshXsHPfaUqWzFxqlexEViyXlbS3k+uqVc2UbZm9+9+75TKzyGQRUkouXbpEUFAQFStWTBeBdOfOHSpWqISVvjBWSlckOuK5T4nyHsyf/wdnzpxh3759bN6wlRKWpqnbEw1RRFqf58Klc2kZC+bNm8/IEaNwFgUQUhCBH2PHjeabDL5kszMTxn/H0fk7aW1fzaT9lwdrCdNGo1AoKF26NDVq1KBGjRpUr16d3t16YhkQS1uHslgp1Bx7cpfdibe5dvtGunDrp0gp2b9/Pzu3bcMmhy09e/d6pRhHR0czZ9Ys9u78G5ecLgz68guaNm36QvtWjRtTJCiA/vk90s75w+173LN3RKjUXLp0Kc3fVaVKFVIS4ikcG8JP5Z/VIfrtZghB+cqwacfOf3MbswV//vknC6YOZf9YiZXGeD2rjmqZdjA3V2/4vpNlpbNEZOzs5Jpq1V5tCJTbty9biExqIuNXYcioOFq6Y5lF5r8TFhZG0ybN8PX1Q6O2Jj4xin59+zFn7uy0D9aQz79g7bK92CqeLQFJaSAo4RAGqQWM+dGSEpLJr2qIleJZ2PBj/Q3qtC3G2vVrTM7r5+fH5s2b0ev1tGvXLltFggUEBLBo4SIe+AVQs24tevXqlS4jQEBAAN07d8Ptvopa9qbJIFZFHKDRgLaMHz8+Xbbm6Ohohg35kg0bN6DV66lVtTqzF/yRLhPxm8bPz4/6NWtSQKWkhIWa8wlJJNracejECZydnXny5AknTpzgyJEjHDlyhMvnz7K/aWk8czybtcZq9VTceZW4hMR3Yu/R8+j1ej7p050De3fRqrzgfriKa0EK/t5zMMNAiXeBrBCZEnb2ck3VzIlM+f17s4vIJGHc9P6yJwOllNLzJe8bj2UWmZeTlJTE3LlzWb16LRqNmkGDBvLxxx+bODEbNmzM2VM3UOOGEAKD1KFXBjHi6y8pUKAAly9fZvmylSgS82KjMi3zG6G7yIDPjMW2ihYtypIlS/l6+GgctMWxVNgTJ4OJ1/hz5tzpbCUiL+Pw4cO0a92OEprCOEo7/MVDDE6CE2dO4ufnx/bt29m2bRtXrlwBIL9VLobkbpcmyMkGLb+GbuD0xbMvveanzvqsLlL2X0hISGDjxo3cvXuXsmXL0q5duxdG6rk6OrClRr50IlNu6yW+Hj2ajz76iAoVKqTdl7i4OKZPncpfG9agVqnp8nFfvvxyaLa6foBLly5x7Ngx3NzcaNOmTYYh4u8KWSUyq6tUz5RthQN7sovIXJJSvnRzT2Zs4AMXGYPBwP79+7l27RpFihShefPmJk+POp2OWrVqc/3abVKSjUmkNZZaWrVqxtq1awHjLMbDwxMbZXGTAmgp+ifEJfsBBqysrHByciY2HBzVz562DVJHuP4kd+7eNlmD//vvv/lp8i8EBQZRvWZ1Jkwc/84IjJSSwvkLUTmhJEWsCqS17Yg+gL94SExsDAqFgpo1a9K2bVuaNm1Kz649UD1KoaqlF0mGFI4mX6NO60Ysec/LAQwe0J/Yo978WDZPmpBMvx7MlsfJPIqIQq/X4+npSYcOHWjTpg3fjPwKt7ggBnpZozVIZt5IwL54Zbbs+PudXIp6F8gqkVlRqWambCsf8s4uImMppUz6rzbwAYvMkydPqFOnDn5+/iQn67GwUJEzpwsnThwnVy7jbGPr1q307t0PbZJt2odYSgMGwmjazFi34/r16yQmJONgVcbkg67Tx2NhG82Ro4coWrQokZGRlCxRCl28HVYiN3qZTLLyAR06tWLJ0kVv5V68Du7fv0/lMpX4zLGHyf0ISg5hW/w+fpszg5YtW5IzZ86092JiYpgx/Tf+2rgFa2tr+g76hE8++eS9D3mNjIykYe2aqGMiqWKn4mq8gUdSzcHjJ7CysmLHjh1s2bKFvXv3kpKSQgknSw53zJd2X1P0kprbHrFu516qVs2cY9nMvyMrRKa4rb1cUalWpmyrHP47u4jMeCBBSjn9vx7r/f4Uv4RRo0Zx+7YvcXF6dDpBfLyewMBH9OrViz179jB37lwmTvyexARp8mUphAK9TsXRo0dxcHDgk08+wc7eDp0h1uT4BmUM3bp3pXjx4iiVSnLmzMn5C+do9VFNtNZ3yJE7iok/jmHR4gVv+tL/by5dukTXj7pSpngZenbrybVr19Lek1Jy+vRpJk+eTGxCLHoMJn2TDckULFiQPn36mAgMGH1RE76fyOUbVzl5/jQDBgx47wUGjLVkzl3x4ZvZC3Dr+imDf57BtTt38fDwwMXFhb59+7Jjxw7Cw8Np06ol7QvZmvwtapSCerk1nD59+oXn+NAeIrMnAoPM3Csb0QuY989GIUT/1ArGmeaDncnY29sTG6szWeKSUiJlfNr/1Wo10mCBWmma90ltGcfSpcYEkwB79uyhY8ePUBjsMejVKDVJ2NmruXDx/Aujnd41jhw5QtuWbSmtLIubyo1HumCu668xf/F8rl+/zpo1a7h//z4WFhY42jrgpStArRyVEEKQYtCyKd6bkT+N4dNPP33bl/JOMnPmTE4snMIftUyDfhpt8eORwp4BAwbQo0ePtBLLhw4d4puvh3Lm0jXy5HTk8y+HMWrMN29lo+27TNbMZBzknxVqv9oQqH50Z3aZyVyRUqaL1kgteX9RSpnpePQPVmRsbW2JjzekExkhEtm/fz/FihVDSknRol5ok61RCEsADDIeOwcFQUGBJpvmbt26xZzZc/C970fDhvXp379/hrVb3lUqlKmI6wNXilgVTWu7mXCDo7FH0As9DRs2pHv37rRv357Y2Fga129MfEQsLipH7sc/oH3HDixZtuSDmKG8DiIiIihRpBDfl7OmQ2E79BL+vPmE2beSKFW+EgcPHsRgMFChQgXq1q3LyiULmFHfkpaFLbkbqWP44WRqdejLL9NmvO1LeafIKpFZWr5OpmxrHNuRXUTmNMZy9o8yeC9DAXrhsT5UkenZsxcbNmxBr3/2pSeEjvr1a7Nv3960tsOHD9O1azcSEhIxGAzkzp2LrVv/eic3lr2M5ORkkpOTM8yxZTAYUKlUfOb6uUnNmRRDCksjFhMYFJjmx3q+z7FjxwgKCqJKlSoZ1iZ53RgMBnbv3s3+vftwdnGmV+/eJpVRX8TFixf59cfJXL92jRKlSjJq3DgqVsxc7qnXyYULF+jfuwcPg4LQGQyULFGCpavWUqRIEUJCQli3bh2rV6/mxuULTKhjy+BKz0K/Q+L0VF7xhAfBoelCws28mKwQmWI5HOTicvUyZVv7xLbsIjKdgJEYs+QHPNfuCuzJTFRZWp8PVWTCwsKoWrUq4eFRxMcnYmNjhbW1JadPn6JAgQImfQwGA9euXUOj0eDl5fVeRfLExcUx5LMhbNi4AYPBQNHCXvyxcC61atVCq9WyZ88eVq5cyZaNW+ji3A1H1bP9O2HaME6ojhEUEvSSM7wdtFot7Vu14fb5K1S1cCMKLSdjHrBy3RpatWr1wn5Hjx6lQ6vWdHPJT2lbJ67FRbHmsR+bd2xPqxL6NpFSEhgYiEqlIk+ePBnalCjkycJaSZTLZRraXPbPJ2zZdzzdnpXIyEiOHDlCjhw5qFevXrZOjvqmyRqRcZQLy9bLlG3dk1uzhcgACCE+BqYDp4HLGH34nYCJUsrVmT3Ou7XbKwtxdXXl1q1bbN68mcuXL1O8eHE6d+6cYT4xhUJBmTJl3sIoXz8d23bE/1wwLa16oBGWBD64R/MmzWn/UXt2797N48ePcXZ2pnyF8hy/c4xGisZYKaxI0CdwRneKL7/+8m1fQoasWrWKBxevM9mjQVqes9o5POjb62OCQoIzzA8mpWTM8K8YnNuLhi7GkHKvHI44qDSM/WoEJy+8eH+VlJK9e/fy18aNaDQauvXqRfXqmdsb8W8QQrxyNla2fAVOPjxiIjKPYvU8jIyjUaNGdOvWjZ49e1K5cmX+mDuHcWNHUa2AFVEJkpBENX/t2E2FCplLTW/m1UhAvnRPY+YRQiwFWgFhUspSqW1OwHogP+APdJZSRmXQtxkwE2ONr8VSyp9fOm4plwshtgDtgZJAPNBNSvmvdrO/cCYjhPgbGCyl9P83B8zuvCup/t8Et2/fpkqFarS06IFSPHMIX0w4zh2tD+07tKNnz540a9YMhULB0CFDWb58OY5WjkQnRTNg4ACm/TbtjfhZtm7dyo/jv+euny8lihZjwpRJNGvWLEPblJQUmtStT/lHCmo7ms5Kh97eTpKNGqVSiVarTXvpdDp0Oh0C2F2tDRaKZ/cjxaCn2ZkdzPj9d0qUKEGJEiXInTv3c2HtkgF9+3Jk507aOjuRIiVbHj/m02HD+HbCxNd1S17IxYsXadagDj/X1tCqiCV3InSMOJJCgUoN0AslO3bsIDk5GU9PTxKjQjj6qYYCTsbf4RYfLaMP2eAbEGye0ZA1MxmvHI5yQZkGmbKtf2rLS88nhKgDxAErnhOZX4FIKeXPQogxgKOUcvQ/+imBO0BjjGXrz2EUjBv/zzX9G142k1kG7BVCLAd+lTI194mZd4Y7d+4wZ/Zc7t/zo3a9mgwcONCkyuW5c+ewUziYCAyAiyo3bpUd2bBhg0n73Plz+fGnHwkICKBAgQLY29vzJli/bh1fDvycTnaV6J67NHdCH9GzUzeWr1tFo0aN8PHx4cKFC1y8eJELFy7g4+ODQmeglHvldMcyCEG1atVwd3dHrVajUqlQq9Vpr1nTfyMoMY5CNs+uLTAxDguFkqFDh6a12dvbU6JECYoXL46lpSV7tv7FpooVsE7dzNshT246TJ1Gj94fp1t+fd1UqFCBzTu8GTdyGJ/tuUqenE58PmwsX40YiUKhIDo6ms2bN/PjxPF8VpU0gQHoUFrNzLM6Dh06ZFKM7Cl6vR6FQvFeLRm/CbIqPFlKeVQIkf8fzW2Beqk/LwcOA6P/YVMFuPe0crAQYl1qvwxFRghRHbiZmdxkr+KFIiOl3CCE2AV8B5wXQqyEZ5sfpJS//deTm3l97N+/nw5tO5IHL6z1Diw4sZI5s+aye683x48fZ926dRw+fBglKrSOKajFs6WVcEUw7Wu1yPC4jo6Ob7wc8/gx4+jpUJ1iNkYfREW7AiiFoGfnbsSlJKLT6QBwcHCgYsWKDB06FL1ez5YlK6nq4ImN0nhtp6MfoHbIwdatW18YymulsWDW73P4Ll9ZnDWWRKQkMSv4FuMnTqTfgP7cuHHD5LVz507Cw8IYWLBAmsAAOFtYUDdnTnbv3m1SC+hNUbt2bY6evpDhe0/3dx07uBvXxPSJOC1JYMuWLVSoUAEXFxcAdu7cyfgxw7hyw5c8ro4M/WoUI74eZY4WzBTi36T6dxFCPL/UslBKufAVfdyeRoFJKR+lOuf/iTsQ+Nz/g4AMd/AKIX7AONMZBnTJ7MBfxKt8MlqM63AWgC38Y4edmWyJlJIB/QZS3FAHV1U+UIC7LMq18KOULV0OvdTh5eXFxIkT8bnsw8kDeyghKmEtcuCnu0WYRRBDvhzyti8DMDrw7wX44eVlutxQzMaduEcJjBw9igoVKlCxYkXy589vsoSVkpDEsJWrqGSfl0hDEgHJT9i1x/ule0VGjhlNVGQkfefNw8XKhvDEeD799FNGfzMWhUKBm5sb9evXN+kzetQogjdtTHes0NgYpk+fTlxcHO3bt6dw4cIm78fExLBixQquXbqAV6nS9OnT940KeLPWHZk5fi99KkpUSuN9C4gycDZAy5EFC1i8eDGNGjWiTJkyrFwyh0XdtDQZrOb6o1gGLfqRxIR4vpv4wxsb77uKlKA3ZFqMw1+T4z8jlXtR1NcJoA7G5bX/fuKX+GSaAb8B24FJUsqErDjh2+Z98MkkJSWxbNkytv21AycnJz77fBC1aj1LWxEYGEgJr1LUVfQ0WdZ4on/MNdV+Dh07SJkyxjQ4er2e36b/xh+z5/Ek9gmNGzVmyi+TX1rEKis4fPgwy5b8SWJCIh917USHDh3SvvyllPj4+LBu3TrWrVvHQ/9AvvZsRX6rZ5kCbsUH4625y417t196nlu3bnHo0CGcnJxo3bp1ukzQLyI2NpYHDx7g6en5ypDfu3fvUq1CBf4sW5oCqYEjl6Ki+fyqD4WKFUtLBFqmTBk6dOhA+/btsbe3p26NapS2UlDFTs2lOB1nopM5dPwERYsWfdnpsgydTkfbFo2J8rtIz9IpRCYK5p9TMOrbH6hdtx7r169nw4YNPA72Y3Y3JT2rPhNnv3BJ9ekaHoZEpAuiiIiIICkpiTx58rzzy2pZ4ZMpauMkZ5VMv/SYEc3PrX/l+VKXy3Y+55O5DdRLncXkBg5LKb3+0ac6xqiwpqn/Hwsgpfzp317Pv+VlInMM+FRKef11D+JN8q6LTFJSErVr1OHhvQjskvKhE0mEq28z8YfxtG7Tmq1bt7Jx40bOnTlPE5tPUIlnztvHugckFgzkyvVLb/EKjDVkFsycRyVNMTSouKy/R9laFfl52i9s2LCBdevWcePGDZRKJY0aNcLVJSdHdu7jY8eaeFg645cYxvKok/w8Zzq9evV6q9fylGV//snQIUOo6OKCVkpuPIlmzYaNNG3aFH9/f7Zu3cqWLVs4fvw4Ukqc7WzpnteOESWf1R1afDeUiy6F2LXvwBsbt1arZfPmzfy9dSM57B3o3XcA1Z6rfSKlxDOPM/s+i6Owq6lg5BkNf/19kJo1jckfg4ODGfRJT44eP4lGpSBvXnfmLlhOjRo13tj1ZDVZITJFbJzkrBIvrkP0PC3Or/t/RGYqEPGc499JSjnqH31UGGcmDYGHGJfDur+J7/cPdp9MdiYhIYGwsDBy586d7ilx4cKFTBzxC4V0DdKeEpMMsVxM2YReGn0TZcuWJTEuCUOwDV6Kaggh0MpkLos9TJz6zVtN7RIQEEDp4qX4MmcnciiNswqd1DMzeB3hKdEA1KlTh65du9KxY0dcXV2RUjJ75ix+mjyFqOgocjrn5LtJE19Y1fJtERkZyb59+1Cr1TRt2jTDcPjQ0FC2bdvG0M8Hc6x5GXJaPnsISNTpKb39MknJydkq/Uub5g1o5XKUfjWfjel2iKTSFC1JWihVqhStWrVi66bVdCgTwdh2CixUsPWcjs+Xq7h45Wa2q/SZWbJGZJzl78UzJzKtLqx9VXTZWoxOfhcgFJgAbAU2AJ7AA4wbKCOFEHkwhiq3SO3bAvgdYwjzUinl5Jec56KU8qVx7JmxAbPIZCv0ej2jR41h/vz5KBVqEJJvvhnDqNGj0gSlScNmPDiWgqvKdH3fR7eDTn1aM3bsWAoUKMDjx49p2awVvnfuY6d24XFiEL1692LuvDlv1Vm7ZMkSFoz9nQ45TDc2Ho2+SGwxJWs3rH3hF5KUkoSEBKytrd/5ZRg3J0c2VPMkfw7LtLbwJC01/r7KwSNHqFGjRra5xhMnTtChdRNmdEimeSkFVx9KvthkQcvOn+GW253t27dz5MgRPJ0ld2fZmIx76HJJzirDmTBxUlpbcHAwCxfM4+4tH0qWrcSAAYPSJU3NLmSVyMwolnG4/T9pfXFNttiMKYRIBO6+zASwz0zRsg92M2Z25PuJk1i+cB2ehsZosCbZEMPPP/5GeEQEarWKvXv3cunCZTxVpilOpJSorAR9+vRJC5fNmTMnZ86f5vLlywQGBlK+fHk8PDzexmWlER8fz+nTp3kcFwk5TN9LVKRQp26Tlz7xCiEynB28i/To2ZMZf2/it/IeKIVASsnU68FYqFXUqlWLihUr8sUXX9ClSxcsLS2RUuLt7c3a5UvR6XS079Kdjh07vpEZT82aNVm3eScTvxlB/9XXyOeei2GjxzFw0CCEEAwbNoz58+ezf+XX6YSxpLuWP7dvoW69BlSvXp1bt27RpFEdOtZU09gLjp44Tvk5v3Pk2JnX7gd8W0jeyYipYpmw0WfmQOaZzBsiJSWFCd9NZOGiRSQkxFOvbn1+n/lbWjEyg8GAo4MzebS1sVA8yx8Wpw/FL/kwChVUr16dYsWKsXblBorJZlgp7JBSEmq4hTZXML5+d9/aLCUxMZHly5fjvcObnK45GTR4EJUrG/epPHz4kDlz5rBgwQKioqKwUGno6tyYYtb5AQhNieDPqL8584pKmO8T8fHxtGvRjHvXr1HZxZYrUfG4eOZn3Zat7Nq1i9mzZ3Pjxg1cXFwYOHAg4aGPOLzjL/oXtkSjFCy/n4xXtbqs2bg5W8x4bt68Sf1aFbn3uxIrzbPxNJ2cxMFrOqSUxuJ99haM66JgQMtnwRQ/r43lelwt1m7Yltam0+nYsWMHx44eJlfuPPTq1ZvcuXO/0WuCrJnJFLZ2llO9Mt4S8E86XF6VLWYyWYlZZLKQhw8folAoMvwwdOzwEYf2ncbSUACl0JCgC8ZgFcb582cJDAzk4MGD/PjjZEpbdjUtfiaT8DX8TWhYSFryyjlz5jBm1FjsLVxJ1idg52SD955db+0LOj4+ntrVa5MQFEchChAv47mqvc7nw4bge9+XjRs3YjAYaNeuHcOHD0cIQYc27bFX2KARagLjQ5g7fy4937AT32AwsH79etavXAVAt49706lTpzcm1FJKzp49y7Vr1/Dy8qJmzZomIdiHDh1i1qxZbN++nRwqwaWuhbG3MM5cknQGGnqHMn/tlnQh1W+Lj3t2JsBnN+Pb6nCwESw8KDgekJP9h05y/vx59uzZw7x5c4nZ7onFc0IUGqWneL/HhIRFYm1tTWJiIi2bNyAu8h7t6mjwDYbtR2LZuHk79erVe6PXlFUi86tXy0zZdry80iwy7zqvQ2SuXLlC9249uO/nB1JSvEQJ1q1bkxaK6uvrS5nS5XFRVEM8t7s+MuU68bpgDAbjrNNCbYW7ojq2ymciFam7T75Kao6dOGJyzidPnnDq1Cns7e2pWrXqW/WzzJw5kwXfz6OlVZO0L8kIbSTLw9ZilcOKAQMG8MUXX5jsfNdqtRw+fJikpCTq1av3xjMDSynp2bUblw4epaWtcRlxZ0wglRvXZ8XaTOf+eyNMnDiRu+tnM7OWm0n71IvhiEZ9+PmXX9/SyEzR6XTMmTObVX/OJz4hgZZtOjBm7Pi0DZ0GgwF7O2tuLslJLqdnn4Pr/inU+CKEFL2S8uXLY2VlgaXuJtume6JQGP+edp98wvCZidz1DXyjf+tZITKFrF3kL0UzJzKdrqzIFiIjhFBJmRpJ9B8x+2RegVarZcuWLXh778bNzY3+/T8xSVsfHR1NvXr10SbYYaX0AgF3bzymdu06nDhxPK2glzBYIv6xfm4hnMiZz4LZc2ZSvXp1Dh8+TO+efdHqSmCtcCbeEEq06jbrpnqnG5e9vf0Lc3e9aXb+tZMiopDJDMxZ7USuHG4sWLeQli3Tf8DUajWNGzfOkvOfOnWK36dOJ8DPn2q1ajJi1Nev9D+dPn2ao3v380ehulgojB+D2o55+cx7N2fPnqVKlSov7f/gwQN++3Uq506eJF/BAgwdOfK1lUAuVKgQ5wzp84g9jNeSeM+XlJQUNBpNBj3fLCqVimHDhjNs2PAM31coFPTo3o2xS7ezaHgOVEpBcork22WJtGnXkQIFi3Dq1CkuXzjOih/ypQkMQNPqdih+j+T69euULl36TV1SlmF4957lzwJZkiX1g88J4evry7Zt27h582a695KSkqhdqzYDBnzG6pVbmTVzIeXKleevv/5Ks1m3bh1Sb4mFyhkhBEIINEoXIiPiKFKkCO3atWPjxo0kaZ8gpan7T6ri6fhRB1q0aIGjoyPt27dn+86/KFjVijjHq5Rp6MahIwey9T6D2NhYHoc/JkFvuldXSolWoXthOvqsYtOmTbRu0hzLMw9pGJ2Te5uOULlcBfz8/EzsDAYDgYGBHDlyhD///JOxY8dSzcolTWAALJUqqlq5MGbMGP7880+OHj1KUFAQBoPp783X15cq5csT5b2b3ihx97lJ6yZN2LJly2u5xrZt23IuLJFDQXFpbZcfJ/LX/Vi2bNlCwYIFmTFjBvHxxqqujx8/5odJE2nfojHDvxzCnTtZsnE7S5g6fRbhshRF+0bSaXIihftEYJWrFsuWr2LKlCkcOnSIChUrkpRi+q0sJSQl67OFmP4/SESmXtmILBvMB7tclpKSQrdu3fj7b28sLCzRapOpVq0a27dvT4tgmjt3LmNGj0eb/Cws02BIRqWJ46sRX3H79m0OHjxEQowaK7WpHyZRF0SzljUZOXIkZcuWpX27jpw7eQNrWRCl0BCne4hO85Br16++9aivl3HlyhV+m/obvnd9qVarOsO/Goa7uzvh4eHMmjWL2bNnEx0dja06Bz2cO2GrtEVKyeVEHx66hHL99vXX5pjW6/Xkd/egj3V5vGyeLSVtfnyJR3nVVKxamfv373P//n38/f1JSUlJsxFCUMPBne8Kmwr4xHsnOB0dzPOfC41GQ4ECBShYsCAFCxbk/OnTlI2KYWD+Z9FQF6MimRIahG/g61nOOXr0KN0+6kBuS4FGpeBuZCIL/1yOjY0NP/30E4cPH8bZ2ZnevXuzYc0KGuaRNMoLVyMky66nsGnbrmxRD+cpV69e5c6dO5QqVYpixUwDmZYuXcrCmaPYPdsDa0vjvfxzewQLdlpx4dKNNxrokBXLZQWtXOSPhVtnyrbHtWXZZbksCGPGlwz5N7krP1iRGTduHDNmzCIpSSJSQ0gtLKBr106MHz+ee/fu8dlnnxMYEIVSYZqKJEkbDOgpVKgQTk5O+Fy9jZWikInTVq/yZ+eubdSubaztnZCQwFfDR7BixQqSU5KoUqU6f/wxm/LlM11g7o2ze/duunzUlRKKUjgqnHnEQwKFP23at2H9+vUkJCTQvn17xo4dy8H9B/nxhx/Ja5OHGF0sNo45+Hvv3+nydWUlAQEBVCxVlt/zdzBpD0qK4vv7u7CwtaZQoUJp4vD8y9rampJexRidpzzl7YwCdeFJCFMfXebm3TvExcWlCdTzL19fX7RxcSyvVJ0CNs/isKWUND93gks3X9/GQ61Wy7Fjx9DpdNSuXRsrK6u0906dOsVPP/3E3r93MLiiLd/XeZZFeufdRH6548Sl67ezRSTaq9Dr9fT/pBf7du+kaQ07/IJ13AuSeO85+MYr0maVyEwq3CZTtr2u/ZldROYRMI8XzGiklN9n+lgfqsi4uOQkMjLexBEvpQHTFG0CtdIRpcLmORuJUhPN/v17qV69OjqdjqpVqnH3ThDojB9soY6mQqVSHDy4P92HWkqJwWDIVju6M0JKSeH8hSn2pDQeFvnS2s/FneJq4iW69ezG6NGjTT70ERERnDp1CmdnZ6pVq/bavtCelnZesGABm9ZtYHaxLtgon2VGuBjzgOMOkZy9cvGlxzl48CA9OnfBQaFBAjFSy5qNG14ZwVS5TBl6CjW1XJ4lu32iTaH5icN07t6dAQMGULt27bfyhe7u6sTONhoKOz7z4RikJN+8cO4FBKU54d8Frl69yvHjx3Fzc6NVq1YZFpp73WSFyBSwcpGTCrXNlG3v60uzi8hkajd/ZvhgfTIJCQmkF2mjT2XhwoUcPXqUJUsWY2GpN/GlGGQCrq450/I7qVQqjhw9zLCvBpLT3UAuDxg9dii7d/+d4ZeMECLbCwxAWFgYYWFh5NWYbugtalkcJydnVqxYke6p0tnZmVatWlG9evX/6wtWq9WyfPly2rVsQ48u3dm/f7/J+/7+/kyaNInChQtTr149du7cScGCBVkdfp5kgzEQJiIlji0x1xg2+utXnq9BgwY8eBTMws3rWLxlPQHBDzMVIvvlyJH8EfyA0KQkAJL0eqbdv0ehAgXZunUrdevWpXDhwvzwww88ePDApO++ffvo1aULH7VuxYoVK9Bqs7ZMk7OTI2Hxpj6kJ8mSZK2WGzfSlw5JSkoiODg4rVxCdqJMmTIMHjyYjh07vhWByToEBpm5VzbC7JP5f3k6k2nZsiW7dx/k+QA7KbVUrFiGc+fOpv5fMnz4cBYsWIhGkwOBAQtLFQcPHnjj0/bXQWRkJJcuXSJPnjwUL148rV1KybZt2+jUsRM9nPphqXiW+iQo5QEBbvfwueWTpWPR6XQ0b9yMoKu+VFQXJMmQwsnk2/Qd3J9iJYqzbNkyDh48CBjFoW/fvrRv3x4pJb279eDgwYO42TgQEh/NyFEjGffd+Nc2k5BS8sPE7/lt+jQ8bO0Iio2hcaNGLF21CiEEW7Zs4c8//+TQoUMIIdLGe8PnKmsWLaSPhxM2KgUbQmLIWbw023fvybIHj5kzf2f9zIlsbGWDnYUCnUEydH8M2+4mE5OYQv369RkzZgwNGjRgwrdjmTfvDzQKUKg1fDthEoM//yJLxvG+kDUzmZxyQsHMzWT63liSXWYyTlLKyCw51ocqMnfv3qVKlaokJWlJTtai0ahQqxUcOXI4XX1zf39/jh49iouLC40bN37ny9JKKZkwfgK//TYDF6tcPEmOpHjJYmz6ayMHDhxg6tSp+Pj4YGttSx6Rl1rW9VEJFYmGBA6k7ObbX8ZleZLNTZs2MXbQV3zm1BylME6wY3WJTPJfjVbqKFiwIH369KF3797ky5cvXf+HDx/y8OFDihUrlrZp9XUTExPDzVQfjLu7e7r3/f39Wb58OcuXL8fPzw8rpYIjTSvibGH8+9EZJJ3P3GPivIW0a9cuS8ak1+v54rOBrFu7hop5bbkRlkipsuVZsmIN69ev57fffiM4OJi8ud3IaxnLsg4q8jkquBaip/tmyffTF9KtW7csGcv7QFaITH6rnPK7Au0yZfvJzcXZQmSykg9WZABCQkL4448/OHPmLGXLlmHIkCF4er4y39s7z4YNG/ii/zCqiRZYKWwwSANXU04QJO8SnxRHyZIlGTlyJK1bt6Z3j94cO3oMZysXwhJC+ezTz/h1+q9ZPkv45OO+RHvfpY6D6R6IJWF7aTOkG5MmTXpnqzAaDAbGjRvHxVVLmFe5iMl7f94LJrxKA+YtXpKl5wwMDMTHx4d8+fKZzLqTk5NZsWIFw4Z8yrnPbSjo/GwGtfeOlh8ue3DuSvpw/g+VrBKZcfnbZ8p24K1F753IfNCbMXPlysWkSZNebfieMWvGHArry2GlMQY0KISCUprq3I+9zsqVK+nRo0eaiOz03om/vz8PHjygZMmSODs7v5Yx6Q0Gnujj07VrNZJq1aq9swIDxk2I1apV48jq5eneC0nSIl/DTj0PD48MQ+MtLCzo1KkTXw0dQgEn03taKpcS/wdB6fro9Xr8/PxwcHB4pwIHsgtSkt38LW+U1/bJFUJ4CCEOCSFuCiGuCyGGprY7CSH2CSHupv7r+FyfsUKIe0KI20KIps+1VxRC+KS+N0ukfgMKISyEEOtT28+kFvP54NFqtWzdupUZM2Zw9OhRkz0fBoOBoAeBWClM0yCrhAp7GwcqVqyYbpaSP39+6tSp81oEJjg4mH79+rF81QqOR1/nUfKzZeBLsfeIlgk0aZK5qoL/lSdPnrBgwQK+GTuWrVu3ZqkzvFmzZvgnpuD9MDyt7faTeNb6hbB02TL69+9PcHBwlp3vZdjb25MrpzMnA0yT6O67qyUpIY6WLVvi7e2NwWDgr7/+onD+3DSsWY7CBfLSsU0zIiOzZKn+g0Jm8vU+8tqWy1LLgOaWUl4UQtgCF4B2QB8g8rkqbo5SytFCiBLAWqAKkAfYDxSVUuqFEGeBocBp4G9glpTSWwgxGCgjpfxUCNEVaC+l7PKycWXnejJZQUBAAHVr1UMXK7DSOxItgileuiir161i3bp1zJ8/H7/7/hTQFKeydcO0fuG6R/hYHOFhyENUqqyd4EZHR6PX601EKi4ujqlTpzJt2jR0Oh1ffvklhQoWZPTI0bhb5yRRn4zeArbt2vFG9hL5+PjQuF59Slo54CEsuJgSjVUeN/YfPZJledUuXLhAx9atyCH12KpV3I6O5edp07l9+zazZ89GrVYzatQovv76a5OSBhERESiVShwcHLJkHABr1qxmzNBBTGkoqZBHyUFfPd8fgbYfdWPXrl2EhITg4eFBfFQIm/pDrcIK4pMl3+5ScldWYM/B41k2luxMViyX5bPMKUfn65gp28/vLHjvlsvemE9GCLENmJP6SleP+p81p4UQe4CJgD9wSEpZLLW9W2r/QU9tpJSnUsuLhgA55Usu6n0Xmfp1GhJyPpGCSmPwgpQGLml3E64PRKfXUadOHbp3786P30/GOu5/7Z1leFRHF4Df2d24QYAIhKBBg7u7aynuDoUipaWF9itQXIuUAsUpUIq7u0MgeHBIiBBIICFuuzvfjw0Ji5QACZLcl+c+u5k7M3dm2b3nnjNnzsmMgz4nkTKM++Iai5ctpE2bNqk2lgcPHtCzSw9Onz2NECrcixRl4bJFnDt3jl9//ZVHjx7Rrl07Jk6cSN68eQGD8Dl58iSWlpZUrlz5nbyuPD09mTdnLoH+AdSoV5t+/fun+MZcsVRpqoSraOKQGzA4R0z2vUSF7u0YP3Hiu079jeh0Ok6dOkVMTAxVqlRJEib37t1j5MiRrF+/HmdnZ8aPH0+pUqX4tk8vrl2/jl5C1coV+WvZ36m2brh7925mTBzDfW8fipcowc+jx1O+fHni4+PZuHEjP/0whD5lQhjRIPmhQ6uT5B+r4dDJCxkiLUNqCBlX82zyxxQKmUGKkHnPixjMWMcAd8BXSpnphXOhUsrMQoi5wBkp5arE8iXAbgxCZrKUsm5ieTXgJyllUyHENaChlNI/8dw9oIKUMtkmYSjvC/QFcHV1LfPgwYO0nG6ac+fOHfz9/SlevLiRdhAWFoaTgxM1TLqhFsk3hjBdENfUBzh55njSIvDTp0+Z9+c8Du0/Qq7cORk0dBBlypR55VrvS0JCAgXzFSBvVHbKW5VAILgcdYMDYSeJ08VTuXJlZsyYYZRP/kP4d80avu37DfVtC+CoscIzLpBA8wTOeHq81swXHx9PQEAAfn5+XLt2jR+/G8bmUo2TPNsAbkaGMCfSh5ve91NljCnh1KlTfP/995w5cwZLUw1jyzrSPn9mEvSSBTdC2BJqyrVbd1Nd23wdjetVpU++szQtZizoq85UMXTckiQvtCdPnjBl0nj27NyClZUlXXoOpH///l/EfrC3kTpCxkEOd02ZkBl8Z0G6EzJp/k0VQlgDG4GhUsrw//BKet0J+R/l/9XGuEDKhcBCMGgybxvz50poaChftfiaC54XsTHLTGhMEEMGD2bi5AmEh4ezcuVKEhK0CBPjj0Wgxtra2sjLKEuWLPw66ld+HfVrmox1586dqKNVVLZOFlylrd25G/uAah1rs3DhwlTzUIuPj2fIwEF851SNvBaGheny5Gbho9P069OXSlUq4+fnZ3Q8fvzYOD6ZUKGXoH5hSDopCfAPoGXLltSrV4/69euTP3/+N447Li6O06dPo1arqVSp0nsJgsqVK3Pq1Cl69ezJ48Ob6VzAHgCNSvBdsawcPvSIPXv20LRp03fu+10pX7kW2w9dpGmx5LWbx+GSyw9i6NixI4sWLaJNmzbM/n0SNXI/ZUkXPSGRknHzRnD54lkWLv47zcf4JSABXSos/AshCgJrXyjKC4ySUs56oU5NYCvwPELsJinlJ/VuSlMhI4QwwSBgVkspn4eofSyEcH7BXBaUWO4PvOgO4wI8TCx3eU35i238E81ldkC6XZXs2rk79z2f4K5vhSpWRQ6imT9nMQcO7efq1avExcVhaWaNn/YGuUzcAYPZx191jdZtU/YklVo8ePCArGR6pTy7iSO2Nrap6gJ948YNLIRJkoB5TlXr3MzYup2NmzdhZWWV5HFVrFixpPfPjz7durM16D6tnQyx1nRSz5qguxQpWZwrV66wdasha2Pu3LmTBE7t2rWxtzcIgV27dtGjc2eym5ujlXqe6SX/btpElSpV3nk+Qggy2dmQI6vFK+eK2GpeiTCdVgz8djDlly5i+OZndCijx/+Z5Le95vTp252sDtlZuXIlAwYMoG4xFfN6mPPcj6iSmw63Hzbw08jRRimVpZQEBARgZWVF5syZ33DV9ElqOBBKKW8BJQGEIR5WALD5NVWPSynT/ikkhaSZkEn0AFsC3HgpYuc2oBswOfF16wvl/wghfsew8O8GeCQu/EcIISoCZ4GuwB8v9XUaaA0c+q/1mM+dBw8eMG/efG7fvEPlqhXp3bt30o8xJCSEAwcPUFK0QZVo0jEVljjrSnL10gn6D+xPx44dsbKyoma1WkTpgjGNtSHKIgg7ZyvG/Db6o87FxMSE6+F3qGNZKWm8Ukr81Y/pXzF18674+PjwJDwUrbMOjSrZRBOqjaF0mdJs37ubTJky/adgW/7PaurWqMn5B6Hk0ljiGfWUfMWKsn3PbszNzbl37x779u1j3759rF27lkWLFqFSqShbtiwVK1Zk+aJFzC1WlJKJa0DHg5/QskkT7vv5vZfjQLkKlZi39V8GSpk0bq1essf7KZU+UoiVbNmycfLsBaZOHk+frbvIkiULP00YRseOHRFCMGrUKJo1qk1L11NG7azNBZULCI4ePZokZA4cOMCgAb0IefqE2Hgd9erWZsGivzOMS3Qa3JTqAPeklJ+97T8tvcuqAseBq8DzYEo/YxAU6wBXwBdo8zx8gRDiF6AnoMVgXtudWF4WWA5YYFinGSSllEIIc2AlUAqDBtNeSvmfBvTPdeH/zJkz1K/XEGvpgjrBBq3pU7CK4rynBzExMaxcuZIpE6ZR1rSTUbtI/RPCHK7g7XsvqSw8PJx//vnHkPekfHlatmz50aIUhIWFMXLkSObPn4+1uTUupk5UtiiFWqi5EOdFnKPE87JnquQFOXbsGOPHj2f//v1YmZhT174AbbKVRCVUhCZEM+XREWYtXcBXX6VsI1xcXBzbtm3D19eXcuXKvTHIpVarxcPDg3379rF//35Onz5NUydHJhRzN6r33a3bdB07jq5du77z3OLj46lQqgSFZQh93GyJ1UlmeoVyPjiG0KgYBg4cyMSJEz9adIM38cvPPxF9ZS7TOyaXSSnJOySWh89U1KpVi/Lly/PXvJksH2pOwzKmRMVKRq2O4/KTAhw57vHpBp8CUmNNxsXMQQ5xSZlDzY/35z0AXlxTXpho7n95XEuBC1LKuS+V18RgPfLHYPH5QUrp9X4jTx0y9I7/j0lsbCwbN27kxo0bFC1alFatWhkF/XMvUoLw+9Zk0iSHTHmUcIl480eEhYcCYKI2o6C6LnYvpGf2k+do1LUyC/6a99HmIqXkxIkTnDhxAicnJ1q3bo2NjQ1bt25l4MCBBAYGMnToUH7++Wf+mD2HVStWodVqad2uDf8b9b8PcsWVUnLgwAHGjRvH8ePHcXBw4IcffqBly5Z0adeRB/fu42iZifthj/hh+HBG/TYm1eb9JoYNHUrsju18ky+vUfn4O3epPGQoQ4YMea9+Q0NDmTD2N7Zu3ICJiYYOXXvwzcCBjB8/njlz5pA9e3bmz59Ps2bNCA8PZ8OGDTx+/Jhq1apRpUqVjxIF2sfHh3Kl3VnUM4GmpdTEJsCkbbDFy4EmLdqyfft27t+9yZAWVkzqkazR6XSSAv2j2Lr7BCVKlAAMZs+xo0dy9NgxHLJlod+A7+jf/5tPmp4gtYTMoBQKmRH35731ekIIUwwCpKiU8vFL52wBvZQyUgjRGJgtpXR7XT8fC0XIfAQCAgKoVLEy0RF6tDGmaCzisLYz4czZ0zg5OfHw4UNy58pLQdOWiBe8m+L0ETzQHmDajKk0btyYa9eu0aVjN7JqC2GOHZEmD4m3fILnxfOvjZ2VFiQkJNCqRSvOnTxHTpGTaHUUgdpHlC5XmoMHD1K8eHEWL15MuXLl3qv/+Ph4lixZwobVazExNaVr7+60b98eIQQ7duxg/PjxeHh4kCNHDn766Sd69+5tlFflypUrPHr0iDJlyqRZdIKXOXjwIP3bt+PfkiUwTYxMEKXVUv/YCXoMGMC0adNSPaPj2bNn6d27N9euXaNu3bpcOu9B5eym5LLUsctXR8mK1fh345aP4oV29OhRBvTtytMnwcTG66lSuSKLl6/B2dnwMNSofjW6lrpK2+rGa0y1RoSRs/hX9OvXDwcHB2pUq8h37axoU8cGn8B4fpoXRv1mPZk4aZpRO71ez5MnT7C1tcXc3Jy0JDWETA4zBzkwR9sU1f3F+8+UCJkWwEAp5Vt3KQshfICyL3vcfkwUIZMK3L59m4kTJnHe05PChQsxcuQIoyCbLVu24ti+q9io8ySVhWvv4pzHkqxZ7Tl79iwJ8VoKW36FWiTfjKJ0T9A73MP7QbIp7OLFi8z6fTb37/lQo3Y1Bg8ehINDcl6TtGbevHnM+HkGjS0aoU7MxXMr5jYHww4yZvwYhg8f/t6mOZ1OR4M69Xl01ZuKZgXQSi3H426St0RBgkOfcvnyZfLkycPIkSPp2rXrZxP+XUpJ25YtuXP2LG2zZSVBr+efx0EIOztu3b9P4cKFWbBgAdWrV0/V68bHxzN16lQmjx3Nn/Wy0NLNsOcmTitptSucLj9Nol+/fql6zTchpcTPzw8LCwuyZctmdG7KlElcOzCV5UOTBcKzSD25uj8hKtZgSbcw1zDg68xMGuiUVOdxSALFOvly39s/aW3y33/X8MvIHwgLC0Onh+7duzNl6u9plpY5tYTMgOwpEzL/80mRkPkX2CulXPaac07A48TlhPLABiDXp1yr/nIDQn1Ebty4wb///su5c+d4+f/q8uXLlClTjo3rDuB7N47d289QrVqNpFwo0dHR7Ny5HSuVcbZEK1VObty4TlxcHIMGDaJixYo8xSupf73UEq65Rf8BxjeJUqVKsWLlco6fOsL48eM+qoABWLVsFUVVRZMEDEABczdsLW0+eO1n9+7deF+9TW/7epSwzkMZGze+sW/IyWMnCAsL4++//+b27dv06dMnTQWMlJKjR48yf/58jhw58sr/+csIIfh30yaGz5iBp2surrsVYPKiRdy4e5cdO3YQExNDjRo16NmzJ0+epN4DpampKS1atCCrrSUt8idnbzXTCAYUNWH9qlfuQWmGEAJXV9dXBAxAnz79OHXHgu+XxHD5fgL7L8bReGwsvXr3ISQkhK1bt5LDOQsNKhqHOnK0NyFHVhUTJ07Ew8OD3bt388N3/Vk0zhnf4xU4v6UUNy9tZth33xq1i4qK4q+//qJ3726MHfsbAQEBaTr3lKBHpOh4G0IIS6AesOmFsv5CiOdh0VsD14QQl4E5GNapP6kmkeE1mcjISB48eICLiwt2dnZGdePj42nTpi0H9h/A1NQSrS6OggULsG/f3iTX1Xp163P6+E3MNMk/rnjtM9TmIbjmyomXlxd6vSSHVXUjLUWrjyVEf56YGEMmzpCQEBo1aMKtm3ew1NgTHveIZs2asnL13x/F5JFSKpapiKO3A3nMk7UyKSVrov7l8OnDH5RnZ9jQ77iz6hT17Y1TLfwbcpwOY/rz7bffvqFl6hEWFkajOnUJ8vHF3SoTXlHPyOLqwp5DB997LSk6OpqxY8cyY8YM7OzsmD59Ot26dUv2GtNqiY+Px9LS8i09vcrVq1dpWbcqnu0zG61d7LofzaKnuTh08vNYWA8MDGTSxN/Yv2cndna2dO89iL59+yYFPu3RtT2F7Y7zXccXQg9F63BpepPoRG3HxkrDjJ8L0Lll8ppkcEg8xZt44usXiK2tLU+fPqV6tYq4ukga1HHA62YkW7b7sm37bipVqvTO404NTSa7mYPs5/yf0a6SGPNgbrrbjJlhNRkpJT///DMODo5UqlQFJydnBgwYYBQUceLEiRw8cBRdQmZio81JiLXlutc9unXrzrFjx/jrr784cvQIJupMRn2bqO0ICw8je/bs/Pzzz1SpXIVovW/SE7GUkhj8ad26dVIbe3t7znic4uCRvfyxeBKXrlxgzdp/PisBc/z4cXwCfPCIPIdOJm/Quxt7F5vMNhQpUuSD+ndwdOQZ0a+UR6riUqSxSSk5e/Ysf/75J9u3b3+vAJc/ff89WR49Y3GBynznUpRFBSrjGBzO8O+GvXNfz7G0tGTy5MlcuGAIxdKjRw9q1arFhQsX+LZfX7LY2WKfyY7yJYpz4sS7xQQrWrQoaktbdtxL/twSdJIZHs+46e3HyZMn33vcqYmzszNz/ljAjTt+nDnvRf/+/Y0iaw8a+iMz1oSz+1Q4UkoePU2g96QntGrVCl9fXzZt2oStrQ3FCxlrO9nsTTEz0dGoUSOGDh1Kx47tKF/GhHUrqtOrayF+n1iW6RNKMWBAr7dqpGmJlCk70iMZVpOZPXs2v/zyP6Kj9QihQkqJhYVg8OBvmThxIsHBwRQt4k54mArVCxqIlDritMnRcoVQY22aDxN18pdfp48jQeVDeHgYarWaoKAgqlSpRkhwOCRYIjXRODhn5uTJ4x9tcTql+Pv7s/Cvhdy5eYdK1SrRvXt3dDodP/74I4sXL8bV1RUHewcCvANw0bsQrYnmoe4he/bvoXz58u99Xa1Wy5AhQ1g0/y/6ZW9MAcscSCm5EHmX3fFX8PF/YLTA/zJxcXF83bwlF8+ex93SkQBtBLEWag4eO/zaJGcvkpCQwMOHD/Hz86NhvXosK1oTB7Pkaz2Jj6G711Eiol8VgO+KXq9n6dKl/Pjjj8RFhlPdOTNjS+Qgq5kJuwNCGe0VxAmPc+8UF+zMmTO0aNyAqtlNyW2pZae/xD5HXvwfP8HPz4++ffsyefJkVCoVy5cv58LZE+RxK0TvPv1wcXF5+wU+Env37mX4sIH4+PojhIouXTozbfrspP/3bl3a4ZbtIt/3To7ddscnmqrtLuBWoCg3b95EJeLZs7kxxd2Tf1d6vSRf8Q1cuXqL7Nmzv9OYUkeTcZS9nVKmyYzz/SPdaTIZVsi4uLjw8GEI4oW1BSn1CBGLubk50dHRgMBU44TqhThgUkoS9IFs2LCeMmXKsHHjRkaPmoBalx2VMEEvtejVj+jeswOzZ89KaqfVatm1axc3b96kSJEiNGrU6LOL7XT27Fka1mtITpEXW11mgk0CCVUFoxd6nj17xrBhwxg9ejSWlpYcPnyYEydO4OjoSLt27T7ILTkoKIj27dtz+PBhGjduzIWz5zGXGuL1WizsrFm/ecNbIzFPmjCRTbMXM9SpKppED72tT67xKI8ly1avxN/fHz8/v9e+Pnr0KOkpVy0Em8s2xtYk+cEiQhtPK889hEdGppo307lz56hbrQrnmhbHXJ38RP/7jUfoqjTij/l/vVN/z549Y+3atUkuzDVr1iQqKorRo0cza9Ys7O3tMRE6KmeX1HXVcvmJmo039ezce/C9PQHTAiklz549w9LS8pV1t+vXr1OzRiWG93Kiae2s3LgXxc8z/Oj/7c8MHfo9er2ekiUKMeW3/FStlOxAEB2tpUDpDXh7+yeZuVNKaggZZ1NH2TOFQmainyJkvnieCxkLCwvi4tRGdmwpJVJGMWjQIPLnz8/GjZs4c/oyKl7w79dHUcTdlUuXLgKGJ9MffhjO/PnzsTC3JiY2kjZt2rB48aI083hJK4oXKYG9nzN5zZKfos9EHSXE5hF79u2hZMmSqX7NM2fO0Lp1a54+fcr8+fPp3r07Wq2WCxcuYGpqSokSJVK0T6JI/gK0Jz8FrZLNavF6Hb281pAgjfOmWFtbJ4WTcXFxMXqdOXUa2e8F0i1H8mew3O8mawJuY+/owJAhQ+jXr98Hh90/ePAgo3p3YU15Y03i4MNnrFU7sefIsQ/q/0UuXLhAs0b1+SpPFNMaJGvca67Essg3D6c9r6TatdKaK1euMG7s/zh75gw5XLIzeMhPRumif/99Bts2/8G6FdWxsNAgpWT8tCtcv2PPjh373/l6qSVkujumTMhM9leEzBfPcyFTpUpVTp8+jyG8mgEpteTP78rt27cAg+mobJmyREVpiY3VY2oqUGu0HD586JWIxc+ePePu3bvkypXrtR42nztPnz4lZw5X2lr1TAoDA/BMF8IZk4M8DErdhFpSSubPn8/QoUNxcXFh06ZNHyTE3HLlpZdpUfJYvmAmkXp631zHuMkTKVKkSJIwednB40V8fX2pVrESeVRmuJtYcz0hiru6GMZPmczff//NwYMHsbGxoW/fvkljfx8CAwMp4paf4/UKYmuarCmPvuRH1ibtmfb7zPfq903kcs7G9q91uL2Qblmrl2SfEYHfw8epmqvmU6LVaunRozMHDuyheuXseN18holJJnbuOvDOpjJIPSHTLYVCZko6FDKfz6ryR2bmzN+pVas2sbFapBQIIbGwUDF37h9JdVxcXLh56yZLlizh9OkzFClSmH79+r1242OmTJkoW/bL/W6o1Wp0Oi06tKhI1sDi9HFGCbTeh+vXr7P4r0U8fvSY+o0b0Lx5cwYPHsyqVato0qQJK1eu/KCAiQEBAUgVbAu+xmDX6kmaz4ln3hQuVIhhw1K+aO/q6sq1WzdZvXo1Xleu0KZYMTp37oyNjQ1du3blwoULTJ8+nVmzZjF79mw6duzIDz/8QLFixd5pzM7OznTo0IG+e7YxomBWnC1N2fQghH/vPaa85wXCw8NTNWSMlZUFoTHhQLKQiYqX6HT6z85s+yFoNBpWrvyX69evc/78eb4Z5Er16tU/afpuScZOv5xoIso4R5kyZeRzrly5Ilu3bi3z5MkrGzduIs+cOSPTM97e3rJP776ySIGiskGdhnL//v1Sr9fLHTt2yCJFikgNGlnEooTsbj9I9sgyWHaxHyBz2+aTkydNfu9rrl27VtpZ2cqa9hVkM/ta0i1THmlraSMBOXbsWKnT6d67b71eL1etWiUzZcokzc3NpatzDlk8Wy7ZyamMrOlUWGbNZC8vXLjw3v3/F97e3nLw4MHS0tJSArJhw4by0KFDUq/Xy5iYGDlh3DhZvICbdM+fX47+9VcZGRn5Sh9arVZOnTJFurm6SHtbG9mmeTM5btw4qVarZbFixaSvr2+qjXfihPGybkFbGfJzFhk9KquM+jWL7FvOQlqaIN3d3eWuXbukXq+Xe/fulc0b1pZli7nJgf37SB8fn1Qbw5cIcF5+4D3H0cRB/pB9cIqO1Lje53ZkWHNZRsPb25uypcvhlJAPR3IRoQ/lNufJkcuZGzdv4ObmZog1NvMP/H0eYq/JysNYPxo2asCqNavea5NlbGwsORyz09qyHtnNDGslUkr+DtpKg+5NmT9//nvPJygoiG+++YZNmzZRuXJlli9fTq5cudi4cSNnT50md768dOnSJc2990JCQpg/fz5z5swhKCiI0qVLo4+NxT78GT1cHFELwd8BQUQ4OnM0MdfM29i/fz+tW7fGysqKHTt2GEWPeF8SEhLo3qkdB/fvpUpuc64+1pI1R176DBjMhAkTuHfvHkWLFCbssQ+j6+oo6CDYfl2w6oo5pzwukjt37g8ew5dIapjLHE0dZaes7VNUd2bgnHRnLlOETAahZ/deeKz3orBJspvxM10wR6I2Mn3mNAYMGICJiQlSGvaa+Pj4ULJkSQoVKvTe1zx58iRdmnekm01zo/Kb0fd5XCCKQyeOvFe/mzdvpl+/foSFhTF+/HiGDRv2yU0+sbGx/P3334wbNw7dk2D21qqEOtFsp5eSjhevM3HRkhQnG7t27RpNmjThyZMn/PvvvzRr1ixVxnnjxg0uX75M7ty5qVChAkII4uPjmTt3Lv8b+QPHvzWjWPZk09Kve/RE5O3IvL+WpMr1vzRSS8h0SKGQmZ0OhUyG3YyZ0Th+9DhOqjxGZZnU2bCxsqVx48ZJmooQgooVK9K+ffsPEjBg8OKK1sbw8oNMjD4Wm/dYbwgNDaVLly60atWKnDlzcuHCBYYPH/7JBQyAubk5ffv2ZeDAgdTP4ZQkYABUQlDVxhIPj5Tvvnd3d+fs2bMUKVKEli1bMmnSJIYNGUSBXC6UKJSfaVOnkpCQ8M7jLFy4MO3bt6dixYpJa1empqY0btyY7FmsjAQMQMuiklPHDr/zdRReQBqSlqXkSI8oQiadEB8fz6hfR+PkkB0rS2uaNW7O7du3kdIQhyssLIxIXahRmwQZR5w2Ns0SRxUuXJgEtJyLuJpUFqWL4ZzWi97f9Hlju7CwME6fPo2fn19S2Z49e3B3d+fff/9lzJgxnDlz5oNC2KQVrq6ueCfoXim/G6/F1dX1NS3ejJOTE0eOHKFRo0aMG/ULwfv+YVEZUya4adm1YCpd2qcsfHxKyJYtG08jtETEGt/p7gRLnoWFcfz4caSU3Lp1izYtG5PJ1pLcLtkY+9vo9xJ2GQn5Dkd6JMN6l6U3unTqxsk958mnq46psODOoduULV2OPPlyc+XKFWxtbbmuO0smXTZs1JlJkPFck6do1rRZmqTCjYmJoV27doSEh3LW7hrXI7yxU9twP9KXQYMHvdZsJKVkzK+jmfn7TByt7AmKDqVatWpkc3Zg+fLlFClShG3btr3iPv458dVXXzFi2DBWPwigbU5nBLDZP5CTDx+zsG7dd+7PysqKZs2aEXn1BDOrOiaVr8pmTrnNB7l69eo7e7a9jixZstCkcSOGbt/H7OZ6rM0EN4P0/LIHwrVaqlevTsmSJfHzvs2P9eOZPUbwKPwZIzdPp+/dmyxbufbtF8nApFctJSUomkw64P79++zauZPC+trYqLJgJizJrSmJTVx2/P0CWLBgAY8ePWL81N84w3aOyfXsj19FqbqFWbxsUaqPJywsjAYNGrBjxw7mzZvH46dBLF63jJ/njubGnZtMmDzxtRssV61axYo/F/OD01d8m7kx/3NuR+Cp26xesYoff/wRT0/Pz1rAAFhYWLD/6FGOWthS89g5ah4/x7oYHVohaNmyJU+fPn3nPi+cPU0jF+NIA2ZqFdVyWJOa64sLlvyN3rUe+SZJis/SUHeRCSPHTicwMJD58+cT4OdDy+KxDKuvwsFWUNxFxbo+CWzfvg0fH59UG0d6RGbg2GWKkPlCuH37Nl+1aEUmW3ty5czDtKnT0OkMZpnLly9jp3FALYwV02xqV8qVKU+/fv2wsLBg8JDBPAp+xMGT+/Hx9Wb9pnVYW1u/7nLvzePHj6lZsyanT5/mn3/+4ZtvvkGtVlOnTh3atm37n8nV/pgxiwaWJbHTGPblmKo0tM5WDY2Jhl9++SXNE1SlFgULFuTEuXPcuHcPrzt38bp7l+3bt3Pz5k3q1atHaGjo2zt5gVz58nMjwrhMSolXSNxb47K9C9bW1qxet5lb9x6wYfdJfB8GMWDgICwtLenfvz+Vy5eiflHjW4aVmaB4Tg1XrxpMolqtlqlTJ1MovwuOWe3o1O4r7t69m2pj/BKRgFam7EiPKOayL4CAgAAqlq+MbUxe8qkaEB8cxbRxczl54hSuuXOyatUqIiKiKGKpQ/VCLLYozVOKlahl1Je5uTnu7u4vX+K9uH//Pr+M+IWDBw+S2S4T7bt0YPXq1QQGBrJ9+3YaNmz4Tv0FBQdjr8lvVGahMsXcxIywsLBPns/+XXFySo6fVb9+fTZv3kzLli2pX78++/fvT/Eu+x49e1Fi+jQqZw2jRR5b4vSSGRee4BcalSYZUR0cHF4b9dqtcHHO3TxNqzL6pLK4BInn3Ui6d+9O586deeh3n+B7R1nWS0/2zCpWHd9H9SpH8bzklZQpMyOSTuVHilBcmD8Tnjx5wqpVq/Dz86dKlco0b948Kcz/8OE/snbeXlxkciBDrYzHM/YfNKZqWrRowb3b3jy5G0UefXlMhTmB2tv4mV7k8rVLqfq0+5zAwEBKuJeggC4/Bc0KEKmL5Ej4MSJVURw4fOC9cnf06NKNwN1eNLJPnufd6Ids01/A2//BJ921nVrs2LGDVq1aUapUKfbt2/efIW5exMPDgwG9unPf2wetXk/pkiW4cvMOJiYm7N27N03iyr2Mt7c3FcoWZ1LzGDpUUBEcAT9uMiFAFsQ5Zz62bduGmngCFtpia5lsDh28TEfmUgMZP2EyYNB2tm7dytkzp8jh4krnzp0/u2jkz0kNF+asJo6yRaaUuTAvfaK4MCukAefOnSN/Pjcmj5rPqj/20bfHYCpWqExUVBTR0dHs3bUPS62jURuNMMXeypn169ezbt06jp08QsMO1fGQ6zkUuxir4jEcOLw/TQQMwB+z/8BV5qSCVTkyaexwMctB6yxfAbz3xr1mX7XgUMhlNgaf4Ha0P0fDrvJP2DFm/TknXQgYgKZNm7J+/XouXLhAo0aNiIiIeHsjoHz58py/ep0b97x5EBDIkVNnOXXqFGZmZtSoUeOd89C8D3ny5GHnnkOsulMSu291FPtNjUOpTuw7dIL169fzzz//ULaAtZGAAahTVM+RA7uIjo4mMjKSGlXLMf23Ptg9XYrHznEUKZQvVdeWPjtSuB6TXp/3FU3mI/B8o97WLdvJmjULAwZ+Q4UKFQCDbb1A/kLEBmTBTuOaVBaoO4N9DhP8A/yJj0sgu6YYribJDzh6qcNLbOLytYvkzZs3uVyvR6fTfVAa5JRQp1ptbK5bkc88r1H59vjdzFszj7rv6Enl7+9P2bJlMTMzo0nDxlzyvEiuPLn5bviwD8pT87myadMm2rZtS6VKldi9e/d7r435+vpSv359fH19Wb58Od7373HqyAGccuSk/7dD3poi4X2Jj49Ho9EYCf+7d+9StUIJvOdqMNUkC5qRq2OYvTMeoTbDNWcO3J2DWfu/5Eyeaw5FMXOXPZ6XbiaVnTlzhqVLFhAW+oR6DVvSuXPnT7ImlyqajMZRNk2hJrPiqaLJKLyBBw8e4OXllbQY/5yYmBgqV67KiB9+4+whb7avP03d2vWZP38BAHfu3OHhw4fYqnMmtRFCYCfyE+AfyMCBA1m8ZBFhpt481XkjpZ54GY2f6gzVa1Q3EjAAKpUqzQUMgFshN4K0wUZlOqkjKDronTWZ6OhoWrRoQXR0NLt27WLeX/M5df4Ma9b/my4FDECrVq1Ys2YNp0+fpkmTJoSGhrJ161YWLVrErVu3UtyPq6srx48fx83NjR6d2+Px9xRam1zB+fZ2GtWuxrp169Jk/Kampq9ol/nz56dS5ar0WSh5/EyPTi9ZfyqeZcdMWLBwKQMGDCDkSQBDW1kaeRe2q2mJv78f9+/fB2D+vD9p/VV98pgfpKH7NdYs+YX6dasRGxtrdD2dToeXlxe+vr5pMsfUwhAgM3U2YwohfIQQV4UQl4QQrzwtCwNzhBB3hRBXhBAfHpPoA1EW/lOIlPK1brd+fn583ao117y80GhMMDc3Y9myJTRp0gSA5cuX43P3Edb6IggTQ/sEfVaGDB7CihXLuXTpEglxOrCUwAu5bdCRP39+ZsyYAYCbmxvf9BuI553jqNUmdGzbgTlzZ6f9xF+DlBKViZpz4Z5kU2cln3leYvWxnIw7TeUqlcifP//bO3mhr549e3Lx4kW2bdv2WW6wTCvatGmDVqulU6dO5MrujLtDJnJaavjl+2e0bteePxcuSlEunWzZslG/Tm3cdd7Mr58pqbxGTlO6DPqGVq1afbQ03ivXbOSHYd9S6Lt/0ep0FC9agC3bF1KlShUAThzZTXyCsXedTg/R0bEULVqUUqVKcfWKJ+dWFiCfiyFpWYeGkqbf+bJq1Sp69+4NGNa2Bg7ojYlaS3hEHO7u7vy9av1rUy+86bf7MdGlrsGolpTyyRvONQLcEo8KwPzE109GhtdkpJTExcW9Evrk+bk//vgDJydn1Go1hQoVZufOnUbn69Spy/VrAZiRH40uNzHhNrRr256LFy9y7tw5/vxzAap4e6MvuYnKCvRmhIeHM2DAAFxzufJMfz/pvF7qiNTcp0ev7kll1apV49r1K4SEhhAe8YwlyxZ/cAj+9yEhIYHevXszf/586jasy+0s91jwdDErnq2mRONSrN34bk/OEydOZO3atUyaNCnFcb3SE+3btyeXsyP/K+bIuiouzCjlxLEGbpzcuYU1a9akuJ9jh/bRpYilUVkZJzMsVXpu3LiR2sN+I9bW1ixYuJynoREEBYdy5rxXkoABaNepJ1PXxxOfkPx7W7A9ijx58jBgwACePXtGQVeTJAEDoFIJujSyZOmiPzh//jyenp707NGRxZNzc2Vvee4crULVkqG0aNbA6He8Y8cOypRxR6PRkD9fTubN+/ONv/M33QNSi4+4JtMC+DsxiPQZIJMQ4pO69WVoIbNixQpy5HDB0tISBwcH/vjjD6Mv2pQpUxg58n+EPtFjqs7B/btPaNu2HQcPHgQMASAfBQZjIrImCRETtTW6eEtKly5D+fLlue51DZ2MM7qulBJLKzOWLVvG77//zt59u9HbBRKsOcNTcYWHqkNUqFaCQYO+fWXM1tbWH8UcBoZYYVOmTKFJg6Z8O3AQnp6etGjRgqVLl/Lrr7+ya9curt++jn+gP0+fPeXv1X9jY2Pz9o4T2bJlC//73//o1KkTP/74YxrO5PPl+vXr6GNj6JAvObSPtYmafnlsWbl4YYr7yZw5M4FRxqbaOK0kJCrukyQkMzExee0606BBQ7B2roB731AG/RlJ3RGR/LHTlE1b9/D777+zZMkSYrXmr9zwHz9N4OLlq5QrV47KlcrRtVU2qpS1T7yWip++yUNkxGNOnz4NGCJZ9+nThRHfuRD8oAeL5pZh/rwJzJr1e1KfhofIOeTKlR1raysKFcrHqlWrUv2zkIA+hQeQVQhx/oWj72u62yeE8HzNOYAcgN8Lf/snln0yMqy5bO3atQwYMJCYGD1gwdOnUYwc+TMAgwYNQqvVMmnSJBLiLFGpDDd1tbAgIU5PmzbtcHHJzu3bt9ElmGBjbqyKq1RmFC5chAkTxhETE0O/vgPQ6h3QqCyQUhKte0jmbLZJ6w0FChTA58F9duzYQUBAAJUqVfrkedcfP35MudLlsI62w1nnwpnT51i0YCEJMoG//vqLvn2Tv9/vmjcdDGl0O3fuTLly5Vi0KGVmofRIbGwsFiaaV+ZvqVERGxOT4n56DxzKr4N7U9VFh6OVGp1eMu5U6GcRPPRFTE1N2bhlFx4eHpw9e5Z6Li40bdo0KVV5xYoV0atsWLYthB7NDRYAn4dxzF0fwZKlqzA3N2fC+F8plM/41iWEwMFeT+3atSlQoADPQh8xaUxpGtYzONOULe3A0nlVaN52EoMGDUGj0fDHH3NYuGgGa9a2o3iJ7Jw65UO/3t9jbm5O69atU3Xe+pSrKU/esvBfRUr5UAjhAOwXQtyUUr6Yq/t1P6RP6t2VYYXMr7/+SkyMDpG0S15NdLSO4cN/ZNu2bTx48IDw8AjMTYz3MaiEGeHhweTOXZny5cvz94qV6KUWVWI/Uko0ZvF8++0AvvrK4NIbGBjIr7+OwtokC1pdHLZZLNmzZ4/RjcXMzIyvv/76o8w9JYwbO57MEdmoYF4VEhWnbConLpmcpU+fNwe3fBOhoaFs27aNuLg4ypcvT8uWLbGzs2PLli1YWFik8ui/HEqUKEEUKk49jqCyo0EL1EvJ3z7htBw2KMX9fP3111y7fInys36nhLM13qGx2GZxICrhEeXLl2fLli1UqFCBiIgIfH19yZkz5yfb3CqEoEKFCkkeli+iUqnYvHUPLZs34M8NvjhlMeX89TB+GzuBjh07AobNyVu3T6dDi+xJv6GQZ/FcvhFN586defz4Md73b1GxvLHbf6GCmQkPD6No0aLkypWLc+dOs2tPb4oVN6RlrlIlD7/PasqkCeNTXcik1l1eSvkw8TVICLEZKA+8KGT8gZwv/O0CpG7u9Hckw7owm5tbEB+vNrrRGzK5RVGuXDlcXFzYuXMX6DOjEsnmKZ0+ijLlCnL69CkABg0azIrlq9HH2yKEBqGOwDG7LZcuXTRaMwkJCeHUqVNkzpyZSpUqffb7PvK55qNERHmymiTv/JZSsiFmJZe83m2D5/bt2+nUvhN5LXNigpqrobeQAk6cOvHJNbbPgX379tGh9dc0z2mHi6lgg89TgnVq7vsHvLMgePLkCZ6enjg7O1O8eHG8vLxo1qwZAQEBNGlYj8OHDuFoa8rj8Hh69e7FlOmzPjttBwyu+KdOneLZs2dUqVLFKIhrZGQklSuVpphbAl1bOfA0NIEpC/xp0LgzU6cZzGF16lSlc1szWrfMl9Tuxs0QGrTYTc1a9fH39+fSpQuEhE0yugeEhERTvOh0nj0z7F9KDRfmzGoHWcu6XYrqbg6f+8brCSGsAJWUMiLx/X5grJRyzwt1mgDfAo0xLPjPkVJ+UhfNz/tOl4a4ueUHXg7JrsfZOTtnz55l06ZNjB37G6ZmMej1hkVBnT4GE7M4JkwYn9RizpzZzF8wh2KlnMmZ14whw/py7pzHK4vy9vb2NG3alCpVqnz2AgbAxtaWGBltVKZFS7wu4Z32dISFhdGpfSfa2zbkK6vaNLWqwQCnjphpTD/a2tLnTv369bl4zYu87fryrGITmvcdxNOISKZNm/bOfWXNmpUGDRpQvHhxAIoWLYqHhwc5XXJw58wezvcx52JvEy72tcBjx99MmjAutaeTKqhUKqpWrUrTpk1fiRJubW3N0WNnyV+sM6PmRLNsqyU//jyTKVNnJNUZOXIMP4/2ZPe+B8TH6/DwfEyPb04yesw4Nm/ejIeHB7lyuXDunLH78/Fj93B3L5Kqc0lFF2ZH4IQQ4jLgAeyUUu4RQvQXQvRPrLMLuA/cBRYBA1J1Mu9BhtVkdu3aRZs2bRLXZNSADgsLNfPm/Um3bt0Aw5P7vHnzmDBhIo8fP6JgwULMmDGdRo0afdI5pDZhYWEkJCQk5ZXx9vamTu06hPqF0TxTG8xUZuilHs/4M2Sv6MDOvTvf0mMyq1evZurQCbSyqmNUfjjcg3I9qzNt+rvfSDMC3bt3Z9WqVZw6dSpV9grlcXFkVaN4SmdPtpDfCNbSdL3gYXDIB/f/ObJz507GjBnJpUvXyZ07B99/P4J+/fonaS7Lly9j7NiRzJrTjNJlcnLs6D2+H7aDZUtXJ8XdSw1NJpPaQVa3Spkmsz3izZrMl0qGXZNp3Lgx69ev56efRnDnzh1cXXMybtw42rVL/jIIIRg4cCADBw78hCNNOwICAujepQcnTp5ACEFBt4J07NqBCRMmoNfrqVqnKhuPrSaHlQtP456Qv2A+lq9a/k7XSEhIQP0ahVmNioR4JdnVm5g9ezaHDh2ia9euXLx48YPXrR4Fh1Igq7HpzS2LmkdPQ9Dr9V+Edv2uNGnSJGm/2uvo3r0H5uYWjBk9gbt31uDuXthIwKQmGe1h/kUyrCaT0dHpdBQuUATLIHsKakqhQo1P/E3ORR+meKnibNy4kTx58hAQEMCFCxfImTPnewVhfPToEW5589Mr89dkNjHc5GL18SwL28y67RuoXr16Ks8s/XDw4EHq1q3LkCFDmDVr1gf1VbtKeTo73KBD8eTQLFtuxPHTMQ1Xb3ljZ2eHXq/n6tWrCCEoVqxYhvX4e5HU0GTs1A6yqmXbFNXdFfmnoskopA8OHjxIdEgs5UySTTF5zYoQLB/Stm1b8uTJA0COHDk+KJy8k5MTrVp/zfxVayhrVwxTYcJ17T1atf+aatWqffA80jN16tTh22+/Zfbs2bRo0YJatWq9vdEbGDd1Jl81bcCTmFgq51Tj4a9j7LE4wmO0uLu789133zF/zgxIiEDqQWOZiZX/blQcM1KJjPYw/yLpT0dWSBE+Pj7YyFfTLtuRBZ/7Pql2naCgIHbs3EGREkWpNaARZXtUZdPuLcz7a77ypJwCpkyZYohL1qMHPj4+HD9+HD8/v7c3fIkqVaqw7/AJrtjVZ/CprJyzqsOBo6c4ffo0lpaW/PLT90yu9ZRrQ3V4DdMxunIQzRrVS3GUaIU3Y0haJlN0pEcUTSadc+7cOUb8MJLzF87j5ODE8JE/0KlTJ7y8vPAOv01Ju6pJic6klISaPqJSlV6pdv2hQ4cSGRnJ6tWrKVIkdb12MgKWlpYsX76c2tWr4l7QDffs9tx5Ekm9evVYuuofLC0t395JIiVLlmTV2o2vlA8cOJAjS3+iWdFkV+avS2j41ws2bNhAjx49UmUuGRmZgdOWpZkmI4RYKoQIEkJce6HMXgixXwhxJ/E18wvnRiZGDr0lhGjwQnmZxKijdxOji4rEcjMhxNrE8rNCiNxpNZcvlUuXLlGnVl2entVTSX5N1sDC/DjoZ1xyuDBnzhwyZ83EKe0enmgDeaZ7wkXtcTRZBG3bpsx+/DZ27tzJmjVr+OWXXxQB8wFcvHiBAlks8Wybhx11s3CpdU7ir59i2ODUcUh5+vQpBbPqXynPZRPL48ePAYiKimLp0qWMHDmCtWvXEh8fnyrXzii8Q1iZdEdamsuWAy+7aYwADkop3YCDiX8jhCgCtAeKJraZJ0RSHuH5QF+SI4s+77MXECqlzA/MBKak2Uy+UMaNGU9uXQlymxbFXGVJNo0LZdQNCQ+LYOfOnTzw96HvTz24Z3+RK5bHqde9Oqc9TqXKDvyIiAi++eYbihYtyogRI1JhNhmXv+bMYny5rGQxNxgeLDQqxpfJxD9r/iUuLu4trd9OjRo12HrLjIQXQgXHaSXrLsaxaNEi5s6dS9GCedn851AsvKYzf1wfypUqypMnbwoErPAiEok+hUd6JM2ETGI8nZcd8FsAKxLfrwBavlD+r5QyTkrpjWEjUfnE6KG2UsrT0rBy9vdLbZ73tQGoIzKgkV+n07FgwQJKlyhLIbci/O+X/xEWFgbABc8LZFUZL9pbqeywtcpEgQIFMDU15Zf//cJdnzv4Bfoy54/ZH5QGV0qJj48PwcHB/Pzzz/j7+7No0aKkuFQK78eTkFBcrI0t21kt1CAl0dHRb2iVcmrVqoVbsQo0Xa5i2zUtW69qabRURf4ipdFoNIz4fhB9yj5lc584fm6sZv/AWCo7+jH6f8rDQ4qQhlBBKTnSIx974d9RShkIkPj6PGbJmyKH5kh8/3K5URsppRYIA157hxRC9H0e1TQ4OPh1Vb5YenTryZjhk5C3HLHxK8jKWZspW6ocw4YN49Hjx4Tqg4zqx+qjiNPG4OTklKrjOHToEPlz56OUeylyueTirz8X0LNnTypVqpSq18mI1KxZg83ekUZlB/wiyeXikioRloUQbNi6i3ZDpvGXd0kWPShF9x9ncuTEWS5cuECCXsWg2iqj+t/V0rNp4wbA8KCzdOlS6tWsQM0qpZk58/dXEoxldGQK/6VHPpeF/zdFDv2viKIpjjYqpVwILATDPpn3GeCnJDIykg0bNvDgwQPKlStHgwYNUKvV3Lp1i82btlCONqjVhhAtdtKR8w+2MGvWLKpVq8YFj/NYaG3IpnYhWoZzQ3WCXj16vXe639dx//59WjVvRT3z6uTNlAsdOk6En+XsyTOfRcKoL50xEyZTo3IFQuNDqOlkysUnscy+HMKajZtT7bM1MTGhf//+9O/f36hcp9OhUqvQvbRgkKCD6OgoVqxYwb7dW7l/ZT/DG8ZjqhH8uXo0u7ZtZM+BY59lXLSPjQS06XbF5e18bE3m8fMEOomvzx+z3xQ51D/x/cvlRm2EIZSyHa+a5754bt68Sd7c+fhlyEQWTdhMt/Z9qVi+MlFRURw5coRMwhn1CwE8hRA4qd1o3aoNR48eZeWaFTzKdo09sYvwENvo3L8dM2ZOT9Ux/jV/AUVMC5DPIjdCCDRCQw3byjwNfMqZM2dS9VoZkQIFCnD2wmXMa7ZjfrgzV7KUJCpBx6lTp9L82mZmZjRtWI9p+5OFmV4vmbAbTMws6N69O3t2bmH/jzpalNXQqKSarUN1PHt4LSnBX3x8PAsXLqRFk9q0b92MHTt2ZLB9IynVY9LnZ/KxNZltQDdgcuLr1hfK/xFC/A5kx7DA7yGl1AkhIoQQFYGzQFfgj5f6Og20Bg7JL/Sbe/HiRaZP+53bt+5QqXIFfhj+Pa6uhjwYnTt2xSoiHw7qQqABmSDx8TpGMfdi+Pr5Yqq3hpfW6RNMIylUuCAALVu2pEWLFkRFRWFhYZEmT5Y+9x+QGeOUCEIIspra4+/v/4ZWCu+Cq6sr02cmp9vu2bMn06dPp0OHDknBMNOK2fMWU7dmZY7NCaWsSzxH7ppglTUf97yPMGbMGMIuz8PCNFkIqVWCliVj2Lp5A40aNaJZ4zokhFylT11JRIxk+LdHOXm8L5OmJD/sSCnx8/NDrVZ/0ObfzxFD0rIv8taUKqSlC/MaDAKgoBDCXwjRC4NwqSeEuAPUS/wbKaUXsA64DuwBBkopn4dI/gZYjMEZ4B6wO7F8CZBFCHEXGEaip9rnSGxsLBs3bmTRokXcu3fP6NyePXuoVrUGhzZfJei6GeuWHqBE8VLcuXOHoKAgrnldI6uqQFJ9IQTZKMLDgEcMHToUe0cbfPWX0UsdUkqe6B4QjDe9+/Q2amNtbZ1mpouqNavyQBgLkzh9PD6RfpQtm64iZHw2TJs2jcyZM9O3b190upejiacu2bNn57LXHYZP+huX+uOY9tdGjp/xxM7OjsqVK+P37FVvRC9/PUuXr8TR0ZHH3ufZM8qUttXM6VXfgmMTzVi0cB4+Pj4AXLhwgbKlilCudBFKFHOjWuUy3L59O03n9FERoBf6FB3pESV2WSoQGBjIkSNHsLW1pV69ekbeVJ6entSr1wCVtEDoNUQnPKF3n17MmjUTgHx53NA+csZak5yG+0nCDTT2ocTERhH2LIIy5p1RieTngUh9MNGON/B+cJcHDx7Qvk1Hrl69gkZtQqbMdixfuYyaNWum6hz/i4iICPLmyotTXDZKWxcjRh/LOe0l6n5Vj0VLF3+0cWQ0Vq9eTefOnWnfvj0WasiRKw+9+vQld+7cH20MsbGxuOV1YUyzCLpWUyME7L6sp8ciNSN++Y0li+bRt3owg5sbbxptOyWaXOX70LdvX2pWr8TkfhZ0qGuLXg9/bQ1j1ibJrTsPMDMzQ6vVMn36VBYv/JOQ0HBq1KjKhIkzXrv3KrXXAFMjdpmVOqssZP7mQJ0vciH673QXu0wJK/MWAgMDmTZtGt9//z27du1Crzd+2hg/fjx58+Zj4Dc/0KVzL7I758DT0xMwLJo2bdocEeOMhbYg5vp8ZFKVZvnSlcyYMYM//vgDP38/rNTGnl626pwEBwfz9ddfkztXboL1N5POSaknRHOTzl0NWQJz5crFaY+T3Lp7k/OXPPD2vf9RBQyAv78/YZFhxOfQcdryAned/Php0kj+eocc9QrvTqNGjchiY4n/8a0UDzhIyN5FlCtZjMOHD3+0MZibm7N73xH+OOlK/h9UFB6h4bt19mzaupsffviBVl+3JSD01dvM/YexzJw5k8KFC1OxkI5O9e1QqQQajWDg15nI66Rn27ZtAAwe1J/dm+fw90QHLm0qSiW3O9SuVQVf3+RcMMePH6dqlbJoNBqyO2dl3LjfXqvh3blzhyNHjhAaGpp2H8pLSCS6FP5Lj2RoTeb48eOMHPkz169fJ1++vIwbN84ozPehQ4do3rw56M2Ii9NiYaWidOmS7Nu3F1NTU44dO0aTxs1Q63MmZc+M1z7DKlMMFy9eYNeuXXw35EcyqUobjSEqIYBncbeR6BGoyG/ZFI0wSz6vC8LM5TG379zg9u3bVK9aA1WcFapYK2LNgnErnIeDh/e/U0iRtEKn01G1alXu3LmDl5cXjo6Ob2+kkCr8MvInvLcv5s+amZKe3vf6RDHKy4Sb9x58VK8+KSU3b94kISEBd3f3pNQBd+7coXKFkuz81Ywy+U2QUvLvsThG/mPCilXrmDRpAtVyX2Fk16xG/Q2YFsjaI3qKFi3KtSue3N1XFjub5CXkkTN9Udu3ZPqMWVy6dIn69WowdXQRWjTMwT2fSL4f5UXp8i2YOWsuYMhM26FDay5fvkjevFm4ceMx3333Pb/+Otroczp69CirVq0gJjaaZk2/on379h+sWViqs8j8Fg3eXhG4GrUm3Wkyn4sL80fn8OHDNG3alJgYHaDG0/MqX3/9NStWrKB169bodDratWtPfKwlapU5GjXEx0g8z19i2rRp1K1bl1G/jkafYIOJJtm7y1STiSfBgUmLlxphCcZJMhGoKV6iBBs2rGPc2Ans3nQce1kcldCglbFEaG4xYtgowOBZ5P3gPps2bUpyYa5Tp84nzf9x48YNlixaQtDjIHToOHPmDKtXr1YEzEdm19ZNTCliYXSTrJ/LkmEng7h//z758uX7j9apixCCwoULv1Lu5ubG/IUraNq/J3mcBJHROrQqW3bs3kGJEiUIDw9n0qje/NRZolIZ5pGglew7H0+1arXw9fUlb04zIwEDUKOsNf3HLObS5Ws8DPBmaN88tGlucJYpXMCOFX+WplSt5YweM55MmTLRq1dX8uSO5J9VPTExURMYGMlXXy+iYMHCSTmkJkwYx6LFfzJgYDWsbcyYPuN/qfLZGHb8p8/1lpSQYTWZMmXKcPGiF+IF918ptWTObMXIkSO4du0aa/5Zi4psRu11+mgSdCEYfEZUWJrmwExjvAc0Tu9D565tqV+/Pt269cBKXwhTtW3iNfREqW4wc84kunfvTlRUFJ06dmH//v1YmWUiMjaUAQO+Ydr0qZ/l/pK1a9fSt1c/CmkKYikt8Yr2Aht4EPAgVcLRKKScKmVLMDR7EPVyJT/FxOkkRVYGcu32PZydnf+j9cclNjaWs2fPYmFhQdmyZZMekrRaLbWqV8TB4gGDv7YkQSuZtiYai6xl2LxtD35+fpQuWYTbu0tgaZHsuDJ2ni+bj6jJlNmB27cus2FpZcqXNv4dFq68g9AwFdmyZePxY3/u3RmIpWXy733b9tvMnHWX2bMXEBcXR+vWX3Hhys84ORk8JePjtWSyHvzBmoWF2l7msaiboro3otYrmkx6wcvrOq9OX01IyFOGDx+OWq1GrwdT9asLiW5ubsyc+TsXL15k6pRZSJ19Uh2dPhZUCUybNg1bW1uEEHTp0g0zmQ19ghphHk7pssXp1KkTAFZWVmzZugk/Pz/8/PwoVKgQ9vb2H+ETeHdiY2Pp36c/jc0bkc3EEKzB3aIYu2N3sWzZMgYM+OTpxDMUXfsMYPrEkVRytsDaVIWUkpmeoZQoUeKzEjBgWLupUaPGK+UajYY9+48yY8Y0vvvrHzQaDW07DGLw4CEIIXB1daV+/fr0GnWWaT+44JTFlE37g1m8IYTjJ89RsGBBunfryCmPG0ZCJuhJLKHPdHTs1Bl/f3+io4ONBAxAjuw23LlzJymvUaPG7kkCBsDUNLVujwZd5kMRQuTEEFrLCUM8zYVSytkv1amJYWuId2LRJinl2A+++AeQYYWMs7MzDx4EYvwR6LG1tcXX1xcbGxty587Do4dRqIVh7UNKPWYWOkaN+pUmTZpQv359Dh06jOf5yyTEmqNSS6QqnDlzZmNra9BcWrVqRcmSJVm+fDnBQU9o3KQRjRs3fsWdOGfOnOTMmZPPGQ8PD+xM7JIEDBjMJAVEATav26wImY9Mnz59uOBxmlL/rqdaTmtuPInB92kkLdvm/dRDeyesrKwYNWoMo0aNee35JctWM3LED5T5ejkxsXGULe3O5q27KVjQsBfs+x9GUqd2VRyymdKikQv3vCP4Ycx1+vXvz/Tps9DpdOTJ44KHRwDlyyfvwVm3/hbNm31Ft+692LNnD2c9dqbJ/CSklnuyFvheSnlBCGEDeAoh9kspr79U77iUsmlqXDA1yLBC5tdf/8fgwUOIjtYhhBop9VhaqhkxYgR2doanma1bt1CnTh30umi0WpDE0bx5Czp2NHh2mZiYsG/fXrZu3cqWLVvJnDkzvXv3emVzXN68eRk79pM+TKQKVlZWxGpjkSbG2l2cPg5bG9v/aKmQFqhUKv5aspzhI/+Hh4cHOXLkYPfu3UyZMgVbW1uePHyAmbkFnbr3pmHDhp+l+TUlWFhYMGv2n/w+8w8SEhIwMzMzOl+sWDG2bN3NL798z7cjtuHkmIUBA4cwfPhPAKjVambMmEOnLn0Z9G1JChawZ9duH44cfcypU1txdnamWrVq5M79Nzt3XKFJU8Pv9+aNwFSagURHwof3Yoj3+Dz2Y4QQ4gaGGI4vC5nPigy7JiOlZM6cOYwZM4bY2FhMTEz4/vvvGTVqlNGPMTo6mm3bthEcHEyNGjXSfHf154yUklw5cuEWVYCilkUBiNHHsD12G0v+WUKTJinbC6CQdsTHx5PHxYksRDKwrDUxCZL51/R81bk3k6fN+NTD+6ScO3eO+fPnEBDgR6VK1Rk4cBDZsiWvuZ45c4bWrVvi4pIJaxszLnj6EBoa/sFrJGZqO5nDsmqK6npH7krR9RLzZx0D3KWU4S+U1wQ2Ygi79RD4IXGz+ycjwwqZ52i1WkJCQsicOTMmJib/0TJj4uHhweqVq0nQaqlWvSrffvstkWGRONk4Y6O24UG0D4MGD2LCpAlf7JNyemLnzp2M7NeRI21tMFEb/j9CYvSUXfmMsxevkjfvl2VK+9gkJCRw9OhRYmJiqFGjBnZ2dqkiZJwtK6eo7oPIPQ+AFxP1LEwM8JuEEMIaOApMkFJueumcLaCXUkYKIRoDsxPzd30yMqy57DkajQYHB4e3V8yAjP1tHLOmzSKfKIAKNSsXrUSn1nLuwjkCAwN5+vQp1atXx8XF5e2dKXwU9u3eRZt8IknAANhbqKiX14KDBw8qQuYtmJiYULduyjzBUo5hO2YKefJfQk0Y3GE3AqtfFjAAL2o1UspdQoh5QoisUspPlmEuwwsZhddz//59pk2ZRgvLtliqDC6yhc3c2Rq9jujoaBo0SNnmMoWPSyZ7ex7HvrqH6lG0JHPmzK9poZDWGAJkpop3mcAQs/GGlPL3N9RxAh5LKaUQojyGqC5PP/jiH4ASVkbhtezevZvcZnmTBAyAqcqMvCo3tm7Z+h8tFT4lXbt159+bcVx6HJ9UtvNuDGd9wrh65TKliuQnv6szA/v3ITAwtRa2Fd5GShMwv4UqQBegthDiUuLRWAjRXwjxPBFQa+CaEOIyMAdo/6mj0yuajEISnp6enDx5EmdnZ9RqNQnyVY8YnUr3WYSzUXg9+fLlY/7i5XzVpycFs+qIStDzOEoCkl1LpzCljiVZLFWsuLKWqhV24nnleqpk11R4MzL1vMtO8PpkjS/WmQvM/eCLpSKKkFFAq9XSvnV7Dh88grPKlWh1JKHaYCIiIyhk546DiSGA5zNtKPd1d+jQscMnHrHCf9GmTRuaNm3KiRMnMDc3x9HRkUplirOrsw1WiXlfJtfR8Gh7DEuXLmHYsO8/8YjTOxK9TJ/BL1OCImQUWLhwIR6HPWlo0g61MHwlbumucEVzlgNxu8iuyoEaDX4xPsz5cw758+f/xCNWeBsWFhbUq1cPgPXr11M1r3WSgHlOPVcdh04dZWfBQhw6sA/7rNno2rXbZ78p+EskNXb8f6koQiaDIaXk2LFjbN28FUsrSzp17sSyRctx0xdHrUn+OriZuXOLSxw5eZhbt26h1Wpp2LAhWbJk+Y/eFT5HcufOjVdQPHpphuoFN/NzAQmceXSGm55H+bpgHH6RJpSaNom//1lP48aNP+GI0xvv5F2W7lCETAZCSkmPbj3ZuWUXTgl50au1zJn1B9ZWNmQSxm7IAoFapcbc3DwpSq3Cl0nZsmVxypmfEQfv8Ws1E6xMBdtuxrPiUhzFnOI52tsKjdqwi76du56O3TrxIOAxer0eDw8PLC0tKVOmjLIP6j2RgF4qmoxCOiMmJoa1a9dy/pwnBQsVoEuXLpw7d45dW/ZQTbRCY2bYeJpLV5g9wavBxBMnjUvSjcQv4T529nZJ8aEUvlyEEGzZtY9venfHbe4BNCpB7lw5KV8mD/3z3Ubzwp6ayrk1ONvAtKlTmTNzGq72gogYPSqLzKzdtINixYp9wpl8oUiJ/jVONBkFRch84eh0Onx8fMicOXNS9OagoCAqlquE7pkaq9hs7DI/xNjR46hTtzbOCfmSBAyAtToT2S1yY+Gk5nDIVrLF5yDWNIpHwpeda3YqT6/phKxZs7J+yw7Cw8OJiYnBwcGB1i0aEau9ZVRPSkng03CmTvqNvf1VlHE1RHdedS6Qpg3rcNcngGfPnrF48UKuXz5PwaKl6N2nL05OTm+4skJGzyej7JP5AoiNjcXPz4/4+Hij8vXr15PdyYUyJcrjkj0nX7X4mrCwMEb+9DPqJ3YU19cnn2kpiupr4RhdiK1btqKV8a/0b2quYfykcfy5Yg61+1eiz6hu3L53m8qVUxYKQ+HLwdbWFkdHR4QQdOjam9lnTQiPTd5Gsemalog46F5OUsbVcHsQQtClvBoXm3iWL19OyWIFub1vErWsduB7ZAqlihfi+nVDjEa9Xs/+/fuZOHEi//zzDzExMZ9knp8bUupTdKRHMnzsss+BR48ecfjwYWxtbalXrx6mpqaA4Qc7etQYZs2ahUCNEJKfRv7EyJEj8PDwoF7thuTX1cBO7YRWxuMrzlGwYnY8znlQWtcUK1Vybgyd1LInaiGWplbUMmuDhcoagCfah3iKAwQE+mNtbf1J5q/waZBSMnhgP9avWUWjQib4R6jwChJUrlKZqqq9DKxubOj4anECFx9bM7B6FD82Tk5VMfegngNPKrN2006aNapDyMMb1CuawNWHptx8ZMb+QydwczOEzzp37hwr/15CVGQETZp9TYsWLV5Je/H8nvQ5aNFCiA+OXaZWmUtLs1wpqhsZezvdJS1TNJkUIKVEp3uzd8itW7dYvXo1J06c4GWhHRYWxqhRo3EvWpyKFSqzcuVKozoTJkwkb558DBvwKz06f0OO7Dnx9PQEYOrUaSyYvZQ8uvoUlC1w1dZmxqQ5LFiwgN+nz8RRWwQ7tcFMoRGm5JYVOXToMJERkeil1mgcenSYmJjy0y8/cjhhPZc5iqc4wHn2s27DWkXAZECEEPwxbyFHTl+gfNfJ9Bn1F/ceBNCmfRfWXrVAp0/+nj6Nkhy7C8EhYfSubnzb6FlVsOfAMb7p14fM2mucG6dnckcNO3/QM7h2OP17dwZg9qzfadmkFtnC/6WExU4m/NKTdq2bJ/22Hj58SOcOX2NlaY6NtQU9unUgKCjI6Fq+vr5Mnz6d3377Lel38jLR0dHcu3fvs9KiFE0mA/GiJnP37l2mTp3KuXPncXd356effsTd3T2pblRUFN99N4yVK1cSHx9H+XIVWPDXfEqUKAEYNjF26tSZHdt3YG6WCa0uBhcXZw4dPoijoyPR0dGUKlWG4IAo1LpsSBLQmjyiQ6c2zJ//J8eOHaNZ45Zk01fCRGVIXRyu9Udr+wBfPx+yO+XAKbYKlqrkmFORuiC89UeQOkkhkzrYq429wi7pN+NepiC+F4MoJmojhMGmfkd6UKi2C1u3b8bPz489e/ZgYWFB8+bNkxKsKSiAIRJxo7rVEU+v0atcHBGxkpknzGnRoS/Lli3myLBY8jsmaxn+IZKCI+IxM4F9v1pSLl+yZhKvlWTrE8uUabP4ZcT3XJhrh6uDQUOKT5BU/TGG0VOW06BBA0oWL0TzSnEM65AZvR6mrAzlyDUbPC9eR6PR8M8/qxn0bT++qp8NWyvBhj0hfN2mM7/P/AMhhEHzH/0Lf86di62tGRER8Qz9bhj/+9/o99aKUkeTMZPmpikLIhsddz/daTIZVshcvnyZqlWrEhurQ6eTqFRgbq5m165dVK9eHYA6depy5vQFdAnmgBq9jMbcUsv16164uLgwY8YMfhszGbUue9LNXEswFasUZf/+fSxcuJCRw8dioSuY9CXXywSeJngwe84sViz7m3sXI7A3KWA0Ru/YfcTrI5FSUsaiq9EPRCcTuBy7llKlShHkFUs+dZWkc3H6KC6LLdy9d5t2rdtz/eot7HEmQvUUOwdrjh4/jKOjY9p/yApfPHFxcSxbtoydm9dgYWlFl57f0LRpU378YSjeJxezsqcWE41Aq5P0WqHBwu0rDh/cx5pvoiiTN1nIJGglmXtEEpsAtUuasndiVqPrzN0WyeIj2ciTvzBhASc4+GfyRlApJdW/CeS7n/+kXr165MvryoG/3SmS36B1h0VoqdLuCkuWb6JmzZpMnTqJjevmsmJeOVyyW/HAL5Iu/c/Rredwhgz57r0+h9QQMiqVqTTTpMwxIjbBTxEyXzrPhUzt2rU5cuQUhsjZBqRMwM0tN7t27cTLy4t27dojtVmMbvJShFOjZgXq1q3L5MlTiY/KhIna+oU+9ITFXqNgwQL4+vpjpsuJlUl2ozEER18gTh+KQI2jaUkymeQ2Oh+gPUHD5tU5duQkNuGFyfSCthKi9ca+aCzbdm6hRLFSWEXlIAt5iNVH8Mj0Ct8O68+Y30YjpeTUqVNcuXKFvHnzUq9ePVQqxTqq8GHExMTQsW0Lzp05SYX8Jpy7n0CxkuVYu3EHkyaO497xP1k5QKBSGX4z8/Zp+feaG1+368bGZb9xdKqxWXbMygjm7dITHhnLyG5ZGNXb+CHo+1kP+WPdU4QQVC+fid1LSxudn77Ih3X7NdSoWZd//lnOrrXVcS+crPl7XnpKryFe3L3n917zTS0hY6pJWTqRuIQARch86TwXMhYWFsTFqY0FiJRIGZX0txCmmGmMv/Q6fRQJulAMW6xU2Ji7oUk0dT3vIzzOiwYN6uH7wBe/e5HYmuQ3Ps8lZs6eSmRkJGN/nUo2XQWEMAiAOH0EjzlJ4KOHHD9+nA5tO5FF6461KhsR+sc81XixfedWatasiZ+fH+N+G8+B/QfJmjUrw4YPpV27dp/FgqlC+ubatWtcv36dggULJpmPIyMjaVi3OnHP7lO/aCxXA8y56Kth/6ET5MmTh9yuzvw1QNC4vDkA3o+01Pgpih17jnHz5k0Wzx7K3lnJT/xSSir19qNY+ZaEh4fz7NEJdi42zkw7eYE3c1cFgzAhJCSEUO/2aDTJD1PRMVpci20mNvZVr8qUkCpCRphKE03Wt1cE4rWB6U7IJN5YM85RpkwZKaWUjo5OUggLqVJZJx1CWEoTE1O5bNkyOXPmTGlqai7NNC7S3CRn0mFpnlkOG/a9jIiIkP37fyOtLZxkZsuSSYeVaW7p5lZQ6vV6efv2bWllaS2zmpeWLtZ1ZA6rWjKzhZvMmze/1Ol0Mj4+XtauVVfa2zhLR9OS0sG8qLS2tJWLFy+Wzzl8+LCsUa22dHbMIevWri9PnjwpFRQ+V7Rardy+fbscPXq0XLZsmYyMjEw6d/r0aensmFlWLWEvm1bJKjPZWsi5c+dIKaWMjY2VhQrklt93dpIBOwtL3+2F5LdtHWWJYgVkQkKCDAsLk5kzWcuT68vJaK86MtqrjvQ9UU3mcskkT5w4IaWUsmzZYvKfRdVkhF/HpGPZ3MqyatVy7z0f4Lz8wHuOQCNNNI4pOlLjep/b8ckH8LGP50Jm4sSJ0tLSWgphlShgrKSlpbUcMmSIfE6zZs2llWUmaapxkmaa7NJEk1lmypRZBgYGSimlDAoKkq6uuaSdjaO0NM0pbayyS2trWyNBsGvXLumQzVHa2dhLSwtrWaZMOenj45N0PiEhQW7YsEF27tRFDh40RF6+fFkqKKRXYmNj5c6dO+W6devkkydPjM4FBgbKrp3bSitLM2ljbS579ugkg4ODk85v2rRJZs5kJTs0zyX7dsgtHbJay19+/inp/N69e6VDNls5Z0oF6XGgsZw5oZzMltVWHj58+L3Hmxo3fdBIjTprio70KGQyrLlMp9MxcOBAVqxYgZmZBXFxMbRs+RXLly/DzMwQxykuLo5Ro0azaNEioqOjqV27NrNmzaRAgeSF+sjISFasWMHRo8cpUCA//fr1eyWKrU6n4+bNm1hZWZE7d+6POV0FhXRFUFAQGzduJDo6miZNmlCoUCGj86dOnWLqlHHcunWDIkXd+emnUZQvX/69r5ca5jIhNFKjtnt7RUCrC0l35rIMK2SeExwczJ07d8iTJw/Ozs6fcGQKCgqfG6kjZNRSpUrZPjS9PjzdCZkMH7ssW7ZsZMuW7VMPQ0FBIV2TPjdapoQML2QUFBQU0px0ups/JSgbJxQUFBTSFIlEn6LjbQghGgohbgkh7gohRrzmvBBCzEk8f0UIUfp1/XxMFCGjoKCgkOboU3i8GSGEGvgTaAQUAToIIYq8VK0R4JZ49AXmp9oU3hNFyCgoKCikKZJUCpBZHrgrpbwvpYwH/gVavFSnBfB3ogf2GSCTEOKTejRluDUZT0/PJ0KIB596HKlIVuDJpx5EGpFe55Ze5wXpb24pi9H/3+wFbcq2/IO5EOLFXCQLpZQLE9/nAF6Mj+MPVHip/evq5AAC32G8qUqGEzJSynTlSiaEOJ/eXB6fk17nll7nBel7bu+LlLJhKnX1unhRL+9BSUmdj4piLlNQUFD4MvAHXtzp7QI8fI86HxVFyCgoKCh8GZwD3IQQeYQQpkB7YNtLdbYBXRO9zCoCYVLKT2YqgwxoLkuHLHx7lS+W9Dq39DovSN9z+6RIKbVCiG+BvYAaWCql9BJC9E88vwDYBTQG7gLRQI9PNd7nZLiwMgoKCgoKHw/FXKagoKCgkGYoQkZBQUFBIc1QhMxngBAipxDisBDihhDCSwgxJLHcXgixXwhxJ/E18wttRiaGjrglhGjwQnkZIcTVxHNzRGKaTCGEmRBibWL5WSFE7o84P7UQ4qIQYkc6m1cmIcQGIcTNxP+7Sulobt8lfhevCSHWCCHM08vcFD4ynzqhjXJIAGegdOJ7G+A2hrARU4ERieUjgCmJ74sAlwEzIA9wD1AnnvMAKmHwl98NNEosHwAsSHzfHlj7Eec3DPgH2JH4d3qZ1wqgd+J7UyBTepgbhs173oBF4t/rgO7pYW7K8fGPTz4A5XjNfwpsBeoBtwDnxDJn4Fbi+5HAyBfq7038ITsDN18o7wD89WKdxPcaDLuyxUeYiwtwEKj9gpBJD/OyTbwRi5fK08Pcnu8at0+87g6gfnqYm3J8/EMxl31mJJoNSgFnAUeZ6OOe+OqQWO1NoSNyJL5/udyojZRSC4QBWdJkEsbMAn7EOPpfephXXiAYWJZoClwshLAiHcxNShkATAd8MYQjCZNS7iMdzE3h46MImc8IIYQ1sBEYKqUM/6+qrymT/1H+X23SDCFEUyBISumZ0iavKfvs5pWIBigNzJdSlgKiMJiQ3sQXM7fEtZYWGExf2QErIUTn/2rymrLPcm4KHx9FyHwmCCFMMAiY1VLKTYnFj59HUE18DUosf1PoCP/E9y+XG7URQmgAOyAk9WdiRBWguRDCB0PE2NpCiFV8+fN6fl1/KeXZxL83YBA66WFudQFvKWWwlDIB2ARUJn3MTeEjowiZz4BEj5slwA0p5e8vnNoGdEt83w3DWs3z8vaJHjp5MOSO8Eg0YUQIISom9tn1pTbP+2oNHJJSpumTo5RypJTSRUqZG8Pi7iEpZecvfV6Jc3sE+AkhCiYW1QGukw7mhsFMVlEIYZk4pjrADdLH3BQ+Np96UUg5JEBVDKaCK8ClxKMxBhv1QeBO4qv9C21+weDFc4tEj53E8rLAtcRzc0mO6mAOrMcQbsIDyPuR51iT5IX/dDEvoCRwPvH/bQuQOR3N7TfgZuK4VmLwHEsXc1OOj3soYWUUFBQUFNIMxVymoKCgoJBmKEJGQUFBQSHNUISMgoKCgkKaoQgZBQUFBYU0QxEyCgoKCgpphiJkFDIswhD92lsIYZ/4d+bEv3N96rEpKKQXFCGjkGGRUvoB84HJiUWTgYVSygefblQKCukLZZ+MQoYmMZyPJ7AU6AOUklLGf9pRKSikHzSfegAKCp8SKWWCEGI4sAeorwgYBYXURTGXKShAIwwh7d0/9UAUFNIbipBRyNAIIUpiSBBXEfjueZRhBQWF1EERMgoZlsTIwPMx5O/xBaZhSNaloKCQSihCRiEj0wfwlVLuT/x7HlBICFHjE45JQSFdoXiXKSgoKCikGYomo6CgoKCQZihCRkFBQUEhzVCEjIKCgoJCmqEIGQUFBQWFNEMRMgoKCgoKaYYiZBQUFBQU0gxFyCgoKCgopBn/B/3Ei2Tht4fTAAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 432x288 with 2 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"Particle_data = xr.open_dataset(\"InitZero.nc\")\n",
"\n",
"plt.figure()\n",
"ax = plt.axes()\n",
"ax.set_ylabel('Y')\n",
"ax.set_xlabel('X')\n",
"ax.set_ylim(1000, 49000)\n",
"ax.set_xlim(1000, 99000)\n",
"ax.plot(Particle_data.lon.transpose(), Particle_data.lat.transpose(), c='k', zorder=1)\n",
"T_scatter = ax.scatter(Particle_data.lon, Particle_data.lat, c=Particle_data.temperature, \n",
" cmap=plt.cm.inferno, norm=mpl.colors.Normalize(vmin=0., vmax=20.), \n",
" edgecolor='k', zorder=2)\n",
"plt.colorbar(T_scatter, label='T [$^{\\circ} C$]')\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Sampling initial values"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In some simulations only the particles initial value within the field is of interest: the variable does not need to be known along the entire trajectory. To reduce computing we can specify the `to_write` argument to the temperature `Variable`. This argument can have three values: `True`, `False` or `'once'`. It determines whether to write the `Variable` to the output file. If we want to know only the initial value, we can enter `'once'` and only the first value will be written to the output file."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [],
"source": [
"class SampleParticleOnce(JITParticle): # Define a new particle class\n",
" temperature = Variable('temperature', initial=0, to_write='once') # Variable 'temperature'\n",
" \n",
"pset = ParticleSet(fieldset=fieldset, pclass=SampleParticleOnce, lon=lon, lat=lat, time=time)"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"INFO: Compiled SampleParticleInitZeroSampleT ==> C:\\Users\\GEBRUI~1\\AppData\\Local\\Temp\\parcels-tmp\\a7be8026cea52a1209527ece608da439_0.dll\n",
"INFO: Compiled SampleParticleOnceAdvectionRK4 ==> C:\\Users\\GEBRUI~1\\AppData\\Local\\Temp\\parcels-tmp\\a89daffb525400878a75fcf5f9700e46_0.dll\n"
]
}
],
"source": [
"pset.execute(sample_kernel, dt=0) # by only executing the sample kernel we record the initial temperature of the particles\n",
"\n",
"output_file = pset.ParticleFile(name=\"WriteOnce.nc\", outputdt=delta(hours=1))\n",
"pset.execute(AdvectionRK4, runtime=delta(hours=24), dt=delta(minutes=5),\n",
" output_file=output_file)\n",
"output_file.close()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Since all the particles are released at the same x-position and the temperature field is invariant in the y-direction, all particles have an initial temperature of 0.4$^\\circ$C"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZMAAAEKCAYAAADXdbjqAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAACpDUlEQVR4nOyddXgVRxeH37lxNyKQEBII7u7u7u5QvIUWh34tFChQCoVCKVLaYsUdirsGl+AQiAOBuCf33vn+SHrhEqChJEDIvs+zT2B2ZnZ2CfvbmXPmHCGlREFBQUFB4V1QfegBKCgoKChkfxQxUVBQUFB4ZxQxUVBQUFB4ZxQxUVBQUFB4ZxQxUVBQUFB4ZxQxUVBQUFB4ZxQxUVBQUMgmCCH+EEKECiGuv+a8EELMF0LcF0JcE0KUe19jU8REQUFBIfuwHGjyhvNNgYJpx0Bg0XsYE6CIiYKCgkK2QUp5HAh/Q5XWwEqZijdgK4TI/T7GZvg+LvIxkStXLunh4fGhh6GgoJANuHjx4jMppeO79NG4SSkZ9iw2g9d7eANIfKFoqZRy6VtczhUIfOHvQWllj96ij/9EjhMTDw8PLly48KGHoaCgkA0QQvi/ax9hz2I5e2Fqhuoaih6JUsoK73A58Yqy9xIzK8eJiYKCgsL7RCLRajXv63JBQN4X/u4GhLyPCytioqCgoJCVSIlWm/S+rrYD+FwIsQ6oDERJKbN8iQsUMVFQUFDIUiQSrVRnSl9CiLVAHSCXECIImAQYAUgpFwO7gWbAfSAe6JspF84AipgoKCgoZCkSmUliIqXs+i/nJTAsUy72lihioqCgoJClZJ6YfMwoYpIDSU5OxtDQEJVK2WakoJDlSInUfvpiorxNchDHjx+nQulymJuZY2dty+ivRpGcnPyhh6Wg8Okj1Rk7sjGKmHwCXLlyhZ5dulOxVDk+69uf27dvp6tz/fp1WjdvSemnDswt0I/RTi05tGoHA/t+9gFGrKCQk9AiNQkZOrIziph8xISHh/Prr7/yv//9j71796LVatPVOXr0KHVr1Cb+yENqRuQl9O/rVK1YhUuXLunV+2nWbGqbF6W8VQEMhAoHIyt62tVky9atPH78+H3dkoJCjkPKVJtJRo7sjGIz+QBIKTl//jzPnj2jcuXKODg4pKtz9uxZmjVqQmHTPNhpzFjz6594lijE3/v3YGpqqqs38osv6WBdmbJW+QHwMs+NhTChd9ceNGvTEn9/f/z8/Lh52Ye+TvX0rmGqMia3pQMPHz7ExcUla29aQSHHIiEH2EwUMclkoqKiiIiIIG/evBgYGKQ77+fnR4vGzYgMDcPB2JoHMY/43/++ZtzECbo6Ukp6dO5GW4uKlEsTiaZSy283DvG/r7+mVu3a+Pn58eDBA65cv0a/gvpLVeWs8rPx7inuzvPF3d2dfPny4e7pwd2wEAqbu+rqxWoSeRT7jIIFC2bR01BQUEAqYqLwAlJKkpKSMDExQYj04W9iYmIY1H8gO3buwMzIBBMzU35aMI9OnTrp9dG2RWsKRdlS37EmQggiLGL5+Ye5lC5XlvLly+Pv78/p06cJe/KUsnkb6NqqhIqaZkVYOG8Bc376CQBTU1OMVAaEp8SSy9haV/dZSjR5XHLjFxyg89i6f/8+lcpVxCbSnHJWBQhPiWF77EX69O1Lrly5suqxKSgoQLY3rmcExWYCr7RFvHju+6nTcLLPhZWlFUXyF2LLli3p6vXq1oOAIz5Mdu3Ed7k70cWkEkP7D+L06dMApKSksH//foL8AqhnXVInSHZGltQ1LUq7lm1wcnKiYsWKjBgxgqTk5HTR2bRS4unhyblz5wgNDSU+Pp4vv/qKzTFnidekhmuIUSewLeYCw0d+qef66+XlxZETR4kqYc6U4I2sTTlH3zFDmTt/3js9OwUFhTcjpBahTszQkZ3J0TOTtWvWMGnit9zz98U9txsTv/0fAwcN1Jt5TP5mEusXrWCITQOcHW25HR/MwN79sba2pkGD1JlDYGAghw8d5jvXThirjADIb+ZCvaTitGvZBkMzY0JCQpBS4mRkg+qlmY21oRkuTs58OW5U6pKUuzvdOnbhXMw9qlgXAkAtNRxLvMXQCaOoWLGiru20Gd8THhbGlPXrcbKwJzQunAEDBjBy1Mh091u6dGn2HNqX6c9RQUHhTSjLXJ80mzdv5svBX9DVpjoFC9bHLzGUaeMnodVqGTJ0CABJSUnM//lnRjm1xMHICoCiFm600JSjb/deeBb2IjAwkMDAQOxUFjoh+Yc8xvZoEzU0atQId3d3XFxcGDtyNCFJ4eQxsQdSl74uJPsxdOznDB8+XNd2/ZaNNKzXgOuRwdhLc24mBVOpRhUGDRqkdw0jIyN++/N3ps+aib+/PwUKFMDOzi4rH52CgsJbIRE5YJkrx4rJ1G8m08G6MoXM8wDgaeZMN1Gd8WPGsnffXkJCQggICCA5IUknJP/gYepEWNAp8gtB9erVcXR0ZOmviwlPicH+hbo3k4Lo1qsH8xb8rCszNTVl9BdfUdO8CHYqC66qA1A7mjBo8GC9a5QqVYqHAX5s2bKFR48eMbVGDapUqfJKew2Ao6Mjjo7vlMNHQUEhK5DA+wtB/8HIsWJy/+EDerjq56BxN8lFTHwcvr6+uLm5UaJECTau3cDj5AhcjJ9/7d9LCKFunTr8fWCvriyXfS6WzFlAU4sy5DKy4kq8H1c1Qfw+drTeNfr06UPx4sVZ8utiQh89pk/zL+jXrx8WFhbpxmhubk6PHj0y+c4VFBTeLxKhLHN9uhTyKsj98EeUsvTQlT1MfELe3K74+PjoZgAli5dg3rQfaWdVCVcTe27EBbA79gq7p+zV62/i/yZSoGAB5s+ex5Mnd6jTrC7ekzaQN29eXqZixYpU/LNiunIFBYVPEanMTD5lvps+lX7deqNCUMg8D36JoWyI9mba3B/0lpK+GjUSWztbfpz+A0EhwZQtVYYdP+6iatWqev0JIejSpQtdunR537eioKDwMSMlQv3ekmN9MHKsmLRs2ZLf/1rOt+P/xx/3D+OZNx+zFs5Nt6wkhKBf//7069//A41UQUEhWyOVmcknT6tWrWjVqtWHHoaCgsInjlDEREFBQUHh3VBmJgoKCgoK74iQMkfMTJRwKgrvxNq1aylVpATWFlbUqFSNI0eOfOghKSh8XEiJUCdn6MjOKGKikA4pJWfPnmXq1Kn8/PPPr813snTJUkYNHkGt2Hz8L3c7CgWa075lW44ePfp+B6yg8LGj1WTsyMYoYpIDkfLlEJL65/r37kvrRs05+fNWNk1fRhGvQvz999969bRaLd99M4letjUpZpEXSwMzKlh70cqqHN99/W1W34KCQjZCIrTaDB3ZGcVmkkOQUrLwl4X8OOMHgh6HULxwUWbM/oHmzZvr1duxYwdHdu1nnFNrTNJijVUx8aJ7l26sXvsXQUFB+Pr6cvv2bZ6FPcPdSz+ESyFzV3bd2P3e7ktB4aNHCaeikF149uwZmzZtIjY2liZNmlCiRIl0dWb/OJtfZ8yli3UV3LwcuBUdRO8uPVi3dSMNGjQgJSWFhw8f8vPsn6hi5KUTEkiNW2b5xIiWLVsCYGxsjIeHBwYGBulCzfgnPiW/h2fW37SCQrYhZ3hzKctc2Zy///4bL4/8rJy0gN2zVlOnak1GfTlSbylLrVbzw/SZ9LSpST5TJwyEASUs89HSshw9OnXFy8sLMzMzChcuzMlTp5HpMqmAqZkps2bNIiAggISEBO7cucM3337LmqhTPEqKQErJ/YRHbIs5z/+mKMtcCgovIqQ2Q0d2RpmZfKQ8e/aMMV+NYvOWzWi1kjatWjP755/0crXHxcXRo0t3BtjXx9PMGYBm1mX56c9V5PVwx8rKirt37+Lj40NsTAwuzvqh6QuYuRD97BS1G9ajS5cuFCxYkKdPn/LztNlU0hbEVGUMwP34R0QSz/DhwzExMdG1H//1BAwMDZg9azZRMdHkcXbhp19/VjaCKii8iJSgTvnQo8hyFDH5AFy9epX169ahUWto37EDlSpV0juv0WioV7MODs8MGO/SFgNUHD7iQ80q1bl+5yYmJiZERUWxbNkyXIxsdUICYG5gQhVjL8aMHI1aajA2NqZAgQKoDAx4nBSBi8lzQfFNeEzFihVZv369rkxKie/d+8xct4FSJvmIVyVzMy6QDVs26QkJpIaaGTt+HKPHjiExMREzM7PXhshXUMixSAnZ3LieEZRlrkxESsmNGzc4d+4cKSmv/hKZ+f106teow6Vl+7m+/DAtGjRlwtjxenX27NlD4tNoOthVwdbQAitDM1rbVYKwJEqXLo2zszO2traMHj2axISEdNdQCRX169XjwYMHxMfHc/PmTaZ8P5WVkcd5mPCEFK2Ga7F+7Ii9yLdTJ+u1FUKwaOli9h8/TKMxXen13Rf4+j+kUaNGr71vlUqFubm5IiQKCq9BaDUZOrIzyszkLZBSvvaFeffuXTq0bkdoyGPMDE2Jk0n89ucyWrduravj6+vLzOkzGefSGhvD1PwltTUlmLlwMbmcHVGr1dy/f59Dhw6RT2OT7lqFTXLjEx9Ky5YtKVSoEHnz5mVg/wEEJj4jr2kuABK1yZxN9mXZmBV4ej43hI8aPQpzc3N+nPEDgQ+CKVGkGKt+W0P9+vVfeT9lypShTJky7/K4FBQUgFQD/Kc/M1HE5F/QaDTM+H46C36ez7OIcCqUKcfsn3+iZs2aenUa12tIFU0+BjpXRyUEDxIe06d7L7wvnsPOzo4HDx6wcOFCSpjm1QkJgKWBKWWN3Rk9OjWJlpOTE/b29jxICU0nXoGqCKbPmE737t11ZcbGxvTr1YfSFh6YSSOuJPnTtlP7dDMJIQRDhw1l6LChWfWoFBQUXoUkR4hJjl7mOnPmDM0aNCGviyv1atbh4MGD6eqM+nIka37+nQFWdZnr1Y/ij2xo1bQFly9f1tXZvXs3qngNNa2LoUp7+ec3c6GcsQdlSqUuS1WtWpXVq1cTn5yY7hoaA/j888+JjIzkyZMn+Pj4YJnHnq2R54hRJxCnSWRXxEViTNW0b99er2379u25efc2bcb3pdrnrdl1aC+Lly1VlpwUFD4a0mYmGTmyMTl2ZnLs2DHaNG9FM8sy9Derhd/9ULq07chvK/+gbdu2AERGRvLH77/zde72WBmaAVDB2otITTztW7UlV24n/Pz8ePr0KUXN3dJdw8nIBi/PAnw2ZCAFChTAysqKls1aEJIUTh4TewBCk6O4kuDHH19tw8bGBgBDQ0OOnjrOV5+PYPK2DUippVWLVpxYsA1TU9N013F1dWXkyJFZ9agUFBTeASElQvHmeneEEAbABSBYStlCCGEPrAc8AD+gk5QyIq3uBKA/oAGGSyn3pZWXB5YDZsBuYISUUgohTICVQHkgDOgspfTLyLi+HjOB1lYVqGRdEAAnYxusDMwY8tkg9u3bR0BAAHfv3sVILXRC8g8FTJ05FHqNgsUKU7ZsWWxsbPj151+I1yRhbpDq8SSl5JomkPFfT6Fnz566tkt+W8KgAYMoZuWOkHAjxp/Zc38if/78etdwdHRk9fo1rErbL6LMNBQUsjHZfNaREd7HzGQEcAuwTvv7eOCQlHKmEGJ82t/HCSGKAV2A4kAe4KAQopCUUgMsAgYC3qSKSRNgD6nCEyGl9BJCdAF+ADpnZFBXfK7SxrWTXlkRc1dCg1N3k+fLl4/ChQtz2D+IaHU81obmunoPkp7QvFVL1mxYqyvTJKtZsGItdU2LYa4yxjvZF8t8jnTqpH+Nrt260bBRI3bu3IlGo6FFixZ6e0deRhERBYVsTg6xmWSpmAgh3IDmwPfAP+swrYE6aX9eARwFxqWVr5NSJgEPhRD3gUpCCD/AWkp5Jq3PlUAbUsWkNTA5ra9NwC9CCCHfFMkwDbfceQhOCqOgeR5d2ePkSBxs7Qh9+lT3Eh814iuWr95CO6tKOBlZcyX2IYfjb3D060V6/c2eO4eqNarx++LfiIuJpkenwQweMjjd3gyAXLly0bdv338booKCwidBzvDmymoD/DxgLPDik3SWUj4CSPvplFbuCgS+UC8orcw17c8vl+u1kVKqgSjA4eVBCCEGCiEuCCEuPH36FIDRE8ayOeYcj5MjAAhLiWF99BlGjh6lNxuY9dNseo8axIr4k4x5uJJ7eRPYtXc3pUuXfvkadOjQgT0H93H87ClGjhqJubk5Cm9PQkICc2bPoVr5ytSrUZtVq1ahzQH/GRU+USSglRk7/gUhRBMhxB0hxP20lZ2Xz9sIIXYKIa4KIW4IId7bV2uWzUyEEC2AUCnlRSFEnYw0eUWZfEP5m9roF0i5FFgKUKFCBQnQ/7PPiIqKZsa075EaLVokw0eMYNwE/X8fAwMDJkycyISJEzNwCwpvwtfXl8OHD2Nra0uLFi0wMzNLVyclJYX6teqS6BdOVRMvkrVqvhsxgeOHj/Hbn8s+wKgVFN4VCWr1O/eSZn9eCDQk9aP6vBBih5Ty5gvVhgE3pZQthRCOwB0hxF9SyizPvJWVy1zVgVZCiGaAKWAthFgNPBFC5JZSPhJC5AZC0+oHAXlfaO8GhKSVu72i/MU2QUIIQ8AGCM/I4IQQjBo9iuEjhhMaGkquXLleuSSl8O5IKRk3eixLFy+hhFU+YrQJDBs0hF17d6cLJbN161bCHz7mc/vGOjfrohZ5mbZxE6PGjaZIkSIf4hYUFP47/8xM3p1KwH0p5QMAIcQ6Upf6XxQTCViJ1OUVS1Lfh++uZBkgy8RESjkBmACQNjMZLaXsIYT4EegNzEz7uT2tyQ5gjRDiJ1IN8AWBc1JKjRAiRghRBTgL9AIWvNCmN3AG6AAczoi95EWMjIxwdXX994oK6UhKSmLp0qVsXrMBE1NTeg/oS5cuXVCp9FdP9+zZw5rfV/J17nZYGKS6Nl+NfUi7lm04euo4gYGB+Pv74+fnx8Z16ymhyqMTEgBTlRHFLPNy8uRJRUwUsicZjwicSwhx4YW/L01bWYFXmwIqv9T+F1LfiyGAFakeru9ljfhD7DOZCWwQQvQHAoCOAFLKG0KIDaSqrBoYlubJBTCE567Be9IOgN+BVWnG+nBSvcEU3gNqtZrG9RsRfjuIaiYFSdaq+ebzsRw9eISlf/ymq5eYmMiCn36mpklhnZAAlLb0ZMtDbwoWLKgrE0JgZWmFvUF6U164Ng5nZ+d05QoKHz8Zs4ek8UxKWeE15zKyrN8YuALUAwoAB4QQJ6SU0RkdwH/lvYiJlPIoqV5bSCnDgFcGhJJSfk+q59fL5ReAdBmfpJSJpImRQuag1WpZuOAXFsz9mdCwZ9SoVp3pP86kVKlSevV27txJyK2HDHdogkqkvvxLaPMxec1aElISefr0KXfu3MHf3x9jDOjsXDPdtaxMLeg9fABNmzbFw8MDNzc3njx5QqliJSkbH0QRcze0UnIm5jYxBkk0adLkvTwDBYVMJfOWuV5nCniRvsDMtBWa+0KIh0AR4FxmDOBN5Ngd8DmVuLg4DA0NX2sfGj92HNv+WE8ry3LkcrLm0pWH1KlRG+8LZylYsCCPHz/mxo0bzJszl+KqPDohgdTlqIJGLmzYsIESJUpQtWpV+vTpQ2hoKAfW7KCCVQEMhAEAAYlPiSSeqVOn6hni3d3d2bh1E3179EbEXiBJk4KLa24ObD2EkZFRuvEqKGQLMkdMzgMFhRCeQDCpKzHdXqoTQOrH+gkhhDNQGHiQGRf/NxQxySFcvXqVoQMGc+HyJVQqQdtWbfhlya/Y29vr6kRGRrL410VMzN1Ot0mzjm1xYjUJ1K9dl/jkRMLDU/0bBFDVJr39ItFEw9oVa2nXrp2uTK1W0+b+Q+ae301pg7zEiCQuxPuybPkfr/ToatiwIf4hgfj4+GBqakrhwoWVzZsK2RYpQarfXUyklGohxOfAPsAA+CPNPDA47fxiYCqwXAjhQ+p/03FSymfvfPEMoIjJJ0BsbCy3b9/GxcUFN7f0McIeP35M/dr1aGxaki6evUjSqtl97BLNGjbhhPcp7t27x7Vr19i3bx8WmOjt9gcoYubK2UhfOnTrRIkSJShRogS2trbUrVmHu/EhFDLPg5SSszH3iFAl0rx5c732hoaG7Niziz179rB39x7sHRxY2qd3uhAyL2JgYKCEwFf4NJDo77R7l66k3E1qFJAXyxa/8OcQ4PXJh7IQRUyyOT/O+pFpU6aSy9SGsIQoatWuxep1a7C2ttbVWfbbMkqYuFE9bSZhbmBAO9sqfHt9DRYWFrpEXgYGBhhIQYImCTOD58tgAcnPaNKsKUuWLNG79vrNG+jToxcmcQYka9VY2duwb/v+Vy6hqVQqmjdvnk5oFBRyBDlgz60iJh8pUkpOnDjB+fPnyZcvHy1btkz3kt6yZQs/T5/NKKcW5DKyJlmrZvOFs/Tr2Ydvp07m2rVrXLt2jfWr11ID/VmASgjymTrhWrMoXbp0oVSpUhQpUoRB/Qewes9J2ltXwtbQEp84fw7FXefQuAW8TOPGjQl8FMyVK1cwMTGhRIkSynKUgsKryBSTyceNeMttGdmeChUqyAsXLvx7xQ9IYmIiLZs05/bVGxQ2ys0Took2SubIiWN6S0N1qtXEy8+UclYFnrfVJjPedyUpaV7VxsbGODo64hhrwgDnhrp6aqlh6qPNHD59jJIlS+rKk5OTGT9mHMuWLSMpOYnCBQoyZ8E8GjZ83lZBIacghLj4BlfdDFHeXSW9xxlnqK7x50nvfL0PRY5OjvUhCAoK4vMhQylRsCj1atZh27Zt6erM+mEWYdcDGOvYinZ2lRli15AK6rx0aNWWJUuW8Pnnn1O7dm3Onz9PLiNrvbamKmOsTCyYM2cO169fJzY2lhs3bhBmnsTOiAuEpcQQlBTGn+FHqVazup6QQKr4/PTzXCKiIwmPjODa7RuKkCgovCvaDB7ZGEVMMpG4uDj27NnDoUOHdHaIF3n06BGVylXg7mZvmiUVxeO+IcN6D2T2j7N1dWJjY1n+2+/UNy+BwQtut7Wsi+Nz8waDBw9m5cqVqNVq8nsV4FKcvtdfQOJTjCxM+OKLLyhevDhGRkbY2Nhw+pw3Tg2L8nP4XlYnnaHVkK5s2LrptfdiYGCAhYXFa88rKChkEAlSrcrQkZ1RbCaZxPr16xn02UDczHORolUTJRPYvH0r1atX19X5afYcipGbNnap8ag8zJzwMHPi26+/Yf+B/dy9exd/f39MVEao3PR/sVRCYGxkxJlT3pQvXx4hBAEBAVQqVxEZcY7iJm48SYnkYPx15i78Od2eDDc3N1b8tSrrH4SCgsJLCNB++rbE7C2F74GUlBS+mzQZN+c8WJlb0qppC27duqVXx9fXl0H9BjDEviFDbRsywr4p7U0r0KpZC27cuMGePXuYN28ea1f9RQkTfdfdXEbWWGKMn58f1atXZ9q0abRo3ZKjsTd40Z7lHX2X4kWLU6FCBZ2R293dnYtXL1Gya21OO4SQXMmBLX9vp8cLmR0VFBQ+AqTI2JGNydEzEz8/P+bO/okrFy9TtHhRvhw9Ml0gwc969+PyvtP0tqqOjZU55y7do2a1Gly9fg1XV1eklCz69VfKmXuS1zSXrl1xC3fswi9TosTzKDAWxmY8to2kkPnzwJIpWjXJRpJDhw6RN29qpISYmBjq1qzN/KC9FMKZUINYHqY85dCqw+nuwdXVlZ9+npvZjyZbIaXkyZMnGBsb623CfBWhoaEs+Hk+p46ewM09L1+MHEHFihXf00gVciQSpDIz+XS5fv065UuX487G05QItCJ45xWqVazCqVOndHUCAgLYvn07fe3r4GrigKWBGfVsS1FClYf6detRqlQpLC0tmfvTXCxk+r0VDqY29OjRg+PHjxMaGsruA3s5lHCDwMTUDalJ2hS2Rp2jRo0aOiEBsLKywvvCOWb+No/i/evR97vh3Ht4P52xXAHOnz9PmWKlKJy/IO558tKobgOCgoJeWTckJIRypcpw/LcdFPEzJ+7wA5rUa8imTa+3HSkoZApaVcaObEyOdQ1u3qgp5ldjqGv7fOZwIfo+J4wf0L1vL/z8/Lh06RKx90MZnbeNXh9XYx+yKfoc1evWxMvLi+TkZLat3MAY59YYqVJjT8VqEpn+aAsXr12mQIHnrrsrV65k9JcjMZIGxCTGUb9+fZb/tRIbG5v3cv/ZgT179jB31hxCgoKpUbsm4/83EQ8Pj3T1Hj9+TPHCRWltXp5yVgVQSw2Hoq/hax3N9Ts304XCHz7sC25uPEk7u+dRux8kPGZt4lkCHgVhYGCQ1bemkM3IFNdgV0N5aqhVhuqa/S8y27oG59hlrhOnTvC/3O31yspa5Wf5vcN89913uLm54ezsTKg6ihStRicSAAHqMHr366NbXtJqtTwKCOaXU3upZJSfFKnhVNI9Bg8drCckAL169aJr167cv38fBwcHnJycUHjO4kWLmTz+fzQxL0VZ46Jc23GJSlsqcv7yBfLly6dX949lv1PcxI0K1l4AGAtDmtiUZWbIVtq3b4+trS0xMTG648alawx2bqzXR34zFzRRanx9fSlUqNB7u0+FHEY2n3VkhBwrJrbWtoSnxGJp8DzQYJQ6DnNTM55FhGFqmpp7o23L1vx15gStrStgZWjGhej7nE3wZeGIDbp2KpWKDVs3sXnzZjat3YCpqSnL+0167f4MIyMjihYtmrU3+BERFhbG2FFj2LRpE1JqadumLT/OnZNOSJOSkvh6wkSG2DUgj0mq7SOfqRPaMC09unSjUrUqBAYG6o7QkMe0yVVFrw8hBI7Cin379uHg4IC1tTVWVlZYWVlhYWFBREos+UwddfWTtSnEJydgZ2eX9Q9CIUcic4jNJMeKyZAvhrJqzm/0N6qDmYEJydoUtkafZ8Bnn+mEBGDNhnWMGTmamStWkJCUSOVyFdj36/50QQoNDAzo1KkTnTp1et+38lGjVqupW6M2Ds8MGOvUCiEEhw9cp1bVGly7dR0DAwP8/Py4desWR44cQSRpdULyD6XNPVhwbhcXr14mb968uLm50aBBA8LCwrhx0ofasrjOwy1FqyFIRODt7Z0uB8u6desYN/grPMycsDW0QC017Ii6SN26dXF0dERBIWvIGa7BOVZMxo4bh/8DP75bswY3KyeCY57SvHlzZvz4g149MzMzflm0kPkLF6DRaJScGmmo1Wp+++03Vv++ArVaTcfuXRj2+bB0IeX37NlD4tMYOtg30b3w29lVZk7IDgoVKsSTJ09ITEzU1TdWGZKoTcZU9Tz8xJOUSKpWq8ah40f0Yn8lJCRQvlRZ1kecprp5YZK0KRyI96Fm3TrphASgc+fO3L55ixmz55DX0okn8eGUKVeWP1evyOSno6Cgj8zmbr8ZIcca4P/h8ePH3LlzhwIFCrwyfLvCq+nYtj3Xj1+krmlRDIQBJxPvYFXIhSMnjiKE4N69e1y8eJFFixZhfCOa9o5V9dr//ewCd+2iaN2mNUWLFqVYsWIULVqUgf0GEHziJu1tK2OqMiYkKZxlEYdZvn71KzMthoeHM+27qezYug0TE1P6DOjLl1999UbRj4iI4Nq1a+TJk0cvbbCCwstkhgG+XG4jebK/Q4bqWnz/JNsa4HO8mCjok5yczPbt23nw4AHlypWjfv366byiLly4QIt6TZjg3AYjVerkViu1/BCyDRsPJwICAoiJiQFSc5nkMbJjXN52en0sjjjI+HlT6NZNP1FcbGws/Xv3Zc+ePdiYWpKgTeH7mdMZNHhQFt61gsKryRwxMZbH++T694qA1cxH2VZMcuwyl0J6/P39qVO9FpbJhuSWNizRzMe5QF4OHDmIpaUlAE+fPmXp0qUUMnLRCQmASqgoa+rBxfBgevXqRfny5SlfvjxeXl6UK1mG7RHnaWBdEoHgSPR1Yk3VetkY/8HS0pL1mzfy7NkzQkNDKVCgwGtTDCsoZAskijeXwqfFo0ePSElJIW/evK/MOzKw72eUSslNY7syAGilZOWDY7Rr3Ran3M54e3vj6+sLgKdpepfmcFU8o8eM5quvvtIrP3rqOF99PoJvdqxFSknL5i05/stWPUeHl8mVKxe5cmXsa05B4WMnJ3hzffpyqcCDBw+oUbkaRQoUokyxUpQsXJxz587p1YmNjeX4yRPUtS6uK1MJQUOrkhw7cpTDhw9TunRpZs2axYEDB0iwhNPRt9FKiZSSq7EPuZUUTI8ePdJd38XFhbWb1pOQlEhichKbtm1W7FMKOQZJqgE+I0d2RpmZfOKkpKRQv1Zdyqtd6ezWBYGKy7G+NGnYmI1bNnHr1i3OnDnDqVOnSElJQaD/Cy0QODg4EBwcrDebOXj0MF07dGZv0FUMVQZY2lqzc8/fb3SxVbIwKuRIpFCWuRQ+bsLDw/nfhK/ZsmkzKpWKTl06M+X7qXr53/fs2YNpkop69s9dZctbeXE11o8GDRoAkCdPHqpVq4aJyogT0TepZ5taV0rJ0bibdO7aJZ0QFC9enKs3ffD19UWtVlO4cGFFLBQUXkNOWOZSxCSbkpKSQu3qtbB/pmKwdX0kkoPrDlL/5ElOep/m+vXrnDlzhpUrV2KTnD5laF6TXDhVK8jipUt0NpR79+5Rp0YtHkaE4aK1wpdnmLrYMGnK5FeOQQiBl5dX1t6ogkJ2Rwqk5tOP+6aIyUdIUlISs3+czao/VpCcnESb9u34ZvK3eiE/duzYgfppHJ3sG+lmBN3sajDt9kasrKx0mR4dHBxQJybqxReTUnJHPmFS369wd3fX9VmwYEHuPrjPhg0bePDgAZ+VK0fLli0xNFR+TRQU3gVlZqKQJcg0o/XL+zf+oUPrdgSev0MLixIYGxpxYs1Bauzdx8Wrl4iPj+f8+fP8smAB+aWD3tKSEIJiZm4kF7fh888/p2rVquTNm5f2rdqy7PQh6pkXx0gYcCrhLqZ5bGjbtm26a1tYWNC3b98su/ePgdjYWGJjY3F2dlaW5hSynH8M8J86n75V6CNCo9EwZfIUnOwdMTQ0pFzJMhw6dEivzvnz5zl/5iz9HeqS38wFNxMHuthVIzkkinz58uHg4ECTJk04euwY95Mep7vGE8NYvvzySzp37oy7uztCCNZv2Ui/r7/guLU/u41v02BgO46dOoGxcfrlr+yGlJIbN27g4+ODVqt9Y93o6Gi6deqKi6MThfMXpJCnF/v27Xtjm6NHj1KvZh1yO7pQt3qtdP9eCgr/Slqgx4wc2RllB3wm4uvry/nz58mTJw81atRIN/P4aviX7PtrGx2sK+NkZMO1WH82Rnuz/8hB8uXLx+XLl1m0aBFPjt2hp1NtvbaHIq5xzSqU/gM+o2LFihQtWpTK5StSQetObetiaIHDUT7cMn3Krft3Pgmh+DcuXbpEl/adiA6PQiUEZtbmrF6/lqpVq76yftMGjYm9Gkxrm4qYqYy5GR/I2qjTHDt94pWJx/bt20e39p1pYVUOL7PcPEh4zM7YS6xYt5rmzZu/8hoJCQmsW7eOs6fO4FHAk779+uHs7Jyp963w/siMHfBlHM3kwXYeGarruPR2tt0Br4hJJqDVahn82UA2rN9AYSs3niRHYuFow75DB3T7KaKjo3F1ycPXudthbWiua3s0wod9sdeITojVleUxsefrfB31rrEm8hTtxvVl5MiRurKHDx8ypP8gjp48BkDDeg1YtGxJtt7DkZSUxKFDh0hISKBevXqvDQ0fGxtLfncPWpiUobxVas6Ya3F+bIo9x72Hvnrpe5OTk7lw4QLNGzThO7fOGIrnxtC9EZdJKmnNiFFfYWhoiJGRke5n/559qBGfj9KWnrr612P9OWkdyLVb19ONKTw8nBqVq2EUqaaQcCZUxHA9MZC9B/crqYGzKZklJgda5//3ioDT7zezrZgoNpN/ISkpiVk//MCqP1aQlJxMm3Zt+fa7STg4PA/ctmzZMo5u28+3eTpgqjJGSsm+yCt0atuBb6ZM4vr165w8eRIjjUpPSCA1OZNx0m3mTJtD2bJlKVmyJNUrVWVv5GXqWZfEQKg4F3OP20kh9OrVS6+tp6cnew/v10XdfdOO8uzAqVOnaNuyNbkMrTEVRvSNDWH2T3MYOGhgurqbNm0ir6GDLjEWQGlLT87H+VK9enXMzc0JCwsjLCyM2NhUoXY1ttcTEgBXI3uWHznE/sMH011DIBjoVUOvrKhFXhbd3kujRo1wc3PDzc0NV1dXXF1d2bBuPQ4RhnSxr62zxeSPvseA3v24ctPnnZ+PQjZFyWfy6RMTE8PKlSu5evEyRYoXo0/fPnpftADtWrUh5OJ92piXxtjYkBPrj1Jj7z4u+VzBzMwMtVrNr/N+oYFZCV3YdCEEDWxKMebicpo1awak7gKP1yQSmRKHrZGFrv/7iY+p16Ce3ozj4LHD9O/Vl6/PrEElBIULFubAioOvDS+S3UUEUpeHWjdvSWfLKhS3SPUwCzWPYvyoseRxzYNWq+X27du648qVK1QyTv+152RgzfXoUPLnz0/x4sVxcHDAwcEBIyMjpnw7mVhNgl5CtNspIXTr3YNBQwaTkpKCWq0mJSWFlJQU+vXsQ1BSGJ5mz5epgpPCsDK1IDIykhs3bvD48WOdrcZEGPFV3lZ6Rv3yVgXY4neOx48f4+LiklWPT+EjRiKQ8tM3T+dYMQkMDKR65aq4qK3wwIHNf3vzw/SZHDt1nCJFigCpxvBL3heY6NwGg7Qv2k7GVVnwZA81atQgMTGR+/fvo1JLGrrqp+c1QIWFqTnLf19M48aNsbe3Z+K48Sz/bQ1trSribGzD1Vg/DsVd58g3C/Xa5s2bl/1HDhIREYFarc7WiZvu37/PjGnTOXvqDPk88jFqwljq1auXrt7evXvJbWyvExIAJ2MbKhh70LplK7SkLse6uLhQuHBhGjVqxKn9x/RcnjVSwy3tI5avWKXbkPkiTx89YenKjTQzL42tkQUXYh9wSz5m7Yzpr3zRf/PdJGZ9PZVeqlq4mNjxJDmSDdHeTJ3xPSO+HAGk5nV5/PgxwcHBdG7bkSSZoteHWmrRaLU5woal8HqUmcknzPhRYymhdqGF3fPlySORPvTs3J0Bwwbh6+vLgQMHcBf2OiGB1FlHCRM3jj64Q43aNWnRogU3fK5z+uwdPEyddF+lN+MDsctlT5cuz3ePT5sxnVxOTvw8Zy6hj59SsVwF/p6zhzJlyrxyjNk9lezdu3epWrEKVU28aG5WlBCfcDq37sC8RfPp2q0bt27dwtvbmzNnzrBnzx7s4gzgpVu2MjSnTq3aTJ81k8KFC2NrawukenG1b9WWxacPUMu0CCoEJ5PuULRcSerXr//K8fw4dw4FixZm0c8LCY8Ip36T+nhP3fjaGcOQoUOIj49n5vcz0KSoURkZMGbMaIaPGK6rY2hoqFvuGjpiGKt/XEo+EyedwB2O9qFa1arpZrwKOQiZM1yDc6wB3tbKhrFOrbA1fL7klKxVM/L+H0gkRkZGqTnKwxOZmLeDXh9rIk/RbmxfRo5KXZqKiIigeqWqmEZqKWqQm6faGM4n+LJp25bXvthyAj06dyPmiC+N7crqyh4mPGHRk30YmBoRHR0NpIpmmTJl8D55mv+5ddQtA6ZoNcwL280vq5a+0ntKrVbz+++/89efK9FqtHTp3Z2BAwdm+ixArVYTFhaGvb39G5NupaSk0KV9J44fOUYRCzceqSMwsjXnwNFD2dopIieTGQb40g7mck+zwhmq67r6ynszwAshMvKFo5VSRmakvxw7MzExNiZJq78kkSxTMDI05PbdO7qd4SUKF2N35CUaWJfEQBhwNuYed5JD6NX7uTHczs6O81cusnr1ak4cPkYFz3wsHjggXZ74T4Vz587xzbiJXLh0EdfcroyeOJaePXvq2Qri4+M5fOgwn1nquzh7mjmDVtKiRQsaNWpElSpVKFSoEEIIfpgxkzkzZlHNtBCmwojzKQ8pW6MiTZs2feU4DA0NGTRoEIMGZW3iLENDwwy59xoZGbF5x1auXLnChQsXyJcvH/Xq1cPA4NMPpaHweiQC7ccZTiUk7XjTtMkAcH/DeR1ZNjMRQpgCxwETUkVrk5RyUpoargc8AD+gk5QyIq3NBKA/oAGGSyn3pZWXB5YDZsBuYISUUgohTICVQHkgDOgspfR707j+mZmM+nIkJ1fvoad9TVRChZSSTZHeuNUvwaq1f+nqBwcH81nvfhw/eRwQFC9SjKXLl712aepT59KlS9SvXZdm5mUoYelOSFIE22Iv8OXXo6lWozqHDh3i4MGDnDlzBpEi6Z27rp5rbawmgakhmwl58ggrK6t0/Z85c4YVfywnIS6eNh3b0apVK+VlrPDByIyZSSl7C/l3o2IZquu+/sL7nJlcllKWfdc6urpZKCYCsJBSxgohjICTwAigHRAupZwphBgP2EkpxwkhigFrgUpAHuAgUEhKqRFCnEtr602qmMyXUu4RQgwFSkkpBwshugBtpZSd3zSuf8QkLi6OVk1bcPPqdbzMcxOQ9BQn9zzsO3zglevb0dHRpKSk6LkE50TatmiN8YVwats8z3vyODmCmf5bSJFqhBCUKVOG+vXrY2xszPJffmOAfX2cjG1I0CSxLvIMpZpX5fcVf37Au1BQyBiZJSa7Ghb/94pAvg3n33g9IUQT4GdSZwzLpJQzX1GnDjAPMAKeSSlrv1wnrZ6plDLxTePJSJ1/yLJlLpmqUv/sxDNKOyTQGqiTVr4COAqMSytfJ6VMAh4KIe4DlYQQfoC1lPIMgBBiJdAG2JPWZnJaX5uAX4QQQmZAIS0sLDh47DDnz5/Hx8eHQoUKUaNGjdfGanoxrPunSFxcHN9M/B+rV60iKTmZFs2a88NPP+qt9UdGRuJ9xpsBVnX02roY22FubMr0n36gU6dOei7MuewdmDL5OyyNzIhMiKFd23b8svjX93VbCgofBZlhgBdCGAALgYZAEHBeCLFDSnnzhTq2wK9AEyllgBAifUrU54wRQsRLKee8ftwZExLIYptJ2s1fBLyAhVLKs0IIZynlIwAp5aMXbtaV1JnHPwSllaWk/fnl8n/aBKb1pRZCRAEOwLOXxjEQGAjoRckVQlCpUiUqVaqUCXebfZFS0qJxM+JvhzLEpkFqXpOjt6heuSqr1v7F8ePH2bt3L97e3hhqVQQYP8XF5LnbVaQ6Dq0B9OnTB3Nz/U2ZX40ayeChQ3j48CHOzs45fmankAORmRZ3qxJwX0r5AEAIsY7UD+qbL9TpBmyRUgYASClD39BfT6DMy4VCiM8ARynljLcZXJaKiZRSA5RJU8utQogSb6j+qqct31D+pjYvj2MpsBRSl7neNOZPlWfPnmFoaKhzrX2Rs2fPcvf6LSY4tUElUjdXtbSrgH/wbmrXTp0hly9fnvHjx5MrVy6+/2YKdoaWeJnlJiwlhvXRZxg4YEA6IfkHMzMzihXL2JqxgsKnhgS02gzb/XIJIV6M97Q07f0FL3w8pxEEVH6pfSHASAhxFLACfpZSrnzNtRKklPGvKF8FXAI+HjH5ByllZNrNNQGeCCFyp81KcgP/KGcQkPeFZm6kehoEpf355fIX2wQJIQwBGyA8y24kG3LlyhUG9O7HrTu3kUhqVKvB7yv/1C1fpaSksGXLFtwNHHRC8g8lzN3JU8GLNRvWpbpJp+Hq6sq4kWN47L8fE2MThg4bxnfTprzX+1JQyE5oM77M9ewNNpOMfDwbkuqQVJ9Uh6UzQghvKeXdV7RN+OddrNehlElCCHVGB/zihbMEIYQjkJImJGZAA+AHYAfQG5iZ9nN7WpMdwBohxE+kGuALAufSDPAxQogqwFmgF7DghTa9gTNAB+BwRuwlOYVnz57RoG59mpqWopd7DzRSy6Eb16hTvRZjJo5j//79HDx4kOjoaOwNLZEOUs9mFCQi6NRmgJ6QAHTs2JEOHToQExODubl5tkmeFRQUxP79+7GwsKB58+ZYWlr+a5uEhASuXr2Kvb09hQoVeg+jVPjkyLxlrtd9cL9c55mUMg6IE0IcB0oDrxKTOcB2IURHKaX/P4Vppoc353N4BVkZMCY3cEQIcQ04DxyQUu4iVUQaCiHukWpImgkgpbwBbCB1/W8vMCxtmQxgCLAMuA/4kmp8B/gdcEgz1o8Exmfh/Xx0+Pv7M3fuXGbPns29e/fSnV+5ciVFjPNQ1bowBkKFscqQprbliH0UweDBgzl//jydOnVi48aN5CtSgM2R3sRqEkjWpnA40gdfzVN69+79ymsLIbC2ts42QjLz++kUK1SUZRN/4ofh3+Cex40jR468sc0ff/yBq3NuerToSLXylalWsQrBwcHvacQKnwr/JMfKyPEvnAcKCiE8hRDGQBdSP6hfZDtQUwhhKIQwJ3UZ7NYrxyXlRlIN+heFELuEENOEENOBU8Dst73PHLsDPruzdMlSxowcRVkLTwSCy3EPmfjN14wdPw61Ws2FCxcYOeJLcj9UUd+ulF7bv8JOUH9oe7777jvdTCQ8PJwRw75g05bNqDUa6taszYLFCylcOGM7d98nCQkJTP52Eiv/XEFCUiJNmzRh5uxZ5MuX75X1z549S8uGTfnSsbku4sHd+GBWRZ8k6HEIZmZm6dqcPn2aVo2bM9ihIXlM7NFILfuirvAkt4bzVy6+dmzJycns3LkTX19fSpUqRaNGjV6bUVPh4yczXINL2FrJzTXLZahukV3H/801uBmpbr8GwB9Syu+FEIMBpJSL0+qMAfqSOrtYJqWc96ZrCiGsgLZAcSAO2C2lfOuXpCImHylRUVE8ffoUd3f3dOFBgoKCKFaoKCOdW+BkbANAZEocM0O2ULF6FS5cuKALVVLAPDdfubbUiYZGapj+ZBs7D+2hQoX0v7MajQatVvvGsCEfmmaNmhJ66QFNLctgZmDMqZjbXFUFc/32TT0Hg+joaAIDA5kwdjyce0ITe/3/0D+F7MSjclHy58+PgYEBhoaGup/7d++l0DNr6r0gxFqpZcqjzRw4eZjSpUunG1dwcDC1q9XEOB7chC2+mlDs3Z05dOzIJ+9a/qmSWWKyqUb5DNUt+vex97lpsSpwK6PhUv6N7LFGkYNITExk2KAhbNi4EUtjM1LQMm3G9wweMlhXZ9u2bZSyzKcTEgBbIwvKm3ly+fJlunTpQoMGDahatSqN6zVkfcRpaloUIVmr5kC8D+WqVHilkAAYGBh8kB3nWq2Wu3fvYmZm9toZBqQ6FFzwPsc3Lu10ATib25XnydMomjVthq2dLQEBAQQGBuoE1VAY0CbXy04vYCgFly9f5saNG2g0GjQaDWq1Go1Gg0xUU9VZf6+XSqgwSoYKFSrg5eWFl5cXBQoU0P2cM/NHCifmonmaaEkpWRN0im8m/o+ff5mfWY9KIZshpUDzkYVTEUJMJXXZ7EvgjRu9M4oiJu8ZKSXPnj3D3NwcCwuLdOc/HzyUq7tP822eDlgYmBKcFMbk8f8jMSkRlUrF8ePH2bdvH4VF+lhRhoZGjPh8BJMmTdKVnfA+xZRJ3/HXlq2YGBvTc0Qfxowdk6X3+LYcPnyYfr36kBgTT5I6hcJFCrNm4zq92GYajYYbN27w888/42ZgpxfJGaCwUW52XrlIwWKFKViwIPXq1SNv3rzkzZuXoKAgFkybQ3VtUYxVqb/yoclRBGsj8b8X8MqIB7N++IEts5dTmuehYMJSYoggnmHDhhEYGMj9+/c5cuQIcXFxAKgQ/OjVR1dfCEEDyxIsXrvutWKiVqv5+++/dRtnW7dujYmJyX9+lgofJx9h1OBTQC1ebZj/TyjLXO+Ro0ePMmzgEAICA9BKSasWLVm0bIluaeaf1L7f5OmApcHzhFcXY+7z1+PjJMkUPDw8KFeuHPt27WFsnjbkMk5dPolSx/Hjk52cPHc6W+3pCAgIoHTxUnSzqUYx87xokRyLvs4loxAWLl3E2bNnOX36NN7e3sTExABgY2jBNM/uqF7wPFsXeZomw7sw8euJ6a6h1Wrp2bU7J/YfoZyhB4kihXPxvvzw048MGDjgleOKioqicrmK2McYUc7Yg0h1HIcSbjDq67GMfkGMpZQ8efKEmzdv0rhRY3707IWx6vkS4dPkKKb7b6JqrerUrl2b2rVrU6VKFczNzQkPD6dujdokhkbjKXIRIqKINVVz/PRJJcrwR0JmLHMVt7GW66qknxm/ilL7D2bbtL2KmGQSUkouX75MUFAQ5cuXx9XVVe/83bt3qVy+Ip2sq1DSwoNEbTI7oy9iWMSe+YsWcvbsWQ4cOMDfm7YzM79+et7gpDCWx57gzKVzuh38ixctZvzosZS18EQlBZfiHzJu4jjGv+Jl+jEz6dtvObVkJ+1s9f+zTXm4jicpUahUKkqWLEm1atWoVq0aVatWpVfXHhg+jKOZdVlMVUacib7LoeSb3LhzM50b8z9IKTl48CA7t+/A0tKSHr16/qvoRkZGsmD+Avbt3E0ux1wMGfE5jRs3fm39pg0aY+oTTUPb0rprrg8/TWweQ1TGBly+fFlnj6pUqRIJsfFYBCbT2aG6zqa1O+IihhVzs+3vl510FD4EmSIm1tZyTZUqGapb5sABRUyyC1khJqGhobRo3IygB/7kNnPgXnQQffr25edf5uteEiM+H869jWdoYfvcEKeRWsY/WEm8JglIjf+lTkhmRJ4WuJk8DzuyL/IK1vUK6EUzBnj48CGbN29Go9HQpk2bj8rzyt/fn2VLfyPAz59qtWrQs2fPdDvk/f396dapK25+Kmrb6gdH+PPpYep+1oZvvvkmXXThyMhIvvx8OOs3bkCt0VCjclUWLPmVEiXeFGAh63n48CG1qtXAUWNBbq01D0UYwt6M46dP4ODgQFRUFKdOneLYsWMcO3aMS+cu8D+PTuQyem6cT9AkM9F/NXEJ8dnG7fpTJjPEpJi1jVxTOWNiUvbg/vdpgL8kpXyjm1lG6ujqKmLyZhITE/l14a9sXrsBIyMjeg/sR+/evfXcPZs2aIz22jNa2lZAJQTxmiQWhx2g55cD8PT05MqVK6xd8RfNTUpTzko/x8nPj/+mef+ODBw4kEKFCvHH73/wv9HjaWZehtwmdvgkBHAq8R6nz535qMTiTRw9epS2LdtQ3swTJ2HFLe1jkmxVnDx7mocPH7Jjxw62b9/O1atXAchv7sJI1+e505O0KUx9tIkzF8+98Z7/MZp/TClx4+Pj2bhxI/fu3aN06dK0adPmtZ5xDjZ2jHBomk5Mxj5YwdhxY+nQoQPlypXTPZfY2Fhm//gjG9dswMjIkB59ezN8xPCP6v4/NTJLTP6qVDVDdcsd2vc+xSQBSL9B7YUqgI2U8sPmM/lYeVFMtFotBw8e5Pr16xQsWJCmTZvqfQ2q1Wrq1qxN7L1QqpkWJEWr4WjiLao0qcXKNauB1FlJfncPpuXtpjPuAlyPDeDPRwdJlCmYmZmRy94B1zhLejo99xBK0CTzXcgGbt69rbdGvnv3bmbPmEVQYBBVqlXh60nfZBshkVJS0KMADdWFKWmZT1e26ukxbmseERUTjUqlonr16rRu3ZrGjRvTo0t3TB4nU82sIInaZA4l3KRmy/qffJj6wZ8N5PZ2bzraVdUJxq7wC1whkNCIMDQaDe7u7rRrl5rXZdzIMRAYSy3zIqillsMJN8hXsSg7du98bbRrhXcjs8RkZYXqGapb8cie9ykmr3ebfI5GShn079VysDdXVFQUDerUIyzgCfkNHAnSRjDOzpTDJ47qcoLv2rWLJ3cDGe7QVGfsLWbhxuStG2jVqhWPHz/mxo0byBQNRi95F1kZmpHL0ZH9Rw9SqFAhwsPDKV28FDsjLlDJwotodTx74q/StWu3dMbWZs2a0axZs/fyHDKbhw8fEhkeQYnc+tGZa1oV5V7EE/7880+aN2+Oo6Oj7vzx0yeY+9NPbNuwBXMLc8YM/Ib+/ft/iOG/V6bPmkntU7VY8HQfHjgQoko1wJ89fQEzMzN27tzJ1q1bWbRoEfPmzcPVxIEJ7u11wpHfzJkZp7dx7tw5KlfOmIFX4f0jP9Ic8C+GUMkMcqyYTBw3AdOgJEY5NNf959wecZ5+vfoyYtSX3L9/nz+W/U4xVR49ryFjlRGFjFw4fvw4lSpVon///qxbtYbb8cEUtXguCufi79OxWyeKFi0KgKOjI94XzjL5f9+ybO8+bKxtGDp6FJ9/8fn7vfF34PLly/w4/Qdu3bhJydKlGPv1eJ2dQkrJ2bNn+e2334iJj0UttXoCG69NIn9+T/r06ZOuX2trayZNnsykyZPf0518HNjb23PZ5wq7du3Cx8eHggUL0rZtW51rcN++fenbty8xMTF079Yd4f1EbwZiKAwoaurK2bNnFTH5qBFvE+gx25JjxWT9uvUMt2us95+zoXUpxh1YwZ4DewEwNjLG2NwzXdsEEy2/L/6d9u3bA9C8eXO6duhM1ZSCOKtsuKkJIdQ0nvVfT9Br5+7uzh8rl2fdTWUhx44do22L1tQzL059k/z4Hval5q7qLPptCTdu3GDNmjU8ePAAExMTHOwdOBh1lSa2ZRFCkKRN4WD8Db7634R/v1AOw9DQkDZt2tCmTZvX1rGysqJ+g/qsP/dbunOhMiad56DCx8fHODPJbHJs0CCtVqM344DUHc4qlYrDhw8TEhLCQ7+H3NY85kZcAFJKtFJyOvoOYSKeFi1a6No1btyY0+e98epYlfCy5nQc259LPlde66aaHRk1/CvaWlWknm1J8pu50NC2NC0sytGnWy+mT59OgQIF+PPPP3ny5AnnLl/ggW0Ms8N2sSr6BFNCNlG9RV0GDhz4oW8j29KjRw/uJoVwLvoeWinRSA1Ho64TbZhEy5YtP/TwFP6FTAr0mKmkpe3INHLszKR169Yc3XeNdnbPlweORd+gcYNG1K1bV1e2dec2enXtwfanF0nWqHF0ceLA1oPpdikXKVIkW4fMSEpKIikp6ZUxpLRaLZd8rtDb6zO98rJWnqx/dpLgoGCdnQnAxsYGn9s3OHHiBEFBQVSqVImCBQtm+T28jFarZe/evRzcdwAHRwd69uqll2nzdVy6dImZU6dzw+c6xUoUZ/w3EylfPmOxlbIKBwcH9h06QJ/uvdgRdAGNVkuxosU4tO6I4s31kSMlaLQf5Xf7OSBjESgzQI715goNDaVmleoYx2jxlA4Eq6IINYjl+OmTeHrqL21ptVquX7+OsbExhQsX/qQ8Z2JjYxk+9HPWb9iAVqulSMFCLFjyKzVq1CAlJYV9+/axatUqtm7czIR8HXA2ttW1DUh8yl9J3gQ+/vjCsqekpNCmeStuXrhGKQM3YkQSl+IfsnrdX3qzypc5fvw4bZq3pL55CQqYuvAg8QkH433YumuHLuvkh0RKSWBgIIaGhuTJk+dDD+eTJzO8uYpY2smlpetkqG7t09vepzfXZSll2czqL8fOTJycnLh26zqbN2/m6pWrtC1ahE6dOr0yXpZKpaJUqVKv6CX707FNe6KvBvGta0csDEy4HPGQ5o2b0rp9W/bu3cvTp09xcHCgbPlybLh/hr4OdbE0MCVaHc+2mAt8MXbEh76FV7J69WoeXLzFyFzNdHG8ypt60rdnb4Ieh7wy/pWUkrFfjqKNZUUqWHsB4G7qiKXKlHFfjcb70vnXXk9Kyf79+9m8fhPGJkZ079WTqlUztrfgbRBCZGh2pfDxIAH5yiSJHxxHIcTI152UUv70Np29du4lhNgthPB4m86yGyYmJnTr1o0fZv1A3759XykknzJ37tzhnPdZOttVw8rQDJVQUd6qAJVM8rN+zTrq1KnD9u3bCQkJ4dSZ09Tv3IKpIZuYHbaL6Y+20KJXe0aPHf1exrpt2zbKlyyLjaU1VcpVYu/eva+tm5yczJ9LfqeqsZdeQEhPM2cMEyRubm64uLjg4OCAtbU1ZmZmGBkZoVKpOHf5AqUtPfT6K23pybkrF5k/fz4HDx4kJCSEF2f0Ukr69+nHgC69ebbzOoGbL9KmcQumTP4u05+DQvbkY7SZkJoTxZLUXPGvOt6KN81MlgP7hRArgFlSypS3HqrCB+Xu3bv8umAhfr4PqVa7OgMGDsTOzk53/vz58zgZ2WD40h4ZT1MXRMlcbNiwQa/8l8ULmTpjGv7+/nh6emJjY8P7YP26dQwfOIx2VhXp7FKKe48f0aNjV1asW02DBg3w8fHh4sWLXLp0iYsXL+Lj44NI0ZLPKf1GMamCKlWq4OrqipGREYaGhhgZGemOebPnEpoShesL4WxCUyIxFoaMGPF8FmZjY0OxYsUoWrQopqam/L15B+Nyt8E0LchjVXVhZv44h569e6VbNlXIeXykrsGPpJRTMquz14qJlHKDEOJv4FvgghBiFS/kBX7bKZDC++XgwYN0bNuequYFcVHZsvXCCn5dsJC/9+3h5MmTrFu3jqNHj2IsDEnMlYyp6rkR957mCTVqvNquYGdnpydI74Nvxv+PrjbVKGSe6gJb1io/KqGie8euxKUkoFarAbC1taV8+fKMGDECjUbDxmV/UcbSEzOD1CWtKzEPMLG1YNu2ba/N2WJqbMLy2YvpbVcLG0MLotTxbI4+x7ffTab/gP7cvHlT79i1axdPQ0NpYl9OJyQA1obmlLBwZ+/evQwZMiSLn5DCx80HmXVkhEwd1L/ZTFJITeNoQuq0562TzCu8f6SUDO4/kG421Slukbq+XgEv1oeepGyp0qRoNRQuXJjJkydz46oPy44dprlFWWwMzTkXe5+bmhDWfiSbKVNSUrjv/4CCBevrlRc2dyXucTxjxo2lXLlylC9fHg8PD51zhJSSpPhEvl+1mhIW+YiWCYSoI/h73543Jv8aO34c4eHhzFi0GFsTSyKTYhk0eDDjJ45HpVLh7Oys5+0HMG7sWC7+sT9dX2FxUcyZM4fY2Fjatm2Ll5eX3vno6GhWrlzJ1YuXKVayBH369nnvQq2Q9XzE3lz1/71KxnmtN5cQognwE6kJ66dIKeMz88IfiuyStvdNJCYmsnz5cnZv24mdvT0Dhg6iRo0auvOBgYGULlKCqa5d9DzPAhOfsSzqCAePHaZUqVIIIdBoNPw05yeW/LKIyOgoGjVsyNSZ31OgQIEsvYejR4+y4vc/SYhPoH2XjrRr1073kpdS4uPjw7p161i3bh3BfoF8mbcV+Uyfh2C5Gx/MfpO73Lx/543XuX37NkeOHMHe3p6WLVumi1z8OmJiYggICMDd3T1d1OKXuXfvHpXKVuALxya4GKeKgW/CYxY/2UfBooV1AS1LlSpFu3btaNu2LTY2NtSoUo08Gms8hAOBRPJA85Tjp09QqFChDI1RIevJDG+uQhb2cn7xRhmq2/T8+k8vBL0Q4gQwWEp54/0OKWvJ7mKSmJhInRq1SPALp7yRBzHaBI4l3Obr776hRauWbNu2jY0bN3Lx3AVmFeiNyQtLL7fiAjltF8xFnysf7gaASd98y9L5i6huUggTYcjZlAeUqlGeGT/+wIYNG1i3bh03b97EwMCABg0a4JTLkaO7DtDDtiZuJg74JYTyV9RJZv4yh549e37Qe/mHP//8k+HDvqCQtRsaqcE//inrNq2ncePG+Pn5sW3bNrZs2cLJkyeRUmJraUNVkwK0cKio6+NwpA+xxS3Yezj9LEfhw5AZYlLQwl7OL/b6PDgv0uzCuk9PTD5VsoOYxMfHExoaSu7cudO5sC5dupRfJv7AIPsGullHWEoM0/w3kKxNtR2ULl2a5LhE8kSa0cauEiohSNAksTj8IKOmf83gwYPTXfN94e/vT6miJZiYux1WhmYApGg1TA/cRGhSJAC1atWiS5cutG/fHicnJ6SULPh5PjOmTSc8KhInh1x8O2Xya7MkfijCw8M5cOAARkZGNG7c+JXegU+ePGH79u18MfRzvsvXBWvD5zOlZG0Kox+sICk56Y1LcQrvj8wREwc5r2jGxKTFxbXZVkxy7D6TjxGNRsPEceNZvHgJpgZGqNEyfuIERo8d8zwY5cYtlDPy0Fu+cjCyws3MkfrdWjBhwgQ8PT15+vQprZq24Pt7W8hj5sD96GB69Oz5wUOaHDx4kOJW+XRCAmCkMqCaVWHCyhmyZsO6dFGUhRAM/3IEX4wYTnx8PObm5h/lxlF7e3s6d+78xjrOzs4MHDiQiWMnkKhN4cV4A0laNQKBt7c31apV+yjvUeG/8TEa4IUQMaRug0l3CpBSyvThMN6AIiYfEVO/m8KOPzcy1qkVdkaWPEmO5JcZc3n67BmGRobs37+fa5eu0MxB/8NFSonGBPr06aNzQ3V0dOT0eW+uXLlCYGAgZcuWJW/evB/itnTExcXh7e1NaGw42Oqfi1elULNOvTfmPhdCfDJ7gXr07MHetfvpYV8TlVAhpWRnxHmMDQ2pUaMG5cuX54svvqBz586YmpoipWTPnj2s+mMFarWajt060759e2UGkw2QfJyeS1LKt95L8iaUZa73RHJyMt9Nmszvvy0jNi6OenXq8uO8ObqkV1qtFkc7Bz63b6wXsuRufAiLg/eiMZBUrVqVIkWKsPmvDQx3aoqjsQ1SSk5F3+a8aRB3HtzTywD5PklISGDFihXs27mHXE6ODBw6iIoVU+0BwcHB/PLLLyxZsoSIiAhMDI3p51SfEpapnmYhSeEsfLYX74vns00SsHclLi6OFo2bcef6LQqYueCf+JTc+d3YtG0Lf//9NwsWLODmzZvkypWLgQMHEvroCXu37KK6SUEMhQHeyb6Uq1OZ9Zs3KjOYLCQzlrm8zB3kj4Uzlp+o3ZXVH2SZSwhhBxQETP8pk1Ief5s+lJlJJhIcHIxKpSJ37tzpzvXs2p07xy4zwLIuVrameF+8S42q1fE+f5bAwEAOHz5MVEw0Ts76GwHzmNhhaGJE6JNHuiCMpUuVZuK48bhbOhOdEoeJjQW79u7+YEISFxdH7Wo1UYfEUMYwL8+0oTTd1IghX36Or68vGzduRKvV0qZNG7766iuEELRv3ZbDyTcxVhnhH/eEhYsWvnch0Wq1rF+/nrUr/wKge5+edOzY8b08RwsLCw6fOMq5c+e4fv06hQsXpnr16gghGDx4MIMGDeLIkSPMnz+fGTNmYCIMmerZHfO0PTMVtV7MPrKLo0ePpnNVVvj4+EjDqQAghPgMGAG4AVeAKsAZoN7b9KOISSZw9epV+nTrxYOHD5BIihctzoq1q3Qunr6+vhzYt59JuTtilJbat4FdaZ6ERlGkUGHUWg0Alibm6ZJsXY8NoGL5CnrRfId9PowePXtw5swZbGxsqFy58gcTEoBly5ahDYllgF093VdySXN3Znw/A1MLM7744gu++OILvZ3ggY+COXr0aKp3Wp06/+p+m9lIKenRpRvnDp6iuklqROOJQ0axa9sOVq39672MQQhB5cqVX5nYSghBvXr1qFevHpMnT+bA/A06IQEwUhlS2jAve/fsVcTkI0d+/MmxRgAVAW8pZV0hRBHgrWMBKWLyL6SkpLBlyxYO7t2Po7MTffv30wunHhkZScO69WlsUpL+bpWRSE4E36ZerTocPXlclzjKSWWtE5J/KGLmSriDhjnz51K1alWOHj3KgF79aK4pSz4TR+4mhLA/3odds3anG5eNjQ1NmjTJ8vvPCLu37aT8S04BLsZ25LVyYsGa32jevHm6NkZGRjRs2DBTrn/mzBnmzppDgJ8/VWpUY9TY0f9qH/L29ubIvkOMc2qNcdq/S1mtJzN3b+fcuXNUqlTpje0DAgKYM2s2Z0+dIV9+D0aOHZ1l2Q4LFCjALqP0q+4RKbHc971PcnKyEob+I0f7cVsTEqWUiUIIhBAmUsrbQoi3Xib4KLdlvk98fX3Zvn07t27dSncuMTGRerXqMGnYOKL+vsPFP/dTqWwFtm7dqquzbt06PA2dqGpdGJVQYSAMqGNTHONoLQULFqRNmzZs3LiRwIRnqKVGr/8ATRit27WlWbNm2NnZ0bZtWzbu2EJIYcFqtTeJFezYf+Qg1apVy/Ln8F+JiYnh6bNnxKgT9MqllCQKdZaHSd+0aRMtGjWD04+p8iw3N9efoEKZ8jx8+FCvnlarJTAwkGPHjvHnn38yYcIEShi66oQEUlMyFzdwZfz48fz5558cP36coKAgtFr9F7mvry8VypTn9sZTVHmWG3nyEc0aNGHLli1Zco+tW7fmYeITbsUF6sr8E59yMdaXLVu2kD9/fubOnUtcXBwAT58+Zcp339GiUVNGfD6cu3fvZsm4FDKORGTo+EAECSFsgW3AASHEdiDkbTvJsQb45ORkenfryd49e8lvnRv/2CdUrFKJTdu26DyGFi5cyJJJcxloX1+XldEvIZSl4Qf54qsR3LlzhyOHj1AZD5o56CdP2vjsFHa1CzJmzBhKly5Np3YdeHrhIa2sy2NpYMa56LvsTfThyvWrH9zL6k1cvXqVebN/4sE9XypVr8KXI7/C1dWVZ8+eMX/+fBYsWEBkZCS2xpaMdm2NnZElUkqORd/khvUzrt+5mWUGYo1Gg4erOx2NK+Bl9txOtSv8AuH5VJSvXJEHDx7w4MED/Pz8SE5O1tURQlDa0pMBufVnR0tC9uET568XFdjY2BhPT0/y589P/vz5OXfmLI4B0Nz++b/5vfgQNmsu4xfknyVLjsePH6djuw7YCDOMhAGPEsP5fcWfWFhYMGPGDI4ePYqDgwO9evVi7aq/KCicKWToQogmnDPx99j2keRjyW5khgE+v1kuOc0rY9kwu19f/kH3mQghagM2wF4pZfK/1X+RHLvMNW3KVG4ducikPB0xVhmisdKw5sopvvpiBOP/N5H79+/z67xfqG6cXy+9r4eZE8bJgmnTplGgQAE883vic8ufJrKcrp5Garmvfcqar37V5bTYsGUTY0aOZubKlSQkJVCjcjUOLjz0UQvJ3r176dqhM3UsilHCyI7Lqw5R5o/ltGzbivXr1xMfH0/btm2ZMGECRw4dZtqUqeS3zkNEcgxmdlbs2r07Sz2NgoKCiI+Nw8tV3+GhnEV+Zl/axu37dylQoAClSpWiTZs2OjHInz8/5ubmFCtUhNvxQRQxT7VR3YoLIoBwHj16RGxsrE6IXjxOnz5NYnQ8Y93b6l3Tyyw3sSHHCAkJeaN783+lVq1aBD0K5sSJE6jVamrWrImZWepenUaNGnHmzBlmzJjBgnnzqWtbkjaOqUtu5chPXkMHhg0Ygs+dG4rn1wdC+xEb4F9ESnnsv7bNsTMTV6fc9DGvoRdqPEodxzcP1qBJ8wo3EYZ0cqpBFZvny4dSSqY93sKWfTuoWrUqarWaGlWqofWLppZ5EbRScjjhJs6lPNh7aH+6/7xSSrRa7Ue/P0BKSSFPLxqri1DM4rng7Xx2nsOR1+jcvSvjxo2jePHiunNhYWGcOXMGBwcHqlSpkmUvLq1Wy4kTJ1iyZAkb121gRv6eesZpn1g/LuQK5fzVS2/s5/Dhw3Tt2AUrYYIE4khm3ab11KlT543typUoQ5WI3JSwzKcri9MkMvHBarp078qAAQOoWbPmB3lxO9s7MsSmAU7Gz70CtVIyIXA1DwP9yZUr13sfU3YmM2Ymnma55JQCrTNUt9eNP95npsWTUsoar9i8+J82LeZYm0lMXCxWBmZ6ZRYGpkiRGrLk+PHj/LpsCceSbhOvSdLV8Y65i3UuW6pUqQKAoaEhB48eptnQzuw2vs0B83t0HtmPHXt2vfJlIoT46IUEIDQ0lNDQUIqa639lV7YuhIOdPStXrtQTEkjNU96iRQuqVq36n16kKSkprFixgjbNW9G9czcOHjyod97Pz48pU6bg5eVFnTp12LVrFwU887M5wptkbWq6nYiUWP6Ou8pX4/49aVe9evUIehzMn1vXsGLbWgIfBf2rkAB8NW4Uu+OvEpESC6SGQdkccZb8+fOzbds2ateujZeXF1OnTiUgIECv7YEDB+jWqSttm7di5cqVpKRkbpoge3t7otX6MVkTtckkpSRz8+bNdPUTExMJCQnRhfFXyApSvbkycrxPpJT/RIddJKW0fuGwAha/bX85dmbStkVrOBdKQ7vSunOno27jny+ZE2dPA6lf52NGjmbZ0t8oZuVOhCaOGINk9h3an+5Fmh0JDw/n8uXL5MmTh6JFi+rKpZRs376dTu078r1ndywMdPuYuB0XxDErf67e8snUsajVapo1bELQtftUNM5PgjaFk4l36Dv0M4oUK8ry5cs5fPgwkCoCffv2pW3btkgp6dm1O0cOH8HR3JYn8RGMGTuW/337vyybGUgpmTL5O+bMnoOzuR2hcRE0aNiAFX+tQgjBli1b+PPPPzly5IjOxbdv375cv+bDisV/UNO0MKYqI84lPyBfmUL8vf/NYfHfhp/n/cyiqT8xwK4+ZgbGaKSW9c9OcjnOj/jkBOrVq8e4ceOoV68e30z8ml9/XYQBKgyNDZn03WSGfSSpBz4WMmdm4ign5c/YzKTvzd/fu81ECHFJSlnupbJrUsq3ylWeY8Xk3r17VK9cjWKGeShg6EiAJpyLiQ85eOQQ5crpPVf8/Pw4fvw4uXLlomHDhhgZGb2m9+yBlJLJ305i7pyfcLdyJjQhgsLFirJ+y0YOHTrEjz/+iI+PD9bmVhQxyUM3hxoYqQyJUSfwW8Qhxkz/H4MyOVjkpk2bmDhoJF84NMFApE6YY9QJfPtwDclSTf78+enTpw+9evUiX7586doHBwcTHBxMkSJF9PbkZCXR0dHcunULNzc3XF1d05338/NjxYoVrFixgocPH2IsDJni2U0Xl0wjtfwctofZvy+gTZs2mTImjUbD0IGDWbt2Lfmt8xAc94xSZUuzYs0q1q9fz08//URISAh5nHNjkaCip0NtHIysCE4KY0XEcX5cPI+uXbtmylg+BTJDTDzMHOW3nm0yVLf/rWXvc5lrCDAUKADcf+GUFXBaStn9rfrLqWIC8PjxYxYvWsTlc5coWrI4Qz8firu7+wceYdazYcMGxgwcwWCHBtgYWqCRWraFn+V8nC8xiXEUL16cMWPG0LJlS/r06MWJYyfIbeFAUGwog4YMYdbsWZn+1d+/d19i9tyjjl0JvfKlT/bT4vNuTJky5YNuzHwXtFotX3/9NXsXbWSAcwO9c4cjrmHfojhL//gtU68ZGBiIj48P+fLl05tFJyUlsXLlSj4fMoyJedvj+IJt5UZcAKesg7hy81qmjiU7k1li8rVH23+vCAy8/dv7FBMbwA6YAYx/4VSMlDL8bfvLsd5cAC4uLkz+7q03emZ7fp33Cw3NS2JjmOoCbSBUtLSryKnIW6xatYru3bvrxGLH7l34+fkREBBA8eLFcXBweFPX/xmNVkuUJi5debJxas727CokACqViipVqrDz9w3pzkVq4rF5af9RZpA3b95XegqamJjQsWNHRnw+nFxG+jM4VxMHAoO9M30sOR0pMy8HfFrSwp8BA2CZlHLma+pVBLyBzlLKTa8el4wCooBMmYpm2f9QIUReIcQRIcQtIcQNIcSItHJ7IcQBIcS9tJ92L7SZIIS4L4S4I4Ro/EJ5eSGET9q5+SLtTSeEMBFCrE8rPyuE8Miq+8lOpKSksG3bNubOncvx48f19kxotVqCAgOxNdTPOGisMsTBMjWH+suzDg8PD2rVqpUlQhISEkK/fv1YsXolxyJvEJL0/IPoYowvETKeRo0ylqXuXYmKimLJkiVMnDCBbdu2ZapRukmTJjzTxnAp5oGuLDgpjJORN/lzxXI+++wzQkLeep/Yf8LGxganXI74Jj7WK78ZF0j5smXfyxhyGjKDx5sQQhgAC4GmQDGgqxCi2Gvq/QDs+5f+Tqb9jBFCRL9wxAghot/m/iBrZyZqYJSU8pIQwgq4KIQ4APQBDkkpZwohxpM6vRqX9lC6AMWBPMBBIUQhKaUGWAQMJFVpdwNNgD1AfyBCSuklhOhC6gN8c0KJTxx/f3/q1ayDSQLkUdkyN3kWBYoXYuXa1axbt47FixfjHxSAt40Z+c1cdO0eJjxBayT0QsVkFpGRkWg0Gj0xio2N5ccff2T27Nmo1WpGjx5Ngfz5GTdmHG7mjiRoklCbwO79e95LqBAfHx/q16mHp0EuHLWWbP5tDd/nncrh40czJW6YiYkJf+/bQ5sWrTjy7CamBiYEJzxj/qJfuHPnDgsWLGDt2rWMHTuW0aNH64XaDwsLw8DAAFtb23ceB6R6FE6fNYMvhwynpboc7ia5uJ0Qwr64q+yeuTdTrqGgTybNTCoB96WUDwCEEOuA1sDLbnpfAJtJjbf1Wv7x5sqsUPRZJiZSykfAo7Q/xwghbgGupN58nbRqK4CjwLi08nVSyiTgoRDiPlBJCOEHWEspzwAIIVYCbUgVk9bA5LS+NgG/CCGEzGmGoBf4rHc/SiQ509i+DABaqeW3awco4JmfFI2aWrVqMXbsWKZP+Z41EScpbuTGU3UUx+JvsfiP3zA0zLxfCX9/f/r36ssZ7zMIIShRrDhL/lzG+fPn+eabb3j8+DGdO3dm+vTp5M+fH4AePXty6tQpzM3NqVat2lt5OV28eJFf5/9CSGAwdRrVY9DgwRl+Affv2ZeGRsWpblMESHVSWBV4nB9mzGTa9O/f+t5fRfny5fELCuD06dMkJCRQvXp1nWgMHTqUCRMmMHnyZJYsWcK0adMoW7Ysg/sN4Matm0gk1apU4/eVf2aKXa9b9+7Y2dsz47vv2e93nNKlS7N36v5/jUmm8Pa8ZT6TXEKIF3NkLJVSLk37sysQ+MK5IEAvIJwQwhVoS2rE3zeKSWbzXgzwactPx4ESQICU0vaFcxFSSjshxC+kRq1cnVb+O6mC4QfMlFI2SCuvCYyTUrYQQlwHmkgpg9LO+QKVpZTPXrr+QFJnNri7u5f39/fPytvNcu7du0dQUBClSpXS+9qPiooij7ML3+ftrhdzKiDxKcsiDnPszEmdMTYsLIxfF/7K8YNHyOvhzrARX1C+fPl01/qvpKSkUKRAIUomuVDXujgqIfCOvsuWMG8S1clUq1aNOXPm6PbrvCvr1q5l2MCh1DYvgoOBFdfVQTwzT8L74rlXLs8lJycTHBxMYGAg169fZ8yXo5jp0VPnSQbgnxjKVnGVu36+mTLGjHD69GlGjRqFt7c3pobGtHOoQhXrwmiklsPR17ll9pRb9+9kqugrvJ7MMMC7mzrJMe7tM1R3+L3Fr72eEKIj0FhK+Vna33sClaSUX7xQZyMwR0rpLYRYDux6nc3khTYmQHvAgxcmGFLKKRkadBpZ/hsphLAkdcr1pZQy+g1eQK86Id9Q/qY2+gWpyr4UUr25/m3MHysRERF0bNOeK5cu42xuT0DME4YPH860Gd8THR3NqlWrSElRY/DSMzYQKiwtrfS8ehwcHPjm22/g22+yZKx///03JgnQyP75Pp7qNkW5HhdApS4NWLp0aaZ5hCUnJzN82HAG2NfD3dQRgLLk56+wEwwaMJCq1asRGBiodzx58kTPlmQkDJAv/epopJag4GDatGlDw4YNadSoEV5eXq8dd1JSEmfOnMHAwICqVav+pxd+tWrVOH36NP369ePK5uNUt0nd/2MgVDSxLcPd8L3s3buXFi1avHXfCh8GCWgyZ5krCHjRq8KN9AEZKwDr0n5HcwHNhBBqKeW2N/S7nVRD/EUg6Q313kiWiokQwohUIflLSvlPSNUnQojcUspHQojcQGha+eseVFDan18uf7FNkBDCkNQAZW/t0pZd6NezD5pbYUzK3QEDYUC0ZTwLFy5j/6ED+Pj4kJSUhLWpBaeiblPLNlU4pJQci7tFu24Z+zLKLPz9/XFR2aQr9zB1wsbKOlNdi2/duoUphjoh+YeKZgVYsn0Xm7emBu/8x8OpZMmSuj//c/Tv1ZfjgTepZ1MSSBWSAzE+lChbimvXrrF9+/bU8Xt46ISlXr162NvbA7B79256d++JvaEVGqkhXpXCxq2bqV69+lvfjxACWysbPEwc053LrbJNFxFZ4eMnk0LQnwcKCiE8gWBSbczdXqwgpdQlDXphZrLtX/p1k1K+cz6LLBOTNI+r34FbUsqfXji1A+gNzEz7uf2F8jVCiJ9INcAXBM5JKTVp3gVVgLNAL2DBS32dAToAh7OzvcTf35/Fvy7G985dKlWvQv/PPsPOLtXZLTw8nAOHDjLFrQsGItWOYG1oTnPrcvx17QSDhwymW7duWFhYUK9WXR5GPMNZa8V98RQjR0u+/W7Se70XIyMjrkT40tamkm7pSErJfZ7SvUrm5v3w8/MjLCYCdS4NhuK5jSVKHUe5cuXYtX83tra2bxSwlWtXU69WHe5GPMEJK+6kPKJwqWLs2rcbU1NTfH192b9/P/v372f9+vX89ttvqFQqKlSoQJUqVfhj6e8Mcmygc2q4HhtAq2Yt8AsK+E8G/EpVK3Ng7Q4aSKkbt0ZquRJxn64mJv/SWuFjIzNeSlJKtRDic1K9tAyAP6SUN4QQg9POv3UIlDROCyFKSinfKaxFltlMhBA1gBOAD8/tTxNJFYQNgDsQAHT8Z4OMEOJroB+pnmBfSin3pJVXAJYDZqTaUb6QUkohhCmwCihL6oykyz+eDq/jQ+WA/ze8vb1p1qgp5c08yaOy5Z7mCYEGkXhfOEdCQgKrVq1i7ozZzPTsqdcuMPEZm8VlvXX96Oho1qxZwwNfXypWqkSbNm3e2679qKgoJkyYwKJFi7AysyC/iTONrEpjqDLgeNwtYhwF569czBQPrePHjzNt2jQOHDiAuZEpNa2L0cK+PCqhIlIdx6KwA8z/cxFt22Zsw1hSUhI7duwgICCAihUrvjZYo1qt5ty5c+zfv58DBw5w5swZKlp50dtFP8vpH5FHGf7jRHr16vXW95acnEz50uWwfQa1LIqSotWwL+YqD5OeEJMQx7Bhw5g+ffp72+2fU8kMm4mbiZMc4dYxQ3XHPvj1Q4RTuUnqx/sDUpe5/gn0qIRTeRMfSkwSExPZvHkzt27donjx4rRr1w6TF74wy5UoTZkwRypYe+nKtj47y2WNP2FREQCYGZkwyLkRBc2fJ5zaFnGOgu2qsHDxr+/tXqSUnDx5kpMnT+Li4kKHDh2wsrJi+/btDBs2jEePHvHll18yceJEFsyfz5oVq0lJUdO+cwf+9+037+TiKqXk4MGDTJ06lRMnTuDk5MTo0aNp06YNPTp3w9/3IY6mtvjFPGb0mDFMeg8zsq++/Iq7q0/Q3EH/HbAh4jRtv+7PiBEj/lO/ERERTJ08ha2btmBkZEiPvr0YOmwY06ZNY/78+eTJk4dFixbRsmVLoqOj2bRpE0+ePKFmzZq6fPIK70ZmickXGRST8R9GTNxJE5AXy6WUAa9u8Zp+FDHJeoKDg6lVtQaWiQa4aW0JFJEkWEhOeJ/CxcWFkJAQvDzyM8ujF6oXvIlCk6OYHbKdGbN/oFmzZly/fp2+3XtTx6Iozoa23EoJ5p54yrlLF14ZGyorSElJoUPrdlw8fY5iRq5EqOJ5kBhK2YrlOHToEKVKlWLZsmVUrPjfvBKTk5P5/fff2fTXeoyMjen1WR+6dOmCEIJdu3Yxbdo0zp07h6urK+PGjeOzzz7T5fUAuHbtGo8fP6Z8+fJZtlv/ZQ4dOkTfDt0ZlaslRqrUZbZEbTL/e7CGAZ8P4scff8z0vTJnz57ls88+4/r16zRo0ICL5y7gZeqCrdaMGylBVKpRlY3bNiteX+9IZoiJq4mTHObaKUN1v3648H2GU3k59LzuFP8hBL0iJpnA3bt3mTXjB65cvEyhIoUZPX6MXrDIjm07EHfKnxZ2z11vt4Wd44lzCjYOdpw9exZNspofCvTC7IW8HA8SHrPT4Dp3Hj6PwXb58mUWzP0Zvwd+1KhTk8+Hf4GTk1Om3s+b+PXXX1n4zY8Mcmigs09ciL7PmtDjfDt1MmPGjPnPS2oajYbG9Rvy+Lof1YwLopYajiXdJn/pwjyNCOPq1at4enoyYcIEevXqpTez+5BIKenQuh0+Jy9S1cQLjdRyIvEOxvYW3H/oS9GiRVm8eDG1atXK1OsmJycza9Yspk2aQg/n2pSzKgBAilbD4vADfDl9AoMGDcrUa+Y0MktMhubJmJj8z+/9iUlmk30DHr1Hbt26xbp16zh//jwvi+/Vq1epUqEyT3b7UCsiL8nHAqhfq64uF0d8fDw7du2gnrV+AMN6NiW4cfMmSUlJfPHFF1SrWpVdUZfQpvWfrE1hb9w1+g8eqNeubNmy/LFyOYdPHmXKtKnvVUgA1i5fTS3TInqG7vJWBbAxt3pn28yePXt46HOXQfYNKGPlSQVrL4Y5NObU8ZNERUWxcuVK7t69y4ABA7JUSKSUHDt2jEWLFnH06NF0/+YvI4Rgw9ZNTFowg8iyFiRWtmfen79y1/ceu3btIiEhgdq1a9OvXz+ePXv2xr7eBmNjY1q3bo2thTVlLfPryo1UBtQyLcKa5asy7VoK74YWkaEjO5Pj58CxsbH4+/vj5uaGjY2+K2tycjLdOnXlyMFDFLRyJSDhKR4F87Nr326dS+jEMeNpaFaC2mmuuF7muXEwtKJbxy645M3DjRs3QCvRSP09sFokpmamnD17Fkj11mrZpDnT72zB1SwX92NCaNGyBSNHjXwPTyHjaLSv/pVXGaj+9aX7bxw+eIgSKle9jYOmKiPK2RWky6jB9OzZ8w2tM4eoqCga12/IowdBeBo74pf8FKd8edh/5OAbbT0GBgZ0796d7t31o3Y3b96cunXrMmXKFObMmcOOHTuYPXs2vXv31tk01Go1ycnJmJubv6rrf+VVQTAFoNW8xb5rhSxDkmmuwR81OXZmIqXkm4n/w9U5N01rNiBvbleGD/tCL7jfzBkzuHfyKt/m7kgv65pMdGqLiX8CA/r25/jx4yxZsoTDR49Q7oWvQoCSFvkIi4wgT548TJw4kZrVa3Ag+qruZSul5GC0Dx3bd9C1sbe35+TZ0+w8vJfxC6dx/upFVq3766Na8z5x4gQPgvzYG34ZzQuRbi/HPsTCxopixdLFnHsrnJydiZDx6cpjDJIyNAOTUnL27FkWLlzIzp07/1OgxrEjR2Pkn8DYXC3pZFOVMblaYhaUzOivRr11X/9gbm7OzJkzuXTpEoULF6Zv377UrVuXS5cuMWTgYOysbbCzsaV8yTKcPHnyrfouXrw4ZtbmXI3105VppIa9YZfwDfTj1KlT/3ncCpmHlBk7sjM51may4Of5/Dx5Fn3t6mBnZEmMOoFVkcdpM6gbU7+fxtOnTylXojQ9zKrpbYaL0yQywXeVLk+8qcqYYa5N9YImhqXEMDt0J+FRERgYGBAaGkrdGrVRh8eTT+WAn/YZJo7WHD157L0ZiTNKUFAQvy1Zyv0796hcoyp9+vRBo9EwduxYli1bhru7O84Ojjx+GEwxg9xEGCTim/SY3fv3vlNcJ7VazYgRI/ht0RKGujalkLkrUkouxvjyd8o1/AL99QztL5OUlES7Vm245H2BIqauPNZGkWIuOHT8yCuTab1ISkoKISEhBAYG0rhBIybmaYedkaXufKQ6jukhW4hNSB8i/23RarX88ccfjB07lvjoWIpZutPRoSpWBmZcjn3I1pjznLlwlsKFC2e4T29vb1o0aYaXiQu2GlNuah6R29ONR8+eEBgYyMCBA5k5cyYqlYrly5dz7pQ3XkUKMmDgQNzc3P79AjmYzLCZ5DFxlp+5ZCz+7NSABdnWZpJjxaSAuydtKa0nAqHJUcwI3IyhiRHx8fEYCQP+59FJL++DRmoY9WA56zduoHz58mzZvIWFU+fQ364u1obmxGuSWB15kvo9WjJn3vO9mmq1mt27d3P79m2KFStG06ZNP7pc8GfPnqVpwyaUNfMgt7DhnvYJ/pow1EJLZGQkI0eOZNKkSZibm3PkyBFOnjyJs7MznTt3fid339DQULp06cKRI0do1qwZl85ewFQakqJVY2pjycatmyj7L6HRp38/nQ0//UF/h7q6TZ37I68QVdCE5X+tJCgoiMDAwFf+fPz4sW7WqEIws0AvvVTF8ZokJvitJiY2BlNT01de/205f/48darXYnq+7hi9EEdtd+Ql3NuU59cli96qv8jISNavX69zDa5Tpw5xcXFMmjSJefPmYW9vj0oDHoaOFFQ58UhGcTnRj30H9/9nz7ucQGaISW5jZ9kvg2IyPVARk2zDP2JiZW7Bt3k66r00tFIy4v5vDPv8c7y8vNixZRuGN6JoZf/8P5t31B3u5onF+9L51DZaLePGjGPxokU4W9gTGhdOx44dWfTbkvcSOj0zKVu8NGXD9fe6bAg9yR2jZ+zZv5cyZcpk+jW9vb3p0KEDYWFhLFq0iD59+qBWq7l06RLGxsaULl06Q/slihYoTPOUonofBylaNaN9l6N+KfmUpaWlLoyKm5ub3s85P/yI8fVomtk998bbHXaBA+FXcXBxZMSIEQwaNOidw8EfOnSIL7sPYoiNfuZFn1h/7uZP5NCJI+/U/4tcunSJZo2aUkzjRAen5+FdzkXf5bpTJBeuXsq0a31qZJaY9HHOmJjMDMq+YvLxLMi/ZyqVr8jVe35USws5DnAjzp/ihYoyf/58ANq1a0fVipWJijiBl8qRYBnJ1cQA9v92QNdGpVLx45wf+fqbr7l//z758uXD0TF9TKWPnbCwMO753qO/u36ok1q2xbkffyLThURKyaJFi/jyyy9xc3PjzJkzumsYGhq+9ZJZijpFz8MMUoMjGhka8sPMWRQrVkwnGi87WrxI0aJFqV65Kk8iosmHPQFEEGIYxW/Lf2flypWMHz+e77//noEDB+rG/l8oVqwY/tFPSLBM0nMHv50YTPkKDf9Tn6+jXLlyqISgpm1xvfLyVl5suL2KyMjITMuVovBqcsIne441wM+YM4u/4y5zMPIaAYlPOR51g/VR3syeP1dXx83NDZ9bN+g4rj/ami7UGtSaazd9Xhmq3dbWlgoVKmRLIYFUbyS1RkOy1Ddax2uSsHwhUdN/4ebNm4wc8RU9OndjxYoVRERE0KtXL4YNG0ajRo24ePHiO4lVcHAwqAQHI67qeZSdj7lP0cJFGDlyJE2aNKF48eJvFBIAd3d3bt69Tf8pX+LSvix9vxvOrXt36NWrFwcPHuTixYu0aNGCefPm4enpSe/evfHxefuQRrlz56Zr1y78HnEEv4RQItVxHIi4wqmIm5y/dIHo6LdOdPdGLMxTl2BfJFmbglar/eiWWz81Ur25RIaO7EyOFZNKlSpx/PRJTGvnY6fxDZIrOrDn0L50KWJtbW0ZOWokf21cx+Qp3723neZZgZ+fH4MHDKJ0kRI0b9iEgwcPIqXk77//pnr16kiNlh1hz/fSJGvV7Iu7Rt+Bn/3na27YsIHqlapyZ+1J5NFgZo2cjIdbPlavXs2UKVPYsWOHLpjl2yKl5K+//qJEiRIEPw4h1CKRXyMOcCD8Cn9FnuTvxKssW/nnW/drZWXF4MGD+WXRQoYMGaIXqLFcuXKsWbOG+/fvM3ToUDZt2kSpUqVo2rQpR44cQUpJYmIi30/7nuIFi1K0QGEmffstcXHpjfe/Ll1Mn7FD2SQv8WPoDkRlF76dMplTp05Ro0YNAgMD07X5r/Qd+Bn74q6Rok39WJBSsiP8PFKjpVq1auzZswcpJfv376dpg8aULlKCIQMHk91z/3wsKN5cnyAfa6DHrObhw4dUKl+RCoYelDDNy+PkSPbEXsEpb25u3b5FwYIFmThxIgvnLeCxfzCuJg7cjQ2mcdPGrFyz+j9tRkxMTMTNJQ+f2dTVecRJKVkQ/Dd1e7Vk0aK3MzK/SGhoKEOGDGHLli1Uq1aN5cuXky9fPjZv3szZ02fwKJCfnj17Zrm3XHh4OIsWLWL+/PmEhoZSrlw5UuKTMHyaRF3z4qgQHIu/hYGnLSe9T2VoFnDgwAE6dOiAhYUFu3bt0oum8F9JSUmhR+duHNh/gEKWrgQlPSOPR16GDB/G999/j6+vL8WKFiU04BFNLMvgYmzL9cQALqoDOHfpPB4eHu88huxIZthMnI2dZfdcXTJUd+6j+dnWZqKISQ7hs779efT3NZq/ENIlMPEZPwXtYNZPPzJ06FCMjIx0ezX8/PwoU6YMRYoUeUOvb+bUqVP0ad2Vrxya6ZVfjfXjvmcih04e/U/9bt26lUGDBhEVFcW0adMYOXLkB1+qSUxMZOXKlUydOpW4x5FM8eyqi7OmlZJ5YbuZt2JRhpNaXb9+nebNm/Ps2TPWrVtHy5YtM2Wct27d4urVq3h4eFC5cmWEECQnJ/PLL78wYcw4Rudtg6vJcwHeGXGBfK3KsXjZ0jf0+umSWWLSNYNi8nM2FpMcu8yV0zh57ASlzPT3W+Q1zYWdpTXNmjXTzTyEEFSpUoUuXbq8k5BAqtdUXEpCup3x8ZpErKzfPsdHREQEPXv2pF27duTNm5dLly4xZsyYDy4kAKampgwcOJBhw4ZRzqaAXsBOlRAUEs6cO3cuw/2VKFGCs2fPUqxYMdq0acOMGTP48osR5HfLRzGvIvw4axYpKSlvPc6iRYvSpUsXqlSpovOSMzY2plmzZjhY2ekJCUAps3wcP3rsra+j8AIydQd8Ro7sjCImnwjJyclM/nYSbs55sLawpE3zVty9e1cXZyoqKorQlEi9NgmaJOKSE8iVK1eWjKlo0aIko+FE5A1dWYw6gaOJt+k/ZOBr20VFRXHmzBk9m8HevXspUaIE69atY/LkyXh7e+ulIf5YcHd355kqvX0kVBWLu7v7W/Xl4uLC0aNHadq0KZO//pYLfx2kq2ElmiQXZuUPi+naMWNfuxnB0dGR2OR4ErXJ+uNOjiQyMooTJ04gpeTOnTu0ad4KawtL3Jzz8N2kyf9J1HIS8i2O7EyOdQ3+1OjTozc3Dp+nt2V1rC3NOXvhLpXLV8Q9vwfXrl3D2tqa7QkXcDPJhbOxLYnaZDZHnaNly1b/2QD+JhISEujcuTNh0REctLnFhTB/7A0tuR0dxBfDv3jlco+UksnfTGLu3Lm4mNsTGh9OjZq1cMztxPLlyylWrBg7dux4pTfdx0Lbtm0Z89UojkXdoIZ1EUBwJuoONyIe0qBBg39t/zIWFha0bNmShyd86OZYU1eez8SJqYc24ePjQ8mSJd953A4ODjRt2pTNx8/S3rYKpiojHidHsDPyAslGklq1alGmTBke3ntAPfNifO3SnmhNPJt/WcX9O/dYte6vdx7Dp0x2n3VkBEVMPgEePHjA7r//ZnKeThin7aZuYFuaR4kR3AsKZvHixfTq1YtlS39j0jffYmloRmRiDE2bNmXpH79l+niioqJo2bIlJ0+e5Ndff2XgwIEcPXqUsLAwqlev/lqPuNWrV7Ni4TLGu7TB1tCCZFs1q08fY3/sfsaOHct3332XaTvQswozMzMOHz9Kn269+PrWWgSC3Llzo42ENm3acOjQobd2Cjh/5iwlTPPqlRmpDChi4caFCxcyRUwAfl/xJ/169WXy3vXYmloRp0lkyqzv6du/HytWrOCbr/9HCYM8NLArDYCVoRl9jerw3c4N+Pn55VgjfUbICaZpRUyyCXfv3mXi2AkcOXIEOxtbBn0+hJGjUg3PV69exd3MUSck/1DcIi8OJfLrclp8MWI4AwYN5P79+zg7O2fJnpgnT57QpEkTrl+/zpo1a+jSJXUppn79+v/adsGceTQzL4OtYeq+FmOVIV2canArKYivv/76oxeSfyhcuDBnLp7VhWnJnTs3+/fvp1WrVjRs2JBDhw691WzQ06sAB7ioVyalJCgp7F/jjr0NlpaWbNiykdDQUEJDQ/Hy8tI98yFDhrBz83Zcb+pHIjZRGeFplYebN28qYvIaJKDOAWKi2EyyAcHBwVSvUg316WBGOjSjLaX544eFdGrXgeHDh9O/f3/uRQSlCxsSqAmnWCl9u4KpqSklSpTIFCF58OAB3Tt1xcXBiSIFCjF50iSqV6/O3bt32blzp05IMsrTp09xMNI3zJupjDExMiEqKuqdx/u+cXFxIXfu3AA0atSIrVu3cuPGDRo1akRkZGSG++nXvx8+iQFciL6PVmpJ1qawPewcT+MismTfk5OTEyVKlEgn3kVLFCNQE65XlqLV4B/7hIIFC2b6OD4lcoLNRBGTj4Rnz54xb948xowazZYtW/TCp8+f9zOljfLSyK4MdkaWeJo585ldXXbu3MmSJUto0KABJUuVZE34SSLVcailhjNRtzmf8IBhX3yeJeN99OgRVStWIfqoL0OtG9AsuSi/z/qVx0GPOHjwIE2aNHnrPuvUq8vFOF+9svsJj7CytsrWm0X/oWnTpmzevJmrV6/SuHHjDAtk7ty52XNgH5fsnjAxaA1fB64l3ssME0szatWqxZUrV7J24Gl8PuILziX4cibqDmqpITIljrWRJ6lRq4YiJm/gn3wmijeXQpZz/vx5ingVYuP0ZdxZcZwJA7+iRpVqxMXFER8fz8G9Byho6KzXxszABE+bPGzcuJENGzZw5OQxyrarzfSQLYz0/ZMH7knsP3wgU5dBXmTBzwsobpCHpnblyGVsjZd5bka4phrV/+tyR8u2rTkYdpUNT09xOz6II1E+rIw8wbyF81+ZACo70qJFCzZu3MilS5do2rQpMTExGWpXqVIlrtz04d5DX4IeBXPy7GlOnz6NiYkJtWvXfus8KP8FT09P9h3azwP3REb6/sn0R1so164O6zZtyPJrZ2syuPs9u9tVlE2L74F/NrTt3fE3drkcGDhkEJUrpwZUlFJSvFBRqsa5Ud4qNVqvVkr+CD1ETC4IDApCnZRCA7vStHJ8HvwwRavhu0cbuHDtMvnzP0/OpdVq0Wg075Q+NyM0rFUPL19jSlp66JUvijzI3L8Wv7XnUlBQEBUqVMDExITmTZpx5eJlPDw9+HLMyHfKk/KxsmXLFjp16kTVqlXZs2cPlpaW/97oFQQEBNCoUSMCAgJYvnw5D3wfcPzQEfLkdWPY8M//NXT/fyU5ORlDQ8NPRuRfR2ZsWsxl6Cxb2GZsyXdFWPbdtKgY4DMJf39/YmNjKVKkiN4muoSEBOrUqE28fxjljPIRoQ2l+eYmTJs1g8FDBnPv3j0eBYdQ1q22ro1KCOpYFef34EMMGzaM4sWLM2rEV7jFOFDG0pMYTSI7oi9Qs1YtPSGB1CjG7+M/eIHCBQm4dYmSeOjK1FJDcNyzt56ZxMfH07p1a+Lj4zl06NBHuX8ks2nXrh1r166la9euNG/enG3btnH8+HFCQ0OpVatWhpNjubu7c+LECRo0aEDPrt0pbZOf0qb5eOZzgwab6rLo96V06tQp08ef3dIrfEhyStpeRUwyiJTylXk1AgMD6dqhMzeu38DcyBRhYsCSP36jefPmACxfvpxE/3AG2zfQtS9l7sHIEV+yfMXy1PXuZA0SCS9kV1dLDV4FvJgzZw4ABQsWZPjgYay6exwjQ0O6de3K3AU/Z/l9vwopJSojAw6GXcHN2J6SFh7EaxPZHnWBqtWq4uXl9e+dvNBXv379uHz5Mjt27MgRQvIPHTt2RK1W0717d9xcXPH4f3vnHVdl9T/w9+EyLusiOJiCgODeK/femZqVmivnz8yW9XVku8yBOStnjsrMXEiuNLU0TVHce6LgAEFE9rj3/P64VwRHYmw4b1/P697nPOec53wAn89zzvkMnQtOGjvGxb/Py717M3/xgmzlcilbtizt2rTF5moKA8q2yij3s3LjrVGjefHFFwtV+ueSiL4EKJPiPUfNBlJKUlJSHgn5cf/aN3O/wdPVA41GQ+2qNdi0aVOW653adaB0qIHP3V9honNPXrasz4A+/Thy5AgHDx5k8XcLqGdRIctDoZylA6XN7Lh37x6jRo3C08uLvffOZFxPl3p2Jp2m/5BBGWXNmzfnyKnjRMdEE3PvLguXLMY2h6Hh/wtpaWkMGzaMefPm0aZjO/62vca4az/y+fXV+HWsxy9rn239/KuvvmLVqlVMnjw523GrihN9+vTBw9mNHqUa8IZTB/o6NOFD1178sX4zK1euzHY/u7btoLF91tlMBetymOvNOHPmzBNaKfKLkrBnUqKVyfLly/EpXwFbG1s8nN34Zu43WZTK9GkBfP3xV/S1bMjsikNpHOvBwN792LFjB2AMZBgXGUMHh1oZqWL9bNyoZ1GBBnXr07BhQ06cOsm99MQs95VSIqwtWLp0KTNmzGDj75vZKy7zXcx21tzdz+SIQCo+V53Rj7HEsrOzy/P9kPvExMQwbepUXujUlbfeeJOQkBC6d+/OkiVL+Oijj9i8eTMnz50m7EY4UTF3WPbTD1nCtT+NwMBAPvzwQ/r168fYsWPzUJLCy+nTp0lNTMmSpE1rZkkrbWWWLvg+2/04OjkSq88axiXNoCc+NVElvipgJGDI5lGUKbFz31WrVjHuzffoV6oZPr6dCEuJIuCjSQCMfnM06enpTJ08hVGO7XGxNDqY1bDzItmQyoDer1LGzZnz58/jZVb6kaUIF8tSVK9ajU++/IykpCTeHfkmtdO8cbKwR0rJ3ntnsXa0zdhY9vf352LoZTZu3Mj169eZ2rhxgefljoiIoFG9Bril2lPF3JVLh/fTbMFCUgxpLFiwgBEjHsTWcnJyeub+jx8/Tv/+/WnQoAGLFi3K1nJOcSQ5ORkrjcUj8lsKC5KTsu9b8/rboxkzbDQVrd1wMLfBIA38Fh1c7DfIiwqGoj7tyAYlVplM+uRzXtI1wteUM9xTW5a+NOGDcePZELTBuKEeF4+Lc1ZPZR9rF+5G7aV+k0Y0bNiQlT+uIFGfgo0p9aqUkpP6G4x44x169uwJQMTNW3zy0cd427tyLz0Rc3stG7dszvIAsbKyolevXvkk/dOZ9PmX+KY40cvpuYwyb8tyrE89zPDhw5+5v5iYGIKCgkhJSaFhw4b06NEDBwcHAgMDsba2zs2hFylq1apFmrmB84nX8bcx+tIYpGRv0nmG9nsr2/306tWL40ePMXnGTCrYuxCZfBfHsqVJvZVOw4YNCQwMpFGjRsTFxXHt2jXKly+PTqfLK7EUD1H8VUkJNg22s7blU/dXMpQAGBXBmxcWUb9BfTw8PNi2eStjXLrhYvVAoQTfu8BVnzR27d0NwLtvvs2Gn9bQzroathotB5IvEetoIPjIoSx7Gnfu3GHfvn04OjrSuHHjQv/G6Ofly0vUobz2QURhKSWf3PyVkJNHn8l/5bfffqN/335UsnXHEnMORZ9HCsnf+/YW+AysMLBt2zZeefFl6tn64GDQciDuPInm6Vy9EfbMD/yoqChCQkJwdXWlZs2anDp1im7dunH9+nU6t+/Izl27KGVlx93keIYOG8r0mV8XihD+hZXcMA121JSTre16Z6vu+nvfKNPgokZl/0pciLpBLTvvjLLLyRF4uZfnwIEDCCEImBbAt5Nn8rJ9IzysynAmMYzf4kNY/cW6jDYz5syi/nMNWfTtAu7FRtBtcC/eHTPmkc1xJyenIrXBrNPpuBeTda8nVaaTkp76TD4RsbGx9O/bj5Gl2+GlLQdAZ9taBNzckG97P4WdDh06cPz0CZYtXcatGzfpX6oF06ZNIyAggC+++OKZ+ipTpgwdO3bMOK9WrRrBwcE0atiQg9v3Mt7DGETzXnoiP6wIxKm0Ex998nFui6TIhDINLuZ8PvlLBvbuB4CftRtXkyNZfe8AU+d+nbH89P7/3sfW1pZpX00h/PINalapxk+LV9KmTZuMfoQQ9OvXj379+hWIHLlBbGwsaWlpGXlNrly5Qkx8LOtuX8Vb64yNxgqDNLAl9gitWrZ6pqi3GzduxM/WLUORADha2NHYrhI//7SC2rVr57Y4RRJPT08+zvRQj4iIYPLkyXTr1i3HTptlypQhNTGFAS6tMoJo6sxt6GXfiLmz5yplkg8U9c317FC411rykC5duvDDqhUcLhPFp9d/5S+7UGYv+pZBgx6Y4wohGPXGKEKvXyNdn87hk8fo3LlzAY46d7l+/Tqd2nbAzdmFCh6e1K9Zl4CAAOrUqUNUdBR1Wz/H5zfWsDh2F19GrCPey5IlPy57pnukpaVhzqPLKBaYkZaa+pgWCoDZs2fj5ubGwIEDSUpKynF/t+9EUc6yVJaycpYORN2NxmAoCY+6gkVKma2jKFNiZyZgVChdunR5esViiF6vp13LNvjGOTCp/KtohIbgyAtMHDeB6rVrsnbtWry9vbl+/TqHDx+mfPny/2kW0alTJ94aNZoo21qUsTCu/yfpUzmUGsr7L03PZamKDw4ODixdupR27doxYcIEZs2alaP+GtSpx/FrV2io888oOx4firNjWeLi4nBwcMBgMHDixAmEENSoUaPEWtjlNvdNg4s7JVqZlGR27NhB+t0kupRunVHW2KESF1Jv0uOVV/D2Nu4lubu75yhir4uLCz1f6sVXP/1Mc6dqWAkLQlJD6dG7F82bN396ByWYtm3bMnr0aGbPnk337t1p3br10xs9gSkzAujWqSvxhhR8tS5cSY5g893DJKYlU716dd59913mzphNWkIyBimxcbBj5ZpVykAil8itWYcQohMwG9AAi6WUUx663g8YZzqNB16XUh7LlZs/hRK7zFXSCQ0NxUVT6pFyD3Mnrl4OzbX7REZGsnHTRqrUqk6j/3ueKoNasmZzIN8tmKfefLPB1KlT8fPzY/DgwYSGhrJnzx7CwsKeuZ+mTZuyc8+fmDd3Z5PlaWRjZ/7cu5t//vkHGxsbxr8/lo6yChPK9mBiuZ60SvOlS4dO2Y5qrHgyxuRYMlvHvyGE0ADfAp2BqkBfIUTVh6pdAVpKKWsCXwALc1+ix6NmJsWcgwcPMvF/4zl0OARXZxfGjHufV/v149SpUxyNvsArDo0yvPellFzgNt2aNs61+7/zzjvEx8ezYsUKqlZ9+O9e8TRsbGxYtmwZrZq1oIpfJSo4unEzIZp27dvxw88/YWNjk+2+ateu/dhw8W+88QbLP5lLzUwRoOva+3JMH8aaNWsYPHhwbohSopG542nSELgopbwMIIT4BegOnM64j5T7MtXfD3jkxo2zQ57NTIQQS4QQkUKIk5nKnIQQ24UQF0yfjpmuTRBCXBRCnBNCdMxUXk8IccJ0bY4wvc4KIayEEKtM5QeEEBXySpaiytGjR+nQph1lz6QztuwLtE/245N3P8DT3YM5c+agK12KRVE7uZIUwfWUaH6N+YdUnVmuRZndtGkTK1euZOLEiUqR5IAjh4/galOaz7z68KZjRz51e4XwvWd4+43sOzX+G9HR0ZTTPOrP4qDXEhERAUBCQgJLlixhwvjxrFq1ilRlPPFMPEM4lTJCiEOZjhGZunEHMk9Lw01lT2IosCWXRHgqebnMtQx4ON3eeGCHlNIP2GE6xzRV6wNUM7X5zjSlA5gHjAD8TMf9PocCMVLKisBMYGqeSVJEmfTZl7SzqU7TUlXQmdvgb+PO8DJtibsXx6ZNm7gSdpXeY4YQpDnJirQD1OnTmr8P7MsVj/S4uDhef/11qlWrxvjx43NBmpLLN7Pm8KJjI+w0xt+LpZk5PXQNWPnLSlJSUnLcf8uWLTmlv4E+U9rnNIOeg3fPs2jRIr755hsq+frx7fipnFy8ky9GT6BO9VpERUXl+N4lAYnEkM0DiJJS1s90ZF6mety68GOnPEKI1hifkeMedz0vyDNlIqXcDdx5qLg7sNz0fTnQI1P5L1LKFCnlFeAi0FAI4QropJT/SOMO1g8Ptbnf1xqg7f1ZS0lCr9czf/58GtWpT41KVflo4ocZ6WCPhBzG39otS/2ylg442jng7++PpaUlEz+cyLkrFwi9fo1Zc2c/kw/Jw0gpCQ0N5fbt23zwwQeEh4ezaNEilfsih9y5cwcni6wBNO001kgpSUxMfEKr7NO6dWtqNKjN/Og/OBYfytG4K8y7s40qtatjbm7Oe2+9Sz19eYY6tqZz6bq87tiecjGWfDhhYo7vXSKQxhA52TmeQjhQPtO5B3Dj4UpCiJrAYqC7lDI61+R4Cvm9Ae8spbwJYPq878n2pOmbu+n7w+VZ2kgp04FY4LFPQiHEiPvTxtu3b+eSKIWDYa8NYeYHk6l/uxwdk/zZsXA9jeo1YMyYMURE3OJaclZ5Y9MTSUhLxsXFJVfHsXPnTvwq+FKvem0qeHiy6Nv5DBkyhMaNc2//paTSslUrQuIvZSk7lXANT/fyuRIRWAhB4KYg3pw0jnOeCVzwTuL9qR/x9/59HD58GIMZtC5VPUv91nbVWLtmLWB8oVmyZAktGzejSb1GzJwxk+Tk5ByPqzghs/nvKRwE/IQQ3kIIS4yrOUGZKwghPIF1wAAp5fk8EeYJFJYN+CdN3/5tWpftKZ9pqrgQjLG5/ssAC5L4+HjWrFnD1atXadCgAR07dkSj0XDu3Dk2rA/kI9eXsDIzhibx1jozI2wDs2bNonnz5mw8eBhHczsq2bgTnRbHr/f+YejQof85TezjuHz5Mr2696SvrinV3MqTLvVsig4heO/+JyYVU2SfL6dMommjJiTFpOFv6crV5Ei23z3Kr+vX5trP1sLCgpEjRzJy5Mgs5Xq9Ho2Z2f0lmAflGEhMTOCHH35gU9BGju7cTyvrKpgLDcu++pYN6wLZ8ddOFfcLkzVXLniaSCnThRCjgd8xmgYvkVKeEkKMNF2fD3yM8aX6O9PfRnp+xfrK75lJhGnpCtNnpKn8SdO3cLJaI2Se1mW0EUKYAw48uqxW5Dl79ix+3hWZO3Yy++cG8eaAETR7rikJCQn8+eefVNS6ZigSML41NtD50bvXy/z1118s/fkHtlqc5b3QZcyM2swLw/oQMCN3nQUXzJtPQ5uKVLfzRAiBhZk53cs0JOZWFPv378/Ve5VE/P39CTl2mGp9W3DUPYb0uk4k69PYt2/f0xvnECsrKzq178gfsScyygxSsvXuEay0WgYNGsSmwCBeL92BWnbeVLP1ZLhTG8LPXM6SSK5kk915ydPfc6WUm6WU/lJKXynlJFPZfJMiQUo5TErpKKWsbTryLWhkfs9MgoBBwBTT54ZM5T8LIWYAbhg32oOllHohRJwQ4jngADAQmPtQX/8ALwE7ZRGNR3DkyBFmTZ/BpfMXadC4Ee++PwZPT08ABvcbREuNHy0cjOlsDVKy9OIOataoydVrV3Eys31kce828TSrYsy616NHD7p3705CQgLW1tZ58qZ47fJVyoms1kBCCFytHAkPD39CK8Wz4OnpyYzZMzPOhwwZwvTp0+nbty81a9bM03t/t2g+rZq2YO6d3/EQjlxKj6CMtxtXdgXz6aefcnD5NizNHjxKzIQZ1czc+GvXn7zwwgt5OraigNEDvkg+mp6JvDQNXonxQV9JCBEuhBiKUYm0F0JcANqbzpFSngJ+xWgvvRV4Q8oM05LXMW4mXQQu8cDU7XugtBDiIjAGk2VYYSQ5OZm1a9eyaNEiLl3Kuva9detW2jRvRdwfF6l7szSnf9lDvVp1uXDhApGRkZw4dYKmugdZ+MyEoJ2uJpHXb/HOO+9gXUbH9rvHSJd6Yy6V+KscTrzC0GHDMtoIIbCzs8uzJYcmrZpxxpB1HzDZkMr5uHDq1y+S0bQLPQEBATg6OjJixAj0ev3TG+QANzc3Tp0/w5TFs+g49lUWrFrG/kMHcHBwoEmTJsSZP2pRFmOWhKu722N6K4EIMAhDto6iTInNZ5Kb3Lx5kz///BOdTkf79u2zWC+FhITQpUMnnDUOOJhZczLuGkOGG/NIAFT29addqh/VbD0z2my9c5ijFjeIS0ogITaOrysOznAsBAhNimSD5jjnrlzk6tWr9O/9KieOH8fS3AL7Ug58/8NSWrVqlasy/htxcXFU9PLBR+9Ei1LVSdAnsz3xBC17dGDhksX5No6SxooVK+jfvz99+vTBQmjwrODFsBHDqVChQr6NITk5Ge/yFWhnXoVG9v4I4FRCGL/E7ePMhXM4Ozvn21jygtzIZ2KrKSMra7tmq+7hxB9UPpPiys2bN/npp5+IjIigdZs2dOrUKUtiq8lffsXkr76iss6TeEMydwwJbPp9M/Xq1UOv19OzW3e6WdWhrr0PAIl29Zm97GdcPdywtLTkWtg1qnq3yXLP+nYV+SP8OK8O6s+eHX+xO/ZMhjWNQRrYlXiKPq+/CoCXlxd79u/l+vXrJCUl4evrm+8b3uHh4cTExxJTwYnAtOPYO9jz7ocfZEntq8h9OnfujIOtPSFBu6lv58sBTvPt3G9ZF7Q+R3G8ngWtVsv2XX/Q+8WX2XbrBOZmGixsrQjcGFTkFUluIZHoydvZY2GgRCuTPXv28NnEjzl1+jS+Pr58+PnHdOr0wM9y586d9OrekxrWXjgYtKxd8gsVa1Vm4++bsbS0ZPfu3cyaNoMJrj1xMOWJOBJ3me5duxF8+BCbN2/GEJ9KXVefjD5tNFa00FZi4tgJpMp0zIUZ8fpk7M0fOAreSY/Dx9uHxYsXc/78eVo3b8nFmEjKGew4b4jAo1IFxk3IuqqXk2CMOUGv1zNkyBB0Oh1/7dmtHiD5SMDUAKppPXjVqXnGC4SfuTPDBg3h4tXL+fZSUb16dU6eO83Zs2dJS0ujevXqhT6TaH5T1JewskOJVSa7du2iV7eePG9Xh5a6doSGRzLg5VeZt3QhL730Enq9ngF9+jHAoTmVbY0GZR1kbRYc/4OAgADatWvHF598RnOtf4YiAahj70NQaHDGw93loRwSAFbCgtq1arFi9S9M/mIS6zcfoE+pxliaWRCXnsTG+CO8/4HRIczf35+LoZdZt24dV69e5f0GDWjbtm2B/mc9c+YM3y9aTFTEbdLQs3//flasWKEUST7z27pAOtlUyqI0qtl6svrWAS5fvoyvr2++jUUIQZUqVfLtfkUJowe8UibFloljJ9BTV5969hUBKG1hj51Gy1uvjyY0NJSTJ0+SHp9C5fIPLJM1woymWj++/OgzPvzwQ6yEOS+Xa/pI3w5ae3q81psOHTow9LUhXE2OzMg0qJd6/km9yLi3P6VixYrM+e4bBvUbwKfbV+Ns68TN+ChGjnqd/8tk729tbV1oMjmuWrWKkUNH8JyNHw7Cmn2xZynnWIaePXsW9NBKHDa2NiQlZY2RlS4NpKanPVMASEXeo5RJMeb4yRO86J41oKG/tRu3wiP53//+h0ajwU5YPeJ0ly71+Pn7MfnraRw5coQfZyykofRHI4wzhYjUu0SkxxIQEIBOp0MIwZCBr1Hfxhed1HLMEIZfnWoZysHW1pY1gesICwsjLCyMypUr4+TklH8/iGcgOTmZUSNGMrJ0e8prjSl+mzlUZUH0dpYuXcqoUaMKeIQli6Gvj2DGhEn4WruiNbNASsm2mCPUqlULV1fXgh6eIgPj3KS4U2KVSXk3d8JTovC3ebDXcDM1BicHRy5dvYy9vT3+Pn6ExF2ivs44e0kxpLE7+RyfTJtM165d6dChA3/v2s2co1uoo/EigRT+STzPjDkz0emMfhcvvvgitWvXZvmy5UTfjmJwlw/o0qXLI2a65cuXp3z58hRmgoODKW2py1AkYDRVbmRVkQ2r1yllks8MHz6cg/8c4IvVa6hk78H1pCgi4+7wkk/uRH1W5A4StWdSrBk7cTwfj/mAQRpr3KyciEyN5Zd7+xg7fiwODg4ArF6/hk7tOnA45iqOwpaTidfo2v15Xn3VaEllYWHBxt83s2HDBjZt+A0Px1JMHvr9I05kPj4+fPb5Z/kuY25ja2tLYnrKI7O1JEMKdvaFczZVnDEzM2PxsiWM//ADgoON+3Rbtmxh6tSp6HQ6bl67jlarZdCwwXTq1EmFtSkwJHrSCnoQeU6J9TORUvLNnLl88dkXpKYkozE359333mPiRxOz/KdLTEwkKCiI27dv07Jlyzz3Ni7MSCnx9vCiabo3TUsZN1vj9UnMidrKghVL6No1e7b0irwjNTWV8q7uWCRI2jrWJNWQzp6Uc7w6dCDTvg4o6OEVOXLDz8RK4yDdbZplq+6V+M3Kz6SoIYTgzbff4vU3RnHnzh0cHR2xsLB4pJ6NjQ19+vQpgBEWDoKDg/n5xxWkp6fTtEUz4pITWHdvPwf1V3A0t+fMvWu8+dabdOnSpaCHqgC2b9+OjcGCMZ5dMxxd6+p9mDR/ASPfeB0fH5+n9KDIC9QGfAnA3NyccuXKPb1iCeSLz75g7tczaaStiDlmvPH9D6QIPQdCDnLz5k2io6Np0aIFHh75lhlU8RS2bt5CbXPPLBETbDVaqtt7sWPHDqVMCgSj22Jxp8QrE8XjuXz5Ml9PC2CcSw8czI1mps10VZlyaz2JiYl07NjxKT0oCgJHJyfOikdjZd3TJ+Ho6PiYFoq8xhjosfjPTJSbquKxbNmyhZp2FTIUCYC1xpIGWl82BG74l5aKgmTQa4M4mHApS1K0Y/GhnI+5xvFjx6nmVwUv1/KMHP5/3Lx5swBHWrLIbuLeooyamSgyCAkJYe/evbi6uqLRaEiWqY/USRV65RBXiPH19WXRsu8ZMWQ4rtZOpBjSiNMnAfDj1wvoUboRdlbW7N8QzHObG3Ls1IlcydaoeDKyhFhzKWWiID09nVdf6cPuP/6kirUH0TKe6ynRxMXFEaqtSgVr455SROpdQpIuMf/VvgU8YsW/8fLLL/P888/z999/o9VqcXZ2pn6turzl/nxGIrWeVo34IWY3S75fwpj3xhTwiIs7EoNUeyaKEsDChQs58dchJjj3wMKU5GjP3VMEJR9ifvR2Ktq5YS40nLl3jdnfzKFixYoFPGLF07C2tqZ9+/YArF69msqlPLNk5ASopHHhn91/s6lyJXZs+4PSZUszcNCgQu88WxQp6ktY2UEpkxKGlJLdu3cTFLgBaxsb+vXvx4+Ll9FaWzVDkQA0dajCtoQT7Pj7T86dO0d6ejqdOnWidOnS/9K7ojBSoUIFridFYbCXmGXyoQpNiuTS/rMc3hNMDY07R0UKAVMC+PnXlcrUO1dR1lyKYoaUkqGvDeH3DZupZ+FFitDz7ey52Nva0cAyq3m0QGBuZo5Wq6V3794FNGJFblC/fn08fLwIDA+mi0MdLIUFx+KvsO/eWdwsnXjHs0dGbLk62gq81n8g4bduYDAYCA4OxsbGhnr16ikP+v+IxJiHqLijlEkxJSkpiVWrVnH4UAh+lfwZMGAABw8eZHvQFt4v+2DtvLGtP1+G/sp2m2P4W7tnvLkeiw/F3lFHpUqVClIMRS4ghGDTti0Mf20oH/3xCxozM7zKe1LXuQ7VI0plKBIAX2sXdInWTJs2jVnTZ+BkYU9SegraUrasCwqkRo0aBShJEUVKDFJtwCsKOXq9ntDQUBwdHTOiDUdGRtK0YWNsE83wkWUINtvBl59+Qdt2bahvUSHL2nk5SweqOHiSWtqC2dFbqCJciNEkcTo5nN+2bFJvo8WEMmXKsH7jBu7du0dSUhLlypWje5dupN9KzFJPSknUvRgmfz6J0a5d8NKWRUpJcNwFOrXrQGj4tcdGilA8mZKSz0T5mRQBkpOTCQsLIzU1q6nu6tWr8XT1oHGdhni5l+elHr2IjY1l4rgP8ErUMcKxLe2cajGwVAtamPsTFLiBFP2jb0jmVhZ8/tUXTF8yF/9Bzek5bjBnL56nSZMm+SWiIp/Q6XQ4OzsjhGDg0NfYnXyWJP2Dv6sj8ZdJNqTRyNYPL21ZwDizaaTzR2fQsn379oIaepFGSkO2jqKMmpkUAm7dusWuXbvQ6XS0b98eS0tLAAwGA599/CmzZ83GXGgwCAPjxo9j7ITxBAcHM3LICAY7tsTH0YVkQyob9h2kT69XCD4YzNtOnbPco5muMusi97Ev4TzNSlWllCk75KWkW4QmRtK1a1fs7Ozo3r17vsuvKBh69erFzu07mLRiJdVtPYmVSdzS36Vz585YHIh6pH4pjQ1RUY+WK56G2oBXmJBSYjAYHslBcp9z585x6NAhvLy8aNq0aZalodjYWGbOmMFvazdgZ2/HsFH/R//+/TPqTJn0FV9N+orKOk/iDcnEyEQ2bt1EvXr1mD4tgJXfLeO9cs9T2sKeyNRY5gfMRedYij27/qKNTVV8rF0A0JpZ8qLDc4zbtRwpJamO6VnGmC71WFhY8v4HY5kyZRo1dF6kyHQuJt5k1ZpfsbOzy6OfnqKwIoTguwXzeOvdt9m1axelS5emW7duBAUF8fG+sbSQVTEz7afE65M5fe8aLVu2LOBRF02K+qwjO5TYEPQAFy9e5Otp0zl2+CiVq1ZmzNj3qV69ekbdhIQE/jfmfX788UeSUpJo1qgps+fNpVatWoDR2e+1fgPZvGkzlew9uJESjaNbWX7fsR1nZ2cSExNpVLcBdtGSRtqKJOqT2ZF8mi59ejD3u2/YvXs3rzz/Im+V7ZwxUzgcd5kt+hNcvhaKp6sHw3StcLd6YI57OekWCyK3I/UGBju3pYpt1iCLU26sx7tWJRLPRDCodEvMhBlSSoLuHsLuufKsDQokLCyMrVu3Ym1tzQsvvJCRyEuhAEhLS6NdqzbcOXeDRpa+JBtS2Z1ylr5DBzB1eskKY58bIeg1ZlZSa5m9YKiJKZdVCPqixrFjx2jdvBWNtRWpb+XMtbCztFjfjMBNQbRo0QKAl3q8yN2jYUxw6YmtRsuBy+dp06I1x04dx8PDgzmz53D4j3/42PUlLM3MkVKy8XYIQwa8xqZtW/jpp58wj06lv2ObjJmIv407ny1ZSvVaNVix/EeaaP0zFAlAXXsfNl49iLW1NVJKXMtkTTrlZuVEcloKdWrX4Xjo1SzK5G5aAncNifyyehWvvtyHKSc34Kd1JSw9GqvS9uxctAAwZnUcPnx4Xv+IFUUUCwsLtu38g6VLl7J+1RpsbB349v8W8fzzzxf00IokEonBUPytuUrszKRz247oTibSslS1jGshcZc45HCLdRsDOXXqFK/1HcBn7q9kCef9a/Q+bOq707ptG2ZO/Zre1g3xs3HLuJ5qSGPs5R/w9a/IrbAbdLWrQxOHylnGMDd8I2cTr2MpzHm5XNNHrs+8uZE6nZrwz+69dNPUorqdZ6YxXuS0Wxzrfgukbs061BTu1LX25k56HFsTjjP0nZF8/OknSCnZt28fx48fx8fHh/bt22NmpuwtFIpnITdmJmZmltLSPHtpLlLSrquZSVHj73/28pFbryxlte28WXp2R0a4kIrWrlkUCYCPRTl+3raDLb9vxUpYYONpleW6uTBHI8zw9vbGQmNOxK3YLNellCSYp7N48WLi4+OZ9/kMGkn/DFv/iNS7ROhjWbx4MXv27GFgn37E65PwtnbmYuJNNiccZf3PG3B1dSX48EEmff4la7fvoKxbGaa+NzPDwVAIQdOmTWnatGmu/twUCsUzIkvGnkmJfVV1KuXInbT4LGV30xPQWlqxdOlSZs6cSaSMI82Q1Qrjkj6SN8e8TVxcHMNGjmBfwvks14/GX6Gib0U2bdrE2vXrOJR8mfOJNwDQSwN/xB7HtqwDgwcPZtSoUVSoXYk50Vv56+5JNseE8M3trcycMwudTkfXrl1Z+1sgNyubsSx5LzE1rNm0bQutWrUCjMtV8xct4HzoRfYe3E+fPn2UX4hCUeiQJSIEfYld5po6eSrLps9jiGMrbDVakg2p/BSzhzYDXmD6zK8B6NX9Ra7sPcHzdnWxM9eyP+48f6dd5PjpE7i4uHD79m2aNHgOh0RzKgkXbnGPI0mhbNy6KcNHY8sWo+exTNWTlJZM5SpVWLlmFV5eXoBxE3/Dhg1sDAyilKMjg4cNKdF55hWKwkRuLHMJYSHNNaWyVTddH1Vkl7lKrDLR6/W8M/ptli9fhqtdGW7GR9OzRw8WLl2MlZVx6SolJYXPPvmUJYu/Jz4hgXZt2jJt5nT8/f0z+ouPj2f58uX8s3svPn6+DP+/EY9EXdXr9Zw9exZbW1sqVKiQn+IqFIockDvKxFyaaxyyVTddf0cpk6JCZtNggNu3b3PhwgW8vb1xdXUtwJEpFIrCRu4oE400M8ueH5fBcK/IKpMSuwF/n7Jly1K2bNmCHoZCoSjWFO39kOxQ4pWJQqFQ5DnKmkuhUCgUOSP3rLmEEJ2EEOeEEBeFEOMfc10IIeaYrh8XQtTNE5Eeg1ImCoVCkecYsnk8GSGEBvgW6AxUBfoKIao+VK0z4Gc6RgDzck2Ep6CUiUKhUOQpMrdC0DcELkopL0spU4FfgIfDfHcHfpBG9gOlhBD5YllU4vZMQkJCooQQVwt6HLlIGaC4xgUvrrIVV7mg+MnmlQt9/A7pZbJZVyuEOJTpfKGUcqHpuzsQlulaONDoofaPq+MO3HyG8f4nSpwykVIWK9MtIcShompK+DSKq2zFVS4o3rL9V6SUnXKpq8eFt3jYtyM7dfIEtcylUCgURYNwILNHtAdw4z/UyROUMlEoFIqiwUHATwjhLYSwBPoAQQ/VCQIGmqy6ngNipZR5vsQFJXCZqxiy8OlViizFVbbiKhcUb9kKFClluhBiNPA7oAGWSClPCSFGmq7PBzYDXYCLQCIwOL/GV+LCqSgUCoUi91HLXAqFQqHIMUqZKBQKhSLHKGVSCBBClBdC7BJCnBFCnBJCvG0qdxJCbBdCXDB9OmZqM8EUMuGcEKJjpvJ6QogTpmtzhClblhDCSgixylR+QAhRIR/l0wghjgghNhYzuUoJIdYIIc6afneNi5Fs75r+Fk8KIVYKIbTFRTZFHiGlVEcBH4ArUNf03R44jzFcwjRgvKl8PDDV9L0qcAywAryBS4DGdC0YaIzR3nwL0NlUPgqYb/reB1iVj/KNAX4GNprOi4tcy4Fhpu+WQKniIBtGJ7crgLXp/FfgteIgmzry8O+moAegjsf8UmAD0B44B7iaylyBc6bvE4AJmer/bvoP6wqczVTeF1iQuY7puzlGL2WRD7J4ADuANpmUSXGQS2d64IqHyouDbPe9qJ1M990IdCgOsqkj7w61zFXIME336wAHAGdpshE3fZYzVXtSyAR30/eHy7O0kVKmA7FA6TwRIiuzgLFkjWJXHOTyAW4DS01LeIuFELYUA9mklNeB6cA1jGE4YqWU2ygGsinyDqVMChFCCDtgLfCOlPLev1V9TJn8l/J/a5NnCCGeByKllCHZbfKYskInlwlzoC4wT0pZB0jAuPTzJIqMbKa9kO4Yl6zcAFshRP9/a/KYskIpmyLvUMqkkCCEsMCoSFZIKdeZiiPuR/w0fUaayp8UMiHc9P3h8ixthBDmgANwJ/clyUJT4AUhRCjGCKdthBA/UfTlun/fcCnlAdP5GozKpTjI1g64IqW8LaVMA9YBTSgesinyCKVMCgEmC5fvgTNSyhmZLgUBg0zfB2HcS7lf3sdkEeONMXdBsGnpIU4I8Zypz4EPtbnf10vATillnr4JSiknSCk9pJQVMG6y7pRS9i/qcplkuwWECSEqmYraAqcpBrJhXN56TghhYxpTW+AMxUM2RV5R0Js26pAAzTBO8Y8DR01HF4xryDuAC6ZPp0xtJmK0mjmHyULGVF4fOGm69g0PohxogdUYwywEAz75LGMrHmzAFwu5gNrAIdPvLRBwLEayfQacNY3rR4yWWsVCNnXkzaHCqSgUCoUix6hlLoVCoVDkGKVMFAqFQpFjlDJRKBQKRY5RykShUCgUOUYpE4VCoVDkGKVMFCUWYYzWfEUI4WQ6dzSdexX02BSKooZSJooSi5QyDJgHTDEVTQEWSimvFtyoFIqiifIzUZRoTGFsQoAlwHCgjpQytWBHpVAUPcwLegAKRUEipUwTQvwP2Ap0UIpEofhvqGUuhQI6Ywy1Xr2gB6JQFFWUMlGUaIQQtTEmInsOePd+VFyFQvFsKGWiKLGYItnOw5g/5hoQgDEplEKheEaUMlGUZIYD16SU203n3wGVhRAtC3BMCkWRRFlzKRQKhSLHqJmJQqFQKHKMUiYKhUKhyDFKmSgUCoUixyhlolAoFIoco5SJQqFQKHKMUiYKhUKhyDFKmSgUCoUix/w/jWZNpxJXbzMAAAAASUVORK5CYII=\n",
"text/plain": [
"<Figure size 432x288 with 2 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"Particle_data = xr.open_dataset(\"WriteOnce.nc\")\n",
"\n",
"plt.figure()\n",
"ax = plt.axes()\n",
"ax.set_ylabel('Y')\n",
"ax.set_xlabel('X')\n",
"ax.set_ylim(1000, 49000)\n",
"ax.set_xlim(1000, 99000)\n",
"ax.plot(Particle_data.lon.transpose(), Particle_data.lat.transpose(), c='k', zorder=1)\n",
"T_scatter = ax.scatter(Particle_data.lon, Particle_data.lat, \n",
" c=np.tile(Particle_data.temperature, (Particle_data.lon.shape[1], 1)).T,\n",
" cmap=plt.cm.inferno, norm=mpl.colors.Normalize(vmin=0., vmax=1.), \n",
" edgecolor='k', zorder=2)\n",
"plt.colorbar(T_scatter, label='Initial T [$^{\\circ} C$]')\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Sampling with repeatdt"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Some experiments require large sets of particles to be released repeatedly on the same locations. The [`particleset`](https://oceanparcels.org/gh-pages/html/#module-parcels.particleset) object has the option `repeatdt` for this, but when you want to sample the initial values this introduces some problems as we have seen [here](#repeatdt_error). For more advanced control over the repeated release of particles, you can manually write a for-loop using the function `particleset.add()`. Note that this for-loop is very similar to the one that `repeatdt` would execute under the hood in `particleset.execute()`.\n",
"\n",
"Adding particles to the `particleset` during the simulation reduces the memory used compared to specifying the delayed particle release times upfront, which improves the computational speed. In the loop, we want to initialise new particles and sample their initial temperature. If we want to write both the initialised particles with the sampled temperature and the older particles that have already been advected, we have to make sure both sets of particles find themselves at the same moment in time. The initial conditions must be written to the output file before advecting them, because during advection the `particle.time` will increase.\n",
"\n",
"We do not specify the `outputdt` argument for the `output_file` and instead write the data with `output_file.write(pset, time)` on each iteration. A new particleset is initialised whenever time is a multiple of `repeatdt`. Because the particles are advected after being written, the last displacement must be written once more after the loop."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"INFO: Compiled SampleParticleInitZeroSampleT ==> C:\\Users\\GEBRUI~1\\AppData\\Local\\Temp\\parcels-tmp\\d441e19c77676cd806da7f8e4c974550_0.dll\n",
"INFO: Compiled SampleParticleInitZeroAdvectionRK4SampleT ==> C:\\Users\\GEBRUI~1\\AppData\\Local\\Temp\\parcels-tmp\\d1281aa8d15fe9594b477ca71b782dce_0.dll\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Length of pset: 10\n",
"Length of pset: 10\n",
"Length of pset: 10\n",
"Length of pset: 10\n",
"Length of pset: 10\n",
"Length of pset: 10\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"INFO: Compiled SampleParticleInitZeroSampleT ==> C:\\Users\\GEBRUI~1\\AppData\\Local\\Temp\\parcels-tmp\\01fc394199c11f84c25331b4797a64a0_0.dll\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Length of pset: 20\n",
"Length of pset: 20\n",
"Length of pset: 20\n",
"Length of pset: 20\n",
"Length of pset: 20\n",
"Length of pset: 20\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"INFO: Compiled SampleParticleInitZeroSampleT ==> C:\\Users\\GEBRUI~1\\AppData\\Local\\Temp\\parcels-tmp\\1dcf704643338d59fe9815a88cd8967c_0.dll\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Length of pset: 30\n",
"Length of pset: 30\n",
"Length of pset: 30\n",
"Length of pset: 30\n",
"Length of pset: 30\n",
"Length of pset: 30\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"INFO: Compiled SampleParticleInitZeroSampleT ==> C:\\Users\\GEBRUI~1\\AppData\\Local\\Temp\\parcels-tmp\\0364537a5edb2a00eaf61893bcae1143_0.dll\n"
]
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"Length of pset: 40\n",
"Length of pset: 40\n",
"Length of pset: 40\n",
"Length of pset: 40\n",
"Length of pset: 40\n",
"Length of pset: 40\n"
]
}
],
"source": [
"outputdt = delta(hours=1).total_seconds() # write the particle data every hour\n",
"repeatdt = delta(hours=6).total_seconds() # release each set of particles six hours later\n",
"runtime = delta(hours=24).total_seconds() \n",
"\n",
"pset = ParticleSet(fieldset=fieldset, pclass=SampleParticleInitZero, lon=[], lat=[], time=[]) # Using SampleParticleInitZero\n",
"kernels = AdvectionRK4 + sample_kernel\n",
"\n",
"output_file = pset.ParticleFile(name=\"RepeatLoop.nc\") # Do not specify the outputdt yet, so we can manually write the output\n",
"\n",
"for time in np.arange(0, runtime, outputdt):\n",
" if np.isclose(np.fmod(time, repeatdt), 0): # time is a multiple of repeatdt\n",
" pset_init = ParticleSet(fieldset=fieldset, pclass=SampleParticleInitZero, lon=lon, lat=lat, time=time)\n",
" pset_init.execute(sample_kernel, dt=0) # record the initial temperature of the particles\n",
" pset.add(pset_init) # add the newly released particles to the total particleset\n",
" \n",
" output_file.write(pset,time) # write the initialised particles and the advected particles\n",
"\n",
" pset.execute(kernels, runtime=outputdt, dt=delta(minutes=5))\n",
" print('Length of pset at time %d: %d' % (time, len(pset)))\n",
" \n",
"output_file.write(pset, time+outputdt) \n",
"\n",
"output_file.close()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In each iteration of the loop, spanning six hours, we have added ten particles."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[ 0 0 0 0 0 0 0 0 0 0 6 6 6 6 6 6 6 6 6 6 12 12 12 12\n",
" 12 12 12 12 12 12 18 18 18 18 18 18 18 18 18 18]\n"
]
}
],
"source": [
"Particle_data = xr.open_dataset(\"RepeatLoop.nc\")\n",
"print(Particle_data.time[:,0].values / np.timedelta64(1, 'h')) # The initial hour at which each particle is released\n",
"assert np.allclose(Particle_data.time[:,0].values / np.timedelta64(1, 'h'), [int(k/10)*6 for k in range(40)])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's check if the initial temperatures were sampled correctly for all particles"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[0.4040816 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816\n",
" 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816\n",
" 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816\n",
" 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816\n",
" 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816\n",
" 0.4040816 0.4040816 0.4040816 0.4040816 0.4040816]\n"
]
}
],
"source": [
"print(Particle_data.temperature[:,0].values)\n",
"assert np.allclose(Particle_data.temperature[:,0].values, Particle_data.temperature[:,0].values[0])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"And see if the sampling of the temperature field is done correctly along the trajectories"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZkAAAEKCAYAAADAVygjAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/d3fzzAAAACXBIWXMAAAsTAAALEwEAmpwYAADzh0lEQVR4nOyddXRU1xaHvzszcZIQIQlxCCG4BXd3p0WLFC2UFrdCi7sXKBQrUtzd3d09SoR4IJ6MnPfHpBOmCfLeCy0y31qzkpzZ51pm7u+effbZWxJCYMCAAQMGDHwIZP/2ARgwYMCAgc8Xg8gYMGDAgIEPhkFkDBgwYMDAB8MgMgYMGDBg4INhEBkDBgwYMPDBMIiMAQMGDBj4YBhExoABAwY+ASRJcpMk6ZQkSY8kSXogSdKgzHZbSZKOSZL0LPOnzRv6N5Yk6YkkSX6SJI3+x47bsE7GgAEDBj5+JEnKD+QXQtyUJMkSuAG0BnoAcUKIGZniYSOEGPW3vnLgKdAACAWuAZ2EEA8/9HEbRjIGDBgw8AkghHghhLiZ+Xsi8AhwAVoBazPN1qIVnr9TEfATQgQIITKAzZn9PjiKf2InHxP29vbC09Pz3z4MAwYMfALcuHEjRgiR7//ZRqPGpURsTNJ77i/wAZD2WtNyIcTyv9tJkuQJlAWuAI5CiBegFSJJkhxy2LQLEPLa36FApfc6qP+TL05kPD09uX79+r99GAYMGPgEkCQp+P/dRmxMEleuT34vW4X0TZoQovw7jikPsAMYLIRIkCTpfTadk9E/MlfyxYmMAQN/zUO+55fTgIH/C4FAo1HnyrYkSTJCKzAbhBA7M5sjJUnKnzmKyQ9E5dA1FHB77W9XIDxXDuodGOZkDHy0BAUF8fDhQzQazRtt1Go1a9asoXGd+jSuU5+1a9eiVuf8hQ4KCqJ1sxaYGBtjaW5Bz27diY+Pz9E2MDCQ9m3aYGVugaOtHcOHDCUlJSVHW6VSyebNm+nVtSvDhw7lwYMH7zw3Q8DNF4QQaDTp7/V6G5L2qWgV8EgIMe+1t/YC3TN/7w7syaH7NcBbkqQCkiQZAx0z+31wDCJj4B9DrVZz7Ngx1qxZw6NHj95oFxgYSGXfipQtUZr6VWvj6erBsWPHstkJIej4VXtmDv+ZQv4qCvmrmDF0HJ3bd8x2E09MTKRG5apY3Q1lffHWLPVuTOTxqzSuWz+bbXx8PDUqV8H69lM2lKjJ/AJlub11F1+1yj5Pmp6eTuO6dZk9dCiO16+TsG8ftatUYcOff+Z4bseOHaNi6VLI5XLcnRyZM2vmW0U0MTERPz8/0tPffgMy8PEiEGiE6r1e76Aa0BWoK0nS7cxXU2AG0ECSpGdoo8dmAEiS5CxJ0kEAIYQKGAgcQRswsFUI8e6noVzA4C4z8H/z6NEjLl++jLOzM/Xr10cul2ezef78OfVr10P1Kh17uQ1DU4Jp0rwp6zas17NXq9U0qtuAEqkOdHLugAyJJylhtG/7FTfv3qZAgQI62wsXLnD59DkmOTfBSKbdRjlLd34+fohDhw5RunRp0tPTycjIYMOGDXgIM9o7FAPAQg7fOZXlx4DjLFiwgHLlyiFJEpIksWXzZoorzOju4g2ADSaM8yxJpytnOXLkCL6+vpiammJqasr69etJCQhgRfHiyDPdbw3t7ek3YABt2rbF3Nxc73i7tGvLxGIu/NmyMs8SUxg3fw5JCYlMmDJF73plZGQwbNAPrF+/nrxmJiSrNPw8fgI/Dh7yxv9DXFwcQgjs7Oz+23+hgQ+KQLxbQN69FSHOk/PcCkC9HOzDgaav/X0QOPh/H8h/iUFkDOSIEII7d+6QlJRE+fLlMTU1zWajVqvp0bUH+/fux8PUnZeaV8gsZZw4fUJPDAC+6dCFgokO1LAqC4DSrAobjx5h6dKlDBw4kLS0NGJjYzlw4AAZ8SnUdSyl61vEwpXSqR60bd2GQoW9SUxMJDExEX9/f3wVjjqBATCWKShp5ECzZs309q9ARneX0nptkiRRQG7B0KFD9dpNZXJ+KFBCv78ko6DClMaNG+u1WygUjCtSRCcwAN6WljjIZDRu3Bhvb2+srKywtrZm95bNDPZypJGzVgSKWlvwa2l3Wi1cyKixYzEzM9NtY/TwYTw6sosLLTyxN1Xw7GUaPadNwjG/Mx06dNA7hoCAAPr2+Iar128iSVCqRHF+/2M9xYoVy/Y/M/BvkDsi86liEJkvkIyMDBQKBTJZzt7Sx48f06p5a+Kj4jFVmJKoSmDZimXZbm4rV67k/MFzdLXshJHMCIAbCbfo9HUnzl8+T1RUFBERETx8+JDrN64zyrmHrq+RTEE141KMGTaKUaNG6c13FLdwz3ZMjgprbvvfIV2ZgaWlJZaWljg5ORHzPCGbbbxIo2PHjtStWxcTExOMjY05ffo0d3ce0VtAIIQgQJ3E/PnzKVWqFEIIhBBs3riRB0dP0/I1W40QBKpS+emnn3ByciItLY20tDR2bNpEokr/BiKEIFGlIi0khICAAF69ekVSUhIWChm+tUrp2bqYmyIy0rC1tcXBwYF8+fJhY2PDhTOnudSmEPam2q+od15TfillzZypk2jXrh0KhbY9PT2d+rWq07NABht7OiGTYP3D5zSsU5NHfoFYWlrq7e/gwYNM+WU0Dx4/o7CXJ6N/mUK7du2yXUMDuYgQCI1BZAx8AZw9e5ZB3w/m3sO7mJma06dPH2bMmo6xsbHORq1W06h+I9wSClHNuCGSJBEjoujbsy8lS5akSJEiREVFERoayryZ8ygrL60TGIAyZqVYenM5RkZGevs2lYyR/20K0EQywtTUlG69e2BnZ4ednR0ZGRmMGzmGNE0GpjLtcQkheKgJZ/6ihXz77be6/nFxcRTyLMjtxBDKWGoDZ24nhuCniuPI0qXkzZtXZ9u8eXOK793Pxsj7NLMrRIZGzeaYRzgXKsCgQYP0Is1Kly5NyT1F2f4ikBYO7iSplax84UfhEiWYMmWKnm3FihXp17kz9R0dsc28jgcjIjC1s+Opv79OyNVqNa2aNOJ6TBDeVlkutNDkNFQyOf369SM+Pp6YmBjCw8ORIXAy17+GhfOa8vDMI4yNjbG3tyd//vxIkoQDCfxQLmspR8+SeTj5IpGNGzfSr18/XfuBAwfo260D8xrIqFHfjKuhYQzq35309DQ6d+6it6+MjAzWr1/Pvh0bMTM3p0uPfjRr1swQkfe/YhjJGPiUuX37NjOnz+bRg0eU9S3LqDEjKFKkiJ7N/fv3ad60BcU0VWmV5ztSRRI7V+8nOjqa9RvWAdqb+c6dO1EmqPExyXIX2Ssc8MwoTNXKVUlOTUaV+eRuLBlTxrak3n5kyDA2MqFv334UL14cJycnHB0d6dK+M49TAylqXlC3rxsZT+jdvy/TZ0zXP9bb91i26xB1zYpjJjPmctozZA7mdOrUSc/O1taWPQf20fnrDuxIvI8ANMYy9h7crycwAHny5OHc5YuMGDSEvocOYqQwomPHDsycOyfbjTNfvnycPHeWIQMGsuT8IYwVRnTp1Ik/F8zPZtuoUSN6DBhA23nzqOjgQExGBlFqNQeOHtUbKcrlcsZOnEyrxo2wNpJT18mGpwmpTHgczshRo/h5wkSdrUajwcvNhWtRyVRwsNC1HwlJpHjxEjRt3ZYXL17w4sULbt26RRO77CPSElZqBgzoz7Rp03B1dcXNzY3LZ0+woKGM5kW0YtjI25gVRkoG/TxGT2RUKhWtmjYgLfwmvSqkk5wuGPHdac536sOM2fOy7Ss+Pp5du3aRlJREo0aN8PHxyWbzZaNBqFP/7YP41/jicpeVL19efCqLMePi4ti8eTPh4eFUr16dhg0bZnNxnT59mhbNWuGsLo4lDiRIEUTIH3P67EnKlSuns+vRtQc3dz7Dx8hX16YUGRxKXkOFyuWJjIwkJCSE9PR0nI3caGzdRm8/T9LuE2EfTPtO7XF1dcXFxYUD+w9wcdsFGprX0918A9ICuWNxH/9gf70b8vnz52nZtAVFjT2xFZYESC+Q7I05f/lCNkHQaDSsW7eOVUuXk5yUTOv27Rg8ZDBWVlY5Xie1Ws2NGzeQJIly5crlGHjwv6JWq5HJZO98gg8LC+PMmTPY2tpSr169bCO5vzh58iTjRgzn+t27uDo4MGj4CH4cPDjb9jdu2MDIH/ozuoQ1JWzNOBmezG9PEjhx9jylS5fW297Ab9px/itr5DLtNoQQ1Nkeh1eVhpibmxMaGkpISAhBAX6EjbLF0iRrX0II8kyMo1bt2nh6euLh4UFMTAwXD/zBhR/UKORa27hkQfGZEtduP9Sbbzty5AidO7SjbnE5tuZqdt/Q0KvvAKbNmJPj+YeEhBAdHU2xYsVynOf72JAk6ca7Fke+i7Jl84szZ759tyFgbT39/97fx4ZBZP4FhBBcu3aNmJgYKlWqlGM00JUrV2jYoDEWOEKaKRmmURQrXZijxw7rfTlLFS8Dfo44Kgrq2kKVDxGe0bRq04KgoCCCg4O5e/MeFYwb4qBw09vP0aQNuBd1pnjx4ri7u2NlZcW0ydNonacLZjJz3fGeUh1g4q/j6datm65vQkICNarUIOVFMm5qVxLkifgp/dmzfw+1atXKdk5hYWGsWrmK54HBVK9dg44dO34SN5p/i+PHjzN/+lQCAwPwrVCR0b9MoHjx4no2Qgjq16qORfQjhpQ2RS6D3+6lE2jkyoWrN3RzNwClixZiesVo6hTMEsCb4SpabEynSMmyBAcH8+LFC4zlginNFQyqre/o6LhGQ2r+erRo0QIPDw8cHR1p3KA2OwZmUK2wVthjEwVVpyhYuWEftWvX1vWNi4ujR9evuXTpEvntTImIVzF12mz69O3Hx0zuiIyTOHOq27sNAWub2QaR+dT50CLz6tUr4uPjcXNzy/GJOigoiEYNmxAZEYOJwpzE1BjG/TyOn34ao7MRQlDQsxBShBs2Co/MNg2hsvN07deWWrVqERQUREBAAL8u/JW6Zn2QpKwRjlKkcTZ1HUbGCtzd3fHw8CA8NByC81DcpLLOLl2TyknlJoJCgrC3t9e1jx0zlpVLVlFYlMBYMiVI9hQ7LxvOXTyLiYmJ3vmkp6ezdetWzp46i5uHGz179cTV1TXXrqeBd5OSksKsGdPZumEdao2Gtu07Mmbsz9lGfhs3buTnof1Y1VxGRVcFdyLU9N6v4fsx0xjw/UAgM3R66GDkj1Yzu6X+6KrKPCW3w9Bb7OpbQOLKJP0HhbkHVZyJq8G0mfPw9PTE2tqa5o3r4Gl6mxnfmmFqLPHwuZIWE1JZ/edu6tXLir5Vq9XMmjWd3xYv5EVkHFUrlWHqjAXUqFEjty/be5ErIlPGUZw52eXdhoC13XyDyHzq/K8iI4QgPT0dExOTHF0niYmJ9OrZm7379qJQGGNubsbixb/Svn17vW2ULFGaqEANljJPJElCpUklXnaLLds24OvrS3BwMBcvXmT0iHEUkbfW21eCOoyA9LNoUAJgamqKMkNFJeP2mMuybiiv1FGE5b1CSPhznXvNz8+P8mUrUFBdBldFIVJEIo+lK7T+pjmLf1uU7Vz379/P8t9WkJSYRJv2renTp49eiK2BT5M/Vq9myoSxhEZE42Rvw8iffmHA9wP1Pmd+fn5UqVCa/b1UlHOTIYRg6y0No49Y8iwwlPj4eIKCgti+fTs3jy3jxCj9fSw6omLMFiVp2o8plpaWSOpkwjc5YmKUtZ+Vh5M55Fee3fuP6fY/YvggLp/awK9D7SjkZsKeM68YujCOI8fOUrZsWV1fIQSbNm1i2dL5xETHULN2XX76aTzu7tkjE/8fck1kTnR4tyFgbb/IIDKfOjmJjEajeWM4r0ajYcqUqcybN5fExCTc3NyYN28ubdu21bNr3rwF507fQCEckUkKlOokVPIwjh49TNWqVVEqlZw8eZJ2bdrjKKuhLx7KYOJVT1CpM3RtcowpZdZBz+6VOhScQ9i0ZQOenp7Y29szcsQoNv6+E291TYwkEzJEKk/kpxj2yw+MGDFc7xjv3LnDiCEjOX/pPLZ5bflh0A8MHzEsV+cwDHz8CCFIS0vD1NT0jXNN27dvZ0C/nhS0l5OUpiFdlodtuw5QpkwZnU1CQgKebvk5MUpNKXft9yc5TVBlipzegybj6upKUFAQV69e5c7lfTxcru8WPn0nnXaT41Bhhru7O87Ozly+dJYn2wvjYJvl0luwKYZ70ZVZv3G7rm3KlIls+nMxE4Z44uZszo6DEWzaG8/Va7dxdnbWO9ft27ezZs3vJCcn0aRJa77/fiB58uR5r2uVGyJTrnQ+ceZom3cbAlZOKwwi86nzushs3LiRMWPG8Pz5c5ycnBg/fjz9+vXT++KNHTuWXxf+hjLDHAkFGpGGwjiZPXt2U79+fUA7mVm4cBEsZD5oawNpSVVGYWKRjJm5KeHh4QghMJIscLeoo3dMyapIZDYRjBo9HA8PD9zd3fm6XQfUYQ7YKrwA0Ag1YfJz/DJ9BAMHDtT1VSqV9OvzHVu2bMHK1JaEtDj69OnDvAVz3yicBgy8D2lpaVy+fBkzMzMqVKiQ4+dpy5bNfP9dT9pXlLAxU7L5mjF1G7dl+cq1uu9RSkoK7q6OnJ1pTmHXrHme75ckEZRenuIlSxMcHMzjx49JjPXDb3dRvX1ce5BCy2HB+BTzxc3NDUdHR/5YvZxbh6vj7JQ1uh4+5QmWji2ZOTMr6GDkyGEcPLCJoYNKkdfGhHXrnxIeYcrZs5feaz4wd0TGXpw53PLdhoCV8x8GkfnU+UtkduzYQbdu3UlNVQNyQIO5uZxZs2YyYMAAQDvfYGtrh1qZF5mU9eVQqZOwtpFRtGgRQkJCCAkJQWgU2Jrrh/NmqBMQiki++rot7u7uODk5MXTIMOyk8pjIte4tIQSvpPuM+uV7RowYoet79+5d6tauj7HGCinDjBR5BNVqVGHXnh05Ri5FR0cTHByMl5cXNjY5Vl81YOCDEBwczKZNm0hMTKBZs+ZUqVIl2whpyZJfmTNtLGPbK/DKL2fbBTWHbplw+dodHB0dAe18pqeHM3c3euL42khm/sZo1hwxxsXNi+fPnxMcHIyHixG3j+o/rJ28EE2/MU+oXacprq6umJubM3/+LG5f74KtjVZQhBC0bX+Yb7r+pLfm6k3kjsjYibOHmr3bELB0Wf/ZicwXu05m7NixpKaqkXTiISclRc2wYcM5cuQI4eHhPH/+nJSUFMyM7fX6ymQmxMdHIUkS1apVI1++fPy2ZClqTTpy2WsT47IUuvfoyqJFWXMepqam/DBwEKYqV2TCBLVxLA4uefjuu+/09lGqVCmehwaxc+dOXrx4QfXq1alcufIb3Rv58uUjX77/q7aSAQP/Ex4eHowe/faS8d9//yOFCvmwbPFcIi+EU6N2Iy79PkInMADW1tb06dOHTuP+ZOFQO7zdTNh9+hVzNiRw7MQ5nasuKCiI8r4lSEtXY2qS5Tl4+DQRhdyEy5cvExoaSkZGBnVqu+kEBrSphFq1cOPMmWPvJTK5ggByKdX/p8gXKzJBQcFoRzCvIyMtLRl/f39cXV0pUaIEGzduQiOUyKSsJysh0qlduzbHj2dlBraxsWXO7PmolLbIZSaoRQIKs1RGjhypt4cePXpQvHhxlixeSkREBM2af0vPnj2xsLDg75ibm/PNN9/k5mkbMPCv0ahRIxo1avRWm+kz5jJ7tgNtxywgPCKOapXLsmvPBr25IE9PT6pXr8HQSU+YMdobK0sjLt2IY/7KUHbvPUqlSpUQQrB7925++WVgtn0EBSfj4OCcrf3DIZC+4LQyX6y7rHjx4jx6FPDaSAaEUOPoaE14eLhuxDBnzhwmTJiMMt0MmWSEWpOKkUkax48fo0qVKq/1FWzZsoXZs+YSGRVJvbp1mTBxfLZEkQYMGPj/SUhIoP93Pdm//yCWeYwxMjZj9pxFfPXVVzobtVpN8WLe9OjmRr8+JZHLZVy99oLOXY9x7vyV98pMkCvuslI24tzebEmScyRPgR2fnbvsixWZffv20bFjR1JTNWhHNGrMzOQsWvQrPXv21NkLIVi9ejVTpkwjIuIFJUuWYu7c2f9a3L4BAwayiI+P5+XLl7i7u+cYJenv70+nTu0IDw/BysqUhAQVv/22gpYt328iPldEpmRecX7X+90vLLz3G0TmU+f16LK9e/cycuQo/P39cHV1Y/LkSQb31GfOXyUMwsLC8PX1xcnJ6a32UVFR+Pn5UahQIRwcHP6hozSQ2zx58oSkpCRKlSr1xpQ/OZErIlPCWpzfWe29bC18Dn12IvNFx7i2bNmSx48foVQqCQwMMAjMR4QQgtu3b3Px4sW3VoXMyMjg55/Gkj+fIxZm5rRs0ozHjx/naBsVFUW1ChVpXrs+k/r+iE9BL0YMHZZjKWSlUkm/Xr3w9ixA/3bttT9799ElB/07ISEhDB00iBoVytO1QweuXbv2v524gQ+Cj48Pvr6+/5XA5CaSRv1er8+RL1pkDPzz+Pv7c+PGDTIyMt5o8+jRI4oVLkLT2g3p1rIDLk7O7NixI0fb7p2/4dCKzQzOW405nq2xvBNNzarVCQ8Pz27bqQsuEWks9WrAL/krsaxwY/au3cj69euz2U6ZNIk7B46yuVRtlniVZ3Op2tzcf5gpkybleE4Vy5Qh7sB+uglB/rt3aFavHnv35lxC/erVqzStVxd7a2vKFC3CmjVrchQ6A58LQhtd9j6vz5Av2l1m4J8jNDSUr9t8xZNHT8hjbE6qSGfR0sV07NhRz06lUuHlUYBqmoJUsSyCJEkEp0WxMvYEl29c1Zus9fPzo0Lpcsz1bI2xLCuAY13UFayrF6VNu7a64mLR0dHMmjqd9SVaYvKa7ZWXoaxPCaB91y66bMsymYxF8+azpEhlPM2zin4FpiQw2O86K9aswcLCAgsLC8zNzZk6YQJOjx7yXcGsII+rcXFMj4zmaVCQ3iLGmzdv0rB2LYYXcqBu/rw8TUhl8pMI+o0Yw9DX1kn9xb1795g7fRr3797Cp2hxho0Zq5dd28CHJTfcZb7FLcWFLe+3CbOSp9+6P0mSVgPNgSghRInMti3AX1+MvMBLIUSZHPoGAYmAGlD9U265LzaE2UDusGnTJqZOnEpwSDClipdkysyp1Kmjv0hOCEHzRs2wj7TgR/vOyCUZ4elRDOj9HT4+PpQtWxYhBPHx8Wzfvh1FiqCqQ9aqbw9TB3xNCtCkURPsHeyJj4/XvbxM7fUEBsDHxIGVu/eyfaf+6MdSboyxpD85nNfIjOjoaH799Vc0Gg0ajQYhBBq1mvwm5nq2+U3MiU9MzFZJ0lwuZ1PlinptFWxsiLxzjzp16uDi4oKdnR329vbs37mDAQXs6VBAO7+Tz9SY38yM6Th1Ct//+KNeAtIrV67QrGF9BvhY0qGAKddDLtGoTi227t6b7RqDNn/ezp07iY2NpU6dOnq5vgz8iwiBpHrzyP2/ZA2wGFiXtXmhS4wmSdJc4NVb+tcRQsTk1sG8DwaRMZANIQRXr17l6NGjWFlZ0aFDhxwnyJf/vpyfR4yjulFValpWJdgvhDYt2rB7/269NO8XLlzgRUg4bW2zcrE5mzhQ1rgITRs1wcjUmIiICJRKbUbFouZu2fZlp7DkYUoE9vb2FCpUCBsbG9RqNZvWrEelUaOQZYmHf0Ycnbt9w6gxozE1NcXU1BQjIyNKFyvOvaQoSllmLQA89eo53w38njnz9Ytx1a5SlRMxYTR1zEq4eCImjEply7Hsj9UkJyeTnJxMSkoKowYNIiw1lQKvrXVKUKlQCUFKSgrXrl0jNjaW+Ph4LBQyptYuobevgpZmqNNSqVixIgULFsTZ2RkXFxe2rF/DL6Ws6OitzeDgm88cZ3M5Pw0bzKWbd/S2cfnyZVo1bUzF/Ea4mGmYP208DZu1YsUf6wzphT4GcskVJoQ4K0mSZ07vSdovV3ugbq7sLJcwiMwXiBDijZkDhBB8270n+3ftx0V4olJk8PNPP7Np6yaaNctKjaHRaBj/83gamNTD0Vj7VF7ErDAaoaFb5274VvLVpQCJjY3Fxdgh2z7tFHmRhETdunVxcnIif/78KBQKRg8bSbI6DQu5dqW2RgjuqUOZvXAuXbrop0wPDw5hxY3LdLAtg6XclAsv/bmS+pxbE/dly8i7dOUKunXsTJO8BXA1ysO1tCiCFOmsGpN9tfrMBfNp2qAhUap0Slrk5V7yS3bFhnJowzG9omGgrZUye9RICuexxMHUhFS1mlkBgXTq0IHVf/6ps1OpVDSuU5t78RF6JZijUjNI14C9vT1+fn6cOXOG+Ph4FBI089WvcNrE3Yo+p+7yww8/ULBgQTw9PXFzc6Nju9YsqGFMMy/tdsdX0dBszwG2bt2azSV58+ZNRg/7gdPnr2BrnYfeffvxy4TJemW4DeQmAkmj+Sd2VAOIFEI8e+OBwFFJkgTwuxBi+T9xUAaR+UIQQrB48RJmTptJeGQ4Rb2LMmveTD3hAG1Y99E9R2lq8jVGmVkOCuJD5w6d2bB5A6GhoQQEBPDo0SNiYmNwdNIP63U3ceV4xEmePXuGu7s7FStWxNbWlvlz5pGoSsZSkfW0/1TznJHjRjF48GC9bTwPDGLJqvXUNCmKmdyYa+n+5C3oyNdff53tvDbv2MaoYSMYu3YNqelpVKtYhWNLTuSY8r1Zs2acvXyRpYsW8ygomMZ1W9Knb99slTkBKlWqxIWrV5g/azbb7t6lRKUqXBgxPFtZa9BmcQjy96fd/Pl4WFsTkpBAvXr1+HXZMj07hULBmAkT+aZdG/KbG1PZ3oqQlHR+ehDOgIHfM3vefJ1tamoqRQp6EJCQQWn7rCSQQYkZmBnJ+eOPP0hOTta1u1rKaeaVVcfHwkhG/+Jyfps/m4oVK+Lu7o5CoSAgIIDG9WszoYaazaOtCE3QMGrPMvqFPOeP9ZuynVt0dDQ7duwgOTmZJk2aUKxYsWw2Bt7Bf5dWxl6SpNcnjZf/F2LQCcj+T8yimhAiXJIkB+CYJEmPhRBn3/fA/lcME/+fATExMWzfvp2kpCQaN25MiRIlstnMmjmbuVMXUExTnbwyeyJVz3konWf7nm3Ur18/M4w7kD49+6K6LaOImX6yz93xG4lTa125xsbGeHp6EhwQTCebr7E1stXZ+aX6E+YWwfU7+td4wi/jWbHwd6oYlyKP3Jz7Sj+SbJRcu3UdS0tLPVshBHv37mXl0uUkJybRukO7d9azEUKg0Wj+1bIFL1++5NGjR7i5ub21cNuOHTsYO3woIeERmJqaMGDA94yfPFmviiXA3Nmz2fLrDFZXs8fB3IjYNBX9LsZQt+t3jJ80WVfX5ciRI6xdMJWrXfRz7O14ksyPx2JJUgoUCgWenp6gzqClazRTG2Rdy6R0gc+vadx5+FTvuPft20f3bzrQuJicvCZqdt2T6NazLzNmzXtnOerPhVyZ+C9qLi79Ufi9bE2q3Hnn/jLdZfv/mvjPbFMAYYCvECL0XfuRJGkCkCSEyLlOdi5iEJlPnAMHDtCxfSfs5G7I1EbEEkzP3t8yb8Fc3Y1ApVLhYO+Ir6oJVvIsQQhRPiHA5BZ57awICgpCrVYjR0FFi+oUNSult5/DaTsZ/MuPdOzYERcXF2QyGdOmTGPZnKXUNa6FrcKW8IwXHE8/xeoNq7OtqBZCsGfPHpb++hvx8fE0b9WcHwcPynEU8SUghCAxMRELC4s3CqNGo+GnkSP4fdkynK3MCE9IoXuPHsxZ8KueIKlUKjxdnFhaQ04td614ZKgFzfe8onbH7yhcuDB+fn74+/tz/sRBFjeGJj76rrEqyxIxdi1L5cqVKVy4MG5ubvTo2pH9fVRU8NDO6cQlC6ouNGLVpv16c25CCJYtXcqiBTMIDY+iUvkyTJo+Xy/t0qdKbonM5dWF3svWuOq9/1VkGgNjhBDZ655r37cAZEKIxMzfjwGThBCH3/M0/mcMIvOREhMTw9DBw9ixcwdCCFq2bMWChfP0JuCTk5PJ7+RCEWVdrOXayWylSOeubB+/TBmLpaUlT58+5d69exw7fJyWlvqZnlM0iZxM3UTrdq3w9vbG29ub6OhoZk+aQyOjNhjJtDeiCGUYl8RJXkS90It+EkIwa8Ys5syeQ0JiAvkdnZgyY6phUWsuk5CQQGBgIB4eHm8U5RMnTtChbWuaFDDB2VTF3udQrHw1tuzcoydIg3/4HuP765lUN2tRYlK6oODcBNy9ihAUFKRzw1XylDg3VF+M5pxQc000ZOny1Tg4aOfZpkyewM61c1nQRUkxVxn7b6oZsUXBkePnsoVbp6WlsXv3bgICAihTpgyNGjX6qIvm5YrIFDETl1d4vpetcc3H7wph3gTUBuyBSGC8EGKVJElrgMtCiGWv2ToDK4UQTSVJKgjsynxLAWwUQkz9H07nv8YgMv8Cd+7cYdOmzajVar7++isqVtQPf1Wr1ZQoXopXz8FOFEOSJGLFY4wdknn89CEmJia8evWKlStXMnv8IkqKJnr9gzPu4K+6igY1xsbGeHl5EeAXSA3jdtlGMsalUjh/+ZyuTQhB/7792bppG66yAqgUGYRmBLN95zYaNmyY4/loNBrS0tIwMzP7YtwoHyORkZFs2rSJmOho6tarR506dbL9P/z9/alSoSwTaqjpWMpEOydzXOBUtgl//LkZIQQRERGsWLGCM1tmcvg7/bmE+SdU/HJATboKrKysKFSoEE8e3eXOdAWe+bKi2BYdUXE5uSGbt+/TtQUGBlK/TjUKOmRQtoCak3clTKw9OHT0DFZWVvyd9PR0Xr16hb29/b8WIZcrIuNjKi4v93gvW+PaTz+7tDIGkclFhBA8fPiQ5ORkypYtm2MKi6lTpzFj2kxMNE4gIEMRxXf9+zJr9kydzf79++nZpT+uSv2bhL/qKE4FrImPjycqKgoAK8mBimb6paCfq+7iXt2C5St/1yUOnD1rDnMmz6OYpjrW8nxEqoJ5KF1g597t1KuXPUPs7du3dSHMX3/9NXZ2dtlsDHya/BVddurcZezyWtKrT1/GT5yiF132V2nlo/2VlHbR3uATUgVVFiro8f1Y8uTJw9OnT7l16xb+Dy4T9pt+lcm7zzU0nClo0aYzhQsXxtvbm1/nz6ChTwCj2muDP4QQfDsvGefSPZg1OyuEXKVSMW7sKJYv/x0JDZaWlkyaMotu3br/A1dHn9wSmSvL3jxH9zpGdf0/O5ExRJf9F7wt9Pfp06e0bNmasLBwFHIjJEnDH2tW06pVK52Nv78/06ZOJ59UGYVC+6VUC0+WLFmKo5MDKpUKPz8/Tpw4gZRiiWSsvy9z4UhKSjwtWrTQ+c179+xDgiYGK5l20lclMog19ufXkWv1ygwMHzEMCwtzZkybSXhEGEV9irFpzoYcBQagTJkyejU8DHw+lCtXjqOnLrzVxsrKimUr/qBRnx60KQ15TVRsu2tMi7adGDNmjO57kJSUhJuLA+HxGpxtskYbV/w0mJqYc+jQIf744w8AjBSwf6SLzkaSJIa3M6bZ+D/4pmsPvLy8sLCw4KcxI7h+bgPX1hXAzdGYaw+S6fLTj9jZ2ecYDbls6QJiYqKoXacRw4aN1CuE9nEg4J8JYf4oMYxk3oFarWbKlKksXLiQly/jKVWqNIsW/aqX6l+tVuPh7klCnAJjmR2SJKFUJ6GUhXLz5nVsbGwICAhgyZIl7N9+HjuFfvRXTPoDXikDAXBwcMDW1pawgFgKyRvriVq44jxzfpukt1Zkx44ddO/ag3yyAkgqI+IUQXzdoR3LV/5ucF0Z+L8JDQ1ly5YtJCUl0axZM8qXz/6QPWrEEC4dXsmy7iq8nSQO3dHQd7WcHXuPUq1aNRITE7lz5w4N69chcqsjZiZZYvQgSEm1wZEkp2nvQ46OjiS+iuH+tqK4OGSNrHaciGfFEQdOnr6sa5szZya//zaLMd+74+5izrYDkRw7n8qVq7ezVYm9evUqmzb9iUqlok2br3J0JeZEroxkCpuIK0vyv5etUcPgz24k80WLzKVLlxg3bhz37t3H27sQEydOpH79+nr2Awf+wNo1f6JMN0OSjFBrUjAySeX8+XO6tB379u3jmy7fYqzRL1CWnBGCiniUyqyUEhby/DiZ+erZxake0qV3U6ZMmYK1tTUqlYriRUuQFGaEHcWQ0M7JyOxe8tTvMaam+q6JsLAwtmzZQmJiIk2bNqVChQq5dr0MGHgXarWaqVMmsmTRQuJeJVGySEGmzFxI06ZN9eyaNKxJbY/7DPsqD6D1DPRekAT5mtCsRWv8/f25c+cORw/tJOKYfgj9s+dpVOn+hAKFilOgQAFcXFxYv24VV/dXw90la2HrwHGPcPPpxMSJk3VtU6dOZunSBfToVgQjIxl/bnhGw0atWLx42TuFJndExlhcWfT2khJ/YdQ4xCAynzp/icyZM2do2rQpqalqsoqWKfjzz/W0adMG0K57yJ/fGdR2SK/lvFKpE3BwssDZOT9BQUFER0djJLfC2lQ/Fj5VGYWLpzkDBnyHl5cXlpaWNGnSDDt8MZFrJzqVmmRixDXu3b9DwYIFdX2jo6P5YeAgdu/eiUYImjdrwaLFC3FxccGAgY8RIQRKpfKNmQP8/f2pX6c6RVyUlPVUcvyuHMnMhaMnzmNtbQ1o52M83BzZO8eBkt5Z4rFkazQrDygoWKg4gYGBPHv2DE9XI24d0c/hdvRsFEMmBvJV++54eHhgYmLCqFFDuHKhC46O2rmgxMQMqtfeysaNe94ZZp0bIlPe20hcWWD/bkNA0TzisxOZDz4nI2nvzteBMCFEc0mSbIEtgCcQBLQXQsRn2o4BeqHNEvqjEOJIZrsv2sRwZsBBYJAQQkiSZII2UZwvEAt0EEIEvc9xDR8+nNRUNZL01+S8jNRUFT179uLIkSM8f/6cp0+fkp6uxNRIP8RSJpkQFRVN8eLFKFu2LNbW1ixc8CsaoUKWWc5ZCIHCJI1x46bQtWtXXd+VK5fTu3dfLDNDjhNVEcxfMF9PYADy5cvH5i0bdSngDa4vAx87kiS9NTWNl5cXD58EsH37dgIDAxnXqQxNmzbVC7FWKBT8Mn4KHX4aw8wf7ChZyIzDFxOY9kc8R46d0YVEP3v2jOpVy6FUajAyynK/PQtMIiU1g0WLFunqEH3VzkcnMACWlsa0/8qLffv2/nNreb7gOZl/YuJ/EPAI+CtGcTRwQggxQ5Kk0Zl/j5IkqRjQESgOOAPHJUkqLIRQA0uBvsBltCLTGDiEVpDihRCFJEnqCMwEOvAe3Lt3n+ynL+flS20mYA8PD3x8fAgKCkYItd5IBklJq1Yt2bZtq64pPT2DNavXo1FaI0OOZJRIwUKutG/fXm8PnTt3pmHDhuzbtw+1Wk3z5s3fWp3RIC65T1paGgEBAeTPnx8bG5t32mdkZKDRaLK5KQ3895iZmek9dOVEv+/6Y2efj/lzpxL8PITyvuU5fHSq3pobb29vypT1ZeysZ0waXghTEzl3Hr5iwcowdu46QJUqVYiKimLx4sXcvZO9FlFSkgonZ/Ns7R8EwRctMgghPtgLcAVOoM0Kuj+z7QmQP/P3/MCTzN/HoF2x+lffI0CVTJvHr7V3QpvcTWeT+bsCiCHTBfiml6+vrxBCCA8PTyFJZkImy6N7SZK5sLa2FhqNRvzFDz/8KPJY5BUmivzC1MhNGMnthLm5hbh9+7Z4HY1GI7Zt2ybq1qknKlSoJObMmSOSk5OFgQ/P8ePHRfvW7UT9GrXE7FmzRUJCwhtt586eI2wtrYWHrYOwNDMX337TTaSmpuZoGxERIb5q1UqYGhsLY4WRqF+jpnj8+PEbt63RaMTp06fFypUrxdWrV/U+RwZyn5iYGNGsaX1ha2MhfArlE06OtmLt2jV6NrGxscLW1kqcPNpJvIodIl7FDhE3rvQQ9vZW4tmzZ+/cB3Bd/J/3QV8vuVDttH2vV27s72N7fWiR2Y7WlVX7NZF5+Teb+Myfi4FvXmtfBXwFlAeOv9Ze47Vt3QdcX3vPH7DP4Tj6onXZXXd3dxdCCLF8+XJhYaEVlr8ExsIij5g8ebLeh0ylUokpU6YIe/t8Qi6XC1/fCuL8+fPCwIcjJSVFzJk9R1QpV1HUqVZTrFu3TqjV6hxt586eI5ys7ER35ypisHtdUdnBW5QsUkwkJiZms92yZYvwyGsvfi/eXOz37SQ2l24nqjsWFP169c5mq1KpREkfH9HFw0ccrtxEnKjaTPzoVVLkt88nXr58mc0+JiZGVChdWhTOZy/aeBUQ7jY2olGdOm990IiLixOnT58WT58+/S+ujoG/ExoaKu7evSvS09NzfH/fvn3C1tZKNGxYRLRoXlxYW1uIVatWvte2c0VkCsqFarvNe70+R5H5YO4ySZL+qt52Q5Kk2u/TJYc28Zb2t/XRb9BmMV0O2ol/gN69e/Py5UsmT56CSqVCJpMYPHgQP/30k15fuVzO2LFjGTt27HucgoG34e/vz8mTJ8mbNy/NmzfPMeGlUqmkXs06pAXFUdmkEBkaFRMHjeHsyTOs+GOlnu3Lly+ZMH48k1ybYm+sjVgqZ+nO4qhzzJk9m06dO5OSkqJ7TfxpHN3siuJiqk3ImUdhzHeOpemzfj0ly5bB3NwcuVyOTCbj/v37pEfF8l2xKjqXZfv8BXiQmsiiRYv44YcfsLS01K1EHzRgAN6JrxhdthSSJKHSaBj9+BkTx49n5uzZescthGDKxAnMnTOHwrZWBL9KolSZsmzeucuw6PV/wMXF5a0BMc2bNycoKJRDhw6hVCr5Y03jf/g6C1Cp/sH9fVx8yDmZakBLSZKaAqaAlSRJfwKRkiTlF0K8kCQpPxCVaR8KvF6tyhUIz2x3zaH99T6hmVlIrYG49zk4SZIYMWIEgwcPJioqCnt7e728XAZyDyEEI4ePZPmy3/GxKECSSGVAv/4cOHwwW0qdXbt2ERcYwQDbRsgyb+5FLdyYvGULRUsWw8jIiOjoaKKiorh37x4OMgudwID2/1rR1I1ZU6YzcdIkvW2byhS4FNWPAMxrZIqkUjNw4MBsx93YwS3bnJiPsTkTfvmFn3/+GUmSsLS0xMrKiojwcE7Xqq6zV8hk9Hd3oc+KFTRt3hxnZ2ecnZ2xsLBg27Zt/PnbIo7U8sHRzBilRsO0R4H06voNuw8eynYckZGRLJw3l4unT5Lf1ZUBg4fprdMy8G4sLS2zzY/+YwhA82VF8b7OBxMZIcQYtPMsZI5khgshvpEkaTbQHZiR+XNPZpe9wEZJkuahnfj3Bq4KIdSSJCVKklQZuAJ0Axa91qc7cAmta+1k5hD3vTEyMjKEBf+PpKens3z5crZt2IqJqSnf9v2Wjh07ZsszdejQITasWs8Auw6YZxYie5QcQJsWrTlz4SwhISEEBwcTFBTEts1bKCZz1gkMgInMiAJyB4YNGwZohcTe3p48efKQoExBCP1MDLHKZHwrlGfAoB8wNzfHzMwMc3Nzpk2cxOXHYXxlmpUn63FSDHltbXlw7QqSJKFWq9FoNFy5coVxA39ELQTy17Z9I+Ul3Xr0oESJErx69YpXr14RFxfHpg1/YirXP28LuYKExES9jMVWVlYYa9RMKuGMo5k2EstIJmOkjxNVjp0mLCxM7/P44sULKvuWpZ49DHQxwT8inI6tmjFt3q9079Hjjf8btVr9USee/OIQX+7E/7+RVmYGsFWSpF7Ac+BrACHEA0mStgIPARXwvdBGlgH0JyuE+VDmC7TzNuslSfJDO4LRLwFo4IOhUqloWLchLx6GU0xWBKVQMWrAKE4dP8WK1St0dmlpafw6byHlFUV1AgNQ1KIgR0LP4+3trWuTJAnLPJbYyLMnQ0w2UrJ48WLat2+Pra0tcrkcIQSli5XgUPxDGtsUQyZJvEh/xfFkP/bMP5AtPHXurwupUaUqKgS+eRwJSn3F5vgnzPttsbbWymt4eXmx8relTAm8RzenApjIZOyIek68uQlLlizJ5up7ERTEjvAXdHbLGnRvDntB06ZN+X7wYMLDw3WvrevWkN9MP9TXTCFHoVbh7u6Oh4cHXl5eeHl58eTRAxrYaZheUbuCvZYLVHAwo8uwIXTq3DlbyPCK5b8zY/IEAsMi8fZ04eeJ0/jmHdFcBj40wjCS+dAIIU4DpzN/jwVyTJgltKmns6WfFkJcB7JV4hJCpJEpUgZyB41Gw+JFi1k471eiY6OpXrUaM+bMoFQp/foy+/btI/hhEG3MWiKTtKJQUOPJHxvWk6ZMIzo6midPnhAcHIwRCprbZS9zYWGah2/79aFJkyZ4enri6upKZGQkpYqV5ElKKD7mrmiE4FLiY1JN1PTt21cv6agkSew9dIA2zVtyOnQfeY0tCE+NZ9acOTmufyhatCiXrl1lxpSprLp4CY/CBdg4egd162YviS5JEvuPHmHCz78wZsMGMpRKWrVqxdkZ03OcS1q4bBn1atbkYWoaxUxMuJGaxjO1hnPLlmUbKcuFYO/RXZSxzXLz3YpLQmZqzqih3xMYGIi/vz/bt28nIyGe4Y30q3yWtDPFSJ3OpEmTqF+/PkWLFsXBwYEVy39n7oRRrKhriq+TC5fCMug/dABGxsZ06JBzZH9QUBBCCDw9PQ3h8h+KL9xd9sWu+P9SSU5ORqFQvHH+acSwEWxeuZUyUiUs5dYEZfjxSLrNletX8Pb2JiIiggcPHjBpwiS4p6FCHv0UOfvjDhGkCaZEiRL4+Pjg4+NDVFQUhzbso1ve5sgz1xuFp0exOekI4ZEvst20jx07xrffdEfK0JCuVuLkkp+tu7bnWPoYtHM+9+/fJy4ujvLly2NhYZGj3YcmNjaWNX/8wbNHjyhdvjzffPNNtqqfoHWBVSlfjqp55NS3tyAgOYMVgbEsWrEy27xBo9o1aCMF0s7LWteWqtJQdMNTUlRZLhgbGxtEejI7WuelfP6s/+3JoDQmPsrLrQdP9bZ7//59en7TnufBwUgSOLu4smr9FkNS1L+RKyv+C8jElfFvXqT6Oopv0z+7Ff8GkflCuHPnDv16f8fN2zeRSRKtWrZm6fLfsLXNqi/z8uVLXJ3daGnWETNZ1kK1mymXibIMJU2ZRlxcVlxFSfPiNMirPyjdk7qfWStn07ZtVvkBlUpFq2YtuX/1Lj6SBymydO6lPmXV2tV89dVXOR6vWq3m3r17mJqa4uPj89k9ZUdHR7P414VcOn0aZ3d3vh88JMecc/v27WNwz65sqZsPD0tj0tUaJtyII9qlNIuXr+LRo0c8evSIBw8esHLlCuKHuOpdq6QMDZ6/hdOnX39KlixJyZIlKVCgABXKluSXaml0LasdGW6+o2TsGWOe+AfnWNvl7t27hIeHU7Zs2Y8wy/GHI1dyl3nKxJVx2ct+5IRRnwyDyHzqfI4ik5SUxOPHj3FycsqxtnxERATFfIpTQFkGd0URVCh5qrmOVWEFF69c4NmzZ9y9e5cjR46wZ9M+2lh20e+vDOOC6gQdurSnRIkSlChRgrx581K7Rm0amdbHzcQVIQSPUh9z2+geQSFB2UZKGo2GQ4cOcfjAIWzt7ejeo3u2VDoGcmbenNlMmTgRj7xmhL5KoWKlSqzfsl3vAQHAp6Abv1bMoIpr1rU/EpDK9ydTSBcKEhISdO21ChpxuKf+iK/TdkHTAbPp06ePri06OpqvWjUhyP8x3k5G3AhMo1+//kyfNfezE/6cyBWR8ZCJK2PfU2T6fX4iY6gn84kza+ZsJk2aTB4ja5LSX1GrVk02bd2o9zS6YsVK8gl3PI2KA2CMnOKyahy5uxYLCwuUSiWgXRMkCRkZmnSMZVk3qlh1NE2bNeH333/X2/fWHVvp3qU78hQ5Ko0Sa7u8HN1zNEdXnEwmo1mzZtnqgRh4N0OHj6BPv+948OABTk5O2YIU/mLchKl8N+x75tcSVHQ25kJoOkPOpLFy3SZatGjB8+fPuXfvHosXL6Zw0pls/b2t0vjll1+4cOECpUuXplSpUsyZMRHfPPc5+osGuUxJTJKg8dIVFC9VNlt6GKVSyb59+3jy5AklSpSgadOmhgi3v/hyg8sMI5mPFSEE586d49q1a3h4eNCiRYtsN++dO3fSp1t/fNT1MZNZoRYqAqXLlK3nzaQpE7h79y53795l4/pNOLz0poCxfuzE1fRDlK7vQ8eOHSlVqhRFihShT88+XNh3GV95NSxkeXieEcA1zXlOnT2ZrV47aF1ht2/fxsTEhBIlSnwRT7cfM5s2bWLm5F94GhBMscJe/Dx5hl7hPIDTp0/T/5uWXO0rw0iu/X+pNQLfJelYuBQjPDyciIgIAMyMIHK2EWavFdDbd1fDgtslOHPplq7txYsX1K9TFVujeCoXSOfsMxPUJvk5evJCthHXp0SujWRGv+dIZsDnN5IxiMxHSFpaGk0aNePOrfuYqR1QGyUhN1Nx7sIZPRdTtco1SbhlioPCS9emEhmcT12LBm30t7GxMfny5UOKMaOiSROdnUaoOaXZxLlLZyhZMqt2R0ZGBiOHj2LVqpWkZ6TjXbAwCxbPp0GDBv/AmRv4JxBC0LxxPVSh1xlSSYNMgoVXZWTYl+LIibPIZDKioqI4ePAgPw3tR/AU/XVI14I0NP5VhWfhUpQsWZJSpUpx5OAuyue9w7QOct0+Bq4BqUB7lv6+Wm//d+7cYcG8Gfg/e0TJMhUYMnQUhQoV+icvwXuTKyLjLhOXR73fxL/xwLdP/EuStBr4K5tKicy2CUAfIDrT7CchxMEc+jYGFqKtbbJSCDHjvzmP/xWDyPzDhIaGMnXKNI4fP4mjowPDRwyldevWejYTJ07it9lrcdFURcoMD45WP8TaK4OBPw7g3r173Lt3j0vnr1DauDlWMv0qgFdUG5k0fTyNGjWicOHCpKSkUKxIcawTXPCQFSVDpOMnu0nJaj7sP7Q3x+NUq9WkpaX9a5FaBj4s6enpLFr0K9s2/IEQgnaduvPjj4P0Iv3UajXeBVxY0S6WWoWz1i4N3CK4m1YKGztH7t69S2hoKHIZRP5uQV6LLDEKjtZQ/mdB4PMXunoxJ0+epOPXLRna1oQKPkacvqvk94NKjp88ny1MHrTZDqKjo/H29v5XMnLkmsiMeE+R+fGdIlMTSALW/U1kkoQQc97STw48BRqgzZRyDegkhHj4vufxv2IQmVwkOTmZs2fPYmxsTM2aNfXWdIDWpVC6VBnUyVaY4oBSk0K60XPG/TyaESNHANpJ/CKFi5MnrjgW8izx0Ag1d1I3I1BjaWlJyZIliY99SWqQCQXllXR2CZpogszOEh4Zprf/0NBQxowcw4EDBzEzM6Nn756M+3msIZWOgbeyf/9+enbtwPc1VBRx1LD3gQlXwq24cOWWLsosJiYG5/yORC4zw8o8S2RCYzX4DEkhXQVubm6UKFGCB3evMreXjNbVs6IXF+9O5PRzX3bvO6prS0hIoG/vrhw9ehxHezPiXqmYMm0mffr0++dOnlwSGTeZuDT0/cpEmAxNfef+JEnyRJsk+L8RmSrABCFEo8y/xwAIIaa/14H9Hxgm/nOJLVu20KtXb0yM8iCEBkmuZu/ePVSrVk1nM2f2XDSpVljLtfmzTOR5MdHkZey4nzl2/BhPnz4lODgYGQq8TfTnTyQkjIyMuHDxMr6+vkiSxPPnz/EtW4HAtCvkVbuSIl4RYXSPRQsXZhM4V1dX1m9c/+EvhIHPiubNm3Pi7GWWLVnI7ZBAKrWox6J+3+nNs9jb29O6RWPmHTrFhHZZ7rLZBwR169ahZp2GPHjwgLt37xL2IpYWVfQXl7avZc7P355m9erVFC1alKJFi9K3d1csVDfx31cECzM5D/1TaT1sFB4eBWjYsKGurxCCrVu3snHDapTKDFq26kDPnj3fWjztn0cCzXvPVdpLkvT6U/DyzAS/72KgJEnd0GabHyYyC0G+hgsQ8trfoUAl/gEMI5l3oFQqmTJlCkt/W0piUhK1atVi/vx5FC1aVGfj7+9PqZKlMRYeKOTaJ7QM1SuEcRSXLl3g+fPnPHnyhKlTZqBI9sRMoZ8BNiT5NAUKuVChQgWKFSvGjRs3uXD4Li5kZQCOVT3Dpkg6t+7c0OsbFhbG7FlzOHPqHO4ebgwfOdSQPNHAP05oaCh1alamgE0SlTxTOfPMjHiVHSfPXCZfPu2IXK1WY29rxY3fbHB3yHq+vfwonSajo0hKzQrBMjeVEXq0DBZmWdFpa/dGs/9WIfbsO6ZrGzCgDxfP7ePHni6YmMhZsSEcMysf9u8/mi2y7cGDB5w6dQo7OztatWqFufm7i5blzkhGLi4Nyp4lIidMRiT/LyMZR7S1tAQwGW29rp5/6/M10EgI0Tvz765ARSHED//l6fzXfNEjmaCgIObMmcO1a9coUaIEI0aMyLaqvFu37uzbdxhVuimSZMepE1epUrkKDx4+wMXFBSEES5b8hkxY6QQGwFhhzcvkF5QokTUiMTYyxVKWhBlZIqMRaoxNZZw4cQI3N20S6sTERGpUq0Vo8GkUqXZgmkK6cSz7/jyV7RxcXFxYsHB+bl+aTwohBJGRkRgbG78zkikqKopFC3/l4pmzuLq7MXDI4BwXQf5FYmIimzZt4tH9B5QsU5oOHToY5qlywNXVlXsP/di5cydPnjzhh44laNWqld6IQi6X06t3Lwb99ifrRubB0lxG9Es1I1akMWHyTFq1as2jR484efIke7at0BMYgMIeppxdcJoSJUpQuHBhbG1t2bN7E/dO1sYyj3bk3ry+E7XaXeXw4cO6cHkhBAMG9GX37u00bVyQ0LBkhg79gX37DlO+/D8QyCVAvP9I5r/fvBCRf/0uSdIKYH8OZm/Kcv/B+WJHMvfv36dq1aqkp6tRKjXI5RImJjKOHDmic3E9f/4cH58ioLbXTcADqMVL3D0cMDMzxd/fn5SUFMyMnLEwdtbbV6o6mDZfNaJv374UKVKER48e0axpS6w0JTCRW6MRKpLww7dqYY4c1U/xrlKp2LdvH5cvX6FAAU86deqkmzw1kMW1a9fo3f1bgoKCUAsN1SpXYdX6tTkuSg0PD6dSufKUlFtT0dyB0PQkdsf7seyPVTlmHggMDKRW1aoUkptS1MicexnJhMk0nLtyGWdn52z2oI2cWrNqFa/i4mjcsiVt27bVq2H/pZOens6A73qya9cuvFzM8QtNoXfvPsycPV+XvTstLQ03VweOL/WgaIGsEcCI+aFcfuaEU343nj59ytOnT/mqeX5Wz9cXirnLnnLgjDk9evTCy8uLx48fs3rVbA7ua0WePFrR2733KZOn3OPJ08BsWcNfJ1dGMq5ycXFgnncbAqZjEv6XkUx+IcSLzN+HAJWEEB3/1keBduK/HhCGduK/sxDiwX95Ov81X6zI1K9fn5MnzyNJWXMXQihxcclHr169CAoK4ubNmzx88AxjhX4aDbUmBYVxCvXq1aVQoUJkZGTwx+o/MZO8dGKkESpSxTPu3buDl1dWiPG6desYPGgIGrVEujKVenXrsWHjeoOAvMahQ4eYP2su4aFhVK9Vg9HjfspxAWJERATFfYrS0ao0lawLoBJqDsQ/4JFFEvefPMp28xg0cCAhu07RK39pXdujpBgWxN8lODwsm3ulVZOmOD0JpptLVnjt8pAnqCuV4c8tm7Mdz6qVKxkzdChf53fERi7nQPxLHIsVY9/hI9nmyP5CCEFCQgIWFhZflBhFRkYSFBSEt7d3jqPPpb8tYfaMsfzc25ZCbqbsPp3IlmNpXL56S/cAsWnTJlYuHcXeNfrrt/qPus2m3aGoVNow/jx5jJg3ux4d2me5uIUQVK62hXXr97x1JJsrIuOiEBcGZM9hlxNm416+K7psE9pKw/ZAJDA+8+8yaN1lQUC/zHpdzmhDlZtm9m0KLEAbwrw6MyHxB+fL+VT/jYsXL5L99BWEhoYyceJEXF1dtdEzkipbvRK5QkOvXr349deFgDZlyvPgEM6euYg63QIQSMYJfN+vv57AAHTr1o1OnTrh5+eHnZ0dDg4OH/ZEPzGWLV3GhNHjaGhWmlLGxbi/9yYVd1bg2q3reHh46NmuXrmKMmbOVMmrXTtkLClobVuK68H7adu2LTY2NiQmJpKYmEhCQgKPbt9lgmd1vW0UzWNPkv9LbGxsMDExQaFQIJfLkcvlhIaEcLhyEz37do4edNi1E++JE7G3t8fe3p58+fJhYmLC0EGD2FCuNJ4WWrfpV67O9L73kC1btvDNN99kO9cdO3bw07ChhEVEYGJiQv/+/ZkwZeoXITaOjo5vzYHWf8D3eBYoyJJFs4nYFU61Gi25dGW03gi1devWDB/2I9v2hfJVcxckSeLclRgOnozD3z8AmUxGQEAAw4Z+j5Gx/gOHJEkYmyh02S4+OJo3j5b+G4QQnXJoXvUG23Cg6Wt/HwSyrZ/50Hz+n+Y3YGVlRVpaAlpR/wuBiYkpL1/GY2qqDTls3qw5p09fRK00B+SoNcmYGGcwePAgXS+ZTMau3TvZsWMHGzduwszUjJ69vn3jAkYjIyO9wIHPndjYWEYMHcGOHdvRaDS0ad2GOQvmZhPY9PR0xo7+iX55G5DfRPt062HqgCZO8E3HzlSsWpmQkBDdK+pFBB0d9R/6JEnCUWbB0aNHsbOz01WutLS0xMLCguiMFLwtsubE0jQqMiRBlw4dMDIyQq1Wo1KpUCqVbN6wkQyNGnN51tckQ6NBqDVMmDAh23kWt7LUCQxoq2O2srdl4exZWFlZ4eXlRcGCBTEzM+PkyZMM7PUt88q4UKVCaUJTMhi9YQ1j0tOZPX/BG69lamoqRkZGX4QQNWnShCZNmrzxfTMzM/YfOErHDm2YtigYM1MFMXEqNmzchru7NoLN1dWV7/oPZtXqabRoVggjI+33/fyFUGJi0t46isktxAeek/nY+WLdZVOnTmXatBmkpmpHKUIITE0levXqwaJFi3T2qampDBkylLVr15KRkU6ZMuVYtuy3f+TD+TmgUqkoW7IMFpFGVDUvgwRcSb1LdN5E7j26j1wuJygoiEePHnHq1CnW/raK8W76D2vBaZEsCduPZKLAzc0NV1dX3NzciI2NJfjCXUY419WNNJUaNaND9nHs/Olsi/s2b97M2AGDGO9aBTtjc5QaNX9E3kNWpiC7DmSfK+3eqTOpF6/zo1sRJElCIwSzgh/g0awhCxYvIjY2lpiYGGJiYjh9+jSbfv2V7RXK6m1jTWAwi/0CSNdkRU45Ozsj0lIZ7mVDO097XXtUagYNTj0lLDIqW3DBlStXGPr9d1y/cw9jIwVdOndizoJF5Mnzfr7+zxmNRsOtW7dQKpX4+vpmc00qlUratm1BUNB9WrfwICw8lb37/dmwYSuNGjV667Zzw11WztlIXOiT971szSfFGNLKfOr8JTJqtbYI1oYNGzEzMyMtLZVmzZrx559/6kYxr6PRaFCr1W/0rX9pqFQqVqxYwbpV61CpVHTo0oHvB36frTbMvn37GNxjIF3ztNBzOa6O3omUz4jIyEjS0tJ07UYyBVMLdMNUlhWVdDXhKWHeak6cPaW3jdTUVHxLlSV/gpw6loVI1yjZl/iIQlXLsH3PrmzHLIRg0vgJzJ0zhwLW9oQnvaR0ubJs3bUzx3mB2NhYGtSqTVpUDEXNrLiX/BI7DzeOnDqZLR2+SqXCy92dHx3saOSkdQNFpaXT/c59lqxdi6OjI/7+/gQEBODv78/ebVvYXM2Lwtb6YbS++25TvVETqlatqktSmZKSQhXfskwqa0nrglbEpamZcPMl6Z5l2HPoKAbejUaj4ejRo5w8eRw7u3x07dr1jcEbr5NbInO+t8172VpMjjaIzKfO39fJRERE8OTJE7y8vHKMSDKQM+1at+PW6VuUkpVALsl5oHlIviIOnD5/GkmSePbsGTdu3GDp0qWo7ybRyEZ/LuTUyyuE2cfTqnUrihYtSrFixbSL8Hr2IfTcQ9pYV8ZUZsyL9DhWvzzBmi1/0rhx42zHERcXx9RJk9mzczempiZ0792TwUOGvPVhID4+nrt37+Ls7KxX/jknNBoNJ06c4MmTJxQvXpzatWu/MQnozZs3adWkCQ4KObZGRlyLjuGnceMYOWZMNtsOrVtRNPgO33pnzUsEJKbS4uRj8uZzICwsTNduaWFG14LmTKyU5V7MUAt8d4Vy+vJ1fHx89LYdGBjInJnTuH75Au6eBRk0fDTVq+tffwPvR66ITH4jcb6X3bsNAYupkQaR+dT5t3OXfexkZGSwZ88eAgICKFeuHPXq1csWpXX9+nWa1GlMpzwdUEjauQGN0LDp1VbyFczH8+fPSUxMBEChUOCgsKWvo37Fxy1Jhxn360Q6d+6s156UlESv7t9y8NAhrE3ykCaUTJ0xjX7f/bPpRP5XlEolx48fJyEhgdq1a79xcvvWrVs0qFWT4YXtqZc/L08TUpn8KIo+w0czbORI4uLiuHfvHnfu3GHJvFmMLgQtCuiPnlocCMGxYj06duxIhQoVKFiwIH5+ftSoXIGuRWQ09FDwIEbFzOsZLFy2OlvVTQPvJndExlic7WH/bkPAcsYLg8h86hhE5s0EBwdTs1pN5CnGWCrzEi1/gVshV06cPq7z/UdHRzN27Fiubr5C3Ty19fpfSbxGkGUwbdq2wdfXF19fXwoVKkTZkmVwfGlNFfMySJLEleS7BJlH8OjZ4xxdk6DNhxUVFYWXl9dnm1/t2rVrTPhpNFevXcfVOT+DR42hW7du2UZK438eR+jelcysmOXSS1ZqKLHJD6WkID09HQBbW1uszI3p4pnKqMpZIbOXw9Lpe0bCP+RFtgeGuLg4du/eTXJyMk2aNPlosyH/W+SKyDgZi7Pd3y+K1HJWmEFkPnW+ZJF58eIFSqUSNze3HF0+Deo04OX1VEqa+ALaOYwLGcdxr+iCU35HLl++jL+/PwD5jZzoaK//ZHwy7TTdf+7BkCFD9NojIiIYPHAQu/buBiFo0awFCxYvNLgn35OIiAjKlixOr4JGdPSyJDJVxeTbiXjVaMyyVX9w//59rl27xtWrV9mxaR3HO9hS2O719V+CAsuiWbdlJw0bNtS5Eg8dOsQ3Hb+mTiEjrI3V7H2oYsCPg5k4edq/daofHbklMme6vl/Jaqs5oQaR+dT5EkUmICCALh2+4d79e8hlcpydnVm7YQ0VK1bU2SQlJWFna08Hy54oXlugGqeK4cCrbeTLb0+VKlWoXLkyZcuWpUvHLpRWl6S4aTEA/NMDOKe6wFP/p7pcVX/nr8+aobDZf8+zZ8/4ZfRIjp84gbWVJT379mfk6NHZQpmrVyjDj26hNPHKCsCITVXjs+wFGWpt2G/58uXx9fXlj5XL2NNFTmV37TaikzVUX6Hhz52Hc5zDiY+PJyoqCk9Pz892dPl3ckNkyjoZizPfOL2XrfXckM9OZD7/YPsvHKVSSe0adbCJd6e+UVckZISF+dGwfiN27NrOo0ePuHTpEhcuXEClVAL6AiAhYWdnS1hYmJ44nDxzkg7tOnA99CZymRwrGysObDrwRoEBg7j8P3h7e7NpR/aIub/z/dBRTBj2HcXsjfCwVpCYoWHE2TS+atuWVl914NKlS1y6dIlFixbh6wyV3bPEIp+FjN7lVGz6c42eyKSmpjKwfy927NiJvZUxiekwfuI0Bnw/8IOc62eHkHJtMeaniEFkPmHi4uL4acxYtm/bgUwmo2OnDkyZOlkvvPbQoUOIFDleRmV0ba5G3oSnBFC/fn1Au26jatWqGEnGPIm+R3FT7VoPIQRPNHfp2LljNoEoXrw49x7dw9/fH5VKhY+Pj0FEPgI6duzI86AAak6fhou1CWEv02jWrBm/r16Lubm5bvJ/w4YNrJ8+IFt/Y5mGtWvW8uCxH1WrVqVKlSps27yelGcHeDZBg41FOg9fCNpOHY2Lq1u20s5/odFo3poT7EvDsBjzC+JzcZcplUpKlyxLSoiM/JriCCBcdg/7QqZcunqB+/fvc+nSJdatW0fknUR8Tevr9X+afhPXWlYsX/G7bo7m2bNn1KxWC0ulNRbp1sSZRGLtbMXZC2fImzfvv3KeBv43kpKSePbsGc7OzjlGuL18+ZKC7i6c+FZGMUftKvikdEGlZUpKVGlIWFgYt2/fRqVSYaKA4OlG2OXJulFuv6Fh1dNyHDtzRdem0WiYO2cWvy6YTVhEPOVL+zBl5kK9+i+fGrniLnMwFac6vN/8o81if4O7zMCHJz09ndmz5/DHqjVkZGTQ7qu2jJ/wCzY2WQu69u7dy8sXyRQRjZBk2i9/IVGdaw+3YmlpqcvJZGdnR6omHbVQI5eyCkq9MnnBzz1/1KXfAK1Lxi/wGVu3btWFMLdo0eKLSGHyuZEnTx7Kli37xvfz5s3LoqW/02BAX9qXBGtjFVsfKmjQsgNLl69GkiRSUlK0i2m/64bd3xILFHGCW1tvM3z4cCpVqkSlSpVYtWIpR7YvYe9gNcVcLTh4K4hunduwffeRHOd41Go1arX6Iysw9mEwjGS+ID6GkYwQAiHEG90JjRs15eaFR9iofJAkBa9kfli5SNy5e4uUlBSuXbvG9OnTCb6QREFj/fQ2z5QX8ahkxcCBA6lSpQpubm60btGGm2fv4akuhQw5obJHWHoac/XGlS/iC/53kpKSSEpKwtHR8Yt38QUGBrJp0yaSkxJp1rwFVapU0bsmKpUKDxcHdvdOpKxb1ud16kENK69ZEx2fpAuhNjWWeDjPHHf7LLtVJzM4GFad3fuP69qSk5MZOXwQ6//cQGpaBlUrlmXuwmX/TG2X/5LcGMmUcTAVJ79yf7chYLf02Wc3kjE4Tf9B1Go1EyZMxNbGHoVCQYnipTlx4oSezbVr17h84QoumqpYyPNhLrPBSZQnMvglHh4e2NnZ0bhxY86cOUMCEdn3YZ7E4MGD6dChA+7u7kiSxPZd2xgyYSAv3QN44XSfTj+24dzFs5+FwAghePDgAffu3UPzWn6wnEhISOCbDh1xyudAUS9vfAp4ceTIkbf2OX36NA1q1sLVwYF61Wtk+3996hQoUICffvqJqdOmU7Vq1Wyiq1AomDJ9Dl+tNObPK2puhWiYchB+u2jGiTMXSUhI4OrVq4wfPx5rc4WewABUKSzn0sWLzJkzh1OnTvHq1Su6dGxDvN8uHqywI2GvK92rBtG0cV2CgoKyHV9aWhpnz57l2rVr7/z/frRkJsh8n9fniGEkk4v4+/tz7do1nJ2dqV69eraRyo8/DOLPNdsw13hjJFmQoo4kWfaMU6dP4OHhwa1bt1i6dCkXDj3ATVFZr2+U8iEmrq/o07c3FSpUoGjRopQvV4E8rzxwloohgDBxF6V9NM/8n3wWAvIubt68Saev2pMQ9xIZEqZWFvy5ZRNVqlTJ0b5Zg4aoHwTzrUNJLORG3Ex4wa+Rtzh14TwlS5bMZn/kyBG++bo93+X3orSVHfcS4lj2wo/Vmzbqqi7+ndTUVDZv3szVixfxKFiQb3v2fGtK+0+FI0eOsGjuNEJCnlOhcjVG/TReLyVPWloaLvntuTIJCjhkfe6XHc1g/A6J2FdZ+elsLOWEbXHBSJF1Ux21Mgkjzx7MmDlH17Zz5076f9cTj/ymJCQrQWbJlm17KF06qx7QhyZXRjL5zMTxtp7vZZtv+ePPbiRjEJlcQKPR0LtXHzZv2YKZcV7UIg0HRztOnjyhW3CYkJCAk2N+8smqIJdlhY0mZASRLAsiLS1F12Ymz0sRk+Z6+4iQXWf4xD4MHTpU1xYYGEifnv04e/4MAPXq1mfFqt8/6UWO6enpnDhxgtTUVOrWras3D/U6SUlJFHT35GuLklSyKgDAzcTnrH91g2eB/noJLzMyMrh+/TrNGzRitU9TjGRZ5R22RD4kqnA+fhw2BIVCoUujb2RkRJ9u3emssKamXX6d/cW4SDaKRG49zF5QMC4ujpqVK2ObmkK1POb4ZSg5HRvPwWPHvois3VMmj2f3+nks6q6hhJuM/TdUDFovY+/BE3h5eXHjxg02bNhA8L1dnJytn2Zl+9lkflor0fGb3pQuXZq8efPyTeev2LPQA99ieRBCsPlQHD8vfYV/YKjeQ1RoaCi//baIhw9u41OkJAMG/JCt9tD/Sm6JzLFWBd/L1mHVw89OZAwzuu8gPT2dGTNmsGrVajIyMvjqq3ZMnDgRO7ushHcrV65kx469mEmFkankSEIQERpF69ZtmTx5Ivfv3+f8+fOolCA301/EZiK3QSkPZ+rcyZQtW5aSJUtSsUJloiIeYC/5ICEjXh1Eqmkk3bp10+tboEABjp86qsti/KYULZ8KFy5coHWLVtgrrDCRjPg2MZw58+fSt1/fbLbbt2/H08iWytZZX15fKw8uJgZQrVo1zM3NiY2NJTY2lqSkJAAKmOXVExiAAibW7Dh9hiMnj/N3ZEClqvojloo2+Rh54QoNGjTAzc0NFxcXXF1dcXFxYfvmzRRRpjOheGGd2+lAeATfffstN+7fz/GcVSoVhw4dIjg4mPLly1OpUqVPdp5o7LgJWFnb0G3+LELCo6lYrgRbd86ncmXtqLxx48b4+PhQ0XcnKWkazE2zRjzHbmSQpjRl9uzZqFQq5DL4rr0jvsW0EQeSJNGpqR0rdydw+PBhWrZsCcCDBw+oV7cG7Zo58nXjvFy9dZAK5Vdy5OipbIEPKpWKCxcukJ6eTvXq1TE318+A/cEw1JP5ckcyiYmJrFu3juvXr1OiRAm+/fbbbCnfGzZoxMVL11ClmwASMkUa+Z1tuX//HmZmZqhUKkqWLE14YAbGiry6fkJoiE25DWj9yE5OTkRHxeBsWhOFLEsMElRB1GpSlB07t+vaQkJC6Na1B5cuXUKSJAp7F2bNutVvjRb61ElNTcUtvwvtLKpQzEI7SRqd8YrfYg6ybvOfaDQaHj9+rHvdvn2baqaedHPWd41ti7zBTeMYSpcpjZ2dne5lZGTE5PETWF6kKdaKLKFf9uIWjg2r0Lf/dyiVSl3BMqVSSZ9u3fnZ2YcSVlmficdJLxn25DqFSxQnLCyMiIgI3VyBuVzOukrlKGKVlTdMLQQ1zlzk4PETVK5cWa/Ec3BwMA1r18JalYpPHmPORydRrFx5du7b/1mvqO/+TXsi/Y4ztYcpjjZy1h9LYdF+wc3bD7GxseHRo0eMHDGYhqUD+aFzfr2+7YY84cTVNEqXLk2xYsW4eeMSXVqbMODbrJxrqzcGsu+UBUePndW1Xb58mfbt22Bvb4KZmYInT2JYunQFX3/99VuPNTdGMqXtzcXRFu+XE85pzT3DSOZzISQkhAoVKpKUlEJKShpmZiZMnTqVixcvUqRIEUA7CX/x0iXUGTbIMsOEhdqIsNBIqlevTlpaGn5+fmRkqLA2Lfy3PUiYmJjyxx8radSoEba2towcOZoVy9ZgrvLCSJaHZFUkafIQfv5lg15PNzc3Tp0+QXx8PCqV6q2r6D92/Pz8mDZ5GlcuXsbd050RY0ZSt27dbHaHDx/GychWJzAA+YytKWdcgFYtWqJB+zDk5OSEj48PDRs25OKx0yg1at3oRCU03FNHsmbtet1C09eJjohkyvrNdLEtgp2xOWdePud6Riy3pk/DySl72o+xEyYw95cJjPcsgae5Jc9Tk5gT+phJ06by4+DB2n2qVERERBAWFkbndm1JUav1tqHUaEjLUOqenEuWLEnp0qUpXbo061etoKWV4IciHjrb767fY87sWYwd9/P/dsE/AVb+sYHp06bw1bRlvEpIoEH9Opw+O1f3PyhTpgx9+w1k9uQBDOggkMu13724VyrO306lffsOhIaGcujQIWKiI+myvoXe9ju3c2fwz3tYtWoVPj4+uLi40Lp1cxbOr0mTJtqb/Z27kbRp2xtfX18KFnw/V9b/Q26NZCRJWg00B6KEECUy22YDLYAMwB/4VgjxMoe+QUAioAZU/5SYfbEjma+/bs/u3fvRaF53n6goXtybgQMH4u/vz7Fjx7h/9xkKuX4tCJU6AQtLQa1atfDx8eHu3XucP3MTE8lV5+rIUL3CKl86z58H6do0Gg3z589n7pz5xMRG41uuPHPnzaZq1ar/1On/ozx9+pQqFSpTSlGYQkbuRCljOZ9xi4VLf6Vz5848evSIy5cvc+nSJQ4dOoT1Szn9XPTdU6fi75BQzJTps6bj4+OjWxQqhKBdqzY8vXiL+ubeyCSJkyl+OJUqxKHjR3N0OQkhWL58Ob//upi4uDjqNqjPL5Mm4unpmePxCyGYP2cOM6ZNR61UIlMoGDZyBKPGjMlx+7NmzmTfooX8WtwH48ygj6WBwdyxsqVn//7cvn2bO3fucOfOHV6+fImxTOJem3KYyrPcRjdikhgXnMYDv4Bs24+JiWHpkiVcOnMCZzcPBgwaQrly5d733/FJoVKpaNK4Lurkp/RubUliipoFG17Ssu23zJw1V2eX38mOAxt88fHKynIRHJpMuXpHSc/IikarVNGFo0f0y0qM+ekM+RwaM2HCxDceR66MZOzMxeFmf38IzRnn9Xfeuj9JkmoCScC610SmIXBSCKGSJGkmgBBiVA59g4DyQoiY//4s/ne+WJHJkycPKSkCScr6gmvXryQDYGRkhIODA1GRsShk+tFBcqNkJkwczbBhwwBt4sAKFSoRG52IKs0EmUKNWnrJnj27qVev3j93ch8ZXTp0JvJYENUtfXVtoekRbIo/iMJUQUJCAgA2NjaUKVOGy+cvMsr1a/IqtH54lUbN4rgDLF6/PMdoLpVKxapVq9jwxzo0ag0du3ehb9++uR5Zp1KpiI2NxdbW9q3F0JRKJZ2/+ooLZ85Qxd6WZ8kpqPNYcuTUKb1gDCEEt2/fpmaVytxpUQqFLEuwHsSn0P70Y6rVrU+NGjWoWbMmFSpU4OXLl1QpX45qNmoaOxvx7JWKZY+T+W3VGtq1a5er5/uxkJ6ezpo1a9i/dyvmZuZ06daHFi30K6yOGzeGm5c3sW5xWcxM5aSlq+k15DYFfZoz4PtBPHv2jLVr16JW3WfVyqZ625+/4ArxL0uzYMGvbzyG3BKZQ0193m0IuPx5+537kyTJE9j/l8j87b02wFdCiC45vBeEQWQ+PH+JjI2NLa9epWcTGbk8nadPn+pWwhf29iE8LB6EBSChEcmYWajw8/PD3j4rQiY5OZk///yTkydO4VnAk379+v4jw/B/g6tXrzJ21Fiu37iOi7MLI38aSdeuXfW+/CkpKXi5F6StcT3yGenPc80KW0mbDm1p2LAhlStXpnBh7UT5zOkzmDNtFpXNfDBFwQ1VIGWql2f77p2fVB6s27dvc/36dTw8PKhbt67ePMzrVClXhnaKBNoX0H6OhBAMvxFCoJUTaUoVDx5oI9hMTExwymdH3bxpzKqaVZfkakQK311NJTD0xRv38bmTkZHBtz26cPToYcqUzMed+zHUrlOXtWs36UqB+/v7U7lyOa5d7YatjVlmPzV16m1l1qzlNGnS5I3bzw2RKWVnIQ42Kvpetm6bbgQDr4vAciHE8r8dkydvFpl9wBYhxJ85vBcIxAMC+P3v2/1QfDCRkSTJFDgLmKCd+9kuhBgvSZItsAXwBIKA9kKI+Mw+Y4BeaH2GPwohjmS2+wJrADPgIDBICCEkSTIB1gG+QCzQQQgR9Lbj+ktkBg8ezO+/ryQ9XRu5IoTA2BhatWrOli2bdfZhYWF069qd8xfOARJFihRh7do1lClTJjcu0yfHzZs3qVOzDhUU5SlgUoAYVSyXlZcZNm4Y1WpU48SJExw/fpxLly6BUtDGrgFFzLPENkWdym9xm3kR+QJLS8ts27906RJrV68hJTmFNl+3pWXLlp/tDfTOnTs0qluHqnZmFDGTcSZeSYqlDacuXCJv3rzExsZy/vx5zp07x9rff2NDfQfKOZjpbaPctlAOnr1EiRL695v79++zYM5MHj+4S7GSZRgyYjRFi77fje5TJCAggMePH1O4cOEcC6+NHj2CnTvW069fSczNjfhjzSNcXEqwY8eetz7A5IrI2FqIAw2LvZet+5br//NIRpKksUB5oK3I4cYuSZKzECJckiQH4BjwgxDi7N/tcpsPKTISYCGESJIkyQg4DwwC2gJxQogZkiSNBmyEEKMkSSoGbAIqAs7AcaCwEEItSdLVzL6X0YrMr0KIQ5IkDQBKCSG+kySpI9BGCNHhbcf1l8gkJyfTuHFjbt26jSTJAQ0FCxbg1KlT2SLMQLvORalU6oUuf4m0bt6aV+dfUdq8lK4tThXHppjNqIQKSZIoU6YM9erVw9jYmNWLVvJVnobYGeUlTZPOoeRz+Laowuq1q//Fs/h4iIuLY/369QQH+FOhchXatWuXo7uvbtVKdM8TRrMCWcKcotJQZO0z5GYW1KtXj4YNG9KwYUMiIiJo07wx35cxonJ+BRfCVCy7q+LA0RN6NYS+JIQQHDlyhI0b15KenkarVl/Tvn37d+blyy2R2d+g+HvZemy99j+JjCRJ3YHvgHpCiJQ39X3NfgKQJISY8y7b/5cPFl2WqaRJmX8aZb4E0Aqondm+FjgNjMps3yyESAcCJUnyAypm+hGthBCXACRJWge0Bg5l9pmQua3twGJJkqScVPzvWFhY6NJV3Lt3j8KFC1O9evU3rlF4PX3+50hycjLjfhrH+nV/kpGRTrNmzZg9b7beXMLLly+5dOkSjYz0s+raKmwxNTJl5vyZtG/fXs+NaGdrx6QJk7BQmPEqLZG2bdqwZNmSf+y8PnZsbW0ZNGjQO+36/jiEyUP6U97RDEdzBSqNYNrNl5QuXYpS5Stx5MgR9uzZo91mHhNm1zanfTHtOpDq7ibkt0hm7IghHDtz4YOez8eKJEk0btyYxo0b/yv7F+LDrZORJKkx2ntorTcJjCRJFoBMCJGY+XtDYNIHO6jX+KAhzJJ2iHADKAQsEUJckSTJUQjxAkAI8SJz6Abggnak8hehmW3KzN//3v5Xn5DMbakkSXoF2KHv00SSpL5AX0Av67AkSVSsWPGLfbr7CyEETRs148XdaGrIm2BkYsSjQ/epcr4KGzZv4OzZsxw+fJjLly8j08iIsorC9rV5liR1EsihR48e2Ra4DR02lP4D+hMYGIijo+MXPxL8X+nQoQOPH9yj+vz5FHe0JDA+laIlSrJ/117s7OwQQuDn58eRI0f48ccfaO2jf53bFjFjyJIr2eq8vHz5ktkzp3Nwz3YsLCz4ptcA+vbt+0nNgX30iNzLSyZJ0ia0D+n2kiSFAuOBMWinJY5lPiRfzvTuOAMrhRBNAUdgV+b7CmCjEOJwrhzUO/igIiOEUANlJEnKi/YEs01UvUZO/wXxlva39fn7cSwHloPWXfa2Y/5ciYmJQaFQ5FgX5sqVKzy6+4jGRu2RZQZClDGpzLHY3dSqVQsAX19fRo8ejb29PZPGTSJPeh5cjF1IUCdwNuMcffr2eeMKajMzM4oVez+ftIGckSSJCZOn8sPgody+fRsXFxfdeq6/3vf29sbb25vJ48cS9FJFYbusSLigl2oUQoOTkxONGjWicePGVK9enVZNG1DSIpwFtQQJaTB97khuXLnIij/W/Run+Vki4G9LJf6PbQnRKYfmVW+wDQeaZv4eAPxzSd9e4x9ZjCmEeClJ0mmgMRApSVL+zFFMfiAq0ywUcHutmysQntnumkP7631CJUlSANZA3Ac7kU+Q27dv8223Xjx58hiBhmpVq7Nm/R86N5hSqWTnzp3k1djrBOYvXBUF8KlSiM1bN+HgkBXV5OLiwsghIzgQdRATExMGfD+ASVP+kZH3F4+dnd07w+L79f+eEVuXsraJnLymMmJT1Yw8m07z1m0xMjHl8OHD/PmnNvioppcRK74x1bmJqxUQFJ2/nZE//ayXAPMvUlJSkMvln3VGgg+B5gO6yz52PtiYWJKkfJkjGCRJMgPqA4+BvUD3TLPuwJ7M3/cCHSVJMpEkqQDgDVzNdK0lSpJUOTOYoNvf+vy1ra/QLkj6IkcqORETE0Pd2vWQntlQ37gH9Y178OJqEjWq1uT333+nXbt22NvbM3v2bMJTQ/j7pUswjqVl6xZ6AgPw9ddfExASSGRMJDHxMUybMe2TKGwWGhrK6tWr2bJliy6f2btITU3l8uXLPH369AMfXe7x8/iJ+NRuS8nV8dTckkrp1S8p27gjGzdv4c8//yQyMpKrV69SqVxJvi4p15uHtDCWqOYh48CBA3rbfPz4MY3qVsPO1hoba0s6tG1OZGTkP31qnybi/dL8f675zT5kdFkptBP7crRitlUIMUmSJDtgK+AOPAe+FkLEZfYZC/QEVMBgIcShzPbyZIUwH0Ibeicyw6TXA2XRjmA6Zg4L38jHULQstwgODmbnzp2o1WpatWqV7clz3rx5/DZhDSWopdd+ImkDSSIeNzc3GjVqRKNGjZg8YQrq5zJKKMqjkBQ8y3hAoPEjnvg9eWMm5E+JGVOnMX3aNMrndSVZqHiWHMP23buoU6fOG/v8sXo1w4cMwcnMgpiUFLyL+LBl105cXFze2OdjIjo6msDAQLy8vHKcC/vl57HEn/mVOU3114oVm5NEYJzAx8eHRo0aUbVqVYb8+B0j6yTRp5pEugqmHZFxPNSdm3cff9bzN7kRXVYir6XYWfP98g767Dv32eUu+2IXY37qLP99OUOHDMNeVgCERIwIZNzPYxk9ZhQqlYrr168z6MfBJN9VUMhY/wN+V3Wab4a3YeLEibqn2Li4OH4Y8AM7du5ArVFTs3otfvt9CT4+77dS+Z8kNTWVCb+MZ92ataSmpdGkcWNmzJn1xvTuV65coVWDxkz3qI2dsXbe6G5iJAuibhDyIly3aO91Ll68SJsmTZnjVZaCFlaohIZ1Yf7cz2vKlVs333hsGRkZ7Nu3D39/f0qVKkXDhg0/2ptwcHAw5csUZ3lLDU2KKFCqYd55NRuf2tL3+8EcO3aMM2fOkJaWRvNSErv6Z83xCCGoMs+MaUu20bBhVrShWq3m0KFDnD1zCgfH/HTt2vWTrqeTWyKzo8b7pf8psv+sQWQ+dT4VkXn16hXR0dG4u7tnWzcRGhqKj3dRStAcc5k1AOmaZG6pd1K1RmWuX7+uS9liZ+RMNZM2WfnThJoLbOPIqUM5lrtVq9VoNJq3pk/5t2nWsDExtwNoaVUSc5kxZxKecoMX3Hv8UC+wISEhgZCQEH4aORrL2yG0d9JfqzDa/wTO5UtQsGBB5HI5CoVC9/P4wUPUTJPo4OKls1cLQcd75zh09nSOhbPCwsKoU706NsoMipmZcC0xmTzOLhw9ffqjDYE/ffo03/XqStKreFIz1JQtU4Y/NmzFzU07PZqWlkaXTl9TWX6IIfX1J697r9eQ4tKGX375heLFi5ORkUHLpvWJCblL63JpBMaYsO+mYNvOfdSuXftfOLv/n9wSme3Vfd9tCBQ9cOazE5mP35H+hZGWlka/vv3Ztm0rxgozJJmGaTOm0r9/f53N7t27sZd7YC6sdW0mMgvsVAW4dfMWHTt2pH79+lSpUoX6dRrw4MU53DTFUKMiSHaHClUqvLGeulwu/1dW2Gs0Gp4+fYqZmdlbC07dvn2b65evMtW1NYrMQIXWdmV5EZFA0yZNyGtjw/PnzwkJCdEJrZEko7tLmWzbMhISt27d4sGDB6jVatRqNSqVCrVajSwjgw6F9PvIJQlzlYby5ctTqFAhChUqhJeXl+7nglkzqWcsZ2Bm1JcQgl+e+PHL2LEsWLQody5ULlO7dm0e+T0nICAAc3Nz8ufXT61vampKi1bt2LLwDEPqp+va1RrB8Ucawi5uY9u2bTg4OODq4kJe9WMuTZTrCvMdvq2mZ/eO+AWG643ohBDcuHGDsLAwypUrpxO1zxEhJNTqzzNrxftgEJl/GCEEMTExmJubY2Fhke397/oN4PDOcxSUmqLQmJCqimf0iHGkp6cjk8k4e/YsR44cwSzNURsZ/xoKhRGDBg9i/PjxuraLVy4wYfxEdm3fhbGJMX169WDkyBEf+jT/K06ePEnPrt+SmpRMukpJkSI+bNy2WS/3m1qt5sGDByxcuBB3hY1OYP6imIkjO27fxruYD97e3tStWxc3Nzfc3Ny0lROnzaahphAmMu1HPjwtgUBlAkGBITlmeJg1cyYnFv2uVxUzIi2FCHU633//PSEhIfj5+XHq1CmSk7VJVeWSxOR6NXT2kiTR09WZvps2vVFkVCoVBw4c0C0IbtWq1T8euSVJEl5eXm98v0OHDsycOp6h2yMZWEtDqlIw9YgxxUpX4Oyq9Zw+fZpTp05xaO9WfuknR/5aws9GpeXI1idx69YtfH21T/NRUVG0btGQqBeBFPEw5eK9RLp26878BUs+Wtfi/8uHXIz5sWNwl/2DnD59mj69+xESGgJC0Lx5c1auWqFz8fxVormg1BSFlHWjiVcFEZpxBQ0qPD09KVeuHAf2HaKMvDVmMq0bJl0kc1/ax+VrFz+pNSnPnz+ndPFSfJWnGkXM3dEgOJ94j3smYSxZvpQrV65w8eJFLl++TGJiIgB5jcyZW6gjsteiotbFXqHBD50YM/anbPvQaDR069SFC8dOUsPcmVSh4mTCc2bMnUOfvn1yPK5Xr15Rxbc8HukaGlg7EJ2eyoaYEAaNGc2w10RaCEFkZCQPHz6kccOGXKxbHbPXRoLPU1Joe+EqlarXoFatWtSqVYvKlStjbm5OXFwc9WtWR/YylsrWRtxJVhMhjDh14eJHV0I7MjKS8eNGs3fPboyNFXTq0oOfx0/UWxvVqF5V+pS5RZuK+nM3zv2SSVGbU716dapVq8bRQ7up5BHMtJ6WyGQSL5PUNB2bQJ9Bs+jTR///ERERwYkTJ8iTJw+NGjX6x6u/5oa7rLi1ldhcudJ72ZY6evyzc5cZRCaXEEJw69YtQkND8fX1zRaB9PTpU3zLlcdMXQgzuQMCFckEUKysG8uW/caVK1c4duwYO7buppipfur2VE08cebXuXHrmi5jwdKlyxgxbCR2UgEkIRFLIGPGjuKnHG6yHzPjf/6Fs8v208K6sl77zOebiFK+RCaTUbJkSapWrUrVqlWpUqUK3Tp9g2lwIq3ylsZMZsS5V884nPqE+08eZgu3/gshBMePH2f/nj1Y5LHkm25d3ynGL1++ZPGvv3J0/0Hs89nT78cfaNSo0RvtmzdogHdoML093XT7nPzEDz9rGySFEbdu3dLNd1WsWJGMlGQKJUYwvWxWHaJ5jyII9SjF9n37/5vL+FHwxx9/8PvsQRwfIzAz1p7P+rNKJu61pFGztly8eJF79+5hZiwRucsdM5OsUcvhqylM3+PIhct3dG1z585iyuQJ1KloS3yCmseB6ezYtf8frb+UKyJjZSU2Vq78bkOgzLFjH4XIZCYyfheanIqjZduWQWT+f6KiomjUsDH+/oEYG5mTnBpPz297snjJIt3NY+D3P7BpzVEsZVkuICE0hKacQiOUgDY/WlpKOp6KepjJssKGo9UPqdmqCJu2bNTbb2BgIDt27ECtVtO6deuPKhIsODiYFctX8DwwmGq1qtO1a9dsGQGCg4Pp3L4TjgEKqlvrJ4P4M/YE9fu04ueff86Wrfnly5cMHvgjW7dtRalWU71SFRb9/lu2TMT/NIGBgdSpVo0CCjnFTIy4npJGqqUVpy5cwM7OjlevXnHhwgXOnDnDmTNnuH39KscblcQ9T9aoNVGpxnf/XZJSUj+JtUevo1ar6dWjMyeOHqB5WYmAGAX3Q2UcPHJSFyhx584dGtWrQshmR731OTeeptNoRCTlKtakfPnyWFlZsXTxTM6t8sLVURv4cujCS/pPjyXo+Qu9YJhbt26xfPkSIl6EUq16Pfr06Yu1tTW5QW6ITDEra7Gx0vuJTNnjRz8WkUlDu+j9bX4+uRDC/S3va7dlEJm3k5aWxpIlS9iwYRPGxkb069eX7t276/mO69VrwNVLDzFC+8XRCBVqeSjDhv9IgQIFuH37NmvXrEeW6oqFQr/Mb6zqJn36a4ttFS5cmFWrVjN8yCjyKotiKrMmSYSTbBzElWuXPyoReRunT5+mdYvWFDMuhI2wIkgKQ2MrceHKRQIDA9m7dy979uzhzh3tU6unmRMD87fW3XTSNUpmRW7l8s2rbz3nvybrc7tI2f9DSkoK27Zt49mzZ5QuXZrWrVu/MVLPwSYvO6t6ZBOZMrtvMXzUKL766ivKlSunuy5JSUnMnT2bXVs3YqQwokP3b/nxx0Ef1fmD9qZ/7tw5HB0dadmypV6IuEajoWhhDxb0UdKgfNZDx/cL47kR6o5MYcKdO3eQhJIxvZwZ08tZb9u1+gTx06RVtGihLbm8detWfhzYh/7d3SjoYcbeI7E88JM4f+Fatrm2xMRE7t69i5OT01vnoF4nt0RmQ8Uq72Vb7sSRj0Vkbgkh3rq4531s4AsXGY1Gw/Hjx7l//z7e3t40adJE7+lRpVJRvXoNHtx/Qka6Nom0samS5s0bs2nTJkA7inFzc8dCXlSvAFqG+hVJ6YGABjMzM2xt7UiMARujrKdtjVARo77I02dP9HzwBw8eZPrUmYSGhFKlWhXGT/j5kxEYIQSFPL2okFIcb7MCurZ9L08QJIWRkJiATCajWrVqtGrVikaNGvFNxy4oXmRQydSHNE0GZ9PvU7NFfVZ95uUABvTpTeLZQ0wp7awTkrkPwtkZnc6L2HjUajXu7u60bautq/PTiKE4JoXS18ccpUaw8GEK1kUrsHPfwTdmD/8YOXbsGF06tqV3ExOKuMs4cEXDrSAzzl+6gYODAxkZGXT4uhV1ijziu6/13Z/1+j7i0t1UihcvTokSJTh8aC+7VpfDt1TWyP+7UfcoWKwzEydO1rXNmTOLadOmUMjLnuDncZQpU5aNG7e/M2FrbonMuvLV3su2wqlDH4vImAoh0v5fG/iCRebVq1fUrFmTwMAg0tPVmJgoyJfPngsXzuPkpB1t7N69m27deqJMs9R9iYXQoCGKRo21dTsePHhAako6ec1K6X3RVepkTCxfcubsKQoXLkxcXBzFi5VAlWyFmZQftUgnXf6ctl83Z9XqFf/KtfgQBAQEUKFUefrbdNG7HqHpEexJPsa8xfNp1qwZ+fLl072XkJDA/Lnz2LVtJ+bm5nzbrxe9evX6bCON/iIuLo56NaphlBBHRSsFd5M1vBBGnDx/ATMzM/bt28fOnTs5evQoGRkZFLM15XQ7D911zVALqu15web9R6lU6f0mlj8Wnjx5wvLflxD2PIAKVWrTu3cfPRfXzp07mfpLP86s8MDYSPs58A9No1LXp3zbsx9+fn5cv34dhZTA04v682RnL8cw6JcgZs1ZTJEiRXj48CGjRvZn144WuLtZoVSq+Xn8RULCbNm378hbjzM3RKaopbVYV776e9lWPH3wYxGZn4EUIcTc/3tbX6rI9OvXj7VrN5CRge5LK5drqFWrKsOHD8fPz48VK1by4H4QRnJ9/26GMoY8VgoqVqxIkSJFWLfuTzRpdhjJsxbcZfCCnr3bs3DhAl3b8+fPGTfuFw4fOoyVlRU//Pg9P/zwwydzM7116xYzp87k4YOHlCpTitFjR+vmQYQQXLlyhRUrVrD+j3UMc+mLQsqKsvJPDeZp/lCu373xbx3+R4lKpWL//v3cu3cPb29v2rRpky2EOTExkW86d6Jk5FUGl9V/8h5xKYYyvca9sSaNEOKTGuX8hVqtpsPXrfB7fJmuTcyJSxCs2v2SCZNn8t13A4DMjAW+JXh2oQ5GRlnfoa17Q/lx3B2SklUAWFoaM39OPb7+KitrdVqaimIl13D33mOcnfVdcq+TOyKTV6zxfT+RqXzmwMciMk+BMn+vTyNJUm8gnxBi+vtu69OaWcxFNm/eTEaG0HNxqVQSx48f5/jx4wCZvvTsaxYsLE1ZtUqbYBKgWbNmtGv3FUpNKhq1EXLjNPJaGzH2b5Fe7u7urFu35oOd04fkzJkztGrWipLy0hRWFCHwYBDV91Vn2cplPHjwgI0bNxIQEICJiQl2dnZcSrpJ9TzlkSSJDI2SK6o7jBgw+t8+jY8OhUJB69atad269RttLC0tqVu/AReWX8v23q0XiRycNo3o6Gi6dOmiK7F86tQpfho+iCu37uOcz4bvfxzMyNE/fTKlrOVyOVu27eHAgQMcPLCbPFZWHDn+rV6mBQ8PD0qXKs2MJX6M/dEbmUwiMjqNWb8Fs+S3VRQpUoQnT54w/pdRuLrqB4+Ymiqwt89DbGzsW0Umt/gE18mkvqEA2nrgJvDeIvPFjmQsLS1JTtboiYz2qS+V48ePU6RIEYQQFC7sgzLdHJmkjc/XiGSs8soIDQ3Re+J8/Pgxixctxj8gkHr16tC7d+8ca7d8qpQr5YvDcwe8zQrr2h6lPORs4hnUkpp69erRuXNn2rRpQ2JiIg3qNCA5NhF7hQ0Byc9p064tq9as+mRGbR8bsbGxFPP2YmIZc9oWskIt4I9Hr1j0OI0SZctz8uRJNBoN5cqVo1atWqxf9Tvz65jSrJApz+JUDDmdTvW23zJzzvx/+1RylfDwcNq2bUZUxHMKuFty8240gwYPZfz4SboR3MiRw3n18jSzZ9TU9bt7L4qvOx4mODj8rYETuTWSWV225rsNgarn9n0sI5nLaMvZv8jhvTtCiPeuTfPFisw333Rl69adqNVZNz1JUlGnTg2OHTuqazt9+jQdO3YiJSUVjUZD/vxO7N69i+LF369m96dCeno66enpOebY0mg0KBQK+jt8r1dzJkOTwerYlYSEhujmsV7vc+7cOUJDQ6lYsWKOtUk+NBqNhsOHD3P86DHs7O3o2q2bXmXUN3Hz5k1mTZnKg/v3KVaiOCPHjtWtVv83uXHjBr27dSEsNBSVRkPxYsVY/ecmvL29iYiIYPPmzWzYsIGHt28wvqYlA8pnPb1HJKmpsO4Vz8Mjs4WEf+oIIbh9+zYRERGUL19eb74PtAtJq1QuT62a9rRoXoCAgJfM//UO06fPo1u37m/YqpbcEJkiefKKlWVqv5dtjQt7PhaR+RoYgTZLfvBr7Q7AkfeJKtP1+VJFJioqikqVKhETE09ycioWFmaYm5ty+fIlChQooNdHo9Fw//59jI2N8fHx+SR93G8iKSmJgf0HsnXbVjQaDYUL+fDb8iVUr14dpVLJkSNHWL9+PTu37aSDXSdsFFlRPFHKKC4ozhEaEfqWPfw7KJVK2jRvyZPrd6hk4kg8Si4mPGf95o00b978jf3Onj1L2+Yt6GTvSUlLW+4nxbMxOpAd+/bqqoT+mwghCAkJQaFQvNHNU8zLneXV0yjjpP+EXvqPV+w8dj5bcs//tHfW4VEdXRx+ZzfuBiEQLLhLcHd39wLFCkVKP6xKgaLFKe5S3N3d3R2iBKLEZWW+PzYkWaQEGoFkX5777O7ce+fOhN37u3PmzDnBwcGcPHkSKysratWq9UUHR/1cAgICmDt3NmfPHsfFxZXvvhtC1aof9/hKGZGxl4tL1UrWsTXP7fgiRAZACPENMB24ANxAl7KlPTBWSrku2fVkVpEB3dP71q1buXHjBkWKFKFDhw7vjSeWkWlYtyEel19QUlkJE2GGd9wTrmvP0Lpdaw4cOEBAQACOjo645XHD/1EA9czrY64wJ0oTxdG4wwwcPZCRo0emdzfeYcWKFcwc+Tu/5KiREOfsUWQA0wMu4fPyxXvjg0kpqVquPPUiFNR1SnQpPxrowxErLeeufnh9lZSSQ4cOsX3zZkxMTOjcvTuVKydvbURK07ldK8q8PslA98Tvsl+4hhKLX2Jt70Tnzp3p1q0b5cuXZ/7f8/h5zEgq5TUnJEryMtqY7bsPULZs8kLTZ3RSQmQKWdnLxaU+nLcoKbXObf/X6wkhlgPNAH8pZfH4MgdgI5AH8AA6SClD3nNuI2A2uhxfS6WUkz/WHiGENdAaKAZEAvuklJ+0mv2DIiOE2AcMlFJ6fEqFXzpfS6j/tODhw4dUKFuJpqZdUSbxBLsWdYZHqtu0btOKbt260ahRIxQKBUO/H8qqVauwN7fndcxr+vbry18z/kqTeZYdO3Yw4dc/ePz8KUULFub3ieNo1KjRe4+Ni4ujQc3alPFTUN1ef1Q69OEuYiyNUSqVqFSqhE2tVqNWqxHAgUotMFUk/j3itBoaXdzNzFmzKFq0KEWLFsXFxSWJW7ukb69enNyzh5aODsRJybaAAAYMG8Yvv49NrT/JB7l27RqN6tRgcnUTmhUw41GQmh9PxpG3XB00Qsnu3buJjY0lV65cRIe85NQAE/I66P4Pt91WMeq4JU89X2TIEc2nklIis6hknWQdW/v8to+JTA0gAlidRGSmAsFSyslCiNGAvZRy1FvnKYFHQH10aesvA52llPc+p0+fwr95l60EDgkhVgFTpYyPfWLgq+HRo0fMm/s3z548p3qtqvTr108vy+Xly5exUdjpCQyAk5ELzuXt2bRpk1753wv/ZsKkCXh6epI3b94UC93xMTZu2MCQfoNob1OOLi4lePTKj27tO7Nqw1rq1avH7du3uXr1KteuXePq1avcvn0bhVpL8Rzl36lLKwSVKlUiR44cGBsbY2RkhLGxccI2Z/oMfKIjyGeZ2Dfv6AhMFUo9N2FbW1uKFi1KkSJFMDMz4+CO7WxxL4tF/GLeNtldaDPtL7r2+OYd82tqU7ZsWbbu3s/PI4bx3cFbZM/iwKBhYxj+4wgUCgWvX79m69atTBj7K99VJEFgANqUMGb2JTXHjx/XS0b2Bo1Gg0KhyFAm47RAm0LeZVLKU0KIPG8VtwRqxb9fBZwARr11TAXgyZvMwUKIDfHnvVdkhBCVgfvJiU32MT4oMlLKTUKIvcBvwBUhxBpAm2T/jP96cQOpx5EjR2jTsi3ZKYSFxo5FZ9cwb87fHDi0nzNnzrBhwwZOnDiBEiNU9nEYi0T7faDiBa2rNXlvvfb29mmejvnX0T/Tza4yhS11cxDuNnlRCkG3Dp2JiItGrdath7Czs8Pd3Z2hQ4ei0WjYtmwNFe1yYanU9e3Cay+M7azYsWPHB115zU1MmTNrHr/lLoWjiRlBcTHMefGAX8eOpXffPty7d09v27NnD4H+/vRzy5sgMACOpqbUzJKFAwcO6OUCSiuqV6/OqQvvX5NkZ2fHt99+y+ljB8ga/W4gTjOi2LZtG2XLlsXJyQmAPXv28OvoYdy895TsWe0ZOnwkP/5vpMFbMFmIT3FhdhJCJDW1LJZSLv7IOc5vvMCklH7xk/NvkwPwTvLZB3jvCl4hxHh0I51hQMfkNvxDfGydjAqdHc4UsCaJyBj4cpFS0rd3P4poa5DVKDcoIIcsyJ3AU5QqURqNVFOoUCHGjh3L7Ru3OXf0IEVFOSyEFc/VD/A39eH7Id+ndzcA3QT+E8/nFCqkb24obJmDCL8oRowaSdmyZXF3dydPnjx6Jqy4qBiGrVlLOVtXgrUxeMaGsvfg/n9dKzJi9ChCgoPptWABTuaWBEZHMmDAAEb9NAaFQoGzszO1a+vb10eNHMmLLZvfqetVeBjTp08nIiKC1q1bkz9/fr39YWFhrF69mjvXr1KoeAl69uyVpgLeqHlbZv96iJ7uEiOl7u/mGaLlkqeKk4sWsXTpUurVq0fJkiVZs2weSzqraDDQmLt+4fRfMoHoqEh+Gzv+I1cxICVotMkW48BUmvh/n8p9aEL+LFADnXntv1/4X+ZkGgEzgF3AuA8szPnqyAhzMjExMaxcuZKd23fj4ODAd4P6U61a4opib29vihYqTk1FNz2zRqgmgDtGRzh++hglS+rC4Gg0GmZMn8H8uQsIDQ+lfr36TJzyZ7IDCH4uJ06cYOWyFURHRdOuU3vatGmTcPOXUnL79m02bNjAhg0b8PXw5n+5mpHHPNE19UHkC/abPObek4f/ep0HDx5w/PhxHBwcaN68+TuRoD9EeHg4Xl5e5MqV66Muv48fP6ZS2bKsKFWCvPGOI9dDXjPo1m3yFS6cEAi0ZMmStGnThtatW2Nra0vNKpUoYa6ggo0x1yPUXHwdy/EzZylYsOC/XS7FUKvVtGxSn5Dn1+hWIo7gaMHCywpG/jKe6jVrsXHjRjZt2kTAi+fM7aykW8VEcX4eKKk83QTfl0HvOFEEBQURExND9uzZv3qzWkrMyRS0dJBzir1renwfjS9v/Oj14s1le5LMyTwEasWPYlyAE1LKQm+dUxmdV1jD+M9jAD5l5f7n8m8icxoYIKW8m9qNSEu+dpGJiYmhepUa+D4JwiYmN2oRQ6DxQ8aO/5XmLZqzY8cONm/ezOWLV2hg+S1GInHyNkDtRbSbNzfvXk/HHuhyyCyavYByJoUxwYgbmieUqubO5L+msGnTJjZs2MC9e/dQKpXUq1ePrE5ZOLnnMN/YVyWnmSPPo/1ZFXKOyfOm071793TtyxtWrljB0O+/x93JCZWU3At9zT+bNtOwYUM8PDzYsWMH27Zt48yZM0gpcbSxpourDT8WS8w7tPTxK6455WPv4aNp1m6VSsXWrVvZt2MzVrZ29OjVl0pJcp9IKcmV3ZHD30WQP6u+YGQfBdv3HUtwBX7x4gX9v+3GqTPnMDFS4Oqag78XrUrT/C8pTUqITAFLBzmn6IfzECWlyZUNnyMy04CgJBP/DlLKkW+dY4RuZFIX8EVnDuuSFvf3TO3C/KUSFRWFv78/Li4u7zwlLl68mLE/TiGfuk7CU2KMNpxrcVvQSN3cRKlSpYiOiEH7wpJCikoIIVDJWG6Ig4yd9hMDBgxI8z69wdPTkxJFijMkS3uslLpRhVpqmP1iA4FxrwGoUaMGnTp1om3btmTNmhUpJXNnz2HSnxMJeR1CFscs/DZu7AezWqYXwcHBHD58GGNjYxo2bPhed/hXr16xc+dOhg4ayOnGJclilvgQEK3WUGLXDWJiY7+o8C8tGtehmdMpeldNbNPDl5JyE1XEqKB48eI0a9aMHVvW0aZkEGNaKTA1gh2X1QxaZcS1m/e/uEyfySVlRMZRziqSPJFpdnX9x7zL1qOb5HcCXgG/AzuATUAuwAvdAspgIUR2dK7KTeLPbQLMQufCvFxK+ee/XOealPJf/diTcwwYROaLQqPRMGrkaBYuXIhSYQxC8tNPoxk5amSCoDSo2wiv03FkNdK3799W76Z9z+aMGTOGvHnzEhAQQNNGzXj66Bk2xk4ERPvQvUd3/l4wL10na5ctW8aiMbNoY6W/sPHU62uEF1ayftP6D96QpJRERUVhYWHx1ZthnB3s2VQpF3msEtMJB8aoqLLvFsdOnqRKlSpfTB/Pnj1Lm+YNmNkmlsbFFdzylQzeYkrTDt/h7JKDXbt2cfLkSXI5Sh7PsdRr99BVkiwVfuD3seMSyl68eMHiRQt4/OA2xUqVo2/f/u+s0v9SSCmRmVn4/e72b9P82j9fxGJMIUQ08PjfDgFsk5O0LNMGyPwS+WPsOFYt3kAubX1MsCBWG8bkCTMIDArC2NiIQ4cOcf3qDXIZ6Yc4kVJiZC7o2bNngrtslixZuHjlAjdu3MDb25syZcqQM2fO9OhWApGRkVy4cIGAiGCw0t8XrYijRs0G//rEK4TIMItlu3brxsx9W5hRJidKIZBSMu3uC0yNjahWrRru7u4MHjyYjh07YmZmhpSS/fv3s37VctRqNa07dqFt27ZpMuKpWrUqG7buYexPP9Jn3R1y58jGsFE/069/f4QQDBs2jIULF3Jkzf/eEcZiOVSs2LWNmrXqULlyZR48eECDejVoW9WY+oXg1NkzlJk3i5OnL6b6PGB6IfkqPaYKf/wQNMmpyDCSSSPi4uL4/bexLF6yhKioSGrVrM2s2TMSkpFptVrs7RzJrqqOqSIxfliE5hXPY0+gMILKlStTuHBh1q/ZRGHZCHOFDVJKXmkfoMr2gqfPH6fbKCU6OppVq1axf/d+smTNQv+B/SlfXrdOxdfXl3nz5rFo0SJCQkIwNTKhk2N9ClvkAeBVXBArQvZx8SOZMDMSkZGRtGrSiCd371DeyZqbIZE45crDhm072Lt3L3PnzuXevXs4OTnRr18/Al/5cWL3dvrkN8NEKVj1LJZClWryz+atX8SI5/79+9Su5s6TWUrMTRLb0/DPGI7dUSOl1CXvszXl544K+jZNdKaYvD6cuxHVWL9pZ0KZWq1m9+7dnD51gmwu2enevQcuLi5p2idImZFMfgtHOa3Q+5cEvE2bG2u/iJFMSmIQmRTE19cXhULx3h9D2zbtOH74AmbavCiFCVHqF2jN/bly5RLe3t4cO3aMCRP+pIRZJ/3kZzKGp9p9vPJ/mRC8ct68eYweOQZb06zEaqKwcbBk/8G96XaDjoyMpHrl6kT5RJCPvETKSG6p7jJo2Pc8ffaUzZs3o9VqadWqFT/88ANCCNq0aI2twhITYYx35Ev+Xvg33dJ4El+r1bJx40Y2rlkLQOdvetC+ffs0E2opJZcuXeLOnTsUKlSIqlWr6rlgHz9+nDlz5rBr1y6sjATXO+XH1lQ3colRa6m7/xUL1297x6U6vfimWwc8bx/g15Zq7CwFi48Jznhm4cjxc1y5coWDBw+yYMHfhO3KhWkSIXoVoqFI7wBe+gdjYWFBdHQ0TRvXISL4Ca1qmPD0Bew6Gc7mrbuoVatWmvYppURmaqGmyTq27Y01BpH52kkNkbl58yZdOnfl2fPnICVFihZlw4Z/ElxRnz59SskSZXBSVEIkWV0fHHeXSPULtFrdqNPU2JwcispYKxNFKlj9jNzljDl99qTeNUNDQzl//jy2trZUrFgxXedZZs+ezaI/FtDUvEHCTTJIFcwq//WYW5nTt29fBg8erLfyXaVSceLECWJiYqhVq1aaRwaWUtKtU2euHztFU2udGXFPmDfl69dm9fpkx/5LE8aOHcvjjXOZXc1Zr3zatUBEvZ5MnjI1nVqmj1qtZt68uaxdsZDIqCiatmjD6DG/Jizo1Gq12NpYcH9ZFrI5JP4O7nrEUWXwS+I0SsqUKYO5uSlm6vvsnJ4LhUL3fTpwLpQfZkfz+Kl3wnc9KiqK2bNnsWvnRkxMTOncpTd9+/ZNURNiSohMPgsnOaVg8kSm/c3VX4TICCGMpIz3JPqPGOZkPoJKpWLbtm3s338AZ2dn+vT5Vi9s/evXr6lVqzaqKBvMlYVAwON7AVSvXoOzZ88kJPQSWjPEW19+U+FAltymzJ03m8qVK3PixAl6dOuFSl0UC4UjkdpXvDZ6yIZp+99pl62t7Qdjd6U1e7bvoYDIpzcCczR2IJuVM4s2LKZp03d/YMbGxtSvXz9Frn/+/HlmTZuO53MPKlWryo8j//fR+acLFy5w6tAR5uerialC9zOobu/Kd/sPcOnSJSpUqPCv53t5eTFj6jQunztHbre8DB0xItVSIOfLl4/L2nfjiPlGqoh+8pS4uLh/zYmSVhgZGTFs2A8MG/bDe/crFAq6dunMmOW7WPKDFUZKQWyc5JeV0bRo1Za8bgU4d+4cN6+dZfX43AkCA9Cwsg3av/w5evQo9erVQ61W07B+TRys/fllYHZiYjRMXzKO82dPsGrNBr3rqtVqTp8+rRtxV6+eZuGQkqL9+p7lLwEpEiU104vM06dPuXPnDgULFkzIKviGmJgYatWsxb37j4iOlBgZC+bNm8fatWto3bo1oMuwKTVmmBolpsU1UToRHPQwQYyEECiEMdLorSRpRpG0bdeGJk109trWrVuza48df/w+gSdPblGqdEn+GDefcuXS/cHmg4SHhxMQGEAWjf5KdSklKoU61bMObtmyhQG9+tDUpgh1TbJwc8tJyv/zD+evXNIbOWm1Wnx9fXn27BnPnj1j1apVVDJ3ShAYADOlERXNnRg9ejTdu3cnX758uLm5kT17dr2R4tOnT6laoQIN7RzoYWvPk9v3ad6gAQtXrKBNmzYp3seWLVvy45DvOe4TQW1XncfEjYBotj8LJ+rhNtzc3Pjxxx/p168flpaWBAQEsHDB31y7cJY8+Qvx3fdD0myB58eYNn0OHdo+o2Cva7gXsuDC3Uiq16jNylVrE9z169auRExcgN55UkJoeBQNGjTAyckJFxcXjHjB/hWVEsSoVhUnSjU4wK1btyhZsiSgCxbapk1zHB2MsLU1pXt3P6ZNm0GfPmnr/i7fu+D+iybFGpxpzWVxcXF07tyZffv2Y2pqhkoVS6VKldi1a1eCB9Pff//N6FG/oopNdMvUamMxMolg+I/DefjwIceOHScqzBhzY/15mGi1D42aVmXEiBGUKlWK1q3acvncPSykG0phQoTaF7WJL3fu3kp3r69/4+bNm8yYNoOnj59SqVplfhg+jBw5chAYGMicOXOYO3cur1+/xtrYiq6O7bFWWuuSSEXfxtfpFXcf3k21iWmNRkOeHDnpaVGGQpaJpqStAdfxczXGvWL5BFHx8PAgLi4u4RghBFXscvBbfv2FgmOfnOXC6xck/V2YmJiQN29e3NzccHNz48qFC5QKCaNfnkRvqGshwUx85cNTb+9UMV2eOnWKzu3a4GImMDFS8Dg4msUrVmFpacmkSZM4ceIEjo6O9OjRg03/rKZudkk9V7gVJFl5N44tO/d+Eflw3nDr1i0ePXpE8eLFKVxY35Fp+fLlLJ49kgNzc2JhpvtbLt8VxOzNMPD7H7lx4wb79+/h+x6ODOuj75HWd+QtQuNK0KNHD/Lnz0+LFo2ZON6dVi10Lv9PnoTQuMVuDh06+U5enfeREuYyN3MnOSF/82Qd2/XOyi/FXOaDLuLLe/mU2JWZVmR+/vlnZs6cQ0yMRMS7kJqaQqdO7fn111958uQJ3303CG/PEJQK/VAkMaoXgIZ8+fLh4ODA7VsPMVfk05u01Rh5sGfvTqpXrw7o7MfDf/iR1atXExsXQ4UKlZk/fy5lyiQ7wVyac+DAATq260RRRXHsFY744Yu38KBF6xZs3LiRqKgoWrduzZgxYzh25BgTxk/A1TI7YepwLO2t2Hdo3zvxulIST09P3IuXYlYe/dGDT0wIfzzbi6m1RcJo5O3NwsKCYoUKMyp7GcrY6ATqauhLpvnd4P7jR0RERCQIVNLt6dOnqCIiWFWuMnktE/2wpZQ0vnyW6/dTb+GhSqXi9OnTqNVqqlevjrm5ecK+8+fPM2nSJA7t281Ad2v+qJFoEtrzOJopjxy4fvfhF+GJ9jE0Gg19vu3O4QN7aFjFhucv1Dzxkew/eCwhI+2UKZN5eH0p8yboWx+qtT7D9TuvEz4XLerI+VNd9I6ZNOUSseqKzJgx+6NtSSmRGZe/RbKO7X5nxZciMn7AAj4wopFS/pHsujKryDg5ZSE4OFJvIl5KLfoh2gTGSnuUCsskx0iUJq85cuQQlStXRq1WU7FCJR4/8gG17octjF9Ttlxxjh078s6PWkqJVqv9olZ0vw8pJfnz5KdwaAlymuZOKL8ccZ5b0dfp3K0zo0aN0ktDHRQUxPnz53F0dKRSpUqpdkN7k9p50aJFbNmwibmFO2KpTIyMcC3MizN2wVy6ee1f6zl27BhdO3TETmGCBMKkin82b/qoB1P5kiXpJoyp5pQY7DZUFUfjsyfo0KULffv2pXr16ulyQ8+R1YE9LUzIb584h6OVktwLAnni6ZMwCf81cOvWLc6cOYOzszPNmjXTi37x8uVLShQvxII/C9G4Tla0Wli2wYvZKwK5fuMeHh4eLF++nAf397Flg7778JLlt7j3IBfLlq3+aBtSQmTymjvJcflaJuvYHneXfykik6zV/Mkh08bpjoqK4l2RFgghWLx4MadOnWLZsqWYmmmQMnEplVZGkTVrloT4TkZGRpw8dYJhw/uRJYeWbDlh1JihHDiw7703GSHEFy8wAP7+/vj7++Nqor+gt6BZERwcHFm9erWewAA4OjrSrFkzKleu/Fk3WJVKxapVq2jVtAVdO3bhyJEjevs9PDwYN24c+fPnp1atWuzZswc3NzfWBV4hVqtzhAmKi2Bb2B2GjfrfR69Xp04dvPxesHjrBpZu24jnC99kucgOGTGC+S+8eBUTA0CMRsNfz56QL68bO3bsoGbNmuTPn5/x48fj5eWld+7hw4fp3rEj7Zo3Y/Xq1ahUKZumydHBHv9I/aV/obGSWJWKe/feTR0SExPDixcvEtIlfEmULFmSgQMH0rZt23fCK2XLlo1t2/fw8/RXFK1zjoI1TvPPHsGBg8exs7OjdOnS/PTTT1y+8pIXfhEJ56nVWjZuek6jRskzX6UMAq1M3vYFYZiT+VzejGSaNm3KgQPHSOr7IKUKd/eSXL58Kf6z5IcffmDRosWYmFgh0GJqZsSxY0ffucF+jQQHB3P9+nWyZ8+u5/QgpWTnzp20b9uerg69MVMkhj7xifPC0/kJtx/cTtG2qNVqGtdvhM+tp7gbuxGjjeNc7EN6DexD4aJFWLlyJceOHQN04tCrVy9at26NlJIenbty7NgxnC3teBn5mhEjR/Dzb7+m2khCSsn4sX8wY/pf5LS2wSc8jPr16rF87VqEEGzbto0VK1Zw/PhxhBAJ7b13+xb/LFlMz5wOWBop2PQyjCxFSrDrwMEUe/CYPXsWG2ePZXMzS2xMFai1kqFHwtj5OJaw6Dhq167N6NGjqVOnDr//MoYFC+ZjogCFsQm//D6OgYMGp0g70gqtVsujR48wMTHBzc3tnf3Tpk1h7txp9O9TBDs7U9ase4KDYwF27dqPkdHH/Z5SZiSTRf7ulryRTK97y76UkYyDlDI4RerKrCLz+PFjKlSoSEyMithYFSYmRhgbKzh58sQ7+c09PDw4deoUTk5O1K9f/6tPSyul5Pdff2fGjJk4mWcjNDaYIsUKs2X7Zo4ePcq0adO4ffs21hbWZBeuVLOojZEwIlobxdG4A/wy5ecUD7K5ZcsWxvQfzncOjVHGe+CFq6MZ57EOlVTj5uZGz5496dGjB7lz537nfF9fX3x9fSlcuHDCotXUJiwsjPvxczA5cuR4Z7+HhwerVq1i1apVPH/+HHOlgpMN3XE01X1/1FpJh4tPGLtgMa1atUqRNmk0GgZ/148N6//B3dWae/7RFC9VhmWr/2Hjxo3MmDGDFy9e4OrijKtZOCvbGJHbXsGdlxq6bJX8MX0xnTt3TpG2fCmcOXOG1auXExERRtOmrenQoUOyf8MpITJ5zLPI3/K2Stax395f+kWITEqSaUUGdHbd+fPnc/HiJUqVKsn3339Prlwfjff21bNp0yYG9xlGJdEEc4UlWqnlVtxZfORjImMiKFasGCNGjKB58+b06NqD06dO42juhH/UK74b8B1Tp09N8VHCt9/04vX+x9SwK6FXvsz/EC2+78y4ceO+2iyMWq2Wn3/+mWtrl7GgfAG9fSuevCCwQh0WLF2Wotf09vbm9u3b5M6dW2/UHRsby+rVqxn2/QAuD7LEzTFxBHXokYrxN3Jy+eb9FG3L10xKiczPeVon69h+D5ZkOJHJ1OtksmXLxrhx4z5+YAZjzsx55NeUxtxE59CgEAqKm1TmWfhd1qxZQ9euXRNEZM/+PXh4eODl5UWxYsVwdHT8t6o/G41WS6gm8p1ylYmkUqVKX63AgG4RYqVKlTi5btU7+17GqJCpsFIvZ86c73WNNzU1pX379gwf+j15HfT/psWzKfHw8nnnHI1Gw/Pnz7Gzs/uqHAe+FKTkS5tvSVNS7ZcrhMgphDguhLgvhLgrhBgaX+4ghDgshHgc/2qf5JwxQognQoiHQoiGScrdhRC34/fNEfF3QCGEqRBiY3z5xfhkPpkelUrFjh07mDlzJqdOndJb86HVavHx8sZcoR8G2UgYYWtph7u7+zujlDx58lCjRo1UEZgXL17Qu3dvVq1dzZnXd/GLTTQDXw9/wmupW4CXFoSGhrJo0SJ+GjOGHTt2pOhkeKNGjfCIjmO/b2BC2cPQSNY/f8nylSvp06cPL168SLHr/Ru2trZky+LIOU/9ILqHH6uIiYqgadOm7N+/H61Wy/bt28mfx4W6VUuTP68rbVs0Ijg4RUz1mQqZzC0jkmrmsvg0oC5SymtCCGvgKtAK6AkEJ8niZi+lHCWEKAqsByoA2YEjQEEppUYIcQkYClwA9gFzpJT7hRADgZJSygFCiE5Aayllx39r15ecTyYl8PT0pGa1WqjDBeYae16LFxQpUZB1G9ayYcMGFi5cyPNnHuQ1KUJ5i7oJ5wWq/bhtehLfl77JmhD9FF6/fo1Go9ETqYiICKZNm8Zff/2FWq1myJAh5HNzY9SIUeSwyEK0JhaNKezcuztN1hLdvn2b+rVqU8zcjpzClGtxrzHP7syRUydTLK7a1atXadu8GVZSg7WxEQ9fhzP5r+k8fPiQuXPnYmxszMiRI/nf//6nl9IgKCgIpVKJnZ1dirQD4J9/1jF6aH8m1pWUza7k2FMNf5yElu06s3fvXl6+fEnOnDmJDHnJlj5QLb+CyFjJL3uVPJZlOXjsTIq15UsmJcxluc2yyFG52ybr2EGPFmU4c1mazckIIXYC8+K3d/JRv51zWghxEBgLeADHpZSF48s7x5/f/80xUsrz8elFXwJZ5L90KqOLTO0adXl5JRo3pc55QUot11UHCNR4o9aoqVGjBl26dGHCH39iEWFPVm1OImQoz8Qdlq5YTPv27VOsLZ6envTu3ovzF88jhILiRYuxeMUSLl++zK+//srLly/p2LEjEydOTPAMioiI4OzZs1hYWFClSpVP8rq6evUq8+fMw8/Hl5r169B/wIBk35grlSlL1TAFTbPmAXTOEZO9blCxZ0cmTJz4qV3/IBqNhnPnzhEdHU3VqlUTxOTp06eMGTOGzZs34+LiwoQJEyhTpgzf9/2WO/fuoZVQrUolFq1YnWLzhvv372f6xLE8e+5ByVKl+On3CVSoUIG4uDi2bt3KqP8Npa97MKMbJj50qDWS/OOMOHb2WqZIy5ASIpPLLIscmUyRGWwQmc+8iM6MdQooDnhJKe2S7AuRUtoLIeYBF6SUa+PLlwH70YnMZCllvfjy6sAoKWUzIcQdoJGU0id+31OgopQy0SahK+8H9APIlSuXu6enZ2p2N9V5/PgxPj4+lCxZUm90EBoaSras2ahp/A1KkXhjCNX4c0d5hLMXTidMAgcFBTH/7/kcO3yC3HlyMnjYYNzd3d+51ueiUqkolK8gbpHZqWBZCoHgZuR9joSeJVYTR5UqVZg+fbpePvn/wob16/m+33c0sCmIs5ElV2P98DNTceHqpfea+eLi4vD19cXb25s7d+4w8ofhbC/TJMGzDeBBRDBzIjx48PxZirQxOZw7d44ff/yRCxcuYGFixLhyznTKb49KK1l4P5gdISbcefgkxUeb76NJ/Wr0zXeRZiX0hb7aTAXDxi9L8EILDAxkyqQJHNi7A0tLC7r3HsSAAQO+ivVgHyNlRCarHJEreSIz5PHCDCcyqf5NFUJYAVuBYVLKsH/xSnrfDvkv5f92jn6BlIuBxaAbyXyszV8qISEhtG7ZlmtXr2Ntak9ItD9Dhwxh4uQ/CQsLY82aNahUaoSx/p9FoMTKykrPy8jR0ZFff/uVX3/7NVXaunfvXpRRCqpYJQpXWaviPInxpHqXOixevDjFPNTi4uIYOmgwP2Srjpu5bmK6AnlY/PI8/fv2o3LVKnh7e+ttr1690o9PJhRoJSiTNEkjJb4+vrRq1Yr69evToEED8ufP/8F2x8bGcv78eZRKJZUrV/4sIahSpQrnzp3j2969eXV8O90KOgBgpBD8UMKJ48decuDAAZo1a/bJdX8qFarUZvex6zQrkTh38ypMctMzmi5durBkyRLat2/P7BmTqJkniGXdtQRHSMbPH83N6xdZvPTjK+ozAxLQpMDEvxCiELAxSZEb8JuUclaSY2oBO4Hn8UXbpJTp6t2UqiIjhDBGJzDrpJTb4otfCSFckpjL/OPLfYCk7jCuwIv4ctf3lCc9xyfeXGYLZNhZyR7devLsaiDFtW1QxCjIQRQL5izlyLHD3L59m9jYWCxMrfBW3ye3cXFAZ/bxUdyhXYfkPUmlFJ6enjhh9055dmNnbKxtUtQF+v79+5gL4wSBeUM1qzxM37mbrdu3YWlpmeBxVaJEiYT3b7a+3/Rkp/8z2mXTxVrTSC3r/Z9QtHRJbt26xc6duqyNefLkSRCcOnXq4OCgE4F9+/bRq1s3spuZoZZaXmslG7Zto2rVqp/cHyEEdrbW5HAyf2dfURsjnj9//p6zUp5B3w+hwvIljNj+ms7uWnxeS/44aEbffj1xypqdNWvWMHDgQOqVUDC/lxlv/IgqF9BQ4H9bGDXmd72UylJKfH19sbS0xN7e/gNXzZikhAOhlPIhUBpA6OJh+QLb33PoaSll6j+FJJNUE5l4D7BlwP23InbuAr4BJse/7kxS/o8QYga6if8CwKX4if9wIUQl4CLQA5j7Vl3ngXbAsX+bj/nS8fT0ZP78BTx68Jgq1SrRp0+fhB9jcHAwR44eobRojyLepGMiLHDRlOb2jTMMGDSALl26YGlpSa3qtYnUBGASY02kuT+2LpaM/eP3NO2LsbEx98IeU9eickJ7pZT4KF8xoFLK5l3x8PAgMCwEtYsGI0WiiSZEHU1Z97LsPrgfOzu7fxW2lf+so17NWlzxDCG3kQVXI4PIV6IYuw/sx8zMjKdPn3Lo0CEOHTrExo0bWbJkCQqFgnLlylGpUiVWLlnCvBLFKB0/B3Q6IJBWTZvyzNv7sxwHyleszPydGxgkZUK71VrJgedBVH4rxEpqkSVLFs5evMbUyRPou3Mfjo6OjPpzOF26dEEIwW+//UbzxnVoleuc3nlWZoIqBQUnT55MEJkjR44weOC3BAcFEhOnoX69OixcsjrTuESnwk2pLvBUSvnF2/5T07usGnAauA28Cab0Ezqh2ATkAryA9m/CFwghfgZ6A2p05rX98eXlgJWAObp5msFSSimEMAPWAGXQjWA6SSn/1YD+pU78X7hwgQb1G2ElXVGqrFGbBIFlJFeuXiI6Opo1a9Yw5c9plDPpqndehDaQ0Ky3eO71NKEsLCyMf/75h6dPn1KhQgVatWqVZlEKQkNDGTNmDAsWLMDKzApXk2xUMS+DUii5FnuXWGfJ1ZtXUyTJ1qlTp5gwYQKHDx/G0tiMeg4FaZ+lNAqhIEQVxZSXJ5i1fGFC7p+PERsby65du/Dy8qJ8+fIfDHKpVqu5dOkShw4d4vDhw5w/f55m2Zz5s0RxveN+ePiIHuPG06NHj0/uW1xcHBXLlKKIDKZvARtiNJKZd0O4EhBNSGQ0gwYNYuLEiWkW3eBD/PzTKKJuzeOvJIGOpZS4DY3hxWsFtWvXpkKFCiyaP5OVw8xo5G5CZIzkt3Wx3AwsyInTl9Kv8ckgJeZkXE2zyqGuyXOoGflsvieQdE55cby5/+12LQeuSSnnvVVeC531yAedxed/Usq7n9fylCFTr/hPS2JiYti6dSv379+nWLFitGnTRi/oX/GipQh7ZoWdUWLIlJeqG8SZvSQ0LAQAY6UphZT1sE2SntlbXqZxjyosXDQ/zfoipeTMmTOcOXOGbNmy0a5dO6ytrdm5cyeDBg3Cz8+PYcOG8dNPPzF39hzWrlqLWq2mXcf2/PLbL//JFVdKyZEjRxg/fjynT58ma9as/O9//6NVq1Z079gFz6fPcLaw41noS/43YgS//TE2xfr9IYYPG0bMnt18l08/dtaEx0+oMnQYQ4cO/ax6Q0JC+HPcH+zcugVjYyM69+jFd4MGMWHCBObMmUP27NlZsGABzZs3JywsjC1btvDq1SuqV69O1apV0yQKtIeHB+XLFmdJbxXNyiiJUcGkXbDjblaatuzA7t27efbkAUNbWjKpV+KITqORFBwQyc79ZxLyuty/f59xv4/h5KlTZM3iSP+BPzBgwHfpmp4gpURmcDJFZvSz+R+9nhDCBJ2AFJNSvnprnw2glVJGCCGaALOllAXeV09aYRCZNMDX15fKlaoQFa5FHW2CkXksVrbGXLh4nmzZsvHixQvy5HajkEkrvcyZsdpwPNVHmDZ9Kk2aNOHOnTt07/INTurCmGFLhPEL4iwCuXr9yntjZ6UGKpWKNi3bcPnsZXKKnEQpI/FTv6Rs+bIcPXqUkiVLsnTpUsqXL/9Z9cfFxbFs2TK2rNuIsYkJPfr0pFOnTggh2LNnDxMmTODSpUvkyJGDUaNG0adPH728Krdu3eLly5e4u7unWnSCtzl69CgDOnVkQ+lSmMRHJohUq2lw6gy9Bg5k2rRpKZ4e+eLFi/Tp04c7d+5Qr149bly5RJXsJuS20LDPS0PpStXZsHVHmnihnTx5koH9ehAUGEBMnJaqVSqxdOV6XFx0D0ONG1SnR5nbdKihP8dUe3QoOUu2pn///mTNmpWa1SvxQ0dL2te1xsMvjlHzQ2nQvDcTJ03TO0+r1RIYGIiNjQ1mZmakJikhMjlMs8pBOTok69ifn/+dHJFpCQySUn50lbIQwgMo97bHbVpiEJkU4NGjR0z8cxJXrl6lSJHCjBkzWi/IZqtWbTh16DbWysR0wGHqJ7jktcDJyYGLFy+iilNTxKI1SpF4M4rUBKLN+pTnnommsOvXrzNrxmyePfWgZp3qDBkymKxZE/OapDbz589n+k/TaWLeGGV8Lp6H0Y84GnqUsRPGMmLEiM82zWk0GhrWbcDL28+pZFoQtVRzOvYBbqUKERASxM2bN8mbNy9jxoyhR48e74R/Ty+klHRo1YrHFy/SIYsTKq2Wf175I2xtefjsGUWKFGHhwoXUqFEjRa8bFxfH1KlTmTzud/6u70irAro1N7FqSZt9YXQfNYn+/fun6DU/hJQSb29vzM3NyZIli96+KVMmcefIVFYOSxSE1xFacvcMJDJGZ0k3NzNiYFt7Jg3KlnDMq2AVJbp68ey5T8Lc5IYN6/l5zP8IDQ1Fo4WePXsyZeqMFBfxN6SUyAzMnjyR+cUjWSKzATgopVzxnn3ZgFfx0wkVgC1A7vScq/56A0KlIffv32fDhg1cvnyZt/+vbt68ibt7ebZuOoLXk1j2775A9eo1E3KhREVFsXfvbiwV+tkSLRU5uX//HrGxsQwePJhKlSoRxN2E+rVSTZjRQwYM1L9JlClThlVrVnL63AkmTBifpgIDsHbFWoopiiUIDEBBswLYWFj/57mf/fv38/z2I/o41KeUVV7crQvwnUMjzp46Q2hoKKtXr+bRo0f07ds3VQVGSsnJkydZsGABJ06ceOf//G2EEGzYto0R06dzNVdu7hUoyOQlS7j/5Al79uwhOjqamjVr0rt3bwIDU+6B0sTEhJYtW+JkY0HL/InZW02NBAOLGbN57Tv3oFRDCEGuXLneERiAvn37c+6xOT8ui+bmMxWHr8fSZFwM3/bpS3BwMDt37iSHiyMNK+mHOnJ2MCaHk4KJEydy6dIl9u/fz/9+GMCS8S54na7IlR1leHBjO8N/+F7vvMjISBYtWkSfPt8wbtwf+Pr6pmrfk4MWkaztYwghLID6wLYkZQOEEG/CorcD7gghbgJz0M1Tp+tIItOPZCIiIvD09MTV1RVbW1u9Y+Pi4mjfvgNHDh/BxMQCtSaWQoUKcujQwQTX1fr1GnD+9ANMjRJ/XHHq1yjNgsmVOyd3795Fq5XksKyhN0pRa2MI1l4hOlqXiTM4OJjGDZvy8MFjLIwcCIt9SfPmzVizbnWamDySSyX3Sjg/z0pes8RRmZSS9ZEbOH7++H/KszN82A88XnuOBg76qRY2BJ+m89gBfP/99x84M+UIDQ2lcd16+Ht4UdzSjruRr3HM5cqBY0c/ey4pKiqKcePGMX36dGxtbfnrr7/45ptvEr3G1Gri4uKwsLD4SE3vcvv2bVrVq8bVTvZ6cxf7nkWxJCg3x85+GRPrfn5+TJr4B4cP7MXW1oaefQbTr1+/hMCnvXp0oojtaX7okiT0UJQG12YPiIof7VhbGjH9p4J0a5U4JxkQHEfJplfx8vbDxsaGoKAgalSvRC5XScO6Wbn7IIIdu73YtXs/lStX/uR2p8RIJrtpVtnf5V+jXSUw1nNehluMmWlHMlJKfvrpJ7JmdaZy5apky+bCwIED9YIiTpw4kaNHTqJR2RMTZYYqxoZ7d5/yzTc9OXXqFIsWLeLEyRMYK+306jZW2hIaFkr27Nn56aefqFqlKlFar4QnYikl0fjQrl27hHMcHBy4cOkcR08cZO7SSdy4dY31G//5ogTm9OnTePh6cCniMhqZuEDvScwTrO2tKVq06H+qP6uzM6+Jeqc8QhGbrBGblJKLFy/y999/s3v37s8KcDnqxx9xfPmapQWr8INrMZYUrIJzQBgjfhj+yXW9wcLCgsmTJ3Ptmi4US69evahduzbXrl3j+/79cLS1wcHOlgqlSnLmzKfFBCtWrBhKCxv2PE38u6k0kumXXvPguTdnz5797HanJC4uLsyZu5D7j725cOUuAwYM0IusPXjYSKavD2P/uTCklLwMUtFnUiBt2rTBy8uLbdu2YWNjTcnC+qOdLA4mmBpraNy4McOGDaNLl45UcDdm06oafNujMDMmluOvP8swcOC3Hx2RpiZSJm/LiGTakczs2bP5+edfiIrSIoQCKSXm5oIhQ75n4sSJBAQEUKxoccJCFSiSjECk1BCrToyWK4QSK5N8GCsTv/wabSwqhQdhYaEolUr8/f2pWrU6wQFhoLJAGkWR1cWes2dPp9nkdHLx8fFh8aLFPH7wmMrVK9OzZ080Gg0jR45k6dKl5MqVi6wOWfF97our1pUooyheaF5w4PABKlSo8NnXVavVDB06lCULFtE/exMKWuRASsm1iCfsj7uFh4+n3gT/28TGxtK2RSuuX7xCcQtnfNXhxJgrOXrq+HuTnCVFpVLx4sULvL29aVS/PiuK1SKraeK1AuOi6Xn3JOFR7wrgp6LValm+fDkjR44kNiKMGi72jCuVAydTY/b7hvD7XX/OXLr8SXHBLly4QMsmDamW3YQ8Fmr2+kgccrjh8yoQb29v+vXrx+TJk1EoFKxcuZJrF8+Qt0Bh+vTtj6ur68cvkEYcPHiQEcMH4eHlgxAKunfvxrS/Zif8v3/TvSMFslznxz6Jsdsee0RRreM1ChQsxoMHD1CIOA5sb0LJ4om/K61Wkq/kFm7dfkj27Nk/qU0pM5Jxln2yJW8kM95rboYbyWRakXF1deXFi2BEkrkFKbUIEYOZmRlRUVGAwMQoG4okccCklKi0fmzZshl3d3e2bt3K77/9iVKTHYUwRivVaJUv6dm7M7Nnz0o4T61Ws2/fPh48eEDRokVp3LjxFxfb6eLFizSq34icwg0bjT0Bxn6EKALQCi2vX79m+PDh/P7771hYWHD8+HHOnDmDs7MzHTt2/E9uyf7+/nTq1Injx4/TpEkTrl28gpk0Ik6rxtzWis3bt3w0EvOkPyeybfZShmWrhlG8h97OwDu8zGvBinVr8PHxwdvb+72vL1++THjKVQrB9nJNsDFOfLAIV8fR5uoBwiIiUsyb6fLly9SrXpXLzUpipkx8op9x/yWaqo2Zu2DRJ9X3+vVrNm7cmODCXKtWLSIjI/n999+ZNWsWDg4OGAsNVbJL6uVSczNQydYHWvYePPrZnoCpgZSS169fY2Fh8c68271796hVszIjvs1GszpO3H8ayU/TvRnw/U8MG/YjWq2W0qUKM+WP/FSrnOhAEBWlpmDZLTx/7pNg5k4uKSEyLibOsncyRWait0FkvnreiIy5uTmxsUo9O7aUEikjGTx4MPnz52fr1m1cOH8TBUn8+7WRFC2eixs3rgO6J9P//W8ECxYswNzMiuiYCNq3b8/SpUtSzeMltShZtBQO3i64mSY+RV+IPEmw9UsOHDpA6dKlU/yaFy5coF27dgQFBbFgwQJ69uyJWq3m2rVrmJiYUKpUqWStkyiavyCdyE8hy0SzWpxWw7d316OS+nlTrKysEsLJuLq66r3OnDqN7E/9+CZH4t9gpfcD1vs+wsE5K0OHDqV///7/Oez+0aNH+a1Pd9ZX0B9JHH3xmo3KbBw4ceo/1Z+Ua9eu0bxxA1rnjWRaw8QR9/pbMSzxysv5q7dS7Fqpza1btxg/7hcuXrhADtfsDBk6Si9d9IwZ09m1fS6bVtXA3NwIKSUTpt3i3mMH9uw5/MnXSymR6emcPJGZ7GMQma+eNyJTtWo1zp+/gi68mg4p1eTPn4tHjx4COtNROfdyREaqiYnRYmIiUBqpOX782DsRi1+/fs2TJ0/InTv3ez1svnSCgoLImSMXHSx7J4SBAXitCeaC8VFe+KdsQi0pJQsWLGDYsGG4urqybdu2/yRiBXK78a1JMfJaJDGTSC19Hmxi/OSJFC1aNEFM3nbwSIqXlxfVK1Umr8KU4sZW3FNF8kQTzYQpk1m9ejVHjx7F2tqafv36JbT9c/Dz86Nogfycrl8IG5PEkfLvN7xxatqJaTNmfla9HyK3SxZ2t9VQIEm6ZbVWkn16ON4vXqVorpr0RK1W06tXN44cOUCNKtm5++A1xsZ27N135JNNZZByIvNNMkVmSgYUmS9nVjmNmTlzBrVr1yEmRo2UAiEk5uYK5s2bm3CMq6srDx4+YNmyZZw/f4GiRYvQv3//9y58tLOzo1y5r/e7oVQq0WjUaFCjIHEEFquN1Uug9Tncu3ePpYuW8OrlKxo0aUiLFi0YMmQIa9eupWnTpqxZs+Y/BUz09fVFKmBXwB2G5KqRMPI58/o5RQoXZvjw5E/a58qVizsPH7Bu3Tru3rpF+xIl6NatG9bW1vTo0YNr167x119/MWvWLGbPnk2XLl343//+R4kSJT6pzS4uLnTu3Jl+B3YxupATLhYmbPMMZsPTV1S4eo2wsLAUDRljaWlOSHQYkCgykXESjUb7xZlt/wtGRkasWbOBe/fuceXKFb4bnIsaNWqka/puSeZOvxxvIso8m7u7u3zDrVu3ZLt27WTevG6ySZOm8sKFCzIj8/z5c9m3Tz9ZtGAx2bBuI3n48GGp1Wrlnj17ZNGiRaURRrKoeSnZ02Gw7OU4RHZ3GCjz2OSTkydN/uxrbty4Udpa2shaDhVlc4fasoBdXmljYS0BOW7cOKnRaD67bq1WK9euXSvt7OykmZmZzOWSQ5bMklt2zeYua2UrIp3sHOS1a9c+u/5/4/nz53LIkCHSwsJCArJRo0by2LFjUqvVyujoaPnn+PGyZMECsnj+/PL3X3+VERER79ShVqvl1ClTZIFcrtLBxlq2b9Fcjh8/XiqVSlmiRAnp5eWVYu2d+OcEWa+QjQz+yVFG/eYkI391lP3Km0sLY2Tx4sXlvn37pFarlQcPHpQtGtWR5UoUkIMG9JUeHh4p1oavEeCK/I/3HGfjrPJ/2Ycka0uJ631pW6Y1l2U2nj9/Trmy5cmmyoczuQnXhvCIK+TI7cL9B/cpUKCALtbYzLn4eLzAwciJFzHeNGrckLXr137WIsuYmBhyOGennUV9spvq5kqklKz230nDns1YsGDBZ/fH39+f7777jm3btlGlShVWrlxJ7ty52bp1KxfPnSdPPje6d++e6t57wcHBLFiwgDlz5uDv70/ZsmXRxsTgEPaaXq7OKIVgta8/4c4unIzPNfMxDh8+TLt27bC0tGTPnj160SM+F5VKRc+uHTl6+CBV85hx+5Uapxxu9B04hD///JOnT59SrGgRQl958Hs9DYWyCnbfE6y9Zca5S9fJkyfPf27D10hKmMucTZxlV6dOyTp2pt+cDGcuM4hMJqF3z2+5tPkuRYwT3YxfawI4EbmVv2ZOY+DAgRgbGyOlbq2Jh4cHpUuXpnDhwp99zbNnz9K9RRe+sW6hV/4g6hmvCkZy7MyJz6p3+/bt9O/fn9DQUCZMmMDw4cPT3eQTExPD6tWrGT9+PJrAAA7Wrowy3mynlZIu1+8xccmyZCcbu3PnDk2bNiUwMJANGzbQvHnzFGnn/fv3uXnzJnny5KFixYoIIYiLi2PevHn8MuZ/nP7elBLZE01Lvx7QEu7WhfmLlqXI9b82UkpkOidTZGZnQJHJtIsxMxunT54mmyKvXpmdMgvWljY0adIkYaQihKBSpUp06tTpPwkM6Ly4otTRvP0gE62Nwfoz5htCQkLo3r07bdq0IWfOnFy7do0RI0aku8AAmJmZ0a9fPwYNGkSDHNkSBAZAIQTVrC24dCn5q++LFy/OxYsXKVq0KK1atWLSpEkMHzqYgrldKVU4P9OmTkWlUn1yO4sUKUKnTp2oVKlSwtyViYkJTZo0IbujpZ7AALQqJjl36vgnX8dAEqQuaVlytoyIQWQyCHFxcfz26+9ky5odSwsrmjdpwaNHj5BSF4crNDSUCE2I3jkqGUusOibVEkcVKVIEFWouh99OKIvURHNZfZc+3/X94HmhoaGcP38eb2/vhLIDBw5QvHhxNmzYwNixY7lw4cJ/CmGTWuTKlYvnKs075U/i1OTKles9Z3yYbNmyceLECRo3bsz4334m4NA/LHE34c8CavYtnEr3TskLH58csmTJQlC4mvAY/Tvd4wDJ69BQTp8+jZSShw8f0r5VE+xsLMjjmoVxf/z+WWKXmZCfsGVEMq13WUaje9dvOHvgCvk0NTAR5jw+9ohyZcuTN18ebt26hY2NDfc0F7HTZMFaaY9KxnFHnqN5s+apkgo3Ojqajh07EhwWwkXbO9wLf46t0ppnEV4MHjL4vWYjKSVjf/2dmTNm4mzpgH9UCNWrVyeLS1ZWrlxJ0aJF2bVr1zvu418SrVu3ZvTw4azz9KVDThcEsN3Hj7MvXrG4Xr1Prs/S0pLmzZsTcfsMM6s5J5SvzWJG+e1HuX379id7tr0PR0dHmjZpzLDdh5jdQouVqeCBv5afD0CYWk2NGjUoXbo03s8fMbJBHLPHCl6GvWbM9r/o9+QBK9Zs/PhFMjEZdZSSHAwjmQzAs2fP2Ld3L0W0dbBWOGIqLMhjVBrr2Oz4ePuycOFCXr58yYSpf3CB3ZySmzkct5Yy9YqwdMWSFG9PaGgoDRs2ZM+ePcyfP59XQf4s3bSCn+b9zv3HD/hz8sT3LrBcu3Ytq/5eyv+yteZ7+yb84tIRv3OPWLdqLSNHjuTq1atftMAAmJubc/jkSU6a21Dr1GVqnb7MpmgNaiFo1aoVQUFBn1zntYvnaeyqH2nAVKmgeg4rUnJ+ceGy1Whz1SffJEnJWUbUW2LMmHF/4efnx4IFC/D19qBVyRiGN1CQ1UZQ0lXBpr4qdu/ehYeHR4q1IyMiM3HsMoPIfCU8evSI1i3bYGfjQO6ceZk2dRoajc4sc/PmTWyNsqIU+gPTLMpclHevQP/+/TE3N2fI0CG8DHjJ0bOH8fB6zuZtm7Cysnrf5T6bV69eUatWLc6fP88///zDd999h1KppG7dunTo0OFfk6vNnT6LhhalsTXSrcsxURjRLkt1jIyN+Pnnn1M9QVVKUahQIc5cvsz9p0+5+/gJd588Yffu3Tx48ID69esTEhLy8UqSkDtffu6H65dJKbkbHPvRuGyfgpWVFes2befhU0+27D+L1wt/Bg4ajIWFBQMGDKBKhTI0KKZ/y7A0FZTMacTt2zqTqFqtZurUyRTO74qzky1dO7bmyZMnKdbGrxEJqGXytoyIwVz2FeDr60ulClWwiXYjn6IhcQGRTBs/j7NnzpErT07Wrl1LeHgkRS00KJLEYos0CqJEqdp6dZmZmVG8ePG3L/FZPHv2jJ9H/8zRo0ext7WjU/fOrFu3Dj8/P3bv3k2jRo0+qT7/gAAcjPLrlZkrTDAzNiU0NDTd89l/KtmyJcbPatCgAdu3b6dVq1Y0aNCAw4cPJ3uVfa/e31Lqr2lUcQqlZV4bYrWS6dcC8Q6JTJWMqFmzZn1v1OsCRUpy+cF52rhrE8piVZKrTyLo2bMn3bp144X3MwKenmTFt1qy2ytYe/oQNaqe5OqNuwmZMjMjGVQ/koXBhfkLITAwkLVr1+Lt7UPVqlVo0aJFQpj/ESNGsnH+QVxlYiBDtYzjasw/GJkoadmyJU8fPSfwSSR5tRUwEWb4qR/hbXKdm3dupOjT7hv8/PwoVbwUBTX5KWRakAhNBCfCThGhiOTI8SOflbujV/dv8Nt/l8YOif18EvWCXdprPPfxTNdV2ynFnj17aNOmDWXKlOHQoUP/GuImKZcuXWLgtz159twDtVZL2dKluPXgMcbGxhw8eDBV4sq9zfPnz6lYriSTWkTTuaKCgHAYuc0YX1kIl5z52LVrF0ri8F1sg41Fojl0yAoN9mUGMeHPyYButLNz504uXjhHDtdcdOvW7YuLRv6GlHBhdjJ2li3tkufCvDzQ4MJsIBW4fPky+fMVYPJvC1g79xD9eg2hUsUqREZGEhUVxcF9h7BQO+udYyRMcLB0YfPmzWzatIlTZ0/QqHMNLsnNHItZimXJaI4cP5wqAgMwd/ZccsmcVLQsj52RLa6mOWjn2BrgsxfuNW/dkmPBN9kacIZHUT6cDL3NP6GnmPX3nAwhMADNmjVj8+bNXLt2jcaNGxMeHv7xk4AKFSpw5fY97j99jqevHyfOXeTcuXOYmppSs2bNT85D8znkzZuXvQeOsfZxaWy/11DiDyVZy3Tl0LEzbN68mX/++YdyBa30BAagbjEtJ47sIyoqioiICGpWK89ff/TFNmg5l/aOp2jhfCk6t/TFkcz5mIz6vG8YyaQBbxbq7dyxGycnRwYO+o6KFSsCOtt6wfyFifF1xNYoV0KZn+YCDjmM8fH1IS5WRXajEuQyTnzA0UoNd8U2bt65jpubW2K5VotGo/lPaZCTQ93qdbC+Z0k+Mze98t1x+5m/fj71PtGTysfHh3LlymFqakrTRk24cfU6ufPm4YcRw/9TnpovlW3bttGhQwcqV67M/v37P3tuzMvLiwYNGuDl5cXKlSt5/uwp504cIVuOnAz4fuhHUyR8LnFxcRgZGemJ/5MnT6hWsRTP5xlhYpQoNGPWRTN7bxxCaUqunDko7hLAxl8SM3muPxbJzH0OXL3xIKHswoULLF+2kNCQQOo3akW3bt3SZU4uRUYyRs6yWTJHMquCDCMZAx/A09OTu3fvJkzGvyE6OpoqVaox+n9/cPHYc3ZvPk+9Og1YsGAhAI8fP+bFixfYKHMmnCOEwFbkx9fHj0GDBrF02RJCTZ4TpHmOlFriZBTeigvUqFlDT2AAFApFqgsMQIHCBfBXB+iVaaQG/yj/Tx7JREVF0bJlS6Kioti3bx/zFy3g3JULrN+8IUMKDECbNm1Yv34958+fp2nTpoSEhLBz506WLFnCw4cPk11Prly5OH36NAUKFKBXt05cWj2Fdsa3cHm0m8Z1qrNp06ZUab+Jick7o8v8+fNTuUo1+i6WvHqtRaOVbD4Xx4pTxixcvJyBAwcSHOjLsDYWet6FHWtZ4OPjzbNnzwBYMP9v2rVuQF6zozQqfof1y36mQb3qxMTE6F1Po9Fw9+5dvLy8UqWPKYUuQGbKLMYUQngIIW4LIW4IId55WhY65gghngghbgkh/ntMov+IYeI/mUgp3+t26+3tTds27bhz9y5GRsaYmZmyYsUymjZtCsDKlSvxePISK21RhLHufJXWiaFDhrJq1Upu3LiBKlYDFhJIktsGDfnz52f69OkAFChQgO/6D+Lq49MolcZ06dCZOfNmp37H34OUEoWxksthV8midCKfmRsx2hjOxp6nStXK5M+f/+OVJKmrd+/eXL9+nV27dn2RCyxTi/bt26NWq+natSu5s7tQPKsdOS2M+PnH17Tr2Im/Fy9JVi6dLFmy0KBuHYprnrOggV1Cec2cJnQf/B1t2rRJszTea9Zv5X/Dv6fwDxtQazSULFaQHbsXU7VqVQDOnNhPnErfu06jhaioGIoVK0aZMmW4fesql9cUJJ+rLmlZ50aSZj94sXbtWvr06QPo5rYGDeyDsVJNWHgsxYsXZ/XazV9Ups+kaFLWYFRbShn4gX2NgQLxW0VgQfxrupHpRzJSSmJjY98JffJm39y5c8mWzQWlUknhwkXYu3ev3v66detx744vpuTHSJOH6DBrOnboxPXr17l8+TJ//70QRZyD3s3CWGEJWlPCwsIYOHAguXLn4rX2WcJ+rdQQYfSMXt/2TCirXr06d+7dIjgkmLDw1yxbsfQ/h+D/HFQqFX369GHBggXUa1SPR45PWRi0lFWv11GqSRk2bv20J+eJEyeyceNGJk2alOy4XhmJTp06kdvFmV9KOLOpqivTy2TjVMMCnN27g/Xr1ye7nlPHDtG9qIVemXs2UywUWu7fv5/Szf4gVlZWLFy8kqCQcPwDQrhw5W6CwAB07NqbqZvjiFMl/t4W7o4kb968DBw4kNevX1Mol3GCwAAoFILujS1YvmQuV65c4erVq/Tu1YWlk/Nw62AFHp+sSrXSIbRs3vC9v+MvgTSck2kJrI4PIn0BsBNCpKtbX6YWmVWrVpEjhysWFhZkzZqVuXPn6n1Jp0yZwpgxvxASqMVEmYNnTwLp0KEjR48eBXQBIF/6BWAsnBJExFhphSbOgrJl3alQoQL37t5BI2P1riulxMLSlBUrVjBjxgwOHtqP1taPAKMLBIlbvFAco2L1Ugwe/P07bbayskoTcxjoYoVNmTKFpg2b8f2gwVy9epWWLVuyfPlyfv31V/bt28e9R/fw8fMh6HUQq9etxtra+uMVx7Njxw5++eUXunbtysiRI1OxJ18u9+7dQxsTTed8iaF9rIyV9M9rw5qli5Ndj729PX6R+qbaWLUkODI2XRKSGRsbv3eeafDgoVi5VKR4vxAG/x1BvdERzN1rwradB5gxYwbLli0jRm32jli8ClJx/eZtypcvT5XK5enRJgtVyznEX0vBqO/yEhnhz4ULF9Kkf5+CBLTJ3AAnIcSVJFu/91R3SAhx9T37AHIA3kk++8SXpRuZ1ly2ceNGBg4cRHS0FjAnKCiSMWN+AmDw4MGo1WomTZqEKtYChUJ3U1cKc1SxWtq374ira3YePXqERmWMtZm+SUOhMKVIkaL8+ed4oqOj6d9vIGptVowU5kgpidK8wD6LTcJ8Q8GCBfHwfMaePXvw9fWlcuXK6Z53/dWrV5QvWx6rKFtcNK5cOH+ZJQsXo5IqFi1aRL9+id/vT82bDro0ut26daN8+fIsWZI8s1BGJCYmBnNjo3f6b2GkICY6Otn19Bk0jF+H9KGaqwZnSyUarWT8uZAvInhoUkxMTNi6Yx+XLl3i4sWL1Hd1pVmzZgmpyitVqoRWYc2KXcH0aqGzAHi8iGXe5nCWLV+LmZkZf074lcL59G9dQgjy5bHCz88vPbr1UbTJH6YEfmTiv6qU8oUQIitwWAjxQEqZNFf3+35I6Tq8y7Qi8+uvvxIdrUEkrJJXEhWlYcSIkezatQtPT0/CwsIxM9Zfx6AQpoSFBZAnTxUqVKjA6lVr0Eo1ivh6pJQYmcbx/fcDad1a59Lr5+fHr7/+hpWxI2pNLDaOFhw4cEDvxmJqakrbtm3TpO/JYfy4CdiHZ6GiWTWIHzhlUWTjhvFF+vb9cHDLDxESEsKuXbuIjY2lQoUKtGrVCltbW3bs2IG5uXkKt/7roVSpUkSi4NyrcKo460aBWilZ7RFGq+GDk11P27ZtuXPzBhVmzaCUixXPQ2KwccxKpOolFSpUYMeOHVSsWJHw8HC8vLzImTNnui1uFUJQsWLFBA/LpCgUCrbvPECrFg35e4sX2RxNuHIvlD/G/UmXLl0A3eLknbv/onPL7Am/oeDXcZy/4s/i99T5JZBSd3kp5Yv4V38hxHagApBUZHyAnEk+uwIpmzv9E8m0LsxmZubExSn1bvS6TG6RlC9fHldXV/bu3QdaexQi0Tyl0UbiXr4Q58+fA2Dw4CGsWrkObZwNQhghlOE4Z7fhxo3renMmwcHBnDt3Dnt7eypXrvzFr/vIlysfpcIr4GScuPJbSsmW6DXcuPtpCzx3795N105dcbPIiTFKboc8RAo4c+5Muo/YvgQOHTpE53ZtaZHTFlcTwRaPIAI0Sp75+H6yEAQGBnL16lVcXFwoWbIkd+/epXnz5vj6+tK0UX2OHzuGs40Jr8Li+LbPt0z5a9YXN9oBnSv+uXPneP36NVWrVtUL4hoREUGVymUpUUBFjzZZCQpRMWWhDw2bdGPqtBkp2o6UcGG2V2aVta06JuvY7WHzPng9IYQloJBShse/PwyMk1IeSHJMU+B7oAm6Cf85Usp0ddHMtCJTokQJ7t59kmQkA1JqyJbNHl9fH4QQTJkyhQnjJxEXY4oQJmhlDMam0ezevYs6derEnyP5559/mDf3b0LDwmjbtg0//jg8XezgKUnp4mVw8clFTpM8CWUqqWJTxGq8fDyTvUI7NDSUnNlz0smmETlMdQtKQ9URLA3awqnzp9NkpfrXgJeXF6tWrsTf7wUWNrZMnTqVX375hfHjx//nugMDA6lUsQLmEV7s6GpDdmslryK09NilpkH3H/jlt7H/vQNpTEhICLNmzeDA/h3Y2NjSs9d3dOnSJcXNrikhMnbKrLKWZfJEZmf4v4qMG7A9/qMR8I+U8k8hxAAAKeVCofsDzAMaAVFALylluq50zbQis2/fPtq3bx8/J6MENJibK5k//2+++eYbQCcg8+fP588/J/Lq1UsKFSrM9Ol/0bhx43TtQ0oTGhqKSqVKyCvz/Plz6tapS4h3KC3s2mOqMEUrtVyNu0D2SlnZe3DvR2pMZN26dUwd9idtLOvqlR8Pu0T53jWY9te0FO1LRqFnz56sXbuWc+fOpchaobyuzqxtHEfZ7IkPVfcD1DTbLHgREPyf68+opJTI1EimyOz+F5H5WvmybTapSJMmTdi8eTPFihXAxERD/vw5Wb58WYLAgM52PGjQIF688EWj0XDv3t0MJTC+vr7Ur9OAbFldyOWamzIlyjJt2jTKlClDYFAgletWZGvkOk5qD7EjZgOmBZSsXLvyk66hUqlQvudrpkSBKs6Q7OpDzJ49m+zZs9OjRw+iP8EB4EO8DAihoJO+WayAo5KXQa/RarUfOMtASqEzxX98y4hkWpEBndDcvn2LmJhoHj16RMeOyXvayAhoNBpq16hDwOVwWlj0pKV5b8yeOTJm5Bjc3Ny4efMm+w7u4+GTB/y1YipHTh/mwpULZMmS5ZOu06hRIx5HehCiCksoi9HGcVfzlDbt2qR0tzIMtra2rFixgocPHzJmzJj/XF/lcqXZ/UDflX7Pwzhcs9olxE/TarXcvHmTW7duZdgbXnrwiS7MGY5M612W2Tl69ChRwTGUN040xbiZFiVAvqBDhw7kzZsXgBw5cvyncPLZsmWjTbu2LFi7nnK2JTARxtxTP6VNp7ZUr179P/cjI1O3bl2+//57Zs+eTcuWLaldu/bHT/oA46fOpHWzhgRGx1Alp5JLPhrGnYolLFpN8eLF+eGHH1gwZzqowpFaMLKwY82GrQbHjBQiM4t2ph7JZGY8PDywlu+mXbbFEY9nHil2HX9/f/bs3UPRUsWoPbAx5XpVY9v+HcxftCDTro35FKZMmaKLS9arFx4eHpw+fRpvb++Pn/gWVatW5dDxM9yybcCQc05ctqzLkZPnOH/+PBYWFvw86kcm1w7izjANd4dr+L2KP80b1092lGgDH0aXtEwma8uIGEYyGZzLly8z+n9juHLtCtmyZmPEmP/RtWtX7t69y/OwR5S2rZaQ6ExKSYjJSypX/TbFrj9s2DAiIiJYt24dRYsWTbF6MwsWFhasXLmSOjWqUbxQAYpnd+BxYAT169dn+dp/sLCw+Hgl8ZQuXZq1G7e+Uz5o0CBOLB9F82KJczZtSxmx4S5s2bKFXr16pUhfMjMyE6ctS7WRjBBiuRDCXwhxJ0mZgxDisBDicfyrfZJ9Y+Ijhz4UQjRMUu4eH3X0SXx0URFfbiqE2BhfflEIkSe1+vK1cuPGDerWrkfQRS2VZVuc/IowcvBPuOZwZc6cOdg72XFOfYBAtR+vNYFcV5/GyFHQoUOHFLn+3r17Wb9+PT///LNBYP4D169fo6CjBVc75GVPPUdutMtJ3L1zDB8yKEXqDwoKopDTuzMCua1jePXqFQCRkZEsX76cMWNGs3HjRuLi4lLk2pmFzDwnk5rmspXofLWTMho4KqUsAByN/4wQoijQCSgWf858IRLyCC8A+pEYWfRNnd8CIVLK/MBMYEqq9eQrZfzYCeTRlCKPSTHMFBZkMXLFXdmIsNBw9u7di6ePB/1G9eKpw3VuWZymfs8anL90LkVW4IeHh/Pdd99RrFgxRo8enQK9ybwsmjOLCeWdcDTTGR7MjRRMcLfjn/UbiI2N/cjZH6dmzZrsfGiKKkmo4Fi1ZNP1WJYsWcK8efMoVsiN7X8Pw/zuXywY35fyZYoRGPihQMAGkiKRaJO5ZURSTWTi4+m87YDfElgV/34V0CpJ+QYpZayU8jnwBKgQHz3URkp5Xupmzla/dc6burYAdUUmNPJrNBoWLlxI2VLlKFygKL/8/AuhoaEAXLt6DSeF/qS9pcIWG0s7ChYsiImJCT//8jNPPB7j7efFnLmz/1MaXCklHh4eBAQE8NNPP+Hj48OSJUsS4lIZ+DwCg0NwtdK3bDuZK0FKoqKi/nP9tWvXpkCJijRbqWDXHTU7b6tpvFxB/qJlMTIyYvSPg+lbLojtfWP5qYmSw4NiqOLsze+/GB4ekoXUhQpKzpYRSeuJf2cppR9A/OubmCUfihyaI/792+V650gp1UAo8N47pBCi35uopgEBAe875Kul1ze9GTtiEvKhM9behVgzazvlypRn+PDhvHz1ihCtv97xMdpIYtXRZMuWLUXbcezYMfLnyUeZ4mXI7ZqbRX8vpHfv3lSuXDlFr5MZqVWrJtufR+iVHfGOILera4pElhBCsGXnPjoOncai56VZ4lmGniNncuLMRa5du4ZKq2BwHYXe8T/U1rJt6xZA96CzfPly6teqSK2qZZk5c8Y7CcYyOzKZ/zIiX8rE/4cih/5bRNFkRxuVUi4GFoNuxf/nNDA9iYiIYMuWLXh6elK+fHkaNmyIUqnk4cOHbN+2g/K0R6nUxVezlc5c8dzBrFmzqF69OtcuXcFcbU0WpStRMoz7ijN82+vbz073+z6ePXtGmxZtqG9WAze73GjQcCbsIhfPXvhgsjcDyWfsn5OpWaUiIXHB1MpmwvXAGGbfDGb91u0p9rc1NjZmwIABDBgwQK9co9GgUCrQvDVhoNJAVFQkq1at4tD+nTy7dZgRjeIwMRL8ve539u3ayoEjp77IuGhpjQTUGXbG5eOk9Ujm1ZsEOvGvbx6zPxQ51Cf+/dvleucIXQAyW941z331PHjwALc8+fh56ESW/Lmdbzr1o1KFKkRGRnLixAnshAvKJAE8hRBkUxagXZv2nDx5kjXrV/Eyyx0OxCzhkthFtwEdmT7zrxRt46IFCylqUpB85nkQQmAkjKhpU4Ugv6AvMr/H10bBggW5eO0mZrU6siDMhVuOpYlUaTh37lyqX9vU1JRmjeoz7XCimGm1kj/3g7GpOT179uTA3h0cHqmhZTkjGpdWsnOYhtcv7iQk+IuLi2Px4sW0bFqHTu2as2fPnky2biS545iM+TdJ65HMLuAbYHL8684k5f8IIWYA2dFN8F+SUmqEEOFCiErARaAHMPetus4D7YBj8iv95l6/fp2/ps3g0cPHVK5Skf+N+JFcuXIB0K1LDyzD85FVWRiMQKokHndPUaJ4Cby8vTDRWsFb8/QqkwgKFykEQKtWrWjZsiWRkZGYm5unypOlxzNP7NFPiSCEwMnEAR8fnw+cZeBTyJUrF3/NTEy33bt3b/766y86d+5MyZIlU/Xas+cvpV6tKpyaE0I51zhOPDHG0ikfT5+fYOzYsYTenI+5SaIIKRWCVqWj2bl9C40bN6Z5k7qogm/Tt54kPFoy4vuTnD3dj0lTEh92pJR4e3ujVCr/0+LfLxHdiv+v8taUIqSmC/N6dAJQSAjhI4T4Fp241BdCPAbqx39GSnkX2ATcAw4Ag6SUb9L8fQcsRecM8BTYH1++DHAUQjwBhhPvqfYlEhMTw9atW1myZAlPnz7V23fgwAGqV6vJse238b9nyqblRyhVsgyPHz/G39+fO3fv4KQomHC8EIIsFOWF70uGDRuGg7M1XtqbaKUGKSWBGk8CeE6fvn30zrGysko100W1WtXwFPpiEquNwyPCm3LlMlSsvy+GadOmYW9vT79+/dBoNB8/4T+QPXt2bt59zIhJq3FtMJ5pi7Zy+sJVbG1tqVKlCt6v3/VGvOujZfnKNTg7O/Pq+RUO/GZCh+pmfNvAnFMTTVmyeD4eHh4AXLt2jXJlilK+bFFKlShA9SruPHr0KFX7lKYI0AptsraMSKaNwpyS+Pn5ceLECWxsbKhfv76eN9XVq1epX78hCmmO0BoRpQqkT99vmTVrJgD58hZA/dIFK6PENNyBqvsYOYQQHRNJ6Otw3M26oRCJzwMR2gCinO/z3PMJnp6edGrfhdu3b2GkNMbO3paVa1ZQq1atFO3jvxEeHo5bbjeyxWahrFUJorUxXFbfoF7r+ixZvjTN2pHZWLduHd26daNTp06YKyFH7rx827cfefLkSbM2xMTEUMDNlbHNw+lRXYkQsP+mll5LlIz++Q+WLZlPvxoBDGmhv2i0w5QoclfoS79+/ahVozKT+5vTuZ4NWi0s2hnKrG2Sh489MTU1TbO+vI+UiMJsqXSShc2aJuvYa1GrM1wU5i9l4v+Lxc/Pj7Vr1/Ly5Uvq1q1Lo0aN9BKOTZgwgT//nIi5qT0IDQqFhoOHDuDu7o5Go6FZsxaIaBfMjXS5VEwUuVi5fA05c7piYmKCt483+U3L6F3TRpkTz4BHfNOzO8eOnCDA7wHOSt1iRim1BBs9oE8PXZbA3Llzc/7SWXx9fYmOjiZfvnxpPtHu4+NDaEQoDnkcOK+6hpWVNaMGjdFL0Wwg5WncuDGO1hb4nN5J2wJWPH4gKf/3XDZt3/Wf4px9CmZmZuw/dIJunVozbqcfJsYKpNKKbTs3UKNGDUKCA/F9tOCd8569iGHbzJnMnDmTltWt6dpAZ25VKGBQWzt2nw9i165dtG/fPk36kZpIJBpSd7T5JZOpReb06dOMGfMT9+7dI18+N8aPH0+jRonrR48dO0aLFi1Aa0psrJolS5ZTtmxpDh06iImJCadOnWLK5GmYCjdQ6SbfY9SvadKkKdevX2Pfvn1EhEVjFy8wAAphjFKVlZEjRiHRIlCgIQ4jEp/YVDKKvHndWLp0KY8ePaJGtZp4xwaiiLEkxjSAAkXyMmaMvnUwvezYGo2G3r17Y2Njw6nTp3B2dv74SQZShOnTptAglxl/17JLeLCo4WLEgG+/4cFTzzR72ChevDjXbz/iwYMHqFQqihcvnvAg1rPXt1SpOJcOVVW45zdGSsmGU7EExthy9OgmJk36k7J5br1TZ5FcIkPN52VUU1hyyLQic/z4cZo1a0Z0tAZQcvXqbdq2bcuqVato164dGo2Gjh07ERdjgVJhhpES4qIlV6/cYNq0adSrV4/ffv0drcoaY6NE7y4TIzsCA/wSbvpGwgIs9a8tUFKyVCm2bNnE+HF/sn/baRxkSRTCCLWMIdzoIaOH/wboPIueez5j27ZtCS7MdevWTdf0zffv32fZkmX4v/JHg4YLFy6wbt06g8CkMft2bmNKUXM9MWmQ24LhZ/159uwZ+fLlS7O2CCEoUqTIO+UFChRgweJVNBvQm7zZBBFRGtQKG/bs30OpUqUICwtj0m99GNVNolDo+qFSSw5eimXVDxXTrP2piW7Ff+YVmUw7J+Pu7s7163cRSdx/pVRjb2/JmDGjuXPnDuv/2YgC/fwpGm0UKk0wOp8RBRYmOTA10l8DGqv1oFuPDjRo0IBvvumFpbYwJkqb+GtoiVTcZ+acSfTs2ZPIyEi6dunO4cOHsTS1IyImhIEDv2PaX1O/yPUlGzdupN+3/SlsVAgLacHdqLtgDZ6+nikSjsZA8qlarhTDsvtTP3fiU0ysRlJ0jR93Hj3FxcXlX85OW2JiYrh48SLm5uaUK1cu4SFJrVZTu0Ylspp7MqStBSq1ZNr6KMyd3Nm+60C6/wZSYk7GXOkg85rXS9ax9yM3Z7g5mUwrMmZm5sTFKfW+xLrsdJEAKJVKtFowUbroHaPRRpHHzZGZM2dw/fp1pk6ZhVLjmnCMRhuDWuGNn98LbGxs2LZtG927f4OpyIJWpUSYhVG2XEkOHNiHsXGiwHl7e+Pt7U3hwoVxcHBIo7/GpxETE4NLVhcamTQii7EuWIOUkv0x+xg+cTgDBw5M5xZmLhYtWsTyiWPY2sgOKxMFUkqmXA7hknEhjp05n97NSzaRkZFMnz6NHVv/wcjIiA6dezFkyNAvIhxRyoiMvcxjXvfjBwIPIrd+8HpCiJzoQmtlQxdPc7GUcvZbx9RCtzTkeXzRNinluM9recqQaUUmb143PD390K3j1CGlBmtrY7y8vLC2tiZPnry8fBGJUmERv1+LsVkkCxbMpVu3bqhUKho2bMTVKzdRxZihUEqkIow5c2bx7beJ4fKfPXvGypUrCfAPpEnTxjRp0uSrXAl96tQperTuQQuTlnrlT2Ieoyql4vCJw+nUssyJVqvlu7692bZlM9VzWnE/MBqvoAhadejMunXr0rt5GYKUEBkzpb3MbZE8R4xHEdv/TWRcABcp5TUhhDVwFWglpbyX5JhawP+klM3+S5tTkkw7J/Prr78wZMhQoqI0CKFESi0WFkpGjx6Nra3O02Xnzh3UrVsXrSYKtRoksbRo0ZIuXXSeXcbGxhw6dJCdO3eyY8dO7O3t6dPn23cWx7m5uTFuXLo+TKQIlpaWxKhjkMb6oWJitbHYWNukY8syJwqFgkXLVjJizC9cunSJHDlysH//fqZMmYKNjQ2BLzwxNTOna88+NGrUKN1NT5kXiQbVf69FF+/xTezHcCHEfXQxHO/964npTKYdyUgpmTNnDmPHjiUmJgZjY2N+/PFHfvvtN70fY1RUFLt27SIgIICaNWum+urqLxkpJblz5KZAZEGKWRQDIFobze6YXSz7ZxlNmyZvLYCB1CMuLo68rtlwJIJB5ayIVkkW3NHSulsfJk+bnt7N++pIiZGMqdJW5rColqxjn0fsS9b14vNnnQKKSynDkpTXAraiC7v1At2o5u6ntzrlyLQjGSEEQ4cOZdCgQQQHB2Nvb683R/IGCwsLOnXqlA4t/DK4dOkS69asQ6VWU71GNSJjIzkTeZoniidYK63xjPJg8JDBNGnSJL2bagA4fPgwjiYaTnTIirFS97DUupCWcosX0u+7Qbi5uaVzCzMnn+Bd5iSESLpafHF8gN8EhBBW6IRkWFKBiecakFtKGSGEaALsQBemK93ItCLzBiMjI7JmzfrxAzMh4/4Yz6xps8gnCqJAyZola9Ao1Vy+dhk/Pz+CgoKoUaMGrq6uH6/MQJpwaP8+2ucTCQID4GCuoL6bOUePHjWITLqgW46ZTAL/bSQjdO6wW4F1Uspt71wpiehIKfcJIeYLIZyklOmWYS7Ti4yB9/Ps2TOmTZlGS4sOWCh0LrJFTIuzM2oTUVFRNGzY8CM1GEgP7BwceBXz7hqql1ESe3v795xhILXRBcj87+tk4pMyLgPuSylnfOCYbMArKaUUQlRAF58y6D9f/D+Qfiv6DHzR7N+/nzymbgkCA2CiMMVNUYCdO3b+y5kG0pMe3/Rkw4NYbryKSyjb+ySaix6h3L51kzJF85M/lwuDBvTFz88vHVuauUhuAuaPUBXoDtQRQtyI35oIIQYIId4kAmoH3BFC3ATmAJ3SOzq9YSRjIIGrV69y9uxZXFxcUCqVqOS7HjEahQYLC4v3nG3gSyBfvnwsWLqS1n17U8hJQ6RKy6tICUj2LZ/ClLoWOFooWHVrI9Uq7uXqrXspkl3TwIeRKedddob3J2tMesw8YN5/vlgKYhAZA6jVajq168TxoydwUeQiShlBiDqA8IhwCtsWJ6uxLlXza3UIzzSP6dylczq32MC/0b59e5o1a8aZM2cwMzPD2dmZyu4l2dfNGsv4vC+T6xrxcnc0y5cvY/jwH9O5xRkdiVYaAmQayMQsXryYS8ev0si4I8r4xakPNbe4ZXSRI7H7yK7IgRIjvKM9mPP3HPLnz5/OLTbwMczNzalfvz4AmzdvppqbVYLAvKF+Lg3Hzp1kb6HCHDtyCAenLPTo8Q05c+Z8X5UG/gPJMIVlWAwik8mQUnLq1Cl2bt+JhaUFXbt1ZcWSlRTQlkRplPh1KGBanIfc4MTZ4zx8+BC1Wk2jRo1wdHT8l9oNfInkyZOHu/5xaKUpiiRrwC77qrjw8gIPrp6kbaFYvCOMKTNtEqv/2WxwSU9RPsm7LMNhEJlMhJSSXt/0Zu+OfWRTuaFVqpkzay5WltbYCX03ZIFAqVBiZmZGx44d06nFBlKCcuXKkS1nfkYffcqv1Y2xNBHsehDHqhuxlMgWx8k+lhgpdakmOhbX0uWbrnj6vkKr1XLp0iUsLCxwd3c3RAz4TCSglYaRjIEMRnR0NBs3buTK5asUKlyQ7t27c/nyZfbtOEB10QYjU93C09yaIhwIWAfGV8lmlBjo01v1DFsHWwoVKpSe3TCQAggh2LHvEN/16UmBeUcwUgjy5M5JBfe8DMj3CKMka2qq5DHCxRqmTZ3KnJnTyOUgCI/WojC3Z+O2PZQoUSIde/KVIiXa9zjRZBYMIvOVo9Fo8PDwwN7ePiF6s7+/P5XKV0bzWollTBb2mR1j3O/jqVuvDi6qfAkCA2CltCO7eR7Msyk5HryTLHE5iDGJ5KXwYu/6vYan1wyCk5MTm3fsISwsjOjoaLJmzUq7lo2JUT/UO05KiV9QGFMn/cHBAQrcc+miO6+97EezRnV54uH73sgYBj5MZs8nY1gn8xUQExODt7c3cXFxeuWbN28mezZX3EtVwDV7Tlq3bEtoaChjRv2EMtCWktoG5DMpQzFtbZyjCrNzx07UMu6d+k3MjJgwaTx/r5pDnQGV6fvbNzx6+ogqVaqkVRcNpBE2NjY4OzsjhKBzjz7MvmhMWEziMoptd9SEx0LP8hL3XLrbgxCC7hWUuFrHcfiwIdL25yClNllbRsQwkvkCePnyJcePH8fGxob69esn5NHQarX8/ttYZs2ahUCJEJJRY0YxZsxoLl26xLc9+5FfUxNbZTbUijiuHblM+zYduHT5EmXRj/Sdy6go9yLP4GlyHzdtccwVVgAEql8QJF7RtGlTrKysaNmy5TvtM5Axadu2LSePHaLE7LU0LmyMT7iCu/5mNGpch7yKg+8c72onCQxMt+gkXzGGiX8DH0FKiVar/WAOmIcPH3LlyhVy585N1apV9UxMoaGhTJ8+g21bt2NlZcWg77+jW7duCcf8+edE/pzwJ7ZmLmiIQypjOXBwH+7u7kydOo2Fs5eTV9MAU4UVMZowpk+ag729HSeOncRZXRRbI90aFiNhQh5ZiWPHVgESrblar41aNBgbmzDq55FMmTSVHKZuqIWKAHzZvGUTVlZWqfPHM/DFIoRg7vzFDBoynOPHj9PY0ZHmzZuza9cuZv16igHV4lDGp0QOipQcuR/H1Jo107nVXycZdZSSHDJtqH+AJ0+eMHXqVC5fvkLx4sUZNWokxYsXTzg2MjKSH34Yzpo1a4iLi6VC+YosXLSAUqVKAbpFjF27dmPP7j2Ymdqh1kTj6urCseNHcXZ2JioqijJl3AnwjUSpyYJEhdr4JZ27tmfBgr85deoUzZu0Iou2MsYKXeriMLUPahtPvLw9yJ4tB9liqmKhSIw5FaHx57n2BFIjKWxcFwelvlfYDe12irsXwuu6PyVEHYTQ2dQfy0sUruPKzt3b8fb25sCBA5ibm9OiRQtsbAy5YAwkolKpaFyvBiLoDt+WjyU8RjLzjBktO/dj0tTMlS4gJUL9KxWm0swkeUFko2KfGdIvf+28EZmbN29SrVo1YmI0aDQShQLMzJTs27ePGjVqAFC3bj0unL+GRmUGKNHKKMws1Ny7dxdXV1emT5/OH2Mno9RkT7iZqwmgUtViHD58iMWLFzNmxDjMNYUSRi5aqSJIdYnZc2axasVqnl4Px8G4oF4bn8ccIk4bgZQSd/Me+umfpYqbMRspU6YM/ndjyKesmrAvVhvJTbGDJ08f0bFdJ+7dfogDLoQrgrDNasXJ08dxdnZO/T+yga+e2NhYVqxYwd7t6zG3sKR77+9o1qxZpnMESQmRUShMpGm8xeFjxKi8DSLztfNGZOrUqcOJE+fQRc7WIaWKAgXysG/fXu7evUvHjp2Qake9H5YUYdSsVZF69eoxefJU4iLtMFZaJalDS2jMHQoVKoiXlw+mmpxYGmfXa0NA1DVitSEIlDiblMbOOI/efl/1GRq1qMGpE2exDiuCXZLRSrD6OQ7FYti1dwelSpTBMjIHjuQlRhvOS5NbfD98AGP/+B0pJefOnePWrVu4ublRv359FAqDn4cBA59CSomMiVHy0onEqnwNIvO180ZkzM3NiY1V6guIlEgZmfBZCBNMjfSf/DXaSFSaEHRLrBRYmxXAKN7U9aaOsNi7NGxYHy9PL7yfRmBjnF9/PzeYOXsqERERjPt1Klk0FRFCJwCx2nBecRa/ly84ffo0nTt0xVFdHCtFFsK1rwgyusvuvTupVasW3t7ejP9jAkcOH8XJyYnhI4bRsWPHTPe0acBAapEiIiNMpLGRU7KOjVP7ZTiRybSPtra2dvCO77rE2NiEFStWMHPmTIyNdSawpBgbS4YPH054eDgDBvRHilC9/SpNKPny5WPv3r1s37EdjTKIGHWIrnapJUrrTRZnB3r16sXAgQMpXa4oAcoLhKieEqx5QIC4wJy5s7GxsaFp06bs2ruD3BVNCbK9TIFq1hw8vJ9atWoBkDNnThYvXcQzzydcunqBTp06GQTGgIEvDplSof6/TnRP75lnc3d3l1JKOXHiRGlhYSWFsJQKhe7VwsJKDh06VL6hefMW0tLCTpoYZZOmRtmlsZG9tLOzl35+flJKKf39/WWuXLmlrbWztDDJKa0ts0srKxt59uzZhDr27dsns2ZxlrbWDtLC3Eq6u5eXHh4eCftVKpXcsmWL7Na1uxwyeKi8efOmNGDAwJcBcEX+x3sOGEkjpVOytpS43pe2ZVpzmUajYdCgQaxatQpTU3NiY6Np1ao1K1euwNRUF8cpNjaW3377nSVLlhAVFUWdOnWYNWsmBQsmTtRHRESwatUqTp48TcGC+enfv/87UWw1Gg0PHjzA0tKSPHnypGV3DRgw8B9ICXOZEEbSSGmbrGPVmuAMZy7LtCLzhoCAAB4/fkzevHlxcXFJx5YZMGDgSyNlREYpFYrkrUPTasMynMhk+sWYWbJkIUuWLOndDAMGDGRoMuh8SzLI9CJjwIABA6lOJl7xn2m9ywwYMGAgbUg57zIhRCMhxEMhxBMhxOj37BdCiDnx+28JIcqmSpc+AYPIGDBgwECqo03m9mGEEErgb6AxUBToLIQo+tZhjYEC8Vs/YEGKdeEzMYiMAQMGDKQqkhQK9V8BeCKlfCaljAM2AG+HTW8JrI73wL4A2Akh0tWjKdPNyVy9ejVQCOGZ3u1IQZyAjBp/PaP2LaP2CzJe33KnQB0HQZ28Jf9gJoS4kuTzYinl4vj3OQDvJPt8gIpvnf++Y3IAfp/Q3hQl04mMlDJDuZIJIa5kNJfHN2TUvmXUfkHG7tvnIqVslEJVvS+cx9trUJJzTJpiMJcZMGDAwNeBD5B0pbcr8OIzjklTDCJjwIABA18Hl4ECQoi8QggToBOw661jdgE94r3MKgGhUsp0M5VBJjSXZUAWf/yQr5aM2reM2i/I2H1LV6SUaiHE98BBQAksl1LeFUIMiN+/ENgHNAGeAFFAr/Rq7xsyXVgZAwYMGDCQdhjMZQYMGDBgINUwiIwBAwYMGEg1DCLzBSCEyCmEOC6EuC+EuCuEGBpf7iCEOCyEeBz/ap/knDHxoSMeCiEaJil3F0Lcjt83R8RnMRNCmAohNsaXXxRC5EnD/imFENeFEHsyWL/shBBbhBAP4v/vKmegvv0Q/128I4RYL4Qwyyh9M5DGpHdCG8MmAVyAsvHvrYFH6MJGTAVGx5ePBqbEvy8K3ARMgbzAU0AZv+8SUBmdv/x+oHF8+UBgYfz7TsDGNOzfcOAfYE/854zSr1VAn/j3JoBdRugbusV7zwHz+M+bgJ4ZoW+GLe23dG+AYXvPfwrsBOoDDwGX+DIX4GH8+zHAmCTHH4z/IbsAD5KUdwYWJT0m/r0RulXZIg364gocBeokEZmM0C+b+BuxeKs8I/Ttzapxh/jr7gEaZIS+Gba03wzmsi+MeLNBGeAi4CzjfdzjX7PGH/ah0BE54t+/Xa53jpRSDYQCjqnSCX1mASPRj/6XEfrlBgQAK+JNgUuFEJZkgL5JKX2BvwAvdOFIQqWUh8gAfTOQ9hhE5gtCCGEFbAWGSSnD/u3Q95TJfyn/t3NSDSFEM8BfSnk1uae8p+yL61c8RkBZYIGUsgwQic6E9CG+mr7Fz7W0RGf6yg5YCiG6/dsp7yn7IvtmIO0xiMwXghDCGJ3ArJNSbosvfvUmgmr8q398+YdCR/jEv3+7XO8cIYQRYAsEp3xP9KgKtBBCeKCLGFtHCLGWr79fb67rI6W8GP95CzrRyQh9qwc8l1IGSClVwDagChmjbwbSGIPIfAHEe9wsA+5LKWck2bUL+Cb+/Tfo5mrelHeK99DJiy53xKV4E0a4EKJSfJ093jrnTV3tgGNSylR9cpRSjpFSukop86Cb3D0mpez2tfcrvm8vAW8hRKH4orrAPTJA39CZySoJISzi21QXuE/G6JuBtCa9J4UMmwSohs5UcAu4Eb81QWejPgo8jn91SHLOz+i8eB4S77ETX14OuBO/bx6JUR3MgM3owk1cAtzSuI+1SJz4zxD9AkoDV+L/33YA9hmob38AD+LbtQad51iG6JthS9vNEFbGgAEDBgykGgZzmQEDBgwYSDUMImPAgAEDBlINg8gYMGDAgIFUwyAyBgwYMGAg1TCIjAEDBgwYSDUMImMg0yJ00a+fCyEc4j/bx3/Ond5tM2Ago2AQGQOZFimlN7AAmBxfNBlYLKX0TL9WGTCQsTCskzGQqYkP53MVWA70BcpIKePSt1UGDGQcjNK7AQYMpCdSSpUQYgRwAGhgEBgDBlIWg7nMgAFojC6kffH0bogBAxkNg8gYyNQIIUqjSxBXCfjhTZRhAwYMpAwGkTGQaYmPDLwAXf4eL2AaumRdBgwYSCEMImMgM9MX8JJSHo7/PB8oLISomY5tMmAgQ2HwLjNgwIABA6mGYSRjwIABAwZSDYPIGDBgwICBVMMgMgYMGDBgINUwiIwBAwYMGEg1DCJjwIABAwZSDYPIGDBgwICBVMMgMgYMGDBgINX4P6BPNwQPuSuBAAAAAElFTkSuQmCC\n",
"text/plain": [
"<Figure size 432x288 with 2 Axes>"
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"Release0 = Particle_data.where(Particle_data.time[:,0]==np.timedelta64(0, 's')) # the particles released at t = 0\n",
"\n",
"plt.figure()\n",
"ax = plt.axes()\n",
"ax.set_ylabel('Y')\n",
"ax.set_xlabel('X')\n",
"ax.set_ylim(1000, 49000)\n",
"ax.set_xlim(1000, 99000)\n",
"ax.plot(Release0.lon.transpose(), Release0.lat.transpose(), c='k', zorder=1)\n",
"T_scatter = ax.scatter(Release0.lon, Release0.lat, c=Release0.temperature, \n",
" cmap=plt.cm.inferno, norm=mpl.colors.Normalize(vmin=0., vmax=20.), \n",
" edgecolor='k', zorder=2)\n",
"plt.colorbar(T_scatter, label='T [$^{\\circ} C$]')\n",
"plt.show()"
]
}
],
"metadata": {
"celltoolbar": "Raw-celnotatie",
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.11"
},
"pycharm": {
"stem_cell": {
"cell_type": "raw",
"source": [],
"metadata": {
"collapsed": false
}
}
}
},
"nbformat": 4,
"nbformat_minor": 4
} | mit |
rishuatgithub/MLPy | torch/10. JPEG - CNN + AlexNet.ipynb | 1 | 1910035 | null | apache-2.0 |
Luke035/dlnd-lessons | gan_mnist/Intro_to_GANs_Solution.ipynb | 1 | 209536 | {
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Generative Adversarial Network\n",
"\n",
"In this notebook, we'll be building a generative adversarial network (GAN) trained on the MNIST dataset. From this, we'll be able to generate new handwritten digits!\n",
"\n",
"GANs were [first reported on](https://arxiv.org/abs/1406.2661) in 2014 from Ian Goodfellow and others in Yoshua Bengio's lab. Since then, GANs have exploded in popularity. Here are a few examples to check out:\n",
"\n",
"* [Pix2Pix](https://affinelayer.com/pixsrv/) \n",
"* [CycleGAN](https://github.com/junyanz/CycleGAN)\n",
"* [A whole list](https://github.com/wiseodd/generative-models)\n",
"\n",
"The idea behind GANs is that you have two networks, a generator $G$ and a discriminator $D$, competing against each other. The generator makes fake data to pass to the discriminator. The discriminator also sees real data and predicts if the data it's received is real or fake. The generator is trained to fool the discriminator, it wants to output data that looks _as close as possible_ to real data. And the discriminator is trained to figure out which data is real and which is fake. What ends up happening is that the generator learns to make data that is indistiguishable from real data to the discriminator.\n",
"\n",
"\n",
"\n",
"The general structure of a GAN is shown in the diagram above, using MNIST images as data. The latent sample is a random vector the generator uses to contruct it's fake images. As the generator learns through training, it figures out how to map these random vectors to recognizable images that can foold the discriminator.\n",
"\n",
"The output of the discriminator is a sigmoid function, where 0 indicates a fake image and 1 indicates an real image. If you're interested only in generating new images, you can throw out the discriminator after training. Now, let's see how we build this thing in TensorFlow."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"%matplotlib inline\n",
"\n",
"import pickle as pkl\n",
"import numpy as np\n",
"import tensorflow as tf\n",
"import matplotlib.pyplot as plt"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"'1.1.0'"
]
},
"execution_count": 2,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"tf.__version__"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Extracting MNIST_data/train-images-idx3-ubyte.gz\n",
"Extracting MNIST_data/train-labels-idx1-ubyte.gz\n",
"Extracting MNIST_data/t10k-images-idx3-ubyte.gz\n",
"Extracting MNIST_data/t10k-labels-idx1-ubyte.gz\n"
]
}
],
"source": [
"from tensorflow.examples.tutorials.mnist import input_data\n",
"mnist = input_data.read_data_sets('MNIST_data')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Model Inputs\n",
"\n",
"First we need to create the inputs for our graph. We need two inputs, one for the discriminator and one for the generator. Here we'll call the discriminator input `inputs_real` and the generator input `inputs_z`. We'll assign them the appropriate sizes for each of the networks."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [],
"source": [
"def model_inputs(real_dim, z_dim):\n",
" inputs_real = tf.placeholder(tf.float32, (None, real_dim), name='input_real') \n",
" inputs_z = tf.placeholder(tf.float32, (None, z_dim), name='input_z')\n",
" \n",
" return inputs_real, inputs_z"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Generator network\n",
"\n",
"\n",
"\n",
"Here we'll build the generator network. To make this network a universal function approximator, we'll need at least one hidden layer. We should use a leaky ReLU to allow gradients to flow backwards through the layer unimpeded. A leaky ReLU is like a normal ReLU, except that there is a small non-zero output for negative input values.\n",
"\n",
"#### Variable Scope\n",
"Here we need to use `tf.variable_scope` for two reasons. Firstly, we're going to make sure all the variable names start with `generator`. Similarly, we'll prepend `discriminator` to the discriminator variables. This will help out later when we're training the separate networks.\n",
"\n",
"We could just use `tf.name_scope` to set the names, but we also want to reuse these networks with different inputs. For the generator, we're going to train it, but also _sample from it_ as we're training and after training. The discriminator will need to share variables between the fake and real input images. So, we can use the `reuse` keyword for `tf.variable_scope` to tell TensorFlow to reuse the variables instead of creating new ones if we build the graph again.\n",
"\n",
"To use `tf.variable_scope`, you use a `with` statement:\n",
"```python\n",
"with tf.variable_scope('scope_name', reuse=False):\n",
" # code here\n",
"```\n",
"\n",
"Here's more from [the TensorFlow documentation](https://www.tensorflow.org/programmers_guide/variable_scope#the_problem) to get another look at using `tf.variable_scope`.\n",
"\n",
"#### Leaky ReLU\n",
"TensorFlow doesn't provide an operation for leaky ReLUs, so we'll need to make one . For this you can use take the outputs from a linear fully connected layer and pass them to `tf.maximum`. Typically, a parameter `alpha` sets the magnitude of the output for negative values. So, the output for negative input (`x`) values is `alpha*x`, and the output for positive `x` is `x`:\n",
"$$\n",
"f(x) = max(\\alpha * x, x)\n",
"$$\n",
"\n",
"#### Tanh Output\n",
"The generator has been found to perform the best with $tanh$ for the generator output. This means that we'll have to rescale the MNIST images to be between -1 and 1, instead of 0 and 1."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [],
"source": [
"def generator(z, out_dim, n_units=128, reuse=False, alpha=0.01):\n",
" with tf.variable_scope('generator', reuse=reuse):\n",
" # Hidden layer\n",
" h1 = tf.layers.dense(z, n_units, activation=None)\n",
" # Leaky ReLU\n",
" h1 = tf.maximum(alpha * h1, h1)\n",
" \n",
" # Logits and tanh output\n",
" logits = tf.layers.dense(h1, out_dim, activation=None)\n",
" out = tf.tanh(logits)\n",
" \n",
" return out"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Discriminator\n",
"\n",
"The discriminator network is almost exactly the same as the generator network, except that we're using a sigmoid output layer."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [],
"source": [
"def discriminator(x, n_units=128, reuse=False, alpha=0.01):\n",
" with tf.variable_scope('discriminator', reuse=reuse):\n",
" # Hidden layer\n",
" h1 = tf.layers.dense(x, n_units, activation=None)\n",
" # Leaky ReLU\n",
" h1 = tf.maximum(alpha * h1, h1)\n",
" \n",
" logits = tf.layers.dense(h1, 1, activation=None)\n",
" out = tf.sigmoid(logits)\n",
" \n",
" return out, logits"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Hyperparameters"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [],
"source": [
"# Size of input image to discriminator\n",
"input_size = 784\n",
"# Size of latent vector to generator\n",
"z_size = 100\n",
"# Sizes of hidden layers in generator and discriminator\n",
"g_hidden_size = 128\n",
"d_hidden_size = 128\n",
"# Leak factor for leaky ReLU\n",
"alpha = 0.01\n",
"# Smoothing \n",
"smooth = 0.1"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Build network\n",
"\n",
"Now we're building the network from the functions defined above.\n",
"\n",
"First is to get our inputs, `input_real, input_z` from `model_inputs` using the sizes of the input and z.\n",
"\n",
"Then, we'll create the generator, `generator(input_z, input_size)`. This builds the generator with the appropriate input and output sizes.\n",
"\n",
"Then the discriminators. We'll build two of them, one for real data and one for fake data. Since we want the weights to be the same for both real and fake data, we need to reuse the variables. For the fake data, we're getting it from the generator as `g_model`. So the real data discriminator is `discriminator(input_real)` while the fake discriminator is `discriminator(g_model, reuse=True)`."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [],
"source": [
"tf.reset_default_graph()\n",
"# Create our input placeholders\n",
"input_real, input_z = model_inputs(input_size, z_size)\n",
"\n",
"# Build the model\n",
"g_model = generator(input_z, input_size, n_units=g_hidden_size, alpha=alpha)\n",
"# g_model is the generator output\n",
"\n",
"d_model_real, d_logits_real = discriminator(input_real, n_units=d_hidden_size, alpha=alpha)\n",
"d_model_fake, d_logits_fake = discriminator(g_model, reuse=True, n_units=d_hidden_size, alpha=alpha)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Discriminator and Generator Losses\n",
"\n",
"Now we need to calculate the losses, which is a little tricky. For the discriminator, the total loss is the sum of the losses for real and fake images, `d_loss = d_loss_real + d_loss_fake`. The losses will by sigmoid cross-entropys, which we can get with `tf.nn.sigmoid_cross_entropy_with_logits`. We'll also wrap that in `tf.reduce_mean` to get the mean for all the images in the batch. So the losses will look something like \n",
"\n",
"```python\n",
"tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=labels))\n",
"```\n",
"\n",
"For the real image logits, we'll use `d_logits_real` which we got from the discriminator in the cell above. For the labels, we want them to be all ones, since these are all real images. To help the discriminator generalize better, the labels are reduced a bit from 1.0 to 0.9, for example, using the parameter `smooth`. This is known as label smoothing, typically used with classifiers to improve performance. In TensorFlow, it looks something like `labels = tf.ones_like(tensor) * (1 - smooth)`\n",
"\n",
"The discriminator loss for the fake data is similar. The logits are `d_logits_fake`, which we got from passing the generator output to the discriminator. These fake logits are used with labels of all zeros. Remember that we want the discriminator to output 1 for real images and 0 for fake images, so we need to set up the losses to reflect that.\n",
"\n",
"Finally, the generator losses are using `d_logits_fake`, the fake image logits. But, now the labels are all ones. The generator is trying to fool the discriminator, so it wants to discriminator to output ones for fake images."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [],
"source": [
"# Calculate losses\n",
"d_loss_real = tf.reduce_mean(\n",
" tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_real, \n",
" labels=tf.ones_like(d_logits_real) * (1 - smooth)))\n",
"d_loss_fake = tf.reduce_mean(\n",
" tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_fake, \n",
" labels=tf.zeros_like(d_logits_real)))\n",
"d_loss = d_loss_real + d_loss_fake\n",
"\n",
"g_loss = tf.reduce_mean(\n",
" tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_fake,\n",
" labels=tf.ones_like(d_logits_fake)))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Optimizers\n",
"\n",
"We want to update the generator and discriminator variables separately. So we need to get the variables for each part build optimizers for the two parts. To get all the trainable variables, we use `tf.trainable_variables()`. This creates a list of all the variables we've defined in our graph.\n",
"\n",
"For the generator optimizer, we only want to generator variables. Our past selves were nice and used a variable scope to start all of our generator variable names with `generator`. So, we just need to iterate through the list from `tf.trainable_variables()` and keep variables to start with `generator`. Each variable object has an attribute `name` which holds the name of the variable as a string (`var.name == 'weights_0'` for instance). \n",
"\n",
"We can do something similar with the discriminator. All the variables in the discriminator start with `discriminator`.\n",
"\n",
"Then, in the optimizer we pass the variable lists to `var_list` in the `minimize` method. This tells the optimizer to only update the listed variables. Something like `tf.train.AdamOptimizer().minimize(loss, var_list=var_list)` will only train the variables in `var_list`."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"scrolled": true
},
"outputs": [],
"source": [
"# Optimizers\n",
"learning_rate = 0.002\n",
"\n",
"# Get the trainable_variables, split into G and D parts\n",
"t_vars = tf.trainable_variables()\n",
"g_vars = [var for var in t_vars if var.name.startswith('generator')]\n",
"d_vars = [var for var in t_vars if var.name.startswith('discriminator')]\n",
"\n",
"d_train_opt = tf.train.AdamOptimizer(learning_rate).minimize(d_loss, var_list=d_vars)\n",
"g_train_opt = tf.train.AdamOptimizer(learning_rate).minimize(g_loss, var_list=g_vars)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Training"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Epoch 1/100... Discriminator Loss: 0.3476... Generator Loss: 4.4379\n",
"Epoch 2/100... Discriminator Loss: 0.3773... Generator Loss: 3.6476\n",
"Epoch 3/100... Discriminator Loss: 0.4128... Generator Loss: 2.9022\n",
"Epoch 4/100... Discriminator Loss: 1.3566... Generator Loss: 1.9196\n",
"Epoch 5/100... Discriminator Loss: 0.5184... Generator Loss: 6.9337\n",
"Epoch 6/100... Discriminator Loss: 1.8136... Generator Loss: 1.5963\n",
"Epoch 7/100... Discriminator Loss: 1.3852... Generator Loss: 2.7554\n",
"Epoch 8/100... Discriminator Loss: 1.4262... Generator Loss: 5.0319\n",
"Epoch 9/100... Discriminator Loss: 1.6795... Generator Loss: 4.5466\n",
"Epoch 10/100... Discriminator Loss: 2.1964... Generator Loss: 0.6939\n",
"Epoch 11/100... Discriminator Loss: 1.3391... Generator Loss: 1.0769\n",
"Epoch 12/100... Discriminator Loss: 2.0142... Generator Loss: 1.4427\n",
"Epoch 13/100... Discriminator Loss: 0.6645... Generator Loss: 3.5429\n",
"Epoch 14/100... Discriminator Loss: 1.9441... Generator Loss: 2.2589\n",
"Epoch 15/100... Discriminator Loss: 3.1723... Generator Loss: 0.7948\n",
"Epoch 16/100... Discriminator Loss: 1.6960... Generator Loss: 1.7192\n",
"Epoch 17/100... Discriminator Loss: 2.5293... Generator Loss: 1.7526\n",
"Epoch 18/100... Discriminator Loss: 0.8310... Generator Loss: 2.8067\n",
"Epoch 19/100... Discriminator Loss: 1.1654... Generator Loss: 1.2197\n",
"Epoch 20/100... Discriminator Loss: 1.8485... Generator Loss: 1.1577\n",
"Epoch 21/100... Discriminator Loss: 1.1272... Generator Loss: 1.4185\n",
"Epoch 22/100... Discriminator Loss: 0.7266... Generator Loss: 2.6219\n",
"Epoch 23/100... Discriminator Loss: 0.9997... Generator Loss: 1.5696\n",
"Epoch 24/100... Discriminator Loss: 0.7488... Generator Loss: 3.1071\n",
"Epoch 25/100... Discriminator Loss: 0.9664... Generator Loss: 1.3132\n",
"Epoch 26/100... Discriminator Loss: 0.9947... Generator Loss: 2.1388\n",
"Epoch 27/100... Discriminator Loss: 1.2071... Generator Loss: 1.8175\n",
"Epoch 28/100... Discriminator Loss: 0.7611... Generator Loss: 2.3673\n",
"Epoch 29/100... Discriminator Loss: 0.8222... Generator Loss: 2.3087\n",
"Epoch 30/100... Discriminator Loss: 0.9604... Generator Loss: 2.3985\n",
"Epoch 31/100... Discriminator Loss: 1.1468... Generator Loss: 2.0511\n",
"Epoch 32/100... Discriminator Loss: 1.2076... Generator Loss: 1.5616\n",
"Epoch 33/100... Discriminator Loss: 1.1870... Generator Loss: 2.2151\n",
"Epoch 34/100... Discriminator Loss: 1.0174... Generator Loss: 1.8403\n",
"Epoch 35/100... Discriminator Loss: 1.1196... Generator Loss: 1.4938\n",
"Epoch 36/100... Discriminator Loss: 0.8838... Generator Loss: 2.5240\n",
"Epoch 37/100... Discriminator Loss: 1.1113... Generator Loss: 1.9427\n",
"Epoch 38/100... Discriminator Loss: 0.7654... Generator Loss: 3.5077\n",
"Epoch 39/100... Discriminator Loss: 0.6580... Generator Loss: 2.7958\n",
"Epoch 40/100... Discriminator Loss: 1.2465... Generator Loss: 1.9984\n",
"Epoch 41/100... Discriminator Loss: 0.9223... Generator Loss: 1.9843\n",
"Epoch 42/100... Discriminator Loss: 1.0616... Generator Loss: 2.2574\n",
"Epoch 43/100... Discriminator Loss: 1.3891... Generator Loss: 1.5796\n",
"Epoch 44/100... Discriminator Loss: 0.9016... Generator Loss: 1.9284\n",
"Epoch 45/100... Discriminator Loss: 0.8242... Generator Loss: 2.7717\n",
"Epoch 46/100... Discriminator Loss: 0.7974... Generator Loss: 2.0371\n",
"Epoch 47/100... Discriminator Loss: 0.9277... Generator Loss: 1.6320\n",
"Epoch 48/100... Discriminator Loss: 1.1799... Generator Loss: 1.9311\n",
"Epoch 49/100... Discriminator Loss: 1.0351... Generator Loss: 1.4160\n",
"Epoch 50/100... Discriminator Loss: 0.8978... Generator Loss: 2.0509\n",
"Epoch 51/100... Discriminator Loss: 0.8651... Generator Loss: 2.2080\n",
"Epoch 52/100... Discriminator Loss: 0.7782... Generator Loss: 2.2180\n",
"Epoch 53/100... Discriminator Loss: 0.9958... Generator Loss: 1.9843\n",
"Epoch 54/100... Discriminator Loss: 1.0633... Generator Loss: 1.4747\n",
"Epoch 55/100... Discriminator Loss: 1.0347... Generator Loss: 2.0532\n",
"Epoch 56/100... Discriminator Loss: 1.0908... Generator Loss: 1.8969\n",
"Epoch 57/100... Discriminator Loss: 1.0056... Generator Loss: 2.0256\n",
"Epoch 58/100... Discriminator Loss: 1.0669... Generator Loss: 1.7931\n",
"Epoch 59/100... Discriminator Loss: 0.8461... Generator Loss: 1.8467\n",
"Epoch 60/100... Discriminator Loss: 0.9207... Generator Loss: 1.9543\n",
"Epoch 61/100... Discriminator Loss: 0.9859... Generator Loss: 1.7968\n",
"Epoch 62/100... Discriminator Loss: 1.1813... Generator Loss: 1.6643\n",
"Epoch 63/100... Discriminator Loss: 0.9457... Generator Loss: 2.2089\n",
"Epoch 64/100... Discriminator Loss: 1.0183... Generator Loss: 1.8519\n",
"Epoch 65/100... Discriminator Loss: 1.0323... Generator Loss: 2.1944\n",
"Epoch 66/100... Discriminator Loss: 0.7799... Generator Loss: 2.6862\n",
"Epoch 67/100... Discriminator Loss: 0.9300... Generator Loss: 2.2780\n",
"Epoch 68/100... Discriminator Loss: 1.0825... Generator Loss: 1.6308\n",
"Epoch 69/100... Discriminator Loss: 1.0393... Generator Loss: 1.7590\n",
"Epoch 70/100... Discriminator Loss: 1.2438... Generator Loss: 1.7331\n",
"Epoch 71/100... Discriminator Loss: 1.0732... Generator Loss: 1.9556\n",
"Epoch 72/100... Discriminator Loss: 1.0529... Generator Loss: 1.7048\n",
"Epoch 73/100... Discriminator Loss: 1.0301... Generator Loss: 1.6153\n",
"Epoch 74/100... Discriminator Loss: 1.0944... Generator Loss: 1.8231\n",
"Epoch 75/100... Discriminator Loss: 0.9399... Generator Loss: 2.0286\n",
"Epoch 76/100... Discriminator Loss: 1.1016... Generator Loss: 1.5947\n",
"Epoch 77/100... Discriminator Loss: 0.9712... Generator Loss: 2.0750\n",
"Epoch 78/100... Discriminator Loss: 1.1852... Generator Loss: 1.4842\n",
"Epoch 79/100... Discriminator Loss: 1.0053... Generator Loss: 1.3980\n",
"Epoch 80/100... Discriminator Loss: 0.9162... Generator Loss: 2.0734\n",
"Epoch 81/100... Discriminator Loss: 1.3742... Generator Loss: 0.9680\n",
"Epoch 82/100... Discriminator Loss: 1.0276... Generator Loss: 1.8480\n",
"Epoch 83/100... Discriminator Loss: 1.0645... Generator Loss: 1.5863\n",
"Epoch 84/100... Discriminator Loss: 1.2115... Generator Loss: 1.4543\n",
"Epoch 85/100... Discriminator Loss: 1.0001... Generator Loss: 1.9772\n",
"Epoch 86/100... Discriminator Loss: 0.8218... Generator Loss: 2.1147\n",
"Epoch 87/100... Discriminator Loss: 1.1014... Generator Loss: 1.5176\n",
"Epoch 88/100... Discriminator Loss: 0.8500... Generator Loss: 1.8422\n",
"Epoch 89/100... Discriminator Loss: 0.9565... Generator Loss: 1.6739\n",
"Epoch 90/100... Discriminator Loss: 1.2104... Generator Loss: 1.4702\n",
"Epoch 91/100... Discriminator Loss: 0.8567... Generator Loss: 2.1475\n",
"Epoch 92/100... Discriminator Loss: 1.0398... Generator Loss: 1.5363\n",
"Epoch 93/100... Discriminator Loss: 1.2562... Generator Loss: 1.2255\n",
"Epoch 94/100... Discriminator Loss: 1.2859... Generator Loss: 1.3106\n",
"Epoch 95/100... Discriminator Loss: 1.0269... Generator Loss: 1.8969\n",
"Epoch 96/100... Discriminator Loss: 0.9509... Generator Loss: 2.1518\n",
"Epoch 97/100... Discriminator Loss: 1.0212... Generator Loss: 1.9379\n",
"Epoch 98/100... Discriminator Loss: 1.0222... Generator Loss: 1.9024\n",
"Epoch 99/100... Discriminator Loss: 1.0340... Generator Loss: 1.5095\n",
"Epoch 100/100... Discriminator Loss: 1.0565... Generator Loss: 1.4482\n"
]
}
],
"source": [
"batch_size = 100\n",
"epochs = 100\n",
"samples = []\n",
"losses = []\n",
"# Only save generator variables\n",
"saver = tf.train.Saver(var_list=g_vars)\n",
"with tf.Session() as sess:\n",
" sess.run(tf.global_variables_initializer())\n",
" for e in range(epochs):\n",
" for ii in range(mnist.train.num_examples//batch_size):\n",
" batch = mnist.train.next_batch(batch_size)\n",
" \n",
" # Get images, reshape and rescale to pass to D\n",
" batch_images = batch[0].reshape((batch_size, 784))\n",
" batch_images = batch_images*2 - 1\n",
" \n",
" # Sample random noise for G\n",
" batch_z = np.random.uniform(-1, 1, size=(batch_size, z_size))\n",
" \n",
" # Run optimizers\n",
" _ = sess.run(d_train_opt, feed_dict={input_real: batch_images, input_z: batch_z})\n",
" _ = sess.run(g_train_opt, feed_dict={input_z: batch_z})\n",
" \n",
" # At the end of each epoch, get the losses and print them out\n",
" train_loss_d = sess.run(d_loss, {input_z: batch_z, input_real: batch_images})\n",
" train_loss_g = g_loss.eval({input_z: batch_z})\n",
" \n",
" print(\"Epoch {}/{}...\".format(e+1, epochs),\n",
" \"Discriminator Loss: {:.4f}...\".format(train_loss_d),\n",
" \"Generator Loss: {:.4f}\".format(train_loss_g)) \n",
" # Save losses to view after training\n",
" losses.append((train_loss_d, train_loss_g))\n",
" \n",
" # Sample from generator as we're training for viewing afterwards\n",
" sample_z = np.random.uniform(-1, 1, size=(16, z_size))\n",
" gen_samples = sess.run(\n",
" generator(input_z, input_size, n_units=g_hidden_size, reuse=True, alpha=alpha),\n",
" feed_dict={input_z: sample_z})\n",
" samples.append(gen_samples)\n",
" saver.save(sess, './checkpoints/generator.ckpt')\n",
"\n",
"# Save training generator samples\n",
"with open('train_samples.pkl', 'wb') as f:\n",
" pkl.dump(samples, f)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Training loss\n",
"\n",
"Here we'll check out the training losses for the generator and discriminator."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.legend.Legend at 0x7f90b983ddd8>"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAW4AAAEICAYAAAB/Dx7IAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXd4XNWZ/z9nRhr1YjU32ZZccTeugOnNQGjJwpIECKQB\nGyAJJYH9pUE2m00hhRbKJkDC0kJvIQSMDbhg3Hvvsq3eR2Xa+f1x7p2500fVGut8nkfPSDP33jma\n8r3v/b7veY+QUqLRaDSa5MF2vAeg0Wg0mq6hhVuj0WiSDC3cGo1Gk2Ro4dZoNJokQwu3RqPRJBla\nuDUajSbJ0MKtOe4IIexCiFYhxOje3FajOVERuo5b01WEEK2WPzOBTsBr/H2zlPK5/h9VzxFC/AIo\nlVLeeLzHotHEIuV4D0CTfEgps83fhRAHgG9JKT+Mtr0QIkVK6emPsWk0gwFtlWh6HSHEL4QQLwkh\nXhBCtADXCSFOFUJ8JoRoFEIcE0I8JIRINbZPEUJIIUSZ8ff/GY+/J4RoEUKsFEKUd3Vb4/GLhRC7\nhBBNQoiHhRDLhRA3duN/miqE+NgY/2YhxBcsj10qhNhuPH+FEOIO4/4SIcQ/jH3qhRCfWPYpFUK8\nLoSoEULsF0LcannsFCHEOiFEsxCiSgjx266OV3Nio4Vb01d8EXgeyANeAjzA94AiYCFwEXBzjP2/\nCvwEKAAOAf/V1W2FECXA34EfGM+7H5jf1X9ECOEA3gHeBYqBO4CXhBDjjU2eBr4ppcwBZgAfG/f/\nANhn7DMM+LFxPJtxvNXASOAC4AdCiPOM/R4GfiulzAXGA690dcyaExst3Jq+YpmU8m0ppU9K2S6l\nXC2lXCWl9Egp9wFPAmfF2P8VKeUaKaUbeA6Y1Y1tLwU2SCnfNB77A1Dbjf9lIeBAianbsIXeA75s\nPO4GpgghcqSU9VLKdZb7RwCjpZQuKaUZcZ8K5Eopf2ncvwf4S8jxJgghCqWULVLKVd0Ys+YERgu3\npq84bP1DCHGSEOJdIUSlEKIZ+DkqCo5GpeX3NiA72oYxth1hHYdUmfiKBMYeygjgkAzO5B9ERcug\nri4uBw4JIZYKIRYY9//K2G6xEGKvEOIHxv1jgNGGhdIohGgEfoiKygG+DkwBdgohPhdCXNKNMWtO\nYLRwa/qK0HKlJ4AtwHjDAvgpIPp4DMeAUvMPIYQgILZd4SgwytjfZDRwBMC4krgcKEFZIC8a9zdL\nKe+QUpYBVwL3CCHOQp1Mdksp8y0/OVLKy4z9dkopv2wc73fAq0KI9G6MW3OCooVb01/kAE2AUwgx\nmdj+dm/xDjBbCHGZECIF5bEXx9nHLoRIt/ykAStQHv1dQohUIcS5wCUonztDCPFVIUSuYce0AD4A\n43nHGYLfhCqZ9AErAZcQ4i7jOexCiOlCiDnGftcLIYqklD5jP2keU6MBLdya/uMu4AaUsD2BSlj2\nKVLKKuAa4PdAHTAOWI+qO4/GdUC75WenlLITuAy4AuWRPwR8VUq529jnBuCgYQF90zgGwCTgI6AV\nWA48KKX81CiNvASVKD1gHPMJINfY7xJgu1GR8wBwjZTS1f1XQnOioSfgaAYNQgg7yva4Skr56fEe\nj0bTXXTErTmhEUJcJITINyyPn6AqNj4/zsPSaHqEFm7Nic7pqFrqGmAR8EXD+tBokhZtlWg0Gk2S\noSNujUajSTL6pMlUUVGRLCsr64tDazQazQnJ2rVra6WU8cpVgT4S7rKyMtasWdMXh9ZoNJoTEiHE\nwUS31VaJRqPRJBlauDUajSbJ0MKt0Wg0SUZcj1sIMYng6cljgZ9KKf/YZ6PSaDQ9xu12U1FRQUdH\nx/EeisZCeno6paWlpKamdvsYcYVbSrkTo7+xMWX4CPB6t59Ro9H0CxUVFeTk5FBWVkZwY0PN8UJK\nSV1dHRUVFZSXl8ffIQpdtUrOA/ZKKRPOfmo0muNDR0cHhYWFWrQHEEIICgsLe3wV1FXh/jLwQpQB\n3SSEWCOEWFNTU9OjQWk0mt5Bi/bAozfek4SF21h373Lg5UiPSymflFLOlVLOLS5OqIa851Rvh4Mr\n+ue5NBqNZoDQlYj7YmCd0eN4YPDxb+CdO473KDQaTRTsdjuzZs1i6tSpzJw5k9/97nf4fGpNiDVr\n1vDd7363x8/x+OOP87e//a1L+5x22mndfr5nnnmGo0ePdnv/3qArMye/QhSb5Ljh6VA/Go1mQJKR\nkcGGDRsAqK6u5qtf/SrNzc3cf//9zJ07l7lz5/bo+B6Ph1tuuaXL+61Y0f0r9WeeeYZp06YxYsSI\nhPfxer3Y7fZuP2coCUXcQogs4ALgtV575t7A6wav53iPQqPRJEBJSQlPPvkkjzzyCFJKli5dyqWX\nXgrAxx9/zKxZs5g1axYnn3wyLS0tAPz6179m+vTpzJw5k3vvvReAs88+m+9///vMnTuXBx98kPvu\nu48HHnjA/9gdd9zB3LlzmTx5MqtXr+ZLX/oSEyZM4Mc//rF/LNnZaj3ppUuXcvbZZ3PVVVdx0kkn\nce2112J2TP35z3/OvHnzmDZtGjfddBNSSl555RXWrFnDtddey6xZs2hvb2fx4sWcfPLJTJ8+nW98\n4xt0dqquwWVlZdxzzz3Mnj2bl1+O6DB3m4QibimlEyjs1WfuDXxu9aPRaGJy/9tb2Xa0uVePOWVE\nLj+7bGqX9hk7dixer5fq6uqg+x944AEeffRRFi5cSGtrK+np6bz33nu8+eabrFq1iszMTOrr6/3b\nu1wufz+k++67L+hYDoeDNWvW8OCDD3LFFVewdu1aCgoKGDduHHfccQeFhcFStn79erZu3cqIESNY\nuHAhy5cv5/TTT+e2227jpz/9KQDXX38977zzDldddRWPPPIIDzzwAHPnzqWjo4Mbb7yRxYsXM3Hi\nRL72ta/x2GOP8f3vfx+AwsJC1q1b16XXKBGSe+ak16Oibo1Gk9QsXLiQO++8k4ceeojGxkZSUlL4\n8MMP+frXv05mZiYABQUF/u2vueaaqMe6/PLLAZg+fTpTp05l+PDhpKWlMXbsWA4fPhy2/fz58ykt\nLcVmszFr1iwOHDgAwJIlS1iwYAHTp0/no48+YuvWrWH77ty5k/LyciZOnAjADTfcwCeffJLQOHtC\nn3QH7Dd8bvBpq0SjiUdXI+O+Yt++fdjtdkpKSti+fbv//nvvvZcvfOEL/OMf/2DhwoW8//77MY+T\nlZUV9bG0tDQAbDab/3fzb48nXC+s29jtdjweDx0dHXznO99hzZo1jBo1ivvuu69btdexxtkTkjzi\ndumIW6NJEmpqarjlllu47bbbwmqZ9+7dy/Tp07nnnnuYN28eO3bs4IILLuDpp5+mra0NIMgq6WtM\nkS4qKqK1tZVXXnnF/1hOTo7fg580aRIHDhxgz549ADz77LOcddZZfT6+5I64vR7tcWs0A5j29nZm\nzZqF2+0mJSWF66+/njvvvDNsuz/+8Y8sWbIEm83G1KlTufjii0lLS2PDhg3MnTsXh8PBJZdcwi9/\n+ct+GXd+fj7f/va3mTZtGsOGDWPevHn+x2688UZuueUWMjIyWLlyJU8//TRXX301Ho+HefPmdavK\npav0yZqTc+fOlf2ykMKjC6BmB/ysEfQMMY0miO3btzN58uTjPQxNBCK9N0KItVLKhOojk9wqMaJt\n7XNrNJpBhBZujUajSTKSW7hNf1snKDUazSAiuYVbR9wajWYQktzCrSNujUYzCElu4fZH3Fq4NRrN\n4OHEEG4dcWs0A5aqqiq++tWvMnbsWObMmcOpp57K668fn9UPly5d2qPOgAOF5BVuKQORtva4NZoB\niZSSK6+8kjPPPJN9+/axdu1aXnzxRSoqKvrsOSNNazfpjnDHOt7xInmF2+cN/K4jbo1mQPLRRx/h\ncDiCZhOOGTOG22+/Ha/Xyw9+8APmzZvHjBkzeOKJJ4DYrVbXrl3LWWedxZw5c1i0aBHHjh0Dwlu9\nvv322yxYsICTTz6Z888/n6qqKg4cOMDjjz/OH/7wB2bNmsWnn37KgQMHOPfcc5kxYwbnnXcehw4d\nAgKzIxcsWMAPf/jDfn7V4pO8U96tvrb2uDWa2Lx3L1Ru7t1jDpsOF/8q5iZbt25l9uzZER/7y1/+\nQl5eHqtXr6azs5OFCxdy4YUXApFbrS5YsIDbb7+dN998k+LiYl566SV+9KMf8dRTTwHBrV4bGhr4\n7LPPEELw5z//md/85jf87ne/45ZbbiE7O5u7774bgMsuu4wbbriBG264gaeeeorvfve7vPHGGwBU\nVFSwYsWKXl0AobdIXuH2uiy/D7xLGY1GE86tt97KsmXLcDgcjBkzhk2bNvkbODU1NbF7924cDoe/\n1Srgb7Wan5/Pli1buOCCCwC1qszw4cP9x7a2UK2oqOCaa67h2LFjuFwuysvLI45n5cqVvPaaWh/m\n+uuvD4qur7766gEp2pDUwm0Rax1xazSxiRMZ9xVTp07l1Vdf9f/96KOPUltby9y5cxk9ejQPP/ww\nixYtCtpn6dKlEVutSimZOnUqK1eujPhc1haqt99+O3feeSeXX345S5cuDVtsIRH6qiVrb5DEHrdF\nrLXHrdEMSM4991w6Ojp47LHH/PeZbVoXLVrEY489htutvr+7du3C6XRGPdakSZOoqanxC7fb7Y64\nuAGo6H3kyJEA/PWvf/Xfb23JCmrR4BdffBGA5557jjPOOKM7/2a/k7zCbRVrXVWi0QxIhBC88cYb\nfPzxx5SXlzN//nxuuOEGfv3rX/Otb32LKVOmMHv2bKZNm8bNN98cs4LD4XDwyiuvcM899zBz5kxm\nzZoVtULkvvvu4+qrr2bOnDkUFRX577/ssst4/fXX/cnJhx9+mKeffpoZM2bw7LPP8uCDD/b6a9AX\nJG9b17q98LCR9Lj2FZhwQd8+n0aTZOi2rgOXwdvW1Rpla6tEo9EMIhISbiFEvhDiFSHEDiHEdiHE\nqX09sLh4dTmgRqMZnCRaVfIg8E8p5VVCCAeQ2YdjSgydnNRo4iKlDFvfUXN86Q17Om7ELYTIA84E\n/mI8qUtK2djjZ+4pOjmp0cQkPT2durq6XhEKTe8gpaSuro709PQeHSeRiLscqAGeFkLMBNYC35NS\nBtXtCCFuAm4CGD16dI8GlRBeHXFrNLEoLS2loqKCmpqa4z0UjYX09HT/5KLukohwpwCzgdullKuE\nEA8C9wI/sW4kpXwSeBJUVUmPRpUIesq7RhOT1NTUqDMGNclNIsnJCqBCSrnK+PsVlJAfX6wzJ/WU\nd41GM4iIK9xSykrgsBBiknHXecC2Ph1VIuiIW6PRDFISrSq5HXjOqCjZB3y974aUIEFNprRwazSa\nwUNCwi2l3AAkNKOn39B13BqNZpByYsyctC6qoNFoNCc4ySvcuhxQo9EMUpJYuC0et7ZKNBrNICJ5\nhdunywE1Gs3gJHmF27RHhF1H3BqNZlCRvMJtinVqpva4NRrNoCJ5hdsU69QMHXFrNJpBxQkg3Ona\n49ZoNIOK5BVunxtsqepHR9wajWYQkbzC7XWDPVX9aI9bo9EMIpJXuH0eJdq2FL2QgkajGVQkr3B7\nXYZVkqIjbo1GM6hIYuG2WCU64tZoNIOI5BVun8eSnNTCrdFoBg/JK9xeN9hT1I+2SjQazSAiiYXb\nBXaHLgfUaDSDjuQVbtMq0eWAGo1mkJG8wm1aJbocUKPRDDKSV7jNmZM64tZoNIOM5BVur0d73BqN\nZlCSxMLtMqpKUnWTKY1GM6hIaJV3IcQBoAXwAh4p5fFf8d3fZEovpKDRaAYXCQm3wTlSyto+G0lX\n8Zq9SuJ43B1NcGQdjDun/8am0Wg0fUjyWiW+BKe8b3wRnr0Smir6b2wajUbThyQq3BL4UAixVghx\nU6QNhBA3CSHWCCHW1NTU9N4Io2FtMhVLuNsb1e2RtX0/Jo1Go+kHEhXu06WUs4CLgVuFEGeGbiCl\nfFJKOVdKObe4uLhXBxkR0yqJVw7odqrbijV9PyaNRqPpBxISbinlEeO2GngdmN+Xg0oIn1tF22Y5\noJSRt3MZwn1kXf+NTaPRaPqQuMIthMgSQuSYvwMXAlv6emBxsbZ1BfB5I2/nalO3R9dH30aj0WiS\niEQi7qHAMiHERuBz4F0p5T/7dlgJ4HUbE3CMwphoJYGuVnXrdkLNzv4Zm0aj0fQhccsBpZT7gJn9\nMJauYVolZsTtdUNqRvh27jZIz4eORpWgHDqlf8ep0Wg0vUzylgOaVonNtEqiVJa4nDBsOqTl6coS\njUZzQpCcwi2lpcmUcdEQrbLE5QRHNow8WQu3RqM5IUhO4TaTjGaTKYjhcTvBkQUj50DVVnC3988Y\nNRqNpo9ITuH2utSt2Y8bokfc7jZwZCrhll44tql/xqjRaDR9RHIKtxld26zlgDE8bke2Em7QdolG\no0l6klO4zTau9tTYEbeUSrhTMyFnGOSWauHWaDRJT3IKtz/iTokdcXs6lT3iyFJ/j5ythVuj0SQ9\nySncfo87TnLSbcya9Av3HGjYD231fT9GjUaj6SOSVLgNkbZbywEjRNzmrElTuPNK1W1bXd+OT6PR\naPqQ5BRu0xYxm0xB5Ijb7FOSmqluTVvF09m349NoNJo+ZOAIt88L//ghbHsz/rZBEXdq8H1WzM6A\njmxj+zRjWy3cGo0meRk4wm2zw+aXYe+S+NtG9LhjWSVGxJ3iULceV8/GqtFoNMeRgSPcAEPGQOPB\n+Nv5rZI4U95Dk5P+iFsLt0ajSV4GmHCXQcOB+Nv5rZJ4HrdhlaQawp2ihVuj0SQ/A0u488dA4+H4\nCx5YZ07GmoDj97jNiFsnJzUaTfIzsIR7yBglyi3HYm/nnznpiD0Bxy/cZlWJTk5qNJrkZ2AJd/4Y\nddsQx+dOtMmUO9Qq0clJjUaT/Aws4R5Spm7jJSgjNpmKYpXYUgOCrZOTGo3mBGBgCXdeKSASiLgt\nddy2GIsFu9oC/jbo5KRGozkhGFjCnZIGuSPjV5ZYZ07GKgc0F1Ew0clJjUZzAjCwhBsSq+VOuMlU\nqHDr5KRGo0l+EhZuIYRdCLFeCPFOXw6I/DFds0riTXk3+5SAEnrQyUmNRpPUdCXi/h6wva8G4mfI\nGFUOGMvOsM6cjDnlvS3QpwTAZlPb64hbo9EkMQkJtxCiFPgC8Oe+HQ5GSaBUE3GiETRz0gbCFiXi\nbg3UcJukpEVfn1Kj0WiSgEQj7j8CPwR80TYQQtwkhFgjhFhTU1PT/RH5SwIPRN/G6nGDiqKjLaRg\n9bhBWSs6OanRaJKYuMIthLgUqJZSxlzzS0r5pJRyrpRybnFxcfdHNCSBSThWqwSUGEdcSMEZmHxj\nYk/TVolGo0lqEom4FwKXCyEOAC8C5woh/q/PRpQ9TIlrrJJA0+qw2QO30SbghEbcKQ6dnNRoNElN\nXOGWUv6nlLJUSlkGfBn4SEp5Xd+NyAb5o2KXBPrcKtoWwtgnNbE6btARt0ajSXoGXh03xC8J9LoD\n/jYoqyQ04va41H06OanRaE4wuiTcUsqlUspL+2owfuJNwvG6AzMmwYi4Qzxud8iyZSY6OanRaJKc\ngRlxDymD9gboaI78uGmVmNhTwuu4QxcK9m+rrRKNRpPcDEzhNtu7Rou6ve7AjEmIXA4YuoiCiU5O\najSaJGdgCre/JPBA5Md9npCIO5ZVopOTGo3mxGJgCne8BRW8rpCIO6ULEbdOTmo0muRmYAp3xhBI\ny0vcKrFHKAcMXSjYuq1OTmo0miRmYAq3EMouSdQqsaVGSE5qq0Sj0ZyYDEzhBigoh/p9kR8LLQe0\np0SPuMPquHVyUqPRJDcDV7iHlCuPO9KSZF5X8AScSB632ygHDKvj7kLE7fPBe/dC9Y7Ex63RaDR9\nzMAV7oJyJcbNR8Ifi2SVhEXcreo2tI67K8nJtlpY9Rjs6Nu1I04o3B3wz/+EtvrjPRKN5oRl4Ar3\nkHJ1W78//LEwqySSx90Gwh5YINi6baLJyc4WdatFKHGOroPP/gS73j/eI9FoTlgGrnAXmMIdwecO\nnTlpi+JxO7ICjahM7Glqf1/U1uLBxwAVeWsSo71R3dbvPb7j0GhOYAaucOeOVD52Q6SI2xO/yVTo\nQsEmKcZ+3gQSlKbd0laX2Jg10NGkbqMlljUaTY8ZuMJts6uJOBGtEld4k6nQJGboQsEmXVnp3R9x\na+FOmA4j4q7TEbdG01cMXOEGZZdEirgjNZkKs0oiLFsGAc87kQSl6XE7tXAnjN8q2QdSHt+xaDQn\nKANbuIeUQ/2BcAHwehJoMtUaWbhNiyWRBKWOuLuOGXF3NoNT5wY0mr5gYAt3QTm4WsIFwOdWCUmT\niE2mokTcpnAnZJUYHrfbCe72xMc9mDE9btAJSo2mjxjYwm2WBIbaJYlMwInmcZvJyURmT5rCDTrq\nTpT2RnDkqN91glKj6RMGtnAXRKnlDrVKIjaZagufNQldS052WoRbX/YnRkcjDJumauh1glKj6RMG\ntnDnjwFEeMQdapWYEbfVC3e1hvcpgUByMqGI2xn4PSTifnVtBVuONKEJob0RMgshf7S2SjSaPmJg\nC3dquqrnDou4I6yAA8ElgXE97q5aJcGzJ3/65haeXRljXczBSkcTZORD4TgdcWs0fcTAFm4I7xIo\npYqugybgGNG36XP7vODpCO/FDV1PTmYPU79bZk+2u7w4XV4a2/upy6CrDT74aWAdzYFMRyOk50PB\nWF0SqNH0EXGFWwiRLoT4XAixUQixVQhxf38MzM+QsmCrxOxJEtpkCgI+d7Re3NC15GRnK+SNBGEL\nskrqnEr0G9v6aSWdQytg+YPqdiDjcakrnYx8KBinTnyt1cd7VBrNCUciEXcncK6UciYwC7hICHFK\n3w7LQkE5OGsCk2FMcQ5tMgUBUY/Wixu6PnMyLQcyCoKSk/VOJfpN7f0k3Oaklmir3g8UzBrudMMq\nAV1ZotH0AXGFWypMszfV+Om/619/SeABdWvaIaFNpiAg6tF6cUMXk5Ot6hhZRSERd38Ld4O67Rzg\nwt1uEe6Csep3naDUaHqdhDxuIYRdCLEBqAY+kFKuirDNTUKINUKINTU1Nb03Qr8AGJGbOdEmtBwQ\nLBF3lF7c0PXkpCNbVUlYhbtV7dtvVol/NmJL/zxfdzEn32Tkq4ogW4pOUGo0fUBCwi2l9EopZwGl\nwHwhxLQI2zwppZwrpZxbXFzceyMMreU2BTdiVYnpcZsRdw+Tk52tkBYu3PWGx93u9tLpibBCT2+T\njFaJPcVoEqaFW6PpbbpUVSKlbASWABf1zXAikJ6nPGYzQRnJKjFF3BvqccdoMpVoHbcjKzzidgb2\n7Re7JFkibr9VkqduC8ZCnfa4NZreJpGqkmIhRL7xewZwAdC/izAOGQONh9Tv/uRkBI/bFHV3DOFO\nNOL2utU2jhxDuOv9iy+YVglAU3/YJe2Wxk0DGfMEk5GvbgvH6ZJAjaYPSCTiHg4sEUJsAlajPO7+\nXYQxZwQ0H1O/+8sBI1SVhJYDRuxVkmDEbfrkjiyVnJRevzDVWyLuxn6JuJuCbwcqVqsEVEmg2wmt\nVcdvTBrNCUhKvA2klJuAk/thLNHJHQ4Hl6vf/R63tclUqMdtRtwRqkpsKYCIn5w0j5GWDSnp6ve2\nOsgsoM7pYkhmKg1t7tgJyr1LlNhOvTL2c8WjPYmsktTMQK18oZFYrtsLOcOO37g0mhOMgT9zEiBn\nuIrm3O2xrZIwjztCxC2EEv14VkmnJeLOLFS/Gz53XWsnY4vVSaGxLcYJYNkfYOn/xH6eROhIIqvE\n9LdBRdzQO7XcB1fCzvd6fhyN5gQgeYQboPlo5JmToVPeXa2AgJSMyMdLSUvAKjHFPydMuOudLsYW\nKf88ZnKytSoQLfeEZKkqaW8M2CQAeaVq1mljL/R0Wfo/8N4Pe34cjeYEIK5VMiDINYS7pTJwX+ia\nkxCIxg1LA1uU81IiEbfLsCWsEbezlnaXlzaXl7KiLGwijnC3VCa20k4svJ7AWAa6VWI2mDKxp0Ju\nKTT0gnA3HoKmCnXCTXHE316jOYFJkoh7hLptORaIqkNXeYdANN5aDVkl0Y/XlYjbrOMGaKvz9ykp\nynaQl5Ea3eN2dyjrwNPeM/E2E5Ip6UlileQH35c/uucRt88HzUdA+gLVRYONtnr43Ukqb6IZ9CSH\ncOdarBJvAlPenbWQHWMSkN0RPznp97izlVeemgltdf6KkoKsNCXc0SJuayVFotUgUvpLDgP7GjZJ\n3ijV8TCR+vPjRXtTsMcNqpSzpxF3a1Xg/RqsvU8Or1KBy7Y3j/dINAOA5BDutFwlnC2VcZpMmcJd\nDVnxhDueVWIRboBM1a/ErOEuyHKQl+mIbpVYhTtRn3vPh/DrMcFCb+6bP1rdDmS7pKMx2CoBNXuy\ntbJna3Y2HQ78HrqoxmDhyFp1e2DZ8R2HZkCQHMIthEpQthyN0mQq1CqpiWOVOLpWxw3KM3fW+mdN\nFmU7yM9IpSlaVYnVj0804q7crOwQs6EWQIfRYCp/lLrtHKC13D6vGnuoVTJkjLptquj+sa32yGCN\nuI+sU7d1uwNzGjSDluQQboBcYxJOpHJA65R3d7tK5mUVRT+WPS2BiNsJiMAkHmPau9mnpCDLQX5m\nuFVS1dxBdUtHiFWSYMRtto5tiRCtD7SIW8rgKhdrgykr+YZw98QuMSPuIeWDU7ilhKPrYNgM9bc5\np0EzaEke4c4Zpjy+eFPenUZnwuweJic7W1W0bVamZAWsEofdRnZaSsTk5HdfWM//e21z9yJuc+yt\nln3Nlq6mAA6UksC9i+G34wORdEdInxITM+JuPND952o8rCL5YdMHp3A37Fefgzk3KNvwwKfHe0Sa\n40wSCfdww+M2BDdikym3skkgtlWSSHLSbOlqYkTcdU4XhdkOhBDkZ6TS3OHG5wv04thb46SquVNF\n3Gbliym+8TCFuyVCtJ5nWiUDJOKu2qauWsxL+PaQ6e4m2cPUFU5PI+78UappVcPB4LVFBwPma1w6\nD8acpn1uTRIJd+4IJRROYymsiG1dPQHx643kpLVJVWYhuFppbmmlIEsJcl6mAymhpUN56x1uL7Wt\nnbR0uJWpLKbjAAAgAElEQVRwmzMHE464DaskNLGZkhGwfgZKSaA5xupt6jaaVWKzKdHtSUlg42HI\nG62E2+fumV+ejBxdr8pBS6ZA2elQt0f73IOc5BFus9eFmagKSk7a1a3XHRD2WOWACSUnnaqG28So\n5fa01PiFOz9DjcFcNPhIo6qcaO7wqKuD/NFKdBP1uM0Fia1WiVmpkZZr/N1D4a7e3ju10C2GcFRt\nVbehDaas5PegJFDK4IgbBp9dcmSt8rftqUq4QUfdg5wkEm5jEo4pOhFXwHEnGHEnkJzsDLFKjIjX\n11ZHUbbqMJhnCrfhc1c0KOFu6XAjW6sgZ6jyfBOJuKWMbJWY08jTDeFONOLe/2lAVE3WPwePnw6v\nfjuxY8SiJSTiDu3FbaUnk3DaG9TVT/7owKIag6kk0OuBYxth5Gz197AZkJanfe5BTnJMeYfAJJxI\nwm2d8u6sVf1FUqP0KYEEZ062QvbQwN9GxG1vrwtE3JlmxK2E+4gh3F6vV4lw9jAVLSdSx93RaCln\nDElsZuSrMdsdiQm3pxP+70vqeLO/Buf8GNY8BUt/qb70h1eBsw6yCuMfKxpmxF2/T1XyhPbitjJk\njBLgjubACShRzIqSvFHq5G1PG1wRd80OtYbqyDnqb5td+9yaJIq4sw2rxPQ3IyUnfR5llcSySaD7\nHjeQ5WkKE25zEs6RRrVkWiFNCOmzRNwJCLfpb+cMV9GsufiAtXFTWm5iVknNDpV8HX0qrP8/+MMU\nJdozvwLXvgxINdmnJ7RWQe5INQ29Zoc6wdhSI/dANytiumPRmPvkj1J+eUF5YBm7wcBRIzE5Ynbg\nvrLT1ZJwzUePz5g0x53kEe4Uh5q96K8qsQces9lRPbYNqySWTQIJVpWEetzKKhkiWijKNpKTGerW\nnIRjWiUlwhDq7KFKdBOxSkybZOg0dVIxxd46GzEtJ7Gqksot6vayB+E/VsJJX4BzfwJXPqYqE7JK\nYNc/4x8nGp0t6sQ27hz1d9U2dYLJyFeTpULxlwRGsUs6WwMteUNpNCNuo459sNVyH1mnrpJMfx+0\nz61JIuGGgF1id4QLhD1VedytCQh3IsnJUI87Ix+JoEA0U5AV2eM+0tCOEFbhHqYi7kSsEjPiHmas\nw2x6yNaIOz03MaukcrOKfAvGQvFEuPoZOPNu9ZrZbDDxQlWH7Y3R2TAW5thGn6aSr9XbwntxW8kv\nU7eREpReNzx2Kiz5ReR9mw6r/yWzQP1dMFZF3INlObQja2HkycGdLodNV5ZR5abjNy7NcSW5hNtM\nUFptEhNbqoraEoq405DeTjYejiKoUobXcdvseBy55BMoB3Sk2Mh02P0ed0VDO+WFWRSbwp0zVEWh\nXY24QfncZkvXDItVklDEvRmGTg2+KrEyYZEa0+FVkR/f9Hd49VvRj2968LkjoHiSSoKG9uK2klmg\nXstIEfeeD5UdYvbiCKXxkPK3zRN1QbnquGid4NQVnLXw+i3w5/PhD9PhV6OPf+TafBTevTu8n4u7\nQ50UrTYJqPe1cDzU7u6/MWoGFEkm3IbPbY+QU7WnqO55bXWxZ00CpKQhpI8vPfoJmysiiKq7DZBh\niw13puSSJ5x+qwRUSWBTuxuXx0dVSweTh+dSgtUqMapKQrv+hWJG3CVT1G1LVUDwu+JxSwlVmwMn\ngEiMO0ed6KLZJVvfgM0vB/dMsWKKZs4wdYKo3hbei9uKENFLAjc8p25r90Te1ywFNOlpSeC7d8Hm\nV1QUP+ZU9Tp8+vvuHau32PIarP5f2LM4+P4ja1XexkxMWimaADU7+2d8mgFHcgl3bpyIu7UKkIl5\n3IADN/vrnOGPW3txW2iz55KP0x9xg5qE09jm5lhTO1LC5OE5lIhGOlPzVCVIer4akytOpOysUdvm\nlaq/WyvDKzVCrRIpYflDwZMxmg4rER02PfpzpeVA2ULY9a/Ij9fuUrfRej9bhbtkinrdG/ZHj7hB\n+dyhEbezDnb+E1KzVAMxs5WulcbDgVmj0LOSwO1vw7Y34Ox74Ia34EtPwim3KNuoekfXj9dbVG5W\nt3s+CL5/1z9VO4fyM8P3KZ6kXk93R9+PL1lpPgrPXBpcXpsoUqp9l/TC0oN9QHIJt7mEmT2CcNtT\nA1n2BIU7FY+/hC8I044IWWy41ZbDEFsr2WmBiF9F3C7/cSYPz6VENOJ0GDMdTd83ns9tWjxpOUYL\n26rwaeRpOcHCXb8PPvgJrHwkcJ8pAmZDomhMvAhqd4ZXaHjdAVHc+1HkfVuOKY81PR+GGlcI7Q3R\nPW4IRNxWb3rLKyovceqtxv+zN3gflxPa64Mj7rzRSsy6GnG3N6hoe9h0WPj9wP1zvq5mJa56rGvH\n603M92z3B8Gvz673YczCyCWURRNVRU/oa3ai8env4e3vdW/ffR+revfu1LwfXK72W/5goI3GACKu\ncAshRgkhlgghtgkhtgohuvkq9gKxhNuWGqgtjmOVSEO40/D4S/iCiLJKfCPZFNjaEJbEqNloyqwo\nmVCiIu7mFKNG2oyW4/ncbXVKuIVQFktrZaCla6jHbX65zQh2+9uB+yq3ACIgqNGYcKG63R0Sddfv\nV5fn6Xmw/+PIfUFaq1S0LQSUTA3cH80qARVxu51qJReTDc/B8Jkw5Qr1d6hna1aUmOWEoCyx/NFd\nF+73f6TsqCseDf78ZBXBjH+HjS8Gj81KXyZC3R3qBJo7Uq3yU71d3V+/T90/6eLI+xVNVLfm1VF/\n4ayF9+6N3V9dSvj0dz1vTbDrfVh8P2x4IXrVUSzqDPvNfE27wpqn1fff03F8T+pRSCTi9gB3SSmn\nAKcAtwoh4qhCH2FWlUSySuwpgf4ZsRpMAY1uJbwO3BxtjHCpGdqL26DBl0UewZfz+ZnK465obMcm\nYHh+OsNsjTTahqgNzCg0Xi23sybQjyRnmFp+LTTiTs9VUZZ5YjFrnBsPBqK2yk1QOC5s7GEUjoPC\nCerLYcUUgtlfUyebo+vD922pDOQbsksCS7vFskrMtrRml8DKLWpG4Kxr1VgQUBcSPVon31jpaklg\nxVp1klj4PXWiCOWU76gv6Nqnwx+TEp44Az68P/wxV1vPFogAVQPv88Cpt6m/zROp+b5MXBR5v8Lx\ngICaPhJujyuyfbT1dSVksVrL1u2BxT+HLa92//mbjqgksjnLuTvWWJ0RCNR00QZz1sH2t+Dk62DK\n5fD5//bOot+9SFzhllIek1KuM35vAbYDI/t6YBExq0oiRtwpStQgdi9u4HCTiiKHZdvCrJI2l4ff\nvWNMekjLCXqs1pNBtmwNSjTmGT25KxraGJqbTqpNUEQDdcIU7gQjbms1TPZQJY6hHrc5HtMuaTwE\nwq5WUt/xjrqvcnNsf9tK2elQsSY4cVprJLzmfQsQke0Sq3ALEUioxoq4zah594dKoNc/q07A065S\ns1zzRgW+aCbWyTdWik9SiblE1/I0q2dO+U7kx0smw9hz1Bc0tESytVq9psv+AIcsVTjOWnh0Abzw\nlcTGEA2zpG/iIhg6PTAxaud7UDQpuH7biiNTvS59FXF/+DPVHsFMmpuY1T9V26Lva145tVZ377m9\nHnj1m2quxZV/UvdVx3i+qOPoZsS94Tn13HNuhDPuUt+31f/b9efvQ7rkcQshyoCTgbA6MiHETUKI\nNUKINTU1feQJZRYofzpachLU47G8VuBgo7rsOr0sh6ONwcK9uaKJfUeMyD0kaq30ZGJDBq1Ck5/h\nwOXxsbe6ldIhGdDegAMP1dKMkhPwuL0edZkeFHFH8rhDGk01HlLJzNGnKruko0lF37EqSqyMnK3+\nF2v0WrtbnSCHlMGIWdGF25zJCqqyxPq/RqKgXF16Lv0lPDwbVj0Oky4KTLsvHBdulTQdVu+r9blA\nJVY9Heqkkwi1OyGjIPaM2lO+o6y2He8G319t9HuxO+Ct25S14fXAyzdC0yHYtwSOboj9/LEqiio3\nq9dlSDlMOB8OrVTR5sHl0aNtk6JJgRNtPLyexO2GlkrVIsHnhkOfBT9mvuaxxLCuh8K97A/qdbj0\njzDpEkB0XXx9hv8v7CpaTzSJKyWsfQZGnaJO6MNnKltx5Z8CV7oDgISFWwiRDbwKfF9KGVaTJqV8\nUko5V0o5t7g4TnKwuwihRC1ictJIGJo+cQz2NajJN2PyU2jp9AStG7mv1kmmMN7kEOE+1pmufrH0\n1zYn4eyobGFkfobfrqn0GSKWiMfdXk9QNUz2UHWWbzmmEmepxvOawmgmTxsPKwti8mUqItn2lro/\nXmLSxCwzs9ZQ1+5SpWYA486Fw58HlyC6nKpCJscipmbEHcsqcWTB9zfD19+DK/4EZ/8/OO++wONF\nE1QkbvWTGw9D3sjgySegenUgwpNOLiccXh3+3DU7VRVGLMafp6pbDq0Mvt9s1HXFo+q1+fjX8MFP\n1XNf/Bslup9F8UB9XtXQ65G50d//SqN002aD8Rco2+SDn6rbaP62SdFEFVXGKzUFeP5qeOHL8bcD\nlZDzutXJyvp6tDcGRLl6a+R9IeAtt3ajmgNg62uqkmbG1erKoqC86xF3c4U6uZedrq7EE70y2f+J\nEvy5Xw/cd8Zd6jv64f0DJlGZkHALIVJRov2clPK1vh1SHPJGRW4gZUbc8SpKgD31SqiHZal/3xp1\n7691ko3xtyU52e7yUu0x+nBYhNvsV9Lp8VE6JNP/YT3qNUTWkaOsjFget3k5ao24QQmOVQz9Vokh\nAo2HlHCfdKn6+5PfqttErZKiSaqCxeyHIaWKes3E17hzQXqDBdJaCmgycRFMvjyyf2wls0CJ7snX\nqpK8ovGBxwonqBOC9ctes1NF/qFkDFH/Y+jEmaW/gqcWKY/SSiLCbbOrY4ZGz1Xb1Il0xtUw6zpY\n/kf47FGYfzMsuFn5oFteDZ8Q5PPBW7fD5r8b1T8/DX9On095/eb7NWq+mt6+5RX1vpfOjz3m4olq\nMpJ1MeVIHF6trpz2fBC/9tuMtmd+BUbODRZu83MydJo6TrQFLUyLwtkNkXO1KU961ILAfSVTuh5x\nm1dvky9Tt4n63GufUa+9mTAHGH0KTP0ifP4E/G4i/O3K8CuRfiaRqhIB/AXYLqU8zjMVgIt+BYv+\nO/x+MwqPU1FS1dxBjaHLJZkqMrf63PtqWsnE8E4twl3f5qJRGn9bhTsjEP2PHJLhrxk91GnYGjab\nMXEmRsQd2orW7EpYsyPYN7ZaJZ5OFZHnj1Ze5/BZyibJLAwW1VjYU9R+ZsTdWqUifVPkSuerKNRq\nl0QS7pxhcM2zsT3ueBQai06YX7jmY2oiUaQaZlD3H/48cAns86mJLNILxyzi66xV0VJRHOEGGHGy\n8pytglS9NXBFsegXykYac3rgM7jgZhUdf27xQKWE936ovNKz/xNOu00Jwv5Pgp+v8YA6WZnCbU+F\ncWer3ydcGHmimRV/ZUmcGZQrHlRXa7ZUJcqxWP6QirbPvEsJ1rGNAYvA/JzMulZFs9EmaPmtkm5E\n3NXbVIRsDQJKJqursa7UrJtR/8SLVP4rEeH3upVVNv3q8ODw6mdU35/T71BXYW/emvhY+oBEIu6F\nwPXAuUKIDcbPJX08rugMn6G+YKHYLFZJDDZXNOGSatsi47050mgVbifZoh03qaqniUGD00UThnVi\n8avzMgPCXTokwz8d/IDLktgMae363uZj3P6CpVojVLhNUTQn5Zj4I+4Wo9RKBqo1zMhi2PS4VlEQ\nI2fDsU3qQ2teTppWSYoDys8IntFnTncP9Z17ivmc5hfOrK6YeFHk7cvOUNUGFZ+rvys+V5fHECzc\nZqRVPDH+GEbMUrNmzdfB61GVFaaHnzEEbl2lJu+YgULBWNXEa81TqsKk8TC8dpNKZp16G5x1j7KF\nCsbCW99VEaWJv+becoVklmnG87chcDKK5XPX7oHt78D8m1SFxIYXgsdgpaUK1vwFZn5ZjXf0qeqk\nZPraFWvVldHoU9Tfof3eQX3OnTXqSrOtLjzZ+/p/qJYK0TDfu1Dhlt7g5PXR9fCvH8eI+nerQCev\nVK1ElUjEXbdHfaZK50V+fOgUOO+nqjqpbo/KRRwnEqkqWSalFFLKGVLKWcbPP/pjcF2htt2sKIkj\n3EeacAn1pctN9eFIsfmtErfXx6H6NjLpoF2kB+1X53TRFCHizrNG3Pkq4nbb0qnqTMFrrkUZspjC\ne1sqeXvjUbXEGQSsEqMDYVAfcGsUa11MIbRUzhTuRBOT/kHPVh/Wqq0W4baI3LjzVHLHLNWLFHH3\nBrmlqmGVVbhzSwPRbihjTlUW1H7DxtnyqsoH5IwItjtMa6D4pPhjMAMCswSyfp96bYZaatXTssN7\nwJzyHRXVP3e1SrxuewPOuBsu/IU6iToy4fKH1eu4xHK1WLlZJc+s/+O0q+ALvw++VI9GVqFKusby\nb1c+rLzq+TfD3G8qmy1amd4KI9o+4y7196j5gFC2gJQq4i6da7yWURKG5vtnirvVLvG4YOMLsOSX\n0X35YxvVCdJaAmq+PtbnW/ZHWPFw5BJOcxyF44yqp5MSi7jNE1G8ORBjz1K3+z+Of8w+IrlmTsag\nyqk+CG2pBTG323q0iWFDlADafG5G5KVTYQj3ofo2PD5Jjq0DJ8HCHS3izs8MROUj8lXE3ZZWDAha\nO40sfnp+kMe9r1bVgh+sMyIfZ40SoQyjhDCjIHAFYY24HZaI218qZ0TcxZNUAm3BLTH//zDMBkZH\n16maYEd2YKITqE6CEKgrbqlUQmCOtbew2QKVJZ5ONd1+4oXRrx7S81RUdmCZirq2vqGi1dELgiPu\nWuN/yk2ggrVwvLKGTOE3E3DRTh4mY05Ton9whYpWb18H5/0keOxlp8Pcb8DKRwNXMMc2qfct1fJZ\nS02Hed+MnICPRPGk4FpuZ20gsGipUhH2ydeqipoxpynRjWSXtNbA6r+oyUimbZWRr05ah1aoQMFZ\nrRLasRKGpnCXLTSOa6ksaTkGSHUCOxilsdexjep9tb52BeMMu8N4PneHUTYp4MOfR65eqdujrg4A\niicrWyfalYZJ9TZ1Ii2Kc3VWMlVZkqHWVz9ywgh3h1f9K3vaYqx8g4q4y4cZ4u5xMXJIhj/i3lej\nvLzhGV5afeERt5sUZGpWUMSd5bDjsEkuyNpL+oc/gj0f4spQPnuzWa1iae0qpWS/8TwHzD4pbbUq\n2jarJ2y2QNRtjbhtNiXeHc2BGm6rIJ18XXjNczyGlKkTxZG1gYoS65dmSJn6spsNqcxSwK7YMYlS\nOE594Q4uV7MsJ8SxC8rOgIrV6kvsrIZpXzK8/kOBWZA1O8L/p2jY7Eo0zIi7aqs6ocaL1oWAa1+B\n721UkXW09+DC/1YngVe/pSyVrtTcR6NoQiDirtsLD8+BX5fD42eokkWvKzC5Rwh18ji6Lnxi1YqH\n1NXFGXcH3z/6VJXcNGvYzUqkkimRhbt2t/pcmolVq6haZ1Ku+1v4vh6XSgYPnxV8f4pDibA5IWjf\nUjVJ7qL/UdZWaOLX1aZONKb9VnISIMPnCYRSvV3tk5IWezubTX329n183NoLnzDC3e5VX8xNjY6o\n21S3dFDV3Mm44YZwezsZmZ/hT07uq1GRcEmahxaZhtsbuJxrcLqw2wRkDgkSbiEET6c9wP96f6Ii\nmTGns3fGnUBg9Xdra9ealk6cLuXLBSLu2nCLxxTu0BI7s9FU4yEl2vESWPEQQtklR9YHV5RYmbhI\nRZMdzcrj7m2bxKRwgoqMtr+jbI9oiUmT8jNVrfG/fqwi5QmLlE8NKnIDFY0mkpg0GTFLCarXo0Sk\ncHxwRByNrKL4J01Hpkri+jzw/DWqsVaPhXuSOvE3HoKXrlPv55k/UMHCkbUq0WZG0AAzrlGVRJ89\nHhAdZy2s/rOyaayVPqAsD7dTJVftaQErrmRK5IRh3W51svc3S7MkKE3hHneuKl0NbTFQvU29n5Gq\nk0omB04UO95R/vXcb8LC7yr75YBlJqc5L8H8v80Tb7xGYlVb1fMkwtiz1PtnXmH0MyeMcLcZEffn\n1VF6UIO/hesEU7g9nYzIz6C6pZNOj5d9NU4Ksxzk2DpxynQa2gKLLdQ5XQzJTEVkBAs3wAx2syXv\nLPjhXvjK83hLlb/n97Aty5ftrQkU8e+vNX63Tnc3McUxtFLDbDTVeKjr0XU0Rs6Bmu0quWdGKVYm\nLFJfqH1LjFmTQ8O36Q2KJqgk1MYXlSg7IiyDZmX0KSq6q92lap4dmYEv/bEN6mTZcjR+KaCVESer\nErvaXcEVJb1F4Tg1G9C0YXos3MaJ9vlr1NXFVU/BuT+CG9+B/3cEvvhE8PYZ+Srq3vQivHePsplW\nPqoSq2feHX780aeq24PL1GtrJuzNhGGov167R72PZnWX0xpxG3mZs/9TRfehSUrzZBtRuKeoqqmO\nJjWrdMKFaixn3K0aj717V2CCkRlZm1aJabXUxPC5O1vU8a29d2JRfnx97hNHuI337LNqO07TWw7h\nzQ1HyU1PYepo40PldamEIlDZ1MG+2lbGFmeR7mvDSYZ/ZRtQEfeQTMPbtQq3y0mObGXS7LP8VR+5\n6cqfbO6weNyeDnB3+MV6ZH4GB+tiCLffKgnxks2e3Obkm95g5JxAu4BIEfeoBerks+t95ZtaPfDe\npNCI9tzOQHVFLNJyAgnFaf+mbjOGqOn1RzcEyuS6ItzmZfqBZSr672qyNxEmX6Y6FKZkxK99j4dZ\nLVO9Dc6/T0WzJvbU8MlLABf8l7JPPn8CXvwqfP6kqlOO9DrljQx8zqx9wSMlDM3ZioXjVTldWm64\nVZJZqJKeI06GdX8NthqObVT7DCkPH4cZCa/9q7rCmGzMXXBkwkW/VKK86SV1n1lHbkbcKQ41plgR\nt/lYvMSkScFYlTzfp4W723S4vXR4bfgQ1PmyWXeoIWybutZO/rmlkn+bU0p6mnHpaxHuIw3t7K91\nMrYoG4e3HSdpNDgDEXe906X6cIcKt9FKNjW/1H9XTrqyL4IiboCOJvbVtJKWYuO0cYUciGWVmBF3\nJKukrV5Fkr0l3NYVViIJtz1Fzerb+Q9VlZDdRxF3oeUyPZFyOICTLlGVJOPPC9w3YpaKuM2Kkq5Y\nJYXjVTJz4/Pq70S/yF3l/Pvg7p09T/LmjVafnWlXwWnfTWwfm03VoV/8G3UydrUqeyUaZtRdOjdw\nX+E4laS2+tzmbEXzfcwuCbZKmo8ELJTZN6h9j6wLPH5so5r1G+lkYwr3ioeVZTP+/MBjJ12qToCf\n/EZVxdTtVjaideZz8UmxI27z/0j0CksIZZcc+DSxmau9zAkh3A1tLqoooDlzDFLYWb0/vD3nK2sr\ncHl9XLtgdCD5YCQnAbZXtlDb6mJscRYp3jacMiPIKqlviybcRi1nXiBJmGuUCPqTk+aXs6OJ/bVO\nyouyKC/Ooqalk1anU1kfUSPuCFZJ7S4VIfeWcGcXKwEQ9uhNjSYuCvzffRVxZ+QrESqenPj/tvAO\n+N6G4ITS8FkqWj68SolLpNmX0bDZghOUQxO8dO4qQsTtqZMQNpuqYvnS/3Y9YbzgZrjuVZVQjXWC\nGneushqssxntqeokbxVu8wrHtNuyh4ZH3GaZ37R/U177st+rqNvrgaot0a9AhpSpKxRnNYw9O7gB\nnBDKfmk4oKLuuj3BQQAo4W84GL2ypHqbypNYWwjHo/ws9Z04Dmt/nhDCXe908YjnSlZf8CrTRuax\nKkS4fT7J858fYn55AeNLclT1gLCDt5NheekIAct2q3rTscXZ2N1O2kinIcQqCRJu8xLPLMI3V+fB\nGnGbVkmgtasp3GWFKho4csTw/UIj7tJ56pIx9AOYlqv8QQhvd9oTyk5XX95oGfXx56sKC+g7jxvg\n3B/D+T9LfHubLXzMZoJy2xvq9etqAte0XxzZgdXlBzLpuZGj1EQYf55q4RuL6f8O310fnlMJnYpu\nJupMbzm7JIJwlwbGfNY9KtG46gkVjHg6Au9dKDZ7wMoxbRIrEy9SJ+yPfxPw2a0UG5Ul0SYrVW1V\n1SddeR3N5PlxKAs8YYTbTQp5+QXMKytgw+FGOj2BGVUr9tZxsK5NRdsmKWng6SQtxU5xdhqf7VNi\nP7bAgfB20irTqTesEp9P0mCNuH3uwDRgc9WdnIBwp9ptZKTaafZbJSpq9rQ1cKi+jbHFAeGuqTQy\n7aHCPWyaiiRDI3Hraii9FXEDXPJb+Npb0R/PLAhEXL09a9LKnBvjN1eKh+lTdzTFr8mNtX/J5O4L\n4omEzRb5s1Yy2Vgqz2hCZs5WNBOTWRbh7mhSV5bW8tWF34NJX4B//Uj57BDb8y+ZooKHSREmbptR\nd+NBZeeFBjzmcQ+uiHzs6u1dT0TnDlefr62vhxUs9DUnxKfSFNiCrFTmlRXQ6fGx5UhgpuJzqw5S\nkOXgomkWwbE7VI0rqsdIu9tLik0wOltF0i57Bo2GVdLU7sYnCQg3BN6o5gpVgx1SMpaTnhIWcdfV\nVuPxScqLshlTqComGmoM4c8MEehomP1KhC2xSSWJkpatxDkWJ12qXre8XnzeviCzIHhiUlcxo76+\nsklOFEyh2/yyuq3brQTTtGyyS5SIutsDpYB5gVwQQsAXH1Pv1dqnlXUSKrhWTr9DWULR+u1PXBTI\n1xSGRNwF5SrRvC1CcNJarRKe3Xm/T/kPlU95eA6se7bf/O4TQrgb/MKdxrwyJayf71fCWt3cwb+2\nVXHVnFLSUiylgnaHvxG/maAcXZBJqiewbFm9U0XMdf7jOwLJQr9wHw2ySUxy0lMCEbfhUzfUKTum\nvCiLrLQUinPScNYby63FWfzBjyncOSOCeqn0C6f8B3zns96fNdkXmFFzd4S7YJzyYKd+qXfHdKIx\n9mw1EeXdO2HxfymLwiq8Zp6mtdoi3CF2S3oe/Puzyr8eNiO8nYCV4okw/arojwsBF/xcWYyRLJcp\nV8LhzwJXySbmVPdEa7itzP0G3PyJOlG8dRv85YL4MzR7gR7O3hgY1Le5EUL1DbHbBONLslm8vYqG\nNqkN/iYAACAASURBVBevrK1ASslX5odc6qWk+RvgmMJdXpTlfxNb0kf6I24zSVmQ5YCU0Ig7cnVH\nbkZqWMTd0lgLTGJcsbJJyguzkIkucGxiJmV6q4a7K9jswZM5+gCvT2ITBK3r2S1GzFLLT3WlosTE\nZlP10JrYpKbDda/BP+6CTx9Q91m9ZX8td03kiNtk2DS44e34dfuJUH6GshgjMeUKWPILtejIgpsD\n9/srSrp5hTVsOnzjn2r+wZG1vfN/xCHpIm6vTwaaNxnUOzvJN0QbYF5ZAWsONvDUsv3MLyvghW+f\nokTZit3hT/KZlSVji7PU9OnUTI7lzaTeEOy6VnXrr+OGQO+RpoooEXdqoI47JQ1SMmhvrmdIZqq/\nv8mYggzmtixRkUaklbwjYW7Xm/72AOKaJ1bykze39PxAJ18P59/f+xNoNMGkOOCyh9R0fmEPrjwx\nhPsfn22g7ug+YzWjKIntUfP63poqnqgqlra9GXx/9TYVOMVaISkeQsCsr8AXHujZGBMk6SLuu/6+\ngU6Pj8euC0wGaHC6GZIVsA2+c/Y4Jg/P4aKpwyjJjTJd2UhOAozIM4U7Gz5bDGVnkC2yOHhUJV3M\niLsw2wFYIm6XUwl4BK85Nz2FinrLJVN6Hh5nvXoOg/lpB5nAQVwzf0vCpkfaiSvcB+ucrDnYQE1r\ngmtJxiK7BE7/fs+Po4mPEKrn+PxvB1f4GCK9bP02SgoPUpg7/Pgne6deqRbcaKkKVEdVbUu6E3zS\nRdxbjjazqSJ4UYJ6p4tCi3CPKsjka6eWRRdtCEpOzhyVz8zSPM4qbFF9DsafT0GWwy/YZvIzKOJu\nb1DN/iGicAdF3AAZ+ciOpqDIf37DO7RLB/uHd6G9ud8qOfGE+4NtarLGwbq2oMlPmiQhtCzTsP+K\naUQ0H0HmRrBJ+pspVwBS2WiguiLW7NDC3ddUNnVQ2dyBx9IAqt6cjt4VLMnJ4pw03rztdEbUGaVC\n488jP9NBU7sbr09S73SR5bCTnmpXU3ntaYZwG75dBKskN8OSnAS8jlzSPS0B4e5spfTIu7zrO4V9\nLTESMqEMnQan3Bq5JCrJ+dfWKtJS1EdyY0WMpd40yYE9lTZ7HkWiiaGyhvqU2KtT9Qslk6FoEq7N\nr/Pehx9Q+8eFdLjdfOxYeLxH1iWSSrhbOty0dnrw+iSVzYGuZP5ZjV3Bkpz0s2exmqFVOI4hmalI\nqUoB652ugBUjRGASjplYjFAel5ueisvjo8Ot6smdtmzyhNOfmGTra9jdTl7wnBOY+p7QuB2qN0Oi\nVSgDBI/Xx23Pr2Ptwcj1rrWtnaw5WM/1p4xBCNh4OMZSb5qE+Muy/byz6Wj8DfuQGvIZn9HCUBrY\n2dGDpe16kcbyi7EfWsEZn16H9Li5yf4LfrUlH3mcWrR2h6QS7iqLWFcYrVillKoBVFeF25KcBFT0\nvf8Tfw8E80RQ73SFWTEB4TZmTeZEiLhDZk82kkOZqGR6yzI163Ld36BoEgczpweaTfUAKSWPLtnD\nnuqWLu/r8fp4btVBfvbmFv6++jDbjjYHtbTtDfbVOnln0zGeWr4/4uMfba/GJ+FLs0sZV5zNJh1x\n94hdVS384t1t3PX3jRyu7/vytEh0uL1UuHOYIg6SKrysro9ebfHEx3t5afWhHj/n4fo2fvDyRtpc\nkRvNATzTdDICsJVMoujO5Vx4wcVsPxZuwQ5kkkq4jzUFhNvsod3S6cHjk8HCmggpaapxu8mhz1RX\nOkO4zcqPxjZXcMQNhnA3qunumYUR+zXnGB0CzUZTS4q+SoUsZuT734JnLlULAMz+GmVFWYH2rj1g\nyc5qfvv+Tv664mCX9lt9oJ7LHlnOj17fwourD/PDVzdxyUOfcsmDn8b88HeVnZXqhLJ0R7X/KsTK\n+1srKR2SweThOcwszWdjRWOXI6A1B+q5/YX1UbtDDiRW7Knl2j9/1mdjfWjxbjJT7dhtgp+/E2HB\ng15gZ2ULC3/1UcSmbqAWLamWeeS51HJ365uzqGgIP4m8v7WS/3lvBz97ays1LT1LTD/28V5eXlvB\nkh2RV5ivbOrgT1vTePSkZ8i86V+I3BFcMWsEGal2XuyFE0d/kbzCbaxaU28t1esKoRH3ng9VuVLZ\nGQAUZAZH3AURI+6jUWcvhvYr+aShkFuz/6DKpo5tUD75zC9TVpQVWFChm0gpefgj1SdiTRQrIhK/\n/9dOrn58JU1tLv507Wy2//wiPrrrLP7riqnsrm7l0SW91yTeFG6ny8uKvbVBjzk7PXy6p5YLpwxD\nCMGsUXnUtrqCFnFOhN+8v5O3Nx7l52/3jVD1Fl6f5L63t7J8Tx2vrauIv0MX2VXVwrubj3HjwjK+\ne94EPthWxUc7urHiehwe+mg3Rxrbue+trfh84SfZtQcbqJWBRlpHZRFLdgQvM1bT0sl/vraZscVZ\nuDw+/rIs8hVZIrR2enhzvboKXrIzwnJmwJ8/3YdXSq5cdKE/4MpJT+XSGcN5a8PRwHKDA5ykEu5K\nQ7jzMlL9EXe9dXJMV7AkJwHY+5FqzJ+myvXyjdXbG9uUx12QGcUqiSLc/g6BHW7aXV6W7anljJNG\nqLKp29fCtz+CrCLKi7KobO6gqd0d8TiJsHJvHesPNTKmMJOdlc2BdrIx2F3VwiNL9nD5zBF8eNdZ\nXDJ9ODabYGxxNtefWsaXZo/kyU/2sddYFQjgkY92c+4DS8MqPo42tnPb8+tiVoLsrGphTGEm2Wkp\n/GtrsIh8sqsGl8fHhVNVedbMUcoL7YrPvbuqhc/311NWmMlLaw7zzy2VCe/bFVo7PT22kd7aeIRd\nVa3kpKfw9IoDEUWvJzxoRNvfOn0s31hYzrjiLO57a1vEKx0rbS5PxJNlc4ebdzcdCxrn3ppW/rH5\nGFOG57Kpook3NoSveL7uYAOejEBtdMqQUSy2CLeUknte3URrp4cnrpvDpTNG8OzKA/6Jb6FUNLTx\nya7IkTTAWxuO4nR5GVecxdKdNWGva4PTxfOfH+KyGcMZVRBs23x5/micLi9vbzy+OYFEiSvcQoin\nhBDVQohemBXRM441dVCY5aC8KIuKRhWlmmLRZY87xRFITjYfUy0lLT1+zeMdbWqn3e2lINsq3PkB\n4Y7St8MacX+6u4ZOj48Lphh1oznD1GwxYM4Yc4p+eCvaRHlkyR5KctL4yRem4JOw/lB8f/hX7+0g\ny5HCfZdPJdMRXs7/nxdPJj3Vzn1vbUVKyR8+2MUD/9rFvlonL4RcUv5p6R7e2XSMf2w5FvX5dla2\nMG1kHuecVMIH26qCJlH9a1sVQzJTmWu8FicNy8Vht3XJ535u1SFS7YKXbj6V6SPzuPe1TUE5ka6y\n5UgThyxXQm0uDw8t3s2C//6Qyx9ZHiZwGw83ss2o+4+Fy+Pj9x/sYuqIXO6/fCr7apx8sju6GMWj\n3eXluj+v4vYX1rPmQD07K1v4hxFtD8ly4Eixcf/l0zhU38Zdf9/IO5uOcrDOGWZDfbCtivN+9zHn\nPrCUPdWtQY/9v9c2c+vz63joo8CajY8t3Utaio2/fmM+M0vz+PU/dwRZa1JK1h1qJLfY+H6k5XHK\n5HJW7K2jzaUKDP6ybD8f7ajm3otOYsLQHG49ZzxOl5enlx+I+L/e//Y2vv7M6ojvq5SS51Yd5KRh\n6ji1rZ1sDXk//rryAG0uL/9xdng/lNmj85k4NJsXP+++XeLy+HolX5UIiUTczwAX9fE4EqKquYNh\neemMHBJYJ9Ksse6yx21PC1gl+5aoW8vqIVkOOw67zb+AcHDEna8WKW1viFgKCJZVcNrdfLi9ipz0\nFOaXhzdxOnl0PmkpNlbureva+A3WHmxgxd46bjpzLAvGFmATRK3cMFm5t47FO6r5zjnjo16pFOek\ncfeFk/h0dy3feGY1Dy7ezdVzSjltXCHPrjzojzobnKqtAKgEYyScnR4O1bcxaWgOi6YOpc7p8o9x\nb00r/9xSyfmTh5JiVx9HR4qNySNy2XA4MeFud3l5dV0FF08bztDcdP745Vl0un3c/fLGLkezda2d\n3P7Cei59eBln/nYJZ/92Cfe8somzfruU33+wiwVjC6mob+OKR5az9mAD1S0d3PnSBq54dDlfe2pV\n3Kj2pTWHOVzfzt2LJnHpjBEU56SFCZXPJzna2M7KvXW8u+lYzAj/t+/vZNmeWpbuqOaqx1fypT8t\nJ8uRwrdOD/RVP31CEV9fWMa/tlVy2/PrOeu3S5n18w/4+tOf8/Di3dzy7Fq+/bc15Kankp5q5wev\nbPSfWD/aUcU7m44xMj+DBxfvZsmOaioa2nhj/RG+PG80xTlp/OTSKVQ1d/L4x/v8z1nR0E5taydD\nRxjzDfJKOfekElweH3e8tIGFv/qIX7y7nTMmFHHjaWUATBqmPh9PL98fdtVY73SxZEc1Xp/kpdWH\nw16HTRVNbD3azLULRnPWxGKECLZLnJ0enllxgPMnlzBpWE7Y/kIIvjxvNBsrmiKegL0+SVO7m8Y2\nF3WtneyraWX5nlpeXnOY/353G1c9toLp973Pvz+xsl+qU+LOnJRSfiKEKOvzkSTAsaYORuanU5qf\nwQdbq/AZNdbQnYjbkpzct1R157MsUyWEID8z1W8VhHncJnE87sZ2N4u3V3POpBJS7eHnybQUO3PL\nhoT5vi6Pj0921XDe5JKofTtcHh8PLd7NkMxUvrpgNJmOFCYNy40p3D6f5H/e287wvHS+vrAs6nYA\n1y4YzUurD7NkZw1Xzynl1/82g492VPOtv63h/a2VXDpjBP/32UE63D4Wji9k2Z5a2l1eMhzBdem7\njQhu0rAcThtXiMNu4/2tlcwozeP259eTnmrjrguDe4rMKs3j5bUVeH3S38ogGm9vOkpLh8fftndc\ncTY/vnQyP3p9C09+uo9bzkqsv8p7m4/x4ze20Nzh5nvnTWBIZiof76rh7U1HmTI8l8evm82cMQXs\nqW7hm39dw1ee/Iy0FBudHh9XzhrBGxuO8sraCq47JXIz/naXl4cX72Ze2RDOnliMEILrTxnD7z/Y\nxZ7qVsYWZfHU8v384YNd/gWlAX5+xVS+dmpZ2PFW7avj6RX7ueHUMdxz8Um8sf4of19zmMtnjgj7\nPvzssqnce/FJ7KpsZfORJjYebmTdoQaW7KwhLcXGDy+axLfPGMu7m47x/Zc28PTy/Xxl/mh+8sZW\nJpRk8+p3TuPLT3zG915cz6njChECbjpTnRzmlhVw6YzhPPHxXr548kjKi7L8n8GyMeWwBsgbyfzy\nAvIzU1m8vZqzJxXz40snc8GUodgs7+9t50zg/a1V/G3lQW49JxAZv73xKB6fZGxRFi98fojvnD3O\nf6IHeH7V/2/vzMOiuu4+/jmzsAz7joBsAiKKRBZxQeMWozHVmmiqklRT39rGNtqkTZq8yfs8Xd40\na/smbVNba2x9qk3aqrWJ1WjVbBo1NSYuURHUiiB7FGWRRc77x50BhmFANmGG83keHmbu3LlzfjP3\nfs/v/s7v/E4+7kY988aE4+1mJCXCl/dySlk1Xaud8rsPz3O1psHqmG25LzWcl3ad4dE3j/J6diqJ\nod7N3/MTm4+Tbyc7x8WgIznch4fGRZEa5YeUXV/Toqv02pR3IcQKYAVAZGTfzOorrqwlNdKXCD93\n6m82UV5Vx5c19bjodXi4dGESC7QMTkqpCXfsnTbTcf09XFo87i4Kt4eLAZ3Q4rcV1fXMSLK/+MCE\nYYG8vCvHahB046GL/GT7KX7/9fSWEAvaLeHmTwvY9UUJB8+VU11/kyfuHt4c7kiP8mPr0QIabzZZ\nndgW3jl+meMFlbyyMEWbUNQBBr2O17NT2Z9bRnZmFDqdYFpiMFEBJtbvv8CMESFsOHiROxOC+EZW\nDAfyPuHg+XKmJVrbmlOseTDDQ7zwcjMyMS6AXV8U03iziVNF11i/LJ1QH+vMnJShvmw4eJG80qp2\nPaTWbDqcT1ywp9UdzZKxkXycV8HLu3LIiPYjLarjkrUnCyt5ZNNRksN92LQws/miXTYxBimlVecZ\nF+zFtpUT+cHfjiEEPDMniegAExfKq/n9R+dZPDbSprMpu17Hs9tOUHq9jl8vSW0+3pLMSH79Xh6v\n7jnL1ZoG9ueVM3V4EDOSQojy9+D5naf58+F8c357yzFr6ht5YvNxhvqZ+OHsREwuBpZkRrIk0/61\n52rQkxzhQ3KET/N+lebFQnzMYzrz7ghj+/HLvLwrh6P5Vyi8WsuWR8bj7Wbkdw+lce+v9rPrixK+\nlj6UMHNxNoCnZifyUW45C3/7MW8szeBo/hVMLnpNuAF8InAx6NixahJuRr3dO73kCB+mDg9i7Yfn\nWTI2srkD2nq0gBFDvFk9PZ5vb/yU93LKmq+LazcaePvYZeamhDXf6U4dHsyre8/yZXU99Y1NrP3w\nHHNGD2FMpP3Klr4mF9Yvy2D1W58z79cH+J97k7hYUc26/ReI9Dfx3/ckYtTr0AmBp6uBMF93wn3d\nCfVxw8Vwe4cLe+3TpJRrpZTpUsr0oKAeFGuxw42Gm1ypaWCIOVQCcOlKrTmH29j1anKWKe+lp7R1\n8WKn2uziazJSa771tS/c7YdKdDrtxz14vgKDTjBluP3vZFxsAACHzreESyzhh02HrdP7dp4s5onN\nx8kpucZXx4Sz9qE0HmnlUaZH+1Fdf5Mzxbb53BVVdfxsx2lGDPFm/phbq6kdE+jBQ+Ojm70inU6w\ndHw0R/Ov8tPtpyivquObk2LJjPHH5KJn3xnbcElOcRXuRj2R5gGhu0eGUnCllg0HL7I8K8ZG6KH1\nAGXH4ZKTZu8xOzPS6hwQQvD8/cmE+7rz6J8/63QK/ZoPzuHlamDTN1tEu/Wx2uLn4cIbyzJYtzSD\nmEAPhBB8+85hXKyosRoYlVLy139fYsYvPuC9M2X8cFaiVQcT6OnKvJQwth8v4tOLV3j+vmTWL8sg\nOzOKrPhAHhoXxZni6zYpdy/uPEP+lzW8vGB0u2MUt4qPydgs2hZbn5ufjKtBx44TxTw4LrK50xvq\nb+JXi8cwMsyblVOt72Ii/ExseWQ8bkY9i9YeYufJYlIifDF4BmklT83Fp8J83TtNJHj6nhFU1TXy\nf3u0FeTzSqs4VlDJ/anhzBgRTIi3KxsPadeFlJKX3j1DbcNNq05ramIQUmqO0yu7c2hqgqdmJXb6\nfUwYFsiOVZMYG+PPs9tO8vuPLrBkbCQ7Vk1ixeRhPDwxhqUTork/LYLxwwKIDDDddtEGB8oqsQxI\nhPq4E+6rCUDh1Vq+rG7oeiogtNSyzt2t/Y+dYrNL6xOsqx43aJklUmrCbPEE2mN0hA8eLvrmOPcX\nlys5VXSNqAATH5wta55AIaVkzfvniAn04P0fTOW5+cnMHBlqdatpGexsGy5papJ8/2/HuFLTwCsL\nR3cafuiIhekReLoa2HQ4n8RQLybGBeBm1JMVF8i+06U2Mb6ckmskhHg2t3NGUgg6AcnhPvzQzsUU\nE+CBl5vBbo4waHHH53eext2o574xtnUwvN2MvL4klfKqeh7/6+d2sxUulFez80QR2eOiOvydOmPm\nyFBiAj347QfnkFJSdr2OZX/4N09uOU5CiCc7VmfxyBTbsM2q6fF8LX0o/1yVxeKx1h3QV1LCtA7l\nUMug2cd55Ww4eJGHJ0aTae70e5MQbzdeWpDCpPhAnmzz+0xOCOKfqyYRFeBh8764YC/+vnIi8SGe\nlF2v085FnQ4ePQIpi2758xNCvMjOjGTT4XzOllzn758VoBMw944wDHodizIi+TC3jPyKGl549wwb\nD+XzX1kxzZ09wKgwHwI9XVi3/zxbjhbw8MRom0wSewR5ubLh4bH8bH4yG5dn8tz8ZDxcB1Y9PocR\nbksOd2uPu/BKLV9W15mr9nURvbkgztndWvH3dupbWybh6HXC+oK2CLedyTcWLJNw7uogTALaUmcZ\nMf7Nce4tnxZi1AvWZKehE4JNh7WLdn9eOScKK/nW5Fi7whvu606ot5uNcK/bf573c8p4ds4IRob1\nbJFaLzcjC9I0oVwxObZZaKYlBnO58oaNt59TXEVCSEu4I9DTlY3LM1m/LMOut6LTCSYnBPGXI5f4\n+e4cm1K+AK/szuFAXgU/njvSymtsTXKED8/eO4L3cspI+989PLjuMJsOX6S+sWXAb+2H5zDodXwj\nK7pL30Nb9DrBNyfFcqKwktf25jL7tY84eF5r319WjNfWO22Hof4mXlww2qpypAUPVwPzU8PZfqKI\nK9X1XLvRwBObjxMb6MGTd3fuQXaXWaNC+dPyzC53ZEFerry1YhxPzhrO18d3YeHdNjw2IwFPVwM/\neecU2z67zKT4IIK9tGtt0dih6ITg4T9+wu8+OM+D4yJ5Zo71Igg6neDOhGBOFl7D193Iyg5i2+2h\n0wmWZEaSFT8wS0vcSjrgm8BBYLgQokAIsbzvm2WLJYc7xNsNT1cDviYjhVdruFLTXY/bLNyXDrfr\nbQP4mcXAz2S08mqbhdtOmMSCZdr79BGdF9eZMCyAc2XVFF6t5R+fFzJjRAhJYd5MTwzmb0cuUdd4\nkzXvnyPE25X5qfa9fCEEaVF+VsL9Wf4VXno3h1kjQ3nIzsBZV3l0WhxPzU7kKykt38HURM3O1uGS\niqo6yqvqbOLUE+ICCfKyszCxmVcWpLAwLYJf7csje92h5nMA4N2Txax5/xyLx0byQEbHi0p8fXw0\n73w3ixWTYym8Wsszfz/J0vWfUFnTQMm1G2z5tJAH0iOahaEn3JcaTqCnK6/uycXfw8jb353I0gnR\n1udPF1mSGUl9YxNbjhbw03dOUVRZy88fSLEZBB4omFwMrJwS13F1zk7w83DhezPi2Z9XTuHVWu5r\ndc4P8XFnemIw58qqWZAWwU/mjmo3nDXNfD5+b0YCPu7dv5MaiNxKVsni29GQzrB43JZBrHBfdwqu\n1NrOarxV9Ob3yJvtxrehZTamzfFdvbWi8Z2UqYwKMNHYJInw6/wWbXys1rM/v+M0FdX1zR5t9rgo\ndp8q4cWdOXx8roJn7hlhvQRbO6RF+fHPE0UUXq1lf24ZL+w8Q6iPGy8uGN3zlWXMBHi62mRrhHi7\nkRzuw97TJc2j95YZk50NMLaHu4uelxakMDYmgGe3nWDCC3sZFe5DZow/b35yiZShvvxo7q2V47QM\nyj1593C2Hi3k6a0nmP+bA4wK96GxqYkVk3pnZR83o56fzR/FicJKVk6J6xVxTQz1Ji3Kj1/uzeXa\njUa+M3VYh4NszsKD46LYeOgiJdfqmJlkvUD1s3OSGBcb0GGnOHtUKH98OIPJ8b0/5tbfDKzATQcU\nV9bi5WbA0xxrivBzJ7ekisrabnrcFuEWOojOancXy3Ftji+EFloJ6ngF8efmJ9N489ZyOpPCvPF2\nM7D9eBGBnq5MTtBOtklxgUT6m1h/4AI+7kYWd5A1YCHdvO7m/NcPUHq9jvQoP164f/Rt8TqmJQbz\ny325VFTVEeDpSk5J94XbwoK0CFIjffnH55f5+Fw5fzjwH3xNRtZkp3baibVFCMH9aREM9TfxrT8d\n4e1jl5l3RxiRAb233NTMkaHMHBna+Y5dIDszksf/esycWdGNlesdEKNexxtLM6iorrPpACMDTHwj\nK6bD9+t0ginDB0Ap2T7AcYT72g2GtEoZC/c1sdtceL9bMW5LqCQ8rXkx37ZYPO12j7/8X+BiG5Ns\njVGvo5OMu2b0OkFmbAD/OlXC/DFhzTnflljbCzvPsHR8VHPH1REjhnjjZzLSJOEXD6Qwf0x4r3na\nnXH3yFBe25vLU1tP8JvsVHKKr+NnMhLk2XFYpDNigzx57K4EHrsrgWpzYbGedERjY/zZ9p2J/HJv\nHqunx3f+hn5mzugh5JZWsTAtol+yGPqL6EAPotsuO6hwIOGuvEGoT0veaLifO5bkhR553LFT7O7i\n2xzjbuf4nr3fk09OCGLP6RIWpFnHbLMzI7lW28DySbF23mmNUa9j5+rJeLa6Q7ldJIV586OvJPGj\nd7SSohcrqhke6tWrHUdvjfBHBXjw8wdSeuVYfY2rQW83A0cx+HAY4S6qvGF1ux3h1yLi3YpxWxYi\niJ9pdxfLcbt1/G6wOGMoY6P9bcIKXm5Gm7Sszmg7oeV2smxiDDUNN3np3RztuXlKs0Kh6B0cQrgb\nbjZRVlVn7XG3mrXVLY87cjx89wgE2r9NDvJyxcvNQFxwxyGR3sKg1/UoFjyQWDklTpvivS+PpCG3\nuIK9QqG4JRxCuEuv1yElVjHu1h53t2LcQnQo2qClNR16ejqmAZp2NdB5/K4EsuICrSZGKBSKnuMQ\noxzFbVIBQavJbYnf+tqZfNEbeLgabtvAnrMhhDbg2llNFIVC0TUcS7hbJfQLIQj3dcfT1dDllDCF\nQqFwZBwiVFJUqdXeHtJmwC3Cz725CJRCoVAMFhxCuIsrb+Bm1Nnk7T4+M4Er1d1f8kuhUCgcEYcQ\n7qJrNxji424Ta+5psSSFQqFwRAa0cNfUN7LndCmfXbzSq1OSFQqFwpEZcMJdUVXHB2fL2HemlH1n\nSqmpv0mwlyuLMvpmVR2FQqFwNAaMcN9ouMmitYc4VnAVKc0rg9wRztyUMMbG+Peo8L9CoVA4EwNG\nuN2MeqIDTEwdHsy0xGBGhnn3qIaxQqFQOCsDRrgBXl00pr+boFAoFAMeh5iAo1AoFIoWlHArFAqF\ng6GEW6FQKBwMJdwKhULhYCjhVigUCgdDCbdCoVA4GEq4FQqFwsFQwq1QKBQOhpCWpdJ786BClAEX\nu/n2QKC8F5vjCAxGm2Fw2j0YbYbBaXdXbY6SUgbdyo59Itw9QQhxREqZ3t/tuJ0MRpthcNo9GG2G\nwWl3X9qsQiUKhULhYCjhVigUCgdjIAr32v5uQD8wGG2GwWn3YLQZBqfdfWbzgItxKxQKhaJjBqLH\nrVAoFIoOUMKtUCgUDsaAEW4hxCwhRI4QIk8I8VR/t6evEEIMFUK8J4Q4JYT4Qgix2rzdXwjxSQk1\nDQAAAzxJREFULyFErvm/X3+3tbcRQuiFEJ8JIbabnw8Gm32FEJuFEGeEEKeFEOOd3W4hxGPmc/uk\nEOJNIYSbM9oshFgvhCgVQpxstc2unUKIp836liOEuLsnnz0ghFsIoQdeB2YDScBiIURS/7aqz2gE\nvi+lTALGAd8x2/oUsFdKGQ/sNT93NlYDp1s9Hww2vwa8K6VMBFLQ7Hdau4UQ4cAqIF1KOQrQA4tw\nTpv/CMxqs61dO83X+CJgpPk9vzHrXrcYEMINjAXypJTnpZT1wFvAvH5uU58gpSySUh41P76OdiGH\no9m7wbzbBuCr/dPCvkEIEQHMAda12uzsNvsAk4E3AKSU9VLKqzi53WhLIroLIQyACbiME9ospfwQ\n+LLNZnt2zgPeklLWSSkvAHloutctBopwhwOXWj0vMG9zaoQQ0cAY4DAQIqUsMr9UDIT0U7P6ileB\nJ4GmVtuc3eYYoAz4gzlEtE4I4YET2y2lLAReAfKBIqBSSrkbJ7a5Dfbs7FWNGyjCPegQQngCW4Dv\nSSmvtX5NajmaTpOnKYS4FyiVUn5qbx9ns9mMAUgF1kgpxwDVtAkROJvd5pjuPLROKwzwEEI82Hof\nZ7PZHn1p50AR7kJgaKvnEeZtTokQwogm2puklFvNm0uEEEPMrw8BSvurfX3ARGCuEOI/aGGwaUKI\njTi3zaB5VQVSysPm55vRhNyZ7Z4BXJBSlkkpG4CtwASc2+bW2LOzVzVuoAj3v4F4IUSMEMIFLYj/\ndj+3qU8QQgi0mOdpKeUvWr30NrDU/Hgp8I/b3ba+Qkr5tJQyQkoZjfbb7pNSPogT2wwgpSwGLgkh\nhps3TQdO4dx25wPjhBAm87k+HW0cx5ltbo09O98GFgkhXIUQMUA88Em3P0VKOSD+gHuAs8A54Jn+\nbk8f2pmFdvt0HPjc/HcPEIA2Cp0L7AH8+7utfWT/FGC7+bHT2wzcARwx/97bAD9ntxv4MXAGOAn8\nCXB1RpuBN9Hi+A1od1fLO7ITeMasbznA7J58tpryrlAoFA7GQAmVKBQKheIWUcKtUCgUDoYSboVC\noXAwlHArFAqFg6GEW6FQKBwMJdwKhULhYCjhVigUCgfj/wHR4MZc4lp7GgAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f90c6cd27f0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fig, ax = plt.subplots()\n",
"losses = np.array(losses)\n",
"plt.plot(losses.T[0], label='Discriminator')\n",
"plt.plot(losses.T[1], label='Generator')\n",
"plt.title(\"Training Losses\")\n",
"plt.legend()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Generator samples from training\n",
"\n",
"Here we can view samples of images from the generator. First we'll look at images taken while training."
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [],
"source": [
"def view_samples(epoch, samples):\n",
" fig, axes = plt.subplots(figsize=(7,7), nrows=4, ncols=4, sharey=True, sharex=True)\n",
" for ax, img in zip(axes.flatten(), samples[epoch]):\n",
" ax.xaxis.set_visible(False)\n",
" ax.yaxis.set_visible(False)\n",
" im = ax.imshow(img.reshape((28,28)), cmap='Greys_r')\n",
" \n",
" return fig, axes"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [],
"source": [
"# Load samples from generator taken while training\n",
"with open('train_samples.pkl', 'rb') as f:\n",
" samples = pkl.load(f)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"These are samples from the final training epoch. You can see the generator is able to reproduce numbers like 1, 7, 3, 2. Since this is just a sample, it isn't representative of the full range of images this generator can make."
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZwAAAGRCAYAAABR3wXnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztvXm8VWP//38dUyhSpyQNjkqIQiEhRbjJlBAyz9OdebzN\nxc2NDLd56jZ8jPUl85QxkQZDQklEE5JUQqbz++P3WG/PrX111jp7r2uvfXo9H4/z8Hose6+99rrW\nWlfv136/31dFdXW1E0IIIdJmuVIfgBBCiGUDTThCCCGCoAlHCCFEEDThCCGECIImHCGEEEHQhCOE\nECIImnCEEEIEQROOEEKIIGjCEUIIEYbq6urYf5WVldXOOf0V6a9Lly7Vzrk5ScZA41Ie41JZWRnt\nR3/F+0v1XqmoqLC/DHzXsvhLeq8kinCqqqq8/6+iosL+RDzGjRvnnHNfFrqfpY2LSE4xxqWqqira\njygeqd4rK6ywgv0tqyR9jie9V2SpCSGECELiqXy55f6ao/7880/TnBGTNgQt5L21/Rzi+0zfdxXp\n0bBhQ9Pz588v4ZHUffLdD8tyM9/ffvst1f0nec75XsvtvFd++OGHIMdVKIpwhBBCBEETjhBCiCAk\nttR81pIvFIsTrhU7jIvzg1ecz5SNFh7ZaOFYlu2zfKRtoSc533GelYXYaIVQSGKYIhwhhBBB0IQj\nhBAiCEVLOA9llzmXG/oyZ/7XX391zvkznXgsccLnpFltK6200hLHIkREnGvOl5FUakaNGmV6m222\nMX3AAQeYfvjhh4MeUzFo0qSJ6e+++y7va/iM+f33302HzO5KE981l8YzXRGOEEKIIGjCEUIIEYTE\nllrQIiGPBbHGGmuYnjdvnunll1/eOefcTz/9VOO+4xR78jVxwk7ZaH+xyiqrmG7atKlzzrlvv/3W\ntv3yyy9537fjjjua/vHHH03ffffdpr/55hvTO+ywg+ksWhyvv/666R49etT4+kJstPXWW8/0lClT\nanx9dL88+uijtq1v376m//jjD9P77rtv3n2Uo43Gc+yz0UhSG40WHM8hX7/iiiuaTrvgtBgU695S\nhCOEECIImnCEEEIEIbGlFtKqYBhHzTC1WbNmptdaay3nnHMbbbSRbRsxYoRphq60zurXr2+aVs/C\nhQtN//zzz6YjK+Lvx5I026Muw/M1a9Ys55w/M4vnk9lQZ511lulevXqZph1Bsnie49hoxYI2Wpzr\nLyocbNCgQd7/z3th+PDhxTjETJBGr0e+Zp111jHdokUL06NHjzbN7Dg+Q+bMmeOcy70naOnFOXba\n2Xy28eeHDTfc0PTEiRPz7t+XncdjS4oiHCGEEEHQhCOEECIIRSv89NlfhfQk4nsbNWpkmhbA5ptv\nbjoK9RYvXpz3/0+YMMH01ltvbfqtt97Ke+zMOqMFx5CVtlu5ZZ6Eol69es455/r372/bXnjhBdNR\nFptzzj300EOmhw0bZvof//iH6XvvvTeV4ywVvuumEFs2zutPO+0055xzd9xxR97PPOeccxJ9ZrmQ\n9LzSWhowYIDp6667znSrVq1M77HHHqb5zJkxY4Zp2p+dO3c2/cQTTzjnnPv+++9t26WXXmqaWXV8\nDjEz9+KLLzY9ZMgQ0127djXN+88HbTRCCzApinCEEEIEQROOEEKIICS21BjGMRPJVyTpg2Etsx74\nXvZEY7Hnsccea3r99dc3HYWpX3751xLbH3/8sentttvO9AcffGB6tdVWM83iRFp61CxIpNVGO2TV\nVVc1HacQta7BMf3000+dc7l2ALMLef7ff/9900cffbRpXnfPPfecaV8mYVaIY9/47Ne0s+54HiMW\nLFhgmvdfXYIWLr+vrxiZ9zKzy2iR8ZnAwuQrr7zSNK1T7ofXyP777++cy7Wt+EzitcKfAqLsNuf+\nsrCdc+7AAw80PXToUJcPX9ZtGijCEUIIEQRNOEIIIYKQ2FLzhZ2FwGwIhp20XXbeeWfTzLZo3Lix\n6SjEXbRokW1r27Zt3v1xtbzI8nEu15aJ09eKltrqq69u2nee+PpyxZeR+NFHH5nm948KcjnOH374\noenbb7/d9Jprrpl332T69OmmW7dubdpnqTHDkcVvIeB4p21XJGXq1KnOudzzzELBd999N/gxhWDu\n3LmmaZX77E8+T6IsMudy7Xra/B07djRNy47WHD+LFli0nZ9Py4sZunz2rbzyyqa32mor0yNHjjTN\ne5LP2TSe6T7K/+knhBCiLNCEI4QQIgipFH7Gya7xvYa2A20vZjJFvbmcy11l8+2333bO5RZNderU\nyTRtHFoHDGmZBRJnxTvf8fr6DfF4Q5BGTzeeu969e5tmDylmlUUhe/fu3fPuj+cqjo3J13BFV14j\nzF4LbaORrNloZNKkSc455zbZZBPbxrGoq8tt0EbjPcEi8XHjxpmmRTZ27FjTp556qmle7w888IBp\nX5H63nvvbToqwCXRs8y53GeGb2kO/nTAY4zG2Lnc51MhGZ3qpSaEECLzaMIRQggRhIKWJ0jDrmG4\nywwkhoNdunQx/fTTT5uOrJP33nvPtrGvGi0falptvrbgxPe94/SQC5kR4lzxxoUZfoMHDza95557\nmqY1yR5SUdYMw3jaBMy2icPll19umueTn9+8eXPTs2fPNs3sHI5Rlq2vtKBVlI+6WrDsu2dpozG7\nkNmXvGbYa47XHl9Dy5fXGAtFuQxHVGzLImley3xusb8g980C92uuucY0M+YKoZD+mIpwhBBCBEET\njhBCiCAUlKWWRq8nhrL77ruv6Z122sk0Q0wWX6299trOuXgFa+utt55pWj0+a4UWEF9DXVlZaZrF\nZeXKoEGDTDPb5qCDDjJNS4vf+d///rfpfBkx7I3HXlFRkahzuXYoNdu10yI788wzTd92222maZtk\nfdmIc8891zT7cJUCWs1p4+vRmDY+e5ya1z4zHnlNMnOW+DJa+ZyjdRmtxMksS/ZJo53NzDTuj9Yg\nj7dYtnEhz31FOEIIIYKgCUcIIUQQilb4WSxoXdGuYXEas8e40t7o0aOdc85VVVXZNlo022yzjWn2\n42IGnM9yiVMEx8ySOAWMWYch+GGHHWaa/aT2228/08zUqckW6dOnj2kuJ0G91157mWaxKWH/OloJ\n3A8tkdBZgiTOkhUhbbSarlH2EEsb2lMhiZN1y+cDX0MrmKuC8vnks5/4nKO9HC2bwkww9knbdddd\n8+6D5++GG24wzWy4tJe7iIMiHCGEEEHQhCOEECIImbPUmK1CS4XQ9mIGRxTW9u3b17axuO2pp54y\n/fLLL5tmRogv7CxWr7isw8w0ZgDSLrv++utN0z6gBVdTcRhtClqdXGWSPfFYkMvMtGnTpplu166d\naVqgtCRKaalloZDSt7RERKn6pxVSTFgIPkuN+I6tWNmPLHyO7jNa/j179sz7mbz3XnvtNdMsNk2j\nOL+QnwsU4QghhAhC5iIc/kuBC6PxXwH8Fy7rab766ivnnHM9evSwbfzRjJqRUZx/wZRrxJKUk08+\n2TS7L7MzLhd18tUu1AQjTMLIh3AsGLEccMABpr/++mvTbK2T9dqbkLCTcBSRJu3WXe7Eqb3xwXqX\nQqIyRpJ8zkUw6o9qc5xz7qGHHjK9zz77mGbNFDtKsyUVWzwlpVjPQkU4QgghgqAJRwghRBAyZ6kx\nn/zCCy803bJlS9NNmjQxTdsnarnCH54/++wz05MnTzYdp31GnB8U64LVNmzYMNP8PrQM7rjjDtPF\naJHB9kRMDrj55ptNH3fccaY5/rQjaI0OGTLENK8j1vCErC3JIuwknO9ccGxptdWlbtpx7ll2ZY6s\n+rjvjYNvEbjonPNZRXbbbTfTXKRt/Pjxpnv16mX6kUceMU07kM+zOGNbrO+tCEcIIUQQNOEIIYQI\nQuYsNYaaDGWZgURLZf/99zcdtbG59dZbbRstN9aVxKk3SGqjxWldkhXYfZuwVQxrVo4//njTrMNJ\nAi0aru/OVkRHHnmkadoKzLxhxuLEiRNN81pgls/QoUNNM4Mxi6RtY7Vv336p/58ZgHXVUosDWyOR\nNLL4aHVFVjOfH7SER40aZZo1i+zgHrX4ci63Pod1aqXKzFWEI4QQIgiacIQQQgQhc5Ya8XWOZmdW\nhoavv/76Eu+7//77TbM9C7OYfOElt8cJNX02WhYLSFm8+eKLL+Z9DY+VbYGmTp1qmotAEdoEUTEp\n14ZnMeb//d//5X0fbTGOBbtys/CX2Yts+5F1G42kbV0xOzAfvC84tp988klqx5R1aJXzuvV1hY5z\nv7du3dp0o0aNTEdtaQ499FDbxjY3XOSRBfD8yYHZvddcc41pZrJ16dIl73Gl/XxShCOEECIImnCE\nEEIEIROWmq+DLRcmYshIa+yNN94wHXV9btGihW1jHyLuY8GCBabZv8u3YFEhWR1ZsdEILUrfd+B2\nFocOHDjQNG2vNm3amL7vvvuW+MxocSnnnLvnnntMczz5+cyY49rsZMqUKXm3i/w0bdp0qf+fmWl1\n1UaLc8/yPNAqT2qP8/W0i7fcckvTXCQysohZoPvggw+aZsH6F198YZqLwXXv3t30rFmzTNNGK9Uz\nSRGOEEKIIGjCEUIIEYRMWGqE9grD0fPPP9/0559/brpz586mI5ts5syZtu2QQw4xzb5bTz75pOkx\nY8aY9i0i5mtLnkW7rBC233570wzln3jiCdN33XWXaWYM1kSnTp1MX3vttaZ9fZ2YnSOKAxckzMfz\nzz9vOovZlcXAZxtT01KLc7/7zhX3Q4v4lVdeMb3tttsuoVnofNhhh5mmtc2lCpixxkJR3qutWrUy\nzaL6OAsUstiavQ+ToghHCCFEEDThCCGECEImLDWGoCw8owXGlQoZDu69996m33//fedc7qqVhP2R\nWOzIYq6k65rXNZgFw75mhx9+uOkkNhrx2Q7s/XTggQeaXlbOeUiYYRj1x2vQoIFtY3EgrZY4y3mU\nC3FW/GRRJ3uW8fnE19Nypy3M17CQdueddzbNDLOowPqKK66wbZMmTTJNq43LsNB+Puqoo0wzM/eZ\nZ54xTQvOZ6MRX5ZoUhThCCGECIImHCGEEEFI7I2knblCG4Wavb823XRT048//rjpKGON2SAMgdlX\n7Z133jFNS60uZePUhvfee880l3Zgi//awoxCfg5Jo/17KaGNwh50IWGmFK9vWmYRF110kWmu8krb\npVj3SKmy4JJmmtFO5Hb2paN1xecTswLHjRtnmkWbLJ6OrLY111wz7zGydyCzazmW//vf/0xzeQJm\nrzHTjPYan4VEK34KIYQoKzThCCGECEJiSy3t0Jc2GnsYcYVO9jtjf64o24bZaMy6efPNN/PuQ/wF\nzzOLY4cMGWL6n//8p2lm55BoqQjnnOvZs2fsz69rlmZSGy0Nm4mWmm9Fz3yfecQRR5i+/PLLi3Is\nvs8qFb6iRy5x4sti3XHHHU0PHz7c9FlnnWXaZyMz05PnIcokY7EnC9mZXcsVjDmW7GPIbDs+T0uV\ngagIRwghRBA04QghhAhCKoWfxbIFGCZSs1CK/YGilfkmTJhg21gkGme5AR91ta/U0mARJs8zC2t5\nLpjVtmjRopSPrm6SxrVFm5SrpUafxXuB9lEaNlrW8C3T4euf1r59e9OPPfaYaRZGcwmIdu3amWZm\n2GabbWaamWS77babc865uXPn2jZmvbHYk2PFYlMeY1VVleldd93VNG1xwow1X1/JQlCEI4QQIgia\ncIQQQgQhFUutEFvAZ12xbX63bt1Mz5gxw3QUyjJ7Y+LEiab79etn+qqrrkp0XMuKjUZoR1LXteLM\nZZXIpu7atattY8/CZQ1fLzVe77NnzzbNrC/aa1E/NOec22KLLUy/9dZbpnfaaSfTfJ5FllmjRo1s\n2y233GKazzB+Dq1BHjuXQWAvNd/zzFf4WSwU4QghhAiCJhwhhBBBSGyp+Va+9JE0u4uvYZbEiBEj\nTL/xxhumW7dubTpq4z158mTbxgKrl19+ucbjWhaz0UR6sPfVlClTanw9szF5/acJ+wqKJeESKCyG\n5vOBVhuh5c9Vi7n8QJRd69xffdA++ugj28YlCdhjjTYan8VczoBZbbQASchrThGOEEKIIGjCEUII\nEYTEllrSAqBi2VLMvGAmBe2zaFU6FobG+fykNppst79IarEua8Sx0UgoGy0kbIvPayTLq4jyHmcG\nWhyOOeYY03feeafpQYMG5X39bbfdZrpLly7OudzC6SZNmpj2rc7ps8Xmz5+f9/WNGzc2zYJUwn5y\nLB4uBEU4QgghgqAJRwghRBBK1kstqRXD/fjey1X3kpDURhN/IRutdjB7knaxDxZnJs0qK7UFTOus\nXK6XpOeJzyTaaEnhcioRtNF81llSK9ZnoxGfjVbIs1ARjhBCiCBowhFCCBGEiiShY0VFxRzn3Jc1\nvlAkYZ3q6uqmNb/Mj8YlFQoaF41JKuheySaxxyXRhCOEEELUFllqQgghgqAJRwghRBA04QghhAiC\nJhwhhBBB0IQjhBAiCJpwhBBCBEETjhBCiCBowhFCCBEETThCCCGCoAlHCCFEEDThCCGECIImHCGE\nEEHQhCOEECIImnCEEEKEobq6OvZfZWVltXNOf0X669KlS7Vzbk6SMUh7XCoqKuyv1OennMelsrIy\n2o/+iveXqXtFf8nvlUQRTlVVVZKXixoYN26cc0VYDGpp41JRUWF/cVh55ZXtr9gst9xy9pdlijEu\nVVVV0X5E8Uj1XhHJSXqvZPvOF0IIUWdYodQHIIoDI5JffvnFNFd0ZZTjW+n1559/rvH13M5o5Y8/\n/ljqMf755595t6+44oqmf/vtt7yv4efUr1/f9MKFC5f6mXGJGwGmQcOGDU3Pnz+/ZMfhXLxrxAfH\nyDfWYtlGEY4QQoggaMIRQggRBFlqdQTaaMRntcWxP3yWCrfXZKP5oHXjs9EIj5G2X9LPivOdQlNq\nG40Uch5kqdUOXp+rr766c865k046ybb17t3b9AMPPGD61ltvDXB0xUURjhBCiCBowhFCCBGE1C01\nn6UjiovPNlq8eHHe15fC8ohjba200kqmf/3117yv+f333xPts5DMq9C0bdvW9NSpU2u9n+WXX960\nz/Zs0KCBc865RYsW2Tbf+dlll11Mv/DCC3lfz3Eh5XT+Q+HLilxhhf//kXzjjTfatqFDh5qeMmVK\nugeWMopwhBBCBEETjhBCiCCkbqmlYaO1adPG9DfffGM6ynZi1pMvhF9llVVM+6wA2hJZtwMLyb5K\nann4CjXj2GERzGiKbIS/a9p+a6yxhukffvjBNO0ivpdjGsc+5HtLSSE2GuF5ueCCC0wzs2nVVVd1\nzuVaaqRJkyamL7nkEtNnn3226W7duplm9mBlZaVpn723rNlrvvts4403Nh2dwzfffNO27bzzzqZ5\n7/G69tmmvnuiVCjCEUIIEQRNOEIIIYKQDR8BtGjRwvTMmTPzbm/UqJHpBQsWmI56UjVr1sy2ffbZ\nZ6avvPJK01tvvbXpDTbYwDRD3Xfffdf0/vvvb/rbb781TUupnLJxCjlWWiQ+GjdubHqTTTZxzuVa\nOx9//LHpV1991fSXX/7VeHattdYyzWshsoKcc27OnDmm49h7vu+dBbuhmPB78rrn9/z++++dc7nj\nyT51F154oWnaPjy3vs7fs2fPNs37i9b0euutZ/rDDz/0fZWy5h//+Ifpl156yTSzdydPnmz6+eef\nd8459/7779u2pk2bmu7atavpe++917TPNs7ada0IRwghRBA04QghhAhC5iw1WifkmGOOMU1L67jj\njjO9zTbbOOecu+OOO2wbrbDWrVub7tSpk2mfLUDbjZkiLVu2NH3ZZZeZzrqNViwYvnfo0ME0F7fa\nfPPNTR999NHOuVwbYauttjIdWW7O5VoAtF84dkcddZRp9iGjdfPee+/lPa5p06bl+UZ1G5+tEmWY\n0Xbma6+44grTJ5xwgmlmPtG6o37ttddMP/3006ZpMWXZRouzZEYcRo8ebZrW8bx580yvs846pj/6\n6CPnnHPnnHOObWP23+uvv246TmZaMfoeFhNFOEIIIYKgCUcIIUQQMmep+bjmmmtMM4ODBZxRKHnu\nuefaNq6mWK9evbz7ZqjJjB1aBHfeeWfez+zfv7/phx9+OO8+QxOnj1bSglBmhq277rqmeX4POeQQ\n07SxomyouXPn2jbaKSx2ZHZT8+bNTfN7MMONdsfEiRNN06Zg5tuygm98eW1E2VH77LOPbTvvvPNM\nMzOUVhstaN/90rdvX9MnnniiaVrmLOCmffrTTz/lPfaQxLHRmK235557mmY22gcffGB6tdVWMx0t\nQ+Ccc+PGjTMd/XTgKzT32f+E9wqzRWk/8/Oj+zMEinCEEEIEQROOEEKIIGTaUlt77bVNX3755aa/\n++470wwZo4JPhq4s+qNm2B5lhjiXayO0atXK9CeffGI6yoZzzrnhw4ebLqWNRjujWMdBW8ZXWEZ7\ncdasWaZpe02YMME5l2tBsH8XrU6O3eeff573WPiZtB54Dn788UfTzFR89NFH836nUvZSK1ZGVBwO\nPPBA05FNzUJpns+FCxea5jHSgqFlxPuV+6Fl98Ybb5jeYostTHPJA5K1VUR5PHyeMBNvjz32MM2e\ncryGaUUyYy2yLn2v9cFrn4Xxt912m2neBxzbOPskBa0KW+t3CiGEEAnQhCOEECIImbDUGLrRLunc\nubNpZhoxlGWx33PPPeecyy0SpRXAjDJ+JsN/Wjq0iNizi8fiW1HThy9MLRR+T56fJEsG/B0eK9/L\n/nU9evQwTVuK2WuRBfrVV1/ZNl9/KGb7MKvmrbfeMs3zT3uHmVS0DJg96KOUdmjaNtpee+1l+qab\nbjIdjSktEl5HtB+5JATvF76G48Vrh0W+zB702WgkCzYa4fHwXLGomQWz3E5rjMuq9OnTx3S+a4Gf\nybHy9QXkPh555JEaX+8jjUJ2RThCCCGCoAlHCCFEEDJhqTHTjNljtEtYeEiLYOzYsaa3224755xz\np556qm0bOXKk6U8//dQ0w0WGvWyZzrbhtGsYSiclrX5rtLx8mTTFglkwLPA84ogjTLOfXXQ8HFuu\nFNm7d2/TG220kWlamrRxXn75ZdM+K8z3vWkr8Dxloc9UMeH9MmzYMNO8/iL7mP3leO8888wzpn0r\nq7J4k9mjtMZ5v7DIt5yW88gHrStauCyepaXFc8h+kL7lM/LBceX9xPddf/31pmlF83rv16+f6Qce\neGCpn1lMFOEIIYQIgiYcIYQQQSiZpebLEmPYyQwrFgGyCJShbNTLi1YMQ3ifbeIrAqUV0LNnT9Ns\nM86snwEDBpgu5Up7xcrs8dkcO+20k2kWEvJ8tWvXznRUQEubhUW1tOiouVIlbR/2W+N15PvetIB4\nDdQ1G43nn1bn9OnTTTdp0mSJ17MHHQsY46wiyfuS9hp7D+64446mTzvtNNPlaKP54LXEYlhCy5HL\nnZBoGY4ZM2bYNo6rz0bzZX1y1VxmlDLTlFmcvoy4YqEIRwghRBA04QghhAhCUEvNl5VCy6NBgwam\nGYIyNGRxJvtAjRo1yjmXm2n27rvvmqbV5oMhJYs633zzzbzHwpUQy4k4SxgQZrjwPHIsuE/abpEF\n9uSTT9o2jjMt1WgMncsdOy5nwD5pcexDWkBpFd6GxFcozevy6quvNs1sT1ovN998s3POuXfeece2\nxeldxs/nSqz169c3zYzQSy+91PS//vWvvPssF+LcN9zue56wx1qUXeucc0OHDnXO+ceB25lde/DB\nB5tmJhtXWGXhNYtxQ1rLinCEEEIEQROOEEKIIJQsS43hN0PGTTfd1PSxxx5rmj2YmEnD1T+j8HHM\nmDG1Pi72AGMIzCUJaPuEbC1fG3w2ZtIwmq+nXcKsGa4iSKIiT47hzz//bPq9994zzXNLG43ZiIVY\nAOWUGcWxo33C7//QQw+Z5jXKvmbMDNtyyy1Nf/3118653PvFl13JY2Fx7ogRI0zz3PJaYFZp1pYb\nSIpvdWA+B8aPH2+aRZ20PNkPkPdTtM+2bdvaNvax4/iwZ1vHjh1N8z7juHHplc0228z0K6+8Yppj\nkobVpghHCCFEEIJGOIwe+C82zrZnnHGG6VtvvdX03LlzTTPPnAt9RT+4+dq8UPv+5c/OrUcddZTp\no48+2jTrg7Kw/vrSKNa/6PkvH0YkN954o+nTTz/dNKO9KFmA/2LimDPxgGPkq89aVuC/oHlNR13R\nnXNuhx12MM3FttjOhv/6HjhwYN595oPvY30UF1RbY401TPO+YD2b71/Q5Q6/C7vWc3FBPrcYsfO5\nke8eZTdpRpSMVpmYwyQc3kOEyVkXX3yx6RdffNE0x1wRjhBCiLJFE44QQoggBLXUmCjAeoDox0vn\n/O1h2EKD66IzHM0XmjLspY1Gu4I2Q9++fU1fd911ptdcc03Tn3322RKfsyzBUNvXmZYhfmTHsMUJ\n7RcubseQvl69eqZpry2LMJmCbYM4FuwAfMMNN5jm9ZrEYuVruTDe+eefb5rjxfqsM8880zQ7uicl\nax2l+dxgDRTbMPGc8D7YYostTLds2dI0bdGorvDwww+3bbQz+RyiJcrnHI+R0MZjchZ/6mCCQhoo\nwhFCCBEETThCCCGCkLqlxsXVaIuw+2+HDh1Mc9Ez1mrE6QpcE746lJNOOsn0zJkzTQ8aNCivHjdu\nnOlSdoUuFRwLhvXsOszWGc2bN3fO5daG8P9zkTzaP4UsdOc73izYMkuDXZ7ZroTX3+OPP26aNRz7\n7ruvabazSfKdea6ouW+OC+9FLipWjPvVueyNF58bvPc/+eQT08zAZW0UszGZseZbrC7fZ7KtE7tS\n83N8sOXNYYcdZpo2WnSvOpebYVeshRwV4QghhAiCJhwhhBBBSN1SY7j2wgsvmGamy7///W/TXJio\nWGF5BLM3mJnBrtTMAGLIfNVVV5n+73//W/CxlDPsdMsCzz322MM0F3uKigA33nhj28YCX9omHHO2\n6Jg3b57ppAVpPlsmacfsENCWOuuss0z7CpifffZZ0+uuu67pSZMm1erzef5p19Fq8Y0Xs6DYQuf5\n55+v1bExiJf3AAAgAElEQVRkEZ57Xu/MwGQRKIstCZ8/JDq3PK+0mVloy+Jp/vzAbGDCfdIu43Y+\nr4tloxFFOEIIIYKgCUcIIUQQUrfU2KGUxWDnnHOOaYaGzGpjP6HawnCRhYSHHHKI6bXXXts0LSKG\nqbvuuqtpZnsw864u9YlyLtc+YJjOQjVaQLRgmCUVdcalzUKrgeeZfahoc3Hs4vSv4/59mYRZsdFo\nUXJBs+HDh5tmUSevUWY7scdabeF9we7GPJ+01GjN0A7nONYleI9PmTLFNC33e+65x7TvGvP1O4te\nz//PZyI18Vl3hFZf9+7d8+6T45kGinCEEEIEQROOEEKIIKRuqU2fPt00F05jy23aXrvttptpWgqk\nprCP4Sj7ELHAk+25+fkMgdlviNYZLR2+t5SkUdzILC4W59Im7dmzp+mbbrrJNK22yA7jUgbt27c3\nTfutS5cupmkRJV0GopwKcnk9MxuvV69eptl7zlecydfQdqvpejjwwANN33nnnaZp0/iur1NOOcV0\nsWy0LC9qyHuCiz9yITyeBxaBJilkpnXHceC+WUjK5xY1i635DBsyZIjpkMW1inCEEEIEQROOEEKI\nIKRuqe2+++6mGfIzjGPYTFvmpZdeMr355pubZi8pFrtF66jffPPNto3WTZMmTfIeI4+FyyDwMx9+\n+OEa31tKinUctE6YPcVwnCt+0rKkjUXbLSpC5PlkZiBbtXPpiQULFpimTZpGNmBWrNHx48eb5vn3\nFUFzGYIHH3zQdNTm3rnc5T9YwBkVjdI6jsOMGTNMc2XRYtm6WbPRCO0q2msbbrihad4fnTp1Mu0r\nmM3X45FjxucW7bVoJV3nnDv77LNN82eMrC3roQhHCCFEEDThCCGECELqlhoz09i+nivksaiNGTsM\nTVlsyCUMaLudcMIJzrl49ghDzbfffts0i7aYecJQtq4VePpg9hiXE+jTp49pZo8dccQRprmKZ5Qd\nuP7669s2Zuywrx5XjYxTVFtOSw/EgUXQPOfsR8Y+XMyCog3Tu3dv08ymYt9AZorWBK0hFpsuy/iK\nOjt37mx6k002Mc3rvE2bNqZZhBnZibQVWYDL/ma8P+OQhXtFEY4QQoggaMIRQggRhNQtNfLVV1+Z\nfuWVV0zTomFfH2Y9jR492jSz3dq2bWs6n5XG0JHhaLdu3UyzBxj7evky6eoyvu/M7ClaY8w8o+3J\n/USZURy3sWPHmmY2mq9QzmdfFMsayIodx2t4l112MU170Wepsd/cqFGj8u7fl6kZES0l4VyuHZRG\n37m0Mw9LBa8l2pn77bdfrfZHq7QQsnCNK8IRQggRBE04QgghghDUUiPs5cMMnBEjRphmyM3XHHfc\ncabzWV3s2bXKKquYZnFUnIKoLGR1FBOeC1qHcZg9e7bpMWPGmPadF7ZCjwrkWFT7zjvvmGamGy2d\nOL2nCrFlsji+PA5mY/Kav+WWW0wzg4nXdP/+/U1zhdrzzjvP9BNPPOGcK91SAr7xqqtWWynI2jWu\nCEcIIUQQNOEIIYQIQlBLjeExNVtos8CMmTHstxWtIOmcc4MHD867z2KQhRC0mPhstDhhd6tWrUwz\nw4xZOMxYY+Fn9F6uGsqi3sWLF5vmmHM8fcdVyBixmDeLWYgsPGbfrhdffNE0LbJbb73VNDP/2G+w\nHCyqcjjGcoH3B6+hUq12qwhHCCFEEDThCCGECELJstQILTUfX3zxhemrr746zcMpS5jZwzCa2xlG\n005iwaAvY4nn3/e5hx56qGmuVhlZdixG5DH+8MMPNR5vGoSw0ZJmCfkytHguaI1edNFFhR6iWEYo\nlY1GFOEIIYQIgiYcIYQQQciEpSYKx5fZ4wuj2aeOmiTNAGPh4TPPPGM6yo6JE9LzexRStJb0vczg\nKSZcEZXWoW+8lKEl6jKKcIQQQgRBE44QQoggyFKLSdZ6EtWGON/Bt7JpHAvI16stiU2UtDiNx0t8\nNqGPtKysOKsy1oVr6+/Uxe8kCkcRjhBCiCBowhFCCBGEiiThbkVFxRzn3Jc1vlAkYZ3q6uqmhexA\n45IKBY2LxiQVdK9kk9jjkmjCEUIIIWqLLDUhhBBB0IQjhBAiCJpwhBBCBEETjhBCiCBowhFCCBEE\nTThCCCGCoAlHCCFEEDThCCGECIImHCGEEEHQhCOEECIImnCEEEIEQROOEEKIIGjCEUIIEQRNOEII\nIcJQXV0d+6+ysrLaOae/Iv116dKl2jk3J8kYaFzi/dWvX9/+SjEulZWV0X70V7w/3SsZ+0t6rySK\ncKqqqpK8vGAqKirsry4ybtw454qwGNTSxmX55Ze3v2WJTTfd1P6SUoxxqaqqivaTl+WWW87+ypnA\n92iq90pS6soYFkLSe2XZPVNCCCGCskKxdsR/4SRdRdT3Xuok+/e9tpBjzDq+7/bHH38E+6wsMWrU\nqESvX2WVVVI6kvz8+eefQT8vH9G/zH3HwnFee+21Tc+cOdN0Vse/UHg9/Pzzz3lfk4UxLDcU4Qgh\nhAiCJhwhhBBBKJqlVoh1VazX1PTaLIT/af24Gue78bPXWGMN0/PmzSv6Z5UbPtski6ywwl+37e+/\n/17r/dRkCXGcaaMVclwNGzY0PX/+/Br3WSqSXg/lYDNnAUU4QgghgqAJRwghRBASW2o+S8iXXbYs\nESeszsq5+eGHH2p8jWyC8MSxpZLaaCuuuKLp3377rXYHFoM4x5VlG81Hs2bNTH/zzTd5X1Os++Pu\nu+92zjl3zDHH2DbW0KU5fiFQhCOEECIImnCEEEIEIbGlFtJaKbcCziwdSz6SHl/Wv09dJKldxrYq\n++67r+nHHnvM9Kqrrmp6q622Mr399ts755x75plnbNunn35qevHixaZ32WUX0/Xr1zd96aWX5n3N\ntGnTTP/4448xvkl28dlohfDLL7+Y5hhG9lnfvn1t2/HHH2/6wgsvNE2rtHnz5qY//PBD0xxvvr5U\nRauKcIQQQgRBE44QQoggFK3wMw18lg5DUIaGxbCAuO+OHTua/uijj0wXUmwnSgszftLoMxca9vwa\nNmyYad4LvEd4fY8cOdI559yCBQtsG/Xee+9t+uCDDzbNDtzjx483vcMOO5j+73//m+BbZNcmLybM\nQOzUqZPpfv36mY4sShbIRplrzjm38sorm+Y5o6aN9uuvv5q+6aabTJ900kl538vrI43nnCIcIYQQ\nQdCEI4QQIggFWWpxwmBfuBbHzlhppZVMV1ZWmp49e/ZS38fPYYYOs264b26nRTFhwgTTdSHM53dm\nqJ3GPjnue+yxh3POuZtvvtm2MbxnlhR7WH3xxRemi5VVk0UbzXcfNWjQwLQv02vRokV5t/Me4Gue\nf/75JT7Xd22/9957pq+//nrTvKc6d+5s+pBDDsm7nzjUhfurJjbZZBPTH3zwgekHHnjAdNOmTZ1z\nzr300ku2bfr06ab5fHr99ddNMwON19Po0aNN00bzFeqnnb2mCEcIIUQQNOEIIYQIQkGWWtJlBRiu\nMexj9gZXFrziiitMn3vuuaYZus+YMcP01KlTnXPOtWnTxraxSI0FVOzpxNfT6nn00UdNZz0zjRl1\nH3/8sWme86Q2Gu0ywv2wt9Nmm21metasWabbtWvnnMvNvDnvvPNMH3XUUaaPOOKIJd7nnHNjxowx\nnXQ5hVJyzTXXmD7zzDPzvsZ3H/lsNJ8Fx/uI2zmOtCxrun9pAd14442mWeDJ+yVOfz5fhumywLvv\nvmv6tNNOM81zG233PSufffZZ099++61p9nvjdbD++uubXmuttUzzZ4mQY6IIRwghRBA04QghhAhC\nYkutkMI5hvAMARkaMrz87LPPTNPe2njjjU0zA2fhwoXOudzVLKNtzuXadb7suUaNGuU93mLBwq1i\nwv5JxcJnwTEjpmXLlqZ33nln07RuIivtu+++s20spOX5P/3000337NnTdI8ePUyzODGLWWfkrLPO\nKvo+eb54jfJcrLPOOqZ/+ukn0/msYW7j/X3OOeeY3nDDDfMey7hx4+IetnNu2bPRyBZbbGG6qqrK\nNC3P6N7iTwFff/216auvvto0sz5pOV911VWmaa9xPyTpmPD+T4oiHCGEEEHQhCOEECIIiS01n4XB\nENBXjEbY8pth/IABA0zvvvvuptnXiRlmUaGUc39lrM2cOdO2rbvuuqZpEdWrV8807TVafWmE/2wj\nXq5ccMEFpmnpsCiNRZuDBg1yzjl35ZVX2jaec4boHP8+ffqYPvvss00fd9xxpmndFUJaVmfSYuc4\nGUO+/fA80hqeO3euaWYVRmPAsTj//PNNb7DBBnn3TYuuLlGsfm4cw4EDB5pmZhrPIZ+dUbHtnnvu\nadvYd22fffYxPWLECNMsFKW9lsbPArLUhBBCZB5NOEIIIYJQtOUJ4thoPmgRsJCT7dbZ74whJguh\nIpvslVdesW0dOnQwzZ5FtNqY9cTiqDSg1VRO0HJi4R+tG/Z2Gjx4sOnIGuIqh4QFo0ceeaRpWhO7\n7rqraVp3hVhqtFB8x1YoSbPoCrFxaZcxa7GmouXGjRubPvbYY01zzPk9TjjhBNMs8C0WpVqqoJDP\nYtYZ+8udccYZpmnjsx9d//79TR966KHOudwiWo7rpEmT8u6bmW7ct++5zHNM4pyDQixVRThCCCGC\noAlHCCFEEDK34ictBWagMcSkdcNMjchqof0W9VdzLrcIinD72LFjTRcSYtOOSMuu8VEsS4LnhQV+\n7M/E88tzN2fOHNPMQozo2rWraVp0tCYILQNaoIVQl1vix+n9F1kvbJXP4mjCa5iWdSFWuo8sjEvS\ne4jXJItk8137zvnHJ3o9l2N57LHHTH///fd5j4u2W779/V0zYzdphnEhKMIRQggRBE04QgghgpA5\nS42hLDOgttxyS9OvvvqqaVpw7JsWQXuNYSTfx2y4u+66qzaHvQShbTRSLEuCY+HrzUXbk6F/vl51\nHE8W2J5yyil538fvceedd5rO+lIRWYbWZL9+/ZxzuWNBeP4vvvhi0zWtuFsbSpWZ5iPpMXDJjCjT\nzLnc70X7mRYce0NGWZfMxOzdu7dp3m/sQUkLjtlw/Bzet7TX0rbRiCIcIYQQQdCEI4QQIgiZs9QY\nyjIbitsnTJiQd3sEw1hmQNFO4GqKbPmdhXC+mPA7J13xk8V+7J9Ezew1Fs3yczfaaCPnXK4td8AB\nB5hmoZrv8y+//PJExy7yw3E5+OCDnXO5BbaE5/+ee+4xncY9Ui73Ha/h6dOn531NixYtTPN73Xrr\nraavvfZa07SaoyUh9tprL9vG4mb+bMBlWNgDr3v37qZZaL799tub5mq6cVZqLRaKcIQQQgQh0xEO\nf4Tmj2jsfpsP/gv8mGOOMc1/4TNvnQu91TWSRjWELWf4IyMjyI4dO5rmInn83CiC7NWrl21jrQKT\nAPivbY5zsWpvlhV4Hhl5vvzyy6ajf637frAfMmSIaY5nnI7WdZUvv/wy73Z2gWfCEO8P33uZcHDu\nuefm/Ne53OcZx4c1U+wizWNhmx0+544//njT7OKeNopwhBBCBEETjhBCiCBkzlIj/DGLlgrD+Hw/\nNrZq1co0W6Wsueaapk899VTThdhOSfF1aQ2BL4HAZ6nwR1Hm6q+22mqmORZNmjQxzVqEaCEv7o/t\nVLp165Z3fyeffLLppF2Xk1LKcUkbntPPP//cNBdYi+CPzBdeeKFp1nawFcrXX39tmrZrTffo3ykX\nm44/1PMHfLaBYof67777znRtv5evbQ2fj6yl4jjQrp48ebLpfDWLIVCEI4QQIgiacIQQQgQh05aa\nLyz3hehRKBnVfTjnXNu2bU2zbc39999ftOOMiGMLlLLeII6NRpg9w4XudthhB9MjR440Ha3H7lxu\nRs62227rnMttT8MWHX379s17LGw5lDblUgcSF1o8zFpijUhkU77zzju2beDAgaZpB/Ha5rXDz4lz\njxLaQN98802Nry8VtKhoY/E80GZkp/Q0ryv+zOB79vDYafWxDigkinCEEEIEQROOEEKIIBRkqaXd\n4TVp5kpkEbCQiUVYzMxI43hLmV2T9FzF+f7Mjjn88MPzfhazYBo0aJB3P9ddd51zLtcC4Gtpe7JQ\nN8vZSnEpJHMrKbTLaP2wpUqnTp2WeF/UNdo5fydoHjs1ixJ5LfB7+zIMs2yjER4/LURmfbKb9okn\nnmiaz0i2qKkt3B9bQjGLtGHDhqY5VszYZcf9kCjCEUIIEQRNOEIIIYJQkKWWdmZP0v03btzYOedc\ny5YtbRsL1saOHWuaoXHIws+0SNt+inOOauo6y3PORde4kFQ0hs7lZkmVKyELVrmQFzsD00bjPXXL\nLbc455z7/vvvbVvS68hXlMjvzWNkxhztOx5X1hZjW3nllU3ToueiZzzftK5Y4Fzb4lbeN3wf98de\nk7Q2uegae1PGsTzTQBGOEEKIIGjCEUIIEYRMF34m5eyzz3bO5WZvMOT3ZW+IMPCc77nnnqaZvcPF\n9T799NNUjydr1k1cfEtF0D4+44wz8r6e3/Oiiy5yzhWWPUW7h9aMrwiU9hS30x5i9hctrFLBY9hy\nyy1Nv/7666Z57rmswz//+U/T7Ds3derUpX4ms/9YyN6+fXvT9913n2mOMeESI+yTx3Mfx17z2YpJ\nUYQjhBAiCJpwhBBCBKEgS43hNDMj0sBnf3DlyKglPkPEmTNnmh4/frzpkJkZoWndurXpr776qoRH\nkgt7Ob3wwgum2Saf45W25VVONhqhNUkrh5lKPpipWdu17Gn3sIDX12eMTJs2Le9r+J2yYKMRHif7\nCPI8LF682DSzAjfddFPTn3zyiWmeBz6vGjVq5JzL7VHIvoNcHoHwWuaxzJgxI+9rSJxnYbHGRBGO\nEEKIIGjCEUIIEYSCLLW0bTRfBgxthPPPP980Q88IhsMff/yxaWbF1DV7LUs2GuFqk2+99ZZpZt5w\nVdY0KNfMNOLL7ho0aFDe7fzO7FVXE7R61l9/fdPMdpo/f37e4/Kd565du5rmsghZhsf/n//8xzTP\nz2WXXWaaRdI33nijaT5naCGyCJp975IcFws8BwwYkPdYsoAiHCGEEEHQhCOEECIImV6egEWb/Kx1\n113XNAuSotcwXGVRW7t27UxPnDixuAfrStefaGlkyUJiVg/73bG/1sknn2z6iSeeMF1IK/uQ2ZTF\nJM7YNWnSxDRb1Pvey2LBLl26OOdyz0+UJeVcbo81ZlgVch3RRmNWHe/TUl+ncbn99ttNc6VUnk/i\nWx01iY3G63e//fYzzfPqW2IiCyjCEUIIEQRNOEIIIYKQ6eUJfJ/FbJxu3bqZjiwthufPPvusaWZv\n0f4qls2SFRuttm3Q04Z9nfr372+axYPsN1Ws85kVGy2pvRnnNbym2UOQq6vyfmAb/dVXX32J/XFJ\nCF8/tDj4Xu/LrCoXOIY8VzyXTz75ZF791FNPmR41apRpFmo2a9bMOefc9ddfb9vmzp1revDgwabL\nxXokinCEEEIEQROOEEKIIGRieQJaQIR2EJcW6N69u2kWoUUr8L322mu2jaEpM3pYsFYsspKllgUb\njdbDgQce6Jxz7pxzzrFtzFLj8TIzim3q6wJxLJBCMupYnJlkn6WyYLNq/S4N33EyQ7BXr1417oeZ\nmcsSinCEEEIEQROOEEKIICS21JKG/I0bNzZNu4T4wlTaMqeddpppFoSyFXjU0ptFUNtss43pYcOG\nmU6jGLCUNhrtiTjZRTy3kRXpXG7mTSFw//PmzXPO5S49wCUJaEXOmTPH9KxZs4pyLOVEGplHNV3f\npbKzsmCjxckc7Nmzp2mu8lmOWWKlRhGOEEKIIGjCEUIIEYTElhrD8zjhqM9Gi4Ov2JN9i7bbbjvT\nV1xxhXPOuUsvvTTR5yQtyPOtZljKEJu2FC3HOBTLRiO0S6ZPn+6cc2633XazbVxiok+fPqYfeeQR\n04WMC/t0lVOBYamLh4vVey9LPfyWRpxjY9arKAxFOEIIIYKgCUcIIUQQUumlVogV4ns9rYbWrVub\nZrjLvmpJSPo9aAf98ssviT6LLfqLSRwbjYWvadhovvOVbykInreHH3447z4KOc9JbTSfTZp1im1d\nFbKPcizk9FEulmC5oQhHCCFEEDThCCGECEJFknCxoqJijnPuy/QOZ5lknerq6qaF7EDjkgoFjYvG\nJBV0r2ST2OOSaMIRQgghaossNSGEEEHQhCOEECIImnCEEEIEQROOEEKIIGjCEUIIEQRNOEIIIYKg\nCUcIIUQQNOEIIYQIgiYcIYQQQdCEI4QQIgiacIQQQgRBE44QQoggaMIRQggRBE04QgghgqAJRwgh\nRBiqq6tj/1VWVlY75/SHvw4dOthf0vd26dKl2jk3J8kYaFzS/yvGuFRWVkb7qfVfRUWF/aX5fZdb\nbjn7K/W5r+Ev1Xsl7fOdZP9ZOpal/SW9V1ZwCaiqqnJz585N8pY6Q0VFhWkuWvfwww+b7tSpU6J9\njhs3zlVUVBS8+uCyPC5pUIxxqaqqivZT632ssMJft+dvv/1WyOEslfr165teuHBhovf67gsfyy33\nl6ny559/JvosV4SVOv9+r/D4fefbN4bLL7+86d9//9207zuuuOKKpn/99delHiePhfuOc47jjAn3\n/8cff+Q93jgkvVcSTTjlQsOGDU3Pnz8/72s4KLxAePKJb+CSTjIimxQyMSwNPpR4bfHzfA+uNCcZ\nEmeSSTqx+Ej6QItzLydllVVWMf3zzz+b5rHFuR44Vpy0Fy1alGg/JHq9b+x5rRAee5xJvZBri/tP\n/N5av1MIIYRIgCYcIYQQQUjdUlt55ZVN//LLL2l/nHMuXuhNW8Bno4llh0JsoqURx6KNY82UgpVW\nWsm07zeHtM5bRLFsNEIbjZYXf2Phs4oWku/7/vTTT3m3c/8+GyufXclz7/s9yfe7EWnQoIHpH3/8\nscbPj2PHFTLminCEEEIEQROOEEKIIBRkqflS90goG02ILOLLUqItQRuDdk+poY32//7f/zO9zz77\nlOJwUoffl9lgtJZ8dpJvuy/zraZML9poPvufFiCfv/xMn9WXFB5DIRmdinCEEEIEQROOEEKIIBRk\nqflsNCHyZdmcdtpptu366683XYuK87LBZz9wu+/7r7rqqqaLZY2QKCOO9g3HjcdYl2y0OJaQL7sw\nTgGsr3sBWXPNNU0zEy+yyZhR5rNffTYXX0NrkNt9GXNpZ+wqwhFCCBEETThCCCGCUCd7qWWBYvWe\nyiK+/mCrrbaa6e+++840bZqIwYMHm2Z2EPtc1QWrLel3oO0Rx0bjWJxxxhmmJ0yYYLp9+/amBwwY\nYLpJkybOudxzPnPmTNPrrLOOaV7DHM9yvLbjWGFx3uu7x7n92GOPNX3fffeZpqXWs2dP01Gxb9Om\nTW3bt99+a7qysjLv9nnz5i2xD+ecmzRpkmlmDNOu9WVG+u5zFX4KIYTIPJpwhBBCBCEVSy2N/mks\ncmKGBcO+gw46yDnn3IsvvmjbPvnkE9P16tUzTauD/YaKRRathjiFunHgd+N59LVIj17vsx14XNOm\nTTO9ySabmP7hhx/yfn454etT5RuX7bff3vSbb75perPNNjP91FNPmZ46darpgQMHmub54mfly6Bq\n06ZN3mMcOXKkaY5do0aNTH///fdL7C+LcBx834VZYosXLzbNc+m7DvlMGjZsmOl+/fqZpl3KJU4+\n/PBD55xz33zzjW2jzUm93XbbmabN+fXXX5v+4osvTNMW8/Vho46zxk9SFOEIIYQIgiYcIYQQQUhs\nqcUJrWijMXMp6fK1hHYYQ0baYZHtFicLha9ZsGCB6R49epiOwtu/fw7tnUMPPdQ0s1CySFIbbeut\ntzb99ttvm2ahGu0GWqkM36Pzxcwbnv+uXbuaHj9+vOljjjnGNDNy2Ncr6zRv3tw0r1viG5dXX33V\ndOvWrU1fc801pnl/de7c2TTHi9bkjBkzTK+99tpL7IPj9vTTT5v+8su/VhFmNlyrVq1MX3zxxaaZ\nNZU1fAW1XHraZ//6niFcVoLPxa222so0n520LpklFl0LtM44Js2aNTPNnw46dOiQ9zvxnmQ2KI+d\nz1a+d4sttjA9ZswYVwwU4QghhAiCJhwhhBBBSGypJc1QKMRGIwcccIBpZpMwHI2yQ3ytxX2hMS0F\n2gKPP/646UceecQ0C+n4mrrGW2+9ZZq2D7MEGY4TjkGEz+qk1dSuXTvT1157rWlmVPGaaty4cd59\nZgVagYVk19Hq+N///md68803N33XXXeZHj58uGlmXDFrKbLgrr76att25ZVX5v18Wp20V5g9yky6\noUOHmk76vWlP0bItVu9GWv6+55lvJVBfhiy/I6/JDTfc0HTLli3z7jMqwCWR3emcc59//rlpZgLS\nLuN54nHRPuT5Y3Eoj50WKTNGuU8WrSZFEY4QQoggaMIRQggRhMz1UmMoy6wRZslMnjzZ9AYbbGA6\nyuaYNWuWbWNmVE2r7Dnn3Lbbbmv6hBNOWGLfzjn36aefml5jjTVq3Ge5km+JAedyQ3kfHANakBEM\n9Tnm77zzjmmfXcdi3qzja/ceZ+kBXq+0Zh599FHTzIxs2LChadokzKrkuY4y2Zjd5ltpklma7L3G\n/V1yySWmmeGZdLxo96QBzxMtKmaAsfDS10fMZ13xvmEGLLPE2OuOllpktXHs2T+Nz54uXbrk3Tft\nNRYJv/baay4ftFxpN3JseQ4KWZVWEY4QQoggaMIRQggRhExYaszYYDYS7ao+ffqYfuyxx0wzG+bI\nI490zuWGvSygYijtg9YBW+z7VsijXVHXYHEa29rfeeedpn1ZPrQj99tvP+eccw888IBtu+GGG0wf\nffTReffnaxd/++2313jsWYH2CrOE4iw9wHuBvcyIzx6i3cP98PxGx8Dj8mWUMWvKV/x9xx13mG7R\nooVp9nij9VMqfJlezJZMulIrrSg+zzgOLKRlnzxaVJEFNnr06Lz7Y1Yij4WWHi3SiRMnmua59/U9\npD4JNtQAAAz/SURBVHXm6zlXyDNPEY4QQoggaMIRQggRhJJZahtvvLHpm2++2TQLL08++WTTxx9/\nvOmrrrrKNC217t275/zXudyMF4a3viUJGGr6bLRlhdmzZ5v2nQtmEt54442maanssMMOzjnn+vfv\nb9u4yiH3TfvAx/3331/ja7ICbQyuoMmsS59942sPz8JIFhkyO4ma1zr74K211lrOudwsJf5/wr52\nvgLqnXbayTS/KzO+mLHG7+TLjksD7p/jw+PxFY/z+vStgsrzzSUEfD0Iq6qqTEc98/hzAovOaQcy\nAzdO5iyz3Vjs/vHHH5v2FbMWa0wU4QghhAiCJhwhhBBBKMhS87XqjsNHH31k+pZbbjHN7AwWD/I1\nLAjk9k033dQ5lxuuMuyMY9ccccQRNb4mDsVaXbOU0K556KGHTNPSPPjgg02zyO2NN95YYj/sx8Vs\nGF8Wle/6uueee0wfdthhMb5J6eB3+Oqrr/K+xnfvsK/cZ599ZprXNy1jXme0RpgFxWymyELy2Wgs\nSOR9weOlFUZrhn3w+D24T99yDSHxnXufzesrAmUxLJeDmD59uuktt9zSNAsymQ0anZNx48bZNva/\n43gzA5c2Go+dmnYcr0WfdeZbubkQe00RjhBCiCBowhFCCBGEgiy1QkIrtlj/17/+ZTrKnHEu1wqg\njcawluFrp06dnHO52SYMR9ddd928x8LvwaLSQki6jEMpYYYNz123bt1Mc7wGDx5smlYbX0+bLLLX\n2Pqcq3ZefvnlplnUyZVAeYwHHXSQ6VNOOcV0Fotw49wjvkLKKVOmmPa1yKeNRvvOl1WYryce30dr\nhssWcDy5bAVXmnzwwQdNn3322aZPP/1003GKrwmtQV9fukLw3af8XN+55DVJy4kr5dJqY59Gngdm\nHUYZfb5iWdqW3EfHjh1N85pjhiA/h89WngO+t1g2GlGEI4QQIgglq8PhD8977bWX6dtuu800f7Ti\nv5569eplmvnkEZyNueiRD76+WD/w+/7VmkX4Lyj+S/ruu+82zX/hMqrgGPFfvvz+G220kXMuN8GA\nEQ7P/3nnnWeaC3oR/uuTESwTRMopUSPO9cHX8F+q/Nd3nP3wXEcLe/F8sls3WzudddZZplkHxXPO\ndj3z5s0z7avtiJN0lEZUE6dTt+94eMy8xtj6h9+dY8Vz62shE0UwrFfiQmh8H+89nmMmIXA/vk7Q\nceptfLVXSVGEI4QQIgiacIQQQgQhFUuNP6b5usOyJQoXlGJIR7uMC1AxTM3Hq6++apo/XjK3nRRS\nT+SjnCyde++91zTbCXGMfGua+xaKotUTtXHxJWSwFQhrFeLAug62X6E1m0XiXHP8UZg1Try2mDSz\n/vrrm2Znbtow/NzIvonaqfz9/1944YWmn3nmGdMcW9aZkCuvvNI0ExFYC+LrUpw2cTp1+6C17Gtz\nw7ZFL730kmmOG2up+LyMEl98bXb4E0FUd+hcbtsofs4TTzxhmueYz1BeWySNFkOKcIQQQgRBE44Q\nQoggpGKpxVlkifnhPubMmWOa9kJNWRIvvviiaS4K5SPrWWRp42sPw7qZnXfe2fTzzz+f9/XM7Wf7\nmUsvvdQ5lzturE9g6E5bLk5Iz067WbfRSJxsILacoX3Deie2nPnggw9MN2vWzDTtE1rTUTYT77Pr\nrrvO9FNPPWWaGU5x7hfaOm3btjVNS2311Vc3zcyuNCzupPAYfF2taXXRfiasDaN1xfdusMEGptdb\nbz3nXG52GW00trZp3ry5aXbIZwYwrxUuxhanxsZ3DgqxPxXhCCGECIImHCGEEEEoWeFnHBjqMduM\nWVUMDaOCUHZiZRaPj379+hV0nHUVFvU9+eSTeV/DMWIGz5lnnmk6GiNfJ9ozzjjD9DbbbJP3c2jT\nMmOKHcWzCK2IOAV2tBq7dOlieuHChaaZyRctbuecc5MnTzZ97LHHmj7ppJNMP/fcc6aHDBninMs9\nh8OHDzfty6TiPeeDrajGjh1rmuNOG41kwUbz2UZ8Da/3zp07m6bNS+vshRdeMM1nFG3OKMONmaC0\n65iNts8+++Q9rt133900C6yJL4vWV5hLeE0nRRGOEEKIIGjCEUIIEYRMW2pkxIgRptmTixZBtNAX\nC68Y0pI0OkTXNb799lvTPXr0MM1CXYb+7FFVUyYTrU4WbDJLjSE9x5EFjsyMyyJJMyCZBcVecizO\nZCdhFs2y39n5559vmt3Yhw4dajo6vz/++KNtYzYci2ppo3DhNI6Lr+s0radnn33WtM/uTjtrNE6f\nQ1/hJV9Pa5FWKK3oqIO9c85NmDDBNO3Kt99+23S0MCUz0DgO3HejRo1M0/Ik77//vmmOM68bZtLx\nueizgwsZH0U4QgghgqAJRwghRBDKxlJjcRoX/WKoF2XyXHHFFTXujxk9xYJ2kK8QrFwZM2aM6UMP\nPdQ0i2xJTbYFe235bDRmCkV26d+3Z504fQUJLTWeZy4J8O6775pmNhjvBS6exgXuaKtE55FjReuU\nxYcsAr7gggtMR4vrOZfbfn/SpEmmaTex/xevCxZ2MwuPvciKhc8S8mXHcUx8bfrZU45F7bxvWABL\nuzqy0Zz7y2qj5casN2q+htmF//nPf/J+Di1v2mg+y5D3Ga9j34J0cVCEI4QQIgiacIQQQgShIEuN\nq9ylXYAXp91/9BquCOqjd+/eBR/T36lrNhphqP3aa6+ZZhEuVwg999xzTUd2aIcOHWwbM5TiFJgx\nG45ZWlknjo1GaD+xZx37adHqat++vWmfNclVVNlvLrJMDjnkENvGVT6ZAcjstcMPP9z0kUceaZrX\nPy1Qn03q6xuXho3mg+c7Tn8xbqcVxT5lzB7jUggtWrQwzeclz0mk+T7fyp4vv/yyafaMZL86FtfS\ngvOtXOqD17EKP4UQQmQeTThCCCGCUJCllrU+VlGYyJDWB62IL774IrVjquvQSmB24KBBg0zfdNNN\nzrnc7BlfoRq56KKLTJeTjUaSttqnjdW1a1fTXHqgZ8+eptnanlbU008/bXqttdYyfdxxx5mO7t+Z\nM2faNhZm8thPPPFE0xw7Wjy00Wjr+IpTeT34zhP3n0Z2Is+3LwPN118snxXmXG7vOI4Ps9d4rtgn\nL7L4eI5Z9EtrmxZ2tHqrc7kWGY+Ly0HQwkx6jgvpdacIRwghRBA04QghhAhC2RR++mA4GIWJvqwn\nhoJsFS5qz+23326aKw3SAovO+7777lvj/mbMmGH6sssuK8YhlpSk9gOv59GjR5umTbzxxhubHjVq\nlGlmsrH/1q677mp65MiRpqOiQFp3zNoaMGBA3n3wGGfPnm36hhtuMH3LLbeYpr3KHm8+C46kXeSb\n1PL02Wu0ulhgOW3aNNNceoM2GolsTtqmzOhkfz1fHzvum9YcVxyNsxQDKdYqrIpwhBBCBEETjhBC\niCCUpaXG1t0DBw40Xb9+/aW+j0WKIYnTDr1cYbEc+6pxtcrIpmFmDIsUaRl8/vnnqRxnueDLfGJB\n5iWXXGKaFguvM2ZEcbVWFv899dRTzrncTEO+lsWefA0tFWZ7Dh482DSLwll4Snw2WqnwWfE+fNYS\nzxszBGm1de/e3TQzzLbddlvnnHMdO3a0bVtvvbVpZpqxvx6XLeD3YDEuP3/RokWm4zyfZKkJIYQo\nKzThCCGECEJZWmrs68NeThEM+dhKO99rQ1DXbDQfe+yxR6kPoezxrbjJbDBaVLzWfT2x2E+Lfbke\nfPDBJfbHpQciy825XIuU29nzi8fCdv1ZxtcXjPesz2rz9SOjFcrzwwJYWma0mtu0aeOcc2699daz\nbVxKhfYbi1ZpofIzeVy+64Pf1WevFetnAUU4QgghgqAJRwghRBCCWmqrrbaaaV/hUxyYeUGLIAoZ\nGdrTRisku0KIQoljS9ACpjVCfNldtOO4H173tGHuuece55xzd911l23jMhBcZXfKlCl5P7MciWOR\nxclAo7XP99LeYp86FjUzw4yrnUZwjLmsB+21FVb46/HNlVyTZtv5CliTLmEQB0U4QgghgqAJRwgh\nRBCCWmoM+4oFrYOotxCzRIYMGVL0zxSiNsTJ7vGtgumDNh3vhTjks0mi/mrFpFhFg8UiaR8xHrPP\nRiO+fbL3GX8W4M8L9erVW2IfXO7AZ5vSXuO48tjjvIbficdbrHFThCOEECIImnCEEEIEIRVLLU62\nTBoUo5V51sJ/UTfhcgMszEx6zSUtwivF9e37HN8Km1kolI6zAmkcK4q9BmlXchkIZg5GVpfPLqOl\nR3x2Kj+HffR8q3zyO9GujWMlxkERjhBCiCBowhFCCBGEiiRhdUVFxRzn3JfpHc4yyTrV1dVNa36Z\nH41LKhQ0LhqTVNC9kk1ij0uiCUcIIYSoLbLUhBBCBEETjhBCiCBowhFCCBEETThCCCGCoAlHCCFE\nEDThCCGECIImHCGEEEHQhCOEECIImnCEEEIE4f8DUFXK4jYBfhMAAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f90b98887b8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"_ = view_samples(-1, samples)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Below I'm showing the generated images as the network was training, every 10 epochs. With bonus optical illusion!"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZwAAAKhCAYAAABkTRjXAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsnXeYJFX1ht8N5CXnoOQsGQUJIiwZJEsQkCA5iiig/iSD\nkSBZMQFKlChJQFAykkFyEgmSRHKG+f2B79zps1PbXT09vSOe73l4mp7trq766txb3wn33GE9PT0k\nEolEIjHYGD6uTyCRSCQS/xvIB04ikUgkuoJ84CQSiUSiK8gHTiKRSCS6gnzgJBKJRKIryAdOIpFI\nJLqCfOAkEolEoivIB04ikUgkuoJ84CQSiUSiKxhZ58OTTDJJz1RTTcWwYcMAGH/88QF48cUXAZh2\n2mkBeOGFFwCYddZZAXjnnXcAeOmllzwOAG+99RYAE0wwQcPvfPTRRw3/PmLEiIZ/n3rqqRs+9+GH\nHwLw6quvAjDDDDMA8PrrrwPw/vvvA/Dvf/8bgCmnnBKADz74AIDhwz9+7r788ssv9fT0TNsKF6NG\njeqZcsope7kYb7zxGriYbrrpAHj++ecBmG222VriQk49brtcvPLKKwDMOOOMDVy89957Df/eHxdv\nvvkm77zzzrBWeBgbF16jdvG/zMX/ol04XwjHufODXNSdLwabi1bmi3btQsS5s9N28eabbwIwcmTj\nFD+u7aLWA2f66afn0EMP7b3In//85wAsscQSAMw888xAIUcSfe/JPvDAAwC8/fbbADzxxBMALLjg\nggBsscUWANx9990AXH311UAh4fjjjwfg8ccfB+Cee+4BioFMOOGEDZ//4he/CJSb5E179tlnAZh0\n0kkB2HfffZ9slYvpppuOQw45pJeLk08+GYAll1wSgFlmmQUY06B8LxcPPvhgw7n9/e9/HysXV111\nFQBvvPEGACeeeCIAjz32WAMXL7/8MgATTTRRS1w888wzAEw22WQcc8wxrdLQwIUTinZRl4v7778f\nKIMscvGVr3wFgHvvvbdfLk444QRgTLuoy0Vfu2iXi2Z2ER/Gg20Xcvavf/0LgIknnhiA1157baxc\naBeTTjopxx57bC0ums0XVXbRbL6QiwUWWKBfLqrmi0cffRSAv/3tb8DA5ou6djHttNNy8MEH9/5W\ns/lCu5CLKaaYAoCHHnoIKPdZLhZaaKF+udAuvM8nnXQSUMZItIs4RlZYYQWgcO+/y8Vkk01Wyy4y\npJZIJBKJrqCWh/P2229zzz33cN111wHlKTjXXHMBRTWpqlZffXUAbr31VqC4b5/+9KcBuPLKKwHY\nd999ATj77LMBuOuuuwD405/+BBQlsvDCCwPlKevnttpqKwAOOuggoDz1l19+eYDe81Ud/vWvfwXg\nySc/dmi23377OjQAH6ufe+65h+uvvx4oLqxceI6RC39bl1YurrjiCgD22WcfAM455xwA7rzzTqCo\nNtX6IossAhR1pqL56le/2sCF3//CF77QwIXq8JZbbgHgqaee6uUiuuHd4sIwQhUXXuOf//xnoLld\nbL311gAceOCBbXGx3XbbDRoXqu3VVlutXy4ML/3xj3/slwuvpYqLKrs45JBDanHxj3/8A2jPLuJ8\n0cwu1lhjjQYuquYLuWg2X3zmM59p+B093mgXrc4XctGOXbz99tvce++9vcfWY5hzzjn75SLahU2W\n43zh3Kld3HHHHQD85S9/Acp8oQfU6nwhFzfccAMA8803HwA333wzAE8//TRQ3y7Sw0kkEolEV1Dv\nMc3HSah55pkHgM9//vPAx3E8KJ7Cd77zHaAkwD71qU8BcOGFFwIlEWU8UTUljPlusMEGACy66KIA\nPPzwwwCcccYZQCkOOP/884ESD5177rmBkiDz6W9cfJlllgFKctC4aR0MGzaMkSNHMu+88wLwuc99\nDiix1sjFc889BxQuLr74YqAonZ/97GdA4UJFo3rYcMMNgaJgH3nkkX65OO+884ASJ1dBTTPNNA1c\nGBdfdtllG7h44YUXehOCg8VFtItWuTABv/766wPFy4t2YeLz3HPPbYsLr//FF1/sGBfmI7bbbru2\nuFBZRruQi1btYrHFFgNg9tlnb4mLvmOkLheeZ6vzxT//+c8GLuJ8YQ7opptuauCi1fki2oXzhR7X\nYHIxbNgwRowYwfzzzw/AZz/7WWBMu/j2t78NjGkXl1xyCVDySnGM6BnHMaJno0d95plnAsUu5GLx\nxRcHxhwjP/3pT4GS99Lz8fqfe+65Xl5aQXo4iUQikegKank4r776KhdffHHv0/jaa68FSnXRpptu\nCpSnn7FRY7MqBuPExrl92q611loNv6caUAVYPmlVmTmjd999Fyi5ohgLNh5urHf06NFAUQWqyjp4\n9dVXueSSS3q5MDbrNW622WZA4UL15rnpbcmF31eFrb322g2/14wLY8BWeMmFnKqEIhcrr7wyUNTi\nRRdd1FsCOVhcWJW45pprDogLPagqu2iXi7520Q4Xf/jDH9hhhx1a4sIxYl6r03YxUC60i3a5aGW+\nMFcjF9pFnC/8vvNFMy70EpqNkWbzhVx4z9rl4rLLLqscI1ZgRi7ifGFeSS60iy996UtAKY+uO3d6\n7R5HjzpyseqqqwLFLi699NLe5SitID2cRCKRSHQFw+psMT3XXHP1HHHEEb1PP5/KVr6YpzA+bK22\ntfzTTz89UGKi22yzDQCXX345UCoofKp7PJ/2LiLziTrTTDMBJd7t0101YLWKsVz/XYVkbPmAAw4A\n4Iknnri9p6dnyTpcGE+Wi0MPPbTh2ueYYw6geDjtcqFas34+cuEaKLlwMasKSi6s43dxnOdh3uuA\nAw7g2Wef5d133215Udtcc83Vc+SRR3LjjTe2xYVrDowPb7vttgBcdtllY+VCT0kVF7lQyUa7sHJH\nLuRKLsy/HHDAATzzzDMD4kKP5rDDDhsrF/7d2HnkQrtwrdNAuWjVLhwj+++/f1t20c35InLhGNEb\niWMk2oWf833VGDnwwAPbtgurvqrGiDkUOdA+HCPLLbccMKZdNJsvtAvX4zh36uFU2YVcmDN0rVTf\nubOOXaSHk0gkEomuoJaHM/nkk/d8/vOf71VhKgWrQ4w/ujbAKjFX6qrqfLWW3PfrrrsuUJ7CKg6/\nbzzRVbFWl6mgfCqvuOKKQFmla/zRahdVotVtv/3tbwGYZ555WvZwJptssp6ll16694nvGoONNtqo\ngYtrrrmmXy5UMl676y38exUXo0aNAko9vlwYo5ULP7/SSis1cGWdvvFoubBa5fTTT2eDDTbg3nvv\nbVm9dZqLgdpF5EK1r11UcaFK/P3vf/8/w4Vj5Pbbbx90LgY6XzQbI16b349jpNl84eciF/3NF+1w\nsdRSS/V6S3YKsPrUvKF24RzbbO7UO7QqzbWRXlucL7zf2oU5vKr5Qi48PysCtYszzzyT9ddfv2Uu\n0sNJJBKJRFdQq0pt5MiRTDPNNL2qTc/BqhLjkL5X2ViV4tPZGKtPb5+qruT1c9acG4/0qWxtujFg\nFYqfV7n6765QdlW1uQFr3o2v18F4443HdNNNNwYXVv8Ye/W9yua+++4DikozxqoSkQtXu6tgVIce\nVy7sweTf/b6fV6HIhauxzRFELg499NDeYw2UC6uItItmXJiri3ZRxYXXpBprlQv/XS60i0svvRSA\n7373uwPmQgXriu527aJVLjyuCtZ8RV0utItOcuFvOi7bnS/iGInzRdUYqTtfRLvQs+o7X7TDxfTT\nT99rF1VjxPdyoV24VijOF6ussgpQ7MJuHV6bx213vrDDSZwvXDt1yCGH1OIiPZxEIpFIdAW1PJzp\nppuO3XbbjY033hiA0047DSgxWOOOPm2tcFhqqaWAUjVilZDrYYQxU5WLNeaqNTubGvu1msjj+j1j\nula1qBqtKNt8882BolyMHdfBdNNNx+67786Xv/xloHBhDyO58Jys/nC1tVUjk08+OVDNhVxaWWd1\nSeTCunu58HvGZu0fpVKKVVR6gdNOO23tPlED5cJzNoZufyfzi5EL7UIu7JHl5yIX/q5cWOFj1ZFc\nRLvoBBennnoqUNZNtGsXrXKhXVRxEe3CMRK50C4GykU788XSSy8NlHHpfBHXBlXNF1VctDtfRC6m\nmWaajtuF1+o56eXZFaVVu7DHWat24e96D8z9OF/IRafmi/RwEolEItEV1KpSm2qqqXpGjx7dGxP1\nqWtc0vUM1oYbK/VpaXWISsWnsdVjVtio5n/5y182vFf5GNN1pbl9fqyk8Jp8ahtjtNrE3xM+oY85\n5piWq9TkwpioqqkZF3a2dmWvSkUu7EtkVUkVF3qN5j2quNADMpbraxUXI0aM4KyzzuL5559vuQJn\nyimn7Bk9enTvOcuFFTMD5UJ7U7XJhe/tV1bFhRzISVzjMDa7OPPMM9viwnNWQcqF6x1Uy3KhV+fq\n97pcVNmFithcQDMurE5zfYZoxy7ifBHtwnFnvsh9aPQ0rKCKXIyr+cJ7N2LEiHFmF86dnqvn5tiL\ndmGOsIqLaBe+xrVy2kXsmzZ8+PBadpEeTiKRSCS6glqByGHDhjH++OP3KtL11lsPKFVkrgj277/7\n3e+AomztaOvT2XyCcUWfukcffTRQ4pd2l7XSwk6rqnVjs+YA4upqV8W6M92PfvQjAI466qiPSagZ\nj+3LhcrDNQFVXLjWRwVTlwuPJxdWZrXKhSucjdW7Y2F/XNTp/gofq5wJJpig1y5a5cK1BHa0bcaF\nnWvNd6jeq7hwD49YuaUq9N/luFNcTDjhhJV2oU27bkIujInLhbF871erY6QZF7GiT09mMLiomi+s\ngNIu1llnHWDg84XHs19Yq/OFXFTNFz/84Q8bfmcgYyTahVx4H+PcqV24t497eDWzizhfyIXRAD2X\naBeOEXM2chXt4sgjj2yLi/RwEolEItEV1MrhzDDDDD1bbLFFr0q315BrCozVqzyNN/oUd02Bq1Xt\nAnv44YcDpROp37diQhVmzPW2224DSv2+FRfuEeE1Gcd2BbLVMipef3fvvfcGYJdddmk5hzPDDDP0\nbL755r0q3Rhs7Nqq8miVix/84AcNn49cqM5VNtbNV3EhjN1anSQXqry+XPzgBz/gySefbDk+XcWF\nytX3VXZh51pj5lVcqNa8hrp2MRS4EOY/zU/UtQu50C5Ume3ahWPEKqrB4OK/Zb7QLjbZZBOg//mi\nLhfTTz99z+abb947d3rtejoi2oW5FNfdVNmFn49caBe+xrVQzezC41SNkW9+85u1uEgPJ5FIJBJd\nQa3kxYQTTsi8887bu6ugcUSrQuxoaqxUlaVCsDLD2m5r0ffaay+gKBuf/tblG1N1Va1xRave3OfC\nfcDtDu1T3xXwqgsVjR1b/X5dLuaff/7ePci9piouVBbGSuXCVdKnnHIKAHvuuWcDF7GjrVzYFdYY\nrGsGqrhwRXHkQvTlQv7rcDHffPONwYWrpX1txkW0i8iF52VnY+2vyi70nFTC2m2rXEw88cQd48Jq\noVbtohkX2oX3Vy6iXTTjIq66Hwwu3G3SHEzdMRK5+PrXvw6UvETVGKk7X+hhWWk6tvmiLhcTTTQR\nCyywQG+ngDhG5ML722y++M1vfgPAHnvs0fC9OEbk3MiLHk3VfOH3tAs7EJhXE+3aRXo4iUQikegK\nauVwZp555p6dd965VzFYz65S9Olr/x3XBFgDrhIxTulT3fp6j2dc0+PqKXkc45HGE41r2gPJPeyt\ncbeflRUeVmi4gtkqtauuuqrlHM7MM8/cs9NOO/UqSVfyqhTlwu6vVodELszxqHQ8N7kw9h+5sFLL\neLXXUsVF7OEkF1YA9eXi1ltv5bXXXms5Pl3FheesmotcaB8qpIFyYX6rmV0048IY/vDhwzvGRat2\nIRwjA+XC6IL5Mceme9gPNhednC/kIs4XVVzE+UIbH2+88YDW7SLOF+1yseOOO/Z6GM3sQi60jzhG\nondYxYX5K6vgnC/iGPF3q+zC/Jbc+/2RI0dy2223tcxFejiJRCKR6Apq5XA+/PBDXnvttV7PwRin\nT01VlWsM7JV0ySWXAB/vGghlLwWVj72MXIVrvNAqERWLT2NjsXZzVan4fc/LmndXyRqPtNbcVbUq\nmLpcvP76673n7m/Kga8qDhVJ5MJ9aIw7ezzPsYoLVZr18nKhWnRtgd+XC2O2KiB/R0/36aef7uWl\nU1yoMCMXrjAfKBfahXFpO9vas6tVLvycXDzzzDMD5sIKrThGIhcXX3wxUHafrRojrdpF5EK7iN+X\nC3M8Kls/17cjQTtcdGK+qLKLeF8jF3p1decL7ULvo7/5ol27sBrQrstWFcqFuRa9OcdItAu50AO1\nZ1rkQi/RMVI1X8TvR7vwHsp5u3aRHk4ikUgkuoJaHs7w4cOZeOKJe+OP7snhU8+noauq7evj0zhW\nF/nUtGrFWnNVnR1TrbxRqajajLFarWKuwO/7Oev/fZqrLt1b3XUBxjvrcGHs1H0oVE2uIfDcVEle\nuxU1VpHIhZzJpbmAyIV9plZYYYUGLozZGxOWCxWNsWBjtubLDj74YOBjhWVceKBc2N+pigvtolUu\nvBb7P0UuvMZoF5ELOZML7SJysdZaa9X2fiMX9vtqxoXnJhdxjAyUiyq7kAuhV+iK94MOOgj4eJ+W\ndu3C+SKOkVbni2gXrc4XzezC41bNF44R5wvtYu21127LLiaZZJLe++XcqV14LXEPH+3Aa3OOkwvt\nJ84X0S7s9lA1X3g+zeYL7eLAAw/s5aKOXaSHk0gkEomuoJaH8/rrr3PNNdew4IILAuVpbMzbp6kx\nWP99hx12AIpyiB2VrTV37cKiiy4KlAoM+0ottthiQKkW8Xf1sKxKueiii4BSuWE81HjmzjvvDMC+\n++4LlJhwO1y44lelIOTCGKzXGLkwfyAXcuY5yYWKKnJhtYhcqBKtcpELFY9xcrnYfvvtgbKb4euv\nv94b+67LhXYhF/7G6quv3lEutAsrqSIXwrh05EK7aMbFG2+80RYXV199dW/vq8hFHCOtcuHnzAF0\nigu9D3NJnud2223XwMVA7MIx4jWIuvOF7+vOF3GMOF9U2YXzhfB8BsrF1VdfXTlGXAdjDsV/r7KL\nyIUdAawys5pMLvx7tAvnC6sbL7zwQqBwEe3CvaTc8bPuGEkPJ5FIJBJdQS0PZ7zxxmPGGWfsraiw\nplwVptI455xzgLK/xfe//30AvvWtbwFwxhlnACUmapdW48U+bY1jWnljTNc+UvYZUr25Wt94plVp\nv/71rwFYcsmPl9joLcR95NvhwgosY6cqD9XV2Wef3cCFPYj0rk4//fSxcqHXZqy3GRfGdF2VbYWe\nykg1ZwddVyj3jRGrZupyEbswN+NCu9hnn31qcaFdWHnTjAvtIlalWRnmOoxOcTHTTDONMUbkwjFy\n1llndZWLOEZiJZYr16u4mGOOOdq2C8dIq/NFHCNnnnlmw7Vb5WYeYaDzhVw4X7iXjGtgzDF1YozE\n+cI1gPLejAu7SJt/jnbhehtzh63OF3Kht+IY0ft0DOuFmmucffbZa3GRHk4ikUgkuoK29sNREVhD\n7lM0xqON2W+xxRZAibnG1dMqTWOqPn1VWSohn7rGx62oMc6ognJVrE9j+1Dp0ey3335AiQ2rvNvh\nQg/CWnSVplzsuOOOQFEKW265JVB6WTXjQg7kRKVRxYXHU0FFLuxbZ4xWLqx6Oeuss3pzZIPNhXbR\njAsVrFxEu1Clu5eM+8R7PHMI9rGKdiEXqkjtohNcuF4hjpFmXNh7rZldNOMijpF2uTjnnHPa5qLu\nfOEYsQeb596p+UK7iPOFnoxjxPlCr3OgdjHBBBP0ehDaRczRRbtwx0/twgo9ufBzzbhoNkacL+wS\n3apdnH322bW4SA8nkUgkEl1BrV5q448/fs+0007L1ltvDYy5Ytc4pOrO6iRXCrsHgxUYKh9jgCog\n44zuUmk1ixU6KiR39nNlsbFZVYMKyaezMVhX87pK19jt/vvv33IvNblQgbiWQy7MF0Uuzj//fKBU\npVg1Yt5JLswBuL/F9ddf38CFlVtyIWeuJariwqqkBx54APi4jr7v8d566y1OOukknnnmmZYDs+3a\nRatcGPeOduFxhjIXV111VQMX2kXs3uwY8f62aheDxYVr0/R8x4Vd+L7T84WdmK3QkgsjMHLhfKFd\neLy33367bS6q5gu5iN2bzzvvvAYu9CaiXZjXinYRudDDkgs7CpjLiXZxzz33ACVnM1C7SA8nkUgk\nEl1BrRzOiBEjmHzyyXvr3TfaaCOgdBR1hfDPf/5zoCgXa8B9qlshpXL1ae3KXysv3H3QWKx/d/Xt\nnXfeCZQYrXFHn8o+te02a1zc87QyyKd1XS4mm2yy3rivO+J5TsZETzrpJKAoi0UWWQQoK3dVvCoU\nV6Iba9f7kgtjsZEL74ExWs/LTtkq26mmmgoosVtXFsvFa6+91quG6nJh/Fi7aJWLaBeq+GgXcuHx\nW+VCu4jKthtceN/kwrzBiSeeCBT1bW4uctHMLppx4f2vaxfes05w4XwRuYh24XzRzC7kwmuMY6Rq\nvtAu4jpCuXB9TpwvtAt312yHi+HDhzNq1KjK+UK7OOGEE4Axx4j5Jz0hr00unAO1g6r5wrlPLhZe\neGFgTLtwjLgPj3m0OEZeffXVWlykh5NIJBKJrqCWhzPJJJP0VgxB6UhrnND44U477QSUSgpVnErD\nuKWro10H41NctWUtuXFKj+dx/L7Kx/i1sVif6ldeeSVQFIy71e29995Aqaoy7tkqF8sss0zv6mW7\nsMqFvZHsauDKXyu3VO1y4b9HLlRbcmGMtYoLFbFcWI3k380pqGw322wz4OO9yeXC1cmtYtSoUSy7\n7LK9XGgX5uyaceE1uNaomV34OblQQTfjwri0djEuuFCRyoX3cbC48Pz1AlT/jpHBtAvHiIhjxDxC\nM7sYrPnCHG7VGDFC0h8X9iJrFaNGjWK55ZbrrU6rmi923XXXBi70+rxm73fVfBHtwvVf2oUejlw4\nFozy1J0vPvroo95zaQXp4SQSiUSiK6jl4Uw44YTMNddcvXt8WON9wQUXAKWyYtlllwVK9UjcP9t4\no09f44c+nVVrdrY98sgjAVhuueWAolxUi7/97W8B2HTTTYFSkRO7TPt96+49jkqmDiaYYALmmGOO\nXgVgrNWqEn9bhaeCifuqG1uXC+PKcqFa0yOSCzn2Gsx3nHbaaUBRIpEL74VcxF0N2+Fi/PHHZ/bZ\nZ++1C3N2sQpNLlS20S6quNDLi1wcccQRDdfiNagK5UKP1mpGvY3B5EK7cIxUcRHtwvtY1y6quPB4\njpFucuF8YX8w7aJqvoh24X1sdb5Q7TcbI3bhqBojgzVfzD777L2VenG+sArNc3Zui3ZhzsUOBa7f\nMdci9Oq0i8iF3Ea7sKu0++/oifn9aBdGjVpFejiJRCKR6ApqeThvvfUWd999d2882NiqCkTVZKxX\nJWInU6s+rMxyfYxVKCoWn752APD39Jiuu+46oMTkrdSxT5hPez9n7btxSc9LpVIndyPefvtt7r33\n3t4qEGOmKtPIhSt/jRvX5cIeS8bgq7iwOkUurC5xHc9WW23VwIXnZYz2+uuv711FXJcL48HahVyo\nIFvlwhXevvd+Ri7kXi68Rldly4UdcD1O5MLz7iQX0S4cI1bKNePCaqTIRZVd1OWiyi46yYXzhbbW\nbL6o4sIx0eoYiVw0GyPRLuJ8Ebm44YYb2rYLv2e+qWq+iHOnHQbifOF7owBGCyIX5tflItqFXqec\nV80X5oJcm3TttdfW4iI9nEQikUh0BbU8nEknnZQvfOELvfG+3XbbreHfYx28ysPd5Nx/xLigdfj2\nA/LfXVk8evRoAP7yl780HNd9vY2x/uIXvwBKHyHVg8e3Ss6ad/sOGQdXXdSBXBgHtrrEOPOGG27Y\ncM4qD5VIMy5UXa44lwvX70QujLHa6dbKEbm3OsUKILmw6rAvF6qiTnGhBxq5UKF6rcbuW7ULufB8\nVXXjmosVVlihY3bh+oy6XNi5wGuSC6uTzI92wy7ifOEx43zRaS48rnkSr8n5wjxE3O0yzhd+z1xR\nO1yMGjWqgYtddtkFKLmYDTbYoOGczdlMMcUUQPFIjcbIhf3nHENysfLKK/fLhfOFOcQquzA36Hog\nufB7cnHHHXfU4iI9nEQikUh0BbU8nHfffZfHH3+8VwkY6/TpqeKw1txVqyuuuCJQKhzsH2X9vRUb\ncW9s3/u0P/744wHYZpttgFKNYpzRKhUrLVSVft+4pKpChbPSSisB8Ktf/ao2FypEz0kuVCRy4cpe\nfyty4dqlyIXrOaq4sE/VUUcd1S8X7uuuglVFGstVzeltjB49ujfO3ykuol3Ihavr2+XCaznuuOMG\nxEW0i4Fy8dhjj/VWCblDonHuunbhGLE6qRkXxx57LFA6Lh999NEN3KhgW7ULvY2B2IXzhfdDLlTl\nvqqi684XzcaI81SVXbQ6X3ieK620Um0u3nvvPZ544oneMaJdVM0XcqHXZqXceuut18CFdmF0xzWF\nVWPEa492oZenXRidimNEuzBqMHr06N5cWCtIDyeRSCQSXUEtD2f88cdnttlm682pWLkgrMnWc/Bp\nbqWNq1mNM/q0NU/hinCrmnzqW7GharTPj3vQ2zvN31EN2O1Vhe33Tz75ZKA8te2AWgeut3BfCat7\n4r7pKgFVntUlKhu5UGn4Xq7kwh5XVszIrZV2rXIhp5ELle3aa6/dq7JahWuS6nIR7cI1BXJRZRdy\noV3Ihb9Tlwvj1YPBhRWW7XLRbIzU5UL764ZdOEacL7QLUTVfeI56Qq3OF1VjxOqygY6RvvNFu1xU\n2YXj2FyKecxW5wu5sPuzVW2RCysFv/a1rzUcX06skpMLOXWMmP9q1y7Sw0kkEolEV1C7W/Rkk03W\nq8Ksczfup8djhY57jlv/blzZqjBrw12VbZxx3XXXBcoeDA8//DBQlIfxU+PLqjvjmZ6He6GrcDbZ\nZBMAvv71rwNlZbO18H6+VS4mnXTS3jUDHityYVWKK3etf49cyKVcGH9eZ511+uVC5WH9fOTCa/I8\nzjjjDKDFNDz4AAAgAElEQVQoKSuE5MLfX2ihhXpVUqsYPnw4k0wyyRh7bciFynbzzTcHYP/99wfG\ntAvXqGgX9sCr4iLuguhq/iouPI+zzjoLKHYhF+702NcuBpuLKrsYKBfN7KIZF52wC8eI6rvb84Vj\npNX5Io6Rsc0X7XAxatSojo0RuYx2IRfua/TQQw8BJSpkxZ55SrlwbZR95pwL5cJK08jFwgsvXIuL\n9HASiUQi0RXU2vFz2LBhLwL12qT+d2HWnp6eaVv54Ceci5Z5gOSiL5KLguSiILn4GLUeOIlEIpFI\ntIsMqSUSiUSiK8gHTiKRSCS6gnzgJBKJRKIryAdOIpFIJLqCfOAkEolEoivIB04ikUgkuoJ84CQS\niUSiK8gHTiKRSCS6gnzgJBKJRKIrqNW8c9iwYT3hPVBabMf38XMifr6f3wHKZkTNfqfq+FXHrTq/\nnp6el2q0tvlEt2jo6enp/+b0g25xUXX/BhvJRUFyUTAUuXDr57rbJwwUrXJR64EDjZO7u795cV6s\nu8752fj6/vvvf/zjIxt/3n93F0I7qEaDir/jTn3igw8+6Pd7fs738Xjvv/9+272Oqh6ezT4fH6oR\nnrPXWoV2H779fX+gA7cZF/H4cZBUfV97036aHb/qOGMRHGP8vR0u+n4v2lyzybFVu3CM2N232XHk\nWFRNSH6uvzHSzAaboa5dtCAQgTKPOO6bfb4TAnWwx0g8t3hfquBOne630+y4rd6TTs0XdT0cxhtv\nvF7Diwbo+2jcVRNM1YlqOPF9fLBEeNw4yOOD0X+PD6a6GD58eOU1tDrpNfvtyHHV95q9b4Z2OWjl\n+/Gc40Budk3+e3zQtDqJx883u4aBTiZ97SIeKz5Iqrhodo7NuIifrzpOq+/bxUDsotkx/HucL1r5\n7TrolF0MGzas8pyaCYyq345z6UAfNIPtJWYOJ5FIJBJdQS0Pp6enh/fff7/36Rg9jmbKpOrzPqUN\nE8TjG1pz8yI3TPJ9VIe62KpAww7R9W6mKpqhb1iirkJspuaqwn/+ZryWZuHC6CnVzas1Q9/raPUY\nVZ5w5MQwQVT1cjHxxBMD8NZbbwHVYchWPduBKuMPP/yw9xjxGqt+I6r8GPKK4eZoD15THCPaSTxe\ntIsYemvV42qGduyiVU/Ya62yC+1GLrz/kYtoF1XXMFC76OnpaTl/HcdvtIvIiWMgpiH8vBumuXlm\n1Vjw783C1m1Hhdr6ViKRSCQSNVG7aGDEiBFjqJ6q9zGp79NWlSZ8mvq5N998EygKxa1lfaoap/Tz\nUa3F84kqLz7N263oqJMwq1I2VZ6J8JrMQ/ka49e+j95d33Ntdi0Dwdi4aBa3jvcxHsdrkQvtQY+m\n6r6OGjUKgFdffbXfzw0WxpbDEVWqPd5HEW1Ur90xol3IoUrX4/h3v9dqXrWTdlF1rRHxc3GMiBip\nmGSSSYDqQgqvcaKJJgLKPNMtu2hljFTl/OSgai7zfvt3t5B2e2/HUMxzTzHFFAD861//AqqLkzqW\n3xzQtxOJRCKRaBF1t5juGTly5Bgln7EMOv67UFn4tFWB+lSeccYZgfLUfeWVVwCYd955AXjppZcA\neOKJJwCYc845AbjrrruAEtP1qa7qUwmLqBZ9/9FHH93e09OzZHMmPuaijiKqKuX0vepMbuRC6NUt\nvPDCADz44IMAvPHGGwDMMMMMAPz9738HCvf+u1wYz65CHzVae41BVfy5WWll5GKmmWYC4MUXXwTg\n85//PACPPfYYUOLQW2+9NQCnnnoqANNMMw1Q7qd2IHe+j7H9FryQWlz09XDqepZ6/46pySabDCh2\n8elPfxoo3HpNn/3sZwH429/+BhSv7lOf+hQADz30EFDswn+PSxBEf1GL//w3YLtoNX8R1fy0007b\ncO6LLbYYAM888wxQPJYNNtgAgIsuuggo845j4OWXXwYKp3IY819V6MYYiTmYWGk7xxxzAPDUU08B\nMHr0aKDcf69p1113BeDEE08Eij3Ilffdz8utnLViF/95bYmL9HASiUQi0RW05eH0eQ8UNRbjxSoG\n/66KV2XNN998ADz33HMALL/88kB5yi6xxBJAqcBQ7enR6PHoCV1xxRVAqcgwLunTWmUccz59FowN\n2MOJykXIga8xF6MXJxezzz47UFS73pyf1wO67777APjHP/4BFHV2xx13AGNW6jVTtO2qt77x6WYq\nTrvwvsbKOxXqBRdc0PC5jTbaCCgeysMPPwwUu1G5qmxnnXVWAO69915gTO/Pe6AX2Od6Gs6rHQ8n\noqrqyPsRX/33xRdfHCje3QILLAAUG59nnnkaPj/LLLP0e83a+HXXXddwbbECVOVblUscTLvwfjhe\nhXaxxhprAHDllVcCZT5Yc801gcLJk08+CcDSSy8NwD//+U8ArrrqKgCmn356oIyR559/vuH3vAdy\nETEYYyTmqbwf0cP13LbYYgsAfvOb3wBlbt1qq60afveee+4BigekrZ911lkAzD333EAZS/fffz9Q\nOI9Ro3j+dcdIejiJRCKR6ApqV6n19PSMoUhjlZHwvTF0VbyehpUUCy64IACf+cxngPK0nm222QC4\n/vrrAVhllVWA4rmoVHyvInnggQcafj+uw+lUXX1/x2pWkaXSNB6twvRajNEbn5YDlYaq7Etf+hJQ\nlKexWa9dD0l19+9//xsoXHSq6qQVxN/wHFS03u9YNaRdqGD1iB9//PGG13XXXReA3/72twDsueee\nAJx++ulAue/mhvwdPaJOrz3pew3Ro4m8+zk9Uz1X845TTjklAMsttxxQ7ML7rfd34403ArDSSis1\nXKNennYhh+Y9VM6O0ao822CgyotyjKju5cJzW3TRRYGi2r0mPRWvTbs488wzAdhuu+0AOP/884FS\n7eg9kDPV/GDYRRXibzhGfHX866F4v5wz11prLaDMsTFn53xx2mmnAfCd73wHgF/96lcNv6NdaY/O\nH5GLdit708NJJBKJRFcwoOadcTV11XoKVZtVR8alzU/4tI7qzTj0HnvsAZTcjmpPhaqyjXFt451+\nLq7b8DxV2lX1+3VQtcLcc1GR6uWp0jx3FafXqCpXzX/7298GSnWKXL7wwgtAicFatfSnP/2p4Xzk\n0N+JimXYsGFtqZf+1J9cyK8K1oo6VZSqbeeddwbK/Vep6tlqJ17DEUccARQP2Modla5c6+moArU7\nOVDZxvzWiBEjOtawMtqFr+aj9PLMR+qpeK7ayzLLLAPAdNNNB5Tczn777QcUzsx/Oub0jJdc8uMU\nZezK4BiJub2+a+Ta4WJsdhGr0Kaeemqg2Il2YV5C719vbrXVVmv4vK8/+clPgHLN5inMj8r50Ucf\n3XB8Iy4eJ67367uWpdNjRA/GOUhb1tbl4utf/zpQcrrmXlZddVWgRDKs9D3yyCMBuPrqq4Hi8Zrn\n8nfNe66wwgpAicDIgfZnfs3zGTlyZGWHhv6QHk4ikUgkuoJaVWrDhw/vGTly5BirX0VsH68682mp\n56HHM//88wNFgXjcz33uc0BRqj71fXobs3300Ucbfu+WW24Bisr3qe55ejyv2e8NZB1Osw4CsZeR\n6srKKtciyZHK1uqir3zlKwBce+21QFFhd999N1Di1H/+85+B4hEZm1UhqQpVIyqWfqrTfB1wBU4V\nF8bO/fw3vvENAJ5++mmgeBp6eXow3//+9wE46KCDgKLir7nmGqCo/N/97ncAbLvttgCsv/76QLE/\nq5XkQPuKSq2T63Cit6ftmaPRw1Fh+l5Vr8f67LPPArDeeusBcNtttwHFjhwT2tHNN98MFK/SNUt6\nUtqN1+7f+4yJXi7aWYdTxy7M2fi5HXbYASjjXrvQ49WmDzjgAAB+8IMfALDUUksBpZrtW9/6FlDs\nYpNNNgFgyy23BMp8pB3p/entVXVs7wQXVV1P9FD87e9973tA8Wj1kJ0r//KXvwDF6zcSokdrdaK5\nG+3AdTpWABpl+uMf/wiUfJb2ETtV5DqcRCKRSAxJtOXhxKe0T+HY18mnolUlxiVVuK4gV8Wp6lQY\nxmBXX311YMzqImP0Po1VyFZWGLN1VX6zzaree++9jq3DUbHE+npj73p1Koq55poLKMrF6jRzNXpn\nX/ziF4HC8a233gqU9Rnms7wnXrvfl5uqzar8WzvqrQpxXZbwGsxjuf5GVRXXiDzyyCNAWWsS1ypZ\nfWSeQy60L9cqGfc2vxFVXF+0w8XY1uGYt1Ctq2i9Jivz9OKtOtJD1n7M1Xg/9Yy0N9dfyNHZZ58N\nFE71oD2OMf3YfaHvWP/www8HZBdx3ohd4v138wRe09prr93w7+YP9AK0C71FuTNqcO655wKw4oor\nAvDLX/4SKJ6NXqHeg3bh7/SXuxqsMRLXIHk/9UC+/OUvA+W+ez/9vlw4n3iNerhy4Rg544wzgJIT\n8rhWucmFax776yJdh4v0cBKJRCLRFbRVpRY7lerZCCsbfLoad95www2BojSNqdv/x6epT2vjyRde\neCEAK6+8MjDmqmy9BZ++t99+O1A8Iv/eaq+kgSDmtVRHqnDVtDkclYSei9dsnsE8l96aFVdf+9rX\ngKKMVX8zzzwzUJS0MXrfV/W9E3U6YFehqpeeHoTemN6X9/Woo44CYLfddgOKJ2x8+pvf/CYA3/3u\nd4Gi2n/9618DRc3rIetBqQo322wzoFT06AH1x0G8ljroj8PY/Vlv25ybeYpll10WKBWa5iv0UK06\n1PPRA3Z9hXahvQntwnuiXRgl8HwcewPdDXdsiB6gv6XK1vvS8zUfudNOOwHFkzFHu/vuuwNw6KGH\nAnDppZcCcPzxxwNlftBjcb6yalHOzIdcfPHFQOftoi+q+gg6Ps29GMGQiwMPPBAo16zna47GsbHX\nXnsBxWszf2XkJHYO2HzzzYGS7zTPdeyxxwLV+yn1PedWkB5OIpFIJLqCAXWLjp1thU9dX10rouej\nslC1mdvx3+0GrWIV9kYSxuJdg2JHVH83rratWmPQiRxOlRKUo7jaXZXmKvrYQ00OrDKzOs0Yvlzo\ntV122WVA8d4uv/zyhmuWa9Vk3Duorx10Kj4d/xb7yXmfvDa9PNW+Mfff//73DedoRZZrCszxeRwr\nb1S2XruetjlAX+MuimIgVWp93je8ClW29091H9W35+61uB5LjuxQoT0Zm9fuVOteo9EC778ekmOh\nan2W/98Nu9CzdV2OFXdes7lfbTzmkJ1PtAur3/bZZx+grPPSk3LsmadQ/XfaLsbGRaxidM4yr22+\n6gtf+AIw5jo+Ix8eR8/V/KWdBrQTvTq7zzvPmAd3bGh/kYvspZZIJBKJIY1aOZxhw4YxbNiw3vhd\n3Cs8xiF9yuqJGKtXvbu2IK4Jsbok7nehglGZqPZVfeYzrNTw943d+lSOO0hW7TtfB1W7BqraVFle\nq/FiVZuxVa9Rta6Cdb1N7HhrhZ7dY08++WSgKBvXJI3L3mnCSplYDWYVo+snYq89Falx7XXWWQeA\nH//4xw2/5wpz497GsfWE/vrXvwKlIktU9Q8bSD4rKsCqzsh6eeYvHSOqbHN42pEK1RyN1UvG8LUz\n15S4jsuuwnrQ5oiq7KK/KrWBoopLrymOQ+3Cyr24s6fjXY7sJu5aFDkzD2H+y3Vf2tdNN90EFG9P\nDIZdVMHjaesxGuNcqX04b+gFauN6uNqFa9fMZ59wwglA6TIvF4sssghQ1jKa+xHem5jLqctFejiJ\nRCKR6ApqeTh2io77a0fV5t+NjfrUVbWpUP2ecUOVr9Vt5jtU6x5XdWf1kkpHVaBisuJLD6eq6qQT\naiWqId97TZ6b1UJ6ZeZiVCy+eq12wtY7MIar0rAPlPX13gO9yLjuI9bRd6MTrlxY428llhzohVm1\n6LoIY/GqL3M5rrLXDjyO6s1cnty5Gj/uCRQ78Eb11glOqjqoex+0i9gHzjGjDev1eT8dS3q6cuq/\nW3VkDsf1HUYHvHZfYz4zYjDsw98yX2D1otdm9WrsEm40wEo9q9L05pwvvNaf/vSnQFl/I6eqeSM1\n2kXM+VblctpB9Hzj3z1nIxqeox6JHqr5ab07PSArL/Vw9HiN+hgBOe6444CS/zZS4nnF3o/meAbK\nQXo4iUQikegKaudw+nZKjZ6NSsGnok/JuBra+KCqTqVqTFVFYzzTp6u/qwowbqm61wtQGXk+xslV\nNqq52K22E6hSMJEbFYhq3pzOnXfeCZSqJD0ir02larxZBWQloLF7lavKuIqLqh0IB4KqvV98r0fj\nWgJj9a4lcR3OKaecApRrtupID9bOuao61+XYg02PyOpHc3Zx75mYQxyMfEXsyiHifidW6qlI9YDt\nHOAKcr1685jmNcx3+vmFFloIKL34vP/aj1yohK3UivnNwYgCRL49J/OR3kcr67bffnug3G89HCuw\nvDb3vTnvvPOAMj9Y3aadeO16Mr43hyyXnRwjVb3U4to180quq/G+68XvvffeQFmj5H0yx2NVmz3V\nfvaznwGlms3qNrtzOEbiTrB6k0ZeBjpG0sNJJBKJRFfQ1jqcKtUT96pXfakYjDOq1vU0jFfbgUBP\nyHp8V47rAekxnXPOOUDxElyfobJRpanmzafEvUD8XDvdovu8b+BEjlSOVp/56gpy1bte3KabbgoU\nL00lojcXPRx/56STTgKKKpNz9y6v6hIdY/edWGNQ5dkYf/Y3VfdWF6nSvZ92BrDqzO7QsTef3aPt\n/qsqlCvj3KpDf1+7ELEvVd01BnIxfPjwSjWvzWnLXrNjxi4IqnXzGa7LMTpgLk8vzWiCHoowZq9d\nGE1wF0ztIkYR+uNioOuzquxCby2uDbO3nhwZ2TA/pV3oBWoX5n693+6bY1dp74FRBHN+sWO2iF0Y\n2rWLVrgwj2VVmZ7HxhtvDBS7sEuHHN11111Aqegz4mFe1DVIduB2jOgJ6Qmb23GMmF/z/Jw72+Ui\nPZxEIpFIdAVtrcNptdrLld2uoladWTuuqlLRGpP1qaqyiPFOn+YqGlWAaxFUtO6jopdh1VKsrutk\nzD5WJcX4sNdovzerzOxtJRdW2ujluYZEJaxCdm2Bq7GN/RqblWur1uKOfdFb7eQag7jHh16ZalzP\nxnN2PxPvmyrLXJ6VWK63kRvX57jeQiWrl2gc21yjKk070H5i/q1dLvrb9yTaRdxzxb3pzb3Y00qv\nX+70BvSU/bycahdWcBrTN9en968XYPVT9LQ7mbsRcYz43mpW748VWjfccANQPNhYVRb3CtKjcbxb\n3aiXt++++wJl7B1yyCFAuXbnB7n0HnXKLvpD7HHo+DdapDfn3j8//OEPgZKrdYx5P50H7Ctn1Ecv\n8JhjjgHg8MMPB8oaSdfjeDw59vyqPJtch5NIJBKJIYm21uGIqtXUcf8TKxyMHxuLVdXFLtFWRpjr\n8akfd/y02klV5+898MADwJj19NETq+oOUAdVvYW8lrgOxhi7n3NHRmOu1te7HsPvWWGjIlXxqGhc\ni+C1Gvc2ByAGq1N23y7iInam9v6YdzCvoCest2YPtQsuuAAo+SsrrYxH68Go9tzN0JXmXqsethVg\nqsS490unOiP/J9cxxt+g2GTseO56COG1GdO3ak3vX/vSu9NutCc5dNdLr1XFa57C48SV7fG8B6Lq\nq8ZItAu9ce1BToxcmLe66KKLgFLBadfoXXbZBSjj36jBnnvuCZTu0Xr3eov2E7PreLN9s9pFfxW+\ncYzouToHOkZcq6j37/21Ai+Okf/7v/8DynxxxRVXAMVb/NGPfgSUvJVzqlEHq+C0i7F1zq6D9HAS\niUQi0RXU3g8HxozjxX1PfK9HY1WZytZYqU9vKytU//7dp7816D5tVXPGfFUyVnComHx6e57G6v2e\nGEg8tqo6La7gj2t+jBubp7j77ruBomg9jorVa7HSywotlYvHt3LH45s3855ETjqp6uP/xxyOv61H\na1dn33tfXPXsTo/ai5VVKmAVsRV/qjLtRY/J83G/HdWjnnMnV5KLqvUV8bfizp/mH1ThevGqcD0V\n12vJqdek0tUutAPtyLGh96CdOdbi+ptO7odTNUa8Br1xczJGNPy8nqyVfOabXKfje+cd81ff+973\ngJLzMTck3PXSqlrnq2Z7R9WFlX59jxn59/7a7898pB6OY0Qvz64bnrNrlMz5aU+OJcec88wll1zS\ncG1GCcyPmzuO81m7XKSHk0gkEomuoHaV2ogRI8ZQQz51fZqqNMzBqET9vPkFPRYrJVTv1s2734Ur\ny61Ndy2J8WirmFR1Kqa4e2FUmQNVb2OLa6tcjQe7LsZrVoX57+YZVPPGl61SMRavZ6NHJCceXw7t\nH2ZVm78bVVsnUbW2QPuI6y6MmceOFO5q6OpolaprCIzZmwNUoaoO/bsqUftzz6DIhajKu9RF33xW\nPIYeh+dgdZF2ECso5UqFq/fmuhxj9v6eXlu0Cz0gK7RiH7k4ZgajA4XwmHEXVPvCeZ+0XfOZO++8\nMwB/+MMfgJLX1C70gBwj5jfk2jUpRlRiX7rYkaKqa0gnIyIxj+Uc5TVYuenf9e7NU5qP1IPZcccd\ngTJGzA27Hs9qMz0YPSHtyu4cfq7ZtdflIj2cRCKRSHQFbXUaULGqilQKKhIVpepKz8dVrXo4xhHd\nB8W4sipddafH5FPfPR78XdVf3N1QbyFWhMQ8hvjwww9rdxqoUiyem9esRxN34lPZ6KXpFbqq3n83\nz+HaAr0+lY7cec2qPZWziiVy0d++J+2sKB8+fHil2tFePGfVduxAIDfG7uVuv/32A0plletwXFNg\n7s61BSpV1Zv5C5Vs3NUyVqv1RTtcjBgxorJq0ftpZaV5Ta/d++97x0DM3Tmm9GTk1DyEduHY0X6M\nGjTrPNHfDo+d2vFTOEbivkd6vL6XC++TdmEvPb00OwboFfi9ww47DChcOV+Yy5GD2EndsdMpuxjb\nGNEuHCN6HML5Qg/ZaICf33///YEy/q1Gs0O29uL6HM/DdV6OEcde3LPKMTVQLtLDSSQSiURX0FaV\nWpWHYKzUdTaxQsc8hZUV1sv79FTt+Tnh8VQmPoVVPMaxrWE35iuimo87lA4EVcfwN628i+sdjN2v\nueaaQMk32CXBSjy5skOBawlUvqp4j2udflwxHM9LDEaVWkTkwvukAnWNietrrFK0v5P7mcTOt+Yx\n7CJtfymP72p7PaCoYCM3VetE6qK/dTjCc1Chep9Uqno4rrbXDqw+07b1dPUe7aWnMpZDVbqVnHIT\n1/1Ebqp2eOwktAu9Lz0bVbywe7j5C/MSv/jFL4BSnahXZw8+111ZqSlX2oX253zm/a5an9Xpys6+\nkH/vixxou1Yrur7G++v6GdfV+O+nnnoqUCo43YPMMeJxzfUYlfJexN5poj/PPTsNJBKJRGLIoVYO\nZ/jw4T2xsqQvVGs+nY0bmrOxOkQPxteYl1AJG4/2vapQlefqej0lP6fH5LmqWHwqVymVdnI4Y/l3\nYMyd83xvJZWxdz0W49aqOL25WK2kUlGRWIUiB8arY5eFZpVZ7eZw6nARO2cvtthiQPHuYg8r981R\n4RrP9hpVf37PHlnCz5nDqbKDTuWzRowYUbkyO1YlqTTlInbCdgzEseIY0C5Uxu6KqV24/4ncyUFU\nrtEu+tuRstM5nJjvdIzIjWNAu/Ac/bz73siFY8eczr333guUPJZegNfm52Ieq1llVifHSLQLvTDn\nUF/lwjnU++u52QvNiIc5Pz1cOw7ozekJxV5pdrLo00G/4fwGOkbSw0kkEolEV1C7l1pPT88YT2Wf\nhno4sftu3NvDp7OfV2n49DZnozIxXqla92kdczp9zxNKXDT2ePM4cc1DXfTlogqeQ+xQbDVJhB2Q\nXUfjugo5VoH4qnK1466/U6VYm+262C764yK+jxVQ3n/PXXXmSnJ3RbWnmmtIXH+lWpMLqyJjNVr0\ncKvWEnSKi48++qhyR0ffqzy1fb2/aBd+3kquO+64Ayi5nciBY0a7cCz5O1XViRFV3c/ropUx4jnF\nfaq0CyMbyy+/PFD2iLIq1a4LRlK833Ki5yQ3cu9rq3mqTo6RKvvwfuqVRy70YM1fmgO2C7idAbQX\nufXajQ5oD44R58Q63n87SA8nkUgkEl1BWzmcqqoNn8aqIt/HqjBVvDFXVwDrCekhGcu1h5YKxt/T\n8zH3UxWLjedZpfY/+OCDjuVw+nwOGHNVtRwZo/UaXK9jrN46ebmxz5jHU6HImUq5qit0lbrvey3t\nxqdbVT/eV9WX72P1mte20047AWVtkXZg3ziPE1Wa5xE7ITdT9f2outrrLapW6Edl6/0S2oVenPZg\nLke70IORM1ffezy509vzc9pJvOZW7GKgOZxm9mH+IvaZi3bh97/61a8CZT2N84rdpeM6q9gnLkZi\nqlR8p+yizhjxmvV4tHn/Hsf5XnvtBZT5wc8bFfDa9Zzi71ft/dMKMoeTSCQSiSGHtjoNNKvRj0/P\n2J3Zf1e1+RRXcaj6VfF+3kqcqOLia1U/KOHv9XPtHfNwqn47duH1c9bBe26xSiSiao+fGKNvhrGo\n/Y4p2WYqP94v1xyZz4jqLNpfvJ/azdhWirdynn0+V9vDqUL8zchBtBfX5XgtsUtC5C4q1ZjPjCq/\n6t7EHGCf8x9ndmFFp5EM73vVWKjiaizjv6Xz7PO5jlXsVdmFiH0g7URiHtv7pUcbPx+5cE6OkZAq\nT7fZnJ8eTiKRSCSGFNrycGJeIqomn4Lx734+7g0T8xsqEOOVPrVj7N/jxpXBVZ0Eqq7Vp/3bb7/d\ndi+1iGa8RhVXtbdQlSLpb2/xvu+rfq8ZJwNZYxCVfYyJx9+Kn497g0Q78d/1cGNupqqyJiL+ztgU\ndztc9M3hVFUFxvfx8167YyHmN7xWx0Ss8IpcNOsw0Yq9fvjhhwOyi2bVgfHc4hiJ1bCRuyq7aNVj\nqcrxdnKMxPEdKyebeTqRC+0icqNdxB5orc6Jcf+sZt5ZejiJRCKRGFKoXaU23njjVa7ErVK4VWqq\nWU3N+gkAACAASURBVI1//H7c16ZZxUf0GqrUf59qto5XqbWKZhUxEVUx/IFiIBU4dVF1jVXeW7Nr\nbPd7VQrbf6vLRX+dBlr4Xr/nUvf+Rm+wrrofm721q+o7hbpjJH6vipsqVNnFQKoXq45ddc5Vn3dO\na8VL7/v3VsdIVeVef+eXHk4ikUgkhhzq5nBeBJ4cvNMZ55i1p6dn2lY++AnnomUeILnoi+SiILko\nSC4+Rq0HTiKRSCQS7SJDaolEIpHoCvKBk0gkEomuIB84iUQikegK8oGTSCQSia4gHziJRCKR6Ary\ngZNIJBKJriAfOIlEIpHoCvKBk0gkEomuIB84iUQikegKRjb/SMGwYcM+6W0JXqrR2uYTzUXdxoSD\neS7jGslFwWByEZtqDvUuKGkXBa1yUeuB8z+AT2qvo0RinGDEiBGVHY1jx+PYwbiqs7Fott9R7A5f\n9f1W90/6b3kQDmVkSC2RSCQSXUF6OInEJwCt7g3TbXz00UeVe7LE3Stb9STi9+PxJ554YgDefPPN\nfo+jZ/X+++83/L3Z7r1Djdv/RqSHk0gkEomuYEh5OFFhVO3wF2O68e+JxCcVre5WWZUH6bZKH9vv\n6WFUeRb+XY8kIu7kO9tsswHwz3/+E4BRo0YBxdPps7Nvv8f1XPW4Ep1HejiJRCKR6Aq66uGoWCaa\naCKgKByVxXjjjffxSY38+LT67gEO8N577wEw6aSTAkWJvP766w2f8/tvv/12w/H/m9DMe2tW8fPf\niKo8RLPYfqtcDNU8R39wjHjt2vJkk00GlGtQvfu5mL+YfPLJAfj3v//d8Dk5evfddxuONxiIttzq\n/XMcTzDBBA3vJ5xwQqBcy2qrrQbAY489BsBCCy0EwCuvvALA/fffD8AMM8wAwAcffADAM888A8A7\n77zT8Pcqb/C/wX5a5XhcXUt6OIlEIpHoCgbVw4keSqwqMcYq5p57bqB4OrPMMgsA00wzDVAUzlNP\nPQXA448/DsC//vUvAJ5//vmG41Upq6GsUGJcevzxxwfg85//PAB33XUXUK5Bb89r9+//TfmsqvUW\n0VPx/ac+9SkAXn755X6P99prr/V73KF4371/0YN59dVXgeLpOBa8timmmAKAzTffHIB//OMfQOFI\nr//uu+8GYOqppwbgpZdeAsYcG7FibDDgfYjzQrNcTYx8rLTSSgAstdRSANx4440AnHnmmUCZD/z8\nn//8ZwDmmmsuAI4//nigcC4399xzD1DugV6i0BMaSqhac/SFL3wBKNwIvcN4bd1CejiJRCKR6AoG\nxcOJ6kmFoiozFzP99NMDJc68zDLLAOUpPNVUUwEw3XTTAfDpT38agIsuuqjh91SJ/p7qMFalqAbG\npVKpqsSLeSk5+OxnPwsUpWt8ep555gHgd7/7XcPx5Cp6PFVKaFyiKq487bQfdxdSpatUt956awBu\nvvlmoOQfJplkEgD+/ve/A0Upa296QjFHYMx+XMSz/c233noLKJ6s98e8xejRowF46KGHgDJWDjjg\nAKAoWO3HVyu1fL/44osDcM011zT8vnDMGHV44403BnyN/k5V3iDmavQs9Dy+9KUvAeV+r7vuukC5\n73osW221FVDupx6w1zLrrLMCcN555wGw2WabASX3c8sttwDw8MMPN5yfdqUdeo+cv7qJyJ124H1y\nvpBD5zjHkhz89a9/bTjuTDPNBBR7GewcT3o4iUQikegKhtV5grXagE6PRrXm01iVvdxyywFFQfh0\nNk+x5JJLAuXpuvDCCwNwww03NPzOJZdc0vD+97//PVCUk8rWp32sRukHt/f09CzZyjW224xPNSdU\nbRdeeCFQPBSVrde+wgorALDIIosAcOyxxwKl8uYPf/gDUNSgcWw9Jq/Z12b3fTAaE0bVJBfawVpr\nrQWUWLxqzb/r3a288soALLjgggCcdtppADz55Met8IxPn3POOcCY9197VNWJKk4Ggws9VtWyalyv\nfs011wSKB+u16uUZHTC3M//88wNw+umnNxzHnM+ll14KFM/XCi2Pe8UVVwDFPqpUfCe4iDmcWJU6\nxxxzAPDcc88BsMQSSwDl/u+1115A8YSswPOaPXfnHzm69957vQYAjjrqKABuuukmoHgwjp04VvrO\nGz09PV1p3hlzunpzp5xyClDGzmc+8xmg5Lt/+MMfAiUvvsEGGwCw6qqrAvDII48A8LOf/Qwoc3aM\n/rSa02uVi/RwEolEItEVdNTDibkb49DG0lUyKgk9nZlnnhkoMVtjpsYfH3zwQaBUk6h8b731VqBU\n3liRYzza+LjKRuXjU7ufax80D0f15mpoYcXdDjvs0PD3+eabDyiKVtV15ZVXArDlllsCpWptww03\nBIoKvO+++4Ci/uK6jWYYTPWmattoo40AePHFF4Hinanqf/7znwOw0047AcW7U8X95Cc/AeD//u//\nAHjiiScA+NznPtfwO1G9aV9jsYMGdJKLmDvRu9ej0XO5+OKLgaJA9d6//OUvA8WzNa/5gx/8AIDv\nfve7QPFg9t57b6B4A/6eY/C6664DytgwP1LFTV0u+uZwYpWq72NuxHnC8a+Kd+x4v/XK9NL+9re/\nAWXc+6r3t8466wAlmiAnRkqcV1zPoz15PrE322COETnSG3cOtRrReWH55ZcHCodGTJxXnCM33XRT\noMyFfk97c86Maxpjv7kqpIeTSCQSiSGFjlap6dGoKGMPI2Ec0Uorlac5F+PZqnnr7VUkUcmq6uad\nd16gVGIYvzZe7u90sxpJZeKqZxWKCkZlaz7hm9/8JgDHHXccUDhV2V5//fVAuXbXDujRqOL0HjyO\ninW99dYD4IILLujYNbYK14zowZx//vkN/77YYosB8Mtf/rLhVQ/nO9/5DlAqblSkjz76KAC33347\nUKqNDj74YKBcu/kNlbVVkddee20nLq8lqJZVnJ6TeQTPdZVVVmn498MPPxyAb33rWwDsvPPOQLEP\n8xfmOc03nHDCCQD86le/ajgPczpWselN3HHHHUBnx0jslqGX5Tj3XB3fSy+9NFAiF1aVmdPxWmaf\nfXagjHfnCz0hufF3zXM6hhZYYAGgeAOOUeeNfry72tdeF1bYeU6ei56H+W1t3rnvxz/+MVCuYfvt\ntwfgG9/4RsP3nGNfeOEFoHhKcnnEEUcA5VrNgzr/DBTp4SQSiUSiK+hoDkf1pqJQgara9EBUICoM\nY7TGj32qWyOusjFWG5WI8WqrlFyPEb2JcVGlFtciGac2H6GyMN9gbN76epWLlTk77rgjUJSsytj8\n1lVXXQWUnI+/r3pU3Y+FA2Bwq9RU497HjTfeGCjVSc8++yxQPGS5U62r7r/2ta8BxX6M7Vuxc/bZ\nZwPFTrxm49Jy0SxO3Uku/E29bteSaLO77babxwGKF+AYULVHBWs14/rrrw/Aj370IwDmnHNOoKzj\nMT9hbi+OCZX0YFSpxfyV80XM7Tp/eE3mYrbddlugjBU5MXdrvsNr9PMPPPAAUO6z9iA3f/zjHxu+\nF9dCOb/07Vgx2FVqscuGUR7zl3ZZcU50vF9++eVAqWYzD3rkkUcCJe9lrufAAw8ExhwD2kOr6/cy\nh5NIJBKJIYWO5nDiPhN6LMaJp5xyyo9/9D+KRuWiijNeaCxfD8eYvWsIXKNiVZPxSKvZ/F2huh8X\nq+zjLoSeg6pLRWpOxTUDVimp4sxHGGNVgZoPMy6uclW1qWBj14VxgdjLTpVv1ZBrB1yHo3o/9NBD\nAfjqV78KwMknnwzANtts03AcqxxVg/6OKi+uzxgXnbU9JxWl98tcn/mt733ve0DpqrH66qsDhavD\nDjsMKNwcdNBBQIntm8szJ6BSNeenIq6qSuvUSvOqvW76/qbwHPVY9XD0iM1zOpbM3ay44opAyQla\neWVln/ZgzthqNq/dXJEejV6enpCeVze7z3vtVpXddtttwJgVnHpp2oljxrGgJ2zUQK/PDibmCPWA\n49zZ6fkiPZxEIpFIdAUd9XBip2LVjZ1LVVeLLrooUJSDcUg9l1jF4loDPSef5v5dhaKCVak021Gw\nmzAnE3tVqVhdK2BeQy/QlcJnnXUWAMcccwwAv/3tb4ESv1522WWBMSts5HIo7A3k/dOzNeZu5Yy9\nrrQXFavK1y4McmaHAbmJa4/iGiSVs9yPCy78TW3U9Q/asp6HObq1114bKHu6GC3Qq/vLX/4CwE9/\n+lOg5PCM8evh6hX4PvbQUtl2uk9YX47jOJSD6GWZ2/W73i8jJOaCtW3tQW/OnKCekXanPWhvVqtp\nF7GjgGNGe+1mzz3nSs/duUwPxqpCPRPnC+3C/LkdCfR0rOR0nnE+8r7H/ZQ6jfRwEolEItEVDEq3\naJWHno6VVOZihE9h8xU+zVW0Kho7EpiXMO/h9/RwhDHYodQhWVXkuVmppyLZc889gRKrN94sRyoc\nV5TbB8r1GnoLKhi/5yr+obAXjApWVeW5mbMzR6cqM46tmnM9hjkcvYOvf/3rQFm/Yfxaj2nGGWcE\nSiWYGJddomPHY/OQX/ziF4FSGWUuxnyEY2uTTTYBSkxfNf+Vr3wFgF122QUonSd+85vfAKVr9J/+\n9KeG81Hlx114B4oRI0aMkduNff1U1bE7s3kLe+lp49r8GWecARQ7MZ+h9+bv6i3oGelBee1GCWI3\n+zhvjIt5xHPx2owKnXvuuUBZj+eYip6NuT67isuha5LMFVo1e+eddw7WpQDp4SQSiUSiSxiUHI7q\nzaexnopxaqGKtxLDeLVPc1fHqmT1Cty/wp3/VGsx9qqiHgo7P8ZzUY2rYFRhxk5VXyqQmNux0kaF\nY4We127ceyjuw26eyXPzvlqhd8ghhwAl36DytRrJ72kf9gNT9duhQG5djyWGAhfaoivKzWc4Jrxm\nq5H8nF3DzXP5d8eOeSy9PNdlmBvSy4s5JNFpe/noo4+a7rTruNXb1x707lxf57zyi1/8Aij5TVW9\neUzXban6zVPZjd7cnzkdx5Zr2Twfx1rMPXXDfmIFn70Tzdl5DZ67c6ydKOK6Gr1Gqxldy+Z8Mdie\njUgPJ5FIJBJdwaDkcFTxxgtVtKorY/KuHLdqTSXi6ns9H6tPrNAx3mgew+ol17YY5xbjch1O3PvD\n9+ajVGX77LMPUCr2VLKqLGOxvqrCXJ1/2WWXNXzfuPRQUPPCa49719v7TAXr+irzG8bwvX+u17LL\nuOrdfIU5G5Wv6zWGQrWi90NbdozojcVOx3KhnajqVbB6utrB008/DRQ7EGussQYAxx9/PFC8gHhe\nnR4jPT09lV5T7KYg9PKtzNMLM9cjZ37fHK5c6aloHx7fCk87q1vRJ3dGSrwXcUfYvtW33RpXjn97\n6RkZcT2eNu6YcO5z/vCa7DDgWJFjx4xz7WAjPZxEIpFIdAWDuh+OMVmfulaHqDzMM6jGrGIzHml+\nwqey8UpzQ65FcTW+T2nVX6zQ8nUsK8wHfcfPuEeLqt6Yut6aFTW+2mnAa7XnmiuIt9tuO6DsfxHr\n90Wr97sbe33E93HtkEpWO5Aj77tegB6sSnj33XcH4Oqrr244flwf1qqaHwwuvD+OEW3aV/NX5qnk\nxH2SvK/f//73gZKPULk6tqxGcodY7c7v+yqXjo0qbtrZD6cKcmCFnRV6qno7mzv+nR9cY2TFnVx5\nPD0j8xZes/OM+QpfHWNWvfl7wnmn7zzSrR0/495B3p/oHbqOz7nTNWyuOfLv3m979jmW4hism8vL\nXmqJRCKRGFLoaA7Hp6IKxVioCkOPQzWmsnB/bVVc7D/mjnwqXZ/esReSSte/x1xBp1dRtwMVipzE\nVc7mLaxacx8K1whYiWX1kvmN2GcqVqkNhbVIIqomOfAcVWF6wuZ47EShfbmb5a677grAyiuvDBQ7\niN5C/P1xUcGnUvXVc9Nm7XFlbN7qQyu2PFcVq9/X09Fe7JwtjC4YBYgrybWbuONjJxF51rvzPtit\nWc/FcW8O11yvXr0cyJU5HPNYdg2XU7kyb2Gu2M7akVPnFe1yXKzri5w5b3gOvrc60fse1/eZu7NS\nOO6uGrvHD9aYSA8nkUgkEl3BoKzD8dVqEdW2K8mNxarKzVu4rsYOAnoyKhXXFBivFLHTgE9vlVOn\nV0+3g6imVbSem4rlrrvuAsqOjPZAUsHYR85qlS222AIonZajhzOUPBsRuYjemDBWby7mgAMOAErv\nNPf4cKW5XFnBIxdy7e+Nyw4UUS2rRPV8rS7U6xPmJfbff3+gdPm1OmmPPfYAyh5B3/72t4Hi/Zm/\nkAvPI67u7/QY6a+XWoxgRA8mrr+y4koVbqWe6/XsPKHaN7/p2HK+iWpee1L1m++I+yX1lz/p9lzi\nb8f8s+dqPzk7qlsFaV5Kjl3jtu+++zZ8zqjTYCM9nEQikUh0BYOyDsfYeYwHG2t15bfKQ4VrhZVK\nR8/FdTw+hf27VUlWm5gDMj4du9COS0RFpNry3Mw3yYW9s9zvxhXCJ510ElC8R9ciGY92PxQxlPrJ\niar1GDHfpP1YSaNnu+mmmwJl3xxj9K6zcD8UY/1xLdS45CLmOYVK1Yot/10bN49lTseuDK5A117M\nY1nVaMeBX/3qV0DJUziWrE4bTETP1fvh/XU8+2q+0gosx4j95rR9e63FfJd95GIORo7NZzhmzBXZ\ntSHuehq90qGwtk1OnS/MW9lncocddgDKtelN6vn6vluejUgPJ5FIJBJdwaB4OHoWehxxL3kViv2g\nnnjiCaD0kbI3lupeBbPRRhsBZYWwcW1Vmwol7l4Yu9SOC0RPI57LEkssAcAdd9wBlPUX5r1OPfVU\noHTeNv5sp2RzPENp/5tWEXN/2oGdKVS8xuz1eKwuMo9lZZ/2ZH5ELoYC4lowPRlfHTt66eZkvO/a\nshV8dsR2Jbndol1LYgcKKzyvvfZaYMyuD3HMdBJV3r1QpZvT9X6594sehxERcztW3tl9Y/nllwdK\nFVr0cOyk7nFOPPHEhvOrqtgaCvNHhHkq1+WZfzIfZYcBezFqJ1Z66tl0u1IzPZxEIpFIdAWD0mlA\npWCcUDVlfNrYqetwjM2r7tx32zUDKhPX8RirtW7fWKsKySoXPaoaOZxB7zQQ8wlR7cmRFTfu/Kiq\nN65tzF4vQO9ODydWI9VFN1ZRRy7iuinh/ibu6WGFlvamd3fBBRcAZWX4UOSiKodjpaac2A9O2/Wa\n7JhtjsZqxlj5qUdsXtTKLvfZURnHCqxmqMPF8OHDe8Ybb7wxqkT9TecH80yObzsOeK16Fno0vtf2\n5dKKLPsSer+dJ8wFW+UoN3qTek6uCxRxdX+frvNd6zQQ144J5wnz5kZ9zFN5rl5rvObo4baL7DSQ\nSCQSiSGFQVmHE3f086lsHygrY4wzG7M1Lq1K8+ms4nF1vVD1+Rr7hw2F6rQq2BdMzlRX5iP0WFT3\ndgV2v4sf//jHQInF6hnJhWsXrrnmmkG8ioEhxs7jfup6de49P8000wCl0/aBBx4IlP1v9GTiLqmu\nvlfZjkvEMaIXplfuuVuFZk7v7LPPBorH6+dct6X6v/LKK4EytuKOolaA+rnBzEv09PQ0dPeIat1x\n77mYc7ObvJ/zPvp3r+2hhx4CynxhDz29P+3B/XX8HceS85BeghxFr89/H5fzSazkdKzYlUHuXG9j\nPvMnP/kJUMaIXDrfONZcu2b3jsFCejiJRCKR6Ao6msPp8zmgKAMVgxUU7j/hHh+xp5KqPXY6Vd1Z\nhaQqVKn4tI4KpcY1DnoOx2vUI/FajTubz3JHP/NZekSuMbAa6eijjwaKJ2RV20CVazfi03qk0TO1\nw4Q7PRqP1kOxylG1ftxxxwGw1VZbASVHaL4i9g2ri8HgQjvwvlqJp+1q06py15zYbcMOAuZ67Kxs\nF+BDDz0UKJV92oWecz/5iJaubyDdomOlZuycruo20qFa33jjjYEx8056OHGnX8eWeU6PZ+cKvUrn\nh7jraVVX+b45qP/sZNq1HI5RAMfIueeeCxTbdj2ea9G8RqNDdihxnZZ7inVq36zM4SQSiURiSGFQ\nPBwR9wSPuwwaW9WTWW211YCyQ6MKyBitisOneuxKLQYQax10DyfCa4jcWIll/sFYrfFnoRLudEeB\nbqi3CHM03l89X9eO6NG4Hssea95vY/v/TVxYXRQ7TpjDiXmGX//610CxC9drWbmputdOYuWf3kDc\nG2gwPRy9uNi1O+71YgWm4zmuNbESz3OXMz/vuhuPGzueRC7iNcdOJVWfGzZsWNc8nIi4fkq7cPdk\nIyJ2oDAqIGfNukS3i/RwEolEIjGkMKgejohP5Rgj9e9xXYb/rtKNCikq2A4o2q55OM32eY+vQo7i\nTp6dRjfVW+xRFavXfI3315i/lXliEDoeDzoXquuY31CR+u9xLKlQ3R3VXI3qvqpzersYzHyW1xa9\nPj0kPY9oHzEHGD1cudFOPF7kJuazqvaSGjFiBB9++GFXx0gzT9Rrjp/z74PdJSE9nEQikUgMKXTF\nw+nz/X7fx55nKgqVjvX0VbH5DirarudwWoUqLVbUDBbGRXy6hd8Byp4fp5xySjd+dpxyEb3+uEeL\nFVzm/Ko85nGZz4rjvuoc4/iO126OJ3a4roqYRES1H9838yLivw/FMSKsXjT/PdhIDyeRSCQSQwpd\n9XD+CzBkPZxuYyirt24juSio20tt5MiRvR5EVSSjz7HHeryY14x9wKr6wjXrBt3MA4s5xhEjRvDB\nBx+kXfRBejiJRCKRGFKo20vtJeDJwTiRIYJZa3z2k8xFHR4gueiL5OI/6Onpeen9998fg4t218nF\nKsa6VapVlVrNPKt43P8cJ+2ioGUuaoXUEolEIpFoFxlSSyQSiURXkA+cRCKRSHQF+cBJJBKJRFeQ\nD5xEIpFIdAX5wEkkEolEV5APnEQikUh0BfnASSQSiURXkA+cRCKRSHQF+cBJJBKJRFdQq7XNJ70B\nHfBST0/PtK188JPORTYmLEguCpKLgk5w4RbRndpQMW7x0OpW0q1uNV71uVa5qNtLbVBRd3/1QcAn\ntddRIjFOMGzYsDG6PNftpVbVzTnue1N13FYnXRG7WXdqT6Fhw4aNsU+N5zTzzDMD8PbbbwPw8ssv\n93uMuEeQe4ZNPPHEAPz73/9u+PcqTjzOFFNM0fC9OAc328OsLjKklkgkEomuYJzshxOfmvHvrSqJ\n6D52wEPK/XD+gwydFCQXBeOCiziuVfN6B6r4Zp7TlFNOCcArr7wCFE/G48T9dZphILufRu8s7joa\n58Jm5xa9sgkmmACA9957DxjTk4mfn2222QD4xz/+0fA7hvw8TpW3mfvhJBKJRGJIYZzkcJrtGV4F\n9zR/8803gTE9nE/yVgvxWv+XEBXuRBNNBJR49xDI/XUNg+DVdx11zzl+7q233gJg0kknBeD111/v\n93vmS1577TWg5Ds8XtVOoXU9nTqIv121C6oeSrTx2WefHYAnn3yy4fOHHXYYAPvttx8A77zzTsPv\nmhPyWvWo5PD555/v97z0bMRkk00GwKuvvlrrukV6OIlEIpHoCsZJDic+zWN8UU9mvfXWA+DMM88E\nYNppP65YnmaaaYDylI0VH5NMMgkAb7zxRt1TyxzOfzAuYvVx7/iqnJ6fixU7ft6qJNWhnzP2X9cu\nBpOLgZajRkQPqNOe8UDyFvG+xmupKhGOOZuVVloJgMsvvxyAhRZaCIDddtsNgL322guAb3zjGwCc\ncsopAEw33XQA3HPPPQ3Hi/NPn/NveI0ctsOFXpa/XVUNFj0RcyxPPfUUAJNPPjkA8803HwA33XQT\nAHPNNRcAG2ywAQDHHXccAL///e8BWHPNNYHC6bvvvtvwO44duXJujefZt/Kvp6cncziJRCKRGFpo\nK4fTbtxYBaMHooei57LYYosBsOqqqwJw6623ArD66qsD8K1vfQuAm2++GYBzzjkHgIUXXhiARx99\nFIBtt90WgH322QdoHuv9b0JVlcgnAVXrHvSI47Xr6WpXcS2BKs73ejaDGaOvi2b5zKp/dwypdOeZ\nZx4AvvzlLwNwxBFHACWW36eaCCgx+09/+tNAUc6DkSOM11J1TXo2fn733XcH4JFHHgHKuHd8P/PM\nMwD86U9/AuCWW24ByrhfZpllAFh//fUB2GijjQBYeeWVgZKPOPDAAwGYf/75gZIneeKJJxrOp+/1\ntDvuYk5k7rnnBuCll14Cig17H370ox8BMOecczZcg977Zz7zGaB4bX/+85+BMlc+9NBDAOy9995A\nsYuHH3644Xe22WYboHCmp+S/P/fcc0DxvBxzPT09La9vgvRwEolEItEldCWHo0LQk3nhhReAEs9U\naUw11VRAeYr6PT2cddZZB4DzzjsPKE97n+Z+X2Xr54zRetyqVbwMwRyO5zzLLLMARbGeddZZQOGk\n095bN3M4UUHqgfSnpqAo0aeffhqAddddF4Abb7wRKJ6uuUCrmuSuroofl+twjJV77QcddBBQvDNj\n+17blltuCZSYvYr31FNPBQonrkWpm+PpJBdVORLfzzDDDEDJI8wxxxwALLfcckCJkEw44YRAmUf0\nTLbYYgsAjjrqKADOPvtsAE444QQArrzySgDWXnttoHgTrvpfYIEFGj7nvKI91eWivyrcOP9WRTDM\nqSyxxBJA8VBuu+02oIwR8916cTvuuCNQ5gs9I/Ng2o2VfF6bn3OsPfjggw3n57159tlnPc/M4SQS\niURi6KArHk5V5YzwHFTxBx98MABHH300ADvttBMA11xzDVCersZ2rci47rrrAHjssccAePHFFwHY\ndNNNG447lvj4oHs4Vb+tSjMeamxd700ls8MOOwClMkeVb5XKiSeeCJR4drux5m6o+lht5rm6IlyV\npWe89NJLAyVevcoqqwAlH+G6iwceeKDh79qJaxv0cOMq6iqMy9X1vpqzsXJTj+UPf/gDAKNHjwaK\nUtWrlyvHzsknnwyUMaSdaG9xfUe7TRr/c+5tceFYENpHXO1uhOTb3/42UPITX/3qV4GS4zUfS4Jg\nNwAAIABJREFUYRRAL9Cc8VZbbQXA4osvDhSvYI011gCqc36d5MK1ZY5/vTV/23/XDpZaaikA7rjj\nDqB4rl6Lnq3e2+GHHw7A+eefD5Rrdyw415577rlAGYOOIXNBcV3QhBNOyDvvvMOHH36YHk4ikUgk\nhg660mkgxmZ7f/w/8WkViNVmxh9nnXVWAG644QagKFTVnVUsKhs/r0dz//33AyVmG1XjuKjw8jfj\nmgM5uO+++4ASm1eV7brrrg1/F//617+AwpEKtVX1Pi4Q74MKVhU377zzAiUXo5rbc889gcKRSlaV\nrnf3uc99DijqzVj8BRdcABRP2sqscYloi1FNX3vttUCp2Nxwww2BUnG31lprASX2rnevElUR6yFb\nDaVy1Ut4/PHHO3xl1ajKG8mFa0N8r7fmuVrF6v3dbLPNAPj73/8OlHlAz/jOO+8ECneuytczOu20\n04DiFbh+J3ZUdqy1W6XWN7LjfTY346vnam720ksvBYrH4dzneNcuYgcC81DOpUZK9thjD6BEfxZd\ndNGG73teesbm22MUQrzzzju1cqLp4SQSiUSiK+hqLzUVrE9JlcOKK64IFJVvBYa5G3MvVpsYj3SV\nrR1OjWOqCsxrqAar1gF0s0+Z8WlVnF6eHKja5MrYqkrXyjtXT5u/slpEBVunNr7bqFKHU089NfD/\n7J11vC1V+Yefey8pgnQKF6S7u0s6pQQkpCQlpFNAUEo6Lt3SId2ohEiXdEhKh4Xy4/7+wOeus9c5\nc3fNnr0vvs8/+3P22Xv2zJo1M+/3rQWTTTYZkKwuz4tW+q233gqkLKRLLrkESBk8Khm34/m3ZkVL\n1XOR952qknwsVDaef9W751sr/4QTTgDg4osvBpJ3wLiDFqxKRwvZY/b/eg3qLQTWTu1JTtF1lm9/\n9tlnH/HbkK6N3Bo/6aSTgHTdL7PMMkCK3W2zzTZAqlGyZslMvbPOOgtIWY55TZLzRb71rW+NGNdm\nGDx48Ijr0m1bS2Qmnhhz8/p2H73nXX/99QBsvPHGQKrHMcabx69VPN539t9/fyDFAI3tOQ8OP/zw\nmv1xXsZ6OEEQBMEoQUez1Ir802Zg+FTWipt66qmB5Gs1394MGqtw9dnrv9RHb4aO1r6ZOE899VTN\n/oxkOdfK6nC0JHxVZVlz5DHaGfu8884D0tjpe9VHv+iiiwIpe+3cc89tZ/cqzVJT5emb1/fuq751\nYy9mq/mqwjG7SD+1qvG4446r+b5+6ZHUY9XQjSw16x+sq9Cy1Wo/+uijgRR7UcE4plqwxr1Uyosv\nvjiQLFbjHdau1KOMXmpF5CpLj4XHbh2M14IqQ+Xi3FcdqmROP/10IKkIY4SOsWrDei7jpe5HroBV\ne82OxZAhQ/plunmPMqaWj1XeyVoVZ3bqJptsAqR7pfPDz5vF5v3BTF7vH6o3vQv2p/P3vSaLGDx4\nMF999VXU4QRBEAS9RUcVTlFsRN+6FohV0Vos+lL11eqT14998MEHA3DRRRcByRKZcsopgaR89I82\n4p8GGD58eGUKR7Xnq/tuDCbPYtHKMnNLNac1l1cUtxvDqcKqtzOEx6afWWWjAvH/WnEqWBWL51fF\nrNXmfNIi1mJutm9YN7ouqFjMyFPJ2tPKvmJmVGmJGsfyGnMMfvnLXwL9lUyVXReKrkPnuvEl98nz\n7rFZ7a6VbgxYq95aEdWcWapm8pl5teCCCwLp/uL8MMNrpZVWAuC2226r2U/vlRNNNBGffPIJX375\nZdvzwvOtGvfYvH5V9x6DPdVU6capb7jhBiDV11hrpHdIJew8Ms7lNef/jY9b0+a1aBzUbMgB1iIL\nhRMEQRD0DpVkqZlZIz6lzULz6akFk/veffpaRavicTtmWmjZ5r75kcRsgO7U42jZaMnYF2ruuecG\nkjWmj9fMLD9nB2w74/Zdn6LXcT6o0sxONGtIH3teJ2MHAWN5+vZVso6B88l5olWWd+LtBXKfvcdg\nHOGJJ54A0ly3DuPGG28EUvzSMTVGYz2O65/oFfD3utEpu+g69HyYQWWc0qxCsX5GJaOat3u08Q2V\nrMrIDE/VX16rpNI2xqOyKVoHJ89aa4a8nsXXxx9/HEhjZO2gdTTGZD027wcqGu+ZxoI8Nut1XBfH\n+4e/6+fsVOF8coy9Fh1L+8rpWTHG3PDxN/XpIAiCIGiRUhROUYfTvB+TT2ezi3wa65O3it6nq7nk\n5tm7op8WibnqW221FZCy3fIMsNzq7+YaMrmFqcWjdafv3mMyHz5fnVC/tyoh9zf3Irmq00+sinN+\naK1bW+Ixar37f3upOWb2zlIN2HHA2iW/Z/eFXlI6eY2aKj2vu9A379gY59hwww2BNC/03ecWby+s\nAWS2Wb4iq+fD8+T9YIMNNgBSnNNMKuMNxnydJ6p+7wfGQY1/qYzsYOHYe19xO52ozyrquqL6dt9V\nZcaVnA/GXLyHmsXo5+xM4hpAv/rVr4Ckyoz9OYbOG+eVXiZ/x/lkPY/3mb7dIJq5n4bCCYIgCCqh\nFIWT54qLud35etj6Ba2K1ceuP1CrzGwTffwqGut0/L077rgDSNagvn7pZu+0nLwmyX3Tun/kkUeA\nFMtxLFwLJM8SMavFrJVRAS1YLUiP3RU8/fvee+8FUn2WlvGBBx4IpBifdRjGbpwnKmWr6XN/c5Xz\nol7PNMfCTC0tVS1SM6ccG63xpZdeGkh95IyLmrllDMf5ow+/KnU3kAWsItVKdl923XVXIMUn/J6r\nYi655JJAUrqOkda9NWx2SN5iiy2AFONT4aiM7MFmfMRry3oe46hlrRDbdyycD3phnNuuyWOfQOPW\nKiCPyXugx2y9lXEse6cZB/PaOPvss4F0f1E1LrXUUkDqK+f+mdFntxf337Fo9toJhRMEQRBUQikK\nJ++zI/odzbyx2tVMBy2dNdZYA0gWqyt52iPNp7x+af+vH9Ou0caC8gr2PDumFxRPPmb6WO0XpiWj\npTps2DAgqQOtOq32gVYT7DUc77yCW1WnktESPeaYY4C05ryWr2OjJWrWkX5naxfcflHfqyrPf1HP\ntPz/Wv1mFxlnsGbEfoJeA553lY3xKa89LV/rcKqOWw00xioOPSDOYfvCicdkvZ1Zi8budtttNyAp\nIM+3SsisNjO+dthhByDVrJkZ5phbm+J8zHs+tpOd1nd7kM6D58uaxBNPPBFI94HrrrsOSDE7Vy21\nu4b3Uq8dOw/Ye02vgceqojFW5N92Wdhjjz2AlLHnNZXPm+ilFgRBEPQ0Hek0kK9zop9SS1X/of18\ntFDtbWT9hNkl+jV/9rOfAamq9s477wRSlpMZFtZz+FTOfbDdXPGzCH3z+lzNsNGHmnck0Kdv5bB1\nGWVZ7Z2srndeeExaUWYLafWp5uz26+etflYZm4njdvVDm22k/7uoW3g9quw0oOq3HsKYi8dkDy3H\nSJWnAjrnnHOA1IVBZew1U7SSZ6O0MhZ5dmB+/Rm/cO5rrV966aU176uMje1Zi6aiNaZjRp+Znioj\n7zt2YTDjyu051na0cDt5h/c+86jteaEXxuvY+Lb3TJWIKk8V6Dyx04DXgO/bT9AxV72peBdY4Ovb\n3AEHHACkTD9jgvZyVPmo+orWkIpOA0EQBEFPUWqW2oiN/vepbS64mTb6E4888kggZWL4FNZCMeNK\ni2PrrbcG0lPXjAk/5/o5fl60Gpqthu0G+Zo9Bx10EJCsMK1ErTH9166H0QsZeI1iJbmvKhAVjP3k\n9PE7L8xq9FiNY/n+PvvsA6Rsozwjq2jVwl6I6Xl+HQs7DWilW29hxp3xCtW9qs96ip///OdAipc0\ne4xljkm+6qwxEc+r9VjGI6yTUfk4FsZqVDZW2esh0bORZ6vaK00r/aGHHgLSfcN6LRW23RzyFUjL\nnB+e77yezjlthwFX/jSG473PzgB2g7bbwhlnnAGkrDOPTa+Rmb977703kBSzSsZjVOnYxcV7d1HN\nZaOEwgmCIAgqodQYjr5RlYe+T/3MosWjhatF6/eM5Wjt6Us199x4h1lrWn1aRlq4LVgkXYvhiOrQ\neJVjYqaNqyAajzKjq+yq6DLjFrlVlK8B5KvzQgtWrHK204TK1Q4UWmlarL7q8/e1yrhFszhGebzA\nGjS7PG+55ZZAuibsHv6HP/wB6N9t2HVztKTr9RWsRzNjMXjw4OFjjjlmP4XgHDdGYz2McSgVxtNP\nPw0kleZ59Zitk5lvvvlq/m92o14Cx9Zryrot6360/vtWz/fd36J508688Hzk14LKx1oyYy16hfK4\nuNmHegM873ZpseuGysYOA2a7eQ5UVq4wWpTNmMfDXeMnYjhBEARBT1Gqwsmf0j4F9f/ps9UfqWLx\naauFoi/Vp3e+up1WnBaKT3vz5P3dFiqDu65wHEOtNlWex6I/2h5IdiIom05a9XmVdV61rPK1NsFY\noPPFzCutv3wdlDyWl8dwcuutXryiG+vhODZeS6oAsxFVLlaWq/bsrK4SMr6h6m+XMsbCY7R7sx4K\nr3OtctW7PfI8r9brmXmn4jUzyxjNNddcA6SaEjO+rHUx+9GuDa63lcfJiuZHs2pv9NFHL8zUU9V7\nLP7fDhFm4hmvtAbR+WF2ovuu18h5s8oqqwApDuY92RpHYz+ujqwnxS7U22+/PZDUYb62USicIAiC\noKfoSB2OCsUMGnsbGWMxS0WLxQwNfbeux26fIH25WrrmlPt/4xz6F7WQW+gv1nWF4zGYoaPletdd\ndwGp1siVIPNeXGXRCas+j+V4rHkHXWN0joGV5XbOdkVX54sq0POtpWyHAa2xVrONuqFwVGNmn2nJ\nmtnpSp+S1xxZWa5lWlamVbNjoY+/L8ZwjPlqxdv/ywwrr3ePzfNpvMGeaMY7rBHRk7LffvsBSQ2o\nhO07Z5zDOIbZbY3Wa7UyL4rWrfJ9r3PVumrOfXRdI5Xs0KFDgdQ9wdpGlY4dB1QyvqqM9aRY36eq\ntDbOOLldX/ocj2PgayicIAiCoHcoVeH41FPh5FaV61poSVx55ZVAqoo208ZsFatf9XtqKdmTzae4\na5dbkZz78JugawpHa9+xssOA1pr+bscsH5OyqaLTgGjdqWisAXC1S2sOrKNQ4ZpxY5zC7eRjY+ZX\nqyqwSoXjMbjP1l3YJ9CVF/3ba0qL2XoMlbDegT77B7Rei1SGwhGPVUXr39437OKsQt13331r/q/S\n8T7w2GOPAUk5GQ855ZRTgGTFm/WoerD6vlmajeGMNtpoI8bX86Vy9Risx1OpqFjNvLMz/hxzzAGk\n7FXHyNojx9L7h10WvKb0GugNcL9ee+01oP96Xe5vHge1A3YonCAIgqCnKKXTgORPb5+Sud/SDqj2\nAzPTyjx5eynZP8jv689WwfhUN5vJLLf871EBx87+YFoe+lpdtdKaAbNDeqFKvlm0jrTinSd2hLAz\nhVaf1c52Dz7zzDOBlJXoGNhHygwdf0eLuChLrRfQKyDGK7xmVP1mZtk12mPRctV7YFbTANlEQOO1\nJu3yf//3f4XryXhseiaMExiDVZGamamaM5NK5atyMd7pNeRYnHzyyUCKf9ldXmVjZ22z1UTFXUaG\n3/Dhw2tqoFR1bnuxxRYDUicRlannXS+OPfXsqWbPvZtvvhlIPRhV/Waj2X3c+Lj3EePpziMVjnE1\nYzjGjPJO/HkXiXqEwgmCIAgqoSNZaq5X4tNYS9W6CS0Ys0a0dPRTaqlaWe5T3rVhVC5aCfo9pYnu\n0Dmlx3Bcz8Q+cKKFII6R2SFarH7O2gFrkVSBuYVaVkynE3GL3GLMV4C1olxL0Hmiz11l7Oe03t2O\nqqBoHaRW6cRYWBtiHzEtRzM6neP62rUwvaY8Nqvt3Z59B3MF3GztURFljoUKV6VhPEJPhta7VfTG\n8LxWzD6zp5oZXMY7vRasXdJqt2uD5B6YohWM+xxXU3GL/35nuN+FdC3kfR5Vup4/98nzZ+cJ/6/C\nsDean3PeOI/MctNj4tg7hiog18Oxzsv6ILPXjBGqOv3NiOEEQRAEPUVHFI5oOfgbuT/Zp7ydB/Td\nTzvttECy8otW4usAHctSK7Io9aGq5rTerCjWYtHa14I1W00LqMiSbZUqOg0Uve+8ySu+zWYUlU5e\n01B2jKaTY6Ea91hVf1qWxq3sruC1sPbaawPJmre7cB6/KoqftEon67O8P2i1e3/w73wFTjO4XDfL\n2iPHyEy9IorGpqheLJ9nzY6Fyqjvb9RToMannOu5AsqzyVSHiy++OJDGRIVinMpjURl7zfmaZ3T6\nu/nquZGlFgRBEPQkHVU4Us/Kyusy3Kf8exVkYnWtDscxMFZjFok+WP3Y+uwdi3p9wlqlytqTAbYH\nJAtXqyq3PItWryw7c6+bY5H31nOte+OXxgCKvAjdnheDBw9u+rfz2Gx+DHl2Yx6rzedFo/Oh2XnT\nTgzH3yg6P7miKFol9cADDwRSjVLeGcB7aJ99BlL9j0omv9fmca0i1XfYYYdx8skn8+abb4bCCYIg\nCHqHShROtyjqWzQSut5Lrc/2ge7V13TTqu81enks2l2BsVnKHItm40u5Gmj0+vZ3/H5R9qJZbGYE\n5vQd61ay1AYPHjxQx+mRfq8og67RrEMzAE844QQgKZui+pm8l1+uHov2O2I4QRAEQU/xjVY4LdAz\nCqfb9LJVXzUxFol2xqLeyq/tdjzP41f57xbd64q+l9fK9Y1ntFqHk1PUFaXePhcpkRwzfu2knX/O\nY89VYlFmXr5fY4wxBv/5z3/46quvQuEEQRAEvUOzCud94PXO7U7XGTp8+PBJGvngN3wsGh4HiLHo\nS4xFIsYiEWPxNU09cIIgCIKgVcKlFgRBEFRCPHCCIAiCSogHThAEQVAJ8cAJgiAIKiEeOEEQBEEl\nxAMnCIIgqIR44ARBEASVEA+cIAiCoBLigRMEQRBUwmj1P5L4pjcmBD5oorXNN2os8qZ8zTQmnGii\niYYPHTqUxx57rNR9qPf/iSeeGEjLKneKaN6ZiLFIxFgkvlHLEwwaNKhfp9kOba/tXkdue/DgwQwe\nPLjuvjf6f7fX6PfE7+Xfzxl99NFHdI5tlqFDh3LvvfcW/n/IkCH9Vh4ciLHGGmvEao4DMeaYYzLm\nmGOO+Hvddddl3XXXbW5ng65Rbw42S34NlL39UYn8Gmv2/lAVPbk8QauLj+VL07ZAx5YnqGpBNX8n\nX2533HHHBVIL9nqt4MtoQ9/qsTa6MNc444wDpGWWi5h//vkBeOSRRxr6/XbUXliyibLGwrn7+eef\nl7G5lpcryBkV50WjS443u7DfN0rhBEEQBKM+bSmcFpZw7nWaVjhaQ1oE+dKtzVr7U089NZAWTCqL\nySefHIB33323oc83a725KBXAt771LQD+8Y9/+H+32fgOt/G9Rsn3s4hR0ZLtFKPCWOQKeYIJJgDg\n448/Bhjhtm13wbdeGItG457isX/xxRc17/dR8y3tRyicIAiCoKdoKkstpyxlM9FEEwHw4Ycf1rw/\n9thjA8nvWOSrb9QSHmOMMYD+KqQdtJ7ee++9Af/vPuW+0zzW4v/ff/99oL96bNSvXESubBZffHEA\n7rvvvpr3+yqVZuj7Ha0olYP/W3PNNQG4/vrrm95mJ6inbIL2aXU+1dsmFM8PY7n//Oc/gXTNqHz8\nvwrIazKPGfo7KuF6scJGaDSGUkR+7G7PY/P9RRddFIAXX3wRSPcV733+vt/zXlt0jI3GVesRCicI\ngiCohKZjOO1YLPUsk1lmmQVIT2VTYFdddVUA7r//fiDFOaaaaioAbr75ZiA9pT/66KOW9o8mYjhj\njjnm8KmmmopXX321oQ2rrlQs77zzDgAzzDBDzedeeuklgH4pyk899RQAU0wxBQBbb701AL///e+B\npIjM3Prkk09qvp/HK4rib57fXvBPd4uHH34YgAUW+Hoq/C+PRU4rY9GoddyopyL/nNf9+OOPDyQr\nfpJJvi6p22WXXQDYY489gP5eCb+nWvD9evvTTpyzHvn17xh6bJNNNlnNvruv4403HpDupd5nnn/+\neSAdm8dqHCv3vPi3+1vvHEYMJwiCIOgpKq3D8am64IILAvDHP/4R6P/01Eo/5ZRTAHjllVcAWGWV\nVQCYe+65Adhrr72AFBv47LPPANh0002B9LTX2tc6GIkftekstSmnnBJIlkS98fTz+pfdB6vmVXdm\nqani9EO7/dVXXx2AddZZB4B99tkH6O+DreczLsrYacWS3WGHHQA49dRTgfbjTjPOOCOQxqQIj9Hf\n8Xy7H4cccgjQ31efF7ydccYZAGy33XbA1yrwyy+/7AmFo1X+6aef1rzvteJ8Urlq3b/55pvuF9B4\n7KDIui9jLBpVMnn9lOfLOa9n46ijjgJguummA+Ctt94C4Lvf/S4Ac8wxBwBLL710zfa85hwz56tj\nWk/pdHJe5LFdr4W//OUvAMw888xAUjKvv/51zbr3yCWWWAKAk046CWBEYbb3wFzZSD0VWnQ/CYUT\nBEEQ9BQdUTh57rcWhBaolsR3vvMdIFUSq1wWWmghICkVn6r596w89ql98cUXAyn2c9hhhwFN9doq\nvdOA6s1XFYsWyTPPPAPA0UcfDSRVd8sttwBp36+88koAzjvvPAAuuugiAB566CEA7rjjDgC23HJL\nAM455xwgqb7cIqmnfMq03hrNzFElas2r1iaccMKaz3m+nWeXX345AJtssknN5/L41IEHHgjAFVdc\nAcDLL78MwLBhwwDYdtttB9yvKhVO7ou3a4bHpvJVtZ1//vkA7LzzzgCsuOKKACyzzDJAmkeOZbsZ\nY50YC2MwqrQBtgOkeMXyyy8PMKJ33zHHHAPAFltsAcCTTz4JwJlnngkkpTTXXHMBcO211wJJwah8\njBU7D7yGirJxOzEW3ifyLDKVx7LLLgukOPWuu+4KwMEHHwzAeuutB8ADDzwAJAV09913AymG67zS\nw2GNUgMdBYreD4UTBEEQ9A4djeEUNY/zqbrNNtsA/ZXMb3/7WyD50m3QqBo44ogjgGTReAxud7HF\nFqvZnpldWlK/+c1vavavzxh0rJfa9NNPD6QaAP3M8847L5CssD//+c9AslzNyLvkkkuAZN3ttNNO\nABx77LEAbL755kCy6nbccUcgWTK33347UFxrUKV/WvRLX3bZZUDK5Jt99tkH/PzTTz8NJBX4y1/+\nEoBnn30WSL56FbPH5DF67M63q666CuivmHKqGAt/2/mhJTrnnHMCsOeeewJJ7anOjNHou//Tn/4E\nwNVXX13zf+dbnn3ULFXELfJ9y7uC5+dJz4ixF2OJl156KZCuKeNfd955JwAzzTRTzXaXWmopIKnI\nvFNBnv1a5lh4TN6j7AQw6aST1vztNbPyyisDqXbReaOi3XDDDYEUy/Ga8f6hInLMvAYcizzGXFbG\nXiicIAiCoBI6onByv2OuNLbaaisADjroIACuu+46IPmZtSj2228/IFm2Po1VMhdeeCGQaln0a2vx\n6OM1/tFAtlTTCqcoPqFFYNxJC0ILdckllwRSZpR1Mmaf/PWvfwVSPMpMvHPPPRdIlpDqQAW1wgor\nACl2I/l5LrvGAPr3rNLa0hrLyWsLitqkG5tTmdiZwlifinjvvfcG4Be/+AWQxt555fa1BuuNweDB\ng/nqq68qUTie15/97GdAOu8qWf8+8cQTgWSNm200dOhQIJ1/vQN+z/quVivcpcyxMCaT14zVw/O4\nxhprAGnuq3Q9v2ajqfKMzTgvVf/WW/m+NS525yjqM1bmWOTLd3iezDb0mLwPqFi9zr3X+rlpppkG\ngB/84AdAuq94zzRrzZozlZLHOJJ6m6L3Q+EEQRAEvUMldThaksYXzJ9XsWjl61988MEHgWLLQr/m\naqutBsAJJ5wApKw1t6Mf3Nz1BmhK4VinAf27sLrPZuj5qjIxU8ZMOrOK9K3m6lArULWnWjNLRYvH\nGidjNnl8wu3Vy7dvx3rTWrMOwow8rXPjVWbcFHWudWyN7RTh/+2+oDK25kkFbf1Gs1SZpebc9vXt\nt98GUoaV14ZjYzabamHWWWcFksr3WnvuueeA4kywRulGTVJez+X8UtkatzL2l2d4ei3YMd3PPf74\n40B/he2Y16OdTgO5us6vT983FqMiUbkYp1TtO188Zu+N3/ve94DUqcTzb0zY+0B+X8nvX/n7OaFw\ngiAIgp6iEoWTP7XNCdcStZOAcQx9p/l6Klo2G220EQCHHnookOpyjAlpyfg7d911V6O72rDCGTJk\nyPCxxx57RHxAS0Ofuu+77/pOv//97wOpHkdlpD/ZMVL9mVdvfY2W63LLLQf0t8byTJq8b5TWohZy\nfv6riFuodI3l5VlH+XwpQivPmiS7L6h0VT6nnXYakOIjzWZoVWHVa0n22Q6QLMuiMXIMfve73wGp\nHkvLVRXw6KOPAu3X45Q5Fo2up+V9wX12jnt+tdpVsqp8Mz2PO+44II2VnzeTz9hgXq9XlNHXyWvE\nY8pjOr5vrZD3NO+FxknNvPvDH/4ApHuomXpmNxobsnO7Ki/30IjzKRROEARBMErQ1no4ReRWtBaK\nGTNaoPr4ffrutttuQKoIz1EV+LTVavd9LRZVhnEPM8Pa6CLdj6+++qpmPZV8LZ98vRszqLSmzNjL\ns0NES0PL1DiV1fjGpfIMLH25jo3Kyf//8Ic/BOCCCy4oPK52yTP3ckvWWIuWpnGtZmtEPLbtt98e\nSPEM42NaiVq4Oda46N/uBmYVeSySd6hwzueV6GarWVui5eu1ZcynnoXaDZpdT8tYb77KrvcTa9p+\n9atfASku4ef0Jjhm3h+8jhtd66WMayTHa8R9yNfg8br2/KnixPlz2223AWmeGLvze46VXe6Nd9t1\n3mPLM3rLmjehcIIgCIJK6GgMJ7fO5plnHiD5C421aIloafh/8+z1M/oUtzvsvvvuC8A999wDpGrr\nvDI4t1xGcsyldxoo6iunTzZfFVPMTrG+YoMNNgBS9bSvWntmqXmsZjVpvas68lqXvFas+A3zAAAg\nAElEQVRFyshSK7IY/U196u77bLPNBtBvjSE/p9VltpsdJay+tm9Uo2sU5RTVhXSzW3S+kqP1FNZX\n2CVcS9ZYokrWXntlWeXd6CtnppVruuTxDa12MXar8rWmzY4Fqgfrb+w4kY9RWWvA/PdYGhoLr41c\n6bivxqut41Pp5F0U9CapoFUwdiDZfffdgVTH4/1Iz4h/6y3y76IYT8RwgiAIgp6iLYVTr8urFoJP\nZZ+mWtnWYZhHrwVrfzDz57VgrrnmGiA9pX36Wmtw1llnAbD++usD/S2WBtZnKV3h5Fkn7nO9cffz\nKhXz8PPeSnk+v6+LL744kNYccix8tUpfC7jPcbW94qe1IMbmisj91vmYuB0t1R//+MdAyuATK8y1\n9owF2nGgVXpp9VN76hl/0EI1a9ExNMPTvnLOt1bXJMqpciy8b2i1zzfffG4XSMf8/vvvA3DyyScD\nKQtSpWqHgfvuuw9I1frHH388kMYmrzWpF2PqxFh4TahQjEv6vuffa8JO6d6LVfvOAzuj6z3Qe+S1\nZVabnhC7enif0fvkPdvv54TCCYIgCHqKtrLUipSNfsc8W8wsE2sDtFxeeOEFICka/dNmq5lPry/W\n+pvc72jNiiv/6cvPV7VsdMXBdqhnEdRD681qaOMLKhQtE+MfWndaMqo8/daLLLIIkPzbqspOUKRs\n8hU8tSCLujTfeOONQLLuVX32avN8en7NUmpV2Rj/KMoc7AYes5at59V4VZ7ZZ0amaj7PfhuVyFfu\nza9b45/Ocetw8ro9/2+Nku/bkcBaNl+7cd7zFVk9Nu8jrnd06623AuleqZLxvJt9qjLxmltrrbWA\npIidP6pDx8K+dGbHem3lMd5WCYUTBEEQVEKpWWp5jYBWuU9ZV+Izi8z6CGM5rlJ3//33A6kTgZaw\nMaDTTz8dSFkrZr+Z1WZ8oujYRqJwmo7hFNVRlE2eMePYOjaOqRaP/mrVoeqyKGNvgFhQx9aub1Rh\nHn744UCy3vRbi6rN+aC6M6vNLDazGJtlwgkn5NNPP+XLL7/segzHmMypp54KpGNzXjj/rJZfdNFF\ngaT+R4UsNa15PRfG5Mwic857H7ALtFa93Ra8zxj3sJefcRFf/dyRRx4JpDq+RudnJ8bC33YfrddT\nsZp5qxdp2mmnBfpnI3oN+Dm7jtvdQ2644QYgdS5x3RxjQ86nvBNKTsRwgiAIgp6i6RhO346nOfk6\n3D6t9Sfav8esEfv9uJKnmRNW5WvR6KvXd2+WiWt8uCaMnZfdv6K+YWX6aIuUTZ4R12jfqCLybtRa\nefpc7UDg2BvHuOmmm4B0bkayeiHwdWxIi7BZPG9Weo/EGhrpdrR03UdrTcw++/Wvf12zHdcvscra\nmgTrN5rFc1VmZ4pWMfvI+IJWvz5+LVnPv9eI157H0mossUryWo+VVloJSMeoOnftILsqqFS05v3c\nxhtvXPO3cQjHwm4MZr9uttlmQOp7WCV5ZxIz8qy7MsbivU/Vp1dIPN9mclq/Y/zb+KRxMd93bKzn\n8j6l0irKdhzZ82AgQuEEQRAElVBKDKdo1Uu79Lr2vFaalsf+++8PJEtUyzRfv8Yq2RVXXBFIfmyt\ndS1b+0bVqxAeCaXV4eR+YK00LYdG1yXJ18nw2FRQZvRp4erX1ldrPMueSWKevVluOa34p4vW+GhV\nUeZrAllvYw+0fL5Zc6AVaEeCPffcc6S/U68+q5t1OI6hx66XwPe9Vo4++mggZR9qwWqxlpVl1Mna\nE+eqnguvEbPM7Padx3ZVLM4Hx0blqxow1nvOOecAqQfjuuuuC/TvPl2PTo7FwgsvDCTV5uqleVai\nStf7gorEMfP/xkPtNu1cz1fT1evkvVkF5OejDicIgiAYJWirDie3YI256IPdYYcdgLQGjNa0/kgz\nIvTRW1tiZwGr5PVbm7FhPMMalSeeeAJoS9m0jatLqjQcEzsja6Go4lQiWjDWKmlty29+8xsAttlm\nGyBZMHZXMM5gb7UZZpgBgE022QRIFemOifn3ZviVWZPkNqwQ91ibZfPNNweSNeW+ulJormzMFNRS\ndV65zlK9eVFWFX4n0OJ1TIYNGwakuMNJJ50EpHmzxBJLAGnMtNarqD1rFRWsmVbeB9x3Yytmr3p/\nMa7g9413+Wofwtdeew1IWWjel+xH5tj1QpzLa8c5aRaa6ksvkXFxYzWqPa8Ra8q8L5mF5tipZPzb\ne+nZZ59d83v1lE2zhMIJgiAIKqEthZNbS/qN9StraVgd6zrae+yxB5Cq3u0oYG8jLZJddtkFSIrH\nzKxDDjkESKvc5T7XPCOsCusuX3nTTtjrrLMOkFYjVbG4j2Z2aVHYO80YjGOlpbLddtsBqZ+cGTVa\nha4Mmvv4/Zzf76QKNFMq70zdKFrxKhMt0qJ9NlPQ6mjHxjFudT9efvnlERXa3UIrXEvXLtDON2Mz\nqj69B157ncjMLAuVhTFdr+dpppkGSN0VtOa1wrW28+vaayRfvXLttdcGUj3WMsssA6TOJGY95p2a\npaz7x8gyuvR0eC/T46FStWuK90LvtWapqmhUSCpix9KuHd4fjAkaWzZWYx1fvkZVWYTCCYIgCCqh\npSw1rfHcr6cloKXgetv6m32q6j9U4Vhf4Xo2WiBaKFr9Wqw+xf2emRjGN/JOyvVqEfr4+JvOUtN6\n9re0GOz/ZRzB/1sXY2admXezzz47kCwKYzT2mfvRj34EpFiNx6TqsxJdpWNNk10cjJ/5ef3fAxxX\naR2Sm609coy03rT2GvUfq4ycd8arcvUp+r/rZXD1wno4vuaZVLk1ntes+LmyFE4ZY2HMzevWeeJ9\nw/NlDDDPblVBOxb+nSta4xYPP/wwkOKbxoKclypos18bpcxuHLmKcizy+Ld1NJ5f183So+Lcd0wc\na2vr7DxhrNm4mYrKWHO+NlnRNdjs/SIUThAEQVAJpdbh+OrT15iMdRBa+2azacXvtddeQIrN2PfL\np68qwKeyPl2VjtafT/98vQwtnwaykdquw/HYcmtdC0SfrCpMa0tlogKxh5HvOxbm1+u79ff0vdq3\nzriGlolj0Kkag9FGG63lLgriMVmPoZqrh+dZ1WgswA4WVm23mmnTDYWTd9DO1Xoen/S8q9qsvndM\nnXftKp0yxyI/JnvjqUjsB+e145x2rqv+vQ+Yoef5NkZjpqZ1WWYzOkatZvJ1Yl7kHhNjO3pvrMPy\nVUW7wgorAGnuW5PmteS9147adtxXNapwzABWXTbaIzIUThAEQdBTlKJwfBpbva6V7lPV7BLjE2be\n2AvJ+pqf/OQnQIp/+H8tIGM+Wj5FcYg2Oji3rXByqy1f1XLfffcFkiVqB2R9trkS0Wo3C8WsKeMO\nxnYuuuiimt9v1Zrv5CqX1h7ZOSJXaVY3m1HnmDhWRee7aA7b6eK8884D+q9uWoRjrDVYpcLJa4ac\nD67xpMp3juc99jxma06uvPJKIPnk26WTHZJVKo77EUccAaQYsHNaT4adju0o4DHrBTBu4Wq54ljU\ny8DKu3wM0Gm9Y/PC3/b8+rdrPqlA7JDutaW6y9dD8ppTKXlvdt44ts3WMkYMJwiCIOhJSl0PR3wq\nm8tttoidT824MP/dp7f9oLQ89LVaj6OlYdxD/2WuZPLV8wY4jpq/+4xBUwpnoLhFkR9Yi1QLxTGx\nUtwsM7PKjjnmGAAOPvhgIHXCNg+/CMcor78o6ndXtL9lWG9aqPa+EmsCHAPnSxF51wb7g9mBIl+b\nXuvO79mr74033gCar7OoUuHYH1AFm6/k6avzyM+tttpqQFJCZjfldDOGU896zs+D581aNvuBudaT\nY+E8s1blqaeeApLSOfPMM4E0Rjmtdiipcl6Ykafi9Tr2uvYacv6ogPSU+P38Xun9K1fKRffOovtI\nKJwgCIKgpyhV4eQWigpFi1QLxHx3OxhbP/HYY48Bab3uPA5RZIloyZjZVW+/RkLLMZxGfyPvZGsv\nNI/JrLQXX3yx5v2y6igarY1px3rLx8Lf0kevxWnVfKOoYKyKdj2TfGzsiOsKkFp7zpN6Pd7szmCV\ndi9kqdlpILdstUjvvPNOINWsdao/XC90zvbasaZE691rxdd2q+TNECuKf/XCWBjf9BrIj9m4Z94R\nPf+7KuUbCicIgiCohKYVzuDBg/ut7JkrjrwuRwtXn6tVsHl8we3l1lnR7zS6/koVCkffuSpOGu2c\n3GvdfNux3lyXyLoKsTbA3P9cwWqtOb+KstIk9ydvsMEGQFopcv311wdSLZRW3dJLLw2krMd6vvtu\nWrIj+R2g+vlSZnV9r8z1VinTC9AsRRl0eR1P0dzOr5129ycUThAEQdBTdDSG06uMZD9LW/GzbAui\nU+RqpJN1OGVRlCnjOjjXX389kGqY8nPgyo/Wh9Wjl8eiar7JY9HNTgO9en/IaTerNRROEARBUAkd\nqcPpNNbf1KtJaYHSFE5OUXZYkbXeKEUWR7M1DzllWG95JozkmTJFnSHyLKFWqqChuFK8HnvuuScX\nXHAB77777jfWqm+WbnZd6BStXoO9pPYaVUjt3m+KCIUTBEEQ9BTNKpz3gdc7tztdZ+jw4cMnaeSD\n3/CxaHgcIMaiLzEWiRiLRIzF1zT1wAmCIAiCVgmXWhAEQVAJ8cAJgiAIKiEeOEEQBEElxAMnCIIg\nqIR44ARBEASVEA+cIAiCoBLigRMEQRBUQjxwgiAIgkqIB04QBEFQCaM18+FvemNC4IMmWtt8o8ei\nlxoTdpsYi0SMRSLGItHTzTsHDRrUb832btJnf76pvY4qYfDgwSO60XaCRufNkCFDRnQa7gatzO1G\n93mfffZhn332aWW3ukIV13nZ95Oi7Tm/e+neNaoRLrUgCIKgEjqyHk69NReqXt2u6PcGeL/09XDK\nWn8i31f/9lXr2P+7hkijY5xvvxV3QdXn1bHNx2SyySYD4J///GfN5z766KOWfmdUdJ2UdS7KmBcb\nbrghAJdddtmAn5t44okB+OyzzwD497//3eruVsqoOC86RU+71IIgCIL/PUbJFT/bZSTWX8dW/GyW\nfLXMscceG0jWn6th/v3vfweSwpliiikAePfdd2s+3yydsN48BpVHEUOHDgXg7bffBuAnP/kJACef\nfDIA0047LQAzzDADkMbi97//PQArrbQSAIsssggABx98MACffPJJI7vZj25asmeccQYA22233YD/\nL1pJtlP8L1n1+TWYeyv+l8aiHqFwgiAIgp6iqbToXqdRv3UnYgzN+sxzyzTPfPH/k046KQCLLbYY\nAHPPPTcA448/PgA333wzkKz5Qw89FKBfxlNunVUdb4H+ysZ9mnrqqQF44403gKRYvv3tbwMw1lhj\nAbDpppsCcNRRRwFwzTXXALDKKqsAcMopp9T8/f3vfx+ABRdcEIAHH3yw1OMpk6JYX65sHJt//OMf\nNZ+fZ555AHj88cc7up/NMnjw4H7HlMfeenURSJWNtBuHDULhBEEQBBXRUYVTL7Mqt+r1mX7xxRc1\n/x9zzDGBpAZ8/c53vgPAp59+CiTLyQytov3oBPW2nR+r1pJKxFetccfiu9/9LgCzzTYbAEsvvTQA\nn3/+OQDvv/8+AKeeeiqQxsQx/Ne//lWzf+5H0VhVQa7u1llnHQD+9Kc/Aclav//++wG46667AFh5\n5ZUBuPvuuwHYeOONgRS7UfXddNNNQBrTZ555plOHUojjvP766wNw+eWXj/TzRRmUzn1jcqutthqQ\n4lT77bcfkJRwr/HVV1+NOA/O+bKUgmM03njjATDXXHMBMP/88wMpK85rZZxxxgFS3PP5558HYJpp\npgG6cy2UhdeUY6tXYJJJvq5jf/313igxDIUTBEEQVEJHs9RyZaFVrSVq1tL3vvc9IGUlLb744gBM\nP/30QLJgzTLSEvnLX/4CJH+2Vn0bFlTpWWq5snEstEhUMv7t2JiJZWxGy9Y4hFb8lFNOCcCNN94I\nJKteq84xV000er47kYGz6667AnD22WcPuI8TTDABkCzWZZddtuZzY4wxBsCISnuz2R555BEgZehp\n4eqD97VVhdvJbKRc4bqvhxxyCJAy7C666CIAVlhhBSApWbMQxx13XADmnXdeAJ544olmdqNh2hkL\nj7FZJWFM7o9//CMA9913H5DuG15Dxgi9rzjnn376aSDNF2OFM844I5CuKRXRsGHDgPpxz25kqXme\nvSZUtksuuSQAf/vb34A0j8477zwAttlmGyDdS71n1qOJuHhkqQVBEAS9Q0diOPlTUctGv6KW6kwz\nzQTAXnvtBSQf7AcffFDzqrV/7733AsnHb12GyiavTelm9ktuHfm3Y+EY+L4ZWdNNNx0Am2++OZDi\nFldffTWQxujOO+8EkrVoptc777wDJN9/rvYck6rqNvpy/PHHA/3HQgvVMbEjgFb9nnvuCSRFe9JJ\nJwGpPkfL1zFzLP/617926lCapshSVLWr6vyc8SyVr9mHsv/++wPw8ssvA7DTTjsBnVM2ZaDy0Aov\nwpidc3SZZZYBUhzLOe18Ea//fIy9XxjP9D7k2O68884AvPbaawBMNNFEAHz44YcATD755DW/P1Dm\nXafIO4l4b5twwgkB+PjjjwE4/PDDAbj22muBpPKnmmoqINWszT777ABccMEFQPIiGBd1+6rFsu+h\noXCCIAiCSuhoDEdLUz+jFsLMM88MwAEHHACkp68W0EMPPQTAe++9BySf7UILLQQkP+Ydd9wBwG23\n3QYkv7aZWy1U2ZcWw8ljN1oo7rsWkkrEY996660BmGOOOYBUd2PNyVNPPQUkS0Sr7s9//jOQMm/8\nPa26vK9Yn2rpAfe/k/5p98GYi/vi+TLrUEszj/U4ZmeddRaQeqe9+OKLAOyyyy5A6s3VrpXWylg0\n2wEgV315DYgWq+ffOKdK1zFceOGFgRTXKpsy50V+jRxxxBEA7LvvvkCKS/qqR0NV7xjnMSGVrfeB\n6667DoBVV10VgGeffRaANddcE0hj533K+eV8LOpLWGUMJ1fI9p/zuheVcq7+ci9QjopJJb3DDjsM\n+LtFRAwnCIIg6ClKjeHoG9Wq9tX8dzMpfCr/4Q9/AFJmlnEIfae33norkHLIjeVo9asC9D/6PZ/u\n7WYntYOWgdaTVpJKQ7/0m2++CSRfq9bZBhtsACRLVavsscceA5Ilo0rQQjZzR9+unzP+kXcg6Ebt\ngfvqseZj5asWap7dpAV64oknAknpPPDAAzWf72YML1c2RZZifmxeK7nCefTRR2v+vuWWW2q26/f3\n2GMPINUo5dTrXl5Wd/NGyGO8Bx10UM0+bLTRRgCsvfbaQFKsnn89IXZX2HHHHYE0JmZFbrvttkC6\nv3gt6XExIzDv9VfPC1AlxxxzDJDU31prrQWkOKYeD71K1n2577/4xS9qtuexOs/MEDWmaFxVJX3P\nPfeUchyhcIIgCIJKKEXh5BaqSkcrT5+8T1ufmr4/yyyzAHD++ecDcNxxxwHJ0tBaM5/e6lkzslQH\nL7zwApCe9lVQZLnmufv5q1lIfk7ra4EFFqh539oA1ZudCIxrqHC0/l555RUgja1j4fY6qfrqWcf6\nyI3N1dtOUQ2TMRvn15lnngmkOi4Vs7UGKu1uUjRPcoXpec3rLYxnOYZaoKKq1xdfRD3l0gllUxTP\n8n3Ja8WcB875o48+Gki1ScsvvzzQ//way73qqquAFBsS1+fxWtPj4n3JWpVe6Lkoe++9N5DmuN4B\n1b2ZmsapvM71/qhw/F2vDRWR8SqzHx37hx9+uKn9rEconCAIgqASSo3h+FRVgfgU1XLR2jaWY72F\nykb/oZaPVp1qwG7B9hczBuTvaOXl2Wmd7KXWROU+kCxXj91j8VULRh+r2O/JGI6qTmtfH7/WXq5s\npJNjUc86rqdsxH0rqvDWitN3bwW5lu0NN9wAdKfWqIhmlYPKJu9EoMrP1Z/K1up5aTRb7oc//CEA\nl156aVP72QhFc60ozuUx2BFAZWMNmjEZrxXjll4zbse6GjFT68orrwRSDZMemd/97nc1n889NWXM\np2avO4/Fe5s9FfXuXHjhhUDycJjFaBd5M3l32223mu95LOeeey6QYofifK1XM9UsoXCCIAiCSihF\n4eSdiFUq+gH9255IrmK44oorAskvrYWiZaEFs9xyywHw5JNPAsna14Ixw8KskyLff5VrwBT1kbN7\ngseqL9YxULlcf/31QKqS1sLVmnN7VkFrAWnp+H9VZx5nqzIbqVXcR9Fat0raWgEtU7MXretSGY8K\nx1qEMR4rxLVM8xiOKs8MLlE559Z+TieUjXgMjWbIvfTSS0DKsPzpT38KpD5yduNwPqicnfu5qsv/\ndrt2svjBD34w4P5UEfurd0/yfftKWkfjPVDVpudEBew6Sr/97W8B2GyzzYCU+bn77rsDaX4M0Ceu\nzSMbmFA4QRAEQSWUGsPxqWgMxYwZn57mcuuDn3XWWYEUl1ChqHDWXXddIFlzZqXob9Sqc/tup97+\nVcEAVclAslC0+ow7qOZ837iUY2LfOddXUdGoHkXF4/f1g0u+2mIvka/VoyWshZorV+eXPn4zbIwh\nunaQGTz5iqOjEqo4x8Lzp4J1Pjh//Ftl040VXnPqKcxcCZlpeeSRRwJJwZills8HPR15Rqi/u/32\n2wOpXssYTjdp9HwYm3HOq+btL+k8cI7bxcW1oFTIziMzgY2L27HC+1ARefZks4TCCYIgCCqh1Dqc\nPF6hRaJC8X0VjPnuWvmu/Ghcw95YWrD6G/VD2lvJ7BUpWj2xCuuuyE/t+/pc875gWq7GavIVOR0j\nYzjmz1un8/Of/xyA9dZbD0jWoRQprrIYNGhQw9ssmi9a5XaQMEPGGiWtNTtna7X5fftLabU5Fvri\ni+ZBL1j/jWIHiiuuuAJI15Yqzu7idumQ/Nh6Oa6V75P3EeMOufLNv5fHbnzfeh6zGGVUOv9mt5qh\ne8kllwAppqPXx/uEmb52Xci7J5jl1iitKhsJhRMEQRBUQqlZauJTVKtci0NL0+wh8+2NU7z66qtA\nUjb6C83YMtNizjnnBJIayPuJPffccwPuXxVWXb0MnFzJ2B9O36k9z1zJ0+7PZtYYs7HOxvetw9Hi\n1dLx+3n2Sdlj0Yx1WNRPTOvcTgEqHNcr0W/t57V89V+bbeR6Ko61nSouvvjitve9W3gN6WtXKauQ\nzWa0o7qfy3uyVa1smlG+ReT1fXYU8f7geTZ+YWxm0UUXBdLY6Q3w2jJGfM4557S1f93AMTHjV0Wb\nqz69A7fffjuQVhDOqUrlhcIJgiAIKqHULLX8Kak1nlvV5orbH0yr3L/zHHOtMfPz9fEby8mr7ev1\nN6sC9yGvl9Da8v/GWuyIrdWmMjE+lfdAMiPP+h3f13pze3l36LyKv0rytea1xlTCVkObzXjggQcC\naR7k3chVeXZONobjdsxmtA9VXo/h2PRSV+B62AU8P68e27Bhw4D+a8Z4zEXnvVMWbpnb06o3W1Wv\ngPcD45gqXzOxVMgqGev/rMMZlXHu2zHALgyiAnY9pSKqmvuhcIIgCIJK6EgdTj2FodVlxoN1O1qw\n9oXy83Y8tVOBqkGLxew2fbdVdosuIlcSuXXvGKlMtET82/iF6+Hoj9b69xiXWGIJIPlyrbJXXaoC\ni7ovVIk+ds+fNUOu6WH8wewzLVrHxrH02F3/RAvXGJ9xMCvUjWfYV0o6XVXdCY466iigv8LRe2B8\nVC9BruZcQyhfO6aba0Y1+9vGevPO2Ntssw2QVnz1WjKTy67iZnB5baiwRwUcM2uO7Exi5ma973U7\nIy8UThAEQVAJpSocqff0VNFo6fp5FU9eLe2qmNbhmIXmuhaufqd/uyoaycAx40rr3qwRa43yjKt8\nlVS7w3rsVgqrBvfZZx8gqT99+HaFzVfRzOlGPYZWt2NgVpljY/2MY5OPlf2hHDOzGO25t+yyywJp\nDKxZMBYko1JtipapXZ1zxerfZicWrbujspH8c6oG6z06SbNWthmdxuqsSbrvvvsAuPbaa4G0Do7x\nDbt7LLXUUjWfN+aTr7qak68g28354T449+0rd9JJJwEpk2/mmWcG0rxYY401ar7fLULhBEEQBJXQ\nEYVTRG5J5GuH5/5FlZA+VhWPvv/TTjsNSP2iqq45GJm1YJzK7tDWHOW1A3a69dhULsYxjE94DFou\nqkOz0U4//XQA3nrrLSD5r6XIiuuGxeNvao25dr1xp5tuuglI3YHFeeC8UQXaWcAxdqxUg3nX6SJl\nU2W9VrOolPfaay8gxSXEa6XZfc7nRRXKplFUJqp+FWrel9C4patfHn744UC6pqym1yNifNT55LGb\n4Zn3EytSPt1EL4GZu3lXFu+lfs77RKMUxXryTNFmCYUTBEEQVEJLCqfVTIei/mK5halF4d/GMbS+\ntOa05vXN3nbbbTXb6wVfq1kkxqFc10IFowLSP52v8GfPNNWAsRwzrlQFvuarnUqRiuxmdpLZZPbI\ncmx+9rOfASlDz7iE2WbWT2jVqfquu+46APbbbz8gVVerDowRzjvvvEBarz2vx+mmRetczmN1Wqp5\njzQtTTP0clTSqkGvId83DrLYYosBKcOrynmhMjWGpzpfYIEFgBTTsweax+IY2QV6pZVWAtJYeR/w\n+wsvvDCQ1tVyLPxdY371KKN7Qlnk+2HH9FNPPRVIqrBoPSTnvp4X1V/R6qbtrhEUCicIgiCohEHN\nPKkHDRpU8+FmlUTReie5jz3//CmnnAIka19LeKeddgLg2WefrdleG0/hR4YPH75AIx/MxyIn71Rr\nNwRrSjxm62i0QLbeemsgdRDQT20tktadfmmtQbs0GN/IuzQ0yuDBg/nqq68YPnz4oPqf/pp6Y9HA\n9wH48Y9/DCSFseWWWwJJ/VlFrdIRVYDKSOVkN3K35xg3q+6qHIsinAd2/73//vuBdJ4dI+szVHM3\n3ngjkDI5rXmy03qzNDsWfdXAkksuCaSswXz8vb69VsxGtRuHc95jcD64rpbr5HzQL3kAACAASURB\nVKiY7NZhTZKKyXnheknWsOQx4D7HMeD+9sK8ELPVvIbMXlXBeN8p8iJtvvnmAJx//vkt/X6jYxEK\nJwiCIKiEthROyz+a1RDkPnStNP2KV155JZBiNg899BCQfPT2ZtO6b8O/WprCyVWctQN5ZoxWnRaI\nGXh2RnYdC1f8s5LcqmljQFbf1+sL1stWfa6AHTNrDlR9rmJqnMvvOY/yTha5f9rPa9HaBaJoRdB2\nxsLOAGaXtYr7akaW2Un5teQ8Uc3ZhUNl5Fhab2ONU6Nx2U7OC2N1doN2HuTdEjy/ZqMZy7P+Riv/\nvPPOA5JXwFiNatEYUKt0wwuQnx+7hOvlyWvNxJok41157LddQuEEQRAEPUVXFI4xGK2wfK0Y13ix\ny6tWvL2S9OX++c9/BlKXaDPBmlU4fdRIaQqnz+dq9sm/zZzaaqutgFRXYfaaVpjWtzEa/dIqJDNr\n8nqKoqy0RvZ3+PDhXfVPF1XRF8WjrEnK1Z1jmCsbx6ooE0dGG200vvzyy5bGIu/SXBb2GXT1U+MS\nHqPxCuNaRf0NW800LXNe5F4A17lynRrrqzwm57ZWvNfGE0884b4Bqe+g9xEzRV13y99T7TUa58zP\naTeukTyjV8+I9wWzWPMVg/Ps17I7pIfCCYIgCHqKriicPtsDUhzDehstmPnmmw9IXX/1yVqZfvzx\nxwOpF5f+6DYoXeEUoZWtxaElolVuzyy7Q5t556udbrVw8vhVu5ZLK9ZbL9Q/9aWszridsGSL9q3e\nGObqz2vHeZNfA0XbM07abP/BMsaiSG15TahMXPfm0ksvrfm/c10VZ4zXLDXra3xVkeg9MLvNmqNW\n6QUvgMd08803A+l+YN2eY+X86BShcIIgCIKeoiWFk6+t0KpFW1R/41Pa2gHjHfla9cZwmrVgR9Id\ntmWFU8+arvd/lY5olfm+efauBaLSMX5RVEPQKr1UY1A2RWsDdaPewjiF3RPcB2tLzD7qFZoZi8GD\nBw8fffTRR8zNornv9ez9wM9fc801QIpTWpdlTMb7hEpGxVOUeVW2Aq/yGinad9/PPSZ6icqOIRYR\nCicIgiDoKboawxnJ7wD91+awlkC/cwfWoq8shtMsZa/UV29732SF0yzfxLHoZpZao0pjiimmAJLC\n0Xov6hc4kv0Ayu8PNyrMi7JW+q13zkLhBEEQBD1FpQqn17KYBqA0hdP1tcPbHOtWrLduH3O7jAo9\ns7pNmQrH2I2Kxb/zPl9lk8dw9ZxY69YoZc6LTtVtVUUonCAIgqCnaHY9nA+A5paO60MPKxsZ2sRn\nRzoW3bby2xzrZsYB/jsW3T7mdinY/5bGov296UlKGQvnZh6Lqcq6z7NTm1U2/6XUeTGqKpv/0vBY\nNOVSC4IgCIJWCZdaEARBUAnxwAmCIAgqIR44QRAEQSXEAycIgiCohHjgBEEQBJUQD5wgCIKgEuKB\nEwRBEFRCPHCCIAiCSogHThAEQVAJTbW2abQx4ZRTTgnA22+/3cIulc9kk00GNLQE9QfDhw+fpJFt\nRpPGRIxFoltj0amF+HJGhbGoik6Mxdhjjw2kpaFHFRodi6a7RQ8ZMmSglTLbotVOqR3oTtxwt+ix\nxx57+HTTTTdi1dGcccYZB4C///3vZe1bpTRzMQ0ZMmT4WGONxT/+8Y9O7lLDjMorOxax0EILAfDQ\nQw+1tZ1udBHvNeqNQaP3lWbHYvDgwW3/Zqdo9/ejW3QQBEHQU7S0Hk5ZazdMPfXUALzxxhsAfO97\n3wPgzTffBOBb3/oWfX/vgw8+aGi7bexfz674mVtl//rXv4C0jnvZdNOS7bV1k5pVe2OPPfYoq2zr\n0c150ajXoGy14Hx0e31eR3m1lzPuuOMC8Pnnnzf1vVA4QRAEQU/R1oqf+pP1LxeRWyZzzDEHAM89\n9xyQ1ipX0ahwtCwMiGrxasFcd911QAqUbrDBBgP+fpGFMgAtK5x99tkHgF/+8peNfH3EWDg2vUY7\n1lu3/dHNUk8RfxMt2VZpZyzylTbbxXmWX98TTDABwIiYYn5evY/42um4xX/3NeYFoXCCIAiCimhL\n4TSKFsh3vvMdAD755BMgpQCaPu3/m+Wxxx4DYJFFFgH6ryRYxACWbc/GcKqmG9bbFFNMAcBnn30G\npPP4/vvvA3DVVVcBsPfeewOw7bbbArDmmmsCMP/88wNJMedzu15sqCgltcqxePzxxwF47bXXANh9\n990B+O53vwvA7373OwBWXnllAG655RYAVlllFQBuvvnmmu1NPvnkALz77rs17zeqNmaccUYAXnzx\nRaC3rHrPp3HMbbbZBoAtttgCSMf4pz/9CYAdd9yx5vvGQVull8aiXSJLLQiCIPhG0ZLCaTSL6KOP\nPgJgwgknrHlfhTPLLLMASeH4lG0UrbOJJ564ZrttPK2bVjiNjoXHaFFsr9NJ661ISZgZc+655wKw\n0047AbDddtsBsMMOOwDw6aefAikOttFGG9X87fkvK1bQzlgYXzQOKbnCcJ8//PBDAMYbbzwADjvs\nMCBZ7yqc+eabD4DZZ58dgEkm+bpeefnllwfgoosuyo+h5vMPPPAAAOOPP36jh+Z2mh6LTmUdul2v\n//vvvx9I2a8qZNXdwQcfDMCzzz4LwKuvvgokRd3s/aKdsfD8+5qrrSeffBKAueaaq6l9qoe/7zXo\n3157+b1z1llnBSisN5RQOEEQBEFPUUkMR9Zaay0AbrjhBiBZqq1mamkh33HHHUDy5bdB12M4WhxH\nHXUUkMZIy/fUU0+tt19A+xliVfqnVbpLLbUUkI5R699Y21tvvQXAVlttBcCDDz4IwEQTTQSkOi3H\nbtdddwUaj+kV0YmMPWMr77zzDpAyqszU/Mtf/gLA4YcfDsAXX3wBwH333Qek2jVVg2Ol9T7zzDOP\n9PeXXHLJmu01Si/ELVQF3//+94GU7Xr99dcDMNtss/n7QLLel1lmGQBeeOEFoP0uIL0wFs1irePq\nq68OJIVrjHDhhRcGYIEFvr4NOnb16v1C4QRBEAQ9RVPNO4sosqLy962bkWHDhgGwyy67AMlyyfH7\nxoTOOussIFm41157bXsH0EU85rXXXhuA4447DoBpppmm5nP6dE8//XSgvz/cDJwTTzyx5v95F4de\nQNW28cYbA0nxGu9QkRj30L+tj/7222+v2d7f/vY3AL797W8D8N577wFw6aWXAvDDH/6wZrtVUnRN\nGFfw/3vuuScAJ598MpB853l/Or+fKyS//8QTTwAw00wz1XxeBeQ106yy6SWshnfsjMF4HzBO6jGb\nhbrooosC8PTTTwO919FiZDTaPcVMTz0ir7zySs37jpn3Hf92DIw1ez8xVqjybrdfYiicIAiCoBJa\nUjgbbrghAJdddhlQHC8oel/LwpoDfar64n1V0VxzzTU1fxsL0rrTv9huXn0VaJ2vtNJKQIpD5VlM\nOWaraLWpFlddddUBv+8Y64uVJpZq6BgqkRtvvBGA448/HkhWux0j7r77biDFbIzhFJF3Unb71qzo\n4+8m+TXh36eddhqQVH9uyeY9rlRIZhtdccUVQOri4fkXLeTNN9+8hKNojrKUxNChQ4GkhP/whz/U\n/N+ss2OPPbbm/8YlrrzySqC/Vd+LPPPMM0DKKqynbLz+rd9yzD3v9fDzXmPegx3TI444AoDddtut\noe0V/k5b3w6CIAiCBiklS83K7mZ95H7vkEMOAVLdxT333APA2WefDaTsI5/ic845Z83nzXIqoXdX\nx7LU9KVbJW/cyhqCegrnpZdeApJv3+0tvvjiQFIDjoFxDS1g+0v5fj06kYHjPhvDMavQfdfidB/t\nHFGvBkBFtP766wOw3nrrAcmyNQPn6quvbmQ3+1HGWHjef/WrX7W0D+LYTT/99EBS/TPMMAOQMj4f\nfvhhoH+fMeeb32uWbmRmaaVPOumkQLofeP8wg2/rrbd2H4GUqef9xE4ml19+OZDuVw30WByQMsbC\nOOYll1zS1G+LsRhjfz/5yU+AFLt9+eWXgZSV6DE2qnxE74HXVE5kqQVBEAQ9RUc7DTRKngFhpbkV\n5j7FzbyxN9K+++4LwG9+8xugvo+/CK2+Dz74oHSFo1X1gx/8AEjWlTEcq6J/9KMfASkrRN/pSSed\nBMCvf/3rAbdvjystXDHuoWViZk49VlxxRR588EE+++yzjluydoYYc8wxgWSx+rraaqsBKfbiPHDe\nqQrtN3bkkUcCKSZoHc4ee+wBwAorrNDU/g0aNIjhw4f3RL3FdNNNB8Drr78OwPbbbw/AKaecAsCm\nm24KJK+AYygqI2MCrV4r3VQ43qusHfGYzD7zvNux/fzzzwdSzFClrLIxBuz9rFEPTS/NC5Wqno88\ntif+vddeewEpC817r16F/Br0/mJt00ji9aFwgiAIgt6hrRhO2eue+LS1lkR/5LrrrgskJaOFa675\nVFNNBaQMrmb3R7Vx6623drzTgFaXdRMew2233QakbDQztor6gWmVOVZaLB67mXtFVls314BRmXjs\nZmCZfaQisd7KTL48VqjV/9vf/hZIKi+vv/jjH/8IpMr0nGmnnRZIGT453bRkrY63fsaq+uWWWw5I\nFm1R1bzzwWM0c884aKMMHTqUd955hy+++KJrY5H3WvTYnAd6C2SzzTYDUl85u4nfe++9QKrXsqtD\ns1Q5Lzx2X417Oue9NlR/RTFh7xt2YDe263aXXXZZIHmRGu3GEAonCIIg6Cna6jRQlrLRN6+FayaP\nnXFdk0PyHPN6Oer1Yk633nprK7vdFGYp5Zk0WuOuZ9KoH9kxsoOyWM/hdszQ0VKWemPWCTwPZlKp\nbEQry64I/q31ZgW5VtmZZ54JJP+yOKbzzjsvkHz7c889N5Cq8aVI2fQCxuDyim+zFvNrMO9Obd2O\nVnyRsqm3Po6xo14gP2Yzp+zWsfTSS9f8304TZm45dtYBtppl2wlU9XYH91ifeuopIGWzLbbYYkC6\np/30pz+t+X4Rd911F5Biy8ZuHDPnm6pQFej9q11C4QRBEASVUEovNS3Ojz/+uKnvFa1bYvW8T+98\nzQ6/Zy2LMZ6iOoteqCi+8847gaQsiirO6+Gxq+78O1+nXQs3z8zKK9arxH1zDLSuPBbjTsbk8r5N\nef8xffRad2apud1DDz0UgJ133hlI1dNWTe+3334lHVkxxhfMOmwU41IqC8fOY899+pL77htd76be\n2kFmZnWT/PdVZSqVc845B0hdF+w+7hio8uy2kc9H6WaPNT0g4uqlqri8js7uKvZYrLemmN0avLbM\nEPXerdKxb2HZhMIJgiAIKqHpLLUhQ4aUtpKi/mgrys28+PGPfwyk6lmfwmYr+T3/XmeddYCU6eUx\nmbWi77YBur4ezkh+D0g90LR87ZXmMWudtao6pZMZOFppWuNFfZ/sQPHzn/8cSPUU+tzdTu57V8XZ\nt84xMr5hXEslXe8aKHMsrLe68MILR7od41VvvvlmzT7m3X5ztNaff/55INXnqALapdmxKFMZ5V0T\nXBV1wQUXBFLdlvEula/eBc+7XaVVkdaDNUsVWWqef+e63RNEFWYtoWPjMeVqzT6UZi3aqcQuHcZP\nvbfqVaiXkRxZakEQBEFP0XQMpyx1A+mpq0UiWn9mXPlUzVdFFC1Zn+buoz2XeoF2/cJ2HNCqs6ZA\nup1h04jyVXHqQ7fq3bVZtKrMjLnggguA/tXQ/l1kbZmdZudk6y7sHmx36m7EJJzb1ju4T3k2kuf5\n97//PZDiEfWwTsc4htX4+fxTIakGW7XyR8aQIUMYd9xxW952blX7t/uuircGzfl09NFH13z+0Ucf\nBVIvtosvvhjojdhujvt80EEHATDPPPMA6ZrI99nPu8qtWatm9pqRaR2X80i1r+K2L6W1cXZ1yeOm\n7RIKJwiCIKiEUrpFj+TzQHHevDGbm266CUj58WZquJKf3X7NyLCOwz4/K664IpCe/mY5mVPeREeE\njsVw6tU5FKFlqgq0al5fvXEQ4xq+32iNUhGd9E8fdthhQIrRWPWsctGq0p/sec0z7IrWQTIzzPnh\n2Ocrifq3faba9U9D82Ph+XEf7LKQ97pyn41j5XPaeaXF6lpVft4uCyomLWbp021jpPvbybHIj8k5\nnMfu7J1m3MEY7s033wyk9bPsquDYGMszlpMrp6K/i+jkWHjvm3DCCQF47LHHgBSrsY7GzEu9A14j\njpXXVt59w7i4tWn2mcuzXVWnebZjfj+LGE4QBEHQU5SqcPp0Xa55X7+hlsUA2wXS0/eRRx4B0lPc\np7RrOohPYS1elY9Pd/3h+vKtsvb9AeIqlWWpaZnoMy16XyvfrCOtPi0LLY16+ffNUkUGjrE3/c9m\nDaloPT+5NV5kgRrXMi6iAhKzmexgYa8+Y0WSV563MhYqEn3lRbiWS1F3Z68Bj9VrxBiP1fV2W9D3\nn2PcQjWQd2jP46JFVNk/TKva2Iz9BVVvjp3q0KxWu0V7P9CDYp/CPN7ZqNch9xq0MhZFnoei950X\nV111FZBigMbojNnYNVycP14DnmfH1N8x3mXX6WOOOaah43HMVVahcIIgCIKeopROA6Kyyaug7d+T\n14r025n/PuX1wWvFFdUc5Bkbft61YMxWEpXNCSecAKQqXq3IKrE+JremtTQcO7OO8hoVx6TZrr+d\npF5PKo/J87/yyisDyeqyuln/ssq2aDu5wtHizZWNnzOmp7Wnrz+njIy/espGjD+piDyGfE56DMY/\n/Z51FHZTyFEVuA7K6quvDsC2224LJGVjBfrbb79ds/+txh7bIR+LW265BUid1j0/7rtjsdBCCwEp\nG9IsNmM93h+cV94/6sVsirwRrVAUU83fN5PTPn96j/R4uK+5srHXmmPj+TMO5vfsAn3ssccC/ed8\nUWduUdk0SyicIAiCoBJKjeHoT7bu4bjjjgNgk002AYrXaJCiLJEiZeT7WirGBFQDWtB5Hyqf9lq6\n3Yjh5OQZV1o4ZmzlaKFoCZdtgXbSV28PtPPOOw9InSDMlHEtDnuhaW17Xl0DxN5YWltmNw4bNqzm\n9/J4l/Mgz/Arsto6MRZ53NLqd6+hfK6bpWQcyn2eYoopAHjllVcG/B0/Z9ZTvl3nmdu3Ar2IKmI4\n7rMrthrTy5WKn/N8XnnllUCKa/g9rxUVk906nBf1FE7uselzP2l7LKyXsdee88H7gXN54403BlLN\nmt1YHBP/9tpwX72fqOqmn376mmPwd3KvgDGgRrNcI4YTBEEQ9BSlxnBce961XbRki2I2OUWZVvW+\n75r2VhIfeOCBAEwyySRA/9jSHXfcAaQeblVSZE1piWhpFCkb6ZSy6QSeP18POOAAoH+38JdffhlI\nq1kaa1PJaN153qwZWX755YHiTCutNF/tNODv7rPPPgAcfPDBLR9js+RZZ3Y8z8+nlqiZWWbU6buv\n103DWrc8o8v6CuMS3ei6UBQfUsmqgI03+XkVi+c7XytGzG60A/LTTz8N9L+2Gqi3aehzrWCtmErH\n7u7WJDovjL256rEdBMzEK9pnYz/5yp1+z/f1IuTxsbLXzQqFEwRBEFRCqQpHa0yL06wjLYr11luv\nqe3VqwDefPPNgfTUNzvF/+f1G2JX2SrIVVuuunJfar1MmLyyvFG6kW0keTah9RCuIuiKjOeeey6Q\nFIzKxliL3Ra0zvTRG3+w3ssxssZA/7eWs4rGTEGzmbpBXmO2wQYbACnjymvJtX7MUsqzF3fbbTcg\nrQllN3FVpQonzwDzGlJdVkk+F71WjK0aq9EK93rOa4gcG8kzsewjlnfebpROXjvWCKq+PA+u9eWx\nutaPY1KkPIzVGZvLu3BIrnjya9T5UTahcIIgCIJKKCVLLbcAfCpb9bz//vsDqT+UvvnrrrsOSGt1\naN394he/AJLfWuvPDBozeorWeimq2s33cwDLpWNZavlKnFoqZmY5ZnmvrBz3udOdbtvJwCmqsleZ\n6Cf2GFz7xZqSG264AYBnn30WSErG82Qml5ZrPg/srWfFub594x9mKfXZf6A7vdTE+KPzwAw9a9jM\nQlpiiSVqvmdfOlX7NttsAyTfvWvTP/nkk0D/FWCtefKcGBs0Symnyk4DqrM111wTSH2/PP9mpdpJ\nwLiG59FjyLPLWqXV6vr/7kNDY+G9yxib8Wjj1F4LOd7r8sy9qogstSAIgqCnaErhDBkyZPhYY43V\nb635bxClKxytIn2ixhns52XsxrVecmtMy9PaAuMcnaYKS7ZIWajyVES5IinCTtrGgFTGjnUTXcNr\n6GQdTqP7Yhdg54kxHnvsWV9hPMvuDVbp2ynZeZV3rmiUbigc99XOydZb2fdLRa3yKIq1lG31VzEW\nxq3shJ135TD+6bo57dLpayQUThAEQVAJHV0PZ1ShT9foyjoN5P5gq+tdD8X1S8zoci3yqnyzZVpv\njXZO7lXKHAv7BFpZXjVmctrdoR55TKdKhdPrdHIsvGasMbLrgurNWsKy7gcbbbQRkDJ+myUUThAE\nQdBTtOTIzatUc7pZ89EMZWWvtIL58fZCskeWmEef15aMivSKsmnVP10m3VI2orIZYC2oASnKVusk\no8r9o5N4zZit9swzzwDwwgsvAMlD0uh5rIfKptPXSCicIAiCoBLaiuH0gsU4EG3sV+XdorVQtCSt\nw9B3blZS1YSvPhFjkYixSMRYJCKGEwRBEPQUTcVwRhttNCaccMIRueGNKggVhzUn9VaLq7faXD16\nTXGNDH2v1ln0qmpshk754PMeWqMivXp+I27SW9TrIzmqEgonCIIgqIRmYzjvA693bne6ztDhw4dP\n0sgHv+Fj0fA4QIxFX2IsEjEWiRiLr2nqgRMEQRAErRIutSAIgqAS4oETBEEQVEI8cIIgCIJKiAdO\nEARBUAnxwAmCIAgqIR44QRAEQSXEAycIgiCohHjgBEEQBJUQD5wgCIKgEppq3tlui20bVH7++eft\nbKaTfNBEa5tvdIuGdlqvf1MaDUq0oU/EWCRiLBI9uTzBAgsswAILNLTcTLf4pvY6qsuQIUNGdAxu\nlUGDBjFo0CBGG200Rhutvy1T9H697XXq80E1DB48eMS6T52k0+e/2fk7EP/rc7StBdjmnntuAJ54\n4gn/D/SeZesk+fLLL+t9tPIF2MqmrHNQpfU2xhhjAPDvf/97pJ974IEHAFh00UXb+bmmCUs20Ytj\nkc/5evOp6Bqpd+3k/+/FsegWPalwgiAIgv9dmtKHM8wwA8cddxxrrrkmkJSNtLtYkLLbRcnKogFl\n842h19RlX1w22xie57meshl99NEBOPHEEwfcnstzt0ruSoxFyKqlUcVRdH/Iv5fPJ+fPf/7znwE/\nX7SdZv8f1CcUThAEQVAJbcVwuk0HFNEoH8Mpi3b802UtBf3WW28BcM011wCw0047tbW9IhZaaCEA\nHnrooQH/301fvWM55phjAvDxxx+XufmmaXYsRhtttEIPQ6/GfIvuKxHDKT5nEcMJgiAIeopKFc5U\nU00FwNtvvw3AzTffDMB6660HpDqdL774AoDnnnsOgPnnnx+AI488EoDNNtsMgMknn7xme0V8+9vf\nBuBvf/tbvV0cZRSOVthPf/pTAH79618Do1aWmufb83LYYYcBcNBBBwHlx/JapZuWrGNwzjnnALDn\nnnsC8MknnwAw33zzAXD55ZcDSQU+//zzALzyyitl7k5LY+Gc9Drs1Tq8Zq+dXlY4RZl6ZcU9c0Lh\nBEEQBD1FU1lqQ4YMYfzxx+fDDz+seb9e3vsee+wBwCKLLALAtttuC8AEE0wAwCOPPALAlFNOCcA4\n44xTs73XX/+6HlPLY+mllwZg7bXXrvmcVv97771X8/sNKJuO0W6cadZZZwXgmWeeAZIVJldffTUA\nRx11FJBUpMc8xxxzAPDwww+3tR/tMOmkkwJp399//33g66xHgM8++wyAAw88EOg9n34VmBlnzZi1\nRqr8F198EYCPPvoISCrh9ttvB2DaaacF4JZbbgHSGDZRg9YRBg0aNGJfcmVTdgxH6937ymuvvVbz\nOwsvvDCQ7jc77rgjACeffDKQ7jvOR7Pb6mVRdgO9Qk8//TQAM800EwDXXnstAPfffz+Q7rmO8T//\n+U8geRe8Bn/0ox8BsM466wBprP71r3+Vut+hcIIgCIJKaErh/N///V8/dQNJcWht5Rx77LFAUh7G\naLTiZpllFgAee+yxmu+ZmZMz0UQTATDJJF+3PdP61xLRqtNqLLKgrL/oRN3F2GOPDSSLQooyuFSJ\nU089NQB33XUXANNMM81If0eL5O677wZg/PHHB1JcS9XYTdXgeXz33XeBNO4zzjgjAMsvvzwAe+21\nFwB///vfgfpWeSfPX1WogF944QUA3nzzTQAuuOACAGabbTYAttxySyAd6w477ADApZdeWrOd/Dx3\nuwZtZPOu0TnptSHGrU477TQALrnkEgAefPBBAOacc04gKWtV/yabbAIwor2WMUMz/xxzlc5cc80F\npA4X3biGvB84L9wH73lPPfUUQL+WO4svvviA21PZuJ2XXnqp5m9rLMtWNhIKJwiCIKiE9jrR/ReV\njVljWrJaFvrstThyfvjDHwL1OxX4vurh1FNPBZLC0gpo1KrrpGWsslHVeexFtSmqs2WWWQZIyqQe\njpGWi1ac7xsX2XnnnZva/zLRGtt6660BuOyyywC48847geRn9v+rrbYaAMsttxyQ6mPMxPv9738P\npPN80003ASne5f9VidIrWW992X777YF0nq666iqgf6zu3HPPrXnN8drTMjWLbVRWf2anemwzzzwz\nAPvttx+QMq3WX399IMVk/LxxTOebcYlVVlkFSGP0xhtvAEkl6oVwPqlwqmCsscYC0nl03+See+4B\n4NVXXwX6K5tGyeeXf//2t78FkldChfXyyy+39Ds5oXCCIAiCSihF4YjKRqwUL8JYjJk3WqAqIrPb\nrMvQtzrZZJMBSUEZxzj99NOBxrNKOtW7rS9Fqk7MhFGd7bbbbkCx5eK+ouhygQAAIABJREFUrr76\n6kAa83feeQdISueAAw4Ako+3SnKFqoJxX8y4UsHk1paK5dFHHwWSCnBMNthgg5rvqYgmnHDCmu3Y\nO0sL+LrrrmvzyMrHuEGewVUULyias84Dv2f8QWvdrKWq6Zul1ve9vq8ei7Fc41l6CYYOHQokZaOy\n/etf/wrAeOONB6RMqzPOOANI1rrXmPV7ZrM5Nqp/e0MaQ+xGdmt+Xr2eVXt6c3ztFMbZy15KIRRO\nEARBUAmlKpxm0Qerv1JLSAXj31oqa6yxBpB8+X7/iiuuAJJF2yjd8OlrhavqPMYpppgCSNadaJ0V\nZdxp8Tpm1h74ea24KnGftUxzlWd2WhFasFtssQWQagVWWmklADbddFMgxbmK/Mvux9FHHw30psJp\nturezDznbq4Szj//fCBZ/Vr73aLvfK1XE2R3BI/JGiTVmnPa82q848ILLwSSEl5rrbUAWGyxxYBU\nq6YStuu4XRi89rwP7bvvvkCKETfabbodHn/8cQDmmWeemvedHwsuuGDNbxcpj0bj4PXolLoLhRME\nQRBUQle7RWvtazmYGfHBBx/4e0CyjKxJOPTQQ4HU5ddq+lw15DRQn9O1XmoTTzwxkOJX1tUY5ygi\nt77yHmvDhg0DksVrrEeKalnK6BNl9fuZZ54JpHqbIivLOIQWZ7MUnXfHJq/naGK7PdszSyvf7DYz\nsYyPtnvsOVWMhXPYbFSzGV1hWOv7kEMOAVI38byDhUpKdeD1b78556d96FRA6667LpDqArfZZhsg\nzWMpYyzqxZG9L6j+vI6LYrzGvfT6nHfeeUBSc0sttRSQOpOY0VeE/zdeZtac2WsSvdSCIAiCnqKr\nMRyzRbQcrJq2ctj+QObN67vXL22MQCu9nlrT4imqyq6C3LeqhZorjxVWWKGh7eXKRkvJnkr2hSqy\niHJlM2TIkNJqN4wnGbMx9rb77rsDaQzMCmpV2UiRf3vVVVdta7u9jOe/6BjtyF5FRmaz5NdCHuNR\nvavO9IA4j6zvUtmYxbr//vsDaW77uSWWWAL4//bOPN63udzj73OcdAhlSskQKrMMSZFMkaSIuIYy\nZHZD3FDqkswKTZJS5jGEzEXGRCVk7KqkNFHIkFucc//ovs93/56z11lr/aa96Xn/s1977/Vbw3d9\n1289n+8zwSKLLAKU6tXm43g8832MWovKpp94P1ZffXWg5JC5emOEp2oudr0VFYgrGo5R7J+kv+vq\nq68Gpo8sjhhZqh82KpsZ9TsajVQ4SZIkyVDoSeFES7JOMWhlabEYmWEklVn25t+YZ2MvENdu119/\nfQCuv/56oPh8mjJMKy9alrE/u2urWneuW1edo2pOtOLi9ion16FVEfrNqmol9UPdeG3iWrnnqFXu\ntah0u8V5aP6VlrDWoj6ApoxHNSDx3MyXqOLMM88EulfzvVZ0Hi0PR6rqvnlM6wJqZfs9cdlllwFl\nLFTQVn3Wh+Ocd7XAaEX9oieddFLHfrTex2Llw7kqVrS2Ppz/jyreSF0j+VzRqKuFpiJyHsVnVl9Q\nVR6hx29bqy8VTpIkSTIUWiuckWv8bS0BLVkjL8yijVaUNYy0hLfYYgugrLUusMACAJxxxhn/uoj/\nVwdt+1YMw5KN+1Zh2J8mRonUWQyOfV08vWu3VtRWFQ6qCuxIqnrBH3nkkQB84hOfAIovrtfxN3In\nVhd3zb7tPB2PysZVAVV/XSdPrXej18aqWvjUqVNbqyR9KUbaWVXeXDN9u/o9VXGuDqiMPK6RVQcf\nfDBQnnv9F4cffjhQvldi/bJ+9+1pgvfbYxtdFlHRxB5gdbi6EJWN1+g8q6LbsUiFkyRJkgyF1gqn\nlzV+FYqRM5FoWdrTRav/Yx/7GACXXnopUCrsGpHVlmFasloUqjEjslxnbtqZ0TXVOovmvvvuA4q1\np78rZqoPEvOm7r33XqBkcJvx368K1uYcRPT5mV9h1V/ztV4MGEmlNW4kVhWxSnivPrl+WPVN9+Hc\n1LrfdNNNgeKPNI/L/8ccMxWOaL1bkcLajocddhhQVlgkKpux7JYaq8pH380OO+wAlA6vbfHZjLj/\n2MerX6TCSZIkSYZCa4Uzo6iTOvyca+vWKrJGmhapUWq/+c1vgOKbMWJDS8iokm4rmg7SgnENVKtK\nv9XDDz8MlEoAWqJ2KaxjtI6ro+Fxjed3DXhQyma0eaGycU3e++Q1xHFv61Mz32Ldddcd9f/Wodp4\n442B4guwkvYgqers2hTnphFWRi2Zr1E1531m6vIrhhWJN2HChGkqO+aERGKtNPtsWSvP6DJ9t1ba\n1jfjmHlN3n/vgRUFXGlxZUSF5Hb6jqM6HDnm/fbnLLbYYkC5Vr/jPBd/2q3U/BxXgZqiWtRfFdF/\nrm+oXxUqJBVOkiRJMhTGpJaa1p/9s+2PouXrWqoWhpnpxxxzTMd+7H+jJWTPD2PMu7BC+lZLrSqy\nRevLn/YeN2qtas09RpPUWabxuP7umO2+++51n29dJ6pKMZonYWRVrHTsuRllZmSVytftnTf7778/\nUPokRcxNcI3+pptuAopPoG3e1ljUUlMRq1S1OI3cigpHa15rvYqq2nlNFU8/xyIe02taccUVgeLn\n1B/pasCuu+4KwFFHHQXAzjvvDBRr3PlkV8z11lsPKMomVriIuWxWMLFHVRyr2WefnWeeeYYXXnih\nb2OhgrFrqf6p+Bz7Heh20W8ViV2Yvf/mb8W8Pp/dOJZ1ZC21JEmSZFwxJrXUzAW55JJLAHjwwQeB\nUifIjGDXcq0jFPEtvOWWWwJFMe24445AeVtXWXWDJFoGWv9aqvqp7r777o7tq8616Vp7lT/KelKD\nzCWoOrYK1jwsFYjnEqsAe/+NlFGxmi+x7bbbAtNnSbs/P2dEl/tvq2zGEiPpjKg66KCDgKICHJND\nDjkEKH6NOlzD1y+qZe1Y+ky1zWnrhjinvX/OVTu++kxsv/32QLmvWulRIYn+rujPcjvVgWPivNEP\nFlcV/FzbHkZN8LtOZasvJWLlaqstOCZGasY+NvHaHauobMT5NKjviVQ4SZIkyVDoyofjG97aZ0bQ\ntNgPAGuttRZQLBpzTKz+6s/zzz8fKJ38xOOa12HNNS1o12hj18wZqIXWPhyznmOnzoiRUlaidZ3Y\nSKu6CJ6meG/M31B1uM5tf4y6+97NWr3qrc6PUEdUeZdffjlQ8nbsFWRUkXkWWr7m+1gR15p9TRml\n/l3ffTixj9GIzwNlztubRfbbb7+OzztG+jPqqFIw8ZqtqKwfRNqOxcSJE6dFk6oc6vjgBz8IFF+e\nfgjvt+fqCol+UM/d741FF10UqM4pcdVB32FV7ksVg/TtGa3mNUT0h/odp4qP52xlk2222QaAY489\n1vPp2M7POdZtKxekDydJkiQZV/QlSq3bWkMLLbQQANdddx1QLBUtGH8aZWTsuG91LV0tXyN6Yr2x\nFufV946f1nsy4sZupa6VqkBiFem2+RHm8dx1110df9eSNR/HHh91jMcul3FN3bV317vtdmn/kqpe\nQZG6qufDGIs555wTmL6qd+yTdOuttwLlWrVI9flExSSqxlVXXRUoPkSVtzimVTX3BjkW5q55Ld4X\nz10Vp7L58pe/DJQcFtGvYZ5OvJ/xfvt722duEGPhd1dVjy+/L1Rn+vJiTUb9U/akqqr67P5uvvlm\noKxatSUVTpIkSTKu6CpKzfVj+5wYhTRtpyEfQwvCn0Yrueavv8GfVjj+4he/CJT8i2jxGIFhFWIV\njlFObdchB4HKJtZS06+wzDLLdGzf1MrS8tVyida/aP1r6QySQWevR6vPNXd7/ujT0+9x4YUXzvB8\nYv8c96t1OKh6UqPhGrx131xzj6hsxDkvXrsqwGfDKKall16643dxLPqdWd4E/QrnnHMOUHw3Rt65\ngmHUmhUDYi0082a8NudjVcUA/x8Vjj4n1cMwIvakLq/G7w99OH4Hx+9IfblVFSniisoDDzzQw1k3\nJxVOkiRJMhR68uFES8G1VN++Khzf2sbNn3DCCR373W677QA44IADgJJXs8IKK3Rs5+e1SK2U6jq0\nForr4dZq23zzzTv2M4M6V3334YiqLq5PR+tqww03BMqY6b9SzVVZLK65r7zyyv+6kP+39mOPmKb0\nY31aq8nIvF5xftlPx4xzr9H7GvNt9BXGasDOfbP3q+rUDWKtPvoXrfxw/PHHA9Nb5VHdxXlg9OHR\nRx8NlOoOPiPRStfXE+vcjWVklh07vZ/3338/ALvtthtQVj78v9a+12IF5bPPPttzrTqvjt9jHk5T\nBjkW3i/vT4Nz8TiNtvc7O45ht6QPJ0mSJBlX9LWWWqzbE3MN9NG4rrzVVlsBxZq3ntjyyy8PlLev\nSuSGG24Aytv5uOOOA0qUW8T1aK3FBpUGBqZwxOquWmteo7S1VOoyh81NMfqpKb1Yb71WSo54v6Mf\nrM4ijWv09gQy/8uIHCN0PN84b8ciYk8f3d577w0Uq937rVpbYoklgO47ubatLDDInKStt94aKNes\nD1fV5v33e8Tn+bbbbgNKNem2HYm79T0OY17ol6rrwNkUxyZ+70Sq8sSqSIWTJEmSjCv64sNxH0aR\nrLTSSh1/N2JGhWIugb4Xt7NvhtnN66+/PlDW7H3rxn4ZkR6ipQaucIweca1+zz33BKqjg6KfTEvW\n7auUTa+MpzycGDXW1N9gV0M/F7PmmzKexmKs6cdY1OU9GX1mRN6JJ54IlOoc8XtFBWS0bKwKHY8T\no11jBfem9DIWTb+jrJriOavu2vYAq1sJ6ZVUOEmSJMm4Yij9cGI136rM3/j3qs+95z3vAeCaa64B\nuo+TH8XKGLjC6RY7P2qlW2tpULwUrHrnlfle5jzV1fSKiuqlMBb9opexaFq13W6W+mZ22WUXoDwD\n1hezeri1FGPVjl6rd9QxlvNCH4xz1ZUTK1QcccQRQBm7pnRbNSYVTpIkSTKu6KvC6fbt2JZoKVVF\nRZmF2yLLftwqHLHbZdPqwBEj+upqJr2YrHrng/PPCC9zUVzTl1iJoI4X01i0JVYFsaumtf4i3YxF\nXZdRf8bKJLF/klUzjII1p62q02yL8wSqV1iqlNFLeV60JRVOkiRJMq4Yig8ndtjrV35GvzDy4+mn\nnx73CmdYDNN623fffQH4/ve/D8AWW2wBFJ+L1ResN+bavjko5mPFfkn9op9jMaxVgEHRzVjEnA7H\nwKhUe0HFvCkxItNKI/Zbisq139Tdq1Q4hVQ4SZIkybhiTH049u+u6zXftJ9JjLOvq6U0yv9fMgqn\naURQFWNpvXm/rZllLbaqzp0xr8K1/L322gsoGevd0s+xGHRF7UEzjLpyvc7dOqruQdsKGalwCqlw\nkiRJknFFW4XzKNCsMfmLk4WnTp06b5MNX+Jj0XgcIMdiJDkWhRyLQo7Fv2j1wkmSJEmSbskltSRJ\nkmQo5AsnSZIkGQr5wkmSJEmGQr5wkiRJkqGQL5wkSZJkKOQLJ0mSJBkK+cJJkiRJhkK+cJIkSZKh\nkC+cJEmSZChMarNxVQG6F3tBwhE81qK0zUu6REM3hQlfrKX355xzTqCUu4/nn0UaC/9OY1HX2O3f\naSzqaDoWrV44VbzYXjTrr78+AFdeeWX810u11tHAmTBhQmW1bvus/+1vfwOad2asqxrscfwZ52HV\n5+P52Y8lMv/88/Poo482OtemaJx57H6/nCdPngyUsfjHP/7R6HzcftCVmmHwhkm3+49jUTVPR871\nQfNiNeKqyCW1JEmSZCgMpePnoK26PjL0fjjj1YIZxpKa88JOnj/72c+A0hnWDo9NFXTd0m5cIqk6\nXztMqg4G0fHzla98JVDdtbKt0ohdNZtSd8/syjliuXFoy0j9Ult11xjvd9XnXvGKVwDwzDPP+PeB\n9waq6hUUFWnTVQOfrZVXXhmAhx9+GIBHHnkEgC233BKA0047DaieV/HeZD+cJEmSZFwxEIVT52wb\nx7xkOn42JVpt0tZ6m9G6tn6FZZZZBoCf/OQnQL0i0Yry856jn9t8880BOOecczwPzx2Aj3zkIwD8\nz//8DwA333zzqMdbdNFFAfjVr34Vr4upU6e2GouZZppp6iyzzDLdeNZRNRbRkpxtttkAuOqqqwBY\nffXVR/1cxGfSMdJijWPmWD/33HOj7mcQ3U/7vfLRtANw3d+rfIMyCIVT9TyOsj+gjKEq7TWveQ1Q\n/KWvf/3rAdhggw0A2GWXXQC44oorANhqq60AuOaaawDYZJNNgHLNTebV888/nwonSZIkGV8MxYfT\nbwbo9/i3UzhV9EPhtL1P0bL0c1rnWvurrroqADfccAMA3/3udwFYeOGFATjzzDM79qO/5M477wTK\nuvUPf/hDAOaee24A/vSnP416Xr1YslEx1Fnf73//+wG4/vrrATjkkEMAuPfeewE49thjO4533nnn\nASUSUL/Xfvvt1/G70XZarCqm+eefH4A//OEP8ZpHvb5+zAvv54j1/6a77ApVQJxfnsess84KwNNP\nPw0UX47z5sknn+zYXzfKt+33Rbf+UD/nNb3hDW8A4AMf+AAAp556KgCLLLIIUFICbrvtNgC23npr\nAH73u98BxZdT509LhZMkSZKMK15UCse37EUXXQTAe9/73o7/u2754x//GIB111230X5HWBMDVzh/\n//vfgRIt8qUvfQmAffbZB4B3vvOdAPzxj38EimUbz1Wi5bHiiisCcPvttwPdW4+9WG9t1+bjerTb\nO0YxL8LImaOPPhqA1772tQBstNFGHZ/XStPHc9BBB3Xsxwgs83D6ZdWP9vc3velNAPziF79otB+V\nkWPjuarqXJv3/16rSuorX/kKAGeffTZQrtExdgy0cH12nEcLLrggAL/97W87zqsf0YuDjsz0Gp0/\n8803HwCnn346AN/73vcAuO+++4Diz1Ipq3ifeuopoNqfMp4SP/XhqGi85pe//OVA+R6JCsX7v9Za\nawElN/E3v+lMSfQZjD5ASYWTJEmSjCv6Ummgile/+tUA/PnPf+5pP3vuuScA//Ef/wGUNXzfulpK\n5nFcdtllwPSRP77Ff/CDH3Tsfxg5MK4X33XXXUBRMHfccQdQIq4+9KEPASVaRCtNy/XDH/4wAGed\ndRYASy65JFAsGqNPtETOP/98ALbYYov+X9QIRqs0IHXj6/+9TzEPx7Ez0uZHP/oRAF/84heBomhF\n6+uWW24BiuVqhJf704r3OH5OK7Af2faOhcqmqXWvH0HfjEpYRSvux+gk/VP/+Z//CZRotpi34Xwy\nv+b3v/89UMZExaQv4O9//3vXz4mKdEReU1f7qUIr3Z9zzDEHAJ/73OeAcm033ngjUCKzVI0PPfQQ\nAH/961+B4hfbeOONAfj1r38NTO/nasvI56LfY+Bc9Vz9Gee0+N34hS98ASjfiYsvvjhQVoeWWGIJ\nAPbaay+g3MtuSYWTJEmSDIW++HC0wrQQIq6JalW1zVEwWsQ8CS2ZaEmL16SlY/RJA/ruw9EiePbZ\nZzt+am17DVpj+nDe/va3A9PH5S+77LIA7LvvvgCsvfbaQLFwXZvXmlxppZWAkovSlDbr0y972cum\nzjXXXNOUbLcZ4jF6SRwjlY9jqPX1vve9Dyh5N87DTTfdFCh+M/0UztfHHnts1POIlmibsZg4ceLU\nSZMmVWb8ty10e9111wHl/t50000A3HrrrUAZE31EO+64I1DuwU9/+lOgRB+prH0W9RXpA9DXY/Sa\n6kCG4bdo6+NRlTkPjNBzPvksOOaXXHIJUMbEMV1zzTUBWG211QD45S9/2XEeMaquzVjMPPPMU+eZ\nZ57pVFKvhY+j/9P7Hr93qiJIP/WpTwFFETs/9t57b6A8Q6pCx/Zb3/pWx37Th5MkSZKMK/riw6lS\nNiqTv/zlL432o7W2wgorAMW6822sBV2lbMS3umvzY4k+FS1QVVrM5P3mN78JwIUXXghMb6kstdRS\nAGy//fZAWXtXAcWMY39qxXdba6sJL7zwAo8//vi0+9JW2cTIqSrc/wILLADAZpttBsAOO+wAFOV7\n6aWXAmWMVDgS52NUViOj5dqutU+dOrVjjKO13tSSVekaUfWud70LKHkRWuWxzpcKx2tQzemv0ML2\n2dQfql/sPe95DwDrrLMOUCzabi1wM9Hb4DXVWf/zzDMPAN/4xjeA6SOyzJ+xTti73/1uoESn+czF\nGmqOperP+TPyvNqOxz//+c9RfUBt96NPbaGFFpp2LiP389a3vhWAe+65Byg+4vhMOue9/46lqwA+\nW/q9dt99d6C6hUdTUuEkSZIkQ2EgUWrRujKePeZlaP3Zn8a1VSNk3vGOdwAlCsnPaXFogcS3rVbA\nIKz5OqLFoaWoD8W8Bq10M8ddL1aJqPa02lxzP+qoowD46Ec/2vH/aCl5HkadaMEOgmjVR+p8OnVW\nXlRO5t8Ytaaac54dc8wxwAzrgY2637hW3w0TJ05k8uTJ01nFbbFGmvlZqnvzcCKqCK9ZFed9X2yx\nxYBi7Ts/tLpVwlrE5mP0Gk3VTT1F72fVnPK+GUVm7om+HK1yf1577bVA8Tu48uGzpno0skuFVOUD\nHov+X16zysN8uze+8Y1AUTyeqxXY9WtZK01ls8YaawAlctf7ZE7bz3/+c6DMP5W29Qi7JRVOkiRJ\nMhRaKZxZZ52VJZdcclrkSxVaAFoMEuv8mAG+4YYbdvzft7D1fUSr3zV7a2aJb3cVUmQYvWe89jPO\nOAMo68Na+Vph999/P1CiRGLuh3k1V199NVCi2MwcV9m4Tu32Hs//P/jgg0B11FE/qVpz7zWfxbpP\nRg9ZYUILVave42jBNs3/6SdTpkyZ5kPsBmupqWDN2zICrw7zddZbbz0ALr74YqBU6FYFeo5xPvSa\na9ILsXZZVeVkVfuBBx4IlAg+n3utcH15oq/ZzxuRZ/7eySefDBR/l7X1hpGnV/fdZJTYpz/9aaAo\nGhWvdQHN0/MZNELYsXXVyXw/lbhqcttttwXK95PKSB+0UWwjz7vN+KTCSZIkSYZCK4Xz7LPP1qqb\nGeGb0CgR1wvj2/3EE08c9fNW0B3Rca/jp+vT5p5UHX8YmJmrJeFPoz1cQ61ap9YC1aqP68hGi+y/\n//5AqQLr+rdWv9biMPxZVQqnW2WpKnTd2jV777+qzuOaS2CkTbcMMiO8ClW/qt376N+1xqtYeuml\nO7Y3umz22WcHyv13laAqF868iwsuuKCLq+gN1VddhRJXOGJdLxWPqt5rjJFVqn+Vjj5iq3G48hK7\na/aaMzMjquaZ989qCEaT+f0Qo19V+T4zKpK4yqB6M5rthBNOAIqvxu1VRo5p0/OuIhVOkiRJMhQG\nWkstYsdHI7S0GESLxcitWPX1lFNOAUqHRlWC1r9Z965LDsNnU4Vr5q6JX3755UBZQ62L3tHaq8Ix\n0kqLdeXuvvtuoLse992M14QJE6ZdUxz3bsdf605cr951112B4q8yIsvILhWOY97WIu11vnQzhqp9\n0Q+lcjn00EOBUpPNqEZVvVa/98Dt9Fv4d8eiKi/LPDCfuZjDNAg8F8/N3j3ef/+ugvX++/2g+rP+\nl/XkVPla6foztN5VNl/72teAsvpQlZ0/MtetXzl+sY+N5xZzDe1n44qF88XoQn03jqWV0Y844gig\nqEWrKVgN2nqDRgjHnkEeL6q9bnOSUuEkSZIkQ2GgCsf1xc985jNAqfZcVSlAq94IDCMlrAqsFRfR\nEmratXAYGFklnqMqTItBy1NLx7yJVVZZBai+Bq03I3litnRVpF4dPfTP6XkfopWm/0r/lH4x/Vb6\nKfRb2CNGq+8tb/lXWbyYx9XmPLrJI+lG4Vhdwxwj57r318g8e9JHFam/wnwvLeBYFVqqlG/MdZNu\nx6IJWsjzzjsvUBSOxzOK1cg9o1jjs2N9OXPdHDt9Qq6EqBodGxVO7IsUx9jjvfDCC337bqlSB34/\nOCYPPPAAUNSa52b0qc+MY+P9XW655YDSDVc/uD6e73//+0AZq6qVlahs6s6/ilQ4SZIkyVBopXAm\nTZrEq171qukqH1fh29NaR3F9UHxrmt1slqtv+braaf5fVaClMx5wbVUrvao6gnWdVHfmElRFs3nN\nxueL0U1We30xYS00o9H0U3gt5ghojbm+rFVm5M0hhxwClK6XUU02pdvIvilTpky7DzEPqyonyXwb\nLdU777wTKDkh+j+15mN3VCOv9BFahcF5ZF3CbhlklKNjouKI9QD13Wjtu73zwO0OO+wwoHzvqPJU\nd/r2rNTuWDk2satlVYXlbtXNSOXrXK+KPnSu6oMzJzHOdfvYWC3B+/Sd73wHKCsmRh+qiBwjV14c\nG1VgvEbHukXl/VFJhZMkSZIMhVYK5/nnn+exxx6rVRxy3HHHAcWHU/W5WCcoouXj+qQ/fQurtFyr\nH2S8fFv0M6hEosWrZWL0iOvNWnMHH3wwUOLp7QyqFb/TTjsBJQ7fbqdW/TW+/sWA68wrr7wyUCJt\nzLeJa/eHH344UGrxWS/M9W6tNn0Adv6sUhn9nDfRp1ZXbcHIKi1Xo8S8Vv9uxYnY40Vl5LyyX1LT\n2lfd9jBqQ1QIsbJIjIjSX+HvPgPOkxjZFStOqGSsN6Y6MMfIytoqnEFXppg6deq0c44+NRWPf3cu\nqiyc2yoY67xZZcE8P78DVX0q5Ntvvx0oUWt2+rSavdtXobKJ97Ctby8VTpIkSTIU+tLxswpzRVxP\nNmqtqUKqw1hyFZTWwUUXXdTtLvve8bMOI7Fcg7d2WuzDvskmmwDFwtHq0yekyjMj2L4Y3a69D6Oz\no3gNrjs7JkYrmT9hJJZjZJa0f9fP8brXvQ4oY/Lxj38cKOvhTWutST/GIqqzGXw+HhuYPl/DMdMC\nNkPcLqhub37FNttsA1TnmDRlEPPCsfGc/V1/phF722233ajbqw6d+wcccABQngHzs6666iqg5HM5\nb4zI8xlsWgtvkM+Iz7c/reKtapPPfvazQMlRjHk8XpM10bxmx8qigej2AAAgAElEQVRK2j5TKpkq\npVs1j7PjZ5IkSTKuGEgejm9J8yN825o/YU+XKmLtooj5NlYc0AoYi/43dXiO+lh22203oESl2ckz\n1gUzgsb6TuI6tZZOtIjN84kWrGNkhz+V0yCostLj+q8RMvbkMEdAJeLYeO5aqq7lb7TRRkCx3l3z\nd2yM/Io1uaqse6OaBlExucpibFqVIT4TWqr6cvT5xLV477fPhp+P56Nicn55b8xtMnK0n3hfPWet\ncf2XnrNVM4zc00/h5+1zo9JREZmd//a3vx0o9chUznZNdWx7qfLdlviMqBz0xenLNZ/O+xYrWVsl\nWuI8cl54v/1eiZUKHOs6H15VNZGmpMJJkiRJhsJAFI6WhBFSRkR8/vOfB0qdsT322AMoMeFaU+ae\naGUZZeJbXl+Qlsl4iEaLaH0ZB28UmrWLtExde9XCOPfcczv+b5UFP6cV5tgZvaLPJ1aV1VJyjFQ2\ng8xZ0uqJkU9R6diNUB+LikSr3PphZs97DdEK0+dj/yX/b/6Ox6vKx9G61MIeBFWKs2nuR9yPlrDq\nIFZQj/tbfvnlgaIOxGcq5sAY0aWymXnmmfu2guC5aa0bneZc9rk3R0VrXF+LFSR8NlQ2PjMqJP1b\n5qpYJy5GXKkChqlw4jPi2Pp36wMahWr9yVh3zrkc57TXpur3+8Br9xkzErRtzbxufYCpcJIkSZKh\nMBCFY7SQlqcZ477NjYzQx+PvWhj24zYyQ9xPr9muw8DIKhVGFdFqNL7eunMqGf0WjuExxxwDFEvD\nvu5G6mmxWjXYmkoyCGUTreqqysSeq7kD1rJS0WhxfvKTnwRKdJFKyPwJFYw5J0ataZU7BrEWljiW\n/l912M8q41HluW/rgnnMGEWkdW5OknNfa95rMQ/D+RYtXv0fqse6qgtVqwUxr6gXHFeVjQrTa9bf\n6Tm6nfky5us5t93fiiuuCJRcNTt52lVXf4jXoprzeydWbxhELcbY1dR5seSSSwJlzuqjMXJTf6b+\nym9/+9vA9F2VxWfOKg3OE//uvHA+Vvn2qhip0LPjZ5IkSTLuGGi1aLOczQ0wQsIopNhzXOzYGd+c\nRnKNJ6qs4RgZ1dRq1iqr6qwa13o9jmOjBWV1Yf1jWoveCytx94vRKiT7u+es2tN/dN555wGlCrRr\n7+bJGDnlfDDDXOWrlee8MuLG9ei6sdaqG0R0Y7SWI1aYsAKF16xfQhVnfTDVm1a5fg4jsL785S8D\nxZr3vts7JuauxP44MUpNmuYPzYiqKgZR2ahoVb5eo1a6vhgrTKhU/LzKR1+c88ZnJKq0WKsx+tMi\n/ahEUVWN2efRigPm3TkGO++8M1C+H1REPs/33nsvUOaHeTaumDgmPhtHHnlkx3HbXlO3FSlS4SRJ\nkiRDYSgdP7UMVDZ1uIYbLQ0jN8YTdRVljcSJtZOqiLlH0fJYdtllgWIdqho8rtnYrvU7ZqqDfisb\nmZGacN1YS1Mlo/WuMnFd2+39ad6E69pGL2nptq0cIFUWbT/W7uO+/ek1bbnllkCJwFJlWf/NnBO3\n875p/ZuFbx6G+V7mMmnBxugj54s9YyQqm352/Iz+K8fXY3r/jGbVmveZMS9KP4RzO0YfGs2q2jMC\nVL9YpOraqlYjRt7TbudIlZJwf35H+ryus846AJx44okdv9vd1Hlifp9qT/+4ylUf3kc+8pGO3+uu\no2osuq29lwonSZIkGQp9UTjHH388UNZaI23XB12rjZx//vnA4PwQg0ArraqHvKhs9G8YRaIVZoTW\nPvvsA5T1aNdmtRKtlOzY6NNxDV5l1G9GqoSYC+KxtcIvvvhioFQEMFLLnkFaTUYP2QXTeaRS6lWJ\n1GX/d3uMkX3e4+e9bx5bxaqisA5cVLLWJYzRRv5uFWCj32KEnnkYkVirzfPuh7KpOlYVVtVwTqtk\nvFZ7wqhwVb5a2/aeUtHUfe/UKZlur6MJdXlXqneVqr44vxeMWvV3n3/9YCpllZHRbiqgpj2iqq41\n83CSJEmScc1Aq0W3xdwQq7xGFl98caDE3w+AvleLrusBEi1M/RlGnb3tbW8DylqtXS/NWdEadM1W\nC7rX6KJ+VMKNvhGre5tToIIxw9z1ZuvBuQZvZM+gKkrURRD2Yyz0nXjN3i/vt9dufpVKVx+PCsio\nJa14fTp2y7Uu3SOPPAIUxWsE11lnnQV0Pz/6WSFZ5bLIIot0nLO/77777gBsvfXWQPl+MDrR3CXV\nm5Gdqsc6P0NVZF5ThllRXSWrn9P54+9+f9gt17E0otPvCVdYqqLlqujXM5IKJ0mSJBkK40LhGDtu\nzLhrs6Jlq8UyQIbWD0eLwUxyI3G07vVnVOFYWK9Oa1CL1egmc6FcD29KW+ttwoQJ0yLkTj755FG3\n0z+h9TVeiJZw9Ld1MxZGkanq6o454vMd/19wwQUBOOmkk4CSu6Yfy9p7UanYw97999AjqoNuxqLu\nO8Zr1Uo3f8aoRH3D+iOtS2guk6re742mqq3Or9pv5TtyLOp8OPHvfkfGXKK4vWPptTkWcZ7F84h/\nb0sqnCRJkmRcMS4UTsTIDN/mBx54YE/7ixUOZsDQFI6WiNdqPTAtU/uu131+UD3oh7k+3c/aZU2o\n81/E/w9zLCR2dI1jpA+nykeoMlJNavFGf0W08ofhz2qKimfppZcGSjZ97A3kM1B1X6tyimLFbmmS\nmzJ16tSBjkXbZyJubzRa0w6vjp3zLVYfryMVTpIkSTKuaK1wJk2a1FNdpSaYHW8F3EExivJppXB6\nyTjuFbOq7RXTb9pYb3PMMcfUVVZZZVr9rsiwFUzb40YrP+ak9GLJVp2Dx9AStQK6fopYmcLtzcew\nwnZd5F6dn6KKqrX9NmMxyyyzTF100UWnKZOmxxyrZ6otg/BnVSnW+Lu1Eo1OtEeQeTkqmzg/2q6M\nVPmOIqlwkiRJknHFuPLhdGuNNUXFNIOabEPz4Yx3+mHVj9hX0/109ble0eozVyF2fuzHWr15E912\nlez28/1WDWPhzxqxP8+hn7vtmm7Gom2txbpoxhHn0vRUuqLueKlwkiRJknFFW4XzKDB6YsFLg4Wn\nTp06b5MNX+Jj0XgcIMdiJDkWhRyLQo7Fv2j1wkmSJEmSbskltSRJkmQo5AsnSZIkGQr5wkmSJEmG\nQr5wkiRJkqGQL5wkSZJkKOQLJ0mSJBkK+cJJkiRJhkK+cJIkSZKhkC+cJEmSZChMarNxXTG+8VZc\nrwsea1Ha5kV7kU0YyyKN440ci0KORSHHojCQ4p0ve9nLeO1rXzvt9wkTJnRUEf3/Lnhtdvmvk5g4\ncVq/j27w8/F8qphpppmmVWENdF3rqOmx/x1wLKruy/LLL8/yyy9f+flJkyZN60AI/6qoa1Xd0Xjl\nK185rY9ME2adddZp1ZdHHm+++eZjvvnma7yfXohjNKzjVf0+DGabbTZmm222oR7z34UZfKc1Yljz\nIZfUkiRJkqHQUz+c2WefHYCnnnqqY7uqHuKxk2Jdb3nfuHPMMQcATz755Az3V/X5Fl32xqwfzqB7\nAbVlEMsFjzzyCACve93rRv2/XQUXXHBBAP70pz8B0/cEec1rXgPAH//4x6an2MGNN94IwDvf+U5g\n+vkRjzeIjp/2jn/uuedmuL9eO7uOdT+cXrrixnM/44wzAPjQhz7UsZ33y++Jxx9/vKvjteWl0Buo\nX/vJfjhJkiTJuGIgHT/jWzMqkW7fqn5OC/h3v/tdx37b7meU4/dd4dRd+0c/+lEALrjgAgBuueUW\nAM4991wA9thjDwDuuusuAD75yU8CcPjhhwNw8MEHA/C9730PqO5VXqcGI22st5lmmmmqqhZKV8qm\nytJz9hz33XdfAD73uc91bH/DDTcARZl0S5Uylz333BOAL33pS8BLyzlcNw/qet73YyzmnHNOoLkS\n0d/28MMPA7DBBhsAcN111wHlnLfaaiuAaX6iU089FYCZZ54ZKAq6X4zlvKi7T8MmFU6SJEkyrhiI\nwhkUWjr/+7//CxQLWmstWm/+vv322wPwrW99q+Nzo9BK4XSzPu3avef4hz/8ASjXpH9ixHE6fq+6\n1qOOOgooVrn+rjhGTa28bqw3ra6dd94ZgBNOOAFgWgRZ9MGN+DwAK664IgA//elPGbm/aMW97W1v\nA+ADH/gAADvttBMAc801FzD92ET/mJFojz76aMd2VbyUFE4ddasPwxwLfXTzztuZqRCj+vQB6xNe\ndNFFgaKImqqAV7ziFQA888wzjbZ/Mc6Lqvvrd6vq02ej398XqXCSJEmSodCVwhlWgqeWqcdbfPHF\nATj00EOB4s8wmsnt9H+st956wPQ+AhnFsh14lJq+DqOT/uu//guA1VZbDYBFFlkEgIUWWggo69H6\ncJZddlmgjI38+te/BopF4vr1VVddBcCdd94JDMaH41i09RM12O+ofz/55JMB+MxnPgPAQw89BMCB\nBx4IwH333QfAhRdeCJR5c8UVVwDwhje8ASiKZ8cddwTgpJNOGvV4/bBkB/XMOD+cT1r5zo8YBee1\n/+IXv+g4H/2iv/nNjFPRBmnVv/WtbwXg+uuvB4raf+KJJxp93lUC/aLe/7/+9a+jbh+jZFdddVUA\nfvjDH466/Sg5h63HYqyS410tWHLJJQH4/e9/DxR/6xJLLAHAHXfcQTfnmQonSZIkGVe0Km0jvvVi\nLoHRIAsvvDDQPndAi8Moot133x2ATTfdFICll14aKBb0uuuu2/H7gw8+CMCZZ57Zsd/NNtsMgG9/\n+9tAUQ+u9RrtMgii1W9u0jzzzAOUsTJHRWtdC/XVr351xznr89H6czuvRWstZh0Pw6KqUjb6TJwv\nVVb0Jz7xCQCOPPJIoCiQs846C4BtttkGKMrG/fz5z38Gylh9+MMf7tiv98CxjqhsFltsMQB+9atf\nAf0ds15zUfxpxQWfBXNPbr755o7jqKRf//rXA2V+3H333R37d+3e+RdVpfvrJZ+mjs9+9rNAUajm\nad1///0z/Jxz3RUMvz9USFXKJn7eMahSNtKP64/7qPIvumrTFu/f/PPPD8A+++wDlGfPyMBLLrkE\nKHPdZ6kuN7JXUuEkSZIkQ6GnKLVe1yP9fLRMVl555Y6/azlrxemnWHPNNYGyDnnttdcCZY1f5XLb\nbbcBxfL191EYuA/nK1/5ClByTFRzCyywAFDW2L2Wxx57DIC//e1vHfvZa6+9gJKHM7L22MjP6Z9w\nf45VHWMRgaNSfvnLXw6U++78ete73gWUa1f5asmq6rQajVI67bTTgOL7q2K0KMcpU6YMdSyiMt14\n442BonwPO+wwoFiqRnB97GMfA4pyVrGogFZffXUAbrrpJqBE+hmNdOWVVwJlno1llJrfA0Ytap3H\nqMWf/exnQPF/xohMrz36gLzPrhI4r3784x8DRVnVfa+Nhyg1r8UIu7nnnhso12KE6C9/+UugKGTV\n5Nlnnw2UMdMPVhXZV/Wdnz6cJEmSZFwxJnk4viVdO3Wd8aCDDgKKJaOSMX/G/xvJdcwxxwAlcsto\nJK0039qqhrXXXhuATTbZBCgKacS65cAUTrSeXafWmncN1e3qaqq5nfk3Wi4bbbQRUCwUI388rpZv\nHW2st4kTJ06dPHnydBFRTeeW69ZWjvD+R/9FxPyqZZZZBijzyOMed9xxAOy3337A9FZblb9Cbrzx\nRnbccUfuv//+vtdSq2OFFVYAioXqHN9yyy0BplXbvvTSS4FyjU8//TQAyy23HDC9f/WrX/0qUBS2\nfs+f/OQnQPGDeS8cs9lmm41nn32WF154YeCRWV6b+Vj6E7xGq2oYjVi136rjOqY+Y6p+1eTFF188\nw/1uuOGG3HjjjTzxxBMDUzhNx8xnZaWVVgLKfPA5P/roo4HyXav/01w5lZCrBHURplW5calwkiRJ\nknFFXxRO1ds4/t11RmshmSez3XbbAeWtqRV2+umnAyUHJb5VtYyNyDGT3d/NRDfjXWbwFh+YwnEs\nHAPX2lU23frBohq49dZbgRKV5LW6jm0kVhXzzDMPTzzxBP/85z+Htj7turFWuKhUq3rdRDWoInY/\n/l0fQB1VVc6HsVYfFfCb3/xmoKj5448/Hig+m3vuuQeAyy67DCiRXj4jPhuq+XXWWQcoysnVAvO0\nfHa89tGqNTz//PNMmTJl4GOhMjVXRJ+c99dqGt3WRtP3YzTrscceCxR/59e//vVG+xkP1aKNRrNP\nmXk2jpn317/r23VsrScY53zdcdOHkyRJkoxrusrDidRZ51pLrpW69up6YqyNZnSZlkhEn4tva/0g\nvqVd89WCsT5QXVz+IDEfQrW1/vrr97Q/LQ3X3LXmja9XyejfcI3XfB4juETl5Zh2cz7dqjQVrvk2\nWl9VfXNE61uVF5Wr+2mK82csssE9pupMf4URm9aJ0ydzzjnnAPC1r30NKPffc/YZ8H7qv1QVWH9O\nReTYVzHMPk3//d//DZT7am2zqHTqqPIBuoLyne98p+PvTZXNeMDnXsWrb8/IPpWvz5Dfgd5n/d1d\nRKMB3VcVSYWTJEmSDIW+KJwqXHt3fdH4dmPCL7/8cqBUFPj5z38OwHe/+91R9xffur61o1WukvLt\nrTUwTD74wQ8Cpc+N57711lv3tF+tPsdAP4cW8Kc//WmgWMJGcsXclEjTCrmjMXHiRCZPntw4x2fk\n5wC++c1vAiWixo6cTZWGY+D21gl7y1saueOmEY8366yz1nbk7JZ4LOeF0WUqEvO03M5qCz470dp3\nv37O/eqfcnVA9a/Pr6oqeT9pahXvvffeQLHGXQFp6mcQx8woVStSqALOP/98YPpnath1zrrBaFR7\nR5lLtMUWWwBwyimnAKV3lPk2PhtGtVZVcK8bg27nRyqcJEmSZCgMVOEYGeVbVCtKa+u3v/0tUN6W\nKpH4dtUq8/Pvfve7gRKBEYnVoc2mjlFIg7RktJ7EmkXmGPzlL39ptb9oHcbKAtaJs36dVai1lOP5\n9JMpU6a0VjdQOnh6XzxnfXxanrGuk/PAMdEvpY/OGnuxo2eVYtLyVYk7f7q5pqaMrFEGpUaeFdBj\nV0zv6+233w5Mb2G6H8dC1fiOd7yjYzvngX4zt/OaXfNvmq/VhqZW8YknnggU5RqrvNfh9lZANhfN\nah76OZ0f+oys4tDvzqC9EOesFa033HBDoPQM8tytnuB273vf+4CiEo1e1Wc7CCU7I1LhJEmSJEOh\nK4VjDw6zmquIWam+pbXOVRoxT0JLUwvE9WatO+Pw6yJn4ts7WqyrrLIKUNaxB4Fj4E/9VG3RajMi\nzzVYfzfqxLH1mszKtlJyXb+TXohWex2qL+dR9C9YEVlr3+hFa2Rp/WuRmple5aeqirCJPr5+9Itv\n6n/S0tQa9746Fj4Dsf6f16BvTiWjOtCa91r0RTnWrhLEaxyEsmmKYxarP3stfk+YgxSffz9vRKg9\noKxIoppbY401gJLDYgVt51X0Cfezz1MXfWY6PqeCedOb3gQURevfzVmMUbDOE/3jsWr4sEiFkyRJ\nkgyFVgpn4sSJzDLLLNMpG62oQw45BIADDjgAKNZ3VBb6L3xruw5pNrSRVlo4ViTw7W30mxZuU6J1\nYR2hQaK15k+jyTz3aMFEf1Xs+aG1tdVWWwGlh4yq086fWsZ+ztpYgyRWCqhTPGY/WxHCauBGMS61\n1FId25uXpTI2B+VHP/oRUKz7Oiuyyv/h9r0om8mTJ7Poooty7733Ntpe5aGfUz+U99PoQcfISE/X\n4n0W9X/pD/OnmHPis+XnvGdtI8AGgeOv79f7pN9T5WHuScyzilFm9reJvaOcZ66k2BlUBRUVTT/9\nHL1W1reStisWqnuj1awH52qQkZqueFgleqxIhZMkSZIMhVYKZ8qUKaPma2gRaj2peKqifHzLu6Z6\nxhlnAPDGN74RgLXWWgsodaTcn7Hn9nYxys3ja8momCLRDzLIKCSrKBg9oipTsXguXpu11RxD1Zcq\nwAoF5tW4nZaP98V+Ox7HsdaS1aKeUYXdtlbYUkstxVlnnTXNEh25rxmh/8KsaKOJzJtwDLTStN6M\n0PnCF74AwA477AAUC7ZO4agOzfOIlSh66Xr43HPPNVY3UCpBeM2OiXkTVojQmneM9Plcc801QMm7\ncV557SrbPfbYA6j2e3rcqnwsewP1k7r75N/14diZ1bHxGfCajcSy548KxjGUj3/840BZDbCHjArK\n6+y1+2Y/8ZxcGdHvaDSaVeONyHVOx9xHvzPHilQ4SZIkyVDoS7Vo37ZHHHEEUCzOEZ8Dpre2tUwW\nXHBBoLzFjZPX4tRKM+JKa8+oEv/uOnhbS2zE+XVdLXq06rpQrGU7LLq2qi/HOHktUP+utaYvRstU\nv0ZUD6oBOz+6fu12jpX7c42/yqJtWwm3Gwv4vPPOA2DzzTcf9f+uqavK7OnhOra5K+9973uBcg/c\nrle/hGqvl6rAMeKtqoK6z46Rk1Z/Nhop9naKuSWxorb9bex74zMS1UBVrlMVg6iQ7LPiOUS1tcsu\nuwDTV333mfAaYr6O/9e699ly7ruqoBpwvvn9UhcFO4xq0XU9mxwrv0PtHWaEp2NrtXF9Pf0mq0Un\nSZIk44q+dvzUQtCaiz3m9ZmYde9at3kTZstrYZiToNLRYt1///2Boh604szGFi0efzaw4nruh6P1\n5LUZHaTlaldKr2nbbbcFSoRe7NSota6lo/9JvKaLLroIKFWiXbfWAjIqSWvOLO4qf1Yv1pv+BdeP\n29I0VyFGJakCrB927rnnjvq5qjybeNxXvepVPPXUUzz//PMDs2RjVry/myfhs6OPxvmistl0002B\nErllnpV5NlrpVlOoqhdWNeZRuQ/CqleduULhc+0zc9pppwElMi/iuUWFY2TWAw88AJQox8MPPxwo\nY+azYg0/fUNG3VYxzD5J4rXGahuuYLiyYV6e2zmWMZ+rV9r2SUqFkyRJkgyFrioNVGXeGnFjDoHW\nlfkzvoWtFGC0iT+NMnONPq57f+pTnwKKBatS0qpzO1WBMepVa7Faj/3o9RH7mbg+rG9G7DluRJ7r\nyq7Buh8VjtafVnlES3jNNdcEynr1nnvu2bGddee0HlU4/cy/0I+kf6EKrz0qUqlTNt7XmOfjfIx1\n46I1uNlmmwGlp0zVcc0H6YWmOUFGQsW6g87NmENihKfbeS1GWnlfjWqKlrHPiMq2ac5SP/F7IlYs\nVrVrjTs2UeFUnZt/32233YCiWFSHjo0/9as6Bvq7xhLvk8+988Dnd4TiBIpPTpWmYnYsfSb7rXDa\nfnemwkmSJEmGQiuFM99887HNNttM85lEv4Jx7a4jain4f9dSY+0i824kWqxaQuakXH311R37sU+7\n+RrmJkQLWvVRp3yaMtNMM01XJ86IPRWEtdOMUtMvtfPOOwOl/peROF6zdZ6qLE8VkBaQdaNc23ds\nN9hgA6DUkzJKTWXVj4rZEyZMYPLkydO6U5rXILEydrwvKg59eJ5b7NDqud9yyy1AsfZ+8IMfANNX\nPq7y4UVls+yyywIlx0k/WzdMmDCBSZMmTdeBc7TtRqKvzb977d5Hr8nctGjtW2Hb6gtGeEUV6O+D\nzEGTWWaZhcUXX5w77rhj1P/HqszeJ++r/7e3VMwhcUxUf+K1mq/ls2IkoNU5PJ7+zejvsIJFP5g0\naRJzzz1345we75PVu33OXcGIqzOeu1Gv4ucefPDBrs67H3UFR5IKJ0mSJBkKXUWpRWvJt61vQyuS\nfv7znwdKtr0VbX0rx7emCiRah/5dS9bIHNcttVC07vXpxHXrqpyDET6pnqPUPJZdBU899VSgRI14\nDm6nEjIKSaJl6nqzOUmue7t//Q3eC7uoei9OP/10AC6++GKgRPpdeeWVo15fLxE4TTP1vTbXl6uq\ndmuNGwUZ5533X79E0+q+Md/D8/ZerLXWWlx77bU8/vjjfY9GigrHa/GcY6TnfvvtB5T7ZjSk+Tb2\ntDfis9+9nvqRk1SHOWauhMQxkK9+9asA7LTTTtPObTRiPUHnj/f9zW9+M1BWUFSJ+r3i99MwIvaq\ncHXH77bY08u5q//y/e9/f8e5qvaqnvdumWuuuXjyyScbR3KmwkmSJEmGQl/ycLRA7Fao1X7QQQcB\nxdfi2r3+itj/QuI5mTtiXoWdIo2n9y2u1adlHdc3G1xrzwrHSDv7iqy22mpAqe/kOcV8Gs9t1113\n7fi7/ir9IH7ONf6ohIxO01pU6fg5fUqej50f49j0w3rzGLHrZESFo5VmpJWKR7+X52hOyQUXXADA\nwQcfDJQxUi24du/v1lBTFTa4rr5Z9VVr4bGmnnNXq3uTTTYByly3vpf30fqCVT2A+k0/xsK5qt/R\n1YCodKv8BipZ50msjD3iXIGidPycYxyrQ3sPjCytqks4Yv+txmK0OoVN1bjbxU6wUe1bb85VINW7\n1aUHVRU8Kw0kSZIk44q+VhqIfSb0sWiJWE3YKCCjkrR4Yi00/+7bW8vUePqq3uMxx0BiRrOMsD57\nVjiite7aq+pOhWOF7BjVpmUiVZnh3dIii7+x9bbccstNveyyy6bF/sdxb1t92ftkRE+VGtTa04K1\n++FDDz3Usb0+QGu3WXVaqqzM+eefn0cffZR//OMfPdeVi/2OovXu9lrdjpXq0Kx3K0n47Fgbq+pZ\n6DeD9Fs4Nv70+6Nqrlr12bpzjrFRtPbRsgOoUbT6blQyp5xySsdx4vfPDKpZD82HU4Vz17w/qyn4\n++WXXw6UMTHCs98+vlQ4SZIkybiitcKZkfWmErFGkUrCyCotUdcVzTU5+uijgRInH6NTtFDXXntt\noLylY55GW0ZZV++bwpHYn8QxGpZFGmkaV9+L9eY1es1NlU20bMX5o3KO801cyzdiz+3r5om9i/w5\nMmLshRde6KslGyPjovLxnK32q5Kxz4lVOcw5stpGW4s1Wu+DUL5tI/Y8dtUKRdv9xL/7veR8iPOy\nha/X7YaucKoq75uvY97doYceCkzfTbcfVVVGIxVOkiRJMvPxf9wAAAKoSURBVK5oXUttypQp096y\nsSKAlqERWvbycD1RC/See+4BSk01o5mi1W0+hJFf9nRwHTvSNiu21+zZJt0xoxocK2Uj/coYnhFN\nrSjvl5UJjD5T+Vo13DpzRm5VWb5G4DhvjOQyB6oKlU3b829CnJMqGyPvYu00FZAKx/mj8tEfoV+0\n27X4USKuutpPHU2ekfj/bqsg1HUONV+rSnEPagxGo62Ki7lGVuMw3+aKK64AisIxWs35Yn3KplFx\ngyIVTpIkSTIU+hqlJjEq6Rvf+AZQckxirasqn5A/rY1mTouW7BprrAFQWatJRaWqaGDd992HM96J\ncf0yjPVp64Hph4iomK07Z8fHKuvMeWfNLSMEY9VnfYHXXnvtDM9Pf2UvY1HlK5Ho2zOvRgvWSCtX\nCZzD/r0qryfuPz7nKia7pjZlPERmDZsq3854GIuqmmpxnnWraPrt20uFkyRJkgyFgSicBvsBmq+Z\nGjev76dqDbbtfkfZ/t9O4VTRD+tNP4UKI1aBrvK5aX2bm2RlimOPPbbpKc2QqMDr1rWHack6J60A\nYe272MOl1/334PsZc6t+vDCWYxGjX0ecUz8P05hUOEmSJMm4onWU2ozycHy71kWLuZ3RRObnVHXg\ntObSaOcC03e/S8YW70v0nayzzjpAyS0R54+Z31//+teBUkfOn22J80uqsvwjTSKs+o3Hi/Xe+hVV\n1Gu+TjIcqr5Dq3yAVYqnKa4iVX3XVtH2GUmFkyRJkgyFtj6cR4HfDO50xpyFp06dOm+TDV/iY9F4\nHCDHYiQ5FoUci0KOxb9o9cJJkiRJkm7JJbUkSZJkKOQLJ0mSJBkK+cJJkiRJhkK+cJIkSZKhkC+c\nJEmSZCjkCydJkiQZCvnCSZIkSYZCvnCSJEmSoZAvnCRJkmQo/B+upgo4r1EqBAAAAABJRU5ErkJg\ngg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f90b8318c50>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"rows, cols = 10, 6\n",
"fig, axes = plt.subplots(figsize=(7,12), nrows=rows, ncols=cols, sharex=True, sharey=True)\n",
"\n",
"for sample, ax_row in zip(samples[::int(len(samples)/rows)], axes):\n",
" for img, ax in zip(sample[::int(len(sample)/cols)], ax_row):\n",
" ax.imshow(img.reshape((28,28)), cmap='Greys_r')\n",
" ax.xaxis.set_visible(False)\n",
" ax.yaxis.set_visible(False)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"It starts out as all noise. Then it learns to make only the center white and the rest black. You can start to see some number like structures appear out of the noise like 1s and 9s."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Sampling from the generator\n",
"\n",
"We can also get completely new images from the generator by using the checkpoint we saved after training. We just need to pass in a new latent vector $z$ and we'll get new samples!"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"INFO:tensorflow:Restoring parameters from checkpoints/generator.ckpt\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZwAAAGRCAYAAABR3wXnAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztvXncVeP+/39lKkNUd0WGuqkopShThkPGhCRDiHAKIc4R\nMs8+jqGjrylk5nA6KJKZIkNIQkKEBkPzqJCp3z+/9fa8tS73Wvfe+9pr3/fr+XjsR6/Hau21rr2u\ntfZ1X6/9fr+vWitXrnRCCCFEoVmt2A0QQghRM9CAI4QQIggacIQQQgRBA44QQoggaMARQggRBA04\nQgghgqABRwghRBA04AghhAiCBhwhhBBhWLlyZeJXWVnZSuecXnl6dezYcaVzbl6aPlC/lEa/lJWV\nRceJfa211lr2Kvbnbd26tb0Kfa5atWrZqwrvL+izssYaa9ir2H0S8tW2bVt7pX1v2mdlDZeC8vJy\nt2DBgjRvEX/BhAkTXK1atWbkehz1S37JR7+Ul5dHx4n9/0022cT0tGnTYvdZbbU/DIjff/89l+b8\nJQ8//LDpDh06pHovP1+SMll16tQx/eOPP6Y6l3OuoM9Kw4YNTc+ePTvXUwUlbT+QkSNHmm7evHmq\n96Z9VmSpCSGECEKqGY4QhWb11Vc3/dtvvxWxJfmhvLzc9PTp001zVrPWWmuZ/vnnn03nMqvZfPPN\nY88VR9pZDUn713TaWU3v3r1NP/jgg6nemxbOanKZMYRinXXWMf3DDz9U+TgtWrTIR3MSoRmOEEKI\nIGjAEUIIEQRZaiJT5MtGy5fdkCu00QgtG9pou+yyi+lx48ZV+byV2Wikfv36po855hjTt99+u+lC\nBi38FYW20ZJw2GGHmR4+fHgRW1KRfN3XaS1DBrOkRTMcIYQQQdCAI4QQIgiy1ETeyFJkTzFtNOK7\nJmuuuaZpWmrjx48P0zCw0UYbmR47dqxptpfal1tUneDnTWKj+XKm1ljjj6/YX3/9NU+tKy652Kua\n4QghhAiCBhwhhBBBkKUmUnP99debHjhwoOmq2mi0aGrXrm36p59+Ml2vXj3Ty5cvN/3LL79U6Zyh\nYATYwoULTdNGI7RdCm1RHnDAAc455+rWrWvbLrnkEtNMCGVbkvRXlllvvfVML1u2LC/H9NlMxYru\nyyqa4QghhAiCBhwhhBBBqJaWmq82VVpY18sXsVPsaKxQ0EahjZaP45111lmmI5vHOec22GAD05dd\ndpnpvffe2/Q555xT5fOG6DvaaGkpdPteeOGFVbY9+uijpln37JVXXjHdtWtX06Vio5F82Wg+eI/x\nO0T2mmY4QgghAqEBRwghRBCqlaUWTWU5jW3fvr3pTz/91DSnt0kSsmhv7LHHHqZfffXVKrU1S/zt\nb38z/dprr8Xuk297p0GDBqavuOIK0+uuu67pFStWmD755JNNH3rooVU+bxYtUCYH8r7ccsstTU+Z\nMiXv540i/Hy1sXit9tprL9O0rLlP1iMG08AF8ubNm2eaSbLff/+96UWLFpn2XZMhQ4aYPu2002LP\nG/VFdbXfNMMRQggRBA04QgghglCSlhotAJah/7//+z/nnHP9+/e3bb5y9x07djQ9efJk07Tjunfv\nHquPPfbYqjS7oCxdutT0+uuvn+q9PhutkNAyWHvttU3T9mQUVT4i44pBkhVMfZZuIWw0MmbMGOec\nc/vss0/s/7/11lum2V+0ke+44w7Tw4YNM51LdGixaN68uekvv/zSND8L7URy6623mmbkJG3h8847\nz/Suu+5qmsnBgwYNcs798V3mnHMTJkwwzeUr7rnnHt9HySya4QghhAiCBhwhhBBBKBlLjTYa7ZWL\nLrrINGskRTAJi9YFI0YYdUbbY7/99jNNC26nnXYy/fXXX5ueNWuW6dDRUGlttJBEpfgZgcZEQtpO\nrVq1Mt2oUSPTAwYMKGQTC0a+VjDNF3we+vXr55yraClPmjTJ9GOPPWZ6wYIFpm+88UbTd911l+kX\nX3zR9OzZs/Pe3kI/U7TRiM9G4xITtMB4DRlpyBVUubIqo+CiZGeudMp7iM9Kly5dTB9xxBGxbcwa\nmuEIIYQIggYcIYQQQcibpeZb8S4XOGXltPKCCy4wTRstmnL7Sqk//vjjphkxwn34OR544AHT06dP\nN80otTPOOCPBJ/mDhg0bptq/OhAlvzGSrl27drH78vqXYp2urENbKrKQ4p4h5/zP8WGHHWb64IMP\nrnT/XMhaom7Pnj1Ns21csoNW1/PPP2+aS2zMmTPHNJNJ46CNRnr06GGaPxfUqVMndnu+8LUnCZrh\nCCGECIIGHCGEEEHIm6VWiOk0p26bbrqpaUZk0WqLrDFG3Xz00Ueme/fuHfs+MnbsWNMsic8EtyVL\nliT7ADHMnz+/yu8tdXzRPj4YDViq0CJs1qyZ6WnTphWjObGkjaT7/PPPTdOyWbx4cd7aVAxorTdt\n2tQ0Ez8ZuXrqqaeaHj16tGlG9NFG22233Uxz6QceP6qrx0jc6667zjS/E3018C6++GLTl19+eew+\nuZBL5KVmOEIIIYKgAUcIIUQQCp74maSWlI+tttrK9BtvvBF7HE5927Rp45yrmHjFaBAfnErvuOOO\npkeMGGGapcjLy8srPaZYFdpIvOY+WIeqVKHV/O233xaxJbnBmoVnn3226XzVT9t9991Nv/7661U+\nTi4wKpb2IKMr+/bta5rfQ0xMZl21Tp06meZ3y8SJE02zrlr0XHBZAz43w4cPr/RzdOvWzXQhLLVc\n0AxHCCFEEDTgCCGECELBLbW00Wu0WhjJwWiYL774wvR2221n+tlnn3XOVUzISlKLidFrbO8tt9xi\nmqtSZi0ZLYvwukeJhWVlZZW+j/WsFi5cmP+GFZFCJOEVEq5ESnuT1hnttVwolo1G+Ll89iCTKpkw\nu/3225vmdwi/K9555x3TaSIwaen54Dl33nnnxMf+M4WuXacZjhBCiCBowBFCCBGEgltqaadlTGbi\nezm9f+6550wzei2KHmMU2Ycffmia5fEZMTJ06FDTF154oen/9//+n+lCJLZWZ2rXrm06sl0YBeTD\nV2OtOlAK9xCjSplgzecvKqHvXGFW9gy5JEFaaIu+/PLLpg855BDTjEx78803cz4nl/Lw/VzAdjFJ\n/quvvoo9pu8aU+cSYexDMxwhhBBByNwCbBxJp06danrDDTc0zRh1lkuJ4tW5KBqrQp9//vmmOZJf\nffXVpgcPHmyaVVy/++67FJ9CsO84s4yDgQI1sUI0Z368t4sB820YtMN+KfSsIwuzGl/1e34/cZE0\nLqJGV2WHHXYw7ZtV8Dss6n8G2HD2Qs37hvqbb76J/1CAQQtvv/127D6cvXK2o2rRQgghMo8GHCGE\nEEHInKXm44cffojdHmdBcNrJRYr4QzbXAI/yd5yrONWVjVZ1tt12W9NxFbJ5nbmgXSn8sJ5v8vWD\nbNof2yPb6L333rNtLN3C7TUNBknwO2bRokWmZ82aZZrfT3vssYdp9smee+5p+v777489ZmRjcRG3\nVq1amU4SeOOrIk0mTJgQuz8/t+9cuTyjmuEIIYQIggYcIYQQQSgZSy0Nffr0Md2hQwfTXDjtqaee\nMp2FqJjqximnnLLKNl/U0/jx44O0qRgw2ogLc5F82YiMMKPF47u/ly9f7pxz7rbbbrNtNdlGI778\novr165tu2bKlaX638N6mpcYFHRs2bGiaNlYUYcuyWj179qy0vcxNTBLpyZ8dGEWa5L7J5ftSMxwh\nhBBB0IAjhBAiCNXKUosSkq6//nrbxqkxS1HIRss/jLw5/vjjV/l/RsM0a9Ysdnt1i1Kj1ZIkiozb\nBw0aZPrcc8+t9FxMjuaiXaxqHC1S6Nwfz0tcFKGIZ/r06abHjh1rmhXnfbB/aH8ykfKMM85wzlVc\n8JHJo7TxeK/069ev0vPTuqOlFlmrf7VPvtAMRwghRBA04AghhAhCtbLUosqsrHLLaSGj10R+YOVg\nJnDGwUW8GElTaguTpYGfjZaaD1+1dEYS0QIh++yzj2lWQCdMVhw+fLhzrmKUWk3GZ3n6rOC0HHro\noaYZPcsFJT/++GPnXMVosRYtWsQejwuzsX6kD99z5qs6XQg0wxFCCBEEDThCCCGCUPKWWpMmTUzH\nrRMeTVGdS1ZjSFQOryOTGX1ly6PIM9aYKnYZ/lDkspgYbZLNNtvM9Nprr2365ptvNs1INpa8pz1T\nt25d0xdffLFzrmJEVBZgVN2yZcuCndfXP/mKnJwyZUqsZn8yOTqCzxgTRvnTQZIlLvhdSWs1ZMSu\nvoGFEEIEQQOOEEKIIJSkpcbkpMqWEBgxYoTpmriaZCGgxcDExgYNGsTuH9VKmzx5cmEblkGS2BW+\nEvb9+/c3/emnn5pu166daa46yUg2LnnAyCO+d/To0ZW2LQ5aQIw8zJf1FNJGy8Jqq3E2GrnoootM\n33nnnaZ537DG29y5c2OPQxutWGiGI4QQIggacIQQQgQh05Yao54YkbFw4cK/fB9tDNb3qmzqKpKx\nzTbbmGY5+3333dc07YlRo0Y55/K3smV1Y+ONNzb94osvmqZFxXu6Tp06ppk0SKvZF3n2wgsv5NZY\n57emk9TES1s3j/XH5syZk7SJiSmFpONrr7220n18S19kDc1whBBCBEEDjhBCiCAUzVJLkhBH6+DZ\nZ5+t9JjRcXr06GHbZs6cWdUmCg+8prvvvnvsPrR3HnnkEedcxYgg34qKhYDRc5XZscXg22+/NU0r\nrF69eqZpB++1116mudJjIaOs2J+svcaVXZNE5KWNZCuEjUayukwJIw4ZgeajVJb10AxHCCFEEDTg\nCCGECELRLDVOZVlWncloRx55pGmW8yaDBw82feGFFzrnlOBZaFgTjZGE7NMPP/zQdJTMyCTFkGTR\nRiM77rijadp/tFLmzZtnmpbWpptuWrB20UZjhGGS1SXzRS616EoZLvvhg4nUpXJtNMMRQggRBA04\nQgghgpCTpcYS6LlEHdFSYDTatGnTYs/F+k0DBgyo8nlF1XjqqadMs19OOukk03fdddcq+zDyJmsl\n8YtJVGvOuYoW5aJFi0zT3spXAnNk33HlSCZCcpkA1swLad+UilWUb1gj0rdMBaM+8wXvPybdVlaz\nMima4QghhAiCBhwhhBBByMlSS2KjnXHGGaZvueWW2H2uueYa09ddd51pWgdMAGvatGmqdoow0EYj\n0X0SMtmzVGE0GC3I5cuXm+byAIQJuc2aNTPts6Uqi95jOfv999/f9GuvvfaX76tucJXN+fPnBz8/\n66SxpmQhkj15/xUi6VYzHCGEEEHQgCOEECIIBU/89NloPsrKykxzKskS7ozY8dkOItukLVNfquSS\nuJjkfu7cubPp5s2bV+lcjEajjd2oUSPTuazCyXZNnz7dNO2bLCd4hrTRWrVq5ZyrmOhO67N9+/am\nWWuvEBRiORHNcIQQQgRBA44QQoggZG7Fz7lz55pu0qRJ7D4sw17IkuyicFRnG4347KG6deua9iXB\nJrGZ3njjDdNpn4Xo+D67zLc9rR365Zdfxm4v9GqeubB48WLThbCufP0/ZcqUCv8698fyHklJct/w\nM/GzJoH9nxbNcIQQQgRBA44QQogg1EoTEVKrVq15zrkZhWtOjaTZypUrG1W+mx/1S0HIqV/UJwVB\nz0o2SdwvqQYcIYQQoqrIUhNCCBEEDThCCCGCoAFHCCFEEDTgCCGECIIGHCGEEEHQgCOEECIIGnCE\nEEIEQQOOEEKIIGjAEUIIEQQNOEIIIYKgAUcIIUQQNOAIIYQIggYcIYQQQdCAI4QQIgwrV65M/Cor\nK1vpnNMrT6+OHTuudM7NS9MH6pfS6JeysrLoOHrl76VnJWOvtM9KqhlOeXl5mt2DUKtWLXuVGhMm\nTHAuD4tBFbNfVlttNXtllbRtzEe/lJeXR8cR+SPYsxLye2X11Ve3V0Quz1UubS/0s5LdbwkhhBDV\nijXSvoGjZr5WC11jjT+a8euvv6Z6b8olslMdI5d21RR+//332O1rrbWW6Z9//jmv50x7D/raKPIL\n/yrO8jVP0s5CfM/5+O2331bZ5mvXBhtsYHrJkiWx+7C966yzjukff/wxdh/fedN+XyZBMxwhhBBB\n0IAjhBAiCKktNd90at111zW9fPnyVMcMZVelnQpWNxstF5sgrb1IGy2yMPr372/bbr755iq3q9AW\nRwhCWjahyLKNRpK0k/tsuOGGpufMmVOQNiXFZ6P5+OGHHyrdx3cv+u5LBjekRTMcIYQQQdCAI4QQ\nIgipLTUfPhutEJFenNLFRXiQkJEzvsisrNgnuZybfef7PNy+5pprmo6uxX333Zf3dpUqhY6MTBOJ\nxX0re56qM7xnee3nzZtXjOZUSllZmekFCxZU+ThJrDPeF7ncI5rhCCGECIIGHCGEEEFIbanVqVPH\n9E8//VTp/oWI9KrqlI7Wwfrrr2/6+++/N92wYUPTS5cuNc2kKR++BMdSsox8dlndunVN83oR7t+t\nWzfTXbp0cc45d9JJJ+W9XdWNfD0vtNG22WYb05MnTzYdXdN8Wc1JrNYs990vv/wSuz1Lbea1XLRo\nUez2I4880vTJJ59seu+99zad5GcJ3/ZcylhphiOEECIIGnCEEEIEIbWllsRGKzac8vXo0cP0lVde\naXrTTTc1fc8995i+9957Tffq1cv0jTfeaDqJRVAqNsKf8bXVZ6Nxav7KK6+Y3nLLLU3Pnz/fOefc\nueeea9vuvvtu04wO8iXWsV1pohRrKox2Y5RV/fr1V9mHNvLMmTNN++w9X40tHpv9mMSyy/LzkqRt\nvujCtdde2zS/O3nPM2k+SjJ99NFHbRv7h7XUpkyZYvqiiy4yPX36dNNPPvmk6R133NH0119/bTp6\nPp3z24okFwtWMxwhhBBB0IAjhBAiCDklfma1HDmnoFdccYXprbbayjSnxnvssYfp66+/3vTgwYNj\nj59kip01W8C5wtgWPE7nzp1Nf/7556aXLVvmnKs4dV+8eLHptJYLE2yTRA/WRBiFSZukRYsWpvv0\n6eOcq9hXY8eONf3pp5+a7t69u2n2OS3NcePGmWZ/1atXzzQjq0jWnpe09dNoo9Euo4223nrrmd5h\nhx1MX3LJJaanTp3qnKtoT7ItfFbatm1r+o477jDNfhgwYIBpLlVw3XXXme7du3f8hwL5+q7XDEcI\nIUQQNOAIIYQIQmpLbeONNzb93Xff5bUxuRJN+2idcTrK6f+zzz5r+v777zc9d+5c00lWxcsivulv\nIWwLHn/XXXc1zSTPyOL8/9c/d875E2/ZR7RlmjRpYpr2RSlZaiEjsXhNjzrqKNPbbrut6SghdOut\nt7Zt7du3N73RRhuZvvbaa02z7Xy+mBRO25P2qe8aZM2eT2Kjsc2MHluxYoXpVq1amaalzOU5+Czs\nvPPOzjnnateuHXtORmjy/LTxaFvyPmC0YhIbjeSrTzTDEUIIEQQNOEIIIYKQ2lKbNWtWIdpRZTjF\n3GmnnZxzFWsJMfGKds27775revz48bH7pCWJZULboVCEtCQ4re/UqZPp559/3vTs2bOdc87tvvvu\ntu2hhx4y7WsvbYKoHptzzv3rX/8yHVkQzjk3bdq0VG0PTaGThBkFtddee5mmDc56Wo0bN3bOVbSD\n+Lx8+OGHpn19x+coiV3GPiW+hHK2J6R9mqRPeN/SuqKdyEi/6Hr/eR8uLRDVY9xkk01i/59Joow+\n5PEuvvhi01zxM5d7i9fDl/ibBM1whBBCBEEDjhBCiCCkttQYPcFpcMgIHNYtokUVJbCxThCn8Jxe\nMhqnEEmQPqpD7S8mpTECifcGbc3bbrvNOVfRZvNNy7l9l112MX3DDTeYZlRP165dTQ8ZMsR01hIJ\n/0whVvbkEhJchoC2I62Xhx9+2DlXsd5geXm5aSYT8tmh5ncA7+0kNlTW+ijJdxivN/fh5+L14f7c\nzrqOtMBef/1155xzLVu2tG28PxhlSEuN9SCjROu/+hxpyddxNMMRQggRBA04QgghgpC35QlCTo9p\nR3AqGyUYfvnll7aNUWy0HPbcc0/TSUpy5wKn6oU+VwgYLcTP9thjj5lm0mDUB0ymY1+wP2lBnHDC\nCaYZSUXYv6RBgwamFy5cGLtPaHit8mWj+WwdJsoeffTRpl999VXTUeLn7bffbttat25tmhFWLIW/\nZMkS07RRaRmRXFYCLURkmu+8Sb7DfBGVSSxEXrcXX3zRNJcNeOqpp5xzzn3yySe2jUumTJo0yTQj\n4/79739X2pZ8kcvxNcMRQggRBA04QgghgpDT8gQhYXRNt27dTD/xxBOmIxuHERs++4GWDst254ss\nr2BYFfh5zjnnHNOsw0Ubi+XsI/vy5Zdftm2MtmEyG+s9MWGR/UgY7TN06FDTWbHRSL7uA9o0tCN3\n220307Q0v/jiC9NcAfLggw92zlW0rV566SXTH3zwgWnuw8/hs1f5TC1fvtw0o0Z5nFwsxrQk6YdC\nJJzy+eCSDTNmzDB9+eWXO+ecGz16tG376KOPTPM6se4jreVcEjPJ5ptvbjpfSdWa4QghhAiCBhwh\nhBBBKBlLjdEwrOvUqFEj09EUM6pH5FxF+4ERYm+99ZbpQiyzUB1sNNo1tC4fffRR0wMHDjTNFVJp\nSURW2iGHHGLbaIWxVlS7du1M+2w0WgaXXXaZaV8EZXWGic/8/IcddphplsVnYmcUCbX99tvbNtYV\n5DNHWynJ8he+iLVSidL0WYVpn2teK9amY907Xudhw4Y55yr+hEBLsm/fvqbZr0zGjmy5XClEbULN\ncIQQQgRBA44QQogglKSlxig0TiUje62srMy2ccrPlfCYVFgd6pvlC1/5+M0228w0rz+v3XbbbWe6\nc+fOps8//3znXMX6dbQJmjZtapoWka8kOi1TLlVw0003xba9OsPrRcuSibKsYceIp2bNmjnnKlon\ntJfZtzwPI6VqwrOTiz1+5plnmmYyLq02XsMjjjhilWMwGo2Rbvyei0u0di4bq6cSzXCEEEIEoWRm\nOJydMFCgY8eOpr/66ivnnD9PoH///qa//fZb09XhB/58wfwk5mzwx3z+OM2/oLhPVCHauT9mJJw9\nMaiAeSLRX91/bosvT4M/xNYUONvjX7ODBg0y3bx5c9P8q5glat544w3nXEWXgEEFXASMMx/+8M+/\n1KlD5tVkmV69epn25cfwusXlBG666aamfQ7EAQccYJqzHVbOzwKa4QghhAiCBhwhhBBBKBlLjT+s\n0RaYPn266che4XSeFVpfeeWV2OPVdM477zzTBx54oGmWnPFV+aUd9sILL5geMWKE6ciOYbVolq1p\n1aqV6VtvvdU0cxFoO/hs0poC+4K5GEuXLjXNQADuH7dIGvuFwRwMFOD1533BAA5f7k0uFKtEFK3K\nXL4rzj33XNPPPPOMaV5bHj+6zmmrajMg4YEHHjC9//77m85XDlQupXM0wxFCCBEEDThCCCGCUDKW\nGuG0klPTKJ/joYcesm2sZsxIt5rOihUrTDMajNP7Sy+91DQj05jDNHLkSNO0Mhm9Fk3B2W+c3jNn\nhBFVtHFo3TH3JopMrKmwv6pajoXXmRWCec1pMdEOZRRUIeyvYkWQxt2/zqVvz+uvv276lFNOMb3l\nllua5vWMrv/w4cNtGyPXjjnmGNNt2rQxzTJUUXkc55xr0aKFaS6olwtagE0IIUTm0YAjhBAiCCVp\nqXF6z4WKomnlkUceadv23nvv2PfFResUitCRNpyCM3KI9iP3oXVGq4sL3dEO6NOnj2lGo/H4jF6K\nrrWv5Mbpp59u2hdR1alTJ9O07hhVJf4gzX3G+5MWGatIczuTdhmxRts1ywsQ+qpdk0K0+emnnza9\nww47mH777bdNR1Y3S3kxWvPjjz82zZ8Ovv/+e9Ndu3Y1fd999+Xa7LyiGY4QQoggaMARQggRhJK0\n1FhPiMmcrVu3ds5VnI4ySo11t0JO80OcizaBLwFvv/32M83p/dVXX236jjvuMM0K0aw9RwuO+KoI\nR/YdbbGpU6eafvzxx03zWtHSofXBCLt8ka914POJz5bKt13VsGFD06z4Xa9ePdOs58W++Oyzz/La\nlhCErKDM54CJuVEdO+cq2thRBWhu4/NMa5ORaYx04/ffqaeeavrmm29O/wHyjGY4QgghgqABRwgh\nRBBKxlJjBBTXA2eEUzTFZLTMggULTGfRNskXSWwCJqFxOk598sknV3ocRrgx8oyWCiOZIgts5513\ntm1bbbWV6cgKdc65tm3bmj7nnHNMF7r0fRbtIJ+NlsRSS7MP+4W1v/ic0aY58cQTTTMasabBa8xn\nyHd/MjKN0WZcbqVDhw7OuYpLg/C779hjjzXNZ48/MzCRm3XyuNwEtyd5nmiv57LkgWY4QgghgqAB\nRwghRBBKxlJjZBKnprRaoikuE6VefPFF0/kqz12qsJYcI5C4hAOtMF+0G5PMfHCaHvXL3//+d9vG\n+mm0PZ977jnTXLXysMMOM33vvfdWev4skkt0GfdPErFGi4f3PW2y6PqynD3fR5uGNjUjDLNoRYaC\n3z29e/c2fdBBB5m+4IILTDPq0nedI6uNdpnPzoxbHfTP21kPj1FybHsS8rVyqGY4QgghgqABRwgh\nRBBSW2ohayT5znX33XfHbo+SrGbMmGHbQiZ5lRKLFy+O3U4bLV8WUHQu1t2ijde9e3fTrP10ww03\nmGZUT6mSr+fFZ4f4agUyaolJnlHyIW02QhuNK0fSmi1FSy3Jfc1rwnp9PjuTq+ZyiQ0mpjMJ86ij\njjJNCyxaYoLLbtAWSxKtyGUqaF2/+eabptu1a+fiYAJptFJvPtEMRwghRBA04AghhAhCakutWDXI\nGNXBqA3us2zZMuecc0OHDrVttBbEHySxFdL2Na0eRphFUYM8Hmtz0bo588wzY/eZNGlSpefPckn8\nfEKbmEmBtNRIs2bNTK+//vqrHIfXauHChaYHDBhg+r333jNd6tc2SftpLfv279mzp2nWKRw8eLDp\nKVOmmD7//PNNM7GTq3JeddVVzjnnevToYdsuuugi077INN4TJ510kmmuzksbzWfN0UYrxPOkGY4Q\nQoggaMA7uEq3AAAgAElEQVQRQggRhEwnftKi6dKli2lGUpAoCoqJbCKeQtgi7C9aDFESaP369W0b\nbTTyzjvvmGZCnI/qYKOl/Qzcn9eR14sWC22yyHZ27o9lJmgfzZ0713QuSdNJVtXMAkx0ZnQXrzEj\n1piA/sQTT5hmTTmuiMs6gbQlr7vuOtPDhw83PW7cOOdcRfuNkWZc1uCee+4xTWuVddKOP/5400nq\nvRW63qRmOEIIIYKgAUcIIUQQMm2pcSr+zTffmGbkGfeJpvETJkywbdtss41p1gDL8jQ/NLQMaLn4\n8E27OU3nFL9jx47OOb+N5iOJjVNKNprPZkproxFeZ14vJnvyeaHd8t///tc5V7HGFm2XtO3i/ll+\nvthm2miE18yX+Om7P2lhMtmScJVbMnDgwFW2jRw5stJzNm3a1DTrnjHS01cPLeQzpBmOEEKIIGjA\nEUIIEYTUlhprMc2fPz/Ve3OJKPrggw9MM3mNkU+MsBF/De2dJDYa8fUdj/nYY4+ZnjlzZsrWVR98\nUVA+GGlG+8R3zWlT8vny1crjPlFkFe0vap4/bbuyTC51AWk5+q5bvmEEnO871PeM5WtZgXyhGY4Q\nQoggaMARQggRhNSWWlobjeQy/WadKE7pGzdubDrOUit0YmCpJLj9mUK0lcesyTYaKURkXi5wiYiW\nLVs65yra1bRvQrYrJEm+E3z7+BImQ5GvuofFSpjWDEcIIUQQNOAIIYQIQtESP9NO6ZiIFZW7d865\nyZMn/+X70k6Zk8D3prWmCl2rqCaTxbpquSRPFuJcjEh8//33q3yuyqDVzHZloV/yZT+l3Z4limXB\naYYjhBAiCBpwhBBCBKFWmulRrVq15jnnZhSuOTWSZitXrmyUywHULwUhp35RnxQEPSvZJHG/pBpw\nhBBCiKoiS00IIUQQNOAIIYQIggYcIYQQQdCAI4QQIggacIQQQgRBA44QQoggaMARQggRBA04Qggh\ngqABRwghRBA04AghhAiCBhwhhBBB0IAjhBAiCBpwhBBCBEEDjhBCiDCsXLky8ausrGylc06vPL06\nduy40jk3L00fqF/Sv2rVqmWvUP1SVlYWHSf2tdpqq9mr2NenhF56VjL2SvuspJrhlJeXp9ldVMKE\nCROcy8NiULn2y2qrrWavJNSqVavSVz5gu9Iem+9dc8017ZWEfPRLeXl5dJxY1llnHXslId/Xtlik\nvdf+RNGfFVGRtM+KLDUhhBBBWKPYDRD5h389ckVX3+quv//+e6XHXH311U3/9ttvptdee23TP/74\n418eg3+dsy1s7wYbbGB60aJFlbbLBz/Tzz//XOn+VfyLu1J43dim5cuXm15jjT8ew19//TX2OLxe\nSWY59erVM83rGNePvn7hjJBtZ//zvdS+eyoLKwz7Pm/Wjlkd0QxHCCFEEDTgCCGECIIstWqIz87w\nWTFJLADaKMRno9GiirTPLmJ709poPqsvLYWy1JK0if3CdiSxOn3WpO868nptttlmzjnnhg0bZtuO\nPPJI0926dTN92223mabVxj713V9JrNQk1m++8B3fd+2T2GVZtdGyZvVphiOEECIIGnCEEEIEQZZa\nNaFu3bqmf/jhB9O52Ew+klhztCSSWENVJV+fz2f35YovimuttdYyvWLFCtNJbI8k0Ya0h55//nnT\n5513nuklS5Y455zr3bu3bZs5c6Zp2mj169c3vXDhwtjz52LZ5vLefJHlyLqqkrW2a4YjhBAiCBpw\nhBBCBEGWWjXh+++/N80oIlpOaZMHfay77rqmly1bZjpJAmOW8EVJFeoc7IuffvrJdJLoLl8kW4MG\nDUzPmzcvdv+XX37ZdL9+/UxHSbunnHJK7LFJZL8551ydOnVMM+qtssTfP5MkmjJt1F51Icnz6btn\n+d7atWubZgJ0sa6lZjhCCCGCoAFHCCFEEKqlpVZq1k6++eWXX0z7Er9803FGIzF5kMe5//77Tfft\n29d08+bNTU+ZMsU064ZVFfbpvffea/rEE080nTZiLYStkDbx09dH3If39Ny5c00zUpGf7dtvvzXd\npk0b00OGDFll2wcffBB7DNa4a9q0qenp06ebTmup+ShWZFWxkiRpgUe6c+fOtm3GjD+KMdPO/Oqr\nr0zz2jdq1Mg0q5FPnTrV9OGHH256+PDhse0qxDXQDEcIIUQQNOAIIYQIQslbaoySueSSS5xzFa0F\nJthFFoJzFZMjOWWtbvhsGeomTZqYpv3CfY477jjTnLJzmt6hQwfTvL6VnT+JjcTkxH/+85+mC5HY\nWih8kUf77befaSZpJin3T3jNd911V9OtWrUy3aVLF9NR9Nqrr75q23zXk+efNGmS6fXXXz9VG5NQ\nLGvLd+/lqw20zvi9tNFGG62yz8SJE22b77pyaRB+522//fam+TzzPO+//75pRgKut956phmZmC80\nwxFCCBEEDThCCCGCUJKW2sUXX2z6qquuWuX/fVPg/v37m/bVr+rUqZNpRuyUKr7kRl8UE60E2i83\n3HCDaVpqrKvFvqDttXTp0lWOzWibXr16mX7rrbdMH3zwwaYZebfPPvuYfuyxx0xnrW6UcxWTZJl4\nx89DGy1JiXzfPj6L5fjjjzfdsGFD02effbZzzrnnnnsu9jybbLKJaUapfffdd6YXL14c+95c+iIL\n/Zi2Db7PzmvYrl0702eeeabpzTff3PTTTz/tnKv43cOEXkaRjh07NnY77brWrVubpqW3YMEC082a\nNTM9bdo004WI9tUMRwghRBA04AghhAhCSVpqcTYa4fSW1gWniJx2cv9Zs2blo4nB8U3pk0QO8b20\nZT7//HPTtGJYt402UY8ePUyPGjXK9AsvvOCcq2ijlZeXm77mmmtMR/abcxXtiBEjRph+8sknTefL\nfqH1lU9YMy1J7askJfIZScb+2nHHHU2zxlq9evVijxlFKtE6feKJJ0wz0o0WDPuREWt81vJFqdRS\nY7QsnxUmSbdt29Y0I8ZIZG9NnjzZtg0dOtQ0E219x2P/MEmXSaC0onk/cX9f9G4udRg1wxFCCBEE\nDThCCCGCUJKWmo/IdmDkDC0HTsmZJMcpaCFsgRAkWXqA035GnfC9rMnEJDBeU+7P6Jj33nvPNCPf\non1ol82fP9807RomEvI8O++8s+lvvvnG5Zt81HuLg5FBtNcYRUaLMgnsR0aP8Vy0WK6++mrT7du3\nNx0lfE6YMMG28VmYPXt2bNt577AtpfrsRPC7gs+Bz67m9eYyAC1btjRNW5L78Bry+NG9PW7cuNj/\n588CLVq0iN3OxE/uc8stt5hmX7Fmom81VyJLTQghRObRgCOEECIIJWOpnXPOOZXuE01TmUj4r3/9\ny/TWW29tmglOO+ywg2laBKWEb9rPKJ8kyVt870cffWT6nXfeMc1IGVpdnLKPHz/edDTd5zSeK4XS\natt0001jz8MIm3yVwWekIqPt8gmtKEbd0XJMC61hJgU2btzY9GeffWaa9/dNN91kOvrMX3/9tW2j\npTZz5kzTPju20M9LoZNA+Xz47ivfKqiM7uL9w+vJemS+unNMqv7kk0+cc86NGTMm9n20UPms0MY7\n8MADTX/44Yem33jjDdM+C5nXm33Lz5pLtKBmOEIIIYKgAUcIIUQQMm2pcUrHaSfhFDCayh566KG2\njXWKGA201VZbmWbSX77smtD4rAdOf7ki55dffpnqmLTLaFMyqoUrB/K8cZYaYZQMYY0nX1RPLpYL\nbZAQVirtL+L7PL5oIN6vtDq22WYb07RDmTRLK+9vf/ubc865jz/+uNLz+EresyYhr2cSizJJPxba\nUvPZQ74ahL73+pLKeQ3Z/1y19tZbbzUd9Se/h/i9xehOWmpM2PTdN/xMjMjz9VUu0Wg+NMMRQggR\nBA04QgghgpBpSy3JlI779OzZ0zlXMRqtb9++pjk1pkXDcvtfffVV1RpbAiSx0Qiv1xdffGGaES7c\nx1fOPG71T0JLZ/fddzfNZNN+/fqZ9lkxjLBidJgPHifEyqE+SzHJqqzchwmEtG+4+irr2tHWueuu\nu0w//vjjq5yHx6ONxtp3tGZYe9AXzZULxVr9k3aZL1qL8N7bf//9TdNGY/8zeZnLFkSRZDw/ryuv\nB59D2mtz5swxfe2115pmXyX56SBfSxIQzXCEEEIEQQOOEEKIIGTaUmPUjQ8mJEZ1g+68807b5rMo\naP+wlld1wGcBpC31zuu15ZZbmmaE36effmo6iY0VwSiZbt26mWZ9Ktqbr732Wmy7eJwk5w+R7JkE\nn1Xk0+w7JhNyFdsLL7zQNKOZhgwZEnucuG2s8bbHHnuYZjLhpZdearpDhw6mfYmivAf53PEeLFaU\nWhJ8NprPkmX9Mq6m2qZNm9h9eK0i25vRn7xmvkgzRuPynExCpRVbrGhczXCEEEIEIdMzHC7u5MvD\nYL7B//73P+ecc4MGDbJtLCdC+NcVy6xUB3x/kaUtScFyMvyL+bLLLjMd/fCcBPbbaaedZpp9xL/g\nNtxwQ9OcYfGHUP5Ayx/HfX3KWQ1nO4WqdJzkB2cfvqCZTp06md5zzz1Ns7+4CNj1119vesqUKaYH\nDx7snKs4k+EPyzw2r8/cuXNNM1CBf3EzUMRXFockyUXKwmyH8F7deOONTfP6sCzNI488YprBBE2a\nNDEdVfPmLJb3Nfft3r27aT7bdGwYkMByR8Va2E4zHCGEEEHQgCOEECIImbbUONVjlVtaBJyaHnHE\nEc65ink1Pk444QTTIXIwQpIve4K2SFTF1rmK1g1/NH7ppZdMx1mgf//7323bNddcY5qWC/ucQQDP\nP/+86YkTJ5pmAAPbSHyfO0RpmyT3ls/e8OXH8AffnXbayTStF+aF+Ij6gIEatC65AB/zd7g9euac\nc+6JJ54wzXIsvvI3/Hzch9esWDZakurr3M6csVdeecX0jBkzTLMPaT/S/o3y0Hhf016jhcySULTu\n+Oy9++67ptnPxfrO0wxHCCFEEDTgCCGECEKmLTVOWc8880zTzBUYMGCA6WHDhjnn/NE9tCsefvjh\nvLUza+SS0+Czd5gLwIXRrrrqKtOcytNWOPbYY51zzt1xxx22jRYW28W13FmVmH3KyJuOHTuaZhSO\nzzLgAla0fUJG6vyZJLYnry3tJ9pr3E6b5oMPPjDNZyeyQ1kKpV69eqZpf7GMCquxv/3226a32247\n06NHj45tI6Pd2Be0b7MQmebrE1/JG9pejJz1PUN877bbbmu6a9euzjnnysrKbBuvE21mX0Tn2LFj\nTdP+5nuLdV01wxFCCBEEDThCCCGCkGlLjQwdOtQ0K+Eed9xxpiurLl3dStj4yCWpi5E0tKVYxfmB\nBx6I3WfkyJGx2x999FHnnHO33XZb7P/TcmFSKe2XUaNGmT7rrLNMs4r0/fffb9pny9D6KCZpbSNG\nndH2onXGCsSXXHKJaZaiWbp0qenIgmRf0ArdbbfdTDM5lNFwjFI855xzTJ9yyimmGWHKPt1oo41M\ns1+ylvjpOy9tMUbusc28VrNnzzbNZGdGj0WRfrSNGzdubDpKDHWu4vVjFCevMRN5+WynKUOVTzTD\nEUIIEQQNOEIIIYJQMpbaGWecYZrWSVQ/zTnntthii1Xex+geVlStzuQSceWbao8ZM8Y0+4LJfoxk\nIlG003777WfbuKb7f//7X9O0A1mJmgmJtCB4L5Cs1N1KUhU6yf68trTRWFWYC9kxEZHXlwmHzZs3\nd84599Zbb9m2N9980/Trr79umtYl7SBaYQcddJDp8847z/TBBx9s+vPPPzfN6DnfImPFjB6sDFpX\njLJjZBgjzJioydqE06ZNMx1dWyYx832skcdjM6KTFlxVq7kXCs1whBBCBEEDjhBCiCCUjKXGZLNm\nzZqZjrPRfO/zWT41hVwifmjjcEkCJhv6iKKgWBqfFg0jsHbZZRfTrCfF5ETWbEv7mbIQ9fRXJEna\n5UJn559/vmnax7169TLNaCb2Y2SHPv3007aNCYd8zhgZx2hPWjlc+JDnHDFihGmW1/dZZ2xDliNL\nfXX5+Flol9WvX980IzNZDzKyvWiD8plg8ii57777TDNaMYmNFnKpAs1whBBCBEEDjhBCiCCUjKXG\naTkjaSqDdkFNgVFEtKJ8qy2mJclxaJdECXJHHXWUbeO664cffrhplnOntcJIKlqjviggH6FtNF9p\n+1ysC9pM1LzmjF7j9dp0001NR+vdM2mRllufPn1Msy8aNGgQezxGqXE5A35W3o8+2PZirUyZBEZL\nMgmUmnYxIy15HWi1RXXQaNFNmDDBNJchYF/xmeR18q2UzPtSK34KIYSodmjAEUIIEYSSsdQIozbi\n4CqINZHvvvvOdCEspCRTcE7fo2gnRs8wiooROwcccIDpU0891TSjnmhHMJKKlpqvrl4xI9MKbV3w\nszE6yme1RTYZrz8tLF7///znP6ZZe4010xixxqg2ntO34qfvc2QtkpBt9lnLXAKiS5cupvm9xdp0\nV1xxhenoWvlWe2XiJ/uN157t4vWj1acVP4UQQlRrNOAIIYQIQslYaix9TjhlfOONN5xzzo0fPz5I\nm7JKSBuC52IpdtpH0T5McGMSKJckuOiii0wzqZf1uLhCYvfu3U2zThjthtatW5tmbSnCtlcH2C9M\nFuT2yJr0WS1MGmTtu8MOO8w0a6Oxzxlt6Is043afjZY1S823dAIpLy83zeuw//77m6b927dvX9MD\nBw50zlVMkG3VqpXprbfe2jQjdxmJyBpvbGOxbDSiGY4QQoggaMARQggRhExbaizzzRUMOa098MAD\nTTOZUBQOX7QVI5CYHHjttdc65yomA3KFQkbecDXR22+/3TTfO2jQINO0i2ijEZ+NRkLU2fNZMLSW\nCmF7xCXhOvfHc8Rz+iwsrgR64oknmn7kkUdM0yalZXT22WfHtoXnzXqNuwhfHzIJlM8BoyiZqMmV\nO1kbcM8993TOOTd69GjbxmU9+Kww6TdJDb4soBmOEEKIIGjAEUIIEYScLLUk0+AktZB801RuZw2h\nuXPnmh43blyyxlZz0iZ1scaTr4Q5E84Y+eLra+7D5MzevXs75youZcBjcDtXrWRCHNvI+4KWmu9+\nZA2rqVOnxu7juwfzie+68bnIl7XE+4H4+qAypk+fbnrfffc1zeURhgwZYpoRiUmiznx9kTVLyLek\nAu3cqEadcxXvN35X3X333aa3224709H33M4772zbRo0aZZp1JGnR0dLjc5g1NMMRQggRBA04Qggh\ngpCTpZZkulu7dm3TvigiJuyxDtGkSZNMs2bTxRdfbHrp0qXJGlvN4fTeZ6/RDmAkjY8kNloSKlt1\n8MEHHzQ9ZsyY2Pf5bJYk9gGTE33JoSGsG5/t4VvCgPisHB/sd989UBk//PBD7Pt470ycONH0/Pnz\nTeeSvJllGy1J23h9aGEyIZT1zp555hnTkU3GqEk+z76VRfO19Eih0QxHCCFEEDTgCCGECELBEz99\nNhrh1J2akS7vvvuu6aZNm5r21WMqJIzeSmJNhYBJspzGE14fX6Kab39O6+PqpP2ZuGRDTvsZXda4\ncePYtiSJpGMZfL6XqyjOmjXLdJL7sVAksT18dlmS65ykFH1VnxHf+0aOHFnpe5kEzKUKSMuWLU0z\nsisLJLlmPpuX156r1qbBZxtnbemBJGiGI4QQIggacIQQQgQh07XU2rZtW+k+hV5FMY6s2GgkSS2w\ntFFqSepekSuvvNL0pZdeajrOSqIdwBVKk8ClBBYvXhy7D63ZJBQz8TOtRZskmZr9lWQZgMpIUube\n1y7aaD7rJ2s2mg9eB1/koM/+9UUjxi3ZkDYZ2NcnWUui1QxHCCFEEDTgCCGECEKtlNPqec65GZXu\nKNLQbOXKlY1yOYD6pSDk1C/qk4KgZyWbJO6XVAOOEEIIUVVkqQkhhAiCBhwhhBBB0IAjhBAiCBpw\nhBBCBEEDjhBCiCBowBFCCBEEDThCCCGCoAFHCCFEEDTgCCGECIIGHCGEEEHQgCOEECIIGnCEEEIE\nQQOOEEKIIGjAEUIIEQQNOEIIIcKwcuXKxK+ysrKVzjm98vTq2LHjSufcvDR9UOh+qVWrlr3y/XlX\nX311exX72he6X8rKyqLj6JW/V6aeFb3SPyupZjjl5eVpdheVMGHCBOfysPpgPvtlzTXXtFcSatWq\nZa/K9qlbt6698kWS86clH/1SXl4eHUfkj0w9K9WF1VZbzV5pSfusrJH6DCKTrLPOOqZ/+OGHSrf7\n+Pnnn1Odlzfpb7/9FrtPtKrs4sWLUx07CVqxNgxrrbWW6bT3SKnAP1pq0n31+++/BzuXfsMRQggR\nBA04QgghgpDaUsvytDNqz8KFC21bgwYNVvl/51yV/Mos47PLGjVqZHrGjD+s1o4dO5p+7733qnxe\nn41W2X1Cq++nn34yHXJ6T+rUqVOU85YK1dVGI77vsyx/55Ua1etbVwghRGbRgCOEECIIqS21Qkwp\nN998c9PTpk0z7Qt1bdu2remJEyeu8v+00RgZVb9+/ZzaWYrQRiNJbLQNN9zQ9Jw5c0yzX9Zdd93Y\n7d9///1fHpsWIEOw27dvb/r999+vtI35grZeoaCN67MOr776atMXX3xxwdv0Z2QfrYquQ/7QDEcI\nIUQQNOAIIYQIQiYSP2mjJWGnnXYyvcYaf/0R/vGPf1SpTTWJ1Vdf3TSjzmijkbXXXtv0smXLTPfv\n39/0rbfeajqKSKONtvHGG5tu3ry56alTp5pu3bq16enTp5tmxBTbm4sdFCJqMUkEXiFsNNqeH330\nkel9993XOefcFVdcYduOOeYY07yebHuLFi1M0zqdP39+nlosqiua4QghhAiCBhwhhBBByISl5rNC\nXn/9ddODBg0yfeWVV5qOS/LkMYYNG5bfxmYU3zX0RfpxH1/ypg9fkiltNLJixQrnnHPbb7+9bTvo\noINMH3XUUaafe+4505Hl45xzd911l+lPPvnE9Msvv2w6iY3Gc/HeKFbCaa4k6XdakI0bNzb9xRdf\nJD4PLcc+ffqYLkYkXRZRdF8yNMMRQggRBA04QgghglAQS+3yyy+P1Sxx/ssvv/zRCESa/frrr6Z3\n2203077EPB4z4sILL4w9T3UmyTSe15n785rnC1owZWVlzjnnBg4caNs6d+5smpFuvqjCG2+80TSj\n1xiBtXz5ctO+61FKFqvvsxHf5zzrrLNMn3POOaYPP/xw09ddd51zrmKCb7169UzXrl079tg8Hu3t\nmlBvzUeS56+qtlva92XZ3tMMRwghRBA04AghhAhCwS01wil3jx49TDMCac899zQdRTc551y/fv1M\n33333bHHv+eee5xzzl177bWp2lud4ZS6EPYik0BZE2/o0KGmo6UQFixYYNtouTFh8KWXXjJ93HHH\nmWYk3aGHHmp6yJAhprNmHzjn3HrrrWea1mESfDZaEmhBfvbZZ6bHjh1rOooa9NnbfP7Ylrlz55ou\nhB1b6rDPR44cafrOO+803aZNG9M33XST6bgahA0bNjTNe/++++4z3a5dO9NMjH/iiSdM8/5btGhR\nJZ+iMGiGI4QQIggacIQQQgShaImfI0aMMP3CCy+Yvu2220yfcMIJpllLi1NJ2gGnnHLKX54zSXn4\n6kYhIlYYJbb//vub/ve//22aFtg333zjnHNuq622sm1ckoC2HOu6sW/nzZtnmrX3tt56a9Pjx483\n7VvdlduZBFmoOmBpbbRC8Mwzz8Ruj6tDyH6jvcN9uU9NeY4qg8/ZmDFjTNPy5T18/vnnm+b9P2DA\nAOec/7uK22nFcTuT4Xv27GmaP1cU67tQMxwhhBBB0IAjhBAiCDlZarnYNXwvI2B8iX9du3Y1TauF\nK1f26tXLOefcgw8+GHsMJrL9+OOPqdqbdaIlAJyrWOssFxvN178sZ8+kQUahMfk2LqqQfeirzfbP\nf/7TNK02RsP5Vg7l8WkZ8DNx+QUmWdYU4iLMHn30UdO8hrw+IZZyyBK+eoS8JpMnTzbdqFEj0/fe\ne69p3ofU55577l+en9ebbWH/MQF+gw02ME3LuW7duqZp9YZM2K1Zd44QQoiioQFHCCFEEHKy1HKx\na3zvXbJkiWmWs6dNRuuEU8MttthileNxCsppL1ctzGLCYFpoLeWSbEh8kV60N6MINOecmzlzpun/\n/Oc/VT5vhC9RlfcIE9hOO+0000wm9tVYo/XAY9YUIpty1KhRtu2AAw6o9H2+ZSiqK7xnGK3H+o7R\n0ijOOVenTh3T/P7hM0SLmMeJvtu++uor27bJJpuY5nPOZ4/JodyfNjeTQ7nyK/cpNJrhCCGECIIG\nHCGEEEHIxIqfPt544w3TvlLp2223neldd93VOVcxiorRW6effrrpYpXw9kW85BPaaLl8TloAviUk\naG8effTRpn3LSVQG20vNZENGl+23336mmUxMW9EXtUcbjZ+jpvDOO+845/6odZcURg8y+bDUoc3F\ne5/WLu/9Jk2amOb3DPGtwnrzzTeb5qqp0VIeTHT3sdlmm5lmvTyep3nz5qZHjx5tmhac79kuBJrh\nCCGECIIGHCGEEEFIbamFtKKSJJgxOiRuf9Zju+aaa0xz6tihQwfTjLTiVJPTatYS+/TTTyttIwkd\nEec7ny+ZzFcna/311zfdqlUr023btjWd7wQyX7vIc889V+lxfPdRoZduyCK0W9PU0OK+aS24UoH3\nmO9+22ijjUyz/h4TyVkbzXcPX3DBBaZp+cYtT0B4LzOi0PeTA+/xSZMmmWYkG6N3C41mOEIIIYKg\nAUcIIUQQUltqhbaEWBMorny6c8599913pjk1jGDEyBdffGGatYQ41W3fvr1prpDHSCdGdWyzzTam\nDz/8cNOPP/547PGzmFiatiQ57QNG57z55pux2yv7/Px/JsqxTtonn3ySqo0+VEL/DxjJx6jCyrjq\nqqtMZ2HJhWJB6+r11183zahM1ljjfc7IM1/9wMrgasZnn322aZ9tzKU8aAd+/vnnsfvXr1/f9OLF\ni6YBafsAAAiPSURBVE3n6ztMMxwhhBBByFweDmc4H3/8sWn+ON20adO/PAZLONxzzz2mfTkww4cP\nN+2bVXGEZ6AA/2rgzIelI0LAfKT333+/0v35w2baytmzZ882zWvKchzMa4muHWej0UJTzlWcJR57\n7LGm8zXD8ZH1WWi+YH5Jt27dTMc9D7wO/FF67Nixpvnjd025hhEsA9OyZUvT9erVi92fwSj77rtv\nlc55++23m+Yik0ly+ujSdO7c2fTAgQNNX3311aZZKqoQaIYjhBAiCBpwhBBCBCFzlhrtHea7EP6A\nz9yPCRMmOOcqlnxIUrKElkMSGHzQpUsX0/xBNjRJbDSSywJ0tE58Ngptl+iHVlYlpv1IaLW98sor\nVW4j8dk+NcECcq5i0ESnTp1MR5Yln6G99trL9Ntvv23al5fCH8j5w7lv/1KHP/bPmjXLNO1/Wvq0\n1BicxB/zaeNvu+22zjnnHnvsMdtWXl5e5fbyu6px48amBw8eXOVj5oJmOEIIIYKgAUcIIUQQMmep\nMSfDF1vOKClfNdbKoP11yCGHmPbZazz2oEGDTD/55JOmGbfOdc1DlE1hiZ+FCxfG7sPpdWUlNJyr\n+JlpTdIu4fXiPjvuuKPpaPrORe98jBkzJvbYuVg0NcU6I3x2mJdGK2fFihWr/H+SckKEfc6F7qor\ntCe5QCQXHIxsMecqfrc8/PDDpnlvs8wWLcp8tJFRZ8y98eUB+fLjcrHgiWY4QgghgqABRwghRBAy\nZ6kNGzbMdBKLrLJ9ItvAuYpRNA8++KBpWl49e/as9JyXXnqpaU5fmbQYuvqwz0YjtNF8kVuc6jOZ\ndJ999jHdu3dv0yzXwSicDTbYwHRkGTDZlDYCrxUT1Til9y2i5luwjZZSoReVyjqvvfaaado9EWlt\nNFLTytzwWh144IGmjz/+eNO0GVmGi5Yj7W2WjXr33Xedc87tscceto3PLau2++5rPitsI+09JpMS\nPlv5stGIZjhCCCGCoAFHCCFEEDJnqTG6iXZVksXYImjR0EZjNM4jjzximvXbOKVkQhzfywXImPCV\nNoG0mCSpgXXccceZ7tevn2n2C5NwaYdNnTp1leOxEjTXYKftyag/JsT52uiLqqGt4Pus1bkOGO/F\nDz/80DRtz8g+o02TtpZWTbMreZ+wBqMPJnCymjzvVX5HRdWazzzzTNt26qmnml66dKnpBx54wDTr\nS55++ummWePNZ6Px+4/fnYV4JjTDEUIIEQQNOEIIIYKQOUttww03NE1bhBFOaaBd4EtkJIzS6dq1\na+w+U6ZMiT0mKSsrM82S5lkhyaJkRxxxhGn2BZMHr7zyStPffPON6YkTJ5qOaqkxco3RgOeee67p\nZs2amaZdSXuNNg4/B6NqGDXEBL0zzjjDdHWz0Qgjkniv05qO7l32S6HL09dkkkSALVmyxDlXcSHI\nf/zjH6bfeust06+++qppRiLyOyxJgjd/Oig0muEIIYQIggYcIYQQQcicpUZYV+iKK64wfckll/zl\n+5IsSUA41Y2WOHDOuXHjxpn2WVC0KLhPMW002pJz5swxnaQ22cYbb2z6hhtuMM3127/88kvTSSyY\nyD7gOf/3v/+ZPvroo02z3lOS9vpqyD300EOma1pyonMVo/0YKUUiS22LLbawbUzkFeGJ7M0333zT\ntvHnBC6H0r1790qPl7VITM1whBBCBEEDjhBCiCBk2lLjFJD1y4YMGWL6lltuMX344YdX6dhNmjQx\nfdRRR5lmQpaPJNFeoaGNRnz2H7cz0uzWW281PXPmTNNt2rSpUrsYXcYVP5lsxig1ntNXm85n6fHz\nJUnQqw7QDmWEX2UwMdTH3LlzTdOCq4l2ZSHZYYcdnHMVbTTaYlwGwfc8kyzYaEQzHCGEEEHQgCOE\nECIImbbUfHDFTyYnRlFNTLrklL9v376mb7755lXe9+ft1Q3aUvzMvkgWJlu2bNkydjvrMBEeJzov\na6ntuuuupmmj9ejRw/TLL7/s+yix5/HBGm+8HxjNmEVrNC1M9mQNrcqYN2+eaSaB8lo1btw4x9YJ\nH7TGou8zbmPk4AcffGC6WPdsmpWV/4xmOEIIIYKgAUcIIUQQStJS8xElBzKihtAuS7LKISNFWEK/\nVO0XljNnrTGWSue14GemdeUr8U9ozSxevNg559y3335r27j0weTJk03TDk1ilyVJbPNFUoVelbXQ\n0IJM0kcRffr0MZ2k9pbIL9GSBM45d8IJJzjnKvYfa6aNGjUqVLO85BL5phmOEEKIIGjAEUIIEYRq\nZalVRtq6QiwhzhU/aTX57Lhi4vuctNEYXcYEV26ndcjj8DP7rJvIRiM8D5NHx44da/rII480zdUp\nfcmJWUtsKyZcZTXNCrmiuDDxPOq3yFpzzrkHH3ww7+csVo013ZVCCCGCoAFHCCFEEIpmqRVjSpfL\nebjiZRbh9WSioy/qiKv8MamPEX5cHoLHZ9QXE0K/+OKL2P3jrjvPv9NOO5necsstTSep8UWyVord\nuYoWZZKVFbP4GUQ6ktQ4I5988onpKDmdy2sUgmLdW5rhCCGECIIGHCGEEEEomqUmuyC/0IpJm7zn\nS5Rdvnx57HZacIyMSoPPauCKn2lhbbQk9lUI0rajuj8XTKZmFGh1gve2L+qT9QgZvbn33ns75yqu\n2MolOPJ1f5x55pmmQ9aP1AxHCCFEEDTgCCGECEKNSvysziSZajPqzGeX+eByBrTgih1VxfNnxUYT\nfqqrjebDd09y9Vvew7169Sp4m5wr3jIsmuEIIYQIggYcIYQQQaiVxgapVavWPOfcjMI1p0bSbOXK\nlY1yOYD6pSDk1C/qk4KgZyWbJO6XVAOOEEIIUVVkqQkhhAiCBhwhhBBB0IAjhBAiCBpwhBBCBEED\njhBCiCBowBFCCBEEDThCCCGCoAFHCCFEEDTgCCGECML/B2p+AB2SZaWtAAAAAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x7f90c6cee048>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"saver = tf.train.Saver(var_list=g_vars)\n",
"with tf.Session() as sess:\n",
" saver.restore(sess, tf.train.latest_checkpoint('checkpoints'))\n",
" sample_z = np.random.uniform(-1, 1, size=(16, z_size))\n",
" gen_samples = sess.run(\n",
" generator(input_z, input_size, n_units=g_hidden_size, reuse=True, alpha=alpha),\n",
" feed_dict={input_z: sample_z})\n",
"_ = view_samples(0, [gen_samples])"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.5.3"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
| mit |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.